problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Prove that
$$
\frac{\sigma(1)}{1}+\frac{\sigma(2)}{2}+\frac{\sigma(3)}{3}+\cdots+\frac{\sigma(n)}{n} \leq 2 n
$$
for every positive integer $n$.
|
This is similar to the previous solution. If $d$ is a divisor of $i$, then so is $i / d$, and $(i / d) / i=1 / d$. Summing over all $d$, we see that $\sigma(i) / i$ is the sum of the reciprocals of the divisors of $i$, for each positive integer $i$. So, summing over all $i$ from 1 to $n$, we get the value $1 / d$ appearing $\lfloor n / d\rfloor$ times, once for each multiple of $d$ that is at most $n$. In particular, the sum is
$$
\frac{1}{1}\left\lfloor\frac{n}{1}\right\rfloor+\frac{1}{2}\left\lfloor\frac{n}{2}\right\rfloor+\frac{1}{3}\left\lfloor\frac{n}{3}\right\rfloor+\cdots+\frac{1}{n}\left\lfloor\frac{n}{n}\right\rfloor<\frac{n}{1^{2}}+\frac{n}{2^{2}}+\cdots+\frac{n}{n^{2}} .
$$
So now all we need is $1 / 1^{2}+1 / 2^{2}+\cdots+1 / n^{2}<2$. This can be obtained from the classic formula $1 / 1^{2}+1 / 2^{2}+\cdots=\pi^{2} / 6$, or from the more elementary estimate
$$
\begin{aligned}
1 / 2^{2}+1 / 3^{2}+\cdots+1 / n^{2} & <1 /(1 \cdot 2)+1 /(2 \cdot 3)+\cdots+1 /((n-1) \cdot n) \\
& =(1 / 1-1 / 2)+(1 / 2-1 / 3)+\cdots+(1 /(n-1)-1 / n) \\
& =1-1 / n \\
& <1 .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that
$$
\frac{\sigma(1)}{1}+\frac{\sigma(2)}{2}+\frac{\sigma(3)}{3}+\cdots+\frac{\sigma(n)}{n} \leq 2 n
$$
for every positive integer $n$.
|
This is similar to the previous solution. If $d$ is a divisor of $i$, then so is $i / d$, and $(i / d) / i=1 / d$. Summing over all $d$, we see that $\sigma(i) / i$ is the sum of the reciprocals of the divisors of $i$, for each positive integer $i$. So, summing over all $i$ from 1 to $n$, we get the value $1 / d$ appearing $\lfloor n / d\rfloor$ times, once for each multiple of $d$ that is at most $n$. In particular, the sum is
$$
\frac{1}{1}\left\lfloor\frac{n}{1}\right\rfloor+\frac{1}{2}\left\lfloor\frac{n}{2}\right\rfloor+\frac{1}{3}\left\lfloor\frac{n}{3}\right\rfloor+\cdots+\frac{1}{n}\left\lfloor\frac{n}{n}\right\rfloor<\frac{n}{1^{2}}+\frac{n}{2^{2}}+\cdots+\frac{n}{n^{2}} .
$$
So now all we need is $1 / 1^{2}+1 / 2^{2}+\cdots+1 / n^{2}<2$. This can be obtained from the classic formula $1 / 1^{2}+1 / 2^{2}+\cdots=\pi^{2} / 6$, or from the more elementary estimate
$$
\begin{aligned}
1 / 2^{2}+1 / 3^{2}+\cdots+1 / n^{2} & <1 /(1 \cdot 2)+1 /(2 \cdot 3)+\cdots+1 /((n-1) \cdot n) \\
& =(1 / 1-1 / 2)+(1 / 2-1 / 3)+\cdots+(1 /(n-1)-1 / n) \\
& =1-1 / n \\
& <1 .
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-team-solutions.jsonl",
"problem_match": "\n15. ",
"solution_match": "\nSolution: "
}
|
d6e6aba0-1f33-5056-a86f-61fa2850d0f6
| 611,302
|
Now suppose again that $n$ is odd. Prove that
$$
\sigma(1)\left\lfloor\log _{2} n\right\rfloor+\sigma(3)\left\lfloor\log _{2}(n / 3)\right\rfloor+\sigma(5)\left\lfloor\log _{2}(n / 5)\right\rfloor+\cdots+\sigma(n)\left\lfloor\log _{2}(n / n)\right\rfloor<n^{2} / 8
$$
|
The term $\sigma(i)\left\lfloor\log _{2}(n / i)\right\rfloor$ is the sum of the divisors of $i$ times the number of even numbers $\leq n$ whose greatest odd divisor is $i$. Thus, summing over all odd $i$,
we get the sum of $d$ over all pairs $(d, j)$, where $j<n$ is even and $d$ is an odd divisor of $j$. Each odd number $d$ then appears $\lfloor n / 2 d\rfloor$ times, since this is the number of even numbers $<n$ that have $d$ as a divisor. So the sum equals
$$
\begin{aligned}
\lfloor n / 2\rfloor+3\lfloor n / 6\rfloor & +5\lfloor n / 10\rfloor+\cdots+n\lfloor n / 2 n\rfloor \\
& \leq(n-1) / 2+3(n-1) / 6+\cdots+m(n-1) / 2 m
\end{aligned}
$$
where $m$ is the greatest odd integer less than $n / 2$. (We can ignore the terms $d\lfloor n / 2 d\rfloor$ for $d>m$ because these floors are zero.) This expression equals
$$
(n-1) / 2+(n-1) / 2+\cdots+(n-1) / 2=(n-1)(m+1) / 4 \leq(n-1)(n+1) / 8
$$
which is less than $n^{2} / 8$, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Now suppose again that $n$ is odd. Prove that
$$
\sigma(1)\left\lfloor\log _{2} n\right\rfloor+\sigma(3)\left\lfloor\log _{2}(n / 3)\right\rfloor+\sigma(5)\left\lfloor\log _{2}(n / 5)\right\rfloor+\cdots+\sigma(n)\left\lfloor\log _{2}(n / n)\right\rfloor<n^{2} / 8
$$
|
The term $\sigma(i)\left\lfloor\log _{2}(n / i)\right\rfloor$ is the sum of the divisors of $i$ times the number of even numbers $\leq n$ whose greatest odd divisor is $i$. Thus, summing over all odd $i$,
we get the sum of $d$ over all pairs $(d, j)$, where $j<n$ is even and $d$ is an odd divisor of $j$. Each odd number $d$ then appears $\lfloor n / 2 d\rfloor$ times, since this is the number of even numbers $<n$ that have $d$ as a divisor. So the sum equals
$$
\begin{aligned}
\lfloor n / 2\rfloor+3\lfloor n / 6\rfloor & +5\lfloor n / 10\rfloor+\cdots+n\lfloor n / 2 n\rfloor \\
& \leq(n-1) / 2+3(n-1) / 6+\cdots+m(n-1) / 2 m
\end{aligned}
$$
where $m$ is the greatest odd integer less than $n / 2$. (We can ignore the terms $d\lfloor n / 2 d\rfloor$ for $d>m$ because these floors are zero.) This expression equals
$$
(n-1) / 2+(n-1) / 2+\cdots+(n-1) / 2=(n-1)(m+1) / 4 \leq(n-1)(n+1) / 8
$$
which is less than $n^{2} / 8$, as required.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-team-solutions.jsonl",
"problem_match": "\n16. ",
"solution_match": "\nSolution: "
}
|
89479a26-3dcb-5666-bda3-95879b79f5a2
| 611,303
|
Suppose $0<a \leq b$ and $4 \nmid m n$. Prove that the number of ways in which an $m \times n$ rectangle can be partitioned into dominoes of type ( $a, b$ ) is even.
|
If the rectangle is tileable, it can be partitioned into an odd number of dominoes. Consider the reflection of the partitioned rectangle over one axis. This gives another partition of the rectangle. In fact, it cannot be the same partition, for suppose it were. Then we can pair each domino with its reflected image, but since there are an odd number of dominoes, one must reflect into itself. Since $a>0$, this is not possible. Therefore, we can pair off partitions and their reflections, and it follows that the total number of partitions is even.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Suppose $0<a \leq b$ and $4 \nmid m n$. Prove that the number of ways in which an $m \times n$ rectangle can be partitioned into dominoes of type ( $a, b$ ) is even.
|
If the rectangle is tileable, it can be partitioned into an odd number of dominoes. Consider the reflection of the partitioned rectangle over one axis. This gives another partition of the rectangle. In fact, it cannot be the same partition, for suppose it were. Then we can pair each domino with its reflected image, but since there are an odd number of dominoes, one must reflect into itself. Since $a>0$, this is not possible. Therefore, we can pair off partitions and their reflections, and it follows that the total number of partitions is even.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team1-solutions.jsonl",
"problem_match": "\n2. [25]",
"solution_match": "\nSolution: "
}
|
1ef5386c-bf0a-5ddd-ab15-cd2600c89aea
| 611,395
|
Show that no rectangle of the form $1 \times k$ or $2 \times n$, where $4 \nmid n$, is $(1,2)$-tileable.
|
The claim is obvious for $1 \times k$ rectangles. For the others, color the first two columns black, the next two white, the next two black, etc. Each $(1,2)$ domino will contain one square of each color, so in order to be tileable, the rectangle must contain the same number of black and white squares. This is the case only when $4 \mid n$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Show that no rectangle of the form $1 \times k$ or $2 \times n$, where $4 \nmid n$, is $(1,2)$-tileable.
|
The claim is obvious for $1 \times k$ rectangles. For the others, color the first two columns black, the next two white, the next two black, etc. Each $(1,2)$ domino will contain one square of each color, so in order to be tileable, the rectangle must contain the same number of black and white squares. This is the case only when $4 \mid n$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team1-solutions.jsonl",
"problem_match": "\n3. [10]",
"solution_match": "\nSolution: "
}
|
e6a7400c-501c-599d-a775-91327cf1f2ab
| 611,396
|
Show that for $b$ even, there exists some $M$ such that for every $n>M$, a $2 b \times n$ rectangle is $(1, b)$-tileable.
|
Recall from above that we can tile a $2 \times 2 b$ rectangle. Four columns of a $(b+1) \times 2 b$ rectangle can be tiled as shown below, and repeating this $\frac{b}{2}$ times tiles the entire rectangle. Since any integer at least $b$ can be written as a positive linear combination of 2 and $b+1$, we can tile any $2 b \times n$ rectangle for $n \geq b$.
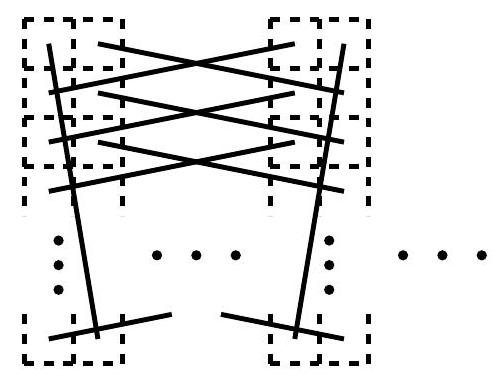
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Show that for $b$ even, there exists some $M$ such that for every $n>M$, a $2 b \times n$ rectangle is $(1, b)$-tileable.
|
Recall from above that we can tile a $2 \times 2 b$ rectangle. Four columns of a $(b+1) \times 2 b$ rectangle can be tiled as shown below, and repeating this $\frac{b}{2}$ times tiles the entire rectangle. Since any integer at least $b$ can be written as a positive linear combination of 2 and $b+1$, we can tile any $2 b \times n$ rectangle for $n \geq b$.

|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team1-solutions.jsonl",
"problem_match": "\n5. [25]",
"solution_match": "\nSolution: "
}
|
c3aabc05-fcbf-5333-9ffc-992658c9a7f0
| 611,398
|
Show that for $b$ even, there exists some $M$ such that for every $m, n>M$ with $m n$ even, an $m \times n$ rectangle is $(1, b)$-tileable.
|
By the diagram below, it is possible to tile a $(2 b+2) \times(4 b+1)$ rectangle. Since we can already tile a $(2 b+2) \times 2 b$ rectangle by above, and $2 b$ is relatively prime to $4 b+1$, this will allow us to tile any $(2 b+2) \times n$ rectangle for $n$ sufficiently large. Combining this with the previous problem, this will allow us to tile any $m \times n$ rectangle for $m$ and $n$ sufficiently large and $m$ even, completing the proof.
To tile the $(2 b+2) \times(4 b+1)$ rectangle, we first tile the following piece:

This is then combined with two $2 \times 2 b$ rectangles, a $2 b \times b$ rectangle, and a $2 b \times(2 b+1)$ rectangle as follows:
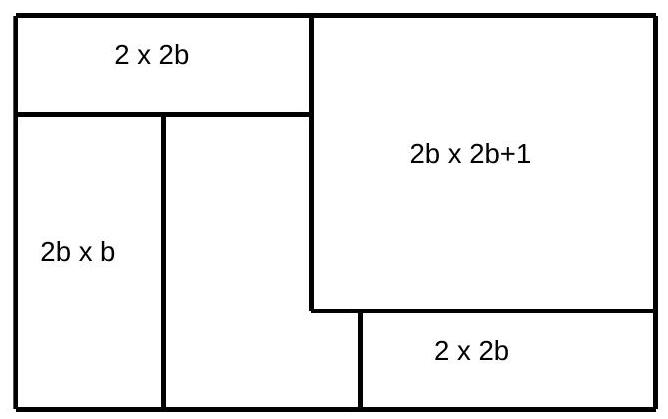
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Show that for $b$ even, there exists some $M$ such that for every $m, n>M$ with $m n$ even, an $m \times n$ rectangle is $(1, b)$-tileable.
|
By the diagram below, it is possible to tile a $(2 b+2) \times(4 b+1)$ rectangle. Since we can already tile a $(2 b+2) \times 2 b$ rectangle by above, and $2 b$ is relatively prime to $4 b+1$, this will allow us to tile any $(2 b+2) \times n$ rectangle for $n$ sufficiently large. Combining this with the previous problem, this will allow us to tile any $m \times n$ rectangle for $m$ and $n$ sufficiently large and $m$ even, completing the proof.
To tile the $(2 b+2) \times(4 b+1)$ rectangle, we first tile the following piece:

This is then combined with two $2 \times 2 b$ rectangles, a $2 b \times b$ rectangle, and a $2 b \times(2 b+1)$ rectangle as follows:

|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team1-solutions.jsonl",
"problem_match": "\n6. [40]",
"solution_match": "\nSolution: "
}
|
75355ccb-4af4-5efc-b693-70247d8a9b7f
| 611,399
|
Let $P(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0}$ be a polynomial with real coefficients, $a_{n} \neq 0$. Suppose every root of $P$ is a root of unity, but $P(1) \neq 0$. Show that the coefficients of $P$ are symmetric; that is, show that $a_{n}=a_{0}, a_{n-1}=a_{1}, \ldots$
|
Since the coefficients of $P$ are real, the complex conjugates of the roots of $P$ are also roots of $P$. Now, if $x$ is a root of unity, then $x^{-1}=\bar{x}$. But the roots of
$$
x^{n} P\left(x^{-1}\right)=a_{0} x^{n}+a_{1} x^{n-1}+\cdots+a_{n}
$$
are then just the complex conjugates of the roots of $P$, so they are the roots of $P$. Therefore, $P(x)$ and $x^{n} P\left(x^{-1}\right)$ differ by a constant multiple $c$. Since $a_{n}=c a_{0}$ and $a_{0}=c a_{n}, c$ is either 1 or -1 . But if it were -1 , then
$$
P(1)=a_{n}+a_{n-1}+\cdots+a_{0}=\frac{1}{2}\left(\left(a_{n}+a_{0}\right)+\left(a_{n-1}+a_{1}\right)+\cdots+\left(a_{0}+a_{n}\right)\right)=0,
$$
a contradiction. Therefore $c=1$, giving the result.
## Early Re-tile-ment [125]
Let $S=\left\{s_{0}, \ldots, s_{n}\right\}$ be a finite set of integers, and define $S+k=\left\{s_{0}+k, \ldots, s_{n}+k\right\}$. We say that two sets $S$ and $T$ are equivalent, written $S \sim T$, if $T=S+k$ for some $k$. Given a (possibly infinite) set of integers $A$, we say that $S$ tiles $A$ if $A$ can be partitioned into subsets equivalent to $S$. Such a partition is called a tiling of $A$ by $S$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0}$ be a polynomial with real coefficients, $a_{n} \neq 0$. Suppose every root of $P$ is a root of unity, but $P(1) \neq 0$. Show that the coefficients of $P$ are symmetric; that is, show that $a_{n}=a_{0}, a_{n-1}=a_{1}, \ldots$
|
Since the coefficients of $P$ are real, the complex conjugates of the roots of $P$ are also roots of $P$. Now, if $x$ is a root of unity, then $x^{-1}=\bar{x}$. But the roots of
$$
x^{n} P\left(x^{-1}\right)=a_{0} x^{n}+a_{1} x^{n-1}+\cdots+a_{n}
$$
are then just the complex conjugates of the roots of $P$, so they are the roots of $P$. Therefore, $P(x)$ and $x^{n} P\left(x^{-1}\right)$ differ by a constant multiple $c$. Since $a_{n}=c a_{0}$ and $a_{0}=c a_{n}, c$ is either 1 or -1 . But if it were -1 , then
$$
P(1)=a_{n}+a_{n-1}+\cdots+a_{0}=\frac{1}{2}\left(\left(a_{n}+a_{0}\right)+\left(a_{n-1}+a_{1}\right)+\cdots+\left(a_{0}+a_{n}\right)\right)=0,
$$
a contradiction. Therefore $c=1$, giving the result.
## Early Re-tile-ment [125]
Let $S=\left\{s_{0}, \ldots, s_{n}\right\}$ be a finite set of integers, and define $S+k=\left\{s_{0}+k, \ldots, s_{n}+k\right\}$. We say that two sets $S$ and $T$ are equivalent, written $S \sim T$, if $T=S+k$ for some $k$. Given a (possibly infinite) set of integers $A$, we say that $S$ tiles $A$ if $A$ can be partitioned into subsets equivalent to $S$. Such a partition is called a tiling of $A$ by $S$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team1-solutions.jsonl",
"problem_match": "\n11. [25]",
"solution_match": "\nSolution: "
}
|
10330a60-30da-5d9b-8dd3-27b580f5f6cd
| 611,404
|
Suppose the elements of $A$ are either bounded below or bounded above. Show that if $S$ tiles $A$, then it does so uniquely, i.e., there is a unique tiling of $A$ by $S$.
|
Assume $A$ is bounded below; the other case is analogous. In choosing the tiling of $A$, note that there is a unique choice for the set $S_{0}$ that contains the minimum element of $A$. But then there is a unique choice for the set $S_{1}$ that contains the minimum element of $A \backslash S_{0}$. Continuing in this manner, there is a unique choice for the set containing the minimum element not yet covered, so we see that the tiling is uniquely determined.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Suppose the elements of $A$ are either bounded below or bounded above. Show that if $S$ tiles $A$, then it does so uniquely, i.e., there is a unique tiling of $A$ by $S$.
|
Assume $A$ is bounded below; the other case is analogous. In choosing the tiling of $A$, note that there is a unique choice for the set $S_{0}$ that contains the minimum element of $A$. But then there is a unique choice for the set $S_{1}$ that contains the minimum element of $A \backslash S_{0}$. Continuing in this manner, there is a unique choice for the set containing the minimum element not yet covered, so we see that the tiling is uniquely determined.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team1-solutions.jsonl",
"problem_match": "\n12. [20]",
"solution_match": "\nSolution: "
}
|
0e4e08fd-98fd-5f00-8dea-eb4dd8be20b5
| 611,405
|
Let $B$ be a set of integers either bounded below or bounded above. Then show that if $S$ tiles all other integers $\mathbf{Z} \backslash B$, then $S$ tiles all integers $\mathbf{Z}$.
|
Assume $B$ is bounded above; the other case is analogous. Let $a$ be the difference between the largest and smallest element of $S$. Denote the sets in the partition of $\mathbf{Z} \backslash B$ by $S_{k}, k \in \mathbf{Z}$, such that the minimum element of $S_{k}$, which we will denote $c_{k}$, is strictly increasing as $k$ increases. Since $B$ is bounded above, there exists some $k_{0}$ such that $c_{k_{0}}$ is larger than all the elements of $B$. Let
$$
T_{l}=\bigcup_{k=l}^{\infty} S_{k}
$$
Suppose $l \geq k_{0}$. Note that any element in $S_{k}, k<l$, is at most $c_{l}-1+a$. Therefore, $T_{l}$ contains all integers that are at least $c_{l}+a$. Since the minimum element of $T_{l}$ is $c_{l}, T_{l}$ is completely determined by which of the integers $c_{l}+1, c_{l}+2, \ldots, c_{l}+a-1$ it contains. This implies that there are at most $2^{a-1}$ possible nonequivalent sets $T_{l}$ when $l \geq k_{0}$ (here we extend the notion of equivalence to infinite sets in the natural way.) By the Pigeonhole Principle, there must then be some $l_{2}>l_{1} \geq k_{0}$ such that $T_{l_{1}} \sim T_{l_{2}}$. But then it is easy to see that the set $S_{l_{1}} \cup S_{l_{1}+1} \cup \cdots \cup S_{l_{2}-1}$ tiles Z, so $S$ tiles Z.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $B$ be a set of integers either bounded below or bounded above. Then show that if $S$ tiles all other integers $\mathbf{Z} \backslash B$, then $S$ tiles all integers $\mathbf{Z}$.
|
Assume $B$ is bounded above; the other case is analogous. Let $a$ be the difference between the largest and smallest element of $S$. Denote the sets in the partition of $\mathbf{Z} \backslash B$ by $S_{k}, k \in \mathbf{Z}$, such that the minimum element of $S_{k}$, which we will denote $c_{k}$, is strictly increasing as $k$ increases. Since $B$ is bounded above, there exists some $k_{0}$ such that $c_{k_{0}}$ is larger than all the elements of $B$. Let
$$
T_{l}=\bigcup_{k=l}^{\infty} S_{k}
$$
Suppose $l \geq k_{0}$. Note that any element in $S_{k}, k<l$, is at most $c_{l}-1+a$. Therefore, $T_{l}$ contains all integers that are at least $c_{l}+a$. Since the minimum element of $T_{l}$ is $c_{l}, T_{l}$ is completely determined by which of the integers $c_{l}+1, c_{l}+2, \ldots, c_{l}+a-1$ it contains. This implies that there are at most $2^{a-1}$ possible nonequivalent sets $T_{l}$ when $l \geq k_{0}$ (here we extend the notion of equivalence to infinite sets in the natural way.) By the Pigeonhole Principle, there must then be some $l_{2}>l_{1} \geq k_{0}$ such that $T_{l_{1}} \sim T_{l_{2}}$. But then it is easy to see that the set $S_{l_{1}} \cup S_{l_{1}+1} \cup \cdots \cup S_{l_{2}-1}$ tiles Z, so $S$ tiles Z.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team1-solutions.jsonl",
"problem_match": "\n13. [35]",
"solution_match": "\nSolution: "
}
|
11cd0c23-92cf-5534-a79c-6d68b5d10609
| 611,406
|
Suppose $S$ tiles the natural numbers $\mathbf{N}$. Show that $S$ tiles the set $\{1,2, \ldots, k\}$ for some positive integer $k$.
|
Using the notation from above, we can find $l_{1}<l_{2}$ such that $T_{l_{1}} \sim T_{l_{2}}$. By the same argument as in problem 12, as long as $T_{l_{1}} \neq \mathbf{N}$, there is a unique choice for $S_{l_{1}-1}$ that contains the largest integer not in $T_{l_{1}}$. Since the same can be said for $T_{l_{2}}$, we must have that $T_{l_{1}-1} \sim T_{l_{2}-1}$. Continuing in this manner, we find that there must exist some $l$ for which $\mathbf{N} \sim T_{l}$; then $S$ tiles $\mathbf{N} \backslash T_{l}=\left\{1,2, \cdots, c_{l}-1\right\}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Suppose $S$ tiles the natural numbers $\mathbf{N}$. Show that $S$ tiles the set $\{1,2, \ldots, k\}$ for some positive integer $k$.
|
Using the notation from above, we can find $l_{1}<l_{2}$ such that $T_{l_{1}} \sim T_{l_{2}}$. By the same argument as in problem 12, as long as $T_{l_{1}} \neq \mathbf{N}$, there is a unique choice for $S_{l_{1}-1}$ that contains the largest integer not in $T_{l_{1}}$. Since the same can be said for $T_{l_{2}}$, we must have that $T_{l_{1}-1} \sim T_{l_{2}-1}$. Continuing in this manner, we find that there must exist some $l$ for which $\mathbf{N} \sim T_{l}$; then $S$ tiles $\mathbf{N} \backslash T_{l}=\left\{1,2, \cdots, c_{l}-1\right\}$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team1-solutions.jsonl",
"problem_match": "\n14. [35]",
"solution_match": "\nSolution: "
}
|
194b686b-1c2f-5fb5-a40a-6a4c38ab18a2
| 611,407
|
Suppose $S$ tiles N. Show that $S$ is symmetric; that is, if $-S=\left\{-s_{n}, \ldots,-s_{0}\right\}$, show that $S \sim-S$.
|
Assume without loss of generality that the minimum element of $S$ is 0 . By the previous problem, $S$ tiles the set $\{1,2, \ldots, k\}$ for some positive integer $k$. Then let $P(x)$ be the polynomial $\sum_{i=0}^{n} x^{s_{i}}$. To say that the set $\{1,2, \ldots, k\}$, or equivalently the set $\{0,1, \ldots, k-1\}$, is tiled by $S$ is to say that there is some polynomial $Q(x)$ with coefficients 0 or 1 such that $P(x) Q(x)=1+x+\cdots+x^{k-1}=\left(x^{k}-1\right) /(x-1)$. It follows that all the roots of $P(x)$ are roots of unity, but $P(1) \neq 0$. By question 11 above, this implies that $P(x)$ is symmetric. Therefore, $s_{0}+s_{n}=s_{1}+s_{n-1}=\cdots=s_{n}+s_{0}$, so $S$ is symmetric.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Suppose $S$ tiles N. Show that $S$ is symmetric; that is, if $-S=\left\{-s_{n}, \ldots,-s_{0}\right\}$, show that $S \sim-S$.
|
Assume without loss of generality that the minimum element of $S$ is 0 . By the previous problem, $S$ tiles the set $\{1,2, \ldots, k\}$ for some positive integer $k$. Then let $P(x)$ be the polynomial $\sum_{i=0}^{n} x^{s_{i}}$. To say that the set $\{1,2, \ldots, k\}$, or equivalently the set $\{0,1, \ldots, k-1\}$, is tiled by $S$ is to say that there is some polynomial $Q(x)$ with coefficients 0 or 1 such that $P(x) Q(x)=1+x+\cdots+x^{k-1}=\left(x^{k}-1\right) /(x-1)$. It follows that all the roots of $P(x)$ are roots of unity, but $P(1) \neq 0$. By question 11 above, this implies that $P(x)$ is symmetric. Therefore, $s_{0}+s_{n}=s_{1}+s_{n-1}=\cdots=s_{n}+s_{0}$, so $S$ is symmetric.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team1-solutions.jsonl",
"problem_match": "\n15. [35]",
"solution_match": "\nSolution: "
}
|
fa0fb7d0-25c4-5339-b28b-63e80f226987
| 611,408
|
Prove that an $m \times n$ rectangle is $(b, b)$-tileable if and only if $2 b \mid m$ and $2 b \mid n$.
|
Color the first $b$ rows of an $m \times n$ rectangle black, the next $b$ white, the next $b$ black, etc. Any $(b, b)$ domino covers one square of each color, so for the rectangle to be $(b, b)$-tileable, there must be the same number of black squares as white squares. This is possible only when $2 b \mid m$. Similarly, we must have $2 b \mid n$. It is easy to exhibit a tiling of all such rectangles, proving the claim. (It is also possible to prove this using the lemma described below.)
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Prove that an $m \times n$ rectangle is $(b, b)$-tileable if and only if $2 b \mid m$ and $2 b \mid n$.
|
Color the first $b$ rows of an $m \times n$ rectangle black, the next $b$ white, the next $b$ black, etc. Any $(b, b)$ domino covers one square of each color, so for the rectangle to be $(b, b)$-tileable, there must be the same number of black squares as white squares. This is possible only when $2 b \mid m$. Similarly, we must have $2 b \mid n$. It is easy to exhibit a tiling of all such rectangles, proving the claim. (It is also possible to prove this using the lemma described below.)
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team2-solutions.jsonl",
"problem_match": "\n4. [30]",
"solution_match": "\nSolution: "
}
|
cce3a92f-2b45-56e9-b575-eb9734d01fcd
| 611,412
|
Let $k$ be an integer such that $k \mid a$ and $k \mid b$. Prove that if an $m \times n$ rectangle is ( $a, b$ )-tileable, then $2 k \mid m$ or $2 k \mid n$.
|
We prove the following lemma.
Lemma. Let $k$ be a positive integer such that $k \mid a$ and $k \mid b$. Then an $m \times n$ rectangle is ( $a, b$ )-tileable if and only if an $m^{\prime} \times n^{\prime}$ rectangle is $\left(\frac{a}{k}, \frac{b}{k}\right)$-tileable for $\left\lfloor\frac{m}{k}\right\rfloor \leq m^{\prime} \leq\left\lceil\frac{m}{k}\right\rceil$ and $\left\lfloor\frac{n}{k}\right\rfloor \leq n^{\prime} \leq\left\lceil\frac{n}{k}\right\rceil$. (Here, $\lfloor x\rfloor$ denotes the greatest integer less than or equal to $x$, while $\lceil x\rceil$ denotes the least integer greater than or equal to $x$.)
Proof. Number the rows and columns in order. For each pair $0 \leq i, j<k$, consider the set of squares in a row congruent to $i$ modulo $k$ and in a column congruent to $j$ modulo $k$. If one square of a type $(a, b)$ domino lies in this set, then so does the other. We can therefore partition the rectangle into these sets and then tile these sets instead. Each such set is a rectangular array of dimensions $m^{\prime} \times n^{\prime}$, with $\left\lfloor\frac{m}{k}\right\rfloor \leq m^{\prime} \leq\left\lceil\frac{m}{k}\right\rceil$ and $\left\lfloor\frac{n}{k}\right\rfloor \leq n^{\prime} \leq\left\lceil\frac{n}{k}\right\rceil$, and a type $(a, b)$ domino on the original rectangle is a type $\left(\frac{a}{k}, \frac{b}{k}\right)$ domino on this new array. Since all possible pairs $\left(m^{\prime}, n^{\prime}\right)$ occur, the result follows.
Suppose $2 k \nmid m$ and $2 k \nmid n$. Then at least one of $\left\lfloor\frac{m}{k}\right\rfloor$ and $\left\lceil\frac{m}{k}\right\rceil$ is odd, so we can choose $m^{\prime}$ odd. Likewise we can choose $n^{\prime}$ odd. But then an $m^{\prime} \times n^{\prime}$ rectangle has odd area and so cannot be tileable, implying that the $m \times n$ rectangle is not tileable.
An Interlude - Discovering One's Roots [100]
A $k$ th root of unity is any complex number $\omega$ such that $\omega^{k}=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $k$ be an integer such that $k \mid a$ and $k \mid b$. Prove that if an $m \times n$ rectangle is ( $a, b$ )-tileable, then $2 k \mid m$ or $2 k \mid n$.
|
We prove the following lemma.
Lemma. Let $k$ be a positive integer such that $k \mid a$ and $k \mid b$. Then an $m \times n$ rectangle is ( $a, b$ )-tileable if and only if an $m^{\prime} \times n^{\prime}$ rectangle is $\left(\frac{a}{k}, \frac{b}{k}\right)$-tileable for $\left\lfloor\frac{m}{k}\right\rfloor \leq m^{\prime} \leq\left\lceil\frac{m}{k}\right\rceil$ and $\left\lfloor\frac{n}{k}\right\rfloor \leq n^{\prime} \leq\left\lceil\frac{n}{k}\right\rceil$. (Here, $\lfloor x\rfloor$ denotes the greatest integer less than or equal to $x$, while $\lceil x\rceil$ denotes the least integer greater than or equal to $x$.)
Proof. Number the rows and columns in order. For each pair $0 \leq i, j<k$, consider the set of squares in a row congruent to $i$ modulo $k$ and in a column congruent to $j$ modulo $k$. If one square of a type $(a, b)$ domino lies in this set, then so does the other. We can therefore partition the rectangle into these sets and then tile these sets instead. Each such set is a rectangular array of dimensions $m^{\prime} \times n^{\prime}$, with $\left\lfloor\frac{m}{k}\right\rfloor \leq m^{\prime} \leq\left\lceil\frac{m}{k}\right\rceil$ and $\left\lfloor\frac{n}{k}\right\rfloor \leq n^{\prime} \leq\left\lceil\frac{n}{k}\right\rceil$, and a type $(a, b)$ domino on the original rectangle is a type $\left(\frac{a}{k}, \frac{b}{k}\right)$ domino on this new array. Since all possible pairs $\left(m^{\prime}, n^{\prime}\right)$ occur, the result follows.
Suppose $2 k \nmid m$ and $2 k \nmid n$. Then at least one of $\left\lfloor\frac{m}{k}\right\rfloor$ and $\left\lceil\frac{m}{k}\right\rceil$ is odd, so we can choose $m^{\prime}$ odd. Likewise we can choose $n^{\prime}$ odd. But then an $m^{\prime} \times n^{\prime}$ rectangle has odd area and so cannot be tileable, implying that the $m \times n$ rectangle is not tileable.
An Interlude - Discovering One's Roots [100]
A $k$ th root of unity is any complex number $\omega$ such that $\omega^{k}=1$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team2-solutions.jsonl",
"problem_match": "\n6. [40]",
"solution_match": "\nSolution: "
}
|
668dd1f0-70cd-5d99-9ccd-8e9d58d9ee83
| 611,414
|
Let $x$ and $y$ be two $k$ th roots of unity. Prove that $(x+y)^{k}$ is real.
|
Note that
$$
\begin{aligned}
(x+y)^{k} & =\sum_{i=0}^{k}\binom{k}{i} x^{i} y^{k-i} \\
& =\frac{1}{2} \sum_{i=0}^{k}\binom{k}{i}\left(x^{i} y^{k-i}+x^{k-i} y^{i}\right)
\end{aligned}
$$
by pairing the $i$ th and $(k-i)$ th terms. But $x^{k-i} y^{i}=\left(x^{i} y^{k-i}\right)^{-1}$ since $x$ and $y$ are $k$ th roots of unity. Moreover, since $x$ and $y$ have absolute value 1 , so does $x^{i} y^{k-i}$, so $x^{k-i} y^{i}$ is in fact its complex conjugate. It follows that their sum is real, thus so is $(x+y)^{k}$.
This can also be shown geometrically. The argument of $x$ (the angle between the vector $x$ and the positive $x$-axis) is an integer multiple of $\frac{2 \pi}{k}$, as is the argument of $y$. Since $x+y$ bisects the angle between $x$ and $y$, its argument is an integer multiple of $\frac{\pi}{k}$. Multiplying this angle by $k$ gives a multiple of $\pi$, so $(x+y)^{k}$ is real.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $x$ and $y$ be two $k$ th roots of unity. Prove that $(x+y)^{k}$ is real.
|
Note that
$$
\begin{aligned}
(x+y)^{k} & =\sum_{i=0}^{k}\binom{k}{i} x^{i} y^{k-i} \\
& =\frac{1}{2} \sum_{i=0}^{k}\binom{k}{i}\left(x^{i} y^{k-i}+x^{k-i} y^{i}\right)
\end{aligned}
$$
by pairing the $i$ th and $(k-i)$ th terms. But $x^{k-i} y^{i}=\left(x^{i} y^{k-i}\right)^{-1}$ since $x$ and $y$ are $k$ th roots of unity. Moreover, since $x$ and $y$ have absolute value 1 , so does $x^{i} y^{k-i}$, so $x^{k-i} y^{i}$ is in fact its complex conjugate. It follows that their sum is real, thus so is $(x+y)^{k}$.
This can also be shown geometrically. The argument of $x$ (the angle between the vector $x$ and the positive $x$-axis) is an integer multiple of $\frac{2 \pi}{k}$, as is the argument of $y$. Since $x+y$ bisects the angle between $x$ and $y$, its argument is an integer multiple of $\frac{\pi}{k}$. Multiplying this angle by $k$ gives a multiple of $\pi$, so $(x+y)^{k}$ is real.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team2-solutions.jsonl",
"problem_match": "\n8. [25]",
"solution_match": "\nSolution: "
}
|
da836a82-1bee-5bf5-a4c0-a11a330fd90c
| 611,416
|
Let $x$ and $y$ be two distinct roots of unity. Prove that $x+y$ is also a root of unity if and only if $\frac{y}{x}$ is a cube root of unity.
|
This is easiest to see geometrically. The vectors corresponding to $x, y$, and $-x-y$ sum to 0 , so they form a triangle. In order for them all to be roots of unity, they must all have length one, so the triangle must be equilateral. Therefore the angle between $x$ and $y$ is $\pm \frac{2 \pi}{3}$, that is, $\frac{y}{x}$ is a cube root of unity.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $x$ and $y$ be two distinct roots of unity. Prove that $x+y$ is also a root of unity if and only if $\frac{y}{x}$ is a cube root of unity.
|
This is easiest to see geometrically. The vectors corresponding to $x, y$, and $-x-y$ sum to 0 , so they form a triangle. In order for them all to be roots of unity, they must all have length one, so the triangle must be equilateral. Therefore the angle between $x$ and $y$ is $\pm \frac{2 \pi}{3}$, that is, $\frac{y}{x}$ is a cube root of unity.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team2-solutions.jsonl",
"problem_match": "\n9. [30]",
"solution_match": "\nSolution: "
}
|
d5a65212-521c-5fae-b528-a9aef01c9912
| 611,417
|
Let $x, y$, and $z$ be three roots of unity. Prove that $x+y+z$ is also a root of unity if and only if $x+y=0, y+z=0$, or $z+x=0$.
|
Again, we consider the geometric picture. Arrange the vectors $x, y, z$, and $-x-y-z$ so as to form a quadrilateral. If they are all roots of unity, they form a quadrilateral all of whose side lengths are 1. If the quadrilateral is degenerate, then two of the vectors sum to 0 , which implies the result. But even if it is not degenerate, the quadrilateral must be a rhombus, and since opposite sides of a rhombus are parallel, this again implies that two of the four roots of unity sum to 0 .
## Early Re-tile-ment [150]
Let $S=\left\{s_{0}, \ldots, s_{n}\right\}$ be a finite set of integers, and define $S+k=\left\{s_{0}+k, \ldots, s_{n}+k\right\}$. We say that $S$ and $T$ are equivalent, written $S \sim T$, if $T=S+k$ for some $k$. Given a (possibly infinite) set of integers $A$, we say that $S$ tiles $A$ if $A$ can be partitioned into subsets equivalent to $S$. Such a partition is called a tiling of $A$ by $S$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $x, y$, and $z$ be three roots of unity. Prove that $x+y+z$ is also a root of unity if and only if $x+y=0, y+z=0$, or $z+x=0$.
|
Again, we consider the geometric picture. Arrange the vectors $x, y, z$, and $-x-y-z$ so as to form a quadrilateral. If they are all roots of unity, they form a quadrilateral all of whose side lengths are 1. If the quadrilateral is degenerate, then two of the vectors sum to 0 , which implies the result. But even if it is not degenerate, the quadrilateral must be a rhombus, and since opposite sides of a rhombus are parallel, this again implies that two of the four roots of unity sum to 0 .
## Early Re-tile-ment [150]
Let $S=\left\{s_{0}, \ldots, s_{n}\right\}$ be a finite set of integers, and define $S+k=\left\{s_{0}+k, \ldots, s_{n}+k\right\}$. We say that $S$ and $T$ are equivalent, written $S \sim T$, if $T=S+k$ for some $k$. Given a (possibly infinite) set of integers $A$, we say that $S$ tiles $A$ if $A$ can be partitioned into subsets equivalent to $S$. Such a partition is called a tiling of $A$ by $S$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team2-solutions.jsonl",
"problem_match": "\n10. [30]",
"solution_match": "\nSolution: "
}
|
d0e2cf5f-a19e-5b97-bc86-db9aa70b80a2
| 611,418
|
Let $A$ be a finite set with more than one element. Prove that the number of nonequivalent sets $S$ which tile $A$ is always even.
|
Suppose $A$ can be partitioned into sets $S_{0}, \ldots, S_{m}$, each equivalent to $S$. (This partition is unique, simply by choosing $S_{0}$ to contain the smallest element of $A$, $S_{1}$ the smallest element of $A$ not in $S_{0}$, etc.) Then if $S_{j}=S+t_{j}$, each element of $A$ can be written uniquely as $s_{i}+t_{j}$ for some $i$ and $j$. But then the set $T$ containing all $t_{j}$ also tiles $A$ by translation by the $s_{i}$. We cannot have $S$ and $T$ equivalent, for if so, since $A$ has more than one element, both $S$ and $T$ would as well. This would imply that $s_{0}+t_{1}=s_{1}+t_{0}$, an overlap in the tiling of $A$. We can thus pair together $S$ and $T$, each of which tile $A$, so that the total number of sets tiling $A$ must be even.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $A$ be a finite set with more than one element. Prove that the number of nonequivalent sets $S$ which tile $A$ is always even.
|
Suppose $A$ can be partitioned into sets $S_{0}, \ldots, S_{m}$, each equivalent to $S$. (This partition is unique, simply by choosing $S_{0}$ to contain the smallest element of $A$, $S_{1}$ the smallest element of $A$ not in $S_{0}$, etc.) Then if $S_{j}=S+t_{j}$, each element of $A$ can be written uniquely as $s_{i}+t_{j}$ for some $i$ and $j$. But then the set $T$ containing all $t_{j}$ also tiles $A$ by translation by the $s_{i}$. We cannot have $S$ and $T$ equivalent, for if so, since $A$ has more than one element, both $S$ and $T$ would as well. This would imply that $s_{0}+t_{1}=s_{1}+t_{0}$, an overlap in the tiling of $A$. We can thus pair together $S$ and $T$, each of which tile $A$, so that the total number of sets tiling $A$ must be even.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team2-solutions.jsonl",
"problem_match": "\n12. [35]",
"solution_match": "\nSolution: "
}
|
db1c4c32-ba8c-5952-86ee-ce15a78da2d4
| 611,420
|
Suppose that $S$ tiles the set of all integer cubes. Prove that $S$ has only one element.
|
Let the difference between the smallest and largest element of $S$ be $a$. Then the set equivalent to $S$ that contains $b^{3}$ can only contain integers between $b^{3}-a$ and $b^{3}+a$, inclusive. But for sufficiently large $b, b^{3}$ is the only cube in this range, so $S$ can only have one element.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Suppose that $S$ tiles the set of all integer cubes. Prove that $S$ has only one element.
|
Let the difference between the smallest and largest element of $S$ be $a$. Then the set equivalent to $S$ that contains $b^{3}$ can only contain integers between $b^{3}-a$ and $b^{3}+a$, inclusive. But for sufficiently large $b, b^{3}$ is the only cube in this range, so $S$ can only have one element.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team2-solutions.jsonl",
"problem_match": "\n14. [30]",
"solution_match": "\nSolution: "
}
|
f82b0bd2-1189-5277-973c-187a8411ecd7
| 611,422
|
Suppose that $S$ tiles the set of odd prime numbers. Prove that $S$ has only one element.
|
Consider the set $S_{0}$ equivalent to $S$ that contains 3. If it contains 5 but not 7 , then the set $S_{1}$ equivalent to $S$ containing 7 must contain 9 , which is not prime. Likewise, $S_{0}$ cannot contain 7 but not 5 , because then the set $S_{1}$ containing 5 must contain 9 . Suppose $S_{0}$ contains 3,5 , and 7 . Then any other set $S_{1}$ of the tiling contains elements $p, p+2$, and $p+4$. But not all of these can be prime, because one of them is divisible by 3 . Finally, suppose $S_{0}$ contains 3 and has second-smallest element $p>7$. Then the set $S_{1}$ containing 5 does not contain 7 but does contain $p+2$, and the set $S_{2}$ containing 7 contains $p+4$. But as before, not all of $p, p+2$, and $p+4$ can be prime. Therefore $S$ has no second-smallest element, so it has only one element.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Suppose that $S$ tiles the set of odd prime numbers. Prove that $S$ has only one element.
|
Consider the set $S_{0}$ equivalent to $S$ that contains 3. If it contains 5 but not 7 , then the set $S_{1}$ equivalent to $S$ containing 7 must contain 9 , which is not prime. Likewise, $S_{0}$ cannot contain 7 but not 5 , because then the set $S_{1}$ containing 5 must contain 9 . Suppose $S_{0}$ contains 3,5 , and 7 . Then any other set $S_{1}$ of the tiling contains elements $p, p+2$, and $p+4$. But not all of these can be prime, because one of them is divisible by 3 . Finally, suppose $S_{0}$ contains 3 and has second-smallest element $p>7$. Then the set $S_{1}$ containing 5 does not contain 7 but does contain $p+2$, and the set $S_{2}$ containing 7 contains $p+4$. But as before, not all of $p, p+2$, and $p+4$ can be prime. Therefore $S$ has no second-smallest element, so it has only one element.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-team2-solutions.jsonl",
"problem_match": "\n15. [40]",
"solution_match": "\nSolution: "
}
|
b440dade-f42b-5fc6-a371-6e74beebc0d7
| 611,423
|
Let $n$ be an integer at least 5. At most how many diagonals of a regular $n$-gon can be simultaneously drawn so that no two are parallel? Prove your answer.
|
Let $O$ be the center of the $n$-gon. Let us consider two cases, based on the parity of $n$ :
- $n$ is odd. In this case, for each diagonal $d$, there is exactly one vertex $D$ of the $n$-gon, such that $d$ is perpendicular to line $O D$; and of course, for each vertex $D$, there is at least one diagonal $d$ perpendicular to $O D$, because $n \geq 5$. The problem of picking a bunch of $d$ 's so that no two are parallel is thus transmuted into one of picking a bunch of $d$ 's so that none of the corresponding $D$ 's are the same. Well, go figure.
- $n$ is even. What can I say? For each diagonal $d$, the perpendicular dropped from $O$ to $d$ either passes through two opposite vertices of the $n$-gon, or else bisects two opposite sides. Conversely, for each line joining opposite vertices or bisecting opposite sides, there is at least one diagonal perpendicular to it, because $n \geq 6$. By reasoning similar to the odd case, we find the answer to be $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be an integer at least 5. At most how many diagonals of a regular $n$-gon can be simultaneously drawn so that no two are parallel? Prove your answer.
|
Let $O$ be the center of the $n$-gon. Let us consider two cases, based on the parity of $n$ :
- $n$ is odd. In this case, for each diagonal $d$, there is exactly one vertex $D$ of the $n$-gon, such that $d$ is perpendicular to line $O D$; and of course, for each vertex $D$, there is at least one diagonal $d$ perpendicular to $O D$, because $n \geq 5$. The problem of picking a bunch of $d$ 's so that no two are parallel is thus transmuted into one of picking a bunch of $d$ 's so that none of the corresponding $D$ 's are the same. Well, go figure.
- $n$ is even. What can I say? For each diagonal $d$, the perpendicular dropped from $O$ to $d$ either passes through two opposite vertices of the $n$-gon, or else bisects two opposite sides. Conversely, for each line joining opposite vertices or bisecting opposite sides, there is at least one diagonal perpendicular to it, because $n \geq 6$. By reasoning similar to the odd case, we find the answer to be $n$.
|
{
"resource_path": "HarvardMIT/segmented/en-92-2006-feb-team1-solutions.jsonl",
"problem_match": "\n6. [15]",
"solution_match": "\nSolution: "
}
|
e4a71759-4eab-5f2e-a8a3-63294b84897b
| 611,526
|
Given a convex $n$-gon, $n \geq 4$, at most how many diagonals can be drawn such that each drawn diagonal intersects every other drawn diagonal either in the interior of the $n$-gon or at a vertex? Prove your answer.
|
First of all, assume without loss of generality that the $n$-gon is regular (this has no effect as far as diagonal intersection is concerned). Also, treat $n=4$ as a special case; obviously the answer is 2 here.
If $n$ is odd, simply draw $n$ diagonals, connecting each vertex to the ones $(n-1) / 2$ vertices away (in either direction).
If $n$ is even, first draw the $n / 2$ diagonals connecting pairs of vertices $n / 2$ vertices apart. Then, there are $n$ diagonals connecting pairs of vertices $n / 2-1$ vertices apart; they come in $n / 2$ pairs of parallel diagonals; from each such pair, randomly pick one diagonal and draw it.
To see that these constructions work, note that two diagonals, each connecting pairs of vertices at least $n / 2-1$ vertices apart, can fail to intersect or share a vertex only if they are parallel.
The previous problem shows that these constructions are optimal.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Given a convex $n$-gon, $n \geq 4$, at most how many diagonals can be drawn such that each drawn diagonal intersects every other drawn diagonal either in the interior of the $n$-gon or at a vertex? Prove your answer.
|
First of all, assume without loss of generality that the $n$-gon is regular (this has no effect as far as diagonal intersection is concerned). Also, treat $n=4$ as a special case; obviously the answer is 2 here.
If $n$ is odd, simply draw $n$ diagonals, connecting each vertex to the ones $(n-1) / 2$ vertices away (in either direction).
If $n$ is even, first draw the $n / 2$ diagonals connecting pairs of vertices $n / 2$ vertices apart. Then, there are $n$ diagonals connecting pairs of vertices $n / 2-1$ vertices apart; they come in $n / 2$ pairs of parallel diagonals; from each such pair, randomly pick one diagonal and draw it.
To see that these constructions work, note that two diagonals, each connecting pairs of vertices at least $n / 2-1$ vertices apart, can fail to intersect or share a vertex only if they are parallel.
The previous problem shows that these constructions are optimal.
|
{
"resource_path": "HarvardMIT/segmented/en-92-2006-feb-team1-solutions.jsonl",
"problem_match": "\n7. [25]",
"solution_match": "\nSolution: "
}
|
d189fc18-aa52-5836-ad8e-3cd6aba6ac1c
| 611,527
|
Let $n \geq 3$ be a positive integer. Prove that given any $n$ angles $0<\theta_{1}, \theta_{2}, \ldots, \theta_{n}<$ $180^{\circ}$, such that their sum is $180(n-2)$ degrees, there exists a convex $n$-gon having exactly those angles, in that order.
|
We induct on $n$. The statement holds trivially for $n=3$, as all triangles are convex. Now, suppose that the statement is true for $n-1$, where $n \geq 4$. Let $\theta_{1}, \theta_{2}, \ldots, \theta_{n}$ be $n$ angles less than $180^{\circ}$ whose sum equals $180(n-2)$ degrees. The statement is clearly true if $n=4$ and $\theta_{1}=\theta_{3}=180^{\circ}-\theta_{2}=180^{\circ}-\theta_{4}$ since we can easily form a parallelogram, so assume otherwise.
I claim that there exist two adjacent angles whose sum is greater than $180^{\circ}$. Assume otherwise. Then, we have $\theta_{i}+\theta_{i+1} \leq 180$ for $i=1,2, \ldots, n$, where $\theta_{n+1}=\theta_{1}$. Summing these inequalities over all $i$ yields $2 \cdot 180(n-2) \leq 180 n$, which is equivalent to $n \leq 4$. Of course, we can have $n=4$ if and only if we have equality in each of the above inequalities, forcing us to have a parallelogram contrary to our assumption.
Hence, we have two adjacent angles with sum greater than $180^{\circ}$. Without loss of generality, let these angles be $\theta_{n-1}$ and $\theta_{n}$, relabeling if necessary. By the inductive hypothesis, we may construct an $(n-1)$-gon with angles $\theta_{1}, \theta_{2}, \ldots, \theta_{n-2}, \theta_{n-1}+\theta_{n}-180^{\circ}$, as these angles are each less than $180^{\circ}$ and their sum equals $180(n-3)$ degrees. Consider the vertex with angle $\theta_{n-1}+\theta_{n}-180^{\circ}$. Note that we can "clip off" a triangle with angles $\theta_{n-1}+\theta_{n}-180^{\circ}, 180^{\circ}-\theta_{n-1}$, and $180^{\circ}-\theta_{n}$ at this vertex, yielding an $n$-gon with the desired angles, completing the inductive step.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $n \geq 3$ be a positive integer. Prove that given any $n$ angles $0<\theta_{1}, \theta_{2}, \ldots, \theta_{n}<$ $180^{\circ}$, such that their sum is $180(n-2)$ degrees, there exists a convex $n$-gon having exactly those angles, in that order.
|
We induct on $n$. The statement holds trivially for $n=3$, as all triangles are convex. Now, suppose that the statement is true for $n-1$, where $n \geq 4$. Let $\theta_{1}, \theta_{2}, \ldots, \theta_{n}$ be $n$ angles less than $180^{\circ}$ whose sum equals $180(n-2)$ degrees. The statement is clearly true if $n=4$ and $\theta_{1}=\theta_{3}=180^{\circ}-\theta_{2}=180^{\circ}-\theta_{4}$ since we can easily form a parallelogram, so assume otherwise.
I claim that there exist two adjacent angles whose sum is greater than $180^{\circ}$. Assume otherwise. Then, we have $\theta_{i}+\theta_{i+1} \leq 180$ for $i=1,2, \ldots, n$, where $\theta_{n+1}=\theta_{1}$. Summing these inequalities over all $i$ yields $2 \cdot 180(n-2) \leq 180 n$, which is equivalent to $n \leq 4$. Of course, we can have $n=4$ if and only if we have equality in each of the above inequalities, forcing us to have a parallelogram contrary to our assumption.
Hence, we have two adjacent angles with sum greater than $180^{\circ}$. Without loss of generality, let these angles be $\theta_{n-1}$ and $\theta_{n}$, relabeling if necessary. By the inductive hypothesis, we may construct an $(n-1)$-gon with angles $\theta_{1}, \theta_{2}, \ldots, \theta_{n-2}, \theta_{n-1}+\theta_{n}-180^{\circ}$, as these angles are each less than $180^{\circ}$ and their sum equals $180(n-3)$ degrees. Consider the vertex with angle $\theta_{n-1}+\theta_{n}-180^{\circ}$. Note that we can "clip off" a triangle with angles $\theta_{n-1}+\theta_{n}-180^{\circ}, 180^{\circ}-\theta_{n-1}$, and $180^{\circ}-\theta_{n}$ at this vertex, yielding an $n$-gon with the desired angles, completing the inductive step.
|
{
"resource_path": "HarvardMIT/segmented/en-92-2006-feb-team1-solutions.jsonl",
"problem_match": "\n9. [40]",
"solution_match": "\nSolution: "
}
|
59e88209-ed56-58ce-8a18-7ce8dca906d5
| 611,529
|
Having lost a game of checkers and my temper, I dash all the pieces to the ground but one. This last checker, which is perfectly circular in shape, remains completely on the board, and happens to cover equal areas of red and black squares. Prove that the center of this piece must lie on a boundary between two squares (or at a junction of four).
|
Suppose, for the sake of contradiction, that the problem is false. Evidently, at least one boundary between adjacent squares must lie within our checker, or else the checker would exist entirely within one square, meaning it would cover only one color. Note also that a checker's diameter is smaller than the side of any square of the board, so there are at most two such boundaries within our checker (one in each direction). Let $\ell$ be this, or one of these, boundaries. Draw a diameter $d$ of the checker parallel to $\ell$. Presumably, the strip of the checker between $\ell$ and $d$ is part red, part black. These red and black areas are unequal, however, because the center of the checker does not lie on any boundary between squares. But, if we were to swap colors within this strip, then the checker would have equal red and black areas, because then it would be
colored in a way such that flipping it across $d$ swaps the colors. This shows that, the way it is currently colored, the checker does not have equal red and black areas. This gives us the desired contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Having lost a game of checkers and my temper, I dash all the pieces to the ground but one. This last checker, which is perfectly circular in shape, remains completely on the board, and happens to cover equal areas of red and black squares. Prove that the center of this piece must lie on a boundary between two squares (or at a junction of four).
|
Suppose, for the sake of contradiction, that the problem is false. Evidently, at least one boundary between adjacent squares must lie within our checker, or else the checker would exist entirely within one square, meaning it would cover only one color. Note also that a checker's diameter is smaller than the side of any square of the board, so there are at most two such boundaries within our checker (one in each direction). Let $\ell$ be this, or one of these, boundaries. Draw a diameter $d$ of the checker parallel to $\ell$. Presumably, the strip of the checker between $\ell$ and $d$ is part red, part black. These red and black areas are unequal, however, because the center of the checker does not lie on any boundary between squares. But, if we were to swap colors within this strip, then the checker would have equal red and black areas, because then it would be
colored in a way such that flipping it across $d$ swaps the colors. This shows that, the way it is currently colored, the checker does not have equal red and black areas. This gives us the desired contradiction.
|
{
"resource_path": "HarvardMIT/segmented/en-92-2006-feb-team1-solutions.jsonl",
"problem_match": "\n13. [40]",
"solution_match": "\nSolution: "
}
|
c5efa2ce-005a-558d-a620-bc242c91529a
| 611,533
|
Find, with proof, all positive integer palindromes whose square is also a palindrome.
|
A palindrome satisfies the requirement if and only if the sum of the squares of its digits is less than 10 . We may categorize these numbers this way:
- 3
- Any palindromic combination of 1 s and 0 s with at most nine 1 s .
- Any palindrome consisting of a single 2 in the middle and 1 s and 0 s elsewhere, with at most four 1s.
- 2000... 0002
- 2000... $0001000 \ldots 0002$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Find, with proof, all positive integer palindromes whose square is also a palindrome.
|
A palindrome satisfies the requirement if and only if the sum of the squares of its digits is less than 10 . We may categorize these numbers this way:
- 3
- Any palindromic combination of 1 s and 0 s with at most nine 1 s .
- Any palindrome consisting of a single 2 in the middle and 1 s and 0 s elsewhere, with at most four 1s.
- 2000... 0002
- 2000... $0001000 \ldots 0002$
|
{
"resource_path": "HarvardMIT/segmented/en-92-2006-feb-team1-solutions.jsonl",
"problem_match": "\n15. [50]",
"solution_match": "\nAnswer: "
}
|
95d72029-3d99-5c9e-89a7-be0347ecff08
| 611,535
|
Find, with proof, all positive integer palindromes whose square is also a palindrome.
|
Let $n:=\sum_{i=0}^{d} a_{i} \cdot 10^{i}$ be a palindrome, where the $a_{i}$ are digits with $a_{i}=a_{d-i}$ and $a_{d} \neq 0$. Then, if we let
$$
b_{k}:=\sum_{i+j=k} a_{i} a_{j}
$$
for all $0 \leq k \leq 2 d$, then
$$
n^{2}=\sum_{k=0}^{2 d} b_{k} \cdot 10^{k}
$$
(this is not necessarily the decimal expansion of $n^{2}$, however). We have to show that $\sum_{i=0}^{d} a_{i}^{2}<10$ if and only if $n^{2}$ is a palindrome.
Suppose $\sum_{i=0}^{d} a_{i}^{2}<10$. Then, by the AM-GM inequality, we have
$$
b_{k}=\sum_{i+j=k} a_{i} a_{j} \leq \sum_{i+j=k} \frac{a_{i}^{2}+a_{j}^{2}}{2} \leq \sum_{i=0}^{d} \frac{a_{i}^{2}}{2}+\sum_{j=0}^{d} \frac{a_{j}^{2}}{2}<\frac{10}{2}+\frac{10}{2}=10
$$
Thus, loosely speaking, no carrying is ever done in computing $n \times n$ by long multiplication, so the digit in the $10^{k}$ place in $n^{2}$ is precisely $b_{k}$, and it's easy to see that $b_{k}=b_{2 d-k}$ and that $b_{2 d}=a_{d}^{2} \neq 0$. So $n^{2}$ is indeed a palindrome, as desired.
Now suppose $\sum_{i=0}^{d} a_{i}^{2} \geq 10$. Here note that
$$
b_{d}=\sum_{i+j=d} a_{i} a_{j}=\sum_{i=0}^{d} a_{i} a_{d-i}=\sum_{i=0}^{d} a_{i}^{2} \geq 10
$$
Thus, it cannot be true that, for all $k, b_{k}$ represents the $10^{k}$ digit of $n^{2}$, because no digit can be greater than or equal to 10 . Let $\ell$ be the greatest such that $b_{\ell}$ does not represent the $10^{\ell}$ digit of $n^{2}$. We are trying to prove that $n^{2}$ cannot be a palindrome. Consider three cases:
- $a_{d}=a_{0} \geq 4$. In this case we must have $\ell \geq 2 d$, because $b_{2 d}=a_{d}^{2}>10$.
If $a_{0}=4$, then $n^{2}$ ends in the digit 6 , but lies in the interval $\left[16 \cdot 10^{2 d}, 25 \cdot 10^{2 d}\right.$ ), and so starts with either a 1 or a 2 ; thus, $n^{2}$ cannot be a palindrome. Similarly, if $a_{0}=5$, then $n^{2}$ ends in 5 but starts with 2 or 3 ; if $a_{0}=6$, then $n^{2}$ ends in 6 but starts with 3 or 4 ; if $a_{0}=7$, then $n^{2}$ ends in 9 but starts with 4,5 , or 6 ; if $a_{0}=8$, then $n^{2}$ ends in 4 but starts with 6,7 or 8 ; if $a_{0}=9$, then $n^{2}$ ends in 1 but starts with 8 or 9 .
- $\ell \geq 2 d$ and $a_{d}=a_{0} \leq 3$.
Here we do something similar, but with a slight twist. The units digit of $n^{2}$ is $a_{0}^{2}$. Because $\ell \geq 2 d, n^{2}$ must be in the interval $\left[\left(a_{0}^{2}+1\right) \cdot 10^{2 d},\left(a_{0}+1\right)^{2} \cdot 10^{2 d}\right)$,
which is certainly a subset of the interval $\left[\left(a_{0}^{2}+1\right) \cdot 10^{2 d}, a_{0}^{2} \cdot 10^{2 d+1}\right)$. No integer in even this larger interval manages to start with the digit $a_{0}^{2}$, so $n^{2}$ cannot be palindromic.
- $\ell<2 d$.
Here we can rest assured that $n^{2}$ does have $(2 d+1)$ digits - that is, the first digit is in the $10^{2 d}$ place. In order for $n^{2}$ to be a palindrome, the digits in the $10^{k}$ and $10^{2 d-k}$ places must always be the same.
Now $b_{\ell}, b_{\ell+1}, \ldots, b_{2 d}$ had all better be less than 10 , or else $\ell$ would be greater than what it is. Thus, the numbers just listed do appear as the lowest digits of $n^{2}$ in left-to-right order, although they don't appear as the highest $(2 d+1-\ell)$ digits of $n^{2}$ in right-to-left order. Thus, $n^{2}$ cannot be a palindrome.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Find, with proof, all positive integer palindromes whose square is also a palindrome.
|
Let $n:=\sum_{i=0}^{d} a_{i} \cdot 10^{i}$ be a palindrome, where the $a_{i}$ are digits with $a_{i}=a_{d-i}$ and $a_{d} \neq 0$. Then, if we let
$$
b_{k}:=\sum_{i+j=k} a_{i} a_{j}
$$
for all $0 \leq k \leq 2 d$, then
$$
n^{2}=\sum_{k=0}^{2 d} b_{k} \cdot 10^{k}
$$
(this is not necessarily the decimal expansion of $n^{2}$, however). We have to show that $\sum_{i=0}^{d} a_{i}^{2}<10$ if and only if $n^{2}$ is a palindrome.
Suppose $\sum_{i=0}^{d} a_{i}^{2}<10$. Then, by the AM-GM inequality, we have
$$
b_{k}=\sum_{i+j=k} a_{i} a_{j} \leq \sum_{i+j=k} \frac{a_{i}^{2}+a_{j}^{2}}{2} \leq \sum_{i=0}^{d} \frac{a_{i}^{2}}{2}+\sum_{j=0}^{d} \frac{a_{j}^{2}}{2}<\frac{10}{2}+\frac{10}{2}=10
$$
Thus, loosely speaking, no carrying is ever done in computing $n \times n$ by long multiplication, so the digit in the $10^{k}$ place in $n^{2}$ is precisely $b_{k}$, and it's easy to see that $b_{k}=b_{2 d-k}$ and that $b_{2 d}=a_{d}^{2} \neq 0$. So $n^{2}$ is indeed a palindrome, as desired.
Now suppose $\sum_{i=0}^{d} a_{i}^{2} \geq 10$. Here note that
$$
b_{d}=\sum_{i+j=d} a_{i} a_{j}=\sum_{i=0}^{d} a_{i} a_{d-i}=\sum_{i=0}^{d} a_{i}^{2} \geq 10
$$
Thus, it cannot be true that, for all $k, b_{k}$ represents the $10^{k}$ digit of $n^{2}$, because no digit can be greater than or equal to 10 . Let $\ell$ be the greatest such that $b_{\ell}$ does not represent the $10^{\ell}$ digit of $n^{2}$. We are trying to prove that $n^{2}$ cannot be a palindrome. Consider three cases:
- $a_{d}=a_{0} \geq 4$. In this case we must have $\ell \geq 2 d$, because $b_{2 d}=a_{d}^{2}>10$.
If $a_{0}=4$, then $n^{2}$ ends in the digit 6 , but lies in the interval $\left[16 \cdot 10^{2 d}, 25 \cdot 10^{2 d}\right.$ ), and so starts with either a 1 or a 2 ; thus, $n^{2}$ cannot be a palindrome. Similarly, if $a_{0}=5$, then $n^{2}$ ends in 5 but starts with 2 or 3 ; if $a_{0}=6$, then $n^{2}$ ends in 6 but starts with 3 or 4 ; if $a_{0}=7$, then $n^{2}$ ends in 9 but starts with 4,5 , or 6 ; if $a_{0}=8$, then $n^{2}$ ends in 4 but starts with 6,7 or 8 ; if $a_{0}=9$, then $n^{2}$ ends in 1 but starts with 8 or 9 .
- $\ell \geq 2 d$ and $a_{d}=a_{0} \leq 3$.
Here we do something similar, but with a slight twist. The units digit of $n^{2}$ is $a_{0}^{2}$. Because $\ell \geq 2 d, n^{2}$ must be in the interval $\left[\left(a_{0}^{2}+1\right) \cdot 10^{2 d},\left(a_{0}+1\right)^{2} \cdot 10^{2 d}\right)$,
which is certainly a subset of the interval $\left[\left(a_{0}^{2}+1\right) \cdot 10^{2 d}, a_{0}^{2} \cdot 10^{2 d+1}\right)$. No integer in even this larger interval manages to start with the digit $a_{0}^{2}$, so $n^{2}$ cannot be palindromic.
- $\ell<2 d$.
Here we can rest assured that $n^{2}$ does have $(2 d+1)$ digits - that is, the first digit is in the $10^{2 d}$ place. In order for $n^{2}$ to be a palindrome, the digits in the $10^{k}$ and $10^{2 d-k}$ places must always be the same.
Now $b_{\ell}, b_{\ell+1}, \ldots, b_{2 d}$ had all better be less than 10 , or else $\ell$ would be greater than what it is. Thus, the numbers just listed do appear as the lowest digits of $n^{2}$ in left-to-right order, although they don't appear as the highest $(2 d+1-\ell)$ digits of $n^{2}$ in right-to-left order. Thus, $n^{2}$ cannot be a palindrome.
|
{
"resource_path": "HarvardMIT/segmented/en-92-2006-feb-team1-solutions.jsonl",
"problem_match": "\n15. [50]",
"solution_match": "\nSolution: "
}
|
95d72029-3d99-5c9e-89a7-be0347ecff08
| 611,535
|
Prove that, given any formation, each mobot may be colored in one of three colors - say, white, black, and blue - such that no two adjacent clumps of grass are mowed by different mobots of the same color. Two clumps of grass are adjacent if the distance between them is 1 . In your proof, you may use the Four-Color Theorem if you're familiar with it.
|
We can divide the coordinate plane into regions: Let's say a point belongs to Region 0 if the closest lattice point to it is not on the lawn, and each mobot $M$ owns a region that is the set of points for which the closest lattice point is on the lawn and mowed by $M$. Applying the Four-Color Theorem to these regions, we note that all the conditions demanded in the problem are satisfied. In particular at most 3 colors are used on the mobots because every mobot region borders Region 0 and hence is not colored the same color as Region 0.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Prove that, given any formation, each mobot may be colored in one of three colors - say, white, black, and blue - such that no two adjacent clumps of grass are mowed by different mobots of the same color. Two clumps of grass are adjacent if the distance between them is 1 . In your proof, you may use the Four-Color Theorem if you're familiar with it.
|
We can divide the coordinate plane into regions: Let's say a point belongs to Region 0 if the closest lattice point to it is not on the lawn, and each mobot $M$ owns a region that is the set of points for which the closest lattice point is on the lawn and mowed by $M$. Applying the Four-Color Theorem to these regions, we note that all the conditions demanded in the problem are satisfied. In particular at most 3 colors are used on the mobots because every mobot region borders Region 0 and hence is not colored the same color as Region 0.
|
{
"resource_path": "HarvardMIT/segmented/en-92-2006-feb-team2-solutions.jsonl",
"problem_match": "\n3. [15]",
"solution_match": "\nSolution: "
}
|
0cd25827-b07e-5210-a8ba-dd615ab99d68
| 611,538
|
Given a convex $n$-gon, $n \geq 4$, at most how many diagonals can be drawn such that each drawn diagonal intersects every other drawn diagonal strictly in the interior of the $n$-gon? Prove that your answer is correct.
|
If $n$ is even, simply draw all $n / 2$ diagonals connecting a vertex to the one $n / 2$ vertices away. If $n$ is odd, pretend one of the vertices does not exist, and do the above for the ( $n-1$ )-gon remaining.
To show this is optimal, consider any given drawn diagonal: it divides the remaining $n-2$ vertices into two camps, one of which therefore has size at most $\lfloor n / 2\rfloor-1$, and one cannot draw two diagonals sharing a vertex.
## What do the following problems have in common?
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Given a convex $n$-gon, $n \geq 4$, at most how many diagonals can be drawn such that each drawn diagonal intersects every other drawn diagonal strictly in the interior of the $n$-gon? Prove that your answer is correct.
|
If $n$ is even, simply draw all $n / 2$ diagonals connecting a vertex to the one $n / 2$ vertices away. If $n$ is odd, pretend one of the vertices does not exist, and do the above for the ( $n-1$ )-gon remaining.
To show this is optimal, consider any given drawn diagonal: it divides the remaining $n-2$ vertices into two camps, one of which therefore has size at most $\lfloor n / 2\rfloor-1$, and one cannot draw two diagonals sharing a vertex.
## What do the following problems have in common?
|
{
"resource_path": "HarvardMIT/segmented/en-92-2006-feb-team2-solutions.jsonl",
"problem_match": "\n10. [40]",
"solution_match": "\nSolution: "
}
|
b6d75a83-6a3b-520d-87d8-992f0ec9bee4
| 611,545
|
A sequence of real numbers $a_{0}, a_{1}, a_{2}, \ldots$ is defined by the formula $$ a_{i+1}=\left\lfloor a_{i}\right\rfloor \cdot\left\langle a_{i}\right\rangle \quad \text { for } \quad i \geq 0 \text {; } $$ here $a_{0}$ is an arbitrary real number, $\left\lfloor a_{i}\right\rfloor$ denotes the greatest integer not exceeding $a_{i}$, and $\left\langle a_{i}\right\rangle=a_{i}-\left\lfloor a_{i}\right\rfloor$. Prove that $a_{i}=a_{i+2}$ for $i$ sufficiently large. (Estonia)
|
First note that if $a_{0} \geq 0$, then all $a_{i} \geq 0$. For $a_{i} \geq 1$ we have (in view of $\left\langle a_{i}\right\rangle<1$ and $\left\lfloor a_{i}\right\rfloor>0$ ) $$ \left\lfloor a_{i+1}\right\rfloor \leq a_{i+1}=\left\lfloor a_{i}\right\rfloor \cdot\left\langle a_{i}\right\rangle<\left\lfloor a_{i}\right\rfloor $$ the sequence $\left\lfloor a_{i}\right\rfloor$ is strictly decreasing as long as its terms are in $[1, \infty)$. Eventually there appears a number from the interval $[0,1)$ and all subsequent terms are 0 . Now pass to the more interesting situation where $a_{0}<0$; then all $a_{i} \leq 0$. Suppose the sequence never hits 0 . Then we have $\left\lfloor a_{i}\right\rfloor \leq-1$ for all $i$, and so $$ 1+\left\lfloor a_{i+1}\right\rfloor>a_{i+1}=\left\lfloor a_{i}\right\rfloor \cdot\left\langle a_{i}\right\rangle>\left\lfloor a_{i}\right\rfloor $$ this means that the sequence $\left\lfloor a_{i}\right\rfloor$ is nondecreasing. And since all its terms are integers from $(-\infty,-1]$, this sequence must be constant from some term on: $$ \left\lfloor a_{i}\right\rfloor=c \quad \text { for } \quad i \geq i_{0} ; \quad c \text { a negative integer. } $$ The defining formula becomes $$ a_{i+1}=c \cdot\left\langle a_{i}\right\rangle=c\left(a_{i}-c\right)=c a_{i}-c^{2} . $$ Consider the sequence $$ b_{i}=a_{i}-\frac{c^{2}}{c-1} $$ It satisfies the recursion rule $$ b_{i+1}=a_{i+1}-\frac{c^{2}}{c-1}=c a_{i}-c^{2}-\frac{c^{2}}{c-1}=c b_{i} $$ implying $$ b_{i}=c^{i-i_{0}} b_{i_{0}} \quad \text { for } \quad i \geq i_{0} . $$ Since all the numbers $a_{i}$ (for $i \geq i_{0}$ ) lie in $\left[c, c+1\right.$ ), the sequence $\left(b_{i}\right)$ is bounded. The equation (2) can be satisfied only if either $b_{i_{0}}=0$ or $|c|=1$, i.e., $c=-1$. In the first case, $b_{i}=0$ for all $i \geq i_{0}$, so that $$ a_{i}=\frac{c^{2}}{c-1} \quad \text { for } \quad i \geq i_{0} $$ In the second case, $c=-1$, equations (1) and (2) say that $$ a_{i}=-\frac{1}{2}+(-1)^{i-i_{0}} b_{i_{0}}= \begin{cases}a_{i_{0}} & \text { for } i=i_{0}, i_{0}+2, i_{0}+4, \ldots \\ 1-a_{i_{0}} & \text { for } i=i_{0}+1, i_{0}+3, i_{0}+5, \ldots\end{cases} $$ Summarising, we see that (from some point on) the sequence $\left(a_{i}\right)$ either is constant or takes alternately two values from the interval $(-1,0)$. The result follows. Comment. There is nothing mysterious in introducing the sequence $\left(b_{i}\right)$. The sequence $\left(a_{i}\right)$ arises by iterating the function $x \mapsto c x-c^{2}$ whose unique fixed point is $c^{2} /(c-1)$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A sequence of real numbers $a_{0}, a_{1}, a_{2}, \ldots$ is defined by the formula $$ a_{i+1}=\left\lfloor a_{i}\right\rfloor \cdot\left\langle a_{i}\right\rangle \quad \text { for } \quad i \geq 0 \text {; } $$ here $a_{0}$ is an arbitrary real number, $\left\lfloor a_{i}\right\rfloor$ denotes the greatest integer not exceeding $a_{i}$, and $\left\langle a_{i}\right\rangle=a_{i}-\left\lfloor a_{i}\right\rfloor$. Prove that $a_{i}=a_{i+2}$ for $i$ sufficiently large. (Estonia)
|
First note that if $a_{0} \geq 0$, then all $a_{i} \geq 0$. For $a_{i} \geq 1$ we have (in view of $\left\langle a_{i}\right\rangle<1$ and $\left\lfloor a_{i}\right\rfloor>0$ ) $$ \left\lfloor a_{i+1}\right\rfloor \leq a_{i+1}=\left\lfloor a_{i}\right\rfloor \cdot\left\langle a_{i}\right\rangle<\left\lfloor a_{i}\right\rfloor $$ the sequence $\left\lfloor a_{i}\right\rfloor$ is strictly decreasing as long as its terms are in $[1, \infty)$. Eventually there appears a number from the interval $[0,1)$ and all subsequent terms are 0 . Now pass to the more interesting situation where $a_{0}<0$; then all $a_{i} \leq 0$. Suppose the sequence never hits 0 . Then we have $\left\lfloor a_{i}\right\rfloor \leq-1$ for all $i$, and so $$ 1+\left\lfloor a_{i+1}\right\rfloor>a_{i+1}=\left\lfloor a_{i}\right\rfloor \cdot\left\langle a_{i}\right\rangle>\left\lfloor a_{i}\right\rfloor $$ this means that the sequence $\left\lfloor a_{i}\right\rfloor$ is nondecreasing. And since all its terms are integers from $(-\infty,-1]$, this sequence must be constant from some term on: $$ \left\lfloor a_{i}\right\rfloor=c \quad \text { for } \quad i \geq i_{0} ; \quad c \text { a negative integer. } $$ The defining formula becomes $$ a_{i+1}=c \cdot\left\langle a_{i}\right\rangle=c\left(a_{i}-c\right)=c a_{i}-c^{2} . $$ Consider the sequence $$ b_{i}=a_{i}-\frac{c^{2}}{c-1} $$ It satisfies the recursion rule $$ b_{i+1}=a_{i+1}-\frac{c^{2}}{c-1}=c a_{i}-c^{2}-\frac{c^{2}}{c-1}=c b_{i} $$ implying $$ b_{i}=c^{i-i_{0}} b_{i_{0}} \quad \text { for } \quad i \geq i_{0} . $$ Since all the numbers $a_{i}$ (for $i \geq i_{0}$ ) lie in $\left[c, c+1\right.$ ), the sequence $\left(b_{i}\right)$ is bounded. The equation (2) can be satisfied only if either $b_{i_{0}}=0$ or $|c|=1$, i.e., $c=-1$. In the first case, $b_{i}=0$ for all $i \geq i_{0}$, so that $$ a_{i}=\frac{c^{2}}{c-1} \quad \text { for } \quad i \geq i_{0} $$ In the second case, $c=-1$, equations (1) and (2) say that $$ a_{i}=-\frac{1}{2}+(-1)^{i-i_{0}} b_{i_{0}}= \begin{cases}a_{i_{0}} & \text { for } i=i_{0}, i_{0}+2, i_{0}+4, \ldots \\ 1-a_{i_{0}} & \text { for } i=i_{0}+1, i_{0}+3, i_{0}+5, \ldots\end{cases} $$ Summarising, we see that (from some point on) the sequence $\left(a_{i}\right)$ either is constant or takes alternately two values from the interval $(-1,0)$. The result follows. Comment. There is nothing mysterious in introducing the sequence $\left(b_{i}\right)$. The sequence $\left(a_{i}\right)$ arises by iterating the function $x \mapsto c x-c^{2}$ whose unique fixed point is $c^{2} /(c-1)$.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
08372ea3-6a52-5bb0-88a0-f03c63bb75d4
| 23,526
|
The sequence of real numbers $a_{0}, a_{1}, a_{2}, \ldots$ is defined recursively by $$ a_{0}=-1, \quad \sum_{k=0}^{n} \frac{a_{n-k}}{k+1}=0 \quad \text { for } \quad n \geq 1 $$ Show that $a_{n}>0$ for $n \geq 1$. (Poland)
|
The proof goes by induction. For $n=1$ the formula yields $a_{1}=1 / 2$. Take $n \geq 1$, assume $a_{1}, \ldots, a_{n}>0$ and write the recurrence formula for $n$ and $n+1$, respectively as $$ \sum_{k=0}^{n} \frac{a_{k}}{n-k+1}=0 \quad \text { and } \quad \sum_{k=0}^{n+1} \frac{a_{k}}{n-k+2}=0 $$ Subtraction yields $$ \begin{aligned} 0=(n+2) \sum_{k=0}^{n+1} & \frac{a_{k}}{n-k+2}-(n+1) \sum_{k=0}^{n} \frac{a_{k}}{n-k+1} \\ = & (n+2) a_{n+1}+\sum_{k=0}^{n}\left(\frac{n+2}{n-k+2}-\frac{n+1}{n-k+1}\right) a_{k} . \end{aligned} $$ The coefficient of $a_{0}$ vanishes, so $$ a_{n+1}=\frac{1}{n+2} \sum_{k=1}^{n}\left(\frac{n+1}{n-k+1}-\frac{n+2}{n-k+2}\right) a_{k}=\frac{1}{n+2} \sum_{k=1}^{n} \frac{k}{(n-k+1)(n-k+2)} a_{k} . $$ The coefficients of $a_{1}, \ldots, a_{n}$ are all positive. Therefore, $a_{1}, \ldots, a_{n}>0$ implies $a_{n+1}>0$. Comment. Students familiar with the technique of generating functions will immediately recognise $\sum a_{n} x^{n}$ as the power series expansion of $x / \ln (1-x)$ (with value -1 at 0 ). But this can be a trap; attempts along these lines lead to unpleasant differential equations and integrals hard to handle. Using only tools from real analysis (e.g. computing the coefficients from the derivatives) seems very difficult. On the other hand, the coefficients can be approached applying complex contour integrals and some other techniques from complex analysis and an attractive formula can be obtained for the coefficients: $$ a_{n}=\int_{1}^{\infty} \frac{\mathrm{d} x}{x^{n}\left(\pi^{2}+\log ^{2}(x-1)\right)} \quad(n \geq 1) $$ which is evidently positive.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
The sequence of real numbers $a_{0}, a_{1}, a_{2}, \ldots$ is defined recursively by $$ a_{0}=-1, \quad \sum_{k=0}^{n} \frac{a_{n-k}}{k+1}=0 \quad \text { for } \quad n \geq 1 $$ Show that $a_{n}>0$ for $n \geq 1$. (Poland)
|
The proof goes by induction. For $n=1$ the formula yields $a_{1}=1 / 2$. Take $n \geq 1$, assume $a_{1}, \ldots, a_{n}>0$ and write the recurrence formula for $n$ and $n+1$, respectively as $$ \sum_{k=0}^{n} \frac{a_{k}}{n-k+1}=0 \quad \text { and } \quad \sum_{k=0}^{n+1} \frac{a_{k}}{n-k+2}=0 $$ Subtraction yields $$ \begin{aligned} 0=(n+2) \sum_{k=0}^{n+1} & \frac{a_{k}}{n-k+2}-(n+1) \sum_{k=0}^{n} \frac{a_{k}}{n-k+1} \\ = & (n+2) a_{n+1}+\sum_{k=0}^{n}\left(\frac{n+2}{n-k+2}-\frac{n+1}{n-k+1}\right) a_{k} . \end{aligned} $$ The coefficient of $a_{0}$ vanishes, so $$ a_{n+1}=\frac{1}{n+2} \sum_{k=1}^{n}\left(\frac{n+1}{n-k+1}-\frac{n+2}{n-k+2}\right) a_{k}=\frac{1}{n+2} \sum_{k=1}^{n} \frac{k}{(n-k+1)(n-k+2)} a_{k} . $$ The coefficients of $a_{1}, \ldots, a_{n}$ are all positive. Therefore, $a_{1}, \ldots, a_{n}>0$ implies $a_{n+1}>0$. Comment. Students familiar with the technique of generating functions will immediately recognise $\sum a_{n} x^{n}$ as the power series expansion of $x / \ln (1-x)$ (with value -1 at 0 ). But this can be a trap; attempts along these lines lead to unpleasant differential equations and integrals hard to handle. Using only tools from real analysis (e.g. computing the coefficients from the derivatives) seems very difficult. On the other hand, the coefficients can be approached applying complex contour integrals and some other techniques from complex analysis and an attractive formula can be obtained for the coefficients: $$ a_{n}=\int_{1}^{\infty} \frac{\mathrm{d} x}{x^{n}\left(\pi^{2}+\log ^{2}(x-1)\right)} \quad(n \geq 1) $$ which is evidently positive.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
1d0c3c80-a19d-596c-b792-15d6496de511
| 23,530
|
Prove the inequality $$ \sum_{i<j} \frac{a_{i} a_{j}}{a_{i}+a_{j}} \leq \frac{n}{2\left(a_{1}+a_{2}+\cdots+a_{n}\right)} \sum_{i<j} a_{i} a_{j} $$ for positive real numbers $a_{1}, a_{2}, \ldots, a_{n}$. (Serbia)
|
Let $S=\sum_{i} a_{i}$. Denote by $L$ and $R$ the expressions on the left and right hand side of the proposed inequality. We transform $L$ and $R$ using the identity $$ \sum_{i<j}\left(a_{i}+a_{j}\right)=(n-1) \sum_{i} a_{i} $$ And thus: $$ L=\sum_{i<j} \frac{a_{i} a_{j}}{a_{i}+a_{j}}=\sum_{i<j} \frac{1}{4}\left(a_{i}+a_{j}-\frac{\left(a_{i}-a_{j}\right)^{2}}{a_{i}+a_{j}}\right)=\frac{n-1}{4} \cdot S-\frac{1}{4} \sum_{i<j} \frac{\left(a_{i}-a_{j}\right)^{2}}{a_{i}+a_{j}} . $$ To represent $R$ we express the sum $\sum_{i<j} a_{i} a_{j}$ in two ways; in the second transformation identity (1) will be applied to the squares of the numbers $a_{i}$ : $$ \begin{gathered} \sum_{i<j} a_{i} a_{j}=\frac{1}{2}\left(S^{2}-\sum_{i} a_{i}^{2}\right) \\ \sum_{i<j} a_{i} a_{j}=\frac{1}{2} \sum_{i<j}\left(a_{i}^{2}+a_{j}^{2}-\left(a_{i}-a_{j}\right)^{2}\right)=\frac{n-1}{2} \cdot \sum_{i} a_{i}^{2}-\frac{1}{2} \sum_{i<j}\left(a_{i}-a_{j}\right)^{2} . \end{gathered} $$ Multiplying the first of these equalities by $n-1$ and adding the second one we obtain $$ n \sum_{i<j} a_{i} a_{j}=\frac{n-1}{2} \cdot S^{2}-\frac{1}{2} \sum_{i<j}\left(a_{i}-a_{j}\right)^{2} $$ Hence $$ R=\frac{n}{2 S} \sum_{i<j} a_{i} a_{j}=\frac{n-1}{4} \cdot S-\frac{1}{4} \sum_{i<j} \frac{\left(a_{i}-a_{j}\right)^{2}}{S} . $$ Now compare (2) and (3). Since $S \geq a_{i}+a_{j}$ for any $i<j$, the claim $L \geq R$ results.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove the inequality $$ \sum_{i<j} \frac{a_{i} a_{j}}{a_{i}+a_{j}} \leq \frac{n}{2\left(a_{1}+a_{2}+\cdots+a_{n}\right)} \sum_{i<j} a_{i} a_{j} $$ for positive real numbers $a_{1}, a_{2}, \ldots, a_{n}$. (Serbia)
|
Let $S=\sum_{i} a_{i}$. Denote by $L$ and $R$ the expressions on the left and right hand side of the proposed inequality. We transform $L$ and $R$ using the identity $$ \sum_{i<j}\left(a_{i}+a_{j}\right)=(n-1) \sum_{i} a_{i} $$ And thus: $$ L=\sum_{i<j} \frac{a_{i} a_{j}}{a_{i}+a_{j}}=\sum_{i<j} \frac{1}{4}\left(a_{i}+a_{j}-\frac{\left(a_{i}-a_{j}\right)^{2}}{a_{i}+a_{j}}\right)=\frac{n-1}{4} \cdot S-\frac{1}{4} \sum_{i<j} \frac{\left(a_{i}-a_{j}\right)^{2}}{a_{i}+a_{j}} . $$ To represent $R$ we express the sum $\sum_{i<j} a_{i} a_{j}$ in two ways; in the second transformation identity (1) will be applied to the squares of the numbers $a_{i}$ : $$ \begin{gathered} \sum_{i<j} a_{i} a_{j}=\frac{1}{2}\left(S^{2}-\sum_{i} a_{i}^{2}\right) \\ \sum_{i<j} a_{i} a_{j}=\frac{1}{2} \sum_{i<j}\left(a_{i}^{2}+a_{j}^{2}-\left(a_{i}-a_{j}\right)^{2}\right)=\frac{n-1}{2} \cdot \sum_{i} a_{i}^{2}-\frac{1}{2} \sum_{i<j}\left(a_{i}-a_{j}\right)^{2} . \end{gathered} $$ Multiplying the first of these equalities by $n-1$ and adding the second one we obtain $$ n \sum_{i<j} a_{i} a_{j}=\frac{n-1}{2} \cdot S^{2}-\frac{1}{2} \sum_{i<j}\left(a_{i}-a_{j}\right)^{2} $$ Hence $$ R=\frac{n}{2 S} \sum_{i<j} a_{i} a_{j}=\frac{n-1}{4} \cdot S-\frac{1}{4} \sum_{i<j} \frac{\left(a_{i}-a_{j}\right)^{2}}{S} . $$ Now compare (2) and (3). Since $S \geq a_{i}+a_{j}$ for any $i<j$, the claim $L \geq R$ results.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9fe3c2d5-810f-5217-942b-b6e528059ff5
| 23,535
|
Prove the inequality $$ \sum_{i<j} \frac{a_{i} a_{j}}{a_{i}+a_{j}} \leq \frac{n}{2\left(a_{1}+a_{2}+\cdots+a_{n}\right)} \sum_{i<j} a_{i} a_{j} $$ for positive real numbers $a_{1}, a_{2}, \ldots, a_{n}$. (Serbia)
|
Let $S=a_{1}+a_{2}+\cdots+a_{n}$. For any $i \neq j$, $$ 4 \frac{a_{i} a_{j}}{a_{i}+a_{j}}=a_{i}+a_{j}-\frac{\left(a_{i}-a_{j}\right)^{2}}{a_{i}+a_{j}} \leq a_{i}+a_{j}-\frac{\left(a_{i}-a_{j}\right)^{2}}{a_{1}+a_{2}+\cdots+a_{n}}=\frac{\sum_{k \neq i} a_{i} a_{k}+\sum_{k \neq j} a_{j} a_{k}+2 a_{i} a_{j}}{S} . $$ The statement is obtained by summing up these inequalities for all pairs $i, j$ : $$ \begin{gathered} \sum_{i<j} \frac{a_{i} a_{j}}{a_{i}+a_{j}}=\frac{1}{2} \sum_{i} \sum_{j \neq i} \frac{a_{i} a_{j}}{a_{i}+a_{j}} \leq \frac{1}{8 S} \sum_{i} \sum_{j \neq i}\left(\sum_{k \neq i} a_{i} a_{k}+\sum_{k \neq j} a_{j} a_{k}+2 a_{i} a_{j}\right) \\ =\frac{1}{8 S}\left(\sum_{k} \sum_{i \neq k} \sum_{j \neq i} a_{i} a_{k}+\sum_{k} \sum_{j \neq k} \sum_{i \neq j} a_{j} a_{k}+\sum_{i} \sum_{j \neq i} 2 a_{i} a_{j}\right) \\ =\frac{1}{8 S}\left(\sum_{k} \sum_{i \neq k}(n-1) a_{i} a_{k}+\sum_{k} \sum_{j \neq k}(n-1) a_{j} a_{k}+\sum_{i} \sum_{j \neq i} 2 a_{i} a_{j}\right) \\ =\frac{n}{4 S} \sum_{i} \sum_{j \neq i} a_{i} a_{j}=\frac{n}{2 S} \sum_{i<j} a_{i} a_{j} . \end{gathered} $$ Comment. Here is an outline of another possible approach. Examine the function $R-L$ subject to constraints $\sum_{i} a_{i}=S, \sum_{i<j} a_{i} a_{j}=U$ for fixed constants $S, U>0$ (which can jointly occur as values of these symmetric forms). Suppose that among the numbers $a_{i}$ there are some three, say $a_{k}, a_{l}, a_{m}$ such that $a_{k}<a_{l} \leq a_{m}$. Then it is possible to decrease the value of $R-L$ by perturbing this triple so that in the new triple $a_{k}^{\prime}, a_{l}^{\prime}, a_{m}^{\prime}$ one has $a_{k}^{\prime}=a_{l}^{\prime} \leq a_{m}^{\prime}$, without touching the remaining $a_{i} \mathrm{~s}$ and without changing the values of $S$ and $U$; this requires some skill in algebraic manipulations. It follows that the constrained minimum can be only attained for $n-1$ of the $a_{i}$ s equal and a single one possibly greater. In this case, $R-L \geq 0$ holds almost trivially.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove the inequality $$ \sum_{i<j} \frac{a_{i} a_{j}}{a_{i}+a_{j}} \leq \frac{n}{2\left(a_{1}+a_{2}+\cdots+a_{n}\right)} \sum_{i<j} a_{i} a_{j} $$ for positive real numbers $a_{1}, a_{2}, \ldots, a_{n}$. (Serbia)
|
Let $S=a_{1}+a_{2}+\cdots+a_{n}$. For any $i \neq j$, $$ 4 \frac{a_{i} a_{j}}{a_{i}+a_{j}}=a_{i}+a_{j}-\frac{\left(a_{i}-a_{j}\right)^{2}}{a_{i}+a_{j}} \leq a_{i}+a_{j}-\frac{\left(a_{i}-a_{j}\right)^{2}}{a_{1}+a_{2}+\cdots+a_{n}}=\frac{\sum_{k \neq i} a_{i} a_{k}+\sum_{k \neq j} a_{j} a_{k}+2 a_{i} a_{j}}{S} . $$ The statement is obtained by summing up these inequalities for all pairs $i, j$ : $$ \begin{gathered} \sum_{i<j} \frac{a_{i} a_{j}}{a_{i}+a_{j}}=\frac{1}{2} \sum_{i} \sum_{j \neq i} \frac{a_{i} a_{j}}{a_{i}+a_{j}} \leq \frac{1}{8 S} \sum_{i} \sum_{j \neq i}\left(\sum_{k \neq i} a_{i} a_{k}+\sum_{k \neq j} a_{j} a_{k}+2 a_{i} a_{j}\right) \\ =\frac{1}{8 S}\left(\sum_{k} \sum_{i \neq k} \sum_{j \neq i} a_{i} a_{k}+\sum_{k} \sum_{j \neq k} \sum_{i \neq j} a_{j} a_{k}+\sum_{i} \sum_{j \neq i} 2 a_{i} a_{j}\right) \\ =\frac{1}{8 S}\left(\sum_{k} \sum_{i \neq k}(n-1) a_{i} a_{k}+\sum_{k} \sum_{j \neq k}(n-1) a_{j} a_{k}+\sum_{i} \sum_{j \neq i} 2 a_{i} a_{j}\right) \\ =\frac{n}{4 S} \sum_{i} \sum_{j \neq i} a_{i} a_{j}=\frac{n}{2 S} \sum_{i<j} a_{i} a_{j} . \end{gathered} $$ Comment. Here is an outline of another possible approach. Examine the function $R-L$ subject to constraints $\sum_{i} a_{i}=S, \sum_{i<j} a_{i} a_{j}=U$ for fixed constants $S, U>0$ (which can jointly occur as values of these symmetric forms). Suppose that among the numbers $a_{i}$ there are some three, say $a_{k}, a_{l}, a_{m}$ such that $a_{k}<a_{l} \leq a_{m}$. Then it is possible to decrease the value of $R-L$ by perturbing this triple so that in the new triple $a_{k}^{\prime}, a_{l}^{\prime}, a_{m}^{\prime}$ one has $a_{k}^{\prime}=a_{l}^{\prime} \leq a_{m}^{\prime}$, without touching the remaining $a_{i} \mathrm{~s}$ and without changing the values of $S$ and $U$; this requires some skill in algebraic manipulations. It follows that the constrained minimum can be only attained for $n-1$ of the $a_{i}$ s equal and a single one possibly greater. In this case, $R-L \geq 0$ holds almost trivially.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9fe3c2d5-810f-5217-942b-b6e528059ff5
| 23,535
|
Let $a, b, c$ be the sides of a triangle. Prove that $$ \frac{\sqrt{b+c-a}}{\sqrt{b}+\sqrt{c}-\sqrt{a}}+\frac{\sqrt{c+a-b}}{\sqrt{c}+\sqrt{a}-\sqrt{b}}+\frac{\sqrt{a+b-c}}{\sqrt{a}+\sqrt{b}-\sqrt{c}} \leq 3 . $$ (Korea)
|
Note first that the denominators are all positive, e.g. $\sqrt{a}+\sqrt{b}>\sqrt{a+b}>\sqrt{c}$. Let $x=\sqrt{b}+\sqrt{c}-\sqrt{a}, y=\sqrt{c}+\sqrt{a}-\sqrt{b}$ and $z=\sqrt{a}+\sqrt{b}-\sqrt{c}$. Then $b+c-a=\left(\frac{z+x}{2}\right)^{2}+\left(\frac{x+y}{2}\right)^{2}-\left(\frac{y+z}{2}\right)^{2}=\frac{x^{2}+x y+x z-y z}{2}=x^{2}-\frac{1}{2}(x-y)(x-z)$ and $$ \frac{\sqrt{b+c-a}}{\sqrt{b}+\sqrt{c}-\sqrt{a}}=\sqrt{1-\frac{(x-y)(x-z)}{2 x^{2}}} \leq 1-\frac{(x-y)(x-z)}{4 x^{2}} $$ applying $\sqrt{1+2 u} \leq 1+u$ in the last step. Similarly we obtain $$ \frac{\sqrt{c+a-b}}{\sqrt{c}+\sqrt{a}-\sqrt{b}} \leq 1-\frac{(z-x)(z-y)}{4 z^{2}} \quad \text { and } \quad \frac{\sqrt{a+b-c}}{\sqrt{a}+\sqrt{b}-\sqrt{c}} \leq 1-\frac{(y-z)(y-x)}{4 y^{2}} $$ Substituting these quantities into the statement, it is sufficient to prove that $$ \frac{(x-y)(x-z)}{x^{2}}+\frac{(y-z)(y-x)}{y^{2}}+\frac{(z-x)(z-y)}{z^{2}} \geq 0 . $$ By symmetry we can assume $x \leq y \leq z$. Then $$ \begin{gathered} \frac{(x-y)(x-z)}{x^{2}}=\frac{(y-x)(z-x)}{x^{2}} \geq \frac{(y-x)(z-y)}{y^{2}}=-\frac{(y-z)(y-x)}{y^{2}} \\ \frac{(z-x)(z-y)}{z^{2}} \geq 0 \end{gathered} $$ and (1) follows. Comment 1. Inequality (1) is a special case of the well-known inequality $$ x^{t}(x-y)(x-z)+y^{t}(y-z)(y-x)+z^{t}(z-x)(z-y) \geq 0 $$ which holds for all positive numbers $x, y, z$ and real $t$; in our case $t=-2$. Case $t>0$ is called Schur's inequality. More generally, if $x \leq y \leq z$ are real numbers and $p, q, r$ are nonnegative numbers such that $q \leq p$ or $q \leq r$ then $$ p(x-y)(x-z)+q(y-z)(y-x)+r(z-x)(z-y) \geq 0 \text {. } $$ Comment 2. One might also start using Cauchy-Schwarz' inequality (or the root mean square vs. arithmetic mean inequality) to the effect that $$ \left(\sum \frac{\sqrt{b+c-a}}{\sqrt{b}+\sqrt{c}-\sqrt{a}}\right)^{2} \leq 3 \cdot \sum \frac{b+c-a}{(\sqrt{b}+\sqrt{c}-\sqrt{a})^{2}} $$ in cyclic sum notation. There are several ways to prove that the right-hand side of (2) never exceeds 9 (and this is just what we need). One of them is to introduce new variables $x, y, z$, as in Solution 1, which upon some manipulation brings the problem again to inequality (1). Alternatively, the claim that right-hand side of (2) is not greater than 9 can be expressed in terms of the symmetric forms $\sigma_{1}=\sum x, \sigma_{2}=\sum x y, \sigma_{3}=x y z$ equivalently as $$ 4 \sigma_{1} \sigma_{2} \sigma_{3} \leq \sigma_{2}^{3}+9 \sigma_{3}^{2} $$ which is a known inequality. A yet different method to deal with the right-hand expression in (2) is to consider $\sqrt{a}, \sqrt{b}, \sqrt{c}$ as sides of a triangle. Through standard trigonometric formulas the problem comes down to showing that $$ p^{2} \leq 4 R^{2}+4 R r+3 r^{2} $$ $p, R$ and $r$ standing for the semiperimeter, the circumradius and the inradius of that triangle. Again, (4) is another known inequality. Note that the inequalities (1), (3), (4) are equivalent statements about the same mathematical situation.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be the sides of a triangle. Prove that $$ \frac{\sqrt{b+c-a}}{\sqrt{b}+\sqrt{c}-\sqrt{a}}+\frac{\sqrt{c+a-b}}{\sqrt{c}+\sqrt{a}-\sqrt{b}}+\frac{\sqrt{a+b-c}}{\sqrt{a}+\sqrt{b}-\sqrt{c}} \leq 3 . $$ (Korea)
|
Note first that the denominators are all positive, e.g. $\sqrt{a}+\sqrt{b}>\sqrt{a+b}>\sqrt{c}$. Let $x=\sqrt{b}+\sqrt{c}-\sqrt{a}, y=\sqrt{c}+\sqrt{a}-\sqrt{b}$ and $z=\sqrt{a}+\sqrt{b}-\sqrt{c}$. Then $b+c-a=\left(\frac{z+x}{2}\right)^{2}+\left(\frac{x+y}{2}\right)^{2}-\left(\frac{y+z}{2}\right)^{2}=\frac{x^{2}+x y+x z-y z}{2}=x^{2}-\frac{1}{2}(x-y)(x-z)$ and $$ \frac{\sqrt{b+c-a}}{\sqrt{b}+\sqrt{c}-\sqrt{a}}=\sqrt{1-\frac{(x-y)(x-z)}{2 x^{2}}} \leq 1-\frac{(x-y)(x-z)}{4 x^{2}} $$ applying $\sqrt{1+2 u} \leq 1+u$ in the last step. Similarly we obtain $$ \frac{\sqrt{c+a-b}}{\sqrt{c}+\sqrt{a}-\sqrt{b}} \leq 1-\frac{(z-x)(z-y)}{4 z^{2}} \quad \text { and } \quad \frac{\sqrt{a+b-c}}{\sqrt{a}+\sqrt{b}-\sqrt{c}} \leq 1-\frac{(y-z)(y-x)}{4 y^{2}} $$ Substituting these quantities into the statement, it is sufficient to prove that $$ \frac{(x-y)(x-z)}{x^{2}}+\frac{(y-z)(y-x)}{y^{2}}+\frac{(z-x)(z-y)}{z^{2}} \geq 0 . $$ By symmetry we can assume $x \leq y \leq z$. Then $$ \begin{gathered} \frac{(x-y)(x-z)}{x^{2}}=\frac{(y-x)(z-x)}{x^{2}} \geq \frac{(y-x)(z-y)}{y^{2}}=-\frac{(y-z)(y-x)}{y^{2}} \\ \frac{(z-x)(z-y)}{z^{2}} \geq 0 \end{gathered} $$ and (1) follows. Comment 1. Inequality (1) is a special case of the well-known inequality $$ x^{t}(x-y)(x-z)+y^{t}(y-z)(y-x)+z^{t}(z-x)(z-y) \geq 0 $$ which holds for all positive numbers $x, y, z$ and real $t$; in our case $t=-2$. Case $t>0$ is called Schur's inequality. More generally, if $x \leq y \leq z$ are real numbers and $p, q, r$ are nonnegative numbers such that $q \leq p$ or $q \leq r$ then $$ p(x-y)(x-z)+q(y-z)(y-x)+r(z-x)(z-y) \geq 0 \text {. } $$ Comment 2. One might also start using Cauchy-Schwarz' inequality (or the root mean square vs. arithmetic mean inequality) to the effect that $$ \left(\sum \frac{\sqrt{b+c-a}}{\sqrt{b}+\sqrt{c}-\sqrt{a}}\right)^{2} \leq 3 \cdot \sum \frac{b+c-a}{(\sqrt{b}+\sqrt{c}-\sqrt{a})^{2}} $$ in cyclic sum notation. There are several ways to prove that the right-hand side of (2) never exceeds 9 (and this is just what we need). One of them is to introduce new variables $x, y, z$, as in Solution 1, which upon some manipulation brings the problem again to inequality (1). Alternatively, the claim that right-hand side of (2) is not greater than 9 can be expressed in terms of the symmetric forms $\sigma_{1}=\sum x, \sigma_{2}=\sum x y, \sigma_{3}=x y z$ equivalently as $$ 4 \sigma_{1} \sigma_{2} \sigma_{3} \leq \sigma_{2}^{3}+9 \sigma_{3}^{2} $$ which is a known inequality. A yet different method to deal with the right-hand expression in (2) is to consider $\sqrt{a}, \sqrt{b}, \sqrt{c}$ as sides of a triangle. Through standard trigonometric formulas the problem comes down to showing that $$ p^{2} \leq 4 R^{2}+4 R r+3 r^{2} $$ $p, R$ and $r$ standing for the semiperimeter, the circumradius and the inradius of that triangle. Again, (4) is another known inequality. Note that the inequalities (1), (3), (4) are equivalent statements about the same mathematical situation.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8bc5e4d1-2dd4-5f35-9c35-d17f143a3d92
| 23,539
|
Let $a, b, c$ be the sides of a triangle. Prove that $$ \frac{\sqrt{b+c-a}}{\sqrt{b}+\sqrt{c}-\sqrt{a}}+\frac{\sqrt{c+a-b}}{\sqrt{c}+\sqrt{a}-\sqrt{b}}+\frac{\sqrt{a+b-c}}{\sqrt{a}+\sqrt{b}-\sqrt{c}} \leq 3 . $$ (Korea)
|
Due to the symmetry of variables, it can be assumed that $a \geq b \geq c$. We claim that $$ \frac{\sqrt{a+b-c}}{\sqrt{a}+\sqrt{b}-\sqrt{c}} \leq 1 \quad \text { and } \quad \frac{\sqrt{b+c-a}}{\sqrt{b}+\sqrt{c}-\sqrt{a}}+\frac{\sqrt{c+a-b}}{\sqrt{c}+\sqrt{a}-\sqrt{b}} \leq 2 . $$ The first inequality follows from $$ \sqrt{a+b-c}-\sqrt{a}=\frac{(a+b-c)-a}{\sqrt{a+b-c}+\sqrt{a}} \leq \frac{b-c}{\sqrt{b}+\sqrt{c}}=\sqrt{b}-\sqrt{c} . $$ For proving the second inequality, let $p=\sqrt{a}+\sqrt{b}$ and $q=\sqrt{a}-\sqrt{b}$. Then $a-b=p q$ and the inequality becomes $$ \frac{\sqrt{c-p q}}{\sqrt{c}-q}+\frac{\sqrt{c+p q}}{\sqrt{c}+q} \leq 2 $$ From $a \geq b \geq c$ we have $p \geq 2 \sqrt{c}$. Applying the Cauchy-Schwarz inequality, $$ \begin{gathered} \left(\frac{\sqrt{c-p q}}{\sqrt{c}-q}+\frac{\sqrt{c+p q}}{\sqrt{c}+q}\right)^{2} \leq\left(\frac{c-p q}{\sqrt{c}-q}+\frac{c+p q}{\sqrt{c}+q}\right)\left(\frac{1}{\sqrt{c}-q}+\frac{1}{\sqrt{c}+q}\right) \\ =\frac{2\left(c \sqrt{c}-p q^{2}\right)}{c-q^{2}} \cdot \frac{2 \sqrt{c}}{c-q^{2}}=4 \cdot \frac{c^{2}-\sqrt{c} p q^{2}}{\left(c-q^{2}\right)^{2}} \leq 4 \cdot \frac{c^{2}-2 c q^{2}}{\left(c-q^{2}\right)^{2}} \leq 4 . \end{gathered} $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be the sides of a triangle. Prove that $$ \frac{\sqrt{b+c-a}}{\sqrt{b}+\sqrt{c}-\sqrt{a}}+\frac{\sqrt{c+a-b}}{\sqrt{c}+\sqrt{a}-\sqrt{b}}+\frac{\sqrt{a+b-c}}{\sqrt{a}+\sqrt{b}-\sqrt{c}} \leq 3 . $$ (Korea)
|
Due to the symmetry of variables, it can be assumed that $a \geq b \geq c$. We claim that $$ \frac{\sqrt{a+b-c}}{\sqrt{a}+\sqrt{b}-\sqrt{c}} \leq 1 \quad \text { and } \quad \frac{\sqrt{b+c-a}}{\sqrt{b}+\sqrt{c}-\sqrt{a}}+\frac{\sqrt{c+a-b}}{\sqrt{c}+\sqrt{a}-\sqrt{b}} \leq 2 . $$ The first inequality follows from $$ \sqrt{a+b-c}-\sqrt{a}=\frac{(a+b-c)-a}{\sqrt{a+b-c}+\sqrt{a}} \leq \frac{b-c}{\sqrt{b}+\sqrt{c}}=\sqrt{b}-\sqrt{c} . $$ For proving the second inequality, let $p=\sqrt{a}+\sqrt{b}$ and $q=\sqrt{a}-\sqrt{b}$. Then $a-b=p q$ and the inequality becomes $$ \frac{\sqrt{c-p q}}{\sqrt{c}-q}+\frac{\sqrt{c+p q}}{\sqrt{c}+q} \leq 2 $$ From $a \geq b \geq c$ we have $p \geq 2 \sqrt{c}$. Applying the Cauchy-Schwarz inequality, $$ \begin{gathered} \left(\frac{\sqrt{c-p q}}{\sqrt{c}-q}+\frac{\sqrt{c+p q}}{\sqrt{c}+q}\right)^{2} \leq\left(\frac{c-p q}{\sqrt{c}-q}+\frac{c+p q}{\sqrt{c}+q}\right)\left(\frac{1}{\sqrt{c}-q}+\frac{1}{\sqrt{c}+q}\right) \\ =\frac{2\left(c \sqrt{c}-p q^{2}\right)}{c-q^{2}} \cdot \frac{2 \sqrt{c}}{c-q^{2}}=4 \cdot \frac{c^{2}-\sqrt{c} p q^{2}}{\left(c-q^{2}\right)^{2}} \leq 4 \cdot \frac{c^{2}-2 c q^{2}}{\left(c-q^{2}\right)^{2}} \leq 4 . \end{gathered} $$
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8bc5e4d1-2dd4-5f35-9c35-d17f143a3d92
| 23,539
|
We have $n \geq 2$ lamps $L_{1}, \ldots, L_{n}$ in a row, each of them being either on or off. Every second we simultaneously modify the state of each lamp as follows: - if the lamp $L_{i}$ and its neighbours (only one neighbour for $i=1$ or $i=n$, two neighbours for other $i$ ) are in the same state, then $L_{i}$ is switched off; - otherwise, $L_{i}$ is switched on. Initially all the lamps are off except the leftmost one which is on. (a) Prove that there are infinitely many integers $n$ for which all the lamps will eventually be off. (b) Prove that there are infinitely many integers $n$ for which the lamps will never be all off. (France)
|
(a) Experiments with small $n$ lead to the guess that every $n$ of the form $2^{k}$ should be good. This is indeed the case, and more precisely: let $A_{k}$ be the $2^{k} \times 2^{k}$ matrix whose rows represent the evolution of the system, with entries 0,1 (for off and on respectively). The top row shows the initial state $[1,0,0, \ldots, 0]$; the bottom row shows the state after $2^{k}-1$ steps. The claim is that: $$ \text { The bottom row of } A_{k} \text { is }[1,1,1, \ldots, 1] \text {. } $$ This will of course suffice because one more move then produces $[0,0,0, \ldots, 0]$, as required. The proof is by induction on $k$. The base $k=1$ is obvious. Assume the claim to be true for a $k \geq 1$ and write the matrix $A_{k+1}$ in the block form $\left(\begin{array}{ll}A_{k} & O_{k} \\ B_{k} & C_{k}\end{array}\right)$ with four $2^{k} \times 2^{k}$ matrices. After $m$ steps, the last 1 in a row is at position $m+1$. Therefore $O_{k}$ is the zero matrix. According to the induction hypothesis, the bottom row of $\left[A_{k} O_{k}\right]$ is $[1, \ldots, 1,0, \ldots, 0]$, with $2^{k}$ ones and $2^{k}$ zeros. The next row is thus $$ [\underbrace{0, \ldots, 0}_{2^{k}-1}, 1,1, \underbrace{0, \ldots, 0}_{2^{k}-1}] $$ It is symmetric about its midpoint, and this symmetry is preserved in all subsequent rows because the procedure described in the problem statement is left/right symmetric. Thus $B_{k}$ is the mirror image of $C_{k}$. In particular, the rightmost column of $B_{k}$ is identical with the leftmost column of $C_{k}$. Imagine the matrix $C_{k}$ in isolation from the rest of $A_{k+1}$. Suppose it is subject to evolution as defined in the problem: the first (leftmost) term in a row depends only on the two first terms in the preceding row, according as they are equal or not. Now embed $C_{k}$ again in $A_{k}$. The 'leftmost' terms in the rows of $C_{k}$ now have neighbours on their left side- but these neighbours are their exact copies. Consequently the actual evolution within $C_{k}$ is the same, whether or not $C_{k}$ is considered as a piece of $A_{k+1}$ or in isolation. And since the top row of $C_{k}$ is $[1,0, \ldots, 0]$, it follows that $C_{k}$ is identical with $A_{k}$. The bottom row of $A_{k}$ is $[1,1, \ldots, 1]$; the same is the bottom row of $C_{k}$, hence also of $B_{k}$, which mirrors $C_{k}$. So the bottom row of $A_{k+1}$ consists of ones only and the induction is complete. (b) There are many ways to produce an infinite sequence of those $n$ for which the state $[0,0, \ldots, 0]$ will never be achieved. As an example, consider $n=2^{k}+1$ (for $k \geq 1$ ). The evolution of the system can be represented by a matrix $\mathcal{A}$ of width $2^{k}+1$ with infinitely many rows. The top $2^{k}$ rows form the matrix $A_{k}$ discussed above, with one column of zeros attached at its right. In the next row we then have the vector $[0,0, \ldots, 0,1,1]$. But this is just the second row of $\mathcal{A}$ reversed. Subsequent rows will be mirror copies of the foregoing ones, starting from the second one. So the configuration $[1,1,0, \ldots, 0,0]$, i.e. the second row of $\mathcal{A}$, will reappear. Further rows will periodically repeat this pattern and there will be no row of zeros.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
We have $n \geq 2$ lamps $L_{1}, \ldots, L_{n}$ in a row, each of them being either on or off. Every second we simultaneously modify the state of each lamp as follows: - if the lamp $L_{i}$ and its neighbours (only one neighbour for $i=1$ or $i=n$, two neighbours for other $i$ ) are in the same state, then $L_{i}$ is switched off; - otherwise, $L_{i}$ is switched on. Initially all the lamps are off except the leftmost one which is on. (a) Prove that there are infinitely many integers $n$ for which all the lamps will eventually be off. (b) Prove that there are infinitely many integers $n$ for which the lamps will never be all off. (France)
|
(a) Experiments with small $n$ lead to the guess that every $n$ of the form $2^{k}$ should be good. This is indeed the case, and more precisely: let $A_{k}$ be the $2^{k} \times 2^{k}$ matrix whose rows represent the evolution of the system, with entries 0,1 (for off and on respectively). The top row shows the initial state $[1,0,0, \ldots, 0]$; the bottom row shows the state after $2^{k}-1$ steps. The claim is that: $$ \text { The bottom row of } A_{k} \text { is }[1,1,1, \ldots, 1] \text {. } $$ This will of course suffice because one more move then produces $[0,0,0, \ldots, 0]$, as required. The proof is by induction on $k$. The base $k=1$ is obvious. Assume the claim to be true for a $k \geq 1$ and write the matrix $A_{k+1}$ in the block form $\left(\begin{array}{ll}A_{k} & O_{k} \\ B_{k} & C_{k}\end{array}\right)$ with four $2^{k} \times 2^{k}$ matrices. After $m$ steps, the last 1 in a row is at position $m+1$. Therefore $O_{k}$ is the zero matrix. According to the induction hypothesis, the bottom row of $\left[A_{k} O_{k}\right]$ is $[1, \ldots, 1,0, \ldots, 0]$, with $2^{k}$ ones and $2^{k}$ zeros. The next row is thus $$ [\underbrace{0, \ldots, 0}_{2^{k}-1}, 1,1, \underbrace{0, \ldots, 0}_{2^{k}-1}] $$ It is symmetric about its midpoint, and this symmetry is preserved in all subsequent rows because the procedure described in the problem statement is left/right symmetric. Thus $B_{k}$ is the mirror image of $C_{k}$. In particular, the rightmost column of $B_{k}$ is identical with the leftmost column of $C_{k}$. Imagine the matrix $C_{k}$ in isolation from the rest of $A_{k+1}$. Suppose it is subject to evolution as defined in the problem: the first (leftmost) term in a row depends only on the two first terms in the preceding row, according as they are equal or not. Now embed $C_{k}$ again in $A_{k}$. The 'leftmost' terms in the rows of $C_{k}$ now have neighbours on their left side- but these neighbours are their exact copies. Consequently the actual evolution within $C_{k}$ is the same, whether or not $C_{k}$ is considered as a piece of $A_{k+1}$ or in isolation. And since the top row of $C_{k}$ is $[1,0, \ldots, 0]$, it follows that $C_{k}$ is identical with $A_{k}$. The bottom row of $A_{k}$ is $[1,1, \ldots, 1]$; the same is the bottom row of $C_{k}$, hence also of $B_{k}$, which mirrors $C_{k}$. So the bottom row of $A_{k+1}$ consists of ones only and the induction is complete. (b) There are many ways to produce an infinite sequence of those $n$ for which the state $[0,0, \ldots, 0]$ will never be achieved. As an example, consider $n=2^{k}+1$ (for $k \geq 1$ ). The evolution of the system can be represented by a matrix $\mathcal{A}$ of width $2^{k}+1$ with infinitely many rows. The top $2^{k}$ rows form the matrix $A_{k}$ discussed above, with one column of zeros attached at its right. In the next row we then have the vector $[0,0, \ldots, 0,1,1]$. But this is just the second row of $\mathcal{A}$ reversed. Subsequent rows will be mirror copies of the foregoing ones, starting from the second one. So the configuration $[1,1,0, \ldots, 0,0]$, i.e. the second row of $\mathcal{A}$, will reappear. Further rows will periodically repeat this pattern and there will be no row of zeros.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c0d39c62-a6aa-5dd0-b185-8e0ecc0608e3
| 23,545
|
Let $S$ be a finite set of points in the plane such that no three of them are on a line. For each convex polygon $P$ whose vertices are in $S$, let $a(P)$ be the number of vertices of $P$, and let $b(P)$ be the number of points of $S$ which are outside $P$. Prove that for every real number $x$ $$ \sum_{P} x^{a(P)}(1-x)^{b(P)}=1 $$ where the sum is taken over all convex polygons with vertices in $S$. NB. A line segment, a point and the empty set are considered as convex polygons of 2,1 and 0 vertices, respectively. (Colombia)
|
For each convex polygon $P$ whose vertices are in $S$, let $c(P)$ be the number of points of $S$ which are inside $P$, so that $a(P)+b(P)+c(P)=n$, the total number of points in $S$. Denoting $1-x$ by $y$, $$ \sum_{P} x^{a(P)} y^{b(P)}=\sum_{P} x^{a(P)} y^{b(P)}(x+y)^{c(P)}=\sum_{P} \sum_{i=0}^{c(P)}\left(\begin{array}{c} c(P) \\ i \end{array}\right) x^{a(P)+i} y^{b(P)+c(P)-i} . $$ View this expression as a homogeneous polynomial of degree $n$ in two independent variables $x, y$. In the expanded form, it is the sum of terms $x^{r} y^{n-r}(0 \leq r \leq n)$ multiplied by some nonnegative integer coefficients. For a fixed $r$, the coefficient of $x^{r} y^{n-r}$ represents the number of ways of choosing a convex polygon $P$ and then choosing some of the points of $S$ inside $P$ so that the number of vertices of $P$ and the number of chosen points inside $P$ jointly add up to $r$. This corresponds to just choosing an $r$-element subset of $S$. The correspondence is bijective because every set $T$ of points from $S$ splits in exactly one way into the union of two disjoint subsets, of which the first is the set of vertices of a convex polygon - namely, the convex hull of $T$ - and the second consists of some points inside that polygon. So the coefficient of $x^{r} y^{n-r}$ equals $\left(\begin{array}{l}n \\ r\end{array}\right)$. The desired result follows: $$ \sum_{P} x^{a(P)} y^{b(P)}=\sum_{r=0}^{n}\left(\begin{array}{l} n \\ r \end{array}\right) x^{r} y^{n-r}=(x+y)^{n}=1 . $$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a finite set of points in the plane such that no three of them are on a line. For each convex polygon $P$ whose vertices are in $S$, let $a(P)$ be the number of vertices of $P$, and let $b(P)$ be the number of points of $S$ which are outside $P$. Prove that for every real number $x$ $$ \sum_{P} x^{a(P)}(1-x)^{b(P)}=1 $$ where the sum is taken over all convex polygons with vertices in $S$. NB. A line segment, a point and the empty set are considered as convex polygons of 2,1 and 0 vertices, respectively. (Colombia)
|
For each convex polygon $P$ whose vertices are in $S$, let $c(P)$ be the number of points of $S$ which are inside $P$, so that $a(P)+b(P)+c(P)=n$, the total number of points in $S$. Denoting $1-x$ by $y$, $$ \sum_{P} x^{a(P)} y^{b(P)}=\sum_{P} x^{a(P)} y^{b(P)}(x+y)^{c(P)}=\sum_{P} \sum_{i=0}^{c(P)}\left(\begin{array}{c} c(P) \\ i \end{array}\right) x^{a(P)+i} y^{b(P)+c(P)-i} . $$ View this expression as a homogeneous polynomial of degree $n$ in two independent variables $x, y$. In the expanded form, it is the sum of terms $x^{r} y^{n-r}(0 \leq r \leq n)$ multiplied by some nonnegative integer coefficients. For a fixed $r$, the coefficient of $x^{r} y^{n-r}$ represents the number of ways of choosing a convex polygon $P$ and then choosing some of the points of $S$ inside $P$ so that the number of vertices of $P$ and the number of chosen points inside $P$ jointly add up to $r$. This corresponds to just choosing an $r$-element subset of $S$. The correspondence is bijective because every set $T$ of points from $S$ splits in exactly one way into the union of two disjoint subsets, of which the first is the set of vertices of a convex polygon - namely, the convex hull of $T$ - and the second consists of some points inside that polygon. So the coefficient of $x^{r} y^{n-r}$ equals $\left(\begin{array}{l}n \\ r\end{array}\right)$. The desired result follows: $$ \sum_{P} x^{a(P)} y^{b(P)}=\sum_{r=0}^{n}\left(\begin{array}{l} n \\ r \end{array}\right) x^{r} y^{n-r}=(x+y)^{n}=1 . $$
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
89911f96-cdd5-54ec-8c1c-469d49aba25a
| 23,552
|
Let $S$ be a finite set of points in the plane such that no three of them are on a line. For each convex polygon $P$ whose vertices are in $S$, let $a(P)$ be the number of vertices of $P$, and let $b(P)$ be the number of points of $S$ which are outside $P$. Prove that for every real number $x$ $$ \sum_{P} x^{a(P)}(1-x)^{b(P)}=1 $$ where the sum is taken over all convex polygons with vertices in $S$. NB. A line segment, a point and the empty set are considered as convex polygons of 2,1 and 0 vertices, respectively. (Colombia)
|
Apply induction on the number $n$ of points. The case $n=0$ is trivial. Let $n>0$ and assume the statement for less than $n$ points. Take a set $S$ of $n$ points. Let $C$ be the set of vertices of the convex hull of $S$, let $m=|C|$. Let $X \subset C$ be an arbitrary nonempty set. For any convex polygon $P$ with vertices in the set $S \backslash X$, we have $b(P)$ points of $S$ outside $P$. Excluding the points of $X-$ all outside $P$ — the set $S \backslash X$ contains exactly $b(P)-|X|$ of them. Writing $1-x=y$, by the induction hypothesis $$ \sum_{P \subset S \backslash X} x^{a(P)} y^{b(P)-|X|}=1 $$ (where $P \subset S \backslash X$ means that the vertices of $P$ belong to the set $S \backslash X$ ). Therefore $$ \sum_{P \subset S \backslash X} x^{a(P)} y^{b(P)}=y^{|X|} $$ All convex polygons appear at least once, except the convex hull $C$ itself. The convex hull adds $x^{m}$. We can use the inclusion-exclusion principle to compute the sum of the other terms: $$ \begin{gathered} \sum_{P \neq C} x^{a(P)} y^{b(P)}=\sum_{k=1}^{m}(-1)^{k-1} \sum_{|X|=k} \sum_{P \subset S \backslash X} x^{a(P)} y^{b(P)}=\sum_{k=1}^{m}(-1)^{k-1} \sum_{|X|=k} y^{k} \\ =\sum_{k=1}^{m}(-1)^{k-1}\left(\begin{array}{c} m \\ k \end{array}\right) y^{k}=-\left((1-y)^{m}-1\right)=1-x^{m} \end{gathered} $$ and then $$ \sum_{P} x^{a(P)} y^{b(P)}=\sum_{P=C}+\sum_{P \neq C}=x^{m}+\left(1-x^{m}\right)=1 $$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a finite set of points in the plane such that no three of them are on a line. For each convex polygon $P$ whose vertices are in $S$, let $a(P)$ be the number of vertices of $P$, and let $b(P)$ be the number of points of $S$ which are outside $P$. Prove that for every real number $x$ $$ \sum_{P} x^{a(P)}(1-x)^{b(P)}=1 $$ where the sum is taken over all convex polygons with vertices in $S$. NB. A line segment, a point and the empty set are considered as convex polygons of 2,1 and 0 vertices, respectively. (Colombia)
|
Apply induction on the number $n$ of points. The case $n=0$ is trivial. Let $n>0$ and assume the statement for less than $n$ points. Take a set $S$ of $n$ points. Let $C$ be the set of vertices of the convex hull of $S$, let $m=|C|$. Let $X \subset C$ be an arbitrary nonempty set. For any convex polygon $P$ with vertices in the set $S \backslash X$, we have $b(P)$ points of $S$ outside $P$. Excluding the points of $X-$ all outside $P$ — the set $S \backslash X$ contains exactly $b(P)-|X|$ of them. Writing $1-x=y$, by the induction hypothesis $$ \sum_{P \subset S \backslash X} x^{a(P)} y^{b(P)-|X|}=1 $$ (where $P \subset S \backslash X$ means that the vertices of $P$ belong to the set $S \backslash X$ ). Therefore $$ \sum_{P \subset S \backslash X} x^{a(P)} y^{b(P)}=y^{|X|} $$ All convex polygons appear at least once, except the convex hull $C$ itself. The convex hull adds $x^{m}$. We can use the inclusion-exclusion principle to compute the sum of the other terms: $$ \begin{gathered} \sum_{P \neq C} x^{a(P)} y^{b(P)}=\sum_{k=1}^{m}(-1)^{k-1} \sum_{|X|=k} \sum_{P \subset S \backslash X} x^{a(P)} y^{b(P)}=\sum_{k=1}^{m}(-1)^{k-1} \sum_{|X|=k} y^{k} \\ =\sum_{k=1}^{m}(-1)^{k-1}\left(\begin{array}{c} m \\ k \end{array}\right) y^{k}=-\left((1-y)^{m}-1\right)=1-x^{m} \end{gathered} $$ and then $$ \sum_{P} x^{a(P)} y^{b(P)}=\sum_{P=C}+\sum_{P \neq C}=x^{m}+\left(1-x^{m}\right)=1 $$
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
89911f96-cdd5-54ec-8c1c-469d49aba25a
| 23,552
|
A cake has the form of an $n \times n$ square composed of $n^{2}$ unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement $\mathcal{A}$. Let $\mathcal{B}$ be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement $\mathcal{B}$ than of arrangement $\mathcal{A}$. Prove that arrangement $\mathcal{B}$ can be obtained from $\mathcal{A}$ by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle. (Taiwan)
|
We use capital letters to denote unit squares; $O$ is the top left corner square. For any two squares $X$ and $Y$ let $[X Y]$ be the smallest grid rectangle containing these two squares. Strawberries lie on some squares in arrangement $\mathcal{A}$. Put a plum on each square of the target configuration $\mathcal{B}$. For a square $X$ denote by $a(X)$ and $b(X)$ respectively the number of strawberries and the number of plums in $[O X]$. By hypothesis $a(X) \leq b(X)$ for each $X$, with strict inequality for some $X$ (otherwise the two arrangements coincide and there is nothing to prove). The idea is to show that by a legitimate switch one can obtain an arrangement $\mathcal{A}^{\prime}$ such that $$ a(X) \leq a^{\prime}(X) \leq b(X) \quad \text { for each } X ; \quad \sum_{X} a(X)<\sum_{X} a^{\prime}(X) $$ (with $a^{\prime}(X)$ defined analogously to $a(X)$; the sums range over all unit squares $X$ ). This will be enough because the same reasoning then applies to $\mathcal{A}^{\prime}$, giving rise to a new arrangement $\mathcal{A}^{\prime \prime}$, and so on (induction). Since $\sum a(X)<\sum a^{\prime}(X)<\sum a^{\prime \prime}(X)<\ldots$ and all these sums do not exceed $\sum b(X)$, we eventually obtain a sum with all summands equal to the respective $b(X) \mathrm{s}$; all strawberries will meet with plums. Consider the uppermost row in which the plum and the strawberry lie on different squares $P$ and $S$ (respectively); clearly $P$ must be situated left to $S$. In the column passing through $P$, let $T$ be the top square and $B$ the bottom square. The strawberry in that column lies below the plum (because there is no plum in that column above $P$, and the positions of strawberries and plums coincide everywhere above the row of $P$ ). Hence there is at least one strawberry in the region $[B S]$ below $[P S]$. Let $V$ be the position of the uppermost strawberry in that region.  Denote by $W$ the square at the intersection of the row through $V$ with the column through $S$ and let $R$ be the square vertex-adjacent to $W$ up-left. We claim that $$ a(X)<b(X) \quad \text { for all } \quad X \in[P R] $$ This is so because if $X \in[P R]$ then the portion of $[O X]$ left to column $[T B]$ contains at least as many plums as strawberries (the hypothesis of the problem); in the portion above the row through $P$ and $S$ we have perfect balance; and in the remaining portion, i.e. rectangle $[P X]$ we have a plum on square $P$ and no strawberry at all. Now we are able to perform the required switch. Let $U$ be the square at the intersection of the row through $P$ with the column through $V$ (some of $P, U, R$ can coincide). We move strawberries from squares $S$ and $V$ to squares $U$ and $W$. Then $$ a^{\prime}(X)=a(X)+1 \quad \text { for } \quad X \in[U R] ; \quad a^{\prime}(X)=a(X) \quad \text { for other } X $$ And since the rectangle $[U R]$ is contained in $[P R]$, we still have $a^{\prime}(X) \leq b(X)$ for all $S$, in view of (2); conditions (1) are satisfied and the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A cake has the form of an $n \times n$ square composed of $n^{2}$ unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement $\mathcal{A}$. Let $\mathcal{B}$ be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement $\mathcal{B}$ than of arrangement $\mathcal{A}$. Prove that arrangement $\mathcal{B}$ can be obtained from $\mathcal{A}$ by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle. (Taiwan)
|
We use capital letters to denote unit squares; $O$ is the top left corner square. For any two squares $X$ and $Y$ let $[X Y]$ be the smallest grid rectangle containing these two squares. Strawberries lie on some squares in arrangement $\mathcal{A}$. Put a plum on each square of the target configuration $\mathcal{B}$. For a square $X$ denote by $a(X)$ and $b(X)$ respectively the number of strawberries and the number of plums in $[O X]$. By hypothesis $a(X) \leq b(X)$ for each $X$, with strict inequality for some $X$ (otherwise the two arrangements coincide and there is nothing to prove). The idea is to show that by a legitimate switch one can obtain an arrangement $\mathcal{A}^{\prime}$ such that $$ a(X) \leq a^{\prime}(X) \leq b(X) \quad \text { for each } X ; \quad \sum_{X} a(X)<\sum_{X} a^{\prime}(X) $$ (with $a^{\prime}(X)$ defined analogously to $a(X)$; the sums range over all unit squares $X$ ). This will be enough because the same reasoning then applies to $\mathcal{A}^{\prime}$, giving rise to a new arrangement $\mathcal{A}^{\prime \prime}$, and so on (induction). Since $\sum a(X)<\sum a^{\prime}(X)<\sum a^{\prime \prime}(X)<\ldots$ and all these sums do not exceed $\sum b(X)$, we eventually obtain a sum with all summands equal to the respective $b(X) \mathrm{s}$; all strawberries will meet with plums. Consider the uppermost row in which the plum and the strawberry lie on different squares $P$ and $S$ (respectively); clearly $P$ must be situated left to $S$. In the column passing through $P$, let $T$ be the top square and $B$ the bottom square. The strawberry in that column lies below the plum (because there is no plum in that column above $P$, and the positions of strawberries and plums coincide everywhere above the row of $P$ ). Hence there is at least one strawberry in the region $[B S]$ below $[P S]$. Let $V$ be the position of the uppermost strawberry in that region.  Denote by $W$ the square at the intersection of the row through $V$ with the column through $S$ and let $R$ be the square vertex-adjacent to $W$ up-left. We claim that $$ a(X)<b(X) \quad \text { for all } \quad X \in[P R] $$ This is so because if $X \in[P R]$ then the portion of $[O X]$ left to column $[T B]$ contains at least as many plums as strawberries (the hypothesis of the problem); in the portion above the row through $P$ and $S$ we have perfect balance; and in the remaining portion, i.e. rectangle $[P X]$ we have a plum on square $P$ and no strawberry at all. Now we are able to perform the required switch. Let $U$ be the square at the intersection of the row through $P$ with the column through $V$ (some of $P, U, R$ can coincide). We move strawberries from squares $S$ and $V$ to squares $U$ and $W$. Then $$ a^{\prime}(X)=a(X)+1 \quad \text { for } \quad X \in[U R] ; \quad a^{\prime}(X)=a(X) \quad \text { for other } X $$ And since the rectangle $[U R]$ is contained in $[P R]$, we still have $a^{\prime}(X) \leq b(X)$ for all $S$, in view of (2); conditions (1) are satisfied and the proof is complete.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
bcbc9fc6-af5c-547e-9bbd-cfcb813de78e
| 23,554
|
An $(n, k)$-tournament is a contest with $n$ players held in $k$ rounds such that: (i) Each player plays in each round, and every two players meet at most once. (ii) If player $A$ meets player $B$ in round $i$, player $C$ meets player $D$ in round $i$, and player $A$ meets player $C$ in round $j$, then player $B$ meets player $D$ in round $j$. Determine all pairs $(n, k)$ for which there exists an $(n, k)$-tournament. (Argentina)
|
For each $k$, denote by $t_{k}$ the unique integer such that $2^{t_{k}-1}<k+1 \leq 2^{t_{k}}$. We show that an $(n, k)$-tournament exists if and only if $2^{t_{k}}$ divides $n$. First we prove that if $n=2^{t}$ for some $t$ then there is an $(n, k)$-tournament for all $k \leq 2^{t}-1$. Let $S$ be the set of $0-1$ sequences with length $t$. We label the $2^{t}$ players with the elements of $S$ in an arbitrary fashion (which is possible as there are exactly $2^{t}$ sequences in $S$ ). Players are identified with their labels in the construction below. If $\alpha, \beta \in S$, let $\alpha+\beta \in S$ be the result of the modulo 2 term-by-term addition of $\alpha$ and $\beta$ (with rules $0+0=0,0+1=1+0=1$, $1+1=0$; there is no carryover). For each $i=1, \ldots, 2^{t}-1$ let $\omega(i) \in S$ be the sequence of base 2 digits of $i$, completed with leading zeros if necessary to achieve length $t$. Now define a tournament with $n=2^{t}$ players in $k \leq 2^{t}-1$ rounds as follows: For all $i=1, \ldots, k$, let player $\alpha$ meet player $\alpha+\omega(i)$ in round $i$. The tournament is well-defined as $\alpha+\omega(i) \in S$ and $\alpha+\omega(i)=\beta+\omega(i)$ implies $\alpha=\beta$; also $[\alpha+\omega(i)]+\omega(i)=\alpha$ for each $\alpha \in S$ (meaning that player $\alpha+\omega(i)$ meets player $\alpha$ in round $i$, as needed). Each player plays in each round. Next, every two players meet at most once (exactly once if $k=2^{t}-1$ ), since $\omega(i) \neq \omega(j)$ if $i \neq j$. Thus condition (i) holds true, and condition (ii) is also easy to check. Let player $\alpha$ meet player $\beta$ in round $i$, player $\gamma$ meet player $\delta$ in round $i$, and player $\alpha$ meet player $\gamma$ in round $j$. Then $\beta=\alpha+\omega(i), \delta=\gamma+\omega(i)$ and $\gamma=\alpha+\omega(j)$. By definition, $\beta$ will play in round $j$ with $$ \beta+\omega(j)=[\alpha+\omega(i)]+\omega(j)=[\alpha+\omega(j)]+\omega(i)=\gamma+\omega(i)=\delta $$ as required by (ii). So there exists an $(n, k)$-tournament for pairs $(n, k)$ such that $n=2^{t}$ and $k \leq 2^{t}-1$. The same conclusion is straightforward for $n$ of the form $n=2^{t} s$ and $k \leq 2^{t}-1$. Indeed, consider $s$ different $\left(2^{t}, k\right)$-tournaments $T_{1}, \ldots, T_{s}$, no two of them having players in common. Their union can be regarded as a $\left(2^{t} s, k\right)$-tournament $T$ where each round is the union of the respective rounds in $T_{1}, \ldots, T_{s}$. In summary, the condition that $2^{t_{k}}$ divides $n$ is sufficient for an $(n, k)$-tournament to exist. We prove that it is also necessary. Consider an arbitrary $(n, k)$-tournament. Represent each player by a point and after each round, join by an edge every two players who played in this round. Thus to a round $i=1, \ldots, k$ there corresponds a graph $G_{i}$. We say that player $Q$ is an $i$-neighbour of player $P$ if there is a path of edges in $G_{i}$ from $P$ to $Q$; in other words, if there are players $P=X_{1}, X_{2}, \ldots, X_{m}=Q$ such that player $X_{j}$ meets player $X_{j+1}$ in one of the first $i$ rounds, $j=1,2 \ldots, m-1$. The set of $i$-neighbours of a player will be called its $i$-component. Clearly two $i$-components are either disjoint or coincide. Hence after each round $i$ the set of players is partitioned into pairwise disjoint $i$-components. So, to achieve our goal, it suffices to show that all $k$-components have size divisible by $2^{t_{k}}$. To this end, let us see how the $i$-component $\Gamma$ of a player $A$ changes after round $i+1$. Suppose that $A$ meets player $B$ with $i$-component $\Delta$ in round $i+1$ (components $\Gamma$ and $\Delta$ are not necessarily distinct). We claim that then in round $i+1$ each player from $\Gamma$ meets a player from $\Delta$, and vice versa. Indeed, let $C$ be any player in $\Gamma$, and let $C$ meet $D$ in round $i+1$. Since $C$ is an $i$-neighbour of $A$, there is a sequence of players $A=X_{1}, X_{2}, \ldots, X_{m}=C$ such that $X_{j}$ meets $X_{j+1}$ in one of the first $i$ rounds, $j=1,2 \ldots, m-1$. Let $X_{j}$ meet $Y_{j}$ in round $i+1$, for $j=1,2 \ldots, m$; in particular $Y_{1}=B$ and $Y_{m}=D$. Players $Y_{j}$ exists in view of condition (i). Suppose that $X_{j}$ and $X_{j+1}$ met in round $r$, where $r \leq i$. Then condition (ii) implies that and $Y_{j}$ and $Y_{j+1}$ met in round $r$, too. Hence $B=Y_{1}, Y_{2}, \ldots, Y_{m}=D$ is a path in $G_{i}$ from $B$ to $D$. This is to say, $D$ is in the $i$-component $\Delta$ of $B$, as claimed. By symmetry, each player from $\Delta$ meets a player from $\Gamma$ in round $i+1$. It follows in particular that $\Gamma$ and $\Delta$ have the same cardinality. It is straightforward now that the $(i+1)$-component of $A$ is $\Gamma \cup \Delta$, the union of two sets with the same size. Since $\Gamma$ and $\Delta$ are either disjoint or coincide, we have either $|\Gamma \cup \Delta|=2|\Gamma|$ or $|\Gamma \cup \Delta|=|\Gamma|$; as usual, $|\cdots|$ denotes the cardinality of a finite set. Let $\Gamma_{1}, \ldots, \Gamma_{k}$ be the consecutive components of a given player $A$. We obtained that either $\left|\Gamma_{i+1}\right|=2\left|\Gamma_{i}\right|$ or $\left|\Gamma_{i+1}\right|=\left|\Gamma_{i}\right|$ for $i=1, \ldots, k-1$. Because $\left|\Gamma_{1}\right|=2$, each $\left|\Gamma_{i}\right|$ is a power of 2 , $i=1, \ldots, k-1$. In particular $\left|\Gamma_{k}\right|=2^{u}$ for some $u$. On the other hand, player $A$ has played with $k$ different opponents by (i). All of them belong to $\Gamma_{k}$, therefore $\left|\Gamma_{k}\right| \geq k+1$. Thus $2^{u} \geq k+1$, and since $t_{k}$ is the least integer satisfying $2^{t_{k}} \geq k+1$, we conclude that $u \geq t_{k}$. So the size of each $k$-component is divisible by $2^{t_{k}}$, which completes the argument.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
An $(n, k)$-tournament is a contest with $n$ players held in $k$ rounds such that: (i) Each player plays in each round, and every two players meet at most once. (ii) If player $A$ meets player $B$ in round $i$, player $C$ meets player $D$ in round $i$, and player $A$ meets player $C$ in round $j$, then player $B$ meets player $D$ in round $j$. Determine all pairs $(n, k)$ for which there exists an $(n, k)$-tournament. (Argentina)
|
For each $k$, denote by $t_{k}$ the unique integer such that $2^{t_{k}-1}<k+1 \leq 2^{t_{k}}$. We show that an $(n, k)$-tournament exists if and only if $2^{t_{k}}$ divides $n$. First we prove that if $n=2^{t}$ for some $t$ then there is an $(n, k)$-tournament for all $k \leq 2^{t}-1$. Let $S$ be the set of $0-1$ sequences with length $t$. We label the $2^{t}$ players with the elements of $S$ in an arbitrary fashion (which is possible as there are exactly $2^{t}$ sequences in $S$ ). Players are identified with their labels in the construction below. If $\alpha, \beta \in S$, let $\alpha+\beta \in S$ be the result of the modulo 2 term-by-term addition of $\alpha$ and $\beta$ (with rules $0+0=0,0+1=1+0=1$, $1+1=0$; there is no carryover). For each $i=1, \ldots, 2^{t}-1$ let $\omega(i) \in S$ be the sequence of base 2 digits of $i$, completed with leading zeros if necessary to achieve length $t$. Now define a tournament with $n=2^{t}$ players in $k \leq 2^{t}-1$ rounds as follows: For all $i=1, \ldots, k$, let player $\alpha$ meet player $\alpha+\omega(i)$ in round $i$. The tournament is well-defined as $\alpha+\omega(i) \in S$ and $\alpha+\omega(i)=\beta+\omega(i)$ implies $\alpha=\beta$; also $[\alpha+\omega(i)]+\omega(i)=\alpha$ for each $\alpha \in S$ (meaning that player $\alpha+\omega(i)$ meets player $\alpha$ in round $i$, as needed). Each player plays in each round. Next, every two players meet at most once (exactly once if $k=2^{t}-1$ ), since $\omega(i) \neq \omega(j)$ if $i \neq j$. Thus condition (i) holds true, and condition (ii) is also easy to check. Let player $\alpha$ meet player $\beta$ in round $i$, player $\gamma$ meet player $\delta$ in round $i$, and player $\alpha$ meet player $\gamma$ in round $j$. Then $\beta=\alpha+\omega(i), \delta=\gamma+\omega(i)$ and $\gamma=\alpha+\omega(j)$. By definition, $\beta$ will play in round $j$ with $$ \beta+\omega(j)=[\alpha+\omega(i)]+\omega(j)=[\alpha+\omega(j)]+\omega(i)=\gamma+\omega(i)=\delta $$ as required by (ii). So there exists an $(n, k)$-tournament for pairs $(n, k)$ such that $n=2^{t}$ and $k \leq 2^{t}-1$. The same conclusion is straightforward for $n$ of the form $n=2^{t} s$ and $k \leq 2^{t}-1$. Indeed, consider $s$ different $\left(2^{t}, k\right)$-tournaments $T_{1}, \ldots, T_{s}$, no two of them having players in common. Their union can be regarded as a $\left(2^{t} s, k\right)$-tournament $T$ where each round is the union of the respective rounds in $T_{1}, \ldots, T_{s}$. In summary, the condition that $2^{t_{k}}$ divides $n$ is sufficient for an $(n, k)$-tournament to exist. We prove that it is also necessary. Consider an arbitrary $(n, k)$-tournament. Represent each player by a point and after each round, join by an edge every two players who played in this round. Thus to a round $i=1, \ldots, k$ there corresponds a graph $G_{i}$. We say that player $Q$ is an $i$-neighbour of player $P$ if there is a path of edges in $G_{i}$ from $P$ to $Q$; in other words, if there are players $P=X_{1}, X_{2}, \ldots, X_{m}=Q$ such that player $X_{j}$ meets player $X_{j+1}$ in one of the first $i$ rounds, $j=1,2 \ldots, m-1$. The set of $i$-neighbours of a player will be called its $i$-component. Clearly two $i$-components are either disjoint or coincide. Hence after each round $i$ the set of players is partitioned into pairwise disjoint $i$-components. So, to achieve our goal, it suffices to show that all $k$-components have size divisible by $2^{t_{k}}$. To this end, let us see how the $i$-component $\Gamma$ of a player $A$ changes after round $i+1$. Suppose that $A$ meets player $B$ with $i$-component $\Delta$ in round $i+1$ (components $\Gamma$ and $\Delta$ are not necessarily distinct). We claim that then in round $i+1$ each player from $\Gamma$ meets a player from $\Delta$, and vice versa. Indeed, let $C$ be any player in $\Gamma$, and let $C$ meet $D$ in round $i+1$. Since $C$ is an $i$-neighbour of $A$, there is a sequence of players $A=X_{1}, X_{2}, \ldots, X_{m}=C$ such that $X_{j}$ meets $X_{j+1}$ in one of the first $i$ rounds, $j=1,2 \ldots, m-1$. Let $X_{j}$ meet $Y_{j}$ in round $i+1$, for $j=1,2 \ldots, m$; in particular $Y_{1}=B$ and $Y_{m}=D$. Players $Y_{j}$ exists in view of condition (i). Suppose that $X_{j}$ and $X_{j+1}$ met in round $r$, where $r \leq i$. Then condition (ii) implies that and $Y_{j}$ and $Y_{j+1}$ met in round $r$, too. Hence $B=Y_{1}, Y_{2}, \ldots, Y_{m}=D$ is a path in $G_{i}$ from $B$ to $D$. This is to say, $D$ is in the $i$-component $\Delta$ of $B$, as claimed. By symmetry, each player from $\Delta$ meets a player from $\Gamma$ in round $i+1$. It follows in particular that $\Gamma$ and $\Delta$ have the same cardinality. It is straightforward now that the $(i+1)$-component of $A$ is $\Gamma \cup \Delta$, the union of two sets with the same size. Since $\Gamma$ and $\Delta$ are either disjoint or coincide, we have either $|\Gamma \cup \Delta|=2|\Gamma|$ or $|\Gamma \cup \Delta|=|\Gamma|$; as usual, $|\cdots|$ denotes the cardinality of a finite set. Let $\Gamma_{1}, \ldots, \Gamma_{k}$ be the consecutive components of a given player $A$. We obtained that either $\left|\Gamma_{i+1}\right|=2\left|\Gamma_{i}\right|$ or $\left|\Gamma_{i+1}\right|=\left|\Gamma_{i}\right|$ for $i=1, \ldots, k-1$. Because $\left|\Gamma_{1}\right|=2$, each $\left|\Gamma_{i}\right|$ is a power of 2 , $i=1, \ldots, k-1$. In particular $\left|\Gamma_{k}\right|=2^{u}$ for some $u$. On the other hand, player $A$ has played with $k$ different opponents by (i). All of them belong to $\Gamma_{k}$, therefore $\left|\Gamma_{k}\right| \geq k+1$. Thus $2^{u} \geq k+1$, and since $t_{k}$ is the least integer satisfying $2^{t_{k}} \geq k+1$, we conclude that $u \geq t_{k}$. So the size of each $k$-component is divisible by $2^{t_{k}}$, which completes the argument.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a951fbeb-4c5c-531e-9eea-461d8947cde0
| 23,557
|
Let $A B C$ be a triangle with incentre $I$. A point $P$ in the interior of the triangle satisfies $$ \angle P B A+\angle P C A=\angle P B C+\angle P C B . $$ Show that $A P \geq A I$ and that equality holds if and only if $P$ coincides with $I$. (Korea)
|
Let $\angle A=\alpha, \angle B=\beta, \angle C=\gamma$. Since $\angle P B A+\angle P C A+\angle P B C+\angle P C B=\beta+\gamma$, the condition from the problem statement is equivalent to $\angle P B C+\angle P C B=(\beta+\gamma) / 2$, i. e. $\angle B P C=90^{\circ}+\alpha / 2$. On the other hand $\angle B I C=180^{\circ}-(\beta+\gamma) / 2=90^{\circ}+\alpha / 2$. Hence $\angle B P C=\angle B I C$, and since $P$ and $I$ are on the same side of $B C$, the points $B, C, I$ and $P$ are concyclic. In other words, $P$ lies on the circumcircle $\omega$ of triangle $B C I$.  Let $\Omega$ be the circumcircle of triangle $A B C$. It is a well-known fact that the centre of $\omega$ is the midpoint $M$ of the $\operatorname{arc} B C$ of $\Omega$. This is also the point where the angle bisector $A I$ intersects $\Omega$. From triangle $A P M$ we have $$ A P+P M \geq A M=A I+I M=A I+P M \text {. } $$ Therefore $A P \geq A I$. Equality holds if and only if $P$ lies on the line segment $A I$, which occurs if and only if $P=I$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$. A point $P$ in the interior of the triangle satisfies $$ \angle P B A+\angle P C A=\angle P B C+\angle P C B . $$ Show that $A P \geq A I$ and that equality holds if and only if $P$ coincides with $I$. (Korea)
|
Let $\angle A=\alpha, \angle B=\beta, \angle C=\gamma$. Since $\angle P B A+\angle P C A+\angle P B C+\angle P C B=\beta+\gamma$, the condition from the problem statement is equivalent to $\angle P B C+\angle P C B=(\beta+\gamma) / 2$, i. e. $\angle B P C=90^{\circ}+\alpha / 2$. On the other hand $\angle B I C=180^{\circ}-(\beta+\gamma) / 2=90^{\circ}+\alpha / 2$. Hence $\angle B P C=\angle B I C$, and since $P$ and $I$ are on the same side of $B C$, the points $B, C, I$ and $P$ are concyclic. In other words, $P$ lies on the circumcircle $\omega$ of triangle $B C I$.  Let $\Omega$ be the circumcircle of triangle $A B C$. It is a well-known fact that the centre of $\omega$ is the midpoint $M$ of the $\operatorname{arc} B C$ of $\Omega$. This is also the point where the angle bisector $A I$ intersects $\Omega$. From triangle $A P M$ we have $$ A P+P M \geq A M=A I+I M=A I+P M \text {. } $$ Therefore $A P \geq A I$. Equality holds if and only if $P$ lies on the line segment $A I$, which occurs if and only if $P=I$.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
93e50702-194f-5093-8813-f0b7bfd61979
| 23,567
|
Let $A B C D$ be a trapezoid with parallel sides $A B>C D$. Points $K$ and $L$ lie on the line segments $A B$ and $C D$, respectively, so that $A K / K B=D L / L C$. Suppose that there are points $P$ and $Q$ on the line segment $K L$ satisfying $$ \angle A P B=\angle B C D \quad \text { and } \quad \angle C Q D=\angle A B C \text {. } $$ Prove that the points $P, Q, B$ and $C$ are concyclic. (Ukraine)
|
Because $A B \| C D$, the relation $A K / K B=D L / L C$ readily implies that the lines $A D, B C$ and $K L$ have a common point $S$.  Consider the second intersection points $X$ and $Y$ of the line $S K$ with the circles $(A B P)$ and $(C D Q)$, respectively. Since $A P B X$ is a cyclic quadrilateral and $A B \| C D$, one has $$ \angle A X B=180^{\circ}-\angle A P B=180^{\circ}-\angle B C D=\angle A B C . $$ This shows that $B C$ is tangent to the circle $(A B P)$ at $B$. Likewise, $B C$ is tangent to the circle $(C D Q)$ at $C$. Therefore $S P \cdot S X=S B^{2}$ and $S Q \cdot S Y=S C^{2}$. Let $h$ be the homothety with centre $S$ and ratio $S C / S B$. Since $h(B)=C$, the above conclusion about tangency implies that $h$ takes circle $(A B P)$ to circle $(C D Q)$. Also, $h$ takes $A B$ to $C D$, and it easily follows that $h(P)=Y, h(X)=Q$, yielding $S P / S Y=S B / S C=S X / S Q$. Equalities $S P \cdot S X=S B^{2}$ and $S Q / S X=S C / S B$ imply $S P \cdot S Q=S B \cdot S C$, which is equivalent to $P, Q, B$ and $C$ being concyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a trapezoid with parallel sides $A B>C D$. Points $K$ and $L$ lie on the line segments $A B$ and $C D$, respectively, so that $A K / K B=D L / L C$. Suppose that there are points $P$ and $Q$ on the line segment $K L$ satisfying $$ \angle A P B=\angle B C D \quad \text { and } \quad \angle C Q D=\angle A B C \text {. } $$ Prove that the points $P, Q, B$ and $C$ are concyclic. (Ukraine)
|
Because $A B \| C D$, the relation $A K / K B=D L / L C$ readily implies that the lines $A D, B C$ and $K L$ have a common point $S$.  Consider the second intersection points $X$ and $Y$ of the line $S K$ with the circles $(A B P)$ and $(C D Q)$, respectively. Since $A P B X$ is a cyclic quadrilateral and $A B \| C D$, one has $$ \angle A X B=180^{\circ}-\angle A P B=180^{\circ}-\angle B C D=\angle A B C . $$ This shows that $B C$ is tangent to the circle $(A B P)$ at $B$. Likewise, $B C$ is tangent to the circle $(C D Q)$ at $C$. Therefore $S P \cdot S X=S B^{2}$ and $S Q \cdot S Y=S C^{2}$. Let $h$ be the homothety with centre $S$ and ratio $S C / S B$. Since $h(B)=C$, the above conclusion about tangency implies that $h$ takes circle $(A B P)$ to circle $(C D Q)$. Also, $h$ takes $A B$ to $C D$, and it easily follows that $h(P)=Y, h(X)=Q$, yielding $S P / S Y=S B / S C=S X / S Q$. Equalities $S P \cdot S X=S B^{2}$ and $S Q / S X=S C / S B$ imply $S P \cdot S Q=S B \cdot S C$, which is equivalent to $P, Q, B$ and $C$ being concyclic.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8a9ab4e9-3e41-5359-a29f-defa936e41c9
| 23,570
|
Let $A B C D$ be a trapezoid with parallel sides $A B>C D$. Points $K$ and $L$ lie on the line segments $A B$ and $C D$, respectively, so that $A K / K B=D L / L C$. Suppose that there are points $P$ and $Q$ on the line segment $K L$ satisfying $$ \angle A P B=\angle B C D \quad \text { and } \quad \angle C Q D=\angle A B C \text {. } $$ Prove that the points $P, Q, B$ and $C$ are concyclic. (Ukraine)
|
The case where $P=Q$ is trivial. Thus assume that $P$ and $Q$ are two distinct points. As in the first solution, notice that the lines $A D, B C$ and $K L$ concur at a point $S$.  Let the lines $A P$ and $D Q$ meet at $E$, and let $B P$ and $C Q$ meet at $F$. Then $\angle E P F=\angle B C D$ and $\angle F Q E=\angle A B C$ by the condition of the problem. Since the angles $B C D$ and $A B C$ add up to $180^{\circ}$, it follows that $P E Q F$ is a cyclic quadrilateral. Applying Menelaus' theorem, first to triangle $A S P$ and line $D Q$ and then to triangle $B S P$ and line $C Q$, we have $$ \frac{A D}{D S} \cdot \frac{S Q}{Q P} \cdot \frac{P E}{E A}=1 \text { and } \frac{B C}{C S} \cdot \frac{S Q}{Q P} \cdot \frac{P F}{F B}=1 $$ The first factors in these equations are equal, as $A B \| C D$. Thus the last factors are also equal, which implies that $E F$ is parallel to $A B$ and $C D$. Using this and the cyclicity of $P E Q F$, we obtain $$ \angle B C D=\angle B C F+\angle F C D=\angle B C Q+\angle E F Q=\angle B C Q+\angle E P Q $$ On the other hand, $$ \angle B C D=\angle A P B=\angle E P F=\angle E P Q+\angle Q P F, $$ and consequently $\angle B C Q=\angle Q P F$. The latter angle either coincides with $\angle Q P B$ or is supplementary to $\angle Q P B$, depending on whether $Q$ lies between $K$ and $P$ or not. In either case it follows that $P, Q, B$ and $C$ are concyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a trapezoid with parallel sides $A B>C D$. Points $K$ and $L$ lie on the line segments $A B$ and $C D$, respectively, so that $A K / K B=D L / L C$. Suppose that there are points $P$ and $Q$ on the line segment $K L$ satisfying $$ \angle A P B=\angle B C D \quad \text { and } \quad \angle C Q D=\angle A B C \text {. } $$ Prove that the points $P, Q, B$ and $C$ are concyclic. (Ukraine)
|
The case where $P=Q$ is trivial. Thus assume that $P$ and $Q$ are two distinct points. As in the first solution, notice that the lines $A D, B C$ and $K L$ concur at a point $S$.  Let the lines $A P$ and $D Q$ meet at $E$, and let $B P$ and $C Q$ meet at $F$. Then $\angle E P F=\angle B C D$ and $\angle F Q E=\angle A B C$ by the condition of the problem. Since the angles $B C D$ and $A B C$ add up to $180^{\circ}$, it follows that $P E Q F$ is a cyclic quadrilateral. Applying Menelaus' theorem, first to triangle $A S P$ and line $D Q$ and then to triangle $B S P$ and line $C Q$, we have $$ \frac{A D}{D S} \cdot \frac{S Q}{Q P} \cdot \frac{P E}{E A}=1 \text { and } \frac{B C}{C S} \cdot \frac{S Q}{Q P} \cdot \frac{P F}{F B}=1 $$ The first factors in these equations are equal, as $A B \| C D$. Thus the last factors are also equal, which implies that $E F$ is parallel to $A B$ and $C D$. Using this and the cyclicity of $P E Q F$, we obtain $$ \angle B C D=\angle B C F+\angle F C D=\angle B C Q+\angle E F Q=\angle B C Q+\angle E P Q $$ On the other hand, $$ \angle B C D=\angle A P B=\angle E P F=\angle E P Q+\angle Q P F, $$ and consequently $\angle B C Q=\angle Q P F$. The latter angle either coincides with $\angle Q P B$ or is supplementary to $\angle Q P B$, depending on whether $Q$ lies between $K$ and $P$ or not. In either case it follows that $P, Q, B$ and $C$ are concyclic.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8a9ab4e9-3e41-5359-a29f-defa936e41c9
| 23,570
|
Let $A B C D E$ be a convex pentagon such that $$ \angle B A C=\angle C A D=\angle D A E \quad \text { and } \quad \angle A B C=\angle A C D=\angle A D E \text {. } $$ The diagonals $B D$ and $C E$ meet at $P$. Prove that the line $A P$ bisects the side $C D$.
|
Let the diagonals $A C$ and $B D$ meet at $Q$, the diagonals $A D$ and $C E$ meet at $R$, and let the ray $A P$ meet the side $C D$ at $M$. We want to prove that $C M=M D$ holds.  The idea is to show that $Q$ and $R$ divide $A C$ and $A D$ in the same ratio, or more precisely $$ \frac{A Q}{Q C}=\frac{A R}{R D} $$ (which is equivalent to $Q R \| C D$ ). The given angle equalities imply that the triangles $A B C$, $A C D$ and $A D E$ are similar. We therefore have $$ \frac{A B}{A C}=\frac{A C}{A D}=\frac{A D}{A E} $$ Since $\angle B A D=\angle B A C+\angle C A D=\angle C A D+\angle D A E=\angle C A E$, it follows from $A B / A C=$ $A D / A E$ that the triangles $A B D$ and $A C E$ are also similar. Their angle bisectors in $A$ are $A Q$ and $A R$, respectively, so that $$ \frac{A B}{A C}=\frac{A Q}{A R} $$ Because $A B / A C=A C / A D$, we obtain $A Q / A R=A C / A D$, which is equivalent to (1). Now Ceva's theorem for the triangle $A C D$ yields $$ \frac{A Q}{Q C} \cdot \frac{C M}{M D} \cdot \frac{D R}{R A}=1 $$ In view of (1), this reduces to $C M=M D$, which completes the proof. Comment. Relation (1) immediately follows from the fact that quadrilaterals $A B C D$ and $A C D E$ are similar.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E$ be a convex pentagon such that $$ \angle B A C=\angle C A D=\angle D A E \quad \text { and } \quad \angle A B C=\angle A C D=\angle A D E \text {. } $$ The diagonals $B D$ and $C E$ meet at $P$. Prove that the line $A P$ bisects the side $C D$.
|
Let the diagonals $A C$ and $B D$ meet at $Q$, the diagonals $A D$ and $C E$ meet at $R$, and let the ray $A P$ meet the side $C D$ at $M$. We want to prove that $C M=M D$ holds.  The idea is to show that $Q$ and $R$ divide $A C$ and $A D$ in the same ratio, or more precisely $$ \frac{A Q}{Q C}=\frac{A R}{R D} $$ (which is equivalent to $Q R \| C D$ ). The given angle equalities imply that the triangles $A B C$, $A C D$ and $A D E$ are similar. We therefore have $$ \frac{A B}{A C}=\frac{A C}{A D}=\frac{A D}{A E} $$ Since $\angle B A D=\angle B A C+\angle C A D=\angle C A D+\angle D A E=\angle C A E$, it follows from $A B / A C=$ $A D / A E$ that the triangles $A B D$ and $A C E$ are also similar. Their angle bisectors in $A$ are $A Q$ and $A R$, respectively, so that $$ \frac{A B}{A C}=\frac{A Q}{A R} $$ Because $A B / A C=A C / A D$, we obtain $A Q / A R=A C / A D$, which is equivalent to (1). Now Ceva's theorem for the triangle $A C D$ yields $$ \frac{A Q}{Q C} \cdot \frac{C M}{M D} \cdot \frac{D R}{R A}=1 $$ In view of (1), this reduces to $C M=M D$, which completes the proof. Comment. Relation (1) immediately follows from the fact that quadrilaterals $A B C D$ and $A C D E$ are similar.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
63ec2e9c-8072-5175-84b4-06a9674676a1
| 23,575
|
A point $D$ is chosen on the side $A C$ of a triangle $A B C$ with $\angle C<\angle A<90^{\circ}$ in such a way that $B D=B A$. The incircle of $A B C$ is tangent to $A B$ and $A C$ at points $K$ and $L$, respectively. Let $J$ be the incentre of triangle $B C D$. Prove that the line $K L$ intersects the line segment $A J$ at its midpoint. (Russia)
|
Denote by $P$ be the common point of $A J$ and $K L$. Let the parallel to $K L$ through $J$ meet $A C$ at $M$. Then $P$ is the midpoint of $A J$ if and only if $A M=2 \cdot A L$, which we are about to show.  Denoting $\angle B A C=2 \alpha$, the equalities $B A=B D$ and $A K=A L$ imply $\angle A D B=2 \alpha$ and $\angle A L K=90^{\circ}-\alpha$. Since $D J$ bisects $\angle B D C$, we obtain $\angle C D J=\frac{1}{2} \cdot\left(180^{\circ}-\angle A D B\right)=90^{\circ}-\alpha$. Also $\angle D M J=\angle A L K=90^{\circ}-\alpha$ since $J M \| K L$. It follows that $J D=J M$. Let the incircle of triangle $B C D$ touch its side $C D$ at $T$. Then $J T \perp C D$, meaning that $J T$ is the altitude to the base $D M$ of the isosceles triangle $D M J$. It now follows that $D T=M T$, and we have $$ D M=2 \cdot D T=B D+C D-B C \text {. } $$ Therefore $$ \begin{aligned} A M & =A D+(B D+C D-B C) \\ & =A D+A B+D C-B C \\ & =A C+A B-B C \\ & =2 \cdot A L, \end{aligned} $$ which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A point $D$ is chosen on the side $A C$ of a triangle $A B C$ with $\angle C<\angle A<90^{\circ}$ in such a way that $B D=B A$. The incircle of $A B C$ is tangent to $A B$ and $A C$ at points $K$ and $L$, respectively. Let $J$ be the incentre of triangle $B C D$. Prove that the line $K L$ intersects the line segment $A J$ at its midpoint. (Russia)
|
Denote by $P$ be the common point of $A J$ and $K L$. Let the parallel to $K L$ through $J$ meet $A C$ at $M$. Then $P$ is the midpoint of $A J$ if and only if $A M=2 \cdot A L$, which we are about to show.  Denoting $\angle B A C=2 \alpha$, the equalities $B A=B D$ and $A K=A L$ imply $\angle A D B=2 \alpha$ and $\angle A L K=90^{\circ}-\alpha$. Since $D J$ bisects $\angle B D C$, we obtain $\angle C D J=\frac{1}{2} \cdot\left(180^{\circ}-\angle A D B\right)=90^{\circ}-\alpha$. Also $\angle D M J=\angle A L K=90^{\circ}-\alpha$ since $J M \| K L$. It follows that $J D=J M$. Let the incircle of triangle $B C D$ touch its side $C D$ at $T$. Then $J T \perp C D$, meaning that $J T$ is the altitude to the base $D M$ of the isosceles triangle $D M J$. It now follows that $D T=M T$, and we have $$ D M=2 \cdot D T=B D+C D-B C \text {. } $$ Therefore $$ \begin{aligned} A M & =A D+(B D+C D-B C) \\ & =A D+A B+D C-B C \\ & =A C+A B-B C \\ & =2 \cdot A L, \end{aligned} $$ which completes the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
bd01618d-8945-5460-b4a5-e745aa4e960b
| 23,577
|
Circles $\omega_{1}$ and $\omega_{2}$ with centres $O_{1}$ and $O_{2}$ are externally tangent at point $D$ and internally tangent to a circle $\omega$ at points $E$ and $F$, respectively. Line $t$ is the common tangent of $\omega_{1}$ and $\omega_{2}$ at $D$. Let $A B$ be the diameter of $\omega$ perpendicular to $t$, so that $A, E$ and $O_{1}$ are on the same side of $t$. Prove that lines $A O_{1}, B O_{2}, E F$ and $t$ are concurrent. (Brasil)
|
Point $E$ is the centre of a homothety $h$ which takes circle $\omega_{1}$ to circle $\omega$. The radii $O_{1} D$ and $O B$ of these circles are parallel as both are perpendicular to line t. Also, $O_{1} D$ and $O B$ are on the same side of line $E O$, hence $h$ takes $O_{1} D$ to $O B$. Consequently, points $E$, $D$ and $B$ are collinear. Likewise, points $F, D$ and $A$ are collinear as well. Let lines $A E$ and $B F$ intersect at $C$. Since $A F$ and $B E$ are altitudes in triangle $A B C$, their common point $D$ is the orthocentre of this triangle. So $C D$ is perpendicular to $A B$, implying that $C$ lies on line $t$. Note that triangle $A B C$ is acute-angled. We mention the well-known fact that triangles $F E C$ and $A B C$ are similar in ratio $\cos \gamma$, where $\gamma=\angle A C B$. In addition, points $C, E, D$ and $F$ lie on the circle with diameter $C D$.  Let $P$ be the common point of lines $E F$ and $t$. We are going to prove that $P$ lies on line $A O_{1}$. Denote by $N$ the second common point of circle $\omega_{1}$ and $A C$; this is the point of $\omega_{1}$ diametrically opposite to $D$. By Menelaus' theorem for triangle $D C N$, points $A, O_{1}$ and $P$ are collinear if and only if $$ \frac{C A}{A N} \cdot \frac{N O_{1}}{O_{1} D} \cdot \frac{D P}{P C}=1 $$ Because $N O_{1}=O_{1} D$, this reduces to $C A / A N=C P / P D$. Let line $t$ meet $A B$ at $K$. Then $C A / A N=C K / K D$, so it suffices to show that $$ \frac{C P}{P D}=\frac{C K}{K D} $$ To verify (1), consider the circumcircle $\Omega$ of triangle $A B C$. Draw its diameter $C U$ through $C$, and let $C U$ meet $A B$ at $V$. Extend $C K$ to meet $\Omega$ at $L$. Since $A B$ is parallel to $U L$, we have $\angle A C U=\angle B C L$. On the other hand $\angle E F C=\angle B A C, \angle F E C=\angle A B C$ and $E F / A B=\cos \gamma$, as stated above. So reflection in the bisector of $\angle A C B$ followed by a homothety with centre $C$ and ratio $1 / \cos \gamma$ takes triangle $F E C$ to triangle $A B C$. Consequently, this transformation takes $C D$ to $C U$, which implies $C P / P D=C V / V U$. Next, we have $K L=K D$, because $D$ is the orthocentre of triangle $A B C$. Hence $C K / K D=C K / K L$. Finally, $C V / V U=C K / K L$ because $A B$ is parallel to $U L$. Relation (1) follows, proving that $P$ lies on line $A O_{1}$. By symmetry, $P$ also lies on line $A O_{2}$ which completes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Circles $\omega_{1}$ and $\omega_{2}$ with centres $O_{1}$ and $O_{2}$ are externally tangent at point $D$ and internally tangent to a circle $\omega$ at points $E$ and $F$, respectively. Line $t$ is the common tangent of $\omega_{1}$ and $\omega_{2}$ at $D$. Let $A B$ be the diameter of $\omega$ perpendicular to $t$, so that $A, E$ and $O_{1}$ are on the same side of $t$. Prove that lines $A O_{1}, B O_{2}, E F$ and $t$ are concurrent. (Brasil)
|
Point $E$ is the centre of a homothety $h$ which takes circle $\omega_{1}$ to circle $\omega$. The radii $O_{1} D$ and $O B$ of these circles are parallel as both are perpendicular to line t. Also, $O_{1} D$ and $O B$ are on the same side of line $E O$, hence $h$ takes $O_{1} D$ to $O B$. Consequently, points $E$, $D$ and $B$ are collinear. Likewise, points $F, D$ and $A$ are collinear as well. Let lines $A E$ and $B F$ intersect at $C$. Since $A F$ and $B E$ are altitudes in triangle $A B C$, their common point $D$ is the orthocentre of this triangle. So $C D$ is perpendicular to $A B$, implying that $C$ lies on line $t$. Note that triangle $A B C$ is acute-angled. We mention the well-known fact that triangles $F E C$ and $A B C$ are similar in ratio $\cos \gamma$, where $\gamma=\angle A C B$. In addition, points $C, E, D$ and $F$ lie on the circle with diameter $C D$.  Let $P$ be the common point of lines $E F$ and $t$. We are going to prove that $P$ lies on line $A O_{1}$. Denote by $N$ the second common point of circle $\omega_{1}$ and $A C$; this is the point of $\omega_{1}$ diametrically opposite to $D$. By Menelaus' theorem for triangle $D C N$, points $A, O_{1}$ and $P$ are collinear if and only if $$ \frac{C A}{A N} \cdot \frac{N O_{1}}{O_{1} D} \cdot \frac{D P}{P C}=1 $$ Because $N O_{1}=O_{1} D$, this reduces to $C A / A N=C P / P D$. Let line $t$ meet $A B$ at $K$. Then $C A / A N=C K / K D$, so it suffices to show that $$ \frac{C P}{P D}=\frac{C K}{K D} $$ To verify (1), consider the circumcircle $\Omega$ of triangle $A B C$. Draw its diameter $C U$ through $C$, and let $C U$ meet $A B$ at $V$. Extend $C K$ to meet $\Omega$ at $L$. Since $A B$ is parallel to $U L$, we have $\angle A C U=\angle B C L$. On the other hand $\angle E F C=\angle B A C, \angle F E C=\angle A B C$ and $E F / A B=\cos \gamma$, as stated above. So reflection in the bisector of $\angle A C B$ followed by a homothety with centre $C$ and ratio $1 / \cos \gamma$ takes triangle $F E C$ to triangle $A B C$. Consequently, this transformation takes $C D$ to $C U$, which implies $C P / P D=C V / V U$. Next, we have $K L=K D$, because $D$ is the orthocentre of triangle $A B C$. Hence $C K / K D=C K / K L$. Finally, $C V / V U=C K / K L$ because $A B$ is parallel to $U L$. Relation (1) follows, proving that $P$ lies on line $A O_{1}$. By symmetry, $P$ also lies on line $A O_{2}$ which completes the solution.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
50cd4164-5dd9-59eb-8018-855a9e0b3fc2
| 23,584
|
Circles $\omega_{1}$ and $\omega_{2}$ with centres $O_{1}$ and $O_{2}$ are externally tangent at point $D$ and internally tangent to a circle $\omega$ at points $E$ and $F$, respectively. Line $t$ is the common tangent of $\omega_{1}$ and $\omega_{2}$ at $D$. Let $A B$ be the diameter of $\omega$ perpendicular to $t$, so that $A, E$ and $O_{1}$ are on the same side of $t$. Prove that lines $A O_{1}, B O_{2}, E F$ and $t$ are concurrent. (Brasil)
|
We proceed as in the first solution to define a triangle $A B C$ with orthocentre $D$, in which $A F$ and $B E$ are altitudes. Denote by $M$ the midpoint of $C D$. The quadrilateral $C E D F$ is inscribed in a circle with centre $M$, hence $M C=M E=M D=M F$.  Consider triangles $A B C$ and $O_{1} O_{2} M$. Lines $O_{1} O_{2}$ and $A B$ are parallel, both of them being perpendicular to line $t$. Next, $M O_{1}$ is the line of centres of circles $(C E F)$ and $\omega_{1}$ whose common chord is $D E$. Hence $M O_{1}$ bisects $\angle D M E$ which is the external angle at $M$ in the isosceles triangle $C E M$. It follows that $\angle D M O_{1}=\angle D C A$, so that $M O_{1}$ is parallel to $A C$. Likewise, $M O_{2}$ is parallel to $B C$. Thus the respective sides of triangles $A B C$ and $O_{1} O_{2} M$ are parallel; in addition, these triangles are not congruent. Hence there is a homothety taking $A B C$ to $O_{1} O_{2} M$. The lines $A O_{1}$, $B O_{2}$ and $C M=t$ are concurrent at the centre $Q$ of this homothety. Finally, apply Pappus' theorem to the triples of collinear points $A, O, B$ and $O_{2}, D, O_{1}$. The theorem implies that the points $A D \cap O O_{2}=F, A O_{1} \cap B O_{2}=Q$ and $O O_{1} \cap B D=E$ are collinear. In other words, line $E F$ passes through the common point $Q$ of $A O_{1}, B O_{2}$ and $t$. Comment. Relation (1) from Solution 1 expresses the well-known fact that points $P$ and $K$ are harmonic conjugates with respect to points $C$ and $D$. It is also easy to justify it by direct computation. Denoting $\angle C A B=\alpha, \angle A B C=\beta$, it is straightforward to obtain $C P / P D=C K / K D=\tan \alpha \tan \beta$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Circles $\omega_{1}$ and $\omega_{2}$ with centres $O_{1}$ and $O_{2}$ are externally tangent at point $D$ and internally tangent to a circle $\omega$ at points $E$ and $F$, respectively. Line $t$ is the common tangent of $\omega_{1}$ and $\omega_{2}$ at $D$. Let $A B$ be the diameter of $\omega$ perpendicular to $t$, so that $A, E$ and $O_{1}$ are on the same side of $t$. Prove that lines $A O_{1}, B O_{2}, E F$ and $t$ are concurrent. (Brasil)
|
We proceed as in the first solution to define a triangle $A B C$ with orthocentre $D$, in which $A F$ and $B E$ are altitudes. Denote by $M$ the midpoint of $C D$. The quadrilateral $C E D F$ is inscribed in a circle with centre $M$, hence $M C=M E=M D=M F$.  Consider triangles $A B C$ and $O_{1} O_{2} M$. Lines $O_{1} O_{2}$ and $A B$ are parallel, both of them being perpendicular to line $t$. Next, $M O_{1}$ is the line of centres of circles $(C E F)$ and $\omega_{1}$ whose common chord is $D E$. Hence $M O_{1}$ bisects $\angle D M E$ which is the external angle at $M$ in the isosceles triangle $C E M$. It follows that $\angle D M O_{1}=\angle D C A$, so that $M O_{1}$ is parallel to $A C$. Likewise, $M O_{2}$ is parallel to $B C$. Thus the respective sides of triangles $A B C$ and $O_{1} O_{2} M$ are parallel; in addition, these triangles are not congruent. Hence there is a homothety taking $A B C$ to $O_{1} O_{2} M$. The lines $A O_{1}$, $B O_{2}$ and $C M=t$ are concurrent at the centre $Q$ of this homothety. Finally, apply Pappus' theorem to the triples of collinear points $A, O, B$ and $O_{2}, D, O_{1}$. The theorem implies that the points $A D \cap O O_{2}=F, A O_{1} \cap B O_{2}=Q$ and $O O_{1} \cap B D=E$ are collinear. In other words, line $E F$ passes through the common point $Q$ of $A O_{1}, B O_{2}$ and $t$. Comment. Relation (1) from Solution 1 expresses the well-known fact that points $P$ and $K$ are harmonic conjugates with respect to points $C$ and $D$. It is also easy to justify it by direct computation. Denoting $\angle C A B=\alpha, \angle A B C=\beta$, it is straightforward to obtain $C P / P D=C K / K D=\tan \alpha \tan \beta$.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
50cd4164-5dd9-59eb-8018-855a9e0b3fc2
| 23,584
|
Let $A B C D$ be a convex quadrilateral. A circle passing through the points $A$ and $D$ and a circle passing through the points $B$ and $C$ are externally tangent at a point $P$ inside the quadrilateral. Suppose that $$ \angle P A B+\angle P D C \leq 90^{\circ} \quad \text { and } \quad \angle P B A+\angle P C D \leq 90^{\circ} \text {. } $$ Prove that $A B+C D \geq B C+A D$. (Poland)
|
We start with a preliminary observation. Let $T$ be a point inside the quadrilateral $A B C D$. Then: $$ \begin{aligned} & \text { Circles }(B C T) \text { and }(D A T) \text { are tangent at } T \\ & \text { if and only if } \quad \angle A D T+\angle B C T=\angle A T B \text {. } \end{aligned} $$ Indeed, if the two circles touch each other then their common tangent at $T$ intersects the segment $A B$ at a point $Z$, and so $\angle A D T=\angle A T Z, \angle B C T=\angle B T Z$, by the tangent-chord theorem. Thus $\angle A D T+\angle B C T=\angle A T Z+\angle B T Z=\angle A T B$. And conversely, if $\angle A D T+\angle B C T=\angle A T B$ then one can draw from $T$ a ray $T Z$ with $Z$ on $A B$ so that $\angle A D T=\angle A T Z, \angle B C T=\angle B T Z$. The first of these equalities implies that $T Z$ is tangent to the circle $(D A T)$; by the second equality, $T Z$ is tangent to the circle $(B C T)$, so the two circles are tangent at $T$.  So the equivalence (1) is settled. It will be used later on. Now pass to the actual solution. Its key idea is to introduce the circumcircles of triangles $A B P$ and $C D P$ and to consider their second intersection $Q$ (assume for the moment that they indeed meet at two distinct points $P$ and $Q$ ). Since the point $A$ lies outside the circle $(B C P)$, we have $\angle B C P+\angle B A P<180^{\circ}$. Therefore the point $C$ lies outside the circle $(A B P)$. Analogously, $D$ also lies outside that circle. It follows that $P$ and $Q$ lie on the same $\operatorname{arc} C D$ of the circle $(B C P)$.  By symmetry, $P$ and $Q$ lie on the same arc $A B$ of the circle $(A B P)$. Thus the point $Q$ lies either inside the angle $B P C$ or inside the angle $A P D$. Without loss of generality assume that $Q$ lies inside the angle $B P C$. Then $$ \angle A Q D=\angle P Q A+\angle P Q D=\angle P B A+\angle P C D \leq 90^{\circ} \text {, } $$ by the condition of the problem. In the cyclic quadrilaterals $A P Q B$ and $D P Q C$, the angles at vertices $A$ and $D$ are acute. So their angles at $Q$ are obtuse. This implies that $Q$ lies not only inside the angle $B P C$ but in fact inside the triangle $B P C$, hence also inside the quadrilateral $A B C D$. Now an argument similar to that used in deriving (2) shows that $$ \angle B Q C=\angle P A B+\angle P D C \leq 90^{\circ} . $$ Moreover, since $\angle P C Q=\angle P D Q$, we get $$ \angle A D Q+\angle B C Q=\angle A D P+\angle P D Q+\angle B C P-\angle P C Q=\angle A D P+\angle B C P . $$ The last sum is equal to $\angle A P B$, according to the observation (1) applied to $T=P$. And because $\angle A P B=\angle A Q B$, we obtain $$ \angle A D Q+\angle B C Q=\angle A Q B \text {. } $$ Applying now (1) to $T=Q$ we conclude that the circles $(B C Q)$ and $(D A Q)$ are externally tangent at $Q$. (We have assumed $P \neq Q$; but if $P=Q$ then the last conclusion holds trivially.) Finally consider the halfdiscs with diameters $B C$ and $D A$ constructed inwardly to the quadrilateral $A B C D$. They have centres at $M$ and $N$, the midpoints of $B C$ and $D A$ respectively. In view of (2) and (3), these two halfdiscs lie entirely inside the circles $(B Q C)$ and $(A Q D)$; and since these circles are tangent, the two halfdiscs cannot overlap. Hence $M N \geq \frac{1}{2} B C+\frac{1}{2} D A$. On the other hand, since $\overrightarrow{M N}=\frac{1}{2}(\overrightarrow{B A}+\overrightarrow{C D})$, we have $M N \leq \frac{1}{2}(A B+C D)$. Thus indeed $A B+C D \geq B C+D A$, as claimed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral. A circle passing through the points $A$ and $D$ and a circle passing through the points $B$ and $C$ are externally tangent at a point $P$ inside the quadrilateral. Suppose that $$ \angle P A B+\angle P D C \leq 90^{\circ} \quad \text { and } \quad \angle P B A+\angle P C D \leq 90^{\circ} \text {. } $$ Prove that $A B+C D \geq B C+A D$. (Poland)
|
We start with a preliminary observation. Let $T$ be a point inside the quadrilateral $A B C D$. Then: $$ \begin{aligned} & \text { Circles }(B C T) \text { and }(D A T) \text { are tangent at } T \\ & \text { if and only if } \quad \angle A D T+\angle B C T=\angle A T B \text {. } \end{aligned} $$ Indeed, if the two circles touch each other then their common tangent at $T$ intersects the segment $A B$ at a point $Z$, and so $\angle A D T=\angle A T Z, \angle B C T=\angle B T Z$, by the tangent-chord theorem. Thus $\angle A D T+\angle B C T=\angle A T Z+\angle B T Z=\angle A T B$. And conversely, if $\angle A D T+\angle B C T=\angle A T B$ then one can draw from $T$ a ray $T Z$ with $Z$ on $A B$ so that $\angle A D T=\angle A T Z, \angle B C T=\angle B T Z$. The first of these equalities implies that $T Z$ is tangent to the circle $(D A T)$; by the second equality, $T Z$ is tangent to the circle $(B C T)$, so the two circles are tangent at $T$.  So the equivalence (1) is settled. It will be used later on. Now pass to the actual solution. Its key idea is to introduce the circumcircles of triangles $A B P$ and $C D P$ and to consider their second intersection $Q$ (assume for the moment that they indeed meet at two distinct points $P$ and $Q$ ). Since the point $A$ lies outside the circle $(B C P)$, we have $\angle B C P+\angle B A P<180^{\circ}$. Therefore the point $C$ lies outside the circle $(A B P)$. Analogously, $D$ also lies outside that circle. It follows that $P$ and $Q$ lie on the same $\operatorname{arc} C D$ of the circle $(B C P)$.  By symmetry, $P$ and $Q$ lie on the same arc $A B$ of the circle $(A B P)$. Thus the point $Q$ lies either inside the angle $B P C$ or inside the angle $A P D$. Without loss of generality assume that $Q$ lies inside the angle $B P C$. Then $$ \angle A Q D=\angle P Q A+\angle P Q D=\angle P B A+\angle P C D \leq 90^{\circ} \text {, } $$ by the condition of the problem. In the cyclic quadrilaterals $A P Q B$ and $D P Q C$, the angles at vertices $A$ and $D$ are acute. So their angles at $Q$ are obtuse. This implies that $Q$ lies not only inside the angle $B P C$ but in fact inside the triangle $B P C$, hence also inside the quadrilateral $A B C D$. Now an argument similar to that used in deriving (2) shows that $$ \angle B Q C=\angle P A B+\angle P D C \leq 90^{\circ} . $$ Moreover, since $\angle P C Q=\angle P D Q$, we get $$ \angle A D Q+\angle B C Q=\angle A D P+\angle P D Q+\angle B C P-\angle P C Q=\angle A D P+\angle B C P . $$ The last sum is equal to $\angle A P B$, according to the observation (1) applied to $T=P$. And because $\angle A P B=\angle A Q B$, we obtain $$ \angle A D Q+\angle B C Q=\angle A Q B \text {. } $$ Applying now (1) to $T=Q$ we conclude that the circles $(B C Q)$ and $(D A Q)$ are externally tangent at $Q$. (We have assumed $P \neq Q$; but if $P=Q$ then the last conclusion holds trivially.) Finally consider the halfdiscs with diameters $B C$ and $D A$ constructed inwardly to the quadrilateral $A B C D$. They have centres at $M$ and $N$, the midpoints of $B C$ and $D A$ respectively. In view of (2) and (3), these two halfdiscs lie entirely inside the circles $(B Q C)$ and $(A Q D)$; and since these circles are tangent, the two halfdiscs cannot overlap. Hence $M N \geq \frac{1}{2} B C+\frac{1}{2} D A$. On the other hand, since $\overrightarrow{M N}=\frac{1}{2}(\overrightarrow{B A}+\overrightarrow{C D})$, we have $M N \leq \frac{1}{2}(A B+C D)$. Thus indeed $A B+C D \geq B C+D A$, as claimed.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
10d7ed27-a47a-52d8-89ba-b9a03d157b86
| 23,591
|
Points $A_{1}, B_{1}, C_{1}$ are chosen on the sides $B C, C A, A B$ of a triangle $A B C$, respectively. The circumcircles of triangles $A B_{1} C_{1}, B C_{1} A_{1}, C A_{1} B_{1}$ intersect the circumcircle of triangle $A B C$ again at points $A_{2}, B_{2}, C_{2}$, respectively $\left(A_{2} \neq A, B_{2} \neq B, C_{2} \neq C\right)$. Points $A_{3}, B_{3}, C_{3}$ are symmetric to $A_{1}, B_{1}, C_{1}$ with respect to the midpoints of the sides $B C, C A, A B$ respectively. Prove that the triangles $A_{2} B_{2} C_{2}$ and $A_{3} B_{3} C_{3}$ are similar. (Russia)
|
We will work with oriented angles between lines. For two straight lines $\ell, m$ in the plane, $\angle(\ell, m)$ denotes the angle of counterclockwise rotation which transforms line $\ell$ into a line parallel to $m$ (the choice of the rotation centre is irrelevant). This is a signed quantity; values differing by a multiple of $\pi$ are identified, so that $$ \angle(\ell, m)=-\angle(m, \ell), \quad \angle(\ell, m)+\angle(m, n)=\angle(\ell, n) . $$ If $\ell$ is the line through points $K, L$ and $m$ is the line through $M, N$, one writes $\angle(K L, M N)$ for $\angle(\ell, m)$; the characters $K, L$ are freely interchangeable; and so are $M, N$. The counterpart of the classical theorem about cyclic quadrilaterals is the following: If $K, L, M, N$ are four noncollinear points in the plane then $$ K, L, M, N \text { are concyclic if and only if } \angle(K M, L M)=\angle(K N, L N) \text {. } $$ Passing to the solution proper, we first show that the three circles $\left(A B_{1} C_{1}\right),\left(B C_{1} A_{1}\right)$, $\left(C A_{1} B_{1}\right)$ have a common point. So, let $\left(A B_{1} C_{1}\right)$ and $\left(B C_{1} A_{1}\right)$ intersect at the points $C_{1}$ and $P$. Then by (1) $$ \begin{gathered} \angle\left(P A_{1}, C A_{1}\right)=\angle\left(P A_{1}, B A_{1}\right)=\angle\left(P C_{1}, B C_{1}\right) \\ =\angle\left(P C_{1}, A C_{1}\right)=\angle\left(P B_{1}, A B_{1}\right)=\angle\left(P B_{1}, C B_{1}\right) \end{gathered} $$ Denote this angle by $\varphi$. The equality between the outer terms shows, again by (1), that the points $A_{1}, B_{1}, P, C$ are concyclic. Thus $P$ is the common point of the three mentioned circles. From now on the basic property (1) will be used without explicit reference. We have $$ \varphi=\angle\left(P A_{1}, B C\right)=\angle\left(P B_{1}, C A\right)=\angle\left(P C_{1}, A B\right) . $$  Let lines $A_{2} P, B_{2} P, C_{2} P$ meet the circle $(A B C)$ again at $A_{4}, B_{4}, C_{4}$, respectively. As $$ \angle\left(A_{4} A_{2}, A A_{2}\right)=\angle\left(P A_{2}, A A_{2}\right)=\angle\left(P C_{1}, A C_{1}\right)=\angle\left(P C_{1}, A B\right)=\varphi \text {, } $$ we see that line $A_{2} A$ is the image of line $A_{2} A_{4}$ under rotation about $A_{2}$ by the angle $\varphi$. Hence the point $A$ is the image of $A_{4}$ under rotation by $2 \varphi$ about $O$, the centre of $(A B C)$. The same rotation sends $B_{4}$ to $B$ and $C_{4}$ to $C$. Triangle $A B C$ is the image of $A_{4} B_{4} C_{4}$ in this map. Thus $$ \angle\left(A_{4} B_{4}, A B\right)=\angle\left(B_{4} C_{4}, B C\right)=\angle\left(C_{4} A_{4}, C A\right)=2 \varphi \text {. } $$ Since the rotation by $2 \varphi$ about $O$ takes $B_{4}$ to $B$, we have $\angle\left(A B_{4}, A B\right)=\varphi$. Hence by (2) $$ \angle\left(A B_{4}, P C_{1}\right)=\angle\left(A B_{4}, A B\right)+\angle\left(A B, P C_{1}\right)=\varphi+(-\varphi)=0 $$ which means that $A B_{4} \| P C_{1}$.  Let $C_{5}$ be the intersection of lines $P C_{1}$ and $A_{4} B_{4}$; define $A_{5}, B_{5}$ analogously. So $A B_{4} \| C_{1} C_{5}$ and, by (3) and (2), $$ \angle\left(A_{4} B_{4}, P C_{1}\right)=\angle\left(A_{4} B_{4}, A B\right)+\angle\left(A B, P C_{1}\right)=2 \varphi+(-\varphi)=\varphi $$ i.e., $\angle\left(B_{4} C_{5}, C_{5} C_{1}\right)=\varphi$. This combined with $\angle\left(C_{5} C_{1}, C_{1} A\right)=\angle\left(P C_{1}, A B\right)=\varphi$ (see (2)) proves that the quadrilateral $A B_{4} C_{5} C_{1}$ is an isosceles trapezoid with $A C_{1}=B_{4} C_{5}$. Interchanging the roles of $A$ and $B$ we infer that also $B C_{1}=A_{4} C_{5}$. And since $A C_{1}+B C_{1}=$ $A B=A_{4} B_{4}$, it follows that the point $C_{5}$ lies on the line segment $A_{4} B_{4}$ and partitions it into segments $A_{4} C_{5}, B_{4} C_{5}$ of lengths $B C_{1}\left(=A C_{3}\right)$ and $A C_{1}\left(=B C_{3}\right)$. In other words, the rotation which maps triangle $A_{4} B_{4} C_{4}$ onto $A B C$ carries $C_{5}$ onto $C_{3}$. Likewise, it sends $A_{5}$ to $A_{3}$ and $B_{5}$ to $B_{3}$. So the triangles $A_{3} B_{3} C_{3}$ and $A_{5} B_{5} C_{5}$ are congruent. It now suffices to show that the latter is similar to $A_{2} B_{2} C_{2}$. Lines $B_{4} C_{5}$ and $P C_{5}$ coincide respectively with $A_{4} B_{4}$ and $P C_{1}$. Thus by (4) $$ \angle\left(B_{4} C_{5}, P C_{5}\right)=\varphi $$ Analogously (by cyclic shift) $\varphi=\angle\left(C_{4} A_{5}, P A_{5}\right)$, which rewrites as $$ \varphi=\angle\left(B_{4} A_{5}, P A_{5}\right) $$ These relations imply that the points $P, B_{4}, C_{5}, A_{5}$ are concyclic. Analogously, $P, C_{4}, A_{5}, B_{5}$ and $P, A_{4}, B_{5}, C_{5}$ are concyclic quadruples. Therefore $$ \angle\left(A_{5} B_{5}, C_{5} B_{5}\right)=\angle\left(A_{5} B_{5}, P B_{5}\right)+\angle\left(P B_{5}, C_{5} B_{5}\right)=\angle\left(A_{5} C_{4}, P C_{4}\right)+\angle\left(P A_{4}, C_{5} A_{4}\right) . $$ On the other hand, since the points $A_{2}, B_{2}, C_{2}, A_{4}, B_{4}, C_{4}$ all lie on the circle $(A B C)$, we have $$ \angle\left(A_{2} B_{2}, C_{2} B_{2}\right)=\angle\left(A_{2} B_{2}, B_{4} B_{2}\right)+\angle\left(B_{4} B_{2}, C_{2} B_{2}\right)=\angle\left(A_{2} A_{4}, B_{4} A_{4}\right)+\angle\left(B_{4} C_{4}, C_{2} C_{4}\right) . $$ But the lines $A_{2} A_{4}, B_{4} A_{4}, B_{4} C_{4}, C_{2} C_{4}$ coincide respectively with $P A_{4}, C_{5} A_{4}, A_{5} C_{4}, P C_{4}$. So the sums on the right-hand sides of (5) and (6) are equal, leading to equality between their left-hand sides: $\angle\left(A_{5} B_{5}, C_{5} B_{5}\right)=\angle\left(A_{2} B_{2}, C_{2} B_{2}\right)$. Hence (by cyclic shift, once more) also $\angle\left(B_{5} C_{5}, A_{5} C_{5}\right)=\angle\left(B_{2} C_{2}, A_{2} C_{2}\right)$ and $\angle\left(C_{5} A_{5}, B_{5} A_{5}\right)=\angle\left(C_{2} A_{2}, B_{2} A_{2}\right)$. This means that the triangles $A_{5} B_{5} C_{5}$ and $A_{2} B_{2} C_{2}$ have their corresponding angles equal, and consequently they are similar. Comment 1. This is the way in which the proof has been presented by the proposer. Trying to work it out in the language of classical geometry, so as to avoid oriented angles, one is led to difficulties due to the fact that the reasoning becomes heavily case-dependent. Disposition of relevant points can vary in many respects. Angles which are equal in one case become supplementary in another. Although it seems not hard to translate all formulas from the shapes they have in one situation to the one they have in another, the real trouble is to identify all cases possible and rigorously verify that the key conclusions retain validity in each case. The use of oriented angles is a very efficient method to omit this trouble. It seems to be the most appropriate environment in which the solution can be elaborated. Comment 2. Actually, the fact that the circles $\left(A B_{1} C_{1}\right),\left(B C_{1} A_{1}\right)$ and $\left(C A_{1} B_{1}\right)$ have a common point does not require a proof; it is known as Miquel's theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Points $A_{1}, B_{1}, C_{1}$ are chosen on the sides $B C, C A, A B$ of a triangle $A B C$, respectively. The circumcircles of triangles $A B_{1} C_{1}, B C_{1} A_{1}, C A_{1} B_{1}$ intersect the circumcircle of triangle $A B C$ again at points $A_{2}, B_{2}, C_{2}$, respectively $\left(A_{2} \neq A, B_{2} \neq B, C_{2} \neq C\right)$. Points $A_{3}, B_{3}, C_{3}$ are symmetric to $A_{1}, B_{1}, C_{1}$ with respect to the midpoints of the sides $B C, C A, A B$ respectively. Prove that the triangles $A_{2} B_{2} C_{2}$ and $A_{3} B_{3} C_{3}$ are similar. (Russia)
|
We will work with oriented angles between lines. For two straight lines $\ell, m$ in the plane, $\angle(\ell, m)$ denotes the angle of counterclockwise rotation which transforms line $\ell$ into a line parallel to $m$ (the choice of the rotation centre is irrelevant). This is a signed quantity; values differing by a multiple of $\pi$ are identified, so that $$ \angle(\ell, m)=-\angle(m, \ell), \quad \angle(\ell, m)+\angle(m, n)=\angle(\ell, n) . $$ If $\ell$ is the line through points $K, L$ and $m$ is the line through $M, N$, one writes $\angle(K L, M N)$ for $\angle(\ell, m)$; the characters $K, L$ are freely interchangeable; and so are $M, N$. The counterpart of the classical theorem about cyclic quadrilaterals is the following: If $K, L, M, N$ are four noncollinear points in the plane then $$ K, L, M, N \text { are concyclic if and only if } \angle(K M, L M)=\angle(K N, L N) \text {. } $$ Passing to the solution proper, we first show that the three circles $\left(A B_{1} C_{1}\right),\left(B C_{1} A_{1}\right)$, $\left(C A_{1} B_{1}\right)$ have a common point. So, let $\left(A B_{1} C_{1}\right)$ and $\left(B C_{1} A_{1}\right)$ intersect at the points $C_{1}$ and $P$. Then by (1) $$ \begin{gathered} \angle\left(P A_{1}, C A_{1}\right)=\angle\left(P A_{1}, B A_{1}\right)=\angle\left(P C_{1}, B C_{1}\right) \\ =\angle\left(P C_{1}, A C_{1}\right)=\angle\left(P B_{1}, A B_{1}\right)=\angle\left(P B_{1}, C B_{1}\right) \end{gathered} $$ Denote this angle by $\varphi$. The equality between the outer terms shows, again by (1), that the points $A_{1}, B_{1}, P, C$ are concyclic. Thus $P$ is the common point of the three mentioned circles. From now on the basic property (1) will be used without explicit reference. We have $$ \varphi=\angle\left(P A_{1}, B C\right)=\angle\left(P B_{1}, C A\right)=\angle\left(P C_{1}, A B\right) . $$  Let lines $A_{2} P, B_{2} P, C_{2} P$ meet the circle $(A B C)$ again at $A_{4}, B_{4}, C_{4}$, respectively. As $$ \angle\left(A_{4} A_{2}, A A_{2}\right)=\angle\left(P A_{2}, A A_{2}\right)=\angle\left(P C_{1}, A C_{1}\right)=\angle\left(P C_{1}, A B\right)=\varphi \text {, } $$ we see that line $A_{2} A$ is the image of line $A_{2} A_{4}$ under rotation about $A_{2}$ by the angle $\varphi$. Hence the point $A$ is the image of $A_{4}$ under rotation by $2 \varphi$ about $O$, the centre of $(A B C)$. The same rotation sends $B_{4}$ to $B$ and $C_{4}$ to $C$. Triangle $A B C$ is the image of $A_{4} B_{4} C_{4}$ in this map. Thus $$ \angle\left(A_{4} B_{4}, A B\right)=\angle\left(B_{4} C_{4}, B C\right)=\angle\left(C_{4} A_{4}, C A\right)=2 \varphi \text {. } $$ Since the rotation by $2 \varphi$ about $O$ takes $B_{4}$ to $B$, we have $\angle\left(A B_{4}, A B\right)=\varphi$. Hence by (2) $$ \angle\left(A B_{4}, P C_{1}\right)=\angle\left(A B_{4}, A B\right)+\angle\left(A B, P C_{1}\right)=\varphi+(-\varphi)=0 $$ which means that $A B_{4} \| P C_{1}$.  Let $C_{5}$ be the intersection of lines $P C_{1}$ and $A_{4} B_{4}$; define $A_{5}, B_{5}$ analogously. So $A B_{4} \| C_{1} C_{5}$ and, by (3) and (2), $$ \angle\left(A_{4} B_{4}, P C_{1}\right)=\angle\left(A_{4} B_{4}, A B\right)+\angle\left(A B, P C_{1}\right)=2 \varphi+(-\varphi)=\varphi $$ i.e., $\angle\left(B_{4} C_{5}, C_{5} C_{1}\right)=\varphi$. This combined with $\angle\left(C_{5} C_{1}, C_{1} A\right)=\angle\left(P C_{1}, A B\right)=\varphi$ (see (2)) proves that the quadrilateral $A B_{4} C_{5} C_{1}$ is an isosceles trapezoid with $A C_{1}=B_{4} C_{5}$. Interchanging the roles of $A$ and $B$ we infer that also $B C_{1}=A_{4} C_{5}$. And since $A C_{1}+B C_{1}=$ $A B=A_{4} B_{4}$, it follows that the point $C_{5}$ lies on the line segment $A_{4} B_{4}$ and partitions it into segments $A_{4} C_{5}, B_{4} C_{5}$ of lengths $B C_{1}\left(=A C_{3}\right)$ and $A C_{1}\left(=B C_{3}\right)$. In other words, the rotation which maps triangle $A_{4} B_{4} C_{4}$ onto $A B C$ carries $C_{5}$ onto $C_{3}$. Likewise, it sends $A_{5}$ to $A_{3}$ and $B_{5}$ to $B_{3}$. So the triangles $A_{3} B_{3} C_{3}$ and $A_{5} B_{5} C_{5}$ are congruent. It now suffices to show that the latter is similar to $A_{2} B_{2} C_{2}$. Lines $B_{4} C_{5}$ and $P C_{5}$ coincide respectively with $A_{4} B_{4}$ and $P C_{1}$. Thus by (4) $$ \angle\left(B_{4} C_{5}, P C_{5}\right)=\varphi $$ Analogously (by cyclic shift) $\varphi=\angle\left(C_{4} A_{5}, P A_{5}\right)$, which rewrites as $$ \varphi=\angle\left(B_{4} A_{5}, P A_{5}\right) $$ These relations imply that the points $P, B_{4}, C_{5}, A_{5}$ are concyclic. Analogously, $P, C_{4}, A_{5}, B_{5}$ and $P, A_{4}, B_{5}, C_{5}$ are concyclic quadruples. Therefore $$ \angle\left(A_{5} B_{5}, C_{5} B_{5}\right)=\angle\left(A_{5} B_{5}, P B_{5}\right)+\angle\left(P B_{5}, C_{5} B_{5}\right)=\angle\left(A_{5} C_{4}, P C_{4}\right)+\angle\left(P A_{4}, C_{5} A_{4}\right) . $$ On the other hand, since the points $A_{2}, B_{2}, C_{2}, A_{4}, B_{4}, C_{4}$ all lie on the circle $(A B C)$, we have $$ \angle\left(A_{2} B_{2}, C_{2} B_{2}\right)=\angle\left(A_{2} B_{2}, B_{4} B_{2}\right)+\angle\left(B_{4} B_{2}, C_{2} B_{2}\right)=\angle\left(A_{2} A_{4}, B_{4} A_{4}\right)+\angle\left(B_{4} C_{4}, C_{2} C_{4}\right) . $$ But the lines $A_{2} A_{4}, B_{4} A_{4}, B_{4} C_{4}, C_{2} C_{4}$ coincide respectively with $P A_{4}, C_{5} A_{4}, A_{5} C_{4}, P C_{4}$. So the sums on the right-hand sides of (5) and (6) are equal, leading to equality between their left-hand sides: $\angle\left(A_{5} B_{5}, C_{5} B_{5}\right)=\angle\left(A_{2} B_{2}, C_{2} B_{2}\right)$. Hence (by cyclic shift, once more) also $\angle\left(B_{5} C_{5}, A_{5} C_{5}\right)=\angle\left(B_{2} C_{2}, A_{2} C_{2}\right)$ and $\angle\left(C_{5} A_{5}, B_{5} A_{5}\right)=\angle\left(C_{2} A_{2}, B_{2} A_{2}\right)$. This means that the triangles $A_{5} B_{5} C_{5}$ and $A_{2} B_{2} C_{2}$ have their corresponding angles equal, and consequently they are similar. Comment 1. This is the way in which the proof has been presented by the proposer. Trying to work it out in the language of classical geometry, so as to avoid oriented angles, one is led to difficulties due to the fact that the reasoning becomes heavily case-dependent. Disposition of relevant points can vary in many respects. Angles which are equal in one case become supplementary in another. Although it seems not hard to translate all formulas from the shapes they have in one situation to the one they have in another, the real trouble is to identify all cases possible and rigorously verify that the key conclusions retain validity in each case. The use of oriented angles is a very efficient method to omit this trouble. It seems to be the most appropriate environment in which the solution can be elaborated. Comment 2. Actually, the fact that the circles $\left(A B_{1} C_{1}\right),\left(B C_{1} A_{1}\right)$ and $\left(C A_{1} B_{1}\right)$ have a common point does not require a proof; it is known as Miquel's theorem.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ff3f4272-f6f9-53b3-9e49-d5cd8571a1ae
| 23,593
|
To each side $a$ of a convex polygon we assign the maximum area of a triangle contained in the polygon and having $a$ as one of its sides. Show that the sum of the areas assigned to all sides of the polygon is not less than twice the area of the polygon. (Serbia)
|
Lemma. Every convex $(2 n)$-gon, of area $S$, has a side and a vertex that jointly span a triangle of area not less than $S / n$. Proof. By main diagonals of the $(2 n)$-gon we shall mean those which partition the $(2 n)$-gon into two polygons with equally many sides. For any side $b$ of the $(2 n)$-gon denote by $\Delta_{b}$ the triangle $A B P$ where $A, B$ are the endpoints of $b$ and $P$ is the intersection point of the main diagonals $A A^{\prime}, B B^{\prime}$. We claim that the union of triangles $\Delta_{b}$, taken over all sides, covers the whole polygon. To show this, choose any side $A B$ and consider the main diagonal $A A^{\prime}$ as a directed segment. Let $X$ be any point in the polygon, not on any main diagonal. For definiteness, let $X$ lie on the left side of the ray $A A^{\prime}$. Consider the sequence of main diagonals $A A^{\prime}, B B^{\prime}, C C^{\prime}, \ldots$, where $A, B, C, \ldots$ are consecutive vertices, situated right to $A A^{\prime}$. The $n$-th item in this sequence is the diagonal $A^{\prime} A$ (i.e. $A A^{\prime}$ reversed), having $X$ on its right side. So there are two successive vertices $K, L$ in the sequence $A, B, C, \ldots$ before $A^{\prime}$ such that $X$ still lies to the left of $K K^{\prime}$ but to the right of $L L^{\prime}$. And this means that $X$ is in the triangle $\Delta_{\ell^{\prime}}, \ell^{\prime}=K^{\prime} L^{\prime}$. Analogous reasoning applies to points $X$ on the right of $A A^{\prime}$ (points lying on main diagonals can be safely ignored). Thus indeed the triangles $\Delta_{b}$ jointly cover the whole polygon. The sum of their areas is no less than $S$. So we can find two opposite sides, say $b=A B$ and $b^{\prime}=A^{\prime} B^{\prime}$ (with $A A^{\prime}, B B^{\prime}$ main diagonals) such that $\left[\Delta_{b}\right]+\left[\Delta_{b^{\prime}}\right] \geq S / n$, where $[\cdots]$ stands for the area of a region. Let $A A^{\prime}, B B^{\prime}$ intersect at $P$; assume without loss of generality that $P B \geq P B^{\prime}$. Then $$ \left[A B A^{\prime}\right]=[A B P]+\left[P B A^{\prime}\right] \geq[A B P]+\left[P A^{\prime} B^{\prime}\right]=\left[\Delta_{b}\right]+\left[\Delta_{b^{\prime}}\right] \geq S / n $$ proving the lemma. Now, let $\mathcal{P}$ be any convex polygon, of area $S$, with $m$ sides $a_{1}, \ldots, a_{m}$. Let $S_{i}$ be the area of the greatest triangle in $\mathcal{P}$ with side $a_{i}$. Suppose, contrary to the assertion, that $$ \sum_{i=1}^{m} \frac{S_{i}}{S}<2 $$ Then there exist rational numbers $q_{1}, \ldots, q_{m}$ such that $\sum q_{i}=2$ and $q_{i}>S_{i} / S$ for each $i$. Let $n$ be a common denominator of the $m$ fractions $q_{1}, \ldots, q_{m}$. Write $q_{i}=k_{i} / n$; so $\sum k_{i}=2 n$. Partition each side $a_{i}$ of $\mathcal{P}$ into $k_{i}$ equal segments, creating a convex $(2 n)$-gon of area $S$ (with some angles of size $180^{\circ}$ ), to which we apply the lemma. Accordingly, this refined polygon has a side $b$ and a vertex $H$ spanning a triangle $T$ of area $[T] \geq S / n$. If $b$ is a piece of a side $a_{i}$ of $\mathcal{P}$, then the triangle $W$ with base $a_{i}$ and summit $H$ has area $$ [W]=k_{i} \cdot[T] \geq k_{i} \cdot S / n=q_{i} \cdot S>S_{i}, $$ in contradiction with the definition of $S_{i}$. This ends the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
To each side $a$ of a convex polygon we assign the maximum area of a triangle contained in the polygon and having $a$ as one of its sides. Show that the sum of the areas assigned to all sides of the polygon is not less than twice the area of the polygon. (Serbia)
|
Lemma. Every convex $(2 n)$-gon, of area $S$, has a side and a vertex that jointly span a triangle of area not less than $S / n$. Proof. By main diagonals of the $(2 n)$-gon we shall mean those which partition the $(2 n)$-gon into two polygons with equally many sides. For any side $b$ of the $(2 n)$-gon denote by $\Delta_{b}$ the triangle $A B P$ where $A, B$ are the endpoints of $b$ and $P$ is the intersection point of the main diagonals $A A^{\prime}, B B^{\prime}$. We claim that the union of triangles $\Delta_{b}$, taken over all sides, covers the whole polygon. To show this, choose any side $A B$ and consider the main diagonal $A A^{\prime}$ as a directed segment. Let $X$ be any point in the polygon, not on any main diagonal. For definiteness, let $X$ lie on the left side of the ray $A A^{\prime}$. Consider the sequence of main diagonals $A A^{\prime}, B B^{\prime}, C C^{\prime}, \ldots$, where $A, B, C, \ldots$ are consecutive vertices, situated right to $A A^{\prime}$. The $n$-th item in this sequence is the diagonal $A^{\prime} A$ (i.e. $A A^{\prime}$ reversed), having $X$ on its right side. So there are two successive vertices $K, L$ in the sequence $A, B, C, \ldots$ before $A^{\prime}$ such that $X$ still lies to the left of $K K^{\prime}$ but to the right of $L L^{\prime}$. And this means that $X$ is in the triangle $\Delta_{\ell^{\prime}}, \ell^{\prime}=K^{\prime} L^{\prime}$. Analogous reasoning applies to points $X$ on the right of $A A^{\prime}$ (points lying on main diagonals can be safely ignored). Thus indeed the triangles $\Delta_{b}$ jointly cover the whole polygon. The sum of their areas is no less than $S$. So we can find two opposite sides, say $b=A B$ and $b^{\prime}=A^{\prime} B^{\prime}$ (with $A A^{\prime}, B B^{\prime}$ main diagonals) such that $\left[\Delta_{b}\right]+\left[\Delta_{b^{\prime}}\right] \geq S / n$, where $[\cdots]$ stands for the area of a region. Let $A A^{\prime}, B B^{\prime}$ intersect at $P$; assume without loss of generality that $P B \geq P B^{\prime}$. Then $$ \left[A B A^{\prime}\right]=[A B P]+\left[P B A^{\prime}\right] \geq[A B P]+\left[P A^{\prime} B^{\prime}\right]=\left[\Delta_{b}\right]+\left[\Delta_{b^{\prime}}\right] \geq S / n $$ proving the lemma. Now, let $\mathcal{P}$ be any convex polygon, of area $S$, with $m$ sides $a_{1}, \ldots, a_{m}$. Let $S_{i}$ be the area of the greatest triangle in $\mathcal{P}$ with side $a_{i}$. Suppose, contrary to the assertion, that $$ \sum_{i=1}^{m} \frac{S_{i}}{S}<2 $$ Then there exist rational numbers $q_{1}, \ldots, q_{m}$ such that $\sum q_{i}=2$ and $q_{i}>S_{i} / S$ for each $i$. Let $n$ be a common denominator of the $m$ fractions $q_{1}, \ldots, q_{m}$. Write $q_{i}=k_{i} / n$; so $\sum k_{i}=2 n$. Partition each side $a_{i}$ of $\mathcal{P}$ into $k_{i}$ equal segments, creating a convex $(2 n)$-gon of area $S$ (with some angles of size $180^{\circ}$ ), to which we apply the lemma. Accordingly, this refined polygon has a side $b$ and a vertex $H$ spanning a triangle $T$ of area $[T] \geq S / n$. If $b$ is a piece of a side $a_{i}$ of $\mathcal{P}$, then the triangle $W$ with base $a_{i}$ and summit $H$ has area $$ [W]=k_{i} \cdot[T] \geq k_{i} \cdot S / n=q_{i} \cdot S>S_{i}, $$ in contradiction with the definition of $S_{i}$. This ends the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
34146db4-37d6-5f0c-8675-80499ea38577
| 23,597
|
For $x \in(0,1)$ let $y \in(0,1)$ be the number whose $n$th digit after the decimal point is the $\left(2^{n}\right)$ th digit after the decimal point of $x$. Show that if $x$ is rational then so is $y$. (Canada)
|
Since $x$ is rational, its digits repeat periodically starting at some point. We wish to show that this is also true for the digits of $y$, implying that $y$ is rational. Let $d$ be the length of the period of $x$ and let $d=2^{u} \cdot v$, where $v$ is odd. There is a positive integer $w$ such that $$ 2^{w} \equiv 1 \quad(\bmod v) $$ (For instance, one can choose $w$ to be $\varphi(v)$, the value of Euler's function at $v$.) Therefore $$ 2^{n+w}=2^{n} \cdot 2^{w} \equiv 2^{n} \quad(\bmod v) $$ for each $n$. Also, for $n \geq u$ we have $$ 2^{n+w} \equiv 2^{n} \equiv 0 \quad\left(\bmod 2^{u}\right) $$ It follows that, for all $n \geq u$, the relation $$ 2^{n+w} \equiv 2^{n} \quad(\bmod d) $$ holds. Thus, for $n$ sufficiently large, the $2^{n+w}$ th digit of $x$ is in the same spot in the cycle of $x$ as its $2^{n}$ th digit, and so these digits are equal. Hence the $(n+w)$ th digit of $y$ is equal to its $n$th digit. This means that the digits of $y$ repeat periodically with period $w$ from some point on, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For $x \in(0,1)$ let $y \in(0,1)$ be the number whose $n$th digit after the decimal point is the $\left(2^{n}\right)$ th digit after the decimal point of $x$. Show that if $x$ is rational then so is $y$. (Canada)
|
Since $x$ is rational, its digits repeat periodically starting at some point. We wish to show that this is also true for the digits of $y$, implying that $y$ is rational. Let $d$ be the length of the period of $x$ and let $d=2^{u} \cdot v$, where $v$ is odd. There is a positive integer $w$ such that $$ 2^{w} \equiv 1 \quad(\bmod v) $$ (For instance, one can choose $w$ to be $\varphi(v)$, the value of Euler's function at $v$.) Therefore $$ 2^{n+w}=2^{n} \cdot 2^{w} \equiv 2^{n} \quad(\bmod v) $$ for each $n$. Also, for $n \geq u$ we have $$ 2^{n+w} \equiv 2^{n} \equiv 0 \quad\left(\bmod 2^{u}\right) $$ It follows that, for all $n \geq u$, the relation $$ 2^{n+w} \equiv 2^{n} \quad(\bmod d) $$ holds. Thus, for $n$ sufficiently large, the $2^{n+w}$ th digit of $x$ is in the same spot in the cycle of $x$ as its $2^{n}$ th digit, and so these digits are equal. Hence the $(n+w)$ th digit of $y$ is equal to its $n$th digit. This means that the digits of $y$ repeat periodically with period $w$ from some point on, as required.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
113b47a5-d06c-50f3-9592-473177ed884b
| 23,603
|
The sequence $f(1), f(2), f(3), \ldots$ is defined by $$ f(n)=\frac{1}{n}\left(\left\lfloor\frac{n}{1}\right\rfloor+\left\lfloor\frac{n}{2}\right\rfloor+\cdots+\left\lfloor\frac{n}{n}\right\rfloor\right), $$ where $\lfloor x\rfloor$ denotes the integer part of $x$. (a) Prove that $f(n+1)>f(n)$ infinitely often. (b) Prove that $f(n+1)<f(n)$ infinitely often. (South Africa)
|
Let $g(n)=n f(n)$ for $n \geq 1$ and $g(0)=0$. We note that, for $k=1, \ldots, n$, $$ \left\lfloor\frac{n}{k}\right\rfloor-\left\lfloor\frac{n-1}{k}\right\rfloor=0 $$ if $k$ is not a divisor of $n$ and $$ \left\lfloor\frac{n}{k}\right\rfloor-\left\lfloor\frac{n-1}{k}\right\rfloor=1 $$ if $k$ divides $n$. It therefore follows that if $d(n)$ is the number of positive divisors of $n \geq 1$ then $$ \begin{aligned} g(n) & =\left\lfloor\frac{n}{1}\right\rfloor+\left\lfloor\frac{n}{2}\right\rfloor+\cdots+\left\lfloor\frac{n}{n-1}\right\rfloor+\left\lfloor\frac{n}{n}\right\rfloor \\ & =\left\lfloor\frac{n-1}{1}\right\rfloor+\left\lfloor\frac{n-1}{2}\right\rfloor+\cdots+\left\lfloor\frac{n-1}{n-1}\right\rfloor+\left\lfloor\frac{n-1}{n}\right\rfloor+d(n) \\ & =g(n-1)+d(n) . \end{aligned} $$ Hence $$ g(n)=g(n-1)+d(n)=g(n-2)+d(n-1)+d(n)=\cdots=d(1)+d(2)+\cdots+d(n), $$ meaning that $$ f(n)=\frac{d(1)+d(2)+\cdots+d(n)}{n} . $$ In other words, $f(n)$ is equal to the arithmetic mean of $d(1), d(2), \ldots, d(n)$. In order to prove the claims, it is therefore sufficient to show that $d(n+1)>f(n)$ and $d(n+1)<f(n)$ both hold infinitely often. We note that $d(1)=1$. For $n>1, d(n) \geq 2$ holds, with equality if and only if $n$ is prime. Since $f(6)=7 / 3>2$, it follows that $f(n)>2$ holds for all $n \geq 6$. Since there are infinitely many primes, $d(n+1)=2$ holds for infinitely many values of $n$, and for each such $n \geq 6$ we have $d(n+1)=2<f(n)$. This proves claim (b). To prove (a), notice that the sequence $d(1), d(2), d(3), \ldots$ is unbounded (e. g. $d\left(2^{k}\right)=k+1$ for all $k$ ). Hence $d(n+1)>\max \{d(1), d(2), \ldots, d(n)\}$ for infinitely many $n$. For all such $n$, we have $d(n+1)>f(n)$. This completes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
The sequence $f(1), f(2), f(3), \ldots$ is defined by $$ f(n)=\frac{1}{n}\left(\left\lfloor\frac{n}{1}\right\rfloor+\left\lfloor\frac{n}{2}\right\rfloor+\cdots+\left\lfloor\frac{n}{n}\right\rfloor\right), $$ where $\lfloor x\rfloor$ denotes the integer part of $x$. (a) Prove that $f(n+1)>f(n)$ infinitely often. (b) Prove that $f(n+1)<f(n)$ infinitely often. (South Africa)
|
Let $g(n)=n f(n)$ for $n \geq 1$ and $g(0)=0$. We note that, for $k=1, \ldots, n$, $$ \left\lfloor\frac{n}{k}\right\rfloor-\left\lfloor\frac{n-1}{k}\right\rfloor=0 $$ if $k$ is not a divisor of $n$ and $$ \left\lfloor\frac{n}{k}\right\rfloor-\left\lfloor\frac{n-1}{k}\right\rfloor=1 $$ if $k$ divides $n$. It therefore follows that if $d(n)$ is the number of positive divisors of $n \geq 1$ then $$ \begin{aligned} g(n) & =\left\lfloor\frac{n}{1}\right\rfloor+\left\lfloor\frac{n}{2}\right\rfloor+\cdots+\left\lfloor\frac{n}{n-1}\right\rfloor+\left\lfloor\frac{n}{n}\right\rfloor \\ & =\left\lfloor\frac{n-1}{1}\right\rfloor+\left\lfloor\frac{n-1}{2}\right\rfloor+\cdots+\left\lfloor\frac{n-1}{n-1}\right\rfloor+\left\lfloor\frac{n-1}{n}\right\rfloor+d(n) \\ & =g(n-1)+d(n) . \end{aligned} $$ Hence $$ g(n)=g(n-1)+d(n)=g(n-2)+d(n-1)+d(n)=\cdots=d(1)+d(2)+\cdots+d(n), $$ meaning that $$ f(n)=\frac{d(1)+d(2)+\cdots+d(n)}{n} . $$ In other words, $f(n)$ is equal to the arithmetic mean of $d(1), d(2), \ldots, d(n)$. In order to prove the claims, it is therefore sufficient to show that $d(n+1)>f(n)$ and $d(n+1)<f(n)$ both hold infinitely often. We note that $d(1)=1$. For $n>1, d(n) \geq 2$ holds, with equality if and only if $n$ is prime. Since $f(6)=7 / 3>2$, it follows that $f(n)>2$ holds for all $n \geq 6$. Since there are infinitely many primes, $d(n+1)=2$ holds for infinitely many values of $n$, and for each such $n \geq 6$ we have $d(n+1)=2<f(n)$. This proves claim (b). To prove (a), notice that the sequence $d(1), d(2), d(3), \ldots$ is unbounded (e. g. $d\left(2^{k}\right)=k+1$ for all $k$ ). Hence $d(n+1)>\max \{d(1), d(2), \ldots, d(n)\}$ for infinitely many $n$. For all such $n$, we have $d(n+1)>f(n)$. This completes the solution.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
eef2899b-7965-5392-ac9a-0bbc2a8b9f82
| 23,606
|
Let $P$ be a polynomial of degree $n>1$ with integer coefficients and let $k$ be any positive integer. Consider the polynomial $Q(x)=P(P(\ldots P(P(x)) \ldots))$, with $k$ pairs of parentheses. Prove that $Q$ has no more than $n$ integer fixed points, i.e. integers satisfying the equation $Q(x)=x$. (Romania)
|
The claim is obvious if every integer fixed point of $Q$ is a fixed point of $P$ itself. For the sequel assume that this is not the case. Take any integer $x_{0}$ such that $Q\left(x_{0}\right)=x_{0}$, $P\left(x_{0}\right) \neq x_{0}$ and define inductively $x_{i+1}=P\left(x_{i}\right)$ for $i=0,1,2, \ldots$; then $x_{k}=x_{0}$. It is evident that $$ P(u)-P(v) \text { is divisible by } u-v \text { for distinct integers } u, v \text {. } $$ (Indeed, if $P(x)=\sum a_{i} x^{i}$ then each $a_{i}\left(u^{i}-v^{i}\right)$ is divisible by $u-v$.) Therefore each term in the chain of (nonzero) differences $$ x_{0}-x_{1}, \quad x_{1}-x_{2}, \quad \ldots, \quad x_{k-1}-x_{k}, \quad x_{k}-x_{k+1} $$ is a divisor of the next one; and since $x_{k}-x_{k+1}=x_{0}-x_{1}$, all these differences have equal absolute values. For $x_{m}=\min \left(x_{1}, \ldots, x_{k}\right)$ this means that $x_{m-1}-x_{m}=-\left(x_{m}-x_{m+1}\right)$. Thus $x_{m-1}=x_{m+1}\left(\neq x_{m}\right)$. It follows that consecutive differences in the sequence (2) have opposite signs. Consequently, $x_{0}, x_{1}, x_{2}, \ldots$ is an alternating sequence of two distinct values. In other words, every integer fixed point of $Q$ is a fixed point of the polynomial $P(P(x))$. Our task is to prove that there are at most $n$ such points. Let $a$ be one of them so that $b=P(a) \neq a$ (we have assumed that such an $a$ exists); then $a=P(b)$. Take any other integer fixed point $\alpha$ of $P(P(x))$ and let $P(\alpha)=\beta$, so that $P(\beta)=\alpha$; the numbers $\alpha$ and $\beta$ need not be distinct ( $\alpha$ can be a fixed point of $P$ ), but each of $\alpha, \beta$ is different from each of $a, b$. Applying property (1) to the four pairs of integers $(\alpha, a),(\beta, b)$, $(\alpha, b),(\beta, a)$ we get that the numbers $\alpha-a$ and $\beta-b$ divide each other, and also $\alpha-b$ and $\beta-a$ divide each other. Consequently $$ \alpha-b= \pm(\beta-a), \quad \alpha-a= \pm(\beta-b) . $$ Suppose we have a plus in both instances: $\alpha-b=\beta-a$ and $\alpha-a=\beta-b$. Subtraction yields $a-b=b-a$, a contradiction, as $a \neq b$. Therefore at least one equality in (3) holds with a minus sign. For each of them this means that $\alpha+\beta=a+b$; equivalently $a+b-\alpha-P(\alpha)=0$. Denote $a+b$ by $C$. We have shown that every integer fixed point of $Q$ other that $a$ and $b$ is a root of the polynomial $F(x)=C-x-P(x)$. This is of course true for $a$ and $b$ as well. And since $P$ has degree $n>1$, the polynomial $F$ has the same degree, so it cannot have more than $n$ roots. Hence the result. Comment. The first part of the solution, showing that integer fixed points of any iterate of $P$ are in fact fixed points of the second iterate $P \circ P$ is standard; moreover, this fact has already appeared in contests. We however do not consider this as a major drawback to the problem because the only tricky moment comes up only at the next stage of the reasoning - to apply the divisibility property (1) to points from distinct 2-orbits of $P$. Yet maybe it would be more appropriate to state the problem in a version involving $k=2$ only.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P$ be a polynomial of degree $n>1$ with integer coefficients and let $k$ be any positive integer. Consider the polynomial $Q(x)=P(P(\ldots P(P(x)) \ldots))$, with $k$ pairs of parentheses. Prove that $Q$ has no more than $n$ integer fixed points, i.e. integers satisfying the equation $Q(x)=x$. (Romania)
|
The claim is obvious if every integer fixed point of $Q$ is a fixed point of $P$ itself. For the sequel assume that this is not the case. Take any integer $x_{0}$ such that $Q\left(x_{0}\right)=x_{0}$, $P\left(x_{0}\right) \neq x_{0}$ and define inductively $x_{i+1}=P\left(x_{i}\right)$ for $i=0,1,2, \ldots$; then $x_{k}=x_{0}$. It is evident that $$ P(u)-P(v) \text { is divisible by } u-v \text { for distinct integers } u, v \text {. } $$ (Indeed, if $P(x)=\sum a_{i} x^{i}$ then each $a_{i}\left(u^{i}-v^{i}\right)$ is divisible by $u-v$.) Therefore each term in the chain of (nonzero) differences $$ x_{0}-x_{1}, \quad x_{1}-x_{2}, \quad \ldots, \quad x_{k-1}-x_{k}, \quad x_{k}-x_{k+1} $$ is a divisor of the next one; and since $x_{k}-x_{k+1}=x_{0}-x_{1}$, all these differences have equal absolute values. For $x_{m}=\min \left(x_{1}, \ldots, x_{k}\right)$ this means that $x_{m-1}-x_{m}=-\left(x_{m}-x_{m+1}\right)$. Thus $x_{m-1}=x_{m+1}\left(\neq x_{m}\right)$. It follows that consecutive differences in the sequence (2) have opposite signs. Consequently, $x_{0}, x_{1}, x_{2}, \ldots$ is an alternating sequence of two distinct values. In other words, every integer fixed point of $Q$ is a fixed point of the polynomial $P(P(x))$. Our task is to prove that there are at most $n$ such points. Let $a$ be one of them so that $b=P(a) \neq a$ (we have assumed that such an $a$ exists); then $a=P(b)$. Take any other integer fixed point $\alpha$ of $P(P(x))$ and let $P(\alpha)=\beta$, so that $P(\beta)=\alpha$; the numbers $\alpha$ and $\beta$ need not be distinct ( $\alpha$ can be a fixed point of $P$ ), but each of $\alpha, \beta$ is different from each of $a, b$. Applying property (1) to the four pairs of integers $(\alpha, a),(\beta, b)$, $(\alpha, b),(\beta, a)$ we get that the numbers $\alpha-a$ and $\beta-b$ divide each other, and also $\alpha-b$ and $\beta-a$ divide each other. Consequently $$ \alpha-b= \pm(\beta-a), \quad \alpha-a= \pm(\beta-b) . $$ Suppose we have a plus in both instances: $\alpha-b=\beta-a$ and $\alpha-a=\beta-b$. Subtraction yields $a-b=b-a$, a contradiction, as $a \neq b$. Therefore at least one equality in (3) holds with a minus sign. For each of them this means that $\alpha+\beta=a+b$; equivalently $a+b-\alpha-P(\alpha)=0$. Denote $a+b$ by $C$. We have shown that every integer fixed point of $Q$ other that $a$ and $b$ is a root of the polynomial $F(x)=C-x-P(x)$. This is of course true for $a$ and $b$ as well. And since $P$ has degree $n>1$, the polynomial $F$ has the same degree, so it cannot have more than $n$ roots. Hence the result. Comment. The first part of the solution, showing that integer fixed points of any iterate of $P$ are in fact fixed points of the second iterate $P \circ P$ is standard; moreover, this fact has already appeared in contests. We however do not consider this as a major drawback to the problem because the only tricky moment comes up only at the next stage of the reasoning - to apply the divisibility property (1) to points from distinct 2-orbits of $P$. Yet maybe it would be more appropriate to state the problem in a version involving $k=2$ only.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e2867a96-e22a-5aa3-9cf9-6fca8362595e
| 23,609
|
Prove that, for every positive integer $n$, there exists an integer $m$ such that $2^{m}+m$ is divisible by $n$. (Estonia)
|
We will prove by induction on $d$ that, for every positive integer $N$, there exist positive integers $b_{0}, b_{1}, \ldots, b_{d-1}$ such that, for each $i=0,1,2, \ldots, d-1$, we have $b_{i}>N$ and $$ 2^{b_{i}}+b_{i} \equiv i \quad(\bmod d) . $$ This yields the claim for $m=b_{0}$. The base case $d=1$ is trivial. Take an $a>1$ and assume that the statement holds for all $d<a$. Note that the remainders of $2^{i}$ modulo $a$ repeat periodically starting with some exponent $M$. Let $k$ be the length of the period; this means that $2^{M+k^{\prime}} \equiv 2^{M}(\bmod a)$ holds only for those $k^{\prime}$ which are multiples of $k$. Note further that the period cannot contain all the $a$ remainders, since 0 either is missing or is the only number in the period. Thus $k<a$. Let $d=\operatorname{gcd}(a, k)$ and let $a^{\prime}=a / d, k^{\prime}=k / d$. Since $0<k<a$, we also have $0<d<a$. By the induction hypothesis, there exist positive integers $b_{0}, b_{1}, \ldots, b_{d-1}$ such that $b_{i}>\max \left(2^{M}, N\right)$ and $$ 2^{b_{i}}+b_{i} \equiv i \quad(\bmod d) \quad \text { for } \quad i=0,1,2, \ldots, d-1 $$ For each $i=0,1, \ldots, d-1$ consider the sequence $$ 2^{b_{i}}+b_{i}, \quad 2^{b_{i}+k}+\left(b_{i}+k\right), \ldots, \quad 2^{b_{i}+\left(a^{\prime}-1\right) k}+\left(b_{i}+\left(a^{\prime}-1\right) k\right) . $$ Modulo $a$, these numbers are congruent to $$ 2^{b_{i}}+b_{i}, \quad 2^{b_{i}}+\left(b_{i}+k\right), \ldots, \quad 2^{b_{i}}+\left(b_{i}+\left(a^{\prime}-1\right) k\right), $$ respectively. The $d$ sequences contain $a^{\prime} d=a$ numbers altogether. We shall now prove that no two of these numbers are congruent modulo $a$. Suppose that $$ 2^{b_{i}}+\left(b_{i}+m k\right) \equiv 2^{b_{j}}+\left(b_{j}+n k\right) \quad(\bmod a) $$ for some values of $i, j \in\{0,1, \ldots, d-1\}$ and $m, n \in\left\{0,1, \ldots, a^{\prime}-1\right\}$. Since $d$ is a divisor of $a$, we also have $$ 2^{b_{i}}+\left(b_{i}+m k\right) \equiv 2^{b_{j}}+\left(b_{j}+n k\right) \quad(\bmod d) . $$ Because $d$ is a divisor of $k$ and in view of $(1)$, we obtain $i \equiv j(\bmod d)$. As $i, j \in\{0,1, \ldots, d-1\}$, this just means that $i=j$. Substituting this into (3) yields $m k \equiv n k(\bmod a)$. Therefore $m k^{\prime} \equiv n k^{\prime}\left(\bmod a^{\prime}\right)$; and since $a^{\prime}$ and $k^{\prime}$ are coprime, we get $m \equiv n\left(\bmod a^{\prime}\right)$. Hence also $m=n$. It follows that the $a$ numbers that make up the $d$ sequences (2) satisfy all the requirements; they are certainly all greater than $N$ because we chose each $b_{i}>\max \left(2^{M}, N\right)$. So the statement holds for $a$, completing the induction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that, for every positive integer $n$, there exists an integer $m$ such that $2^{m}+m$ is divisible by $n$. (Estonia)
|
We will prove by induction on $d$ that, for every positive integer $N$, there exist positive integers $b_{0}, b_{1}, \ldots, b_{d-1}$ such that, for each $i=0,1,2, \ldots, d-1$, we have $b_{i}>N$ and $$ 2^{b_{i}}+b_{i} \equiv i \quad(\bmod d) . $$ This yields the claim for $m=b_{0}$. The base case $d=1$ is trivial. Take an $a>1$ and assume that the statement holds for all $d<a$. Note that the remainders of $2^{i}$ modulo $a$ repeat periodically starting with some exponent $M$. Let $k$ be the length of the period; this means that $2^{M+k^{\prime}} \equiv 2^{M}(\bmod a)$ holds only for those $k^{\prime}$ which are multiples of $k$. Note further that the period cannot contain all the $a$ remainders, since 0 either is missing or is the only number in the period. Thus $k<a$. Let $d=\operatorname{gcd}(a, k)$ and let $a^{\prime}=a / d, k^{\prime}=k / d$. Since $0<k<a$, we also have $0<d<a$. By the induction hypothesis, there exist positive integers $b_{0}, b_{1}, \ldots, b_{d-1}$ such that $b_{i}>\max \left(2^{M}, N\right)$ and $$ 2^{b_{i}}+b_{i} \equiv i \quad(\bmod d) \quad \text { for } \quad i=0,1,2, \ldots, d-1 $$ For each $i=0,1, \ldots, d-1$ consider the sequence $$ 2^{b_{i}}+b_{i}, \quad 2^{b_{i}+k}+\left(b_{i}+k\right), \ldots, \quad 2^{b_{i}+\left(a^{\prime}-1\right) k}+\left(b_{i}+\left(a^{\prime}-1\right) k\right) . $$ Modulo $a$, these numbers are congruent to $$ 2^{b_{i}}+b_{i}, \quad 2^{b_{i}}+\left(b_{i}+k\right), \ldots, \quad 2^{b_{i}}+\left(b_{i}+\left(a^{\prime}-1\right) k\right), $$ respectively. The $d$ sequences contain $a^{\prime} d=a$ numbers altogether. We shall now prove that no two of these numbers are congruent modulo $a$. Suppose that $$ 2^{b_{i}}+\left(b_{i}+m k\right) \equiv 2^{b_{j}}+\left(b_{j}+n k\right) \quad(\bmod a) $$ for some values of $i, j \in\{0,1, \ldots, d-1\}$ and $m, n \in\left\{0,1, \ldots, a^{\prime}-1\right\}$. Since $d$ is a divisor of $a$, we also have $$ 2^{b_{i}}+\left(b_{i}+m k\right) \equiv 2^{b_{j}}+\left(b_{j}+n k\right) \quad(\bmod d) . $$ Because $d$ is a divisor of $k$ and in view of $(1)$, we obtain $i \equiv j(\bmod d)$. As $i, j \in\{0,1, \ldots, d-1\}$, this just means that $i=j$. Substituting this into (3) yields $m k \equiv n k(\bmod a)$. Therefore $m k^{\prime} \equiv n k^{\prime}\left(\bmod a^{\prime}\right)$; and since $a^{\prime}$ and $k^{\prime}$ are coprime, we get $m \equiv n\left(\bmod a^{\prime}\right)$. Hence also $m=n$. It follows that the $a$ numbers that make up the $d$ sequences (2) satisfy all the requirements; they are certainly all greater than $N$ because we chose each $b_{i}>\max \left(2^{M}, N\right)$. So the statement holds for $a$, completing the induction.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5391fbb6-f231-5edf-b646-9d0e143b3970
| 23,617
|
Given a sequence $a_{1}, a_{2}, \ldots, a_{n}$ of real numbers. For each $i(1 \leq i \leq n)$ define $$ d_{i}=\max \left\{a_{j}: 1 \leq j \leq i\right\}-\min \left\{a_{j}: i \leq j \leq n\right\} $$ and let $$ d=\max \left\{d_{i}: 1 \leq i \leq n\right\} $$ (a) Prove that for arbitrary real numbers $x_{1} \leq x_{2} \leq \ldots \leq x_{n}$, $$ \max \left\{\left|x_{i}-a_{i}\right|: 1 \leq i \leq n\right\} \geq \frac{d}{2} $$ (b) Show that there exists a sequence $x_{1} \leq x_{2} \leq \ldots \leq x_{n}$ of real numbers such that we have equality in (1). (New Zealand)
|
(a) Let $1 \leq p \leq q \leq r \leq n$ be indices for which $$ d=d_{q}, \quad a_{p}=\max \left\{a_{j}: 1 \leq j \leq q\right\}, \quad a_{r}=\min \left\{a_{j}: q \leq j \leq n\right\} $$ and thus $d=a_{p}-a_{r}$. (These indices are not necessarily unique.)  For arbitrary real numbers $x_{1} \leq x_{2} \leq \ldots \leq x_{n}$, consider just the two quantities $\left|x_{p}-a_{p}\right|$ and $\left|x_{r}-a_{r}\right|$. Since $$ \left(a_{p}-x_{p}\right)+\left(x_{r}-a_{r}\right)=\left(a_{p}-a_{r}\right)+\left(x_{r}-x_{p}\right) \geq a_{p}-a_{r}=d, $$ we have either $a_{p}-x_{p} \geq \frac{d}{2}$ or $x_{r}-a_{r} \geq \frac{d}{2}$. Hence, $$ \max \left\{\left|x_{i}-a_{i}\right|: 1 \leq i \leq n\right\} \geq \max \left\{\left|x_{p}-a_{p}\right|,\left|x_{r}-a_{r}\right|\right\} \geq \max \left\{a_{p}-x_{p}, x_{r}-a_{r}\right\} \geq \frac{d}{2} $$ (b) Define the sequence $\left(x_{k}\right)$ as $$ x_{1}=a_{1}-\frac{d}{2}, \quad x_{k}=\max \left\{x_{k-1}, a_{k}-\frac{d}{2}\right\} \quad \text { for } 2 \leq k \leq n $$ We show that we have equality in (1) for this sequence. By the definition, sequence $\left(x_{k}\right)$ is non-decreasing and $x_{k}-a_{k} \geq-\frac{d}{2}$ for all $1 \leq k \leq n$. Next we prove that $$ x_{k}-a_{k} \leq \frac{d}{2} \quad \text { for all } 1 \leq k \leq n $$ Consider an arbitrary index $1 \leq k \leq n$. Let $\ell \leq k$ be the smallest index such that $x_{k}=x_{\ell}$. We have either $\ell=1$, or $\ell \geq 2$ and $x_{\ell}>x_{\ell-1}$. In both cases, $$ x_{k}=x_{\ell}=a_{\ell}-\frac{d}{2} $$ Since $$ a_{\ell}-a_{k} \leq \max \left\{a_{j}: 1 \leq j \leq k\right\}-\min \left\{a_{j}: k \leq j \leq n\right\}=d_{k} \leq d $$ equality (3) implies $$ x_{k}-a_{k}=a_{\ell}-a_{k}-\frac{d}{2} \leq d-\frac{d}{2}=\frac{d}{2} $$ We obtained that $-\frac{d}{2} \leq x_{k}-a_{k} \leq \frac{d}{2}$ for all $1 \leq k \leq n$, so $$ \max \left\{\left|x_{i}-a_{i}\right|: 1 \leq i \leq n\right\} \leq \frac{d}{2} $$ We have equality because $\left|x_{1}-a_{1}\right|=\frac{d}{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Given a sequence $a_{1}, a_{2}, \ldots, a_{n}$ of real numbers. For each $i(1 \leq i \leq n)$ define $$ d_{i}=\max \left\{a_{j}: 1 \leq j \leq i\right\}-\min \left\{a_{j}: i \leq j \leq n\right\} $$ and let $$ d=\max \left\{d_{i}: 1 \leq i \leq n\right\} $$ (a) Prove that for arbitrary real numbers $x_{1} \leq x_{2} \leq \ldots \leq x_{n}$, $$ \max \left\{\left|x_{i}-a_{i}\right|: 1 \leq i \leq n\right\} \geq \frac{d}{2} $$ (b) Show that there exists a sequence $x_{1} \leq x_{2} \leq \ldots \leq x_{n}$ of real numbers such that we have equality in (1). (New Zealand)
|
(a) Let $1 \leq p \leq q \leq r \leq n$ be indices for which $$ d=d_{q}, \quad a_{p}=\max \left\{a_{j}: 1 \leq j \leq q\right\}, \quad a_{r}=\min \left\{a_{j}: q \leq j \leq n\right\} $$ and thus $d=a_{p}-a_{r}$. (These indices are not necessarily unique.)  For arbitrary real numbers $x_{1} \leq x_{2} \leq \ldots \leq x_{n}$, consider just the two quantities $\left|x_{p}-a_{p}\right|$ and $\left|x_{r}-a_{r}\right|$. Since $$ \left(a_{p}-x_{p}\right)+\left(x_{r}-a_{r}\right)=\left(a_{p}-a_{r}\right)+\left(x_{r}-x_{p}\right) \geq a_{p}-a_{r}=d, $$ we have either $a_{p}-x_{p} \geq \frac{d}{2}$ or $x_{r}-a_{r} \geq \frac{d}{2}$. Hence, $$ \max \left\{\left|x_{i}-a_{i}\right|: 1 \leq i \leq n\right\} \geq \max \left\{\left|x_{p}-a_{p}\right|,\left|x_{r}-a_{r}\right|\right\} \geq \max \left\{a_{p}-x_{p}, x_{r}-a_{r}\right\} \geq \frac{d}{2} $$ (b) Define the sequence $\left(x_{k}\right)$ as $$ x_{1}=a_{1}-\frac{d}{2}, \quad x_{k}=\max \left\{x_{k-1}, a_{k}-\frac{d}{2}\right\} \quad \text { for } 2 \leq k \leq n $$ We show that we have equality in (1) for this sequence. By the definition, sequence $\left(x_{k}\right)$ is non-decreasing and $x_{k}-a_{k} \geq-\frac{d}{2}$ for all $1 \leq k \leq n$. Next we prove that $$ x_{k}-a_{k} \leq \frac{d}{2} \quad \text { for all } 1 \leq k \leq n $$ Consider an arbitrary index $1 \leq k \leq n$. Let $\ell \leq k$ be the smallest index such that $x_{k}=x_{\ell}$. We have either $\ell=1$, or $\ell \geq 2$ and $x_{\ell}>x_{\ell-1}$. In both cases, $$ x_{k}=x_{\ell}=a_{\ell}-\frac{d}{2} $$ Since $$ a_{\ell}-a_{k} \leq \max \left\{a_{j}: 1 \leq j \leq k\right\}-\min \left\{a_{j}: k \leq j \leq n\right\}=d_{k} \leq d $$ equality (3) implies $$ x_{k}-a_{k}=a_{\ell}-a_{k}-\frac{d}{2} \leq d-\frac{d}{2}=\frac{d}{2} $$ We obtained that $-\frac{d}{2} \leq x_{k}-a_{k} \leq \frac{d}{2}$ for all $1 \leq k \leq n$, so $$ \max \left\{\left|x_{i}-a_{i}\right|: 1 \leq i \leq n\right\} \leq \frac{d}{2} $$ We have equality because $\left|x_{1}-a_{1}\right|=\frac{d}{2}$.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6ff35de1-e8a5-5972-b181-6d35a25df3df
| 23,620
|
Given a sequence $a_{1}, a_{2}, \ldots, a_{n}$ of real numbers. For each $i(1 \leq i \leq n)$ define $$ d_{i}=\max \left\{a_{j}: 1 \leq j \leq i\right\}-\min \left\{a_{j}: i \leq j \leq n\right\} $$ and let $$ d=\max \left\{d_{i}: 1 \leq i \leq n\right\} $$ (a) Prove that for arbitrary real numbers $x_{1} \leq x_{2} \leq \ldots \leq x_{n}$, $$ \max \left\{\left|x_{i}-a_{i}\right|: 1 \leq i \leq n\right\} \geq \frac{d}{2} $$ (b) Show that there exists a sequence $x_{1} \leq x_{2} \leq \ldots \leq x_{n}$ of real numbers such that we have equality in (1). (New Zealand)
|
We present another construction of a sequence $\left(x_{i}\right)$ for part (b). For each $1 \leq i \leq n$, let $$ M_{i}=\max \left\{a_{j}: 1 \leq j \leq i\right\} \quad \text { and } \quad m_{i}=\min \left\{a_{j}: i \leq j \leq n\right\} $$ For all $1 \leq i<n$, we have $$ M_{i}=\max \left\{a_{1}, \ldots, a_{i}\right\} \leq \max \left\{a_{1}, \ldots, a_{i}, a_{i+1}\right\}=M_{i+1} $$ and $$ m_{i}=\min \left\{a_{i}, a_{i+1}, \ldots, a_{n}\right\} \leq \min \left\{a_{i+1}, \ldots, a_{n}\right\}=m_{i+1} . $$ Therefore sequences $\left(M_{i}\right)$ and $\left(m_{i}\right)$ are non-decreasing. Moreover, since $a_{i}$ is listed in both definitions, $$ m_{i} \leq a_{i} \leq M_{i} $$ To achieve equality in (1), set $$ x_{i}=\frac{M_{i}+m_{i}}{2} . $$ Since sequences $\left(M_{i}\right)$ and $\left(m_{i}\right)$ are non-decreasing, this sequence is non-decreasing as well. From $d_{i}=M_{i}-m_{i}$ we obtain that $$ -\frac{d_{i}}{2}=\frac{m_{i}-M_{i}}{2}=x_{i}-M_{i} \leq x_{i}-a_{i} \leq x_{i}-m_{i}=\frac{M_{i}-m_{i}}{2}=\frac{d_{i}}{2} . $$ Therefore $$ \max \left\{\left|x_{i}-a_{i}\right|: 1 \leq i \leq n\right\} \leq \max \left\{\frac{d_{i}}{2}: 1 \leq i \leq n\right\}=\frac{d}{2} $$ Since the opposite inequality has been proved in part (a), we must have equality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Given a sequence $a_{1}, a_{2}, \ldots, a_{n}$ of real numbers. For each $i(1 \leq i \leq n)$ define $$ d_{i}=\max \left\{a_{j}: 1 \leq j \leq i\right\}-\min \left\{a_{j}: i \leq j \leq n\right\} $$ and let $$ d=\max \left\{d_{i}: 1 \leq i \leq n\right\} $$ (a) Prove that for arbitrary real numbers $x_{1} \leq x_{2} \leq \ldots \leq x_{n}$, $$ \max \left\{\left|x_{i}-a_{i}\right|: 1 \leq i \leq n\right\} \geq \frac{d}{2} $$ (b) Show that there exists a sequence $x_{1} \leq x_{2} \leq \ldots \leq x_{n}$ of real numbers such that we have equality in (1). (New Zealand)
|
We present another construction of a sequence $\left(x_{i}\right)$ for part (b). For each $1 \leq i \leq n$, let $$ M_{i}=\max \left\{a_{j}: 1 \leq j \leq i\right\} \quad \text { and } \quad m_{i}=\min \left\{a_{j}: i \leq j \leq n\right\} $$ For all $1 \leq i<n$, we have $$ M_{i}=\max \left\{a_{1}, \ldots, a_{i}\right\} \leq \max \left\{a_{1}, \ldots, a_{i}, a_{i+1}\right\}=M_{i+1} $$ and $$ m_{i}=\min \left\{a_{i}, a_{i+1}, \ldots, a_{n}\right\} \leq \min \left\{a_{i+1}, \ldots, a_{n}\right\}=m_{i+1} . $$ Therefore sequences $\left(M_{i}\right)$ and $\left(m_{i}\right)$ are non-decreasing. Moreover, since $a_{i}$ is listed in both definitions, $$ m_{i} \leq a_{i} \leq M_{i} $$ To achieve equality in (1), set $$ x_{i}=\frac{M_{i}+m_{i}}{2} . $$ Since sequences $\left(M_{i}\right)$ and $\left(m_{i}\right)$ are non-decreasing, this sequence is non-decreasing as well. From $d_{i}=M_{i}-m_{i}$ we obtain that $$ -\frac{d_{i}}{2}=\frac{m_{i}-M_{i}}{2}=x_{i}-M_{i} \leq x_{i}-a_{i} \leq x_{i}-m_{i}=\frac{M_{i}-m_{i}}{2}=\frac{d_{i}}{2} . $$ Therefore $$ \max \left\{\left|x_{i}-a_{i}\right|: 1 \leq i \leq n\right\} \leq \max \left\{\frac{d_{i}}{2}: 1 \leq i \leq n\right\}=\frac{d}{2} $$ Since the opposite inequality has been proved in part (a), we must have equality.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6ff35de1-e8a5-5972-b181-6d35a25df3df
| 23,620
|
Let $n$ be a positive integer, and let $x$ and $y$ be positive real numbers such that $x^{n}+y^{n}=1$. Prove that $$ \left(\sum_{k=1}^{n} \frac{1+x^{2 k}}{1+x^{4 k}}\right)\left(\sum_{k=1}^{n} \frac{1+y^{2 k}}{1+y^{4 k}}\right)<\frac{1}{(1-x)(1-y)} $$ (Estonia)
|
We prove $$ \left(\sum_{k=1}^{n} \frac{1+x^{2 k}}{1+x^{4 k}}\right)\left(\sum_{k=1}^{n} \frac{1+y^{2 k}}{1+y^{4 k}}\right)<\frac{\left(\frac{1+\sqrt{2}}{2} \ln 2\right)^{2}}{(1-x)(1-y)}<\frac{0.7001}{(1-x)(1-y)} $$ The idea is to estimate each term on the left-hand side with the same constant. To find the upper bound for the expression $\frac{1+x^{2 k}}{1+x^{4 k}}$, consider the function $f(t)=\frac{1+t}{1+t^{2}}$ in interval $(0,1)$. Since $$ f^{\prime}(t)=\frac{1-2 t-t^{2}}{\left(1+t^{2}\right)^{2}}=\frac{(\sqrt{2}+1+t)(\sqrt{2}-1-t)}{\left(1+t^{2}\right)^{2}} $$ the function increases in interval $(0, \sqrt{2}-1]$ and decreases in $[\sqrt{2}-1,1)$. Therefore the maximum is at point $t_{0}=\sqrt{2}-1$ and $$ f(t)=\frac{1+t}{1+t^{2}} \leq f\left(t_{0}\right)=\frac{1+\sqrt{2}}{2}=\alpha . $$ Applying this to each term on the left-hand side of (1), we obtain $$ \left(\sum_{k=1}^{n} \frac{1+x^{2 k}}{1+x^{4 k}}\right)\left(\sum_{k=1}^{n} \frac{1+y^{2 k}}{1+y^{4 k}}\right) \leq n \alpha \cdot n \alpha=(n \alpha)^{2} $$ To estimate $(1-x)(1-y)$ on the right-hand side, consider the function $$ g(t)=\ln \left(1-t^{1 / n}\right)+\ln \left(1-(1-t)^{1 / n}\right) . $$ Substituting $s$ for $1-t$, we have $$ -n g^{\prime}(t)=\frac{t^{1 / n-1}}{1-t^{1 / n}}-\frac{s^{1 / n-1}}{1-s^{1 / n}}=\frac{1}{s t}\left(\frac{(1-t) t^{1 / n}}{1-t^{1 / n}}-\frac{(1-s) s^{1 / n}}{1-s^{1 / n}}\right)=\frac{h(t)-h(s)}{s t} . $$ The function $$ h(t)=t^{1 / n} \frac{1-t}{1-t^{1 / n}}=\sum_{i=1}^{n} t^{i / n} $$ is obviously increasing for $t \in(0,1)$, hence for these values of $t$ we have $$ g^{\prime}(t)>0 \Longleftrightarrow h(t)<h(s) \Longleftrightarrow t<s=1-t \Longleftrightarrow t<\frac{1}{2} . $$ Then, the maximum of $g(t)$ in $(0,1)$ is attained at point $t_{1}=1 / 2$ and therefore $$ g(t) \leq g\left(\frac{1}{2}\right)=2 \ln \left(1-2^{-1 / n}\right), \quad t \in(0,1) $$ Substituting $t=x^{n}$, we have $1-t=y^{n},(1-x)(1-y)=\exp g(t)$ and hence $$ (1-x)(1-y)=\exp g(t) \leq\left(1-2^{-1 / n}\right)^{2} $$ Combining (2) and (3), we get $$ \left(\sum_{k=1}^{n} \frac{1+x^{2 k}}{1+x^{4 k}}\right)\left(\sum_{k=1}^{n} \frac{1+y^{2 k}}{1+y^{4 k}}\right) \leq(\alpha n)^{2} \cdot 1 \leq(\alpha n)^{2} \frac{\left(1-2^{-1 / n}\right)^{2}}{(1-x)(1-y)}=\frac{\left(\alpha n\left(1-2^{-1 / n}\right)\right)^{2}}{(1-x)(1-y)} $$ Applying the inequality $1-\exp (-t)<t$ for $t=\frac{\ln 2}{n}$, we obtain $$ \alpha n\left(1-2^{-1 / n}\right)=\alpha n\left(1-\exp \left(-\frac{\ln 2}{n}\right)\right)<\alpha n \cdot \frac{\ln 2}{n}=\alpha \ln 2=\frac{1+\sqrt{2}}{2} \ln 2 . $$ Hence, $$ \left(\sum_{k=1}^{n} \frac{1+x^{2 k}}{1+x^{4 k}}\right)\left(\sum_{k=1}^{n} \frac{1+y^{2 k}}{1+y^{4 k}}\right)<\frac{\left(\frac{1+\sqrt{2}}{2} \ln 2\right)^{2}}{(1-x)(1-y)} $$ Comment. It is a natural idea to compare the sum $S_{n}(x)=\sum_{k=1}^{n} \frac{1+x^{2 k}}{1+x^{4 k}}$ with the integral $I_{n}(x)=$ $\int_{0}^{n} \frac{1+x^{2 t}}{1+x^{4 t}} \mathrm{~d} t$. Though computing the integral is quite standard, many difficulties arise. First, the integrand $\frac{1+x^{2 k}}{1+x^{4 k}}$ has an increasing segment and, depending on $x$, it can have a decreasing segment as well. So comparing $S_{n}(x)$ and $I_{n}(x)$ is not completely obvious. We can add a term to fix the estimate, e.g. $S_{n} \leq I_{n}+(\alpha-1)$, but then the final result will be weak for the small values of $n$. Second, we have to minimize $(1-x)(1-y) I_{n}(x) I_{n}(y)$ which leads to very unpleasant computations. However, by computer search we found that the maximum of $I_{n}(x) I_{n}(y)$ is at $x=y=2^{-1 / n}$, as well as the maximum of $S_{n}(x) S_{n}(y)$, and the latter is less. Hence, one can conjecture that the exact constant which can be put into the numerator on the right-hand side of (1) is $$ \left(\ln 2 \cdot \int_{0}^{1} \frac{1+4^{-t}}{1+16^{-t}} \mathrm{~d} t\right)^{2}=\frac{1}{4}\left(\frac{1}{2} \ln \frac{17}{2}+\arctan 4-\frac{\pi}{4}\right)^{2} \approx 0.6484 $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be a positive integer, and let $x$ and $y$ be positive real numbers such that $x^{n}+y^{n}=1$. Prove that $$ \left(\sum_{k=1}^{n} \frac{1+x^{2 k}}{1+x^{4 k}}\right)\left(\sum_{k=1}^{n} \frac{1+y^{2 k}}{1+y^{4 k}}\right)<\frac{1}{(1-x)(1-y)} $$ (Estonia)
|
We prove $$ \left(\sum_{k=1}^{n} \frac{1+x^{2 k}}{1+x^{4 k}}\right)\left(\sum_{k=1}^{n} \frac{1+y^{2 k}}{1+y^{4 k}}\right)<\frac{\left(\frac{1+\sqrt{2}}{2} \ln 2\right)^{2}}{(1-x)(1-y)}<\frac{0.7001}{(1-x)(1-y)} $$ The idea is to estimate each term on the left-hand side with the same constant. To find the upper bound for the expression $\frac{1+x^{2 k}}{1+x^{4 k}}$, consider the function $f(t)=\frac{1+t}{1+t^{2}}$ in interval $(0,1)$. Since $$ f^{\prime}(t)=\frac{1-2 t-t^{2}}{\left(1+t^{2}\right)^{2}}=\frac{(\sqrt{2}+1+t)(\sqrt{2}-1-t)}{\left(1+t^{2}\right)^{2}} $$ the function increases in interval $(0, \sqrt{2}-1]$ and decreases in $[\sqrt{2}-1,1)$. Therefore the maximum is at point $t_{0}=\sqrt{2}-1$ and $$ f(t)=\frac{1+t}{1+t^{2}} \leq f\left(t_{0}\right)=\frac{1+\sqrt{2}}{2}=\alpha . $$ Applying this to each term on the left-hand side of (1), we obtain $$ \left(\sum_{k=1}^{n} \frac{1+x^{2 k}}{1+x^{4 k}}\right)\left(\sum_{k=1}^{n} \frac{1+y^{2 k}}{1+y^{4 k}}\right) \leq n \alpha \cdot n \alpha=(n \alpha)^{2} $$ To estimate $(1-x)(1-y)$ on the right-hand side, consider the function $$ g(t)=\ln \left(1-t^{1 / n}\right)+\ln \left(1-(1-t)^{1 / n}\right) . $$ Substituting $s$ for $1-t$, we have $$ -n g^{\prime}(t)=\frac{t^{1 / n-1}}{1-t^{1 / n}}-\frac{s^{1 / n-1}}{1-s^{1 / n}}=\frac{1}{s t}\left(\frac{(1-t) t^{1 / n}}{1-t^{1 / n}}-\frac{(1-s) s^{1 / n}}{1-s^{1 / n}}\right)=\frac{h(t)-h(s)}{s t} . $$ The function $$ h(t)=t^{1 / n} \frac{1-t}{1-t^{1 / n}}=\sum_{i=1}^{n} t^{i / n} $$ is obviously increasing for $t \in(0,1)$, hence for these values of $t$ we have $$ g^{\prime}(t)>0 \Longleftrightarrow h(t)<h(s) \Longleftrightarrow t<s=1-t \Longleftrightarrow t<\frac{1}{2} . $$ Then, the maximum of $g(t)$ in $(0,1)$ is attained at point $t_{1}=1 / 2$ and therefore $$ g(t) \leq g\left(\frac{1}{2}\right)=2 \ln \left(1-2^{-1 / n}\right), \quad t \in(0,1) $$ Substituting $t=x^{n}$, we have $1-t=y^{n},(1-x)(1-y)=\exp g(t)$ and hence $$ (1-x)(1-y)=\exp g(t) \leq\left(1-2^{-1 / n}\right)^{2} $$ Combining (2) and (3), we get $$ \left(\sum_{k=1}^{n} \frac{1+x^{2 k}}{1+x^{4 k}}\right)\left(\sum_{k=1}^{n} \frac{1+y^{2 k}}{1+y^{4 k}}\right) \leq(\alpha n)^{2} \cdot 1 \leq(\alpha n)^{2} \frac{\left(1-2^{-1 / n}\right)^{2}}{(1-x)(1-y)}=\frac{\left(\alpha n\left(1-2^{-1 / n}\right)\right)^{2}}{(1-x)(1-y)} $$ Applying the inequality $1-\exp (-t)<t$ for $t=\frac{\ln 2}{n}$, we obtain $$ \alpha n\left(1-2^{-1 / n}\right)=\alpha n\left(1-\exp \left(-\frac{\ln 2}{n}\right)\right)<\alpha n \cdot \frac{\ln 2}{n}=\alpha \ln 2=\frac{1+\sqrt{2}}{2} \ln 2 . $$ Hence, $$ \left(\sum_{k=1}^{n} \frac{1+x^{2 k}}{1+x^{4 k}}\right)\left(\sum_{k=1}^{n} \frac{1+y^{2 k}}{1+y^{4 k}}\right)<\frac{\left(\frac{1+\sqrt{2}}{2} \ln 2\right)^{2}}{(1-x)(1-y)} $$ Comment. It is a natural idea to compare the sum $S_{n}(x)=\sum_{k=1}^{n} \frac{1+x^{2 k}}{1+x^{4 k}}$ with the integral $I_{n}(x)=$ $\int_{0}^{n} \frac{1+x^{2 t}}{1+x^{4 t}} \mathrm{~d} t$. Though computing the integral is quite standard, many difficulties arise. First, the integrand $\frac{1+x^{2 k}}{1+x^{4 k}}$ has an increasing segment and, depending on $x$, it can have a decreasing segment as well. So comparing $S_{n}(x)$ and $I_{n}(x)$ is not completely obvious. We can add a term to fix the estimate, e.g. $S_{n} \leq I_{n}+(\alpha-1)$, but then the final result will be weak for the small values of $n$. Second, we have to minimize $(1-x)(1-y) I_{n}(x) I_{n}(y)$ which leads to very unpleasant computations. However, by computer search we found that the maximum of $I_{n}(x) I_{n}(y)$ is at $x=y=2^{-1 / n}$, as well as the maximum of $S_{n}(x) S_{n}(y)$, and the latter is less. Hence, one can conjecture that the exact constant which can be put into the numerator on the right-hand side of (1) is $$ \left(\ln 2 \cdot \int_{0}^{1} \frac{1+4^{-t}}{1+16^{-t}} \mathrm{~d} t\right)^{2}=\frac{1}{4}\left(\frac{1}{2} \ln \frac{17}{2}+\arctan 4-\frac{\pi}{4}\right)^{2} \approx 0.6484 $$
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
46f5e3d6-c47e-59a6-b292-b65b9e75b059
| 23,627
|
Let $c>2$, and let $a(1), a(2), \ldots$ be a sequence of nonnegative real numbers such that $$ a(m+n) \leq 2 a(m)+2 a(n) \text { for all } m, n \geq 1 \text {, } $$ and $$ a\left(2^{k}\right) \leq \frac{1}{(k+1)^{c}} \quad \text { for all } k \geq 0 $$ Prove that the sequence $a(n)$ is bounded. (Croatia)
|
For convenience, define $a(0)=0$; then condition (1) persists for all pairs of nonnegative indices. Lemma 1. For arbitrary nonnegative indices $n_{1}, \ldots, n_{k}$, we have $$ a\left(\sum_{i=1}^{k} n_{i}\right) \leq \sum_{i=1}^{k} 2^{i} a\left(n_{i}\right) $$ and $$ a\left(\sum_{i=1}^{k} n_{i}\right) \leq 2 k \sum_{i=1}^{k} a\left(n_{i}\right) $$ Proof. Inequality (3) is proved by induction on $k$. The base case $k=1$ is trivial, while the induction step is provided by $a\left(\sum_{i=1}^{k+1} n_{i}\right)=a\left(n_{1}+\sum_{i=2}^{k+1} n_{i}\right) \leq 2 a\left(n_{1}\right)+2 a\left(\sum_{i=1}^{k} n_{i+1}\right) \leq 2 a\left(n_{1}\right)+2 \sum_{i=1}^{k} 2^{i} a\left(n_{i+1}\right)=\sum_{i=1}^{k+1} 2^{i} a\left(n_{i}\right)$. To establish (4), first the inequality $$ a\left(\sum_{i=1}^{2^{d}} n_{i}\right) \leq 2^{d} \sum_{i=1}^{2^{d}} a\left(n_{i}\right) $$ can be proved by an obvious induction on $d$. Then, turning to (4), we find an integer $d$ such that $2^{d-1}<k \leq 2^{d}$ to obtain $$ a\left(\sum_{i=1}^{k} n_{i}\right)=a\left(\sum_{i=1}^{k} n_{i}+\sum_{i=k+1}^{2^{d}} 0\right) \leq 2^{d}\left(\sum_{i=1}^{k} a\left(n_{i}\right)+\sum_{i=k+1}^{2^{d}} a(0)\right)=2^{d} \sum_{i=1}^{k} a\left(n_{i}\right) \leq 2 k \sum_{i=1}^{k} a\left(n_{i}\right) . $$ Fix an increasing unbounded sequence $0=M_{0}<M_{1}<M_{2}<\ldots$ of real numbers; the exact values will be defined later. Let $n$ be an arbitrary positive integer and write $$ n=\sum_{i=0}^{d} \varepsilon_{i} \cdot 2^{i}, \quad \text { where } \varepsilon_{i} \in\{0,1\} $$ Set $\varepsilon_{i}=0$ for $i>d$, and take some positive integer $f$ such that $M_{f}>d$. Applying (3), we get $$ a(n)=a\left(\sum_{k=1}^{f} \sum_{M_{k-1} \leq i<M_{k}} \varepsilon_{i} \cdot 2^{i}\right) \leq \sum_{k=1}^{f} 2^{k} a\left(\sum_{M_{k-1} \leq i<M_{k}} \varepsilon_{i} \cdot 2^{i}\right) $$ Note that there are less than $M_{k}-M_{k-1}+1$ integers in interval $\left[M_{k-1}, M_{k}\right)$; hence, using (4) we have $$ \begin{aligned} a(n) & \leq \sum_{k=1}^{f} 2^{k} \cdot 2\left(M_{k}-M_{k-1}+1\right) \sum_{M_{k-1} \leq i<M_{k}} \varepsilon_{i} \cdot a\left(2^{i}\right) \\ & \leq \sum_{k=1}^{f} 2^{k} \cdot 2\left(M_{k}-M_{k-1}+1\right)^{2} \max _{M_{k-1} \leq i<M_{k}} a\left(2^{i}\right) \\ & \leq \sum_{k=1}^{f} 2^{k+1}\left(M_{k}+1\right)^{2} \cdot \frac{1}{\left(M_{k-1}+1\right)^{c}}=\sum_{k=1}^{f}\left(\frac{M_{k}+1}{M_{k-1}+1}\right)^{2} \frac{2^{k+1}}{\left(M_{k-1}+1\right)^{c-2}} . \end{aligned} $$ Setting $M_{k}=4^{k /(c-2)}-1$, we obtain $$ a(n) \leq \sum_{k=1}^{f} 4^{2 /(c-2)} \frac{2^{k+1}}{\left(4^{(k-1) /(c-2)}\right)^{c-2}}=8 \cdot 4^{2 /(c-2)} \sum_{k=1}^{f}\left(\frac{1}{2}\right)^{k}<8 \cdot 4^{2 /(c-2)} $$ and the sequence $a(n)$ is bounded.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $c>2$, and let $a(1), a(2), \ldots$ be a sequence of nonnegative real numbers such that $$ a(m+n) \leq 2 a(m)+2 a(n) \text { for all } m, n \geq 1 \text {, } $$ and $$ a\left(2^{k}\right) \leq \frac{1}{(k+1)^{c}} \quad \text { for all } k \geq 0 $$ Prove that the sequence $a(n)$ is bounded. (Croatia)
|
For convenience, define $a(0)=0$; then condition (1) persists for all pairs of nonnegative indices. Lemma 1. For arbitrary nonnegative indices $n_{1}, \ldots, n_{k}$, we have $$ a\left(\sum_{i=1}^{k} n_{i}\right) \leq \sum_{i=1}^{k} 2^{i} a\left(n_{i}\right) $$ and $$ a\left(\sum_{i=1}^{k} n_{i}\right) \leq 2 k \sum_{i=1}^{k} a\left(n_{i}\right) $$ Proof. Inequality (3) is proved by induction on $k$. The base case $k=1$ is trivial, while the induction step is provided by $a\left(\sum_{i=1}^{k+1} n_{i}\right)=a\left(n_{1}+\sum_{i=2}^{k+1} n_{i}\right) \leq 2 a\left(n_{1}\right)+2 a\left(\sum_{i=1}^{k} n_{i+1}\right) \leq 2 a\left(n_{1}\right)+2 \sum_{i=1}^{k} 2^{i} a\left(n_{i+1}\right)=\sum_{i=1}^{k+1} 2^{i} a\left(n_{i}\right)$. To establish (4), first the inequality $$ a\left(\sum_{i=1}^{2^{d}} n_{i}\right) \leq 2^{d} \sum_{i=1}^{2^{d}} a\left(n_{i}\right) $$ can be proved by an obvious induction on $d$. Then, turning to (4), we find an integer $d$ such that $2^{d-1}<k \leq 2^{d}$ to obtain $$ a\left(\sum_{i=1}^{k} n_{i}\right)=a\left(\sum_{i=1}^{k} n_{i}+\sum_{i=k+1}^{2^{d}} 0\right) \leq 2^{d}\left(\sum_{i=1}^{k} a\left(n_{i}\right)+\sum_{i=k+1}^{2^{d}} a(0)\right)=2^{d} \sum_{i=1}^{k} a\left(n_{i}\right) \leq 2 k \sum_{i=1}^{k} a\left(n_{i}\right) . $$ Fix an increasing unbounded sequence $0=M_{0}<M_{1}<M_{2}<\ldots$ of real numbers; the exact values will be defined later. Let $n$ be an arbitrary positive integer and write $$ n=\sum_{i=0}^{d} \varepsilon_{i} \cdot 2^{i}, \quad \text { where } \varepsilon_{i} \in\{0,1\} $$ Set $\varepsilon_{i}=0$ for $i>d$, and take some positive integer $f$ such that $M_{f}>d$. Applying (3), we get $$ a(n)=a\left(\sum_{k=1}^{f} \sum_{M_{k-1} \leq i<M_{k}} \varepsilon_{i} \cdot 2^{i}\right) \leq \sum_{k=1}^{f} 2^{k} a\left(\sum_{M_{k-1} \leq i<M_{k}} \varepsilon_{i} \cdot 2^{i}\right) $$ Note that there are less than $M_{k}-M_{k-1}+1$ integers in interval $\left[M_{k-1}, M_{k}\right)$; hence, using (4) we have $$ \begin{aligned} a(n) & \leq \sum_{k=1}^{f} 2^{k} \cdot 2\left(M_{k}-M_{k-1}+1\right) \sum_{M_{k-1} \leq i<M_{k}} \varepsilon_{i} \cdot a\left(2^{i}\right) \\ & \leq \sum_{k=1}^{f} 2^{k} \cdot 2\left(M_{k}-M_{k-1}+1\right)^{2} \max _{M_{k-1} \leq i<M_{k}} a\left(2^{i}\right) \\ & \leq \sum_{k=1}^{f} 2^{k+1}\left(M_{k}+1\right)^{2} \cdot \frac{1}{\left(M_{k-1}+1\right)^{c}}=\sum_{k=1}^{f}\left(\frac{M_{k}+1}{M_{k-1}+1}\right)^{2} \frac{2^{k+1}}{\left(M_{k-1}+1\right)^{c-2}} . \end{aligned} $$ Setting $M_{k}=4^{k /(c-2)}-1$, we obtain $$ a(n) \leq \sum_{k=1}^{f} 4^{2 /(c-2)} \frac{2^{k+1}}{\left(4^{(k-1) /(c-2)}\right)^{c-2}}=8 \cdot 4^{2 /(c-2)} \sum_{k=1}^{f}\left(\frac{1}{2}\right)^{k}<8 \cdot 4^{2 /(c-2)} $$ and the sequence $a(n)$ is bounded.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8ce0da9b-c167-5543-b8e6-2f2545bf127b
| 23,635
|
Let $c>2$, and let $a(1), a(2), \ldots$ be a sequence of nonnegative real numbers such that $$ a(m+n) \leq 2 a(m)+2 a(n) \text { for all } m, n \geq 1 \text {, } $$ and $$ a\left(2^{k}\right) \leq \frac{1}{(k+1)^{c}} \quad \text { for all } k \geq 0 $$ Prove that the sequence $a(n)$ is bounded. (Croatia)
|
Lemma 2. Suppose that $s_{1}, \ldots, s_{k}$ are positive integers such that $$ \sum_{i=1}^{k} 2^{-s_{i}} \leq 1 $$ Then for arbitrary positive integers $n_{1}, \ldots, n_{k}$ we have $$ a\left(\sum_{i=1}^{k} n_{i}\right) \leq \sum_{i=1}^{k} 2^{s_{i}} a\left(n_{i}\right) $$ Proof. Apply an induction on $k$. The base cases are $k=1$ (trivial) and $k=2$ (follows from the condition (1)). Suppose that $k>2$. We can assume that $s_{1} \leq s_{2} \leq \cdots \leq s_{k}$. Note that $$ \sum_{i=1}^{k-1} 2^{-s_{i}} \leq 1-2^{-s_{k-1}} $$ since the left-hand side is a fraction with the denominator $2^{s_{k-1}}$, and this fraction is less than 1. Define $s_{k-1}^{\prime}=s_{k-1}-1$ and $n_{k-1}^{\prime}=n_{k-1}+n_{k}$; then we have $$ \sum_{i=1}^{k-2} 2^{-s_{i}}+2^{-s_{k-1}^{\prime}} \leq\left(1-2 \cdot 2^{-s_{k-1}}\right)+2^{1-s_{k-1}}=1 . $$ Now, the induction hypothesis can be applied to achieve $$ \begin{aligned} a\left(\sum_{i=1}^{k} n_{i}\right)=a\left(\sum_{i=1}^{k-2} n_{i}+n_{k-1}^{\prime}\right) & \leq \sum_{i=1}^{k-2} 2^{s_{i}} a\left(n_{i}\right)+2^{s_{k-1}^{\prime}} a\left(n_{k-1}^{\prime}\right) \\ & \leq \sum_{i=1}^{k-2} 2^{s_{i}} a\left(n_{i}\right)+2^{s_{k-1}-1} \cdot 2\left(a\left(n_{k-1}\right)+a\left(n_{k}\right)\right) \\ & \leq \sum_{i=1}^{k-2} 2^{s_{i}} a\left(n_{i}\right)+2^{s_{k-1}} a\left(n_{k-1}\right)+2^{s_{k}} a\left(n_{k}\right) . \end{aligned} $$ Let $q=c / 2>1$. Take an arbitrary positive integer $n$ and write $$ n=\sum_{i=1}^{k} 2^{u_{i}}, \quad 0 \leq u_{1}<u_{2}<\cdots<u_{k} $$ Choose $s_{i}=\left\lfloor\log _{2}\left(u_{i}+1\right)^{q}\right\rfloor+d(i=1, \ldots, k)$ for some integer $d$. We have $$ \sum_{i=1}^{k} 2^{-s_{i}}=2^{-d} \sum_{i=1}^{k} 2^{-\left\lfloor\log _{2}\left(u_{i}+1\right)^{q}\right\rfloor} $$ and we choose $d$ in such a way that $$ \frac{1}{2}<\sum_{i=1}^{k} 2^{-s_{i}} \leq 1 $$ In particular, this implies $$ 2^{d}<2 \sum_{i=1}^{k} 2^{-\left\lfloor\log _{2}\left(u_{i}+1\right)^{q}\right\rfloor}<4 \sum_{i=1}^{k} \frac{1}{\left(u_{i}+1\right)^{q}} $$ Now, by Lemma 2 we obtain $$ \begin{aligned} a(n)=a\left(\sum_{i=1}^{k} 2^{u_{i}}\right) & \leq \sum_{i=1}^{k} 2^{s_{i}} a\left(2^{u_{i}}\right) \leq \sum_{i=1}^{k} 2^{d}\left(u_{i}+1\right)^{q} \cdot \frac{1}{\left(u_{i}+1\right)^{2 q}} \\ & =2^{d} \sum_{i=1}^{k} \frac{1}{\left(u_{i}+1\right)^{q}}<4\left(\sum_{i=1}^{k} \frac{1}{\left(u_{i}+1\right)^{q}}\right)^{2} \end{aligned} $$ which is bounded since $q>1$. Comment 1. In fact, Lemma 2 (applied to the case $n_{i}=2^{u_{i}}$ only) provides a sharp bound for any $a(n)$. Actually, let $b(k)=\frac{1}{(k+1)^{c}}$ and consider the sequence $$ a(n)=\min \left\{\sum_{i=1}^{k} 2^{s_{i}} b\left(u_{i}\right) \mid k \in \mathbb{N}, \quad \sum_{i=1}^{k} 2^{-s_{i}} \leq 1, \quad \sum_{i=1}^{k} 2^{u_{i}}=n\right\} $$ We show that this sequence satisfies the conditions of the problem. Take two arbitrary indices $m$ and $n$. Let $$ \begin{aligned} & a(m)=\sum_{i=1}^{k} 2^{s_{i}} b\left(u_{i}\right), \quad \sum_{i=1}^{k} 2^{-s_{i}} \leq 1, \quad \sum_{i=1}^{k} 2^{u_{i}}=m ; \\ & a(n)=\sum_{i=1}^{l} 2^{r_{i}} b\left(w_{i}\right), \quad \sum_{i=1}^{l} 2^{-r_{i}} \leq 1, \quad \sum_{i=1}^{l} 2^{w_{i}}=n . \end{aligned} $$ Then we have $$ \sum_{i=1}^{k} 2^{-1-s_{i}}+\sum_{i=1}^{l} 2^{-1-r_{i}} \leq \frac{1}{2}+\frac{1}{2}=1, \quad \sum_{i=1}^{k} 2^{u_{i}}+\sum_{i=1}^{l} 2^{w_{i}}=m+n $$ so by (5) we obtain $$ a(n+m) \leq \sum_{i=1}^{k} 2^{1+s_{i}} b\left(u_{i}\right)+\sum_{i=1}^{l} 2^{1+r_{i}} b\left(w_{i}\right)=2 a(m)+2 a(n) . $$ Comment 2. The condition $c>2$ is sharp; we show that the sequence (5) is not bounded if $c \leq 2$. First, we prove that for an arbitrary $n$ the minimum in (5) is attained with a sequence $\left(u_{i}\right)$ consisting of distinct numbers. To the contrary, assume that $u_{k-1}=u_{k}$. Replace $u_{k-1}$ and $u_{k}$ by a single number $u_{k-1}^{\prime}=u_{k}+1$, and $s_{k-1}$ and $s_{k}$ by $s_{k-1}^{\prime}=\min \left\{s_{k-1}, s_{k}\right\}$. The modified sequences provide a better bound since $$ 2^{s_{k-1}^{\prime}} b\left(u_{k-1}^{\prime}\right)=2^{s_{k-1}^{\prime}} b\left(u_{k}+1\right)<2^{s_{k-1}} b\left(u_{k-1}\right)+2^{s_{k}} b\left(u_{k}\right) $$ (we used the fact that $b(k)$ is decreasing). This is impossible. Hence, the claim is proved, and we can assume that the minimum is attained with $u_{1}<\cdots<u_{k}$; then $$ n=\sum_{i=1}^{k} 2^{u_{i}} $$ is simply the binary representation of $n$. (In particular, it follows that $a\left(2^{n}\right)=b(n)$ for each $n$.) Now we show that the sequence $\left(a\left(2^{k}-1\right)\right)$ is not bounded. For some $s_{1}, \ldots, s_{k}$ we have $$ a\left(2^{k}-1\right)=a\left(\sum_{i=1}^{k} 2^{i-1}\right)=\sum_{i=1}^{k} 2^{s_{i}} b(i-1)=\sum_{i=1}^{k} \frac{2^{s_{i}}}{i^{c}} . $$ By the Cauchy-Schwarz inequality we get $$ a\left(2^{k}-1\right)=a\left(2^{k}-1\right) \cdot 1 \geq\left(\sum_{i=1}^{k} \frac{2^{s_{i}}}{i^{c}}\right)\left(\sum_{i=1}^{k} \frac{1}{2^{s_{i}}}\right) \geq\left(\sum_{i=1}^{k} \frac{1}{i^{c / 2}}\right)^{2}, $$ which is unbounded. For $c \leq 2$, it is also possible to show a concrete counterexample. Actually, one can prove that the sequence $$ a\left(\sum_{i=1}^{k} 2^{u_{i}}\right)=\sum_{i=1}^{k} \frac{i}{\left(u_{i}+1\right)^{2}} \quad\left(0 \leq u_{1}<\ldots<u_{k}\right) $$ satisfies (1) and (2) but is not bounded.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $c>2$, and let $a(1), a(2), \ldots$ be a sequence of nonnegative real numbers such that $$ a(m+n) \leq 2 a(m)+2 a(n) \text { for all } m, n \geq 1 \text {, } $$ and $$ a\left(2^{k}\right) \leq \frac{1}{(k+1)^{c}} \quad \text { for all } k \geq 0 $$ Prove that the sequence $a(n)$ is bounded. (Croatia)
|
Lemma 2. Suppose that $s_{1}, \ldots, s_{k}$ are positive integers such that $$ \sum_{i=1}^{k} 2^{-s_{i}} \leq 1 $$ Then for arbitrary positive integers $n_{1}, \ldots, n_{k}$ we have $$ a\left(\sum_{i=1}^{k} n_{i}\right) \leq \sum_{i=1}^{k} 2^{s_{i}} a\left(n_{i}\right) $$ Proof. Apply an induction on $k$. The base cases are $k=1$ (trivial) and $k=2$ (follows from the condition (1)). Suppose that $k>2$. We can assume that $s_{1} \leq s_{2} \leq \cdots \leq s_{k}$. Note that $$ \sum_{i=1}^{k-1} 2^{-s_{i}} \leq 1-2^{-s_{k-1}} $$ since the left-hand side is a fraction with the denominator $2^{s_{k-1}}$, and this fraction is less than 1. Define $s_{k-1}^{\prime}=s_{k-1}-1$ and $n_{k-1}^{\prime}=n_{k-1}+n_{k}$; then we have $$ \sum_{i=1}^{k-2} 2^{-s_{i}}+2^{-s_{k-1}^{\prime}} \leq\left(1-2 \cdot 2^{-s_{k-1}}\right)+2^{1-s_{k-1}}=1 . $$ Now, the induction hypothesis can be applied to achieve $$ \begin{aligned} a\left(\sum_{i=1}^{k} n_{i}\right)=a\left(\sum_{i=1}^{k-2} n_{i}+n_{k-1}^{\prime}\right) & \leq \sum_{i=1}^{k-2} 2^{s_{i}} a\left(n_{i}\right)+2^{s_{k-1}^{\prime}} a\left(n_{k-1}^{\prime}\right) \\ & \leq \sum_{i=1}^{k-2} 2^{s_{i}} a\left(n_{i}\right)+2^{s_{k-1}-1} \cdot 2\left(a\left(n_{k-1}\right)+a\left(n_{k}\right)\right) \\ & \leq \sum_{i=1}^{k-2} 2^{s_{i}} a\left(n_{i}\right)+2^{s_{k-1}} a\left(n_{k-1}\right)+2^{s_{k}} a\left(n_{k}\right) . \end{aligned} $$ Let $q=c / 2>1$. Take an arbitrary positive integer $n$ and write $$ n=\sum_{i=1}^{k} 2^{u_{i}}, \quad 0 \leq u_{1}<u_{2}<\cdots<u_{k} $$ Choose $s_{i}=\left\lfloor\log _{2}\left(u_{i}+1\right)^{q}\right\rfloor+d(i=1, \ldots, k)$ for some integer $d$. We have $$ \sum_{i=1}^{k} 2^{-s_{i}}=2^{-d} \sum_{i=1}^{k} 2^{-\left\lfloor\log _{2}\left(u_{i}+1\right)^{q}\right\rfloor} $$ and we choose $d$ in such a way that $$ \frac{1}{2}<\sum_{i=1}^{k} 2^{-s_{i}} \leq 1 $$ In particular, this implies $$ 2^{d}<2 \sum_{i=1}^{k} 2^{-\left\lfloor\log _{2}\left(u_{i}+1\right)^{q}\right\rfloor}<4 \sum_{i=1}^{k} \frac{1}{\left(u_{i}+1\right)^{q}} $$ Now, by Lemma 2 we obtain $$ \begin{aligned} a(n)=a\left(\sum_{i=1}^{k} 2^{u_{i}}\right) & \leq \sum_{i=1}^{k} 2^{s_{i}} a\left(2^{u_{i}}\right) \leq \sum_{i=1}^{k} 2^{d}\left(u_{i}+1\right)^{q} \cdot \frac{1}{\left(u_{i}+1\right)^{2 q}} \\ & =2^{d} \sum_{i=1}^{k} \frac{1}{\left(u_{i}+1\right)^{q}}<4\left(\sum_{i=1}^{k} \frac{1}{\left(u_{i}+1\right)^{q}}\right)^{2} \end{aligned} $$ which is bounded since $q>1$. Comment 1. In fact, Lemma 2 (applied to the case $n_{i}=2^{u_{i}}$ only) provides a sharp bound for any $a(n)$. Actually, let $b(k)=\frac{1}{(k+1)^{c}}$ and consider the sequence $$ a(n)=\min \left\{\sum_{i=1}^{k} 2^{s_{i}} b\left(u_{i}\right) \mid k \in \mathbb{N}, \quad \sum_{i=1}^{k} 2^{-s_{i}} \leq 1, \quad \sum_{i=1}^{k} 2^{u_{i}}=n\right\} $$ We show that this sequence satisfies the conditions of the problem. Take two arbitrary indices $m$ and $n$. Let $$ \begin{aligned} & a(m)=\sum_{i=1}^{k} 2^{s_{i}} b\left(u_{i}\right), \quad \sum_{i=1}^{k} 2^{-s_{i}} \leq 1, \quad \sum_{i=1}^{k} 2^{u_{i}}=m ; \\ & a(n)=\sum_{i=1}^{l} 2^{r_{i}} b\left(w_{i}\right), \quad \sum_{i=1}^{l} 2^{-r_{i}} \leq 1, \quad \sum_{i=1}^{l} 2^{w_{i}}=n . \end{aligned} $$ Then we have $$ \sum_{i=1}^{k} 2^{-1-s_{i}}+\sum_{i=1}^{l} 2^{-1-r_{i}} \leq \frac{1}{2}+\frac{1}{2}=1, \quad \sum_{i=1}^{k} 2^{u_{i}}+\sum_{i=1}^{l} 2^{w_{i}}=m+n $$ so by (5) we obtain $$ a(n+m) \leq \sum_{i=1}^{k} 2^{1+s_{i}} b\left(u_{i}\right)+\sum_{i=1}^{l} 2^{1+r_{i}} b\left(w_{i}\right)=2 a(m)+2 a(n) . $$ Comment 2. The condition $c>2$ is sharp; we show that the sequence (5) is not bounded if $c \leq 2$. First, we prove that for an arbitrary $n$ the minimum in (5) is attained with a sequence $\left(u_{i}\right)$ consisting of distinct numbers. To the contrary, assume that $u_{k-1}=u_{k}$. Replace $u_{k-1}$ and $u_{k}$ by a single number $u_{k-1}^{\prime}=u_{k}+1$, and $s_{k-1}$ and $s_{k}$ by $s_{k-1}^{\prime}=\min \left\{s_{k-1}, s_{k}\right\}$. The modified sequences provide a better bound since $$ 2^{s_{k-1}^{\prime}} b\left(u_{k-1}^{\prime}\right)=2^{s_{k-1}^{\prime}} b\left(u_{k}+1\right)<2^{s_{k-1}} b\left(u_{k-1}\right)+2^{s_{k}} b\left(u_{k}\right) $$ (we used the fact that $b(k)$ is decreasing). This is impossible. Hence, the claim is proved, and we can assume that the minimum is attained with $u_{1}<\cdots<u_{k}$; then $$ n=\sum_{i=1}^{k} 2^{u_{i}} $$ is simply the binary representation of $n$. (In particular, it follows that $a\left(2^{n}\right)=b(n)$ for each $n$.) Now we show that the sequence $\left(a\left(2^{k}-1\right)\right)$ is not bounded. For some $s_{1}, \ldots, s_{k}$ we have $$ a\left(2^{k}-1\right)=a\left(\sum_{i=1}^{k} 2^{i-1}\right)=\sum_{i=1}^{k} 2^{s_{i}} b(i-1)=\sum_{i=1}^{k} \frac{2^{s_{i}}}{i^{c}} . $$ By the Cauchy-Schwarz inequality we get $$ a\left(2^{k}-1\right)=a\left(2^{k}-1\right) \cdot 1 \geq\left(\sum_{i=1}^{k} \frac{2^{s_{i}}}{i^{c}}\right)\left(\sum_{i=1}^{k} \frac{1}{2^{s_{i}}}\right) \geq\left(\sum_{i=1}^{k} \frac{1}{i^{c / 2}}\right)^{2}, $$ which is unbounded. For $c \leq 2$, it is also possible to show a concrete counterexample. Actually, one can prove that the sequence $$ a\left(\sum_{i=1}^{k} 2^{u_{i}}\right)=\sum_{i=1}^{k} \frac{i}{\left(u_{i}+1\right)^{2}} \quad\left(0 \leq u_{1}<\ldots<u_{k}\right) $$ satisfies (1) and (2) but is not bounded.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8ce0da9b-c167-5543-b8e6-2f2545bf127b
| 23,635
|
A unit square is dissected into $n>1$ rectangles such that their sides are parallel to the sides of the square. Any line, parallel to a side of the square and intersecting its interior, also intersects the interior of some rectangle. Prove that in this dissection, there exists a rectangle having no point on the boundary of the square. (Japan)
|
Call the directions of the sides of the square horizontal and vertical. A horizontal or vertical line, which intersects the interior of the square but does not intersect the interior of any rectangle, will be called a splitting line. A rectangle having no point on the boundary of the square will be called an interior rectangle. Suppose, to the contrary, that there exists a dissection of the square into more than one rectangle, such that no interior rectangle and no splitting line appear. Consider such a dissection with the least possible number of rectangles. Notice that this number of rectangles is greater than 2, otherwise their common side provides a splitting line. If there exist two rectangles having a common side, then we can replace them by their union (see Figure 1). The number of rectangles was greater than 2, so in a new dissection it is greater than 1. Clearly, in the new dissection, there is also no splitting line as well as no interior rectangle. This contradicts the choice of the original dissection. Denote the initial square by $A B C D$, with $A$ and $B$ being respectively the lower left and lower right vertices. Consider those two rectangles $a$ and $b$ containing vertices $A$ and $B$, respectively. (Note that $a \neq b$, otherwise its top side provides a splitting line.) We can assume that the height of $a$ is not greater than that of $b$. Then consider the rectangle $c$ neighboring to the lower right corner of $a$ (it may happen that $c=b$ ). By aforementioned, the heights of $a$ and $c$ are distinct. Then two cases are possible.  Figure 1  Figure 2 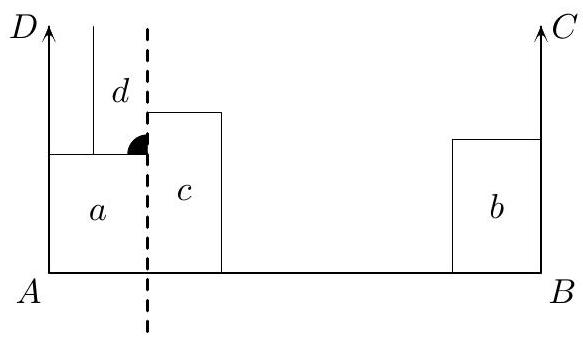 Figure 3 Case 1. The height of $c$ is less than that of $a$. Consider the rectangle $d$ which is adjacent to both $a$ and $c$, i. e. the one containing the angle marked in Figure 2. This rectangle has no common point with $B C$ (since $a$ is not higher than $b$ ), as well as no common point with $A B$ or with $A D$ (obviously). Then $d$ has a common point with $C D$, and its left side provides a splitting line. Contradiction. Case 2. The height of $c$ is greater than that of $a$. Analogously, consider the rectangle $d$ containing the angle marked on Figure 3. It has no common point with $A D$ (otherwise it has a common side with $a$ ), as well as no common point with $A B$ or with $B C$ (obviously). Then $d$ has a common point with $C D$. Hence its right side provides a splitting line, and we get the contradiction again.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A unit square is dissected into $n>1$ rectangles such that their sides are parallel to the sides of the square. Any line, parallel to a side of the square and intersecting its interior, also intersects the interior of some rectangle. Prove that in this dissection, there exists a rectangle having no point on the boundary of the square. (Japan)
|
Call the directions of the sides of the square horizontal and vertical. A horizontal or vertical line, which intersects the interior of the square but does not intersect the interior of any rectangle, will be called a splitting line. A rectangle having no point on the boundary of the square will be called an interior rectangle. Suppose, to the contrary, that there exists a dissection of the square into more than one rectangle, such that no interior rectangle and no splitting line appear. Consider such a dissection with the least possible number of rectangles. Notice that this number of rectangles is greater than 2, otherwise their common side provides a splitting line. If there exist two rectangles having a common side, then we can replace them by their union (see Figure 1). The number of rectangles was greater than 2, so in a new dissection it is greater than 1. Clearly, in the new dissection, there is also no splitting line as well as no interior rectangle. This contradicts the choice of the original dissection. Denote the initial square by $A B C D$, with $A$ and $B$ being respectively the lower left and lower right vertices. Consider those two rectangles $a$ and $b$ containing vertices $A$ and $B$, respectively. (Note that $a \neq b$, otherwise its top side provides a splitting line.) We can assume that the height of $a$ is not greater than that of $b$. Then consider the rectangle $c$ neighboring to the lower right corner of $a$ (it may happen that $c=b$ ). By aforementioned, the heights of $a$ and $c$ are distinct. Then two cases are possible.  Figure 1  Figure 2  Figure 3 Case 1. The height of $c$ is less than that of $a$. Consider the rectangle $d$ which is adjacent to both $a$ and $c$, i. e. the one containing the angle marked in Figure 2. This rectangle has no common point with $B C$ (since $a$ is not higher than $b$ ), as well as no common point with $A B$ or with $A D$ (obviously). Then $d$ has a common point with $C D$, and its left side provides a splitting line. Contradiction. Case 2. The height of $c$ is greater than that of $a$. Analogously, consider the rectangle $d$ containing the angle marked on Figure 3. It has no common point with $A D$ (otherwise it has a common side with $a$ ), as well as no common point with $A B$ or with $B C$ (obviously). Then $d$ has a common point with $C D$. Hence its right side provides a splitting line, and we get the contradiction again.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
babc5382-c694-597d-acdd-c9c4a8d7a544
| 23,650
|
A unit square is dissected into $n>1$ rectangles such that their sides are parallel to the sides of the square. Any line, parallel to a side of the square and intersecting its interior, also intersects the interior of some rectangle. Prove that in this dissection, there exists a rectangle having no point on the boundary of the square. (Japan)
|
Again, we suppose the contrary. Consider an arbitrary counterexample. Then we know that each rectangle is attached to at least one side of the square. Observe that a rectangle cannot be attached to two opposite sides, otherwise one of its sides lies on a splitting line. We say that two rectangles are opposite if they are attached to opposite sides of $A B C D$. We claim that there exist two opposite rectangles having a common point. Consider the union $L$ of all rectangles attached to the left. Assume, to the contrary, that $L$ has no common point with the rectangles attached to the right. Take a polygonal line $p$ connecting the top and the bottom sides of the square and passing close from the right to the boundary of $L$ (see Figure 4). Then all its points belong to the rectangles attached either to the top or to the bottom. Moreover, the upper end-point of $p$ belongs to a rectangle attached to the top, and the lower one belongs to an other rectangle attached to the bottom. Hence, there is a point on $p$ where some rectangles attached to the top and to the bottom meet each other. So, there always exists a pair of neighboring opposite rectangles. 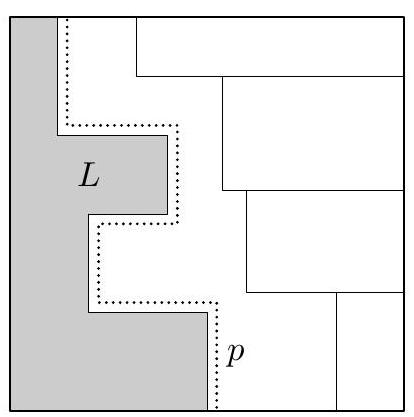 Figure 4 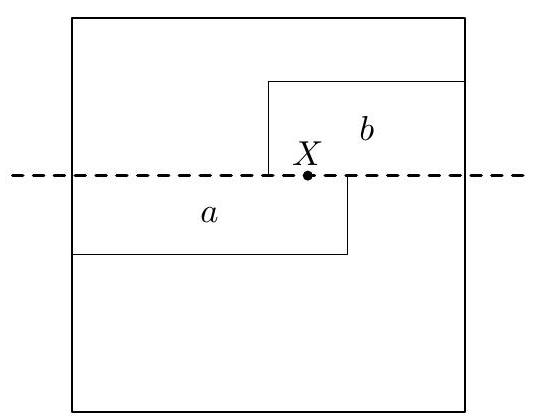 Figure 5 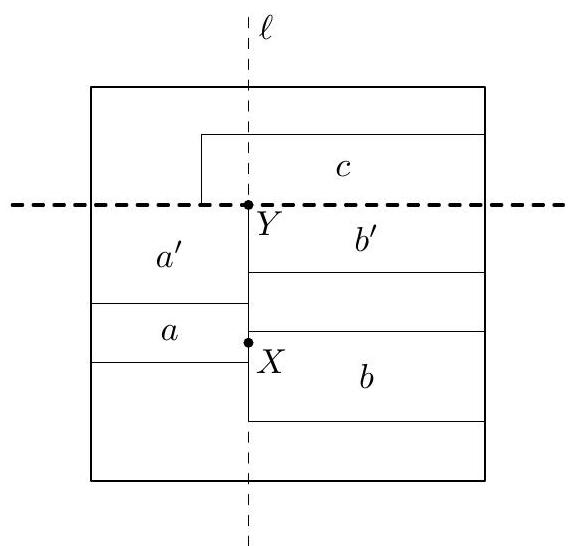 Figure 6 Now, take two opposite neighboring rectangles $a$ and $b$. We can assume that $a$ is attached to the left and $b$ is attached to the right. Let $X$ be their common point. If $X$ belongs to their horizontal sides (in particular, $X$ may appear to be a common vertex of $a$ and $b$ ), then these sides provide a splitting line (see Figure 5). Otherwise, $X$ lies on the vertical sides. Let $\ell$ be the line containing these sides. Since $\ell$ is not a splitting line, it intersects the interior of some rectangle. Let $c$ be such a rectangle, closest to $X$; we can assume that $c$ lies above $X$. Let $Y$ be the common point of $\ell$ and the bottom side of $c$ (see Figure 6). Then $Y$ is also a vertex of two rectangles lying below $c$. So, let $Y$ be the upper-right and upper-left corners of the rectangles $a^{\prime}$ and $b^{\prime}$, respectively. Then $a^{\prime}$ and $b^{\prime}$ are situated not lower than $a$ and $b$, respectively (it may happen that $a=a^{\prime}$ or $b=b^{\prime}$ ). We claim that $a^{\prime}$ is attached to the left. If $a=a^{\prime}$ then of course it is. If $a \neq a^{\prime}$ then $a^{\prime}$ is above $a$, below $c$ and to the left from $b^{\prime}$. Hence, it can be attached to the left only. Analogously, $b^{\prime}$ is attached to the right. Now, the top sides of these two rectangles pass through $Y$, hence they provide a splitting line again. This last contradiction completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A unit square is dissected into $n>1$ rectangles such that their sides are parallel to the sides of the square. Any line, parallel to a side of the square and intersecting its interior, also intersects the interior of some rectangle. Prove that in this dissection, there exists a rectangle having no point on the boundary of the square. (Japan)
|
Again, we suppose the contrary. Consider an arbitrary counterexample. Then we know that each rectangle is attached to at least one side of the square. Observe that a rectangle cannot be attached to two opposite sides, otherwise one of its sides lies on a splitting line. We say that two rectangles are opposite if they are attached to opposite sides of $A B C D$. We claim that there exist two opposite rectangles having a common point. Consider the union $L$ of all rectangles attached to the left. Assume, to the contrary, that $L$ has no common point with the rectangles attached to the right. Take a polygonal line $p$ connecting the top and the bottom sides of the square and passing close from the right to the boundary of $L$ (see Figure 4). Then all its points belong to the rectangles attached either to the top or to the bottom. Moreover, the upper end-point of $p$ belongs to a rectangle attached to the top, and the lower one belongs to an other rectangle attached to the bottom. Hence, there is a point on $p$ where some rectangles attached to the top and to the bottom meet each other. So, there always exists a pair of neighboring opposite rectangles.  Figure 4  Figure 5  Figure 6 Now, take two opposite neighboring rectangles $a$ and $b$. We can assume that $a$ is attached to the left and $b$ is attached to the right. Let $X$ be their common point. If $X$ belongs to their horizontal sides (in particular, $X$ may appear to be a common vertex of $a$ and $b$ ), then these sides provide a splitting line (see Figure 5). Otherwise, $X$ lies on the vertical sides. Let $\ell$ be the line containing these sides. Since $\ell$ is not a splitting line, it intersects the interior of some rectangle. Let $c$ be such a rectangle, closest to $X$; we can assume that $c$ lies above $X$. Let $Y$ be the common point of $\ell$ and the bottom side of $c$ (see Figure 6). Then $Y$ is also a vertex of two rectangles lying below $c$. So, let $Y$ be the upper-right and upper-left corners of the rectangles $a^{\prime}$ and $b^{\prime}$, respectively. Then $a^{\prime}$ and $b^{\prime}$ are situated not lower than $a$ and $b$, respectively (it may happen that $a=a^{\prime}$ or $b=b^{\prime}$ ). We claim that $a^{\prime}$ is attached to the left. If $a=a^{\prime}$ then of course it is. If $a \neq a^{\prime}$ then $a^{\prime}$ is above $a$, below $c$ and to the left from $b^{\prime}$. Hence, it can be attached to the left only. Analogously, $b^{\prime}$ is attached to the right. Now, the top sides of these two rectangles pass through $Y$, hence they provide a splitting line again. This last contradiction completes the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
babc5382-c694-597d-acdd-c9c4a8d7a544
| 23,650
|
Let $A_{0}=\left(a_{1}, \ldots, a_{n}\right)$ be a finite sequence of real numbers. For each $k \geq 0$, from the sequence $A_{k}=\left(x_{1}, \ldots, x_{n}\right)$ we construct a new sequence $A_{k+1}$ in the following way. 1. We choose a partition $\{1, \ldots, n\}=I \cup J$, where $I$ and $J$ are two disjoint sets, such that the expression $$ \left|\sum_{i \in I} x_{i}-\sum_{j \in J} x_{j}\right| $$ attains the smallest possible value. (We allow the sets $I$ or $J$ to be empty; in this case the corresponding sum is 0 .) If there are several such partitions, one is chosen arbitrarily. 2. We set $A_{k+1}=\left(y_{1}, \ldots, y_{n}\right)$, where $y_{i}=x_{i}+1$ if $i \in I$, and $y_{i}=x_{i}-1$ if $i \in J$. Prove that for some $k$, the sequence $A_{k}$ contains an element $x$ such that $|x| \geq n / 2$. (Iran)
|
Lemma. Suppose that all terms of the sequence $\left(x_{1}, \ldots, x_{n}\right)$ satisfy the inequality $\left|x_{i}\right|<a$. Then there exists a partition $\{1,2, \ldots, n\}=I \cup J$ into two disjoint sets such that $$ \left|\sum_{i \in I} x_{i}-\sum_{j \in J} x_{j}\right|<a $$ Proof. Apply an induction on $n$. The base case $n=1$ is trivial. For the induction step, consider a sequence $\left(x_{1}, \ldots, x_{n}\right)(n>1)$. By the induction hypothesis there exists a splitting $\{1, \ldots, n-1\}=I^{\prime} \cup J^{\prime}$ such that $$ \left|\sum_{i \in I^{\prime}} x_{i}-\sum_{j \in J^{\prime}} x_{j}\right|<a $$ For convenience, suppose that $\sum_{i \in I^{\prime}} x_{i} \geq \sum_{j \in J^{\prime}} x_{j}$. If $x_{n} \geq 0$ then choose $I=I^{\prime}, J=J \cup\{n\}$; otherwise choose $I=I^{\prime} \cup\{n\}, J=J^{\prime}$. In both cases, we have $\sum_{i \in I^{\prime}} x_{i}-\sum_{j \in J^{\prime}} x_{j} \in[0, a)$ and $\left|x_{n}\right| \in[0, a)$; hence $$ \sum_{i \in I} x_{i}-\sum_{j \in J} x_{j}=\sum_{i \in I^{\prime}} x_{i}-\sum_{j \in J^{\prime}} x_{j}-\left|x_{n}\right| \in(-a, a) $$ as desired. Let us turn now to the problem. To the contrary, assume that for all $k$, all the numbers in $A_{k}$ lie in interval $(-n / 2, n / 2)$. Consider an arbitrary sequence $A_{k}=\left(b_{1}, \ldots, b_{n}\right)$. To obtain the term $b_{i}$, we increased and decreased number $a_{i}$ by one several times. Therefore $b_{i}-a_{i}$ is always an integer, and there are not more than $n$ possible values for $b_{i}$. So, there are not more than $n^{n}$ distinct possible sequences $A_{k}$, and hence two of the sequences $A_{1}, A_{2}, \ldots, A_{n^{n}+1}$ should be identical, say $A_{p}=A_{q}$ for some $p<q$. For any positive integer $k$, let $S_{k}$ be the sum of squares of elements in $A_{k}$. Consider two consecutive sequences $A_{k}=\left(x_{1}, \ldots, x_{n}\right)$ and $A_{k+1}=\left(y_{1}, \ldots, y_{n}\right)$. Let $\{1,2, \ldots, n\}=I \cup J$ be the partition used in this step - that is, $y_{i}=x_{i}+1$ for all $i \in I$ and $y_{j}=x_{j}-1$ for all $j \in J$. Since the value of $\left|\sum_{i \in I} x_{i}-\sum_{j \in J} x_{j}\right|$ is the smallest possible, the Lemma implies that it is less than $n / 2$. Then we have $S_{k+1}-S_{k}=\sum_{i \in I}\left(\left(x_{i}+1\right)^{2}-x_{i}^{2}\right)+\sum_{j \in J}\left(\left(x_{j}-1\right)^{2}-x_{j}^{2}\right)=n+2\left(\sum_{i \in I} x_{i}-\sum_{j \in J} x_{j}\right)>n-2 \cdot \frac{n}{2}=0$. Thus we obtain $S_{q}>S_{q-1}>\cdots>S_{p}$. This is impossible since $A_{p}=A_{q}$ and hence $S_{p}=S_{q}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $A_{0}=\left(a_{1}, \ldots, a_{n}\right)$ be a finite sequence of real numbers. For each $k \geq 0$, from the sequence $A_{k}=\left(x_{1}, \ldots, x_{n}\right)$ we construct a new sequence $A_{k+1}$ in the following way. 1. We choose a partition $\{1, \ldots, n\}=I \cup J$, where $I$ and $J$ are two disjoint sets, such that the expression $$ \left|\sum_{i \in I} x_{i}-\sum_{j \in J} x_{j}\right| $$ attains the smallest possible value. (We allow the sets $I$ or $J$ to be empty; in this case the corresponding sum is 0 .) If there are several such partitions, one is chosen arbitrarily. 2. We set $A_{k+1}=\left(y_{1}, \ldots, y_{n}\right)$, where $y_{i}=x_{i}+1$ if $i \in I$, and $y_{i}=x_{i}-1$ if $i \in J$. Prove that for some $k$, the sequence $A_{k}$ contains an element $x$ such that $|x| \geq n / 2$. (Iran)
|
Lemma. Suppose that all terms of the sequence $\left(x_{1}, \ldots, x_{n}\right)$ satisfy the inequality $\left|x_{i}\right|<a$. Then there exists a partition $\{1,2, \ldots, n\}=I \cup J$ into two disjoint sets such that $$ \left|\sum_{i \in I} x_{i}-\sum_{j \in J} x_{j}\right|<a $$ Proof. Apply an induction on $n$. The base case $n=1$ is trivial. For the induction step, consider a sequence $\left(x_{1}, \ldots, x_{n}\right)(n>1)$. By the induction hypothesis there exists a splitting $\{1, \ldots, n-1\}=I^{\prime} \cup J^{\prime}$ such that $$ \left|\sum_{i \in I^{\prime}} x_{i}-\sum_{j \in J^{\prime}} x_{j}\right|<a $$ For convenience, suppose that $\sum_{i \in I^{\prime}} x_{i} \geq \sum_{j \in J^{\prime}} x_{j}$. If $x_{n} \geq 0$ then choose $I=I^{\prime}, J=J \cup\{n\}$; otherwise choose $I=I^{\prime} \cup\{n\}, J=J^{\prime}$. In both cases, we have $\sum_{i \in I^{\prime}} x_{i}-\sum_{j \in J^{\prime}} x_{j} \in[0, a)$ and $\left|x_{n}\right| \in[0, a)$; hence $$ \sum_{i \in I} x_{i}-\sum_{j \in J} x_{j}=\sum_{i \in I^{\prime}} x_{i}-\sum_{j \in J^{\prime}} x_{j}-\left|x_{n}\right| \in(-a, a) $$ as desired. Let us turn now to the problem. To the contrary, assume that for all $k$, all the numbers in $A_{k}$ lie in interval $(-n / 2, n / 2)$. Consider an arbitrary sequence $A_{k}=\left(b_{1}, \ldots, b_{n}\right)$. To obtain the term $b_{i}$, we increased and decreased number $a_{i}$ by one several times. Therefore $b_{i}-a_{i}$ is always an integer, and there are not more than $n$ possible values for $b_{i}$. So, there are not more than $n^{n}$ distinct possible sequences $A_{k}$, and hence two of the sequences $A_{1}, A_{2}, \ldots, A_{n^{n}+1}$ should be identical, say $A_{p}=A_{q}$ for some $p<q$. For any positive integer $k$, let $S_{k}$ be the sum of squares of elements in $A_{k}$. Consider two consecutive sequences $A_{k}=\left(x_{1}, \ldots, x_{n}\right)$ and $A_{k+1}=\left(y_{1}, \ldots, y_{n}\right)$. Let $\{1,2, \ldots, n\}=I \cup J$ be the partition used in this step - that is, $y_{i}=x_{i}+1$ for all $i \in I$ and $y_{j}=x_{j}-1$ for all $j \in J$. Since the value of $\left|\sum_{i \in I} x_{i}-\sum_{j \in J} x_{j}\right|$ is the smallest possible, the Lemma implies that it is less than $n / 2$. Then we have $S_{k+1}-S_{k}=\sum_{i \in I}\left(\left(x_{i}+1\right)^{2}-x_{i}^{2}\right)+\sum_{j \in J}\left(\left(x_{j}-1\right)^{2}-x_{j}^{2}\right)=n+2\left(\sum_{i \in I} x_{i}-\sum_{j \in J} x_{j}\right)>n-2 \cdot \frac{n}{2}=0$. Thus we obtain $S_{q}>S_{q-1}>\cdots>S_{p}$. This is impossible since $A_{p}=A_{q}$ and hence $S_{p}=S_{q}$.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9bf91c1c-5cf9-5e21-a78a-3c727318cac4
| 23,657
|
In the Cartesian coordinate plane define the strip $S_{n}=\{(x, y) \mid n \leq x<n+1\}$ for every integer $n$. Assume that each strip $S_{n}$ is colored either red or blue, and let $a$ and $b$ be two distinct positive integers. Prove that there exists a rectangle with side lengths $a$ and $b$ such that its vertices have the same color. (Romania)
|
If $S_{n}$ and $S_{n+a}$ have the same color for some integer $n$, then we can choose the rectangle with vertices $(n, 0) \in S_{n},(n, b) \in S_{n},(n+a, 0) \in S_{n+a}$, and $(n+a, b) \in S_{n+a}$, and we are done. So it can be assumed that $S_{n}$ and $S_{n+a}$ have opposite colors for each $n$. Similarly, it also can be assumed that $S_{n}$ and $S_{n+b}$ have opposite colors. Then, by induction on $|p|+|q|$, we obtain that for arbitrary integers $p$ and $q$, strips $S_{n}$ and $S_{n+p a+q b}$ have the same color if $p+q$ is even, and these two strips have opposite colors if $p+q$ is odd. Let $d=\operatorname{gcd}(a, b), a_{1}=a / d$ and $b_{1}=b / d$. Apply the result above for $p=b_{1}$ and $q=-a_{1}$. The strips $S_{0}$ and $S_{0+b_{1} a-a_{1} b}$ are identical and therefore they have the same color. Hence, $a_{1}+b_{1}$ is even. By the construction, $a_{1}$ and $b_{1}$ are coprime, so this is possible only if both are odd. Without loss of generality, we can assume $a>b$. Then $a_{1}>b_{1} \geq 1$, so $a_{1} \geq 3$. Choose integers $k$ and $\ell$ such that $k a_{1}-\ell b_{1}=1$ and therefore $k a-\ell b=d$. Since $a_{1}$ and $b_{1}$ are odd, $k+\ell$ is odd as well. Hence, for every integer $n$, strips $S_{n}$ and $S_{n+k a-\ell b}=S_{n+d}$ have opposite colors. This also implies that the coloring is periodic with period $2 d$, i.e. strips $S_{n}$ and $S_{n+2 d}$ have the same color for every $n$. 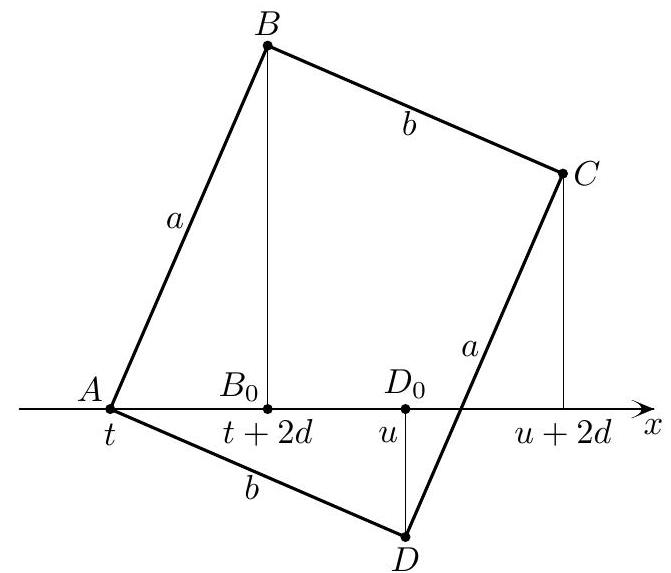 Figure 1 We will construct the desired rectangle $A B C D$ with $A B=C D=a$ and $B C=A D=b$ in a position such that vertex $A$ lies on the $x$-axis, and the projection of side $A B$ onto the $x$-axis is of length $2 d$ (see Figure 1). This is possible since $a=a_{1} d>2 d$. The coordinates of the vertices will have the forms $$ A=(t, 0), \quad B=\left(t+2 d, y_{1}\right), \quad C=\left(u+2 d, y_{2}\right), \quad D=\left(u, y_{3}\right) . $$ Let $\varphi=\sqrt{a_{1}^{2}-4}$. By Pythagoras' theorem, $$ y_{1}=B B_{0}=\sqrt{a^{2}-4 d^{2}}=d \sqrt{a_{1}^{2}-4}=d \varphi \text {. } $$ So, by the similar triangles $A D D_{0}$ and $B A B_{0}$, we have the constraint $$ u-t=A D_{0}=\frac{A D}{A B} \cdot B B_{0}=\frac{b d}{a} \varphi $$ for numbers $t$ and $u$. Computing the numbers $y_{2}$ and $y_{3}$ is not required since they have no effect to the colors. Observe that the number $\varphi$ is irrational, because $\varphi^{2}$ is an integer, but $\varphi$ is not: $a_{1}>\varphi \geq$ $\sqrt{a_{1}^{2}-2 a_{1}+2}>a_{1}-1$. By the periodicity, points $A$ and $B$ have the same color; similarly, points $C$ and $D$ have the same color. Furthermore, these colors depend only on the values of $t$ and $u$. So it is sufficient to choose numbers $t$ and $u$ such that vertices $A$ and $D$ have the same color. Let $w$ be the largest positive integer such that there exist $w$ consecutive strips $S_{n_{0}}, S_{n_{0}+1}, \ldots$, $S_{n_{0}+w-1}$ with the same color, say red. (Since $S_{n_{0}+d}$ must be blue, we have $w \leq d$.) We will choose $t$ from the interval $\left(n_{0}, n_{0}+w\right)$.  Figure 2 Consider the interval $I=\left(n_{0}+\frac{b d}{a} \varphi, n_{0}+\frac{b d}{a} \varphi+w\right)$ on the $x$-axis (see Figure 2). Its length is $w$, and the end-points are irrational. Therefore, this interval intersects $w+1$ consecutive strips. Since at most $w$ consecutive strips may have the same color, interval $I$ must contain both red and blue points. Choose $u \in I$ such that the line $x=u$ is red and set $t=u-\frac{b d}{a} \varphi$, according to the constraint (1). Then $t \in\left(n_{0}, n_{0}+w\right)$ and $A=(t, 0)$ is red as well as $D=\left(u, y_{3}\right)$. Hence, variables $u$ and $t$ can be set such that they provide a rectangle with four red vertices. Comment. The statement is false for squares, i.e. in the case $a=b$. If strips $S_{2 k a}, S_{2 k a+1}, \ldots$, $S_{(2 k+1) a-1}$ are red, and strips $S_{(2 k+1) a}, S_{(2 k+1) a+1}, \ldots, S_{(2 k+2) a-1}$ are blue for every integer $k$, then each square of size $a \times a$ has at least one red and at least one blue vertex as well.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In the Cartesian coordinate plane define the strip $S_{n}=\{(x, y) \mid n \leq x<n+1\}$ for every integer $n$. Assume that each strip $S_{n}$ is colored either red or blue, and let $a$ and $b$ be two distinct positive integers. Prove that there exists a rectangle with side lengths $a$ and $b$ such that its vertices have the same color. (Romania)
|
If $S_{n}$ and $S_{n+a}$ have the same color for some integer $n$, then we can choose the rectangle with vertices $(n, 0) \in S_{n},(n, b) \in S_{n},(n+a, 0) \in S_{n+a}$, and $(n+a, b) \in S_{n+a}$, and we are done. So it can be assumed that $S_{n}$ and $S_{n+a}$ have opposite colors for each $n$. Similarly, it also can be assumed that $S_{n}$ and $S_{n+b}$ have opposite colors. Then, by induction on $|p|+|q|$, we obtain that for arbitrary integers $p$ and $q$, strips $S_{n}$ and $S_{n+p a+q b}$ have the same color if $p+q$ is even, and these two strips have opposite colors if $p+q$ is odd. Let $d=\operatorname{gcd}(a, b), a_{1}=a / d$ and $b_{1}=b / d$. Apply the result above for $p=b_{1}$ and $q=-a_{1}$. The strips $S_{0}$ and $S_{0+b_{1} a-a_{1} b}$ are identical and therefore they have the same color. Hence, $a_{1}+b_{1}$ is even. By the construction, $a_{1}$ and $b_{1}$ are coprime, so this is possible only if both are odd. Without loss of generality, we can assume $a>b$. Then $a_{1}>b_{1} \geq 1$, so $a_{1} \geq 3$. Choose integers $k$ and $\ell$ such that $k a_{1}-\ell b_{1}=1$ and therefore $k a-\ell b=d$. Since $a_{1}$ and $b_{1}$ are odd, $k+\ell$ is odd as well. Hence, for every integer $n$, strips $S_{n}$ and $S_{n+k a-\ell b}=S_{n+d}$ have opposite colors. This also implies that the coloring is periodic with period $2 d$, i.e. strips $S_{n}$ and $S_{n+2 d}$ have the same color for every $n$.  Figure 1 We will construct the desired rectangle $A B C D$ with $A B=C D=a$ and $B C=A D=b$ in a position such that vertex $A$ lies on the $x$-axis, and the projection of side $A B$ onto the $x$-axis is of length $2 d$ (see Figure 1). This is possible since $a=a_{1} d>2 d$. The coordinates of the vertices will have the forms $$ A=(t, 0), \quad B=\left(t+2 d, y_{1}\right), \quad C=\left(u+2 d, y_{2}\right), \quad D=\left(u, y_{3}\right) . $$ Let $\varphi=\sqrt{a_{1}^{2}-4}$. By Pythagoras' theorem, $$ y_{1}=B B_{0}=\sqrt{a^{2}-4 d^{2}}=d \sqrt{a_{1}^{2}-4}=d \varphi \text {. } $$ So, by the similar triangles $A D D_{0}$ and $B A B_{0}$, we have the constraint $$ u-t=A D_{0}=\frac{A D}{A B} \cdot B B_{0}=\frac{b d}{a} \varphi $$ for numbers $t$ and $u$. Computing the numbers $y_{2}$ and $y_{3}$ is not required since they have no effect to the colors. Observe that the number $\varphi$ is irrational, because $\varphi^{2}$ is an integer, but $\varphi$ is not: $a_{1}>\varphi \geq$ $\sqrt{a_{1}^{2}-2 a_{1}+2}>a_{1}-1$. By the periodicity, points $A$ and $B$ have the same color; similarly, points $C$ and $D$ have the same color. Furthermore, these colors depend only on the values of $t$ and $u$. So it is sufficient to choose numbers $t$ and $u$ such that vertices $A$ and $D$ have the same color. Let $w$ be the largest positive integer such that there exist $w$ consecutive strips $S_{n_{0}}, S_{n_{0}+1}, \ldots$, $S_{n_{0}+w-1}$ with the same color, say red. (Since $S_{n_{0}+d}$ must be blue, we have $w \leq d$.) We will choose $t$ from the interval $\left(n_{0}, n_{0}+w\right)$.  Figure 2 Consider the interval $I=\left(n_{0}+\frac{b d}{a} \varphi, n_{0}+\frac{b d}{a} \varphi+w\right)$ on the $x$-axis (see Figure 2). Its length is $w$, and the end-points are irrational. Therefore, this interval intersects $w+1$ consecutive strips. Since at most $w$ consecutive strips may have the same color, interval $I$ must contain both red and blue points. Choose $u \in I$ such that the line $x=u$ is red and set $t=u-\frac{b d}{a} \varphi$, according to the constraint (1). Then $t \in\left(n_{0}, n_{0}+w\right)$ and $A=(t, 0)$ is red as well as $D=\left(u, y_{3}\right)$. Hence, variables $u$ and $t$ can be set such that they provide a rectangle with four red vertices. Comment. The statement is false for squares, i.e. in the case $a=b$. If strips $S_{2 k a}, S_{2 k a+1}, \ldots$, $S_{(2 k+1) a-1}$ are red, and strips $S_{(2 k+1) a}, S_{(2 k+1) a+1}, \ldots, S_{(2 k+2) a-1}$ are blue for every integer $k$, then each square of size $a \times a$ has at least one red and at least one blue vertex as well.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6017efc3-ab53-577b-9807-ba26733e0b00
| 23,660
|
In a mathematical competition some competitors are friends; friendship is always mutual. Call a group of competitors a clique if each two of them are friends. The number of members in a clique is called its size. It is known that the largest size of cliques is even. Prove that the competitors can be arranged in two rooms such that the largest size of cliques in one room is the same as the largest size of cliques in the other room. (Russia)
|
We present an algorithm to arrange the competitors. Let the two rooms be Room $A$ and Room B. We start with an initial arrangement, and then we modify it several times by sending one person to the other room. At any state of the algorithm, $A$ and $B$ denote the sets of the competitors in the rooms, and $c(A)$ and $c(B)$ denote the largest sizes of cliques in the rooms, respectively. Step 1. Let $M$ be one of the cliques of largest size, $|M|=2 m$. Send all members of $M$ to Room $A$ and all other competitors to Room B. Since $M$ is a clique of the largest size, we have $c(A)=|M| \geq c(B)$. Step 2. While $c(A)>c(B)$, send one person from Room $A$ to Room $B$.  Note that $c(A)>c(B)$ implies that Room $A$ is not empty. In each step, $c(A)$ decreases by one and $c(B)$ increases by at most one. So at the end we have $c(A) \leq c(B) \leq c(A)+1$. We also have $c(A)=|A| \geq m$ at the end. Otherwise we would have at least $m+1$ members of $M$ in Room $B$ and at most $m-1$ in Room $A$, implying $c(B)-c(A) \geq(m+1)-(m-1)=2$. Step 3. Let $k=c(A)$. If $c(B)=k$ then $S T O P$. If we reached $c(A)=c(B)=k$ then we have found the desired arrangement. In all other cases we have $c(B)=k+1$. From the estimate above we also know that $k=|A|=|A \cap M| \geq m$ and $|B \cap M| \leq m$. Step 4. If there exists a competitor $x \in B \cap M$ and a clique $C \subset B$ such that $|C|=k+1$ and $x \notin C$, then move $x$ to Room $A$ and $S T O P$.  After moving $x$ back to Room $A$, we will have $k+1$ members of $M$ in Room $A$, thus $c(A)=k+1$. Due to $x \notin C, c(B)=|C|$ is not decreased, and after this step we have $c(A)=c(B)=k+1$. If there is no such competitor $x$, then in Room $B$, all cliques of size $k+1$ contain $B \cap M$ as a subset. Step 5. While $c(B)=k+1$, choose a clique $C \subset B$ such that $|C|=k+1$ and move one member of $C \backslash M$ to Room $A$.  Note that $|C|=k+1>m \geq|B \cap M|$, so $C \backslash M$ cannot be empty. Every time we move a single person from Room $B$ to Room $A$, so $c(B)$ decreases by at most 1. Hence, at the end of this loop we have $c(B)=k$. In Room $A$ we have the clique $A \cap M$ with size $|A \cap M|=k$ thus $c(A) \geq k$. We prove that there is no clique of larger size there. Let $Q \subset A$ be an arbitrary clique. We show that $|Q| \leq k$.  In Room $A$, and specially in set $Q$, there can be two types of competitors: - Some members of $M$. Since $M$ is a clique, they are friends with all members of $B \cap M$. - Competitors which were moved to Room $A$ in Step 5. Each of them has been in a clique with $B \cap M$ so they are also friends with all members of $B \cap M$. Hence, all members of $Q$ are friends with all members of $B \cap M$. Sets $Q$ and $B \cap M$ are cliques themselves, so $Q \cup(B \cap M)$ is also a clique. Since $M$ is a clique of the largest size, $$ |M| \geq|Q \cup(B \cap M)|=|Q|+|B \cap M|=|Q|+|M|-|A \cap M| $$ therefore $$ |Q| \leq|A \cap M|=k $$ Finally, after Step 5 we have $c(A)=c(B)=k$. Comment. Obviously, the statement is false without the assumption that the largest clique size is even.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In a mathematical competition some competitors are friends; friendship is always mutual. Call a group of competitors a clique if each two of them are friends. The number of members in a clique is called its size. It is known that the largest size of cliques is even. Prove that the competitors can be arranged in two rooms such that the largest size of cliques in one room is the same as the largest size of cliques in the other room. (Russia)
|
We present an algorithm to arrange the competitors. Let the two rooms be Room $A$ and Room B. We start with an initial arrangement, and then we modify it several times by sending one person to the other room. At any state of the algorithm, $A$ and $B$ denote the sets of the competitors in the rooms, and $c(A)$ and $c(B)$ denote the largest sizes of cliques in the rooms, respectively. Step 1. Let $M$ be one of the cliques of largest size, $|M|=2 m$. Send all members of $M$ to Room $A$ and all other competitors to Room B. Since $M$ is a clique of the largest size, we have $c(A)=|M| \geq c(B)$. Step 2. While $c(A)>c(B)$, send one person from Room $A$ to Room $B$.  Note that $c(A)>c(B)$ implies that Room $A$ is not empty. In each step, $c(A)$ decreases by one and $c(B)$ increases by at most one. So at the end we have $c(A) \leq c(B) \leq c(A)+1$. We also have $c(A)=|A| \geq m$ at the end. Otherwise we would have at least $m+1$ members of $M$ in Room $B$ and at most $m-1$ in Room $A$, implying $c(B)-c(A) \geq(m+1)-(m-1)=2$. Step 3. Let $k=c(A)$. If $c(B)=k$ then $S T O P$. If we reached $c(A)=c(B)=k$ then we have found the desired arrangement. In all other cases we have $c(B)=k+1$. From the estimate above we also know that $k=|A|=|A \cap M| \geq m$ and $|B \cap M| \leq m$. Step 4. If there exists a competitor $x \in B \cap M$ and a clique $C \subset B$ such that $|C|=k+1$ and $x \notin C$, then move $x$ to Room $A$ and $S T O P$.  After moving $x$ back to Room $A$, we will have $k+1$ members of $M$ in Room $A$, thus $c(A)=k+1$. Due to $x \notin C, c(B)=|C|$ is not decreased, and after this step we have $c(A)=c(B)=k+1$. If there is no such competitor $x$, then in Room $B$, all cliques of size $k+1$ contain $B \cap M$ as a subset. Step 5. While $c(B)=k+1$, choose a clique $C \subset B$ such that $|C|=k+1$ and move one member of $C \backslash M$ to Room $A$.  Note that $|C|=k+1>m \geq|B \cap M|$, so $C \backslash M$ cannot be empty. Every time we move a single person from Room $B$ to Room $A$, so $c(B)$ decreases by at most 1. Hence, at the end of this loop we have $c(B)=k$. In Room $A$ we have the clique $A \cap M$ with size $|A \cap M|=k$ thus $c(A) \geq k$. We prove that there is no clique of larger size there. Let $Q \subset A$ be an arbitrary clique. We show that $|Q| \leq k$.  In Room $A$, and specially in set $Q$, there can be two types of competitors: - Some members of $M$. Since $M$ is a clique, they are friends with all members of $B \cap M$. - Competitors which were moved to Room $A$ in Step 5. Each of them has been in a clique with $B \cap M$ so they are also friends with all members of $B \cap M$. Hence, all members of $Q$ are friends with all members of $B \cap M$. Sets $Q$ and $B \cap M$ are cliques themselves, so $Q \cup(B \cap M)$ is also a clique. Since $M$ is a clique of the largest size, $$ |M| \geq|Q \cup(B \cap M)|=|Q|+|B \cap M|=|Q|+|M|-|A \cap M| $$ therefore $$ |Q| \leq|A \cap M|=k $$ Finally, after Step 5 we have $c(A)=c(B)=k$. Comment. Obviously, the statement is false without the assumption that the largest clique size is even.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
aae8ee72-dac1-5b08-8c13-762e101d28e5
| 23,663
|
Let $\alpha<\frac{3-\sqrt{5}}{2}$ be a positive real number. Prove that there exist positive integers $n$ and $p>\alpha \cdot 2^{n}$ for which one can select $2 p$ pairwise distinct subsets $S_{1}, \ldots, S_{p}, T_{1}, \ldots, T_{p}$ of the set $\{1,2, \ldots, n\}$ such that $S_{i} \cap T_{j} \neq \varnothing$ for all $1 \leq i, j \leq p$. (Austria)
|
Let $k$ and $m$ be positive integers (to be determined later) and set $n=k m$. Decompose the set $\{1,2, \ldots, n\}$ into $k$ disjoint subsets, each of size $m$; denote these subsets by $A_{1}, \ldots, A_{k}$. Define the following families of sets: $$ \begin{aligned} \mathcal{S} & =\left\{S \subset\{1,2, \ldots, n\}: \forall i S \cap A_{i} \neq \varnothing\right\} \\ \mathcal{T}_{1} & =\left\{T \subset\{1,2, \ldots, n\}: \quad \exists i A_{i} \subset T\right\}, \quad \mathcal{T}=\mathcal{T}_{1} \backslash \mathcal{S} . \end{aligned} $$ For each set $T \in \mathcal{T} \subset \mathcal{T}_{1}$, there exists an index $1 \leq i \leq k$ such that $A_{i} \subset T$. Then for all $S \in \mathcal{S}$, $S \cap T \supset S \cap A_{i} \neq \varnothing$. Hence, each $S \in \mathcal{S}$ and each $T \in \mathcal{T}$ have at least one common element. Below we show that the numbers $m$ and $k$ can be chosen such that $|\mathcal{S}|,|\mathcal{T}|>\alpha \cdot 2^{n}$. Then, choosing $p=\min \{|\mathcal{S}|,|\mathcal{T}|\}$, one can select the desired $2 p$ sets $S_{1}, \ldots, S_{p}$ and $T_{1}, \ldots, T_{p}$ from families $\mathcal{S}$ and $\mathcal{T}$, respectively. Since families $\mathcal{S}$ and $\mathcal{T}$ are disjoint, sets $S_{i}$ and $T_{j}$ will be pairwise distinct. To count the sets $S \in \mathcal{S}$, observe that each $A_{i}$ has $2^{m}-1$ nonempty subsets so we have $2^{m}-1$ choices for $S \cap A_{i}$. These intersections uniquely determine set $S$, so $$ |\mathcal{S}|=\left(2^{m}-1\right)^{k} $$ Similarly, if a set $H \subset\{1,2, \ldots, n\}$ does not contain a certain set $A_{i}$ then we have $2^{m}-1$ choices for $H \cap A_{i}$ : all subsets of $A_{i}$, except $A_{i}$ itself. Therefore, the complement of $\mathcal{T}_{1}$ contains $\left(2^{m}-1\right)^{k}$ sets and $$ \left|\mathcal{T}_{1}\right|=2^{k m}-\left(2^{m}-1\right)^{k} . $$ Next consider the family $\mathcal{S} \backslash \mathcal{T}_{1}$. If a set $S$ intersects all $A_{i}$ but does not contain any of them, then there exists $2^{m}-2$ possible values for each $S \cap A_{i}$ : all subsets of $A_{i}$ except $\varnothing$ and $A_{i}$. Therefore the number of such sets $S$ is $\left(2^{m}-2\right)^{k}$, so $$ \left|\mathcal{S} \backslash \mathcal{T}_{1}\right|=\left(2^{m}-2\right)^{k} $$ From (1), (2), and (3) we obtain $$ |\mathcal{T}|=\left|\mathcal{T}_{1}\right|-\left|\mathcal{S} \cap \mathcal{T}_{1}\right|=\left|\mathcal{T}_{1}\right|-\left(|\mathcal{S}|-\left|\mathcal{S} \backslash \mathcal{T}_{1}\right|\right)=2^{k m}-2\left(2^{m}-1\right)^{k}+\left(2^{m}-2\right)^{k} $$ Let $\delta=\frac{3-\sqrt{5}}{2}$ and $k=k(m)=\left[2^{m} \log \frac{1}{\delta}\right]$. Then $$ \lim _{m \rightarrow \infty} \frac{|\mathcal{S}|}{2^{k m}}=\lim _{m \rightarrow \infty}\left(1-\frac{1}{2^{m}}\right)^{k}=\exp \left(-\lim _{m \rightarrow \infty} \frac{k}{2^{m}}\right)=\delta $$ and similarly $$ \lim _{m \rightarrow \infty} \frac{|\mathcal{T}|}{2^{k m}}=1-2 \lim _{m \rightarrow \infty}\left(1-\frac{1}{2^{m}}\right)^{k}+\lim _{m \rightarrow \infty}\left(1-\frac{2}{2^{m}}\right)^{k}=1-2 \delta+\delta^{2}=\delta $$ Hence, if $m$ is sufficiently large then $\frac{|\mathcal{S}|}{2^{m k}}$ and $\frac{|\mathcal{T}|}{2^{m k}}$ are greater than $\alpha$ (since $\alpha<\delta$ ). So $|\mathcal{S}|,|\mathcal{T}|>\alpha \cdot 2^{m k}=\alpha \cdot 2^{n}$. Comment. It can be proved that the constant $\frac{3-\sqrt{5}}{2}$ is sharp. Actually, if $S_{1}, \ldots, S_{p}, T_{1}, \ldots, T_{p}$ are distinct subsets of $\{1,2, \ldots, n\}$ such that each $S_{i}$ intersects each $T_{j}$, then $p<\frac{3-\sqrt{5}}{2} \cdot 2^{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $\alpha<\frac{3-\sqrt{5}}{2}$ be a positive real number. Prove that there exist positive integers $n$ and $p>\alpha \cdot 2^{n}$ for which one can select $2 p$ pairwise distinct subsets $S_{1}, \ldots, S_{p}, T_{1}, \ldots, T_{p}$ of the set $\{1,2, \ldots, n\}$ such that $S_{i} \cap T_{j} \neq \varnothing$ for all $1 \leq i, j \leq p$. (Austria)
|
Let $k$ and $m$ be positive integers (to be determined later) and set $n=k m$. Decompose the set $\{1,2, \ldots, n\}$ into $k$ disjoint subsets, each of size $m$; denote these subsets by $A_{1}, \ldots, A_{k}$. Define the following families of sets: $$ \begin{aligned} \mathcal{S} & =\left\{S \subset\{1,2, \ldots, n\}: \forall i S \cap A_{i} \neq \varnothing\right\} \\ \mathcal{T}_{1} & =\left\{T \subset\{1,2, \ldots, n\}: \quad \exists i A_{i} \subset T\right\}, \quad \mathcal{T}=\mathcal{T}_{1} \backslash \mathcal{S} . \end{aligned} $$ For each set $T \in \mathcal{T} \subset \mathcal{T}_{1}$, there exists an index $1 \leq i \leq k$ such that $A_{i} \subset T$. Then for all $S \in \mathcal{S}$, $S \cap T \supset S \cap A_{i} \neq \varnothing$. Hence, each $S \in \mathcal{S}$ and each $T \in \mathcal{T}$ have at least one common element. Below we show that the numbers $m$ and $k$ can be chosen such that $|\mathcal{S}|,|\mathcal{T}|>\alpha \cdot 2^{n}$. Then, choosing $p=\min \{|\mathcal{S}|,|\mathcal{T}|\}$, one can select the desired $2 p$ sets $S_{1}, \ldots, S_{p}$ and $T_{1}, \ldots, T_{p}$ from families $\mathcal{S}$ and $\mathcal{T}$, respectively. Since families $\mathcal{S}$ and $\mathcal{T}$ are disjoint, sets $S_{i}$ and $T_{j}$ will be pairwise distinct. To count the sets $S \in \mathcal{S}$, observe that each $A_{i}$ has $2^{m}-1$ nonempty subsets so we have $2^{m}-1$ choices for $S \cap A_{i}$. These intersections uniquely determine set $S$, so $$ |\mathcal{S}|=\left(2^{m}-1\right)^{k} $$ Similarly, if a set $H \subset\{1,2, \ldots, n\}$ does not contain a certain set $A_{i}$ then we have $2^{m}-1$ choices for $H \cap A_{i}$ : all subsets of $A_{i}$, except $A_{i}$ itself. Therefore, the complement of $\mathcal{T}_{1}$ contains $\left(2^{m}-1\right)^{k}$ sets and $$ \left|\mathcal{T}_{1}\right|=2^{k m}-\left(2^{m}-1\right)^{k} . $$ Next consider the family $\mathcal{S} \backslash \mathcal{T}_{1}$. If a set $S$ intersects all $A_{i}$ but does not contain any of them, then there exists $2^{m}-2$ possible values for each $S \cap A_{i}$ : all subsets of $A_{i}$ except $\varnothing$ and $A_{i}$. Therefore the number of such sets $S$ is $\left(2^{m}-2\right)^{k}$, so $$ \left|\mathcal{S} \backslash \mathcal{T}_{1}\right|=\left(2^{m}-2\right)^{k} $$ From (1), (2), and (3) we obtain $$ |\mathcal{T}|=\left|\mathcal{T}_{1}\right|-\left|\mathcal{S} \cap \mathcal{T}_{1}\right|=\left|\mathcal{T}_{1}\right|-\left(|\mathcal{S}|-\left|\mathcal{S} \backslash \mathcal{T}_{1}\right|\right)=2^{k m}-2\left(2^{m}-1\right)^{k}+\left(2^{m}-2\right)^{k} $$ Let $\delta=\frac{3-\sqrt{5}}{2}$ and $k=k(m)=\left[2^{m} \log \frac{1}{\delta}\right]$. Then $$ \lim _{m \rightarrow \infty} \frac{|\mathcal{S}|}{2^{k m}}=\lim _{m \rightarrow \infty}\left(1-\frac{1}{2^{m}}\right)^{k}=\exp \left(-\lim _{m \rightarrow \infty} \frac{k}{2^{m}}\right)=\delta $$ and similarly $$ \lim _{m \rightarrow \infty} \frac{|\mathcal{T}|}{2^{k m}}=1-2 \lim _{m \rightarrow \infty}\left(1-\frac{1}{2^{m}}\right)^{k}+\lim _{m \rightarrow \infty}\left(1-\frac{2}{2^{m}}\right)^{k}=1-2 \delta+\delta^{2}=\delta $$ Hence, if $m$ is sufficiently large then $\frac{|\mathcal{S}|}{2^{m k}}$ and $\frac{|\mathcal{T}|}{2^{m k}}$ are greater than $\alpha$ (since $\alpha<\delta$ ). So $|\mathcal{S}|,|\mathcal{T}|>\alpha \cdot 2^{m k}=\alpha \cdot 2^{n}$. Comment. It can be proved that the constant $\frac{3-\sqrt{5}}{2}$ is sharp. Actually, if $S_{1}, \ldots, S_{p}, T_{1}, \ldots, T_{p}$ are distinct subsets of $\{1,2, \ldots, n\}$ such that each $S_{i}$ intersects each $T_{j}$, then $p<\frac{3-\sqrt{5}}{2} \cdot 2^{n}$.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8951a9fb-0f6d-59a4-8dea-a85cec925e26
| 23,666
|
In triangle $A B C$, the angle bisector at vertex $C$ intersects the circumcircle and the perpendicular bisectors of sides $B C$ and $C A$ at points $R, P$, and $Q$, respectively. The midpoints of $B C$ and $C A$ are $S$ and $T$, respectively. Prove that triangles $R Q T$ and $R P S$ have the same area. (Czech Republic)
|
If $A C=B C$ then triangle $A B C$ is isosceles, triangles $R Q T$ and $R P S$ are symmetric about the bisector $C R$ and the statement is trivial. If $A C \neq B C$ then it can be assumed without loss of generality that $A C<B C$.  Denote the circumcenter by $O$. The right triangles $C T Q$ and $C S P$ have equal angles at vertex $C$, so they are similar, $\angle C P S=\angle C Q T=\angle O Q P$ and $$ \frac{Q T}{P S}=\frac{C Q}{C P} $$ Let $\ell$ be the perpendicular bisector of chord $C R$; of course, $\ell$ passes through the circumcenter $O$. Due to the equal angles at $P$ and $Q$, triangle $O P Q$ is isosceles with $O P=O Q$. Then line $\ell$ is the axis of symmetry in this triangle as well. Therefore, points $P$ and $Q$ lie symmetrically on line segment $C R$, $$ R P=C Q \quad \text { and } \quad R Q=C P $$ Triangles $R Q T$ and $R P S$ have equal angles at vertices $Q$ and $P$, respectively. Then $$ \frac{\operatorname{area}(R Q T)}{\operatorname{area}(R P S)}=\frac{\frac{1}{2} \cdot R Q \cdot Q T \cdot \sin \angle R Q T}{\frac{1}{2} \cdot R P \cdot P S \cdot \sin \angle R P S}=\frac{R Q}{R P} \cdot \frac{Q T}{P S} $$ Substituting (1) and (2), $$ \frac{\operatorname{area}(R Q T)}{\operatorname{area}(R P S)}=\frac{R Q}{R P} \cdot \frac{Q T}{P S}=\frac{C P}{C Q} \cdot \frac{C Q}{C P}=1 $$ Hence, $\operatorname{area}(R Q T)=\operatorname{area}(R S P)$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, the angle bisector at vertex $C$ intersects the circumcircle and the perpendicular bisectors of sides $B C$ and $C A$ at points $R, P$, and $Q$, respectively. The midpoints of $B C$ and $C A$ are $S$ and $T$, respectively. Prove that triangles $R Q T$ and $R P S$ have the same area. (Czech Republic)
|
If $A C=B C$ then triangle $A B C$ is isosceles, triangles $R Q T$ and $R P S$ are symmetric about the bisector $C R$ and the statement is trivial. If $A C \neq B C$ then it can be assumed without loss of generality that $A C<B C$.  Denote the circumcenter by $O$. The right triangles $C T Q$ and $C S P$ have equal angles at vertex $C$, so they are similar, $\angle C P S=\angle C Q T=\angle O Q P$ and $$ \frac{Q T}{P S}=\frac{C Q}{C P} $$ Let $\ell$ be the perpendicular bisector of chord $C R$; of course, $\ell$ passes through the circumcenter $O$. Due to the equal angles at $P$ and $Q$, triangle $O P Q$ is isosceles with $O P=O Q$. Then line $\ell$ is the axis of symmetry in this triangle as well. Therefore, points $P$ and $Q$ lie symmetrically on line segment $C R$, $$ R P=C Q \quad \text { and } \quad R Q=C P $$ Triangles $R Q T$ and $R P S$ have equal angles at vertices $Q$ and $P$, respectively. Then $$ \frac{\operatorname{area}(R Q T)}{\operatorname{area}(R P S)}=\frac{\frac{1}{2} \cdot R Q \cdot Q T \cdot \sin \angle R Q T}{\frac{1}{2} \cdot R P \cdot P S \cdot \sin \angle R P S}=\frac{R Q}{R P} \cdot \frac{Q T}{P S} $$ Substituting (1) and (2), $$ \frac{\operatorname{area}(R Q T)}{\operatorname{area}(R P S)}=\frac{R Q}{R P} \cdot \frac{Q T}{P S}=\frac{C P}{C Q} \cdot \frac{C Q}{C P}=1 $$ Hence, $\operatorname{area}(R Q T)=\operatorname{area}(R S P)$.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f32b987e-aa44-514a-b730-6c3a8cda4d17
| 23,671
|
In triangle $A B C$, the angle bisector at vertex $C$ intersects the circumcircle and the perpendicular bisectors of sides $B C$ and $C A$ at points $R, P$, and $Q$, respectively. The midpoints of $B C$ and $C A$ are $S$ and $T$, respectively. Prove that triangles $R Q T$ and $R P S$ have the same area. (Czech Republic)
|
Assume again $A C<B C$. Denote the circumcenter by $O$, and let $\gamma$ be the angle at $C$. Similarly to the first solution, from right triangles $C T Q$ and $C S P$ we obtain that $\angle O P Q=\angle O Q P=90^{\circ}-\frac{\gamma}{2}$. Then triangle $O P Q$ is isosceles, $O P=O Q$ and moreover $\angle P O Q=\gamma$. As is well-known, point $R$ is the midpoint of $\operatorname{arc} A B$ and $\angle R O A=\angle B O R=\gamma$.  Consider the rotation around point $O$ by angle $\gamma$. This transform moves $A$ to $R, R$ to $B$ and $Q$ to $P$; hence triangles $R Q A$ and $B P R$ are congruent and they have the same area. Triangles $R Q T$ and $R Q A$ have $R Q$ as a common side, so the ratio between their areas is $$ \frac{\operatorname{area}(R Q T)}{\operatorname{area}(R Q A)}=\frac{d(T, C R)}{d(A, C R)}=\frac{C T}{C A}=\frac{1}{2} $$ $(d(X, Y Z)$ denotes the distance between point $X$ and line $Y Z)$. It can be obtained similarly that $$ \frac{\operatorname{area}(R P S)}{\operatorname{area}(B P R)}=\frac{C S}{C B}=\frac{1}{2} $$ Now the proof can be completed as $$ \operatorname{area}(R Q T)=\frac{1}{2} \operatorname{area}(R Q A)=\frac{1}{2} \operatorname{area}(B P R)=\operatorname{area}(R P S) $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, the angle bisector at vertex $C$ intersects the circumcircle and the perpendicular bisectors of sides $B C$ and $C A$ at points $R, P$, and $Q$, respectively. The midpoints of $B C$ and $C A$ are $S$ and $T$, respectively. Prove that triangles $R Q T$ and $R P S$ have the same area. (Czech Republic)
|
Assume again $A C<B C$. Denote the circumcenter by $O$, and let $\gamma$ be the angle at $C$. Similarly to the first solution, from right triangles $C T Q$ and $C S P$ we obtain that $\angle O P Q=\angle O Q P=90^{\circ}-\frac{\gamma}{2}$. Then triangle $O P Q$ is isosceles, $O P=O Q$ and moreover $\angle P O Q=\gamma$. As is well-known, point $R$ is the midpoint of $\operatorname{arc} A B$ and $\angle R O A=\angle B O R=\gamma$.  Consider the rotation around point $O$ by angle $\gamma$. This transform moves $A$ to $R, R$ to $B$ and $Q$ to $P$; hence triangles $R Q A$ and $B P R$ are congruent and they have the same area. Triangles $R Q T$ and $R Q A$ have $R Q$ as a common side, so the ratio between their areas is $$ \frac{\operatorname{area}(R Q T)}{\operatorname{area}(R Q A)}=\frac{d(T, C R)}{d(A, C R)}=\frac{C T}{C A}=\frac{1}{2} $$ $(d(X, Y Z)$ denotes the distance between point $X$ and line $Y Z)$. It can be obtained similarly that $$ \frac{\operatorname{area}(R P S)}{\operatorname{area}(B P R)}=\frac{C S}{C B}=\frac{1}{2} $$ Now the proof can be completed as $$ \operatorname{area}(R Q T)=\frac{1}{2} \operatorname{area}(R Q A)=\frac{1}{2} \operatorname{area}(B P R)=\operatorname{area}(R P S) $$
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f32b987e-aa44-514a-b730-6c3a8cda4d17
| 23,671
|
Given an isosceles triangle $A B C$ with $A B=A C$. The midpoint of side $B C$ is denoted by $M$. Let $X$ be a variable point on the shorter arc $M A$ of the circumcircle of triangle $A B M$. Let $T$ be the point in the angle domain $B M A$, for which $\angle T M X=90^{\circ}$ and $T X=B X$. Prove that $\angle M T B-\angle C T M$ does not depend on $X$. (Canada)
|
Let $N$ be the midpoint of segment $B T$ (see Figure 1). Line $X N$ is the axis of symmetry in the isosceles triangle $B X T$, thus $\angle T N X=90^{\circ}$ and $\angle B X N=\angle N X T$. Moreover, in triangle $B C T$, line $M N$ is the midline parallel to $C T$; hence $\angle C T M=\angle N M T$. Due to the right angles at points $M$ and $N$, these points lie on the circle with diameter $X T$. Therefore, $$ \angle M T B=\angle M T N=\angle M X N \quad \text { and } \quad \angle C T M=\angle N M T=\angle N X T=\angle B X N $$ Hence $$ \angle M T B-\angle C T M=\angle M X N-\angle B X N=\angle M X B=\angle M A B $$ which does not depend on $X$.  Figure 1  Figure 2
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given an isosceles triangle $A B C$ with $A B=A C$. The midpoint of side $B C$ is denoted by $M$. Let $X$ be a variable point on the shorter arc $M A$ of the circumcircle of triangle $A B M$. Let $T$ be the point in the angle domain $B M A$, for which $\angle T M X=90^{\circ}$ and $T X=B X$. Prove that $\angle M T B-\angle C T M$ does not depend on $X$. (Canada)
|
Let $N$ be the midpoint of segment $B T$ (see Figure 1). Line $X N$ is the axis of symmetry in the isosceles triangle $B X T$, thus $\angle T N X=90^{\circ}$ and $\angle B X N=\angle N X T$. Moreover, in triangle $B C T$, line $M N$ is the midline parallel to $C T$; hence $\angle C T M=\angle N M T$. Due to the right angles at points $M$ and $N$, these points lie on the circle with diameter $X T$. Therefore, $$ \angle M T B=\angle M T N=\angle M X N \quad \text { and } \quad \angle C T M=\angle N M T=\angle N X T=\angle B X N $$ Hence $$ \angle M T B-\angle C T M=\angle M X N-\angle B X N=\angle M X B=\angle M A B $$ which does not depend on $X$.  Figure 1  Figure 2
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f0d4cc4a-aa60-57a1-89bd-b15906c75e61
| 23,674
|
The diagonals of a trapezoid $A B C D$ intersect at point $P$. Point $Q$ lies between the parallel lines $B C$ and $A D$ such that $\angle A Q D=\angle C Q B$, and line $C D$ separates points $P$ and $Q$. Prove that $\angle B Q P=\angle D A Q$. (Ukraine)
|
Let $t=\frac{A D}{B C}$. Consider the homothety $h$ with center $P$ and scale $-t$. Triangles $P D A$ and $P B C$ are similar with ratio $t$, hence $h(B)=D$ and $h(C)=A$.  Let $Q^{\prime}=h(Q)$ (see Figure 1). Then points $Q, P$ and $Q^{\prime}$ are obviously collinear. Points $Q$ and $P$ lie on the same side of $A D$, as well as on the same side of $B C$; hence $Q^{\prime}$ and $P$ are also on the same side of $h(B C)=A D$, and therefore $Q$ and $Q^{\prime}$ are on the same side of $A D$. Moreover, points $Q$ and $C$ are on the same side of $B D$, while $Q^{\prime}$ and $A$ are on the opposite side (see Figure above). By the homothety, $\angle A Q^{\prime} D=\angle C Q B=\angle A Q D$, hence quadrilateral $A Q^{\prime} Q D$ is cyclic. Then $$ \angle D A Q=\angle D Q^{\prime} Q=\angle D Q^{\prime} P=\angle B Q P $$ (the latter equality is valid by the homothety again). Comment. The statement of the problem is a limit case of the following result. In an arbitrary quadrilateral $A B C D$, let $P=A C \cap B D, I=A D \cap B C$, and let $Q$ be an arbitrary point which is not collinear with any two of points $A, B, C, D$. Then $\angle A Q D=\angle C Q B$ if and only if $\angle B Q P=\angle I Q A$ (angles are oriented; see Figure below to the left). In the special case of the trapezoid, $I$ is an ideal point and $\angle D A Q=\angle I Q A=\angle B Q P$.  Let $a=Q A, b=Q B, c=Q C, d=Q D, i=Q I$ and $p=Q P$. Let line $Q A$ intersect lines $B C$ and $B D$ at points $U$ and $V$, respectively. On lines $B C$ and $B D$ we have $$ (a b c i)=(U B C I) \quad \text { and } \quad(b a d p)=(a b p d)=(V B P D) \text {. } $$ Projecting from $A$, we get $$ (a b c i)=(U B C I)=(V B P D)=(b a d p) . $$ Suppose that $\angle A Q D=\angle C Q B$. Let line $p^{\prime}$ be the reflection of line $i$ about the bisector of angle $A Q B$. Then by symmetry we have $\left(b a d p^{\prime}\right)=(a b c i)=(b a d p)$. Hence $p=p^{\prime}$, as desired. The converse statement can be proved analogously.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The diagonals of a trapezoid $A B C D$ intersect at point $P$. Point $Q$ lies between the parallel lines $B C$ and $A D$ such that $\angle A Q D=\angle C Q B$, and line $C D$ separates points $P$ and $Q$. Prove that $\angle B Q P=\angle D A Q$. (Ukraine)
|
Let $t=\frac{A D}{B C}$. Consider the homothety $h$ with center $P$ and scale $-t$. Triangles $P D A$ and $P B C$ are similar with ratio $t$, hence $h(B)=D$ and $h(C)=A$.  Let $Q^{\prime}=h(Q)$ (see Figure 1). Then points $Q, P$ and $Q^{\prime}$ are obviously collinear. Points $Q$ and $P$ lie on the same side of $A D$, as well as on the same side of $B C$; hence $Q^{\prime}$ and $P$ are also on the same side of $h(B C)=A D$, and therefore $Q$ and $Q^{\prime}$ are on the same side of $A D$. Moreover, points $Q$ and $C$ are on the same side of $B D$, while $Q^{\prime}$ and $A$ are on the opposite side (see Figure above). By the homothety, $\angle A Q^{\prime} D=\angle C Q B=\angle A Q D$, hence quadrilateral $A Q^{\prime} Q D$ is cyclic. Then $$ \angle D A Q=\angle D Q^{\prime} Q=\angle D Q^{\prime} P=\angle B Q P $$ (the latter equality is valid by the homothety again). Comment. The statement of the problem is a limit case of the following result. In an arbitrary quadrilateral $A B C D$, let $P=A C \cap B D, I=A D \cap B C$, and let $Q$ be an arbitrary point which is not collinear with any two of points $A, B, C, D$. Then $\angle A Q D=\angle C Q B$ if and only if $\angle B Q P=\angle I Q A$ (angles are oriented; see Figure below to the left). In the special case of the trapezoid, $I$ is an ideal point and $\angle D A Q=\angle I Q A=\angle B Q P$.  Let $a=Q A, b=Q B, c=Q C, d=Q D, i=Q I$ and $p=Q P$. Let line $Q A$ intersect lines $B C$ and $B D$ at points $U$ and $V$, respectively. On lines $B C$ and $B D$ we have $$ (a b c i)=(U B C I) \quad \text { and } \quad(b a d p)=(a b p d)=(V B P D) \text {. } $$ Projecting from $A$, we get $$ (a b c i)=(U B C I)=(V B P D)=(b a d p) . $$ Suppose that $\angle A Q D=\angle C Q B$. Let line $p^{\prime}$ be the reflection of line $i$ about the bisector of angle $A Q B$. Then by symmetry we have $\left(b a d p^{\prime}\right)=(a b c i)=(b a d p)$. Hence $p=p^{\prime}$, as desired. The converse statement can be proved analogously.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
1fb5a3fc-0e43-5a2f-a6fb-9d9463e7f40a
| 23,678
|
Consider five points $A, B, C, D, E$ such that $A B C D$ is a parallelogram and $B C E D$ is a cyclic quadrilateral. Let $\ell$ be a line passing through $A$, and let $\ell$ intersect segment $D C$ and line $B C$ at points $F$ and $G$, respectively. Suppose that $E F=E G=E C$. Prove that $\ell$ is the bisector of angle $D A B$. (Luxembourg)
|
If $C F=C G$, then $\angle F G C=\angle G F C$, hence $\angle G A B=\angle G F C=\angle F G C=\angle F A D$, and $\ell$ is a bisector. Assume that $C F<G C$. Let $E K$ and $E L$ be the altitudes in the isosceles triangles $E C F$ and $E G C$, respectively. Then in the right triangles $E K F$ and $E L C$ we have $E F=E C$ and $$ K F=\frac{C F}{2}<\frac{G C}{2}=L C, $$ So $$ K E=\sqrt{E F^{2}-K F^{2}}>\sqrt{E C^{2}-L C^{2}}=L E . $$ Since quadrilateral $B C E D$ is cyclic, we have $\angle E D C=\angle E B C$, so the right triangles $B E L$ and $D E K$ are similar. Then $K E>L E$ implies $D K>B L$, and hence $$ D F=D K-K F>B L-L C=B C=A D \text {. } $$ But triangles $A D F$ and $G C F$ are similar, so we have $1>\frac{A D}{D F}=\frac{G C}{C F}$; this contradicts our assumption. The case $C F>G C$ is completely similar. We consequently obtain the converse inequalities $K F>L C, K E<L E, D K<B L, D F<A D$, hence $1<\frac{A D}{D F}=\frac{G C}{C F} ;$ a contradiction. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider five points $A, B, C, D, E$ such that $A B C D$ is a parallelogram and $B C E D$ is a cyclic quadrilateral. Let $\ell$ be a line passing through $A$, and let $\ell$ intersect segment $D C$ and line $B C$ at points $F$ and $G$, respectively. Suppose that $E F=E G=E C$. Prove that $\ell$ is the bisector of angle $D A B$. (Luxembourg)
|
If $C F=C G$, then $\angle F G C=\angle G F C$, hence $\angle G A B=\angle G F C=\angle F G C=\angle F A D$, and $\ell$ is a bisector. Assume that $C F<G C$. Let $E K$ and $E L$ be the altitudes in the isosceles triangles $E C F$ and $E G C$, respectively. Then in the right triangles $E K F$ and $E L C$ we have $E F=E C$ and $$ K F=\frac{C F}{2}<\frac{G C}{2}=L C, $$ So $$ K E=\sqrt{E F^{2}-K F^{2}}>\sqrt{E C^{2}-L C^{2}}=L E . $$ Since quadrilateral $B C E D$ is cyclic, we have $\angle E D C=\angle E B C$, so the right triangles $B E L$ and $D E K$ are similar. Then $K E>L E$ implies $D K>B L$, and hence $$ D F=D K-K F>B L-L C=B C=A D \text {. } $$ But triangles $A D F$ and $G C F$ are similar, so we have $1>\frac{A D}{D F}=\frac{G C}{C F}$; this contradicts our assumption. The case $C F>G C$ is completely similar. We consequently obtain the converse inequalities $K F>L C, K E<L E, D K<B L, D F<A D$, hence $1<\frac{A D}{D F}=\frac{G C}{C F} ;$ a contradiction. 
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
485cbb7d-4b03-5d27-8024-d815e6f2740d
| 23,681
|
Let $A B C$ be a fixed triangle, and let $A_{1}, B_{1}, C_{1}$ be the midpoints of sides $B C, C A, A B$, respectively. Let $P$ be a variable point on the circumcircle. Let lines $P A_{1}, P B_{1}, P C_{1}$ meet the circumcircle again at $A^{\prime}, B^{\prime}, C^{\prime}$ respectively. Assume that the points $A, B, C, A^{\prime}, B^{\prime}, C^{\prime}$ are distinct, and lines $A A^{\prime}, B B^{\prime}, C C^{\prime}$ form a triangle. Prove that the area of this triangle does not depend on $P$. (United Kingdom)
|
Again, we prove that $\operatorname{area}\left(A_{0} B_{0} C_{0}\right)=\frac{1}{2} \operatorname{area}(A B C)$. We can assume that $P$ lies on arc $A C$. Mark a point $L$ on side $A C$ such that $\angle C B L=$ $\angle P B A$; then $\angle L B A=\angle C B A-\angle C B L=\angle C B A-\angle P B A=\angle C B P$. Note also that $\angle B A L=\angle B A C=\angle B P C$ and $\angle L C B=\angle A P B$. Hence, triangles $B A L$ and $B P C$ are similar, and so are triangles $L C B$ and $A P B$. Analogously, mark points $K$ and $M$ respectively on the extensions of sides $C B$ and $A B$ beyond point $B$, such that $\angle K A B=\angle C A P$ and $\angle B C M=\angle P C A$. For analogous reasons, $\angle K A C=\angle B A P$ and $\angle A C M=\angle P C B$. Hence $\triangle A B K \sim \triangle A P C \sim \triangle M B C, \triangle A C K \sim$ $\triangle A P B$, and $\triangle M A C \sim \triangle B P C$. From these similarities, we have $\angle C M B=\angle K A B=\angle C A P$, while we have seen that $\angle C A P=\angle C B P=\angle L B A$. Hence, $A K\|B L\| C M$.  Let line $C C^{\prime}$ intersect $B L$ at point $X$. Note that $\angle L C X=\angle A C C^{\prime}=\angle A P C^{\prime}=\angle A P C_{1}$, and $P C_{1}$ is a median in triangle $A P B$. Since triangles $A P B$ and $L C B$ are similar, $C X$ is a median in triangle $L C B$, and $X$ is a midpoint of $B L$. For the same reason, $A A^{\prime}$ passes through this midpoint, so $X=B_{0}$. Analogously, $A_{0}$ and $C_{0}$ are the midpoints of $A K$ and $C M$. Now, from $A A_{0} \| C C_{0}$, we have $$ \operatorname{area}\left(A_{0} B_{0} C_{0}\right)=\operatorname{area}\left(A C_{0} A_{0}\right)-\operatorname{area}\left(A B_{0} A_{0}\right)=\operatorname{area}\left(A C A_{0}\right)-\operatorname{area}\left(A B_{0} A_{0}\right)=\operatorname{area}\left(A C B_{0}\right) \text {. } $$ Finally, $$ \operatorname{area}\left(A_{0} B_{0} C_{0}\right)=\operatorname{area}\left(A C B_{0}\right)=\frac{1}{2} B_{0} L \cdot A C \sin A L B_{0}=\frac{1}{4} B L \cdot A C \sin A L B=\frac{1}{2} \operatorname{area}(A B C) . $$ Comment 1. The equality area $\left(A_{0} B_{0} C_{0}\right)=\operatorname{area}\left(A C B_{0}\right)$ in Solution 2 does not need to be proved since the following fact is frequently known. Suppose that the lines $K L$ and $M N$ are parallel, while the lines $K M$ and $L N$ intersect in a point $E$. Then $\operatorname{area}(K E N)=\operatorname{area}(M E L)$. Comment 2. It follows immediately from both solutions that $A A_{0}\left\|B B_{0}\right\| C C_{0}$. These lines pass through an ideal point which is isogonally conjugate to $P$. It is known that they are parallel to the Simson line of point $Q$ which is opposite to $P$ on the circumcircle. Comment 3. If $A=A^{\prime}$, then one can define the line $A A^{\prime}$ to be the tangent to the circumcircle at point $A$. Then the statement of the problem is also valid in this case.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a fixed triangle, and let $A_{1}, B_{1}, C_{1}$ be the midpoints of sides $B C, C A, A B$, respectively. Let $P$ be a variable point on the circumcircle. Let lines $P A_{1}, P B_{1}, P C_{1}$ meet the circumcircle again at $A^{\prime}, B^{\prime}, C^{\prime}$ respectively. Assume that the points $A, B, C, A^{\prime}, B^{\prime}, C^{\prime}$ are distinct, and lines $A A^{\prime}, B B^{\prime}, C C^{\prime}$ form a triangle. Prove that the area of this triangle does not depend on $P$. (United Kingdom)
|
Again, we prove that $\operatorname{area}\left(A_{0} B_{0} C_{0}\right)=\frac{1}{2} \operatorname{area}(A B C)$. We can assume that $P$ lies on arc $A C$. Mark a point $L$ on side $A C$ such that $\angle C B L=$ $\angle P B A$; then $\angle L B A=\angle C B A-\angle C B L=\angle C B A-\angle P B A=\angle C B P$. Note also that $\angle B A L=\angle B A C=\angle B P C$ and $\angle L C B=\angle A P B$. Hence, triangles $B A L$ and $B P C$ are similar, and so are triangles $L C B$ and $A P B$. Analogously, mark points $K$ and $M$ respectively on the extensions of sides $C B$ and $A B$ beyond point $B$, such that $\angle K A B=\angle C A P$ and $\angle B C M=\angle P C A$. For analogous reasons, $\angle K A C=\angle B A P$ and $\angle A C M=\angle P C B$. Hence $\triangle A B K \sim \triangle A P C \sim \triangle M B C, \triangle A C K \sim$ $\triangle A P B$, and $\triangle M A C \sim \triangle B P C$. From these similarities, we have $\angle C M B=\angle K A B=\angle C A P$, while we have seen that $\angle C A P=\angle C B P=\angle L B A$. Hence, $A K\|B L\| C M$.  Let line $C C^{\prime}$ intersect $B L$ at point $X$. Note that $\angle L C X=\angle A C C^{\prime}=\angle A P C^{\prime}=\angle A P C_{1}$, and $P C_{1}$ is a median in triangle $A P B$. Since triangles $A P B$ and $L C B$ are similar, $C X$ is a median in triangle $L C B$, and $X$ is a midpoint of $B L$. For the same reason, $A A^{\prime}$ passes through this midpoint, so $X=B_{0}$. Analogously, $A_{0}$ and $C_{0}$ are the midpoints of $A K$ and $C M$. Now, from $A A_{0} \| C C_{0}$, we have $$ \operatorname{area}\left(A_{0} B_{0} C_{0}\right)=\operatorname{area}\left(A C_{0} A_{0}\right)-\operatorname{area}\left(A B_{0} A_{0}\right)=\operatorname{area}\left(A C A_{0}\right)-\operatorname{area}\left(A B_{0} A_{0}\right)=\operatorname{area}\left(A C B_{0}\right) \text {. } $$ Finally, $$ \operatorname{area}\left(A_{0} B_{0} C_{0}\right)=\operatorname{area}\left(A C B_{0}\right)=\frac{1}{2} B_{0} L \cdot A C \sin A L B_{0}=\frac{1}{4} B L \cdot A C \sin A L B=\frac{1}{2} \operatorname{area}(A B C) . $$ Comment 1. The equality area $\left(A_{0} B_{0} C_{0}\right)=\operatorname{area}\left(A C B_{0}\right)$ in Solution 2 does not need to be proved since the following fact is frequently known. Suppose that the lines $K L$ and $M N$ are parallel, while the lines $K M$ and $L N$ intersect in a point $E$. Then $\operatorname{area}(K E N)=\operatorname{area}(M E L)$. Comment 2. It follows immediately from both solutions that $A A_{0}\left\|B B_{0}\right\| C C_{0}$. These lines pass through an ideal point which is isogonally conjugate to $P$. It is known that they are parallel to the Simson line of point $Q$ which is opposite to $P$ on the circumcircle. Comment 3. If $A=A^{\prime}$, then one can define the line $A A^{\prime}$ to be the tangent to the circumcircle at point $A$. Then the statement of the problem is also valid in this case.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c40be71c-354a-57c5-bdc4-f391ecb1f934
| 23,683
|
Given an acute triangle $A B C$ with angles $\alpha, \beta$ and $\gamma$ at vertices $A, B$ and $C$, respectively, such that $\beta>\gamma$. Point $I$ is the incenter, and $R$ is the circumradius. Point $D$ is the foot of the altitude from vertex $A$. Point $K$ lies on line $A D$ such that $A K=2 R$, and $D$ separates $A$ and $K$. Finally, lines $D I$ and $K I$ meet sides $A C$ and $B C$ at $E$ and $F$, respectively. Prove that if $I E=I F$ then $\beta \leq 3 \gamma$. (Iran)
|
We first prove that $$ \angle K I D=\frac{\beta-\gamma}{2} $$ even without the assumption that $I E=I F$. Then we will show that the statement of the problem is a consequence of this fact. Denote the circumcenter by $O$. On the circumcircle, let $P$ be the point opposite to $A$, and let the angle bisector $A I$ intersect the circle again at $M$. Since $A K=A P=2 R$, triangle $A K P$ is isosceles. It is known that $\angle B A D=\angle C A O$, hence $\angle D A I=\angle B A I-\angle B A D=\angle C A I-$ $\angle C A O=\angle O A I$, and $A M$ is the bisector line in triangle $A K P$. Therefore, points $K$ and $P$ are symmetrical about $A M$, and $\angle A M K=\angle A M P=90^{\circ}$. Thus, $M$ is the midpoint of $K P$, and $A M$ is the perpendicular bisector of $K P$.  Denote the perpendicular feet of incenter $I$ on lines $B C, A C$, and $A D$ by $A_{1}, B_{1}$, and $T$, respectively. Quadrilateral $D A_{1} I T$ is a rectangle, hence $T D=I A_{1}=I B_{1}$. Due to the right angles at $T$ and $B_{1}$, quadrilateral $A B_{1} I T$ is cyclic. Hence $\angle B_{1} T I=$ $\angle B_{1} A I=\angle C A M=\angle B A M=\angle B P M$ and $\angle I B_{1} T=\angle I A T=\angle M A K=\angle M A P=$ $\angle M B P$. Therefore, triangles $B_{1} T I$ and $B P M$ are similar and $\frac{I T}{I B_{1}}=\frac{M P}{M B}$. It is well-known that $M B=M C=M I$. Then right triangles $I T D$ and $K M I$ are also similar, because $\frac{I T}{T D}=\frac{I T}{I B_{1}}=\frac{M P}{M B}=\frac{K M}{M I}$. Hence, $\angle K I M=\angle I D T=\angle I D A$, and $$ \angle K I D=\angle M I D-\angle K I M=(\angle I A D+\angle I D A)-\angle I D A=\angle I A D . $$ Finally, from the right triangle $A D B$ we can compute $$ \angle K I D=\angle I A D=\angle I A B-\angle D A B=\frac{\alpha}{2}-\left(90^{\circ}-\beta\right)=\frac{\alpha}{2}-\frac{\alpha+\beta+\gamma}{2}+\beta=\frac{\beta-\gamma}{2} . $$ Now let us turn to the statement and suppose that $I E=I F$. Since $I A_{1}=I B_{1}$, the right triangles $I E B_{1}$ and $I F A_{1}$ are congruent and $\angle I E B_{1}=\angle I F A_{1}$. Since $\beta>\gamma, A_{1}$ lies in the interior of segment $C D$ and $F$ lies in the interior of $A_{1} D$. Hence, $\angle I F C$ is acute. Then two cases are possible depending on the order of points $A, C, B_{1}$ and $E$.  If point $E$ lies between $C$ and $B_{1}$ then $\angle I F C=\angle I E A$, hence quadrilateral $C E I F$ is cyclic and $\angle F C E=180^{\circ}-\angle E I F=\angle K I D$. By (1), in this case we obtain $\angle F C E=\gamma=\angle K I D=$ $\frac{\beta-\gamma}{2}$ and $\beta=3 \gamma$. Otherwise, if point $E$ lies between $A$ and $B_{1}$, quadrilateral $C E I F$ is a deltoid such that $\angle I E C=\angle I F C<90^{\circ}$. Then we have $\angle F C E>180^{\circ}-\angle E I F=\angle K I D$. Therefore, $\angle F C E=\gamma>\angle K I D=\frac{\beta-\gamma}{2}$ and $\beta<3 \gamma$. Comment 1. In the case when quadrilateral $C E I F$ is a deltoid, one can prove the desired inequality without using (1). Actually, from $\angle I E C=\angle I F C<90^{\circ}$ it follows that $\angle A D I=90^{\circ}-\angle E D C<$ $\angle A E D-\angle E D C=\gamma$. Since the incircle lies inside triangle $A B C$, we have $A D>2 r$ (here $r$ is the inradius), which implies $D T<T A$ and $D I<A I$; hence $\frac{\beta-\gamma}{2}=\angle I A D<\angle A D I<\gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given an acute triangle $A B C$ with angles $\alpha, \beta$ and $\gamma$ at vertices $A, B$ and $C$, respectively, such that $\beta>\gamma$. Point $I$ is the incenter, and $R$ is the circumradius. Point $D$ is the foot of the altitude from vertex $A$. Point $K$ lies on line $A D$ such that $A K=2 R$, and $D$ separates $A$ and $K$. Finally, lines $D I$ and $K I$ meet sides $A C$ and $B C$ at $E$ and $F$, respectively. Prove that if $I E=I F$ then $\beta \leq 3 \gamma$. (Iran)
|
We first prove that $$ \angle K I D=\frac{\beta-\gamma}{2} $$ even without the assumption that $I E=I F$. Then we will show that the statement of the problem is a consequence of this fact. Denote the circumcenter by $O$. On the circumcircle, let $P$ be the point opposite to $A$, and let the angle bisector $A I$ intersect the circle again at $M$. Since $A K=A P=2 R$, triangle $A K P$ is isosceles. It is known that $\angle B A D=\angle C A O$, hence $\angle D A I=\angle B A I-\angle B A D=\angle C A I-$ $\angle C A O=\angle O A I$, and $A M$ is the bisector line in triangle $A K P$. Therefore, points $K$ and $P$ are symmetrical about $A M$, and $\angle A M K=\angle A M P=90^{\circ}$. Thus, $M$ is the midpoint of $K P$, and $A M$ is the perpendicular bisector of $K P$.  Denote the perpendicular feet of incenter $I$ on lines $B C, A C$, and $A D$ by $A_{1}, B_{1}$, and $T$, respectively. Quadrilateral $D A_{1} I T$ is a rectangle, hence $T D=I A_{1}=I B_{1}$. Due to the right angles at $T$ and $B_{1}$, quadrilateral $A B_{1} I T$ is cyclic. Hence $\angle B_{1} T I=$ $\angle B_{1} A I=\angle C A M=\angle B A M=\angle B P M$ and $\angle I B_{1} T=\angle I A T=\angle M A K=\angle M A P=$ $\angle M B P$. Therefore, triangles $B_{1} T I$ and $B P M$ are similar and $\frac{I T}{I B_{1}}=\frac{M P}{M B}$. It is well-known that $M B=M C=M I$. Then right triangles $I T D$ and $K M I$ are also similar, because $\frac{I T}{T D}=\frac{I T}{I B_{1}}=\frac{M P}{M B}=\frac{K M}{M I}$. Hence, $\angle K I M=\angle I D T=\angle I D A$, and $$ \angle K I D=\angle M I D-\angle K I M=(\angle I A D+\angle I D A)-\angle I D A=\angle I A D . $$ Finally, from the right triangle $A D B$ we can compute $$ \angle K I D=\angle I A D=\angle I A B-\angle D A B=\frac{\alpha}{2}-\left(90^{\circ}-\beta\right)=\frac{\alpha}{2}-\frac{\alpha+\beta+\gamma}{2}+\beta=\frac{\beta-\gamma}{2} . $$ Now let us turn to the statement and suppose that $I E=I F$. Since $I A_{1}=I B_{1}$, the right triangles $I E B_{1}$ and $I F A_{1}$ are congruent and $\angle I E B_{1}=\angle I F A_{1}$. Since $\beta>\gamma, A_{1}$ lies in the interior of segment $C D$ and $F$ lies in the interior of $A_{1} D$. Hence, $\angle I F C$ is acute. Then two cases are possible depending on the order of points $A, C, B_{1}$ and $E$.  If point $E$ lies between $C$ and $B_{1}$ then $\angle I F C=\angle I E A$, hence quadrilateral $C E I F$ is cyclic and $\angle F C E=180^{\circ}-\angle E I F=\angle K I D$. By (1), in this case we obtain $\angle F C E=\gamma=\angle K I D=$ $\frac{\beta-\gamma}{2}$ and $\beta=3 \gamma$. Otherwise, if point $E$ lies between $A$ and $B_{1}$, quadrilateral $C E I F$ is a deltoid such that $\angle I E C=\angle I F C<90^{\circ}$. Then we have $\angle F C E>180^{\circ}-\angle E I F=\angle K I D$. Therefore, $\angle F C E=\gamma>\angle K I D=\frac{\beta-\gamma}{2}$ and $\beta<3 \gamma$. Comment 1. In the case when quadrilateral $C E I F$ is a deltoid, one can prove the desired inequality without using (1). Actually, from $\angle I E C=\angle I F C<90^{\circ}$ it follows that $\angle A D I=90^{\circ}-\angle E D C<$ $\angle A E D-\angle E D C=\gamma$. Since the incircle lies inside triangle $A B C$, we have $A D>2 r$ (here $r$ is the inradius), which implies $D T<T A$ and $D I<A I$; hence $\frac{\beta-\gamma}{2}=\angle I A D<\angle A D I<\gamma$.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
23b2bc7e-79b8-5d22-aa4d-d058e78bba68
| 23,690
|
Given an acute triangle $A B C$ with angles $\alpha, \beta$ and $\gamma$ at vertices $A, B$ and $C$, respectively, such that $\beta>\gamma$. Point $I$ is the incenter, and $R$ is the circumradius. Point $D$ is the foot of the altitude from vertex $A$. Point $K$ lies on line $A D$ such that $A K=2 R$, and $D$ separates $A$ and $K$. Finally, lines $D I$ and $K I$ meet sides $A C$ and $B C$ at $E$ and $F$, respectively. Prove that if $I E=I F$ then $\beta \leq 3 \gamma$. (Iran)
|
We give a different proof for (1). Then the solution can be finished in the same way as above. Define points $M$ and $P$ again; it can be proved in the same way that $A M$ is the perpendicular bisector of $K P$. Let $J$ be the center of the excircle touching side $B C$. It is well-known that points $B, C, I, J$ lie on a circle with center $M$; denote this circle by $\omega_{1}$. Let $B^{\prime}$ be the reflection of point $B$ about the angle bisector $A M$. By the symmetry, $B^{\prime}$ is the second intersection point of circle $\omega_{1}$ and line $A C$. Triangles $P B A$ and $K B^{\prime} A$ are symmetrical with respect to line $A M$, therefore $\angle K B^{\prime} A=\angle P B A=90^{\circ}$. By the right angles at $D$ and $B^{\prime}$, points $K, D, B^{\prime}, C$ are concyclic and $$ A D \cdot A K=A B^{\prime} \cdot A C . $$ From the cyclic quadrilateral $I J C B^{\prime}$ we obtain $A B^{\prime} \cdot A C=A I \cdot A J$ as well, therefore $$ A D \cdot A K=A B^{\prime} \cdot A C=A I \cdot A J $$ and points $I, J, K, D$ are also concyclic. Denote circle $I D K J$ by $\omega_{2}$.  Let $N$ be the point on circle $\omega_{2}$ which is opposite to $K$. Since $\angle N D K=90^{\circ}=\angle C D K$, point $N$ lies on line $B C$. Point $M$, being the center of circle $\omega_{1}$, is the midpoint of segment $I J$, and $K M$ is perpendicular to $I J$. Therefore, line $K M$ is the perpendicular bisector of $I J$ and hence it passes through $N$. From the cyclic quadrilateral $I D K N$ we obtain $$ \angle K I D=\angle K N D=90^{\circ}-\angle D K N=90^{\circ}-\angle A K M=\angle M A K=\frac{\beta-\gamma}{2} $$ Comment 2. The main difficulty in the solution is finding (1). If someone can guess this fact, he or she can compute it in a relatively short way. One possible way is finding and applying the relation $A I^{2}=2 R\left(h_{a}-2 r\right)$, where $h_{a}=A D$ is the length of the altitude. Using this fact, one can see that triangles $A K I$ and $A I D^{\prime}$ are similar (here $D^{\prime}$ is the point symmetrical to $D$ about $T$ ). Hence, $\angle M I K=\angle D D^{\prime} I=\angle I D D^{\prime}$. The proof can be finished as in Solution 1.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given an acute triangle $A B C$ with angles $\alpha, \beta$ and $\gamma$ at vertices $A, B$ and $C$, respectively, such that $\beta>\gamma$. Point $I$ is the incenter, and $R$ is the circumradius. Point $D$ is the foot of the altitude from vertex $A$. Point $K$ lies on line $A D$ such that $A K=2 R$, and $D$ separates $A$ and $K$. Finally, lines $D I$ and $K I$ meet sides $A C$ and $B C$ at $E$ and $F$, respectively. Prove that if $I E=I F$ then $\beta \leq 3 \gamma$. (Iran)
|
We give a different proof for (1). Then the solution can be finished in the same way as above. Define points $M$ and $P$ again; it can be proved in the same way that $A M$ is the perpendicular bisector of $K P$. Let $J$ be the center of the excircle touching side $B C$. It is well-known that points $B, C, I, J$ lie on a circle with center $M$; denote this circle by $\omega_{1}$. Let $B^{\prime}$ be the reflection of point $B$ about the angle bisector $A M$. By the symmetry, $B^{\prime}$ is the second intersection point of circle $\omega_{1}$ and line $A C$. Triangles $P B A$ and $K B^{\prime} A$ are symmetrical with respect to line $A M$, therefore $\angle K B^{\prime} A=\angle P B A=90^{\circ}$. By the right angles at $D$ and $B^{\prime}$, points $K, D, B^{\prime}, C$ are concyclic and $$ A D \cdot A K=A B^{\prime} \cdot A C . $$ From the cyclic quadrilateral $I J C B^{\prime}$ we obtain $A B^{\prime} \cdot A C=A I \cdot A J$ as well, therefore $$ A D \cdot A K=A B^{\prime} \cdot A C=A I \cdot A J $$ and points $I, J, K, D$ are also concyclic. Denote circle $I D K J$ by $\omega_{2}$.  Let $N$ be the point on circle $\omega_{2}$ which is opposite to $K$. Since $\angle N D K=90^{\circ}=\angle C D K$, point $N$ lies on line $B C$. Point $M$, being the center of circle $\omega_{1}$, is the midpoint of segment $I J$, and $K M$ is perpendicular to $I J$. Therefore, line $K M$ is the perpendicular bisector of $I J$ and hence it passes through $N$. From the cyclic quadrilateral $I D K N$ we obtain $$ \angle K I D=\angle K N D=90^{\circ}-\angle D K N=90^{\circ}-\angle A K M=\angle M A K=\frac{\beta-\gamma}{2} $$ Comment 2. The main difficulty in the solution is finding (1). If someone can guess this fact, he or she can compute it in a relatively short way. One possible way is finding and applying the relation $A I^{2}=2 R\left(h_{a}-2 r\right)$, where $h_{a}=A D$ is the length of the altitude. Using this fact, one can see that triangles $A K I$ and $A I D^{\prime}$ are similar (here $D^{\prime}$ is the point symmetrical to $D$ about $T$ ). Hence, $\angle M I K=\angle D D^{\prime} I=\angle I D D^{\prime}$. The proof can be finished as in Solution 1.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
23b2bc7e-79b8-5d22-aa4d-d058e78bba68
| 23,690
|
Point $P$ lies on side $A B$ of a convex quadrilateral $A B C D$. Let $\omega$ be the incircle of triangle $C P D$, and let $I$ be its incenter. Suppose that $\omega$ is tangent to the incircles of triangles $A P D$ and $B P C$ at points $K$ and $L$, respectively. Let lines $A C$ and $B D$ meet at $E$, and let lines $A K$ and $B L$ meet at $F$. Prove that points $E, I$, and $F$ are collinear. (Poland)
|
Let $\Omega$ be the circle tangent to segment $A B$ and to rays $A D$ and $B C$; let $J$ be its center. We prove that points $E$ and $F$ lie on line $I J$.  Denote the incircles of triangles $A D P$ and $B C P$ by $\omega_{A}$ and $\omega_{B}$. Let $h_{1}$ be the homothety with a negative scale taking $\omega$ to $\Omega$. Consider this homothety as the composition of two homotheties: one taking $\omega$ to $\omega_{A}$ (with a negative scale and center $K$ ), and another one taking $\omega_{A}$ to $\Omega$ (with a positive scale and center $A$ ). It is known that in such a case the three centers of homothety are collinear (this theorem is also referred to as the theorem on the three similitude centers). Hence, the center of $h_{1}$ lies on line $A K$. Analogously, it also lies on $B L$, so this center is $F$. Hence, $F$ lies on the line of centers of $\omega$ and $\Omega$, i. e. on $I J$ (if $I=J$, then $F=I$ as well, and the claim is obvious). Consider quadrilateral $A P C D$ and mark the equal segments of tangents to $\omega$ and $\omega_{A}$ (see the figure below to the left). Since circles $\omega$ and $\omega_{A}$ have a common point of tangency with $P D$, one can easily see that $A D+P C=A P+C D$. So, quadrilateral $A P C D$ is circumscribed; analogously, circumscribed is also quadrilateral $B C D P$. Let $\Omega_{A}$ and $\Omega_{B}$ respectively be their incircles.  Consider the homothety $h_{2}$ with a positive scale taking $\omega$ to $\Omega$. Consider $h_{2}$ as the composition of two homotheties: taking $\omega$ to $\Omega_{A}$ (with a positive scale and center $C$ ), and taking $\Omega_{A}$ to $\Omega$ (with a positive scale and center $A$ ), respectively. So the center of $h_{2}$ lies on line $A C$. By analogous reasons, it lies also on $B D$, hence this center is $E$. Thus, $E$ also lies on the line of centers $I J$, and the claim is proved. Comment. In both main steps of the solution, there can be several different reasonings for the same claims. For instance, one can mostly use Desargues' theorem instead of the three homotheties theorem. Namely, if $I_{A}$ and $I_{B}$ are the centers of $\omega_{A}$ and $\omega_{B}$, then lines $I_{A} I_{B}, K L$ and $A B$ are concurrent (by the theorem on three similitude centers applied to $\omega, \omega_{A}$ and $\omega_{B}$ ). Then Desargues' theorem, applied to triangles $A I_{A} K$ and $B I_{B} L$, yields that the points $J=A I_{A} \cap B I_{B}, I=I_{A} K \cap I_{B} L$ and $F=A K \cap B L$ are collinear. For the second step, let $J_{A}$ and $J_{B}$ be the centers of $\Omega_{A}$ and $\Omega_{B}$. Then lines $J_{A} J_{B}, A B$ and $C D$ are concurrent, since they appear to be the two common tangents and the line of centers of $\Omega_{A}$ and $\Omega_{B}$. Applying Desargues' theorem to triangles $A J_{A} C$ and $B J_{B} D$, we obtain that the points $J=A J_{A} \cap B J_{B}$, $I=C J_{A} \cap D J_{B}$ and $E=A C \cap B D$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Point $P$ lies on side $A B$ of a convex quadrilateral $A B C D$. Let $\omega$ be the incircle of triangle $C P D$, and let $I$ be its incenter. Suppose that $\omega$ is tangent to the incircles of triangles $A P D$ and $B P C$ at points $K$ and $L$, respectively. Let lines $A C$ and $B D$ meet at $E$, and let lines $A K$ and $B L$ meet at $F$. Prove that points $E, I$, and $F$ are collinear. (Poland)
|
Let $\Omega$ be the circle tangent to segment $A B$ and to rays $A D$ and $B C$; let $J$ be its center. We prove that points $E$ and $F$ lie on line $I J$.  Denote the incircles of triangles $A D P$ and $B C P$ by $\omega_{A}$ and $\omega_{B}$. Let $h_{1}$ be the homothety with a negative scale taking $\omega$ to $\Omega$. Consider this homothety as the composition of two homotheties: one taking $\omega$ to $\omega_{A}$ (with a negative scale and center $K$ ), and another one taking $\omega_{A}$ to $\Omega$ (with a positive scale and center $A$ ). It is known that in such a case the three centers of homothety are collinear (this theorem is also referred to as the theorem on the three similitude centers). Hence, the center of $h_{1}$ lies on line $A K$. Analogously, it also lies on $B L$, so this center is $F$. Hence, $F$ lies on the line of centers of $\omega$ and $\Omega$, i. e. on $I J$ (if $I=J$, then $F=I$ as well, and the claim is obvious). Consider quadrilateral $A P C D$ and mark the equal segments of tangents to $\omega$ and $\omega_{A}$ (see the figure below to the left). Since circles $\omega$ and $\omega_{A}$ have a common point of tangency with $P D$, one can easily see that $A D+P C=A P+C D$. So, quadrilateral $A P C D$ is circumscribed; analogously, circumscribed is also quadrilateral $B C D P$. Let $\Omega_{A}$ and $\Omega_{B}$ respectively be their incircles.  Consider the homothety $h_{2}$ with a positive scale taking $\omega$ to $\Omega$. Consider $h_{2}$ as the composition of two homotheties: taking $\omega$ to $\Omega_{A}$ (with a positive scale and center $C$ ), and taking $\Omega_{A}$ to $\Omega$ (with a positive scale and center $A$ ), respectively. So the center of $h_{2}$ lies on line $A C$. By analogous reasons, it lies also on $B D$, hence this center is $E$. Thus, $E$ also lies on the line of centers $I J$, and the claim is proved. Comment. In both main steps of the solution, there can be several different reasonings for the same claims. For instance, one can mostly use Desargues' theorem instead of the three homotheties theorem. Namely, if $I_{A}$ and $I_{B}$ are the centers of $\omega_{A}$ and $\omega_{B}$, then lines $I_{A} I_{B}, K L$ and $A B$ are concurrent (by the theorem on three similitude centers applied to $\omega, \omega_{A}$ and $\omega_{B}$ ). Then Desargues' theorem, applied to triangles $A I_{A} K$ and $B I_{B} L$, yields that the points $J=A I_{A} \cap B I_{B}, I=I_{A} K \cap I_{B} L$ and $F=A K \cap B L$ are collinear. For the second step, let $J_{A}$ and $J_{B}$ be the centers of $\Omega_{A}$ and $\Omega_{B}$. Then lines $J_{A} J_{B}, A B$ and $C D$ are concurrent, since they appear to be the two common tangents and the line of centers of $\Omega_{A}$ and $\Omega_{B}$. Applying Desargues' theorem to triangles $A J_{A} C$ and $B J_{B} D$, we obtain that the points $J=A J_{A} \cap B J_{B}$, $I=C J_{A} \cap D J_{B}$ and $E=A C \cap B D$ are collinear.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
60e4f026-4b2f-5d82-ac1b-bb49299d3dda
| 23,693
|
Let $b, n>1$ be integers. Suppose that for each $k>1$ there exists an integer $a_{k}$ such that $b-a_{k}^{n}$ is divisible by $k$. Prove that $b=A^{n}$ for some integer $A$. (Canada)
|
Let the prime factorization of $b$ be $b=p_{1}^{\alpha_{1}} \ldots p_{s}^{\alpha_{s}}$, where $p_{1}, \ldots, p_{s}$ are distinct primes. Our goal is to show that all exponents $\alpha_{i}$ are divisible by $n$, then we can set $A=p_{1}^{\alpha_{1} / n} \ldots p_{s}^{\alpha_{s} / n}$. Apply the condition for $k=b^{2}$. The number $b-a_{k}^{n}$ is divisible by $b^{2}$ and hence, for each $1 \leq i \leq s$, it is divisible by $p_{i}^{2 \alpha_{i}}>p_{i}^{\alpha_{i}}$ as well. Therefore $$ a_{k}^{n} \equiv b \equiv 0 \quad\left(\bmod p_{i}^{\alpha_{i}}\right) $$ and $$ a_{k}^{n} \equiv b \not \equiv 0 \quad\left(\bmod p_{i}^{\alpha_{i}+1}\right) $$ which implies that the largest power of $p_{i}$ dividing $a_{k}^{n}$ is $p_{i}^{\alpha_{i}}$. Since $a_{k}^{n}$ is a complete $n$th power, this implies that $\alpha_{i}$ is divisible by $n$. Comment. If $n=8$ and $b=16$, then for each prime $p$ there exists an integer $a_{p}$ such that $b-a_{p}^{n}$ is divisible by $p$. Actually, the congruency $x^{8}-16 \equiv 0(\bmod p)$ expands as $$ \left(x^{2}-2\right)\left(x^{2}+2\right)\left(x^{2}-2 x+2\right)\left(x^{2}+2 x+2\right) \equiv 0 \quad(\bmod p) $$ Hence, if -1 is a quadratic residue modulo $p$, then congruency $x^{2}+2 x+2=(x+1)^{2}+1 \equiv 0$ has a solution. Otherwise, one of congruencies $x^{2} \equiv 2$ and $x^{2} \equiv-2$ has a solution. Thus, the solution cannot work using only prime values of $k$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $b, n>1$ be integers. Suppose that for each $k>1$ there exists an integer $a_{k}$ such that $b-a_{k}^{n}$ is divisible by $k$. Prove that $b=A^{n}$ for some integer $A$. (Canada)
|
Let the prime factorization of $b$ be $b=p_{1}^{\alpha_{1}} \ldots p_{s}^{\alpha_{s}}$, where $p_{1}, \ldots, p_{s}$ are distinct primes. Our goal is to show that all exponents $\alpha_{i}$ are divisible by $n$, then we can set $A=p_{1}^{\alpha_{1} / n} \ldots p_{s}^{\alpha_{s} / n}$. Apply the condition for $k=b^{2}$. The number $b-a_{k}^{n}$ is divisible by $b^{2}$ and hence, for each $1 \leq i \leq s$, it is divisible by $p_{i}^{2 \alpha_{i}}>p_{i}^{\alpha_{i}}$ as well. Therefore $$ a_{k}^{n} \equiv b \equiv 0 \quad\left(\bmod p_{i}^{\alpha_{i}}\right) $$ and $$ a_{k}^{n} \equiv b \not \equiv 0 \quad\left(\bmod p_{i}^{\alpha_{i}+1}\right) $$ which implies that the largest power of $p_{i}$ dividing $a_{k}^{n}$ is $p_{i}^{\alpha_{i}}$. Since $a_{k}^{n}$ is a complete $n$th power, this implies that $\alpha_{i}$ is divisible by $n$. Comment. If $n=8$ and $b=16$, then for each prime $p$ there exists an integer $a_{p}$ such that $b-a_{p}^{n}$ is divisible by $p$. Actually, the congruency $x^{8}-16 \equiv 0(\bmod p)$ expands as $$ \left(x^{2}-2\right)\left(x^{2}+2\right)\left(x^{2}-2 x+2\right)\left(x^{2}+2 x+2\right) \equiv 0 \quad(\bmod p) $$ Hence, if -1 is a quadratic residue modulo $p$, then congruency $x^{2}+2 x+2=(x+1)^{2}+1 \equiv 0$ has a solution. Otherwise, one of congruencies $x^{2} \equiv 2$ and $x^{2} \equiv-2$ has a solution. Thus, the solution cannot work using only prime values of $k$.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8dd76b8e-9122-5168-9653-429eb9ef108f
| 23,698
|
Let $X$ be a set of 10000 integers, none of them is divisible by 47 . Prove that there exists a 2007-element subset $Y$ of $X$ such that $a-b+c-d+e$ is not divisible by 47 for any $a, b, c, d, e \in Y$. (Netherlands)
|
Call a set $M$ of integers good if $47 \nmid a-b+c-d+e$ for any $a, b, c, d, e \in M$. Consider the set $J=\{-9,-7,-5,-3,-1,1,3,5,7,9\}$. We claim that $J$ is good. Actually, for any $a, b, c, d, e \in J$ the number $a-b+c-d+e$ is odd and $$ -45=(-9)-9+(-9)-9+(-9) \leq a-b+c-d+e \leq 9-(-9)+9-(-9)+9=45 $$ But there is no odd number divisible by 47 between -45 and 45 . For any $k=1, \ldots, 46$ consider the set $$ A_{k}=\{x \in X \mid \exists j \in J: \quad k x \equiv j(\bmod 47)\} . $$ If $A_{k}$ is not good, then $47 \mid a-b+c-d+e$ for some $a, b, c, d, e \in A_{k}$, hence $47 \mid k a-k b+$ $k c-k d+k e$. But set $J$ contains numbers with the same residues modulo 47 , so $J$ also is not good. This is a contradiction; therefore each $A_{k}$ is a good subset of $X$. Then it suffices to prove that there exists a number $k$ such that $\left|A_{k}\right| \geq 2007$. Note that each $x \in X$ is contained in exactly 10 sets $A_{k}$. Then $$ \sum_{k=1}^{46}\left|A_{k}\right|=10|X|=100000 $$ hence for some value of $k$ we have $$ \left|A_{k}\right| \geq \frac{100000}{46}>2173>2007 . $$ This completes the proof. Comment. For the solution, it is essential to find a good set consisting of 10 different residues. Actually, consider a set $X$ containing almost uniform distribution of the nonzero residues (i. e. each residue occurs 217 or 218 times). Let $Y \subset X$ be a good subset containing 2007 elements. Then the set $K$ of all residues appearing in $Y$ contains not less than 10 residues, and obviously this set is good. On the other hand, there is no good set $K$ consisting of 11 different residues. The CauchyDavenport theorem claims that for any sets $A, B$ of residues modulo a prime $p$, $$ |A+B| \geq \min \{p,|A|+|B|-1\} . $$ Hence, if $|K| \geq 11$, then $|K+K| \geq 21,|K+K+K| \geq 31>47-|K+K|$, hence $\mid K+K+K+$ $(-K)+(-K) \mid=47$, and $0 \equiv a+c+e-b-d(\bmod 47)$ for some $a, b, c, d, e \in K$. From the same reasoning, one can see that a good set $K$ containing 10 residues should satisfy equalities $|K+K|=19=2|K|-1$ and $|K+K+K|=28=|K+K|+|K|-1$. It can be proved that in this case set $K$ consists of 10 residues forming an arithmetic progression. As an easy consequence, one obtains that set $K$ has the form $a J$ for some nonzero residue $a$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $X$ be a set of 10000 integers, none of them is divisible by 47 . Prove that there exists a 2007-element subset $Y$ of $X$ such that $a-b+c-d+e$ is not divisible by 47 for any $a, b, c, d, e \in Y$. (Netherlands)
|
Call a set $M$ of integers good if $47 \nmid a-b+c-d+e$ for any $a, b, c, d, e \in M$. Consider the set $J=\{-9,-7,-5,-3,-1,1,3,5,7,9\}$. We claim that $J$ is good. Actually, for any $a, b, c, d, e \in J$ the number $a-b+c-d+e$ is odd and $$ -45=(-9)-9+(-9)-9+(-9) \leq a-b+c-d+e \leq 9-(-9)+9-(-9)+9=45 $$ But there is no odd number divisible by 47 between -45 and 45 . For any $k=1, \ldots, 46$ consider the set $$ A_{k}=\{x \in X \mid \exists j \in J: \quad k x \equiv j(\bmod 47)\} . $$ If $A_{k}$ is not good, then $47 \mid a-b+c-d+e$ for some $a, b, c, d, e \in A_{k}$, hence $47 \mid k a-k b+$ $k c-k d+k e$. But set $J$ contains numbers with the same residues modulo 47 , so $J$ also is not good. This is a contradiction; therefore each $A_{k}$ is a good subset of $X$. Then it suffices to prove that there exists a number $k$ such that $\left|A_{k}\right| \geq 2007$. Note that each $x \in X$ is contained in exactly 10 sets $A_{k}$. Then $$ \sum_{k=1}^{46}\left|A_{k}\right|=10|X|=100000 $$ hence for some value of $k$ we have $$ \left|A_{k}\right| \geq \frac{100000}{46}>2173>2007 . $$ This completes the proof. Comment. For the solution, it is essential to find a good set consisting of 10 different residues. Actually, consider a set $X$ containing almost uniform distribution of the nonzero residues (i. e. each residue occurs 217 or 218 times). Let $Y \subset X$ be a good subset containing 2007 elements. Then the set $K$ of all residues appearing in $Y$ contains not less than 10 residues, and obviously this set is good. On the other hand, there is no good set $K$ consisting of 11 different residues. The CauchyDavenport theorem claims that for any sets $A, B$ of residues modulo a prime $p$, $$ |A+B| \geq \min \{p,|A|+|B|-1\} . $$ Hence, if $|K| \geq 11$, then $|K+K| \geq 21,|K+K+K| \geq 31>47-|K+K|$, hence $\mid K+K+K+$ $(-K)+(-K) \mid=47$, and $0 \equiv a+c+e-b-d(\bmod 47)$ for some $a, b, c, d, e \in K$. From the same reasoning, one can see that a good set $K$ containing 10 residues should satisfy equalities $|K+K|=19=2|K|-1$ and $|K+K+K|=28=|K+K|+|K|-1$. It can be proved that in this case set $K$ consists of 10 residues forming an arithmetic progression. As an easy consequence, one obtains that set $K$ has the form $a J$ for some nonzero residue $a$.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f3daa498-9e78-5ef7-b220-45949df4d386
| 23,700
|
For every integer $k \geq 2$, prove that $2^{3 k}$ divides the number $$ \left(\begin{array}{c} 2^{k+1} \\ 2^{k} \end{array}\right)-\left(\begin{array}{c} 2^{k} \\ 2^{k-1} \end{array}\right) $$ but $2^{3 k+1}$ does not. (Poland)
|
We use the notation $(2 n-1) ! !=1 \cdot 3 \cdots(2 n-1)$ and $(2 n) ! !=2 \cdot 4 \cdots(2 n)=2^{n} n$ ! for any positive integer $n$. Observe that $(2 n) !=(2 n) ! !(2 n-1) ! !=2^{n} n !(2 n-1) !$ !. For any positive integer $n$ we have $$ \begin{aligned} & \left(\begin{array}{l} 4 n \\ 2 n \end{array}\right)=\frac{(4 n) !}{(2 n) !^{2}}=\frac{2^{2 n}(2 n) !(4 n-1) ! !}{(2 n) !^{2}}=\frac{2^{2 n}}{(2 n) !}(4 n-1) ! ! \\ & \left(\begin{array}{c} 2 n \\ n \end{array}\right)=\frac{1}{(2 n) !}\left(\frac{(2 n) !}{n !}\right)^{2}=\frac{1}{(2 n) !}\left(2^{n}(2 n-1) ! !\right)^{2}=\frac{2^{2 n}}{(2 n) !}(2 n-1) ! !^{2} . \end{aligned} $$ Then expression (1) can be rewritten as follows: $$ \begin{aligned} \left(\begin{array}{c} 2^{k+1} \\ 2^{k} \end{array}\right) & -\left(\begin{array}{c} 2^{k} \\ 2^{k-1} \end{array}\right)=\frac{2^{2^{k}}}{\left(2^{k}\right) !}\left(2^{k+1}-1\right) ! !-\frac{2^{2^{k}}}{\left(2^{k}\right) !}\left(2^{k}-1\right) ! !^{2} \\ & =\frac{2^{2^{k}}\left(2^{k}-1\right) ! !}{\left(2^{k}\right) !} \cdot\left(\left(2^{k}+1\right)\left(2^{k}+3\right) \ldots\left(2^{k}+2^{k}-1\right)-\left(2^{k}-1\right)\left(2^{k}-3\right) \ldots\left(2^{k}-2^{k}+1\right)\right) . \end{aligned} $$ We compute the exponent of 2 in the prime decomposition of each factor (the first one is a rational number but not necessarily an integer; it is not important). First, we show by induction on $n$ that the exponent of 2 in $\left(2^{n}\right)$ ! is $2^{n}-1$. The base case $n=1$ is trivial. Suppose that $\left(2^{n}\right) !=2^{2^{n}-1}(2 d+1)$ for some integer $d$. Then we have $$ \left(2^{n+1}\right) !=2^{2^{n}}\left(2^{n}\right) !\left(2^{n+1}-1\right) ! !=2^{2^{n}} 2^{2^{n}-1} \cdot(2 d+1)\left(2^{n+1}-1\right) ! !=2^{2^{n+1}-1} \cdot(2 q+1) $$ for some integer $q$. This finishes the induction step. Hence, the exponent of 2 in the first factor in $(2)$ is $2^{k}-\left(2^{k}-1\right)=1$. The second factor in (2) can be considered as the value of the polynomial $$ P(x)=(x+1)(x+3) \ldots\left(x+2^{k}-1\right)-(x-1)(x-3) \ldots\left(x-2^{k}+1\right) . $$ at $x=2^{k}$. Now we collect some information about $P(x)$. Observe that $P(-x)=-P(x)$, since $k \geq 2$. So $P(x)$ is an odd function, and it has nonzero coefficients only at odd powers of $x$. Hence $P(x)=x^{3} Q(x)+c x$, where $Q(x)$ is a polynomial with integer coefficients. Compute the exponent of 2 in $c$. We have $$ \begin{aligned} c & =2\left(2^{k}-1\right) ! ! \sum_{i=1}^{2^{k-1}} \frac{1}{2 i-1}=\left(2^{k}-1\right) ! ! \sum_{i=1}^{2^{k-1}}\left(\frac{1}{2 i-1}+\frac{1}{2^{k}-2 i+1}\right) \\ & =\left(2^{k}-1\right) ! ! \sum_{i=1}^{2^{k-1}} \frac{2^{k}}{(2 i-1)\left(2^{k}-2 i+1\right)}=2^{k} \sum_{i=1}^{2^{k-1}} \frac{\left(2^{k}-1\right) ! !}{(2 i-1)\left(2^{k}-2 i+1\right)}=2^{k} S \end{aligned} $$ For any integer $i=1, \ldots, 2^{k-1}$, denote by $a_{2 i-1}$ the residue inverse to $2 i-1$ modulo $2^{k}$. Clearly, when $2 i-1$ runs through all odd residues, so does $a_{2 i-1}$, hence $$ \begin{aligned} & S=\sum_{i=1}^{2^{k-1}} \frac{\left(2^{k}-1\right) ! !}{(2 i-1)\left(2^{k}-2 i+1\right)} \equiv-\sum_{i=1}^{2^{k-1}} \frac{\left(2^{k}-1\right) ! !}{(2 i-1)^{2}} \equiv-\sum_{i=1}^{2^{k-1}}\left(2^{k}-1\right) ! ! a_{2 i-1}^{2} \\ &=-\left(2^{k}-1\right) ! ! \sum_{i=1}^{2^{k-1}}(2 i-1)^{2}=-\left(2^{k}-1\right) ! ! \frac{2^{k-1}\left(2^{2 k}-1\right)}{3} \quad\left(\bmod 2^{k}\right) . \end{aligned} $$ Therefore, the exponent of 2 in $S$ is $k-1$, so $c=2^{k} S=2^{2 k-1}(2 t+1)$ for some integer $t$. Finally we obtain that $$ P\left(2^{k}\right)=2^{3 k} Q\left(2^{k}\right)+2^{k} c=2^{3 k} Q\left(2^{k}\right)+2^{3 k-1}(2 t+1), $$ which is divisible exactly by $2^{3 k-1}$. Thus, the exponent of 2 in $(2)$ is $1+(3 k-1)=3 k$. Comment. The fact that (1) is divisible by $2^{2 k}$ is known; but it does not help in solving this problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For every integer $k \geq 2$, prove that $2^{3 k}$ divides the number $$ \left(\begin{array}{c} 2^{k+1} \\ 2^{k} \end{array}\right)-\left(\begin{array}{c} 2^{k} \\ 2^{k-1} \end{array}\right) $$ but $2^{3 k+1}$ does not. (Poland)
|
We use the notation $(2 n-1) ! !=1 \cdot 3 \cdots(2 n-1)$ and $(2 n) ! !=2 \cdot 4 \cdots(2 n)=2^{n} n$ ! for any positive integer $n$. Observe that $(2 n) !=(2 n) ! !(2 n-1) ! !=2^{n} n !(2 n-1) !$ !. For any positive integer $n$ we have $$ \begin{aligned} & \left(\begin{array}{l} 4 n \\ 2 n \end{array}\right)=\frac{(4 n) !}{(2 n) !^{2}}=\frac{2^{2 n}(2 n) !(4 n-1) ! !}{(2 n) !^{2}}=\frac{2^{2 n}}{(2 n) !}(4 n-1) ! ! \\ & \left(\begin{array}{c} 2 n \\ n \end{array}\right)=\frac{1}{(2 n) !}\left(\frac{(2 n) !}{n !}\right)^{2}=\frac{1}{(2 n) !}\left(2^{n}(2 n-1) ! !\right)^{2}=\frac{2^{2 n}}{(2 n) !}(2 n-1) ! !^{2} . \end{aligned} $$ Then expression (1) can be rewritten as follows: $$ \begin{aligned} \left(\begin{array}{c} 2^{k+1} \\ 2^{k} \end{array}\right) & -\left(\begin{array}{c} 2^{k} \\ 2^{k-1} \end{array}\right)=\frac{2^{2^{k}}}{\left(2^{k}\right) !}\left(2^{k+1}-1\right) ! !-\frac{2^{2^{k}}}{\left(2^{k}\right) !}\left(2^{k}-1\right) ! !^{2} \\ & =\frac{2^{2^{k}}\left(2^{k}-1\right) ! !}{\left(2^{k}\right) !} \cdot\left(\left(2^{k}+1\right)\left(2^{k}+3\right) \ldots\left(2^{k}+2^{k}-1\right)-\left(2^{k}-1\right)\left(2^{k}-3\right) \ldots\left(2^{k}-2^{k}+1\right)\right) . \end{aligned} $$ We compute the exponent of 2 in the prime decomposition of each factor (the first one is a rational number but not necessarily an integer; it is not important). First, we show by induction on $n$ that the exponent of 2 in $\left(2^{n}\right)$ ! is $2^{n}-1$. The base case $n=1$ is trivial. Suppose that $\left(2^{n}\right) !=2^{2^{n}-1}(2 d+1)$ for some integer $d$. Then we have $$ \left(2^{n+1}\right) !=2^{2^{n}}\left(2^{n}\right) !\left(2^{n+1}-1\right) ! !=2^{2^{n}} 2^{2^{n}-1} \cdot(2 d+1)\left(2^{n+1}-1\right) ! !=2^{2^{n+1}-1} \cdot(2 q+1) $$ for some integer $q$. This finishes the induction step. Hence, the exponent of 2 in the first factor in $(2)$ is $2^{k}-\left(2^{k}-1\right)=1$. The second factor in (2) can be considered as the value of the polynomial $$ P(x)=(x+1)(x+3) \ldots\left(x+2^{k}-1\right)-(x-1)(x-3) \ldots\left(x-2^{k}+1\right) . $$ at $x=2^{k}$. Now we collect some information about $P(x)$. Observe that $P(-x)=-P(x)$, since $k \geq 2$. So $P(x)$ is an odd function, and it has nonzero coefficients only at odd powers of $x$. Hence $P(x)=x^{3} Q(x)+c x$, where $Q(x)$ is a polynomial with integer coefficients. Compute the exponent of 2 in $c$. We have $$ \begin{aligned} c & =2\left(2^{k}-1\right) ! ! \sum_{i=1}^{2^{k-1}} \frac{1}{2 i-1}=\left(2^{k}-1\right) ! ! \sum_{i=1}^{2^{k-1}}\left(\frac{1}{2 i-1}+\frac{1}{2^{k}-2 i+1}\right) \\ & =\left(2^{k}-1\right) ! ! \sum_{i=1}^{2^{k-1}} \frac{2^{k}}{(2 i-1)\left(2^{k}-2 i+1\right)}=2^{k} \sum_{i=1}^{2^{k-1}} \frac{\left(2^{k}-1\right) ! !}{(2 i-1)\left(2^{k}-2 i+1\right)}=2^{k} S \end{aligned} $$ For any integer $i=1, \ldots, 2^{k-1}$, denote by $a_{2 i-1}$ the residue inverse to $2 i-1$ modulo $2^{k}$. Clearly, when $2 i-1$ runs through all odd residues, so does $a_{2 i-1}$, hence $$ \begin{aligned} & S=\sum_{i=1}^{2^{k-1}} \frac{\left(2^{k}-1\right) ! !}{(2 i-1)\left(2^{k}-2 i+1\right)} \equiv-\sum_{i=1}^{2^{k-1}} \frac{\left(2^{k}-1\right) ! !}{(2 i-1)^{2}} \equiv-\sum_{i=1}^{2^{k-1}}\left(2^{k}-1\right) ! ! a_{2 i-1}^{2} \\ &=-\left(2^{k}-1\right) ! ! \sum_{i=1}^{2^{k-1}}(2 i-1)^{2}=-\left(2^{k}-1\right) ! ! \frac{2^{k-1}\left(2^{2 k}-1\right)}{3} \quad\left(\bmod 2^{k}\right) . \end{aligned} $$ Therefore, the exponent of 2 in $S$ is $k-1$, so $c=2^{k} S=2^{2 k-1}(2 t+1)$ for some integer $t$. Finally we obtain that $$ P\left(2^{k}\right)=2^{3 k} Q\left(2^{k}\right)+2^{k} c=2^{3 k} Q\left(2^{k}\right)+2^{3 k-1}(2 t+1), $$ which is divisible exactly by $2^{3 k-1}$. Thus, the exponent of 2 in $(2)$ is $1+(3 k-1)=3 k$. Comment. The fact that (1) is divisible by $2^{2 k}$ is known; but it does not help in solving this problem.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
4b775f16-c3c8-5bbe-87cb-b5d0cb0bd57f
| 23,703
|
Let $k$ be a positive integer. Prove that the number $\left(4 k^{2}-1\right)^{2}$ has a positive divisor of the form $8 k n-1$ if and only if $k$ is even. (United Kingdom)
|
The statement follows from the following fact. Lemma. For arbitrary positive integers $x$ and $y$, the number $4 x y-1$ divides $\left(4 x^{2}-1\right)^{2}$ if and only if $x=y$. Proof. If $x=y$ then $4 x y-1=4 x^{2}-1$ obviously divides $\left(4 x^{2}-1\right)^{2}$ so it is sufficient to consider the opposite direction. Call a pair $(x, y)$ of positive integers bad if $4 x y-1$ divides $\left(4 x^{2}-1\right)^{2}$ but $x \neq y$. In order to prove that bad pairs do not exist, we present two properties of them which provide an infinite descent. Property (i). If $(x, y)$ is a bad pair and $x<y$ then there exists a positive integer $z<x$ such that $(x, z)$ is also bad. Let $r=\frac{\left(4 x^{2}-1\right)^{2}}{4 x y-1}$. Then $$ r=-r \cdot(-1) \equiv-r(4 x y-1)=-\left(4 x^{2}-1\right)^{2} \equiv-1 \quad(\bmod 4 x) $$ and $r=4 x z-1$ with some positive integer $z$. From $x<y$ we obtain that $$ 4 x z-1=\frac{\left(4 x^{2}-1\right)^{2}}{4 x y-1}<4 x^{2}-1 $$ and therefore $z<x$. By the construction, the number $4 x z-1$ is a divisor of $\left(4 x^{2}-1\right)^{2}$ so $(x, z)$ is a bad pair. Property (ii). If $(x, y)$ is a bad pair then $(y, x)$ is also bad. Since $1=1^{2} \equiv(4 x y)^{2}(\bmod 4 x y-1)$, we have $$ \left(4 y^{2}-1\right)^{2} \equiv\left(4 y^{2}-(4 x y)^{2}\right)^{2}=16 y^{4}\left(4 x^{2}-1\right)^{2} \equiv 0 \quad(\bmod 4 x y-1) $$ Hence, the number $4 x y-1$ divides $\left(4 y^{2}-1\right)^{2}$ as well. Now suppose that there exists at least one bad pair. Take a bad pair $(x, y)$ such that $2 x+y$ attains its smallest possible value. If $x<y$ then property (i) provides a bad pair $(x, z)$ with $z<y$ and thus $2 x+z<2 x+y$. Otherwise, if $y<x$, property (ii) yields that pair $(y, x)$ is also bad while $2 y+x<2 x+y$. Both cases contradict the assumption that $2 x+y$ is minimal; the Lemma is proved. To prove the problem statement, apply the Lemma for $x=k$ and $y=2 n$; the number $8 k n-1$ divides $\left(4 k^{2}-1\right)^{2}$ if and only if $k=2 n$. Hence, there is no such $n$ if $k$ is odd and $n=k / 2$ is the only solution if $k$ is even. Comment. The constant 4 in the Lemma can be replaced with an arbitrary integer greater than 1: if $a>1$ and $a x y-1$ divides $\left(a x^{2}-1\right)^{2}$ then $x=y$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $k$ be a positive integer. Prove that the number $\left(4 k^{2}-1\right)^{2}$ has a positive divisor of the form $8 k n-1$ if and only if $k$ is even. (United Kingdom)
|
The statement follows from the following fact. Lemma. For arbitrary positive integers $x$ and $y$, the number $4 x y-1$ divides $\left(4 x^{2}-1\right)^{2}$ if and only if $x=y$. Proof. If $x=y$ then $4 x y-1=4 x^{2}-1$ obviously divides $\left(4 x^{2}-1\right)^{2}$ so it is sufficient to consider the opposite direction. Call a pair $(x, y)$ of positive integers bad if $4 x y-1$ divides $\left(4 x^{2}-1\right)^{2}$ but $x \neq y$. In order to prove that bad pairs do not exist, we present two properties of them which provide an infinite descent. Property (i). If $(x, y)$ is a bad pair and $x<y$ then there exists a positive integer $z<x$ such that $(x, z)$ is also bad. Let $r=\frac{\left(4 x^{2}-1\right)^{2}}{4 x y-1}$. Then $$ r=-r \cdot(-1) \equiv-r(4 x y-1)=-\left(4 x^{2}-1\right)^{2} \equiv-1 \quad(\bmod 4 x) $$ and $r=4 x z-1$ with some positive integer $z$. From $x<y$ we obtain that $$ 4 x z-1=\frac{\left(4 x^{2}-1\right)^{2}}{4 x y-1}<4 x^{2}-1 $$ and therefore $z<x$. By the construction, the number $4 x z-1$ is a divisor of $\left(4 x^{2}-1\right)^{2}$ so $(x, z)$ is a bad pair. Property (ii). If $(x, y)$ is a bad pair then $(y, x)$ is also bad. Since $1=1^{2} \equiv(4 x y)^{2}(\bmod 4 x y-1)$, we have $$ \left(4 y^{2}-1\right)^{2} \equiv\left(4 y^{2}-(4 x y)^{2}\right)^{2}=16 y^{4}\left(4 x^{2}-1\right)^{2} \equiv 0 \quad(\bmod 4 x y-1) $$ Hence, the number $4 x y-1$ divides $\left(4 y^{2}-1\right)^{2}$ as well. Now suppose that there exists at least one bad pair. Take a bad pair $(x, y)$ such that $2 x+y$ attains its smallest possible value. If $x<y$ then property (i) provides a bad pair $(x, z)$ with $z<y$ and thus $2 x+z<2 x+y$. Otherwise, if $y<x$, property (ii) yields that pair $(y, x)$ is also bad while $2 y+x<2 x+y$. Both cases contradict the assumption that $2 x+y$ is minimal; the Lemma is proved. To prove the problem statement, apply the Lemma for $x=k$ and $y=2 n$; the number $8 k n-1$ divides $\left(4 k^{2}-1\right)^{2}$ if and only if $k=2 n$. Hence, there is no such $n$ if $k$ is odd and $n=k / 2$ is the only solution if $k$ is even. Comment. The constant 4 in the Lemma can be replaced with an arbitrary integer greater than 1: if $a>1$ and $a x y-1$ divides $\left(a x^{2}-1\right)^{2}$ then $x=y$.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7dbb043e-7757-5d68-a28e-5832d4e839eb
| 23,709
|
For a prime $p$ and a positive integer $n$, denote by $\nu_{p}(n)$ the exponent of $p$ in the prime factorization of $n$ !. Given a positive integer $d$ and a finite set $\left\{p_{1}, \ldots, p_{k}\right\}$ of primes. Show that there are infinitely many positive integers $n$ such that $d \mid \nu_{p_{i}}(n)$ for all $1 \leq i \leq k$. (India)
|
For arbitrary prime $p$ and positive integer $n$, denote by $\operatorname{ord}_{p}(n)$ the exponent of $p$ in $n$. Thus, $$ \nu_{p}(n)=\operatorname{ord}_{p}(n !)=\sum_{i=1}^{n} \operatorname{ord}_{p}(i) $$ Lemma. Let $p$ be a prime number, $q$ be a positive integer, $k$ and $r$ be positive integers such that $p^{k}>r$. Then $\nu_{p}\left(q p^{k}+r\right)=\nu_{p}\left(q p^{k}\right)+\nu_{p}(r)$. Proof. We claim that $\operatorname{ord}_{p}\left(q p^{k}+i\right)=\operatorname{ord}_{p}(i)$ for all $0<i<p^{k}$. Actually, if $d=\operatorname{ord}_{p}(i)$ then $d<k$, so $q p^{k}+i$ is divisible by $p^{d}$, but only the first term is divisible by $p^{d+1}$; hence the sum is not. Using this claim, we obtain $$ \nu_{p}\left(q p^{k}+r\right)=\sum_{i=1}^{q p^{k}} \operatorname{ord}_{p}(i)+\sum_{i=q p^{k}+1}^{q p^{k}+r} \operatorname{ord}_{p}(i)=\sum_{i=1}^{q p^{k}} \operatorname{ord}_{p}(i)+\sum_{i=1}^{r} \operatorname{ord}_{p}(i)=\nu_{p}\left(q p^{k}\right)+\nu_{p}(r) . $$ For any integer $a$, denote by $\bar{a}$ its residue modulo $d$. The addition of residues will also be performed modulo $d$, i. e. $\bar{a}+\bar{b}=\overline{a+b}$. For any positive integer $n$, let $f(n)=\left(f_{1}(n), \ldots, f_{k}(n)\right)$, where $f_{i}(n)=\overline{\nu_{p_{i}}(n)}$. Define the sequence $n_{1}=1, n_{\ell+1}=\left(p_{1} p_{2} \ldots p_{k}\right)^{n_{\ell}}$. We claim that $$ f\left(n_{\ell_{1}}+n_{\ell_{2}}+\ldots+n_{\ell_{m}}\right)=f\left(n_{\ell_{1}}\right)+f\left(n_{\ell_{2}}\right)+\ldots+f\left(n_{\ell_{m}}\right) $$ for any $\ell_{1}<\ell_{2}<\ldots<\ell_{m}$. (The addition of $k$-tuples is componentwise.) The base case $m=1$ is trivial. Suppose that $m>1$. By the construction of the sequence, $p_{i}^{n_{\ell_{1}}}$ divides $n_{\ell_{2}}+\ldots+n_{\ell_{m}}$; clearly, $p_{i}^{n_{\ell_{1}}}>n_{\ell_{1}}$ for all $1 \leq i \leq k$. Therefore the Lemma can be applied for $p=p_{i}, k=r=n_{\ell_{1}}$ and $q p^{k}=n_{\ell_{2}}+\ldots+n_{\ell_{m}}$ to obtain $$ f_{i}\left(n_{\ell_{1}}+n_{\ell_{2}}+\ldots+n_{\ell_{m}}\right)=f_{i}\left(n_{\ell_{1}}\right)+f_{i}\left(n_{\ell_{2}}+\ldots+n_{\ell_{m}}\right) \quad \text { for all } 1 \leq i \leq k $$ and hence $$ f\left(n_{\ell_{1}}+n_{\ell_{2}}+\ldots+n_{\ell_{m}}\right)=f\left(n_{\ell_{1}}\right)+f\left(n_{\ell_{2}}+\ldots+n_{\ell_{m}}\right)=f\left(n_{\ell_{1}}\right)+f\left(n_{\ell_{2}}\right)+\ldots+f\left(n_{\ell_{m}}\right) $$ by the induction hypothesis. Now consider the values $f\left(n_{1}\right), f\left(n_{2}\right), \ldots$ There exist finitely many possible values of $f$. Hence, there exists an infinite sequence of indices $\ell_{1}<\ell_{2}<\ldots$ such that $f\left(n_{\ell_{1}}\right)=f\left(n_{\ell_{2}}\right)=\ldots$ and thus $$ f\left(n_{\ell_{m+1}}+n_{\ell_{m+2}}+\ldots+n_{\ell_{m+d}}\right)=f\left(n_{\ell_{m+1}}\right)+\ldots+f\left(n_{\ell_{m+d}}\right)=d \cdot f\left(n_{\ell_{1}}\right)=(\overline{0}, \ldots, \overline{0}) $$ for all $m$. We have found infinitely many suitable numbers.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a prime $p$ and a positive integer $n$, denote by $\nu_{p}(n)$ the exponent of $p$ in the prime factorization of $n$ !. Given a positive integer $d$ and a finite set $\left\{p_{1}, \ldots, p_{k}\right\}$ of primes. Show that there are infinitely many positive integers $n$ such that $d \mid \nu_{p_{i}}(n)$ for all $1 \leq i \leq k$. (India)
|
For arbitrary prime $p$ and positive integer $n$, denote by $\operatorname{ord}_{p}(n)$ the exponent of $p$ in $n$. Thus, $$ \nu_{p}(n)=\operatorname{ord}_{p}(n !)=\sum_{i=1}^{n} \operatorname{ord}_{p}(i) $$ Lemma. Let $p$ be a prime number, $q$ be a positive integer, $k$ and $r$ be positive integers such that $p^{k}>r$. Then $\nu_{p}\left(q p^{k}+r\right)=\nu_{p}\left(q p^{k}\right)+\nu_{p}(r)$. Proof. We claim that $\operatorname{ord}_{p}\left(q p^{k}+i\right)=\operatorname{ord}_{p}(i)$ for all $0<i<p^{k}$. Actually, if $d=\operatorname{ord}_{p}(i)$ then $d<k$, so $q p^{k}+i$ is divisible by $p^{d}$, but only the first term is divisible by $p^{d+1}$; hence the sum is not. Using this claim, we obtain $$ \nu_{p}\left(q p^{k}+r\right)=\sum_{i=1}^{q p^{k}} \operatorname{ord}_{p}(i)+\sum_{i=q p^{k}+1}^{q p^{k}+r} \operatorname{ord}_{p}(i)=\sum_{i=1}^{q p^{k}} \operatorname{ord}_{p}(i)+\sum_{i=1}^{r} \operatorname{ord}_{p}(i)=\nu_{p}\left(q p^{k}\right)+\nu_{p}(r) . $$ For any integer $a$, denote by $\bar{a}$ its residue modulo $d$. The addition of residues will also be performed modulo $d$, i. e. $\bar{a}+\bar{b}=\overline{a+b}$. For any positive integer $n$, let $f(n)=\left(f_{1}(n), \ldots, f_{k}(n)\right)$, where $f_{i}(n)=\overline{\nu_{p_{i}}(n)}$. Define the sequence $n_{1}=1, n_{\ell+1}=\left(p_{1} p_{2} \ldots p_{k}\right)^{n_{\ell}}$. We claim that $$ f\left(n_{\ell_{1}}+n_{\ell_{2}}+\ldots+n_{\ell_{m}}\right)=f\left(n_{\ell_{1}}\right)+f\left(n_{\ell_{2}}\right)+\ldots+f\left(n_{\ell_{m}}\right) $$ for any $\ell_{1}<\ell_{2}<\ldots<\ell_{m}$. (The addition of $k$-tuples is componentwise.) The base case $m=1$ is trivial. Suppose that $m>1$. By the construction of the sequence, $p_{i}^{n_{\ell_{1}}}$ divides $n_{\ell_{2}}+\ldots+n_{\ell_{m}}$; clearly, $p_{i}^{n_{\ell_{1}}}>n_{\ell_{1}}$ for all $1 \leq i \leq k$. Therefore the Lemma can be applied for $p=p_{i}, k=r=n_{\ell_{1}}$ and $q p^{k}=n_{\ell_{2}}+\ldots+n_{\ell_{m}}$ to obtain $$ f_{i}\left(n_{\ell_{1}}+n_{\ell_{2}}+\ldots+n_{\ell_{m}}\right)=f_{i}\left(n_{\ell_{1}}\right)+f_{i}\left(n_{\ell_{2}}+\ldots+n_{\ell_{m}}\right) \quad \text { for all } 1 \leq i \leq k $$ and hence $$ f\left(n_{\ell_{1}}+n_{\ell_{2}}+\ldots+n_{\ell_{m}}\right)=f\left(n_{\ell_{1}}\right)+f\left(n_{\ell_{2}}+\ldots+n_{\ell_{m}}\right)=f\left(n_{\ell_{1}}\right)+f\left(n_{\ell_{2}}\right)+\ldots+f\left(n_{\ell_{m}}\right) $$ by the induction hypothesis. Now consider the values $f\left(n_{1}\right), f\left(n_{2}\right), \ldots$ There exist finitely many possible values of $f$. Hence, there exists an infinite sequence of indices $\ell_{1}<\ell_{2}<\ldots$ such that $f\left(n_{\ell_{1}}\right)=f\left(n_{\ell_{2}}\right)=\ldots$ and thus $$ f\left(n_{\ell_{m+1}}+n_{\ell_{m+2}}+\ldots+n_{\ell_{m+d}}\right)=f\left(n_{\ell_{m+1}}\right)+\ldots+f\left(n_{\ell_{m+d}}\right)=d \cdot f\left(n_{\ell_{1}}\right)=(\overline{0}, \ldots, \overline{0}) $$ for all $m$. We have found infinitely many suitable numbers.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
45642645-6c72-5b35-b2dd-b551600cbd6e
| 23,711
|
For a prime $p$ and a positive integer $n$, denote by $\nu_{p}(n)$ the exponent of $p$ in the prime factorization of $n$ !. Given a positive integer $d$ and a finite set $\left\{p_{1}, \ldots, p_{k}\right\}$ of primes. Show that there are infinitely many positive integers $n$ such that $d \mid \nu_{p_{i}}(n)$ for all $1 \leq i \leq k$. (India)
|
We use the same Lemma and definition of the function $f$. Let $S=\{f(n): n \in \mathbb{N}\}$. Obviously, set $S$ is finite. For every $s \in S$ choose the minimal $n_{s}$ such that $f\left(n_{s}\right)=s$. Denote $N=\max _{s \in S} n_{s}$. Moreover, let $g$ be an integer such that $p_{i}^{g}>N$ for each $i=1,2, \ldots, k$. Let $P=\left(p_{1} p_{2} \ldots p_{k}\right)^{g}$. We claim that $$ \{f(n) \mid n \in[m P, m P+N]\}=S $$ for every positive integer $m$. In particular, since $(\overline{0}, \ldots, \overline{0})=f(1) \in S$, it follows that for an arbitrary $m$ there exists $n \in[m P, m P+N]$ such that $f(n)=(\overline{0}, \ldots, \overline{0})$. So there are infinitely many suitable numbers. To prove (1), let $a_{i}=f_{i}(m P)$. Consider all numbers of the form $n_{m, s}=m P+n_{s}$ with $s=\left(s_{1}, \ldots, s_{k}\right) \in S$ (clearly, all $n_{m, s}$ belong to $[m P, m P+N]$ ). Since $n_{s} \leq N<p_{i}^{g}$ and $p_{i}^{g} \mid m P$, we can apply the Lemma for the values $p=p_{i}, r=n_{s}, k=g, q p^{k}=m P$ to obtain $$ f_{i}\left(n_{m, s}\right)=f_{i}(m P)+f_{i}\left(n_{s}\right)=a_{i}+s_{i} \text {; } $$ hence for distinct $s, t \in S$ we have $f\left(n_{m, s}\right) \neq f\left(n_{m, t}\right)$. Thus, the function $f$ attains at least $|S|$ distinct values in $[m P, m P+N]$. Since all these values belong to $S, f$ should attain all possible values in $[m P, m P+N]$. Comment. Both solutions can be extended to prove the following statements. Claim 1. For any $K$ there exist infinitely many $n$ divisible by $K$, such that $d \mid \nu_{p_{i}}(n)$ for each $i$. Claim 2. For any $s \in S$, there exist infinitely many $n \in \mathbb{N}$ such that $f(n)=s$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a prime $p$ and a positive integer $n$, denote by $\nu_{p}(n)$ the exponent of $p$ in the prime factorization of $n$ !. Given a positive integer $d$ and a finite set $\left\{p_{1}, \ldots, p_{k}\right\}$ of primes. Show that there are infinitely many positive integers $n$ such that $d \mid \nu_{p_{i}}(n)$ for all $1 \leq i \leq k$. (India)
|
We use the same Lemma and definition of the function $f$. Let $S=\{f(n): n \in \mathbb{N}\}$. Obviously, set $S$ is finite. For every $s \in S$ choose the minimal $n_{s}$ such that $f\left(n_{s}\right)=s$. Denote $N=\max _{s \in S} n_{s}$. Moreover, let $g$ be an integer such that $p_{i}^{g}>N$ for each $i=1,2, \ldots, k$. Let $P=\left(p_{1} p_{2} \ldots p_{k}\right)^{g}$. We claim that $$ \{f(n) \mid n \in[m P, m P+N]\}=S $$ for every positive integer $m$. In particular, since $(\overline{0}, \ldots, \overline{0})=f(1) \in S$, it follows that for an arbitrary $m$ there exists $n \in[m P, m P+N]$ such that $f(n)=(\overline{0}, \ldots, \overline{0})$. So there are infinitely many suitable numbers. To prove (1), let $a_{i}=f_{i}(m P)$. Consider all numbers of the form $n_{m, s}=m P+n_{s}$ with $s=\left(s_{1}, \ldots, s_{k}\right) \in S$ (clearly, all $n_{m, s}$ belong to $[m P, m P+N]$ ). Since $n_{s} \leq N<p_{i}^{g}$ and $p_{i}^{g} \mid m P$, we can apply the Lemma for the values $p=p_{i}, r=n_{s}, k=g, q p^{k}=m P$ to obtain $$ f_{i}\left(n_{m, s}\right)=f_{i}(m P)+f_{i}\left(n_{s}\right)=a_{i}+s_{i} \text {; } $$ hence for distinct $s, t \in S$ we have $f\left(n_{m, s}\right) \neq f\left(n_{m, t}\right)$. Thus, the function $f$ attains at least $|S|$ distinct values in $[m P, m P+N]$. Since all these values belong to $S, f$ should attain all possible values in $[m P, m P+N]$. Comment. Both solutions can be extended to prove the following statements. Claim 1. For any $K$ there exist infinitely many $n$ divisible by $K$, such that $d \mid \nu_{p_{i}}(n)$ for each $i$. Claim 2. For any $s \in S$, there exist infinitely many $n \in \mathbb{N}$ such that $f(n)=s$.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
45642645-6c72-5b35-b2dd-b551600cbd6e
| 23,711
|
(a) Prove the inequality $$ \frac{x^{2}}{(x-1)^{2}}+\frac{y^{2}}{(y-1)^{2}}+\frac{z^{2}}{(z-1)^{2}} \geq 1 $$ for real numbers $x, y, z \neq 1$ satisfying the condition $x y z=1$. (b) Show that there are infinitely many triples of rational numbers $x, y, z$ for which this inequality turns into equality.
|
(a) We start with the substitution $$ \frac{x}{x-1}=a, \quad \frac{y}{y-1}=b, \quad \frac{z}{z-1}=c, \quad \text { i.e., } \quad x=\frac{a}{a-1}, \quad y=\frac{b}{b-1}, \quad z=\frac{c}{c-1} \text {. } $$ The inequality to be proved reads $a^{2}+b^{2}+c^{2} \geq 1$. The new variables are subject to the constraints $a, b, c \neq 1$ and the following one coming from the condition $x y z=1$, $$ (a-1)(b-1)(c-1)=a b c . $$ This is successively equivalent to $$ \begin{aligned} a+b+c-1 & =a b+b c+c a, \\ 2(a+b+c-1) & =(a+b+c)^{2}-\left(a^{2}+b^{2}+c^{2}\right), \\ a^{2}+b^{2}+c^{2}-2 & =(a+b+c)^{2}-2(a+b+c), \\ a^{2}+b^{2}+c^{2}-1 & =(a+b+c-1)^{2} . \end{aligned} $$ Thus indeed $a^{2}+b^{2}+c^{2} \geq 1$, as desired. (b) From the equation $a^{2}+b^{2}+c^{2}-1=(a+b+c-1)^{2}$ we see that the proposed inequality becomes an equality if and only if both sums $a^{2}+b^{2}+c^{2}$ and $a+b+c$ have value 1 . The first of them is equal to $(a+b+c)^{2}-2(a b+b c+c a)$. So the instances of equality are described by the system of two equations $$ a+b+c=1, \quad a b+b c+c a=0 $$ plus the constraint $a, b, c \neq 1$. Elimination of $c$ leads to $a^{2}+a b+b^{2}=a+b$, which we regard as a quadratic equation in $b$, $$ b^{2}+(a-1) b+a(a-1)=0, $$ with discriminant $$ \Delta=(a-1)^{2}-4 a(a-1)=(1-a)(1+3 a) . $$ We are looking for rational triples $(a, b, c)$; it will suffice to have $a$ rational such that $1-a$ and $1+3 a$ are both squares of rational numbers (then $\Delta$ will be so too). Set $a=k / m$. We want $m-k$ and $m+3 k$ to be squares of integers. This is achieved for instance by taking $m=k^{2}-k+1$ (clearly nonzero); then $m-k=(k-1)^{2}, m+3 k=(k+1)^{2}$. Note that distinct integers $k$ yield distinct values of $a=k / m$. And thus, if $k$ is any integer and $m=k^{2}-k+1, a=k / m$ then $\Delta=\left(k^{2}-1\right)^{2} / m^{2}$ and the quadratic equation has rational roots $b=\left(m-k \pm k^{2} \mp 1\right) /(2 m)$. Choose e.g. the larger root, $$ b=\frac{m-k+k^{2}-1}{2 m}=\frac{m+(m-2)}{2 m}=\frac{m-1}{m} . $$ Computing $c$ from $a+b+c=1$ then gives $c=(1-k) / m$. The condition $a, b, c \neq 1$ eliminates only $k=0$ and $k=1$. Thus, as $k$ varies over integers greater than 1 , we obtain an infinite family of rational triples $(a, b, c)$ - and coming back to the original variables $(x=a /(a-1)$ etc. $)$-an infinite family of rational triples $(x, y, z)$ with the needed property. (A short calculation shows that the resulting triples are $x=-k /(k-1)^{2}, y=k-k^{2}, z=(k-1) / k^{2}$; but the proof was complete without listing them.) Comment 1. There are many possible variations in handling the equation system $a^{2}+b^{2}+c^{2}=1$, $a+b+c=1(a, b, c \neq 1)$ which of course describes a circle in the $(a, b, c)$-space (with three points excluded), and finding infinitely many rational points on it. Also the initial substitution $x=a /(a-1)$ (etc.) can be successfully replaced by other similar substitutions, e.g. $x=1-1 / \alpha$ (etc.); or $x=x^{\prime}-1$ (etc.); or $1-y z=u$ (etc.) - eventually reducing the inequality to $(\cdots)^{2} \geq 0$, the expression in the parentheses depending on the actual substitution. Depending on the method chosen, one arrives at various sequences of rational triples $(x, y, z)$ as needed; let us produce just one more such example: $x=(2 r-2) /(r+1)^{2}, y=(2 r+2) /(r-1)^{2}$, $z=\left(r^{2}-1\right) / 4$ where $r$ can be any rational number different from 1 or -1 . Solution 2 (an outline). (a) Without changing variables, just setting $z=1 / x y$ and clearing fractions, the proposed inequality takes the form $$ (x y-1)^{2}\left(x^{2}(y-1)^{2}+y^{2}(x-1)^{2}\right)+(x-1)^{2}(y-1)^{2} \geq(x-1)^{2}(y-1)^{2}(x y-1)^{2} . $$ With the notation $p=x+y, q=x y$ this becomes, after lengthy routine manipulation and a lot of cancellation $$ q^{4}-6 q^{3}+2 p q^{2}+9 q^{2}-6 p q+p^{2} \geq 0 \text {. } $$ It is not hard to notice that the expression on the left is just $\left(q^{2}-3 q+p\right)^{2}$, hence nonnegative. (Without introducing $p$ and $q$, one is of course led with some more work to the same expression, just written in terms of $x$ and $y$; but then it is not that easy to see that it is a square.) (b) To have equality, one needs $q^{2}-3 q+p=0$. Note that $x$ and $y$ are the roots of the quadratic trinomial (in a formal variable $t$ ): $t^{2}-p t+q$. When $q^{2}-3 q+p=0$, the discriminant equals $$ \delta=p^{2}-4 q=\left(3 q-q^{2}\right)^{2}-4 q=q(q-1)^{2}(q-4) . $$ Now it suffices to have both $q$ and $q-4$ squares of rational numbers (then $p=3 q-q^{2}$ and $\sqrt{\delta}$ are also rational, and so are the roots of the trinomial). On setting $q=(n / m)^{2}=4+(l / m)^{2}$ the requirement becomes $4 m^{2}+l^{2}=n^{2}$ (with $l, m, n$ being integers). This is just the Pythagorean equation, known to have infinitely many integer solutions. Comment 2. Part (a) alone might also be considered as a possible contest problem (in the category of easy problems).
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
(a) Prove the inequality $$ \frac{x^{2}}{(x-1)^{2}}+\frac{y^{2}}{(y-1)^{2}}+\frac{z^{2}}{(z-1)^{2}} \geq 1 $$ for real numbers $x, y, z \neq 1$ satisfying the condition $x y z=1$. (b) Show that there are infinitely many triples of rational numbers $x, y, z$ for which this inequality turns into equality.
|
(a) We start with the substitution $$ \frac{x}{x-1}=a, \quad \frac{y}{y-1}=b, \quad \frac{z}{z-1}=c, \quad \text { i.e., } \quad x=\frac{a}{a-1}, \quad y=\frac{b}{b-1}, \quad z=\frac{c}{c-1} \text {. } $$ The inequality to be proved reads $a^{2}+b^{2}+c^{2} \geq 1$. The new variables are subject to the constraints $a, b, c \neq 1$ and the following one coming from the condition $x y z=1$, $$ (a-1)(b-1)(c-1)=a b c . $$ This is successively equivalent to $$ \begin{aligned} a+b+c-1 & =a b+b c+c a, \\ 2(a+b+c-1) & =(a+b+c)^{2}-\left(a^{2}+b^{2}+c^{2}\right), \\ a^{2}+b^{2}+c^{2}-2 & =(a+b+c)^{2}-2(a+b+c), \\ a^{2}+b^{2}+c^{2}-1 & =(a+b+c-1)^{2} . \end{aligned} $$ Thus indeed $a^{2}+b^{2}+c^{2} \geq 1$, as desired. (b) From the equation $a^{2}+b^{2}+c^{2}-1=(a+b+c-1)^{2}$ we see that the proposed inequality becomes an equality if and only if both sums $a^{2}+b^{2}+c^{2}$ and $a+b+c$ have value 1 . The first of them is equal to $(a+b+c)^{2}-2(a b+b c+c a)$. So the instances of equality are described by the system of two equations $$ a+b+c=1, \quad a b+b c+c a=0 $$ plus the constraint $a, b, c \neq 1$. Elimination of $c$ leads to $a^{2}+a b+b^{2}=a+b$, which we regard as a quadratic equation in $b$, $$ b^{2}+(a-1) b+a(a-1)=0, $$ with discriminant $$ \Delta=(a-1)^{2}-4 a(a-1)=(1-a)(1+3 a) . $$ We are looking for rational triples $(a, b, c)$; it will suffice to have $a$ rational such that $1-a$ and $1+3 a$ are both squares of rational numbers (then $\Delta$ will be so too). Set $a=k / m$. We want $m-k$ and $m+3 k$ to be squares of integers. This is achieved for instance by taking $m=k^{2}-k+1$ (clearly nonzero); then $m-k=(k-1)^{2}, m+3 k=(k+1)^{2}$. Note that distinct integers $k$ yield distinct values of $a=k / m$. And thus, if $k$ is any integer and $m=k^{2}-k+1, a=k / m$ then $\Delta=\left(k^{2}-1\right)^{2} / m^{2}$ and the quadratic equation has rational roots $b=\left(m-k \pm k^{2} \mp 1\right) /(2 m)$. Choose e.g. the larger root, $$ b=\frac{m-k+k^{2}-1}{2 m}=\frac{m+(m-2)}{2 m}=\frac{m-1}{m} . $$ Computing $c$ from $a+b+c=1$ then gives $c=(1-k) / m$. The condition $a, b, c \neq 1$ eliminates only $k=0$ and $k=1$. Thus, as $k$ varies over integers greater than 1 , we obtain an infinite family of rational triples $(a, b, c)$ - and coming back to the original variables $(x=a /(a-1)$ etc. $)$-an infinite family of rational triples $(x, y, z)$ with the needed property. (A short calculation shows that the resulting triples are $x=-k /(k-1)^{2}, y=k-k^{2}, z=(k-1) / k^{2}$; but the proof was complete without listing them.) Comment 1. There are many possible variations in handling the equation system $a^{2}+b^{2}+c^{2}=1$, $a+b+c=1(a, b, c \neq 1)$ which of course describes a circle in the $(a, b, c)$-space (with three points excluded), and finding infinitely many rational points on it. Also the initial substitution $x=a /(a-1)$ (etc.) can be successfully replaced by other similar substitutions, e.g. $x=1-1 / \alpha$ (etc.); or $x=x^{\prime}-1$ (etc.); or $1-y z=u$ (etc.) - eventually reducing the inequality to $(\cdots)^{2} \geq 0$, the expression in the parentheses depending on the actual substitution. Depending on the method chosen, one arrives at various sequences of rational triples $(x, y, z)$ as needed; let us produce just one more such example: $x=(2 r-2) /(r+1)^{2}, y=(2 r+2) /(r-1)^{2}$, $z=\left(r^{2}-1\right) / 4$ where $r$ can be any rational number different from 1 or -1 . Solution 2 (an outline). (a) Without changing variables, just setting $z=1 / x y$ and clearing fractions, the proposed inequality takes the form $$ (x y-1)^{2}\left(x^{2}(y-1)^{2}+y^{2}(x-1)^{2}\right)+(x-1)^{2}(y-1)^{2} \geq(x-1)^{2}(y-1)^{2}(x y-1)^{2} . $$ With the notation $p=x+y, q=x y$ this becomes, after lengthy routine manipulation and a lot of cancellation $$ q^{4}-6 q^{3}+2 p q^{2}+9 q^{2}-6 p q+p^{2} \geq 0 \text {. } $$ It is not hard to notice that the expression on the left is just $\left(q^{2}-3 q+p\right)^{2}$, hence nonnegative. (Without introducing $p$ and $q$, one is of course led with some more work to the same expression, just written in terms of $x$ and $y$; but then it is not that easy to see that it is a square.) (b) To have equality, one needs $q^{2}-3 q+p=0$. Note that $x$ and $y$ are the roots of the quadratic trinomial (in a formal variable $t$ ): $t^{2}-p t+q$. When $q^{2}-3 q+p=0$, the discriminant equals $$ \delta=p^{2}-4 q=\left(3 q-q^{2}\right)^{2}-4 q=q(q-1)^{2}(q-4) . $$ Now it suffices to have both $q$ and $q-4$ squares of rational numbers (then $p=3 q-q^{2}$ and $\sqrt{\delta}$ are also rational, and so are the roots of the trinomial). On setting $q=(n / m)^{2}=4+(l / m)^{2}$ the requirement becomes $4 m^{2}+l^{2}=n^{2}$ (with $l, m, n$ being integers). This is just the Pythagorean equation, known to have infinitely many integer solutions. Comment 2. Part (a) alone might also be considered as a possible contest problem (in the category of easy problems).
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
91fbd7ef-b442-539c-934a-5e420560d7cd
| 23,719
|
Let $S \subseteq \mathbb{R}$ be a set of real numbers. We say that a pair $(f, g)$ of functions from $S$ into $S$ is a Spanish Couple on $S$, if they satisfy the following conditions: (i) Both functions are strictly increasing, i.e. $f(x)<f(y)$ and $g(x)<g(y)$ for all $x, y \in S$ with $x<y$; (ii) The inequality $f(g(g(x)))<g(f(x))$ holds for all $x \in S$. Decide whether there exists a Spanish Couple (a) on the set $S=\mathbb{N}$ of positive integers; (b) on the set $S=\{a-1 / b: a, b \in \mathbb{N}\}$.
|
We show that the answer is NO for part (a), and YES for part (b). (a) Throughout the solution, we will use the notation $g_{k}(x)=\overbrace{g(g(\ldots g}^{k}(x) \ldots))$, including $g_{0}(x)=x$ as well. Suppose that there exists a Spanish Couple $(f, g)$ on the set $\mathbb{N}$. From property (i) we have $f(x) \geq x$ and $g(x) \geq x$ for all $x \in \mathbb{N}$. We claim that $g_{k}(x) \leq f(x)$ for all $k \geq 0$ and all positive integers $x$. The proof is done by induction on $k$. We already have the base case $k=0$ since $x \leq f(x)$. For the induction step from $k$ to $k+1$, apply the induction hypothesis on $g_{2}(x)$ instead of $x$, then apply (ii): $$ g\left(g_{k+1}(x)\right)=g_{k}\left(g_{2}(x)\right) \leq f\left(g_{2}(x)\right)<g(f(x)) $$ Since $g$ is increasing, it follows that $g_{k+1}(x)<f(x)$. The claim is proven. If $g(x)=x$ for all $x \in \mathbb{N}$ then $f(g(g(x)))=f(x)=g(f(x))$, and we have a contradiction with (ii). Therefore one can choose an $x_{0} \in S$ for which $x_{0}<g\left(x_{0}\right)$. Now consider the sequence $x_{0}, x_{1}, \ldots$ where $x_{k}=g_{k}\left(x_{0}\right)$. The sequence is increasing. Indeed, we have $x_{0}<g\left(x_{0}\right)=x_{1}$, and $x_{k}<x_{k+1}$ implies $x_{k+1}=g\left(x_{k}\right)<g\left(x_{k+1}\right)=x_{k+2}$. Hence, we obtain a strictly increasing sequence $x_{0}<x_{1}<\ldots$ of positive integers which on the other hand has an upper bound, namely $f\left(x_{0}\right)$. This cannot happen in the set $\mathbb{N}$ of positive integers, thus no Spanish Couple exists on $\mathbb{N}$. (b) We present a Spanish Couple on the set $S=\{a-1 / b: a, b \in \mathbb{N}\}$. Let $$ \begin{aligned} & f(a-1 / b)=a+1-1 / b, \\ & g(a-1 / b)=a-1 /\left(b+3^{a}\right) . \end{aligned} $$ These functions are clearly increasing. Condition (ii) holds, since $$ f(g(g(a-1 / b)))=(a+1)-1 /\left(b+2 \cdot 3^{a}\right)<(a+1)-1 /\left(b+3^{a+1}\right)=g(f(a-1 / b)) . $$ Comment. Another example of a Spanish couple is $f(a-1 / b)=3 a-1 / b, g(a-1 / b)=a-1 /(a+b)$. More generally, postulating $f(a-1 / b)=h(a)-1 / b, \quad g(a-1 / b)=a-1 / G(a, b)$ with $h$ increasing and $G$ increasing in both variables, we get that $f \circ g \circ g<g \circ f$ holds if $G(a, G(a, b))<G(h(a), b)$. A search just among linear functions $h(a)=C a, G(a, b)=A a+B b$ results in finding that any integers $A>0, C>2$ and $B=1$ produce a Spanish couple (in the example above, $A=1, C=3$ ). The proposer's example results from taking $h(a)=a+1, G(a, b)=3^{a}+b$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $S \subseteq \mathbb{R}$ be a set of real numbers. We say that a pair $(f, g)$ of functions from $S$ into $S$ is a Spanish Couple on $S$, if they satisfy the following conditions: (i) Both functions are strictly increasing, i.e. $f(x)<f(y)$ and $g(x)<g(y)$ for all $x, y \in S$ with $x<y$; (ii) The inequality $f(g(g(x)))<g(f(x))$ holds for all $x \in S$. Decide whether there exists a Spanish Couple (a) on the set $S=\mathbb{N}$ of positive integers; (b) on the set $S=\{a-1 / b: a, b \in \mathbb{N}\}$.
|
We show that the answer is NO for part (a), and YES for part (b). (a) Throughout the solution, we will use the notation $g_{k}(x)=\overbrace{g(g(\ldots g}^{k}(x) \ldots))$, including $g_{0}(x)=x$ as well. Suppose that there exists a Spanish Couple $(f, g)$ on the set $\mathbb{N}$. From property (i) we have $f(x) \geq x$ and $g(x) \geq x$ for all $x \in \mathbb{N}$. We claim that $g_{k}(x) \leq f(x)$ for all $k \geq 0$ and all positive integers $x$. The proof is done by induction on $k$. We already have the base case $k=0$ since $x \leq f(x)$. For the induction step from $k$ to $k+1$, apply the induction hypothesis on $g_{2}(x)$ instead of $x$, then apply (ii): $$ g\left(g_{k+1}(x)\right)=g_{k}\left(g_{2}(x)\right) \leq f\left(g_{2}(x)\right)<g(f(x)) $$ Since $g$ is increasing, it follows that $g_{k+1}(x)<f(x)$. The claim is proven. If $g(x)=x$ for all $x \in \mathbb{N}$ then $f(g(g(x)))=f(x)=g(f(x))$, and we have a contradiction with (ii). Therefore one can choose an $x_{0} \in S$ for which $x_{0}<g\left(x_{0}\right)$. Now consider the sequence $x_{0}, x_{1}, \ldots$ where $x_{k}=g_{k}\left(x_{0}\right)$. The sequence is increasing. Indeed, we have $x_{0}<g\left(x_{0}\right)=x_{1}$, and $x_{k}<x_{k+1}$ implies $x_{k+1}=g\left(x_{k}\right)<g\left(x_{k+1}\right)=x_{k+2}$. Hence, we obtain a strictly increasing sequence $x_{0}<x_{1}<\ldots$ of positive integers which on the other hand has an upper bound, namely $f\left(x_{0}\right)$. This cannot happen in the set $\mathbb{N}$ of positive integers, thus no Spanish Couple exists on $\mathbb{N}$. (b) We present a Spanish Couple on the set $S=\{a-1 / b: a, b \in \mathbb{N}\}$. Let $$ \begin{aligned} & f(a-1 / b)=a+1-1 / b, \\ & g(a-1 / b)=a-1 /\left(b+3^{a}\right) . \end{aligned} $$ These functions are clearly increasing. Condition (ii) holds, since $$ f(g(g(a-1 / b)))=(a+1)-1 /\left(b+2 \cdot 3^{a}\right)<(a+1)-1 /\left(b+3^{a+1}\right)=g(f(a-1 / b)) . $$ Comment. Another example of a Spanish couple is $f(a-1 / b)=3 a-1 / b, g(a-1 / b)=a-1 /(a+b)$. More generally, postulating $f(a-1 / b)=h(a)-1 / b, \quad g(a-1 / b)=a-1 / G(a, b)$ with $h$ increasing and $G$ increasing in both variables, we get that $f \circ g \circ g<g \circ f$ holds if $G(a, G(a, b))<G(h(a), b)$. A search just among linear functions $h(a)=C a, G(a, b)=A a+B b$ results in finding that any integers $A>0, C>2$ and $B=1$ produce a Spanish couple (in the example above, $A=1, C=3$ ). The proposer's example results from taking $h(a)=a+1, G(a, b)=3^{a}+b$.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
28583a78-8662-5c07-b0b5-7094ab42ceda
| 23,721
|
For an integer $m$, denote by $t(m)$ the unique number in $\{1,2,3\}$ such that $m+t(m)$ is a multiple of 3. A function $f: \mathbb{Z} \rightarrow \mathbb{Z}$ satisfies $f(-1)=0, f(0)=1, f(1)=-1$ and $$ f\left(2^{n}+m\right)=f\left(2^{n}-t(m)\right)-f(m) \quad \text { for all integers } m, n \geq 0 \text { with } 2^{n}>m \text {. } $$ Prove that $f(3 p) \geq 0$ holds for all integers $p \geq 0$.
|
The given conditions determine $f$ uniquely on the positive integers. The signs of $f(1), f(2), \ldots$ seem to change quite erratically. However values of the form $f\left(2^{n}-t(m)\right)$ are sufficient to compute directly any functional value. Indeed, let $n>0$ have base 2 representation $n=2^{a_{0}}+2^{a_{1}}+\cdots+2^{a_{k}}, a_{0}>a_{1}>\cdots>a_{k} \geq 0$, and let $n_{j}=2^{a_{j}}+2^{a_{j-1}}+\cdots+2^{a_{k}}, j=0, \ldots, k$. Repeated applications of the recurrence show that $f(n)$ is an alternating sum of the quantities $f\left(2^{a_{j}}-t\left(n_{j+1}\right)\right)$ plus $(-1)^{k+1}$. (The exact formula is not needed for our proof.) So we focus attention on the values $f\left(2^{n}-1\right), f\left(2^{n}-2\right)$ and $f\left(2^{n}-3\right)$. Six cases arise; more specifically, $t\left(2^{2 k}-3\right)=2, t\left(2^{2 k}-2\right)=1, t\left(2^{2 k}-1\right)=3, t\left(2^{2 k+1}-3\right)=1, t\left(2^{2 k+1}-2\right)=3, t\left(2^{2 k+1}-1\right)=2$. Claim. For all integers $k \geq 0$ the following equalities hold: $$ \begin{array}{lll} f\left(2^{2 k+1}-3\right)=0, & f\left(2^{2 k+1}-2\right)=3^{k}, & f\left(2^{2 k+1}-1\right)=-3^{k}, \\ f\left(2^{2 k+2}-3\right)=-3^{k}, & f\left(2^{2 k+2}-2\right)=-3^{k}, & f\left(2^{2 k+2}-1\right)=2 \cdot 3^{k} . \end{array} $$ Proof. By induction on $k$. The base $k=0$ comes down to checking that $f(2)=-1$ and $f(3)=2$; the given values $f(-1)=0, f(0)=1, f(1)=-1$ are also needed. Suppose the claim holds for $k-1$. For $f\left(2^{2 k+1}-t(m)\right)$, the recurrence formula and the induction hypothesis yield $$ \begin{aligned} & f\left(2^{2 k+1}-3\right)=f\left(2^{2 k}+\left(2^{2 k}-3\right)\right)=f\left(2^{2 k}-2\right)-f\left(2^{2 k}-3\right)=-3^{k-1}+3^{k-1}=0, \\ & f\left(2^{2 k+1}-2\right)=f\left(2^{2 k}+\left(2^{2 k}-2\right)\right)=f\left(2^{2 k}-1\right)-f\left(2^{2 k}-2\right)=2 \cdot 3^{k-1}+3^{k-1}=3^{k}, \\ & f\left(2^{2 k+1}-1\right)=f\left(2^{2 k}+\left(2^{2 k}-1\right)\right)=f\left(2^{2 k}-3\right)-f\left(2^{2 k}-1\right)=-3^{k-1}-2 \cdot 3^{k-1}=-3^{k} . \end{aligned} $$ For $f\left(2^{2 k+2}-t(m)\right)$ we use the three equalities just established: $$ \begin{aligned} & f\left(2^{2 k+2}-3\right)=f\left(2^{2 k+1}+\left(2^{2 k+1}-3\right)\right)=f\left(2^{2 k+1}-1\right)-f\left(2^{2 k+1}-3\right)=-3^{k}-0=-3^{k}, \\ & f\left(2^{2 k+2}-2\right)=f\left(2^{2 k+1}+\left(2^{2 k+1}-2\right)\right)=f\left(2^{2 k+1}-3\right)-f\left(2^{2 k}-2\right)=0-3^{k}=-3^{k}, \\ & f\left(2^{2 k+2}-1\right)=f\left(2^{2 k+1}+\left(2^{2 k+1}-1\right)\right)=f\left(2^{2 k+1}-2\right)-f\left(2^{2 k+1}-1\right)=3^{k}+3^{k}=2 \cdot 3^{k} . \end{aligned} $$ The claim follows. A closer look at the six cases shows that $f\left(2^{n}-t(m)\right) \geq 3^{(n-1) / 2}$ if $2^{n}-t(m)$ is divisible by 3 , and $f\left(2^{n}-t(m)\right) \leq 0$ otherwise. On the other hand, note that $2^{n}-t(m)$ is divisible by 3 if and only if $2^{n}+m$ is. Therefore, for all nonnegative integers $m$ and $n$, (i) $f\left(2^{n}-t(m)\right) \geq 3^{(n-1) / 2}$ if $2^{n}+m$ is divisible by 3 ; (ii) $f\left(2^{n}-t(m)\right) \leq 0$ if $2^{n}+m$ is not divisible by 3 . One more (direct) consequence of the claim is that $\left|f\left(2^{n}-t(m)\right)\right| \leq \frac{2}{3} \cdot 3^{n / 2}$ for all $m, n \geq 0$. The last inequality enables us to find an upper bound for $|f(m)|$ for $m$ less than a given power of 2 . We prove by induction on $n$ that $|f(m)| \leq 3^{n / 2}$ holds true for all integers $m, n \geq 0$ with $2^{n}>m$. The base $n=0$ is clear as $f(0)=1$. For the inductive step from $n$ to $n+1$, let $m$ and $n$ satisfy $2^{n+1}>m$. If $m<2^{n}$, we are done by the inductive hypothesis. If $m \geq 2^{n}$ then $m=2^{n}+k$ where $2^{n}>k \geq 0$. Now, by $\left|f\left(2^{n}-t(k)\right)\right| \leq \frac{2}{3} \cdot 3^{n / 2}$ and the inductive assumption, $$ |f(m)|=\left|f\left(2^{n}-t(k)\right)-f(k)\right| \leq\left|f\left(2^{n}-t(k)\right)\right|+|f(k)| \leq \frac{2}{3} \cdot 3^{n / 2}+3^{n / 2}<3^{(n+1) / 2} . $$ The induction is complete. We proceed to prove that $f(3 p) \geq 0$ for all integers $p \geq 0$. Since $3 p$ is not a power of 2 , its binary expansion contains at least two summands. Hence one can write $3 p=2^{a}+2^{b}+c$ where $a>b$ and $2^{b}>c \geq 0$. Applying the recurrence formula twice yields $$ f(3 p)=f\left(2^{a}+2^{b}+c\right)=f\left(2^{a}-t\left(2^{b}+c\right)\right)-f\left(2^{b}-t(c)\right)+f(c) . $$ Since $2^{a}+2^{b}+c$ is divisible by 3 , we have $f\left(2^{a}-t\left(2^{b}+c\right)\right) \geq 3^{(a-1) / 2}$ by (i). Since $2^{b}+c$ is not divisible by 3 , we have $f\left(2^{b}-t(c)\right) \leq 0$ by (ii). Finally $|f(c)| \leq 3^{b / 2}$ as $2^{b}>c \geq 0$, so that $f(c) \geq-3^{b / 2}$. Therefore $f(3 p) \geq 3^{(a-1) / 2}-3^{b / 2}$ which is nonnegative because $a>b$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For an integer $m$, denote by $t(m)$ the unique number in $\{1,2,3\}$ such that $m+t(m)$ is a multiple of 3. A function $f: \mathbb{Z} \rightarrow \mathbb{Z}$ satisfies $f(-1)=0, f(0)=1, f(1)=-1$ and $$ f\left(2^{n}+m\right)=f\left(2^{n}-t(m)\right)-f(m) \quad \text { for all integers } m, n \geq 0 \text { with } 2^{n}>m \text {. } $$ Prove that $f(3 p) \geq 0$ holds for all integers $p \geq 0$.
|
The given conditions determine $f$ uniquely on the positive integers. The signs of $f(1), f(2), \ldots$ seem to change quite erratically. However values of the form $f\left(2^{n}-t(m)\right)$ are sufficient to compute directly any functional value. Indeed, let $n>0$ have base 2 representation $n=2^{a_{0}}+2^{a_{1}}+\cdots+2^{a_{k}}, a_{0}>a_{1}>\cdots>a_{k} \geq 0$, and let $n_{j}=2^{a_{j}}+2^{a_{j-1}}+\cdots+2^{a_{k}}, j=0, \ldots, k$. Repeated applications of the recurrence show that $f(n)$ is an alternating sum of the quantities $f\left(2^{a_{j}}-t\left(n_{j+1}\right)\right)$ plus $(-1)^{k+1}$. (The exact formula is not needed for our proof.) So we focus attention on the values $f\left(2^{n}-1\right), f\left(2^{n}-2\right)$ and $f\left(2^{n}-3\right)$. Six cases arise; more specifically, $t\left(2^{2 k}-3\right)=2, t\left(2^{2 k}-2\right)=1, t\left(2^{2 k}-1\right)=3, t\left(2^{2 k+1}-3\right)=1, t\left(2^{2 k+1}-2\right)=3, t\left(2^{2 k+1}-1\right)=2$. Claim. For all integers $k \geq 0$ the following equalities hold: $$ \begin{array}{lll} f\left(2^{2 k+1}-3\right)=0, & f\left(2^{2 k+1}-2\right)=3^{k}, & f\left(2^{2 k+1}-1\right)=-3^{k}, \\ f\left(2^{2 k+2}-3\right)=-3^{k}, & f\left(2^{2 k+2}-2\right)=-3^{k}, & f\left(2^{2 k+2}-1\right)=2 \cdot 3^{k} . \end{array} $$ Proof. By induction on $k$. The base $k=0$ comes down to checking that $f(2)=-1$ and $f(3)=2$; the given values $f(-1)=0, f(0)=1, f(1)=-1$ are also needed. Suppose the claim holds for $k-1$. For $f\left(2^{2 k+1}-t(m)\right)$, the recurrence formula and the induction hypothesis yield $$ \begin{aligned} & f\left(2^{2 k+1}-3\right)=f\left(2^{2 k}+\left(2^{2 k}-3\right)\right)=f\left(2^{2 k}-2\right)-f\left(2^{2 k}-3\right)=-3^{k-1}+3^{k-1}=0, \\ & f\left(2^{2 k+1}-2\right)=f\left(2^{2 k}+\left(2^{2 k}-2\right)\right)=f\left(2^{2 k}-1\right)-f\left(2^{2 k}-2\right)=2 \cdot 3^{k-1}+3^{k-1}=3^{k}, \\ & f\left(2^{2 k+1}-1\right)=f\left(2^{2 k}+\left(2^{2 k}-1\right)\right)=f\left(2^{2 k}-3\right)-f\left(2^{2 k}-1\right)=-3^{k-1}-2 \cdot 3^{k-1}=-3^{k} . \end{aligned} $$ For $f\left(2^{2 k+2}-t(m)\right)$ we use the three equalities just established: $$ \begin{aligned} & f\left(2^{2 k+2}-3\right)=f\left(2^{2 k+1}+\left(2^{2 k+1}-3\right)\right)=f\left(2^{2 k+1}-1\right)-f\left(2^{2 k+1}-3\right)=-3^{k}-0=-3^{k}, \\ & f\left(2^{2 k+2}-2\right)=f\left(2^{2 k+1}+\left(2^{2 k+1}-2\right)\right)=f\left(2^{2 k+1}-3\right)-f\left(2^{2 k}-2\right)=0-3^{k}=-3^{k}, \\ & f\left(2^{2 k+2}-1\right)=f\left(2^{2 k+1}+\left(2^{2 k+1}-1\right)\right)=f\left(2^{2 k+1}-2\right)-f\left(2^{2 k+1}-1\right)=3^{k}+3^{k}=2 \cdot 3^{k} . \end{aligned} $$ The claim follows. A closer look at the six cases shows that $f\left(2^{n}-t(m)\right) \geq 3^{(n-1) / 2}$ if $2^{n}-t(m)$ is divisible by 3 , and $f\left(2^{n}-t(m)\right) \leq 0$ otherwise. On the other hand, note that $2^{n}-t(m)$ is divisible by 3 if and only if $2^{n}+m$ is. Therefore, for all nonnegative integers $m$ and $n$, (i) $f\left(2^{n}-t(m)\right) \geq 3^{(n-1) / 2}$ if $2^{n}+m$ is divisible by 3 ; (ii) $f\left(2^{n}-t(m)\right) \leq 0$ if $2^{n}+m$ is not divisible by 3 . One more (direct) consequence of the claim is that $\left|f\left(2^{n}-t(m)\right)\right| \leq \frac{2}{3} \cdot 3^{n / 2}$ for all $m, n \geq 0$. The last inequality enables us to find an upper bound for $|f(m)|$ for $m$ less than a given power of 2 . We prove by induction on $n$ that $|f(m)| \leq 3^{n / 2}$ holds true for all integers $m, n \geq 0$ with $2^{n}>m$. The base $n=0$ is clear as $f(0)=1$. For the inductive step from $n$ to $n+1$, let $m$ and $n$ satisfy $2^{n+1}>m$. If $m<2^{n}$, we are done by the inductive hypothesis. If $m \geq 2^{n}$ then $m=2^{n}+k$ where $2^{n}>k \geq 0$. Now, by $\left|f\left(2^{n}-t(k)\right)\right| \leq \frac{2}{3} \cdot 3^{n / 2}$ and the inductive assumption, $$ |f(m)|=\left|f\left(2^{n}-t(k)\right)-f(k)\right| \leq\left|f\left(2^{n}-t(k)\right)\right|+|f(k)| \leq \frac{2}{3} \cdot 3^{n / 2}+3^{n / 2}<3^{(n+1) / 2} . $$ The induction is complete. We proceed to prove that $f(3 p) \geq 0$ for all integers $p \geq 0$. Since $3 p$ is not a power of 2 , its binary expansion contains at least two summands. Hence one can write $3 p=2^{a}+2^{b}+c$ where $a>b$ and $2^{b}>c \geq 0$. Applying the recurrence formula twice yields $$ f(3 p)=f\left(2^{a}+2^{b}+c\right)=f\left(2^{a}-t\left(2^{b}+c\right)\right)-f\left(2^{b}-t(c)\right)+f(c) . $$ Since $2^{a}+2^{b}+c$ is divisible by 3 , we have $f\left(2^{a}-t\left(2^{b}+c\right)\right) \geq 3^{(a-1) / 2}$ by (i). Since $2^{b}+c$ is not divisible by 3 , we have $f\left(2^{b}-t(c)\right) \leq 0$ by (ii). Finally $|f(c)| \leq 3^{b / 2}$ as $2^{b}>c \geq 0$, so that $f(c) \geq-3^{b / 2}$. Therefore $f(3 p) \geq 3^{(a-1) / 2}-3^{b / 2}$ which is nonnegative because $a>b$.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a3f6c904-1248-57d8-9bbe-f641957839fc
| 23,724
|
Let $a, b, c, d$ be positive real numbers such that $$ a b c d=1 \quad \text { and } \quad a+b+c+d>\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a} $$ Prove that $$ a+b+c+d<\frac{b}{a}+\frac{c}{b}+\frac{d}{c}+\frac{a}{d} $$
|
We show that if $a b c d=1$, the sum $a+b+c+d$ cannot exceed a certain weighted mean of the expressions $\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}$ and $\frac{b}{a}+\frac{c}{b}+\frac{d}{c}+\frac{a}{d}$. By applying the AM-GM inequality to the numbers $\frac{a}{b}, \frac{a}{b}, \frac{b}{c}$ and $\frac{a}{d}$, we obtain $$ a=\sqrt[4]{\frac{a^{4}}{a b c d}}=\sqrt[4]{\frac{a}{b} \cdot \frac{a}{b} \cdot \frac{b}{c} \cdot \frac{a}{d}} \leq \frac{1}{4}\left(\frac{a}{b}+\frac{a}{b}+\frac{b}{c}+\frac{a}{d}\right) $$ Analogously, $$ b \leq \frac{1}{4}\left(\frac{b}{c}+\frac{b}{c}+\frac{c}{d}+\frac{b}{a}\right), \quad c \leq \frac{1}{4}\left(\frac{c}{d}+\frac{c}{d}+\frac{d}{a}+\frac{c}{b}\right) \quad \text { and } \quad d \leq \frac{1}{4}\left(\frac{d}{a}+\frac{d}{a}+\frac{a}{b}+\frac{d}{c}\right) . $$ Summing up these estimates yields $$ a+b+c+d \leq \frac{3}{4}\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}\right)+\frac{1}{4}\left(\frac{b}{a}+\frac{c}{b}+\frac{d}{c}+\frac{a}{d}\right) . $$ In particular, if $a+b+c+d>\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}$ then $a+b+c+d<\frac{b}{a}+\frac{c}{b}+\frac{d}{c}+\frac{a}{d}$. Comment. The estimate in the above solution was obtained by applying the AM-GM inequality to each column of the $4 \times 4$ array $$ \begin{array}{llll} a / b & b / c & c / d & d / a \\ a / b & b / c & c / d & d / a \\ b / c & c / d & d / a & a / b \\ a / d & b / a & c / b & d / c \end{array} $$ and adding up the resulting inequalities. The same table yields a stronger bound: If $a, b, c, d>0$ and $a b c d=1$ then $$ \left(\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}\right)^{3}\left(\frac{b}{a}+\frac{c}{b}+\frac{d}{c}+\frac{a}{d}\right) \geq(a+b+c+d)^{4} $$ It suffices to apply Hölder's inequality to the sequences in the four rows, with weights $1 / 4$ : $$ \begin{gathered} \left(\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}\right)^{1 / 4}\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}\right)^{1 / 4}\left(\frac{b}{c}+\frac{c}{d}+\frac{d}{a}+\frac{a}{b}\right)^{1 / 4}\left(\frac{a}{d}+\frac{b}{a}+\frac{c}{b}+\frac{d}{c}\right)^{1 / 4} \\ \geq\left(\frac{a a b a}{b b c d}\right)^{1 / 4}+\left(\frac{b b c b}{c c d a}\right)^{1 / 4}+\left(\frac{c c d c}{d d a b}\right)^{1 / 4}+\left(\frac{d d a d}{a a b c}\right)^{1 / 4}=a+b+c+d \end{gathered} $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c, d$ be positive real numbers such that $$ a b c d=1 \quad \text { and } \quad a+b+c+d>\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a} $$ Prove that $$ a+b+c+d<\frac{b}{a}+\frac{c}{b}+\frac{d}{c}+\frac{a}{d} $$
|
We show that if $a b c d=1$, the sum $a+b+c+d$ cannot exceed a certain weighted mean of the expressions $\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}$ and $\frac{b}{a}+\frac{c}{b}+\frac{d}{c}+\frac{a}{d}$. By applying the AM-GM inequality to the numbers $\frac{a}{b}, \frac{a}{b}, \frac{b}{c}$ and $\frac{a}{d}$, we obtain $$ a=\sqrt[4]{\frac{a^{4}}{a b c d}}=\sqrt[4]{\frac{a}{b} \cdot \frac{a}{b} \cdot \frac{b}{c} \cdot \frac{a}{d}} \leq \frac{1}{4}\left(\frac{a}{b}+\frac{a}{b}+\frac{b}{c}+\frac{a}{d}\right) $$ Analogously, $$ b \leq \frac{1}{4}\left(\frac{b}{c}+\frac{b}{c}+\frac{c}{d}+\frac{b}{a}\right), \quad c \leq \frac{1}{4}\left(\frac{c}{d}+\frac{c}{d}+\frac{d}{a}+\frac{c}{b}\right) \quad \text { and } \quad d \leq \frac{1}{4}\left(\frac{d}{a}+\frac{d}{a}+\frac{a}{b}+\frac{d}{c}\right) . $$ Summing up these estimates yields $$ a+b+c+d \leq \frac{3}{4}\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}\right)+\frac{1}{4}\left(\frac{b}{a}+\frac{c}{b}+\frac{d}{c}+\frac{a}{d}\right) . $$ In particular, if $a+b+c+d>\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}$ then $a+b+c+d<\frac{b}{a}+\frac{c}{b}+\frac{d}{c}+\frac{a}{d}$. Comment. The estimate in the above solution was obtained by applying the AM-GM inequality to each column of the $4 \times 4$ array $$ \begin{array}{llll} a / b & b / c & c / d & d / a \\ a / b & b / c & c / d & d / a \\ b / c & c / d & d / a & a / b \\ a / d & b / a & c / b & d / c \end{array} $$ and adding up the resulting inequalities. The same table yields a stronger bound: If $a, b, c, d>0$ and $a b c d=1$ then $$ \left(\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}\right)^{3}\left(\frac{b}{a}+\frac{c}{b}+\frac{d}{c}+\frac{a}{d}\right) \geq(a+b+c+d)^{4} $$ It suffices to apply Hölder's inequality to the sequences in the four rows, with weights $1 / 4$ : $$ \begin{gathered} \left(\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}\right)^{1 / 4}\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}\right)^{1 / 4}\left(\frac{b}{c}+\frac{c}{d}+\frac{d}{a}+\frac{a}{b}\right)^{1 / 4}\left(\frac{a}{d}+\frac{b}{a}+\frac{c}{b}+\frac{d}{c}\right)^{1 / 4} \\ \geq\left(\frac{a a b a}{b b c d}\right)^{1 / 4}+\left(\frac{b b c b}{c c d a}\right)^{1 / 4}+\left(\frac{c c d c}{d d a b}\right)^{1 / 4}+\left(\frac{d d a d}{a a b c}\right)^{1 / 4}=a+b+c+d \end{gathered} $$
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
cf70eb2f-37b5-57bb-8bd8-cc7a1a8c91c4
| 23,726
|
Let $f: \mathbb{R} \rightarrow \mathbb{N}$ be a function which satisfies $$ f\left(x+\frac{1}{f(y)}\right)=f\left(y+\frac{1}{f(x)}\right) \quad \text { for all } x, y \in \mathbb{R} . $$ Prove that there is a positive integer which is not a value of $f$.
|
Suppose that the statement is false and $f(\mathbb{R})=\mathbb{N}$. We prove several properties of the function $f$ in order to reach a contradiction. To start with, observe that one can assume $f(0)=1$. Indeed, let $a \in \mathbb{R}$ be such that $f(a)=1$, and consider the function $g(x)=f(x+a)$. By substituting $x+a$ and $y+a$ for $x$ and $y$ in (1), we have $$ g\left(x+\frac{1}{g(y)}\right)=f\left(x+a+\frac{1}{f(y+a)}\right)=f\left(y+a+\frac{1}{f(x+a)}\right)=g\left(y+\frac{1}{g(x)}\right) . $$ So $g$ satisfies the functional equation (1), with the additional property $g(0)=1$. Also, $g$ and $f$ have the same set of values: $g(\mathbb{R})=f(\mathbb{R})=\mathbb{N}$. Henceforth we assume $f(0)=1$. Claim 1. For an arbitrary fixed $c \in \mathbb{R}$ we have $\left\{f\left(c+\frac{1}{n}\right): n \in \mathbb{N}\right\}=\mathbb{N}$. Proof. Equation (1) and $f(\mathbb{R})=\mathbb{N}$ imply $f(\mathbb{R})=\left\{f\left(x+\frac{1}{f(c)}\right): x \in \mathbb{R}\right\}=\left\{f\left(c+\frac{1}{f(x)}\right): x \in \mathbb{R}\right\} \subset\left\{f\left(c+\frac{1}{n}\right): n \in \mathbb{N}\right\} \subset f(\mathbb{R})$. The claim follows. We will use Claim 1 in the special cases $c=0$ and $c=1 / 3$ : $$ \left\{f\left(\frac{1}{n}\right): n \in \mathbb{N}\right\}=\left\{f\left(\frac{1}{3}+\frac{1}{n}\right): n \in \mathbb{N}\right\}=\mathbb{N} $$ Claim 2. If $f(u)=f(v)$ for some $u, v \in \mathbb{R}$ then $f(u+q)=f(v+q)$ for all nonnegative rational $q$. Furthermore, if $f(q)=1$ for some nonnegative rational $q$ then $f(k q)=1$ for all $k \in \mathbb{N}$. Proof. For all $x \in \mathbb{R}$ we have by (1) $$ f\left(u+\frac{1}{f(x)}\right)=f\left(x+\frac{1}{f(u)}\right)=f\left(x+\frac{1}{f(v)}\right)=f\left(v+\frac{1}{f(x)}\right) $$ Since $f(x)$ attains all positive integer values, this yields $f(u+1 / n)=f(v+1 / n)$ for all $n \in \mathbb{N}$. Let $q=k / n$ be a positive rational number. Then $k$ repetitions of the last step yield $$ f(u+q)=f\left(u+\frac{k}{n}\right)=f\left(v+\frac{k}{n}\right)=f(v+q) $$ Now let $f(q)=1$ for some nonnegative rational $q$, and let $k \in \mathbb{N}$. As $f(0)=1$, the previous conclusion yields successively $f(q)=f(2 q), f(2 q)=f(3 q), \ldots, f((k-1) q)=f(k q)$, as needed. Claim 3. The equality $f(q)=f(q+1)$ holds for all nonnegative rational $q$. Proof. Let $m$ be a positive integer such that $f(1 / m)=1$. Such an $m$ exists by (2). Applying the second statement of Claim 2 with $q=1 / m$ and $k=m$ yields $f(1)=1$. Given that $f(0)=f(1)=1$, the first statement of Claim 2 implies $f(q)=f(q+1)$ for all nonnegative rational $q$. Claim 4. The equality $f\left(\frac{1}{n}\right)=n$ holds for every $n \in \mathbb{N}$. Proof. For a nonnegative rational $q$ we set $x=q, y=0$ in (1) and use Claim 3 to obtain $$ f\left(\frac{1}{f(q)}\right)=f\left(q+\frac{1}{f(0)}\right)=f(q+1)=f(q) . $$ By (2), for each $n \in \mathbb{N}$ there exists a $k \in \mathbb{N}$ such that $f(1 / k)=n$. Applying the last equation with $q=1 / k$, we have $$ n=f\left(\frac{1}{k}\right)=f\left(\frac{1}{f(1 / k)}\right)=f\left(\frac{1}{n}\right) $$ Now we are ready to obtain a contradiction. Let $n \in \mathbb{N}$ be such that $f(1 / 3+1 / n)=1$. Such an $n$ exists by (2). Let $1 / 3+1 / n=s / t$, where $s, t \in \mathbb{N}$ are coprime. Observe that $t>1$ as $1 / 3+1 / n$ is not an integer. Choose $k, l \in \mathbb{N}$ so that that $k s-l t=1$. Because $f(0)=f(s / t)=1$, Claim 2 implies $f(k s / t)=1$. Now $f(k s / t)=f(1 / t+l)$; on the other hand $f(1 / t+l)=f(1 / t)$ by $l$ successive applications of Claim 3 . Finally, $f(1 / t)=t$ by Claim 4, leading to the impossible $t=1$. The solution is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f: \mathbb{R} \rightarrow \mathbb{N}$ be a function which satisfies $$ f\left(x+\frac{1}{f(y)}\right)=f\left(y+\frac{1}{f(x)}\right) \quad \text { for all } x, y \in \mathbb{R} . $$ Prove that there is a positive integer which is not a value of $f$.
|
Suppose that the statement is false and $f(\mathbb{R})=\mathbb{N}$. We prove several properties of the function $f$ in order to reach a contradiction. To start with, observe that one can assume $f(0)=1$. Indeed, let $a \in \mathbb{R}$ be such that $f(a)=1$, and consider the function $g(x)=f(x+a)$. By substituting $x+a$ and $y+a$ for $x$ and $y$ in (1), we have $$ g\left(x+\frac{1}{g(y)}\right)=f\left(x+a+\frac{1}{f(y+a)}\right)=f\left(y+a+\frac{1}{f(x+a)}\right)=g\left(y+\frac{1}{g(x)}\right) . $$ So $g$ satisfies the functional equation (1), with the additional property $g(0)=1$. Also, $g$ and $f$ have the same set of values: $g(\mathbb{R})=f(\mathbb{R})=\mathbb{N}$. Henceforth we assume $f(0)=1$. Claim 1. For an arbitrary fixed $c \in \mathbb{R}$ we have $\left\{f\left(c+\frac{1}{n}\right): n \in \mathbb{N}\right\}=\mathbb{N}$. Proof. Equation (1) and $f(\mathbb{R})=\mathbb{N}$ imply $f(\mathbb{R})=\left\{f\left(x+\frac{1}{f(c)}\right): x \in \mathbb{R}\right\}=\left\{f\left(c+\frac{1}{f(x)}\right): x \in \mathbb{R}\right\} \subset\left\{f\left(c+\frac{1}{n}\right): n \in \mathbb{N}\right\} \subset f(\mathbb{R})$. The claim follows. We will use Claim 1 in the special cases $c=0$ and $c=1 / 3$ : $$ \left\{f\left(\frac{1}{n}\right): n \in \mathbb{N}\right\}=\left\{f\left(\frac{1}{3}+\frac{1}{n}\right): n \in \mathbb{N}\right\}=\mathbb{N} $$ Claim 2. If $f(u)=f(v)$ for some $u, v \in \mathbb{R}$ then $f(u+q)=f(v+q)$ for all nonnegative rational $q$. Furthermore, if $f(q)=1$ for some nonnegative rational $q$ then $f(k q)=1$ for all $k \in \mathbb{N}$. Proof. For all $x \in \mathbb{R}$ we have by (1) $$ f\left(u+\frac{1}{f(x)}\right)=f\left(x+\frac{1}{f(u)}\right)=f\left(x+\frac{1}{f(v)}\right)=f\left(v+\frac{1}{f(x)}\right) $$ Since $f(x)$ attains all positive integer values, this yields $f(u+1 / n)=f(v+1 / n)$ for all $n \in \mathbb{N}$. Let $q=k / n$ be a positive rational number. Then $k$ repetitions of the last step yield $$ f(u+q)=f\left(u+\frac{k}{n}\right)=f\left(v+\frac{k}{n}\right)=f(v+q) $$ Now let $f(q)=1$ for some nonnegative rational $q$, and let $k \in \mathbb{N}$. As $f(0)=1$, the previous conclusion yields successively $f(q)=f(2 q), f(2 q)=f(3 q), \ldots, f((k-1) q)=f(k q)$, as needed. Claim 3. The equality $f(q)=f(q+1)$ holds for all nonnegative rational $q$. Proof. Let $m$ be a positive integer such that $f(1 / m)=1$. Such an $m$ exists by (2). Applying the second statement of Claim 2 with $q=1 / m$ and $k=m$ yields $f(1)=1$. Given that $f(0)=f(1)=1$, the first statement of Claim 2 implies $f(q)=f(q+1)$ for all nonnegative rational $q$. Claim 4. The equality $f\left(\frac{1}{n}\right)=n$ holds for every $n \in \mathbb{N}$. Proof. For a nonnegative rational $q$ we set $x=q, y=0$ in (1) and use Claim 3 to obtain $$ f\left(\frac{1}{f(q)}\right)=f\left(q+\frac{1}{f(0)}\right)=f(q+1)=f(q) . $$ By (2), for each $n \in \mathbb{N}$ there exists a $k \in \mathbb{N}$ such that $f(1 / k)=n$. Applying the last equation with $q=1 / k$, we have $$ n=f\left(\frac{1}{k}\right)=f\left(\frac{1}{f(1 / k)}\right)=f\left(\frac{1}{n}\right) $$ Now we are ready to obtain a contradiction. Let $n \in \mathbb{N}$ be such that $f(1 / 3+1 / n)=1$. Such an $n$ exists by (2). Let $1 / 3+1 / n=s / t$, where $s, t \in \mathbb{N}$ are coprime. Observe that $t>1$ as $1 / 3+1 / n$ is not an integer. Choose $k, l \in \mathbb{N}$ so that that $k s-l t=1$. Because $f(0)=f(s / t)=1$, Claim 2 implies $f(k s / t)=1$. Now $f(k s / t)=f(1 / t+l)$; on the other hand $f(1 / t+l)=f(1 / t)$ by $l$ successive applications of Claim 3 . Finally, $f(1 / t)=t$ by Claim 4, leading to the impossible $t=1$. The solution is complete.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
92ff7412-530e-5a4b-b4d8-ac1dc2a30c97
| 23,728
|
Prove that for any four positive real numbers $a, b, c, d$ the inequality $$ \frac{(a-b)(a-c)}{a+b+c}+\frac{(b-c)(b-d)}{b+c+d}+\frac{(c-d)(c-a)}{c+d+a}+\frac{(d-a)(d-b)}{d+a+b} \geq 0 $$ holds. Determine all cases of equality.
|
Denote the four terms by $$ A=\frac{(a-b)(a-c)}{a+b+c}, \quad B=\frac{(b-c)(b-d)}{b+c+d}, \quad C=\frac{(c-d)(c-a)}{c+d+a}, \quad D=\frac{(d-a)(d-b)}{d+a+b} . $$ The expression $2 A$ splits into two summands as follows, $$ 2 A=A^{\prime}+A^{\prime \prime} \quad \text { where } \quad A^{\prime}=\frac{(a-c)^{2}}{a+b+c}, \quad A^{\prime \prime}=\frac{(a-c)(a-2 b+c)}{a+b+c} ; $$ this is easily verified. We analogously represent $2 B=B^{\prime}+B^{\prime \prime}, 2 C=C^{\prime}+C^{\prime \prime}, 2 B=D^{\prime}+D^{\prime \prime}$ and examine each of the sums $A^{\prime}+B^{\prime}+C^{\prime}+D^{\prime}$ and $A^{\prime \prime}+B^{\prime \prime}+C^{\prime \prime}+D^{\prime \prime}$ separately. Write $s=a+b+c+d$; the denominators become $s-d, s-a, s-b, s-c$. By the CauchySchwarz inequality, $$ \begin{aligned} & \left(\frac{|a-c|}{\sqrt{s-d}} \cdot \sqrt{s-d}+\frac{|b-d|}{\sqrt{s-a}} \cdot \sqrt{s-a}+\frac{|c-a|}{\sqrt{s-b}} \cdot \sqrt{s-b}+\frac{|d-b|}{\sqrt{s-c}} \cdot \sqrt{s-c}\right)^{2} \\ & \quad \leq\left(\frac{(a-c)^{2}}{s-d}+\frac{(b-d)^{2}}{s-a}+\frac{(c-a)^{2}}{s-b}+\frac{(d-b)^{2}}{s-c}\right)(4 s-s)=3 s\left(A^{\prime}+B^{\prime}+C^{\prime}+D^{\prime}\right) . \end{aligned} $$ Hence $$ A^{\prime}+B^{\prime}+C^{\prime}+D^{\prime} \geq \frac{(2|a-c|+2|b-d|)^{2}}{3 s} \geq \frac{16 \cdot|a-c| \cdot|b-d|}{3 s} . $$ Next we estimate the absolute value of the other sum. We couple $A^{\prime \prime}$ with $C^{\prime \prime}$ to obtain $$ \begin{aligned} A^{\prime \prime}+C^{\prime \prime} & =\frac{(a-c)(a+c-2 b)}{s-d}+\frac{(c-a)(c+a-2 d)}{s-b} \\ & =\frac{(a-c)(a+c-2 b)(s-b)+(c-a)(c+a-2 d)(s-d)}{(s-d)(s-b)} \\ & =\frac{(a-c)(-2 b(s-b)-b(a+c)+2 d(s-d)+d(a+c))}{s(a+c)+b d} \\ & =\frac{3(a-c)(d-b)(a+c)}{M}, \quad \text { with } \quad M=s(a+c)+b d . \end{aligned} $$ Hence by cyclic shift $$ B^{\prime \prime}+D^{\prime \prime}=\frac{3(b-d)(a-c)(b+d)}{N}, \quad \text { with } \quad N=s(b+d)+c a $$ Thus $$ A^{\prime \prime}+B^{\prime \prime}+C^{\prime \prime}+D^{\prime \prime}=3(a-c)(b-d)\left(\frac{b+d}{N}-\frac{a+c}{M}\right)=\frac{3(a-c)(b-d) W}{M N} $$ where $$ W=(b+d) M-(a+c) N=b d(b+d)-a c(a+c) . $$ Note that $$ M N>(a c(a+c)+b d(b+d)) s \geq|W| \cdot s . $$ Now (2) and (4) yield $$ \left|A^{\prime \prime}+B^{\prime \prime}+C^{\prime \prime}+D^{\prime \prime}\right| \leq \frac{3 \cdot|a-c| \cdot|b-d|}{s} $$ Combined with (1) this results in $$ \begin{aligned} 2(A+B & +C+D)=\left(A^{\prime}+B^{\prime}+C^{\prime}+D^{\prime}\right)+\left(A^{\prime \prime}+B^{\prime \prime}+C^{\prime \prime}+D^{\prime \prime}\right) \\ & \geq \frac{16 \cdot|a-c| \cdot|b-d|}{3 s}-\frac{3 \cdot|a-c| \cdot|b-d|}{s}=\frac{7 \cdot|a-c| \cdot|b-d|}{3(a+b+c+d)} \geq 0 \end{aligned} $$ This is the required inequality. From the last line we see that equality can be achieved only if either $a=c$ or $b=d$. Since we also need equality in (1), this implies that actually $a=c$ and $b=d$ must hold simultaneously, which is obviously also a sufficient condition.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for any four positive real numbers $a, b, c, d$ the inequality $$ \frac{(a-b)(a-c)}{a+b+c}+\frac{(b-c)(b-d)}{b+c+d}+\frac{(c-d)(c-a)}{c+d+a}+\frac{(d-a)(d-b)}{d+a+b} \geq 0 $$ holds. Determine all cases of equality.
|
Denote the four terms by $$ A=\frac{(a-b)(a-c)}{a+b+c}, \quad B=\frac{(b-c)(b-d)}{b+c+d}, \quad C=\frac{(c-d)(c-a)}{c+d+a}, \quad D=\frac{(d-a)(d-b)}{d+a+b} . $$ The expression $2 A$ splits into two summands as follows, $$ 2 A=A^{\prime}+A^{\prime \prime} \quad \text { where } \quad A^{\prime}=\frac{(a-c)^{2}}{a+b+c}, \quad A^{\prime \prime}=\frac{(a-c)(a-2 b+c)}{a+b+c} ; $$ this is easily verified. We analogously represent $2 B=B^{\prime}+B^{\prime \prime}, 2 C=C^{\prime}+C^{\prime \prime}, 2 B=D^{\prime}+D^{\prime \prime}$ and examine each of the sums $A^{\prime}+B^{\prime}+C^{\prime}+D^{\prime}$ and $A^{\prime \prime}+B^{\prime \prime}+C^{\prime \prime}+D^{\prime \prime}$ separately. Write $s=a+b+c+d$; the denominators become $s-d, s-a, s-b, s-c$. By the CauchySchwarz inequality, $$ \begin{aligned} & \left(\frac{|a-c|}{\sqrt{s-d}} \cdot \sqrt{s-d}+\frac{|b-d|}{\sqrt{s-a}} \cdot \sqrt{s-a}+\frac{|c-a|}{\sqrt{s-b}} \cdot \sqrt{s-b}+\frac{|d-b|}{\sqrt{s-c}} \cdot \sqrt{s-c}\right)^{2} \\ & \quad \leq\left(\frac{(a-c)^{2}}{s-d}+\frac{(b-d)^{2}}{s-a}+\frac{(c-a)^{2}}{s-b}+\frac{(d-b)^{2}}{s-c}\right)(4 s-s)=3 s\left(A^{\prime}+B^{\prime}+C^{\prime}+D^{\prime}\right) . \end{aligned} $$ Hence $$ A^{\prime}+B^{\prime}+C^{\prime}+D^{\prime} \geq \frac{(2|a-c|+2|b-d|)^{2}}{3 s} \geq \frac{16 \cdot|a-c| \cdot|b-d|}{3 s} . $$ Next we estimate the absolute value of the other sum. We couple $A^{\prime \prime}$ with $C^{\prime \prime}$ to obtain $$ \begin{aligned} A^{\prime \prime}+C^{\prime \prime} & =\frac{(a-c)(a+c-2 b)}{s-d}+\frac{(c-a)(c+a-2 d)}{s-b} \\ & =\frac{(a-c)(a+c-2 b)(s-b)+(c-a)(c+a-2 d)(s-d)}{(s-d)(s-b)} \\ & =\frac{(a-c)(-2 b(s-b)-b(a+c)+2 d(s-d)+d(a+c))}{s(a+c)+b d} \\ & =\frac{3(a-c)(d-b)(a+c)}{M}, \quad \text { with } \quad M=s(a+c)+b d . \end{aligned} $$ Hence by cyclic shift $$ B^{\prime \prime}+D^{\prime \prime}=\frac{3(b-d)(a-c)(b+d)}{N}, \quad \text { with } \quad N=s(b+d)+c a $$ Thus $$ A^{\prime \prime}+B^{\prime \prime}+C^{\prime \prime}+D^{\prime \prime}=3(a-c)(b-d)\left(\frac{b+d}{N}-\frac{a+c}{M}\right)=\frac{3(a-c)(b-d) W}{M N} $$ where $$ W=(b+d) M-(a+c) N=b d(b+d)-a c(a+c) . $$ Note that $$ M N>(a c(a+c)+b d(b+d)) s \geq|W| \cdot s . $$ Now (2) and (4) yield $$ \left|A^{\prime \prime}+B^{\prime \prime}+C^{\prime \prime}+D^{\prime \prime}\right| \leq \frac{3 \cdot|a-c| \cdot|b-d|}{s} $$ Combined with (1) this results in $$ \begin{aligned} 2(A+B & +C+D)=\left(A^{\prime}+B^{\prime}+C^{\prime}+D^{\prime}\right)+\left(A^{\prime \prime}+B^{\prime \prime}+C^{\prime \prime}+D^{\prime \prime}\right) \\ & \geq \frac{16 \cdot|a-c| \cdot|b-d|}{3 s}-\frac{3 \cdot|a-c| \cdot|b-d|}{s}=\frac{7 \cdot|a-c| \cdot|b-d|}{3(a+b+c+d)} \geq 0 \end{aligned} $$ This is the required inequality. From the last line we see that equality can be achieved only if either $a=c$ or $b=d$. Since we also need equality in (1), this implies that actually $a=c$ and $b=d$ must hold simultaneously, which is obviously also a sufficient condition.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e5fabb6c-1f03-503a-96dc-d4468dd5139b
| 23,730
|
Prove that for any four positive real numbers $a, b, c, d$ the inequality $$ \frac{(a-b)(a-c)}{a+b+c}+\frac{(b-c)(b-d)}{b+c+d}+\frac{(c-d)(c-a)}{c+d+a}+\frac{(d-a)(d-b)}{d+a+b} \geq 0 $$ holds. Determine all cases of equality.
|
We keep the notations $A, B, C, D, s$, and also $M, N, W$ from the preceding solution; the definitions of $M, N, W$ and relations (3), (4) in that solution did not depend on the foregoing considerations. Starting from $$ 2 A=\frac{(a-c)^{2}+3(a+c)(a-c)}{a+b+c}-2 a+2 c $$ we get $$ \begin{aligned} 2(A & +C)=(a-c)^{2}\left(\frac{1}{s-d}+\frac{1}{s-b}\right)+3(a+c)(a-c)\left(\frac{1}{s-d}-\frac{1}{s-b}\right) \\ & =(a-c)^{2} \frac{2 s-b-d}{M}+3(a+c)(a-c) \cdot \frac{d-b}{M}=\frac{p(a-c)^{2}-3(a+c)(a-c)(b-d)}{M} \end{aligned} $$ where $p=2 s-b-d=s+a+c$. Similarly, writing $q=s+b+d$ we have $$ 2(B+D)=\frac{q(b-d)^{2}-3(b+d)(b-d)(c-a)}{N} ; $$ specific grouping of terms in the numerators has its aim. Note that $p q>2 s^{2}$. By adding the fractions expressing $2(A+C)$ and $2(B+D)$, $$ 2(A+B+C+D)=\frac{p(a-c)^{2}}{M}+\frac{3(a-c)(b-d) W}{M N}+\frac{q(b-d)^{2}}{N} $$ with $W$ defined by (3). Substitution $x=(a-c) / M, y=(b-d) / N$ brings the required inequality to the form $$ 2(A+B+C+D)=M p x^{2}+3 W x y+N q y^{2} \geq 0 . $$ It will be enough to verify that the discriminant $\Delta=9 W^{2}-4 M N p q$ of the quadratic trinomial $M p t^{2}+3 W t+N q$ is negative; on setting $t=x / y$ one then gets (6). The first inequality in (4) together with $p q>2 s^{2}$ imply $4 M N p q>8 s^{3}(a c(a+c)+b d(b+d))$. Since $$ (a+c) s^{3}>(a+c)^{4} \geq 4 a c(a+c)^{2} \quad \text { and likewise } \quad(b+d) s^{3}>4 b d(b+d)^{2} $$ the estimate continues as follows, $$ 4 M N p q>8\left(4(a c)^{2}(a+c)^{2}+4(b d)^{2}(b+d)^{2}\right)>32(b d(b+d)-a c(a+c))^{2}=32 W^{2} \geq 9 W^{2} $$ Thus indeed $\Delta<0$. The desired inequality (6) hence results. It becomes an equality if and only if $x=y=0$; equivalently, if and only if $a=c$ and simultaneously $b=d$. Comment. The two solutions presented above do not differ significantly; large portions overlap. The properties of the number $W$ turn out to be crucial in both approaches. The Cauchy-Schwarz inequality, applied in the first solution, is avoided in the second, which requires no knowledge beyond quadratic trinomials. The estimates in the proof of $\Delta<0$ in the second solution seem to be very wasteful. However, they come close to sharp when the terms in one of the pairs $(a, c),(b, d)$ are equal and much bigger than those in the other pair. In attempts to prove the inequality by just considering the six cases of arrangement of the numbers $a, b, c, d$ on the real line, one soon discovers that the cases which create real trouble are precisely those in which $a$ and $c$ are both greater or both smaller than $b$ and $d$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for any four positive real numbers $a, b, c, d$ the inequality $$ \frac{(a-b)(a-c)}{a+b+c}+\frac{(b-c)(b-d)}{b+c+d}+\frac{(c-d)(c-a)}{c+d+a}+\frac{(d-a)(d-b)}{d+a+b} \geq 0 $$ holds. Determine all cases of equality.
|
We keep the notations $A, B, C, D, s$, and also $M, N, W$ from the preceding solution; the definitions of $M, N, W$ and relations (3), (4) in that solution did not depend on the foregoing considerations. Starting from $$ 2 A=\frac{(a-c)^{2}+3(a+c)(a-c)}{a+b+c}-2 a+2 c $$ we get $$ \begin{aligned} 2(A & +C)=(a-c)^{2}\left(\frac{1}{s-d}+\frac{1}{s-b}\right)+3(a+c)(a-c)\left(\frac{1}{s-d}-\frac{1}{s-b}\right) \\ & =(a-c)^{2} \frac{2 s-b-d}{M}+3(a+c)(a-c) \cdot \frac{d-b}{M}=\frac{p(a-c)^{2}-3(a+c)(a-c)(b-d)}{M} \end{aligned} $$ where $p=2 s-b-d=s+a+c$. Similarly, writing $q=s+b+d$ we have $$ 2(B+D)=\frac{q(b-d)^{2}-3(b+d)(b-d)(c-a)}{N} ; $$ specific grouping of terms in the numerators has its aim. Note that $p q>2 s^{2}$. By adding the fractions expressing $2(A+C)$ and $2(B+D)$, $$ 2(A+B+C+D)=\frac{p(a-c)^{2}}{M}+\frac{3(a-c)(b-d) W}{M N}+\frac{q(b-d)^{2}}{N} $$ with $W$ defined by (3). Substitution $x=(a-c) / M, y=(b-d) / N$ brings the required inequality to the form $$ 2(A+B+C+D)=M p x^{2}+3 W x y+N q y^{2} \geq 0 . $$ It will be enough to verify that the discriminant $\Delta=9 W^{2}-4 M N p q$ of the quadratic trinomial $M p t^{2}+3 W t+N q$ is negative; on setting $t=x / y$ one then gets (6). The first inequality in (4) together with $p q>2 s^{2}$ imply $4 M N p q>8 s^{3}(a c(a+c)+b d(b+d))$. Since $$ (a+c) s^{3}>(a+c)^{4} \geq 4 a c(a+c)^{2} \quad \text { and likewise } \quad(b+d) s^{3}>4 b d(b+d)^{2} $$ the estimate continues as follows, $$ 4 M N p q>8\left(4(a c)^{2}(a+c)^{2}+4(b d)^{2}(b+d)^{2}\right)>32(b d(b+d)-a c(a+c))^{2}=32 W^{2} \geq 9 W^{2} $$ Thus indeed $\Delta<0$. The desired inequality (6) hence results. It becomes an equality if and only if $x=y=0$; equivalently, if and only if $a=c$ and simultaneously $b=d$. Comment. The two solutions presented above do not differ significantly; large portions overlap. The properties of the number $W$ turn out to be crucial in both approaches. The Cauchy-Schwarz inequality, applied in the first solution, is avoided in the second, which requires no knowledge beyond quadratic trinomials. The estimates in the proof of $\Delta<0$ in the second solution seem to be very wasteful. However, they come close to sharp when the terms in one of the pairs $(a, c),(b, d)$ are equal and much bigger than those in the other pair. In attempts to prove the inequality by just considering the six cases of arrangement of the numbers $a, b, c, d$ on the real line, one soon discovers that the cases which create real trouble are precisely those in which $a$ and $c$ are both greater or both smaller than $b$ and $d$.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e5fabb6c-1f03-503a-96dc-d4468dd5139b
| 23,730
|
Prove that for any four positive real numbers $a, b, c, d$ the inequality $$ \frac{(a-b)(a-c)}{a+b+c}+\frac{(b-c)(b-d)}{b+c+d}+\frac{(c-d)(c-a)}{c+d+a}+\frac{(d-a)(d-b)}{d+a+b} \geq 0 $$ holds. Determine all cases of equality.
|
$$ \begin{gathered} (a-b)(a-c)(a+b+d)(a+c+d)(b+c+d)= \\ =((a-b)(a+b+d))((a-c)(a+c+d))(b+c+d)= \\ =\left(a^{2}+a d-b^{2}-b d\right)\left(a^{2}+a d-c^{2}-c d\right)(b+c+d)= \\ =\left(a^{4}+2 a^{3} d-a^{2} b^{2}-a^{2} b d-a^{2} c^{2}-a^{2} c d+a^{2} d^{2}-a b^{2} d-a b d^{2}-a c^{2} d-a c d^{2}+b^{2} c^{2}+b^{2} c d+b c^{2} d+b c d^{2}\right)(b+c+d)= \\ =a^{4} b+a^{4} c+a^{4} d+\left(b^{3} c^{2}+a^{2} d^{3}\right)-a^{2} c^{3}+\left(2 a^{3} d^{2}-b^{3} a^{2}+c^{3} b^{2}\right)+ \\ +\left(b^{3} c d-c^{3} d a-d^{3} a b\right)+\left(2 a^{3} b d+c^{3} d b-d^{3} a c\right)+\left(2 a^{3} c d-b^{3} d a+d^{3} b c\right) \\ +\left(-a^{2} b^{2} c+3 b^{2} c^{2} d-2 a c^{2} d^{2}\right)+\left(-2 a^{2} b^{2} d+2 b c^{2} d^{2}\right)+\left(-a^{2} b c^{2}-2 a^{2} c^{2} d-2 a b^{2} d^{2}+2 b^{2} c d^{2}\right)+ \\ +\left(-2 a^{2} b c d-a b^{2} c d-a b c^{2} d-2 a b c d^{2}\right) \\ \text { Introducing the notation } S_{x y z w}=\sum_{c y c} a^{x} b^{y} c^{z} d^{w}, \text { one can write } \\ \sum_{c y c}(a-b)(a-c)(a+b+d)(a+c+d)(b+c+d)= \\ =S_{4100}+S_{4010}+S_{4001}+2 S_{3200}-S_{3020}+2 S_{3002}-S_{3110}+2 S_{3101}+2 S_{3011}-3 S_{2120}-6 S_{2111}= \\ +\left(S_{4100}+S_{4001}+\frac{1}{2} S_{3110}+\frac{1}{2} S_{3011}-3 S_{2120}\right)+ \\ +\left(S_{4010}-S_{3020}-\frac{3}{2} S_{3110}+\frac{3}{2} S_{3011}+\frac{9}{16} S_{2210}+\frac{9}{16} S_{2201}-\frac{9}{8} S_{2111}\right)+ \\ +\frac{9}{16}\left(S_{3200}-S_{2210}-S_{2201}+S_{3002}\right)+\frac{23}{16}\left(S_{3200}-2 S_{3101}+S_{3002}\right)+\frac{39}{8}\left(S_{3101}-S_{2111}\right), \end{gathered} $$ where the expressions $$ \begin{gathered} S_{4100}+S_{4001}+\frac{1}{2} S_{3110}+\frac{1}{2} S_{3011}-3 S_{2120}=\sum_{c y c}\left(a^{4} b+b c^{4}+\frac{1}{2} a^{3} b c+\frac{1}{2} a b c^{3}-3 a^{2} b c^{2}\right), \\ S_{4010}-S_{3020}-\frac{3}{2} S_{3110}+\frac{3}{2} S_{3011}+\frac{9}{16} S_{2210}+\frac{9}{16} S_{2201}-\frac{9}{8} S_{2111}=\sum_{c y c} a^{2} c\left(a-c-\frac{3}{4} b+\frac{3}{4} d\right)^{2}, \\ S_{3200}-S_{2210}-S_{2201}+S_{3002}=\sum_{c y c} b^{2}\left(a^{3}-a^{2} c-a c^{2}+c^{3}\right)=\sum_{c y c} b^{2}(a+c)(a-c)^{2}, \\ S_{3200}-2 S_{3101}+S_{3002}=\sum_{c y c} a^{3}(b-d)^{2} \quad \text { and } \quad S_{3101}-S_{2111}=\frac{1}{3} \sum_{c y c} b d\left(2 a^{3}+c^{3}-3 a^{2} c\right) \end{gathered} $$ are all nonnegative.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for any four positive real numbers $a, b, c, d$ the inequality $$ \frac{(a-b)(a-c)}{a+b+c}+\frac{(b-c)(b-d)}{b+c+d}+\frac{(c-d)(c-a)}{c+d+a}+\frac{(d-a)(d-b)}{d+a+b} \geq 0 $$ holds. Determine all cases of equality.
|
$$ \begin{gathered} (a-b)(a-c)(a+b+d)(a+c+d)(b+c+d)= \\ =((a-b)(a+b+d))((a-c)(a+c+d))(b+c+d)= \\ =\left(a^{2}+a d-b^{2}-b d\right)\left(a^{2}+a d-c^{2}-c d\right)(b+c+d)= \\ =\left(a^{4}+2 a^{3} d-a^{2} b^{2}-a^{2} b d-a^{2} c^{2}-a^{2} c d+a^{2} d^{2}-a b^{2} d-a b d^{2}-a c^{2} d-a c d^{2}+b^{2} c^{2}+b^{2} c d+b c^{2} d+b c d^{2}\right)(b+c+d)= \\ =a^{4} b+a^{4} c+a^{4} d+\left(b^{3} c^{2}+a^{2} d^{3}\right)-a^{2} c^{3}+\left(2 a^{3} d^{2}-b^{3} a^{2}+c^{3} b^{2}\right)+ \\ +\left(b^{3} c d-c^{3} d a-d^{3} a b\right)+\left(2 a^{3} b d+c^{3} d b-d^{3} a c\right)+\left(2 a^{3} c d-b^{3} d a+d^{3} b c\right) \\ +\left(-a^{2} b^{2} c+3 b^{2} c^{2} d-2 a c^{2} d^{2}\right)+\left(-2 a^{2} b^{2} d+2 b c^{2} d^{2}\right)+\left(-a^{2} b c^{2}-2 a^{2} c^{2} d-2 a b^{2} d^{2}+2 b^{2} c d^{2}\right)+ \\ +\left(-2 a^{2} b c d-a b^{2} c d-a b c^{2} d-2 a b c d^{2}\right) \\ \text { Introducing the notation } S_{x y z w}=\sum_{c y c} a^{x} b^{y} c^{z} d^{w}, \text { one can write } \\ \sum_{c y c}(a-b)(a-c)(a+b+d)(a+c+d)(b+c+d)= \\ =S_{4100}+S_{4010}+S_{4001}+2 S_{3200}-S_{3020}+2 S_{3002}-S_{3110}+2 S_{3101}+2 S_{3011}-3 S_{2120}-6 S_{2111}= \\ +\left(S_{4100}+S_{4001}+\frac{1}{2} S_{3110}+\frac{1}{2} S_{3011}-3 S_{2120}\right)+ \\ +\left(S_{4010}-S_{3020}-\frac{3}{2} S_{3110}+\frac{3}{2} S_{3011}+\frac{9}{16} S_{2210}+\frac{9}{16} S_{2201}-\frac{9}{8} S_{2111}\right)+ \\ +\frac{9}{16}\left(S_{3200}-S_{2210}-S_{2201}+S_{3002}\right)+\frac{23}{16}\left(S_{3200}-2 S_{3101}+S_{3002}\right)+\frac{39}{8}\left(S_{3101}-S_{2111}\right), \end{gathered} $$ where the expressions $$ \begin{gathered} S_{4100}+S_{4001}+\frac{1}{2} S_{3110}+\frac{1}{2} S_{3011}-3 S_{2120}=\sum_{c y c}\left(a^{4} b+b c^{4}+\frac{1}{2} a^{3} b c+\frac{1}{2} a b c^{3}-3 a^{2} b c^{2}\right), \\ S_{4010}-S_{3020}-\frac{3}{2} S_{3110}+\frac{3}{2} S_{3011}+\frac{9}{16} S_{2210}+\frac{9}{16} S_{2201}-\frac{9}{8} S_{2111}=\sum_{c y c} a^{2} c\left(a-c-\frac{3}{4} b+\frac{3}{4} d\right)^{2}, \\ S_{3200}-S_{2210}-S_{2201}+S_{3002}=\sum_{c y c} b^{2}\left(a^{3}-a^{2} c-a c^{2}+c^{3}\right)=\sum_{c y c} b^{2}(a+c)(a-c)^{2}, \\ S_{3200}-2 S_{3101}+S_{3002}=\sum_{c y c} a^{3}(b-d)^{2} \quad \text { and } \quad S_{3101}-S_{2111}=\frac{1}{3} \sum_{c y c} b d\left(2 a^{3}+c^{3}-3 a^{2} c\right) \end{gathered} $$ are all nonnegative.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e5fabb6c-1f03-503a-96dc-d4468dd5139b
| 23,730
|
In an acute-angled triangle $A B C$, point $H$ is the orthocentre and $A_{0}, B_{0}, C_{0}$ are the midpoints of the sides $B C, C A, A B$, respectively. Consider three circles passing through $H$ : $\omega_{a}$ around $A_{0}, \omega_{b}$ around $B_{0}$ and $\omega_{c}$ around $C_{0}$. The circle $\omega_{a}$ intersects the line $B C$ at $A_{1}$ and $A_{2} ; \omega_{b}$ intersects $C A$ at $B_{1}$ and $B_{2} ; \omega_{c}$ intersects $A B$ at $C_{1}$ and $C_{2}$. Show that the points $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ lie on a circle.
|
The perpendicular bisectors of the segments $A_{1} A_{2}, B_{1} B_{2}, C_{1} C_{2}$ are also the perpendicular bisectors of $B C, C A, A B$. So they meet at $O$, the circumcentre of $A B C$. Thus $O$ is the only point that can possibly be the centre of the desired circle. From the right triangle $O A_{0} A_{1}$ we get $$ O A_{1}^{2}=O A_{0}^{2}+A_{0} A_{1}^{2}=O A_{0}^{2}+A_{0} H^{2} $$ Let $K$ be the midpoint of $A H$ and let $L$ be the midpoint of $C H$. Since $A_{0}$ and $B_{0}$ are the midpoints of $B C$ and $C A$, we see that $A_{0} L \| B H$ and $B_{0} L \| A H$. Thus the segments $A_{0} L$ and $B_{0} L$ are perpendicular to $A C$ and $B C$, hence parallel to $O B_{0}$ and $O A_{0}$, respectively. Consequently $O A_{0} L B_{0}$ is a parallelogram, so that $O A_{0}$ and $B_{0} L$ are equal and parallel. Also, the midline $B_{0} L$ of triangle $A H C$ is equal and parallel to $A K$ and $K H$. It follows that $A K A_{0} O$ and $H A_{0} O K$ are parallelograms. The first one gives $A_{0} K=O A=R$, where $R$ is the circumradius of $A B C$. From the second one we obtain $$ 2\left(O A_{0}^{2}+A_{0} H^{2}\right)=O H^{2}+A_{0} K^{2}=O H^{2}+R^{2} . $$ (In a parallelogram, the sum of squares of the diagonals equals the sum of squares of the sides). From (1) and (2) we get $O A_{1}^{2}=\left(O H^{2}+R^{2}\right) / 2$. By symmetry, the same holds for the distances $O A_{2}, O B_{1}, O B_{2}, O C_{1}$ and $O C_{2}$. Thus $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ all lie on a circle with centre at $O$ and radius $\left(O H^{2}+R^{2}\right) / 2$. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute-angled triangle $A B C$, point $H$ is the orthocentre and $A_{0}, B_{0}, C_{0}$ are the midpoints of the sides $B C, C A, A B$, respectively. Consider three circles passing through $H$ : $\omega_{a}$ around $A_{0}, \omega_{b}$ around $B_{0}$ and $\omega_{c}$ around $C_{0}$. The circle $\omega_{a}$ intersects the line $B C$ at $A_{1}$ and $A_{2} ; \omega_{b}$ intersects $C A$ at $B_{1}$ and $B_{2} ; \omega_{c}$ intersects $A B$ at $C_{1}$ and $C_{2}$. Show that the points $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ lie on a circle.
|
The perpendicular bisectors of the segments $A_{1} A_{2}, B_{1} B_{2}, C_{1} C_{2}$ are also the perpendicular bisectors of $B C, C A, A B$. So they meet at $O$, the circumcentre of $A B C$. Thus $O$ is the only point that can possibly be the centre of the desired circle. From the right triangle $O A_{0} A_{1}$ we get $$ O A_{1}^{2}=O A_{0}^{2}+A_{0} A_{1}^{2}=O A_{0}^{2}+A_{0} H^{2} $$ Let $K$ be the midpoint of $A H$ and let $L$ be the midpoint of $C H$. Since $A_{0}$ and $B_{0}$ are the midpoints of $B C$ and $C A$, we see that $A_{0} L \| B H$ and $B_{0} L \| A H$. Thus the segments $A_{0} L$ and $B_{0} L$ are perpendicular to $A C$ and $B C$, hence parallel to $O B_{0}$ and $O A_{0}$, respectively. Consequently $O A_{0} L B_{0}$ is a parallelogram, so that $O A_{0}$ and $B_{0} L$ are equal and parallel. Also, the midline $B_{0} L$ of triangle $A H C$ is equal and parallel to $A K$ and $K H$. It follows that $A K A_{0} O$ and $H A_{0} O K$ are parallelograms. The first one gives $A_{0} K=O A=R$, where $R$ is the circumradius of $A B C$. From the second one we obtain $$ 2\left(O A_{0}^{2}+A_{0} H^{2}\right)=O H^{2}+A_{0} K^{2}=O H^{2}+R^{2} . $$ (In a parallelogram, the sum of squares of the diagonals equals the sum of squares of the sides). From (1) and (2) we get $O A_{1}^{2}=\left(O H^{2}+R^{2}\right) / 2$. By symmetry, the same holds for the distances $O A_{2}, O B_{1}, O B_{2}, O C_{1}$ and $O C_{2}$. Thus $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ all lie on a circle with centre at $O$ and radius $\left(O H^{2}+R^{2}\right) / 2$. 
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
be8d6fd2-bbda-553f-af79-b0b373b74649
| 23,753
|
In an acute-angled triangle $A B C$, point $H$ is the orthocentre and $A_{0}, B_{0}, C_{0}$ are the midpoints of the sides $B C, C A, A B$, respectively. Consider three circles passing through $H$ : $\omega_{a}$ around $A_{0}, \omega_{b}$ around $B_{0}$ and $\omega_{c}$ around $C_{0}$. The circle $\omega_{a}$ intersects the line $B C$ at $A_{1}$ and $A_{2} ; \omega_{b}$ intersects $C A$ at $B_{1}$ and $B_{2} ; \omega_{c}$ intersects $A B$ at $C_{1}$ and $C_{2}$. Show that the points $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ lie on a circle.
|
We are going to show again that the circumcentre $O$ is equidistant from the six points in question. Let $A^{\prime}$ be the second intersection point of $\omega_{b}$ and $\omega_{c}$. The line $B_{0} C_{0}$, which is the line of centers of circles $\omega_{b}$ and $\omega_{c}$, is a midline in triangle $A B C$, parallel to $B C$ and perpendicular to the altitude $A H$. The points $A^{\prime}$ and $H$ are symmetric with respect to the line of centers. Therefore $A^{\prime}$ lies on the line $A H$. From the two circles $\omega_{b}$ and $\omega_{c}$ we obtain $A C_{1} \cdot A C_{2}=A A^{\prime} \cdot A H=A B_{1} \cdot A B_{2}$. So the quadrilateral $B_{1} B_{2} C_{1} C_{2}$ is cyclic. The perpendicular bisectors of the sides $B_{1} B_{2}$ and $C_{1} C_{2}$ meet at $O$. Hence $O$ is the circumcentre of $B_{1} B_{2} C_{1} C_{2}$ and so $O B_{1}=O B_{2}=O C_{1}=O C_{2}$. Analogous arguments yield $O A_{1}=O A_{2}=O B_{1}=O B_{2}$ and $O A_{1}=O A_{2}=O C_{1}=O C_{2}$. Thus $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ lie on a circle centred at $O$.  Comment. The problem can be solved without much difficulty in many ways by calculation, using trigonometry, coordinate geometry or complex numbers. As an example we present a short proof using vectors.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute-angled triangle $A B C$, point $H$ is the orthocentre and $A_{0}, B_{0}, C_{0}$ are the midpoints of the sides $B C, C A, A B$, respectively. Consider three circles passing through $H$ : $\omega_{a}$ around $A_{0}, \omega_{b}$ around $B_{0}$ and $\omega_{c}$ around $C_{0}$. The circle $\omega_{a}$ intersects the line $B C$ at $A_{1}$ and $A_{2} ; \omega_{b}$ intersects $C A$ at $B_{1}$ and $B_{2} ; \omega_{c}$ intersects $A B$ at $C_{1}$ and $C_{2}$. Show that the points $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ lie on a circle.
|
We are going to show again that the circumcentre $O$ is equidistant from the six points in question. Let $A^{\prime}$ be the second intersection point of $\omega_{b}$ and $\omega_{c}$. The line $B_{0} C_{0}$, which is the line of centers of circles $\omega_{b}$ and $\omega_{c}$, is a midline in triangle $A B C$, parallel to $B C$ and perpendicular to the altitude $A H$. The points $A^{\prime}$ and $H$ are symmetric with respect to the line of centers. Therefore $A^{\prime}$ lies on the line $A H$. From the two circles $\omega_{b}$ and $\omega_{c}$ we obtain $A C_{1} \cdot A C_{2}=A A^{\prime} \cdot A H=A B_{1} \cdot A B_{2}$. So the quadrilateral $B_{1} B_{2} C_{1} C_{2}$ is cyclic. The perpendicular bisectors of the sides $B_{1} B_{2}$ and $C_{1} C_{2}$ meet at $O$. Hence $O$ is the circumcentre of $B_{1} B_{2} C_{1} C_{2}$ and so $O B_{1}=O B_{2}=O C_{1}=O C_{2}$. Analogous arguments yield $O A_{1}=O A_{2}=O B_{1}=O B_{2}$ and $O A_{1}=O A_{2}=O C_{1}=O C_{2}$. Thus $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ lie on a circle centred at $O$.  Comment. The problem can be solved without much difficulty in many ways by calculation, using trigonometry, coordinate geometry or complex numbers. As an example we present a short proof using vectors.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
be8d6fd2-bbda-553f-af79-b0b373b74649
| 23,753
|
In an acute-angled triangle $A B C$, point $H$ is the orthocentre and $A_{0}, B_{0}, C_{0}$ are the midpoints of the sides $B C, C A, A B$, respectively. Consider three circles passing through $H$ : $\omega_{a}$ around $A_{0}, \omega_{b}$ around $B_{0}$ and $\omega_{c}$ around $C_{0}$. The circle $\omega_{a}$ intersects the line $B C$ at $A_{1}$ and $A_{2} ; \omega_{b}$ intersects $C A$ at $B_{1}$ and $B_{2} ; \omega_{c}$ intersects $A B$ at $C_{1}$ and $C_{2}$. Show that the points $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ lie on a circle.
|
Let again $O$ and $R$ be the circumcentre and circumradius. Consider the vectors $$ \overrightarrow{O A}=\mathbf{a}, \quad \overrightarrow{O B}=\mathbf{b}, \quad \overrightarrow{O C}=\mathbf{c}, \quad \text { where } \quad \mathbf{a}^{2}=\mathbf{b}^{2}=\mathbf{c}^{2}=R^{2} $$ It is well known that $\overrightarrow{O H}=\mathbf{a}+\mathbf{b}+\mathbf{c}$. Accordingly, $$ \overrightarrow{A_{0} H}=\overrightarrow{O H}-\overrightarrow{O A_{0}}=(\mathbf{a}+\mathbf{b}+\mathbf{c})-\frac{\mathbf{b}+\mathbf{c}}{2}=\frac{2 \mathbf{a}+\mathbf{b}+\mathbf{c}}{2} $$ and $$ \begin{gathered} O A_{1}^{2}=O A_{0}^{2}+A_{0} A_{1}^{2}=O A_{0}^{2}+A_{0} H^{2}=\left(\frac{\mathbf{b}+\mathbf{c}}{2}\right)^{2}+\left(\frac{2 \mathbf{a}+\mathbf{b}+\mathbf{c}}{2}\right)^{2} \\ =\frac{1}{4}\left(\mathbf{b}^{2}+2 \mathbf{b} \mathbf{c}+\mathbf{c}^{2}\right)+\frac{1}{4}\left(4 \mathbf{a}^{2}+4 \mathbf{a} \mathbf{b}+4 \mathbf{a} \mathbf{c}+\mathbf{b}^{2}+2 \mathbf{b} \mathbf{c}+\mathbf{c}^{2}\right)=2 R^{2}+(\mathbf{a b}+\mathbf{a c}+\mathbf{b c}) \end{gathered} $$ here $\mathbf{a b}$, bc, etc. denote dot products of vectors. We get the same for the distances $O A_{2}, O B_{1}$, $O B_{2}, O C_{1}$ and $O C_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute-angled triangle $A B C$, point $H$ is the orthocentre and $A_{0}, B_{0}, C_{0}$ are the midpoints of the sides $B C, C A, A B$, respectively. Consider three circles passing through $H$ : $\omega_{a}$ around $A_{0}, \omega_{b}$ around $B_{0}$ and $\omega_{c}$ around $C_{0}$. The circle $\omega_{a}$ intersects the line $B C$ at $A_{1}$ and $A_{2} ; \omega_{b}$ intersects $C A$ at $B_{1}$ and $B_{2} ; \omega_{c}$ intersects $A B$ at $C_{1}$ and $C_{2}$. Show that the points $A_{1}, A_{2}, B_{1}, B_{2}, C_{1}, C_{2}$ lie on a circle.
|
Let again $O$ and $R$ be the circumcentre and circumradius. Consider the vectors $$ \overrightarrow{O A}=\mathbf{a}, \quad \overrightarrow{O B}=\mathbf{b}, \quad \overrightarrow{O C}=\mathbf{c}, \quad \text { where } \quad \mathbf{a}^{2}=\mathbf{b}^{2}=\mathbf{c}^{2}=R^{2} $$ It is well known that $\overrightarrow{O H}=\mathbf{a}+\mathbf{b}+\mathbf{c}$. Accordingly, $$ \overrightarrow{A_{0} H}=\overrightarrow{O H}-\overrightarrow{O A_{0}}=(\mathbf{a}+\mathbf{b}+\mathbf{c})-\frac{\mathbf{b}+\mathbf{c}}{2}=\frac{2 \mathbf{a}+\mathbf{b}+\mathbf{c}}{2} $$ and $$ \begin{gathered} O A_{1}^{2}=O A_{0}^{2}+A_{0} A_{1}^{2}=O A_{0}^{2}+A_{0} H^{2}=\left(\frac{\mathbf{b}+\mathbf{c}}{2}\right)^{2}+\left(\frac{2 \mathbf{a}+\mathbf{b}+\mathbf{c}}{2}\right)^{2} \\ =\frac{1}{4}\left(\mathbf{b}^{2}+2 \mathbf{b} \mathbf{c}+\mathbf{c}^{2}\right)+\frac{1}{4}\left(4 \mathbf{a}^{2}+4 \mathbf{a} \mathbf{b}+4 \mathbf{a} \mathbf{c}+\mathbf{b}^{2}+2 \mathbf{b} \mathbf{c}+\mathbf{c}^{2}\right)=2 R^{2}+(\mathbf{a b}+\mathbf{a c}+\mathbf{b c}) \end{gathered} $$ here $\mathbf{a b}$, bc, etc. denote dot products of vectors. We get the same for the distances $O A_{2}, O B_{1}$, $O B_{2}, O C_{1}$ and $O C_{2}$.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
be8d6fd2-bbda-553f-af79-b0b373b74649
| 23,753
|
Given trapezoid $A B C D$ with parallel sides $A B$ and $C D$, assume that there exist points $E$ on line $B C$ outside segment $B C$, and $F$ inside segment $A D$, such that $\angle D A E=\angle C B F$. Denote by $I$ the point of intersection of $C D$ and $E F$, and by $J$ the point of intersection of $A B$ and $E F$. Let $K$ be the midpoint of segment $E F$; assume it does not lie on line $A B$. Prove that $I$ belongs to the circumcircle of $A B K$ if and only if $K$ belongs to the circumcircle of $C D J$.
|
Assume that the disposition of points is as in the diagram. Since $\angle E B F=180^{\circ}-\angle C B F=180^{\circ}-\angle E A F$ by hypothesis, the quadrilateral $A E B F$ is cyclic. Hence $A J \cdot J B=F J \cdot J E$. In view of this equality, $I$ belongs to the circumcircle of $A B K$ if and only if $I J \cdot J K=F J \cdot J E$. Expressing $I J=I F+F J, J E=F E-F J$, and $J K=\frac{1}{2} F E-F J$, we find that $I$ belongs to the circumcircle of $A B K$ if and only if $$ F J=\frac{I F \cdot F E}{2 I F+F E} . $$ Since $A E B F$ is cyclic and $A B, C D$ are parallel, $\angle F E C=\angle F A B=180^{\circ}-\angle C D F$. Then $C D F E$ is also cyclic, yielding $I D \cdot I C=I F \cdot I E$. It follows that $K$ belongs to the circumcircle of $C D J$ if and only if $I J \cdot I K=I F \cdot I E$. Expressing $I J=I F+F J, I K=I F+\frac{1}{2} F E$, and $I E=I F+F E$, we find that $K$ is on the circumcircle of $C D J$ if and only if $$ F J=\frac{I F \cdot F E}{2 I F+F E} $$ The conclusion follows.  Comment. While the figure shows $B$ inside segment $C E$, it is possible that $C$ is inside segment $B E$. Consequently, $I$ would be inside segment $E F$ and $J$ outside segment $E F$. The position of point $K$ on line $E F$ with respect to points $I, J$ may also vary. Some case may require that an angle $\varphi$ be replaced by $180^{\circ}-\varphi$, and in computing distances, a sum may need to become a difference. All these cases can be covered by the proposed solution if it is clearly stated that signed distances and angles are used.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given trapezoid $A B C D$ with parallel sides $A B$ and $C D$, assume that there exist points $E$ on line $B C$ outside segment $B C$, and $F$ inside segment $A D$, such that $\angle D A E=\angle C B F$. Denote by $I$ the point of intersection of $C D$ and $E F$, and by $J$ the point of intersection of $A B$ and $E F$. Let $K$ be the midpoint of segment $E F$; assume it does not lie on line $A B$. Prove that $I$ belongs to the circumcircle of $A B K$ if and only if $K$ belongs to the circumcircle of $C D J$.
|
Assume that the disposition of points is as in the diagram. Since $\angle E B F=180^{\circ}-\angle C B F=180^{\circ}-\angle E A F$ by hypothesis, the quadrilateral $A E B F$ is cyclic. Hence $A J \cdot J B=F J \cdot J E$. In view of this equality, $I$ belongs to the circumcircle of $A B K$ if and only if $I J \cdot J K=F J \cdot J E$. Expressing $I J=I F+F J, J E=F E-F J$, and $J K=\frac{1}{2} F E-F J$, we find that $I$ belongs to the circumcircle of $A B K$ if and only if $$ F J=\frac{I F \cdot F E}{2 I F+F E} . $$ Since $A E B F$ is cyclic and $A B, C D$ are parallel, $\angle F E C=\angle F A B=180^{\circ}-\angle C D F$. Then $C D F E$ is also cyclic, yielding $I D \cdot I C=I F \cdot I E$. It follows that $K$ belongs to the circumcircle of $C D J$ if and only if $I J \cdot I K=I F \cdot I E$. Expressing $I J=I F+F J, I K=I F+\frac{1}{2} F E$, and $I E=I F+F E$, we find that $K$ is on the circumcircle of $C D J$ if and only if $$ F J=\frac{I F \cdot F E}{2 I F+F E} $$ The conclusion follows.  Comment. While the figure shows $B$ inside segment $C E$, it is possible that $C$ is inside segment $B E$. Consequently, $I$ would be inside segment $E F$ and $J$ outside segment $E F$. The position of point $K$ on line $E F$ with respect to points $I, J$ may also vary. Some case may require that an angle $\varphi$ be replaced by $180^{\circ}-\varphi$, and in computing distances, a sum may need to become a difference. All these cases can be covered by the proposed solution if it is clearly stated that signed distances and angles are used.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6cce70a2-2632-58ee-b16e-377caa617a01
| 23,759
|
Let $A B C D$ be a convex quadrilateral and let $P$ and $Q$ be points in $A B C D$ such that $P Q D A$ and $Q P B C$ are cyclic quadrilaterals. Suppose that there exists a point $E$ on the line segment $P Q$ such that $\angle P A E=\angle Q D E$ and $\angle P B E=\angle Q C E$. Show that the quadrilateral $A B C D$ is cyclic.
|
Let $F$ be the point on the line $A D$ such that $E F \| P A$. By hypothesis, the quadrilateral $P Q D A$ is cyclic. So if $F$ lies between $A$ and $D$ then $\angle E F D=\angle P A D=180^{\circ}-\angle E Q D$; the points $F$ and $Q$ are on distinct sides of the line $D E$ and we infer that $E F D Q$ is a cyclic quadrilateral. And if $D$ lies between $A$ and $F$ then a similar argument shows that $\angle E F D=\angle E Q D$; but now the points $F$ and $Q$ lie on the same side of $D E$, so that $E D F Q$ is a cyclic quadrilateral. In either case we obtain the equality $\angle E F Q=\angle E D Q=\angle P A E$ which implies that $F Q \| A E$. So the triangles $E F Q$ and $P A E$ are either homothetic or parallel-congruent. More specifically, triangle $E F Q$ is the image of $P A E$ under the mapping $f$ which carries the points $P, E$ respectively to $E, Q$ and is either a homothety or translation by a vector. Note that $f$ is uniquely determined by these conditions and the position of the points $P, E, Q$ alone. Let now $G$ be the point on the line $B C$ such that $E G \| P B$. The same reasoning as above applies to points $B, C$ in place of $A, D$, implying that the triangle $E G Q$ is the image of $P B E$ under the same mapping $f$. So $f$ sends the four points $A, P, B, E$ respectively to $F, E, G, Q$. If $P E \neq Q E$, so that $f$ is a homothety with a centre $X$, then the lines $A F, P E, B G$-i.e. the lines $A D, P Q, B C$ - are concurrent at $X$. And since $P Q D A$ and $Q P B C$ are cyclic quadrilaterals, the equalities $X A \cdot X D=X P \cdot X Q=X B \cdot X C$ hold, showing that the quadrilateral $A B C D$ is cyclic. Finally, if $P E=Q E$, so that $f$ is a translation, then $A D\|P Q\| B C$. Thus $P Q D A$ and $Q P B C$ are isosceles trapezoids. Then also $A B C D$ is an isosceles trapezoid, hence a cyclic quadrilateral. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral and let $P$ and $Q$ be points in $A B C D$ such that $P Q D A$ and $Q P B C$ are cyclic quadrilaterals. Suppose that there exists a point $E$ on the line segment $P Q$ such that $\angle P A E=\angle Q D E$ and $\angle P B E=\angle Q C E$. Show that the quadrilateral $A B C D$ is cyclic.
|
Let $F$ be the point on the line $A D$ such that $E F \| P A$. By hypothesis, the quadrilateral $P Q D A$ is cyclic. So if $F$ lies between $A$ and $D$ then $\angle E F D=\angle P A D=180^{\circ}-\angle E Q D$; the points $F$ and $Q$ are on distinct sides of the line $D E$ and we infer that $E F D Q$ is a cyclic quadrilateral. And if $D$ lies between $A$ and $F$ then a similar argument shows that $\angle E F D=\angle E Q D$; but now the points $F$ and $Q$ lie on the same side of $D E$, so that $E D F Q$ is a cyclic quadrilateral. In either case we obtain the equality $\angle E F Q=\angle E D Q=\angle P A E$ which implies that $F Q \| A E$. So the triangles $E F Q$ and $P A E$ are either homothetic or parallel-congruent. More specifically, triangle $E F Q$ is the image of $P A E$ under the mapping $f$ which carries the points $P, E$ respectively to $E, Q$ and is either a homothety or translation by a vector. Note that $f$ is uniquely determined by these conditions and the position of the points $P, E, Q$ alone. Let now $G$ be the point on the line $B C$ such that $E G \| P B$. The same reasoning as above applies to points $B, C$ in place of $A, D$, implying that the triangle $E G Q$ is the image of $P B E$ under the same mapping $f$. So $f$ sends the four points $A, P, B, E$ respectively to $F, E, G, Q$. If $P E \neq Q E$, so that $f$ is a homothety with a centre $X$, then the lines $A F, P E, B G$-i.e. the lines $A D, P Q, B C$ - are concurrent at $X$. And since $P Q D A$ and $Q P B C$ are cyclic quadrilaterals, the equalities $X A \cdot X D=X P \cdot X Q=X B \cdot X C$ hold, showing that the quadrilateral $A B C D$ is cyclic. Finally, if $P E=Q E$, so that $f$ is a translation, then $A D\|P Q\| B C$. Thus $P Q D A$ and $Q P B C$ are isosceles trapezoids. Then also $A B C D$ is an isosceles trapezoid, hence a cyclic quadrilateral. 
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9e0e1a64-408d-5d02-a5c9-23c5feabb1a4
| 23,762
|
Let $A B C D$ be a convex quadrilateral and let $P$ and $Q$ be points in $A B C D$ such that $P Q D A$ and $Q P B C$ are cyclic quadrilaterals. Suppose that there exists a point $E$ on the line segment $P Q$ such that $\angle P A E=\angle Q D E$ and $\angle P B E=\angle Q C E$. Show that the quadrilateral $A B C D$ is cyclic.
|
Here is another way to reach the conclusion that the lines $A D, B C$ and $P Q$ are either concurrent or parallel. From the cyclic quadrilateral $P Q D A$ we get $$ \angle P A D=180^{\circ}-\angle P Q D=\angle Q D E+\angle Q E D=\angle P A E+\angle Q E D . $$ Hence $\angle Q E D=\angle P A D-\angle P A E=\angle E A D$. This in view of the tangent-chord theorem means that the circumcircle of triangle $E A D$ is tangent to the line $P Q$ at $E$. Analogously, the circumcircle of triangle $E B C$ is tangent to $P Q$ at $E$. Suppose that the line $A D$ intersects $P Q$ at $X$. Since $X E$ is tangent to the circle $(E A D)$, $X E^{2}=X A \cdot X D$. Also, $X A \cdot X D=X P \cdot X Q$ because $P, Q, D, A$ lie on a circle. Therefore $X E^{2}=X P \cdot X Q$. It is not hard to see that this equation determines the position of the point $X$ on the line $P Q$ uniquely. Thus, if $B C$ also cuts $P Q$, say at $Y$, then the analogous equation for $Y$ yields $X=Y$, meaning that the three lines indeed concur. In this case, as well as in the case where $A D\|P Q\| B C$, the concluding argument is the same as in the first solution. It remains to eliminate the possibility that e.g. $A D$ meets $P Q$ at $X$ while $B C \| P Q$. Indeed, $Q P B C$ would then be an isosceles trapezoid and the angle equality $\angle P B E=\angle Q C E$ would force that $E$ is the midpoint of $P Q$. So the length of $X E$, which is the geometric mean of the lengths of $X P$ and $X Q$, should also be their arithmetic mean-impossible, as $X P \neq X Q$. The proof is now complete. Comment. After reaching the conclusion that the circles $(E D A)$ and $(E B C)$ are tangent to $P Q$ one may continue as follows. Denote the circles $(P Q D A),(E D A),(E B C),(Q P B C)$ by $\omega_{1}, \omega_{2}, \omega_{3}, \omega_{4}$ respectively. Let $\ell_{i j}$ be the radical axis of the pair $\left(\omega_{i}, \omega_{j}\right)$ for $i<j$. As is well-known, the lines $\ell_{12}, \ell_{13}, \ell_{23}$ concur, possibly at infinity (let this be the meaning of the word concur in this comment). So do the lines $\ell_{12}, \ell_{14}, \ell_{24}$. Note however that $\ell_{23}$ and $\ell_{14}$ both coincide with the line $P Q$. Hence the pair $\ell_{12}, P Q$ is in both triples; thus the four lines $\ell_{12}, \ell_{13}, \ell_{24}$ and $P Q$ are concurrent. Similarly, $\ell_{13}, \ell_{14}, \ell_{34}$ concur, $\ell_{23}, \ell_{24}, \ell_{34}$ concur, and since $\ell_{14}=\ell_{23}=P Q$, the four lines $\ell_{13}, \ell_{24}, \ell_{34}$ and $P Q$ are concurrent. The lines $\ell_{13}$ and $\ell_{24}$ are present in both quadruples, therefore all the lines $\ell_{i j}$ are concurrent. Hence the result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral and let $P$ and $Q$ be points in $A B C D$ such that $P Q D A$ and $Q P B C$ are cyclic quadrilaterals. Suppose that there exists a point $E$ on the line segment $P Q$ such that $\angle P A E=\angle Q D E$ and $\angle P B E=\angle Q C E$. Show that the quadrilateral $A B C D$ is cyclic.
|
Here is another way to reach the conclusion that the lines $A D, B C$ and $P Q$ are either concurrent or parallel. From the cyclic quadrilateral $P Q D A$ we get $$ \angle P A D=180^{\circ}-\angle P Q D=\angle Q D E+\angle Q E D=\angle P A E+\angle Q E D . $$ Hence $\angle Q E D=\angle P A D-\angle P A E=\angle E A D$. This in view of the tangent-chord theorem means that the circumcircle of triangle $E A D$ is tangent to the line $P Q$ at $E$. Analogously, the circumcircle of triangle $E B C$ is tangent to $P Q$ at $E$. Suppose that the line $A D$ intersects $P Q$ at $X$. Since $X E$ is tangent to the circle $(E A D)$, $X E^{2}=X A \cdot X D$. Also, $X A \cdot X D=X P \cdot X Q$ because $P, Q, D, A$ lie on a circle. Therefore $X E^{2}=X P \cdot X Q$. It is not hard to see that this equation determines the position of the point $X$ on the line $P Q$ uniquely. Thus, if $B C$ also cuts $P Q$, say at $Y$, then the analogous equation for $Y$ yields $X=Y$, meaning that the three lines indeed concur. In this case, as well as in the case where $A D\|P Q\| B C$, the concluding argument is the same as in the first solution. It remains to eliminate the possibility that e.g. $A D$ meets $P Q$ at $X$ while $B C \| P Q$. Indeed, $Q P B C$ would then be an isosceles trapezoid and the angle equality $\angle P B E=\angle Q C E$ would force that $E$ is the midpoint of $P Q$. So the length of $X E$, which is the geometric mean of the lengths of $X P$ and $X Q$, should also be their arithmetic mean-impossible, as $X P \neq X Q$. The proof is now complete. Comment. After reaching the conclusion that the circles $(E D A)$ and $(E B C)$ are tangent to $P Q$ one may continue as follows. Denote the circles $(P Q D A),(E D A),(E B C),(Q P B C)$ by $\omega_{1}, \omega_{2}, \omega_{3}, \omega_{4}$ respectively. Let $\ell_{i j}$ be the radical axis of the pair $\left(\omega_{i}, \omega_{j}\right)$ for $i<j$. As is well-known, the lines $\ell_{12}, \ell_{13}, \ell_{23}$ concur, possibly at infinity (let this be the meaning of the word concur in this comment). So do the lines $\ell_{12}, \ell_{14}, \ell_{24}$. Note however that $\ell_{23}$ and $\ell_{14}$ both coincide with the line $P Q$. Hence the pair $\ell_{12}, P Q$ is in both triples; thus the four lines $\ell_{12}, \ell_{13}, \ell_{24}$ and $P Q$ are concurrent. Similarly, $\ell_{13}, \ell_{14}, \ell_{34}$ concur, $\ell_{23}, \ell_{24}, \ell_{34}$ concur, and since $\ell_{14}=\ell_{23}=P Q$, the four lines $\ell_{13}, \ell_{24}, \ell_{34}$ and $P Q$ are concurrent. The lines $\ell_{13}$ and $\ell_{24}$ are present in both quadruples, therefore all the lines $\ell_{i j}$ are concurrent. Hence the result.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9e0e1a64-408d-5d02-a5c9-23c5feabb1a4
| 23,762
|
In an acute triangle $A B C$ segments $B E$ and $C F$ are altitudes. Two circles passing through the points $A$ and $F$ are tangent to the line $B C$ at the points $P$ and $Q$ so that $B$ lies between $C$ and $Q$. Prove that the lines $P E$ and $Q F$ intersect on the circumcircle of triangle $A E F$.
|
To approach the desired result we need some information about the slopes of the lines $P E$ and $Q F$; this information is provided by formulas (1) and (2) which we derive below. The tangents $B P$ and $B Q$ to the two circles passing through $A$ and $F$ are equal, as $B P^{2}=B A \cdot B F=B Q^{2}$. Consider the altitude $A D$ of triangle $A B C$ and its orthocentre $H$. From the cyclic quadrilaterals $C D F A$ and $C D H E$ we get $B A \cdot B F=B C \cdot B D=B E \cdot B H$. Thus $B P^{2}=B E \cdot B H$, or $B P / B H=B E / B P$, implying that the triangles $B P H$ and $B E P$ are similar. Hence $$ \angle B P E=\angle B H P \text {. } $$ The point $P$ lies between $D$ and $C$; this follows from the equality $B P^{2}=B C \cdot B D$. In view of this equality, and because $B P=B Q$, $$ D P \cdot D Q=(B P-B D) \cdot(B P+B D)=B P^{2}-B D^{2}=B D \cdot(B C-B D)=B D \cdot D C . $$ Also $A D \cdot D H=B D \cdot D C$, as is seen from the similar triangles $B D H$ and $A D C$. Combining these equalities we obtain $A D \cdot D H=D P \cdot D Q$. Therefore $D H / D P=D Q / D A$, showing that the triangles $H D P$ and $Q D A$ are similar. Hence $\angle H P D=\angle Q A D$, which can be rewritten as $\angle B P H=\angle B A D+\angle B A Q$. And since $B Q$ is tangent to the circumcircle of triangle $F A Q$, $$ \angle B Q F=\angle B A Q=\angle B P H-\angle B A D . $$ From (1) and (2) we deduce $$ \begin{aligned} & \angle B P E+\angle B Q F=(\angle B H P+\angle B P H)-\angle B A D=\left(180^{\circ}-\angle P B H\right)-\angle B A D \\ & =\left(90^{\circ}+\angle B C A\right)-\left(90^{\circ}-\angle A B C\right)=\angle B C A+\angle A B C=180^{\circ}-\angle C A B . \end{aligned} $$ Thus $\angle B P E+\angle B Q F<180^{\circ}$, which means that the rays $P E$ and $Q F$ meet. Let $S$ be the point of intersection. Then $\angle P S Q=180^{\circ}-(\angle B P E+\angle B Q F)=\angle C A B=\angle E A F$. If $S$ lies between $P$ and $E$ then $\angle P S Q=180^{\circ}-\angle E S F$; and if $E$ lies between $P$ and $S$ then $\angle P S Q=\angle E S F$. In either case the equality $\angle P S Q=\angle E A F$ which we have obtained means that $S$ lies on the circumcircle of triangle $A E F$. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$ segments $B E$ and $C F$ are altitudes. Two circles passing through the points $A$ and $F$ are tangent to the line $B C$ at the points $P$ and $Q$ so that $B$ lies between $C$ and $Q$. Prove that the lines $P E$ and $Q F$ intersect on the circumcircle of triangle $A E F$.
|
To approach the desired result we need some information about the slopes of the lines $P E$ and $Q F$; this information is provided by formulas (1) and (2) which we derive below. The tangents $B P$ and $B Q$ to the two circles passing through $A$ and $F$ are equal, as $B P^{2}=B A \cdot B F=B Q^{2}$. Consider the altitude $A D$ of triangle $A B C$ and its orthocentre $H$. From the cyclic quadrilaterals $C D F A$ and $C D H E$ we get $B A \cdot B F=B C \cdot B D=B E \cdot B H$. Thus $B P^{2}=B E \cdot B H$, or $B P / B H=B E / B P$, implying that the triangles $B P H$ and $B E P$ are similar. Hence $$ \angle B P E=\angle B H P \text {. } $$ The point $P$ lies between $D$ and $C$; this follows from the equality $B P^{2}=B C \cdot B D$. In view of this equality, and because $B P=B Q$, $$ D P \cdot D Q=(B P-B D) \cdot(B P+B D)=B P^{2}-B D^{2}=B D \cdot(B C-B D)=B D \cdot D C . $$ Also $A D \cdot D H=B D \cdot D C$, as is seen from the similar triangles $B D H$ and $A D C$. Combining these equalities we obtain $A D \cdot D H=D P \cdot D Q$. Therefore $D H / D P=D Q / D A$, showing that the triangles $H D P$ and $Q D A$ are similar. Hence $\angle H P D=\angle Q A D$, which can be rewritten as $\angle B P H=\angle B A D+\angle B A Q$. And since $B Q$ is tangent to the circumcircle of triangle $F A Q$, $$ \angle B Q F=\angle B A Q=\angle B P H-\angle B A D . $$ From (1) and (2) we deduce $$ \begin{aligned} & \angle B P E+\angle B Q F=(\angle B H P+\angle B P H)-\angle B A D=\left(180^{\circ}-\angle P B H\right)-\angle B A D \\ & =\left(90^{\circ}+\angle B C A\right)-\left(90^{\circ}-\angle A B C\right)=\angle B C A+\angle A B C=180^{\circ}-\angle C A B . \end{aligned} $$ Thus $\angle B P E+\angle B Q F<180^{\circ}$, which means that the rays $P E$ and $Q F$ meet. Let $S$ be the point of intersection. Then $\angle P S Q=180^{\circ}-(\angle B P E+\angle B Q F)=\angle C A B=\angle E A F$. If $S$ lies between $P$ and $E$ then $\angle P S Q=180^{\circ}-\angle E S F$; and if $E$ lies between $P$ and $S$ then $\angle P S Q=\angle E S F$. In either case the equality $\angle P S Q=\angle E A F$ which we have obtained means that $S$ lies on the circumcircle of triangle $A E F$. 
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
cddf35f4-1c64-50dd-81a8-49c42b2f3e21
| 23,765
|
In an acute triangle $A B C$ segments $B E$ and $C F$ are altitudes. Two circles passing through the points $A$ and $F$ are tangent to the line $B C$ at the points $P$ and $Q$ so that $B$ lies between $C$ and $Q$. Prove that the lines $P E$ and $Q F$ intersect on the circumcircle of triangle $A E F$.
|
Let $H$ be the orthocentre of triangle $A B C$ and let $\omega$ be the circle with diameter $A H$, passing through $E$ and $F$. Introduce the points of intersection of $\omega$ with the following lines emanating from $P: P A \cap \omega=\{A, U\}, P H \cap \omega=\{H, V\}, P E \cap \omega=\{E, S\}$. The altitudes of triangle $A H P$ are contained in the lines $A V, H U, B C$, meeting at its orthocentre $Q^{\prime}$. By Pascal's theorem applied to the (tied) hexagon $A E S F H V$, the points $A E \cap F H=C$, $E S \cap H V=P$ and $S F \cap V A$ are collinear, so $F S$ passes through $Q^{\prime}$. Denote by $\omega_{1}$ and $\omega_{2}$ the circles with diameters $B C$ and $P Q^{\prime}$, respectively. Let $D$ be the foot of the altitude from $A$ in triangle $A B C$. Suppose that $A D$ meets the circles $\omega_{1}$ and $\omega_{2}$ at the respective points $K$ and $L$. Since $H$ is the orthocentre of $A B C$, the triangles $B D H$ and $A D C$ are similar, and so $D A \cdot D H=D B \cdot D C=D K^{2}$; the last equality holds because $B K C$ is a right triangle. Since $H$ is the orthocentre also in triangle $A Q^{\prime} P$, we analogously have $D L^{2}=D A \cdot D H$. Therefore $D K=D L$ and $K=L$. Also, $B D \cdot B C=B A \cdot B F$, from the similar triangles $A B D, C B F$. In the right triangle $B K C$ we have $B K^{2}=B D \cdot B C$. Hence, and because $B A \cdot B F=B P^{2}=B Q^{2}$ (by the definition of $P$ and $Q$ in the problem statement), we obtain $B K=B P=B Q$. It follows that $B$ is the centre of $\omega_{2}$ and hence $Q^{\prime}=Q$. So the lines $P E$ and $Q F$ meet at the point $S$ lying on the circumcircle of triangle $A E F$.  Comment 1. If $T$ is the point defined by $P F \cap \omega=\{F, T\}$, Pascal's theorem for the hexagon $A F T E H V$ will analogously lead to the conclusion that the line $E T$ goes through $Q^{\prime}$. In other words, the lines $P F$ and $Q E$ also concur on $\omega$. Comment 2. As is known from algebraic geometry, the points of the circle $\omega$ form a commutative groups with the operation defined as follows. Choose any point $0 \in \omega$ (to be the neutral element of the group) and a line $\ell$ exterior to the circle. For $X, Y \in \omega$, draw the line from the point $X Y \cap \ell$ through 0 to its second intersection with $\omega$ and define this point to be $X+Y$. In our solution we have chosen $H$ to be the neutral element in this group and line $B C$ to be $\ell$. The fact that the lines $A V, H U, E T, F S$ are concurrent can be deduced from the identities $A+A=0$, $F=E+A, V=U+A=S+E=T+F$. Comment 3. The problem was submitted in the following equivalent formulation: Let $B E$ and $C F$ be altitudes of an acute triangle $A B C$. We choose $P$ on the side $B C$ and $Q$ on the extension of $C B$ beyond $B$ such that $B Q^{2}=B P^{2}=B F \cdot A B$. If $Q F$ and $P E$ intersect at $S$, prove that $E S A F$ is cyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$ segments $B E$ and $C F$ are altitudes. Two circles passing through the points $A$ and $F$ are tangent to the line $B C$ at the points $P$ and $Q$ so that $B$ lies between $C$ and $Q$. Prove that the lines $P E$ and $Q F$ intersect on the circumcircle of triangle $A E F$.
|
Let $H$ be the orthocentre of triangle $A B C$ and let $\omega$ be the circle with diameter $A H$, passing through $E$ and $F$. Introduce the points of intersection of $\omega$ with the following lines emanating from $P: P A \cap \omega=\{A, U\}, P H \cap \omega=\{H, V\}, P E \cap \omega=\{E, S\}$. The altitudes of triangle $A H P$ are contained in the lines $A V, H U, B C$, meeting at its orthocentre $Q^{\prime}$. By Pascal's theorem applied to the (tied) hexagon $A E S F H V$, the points $A E \cap F H=C$, $E S \cap H V=P$ and $S F \cap V A$ are collinear, so $F S$ passes through $Q^{\prime}$. Denote by $\omega_{1}$ and $\omega_{2}$ the circles with diameters $B C$ and $P Q^{\prime}$, respectively. Let $D$ be the foot of the altitude from $A$ in triangle $A B C$. Suppose that $A D$ meets the circles $\omega_{1}$ and $\omega_{2}$ at the respective points $K$ and $L$. Since $H$ is the orthocentre of $A B C$, the triangles $B D H$ and $A D C$ are similar, and so $D A \cdot D H=D B \cdot D C=D K^{2}$; the last equality holds because $B K C$ is a right triangle. Since $H$ is the orthocentre also in triangle $A Q^{\prime} P$, we analogously have $D L^{2}=D A \cdot D H$. Therefore $D K=D L$ and $K=L$. Also, $B D \cdot B C=B A \cdot B F$, from the similar triangles $A B D, C B F$. In the right triangle $B K C$ we have $B K^{2}=B D \cdot B C$. Hence, and because $B A \cdot B F=B P^{2}=B Q^{2}$ (by the definition of $P$ and $Q$ in the problem statement), we obtain $B K=B P=B Q$. It follows that $B$ is the centre of $\omega_{2}$ and hence $Q^{\prime}=Q$. So the lines $P E$ and $Q F$ meet at the point $S$ lying on the circumcircle of triangle $A E F$.  Comment 1. If $T$ is the point defined by $P F \cap \omega=\{F, T\}$, Pascal's theorem for the hexagon $A F T E H V$ will analogously lead to the conclusion that the line $E T$ goes through $Q^{\prime}$. In other words, the lines $P F$ and $Q E$ also concur on $\omega$. Comment 2. As is known from algebraic geometry, the points of the circle $\omega$ form a commutative groups with the operation defined as follows. Choose any point $0 \in \omega$ (to be the neutral element of the group) and a line $\ell$ exterior to the circle. For $X, Y \in \omega$, draw the line from the point $X Y \cap \ell$ through 0 to its second intersection with $\omega$ and define this point to be $X+Y$. In our solution we have chosen $H$ to be the neutral element in this group and line $B C$ to be $\ell$. The fact that the lines $A V, H U, E T, F S$ are concurrent can be deduced from the identities $A+A=0$, $F=E+A, V=U+A=S+E=T+F$. Comment 3. The problem was submitted in the following equivalent formulation: Let $B E$ and $C F$ be altitudes of an acute triangle $A B C$. We choose $P$ on the side $B C$ and $Q$ on the extension of $C B$ beyond $B$ such that $B Q^{2}=B P^{2}=B F \cdot A B$. If $Q F$ and $P E$ intersect at $S$, prove that $E S A F$ is cyclic.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
cddf35f4-1c64-50dd-81a8-49c42b2f3e21
| 23,765
|
Let $k$ and $n$ be integers with $0 \leq k \leq n-2$. Consider a set $L$ of $n$ lines in the plane such that no two of them are parallel and no three have a common point. Denote by $I$ the set of intersection points of lines in $L$. Let $O$ be a point in the plane not lying on any line of $L$. A point $X \in I$ is colored red if the open line segment $O X$ intersects at most $k$ lines in $L$. Prove that $I$ contains at least $\frac{1}{2}(k+1)(k+2)$ red points.
|
There are at least $\frac{1}{2}(k+1)(k+2)$ points in the intersection set $I$ in view of the condition $n \geq k+2$. For each point $P \in I$, define its order as the number of lines that intersect the open line segment $O P$. By definition, $P$ is red if its order is at most $k$. Note that there is always at least one point $X \in I$ of order 0 . Indeed, the lines in $L$ divide the plane into regions, bounded or not, and $O$ belongs to one of them. Clearly any corner of this region is a point of $I$ with order 0 . Claim. Suppose that two points $P, Q \in I$ lie on the same line of $L$, and no other line of $L$ intersects the open line segment $P Q$. Then the orders of $P$ and $Q$ differ by at most 1 . Proof. Let $P$ and $Q$ have orders $p$ and $q$, respectively, with $p \geq q$. Consider triangle $O P Q$. Now $p$ equals the number of lines in $L$ that intersect the interior of side $O P$. None of these lines intersects the interior of side $P Q$, and at most one can pass through $Q$. All remaining lines must intersect the interior of side $O Q$, implying that $q \geq p-1$. The conclusion follows. We prove the main result by induction on $k$. The base $k=0$ is clear since there is a point of order 0 which is red. Assuming the statement true for $k-1$, we pass on to the inductive step. Select a point $P \in I$ of order 0 , and consider one of the lines $\ell \in L$ that pass through $P$. There are $n-1$ intersection points on $\ell$, one of which is $P$. Out of the remaining $n-2$ points, the $k$ closest to $P$ have orders not exceeding $k$ by the Claim. It follows that there are at least $k+1$ red points on $\ell$. Let us now consider the situation with $\ell$ removed (together with all intersection points it contains). By hypothesis of induction, there are at least $\frac{1}{2} k(k+1)$ points of order not exceeding $k-1$ in the resulting configuration. Restoring $\ell$ back produces at most one new intersection point on each line segment joining any of these points to $O$, so their order is at most $k$ in the original configuration. The total number of points with order not exceeding $k$ is therefore at least $(k+1)+\frac{1}{2} k(k+1)=\frac{1}{2}(k+1)(k+2)$. This completes the proof. Comment. The steps of the proof can be performed in reverse order to obtain a configuration of $n$ lines such that equality holds simultaneously for all $0 \leq k \leq n-2$. Such a set of lines is illustrated in the Figure. 
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $k$ and $n$ be integers with $0 \leq k \leq n-2$. Consider a set $L$ of $n$ lines in the plane such that no two of them are parallel and no three have a common point. Denote by $I$ the set of intersection points of lines in $L$. Let $O$ be a point in the plane not lying on any line of $L$. A point $X \in I$ is colored red if the open line segment $O X$ intersects at most $k$ lines in $L$. Prove that $I$ contains at least $\frac{1}{2}(k+1)(k+2)$ red points.
|
There are at least $\frac{1}{2}(k+1)(k+2)$ points in the intersection set $I$ in view of the condition $n \geq k+2$. For each point $P \in I$, define its order as the number of lines that intersect the open line segment $O P$. By definition, $P$ is red if its order is at most $k$. Note that there is always at least one point $X \in I$ of order 0 . Indeed, the lines in $L$ divide the plane into regions, bounded or not, and $O$ belongs to one of them. Clearly any corner of this region is a point of $I$ with order 0 . Claim. Suppose that two points $P, Q \in I$ lie on the same line of $L$, and no other line of $L$ intersects the open line segment $P Q$. Then the orders of $P$ and $Q$ differ by at most 1 . Proof. Let $P$ and $Q$ have orders $p$ and $q$, respectively, with $p \geq q$. Consider triangle $O P Q$. Now $p$ equals the number of lines in $L$ that intersect the interior of side $O P$. None of these lines intersects the interior of side $P Q$, and at most one can pass through $Q$. All remaining lines must intersect the interior of side $O Q$, implying that $q \geq p-1$. The conclusion follows. We prove the main result by induction on $k$. The base $k=0$ is clear since there is a point of order 0 which is red. Assuming the statement true for $k-1$, we pass on to the inductive step. Select a point $P \in I$ of order 0 , and consider one of the lines $\ell \in L$ that pass through $P$. There are $n-1$ intersection points on $\ell$, one of which is $P$. Out of the remaining $n-2$ points, the $k$ closest to $P$ have orders not exceeding $k$ by the Claim. It follows that there are at least $k+1$ red points on $\ell$. Let us now consider the situation with $\ell$ removed (together with all intersection points it contains). By hypothesis of induction, there are at least $\frac{1}{2} k(k+1)$ points of order not exceeding $k-1$ in the resulting configuration. Restoring $\ell$ back produces at most one new intersection point on each line segment joining any of these points to $O$, so their order is at most $k$ in the original configuration. The total number of points with order not exceeding $k$ is therefore at least $(k+1)+\frac{1}{2} k(k+1)=\frac{1}{2}(k+1)(k+2)$. This completes the proof. Comment. The steps of the proof can be performed in reverse order to obtain a configuration of $n$ lines such that equality holds simultaneously for all $0 \leq k \leq n-2$. Such a set of lines is illustrated in the Figure. 
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
75990731-7cd3-5e33-98fe-1af1bfa6032a
| 23,768
|
There is given a convex quadrilateral $A B C D$. Prove that there exists a point $P$ inside the quadrilateral such that $$ \angle P A B+\angle P D C=\angle P B C+\angle P A D=\angle P C D+\angle P B A=\angle P D A+\angle P C B=90^{\circ} $$ if and only if the diagonals $A C$ and $B D$ are perpendicular.
|
For a point $P$ in $A B C D$ which satisfies (1), let $K, L, M, N$ be the feet of perpendiculars from $P$ to lines $A B, B C, C D, D A$, respectively. Note that $K, L, M, N$ are interior to the sides as all angles in (1) are acute. The cyclic quadrilaterals $A K P N$ and $D N P M$ give $$ \angle P A B+\angle P D C=\angle P N K+\angle P N M=\angle K N M . $$ Analogously, $\angle P B C+\angle P A D=\angle L K N$ and $\angle P C D+\angle P B A=\angle M L K$. Hence the equalities (1) imply $\angle K N M=\angle L K N=\angle M L K=90^{\circ}$, so that $K L M N$ is a rectangle. The converse also holds true, provided that $K, L, M, N$ are interior to sides $A B, B C, C D, D A$. (i) Suppose that there exists a point $P$ in $A B C D$ such that $K L M N$ is a rectangle. We show that $A C$ and $B D$ are parallel to the respective sides of $K L M N$. Let $O_{A}$ and $O_{C}$ be the circumcentres of the cyclic quadrilaterals $A K P N$ and $C M P L$. Line $O_{A} O_{C}$ is the common perpendicular bisector of $L M$ and $K N$, therefore $O_{A} O_{C}$ is parallel to $K L$ and $M N$. On the other hand, $O_{A} O_{C}$ is the midline in the triangle $A C P$ that is parallel to $A C$. Therefore the diagonal $A C$ is parallel to the sides $K L$ and $M N$ of the rectangle. Likewise, $B D$ is parallel to $K N$ and $L M$. Hence $A C$ and $B D$ are perpendicular.  (ii) Suppose that $A C$ and $B D$ are perpendicular and meet at $R$. If $A B C D$ is a rhombus, $P$ can be chosen to be its centre. So assume that $A B C D$ is not a rhombus, and let $B R<D R$ without loss of generality. Denote by $U_{A}$ and $U_{C}$ the circumcentres of the triangles $A B D$ and $C D B$, respectively. Let $A V_{A}$ and $C V_{C}$ be the diameters through $A$ and $C$ of the two circumcircles. Since $A R$ is an altitude in triangle $A D B$, lines $A C$ and $A V_{A}$ are isogonal conjugates, i. e. $\angle D A V_{A}=\angle B A C$. Now $B R<D R$ implies that ray $A U_{A}$ lies in $\angle D A C$. Similarly, ray $C U_{C}$ lies in $\angle D C A$. Both diameters $A V_{A}$ and $C V_{C}$ intersect $B D$ as the angles at $B$ and $D$ of both triangles are acute. Also $U_{A} U_{C}$ is parallel to $A C$ as it is the perpendicular bisector of $B D$. Hence $V_{A} V_{C}$ is parallel to $A C$, too. We infer that $A V_{A}$ and $C V_{C}$ intersect at a point $P$ inside triangle $A C D$, hence inside $A B C D$. Construct points $K, L, M, N, O_{A}$ and $O_{C}$ in the same way as in the introduction. It follows from the previous paragraph that $K, L, M, N$ are interior to the respective sides. Now $O_{A} O_{C}$ is a midline in triangle $A C P$ again. Therefore lines $A C, O_{A} O_{C}$ and $U_{A} U_{C}$ are parallel. The cyclic quadrilateral $A K P N$ yields $\angle N K P=\angle N A P$. Since $\angle N A P=\angle D A U_{A}=$ $\angle B A C$, as specified above, we obtain $\angle N K P=\angle B A C$. Because $P K$ is perpendicular to $A B$, it follows that $N K$ is perpendicular to $A C$, hence parallel to $B D$. Likewise, $L M$ is parallel to $B D$. Consider the two homotheties with centres $A$ and $C$ which transform triangles $A B D$ and $C D B$ into triangles $A K N$ and $C M L$, respectively. The images of points $U_{A}$ and $U_{C}$ are $O_{A}$ and $O_{C}$, respectively. Since $U_{A} U_{C}$ and $O_{A} O_{C}$ are parallel to $A C$, the two ratios of homothety are the same, equal to $\lambda=A N / A D=A K / A B=A O_{A} / A U_{A}=C O_{C} / C U_{C}=C M / C D=C L / C B$. It is now straightforward that $D N / D A=D M / D C=B K / B A=B L / B C=1-\lambda$. Hence $K L$ and $M N$ are parallel to $A C$, implying that $K L M N$ is a rectangle and completing the proof. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
There is given a convex quadrilateral $A B C D$. Prove that there exists a point $P$ inside the quadrilateral such that $$ \angle P A B+\angle P D C=\angle P B C+\angle P A D=\angle P C D+\angle P B A=\angle P D A+\angle P C B=90^{\circ} $$ if and only if the diagonals $A C$ and $B D$ are perpendicular.
|
For a point $P$ in $A B C D$ which satisfies (1), let $K, L, M, N$ be the feet of perpendiculars from $P$ to lines $A B, B C, C D, D A$, respectively. Note that $K, L, M, N$ are interior to the sides as all angles in (1) are acute. The cyclic quadrilaterals $A K P N$ and $D N P M$ give $$ \angle P A B+\angle P D C=\angle P N K+\angle P N M=\angle K N M . $$ Analogously, $\angle P B C+\angle P A D=\angle L K N$ and $\angle P C D+\angle P B A=\angle M L K$. Hence the equalities (1) imply $\angle K N M=\angle L K N=\angle M L K=90^{\circ}$, so that $K L M N$ is a rectangle. The converse also holds true, provided that $K, L, M, N$ are interior to sides $A B, B C, C D, D A$. (i) Suppose that there exists a point $P$ in $A B C D$ such that $K L M N$ is a rectangle. We show that $A C$ and $B D$ are parallel to the respective sides of $K L M N$. Let $O_{A}$ and $O_{C}$ be the circumcentres of the cyclic quadrilaterals $A K P N$ and $C M P L$. Line $O_{A} O_{C}$ is the common perpendicular bisector of $L M$ and $K N$, therefore $O_{A} O_{C}$ is parallel to $K L$ and $M N$. On the other hand, $O_{A} O_{C}$ is the midline in the triangle $A C P$ that is parallel to $A C$. Therefore the diagonal $A C$ is parallel to the sides $K L$ and $M N$ of the rectangle. Likewise, $B D$ is parallel to $K N$ and $L M$. Hence $A C$ and $B D$ are perpendicular.  (ii) Suppose that $A C$ and $B D$ are perpendicular and meet at $R$. If $A B C D$ is a rhombus, $P$ can be chosen to be its centre. So assume that $A B C D$ is not a rhombus, and let $B R<D R$ without loss of generality. Denote by $U_{A}$ and $U_{C}$ the circumcentres of the triangles $A B D$ and $C D B$, respectively. Let $A V_{A}$ and $C V_{C}$ be the diameters through $A$ and $C$ of the two circumcircles. Since $A R$ is an altitude in triangle $A D B$, lines $A C$ and $A V_{A}$ are isogonal conjugates, i. e. $\angle D A V_{A}=\angle B A C$. Now $B R<D R$ implies that ray $A U_{A}$ lies in $\angle D A C$. Similarly, ray $C U_{C}$ lies in $\angle D C A$. Both diameters $A V_{A}$ and $C V_{C}$ intersect $B D$ as the angles at $B$ and $D$ of both triangles are acute. Also $U_{A} U_{C}$ is parallel to $A C$ as it is the perpendicular bisector of $B D$. Hence $V_{A} V_{C}$ is parallel to $A C$, too. We infer that $A V_{A}$ and $C V_{C}$ intersect at a point $P$ inside triangle $A C D$, hence inside $A B C D$. Construct points $K, L, M, N, O_{A}$ and $O_{C}$ in the same way as in the introduction. It follows from the previous paragraph that $K, L, M, N$ are interior to the respective sides. Now $O_{A} O_{C}$ is a midline in triangle $A C P$ again. Therefore lines $A C, O_{A} O_{C}$ and $U_{A} U_{C}$ are parallel. The cyclic quadrilateral $A K P N$ yields $\angle N K P=\angle N A P$. Since $\angle N A P=\angle D A U_{A}=$ $\angle B A C$, as specified above, we obtain $\angle N K P=\angle B A C$. Because $P K$ is perpendicular to $A B$, it follows that $N K$ is perpendicular to $A C$, hence parallel to $B D$. Likewise, $L M$ is parallel to $B D$. Consider the two homotheties with centres $A$ and $C$ which transform triangles $A B D$ and $C D B$ into triangles $A K N$ and $C M L$, respectively. The images of points $U_{A}$ and $U_{C}$ are $O_{A}$ and $O_{C}$, respectively. Since $U_{A} U_{C}$ and $O_{A} O_{C}$ are parallel to $A C$, the two ratios of homothety are the same, equal to $\lambda=A N / A D=A K / A B=A O_{A} / A U_{A}=C O_{C} / C U_{C}=C M / C D=C L / C B$. It is now straightforward that $D N / D A=D M / D C=B K / B A=B L / B C=1-\lambda$. Hence $K L$ and $M N$ are parallel to $A C$, implying that $K L M N$ is a rectangle and completing the proof. 
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
09af0b2d-7b65-5d05-a9c2-71ccb90aecea
| 23,771
|
There is given a convex quadrilateral $A B C D$. Prove that there exists a point $P$ inside the quadrilateral such that $$ \angle P A B+\angle P D C=\angle P B C+\angle P A D=\angle P C D+\angle P B A=\angle P D A+\angle P C B=90^{\circ} $$ if and only if the diagonals $A C$ and $B D$ are perpendicular.
|
For a point $P$ distinct from $A, B, C, D$, let circles $(A P D)$ and $(B P C)$ intersect again at $Q(Q=P$ if the circles are tangent). Next, let circles $(A Q B)$ and $(C Q D)$ intersect again at $R$. We show that if $P$ lies in $A B C D$ and satisfies (1) then $A C$ and $B D$ intersect at $R$ and are perpendicular; the converse is also true. It is convenient to use directed angles. Let $\measuredangle(U V, X Y)$ denote the angle of counterclockwise rotation that makes line $U V$ parallel to line $X Y$. Recall that four noncollinear points $U, V, X, Y$ are concyclic if and only if $\measuredangle(U X, V X)=\measuredangle(U Y, V Y)$. The definitions of points $P, Q$ and $R$ imply $$ \begin{aligned} \measuredangle(A R, B R) & =\measuredangle(A Q, B Q)=\measuredangle(A Q, P Q)+\measuredangle(P Q, B Q)=\measuredangle(A D, P D)+\measuredangle(P C, B C), \\ \measuredangle(C R, D R) & =\measuredangle(C Q, D Q)=\measuredangle(C Q, P Q)+\measuredangle(P Q, D Q)=\measuredangle(C B, P B)+\measuredangle(P A, D A), \\ \measuredangle(B R, C R) & =\measuredangle(B R, R Q)+\measuredangle(R Q, C R)=\measuredangle(B A, A Q)+\measuredangle(D Q, C D) \\ & =\measuredangle(B A, A P)+\measuredangle(A P, A Q)+\measuredangle(D Q, D P)+\measuredangle(D P, C D) \\ & =\measuredangle(B A, A P)+\measuredangle(D P, C D) . \end{aligned} $$ Observe that the whole construction is reversible. One may start with point $R$, define $Q$ as the second intersection of circles $(A R B)$ and $(C R D)$, and then define $P$ as the second intersection of circles $(A Q D)$ and $(B Q C)$. The equalities above will still hold true. Assume in addition that $P$ is interior to $A B C D$. Then $$ \begin{gathered} \measuredangle(A D, P D)=\angle P D A, \measuredangle(P C, B C)=\angle P C B, \measuredangle(C B, P B)=\angle P B C, \measuredangle(P A, D A)=\angle P A D, \\ \measuredangle(B A, A P)=\angle P A B, \measuredangle(D P, C D)=\angle P D C . \end{gathered} $$ (i) Suppose that $P$ lies in $A B C D$ and satisfies (1). Then $\measuredangle(A R, B R)=\angle P D A+\angle P C B=90^{\circ}$ and similarly $\measuredangle(B R, C R)=\measuredangle(C R, D R)=90^{\circ}$. It follows that $R$ is the common point of lines $A C$ and $B D$, and that these lines are perpendicular. (ii) Suppose that $A C$ and $B D$ are perpendicular and intersect at $R$. We show that the point $P$ defined by the reverse construction (starting with $R$ and ending with $P$ ) lies in $A B C D$. This is enough to finish the solution, because then the angle equalities above will imply (1). One can assume that $Q$, the second common point of circles $(A B R)$ and $(C D R)$, lies in $\angle A R D$. Then in fact $Q$ lies in triangle $A D R$ as angles $A Q R$ and $D Q R$ are obtuse. Hence $\angle A Q D$ is obtuse, too, so that $B$ and $C$ are outside circle $(A D Q)(\angle A B D$ and $\angle A C D$ are acute). Now $\angle C A B+\angle C D B=\angle B Q R+\angle C Q R=\angle C Q B$ implies $\angle C A B<\angle C Q B$ and $\angle C D B<$ $\angle C Q B$. Hence $A$ and $D$ are outside circle $(B C Q)$. In conclusion, the second common point $P$ of circles $(A D Q)$ and $(B C Q)$ lies on their arcs $A D Q$ and $B C Q$. We can assume that $P$ lies in $\angle C Q D$. Since $$ \begin{gathered} \angle Q P C+\angle Q P D=\left(180^{\circ}-\angle Q B C\right)+\left(180^{\circ}-\angle Q A D\right)= \\ =360^{\circ}-(\angle R B C+\angle Q B R)-(\angle R A D-\angle Q A R)=360^{\circ}-\angle R B C-\angle R A D>180^{\circ}, \end{gathered} $$ point $P$ lies in triangle $C D Q$, and hence in $A B C D$. The proof is complete. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
There is given a convex quadrilateral $A B C D$. Prove that there exists a point $P$ inside the quadrilateral such that $$ \angle P A B+\angle P D C=\angle P B C+\angle P A D=\angle P C D+\angle P B A=\angle P D A+\angle P C B=90^{\circ} $$ if and only if the diagonals $A C$ and $B D$ are perpendicular.
|
For a point $P$ distinct from $A, B, C, D$, let circles $(A P D)$ and $(B P C)$ intersect again at $Q(Q=P$ if the circles are tangent). Next, let circles $(A Q B)$ and $(C Q D)$ intersect again at $R$. We show that if $P$ lies in $A B C D$ and satisfies (1) then $A C$ and $B D$ intersect at $R$ and are perpendicular; the converse is also true. It is convenient to use directed angles. Let $\measuredangle(U V, X Y)$ denote the angle of counterclockwise rotation that makes line $U V$ parallel to line $X Y$. Recall that four noncollinear points $U, V, X, Y$ are concyclic if and only if $\measuredangle(U X, V X)=\measuredangle(U Y, V Y)$. The definitions of points $P, Q$ and $R$ imply $$ \begin{aligned} \measuredangle(A R, B R) & =\measuredangle(A Q, B Q)=\measuredangle(A Q, P Q)+\measuredangle(P Q, B Q)=\measuredangle(A D, P D)+\measuredangle(P C, B C), \\ \measuredangle(C R, D R) & =\measuredangle(C Q, D Q)=\measuredangle(C Q, P Q)+\measuredangle(P Q, D Q)=\measuredangle(C B, P B)+\measuredangle(P A, D A), \\ \measuredangle(B R, C R) & =\measuredangle(B R, R Q)+\measuredangle(R Q, C R)=\measuredangle(B A, A Q)+\measuredangle(D Q, C D) \\ & =\measuredangle(B A, A P)+\measuredangle(A P, A Q)+\measuredangle(D Q, D P)+\measuredangle(D P, C D) \\ & =\measuredangle(B A, A P)+\measuredangle(D P, C D) . \end{aligned} $$ Observe that the whole construction is reversible. One may start with point $R$, define $Q$ as the second intersection of circles $(A R B)$ and $(C R D)$, and then define $P$ as the second intersection of circles $(A Q D)$ and $(B Q C)$. The equalities above will still hold true. Assume in addition that $P$ is interior to $A B C D$. Then $$ \begin{gathered} \measuredangle(A D, P D)=\angle P D A, \measuredangle(P C, B C)=\angle P C B, \measuredangle(C B, P B)=\angle P B C, \measuredangle(P A, D A)=\angle P A D, \\ \measuredangle(B A, A P)=\angle P A B, \measuredangle(D P, C D)=\angle P D C . \end{gathered} $$ (i) Suppose that $P$ lies in $A B C D$ and satisfies (1). Then $\measuredangle(A R, B R)=\angle P D A+\angle P C B=90^{\circ}$ and similarly $\measuredangle(B R, C R)=\measuredangle(C R, D R)=90^{\circ}$. It follows that $R$ is the common point of lines $A C$ and $B D$, and that these lines are perpendicular. (ii) Suppose that $A C$ and $B D$ are perpendicular and intersect at $R$. We show that the point $P$ defined by the reverse construction (starting with $R$ and ending with $P$ ) lies in $A B C D$. This is enough to finish the solution, because then the angle equalities above will imply (1). One can assume that $Q$, the second common point of circles $(A B R)$ and $(C D R)$, lies in $\angle A R D$. Then in fact $Q$ lies in triangle $A D R$ as angles $A Q R$ and $D Q R$ are obtuse. Hence $\angle A Q D$ is obtuse, too, so that $B$ and $C$ are outside circle $(A D Q)(\angle A B D$ and $\angle A C D$ are acute). Now $\angle C A B+\angle C D B=\angle B Q R+\angle C Q R=\angle C Q B$ implies $\angle C A B<\angle C Q B$ and $\angle C D B<$ $\angle C Q B$. Hence $A$ and $D$ are outside circle $(B C Q)$. In conclusion, the second common point $P$ of circles $(A D Q)$ and $(B C Q)$ lies on their arcs $A D Q$ and $B C Q$. We can assume that $P$ lies in $\angle C Q D$. Since $$ \begin{gathered} \angle Q P C+\angle Q P D=\left(180^{\circ}-\angle Q B C\right)+\left(180^{\circ}-\angle Q A D\right)= \\ =360^{\circ}-(\angle R B C+\angle Q B R)-(\angle R A D-\angle Q A R)=360^{\circ}-\angle R B C-\angle R A D>180^{\circ}, \end{gathered} $$ point $P$ lies in triangle $C D Q$, and hence in $A B C D$. The proof is complete. 
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
09af0b2d-7b65-5d05-a9c2-71ccb90aecea
| 23,771
|
Let $A B C D$ be a convex quadrilateral with $A B \neq B C$. Denote by $\omega_{1}$ and $\omega_{2}$ the incircles of triangles $A B C$ and $A D C$. Suppose that there exists a circle $\omega$ inscribed in angle $A B C$, tangent to the extensions of line segments $A D$ and $C D$. Prove that the common external tangents of $\omega_{1}$ and $\omega_{2}$ intersect on $\omega$.
|
The proof below is based on two known facts. Lemma 1. Given a convex quadrilateral $A B C D$, suppose that there exists a circle which is inscribed in angle $A B C$ and tangent to the extensions of line segments $A D$ and $C D$. Then $A B+A D=C B+C D$. Proof. The circle in question is tangent to each of the lines $A B, B C, C D, D A$, and the respective points of tangency $K, L, M, N$ are located as with circle $\omega$ in the figure. Then $$ A B+A D=(B K-A K)+(A N-D N), \quad C B+C D=(B L-C L)+(C M-D M) . $$ Also $B K=B L, D N=D M, A K=A N, C L=C M$ by equalities of tangents. It follows that $A B+A D=C B+C D$.  For brevity, in the sequel we write "excircle $A C$ " for the excircle of a triangle with side $A C$ which is tangent to line segment $A C$ and the extensions of the other two sides. Lemma 2. The incircle of triangle $A B C$ is tangent to its side $A C$ at $P$. Let $P P^{\prime}$ be the diameter of the incircle through $P$, and let line $B P^{\prime}$ intersect $A C$ at $Q$. Then $Q$ is the point of tangency of side $A C$ and excircle $A C$. Proof. Let the tangent at $P^{\prime}$ to the incircle $\omega_{1}$ meet $B A$ and $B C$ at $A^{\prime}$ and $C^{\prime}$. Now $\omega_{1}$ is the excircle $A^{\prime} C^{\prime}$ of triangle $A^{\prime} B C^{\prime}$, and it touches side $A^{\prime} C^{\prime}$ at $P^{\prime}$. Since $A^{\prime} C^{\prime} \| A C$, the homothety with centre $B$ and ratio $B Q / B P^{\prime}$ takes $\omega_{1}$ to the excircle $A C$ of triangle $A B C$. Because this homothety takes $P^{\prime}$ to $Q$, the lemma follows. Recall also that if the incircle of a triangle touches its side $A C$ at $P$, then the tangency point $Q$ of the same side and excircle $A C$ is the unique point on line segment $A C$ such that $A P=C Q$. We pass on to the main proof. Let $\omega_{1}$ and $\omega_{2}$ touch $A C$ at $P$ and $Q$, respectively; then $A P=(A C+A B-B C) / 2, C Q=(C A+C D-A D) / 2$. Since $A B-B C=C D-A D$ by Lemma 1, we obtain $A P=C Q$. It follows that in triangle $A B C$ side $A C$ and excircle $A C$ are tangent at $Q$. Likewise, in triangle $A D C$ side $A C$ and excircle $A C$ are tangent at $P$. Note that $P \neq Q$ as $A B \neq B C$. Let $P P^{\prime}$ and $Q Q^{\prime}$ be the diameters perpendicular to $A C$ of $\omega_{1}$ and $\omega_{2}$, respectively. Then Lemma 2 shows that points $B, P^{\prime}$ and $Q$ are collinear, and so are points $D, Q^{\prime}$ and $P$. Consider the diameter of $\omega$ perpendicular to $A C$ and denote by $T$ its endpoint that is closer to $A C$. The homothety with centre $B$ and ratio $B T / B P^{\prime}$ takes $\omega_{1}$ to $\omega$. Hence $B, P^{\prime}$ and $T$ are collinear. Similarly, $D, Q^{\prime}$ and $T$ are collinear since the homothety with centre $D$ and ratio $-D T / D Q^{\prime}$ takes $\omega_{2}$ to $\omega$. We infer that points $T, P^{\prime}$ and $Q$ are collinear, as well as $T, Q^{\prime}$ and $P$. Since $P P^{\prime} \| Q Q^{\prime}$, line segments $P P^{\prime}$ and $Q Q^{\prime}$ are then homothetic with centre $T$. The same holds true for circles $\omega_{1}$ and $\omega_{2}$ because they have $P P^{\prime}$ and $Q Q^{\prime}$ as diameters. Moreover, it is immediate that $T$ lies on the same side of line $P P^{\prime}$ as $Q$ and $Q^{\prime}$, hence the ratio of homothety is positive. In particular $\omega_{1}$ and $\omega_{2}$ are not congruent. In summary, $T$ is the centre of a homothety with positive ratio that takes circle $\omega_{1}$ to circle $\omega_{2}$. This completes the solution, since the only point with the mentioned property is the intersection of the the common external tangents of $\omega_{1}$ and $\omega_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral with $A B \neq B C$. Denote by $\omega_{1}$ and $\omega_{2}$ the incircles of triangles $A B C$ and $A D C$. Suppose that there exists a circle $\omega$ inscribed in angle $A B C$, tangent to the extensions of line segments $A D$ and $C D$. Prove that the common external tangents of $\omega_{1}$ and $\omega_{2}$ intersect on $\omega$.
|
The proof below is based on two known facts. Lemma 1. Given a convex quadrilateral $A B C D$, suppose that there exists a circle which is inscribed in angle $A B C$ and tangent to the extensions of line segments $A D$ and $C D$. Then $A B+A D=C B+C D$. Proof. The circle in question is tangent to each of the lines $A B, B C, C D, D A$, and the respective points of tangency $K, L, M, N$ are located as with circle $\omega$ in the figure. Then $$ A B+A D=(B K-A K)+(A N-D N), \quad C B+C D=(B L-C L)+(C M-D M) . $$ Also $B K=B L, D N=D M, A K=A N, C L=C M$ by equalities of tangents. It follows that $A B+A D=C B+C D$.  For brevity, in the sequel we write "excircle $A C$ " for the excircle of a triangle with side $A C$ which is tangent to line segment $A C$ and the extensions of the other two sides. Lemma 2. The incircle of triangle $A B C$ is tangent to its side $A C$ at $P$. Let $P P^{\prime}$ be the diameter of the incircle through $P$, and let line $B P^{\prime}$ intersect $A C$ at $Q$. Then $Q$ is the point of tangency of side $A C$ and excircle $A C$. Proof. Let the tangent at $P^{\prime}$ to the incircle $\omega_{1}$ meet $B A$ and $B C$ at $A^{\prime}$ and $C^{\prime}$. Now $\omega_{1}$ is the excircle $A^{\prime} C^{\prime}$ of triangle $A^{\prime} B C^{\prime}$, and it touches side $A^{\prime} C^{\prime}$ at $P^{\prime}$. Since $A^{\prime} C^{\prime} \| A C$, the homothety with centre $B$ and ratio $B Q / B P^{\prime}$ takes $\omega_{1}$ to the excircle $A C$ of triangle $A B C$. Because this homothety takes $P^{\prime}$ to $Q$, the lemma follows. Recall also that if the incircle of a triangle touches its side $A C$ at $P$, then the tangency point $Q$ of the same side and excircle $A C$ is the unique point on line segment $A C$ such that $A P=C Q$. We pass on to the main proof. Let $\omega_{1}$ and $\omega_{2}$ touch $A C$ at $P$ and $Q$, respectively; then $A P=(A C+A B-B C) / 2, C Q=(C A+C D-A D) / 2$. Since $A B-B C=C D-A D$ by Lemma 1, we obtain $A P=C Q$. It follows that in triangle $A B C$ side $A C$ and excircle $A C$ are tangent at $Q$. Likewise, in triangle $A D C$ side $A C$ and excircle $A C$ are tangent at $P$. Note that $P \neq Q$ as $A B \neq B C$. Let $P P^{\prime}$ and $Q Q^{\prime}$ be the diameters perpendicular to $A C$ of $\omega_{1}$ and $\omega_{2}$, respectively. Then Lemma 2 shows that points $B, P^{\prime}$ and $Q$ are collinear, and so are points $D, Q^{\prime}$ and $P$. Consider the diameter of $\omega$ perpendicular to $A C$ and denote by $T$ its endpoint that is closer to $A C$. The homothety with centre $B$ and ratio $B T / B P^{\prime}$ takes $\omega_{1}$ to $\omega$. Hence $B, P^{\prime}$ and $T$ are collinear. Similarly, $D, Q^{\prime}$ and $T$ are collinear since the homothety with centre $D$ and ratio $-D T / D Q^{\prime}$ takes $\omega_{2}$ to $\omega$. We infer that points $T, P^{\prime}$ and $Q$ are collinear, as well as $T, Q^{\prime}$ and $P$. Since $P P^{\prime} \| Q Q^{\prime}$, line segments $P P^{\prime}$ and $Q Q^{\prime}$ are then homothetic with centre $T$. The same holds true for circles $\omega_{1}$ and $\omega_{2}$ because they have $P P^{\prime}$ and $Q Q^{\prime}$ as diameters. Moreover, it is immediate that $T$ lies on the same side of line $P P^{\prime}$ as $Q$ and $Q^{\prime}$, hence the ratio of homothety is positive. In particular $\omega_{1}$ and $\omega_{2}$ are not congruent. In summary, $T$ is the centre of a homothety with positive ratio that takes circle $\omega_{1}$ to circle $\omega_{2}$. This completes the solution, since the only point with the mentioned property is the intersection of the the common external tangents of $\omega_{1}$ and $\omega_{2}$.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
4f278fd3-4358-5b9a-aac8-f7a3ead469d3
| 23,774
|
Let $n$ be a positive integer and let $p$ be a prime number. Prove that if $a, b, c$ are integers (not necessarily positive) satisfying the equations $$ a^{n}+p b=b^{n}+p c=c^{n}+p a, $$ then $a=b=c$.
|
If two of $a, b, c$ are equal, it is immediate that all the three are equal. So we may assume that $a \neq b \neq c \neq a$. Subtracting the equations we get $a^{n}-b^{n}=-p(b-c)$ and two cyclic copies of this equation, which upon multiplication yield $$ \frac{a^{n}-b^{n}}{a-b} \cdot \frac{b^{n}-c^{n}}{b-c} \cdot \frac{c^{n}-a^{n}}{c-a}=-p^{3} . $$ If $n$ is odd then the differences $a^{n}-b^{n}$ and $a-b$ have the same sign and the product on the left is positive, while $-p^{3}$ is negative. So $n$ must be even. Let $d$ be the greatest common divisor of the three differences $a-b, b-c, c-a$, so that $a-b=d u, b-c=d v, \quad c-a=d w ; \operatorname{gcd}(u, v, w)=1, u+v+w=0$. From $a^{n}-b^{n}=-p(b-c)$ we see that $(a-b) \mid p(b-c)$, i.e., $u \mid p v$; and cyclically $v|p w, w| p u$. As $\operatorname{gcd}(u, v, w)=1$ and $u+v+w=0$, at most one of $u, v, w$ can be divisible by $p$. Supposing that the prime $p$ does not divide any one of them, we get $u|v, v| w, w \mid u$, whence $|u|=|v|=|w|=1$; but this quarrels with $u+v+w=0$. Thus $p$ must divide exactly one of these numbers. Let e.g. $p \mid u$ and write $u=p u_{1}$. Now we obtain, similarly as before, $u_{1}|v, v| w, w \mid u_{1}$ so that $\left|u_{1}\right|=|v|=|w|=1$. The equation $p u_{1}+v+w=0$ forces that the prime $p$ must be even; i.e. $p=2$. Hence $v+w=-2 u_{1}= \pm 2$, implying $v=w(= \pm 1)$ and $u=-2 v$. Consequently $a-b=-2(b-c)$. Knowing that $n$ is even, say $n=2 k$, we rewrite the equation $a^{n}-b^{n}=-p(b-c)$ with $p=2$ in the form $$ \left(a^{k}+b^{k}\right)\left(a^{k}-b^{k}\right)=-2(b-c)=a-b . $$ The second factor on the left is divisible by $a-b$, so the first factor $\left(a^{k}+b^{k}\right)$ must be $\pm 1$. Then exactly one of $a$ and $b$ must be odd; yet $a-b=-2(b-c)$ is even. Contradiction ends the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n$ be a positive integer and let $p$ be a prime number. Prove that if $a, b, c$ are integers (not necessarily positive) satisfying the equations $$ a^{n}+p b=b^{n}+p c=c^{n}+p a, $$ then $a=b=c$.
|
If two of $a, b, c$ are equal, it is immediate that all the three are equal. So we may assume that $a \neq b \neq c \neq a$. Subtracting the equations we get $a^{n}-b^{n}=-p(b-c)$ and two cyclic copies of this equation, which upon multiplication yield $$ \frac{a^{n}-b^{n}}{a-b} \cdot \frac{b^{n}-c^{n}}{b-c} \cdot \frac{c^{n}-a^{n}}{c-a}=-p^{3} . $$ If $n$ is odd then the differences $a^{n}-b^{n}$ and $a-b$ have the same sign and the product on the left is positive, while $-p^{3}$ is negative. So $n$ must be even. Let $d$ be the greatest common divisor of the three differences $a-b, b-c, c-a$, so that $a-b=d u, b-c=d v, \quad c-a=d w ; \operatorname{gcd}(u, v, w)=1, u+v+w=0$. From $a^{n}-b^{n}=-p(b-c)$ we see that $(a-b) \mid p(b-c)$, i.e., $u \mid p v$; and cyclically $v|p w, w| p u$. As $\operatorname{gcd}(u, v, w)=1$ and $u+v+w=0$, at most one of $u, v, w$ can be divisible by $p$. Supposing that the prime $p$ does not divide any one of them, we get $u|v, v| w, w \mid u$, whence $|u|=|v|=|w|=1$; but this quarrels with $u+v+w=0$. Thus $p$ must divide exactly one of these numbers. Let e.g. $p \mid u$ and write $u=p u_{1}$. Now we obtain, similarly as before, $u_{1}|v, v| w, w \mid u_{1}$ so that $\left|u_{1}\right|=|v|=|w|=1$. The equation $p u_{1}+v+w=0$ forces that the prime $p$ must be even; i.e. $p=2$. Hence $v+w=-2 u_{1}= \pm 2$, implying $v=w(= \pm 1)$ and $u=-2 v$. Consequently $a-b=-2(b-c)$. Knowing that $n$ is even, say $n=2 k$, we rewrite the equation $a^{n}-b^{n}=-p(b-c)$ with $p=2$ in the form $$ \left(a^{k}+b^{k}\right)\left(a^{k}-b^{k}\right)=-2(b-c)=a-b . $$ The second factor on the left is divisible by $a-b$, so the first factor $\left(a^{k}+b^{k}\right)$ must be $\pm 1$. Then exactly one of $a$ and $b$ must be odd; yet $a-b=-2(b-c)$ is even. Contradiction ends the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
29470af7-5c72-5a39-8e07-69fab4665828
| 23,777
|
Let $n$ be a positive integer and let $p$ be a prime number. Prove that if $a, b, c$ are integers (not necessarily positive) satisfying the equations $$ a^{n}+p b=b^{n}+p c=c^{n}+p a, $$ then $a=b=c$.
|
The beginning is as in the first solution. Assuming that $a, b, c$ are not all equal, hence are all distinct, we derive equation (1) with the conclusion that $n$ is even. Write $n=2 k$. Suppose that $p$ is odd. Then the integer $$ \frac{a^{n}-b^{n}}{a-b}=a^{n-1}+a^{n-2} b+\cdots+b^{n-1} $$ which is a factor in (1), must be odd as well. This sum of $n=2 k$ summands is odd only if $a$ and $b$ have different parities. The same conclusion holding for $b, c$ and for $c$, $a$, we get that $a, b, c, a$ alternate in their parities, which is clearly impossible. Thus $p=2$. The original system shows that $a, b, c$ must be of the same parity. So we may divide (1) by $p^{3}$, i.e. $2^{3}$, to obtain the following product of six integer factors: $$ \frac{a^{k}+b^{k}}{2} \cdot \frac{a^{k}-b^{k}}{a-b} \cdot \frac{b^{k}+c^{k}}{2} \cdot \frac{b^{k}-c^{k}}{b-c} \cdot \frac{c^{k}+a^{k}}{2} \cdot \frac{c^{k}-a^{k}}{c-a}=-1 . $$ Each one of the factors must be equal to $\pm 1$. In particular, $a^{k}+b^{k}= \pm 2$. If $k$ is even, this becomes $a^{k}+b^{k}=2$ and yields $|a|=|b|=1$, whence $a^{k}-b^{k}=0$, contradicting (2). Let now $k$ be odd. Then the sum $a^{k}+b^{k}$, with value $\pm 2$, has $a+b$ as a factor. Since $a$ and $b$ are of the same parity, this means that $a+b= \pm 2$; and cyclically, $b+c= \pm 2, c+a= \pm 2$. In some two of these equations the signs must coincide, hence some two of $a, b, c$ are equal. This is the desired contradiction. Comment. Having arrived at the equation (1) one is tempted to write down all possible decompositions of $-p^{3}$ (cube of a prime) into a product of three integers. This leads to cumbersome examination of many cases, some of which are unpleasant to handle. One may do that just for $p=2$, having earlier in some way eliminated odd primes from consideration. However, the second solution shows that the condition of $p$ being a prime is far too strong. What is actually being used in that solution, is that $p$ is either a positive odd integer or $p=2$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n$ be a positive integer and let $p$ be a prime number. Prove that if $a, b, c$ are integers (not necessarily positive) satisfying the equations $$ a^{n}+p b=b^{n}+p c=c^{n}+p a, $$ then $a=b=c$.
|
The beginning is as in the first solution. Assuming that $a, b, c$ are not all equal, hence are all distinct, we derive equation (1) with the conclusion that $n$ is even. Write $n=2 k$. Suppose that $p$ is odd. Then the integer $$ \frac{a^{n}-b^{n}}{a-b}=a^{n-1}+a^{n-2} b+\cdots+b^{n-1} $$ which is a factor in (1), must be odd as well. This sum of $n=2 k$ summands is odd only if $a$ and $b$ have different parities. The same conclusion holding for $b, c$ and for $c$, $a$, we get that $a, b, c, a$ alternate in their parities, which is clearly impossible. Thus $p=2$. The original system shows that $a, b, c$ must be of the same parity. So we may divide (1) by $p^{3}$, i.e. $2^{3}$, to obtain the following product of six integer factors: $$ \frac{a^{k}+b^{k}}{2} \cdot \frac{a^{k}-b^{k}}{a-b} \cdot \frac{b^{k}+c^{k}}{2} \cdot \frac{b^{k}-c^{k}}{b-c} \cdot \frac{c^{k}+a^{k}}{2} \cdot \frac{c^{k}-a^{k}}{c-a}=-1 . $$ Each one of the factors must be equal to $\pm 1$. In particular, $a^{k}+b^{k}= \pm 2$. If $k$ is even, this becomes $a^{k}+b^{k}=2$ and yields $|a|=|b|=1$, whence $a^{k}-b^{k}=0$, contradicting (2). Let now $k$ be odd. Then the sum $a^{k}+b^{k}$, with value $\pm 2$, has $a+b$ as a factor. Since $a$ and $b$ are of the same parity, this means that $a+b= \pm 2$; and cyclically, $b+c= \pm 2, c+a= \pm 2$. In some two of these equations the signs must coincide, hence some two of $a, b, c$ are equal. This is the desired contradiction. Comment. Having arrived at the equation (1) one is tempted to write down all possible decompositions of $-p^{3}$ (cube of a prime) into a product of three integers. This leads to cumbersome examination of many cases, some of which are unpleasant to handle. One may do that just for $p=2$, having earlier in some way eliminated odd primes from consideration. However, the second solution shows that the condition of $p$ being a prime is far too strong. What is actually being used in that solution, is that $p$ is either a positive odd integer or $p=2$.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
29470af7-5c72-5a39-8e07-69fab4665828
| 23,777
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.