problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Allen plays a game on a tree with $2 n$ vertices, each of whose vertices can be red or blue. Initially, all of the vertices of the tree are colored red. In one move, Allen is allowed to take two vertices of the same color which are connected by an edge and change both of them to the opposite color. He wins if at any time, all of the vertices of the tree are colored blue.
(a) (20) Show that Allen can win if and only if the vertices can be split up into two groups $V_{1}$ and $V_{2}$ of size $n$, such that each edge in the tree has one endpoint in $V_{1}$ and one endpoint in $V_{2}$.
(b) (40) Let $V_{1}=\left\{a_{1}, \ldots, a_{n}\right\}$ and $V_{2}=\left\{b_{1}, \ldots, b_{n}\right\}$ from part (a). Let $M$ be the minimum over all permutations $\sigma$ of $\{1, \ldots, n\}$ of the quantity
$$
\sum_{i=1}^{n} d\left(a_{i}, b_{\sigma(i)}\right)
$$
where $d(v, w)$ denotes the number of edges along the shortest path between vertices $v$ and $w$ in the tree.
Show that if Allen can win, then the minimum number of moves that it can take for Allen to win is equal to $M$.
(A graph consists of a set of vertices and some edges between distinct pairs of vertices. It is connected if every pair of vertices are connected by some path of one or more edges. A tree is a graph which is connected, in which the number of edges is one less than the number of vertices.)
|
Part (a): First we show that if we can't split the vertices in the desired way then Allen cannot win. To do so, observe that there is a unique way to split the vertices into two groups so that all edges cross between the two groups, since trees are bipartite. Each of Allen's moves either adds one more blue vertex to each group or removes a blue vertex from each group, so the difference in the number of blue vertices between the two groups is invariant. Both groups initially have no blue vertices, so Allen can only possibly arrive at a state where both groups have all blue vertices if both groups were initially of equal size.
To show that Allen can win when the splitting is possible, we induct on $n$. It's trivial for $n=1$. A tree on $2 n$ vertices has $2 n-1$ edges, so the total degree for each of the two $n$-vertex groups is $2 n-1$. Therefore, at least one vertex in each group is a leaf, say $L_{1}$ in one group and $L_{2}$ in the other. Allen can then flip all the vertices from $L_{1}$ to $L_{2}$ since there is a path of even length (in terms of number of vertices) from one to the other, including flipping $L_{1}$ and $L_{2}$, and then flip back all of the middle vertices in the path, with the end result being that $L_{1}$ and $L_{2}$ are blue while all other vertices in the tree remain red. This lets us remove $L_{1}$ and $L_{2}$ from consideration and apply the inductive hypothesis on the remaining graph.
Part (b): For each edge $e$ in the graph, we can determine a minimum number of times Allen must perform an operation on the endpoints of that edge (henceforth, "flip this edge"), as follows. Observe that removing $e$ disconnects the graph into two components. Each component is still a tree which can be split into two groups as before, though not necessarily with an equal number of vertices. In particular, suppose that the two groups differ by $d$ vertices. Flipping any edge other than $e$ does not change the difference in number of blue vertices between the two groups of the component. So $e$ must flip at least $d$ times if Allen is to win. Let $m_{e}$ be the minimum number of times that edge $e$ must flip, as determined in this way, and let $M^{\prime}$ be the total sum of all of the $m_{e}$. And let $T^{\prime}$ be the original tree with every edge duplicated $m_{e}$ times (or removed if $m_{e}=0$ ).
Observe that any permutation $\sigma$ that gives us $n$ paths must have total length at least $M^{\prime}$ for the same reasons as in the above paragraph, so $M^{\prime} \leq M$.
In fact, we will show that $M^{\prime}=M$. To show that $M^{\prime}=M$, it suffices to show that $M^{\prime} \geq M$, which we will show by finding a partitioning of $T^{\prime}$ into $n$ odd-length paths for which every vertex is the endpoint of exactly one path. This will show that $M^{\prime}$ is the sum of path lengths for some permutation, meaning it is at least the sum of path lengths for the optimal permutation. We do this by strong induction. The base case is trivial, and if any $m_{e}$ is 0 then we're immediately done because we can split the $T^{\prime}$ into two smaller trees. Otherwise we repeat the argument from part (a) where we use a path between two leaves, since each group of $n$ vertices must contain a leaf, thereby reducing the number of vertices in our tree by 2 and allowing us to use our inductive hypothesis.
It now suffices to show that Allen can win the game in $M^{\prime}$ moves, but this is exactly the same induction as in the previous paragraph. If any $m_{e}$ is 0 then we're immediately done by splitting $T^{\prime}$ into two smaller trees, otherwise we use the path between the two leaves to use our inductive hypothesis.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Allen plays a game on a tree with $2 n$ vertices, each of whose vertices can be red or blue. Initially, all of the vertices of the tree are colored red. In one move, Allen is allowed to take two vertices of the same color which are connected by an edge and change both of them to the opposite color. He wins if at any time, all of the vertices of the tree are colored blue.
(a) (20) Show that Allen can win if and only if the vertices can be split up into two groups $V_{1}$ and $V_{2}$ of size $n$, such that each edge in the tree has one endpoint in $V_{1}$ and one endpoint in $V_{2}$.
(b) (40) Let $V_{1}=\left\{a_{1}, \ldots, a_{n}\right\}$ and $V_{2}=\left\{b_{1}, \ldots, b_{n}\right\}$ from part (a). Let $M$ be the minimum over all permutations $\sigma$ of $\{1, \ldots, n\}$ of the quantity
$$
\sum_{i=1}^{n} d\left(a_{i}, b_{\sigma(i)}\right)
$$
where $d(v, w)$ denotes the number of edges along the shortest path between vertices $v$ and $w$ in the tree.
Show that if Allen can win, then the minimum number of moves that it can take for Allen to win is equal to $M$.
(A graph consists of a set of vertices and some edges between distinct pairs of vertices. It is connected if every pair of vertices are connected by some path of one or more edges. A tree is a graph which is connected, in which the number of edges is one less than the number of vertices.)
|
Part (a): First we show that if we can't split the vertices in the desired way then Allen cannot win. To do so, observe that there is a unique way to split the vertices into two groups so that all edges cross between the two groups, since trees are bipartite. Each of Allen's moves either adds one more blue vertex to each group or removes a blue vertex from each group, so the difference in the number of blue vertices between the two groups is invariant. Both groups initially have no blue vertices, so Allen can only possibly arrive at a state where both groups have all blue vertices if both groups were initially of equal size.
To show that Allen can win when the splitting is possible, we induct on $n$. It's trivial for $n=1$. A tree on $2 n$ vertices has $2 n-1$ edges, so the total degree for each of the two $n$-vertex groups is $2 n-1$. Therefore, at least one vertex in each group is a leaf, say $L_{1}$ in one group and $L_{2}$ in the other. Allen can then flip all the vertices from $L_{1}$ to $L_{2}$ since there is a path of even length (in terms of number of vertices) from one to the other, including flipping $L_{1}$ and $L_{2}$, and then flip back all of the middle vertices in the path, with the end result being that $L_{1}$ and $L_{2}$ are blue while all other vertices in the tree remain red. This lets us remove $L_{1}$ and $L_{2}$ from consideration and apply the inductive hypothesis on the remaining graph.
Part (b): For each edge $e$ in the graph, we can determine a minimum number of times Allen must perform an operation on the endpoints of that edge (henceforth, "flip this edge"), as follows. Observe that removing $e$ disconnects the graph into two components. Each component is still a tree which can be split into two groups as before, though not necessarily with an equal number of vertices. In particular, suppose that the two groups differ by $d$ vertices. Flipping any edge other than $e$ does not change the difference in number of blue vertices between the two groups of the component. So $e$ must flip at least $d$ times if Allen is to win. Let $m_{e}$ be the minimum number of times that edge $e$ must flip, as determined in this way, and let $M^{\prime}$ be the total sum of all of the $m_{e}$. And let $T^{\prime}$ be the original tree with every edge duplicated $m_{e}$ times (or removed if $m_{e}=0$ ).
Observe that any permutation $\sigma$ that gives us $n$ paths must have total length at least $M^{\prime}$ for the same reasons as in the above paragraph, so $M^{\prime} \leq M$.
In fact, we will show that $M^{\prime}=M$. To show that $M^{\prime}=M$, it suffices to show that $M^{\prime} \geq M$, which we will show by finding a partitioning of $T^{\prime}$ into $n$ odd-length paths for which every vertex is the endpoint of exactly one path. This will show that $M^{\prime}$ is the sum of path lengths for some permutation, meaning it is at least the sum of path lengths for the optimal permutation. We do this by strong induction. The base case is trivial, and if any $m_{e}$ is 0 then we're immediately done because we can split the $T^{\prime}$ into two smaller trees. Otherwise we repeat the argument from part (a) where we use a path between two leaves, since each group of $n$ vertices must contain a leaf, thereby reducing the number of vertices in our tree by 2 and allowing us to use our inductive hypothesis.
It now suffices to show that Allen can win the game in $M^{\prime}$ moves, but this is exactly the same induction as in the previous paragraph. If any $m_{e}$ is 0 then we're immediately done by splitting $T^{\prime}$ into two smaller trees, otherwise we use the path between the two leaves to use our inductive hypothesis.
|
{
"resource_path": "HarvardMIT/segmented/en-212-2018-feb-team-solutions.jsonl",
"problem_match": "\n8. [60]",
"solution_match": "\n## Proposed by: Kevin Sun\n\n"
}
|
fcdc9894-8900-5a21-90fd-e6d30bc1de75
| 609,852
|
Evan has a simple graph with $v$ vertices and $e$ edges. Show that he can delete at least $\frac{e-v+1}{2}$ edges so that each vertex still has at least half of its original degree.
|
Fix $v$. We use strong induction on the number of edges $e$. If $e \leq v-1$, the result trivially holds by removing 0 edges. Now take $e>v-1$ and assume the result has been shown for all smaller values of $e$. Consider a graph $G$ with $v$ vertices and $e$ edges.
Suppose $G$ contains a cycle $C$ of even length $2 k$, where vertices (but not edges) may be repeated in the cycle. Let $G^{\prime}$ be the subgraph of $G$ with the edges of $C$ removed. Then $G^{\prime}$ has $v$ vertices and $e-2 k$ edges. By the inductive hypothesis, it is possible to remove $\frac{e-2 k-v+1}{2}$ edges from $G^{\prime}$ so that each vertex still has at least half its original degree. In the original graph $G$, remove these same edges,
and also remove every other edge of $C$ (so, if the vertices of $C$ are $v_{1}, \cdots, v_{2 k}$ in order, we remove the edges between $v_{2 i-1}$ and $v_{2 i}$ for $1 \leq i \leq k$ ). In total, we have removed $\frac{e-2 k-v+1}{2}+k=\frac{e-v+1}{2}$ edges. Furthermore, all vertices in $G$ still have at least half their original degrees, as desired.
The remaining case to consider is if $G$ has no cycles of even length. Then no two cycles in $G$ can have any vertices or edges in common. Suppose the contrary; then two odd cycles overlap, so their union is connected and has an even number of edges. This union has an Eulerian tour, which is a cycle with an even number of edges, contradicting our assumption.
The number of edges in $G$ is at most $v+c-1$, where $c$ is the number of cycles. So, we must remove at least $\frac{e-v+1}{2}=\frac{c}{2}$ edges from $G$. But we can remove $c$ edges from $G$, one from each cycle. No vertex has its degree decreased by more than 1 , and each vertex whose degree is decreased is in a cycle and so has degree at least 2. Therefore each vertex still has at least half of its original degree, and we have removed at least $\frac{e-v+1}{2}$ edges, as desired.
Thus our claim holds for a graph with $e$ edges, and thus by induction holds for any number of edges, as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Evan has a simple graph with $v$ vertices and $e$ edges. Show that he can delete at least $\frac{e-v+1}{2}$ edges so that each vertex still has at least half of its original degree.
|
Fix $v$. We use strong induction on the number of edges $e$. If $e \leq v-1$, the result trivially holds by removing 0 edges. Now take $e>v-1$ and assume the result has been shown for all smaller values of $e$. Consider a graph $G$ with $v$ vertices and $e$ edges.
Suppose $G$ contains a cycle $C$ of even length $2 k$, where vertices (but not edges) may be repeated in the cycle. Let $G^{\prime}$ be the subgraph of $G$ with the edges of $C$ removed. Then $G^{\prime}$ has $v$ vertices and $e-2 k$ edges. By the inductive hypothesis, it is possible to remove $\frac{e-2 k-v+1}{2}$ edges from $G^{\prime}$ so that each vertex still has at least half its original degree. In the original graph $G$, remove these same edges,
and also remove every other edge of $C$ (so, if the vertices of $C$ are $v_{1}, \cdots, v_{2 k}$ in order, we remove the edges between $v_{2 i-1}$ and $v_{2 i}$ for $1 \leq i \leq k$ ). In total, we have removed $\frac{e-2 k-v+1}{2}+k=\frac{e-v+1}{2}$ edges. Furthermore, all vertices in $G$ still have at least half their original degrees, as desired.
The remaining case to consider is if $G$ has no cycles of even length. Then no two cycles in $G$ can have any vertices or edges in common. Suppose the contrary; then two odd cycles overlap, so their union is connected and has an even number of edges. This union has an Eulerian tour, which is a cycle with an even number of edges, contradicting our assumption.
The number of edges in $G$ is at most $v+c-1$, where $c$ is the number of cycles. So, we must remove at least $\frac{e-v+1}{2}=\frac{c}{2}$ edges from $G$. But we can remove $c$ edges from $G$, one from each cycle. No vertex has its degree decreased by more than 1 , and each vertex whose degree is decreased is in a cycle and so has degree at least 2. Therefore each vertex still has at least half of its original degree, and we have removed at least $\frac{e-v+1}{2}$ edges, as desired.
Thus our claim holds for a graph with $e$ edges, and thus by induction holds for any number of edges, as needed.
|
{
"resource_path": "HarvardMIT/segmented/en-212-2018-feb-team-solutions.jsonl",
"problem_match": "\n9. [60]",
"solution_match": "\n## Proposed by: Allen Liu\n\n"
}
|
6d4c5d63-6dd0-5751-9d19-918ed5046d4d
| 72,418
|
Consider a finite set of points $T \in \mathbb{R}^{n}$ contained in the $n$-dimensional unit ball centered at the origin, and let $X$ be the convex hull of $T$. Prove that for all positive integers $k$ and all points $x \in X$, there exist points $t_{1}, t_{2}, \ldots, t_{k} \in T$, not necessarily distinct, such that their centroid
$$
\frac{t_{1}+t_{2}+\cdots+t_{k}}{k}
$$
has Euclidean distance at most $\frac{1}{\sqrt{k}}$ from $x$.
(The $n$-dimensional unit ball centered at the origin is the set of points in $\mathbb{R}^{n}$ with Euclidean distance at most 1 from the origin. The convex hull of a set of points $T \in \mathbb{R}^{n}$ is the smallest set of points $X$ containing $T$ such that each line segment between two points in $X$ lies completely inside $X$.)
|
By the definition of convex hull, we can write $x=\sum_{i=1}^{m} \lambda_{i} z_{i}$, where each $z_{i} \in T$, each $\lambda_{i} \geq 0$ and $\sum_{i=1}^{m} \lambda_{i}=1$. Consider then a random variable $Z$ that takes on value $z_{i}$ with probability $\lambda_{i}$. We have $\mathbb{E}[Z]=x$. Let $\bar{Z}=\frac{1}{k} \sum_{i=1}^{k} Z_{i}$, where each $Z_{i}$ is an independent copy of $Z$. Then we wish to compute
$$
\operatorname{Var}[\bar{Z}]=\frac{1}{k^{2}} \sum_{i=1}^{k} \operatorname{Var}\left[Z_{i}\right]
$$
Finally, we have
$$
\operatorname{Var}\left[Z_{i}\right]=\mathbb{E}\left[\left\|Z_{i}-x\right\|^{2}\right]=\mathbb{E}\left[\left\|Z_{i}\right\|^{2}\right]-x^{2} \leq \mathbb{E}\left[\left\|Z_{i}\right\|^{2}\right] \leq 1
$$
The second equality follows from the identity $\operatorname{Var}[X]=\mathbb{E}\left[X^{2}\right]-\mathbb{E}[X]^{2}$. Now, we know that
$$
\mathbb{E}\left[\left\|x-\frac{1}{k} \sum_{i=1}^{k} Z_{i}\right\|^{2}\right]=\operatorname{Var}[\bar{Z}] \leq \frac{1}{k}
$$
Thus, there must exist some realization of $x_{i}$ of the $Z_{i}$ such that
$$
\left\|x-\frac{1}{k} \sum_{i=1}^{k} x_{i}\right\|^{2} \leq \frac{1}{k}
$$
and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider a finite set of points $T \in \mathbb{R}^{n}$ contained in the $n$-dimensional unit ball centered at the origin, and let $X$ be the convex hull of $T$. Prove that for all positive integers $k$ and all points $x \in X$, there exist points $t_{1}, t_{2}, \ldots, t_{k} \in T$, not necessarily distinct, such that their centroid
$$
\frac{t_{1}+t_{2}+\cdots+t_{k}}{k}
$$
has Euclidean distance at most $\frac{1}{\sqrt{k}}$ from $x$.
(The $n$-dimensional unit ball centered at the origin is the set of points in $\mathbb{R}^{n}$ with Euclidean distance at most 1 from the origin. The convex hull of a set of points $T \in \mathbb{R}^{n}$ is the smallest set of points $X$ containing $T$ such that each line segment between two points in $X$ lies completely inside $X$.)
|
By the definition of convex hull, we can write $x=\sum_{i=1}^{m} \lambda_{i} z_{i}$, where each $z_{i} \in T$, each $\lambda_{i} \geq 0$ and $\sum_{i=1}^{m} \lambda_{i}=1$. Consider then a random variable $Z$ that takes on value $z_{i}$ with probability $\lambda_{i}$. We have $\mathbb{E}[Z]=x$. Let $\bar{Z}=\frac{1}{k} \sum_{i=1}^{k} Z_{i}$, where each $Z_{i}$ is an independent copy of $Z$. Then we wish to compute
$$
\operatorname{Var}[\bar{Z}]=\frac{1}{k^{2}} \sum_{i=1}^{k} \operatorname{Var}\left[Z_{i}\right]
$$
Finally, we have
$$
\operatorname{Var}\left[Z_{i}\right]=\mathbb{E}\left[\left\|Z_{i}-x\right\|^{2}\right]=\mathbb{E}\left[\left\|Z_{i}\right\|^{2}\right]-x^{2} \leq \mathbb{E}\left[\left\|Z_{i}\right\|^{2}\right] \leq 1
$$
The second equality follows from the identity $\operatorname{Var}[X]=\mathbb{E}\left[X^{2}\right]-\mathbb{E}[X]^{2}$. Now, we know that
$$
\mathbb{E}\left[\left\|x-\frac{1}{k} \sum_{i=1}^{k} Z_{i}\right\|^{2}\right]=\operatorname{Var}[\bar{Z}] \leq \frac{1}{k}
$$
Thus, there must exist some realization of $x_{i}$ of the $Z_{i}$ such that
$$
\left\|x-\frac{1}{k} \sum_{i=1}^{k} x_{i}\right\|^{2} \leq \frac{1}{k}
$$
and we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-214-tournaments-2018-hmic-solutions.jsonl",
"problem_match": "\n2. [7]",
"solution_match": "\n## Proposed by: Henrik Boecken\n\n"
}
|
6ffe823c-2da9-57bf-8323-a3ed5d9ef66b
| 609,855
|
A polygon in the plane (with no self-intersections) is called equitable if every line passing through the origin divides the polygon into two (possibly disconnected) regions of equal area.
Does there exist an equitable polygon which is not centrally symmetric about the origin?
(A polygon is centrally symmetric about the origin if a 180-degree rotation about the origin sends the polygon to itself.)
|
Consider the polygon with vertices
$$
\begin{aligned}
& A(1,0), B(0,1), C(0,5), D(5,0), E(7,0) \\
& F(0,-7), G(-7,0), H(-\sqrt{84}, 0), I(0, \sqrt{84}), J(0,6) \\
& K(-6,0), L(-5,0), M(0,-5), N(0,-1)
\end{aligned}
$$
Notice that its intersection with each of the four quadrants are all trapezoids with angles $45^{\circ}, 45^{\circ}, 135^{\circ}, 135^{\circ}$, and the trapezoids in quadrant 1 and 3 both have area $\frac{5^{2}-1^{2}}{2}=\frac{7^{2}-5^{2}}{2}=12$, and the trapezoids in quadrant 2 and 4 both have area $\frac{7^{2}-1^{2}}{2}=\frac{84-6^{2}}{2}=24$, so by similar triangles, we can show that this polygon is indeed equitable. It is also apparent that this polygon is not centrally symmetric.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A polygon in the plane (with no self-intersections) is called equitable if every line passing through the origin divides the polygon into two (possibly disconnected) regions of equal area.
Does there exist an equitable polygon which is not centrally symmetric about the origin?
(A polygon is centrally symmetric about the origin if a 180-degree rotation about the origin sends the polygon to itself.)
|
Consider the polygon with vertices
$$
\begin{aligned}
& A(1,0), B(0,1), C(0,5), D(5,0), E(7,0) \\
& F(0,-7), G(-7,0), H(-\sqrt{84}, 0), I(0, \sqrt{84}), J(0,6) \\
& K(-6,0), L(-5,0), M(0,-5), N(0,-1)
\end{aligned}
$$
Notice that its intersection with each of the four quadrants are all trapezoids with angles $45^{\circ}, 45^{\circ}, 135^{\circ}, 135^{\circ}$, and the trapezoids in quadrant 1 and 3 both have area $\frac{5^{2}-1^{2}}{2}=\frac{7^{2}-5^{2}}{2}=12$, and the trapezoids in quadrant 2 and 4 both have area $\frac{7^{2}-1^{2}}{2}=\frac{84-6^{2}}{2}=24$, so by similar triangles, we can show that this polygon is indeed equitable. It is also apparent that this polygon is not centrally symmetric.
|
{
"resource_path": "HarvardMIT/segmented/en-214-tournaments-2018-hmic-solutions.jsonl",
"problem_match": "\n3. [8]",
"solution_match": "\nProposed by: Kevin Sun\n"
}
|
e5ad86f6-cf93-5801-8018-47ece3cc839e
| 609,856
|
Let $G$ be an undirected simple graph. Let $f(G)$ be the number of ways to orient all of the edges of $G$ in one of the two possible directions so that the resulting directed graph has no directed cycles. Show that $f(G)$ is a multiple of 3 if and only if $G$ has a cycle of odd length.
|
Let $f_{G}(q)$ be the number of ways to color $G$ with $q$ colors. This is the chromatic polynomial of $G$, and turns out to be polynomial in $q$. Indeed, choose an edge $e$ and let $G \backslash e$ be the graph $G$ with $e$ removed and let $G / e$ be graph $G$ with the vertices on either side of $e$ merged together (multiple edges are removed). It is not hard to see that
$$
f_{G}(q)=f_{G \backslash e}(q)-f_{G / e}(q)
$$
and that for an empty graph $E_{n}$ with $n$ vertices, we have $f_{E_{n}}(q)=q^{n}$. Induction finishes.
Now we can also show that the desired number of ways to direct $G$ to avoid directed cycles is $c_{G}=$ $(-1)^{n} f_{G}(-1)$ where $n$ is the number of vertices of $G$. The way to do it is to show that
$$
c_{G}=c_{G \backslash e}+c_{G / e}
$$
and $c_{E_{n}}=1$. Thus $(-1)^{n} c_{G}$ will satisfy the desired recurrence, after multiplying the above by $(-1)^{n}$, and satisfies the correct initial conditions.
Now all we need to know is that $f_{G}(q)$ has integer coefficients, so that $(-1)^{n} c_{G} \equiv f_{G}(-1) \equiv f_{G}(2)$ $(\bmod 3)$, and $f_{G}(2)=0$ when $G$ is not bipartite and is $2^{c(G)}$ where $c(G)$ is the number of connected components of $G$ otherwise. The result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $G$ be an undirected simple graph. Let $f(G)$ be the number of ways to orient all of the edges of $G$ in one of the two possible directions so that the resulting directed graph has no directed cycles. Show that $f(G)$ is a multiple of 3 if and only if $G$ has a cycle of odd length.
|
Let $f_{G}(q)$ be the number of ways to color $G$ with $q$ colors. This is the chromatic polynomial of $G$, and turns out to be polynomial in $q$. Indeed, choose an edge $e$ and let $G \backslash e$ be the graph $G$ with $e$ removed and let $G / e$ be graph $G$ with the vertices on either side of $e$ merged together (multiple edges are removed). It is not hard to see that
$$
f_{G}(q)=f_{G \backslash e}(q)-f_{G / e}(q)
$$
and that for an empty graph $E_{n}$ with $n$ vertices, we have $f_{E_{n}}(q)=q^{n}$. Induction finishes.
Now we can also show that the desired number of ways to direct $G$ to avoid directed cycles is $c_{G}=$ $(-1)^{n} f_{G}(-1)$ where $n$ is the number of vertices of $G$. The way to do it is to show that
$$
c_{G}=c_{G \backslash e}+c_{G / e}
$$
and $c_{E_{n}}=1$. Thus $(-1)^{n} c_{G}$ will satisfy the desired recurrence, after multiplying the above by $(-1)^{n}$, and satisfies the correct initial conditions.
Now all we need to know is that $f_{G}(q)$ has integer coefficients, so that $(-1)^{n} c_{G} \equiv f_{G}(-1) \equiv f_{G}(2)$ $(\bmod 3)$, and $f_{G}(2)=0$ when $G$ is not bipartite and is $2^{c(G)}$ where $c(G)$ is the number of connected components of $G$ otherwise. The result follows.
|
{
"resource_path": "HarvardMIT/segmented/en-214-tournaments-2018-hmic-solutions.jsonl",
"problem_match": "\n5. [11]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
1b59ffb3-44b5-5f7f-aa4a-8071dc112a59
| 609,858
|
Let $r$ be the radius of the inscribed circle of triangle $A B C$. Take a point $D$ on side $B C$, and let $r_{1}$ and $r_{2}$ be the inradii of triangles $A B D$ and $A C D$. Prove that $r, r_{1}$, and $r_{2}$ can always be the side lengths of a triangle.
|
We must show that $r, r_{1}$, and $r_{2}$ satisfy the triangle inequality, i.e. that the sum of any two of them exceeds the third. Clearly $r$ is the largest of the three, so we need only verify that $r_{1}+r_{2}>r$. Let $K$ and $s$ be the area and semiperimeter of triangle $A B C$. Similarly define $K_{1}$, $K_{2}, s_{1}$, and $s_{2}$. Observe that $s$ is larger than $s_{1}$ or $s_{2}$ and that $K_{1}+K_{2}=K$. While these facts are almost trivial to verify, they must be stated. Then $r=K / s, r_{1}=K_{1} / s_{1}$, and $r_{2}=K_{2} / s_{2}$, so $r_{1}+r_{2}=K_{1} / s_{1}+K_{2} / s_{2}>K_{1} / s+K_{2} / s=K / s=r$.
The correct use of areas and semiperimeters is worth 25 points, each of the critical facts is worth 10 points. I don't know of any other way to do this problem, so attempts at alternate proofs should get at most 15 points for effort unless they really on the right track to another solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $r$ be the radius of the inscribed circle of triangle $A B C$. Take a point $D$ on side $B C$, and let $r_{1}$ and $r_{2}$ be the inradii of triangles $A B D$ and $A C D$. Prove that $r, r_{1}$, and $r_{2}$ can always be the side lengths of a triangle.
|
We must show that $r, r_{1}$, and $r_{2}$ satisfy the triangle inequality, i.e. that the sum of any two of them exceeds the third. Clearly $r$ is the largest of the three, so we need only verify that $r_{1}+r_{2}>r$. Let $K$ and $s$ be the area and semiperimeter of triangle $A B C$. Similarly define $K_{1}$, $K_{2}, s_{1}$, and $s_{2}$. Observe that $s$ is larger than $s_{1}$ or $s_{2}$ and that $K_{1}+K_{2}=K$. While these facts are almost trivial to verify, they must be stated. Then $r=K / s, r_{1}=K_{1} / s_{1}$, and $r_{2}=K_{2} / s_{2}$, so $r_{1}+r_{2}=K_{1} / s_{1}+K_{2} / s_{2}>K_{1} / s+K_{2} / s=K / s=r$.
The correct use of areas and semiperimeters is worth 25 points, each of the critical facts is worth 10 points. I don't know of any other way to do this problem, so attempts at alternate proofs should get at most 15 points for effort unless they really on the right track to another solution.
|
{
"resource_path": "HarvardMIT/segmented/en-22-1999-feb-oral-solutions.jsonl",
"problem_match": "\nProblem O5 [45 points]",
"solution_match": "\nSolution: "
}
|
bc16a371-1ff7-57be-9fa1-373eabdc8c66
| 170,575
|
Let $A B C D$ be a parallelogram. Points $X$ and $Y$ lie on segments $A B$ and $A D$ respectively, and $A C$ intersects $X Y$ at point $Z$. Prove that
$$
\frac{A B}{A X}+\frac{A D}{A Y}=\frac{A C}{A Z}
$$
|
Solution 1. (Similar Triangles)
Let $X^{\prime}$ and $Y^{\prime}$ lie on segments $A B$ and $A D$ respectively such that $Z X^{\prime} \| A D$ and $Z Y^{\prime} \| A B$. We note that triangles $A X Y$ and $Y^{\prime} Y Z$ are similar, and that triangles $A Y^{\prime} Z$ and $A D C$ are similar. Thus, we have
$$
\frac{A C}{A Z}=\frac{A D}{A Y^{\prime}} \text { and } \frac{A Y^{\prime}}{A Y}=\frac{X Z}{X Y}
$$
This means that
$$
\frac{A D}{A Y}=\frac{A D}{A Y^{\prime}} \cdot \frac{A Y^{\prime}}{A Y}=\frac{X Z}{X Y} \cdot \frac{A C}{A Z}
$$
and similarly,
$$
\frac{A B}{A X}=\frac{Z Y}{X Y} \cdot \frac{A C}{A Z}
$$
Therefore we have
$$
\frac{A B}{A X}+\frac{A D}{A Y}=\left(\frac{X Z}{X Y}+\frac{Z Y}{X Y}\right) \cdot \frac{A C}{A Z}=\frac{A C}{A Z}
$$
as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram. Points $X$ and $Y$ lie on segments $A B$ and $A D$ respectively, and $A C$ intersects $X Y$ at point $Z$. Prove that
$$
\frac{A B}{A X}+\frac{A D}{A Y}=\frac{A C}{A Z}
$$
|
Solution 1. (Similar Triangles)
Let $X^{\prime}$ and $Y^{\prime}$ lie on segments $A B$ and $A D$ respectively such that $Z X^{\prime} \| A D$ and $Z Y^{\prime} \| A B$. We note that triangles $A X Y$ and $Y^{\prime} Y Z$ are similar, and that triangles $A Y^{\prime} Z$ and $A D C$ are similar. Thus, we have
$$
\frac{A C}{A Z}=\frac{A D}{A Y^{\prime}} \text { and } \frac{A Y^{\prime}}{A Y}=\frac{X Z}{X Y}
$$
This means that
$$
\frac{A D}{A Y}=\frac{A D}{A Y^{\prime}} \cdot \frac{A Y^{\prime}}{A Y}=\frac{X Z}{X Y} \cdot \frac{A C}{A Z}
$$
and similarly,
$$
\frac{A B}{A X}=\frac{Z Y}{X Y} \cdot \frac{A C}{A Z}
$$
Therefore we have
$$
\frac{A B}{A X}+\frac{A D}{A Y}=\left(\frac{X Z}{X Y}+\frac{Z Y}{X Y}\right) \cdot \frac{A C}{A Z}=\frac{A C}{A Z}
$$
as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-222-2019-feb-team-solutions.jsonl",
"problem_match": "\n1. [20]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
4ca278c7-f7b5-5ef3-a3a8-17a632d761db
| 610,034
|
Let $A B C D$ be a parallelogram. Points $X$ and $Y$ lie on segments $A B$ and $A D$ respectively, and $A C$ intersects $X Y$ at point $Z$. Prove that
$$
\frac{A B}{A X}+\frac{A D}{A Y}=\frac{A C}{A Z}
$$
|
(Affine Transformations)
We recall that affine transformations preserve both parallel lines and ratios between distances of collinear points. It thus suffices to show the desired result when $A B C D$ is a square. This can be done in a variety of ways. For instance, a coordinate bash can be applied by setting $A$ to be the origin. Let the length of the square be 1 and set $X$ and $Y$ as $(a, 0)$ and $(0, b)$ respectively, so the line $X Y$ has equation $b x+a y=a b$. Then, we note that $Z$ is the point $\left(\frac{a b}{a+b}, \frac{a b}{a+b}\right)$, so
$$
\frac{A B}{A X}+\frac{A D}{A Y}=\frac{1}{a}+\frac{1}{b}=\frac{a+b}{a b}=\frac{A C}{A Z}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram. Points $X$ and $Y$ lie on segments $A B$ and $A D$ respectively, and $A C$ intersects $X Y$ at point $Z$. Prove that
$$
\frac{A B}{A X}+\frac{A D}{A Y}=\frac{A C}{A Z}
$$
|
(Affine Transformations)
We recall that affine transformations preserve both parallel lines and ratios between distances of collinear points. It thus suffices to show the desired result when $A B C D$ is a square. This can be done in a variety of ways. For instance, a coordinate bash can be applied by setting $A$ to be the origin. Let the length of the square be 1 and set $X$ and $Y$ as $(a, 0)$ and $(0, b)$ respectively, so the line $X Y$ has equation $b x+a y=a b$. Then, we note that $Z$ is the point $\left(\frac{a b}{a+b}, \frac{a b}{a+b}\right)$, so
$$
\frac{A B}{A X}+\frac{A D}{A Y}=\frac{1}{a}+\frac{1}{b}=\frac{a+b}{a b}=\frac{A C}{A Z}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-222-2019-feb-team-solutions.jsonl",
"problem_match": "\n1. [20]",
"solution_match": "\nSolution 2. "
}
|
4ca278c7-f7b5-5ef3-a3a8-17a632d761db
| 610,034
|
Let $\mathbb{N}=\{1,2,3, \ldots\}$ be the set of all positive integers, and let $f$ be a bijection from $\mathbb{N}$ to $\mathbb{N}$. Must there exist some positive integer $n$ such that $(f(1), f(2), \ldots, f(n))$ is a permutation of $(1,2, \ldots, n)$ ?
|
Answer: No
Consider the bijection $f$ defined by
$$
(f(1), f(2), f(3), f(4), \ldots)=(2,4,6,1,8,3,10,5,12, \ldots)
$$
which alternates between even and odd numbers after the second entry. (More formally, we define $f(n)=2 n$ for $n=1,2, f(n)=n+3$ for odd $n \geq 3$ and $f(n)=n-3$ for even $n \geq 4$.) No such $n$ can exist for this $f$ as the largest number among $f(1), f(2), \ldots, f(n)$ is more than $n$ for all $n$ : for $k \geq 2$, the maximum of the first $2 k-1$ or $2 k$ values is achieved by $f(2 k-1)=2 k+2$. (Checking $n=1$ and $n=2$ is trivial.)
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $\mathbb{N}=\{1,2,3, \ldots\}$ be the set of all positive integers, and let $f$ be a bijection from $\mathbb{N}$ to $\mathbb{N}$. Must there exist some positive integer $n$ such that $(f(1), f(2), \ldots, f(n))$ is a permutation of $(1,2, \ldots, n)$ ?
|
Answer: No
Consider the bijection $f$ defined by
$$
(f(1), f(2), f(3), f(4), \ldots)=(2,4,6,1,8,3,10,5,12, \ldots)
$$
which alternates between even and odd numbers after the second entry. (More formally, we define $f(n)=2 n$ for $n=1,2, f(n)=n+3$ for odd $n \geq 3$ and $f(n)=n-3$ for even $n \geq 4$.) No such $n$ can exist for this $f$ as the largest number among $f(1), f(2), \ldots, f(n)$ is more than $n$ for all $n$ : for $k \geq 2$, the maximum of the first $2 k-1$ or $2 k$ values is achieved by $f(2 k-1)=2 k+2$. (Checking $n=1$ and $n=2$ is trivial.)
|
{
"resource_path": "HarvardMIT/segmented/en-222-2019-feb-team-solutions.jsonl",
"problem_match": "\n2. [20]",
"solution_match": "\nProposed by: Michael Tang\n"
}
|
15e7f43d-4909-5193-aa17-b59badfc3247
| 610,035
|
For any angle $0<\theta<\pi / 2$, show that
$$
0<\sin \theta+\cos \theta+\tan \theta+\cot \theta-\sec \theta-\csc \theta<1
$$
|
We use the following geometric construction, which follows from the geometric definition of the trigonometric functions: Let $Z$ be a point on the unit circle in the coordinate plane with origin $O$. Let $X_{1}, Y_{1}$ be the projections of $Z$ onto the $x$ - and $y$-axis respectively, and let $X_{2}, Y_{2}$ lie on $x$ - and $y$-axis respectively such that $X_{2} Y_{2}$ is tangent to the unit circle at $Z$. Then we have
$$
O Z=X_{1} Y_{1}=1, X_{1} Z=\sin \theta, Y_{1} Z=\cos \theta, X_{2} Z=\tan \theta, Y_{2} Z=\cot \theta, O X_{2}=\sec \theta, O Y_{2}=\csc \theta
$$
It then suffices to show that $0<X_{2} Y_{2}-X_{1} X_{2}-Y_{1} Y_{2}<1=X_{1} Y_{1}$. The left inequality is true because $X_{1} X_{2}$ and $Y_{1} Y_{2}$ are the projections of $Z X_{2}$ and $Z Y_{2}$ onto $x$ - and $y$-axis respectively. The right inequality is true because $X_{1} X_{2}+X_{1} Y_{1}+Y_{1} Y_{2}>X_{2} Y_{2}$ by triangle inequality. Therefore we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
For any angle $0<\theta<\pi / 2$, show that
$$
0<\sin \theta+\cos \theta+\tan \theta+\cot \theta-\sec \theta-\csc \theta<1
$$
|
We use the following geometric construction, which follows from the geometric definition of the trigonometric functions: Let $Z$ be a point on the unit circle in the coordinate plane with origin $O$. Let $X_{1}, Y_{1}$ be the projections of $Z$ onto the $x$ - and $y$-axis respectively, and let $X_{2}, Y_{2}$ lie on $x$ - and $y$-axis respectively such that $X_{2} Y_{2}$ is tangent to the unit circle at $Z$. Then we have
$$
O Z=X_{1} Y_{1}=1, X_{1} Z=\sin \theta, Y_{1} Z=\cos \theta, X_{2} Z=\tan \theta, Y_{2} Z=\cot \theta, O X_{2}=\sec \theta, O Y_{2}=\csc \theta
$$
It then suffices to show that $0<X_{2} Y_{2}-X_{1} X_{2}-Y_{1} Y_{2}<1=X_{1} Y_{1}$. The left inequality is true because $X_{1} X_{2}$ and $Y_{1} Y_{2}$ are the projections of $Z X_{2}$ and $Z Y_{2}$ onto $x$ - and $y$-axis respectively. The right inequality is true because $X_{1} X_{2}+X_{1} Y_{1}+Y_{1} Y_{2}>X_{2} Y_{2}$ by triangle inequality. Therefore we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-222-2019-feb-team-solutions.jsonl",
"problem_match": "\n3. [25]",
"solution_match": "\n## Proposed by: Yuan Yao\n\n"
}
|
085513ab-357e-5e13-9287-ff8df001f57a
| 610,036
|
Scalene triangle $A B C$ satisfies $\angle A=60^{\circ}$. Let the circumcenter of $A B C$ be $O$, the orthocenter be $H$, and the incenter be $I$. Let $D, T$ be the points where line $B C$ intersects the internal and external
angle bisectors of $\angle A$, respectively. Choose point $X$ on the circumcircle of $\triangle I H O$ such that $H X \| A I$. Prove that $O D \perp T X$.
|
Let $I_{A}$ denote the $A$-excenter. Because $\angle A=60^{\circ}, A I$ is the perpendicular bisector of $O H$ and $B, H, O, C$ all lie on the circle with diameter $I I_{A}$. We are given that $X$ is on this circle as well, and since $H I=O I, X I O I_{A}$ is also an isosceles trapezoid. But $I I_{A}$ is a diameter, so this means $X$ must be diametrically opposite $O$ on $(B O C)$ and is actually the intersection of the tangents to $(A B C)$ from $B$ and $C$.
Now $(T, D ; B, C)=-1$, so $T$ is on the polar of $D$ with respect to $(A B C) . B C$ is the polar of $X$ and $D$ lies on $B C$, so $X$ must also lie on the polar of $D$. Therefore $T X$ is the polar of $D$ with respect to $(A B C)$, and $O D \perp T X$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Scalene triangle $A B C$ satisfies $\angle A=60^{\circ}$. Let the circumcenter of $A B C$ be $O$, the orthocenter be $H$, and the incenter be $I$. Let $D, T$ be the points where line $B C$ intersects the internal and external
angle bisectors of $\angle A$, respectively. Choose point $X$ on the circumcircle of $\triangle I H O$ such that $H X \| A I$. Prove that $O D \perp T X$.
|
Let $I_{A}$ denote the $A$-excenter. Because $\angle A=60^{\circ}, A I$ is the perpendicular bisector of $O H$ and $B, H, O, C$ all lie on the circle with diameter $I I_{A}$. We are given that $X$ is on this circle as well, and since $H I=O I, X I O I_{A}$ is also an isosceles trapezoid. But $I I_{A}$ is a diameter, so this means $X$ must be diametrically opposite $O$ on $(B O C)$ and is actually the intersection of the tangents to $(A B C)$ from $B$ and $C$.
Now $(T, D ; B, C)=-1$, so $T$ is on the polar of $D$ with respect to $(A B C) . B C$ is the polar of $X$ and $D$ lies on $B C$, so $X$ must also lie on the polar of $D$. Therefore $T X$ is the polar of $D$ with respect to $(A B C)$, and $O D \perp T X$ as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-222-2019-feb-team-solutions.jsonl",
"problem_match": "\n6. [45]",
"solution_match": "\nProposed by: Wanlin Li\n"
}
|
817bc6b1-47c0-5282-843a-8bd2d7ee62e5
| 610,038
|
A convex polygon on the plane is called wide if the projection of the polygon onto any line in the same plane is a segment with length at least 1 . Prove that a circle of radius $\frac{1}{3}$ can be placed completely inside any wide polygon.
|
## Solution 1.
Lemma. for any polygon including its boundary, there exists a largest circle contained inside it.
Proof. Its easy to see that for any circle inside the polygon, it can be increased in size until it is tangent to at least three sides of the polygon. Then for any three sides of the polygon, there is only one circle tangent to all three, so there are only finitely many possibilities. Therefore there exists a largest one.
Alternatively, one can show that the space of valid $(x, y, r)$ such that the circle with center $(x, y)$ and radius $r$ is compact, e.g. by showing the complement is open and that the complement is open. Then the map $(x, y, r) \rightarrow r$ is continuous and therefore has a maximum.
Now, take the largest circle. It clearly must be tangent to three sides. If the circle lies inside the triangle made by the three lines, we can expand the polygon to that triangle and solve it for the triangle instead. Otherwise, we have the following diagram:
Here the circle is an excircle of the triangle $A B C$ made by the lines $A B, A D$, and $B E$. (Note that $A D$ and $A B$ dont have to be consecutive sides of the polygon, but the ones in between dont really matter.)
Then since the circle is an excircle, we can consider a homothety at $C$ with power $1+\epsilon$, which sends the circle to a slightly larger circle which does not touch line $A B$. If this homothety causes the circle to leave the polygon for small enough $\epsilon$, it must be because the circle was initially tangent to another line $\ell$, for which it would be an incircle of the triangle made by $\ell$ and lines $A D, B E$, bringing us back to the first case.
Thus we can reduce to a case where we have a triangle with each height at least 1 , and we want to show the inradius is at least $1 / 3$. Let $K$ be the area of the triangle, so the heights $\frac{2 K}{a}, \frac{2 K}{b}, \frac{2 K}{c}$ are all at least 1. Then the inradius $r$ satisfies
$$
r=\frac{K}{s}=\frac{2 K}{a+b+c} \geq \frac{2 K}{2 K+2 K+2 K}=\frac{1}{3}
$$
as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A convex polygon on the plane is called wide if the projection of the polygon onto any line in the same plane is a segment with length at least 1 . Prove that a circle of radius $\frac{1}{3}$ can be placed completely inside any wide polygon.
|
## Solution 1.
Lemma. for any polygon including its boundary, there exists a largest circle contained inside it.
Proof. Its easy to see that for any circle inside the polygon, it can be increased in size until it is tangent to at least three sides of the polygon. Then for any three sides of the polygon, there is only one circle tangent to all three, so there are only finitely many possibilities. Therefore there exists a largest one.
Alternatively, one can show that the space of valid $(x, y, r)$ such that the circle with center $(x, y)$ and radius $r$ is compact, e.g. by showing the complement is open and that the complement is open. Then the map $(x, y, r) \rightarrow r$ is continuous and therefore has a maximum.
Now, take the largest circle. It clearly must be tangent to three sides. If the circle lies inside the triangle made by the three lines, we can expand the polygon to that triangle and solve it for the triangle instead. Otherwise, we have the following diagram:

Here the circle is an excircle of the triangle $A B C$ made by the lines $A B, A D$, and $B E$. (Note that $A D$ and $A B$ dont have to be consecutive sides of the polygon, but the ones in between dont really matter.)
Then since the circle is an excircle, we can consider a homothety at $C$ with power $1+\epsilon$, which sends the circle to a slightly larger circle which does not touch line $A B$. If this homothety causes the circle to leave the polygon for small enough $\epsilon$, it must be because the circle was initially tangent to another line $\ell$, for which it would be an incircle of the triangle made by $\ell$ and lines $A D, B E$, bringing us back to the first case.
Thus we can reduce to a case where we have a triangle with each height at least 1 , and we want to show the inradius is at least $1 / 3$. Let $K$ be the area of the triangle, so the heights $\frac{2 K}{a}, \frac{2 K}{b}, \frac{2 K}{c}$ are all at least 1. Then the inradius $r$ satisfies
$$
r=\frac{K}{s}=\frac{2 K}{a+b+c} \geq \frac{2 K}{2 K+2 K+2 K}=\frac{1}{3}
$$
as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-222-2019-feb-team-solutions.jsonl",
"problem_match": "\n7. $[\\mathbf{5 0}]$",
"solution_match": "\nProposed by: Shengtong Zhang\n\n"
}
|
b5865a5f-8242-58c5-b3d8-d0105860cfbb
| 610,039
|
A convex polygon on the plane is called wide if the projection of the polygon onto any line in the same plane is a segment with length at least 1 . Prove that a circle of radius $\frac{1}{3}$ can be placed completely inside any wide polygon.
|
Consider the center of mass $G$. We will use the notion of support lines for convex shapes. (Support lines are the lines that touches the shape but does not cut through it.) If a circle centered at $G$ with radius $1 / 3$ cannot be contained inside the polygon, then there exist a point $P$ on the boundary that $G P<1 / 3$. Let $\ell_{1}$ be the support line passing through $p, \ell_{2}$ be the line parallel to $\ell_{1}$ and passing through $G$, and $\ell_{3}$ be the other support line that is parallel to $\ell_{1}$, touching the polygon at $P^{\prime}$. Suppose $\ell_{2}$ intersects the polygon at $A$ and $B$. Extend $P^{\prime} A$ and $P^{\prime} B$, intersecting $\ell_{1}$ at $A^{\prime}$ and $B^{\prime}$. Then, if we consider the two parts of the polygon that $\ell_{2}$ divides the polygon into, we have:
- the part of the polygon that contains $P^{\prime}$ contains the triangle $P^{\prime} A B$;
- the part of the polygon that contains $P$ is contained in the quadrilateral $A A^{\prime} B^{\prime} B$.
Then we conclude that the center of mass $G^{\prime}$ of the triangle $P^{\prime} A^{\prime} B^{\prime}$ lies between $\ell_{2}$ and $\ell_{1}$, which by assumption is less than $\frac{1}{3}$ away from $\ell_{1}$. However, because the height from $P^{\prime}$ to $\ell_{1}$ is at least 1 , the distance from $G^{\prime}$ to $\ell_{1}$ is at least $\frac{1}{3}$, so we have a contradiction. Therefore no such $P$ exists and the circle can be placed inside the polygon.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A convex polygon on the plane is called wide if the projection of the polygon onto any line in the same plane is a segment with length at least 1 . Prove that a circle of radius $\frac{1}{3}$ can be placed completely inside any wide polygon.
|
Consider the center of mass $G$. We will use the notion of support lines for convex shapes. (Support lines are the lines that touches the shape but does not cut through it.) If a circle centered at $G$ with radius $1 / 3$ cannot be contained inside the polygon, then there exist a point $P$ on the boundary that $G P<1 / 3$. Let $\ell_{1}$ be the support line passing through $p, \ell_{2}$ be the line parallel to $\ell_{1}$ and passing through $G$, and $\ell_{3}$ be the other support line that is parallel to $\ell_{1}$, touching the polygon at $P^{\prime}$. Suppose $\ell_{2}$ intersects the polygon at $A$ and $B$. Extend $P^{\prime} A$ and $P^{\prime} B$, intersecting $\ell_{1}$ at $A^{\prime}$ and $B^{\prime}$. Then, if we consider the two parts of the polygon that $\ell_{2}$ divides the polygon into, we have:
- the part of the polygon that contains $P^{\prime}$ contains the triangle $P^{\prime} A B$;
- the part of the polygon that contains $P$ is contained in the quadrilateral $A A^{\prime} B^{\prime} B$.
Then we conclude that the center of mass $G^{\prime}$ of the triangle $P^{\prime} A^{\prime} B^{\prime}$ lies between $\ell_{2}$ and $\ell_{1}$, which by assumption is less than $\frac{1}{3}$ away from $\ell_{1}$. However, because the height from $P^{\prime}$ to $\ell_{1}$ is at least 1 , the distance from $G^{\prime}$ to $\ell_{1}$ is at least $\frac{1}{3}$, so we have a contradiction. Therefore no such $P$ exists and the circle can be placed inside the polygon.
|
{
"resource_path": "HarvardMIT/segmented/en-222-2019-feb-team-solutions.jsonl",
"problem_match": "\n7. $[\\mathbf{5 0}]$",
"solution_match": "\nSolution 2. "
}
|
b5865a5f-8242-58c5-b3d8-d0105860cfbb
| 610,039
|
Prove that for all positive integers $n$, all complex roots $r$ of the polynomial
$$
P(x)=(2 n) x^{2 n}+(2 n-1) x^{2 n-1}+\cdots+(n+1) x^{n+1}+n x^{n}+(n+1) x^{n-1}+\cdots+(2 n-1) x+2 n
$$
lie on the unit circle (i.e. $|r|=1$ ).
|
Note that neither 0 nor 1 are roots of the polynomial. Consider the function
$Q(x)=P(x) / x^{n}=(2 n) x^{n}+(2 n) x^{-n}+(2 n-1) x^{n-1}+(2 n-1) x^{-n+1}+\cdots+(n+1) x^{1}+(n+1) x^{-1}+n$.
All $2 n$ of the complex roots of $P(x)$ will be roots of $Q(x)$.
If $|x|=1$, then $x=e^{i \theta}$, and
$$
\begin{aligned}
Q(x) & =(2 n)\left(x^{n}+x^{-n}\right)+(2 n-1)\left(x^{n-1}+x^{-n+1}\right)+\cdots+(n+1)\left(x+x^{-1}\right)+n \\
& =(2 n)\left(e^{i n \theta}+e^{-i n \theta}\right)+(2 n-1)\left(e^{i(n-1) \theta}+e^{-i(n-1) \theta}\right)+\cdots+(n+1)\left(e^{i \theta}+e^{-i \theta}\right)+n \\
& =(2 n)(2 \cos (n \theta))+(2 n-1)(2 \cos ((n-1) \theta))+\cdots+(n+1)(\cos (\theta))+n
\end{aligned}
$$
which is real. Thus on the unit circle, we have $Q(x)$ is real, and we want to show it has $2 n$ roots there. Rewrite
$$
\begin{aligned}
P(x) & =(2 n) x^{2 n}+(2 n-1) x^{2 n-1}+\cdots+(n+1) x^{n+1}+n x^{n}+(n+1) x^{n-1}+\cdots+2 n \\
& =(2 n)\left(x^{2 n}+x^{2 n-1}+\cdots+1\right) \\
& \quad-\left(x^{2 n-1}+2 x^{2 n-2}+\cdots+(n-1) x^{n}+n x^{n-1}+(n-1) x^{n-2}+\cdots+2 x^{2}+x\right) \\
& =2 n \frac{x^{2 n+1}-1}{x-1}-x\left(x^{2 n-2}+2 x^{2 n-3}+\cdots+(n-1) x^{n}+n x^{n-1}+(n-1) x^{n-2}+\cdots+2 x+1\right) \\
& =2 n \frac{x^{2 n+1}-1}{x-1}-x\left(x^{n-1}+x^{n-2}+\cdots+x+1\right)^{2} \\
& =2 n \frac{x^{2 n+1}-1}{x-1}-x\left(\frac{x^{n}-1}{x-1}\right)^{2}
\end{aligned}
$$
and thus
$$
Q(x)=\frac{2 n}{x^{n}} \frac{x^{2 n+1}-1}{x-1}-\frac{x}{x^{n}}\left(\frac{x^{n}-1}{x-1}\right)^{2}
$$
Consider the roots of unity $r_{j}=e^{i \frac{2 \pi}{2 n} j}$, for $j=0$ to $2 n-1$. There are $2 n$ such roots of unity: they all have $r_{j}^{2 n}=1$, and they alternate between those which satisfy $r_{j}^{n}=1$ or $r_{j}^{n}=-1$. At those $x=r_{j}$, if
$r_{j}^{n}=1$ but $x \neq 1$, then
$$
\begin{aligned}
Q(x) & =\frac{2 n}{x^{n}} \frac{x^{2 n+1}-1}{x-1}-\frac{x}{x^{n}}\left(\frac{x^{n}-1}{x-1}\right)^{2} \\
& =2 n \frac{x^{1}-1}{x-1}-x\left(\frac{1-1}{x-1}\right)^{2}=2 n>0
\end{aligned}
$$
At $x=1$, we can easily see $Q(1)>0$.
If $r_{j}^{n}=-1$, then
$$
\begin{aligned}
Q(x) & =\frac{2 n}{x^{n}} \frac{x^{2 n+1}-1}{x-1}-\frac{x}{x^{n}}\left(\frac{x^{n}-1}{x-1}\right)^{2} \\
& =-2 n \frac{x^{1}-1}{x-1}+x\left(\frac{-1-1}{x-1}\right)^{2} \\
& =-2 n+\frac{4 x}{(x-1)^{2}} \\
& =-2 n+\frac{4}{x-2+1 / x} \\
& =-2 n+\frac{4}{2 \cos \left(\frac{2 \pi}{2 n} j\right)-2}<-2 n-4<0
\end{aligned}
$$
since the denominator of this second term is strictly negative $(j \neq 0)$.
Thus at each of the $2 n$-roots of unity, $Q(x)$ alternates in sign, and because $Q(x)$ is real and continuous on the unit circle, it has at least one root between every pair of consecutive roots of unity. Since there are $2 n$ of these pairs, and we know that $Q(x)$ has exactly $2 n$ roots (by the Fundamental Theorem of Algebra), we have found all of $Q$ 's roots, and therefore those of $P$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that for all positive integers $n$, all complex roots $r$ of the polynomial
$$
P(x)=(2 n) x^{2 n}+(2 n-1) x^{2 n-1}+\cdots+(n+1) x^{n+1}+n x^{n}+(n+1) x^{n-1}+\cdots+(2 n-1) x+2 n
$$
lie on the unit circle (i.e. $|r|=1$ ).
|
Note that neither 0 nor 1 are roots of the polynomial. Consider the function
$Q(x)=P(x) / x^{n}=(2 n) x^{n}+(2 n) x^{-n}+(2 n-1) x^{n-1}+(2 n-1) x^{-n+1}+\cdots+(n+1) x^{1}+(n+1) x^{-1}+n$.
All $2 n$ of the complex roots of $P(x)$ will be roots of $Q(x)$.
If $|x|=1$, then $x=e^{i \theta}$, and
$$
\begin{aligned}
Q(x) & =(2 n)\left(x^{n}+x^{-n}\right)+(2 n-1)\left(x^{n-1}+x^{-n+1}\right)+\cdots+(n+1)\left(x+x^{-1}\right)+n \\
& =(2 n)\left(e^{i n \theta}+e^{-i n \theta}\right)+(2 n-1)\left(e^{i(n-1) \theta}+e^{-i(n-1) \theta}\right)+\cdots+(n+1)\left(e^{i \theta}+e^{-i \theta}\right)+n \\
& =(2 n)(2 \cos (n \theta))+(2 n-1)(2 \cos ((n-1) \theta))+\cdots+(n+1)(\cos (\theta))+n
\end{aligned}
$$
which is real. Thus on the unit circle, we have $Q(x)$ is real, and we want to show it has $2 n$ roots there. Rewrite
$$
\begin{aligned}
P(x) & =(2 n) x^{2 n}+(2 n-1) x^{2 n-1}+\cdots+(n+1) x^{n+1}+n x^{n}+(n+1) x^{n-1}+\cdots+2 n \\
& =(2 n)\left(x^{2 n}+x^{2 n-1}+\cdots+1\right) \\
& \quad-\left(x^{2 n-1}+2 x^{2 n-2}+\cdots+(n-1) x^{n}+n x^{n-1}+(n-1) x^{n-2}+\cdots+2 x^{2}+x\right) \\
& =2 n \frac{x^{2 n+1}-1}{x-1}-x\left(x^{2 n-2}+2 x^{2 n-3}+\cdots+(n-1) x^{n}+n x^{n-1}+(n-1) x^{n-2}+\cdots+2 x+1\right) \\
& =2 n \frac{x^{2 n+1}-1}{x-1}-x\left(x^{n-1}+x^{n-2}+\cdots+x+1\right)^{2} \\
& =2 n \frac{x^{2 n+1}-1}{x-1}-x\left(\frac{x^{n}-1}{x-1}\right)^{2}
\end{aligned}
$$
and thus
$$
Q(x)=\frac{2 n}{x^{n}} \frac{x^{2 n+1}-1}{x-1}-\frac{x}{x^{n}}\left(\frac{x^{n}-1}{x-1}\right)^{2}
$$
Consider the roots of unity $r_{j}=e^{i \frac{2 \pi}{2 n} j}$, for $j=0$ to $2 n-1$. There are $2 n$ such roots of unity: they all have $r_{j}^{2 n}=1$, and they alternate between those which satisfy $r_{j}^{n}=1$ or $r_{j}^{n}=-1$. At those $x=r_{j}$, if
$r_{j}^{n}=1$ but $x \neq 1$, then
$$
\begin{aligned}
Q(x) & =\frac{2 n}{x^{n}} \frac{x^{2 n+1}-1}{x-1}-\frac{x}{x^{n}}\left(\frac{x^{n}-1}{x-1}\right)^{2} \\
& =2 n \frac{x^{1}-1}{x-1}-x\left(\frac{1-1}{x-1}\right)^{2}=2 n>0
\end{aligned}
$$
At $x=1$, we can easily see $Q(1)>0$.
If $r_{j}^{n}=-1$, then
$$
\begin{aligned}
Q(x) & =\frac{2 n}{x^{n}} \frac{x^{2 n+1}-1}{x-1}-\frac{x}{x^{n}}\left(\frac{x^{n}-1}{x-1}\right)^{2} \\
& =-2 n \frac{x^{1}-1}{x-1}+x\left(\frac{-1-1}{x-1}\right)^{2} \\
& =-2 n+\frac{4 x}{(x-1)^{2}} \\
& =-2 n+\frac{4}{x-2+1 / x} \\
& =-2 n+\frac{4}{2 \cos \left(\frac{2 \pi}{2 n} j\right)-2}<-2 n-4<0
\end{aligned}
$$
since the denominator of this second term is strictly negative $(j \neq 0)$.
Thus at each of the $2 n$-roots of unity, $Q(x)$ alternates in sign, and because $Q(x)$ is real and continuous on the unit circle, it has at least one root between every pair of consecutive roots of unity. Since there are $2 n$ of these pairs, and we know that $Q(x)$ has exactly $2 n$ roots (by the Fundamental Theorem of Algebra), we have found all of $Q$ 's roots, and therefore those of $P$.
|
{
"resource_path": "HarvardMIT/segmented/en-222-2019-feb-team-solutions.jsonl",
"problem_match": "\n10. [60]",
"solution_match": "\nProposed by: Faraz Masroor\n"
}
|
d994e176-fdd0-5870-b618-84510db07944
| 610,042
|
Let $A B C$ be an acute scalene triangle with incenter $I$. Show that the circumcircle of $B I C$ intersects the Euler line of $A B C$ in two distinct points.
(Recall that the Euler line of a scalene triangle is the line that passes through its circumcenter, centroid, orthocenter, and the nine-point center.)
|
Let $O$ and $H$ be the circumcenter and orthocenter of $A B C$. Recall that
$$
\begin{aligned}
\angle B O C & =2 \angle A, \\
\angle B H C & =180^{\circ}-\angle A, \\
\angle B I C & =90^{\circ}+\frac{1}{2} \angle A .
\end{aligned}
$$
As $A B C$ is acute, $A, I, O, H$ all lie on the same side of $B C$.
- If $\angle A>60^{\circ}$, then $\angle B O C>\angle B I C$, so $O$ lies inside ( $B I C$ ).
- If $\angle A<60^{\circ}$, then $\angle B H C>\angle B I C$, so $H$ lies inside ( $B I C$ ).
- If $\angle A=60^{\circ}$, then $O$ and $H$ are on (BIC).
In all cases, two intersections are guaranteed.
Note: For an obtuse triangle, the statement is not necessarily true.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute scalene triangle with incenter $I$. Show that the circumcircle of $B I C$ intersects the Euler line of $A B C$ in two distinct points.
(Recall that the Euler line of a scalene triangle is the line that passes through its circumcenter, centroid, orthocenter, and the nine-point center.)
|
Let $O$ and $H$ be the circumcenter and orthocenter of $A B C$. Recall that
$$
\begin{aligned}
\angle B O C & =2 \angle A, \\
\angle B H C & =180^{\circ}-\angle A, \\
\angle B I C & =90^{\circ}+\frac{1}{2} \angle A .
\end{aligned}
$$
As $A B C$ is acute, $A, I, O, H$ all lie on the same side of $B C$.
- If $\angle A>60^{\circ}$, then $\angle B O C>\angle B I C$, so $O$ lies inside ( $B I C$ ).
- If $\angle A<60^{\circ}$, then $\angle B H C>\angle B I C$, so $H$ lies inside ( $B I C$ ).
- If $\angle A=60^{\circ}$, then $O$ and $H$ are on (BIC).
In all cases, two intersections are guaranteed.
Note: For an obtuse triangle, the statement is not necessarily true.
|
{
"resource_path": "HarvardMIT/segmented/en-224-tournaments-2019-hmic-solutions.jsonl",
"problem_match": "\n1. [5]",
"solution_match": "\nProposed by: Andrew Gu\n"
}
|
6f1598c1-887c-5ed8-ab38-5e7dbfadebcd
| 610,043
|
A cactus is a finite simple connected graph where no two cycles share an edge. Show that in a nonempty cactus, there must exist a vertex which is part of at most one cycle.
|
Let $C$ be the original cactus. For every cycle in $C$, arbitrarily remove one of its edges, yielding a new graph $T$. Observe that since the cycles are edge-disjoint, we removed exactly one edge from every cycle, meaning the graph stays connected. However, there are no longer any cycles, so $T$ is a tree.
Now consider any leaf $v$ of $T$ (note that any nonempty tree must have a leaf). If $v$ is the only vertex in the graph we're trivially done, since then $v$ was the only vertex in $C$. Otherwise $v$ has degree 1 . If $v$ was originally a leaf of $C$, we're done. If not, observe that in the process of turning $C$ into $T$, a vertex's degree cannot decrease by more than half, because for every cycle that a vertex is part of in $C$, it gains a degree of 2 , but can only lose 1 degree from an edge of that cycle being removed. Therefore, the original degree of $v$ in $C$ was at most 2 , meaning it could have been part of at most 1 cycle, as desired.
Remark. The problem originally did not state that the graph is finite. We apologize for the omission.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A cactus is a finite simple connected graph where no two cycles share an edge. Show that in a nonempty cactus, there must exist a vertex which is part of at most one cycle.
|
Let $C$ be the original cactus. For every cycle in $C$, arbitrarily remove one of its edges, yielding a new graph $T$. Observe that since the cycles are edge-disjoint, we removed exactly one edge from every cycle, meaning the graph stays connected. However, there are no longer any cycles, so $T$ is a tree.
Now consider any leaf $v$ of $T$ (note that any nonempty tree must have a leaf). If $v$ is the only vertex in the graph we're trivially done, since then $v$ was the only vertex in $C$. Otherwise $v$ has degree 1 . If $v$ was originally a leaf of $C$, we're done. If not, observe that in the process of turning $C$ into $T$, a vertex's degree cannot decrease by more than half, because for every cycle that a vertex is part of in $C$, it gains a degree of 2 , but can only lose 1 degree from an edge of that cycle being removed. Therefore, the original degree of $v$ in $C$ was at most 2 , meaning it could have been part of at most 1 cycle, as desired.
Remark. The problem originally did not state that the graph is finite. We apologize for the omission.
|
{
"resource_path": "HarvardMIT/segmented/en-224-tournaments-2019-hmic-solutions.jsonl",
"problem_match": "\n4. [10]",
"solution_match": "\n## Proposed by: Kevin Yang\n\n"
}
|
30fdd823-f394-57bb-afdc-958d30039ec2
| 610,046
|
Let $A B C$ be a triangle inscribed in a circle $\omega$ and $\ell$ be the tangent to $\omega$ at $A$. The line through $B$ parallel to $A C$ meets $\ell$ at $P$, and the line through $C$ parallel to $A B$ meets $\ell$ at $Q$. The circumcircles of $A B P$ and $A C Q$ meet at $S \neq A$. Show that $A S$ bisects $B C$.
|
Solution 1: In directed angles, we have
$$
\measuredangle C B P=\measuredangle B C A=\measuredangle B A P
$$
so $B C$ is tangent to the circumcircle of $A B P$. Likewise, $B C$ is tangent to the circumcircle of $A C Q$. Let $M$ be the midpoint of $B C$. Then $M$ has equal power $M B^{2}=M C^{2}$ with respect to the circumcircles of $A B P$ and $A C Q$, so the radical axis $A S$ passes through $M$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle inscribed in a circle $\omega$ and $\ell$ be the tangent to $\omega$ at $A$. The line through $B$ parallel to $A C$ meets $\ell$ at $P$, and the line through $C$ parallel to $A B$ meets $\ell$ at $Q$. The circumcircles of $A B P$ and $A C Q$ meet at $S \neq A$. Show that $A S$ bisects $B C$.
|
Solution 1: In directed angles, we have
$$
\measuredangle C B P=\measuredangle B C A=\measuredangle B A P
$$
so $B C$ is tangent to the circumcircle of $A B P$. Likewise, $B C$ is tangent to the circumcircle of $A C Q$. Let $M$ be the midpoint of $B C$. Then $M$ has equal power $M B^{2}=M C^{2}$ with respect to the circumcircles of $A B P$ and $A C Q$, so the radical axis $A S$ passes through $M$.

|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-team-solutions.jsonl",
"problem_match": "\n3. [25]",
"solution_match": "\nProposed by: Andrew Gu\n"
}
|
23087aa0-db11-51d2-ac6c-6e042f0d23d2
| 610,180
|
Let $A B C$ be a triangle inscribed in a circle $\omega$ and $\ell$ be the tangent to $\omega$ at $A$. The line through $B$ parallel to $A C$ meets $\ell$ at $P$, and the line through $C$ parallel to $A B$ meets $\ell$ at $Q$. The circumcircles of $A B P$ and $A C Q$ meet at $S \neq A$. Show that $A S$ bisects $B C$.
|
Since
$$
\measuredangle C B P=\measuredangle B C A=\measuredangle B A P=\measuredangle C Q P
$$
quadrilateral $B C Q P$ is cyclic. Then $A S, B P$, and $C Q$ concur at a point $A^{\prime}$. Since $A^{\prime} B \| A C$ and $A^{\prime} C \| A B$, quadrilateral $A B A^{\prime} C$ is a parallelogram so line $A S A^{\prime}$ bisects $B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle inscribed in a circle $\omega$ and $\ell$ be the tangent to $\omega$ at $A$. The line through $B$ parallel to $A C$ meets $\ell$ at $P$, and the line through $C$ parallel to $A B$ meets $\ell$ at $Q$. The circumcircles of $A B P$ and $A C Q$ meet at $S \neq A$. Show that $A S$ bisects $B C$.
|
Since
$$
\measuredangle C B P=\measuredangle B C A=\measuredangle B A P=\measuredangle C Q P
$$
quadrilateral $B C Q P$ is cyclic. Then $A S, B P$, and $C Q$ concur at a point $A^{\prime}$. Since $A^{\prime} B \| A C$ and $A^{\prime} C \| A B$, quadrilateral $A B A^{\prime} C$ is a parallelogram so line $A S A^{\prime}$ bisects $B C$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-team-solutions.jsonl",
"problem_match": "\n3. [25]",
"solution_match": "\nSolution 2: "
}
|
23087aa0-db11-51d2-ac6c-6e042f0d23d2
| 610,180
|
Alan draws a convex 2020-gon $\mathcal{A}=A_{1} A_{2} \cdots A_{2020}$ with vertices in clockwise order and chooses 2020 angles $\theta_{1}, \theta_{2}, \ldots, \theta_{2020} \in(0, \pi)$ in radians with sum $1010 \pi$. He then constructs isosceles triangles $\triangle A_{i} B_{i} A_{i+1}$ on the exterior of $\mathcal{A}$ with $B_{i} A_{i}=B_{i} A_{i+1}$ and $\angle A_{i} B_{i} A_{i+1}=\theta_{i}$. (Here, $A_{2021}=A_{1}$.) Finally, he erases $\mathcal{A}$ and the point $B_{1}$. He then tells Jason the angles $\theta_{1}, \theta_{2}, \ldots, \theta_{2020}$ he chose. Show that Jason can determine where $B_{1}$ was from the remaining 2019 points, i.e. show that $B_{1}$ is uniquely determined by the information Jason has.
|
Solution 1: For each $i$, let $\tau_{i}$ be the transformation of the plane which is rotation by $\theta_{i}$ counterclockwise about $B_{i}$. Recall that a composition of rotations is a rotation or translation, and that the angles of rotation add. Consider the composition $\tau_{2020} \circ \tau_{2019} \circ \cdots \circ \tau_{1}$, with total rotation angle $1010 \pi$. This must be a translation because $1010 \pi=505(2 \pi)$. Also note that the composition sends $A_{1}$ to itself because $\tau_{i}\left(A_{i}\right)=A_{i+1}$. Therefore it is the identity. Now Jason can identify the map $\tau_{1}$ as $\tau_{2}^{-1} \circ \tau_{3}^{-1} \circ \cdots \circ \tau_{2020}^{-1}$, and $B_{1}$ is the unique fixed point of this map.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Alan draws a convex 2020-gon $\mathcal{A}=A_{1} A_{2} \cdots A_{2020}$ with vertices in clockwise order and chooses 2020 angles $\theta_{1}, \theta_{2}, \ldots, \theta_{2020} \in(0, \pi)$ in radians with sum $1010 \pi$. He then constructs isosceles triangles $\triangle A_{i} B_{i} A_{i+1}$ on the exterior of $\mathcal{A}$ with $B_{i} A_{i}=B_{i} A_{i+1}$ and $\angle A_{i} B_{i} A_{i+1}=\theta_{i}$. (Here, $A_{2021}=A_{1}$.) Finally, he erases $\mathcal{A}$ and the point $B_{1}$. He then tells Jason the angles $\theta_{1}, \theta_{2}, \ldots, \theta_{2020}$ he chose. Show that Jason can determine where $B_{1}$ was from the remaining 2019 points, i.e. show that $B_{1}$ is uniquely determined by the information Jason has.
|
Solution 1: For each $i$, let $\tau_{i}$ be the transformation of the plane which is rotation by $\theta_{i}$ counterclockwise about $B_{i}$. Recall that a composition of rotations is a rotation or translation, and that the angles of rotation add. Consider the composition $\tau_{2020} \circ \tau_{2019} \circ \cdots \circ \tau_{1}$, with total rotation angle $1010 \pi$. This must be a translation because $1010 \pi=505(2 \pi)$. Also note that the composition sends $A_{1}$ to itself because $\tau_{i}\left(A_{i}\right)=A_{i+1}$. Therefore it is the identity. Now Jason can identify the map $\tau_{1}$ as $\tau_{2}^{-1} \circ \tau_{3}^{-1} \circ \cdots \circ \tau_{2020}^{-1}$, and $B_{1}$ is the unique fixed point of this map.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-team-solutions.jsonl",
"problem_match": "\n4. [35]",
"solution_match": "\nProposed by: Andrew Gu, Colin Tang\n"
}
|
db019661-c2df-58b5-92f4-ce8e39f95bb5
| 610,181
|
Alan draws a convex 2020-gon $\mathcal{A}=A_{1} A_{2} \cdots A_{2020}$ with vertices in clockwise order and chooses 2020 angles $\theta_{1}, \theta_{2}, \ldots, \theta_{2020} \in(0, \pi)$ in radians with sum $1010 \pi$. He then constructs isosceles triangles $\triangle A_{i} B_{i} A_{i+1}$ on the exterior of $\mathcal{A}$ with $B_{i} A_{i}=B_{i} A_{i+1}$ and $\angle A_{i} B_{i} A_{i+1}=\theta_{i}$. (Here, $A_{2021}=A_{1}$.) Finally, he erases $\mathcal{A}$ and the point $B_{1}$. He then tells Jason the angles $\theta_{1}, \theta_{2}, \ldots, \theta_{2020}$ he chose. Show that Jason can determine where $B_{1}$ was from the remaining 2019 points, i.e. show that $B_{1}$ is uniquely determined by the information Jason has.
|
Fix an arbitrary coordinate system. For $1 \leq k \leq 2020$, let $a_{k}, b_{k}$ be the complex numbers corresponding to $A_{k}, B_{k}$. The given condition translates to
$$
e^{i \theta_{k}}\left(b_{k}-a_{k}\right)=\left(b_{k}-a_{k+1}\right)
$$
In other words
$$
\left(e^{i \theta_{k}}-1\right) b_{k}=e^{i \theta_{k}} a_{k}-a_{k+1}
$$
or
$$
\left(e^{-i\left(\theta_{k-1}+\cdots+\theta_{1}\right)}-e^{-i\left(\theta_{k}+\cdots+\theta_{1}\right)}\right) b_{k}=e^{-i\left(\theta_{k-1}+\cdots+\theta_{1}\right)} a_{k}-e^{-i\left(\theta_{k}+\cdots+\theta_{1}\right)} a_{k+1} .
$$
Summing over all $k$, and using the fact that
$$
e^{-i\left(\theta_{1}+\cdots+\theta_{2020}\right)}=1,
$$
we see that the right hand side cancels to 0 , thus
$$
\sum_{k=1}^{2020}\left(e^{-i\left(\theta_{k-1}+\cdots+\theta_{1}\right)}-e^{-i\left(\theta_{k}+\cdots+\theta_{1}\right)}\right) b_{k}=0 .
$$
Jason knows $b_{2}, \ldots, b_{2020}$ and all the $\theta_{i}$, so the equation above is a linear equation in $b_{1}$. We finish by noting that the coefficient of $b_{1}$ is $1-e^{-i \theta_{1}}$ which is non-zero, as $\theta_{1} \in(0, \pi)$. Thus Jason can solve for $b_{1}$ uniquely.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Alan draws a convex 2020-gon $\mathcal{A}=A_{1} A_{2} \cdots A_{2020}$ with vertices in clockwise order and chooses 2020 angles $\theta_{1}, \theta_{2}, \ldots, \theta_{2020} \in(0, \pi)$ in radians with sum $1010 \pi$. He then constructs isosceles triangles $\triangle A_{i} B_{i} A_{i+1}$ on the exterior of $\mathcal{A}$ with $B_{i} A_{i}=B_{i} A_{i+1}$ and $\angle A_{i} B_{i} A_{i+1}=\theta_{i}$. (Here, $A_{2021}=A_{1}$.) Finally, he erases $\mathcal{A}$ and the point $B_{1}$. He then tells Jason the angles $\theta_{1}, \theta_{2}, \ldots, \theta_{2020}$ he chose. Show that Jason can determine where $B_{1}$ was from the remaining 2019 points, i.e. show that $B_{1}$ is uniquely determined by the information Jason has.
|
Fix an arbitrary coordinate system. For $1 \leq k \leq 2020$, let $a_{k}, b_{k}$ be the complex numbers corresponding to $A_{k}, B_{k}$. The given condition translates to
$$
e^{i \theta_{k}}\left(b_{k}-a_{k}\right)=\left(b_{k}-a_{k+1}\right)
$$
In other words
$$
\left(e^{i \theta_{k}}-1\right) b_{k}=e^{i \theta_{k}} a_{k}-a_{k+1}
$$
or
$$
\left(e^{-i\left(\theta_{k-1}+\cdots+\theta_{1}\right)}-e^{-i\left(\theta_{k}+\cdots+\theta_{1}\right)}\right) b_{k}=e^{-i\left(\theta_{k-1}+\cdots+\theta_{1}\right)} a_{k}-e^{-i\left(\theta_{k}+\cdots+\theta_{1}\right)} a_{k+1} .
$$
Summing over all $k$, and using the fact that
$$
e^{-i\left(\theta_{1}+\cdots+\theta_{2020}\right)}=1,
$$
we see that the right hand side cancels to 0 , thus
$$
\sum_{k=1}^{2020}\left(e^{-i\left(\theta_{k-1}+\cdots+\theta_{1}\right)}-e^{-i\left(\theta_{k}+\cdots+\theta_{1}\right)}\right) b_{k}=0 .
$$
Jason knows $b_{2}, \ldots, b_{2020}$ and all the $\theta_{i}$, so the equation above is a linear equation in $b_{1}$. We finish by noting that the coefficient of $b_{1}$ is $1-e^{-i \theta_{1}}$ which is non-zero, as $\theta_{1} \in(0, \pi)$. Thus Jason can solve for $b_{1}$ uniquely.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-team-solutions.jsonl",
"problem_match": "\n4. [35]",
"solution_match": "\nSolution 2: "
}
|
db019661-c2df-58b5-92f4-ce8e39f95bb5
| 610,181
|
Alan draws a convex 2020-gon $\mathcal{A}=A_{1} A_{2} \cdots A_{2020}$ with vertices in clockwise order and chooses 2020 angles $\theta_{1}, \theta_{2}, \ldots, \theta_{2020} \in(0, \pi)$ in radians with sum $1010 \pi$. He then constructs isosceles triangles $\triangle A_{i} B_{i} A_{i+1}$ on the exterior of $\mathcal{A}$ with $B_{i} A_{i}=B_{i} A_{i+1}$ and $\angle A_{i} B_{i} A_{i+1}=\theta_{i}$. (Here, $A_{2021}=A_{1}$.) Finally, he erases $\mathcal{A}$ and the point $B_{1}$. He then tells Jason the angles $\theta_{1}, \theta_{2}, \ldots, \theta_{2020}$ he chose. Show that Jason can determine where $B_{1}$ was from the remaining 2019 points, i.e. show that $B_{1}$ is uniquely determined by the information Jason has.
|
Let $A_{1} A_{2} \cdots A_{2020}$ and $\tilde{A}_{1} \tilde{A}_{2} \cdots \tilde{A}_{2020}$ be two 2020 -gons that satisfy the conditions in the problem statement, and let $B_{k}, \tilde{B}_{k}$ be the points Alan would construct with respect to these two polygons. It suffices to show that if $B_{k}=\tilde{B}_{k}$ for $k=2,3, \ldots, 2020$, then $B_{1}=\tilde{B}_{1}$.
For $2 \leq k \leq 2020$, we note that
$$
A_{k} B_{k}=A_{k+1} B_{k}, \quad \tilde{A}_{k} B_{k}=\tilde{A}_{k+1} B_{k}
$$
Furthermore, we have the equality of directed angles $\angle A_{k} B_{k} A_{k+1}=\angle \tilde{A}_{k} B_{k} \tilde{A}_{k+1}=\theta_{k}$, therefore $\angle A_{k} B_{k} \tilde{A}_{k}=\angle A_{k+1} B_{k} \tilde{A}_{k+1}$. This implies the congruence $\triangle A_{k} B_{k} \tilde{A}_{k} \cong \triangle A_{k+1} B_{k} \tilde{A}_{k+1}$.
The congruence shows that $A_{k} \tilde{A}_{k}=A_{k+1} \tilde{A}_{k+1}$; furthermore, the angle from the directed segment $\overrightarrow{A_{k} \tilde{A}_{k}}$ to $\overrightarrow{A_{k+1} \tilde{A}_{k+1}}$ is $\theta_{k}$ counterclockwise. This holds for $k=2,3, \ldots, 2020$; we conclude that $A_{1} \tilde{A}_{1}=A_{2} \tilde{A}_{2}$, and the angle from the directed segments $\overrightarrow{A_{1}} \tilde{A}_{1}$ to $\overrightarrow{A_{2}} \tilde{A}_{2}$ is
$$
-\sum_{k=2}^{2020} \theta_{k}=\theta_{1}-1010 \pi=\theta_{1}
$$
counterclockwise.
Finally we observe that $A_{1} B_{1}=A_{2} B_{1}$, and the angle from the directed segment $\overrightarrow{A_{1} B_{1}}$ to $\overrightarrow{A_{2} B_{1}}$ is $\theta_{1}$ counterclockwise. This implies $\angle B_{1} A_{1} \tilde{A}_{1}=\angle B_{1} A_{2} \tilde{A}_{2}$, so $\triangle A_{1} B_{1} \tilde{A}_{1} \cong \triangle A_{2} B_{1} \tilde{A}_{2}$. Thus $\tilde{A}_{1} B_{1}=$ $\tilde{A}_{2} B_{1}$, and the angle from $\overrightarrow{\tilde{A}_{1} B_{1}}$ to $\overrightarrow{\tilde{A}_{2} B_{1}}$ is $\theta_{1}$ counterclockwise. We conclude that $B_{1}=\tilde{B}_{1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Alan draws a convex 2020-gon $\mathcal{A}=A_{1} A_{2} \cdots A_{2020}$ with vertices in clockwise order and chooses 2020 angles $\theta_{1}, \theta_{2}, \ldots, \theta_{2020} \in(0, \pi)$ in radians with sum $1010 \pi$. He then constructs isosceles triangles $\triangle A_{i} B_{i} A_{i+1}$ on the exterior of $\mathcal{A}$ with $B_{i} A_{i}=B_{i} A_{i+1}$ and $\angle A_{i} B_{i} A_{i+1}=\theta_{i}$. (Here, $A_{2021}=A_{1}$.) Finally, he erases $\mathcal{A}$ and the point $B_{1}$. He then tells Jason the angles $\theta_{1}, \theta_{2}, \ldots, \theta_{2020}$ he chose. Show that Jason can determine where $B_{1}$ was from the remaining 2019 points, i.e. show that $B_{1}$ is uniquely determined by the information Jason has.
|
Let $A_{1} A_{2} \cdots A_{2020}$ and $\tilde{A}_{1} \tilde{A}_{2} \cdots \tilde{A}_{2020}$ be two 2020 -gons that satisfy the conditions in the problem statement, and let $B_{k}, \tilde{B}_{k}$ be the points Alan would construct with respect to these two polygons. It suffices to show that if $B_{k}=\tilde{B}_{k}$ for $k=2,3, \ldots, 2020$, then $B_{1}=\tilde{B}_{1}$.
For $2 \leq k \leq 2020$, we note that
$$
A_{k} B_{k}=A_{k+1} B_{k}, \quad \tilde{A}_{k} B_{k}=\tilde{A}_{k+1} B_{k}
$$
Furthermore, we have the equality of directed angles $\angle A_{k} B_{k} A_{k+1}=\angle \tilde{A}_{k} B_{k} \tilde{A}_{k+1}=\theta_{k}$, therefore $\angle A_{k} B_{k} \tilde{A}_{k}=\angle A_{k+1} B_{k} \tilde{A}_{k+1}$. This implies the congruence $\triangle A_{k} B_{k} \tilde{A}_{k} \cong \triangle A_{k+1} B_{k} \tilde{A}_{k+1}$.
The congruence shows that $A_{k} \tilde{A}_{k}=A_{k+1} \tilde{A}_{k+1}$; furthermore, the angle from the directed segment $\overrightarrow{A_{k} \tilde{A}_{k}}$ to $\overrightarrow{A_{k+1} \tilde{A}_{k+1}}$ is $\theta_{k}$ counterclockwise. This holds for $k=2,3, \ldots, 2020$; we conclude that $A_{1} \tilde{A}_{1}=A_{2} \tilde{A}_{2}$, and the angle from the directed segments $\overrightarrow{A_{1}} \tilde{A}_{1}$ to $\overrightarrow{A_{2}} \tilde{A}_{2}$ is
$$
-\sum_{k=2}^{2020} \theta_{k}=\theta_{1}-1010 \pi=\theta_{1}
$$
counterclockwise.
Finally we observe that $A_{1} B_{1}=A_{2} B_{1}$, and the angle from the directed segment $\overrightarrow{A_{1} B_{1}}$ to $\overrightarrow{A_{2} B_{1}}$ is $\theta_{1}$ counterclockwise. This implies $\angle B_{1} A_{1} \tilde{A}_{1}=\angle B_{1} A_{2} \tilde{A}_{2}$, so $\triangle A_{1} B_{1} \tilde{A}_{1} \cong \triangle A_{2} B_{1} \tilde{A}_{2}$. Thus $\tilde{A}_{1} B_{1}=$ $\tilde{A}_{2} B_{1}$, and the angle from $\overrightarrow{\tilde{A}_{1} B_{1}}$ to $\overrightarrow{\tilde{A}_{2} B_{1}}$ is $\theta_{1}$ counterclockwise. We conclude that $B_{1}=\tilde{B}_{1}$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-team-solutions.jsonl",
"problem_match": "\n4. [35]",
"solution_match": "\nSolution 3: "
}
|
db019661-c2df-58b5-92f4-ce8e39f95bb5
| 610,181
|
Let $a_{0}, b_{0}, c_{0}, a, b, c$ be integers such that $\operatorname{gcd}\left(a_{0}, b_{0}, c_{0}\right)=\operatorname{gcd}(a, b, c)=1$. Prove that there exists a positive integer $n$ and integers $a_{1}, a_{2}, \ldots, a_{n}=a, b_{1}, b_{2}, \ldots, b_{n}=b, c_{1}, c_{2}, \ldots, c_{n}=c$ such that for all $1 \leq i \leq n, a_{i-1} a_{i}+b_{i-1} b_{i}+c_{i-1} c_{i}=1$.
|
Solution: The problem statement is equivalent to showing that we can find a sequence of vectors, each with 3 integer components, such that the first vector is $\left(a_{0}, b_{0}, c_{0}\right)$, the last vector is $(a, b, c)$, and every pair of adjacent vectors has dot product equal to 1 .
We will show that any vector $(a, b, c)$ can be sent to $(1,0,0)$. This is sufficient, because given vectors $\left(a_{0}, b_{0}, c_{0}\right)$ and $(a, b, c)$, we take the sequence from $\left(a_{0}, b_{0}, c_{0}\right)$ to $(1,0,0)$ and then add the reverse of the sequence from $(a, b, c)$ to $(1,0,0)$.
First, suppose that some two of $a, b, c$ are relatively prime. Here we will suppose that $a$ and $b$ are relatively prime; the other cases are similar. If neither of $a$ or $b$ is 0 , then by Bezout's identity, there exist $p, q$ such that $|p|+|q|<|a|+|b|$ and $a p+b q=1$, so we can send ( $a, b, c$ ) to ( $p, q, 0$ ). (Finding such numbers can be done using the extended Euclidean algorithm.) Clearly $p$ and $q$ must also be relatively prime, so we can apply Bezout's identity repeatedly until we eventually have $(1,0,0),(-1,0,0),(0,1,0)$, or $(0,-1,0)$. Now, starting from $(0,-1,0)$, we can do $(0,-1,0) \rightarrow(1,-1,0) \rightarrow(1,0,0)$, and we can do something similar to convert $(-1,0,0)$ to $(0,1,0)$.
Now suppose that no two of $a, b, c$ are relatively prime. Let $f=\operatorname{gcd}(a, b)$. We claim that we can find $x, y, z$ such that $a x y+b x+c z=1$. Notice that this is the same as $(a y+b) x+c z=1$. Since
$\operatorname{gcd}(a, b, c)=1$, there exists $y$ such that $\operatorname{gcd}(a y+b, c)=1$. Then by Bezout's identity, there exist $x, z$ such that $(a y+b) x+c z=1$. Therefore, we can send $(a, b, c)$ to $(x y, x, z)$. Clearly $x$ and $z$ must be relatively prime, so we have reduced to the case above, and we can apply the process described above for that case.
At the end of this process, we will have $(1,0,0),(0,1,0)$, or $(0,0,1)$. The second of these can be converted into $(1,0,0)$ by doing $(0,1,0) \rightarrow(1,1,0) \rightarrow(1,0,0)$, and a similar sequence shows the same for the third. Therefore, $(a, b, c)$ can be sent to $(1,0,0)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{0}, b_{0}, c_{0}, a, b, c$ be integers such that $\operatorname{gcd}\left(a_{0}, b_{0}, c_{0}\right)=\operatorname{gcd}(a, b, c)=1$. Prove that there exists a positive integer $n$ and integers $a_{1}, a_{2}, \ldots, a_{n}=a, b_{1}, b_{2}, \ldots, b_{n}=b, c_{1}, c_{2}, \ldots, c_{n}=c$ such that for all $1 \leq i \leq n, a_{i-1} a_{i}+b_{i-1} b_{i}+c_{i-1} c_{i}=1$.
|
Solution: The problem statement is equivalent to showing that we can find a sequence of vectors, each with 3 integer components, such that the first vector is $\left(a_{0}, b_{0}, c_{0}\right)$, the last vector is $(a, b, c)$, and every pair of adjacent vectors has dot product equal to 1 .
We will show that any vector $(a, b, c)$ can be sent to $(1,0,0)$. This is sufficient, because given vectors $\left(a_{0}, b_{0}, c_{0}\right)$ and $(a, b, c)$, we take the sequence from $\left(a_{0}, b_{0}, c_{0}\right)$ to $(1,0,0)$ and then add the reverse of the sequence from $(a, b, c)$ to $(1,0,0)$.
First, suppose that some two of $a, b, c$ are relatively prime. Here we will suppose that $a$ and $b$ are relatively prime; the other cases are similar. If neither of $a$ or $b$ is 0 , then by Bezout's identity, there exist $p, q$ such that $|p|+|q|<|a|+|b|$ and $a p+b q=1$, so we can send ( $a, b, c$ ) to ( $p, q, 0$ ). (Finding such numbers can be done using the extended Euclidean algorithm.) Clearly $p$ and $q$ must also be relatively prime, so we can apply Bezout's identity repeatedly until we eventually have $(1,0,0),(-1,0,0),(0,1,0)$, or $(0,-1,0)$. Now, starting from $(0,-1,0)$, we can do $(0,-1,0) \rightarrow(1,-1,0) \rightarrow(1,0,0)$, and we can do something similar to convert $(-1,0,0)$ to $(0,1,0)$.
Now suppose that no two of $a, b, c$ are relatively prime. Let $f=\operatorname{gcd}(a, b)$. We claim that we can find $x, y, z$ such that $a x y+b x+c z=1$. Notice that this is the same as $(a y+b) x+c z=1$. Since
$\operatorname{gcd}(a, b, c)=1$, there exists $y$ such that $\operatorname{gcd}(a y+b, c)=1$. Then by Bezout's identity, there exist $x, z$ such that $(a y+b) x+c z=1$. Therefore, we can send $(a, b, c)$ to $(x y, x, z)$. Clearly $x$ and $z$ must be relatively prime, so we have reduced to the case above, and we can apply the process described above for that case.
At the end of this process, we will have $(1,0,0),(0,1,0)$, or $(0,0,1)$. The second of these can be converted into $(1,0,0)$ by doing $(0,1,0) \rightarrow(1,1,0) \rightarrow(1,0,0)$, and a similar sequence shows the same for the third. Therefore, $(a, b, c)$ can be sent to $(1,0,0)$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-team-solutions.jsonl",
"problem_match": "\n5. [40]",
"solution_match": "\nProposed by: Michael Ren\n"
}
|
37b4f3a7-5622-50b5-9fee-4ccb53210cfb
| 610,182
|
Let $n>1$ be a positive integer and $S$ be a collection of $\frac{1}{2}\binom{2 n}{n}$ distinct $n$-element subsets of $\{1,2, \ldots, 2 n\}$. Show that there exists $A, B \in S$ such that $|A \cap B| \leq 1$.
|
Solution 1: Assume for the sake of contradiction that there exist no such $A, B$. Pair up each subset with its complement, like so:
$$
\begin{aligned}
\{1,2,3, \ldots, n\} & \leftrightarrow\{n+1, n+2, \ldots, 2 n\} \\
\{1,2,3, \ldots, n-1, n+1\} & \leftrightarrow\{n, n+2, \ldots, 2 n\} \\
\{1,2,3, \ldots, n-1, n+2\} & \leftrightarrow\{n, n+1, n+3, \ldots, 2 n\} \\
& \vdots
\end{aligned}
$$
Note that for each pair, we can have at most one of the two in $S$. Since $S$ has $\frac{1}{2}$ of the total number of subsets with size $n$, it must be that we have exactly one element from each pair in $S$. For any $s_{0} \in S$, none of the subsets that share exactly one element with $s_{0}$ can be in $S$, so their complements must be in $S$. This means that every subset with $n-1$ shared elements with $s_{0}$ must be in $S$. Without loss of generality, assume $\{1,2,3, \ldots, n\} \in S$. Then, $\{2,3,4, \ldots, n+1\} \in S$, so $\{3,4,5, \ldots, n+2\} \in S$. Continuing on in this manner, we eventually reach $\{n+1, n+2, \ldots, 2 n\} \in S$, contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n>1$ be a positive integer and $S$ be a collection of $\frac{1}{2}\binom{2 n}{n}$ distinct $n$-element subsets of $\{1,2, \ldots, 2 n\}$. Show that there exists $A, B \in S$ such that $|A \cap B| \leq 1$.
|
Solution 1: Assume for the sake of contradiction that there exist no such $A, B$. Pair up each subset with its complement, like so:
$$
\begin{aligned}
\{1,2,3, \ldots, n\} & \leftrightarrow\{n+1, n+2, \ldots, 2 n\} \\
\{1,2,3, \ldots, n-1, n+1\} & \leftrightarrow\{n, n+2, \ldots, 2 n\} \\
\{1,2,3, \ldots, n-1, n+2\} & \leftrightarrow\{n, n+1, n+3, \ldots, 2 n\} \\
& \vdots
\end{aligned}
$$
Note that for each pair, we can have at most one of the two in $S$. Since $S$ has $\frac{1}{2}$ of the total number of subsets with size $n$, it must be that we have exactly one element from each pair in $S$. For any $s_{0} \in S$, none of the subsets that share exactly one element with $s_{0}$ can be in $S$, so their complements must be in $S$. This means that every subset with $n-1$ shared elements with $s_{0}$ must be in $S$. Without loss of generality, assume $\{1,2,3, \ldots, n\} \in S$. Then, $\{2,3,4, \ldots, n+1\} \in S$, so $\{3,4,5, \ldots, n+2\} \in S$. Continuing on in this manner, we eventually reach $\{n+1, n+2, \ldots, 2 n\} \in S$, contradiction.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-team-solutions.jsonl",
"problem_match": "\n6. [40]",
"solution_match": "\nProposed by: Michael Ren\n"
}
|
18a14c9b-e557-5fb8-ad27-80fe9e509609
| 610,183
|
Let $n>1$ be a positive integer and $S$ be a collection of $\frac{1}{2}\binom{2 n}{n}$ distinct $n$-element subsets of $\{1,2, \ldots, 2 n\}$. Show that there exists $A, B \in S$ such that $|A \cap B| \leq 1$.
|
Let $[2 n]=\{1,2, \ldots, 2 n\}$. Consider the following cycle of $2 n-1$ sets such that any two adjacent sets have an intersection of size 1 :
$$
\begin{aligned}
& \{1,2,3, \ldots, n\} \\
& \{1, n+1, n+2, \ldots, 2 n-1\} \\
& \{1,2 n, 2,3, \ldots, n-1\} \\
& \vdots \\
& \{1, n+2, n+3, \ldots, 2 n\}
\end{aligned}
$$
If $S$ contains two adjacent elements of the cycle then we are done. For each permutation $\sigma$ of [2n], we can consider the cycle $C_{\sigma}$ of sets obtained after applying $\sigma$, i.e. $\{\sigma(1), \sigma(2), \sigma(3), \ldots, \sigma(n)\}$ and so on. In total, each subset of $[2 n]$ with size $n$ appears $(2 n-1)(n!)^{2}$ times across all the cycles $C_{\sigma}$, so
$$
\sum_{\sigma}\left|C_{\sigma} \cap S\right|=|S|(2 n-1)(n!)^{2}=\frac{2 n-1}{2}(2 n)!
$$
where the sum is over all $(2 n)$ ! permutations of $[2 n]$. This means that on average across possible cycles, $\frac{2 n-1}{2}$ of its elements are in $S$. Thus, if we select a cycle $C_{\sigma}$ uniformly at random, with positive probability we will have $\left|C_{\sigma} \cap S\right| \geq n$, so two adjacent elements in this cycle will be in $S$. Therefore, there must exist some two subsets in $S$ that share at most one element.
This proof will work under the weaker condition $|S|>\frac{n-1}{2 n-1}\binom{2 n}{n}$.
Remark. A family of sets such that $|A \cap B| \geq t$ for every pair of distinct sets $A, B$ is called $t$-intersecting. Ahlswede and Khachatrian solved the problem of determining the largest $k$-uniform $t$ intersecting family. See "Katona's Intersection Theorem: Four Proofs" or "The Complete Intersection
Theorem for Systems of Finite Sets" for exact results.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n>1$ be a positive integer and $S$ be a collection of $\frac{1}{2}\binom{2 n}{n}$ distinct $n$-element subsets of $\{1,2, \ldots, 2 n\}$. Show that there exists $A, B \in S$ such that $|A \cap B| \leq 1$.
|
Let $[2 n]=\{1,2, \ldots, 2 n\}$. Consider the following cycle of $2 n-1$ sets such that any two adjacent sets have an intersection of size 1 :
$$
\begin{aligned}
& \{1,2,3, \ldots, n\} \\
& \{1, n+1, n+2, \ldots, 2 n-1\} \\
& \{1,2 n, 2,3, \ldots, n-1\} \\
& \vdots \\
& \{1, n+2, n+3, \ldots, 2 n\}
\end{aligned}
$$
If $S$ contains two adjacent elements of the cycle then we are done. For each permutation $\sigma$ of [2n], we can consider the cycle $C_{\sigma}$ of sets obtained after applying $\sigma$, i.e. $\{\sigma(1), \sigma(2), \sigma(3), \ldots, \sigma(n)\}$ and so on. In total, each subset of $[2 n]$ with size $n$ appears $(2 n-1)(n!)^{2}$ times across all the cycles $C_{\sigma}$, so
$$
\sum_{\sigma}\left|C_{\sigma} \cap S\right|=|S|(2 n-1)(n!)^{2}=\frac{2 n-1}{2}(2 n)!
$$
where the sum is over all $(2 n)$ ! permutations of $[2 n]$. This means that on average across possible cycles, $\frac{2 n-1}{2}$ of its elements are in $S$. Thus, if we select a cycle $C_{\sigma}$ uniformly at random, with positive probability we will have $\left|C_{\sigma} \cap S\right| \geq n$, so two adjacent elements in this cycle will be in $S$. Therefore, there must exist some two subsets in $S$ that share at most one element.
This proof will work under the weaker condition $|S|>\frac{n-1}{2 n-1}\binom{2 n}{n}$.
Remark. A family of sets such that $|A \cap B| \geq t$ for every pair of distinct sets $A, B$ is called $t$-intersecting. Ahlswede and Khachatrian solved the problem of determining the largest $k$-uniform $t$ intersecting family. See "Katona's Intersection Theorem: Four Proofs" or "The Complete Intersection
Theorem for Systems of Finite Sets" for exact results.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-team-solutions.jsonl",
"problem_match": "\n6. [40]",
"solution_match": "\nSolution 2: "
}
|
18a14c9b-e557-5fb8-ad27-80fe9e509609
| 610,183
|
Let $A B C$ be a scalene triangle with angle bisectors $A D, B E$, and $C F$ so that $D, E$, and $F$ lie on segments $B C, C A$, and $A B$ respectively. Let $M$ and $N$ be the midpoints of $B C$ and $E F$ respectively. Prove that line $A N$ and the line through $M$ parallel to $A D$ intersect on the circumcircle of $A B C$ if and only if $D E=D F$.
|
## Solution 1:
Let $X, Y$ be on $A B, A C$ such that $C X \| B E$ and $B Y \| C F$. Then $B X=B C=C Y$. Let $Z$ be the midpoint of $X Y$. Then $\overrightarrow{M Z}=\frac{1}{2}(\overrightarrow{B X}+\overrightarrow{C Y})$, which bisects the angle between $B X$ and $C Y$ because they have the same length. Therefore $M Z \| A D$. Furthermore, by similar triangles we have
$$
A E \cdot A X=A B \cdot A C=A F \cdot A Y
$$
This rearranges to $\frac{A E}{A F}=\frac{A Y}{A X}$, so $E F \| X Y$. Therefore $Z$ is the intersection of the lines in the problem statement. Then
$$
\frac{\sin \angle B Z X}{\sin \angle C Z Y}=\frac{B X \frac{\sin \angle Z B X}{X Z}}{C Y \frac{\sin \angle Z C Y}{Y Z}}=1
$$
iff $Z \in(A B C)$, so $X Y$ is the external angle bisector of $\angle B Z C$ iff $Z \in(A B C)$. Thus if $P=A D \cap X Y$, $P \in(A B C)$ if $Z \in(A B C)$. Additionally the spiral similarity from $B X$ to $C Y$ gives $L_{A} Z \perp X Y$ where $L_{A}$ is the midpoint of $\operatorname{arc} B A C$, so if $P \in(A B C)$ then $Z$ must be on $(A B C)$ because $\angle L_{A} Z P=90^{\circ}$. Therefore $Z \in(A B C)$ iff $P \in(A B C)$.
From the previous length computation, we know that an inversion at $A$ with radius $\sqrt{A B \cdot A C}$ composed with reflection about $A D$ will send $X$ and $Y$ to $E$ and $F$. We have $P \in(A B C)$ iff its image under the inversion is $D$, but since $P$ was defined as $A D \cap X Y$ this is true iff $(A E D F)$ is cyclic. Since $A B C$ is scalene and $A E \neq A F$, this is true iff $D E=D F$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle with angle bisectors $A D, B E$, and $C F$ so that $D, E$, and $F$ lie on segments $B C, C A$, and $A B$ respectively. Let $M$ and $N$ be the midpoints of $B C$ and $E F$ respectively. Prove that line $A N$ and the line through $M$ parallel to $A D$ intersect on the circumcircle of $A B C$ if and only if $D E=D F$.
|
## Solution 1:

Let $X, Y$ be on $A B, A C$ such that $C X \| B E$ and $B Y \| C F$. Then $B X=B C=C Y$. Let $Z$ be the midpoint of $X Y$. Then $\overrightarrow{M Z}=\frac{1}{2}(\overrightarrow{B X}+\overrightarrow{C Y})$, which bisects the angle between $B X$ and $C Y$ because they have the same length. Therefore $M Z \| A D$. Furthermore, by similar triangles we have
$$
A E \cdot A X=A B \cdot A C=A F \cdot A Y
$$
This rearranges to $\frac{A E}{A F}=\frac{A Y}{A X}$, so $E F \| X Y$. Therefore $Z$ is the intersection of the lines in the problem statement. Then
$$
\frac{\sin \angle B Z X}{\sin \angle C Z Y}=\frac{B X \frac{\sin \angle Z B X}{X Z}}{C Y \frac{\sin \angle Z C Y}{Y Z}}=1
$$
iff $Z \in(A B C)$, so $X Y$ is the external angle bisector of $\angle B Z C$ iff $Z \in(A B C)$. Thus if $P=A D \cap X Y$, $P \in(A B C)$ if $Z \in(A B C)$. Additionally the spiral similarity from $B X$ to $C Y$ gives $L_{A} Z \perp X Y$ where $L_{A}$ is the midpoint of $\operatorname{arc} B A C$, so if $P \in(A B C)$ then $Z$ must be on $(A B C)$ because $\angle L_{A} Z P=90^{\circ}$. Therefore $Z \in(A B C)$ iff $P \in(A B C)$.
From the previous length computation, we know that an inversion at $A$ with radius $\sqrt{A B \cdot A C}$ composed with reflection about $A D$ will send $X$ and $Y$ to $E$ and $F$. We have $P \in(A B C)$ iff its image under the inversion is $D$, but since $P$ was defined as $A D \cap X Y$ this is true iff $(A E D F)$ is cyclic. Since $A B C$ is scalene and $A E \neq A F$, this is true iff $D E=D F$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-team-solutions.jsonl",
"problem_match": "\n8. [50]",
"solution_match": "\nProposed by: Michael Ren\n\n"
}
|
41c29e3b-3265-5d84-99ed-e6f61803aed0
| 610,185
|
Let $A B C$ be a scalene triangle with angle bisectors $A D, B E$, and $C F$ so that $D, E$, and $F$ lie on segments $B C, C A$, and $A B$ respectively. Let $M$ and $N$ be the midpoints of $B C$ and $E F$ respectively. Prove that line $A N$ and the line through $M$ parallel to $A D$ intersect on the circumcircle of $A B C$ if and only if $D E=D F$.
|
Let $L_{A}$ be the midpoint of arc $B A C$ and let $M_{A}$ be diametrically opposite $L_{A}$. Let $E F, A L_{A}$, and $B C$ meet at $T$ so $\angle D A T=90^{\circ}$; note that $D E=D F$ iff $D N \perp E F$, which is equivalent to ( $T A N D$ ) being cyclic. Let $A N \cap(A B C)=X$ and $X M \cap(A B C)=Y$, and let $Y^{\prime}$ be the reflection of $Y$ over $L_{A} M_{A}$ with similarly $X^{\prime}$ the reflection of $X$ over $L_{A} M_{A}$. We wish to show $N \in(T A D)$ iff $X Y \| A M_{A}$.
We claim $A Y^{\prime} \| E F$. By projecting $-1=(B, C ; M, \infty) \stackrel{X}{=}\left(B, C ; Y, X^{\prime}\right)$ and reflecting over $L_{A} M_{A}$, we find $\left(X, Y^{\prime} ; B, C\right)=-1$. Then projecting through $A$ gives $\left(N, A Y^{\prime} \cap E F ; F, E\right)=-1$, and since $N$ is the midpoint of $E F$ we find $A Y^{\prime} \| E F$.
Now $(T A N D)$ cyclic iff $\measuredangle D A N=\measuredangle D T N$, and $\measuredangle D T N=\measuredangle Y Y^{\prime} A$ by the parallel lines. But we have $\measuredangle D A N=\measuredangle M_{A} A X$, so $\operatorname{arcs} M_{A} X$ and $Y A$ are equal iff $(T A N D)$ is cyclic. Thus $X Y \| A M_{A}$ iff $D E=D F$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle with angle bisectors $A D, B E$, and $C F$ so that $D, E$, and $F$ lie on segments $B C, C A$, and $A B$ respectively. Let $M$ and $N$ be the midpoints of $B C$ and $E F$ respectively. Prove that line $A N$ and the line through $M$ parallel to $A D$ intersect on the circumcircle of $A B C$ if and only if $D E=D F$.
|

Let $L_{A}$ be the midpoint of arc $B A C$ and let $M_{A}$ be diametrically opposite $L_{A}$. Let $E F, A L_{A}$, and $B C$ meet at $T$ so $\angle D A T=90^{\circ}$; note that $D E=D F$ iff $D N \perp E F$, which is equivalent to ( $T A N D$ ) being cyclic. Let $A N \cap(A B C)=X$ and $X M \cap(A B C)=Y$, and let $Y^{\prime}$ be the reflection of $Y$ over $L_{A} M_{A}$ with similarly $X^{\prime}$ the reflection of $X$ over $L_{A} M_{A}$. We wish to show $N \in(T A D)$ iff $X Y \| A M_{A}$.
We claim $A Y^{\prime} \| E F$. By projecting $-1=(B, C ; M, \infty) \stackrel{X}{=}\left(B, C ; Y, X^{\prime}\right)$ and reflecting over $L_{A} M_{A}$, we find $\left(X, Y^{\prime} ; B, C\right)=-1$. Then projecting through $A$ gives $\left(N, A Y^{\prime} \cap E F ; F, E\right)=-1$, and since $N$ is the midpoint of $E F$ we find $A Y^{\prime} \| E F$.
Now $(T A N D)$ cyclic iff $\measuredangle D A N=\measuredangle D T N$, and $\measuredangle D T N=\measuredangle Y Y^{\prime} A$ by the parallel lines. But we have $\measuredangle D A N=\measuredangle M_{A} A X$, so $\operatorname{arcs} M_{A} X$ and $Y A$ are equal iff $(T A N D)$ is cyclic. Thus $X Y \| A M_{A}$ iff $D E=D F$ as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-team-solutions.jsonl",
"problem_match": "\n8. [50]",
"solution_match": "\n## Solution 2:\n\n"
}
|
41c29e3b-3265-5d84-99ed-e6f61803aed0
| 610,185
|
Let $p>5$ be a prime number. Show that there exists a prime number $q<p$ and a positive integer $n$ such that $p$ divides $n^{2}-q$.
|
Solution 1: Note that the condition $p \mid n^{2}-q$ just means that $q$ is a quadratic residue modulo $p$, or that the Legendre symbol $\left(\frac{q}{p}\right)$ is 1 . We use these standard facts about the Legendre symbol:
- If $p \equiv \pm 1(\bmod 8)$, then $\left(\frac{2}{p}\right)=1$.
- For an odd prime $p$,
$$
\left(\frac{-1}{p}\right)=\left\{\begin{array}{lll}
-1 & \text { if } p \equiv 3 & (\bmod 4) \\
+1 & \text { if } p \equiv 1 & (\bmod 4)
\end{array}\right.
$$
- Quadratic reciprocity: for distinct odd primes $p$ and $q$,
$$
\left(\frac{p}{q}\right)\left(\frac{q}{p}\right)= \begin{cases}-1 & \text { if } p \equiv q \equiv 3 \quad(\bmod 4) \\ +1 & \text { otherwise }\end{cases}
$$
If $p$ is a Fermat prime or Mersenne prime, then $p$ is congruent to 1 or 7 modulo 8 respectively, since $p>5$. In that case $q=2$ works. Otherwise assume $p$ is not a Fermat prime or Mersenne prime, so that $p-1$ and $p+1$ are not powers of 2 .
If $p \equiv 1(\bmod 4)$, then let $q$ be an odd prime divisor of $p-1$, so that $p \equiv 1(\bmod q)$. Then by quadratic reciprocity $\left(\frac{q}{p}\right)=\left(\frac{p}{q}\right)=1$.
If $p \equiv 3(\bmod 4)$, then let $q$ be an odd prime divisor of $p+1$, so that $p \equiv-1(\bmod q)$. Either $q \equiv 1$ $(\bmod 4)$ so that $\left(\frac{q}{p}\right)=\left(\frac{p}{q}\right)=1$ or $q \equiv 3(\bmod 4)$ so that $\left(\frac{q}{p}\right)=-\left(\frac{p}{q}\right)=-\left(\frac{-1}{q}\right)=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p>5$ be a prime number. Show that there exists a prime number $q<p$ and a positive integer $n$ such that $p$ divides $n^{2}-q$.
|
Solution 1: Note that the condition $p \mid n^{2}-q$ just means that $q$ is a quadratic residue modulo $p$, or that the Legendre symbol $\left(\frac{q}{p}\right)$ is 1 . We use these standard facts about the Legendre symbol:
- If $p \equiv \pm 1(\bmod 8)$, then $\left(\frac{2}{p}\right)=1$.
- For an odd prime $p$,
$$
\left(\frac{-1}{p}\right)=\left\{\begin{array}{lll}
-1 & \text { if } p \equiv 3 & (\bmod 4) \\
+1 & \text { if } p \equiv 1 & (\bmod 4)
\end{array}\right.
$$
- Quadratic reciprocity: for distinct odd primes $p$ and $q$,
$$
\left(\frac{p}{q}\right)\left(\frac{q}{p}\right)= \begin{cases}-1 & \text { if } p \equiv q \equiv 3 \quad(\bmod 4) \\ +1 & \text { otherwise }\end{cases}
$$
If $p$ is a Fermat prime or Mersenne prime, then $p$ is congruent to 1 or 7 modulo 8 respectively, since $p>5$. In that case $q=2$ works. Otherwise assume $p$ is not a Fermat prime or Mersenne prime, so that $p-1$ and $p+1$ are not powers of 2 .
If $p \equiv 1(\bmod 4)$, then let $q$ be an odd prime divisor of $p-1$, so that $p \equiv 1(\bmod q)$. Then by quadratic reciprocity $\left(\frac{q}{p}\right)=\left(\frac{p}{q}\right)=1$.
If $p \equiv 3(\bmod 4)$, then let $q$ be an odd prime divisor of $p+1$, so that $p \equiv-1(\bmod q)$. Either $q \equiv 1$ $(\bmod 4)$ so that $\left(\frac{q}{p}\right)=\left(\frac{p}{q}\right)=1$ or $q \equiv 3(\bmod 4)$ so that $\left(\frac{q}{p}\right)=-\left(\frac{p}{q}\right)=-\left(\frac{-1}{q}\right)=1$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-team-solutions.jsonl",
"problem_match": "\n9. [55]",
"solution_match": "\nProposed by: Andrew Gu\n"
}
|
a348f39c-9d7e-52c0-8d3d-e306fe536750
| 610,186
|
Let $p>5$ be a prime number. Show that there exists a prime number $q<p$ and a positive integer $n$ such that $p$ divides $n^{2}-q$.
|
(Ankan Bhattacharya) We assume the same standard facts about quadratic residues as the previous solution.
If $p \equiv 1(\bmod 4)$, then since $p>5$, there exists an odd prime divisor $q$ of $p-4$, which gives
$$
\left(\frac{q}{p}\right)=\left(\frac{p}{q}\right)=\left(\frac{4}{q}\right)=1
$$
If $p \equiv 7(\bmod 8)$, then we can take $q=2$.
If $p \equiv 3(\bmod 8)$, then by Legendre's three square theorem there exist odd $a, b, c$ satisfying $p=$ $a^{2}+b^{2}+c^{2}$. Since $p>3$, these are not all equal and we may assume without loss of generality that $b \neq c$. Then $p-a^{2}=b^{2}+c^{2}$ has a prime divisor $q \equiv 1(\bmod 4)$, which gives
$$
\left(\frac{q}{p}\right)=\left(\frac{p}{q}\right)=\left(\frac{a^{2}}{q}\right)=1
$$
Remark. For an odd prime number $p$, let $l(p)$ be the least prime number which is a quadratic residue modulo $p$ and $h(-p)$ be the class number of the quadratic field $\mathbb{Q}[\sqrt{-p}]$. In the paper "The Least Prime Quadratic Residue and the Class Number" by Chowla, Cowles, and Cowles, the following results were proven:
- If $p>5$ and $p \equiv 5(\bmod 8)$, then $l(p)<\sqrt{p}$.
- If $p>3, p \equiv 3(\bmod 8)$, and $h(-p)>1$, then $l(p)<\sqrt{p / 3}$.
- If $p>3, p \equiv 3(\bmod 8)$, and $h(-p)=1$, then $l(p)=\frac{p+1}{4}$.
The proofs of the second and third results require knowledge of binary quadratic forms.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p>5$ be a prime number. Show that there exists a prime number $q<p$ and a positive integer $n$ such that $p$ divides $n^{2}-q$.
|
(Ankan Bhattacharya) We assume the same standard facts about quadratic residues as the previous solution.
If $p \equiv 1(\bmod 4)$, then since $p>5$, there exists an odd prime divisor $q$ of $p-4$, which gives
$$
\left(\frac{q}{p}\right)=\left(\frac{p}{q}\right)=\left(\frac{4}{q}\right)=1
$$
If $p \equiv 7(\bmod 8)$, then we can take $q=2$.
If $p \equiv 3(\bmod 8)$, then by Legendre's three square theorem there exist odd $a, b, c$ satisfying $p=$ $a^{2}+b^{2}+c^{2}$. Since $p>3$, these are not all equal and we may assume without loss of generality that $b \neq c$. Then $p-a^{2}=b^{2}+c^{2}$ has a prime divisor $q \equiv 1(\bmod 4)$, which gives
$$
\left(\frac{q}{p}\right)=\left(\frac{p}{q}\right)=\left(\frac{a^{2}}{q}\right)=1
$$
Remark. For an odd prime number $p$, let $l(p)$ be the least prime number which is a quadratic residue modulo $p$ and $h(-p)$ be the class number of the quadratic field $\mathbb{Q}[\sqrt{-p}]$. In the paper "The Least Prime Quadratic Residue and the Class Number" by Chowla, Cowles, and Cowles, the following results were proven:
- If $p>5$ and $p \equiv 5(\bmod 8)$, then $l(p)<\sqrt{p}$.
- If $p>3, p \equiv 3(\bmod 8)$, and $h(-p)>1$, then $l(p)<\sqrt{p / 3}$.
- If $p>3, p \equiv 3(\bmod 8)$, and $h(-p)=1$, then $l(p)=\frac{p+1}{4}$.
The proofs of the second and third results require knowledge of binary quadratic forms.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-team-solutions.jsonl",
"problem_match": "\n9. [55]",
"solution_match": "\nSolution 2: "
}
|
a348f39c-9d7e-52c0-8d3d-e306fe536750
| 610,186
|
Let $C_{k}=\frac{1}{k+1}\binom{2 k}{k}$ denote the $k^{\text {th }}$ Catalan number and $p$ be an odd prime. Prove that exactly half of the numbers in the set
$$
\left\{\sum_{k=1}^{p-1} C_{k} n^{k} \mid n \in\{1,2, \ldots, p-1\}\right\}
$$
are divisible by $p$.
|
Solution 1: We work in $\mathbb{F}_{p}[X]$.
We claim that
$$
(1-4 X)^{\frac{p+1}{2}}-1+2 X^{p}+2 X \sum_{k=0}^{p-1} C_{k} X^{k}=0
$$
The solution follows from this claim, as
$$
\sum_{k=1}^{p-1} C_{k} n^{k} \equiv 0 \quad(\bmod p) \Longleftrightarrow(1-4 n)^{\frac{p+1}{2}}-1+2 n^{p}+2 n \equiv 0 \quad(\bmod p)
$$
Since $n^{p} \equiv n(\bmod p)$, this is equivalent to $n \equiv \frac{1}{4}(\bmod p)$ or $1-4 n$ being a non-zero quadratic residue in $\mathbb{F}_{p}$. But we must omit the solution of $n=0$, so we get $1+\left(\frac{p-1}{2}-1\right)=\frac{p-1}{2}$ values of $n$ that work. Now we prove the claim. Observe the following facts:
- $C_{p-1}=\frac{1}{2 p-1}\binom{2 p-1}{p}=-1$ by Lucas' theorem.
- For $\frac{p-1}{2}<k<p-1$,
$$
\nu_{p}\left(C_{k}\right)=\nu_{p}((2 k)!)-\nu_{p}((k+1)!)-\nu_{p}(k!)=1
$$
since $k+1<p \leq 2 k$, so $C_{k}=0$.
We show that the coefficient of $X^{k}$ in the LHS is 0 for $k=0, \ldots, p$. This is obvious for $k>\frac{p+1}{2}$ and $k=0$ by the above facts, as the coefficient is $2+2 C_{p-1}$ for $k=p, 2 C_{k}$ for $\frac{p+1}{2}<k<p$, and 0 for $k=0$.
Now for $1 \leq k \leq \frac{p+1}{2}$, the coefficient is $\binom{\frac{p+1}{2}}{k}(-4)^{k}+2 C_{k-1}=0$. Write
$$
\begin{aligned}
\binom{\frac{p+1}{2}}{k} & =\frac{\frac{p+1}{2} \cdot \frac{p-1}{2} \cdot \frac{p-3}{2} \cdots \frac{p-2 k+3}{2}}{k!} \\
& =\frac{\frac{1}{2} \cdot\left(-\frac{1}{2}\right) \cdot\left(-\frac{3}{2}\right) \cdots\left(-\frac{2 k-3}{2}\right)}{k!} \\
& =\frac{(-1)^{k-1}}{2^{k}} \cdot \frac{1 \cdot 3 \cdots(2 k-3)}{k!} \\
& =\frac{(-1)^{k-1}}{2^{k}} \cdot \frac{(2 k-2)!}{2^{k-1}(k-1)!k!} \\
& =-\frac{2 C_{k-1}}{(-4)^{k}}
\end{aligned}
$$
so the coefficient is 0 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $C_{k}=\frac{1}{k+1}\binom{2 k}{k}$ denote the $k^{\text {th }}$ Catalan number and $p$ be an odd prime. Prove that exactly half of the numbers in the set
$$
\left\{\sum_{k=1}^{p-1} C_{k} n^{k} \mid n \in\{1,2, \ldots, p-1\}\right\}
$$
are divisible by $p$.
|
Solution 1: We work in $\mathbb{F}_{p}[X]$.
We claim that
$$
(1-4 X)^{\frac{p+1}{2}}-1+2 X^{p}+2 X \sum_{k=0}^{p-1} C_{k} X^{k}=0
$$
The solution follows from this claim, as
$$
\sum_{k=1}^{p-1} C_{k} n^{k} \equiv 0 \quad(\bmod p) \Longleftrightarrow(1-4 n)^{\frac{p+1}{2}}-1+2 n^{p}+2 n \equiv 0 \quad(\bmod p)
$$
Since $n^{p} \equiv n(\bmod p)$, this is equivalent to $n \equiv \frac{1}{4}(\bmod p)$ or $1-4 n$ being a non-zero quadratic residue in $\mathbb{F}_{p}$. But we must omit the solution of $n=0$, so we get $1+\left(\frac{p-1}{2}-1\right)=\frac{p-1}{2}$ values of $n$ that work. Now we prove the claim. Observe the following facts:
- $C_{p-1}=\frac{1}{2 p-1}\binom{2 p-1}{p}=-1$ by Lucas' theorem.
- For $\frac{p-1}{2}<k<p-1$,
$$
\nu_{p}\left(C_{k}\right)=\nu_{p}((2 k)!)-\nu_{p}((k+1)!)-\nu_{p}(k!)=1
$$
since $k+1<p \leq 2 k$, so $C_{k}=0$.
We show that the coefficient of $X^{k}$ in the LHS is 0 for $k=0, \ldots, p$. This is obvious for $k>\frac{p+1}{2}$ and $k=0$ by the above facts, as the coefficient is $2+2 C_{p-1}$ for $k=p, 2 C_{k}$ for $\frac{p+1}{2}<k<p$, and 0 for $k=0$.
Now for $1 \leq k \leq \frac{p+1}{2}$, the coefficient is $\binom{\frac{p+1}{2}}{k}(-4)^{k}+2 C_{k-1}=0$. Write
$$
\begin{aligned}
\binom{\frac{p+1}{2}}{k} & =\frac{\frac{p+1}{2} \cdot \frac{p-1}{2} \cdot \frac{p-3}{2} \cdots \frac{p-2 k+3}{2}}{k!} \\
& =\frac{\frac{1}{2} \cdot\left(-\frac{1}{2}\right) \cdot\left(-\frac{3}{2}\right) \cdots\left(-\frac{2 k-3}{2}\right)}{k!} \\
& =\frac{(-1)^{k-1}}{2^{k}} \cdot \frac{1 \cdot 3 \cdots(2 k-3)}{k!} \\
& =\frac{(-1)^{k-1}}{2^{k}} \cdot \frac{(2 k-2)!}{2^{k-1}(k-1)!k!} \\
& =-\frac{2 C_{k-1}}{(-4)^{k}}
\end{aligned}
$$
so the coefficient is 0 .
|
{
"resource_path": "HarvardMIT/segmented/en-234-tournaments-2020-hmic-solutions.jsonl",
"problem_match": "\n4. [9]",
"solution_match": "\nProposed by: Tristan Shin\n"
}
|
f44ea284-eac7-5ece-84e5-ef94d69c2f53
| 610,191
|
Let $C_{k}=\frac{1}{k+1}\binom{2 k}{k}$ denote the $k^{\text {th }}$ Catalan number and $p$ be an odd prime. Prove that exactly half of the numbers in the set
$$
\left\{\sum_{k=1}^{p-1} C_{k} n^{k} \mid n \in\{1,2, \ldots, p-1\}\right\}
$$
are divisible by $p$.
|
We present an alternate proof of the key claim. Use the same starting facts as before.
Let $Q(X)=-2+\sum_{k=0}^{\frac{p-1}{2}} C_{k} X^{k}=-2+X^{p-1}+\sum_{k=0}^{p-1} C_{k} X^{k}$.
Square $Q$ and multiply by $X$ to get
$$
\begin{aligned}
X Q^{2} & =4 X-4 X \sum_{k=0}^{\frac{p-1}{2}} C_{k} X^{k}+X\left(\sum_{k=0}^{\frac{p-1}{2}} C_{k} X^{k}\right)^{2} \\
& =-4 X-4 X Q+X \sum_{k=0}^{p-2} \sum_{j=0}^{k} C_{j} C_{k-j} X^{k}+C_{\frac{p-1}{2}}^{2} X^{p} \\
& =-4 X-4 X Q+\sum_{k=0}^{p-2} C_{k+1} X^{k+1}+4 X^{p} \\
& =-4 X-4 X Q+Q+1-X^{p-1}+4 X^{p} \\
& =(1-4 X) Q-(1-4 X)\left(X^{p-1}-1\right)
\end{aligned}
$$
It follows that
$$
\begin{aligned}
0 & =4 X \cdot\left(X Q^{2}-(1-4 X) Q+(1-4 X) \cdot\left(X^{p-1}-1\right)\right) \\
& =4 X^{2} Q^{2}-4 X(1-4 X) Q+4(1-4 X) \cdot\left(X^{p}-X\right) \\
& =4 X^{2} Q^{2}-4 X(1-4 X) Q+(1-4 X)^{2}-(1-4 X)^{p+1} \\
& =\left(2 X Q+(1-4 X)^{\frac{p+1}{2}}-(1-4 X)\right) \cdot\left(2 X Q-(1-4 X)^{\frac{p+1}{2}}-(1-4 X)\right) .
\end{aligned}
$$
Evaluating the second factor at 0 gives -2 , so it is not the zero polynomial. Thus the first factor is the zero polynomial, from which the claim follows.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $C_{k}=\frac{1}{k+1}\binom{2 k}{k}$ denote the $k^{\text {th }}$ Catalan number and $p$ be an odd prime. Prove that exactly half of the numbers in the set
$$
\left\{\sum_{k=1}^{p-1} C_{k} n^{k} \mid n \in\{1,2, \ldots, p-1\}\right\}
$$
are divisible by $p$.
|
We present an alternate proof of the key claim. Use the same starting facts as before.
Let $Q(X)=-2+\sum_{k=0}^{\frac{p-1}{2}} C_{k} X^{k}=-2+X^{p-1}+\sum_{k=0}^{p-1} C_{k} X^{k}$.
Square $Q$ and multiply by $X$ to get
$$
\begin{aligned}
X Q^{2} & =4 X-4 X \sum_{k=0}^{\frac{p-1}{2}} C_{k} X^{k}+X\left(\sum_{k=0}^{\frac{p-1}{2}} C_{k} X^{k}\right)^{2} \\
& =-4 X-4 X Q+X \sum_{k=0}^{p-2} \sum_{j=0}^{k} C_{j} C_{k-j} X^{k}+C_{\frac{p-1}{2}}^{2} X^{p} \\
& =-4 X-4 X Q+\sum_{k=0}^{p-2} C_{k+1} X^{k+1}+4 X^{p} \\
& =-4 X-4 X Q+Q+1-X^{p-1}+4 X^{p} \\
& =(1-4 X) Q-(1-4 X)\left(X^{p-1}-1\right)
\end{aligned}
$$
It follows that
$$
\begin{aligned}
0 & =4 X \cdot\left(X Q^{2}-(1-4 X) Q+(1-4 X) \cdot\left(X^{p-1}-1\right)\right) \\
& =4 X^{2} Q^{2}-4 X(1-4 X) Q+4(1-4 X) \cdot\left(X^{p}-X\right) \\
& =4 X^{2} Q^{2}-4 X(1-4 X) Q+(1-4 X)^{2}-(1-4 X)^{p+1} \\
& =\left(2 X Q+(1-4 X)^{\frac{p+1}{2}}-(1-4 X)\right) \cdot\left(2 X Q-(1-4 X)^{\frac{p+1}{2}}-(1-4 X)\right) .
\end{aligned}
$$
Evaluating the second factor at 0 gives -2 , so it is not the zero polynomial. Thus the first factor is the zero polynomial, from which the claim follows.
|
{
"resource_path": "HarvardMIT/segmented/en-234-tournaments-2020-hmic-solutions.jsonl",
"problem_match": "\n4. [9]",
"solution_match": "\nSolution 2: "
}
|
f44ea284-eac7-5ece-84e5-ef94d69c2f53
| 610,191
|
Let $C_{k}=\frac{1}{k+1}\binom{2 k}{k}$ denote the $k^{\text {th }}$ Catalan number and $p$ be an odd prime. Prove that exactly half of the numbers in the set
$$
\left\{\sum_{k=1}^{p-1} C_{k} n^{k} \mid n \in\{1,2, \ldots, p-1\}\right\}
$$
are divisible by $p$.
|
We prove the following generalization: Let $q$ be a power of $p$. Then the polynomial $\sum_{k=1}^{q-1} C_{k} X^{k}$ has $\frac{q+1}{2}$ roots in $\mathbb{F}_{q}$ and $\frac{p+1}{2}$ roots in $\mathbb{F}_{p}$. It once again suffices to prove the key claim, just with $p$ replaced by $q$.
Work in $\mathbb{F}_{q}[[X]]$, the ring of formal power series over $\mathbb{F}_{q}$. Then
$$
\begin{aligned}
\sum_{k=0}^{\infty}\binom{2 k}{k} X^{k} & =(1-4 X)^{-\frac{1}{2}} \\
& =(1-4 X)^{\frac{q-1}{2}}\left((1-4 X)^{q}\right)^{-\frac{1}{2}} \\
& =(1-4 X)^{\frac{q-1}{2}}\left(1-4 X^{q}\right)^{-\frac{1}{2}} \\
& =(1-4 X)^{\frac{q-1}{2}} \sum_{k=0}^{\infty}\binom{2 k}{k} X^{q k}
\end{aligned}
$$
Taking both sides mod $X^{q}$,
$$
\sum_{k=0}^{q-1}\binom{2 k}{k} X^{k}=(1-4 X)^{\frac{q-1}{2}}
$$
Then using $\binom{2 q}{q}=2$, we have
$$
\sqrt{1-4 X}=(1-4 X) \cdot(1-4 X)^{-\frac{1}{2}} \equiv(1-4 X) \cdot\left((1-4 X)^{\frac{q-1}{2}}+2 X^{q}\right) \quad\left(\bmod X^{q+1}\right)
$$
so
$$
X \sum_{k=0}^{\infty} C_{k} X^{k}=\frac{1-\sqrt{1-4 X}}{2} \equiv \frac{1-(1-4 X)^{\frac{q+1}{2}}-2 X^{q}}{2} \quad\left(\bmod X^{q+1}\right)
$$
from which the claim follows.
Alternatively, one can also finish by integrating $(1-4 X)^{\frac{p-1}{2}}$, noting that the "constant of integration" is no longer a constant but rather a polynomial of the form $a+b X^{p}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $C_{k}=\frac{1}{k+1}\binom{2 k}{k}$ denote the $k^{\text {th }}$ Catalan number and $p$ be an odd prime. Prove that exactly half of the numbers in the set
$$
\left\{\sum_{k=1}^{p-1} C_{k} n^{k} \mid n \in\{1,2, \ldots, p-1\}\right\}
$$
are divisible by $p$.
|
We prove the following generalization: Let $q$ be a power of $p$. Then the polynomial $\sum_{k=1}^{q-1} C_{k} X^{k}$ has $\frac{q+1}{2}$ roots in $\mathbb{F}_{q}$ and $\frac{p+1}{2}$ roots in $\mathbb{F}_{p}$. It once again suffices to prove the key claim, just with $p$ replaced by $q$.
Work in $\mathbb{F}_{q}[[X]]$, the ring of formal power series over $\mathbb{F}_{q}$. Then
$$
\begin{aligned}
\sum_{k=0}^{\infty}\binom{2 k}{k} X^{k} & =(1-4 X)^{-\frac{1}{2}} \\
& =(1-4 X)^{\frac{q-1}{2}}\left((1-4 X)^{q}\right)^{-\frac{1}{2}} \\
& =(1-4 X)^{\frac{q-1}{2}}\left(1-4 X^{q}\right)^{-\frac{1}{2}} \\
& =(1-4 X)^{\frac{q-1}{2}} \sum_{k=0}^{\infty}\binom{2 k}{k} X^{q k}
\end{aligned}
$$
Taking both sides mod $X^{q}$,
$$
\sum_{k=0}^{q-1}\binom{2 k}{k} X^{k}=(1-4 X)^{\frac{q-1}{2}}
$$
Then using $\binom{2 q}{q}=2$, we have
$$
\sqrt{1-4 X}=(1-4 X) \cdot(1-4 X)^{-\frac{1}{2}} \equiv(1-4 X) \cdot\left((1-4 X)^{\frac{q-1}{2}}+2 X^{q}\right) \quad\left(\bmod X^{q+1}\right)
$$
so
$$
X \sum_{k=0}^{\infty} C_{k} X^{k}=\frac{1-\sqrt{1-4 X}}{2} \equiv \frac{1-(1-4 X)^{\frac{q+1}{2}}-2 X^{q}}{2} \quad\left(\bmod X^{q+1}\right)
$$
from which the claim follows.
Alternatively, one can also finish by integrating $(1-4 X)^{\frac{p-1}{2}}$, noting that the "constant of integration" is no longer a constant but rather a polynomial of the form $a+b X^{p}$.
|
{
"resource_path": "HarvardMIT/segmented/en-234-tournaments-2020-hmic-solutions.jsonl",
"problem_match": "\n4. [9]",
"solution_match": "\nSolution 3: "
}
|
f44ea284-eac7-5ece-84e5-ef94d69c2f53
| 610,191
|
A triangle and a circle are in the same plane. Show that the area of the intersection of the triangle and the circle is at most one third of the area of the triangle plus one half of the area of the circle.
|
Solution 1: (Ankan Bhattacharya ${ }^{1}$ Let $\triangle$ denote the triangle, o denote the circle, and $\triangle^{\prime}$ denote the reflection of the triangle in the center of the circle. Letting overline denote complement,
$$
\begin{aligned}
{[\triangle \cap \circ] } & \leq \frac{1}{3}[\triangle]+\frac{1}{2}[\mathrm{o}] \\
\Longleftrightarrow\left[\triangle \cap \triangle^{\prime} \cap \circ\right]+\left[\triangle \cap \overline{\Delta^{\prime}} \cap \circ\right] & \leq \frac{1}{3}[\triangle]+\frac{1}{2}\left[\left[\circ \cap \triangle \cap \triangle^{\prime}\right]+2\left[\circ \cap \Delta \cap \overline{\Delta^{\prime}}\right]+\left[\circ \cap \bar{\triangle} \cap \overline{\Delta^{\prime}}\right]\right] \\
\Longleftrightarrow \frac{1}{2}\left[\triangle \cap \triangle^{\prime} \cap \circ\right] & \leq \frac{1}{3}[\triangle]+\frac{1}{2}\left[\circ \cap \bar{\triangle} \cap \overline{\triangle^{\prime}}\right] \\
\Longleftrightarrow\left[\triangle \cap \triangle^{\prime} \cap \circ\right] & \leq \frac{2}{3}[\triangle]+\left[\circ \cap \bar{\triangle} \cap \overline{\Delta^{\prime}}\right] .
\end{aligned}
$$
Since $\triangle \cap \triangle^{\prime} \cap \circ$ is centrally symmetric, it's enough to show the following well-known lemma.
Lemma. A centrally symmetric region $\mathcal{R}$ of a triangle can have area at most $\frac{2}{3}$ that of the triangle. Let the triangle be $A B C$ with medial triangle $D E F$. We take two cases.
[^0]- Case 1. The center of symmetry is in one of the outer triangles, say $\triangle A E F$. Then the maximal possible $\mathcal{R}$ is a parallelogram with one vertex $A$ and two other vertices on $\overline{A B}$ and $\overline{A C}$. By enlargening the parallelogram, we may assume its fourth vertex lies on $\overline{B C}$. If this vertex divides $\overline{B C}$ into an $a: b$ ratio with $a+b=1$, then the fraction of the area taken up by the parallelogram is $1-a^{2}-b^{2} \leq \frac{1}{2}$.
- Case 2. The center of symmetry is in $\triangle D E F$. Then the maximal possible $\mathcal{R}$ is a centrally symmetric hexagon with two vertices on each side. Then there are three little triangles similar to $\triangle A B C$ on the hexagon; by equal lengths, the similarity ratios $a, b, c$ sum to 1 . Then the fraction of the area taken up by the hexagon is $1-a^{2}-b^{2}-c^{2} \leq \frac{2}{3}$.
We are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A triangle and a circle are in the same plane. Show that the area of the intersection of the triangle and the circle is at most one third of the area of the triangle plus one half of the area of the circle.
|
Solution 1: (Ankan Bhattacharya ${ }^{1}$ Let $\triangle$ denote the triangle, o denote the circle, and $\triangle^{\prime}$ denote the reflection of the triangle in the center of the circle. Letting overline denote complement,
$$
\begin{aligned}
{[\triangle \cap \circ] } & \leq \frac{1}{3}[\triangle]+\frac{1}{2}[\mathrm{o}] \\
\Longleftrightarrow\left[\triangle \cap \triangle^{\prime} \cap \circ\right]+\left[\triangle \cap \overline{\Delta^{\prime}} \cap \circ\right] & \leq \frac{1}{3}[\triangle]+\frac{1}{2}\left[\left[\circ \cap \triangle \cap \triangle^{\prime}\right]+2\left[\circ \cap \Delta \cap \overline{\Delta^{\prime}}\right]+\left[\circ \cap \bar{\triangle} \cap \overline{\Delta^{\prime}}\right]\right] \\
\Longleftrightarrow \frac{1}{2}\left[\triangle \cap \triangle^{\prime} \cap \circ\right] & \leq \frac{1}{3}[\triangle]+\frac{1}{2}\left[\circ \cap \bar{\triangle} \cap \overline{\triangle^{\prime}}\right] \\
\Longleftrightarrow\left[\triangle \cap \triangle^{\prime} \cap \circ\right] & \leq \frac{2}{3}[\triangle]+\left[\circ \cap \bar{\triangle} \cap \overline{\Delta^{\prime}}\right] .
\end{aligned}
$$
Since $\triangle \cap \triangle^{\prime} \cap \circ$ is centrally symmetric, it's enough to show the following well-known lemma.
Lemma. A centrally symmetric region $\mathcal{R}$ of a triangle can have area at most $\frac{2}{3}$ that of the triangle. Let the triangle be $A B C$ with medial triangle $D E F$. We take two cases.
[^0]- Case 1. The center of symmetry is in one of the outer triangles, say $\triangle A E F$. Then the maximal possible $\mathcal{R}$ is a parallelogram with one vertex $A$ and two other vertices on $\overline{A B}$ and $\overline{A C}$. By enlargening the parallelogram, we may assume its fourth vertex lies on $\overline{B C}$. If this vertex divides $\overline{B C}$ into an $a: b$ ratio with $a+b=1$, then the fraction of the area taken up by the parallelogram is $1-a^{2}-b^{2} \leq \frac{1}{2}$.
- Case 2. The center of symmetry is in $\triangle D E F$. Then the maximal possible $\mathcal{R}$ is a centrally symmetric hexagon with two vertices on each side. Then there are three little triangles similar to $\triangle A B C$ on the hexagon; by equal lengths, the similarity ratios $a, b, c$ sum to 1 . Then the fraction of the area taken up by the hexagon is $1-a^{2}-b^{2}-c^{2} \leq \frac{2}{3}$.
We are done.
|
{
"resource_path": "HarvardMIT/segmented/en-234-tournaments-2020-hmic-solutions.jsonl",
"problem_match": "\n5. [11]",
"solution_match": "\nProposed by: Krit Boonsiriseth\n"
}
|
9c03615a-b781-5b78-97f3-0a7d7e5811c7
| 610,192
|
A triangle and a circle are in the same plane. Show that the area of the intersection of the triangle and the circle is at most one third of the area of the triangle plus one half of the area of the circle.
|
It is also possible to approach this as an optimization problem. Fix a triangle $\triangle=A B C$ on the plane, vary the circle $\odot=\odot(O, r)$, and consider the objective function
$$
f(O, r):=[\triangle \cap \odot]-\frac{1}{2}[\odot] .
$$
By a compactness argument we can show that $f$ reaches a maximum, and at that maximum $\frac{\partial f}{\partial r}=0$ and $\nabla_{O} f=\overrightarrow{0}$ must simultaneously hold.
- We have
$$
\begin{aligned}
\frac{\partial}{\partial r} f(O, r) & =\frac{\partial}{\partial r}[\triangle \cap \odot]-\frac{1}{2} \frac{\partial}{\partial r}[\odot] \\
& =r \cdot((\text { total angle subtended by } A B \cap \odot, B C \cap \odot, C A \cap \odot \text { at point } O)-\pi),
\end{aligned}
$$
therefore
$$
\frac{\partial}{\partial r} f(O, r)=0 \Longleftrightarrow \text { the total angle subtended by the sides of } \triangle \text { inside } \odot \text { is } \pi
$$
- Let $\vec{n}_{a}, \vec{n}_{b}, \vec{n}_{c}$ denote the normal vectors of $B C, C A$ and $A B$. Define $k_{a}$ to be the length of $B C \cap \odot$, and define $k_{b}, k_{c}$ similarly.
$$
\begin{aligned}
\nabla_{O} f(O, r) & =\nabla_{O}[\triangle \cap \odot]-\frac{1}{2} \nabla_{O}[\odot] \\
& =\left(k_{a} \vec{n}_{a}+k_{b} \vec{n}_{b}+k_{c} \vec{n}_{c}\right)-\overrightarrow{0}
\end{aligned}
$$
It is easy to see that $a \vec{n}_{a}+b \vec{n}_{b}+c \vec{n}_{c}=\overrightarrow{0}$ is the only linear relation between $\vec{n}_{a}, \vec{n}_{b}, \vec{n}_{c}$, so
$$
\nabla_{O} f(O, r)=\overrightarrow{0} \Longleftrightarrow k_{a}: k_{b}: k_{c}=a: b: c
$$
Now suppose that $\odot(O, r)$ is chosen so that $\frac{\partial f}{\partial r}=0$ and $\nabla_{O} f=\overrightarrow{0}$, so the angle condition in (1) holds, and $\left(k_{a}, k_{b}, k_{c}\right)=k(a, b, c)$ for some $k$. There are two possible cases:
- Case 1. All vertices of $\triangle$ do not lie inside $\odot$. In this case $\odot$ intersects $\triangle$ at six points. The lines joining $O$ and these six points divide $\triangle \cap \odot$ into three sectors and three triangles. By the angle condition in (1), the three sectors have total area $\frac{1}{2}[\odot]$. The three triangles have total area $k[\triangle]$, and it suffices to show that $k \leqslant \frac{1}{3}$.
As the total angle of the triangles at $O$ is $\pi$, we may join two copies of each of the three triangles to form a cyclic hexagon. Therefore,
$$
\begin{aligned}
2 k \cdot[\triangle]= & 2 \cdot(\text { total area of three triangles }) \\
= & \text { area of cyclic hexagon with side lengths } k a, k b, k c, k a, k b, k c \\
\geqslant & \text { area of hexagon with side lengths } k a, k b, k c, k a, k b, k c \\
& \quad \text { created by six copies of a triangle with side lengths } k a, k b, k c \\
= & 6 k^{2} \cdot[\triangle]
\end{aligned}
$$
and our conclusion readily follows.
- Case 2. A vertex of $\triangle$ lies in the interior of $\odot$. WLOG let that vertex be $A$. Let $\odot$ intersect $A B$ at $X, A C$ at $Y$, and $B C$ at $D$ and $E$. From (2), $A X: A Y: D E=A B: A C: B C, X Y \| B C$ and $X Y=D E$, therefore $\square X Y E D$ is a rectangle. From (1), $\angle X O D+\angle Y O E=\pi$, so in fact $\square X Y E D$ is a square. Let $x$ be the side length of $\square X Y D E$, and let $h$ be the height of the altitude from $A$ to $B C$. Clearly $h>x$. As $A$ lies inside $\odot=(X Y D E), \angle B A C>\frac{3 \pi}{4}$, so $a>3 h>3 x$. Now we are done because $k=\frac{x}{a}<\frac{1}{3}$.
[^0]: ${ }^{1}$ https://artofproblemsolving.com/community/c6h2052367p14590886
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A triangle and a circle are in the same plane. Show that the area of the intersection of the triangle and the circle is at most one third of the area of the triangle plus one half of the area of the circle.
|
It is also possible to approach this as an optimization problem. Fix a triangle $\triangle=A B C$ on the plane, vary the circle $\odot=\odot(O, r)$, and consider the objective function
$$
f(O, r):=[\triangle \cap \odot]-\frac{1}{2}[\odot] .
$$
By a compactness argument we can show that $f$ reaches a maximum, and at that maximum $\frac{\partial f}{\partial r}=0$ and $\nabla_{O} f=\overrightarrow{0}$ must simultaneously hold.
- We have
$$
\begin{aligned}
\frac{\partial}{\partial r} f(O, r) & =\frac{\partial}{\partial r}[\triangle \cap \odot]-\frac{1}{2} \frac{\partial}{\partial r}[\odot] \\
& =r \cdot((\text { total angle subtended by } A B \cap \odot, B C \cap \odot, C A \cap \odot \text { at point } O)-\pi),
\end{aligned}
$$
therefore
$$
\frac{\partial}{\partial r} f(O, r)=0 \Longleftrightarrow \text { the total angle subtended by the sides of } \triangle \text { inside } \odot \text { is } \pi
$$
- Let $\vec{n}_{a}, \vec{n}_{b}, \vec{n}_{c}$ denote the normal vectors of $B C, C A$ and $A B$. Define $k_{a}$ to be the length of $B C \cap \odot$, and define $k_{b}, k_{c}$ similarly.
$$
\begin{aligned}
\nabla_{O} f(O, r) & =\nabla_{O}[\triangle \cap \odot]-\frac{1}{2} \nabla_{O}[\odot] \\
& =\left(k_{a} \vec{n}_{a}+k_{b} \vec{n}_{b}+k_{c} \vec{n}_{c}\right)-\overrightarrow{0}
\end{aligned}
$$
It is easy to see that $a \vec{n}_{a}+b \vec{n}_{b}+c \vec{n}_{c}=\overrightarrow{0}$ is the only linear relation between $\vec{n}_{a}, \vec{n}_{b}, \vec{n}_{c}$, so
$$
\nabla_{O} f(O, r)=\overrightarrow{0} \Longleftrightarrow k_{a}: k_{b}: k_{c}=a: b: c
$$
Now suppose that $\odot(O, r)$ is chosen so that $\frac{\partial f}{\partial r}=0$ and $\nabla_{O} f=\overrightarrow{0}$, so the angle condition in (1) holds, and $\left(k_{a}, k_{b}, k_{c}\right)=k(a, b, c)$ for some $k$. There are two possible cases:
- Case 1. All vertices of $\triangle$ do not lie inside $\odot$. In this case $\odot$ intersects $\triangle$ at six points. The lines joining $O$ and these six points divide $\triangle \cap \odot$ into three sectors and three triangles. By the angle condition in (1), the three sectors have total area $\frac{1}{2}[\odot]$. The three triangles have total area $k[\triangle]$, and it suffices to show that $k \leqslant \frac{1}{3}$.
As the total angle of the triangles at $O$ is $\pi$, we may join two copies of each of the three triangles to form a cyclic hexagon. Therefore,
$$
\begin{aligned}
2 k \cdot[\triangle]= & 2 \cdot(\text { total area of three triangles }) \\
= & \text { area of cyclic hexagon with side lengths } k a, k b, k c, k a, k b, k c \\
\geqslant & \text { area of hexagon with side lengths } k a, k b, k c, k a, k b, k c \\
& \quad \text { created by six copies of a triangle with side lengths } k a, k b, k c \\
= & 6 k^{2} \cdot[\triangle]
\end{aligned}
$$
and our conclusion readily follows.
- Case 2. A vertex of $\triangle$ lies in the interior of $\odot$. WLOG let that vertex be $A$. Let $\odot$ intersect $A B$ at $X, A C$ at $Y$, and $B C$ at $D$ and $E$. From (2), $A X: A Y: D E=A B: A C: B C, X Y \| B C$ and $X Y=D E$, therefore $\square X Y E D$ is a rectangle. From (1), $\angle X O D+\angle Y O E=\pi$, so in fact $\square X Y E D$ is a square. Let $x$ be the side length of $\square X Y D E$, and let $h$ be the height of the altitude from $A$ to $B C$. Clearly $h>x$. As $A$ lies inside $\odot=(X Y D E), \angle B A C>\frac{3 \pi}{4}$, so $a>3 h>3 x$. Now we are done because $k=\frac{x}{a}<\frac{1}{3}$.
[^0]: ${ }^{1}$ https://artofproblemsolving.com/community/c6h2052367p14590886
|
{
"resource_path": "HarvardMIT/segmented/en-234-tournaments-2020-hmic-solutions.jsonl",
"problem_match": "\n5. [11]",
"solution_match": "\nSolution 2: "
}
|
9c03615a-b781-5b78-97f3-0a7d7e5811c7
| 610,192
|
Let $A B C$ be a right triangle with $\angle A=90^{\circ}$. A circle $\omega$ centered on $B C$ is tangent to $A B$ at $D$ and $A C$ at $E$. Let $F$ and $G$ be the intersections of $\omega$ and $B C$ so that $F$ lies between $B$ and $G$. If lines $D G$ and $E F$ intersect at $X$, show that $A X=A D$.
|
Solution 1: In all solutions, let $O$ be the center of $\omega$. Then $\angle D O E=90^{\circ}$, so $\angle D F E=45^{\circ}$, so $\angle D X E=135^{\circ}$. Let $\Gamma$ be the circle centered at $A$ with radius $A D=A E$, and let $X^{\prime}=\overrightarrow{A X} \cap \Gamma$. Then $\angle D X E=\angle D X^{\prime} E=135^{\circ}$, so $X=X^{\prime}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a right triangle with $\angle A=90^{\circ}$. A circle $\omega$ centered on $B C$ is tangent to $A B$ at $D$ and $A C$ at $E$. Let $F$ and $G$ be the intersections of $\omega$ and $B C$ so that $F$ lies between $B$ and $G$. If lines $D G$ and $E F$ intersect at $X$, show that $A X=A D$.
|
Solution 1: In all solutions, let $O$ be the center of $\omega$. Then $\angle D O E=90^{\circ}$, so $\angle D F E=45^{\circ}$, so $\angle D X E=135^{\circ}$. Let $\Gamma$ be the circle centered at $A$ with radius $A D=A E$, and let $X^{\prime}=\overrightarrow{A X} \cap \Gamma$. Then $\angle D X E=\angle D X^{\prime} E=135^{\circ}$, so $X=X^{\prime}$.
|
{
"resource_path": "HarvardMIT/segmented/en-242-2021-feb-team-solutions.jsonl",
"problem_match": "\n2. [50]",
"solution_match": "\nProposed by: Krit Boonsiriseth\n"
}
|
d21bd1d0-a64f-559d-b5d5-1ebc0a2d35ea
| 610,325
|
Let $A B C$ be a right triangle with $\angle A=90^{\circ}$. A circle $\omega$ centered on $B C$ is tangent to $A B$ at $D$ and $A C$ at $E$. Let $F$ and $G$ be the intersections of $\omega$ and $B C$ so that $F$ lies between $B$ and $G$. If lines $D G$ and $E F$ intersect at $X$, show that $A X=A D$.
|
We use complex numbers, with ( $F D E G$ ) being the unit circle, and $d=-1, e=-i$. As $F G$ is a diameter of the unit circle, we have $g=-f$. We have $a=-1-i$, from either intersecting the tangents to the unit circle at $D$ and $E$ or noting that $A D O E$ is a square.
Now, intersecting the chords $D G$ and $E F$, we obtain
$$
x=\frac{d g(e+f)-e f(d+g)}{d g-e f}=\frac{f(i+f)+i f(1-f)}{f+i f}=\frac{f-i-i-i f}{1+i}=-1-i+f \cdot \frac{1-i}{1+i} .
$$
So,
$$
|x-a|=\left|f \cdot \frac{1-i}{1+i}\right|=1 \cdot \frac{\sqrt{2}}{\sqrt{2}}=1
$$
So $A X$ and $A D$ have the same length (1 unit), as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a right triangle with $\angle A=90^{\circ}$. A circle $\omega$ centered on $B C$ is tangent to $A B$ at $D$ and $A C$ at $E$. Let $F$ and $G$ be the intersections of $\omega$ and $B C$ so that $F$ lies between $B$ and $G$. If lines $D G$ and $E F$ intersect at $X$, show that $A X=A D$.
|
We use complex numbers, with ( $F D E G$ ) being the unit circle, and $d=-1, e=-i$. As $F G$ is a diameter of the unit circle, we have $g=-f$. We have $a=-1-i$, from either intersecting the tangents to the unit circle at $D$ and $E$ or noting that $A D O E$ is a square.
Now, intersecting the chords $D G$ and $E F$, we obtain
$$
x=\frac{d g(e+f)-e f(d+g)}{d g-e f}=\frac{f(i+f)+i f(1-f)}{f+i f}=\frac{f-i-i-i f}{1+i}=-1-i+f \cdot \frac{1-i}{1+i} .
$$
So,
$$
|x-a|=\left|f \cdot \frac{1-i}{1+i}\right|=1 \cdot \frac{\sqrt{2}}{\sqrt{2}}=1
$$
So $A X$ and $A D$ have the same length (1 unit), as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-242-2021-feb-team-solutions.jsonl",
"problem_match": "\n2. [50]",
"solution_match": "\nSolution 5: "
}
|
d21bd1d0-a64f-559d-b5d5-1ebc0a2d35ea
| 610,325
|
Let $m$ be a positive integer. Show that there exists a positive integer $n$ such that each of the $2 m+1$ integers
$$
2^{n}-m, 2^{n}-(m-1), \ldots, 2^{n}+(m-1), 2^{n}+m
$$
is positive and composite.
|
Solution: Let $P$ be the set of prime divisors of the $2 m+1$ numbers
$$
2^{m+1}-m, 2^{m+1}-m+1, \ldots, 2^{m+1}+m
$$
We claim that
$$
n=m+1+\prod_{p \in P}(p-1)
$$
works. To check this, let $k$ be any integer with $|k| \leq m$. We can take some prime $q \mid 2^{m+1}+k$, as $2^{m+1}+k \geq 2^{m+1}-m \geq 3$. Let $\prod_{p \in P}(p-1)=(q-1) \alpha_{q}$. Then, applying Fermat's little theorem, we have
$$
2^{n} \equiv 2^{m+1} \cdot\left(2^{q-1}\right)^{\alpha_{q}} \equiv 2^{m+1} \equiv-k \quad(\bmod q)
$$
Thus, $2^{n}+k$ is divisible by $q$ and is bigger than $q$, so it is positive and composite. This works for each of the required $k$, so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $m$ be a positive integer. Show that there exists a positive integer $n$ such that each of the $2 m+1$ integers
$$
2^{n}-m, 2^{n}-(m-1), \ldots, 2^{n}+(m-1), 2^{n}+m
$$
is positive and composite.
|
Solution: Let $P$ be the set of prime divisors of the $2 m+1$ numbers
$$
2^{m+1}-m, 2^{m+1}-m+1, \ldots, 2^{m+1}+m
$$
We claim that
$$
n=m+1+\prod_{p \in P}(p-1)
$$
works. To check this, let $k$ be any integer with $|k| \leq m$. We can take some prime $q \mid 2^{m+1}+k$, as $2^{m+1}+k \geq 2^{m+1}-m \geq 3$. Let $\prod_{p \in P}(p-1)=(q-1) \alpha_{q}$. Then, applying Fermat's little theorem, we have
$$
2^{n} \equiv 2^{m+1} \cdot\left(2^{q-1}\right)^{\alpha_{q}} \equiv 2^{m+1} \equiv-k \quad(\bmod q)
$$
Thus, $2^{n}+k$ is divisible by $q$ and is bigger than $q$, so it is positive and composite. This works for each of the required $k$, so we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-242-2021-feb-team-solutions.jsonl",
"problem_match": "\n3. [50]",
"solution_match": "\nProposed by: Michael Ren\n"
}
|
a9eb5b49-9cb4-5587-a8af-9d873e741557
| 610,326
|
Let $f(x)=x^{2}+x+1$. Determine, with proof, all positive integers $n$ such that $f(k)$ divides $f(n)$ whenever $k$ is a positive divisor of $n$.
|
The answer is $n$ can be 1 , a prime that is $1 \bmod 3$, or the square of any prime except 3 . It is easy to verify that all of these work.
First note that $n$ must be $1 \bmod 3$ since 1 divides $n$ implies $f(1)$ divides $f(n)$.
Next, suppose for sake of contradiction that $n=a b$, with $a>b>1$. We are given that $f(a)$ divides $f(n)$, which means $f(a)$ divides $f(n)-f(a)$. We can write this as
$$
a^{2}+a+1 \mid n^{2}+n-a^{2}-a=(n-a)(n+a+1)
$$
Since we are working $\bmod a^{2}+a+1$, we can replace $a+1$ with $-a^{2}$, so we have
$$
a^{2}+a+1 \mid(n-a)\left(n-a^{2}\right)=a^{2}(b-1)(b-a)
$$
However, $a^{2}+a+1$ cannot share any factors with $a$, and $0<|(b-1)(b-a)|<a^{2}+a+1$, which is a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f(x)=x^{2}+x+1$. Determine, with proof, all positive integers $n$ such that $f(k)$ divides $f(n)$ whenever $k$ is a positive divisor of $n$.
|
The answer is $n$ can be 1 , a prime that is $1 \bmod 3$, or the square of any prime except 3 . It is easy to verify that all of these work.
First note that $n$ must be $1 \bmod 3$ since 1 divides $n$ implies $f(1)$ divides $f(n)$.
Next, suppose for sake of contradiction that $n=a b$, with $a>b>1$. We are given that $f(a)$ divides $f(n)$, which means $f(a)$ divides $f(n)-f(a)$. We can write this as
$$
a^{2}+a+1 \mid n^{2}+n-a^{2}-a=(n-a)(n+a+1)
$$
Since we are working $\bmod a^{2}+a+1$, we can replace $a+1$ with $-a^{2}$, so we have
$$
a^{2}+a+1 \mid(n-a)\left(n-a^{2}\right)=a^{2}(b-1)(b-a)
$$
However, $a^{2}+a+1$ cannot share any factors with $a$, and $0<|(b-1)(b-a)|<a^{2}+a+1$, which is a contradiction.
|
{
"resource_path": "HarvardMIT/segmented/en-242-2021-feb-team-solutions.jsonl",
"problem_match": "\n6. [70]",
"solution_match": "\nSolution: "
}
|
1bdd643d-d02a-5949-b323-a9c2cee9f01b
| 610,328
|
In triangle $A B C$, let $M$ be the midpoint of $B C$ and $D$ be a point on segment $A M$. Distinct points $Y$ and $Z$ are chosen on rays $\overrightarrow{C A}$ and $\overrightarrow{B A}$, respectively, such that $\angle D Y C=\angle D C B$ and $\angle D B C=\angle D Z B$. Prove that the circumcircle of $\triangle D Y Z$ is tangent to the circumcircle of $\triangle D B C$.
|
Solution 1: We first note that the circumcircles of $D B Z$ and $Y D C$ are tangent to $B C$ from our angle criteria. By power of a point, we obtain that $M$ lies on the radical axis of the two circles and clearly $D$ does as well. Therefore, we find that $A$ lies on the radical axis so $A Y \cdot A C=A B \cdot A Z$ implying that $B Y Z C$ is a cyclic quadrilateral.
Next, by Reim's Theorem on $(B Y Z C)$ and $(D Y Z)$, we get that $(D Y Z)$ intersects $A B, A C$ at $B^{\prime}, C^{\prime}$ where $B C, B^{\prime} C^{\prime}$ are parallel. Then a negative homothety maps $B$ to $B^{\prime}$ and $C$ to $C^{\prime}$, so $(D B C)$ gets mapped to $\left(D B^{\prime} C^{\prime}\right)$, and we have tangent circles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, let $M$ be the midpoint of $B C$ and $D$ be a point on segment $A M$. Distinct points $Y$ and $Z$ are chosen on rays $\overrightarrow{C A}$ and $\overrightarrow{B A}$, respectively, such that $\angle D Y C=\angle D C B$ and $\angle D B C=\angle D Z B$. Prove that the circumcircle of $\triangle D Y Z$ is tangent to the circumcircle of $\triangle D B C$.
|
Solution 1: We first note that the circumcircles of $D B Z$ and $Y D C$ are tangent to $B C$ from our angle criteria. By power of a point, we obtain that $M$ lies on the radical axis of the two circles and clearly $D$ does as well. Therefore, we find that $A$ lies on the radical axis so $A Y \cdot A C=A B \cdot A Z$ implying that $B Y Z C$ is a cyclic quadrilateral.
Next, by Reim's Theorem on $(B Y Z C)$ and $(D Y Z)$, we get that $(D Y Z)$ intersects $A B, A C$ at $B^{\prime}, C^{\prime}$ where $B C, B^{\prime} C^{\prime}$ are parallel. Then a negative homothety maps $B$ to $B^{\prime}$ and $C$ to $C^{\prime}$, so $(D B C)$ gets mapped to $\left(D B^{\prime} C^{\prime}\right)$, and we have tangent circles.
|
{
"resource_path": "HarvardMIT/segmented/en-242-2021-feb-team-solutions.jsonl",
"problem_match": "\n7. [70]",
"solution_match": "\n## Proposed by: Joseph Heerens\n\n"
}
|
f9c2d892-0eb4-56dc-912b-11c7fe340784
| 610,329
|
In triangle $A B C$, let $M$ be the midpoint of $B C$ and $D$ be a point on segment $A M$. Distinct points $Y$ and $Z$ are chosen on rays $\overrightarrow{C A}$ and $\overrightarrow{B A}$, respectively, such that $\angle D Y C=\angle D C B$ and $\angle D B C=\angle D Z B$. Prove that the circumcircle of $\triangle D Y Z$ is tangent to the circumcircle of $\triangle D B C$.
|
Let $(D Y Z)$ intersect $A B$ and $A C$ at $B^{\prime}$ and $C^{\prime}$, respectively. We see that $\measuredangle Y C^{\prime} B^{\prime}=$ $\measuredangle Y Z B^{\prime}=\measuredangle Y Z B=\measuredangle Y C B$. Thus, $B C \| B^{\prime} C^{\prime}$. This means that there exists a negative homothety taking $B$ to $B^{\prime}$ and $C$ to $C^{\prime}$ which will map $(D B C)$ to $\left(D B^{\prime} C^{\prime}\right)$ which is also $(D Y Z)$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, let $M$ be the midpoint of $B C$ and $D$ be a point on segment $A M$. Distinct points $Y$ and $Z$ are chosen on rays $\overrightarrow{C A}$ and $\overrightarrow{B A}$, respectively, such that $\angle D Y C=\angle D C B$ and $\angle D B C=\angle D Z B$. Prove that the circumcircle of $\triangle D Y Z$ is tangent to the circumcircle of $\triangle D B C$.
|
Let $(D Y Z)$ intersect $A B$ and $A C$ at $B^{\prime}$ and $C^{\prime}$, respectively. We see that $\measuredangle Y C^{\prime} B^{\prime}=$ $\measuredangle Y Z B^{\prime}=\measuredangle Y Z B=\measuredangle Y C B$. Thus, $B C \| B^{\prime} C^{\prime}$. This means that there exists a negative homothety taking $B$ to $B^{\prime}$ and $C$ to $C^{\prime}$ which will map $(D B C)$ to $\left(D B^{\prime} C^{\prime}\right)$ which is also $(D Y Z)$.
|
{
"resource_path": "HarvardMIT/segmented/en-242-2021-feb-team-solutions.jsonl",
"problem_match": "\n7. [70]",
"solution_match": "\nSolution 2: "
}
|
f9c2d892-0eb4-56dc-912b-11c7fe340784
| 610,329
|
Let scalene triangle $A B C$ have circumcenter $O$ and incenter $I$. Its incircle $\omega$ is tangent to sides $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let $P$ be the foot of the altitude from $D$ to $E F$, and let line $D P$ intersect $\omega$ again at $Q \neq D$. The line $O I$ intersects the altitude from $A$ to $B C$ at $T$. Given that $O I \| B C$, show that $P Q=P T$.
|
Solution: Let $H$ be the orthocenter of $\triangle D E F$. We first claim that $O, I, H$ are collinear. We present two proofs.
Proof 1. Invert about $\omega$. Circle $(A B C)$ inverts to a circle with center on $O I$, but $A, B, C$ invert to the midpoints of $E F, F D, D E$, respectively, so the nine-point center of $\triangle D E F$ is on $O I$. As this center is the midpoint of $I H$, we get that $H, I, O$ are collinear.
Proof 2. Let $Q_{A}, Q_{B}, Q_{C}$ be the second intersections of the $D-, E-$, and $F$ - altitudes, respectively, in $\triangle D E F$ with $\omega$. We claim $\Delta Q_{A} Q_{B} Q_{C}$ is homothetic with $\triangle A B C$. Indeed, as $Q_{B}$ is the reflection of $H$ over $D F$ and $Q_{C}$ is the reflection of $H$ over $D E, D Q_{B}=D Q_{C}$, so the perpendicular bisector of $Q_{B} Q_{C}$ is line $I D$. As $I D \perp B C, Q_{B} Q_{C} \| B C$, whence the homothety follows. This homothety takes the incircle to the circumcircle, so it is centered on line $O I$. However, it also takes the incenter $H$ of $Q_{A} Q_{B} Q_{C}$ to the incenter $I$ of $A B C$, so it is centered on line $I H$. So, $O, I, H$ are collinear.
As $P$ is the midpoint of $Q H$, it suffices to show that $P$ is on the circle with diameter $Q H$, or that $\angle Q T H=90^{\circ}$. As $A T \perp \overline{T H}=\overline{I O}$, it suffices to show that $Q$ is on line $A T$. We also present two proofs of this.
Proof 1. Let $D^{\prime}$ be the antipode of $D$, and let $A D^{\prime}$ intersect $B C$ at $X$. As $X$ is the $A$-extouch point, the midpoint $M$ of $D X$ is also the midpoint of $B C$. We have
$$
\frac{O M}{M X}=\frac{I D}{\frac{D X}{2}}=\frac{D D^{\prime}}{D X}
$$
and $\angle O M X=\angle D^{\prime} D X=90^{\circ}$, so $D^{\prime}, O, X$ are collinear, so $D^{\prime}$ is on line $A O$. As $Q D^{\prime} \| E F, A Q$ and $A D^{\prime}$ are isogonal in $\angle B A C$, so $A Q$ and $A O$ are isogonal, which means $Q$ is on the $A$-altitude, finishing the proof.
Proof 2. Let $\Gamma$ denote the circumcircle of $\triangle A B C$, and let $M$ be the midpoint of arc $B C$ on $\Gamma$ not containing $A$.
Lemma. The intersection $T^{\prime}$ of $M D$ and the $A$-altitude to $B C$ is on the line through $I$ parallel to $B C$.
Proof. Let $D^{\prime}=M A \cap B C$. As $\angle D^{\prime} B M=\angle C B M=\angle C A M=\angle M A B, \triangle D^{\prime} B M \sim \triangle B A M$, and
$$
M I^{2}=M B^{2}=M D^{\prime} \cdot M A
$$
Since $A T^{\prime} \| I D$, we have
$$
\frac{M T^{\prime}}{M D}=\frac{M A}{M I}=\frac{M I}{M D^{\prime}}
$$
so $I T^{\prime} \| D D^{\prime}$, finishing the proof.
By the above lemma, $T$ is on $M D$. Consider a homothety centered at $T$ that takes $D$ to $M$. It takes $\omega$ to a circle centered on line $I T$ that is tangent to $\Gamma$ at $M$; since $O$ is on line $I T$ this circle must be $\Gamma$ itself. So, $T$ is the exsimilicenter of $\Gamma$ and $\omega$. By Proof 2 above, $T$ is the center of the homothety which sends $Q_{A} Q_{B} Q_{C}$ to $A B C$, so $T, Q=Q_{A}$, and $A$ are collinear, finishing the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let scalene triangle $A B C$ have circumcenter $O$ and incenter $I$. Its incircle $\omega$ is tangent to sides $B C, C A$, and $A B$ at $D, E$, and $F$, respectively. Let $P$ be the foot of the altitude from $D$ to $E F$, and let line $D P$ intersect $\omega$ again at $Q \neq D$. The line $O I$ intersects the altitude from $A$ to $B C$ at $T$. Given that $O I \| B C$, show that $P Q=P T$.
|
Solution: Let $H$ be the orthocenter of $\triangle D E F$. We first claim that $O, I, H$ are collinear. We present two proofs.
Proof 1. Invert about $\omega$. Circle $(A B C)$ inverts to a circle with center on $O I$, but $A, B, C$ invert to the midpoints of $E F, F D, D E$, respectively, so the nine-point center of $\triangle D E F$ is on $O I$. As this center is the midpoint of $I H$, we get that $H, I, O$ are collinear.
Proof 2. Let $Q_{A}, Q_{B}, Q_{C}$ be the second intersections of the $D-, E-$, and $F$ - altitudes, respectively, in $\triangle D E F$ with $\omega$. We claim $\Delta Q_{A} Q_{B} Q_{C}$ is homothetic with $\triangle A B C$. Indeed, as $Q_{B}$ is the reflection of $H$ over $D F$ and $Q_{C}$ is the reflection of $H$ over $D E, D Q_{B}=D Q_{C}$, so the perpendicular bisector of $Q_{B} Q_{C}$ is line $I D$. As $I D \perp B C, Q_{B} Q_{C} \| B C$, whence the homothety follows. This homothety takes the incircle to the circumcircle, so it is centered on line $O I$. However, it also takes the incenter $H$ of $Q_{A} Q_{B} Q_{C}$ to the incenter $I$ of $A B C$, so it is centered on line $I H$. So, $O, I, H$ are collinear.
As $P$ is the midpoint of $Q H$, it suffices to show that $P$ is on the circle with diameter $Q H$, or that $\angle Q T H=90^{\circ}$. As $A T \perp \overline{T H}=\overline{I O}$, it suffices to show that $Q$ is on line $A T$. We also present two proofs of this.
Proof 1. Let $D^{\prime}$ be the antipode of $D$, and let $A D^{\prime}$ intersect $B C$ at $X$. As $X$ is the $A$-extouch point, the midpoint $M$ of $D X$ is also the midpoint of $B C$. We have
$$
\frac{O M}{M X}=\frac{I D}{\frac{D X}{2}}=\frac{D D^{\prime}}{D X}
$$
and $\angle O M X=\angle D^{\prime} D X=90^{\circ}$, so $D^{\prime}, O, X$ are collinear, so $D^{\prime}$ is on line $A O$. As $Q D^{\prime} \| E F, A Q$ and $A D^{\prime}$ are isogonal in $\angle B A C$, so $A Q$ and $A O$ are isogonal, which means $Q$ is on the $A$-altitude, finishing the proof.
Proof 2. Let $\Gamma$ denote the circumcircle of $\triangle A B C$, and let $M$ be the midpoint of arc $B C$ on $\Gamma$ not containing $A$.
Lemma. The intersection $T^{\prime}$ of $M D$ and the $A$-altitude to $B C$ is on the line through $I$ parallel to $B C$.
Proof. Let $D^{\prime}=M A \cap B C$. As $\angle D^{\prime} B M=\angle C B M=\angle C A M=\angle M A B, \triangle D^{\prime} B M \sim \triangle B A M$, and
$$
M I^{2}=M B^{2}=M D^{\prime} \cdot M A
$$
Since $A T^{\prime} \| I D$, we have
$$
\frac{M T^{\prime}}{M D}=\frac{M A}{M I}=\frac{M I}{M D^{\prime}}
$$
so $I T^{\prime} \| D D^{\prime}$, finishing the proof.
By the above lemma, $T$ is on $M D$. Consider a homothety centered at $T$ that takes $D$ to $M$. It takes $\omega$ to a circle centered on line $I T$ that is tangent to $\Gamma$ at $M$; since $O$ is on line $I T$ this circle must be $\Gamma$ itself. So, $T$ is the exsimilicenter of $\Gamma$ and $\omega$. By Proof 2 above, $T$ is the center of the homothety which sends $Q_{A} Q_{B} Q_{C}$ to $A B C$, so $T, Q=Q_{A}$, and $A$ are collinear, finishing the proof.
|
{
"resource_path": "HarvardMIT/segmented/en-242-2021-feb-team-solutions.jsonl",
"problem_match": "\n9. [90]",
"solution_match": "\nProposed by: Carl Schildkraut, Milan Haiman\n"
}
|
9d73a855-eede-57aa-9c80-5bbe57109b38
| 610,331
|
Let $A$ be a set of $n \geq 2$ positive integers, and let $f(x)=\sum_{a \in A} x^{a}$. Prove that there exists a complex number $z$ with $|z|=1$ and $|f(z)|=\sqrt{n-2}$.
|
Solution 1: Let $A$ consist of the numbers $a_{1}<a_{2}<\cdots<a_{n}$. Let $d=a_{n}-a_{1}$. Then, note that if we choose $z$ uniformly at random from the set $X=\left\{x: x^{d}=-1\right\}$, then we have
$$
f(z)=\left(z^{a_{1}}+z^{a_{n}}\right)+\sum_{i=2}^{n-1} z^{a_{i}}=\sum_{i=2}^{n-1} z^{a_{i}}
$$
Then, note that
$$
|f(z)|^{2}=f(z) f(\bar{z})=\left(\sum_{i=2}^{n-1} z^{a_{i}}\right)\left(\sum_{i=2}^{n-1} \bar{z}^{a_{i}}\right)=n-2+\sum_{i \neq j, 2 \leq i, j \leq n-1} z^{a_{i}-a_{j}}
$$
However, since $0<\left|a_{i}-a_{j}\right|<d$, for all $2 \leq i, j \leq n-1$ with $i \neq j$, we know that the average value of $z^{a_{i}-a_{j}}$ over all $z \in X$ is just 0 . Thus, the average value of $|f(z)|^{2}$ is $n-2$, and thus, there exists $z_{1}$ and $z_{2}$ on the unit circle such that $\left|f\left(z_{1}\right)\right|^{2} \leq n-2 \leq\left|f\left(z_{2}\right)\right|^{2}$, and thus by Intermediate Value Theorem, there exists $z$ on the unit circle such that $|f(z)|^{2}=n-2$, so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $A$ be a set of $n \geq 2$ positive integers, and let $f(x)=\sum_{a \in A} x^{a}$. Prove that there exists a complex number $z$ with $|z|=1$ and $|f(z)|=\sqrt{n-2}$.
|
Solution 1: Let $A$ consist of the numbers $a_{1}<a_{2}<\cdots<a_{n}$. Let $d=a_{n}-a_{1}$. Then, note that if we choose $z$ uniformly at random from the set $X=\left\{x: x^{d}=-1\right\}$, then we have
$$
f(z)=\left(z^{a_{1}}+z^{a_{n}}\right)+\sum_{i=2}^{n-1} z^{a_{i}}=\sum_{i=2}^{n-1} z^{a_{i}}
$$
Then, note that
$$
|f(z)|^{2}=f(z) f(\bar{z})=\left(\sum_{i=2}^{n-1} z^{a_{i}}\right)\left(\sum_{i=2}^{n-1} \bar{z}^{a_{i}}\right)=n-2+\sum_{i \neq j, 2 \leq i, j \leq n-1} z^{a_{i}-a_{j}}
$$
However, since $0<\left|a_{i}-a_{j}\right|<d$, for all $2 \leq i, j \leq n-1$ with $i \neq j$, we know that the average value of $z^{a_{i}-a_{j}}$ over all $z \in X$ is just 0 . Thus, the average value of $|f(z)|^{2}$ is $n-2$, and thus, there exists $z_{1}$ and $z_{2}$ on the unit circle such that $\left|f\left(z_{1}\right)\right|^{2} \leq n-2 \leq\left|f\left(z_{2}\right)\right|^{2}$, and thus by Intermediate Value Theorem, there exists $z$ on the unit circle such that $|f(z)|^{2}=n-2$, so we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-244-tournaments-2021-hmic-solutions.jsonl",
"problem_match": "\n3. [8]",
"solution_match": "\nProposed by: Milan Haiman\n"
}
|
32360641-f8a5-5c7a-899d-2e6f7b432610
| 610,335
|
Let $A$ be a set of $n \geq 2$ positive integers, and let $f(x)=\sum_{a \in A} x^{a}$. Prove that there exists a complex number $z$ with $|z|=1$ and $|f(z)|=\sqrt{n-2}$.
|
Note that we have
$$
|f(x)|^{2}=f(x) f(\bar{x})=\left(\sum_{a \in A} x^{a}\right)\left(\sum_{b \in A} \bar{x}^{b}\right)=n+\sum_{a \neq b} x^{a-b}
$$
Let $t=1+\max _{a \neq b, a, b \in A} v_{2}(a-b)$. Let $z$ be chosen uniformly at random from $X=\left\{x: x^{2^{t}}=1, x^{2^{t-1}}=\right.$ $-1\}$, the set of all primitive $2^{t}$ th roots of unity. Note that for all distinct $a, b \in A$, we know that the expected value of $z^{a-b}$ is 1 if $v_{2}(t) \geq t,-1$ if $v_{2}(a-b)=t-1$, and 0 if $v_{2}(a-b)<t-1$. However, we know that there exists distinct $\hat{a}, \hat{b} \in A$ such that $v_{2}(\hat{a}-\hat{b})=t-1$, so the expected values of $z^{\hat{a}-\hat{b}}$ and $z^{\hat{b}-\hat{a}}$ are both -1 . Also, we know that the expected value of every other term in this sum $\sum_{a \neq b} x^{a-b}$ is less than or equal to 0 . Thus, the expected value of $|f(z)|^{2}$ is at most $n-2$. Additionally, since $|f(1)|^{2}=n^{2}$, and then finish with Intermediate Value Theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $A$ be a set of $n \geq 2$ positive integers, and let $f(x)=\sum_{a \in A} x^{a}$. Prove that there exists a complex number $z$ with $|z|=1$ and $|f(z)|=\sqrt{n-2}$.
|
Note that we have
$$
|f(x)|^{2}=f(x) f(\bar{x})=\left(\sum_{a \in A} x^{a}\right)\left(\sum_{b \in A} \bar{x}^{b}\right)=n+\sum_{a \neq b} x^{a-b}
$$
Let $t=1+\max _{a \neq b, a, b \in A} v_{2}(a-b)$. Let $z$ be chosen uniformly at random from $X=\left\{x: x^{2^{t}}=1, x^{2^{t-1}}=\right.$ $-1\}$, the set of all primitive $2^{t}$ th roots of unity. Note that for all distinct $a, b \in A$, we know that the expected value of $z^{a-b}$ is 1 if $v_{2}(t) \geq t,-1$ if $v_{2}(a-b)=t-1$, and 0 if $v_{2}(a-b)<t-1$. However, we know that there exists distinct $\hat{a}, \hat{b} \in A$ such that $v_{2}(\hat{a}-\hat{b})=t-1$, so the expected values of $z^{\hat{a}-\hat{b}}$ and $z^{\hat{b}-\hat{a}}$ are both -1 . Also, we know that the expected value of every other term in this sum $\sum_{a \neq b} x^{a-b}$ is less than or equal to 0 . Thus, the expected value of $|f(z)|^{2}$ is at most $n-2$. Additionally, since $|f(1)|^{2}=n^{2}$, and then finish with Intermediate Value Theorem.
|
{
"resource_path": "HarvardMIT/segmented/en-244-tournaments-2021-hmic-solutions.jsonl",
"problem_match": "\n3. [8]",
"solution_match": "\nSolution 2: "
}
|
32360641-f8a5-5c7a-899d-2e6f7b432610
| 610,335
|
Suppose $n \geq 3$ is a positive integer. Let $a_{1}<a_{2}<\cdots<a_{n}$ be an increasing sequence of positive real numbers, and let $a_{n+1}=a_{1}$. Prove that
$$
\sum_{k=1}^{n} \frac{a_{k}}{a_{k+1}}>\sum_{k=1}^{n} \frac{a_{k+1}}{a_{k}} .
$$
|
Solution 1: We will use induction. The base case is $n=3$. In this case, we want to show that
$$
\frac{a_{1}}{a_{2}}+\frac{a_{2}}{a_{3}}+\frac{a_{3}}{a_{1}}>\frac{a_{2}}{a_{1}}+\frac{a_{3}}{a_{2}}+\frac{a_{1}}{a_{3}} .
$$
Equivalently, we want to show
$$
\begin{aligned}
a_{1}^{2} a_{3}+a_{2}^{2} a_{1}+a_{3}^{2} a_{2}>a_{1}^{2} a_{2}+a_{2}^{2} a_{3}+a_{3}^{2} a_{1} & \Longleftrightarrow a_{1}^{2}\left(a_{3}-a_{2}\right)+a_{3}^{2}\left(a_{2}-a_{1}\right)>a_{2}^{2}\left(a_{3}-a_{1}\right) \\
& \Longleftrightarrow\left(a_{3}^{2}-a_{2}^{2}\right)\left(a_{2}-a_{1}\right)>\left(a_{2}^{2}-a_{1}^{2}\right)\left(a_{3}-a_{2}\right) \\
& \Longleftrightarrow a_{3}+a_{2}>a_{2}+a_{1},
\end{aligned}
$$
which is true.
Now assume the claim is true for $n \geq 3$. Then, we have that
$$
\frac{a_{1}}{a_{3}}+\frac{a_{3}}{a_{4}}+\cdots+\frac{a_{n}}{a_{n+1}}+\frac{a_{n+1}}{a_{1}}>\frac{a_{3}}{a_{1}}+\frac{a_{4}}{a_{3}}+\cdots+\frac{a_{n+1}}{a_{n}}+\frac{a_{1}}{a_{n+1}} .
$$
We also have that
$$
\frac{a_{1}}{a_{2}}+\frac{a_{2}}{a_{3}}+\frac{a_{3}}{a_{1}}>\frac{a_{2}}{a_{1}}+\frac{a_{3}}{a_{2}}+\frac{a_{3}}{a_{1}} .
$$
Adding the two inequalities and simplifying gives the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Suppose $n \geq 3$ is a positive integer. Let $a_{1}<a_{2}<\cdots<a_{n}$ be an increasing sequence of positive real numbers, and let $a_{n+1}=a_{1}$. Prove that
$$
\sum_{k=1}^{n} \frac{a_{k}}{a_{k+1}}>\sum_{k=1}^{n} \frac{a_{k+1}}{a_{k}} .
$$
|
Solution 1: We will use induction. The base case is $n=3$. In this case, we want to show that
$$
\frac{a_{1}}{a_{2}}+\frac{a_{2}}{a_{3}}+\frac{a_{3}}{a_{1}}>\frac{a_{2}}{a_{1}}+\frac{a_{3}}{a_{2}}+\frac{a_{1}}{a_{3}} .
$$
Equivalently, we want to show
$$
\begin{aligned}
a_{1}^{2} a_{3}+a_{2}^{2} a_{1}+a_{3}^{2} a_{2}>a_{1}^{2} a_{2}+a_{2}^{2} a_{3}+a_{3}^{2} a_{1} & \Longleftrightarrow a_{1}^{2}\left(a_{3}-a_{2}\right)+a_{3}^{2}\left(a_{2}-a_{1}\right)>a_{2}^{2}\left(a_{3}-a_{1}\right) \\
& \Longleftrightarrow\left(a_{3}^{2}-a_{2}^{2}\right)\left(a_{2}-a_{1}\right)>\left(a_{2}^{2}-a_{1}^{2}\right)\left(a_{3}-a_{2}\right) \\
& \Longleftrightarrow a_{3}+a_{2}>a_{2}+a_{1},
\end{aligned}
$$
which is true.
Now assume the claim is true for $n \geq 3$. Then, we have that
$$
\frac{a_{1}}{a_{3}}+\frac{a_{3}}{a_{4}}+\cdots+\frac{a_{n}}{a_{n+1}}+\frac{a_{n+1}}{a_{1}}>\frac{a_{3}}{a_{1}}+\frac{a_{4}}{a_{3}}+\cdots+\frac{a_{n+1}}{a_{n}}+\frac{a_{1}}{a_{n+1}} .
$$
We also have that
$$
\frac{a_{1}}{a_{2}}+\frac{a_{2}}{a_{3}}+\frac{a_{3}}{a_{1}}>\frac{a_{2}}{a_{1}}+\frac{a_{3}}{a_{2}}+\frac{a_{3}}{a_{1}} .
$$
Adding the two inequalities and simplifying gives the desired result.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-team-solutions.jsonl",
"problem_match": "\n4. [30]",
"solution_match": "\n## Proposed by: Akash Das\n\n"
}
|
2a7c4b43-e25f-57f7-9791-bb0282d82c05
| 610,471
|
Suppose $n \geq 3$ is a positive integer. Let $a_{1}<a_{2}<\cdots<a_{n}$ be an increasing sequence of positive real numbers, and let $a_{n+1}=a_{1}$. Prove that
$$
\sum_{k=1}^{n} \frac{a_{k}}{a_{k+1}}>\sum_{k=1}^{n} \frac{a_{k+1}}{a_{k}} .
$$
|
The points $\left(a_{1}, \frac{1}{a_{1}}\right),\left(a_{2}, \frac{1}{a_{2}}\right),\left(a_{3}, \frac{1}{a_{3}}\right), \ldots,\left(a_{n}, \frac{1}{a_{n}}\right)$ form a counter-clockwise oriented polygon. Thus, we have the area, $A$, which must be positive, can be calculated by Shoelace theorem:
$$
A=\frac{1}{2}\left(\sum_{k=1}^{n} \frac{a_{k}}{a_{k+1}}-\sum_{k=1}^{n} \frac{a_{k+1}}{a_{k}}\right) .
$$
Since $A$ is positive, we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Suppose $n \geq 3$ is a positive integer. Let $a_{1}<a_{2}<\cdots<a_{n}$ be an increasing sequence of positive real numbers, and let $a_{n+1}=a_{1}$. Prove that
$$
\sum_{k=1}^{n} \frac{a_{k}}{a_{k+1}}>\sum_{k=1}^{n} \frac{a_{k+1}}{a_{k}} .
$$
|
The points $\left(a_{1}, \frac{1}{a_{1}}\right),\left(a_{2}, \frac{1}{a_{2}}\right),\left(a_{3}, \frac{1}{a_{3}}\right), \ldots,\left(a_{n}, \frac{1}{a_{n}}\right)$ form a counter-clockwise oriented polygon. Thus, we have the area, $A$, which must be positive, can be calculated by Shoelace theorem:
$$
A=\frac{1}{2}\left(\sum_{k=1}^{n} \frac{a_{k}}{a_{k+1}}-\sum_{k=1}^{n} \frac{a_{k+1}}{a_{k}}\right) .
$$
Since $A$ is positive, we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-team-solutions.jsonl",
"problem_match": "\n4. [30]",
"solution_match": "\nSolution 2: "
}
|
2a7c4b43-e25f-57f7-9791-bb0282d82c05
| 610,471
|
Suppose $n \geq 3$ is a positive integer. Let $a_{1}<a_{2}<\cdots<a_{n}$ be an increasing sequence of positive real numbers, and let $a_{n+1}=a_{1}$. Prove that
$$
\sum_{k=1}^{n} \frac{a_{k}}{a_{k+1}}>\sum_{k=1}^{n} \frac{a_{k+1}}{a_{k}} .
$$
|
For $1 \leq i \leq n-1$, let $r_{i}=a_{i+1} / a_{i}$. Then the inequality becomes
$$
r_{1} r_{2} \cdots r_{n-1}+\frac{1}{r_{1}}+\cdots+\frac{1}{r_{n-1}}>\frac{1}{r_{1} r_{2} \cdots r_{n-1}}+r_{1}+\cdots+r_{n-1} .
$$
If we let $s_{i}=\log r_{i}$ and $f(s)=e^{s}-e^{-s}$, this is the same as
$$
f\left(s_{1}+\cdots+s_{n-1}\right)>f\left(s_{1}\right)+\cdots+f\left(s_{n-1}\right)
$$
This follows from the convexity of $f$ and the fact that $f(0)=0$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Suppose $n \geq 3$ is a positive integer. Let $a_{1}<a_{2}<\cdots<a_{n}$ be an increasing sequence of positive real numbers, and let $a_{n+1}=a_{1}$. Prove that
$$
\sum_{k=1}^{n} \frac{a_{k}}{a_{k+1}}>\sum_{k=1}^{n} \frac{a_{k+1}}{a_{k}} .
$$
|
For $1 \leq i \leq n-1$, let $r_{i}=a_{i+1} / a_{i}$. Then the inequality becomes
$$
r_{1} r_{2} \cdots r_{n-1}+\frac{1}{r_{1}}+\cdots+\frac{1}{r_{n-1}}>\frac{1}{r_{1} r_{2} \cdots r_{n-1}}+r_{1}+\cdots+r_{n-1} .
$$
If we let $s_{i}=\log r_{i}$ and $f(s)=e^{s}-e^{-s}$, this is the same as
$$
f\left(s_{1}+\cdots+s_{n-1}\right)>f\left(s_{1}\right)+\cdots+f\left(s_{n-1}\right)
$$
This follows from the convexity of $f$ and the fact that $f(0)=0$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-team-solutions.jsonl",
"problem_match": "\n4. [30]",
"solution_match": "\nSolution 3: "
}
|
2a7c4b43-e25f-57f7-9791-bb0282d82c05
| 610,471
|
Let $A B C$ be a triangle with centroid $G$, and let $E$ and $F$ be points on side $B C$ such that $B E=E F=F C$. Points $X$ and $Y$ lie on lines $A B$ and $A C$, respectively, so that $X, Y$, and $G$ are not collinear. If the line through $E$ parallel to $X G$ and the line through $F$ parallel to $Y G$ intersect at $P \neq G$, prove that $G P$ passes through the midpoint of $X Y$.
|
Solution: Let $C G$ intersect $A B$ at $N$. Then $N$ is the midpoint of $A B$ and it is known that $\frac{C G}{A B}=2=$ $\frac{C E}{E B}$, so $E G \| A B$. Moreover, since $F E=E B$, we have $[E F G]=[E X G]$. Similarly, $[E F G]=[F Y G]$. Now we have $[P X G]=[E X G]=[E F G]=[F Y G]=[P Y G]$, so $P G$ bisects $X Y$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with centroid $G$, and let $E$ and $F$ be points on side $B C$ such that $B E=E F=F C$. Points $X$ and $Y$ lie on lines $A B$ and $A C$, respectively, so that $X, Y$, and $G$ are not collinear. If the line through $E$ parallel to $X G$ and the line through $F$ parallel to $Y G$ intersect at $P \neq G$, prove that $G P$ passes through the midpoint of $X Y$.
|
Solution: Let $C G$ intersect $A B$ at $N$. Then $N$ is the midpoint of $A B$ and it is known that $\frac{C G}{A B}=2=$ $\frac{C E}{E B}$, so $E G \| A B$. Moreover, since $F E=E B$, we have $[E F G]=[E X G]$. Similarly, $[E F G]=[F Y G]$. Now we have $[P X G]=[E X G]=[E F G]=[F Y G]=[P Y G]$, so $P G$ bisects $X Y$, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-team-solutions.jsonl",
"problem_match": "\n5. [40]",
"solution_match": "\nProposed by: Eric Shen\n"
}
|
adfbde4d-487f-52fa-b3ad-93fbdc8e416b
| 610,472
|
Find, with proof, all functions $f: \mathbb{R} \backslash\{0\} \rightarrow \mathbb{R}$ such that
$$
f(x)^{2}-f(y) f(z)=x(x+y+z)(f(x)+f(y)+f(z))
$$
for all real $x, y, z$ such that $x y z=1$.
|
The answer is either $f(x)=0$ for all $x$ or $f(x)=x^{2}-\frac{1}{x}$ for all $x$. These can be checked to work.
Now, I will prove that these are the only solutions. Let $P(x, y, z)$ be the assertion of the problem statement.
Lemma 1. $f(x) \in\left\{0, x^{2}-\frac{1}{x}\right\}$ for all $x \in \mathbb{R} \backslash\{0\}$.
Proof. $P(1,1,1)$ yields $f(1)=0$. Then, $P\left(x, 1, \frac{1}{x}\right)$ and $P\left(1, x, \frac{1}{x}\right)$ yield
$$
\begin{aligned}
f(x)^{2} & =x\left(x+\frac{1}{x}+1\right)\left(f(x)+f\left(\frac{1}{x}\right)\right) \\
-f(x) f\left(\frac{1}{x}\right) & =\left(x+\frac{1}{x}+1\right)\left(f(x)+f\left(\frac{1}{x}\right)\right)
\end{aligned}
$$
Thus, we have $f(x)^{2}=-x f(x) f\left(\frac{1}{x}\right)$, so we have $f(x)=0$ or $f\left(\frac{1}{x}\right)=-\frac{f(x)}{x}$. Plugging in the latter into the first equation above gives us
$$
f(x)^{2}=x\left(x+\frac{1}{x}+1\right)\left(f(x)-\frac{f(x)}{x}\right)
$$
which gives us $f(x)=0$ or $f(x)=x^{2}-\frac{1}{x}$. This proves Lemma 1 .
Lemma 2. If $f(t)=0$ for some $t \neq 1$, then we have $f(x)=0$ for all $x$.
Proof. $P\left(x, t, \frac{1}{t x}\right)$ and $P\left(t, x, \frac{1}{t x}\right)$ give us
$$
\begin{aligned}
f(x)^{2} & =x\left(x+\frac{1}{t x}+t\right)\left(f(x)+f\left(\frac{1}{t x}\right)\right) \\
-f(x) f\left(\frac{1}{t x}\right) & =t\left(x+\frac{1}{t x}+t\right)\left(f(x)+f\left(\frac{1}{t x}\right)\right)
\end{aligned}
$$
Thus we have $t f(x)^{2}=-x f(x) f\left(\frac{1}{t x}\right)$, so $f(x)=0$ or $f\left(\frac{1}{t x}\right)=-\frac{t}{x} f(x)$. Plugging in the latter into the first equation gives us
$$
f(x)^{2}=x\left(x+\frac{1}{t x}+t\right)\left(f(x)-\frac{t f(x)}{x}\right)
$$
which gives us either $f(x)=0$ or $f(x)=x\left(x+t+\frac{1}{t x}\right)\left(1-\frac{t}{x}\right)=x^{2}-\frac{1}{x}-\left(t^{2}-\frac{1}{t}\right)$. Note that since the ladder expression doesn't equal $x^{2}-\frac{1}{x}$, since $t \neq 1$, we must have that $f(x)=0$. Thus, we have proved lemma 2.
Combining these lemmas finishes the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Find, with proof, all functions $f: \mathbb{R} \backslash\{0\} \rightarrow \mathbb{R}$ such that
$$
f(x)^{2}-f(y) f(z)=x(x+y+z)(f(x)+f(y)+f(z))
$$
for all real $x, y, z$ such that $x y z=1$.
|
The answer is either $f(x)=0$ for all $x$ or $f(x)=x^{2}-\frac{1}{x}$ for all $x$. These can be checked to work.
Now, I will prove that these are the only solutions. Let $P(x, y, z)$ be the assertion of the problem statement.
Lemma 1. $f(x) \in\left\{0, x^{2}-\frac{1}{x}\right\}$ for all $x \in \mathbb{R} \backslash\{0\}$.
Proof. $P(1,1,1)$ yields $f(1)=0$. Then, $P\left(x, 1, \frac{1}{x}\right)$ and $P\left(1, x, \frac{1}{x}\right)$ yield
$$
\begin{aligned}
f(x)^{2} & =x\left(x+\frac{1}{x}+1\right)\left(f(x)+f\left(\frac{1}{x}\right)\right) \\
-f(x) f\left(\frac{1}{x}\right) & =\left(x+\frac{1}{x}+1\right)\left(f(x)+f\left(\frac{1}{x}\right)\right)
\end{aligned}
$$
Thus, we have $f(x)^{2}=-x f(x) f\left(\frac{1}{x}\right)$, so we have $f(x)=0$ or $f\left(\frac{1}{x}\right)=-\frac{f(x)}{x}$. Plugging in the latter into the first equation above gives us
$$
f(x)^{2}=x\left(x+\frac{1}{x}+1\right)\left(f(x)-\frac{f(x)}{x}\right)
$$
which gives us $f(x)=0$ or $f(x)=x^{2}-\frac{1}{x}$. This proves Lemma 1 .
Lemma 2. If $f(t)=0$ for some $t \neq 1$, then we have $f(x)=0$ for all $x$.
Proof. $P\left(x, t, \frac{1}{t x}\right)$ and $P\left(t, x, \frac{1}{t x}\right)$ give us
$$
\begin{aligned}
f(x)^{2} & =x\left(x+\frac{1}{t x}+t\right)\left(f(x)+f\left(\frac{1}{t x}\right)\right) \\
-f(x) f\left(\frac{1}{t x}\right) & =t\left(x+\frac{1}{t x}+t\right)\left(f(x)+f\left(\frac{1}{t x}\right)\right)
\end{aligned}
$$
Thus we have $t f(x)^{2}=-x f(x) f\left(\frac{1}{t x}\right)$, so $f(x)=0$ or $f\left(\frac{1}{t x}\right)=-\frac{t}{x} f(x)$. Plugging in the latter into the first equation gives us
$$
f(x)^{2}=x\left(x+\frac{1}{t x}+t\right)\left(f(x)-\frac{t f(x)}{x}\right)
$$
which gives us either $f(x)=0$ or $f(x)=x\left(x+t+\frac{1}{t x}\right)\left(1-\frac{t}{x}\right)=x^{2}-\frac{1}{x}-\left(t^{2}-\frac{1}{t}\right)$. Note that since the ladder expression doesn't equal $x^{2}-\frac{1}{x}$, since $t \neq 1$, we must have that $f(x)=0$. Thus, we have proved lemma 2.
Combining these lemmas finishes the problem.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-team-solutions.jsonl",
"problem_match": "\n7. [50]",
"solution_match": "\nSolution 1: "
}
|
e4ba1bce-7818-5696-8af3-410053295e71
| 610,474
|
Find, with proof, all functions $f: \mathbb{R} \backslash\{0\} \rightarrow \mathbb{R}$ such that
$$
f(x)^{2}-f(y) f(z)=x(x+y+z)(f(x)+f(y)+f(z))
$$
for all real $x, y, z$ such that $x y z=1$.
|
Suppose $x y z=1$ and $x+y+z \neq 0$ and that $x, y, z$ are not all the same. Then we have
$$
\begin{aligned}
& f(x)^{2}-f(y) f(z)=x(x+y+z)(f(x)+f(y)+f(z)) \\
& f(y)^{2}-f(z) f(x)=y(x+y+z)(f(x)+f(y)+f(z)) \\
& f(z)^{2}-f(x) f(y)=z(x+y+z)(f(x)+f(y)+f(z))
\end{aligned}
$$
Squaring the first equation and subtracting the second equation times the third gives us: $f(x) F(x, y, z)=$ $\left(x^{2}-y z\right) G(x, y, z)^{2}$, where $F(x, y, z)=f(x)^{3}+f(y)^{3}+f(z)^{3}-3 f(x) f(y) f(z)$ and $G(x, y, z)=(x+y+$ $z)(f(x)+f(y)+f(z))$. If $F(x, y, z)=0$, it is not too hard to see that we get $f(x)=f(y)=f(z)=0$. If not, then we can let $K=\frac{G^{2}}{F}$ and we substitute $(f(x), f(y), f(z))=\left(K\left(x^{2}-y z\right), K\left(y^{2}-x z\right), K\left(z^{2}-x y\right)\right)$ into the first equation to get $K^{2} x\left(x^{3}+y^{3}+z^{3}-3 x y z\right)=K x\left(x^{3}+y^{3}+z^{3}-3 x y z\right)$. Thus, we have $K=0$ or $K=1$. Thus, we have either $(f(x), f(y), f(z))=(0,0,0)$ or $(f(x), f(y), f(z))=$ $\left(x^{2}-y z, y^{2}-z x, z^{2}-x y\right)$.
Thus, $f(0.5)=0$ or $f(0.5)=0.5^{2}-\frac{1}{0.5}$. If the former is true, then for all $y$ and $z$ such that $y z=2$ and $y+z \neq 0.5$, we have $f(y)=0$. However, this gives that $f(y)=0$ for all $y$. Likewise, if the latter were true, we would have $f(y)=y^{2}-\frac{1}{y}$ for all $y$, so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Find, with proof, all functions $f: \mathbb{R} \backslash\{0\} \rightarrow \mathbb{R}$ such that
$$
f(x)^{2}-f(y) f(z)=x(x+y+z)(f(x)+f(y)+f(z))
$$
for all real $x, y, z$ such that $x y z=1$.
|
Suppose $x y z=1$ and $x+y+z \neq 0$ and that $x, y, z$ are not all the same. Then we have
$$
\begin{aligned}
& f(x)^{2}-f(y) f(z)=x(x+y+z)(f(x)+f(y)+f(z)) \\
& f(y)^{2}-f(z) f(x)=y(x+y+z)(f(x)+f(y)+f(z)) \\
& f(z)^{2}-f(x) f(y)=z(x+y+z)(f(x)+f(y)+f(z))
\end{aligned}
$$
Squaring the first equation and subtracting the second equation times the third gives us: $f(x) F(x, y, z)=$ $\left(x^{2}-y z\right) G(x, y, z)^{2}$, where $F(x, y, z)=f(x)^{3}+f(y)^{3}+f(z)^{3}-3 f(x) f(y) f(z)$ and $G(x, y, z)=(x+y+$ $z)(f(x)+f(y)+f(z))$. If $F(x, y, z)=0$, it is not too hard to see that we get $f(x)=f(y)=f(z)=0$. If not, then we can let $K=\frac{G^{2}}{F}$ and we substitute $(f(x), f(y), f(z))=\left(K\left(x^{2}-y z\right), K\left(y^{2}-x z\right), K\left(z^{2}-x y\right)\right)$ into the first equation to get $K^{2} x\left(x^{3}+y^{3}+z^{3}-3 x y z\right)=K x\left(x^{3}+y^{3}+z^{3}-3 x y z\right)$. Thus, we have $K=0$ or $K=1$. Thus, we have either $(f(x), f(y), f(z))=(0,0,0)$ or $(f(x), f(y), f(z))=$ $\left(x^{2}-y z, y^{2}-z x, z^{2}-x y\right)$.
Thus, $f(0.5)=0$ or $f(0.5)=0.5^{2}-\frac{1}{0.5}$. If the former is true, then for all $y$ and $z$ such that $y z=2$ and $y+z \neq 0.5$, we have $f(y)=0$. However, this gives that $f(y)=0$ for all $y$. Likewise, if the latter were true, we would have $f(y)=y^{2}-\frac{1}{y}$ for all $y$, so we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-team-solutions.jsonl",
"problem_match": "\n7. [50]",
"solution_match": "\nSolution 2: "
}
|
e4ba1bce-7818-5696-8af3-410053295e71
| 610,474
|
For a nonnegative integer $n$, let $s(n)$ be the sum of digits of the binary representation of $n$. Prove that
$$
\sum_{n=0}^{2^{2022}-1} \frac{(-1)^{s(n)}}{2022+n}>0
$$
|
Solution 1: Define
$$
f_{k}(x)=\sum_{n=0}^{2^{k}-1} \frac{(-1)^{s(n)}}{x+n}
$$
We want to show that $f_{2022}(2022)>0$. We will in fact show something stronger.
I claim that for all $x>0$, for all $k \geq 0$, we have $f_{k}^{(i)}(x)>0$ for even $i$ and $f_{k}^{(i)}(x)<0$ for odd $i$, where $f^{(i)}$ denotes the $i$ th derivative of $f$. We will prove this claim with induction on $k$. The base case of $k=0$ is easy to see because $f_{0}(x)=\frac{1}{x}$, so $f_{0}^{(2 j)}(x)=\frac{(2 j)!}{x^{2 j+1}}>0$ and $f_{0}^{(2 j-1)}(x)=-\frac{(2 j-1)!}{x^{2 j}}<0$ for all $x>0$. Now, assume the claim is true for $k=N$. Then, note that
$$
\begin{gathered}
f_{N+1}(x)=\sum_{n=0}^{2^{N+1}-1} \frac{(-1)^{s(n)}}{x+n}=\sum_{n=0}^{2^{N}-1} \frac{(-1)^{s(n)}}{x+n}+\sum_{n=0}^{2^{N}-1} \frac{(-1)^{s\left(n+2^{N}\right)}}{x+n+2^{N}}= \\
\sum_{n=0}^{2^{N}-1} \frac{(-1)^{s(n)}}{x+n}-\sum_{n=0}^{2^{N}-1} \frac{(-1)^{s(n)}}{x+n+2^{N}}=f_{N}(x)-f_{N}\left(x+2^{N}\right)
\end{gathered}
$$
Thus,
$$
f_{N+1}^{(2 j)}(x)=f_{N}^{(2 j)}(x)-f_{N}^{(2 j)}\left(x+2^{N}\right)>0
$$
since $\left(f_{N}^{(2 j)}(x)\right)^{\prime}=f_{N}^{(2 j+1)}(x)<0$. Similarly, we can show that $f_{N+1}^{2 j+1}(x)<0$, which completes the induction, so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a nonnegative integer $n$, let $s(n)$ be the sum of digits of the binary representation of $n$. Prove that
$$
\sum_{n=0}^{2^{2022}-1} \frac{(-1)^{s(n)}}{2022+n}>0
$$
|
Solution 1: Define
$$
f_{k}(x)=\sum_{n=0}^{2^{k}-1} \frac{(-1)^{s(n)}}{x+n}
$$
We want to show that $f_{2022}(2022)>0$. We will in fact show something stronger.
I claim that for all $x>0$, for all $k \geq 0$, we have $f_{k}^{(i)}(x)>0$ for even $i$ and $f_{k}^{(i)}(x)<0$ for odd $i$, where $f^{(i)}$ denotes the $i$ th derivative of $f$. We will prove this claim with induction on $k$. The base case of $k=0$ is easy to see because $f_{0}(x)=\frac{1}{x}$, so $f_{0}^{(2 j)}(x)=\frac{(2 j)!}{x^{2 j+1}}>0$ and $f_{0}^{(2 j-1)}(x)=-\frac{(2 j-1)!}{x^{2 j}}<0$ for all $x>0$. Now, assume the claim is true for $k=N$. Then, note that
$$
\begin{gathered}
f_{N+1}(x)=\sum_{n=0}^{2^{N+1}-1} \frac{(-1)^{s(n)}}{x+n}=\sum_{n=0}^{2^{N}-1} \frac{(-1)^{s(n)}}{x+n}+\sum_{n=0}^{2^{N}-1} \frac{(-1)^{s\left(n+2^{N}\right)}}{x+n+2^{N}}= \\
\sum_{n=0}^{2^{N}-1} \frac{(-1)^{s(n)}}{x+n}-\sum_{n=0}^{2^{N}-1} \frac{(-1)^{s(n)}}{x+n+2^{N}}=f_{N}(x)-f_{N}\left(x+2^{N}\right)
\end{gathered}
$$
Thus,
$$
f_{N+1}^{(2 j)}(x)=f_{N}^{(2 j)}(x)-f_{N}^{(2 j)}\left(x+2^{N}\right)>0
$$
since $\left(f_{N}^{(2 j)}(x)\right)^{\prime}=f_{N}^{(2 j+1)}(x)<0$. Similarly, we can show that $f_{N+1}^{2 j+1}(x)<0$, which completes the induction, so we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-254-tournaments-2022-hmic-solutions.jsonl",
"problem_match": "\n3. [8]",
"solution_match": "\nProposed by: Akash Das\n"
}
|
9ca718bb-3f30-52d1-b3da-8a532523a2ea
| 610,480
|
Prove that there do not exist pairwise distinct complex numbers $a, b, c$, and $d$ such that
$$
a^{3}-b c d=b^{3}-c d a=c^{3}-d a b=d^{3}-a b c .
$$
|
Solution 1: First suppose none of them are 0 . Let the common value of the four expressions be $k$, and let $a b c d=P$. Then for $x \in\{a, b, c, d\}$,
$$
x^{3}-\frac{P}{x}=k \Longrightarrow x^{4}-k x-P=0
$$
However, Vieta's tells us $a b c d=-P$, meaning $P=-P$, so $P=0$, a contradiction.
Now if $a=0$, then $-b c d=b^{3}=c^{3}=d^{3}$. Then without loss of generality $b=x, c=x \omega$, and $d=x \omega^{2}$. But then $-b c d=-x^{3} \neq x^{3}$, a contradiction.
Thus, there do not exist distinct complex numbers satisfying the equation.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that there do not exist pairwise distinct complex numbers $a, b, c$, and $d$ such that
$$
a^{3}-b c d=b^{3}-c d a=c^{3}-d a b=d^{3}-a b c .
$$
|
Solution 1: First suppose none of them are 0 . Let the common value of the four expressions be $k$, and let $a b c d=P$. Then for $x \in\{a, b, c, d\}$,
$$
x^{3}-\frac{P}{x}=k \Longrightarrow x^{4}-k x-P=0
$$
However, Vieta's tells us $a b c d=-P$, meaning $P=-P$, so $P=0$, a contradiction.
Now if $a=0$, then $-b c d=b^{3}=c^{3}=d^{3}$. Then without loss of generality $b=x, c=x \omega$, and $d=x \omega^{2}$. But then $-b c d=-x^{3} \neq x^{3}$, a contradiction.
Thus, there do not exist distinct complex numbers satisfying the equation.
|
{
"resource_path": "HarvardMIT/segmented/en-262-2023-feb-team-solutions.jsonl",
"problem_match": "\n2. [30]",
"solution_match": "\nProposed by: Rishabh Das\n"
}
|
42c29e70-5bf1-5dc8-a14e-2359529c65cc
| 610,613
|
Prove that there do not exist pairwise distinct complex numbers $a, b, c$, and $d$ such that
$$
a^{3}-b c d=b^{3}-c d a=c^{3}-d a b=d^{3}-a b c .
$$
|
Subtracting the first two equations and dividing by $a-b$ gives $a^{2}+b^{2}+a b+c d=0$. Similarly, $c^{2}+d^{2}+a b+c d=0$. So, $a^{2}+b^{2}=c^{2}+d^{2}$. Similarly, $a^{2}+c^{2}=b^{2}+d^{2}$. So, $b^{2}=c^{2}$. Similarly, $a^{2}=b^{2}=c^{2}=d^{2}$. Now by Pigeonhole, two of these 4 must be the same.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that there do not exist pairwise distinct complex numbers $a, b, c$, and $d$ such that
$$
a^{3}-b c d=b^{3}-c d a=c^{3}-d a b=d^{3}-a b c .
$$
|
Subtracting the first two equations and dividing by $a-b$ gives $a^{2}+b^{2}+a b+c d=0$. Similarly, $c^{2}+d^{2}+a b+c d=0$. So, $a^{2}+b^{2}=c^{2}+d^{2}$. Similarly, $a^{2}+c^{2}=b^{2}+d^{2}$. So, $b^{2}=c^{2}$. Similarly, $a^{2}=b^{2}=c^{2}=d^{2}$. Now by Pigeonhole, two of these 4 must be the same.
|
{
"resource_path": "HarvardMIT/segmented/en-262-2023-feb-team-solutions.jsonl",
"problem_match": "\n2. [30]",
"solution_match": "\nSolution 2: "
}
|
42c29e70-5bf1-5dc8-a14e-2359529c65cc
| 610,613
|
Let $A B C D$ be a convex quadrilateral such that $\angle A B C=\angle B C D=\theta$ for some angle $\theta<90^{\circ}$. Point $X$ lies inside the quadrilateral such that $\angle X A D=\angle X D A=90^{\circ}-\theta$. Prove that $B X=X C$.
|
## Solution 1:
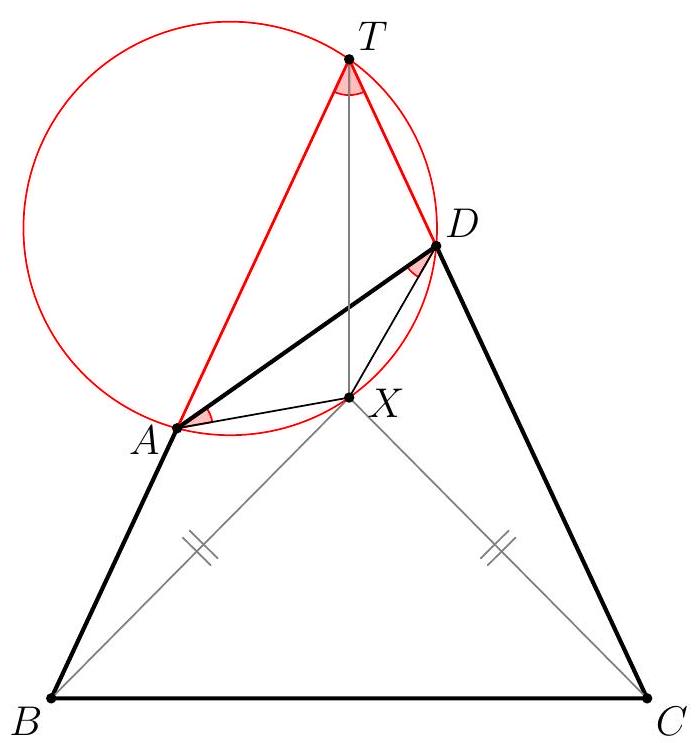
Let lines $A B$ and $C D$ meet at $T$. Notice that
$$
\begin{aligned}
& \angle A T D=180^{\circ}-\angle A B C-\angle D B C=180^{\circ}-2 \theta \\
& \angle A X D=180^{\circ}-2\left(90^{\circ}-\theta\right)=2 \theta
\end{aligned}
$$
Therefore, $A, T, X$, and $D$ are concyclic. In particular, this implies that $\angle X T A=90^{\circ}-\theta=\angle X T D$. Thus, $X T$ bisects $\angle B T C$. However, notice that $\angle T B C$ is isosceles, so $X T$ is actually the perpendicular bisector of $B C$, implying that $B X=X C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral such that $\angle A B C=\angle B C D=\theta$ for some angle $\theta<90^{\circ}$. Point $X$ lies inside the quadrilateral such that $\angle X A D=\angle X D A=90^{\circ}-\theta$. Prove that $B X=X C$.
|
## Solution 1:

Let lines $A B$ and $C D$ meet at $T$. Notice that
$$
\begin{aligned}
& \angle A T D=180^{\circ}-\angle A B C-\angle D B C=180^{\circ}-2 \theta \\
& \angle A X D=180^{\circ}-2\left(90^{\circ}-\theta\right)=2 \theta
\end{aligned}
$$
Therefore, $A, T, X$, and $D$ are concyclic. In particular, this implies that $\angle X T A=90^{\circ}-\theta=\angle X T D$. Thus, $X T$ bisects $\angle B T C$. However, notice that $\angle T B C$ is isosceles, so $X T$ is actually the perpendicular bisector of $B C$, implying that $B X=X C$.
|
{
"resource_path": "HarvardMIT/segmented/en-262-2023-feb-team-solutions.jsonl",
"problem_match": "\n3. [35]",
"solution_match": "\nProposed by: Pitchayut Saengrungkongka\n\n"
}
|
07fc6e22-cb0a-5e7d-846e-6a67b3a4f851
| 610,614
|
Let $A B C D$ be a convex quadrilateral such that $\angle A B C=\angle B C D=\theta$ for some angle $\theta<90^{\circ}$. Point $X$ lies inside the quadrilateral such that $\angle X A D=\angle X D A=90^{\circ}-\theta$. Prove that $B X=X C$.
|
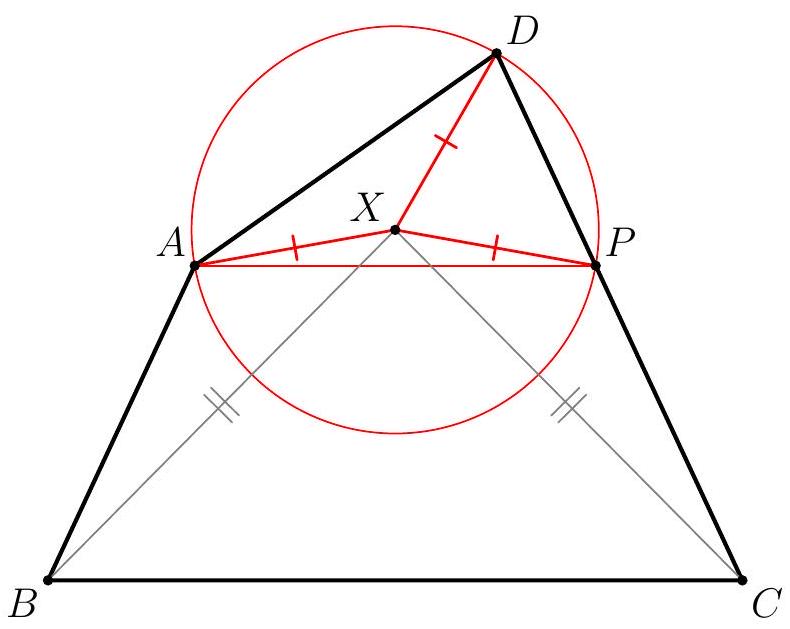
Without loss of generality, let $A B>C D$. Draw the circle $\gamma$ centered at $X$ and passes through $A$ and $D$. Let this circle intersects $C D$ again at point $P \neq D$. Then, notice that
$$
\angle A P D=\frac{\angle A X D}{2}=\theta
$$
implying that $A P \| B C$. Combining with $\angle A B C=\angle B C P$, we get that quadrilateral $A P C B$ is isosceles trapezoid. Since $X \in \gamma$, we have $X$ lies on the perpendicular bisector of $A P$, which is the same as the perpendicular bisector of $B C$, so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral such that $\angle A B C=\angle B C D=\theta$ for some angle $\theta<90^{\circ}$. Point $X$ lies inside the quadrilateral such that $\angle X A D=\angle X D A=90^{\circ}-\theta$. Prove that $B X=X C$.
|

Without loss of generality, let $A B>C D$. Draw the circle $\gamma$ centered at $X$ and passes through $A$ and $D$. Let this circle intersects $C D$ again at point $P \neq D$. Then, notice that
$$
\angle A P D=\frac{\angle A X D}{2}=\theta
$$
implying that $A P \| B C$. Combining with $\angle A B C=\angle B C P$, we get that quadrilateral $A P C B$ is isosceles trapezoid. Since $X \in \gamma$, we have $X$ lies on the perpendicular bisector of $A P$, which is the same as the perpendicular bisector of $B C$, so we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-262-2023-feb-team-solutions.jsonl",
"problem_match": "\n3. [35]",
"solution_match": "\n## Solution 2:\n\n"
}
|
07fc6e22-cb0a-5e7d-846e-6a67b3a4f851
| 610,614
|
Let $A B C D$ be a convex quadrilateral such that $\angle A B C=\angle B C D=\theta$ for some angle $\theta<90^{\circ}$. Point $X$ lies inside the quadrilateral such that $\angle X A D=\angle X D A=90^{\circ}-\theta$. Prove that $B X=X C$.
|
Let the perpendicular bisector of $A D$ intersects $B C$ at point $K$. Notice that
$$
\begin{aligned}
\angle A X K=90^{\circ}+\angle X A D=180^{\circ}-\theta=\angle A B K & \Longrightarrow A, B, X, K \text { are concyclic. } \\
& \Longrightarrow \angle X B C=\angle X A K
\end{aligned}
$$
Similarly, we get that $\angle X C B=\angle X D K$. However, since both $X$ and $K$ lies on the perpendicular bisector of $A D$, implying that $\angle X B C=\angle X C B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral such that $\angle A B C=\angle B C D=\theta$ for some angle $\theta<90^{\circ}$. Point $X$ lies inside the quadrilateral such that $\angle X A D=\angle X D A=90^{\circ}-\theta$. Prove that $B X=X C$.
|

Let the perpendicular bisector of $A D$ intersects $B C$ at point $K$. Notice that
$$
\begin{aligned}
\angle A X K=90^{\circ}+\angle X A D=180^{\circ}-\theta=\angle A B K & \Longrightarrow A, B, X, K \text { are concyclic. } \\
& \Longrightarrow \angle X B C=\angle X A K
\end{aligned}
$$
Similarly, we get that $\angle X C B=\angle X D K$. However, since both $X$ and $K$ lies on the perpendicular bisector of $A D$, implying that $\angle X B C=\angle X C B$.
|
{
"resource_path": "HarvardMIT/segmented/en-262-2023-feb-team-solutions.jsonl",
"problem_match": "\n3. [35]",
"solution_match": "\n## Solution 3:\n\n"
}
|
07fc6e22-cb0a-5e7d-846e-6a67b3a4f851
| 610,614
|
Let $A B C D$ be a convex quadrilateral such that $\angle A B C=\angle B C D=\theta$ for some angle $\theta<90^{\circ}$. Point $X$ lies inside the quadrilateral such that $\angle X A D=\angle X D A=90^{\circ}-\theta$. Prove that $B X=X C$.
|
Fix $\theta$ and points $A, B$, and $C$. Animate point $D$ along the fixed line through $C$. Since $\triangle X A D$ as a fixed shape, it follows that $X$ moves linearly along a fixed line. Since we want to show that $X$ lies on the perpendicular bisector of $B C$, which is fixed, it suffices to prove this for only two locations of $D$.
- When $A D \| B C$, it follows that $A B C D$ is an isosceles trapezoid, implying the result.
- When $D=C$, we notice that
$$
\angle A X C=2 \theta=2 \angle A B C,
$$
implying that $X$ is the circumcenter of $\triangle A B C$, and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral such that $\angle A B C=\angle B C D=\theta$ for some angle $\theta<90^{\circ}$. Point $X$ lies inside the quadrilateral such that $\angle X A D=\angle X D A=90^{\circ}-\theta$. Prove that $B X=X C$.
|
Fix $\theta$ and points $A, B$, and $C$. Animate point $D$ along the fixed line through $C$. Since $\triangle X A D$ as a fixed shape, it follows that $X$ moves linearly along a fixed line. Since we want to show that $X$ lies on the perpendicular bisector of $B C$, which is fixed, it suffices to prove this for only two locations of $D$.
- When $A D \| B C$, it follows that $A B C D$ is an isosceles trapezoid, implying the result.
- When $D=C$, we notice that
$$
\angle A X C=2 \theta=2 \angle A B C,
$$
implying that $X$ is the circumcenter of $\triangle A B C$, and the result follows.
|
{
"resource_path": "HarvardMIT/segmented/en-262-2023-feb-team-solutions.jsonl",
"problem_match": "\n3. [35]",
"solution_match": "\nSolution 4: "
}
|
07fc6e22-cb0a-5e7d-846e-6a67b3a4f851
| 610,614
|
For any odd positive integer $n$, let $r(n)$ be the odd positive integer such that the binary representation of $r(n)$ is the binary representation of $n$ written backwards. For example, $r(2023)=$
$r\left(11111100111_{2}\right)=11100111111_{2}=1855$. Determine, with proof, whether there exists a strictly increasing eight-term arithmetic progression $a_{1}, \ldots, a_{8}$ of odd positive integers such that $r\left(a_{1}\right), \ldots$, $r\left(a_{8}\right)$ is an arithmetic progression in that order.
|
Solution: The main idea is the following claim.
Claim: If $a, b, c$ are in arithmetic progression and have the same number of digits in their binary representations, then $r(a), r(b), r(c)$ cannot be in arithmetic progression in that order.
Proof. Consider the least significant digit that differs in $a$ and $b$. Then $c$ will have the same value of that digit as $a$, which will be different from $b$. Since this becomes the most significant digit in $r(a), r(b), r(c)$, then of course $b$ cannot be between $a$ and $c$.
To finish, we just need to show that if there are 8 numbers in arithmetic progression, which we'll write as $a_{1}, a_{1}+d, a_{1}+2 d, \ldots, a_{1}+7 d$, three of them have the same number of digits. We have a few cases.
- If $a_{1}+3 d<2^{k} \leq a_{1}+4 d$, then $a_{1}+4 d, a_{1}+5 d, a_{1}+6 d$ will have the same number of digits.
- If $a_{1}+4 d<2^{k} \leq a_{1}+5 d$, then $a_{1}+5 d, a_{1}+6 d, a_{1}+7 d$ will have the same number of digits.
- If neither of these assumptions are true, $a_{1}+3 d, a_{1}+4 d, a_{1}+5 d$ will have the same number of digits.
Having exhausted all cases, we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For any odd positive integer $n$, let $r(n)$ be the odd positive integer such that the binary representation of $r(n)$ is the binary representation of $n$ written backwards. For example, $r(2023)=$
$r\left(11111100111_{2}\right)=11100111111_{2}=1855$. Determine, with proof, whether there exists a strictly increasing eight-term arithmetic progression $a_{1}, \ldots, a_{8}$ of odd positive integers such that $r\left(a_{1}\right), \ldots$, $r\left(a_{8}\right)$ is an arithmetic progression in that order.
|
Solution: The main idea is the following claim.
Claim: If $a, b, c$ are in arithmetic progression and have the same number of digits in their binary representations, then $r(a), r(b), r(c)$ cannot be in arithmetic progression in that order.
Proof. Consider the least significant digit that differs in $a$ and $b$. Then $c$ will have the same value of that digit as $a$, which will be different from $b$. Since this becomes the most significant digit in $r(a), r(b), r(c)$, then of course $b$ cannot be between $a$ and $c$.
To finish, we just need to show that if there are 8 numbers in arithmetic progression, which we'll write as $a_{1}, a_{1}+d, a_{1}+2 d, \ldots, a_{1}+7 d$, three of them have the same number of digits. We have a few cases.
- If $a_{1}+3 d<2^{k} \leq a_{1}+4 d$, then $a_{1}+4 d, a_{1}+5 d, a_{1}+6 d$ will have the same number of digits.
- If $a_{1}+4 d<2^{k} \leq a_{1}+5 d$, then $a_{1}+5 d, a_{1}+6 d, a_{1}+7 d$ will have the same number of digits.
- If neither of these assumptions are true, $a_{1}+3 d, a_{1}+4 d, a_{1}+5 d$ will have the same number of digits.
Having exhausted all cases, we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-262-2023-feb-team-solutions.jsonl",
"problem_match": "\n6. [50]",
"solution_match": "\nProposed by: Daniel Zhu\n"
}
|
7f24b751-edf5-5604-a8d1-20f498b49c0b
| 610,617
|
Let $A B C$ be a triangle. Point $D$ lies on segment $B C$ such that $\angle B A D=\angle D A C$. Point $X$ lies on the opposite side of line $B C$ as $A$ and satisfies $X B=X D$ and $\angle B X D=\angle A C B$. Analogously, point $Y$ lies on the opposite side of line $B C$ as $A$ and satisfies $Y C=Y D$ and $\angle C Y D=\angle A B C$. Prove that lines $X Y$ and $A D$ are perpendicular.
|
## Solution 1:
Let $I$ and $I_{A}$ be the incenter and the $A$-excenter of $\triangle A B C$. The key observation is that $X$ is the circumcenter of $\triangle B D I_{A}$. To see why this is true, note that
$$
\angle B X D=\angle C=2 \angle I C B=2 \angle I I_{A} B=2 \angle D I_{A} B .
$$
Analogously, $Y$ is the circumcenter of $\triangle C D I_{A}$. Hence, $X Y$ is the perpendicular bisector of $D I_{A}$, which is clearly perpendicular to $A D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. Point $D$ lies on segment $B C$ such that $\angle B A D=\angle D A C$. Point $X$ lies on the opposite side of line $B C$ as $A$ and satisfies $X B=X D$ and $\angle B X D=\angle A C B$. Analogously, point $Y$ lies on the opposite side of line $B C$ as $A$ and satisfies $Y C=Y D$ and $\angle C Y D=\angle A B C$. Prove that lines $X Y$ and $A D$ are perpendicular.
|
## Solution 1:

Let $I$ and $I_{A}$ be the incenter and the $A$-excenter of $\triangle A B C$. The key observation is that $X$ is the circumcenter of $\triangle B D I_{A}$. To see why this is true, note that
$$
\angle B X D=\angle C=2 \angle I C B=2 \angle I I_{A} B=2 \angle D I_{A} B .
$$
Analogously, $Y$ is the circumcenter of $\triangle C D I_{A}$. Hence, $X Y$ is the perpendicular bisector of $D I_{A}$, which is clearly perpendicular to $A D$.
|
{
"resource_path": "HarvardMIT/segmented/en-262-2023-feb-team-solutions.jsonl",
"problem_match": "\n7. [55]",
"solution_match": "\nProposed by: Pitchayut Saengrungkongka\n\n"
}
|
69a6d3d2-acb1-5850-8e83-2e16cb474c29
| 610,618
|
Let $A B C$ be a triangle. Point $D$ lies on segment $B C$ such that $\angle B A D=\angle D A C$. Point $X$ lies on the opposite side of line $B C$ as $A$ and satisfies $X B=X D$ and $\angle B X D=\angle A C B$. Analogously, point $Y$ lies on the opposite side of line $B C$ as $A$ and satisfies $Y C=Y D$ and $\angle C Y D=\angle A B C$. Prove that lines $X Y$ and $A D$ are perpendicular.
|
Denote $\omega_{B}$ and $\omega_{C}$ as the circumcircle of $\triangle B X D$ and $\triangle C Y D$. Also, let $A D$ intersects the circumcircle of $\triangle A B C$ at $M$. Since $\angle B X D=\angle A C B=\angle A M B$, we get that $M \in \omega_{B}$. Similarly, $M \in \omega_{C}$. From here, there are two ways to finish.
- Note by Law of Sine that the radius of $\omega_{B}$ and $\omega_{C}$ are $D B /(2 \sin \angle M D B)$ and $D B /(2 \sin \angle M D C)$, so they are actually equal. Thus, if $O_{B}$ and $O_{C}$ are the centers of $\omega_{B}$ and $\omega_{C}$, then $X O_{B}=Y O_{C}$. Moreover, $X O_{B}$ and $Y O_{C}$ are both clearly perpendicular to $B C$, so $X O_{B} O_{C} Y$ is parallelogram, implying that $X Y \| O_{B} O_{C} \perp D M$.
- Observe that
$$
\angle M X D=\angle M B D=\frac{\angle A}{2}=90^{\circ}-\angle X D Y
$$
so $X M \perp D Y$. Similarly, $Y M \perp X D$, so $M$ is the orthocenter of $\triangle D X Y$, implying the result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. Point $D$ lies on segment $B C$ such that $\angle B A D=\angle D A C$. Point $X$ lies on the opposite side of line $B C$ as $A$ and satisfies $X B=X D$ and $\angle B X D=\angle A C B$. Analogously, point $Y$ lies on the opposite side of line $B C$ as $A$ and satisfies $Y C=Y D$ and $\angle C Y D=\angle A B C$. Prove that lines $X Y$ and $A D$ are perpendicular.
|

Denote $\omega_{B}$ and $\omega_{C}$ as the circumcircle of $\triangle B X D$ and $\triangle C Y D$. Also, let $A D$ intersects the circumcircle of $\triangle A B C$ at $M$. Since $\angle B X D=\angle A C B=\angle A M B$, we get that $M \in \omega_{B}$. Similarly, $M \in \omega_{C}$. From here, there are two ways to finish.
- Note by Law of Sine that the radius of $\omega_{B}$ and $\omega_{C}$ are $D B /(2 \sin \angle M D B)$ and $D B /(2 \sin \angle M D C)$, so they are actually equal. Thus, if $O_{B}$ and $O_{C}$ are the centers of $\omega_{B}$ and $\omega_{C}$, then $X O_{B}=Y O_{C}$. Moreover, $X O_{B}$ and $Y O_{C}$ are both clearly perpendicular to $B C$, so $X O_{B} O_{C} Y$ is parallelogram, implying that $X Y \| O_{B} O_{C} \perp D M$.
- Observe that
$$
\angle M X D=\angle M B D=\frac{\angle A}{2}=90^{\circ}-\angle X D Y
$$
so $X M \perp D Y$. Similarly, $Y M \perp X D$, so $M$ is the orthocenter of $\triangle D X Y$, implying the result.
|
{
"resource_path": "HarvardMIT/segmented/en-262-2023-feb-team-solutions.jsonl",
"problem_match": "\n7. [55]",
"solution_match": "\n## Solution 2:\n\n"
}
|
69a6d3d2-acb1-5850-8e83-2e16cb474c29
| 610,618
|
Let $A B C$ be a triangle. Point $D$ lies on segment $B C$ such that $\angle B A D=\angle D A C$. Point $X$ lies on the opposite side of line $B C$ as $A$ and satisfies $X B=X D$ and $\angle B X D=\angle A C B$. Analogously, point $Y$ lies on the opposite side of line $B C$ as $A$ and satisfies $Y C=Y D$ and $\angle C Y D=\angle A B C$. Prove that lines $X Y$ and $A D$ are perpendicular.
|
Let $D X$ intersects $A C$ at $P$ and $D Y$ intersects $A B$ at $Q$. Observe that $\angle B C P=\angle B X P$, so $B, C, P, X$ are concyclic. This implies that $C D=C P$ and that $D B \cdot D C=D X \cdot D P$.
Similarly, we have $B D=B Q$ and that $D B \cdot D C=D Y \cdot D Q$. Thus, we actually have $D X \cdot D P=$ $D Y \cdot D Q$, implying that $X, Y, P, Q$ are concyclic.
Now, let $I$ be the incenter of $\triangle A B C$. Since $B D=B Q$, it follows that $B I$ is the perpendicular bisector of $D Q$, so $I D=I Q$. Similarly, $I D=I P$, so $I$ is actually the circumcenter of $\triangle D P Q$.
We then finish by angle chasing:
$$
\angle X D I=180^{\circ}-\angle P D I=90^{\circ}+\angle D Q P=90^{\circ}+\angle D X Y
$$
implying the result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. Point $D$ lies on segment $B C$ such that $\angle B A D=\angle D A C$. Point $X$ lies on the opposite side of line $B C$ as $A$ and satisfies $X B=X D$ and $\angle B X D=\angle A C B$. Analogously, point $Y$ lies on the opposite side of line $B C$ as $A$ and satisfies $Y C=Y D$ and $\angle C Y D=\angle A B C$. Prove that lines $X Y$ and $A D$ are perpendicular.
|

Let $D X$ intersects $A C$ at $P$ and $D Y$ intersects $A B$ at $Q$. Observe that $\angle B C P=\angle B X P$, so $B, C, P, X$ are concyclic. This implies that $C D=C P$ and that $D B \cdot D C=D X \cdot D P$.
Similarly, we have $B D=B Q$ and that $D B \cdot D C=D Y \cdot D Q$. Thus, we actually have $D X \cdot D P=$ $D Y \cdot D Q$, implying that $X, Y, P, Q$ are concyclic.
Now, let $I$ be the incenter of $\triangle A B C$. Since $B D=B Q$, it follows that $B I$ is the perpendicular bisector of $D Q$, so $I D=I Q$. Similarly, $I D=I P$, so $I$ is actually the circumcenter of $\triangle D P Q$.
We then finish by angle chasing:
$$
\angle X D I=180^{\circ}-\angle P D I=90^{\circ}+\angle D Q P=90^{\circ}+\angle D X Y
$$
implying the result.
|
{
"resource_path": "HarvardMIT/segmented/en-262-2023-feb-team-solutions.jsonl",
"problem_match": "\n7. [55]",
"solution_match": "\n## Solution 3:\n\n"
}
|
69a6d3d2-acb1-5850-8e83-2e16cb474c29
| 610,618
|
Find, with proof, all nonconstant polynomials $P(x)$ with real coefficients such that, for all nonzero real numbers $z$ with $P(z) \neq 0$ and $P\left(\frac{1}{z}\right) \neq 0$, we have
$$
\frac{1}{P(z)}+\frac{1}{P\left(\frac{1}{z}\right)}=z+\frac{1}{z}
$$
|
It is straightforward to plug in and verify the above answers. Hence, we focus on showing that these are all possible solutions. The key claim is the following.
Claim: If $r \neq 0$ is a root of $P(z)$ with multiplicity $n$, then $1 / r$ is also a root of $P(z)$ with multiplicity $n$.
Proof 1 (Elementary). Let $n^{\prime}$ be the multiplicity of $1 / r$. It suffices to show that $n \leq n^{\prime}$ because we can apply the same assertion on $1 / r$ to obtain that $n^{\prime} \leq n$.
To that end, suppose that $(z-r)^{n}$ divides $P(z)$. From the equation, we have
$$
z^{N}\left[P\left(\frac{1}{z}\right)+P(z)\right]=z^{N}\left[\left(z+\frac{1}{z}\right) P(z) P\left(\frac{1}{z}\right)\right]
$$
where $N \gg \operatorname{deg} P+1$ to guarantee that both sides are polynomial. Notice that the factor $z^{N} P(z)$ and the right-hand side is divisible by $(z-r)^{n}$, so $(z-r)^{n}$ must also divide $z^{N} P\left(\frac{1}{z}\right)$. This means that there exists a polynomial $Q(z)$ such that $z^{N} P\left(\frac{1}{z}\right)=(z-r)^{n} Q(z)$. Replacing $z$ with $\frac{1}{z}$, we get
$$
\frac{P(z)}{z^{N}}=\left(\frac{1}{z}-r\right)^{n} Q\left(\frac{1}{z}\right) \Longrightarrow P(z)=z^{N-n}(1-r z)^{n} Q\left(\frac{1}{z}\right)
$$
implying that $P(z)$ is divisible by $(z-1 / r)^{n}$.
Proof 2 (Complex Analysis). Here is more advanced proof of the main claim.
View both sides of the equations as meromorphic functions in the complex plane. Then, a root $r$ with multiplicity $n$ of $P(z)$ is a pole of $\frac{1}{P(z)}$ of order $n$. Since the right-hand side is analytic around $r$, it follows that the other term $\frac{1}{P(1 / z)}$ has a pole at $r$ with order $n$ as well. By replacing $z$ with $1 / z$, we find that $\frac{1}{P(z)}$ has a pole at $1 / r$ of order $n$. This finishes the claim.
The claim implies that there exists an integer $k$ and a constant $\epsilon$ such that
$$
P(z)=\epsilon z^{k} P\left(\frac{1}{z}\right)
$$
By replacing $z$ with $1 / z$, we get that
$$
z^{k} P\left(\frac{1}{z}\right)=\epsilon P(z)
$$
Therefore, $\epsilon= \pm 1$. Moreover, using the main equation, we get that
$$
\frac{1}{P(z)}+\frac{\epsilon z^{k}}{P(z)}=z+\frac{1}{z} \Longrightarrow P(z)=\frac{z\left(1+\epsilon z^{k}\right)}{1+z^{2}}
$$
This is a polynomial if and only if $(\epsilon=1$ and $k \equiv 2(\bmod 4))$ or $(\epsilon=-1$ and $k \equiv 0(\bmod 4))$, so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Find, with proof, all nonconstant polynomials $P(x)$ with real coefficients such that, for all nonzero real numbers $z$ with $P(z) \neq 0$ and $P\left(\frac{1}{z}\right) \neq 0$, we have
$$
\frac{1}{P(z)}+\frac{1}{P\left(\frac{1}{z}\right)}=z+\frac{1}{z}
$$
|
It is straightforward to plug in and verify the above answers. Hence, we focus on showing that these are all possible solutions. The key claim is the following.
Claim: If $r \neq 0$ is a root of $P(z)$ with multiplicity $n$, then $1 / r$ is also a root of $P(z)$ with multiplicity $n$.
Proof 1 (Elementary). Let $n^{\prime}$ be the multiplicity of $1 / r$. It suffices to show that $n \leq n^{\prime}$ because we can apply the same assertion on $1 / r$ to obtain that $n^{\prime} \leq n$.
To that end, suppose that $(z-r)^{n}$ divides $P(z)$. From the equation, we have
$$
z^{N}\left[P\left(\frac{1}{z}\right)+P(z)\right]=z^{N}\left[\left(z+\frac{1}{z}\right) P(z) P\left(\frac{1}{z}\right)\right]
$$
where $N \gg \operatorname{deg} P+1$ to guarantee that both sides are polynomial. Notice that the factor $z^{N} P(z)$ and the right-hand side is divisible by $(z-r)^{n}$, so $(z-r)^{n}$ must also divide $z^{N} P\left(\frac{1}{z}\right)$. This means that there exists a polynomial $Q(z)$ such that $z^{N} P\left(\frac{1}{z}\right)=(z-r)^{n} Q(z)$. Replacing $z$ with $\frac{1}{z}$, we get
$$
\frac{P(z)}{z^{N}}=\left(\frac{1}{z}-r\right)^{n} Q\left(\frac{1}{z}\right) \Longrightarrow P(z)=z^{N-n}(1-r z)^{n} Q\left(\frac{1}{z}\right)
$$
implying that $P(z)$ is divisible by $(z-1 / r)^{n}$.
Proof 2 (Complex Analysis). Here is more advanced proof of the main claim.
View both sides of the equations as meromorphic functions in the complex plane. Then, a root $r$ with multiplicity $n$ of $P(z)$ is a pole of $\frac{1}{P(z)}$ of order $n$. Since the right-hand side is analytic around $r$, it follows that the other term $\frac{1}{P(1 / z)}$ has a pole at $r$ with order $n$ as well. By replacing $z$ with $1 / z$, we find that $\frac{1}{P(z)}$ has a pole at $1 / r$ of order $n$. This finishes the claim.
The claim implies that there exists an integer $k$ and a constant $\epsilon$ such that
$$
P(z)=\epsilon z^{k} P\left(\frac{1}{z}\right)
$$
By replacing $z$ with $1 / z$, we get that
$$
z^{k} P\left(\frac{1}{z}\right)=\epsilon P(z)
$$
Therefore, $\epsilon= \pm 1$. Moreover, using the main equation, we get that
$$
\frac{1}{P(z)}+\frac{\epsilon z^{k}}{P(z)}=z+\frac{1}{z} \Longrightarrow P(z)=\frac{z\left(1+\epsilon z^{k}\right)}{1+z^{2}}
$$
This is a polynomial if and only if $(\epsilon=1$ and $k \equiv 2(\bmod 4))$ or $(\epsilon=-1$ and $k \equiv 0(\bmod 4))$, so we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-262-2023-feb-team-solutions.jsonl",
"problem_match": "\n8. [60]",
"solution_match": "\nSolution: "
}
|
24f5eca9-5929-55a1-a7fe-c8740a633bd8
| 610,619
|
One thousand people are in a tennis tournament where each person plays against each other person exactly once, and there are no ties. Prove that it is possible to put all the competitors in a line so that each of the 998 people who are not at an end of the line either defeated both their neighbors or lost to both their neighbors
|
Solution: Take the natural graph theoretic interpretation, where an edge points towards the loser of each pair, and call such a line an alternating path. Consider the longest alternating path, and suppose it doesn't contain everyone. We will show we can make the path longer, which would be a contradiction.
First, assume the path has an odd number of vertices, labeled $v_{1}, \ldots, v_{n}$. WLOG $v_{1}$ points towards $v_{2}, v_{3}$ points towards $v_{2}$, all the way up to $v_{n}$ which points towards $v_{n-1}$ (otherwise, reverse all the edges). Also WLOG $v_{1}$ points towards $v_{n}$ (if not, label the vertices backwards). Let $w$ be a vertex not in the path. Note that if $v_{n}$ points towards $w$, we can make the path longer by adding $w$ to the end. Thus, $w$ must point towards $v_{n}$. But now we can take the path $w, v_{n}, v_{1}, \ldots, v_{n-1}$, which is longer than before, and so a contradiction.
Now assume the path has an even number of vertices, labeled $v_{1}, \ldots, v_{n}$, and WLOG $v_{1}$ points towards $v_{2}$ again. Then $v_{n-1}$ will point towards $v_{n}$. Since 1000 is even, there are at least 2 vertices not in the path, say $w_{1}$ and $w_{2}$. If either one points towards $v_{n}$, we can add it to the end of the path, so $v_{n}$ must point towards both. Similarly, they must both point towards $v_{1}$. But now note that if $v_{n-1}$ points to either, we can make the path $v_{1}, \ldots, v_{n-1}, w_{i}, v_{n}$, which is longer. Thus, $w_{1}, w_{2}$ must both point towards $v_{n-1}$. Now restrict our attention to $v_{1}, \ldots, v_{n-1}$. Note that $w_{1}, w_{2}$ both point towards both ends, so we can WLOG assume $v_{1}$ points towards $v_{n-1}$. Also WLOG $w_{1}$ points towards $w_{2}$. Then we can form the path $w_{2}, w_{1}, v_{n-1}, v_{1}, \ldots, v_{n-2}$, which has $n+1$ vertices. Thus, if the longest alternating path does not contain every vertex, we can make it longer, which is a contradiction, so there must exist an alternating path with all 1000 vertices.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
One thousand people are in a tennis tournament where each person plays against each other person exactly once, and there are no ties. Prove that it is possible to put all the competitors in a line so that each of the 998 people who are not at an end of the line either defeated both their neighbors or lost to both their neighbors
|
Solution: Take the natural graph theoretic interpretation, where an edge points towards the loser of each pair, and call such a line an alternating path. Consider the longest alternating path, and suppose it doesn't contain everyone. We will show we can make the path longer, which would be a contradiction.
First, assume the path has an odd number of vertices, labeled $v_{1}, \ldots, v_{n}$. WLOG $v_{1}$ points towards $v_{2}, v_{3}$ points towards $v_{2}$, all the way up to $v_{n}$ which points towards $v_{n-1}$ (otherwise, reverse all the edges). Also WLOG $v_{1}$ points towards $v_{n}$ (if not, label the vertices backwards). Let $w$ be a vertex not in the path. Note that if $v_{n}$ points towards $w$, we can make the path longer by adding $w$ to the end. Thus, $w$ must point towards $v_{n}$. But now we can take the path $w, v_{n}, v_{1}, \ldots, v_{n-1}$, which is longer than before, and so a contradiction.
Now assume the path has an even number of vertices, labeled $v_{1}, \ldots, v_{n}$, and WLOG $v_{1}$ points towards $v_{2}$ again. Then $v_{n-1}$ will point towards $v_{n}$. Since 1000 is even, there are at least 2 vertices not in the path, say $w_{1}$ and $w_{2}$. If either one points towards $v_{n}$, we can add it to the end of the path, so $v_{n}$ must point towards both. Similarly, they must both point towards $v_{1}$. But now note that if $v_{n-1}$ points to either, we can make the path $v_{1}, \ldots, v_{n-1}, w_{i}, v_{n}$, which is longer. Thus, $w_{1}, w_{2}$ must both point towards $v_{n-1}$. Now restrict our attention to $v_{1}, \ldots, v_{n-1}$. Note that $w_{1}, w_{2}$ both point towards both ends, so we can WLOG assume $v_{1}$ points towards $v_{n-1}$. Also WLOG $w_{1}$ points towards $w_{2}$. Then we can form the path $w_{2}, w_{1}, v_{n-1}, v_{1}, \ldots, v_{n-2}$, which has $n+1$ vertices. Thus, if the longest alternating path does not contain every vertex, we can make it longer, which is a contradiction, so there must exist an alternating path with all 1000 vertices.
|
{
"resource_path": "HarvardMIT/segmented/en-262-2023-feb-team-solutions.jsonl",
"problem_match": "\n10. [90]",
"solution_match": "\n## Proposed by: Maxim Li\n\n"
}
|
ddabb9af-39f8-5c2c-8b4a-5ba4d774dc10
| 610,621
|
A prime number $p$ is mundane if there exist positive integers $a$ and $b$ less than $\frac{p}{2}$ such that $\frac{a b-1}{p}$ is a positive integer. Find, with proof, all prime numbers that are not mundane.
|
The cases $p=11, p=17, p=19$ fail by $3 \cdot 4,3 \cdot 6$, and $4 \cdot 5$, respectively, so assume that $p \geq 21$. The key idea is the following identity:
$$
\frac{1}{10}-\left(-\frac{2}{5}\right)=\frac{1}{2}
$$
To see how to utilize this, notice that $10<\frac{p}{2}$ and $-\frac{5}{2}(\bmod p)=\frac{p-5}{2}<\frac{p}{2}$. Thus, by plugging in $a=10$ and $a=\frac{p-5}{2}$, we see that both $\frac{1}{10}(\bmod p)$ and $-\frac{2}{5}(\bmod p)$ must be greater than $\frac{p}{2}$, so it must lie in the interval $\left[\frac{p+1}{2}, p-1\right]$.
However, their difference is $\equiv \frac{1}{2} \equiv \frac{p+1}{2}(\bmod p)$, giving a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A prime number $p$ is mundane if there exist positive integers $a$ and $b$ less than $\frac{p}{2}$ such that $\frac{a b-1}{p}$ is a positive integer. Find, with proof, all prime numbers that are not mundane.
|
The cases $p=11, p=17, p=19$ fail by $3 \cdot 4,3 \cdot 6$, and $4 \cdot 5$, respectively, so assume that $p \geq 21$. The key idea is the following identity:
$$
\frac{1}{10}-\left(-\frac{2}{5}\right)=\frac{1}{2}
$$
To see how to utilize this, notice that $10<\frac{p}{2}$ and $-\frac{5}{2}(\bmod p)=\frac{p-5}{2}<\frac{p}{2}$. Thus, by plugging in $a=10$ and $a=\frac{p-5}{2}$, we see that both $\frac{1}{10}(\bmod p)$ and $-\frac{2}{5}(\bmod p)$ must be greater than $\frac{p}{2}$, so it must lie in the interval $\left[\frac{p+1}{2}, p-1\right]$.
However, their difference is $\equiv \frac{1}{2} \equiv \frac{p+1}{2}(\bmod p)$, giving a contradiction.
|
{
"resource_path": "HarvardMIT/segmented/en-264-tournaments-2023-hmic-solutions.jsonl",
"problem_match": "\n2. [7]",
"solution_match": "\nSolution 1:\n\n"
}
|
b0b76e4b-d538-5460-91c3-2f45e29d2b8d
| 610,623
|
A prime number $p$ is mundane if there exist positive integers $a$ and $b$ less than $\frac{p}{2}$ such that $\frac{a b-1}{p}$ is a positive integer. Find, with proof, all prime numbers that are not mundane.
|
The case $p=11$ fails by $3 \cdot 4$, so assume $p=2^{k} n+1 \geq 17$ for some odd $n$.
- If $n=1$, then $p=2^{k}+1$. Since $p+1$ cannot have a divisor greater than $2, \frac{p+1}{2}$ must be prime, so both $2^{k-1}+1$ and $2^{k}+1$ are consecutive Fermat primes. Since $k-1$ and $k$ must be powers of 2 , this forces $k=2$, which gives $p=5$.
- If $n=3$, then $p=3 \cdot 2^{k}+1$. Since $2 p+1$ cannot have a divisor greater than 4 , we have $\frac{2 p+1}{3}=2^{k+1}+1$ must be prime, $k=2^{c}-1 . c \in\{1,2\}$ gives $p \in\{7,25\}$; the latter is not even a prime. If $c \geq 3$, then
$$
5 \mid 3 \cdot 2^{2^{c}-1}+1=p
$$
contradiction.
- If $n \geq 5$, then
$$
2^{k+1} \cdot \frac{p-n}{2} \equiv 1 \quad(\bmod p)
$$
shows that this case yields no solutions.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A prime number $p$ is mundane if there exist positive integers $a$ and $b$ less than $\frac{p}{2}$ such that $\frac{a b-1}{p}$ is a positive integer. Find, with proof, all prime numbers that are not mundane.
|
The case $p=11$ fails by $3 \cdot 4$, so assume $p=2^{k} n+1 \geq 17$ for some odd $n$.
- If $n=1$, then $p=2^{k}+1$. Since $p+1$ cannot have a divisor greater than $2, \frac{p+1}{2}$ must be prime, so both $2^{k-1}+1$ and $2^{k}+1$ are consecutive Fermat primes. Since $k-1$ and $k$ must be powers of 2 , this forces $k=2$, which gives $p=5$.
- If $n=3$, then $p=3 \cdot 2^{k}+1$. Since $2 p+1$ cannot have a divisor greater than 4 , we have $\frac{2 p+1}{3}=2^{k+1}+1$ must be prime, $k=2^{c}-1 . c \in\{1,2\}$ gives $p \in\{7,25\}$; the latter is not even a prime. If $c \geq 3$, then
$$
5 \mid 3 \cdot 2^{2^{c}-1}+1=p
$$
contradiction.
- If $n \geq 5$, then
$$
2^{k+1} \cdot \frac{p-n}{2} \equiv 1 \quad(\bmod p)
$$
shows that this case yields no solutions.
|
{
"resource_path": "HarvardMIT/segmented/en-264-tournaments-2023-hmic-solutions.jsonl",
"problem_match": "\n2. [7]",
"solution_match": "\n## Solution 2:\n\n"
}
|
b0b76e4b-d538-5460-91c3-2f45e29d2b8d
| 610,623
|
A prime number $p$ is mundane if there exist positive integers $a$ and $b$ less than $\frac{p}{2}$ such that $\frac{a b-1}{p}$ is a positive integer. Find, with proof, all prime numbers that are not mundane.
|
Assume $p \geq 3$. Let $q>2$ be the smallest prime not dividing $p-1$.
Lemma: $q^{2}<\frac{p}{2}$ unless $p \in S=\{5,7,13,19,31,37,43,61,211\}$.
Proof. Casework on $q$.
- $q=3$ gives $p=5$.
- $q=5$ gives $p \in\{13,19,37,43\}$.
- $q=7$ gives $p \in\{31,61\}$.
- $q=11$ gives $p=211$.
No larger $q$ work because
$$
13^{2}<\frac{2 \cdot 3 \cdot 5 \cdot 7 \cdot 11}{2}
$$
and $p_{n+1}^{2}<\frac{p_{1} p_{2} \ldots p_{n}}{2}$ for $n \geq 5$ by induction using $p_{i+1}<2 p_{i}$, where $p_{i}$ are the primes in increasing order.
Now, $q^{\prime} \mid\left(q^{\prime}-1\right) p+1$ for all primes $q^{\prime}<q$ by minimality of $q$, but $q \mid k p+1$ for some $0<k<q-1$, since $q \nmid p-1$. Therefore, $q \operatorname{rad}(k+1) \mid k p+1$, so
$$
(q \operatorname{rad}(k+1)) \cdot \frac{k p+1}{q \operatorname{rad}(k+1)} \equiv 1 \quad(\bmod p)
$$
If $p \notin S$, the first factor can be bounded as
$$
q \operatorname{rad}(k+1)<q^{2}<\frac{p}{2}
$$
and the second factor as
$$
\frac{k p+1}{q \operatorname{rad}(k+1)}<\frac{(k+1) p}{(k+1) 2}=\frac{p}{2}
$$
Therefore, no $p \notin S$ satisfy the problem condition.
To finish the problem, it suffices to show no $p \in S \backslash\{5,7,13\}$ work. Indeed,
$$
\begin{aligned}
& 4 \cdot 5 \equiv 1 \\
& 4 \cdot 8(\bmod 19) \\
& 5 \cdot 15 \equiv 1 \\
& 4 \cdot(\bmod 31)(\bmod 37) \\
& 4 \cdot 14 \equiv 1 \\
& 8 \cdot 23 \equiv 1 \quad(\bmod 43) \\
& 4 \cdot 53 \equiv 1 \quad(\bmod 61) \\
&\hline \bmod 211),
\end{aligned}
$$
as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A prime number $p$ is mundane if there exist positive integers $a$ and $b$ less than $\frac{p}{2}$ such that $\frac{a b-1}{p}$ is a positive integer. Find, with proof, all prime numbers that are not mundane.
|
Assume $p \geq 3$. Let $q>2$ be the smallest prime not dividing $p-1$.
Lemma: $q^{2}<\frac{p}{2}$ unless $p \in S=\{5,7,13,19,31,37,43,61,211\}$.
Proof. Casework on $q$.
- $q=3$ gives $p=5$.
- $q=5$ gives $p \in\{13,19,37,43\}$.
- $q=7$ gives $p \in\{31,61\}$.
- $q=11$ gives $p=211$.
No larger $q$ work because
$$
13^{2}<\frac{2 \cdot 3 \cdot 5 \cdot 7 \cdot 11}{2}
$$
and $p_{n+1}^{2}<\frac{p_{1} p_{2} \ldots p_{n}}{2}$ for $n \geq 5$ by induction using $p_{i+1}<2 p_{i}$, where $p_{i}$ are the primes in increasing order.
Now, $q^{\prime} \mid\left(q^{\prime}-1\right) p+1$ for all primes $q^{\prime}<q$ by minimality of $q$, but $q \mid k p+1$ for some $0<k<q-1$, since $q \nmid p-1$. Therefore, $q \operatorname{rad}(k+1) \mid k p+1$, so
$$
(q \operatorname{rad}(k+1)) \cdot \frac{k p+1}{q \operatorname{rad}(k+1)} \equiv 1 \quad(\bmod p)
$$
If $p \notin S$, the first factor can be bounded as
$$
q \operatorname{rad}(k+1)<q^{2}<\frac{p}{2}
$$
and the second factor as
$$
\frac{k p+1}{q \operatorname{rad}(k+1)}<\frac{(k+1) p}{(k+1) 2}=\frac{p}{2}
$$
Therefore, no $p \notin S$ satisfy the problem condition.
To finish the problem, it suffices to show no $p \in S \backslash\{5,7,13\}$ work. Indeed,
$$
\begin{aligned}
& 4 \cdot 5 \equiv 1 \\
& 4 \cdot 8(\bmod 19) \\
& 5 \cdot 15 \equiv 1 \\
& 4 \cdot(\bmod 31)(\bmod 37) \\
& 4 \cdot 14 \equiv 1 \\
& 8 \cdot 23 \equiv 1 \quad(\bmod 43) \\
& 4 \cdot 53 \equiv 1 \quad(\bmod 61) \\
&\hline \bmod 211),
\end{aligned}
$$
as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-264-tournaments-2023-hmic-solutions.jsonl",
"problem_match": "\n2. [7]",
"solution_match": "\n## Solution 3:\n\n"
}
|
b0b76e4b-d538-5460-91c3-2f45e29d2b8d
| 610,623
|
Triangle $A B C$ has incircle $\omega$ and $A$-excircle $\omega_{A}$. Circle $\gamma_{B}$ passes through $B$ and is externally tangent to $\omega$ and $\omega_{A}$. Circle $\gamma_{C}$ passes through $C$ and is externally tangent to $\omega$ and $\omega_{A}$. If $\gamma_{B}$ intersects line $B C$ again at $D$, and $\gamma_{C}$ intersects line $B C$ again at $E$, prove that $B D=E C$.
|
Solution 1: Let $\overline{B C}$ touch the incircle at $X$ and the $A$-excircle at $Y$. Since $B X=C Y$, it suffices to show that $B P \cdot B C=B X \cdot B Y$ by symmetry.
The inversion centered at $B$ with radius $\sqrt{B X \cdot B Y}$
- fixes lines $\overline{A B}$ and $\overline{B C}$,
- swaps $X$ and $Y$,
- sends the incircle to a circle $\Gamma_{1}$ tangent to $\overline{A B}$ and tangent to $\overline{B C}$ at $Y$,
- sends the $A$-excircle to a circle $\Gamma_{2}$ tangent to $\overline{A B}$ and tangent to $\overline{B C}$ at $X$, and
- sends the circle through $B$ tangent to the incircle and $A$-excircle to a common tangent $\ell$ of $\Gamma_{1}$ and $\Gamma_{2}$.
Now, $C \in \ell$ since $\ell$ must intersect $\overline{B C}$ at a point $C^{\prime}$ satisfying $B X=C^{\prime} Y$, so the inversion maps $P$ to $C$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangle $A B C$ has incircle $\omega$ and $A$-excircle $\omega_{A}$. Circle $\gamma_{B}$ passes through $B$ and is externally tangent to $\omega$ and $\omega_{A}$. Circle $\gamma_{C}$ passes through $C$ and is externally tangent to $\omega$ and $\omega_{A}$. If $\gamma_{B}$ intersects line $B C$ again at $D$, and $\gamma_{C}$ intersects line $B C$ again at $E$, prove that $B D=E C$.
|
Solution 1: Let $\overline{B C}$ touch the incircle at $X$ and the $A$-excircle at $Y$. Since $B X=C Y$, it suffices to show that $B P \cdot B C=B X \cdot B Y$ by symmetry.

The inversion centered at $B$ with radius $\sqrt{B X \cdot B Y}$
- fixes lines $\overline{A B}$ and $\overline{B C}$,
- swaps $X$ and $Y$,
- sends the incircle to a circle $\Gamma_{1}$ tangent to $\overline{A B}$ and tangent to $\overline{B C}$ at $Y$,
- sends the $A$-excircle to a circle $\Gamma_{2}$ tangent to $\overline{A B}$ and tangent to $\overline{B C}$ at $X$, and
- sends the circle through $B$ tangent to the incircle and $A$-excircle to a common tangent $\ell$ of $\Gamma_{1}$ and $\Gamma_{2}$.
Now, $C \in \ell$ since $\ell$ must intersect $\overline{B C}$ at a point $C^{\prime}$ satisfying $B X=C^{\prime} Y$, so the inversion maps $P$ to $C$, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-264-tournaments-2023-hmic-solutions.jsonl",
"problem_match": "\n3. [9]",
"solution_match": "\nProposed by: Holden Mui\n"
}
|
e6947888-19f8-525e-a765-368fd5e94a3d
| 610,624
|
Triangle $A B C$ has incircle $\omega$ and $A$-excircle $\omega_{A}$. Circle $\gamma_{B}$ passes through $B$ and is externally tangent to $\omega$ and $\omega_{A}$. Circle $\gamma_{C}$ passes through $C$ and is externally tangent to $\omega$ and $\omega_{A}$. If $\gamma_{B}$ intersects line $B C$ again at $D$, and $\gamma_{C}$ intersects line $B C$ again at $E$, prove that $B D=E C$.
|
Here is another solution based on inversion at $B$. First we will need a lemma.
Lemma: Let $A, B, C, D$ lie on a circle, with $A C$ a diameter of this circle. Say $E$ and $F$ are the feet of the altitudes from $A$ and $C$ to $B D$, respectively. Then $A B E$ is similar to $B C F$, and $B E=D F$.
Proof. The former is due to angle chasing, the latter is because the midpoint of $A C$ is the circumcenter of $(A B C D)$ and hence equidistant from $B$ and $D$.
Now, let $X$ be the $A$-intouch point, and $Y$ the $A$-extouch point. The key identity now is that $B D \cdot B C=$ $B X \cdot B Y$. Paired with the symmetric statement this now solves the problem.
To prove the statement, invert about $B$ with radius $\sqrt{B X \cdot B Y} \cdot \gamma_{B}$ is sent to the line (not $A B$ ) tangent to the images of the incircle and $A$-excircle; it suffices to prove that this line passes through $C$. Now, say the centers of these images are $I^{\prime}$ and $I_{A}^{\prime}$. It suffices to prove that $\angle I^{\prime} C I_{A}^{\prime}=90^{\circ}$, or in other words $B I^{\prime} C I_{A}^{\prime}$ is cyclic. Now, evidently $\triangle I^{\prime} Y B \sim \triangle I X B$ and $\triangle I_{A}^{\prime} X B \sim \triangle I_{A} Y B$. Moreover $B X=C Y$. Hence by the lemma above, $I_{A}^{\prime}$ shares two of the same properties as the antipode of $I^{\prime}$ on $\left(B I^{\prime} C\right)$, so thus they're in fact the same point. So $\left(B I^{\prime} C I_{A}^{\prime}\right)$ is cyclic, and so the claim and hence the problem are proved.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangle $A B C$ has incircle $\omega$ and $A$-excircle $\omega_{A}$. Circle $\gamma_{B}$ passes through $B$ and is externally tangent to $\omega$ and $\omega_{A}$. Circle $\gamma_{C}$ passes through $C$ and is externally tangent to $\omega$ and $\omega_{A}$. If $\gamma_{B}$ intersects line $B C$ again at $D$, and $\gamma_{C}$ intersects line $B C$ again at $E$, prove that $B D=E C$.
|
Here is another solution based on inversion at $B$. First we will need a lemma.
Lemma: Let $A, B, C, D$ lie on a circle, with $A C$ a diameter of this circle. Say $E$ and $F$ are the feet of the altitudes from $A$ and $C$ to $B D$, respectively. Then $A B E$ is similar to $B C F$, and $B E=D F$.
Proof. The former is due to angle chasing, the latter is because the midpoint of $A C$ is the circumcenter of $(A B C D)$ and hence equidistant from $B$ and $D$.
Now, let $X$ be the $A$-intouch point, and $Y$ the $A$-extouch point. The key identity now is that $B D \cdot B C=$ $B X \cdot B Y$. Paired with the symmetric statement this now solves the problem.

To prove the statement, invert about $B$ with radius $\sqrt{B X \cdot B Y} \cdot \gamma_{B}$ is sent to the line (not $A B$ ) tangent to the images of the incircle and $A$-excircle; it suffices to prove that this line passes through $C$. Now, say the centers of these images are $I^{\prime}$ and $I_{A}^{\prime}$. It suffices to prove that $\angle I^{\prime} C I_{A}^{\prime}=90^{\circ}$, or in other words $B I^{\prime} C I_{A}^{\prime}$ is cyclic. Now, evidently $\triangle I^{\prime} Y B \sim \triangle I X B$ and $\triangle I_{A}^{\prime} X B \sim \triangle I_{A} Y B$. Moreover $B X=C Y$. Hence by the lemma above, $I_{A}^{\prime}$ shares two of the same properties as the antipode of $I^{\prime}$ on $\left(B I^{\prime} C\right)$, so thus they're in fact the same point. So $\left(B I^{\prime} C I_{A}^{\prime}\right)$ is cyclic, and so the claim and hence the problem are proved.
|
{
"resource_path": "HarvardMIT/segmented/en-264-tournaments-2023-hmic-solutions.jsonl",
"problem_match": "\n3. [9]",
"solution_match": "\nSolution 2: "
}
|
e6947888-19f8-525e-a765-368fd5e94a3d
| 610,624
|
Triangle $A B C$ has incircle $\omega$ and $A$-excircle $\omega_{A}$. Circle $\gamma_{B}$ passes through $B$ and is externally tangent to $\omega$ and $\omega_{A}$. Circle $\gamma_{C}$ passes through $C$ and is externally tangent to $\omega$ and $\omega_{A}$. If $\gamma_{B}$ intersects line $B C$ again at $D$, and $\gamma_{C}$ intersects line $B C$ again at $E$, prove that $B D=E C$.
|
Here is a length bashing solution.
Let $\gamma_{B}$ intersects $A B$ again at $P$. Then, notice that $\omega_{A}$ is the mixtilinear excircle of $\triangle B D P$, so an inversion around $B$ with radius $\sqrt{B D \cdot B P}$ followed by reflection across the angle bisector of $\angle D B P$ sends $\omega_{A}$ to the incircle of $\triangle B D P$. Therefore, under inversion, the corresponding tangent points must be swapped, giving
$$
(s-c)\left(\frac{B D+B P-D P}{2}\right)=B D \cdot B P \Longrightarrow B D+B P-D P=\frac{2(B D \cdot B P)}{s-c}
$$
Similarly, notice that under the $\sqrt{B D \cdot B P}$-inversion, $\omega$ maps to the $D$-excircle, so
$$
(s-b)\left(\frac{B P+D P-B D}{2}\right)=B D \cdot B P \Longrightarrow B P+D P-B D=\frac{2(B D \cdot B P)}{s-b}
$$
Adding these two equations together, we find that
$$
2 B P=2(B D \cdot B P)\left(\frac{1}{s-b}+\frac{1}{s-c}\right) \Longrightarrow \frac{1}{B D}=\frac{1}{s-b}+\frac{1}{s-c}
$$
Analogously, we have $\frac{1}{C E}=\frac{1}{s-b}+\frac{1}{s-c}$, so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangle $A B C$ has incircle $\omega$ and $A$-excircle $\omega_{A}$. Circle $\gamma_{B}$ passes through $B$ and is externally tangent to $\omega$ and $\omega_{A}$. Circle $\gamma_{C}$ passes through $C$ and is externally tangent to $\omega$ and $\omega_{A}$. If $\gamma_{B}$ intersects line $B C$ again at $D$, and $\gamma_{C}$ intersects line $B C$ again at $E$, prove that $B D=E C$.
|
Here is a length bashing solution.
Let $\gamma_{B}$ intersects $A B$ again at $P$. Then, notice that $\omega_{A}$ is the mixtilinear excircle of $\triangle B D P$, so an inversion around $B$ with radius $\sqrt{B D \cdot B P}$ followed by reflection across the angle bisector of $\angle D B P$ sends $\omega_{A}$ to the incircle of $\triangle B D P$. Therefore, under inversion, the corresponding tangent points must be swapped, giving
$$
(s-c)\left(\frac{B D+B P-D P}{2}\right)=B D \cdot B P \Longrightarrow B D+B P-D P=\frac{2(B D \cdot B P)}{s-c}
$$
Similarly, notice that under the $\sqrt{B D \cdot B P}$-inversion, $\omega$ maps to the $D$-excircle, so
$$
(s-b)\left(\frac{B P+D P-B D}{2}\right)=B D \cdot B P \Longrightarrow B P+D P-B D=\frac{2(B D \cdot B P)}{s-b}
$$
Adding these two equations together, we find that
$$
2 B P=2(B D \cdot B P)\left(\frac{1}{s-b}+\frac{1}{s-c}\right) \Longrightarrow \frac{1}{B D}=\frac{1}{s-b}+\frac{1}{s-c}
$$
Analogously, we have $\frac{1}{C E}=\frac{1}{s-b}+\frac{1}{s-c}$, so we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-264-tournaments-2023-hmic-solutions.jsonl",
"problem_match": "\n3. [9]",
"solution_match": "\nSolution 3: "
}
|
e6947888-19f8-525e-a765-368fd5e94a3d
| 610,624
|
Triangle $A B C$ has incircle $\omega$ and $A$-excircle $\omega_{A}$. Circle $\gamma_{B}$ passes through $B$ and is externally tangent to $\omega$ and $\omega_{A}$. Circle $\gamma_{C}$ passes through $C$ and is externally tangent to $\omega$ and $\omega_{A}$. If $\gamma_{B}$ intersects line $B C$ again at $D$, and $\gamma_{C}$ intersects line $B C$ again at $E$, prove that $B D=E C$.
|
Once again, it suffices by symmetry to show $B P \cdot B C=B X \cdot B Y$, or equivalently
$B P=\frac{B X \cdot B Y}{B X+B Y}$. We use Cartesian coordinates, taking $B$ to be the origin and line $B C$ to be the $x$-axis, with $I$ above the $x$-axis and $I_{A}$ below it. Let $I=(t, r)$ and $I_{A}=\left(u,-r_{A}\right)$ (so $t=B X$ and $\left.u=B Y\right)$. Since $B I \perp B I_{A}$, we have $t u=r r_{A}$. Let $\gamma_{B}$ have center $(x, y)$ and radius $z$. Note that $P=(2 x, 0)$. Now we have that
$$
\begin{aligned}
x^{2}+y^{2} & =z^{2} \\
(x-t)^{2}+(y-r)^{2} & =(z+r)^{2} \\
(x-u)^{2}+\left(y+r_{A}\right)^{2} & =\left(z+r_{A}\right)^{2} .
\end{aligned}
$$
Subtracting the first equation from the second yields $-2 x t+t^{2}=2 r(y+z)$, and subtracting the first equation from the third yields $-2 x u+u^{2}=2 r_{A}(z-y)$. Now, multiplying these equations together gives
$$
t u(-2 x+t)(-2 x+u)=4 r r_{A}\left(z^{2}-y^{2}\right)=4 r r_{A} x^{2}
$$
Dividing by $t u=r r_{A} \neq 0$ yields that $4 x^{2}-2 x(t+u)+t u=(-2 x+t)(-2 x+u)=4 x^{2}$, so $B P=2 x=$ $\frac{t u}{t+u}=\frac{B X \cdot B Y}{B X+B Y}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangle $A B C$ has incircle $\omega$ and $A$-excircle $\omega_{A}$. Circle $\gamma_{B}$ passes through $B$ and is externally tangent to $\omega$ and $\omega_{A}$. Circle $\gamma_{C}$ passes through $C$ and is externally tangent to $\omega$ and $\omega_{A}$. If $\gamma_{B}$ intersects line $B C$ again at $D$, and $\gamma_{C}$ intersects line $B C$ again at $E$, prove that $B D=E C$.
|
Once again, it suffices by symmetry to show $B P \cdot B C=B X \cdot B Y$, or equivalently
$B P=\frac{B X \cdot B Y}{B X+B Y}$. We use Cartesian coordinates, taking $B$ to be the origin and line $B C$ to be the $x$-axis, with $I$ above the $x$-axis and $I_{A}$ below it. Let $I=(t, r)$ and $I_{A}=\left(u,-r_{A}\right)$ (so $t=B X$ and $\left.u=B Y\right)$. Since $B I \perp B I_{A}$, we have $t u=r r_{A}$. Let $\gamma_{B}$ have center $(x, y)$ and radius $z$. Note that $P=(2 x, 0)$. Now we have that
$$
\begin{aligned}
x^{2}+y^{2} & =z^{2} \\
(x-t)^{2}+(y-r)^{2} & =(z+r)^{2} \\
(x-u)^{2}+\left(y+r_{A}\right)^{2} & =\left(z+r_{A}\right)^{2} .
\end{aligned}
$$
Subtracting the first equation from the second yields $-2 x t+t^{2}=2 r(y+z)$, and subtracting the first equation from the third yields $-2 x u+u^{2}=2 r_{A}(z-y)$. Now, multiplying these equations together gives
$$
t u(-2 x+t)(-2 x+u)=4 r r_{A}\left(z^{2}-y^{2}\right)=4 r r_{A} x^{2}
$$
Dividing by $t u=r r_{A} \neq 0$ yields that $4 x^{2}-2 x(t+u)+t u=(-2 x+t)(-2 x+u)=4 x^{2}$, so $B P=2 x=$ $\frac{t u}{t+u}=\frac{B X \cdot B Y}{B X+B Y}$, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-264-tournaments-2023-hmic-solutions.jsonl",
"problem_match": "\n3. [9]",
"solution_match": "\nSolution 4: "
}
|
e6947888-19f8-525e-a765-368fd5e94a3d
| 610,624
|
Let $a_{1}, a_{2}, \ldots$ be an infinite sequence of positive integers such that, for all positive integers $m$ and $n$, we have that $a_{m+n}$ divides $a_{m} a_{n}-1$. Prove that there exists an integer $C$ such that, for all positive integers $k>C$, we have $a_{k}=1$.
|
Solution: For convenience, define $g(x): \mathbb{N} \rightarrow \mathbb{N}$ to be $g(n)=a_{n}$.
We first prove that $1 \in \operatorname{Im}(g)$. Assume otherwise. First, note that $\operatorname{gcd}(g(m+n), g(m))=1$ for all positive integers $m, n$, so thus if $g$ never takes the value 1 then $g$ is injective (and the values it takes are pairwise relatively prime.) Now, let $g(1)=a$ and $g(2)=b$. Note that for every $x$, there exists integers $m, n, p$ such that
$$
\begin{aligned}
g(x+1) & =\frac{a g(x)-1}{m} \\
g(x+1) & =\frac{b g(x-1)-1}{n} \\
g(x) & =\frac{a g(x-1)-1}{p} .
\end{aligned}
$$
Hence,
$$
g(x+1)=\frac{b g(x-1)-1}{n}=\frac{a^{2} g(x-1)-a-p}{m p} .
$$
Now, suppose $g(x+1) \geq g(x-1)$. Then we must have $n<b, m p<a^{2}$. Hence there are finitely many choices for $(n, m, p)$, and each such choice leads to finitely many possibilities to $g(x-1)$ unless $b m p=n a^{2}$. But $\operatorname{gcd}\left(b, a^{2}\right)=1$, so this implies that $b \mid n$, and hence $b \leq n$, which is false. Hence this means that if $g(x+1) \geq g(x-1)$ then $g(x-1)$ must take one of a finite set of possible values.
Now, recall that $g$ is injective. Hence this implies that in fact $g(x+1) \geq g(x-1)$ can only occur a finite number of times, and so for all sufficiently large $x, g(x+1)<g(x-1)$. But this is a contradiction to $g$ being injective, and so our hypothesis was false and hence $1 \in \operatorname{Im}(g)$.
Note that this proof works identically if we scale all the inputs by any positive integer, so this implies that every integer has a multiple in $S:=g^{-1}(\{1\})$.
We now finish the problem. Consider the smallest value of $\operatorname{Im}(g)$ not equal to 1 (if it doesn't exist then we are done), and say $g(c)$ is equal to this value. Then note that if $a \in S$, then $g(a+c) \leq g(c)-1$ and so $a+c \in S$. Now, let $k c$ be a multiple of $c$ which is in $S$; then $d c \in S$ for all $d \geq k$. Now, for each residue class modulo $c$, select an element $j$ for which $g(j) \neq 1$ (if no such element exists we'll still be done, as we will see.) Then for all $d \geq k, g(j+d c) \leq g(j)-1$. Hence $g$ is bounded in each residue class, and so $g$ is bounded. Now note that $g$ is injective in $\mathbb{Z}^{+} \backslash S$, so in fact $\mathbb{Z}^{+} \backslash S$ must be finite! So $g(x)=1$ for all sufficiently large $x$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}, a_{2}, \ldots$ be an infinite sequence of positive integers such that, for all positive integers $m$ and $n$, we have that $a_{m+n}$ divides $a_{m} a_{n}-1$. Prove that there exists an integer $C$ such that, for all positive integers $k>C$, we have $a_{k}=1$.
|
Solution: For convenience, define $g(x): \mathbb{N} \rightarrow \mathbb{N}$ to be $g(n)=a_{n}$.
We first prove that $1 \in \operatorname{Im}(g)$. Assume otherwise. First, note that $\operatorname{gcd}(g(m+n), g(m))=1$ for all positive integers $m, n$, so thus if $g$ never takes the value 1 then $g$ is injective (and the values it takes are pairwise relatively prime.) Now, let $g(1)=a$ and $g(2)=b$. Note that for every $x$, there exists integers $m, n, p$ such that
$$
\begin{aligned}
g(x+1) & =\frac{a g(x)-1}{m} \\
g(x+1) & =\frac{b g(x-1)-1}{n} \\
g(x) & =\frac{a g(x-1)-1}{p} .
\end{aligned}
$$
Hence,
$$
g(x+1)=\frac{b g(x-1)-1}{n}=\frac{a^{2} g(x-1)-a-p}{m p} .
$$
Now, suppose $g(x+1) \geq g(x-1)$. Then we must have $n<b, m p<a^{2}$. Hence there are finitely many choices for $(n, m, p)$, and each such choice leads to finitely many possibilities to $g(x-1)$ unless $b m p=n a^{2}$. But $\operatorname{gcd}\left(b, a^{2}\right)=1$, so this implies that $b \mid n$, and hence $b \leq n$, which is false. Hence this means that if $g(x+1) \geq g(x-1)$ then $g(x-1)$ must take one of a finite set of possible values.
Now, recall that $g$ is injective. Hence this implies that in fact $g(x+1) \geq g(x-1)$ can only occur a finite number of times, and so for all sufficiently large $x, g(x+1)<g(x-1)$. But this is a contradiction to $g$ being injective, and so our hypothesis was false and hence $1 \in \operatorname{Im}(g)$.
Note that this proof works identically if we scale all the inputs by any positive integer, so this implies that every integer has a multiple in $S:=g^{-1}(\{1\})$.
We now finish the problem. Consider the smallest value of $\operatorname{Im}(g)$ not equal to 1 (if it doesn't exist then we are done), and say $g(c)$ is equal to this value. Then note that if $a \in S$, then $g(a+c) \leq g(c)-1$ and so $a+c \in S$. Now, let $k c$ be a multiple of $c$ which is in $S$; then $d c \in S$ for all $d \geq k$. Now, for each residue class modulo $c$, select an element $j$ for which $g(j) \neq 1$ (if no such element exists we'll still be done, as we will see.) Then for all $d \geq k, g(j+d c) \leq g(j)-1$. Hence $g$ is bounded in each residue class, and so $g$ is bounded. Now note that $g$ is injective in $\mathbb{Z}^{+} \backslash S$, so in fact $\mathbb{Z}^{+} \backslash S$ must be finite! So $g(x)=1$ for all sufficiently large $x$, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-264-tournaments-2023-hmic-solutions.jsonl",
"problem_match": "\n5. [11]",
"solution_match": "\nProposed by: Kevin Cong\n"
}
|
616437c0-2506-55b3-b200-ed80c090eded
| 610,626
|
Let $A B C$ be a scalene triangle and $M$ be the midpoint of $B C$. Let $X$ be the point such that $C X \| A B$ and $\angle A M X=90^{\circ}$. Prove that $A M$ bisects $\angle B A X$.
|
## Solution:
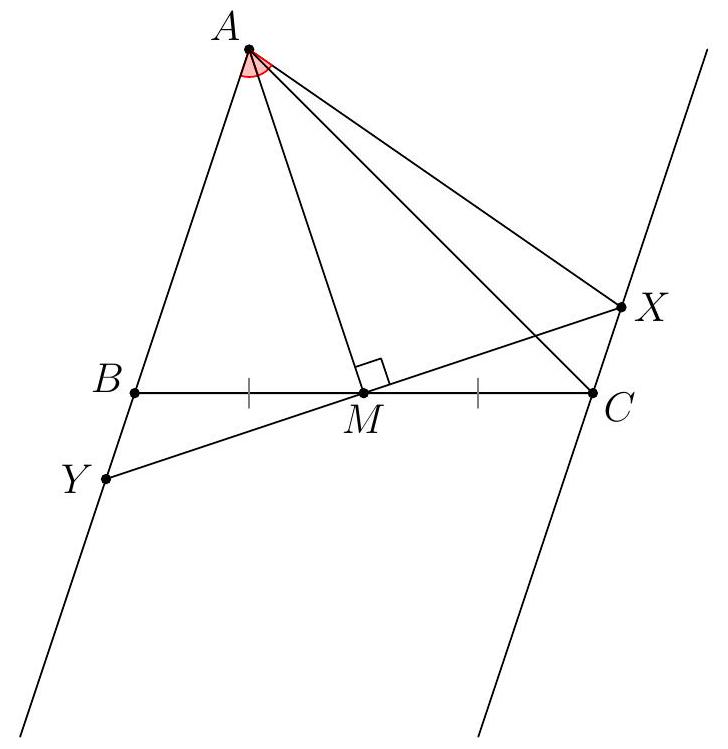
Let $Y$ be the intersection of lines $A B$ and $X M$. Since $B Y \| C X$, we have $\angle Y B M=\angle X C M$. Furthermore, we have $B M=C M$, since $M$ is the midpoint of $B C$. Thus,
$$
\triangle B M Y \cong \triangle C M X
$$
Thus, $M Y=M X$. Combined with the condition $A M \perp X Y$, we get that $A Y X$ is an isosceles triangle with median $A M$. Therefore, $A M$ bisects $\angle Y A X$ which is the same as $\angle B A X$ and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle and $M$ be the midpoint of $B C$. Let $X$ be the point such that $C X \| A B$ and $\angle A M X=90^{\circ}$. Prove that $A M$ bisects $\angle B A X$.
|
## Solution:

Let $Y$ be the intersection of lines $A B$ and $X M$. Since $B Y \| C X$, we have $\angle Y B M=\angle X C M$. Furthermore, we have $B M=C M$, since $M$ is the midpoint of $B C$. Thus,
$$
\triangle B M Y \cong \triangle C M X
$$
Thus, $M Y=M X$. Combined with the condition $A M \perp X Y$, we get that $A Y X$ is an isosceles triangle with median $A M$. Therefore, $A M$ bisects $\angle Y A X$ which is the same as $\angle B A X$ and we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-team-solutions.jsonl",
"problem_match": "\n3. [25]",
"solution_match": "\nProposed by: Pitchayut Saengrungkongka\n\n"
}
|
4799948d-277b-58a7-80d6-889e24241061
| 610,760
|
Let $\mathbb{Q}$ be the set of rational numbers. Given a rational number $a \neq 0$, find, with proof, all functions $f: \mathbb{Q} \rightarrow \mathbb{Q}$ satisfying the equation
$$
f(f(x)+a y)=a f(y)+x
$$
for all $x, y \in \mathbb{Q}$.
|
Let $P(x, y)$ denote the functional equation. From $P(x, 0)$, we have $f(f(x))=x+a f(0)$. Thus, the tripling trick gives $f(x+a f(0))=f(f(f(x)))=f(x)+a f(0)$.
Now, here is the main idea: $P(f(x), y)$ gives
$$
\begin{aligned}
f(f(f(x))+a y) & =a f(y)+f(x) \\
f(x+a f(0)+a y) & =f(x)+a f(y) \\
f(x+a y) & =f(x)+a f(y)-a f(0)
\end{aligned}
$$
In particular, plugging in $x=0$ into this equation gives $f(a y)=a f(y)+(1-a) f(0)$, so inserting it back to the same equation gives
$$
f(x+a y)=f(x)+f(a y)-f(0),
$$
for all rational numbers $x, y$. In particular, the function $g(x)=f(x)-f(0)$ is additive, so $f$ is linear. Let $f(x)=b x+c$. By substituting it in, we have $P(x, y)$ iff
$$
\begin{aligned}
f(a y+b x+c) & =a(b y+c)+x \\
a b y+b^{2} x+b c+c & =a b y+a c+x \\
\left(b^{2}-1\right) x+(b+1-a) c & =0
\end{aligned}
$$
Since $x$ is arbitrary, we can state that $b^{2}-1=0$ and $(b+1-a) c=0$, thus $b= \pm 1$. As $a \neq 0$, we know $b+1-a=0$ only if $b=1$ and $a=2$. When $a \neq 2$ or $b \neq 1$, we know the only solutions are $b= \pm 1, c=0$, while for $a=2, b=1$, the equation is automatically satisfied, so the final answer is
$$
\left\{\begin{array}{l}
f(x)=x \\
f(x)=-x \\
f(x)=x+c \text { for all rational number } c \text { iff } a=2
\end{array}\right.
$$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $\mathbb{Q}$ be the set of rational numbers. Given a rational number $a \neq 0$, find, with proof, all functions $f: \mathbb{Q} \rightarrow \mathbb{Q}$ satisfying the equation
$$
f(f(x)+a y)=a f(y)+x
$$
for all $x, y \in \mathbb{Q}$.
|
Let $P(x, y)$ denote the functional equation. From $P(x, 0)$, we have $f(f(x))=x+a f(0)$. Thus, the tripling trick gives $f(x+a f(0))=f(f(f(x)))=f(x)+a f(0)$.
Now, here is the main idea: $P(f(x), y)$ gives
$$
\begin{aligned}
f(f(f(x))+a y) & =a f(y)+f(x) \\
f(x+a f(0)+a y) & =f(x)+a f(y) \\
f(x+a y) & =f(x)+a f(y)-a f(0)
\end{aligned}
$$
In particular, plugging in $x=0$ into this equation gives $f(a y)=a f(y)+(1-a) f(0)$, so inserting it back to the same equation gives
$$
f(x+a y)=f(x)+f(a y)-f(0),
$$
for all rational numbers $x, y$. In particular, the function $g(x)=f(x)-f(0)$ is additive, so $f$ is linear. Let $f(x)=b x+c$. By substituting it in, we have $P(x, y)$ iff
$$
\begin{aligned}
f(a y+b x+c) & =a(b y+c)+x \\
a b y+b^{2} x+b c+c & =a b y+a c+x \\
\left(b^{2}-1\right) x+(b+1-a) c & =0
\end{aligned}
$$
Since $x$ is arbitrary, we can state that $b^{2}-1=0$ and $(b+1-a) c=0$, thus $b= \pm 1$. As $a \neq 0$, we know $b+1-a=0$ only if $b=1$ and $a=2$. When $a \neq 2$ or $b \neq 1$, we know the only solutions are $b= \pm 1, c=0$, while for $a=2, b=1$, the equation is automatically satisfied, so the final answer is
$$
\left\{\begin{array}{l}
f(x)=x \\
f(x)=-x \\
f(x)=x+c \text { for all rational number } c \text { iff } a=2
\end{array}\right.
$$
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-team-solutions.jsonl",
"problem_match": "\n6. [45]",
"solution_match": "\nSolution: "
}
|
845260f2-5985-558d-9302-9519bcc113cd
| 610,763
|
Let $\mathbb{Q}$ be the set of rational numbers. Given a rational number $a \neq 0$, find, with proof, all functions $f: \mathbb{Q} \rightarrow \mathbb{Q}$ satisfying the equation
$$
f(f(x)+a y)=a f(y)+x
$$
for all $x, y \in \mathbb{Q}$.
|
We will only prove that $f$ is linear. Then, proceed as in the end of Solution 1.
We know $f(f(x))=a f(0)+x$, so as $a f(0)+x$ can take any rational number when $x$ takes every rational number, the range of $f$ is $\mathbb{Q}$, and so $f$ is surjective. If $f\left(x_{1}\right)=f\left(x_{2}\right)$, we have $x_{1}=f\left(f\left(x_{1}\right)\right)-a f(0)=$ $f\left(f\left(x_{2}\right)\right)-a f(0)=x_{2}$, so $x_{1}=x_{2}$, implying $f$ being injective. Thus, $f$ is bijective.
From $P(x, 0)$, we still get $f(f(x))=x+a f(0)$.
Thus, from $\left.P\left(f^{-1}(0)\right), y / a\right)$, we can get $f(y)=a f(y / a)+f^{-1}(0)$. Plugging again $P(f(x), y / a)$, we have $f(f(f(x))+y)=f(x+y+a f(0))=a f(y / a)+f(x)=f(x)+f(y)-f^{-1}(x)$.
Thus, we know $f(x+y)=f(x-a f(0))+f(y)-f^{-1}(0)=f(x)+f(y)-f(0)$. Hence, the function $g(x)=f(x)-f(0)$ is additive, so $g(x)=k x$ for some rational number $k$. Thus, $f$ is a linear function, and we can proceed as in above solution.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $\mathbb{Q}$ be the set of rational numbers. Given a rational number $a \neq 0$, find, with proof, all functions $f: \mathbb{Q} \rightarrow \mathbb{Q}$ satisfying the equation
$$
f(f(x)+a y)=a f(y)+x
$$
for all $x, y \in \mathbb{Q}$.
|
We will only prove that $f$ is linear. Then, proceed as in the end of Solution 1.
We know $f(f(x))=a f(0)+x$, so as $a f(0)+x$ can take any rational number when $x$ takes every rational number, the range of $f$ is $\mathbb{Q}$, and so $f$ is surjective. If $f\left(x_{1}\right)=f\left(x_{2}\right)$, we have $x_{1}=f\left(f\left(x_{1}\right)\right)-a f(0)=$ $f\left(f\left(x_{2}\right)\right)-a f(0)=x_{2}$, so $x_{1}=x_{2}$, implying $f$ being injective. Thus, $f$ is bijective.
From $P(x, 0)$, we still get $f(f(x))=x+a f(0)$.
Thus, from $\left.P\left(f^{-1}(0)\right), y / a\right)$, we can get $f(y)=a f(y / a)+f^{-1}(0)$. Plugging again $P(f(x), y / a)$, we have $f(f(f(x))+y)=f(x+y+a f(0))=a f(y / a)+f(x)=f(x)+f(y)-f^{-1}(x)$.
Thus, we know $f(x+y)=f(x-a f(0))+f(y)-f^{-1}(0)=f(x)+f(y)-f(0)$. Hence, the function $g(x)=f(x)-f(0)$ is additive, so $g(x)=k x$ for some rational number $k$. Thus, $f$ is a linear function, and we can proceed as in above solution.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-team-solutions.jsonl",
"problem_match": "\n6. [45]",
"solution_match": "\nSolution 2: "
}
|
845260f2-5985-558d-9302-9519bcc113cd
| 610,763
|
Let $A B C D E F$ be a regular hexagon with $P$ as a point in its interior. Prove that of the three values $\tan \angle A P D, \tan \angle B P E$, and $\tan \angle C P F$, two of them sum to the third one.
|
## Solution 1:
WLOG let the side length of the hexagon be 1 . Let $O$ be the center of the hexagon. Consider drawing in the circles $(A P D),(B P E)$, and $(C P F)$. Note that $O$ lies on the radical axis of all three circles, since $A O \cdot O D=B O \cdot O E=C O \cdot O F$. Since $P$ also lies on the radical axis, all three circles are coaxial.
Let $X, Y$, and $Z$ be the centers of $(A P D),(B P E)$, and $(C P F)$, respectively. Since the circles are coaxial, $X, Y$, and $Z$ are collinear. WLOG $Y$ lies on segment $X Z$. Note that $X O \perp A D, Y O \perp$ $B E \Longrightarrow \angle X O Y=60^{\circ}$. Similarly, we have $\angle Y O Z=60^{\circ}$. Now, inverting at $O$ and using van Schooten's Theorem gives that $1 / O Y=1 / O X+1 / O Z$.
Furthermore, we have
$$
\angle A P D=180^{\circ}-\frac{1}{2} \angle A X D=180^{\circ}-\angle A X O \Longrightarrow \tan \angle A P D=-\tan \angle A X O=-\frac{A O}{O X}=-\frac{1}{O X}
$$
Similarly, we have $\tan \angle B P E=-\frac{1}{O Y}$ and $\tan \angle C P F=-\frac{1}{O Z}$. Therefore, two of these tangent values sum to the third, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E F$ be a regular hexagon with $P$ as a point in its interior. Prove that of the three values $\tan \angle A P D, \tan \angle B P E$, and $\tan \angle C P F$, two of them sum to the third one.
|
## Solution 1:

WLOG let the side length of the hexagon be 1 . Let $O$ be the center of the hexagon. Consider drawing in the circles $(A P D),(B P E)$, and $(C P F)$. Note that $O$ lies on the radical axis of all three circles, since $A O \cdot O D=B O \cdot O E=C O \cdot O F$. Since $P$ also lies on the radical axis, all three circles are coaxial.
Let $X, Y$, and $Z$ be the centers of $(A P D),(B P E)$, and $(C P F)$, respectively. Since the circles are coaxial, $X, Y$, and $Z$ are collinear. WLOG $Y$ lies on segment $X Z$. Note that $X O \perp A D, Y O \perp$ $B E \Longrightarrow \angle X O Y=60^{\circ}$. Similarly, we have $\angle Y O Z=60^{\circ}$. Now, inverting at $O$ and using van Schooten's Theorem gives that $1 / O Y=1 / O X+1 / O Z$.
Furthermore, we have
$$
\angle A P D=180^{\circ}-\frac{1}{2} \angle A X D=180^{\circ}-\angle A X O \Longrightarrow \tan \angle A P D=-\tan \angle A X O=-\frac{A O}{O X}=-\frac{1}{O X}
$$
Similarly, we have $\tan \angle B P E=-\frac{1}{O Y}$ and $\tan \angle C P F=-\frac{1}{O Z}$. Therefore, two of these tangent values sum to the third, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-team-solutions.jsonl",
"problem_match": "\n7. [50]",
"solution_match": "\nProposed by: Albert Wang\n\n"
}
|
0887cdf7-9f2a-5e1c-8ccd-007ea4602b1a
| 610,764
|
Let $A B C D E F$ be a regular hexagon with $P$ as a point in its interior. Prove that of the three values $\tan \angle A P D, \tan \angle B P E$, and $\tan \angle C P F$, two of them sum to the third one.
|
Firstly, note that $A D, B E$, and $C F$ are diameters of the circle $(A B C D E F)$, so the angles $\angle A P D$, $\angle B P E, \angle C P F$ are all obtuse. Therefore, the desired tangents are well-defined.
WLOG let the side length of the hexagon be 1 . Let $O$ be the center of the hexagon, and let $O P=x$. Finally, let $\angle A O P=\theta$.
Now, by Law of Cosines, we have $A P=\sqrt{x^{2}+1-2 x \cos \theta}$ and $D P=\sqrt{x^{2}+1+2 x \cos \theta}$. Now, by Law of Cosines again we have
$$
\begin{gathered}
\cos \angle A P D=\frac{2\left(x^{2}+1\right)-4}{2 \sqrt{\left(x^{2}+1\right)^{2}-4 x^{2} \cos ^{2} \theta}}=\frac{x^{2}-1}{\sqrt{\left(1-x^{2}\right)^{2}+4 x^{2} \sin ^{2} \theta}} \\
\Longrightarrow \tan \angle A P D=\frac{2 x|\sin \theta|}{x^{2}-1} .
\end{gathered}
$$
Similarly, $\angle(B E, O P)$ and $\angle(C F, O P)$ are $\theta+60^{\circ}$ and $\theta+120^{\circ}$, respectively (here we are using directed angles). Therefore, the desired three values are
$$
\{\tan \angle A P D, \tan \angle B P E, \tan \angle C P F\}=\left\{\frac{2 x|\sin \theta|}{x^{2}-1}, \frac{2 x\left|\sin \left(\theta+60^{\circ}\right)\right|}{x^{2}-1}, \frac{2 x\left|\sin \left(\theta+120^{\circ}\right)\right|}{x^{2}-1}\right\} .
$$
We can scale down the tangent values by $\frac{2 x}{x^{2}-1}$ to get $\left\{|\sin \theta|,\left|\sin \left(\theta+60^{\circ}\right)\right|,\left|\sin \left(\theta+120^{\circ}\right)\right|\right\}$. Now, consider an equilateral triangle with vertices at the third roots of unity rotated by $\theta$ degrees counterclockwise. The three values represent the distances from the three vertices to the real axis. Since the centroid of this triangle is the origin (lying on the real axis), two of these quantities must sum to the third, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E F$ be a regular hexagon with $P$ as a point in its interior. Prove that of the three values $\tan \angle A P D, \tan \angle B P E$, and $\tan \angle C P F$, two of them sum to the third one.
|
Firstly, note that $A D, B E$, and $C F$ are diameters of the circle $(A B C D E F)$, so the angles $\angle A P D$, $\angle B P E, \angle C P F$ are all obtuse. Therefore, the desired tangents are well-defined.
WLOG let the side length of the hexagon be 1 . Let $O$ be the center of the hexagon, and let $O P=x$. Finally, let $\angle A O P=\theta$.
Now, by Law of Cosines, we have $A P=\sqrt{x^{2}+1-2 x \cos \theta}$ and $D P=\sqrt{x^{2}+1+2 x \cos \theta}$. Now, by Law of Cosines again we have
$$
\begin{gathered}
\cos \angle A P D=\frac{2\left(x^{2}+1\right)-4}{2 \sqrt{\left(x^{2}+1\right)^{2}-4 x^{2} \cos ^{2} \theta}}=\frac{x^{2}-1}{\sqrt{\left(1-x^{2}\right)^{2}+4 x^{2} \sin ^{2} \theta}} \\
\Longrightarrow \tan \angle A P D=\frac{2 x|\sin \theta|}{x^{2}-1} .
\end{gathered}
$$
Similarly, $\angle(B E, O P)$ and $\angle(C F, O P)$ are $\theta+60^{\circ}$ and $\theta+120^{\circ}$, respectively (here we are using directed angles). Therefore, the desired three values are
$$
\{\tan \angle A P D, \tan \angle B P E, \tan \angle C P F\}=\left\{\frac{2 x|\sin \theta|}{x^{2}-1}, \frac{2 x\left|\sin \left(\theta+60^{\circ}\right)\right|}{x^{2}-1}, \frac{2 x\left|\sin \left(\theta+120^{\circ}\right)\right|}{x^{2}-1}\right\} .
$$
We can scale down the tangent values by $\frac{2 x}{x^{2}-1}$ to get $\left\{|\sin \theta|,\left|\sin \left(\theta+60^{\circ}\right)\right|,\left|\sin \left(\theta+120^{\circ}\right)\right|\right\}$. Now, consider an equilateral triangle with vertices at the third roots of unity rotated by $\theta$ degrees counterclockwise. The three values represent the distances from the three vertices to the real axis. Since the centroid of this triangle is the origin (lying on the real axis), two of these quantities must sum to the third, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-team-solutions.jsonl",
"problem_match": "\n7. [50]",
"solution_match": "\n## Solution 2:\n\n"
}
|
0887cdf7-9f2a-5e1c-8ccd-007ea4602b1a
| 610,764
|
Let $A B C D E F$ be a regular hexagon with $P$ as a point in its interior. Prove that of the three values $\tan \angle A P D, \tan \angle B P E$, and $\tan \angle C P F$, two of them sum to the third one.
|
We will show either the three sum to 0 or two of them sum to the third one; since they're all negative, the former case is actually impossible.
Let $(A B C D E F)$ be the unit circle, with $a=1, b=\omega$, and so on, where $\omega=e^{\pi i / 3}$. Then $\angle A P D$ is the argument of
$$
\frac{1-p}{\omega^{3}-p}=\frac{(1-p)\left(\omega^{3}-\bar{p}\right)}{\left(\omega^{3}-p\right)\left(\omega^{3}-\bar{p}\right)}=\frac{\omega^{3}-\bar{p}-\omega^{3} p+|p|^{2}}{1+|p|^{2}-\omega^{3} p-\omega^{3} \bar{p}}
$$
Then $\tan \angle A P D$ is the imaginary part divided by the real part of this, which is
$$
-\frac{1}{i} \cdot \frac{\bar{p}-p}{|p|^{2}-1}=c \cdot \operatorname{dist}(P, A D)
$$
for some constant $c$. (Note that $\tan A P D$ might actually be the negative of this, depending on direction; this is why we added the remark at the beginning about them possibly summing to 0 .)
Similarly, $\tan \angle B P E=c \cdot \operatorname{dist}(P, B E)$ and $\tan \angle C P F=c \cdot \operatorname{dist}(P, C F)$. It suffices to show that two $\operatorname{dist}(P, A D), \operatorname{dist}(P, B E)$, and $\operatorname{dist}(P, C F)$ sum to the third. However, this is easy; without loss of generality let $P$ be inside $O A B$, and let the hexagon have side length 1. Then
$$
\operatorname{dist}(P, A D)+\operatorname{dist}(P, B E)=\frac{\sqrt{3}}{2}-\operatorname{dist}(P, A B)=\operatorname{dist}(P, C F)
$$
as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E F$ be a regular hexagon with $P$ as a point in its interior. Prove that of the three values $\tan \angle A P D, \tan \angle B P E$, and $\tan \angle C P F$, two of them sum to the third one.
|
We will show either the three sum to 0 or two of them sum to the third one; since they're all negative, the former case is actually impossible.
Let $(A B C D E F)$ be the unit circle, with $a=1, b=\omega$, and so on, where $\omega=e^{\pi i / 3}$. Then $\angle A P D$ is the argument of
$$
\frac{1-p}{\omega^{3}-p}=\frac{(1-p)\left(\omega^{3}-\bar{p}\right)}{\left(\omega^{3}-p\right)\left(\omega^{3}-\bar{p}\right)}=\frac{\omega^{3}-\bar{p}-\omega^{3} p+|p|^{2}}{1+|p|^{2}-\omega^{3} p-\omega^{3} \bar{p}}
$$
Then $\tan \angle A P D$ is the imaginary part divided by the real part of this, which is
$$
-\frac{1}{i} \cdot \frac{\bar{p}-p}{|p|^{2}-1}=c \cdot \operatorname{dist}(P, A D)
$$
for some constant $c$. (Note that $\tan A P D$ might actually be the negative of this, depending on direction; this is why we added the remark at the beginning about them possibly summing to 0 .)
Similarly, $\tan \angle B P E=c \cdot \operatorname{dist}(P, B E)$ and $\tan \angle C P F=c \cdot \operatorname{dist}(P, C F)$. It suffices to show that two $\operatorname{dist}(P, A D), \operatorname{dist}(P, B E)$, and $\operatorname{dist}(P, C F)$ sum to the third. However, this is easy; without loss of generality let $P$ be inside $O A B$, and let the hexagon have side length 1. Then
$$
\operatorname{dist}(P, A D)+\operatorname{dist}(P, B E)=\frac{\sqrt{3}}{2}-\operatorname{dist}(P, A B)=\operatorname{dist}(P, C F)
$$
as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-team-solutions.jsonl",
"problem_match": "\n7. [50]",
"solution_match": "\nSolution 3: "
}
|
0887cdf7-9f2a-5e1c-8ccd-007ea4602b1a
| 610,764
|
Let $P$ be a point in the interior of quadrilateral $A B C D$ such that the circumcircles of triangles $P D A, P A B$, and $P B C$ are pairwise distinct but congruent. Let the lines $A D$ and $B C$ meet at $X$. If $O$ is the circumcenter of triangle $X C D$, prove that $O P \perp A B$.
|
## Solution 1:
Because the circles have equal radii, $\angle P D A=\angle A B P$, so if $(P D A)$ intersects line $A B$ again at a point $B^{\prime}$, then we have $\angle P B^{\prime} B=\angle P B B^{\prime}$, which means $P B=P B^{\prime}$, similarly for the second intersection of $(P C B)$ with $A B, A^{\prime}$; thus, $(P D A)$ and $(P C B)$ are congruent mirror images across the $P$-altitude, as they are $\left(P A B^{\prime}\right)$ and $\left(P B A^{\prime}\right)$, respectively.
Consider $C^{\prime}$, the reflection of $C$ across the $P$-altitude. We want to prove that $C^{\prime}$ lies on $(X C D)$, as then the circumcenter of $(X C D)$ will lie on the perpendicular bisector of $C C^{\prime}$. Because of our earlier observation, $C^{\prime}, D, P, A$ are concyclic.
We present two approaches to finishing the angle chase from here:
- Add point $C^{\prime \prime}$, the intersection of $C C^{\prime}$ with $(X D A)$. Because $A B$ is parallel to the line between the centers, and so is $C^{\prime \prime} C$, then $A B C C^{\prime \prime}$ is a parallelogram; thus,
$$
\angle C^{\prime} D A=\angle C^{\prime} C^{\prime \prime} A=\angle C^{\prime} C B=\angle C^{\prime} C X
$$
- Add point $B^{\prime}$, the reflection of $B$ over the $P$-altitude. Note that $B^{\prime}$ lies on $(X D A)$; in particular, $C^{\prime} C B B^{\prime}$ is an isosceles trapezoid, as $C^{\prime} B^{\prime}$ is the reflection of $C B$ over the $P$-altitude of $\triangle P A B$. Thus,
$$
\angle C^{\prime} D A=180-\angle C^{\prime} B^{\prime} A=180-\angle C^{\prime} B^{\prime} B=\angle C^{\prime} C B=\angle C^{\prime} C X
$$
Remark. It is possible to do the last angle chasing without adding any additional points (beyond $C^{\prime}$ ). However, the details are much messier.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point in the interior of quadrilateral $A B C D$ such that the circumcircles of triangles $P D A, P A B$, and $P B C$ are pairwise distinct but congruent. Let the lines $A D$ and $B C$ meet at $X$. If $O$ is the circumcenter of triangle $X C D$, prove that $O P \perp A B$.
|
## Solution 1:

Because the circles have equal radii, $\angle P D A=\angle A B P$, so if $(P D A)$ intersects line $A B$ again at a point $B^{\prime}$, then we have $\angle P B^{\prime} B=\angle P B B^{\prime}$, which means $P B=P B^{\prime}$, similarly for the second intersection of $(P C B)$ with $A B, A^{\prime}$; thus, $(P D A)$ and $(P C B)$ are congruent mirror images across the $P$-altitude, as they are $\left(P A B^{\prime}\right)$ and $\left(P B A^{\prime}\right)$, respectively.
Consider $C^{\prime}$, the reflection of $C$ across the $P$-altitude. We want to prove that $C^{\prime}$ lies on $(X C D)$, as then the circumcenter of $(X C D)$ will lie on the perpendicular bisector of $C C^{\prime}$. Because of our earlier observation, $C^{\prime}, D, P, A$ are concyclic.
We present two approaches to finishing the angle chase from here:
- Add point $C^{\prime \prime}$, the intersection of $C C^{\prime}$ with $(X D A)$. Because $A B$ is parallel to the line between the centers, and so is $C^{\prime \prime} C$, then $A B C C^{\prime \prime}$ is a parallelogram; thus,
$$
\angle C^{\prime} D A=\angle C^{\prime} C^{\prime \prime} A=\angle C^{\prime} C B=\angle C^{\prime} C X
$$
- Add point $B^{\prime}$, the reflection of $B$ over the $P$-altitude. Note that $B^{\prime}$ lies on $(X D A)$; in particular, $C^{\prime} C B B^{\prime}$ is an isosceles trapezoid, as $C^{\prime} B^{\prime}$ is the reflection of $C B$ over the $P$-altitude of $\triangle P A B$. Thus,
$$
\angle C^{\prime} D A=180-\angle C^{\prime} B^{\prime} A=180-\angle C^{\prime} B^{\prime} B=\angle C^{\prime} C B=\angle C^{\prime} C X
$$
Remark. It is possible to do the last angle chasing without adding any additional points (beyond $C^{\prime}$ ). However, the details are much messier.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-team-solutions.jsonl",
"problem_match": "\n8. [50]",
"solution_match": "\nProposed by: Pitchayut Saengrungkongka\n\n"
}
|
8aa5c8f6-0a87-5f05-9e9a-292f3d7ea6a4
| 610,765
|
Let $P$ be a point in the interior of quadrilateral $A B C D$ such that the circumcircles of triangles $P D A, P A B$, and $P B C$ are pairwise distinct but congruent. Let the lines $A D$ and $B C$ meet at $X$. If $O$ is the circumcenter of triangle $X C D$, prove that $O P \perp A B$.
|
Invert about $P$. Because the circles $(P D A),(P A B),(P B C)$ all have equal radii and pass through $P$, the resulting lines $D^{\prime} A^{\prime}, A^{\prime} B^{\prime}, B^{\prime} C^{\prime}$ are equal distances away from $P$; letting $H^{\prime}$ be the intersection of lines $D^{\prime} A^{\prime}$ and $B^{\prime} C^{\prime}$, it follows that $P$ is an incenter or excenter of $\triangle A^{\prime} B^{\prime} H^{\prime}$. Also, in the original diagram, the $P$-altitude of $\triangle P A B$ includes the second intersection of the circles $(P D A)$ and $(P C B)$ (as in the first solution); thus this $P$-altitude inverts to line $P H^{\prime}$. Finally, $X^{\prime}$ is the intersection of $\left(P D^{\prime} A^{\prime}\right)$ and $\left(P B^{\prime} C^{\prime}\right)$.
Note that the center of $(X C D)$ lies on the $P$-altitude of $P A B$ iff the inverse of the center of $\left(X^{\prime} C^{\prime} D^{\prime}\right)$ does. Thus we want to show that the center of $\left(X^{\prime} C^{\prime} D^{\prime}\right)$ lies on $H^{\prime} P$. Let $D^{\prime \prime}$ be the second intersection of $X^{\prime} C^{\prime} D^{\prime}$ with $B^{\prime} H^{\prime}$. Then
$$
\begin{aligned}
\measuredangle\left(D^{\prime} D^{\prime \prime}, H^{\prime} P\right) & =\measuredangle D^{\prime} D^{\prime \prime} H^{\prime}+\measuredangle D^{\prime \prime} H^{\prime} P \\
& =\measuredangle D^{\prime} X^{\prime} C^{\prime}+\measuredangle B^{\prime} H^{\prime} P \\
& =\measuredangle D^{\prime} X^{\prime} P+\measuredangle P X^{\prime} C^{\prime}+\measuredangle P H^{\prime} A^{\prime} \\
& =\measuredangle D^{\prime} A^{\prime} P+\measuredangle P B^{\prime} C^{\prime}+\measuredangle P H^{\prime} A^{\prime} \\
& =\measuredangle P A^{\prime} B^{\prime}+\measuredangle P B^{\prime} H^{\prime}+\measuredangle P H^{\prime} A^{\prime} \\
& =90^{\circ}
\end{aligned}
$$
(where the last step follows from the fact that $P$ is an incenter or excenter of $\triangle A^{\prime} B^{\prime} H^{\prime}$ ), and
$$
\begin{aligned}
\measuredangle H^{\prime} D^{\prime} D^{\prime \prime} & =180^{\circ}-\measuredangle D^{\prime \prime} H D^{\prime}-\measuredangle D^{\prime} D^{\prime \prime} H \\
& =180^{\circ}-\measuredangle D^{\prime \prime} H^{\prime} P-\left(\measuredangle D^{\prime \prime} H^{\prime} P+\measuredangle D^{\prime} D^{\prime \prime} H^{\prime}\right) \\
& =90^{\circ}-\measuredangle D^{\prime \prime} H^{\prime} P \\
& =\measuredangle D^{\prime} D^{\prime \prime} H^{\prime},
\end{aligned}
$$
so $\triangle H^{\prime} D^{\prime} D^{\prime \prime}$ is isosceles, and thus $H^{\prime} P$ is the perpendicular bisector of $D^{\prime} D^{\prime \prime}$. Thus the center of $\left(X^{\prime} C^{\prime} D^{\prime} D^{\prime \prime}\right)$ lies on $H^{\prime} P$, which means we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point in the interior of quadrilateral $A B C D$ such that the circumcircles of triangles $P D A, P A B$, and $P B C$ are pairwise distinct but congruent. Let the lines $A D$ and $B C$ meet at $X$. If $O$ is the circumcenter of triangle $X C D$, prove that $O P \perp A B$.
|

Invert about $P$. Because the circles $(P D A),(P A B),(P B C)$ all have equal radii and pass through $P$, the resulting lines $D^{\prime} A^{\prime}, A^{\prime} B^{\prime}, B^{\prime} C^{\prime}$ are equal distances away from $P$; letting $H^{\prime}$ be the intersection of lines $D^{\prime} A^{\prime}$ and $B^{\prime} C^{\prime}$, it follows that $P$ is an incenter or excenter of $\triangle A^{\prime} B^{\prime} H^{\prime}$. Also, in the original diagram, the $P$-altitude of $\triangle P A B$ includes the second intersection of the circles $(P D A)$ and $(P C B)$ (as in the first solution); thus this $P$-altitude inverts to line $P H^{\prime}$. Finally, $X^{\prime}$ is the intersection of $\left(P D^{\prime} A^{\prime}\right)$ and $\left(P B^{\prime} C^{\prime}\right)$.
Note that the center of $(X C D)$ lies on the $P$-altitude of $P A B$ iff the inverse of the center of $\left(X^{\prime} C^{\prime} D^{\prime}\right)$ does. Thus we want to show that the center of $\left(X^{\prime} C^{\prime} D^{\prime}\right)$ lies on $H^{\prime} P$. Let $D^{\prime \prime}$ be the second intersection of $X^{\prime} C^{\prime} D^{\prime}$ with $B^{\prime} H^{\prime}$. Then
$$
\begin{aligned}
\measuredangle\left(D^{\prime} D^{\prime \prime}, H^{\prime} P\right) & =\measuredangle D^{\prime} D^{\prime \prime} H^{\prime}+\measuredangle D^{\prime \prime} H^{\prime} P \\
& =\measuredangle D^{\prime} X^{\prime} C^{\prime}+\measuredangle B^{\prime} H^{\prime} P \\
& =\measuredangle D^{\prime} X^{\prime} P+\measuredangle P X^{\prime} C^{\prime}+\measuredangle P H^{\prime} A^{\prime} \\
& =\measuredangle D^{\prime} A^{\prime} P+\measuredangle P B^{\prime} C^{\prime}+\measuredangle P H^{\prime} A^{\prime} \\
& =\measuredangle P A^{\prime} B^{\prime}+\measuredangle P B^{\prime} H^{\prime}+\measuredangle P H^{\prime} A^{\prime} \\
& =90^{\circ}
\end{aligned}
$$
(where the last step follows from the fact that $P$ is an incenter or excenter of $\triangle A^{\prime} B^{\prime} H^{\prime}$ ), and
$$
\begin{aligned}
\measuredangle H^{\prime} D^{\prime} D^{\prime \prime} & =180^{\circ}-\measuredangle D^{\prime \prime} H D^{\prime}-\measuredangle D^{\prime} D^{\prime \prime} H \\
& =180^{\circ}-\measuredangle D^{\prime \prime} H^{\prime} P-\left(\measuredangle D^{\prime \prime} H^{\prime} P+\measuredangle D^{\prime} D^{\prime \prime} H^{\prime}\right) \\
& =90^{\circ}-\measuredangle D^{\prime \prime} H^{\prime} P \\
& =\measuredangle D^{\prime} D^{\prime \prime} H^{\prime},
\end{aligned}
$$
so $\triangle H^{\prime} D^{\prime} D^{\prime \prime}$ is isosceles, and thus $H^{\prime} P$ is the perpendicular bisector of $D^{\prime} D^{\prime \prime}$. Thus the center of $\left(X^{\prime} C^{\prime} D^{\prime} D^{\prime \prime}\right)$ lies on $H^{\prime} P$, which means we're done.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-team-solutions.jsonl",
"problem_match": "\n8. [50]",
"solution_match": "\n## Solution 2:\n\n"
}
|
8aa5c8f6-0a87-5f05-9e9a-292f3d7ea6a4
| 610,765
|
Let $P$ be a point in the interior of quadrilateral $A B C D$ such that the circumcircles of triangles $P D A, P A B$, and $P B C$ are pairwise distinct but congruent. Let the lines $A D$ and $B C$ meet at $X$. If $O$ is the circumcenter of triangle $X C D$, prove that $O P \perp A B$.
|
Let $A^{\prime}$ be the other intersection of line $P A$ with $(P D X)$ and $B^{\prime}$ be the other intersection of $P B$ with $(P C X)$. Consider circles $\left(P A^{\prime} B^{\prime}\right)$ and $(X C D)$. Note that $A$ and $B$ have equal power with respect to both circles, because of $\left(P D A^{\prime} X\right)$ and $\left(P C B^{\prime} X\right)$. Thus, $A B$ is the radical axis of the two cricles. However,
$$
\measuredangle P A^{\prime} X=\measuredangle P D X=\measuredangle P D A=\measuredangle A B P
$$
and
$$
\measuredangle X B^{\prime} P=\measuredangle X C P=\measuredangle B C P=\measuredangle P A B
$$
where the last step follows from the fact that the circles have equal radii. Because $\measuredangle B^{\prime} P A^{\prime}=\measuredangle B P A$, it follows that $A^{\prime}, X, B^{\prime}$ are collinear, and in fact $\triangle P A B \sim \triangle P B^{\prime} A^{\prime}$. In particular, this means that the $P$-altitude of $\triangle P A B$ passes through the circumcenter of $\triangle P B^{\prime} A^{\prime}$, as the circumcenter and orthocenter are isogonal conjugates. Thus, as the circumcenter of $P A^{\prime} B^{\prime}$ lies on the $P$-altitude, and the line between the centers of $\left(P A^{\prime} B^{\prime}\right)$ and $(X C D)$ must be perpendicular to their radical axis $A B$, then the circumcenter of $(X C D)$ must lie on the $P$-altitude as well, completing the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point in the interior of quadrilateral $A B C D$ such that the circumcircles of triangles $P D A, P A B$, and $P B C$ are pairwise distinct but congruent. Let the lines $A D$ and $B C$ meet at $X$. If $O$ is the circumcenter of triangle $X C D$, prove that $O P \perp A B$.
|

Let $A^{\prime}$ be the other intersection of line $P A$ with $(P D X)$ and $B^{\prime}$ be the other intersection of $P B$ with $(P C X)$. Consider circles $\left(P A^{\prime} B^{\prime}\right)$ and $(X C D)$. Note that $A$ and $B$ have equal power with respect to both circles, because of $\left(P D A^{\prime} X\right)$ and $\left(P C B^{\prime} X\right)$. Thus, $A B$ is the radical axis of the two cricles. However,
$$
\measuredangle P A^{\prime} X=\measuredangle P D X=\measuredangle P D A=\measuredangle A B P
$$
and
$$
\measuredangle X B^{\prime} P=\measuredangle X C P=\measuredangle B C P=\measuredangle P A B
$$
where the last step follows from the fact that the circles have equal radii. Because $\measuredangle B^{\prime} P A^{\prime}=\measuredangle B P A$, it follows that $A^{\prime}, X, B^{\prime}$ are collinear, and in fact $\triangle P A B \sim \triangle P B^{\prime} A^{\prime}$. In particular, this means that the $P$-altitude of $\triangle P A B$ passes through the circumcenter of $\triangle P B^{\prime} A^{\prime}$, as the circumcenter and orthocenter are isogonal conjugates. Thus, as the circumcenter of $P A^{\prime} B^{\prime}$ lies on the $P$-altitude, and the line between the centers of $\left(P A^{\prime} B^{\prime}\right)$ and $(X C D)$ must be perpendicular to their radical axis $A B$, then the circumcenter of $(X C D)$ must lie on the $P$-altitude as well, completing the proof.
|
{
"resource_path": "HarvardMIT/segmented/en-272-2024-feb-team-solutions.jsonl",
"problem_match": "\n8. [50]",
"solution_match": "\n## Solution 3:\n\n"
}
|
8aa5c8f6-0a87-5f05-9e9a-292f3d7ea6a4
| 610,765
|
Let $S$ be a set of nonnegative integers such that
- there exist two elements $a$ and $b$ in $S$ such that $a, b>1$ and $\operatorname{gcd}(a, b)=1$; and
- for any (not necessarily distinct) element $x$ and nonzero element $y$ in $S$, both $x y$ and the remainder when $x$ is divided by $y$ are in $S$.
Prove that $S$ contains every nonnegative integer.
|
Solution: Assume $a<b$. Note that we can get $1 \in S$ via the Euclidean algorithm, and $0 \in S$ from $a \bmod 1$. Suppose $(a, b) \neq(2,3)$. We will show that there exists $c, d \in S$ with $1<c \leq a$ and $1<d \leq b$, with $\operatorname{gcd}(c, d)=1$ and at least one of $c \neq a$ and $d \neq b$ is true. This will show that $2,3 \in S$ by repeatedly applying this sequence of operations. Assume $a>2$.
Unless $b \bmod a=1,(b \bmod a, a)$ works. Thus, assume $b \equiv 1(\bmod a)$. If we can construct any integer $x$ such that $x \not \equiv 0,1 \bmod a$, then we can take $(x \bmod a, a)$; this will be our new goal. Suppose that such an $x$ is not constructable.
Suppose $a^{k}=q b^{\ell}+r$, with $r<a^{k}$. We must have $r \equiv 0,1(\bmod a)$. Taking both sides mod $a$, this means that $0 \equiv q+r(\bmod a)$, so $q \equiv 0,-1(\bmod a)$. Thus, $\left\lfloor\frac{a^{k}}{b^{\ell}}\right\rfloor \equiv 0,-1(\bmod a)$, for all $k, \ell \in \mathbb{N}$. Take $\ell=\left\lfloor k \log _{b} a\right\rfloor$, so $\left\lfloor\frac{a^{k}}{b^{\ell}}\right\rfloor$ is the first digit in the base $b$ representation of $a^{k}$. We can take $k$ such that $0 \leq\left\{k \log _{b} a\right\}<\log _{b} 2$, where $\{\cdot\}$ represents the fractional part operation, since $\log _{b} a$ is irrational. Taking such a $k$, we get the first digit of $a^{k}$ in base $b$ is 1 , which contradicts $\left\lfloor\frac{a^{k}}{b^{\varepsilon}}\right\rfloor \equiv 0,-1(\bmod a)$.
Thus, if $a>2$ then we have shown what we wanted. Suppose $a=2$. Let $2^{k}<b<2^{k+1}$ for some $k$. If $b \neq 3$, then either $b \bmod 2^{k} \neq 1$ or $2^{k+1} \bmod b \neq 1$, and both numbers are less than $b$, so either $(2, b$ $\left.\bmod 2^{k}\right)$ or $\left(2,2^{k+1} \bmod b\right)$ works.
We have shown $2,3 \in S$. Then $4 \in S$, and $5=32 \bmod 27 \in S$. Suppose $n \geq 6$ is the smallest integer that isn't in $S$. Then $n-4, n-2, n-1 \in S$, so $n^{2}-5 n+4, n^{2}-4 n+4$ are both in $S$. A computation shows that $n^{2}-4 n+4<2\left(n^{2}-5 n+4\right)$, and so
$$
n^{2}-4 n+4 \quad \bmod \left(n^{2}-5 n+4\right)=n \in S
$$
a contradiction. Thus, every single nonnegative integer is in $S$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $S$ be a set of nonnegative integers such that
- there exist two elements $a$ and $b$ in $S$ such that $a, b>1$ and $\operatorname{gcd}(a, b)=1$; and
- for any (not necessarily distinct) element $x$ and nonzero element $y$ in $S$, both $x y$ and the remainder when $x$ is divided by $y$ are in $S$.
Prove that $S$ contains every nonnegative integer.
|
Solution: Assume $a<b$. Note that we can get $1 \in S$ via the Euclidean algorithm, and $0 \in S$ from $a \bmod 1$. Suppose $(a, b) \neq(2,3)$. We will show that there exists $c, d \in S$ with $1<c \leq a$ and $1<d \leq b$, with $\operatorname{gcd}(c, d)=1$ and at least one of $c \neq a$ and $d \neq b$ is true. This will show that $2,3 \in S$ by repeatedly applying this sequence of operations. Assume $a>2$.
Unless $b \bmod a=1,(b \bmod a, a)$ works. Thus, assume $b \equiv 1(\bmod a)$. If we can construct any integer $x$ such that $x \not \equiv 0,1 \bmod a$, then we can take $(x \bmod a, a)$; this will be our new goal. Suppose that such an $x$ is not constructable.
Suppose $a^{k}=q b^{\ell}+r$, with $r<a^{k}$. We must have $r \equiv 0,1(\bmod a)$. Taking both sides mod $a$, this means that $0 \equiv q+r(\bmod a)$, so $q \equiv 0,-1(\bmod a)$. Thus, $\left\lfloor\frac{a^{k}}{b^{\ell}}\right\rfloor \equiv 0,-1(\bmod a)$, for all $k, \ell \in \mathbb{N}$. Take $\ell=\left\lfloor k \log _{b} a\right\rfloor$, so $\left\lfloor\frac{a^{k}}{b^{\ell}}\right\rfloor$ is the first digit in the base $b$ representation of $a^{k}$. We can take $k$ such that $0 \leq\left\{k \log _{b} a\right\}<\log _{b} 2$, where $\{\cdot\}$ represents the fractional part operation, since $\log _{b} a$ is irrational. Taking such a $k$, we get the first digit of $a^{k}$ in base $b$ is 1 , which contradicts $\left\lfloor\frac{a^{k}}{b^{\varepsilon}}\right\rfloor \equiv 0,-1(\bmod a)$.
Thus, if $a>2$ then we have shown what we wanted. Suppose $a=2$. Let $2^{k}<b<2^{k+1}$ for some $k$. If $b \neq 3$, then either $b \bmod 2^{k} \neq 1$ or $2^{k+1} \bmod b \neq 1$, and both numbers are less than $b$, so either $(2, b$ $\left.\bmod 2^{k}\right)$ or $\left(2,2^{k+1} \bmod b\right)$ works.
We have shown $2,3 \in S$. Then $4 \in S$, and $5=32 \bmod 27 \in S$. Suppose $n \geq 6$ is the smallest integer that isn't in $S$. Then $n-4, n-2, n-1 \in S$, so $n^{2}-5 n+4, n^{2}-4 n+4$ are both in $S$. A computation shows that $n^{2}-4 n+4<2\left(n^{2}-5 n+4\right)$, and so
$$
n^{2}-4 n+4 \quad \bmod \left(n^{2}-5 n+4\right)=n \in S
$$
a contradiction. Thus, every single nonnegative integer is in $S$.
|
{
"resource_path": "HarvardMIT/segmented/en-274-tournaments-2024-hmic-solutions.jsonl",
"problem_match": "\n3. [9]",
"solution_match": "\n## Proposed by: Jacob Paltrowitz\n\n"
}
|
3e78e125-77ea-50d8-baf9-4b6ba73d8df4
| 610,770
|
Let $A B C$ be an acute, scalene triangle with circumcenter $O$ and symmedian point $K$. Let $X$ be the point on the circumcircle of triangle $B O C$ such that $\angle A X O=90^{\circ}$. Assume that $X \neq K$. The hyperbola passing through $B, C, O, K$, and $X$ intersects the circumcircle of triangle $A B C$ at points $U$ and $V$, distinct from $B$ and $C$. Prove that $U V$ is the perpendicular bisector of $A X$.
The symmedian point of triangle $A B C$ is the intersection of the reflections of $B$-median and $C$-median across the angle bisectors of $\angle A B C$ and $\angle A C B$, respectively.
|
Let $\mathcal{H}$ denote the hyperbola, and also recall a well-known fact that $A, K, X$ are collinear. This solution is split into two independent parts.
Proof of $\boldsymbol{U} \boldsymbol{V} \perp \boldsymbol{A X}$.
Let $T=O X \cap B C$, and let $O X$ intersect $\odot(A B C)$ at points $Y, Z$. Then, we apply Desargues Involution Theorem (DIT) on $B C U V$ and line $O X$. We get an involution that
- swaps $T$ and $U V \cap O X$;
- swaps $B U \cap O X$ and $C V \cap O X$;
- swaps $B V \cap O X$ and $C U \cap O X$;
- from conic $\odot(A B C U V)$, swaps $Y$ and $Z$;
- from conic $\mathcal{H}$, swaps $O$ and $X$.
Thus, we get an involution swapping $(O, X)$ and $(Y, Z)$, and $(T, U V \cap O X)$. Now, notice that since $B, O, X, C$ are concyclic, we have $T Y \cdot T Z=T B \cdot T C=T O \cdot T X$, so this involution is an inversion at $T$. Thus, it maps $T$ to $\infty_{O X}$. Hence, $U, V, \infty_{O X}$ are collinear, implying that $U V \perp A X$.
## Proof of $\boldsymbol{U} \boldsymbol{V}$ bisects $\boldsymbol{A X}$.
Let $M$ be the midpoint of $A X$. Let $A X$ intersect $B C$ at $D$ and $\odot(A B C)$ at $P$. We apply Desargues Involution Theorem (DIT) on $B C U V$ and line $A X$. We get an involution that
- swaps $D$ and $U V \cap O X$;
- swaps $B U \cap A X$ and $C V \cap A X$;
- swaps $B V \cap A X$ and $C U \cap A X$;
- from conic $\odot(A B C U V)$, swaps $A$ and $P$;
- from conic $\mathcal{H}$, swaps $K$ and $X$.
Thus, we have an involution swapping $(A, P)$ and $(K, X)$, and we want to show that it swaps $(D, M)$, or equivalently
$$
(A, X ; M, P)=(P, K ; D, A)
$$
The left hand side is $\frac{A M}{X M} / \frac{A P}{X P}=-2$. To show that $(P, K ; D, A)=-2$, we take any projective transformation that fixes $\odot(A B C)$ and sends $\triangle A B C$ to an equilateral triangle. This transformation preserves $B B \cap C C, C C \cap A A$, and $A A \cap B B$, so it preserves symmedians. The result then become evident.
Remark. Another interesting fact about this hyperbola is that it passes through midpoints of $A B$ and $A C$. We left the proof of this as an exercise for the reader.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute, scalene triangle with circumcenter $O$ and symmedian point $K$. Let $X$ be the point on the circumcircle of triangle $B O C$ such that $\angle A X O=90^{\circ}$. Assume that $X \neq K$. The hyperbola passing through $B, C, O, K$, and $X$ intersects the circumcircle of triangle $A B C$ at points $U$ and $V$, distinct from $B$ and $C$. Prove that $U V$ is the perpendicular bisector of $A X$.
The symmedian point of triangle $A B C$ is the intersection of the reflections of $B$-median and $C$-median across the angle bisectors of $\angle A B C$ and $\angle A C B$, respectively.
|
Let $\mathcal{H}$ denote the hyperbola, and also recall a well-known fact that $A, K, X$ are collinear. This solution is split into two independent parts.
Proof of $\boldsymbol{U} \boldsymbol{V} \perp \boldsymbol{A X}$.
Let $T=O X \cap B C$, and let $O X$ intersect $\odot(A B C)$ at points $Y, Z$. Then, we apply Desargues Involution Theorem (DIT) on $B C U V$ and line $O X$. We get an involution that
- swaps $T$ and $U V \cap O X$;
- swaps $B U \cap O X$ and $C V \cap O X$;
- swaps $B V \cap O X$ and $C U \cap O X$;
- from conic $\odot(A B C U V)$, swaps $Y$ and $Z$;
- from conic $\mathcal{H}$, swaps $O$ and $X$.
Thus, we get an involution swapping $(O, X)$ and $(Y, Z)$, and $(T, U V \cap O X)$. Now, notice that since $B, O, X, C$ are concyclic, we have $T Y \cdot T Z=T B \cdot T C=T O \cdot T X$, so this involution is an inversion at $T$. Thus, it maps $T$ to $\infty_{O X}$. Hence, $U, V, \infty_{O X}$ are collinear, implying that $U V \perp A X$.
## Proof of $\boldsymbol{U} \boldsymbol{V}$ bisects $\boldsymbol{A X}$.
Let $M$ be the midpoint of $A X$. Let $A X$ intersect $B C$ at $D$ and $\odot(A B C)$ at $P$. We apply Desargues Involution Theorem (DIT) on $B C U V$ and line $A X$. We get an involution that
- swaps $D$ and $U V \cap O X$;
- swaps $B U \cap A X$ and $C V \cap A X$;
- swaps $B V \cap A X$ and $C U \cap A X$;
- from conic $\odot(A B C U V)$, swaps $A$ and $P$;
- from conic $\mathcal{H}$, swaps $K$ and $X$.
Thus, we have an involution swapping $(A, P)$ and $(K, X)$, and we want to show that it swaps $(D, M)$, or equivalently
$$
(A, X ; M, P)=(P, K ; D, A)
$$
The left hand side is $\frac{A M}{X M} / \frac{A P}{X P}=-2$. To show that $(P, K ; D, A)=-2$, we take any projective transformation that fixes $\odot(A B C)$ and sends $\triangle A B C$ to an equilateral triangle. This transformation preserves $B B \cap C C, C C \cap A A$, and $A A \cap B B$, so it preserves symmedians. The result then become evident.
Remark. Another interesting fact about this hyperbola is that it passes through midpoints of $A B$ and $A C$. We left the proof of this as an exercise for the reader.
|
{
"resource_path": "HarvardMIT/segmented/en-274-tournaments-2024-hmic-solutions.jsonl",
"problem_match": "\n5. [11]",
"solution_match": "\nSolution 1: "
}
|
3b7cdcd1-60ec-530c-8b0c-20341c0633e7
| 610,772
|
Let $A B C$ be an acute, scalene triangle with circumcenter $O$ and symmedian point $K$. Let $X$ be the point on the circumcircle of triangle $B O C$ such that $\angle A X O=90^{\circ}$. Assume that $X \neq K$. The hyperbola passing through $B, C, O, K$, and $X$ intersects the circumcircle of triangle $A B C$ at points $U$ and $V$, distinct from $B$ and $C$. Prove that $U V$ is the perpendicular bisector of $A X$.
The symmedian point of triangle $A B C$ is the intersection of the reflections of $B$-median and $C$-median across the angle bisectors of $\angle A B C$ and $\angle A C B$, respectively.
|
Let $A K$ meet $B C$ at $Z$, and redefine $U, V$ to be the intersections of perpendicular bisector of $A X$ and $\odot(A B C)$. We will use the following properties of $X$ :
- $X$ lies on $A K$
- $\triangle B X A \sim \triangle A X C$ with ratio $c: b$
- $\angle B X A=\angle A C X=180^{\circ}-A$.
Consider the quadratic function
$$
f(P)=\frac{\operatorname{Pow}_{\odot(A B C)}(P)}{\operatorname{Pow}_{\odot(A B C)}(O)}-\frac{d(P, B C) d(P, U V)}{d(O, B C) d(O, U V)}
$$
It is clear (say, in coordinates) that $f$ is the equation of a conic passing through $B, C, U, V$, and $O$. Hence, it suffices to show $f(X)=0$ and $f(K)=0$.
Since $O X \| U V$, we have
$$
f(X)=\frac{\operatorname{Pow}_{\odot(A B C)}(X)}{\operatorname{Pow}_{\odot(A B C)}(O)}-\frac{d(X, B C)}{d(O, B C)}
$$
The RHS above is a circle (in coordinates) and is 0 when $X \in\{O, B, C\}$, and is hence 0 for any $X$ on $(B O C)$. Thus, $f(X)=0$.
To show that $f(K)=0$, consider the function $f(P)$ for a variable point $P$ on line $A K X Z$. We claim that
$$
f(P)=\frac{P X \cdot P K}{A X \cdot A K} f(A)
$$
after which the result follows from taking $P=K$. The LHS and RHS are quadratic functions that agree at $A$ and $X$. It remains to check that they agree at one more point - we will take $P=Z$. We compute
$$
\begin{aligned}
f(Z) & =\frac{B Z \cdot C Z}{R^{2}}=\frac{a^{2} b^{2} c^{2}}{\left(b^{2}+c^{2}\right)^{2}} \cdot \frac{1}{R^{2}} \\
f(A) & =-\frac{d(A, B C)}{d(O, B C)} \cdot \frac{d(A, U V)}{d(O, U V)}=\frac{d(A, B C)}{d(O, B C)}=\frac{b c}{2 R^{2} \cos A} \\
\frac{Z K}{A K} & =\frac{b^{2}+c^{2}}{a^{2}} \\
\frac{Z X}{A X} & =\frac{[X B C]}{[X A B C]}=\frac{X B \cdot X C \sin (2 A)}{X B \cdot X A \sin (A)+X A \cdot X C \sin (A)}=\frac{2 b c \cos A}{b^{2}+c^{2}},
\end{aligned}
$$
and the desired result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute, scalene triangle with circumcenter $O$ and symmedian point $K$. Let $X$ be the point on the circumcircle of triangle $B O C$ such that $\angle A X O=90^{\circ}$. Assume that $X \neq K$. The hyperbola passing through $B, C, O, K$, and $X$ intersects the circumcircle of triangle $A B C$ at points $U$ and $V$, distinct from $B$ and $C$. Prove that $U V$ is the perpendicular bisector of $A X$.
The symmedian point of triangle $A B C$ is the intersection of the reflections of $B$-median and $C$-median across the angle bisectors of $\angle A B C$ and $\angle A C B$, respectively.
|
Let $A K$ meet $B C$ at $Z$, and redefine $U, V$ to be the intersections of perpendicular bisector of $A X$ and $\odot(A B C)$. We will use the following properties of $X$ :
- $X$ lies on $A K$
- $\triangle B X A \sim \triangle A X C$ with ratio $c: b$
- $\angle B X A=\angle A C X=180^{\circ}-A$.
Consider the quadratic function
$$
f(P)=\frac{\operatorname{Pow}_{\odot(A B C)}(P)}{\operatorname{Pow}_{\odot(A B C)}(O)}-\frac{d(P, B C) d(P, U V)}{d(O, B C) d(O, U V)}
$$
It is clear (say, in coordinates) that $f$ is the equation of a conic passing through $B, C, U, V$, and $O$. Hence, it suffices to show $f(X)=0$ and $f(K)=0$.
Since $O X \| U V$, we have
$$
f(X)=\frac{\operatorname{Pow}_{\odot(A B C)}(X)}{\operatorname{Pow}_{\odot(A B C)}(O)}-\frac{d(X, B C)}{d(O, B C)}
$$
The RHS above is a circle (in coordinates) and is 0 when $X \in\{O, B, C\}$, and is hence 0 for any $X$ on $(B O C)$. Thus, $f(X)=0$.
To show that $f(K)=0$, consider the function $f(P)$ for a variable point $P$ on line $A K X Z$. We claim that
$$
f(P)=\frac{P X \cdot P K}{A X \cdot A K} f(A)
$$
after which the result follows from taking $P=K$. The LHS and RHS are quadratic functions that agree at $A$ and $X$. It remains to check that they agree at one more point - we will take $P=Z$. We compute
$$
\begin{aligned}
f(Z) & =\frac{B Z \cdot C Z}{R^{2}}=\frac{a^{2} b^{2} c^{2}}{\left(b^{2}+c^{2}\right)^{2}} \cdot \frac{1}{R^{2}} \\
f(A) & =-\frac{d(A, B C)}{d(O, B C)} \cdot \frac{d(A, U V)}{d(O, U V)}=\frac{d(A, B C)}{d(O, B C)}=\frac{b c}{2 R^{2} \cos A} \\
\frac{Z K}{A K} & =\frac{b^{2}+c^{2}}{a^{2}} \\
\frac{Z X}{A X} & =\frac{[X B C]}{[X A B C]}=\frac{X B \cdot X C \sin (2 A)}{X B \cdot X A \sin (A)+X A \cdot X C \sin (A)}=\frac{2 b c \cos A}{b^{2}+c^{2}},
\end{aligned}
$$
and the desired result follows.
|
{
"resource_path": "HarvardMIT/segmented/en-274-tournaments-2024-hmic-solutions.jsonl",
"problem_match": "\n5. [11]",
"solution_match": "\nSolution 2: "
}
|
3b7cdcd1-60ec-530c-8b0c-20341c0633e7
| 610,772
|
Let $A B C$ be an acute, scalene triangle with circumcenter $O$ and symmedian point $K$. Let $X$ be the point on the circumcircle of triangle $B O C$ such that $\angle A X O=90^{\circ}$. Assume that $X \neq K$. The hyperbola passing through $B, C, O, K$, and $X$ intersects the circumcircle of triangle $A B C$ at points $U$ and $V$, distinct from $B$ and $C$. Prove that $U V$ is the perpendicular bisector of $A X$.
The symmedian point of triangle $A B C$ is the intersection of the reflections of $B$-median and $C$-median across the angle bisectors of $\angle A B C$ and $\angle A C B$, respectively.
|
We prove the following main claim.
Claim. Let $P$ be a point on $A X$, and let the conic through $B, C, O, X, P$ meet $(A B C)$ again at $U^{\prime}, V^{\prime}$. Then $U^{\prime} V^{\prime}$ passes through a fixed point, and the map $P \mapsto U^{\prime} V^{\prime} \cap A X$ is projective.
Proof. Take a projective transformation sending $B, C$ to the circle points. Then the new problem is the following: We have points $A, X, O$, a fixed circle $\Omega$ passing through $A$, and a point $P$ on $A X$. Let $(P O X)$ meet $\Omega$ at $U^{\prime} V^{\prime}$. Then $U^{\prime} V^{\prime}$ passes through a fixed point and $P \mapsto U^{\prime} V^{\prime} \cap A X$ is projective. First, if we take two points $P_{1}, P_{2}$, by radical axis on $\left(P_{1} O X\right),\left(P_{2} O X\right)$, and $\Omega, U_{1}^{\prime} V_{1}^{\prime}, U_{2}^{\prime} V_{2}^{\prime}$, and $O X$ concur. Thus, $U^{\prime} V^{\prime}$ meets $O X$ at a fixed point. Let this point be $Q$. Now let $O_{1}$ be the center of $\Omega$ and $O_{P}$ the center of $(P O X)$. $O_{P}$ moves linearly w.r.t. $P$, so $P \mapsto O_{1} O_{P}$ is projective. Then $U^{\prime} V^{\prime}$ is the line through $Q$ perpendicular to $O_{1} O_{P}$, and hence also moves projectively. Finally, intersecting $U^{\prime} V^{\prime}$ with $A X$ is projective, so the entire map $P \mapsto U^{\prime} V^{\prime} \cap A X$ is projective, as desired.
We now return to the original problem. Let the tangents to $(A B C)$ at $B, C$ meet at $T$. It is well-known that $A, X, K, T$ are collinear, and $B, O, C, X, T$ are concyclic. We now consider the following cases:
- $\boldsymbol{P}=\boldsymbol{A} \boldsymbol{X} \cap \boldsymbol{B C}$ : The conic $(B C O X P)$ degenerates to the two lines $O X, B C$, so $U^{\prime} V^{\prime}=O X$, and $U^{\prime} V^{\prime} \cap A X=X$. Thus, $A X \cap B C \mapsto X$.
- $\boldsymbol{P}=\boldsymbol{T}$ : The conic $(B C O X T)$ is just the circle $(B O C)$. Then $(B O C)$ meets $(A B C)$ again at the circle points, so $U^{\prime} V^{\prime}$ is the line at infinity, and $T \mapsto(A X)_{\infty}$.
- $\boldsymbol{P}=\boldsymbol{A}$ : In this case, $A=U^{\prime}$ or $V^{\prime}$, so $U^{\prime} V^{\prime} \cap A X=A$ and $A \mapsto A$.
From the first two cases, we see that the fixed point $U^{\prime} V^{\prime}$ passes through is $(O X)_{\infty}$ i.e. $U^{\prime} V^{\prime}$ is always parallel to $O X$. Now note that the cross-ratio $(A, A X \cap B C ; K, T)=-1$, and hence if $K \mapsto f(K)$, we have $\left(A, X ; f(K),(A X)_{\infty}\right)=-1$. Thus, $f(K)$ must be the midpoint of $A X$, and $U V$ is the line through $f(K)$ parallel to $O X$ i.e. the perpendicular bisector of $A X$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute, scalene triangle with circumcenter $O$ and symmedian point $K$. Let $X$ be the point on the circumcircle of triangle $B O C$ such that $\angle A X O=90^{\circ}$. Assume that $X \neq K$. The hyperbola passing through $B, C, O, K$, and $X$ intersects the circumcircle of triangle $A B C$ at points $U$ and $V$, distinct from $B$ and $C$. Prove that $U V$ is the perpendicular bisector of $A X$.
The symmedian point of triangle $A B C$ is the intersection of the reflections of $B$-median and $C$-median across the angle bisectors of $\angle A B C$ and $\angle A C B$, respectively.
|
We prove the following main claim.
Claim. Let $P$ be a point on $A X$, and let the conic through $B, C, O, X, P$ meet $(A B C)$ again at $U^{\prime}, V^{\prime}$. Then $U^{\prime} V^{\prime}$ passes through a fixed point, and the map $P \mapsto U^{\prime} V^{\prime} \cap A X$ is projective.
Proof. Take a projective transformation sending $B, C$ to the circle points. Then the new problem is the following: We have points $A, X, O$, a fixed circle $\Omega$ passing through $A$, and a point $P$ on $A X$. Let $(P O X)$ meet $\Omega$ at $U^{\prime} V^{\prime}$. Then $U^{\prime} V^{\prime}$ passes through a fixed point and $P \mapsto U^{\prime} V^{\prime} \cap A X$ is projective. First, if we take two points $P_{1}, P_{2}$, by radical axis on $\left(P_{1} O X\right),\left(P_{2} O X\right)$, and $\Omega, U_{1}^{\prime} V_{1}^{\prime}, U_{2}^{\prime} V_{2}^{\prime}$, and $O X$ concur. Thus, $U^{\prime} V^{\prime}$ meets $O X$ at a fixed point. Let this point be $Q$. Now let $O_{1}$ be the center of $\Omega$ and $O_{P}$ the center of $(P O X)$. $O_{P}$ moves linearly w.r.t. $P$, so $P \mapsto O_{1} O_{P}$ is projective. Then $U^{\prime} V^{\prime}$ is the line through $Q$ perpendicular to $O_{1} O_{P}$, and hence also moves projectively. Finally, intersecting $U^{\prime} V^{\prime}$ with $A X$ is projective, so the entire map $P \mapsto U^{\prime} V^{\prime} \cap A X$ is projective, as desired.
We now return to the original problem. Let the tangents to $(A B C)$ at $B, C$ meet at $T$. It is well-known that $A, X, K, T$ are collinear, and $B, O, C, X, T$ are concyclic. We now consider the following cases:
- $\boldsymbol{P}=\boldsymbol{A} \boldsymbol{X} \cap \boldsymbol{B C}$ : The conic $(B C O X P)$ degenerates to the two lines $O X, B C$, so $U^{\prime} V^{\prime}=O X$, and $U^{\prime} V^{\prime} \cap A X=X$. Thus, $A X \cap B C \mapsto X$.
- $\boldsymbol{P}=\boldsymbol{T}$ : The conic $(B C O X T)$ is just the circle $(B O C)$. Then $(B O C)$ meets $(A B C)$ again at the circle points, so $U^{\prime} V^{\prime}$ is the line at infinity, and $T \mapsto(A X)_{\infty}$.
- $\boldsymbol{P}=\boldsymbol{A}$ : In this case, $A=U^{\prime}$ or $V^{\prime}$, so $U^{\prime} V^{\prime} \cap A X=A$ and $A \mapsto A$.
From the first two cases, we see that the fixed point $U^{\prime} V^{\prime}$ passes through is $(O X)_{\infty}$ i.e. $U^{\prime} V^{\prime}$ is always parallel to $O X$. Now note that the cross-ratio $(A, A X \cap B C ; K, T)=-1$, and hence if $K \mapsto f(K)$, we have $\left(A, X ; f(K),(A X)_{\infty}\right)=-1$. Thus, $f(K)$ must be the midpoint of $A X$, and $U V$ is the line through $f(K)$ parallel to $O X$ i.e. the perpendicular bisector of $A X$.
|
{
"resource_path": "HarvardMIT/segmented/en-274-tournaments-2024-hmic-solutions.jsonl",
"problem_match": "\n5. [11]",
"solution_match": "\nSolution 3: "
}
|
3b7cdcd1-60ec-530c-8b0c-20341c0633e7
| 610,772
|
Suppose that a positive integer $n$ has the property that $n, 2 n, 3 n, \ldots, 9 n$ are all palindromes. Prove that the decimal digits of $n$ are all zeros or ones.
|
First consider the ones digit $a$ of $n$; we claim that $a=1$. Certainly $a$ cannot be even, for then $5 n$ would be divisible by 10 . If $a$ is 5,7 , or 9 , then $2 n$ has an even ones digit, while its most significant digit is 1 . If $a$ is 3 , then $4 n$ has an even ones digit but most significant digit 1 . Thus $a=1$ is the only possibility. Moreover $9 n$ has the same number of digits as $n$, for otherwise $9 n$ would have most significant digit 1 but least significant digit 9 , which is forbidden.
Now suppose $n$ has at least one digit that is neither a zero nor a one. Let $b$ be the leftmost (i.e., most significant) such digit, so that the left end of the decimal representation of $n$ looks like
$$
\underline{a_{1}} \cdots \underline{a_{r}} \underline{b} \cdots
$$
for some $r \geq 1$ and digits $a_{i} \in\{0,1\}$. When $n$ is multiplied by 9 , there will be a carry out of the column containing $b$. In particular, the $r^{\text {th }}$ digit from the left in $9 n$ will not be $9 a_{r}$. But the right end of the decimal representation of $n$ is
$$
\cdots \underline{a_{r}} \cdots \underline{a_{1}} ;
$$
because each $a_{i}$ is 0 or 1 , there are no carries out of the first $r-1$ columns, so the $r^{\text {th }}$ digit from the right in $9 n$ will be $9 a_{r}$. Thus $9 n$ is not a palindrome, a contradiction. This completes the proof.
Floor functions. The notation $\lfloor x\rfloor$ stands for the largest integer less than or equal to $x$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Suppose that a positive integer $n$ has the property that $n, 2 n, 3 n, \ldots, 9 n$ are all palindromes. Prove that the decimal digits of $n$ are all zeros or ones.
|
First consider the ones digit $a$ of $n$; we claim that $a=1$. Certainly $a$ cannot be even, for then $5 n$ would be divisible by 10 . If $a$ is 5,7 , or 9 , then $2 n$ has an even ones digit, while its most significant digit is 1 . If $a$ is 3 , then $4 n$ has an even ones digit but most significant digit 1 . Thus $a=1$ is the only possibility. Moreover $9 n$ has the same number of digits as $n$, for otherwise $9 n$ would have most significant digit 1 but least significant digit 9 , which is forbidden.
Now suppose $n$ has at least one digit that is neither a zero nor a one. Let $b$ be the leftmost (i.e., most significant) such digit, so that the left end of the decimal representation of $n$ looks like
$$
\underline{a_{1}} \cdots \underline{a_{r}} \underline{b} \cdots
$$
for some $r \geq 1$ and digits $a_{i} \in\{0,1\}$. When $n$ is multiplied by 9 , there will be a carry out of the column containing $b$. In particular, the $r^{\text {th }}$ digit from the left in $9 n$ will not be $9 a_{r}$. But the right end of the decimal representation of $n$ is
$$
\cdots \underline{a_{r}} \cdots \underline{a_{1}} ;
$$
because each $a_{i}$ is 0 or 1 , there are no carries out of the first $r-1$ columns, so the $r^{\text {th }}$ digit from the right in $9 n$ will be $9 a_{r}$. Thus $9 n$ is not a palindrome, a contradiction. This completes the proof.
Floor functions. The notation $\lfloor x\rfloor$ stands for the largest integer less than or equal to $x$.
|
{
"resource_path": "HarvardMIT/segmented/en-52-2002-feb-team-solutions.jsonl",
"problem_match": "\n3. [40]",
"solution_match": "\nSolution. "
}
|
c88a971d-9b55-53ab-a68b-ce5a837fd315
| 611,074
|
Let $n$ be an integer. Prove that
$$
\left\lfloor\frac{n}{2}\right\rfloor+\left\lfloor\frac{n+1}{2}\right\rfloor=n .
$$
|
Suppose $n=2 m$ is even. Then $\lfloor n / 2\rfloor=\lfloor m\rfloor=m$ and $\lfloor(n+1) / 2\rfloor=\lfloor m+1 / 2\rfloor=m$, whose sum is $m+m=2 m=n$. Otherwise $n=2 m+1$ is odd. In this case $\lfloor n / 2\rfloor=\lfloor m+1 / 2\rfloor=m$ and $\lfloor(n+1) / 2\rfloor=\lfloor m+1\rfloor=m+1$, whose sum is $m+(m+1)=2 m+1=n$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be an integer. Prove that
$$
\left\lfloor\frac{n}{2}\right\rfloor+\left\lfloor\frac{n+1}{2}\right\rfloor=n .
$$
|
Suppose $n=2 m$ is even. Then $\lfloor n / 2\rfloor=\lfloor m\rfloor=m$ and $\lfloor(n+1) / 2\rfloor=\lfloor m+1 / 2\rfloor=m$, whose sum is $m+m=2 m=n$. Otherwise $n=2 m+1$ is odd. In this case $\lfloor n / 2\rfloor=\lfloor m+1 / 2\rfloor=m$ and $\lfloor(n+1) / 2\rfloor=\lfloor m+1\rfloor=m+1$, whose sum is $m+(m+1)=2 m+1=n$, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-52-2002-feb-team-solutions.jsonl",
"problem_match": "\n4. [15]",
"solution_match": "\nSolution. "
}
|
2736b02b-adae-5e8a-b584-c3eccb1732c1
| 611,075
|
Prove for integers $n$ that
$$
\left\lfloor\frac{n}{2}\right\rfloor\left\lfloor\frac{n+1}{2}\right\rfloor=\left\lfloor\frac{n^{2}}{4}\right\rfloor .
$$
|
Suppose $n=2 m$ is even; then $\lfloor n / 2\rfloor=\lfloor m\rfloor=m$ and $\lfloor(n+1) / 2\rfloor=\lfloor m+1 / 2\rfloor=m$, whose product is $m^{2}=\left\lfloor m^{2}\right\rfloor=\left\lfloor(2 m)^{2} / 4\right\rfloor$. Otherwise $n=2 m+1$ is odd, so that $\lfloor n / 2\rfloor=$ $\lfloor m+1 / 2\rfloor=m$ and $\lfloor(n+1) / 2\rfloor=\lfloor m+1\rfloor=m+1$, whose product is $m^{2}+m$. On the other side, we find that
$$
\left\lfloor\frac{n^{2}}{4}\right\rfloor=\left\lfloor\frac{4 m^{2}+4 m+1}{4}\right\rfloor=\left\lfloor m^{2}+m+\frac{1}{4}\right\rfloor=m^{2}+m,
$$
as desired.
In problems 6-7 you may use without proof the known summations
$$
\sum_{n=1}^{L} n=n(n+1) / 2 \quad \text { and } \quad \sum_{n=1}^{L} n^{3}=n^{2}(n+1)^{2} / 4 \quad \text { for positive integers } L .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove for integers $n$ that
$$
\left\lfloor\frac{n}{2}\right\rfloor\left\lfloor\frac{n+1}{2}\right\rfloor=\left\lfloor\frac{n^{2}}{4}\right\rfloor .
$$
|
Suppose $n=2 m$ is even; then $\lfloor n / 2\rfloor=\lfloor m\rfloor=m$ and $\lfloor(n+1) / 2\rfloor=\lfloor m+1 / 2\rfloor=m$, whose product is $m^{2}=\left\lfloor m^{2}\right\rfloor=\left\lfloor(2 m)^{2} / 4\right\rfloor$. Otherwise $n=2 m+1$ is odd, so that $\lfloor n / 2\rfloor=$ $\lfloor m+1 / 2\rfloor=m$ and $\lfloor(n+1) / 2\rfloor=\lfloor m+1\rfloor=m+1$, whose product is $m^{2}+m$. On the other side, we find that
$$
\left\lfloor\frac{n^{2}}{4}\right\rfloor=\left\lfloor\frac{4 m^{2}+4 m+1}{4}\right\rfloor=\left\lfloor m^{2}+m+\frac{1}{4}\right\rfloor=m^{2}+m,
$$
as desired.
In problems 6-7 you may use without proof the known summations
$$
\sum_{n=1}^{L} n=n(n+1) / 2 \quad \text { and } \quad \sum_{n=1}^{L} n^{3}=n^{2}(n+1)^{2} / 4 \quad \text { for positive integers } L .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-52-2002-feb-team-solutions.jsonl",
"problem_match": "\n5. [20]",
"solution_match": "\nSolution. "
}
|
6af4bb92-256c-5784-98b5-3b3d38ff7241
| 611,076
|
In this problem suppose that $s_{1}=s_{2}$. Prove that for each board configuration, the first player wins with probability strictly greater than $\frac{1}{2}$.
|
Let $\sigma_{1}$ and $\sigma_{2}$ denote the sequence of the next twelve die rolls that players 1 and 2 respectively will make. The outcome of the game is completely determined by the $\sigma_{i}$. Now player 1 wins in all cases in which $\sigma_{1}=\sigma_{2}$, for then each of player 2's moves bring her piece to a square already occupied by player 1's piece. It is sufficient, therefore, to show that player 1 wins at least half the cases in which $\sigma_{1} \neq \sigma_{2}$. But all these cases can be partitioned into disjoint pairs
$$
\left\{\left(\sigma_{1}, \sigma_{2}\right),\left(\sigma_{2}, \sigma_{1}\right)\right\}
$$
and player 1 wins in at least one case in each pair. For if player 2 wins in the case ( $\sigma_{1}, \sigma_{2}$ ), say on her $n^{\text {th }}$ turn, the first $n$ elements of $\sigma_{1}$ do not take player 1 beyond space 12 , while the first $n$ elements of $\sigma_{2}$ must take player 2 beyond space 12 . Clearly, then, player 1 wins ( $\sigma_{2}, \sigma_{1}$ ) on his $n^{\text {th }}$ turn.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In this problem suppose that $s_{1}=s_{2}$. Prove that for each board configuration, the first player wins with probability strictly greater than $\frac{1}{2}$.
|
Let $\sigma_{1}$ and $\sigma_{2}$ denote the sequence of the next twelve die rolls that players 1 and 2 respectively will make. The outcome of the game is completely determined by the $\sigma_{i}$. Now player 1 wins in all cases in which $\sigma_{1}=\sigma_{2}$, for then each of player 2's moves bring her piece to a square already occupied by player 1's piece. It is sufficient, therefore, to show that player 1 wins at least half the cases in which $\sigma_{1} \neq \sigma_{2}$. But all these cases can be partitioned into disjoint pairs
$$
\left\{\left(\sigma_{1}, \sigma_{2}\right),\left(\sigma_{2}, \sigma_{1}\right)\right\}
$$
and player 1 wins in at least one case in each pair. For if player 2 wins in the case ( $\sigma_{1}, \sigma_{2}$ ), say on her $n^{\text {th }}$ turn, the first $n$ elements of $\sigma_{1}$ do not take player 1 beyond space 12 , while the first $n$ elements of $\sigma_{2}$ must take player 2 beyond space 12 . Clearly, then, player 1 wins ( $\sigma_{2}, \sigma_{1}$ ) on his $n^{\text {th }}$ turn.
|
{
"resource_path": "HarvardMIT/segmented/en-52-2002-feb-team-solutions.jsonl",
"problem_match": "\n9. [30]",
"solution_match": "\nSolution. "
}
|
f453b26e-6af2-505c-874f-f08fd1194651
| 611,080
|
Now suppose that before the game begins, the players choose the initial game state as follows:
- 1. The first player chooses $s_{1}$ subject to the constraint that $2 \leq s_{1} \leq 5$; then
- 2. the second player chooses $s_{2}$ subject to the constraint that $2 \leq s_{2} \leq 5$ and then specifies the board configuration.
Prove that the second player can always make her decisions so that she will win the game with probability strictly greater than $\frac{1}{2}$.
|
If $s_{1} \in\{3,5\}$, take $s_{2}=2$ and put arrows on the even-numbered squares. Player 1 cannot win on his first turn because he can move at most $2 s_{1}$ spaces in a turn. Player 2 wins on her first turn with probability $1 / 2$. Failing that, player 1 might fail to win on his second turn, and player 2 will again have probability $1 / 2$ of winning on her second turn, so her probability of winning the game is certainly greater than $1 / 2$.
If $s_{1}=4$, take $s_{2}=3$ and leave blank only squares $1,4,7$, and 10 . These occupy all congruence classes modulo 4 , so player 1 cannot win on his first turn. But the blank squares lie in the same congruence class modulo 3 , so player 2 then wins on her first turn with probability $2 / 3$.
Finally, if $s_{1}=2$, take $s_{2}=5$ and leave all squares blank. Then player 2 moves 3 squares in a turn on average, hence covers 15 squares on average in her first five turns. Moreover, the distribution of player 2 's distance traveled in five turns is symmetric about 15 . Thus player 2 has probability greater than $1 / 2$ of reaching $E N D$ by the end of her fifth turn. Player 1, on the other hand, cannot win in five turns because he can move at most 10 squares in those turns.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Now suppose that before the game begins, the players choose the initial game state as follows:
- 1. The first player chooses $s_{1}$ subject to the constraint that $2 \leq s_{1} \leq 5$; then
- 2. the second player chooses $s_{2}$ subject to the constraint that $2 \leq s_{2} \leq 5$ and then specifies the board configuration.
Prove that the second player can always make her decisions so that she will win the game with probability strictly greater than $\frac{1}{2}$.
|
If $s_{1} \in\{3,5\}$, take $s_{2}=2$ and put arrows on the even-numbered squares. Player 1 cannot win on his first turn because he can move at most $2 s_{1}$ spaces in a turn. Player 2 wins on her first turn with probability $1 / 2$. Failing that, player 1 might fail to win on his second turn, and player 2 will again have probability $1 / 2$ of winning on her second turn, so her probability of winning the game is certainly greater than $1 / 2$.
If $s_{1}=4$, take $s_{2}=3$ and leave blank only squares $1,4,7$, and 10 . These occupy all congruence classes modulo 4 , so player 1 cannot win on his first turn. But the blank squares lie in the same congruence class modulo 3 , so player 2 then wins on her first turn with probability $2 / 3$.
Finally, if $s_{1}=2$, take $s_{2}=5$ and leave all squares blank. Then player 2 moves 3 squares in a turn on average, hence covers 15 squares on average in her first five turns. Moreover, the distribution of player 2 's distance traveled in five turns is symmetric about 15 . Thus player 2 has probability greater than $1 / 2$ of reaching $E N D$ by the end of her fifth turn. Player 1, on the other hand, cannot win in five turns because he can move at most 10 squares in those turns.
|
{
"resource_path": "HarvardMIT/segmented/en-52-2002-feb-team-solutions.jsonl",
"problem_match": "\n12. [65]",
"solution_match": "\nSolution. "
}
|
b7b272a0-601f-5c36-abbf-f28b273bc3ef
| 611,083
|
Show that, given any 2 -configuration of a set $A$, every element of $A$ belongs to exactly one cell.
|
First, given $a$, let $C_{a}$ be the set of all $b \in A$ for which there exists a sequence $a=c_{0}, c_{1}, \ldots, c_{n}=b$ as in the definition of a cell. Certainly $a \in C_{a}$ (take $n=0$ ); we claim that $C_{a}$ is a cell. If $b, b^{\prime} \in C_{a}$, then there exist sequences $a=c_{0}, c_{1}, \ldots, c_{n}=b$ and $a=c_{0}^{\prime}, c_{1}^{\prime}, \ldots, c_{m}^{\prime}=b^{\prime}$, so the sequence $b=c_{n}, c_{n-1}, \ldots, c_{1}, c_{0}, c_{1}^{\prime}, \ldots, c_{m}^{\prime}=b^{\prime}$ shows that the first condition is met. For the second, suppose that there does exist a sequence $b=c_{0}, c_{1}, \ldots, c_{n}=b^{\prime}$ with $b \in C_{a}, b^{\prime} \notin C_{a}$. Then, concatenating with our sequence from $a$ to $b$, we get a sequence from $a$ to $b^{\prime}$, contradicting the assumption $b^{\prime} \notin C_{a}$. Thus, the second condition holds, and $C_{a}$ is a cell. So $a$ lies in at least one cell.
But now, note that if $C$ is a cell containing $a$, then all $b$ for which such a sequence from $a$ to $b$ exists must lie in $C$ (or the second condition is violated), and if no such sequence exists, then $b$ cannot lie in $C$ (or the first condition is violated). Thus, the elements of $C$ are uniquely determined, so there is exactly one cell containing $a$, and the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Show that, given any 2 -configuration of a set $A$, every element of $A$ belongs to exactly one cell.
|
First, given $a$, let $C_{a}$ be the set of all $b \in A$ for which there exists a sequence $a=c_{0}, c_{1}, \ldots, c_{n}=b$ as in the definition of a cell. Certainly $a \in C_{a}$ (take $n=0$ ); we claim that $C_{a}$ is a cell. If $b, b^{\prime} \in C_{a}$, then there exist sequences $a=c_{0}, c_{1}, \ldots, c_{n}=b$ and $a=c_{0}^{\prime}, c_{1}^{\prime}, \ldots, c_{m}^{\prime}=b^{\prime}$, so the sequence $b=c_{n}, c_{n-1}, \ldots, c_{1}, c_{0}, c_{1}^{\prime}, \ldots, c_{m}^{\prime}=b^{\prime}$ shows that the first condition is met. For the second, suppose that there does exist a sequence $b=c_{0}, c_{1}, \ldots, c_{n}=b^{\prime}$ with $b \in C_{a}, b^{\prime} \notin C_{a}$. Then, concatenating with our sequence from $a$ to $b$, we get a sequence from $a$ to $b^{\prime}$, contradicting the assumption $b^{\prime} \notin C_{a}$. Thus, the second condition holds, and $C_{a}$ is a cell. So $a$ lies in at least one cell.
But now, note that if $C$ is a cell containing $a$, then all $b$ for which such a sequence from $a$ to $b$ exists must lie in $C$ (or the second condition is violated), and if no such sequence exists, then $b$ cannot lie in $C$ (or the first condition is violated). Thus, the elements of $C$ are uniquely determined, so there is exactly one cell containing $a$, and the proof is complete.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-team-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
af81941f-9009-510d-aa5f-36ab88f4d306
| 611,187
|
(a) Show that if every cell of a 2-configuration of a finite set $A$ is $m$-separable, then the whole 2-configuration is $m$-separable.
|
Let $C$ be a 2 -configuration of $A$ with cells $A_{1}, \ldots, A_{n}$, so that there is no element of $C$ with one element in $A_{i}$ and another in $A_{j}$ for $i \neq j$. Suppose that each cell is $m$-separable, so that for each $i, 1 \leq i \leq n$, there is a labeling function $f_{i}: A_{i} \rightarrow\{1, \ldots, m\}$ such that no two elements in the same pair of $C$ are assigned the same number. Then, by combining, we get a function $f$ on all of $A$ whose restriction to $A_{i}$ is $f_{i}$ for each $i$. By the definition of $f_{i}$, within each $A_{i}$ there is no element of $C$ both of whose elements are mapped to the same integer; and as above, we know that there are no elements of $C$ not contained inside any $A_{i}$. Thus, $C$ is $m$-separable, by the existence of $f$.
(b) Show that any barren 2-configuration of a finite set $A$ is 2-separable.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
(a) Show that if every cell of a 2-configuration of a finite set $A$ is $m$-separable, then the whole 2-configuration is $m$-separable.
|
Let $C$ be a 2 -configuration of $A$ with cells $A_{1}, \ldots, A_{n}$, so that there is no element of $C$ with one element in $A_{i}$ and another in $A_{j}$ for $i \neq j$. Suppose that each cell is $m$-separable, so that for each $i, 1 \leq i \leq n$, there is a labeling function $f_{i}: A_{i} \rightarrow\{1, \ldots, m\}$ such that no two elements in the same pair of $C$ are assigned the same number. Then, by combining, we get a function $f$ on all of $A$ whose restriction to $A_{i}$ is $f_{i}$ for each $i$. By the definition of $f_{i}$, within each $A_{i}$ there is no element of $C$ both of whose elements are mapped to the same integer; and as above, we know that there are no elements of $C$ not contained inside any $A_{i}$. Thus, $C$ is $m$-separable, by the existence of $f$.
(b) Show that any barren 2-configuration of a finite set $A$ is 2-separable.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-team-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
6d17bb73-98b6-533d-a51a-4d8f1a58cabf
| 611,189
|
(a) Show that if every cell of a 2-configuration of a finite set $A$ is $m$-separable, then the whole 2-configuration is $m$-separable.
|
It is sufficient to show each cell is 2 -separable, by part (a). A barren 2configuration by definition cannot have any cycles (i.e. subsets $\left\{a_{0}, \ldots, a_{n}\right\}, n \geq 2$, where each $\left\{a_{i}, a_{i+1}\right\}$ and $\left\{a_{n}, a_{0}\right\}$ all belong to the 2 -configuration). For any two distinct elements $a, b$ of $A$ in the same cell of a 2-configuration $C$, define the distance between them to be the smallest $n$ such that there exists a sequence $a=a_{0}, a_{1}, \ldots, a_{n}=$
$b$ with $\left\{a_{0}, a_{1}\right\},\left\{a_{1}, a_{2}\right\}, \ldots,\left\{a_{n-1}, a_{n}\right\}$ all belonging to the 2 -configuration. Notice that the terms of this sequence are all distinct: if $a_{i}=a_{j}$ for $i<j$, then we have the shorter sequence $a_{0}, a_{1}, \ldots, a_{i}, a_{j+1}, \ldots, a_{n}$, contradicting minimality.
Now let $C$ be a barren 2 -configuration of $A$. Pick any element $a$ of $A$; label it and all elements at even distance from it with the integer 1, and label all elements at odd distance from it with the integer 2 . We claim no two different elements with the same label appear in the same element of $C$. Otherwise, let $b$ and $c$ be such elements, and let $a=a_{0}, a_{1}, \ldots, a_{n}=b$ and $a=a_{0}^{\prime}, a_{1}^{\prime}, \ldots, a_{m}^{\prime}=c$ be the corresponding minimal sequences. Consider the largest $p$ such that $a_{p} \in\left\{a_{0}^{\prime}, \ldots, a_{m}^{\prime}\right\}$; write $a_{p}=a_{q}^{\prime}$. We claim the set $\left\{a_{n}, a_{n-1}, \ldots, a_{p}, a_{q+1}^{\prime}, \ldots, a_{m}^{\prime}\right\}$ is then a cycle. It is straightforward to check that all its elements are distinct; the only issue is whether it has at least 3 elements. If not, we would have $a_{p}=a_{n}$ or $a_{m}^{\prime}$. Assume that $a_{p}=a_{n} \Rightarrow p=n \Rightarrow q=m-1$ (by minimality of our sequence $\left(a_{i}^{\prime}\right)$ ), but this means that $m=n+1$, so the distances of $b$ and $c$ from $a$ have opposite parities, contradicting the assumption that they have the same label. The case $a_{q}^{\prime}=a_{m}^{\prime}$ is similar. Thus, our set really does have at least three elements, and it is a cycle. But since $A$ is barren, it contains no cycles, and we have a contradiction.
Thus, after all, no two elements with the same label appear in the same pair of $C$, so the cell containing $a$ is 2 -separable, and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
(a) Show that if every cell of a 2-configuration of a finite set $A$ is $m$-separable, then the whole 2-configuration is $m$-separable.
|
It is sufficient to show each cell is 2 -separable, by part (a). A barren 2configuration by definition cannot have any cycles (i.e. subsets $\left\{a_{0}, \ldots, a_{n}\right\}, n \geq 2$, where each $\left\{a_{i}, a_{i+1}\right\}$ and $\left\{a_{n}, a_{0}\right\}$ all belong to the 2 -configuration). For any two distinct elements $a, b$ of $A$ in the same cell of a 2-configuration $C$, define the distance between them to be the smallest $n$ such that there exists a sequence $a=a_{0}, a_{1}, \ldots, a_{n}=$
$b$ with $\left\{a_{0}, a_{1}\right\},\left\{a_{1}, a_{2}\right\}, \ldots,\left\{a_{n-1}, a_{n}\right\}$ all belonging to the 2 -configuration. Notice that the terms of this sequence are all distinct: if $a_{i}=a_{j}$ for $i<j$, then we have the shorter sequence $a_{0}, a_{1}, \ldots, a_{i}, a_{j+1}, \ldots, a_{n}$, contradicting minimality.
Now let $C$ be a barren 2 -configuration of $A$. Pick any element $a$ of $A$; label it and all elements at even distance from it with the integer 1, and label all elements at odd distance from it with the integer 2 . We claim no two different elements with the same label appear in the same element of $C$. Otherwise, let $b$ and $c$ be such elements, and let $a=a_{0}, a_{1}, \ldots, a_{n}=b$ and $a=a_{0}^{\prime}, a_{1}^{\prime}, \ldots, a_{m}^{\prime}=c$ be the corresponding minimal sequences. Consider the largest $p$ such that $a_{p} \in\left\{a_{0}^{\prime}, \ldots, a_{m}^{\prime}\right\}$; write $a_{p}=a_{q}^{\prime}$. We claim the set $\left\{a_{n}, a_{n-1}, \ldots, a_{p}, a_{q+1}^{\prime}, \ldots, a_{m}^{\prime}\right\}$ is then a cycle. It is straightforward to check that all its elements are distinct; the only issue is whether it has at least 3 elements. If not, we would have $a_{p}=a_{n}$ or $a_{m}^{\prime}$. Assume that $a_{p}=a_{n} \Rightarrow p=n \Rightarrow q=m-1$ (by minimality of our sequence $\left(a_{i}^{\prime}\right)$ ), but this means that $m=n+1$, so the distances of $b$ and $c$ from $a$ have opposite parities, contradicting the assumption that they have the same label. The case $a_{q}^{\prime}=a_{m}^{\prime}$ is similar. Thus, our set really does have at least three elements, and it is a cycle. But since $A$ is barren, it contains no cycles, and we have a contradiction.
Thus, after all, no two elements with the same label appear in the same pair of $C$, so the cell containing $a$ is 2 -separable, and we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-team-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
6d17bb73-98b6-533d-a51a-4d8f1a58cabf
| 611,189
|
Show that every consistent 2-configuration of order 4 on a finite set $A$ has a subset that is a consistent 2-configuration of order 2.
|
First, assume the 2-configuration has just one cell. We claim there exists a sequence $a_{0}, a_{1}, \ldots, a_{n}$ of elements of $A$ (not necessarily all distinct) such that the list
$$
\left\{a_{0}, a_{1}\right\},\left\{a_{1}, a_{2}\right\}, \ldots,\left\{a_{n-1}, a_{n}\right\},\left\{a_{n}, a_{0}\right\}
$$
contains each element of the 2-configuration exactly once. To see this, consider the longest sequence such that $\left\{a_{0}, a_{1}\right\}, \ldots,\left\{a_{n-1}, a_{n}\right\},\left\{a_{n}, a_{0}\right\}$ are all distinct elements of the 2 -configuration. (We may take $n=0$ if necessary. Note that the finiteness condition ensures such a maximal sequence exists.) Each element of $A$ occurs an even number of times among these pairs (since each occurrence in the sequence contributes to two pairs). If every element occurs 4 times or 0 times, then the elements occurring in the sequence form a cell, since they cannot occur in any other pairs in the 2-configuration. Hence, they are all of $A$, and our sequence uses all the pairs in the 2-configuration, so the claim follows. Otherwise, there is some element $a_{i}$ occurring exactly twice. Choose $b_{1}$ so that $\left\{a_{i}, b_{1}\right\}$ is one of the two pairs in the 2 -configuration not used by our sequence. Then choose $b_{2}$ so that $\left\{b_{1}, b_{2}\right\}$ be another pair not used thus far. Continue in this manner, choosing new elements $b_{k}$ with $\left\{b_{k}, b_{k+1}\right\}$ a pair not already used, until we reach a point where finding another unused pair is impossible. Now, our pairs so far are
$$
\begin{gathered}
\left\{a_{0}, a_{1}\right\}, \ldots,\left\{a_{n-1}, a_{n}\right\},\left\{a_{n}, a_{0}\right\}, \\
\left\{a_{i}, b_{1}\right\},\left\{b_{1}, b_{2}\right\}, \ldots,\left\{b_{k-1}, b_{k}\right\} .
\end{gathered}
$$
Every element is used in an even number of these pairs, except possibly $a_{i}$, which is used in three pairs, and $b_{k}$, which is used in an odd number of pairs (so one or three) unless $a_{i}=b_{k}$, in which case this element occurs four times. But since it is impossible to continue the sequence, $b_{k}$ must indeed have been used four times, so $b_{k}=a_{i}$.
But now we can construct the following sequence of distinct elements of the 2-configuration:
$$
\begin{gathered}
\left\{a_{0}, a_{1}\right\}, \ldots,\left\{a_{i-1}, a_{i}\right\},\left\{a_{i}, b_{1}\right\},\left\{b_{1}, b_{2}\right\}, \ldots,\left\{b_{k-1}, a_{i}\right\}, \\
\left\{a_{i}, a_{i+1}\right\}, \ldots,\left\{a_{n-1}, a_{n}\right\},\left\{a_{n}, a_{0}\right\} .
\end{gathered}
$$
This contradicts the maximality of our original sequence. This contradiction means that our original sequence must have used all the pairs in the 2-configuration, after all.
So we can express the 2-configuration via such a sequence of pairs, where each pair's second element equals the first element of the next pair. If $A$ has $n$ elements, then (since each element appears in four pairs) we have $2 n$ pairs. So we can choose the 1st, 3rd, 5th, $\ldots,(2 n-1)$ th pairs, and then each element of $A$ belongs to just two of these pairs, because each occurrence of the element as an $a_{i}$ contributes to two consecutive pairs from our original sequence (or the first and last such pairs). Thus, we have our consistent 2-configuration of order 2, as desired.
Finally, if $A$ consists of more than one cell, then the pairs within any given cell form a consistent 2-configuration of order 4 on that cell. So we simply apply the above procedure to obtain a consistent 2 -configuration of order 2 on each cell, and then combining these gives a consistent 2 -configuration of order 2 on $A$, as desired.
Comments: A note for those who might have found these problems rather foreign - the objects described here are actually of considerable importance; they constitute the elements of graph theory, one of the major research areas of modern mathematics. What we have called a "2-configuration" is generally called a graph, and what we have called a " $k$-configuration" $(k>2)$ is generally called a hypergraph. The graph in problem 3b is the Petersen graph, a ubiquitous counterexample in graph theory. A consistent 2-configuration of order $n$ is an $n$-regular graph; a cell is a component; a barren 2-configuration is a forest (and a forest with one component is a tree); and an $m$-separable configuration is $m$-colorable (and the minimum $m$ for which a graph is $m$-colorable is its chromatic number).
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Show that every consistent 2-configuration of order 4 on a finite set $A$ has a subset that is a consistent 2-configuration of order 2.
|
First, assume the 2-configuration has just one cell. We claim there exists a sequence $a_{0}, a_{1}, \ldots, a_{n}$ of elements of $A$ (not necessarily all distinct) such that the list
$$
\left\{a_{0}, a_{1}\right\},\left\{a_{1}, a_{2}\right\}, \ldots,\left\{a_{n-1}, a_{n}\right\},\left\{a_{n}, a_{0}\right\}
$$
contains each element of the 2-configuration exactly once. To see this, consider the longest sequence such that $\left\{a_{0}, a_{1}\right\}, \ldots,\left\{a_{n-1}, a_{n}\right\},\left\{a_{n}, a_{0}\right\}$ are all distinct elements of the 2 -configuration. (We may take $n=0$ if necessary. Note that the finiteness condition ensures such a maximal sequence exists.) Each element of $A$ occurs an even number of times among these pairs (since each occurrence in the sequence contributes to two pairs). If every element occurs 4 times or 0 times, then the elements occurring in the sequence form a cell, since they cannot occur in any other pairs in the 2-configuration. Hence, they are all of $A$, and our sequence uses all the pairs in the 2-configuration, so the claim follows. Otherwise, there is some element $a_{i}$ occurring exactly twice. Choose $b_{1}$ so that $\left\{a_{i}, b_{1}\right\}$ is one of the two pairs in the 2 -configuration not used by our sequence. Then choose $b_{2}$ so that $\left\{b_{1}, b_{2}\right\}$ be another pair not used thus far. Continue in this manner, choosing new elements $b_{k}$ with $\left\{b_{k}, b_{k+1}\right\}$ a pair not already used, until we reach a point where finding another unused pair is impossible. Now, our pairs so far are
$$
\begin{gathered}
\left\{a_{0}, a_{1}\right\}, \ldots,\left\{a_{n-1}, a_{n}\right\},\left\{a_{n}, a_{0}\right\}, \\
\left\{a_{i}, b_{1}\right\},\left\{b_{1}, b_{2}\right\}, \ldots,\left\{b_{k-1}, b_{k}\right\} .
\end{gathered}
$$
Every element is used in an even number of these pairs, except possibly $a_{i}$, which is used in three pairs, and $b_{k}$, which is used in an odd number of pairs (so one or three) unless $a_{i}=b_{k}$, in which case this element occurs four times. But since it is impossible to continue the sequence, $b_{k}$ must indeed have been used four times, so $b_{k}=a_{i}$.
But now we can construct the following sequence of distinct elements of the 2-configuration:
$$
\begin{gathered}
\left\{a_{0}, a_{1}\right\}, \ldots,\left\{a_{i-1}, a_{i}\right\},\left\{a_{i}, b_{1}\right\},\left\{b_{1}, b_{2}\right\}, \ldots,\left\{b_{k-1}, a_{i}\right\}, \\
\left\{a_{i}, a_{i+1}\right\}, \ldots,\left\{a_{n-1}, a_{n}\right\},\left\{a_{n}, a_{0}\right\} .
\end{gathered}
$$
This contradicts the maximality of our original sequence. This contradiction means that our original sequence must have used all the pairs in the 2-configuration, after all.
So we can express the 2-configuration via such a sequence of pairs, where each pair's second element equals the first element of the next pair. If $A$ has $n$ elements, then (since each element appears in four pairs) we have $2 n$ pairs. So we can choose the 1st, 3rd, 5th, $\ldots,(2 n-1)$ th pairs, and then each element of $A$ belongs to just two of these pairs, because each occurrence of the element as an $a_{i}$ contributes to two consecutive pairs from our original sequence (or the first and last such pairs). Thus, we have our consistent 2-configuration of order 2, as desired.
Finally, if $A$ consists of more than one cell, then the pairs within any given cell form a consistent 2-configuration of order 4 on that cell. So we simply apply the above procedure to obtain a consistent 2 -configuration of order 2 on each cell, and then combining these gives a consistent 2 -configuration of order 2 on $A$, as desired.
Comments: A note for those who might have found these problems rather foreign - the objects described here are actually of considerable importance; they constitute the elements of graph theory, one of the major research areas of modern mathematics. What we have called a "2-configuration" is generally called a graph, and what we have called a " $k$-configuration" $(k>2)$ is generally called a hypergraph. The graph in problem 3b is the Petersen graph, a ubiquitous counterexample in graph theory. A consistent 2-configuration of order $n$ is an $n$-regular graph; a cell is a component; a barren 2-configuration is a forest (and a forest with one component is a tree); and an $m$-separable configuration is $m$-colorable (and the minimum $m$ for which a graph is $m$-colorable is its chromatic number).
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-team-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
1ffd502f-4149-54bf-9c82-a8398a38178e
| 611,190
|
Show that any number in row $n$ (for $n>0$ ) is at most $2^{n-1}$.
|
We use induction on $n$. It is clear that any number in row 1 is at most $1=2^{0}$. Now, if every number in row $n$ is at most $2^{n-1}$, then every number in row $n+1$ is the sum of two numbers in row $n$ and so is at most $2^{n-1}+2^{n-1}=2^{n}$. This gives the induction step, and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that any number in row $n$ (for $n>0$ ) is at most $2^{n-1}$.
|
We use induction on $n$. It is clear that any number in row 1 is at most $1=2^{0}$. Now, if every number in row $n$ is at most $2^{n-1}$, then every number in row $n+1$ is the sum of two numbers in row $n$ and so is at most $2^{n-1}+2^{n-1}=2^{n}$. This gives the induction step, and the result follows.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-team-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
05e87a03-b7db-57dd-9233-9284c35f7feb
| 611,288
|
Let
$$
S(n, r)=\binom{n-1}{r-1}+\binom{n-1}{r}+\binom{n-1}{r+1}+\cdots+\binom{n-1}{n-1}
$$
for all $n, r>0$, and in particular $S(n, r)=0$ if $r>n>0$. Prove that the number in row $n$ of the table, $r$ columns to the left of the 1 in the top row, is at most $S(n, r)$. (Hint: First prove that $S(n-1, r-1)+S(n-1, r)=S(n, r)$.)
|
First, we prove the statement in the hint: adding the $i$ th term of the sum for $S(n-1, r-1)$ to the $i$ th term for $S(n-1, r)$, for each $i$, we get that $S(n-1, r-$ 1) $+S(n-1, r)$ equals
$$
\begin{gathered}
\left(\binom{n-2}{r-2}+\binom{n-2}{r-1}\right)+\left(\binom{n-2}{r-1}+\binom{n-2}{r}\right)+\cdots \\
\cdots+\left(\binom{n-2}{n-3}+\binom{n-2}{n-2}\right)+\binom{n-2}{n-2} \\
=\binom{n-1}{r-1}+\binom{n-1}{r}+\cdots+\binom{n-1}{n-1}=S(n, r) .
\end{gathered}
$$
Now we can prove the main statement by induction on $n$. The base case $n=1$ is clear. If the statement holds for $n-1$, then first suppose $r>1$. Then the number in row $n$, $r$ columns to the left, is the sum of two of the three numbers above it, which, by the induction hypothesis, are at most $S(n-1, r-1), S(n-1, r), S(n-1, r+1)$ respectively. Since the first two of these are greater than the last (because the summation formula gives $S(n-1, r-1)=S(n-1, r)+\binom{n-1}{r-2}$ and $\left.S(n-1, r)=S(n-1, r+1)+\binom{n-1}{r-1}\right)$, we have an upper bound of $S(n-1, r-1)+S(n-1, r)=S(n, r)$ by the above. So the result follows by induction. Finally, in the case $r=1$, the quantity in question is just $2^{n-1}$, and the result holds by Problem 1.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let
$$
S(n, r)=\binom{n-1}{r-1}+\binom{n-1}{r}+\binom{n-1}{r+1}+\cdots+\binom{n-1}{n-1}
$$
for all $n, r>0$, and in particular $S(n, r)=0$ if $r>n>0$. Prove that the number in row $n$ of the table, $r$ columns to the left of the 1 in the top row, is at most $S(n, r)$. (Hint: First prove that $S(n-1, r-1)+S(n-1, r)=S(n, r)$.)
|
First, we prove the statement in the hint: adding the $i$ th term of the sum for $S(n-1, r-1)$ to the $i$ th term for $S(n-1, r)$, for each $i$, we get that $S(n-1, r-$ 1) $+S(n-1, r)$ equals
$$
\begin{gathered}
\left(\binom{n-2}{r-2}+\binom{n-2}{r-1}\right)+\left(\binom{n-2}{r-1}+\binom{n-2}{r}\right)+\cdots \\
\cdots+\left(\binom{n-2}{n-3}+\binom{n-2}{n-2}\right)+\binom{n-2}{n-2} \\
=\binom{n-1}{r-1}+\binom{n-1}{r}+\cdots+\binom{n-1}{n-1}=S(n, r) .
\end{gathered}
$$
Now we can prove the main statement by induction on $n$. The base case $n=1$ is clear. If the statement holds for $n-1$, then first suppose $r>1$. Then the number in row $n$, $r$ columns to the left, is the sum of two of the three numbers above it, which, by the induction hypothesis, are at most $S(n-1, r-1), S(n-1, r), S(n-1, r+1)$ respectively. Since the first two of these are greater than the last (because the summation formula gives $S(n-1, r-1)=S(n-1, r)+\binom{n-1}{r-2}$ and $\left.S(n-1, r)=S(n-1, r+1)+\binom{n-1}{r-1}\right)$, we have an upper bound of $S(n-1, r-1)+S(n-1, r)=S(n, r)$ by the above. So the result follows by induction. Finally, in the case $r=1$, the quantity in question is just $2^{n-1}$, and the result holds by Problem 1.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-team-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
f3b7cc36-5b0b-5eb4-991e-afddb218b2c3
| 611,290
|
Prove that the number of switch pairs in row $n$ is at most twice the number of odd numbers in row $n$.
|
Each switch pair contains an odd number, and each odd number can belong to at most two switch pairs (since it has only two neighbors).
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Prove that the number of switch pairs in row $n$ is at most twice the number of odd numbers in row $n$.
|
Each switch pair contains an odd number, and each odd number can belong to at most two switch pairs (since it has only two neighbors).
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-team-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
9a72272c-ec53-5f9f-bf9d-076657bd37de
| 611,292
|
Prove that the number of odd numbers in row $n$ is at most twice the number of switch pairs in row $n-1$.
|
Each odd number in row $n$ is the sum of two of the three numbers above it in row $n-1$; these three numbers cannot all have the same parity (or else any sum of two of them would be even), so somewhere among them is a switch pair. Since each switch pair in row $n-1$ can contribute to at most two odd numbers in row $n$ in this manner (namely, the two numbers immediately below the members of the pair), the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Prove that the number of odd numbers in row $n$ is at most twice the number of switch pairs in row $n-1$.
|
Each odd number in row $n$ is the sum of two of the three numbers above it in row $n-1$; these three numbers cannot all have the same parity (or else any sum of two of them would be even), so somewhere among them is a switch pair. Since each switch pair in row $n-1$ can contribute to at most two odd numbers in row $n$ in this manner (namely, the two numbers immediately below the members of the pair), the result follows.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-team-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
aab56dc7-1f0f-5e58-b088-5bb86a86a98c
| 611,293
|
Prove that the number of switch pairs in row $n$ is at most twice the number of switch pairs in row $n-1$.
|
If we go sufficiently far to the left or right in row $n$, we get to zeroes. Therefore, row $n$ consists of a finite number of "odd blocks" of the form
$$
E O O O \cdots O E
$$
(where $E$ represents an even number and $O$ an odd number), which are separated by even numbers, except that one even number may simultaneously be an endpoint of two odd blocks. Each odd block contributes two switch pairs to row $n$, so it is enough to show that each odd block has a switch pair somewhere above it in row $n-1$. But the odd block consists of at least one $O$ between two $E$ 's, making for at least three terms. If there were no switch pairs above the block, then in particular, the first three terms immediately above it would be all odd or all even, and then the second term in our block would have to be even, contradicting the assumption that it was $O$. This proves the result.
## Written In The Stars
Suppose $S$ is a finite set with a binary operation $\star$ - that is, for any elements $a, b$ of $S$, there is defined an element $a \star b$ of $S$. It is given that $(a \star b) \star(a \star b)=b \star a$ for all $a, b \in S$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Prove that the number of switch pairs in row $n$ is at most twice the number of switch pairs in row $n-1$.
|
If we go sufficiently far to the left or right in row $n$, we get to zeroes. Therefore, row $n$ consists of a finite number of "odd blocks" of the form
$$
E O O O \cdots O E
$$
(where $E$ represents an even number and $O$ an odd number), which are separated by even numbers, except that one even number may simultaneously be an endpoint of two odd blocks. Each odd block contributes two switch pairs to row $n$, so it is enough to show that each odd block has a switch pair somewhere above it in row $n-1$. But the odd block consists of at least one $O$ between two $E$ 's, making for at least three terms. If there were no switch pairs above the block, then in particular, the first three terms immediately above it would be all odd or all even, and then the second term in our block would have to be even, contradicting the assumption that it was $O$. This proves the result.
## Written In The Stars
Suppose $S$ is a finite set with a binary operation $\star$ - that is, for any elements $a, b$ of $S$, there is defined an element $a \star b$ of $S$. It is given that $(a \star b) \star(a \star b)=b \star a$ for all $a, b \in S$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-team-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
34e78b18-3871-502e-9be4-e3a2db5e6f6d
| 611,294
|
Prove that $a \star b=b \star a$ for all $a, b \in S$.
|
We have
$$
\begin{aligned}
a \star b & =(b \star a) \star(b \star a) \\
& =([a \star b] \star[a \star b]) \star([a \star b] \star[a \star b]) \\
& =[a \star b] \star[a \star b] \\
& =b \star a .
\end{aligned}
$$
Let $T$ be the set of elements of the form $a \star a$ for $a \in S$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that $a \star b=b \star a$ for all $a, b \in S$.
|
We have
$$
\begin{aligned}
a \star b & =(b \star a) \star(b \star a) \\
& =([a \star b] \star[a \star b]) \star([a \star b] \star[a \star b]) \\
& =[a \star b] \star[a \star b] \\
& =b \star a .
\end{aligned}
$$
Let $T$ be the set of elements of the form $a \star a$ for $a \in S$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-team-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
6d93dd63-b0f6-5693-b606-fcb0fecaa9aa
| 611,295
|
If $b$ is any element of $T$, prove that $b \star b=b$.
|
If $b \in T$, then $b=a \star a$ for some $a$, so $b \star b=(a \star a) \star(a \star a)=a \star a$ (by the given property) $=b$.
Now suppose further that $(a \star b) \star c=a \star(b \star c)$ for all $a, b, c \in S$. (Thus we can write an expression like $a \star b \star c \star d$ without ambiguity.)
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
If $b$ is any element of $T$, prove that $b \star b=b$.
|
If $b \in T$, then $b=a \star a$ for some $a$, so $b \star b=(a \star a) \star(a \star a)=a \star a$ (by the given property) $=b$.
Now suppose further that $(a \star b) \star c=a \star(b \star c)$ for all $a, b, c \in S$. (Thus we can write an expression like $a \star b \star c \star d$ without ambiguity.)
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-team-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
b525365f-a251-5f28-acae-a51c6554b9e1
| 611,296
|
Prove that there exists an element $a \in T$ such that the equation $a \star b=a$ holds for all $b \in T$.
|
Choose $a$ whose image contains as few elements as possible - we know we can do this, since $T$, being a subset of $S$, is finite. We claim that this $a$ works. Indeed, suppose $c$ is in the image of $a$. Then, for any $d$ in the image of $c, a \star(c \star d)=$ $(a \star c) \star d=c \star d=d$, so $d$ is also in the image of $a$. So the image of $c$ is contained in the image of $a$. But $a$ was chosen to have image as small as possible, so the two images must coincide. In particular, $a \star a=a$ is in the image of $c$. So
$$
a=c \star a=a \star c=c .
$$
This argument shows that $a$ is the only element of the image of $a$, which gives what we wanted.
Alternative Solution: This can also be solved without using Problem 10: The product of any two elements of $T$ is also in $T$, since commutativity and associativity give $(b \star b) \star(c \star c)=(b \star c) \star(b \star c)$ for $b, c \in S$. Then let $a_{1}, a_{2}, \ldots, a_{n}$ be all the elements of $T$, and put $a=a_{1} \star a_{2} \star \cdots \star a_{n}$; this value does not depend on the ordering of the elements. If $b \in T$, then $a=c \star b$, where $c$ is the $\star$-product of all elements of $T$ different from $b$, and consequently $a \star b=(c \star b) \star b=c \star(b \star b)=c \star b=a$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that there exists an element $a \in T$ such that the equation $a \star b=a$ holds for all $b \in T$.
|
Choose $a$ whose image contains as few elements as possible - we know we can do this, since $T$, being a subset of $S$, is finite. We claim that this $a$ works. Indeed, suppose $c$ is in the image of $a$. Then, for any $d$ in the image of $c, a \star(c \star d)=$ $(a \star c) \star d=c \star d=d$, so $d$ is also in the image of $a$. So the image of $c$ is contained in the image of $a$. But $a$ was chosen to have image as small as possible, so the two images must coincide. In particular, $a \star a=a$ is in the image of $c$. So
$$
a=c \star a=a \star c=c .
$$
This argument shows that $a$ is the only element of the image of $a$, which gives what we wanted.
Alternative Solution: This can also be solved without using Problem 10: The product of any two elements of $T$ is also in $T$, since commutativity and associativity give $(b \star b) \star(c \star c)=(b \star c) \star(b \star c)$ for $b, c \in S$. Then let $a_{1}, a_{2}, \ldots, a_{n}$ be all the elements of $T$, and put $a=a_{1} \star a_{2} \star \cdots \star a_{n}$; this value does not depend on the ordering of the elements. If $b \in T$, then $a=c \star b$, where $c$ is the $\star$-product of all elements of $T$ different from $b$, and consequently $a \star b=(c \star b) \star b=c \star(b \star b)=c \star b=a$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-team-solutions.jsonl",
"problem_match": "\n11. ",
"solution_match": "\nSolution: "
}
|
d2649536-29cc-5bbb-8add-f9c17d5ba6db
| 611,298
|
Prove that
$$
\sigma(1)+\sigma(2)+\sigma(3)+\cdots+\sigma(n) \leq n^{2}
$$
for every positive integer $n$.
|
The $i$ th term on the left is the sum of all $d$ dividing $i$. If we write this sum out explicitly, then each term $d=1,2, \ldots, n$ appears $\lfloor n / d\rfloor$ times - once for each multiple of $d$ that is $\leq n$. Thus, the sum equals
$$
\begin{aligned}
\lfloor n / 1\rfloor+2\lfloor n / 2\rfloor+3\lfloor n / 3\rfloor+\cdots+n\lfloor n / n\rfloor & \leq n / 1+2 n / 2+3 n / 3+\cdots+n / n \\
& =n+n+\cdots+n \\
& =n^{2} .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that
$$
\sigma(1)+\sigma(2)+\sigma(3)+\cdots+\sigma(n) \leq n^{2}
$$
for every positive integer $n$.
|
The $i$ th term on the left is the sum of all $d$ dividing $i$. If we write this sum out explicitly, then each term $d=1,2, \ldots, n$ appears $\lfloor n / d\rfloor$ times - once for each multiple of $d$ that is $\leq n$. Thus, the sum equals
$$
\begin{aligned}
\lfloor n / 1\rfloor+2\lfloor n / 2\rfloor+3\lfloor n / 3\rfloor+\cdots+n\lfloor n / n\rfloor & \leq n / 1+2 n / 2+3 n / 3+\cdots+n / n \\
& =n+n+\cdots+n \\
& =n^{2} .
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-team-solutions.jsonl",
"problem_match": "\n14. ",
"solution_match": "\nSolution: "
}
|
d03c8ae0-e752-56e2-ae8e-2086df71df60
| 611,301
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.