problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $A B C D$ be a convex quadrilateral. Let the diagonals $A C$ and $B D$ intersect in $P$. Let $P E, P F, P G$ and $P H$ be the altitudes from $P$ on to the sides $A B, B C, C D$ and $D A$ respectively. Show that $A B C D$ has an incircle if and only if
$$
\frac{1}{P E}+\frac{1}{P G}=\frac{1}{P F}+\frac{1}{P H}
$$
|
Let $A P=p, B P=q, C P=r, D P=s ; A B=a, B C=b$, $C D=c$ and $D A=d$. Let $\angle A P B=\angle C P D=\theta$. Then $\angle B P C=\angle D P A=$ $\pi-\theta$. Let us also write $P E=h_{1}, P F=h_{2}, P G=h_{3}$ and $P H=h_{4}$.
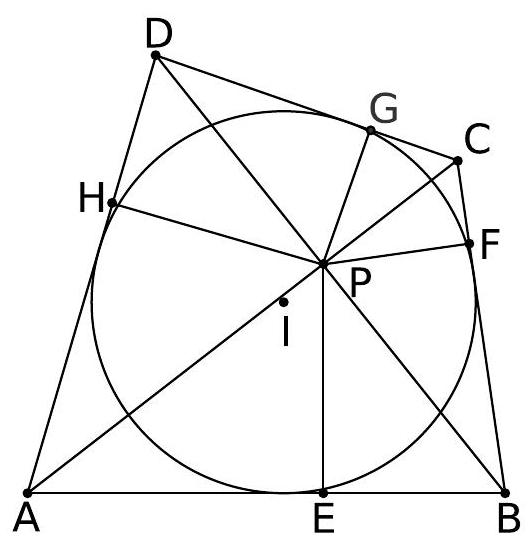
## Observe that
$$
h_{1} a=p q \sin \theta, \quad h_{2} b=q r \sin \theta, \quad h_{3} c=r s \sin \theta, \quad h_{4} d=s p \sin \theta
$$
Hence
$$
\frac{1}{h_{1}}+\frac{1}{h_{3}}=\frac{1}{h_{2}}+\frac{1}{h_{4}}
$$
is equivalent to
$$
\frac{a}{p q}+\frac{c}{r s}=\frac{b}{q r}+\frac{d}{s p}
$$
This is the same as
$$
a r s+c p q=b s p+d q r
$$
Thus we have to prove that $a+c=b+d$ if and only if $a r s+c p q=b s p+d q r$. Now we can write $a+c=b+d$ as
$$
a^{2}+c^{2}+2 a c=b^{2}+d^{2}+2 b d
$$
But we know that
$$
\begin{aligned}
& a^{2}=p^{2}+q^{2}-2 p q \cos \theta, \quad c^{2}=r^{2}+s^{2}-2 r s \cos \theta \\
& b^{2}=q^{2}+r^{2}+2 q r \cos \theta, \quad d^{2}=p^{2}+s^{2}+2 p s \cos \theta
\end{aligned}
$$
Hence $a+c=b+d$ is equivalent to
$$
-p q \cos \theta+-r s \cos \theta+a c=p s \cos \theta+q r \cos \theta+b d
$$
Similarly, by squaring ars $+c p q=b s p+d q r$ we can show that it is equivalent to
$$
-p q \cos \theta+-r s \cos \theta+a c=p s \cos \theta+q r \cos \theta+b d
$$
We conclude that $a+c=b+d$ is equivalent to $c p q+a r s=b p s+d q r$. Hence $A B C D$ has an in circle if and only if
$$
\frac{1}{h_{1}}+\frac{1}{h_{3}}=\frac{1}{h_{2}}+\frac{1}{h_{4}}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral. Let the diagonals $A C$ and $B D$ intersect in $P$. Let $P E, P F, P G$ and $P H$ be the altitudes from $P$ on to the sides $A B, B C, C D$ and $D A$ respectively. Show that $A B C D$ has an incircle if and only if
$$
\frac{1}{P E}+\frac{1}{P G}=\frac{1}{P F}+\frac{1}{P H}
$$
|
Let $A P=p, B P=q, C P=r, D P=s ; A B=a, B C=b$, $C D=c$ and $D A=d$. Let $\angle A P B=\angle C P D=\theta$. Then $\angle B P C=\angle D P A=$ $\pi-\theta$. Let us also write $P E=h_{1}, P F=h_{2}, P G=h_{3}$ and $P H=h_{4}$.

## Observe that
$$
h_{1} a=p q \sin \theta, \quad h_{2} b=q r \sin \theta, \quad h_{3} c=r s \sin \theta, \quad h_{4} d=s p \sin \theta
$$
Hence
$$
\frac{1}{h_{1}}+\frac{1}{h_{3}}=\frac{1}{h_{2}}+\frac{1}{h_{4}}
$$
is equivalent to
$$
\frac{a}{p q}+\frac{c}{r s}=\frac{b}{q r}+\frac{d}{s p}
$$
This is the same as
$$
a r s+c p q=b s p+d q r
$$
Thus we have to prove that $a+c=b+d$ if and only if $a r s+c p q=b s p+d q r$. Now we can write $a+c=b+d$ as
$$
a^{2}+c^{2}+2 a c=b^{2}+d^{2}+2 b d
$$
But we know that
$$
\begin{aligned}
& a^{2}=p^{2}+q^{2}-2 p q \cos \theta, \quad c^{2}=r^{2}+s^{2}-2 r s \cos \theta \\
& b^{2}=q^{2}+r^{2}+2 q r \cos \theta, \quad d^{2}=p^{2}+s^{2}+2 p s \cos \theta
\end{aligned}
$$
Hence $a+c=b+d$ is equivalent to
$$
-p q \cos \theta+-r s \cos \theta+a c=p s \cos \theta+q r \cos \theta+b d
$$
Similarly, by squaring ars $+c p q=b s p+d q r$ we can show that it is equivalent to
$$
-p q \cos \theta+-r s \cos \theta+a c=p s \cos \theta+q r \cos \theta+b d
$$
We conclude that $a+c=b+d$ is equivalent to $c p q+a r s=b p s+d q r$. Hence $A B C D$ has an in circle if and only if
$$
\frac{1}{h_{1}}+\frac{1}{h_{3}}=\frac{1}{h_{2}}+\frac{1}{h_{4}}
$$
|
{
"resource_path": "INMO/segmented/en-inmosol-15.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
e171e5e4-ebb5-5c9a-9bef-59b468411634
| 607,900
|
From a set of 11 square integers, show that one can choose 6 numbers $a^{2}, b^{2}, c^{2}, d^{2}, e^{2}, f^{2}$ such that
$$
a^{2}+b^{2}+c^{2} \equiv d^{2}+e^{2}+f^{2} \quad(\bmod 12)
$$
|
The first observation is that we can find 5 pairs of squares such that the two numbers in a pair have the same parity. We can see this as follows:
| Odd numbers | Even numbers | Odd pairs | Even pairs | Total pairs |
| :---: | :---: | :---: | :---: | :---: |
| 0 | 11 | 0 | 5 | 5 |
| 1 | 10 | 0 | 5 | 5 |
| 2 | 9 | 1 | 4 | 5 |
| 3 | 8 | 1 | 4 | 5 |
| 4 | 7 | 2 | 3 | 5 |
| 5 | 6 | 2 | 3 | 5 |
| 6 | 5 | 3 | 2 | 5 |
| 7 | 4 | 3 | 2 | 5 |
| 8 | 3 | 4 | 1 | 5 |
| 9 | 2 | 4 | 1 | 5 |
| 10 | 1 | 5 | 0 | 5 |
| 11 | 0 | 5 | 0 | 5 |
Let us take such 5 pairs: say $\left(x_{1}^{2}, y_{1}^{2}\right),\left(x_{2}^{2}, y_{2}^{2}\right), \ldots,\left(x_{5}^{2}, y_{5}^{2}\right)$. Then $x_{j}^{2}-y_{j}^{2}$ is divisible by 4 for $1 \leq j \leq 5$. Let $r_{j}$ be the remainder when $x_{j}^{2}-y_{j}^{2}$ is divisible by $3,1 \leq j \leq 3$. We have 5 remainders $r_{1}, r_{2}, r_{3}, r_{4}, r_{5}$. But these can be 0,1 or 2 . Hence either one of the remainders occur 3 times or each of the remainders occur once. If, for example $r_{1}=r_{2}=r_{3}$, then 3 divides $r_{1}+r_{2}+r_{3}$; if $r_{1}=0, r_{2}=1$ and $r_{3}=2$, then again 3 divides $r_{1}+r_{2}+r_{3}$. Thus we can always find three remainders whose sum is divisible by 3 . This means we can find 3 pairs, say, $\left(x_{1}^{2}, y_{1}^{2}\right),\left(x_{2}^{2}, y_{2}^{2}\right),\left(x_{3}^{2}, y_{3}^{2}\right)$ such that 3 divides $\left(x_{1}^{2}-y_{1}^{2}\right)+\left(x_{2}^{2}-y_{2}^{2}\right)+\left(x_{3}^{2}-y_{3}^{2}\right)$. Since each difference is divisible by 4 , we conclude that we can find 6 numbers $a^{2}, b^{2}, c^{2}, d^{2}, e^{2}, f^{2}$ such that
$$
a^{2}+b^{2}+c^{2} \equiv d^{2}+e^{2}+f^{2} \quad(\bmod 12)
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
From a set of 11 square integers, show that one can choose 6 numbers $a^{2}, b^{2}, c^{2}, d^{2}, e^{2}, f^{2}$ such that
$$
a^{2}+b^{2}+c^{2} \equiv d^{2}+e^{2}+f^{2} \quad(\bmod 12)
$$
|
The first observation is that we can find 5 pairs of squares such that the two numbers in a pair have the same parity. We can see this as follows:
| Odd numbers | Even numbers | Odd pairs | Even pairs | Total pairs |
| :---: | :---: | :---: | :---: | :---: |
| 0 | 11 | 0 | 5 | 5 |
| 1 | 10 | 0 | 5 | 5 |
| 2 | 9 | 1 | 4 | 5 |
| 3 | 8 | 1 | 4 | 5 |
| 4 | 7 | 2 | 3 | 5 |
| 5 | 6 | 2 | 3 | 5 |
| 6 | 5 | 3 | 2 | 5 |
| 7 | 4 | 3 | 2 | 5 |
| 8 | 3 | 4 | 1 | 5 |
| 9 | 2 | 4 | 1 | 5 |
| 10 | 1 | 5 | 0 | 5 |
| 11 | 0 | 5 | 0 | 5 |
Let us take such 5 pairs: say $\left(x_{1}^{2}, y_{1}^{2}\right),\left(x_{2}^{2}, y_{2}^{2}\right), \ldots,\left(x_{5}^{2}, y_{5}^{2}\right)$. Then $x_{j}^{2}-y_{j}^{2}$ is divisible by 4 for $1 \leq j \leq 5$. Let $r_{j}$ be the remainder when $x_{j}^{2}-y_{j}^{2}$ is divisible by $3,1 \leq j \leq 3$. We have 5 remainders $r_{1}, r_{2}, r_{3}, r_{4}, r_{5}$. But these can be 0,1 or 2 . Hence either one of the remainders occur 3 times or each of the remainders occur once. If, for example $r_{1}=r_{2}=r_{3}$, then 3 divides $r_{1}+r_{2}+r_{3}$; if $r_{1}=0, r_{2}=1$ and $r_{3}=2$, then again 3 divides $r_{1}+r_{2}+r_{3}$. Thus we can always find three remainders whose sum is divisible by 3 . This means we can find 3 pairs, say, $\left(x_{1}^{2}, y_{1}^{2}\right),\left(x_{2}^{2}, y_{2}^{2}\right),\left(x_{3}^{2}, y_{3}^{2}\right)$ such that 3 divides $\left(x_{1}^{2}-y_{1}^{2}\right)+\left(x_{2}^{2}-y_{2}^{2}\right)+\left(x_{3}^{2}-y_{3}^{2}\right)$. Since each difference is divisible by 4 , we conclude that we can find 6 numbers $a^{2}, b^{2}, c^{2}, d^{2}, e^{2}, f^{2}$ such that
$$
a^{2}+b^{2}+c^{2} \equiv d^{2}+e^{2}+f^{2} \quad(\bmod 12)
$$
|
{
"resource_path": "INMO/segmented/en-inmosol-15.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution:"
}
|
0d5aa8aa-9f75-5c4e-bbe5-6fb86bf5b245
| 607,901
|
Let $\Gamma_{1}$ and $\Gamma_{2}$ be two circles of unequal radii, with centres $O_{1}$ and $O_{2}$ respectively, in the plane intersecting in two distinct points $A$ and $B$. Assume that the centre of each of the circles $\Gamma_{1}$ and $\Gamma_{2}$ is outside the other. The tangent to $\Gamma_{1}$ at $B$ intersects $\Gamma_{2}$ again in $C$, different from $B$; the tangent to $\Gamma_{2}$ at $B$ intersects $\Gamma_{1}$ again in $D$, different from $B$. The bisectors of $\angle D A B$ and $\angle C A B$ meet $\Gamma_{1}$ and $\Gamma_{2}$ again in $X$ and $Y$, respectively, different from $A$. Let $P$ and $Q$ be the circumcentres of triangles $A C D$ and $X A Y$, respectively. Prove that $P Q$ is the perpendicular bisector of the line segment $O_{1} O_{2}$.
|
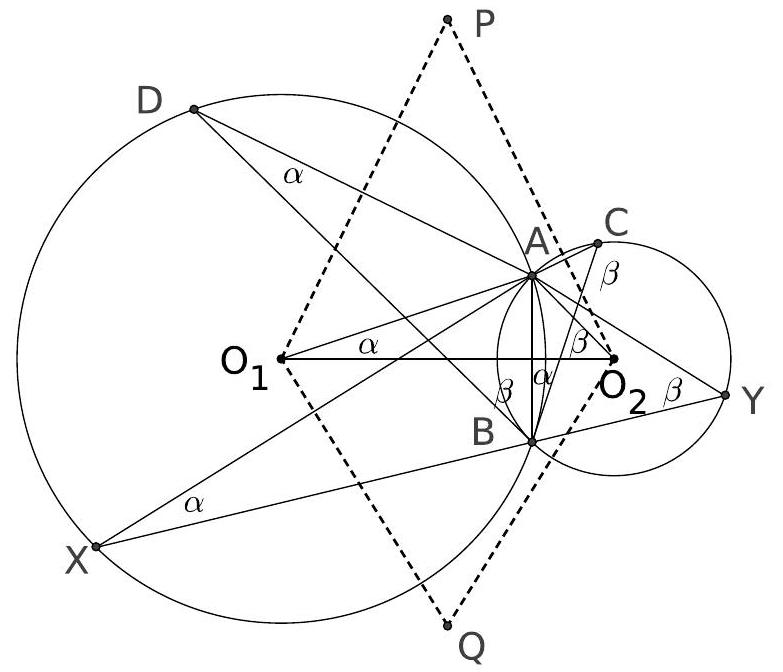
Let $\angle C B A=\alpha$ and $\angle D B A=\beta$. Then $\angle B D A=\alpha$ and $\angle B C A=\beta$. We also observe that $\angle A O_{1} O_{2}=\left(\angle A O_{1} B / 2\right)=\alpha$ and, simiarly, $\angle A O_{2} O_{1}=\beta$. Hence
$$
\angle O_{1} A O_{2}=180^{\circ}-(\alpha+\beta)
$$
We also have
$$
\angle P O_{1} A=\frac{\angle D O_{1} A}{2}=\frac{2 \angle D B A}{2}=\angle D B A=\beta
$$
Hence $\angle P O_{1} O_{2}=\angle P O_{1} A+\angle A O_{1} O_{2}=\beta+\alpha$. Similarly, we can get $\angle P O_{2} O_{1}=\alpha+\beta$. It follows that $P$ lies on the perpendicular bisector of $\mathrm{O}_{1} \mathrm{O}_{2}$.
Now we observe that
$$
\angle X Q Y=360^{\circ}-2 \angle X A Y=360^{\circ}-2\left(180^{\circ}-\alpha-\beta\right)=2(\alpha+\beta)
$$
This gives
$$
\angle O_{1} Q O_{2}=\frac{1}{2}(\angle X Q A+\angle Y Q A)=\frac{\angle X Q Y}{2}=\alpha+\beta
$$
This shows that $A, O_{1}, O_{2}, Q$ are concyclic. We also have
$$
\begin{aligned}
& \angle A B X=\angle A B D+\angle D B X=\beta+\angle D A X=\beta+\frac{\angle D A B}{2} \\
& \angle A B Y=\angle A B C+\angle C B Y=\alpha+\angle C A Y=\alpha+\frac{\angle B A C}{2}
\end{aligned}
$$
Adding we obtain
$$
\angle A B X+\angle A B Y=\alpha+\beta+\frac{1}{2}(\angle D A B+\angle B A C)=\alpha+\beta+\left(180^{\circ}-\alpha-\beta\right)=180^{\circ}
$$
Hence $X, B, Y$ are collinear. Now
$$
\begin{gathered}
\angle Q A X=\frac{1}{2}\left(180^{\circ}-\angle A Q X\right)=90^{\circ}-\beta \\
\angle X A O_{1}=\frac{1}{2}\left(180^{\circ}-\angle X O_{1} A\right)=90^{\circ}-\frac{1}{2}\left(360^{\circ}-2 \angle A B X\right)=\angle A B X-90^{\circ}
\end{gathered}
$$
Hence
$$
\angle Q A O_{1}=90^{\circ}-\beta+\angle A B X-90^{\circ}=\angle A B X-\beta=\frac{\angle D A B}{2}=\frac{\angle O_{1} A O_{2}}{2}
$$
This shows that $A Q$ bisects $\angle O_{1} A O_{2}$ and therefore the chords $Q O_{1}$ and $Q O_{2}$ subtend equal angles on the circumference of the circle passing through $Q O_{2} A O_{1}$. Hence $Q O_{2}=Q O_{1}$. This means $Q$ lies on the perpendicular bisector of $\mathrm{O}_{1} \mathrm{O}_{2}$.
Combining, we get that $P Q$ is the perpendicular bisector of $O_{1} O_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma_{1}$ and $\Gamma_{2}$ be two circles of unequal radii, with centres $O_{1}$ and $O_{2}$ respectively, in the plane intersecting in two distinct points $A$ and $B$. Assume that the centre of each of the circles $\Gamma_{1}$ and $\Gamma_{2}$ is outside the other. The tangent to $\Gamma_{1}$ at $B$ intersects $\Gamma_{2}$ again in $C$, different from $B$; the tangent to $\Gamma_{2}$ at $B$ intersects $\Gamma_{1}$ again in $D$, different from $B$. The bisectors of $\angle D A B$ and $\angle C A B$ meet $\Gamma_{1}$ and $\Gamma_{2}$ again in $X$ and $Y$, respectively, different from $A$. Let $P$ and $Q$ be the circumcentres of triangles $A C D$ and $X A Y$, respectively. Prove that $P Q$ is the perpendicular bisector of the line segment $O_{1} O_{2}$.
|

Let $\angle C B A=\alpha$ and $\angle D B A=\beta$. Then $\angle B D A=\alpha$ and $\angle B C A=\beta$. We also observe that $\angle A O_{1} O_{2}=\left(\angle A O_{1} B / 2\right)=\alpha$ and, simiarly, $\angle A O_{2} O_{1}=\beta$. Hence
$$
\angle O_{1} A O_{2}=180^{\circ}-(\alpha+\beta)
$$
We also have
$$
\angle P O_{1} A=\frac{\angle D O_{1} A}{2}=\frac{2 \angle D B A}{2}=\angle D B A=\beta
$$
Hence $\angle P O_{1} O_{2}=\angle P O_{1} A+\angle A O_{1} O_{2}=\beta+\alpha$. Similarly, we can get $\angle P O_{2} O_{1}=\alpha+\beta$. It follows that $P$ lies on the perpendicular bisector of $\mathrm{O}_{1} \mathrm{O}_{2}$.
Now we observe that
$$
\angle X Q Y=360^{\circ}-2 \angle X A Y=360^{\circ}-2\left(180^{\circ}-\alpha-\beta\right)=2(\alpha+\beta)
$$
This gives
$$
\angle O_{1} Q O_{2}=\frac{1}{2}(\angle X Q A+\angle Y Q A)=\frac{\angle X Q Y}{2}=\alpha+\beta
$$
This shows that $A, O_{1}, O_{2}, Q$ are concyclic. We also have
$$
\begin{aligned}
& \angle A B X=\angle A B D+\angle D B X=\beta+\angle D A X=\beta+\frac{\angle D A B}{2} \\
& \angle A B Y=\angle A B C+\angle C B Y=\alpha+\angle C A Y=\alpha+\frac{\angle B A C}{2}
\end{aligned}
$$
Adding we obtain
$$
\angle A B X+\angle A B Y=\alpha+\beta+\frac{1}{2}(\angle D A B+\angle B A C)=\alpha+\beta+\left(180^{\circ}-\alpha-\beta\right)=180^{\circ}
$$
Hence $X, B, Y$ are collinear. Now
$$
\begin{gathered}
\angle Q A X=\frac{1}{2}\left(180^{\circ}-\angle A Q X\right)=90^{\circ}-\beta \\
\angle X A O_{1}=\frac{1}{2}\left(180^{\circ}-\angle X O_{1} A\right)=90^{\circ}-\frac{1}{2}\left(360^{\circ}-2 \angle A B X\right)=\angle A B X-90^{\circ}
\end{gathered}
$$
Hence
$$
\angle Q A O_{1}=90^{\circ}-\beta+\angle A B X-90^{\circ}=\angle A B X-\beta=\frac{\angle D A B}{2}=\frac{\angle O_{1} A O_{2}}{2}
$$
This shows that $A Q$ bisects $\angle O_{1} A O_{2}$ and therefore the chords $Q O_{1}$ and $Q O_{2}$ subtend equal angles on the circumference of the circle passing through $Q O_{2} A O_{1}$. Hence $Q O_{2}=Q O_{1}$. This means $Q$ lies on the perpendicular bisector of $\mathrm{O}_{1} \mathrm{O}_{2}$.
Combining, we get that $P Q$ is the perpendicular bisector of $O_{1} O_{2}$.
|
{
"resource_path": "INMO/segmented/en-sol-inmo-20.jsonl",
"problem_match": "\n1.",
"solution_match": "## Solution:"
}
|
4ca14b73-618a-5f44-8b16-3f43fdc5338f
| 607,902
|
Suppose $P(x)$ is a polynomial with real coefficients satsfying the condition $P(\cos \theta+\sin \theta)=$ $P(\cos \theta-\sin \theta)$, for every real $\theta$. Prove that $P(x)$ can be expressed in the form
$$
P(x)=a_{0}+a_{1}\left(1-x^{2}\right)^{2}+a_{2}\left(1-x^{2}\right)^{4}+\cdots+a_{n}\left(1-x^{2}\right)^{2 n}
$$
for some real numbers $a_{0}, a_{1}, a_{2}, \ldots, a_{n}$ and nonnegative integer $n$.
|
Changing $\theta$ to $\theta-\pi / 2$, we see that
$$
P(\sin \theta+\cos \theta)=P(\sin \theta-\cos \theta)
$$
This shows that $P(x)=P(-x)$ for all $x \in[-\sqrt{2}, \sqrt{2}]$ and as $\mathrm{P}$ is a polynomial, in fact,
$$
P(x)=P(-x)
$$
for all $x \in \mathbb{R}$. Hence $P(x)$ is an even polynomial; $P(x)=Q\left(x^{2}\right)$ for some polynomial $Q(x)$. This gives
$$
Q(1+\sin (2 \theta))=P(\cos \theta+\sin \theta)=P(\cos \theta-\sin \theta)=Q(1-\sin (2 \theta))
$$
Taking $t=\sin (2 \theta)$, we see that $Q(1+t)=Q(1-t)$. Hence $Q(0)=Q(2)$
Consider $Q(t)-Q(0)$. This vanishes both at $t=0$ and $t=2$. Hence $t(2-t)$ is a factor of $Q(t)-Q(0)$. We obtain
$$
Q(t)-Q(0)=t(2-t) h(t)
$$
for some polynomial $h(t)$. Using $Q(1+t)=Q(1-t)$, it follows that $h(1+t)=h(1-t)$. Hence by induction we get
$$
Q(t)=\sum_{k=0}^{n} b_{k} t^{k}(2-t)^{k}
$$
Hence
$$
P(x)=Q\left(x^{2}\right)=\sum_{k=0}^{n} b_{k}\left(x^{2}\left(2-x^{2}\right)\right)^{k}=\sum_{k=0}^{n} b_{k}\left(1-\left(1-x^{2}\right)^{2}\right)^{k}
$$
Using binomial theorem, we can write this as
$$
P(x)=\sum_{k=0}^{n} a_{k}\left(1-x^{2}\right)^{2 k}
$$
for some coefficients $a_{k}, 0 \leq k \leq n$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Suppose $P(x)$ is a polynomial with real coefficients satsfying the condition $P(\cos \theta+\sin \theta)=$ $P(\cos \theta-\sin \theta)$, for every real $\theta$. Prove that $P(x)$ can be expressed in the form
$$
P(x)=a_{0}+a_{1}\left(1-x^{2}\right)^{2}+a_{2}\left(1-x^{2}\right)^{4}+\cdots+a_{n}\left(1-x^{2}\right)^{2 n}
$$
for some real numbers $a_{0}, a_{1}, a_{2}, \ldots, a_{n}$ and nonnegative integer $n$.
|
Changing $\theta$ to $\theta-\pi / 2$, we see that
$$
P(\sin \theta+\cos \theta)=P(\sin \theta-\cos \theta)
$$
This shows that $P(x)=P(-x)$ for all $x \in[-\sqrt{2}, \sqrt{2}]$ and as $\mathrm{P}$ is a polynomial, in fact,
$$
P(x)=P(-x)
$$
for all $x \in \mathbb{R}$. Hence $P(x)$ is an even polynomial; $P(x)=Q\left(x^{2}\right)$ for some polynomial $Q(x)$. This gives
$$
Q(1+\sin (2 \theta))=P(\cos \theta+\sin \theta)=P(\cos \theta-\sin \theta)=Q(1-\sin (2 \theta))
$$
Taking $t=\sin (2 \theta)$, we see that $Q(1+t)=Q(1-t)$. Hence $Q(0)=Q(2)$
Consider $Q(t)-Q(0)$. This vanishes both at $t=0$ and $t=2$. Hence $t(2-t)$ is a factor of $Q(t)-Q(0)$. We obtain
$$
Q(t)-Q(0)=t(2-t) h(t)
$$
for some polynomial $h(t)$. Using $Q(1+t)=Q(1-t)$, it follows that $h(1+t)=h(1-t)$. Hence by induction we get
$$
Q(t)=\sum_{k=0}^{n} b_{k} t^{k}(2-t)^{k}
$$
Hence
$$
P(x)=Q\left(x^{2}\right)=\sum_{k=0}^{n} b_{k}\left(x^{2}\left(2-x^{2}\right)\right)^{k}=\sum_{k=0}^{n} b_{k}\left(1-\left(1-x^{2}\right)^{2}\right)^{k}
$$
Using binomial theorem, we can write this as
$$
P(x)=\sum_{k=0}^{n} a_{k}\left(1-x^{2}\right)^{2 k}
$$
for some coefficients $a_{k}, 0 \leq k \leq n$.
|
{
"resource_path": "INMO/segmented/en-sol-inmo-20.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution:"
}
|
706b7956-64c7-502c-8384-d5a2b72add00
| 607,903
|
Let $n \geq 3$ be an integer and let $1<a_{1} \leq a_{2} \leq a_{3} \leq \cdots \leq a_{n}$ be $n$ real numbers such that $a_{1}+a_{2}+a_{3}+\cdots+a_{n}=2 n$. Prove that
$$
a_{1} a_{2} \cdots a_{n-1}+a_{1} a_{2} \cdots a_{n-2}+\cdots+a_{1} a_{2}+a_{1}+2 \leq a_{1} a_{2} \cdots a_{n}
$$
|
We use Chebyshev's inequality. Observe
$$
\begin{aligned}
& n\left(a_{1} a_{2} \cdots a_{n-1}+a_{1} a_{2} \cdots a_{n-2}+\cdots+a_{1}+1\right) \\
& \quad=\left(a_{1} a_{2} \cdots a_{n-1}+a_{1} a_{2} \cdots a_{n-2}+\cdots+a_{1}+1\right)\left(\left(a_{n}-1\right)+\left(a_{n-1}-1\right)+\cdots+\left(a_{1}-1\right)\right) \\
& \quad \leq n\left(a_{1} a_{2} \cdots a_{n-1}\left(a_{n}-1\right)+\cdots+a_{1}\left(a_{2}-1\right)+1\left(a_{1}-1\right)\right) \\
& \quad \leq n\left(a_{1} a_{2} \cdots a_{n}-1\right)
\end{aligned}
$$
It follows that
$$
a_{1} a_{2} \cdots a_{n-1}+a_{1} a_{2} \cdots a_{n-2}+\cdots+a_{1}+1 \leq a_{1} a_{2} \cdots a_{n}-1
$$
This gives the required inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geq 3$ be an integer and let $1<a_{1} \leq a_{2} \leq a_{3} \leq \cdots \leq a_{n}$ be $n$ real numbers such that $a_{1}+a_{2}+a_{3}+\cdots+a_{n}=2 n$. Prove that
$$
a_{1} a_{2} \cdots a_{n-1}+a_{1} a_{2} \cdots a_{n-2}+\cdots+a_{1} a_{2}+a_{1}+2 \leq a_{1} a_{2} \cdots a_{n}
$$
|
We use Chebyshev's inequality. Observe
$$
\begin{aligned}
& n\left(a_{1} a_{2} \cdots a_{n-1}+a_{1} a_{2} \cdots a_{n-2}+\cdots+a_{1}+1\right) \\
& \quad=\left(a_{1} a_{2} \cdots a_{n-1}+a_{1} a_{2} \cdots a_{n-2}+\cdots+a_{1}+1\right)\left(\left(a_{n}-1\right)+\left(a_{n-1}-1\right)+\cdots+\left(a_{1}-1\right)\right) \\
& \quad \leq n\left(a_{1} a_{2} \cdots a_{n-1}\left(a_{n}-1\right)+\cdots+a_{1}\left(a_{2}-1\right)+1\left(a_{1}-1\right)\right) \\
& \quad \leq n\left(a_{1} a_{2} \cdots a_{n}-1\right)
\end{aligned}
$$
It follows that
$$
a_{1} a_{2} \cdots a_{n-1}+a_{1} a_{2} \cdots a_{n-2}+\cdots+a_{1}+1 \leq a_{1} a_{2} \cdots a_{n}-1
$$
This gives the required inequality.
|
{
"resource_path": "INMO/segmented/en-sol-inmo-20.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
f726790b-2a68-5500-a348-a668cee8275e
| 607,905
|
Infinitely many equidistant parallel lines are drawn in the plane. A positive integer $n \geq 3$ is called frameable if it is possible to draw a regular polygon with $n$ sides all whose vertices lie on these lines and no line contains more than one vertex of the polygon.
(a) Show that $3,4,6$ are frameable.
(b) Show that any integer $n \geq 7$ is not frameable.
(c) Determine whether 5 is frameable.
|
For $n=3,4,6$ it is possible to draw regular polygons with vertices on the parallel lines (note that when we show a regular hexagon is a framed polygon, it includes the equilateral triangle case).
Figure 1:
Figure 2:
Figure 3:
We will prove that it is not possible for $n \geq 7$. In fact, we prove a stronger statement that we can not draw other polygons with vertices on the lines (even if we allow more than one vertex to lie on the same line).
First observe that if $A, B$ are points on the lines and $C$ is another point on a line, if we locate
Figure 4:
Figure 5:
point $D$ such that $C D$ is parallel and equal to $A B$, then $D$ also lies on a line. Suppose that we have a regular polygon $A_{1} A_{2} \ldots A_{n}$, where $n \geq 6$, with all the vertices on the grid lines. Choose a point $O$ on a grid line and draw segments $O B_{i}$ equal and parallel to $A_{i} A_{i+1}$, for $i=1,2, \ldots, n-1$ and $O B_{n}$ parallel and equal to $A_{n} A_{1}$. The points $B_{i}$ also lie on the grid lines and form a regular polygon with $n$ sides. Consider the ratio $k=\frac{B_{1} B_{2}}{A_{1} A_{2}}$. Since $n>6$, the $\angle B_{1} O B_{2}<360^{\circ} / 6$ and hence is the smallest angle in the triangle $B_{1} O B_{2}$ (note that the triangle $B_{1} O B_{2}$ is isosceles). Thus $k<1$. Hence starting with a polygon with vertices on grid lines, we obtain another polygon with ratio of side lengths $k<1$. Repeating this process, we obtain a polygon with vertices on grid lines with ratio of sides $k^{m}$ for any $m$. This is a contradiction since the length of the side of a polygon with vertices on grid lines can not be less than the distance between the parallel lines. Thus for $n>6$, we can not draw a polygon with vertices on the grid lines.
The above proof fails for $n=5$. In this case, draw $O B_{1}, O B_{1}^{\prime}$ parallel and equal to $A_{1} A_{2}$, in opposite directions (see Figure 5), and similarly for other sides. Then we obtain a regular decagon with vertices on the grid lines and we have proved that this is impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Infinitely many equidistant parallel lines are drawn in the plane. A positive integer $n \geq 3$ is called frameable if it is possible to draw a regular polygon with $n$ sides all whose vertices lie on these lines and no line contains more than one vertex of the polygon.
(a) Show that $3,4,6$ are frameable.
(b) Show that any integer $n \geq 7$ is not frameable.
(c) Determine whether 5 is frameable.
|
For $n=3,4,6$ it is possible to draw regular polygons with vertices on the parallel lines (note that when we show a regular hexagon is a framed polygon, it includes the equilateral triangle case).

Figure 1:

Figure 2:

Figure 3:
We will prove that it is not possible for $n \geq 7$. In fact, we prove a stronger statement that we can not draw other polygons with vertices on the lines (even if we allow more than one vertex to lie on the same line).
First observe that if $A, B$ are points on the lines and $C$ is another point on a line, if we locate

Figure 4:

Figure 5:
point $D$ such that $C D$ is parallel and equal to $A B$, then $D$ also lies on a line. Suppose that we have a regular polygon $A_{1} A_{2} \ldots A_{n}$, where $n \geq 6$, with all the vertices on the grid lines. Choose a point $O$ on a grid line and draw segments $O B_{i}$ equal and parallel to $A_{i} A_{i+1}$, for $i=1,2, \ldots, n-1$ and $O B_{n}$ parallel and equal to $A_{n} A_{1}$. The points $B_{i}$ also lie on the grid lines and form a regular polygon with $n$ sides. Consider the ratio $k=\frac{B_{1} B_{2}}{A_{1} A_{2}}$. Since $n>6$, the $\angle B_{1} O B_{2}<360^{\circ} / 6$ and hence is the smallest angle in the triangle $B_{1} O B_{2}$ (note that the triangle $B_{1} O B_{2}$ is isosceles). Thus $k<1$. Hence starting with a polygon with vertices on grid lines, we obtain another polygon with ratio of side lengths $k<1$. Repeating this process, we obtain a polygon with vertices on grid lines with ratio of sides $k^{m}$ for any $m$. This is a contradiction since the length of the side of a polygon with vertices on grid lines can not be less than the distance between the parallel lines. Thus for $n>6$, we can not draw a polygon with vertices on the grid lines.
The above proof fails for $n=5$. In this case, draw $O B_{1}, O B_{1}^{\prime}$ parallel and equal to $A_{1} A_{2}$, in opposite directions (see Figure 5), and similarly for other sides. Then we obtain a regular decagon with vertices on the grid lines and we have proved that this is impossible.
|
{
"resource_path": "INMO/segmented/en-sol-inmo-20.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
e8b65ce0-399d-5bd7-84b3-f551288c4e0b
| 607,906
|
A stromino is a $3 \times 1$ rectangle. Show that a $5 \times 5$ board divided into twenty-five $1 \times 1$ squares
cannot be covered by 16 strominos such that each stromino covers exactly three unit squares of the board and every unit square is covered by either one or two strominos. (A stromino can be placed either horizontally or vertically on the board.)
|
Suppose on the contrary that it is possible to cover the board with 16 strominos such that each unit square is covered by either one or two strominos. If there are $k$ squares that are covered by exactly one stromino then $2(25-k)+k=163=48$ and hence $k=2$. Thus there are exactly two squares which are covered by only one stromino. We colour the board with three colours red, blue, green as follows. The square corresponding to the $i$-th row and the $j$-th column is coloured red if $i+j \equiv 0(\bmod 3)$, green if $i+j \equiv 1(\bmod 3)$ and blue otherwise. Then there are 9 red squares, 8 green squares and 8 blue squares. Note that each stromino covers exactly one square of each colour. Therefore the two squares that are covered by only one stromino are both red. For each such square $i+j \equiv 0(\bmod 3)$ where $i$ and $j$ are its row and column number.
We now colour the board with a different scheme. We colour the square corresponding to the $i$-th row and the $j$-th column red if $i-j \equiv(\bmod 3)$, green if $i-j \equiv 1(\bmod 3)$ and blue otherwise. Again, there are 9 red squares and hence the two squares covered by only one stromino are both red. For each such square $i-j \equiv 0(\bmod 3)$ where $i$ and $j$ are its row and columne number Thus, each of the two squares covered by only one stromino satisfies $i+j \equiv 0(\bmod 3)$ and $i-j \equiv 0$ $(\bmod 3)$ where $i$ and $j$ are its row and column number. This implies that $i=j=3$. This is a contradiction because there is only one such square.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A stromino is a $3 \times 1$ rectangle. Show that a $5 \times 5$ board divided into twenty-five $1 \times 1$ squares
cannot be covered by 16 strominos such that each stromino covers exactly three unit squares of the board and every unit square is covered by either one or two strominos. (A stromino can be placed either horizontally or vertically on the board.)
|
Suppose on the contrary that it is possible to cover the board with 16 strominos such that each unit square is covered by either one or two strominos. If there are $k$ squares that are covered by exactly one stromino then $2(25-k)+k=163=48$ and hence $k=2$. Thus there are exactly two squares which are covered by only one stromino. We colour the board with three colours red, blue, green as follows. The square corresponding to the $i$-th row and the $j$-th column is coloured red if $i+j \equiv 0(\bmod 3)$, green if $i+j \equiv 1(\bmod 3)$ and blue otherwise. Then there are 9 red squares, 8 green squares and 8 blue squares. Note that each stromino covers exactly one square of each colour. Therefore the two squares that are covered by only one stromino are both red. For each such square $i+j \equiv 0(\bmod 3)$ where $i$ and $j$ are its row and column number.
We now colour the board with a different scheme. We colour the square corresponding to the $i$-th row and the $j$-th column red if $i-j \equiv(\bmod 3)$, green if $i-j \equiv 1(\bmod 3)$ and blue otherwise. Again, there are 9 red squares and hence the two squares covered by only one stromino are both red. For each such square $i-j \equiv 0(\bmod 3)$ where $i$ and $j$ are its row and columne number Thus, each of the two squares covered by only one stromino satisfies $i+j \equiv 0(\bmod 3)$ and $i-j \equiv 0$ $(\bmod 3)$ where $i$ and $j$ are its row and column number. This implies that $i=j=3$. This is a contradiction because there is only one such square.
|
{
"resource_path": "INMO/segmented/en-sol-inmo-20.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution:"
}
|
7828c166-170b-58b3-a42f-a301b8615cd9
| 607,907
|
Let $\mathbb{N}$ denote the set of all natural numbers. Define a function $T: \mathbb{N} \rightarrow \mathbb{N}$ by $T(2 k)=k$ and $T(2 k+1)=2 k+2$. We write $T^{2}(n)=T(T(n))$ and in general $T^{k}(n)=T^{k-1}(T(n))$ for any $k>1$.
(i) Show that for each $n \in \mathbb{N}$, there exists $k$ such that $T^{k}(n)=1$.
(ii) For $k \in \mathbb{N}$, let $c_{k}$ denote the number of elements in the set $\left\{n: T^{k}(n)=1\right\}$. Prove that $c_{k+2}=c_{k+1}+c_{k}$, for $k \geq 1$.
|
(i) For $n=1$, we have $T(1)=2$ and $T^{2}(1)=T(2)=1$. Hence we may assume that $n>1$.
Suppose $n>1$ is even. Then $T(n)=n / 2$. We observe that $(n / 2) \leq n-1$ for $n>1$.
Suppose $n>1$ is odd so that $n \geq 3$. Then $T(n)=n+1$ and $T^{2}(n)=(n+1) / 2$. Again we see that $(n+1) / 2 \leq(n-1)$ for $n \geq 3$.
Thus we see that in at most $2(n-1)$ steps $T$ sends $n$ to 1 . Hence $k \leq 2(n-1)$. (Here $2(n-1)$ is only a bound. In reality, less number of steps will do.)
(ii) We show that $c_{n}=f_{n+1}$, where $f_{n}$ is the $n$-th Fibonacci number.
Let $n \in \mathbb{N}$ and let $k \in \mathbb{N}$ be such that $T^{k}(n)=1$. Here $n$ can be odd or even. If $n$ is even, it can be either of the form $4 d+2$ or of the form $4 d$.
If $n$ is odd, then $1=T^{k}(n)=T^{k-1}(n+1)$. (Observe that $k>1$; otherwise we get $n+1=1$ which is impossible since $n \in \mathbb{N}$.) Here $n+1$ is even.
If $n=4 d+2$, then again $1=T^{k}(4 d+2)=T^{k-1}(2 d+1)$. Here $2 d+1=n / 2$ is odd.
Thus each solution of $T^{k-1}(m)=1$ produces exactly one solution of $T^{k}(n)=1$ and $n$ is either odd or of the form $4 d+2$.
If $n=4 d$, we see that $1=T^{k}(4 d)=T^{k-1}(2 d)=T^{k-2}(d)$. This shows that each solution of $T^{k-2}(m)=1$ produces exactly one solution of $T^{k}(n)=1$ of the form $4 d$.
Thus the number of solutions of $T^{k}(n)=1$ is equal to the number of solutions of $T^{k-1}(m)=1$ and the number of solutions of $T^{k-2}(l)=1$ for $k>2$. This shows that $c_{k}=c_{k-1}+c_{k-2}$ for $k>2$. We also observe that 2 is the only number which goes to 1 in one step and 4 is the only number which goes to 1 in two steps. Hence $c_{1}=1$ and $c_{2}=2$. This proves that $c_{n}=f_{n+1}$ for all $n \in \mathbb{N}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\mathbb{N}$ denote the set of all natural numbers. Define a function $T: \mathbb{N} \rightarrow \mathbb{N}$ by $T(2 k)=k$ and $T(2 k+1)=2 k+2$. We write $T^{2}(n)=T(T(n))$ and in general $T^{k}(n)=T^{k-1}(T(n))$ for any $k>1$.
(i) Show that for each $n \in \mathbb{N}$, there exists $k$ such that $T^{k}(n)=1$.
(ii) For $k \in \mathbb{N}$, let $c_{k}$ denote the number of elements in the set $\left\{n: T^{k}(n)=1\right\}$. Prove that $c_{k+2}=c_{k+1}+c_{k}$, for $k \geq 1$.
|
(i) For $n=1$, we have $T(1)=2$ and $T^{2}(1)=T(2)=1$. Hence we may assume that $n>1$.
Suppose $n>1$ is even. Then $T(n)=n / 2$. We observe that $(n / 2) \leq n-1$ for $n>1$.
Suppose $n>1$ is odd so that $n \geq 3$. Then $T(n)=n+1$ and $T^{2}(n)=(n+1) / 2$. Again we see that $(n+1) / 2 \leq(n-1)$ for $n \geq 3$.
Thus we see that in at most $2(n-1)$ steps $T$ sends $n$ to 1 . Hence $k \leq 2(n-1)$. (Here $2(n-1)$ is only a bound. In reality, less number of steps will do.)
(ii) We show that $c_{n}=f_{n+1}$, where $f_{n}$ is the $n$-th Fibonacci number.
Let $n \in \mathbb{N}$ and let $k \in \mathbb{N}$ be such that $T^{k}(n)=1$. Here $n$ can be odd or even. If $n$ is even, it can be either of the form $4 d+2$ or of the form $4 d$.
If $n$ is odd, then $1=T^{k}(n)=T^{k-1}(n+1)$. (Observe that $k>1$; otherwise we get $n+1=1$ which is impossible since $n \in \mathbb{N}$.) Here $n+1$ is even.
If $n=4 d+2$, then again $1=T^{k}(4 d+2)=T^{k-1}(2 d+1)$. Here $2 d+1=n / 2$ is odd.
Thus each solution of $T^{k-1}(m)=1$ produces exactly one solution of $T^{k}(n)=1$ and $n$ is either odd or of the form $4 d+2$.
If $n=4 d$, we see that $1=T^{k}(4 d)=T^{k-1}(2 d)=T^{k-2}(d)$. This shows that each solution of $T^{k-2}(m)=1$ produces exactly one solution of $T^{k}(n)=1$ of the form $4 d$.
Thus the number of solutions of $T^{k}(n)=1$ is equal to the number of solutions of $T^{k-1}(m)=1$ and the number of solutions of $T^{k-2}(l)=1$ for $k>2$. This shows that $c_{k}=c_{k-1}+c_{k-2}$ for $k>2$. We also observe that 2 is the only number which goes to 1 in one step and 4 is the only number which goes to 1 in two steps. Hence $c_{1}=1$ and $c_{2}=2$. This proves that $c_{n}=f_{n+1}$ for all $n \in \mathbb{N}$.
|
{
"resource_path": "INMO/segmented/en-sol-inmo16.jsonl",
"problem_match": "\n3.",
"solution_match": "## Solution:"
}
|
fd96853e-9e02-57ae-a525-6f700b573e6a
| 607,910
|
Suppose 2016 points of the circumference of a circle are coloured red and the remaining points are coloured blue. Given any natural number $n \geq 3$, prove that there is a regular $n$-sided polygon all of whose vertices are blue.
|
Let $A_{1}, A_{2}, \ldots, A_{2016}$ be 2016 points on the circle which are coloured red and the remain-
ing blue. Let $n \geq 3$ and let $B_{1}, B_{2}, \ldots, B_{n}$ be a regular $n$-sided polygon inscribed in this circle with the vertices chosen in anti-clock-wise direction. We place $B_{1}$ at $A_{1}$. (It is possible, in this position, some other $B$ 's also coincide with some other $A$ 's.) Rotate the polygon in anti-clock-wise direction gradually till some $B$ 's coincide with (an equal number of) $A$ 's second time. We again rotate the polygon in the same direction till some $B$ 's coincide with an equal number of $A$ 's third time, and so on until we return to the original position, i.e., $B_{1}$ at $A_{1}$. We see that the number of rotations will not be more than $2016 \times n$, that is, at most these many times some $B$ 's would have coincided with an equal number of $A$ 's. Since the interval $\left(0,360^{\circ}\right)$ has infinitely many points, we can find a value $\alpha^{\circ} \in\left(0,360^{\circ}\right)$ through which the polygon can be rotated from its initial position such that no $B$ coincides with any $A$. This gives a $n$-sided regular polygon having only blue vertices.
Alternate Solution: Consider a regular $2017 \times n$-gon on the circle; say, $A_{1} A_{2} A_{3} \cdots A_{2017 n}$. For each $j, 1 \leq j \leq 2017$, consider the points $\left\{A_{k}: k \equiv j(\bmod 2017)\right\}$. These are the vertices of a regular $n$-gon, say $S_{j}$. We get 2017 regular $n$-gons; $S_{1}, S_{2}, \ldots, S_{2017}$. Since there are only 2016 red points, by pigeon-hole principle there must be some $n$-gon among these 2017 which does not contain any red point. But then it is a blue $n$-gon.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Suppose 2016 points of the circumference of a circle are coloured red and the remaining points are coloured blue. Given any natural number $n \geq 3$, prove that there is a regular $n$-sided polygon all of whose vertices are blue.
|
Let $A_{1}, A_{2}, \ldots, A_{2016}$ be 2016 points on the circle which are coloured red and the remain-
ing blue. Let $n \geq 3$ and let $B_{1}, B_{2}, \ldots, B_{n}$ be a regular $n$-sided polygon inscribed in this circle with the vertices chosen in anti-clock-wise direction. We place $B_{1}$ at $A_{1}$. (It is possible, in this position, some other $B$ 's also coincide with some other $A$ 's.) Rotate the polygon in anti-clock-wise direction gradually till some $B$ 's coincide with (an equal number of) $A$ 's second time. We again rotate the polygon in the same direction till some $B$ 's coincide with an equal number of $A$ 's third time, and so on until we return to the original position, i.e., $B_{1}$ at $A_{1}$. We see that the number of rotations will not be more than $2016 \times n$, that is, at most these many times some $B$ 's would have coincided with an equal number of $A$ 's. Since the interval $\left(0,360^{\circ}\right)$ has infinitely many points, we can find a value $\alpha^{\circ} \in\left(0,360^{\circ}\right)$ through which the polygon can be rotated from its initial position such that no $B$ coincides with any $A$. This gives a $n$-sided regular polygon having only blue vertices.
Alternate Solution: Consider a regular $2017 \times n$-gon on the circle; say, $A_{1} A_{2} A_{3} \cdots A_{2017 n}$. For each $j, 1 \leq j \leq 2017$, consider the points $\left\{A_{k}: k \equiv j(\bmod 2017)\right\}$. These are the vertices of a regular $n$-gon, say $S_{j}$. We get 2017 regular $n$-gons; $S_{1}, S_{2}, \ldots, S_{2017}$. Since there are only 2016 red points, by pigeon-hole principle there must be some $n$-gon among these 2017 which does not contain any red point. But then it is a blue $n$-gon.
|
{
"resource_path": "INMO/segmented/en-sol-inmo16.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
bd5726ea-a00a-551c-998e-d67562241cc3
| 607,911
|
Consider a non-constant arithmetic progression $a_{1}, a_{2}, \ldots, a_{n}, \ldots$ Suppose there exist relatively prime positive integers $p>1$ and $q>1$ such that $a_{1}^{2}, a_{p+1}^{2}$ and $a_{q+1}^{2}$ are also the terms of the same arithmetic progression. Prove that the terms of the arithmetic progression are all integers.
|
Let us take $a_{1}=a$. We have
$$
a^{2}=a+k d, \quad(a+p d)^{2}=a+l d, \quad(a+q d)^{2}=a+m d
$$
Thus we have
$$
a+l d=(a+p d)^{2}=a^{2}+2 p a d+p^{2} d^{2}=a+k d+2 p a d+p^{2} d^{2}
$$
Since we have non-constant AP, we see that $d \neq 0$. Hence we obtain $2 p a+p^{2} d=l-k$. Similarly, we get $2 q a+q^{2} d=m-k$. Observe that $p^{2} q-p q^{2} \neq 0$. Otherwise $p=q$ and $\operatorname{gcd}(p, q)=p>1$ which is a contradiction to the given hypothesis that $\operatorname{gcd}(p, q)=1$. Hence we can solve the two equations for $a, d$ :
$$
a=\frac{p^{2}(m-k)-q^{2}(l-k)}{2\left(p^{2} q-p q^{2}\right)}, \quad d=\frac{q(l-k)-p(m-k)}{p^{2} q-p q^{2}}
$$
It follows that $a, d$ are rational numbers. We also have
$$
p^{2} a^{2}=p^{2} a+k p^{2} d
$$
But $p^{2} d=l-k-2 p a$. Thus we get
$$
p^{2} a^{2}=p^{2} a+k(l-k-2 p a)=(p-2 k) p a+k(l-k)
$$
This shows that pa satisfies the equation
$$
x^{2}-(p-2 k) x-k(l-k)=0
$$
Since $a$ is rational, we see that $p a$ is rational. Write $p a=w / z$, where $w$ is an integer and $z$ is a natural numbers such that $\operatorname{gcd}(w, z)=1$. Substituting in the equation, we obtain
$$
w^{2}-(p-2 k) w z-k(l-k) z^{2}=0
$$
This shows $z$ divides $w$. Since $\operatorname{gcd}(w, z)=1$, it follows that $z=1$ and $p a=w$ an integer. (In fact any rational solution of a monic polynomial with integer coefficients is necessarily an integer.) Similarly, we can prove that $q a$ is an integer. Since $\operatorname{gcd}(p, q)=1$, there are integers $u$ and $v$ such that $p u+q v=1$. Therefore $a=(p a) u+(q a) v$. It follows that $a$ is an integer.
But $p^{2} d=l-k-2 p a$. Hence $p^{2} d$ is an integer. Similarly, $q^{2} d$ is also an integer. Since $\operatorname{gcd}\left(p^{2}, q^{2}\right)=1$, it follows that $d$ is an integer. Combining these two, we see that all the terms of the AP are integers.
Alternatively, we can prove that $a$ and $d$ are integers in another way. We have seen that $a$ and $d$ are rationals; and we have three relations:
$$
a^{2}=a+k d, \quad p^{2} d+2 p a=n_{1}, \quad q^{2} d+2 q a=n_{2}
$$
where $n_{1}=l-k$ and $n_{2}=m-k$. Let $a=u / v$ and $d=x / y$ where $u, x$ are integers and $v, y$ are natural numbers, and $\operatorname{gcd}(u, v)=1, \operatorname{gcd}(x, y)=1$. Putting this in these relations, we obtain
$$
\begin{aligned}
u^{2} y & =u v y+k x v^{2} \\
2 p u y+p^{2} v x & =v y n_{1} \\
2 q u y+q^{2} v x & =v y n_{2}
\end{aligned}
$$
Now (1) shows that $v \mid u^{2} y$. Since $\operatorname{gcd}(u, v)=1$, it follows that $v \mid y$. Similarly (2) shows that $y \mid p^{2} v x$. Using $\operatorname{gcd}(y, x)=1$, we get that $y \mid p^{2} v$. Similarly, (3) shows that $y \mid q^{2} v$. Therefore $y$ divides $\operatorname{gcd}\left(p^{2} v, q^{2} v\right)=v$. The two results $v \mid y$ and $y \mid v$ imply $v=y$, since both $v, y$ are positive.
Substitute this in (1) to get
$$
u^{2}=u v+k x v
$$
This shows that $v \mid u^{2}$. Since $\operatorname{gcd}(u, v)=1$, it follows that $v=1$. This gives $v=y=1$. Finally $a=u$ and $d=x$ which are integers.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Consider a non-constant arithmetic progression $a_{1}, a_{2}, \ldots, a_{n}, \ldots$ Suppose there exist relatively prime positive integers $p>1$ and $q>1$ such that $a_{1}^{2}, a_{p+1}^{2}$ and $a_{q+1}^{2}$ are also the terms of the same arithmetic progression. Prove that the terms of the arithmetic progression are all integers.
|
Let us take $a_{1}=a$. We have
$$
a^{2}=a+k d, \quad(a+p d)^{2}=a+l d, \quad(a+q d)^{2}=a+m d
$$
Thus we have
$$
a+l d=(a+p d)^{2}=a^{2}+2 p a d+p^{2} d^{2}=a+k d+2 p a d+p^{2} d^{2}
$$
Since we have non-constant AP, we see that $d \neq 0$. Hence we obtain $2 p a+p^{2} d=l-k$. Similarly, we get $2 q a+q^{2} d=m-k$. Observe that $p^{2} q-p q^{2} \neq 0$. Otherwise $p=q$ and $\operatorname{gcd}(p, q)=p>1$ which is a contradiction to the given hypothesis that $\operatorname{gcd}(p, q)=1$. Hence we can solve the two equations for $a, d$ :
$$
a=\frac{p^{2}(m-k)-q^{2}(l-k)}{2\left(p^{2} q-p q^{2}\right)}, \quad d=\frac{q(l-k)-p(m-k)}{p^{2} q-p q^{2}}
$$
It follows that $a, d$ are rational numbers. We also have
$$
p^{2} a^{2}=p^{2} a+k p^{2} d
$$
But $p^{2} d=l-k-2 p a$. Thus we get
$$
p^{2} a^{2}=p^{2} a+k(l-k-2 p a)=(p-2 k) p a+k(l-k)
$$
This shows that pa satisfies the equation
$$
x^{2}-(p-2 k) x-k(l-k)=0
$$
Since $a$ is rational, we see that $p a$ is rational. Write $p a=w / z$, where $w$ is an integer and $z$ is a natural numbers such that $\operatorname{gcd}(w, z)=1$. Substituting in the equation, we obtain
$$
w^{2}-(p-2 k) w z-k(l-k) z^{2}=0
$$
This shows $z$ divides $w$. Since $\operatorname{gcd}(w, z)=1$, it follows that $z=1$ and $p a=w$ an integer. (In fact any rational solution of a monic polynomial with integer coefficients is necessarily an integer.) Similarly, we can prove that $q a$ is an integer. Since $\operatorname{gcd}(p, q)=1$, there are integers $u$ and $v$ such that $p u+q v=1$. Therefore $a=(p a) u+(q a) v$. It follows that $a$ is an integer.
But $p^{2} d=l-k-2 p a$. Hence $p^{2} d$ is an integer. Similarly, $q^{2} d$ is also an integer. Since $\operatorname{gcd}\left(p^{2}, q^{2}\right)=1$, it follows that $d$ is an integer. Combining these two, we see that all the terms of the AP are integers.
Alternatively, we can prove that $a$ and $d$ are integers in another way. We have seen that $a$ and $d$ are rationals; and we have three relations:
$$
a^{2}=a+k d, \quad p^{2} d+2 p a=n_{1}, \quad q^{2} d+2 q a=n_{2}
$$
where $n_{1}=l-k$ and $n_{2}=m-k$. Let $a=u / v$ and $d=x / y$ where $u, x$ are integers and $v, y$ are natural numbers, and $\operatorname{gcd}(u, v)=1, \operatorname{gcd}(x, y)=1$. Putting this in these relations, we obtain
$$
\begin{aligned}
u^{2} y & =u v y+k x v^{2} \\
2 p u y+p^{2} v x & =v y n_{1} \\
2 q u y+q^{2} v x & =v y n_{2}
\end{aligned}
$$
Now (1) shows that $v \mid u^{2} y$. Since $\operatorname{gcd}(u, v)=1$, it follows that $v \mid y$. Similarly (2) shows that $y \mid p^{2} v x$. Using $\operatorname{gcd}(y, x)=1$, we get that $y \mid p^{2} v$. Similarly, (3) shows that $y \mid q^{2} v$. Therefore $y$ divides $\operatorname{gcd}\left(p^{2} v, q^{2} v\right)=v$. The two results $v \mid y$ and $y \mid v$ imply $v=y$, since both $v, y$ are positive.
Substitute this in (1) to get
$$
u^{2}=u v+k x v
$$
This shows that $v \mid u^{2}$. Since $\operatorname{gcd}(u, v)=1$, it follows that $v=1$. This gives $v=y=1$. Finally $a=u$ and $d=x$ which are integers.
|
{
"resource_path": "INMO/segmented/en-sol-inmo16.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution:"
}
|
d40aeb1c-9bf8-5d03-ace6-0d9ab57a49ac
| 607,913
|
Let $A B C$ be a triangle with $\angle A=90^{\circ}$ and $A B<A C$. Let $A D$ be the altitude from $A$ on to $B C$. Let $P, Q$ and $I$ denote respectively the incentres of triangles $A B D, A C D$ and $A B C$. Prove that $A I$ is perpendicular to $P Q$ and $A I=P Q$.
|
Draw $P S \| B C$ and $Q S \| A D$. Then $P S Q$ is a right-angled triangle with $\angle P S Q=90^{\circ}$. Observe that $P S=r_{1}+r_{2}$ and $S Q=r_{2}-r_{1}$, where $r_{1}$ and $r_{2}$ are the inradii of triangles $A B D$ and $A C D$, respectively. We observe that triangles $D A B$ and $D C A$ are similar to triangle $A C B$.
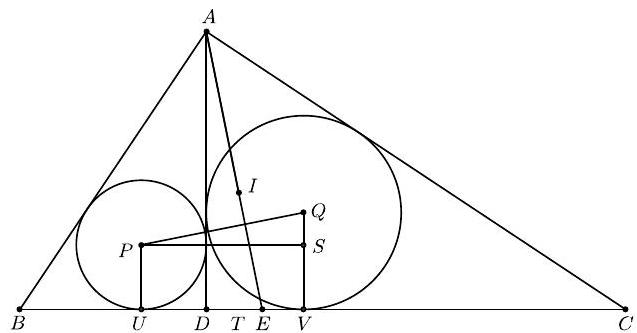
Hence
$$
r_{1}=\frac{c}{a} r, \quad r_{2}=\frac{b}{a} r
$$
where $r$ is the inradius of triangle $A B C$. Thus we get
$$
\frac{P S}{S Q}=\frac{r_{2}+r_{1}}{r_{2}-r_{1}}=\frac{b+c}{b-c}
$$
On the otherhand $A D=h=b c / a$. We also have $B E=c a /(b+c)$ and
$$
B D^{2}=c^{2}-h^{2}=c^{2}-\frac{b^{2} c^{2}}{a^{2}}=\frac{c^{4}}{a^{2}}
$$
Hence $B D=c^{2} / a$. Therefore
$$
D E=B E-B D=\frac{c a}{b+c}-\frac{c^{2}}{a}=\frac{c b(b-c)}{a(b+c)}
$$
Thus we get
$$
\frac{A D}{D E}=\frac{b+c}{b-c}=\frac{P S}{S Q}
$$
Since $\angle A D E=90^{\circ}=\angle P S Q$, we conclude that $\triangle A D E \sim \triangle P S Q$. Since $A D \perp P S$, it follows that $A E \perp P Q$.
We also observe that
$$
P Q^{2}=P S^{2}+S Q^{2}=\left(r_{2}+r_{1}\right)^{2}+\left(r_{2}-r_{1}\right)^{2}=2\left(r_{1}^{2}+r_{2}^{2}\right)
$$
However
$$
r_{1}^{2}+r_{2}^{2}=\frac{c^{2}+b^{2}}{a^{2}} r^{2}=r^{2}
$$
Hence $P Q=\sqrt{2} r$. We also observe that $A I=r \operatorname{cosec}(A / 2)=r \operatorname{cosec}\left(45^{\circ}\right)=\sqrt{2} r$. Thus $P Q=A I$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle A=90^{\circ}$ and $A B<A C$. Let $A D$ be the altitude from $A$ on to $B C$. Let $P, Q$ and $I$ denote respectively the incentres of triangles $A B D, A C D$ and $A B C$. Prove that $A I$ is perpendicular to $P Q$ and $A I=P Q$.
|
Draw $P S \| B C$ and $Q S \| A D$. Then $P S Q$ is a right-angled triangle with $\angle P S Q=90^{\circ}$. Observe that $P S=r_{1}+r_{2}$ and $S Q=r_{2}-r_{1}$, where $r_{1}$ and $r_{2}$ are the inradii of triangles $A B D$ and $A C D$, respectively. We observe that triangles $D A B$ and $D C A$ are similar to triangle $A C B$.

Hence
$$
r_{1}=\frac{c}{a} r, \quad r_{2}=\frac{b}{a} r
$$
where $r$ is the inradius of triangle $A B C$. Thus we get
$$
\frac{P S}{S Q}=\frac{r_{2}+r_{1}}{r_{2}-r_{1}}=\frac{b+c}{b-c}
$$
On the otherhand $A D=h=b c / a$. We also have $B E=c a /(b+c)$ and
$$
B D^{2}=c^{2}-h^{2}=c^{2}-\frac{b^{2} c^{2}}{a^{2}}=\frac{c^{4}}{a^{2}}
$$
Hence $B D=c^{2} / a$. Therefore
$$
D E=B E-B D=\frac{c a}{b+c}-\frac{c^{2}}{a}=\frac{c b(b-c)}{a(b+c)}
$$
Thus we get
$$
\frac{A D}{D E}=\frac{b+c}{b-c}=\frac{P S}{S Q}
$$
Since $\angle A D E=90^{\circ}=\angle P S Q$, we conclude that $\triangle A D E \sim \triangle P S Q$. Since $A D \perp P S$, it follows that $A E \perp P Q$.
We also observe that
$$
P Q^{2}=P S^{2}+S Q^{2}=\left(r_{2}+r_{1}\right)^{2}+\left(r_{2}-r_{1}\right)^{2}=2\left(r_{1}^{2}+r_{2}^{2}\right)
$$
However
$$
r_{1}^{2}+r_{2}^{2}=\frac{c^{2}+b^{2}}{a^{2}} r^{2}=r^{2}
$$
Hence $P Q=\sqrt{2} r$. We also observe that $A I=r \operatorname{cosec}(A / 2)=r \operatorname{cosec}\left(45^{\circ}\right)=\sqrt{2} r$. Thus $P Q=A I$.
|
{
"resource_path": "INMO/segmented/en-sol-inmo_17.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
707e4586-8d22-5acf-b477-0a714b6c8bd3
| 607,918
|
Let $A B C$ be a triangle with $\angle A=90^{\circ}$ and $A B<A C$. Let $A D$ be the altitude from $A$ on to $B C$. Let $P, Q$ and $I$ denote respectively the incentres of triangles $A B D, A C D$ and $A B C$. Prove that $A I$ is perpendicular to $P Q$ and $A I=P Q$.
|
In the figure, we have made the construction as mentioned in the hint. Since $P, Q$ are the incentres of $\triangle A B D, \triangle A C D, D P, D Q$ are the internal angle bisectors of $\angle A D B, \angle A D C$ respectively. Since $A D$ is the altitude on the hypotenuse $B C$ in $\triangle A B C$, we have that $\angle P D Q=45^{\circ}+45^{\circ}=90^{\circ}$. It also implies that
$$
\triangle A B C \sim \triangle D B A \sim \triangle D A C
$$
This implies that all corresponding length in the above mentioned triangles have the same ratio.
In particular,
$$
\begin{aligned}
& \frac{A I}{B C}=\frac{D P}{A B}=\frac{D Q}{A C} \\
\Longrightarrow \quad & \frac{A I^{2}}{B C^{2}}=\frac{D P^{2}}{A B^{2}}=\frac{D Q^{2}}{A C^{2}}=\frac{D P^{2}+D Q^{2}}{A B^{2}+A C^{2}} \\
\Longrightarrow \quad & \frac{A I^{2}}{B C^{2}}=\frac{P Q^{2}}{B C^{2}}, \quad \text { by Pythagoras Theorem in } \triangle A B C, \triangle P D Q \\
\Longrightarrow \quad & A I=P Q
\end{aligned}
$$
as required.
For the second, part, we note that from the above relations, we have $\triangle A B C \sim \triangle D P Q$. Let us take $\angle A C B=\theta$. Then, we get
$$
\begin{aligned}
\angle P S D & =180^{\circ}-(\angle S P D+\angle S D P) \\
& =180^{\circ}-\left(90^{\circ}-\theta+45^{\circ}\right) \\
& =45^{\circ}+\theta
\end{aligned}
$$
This gives us that
$$
\begin{aligned}
\angle A R S & =180^{\circ}-(\angle A S R+\angle S A R) \\
& =180^{\circ}-(\angle P S D+\angle S A C-\angle I A C) \\
& =180^{\circ}-\left(45^{\circ}+\theta+90^{\circ}-\theta-45^{\circ}\right) \\
& =90^{\circ}
\end{aligned}
$$
as required. Hence, we get that $A I=P Q$ and $A I \perp P Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle A=90^{\circ}$ and $A B<A C$. Let $A D$ be the altitude from $A$ on to $B C$. Let $P, Q$ and $I$ denote respectively the incentres of triangles $A B D, A C D$ and $A B C$. Prove that $A I$ is perpendicular to $P Q$ and $A I=P Q$.
|
In the figure, we have made the construction as mentioned in the hint. Since $P, Q$ are the incentres of $\triangle A B D, \triangle A C D, D P, D Q$ are the internal angle bisectors of $\angle A D B, \angle A D C$ respectively. Since $A D$ is the altitude on the hypotenuse $B C$ in $\triangle A B C$, we have that $\angle P D Q=45^{\circ}+45^{\circ}=90^{\circ}$. It also implies that
$$
\triangle A B C \sim \triangle D B A \sim \triangle D A C
$$
This implies that all corresponding length in the above mentioned triangles have the same ratio.

In particular,
$$
\begin{aligned}
& \frac{A I}{B C}=\frac{D P}{A B}=\frac{D Q}{A C} \\
\Longrightarrow \quad & \frac{A I^{2}}{B C^{2}}=\frac{D P^{2}}{A B^{2}}=\frac{D Q^{2}}{A C^{2}}=\frac{D P^{2}+D Q^{2}}{A B^{2}+A C^{2}} \\
\Longrightarrow \quad & \frac{A I^{2}}{B C^{2}}=\frac{P Q^{2}}{B C^{2}}, \quad \text { by Pythagoras Theorem in } \triangle A B C, \triangle P D Q \\
\Longrightarrow \quad & A I=P Q
\end{aligned}
$$
as required.
For the second, part, we note that from the above relations, we have $\triangle A B C \sim \triangle D P Q$. Let us take $\angle A C B=\theta$. Then, we get
$$
\begin{aligned}
\angle P S D & =180^{\circ}-(\angle S P D+\angle S D P) \\
& =180^{\circ}-\left(90^{\circ}-\theta+45^{\circ}\right) \\
& =45^{\circ}+\theta
\end{aligned}
$$
This gives us that
$$
\begin{aligned}
\angle A R S & =180^{\circ}-(\angle A S R+\angle S A R) \\
& =180^{\circ}-(\angle P S D+\angle S A C-\angle I A C) \\
& =180^{\circ}-\left(45^{\circ}+\theta+90^{\circ}-\theta-45^{\circ}\right) \\
& =90^{\circ}
\end{aligned}
$$
as required. Hence, we get that $A I=P Q$ and $A I \perp P Q$.
|
{
"resource_path": "INMO/segmented/en-sol-inmo_17.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution 2:"
}
|
707e4586-8d22-5acf-b477-0a714b6c8bd3
| 607,918
|
Let $A B C$ be a triangle with $\angle A=90^{\circ}$ and $A B<A C$. Let $A D$ be the altitude from $A$ on to $B C$. Let $P, Q$ and $I$ denote respectively the incentres of triangles $A B D, A C D$ and $A B C$. Prove that $A I$ is perpendicular to $P Q$ and $A I=P Q$.
|
We know that the angle bisector of $\angle B$ passes through $P, I$ which implies that $B, P, I$ are collinear. Similarly, $C, Q, I$ are also collinear. Since $I$ is the incentre of $\triangle A B C$, we know that
$$
\angle P I Q=\angle B I C=90^{\circ}+\frac{\angle A}{2}=135^{\circ}
$$
Join $A P, A Q$. We know that $\angle B A P=\frac{1}{2} \angle B A D=\frac{1}{2} \angle C$. Also, $\angle A B P=\frac{1}{2} \angle B$. Hence by Exterior Angle Theorem in $\triangle A B P$, we get that
$$
\angle A P I=\angle A B P+\angle B A P=\frac{1}{2}(\angle B+\angle C)=45^{\circ}
$$
Similarly in $\triangle A D C$, we get that $\angle A Q I=45^{\circ}$. Also, we have
$$
\angle P A I=\angle B A I-\angle B A P=45^{\circ}-\frac{\angle C}{2}=\frac{\angle B}{2}
$$
Similarly, we get $\angle Q A I=\frac{\angle C}{2}$.
Now applying Sine Rule in $\triangle A P I$, we get
$$
\frac{I P}{\sin \angle P A I}=\frac{A I}{\sin \angle A P I} \Longrightarrow I P=\sqrt{2} A I \sin \frac{B}{2}
$$
Similarly, applying Sine Rule in $\triangle A Q I$, we get
$$
\frac{I Q}{\sin \angle P A I}=\frac{A I}{\sin \angle A Q I} \Longrightarrow I Q=\sqrt{2} A I \sin \frac{C}{2}
$$
Applying Cosine Rule in $\triangle P I Q$ gives us that
$$
\begin{aligned}
P Q^{2} & =I P^{2}+I Q^{2}-2 \cdot I P \cdot I Q \cos \angle P I Q \\
& =2 A I^{2}\left(\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}+\sqrt{2} \sin \frac{B}{2} \sin \frac{C}{2}\right)
\end{aligned}
$$
We will prove that $\left(\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}+\sqrt{2} \sin \frac{B}{2} \sin \frac{C}{2}\right)=\frac{1}{2}$. In any $\triangle X Y Z$, we have that
$$
\sum_{c y c} \sin ^{2} \frac{X}{2}=1-2 \prod \sin \frac{X}{2}
$$
Using this in $\triangle A B C$, and using the fact that $\angle A=90^{\circ}$, we get
$$
\begin{aligned}
& \sin ^{2} \frac{A}{2}+\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}=1-2 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} \\
\Longrightarrow \quad & \frac{1}{2}+\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}=1-\sqrt{2} \sin \frac{B}{2} \sin \frac{C}{2} \\
\Longrightarrow \quad & \left(\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}+\sqrt{2} \sin \frac{B}{2} \sin \frac{C}{2}\right)=\frac{1}{2}
\end{aligned}
$$
which was to be proved. Hence we get $P Q=A I$.
The second part of the problem can be obtained by angle-chasing as outlined in Solution 2 .
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle A=90^{\circ}$ and $A B<A C$. Let $A D$ be the altitude from $A$ on to $B C$. Let $P, Q$ and $I$ denote respectively the incentres of triangles $A B D, A C D$ and $A B C$. Prove that $A I$ is perpendicular to $P Q$ and $A I=P Q$.
|
We know that the angle bisector of $\angle B$ passes through $P, I$ which implies that $B, P, I$ are collinear. Similarly, $C, Q, I$ are also collinear. Since $I$ is the incentre of $\triangle A B C$, we know that
$$
\angle P I Q=\angle B I C=90^{\circ}+\frac{\angle A}{2}=135^{\circ}
$$
Join $A P, A Q$. We know that $\angle B A P=\frac{1}{2} \angle B A D=\frac{1}{2} \angle C$. Also, $\angle A B P=\frac{1}{2} \angle B$. Hence by Exterior Angle Theorem in $\triangle A B P$, we get that
$$
\angle A P I=\angle A B P+\angle B A P=\frac{1}{2}(\angle B+\angle C)=45^{\circ}
$$
Similarly in $\triangle A D C$, we get that $\angle A Q I=45^{\circ}$. Also, we have
$$
\angle P A I=\angle B A I-\angle B A P=45^{\circ}-\frac{\angle C}{2}=\frac{\angle B}{2}
$$
Similarly, we get $\angle Q A I=\frac{\angle C}{2}$.
Now applying Sine Rule in $\triangle A P I$, we get
$$
\frac{I P}{\sin \angle P A I}=\frac{A I}{\sin \angle A P I} \Longrightarrow I P=\sqrt{2} A I \sin \frac{B}{2}
$$
Similarly, applying Sine Rule in $\triangle A Q I$, we get
$$
\frac{I Q}{\sin \angle P A I}=\frac{A I}{\sin \angle A Q I} \Longrightarrow I Q=\sqrt{2} A I \sin \frac{C}{2}
$$
Applying Cosine Rule in $\triangle P I Q$ gives us that
$$
\begin{aligned}
P Q^{2} & =I P^{2}+I Q^{2}-2 \cdot I P \cdot I Q \cos \angle P I Q \\
& =2 A I^{2}\left(\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}+\sqrt{2} \sin \frac{B}{2} \sin \frac{C}{2}\right)
\end{aligned}
$$
We will prove that $\left(\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}+\sqrt{2} \sin \frac{B}{2} \sin \frac{C}{2}\right)=\frac{1}{2}$. In any $\triangle X Y Z$, we have that
$$
\sum_{c y c} \sin ^{2} \frac{X}{2}=1-2 \prod \sin \frac{X}{2}
$$
Using this in $\triangle A B C$, and using the fact that $\angle A=90^{\circ}$, we get
$$
\begin{aligned}
& \sin ^{2} \frac{A}{2}+\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}=1-2 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} \\
\Longrightarrow \quad & \frac{1}{2}+\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}=1-\sqrt{2} \sin \frac{B}{2} \sin \frac{C}{2} \\
\Longrightarrow \quad & \left(\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}+\sqrt{2} \sin \frac{B}{2} \sin \frac{C}{2}\right)=\frac{1}{2}
\end{aligned}
$$
which was to be proved. Hence we get $P Q=A I$.
The second part of the problem can be obtained by angle-chasing as outlined in Solution 2 .
|
{
"resource_path": "INMO/segmented/en-sol-inmo_17.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution 3:"
}
|
707e4586-8d22-5acf-b477-0a714b6c8bd3
| 607,918
|
Let $A B C$ be a triangle with $\angle A=90^{\circ}$ and $A B<A C$. Let $A D$ be the altitude from $A$ on to $B C$. Let $P, Q$ and $I$ denote respectively the incentres of triangles $A B D, A C D$ and $A B C$. Prove that $A I$ is perpendicular to $P Q$ and $A I=P Q$.
|
Observe that $\angle A P B=\angle A Q C=135^{\circ}$. Thus $\angle A P I=\angle A Q I=45^{\circ}$ (since $B-P-I$ and $C-Q-I)$. Note $\angle P A Q=1 / 2 \angle A=45^{\circ}$. Let $X=B I \cap A Q$ and $Y=C I \cap A P$. Therefore $\angle A X P=180-\angle A P I-\angle P A Q=90^{\circ}$. Similarly $\angle A Y Q=90^{\circ}$. Hence $I$ is the orthocentre of triangle $P A Q$. Therefore $A I$ is perpendicular to $P Q$. Also $A I=2 R_{P A Q} \cos 45^{\circ}=2 R_{P A Q} \sin 45^{\circ}=P Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle A=90^{\circ}$ and $A B<A C$. Let $A D$ be the altitude from $A$ on to $B C$. Let $P, Q$ and $I$ denote respectively the incentres of triangles $A B D, A C D$ and $A B C$. Prove that $A I$ is perpendicular to $P Q$ and $A I=P Q$.
|
Observe that $\angle A P B=\angle A Q C=135^{\circ}$. Thus $\angle A P I=\angle A Q I=45^{\circ}$ (since $B-P-I$ and $C-Q-I)$. Note $\angle P A Q=1 / 2 \angle A=45^{\circ}$. Let $X=B I \cap A Q$ and $Y=C I \cap A P$. Therefore $\angle A X P=180-\angle A P I-\angle P A Q=90^{\circ}$. Similarly $\angle A Y Q=90^{\circ}$. Hence $I$ is the orthocentre of triangle $P A Q$. Therefore $A I$ is perpendicular to $P Q$. Also $A I=2 R_{P A Q} \cos 45^{\circ}=2 R_{P A Q} \sin 45^{\circ}=P Q$.
|
{
"resource_path": "INMO/segmented/en-sol-inmo_17.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution 4:"
}
|
707e4586-8d22-5acf-b477-0a714b6c8bd3
| 607,918
|
Let $n \geq 1$ be an integer and consider the sum
$$
x=\sum_{k \geq 0}\binom{n}{2 k} 2^{n-2 k} 3^{k}=\binom{n}{0} 2^{n}+\binom{n}{2} 2^{n-2} \cdot 3+\binom{n}{4} 2^{n-4} \cdot 3^{2}+\cdots
$$
Show that $2 x-1,2 x, 2 x+1$ form the sides of a triangle whose area and inradius are also integers.
|
Consider the binomial expansion of $(2+\sqrt{3})^{n}$. It is easy to check that
$$
(2+\sqrt{3})^{n}=x+y \sqrt{3}
$$
where $y$ is also an integer. We also have
$$
(2-\sqrt{3})^{n}=x-y \sqrt{3}
$$
Multiplying these two relations, we obtain $x^{2}-3 y^{2}=1$.
Since all the terms of the expansion of $(2+\sqrt{3})^{n}$ are positive, we see that
$$
2 x=(2+\sqrt{3})^{n}+(2-\sqrt{3})^{n}=2\left(2^{n}+\binom{n}{2} 2^{n-2} \cdot 3+\cdots\right) \geq 4
$$
Thus $x \geq 2$. Hence $2 x+1<2 x+(2 x-1)$ and therefore $2 x-1,2 x, 2 x+1$ are the sides of a triangle. By Heron's formula we have
$$
\Delta^{2}=3 x(x+1)(x)(x-1)=3 x^{2}\left(x^{2}-1\right)=9 x^{2} y^{2}
$$
Hence $\Delta=3 x y$ which is an integer. Finally, its inradius is
$$
\frac{\text { area }}{\text { perimeter }}=\frac{3 x y}{3 x}=y
$$
which is also an integer.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq 1$ be an integer and consider the sum
$$
x=\sum_{k \geq 0}\binom{n}{2 k} 2^{n-2 k} 3^{k}=\binom{n}{0} 2^{n}+\binom{n}{2} 2^{n-2} \cdot 3+\binom{n}{4} 2^{n-4} \cdot 3^{2}+\cdots
$$
Show that $2 x-1,2 x, 2 x+1$ form the sides of a triangle whose area and inradius are also integers.
|
Consider the binomial expansion of $(2+\sqrt{3})^{n}$. It is easy to check that
$$
(2+\sqrt{3})^{n}=x+y \sqrt{3}
$$
where $y$ is also an integer. We also have
$$
(2-\sqrt{3})^{n}=x-y \sqrt{3}
$$
Multiplying these two relations, we obtain $x^{2}-3 y^{2}=1$.
Since all the terms of the expansion of $(2+\sqrt{3})^{n}$ are positive, we see that
$$
2 x=(2+\sqrt{3})^{n}+(2-\sqrt{3})^{n}=2\left(2^{n}+\binom{n}{2} 2^{n-2} \cdot 3+\cdots\right) \geq 4
$$
Thus $x \geq 2$. Hence $2 x+1<2 x+(2 x-1)$ and therefore $2 x-1,2 x, 2 x+1$ are the sides of a triangle. By Heron's formula we have
$$
\Delta^{2}=3 x(x+1)(x)(x-1)=3 x^{2}\left(x^{2}-1\right)=9 x^{2} y^{2}
$$
Hence $\Delta=3 x y$ which is an integer. Finally, its inradius is
$$
\frac{\text { area }}{\text { perimeter }}=\frac{3 x y}{3 x}=y
$$
which is also an integer.
|
{
"resource_path": "INMO/segmented/en-sol-inmo_17.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution:"
}
|
121ad9aa-e98d-5a41-bde5-2af309628235
| 607,919
|
Let $n \geq 1$ be an integer and consider the sum
$$
x=\sum_{k \geq 0}\binom{n}{2 k} 2^{n-2 k} 3^{k}=\binom{n}{0} 2^{n}+\binom{n}{2} 2^{n-2} \cdot 3+\binom{n}{4} 2^{n-4} \cdot 3^{2}+\cdots
$$
Show that $2 x-1,2 x, 2 x+1$ form the sides of a triangle whose area and inradius are also integers.
|
We will first show that the numbers $2 x_{n}-1,2 x_{n}, 2 x_{n}+1$ form the sides of a triangle. To show that, it suffices to prove that $2 x_{n}-1+2 x_{n}>2 x_{n}+1$. If possible, let the converse hold. Then, we see that we must have $4 x_{n}-1 \leq 2 x_{n}+1$, which implies that $x_{n} \leq 1$. But we see that even for the smallest value of $n=1$, we have that $x_{n}>1$. Hence, the numbers are indeed sides of a triangle.
Let $\Delta_{n}, r_{n}, s_{n}$ denote respectively, the area, inradius and semiperimeter of the triangle with sides $2 x_{n}-1,2 x_{n}, 2 x_{n}+1$. By Heron's Formula for the area of a triangle, we see that
$$
\Delta_{n}=\sqrt{3 x_{n}\left(x_{n}-1\right) x_{n}\left(x_{n}+1\right)}=x_{n} \sqrt{3\left(x_{n}^{2}-1\right)}
$$
If possible, let $\Delta_{n}$ be an integer for all $n \in \mathbb{N}$. We see that due to the presence of the first term $\binom{n}{0} 2^{n}$, we have $3 \nmid x_{n}, \forall n \in \mathbb{N}$. Hence, we get that $3 \mid x_{n}^{2}-1$. Hence, we can write $x_{n}^{2}-1$ as $3 m$ for some $m \in \mathbb{N}$. Then, we can also write
$$
\Delta_{n}=3 x_{n} \sqrt{m}
$$
Note that we have assumed that $\Delta_{n}$ is an integer. Hence, we see that we must have $m$ to be a perfect square. Consequently, we get that
$$
r_{n}=\frac{\Delta_{n}}{s_{n}}=\frac{\Delta_{n}}{3 x_{n}}=\sqrt{m} \in \mathbb{Z}
$$
Hence, it only remains to show that $\Delta_{n} \in \mathbb{Z}, \forall n \in \mathbb{N}$. In other words, it suffices to show that $3\left(x_{n}^{2}-1\right)$ is a perfect square for all $n \in \mathbb{N}$.
We see that we can write $x_{n}$ as
$$
\begin{aligned}
x_{n} & =\frac{1}{2}\left(2 \sum_{k \geq 0}\binom{n}{2 k} 2^{n-2 k} 3^{k}\right) \\
& =\frac{1}{2}\left((2+\sqrt{3})^{n}+(2-\sqrt{3})^{n}\right) \\
3 x_{n}^{2}-3 & =\frac{3}{4}\left((2+\sqrt{3})^{2 n}+(2-\sqrt{3})^{2 n}+2(2+\sqrt{3})^{n}(2-\sqrt{3})^{n}\right)-3 \\
& =\frac{3}{4}\left((2+\sqrt{3})^{2 n}+(2-\sqrt{3})^{2 n}-2(2+\sqrt{3})^{n}(2-\sqrt{3})^{n}\right) \\
& =\left(\frac{\sqrt{3}}{2}\left((2+\sqrt{3})^{n}-(2-\sqrt{3})^{n}\right)\right)^{2}
\end{aligned}
$$
We are left to show that the quantity obtained in the above equation is an integer. But we see that if we define
$$
a_{n}=\frac{\sqrt{3}}{2}\left((2+\sqrt{3})^{n}-(2-\sqrt{3})^{n}\right), \quad \forall n \in \mathbb{N}
$$
the sequence $\left\langle a_{k}\right\rangle_{k=1}^{\infty}$ thus obtained is exactly the solution for the recursion given by
$$
a_{n+2}=4 a_{n+1}-a_{n}, \quad \forall n \in \mathbb{N}, \quad a_{1}=3, a_{2}=12
$$
Hence, clearly, each $a_{n}$ is obviously an integer, thus completing the proof. $\qquad$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq 1$ be an integer and consider the sum
$$
x=\sum_{k \geq 0}\binom{n}{2 k} 2^{n-2 k} 3^{k}=\binom{n}{0} 2^{n}+\binom{n}{2} 2^{n-2} \cdot 3+\binom{n}{4} 2^{n-4} \cdot 3^{2}+\cdots
$$
Show that $2 x-1,2 x, 2 x+1$ form the sides of a triangle whose area and inradius are also integers.
|
We will first show that the numbers $2 x_{n}-1,2 x_{n}, 2 x_{n}+1$ form the sides of a triangle. To show that, it suffices to prove that $2 x_{n}-1+2 x_{n}>2 x_{n}+1$. If possible, let the converse hold. Then, we see that we must have $4 x_{n}-1 \leq 2 x_{n}+1$, which implies that $x_{n} \leq 1$. But we see that even for the smallest value of $n=1$, we have that $x_{n}>1$. Hence, the numbers are indeed sides of a triangle.
Let $\Delta_{n}, r_{n}, s_{n}$ denote respectively, the area, inradius and semiperimeter of the triangle with sides $2 x_{n}-1,2 x_{n}, 2 x_{n}+1$. By Heron's Formula for the area of a triangle, we see that
$$
\Delta_{n}=\sqrt{3 x_{n}\left(x_{n}-1\right) x_{n}\left(x_{n}+1\right)}=x_{n} \sqrt{3\left(x_{n}^{2}-1\right)}
$$
If possible, let $\Delta_{n}$ be an integer for all $n \in \mathbb{N}$. We see that due to the presence of the first term $\binom{n}{0} 2^{n}$, we have $3 \nmid x_{n}, \forall n \in \mathbb{N}$. Hence, we get that $3 \mid x_{n}^{2}-1$. Hence, we can write $x_{n}^{2}-1$ as $3 m$ for some $m \in \mathbb{N}$. Then, we can also write
$$
\Delta_{n}=3 x_{n} \sqrt{m}
$$
Note that we have assumed that $\Delta_{n}$ is an integer. Hence, we see that we must have $m$ to be a perfect square. Consequently, we get that
$$
r_{n}=\frac{\Delta_{n}}{s_{n}}=\frac{\Delta_{n}}{3 x_{n}}=\sqrt{m} \in \mathbb{Z}
$$
Hence, it only remains to show that $\Delta_{n} \in \mathbb{Z}, \forall n \in \mathbb{N}$. In other words, it suffices to show that $3\left(x_{n}^{2}-1\right)$ is a perfect square for all $n \in \mathbb{N}$.
We see that we can write $x_{n}$ as
$$
\begin{aligned}
x_{n} & =\frac{1}{2}\left(2 \sum_{k \geq 0}\binom{n}{2 k} 2^{n-2 k} 3^{k}\right) \\
& =\frac{1}{2}\left((2+\sqrt{3})^{n}+(2-\sqrt{3})^{n}\right) \\
3 x_{n}^{2}-3 & =\frac{3}{4}\left((2+\sqrt{3})^{2 n}+(2-\sqrt{3})^{2 n}+2(2+\sqrt{3})^{n}(2-\sqrt{3})^{n}\right)-3 \\
& =\frac{3}{4}\left((2+\sqrt{3})^{2 n}+(2-\sqrt{3})^{2 n}-2(2+\sqrt{3})^{n}(2-\sqrt{3})^{n}\right) \\
& =\left(\frac{\sqrt{3}}{2}\left((2+\sqrt{3})^{n}-(2-\sqrt{3})^{n}\right)\right)^{2}
\end{aligned}
$$
We are left to show that the quantity obtained in the above equation is an integer. But we see that if we define
$$
a_{n}=\frac{\sqrt{3}}{2}\left((2+\sqrt{3})^{n}-(2-\sqrt{3})^{n}\right), \quad \forall n \in \mathbb{N}
$$
the sequence $\left\langle a_{k}\right\rangle_{k=1}^{\infty}$ thus obtained is exactly the solution for the recursion given by
$$
a_{n+2}=4 a_{n+1}-a_{n}, \quad \forall n \in \mathbb{N}, \quad a_{1}=3, a_{2}=12
$$
Hence, clearly, each $a_{n}$ is obviously an integer, thus completing the proof. $\qquad$
|
{
"resource_path": "INMO/segmented/en-sol-inmo_17.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution 2:"
}
|
121ad9aa-e98d-5a41-bde5-2af309628235
| 607,919
|
Do there exist? functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
a) $f$ is a surjective function; and
b) $f(f(x))=(x-1) f(x)+2$ for all $x$ real.
|
We have $f(f(f(x)))=f(f(f(x)))=f((x-1) f(x)+2)$ and also $f(f(f(x)))=(f(x)-1) f(f(x))+2=(f(x)-1)((x-1) f(x)+2)+2=$ $(f(x)-1)(x-1) f(x)+2(f(x)-1)+2=f(x)((f(x)-1)(x-1)+2)$, so
$$
f((x-1) f(x)+2)=f(x)((x-1) f(x)+2-(x-1))
$$
Let $f(a)=0$; then for $x=a$ we get $f(0)=2$, and then for $x=0$ we get $f(2)=0$. Now for $x=1$ we get $f(1)=0$. Taking $f(b)=1$ leads us to $b=-1$, and then to $f(-1)=1$. Finally, taking $f(c)=-1$ leads to $c=2$, but that means $0=f(2)=-1$, absurd. Thus the answer is No.
Comentarii. Jonglerii cu valori particulare (mici), până la obţinerea unei contradicţii ... Important este că undeva pe parcurs trebuie exprimat $f(f(f(z)))$ în două feluri diferite, ceea ce este tipic pentru ecuaţii funcţionale conţinând iterata functुiei.
Ar fi interesant de văzut în ce măsură putem relaxa condiţile, sau ce fenomen se ascunde aici!?! Fără condiţia a) de surjectivitate, o soluţie banală este $f(0)=2, f(x)=0$ pentru $x \neq 0$. Putem oare găsi toate soluţiile?
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Do there exist? functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
a) $f$ is a surjective function; and
b) $f(f(x))=(x-1) f(x)+2$ for all $x$ real.
|
We have $f(f(f(x)))=f(f(f(x)))=f((x-1) f(x)+2)$ and also $f(f(f(x)))=(f(x)-1) f(f(x))+2=(f(x)-1)((x-1) f(x)+2)+2=$ $(f(x)-1)(x-1) f(x)+2(f(x)-1)+2=f(x)((f(x)-1)(x-1)+2)$, so
$$
f((x-1) f(x)+2)=f(x)((x-1) f(x)+2-(x-1))
$$
Let $f(a)=0$; then for $x=a$ we get $f(0)=2$, and then for $x=0$ we get $f(2)=0$. Now for $x=1$ we get $f(1)=0$. Taking $f(b)=1$ leads us to $b=-1$, and then to $f(-1)=1$. Finally, taking $f(c)=-1$ leads to $c=2$, but that means $0=f(2)=-1$, absurd. Thus the answer is No.
Comentarii. Jonglerii cu valori particulare (mici), până la obţinerea unei contradicţii ... Important este că undeva pe parcurs trebuie exprimat $f(f(f(z)))$ în două feluri diferite, ceea ce este tipic pentru ecuaţii funcţionale conţinând iterata functुiei.
Ar fi interesant de văzut în ce măsură putem relaxa condiţile, sau ce fenomen se ascunde aici!?! Fără condiţia a) de surjectivitate, o soluţie banală este $f(0)=2, f(x)=0$ pentru $x \neq 0$. Putem oare găsi toate soluţiile?
|
{
"resource_path": "IZho/segmented/en-2014_zhautykov_resenja_e.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
12041413-1f01-5d1c-ad15-baf7d87e014e
| 604,176
|
Let $U=\{1,2,3, \ldots, 2014\}$. For all $a, b, c \in \mathbb{N}$ let $f(a, b, c)$ be the number of ordered sextuplets $\left(X_{1}, X_{2}, X_{3}, Y_{1}, Y_{2}, Y_{3}\right)$ of subsets of $U$, satisfying the following conditions
(i) $Y_{1} \subseteq X_{1} \subseteq U$ and $\left|X_{1}\right|=a$;
(ii) $Y_{2} \subseteq X_{2} \subseteq U \backslash Y_{1}$ and $\left|X_{2}\right|=b$;
(iii) $Y_{3} \subseteq X_{3} \subseteq U \backslash\left(Y_{1} \cup Y_{2}\right)$ and $\left|X_{3}\right|=c$.
Prove $f(\sigma(a), \sigma(b), \sigma(c))$ does not change, for permutations $\sigma$ of $a, b, c$.
|
In order to avoid any confusion between the letters $a, b, c$ and their numerical values (as cardinalities of sets), the most convenient way will be to denote by $|\ell|$ the cardinality symbolized by any such letter $\ell$. We can now consider the true 3 -element set $\{a, b, c\}$, and the canonical bijection $\phi:\{1,2,3\} \rightarrow\{a, b, c\}$ given by $\phi(1)=a, \phi(2)=b, \phi(3)=c$.
Let us now consider any permutation $\sigma$ of $\{a, b, c\}$. We will denote by $\mathcal{F}_{\sigma}$ the family of ordered sextuplets $\left(X_{1}, X_{2}, X_{3}, Y_{1}, Y_{2}, Y_{3}\right)$ of subsets of $U$ satisfying the conditions of the statement but, under our notations, having $\left|X_{1}\right|=|\sigma(a)|,\left|X_{2}\right|=|\sigma(b)|,\left|X_{3}\right|=|\sigma(c)|$. We will also denote by $\mathcal{F}$ the family of doubletons $\left\{\left(X_{a}, X_{b}, X_{c}\right), Y\right\}$, with $X_{a}, X_{b}, X_{c}$ subsets of $U$ having $\left|X_{a}\right|=|a|,\left|X_{b}\right|=|b|,\left|X_{c}\right|=|c|$, and $\emptyset \subseteq Y \subseteq X=X_{a} \cup X_{b} \cup X_{c}$. The set $Y$ uniquely partitions into 7 classes (some of them maybe empty), indexed by the non-empty subsets $S$ of $\{a, b, c\}$ via $Y_{S}=Y \cap\left(\bigcap_{\ell \in S} X_{\ell}\right) \cap\left(\bigcap_{\ell \notin S}\left(U \backslash X_{\ell}\right)\right)$.
We will now establish a bijection between $\mathcal{F}$ and $\mathcal{F}_{\sigma}$. This will show that $f(\sigma(a), \sigma(b), \sigma(c))=|\mathcal{F}|$ is constant over all permutations $\sigma$. We send an element $\left\{\left(X_{a}, X_{b}, X_{c}\right), Y\right\} \in \mathcal{F}$ into the sextuplet $\left(X_{1}, X_{2}, X_{3}, Y_{1}, Y_{2}, Y_{3}\right)$ given by, and easily verified it actually belongs to $\mathcal{F}_{\sigma}$,
- $X_{1}=X_{\sigma(a)}, X_{2}=X_{\sigma(b)}, X_{3}=X_{\sigma(c)}$ (i.e. $X_{i}=X_{\sigma(\phi(i))}$ for $\left.i \in\{1,2,3\}\right)$,
- $Y_{1}=Y_{\{\sigma(a)\}}$,
- $Y_{2}=Y_{\{\sigma(b)\}} \cup Y_{\{\sigma(a), \sigma(b)\}}$,
- $Y_{3}=Y_{\{\sigma(c)\}} \cup Y_{\{\sigma(a), \sigma(c)\}} \cup Y_{\{\sigma(b), \sigma(c)\}} \cup Y_{\{\sigma(a), \sigma(b), \sigma(c)\}}$.
We also send an element $\left(X_{1}, X_{2}, X_{3}, Y_{1}, Y_{2}, Y_{3}\right) \in \mathcal{F}_{\sigma}$ into the doubleton $\left\{\left(X_{a}, X_{b}, X_{c}\right), Y\right\}$ given by, and easily verified it actually belongs to $\mathcal{F}$, with $\tau$ the permutation of $\{1,2,3\}$ induced by $\sigma$ via $\tau(i)=\phi^{-1}(\sigma(\phi(i)))$ for all $i \in\{1,2,3\}$,
- $X_{a}=X_{\tau(1)}, X_{b}=X_{\tau(2)}, X_{c}=X_{\tau(3)}$ (i.e. $X_{\phi(i)}=X_{\tau(i)}$ for $\left.i \in\{1,2,3\}\right)$, - $Y=Y_{1} \cup Y_{2} \cup Y_{3}$.
It is immediate to see this mapping is a bijection, due to the unicity of the partitioning described in the above. Visualizing the Venn diagrams should tremendously help in understanding our considerations. The only difficulty resides in providing a luminous write-up of the argumentation, the underlying phenomenon being in fact almost trivial. The key element of this solution is to consider the unique partitioning of the set $Y=Y_{1} \cup Y_{2} \cup Y_{3}$ induced by the three sets of cardinalities $a, b, c$.
Comentarii. Pouah ... ce urâţenie de enunţ! Iar cerinţa este aproape evidentă, doar că soluţia este cam lung de scris, formalizat, şi explicat. Evident, valoarea 2014 nu joacă niciun rol.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $U=\{1,2,3, \ldots, 2014\}$. For all $a, b, c \in \mathbb{N}$ let $f(a, b, c)$ be the number of ordered sextuplets $\left(X_{1}, X_{2}, X_{3}, Y_{1}, Y_{2}, Y_{3}\right)$ of subsets of $U$, satisfying the following conditions
(i) $Y_{1} \subseteq X_{1} \subseteq U$ and $\left|X_{1}\right|=a$;
(ii) $Y_{2} \subseteq X_{2} \subseteq U \backslash Y_{1}$ and $\left|X_{2}\right|=b$;
(iii) $Y_{3} \subseteq X_{3} \subseteq U \backslash\left(Y_{1} \cup Y_{2}\right)$ and $\left|X_{3}\right|=c$.
Prove $f(\sigma(a), \sigma(b), \sigma(c))$ does not change, for permutations $\sigma$ of $a, b, c$.
|
In order to avoid any confusion between the letters $a, b, c$ and their numerical values (as cardinalities of sets), the most convenient way will be to denote by $|\ell|$ the cardinality symbolized by any such letter $\ell$. We can now consider the true 3 -element set $\{a, b, c\}$, and the canonical bijection $\phi:\{1,2,3\} \rightarrow\{a, b, c\}$ given by $\phi(1)=a, \phi(2)=b, \phi(3)=c$.
Let us now consider any permutation $\sigma$ of $\{a, b, c\}$. We will denote by $\mathcal{F}_{\sigma}$ the family of ordered sextuplets $\left(X_{1}, X_{2}, X_{3}, Y_{1}, Y_{2}, Y_{3}\right)$ of subsets of $U$ satisfying the conditions of the statement but, under our notations, having $\left|X_{1}\right|=|\sigma(a)|,\left|X_{2}\right|=|\sigma(b)|,\left|X_{3}\right|=|\sigma(c)|$. We will also denote by $\mathcal{F}$ the family of doubletons $\left\{\left(X_{a}, X_{b}, X_{c}\right), Y\right\}$, with $X_{a}, X_{b}, X_{c}$ subsets of $U$ having $\left|X_{a}\right|=|a|,\left|X_{b}\right|=|b|,\left|X_{c}\right|=|c|$, and $\emptyset \subseteq Y \subseteq X=X_{a} \cup X_{b} \cup X_{c}$. The set $Y$ uniquely partitions into 7 classes (some of them maybe empty), indexed by the non-empty subsets $S$ of $\{a, b, c\}$ via $Y_{S}=Y \cap\left(\bigcap_{\ell \in S} X_{\ell}\right) \cap\left(\bigcap_{\ell \notin S}\left(U \backslash X_{\ell}\right)\right)$.
We will now establish a bijection between $\mathcal{F}$ and $\mathcal{F}_{\sigma}$. This will show that $f(\sigma(a), \sigma(b), \sigma(c))=|\mathcal{F}|$ is constant over all permutations $\sigma$. We send an element $\left\{\left(X_{a}, X_{b}, X_{c}\right), Y\right\} \in \mathcal{F}$ into the sextuplet $\left(X_{1}, X_{2}, X_{3}, Y_{1}, Y_{2}, Y_{3}\right)$ given by, and easily verified it actually belongs to $\mathcal{F}_{\sigma}$,
- $X_{1}=X_{\sigma(a)}, X_{2}=X_{\sigma(b)}, X_{3}=X_{\sigma(c)}$ (i.e. $X_{i}=X_{\sigma(\phi(i))}$ for $\left.i \in\{1,2,3\}\right)$,
- $Y_{1}=Y_{\{\sigma(a)\}}$,
- $Y_{2}=Y_{\{\sigma(b)\}} \cup Y_{\{\sigma(a), \sigma(b)\}}$,
- $Y_{3}=Y_{\{\sigma(c)\}} \cup Y_{\{\sigma(a), \sigma(c)\}} \cup Y_{\{\sigma(b), \sigma(c)\}} \cup Y_{\{\sigma(a), \sigma(b), \sigma(c)\}}$.
We also send an element $\left(X_{1}, X_{2}, X_{3}, Y_{1}, Y_{2}, Y_{3}\right) \in \mathcal{F}_{\sigma}$ into the doubleton $\left\{\left(X_{a}, X_{b}, X_{c}\right), Y\right\}$ given by, and easily verified it actually belongs to $\mathcal{F}$, with $\tau$ the permutation of $\{1,2,3\}$ induced by $\sigma$ via $\tau(i)=\phi^{-1}(\sigma(\phi(i)))$ for all $i \in\{1,2,3\}$,
- $X_{a}=X_{\tau(1)}, X_{b}=X_{\tau(2)}, X_{c}=X_{\tau(3)}$ (i.e. $X_{\phi(i)}=X_{\tau(i)}$ for $\left.i \in\{1,2,3\}\right)$, - $Y=Y_{1} \cup Y_{2} \cup Y_{3}$.
It is immediate to see this mapping is a bijection, due to the unicity of the partitioning described in the above. Visualizing the Venn diagrams should tremendously help in understanding our considerations. The only difficulty resides in providing a luminous write-up of the argumentation, the underlying phenomenon being in fact almost trivial. The key element of this solution is to consider the unique partitioning of the set $Y=Y_{1} \cup Y_{2} \cup Y_{3}$ induced by the three sets of cardinalities $a, b, c$.
Comentarii. Pouah ... ce urâţenie de enunţ! Iar cerinţa este aproape evidentă, doar că soluţia este cam lung de scris, formalizat, şi explicat. Evident, valoarea 2014 nu joacă niciun rol.
|
{
"resource_path": "IZho/segmented/en-2014_zhautykov_resenja_e.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
4b57b3a3-8054-5d6b-bfe3-2d0feb1e33a4
| 604,217
|
Each point with integral coordinates in the plane is coloured white or blue. Prove that one can choose a colour so that for every positive integer $n$ there exists a triangle of area $n$ having its vertices of the chosen colour.
|
If there exists some $c$-monochromatic horizontal row $y=k$, then if both rows $y=k-1$ and $y=k+1$ are $\bar{c}$-monochromatic we can find $\bar{c}$-monochromatic triangles of any positive integer area, otherwise they must contain at least a $c$-point, and we can find $c$-monochromatic triangles of any positive integer area. So assume there exists no monochromatic horizontal row. Consider the horizontal row $y=0$. If it contains two $c$-points at distance 1 , then for any positive integer $n$, together with a $c$-point on row $y=2 n$ they will make a $c$-monochromatic triangle of area $n$. Otherwise it will contain two $\bar{c}$-points at distance 2 , which for any positive integer $n$, together with a $\bar{c}$-point on row $y=n$ will make a $\bar{c}$-monochromatic triangle of area $n$.
Comentarii. Extrem de puţin din întreaga diversitate de colorări este utilizat, ceea ce face problema oarecum trivială ... De remarcat că nu este adevărat că se pot întotdeauna obţine triunghiuri monocromatice de orice arie $n / 2$; de exemplu pentru colorarea "în tablă de şah" nu se vor obţine triunghiuri monocromatice de arie $1 / 2$. Iar dacă mărim numărul de culori la trei, există o (simplă) colorare fără triunghiuri monocromatice de arie 1. Presupun că întrebări mult mai interesante şi dificile pot fi imaginate ...
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Each point with integral coordinates in the plane is coloured white or blue. Prove that one can choose a colour so that for every positive integer $n$ there exists a triangle of area $n$ having its vertices of the chosen colour.
|
If there exists some $c$-monochromatic horizontal row $y=k$, then if both rows $y=k-1$ and $y=k+1$ are $\bar{c}$-monochromatic we can find $\bar{c}$-monochromatic triangles of any positive integer area, otherwise they must contain at least a $c$-point, and we can find $c$-monochromatic triangles of any positive integer area. So assume there exists no monochromatic horizontal row. Consider the horizontal row $y=0$. If it contains two $c$-points at distance 1 , then for any positive integer $n$, together with a $c$-point on row $y=2 n$ they will make a $c$-monochromatic triangle of area $n$. Otherwise it will contain two $\bar{c}$-points at distance 2 , which for any positive integer $n$, together with a $\bar{c}$-point on row $y=n$ will make a $\bar{c}$-monochromatic triangle of area $n$.
Comentarii. Extrem de puţin din întreaga diversitate de colorări este utilizat, ceea ce face problema oarecum trivială ... De remarcat că nu este adevărat că se pot întotdeauna obţine triunghiuri monocromatice de orice arie $n / 2$; de exemplu pentru colorarea "în tablă de şah" nu se vor obţine triunghiuri monocromatice de arie $1 / 2$. Iar dacă mărim numărul de culori la trei, există o (simplă) colorare fără triunghiuri monocromatice de arie 1. Presupun că întrebări mult mai interesante şi dificile pot fi imaginate ...
|
{
"resource_path": "IZho/segmented/en-2015_zhautykov_resenja_e.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
951f3ac1-a9c6-52a7-a3fb-8a1cee41bd84
| 604,243
|
Inside the triangle $A B C$ a point $M$ is given. The line $B M$ meets the side $A C$ at $N$. The point $K$ is symmetrical to $M$ with respect to $A C$. The line $B K$ meets $A C$ at $P$. If $\angle A M P=\angle C M N$, prove that $\angle A B P=\angle C B N$.
|
(AoPS - user TelvCohl) Let $M^{*}$ be the isogonal conjugate of $M$ with respect to $\triangle A B C$.
LEMMA. Let $\ell$ be the isogonal conjugate of $A M$ with respect to $\angle B M C$, and let $\ell^{*}$ be the isogonal conjugate of $A M^{*}$ with respect to $\angle B M^{*} C$. The lines $\ell, \ell^{*}$ meet on $B C$ and are symmetrical with respect to $B C$.
Proof. Let $X$ be the meeting point of $B M^{*}$ and $C M$. Let $Y \in B C$ be a point such that $X A, X Y$ are isogonal conjugate with respect to $\angle B X C$.
Since $C A, C Y$ are isogonal conjugate with respect to $\angle M^{*} C M$, so $A$ and $Y$ are isogonal conjugate with respect to $\triangle C X M^{*}$, it follows that $M^{*} Y$, $M^{*} A$ are isogonal conjugate with respect to $\angle B M^{*} C$. Similarly, we can prove $M Y, M A$ are isogonal conjugate with respect to $\angle B M C$.
By easy angle chasing we get $\angle M Y B=\angle C Y M^{*}$, thus $M Y \equiv \ell$ and $M^{*} Y \equiv \ell^{*}$ are symmetrical with respect to $B C$.
From the LemmA we now get that $P K$ is the isogonal conjugate of $B M^{*}$ with respect to $\angle A M^{*} C$, thus from $B \in P K$ we get $P K$ to be the angle bisector of $\angle A M^{*} C$ and $M^{*} \in B K$, therefore $\angle A B P=\angle C B N$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Inside the triangle $A B C$ a point $M$ is given. The line $B M$ meets the side $A C$ at $N$. The point $K$ is symmetrical to $M$ with respect to $A C$. The line $B K$ meets $A C$ at $P$. If $\angle A M P=\angle C M N$, prove that $\angle A B P=\angle C B N$.
|
(AoPS - user TelvCohl) Let $M^{*}$ be the isogonal conjugate of $M$ with respect to $\triangle A B C$.
LEMMA. Let $\ell$ be the isogonal conjugate of $A M$ with respect to $\angle B M C$, and let $\ell^{*}$ be the isogonal conjugate of $A M^{*}$ with respect to $\angle B M^{*} C$. The lines $\ell, \ell^{*}$ meet on $B C$ and are symmetrical with respect to $B C$.
Proof. Let $X$ be the meeting point of $B M^{*}$ and $C M$. Let $Y \in B C$ be a point such that $X A, X Y$ are isogonal conjugate with respect to $\angle B X C$.
Since $C A, C Y$ are isogonal conjugate with respect to $\angle M^{*} C M$, so $A$ and $Y$ are isogonal conjugate with respect to $\triangle C X M^{*}$, it follows that $M^{*} Y$, $M^{*} A$ are isogonal conjugate with respect to $\angle B M^{*} C$. Similarly, we can prove $M Y, M A$ are isogonal conjugate with respect to $\angle B M C$.
By easy angle chasing we get $\angle M Y B=\angle C Y M^{*}$, thus $M Y \equiv \ell$ and $M^{*} Y \equiv \ell^{*}$ are symmetrical with respect to $B C$.
From the LemmA we now get that $P K$ is the isogonal conjugate of $B M^{*}$ with respect to $\angle A M^{*} C$, thus from $B \in P K$ we get $P K$ to be the angle bisector of $\angle A M^{*} C$ and $M^{*} \in B K$, therefore $\angle A B P=\angle C B N$.
|
{
"resource_path": "IZho/segmented/en-2015_zhautykov_resenja_e.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
db1eb405-2b94-5c8a-927c-002c98cb08d3
| 604,251
|
Inside the triangle $A B C$ a point $M$ is given. The line $B M$ meets the side $A C$ at $N$. The point $K$ is symmetrical to $M$ with respect to $A C$. The line $B K$ meets $A C$ at $P$. If $\angle A M P=\angle C M N$, prove that $\angle A B P=\angle C B N$.
|
(Ştefan Tudose on AoPS) Notice that the thesis is equivalent (by Steiner's theorem) with $\frac{B C}{B A}=\frac{M C}{M A}$; stated in other words, that $B$ lies on the $M$-Apollonius circle of $\triangle M C A$.
Let $F$ be the foot of the angle bisector of $\angle C M A$. By dint of the above observation, it is enough to prove that $B \in \odot(M F K)$, which is trivial by simple angle chasing; suppose wlog that $M A>M C$, it then follows $\angle M F K=\pi+\angle M A C-\angle M C A=\pi-\angle K B M$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Inside the triangle $A B C$ a point $M$ is given. The line $B M$ meets the side $A C$ at $N$. The point $K$ is symmetrical to $M$ with respect to $A C$. The line $B K$ meets $A C$ at $P$. If $\angle A M P=\angle C M N$, prove that $\angle A B P=\angle C B N$.
|
(Ştefan Tudose on AoPS) Notice that the thesis is equivalent (by Steiner's theorem) with $\frac{B C}{B A}=\frac{M C}{M A}$; stated in other words, that $B$ lies on the $M$-Apollonius circle of $\triangle M C A$.
Let $F$ be the foot of the angle bisector of $\angle C M A$. By dint of the above observation, it is enough to prove that $B \in \odot(M F K)$, which is trivial by simple angle chasing; suppose wlog that $M A>M C$, it then follows $\angle M F K=\pi+\angle M A C-\angle M C A=\pi-\angle K B M$.
|
{
"resource_path": "IZho/segmented/en-2015_zhautykov_resenja_e.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nAlternative Solution."
}
|
db1eb405-2b94-5c8a-927c-002c98cb08d3
| 604,251
|
Let $A_{n}$ be the set of partitions of the sequence $(1,2, \ldots, n)$ into several subsequences such that every two neighbouring terms of each subsequence have different parity, and let $B_{n}$ be the set of partitions of the sequence $(1,2, \ldots, n)$ into several subsequences such that all the terms of each subsequence have the same parity. 2
Prove that for every positive integer $n$ the sets $A_{n}$ and $B_{n+1}$ contain the same number of elements.
|
For each partition $\pi$ of $\{1,2, \ldots, n\}$, with the elements within each block written in ascending order, denote by $k(\pi)$ the number of blocks of $\pi$ ending in an even number and by $\ell(\pi)$ the number of blocks of $\pi$ ending in an odd number.
Also denote $f_{n}(x, y)=\sum_{\pi \in A_{n}} x^{k(\pi)} y^{\ell(\pi)}$ and $g_{n}(x, y)=\sum_{\pi \in B_{n}} x^{k(\pi)} y^{\ell(\pi)}$.
We will have $\left|A_{n}\right|=f_{n}(1,1)$.
For example
$$
\begin{aligned}
& f_{1}(x, y)=y \\
& f_{2}(x, y)=x(y+1) \\
& f_{3}(x, y)=y(x y+y+x+1) \\
& f_{4}(x, y)=x\left(x y^{2}+y^{2}+3 x y+3 y+x+1\right)
\end{aligned}
$$
A moment of reflection will show us that
$$
\begin{aligned}
& f_{n+1}(x, y)=y\left(f_{n}(x, y)+\frac{\mathrm{d}}{\mathrm{d} x} f_{n}(x, y)\right) \text { for even } n \\
& f_{n+1}(x, y)=x\left(f_{n}(x, y)+\frac{\mathrm{d}}{\mathrm{d} y} f_{n}(x, y)\right) \text { for odd } n
\end{aligned}
$$
This comes from considering where the element $n+1$ may go, and how this affects the number of blocks.
We will also have $\left|B_{n}\right|=g_{n}(1,1) 3^{3}$[^1]
For example
$$
\begin{aligned}
& g_{1}(x, y)=y \\
& g_{2}(x, y)=x y \\
& g_{3}(x, y)=y x(y+1) \\
& g_{4}(x, y)=x y(x y+y+x+1) \\
& g_{5}(x, y)=y x\left(x y^{2}+y^{2}+3 x y+3 y+x+1\right)
\end{aligned}
$$
Another moment of reflection will show us that
$$
\begin{aligned}
& g_{n+1}(x, y)=y\left(g_{n}(x, y)+\frac{\mathrm{d}}{\mathrm{d} y} g_{n}(x, y)\right) \text { for even } n \\
& g_{n+1}(x, y)=x\left(g_{n}(x, y)+\frac{\mathrm{d}}{\mathrm{d} x} g_{n}(x, y)\right) \text { for odd } n
\end{aligned}
$$
This also comes from considering where the element $n+1$ may go, and how this affects the number of blocks.
It is not hard to check that $g_{n+1}(x, y)=y f_{n}(x, y)$ for even $n$ and that $g_{n+1}(x, y)=x f_{n}(x, y)$ for odd $n$. This is seen to hold true for small values of $n$. Henceforth, for even $n, g_{n+1}(x, y)=y\left(g_{n}(x, y)+\frac{\mathrm{d}}{\mathrm{d} y} g_{n}(x, y)\right)=$ $y x f_{n-1}(x, y)+y x \frac{\mathrm{d}}{\mathrm{d} y} f_{n-1}(x, y)$ by induction step on $g_{n}(x, y)=x f_{n-1}(x, y)$, while $y f_{n}(x, y)=y x\left(f_{n-1}(x, y)+\frac{\mathrm{d}}{\mathrm{d} y} f_{n-1}(x, y)\right)$. Alike computation holds for odd $n$. So $g_{n+1}(1,1)=f_{n}(1,1)$ in all cases, and so $\left|B_{n+1}\right|=\left|A_{n}\right|$.
Comentarii. De fapt o partiţie de unul din cele două tipuri poate fi privită şi ca scrierea în cicluri disjuncte a unei permutări convenabile din $\mathcal{S}_{n}$. Odată ce ideea (folosirea unui fel de funcţii generatoare) se iveşte, problema devine aproape trivială. Consideraţii asupra acestor partiţii din $A_{n}$, numite parity-alternating, sunt numeroase, relativ şi la numerele Stirling de a doua speţă $\left\{\begin{array}{l}n \\ k\end{array}\right\}$, legate de numerele Bell $\beta_{n}$ prin relaţia $\beta_{n}=\sum_{k=1}^{n}\left\{\begin{array}{l}n \\ k\end{array}\right\}$; de exemplu http://www.sciencedirect.com/science/article/pii/S0024379513004758
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $A_{n}$ be the set of partitions of the sequence $(1,2, \ldots, n)$ into several subsequences such that every two neighbouring terms of each subsequence have different parity, and let $B_{n}$ be the set of partitions of the sequence $(1,2, \ldots, n)$ into several subsequences such that all the terms of each subsequence have the same parity. 2
Prove that for every positive integer $n$ the sets $A_{n}$ and $B_{n+1}$ contain the same number of elements.
|
For each partition $\pi$ of $\{1,2, \ldots, n\}$, with the elements within each block written in ascending order, denote by $k(\pi)$ the number of blocks of $\pi$ ending in an even number and by $\ell(\pi)$ the number of blocks of $\pi$ ending in an odd number.
Also denote $f_{n}(x, y)=\sum_{\pi \in A_{n}} x^{k(\pi)} y^{\ell(\pi)}$ and $g_{n}(x, y)=\sum_{\pi \in B_{n}} x^{k(\pi)} y^{\ell(\pi)}$.
We will have $\left|A_{n}\right|=f_{n}(1,1)$.
For example
$$
\begin{aligned}
& f_{1}(x, y)=y \\
& f_{2}(x, y)=x(y+1) \\
& f_{3}(x, y)=y(x y+y+x+1) \\
& f_{4}(x, y)=x\left(x y^{2}+y^{2}+3 x y+3 y+x+1\right)
\end{aligned}
$$
A moment of reflection will show us that
$$
\begin{aligned}
& f_{n+1}(x, y)=y\left(f_{n}(x, y)+\frac{\mathrm{d}}{\mathrm{d} x} f_{n}(x, y)\right) \text { for even } n \\
& f_{n+1}(x, y)=x\left(f_{n}(x, y)+\frac{\mathrm{d}}{\mathrm{d} y} f_{n}(x, y)\right) \text { for odd } n
\end{aligned}
$$
This comes from considering where the element $n+1$ may go, and how this affects the number of blocks.
We will also have $\left|B_{n}\right|=g_{n}(1,1) 3^{3}$[^1]
For example
$$
\begin{aligned}
& g_{1}(x, y)=y \\
& g_{2}(x, y)=x y \\
& g_{3}(x, y)=y x(y+1) \\
& g_{4}(x, y)=x y(x y+y+x+1) \\
& g_{5}(x, y)=y x\left(x y^{2}+y^{2}+3 x y+3 y+x+1\right)
\end{aligned}
$$
Another moment of reflection will show us that
$$
\begin{aligned}
& g_{n+1}(x, y)=y\left(g_{n}(x, y)+\frac{\mathrm{d}}{\mathrm{d} y} g_{n}(x, y)\right) \text { for even } n \\
& g_{n+1}(x, y)=x\left(g_{n}(x, y)+\frac{\mathrm{d}}{\mathrm{d} x} g_{n}(x, y)\right) \text { for odd } n
\end{aligned}
$$
This also comes from considering where the element $n+1$ may go, and how this affects the number of blocks.
It is not hard to check that $g_{n+1}(x, y)=y f_{n}(x, y)$ for even $n$ and that $g_{n+1}(x, y)=x f_{n}(x, y)$ for odd $n$. This is seen to hold true for small values of $n$. Henceforth, for even $n, g_{n+1}(x, y)=y\left(g_{n}(x, y)+\frac{\mathrm{d}}{\mathrm{d} y} g_{n}(x, y)\right)=$ $y x f_{n-1}(x, y)+y x \frac{\mathrm{d}}{\mathrm{d} y} f_{n-1}(x, y)$ by induction step on $g_{n}(x, y)=x f_{n-1}(x, y)$, while $y f_{n}(x, y)=y x\left(f_{n-1}(x, y)+\frac{\mathrm{d}}{\mathrm{d} y} f_{n-1}(x, y)\right)$. Alike computation holds for odd $n$. So $g_{n+1}(1,1)=f_{n}(1,1)$ in all cases, and so $\left|B_{n+1}\right|=\left|A_{n}\right|$.
Comentarii. De fapt o partiţie de unul din cele două tipuri poate fi privită şi ca scrierea în cicluri disjuncte a unei permutări convenabile din $\mathcal{S}_{n}$. Odată ce ideea (folosirea unui fel de funcţii generatoare) se iveşte, problema devine aproape trivială. Consideraţii asupra acestor partiţii din $A_{n}$, numite parity-alternating, sunt numeroase, relativ şi la numerele Stirling de a doua speţă $\left\{\begin{array}{l}n \\ k\end{array}\right\}$, legate de numerele Bell $\beta_{n}$ prin relaţia $\beta_{n}=\sum_{k=1}^{n}\left\{\begin{array}{l}n \\ k\end{array}\right\}$; de exemplu http://www.sciencedirect.com/science/article/pii/S0024379513004758
|
{
"resource_path": "IZho/segmented/en-2015_zhautykov_resenja_e.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
d88abb6d-04c7-58ca-b5d6-936e97bf5b6b
| 604,308
|
Let $\alpha, \beta, \gamma$ be the angles of a triangle opposite to the sides $a, b, c$ respectively. Prove the inequality
$$
2\left(\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma\right) \geq \frac{a^{2}}{b^{2}+c^{2}}+\frac{b^{2}}{a^{2}+c^{2}}+\frac{c^{2}}{a^{2}+b^{2}}
$$
|
By the Law of Sines, RHS equals $\frac{\sin ^{2} \alpha}{\sin ^{2} \beta+\sin ^{2} \gamma}+\frac{\sin ^{2} \beta}{\sin ^{2} \alpha+\sin ^{2} \gamma}+\frac{\sin ^{2} \gamma}{\sin ^{2} \alpha+\sin ^{2} \beta}$. Applying Cauchy-Bunyakowski inequality we have
$$
\sin ^{2} \alpha=\sin ^{2}(\beta+\gamma)=(\sin \beta \cos \gamma+\sin \gamma \cos \beta)^{2} \leq\left(\sin ^{2} \beta+\sin ^{2} \gamma\right)\left(\cos ^{2} \gamma+\cos ^{2} \beta\right)
$$
therefore $\cos ^{2} \beta+\cos ^{2} \gamma \geq \frac{\sin ^{2} \alpha}{\sin ^{2} \beta+\sin ^{2} \gamma}$.
Adding similar inequalities for $\cos ^{2} \gamma+\cos ^{2} \alpha$ and $\cos ^{2} \alpha+\cos ^{2} \beta$ we get the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $\alpha, \beta, \gamma$ be the angles of a triangle opposite to the sides $a, b, c$ respectively. Prove the inequality
$$
2\left(\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma\right) \geq \frac{a^{2}}{b^{2}+c^{2}}+\frac{b^{2}}{a^{2}+c^{2}}+\frac{c^{2}}{a^{2}+b^{2}}
$$
|
By the Law of Sines, RHS equals $\frac{\sin ^{2} \alpha}{\sin ^{2} \beta+\sin ^{2} \gamma}+\frac{\sin ^{2} \beta}{\sin ^{2} \alpha+\sin ^{2} \gamma}+\frac{\sin ^{2} \gamma}{\sin ^{2} \alpha+\sin ^{2} \beta}$. Applying Cauchy-Bunyakowski inequality we have
$$
\sin ^{2} \alpha=\sin ^{2}(\beta+\gamma)=(\sin \beta \cos \gamma+\sin \gamma \cos \beta)^{2} \leq\left(\sin ^{2} \beta+\sin ^{2} \gamma\right)\left(\cos ^{2} \gamma+\cos ^{2} \beta\right)
$$
therefore $\cos ^{2} \beta+\cos ^{2} \gamma \geq \frac{\sin ^{2} \alpha}{\sin ^{2} \beta+\sin ^{2} \gamma}$.
Adding similar inequalities for $\cos ^{2} \gamma+\cos ^{2} \alpha$ and $\cos ^{2} \alpha+\cos ^{2} \beta$ we get the desired result.
|
{
"resource_path": "IZho/segmented/en-2018_zhautykov_resenja_e.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution."
}
|
ea8ac919-8ee2-5fe0-94f3-f8ce300f8481
| 604,319
|
Points $N, K, L$ lie on the sides $A B, B C, C A$ of a triangle $A B C$ respectively so that $A L=B K$ and $C N$ is the bisector of the angle $C$. The segments $A K$ and $B L$ meet at the point $P$. Let $I$ and $J$ be the incentres of the triangles $A P L$ and $B P K$ respectively. The lines $C N$ and $I J$ meet at point $Q$. Prove that $I P=J Q$.
|
The case $C A=C B$ is trivial. If $C A \neq C B$, we may suppose, without loss of generality, that $C N$ meets the segment $P K$.
Let the circumcircles $\omega_{1}$ and $\omega_{2}$ of the triangles $A P L$ and $B P K$ respectively meet again at point $T$. Then
$$
\angle L A T=\angle T P B=\angle T K B
$$
and $\angle A L T=\angle A P T=\angle T B K$, that is, $\triangle A L T=\triangle K B T$, hence
$$
A T=T K
$$
It follows from (1) that the quadrilateral $A C K T$ is cyclic; together with (2) this means that $\angle A C T=\angle T C K$, i.e. $T$ lies on the bisector of $C N$.
Let $I J$ meet $\omega_{1}$ and $\omega_{2}$ at $I_{1}$ and $J_{1}$ respectively. Since $\omega_{1}$ and $\omega_{2}$ have equal radii and $A L=B K$, the triangles $A L I_{1}$ and $B K J_{1}$ are equal. We use Mansion's lemma: the midpoint of arc $X Y$ of the circumcircle of $X Y Z$ lies at equal distances from the ends of this arc and the incentre. It follows from this lemma that $I_{1} I=I_{1} L=J_{1} K=J_{1} J$. Moreover, $\angle P I_{1} T=\angle P A T=\angle P K T=$ $\angle P J_{1} T$, therefore, $I_{1} T=J_{1} T$. Thus $T$ lies on the median bisector of $I_{1} J_{1}$ and
Figure 1: image on the median bisector of $I J$.
It remains to prove that $T$ lies on the median bisector of $P Q$. Let $R=A K \cap C T$. Then $\angle A R T=\angle R A C+\angle A C R=$ $\angle R A C+\angle A K T=\angle R A C+\angle K A T=\angle L A T=\angle B P T$. Since $P Q$ bisects the angle $R P B, \angle P Q T=\angle P R T+\angle R P Q=$ $\angle P B T+\angle B P J=\angle T P Q$, therefore $T$ belongs to the median bisector of $P Q$ and $I P=J Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Points $N, K, L$ lie on the sides $A B, B C, C A$ of a triangle $A B C$ respectively so that $A L=B K$ and $C N$ is the bisector of the angle $C$. The segments $A K$ and $B L$ meet at the point $P$. Let $I$ and $J$ be the incentres of the triangles $A P L$ and $B P K$ respectively. The lines $C N$ and $I J$ meet at point $Q$. Prove that $I P=J Q$.
|
The case $C A=C B$ is trivial. If $C A \neq C B$, we may suppose, without loss of generality, that $C N$ meets the segment $P K$.
Let the circumcircles $\omega_{1}$ and $\omega_{2}$ of the triangles $A P L$ and $B P K$ respectively meet again at point $T$. Then
$$
\angle L A T=\angle T P B=\angle T K B
$$
and $\angle A L T=\angle A P T=\angle T B K$, that is, $\triangle A L T=\triangle K B T$, hence
$$
A T=T K
$$
It follows from (1) that the quadrilateral $A C K T$ is cyclic; together with (2) this means that $\angle A C T=\angle T C K$, i.e. $T$ lies on the bisector of $C N$.
Let $I J$ meet $\omega_{1}$ and $\omega_{2}$ at $I_{1}$ and $J_{1}$ respectively. Since $\omega_{1}$ and $\omega_{2}$ have equal radii and $A L=B K$, the triangles $A L I_{1}$ and $B K J_{1}$ are equal. We use Mansion's lemma: the midpoint of arc $X Y$ of the circumcircle of $X Y Z$ lies at equal distances from the ends of this arc and the incentre. It follows from this lemma that $I_{1} I=I_{1} L=J_{1} K=J_{1} J$. Moreover, $\angle P I_{1} T=\angle P A T=\angle P K T=$ $\angle P J_{1} T$, therefore, $I_{1} T=J_{1} T$. Thus $T$ lies on the median bisector of $I_{1} J_{1}$ and

Figure 1: image on the median bisector of $I J$.
It remains to prove that $T$ lies on the median bisector of $P Q$. Let $R=A K \cap C T$. Then $\angle A R T=\angle R A C+\angle A C R=$ $\angle R A C+\angle A K T=\angle R A C+\angle K A T=\angle L A T=\angle B P T$. Since $P Q$ bisects the angle $R P B, \angle P Q T=\angle P R T+\angle R P Q=$ $\angle P B T+\angle B P J=\angle T P Q$, therefore $T$ belongs to the median bisector of $P Q$ and $I P=J Q$.
|
{
"resource_path": "IZho/segmented/en-2018_zhautykov_resenja_e.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution."
}
|
0758ea1d-8de4-560c-9201-52745a4034c7
| 604,330
|
Prove that there exist infinitely many pairs $(m, n)$ of positive integers such that $m+n$ divides $(m!)^{n}+(n!)^{m}+1$.
|
We shall find a pair such that $m+n=p$ is prime and $n$ is even. Applying Wilson's theorem we have
$$
m!=(p-n)!=\frac{(p-1)!}{(p-n+1) \ldots(p-2)(p-1)} \equiv \frac{-1}{-(n-1) \ldots(-2)(-1)} \equiv \frac{1}{(n-1)!} \equiv \frac{n}{n!} \quad(\bmod p)
$$
It follows from Fermat's Little Theorem that $(n!)^{p} \equiv n!(\bmod p)$, therefore
$$
(m!)^{n}+(n!)^{m}+1 \equiv\left(\frac{n}{n!}\right)^{n}+(n!)^{p-n}+1 \equiv \frac{n^{n}+n!+(n!)^{n}}{(n!)^{n}} \quad(\bmod p)
$$
thus it suffices to prove that the number $n^{n}+n!+(n!)^{n}$ has a prime divisor $p>n$ for infinitely many even $n$.
We prove that this condition is satisfied, for instance, by all the numbers of the form $n=2 q$, where $q>2$ is prime. Let $A=(2 q)^{2 q}+(2 q)!+((2 q)!)^{2 q}$. For a prime $p$ and integer $k$ we denote by $v_{p}(k)$ the largest integer $\ell$ such that $p^{\ell}$ divides $k$.
If $r<2 q$ is prime and $r \notin\{2, q\}$ then $A \equiv(2 q)^{2 q} \not \equiv 0(\bmod r)$. The largest degree of $q$ dividing $(2 q)!$ is $q^{2}$, while for $(2 q)^{2 q}$ and $((2 q)!)^{2 q}$ it is $2 q$ and $4 q$ respectively, therefore $v_{q}(A)=2$.
Finally, $v_{2}((2 q)!)=\left[\frac{2 q}{2}\right]+\left[\frac{2 q}{4}\right]+\left[\frac{2 q}{8}\right]+\cdots<\frac{2 q}{2}+\frac{2 q}{4}+\frac{2 q}{8}+\cdots=2 q$, so $v_{2}((2 q)!)<v_{2}\left((2 q)^{2 q}\right)$ and obviously $v_{2}((2 q)!)<v_{2}\left((2 q)!^{2 q}\right)$, thus $v_{2}(A) \leq 2 q-1$. On the other hand, $A>(2 q)^{2 q}>2^{2 q-1} q^{2}$, therefore $A$ has a prime divisor $p>2 q$, q.e.d.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there exist infinitely many pairs $(m, n)$ of positive integers such that $m+n$ divides $(m!)^{n}+(n!)^{m}+1$.
|
We shall find a pair such that $m+n=p$ is prime and $n$ is even. Applying Wilson's theorem we have
$$
m!=(p-n)!=\frac{(p-1)!}{(p-n+1) \ldots(p-2)(p-1)} \equiv \frac{-1}{-(n-1) \ldots(-2)(-1)} \equiv \frac{1}{(n-1)!} \equiv \frac{n}{n!} \quad(\bmod p)
$$
It follows from Fermat's Little Theorem that $(n!)^{p} \equiv n!(\bmod p)$, therefore
$$
(m!)^{n}+(n!)^{m}+1 \equiv\left(\frac{n}{n!}\right)^{n}+(n!)^{p-n}+1 \equiv \frac{n^{n}+n!+(n!)^{n}}{(n!)^{n}} \quad(\bmod p)
$$
thus it suffices to prove that the number $n^{n}+n!+(n!)^{n}$ has a prime divisor $p>n$ for infinitely many even $n$.
We prove that this condition is satisfied, for instance, by all the numbers of the form $n=2 q$, where $q>2$ is prime. Let $A=(2 q)^{2 q}+(2 q)!+((2 q)!)^{2 q}$. For a prime $p$ and integer $k$ we denote by $v_{p}(k)$ the largest integer $\ell$ such that $p^{\ell}$ divides $k$.
If $r<2 q$ is prime and $r \notin\{2, q\}$ then $A \equiv(2 q)^{2 q} \not \equiv 0(\bmod r)$. The largest degree of $q$ dividing $(2 q)!$ is $q^{2}$, while for $(2 q)^{2 q}$ and $((2 q)!)^{2 q}$ it is $2 q$ and $4 q$ respectively, therefore $v_{q}(A)=2$.
Finally, $v_{2}((2 q)!)=\left[\frac{2 q}{2}\right]+\left[\frac{2 q}{4}\right]+\left[\frac{2 q}{8}\right]+\cdots<\frac{2 q}{2}+\frac{2 q}{4}+\frac{2 q}{8}+\cdots=2 q$, so $v_{2}((2 q)!)<v_{2}\left((2 q)^{2 q}\right)$ and obviously $v_{2}((2 q)!)<v_{2}\left((2 q)!^{2 q}\right)$, thus $v_{2}(A) \leq 2 q-1$. On the other hand, $A>(2 q)^{2 q}>2^{2 q-1} q^{2}$, therefore $A$ has a prime divisor $p>2 q$, q.e.d.
|
{
"resource_path": "IZho/segmented/en-2018_zhautykov_resenja_e.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution."
}
|
adfdd6e7-2c17-5d79-90a0-b7c15f545b17
| 604,341
|
Prove that there are at least 100! ways to partition the number 100! into summands from the set $\{1!, 2!, 3!, \ldots, 99$ !\}. (Partitions differing in the order of summands are considered the same; any summand can be taken multiple times. We remind that $n!=1 \cdot 2 \cdot \ldots \cdot n$.)
|
Let us prove by induction on $n \geqslant 4$ that there are at least $n$ ! ways to partition the number $n$ ! into summands from $\{1!, 2!, \ldots,(n-1)!\}$.
For $n=4$, if we use only the summands 1 !, 2 ! there are 13 ways to partition 4 ! as 2 ! can be used from 0 to 12 times. If 3 ! is used 1 time, then $4!-3$ ! = 18 can be partitioned using 1 !, 2 ! in 10 ways. We get at least one more partition if we use 3! two times. So, there are at least 24 such partitions as needed.
Suppose now the statement holds for $n$ and let us prove it for $n+1$. To partition $(n+1)$ !, the summand $n$ ! can be used $i$ times for $0 \leqslant i \leqslant n$. By the hypothesis, for every such $i$, the remaining number $(n+1)!-$ $-i \cdot n!=(n+1-i) \cdot n!$ can be partitioned into the summands $\{1!, \ldots,(n-1)!\}$ in at least $n$ ! ways as follows. For any partition of $n$ ! take each summand appearing say $k$ times and write it $(n+1-i) k$ times. Hence we obtain at least $(n+1) \cdot n!=(n+1)$ ! ways to partition the number $(n+1)$ ! as desired. The original problem follows for $n=100$ then.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Prove that there are at least 100! ways to partition the number 100! into summands from the set $\{1!, 2!, 3!, \ldots, 99$ !\}. (Partitions differing in the order of summands are considered the same; any summand can be taken multiple times. We remind that $n!=1 \cdot 2 \cdot \ldots \cdot n$.)
|
Let us prove by induction on $n \geqslant 4$ that there are at least $n$ ! ways to partition the number $n$ ! into summands from $\{1!, 2!, \ldots,(n-1)!\}$.
For $n=4$, if we use only the summands 1 !, 2 ! there are 13 ways to partition 4 ! as 2 ! can be used from 0 to 12 times. If 3 ! is used 1 time, then $4!-3$ ! = 18 can be partitioned using 1 !, 2 ! in 10 ways. We get at least one more partition if we use 3! two times. So, there are at least 24 such partitions as needed.
Suppose now the statement holds for $n$ and let us prove it for $n+1$. To partition $(n+1)$ !, the summand $n$ ! can be used $i$ times for $0 \leqslant i \leqslant n$. By the hypothesis, for every such $i$, the remaining number $(n+1)!-$ $-i \cdot n!=(n+1-i) \cdot n!$ can be partitioned into the summands $\{1!, \ldots,(n-1)!\}$ in at least $n$ ! ways as follows. For any partition of $n$ ! take each summand appearing say $k$ times and write it $(n+1-i) k$ times. Hence we obtain at least $(n+1) \cdot n!=(n+1)$ ! ways to partition the number $(n+1)$ ! as desired. The original problem follows for $n=100$ then.
|
{
"resource_path": "IZho/segmented/en-2019_zhautykov_resenja_e.jsonl",
"problem_match": "\n№1.",
"solution_match": "\nSolution."
}
|
e899b522-8fa0-5e60-b518-fef883446459
| 604,392
|
The extension of median $C M$ of the triangle $A B C$ intersects its circumcircle $\omega$ at $N$. Let $P$ and $Q$ be the points on the rays $C A$ and $C B$ respectively such that $P M \| B N$ and $Q M \| A N$. Let $X$ and $Y$ be the points on the segments $P M$ and $Q M$ respectively such that $P Y$ and $Q X$ are tangent to $\omega$. The segments $P Y$ and $Q X$ intersect at $Z$. Prove that the quadrilateral $M X Z Y$ is circumscribed.
|
Lemma. The points $K$ and $L$ lie on the sides $B C$ and $A C$ of a triangle $A B C$. The segments $A K$ and $B L$ intersect at $D$. Then the quadrilateral $C K D L$ is circumscribed if and only if $A C - B C = A D - B D$.
Proof. Let $C K D L$ be circumscribed and its incircle touches $L C, C K, K D, D L$ at $X, Y, Z, T$ respectively (see Fig. 1). Then
$$
A C - B C = A X - B Y = A Z - B T = A D - B D
$$

Fig. 1

Fig. 2
Now suppose that $A C - B C = A D - B D$. Let the tangent to the incircle of $B L C$ different from $A C$ meets the segments $B L$ and $B C$ at $D_{1}$ and $K_{1}$ respectively. If $K = K_{1}$ then the lemma is proved. Otherwise $A D_{1} - B D_{1} = A C - B C = A D - B D$ or $A D_{1} - B D_{1} = A D - B D$. In the case when $D$ lies on the segment $B D_{1}$ (see Fig. 2) we have
$$
A D_{1} - B D_{1} = A D - B D \Rightarrow A D_{1} - A D = B D_{1} - B D \Rightarrow A D_{1} - A D = D D_{1}
$$
But the last equation contradicts the triangle inequality, since $A D_{1} - A D < D D_{1}$. The case when $D$ is outside the segment $B D_{1}$ is similar.
Back to the solution of the problem, let $P Y$ and $Q X$ touch $\omega$ at $Y_{1}$ and $X_{1}$ respectively. Since $A C B N$ is cyclic and $P M \| B N$ we have $\angle A C N = \angle A B N = \angle A M P$, i. e. the circumcircle of $\triangle A M C$ is tangent to the line $P M$. Thus $P M^2 = P A \cdot P C$. But $P A \cdot P C = P Y_{1}^2$, and therefore $P M = P Y_{1}$. In the same way we have $Q M = Q X_{1}$. Obviously $Z X_{1} = Z Y_{1}$. It remains to note that the desired result follows from the Lemma because
$$
P M - Q M = P Y_{1} - Q X_{1} = (P Z + Z Y_{1}) - (Q Z + Z X_{1}) = P Z - Q Z \quad \Rightarrow \quad P M - Q M = P Z - Q Z
$$
Fig. 3
Note. This solution does not use the condition that $M$ is the midpoint of $A B$.
## XV International Zhautykov Olympiad in Mathematics
Second day. Solutions
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The extension of median $C M$ of the triangle $A B C$ intersects its circumcircle $\omega$ at $N$. Let $P$ and $Q$ be the points on the rays $C A$ and $C B$ respectively such that $P M \| B N$ and $Q M \| A N$. Let $X$ and $Y$ be the points on the segments $P M$ and $Q M$ respectively such that $P Y$ and $Q X$ are tangent to $\omega$. The segments $P Y$ and $Q X$ intersect at $Z$. Prove that the quadrilateral $M X Z Y$ is circumscribed.
|
Lemma. The points $K$ and $L$ lie on the sides $B C$ and $A C$ of a triangle $A B C$. The segments $A K$ and $B L$ intersect at $D$. Then the quadrilateral $C K D L$ is circumscribed if and only if $A C-B C=A D-B D$.
Proof. Let $C K D L$ be circumscribed and its incircle touches $L C, C K, K D, D L$ at $X, Y, Z, T$ respectively (see Fig. 1). Then
$$
A C-B C=A X-B Y=A Z-B T=A D-B D
$$

Рис. 1

Рис. 2
Now suppose that $A C-B C=A D-B D$. Let the tangent to the incircle of $B L C$ different from $A C$ meets the segments $B L$ and $B C$ at $D_{1}$ and $K_{1}$ respectively. If $K=K_{1}$ then the lemma is proved. Otherwise $A D_{1}-B D_{1}=A C-B C=A D-B D$ or $A D_{1}-B D_{1}=A D-B D$. In the case when $D$ lies on the segment $B D_{1}$ (see Fig. 2) we have
$$
A D_{1}-B D_{1}=A D-B D \Rightarrow A D_{1}-A D=B D_{1}-B D \Rightarrow A D_{1}-A D=D D_{1}
$$
But the last equation contradicts the triangle inequality, since $A D_{1}-A D<D D_{1}$. The case when $D$ is outside the segment $B D_{1}$ is similar.
Back to the solution of the problem, let $P Y$ and $Q X$ touch $\omega$ at $Y_{1}$ and $X_{1}$ respectively. Since $A C B N$ is cyclic and $P M \| B N$ we have $\angle A C N=\angle A B N=\angle A M P$, i. e. the circumcircle of $\triangle A M C$ is tangent to the line $P M$. Thus $P M^{2}=P A \cdot P C$. But $P A \cdot P C=P Y_{1}^{2}$, and therefore $P M=P Y_{1}$. In the same way we have $Q M=Q X_{1}$. Obviously $Z X_{1}=Z Y_{1}$. It remains to note that the desired result follows from the Lemma because
$$
P M-Q M=P Y_{1}-Q X_{1}=\left(P Z+Z Y_{1}\right)-\left(Q Z+Z X_{1}\right)=P Z-Q Z \quad \Rightarrow \quad P M-Q M=P Z-Q Z
$$

Рис. 3
Note. This solution does not use the comdition that $M$ is the midpoint of $A B$.
## XV International Zhautykov Olympiad in Mathematics
Second day. Solutions
|
{
"resource_path": "IZho/segmented/en-2019_zhautykov_resenja_e.jsonl",
"problem_match": "\n№3.",
"solution_match": "## Solution."
}
|
6408879c-6f75-5c6e-a063-7c20b62e5f4f
| 604,409
|
An isosceles triangle $A B C$ with $A C=B C$ is given. Point $D$ is chosen on the side $A C$. The circle $S_{1}$ of radius $R$ with the center $O_{1}$ touches the segment $A D$ and the extensions of $B A$ and $B D$ over the points $A$ and $D$, respectively. The circle $S_{2}$ of radius $2 R$ with the center $O_{2}$ touches the segment $D C$ and the extensions of $B D$ and $B C$ over the points $D$ and $C$, respectively. Let the tangent to the circumcircle of the triangle $B O_{1} O_{2}$ at the point $O_{2}$ intersect the line $B A$ at point $F$. Prove that $O_{1} F=O_{1} O_{2}$.
|
in the triangle $A B C$ we have $\angle A=\angle B$. It is evident that $\angle O_{1} B O_{2}=\angle B / 2$. Let $\ell$ be the straight line passing through $O_{2}$ parallel to $A C$. By the problem condition $\ell$ touches $S_{1}$ (say, at a point $N$ ). Let also $K$ be the tangency point of $S_{1}$ and $B A$. Then the clockwise rotation about the point $O_{1}$ through the angle $N O_{1} K$ transposes $\ell$ to $B A$ and thus transposes the point $O_{2}$ to some point $O \in B A$. Hence $O_{1} O=O_{1} O_{2}$ and $\angle O O_{1} O_{2}=\angle N O_{1} K=180^{\circ}-\angle A=180^{\circ}-\angle B$, so $\angle O_{1} O_{2} O=\angle B / 2=\angle O_{1} B O_{2}$. The latter does mean that the line $\mathrm{O}_{2} \mathrm{O}$ is the tangent to the circumcircle of $\triangle B O_{1} O_{2}$. Hence $F=O$, and $O_{1} F=O_{1} O_{2}$, as was to be proved.
Рис. 1
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
An isosceles triangle $A B C$ with $A C=B C$ is given. Point $D$ is chosen on the side $A C$. The circle $S_{1}$ of radius $R$ with the center $O_{1}$ touches the segment $A D$ and the extensions of $B A$ and $B D$ over the points $A$ and $D$, respectively. The circle $S_{2}$ of radius $2 R$ with the center $O_{2}$ touches the segment $D C$ and the extensions of $B D$ and $B C$ over the points $D$ and $C$, respectively. Let the tangent to the circumcircle of the triangle $B O_{1} O_{2}$ at the point $O_{2}$ intersect the line $B A$ at point $F$. Prove that $O_{1} F=O_{1} O_{2}$.
|
in the triangle $A B C$ we have $\angle A=\angle B$. It is evident that $\angle O_{1} B O_{2}=\angle B / 2$. Let $\ell$ be the straight line passing through $O_{2}$ parallel to $A C$. By the problem condition $\ell$ touches $S_{1}$ (say, at a point $N$ ). Let also $K$ be the tangency point of $S_{1}$ and $B A$. Then the clockwise rotation about the point $O_{1}$ through the angle $N O_{1} K$ transposes $\ell$ to $B A$ and thus transposes the point $O_{2}$ to some point $O \in B A$. Hence $O_{1} O=O_{1} O_{2}$ and $\angle O O_{1} O_{2}=\angle N O_{1} K=180^{\circ}-\angle A=180^{\circ}-\angle B$, so $\angle O_{1} O_{2} O=\angle B / 2=\angle O_{1} B O_{2}$. The latter does mean that the line $\mathrm{O}_{2} \mathrm{O}$ is the tangent to the circumcircle of $\triangle B O_{1} O_{2}$. Hence $F=O$, and $O_{1} F=O_{1} O_{2}$, as was to be proved.

Рис. 1
|
{
"resource_path": "IZho/segmented/en-2019_zhautykov_resenja_e.jsonl",
"problem_match": "\n№4.",
"solution_match": "\nSolution By condition,"
}
|
87541a98-42ea-5151-8a13-a2411c21b79f
| 604,422
|
On a polynomial of degree three it is allowed to perform the following two operations arbitrarily many times:
(i) reverse the order of its coefficients including zeroes (for instance, from the polynomial $x^{3}-2 x^{2}-3$ we can obtain $-3 x^{3}-2 x+1$;
(ii) change polynomial $P(x)$ to the polynomial $P(x+1)$.
Is it possible to obtain the polynomial $x^{3}-3 x^{2}+3 x-3$ from the polynomial $x^{3}-2$ ?
The answer is no.
|
The original polynomial $x^{3}-2$ has a unique real root. The two transformations clearly preserve this property. If $\alpha$ is the only real root of $P(x)$, then the first operation produces a polynomial with root $\frac{1}{\alpha}$, and the second operation gives a polynomial with root $\alpha-1$. Since the root of the original polynomial is $\sqrt[3]{2}$, and thar of the resulting polynomial is $1+\sqrt[3]{2}$, the problem is reduced to the question whether it is possible to obtain the latter number from the former by operations $x \mapsto \frac{1}{x}$ and $x \mapsto x-1$. Let us apply one more operation $x \mapsto x-1$ (so as to transform $\sqrt[3]{2}$ to itself) and reverse all the operations. It appears then that the number $\sqrt[3]{2}$ is transformed to itself by several operations of the form $x \mapsto \frac{1}{x}$ and $x \mapsto x+1$. It is easy to see that the composition of any number of such operations is a fractional-linear function $x \mapsto \frac{a x+b}{c x+d}$, where $a, b, c, d$ are non-negative integers and $a d-b c=1$. Each operation $x \mapsto x+1$ increases $a+b+c+d$, and, since we started with this operation, the resulting function is not identical. Thus $\sqrt[3]{2}$ is transformed to itself by some such composition. This means however that $\sqrt[3]{2}$ is a root of non-zero polynomial $x(c x+d)-a x-b$ with integral coefficients and degree at most 2, which is impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
On a polynomial of degree three it is allowed to perform the following two operations arbitrarily many times:
(i) reverse the order of its coefficients including zeroes (for instance, from the polynomial $x^{3}-2 x^{2}-3$ we can obtain $-3 x^{3}-2 x+1$;
(ii) change polynomial $P(x)$ to the polynomial $P(x+1)$.
Is it possible to obtain the polynomial $x^{3}-3 x^{2}+3 x-3$ from the polynomial $x^{3}-2$ ?
The answer is no.
|
The original polynomial $x^{3}-2$ has a unique real root. The two transformations clearly preserve this property. If $\alpha$ is the only real root of $P(x)$, then the first operation produces a polynomial with root $\frac{1}{\alpha}$, and the second operation gives a polynomial with root $\alpha-1$. Since the root of the original polynomial is $\sqrt[3]{2}$, and thar of the resulting polynomial is $1+\sqrt[3]{2}$, the problem is reduced to the question whether it is possible to obtain the latter number from the former by operations $x \mapsto \frac{1}{x}$ and $x \mapsto x-1$. Let us apply one more operation $x \mapsto x-1$ (so as to transform $\sqrt[3]{2}$ to itself) and reverse all the operations. It appears then that the number $\sqrt[3]{2}$ is transformed to itself by several operations of the form $x \mapsto \frac{1}{x}$ and $x \mapsto x+1$. It is easy to see that the composition of any number of such operations is a fractional-linear function $x \mapsto \frac{a x+b}{c x+d}$, where $a, b, c, d$ are non-negative integers and $a d-b c=1$. Each operation $x \mapsto x+1$ increases $a+b+c+d$, and, since we started with this operation, the resulting function is not identical. Thus $\sqrt[3]{2}$ is transformed to itself by some such composition. This means however that $\sqrt[3]{2}$ is a root of non-zero polynomial $x(c x+d)-a x-b$ with integral coefficients and degree at most 2, which is impossible.
|
{
"resource_path": "IZho/segmented/en-2019_zhautykov_resenja_e.jsonl",
"problem_match": "\n№6.",
"solution_match": "\nSolution I."
}
|
9522b5f7-28bf-510c-9f59-1b48279bb61a
| 604,447
|
On a polynomial of degree three it is allowed to perform the following two operations arbitrarily many times:
(i) reverse the order of its coefficients including zeroes (for instance, from the polynomial $x^{3}-2 x^{2}-3$ we can obtain $-3 x^{3}-2 x+1$;
(ii) change polynomial $P(x)$ to the polynomial $P(x+1)$.
Is it possible to obtain the polynomial $x^{3}-3 x^{2}+3 x-3$ from the polynomial $x^{3}-2$ ?
The answer is no.
|
The original polynomial has one real and two conjugate complex roots. We have seen above that under the two operations these roots are subject to transforms $x \mapsto \frac{1}{x}$ and $x \mapsto x-1$. Note that both imaginary roots of the original polynomial have negative real part. It is easy to check that this property is preserved under the two operations. However the real parts of all the roots of the desired polynomial are positive, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
On a polynomial of degree three it is allowed to perform the following two operations arbitrarily many times:
(i) reverse the order of its coefficients including zeroes (for instance, from the polynomial $x^{3}-2 x^{2}-3$ we can obtain $-3 x^{3}-2 x+1$;
(ii) change polynomial $P(x)$ to the polynomial $P(x+1)$.
Is it possible to obtain the polynomial $x^{3}-3 x^{2}+3 x-3$ from the polynomial $x^{3}-2$ ?
The answer is no.
|
The original polynomial has one real and two conjugate complex roots. We have seen above that under the two operations these roots are subject to transforms $x \mapsto \frac{1}{x}$ and $x \mapsto x-1$. Note that both imaginary roots of the original polynomial have negative real part. It is easy to check that this property is preserved under the two operations. However the real parts of all the roots of the desired polynomial are positive, a contradiction.
|
{
"resource_path": "IZho/segmented/en-2019_zhautykov_resenja_e.jsonl",
"problem_match": "\n№6.",
"solution_match": "\nSolution II."
}
|
9522b5f7-28bf-510c-9f59-1b48279bb61a
| 604,447
|
On a polynomial of degree three it is allowed to perform the following two operations arbitrarily many times:
(i) reverse the order of its coefficients including zeroes (for instance, from the polynomial $x^{3}-2 x^{2}-3$ we can obtain $-3 x^{3}-2 x+1$;
(ii) change polynomial $P(x)$ to the polynomial $P(x+1)$.
Is it possible to obtain the polynomial $x^{3}-3 x^{2}+3 x-3$ from the polynomial $x^{3}-2$ ?
The answer is no.
|
For a polynomial $P(x)=a x^{3}+b x^{2}+c x+d$ we define $\Delta(P)=3 a d-b c$. The first operation transforms $P(x)$ to $d x^{3}+c x^{2}+b x+a$ and does not change $\Delta$. The second operation transforms $P(x)$ to $Q(x)=a x^{3}+(b+3 a) x^{2}+(c+3 a+2 b) x+(d+a+b+c)$, for which $\Delta(Q)=3(d+a+b+c) a-$ $-(b+3 a)(c+3 a+2 b)=\Delta(P)-\left(2 b^{2}+6 a b+6 a^{2}\right)<\Delta(P)$. Thus the permitted operation can not increase $\Delta$. On the other hand, for the original polynomial $\Delta(P)=-6$, and for the resulting polynomial it must be 0 .
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
On a polynomial of degree three it is allowed to perform the following two operations arbitrarily many times:
(i) reverse the order of its coefficients including zeroes (for instance, from the polynomial $x^{3}-2 x^{2}-3$ we can obtain $-3 x^{3}-2 x+1$;
(ii) change polynomial $P(x)$ to the polynomial $P(x+1)$.
Is it possible to obtain the polynomial $x^{3}-3 x^{2}+3 x-3$ from the polynomial $x^{3}-2$ ?
The answer is no.
|
For a polynomial $P(x)=a x^{3}+b x^{2}+c x+d$ we define $\Delta(P)=3 a d-b c$. The first operation transforms $P(x)$ to $d x^{3}+c x^{2}+b x+a$ and does not change $\Delta$. The second operation transforms $P(x)$ to $Q(x)=a x^{3}+(b+3 a) x^{2}+(c+3 a+2 b) x+(d+a+b+c)$, for which $\Delta(Q)=3(d+a+b+c) a-$ $-(b+3 a)(c+3 a+2 b)=\Delta(P)-\left(2 b^{2}+6 a b+6 a^{2}\right)<\Delta(P)$. Thus the permitted operation can not increase $\Delta$. On the other hand, for the original polynomial $\Delta(P)=-6$, and for the resulting polynomial it must be 0 .
|
{
"resource_path": "IZho/segmented/en-2019_zhautykov_resenja_e.jsonl",
"problem_match": "\n№6.",
"solution_match": "\nSolution III."
}
|
9522b5f7-28bf-510c-9f59-1b48279bb61a
| 604,447
|
A positive integer $n$ does not divide $2^{a} 3^{b}+1$ for any positive integers $a$ and $b$. Prove that $n$ does not divide $2^{c}+3^{d}$ for any positive integers $c$ and $d$.
|
Assume the contrary: $n$ divides $2^{c}+3^{d}$. Clearly $n$ is not divisible by 3 ; therefore $n$ divides $3^{k}-1$ for some $k$. Choosing $s$ so that $k s>d$ we see that $n$ divides $3^{k s-d}\left(2^{c}+3^{d}\right)=2^{c} 3^{k s-d}+3^{k s}$. Then $n$ also divides $2^{c} 3^{k s-d}+1=2^{c} 3^{k s-d}+3^{k s}-\left(3^{k s}-1\right)$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A positive integer $n$ does not divide $2^{a} 3^{b}+1$ for any positive integers $a$ and $b$. Prove that $n$ does not divide $2^{c}+3^{d}$ for any positive integers $c$ and $d$.
|
Assume the contrary: $n$ divides $2^{c}+3^{d}$. Clearly $n$ is not divisible by 3 ; therefore $n$ divides $3^{k}-1$ for some $k$. Choosing $s$ so that $k s>d$ we see that $n$ divides $3^{k s-d}\left(2^{c}+3^{d}\right)=2^{c} 3^{k s-d}+3^{k s}$. Then $n$ also divides $2^{c} 3^{k s-d}+1=2^{c} 3^{k s-d}+3^{k s}-\left(3^{k s}-1\right)$, a contradiction.
|
{
"resource_path": "IZho/segmented/en-2020_zhautykov_resenja_e.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution."
}
|
671c5fea-035f-5fe8-ac1e-9c5e111d5554
| 604,483
|
In a scalene triangle $A B C \quad I$ is the incenter and $C N$ is the bisector of angle $C$. The line $C N$ meets the circumcircle of $A B C$ again at $M$. The line $\ell$ is parallel to $A B$ and touches the incircle of $A B C$. The point $R$ on $\ell$ is such that $C I \perp I R$. The circumcircle of $M N R$ meets the line $I R$ again at $S$. Prove that $A S=B S$.
|
In this solution we make use of directed angles. A directed angle $\angle(n, m)$ between lines $n$ and $m$ is the angle of counterclockwise rotation transforming $n$ into a line parallel to $m$.
Let $d$ be the tangent to the circumcircle of $\triangle A B C$ containing $N$ and different from $A B$. Then $\angle(\ell, C I)=\angle(N B, N I)=\angle(N I, d)$. Since $C I \perp I R$, the line $d$ contains $R$ because of symmetry with respect to $I R$.
Let $T$ be the common point of $M S$ and $\ell$. We have $\angle(M N, M S)=\angle(R N, R S)=\angle(R S, R T)$, that is, $R, T, I, M$ are concyclic. Therefore $\angle(R T, M T)=\angle(R I, M I)=90^{\circ}$. It follows that $M S \perp A B$. But $M$ belongs to the perpendicular bisector of $A B$, and so does $S$. Thus $A S=B S$, q.e.d.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a scalene triangle $A B C \quad I$ is the incenter and $C N$ is the bisector of angle $C$. The line $C N$ meets the circumcircle of $A B C$ again at $M$. The line $\ell$ is parallel to $A B$ and touches the incircle of $A B C$. The point $R$ on $\ell$ is such that $C I \perp I R$. The circumcircle of $M N R$ meets the line $I R$ again at $S$. Prove that $A S=B S$.
|
In this solution we make use of directed angles. A directed angle $\angle(n, m)$ between lines $n$ and $m$ is the angle of counterclockwise rotation transforming $n$ into a line parallel to $m$.
Let $d$ be the tangent to the circumcircle of $\triangle A B C$ containing $N$ and different from $A B$. Then $\angle(\ell, C I)=\angle(N B, N I)=\angle(N I, d)$. Since $C I \perp I R$, the line $d$ contains $R$ because of symmetry with respect to $I R$.
Let $T$ be the common point of $M S$ and $\ell$. We have $\angle(M N, M S)=\angle(R N, R S)=\angle(R S, R T)$, that is, $R, T, I, M$ are concyclic. Therefore $\angle(R T, M T)=\angle(R I, M I)=90^{\circ}$. It follows that $M S \perp A B$. But $M$ belongs to the perpendicular bisector of $A B$, and so does $S$. Thus $A S=B S$, q.e.d.
|
{
"resource_path": "IZho/segmented/en-2020_zhautykov_resenja_e.jsonl",
"problem_match": "\n№4.",
"solution_match": "\nSolution."
}
|
0d572c7a-22ed-5b18-8a15-10dce2d14836
| 604,524
|
Prove that for some positive integer $n$ the remainder of $3^{n}$ when divided by $2^{n}$ is greater than $10^{2021}$.
|
We choose a positive integer $M$ such that $2^{M}>10^{2022}$, and consider the remainder of $3^{M}$ when divided by $2^{M}$ :
$$
3^{M} \equiv r \quad\left(\bmod 2^{M}\right), 0<r<2^{M}
$$
If $r>10^{2021}$, then $M$ is the desired number. Otherwise we choose the smallest integer $k$ for which $3^{k} r>$ $>10^{2021}$. Then $3^{k} r<10^{2022}<2^{M}$. Since $3^{k+M} \equiv 3^{k} r\left(\bmod 2^{M}\right)$, the remainder of $3^{k+M}$ when divided by $2^{k+M}$ has the form $3^{k} r+2^{M} s$ with some positive integer $s$, and is therefore greater than $10^{2021}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for some positive integer $n$ the remainder of $3^{n}$ when divided by $2^{n}$ is greater than $10^{2021}$.
|
We choose a positive integer $M$ such that $2^{M}>10^{2022}$, and consider the remainder of $3^{M}$ when divided by $2^{M}$ :
$$
3^{M} \equiv r \quad\left(\bmod 2^{M}\right), 0<r<2^{M}
$$
If $r>10^{2021}$, then $M$ is the desired number. Otherwise we choose the smallest integer $k$ for which $3^{k} r>$ $>10^{2021}$. Then $3^{k} r<10^{2022}<2^{M}$. Since $3^{k+M} \equiv 3^{k} r\left(\bmod 2^{M}\right)$, the remainder of $3^{k+M}$ when divided by $2^{k+M}$ has the form $3^{k} r+2^{M} s$ with some positive integer $s$, and is therefore greater than $10^{2021}$.
|
{
"resource_path": "IZho/segmented/en-2021_zhautykov_resenja_e.jsonl",
"problem_match": "\n№1.",
"solution_match": "\nSolution I."
}
|
a8e5b771-556a-5fe6-9d65-d8401319b5de
| 604,559
|
Prove that for some positive integer $n$ the remainder of $3^{n}$ when divided by $2^{n}$ is greater than $10^{2021}$.
|
We choose a positive integer $k$ such that $2^{k+2}>10^{2021}$. We are going to determine $v_{2}\left(3^{2^{k}}-1\right)$, i. e. the largest $m$ such that $2^{m}$ divides $3^{2^{k}}-1$. According to well-known lifting the exponent lemma,
$$
v_{2}\left(3^{2^{k}}-1\right)=v_{2}\left(3^{2}-1\right)+k-1=k+2
$$
Then the number $n=2^{k}$ satisfies the condition, Indeed, if $r$ is the remainder when $3^{n}$ is divided by $2^{n}$, then $r \equiv 3^{2^{k}}\left(\bmod 2^{2^{k}}\right)$ and therefore $r \equiv 3^{2^{k}}\left(\bmod 2^{k+3}\right)$ (we use the fact that $\left.2^{k} \geq k+3\right)$. Since $2^{k+2}$ divides $r-1$ and $2^{k+3}$ does not, $r \equiv 1+2^{k+2}\left(\bmod 2^{k+3}\right)$, thus $r \geq 1+2^{k+2}>10^{2021}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for some positive integer $n$ the remainder of $3^{n}$ when divided by $2^{n}$ is greater than $10^{2021}$.
|
We choose a positive integer $k$ such that $2^{k+2}>10^{2021}$. We are going to determine $v_{2}\left(3^{2^{k}}-1\right)$, i. e. the largest $m$ such that $2^{m}$ divides $3^{2^{k}}-1$. According to well-known lifting the exponent lemma,
$$
v_{2}\left(3^{2^{k}}-1\right)=v_{2}\left(3^{2}-1\right)+k-1=k+2
$$
Then the number $n=2^{k}$ satisfies the condition, Indeed, if $r$ is the remainder when $3^{n}$ is divided by $2^{n}$, then $r \equiv 3^{2^{k}}\left(\bmod 2^{2^{k}}\right)$ and therefore $r \equiv 3^{2^{k}}\left(\bmod 2^{k+3}\right)$ (we use the fact that $\left.2^{k} \geq k+3\right)$. Since $2^{k+2}$ divides $r-1$ and $2^{k+3}$ does not, $r \equiv 1+2^{k+2}\left(\bmod 2^{k+3}\right)$, thus $r \geq 1+2^{k+2}>10^{2021}$.
|
{
"resource_path": "IZho/segmented/en-2021_zhautykov_resenja_e.jsonl",
"problem_match": "\n№1.",
"solution_match": "\nSolution II."
}
|
a8e5b771-556a-5fe6-9d65-d8401319b5de
| 604,559
|
Prove that for some positive integer $n$ the remainder of $3^{n}$ when divided by $2^{n}$ is greater than $10^{2021}$.
|
Choose a positive integer $k$ such that $3^{k}>10^{2021}$, and a positive integer $m$ such that $2^{m}>3^{k}$. There exists a positive integer $T$ such that $3^{T} \equiv 1\left(\bmod 2^{m}\right)$ (we may take, for instance, $T=$ $=2^{m-2}$ ). Then for all positive integral $s$
$$
3^{k+s T} \equiv 3^{k} \quad\left(\bmod 2^{m}\right)
$$
that is, $3^{k+s T}$ leaves the remainder $3^{k}$ after division by $2^{m}$ and, therefore, a remainder not less than $3^{k}>10^{2021}$ after division by any higher power of 2 . Now we can take $n=k+s T$ such that $k+s T>m$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for some positive integer $n$ the remainder of $3^{n}$ when divided by $2^{n}$ is greater than $10^{2021}$.
|
Choose a positive integer $k$ such that $3^{k}>10^{2021}$, and a positive integer $m$ such that $2^{m}>3^{k}$. There exists a positive integer $T$ such that $3^{T} \equiv 1\left(\bmod 2^{m}\right)$ (we may take, for instance, $T=$ $=2^{m-2}$ ). Then for all positive integral $s$
$$
3^{k+s T} \equiv 3^{k} \quad\left(\bmod 2^{m}\right)
$$
that is, $3^{k+s T}$ leaves the remainder $3^{k}$ after division by $2^{m}$ and, therefore, a remainder not less than $3^{k}>10^{2021}$ after division by any higher power of 2 . Now we can take $n=k+s T$ such that $k+s T>m$.
|
{
"resource_path": "IZho/segmented/en-2021_zhautykov_resenja_e.jsonl",
"problem_match": "\n№1.",
"solution_match": "\nSolution III."
}
|
a8e5b771-556a-5fe6-9d65-d8401319b5de
| 604,559
|
In a convex cyclic hexagon $A B C D E F \quad B C=E F$ and $C D=A F$. Diagonals $A C$ and $B F$ intersect at point $Q$, and diagonals $E C$ and $D F$ intersect at point $P$. Points $R$ and $S$ are marked on the segments $D F$ and $B F$ respectively so that $F R=P D$ and $B Q=F S$. The segments $R Q$ and $P S$ intersect at point $T$. Prove that the line $T C$ bisects the diagonal $D B$.
|
It follows obviously that $B F \| C E$ and $A C \| D F$. We denote the circumcircles of $\triangle A B Q$ and $\triangle D E P$ by $\omega_{1}$ and $\omega_{2}$, respectively. Note that the lines $A D$ and $B E$ are internal common tangents to $\omega_{1}$ and $\omega_{2}$. Indeed, $\angle B A Q=\angle B E C=\angle E B Q$, i. e., $E B$ is tangent to $\omega_{1}$; the other tangencies are established similarly. Note that $C P F Q$ is a parallelogram. Then $C Q=F P=R D$, that is, $C Q R D$ is also a parallelogram as well as $C P S B$. The lines $B C$ and $D C$ are not parallel to $B D$. Therefore $R Q$ and $P S$ intersect the line $B D$; we denote the intersections by $X$ and $Y$ respectively. It follows that $X$ lies on $\omega_{1}$, since $\angle Q A B=\angle C D B=\angle B X Q$. Similarly, $Y$ lies on $\omega_{2}$. Thus
$$
D B \cdot D X=D A^{2}=B E^{2}=B D \cdot B Y
$$
hence $D X=B Y$, or $B X=D Y$. Let $T C$ and $B D$ meet at $Z$. Then it follows from $T X \| C D$ and $T Y \| B C$ that
$$
\frac{D Z}{D X}=\frac{C Z}{C T}=\frac{B Z}{B Y}
$$
which immediately gives $D Z=B Z$.
Note. The equality $B X=D Y$ can be also proved by applying Menelaus theorem to $\triangle B D F$ and the lines $R-Q-X$ and $S-P-Y$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a convex cyclic hexagon $A B C D E F \quad B C=E F$ and $C D=A F$. Diagonals $A C$ and $B F$ intersect at point $Q$, and diagonals $E C$ and $D F$ intersect at point $P$. Points $R$ and $S$ are marked on the segments $D F$ and $B F$ respectively so that $F R=P D$ and $B Q=F S$. The segments $R Q$ and $P S$ intersect at point $T$. Prove that the line $T C$ bisects the diagonal $D B$.
|
It follows obviously that $B F \| C E$ and $A C \| D F$. We denote the circumcircles of $\triangle A B Q$ and $\triangle D E P$ by $\omega_{1}$ and $\omega_{2}$, respectively. Note that the lines $A D$ and $B E$ are internal common tangents to $\omega_{1}$ and $\omega_{2}$. Indeed, $\angle B A Q=\angle B E C=\angle E B Q$, i. e., $E B$ is tangent to $\omega_{1}$; the other tangencies are established similarly. Note that $C P F Q$ is a parallelogram. Then $C Q=F P=R D$, that is, $C Q R D$ is also a parallelogram as well as $C P S B$. The lines $B C$ and $D C$ are not parallel to $B D$. Therefore $R Q$ and $P S$ intersect the line $B D$; we denote the intersections by $X$ and $Y$ respectively. It follows that $X$ lies on $\omega_{1}$, since $\angle Q A B=\angle C D B=\angle B X Q$. Similarly, $Y$ lies on $\omega_{2}$. Thus
$$
D B \cdot D X=D A^{2}=B E^{2}=B D \cdot B Y
$$
hence $D X=B Y$, or $B X=D Y$. Let $T C$ and $B D$ meet at $Z$. Then it follows from $T X \| C D$ and $T Y \| B C$ that
$$
\frac{D Z}{D X}=\frac{C Z}{C T}=\frac{B Z}{B Y}
$$
which immediately gives $D Z=B Z$.

Note. The equality $B X=D Y$ can be also proved by applying Menelaus theorem to $\triangle B D F$ and the lines $R-Q-X$ and $S-P-Y$.
|
{
"resource_path": "IZho/segmented/en-2021_zhautykov_resenja_e.jsonl",
"problem_match": "\n№2.",
"solution_match": "\nFirst solution."
}
|
5a723880-214e-5265-85d4-94cd765f4ce1
| 604,601
|
In a convex cyclic hexagon $A B C D E F \quad B C=E F$ and $C D=A F$. Diagonals $A C$ and $B F$ intersect at point $Q$, and diagonals $E C$ and $D F$ intersect at point $P$. Points $R$ and $S$ are marked on the segments $D F$ and $B F$ respectively so that $F R=P D$ and $B Q=F S$. The segments $R Q$ and $P S$ intersect at point $T$. Prove that the line $T C$ bisects the diagonal $D B$.
|
We follow the first solution, using $B F \| C E$ and $A C \| D F$ to note that $C P F Q$, $C Q R D$, and $C P S B$ are parallelograms.
Let $N$ and $M$ be points on the segments $C Q$ and $R N$ respectively such that $F R N Q$ and $F R M S$ are parallelograms. Then $S M=F R=P D$ and $S M \| P D$, that is, $S M D P$ is also a parallelogram, hence $D M=P S=C B$ and $D M \| C B$, therefore $D M B C$ is a parallelogram, and $C M$ bisects $B D$. It remains to prove that $T, M, C$ are collinear.
Applying Menelaus theorem to $\triangle F R Q$ and the line $P-T-S$ (and bearing in mind the parallelograms found above) we have
$$
1=\frac{F P}{P R} \cdot \frac{R T}{T Q} \cdot \frac{Q S}{S F}=\frac{Q C}{C N} \cdot \frac{R T}{T Q} \cdot \frac{N M}{M R}
$$
that is,
$$
\frac{Q C}{C N} \cdot \frac{R T}{T Q} \cdot \frac{N M}{M R}=1
$$
The collinearity $T, M, C$ follows from (1) immediately by converse Menelaus theorem for $\triangle Q N R$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a convex cyclic hexagon $A B C D E F \quad B C=E F$ and $C D=A F$. Diagonals $A C$ and $B F$ intersect at point $Q$, and diagonals $E C$ and $D F$ intersect at point $P$. Points $R$ and $S$ are marked on the segments $D F$ and $B F$ respectively so that $F R=P D$ and $B Q=F S$. The segments $R Q$ and $P S$ intersect at point $T$. Prove that the line $T C$ bisects the diagonal $D B$.
|
We follow the first solution, using $B F \| C E$ and $A C \| D F$ to note that $C P F Q$, $C Q R D$, and $C P S B$ are parallelograms.
Let $N$ and $M$ be points on the segments $C Q$ and $R N$ respectively such that $F R N Q$ and $F R M S$ are parallelograms. Then $S M=F R=P D$ and $S M \| P D$, that is, $S M D P$ is also a parallelogram, hence $D M=P S=C B$ and $D M \| C B$, therefore $D M B C$ is a parallelogram, and $C M$ bisects $B D$. It remains to prove that $T, M, C$ are collinear.
Applying Menelaus theorem to $\triangle F R Q$ and the line $P-T-S$ (and bearing in mind the parallelograms found above) we have
$$
1=\frac{F P}{P R} \cdot \frac{R T}{T Q} \cdot \frac{Q S}{S F}=\frac{Q C}{C N} \cdot \frac{R T}{T Q} \cdot \frac{N M}{M R}
$$
that is,
$$
\frac{Q C}{C N} \cdot \frac{R T}{T Q} \cdot \frac{N M}{M R}=1
$$
The collinearity $T, M, C$ follows from (1) immediately by converse Menelaus theorem for $\triangle Q N R$.

|
{
"resource_path": "IZho/segmented/en-2021_zhautykov_resenja_e.jsonl",
"problem_match": "\n№2.",
"solution_match": "\nSecond solution."
}
|
5a723880-214e-5265-85d4-94cd765f4ce1
| 604,601
|
Let $n \geq 2$ be an integer. Elwyn is given an $n \times n$ table filled with real numbers (each cell of the table contains exactly one number). We define a rook set as a set of $n$ cells of the table situated in $n$ distinct rows as well as in $n$ distinct columns. Assume that, for every rook set, the sum of $n$ numbers in the cells forming the set is nonnegative.
By a move, Elwyn chooses a row, a column, and a real number $a$, and then he adds $a$ to each number in the chosen row, and subtracts $a$ from each number in the chosen column (thus, the number at the intersection of the chosen row and column does not change). Prove that Elwyn can perform a sequence of moves so that all numbers in the table become nonnegative.
Common remarks. We collect here several definitions and easy observations which will be used in the solutions.
A rook set is nonnegative (resp., vanishing) if the sum of the numbers in its cells is nonnegative (resp., zero). An $n \times n$ table filled with real numbers is good (resp., balanced) if every rook set is nonnegative (resp., vanishing).
Notice that the sum of numbers in any rook set does not change during Elwyn's moves, so good (balanced) tables remain such after any sequence of moves. Also, notice that the rows and/or columns of the table can be permuted with no effect on the condition of the problem, as well as on the desired result.
The proofs of the following two easy propositions can be found in the addendum after Solution 2 .
Proposition 1. Assume that $a_{1}, a_{2}, \ldots, a_{n}$ and $b_{1}, b_{2}, \ldots, b_{n}$ are two sequences of real numbers with equal sums. Then Elwyn can perform a sequence of moves resulting in adding $a_{i}$ to all cells in the $i$ th row, and subtracting $b_{j}$ from all numbers in the $j$ th column, for all $i, j=1,2, \ldots, n$.
Proposition 2. If an $n \times n$ table $B$ is balanced, then Elwyn can perform several moves on that table getting a table filled with zeros.
|
We start with the following known consequence of Hall's lemma.
Lemma. Let $G=(U \sqcup V, E)$ be a bipartite multigraph with parts $U$ and $V$, both of size $n$. Assume that each vertex has degree $k$; then the edges can be partitioned into $k$ perfect matchings.
Proof. Induction on $k$; the base case $k=1$ is trivial. To perform the step, it suffices to find one perfect matching in the graph: removing the edges of that matching, we obtain a graph with all degrees equal to $k-1$.
The existence of such matching is guaranteed by Hall's lemma. Indeed, let $U^{\prime}$ be any subset of $U$, and let $V^{\prime}$ be the set of vertices adjacent to $U^{\prime}$. Put $u=\left|U^{\prime}\right|$ and $v=\left|V^{\prime}\right|$. The total degree of vertices in $U^{\prime}$ is $k u$. so the total degree of vertices in $V^{\prime}$ is at least $k u$; hence $k u \leq k v$ and therefore $u \leq v$, which establishes the conditions of Hall's lemma.
The following claim is the principal step in this solution.
Claim. In any good table, one can decrease some numbers so that the table becomes balanced.
Proof. Say that a cell in a good table is blocked if it is contained in a vanishing rook set (so, decreasing the number in the cell would break goodness of the table). First, we show that in any good table one can decrease several numbers so that the table remains good, and all its cells become blocked.
Consider any cell $c$; let $\epsilon$ be the minimal sum in a rook set containing that cell. Decrease the number in $c$ by $\epsilon$; the obtained table is still good, but now $c$ is blocked. Apply such operation to all cells in the table consecutively; we arrive at a good table all whose cells are blocked. We claim that, in fact, this table is balanced.
In the sequel, we use the following correspondence. Let $R$ and $C$ be the sets of rows and columns of the table, respectively. Then each cell corresponds to a pair of the row and the column it is situated in; this pair may be regarded as an edge of a bipartite (multi)graph with parts $R$ and $C$. This way, any rook set corresponds to a perfect matching between those parts.
Arguing indirectly, assume that there is a non-vanishing rook set $S=\left\{s_{1}, s_{2}, \ldots, s_{n}\right\}$. Each cell $s_{i}$ is contained in some vanishing rook set $V_{i}$. Now construct a bipartite multigraph $G=(R \sqcup C, E)$, introducing, for each set $V_{i}, n$ edges corresponding to its cells (thus, $G$ contains $n^{2}$ edges some of which may be parallel).
Mark each edge with the number in the corresponding cell. Since the sets $V_{i}$ are all vanishing, the sum of all $n^{2}$ marks is zero.
Now, remove $n$ edges corresponding to the cells of $S$, to obtain a graph $G^{\prime}$. Since the sum of numbers in the cells of $S$ is positive, the sum of the marks in $G^{\prime}$ is negative. On the other hand, the degree of every vertex in $G^{\prime}$ is $n-1$, so by the Lemma its edges can be partitioned into $n-1$ perfect matchings. At least one of the obtained matchings has negative sum of marks; so this matching corresponds to a rook set with a negative sum. This is impossible in a good table; this contradiction finishes the proof.
Back to the problem, let $T$ be Elwyn's table. Applying the Claim, decrease some numbers in it to get a balanced table $B$. By Proposition 2, Elwyn can perform some moves on table $B$ so as to get a table filled with zeros. Applying the same moves to $T$, Elwyn gets a table where all numbers are nonnegative, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq 2$ be an integer. Elwyn is given an $n \times n$ table filled with real numbers (each cell of the table contains exactly one number). We define a rook set as a set of $n$ cells of the table situated in $n$ distinct rows as well as in $n$ distinct columns. Assume that, for every rook set, the sum of $n$ numbers in the cells forming the set is nonnegative.
By a move, Elwyn chooses a row, a column, and a real number $a$, and then he adds $a$ to each number in the chosen row, and subtracts $a$ from each number in the chosen column (thus, the number at the intersection of the chosen row and column does not change). Prove that Elwyn can perform a sequence of moves so that all numbers in the table become nonnegative.
Common remarks. We collect here several definitions and easy observations which will be used in the solutions.
A rook set is nonnegative (resp., vanishing) if the sum of the numbers in its cells is nonnegative (resp., zero). An $n \times n$ table filled with real numbers is good (resp., balanced) if every rook set is nonnegative (resp., vanishing).
Notice that the sum of numbers in any rook set does not change during Elwyn's moves, so good (balanced) tables remain such after any sequence of moves. Also, notice that the rows and/or columns of the table can be permuted with no effect on the condition of the problem, as well as on the desired result.
The proofs of the following two easy propositions can be found in the addendum after Solution 2 .
Proposition 1. Assume that $a_{1}, a_{2}, \ldots, a_{n}$ and $b_{1}, b_{2}, \ldots, b_{n}$ are two sequences of real numbers with equal sums. Then Elwyn can perform a sequence of moves resulting in adding $a_{i}$ to all cells in the $i$ th row, and subtracting $b_{j}$ from all numbers in the $j$ th column, for all $i, j=1,2, \ldots, n$.
Proposition 2. If an $n \times n$ table $B$ is balanced, then Elwyn can perform several moves on that table getting a table filled with zeros.
|
We start with the following known consequence of Hall's lemma.
Lemma. Let $G=(U \sqcup V, E)$ be a bipartite multigraph with parts $U$ and $V$, both of size $n$. Assume that each vertex has degree $k$; then the edges can be partitioned into $k$ perfect matchings.
Proof. Induction on $k$; the base case $k=1$ is trivial. To perform the step, it suffices to find one perfect matching in the graph: removing the edges of that matching, we obtain a graph with all degrees equal to $k-1$.
The existence of such matching is guaranteed by Hall's lemma. Indeed, let $U^{\prime}$ be any subset of $U$, and let $V^{\prime}$ be the set of vertices adjacent to $U^{\prime}$. Put $u=\left|U^{\prime}\right|$ and $v=\left|V^{\prime}\right|$. The total degree of vertices in $U^{\prime}$ is $k u$. so the total degree of vertices in $V^{\prime}$ is at least $k u$; hence $k u \leq k v$ and therefore $u \leq v$, which establishes the conditions of Hall's lemma.
The following claim is the principal step in this solution.
Claim. In any good table, one can decrease some numbers so that the table becomes balanced.
Proof. Say that a cell in a good table is blocked if it is contained in a vanishing rook set (so, decreasing the number in the cell would break goodness of the table). First, we show that in any good table one can decrease several numbers so that the table remains good, and all its cells become blocked.
Consider any cell $c$; let $\epsilon$ be the minimal sum in a rook set containing that cell. Decrease the number in $c$ by $\epsilon$; the obtained table is still good, but now $c$ is blocked. Apply such operation to all cells in the table consecutively; we arrive at a good table all whose cells are blocked. We claim that, in fact, this table is balanced.
In the sequel, we use the following correspondence. Let $R$ and $C$ be the sets of rows and columns of the table, respectively. Then each cell corresponds to a pair of the row and the column it is situated in; this pair may be regarded as an edge of a bipartite (multi)graph with parts $R$ and $C$. This way, any rook set corresponds to a perfect matching between those parts.
Arguing indirectly, assume that there is a non-vanishing rook set $S=\left\{s_{1}, s_{2}, \ldots, s_{n}\right\}$. Each cell $s_{i}$ is contained in some vanishing rook set $V_{i}$. Now construct a bipartite multigraph $G=(R \sqcup C, E)$, introducing, for each set $V_{i}, n$ edges corresponding to its cells (thus, $G$ contains $n^{2}$ edges some of which may be parallel).
Mark each edge with the number in the corresponding cell. Since the sets $V_{i}$ are all vanishing, the sum of all $n^{2}$ marks is zero.
Now, remove $n$ edges corresponding to the cells of $S$, to obtain a graph $G^{\prime}$. Since the sum of numbers in the cells of $S$ is positive, the sum of the marks in $G^{\prime}$ is negative. On the other hand, the degree of every vertex in $G^{\prime}$ is $n-1$, so by the Lemma its edges can be partitioned into $n-1$ perfect matchings. At least one of the obtained matchings has negative sum of marks; so this matching corresponds to a rook set with a negative sum. This is impossible in a good table; this contradiction finishes the proof.
Back to the problem, let $T$ be Elwyn's table. Applying the Claim, decrease some numbers in it to get a balanced table $B$. By Proposition 2, Elwyn can perform some moves on table $B$ so as to get a table filled with zeros. Applying the same moves to $T$, Elwyn gets a table where all numbers are nonnegative, as required.
|
{
"resource_path": "IZho/segmented/en-2021_zhautykov_resenja_e.jsonl",
"problem_match": "\n№3.",
"solution_match": "\nSolution 1."
}
|
4b16b1c7-fc89-50b5-b012-c63e876861f1
| 604,626
|
Let $P(x)$ be a nonconstant polynomial of degree $n$ with rational coefficients which can not be presented as a product of two nonconstant polynomials with rational coefficients. Prove that the number of polynomials $Q(x)$ of degree less than $n$ with rational coefficients such that $P(x)$ divides $P(Q(x))$
a) is finite;
b) does not exceed $n$.
|
It is known that an irreducible polynomial $P(x)$ of degree $n$ with rational coefficients has $n$ different complex roots which we denote by $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{n}$.
a) If $P(x)$ divides $P(Q(x))$, then $Q\left(\alpha_{k}\right)$ is also a root of $P(x)$ for each $k \leq n$. It follows that the values of $Q$ at $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{n}$ form a sequence $\alpha_{i_{1}}, \alpha_{i_{2}}, \ldots, \alpha_{i_{n}}$, where all terms are roots of $P$, not necessarily different. The number of such sequences is $n^{n}$, and for each sequence there exists at most one polynomial $Q$ such that $Q\left(\alpha_{k}\right)=\alpha_{i_{k}}$ (since two polynomials of degree less than $n$ with equal values at $n$ points must coincide).
Thus the number of possible polynomials $Q(x)$ does not exceed $n^{n}$.
b) For each polynomial $Q$ satisfying the condition, $Q\left(\alpha_{1}\right)$ equals one of the roots $\alpha_{i}$. However, there is at most one polynomial $Q$ of degree less than $n$ with rational coefficients such that $Q\left(\alpha_{1}\right)=\alpha_{i}$, Indeed, if $Q_{1}\left(\alpha_{1}\right)=Q_{2}\left(\alpha_{1}\right)=\alpha_{i}$, then $\alpha_{1}$ is a root of the polynomial $Q_{1}-Q_{2}$ with rational coefficients and degree less than $n$. If this polynomial is not identically zero, its greatest common divisor with $P$ is a nonconstant divisor of $P$ with rational coefficients and degree less than $n$, a contradiction.
Thus the number of possible polynomials $Q(x)$ does not exceed $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P(x)$ be a nonconstant polynomial of degree $n$ with rational coefficients which can not be presented as a product of two nonconstant polynomials with rational coefficients. Prove that the number of polynomials $Q(x)$ of degree less than $n$ with rational coefficients such that $P(x)$ divides $P(Q(x))$
a) is finite;
b) does not exceed $n$.
|
It is known that an irreducible polynomial $P(x)$ of degree $n$ with rational coefficients has $n$ different complex roots which we denote by $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{n}$.
a) If $P(x)$ divides $P(Q(x))$, then $Q\left(\alpha_{k}\right)$ is also a root of $P(x)$ for each $k \leq n$. It follows that the values of $Q$ at $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{n}$ form a sequence $\alpha_{i_{1}}, \alpha_{i_{2}}, \ldots, \alpha_{i_{n}}$, where all terms are roots of $P$, not necessarily different. The number of such sequences is $n^{n}$, and for each sequence there exists at most one polynomial $Q$ such that $Q\left(\alpha_{k}\right)=\alpha_{i_{k}}$ (since two polynomials of degree less than $n$ with equal values at $n$ points must coincide).
Thus the number of possible polynomials $Q(x)$ does not exceed $n^{n}$.
b) For each polynomial $Q$ satisfying the condition, $Q\left(\alpha_{1}\right)$ equals one of the roots $\alpha_{i}$. However, there is at most one polynomial $Q$ of degree less than $n$ with rational coefficients such that $Q\left(\alpha_{1}\right)=\alpha_{i}$, Indeed, if $Q_{1}\left(\alpha_{1}\right)=Q_{2}\left(\alpha_{1}\right)=\alpha_{i}$, then $\alpha_{1}$ is a root of the polynomial $Q_{1}-Q_{2}$ with rational coefficients and degree less than $n$. If this polynomial is not identically zero, its greatest common divisor with $P$ is a nonconstant divisor of $P$ with rational coefficients and degree less than $n$, a contradiction.
Thus the number of possible polynomials $Q(x)$ does not exceed $n$.
|
{
"resource_path": "IZho/segmented/en-2021_zhautykov_resenja_e.jsonl",
"problem_match": "\n№6.",
"solution_match": "\nSolution."
}
|
ba713fcc-9ea0-50b9-8002-b2074ba7e923
| 604,685
|
In the triangle $\mathrm{ABC}$, the midpoints of $\mathrm{AC}$ and $\mathrm{AB}$ are $\mathrm{M}$ and $\mathrm{N}$ respectively. $\mathrm{BM}$ and $\mathrm{CN}$ meet at $P$. Show that if it is possible to inscribe a circle in the quadrilateral AMPN (touching every side), then $\mathrm{ABC}$ is isosceles.
|
If the quadrilateral has an inscribed circle then $\mathrm{AM}+\mathrm{PN}=\mathrm{AN}+\mathrm{PM}$ (consider the tangents to the circle from $A, M, P, N$ ). But if $\mathrm{AB}>\mathrm{AC}$, then $\mathrm{BM}>\mathrm{CN}$ (see below). We have $\mathrm{AN}=$ $\mathrm{AB} / 2, \mathrm{PM}=\mathrm{BM} / 3, \mathrm{AM}=\mathrm{AC} / 2, \mathrm{PN}=\mathrm{CN} / 3$, so it follows that $\mathrm{AM}+\mathrm{PN}<\mathrm{AN}+\mathrm{PM}$. Similarly, $\mathrm{AB}<\mathrm{AC}$ implies $\mathrm{AM}+\mathrm{PN}>\mathrm{AN}+\mathrm{PM}$, so the triangle must be isosceles.
To prove the result about the medians, note that $\mathrm{BM}^{2}=\mathrm{BC}^{2}+\mathrm{CM}^{2}-2 \mathrm{BC} . \mathrm{CM} \cos \mathrm{C}=(\mathrm{BC}-$ $\mathrm{CM} \cos \mathrm{C})^{2}+(\mathrm{CM} \sin \mathrm{C})^{2}$. Similarly, $\mathrm{CN}^{2}=(\mathrm{BC}-\mathrm{BN} \cos \mathrm{B})^{2}+(\mathrm{BN} \sin \mathrm{B})^{2}$. But $\mathrm{MN}$ is parallel to $\mathrm{BC}$, so $\mathrm{CM} \sin \mathrm{C}=\mathrm{BN} \sin \mathrm{B}$. But $\mathrm{AB}>\mathrm{AC}$, so $\mathrm{BN}>\mathrm{CM}$ and $\mathrm{B}<\mathrm{C}$, so $\cos \mathrm{B}>$ $\cos \mathrm{C}$, hence $\mathrm{BN} \cos \mathrm{B}>\mathrm{CM} \cos \mathrm{C}$ and $\mathrm{BC}-\mathrm{CM} \cos \mathrm{C}>\mathrm{BC}-\mathrm{BN} \cos \mathrm{B}$. So $\mathrm{BM}>\mathrm{CN}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In the triangle $\mathrm{ABC}$, the midpoints of $\mathrm{AC}$ and $\mathrm{AB}$ are $\mathrm{M}$ and $\mathrm{N}$ respectively. $\mathrm{BM}$ and $\mathrm{CN}$ meet at $P$. Show that if it is possible to inscribe a circle in the quadrilateral AMPN (touching every side), then $\mathrm{ABC}$ is isosceles.
|

If the quadrilateral has an inscribed circle then $\mathrm{AM}+\mathrm{PN}=\mathrm{AN}+\mathrm{PM}$ (consider the tangents to the circle from $A, M, P, N$ ). But if $\mathrm{AB}>\mathrm{AC}$, then $\mathrm{BM}>\mathrm{CN}$ (see below). We have $\mathrm{AN}=$ $\mathrm{AB} / 2, \mathrm{PM}=\mathrm{BM} / 3, \mathrm{AM}=\mathrm{AC} / 2, \mathrm{PN}=\mathrm{CN} / 3$, so it follows that $\mathrm{AM}+\mathrm{PN}<\mathrm{AN}+\mathrm{PM}$. Similarly, $\mathrm{AB}<\mathrm{AC}$ implies $\mathrm{AM}+\mathrm{PN}>\mathrm{AN}+\mathrm{PM}$, so the triangle must be isosceles.
To prove the result about the medians, note that $\mathrm{BM}^{2}=\mathrm{BC}^{2}+\mathrm{CM}^{2}-2 \mathrm{BC} . \mathrm{CM} \cos \mathrm{C}=(\mathrm{BC}-$ $\mathrm{CM} \cos \mathrm{C})^{2}+(\mathrm{CM} \sin \mathrm{C})^{2}$. Similarly, $\mathrm{CN}^{2}=(\mathrm{BC}-\mathrm{BN} \cos \mathrm{B})^{2}+(\mathrm{BN} \sin \mathrm{B})^{2}$. But $\mathrm{MN}$ is parallel to $\mathrm{BC}$, so $\mathrm{CM} \sin \mathrm{C}=\mathrm{BN} \sin \mathrm{B}$. But $\mathrm{AB}>\mathrm{AC}$, so $\mathrm{BN}>\mathrm{CM}$ and $\mathrm{B}<\mathrm{C}$, so $\cos \mathrm{B}>$ $\cos \mathrm{C}$, hence $\mathrm{BN} \cos \mathrm{B}>\mathrm{CM} \cos \mathrm{C}$ and $\mathrm{BC}-\mathrm{CM} \cos \mathrm{C}>\mathrm{BC}-\mathrm{BN} \cos \mathrm{B}$. So $\mathrm{BM}>\mathrm{CN}$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A2",
"solution_match": "\n## Solution"
}
|
1ba97342-4c33-51b2-8cd6-a5087819247c
| 604,797
|
Show that if $(2+\sqrt{3})^{k}=1+m+n \sqrt{3}$, for positive integers $m, n, k$ with $k$ odd, then $m$ is a perfect square.
|
We have $(2+\sqrt{ } 3)^{4}=97+56 \sqrt{ } 3=14(7+4 \sqrt{ } 3)-1=14(2+\sqrt{ } 3)^{2}-1$. Hence $(2+\sqrt{3})^{k+2}=14$ $(2+\sqrt{3})^{k}-(2+\sqrt{3})^{k-2}$. Thus if $(2+\sqrt{3})^{k}=a_{k}+b_{k} \sqrt{3}$, then $a_{k+2}=14 a_{k}-a_{k-2}$.
Now suppose the sequence $c_{k}$ satisfies $c_{1}=1, c_{2}=5, c_{k+1}=4 c_{k}-c_{k-1}$. We claim that $c_{k}^{2}-c_{k-}$ ${ }_{1} c_{k+1}=6$. Induction on $\mathrm{k}$. We have $c_{3}=19$, so $c_{2}{ }^{2}-c_{1} c_{3}=25-19=6$. Thus the result is true for $\mathrm{k}=2$. Suppose it is true for $\mathrm{k}$. Then $c_{k+1}=4 c_{k}-c_{k-1}$, so $c_{k+1}{ }^{2}=4 c_{k} c_{k+1}-c_{k-1} c_{k+1}=4 c_{k} c_{k+1}$ $-c_{k}^{2}+6=c_{k}\left(4 c_{k+1}-c_{k}\right)+6=c_{k} c_{k+2}+6$, so the result is true for $k+1$.
Now put $\mathrm{d}_{\mathrm{k}}=\mathrm{c}_{\mathrm{k}}^{2}+1$. We show that $\mathrm{d}_{\mathrm{k}+2}=14 \mathrm{~d}_{\mathrm{k}+1}-\mathrm{d}_{\mathrm{k}}$. Induction on $\mathrm{k}$. We have $\mathrm{d}_{1}=2, \mathrm{~d}_{2}=$ $26, \mathrm{~d}_{3}=362=14 \mathrm{~d}_{2}-\mathrm{d}_{1}$, so the result is true for $\mathrm{k}=1$. Suppose it is true for $\mathrm{k}$. We have $\mathrm{c}_{\mathrm{k}+3}-$ $4 c_{k+2}+c_{k+1}=0$. Hence $12+2 c_{k+3} c_{k+1}-8 c_{k+2} c_{k+1}+2 c_{k+1}{ }^{2}=12$. Hence $2 c_{k+2}{ }^{2}-8 c_{k+2} c_{k+1}+2$ $c_{k+1}^{2}=12$. Hence $16 c_{k+2}{ }^{2}-8 c_{k+2} c_{k+1}+c_{k+1}{ }^{2}+1=14 c_{k+2}{ }^{2}+14-c_{k+1}{ }^{2}-1$, or $\left(4 c_{k+2}-c_{k+1}\right)^{2}+$ $1=14\left(c_{k+2}^{2}+1\right)-\left(c_{k+1}{ }^{2}+1\right)$, or $\mathrm{c}_{\mathrm{k}+3^{2}}+1=14\left(\mathrm{c}_{\mathrm{k}+2}{ }^{2}+1\right)-\left(\mathrm{c}_{\mathrm{k}+1}{ }^{2}+1\right)$, or $\mathrm{d}_{\mathrm{k}+3}=14 \mathrm{~d}_{\mathrm{k}+2}-\mathrm{d}_{\mathrm{k}+1}$. So the result is true for all $\mathrm{k}$.
But $\mathrm{a}_{1}=2, \mathrm{a}_{3}=26$ and $\mathrm{a}_{2 \mathrm{k}+3}=14 \mathrm{a}_{2 \mathrm{k}+1}-\mathrm{a}_{2 k-1}$, and $\mathrm{d}_{1}=2, \mathrm{~d}_{2}=26$ and $\mathrm{d}_{\mathrm{k}+1}=14 \mathrm{~d}_{\mathrm{k}}-\mathrm{d}_{\mathrm{k}-1}$. Hence $\mathrm{a}_{2 \mathrm{k}-1}=\mathrm{d}_{\mathrm{k}}=\mathrm{c}_{\mathrm{k}}^{2}+1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that if $(2+\sqrt{3})^{k}=1+m+n \sqrt{3}$, for positive integers $m, n, k$ with $k$ odd, then $m$ is a perfect square.
|
We have $(2+\sqrt{ } 3)^{4}=97+56 \sqrt{ } 3=14(7+4 \sqrt{ } 3)-1=14(2+\sqrt{ } 3)^{2}-1$. Hence $(2+\sqrt{3})^{k+2}=14$ $(2+\sqrt{3})^{k}-(2+\sqrt{3})^{k-2}$. Thus if $(2+\sqrt{3})^{k}=a_{k}+b_{k} \sqrt{3}$, then $a_{k+2}=14 a_{k}-a_{k-2}$.
Now suppose the sequence $c_{k}$ satisfies $c_{1}=1, c_{2}=5, c_{k+1}=4 c_{k}-c_{k-1}$. We claim that $c_{k}^{2}-c_{k-}$ ${ }_{1} c_{k+1}=6$. Induction on $\mathrm{k}$. We have $c_{3}=19$, so $c_{2}{ }^{2}-c_{1} c_{3}=25-19=6$. Thus the result is true for $\mathrm{k}=2$. Suppose it is true for $\mathrm{k}$. Then $c_{k+1}=4 c_{k}-c_{k-1}$, so $c_{k+1}{ }^{2}=4 c_{k} c_{k+1}-c_{k-1} c_{k+1}=4 c_{k} c_{k+1}$ $-c_{k}^{2}+6=c_{k}\left(4 c_{k+1}-c_{k}\right)+6=c_{k} c_{k+2}+6$, so the result is true for $k+1$.
Now put $\mathrm{d}_{\mathrm{k}}=\mathrm{c}_{\mathrm{k}}^{2}+1$. We show that $\mathrm{d}_{\mathrm{k}+2}=14 \mathrm{~d}_{\mathrm{k}+1}-\mathrm{d}_{\mathrm{k}}$. Induction on $\mathrm{k}$. We have $\mathrm{d}_{1}=2, \mathrm{~d}_{2}=$ $26, \mathrm{~d}_{3}=362=14 \mathrm{~d}_{2}-\mathrm{d}_{1}$, so the result is true for $\mathrm{k}=1$. Suppose it is true for $\mathrm{k}$. We have $\mathrm{c}_{\mathrm{k}+3}-$ $4 c_{k+2}+c_{k+1}=0$. Hence $12+2 c_{k+3} c_{k+1}-8 c_{k+2} c_{k+1}+2 c_{k+1}{ }^{2}=12$. Hence $2 c_{k+2}{ }^{2}-8 c_{k+2} c_{k+1}+2$ $c_{k+1}^{2}=12$. Hence $16 c_{k+2}{ }^{2}-8 c_{k+2} c_{k+1}+c_{k+1}{ }^{2}+1=14 c_{k+2}{ }^{2}+14-c_{k+1}{ }^{2}-1$, or $\left(4 c_{k+2}-c_{k+1}\right)^{2}+$ $1=14\left(c_{k+2}^{2}+1\right)-\left(c_{k+1}{ }^{2}+1\right)$, or $\mathrm{c}_{\mathrm{k}+3^{2}}+1=14\left(\mathrm{c}_{\mathrm{k}+2}{ }^{2}+1\right)-\left(\mathrm{c}_{\mathrm{k}+1}{ }^{2}+1\right)$, or $\mathrm{d}_{\mathrm{k}+3}=14 \mathrm{~d}_{\mathrm{k}+2}-\mathrm{d}_{\mathrm{k}+1}$. So the result is true for all $\mathrm{k}$.
But $\mathrm{a}_{1}=2, \mathrm{a}_{3}=26$ and $\mathrm{a}_{2 \mathrm{k}+3}=14 \mathrm{a}_{2 \mathrm{k}+1}-\mathrm{a}_{2 k-1}$, and $\mathrm{d}_{1}=2, \mathrm{~d}_{2}=26$ and $\mathrm{d}_{\mathrm{k}+1}=14 \mathrm{~d}_{\mathrm{k}}-\mathrm{d}_{\mathrm{k}-1}$. Hence $\mathrm{a}_{2 \mathrm{k}-1}=\mathrm{d}_{\mathrm{k}}=\mathrm{c}_{\mathrm{k}}^{2}+1$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A3",
"solution_match": "\n## Solution"
}
|
3b5e1290-2b94-5e30-a824-da31466cc5a2
| 604,811
|
$\mathrm{ABCD}$ is a convex quadrilateral. $\mathrm{P}, \mathrm{Q}$ are points on the sides $\mathrm{AD}, \mathrm{BC}$ respectively such that $\mathrm{AP} / \mathrm{PD}=\mathrm{BQ} / \mathrm{QC}=\mathrm{AB} / \mathrm{CD}$. Show that the angle between the lines $\mathrm{PQ}$ and $\mathrm{AB}$ equals the angle between the lines $\mathrm{PQ}$ and $\mathrm{CD}$.
|
If $\mathrm{AB}$ is parallel to $\mathrm{CD}$, then it is obvious that $\mathrm{PQ}$ is parallel to both. So assume $\mathrm{AB}$ and $\mathrm{CD}$ meet at $O$. Take $O$ as the origin for vectors. Let $\mathbf{e}$ be a unit vector in the direction OA and $\mathbf{f}$ a unit vector in the direction OC. Take the vector OA to be ae, OB to be be, OC to be cf, and OD to be df. Then OP is $((d-c) a e+(a-b) d \mathbf{f}) /(d-c+a-b)$ and OQ is $((d-c) b e+(a-$ b)cf)/(d - c + a - b). Hence PQ is $(c-d)(a-b)(\mathbf{e}+\mathbf{f}) /(d-c+a-b)$. But $\mathbf{e}$ and $\mathbf{f}$ are unit vectors, so $\mathbf{e}+\mathbf{f}$ makes the same angle with each of them and hence $P Q$ makes the same angle with $A B$ and CD.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$\mathrm{ABCD}$ is a convex quadrilateral. $\mathrm{P}, \mathrm{Q}$ are points on the sides $\mathrm{AD}, \mathrm{BC}$ respectively such that $\mathrm{AP} / \mathrm{PD}=\mathrm{BQ} / \mathrm{QC}=\mathrm{AB} / \mathrm{CD}$. Show that the angle between the lines $\mathrm{PQ}$ and $\mathrm{AB}$ equals the angle between the lines $\mathrm{PQ}$ and $\mathrm{CD}$.
|

If $\mathrm{AB}$ is parallel to $\mathrm{CD}$, then it is obvious that $\mathrm{PQ}$ is parallel to both. So assume $\mathrm{AB}$ and $\mathrm{CD}$ meet at $O$. Take $O$ as the origin for vectors. Let $\mathbf{e}$ be a unit vector in the direction OA and $\mathbf{f}$ a unit vector in the direction OC. Take the vector OA to be ae, OB to be be, OC to be cf, and OD to be df. Then OP is $((d-c) a e+(a-b) d \mathbf{f}) /(d-c+a-b)$ and OQ is $((d-c) b e+(a-$ b)cf)/(d - c + a - b). Hence PQ is $(c-d)(a-b)(\mathbf{e}+\mathbf{f}) /(d-c+a-b)$. But $\mathbf{e}$ and $\mathbf{f}$ are unit vectors, so $\mathbf{e}+\mathbf{f}$ makes the same angle with each of them and hence $P Q$ makes the same angle with $A B$ and CD.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B3",
"solution_match": "\n## Solution"
}
|
348214de-f4d3-5d7a-b5ae-6298ffea349e
| 604,172
|
The sides of a triangle form an arithmetic progression. The altitudes also form an arithmetic progression. Show that the triangle must be equilateral.
|
Let the sides be $a$, $a+d, a+2 d$ with $d>=0$. Then the altitudes are $k / a \geq k /(a+d) \geq k /(a+2 d)$, where $k$ is twice the area. We claim that $k / a+k /(a+2 d)>2 k /(a+d)$ unless $d=0$. This is equivalent to $(a+d)(a+2 d)+a(a+d)>2 a(a+2 d)$ or $2 d^{2}>0$, which is obviously true. So the altitudes can only form an arithmetic progression if $\mathrm{d}=0$ and hence the triangle is equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The sides of a triangle form an arithmetic progression. The altitudes also form an arithmetic progression. Show that the triangle must be equilateral.
|
Let the sides be $a$, $a+d, a+2 d$ with $d>=0$. Then the altitudes are $k / a \geq k /(a+d) \geq k /(a+2 d)$, where $k$ is twice the area. We claim that $k / a+k /(a+2 d)>2 k /(a+d)$ unless $d=0$. This is equivalent to $(a+d)(a+2 d)+a(a+d)>2 a(a+2 d)$ or $2 d^{2}>0$, which is obviously true. So the altitudes can only form an arithmetic progression if $\mathrm{d}=0$ and hence the triangle is equilateral.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A1",
"solution_match": "\n## Solution"
}
|
113f2fa7-4e30-5c37-a5c8-e28f3b6691ca
| 604,192
|
The positive integers $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}, \mathrm{p}, \mathrm{q}$ satisfy $\mathrm{ad}-\mathrm{bc}=1 \mathrm{and} \mathrm{a} / \mathrm{b}>\mathrm{p} / \mathrm{q}>\mathrm{c} / \mathrm{d}$. Show that $\mathrm{q}>=\mathrm{b}+$ $d$ and that if $q=b+d$, then $p=a+c$.
|
$\mathrm{p} / \mathrm{q}>\mathrm{c} / \mathrm{d}$ implies $\mathrm{pd}>\mathrm{cq}$ and hence $\mathrm{pd}>=\mathrm{cq}+1$, so $\mathrm{p} / \mathrm{q} \geq \mathrm{c} / \mathrm{d}+1 /(\mathrm{qd})$. Similarly, $\mathrm{a} / \mathrm{b}>\mathrm{p} / \mathrm{q}$ implies $a / b \geq p / q+1 /(b q)$. So $a / b-c / d \geq 1 /(q d)+1 /(q b)=(b+d) /(q b d)$. But $a / b-c / d=1 / b d$. Hence $\mathrm{q} \geq \mathrm{b}+\mathrm{d}$.
Now assume $\mathrm{q}=\mathrm{b}+\mathrm{d}$. We have $\mathrm{ad}-\mathrm{bc}=1 \leq \mathrm{d}$, so $\mathrm{ad}+\mathrm{cd}-\mathrm{d} \leq \mathrm{bc}+\mathrm{cd}$ and hence ( $\mathrm{a}+\mathrm{c}-$ 1)/(b+d) $\leq c /$ d. So $p \geq a+c$. Similarly $a d-b c \leq b$, so $b c+b+a b \geq a d+a b$, so $(a+c+1) /(b+d)$ $\geq a / b$. So $p \leq a+c$. Hence $p=a+c$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
The positive integers $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}, \mathrm{p}, \mathrm{q}$ satisfy $\mathrm{ad}-\mathrm{bc}=1 \mathrm{and} \mathrm{a} / \mathrm{b}>\mathrm{p} / \mathrm{q}>\mathrm{c} / \mathrm{d}$. Show that $\mathrm{q}>=\mathrm{b}+$ $d$ and that if $q=b+d$, then $p=a+c$.
|
$\mathrm{p} / \mathrm{q}>\mathrm{c} / \mathrm{d}$ implies $\mathrm{pd}>\mathrm{cq}$ and hence $\mathrm{pd}>=\mathrm{cq}+1$, so $\mathrm{p} / \mathrm{q} \geq \mathrm{c} / \mathrm{d}+1 /(\mathrm{qd})$. Similarly, $\mathrm{a} / \mathrm{b}>\mathrm{p} / \mathrm{q}$ implies $a / b \geq p / q+1 /(b q)$. So $a / b-c / d \geq 1 /(q d)+1 /(q b)=(b+d) /(q b d)$. But $a / b-c / d=1 / b d$. Hence $\mathrm{q} \geq \mathrm{b}+\mathrm{d}$.
Now assume $\mathrm{q}=\mathrm{b}+\mathrm{d}$. We have $\mathrm{ad}-\mathrm{bc}=1 \leq \mathrm{d}$, so $\mathrm{ad}+\mathrm{cd}-\mathrm{d} \leq \mathrm{bc}+\mathrm{cd}$ and hence ( $\mathrm{a}+\mathrm{c}-$ 1)/(b+d) $\leq c /$ d. So $p \geq a+c$. Similarly $a d-b c \leq b$, so $b c+b+a b \geq a d+a b$, so $(a+c+1) /(b+d)$ $\geq a / b$. So $p \leq a+c$. Hence $p=a+c$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A2",
"solution_match": "\n## Solution"
}
|
26a07f50-74a2-57c6-afd0-b9ef9869c294
| 604,212
|
$\mathrm{P}$ is a fixed point in the plane. Show that amongst triangles $\mathrm{ABC}$ such that $\mathrm{PA}=3, \mathrm{~PB}=5, \mathrm{PC}$ $=7$, those with the largest perimeter have $\mathrm{P}$ as incenter.
|
Given points $\mathrm{P}, \mathrm{B}, \mathrm{C}$ and a fixed circle center $\mathrm{P}$, we show that the point $\mathrm{A}$ on the circle which maximises $\mathrm{AB}+\mathrm{AC}$ is such that $\mathrm{PA}$ bisects angle $\mathrm{BAC}$. Consider a point $\mathrm{A}^{\prime}$ close to $\mathrm{A}$. Then the change in $A B+A C$ as we move $A$ to $A^{\prime}$ is $A A^{\prime}(\sin P A C-\sin P A B)+O\left(A A^{\prime 2}\right)$. So for a maximal configuration we must have $\sin \mathrm{PAC}=\sin \mathrm{PAB}$, otherwise we could get a larger sum by taking A' on one side or the other. This applies to each vertex of the triangle, so $\mathrm{P}$ must be the incenter.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$\mathrm{P}$ is a fixed point in the plane. Show that amongst triangles $\mathrm{ABC}$ such that $\mathrm{PA}=3, \mathrm{~PB}=5, \mathrm{PC}$ $=7$, those with the largest perimeter have $\mathrm{P}$ as incenter.
|

Given points $\mathrm{P}, \mathrm{B}, \mathrm{C}$ and a fixed circle center $\mathrm{P}$, we show that the point $\mathrm{A}$ on the circle which maximises $\mathrm{AB}+\mathrm{AC}$ is such that $\mathrm{PA}$ bisects angle $\mathrm{BAC}$. Consider a point $\mathrm{A}^{\prime}$ close to $\mathrm{A}$. Then the change in $A B+A C$ as we move $A$ to $A^{\prime}$ is $A A^{\prime}(\sin P A C-\sin P A B)+O\left(A A^{\prime 2}\right)$. So for a maximal configuration we must have $\sin \mathrm{PAC}=\sin \mathrm{PAB}$, otherwise we could get a larger sum by taking A' on one side or the other. This applies to each vertex of the triangle, so $\mathrm{P}$ must be the incenter.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A3",
"solution_match": "\n## Solution"
}
|
98e43018-f002-5d0c-a046-4248edabb354
| 604,231
|
Points $\mathrm{A}_{1}, \mathrm{~A}_{2}, \ldots, \mathrm{A}_{\mathrm{n}}$ are equally spaced on the side $\mathrm{BC}$ of the triangle $\mathrm{ABC}$ (so that $\mathrm{BA}_{1}=$ $\left.A_{1} A_{2}=\ldots=A_{n-1} A_{n}=A_{n} C\right)$. Similarly, points $B_{1}, B_{2}, \ldots, B_{n}$ are equally spaced on the side CA, and points $\mathrm{C}_{1}, \mathrm{C}_{2}, \ldots, \mathrm{C}_{\mathrm{n}}$ are equally spaced on the side $\mathrm{AB}$. Show that $\left(\mathrm{AA}_{1}{ }^{2}+\mathrm{AA}_{2}{ }^{2}+\ldots+\right.$ $\left.\mathrm{AA}_{\mathrm{n}}{ }^{2}+\mathrm{BB}_{1}{ }^{2}+\mathrm{BB}_{2}{ }^{2}+\ldots+\mathrm{BB}_{\mathrm{n}}{ }^{2}+\mathrm{C}_{1}{ }^{2}+\ldots+\mathrm{CC}_{\mathrm{n}}{ }^{2}\right)$ is a rational multiple of $\left(\mathrm{AB}^{2}+\mathrm{BC}^{2}+\right.$ $\left.\mathrm{CA}^{2}\right)$.
|
Using the cosine formula, $\mathrm{AA}_{\mathrm{k}}{ }^{2}=\mathrm{AB}^{2}+\mathrm{k}^{2} \mathrm{BC}^{2} /(\mathrm{n}+1)^{2}-2 \mathrm{k} A \mathrm{AB} \cdot \mathrm{BC} /(\mathrm{n}+1) \cos \mathrm{B}$. So $\sum \mathrm{AA}_{\mathrm{k}}{ }^{2}=$ $n B^{2}+B C^{2} /(n+1)^{2}\left(1^{2}+2^{2}+\ldots+n^{2}\right)-2 A B \cdot B C \cos B(1+2+\ldots+n) /(n+1)$. Similarly for the other two sides.
Thus the total sum is $n\left(\mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{CA}^{2}\right)+\mathrm{n}(2 \mathrm{n}+1) /(6(\mathrm{n}+1))\left(\mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{CA}^{2}\right)-\mathrm{n}$ $(\mathrm{AB} \cdot \mathrm{BC} \cos \mathrm{B}+\mathrm{BC} \cdot \mathrm{CA} \cos \mathrm{C}+\mathrm{CA} \cdot \mathrm{AB} \cos \mathrm{A})$. $\mathrm{But} \mathrm{AB} \cdot \mathrm{BC} \cos \mathrm{B}=\left(\mathrm{AB}^{2}+\mathrm{BC}^{2}-\mathrm{CA}^{2}\right) / 2$, so $A B \cdot B C \cos B+B C \cdot C A \cos C+C A \cdot A B \cos A=\left(A B^{2}+\mathrm{BC}^{2}+C A^{2}\right) / 2$. Thus the sum is rational multiple of $\left(\mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{CA}^{2}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Points $\mathrm{A}_{1}, \mathrm{~A}_{2}, \ldots, \mathrm{A}_{\mathrm{n}}$ are equally spaced on the side $\mathrm{BC}$ of the triangle $\mathrm{ABC}$ (so that $\mathrm{BA}_{1}=$ $\left.A_{1} A_{2}=\ldots=A_{n-1} A_{n}=A_{n} C\right)$. Similarly, points $B_{1}, B_{2}, \ldots, B_{n}$ are equally spaced on the side CA, and points $\mathrm{C}_{1}, \mathrm{C}_{2}, \ldots, \mathrm{C}_{\mathrm{n}}$ are equally spaced on the side $\mathrm{AB}$. Show that $\left(\mathrm{AA}_{1}{ }^{2}+\mathrm{AA}_{2}{ }^{2}+\ldots+\right.$ $\left.\mathrm{AA}_{\mathrm{n}}{ }^{2}+\mathrm{BB}_{1}{ }^{2}+\mathrm{BB}_{2}{ }^{2}+\ldots+\mathrm{BB}_{\mathrm{n}}{ }^{2}+\mathrm{C}_{1}{ }^{2}+\ldots+\mathrm{CC}_{\mathrm{n}}{ }^{2}\right)$ is a rational multiple of $\left(\mathrm{AB}^{2}+\mathrm{BC}^{2}+\right.$ $\left.\mathrm{CA}^{2}\right)$.
|
Using the cosine formula, $\mathrm{AA}_{\mathrm{k}}{ }^{2}=\mathrm{AB}^{2}+\mathrm{k}^{2} \mathrm{BC}^{2} /(\mathrm{n}+1)^{2}-2 \mathrm{k} A \mathrm{AB} \cdot \mathrm{BC} /(\mathrm{n}+1) \cos \mathrm{B}$. So $\sum \mathrm{AA}_{\mathrm{k}}{ }^{2}=$ $n B^{2}+B C^{2} /(n+1)^{2}\left(1^{2}+2^{2}+\ldots+n^{2}\right)-2 A B \cdot B C \cos B(1+2+\ldots+n) /(n+1)$. Similarly for the other two sides.
Thus the total sum is $n\left(\mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{CA}^{2}\right)+\mathrm{n}(2 \mathrm{n}+1) /(6(\mathrm{n}+1))\left(\mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{CA}^{2}\right)-\mathrm{n}$ $(\mathrm{AB} \cdot \mathrm{BC} \cos \mathrm{B}+\mathrm{BC} \cdot \mathrm{CA} \cos \mathrm{C}+\mathrm{CA} \cdot \mathrm{AB} \cos \mathrm{A})$. $\mathrm{But} \mathrm{AB} \cdot \mathrm{BC} \cos \mathrm{B}=\left(\mathrm{AB}^{2}+\mathrm{BC}^{2}-\mathrm{CA}^{2}\right) / 2$, so $A B \cdot B C \cos B+B C \cdot C A \cos C+C A \cdot A B \cos A=\left(A B^{2}+\mathrm{BC}^{2}+C A^{2}\right) / 2$. Thus the sum is rational multiple of $\left(\mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{CA}^{2}\right)$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B1",
"solution_match": "\n## Solution"
}
|
806518c1-f5d0-51c6-9b0c-e3f6ac1980be
| 604,242
|
Let $\mathrm{k}^{3}=2$ and let $\mathrm{x}, \mathrm{y}, \mathrm{z}$ be any rational numbers such that $\mathrm{x}+\mathrm{y} \mathrm{k}+\mathrm{z} \mathrm{k}^{2}$ is non-zero. Show that there are rational numbers $\mathrm{u}, \mathrm{v}, \mathrm{w}$ such that $\left(\mathrm{x}+\mathrm{yk}+\mathrm{z} \mathrm{k}^{2}\right)\left(\mathrm{u}+\mathrm{v} \mathrm{k}+\mathrm{w}^{2}\right)=1$.
|
We need $x u+2 z v+2 y w=1$, $y u+x v+2 z w=0, z u+y v+x w=0$. This is just a straightforward set of linear equations. Solving, we get: $u=\left(x^{2}-2 y z\right) / d, v=\left(2 z^{2}-x y\right) / d, w=$ $\left(y^{2}-x z\right) / d$, were $d=x^{3}+2 y^{3}+4 z^{3}-6 x y z$.
This would fail if $\mathrm{d}=0$. But if $\mathrm{d}=0$, then multiplying through by a suitable integer we have $6 \mathrm{mnr}=\mathrm{m}^{3}+2 \mathrm{n}^{3}+4 \mathrm{r}^{3}$ for some integers $\mathrm{m}, \mathrm{n}, \mathrm{r}$. But we can divide by any common factor of $\mathrm{m}, \mathrm{n}, \mathrm{r}$ to get them without any common factor. But $6 \mathrm{mnr}, 2 \mathrm{n}^{3}, 4 \mathrm{r}^{3}$ are all even, so $\mathrm{m}$ must be even. Put $m=2 M$. Then $12 M n r=8 M^{3}+2 n^{3}+4 r^{3}$, so $6 M n r=4 M^{3}+n^{3}+2 r^{3}$. But $6 M n r, 4 M^{3}$ and $2 r^{3}$ are all even, so $n$ must be even. Put $n=2 N$. Then $12 M N r=4 M^{3}+8 N^{3}+2 r^{3}$, so $6 M N r$ $=2 \mathrm{M}^{3}+4 \mathrm{~N}^{3}+\mathrm{r}^{3}$, so $\mathrm{r}$ must be even. So $\mathrm{m}, \mathrm{n}, \mathrm{r}$ had a common factor 2 . Contradiction. So $\mathrm{d}$ cannot be zero.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $\mathrm{k}^{3}=2$ and let $\mathrm{x}, \mathrm{y}, \mathrm{z}$ be any rational numbers such that $\mathrm{x}+\mathrm{y} \mathrm{k}+\mathrm{z} \mathrm{k}^{2}$ is non-zero. Show that there are rational numbers $\mathrm{u}, \mathrm{v}, \mathrm{w}$ such that $\left(\mathrm{x}+\mathrm{yk}+\mathrm{z} \mathrm{k}^{2}\right)\left(\mathrm{u}+\mathrm{v} \mathrm{k}+\mathrm{w}^{2}\right)=1$.
|
We need $x u+2 z v+2 y w=1$, $y u+x v+2 z w=0, z u+y v+x w=0$. This is just a straightforward set of linear equations. Solving, we get: $u=\left(x^{2}-2 y z\right) / d, v=\left(2 z^{2}-x y\right) / d, w=$ $\left(y^{2}-x z\right) / d$, were $d=x^{3}+2 y^{3}+4 z^{3}-6 x y z$.
This would fail if $\mathrm{d}=0$. But if $\mathrm{d}=0$, then multiplying through by a suitable integer we have $6 \mathrm{mnr}=\mathrm{m}^{3}+2 \mathrm{n}^{3}+4 \mathrm{r}^{3}$ for some integers $\mathrm{m}, \mathrm{n}, \mathrm{r}$. But we can divide by any common factor of $\mathrm{m}, \mathrm{n}, \mathrm{r}$ to get them without any common factor. But $6 \mathrm{mnr}, 2 \mathrm{n}^{3}, 4 \mathrm{r}^{3}$ are all even, so $\mathrm{m}$ must be even. Put $m=2 M$. Then $12 M n r=8 M^{3}+2 n^{3}+4 r^{3}$, so $6 M n r=4 M^{3}+n^{3}+2 r^{3}$. But $6 M n r, 4 M^{3}$ and $2 r^{3}$ are all even, so $n$ must be even. Put $n=2 N$. Then $12 M N r=4 M^{3}+8 N^{3}+2 r^{3}$, so $6 M N r$ $=2 \mathrm{M}^{3}+4 \mathrm{~N}^{3}+\mathrm{r}^{3}$, so $\mathrm{r}$ must be even. So $\mathrm{m}, \mathrm{n}, \mathrm{r}$ had a common factor 2 . Contradiction. So $\mathrm{d}$ cannot be zero.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B2",
"solution_match": "\n## Solution"
}
|
871d0448-1725-5ed7-9abd-6eb9fde7863d
| 604,250
|
Let $S$ be the collection of all sets of $n$ distinct positive integers, with no three in arithmetic progression. Show that there is a member of $S$ which has the largest sum of the inverses of its elements (you do not have to find it or to show that it is unique).
|
Induction on $\mathrm{n}$. For $\mathrm{n}=1,\{1\}$ is obviously maximal. Now suppose $\mathrm{a}_{1}<\mathrm{a}_{2}<\ldots<\mathrm{a}_{\mathrm{n}}$ is a maximal set for $n$. Take $a_{n+1}$ to be the smallest integer $>a_{n}$ such that $\left\{a_{1}, a_{2}, \ldots, a_{n+1}\right\}$ has no three members in AP. Now consider the sequences $\mathrm{b}_{1}<\mathrm{b}_{2}<\ldots<\mathrm{b}_{\mathrm{n}}$ which have no three in AP and $b_{n+1} \leq a_{n+1}$. There are only finitely many such sequences. So we can find one which is maximal. Suppose it is $\mathrm{c}_{1}<\mathrm{c}_{2}<\ldots<\mathrm{c}_{\mathrm{n}+1}$. Now take whichever of $\mathrm{a}_{\mathrm{i}}, \mathrm{c}_{\mathrm{i}}$ has the larger sum of inverses. It is clearly maximal with respect to sequences whose largest member is $\leq a_{n+1}$. Suppose we have a sequence $x_{1}<x_{2}<\ldots<x_{n+1}$ with no three in AP and $x_{n+1}>a_{n+1}$. Then we have $1 / \mathrm{x}_{n+1}<1 / \mathrm{a}_{n+1}$ and, by induction, $1 / \mathrm{x}_{1}+\ldots+1 / \mathrm{x}_{n} \leq 1 / \mathrm{a}_{1}+\ldots+1 / \mathrm{a}_{n}$, so $1 / \mathrm{x}_{1}+\ldots+1 / \mathrm{x}_{\mathrm{n}+1}$ $<1 / \mathrm{a}_{1}+\ldots+1 / \mathrm{a}_{\mathrm{n}+1}$, so it is worse than the sequence we have chosen.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be the collection of all sets of $n$ distinct positive integers, with no three in arithmetic progression. Show that there is a member of $S$ which has the largest sum of the inverses of its elements (you do not have to find it or to show that it is unique).
|
Induction on $\mathrm{n}$. For $\mathrm{n}=1,\{1\}$ is obviously maximal. Now suppose $\mathrm{a}_{1}<\mathrm{a}_{2}<\ldots<\mathrm{a}_{\mathrm{n}}$ is a maximal set for $n$. Take $a_{n+1}$ to be the smallest integer $>a_{n}$ such that $\left\{a_{1}, a_{2}, \ldots, a_{n+1}\right\}$ has no three members in AP. Now consider the sequences $\mathrm{b}_{1}<\mathrm{b}_{2}<\ldots<\mathrm{b}_{\mathrm{n}}$ which have no three in AP and $b_{n+1} \leq a_{n+1}$. There are only finitely many such sequences. So we can find one which is maximal. Suppose it is $\mathrm{c}_{1}<\mathrm{c}_{2}<\ldots<\mathrm{c}_{\mathrm{n}+1}$. Now take whichever of $\mathrm{a}_{\mathrm{i}}, \mathrm{c}_{\mathrm{i}}$ has the larger sum of inverses. It is clearly maximal with respect to sequences whose largest member is $\leq a_{n+1}$. Suppose we have a sequence $x_{1}<x_{2}<\ldots<x_{n+1}$ with no three in AP and $x_{n+1}>a_{n+1}$. Then we have $1 / \mathrm{x}_{n+1}<1 / \mathrm{a}_{n+1}$ and, by induction, $1 / \mathrm{x}_{1}+\ldots+1 / \mathrm{x}_{n} \leq 1 / \mathrm{a}_{1}+\ldots+1 / \mathrm{a}_{n}$, so $1 / \mathrm{x}_{1}+\ldots+1 / \mathrm{x}_{\mathrm{n}+1}$ $<1 / \mathrm{a}_{1}+\ldots+1 / \mathrm{a}_{\mathrm{n}+1}$, so it is worse than the sequence we have chosen.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B3",
"solution_match": "\n## Solution"
}
|
1141e881-bc51-561a-aa16-7b304532d4c7
| 604,261
|
Given positive real numbers $\mathrm{x}, \mathrm{y}, \mathrm{z}$ each less than $\pi / 2$, show that $\pi / 2+2 \sin \mathrm{x} \cos \mathrm{y}+2 \sin \mathrm{y}$ $\cos z>\sin 2 x+\sin 2 y+\sin 2 z$.
|
We have $\sin 2 x+\sin 2 y+\sin 2 z-2 \sin x \cos y-2 \sin y \cos z=2 \sin x(\cos x-\cos y)+2 \sin$ $y(\cos y-\cos z)+2 \sin z \cos z$, so we wish to show that $\sin x(\cos x-\cos y)+\sin y(\cos y-\cos$ $\mathrm{z})+\sin \mathrm{z} \cos \mathrm{z}<\pi / 2(*)$.
We have to consider six cases: (1) $\mathrm{x} \leq \mathrm{y} \leq \mathrm{z}$; (2) $\mathrm{x} \leq \mathrm{z} \leq \mathrm{y}$; (3) $\mathrm{y} \leq \mathrm{x} \leq \mathrm{z}$; (4) $\mathrm{y} \leq \mathrm{z} \leq \mathrm{x}$; (5) $\mathrm{z} \leq$ $\mathrm{x} \leq \mathrm{y} ;$ (6) $\mathrm{z} \leq \mathrm{y} \leq \mathrm{x}$. The first case is obvious from the diagram, because the lhs represents the shaded area, and the rhs represents the whole quarter circle.
In cases (2) and (5) the second term is negative, and - $\sin \mathrm{y}<-\sin \mathrm{x}$, so the sum of the first two terms is less than $\sin x(\cos x-\cos y)+\sin x(\cos y-\cos z)=\sin x(\cos x-\cos z)$. But by the same argument as the first case the two rectangles represented by $\sin x(\cos x-\cos z)$ and $\sin \mathrm{z} \cos \mathrm{z}$ are disjoint and fit inside the quarter circle. So we have proved (2) and (5).
In cases (3) and (4), the first term is negative. The remaining two terms represent disjoint rectangles lying inside the quarter circle, so again the inequality holds.
In case (6) the first two terms are negative. The last term is $1 / 2 \sin 2 z \leq 1 / 2<\pi / 2$, so the inequality certainly holds.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Given positive real numbers $\mathrm{x}, \mathrm{y}, \mathrm{z}$ each less than $\pi / 2$, show that $\pi / 2+2 \sin \mathrm{x} \cos \mathrm{y}+2 \sin \mathrm{y}$ $\cos z>\sin 2 x+\sin 2 y+\sin 2 z$.
|
We have $\sin 2 x+\sin 2 y+\sin 2 z-2 \sin x \cos y-2 \sin y \cos z=2 \sin x(\cos x-\cos y)+2 \sin$ $y(\cos y-\cos z)+2 \sin z \cos z$, so we wish to show that $\sin x(\cos x-\cos y)+\sin y(\cos y-\cos$ $\mathrm{z})+\sin \mathrm{z} \cos \mathrm{z}<\pi / 2(*)$.

We have to consider six cases: (1) $\mathrm{x} \leq \mathrm{y} \leq \mathrm{z}$; (2) $\mathrm{x} \leq \mathrm{z} \leq \mathrm{y}$; (3) $\mathrm{y} \leq \mathrm{x} \leq \mathrm{z}$; (4) $\mathrm{y} \leq \mathrm{z} \leq \mathrm{x}$; (5) $\mathrm{z} \leq$ $\mathrm{x} \leq \mathrm{y} ;$ (6) $\mathrm{z} \leq \mathrm{y} \leq \mathrm{x}$. The first case is obvious from the diagram, because the lhs represents the shaded area, and the rhs represents the whole quarter circle.
In cases (2) and (5) the second term is negative, and - $\sin \mathrm{y}<-\sin \mathrm{x}$, so the sum of the first two terms is less than $\sin x(\cos x-\cos y)+\sin x(\cos y-\cos z)=\sin x(\cos x-\cos z)$. But by the same argument as the first case the two rectangles represented by $\sin x(\cos x-\cos z)$ and $\sin \mathrm{z} \cos \mathrm{z}$ are disjoint and fit inside the quarter circle. So we have proved (2) and (5).
In cases (3) and (4), the first term is negative. The remaining two terms represent disjoint rectangles lying inside the quarter circle, so again the inequality holds.
In case (6) the first two terms are negative. The last term is $1 / 2 \sin 2 z \leq 1 / 2<\pi / 2$, so the inequality certainly holds.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A2",
"solution_match": "\n## Solution"
}
|
826f8f82-19e5-544b-9ddd-a0fff5dd7c23
| 604,283
|
If $\mathrm{a}, \mathrm{b}, \mathrm{c}$, are the sides of a triangle, show that $(\mathrm{a}-\mathrm{b}) /(\mathrm{a}+\mathrm{b})+(\mathrm{b}-\mathrm{c}) /(\mathrm{b}+\mathrm{c})+(\mathrm{c}-\mathrm{a}) /(\mathrm{a}+\mathrm{c})<$ $1 / 16$.
|
Put $\mathrm{f}(\mathrm{a}, \mathrm{b}, \mathrm{c})=(\mathrm{a}-\mathrm{b}) /(\mathrm{a}+\mathrm{b})+(\mathrm{b}-\mathrm{c}) /(\mathrm{b}+\mathrm{c})+(\mathrm{c}-\mathrm{a}) /(\mathrm{a}+\mathrm{c})$. Let $\mathrm{A}, \mathrm{B}, \mathrm{C}$ be the permutation of $\mathrm{a}, \mathrm{b}, \mathrm{c}$, with $\mathrm{A}<=\mathrm{B}<=\mathrm{C}$. If $(\mathrm{A}, \mathrm{B}, \mathrm{C})=(\mathrm{b}, \mathrm{a}, \mathrm{c}),(\mathrm{a}, \mathrm{c}, \mathrm{b})$ or $(\mathrm{c}, \mathrm{b}, \mathrm{a})$, then $\mathrm{f}(\mathrm{a}, \mathrm{b}, \mathrm{c})=\mathrm{X}$, where $X=(B-A) /(B+A)+(C-B) /(C+B)-(C-A) /(A+C)$. If $(A, B, C)=(a, b, c),(b, c$, a) or ( $\mathrm{c}, \mathrm{a}, \mathrm{b})$, then $\mathrm{f}(\mathrm{a}, \mathrm{b}, \mathrm{c})=-\mathrm{X}$.
Put $\mathrm{B}=\mathrm{A}+\mathrm{h}, \mathrm{C}=\mathrm{B}+\mathrm{k}=\mathrm{A}+\mathrm{h}+\mathrm{k}$, where $\mathrm{h}, \mathrm{k} \geq 0$. Since $\mathrm{A}, \mathrm{B}, \mathrm{C}$ are the sides of a triangle, we also have A + B $>$ C or A $>k$. So $X=h /(2 A+h)+k /(2 A+2 h+k)-(h+k) /(2 A+h+k)$ $=\mathrm{hk}(\mathrm{h}+\mathrm{k}) /((2 \mathrm{~A}+\mathrm{h})(2 \mathrm{~A}+\mathrm{h}+\mathrm{k})(2 \mathrm{~A}+2 \mathrm{~h}+\mathrm{k}))$. This is obviously non-negative. We claim also that it is $<1 / 20$. That is equivalent to: $20 \mathrm{~h}^{2} \mathrm{k}+20 \mathrm{hk}^{2}<(2 \mathrm{~A}+\mathrm{h})(2 \mathrm{~A}+\mathrm{h}+\mathrm{k})(2 \mathrm{~A}+2 \mathrm{~h}+$ k). Since $k<A$ it is sufficient to show that $20 h^{2} k+20 h k^{2} \leq(2 k+h)(2 k+h+k)(2 k+2 h+k)$
$=18 \mathrm{k}^{3}+27 \mathrm{hk}^{2}+13 \mathrm{~h}^{2} \mathrm{k}+2 \mathrm{~h}^{3}$ or $18 \mathrm{k}^{3}+7 \mathrm{hk}^{2}-7 \mathrm{~h}^{2} \mathrm{k}+2 \mathrm{~h}^{3} \geq 0$. But $7 \mathrm{k}^{2}-7 \mathrm{hk}+2 \mathrm{~h}^{2}=7(\mathrm{k}-$ $\mathrm{h} / 2)^{2}+\mathrm{h}^{2} / 4 \geq 0$ and $h$ and $\mathrm{k}$ are non-negative, so $18 \mathrm{k}^{3}+\mathrm{h}\left(7 \mathrm{k}^{2}-7 \mathrm{hk}+2 \mathrm{~h}^{2}\right) \geq 0$.
Thus we have established that $0<=\mathrm{X}<1 / 20$, which shows that $\mathrm{f}(\mathrm{a}, \mathrm{b}, \mathrm{c})<1 / 20$, which is slightly stronger than the required result.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
If $\mathrm{a}, \mathrm{b}, \mathrm{c}$, are the sides of a triangle, show that $(\mathrm{a}-\mathrm{b}) /(\mathrm{a}+\mathrm{b})+(\mathrm{b}-\mathrm{c}) /(\mathrm{b}+\mathrm{c})+(\mathrm{c}-\mathrm{a}) /(\mathrm{a}+\mathrm{c})<$ $1 / 16$.
|
Put $\mathrm{f}(\mathrm{a}, \mathrm{b}, \mathrm{c})=(\mathrm{a}-\mathrm{b}) /(\mathrm{a}+\mathrm{b})+(\mathrm{b}-\mathrm{c}) /(\mathrm{b}+\mathrm{c})+(\mathrm{c}-\mathrm{a}) /(\mathrm{a}+\mathrm{c})$. Let $\mathrm{A}, \mathrm{B}, \mathrm{C}$ be the permutation of $\mathrm{a}, \mathrm{b}, \mathrm{c}$, with $\mathrm{A}<=\mathrm{B}<=\mathrm{C}$. If $(\mathrm{A}, \mathrm{B}, \mathrm{C})=(\mathrm{b}, \mathrm{a}, \mathrm{c}),(\mathrm{a}, \mathrm{c}, \mathrm{b})$ or $(\mathrm{c}, \mathrm{b}, \mathrm{a})$, then $\mathrm{f}(\mathrm{a}, \mathrm{b}, \mathrm{c})=\mathrm{X}$, where $X=(B-A) /(B+A)+(C-B) /(C+B)-(C-A) /(A+C)$. If $(A, B, C)=(a, b, c),(b, c$, a) or ( $\mathrm{c}, \mathrm{a}, \mathrm{b})$, then $\mathrm{f}(\mathrm{a}, \mathrm{b}, \mathrm{c})=-\mathrm{X}$.
Put $\mathrm{B}=\mathrm{A}+\mathrm{h}, \mathrm{C}=\mathrm{B}+\mathrm{k}=\mathrm{A}+\mathrm{h}+\mathrm{k}$, where $\mathrm{h}, \mathrm{k} \geq 0$. Since $\mathrm{A}, \mathrm{B}, \mathrm{C}$ are the sides of a triangle, we also have A + B $>$ C or A $>k$. So $X=h /(2 A+h)+k /(2 A+2 h+k)-(h+k) /(2 A+h+k)$ $=\mathrm{hk}(\mathrm{h}+\mathrm{k}) /((2 \mathrm{~A}+\mathrm{h})(2 \mathrm{~A}+\mathrm{h}+\mathrm{k})(2 \mathrm{~A}+2 \mathrm{~h}+\mathrm{k}))$. This is obviously non-negative. We claim also that it is $<1 / 20$. That is equivalent to: $20 \mathrm{~h}^{2} \mathrm{k}+20 \mathrm{hk}^{2}<(2 \mathrm{~A}+\mathrm{h})(2 \mathrm{~A}+\mathrm{h}+\mathrm{k})(2 \mathrm{~A}+2 \mathrm{~h}+$ k). Since $k<A$ it is sufficient to show that $20 h^{2} k+20 h k^{2} \leq(2 k+h)(2 k+h+k)(2 k+2 h+k)$
$=18 \mathrm{k}^{3}+27 \mathrm{hk}^{2}+13 \mathrm{~h}^{2} \mathrm{k}+2 \mathrm{~h}^{3}$ or $18 \mathrm{k}^{3}+7 \mathrm{hk}^{2}-7 \mathrm{~h}^{2} \mathrm{k}+2 \mathrm{~h}^{3} \geq 0$. But $7 \mathrm{k}^{2}-7 \mathrm{hk}+2 \mathrm{~h}^{2}=7(\mathrm{k}-$ $\mathrm{h} / 2)^{2}+\mathrm{h}^{2} / 4 \geq 0$ and $h$ and $\mathrm{k}$ are non-negative, so $18 \mathrm{k}^{3}+\mathrm{h}\left(7 \mathrm{k}^{2}-7 \mathrm{hk}+2 \mathrm{~h}^{2}\right) \geq 0$.
Thus we have established that $0<=\mathrm{X}<1 / 20$, which shows that $\mathrm{f}(\mathrm{a}, \mathrm{b}, \mathrm{c})<1 / 20$, which is slightly stronger than the required result.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A3",
"solution_match": "\n## Solution"
}
|
6bd67bf1-8f9e-5e1e-9744-fe4132729a78
| 604,296
|
The incircle of the triangle $\mathrm{ABC}$ touches $\mathrm{AC}$ at $\mathrm{M}$ and $\mathrm{BC}$ at $\mathrm{N}$ and has center $\mathrm{O}$. $\mathrm{AO}$ meets $\mathrm{MN}$ at $\mathrm{P}$ and BO meets MN at $\mathrm{Q}$. Show that MP.OA $=\mathrm{BC} . \mathrm{OQ}$.
|
The key to getting started is to notice that angle $\mathrm{AQB}=90^{\circ}$.
Angle $\mathrm{BAQ}=90^{\circ}-\mathrm{B} / 2$, so angle $\mathrm{OAQ}=90^{\circ}-\mathrm{B} / 2-\mathrm{A} / 2=\mathrm{C} / 2$. So $\mathrm{OQ}=\mathrm{AO} \sin \mathrm{C} / 2$. Thus we have to show that $\mathrm{MP}=\mathrm{BC} \sin \mathrm{C} / 2$.
Let the incircle touch $\mathrm{AB}$ at $\mathrm{L}$ and let $\mathrm{Y}$ be the midpoint of ML (also the intersection of ML with AO). Angle NMC $=90^{\circ}$ - C/2. It is also A/2 + angle MPY, so angle MPY $=90-\mathrm{C} / 2-$ $\mathrm{A} / 2=\mathrm{B} / 2$. Hence $\mathrm{MP}=\mathrm{MY} / \sin \mathrm{B} / 2$. We have $\mathrm{MY}=\mathrm{MO} \sin \mathrm{MOA}=\mathrm{r} \cos \mathrm{A} / 2$ (where $\mathrm{r}$ is the inradius, as usual). So $\mathrm{MP}=(\mathrm{r} \cos \mathrm{A} / 2) / \sin \mathrm{B} / 2$. We have $\mathrm{BC}=\mathrm{BN}+\mathrm{NC}=\mathrm{r}(\cot \mathrm{B} / 2+$ $\cot \mathrm{C} / 2)$, so $\mathrm{MP} / \mathrm{BC}=(\cos \mathrm{A} / 2) /(\sin \mathrm{B} / 2(\cot \mathrm{B} / 2+\cot \mathrm{C} / 2))$. Hence $\mathrm{MP} /(\mathrm{BC} \sin \mathrm{C} / 2)=($ $\cos \mathrm{A} / 2) /(\cos \mathrm{B} / 2 \sin \mathrm{C} / 2+\sin \mathrm{B} / 2 \cos \mathrm{C} / 2)=\cos \mathrm{A} / 2 / \sin (\mathrm{B} / 2+\mathrm{C} / 2)=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The incircle of the triangle $\mathrm{ABC}$ touches $\mathrm{AC}$ at $\mathrm{M}$ and $\mathrm{BC}$ at $\mathrm{N}$ and has center $\mathrm{O}$. $\mathrm{AO}$ meets $\mathrm{MN}$ at $\mathrm{P}$ and BO meets MN at $\mathrm{Q}$. Show that MP.OA $=\mathrm{BC} . \mathrm{OQ}$.
|

The key to getting started is to notice that angle $\mathrm{AQB}=90^{\circ}$.
Angle $\mathrm{BAQ}=90^{\circ}-\mathrm{B} / 2$, so angle $\mathrm{OAQ}=90^{\circ}-\mathrm{B} / 2-\mathrm{A} / 2=\mathrm{C} / 2$. So $\mathrm{OQ}=\mathrm{AO} \sin \mathrm{C} / 2$. Thus we have to show that $\mathrm{MP}=\mathrm{BC} \sin \mathrm{C} / 2$.
Let the incircle touch $\mathrm{AB}$ at $\mathrm{L}$ and let $\mathrm{Y}$ be the midpoint of ML (also the intersection of ML with AO). Angle NMC $=90^{\circ}$ - C/2. It is also A/2 + angle MPY, so angle MPY $=90-\mathrm{C} / 2-$ $\mathrm{A} / 2=\mathrm{B} / 2$. Hence $\mathrm{MP}=\mathrm{MY} / \sin \mathrm{B} / 2$. We have $\mathrm{MY}=\mathrm{MO} \sin \mathrm{MOA}=\mathrm{r} \cos \mathrm{A} / 2$ (where $\mathrm{r}$ is the inradius, as usual). So $\mathrm{MP}=(\mathrm{r} \cos \mathrm{A} / 2) / \sin \mathrm{B} / 2$. We have $\mathrm{BC}=\mathrm{BN}+\mathrm{NC}=\mathrm{r}(\cot \mathrm{B} / 2+$ $\cot \mathrm{C} / 2)$, so $\mathrm{MP} / \mathrm{BC}=(\cos \mathrm{A} / 2) /(\sin \mathrm{B} / 2(\cot \mathrm{B} / 2+\cot \mathrm{C} / 2))$. Hence $\mathrm{MP} /(\mathrm{BC} \sin \mathrm{C} / 2)=($ $\cos \mathrm{A} / 2) /(\cos \mathrm{B} / 2 \sin \mathrm{C} / 2+\sin \mathrm{B} / 2 \cos \mathrm{C} / 2)=\cos \mathrm{A} / 2 / \sin (\mathrm{B} / 2+\mathrm{C} / 2)=1$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B1",
"solution_match": "\n## Solution"
}
|
a4765c7a-c562-5969-8c0d-c9ec2d3d4c38
| 604,309
|
Show that there are infinitely many solutions in positive integers to $2 a^{2}-3 a+1=3 b^{2}+b$.
|
Put $\mathrm{A}=\mathrm{a}-1$ and the equation becomes $\mathrm{A}(2 \mathrm{~A}+1)=\mathrm{b}(3 \mathrm{~b}+1)$. Let $\mathrm{d}$ be the greatest common divisor of A and $b$. Put $A=d x, b=d y$. Then $x(2 d x+1)=y(3 d y+1)$. Since $x$ and $y$ are coprime, $\mathrm{x}$ must divide $3 \mathrm{dy}+1$. So put $3 \mathrm{dy}+1=\mathrm{nx}$. Then $2 \mathrm{dx}+1=\mathrm{ny}$. Solving for $\mathrm{x}$ and $\mathrm{y}$ in terms of $n$ and $d$ we get $x=(n+3 d) /\left(n^{2}-6 d^{2}\right), y=(n+2 d) /\left(n^{2}-6 d^{2}\right)$.
So we would certainly be home if we could show that there were infinitely many solutions to $\mathrm{n}^{2}-6 \mathrm{~d}^{2}=1$. It is not hard to find the first few: $1^{2}-6.0^{2}=1,5^{2}-6 \cdot 2^{2}=1,49^{2}-6 \cdot 20^{2}=1$. We notice that $49^{2}=2.5^{2}-1$, so we wonder whether $\mathrm{n}=2.49^{2}-1$ might be another solution and indeed we find it gives $d=1960=2 \cdot 49.20$. This suggests we try $\left(2 n^{2}-1\right)^{2}-6(2 n d)^{2}=4 n^{4}-$ $4 n^{2}+1-24 n^{2} d^{2}=4 n^{2}\left(n^{2}-6 d^{2}-1\right)+1=1$. So there are indeed infinitely many solutions to $n^{2}$ $-6 \mathrm{~d}^{2}=1$ and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that there are infinitely many solutions in positive integers to $2 a^{2}-3 a+1=3 b^{2}+b$.
|
Put $\mathrm{A}=\mathrm{a}-1$ and the equation becomes $\mathrm{A}(2 \mathrm{~A}+1)=\mathrm{b}(3 \mathrm{~b}+1)$. Let $\mathrm{d}$ be the greatest common divisor of A and $b$. Put $A=d x, b=d y$. Then $x(2 d x+1)=y(3 d y+1)$. Since $x$ and $y$ are coprime, $\mathrm{x}$ must divide $3 \mathrm{dy}+1$. So put $3 \mathrm{dy}+1=\mathrm{nx}$. Then $2 \mathrm{dx}+1=\mathrm{ny}$. Solving for $\mathrm{x}$ and $\mathrm{y}$ in terms of $n$ and $d$ we get $x=(n+3 d) /\left(n^{2}-6 d^{2}\right), y=(n+2 d) /\left(n^{2}-6 d^{2}\right)$.
So we would certainly be home if we could show that there were infinitely many solutions to $\mathrm{n}^{2}-6 \mathrm{~d}^{2}=1$. It is not hard to find the first few: $1^{2}-6.0^{2}=1,5^{2}-6 \cdot 2^{2}=1,49^{2}-6 \cdot 20^{2}=1$. We notice that $49^{2}=2.5^{2}-1$, so we wonder whether $\mathrm{n}=2.49^{2}-1$ might be another solution and indeed we find it gives $d=1960=2 \cdot 49.20$. This suggests we try $\left(2 n^{2}-1\right)^{2}-6(2 n d)^{2}=4 n^{4}-$ $4 n^{2}+1-24 n^{2} d^{2}=4 n^{2}\left(n^{2}-6 d^{2}-1\right)+1=1$. So there are indeed infinitely many solutions to $n^{2}$ $-6 \mathrm{~d}^{2}=1$ and we are done.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B3",
"solution_match": "\n## Solution"
}
|
b2e7ea8d-ca62-5027-bd26-b5036c69ea1e
| 604,329
|
I is the incenter of the triangle $\mathrm{ABC}$ and the incircle touches $\mathrm{BC}, \mathrm{CA}, \mathrm{AB}$ at $\mathrm{D}, \mathrm{E}, \mathrm{F}$ respectively. AD meets the incircle again at P. M is the midpoint of EF. Show that PMID is cyclic (or the points are collinear).
|
$\angle \mathrm{AEI}=\angle \mathrm{AME}=90^{\circ}$, so $\mathrm{AEI}$ and $\mathrm{AME}$ are similar. Hence $\mathrm{AM} / \mathrm{AE}=\mathrm{AE} / \mathrm{AI}$ or $\mathrm{AM} \cdot \mathrm{AI}=$ $\mathrm{AE}^{2}$. $\mathrm{AE}$ is tangent to the incircle, so $\mathrm{AE} 2=\mathrm{AP} \cdot \mathrm{AD}$. Hence $\mathrm{AM} \cdot \mathrm{AI}=\mathrm{AP} \cdot \mathrm{AD}$, so if $\mathrm{P}, \mathrm{M}, \mathrm{I}, \mathrm{D}$ are not collinear, then they are cyclic.
$\mathrm{f}(\mathrm{x})=(\mathrm{x}+\mathrm{b})^{2}+\mathrm{c}$, where $\mathrm{b}$ and $\mathrm{c}$ are integers. If the prime $\mathrm{p}$ divides $\mathrm{c}$, but $\mathrm{p}^{2}$ does not divide $c$, show that $f(n)$ is not divisible by $p^{2}$ for any integer $n$. If an odd prime $q$ does not divide $c$, but divides $\mathrm{f}(\mathrm{n})$ for some $\mathrm{n}$, show that for any $\mathrm{r}$, we can find $\mathrm{N}$ such that $\mathrm{q}^{\mathrm{r}}$ divides $\mathrm{f}(\mathrm{N})$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
I is the incenter of the triangle $\mathrm{ABC}$ and the incircle touches $\mathrm{BC}, \mathrm{CA}, \mathrm{AB}$ at $\mathrm{D}, \mathrm{E}, \mathrm{F}$ respectively. AD meets the incircle again at P. M is the midpoint of EF. Show that PMID is cyclic (or the points are collinear).
|

$\angle \mathrm{AEI}=\angle \mathrm{AME}=90^{\circ}$, so $\mathrm{AEI}$ and $\mathrm{AME}$ are similar. Hence $\mathrm{AM} / \mathrm{AE}=\mathrm{AE} / \mathrm{AI}$ or $\mathrm{AM} \cdot \mathrm{AI}=$ $\mathrm{AE}^{2}$. $\mathrm{AE}$ is tangent to the incircle, so $\mathrm{AE} 2=\mathrm{AP} \cdot \mathrm{AD}$. Hence $\mathrm{AM} \cdot \mathrm{AI}=\mathrm{AP} \cdot \mathrm{AD}$, so if $\mathrm{P}, \mathrm{M}, \mathrm{I}, \mathrm{D}$ are not collinear, then they are cyclic.
$\mathrm{f}(\mathrm{x})=(\mathrm{x}+\mathrm{b})^{2}+\mathrm{c}$, where $\mathrm{b}$ and $\mathrm{c}$ are integers. If the prime $\mathrm{p}$ divides $\mathrm{c}$, but $\mathrm{p}^{2}$ does not divide $c$, show that $f(n)$ is not divisible by $p^{2}$ for any integer $n$. If an odd prime $q$ does not divide $c$, but divides $\mathrm{f}(\mathrm{n})$ for some $\mathrm{n}$, show that for any $\mathrm{r}$, we can find $\mathrm{N}$ such that $\mathrm{q}^{\mathrm{r}}$ divides $\mathrm{f}(\mathrm{N})$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A2",
"solution_match": "\n## Solution"
}
|
2fe6cc64-ff65-5833-9ab9-fcc0b01df62b
| 604,357
|
The circle $\mathrm{C}$ has diameter $\mathrm{AB}$. The tangent at $\mathrm{B}$ is $\mathrm{T}$. For each point $\mathrm{M}$ (not equal to $\mathrm{A}$ ) on $\mathrm{C}$ there is a circle $\mathrm{C}^{\prime}$ which touches $\mathrm{T}$ and touches $\mathrm{C}$ at M. Find the point at which $\mathrm{C}^{\prime}$ touches $\mathrm{T}$ and find the locus of the center of $\mathrm{C}^{\prime}$ as $\mathrm{M}$ varies. Show that there is a circle orthogonal to all the circles $\mathrm{C}^{\prime}$.
## Answer
$\mathrm{C}^{\prime}$ touches $\mathrm{T}$ at the intersection of $\mathrm{T}$ and the line $\mathrm{AM}$
the locus of the center is a parabola vertex B
the circle center A radius $\mathrm{AB}$ is orthogonal to all circles $\mathrm{C}^{\prime}$
|
Let $\mathrm{O}$ be the center of $\mathrm{C}$. Let the line $\mathrm{AM}$ meet $\mathrm{T}$ at $\mathrm{N}$. Let the perpendicular to $\mathrm{T}$ at $\mathrm{N}$ meet the line $\mathrm{OM}$ at $\mathrm{O}^{\prime}$. Then $\angle \mathrm{O}^{\prime} \mathrm{NM}=\angle \mathrm{MAB}$ ( $\mathrm{O}^{\prime} \mathrm{N}$ parallel to $\mathrm{AB}$, because both perpendicular to $\mathrm{T})=\angle \mathrm{OMA}(\mathrm{OM}=\mathrm{OA})=\angle \mathrm{O}^{\prime} \mathrm{MN}$. So $\mathrm{O}^{\prime} \mathrm{M}=\mathrm{O}^{\prime} \mathrm{N}$. Hence $\mathrm{O}^{\prime}$ is the center of $\mathrm{C}^{\prime}$.
Take B to be the origin and $\mathrm{A}$ to be the point $(2 \mathrm{a}, 0)$, so $\mathrm{O}$ is $(\mathrm{a}, 0)$ and $\mathrm{C}$ has radius a. If $\mathrm{O}^{\prime}$ is $(x, y)$, then we require that $O^{\prime} O=x+a$ or $(x-a)^{2}+y^{2}=(x+a)^{2}$, or $y^{2}=4 a x$, which is a parabola with vertex $B$ and axis the $x$-axis.
Triangles $\mathrm{AMB}, \mathrm{ABN}$ are similar $\left(\angle \mathrm{AMB}=\angle \mathrm{ABN}=90^{\circ}\right)$, so $\mathrm{AM} / \mathrm{AB}=\mathrm{AB} / \mathrm{AN}$ and hence $\mathrm{AM} \cdot \mathrm{AN}=\mathrm{AB}^{2}$. Now consider the circle center $\mathrm{A}$ radius $\mathrm{AB}$. It must meet the circle $\mathrm{C}^{\prime}$, because it contains the point $M$. Suppose it meets at $X$. Then $A X^{2}=A B^{2}=A M \cdot A N$, so $A X$ is tangent to $\mathrm{C}^{\prime}$ and hence the circles are orthogonal.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The circle $\mathrm{C}$ has diameter $\mathrm{AB}$. The tangent at $\mathrm{B}$ is $\mathrm{T}$. For each point $\mathrm{M}$ (not equal to $\mathrm{A}$ ) on $\mathrm{C}$ there is a circle $\mathrm{C}^{\prime}$ which touches $\mathrm{T}$ and touches $\mathrm{C}$ at M. Find the point at which $\mathrm{C}^{\prime}$ touches $\mathrm{T}$ and find the locus of the center of $\mathrm{C}^{\prime}$ as $\mathrm{M}$ varies. Show that there is a circle orthogonal to all the circles $\mathrm{C}^{\prime}$.
## Answer
$\mathrm{C}^{\prime}$ touches $\mathrm{T}$ at the intersection of $\mathrm{T}$ and the line $\mathrm{AM}$
the locus of the center is a parabola vertex B
the circle center A radius $\mathrm{AB}$ is orthogonal to all circles $\mathrm{C}^{\prime}$
|

Let $\mathrm{O}$ be the center of $\mathrm{C}$. Let the line $\mathrm{AM}$ meet $\mathrm{T}$ at $\mathrm{N}$. Let the perpendicular to $\mathrm{T}$ at $\mathrm{N}$ meet the line $\mathrm{OM}$ at $\mathrm{O}^{\prime}$. Then $\angle \mathrm{O}^{\prime} \mathrm{NM}=\angle \mathrm{MAB}$ ( $\mathrm{O}^{\prime} \mathrm{N}$ parallel to $\mathrm{AB}$, because both perpendicular to $\mathrm{T})=\angle \mathrm{OMA}(\mathrm{OM}=\mathrm{OA})=\angle \mathrm{O}^{\prime} \mathrm{MN}$. So $\mathrm{O}^{\prime} \mathrm{M}=\mathrm{O}^{\prime} \mathrm{N}$. Hence $\mathrm{O}^{\prime}$ is the center of $\mathrm{C}^{\prime}$.
Take B to be the origin and $\mathrm{A}$ to be the point $(2 \mathrm{a}, 0)$, so $\mathrm{O}$ is $(\mathrm{a}, 0)$ and $\mathrm{C}$ has radius a. If $\mathrm{O}^{\prime}$ is $(x, y)$, then we require that $O^{\prime} O=x+a$ or $(x-a)^{2}+y^{2}=(x+a)^{2}$, or $y^{2}=4 a x$, which is a parabola with vertex $B$ and axis the $x$-axis.
Triangles $\mathrm{AMB}, \mathrm{ABN}$ are similar $\left(\angle \mathrm{AMB}=\angle \mathrm{ABN}=90^{\circ}\right)$, so $\mathrm{AM} / \mathrm{AB}=\mathrm{AB} / \mathrm{AN}$ and hence $\mathrm{AM} \cdot \mathrm{AN}=\mathrm{AB}^{2}$. Now consider the circle center $\mathrm{A}$ radius $\mathrm{AB}$. It must meet the circle $\mathrm{C}^{\prime}$, because it contains the point $M$. Suppose it meets at $X$. Then $A X^{2}=A B^{2}=A M \cdot A N$, so $A X$ is tangent to $\mathrm{C}^{\prime}$ and hence the circles are orthogonal.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B1",
"solution_match": "\n## Solution"
}
|
35b12489-ea74-5656-9bb4-62fb1af537b9
| 604,380
|
$\mathrm{f}(\mathrm{x})$ is a polynomial of degree 3 with rational coefficients. If its graph touches the $\mathrm{x}$-axis, show that it has three rational roots.
|
Without loss of generality, $f(x)=x^{3}-a x^{2}+b x-c$, where $a, b, c$ are rational. Since the graph touches the $\mathrm{x}$-axis, there is a repeated root, so we may take the roots to be $\mathrm{h}, \mathrm{h}, \mathrm{k}$. Hence $2 \mathrm{~h}+$ $k=a, 2 h k+k^{2}=b, h^{2} k=c$. Hence $a^{2}-3 b=(h-k)^{2}$. Put $r= \pm \sqrt{ }\left(a^{2}-3 b\right)$, where the sign is chosen so that $h=a / 3+r / 3, k=a / 3-2 r / 3$. We need to show that $r$ is rational. If $r$ is zero there is nothing to prove, so assume $\mathrm{r}$ is non-zero.
We have $9 h^{2}=2 a^{2}-3 b+2 a r$. Hence $27 h^{2} k=-2 a^{3}+9 a b+\left(6 b-2 a^{2}\right)$ r. But $27 h^{2} k=27 c$. So $r=$ $\left(27 c+2 a^{3}-9 a b\right) /\left(2\left(3 b-a^{2}\right)\right)$. Note that $3 b-2 a^{2}$ is non-zero because $r$ is non-zero. So $r$ is a rational combination of $\mathrm{a}, \mathrm{b}, \mathrm{c}$ and hence is rational.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
$\mathrm{f}(\mathrm{x})$ is a polynomial of degree 3 with rational coefficients. If its graph touches the $\mathrm{x}$-axis, show that it has three rational roots.
|
Without loss of generality, $f(x)=x^{3}-a x^{2}+b x-c$, where $a, b, c$ are rational. Since the graph touches the $\mathrm{x}$-axis, there is a repeated root, so we may take the roots to be $\mathrm{h}, \mathrm{h}, \mathrm{k}$. Hence $2 \mathrm{~h}+$ $k=a, 2 h k+k^{2}=b, h^{2} k=c$. Hence $a^{2}-3 b=(h-k)^{2}$. Put $r= \pm \sqrt{ }\left(a^{2}-3 b\right)$, where the sign is chosen so that $h=a / 3+r / 3, k=a / 3-2 r / 3$. We need to show that $r$ is rational. If $r$ is zero there is nothing to prove, so assume $\mathrm{r}$ is non-zero.
We have $9 h^{2}=2 a^{2}-3 b+2 a r$. Hence $27 h^{2} k=-2 a^{3}+9 a b+\left(6 b-2 a^{2}\right)$ r. But $27 h^{2} k=27 c$. So $r=$ $\left(27 c+2 a^{3}-9 a b\right) /\left(2\left(3 b-a^{2}\right)\right)$. Note that $3 b-2 a^{2}$ is non-zero because $r$ is non-zero. So $r$ is a rational combination of $\mathrm{a}, \mathrm{b}, \mathrm{c}$ and hence is rational.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B3",
"solution_match": "\n## Solution"
}
|
ceada3e4-afea-5ecb-968e-a71c09074fcd
| 604,403
|
Given three non-collinear points $\mathrm{M}, \mathrm{N}, \mathrm{H}$ show how to construct a triangle which has $\mathrm{H}$ as orthocenter and $\mathrm{M}$ and $\mathrm{N}$ as the midpoints of two sides.
|
Take $\mathrm{H}^{\prime}$ so that $\mathrm{M}$ is the midpoint of $\mathrm{HH}^{\prime}$. The circle diameter $\mathrm{NH}^{\prime}$ meets the line through $\mathrm{H}$ perpendicular to MN in two points (in general), either of which we may take as A. Then B is the reflection of $\mathrm{A}$ in $\mathrm{M}$, and $\mathrm{C}$ is the reflection of $\mathrm{A}$ in $\mathrm{N}$.
To see that this works, note that $\mathrm{M}$ is the midpoint of $\mathrm{HH}^{\prime}$ and $\mathrm{AB}$, so $\mathrm{AHBH}$ ' is a parallelogram. Hence $\mathrm{AH}$ ' is parallel to $\mathrm{BH}$ and hence perpendicular to $\mathrm{AC}$. In other words $\angle \mathrm{NAH}^{\prime}=90^{\circ}$, so A lies on the circle diameter $\mathrm{NH}^{\prime}$. $\mathrm{MN}$ is parallel to $\mathrm{BC}$, so $\mathrm{A}$ lies on the perpendicular to $\mathrm{MN}$ through $\mathrm{H}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given three non-collinear points $\mathrm{M}, \mathrm{N}, \mathrm{H}$ show how to construct a triangle which has $\mathrm{H}$ as orthocenter and $\mathrm{M}$ and $\mathrm{N}$ as the midpoints of two sides.
|

Take $\mathrm{H}^{\prime}$ so that $\mathrm{M}$ is the midpoint of $\mathrm{HH}^{\prime}$. The circle diameter $\mathrm{NH}^{\prime}$ meets the line through $\mathrm{H}$ perpendicular to MN in two points (in general), either of which we may take as A. Then B is the reflection of $\mathrm{A}$ in $\mathrm{M}$, and $\mathrm{C}$ is the reflection of $\mathrm{A}$ in $\mathrm{N}$.
To see that this works, note that $\mathrm{M}$ is the midpoint of $\mathrm{HH}^{\prime}$ and $\mathrm{AB}$, so $\mathrm{AHBH}$ ' is a parallelogram. Hence $\mathrm{AH}$ ' is parallel to $\mathrm{BH}$ and hence perpendicular to $\mathrm{AC}$. In other words $\angle \mathrm{NAH}^{\prime}=90^{\circ}$, so A lies on the circle diameter $\mathrm{NH}^{\prime}$. $\mathrm{MN}$ is parallel to $\mathrm{BC}$, so $\mathrm{A}$ lies on the perpendicular to $\mathrm{MN}$ through $\mathrm{H}$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B3",
"solution_match": "\n## Solution"
}
|
29420675-fd1b-52cb-8f50-061ed3a40257
| 604,454
|
$\mathrm{ABC}$ is an equilateral triangle with side 2 . Show that any point $\mathrm{P}$ on the incircle satisfies $\mathrm{PA}^{2}$ $+\mathrm{PB}^{2}+\mathrm{PC}^{2}=5$. Show also that the triangle with side lengths $\mathrm{PA}, \mathrm{PB}, \mathrm{PC}$ has area $(\sqrt{3}) / 4$.
|
Take vectors centered at the center $\mathrm{O}$ of the triangle. Write the vector $\mathrm{OA}$ as $\mathbf{A}$ etc. Then $\mathrm{PA}^{2}$ $+\mathrm{PB}^{2}+\mathrm{PC}^{2}=(\mathbf{P}-\mathbf{A})^{2}+(\mathbf{P}-\mathbf{B})^{2}+(\mathbf{P}-\mathbf{C})^{2}=3 \mathrm{P}^{2}+\left(\mathrm{A}^{2}+\mathrm{B}^{2}+\mathrm{C}^{2}\right)-2 \mathbf{P} \cdot(\mathbf{A}+\mathbf{B}+\mathbf{C})=15 \mathrm{P}^{2}$, since $A^{2}=B^{2}=C^{2}=4 P^{2}$ and $\mathbf{A}+\mathbf{B}+\mathbf{C}=0$. Finally the side is 2 , so an altitude is $\sqrt{3}$ and the inradius is $(\sqrt{3}) / 3=1 / \sqrt{ } 3$, so $\mathrm{PA}^{2}+\mathrm{PB}^{2}+\mathrm{PC}^{2}=15 / 3=5$.
Take $\mathrm{Q}$ outside the triangle so that $\mathrm{BQ}=\mathrm{BP}$ and $\mathrm{CQ}=\mathrm{AP}$. Then $\mathrm{BQC}$ and $\mathrm{BPA}$ are congruent, so $\angle \mathrm{ABP}=\angle \mathrm{CBQ}$ and hence $\angle \mathrm{PBQ}=60^{\circ}$, so $\mathrm{PBQ}$ is equilateral. Hence $\mathrm{PQ}$ is $\mathrm{PB}$ and $\mathrm{PQC}$ has sides equal to $\mathrm{PA}, \mathrm{PB}, \mathrm{PC}$. If we construct two similar points outside the other two sides then we get a figure with total area equal to 2 area $\mathrm{ABC}$ and to 3 area $\mathrm{PQC}+$ area of three equilateral triangles sides $\mathrm{PA}, \mathrm{PB}, \mathrm{PC}$. Hence 3 area $\mathrm{PQC}=2$ area $\mathrm{ABC}$ - area $\mathrm{ABC}\left(\mathrm{PA}^{2}+\mathrm{PB}^{2}+\mathrm{PC}^{2}\right) / \mathrm{PA}^{2}=(3 / 4)$ area $\mathrm{ABC}=(3 \sqrt{3}) / 4$. So area $\mathrm{PQC}=(\sqrt{3}) / 4$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$\mathrm{ABC}$ is an equilateral triangle with side 2 . Show that any point $\mathrm{P}$ on the incircle satisfies $\mathrm{PA}^{2}$ $+\mathrm{PB}^{2}+\mathrm{PC}^{2}=5$. Show also that the triangle with side lengths $\mathrm{PA}, \mathrm{PB}, \mathrm{PC}$ has area $(\sqrt{3}) / 4$.
|
Take vectors centered at the center $\mathrm{O}$ of the triangle. Write the vector $\mathrm{OA}$ as $\mathbf{A}$ etc. Then $\mathrm{PA}^{2}$ $+\mathrm{PB}^{2}+\mathrm{PC}^{2}=(\mathbf{P}-\mathbf{A})^{2}+(\mathbf{P}-\mathbf{B})^{2}+(\mathbf{P}-\mathbf{C})^{2}=3 \mathrm{P}^{2}+\left(\mathrm{A}^{2}+\mathrm{B}^{2}+\mathrm{C}^{2}\right)-2 \mathbf{P} \cdot(\mathbf{A}+\mathbf{B}+\mathbf{C})=15 \mathrm{P}^{2}$, since $A^{2}=B^{2}=C^{2}=4 P^{2}$ and $\mathbf{A}+\mathbf{B}+\mathbf{C}=0$. Finally the side is 2 , so an altitude is $\sqrt{3}$ and the inradius is $(\sqrt{3}) / 3=1 / \sqrt{ } 3$, so $\mathrm{PA}^{2}+\mathrm{PB}^{2}+\mathrm{PC}^{2}=15 / 3=5$.
Take $\mathrm{Q}$ outside the triangle so that $\mathrm{BQ}=\mathrm{BP}$ and $\mathrm{CQ}=\mathrm{AP}$. Then $\mathrm{BQC}$ and $\mathrm{BPA}$ are congruent, so $\angle \mathrm{ABP}=\angle \mathrm{CBQ}$ and hence $\angle \mathrm{PBQ}=60^{\circ}$, so $\mathrm{PBQ}$ is equilateral. Hence $\mathrm{PQ}$ is $\mathrm{PB}$ and $\mathrm{PQC}$ has sides equal to $\mathrm{PA}, \mathrm{PB}, \mathrm{PC}$. If we construct two similar points outside the other two sides then we get a figure with total area equal to 2 area $\mathrm{ABC}$ and to 3 area $\mathrm{PQC}+$ area of three equilateral triangles sides $\mathrm{PA}, \mathrm{PB}, \mathrm{PC}$. Hence 3 area $\mathrm{PQC}=2$ area $\mathrm{ABC}$ - area $\mathrm{ABC}\left(\mathrm{PA}^{2}+\mathrm{PB}^{2}+\mathrm{PC}^{2}\right) / \mathrm{PA}^{2}=(3 / 4)$ area $\mathrm{ABC}=(3 \sqrt{3}) / 4$. So area $\mathrm{PQC}=(\sqrt{3}) / 4$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A3",
"solution_match": "\n## Solution"
}
|
1248f67a-7bf3-5c8e-83b7-7070c0d3f903
| 604,489
|
We say that two non-negative integers are related if their sum uses only the digits 0 and 1 . For example 22 and 79 are related. Let A and B be two infinite sets of non-negative integers such that: (1) if a $\square \mathrm{A}$ and $\mathrm{b} \square \mathrm{B}$, then a and $\mathrm{b}$ are related, (2) if $\mathrm{c}$ is related to every member of A, then it belongs to $\mathrm{B},(3)$ if $\mathrm{c}$ is related to every member of $\mathrm{B}$, then it belongs to $\mathrm{A}$. Show that in one of the sets $\mathrm{A}, \mathrm{B}$ we can find an infinite number of pairs of consecutive numbers.
|
Suppose there is a member of A with last digit d. Then every member of B must have one of two possible last digits. Suppose there are members of B with both possibilities. Then every member of A must have last digit d. So either every member of A has the same last digit or every member of B has the same last digit (or both). Suppose every member of A has the same last digit d.
But now if $n$ belongs to $B$ and $n+d$ has last digit 0 , then $n+1+d$ has last digit 1 . Moreover, if $m$ is any member of $A$, then $m+n$ has last digit 0 and other digits all 0 or 1 . Hence $m+n+1$ last last digit 1 and other digits all 0 or 1 , so $n+1$ must also belong to B. Similarly, if $n$ is in $B$ and $\mathrm{n}+\mathrm{d}$ has last digit 1 , then $\mathrm{n}-1$ must also belong to $\mathrm{B}$. So in either case there are infinitely many pairs of consecutive numbers in $B$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
We say that two non-negative integers are related if their sum uses only the digits 0 and 1 . For example 22 and 79 are related. Let A and B be two infinite sets of non-negative integers such that: (1) if a $\square \mathrm{A}$ and $\mathrm{b} \square \mathrm{B}$, then a and $\mathrm{b}$ are related, (2) if $\mathrm{c}$ is related to every member of A, then it belongs to $\mathrm{B},(3)$ if $\mathrm{c}$ is related to every member of $\mathrm{B}$, then it belongs to $\mathrm{A}$. Show that in one of the sets $\mathrm{A}, \mathrm{B}$ we can find an infinite number of pairs of consecutive numbers.
|
Suppose there is a member of A with last digit d. Then every member of B must have one of two possible last digits. Suppose there are members of B with both possibilities. Then every member of A must have last digit d. So either every member of A has the same last digit or every member of B has the same last digit (or both). Suppose every member of A has the same last digit d.
But now if $n$ belongs to $B$ and $n+d$ has last digit 0 , then $n+1+d$ has last digit 1 . Moreover, if $m$ is any member of $A$, then $m+n$ has last digit 0 and other digits all 0 or 1 . Hence $m+n+1$ last last digit 1 and other digits all 0 or 1 , so $n+1$ must also belong to B. Similarly, if $n$ is in $B$ and $\mathrm{n}+\mathrm{d}$ has last digit 1 , then $\mathrm{n}-1$ must also belong to $\mathrm{B}$. So in either case there are infinitely many pairs of consecutive numbers in $B$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B3",
"solution_match": "\n## Solution"
}
|
1261cb95-743b-5903-b5b2-36f751eda26a
| 604,570
|
Show that there is a number $1<\mathrm{b}<1993$ such that if 1994 is written in base $\mathrm{b}$ then all its digits are the same. Show that there is no number $1<b<1992$ such that if 1993 is written in base $\mathrm{b}$ then all its digits are the same.
|
Any even number $2 \mathrm{n}$ can be written as 22 in base $\mathrm{n}-1$. In particular $1994=22996$.
We have to show that we cannot write $1993=$ aaa ... $\mathrm{a}_{\mathrm{b}}$. If the number has $\mathrm{n}$ digits, then 1993 $=\mathrm{a}\left(1+\mathrm{b}+\ldots+\mathrm{b}^{\mathrm{n}-1}\right)=\mathrm{a}\left(\mathrm{b}^{\mathrm{n}}-1\right) /(\mathrm{b}-1)$. But 1993 is prime, so a must be 1 . Hence $\mathrm{b}^{\mathrm{n}-1}+\ldots+\mathrm{b}$ $-1992=0$. So b must divide $1992=2^{3} 3.83$. We cannot have $\mathrm{n}=2$, for then $\mathrm{b}=1992$ and we require $\mathrm{b}<1992$. So $\mathrm{n}>2$. But $83^{2}=6889>1993$, so $\mathrm{b}$ must divide 24 . Hence $\mathrm{b}=2,3,4,6$, 8,12 , or 24 . But we can easily check that none of these work:
```
\(1+2+2^{2}+\ldots+2^{9}=1023,1+\ldots+2^{10}=2047\).
\(1+3+\ldots+3^{6}=1093,1+\ldots+3^{\wedge} 7=3280\)
\(1+4+\ldots+4^{5}=1365,1+\ldots+4^{6}=5461\)
```
```
\(1+6+\ldots 6^{4}=1555,1+\ldots+6^{5}=9331\)
\(1+8+8^{2}+8^{3}=585,1+\ldots+8^{4}=4681\)
\(1+12+12^{2}+12^{3}=1885,1+\ldots+12^{4}=22621\)
\(1+24+24^{2}=601,1+\ldots+24^{3}=14425\)
```
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that there is a number $1<\mathrm{b}<1993$ such that if 1994 is written in base $\mathrm{b}$ then all its digits are the same. Show that there is no number $1<b<1992$ such that if 1993 is written in base $\mathrm{b}$ then all its digits are the same.
|
Any even number $2 \mathrm{n}$ can be written as 22 in base $\mathrm{n}-1$. In particular $1994=22996$.
We have to show that we cannot write $1993=$ aaa ... $\mathrm{a}_{\mathrm{b}}$. If the number has $\mathrm{n}$ digits, then 1993 $=\mathrm{a}\left(1+\mathrm{b}+\ldots+\mathrm{b}^{\mathrm{n}-1}\right)=\mathrm{a}\left(\mathrm{b}^{\mathrm{n}}-1\right) /(\mathrm{b}-1)$. But 1993 is prime, so a must be 1 . Hence $\mathrm{b}^{\mathrm{n}-1}+\ldots+\mathrm{b}$ $-1992=0$. So b must divide $1992=2^{3} 3.83$. We cannot have $\mathrm{n}=2$, for then $\mathrm{b}=1992$ and we require $\mathrm{b}<1992$. So $\mathrm{n}>2$. But $83^{2}=6889>1993$, so $\mathrm{b}$ must divide 24 . Hence $\mathrm{b}=2,3,4,6$, 8,12 , or 24 . But we can easily check that none of these work:
```
\(1+2+2^{2}+\ldots+2^{9}=1023,1+\ldots+2^{10}=2047\).
\(1+3+\ldots+3^{6}=1093,1+\ldots+3^{\wedge} 7=3280\)
\(1+4+\ldots+4^{5}=1365,1+\ldots+4^{6}=5461\)
```
```
\(1+6+\ldots 6^{4}=1555,1+\ldots+6^{5}=9331\)
\(1+8+8^{2}+8^{3}=585,1+\ldots+8^{4}=4681\)
\(1+12+12^{2}+12^{3}=1885,1+\ldots+12^{4}=22621\)
\(1+24+24^{2}=601,1+\ldots+24^{3}=14425\)
```
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A1",
"solution_match": "\n## Solution"
}
|
9e9c092c-a2d4-53f1-92bc-34bb8cacfbaf
| 604,584
|
$\mathrm{n}=\mathrm{k}^{2}-\mathrm{k}+1$, where $\mathrm{k}$ is a prime plus one. Show that we can color some squares of an $\mathrm{n} \mathrm{x}$ board black so that each row and column has exactly $\mathrm{k}$ black squares, but there is no rectangle with sides parallel to the sides of the board which has its four corner squares black.
|
We can regard the rows as lines and the columns as points. Black squares denote incidence. So line 3 contains point 4 iff square $(3,4)$ is black. The condition about rectangles then means that there is at most one line through two distinct points.
Suppose we take the points to be ( $\mathrm{a}, \mathrm{b}, \mathrm{c})$, where $\mathrm{a}, \mathrm{b}, \mathrm{c}$ are residues $\bmod \mathrm{p}$, not all zero, and the coordinates are homogeneous, so that we regard (a, b, c), $(2 a, 2 b, 2 c), \ldots,((p-1) a,(p-1) b$, $(\mathrm{p}-1) \mathrm{c})$ as the same point. That gives $\left(\mathrm{p}^{3}-1\right) /(\mathrm{p}-1)=\mathrm{p}^{2}+\mathrm{p}+1$ points, which is the correct number.
We can take lines to be $l \mathrm{x}+m \mathrm{y}+n \mathrm{z}=0$, where the point is $(\mathrm{x}, \mathrm{y}, \mathrm{z})$. In other words, the lines are also triples $(l, m, n)$, with $l, m, n$ residues mod p, not all zero and $(l, m, n),(2 l, 2 m, 2 n), \ldots$, $((p-1) l,(p-1) m,(p-1) n)$ representing the same line.
One way of writing the points is $\mathrm{p}^{2}$ of the form $(\mathrm{a}, \mathrm{b}, 1), \mathrm{p}$ of the form $(\mathrm{a}, 1,0)$ and lastly $(1,0$, $0)$ ) Similarly for the lines. We must show that (1) each point is on $p+1$ lines (so each column has $\mathrm{p}+1$ black squares), (2) each line has $\mathrm{p}+1$ points (so each row has $\mathrm{p}+1$ black squares, (3) two lines meet in just one point (so no rectangles).
(1): Consider the point $\mathrm{P}(\mathrm{a}, \mathrm{b}, 1)$ with a non-zero. Then for any $m$, there is a unique $l$ such that $l \mathrm{a}+m \mathrm{~b}+1.1=0$, so there are $\mathrm{p}$ lines of the form $(l, m, 1)$ which contain P. Similarly, there is a unique $l$ such that $l \mathrm{a}+1 \mathrm{~b}+0.1=0$, so one line of the form $(l, 1,0)$ contains $\mathrm{P}$. The line $(1,0,0)$ does not contain $\mathrm{P}$. So P lies on just $\mathrm{p}+1$ lines. Similarly for $(\mathrm{a}, \mathrm{b}, 1)$ with $\mathrm{b}$ nonzero. The point $(0,0,1)$ does not lie on any lines $(l, m, 1)$, but lies on $(l, 1,0)$ and $(1,0,0)$, so again it lies on $\mathrm{p}+1$ lines.
Consider the point $\mathrm{Q}(\mathrm{a}, 1,0)$ with a non-zero. For any $\mathrm{m}$, there is a unique $l$ such that $\mathrm{Q}$ lies on $(l, m, 0)$. There is also a unique $l$ such that $\mathrm{Q}$ lies on $(l, 1,0)$. $\mathrm{Q}$ does not lie on $(1,0,0)$, so it lies on just p+1 lines. Similarly, the point $(0,1,0)$ lies on the p lines $(l, 0,0)$ and on $(1,0$, $0)$, but no others.
Finally, the point $(1,0,0)$ lies on the $\mathrm{p}$ lines $(0, m, 1)$, the line $(0,1,0)$ and no others. Thus in all cases a point lies on just $\mathrm{p}+1$ lines. The proof of (2) is identical.
(3). Suppose the lines are $(l, m, n)$ and ( $L, M, N$ ). If $l$ and $L$ are non-zero, then we can take the lines as $\left(1, m^{\prime}, n^{\prime}\right)$ and $\left(1, M^{\prime}, N^{\prime}\right)$. So any point (x, y, z) on both satisfies $\mathrm{x}+m^{\prime} \mathrm{y}+n^{\prime} \mathrm{z}=0(*)$ and $\mathrm{x}+M^{\prime} \mathrm{y}+N^{\prime} \mathrm{z}=0$. Subtracting, $\left(m^{\prime}-M^{\prime}\right) \mathrm{y}+\left(n^{\prime}-N^{\prime}\right) \mathrm{z}=0$. The coefficients cannot both be zero, since the lines are distinct. So the ratio $\mathrm{y}: \mathrm{z}$ is fixed. Then *) $^{*}$ gives the ratio $\mathrm{x}: \mathrm{y}$. So the point is uniquely determined. If just one of $l, L$ is non-zero, then we can take the lines as ( 0 , $\left.m^{\prime}, n^{\prime}\right),\left(1, M^{\prime}, N^{\prime}\right)$. We cannot have both $m^{\prime}$ and $n^{\prime}$ zero, so the ratio $\mathrm{y}: \mathrm{z}$ is determined, then the other line determines the ratio $\mathrm{x}: \mathrm{y}$. So again the point is uniquely determined. Finally, suppose $l$ and $L$ are both zero. Then since the lines are distinct y and $\mathrm{z}$ must both be zero. So the unique point on both lines is $(1,0,0)$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
$\mathrm{n}=\mathrm{k}^{2}-\mathrm{k}+1$, where $\mathrm{k}$ is a prime plus one. Show that we can color some squares of an $\mathrm{n} \mathrm{x}$ board black so that each row and column has exactly $\mathrm{k}$ black squares, but there is no rectangle with sides parallel to the sides of the board which has its four corner squares black.
|
We can regard the rows as lines and the columns as points. Black squares denote incidence. So line 3 contains point 4 iff square $(3,4)$ is black. The condition about rectangles then means that there is at most one line through two distinct points.
Suppose we take the points to be ( $\mathrm{a}, \mathrm{b}, \mathrm{c})$, where $\mathrm{a}, \mathrm{b}, \mathrm{c}$ are residues $\bmod \mathrm{p}$, not all zero, and the coordinates are homogeneous, so that we regard (a, b, c), $(2 a, 2 b, 2 c), \ldots,((p-1) a,(p-1) b$, $(\mathrm{p}-1) \mathrm{c})$ as the same point. That gives $\left(\mathrm{p}^{3}-1\right) /(\mathrm{p}-1)=\mathrm{p}^{2}+\mathrm{p}+1$ points, which is the correct number.
We can take lines to be $l \mathrm{x}+m \mathrm{y}+n \mathrm{z}=0$, where the point is $(\mathrm{x}, \mathrm{y}, \mathrm{z})$. In other words, the lines are also triples $(l, m, n)$, with $l, m, n$ residues mod p, not all zero and $(l, m, n),(2 l, 2 m, 2 n), \ldots$, $((p-1) l,(p-1) m,(p-1) n)$ representing the same line.
One way of writing the points is $\mathrm{p}^{2}$ of the form $(\mathrm{a}, \mathrm{b}, 1), \mathrm{p}$ of the form $(\mathrm{a}, 1,0)$ and lastly $(1,0$, $0)$ ) Similarly for the lines. We must show that (1) each point is on $p+1$ lines (so each column has $\mathrm{p}+1$ black squares), (2) each line has $\mathrm{p}+1$ points (so each row has $\mathrm{p}+1$ black squares, (3) two lines meet in just one point (so no rectangles).
(1): Consider the point $\mathrm{P}(\mathrm{a}, \mathrm{b}, 1)$ with a non-zero. Then for any $m$, there is a unique $l$ such that $l \mathrm{a}+m \mathrm{~b}+1.1=0$, so there are $\mathrm{p}$ lines of the form $(l, m, 1)$ which contain P. Similarly, there is a unique $l$ such that $l \mathrm{a}+1 \mathrm{~b}+0.1=0$, so one line of the form $(l, 1,0)$ contains $\mathrm{P}$. The line $(1,0,0)$ does not contain $\mathrm{P}$. So P lies on just $\mathrm{p}+1$ lines. Similarly for $(\mathrm{a}, \mathrm{b}, 1)$ with $\mathrm{b}$ nonzero. The point $(0,0,1)$ does not lie on any lines $(l, m, 1)$, but lies on $(l, 1,0)$ and $(1,0,0)$, so again it lies on $\mathrm{p}+1$ lines.
Consider the point $\mathrm{Q}(\mathrm{a}, 1,0)$ with a non-zero. For any $\mathrm{m}$, there is a unique $l$ such that $\mathrm{Q}$ lies on $(l, m, 0)$. There is also a unique $l$ such that $\mathrm{Q}$ lies on $(l, 1,0)$. $\mathrm{Q}$ does not lie on $(1,0,0)$, so it lies on just p+1 lines. Similarly, the point $(0,1,0)$ lies on the p lines $(l, 0,0)$ and on $(1,0$, $0)$, but no others.
Finally, the point $(1,0,0)$ lies on the $\mathrm{p}$ lines $(0, m, 1)$, the line $(0,1,0)$ and no others. Thus in all cases a point lies on just $\mathrm{p}+1$ lines. The proof of (2) is identical.
(3). Suppose the lines are $(l, m, n)$ and ( $L, M, N$ ). If $l$ and $L$ are non-zero, then we can take the lines as $\left(1, m^{\prime}, n^{\prime}\right)$ and $\left(1, M^{\prime}, N^{\prime}\right)$. So any point (x, y, z) on both satisfies $\mathrm{x}+m^{\prime} \mathrm{y}+n^{\prime} \mathrm{z}=0(*)$ and $\mathrm{x}+M^{\prime} \mathrm{y}+N^{\prime} \mathrm{z}=0$. Subtracting, $\left(m^{\prime}-M^{\prime}\right) \mathrm{y}+\left(n^{\prime}-N^{\prime}\right) \mathrm{z}=0$. The coefficients cannot both be zero, since the lines are distinct. So the ratio $\mathrm{y}: \mathrm{z}$ is fixed. Then *) $^{*}$ gives the ratio $\mathrm{x}: \mathrm{y}$. So the point is uniquely determined. If just one of $l, L$ is non-zero, then we can take the lines as ( 0 , $\left.m^{\prime}, n^{\prime}\right),\left(1, M^{\prime}, N^{\prime}\right)$. We cannot have both $m^{\prime}$ and $n^{\prime}$ zero, so the ratio $\mathrm{y}: \mathrm{z}$ is determined, then the other line determines the ratio $\mathrm{x}: \mathrm{y}$. So again the point is uniquely determined. Finally, suppose $l$ and $L$ are both zero. Then since the lines are distinct y and $\mathrm{z}$ must both be zero. So the unique point on both lines is $(1,0,0)$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A3",
"solution_match": "\n## Solution"
}
|
7b5b6d93-012f-5e79-9594-92bb963c50a1
| 604,732
|
$\mathrm{n}>2$ is an integer. Consider the pairs (a, b) of relatively prime positive integers, such that $\mathrm{a}<$ $\mathrm{b} \leq \mathrm{n}$ and $\mathrm{a}+\mathrm{b}>\mathrm{n}$. Show that the sum of $1 / a b$ taken over all such pairs is $1 / 2$.
|
Induction on $\mathrm{n}$. It is obvious for $\mathrm{n}=3$, because the only pairs are $(1,3)$ and $(2,3)$, and $1 / 3+$ $1 / 6=1 / 2$. Now suppose it is true for $n$. As we move to $n+1$, we introduce the new pairs (a, $\mathrm{n}+1$ ) with a relatively prime to $\mathrm{n}+1$ and we lose the pairs ( $\mathrm{a}, \mathrm{n}+1-\mathrm{a}$ ) with a relatively prime to $\mathrm{n}+1-\mathrm{a}$ and hence to $\mathrm{n}+1$. So for each a relatively prime to $\mathrm{n}+1$ and $<(\mathrm{n}+1) / 2$ we gain ( $a, n+1)$ and $(n+1-a, n+1)$ and lose $(a, n+1-a)$. But $1 / a(n+1)+1 /((n+1-a)(n+1))=(n+1-a+a) /(a(n+1-$ $a)(n+1))=1 /(a(n+1-a))$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
$\mathrm{n}>2$ is an integer. Consider the pairs (a, b) of relatively prime positive integers, such that $\mathrm{a}<$ $\mathrm{b} \leq \mathrm{n}$ and $\mathrm{a}+\mathrm{b}>\mathrm{n}$. Show that the sum of $1 / a b$ taken over all such pairs is $1 / 2$.
|
Induction on $\mathrm{n}$. It is obvious for $\mathrm{n}=3$, because the only pairs are $(1,3)$ and $(2,3)$, and $1 / 3+$ $1 / 6=1 / 2$. Now suppose it is true for $n$. As we move to $n+1$, we introduce the new pairs (a, $\mathrm{n}+1$ ) with a relatively prime to $\mathrm{n}+1$ and we lose the pairs ( $\mathrm{a}, \mathrm{n}+1-\mathrm{a}$ ) with a relatively prime to $\mathrm{n}+1-\mathrm{a}$ and hence to $\mathrm{n}+1$. So for each a relatively prime to $\mathrm{n}+1$ and $<(\mathrm{n}+1) / 2$ we gain ( $a, n+1)$ and $(n+1-a, n+1)$ and lose $(a, n+1-a)$. But $1 / a(n+1)+1 /((n+1-a)(n+1))=(n+1-a+a) /(a(n+1-$ $a)(n+1))=1 /(a(n+1-a))$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B1",
"solution_match": "\n## Solution"
}
|
d5542689-f621-5ac2-9bc6-c13b699a7a21
| 604,749
|
An equilateral triangle of side $n$ is divided into $n^{2}$ equilateral triangles of side 1 by lines parallel to the sides. Initially, all the sides of all the small triangles are painted blue. Three coins A, B, C are placed at vertices of the small triangles. Each coin in turn is moved a distance 1 along a blue side to an adjacent vertex. The side it moves along is painted red, so once a coin has moved along a side, the side cannot be used again. More than one coin is allowed to occupy the same vertex. The coins are moved repeatedly in the order A, B, C, A, B, C, ... Show that it is possible to paint all the sides red in this way.
|
We use induction. It is obvious for $\mathrm{n}=1$ and 2 - see diagram above. Note that A, B, C start and end at vertices of the large triangle.
Now assume that for $\mathrm{n}$ we can find a solution with $\mathrm{A}, \mathrm{B}, \mathrm{C}$ starting and ending at the vertices of the large triangle. Take $\mathrm{n}+1$. We start with the paths shown which bring A, B, C to $\mathrm{A}^{\prime}, \mathrm{B}^{\prime}$, $\mathrm{C}^{\prime}$ at the vertices of a triangle side $\mathrm{n}-1$. Now by induction we can continue the paths so that we bring A, B, C, back to the vertices of that triangle after tracing out all its edges. Finally, note that for each of the points $\mathrm{A}^{\prime}, \mathrm{B}^{\prime}, \mathrm{C}^{\prime}$ there is a path length 2 over untraced segments to a vertex of the large triangle. So we get a solution for $\mathrm{n}+1$ and hence for all $\mathrm{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
An equilateral triangle of side $n$ is divided into $n^{2}$ equilateral triangles of side 1 by lines parallel to the sides. Initially, all the sides of all the small triangles are painted blue. Three coins A, B, C are placed at vertices of the small triangles. Each coin in turn is moved a distance 1 along a blue side to an adjacent vertex. The side it moves along is painted red, so once a coin has moved along a side, the side cannot be used again. More than one coin is allowed to occupy the same vertex. The coins are moved repeatedly in the order A, B, C, A, B, C, ... Show that it is possible to paint all the sides red in this way.
|
We use induction. It is obvious for $\mathrm{n}=1$ and 2 - see diagram above. Note that A, B, C start and end at vertices of the large triangle.

Now assume that for $\mathrm{n}$ we can find a solution with $\mathrm{A}, \mathrm{B}, \mathrm{C}$ starting and ending at the vertices of the large triangle. Take $\mathrm{n}+1$. We start with the paths shown which bring A, B, C to $\mathrm{A}^{\prime}, \mathrm{B}^{\prime}$, $\mathrm{C}^{\prime}$ at the vertices of a triangle side $\mathrm{n}-1$. Now by induction we can continue the paths so that we bring A, B, C, back to the vertices of that triangle after tracing out all its edges. Finally, note that for each of the points $\mathrm{A}^{\prime}, \mathrm{B}^{\prime}, \mathrm{C}^{\prime}$ there is a path length 2 over untraced segments to a vertex of the large triangle. So we get a solution for $\mathrm{n}+1$ and hence for all $\mathrm{n}$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B2",
"solution_match": "\n## Solution"
}
|
881364ce-d14b-5411-be27-e0e2af34f2f0
| 604,761
|
$k>=1$ is a real number such that if $m$ is a multiple of $n$, then [mk] is a multiple of [nk]. Show that $\mathrm{k}$ is an integer.
|
Suppose $\mathrm{k}$ is not an integer. Take an integer $\mathrm{n}$ such that $\mathrm{nk}>1$, but $\mathrm{nk}$ is not an integer. Now take a positive integer $\mathrm{c}$ such that $1 /(\mathrm{c}+1)<=\mathrm{nk}-[\mathrm{nk}]<1 / \mathrm{c}$. Then $1<=(\mathrm{c}+1) \mathrm{nk}-(\mathrm{c}+1)[\mathrm{nk}]<$ $1+1 / \mathrm{c}$. Hence $[(c+1) n k]=(c+1)[n k]+1$. Put $m=(c+1) n$. Then $m$ is a multiple of $n$. But if [mk] is a multiple of [nk], then [mk] - (c+1) [nk] = 1 is a multiple of [nk], which is impossible since $\mathrm{nk}>1$. So we have a contradiction. So $\mathrm{k}$ must be an integer.
## Problem 2
I is the incenter of the triangle $\mathrm{ABC}$. A circle with center I meets the side $\mathrm{BC}$ at $\mathrm{D}$ and $\mathrm{P}$, with D nearer to B. Similarly, it meets the side CA at E and Q, with E nearer to C, and it meets AB at $\mathrm{F}$ and $\mathrm{R}$, with $\mathrm{F}$ nearer to $\mathrm{A}$. The lines EF and QR meet at $\mathrm{S}$, the lines FD and RP meet at T, and the lines DE and PQ meet at U. Show that the circumcircles of DUP, ESQ and FTR have a single point in common.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
$k>=1$ is a real number such that if $m$ is a multiple of $n$, then [mk] is a multiple of [nk]. Show that $\mathrm{k}$ is an integer.
|
Suppose $\mathrm{k}$ is not an integer. Take an integer $\mathrm{n}$ such that $\mathrm{nk}>1$, but $\mathrm{nk}$ is not an integer. Now take a positive integer $\mathrm{c}$ such that $1 /(\mathrm{c}+1)<=\mathrm{nk}-[\mathrm{nk}]<1 / \mathrm{c}$. Then $1<=(\mathrm{c}+1) \mathrm{nk}-(\mathrm{c}+1)[\mathrm{nk}]<$ $1+1 / \mathrm{c}$. Hence $[(c+1) n k]=(c+1)[n k]+1$. Put $m=(c+1) n$. Then $m$ is a multiple of $n$. But if [mk] is a multiple of [nk], then [mk] - (c+1) [nk] = 1 is a multiple of [nk], which is impossible since $\mathrm{nk}>1$. So we have a contradiction. So $\mathrm{k}$ must be an integer.
## Problem 2
I is the incenter of the triangle $\mathrm{ABC}$. A circle with center I meets the side $\mathrm{BC}$ at $\mathrm{D}$ and $\mathrm{P}$, with D nearer to B. Similarly, it meets the side CA at E and Q, with E nearer to C, and it meets AB at $\mathrm{F}$ and $\mathrm{R}$, with $\mathrm{F}$ nearer to $\mathrm{A}$. The lines EF and QR meet at $\mathrm{S}$, the lines FD and RP meet at T, and the lines DE and PQ meet at U. Show that the circumcircles of DUP, ESQ and FTR have a single point in common.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A1",
"solution_match": "\n## Solution"
}
|
bd490e65-ae23-568e-8609-25fda875d82e
| 604,786
|
$n>1$ is an integer. $D_{n}$ is the set of lattice points $(x, y)$ with $|x|,|y|<=n$. If the points of $D_{n}$ are colored with three colors (one for each point), show that there are always two points with the same color such that the line containing them does not contain any other points of $\mathrm{D}_{\mathrm{n}}$. Show that it is possible to color the points of $\mathrm{D}_{\mathrm{n}}$ with four colors (one for each point) so that if any line contains just two points of $\mathrm{D}_{\mathrm{n}}$ then those two points have different colors.
|
Consider the 4 points shown in the diagram. In each case the segment joining them is the diagonal of an $\mathrm{m} \times 1$ parallelogram or rectangle, so it cannot contain any other lattice points. The next points along each line are obviously outside set $\mathrm{D}_{\mathrm{n}}$. That proves the first part.
The second part is the standard parity argument. Color ( $\mathrm{x}, \mathrm{y}$ ) with color 1 if $\mathrm{x}$ and $\mathrm{y}$ are both even, 2 if $\mathrm{x}$ is even and $\mathrm{y}$ is odd, 3 if $\mathrm{x}$ is odd and $\mathrm{y}$ is even, and 4 if $\mathrm{x}$ and $\mathrm{y}$ are both odd. Then if two points are the same color, that means the first coordinates are the same parity and their second coordinates are the same parity. Hence the midpoint of the segment joining them is also a lattice point and they are not the only two points of $D_{n}$ on the line.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
$n>1$ is an integer. $D_{n}$ is the set of lattice points $(x, y)$ with $|x|,|y|<=n$. If the points of $D_{n}$ are colored with three colors (one for each point), show that there are always two points with the same color such that the line containing them does not contain any other points of $\mathrm{D}_{\mathrm{n}}$. Show that it is possible to color the points of $\mathrm{D}_{\mathrm{n}}$ with four colors (one for each point) so that if any line contains just two points of $\mathrm{D}_{\mathrm{n}}$ then those two points have different colors.
|

Consider the 4 points shown in the diagram. In each case the segment joining them is the diagonal of an $\mathrm{m} \times 1$ parallelogram or rectangle, so it cannot contain any other lattice points. The next points along each line are obviously outside set $\mathrm{D}_{\mathrm{n}}$. That proves the first part.
The second part is the standard parity argument. Color ( $\mathrm{x}, \mathrm{y}$ ) with color 1 if $\mathrm{x}$ and $\mathrm{y}$ are both even, 2 if $\mathrm{x}$ is even and $\mathrm{y}$ is odd, 3 if $\mathrm{x}$ is odd and $\mathrm{y}$ is even, and 4 if $\mathrm{x}$ and $\mathrm{y}$ are both odd. Then if two points are the same color, that means the first coordinates are the same parity and their second coordinates are the same parity. Hence the midpoint of the segment joining them is also a lattice point and they are not the only two points of $D_{n}$ on the line.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A3",
"solution_match": "\n## Solution"
}
|
369aae72-95a3-5f49-a77a-a3a68e7851cc
| 604,816
|
$\mathrm{ABC}$ is an acute-angled triangle with orthocenter $\mathrm{H} . \mathrm{AE}$ and $\mathrm{BF}$ are altitudes. $\mathrm{AE}$ is reflected in the angle bisector of angle $\mathrm{A}$ and $\mathrm{BF}$ is reflected in the angle bisector of angle $\mathrm{B}$. The two reflections intersect at $\mathrm{O}$. The rays $\mathrm{AE}$ and $\mathrm{AO}$ meet the circumcircle of $\mathrm{ABC}$ at $\mathrm{M}$ and $\mathrm{N}$ respectively. $\mathrm{P}$ is the intersection of $\mathrm{BC}$ and $\mathrm{HN}, \mathrm{R}$ is the intersection of $\mathrm{BC}$ and $\mathrm{OM}$, and $\mathrm{S}$ is the intersection of HR and OP. Show that AHSO is a parallelogram.
|
We show first that $\mathrm{O}$ is the circumcenter of $\mathrm{ABC} . \angle \mathrm{ABF}=90^{\circ}-\mathrm{A}$. The line $\mathrm{BC}$ is the reflection in $B D$ of the line $B A$ and the line $\mathrm{BF}^{\prime}$ is the refection of $\mathrm{BF}$, so angle $\mathrm{CBF}^{\prime}=90^{\circ}$ A. But if $\mathrm{O}^{\prime}$ is the circumcenter, then $\angle \mathrm{BO}^{\prime} \mathrm{C}=2 \angle \mathrm{BAC}=2 \mathrm{~A}$, so $\angle \mathrm{O}^{\prime} \mathrm{BC}=90^{\circ}-\mathrm{A}$. Hence $\mathrm{O}^{\prime}$ lies on $\mathrm{BF}^{\prime}$. Similarly, it lies on $\mathrm{AE}^{\prime}$ (the reflection of $\mathrm{AE}$ in the angle bisector of $\mathrm{A}$ ). Hence $\mathrm{O}=\mathrm{O}^{\prime}$.
$\angle \mathrm{MBC}=\angle \mathrm{MAC}=90^{\circ}-\mathrm{C}($ since $\mathrm{AH}$ is an altitude $)=\angle \mathrm{FBC}($ since $\mathrm{BF}$ is an altitude $)=$ $\angle \mathrm{HBC}$ (same angle). So triangles HBE and MBE are congruent and HE $=$ EM. [Note: this should be a familiar result.].
$\mathrm{AN}$ is a diameter, so angle $\mathrm{AMN}=90^{\circ}=$ angle $\mathrm{AEC}$, so $\mathrm{BC}$ and $\mathrm{MN}$ are parallel. Hence $\mathrm{P}$ is the midpoint of $\mathrm{HN}$ and of $\mathrm{BC}$. So OP is perpendicular to $\mathrm{BC}$. So $\mathrm{AH}$ and $\mathrm{OS}$ are parallel.
Since $\mathrm{R}$ lies on $\mathrm{BC}$, triangles HER and MER are congruent, so $\angle \mathrm{EHR}=\angle \mathrm{EMR}=\angle \mathrm{AMO}$ $($ same angle $)=\angle \mathrm{MAO}$. Hence HS and AO are parallel. So AHSO is a parallelogram.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$\mathrm{ABC}$ is an acute-angled triangle with orthocenter $\mathrm{H} . \mathrm{AE}$ and $\mathrm{BF}$ are altitudes. $\mathrm{AE}$ is reflected in the angle bisector of angle $\mathrm{A}$ and $\mathrm{BF}$ is reflected in the angle bisector of angle $\mathrm{B}$. The two reflections intersect at $\mathrm{O}$. The rays $\mathrm{AE}$ and $\mathrm{AO}$ meet the circumcircle of $\mathrm{ABC}$ at $\mathrm{M}$ and $\mathrm{N}$ respectively. $\mathrm{P}$ is the intersection of $\mathrm{BC}$ and $\mathrm{HN}, \mathrm{R}$ is the intersection of $\mathrm{BC}$ and $\mathrm{OM}$, and $\mathrm{S}$ is the intersection of HR and OP. Show that AHSO is a parallelogram.
|

We show first that $\mathrm{O}$ is the circumcenter of $\mathrm{ABC} . \angle \mathrm{ABF}=90^{\circ}-\mathrm{A}$. The line $\mathrm{BC}$ is the reflection in $B D$ of the line $B A$ and the line $\mathrm{BF}^{\prime}$ is the refection of $\mathrm{BF}$, so angle $\mathrm{CBF}^{\prime}=90^{\circ}$ A. But if $\mathrm{O}^{\prime}$ is the circumcenter, then $\angle \mathrm{BO}^{\prime} \mathrm{C}=2 \angle \mathrm{BAC}=2 \mathrm{~A}$, so $\angle \mathrm{O}^{\prime} \mathrm{BC}=90^{\circ}-\mathrm{A}$. Hence $\mathrm{O}^{\prime}$ lies on $\mathrm{BF}^{\prime}$. Similarly, it lies on $\mathrm{AE}^{\prime}$ (the reflection of $\mathrm{AE}$ in the angle bisector of $\mathrm{A}$ ). Hence $\mathrm{O}=\mathrm{O}^{\prime}$.

$\angle \mathrm{MBC}=\angle \mathrm{MAC}=90^{\circ}-\mathrm{C}($ since $\mathrm{AH}$ is an altitude $)=\angle \mathrm{FBC}($ since $\mathrm{BF}$ is an altitude $)=$ $\angle \mathrm{HBC}$ (same angle). So triangles HBE and MBE are congruent and HE $=$ EM. [Note: this should be a familiar result.].
$\mathrm{AN}$ is a diameter, so angle $\mathrm{AMN}=90^{\circ}=$ angle $\mathrm{AEC}$, so $\mathrm{BC}$ and $\mathrm{MN}$ are parallel. Hence $\mathrm{P}$ is the midpoint of $\mathrm{HN}$ and of $\mathrm{BC}$. So OP is perpendicular to $\mathrm{BC}$. So $\mathrm{AH}$ and $\mathrm{OS}$ are parallel.
Since $\mathrm{R}$ lies on $\mathrm{BC}$, triangles HER and MER are congruent, so $\angle \mathrm{EHR}=\angle \mathrm{EMR}=\angle \mathrm{AMO}$ $($ same angle $)=\angle \mathrm{MAO}$. Hence HS and AO are parallel. So AHSO is a parallelogram.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B2",
"solution_match": "\n## Solution"
}
|
f11c5c90-a64e-5261-a4bc-3f21521bb609
| 604,842
|
Given 1997 points inside a circle of radius 1, one of them the center of the circle. For each point take the distance to the closest (distinct) point. Show that the sum of the squares of the resulting distances is at most 9 .
|
Let the points be $\mathrm{P}_{\mathrm{i}}$ for $\mathrm{i}=1,2, \ldots$, 1997. Take $\mathrm{P}_{1}$ to be the center of the given unit circle. Let $x_{i}$ be the distance from $P_{i}$ to the closest of the other 1996 points. Let $C_{i}$ be the circle center $P_{i}$ radius $\mathrm{x}_{\mathrm{i}} / 2$. Then $\mathrm{C}_{\mathrm{i}}$ and $\mathrm{C}_{\mathrm{j}}$ cannot overlap by more than one point because $\mathrm{x}_{\mathrm{i}}$ and $\mathrm{x}_{\mathrm{j}} \leq \mathrm{P}_{\mathrm{i}} \mathrm{P}_{\mathrm{j}}$. Also $\mathrm{x}_{\mathrm{i}} \leq 1$, since $\mathrm{P}_{1} \mathrm{P}_{\mathrm{i}} \leq 1$. Thus $\mathrm{C}_{\mathrm{i}}$ is entirely contained in the circle center $\mathrm{P}_{1}$ radius $3 / 2$. Since the circles $\mathrm{C}_{\mathrm{i}}$ do not overlap, their total area cannot exceed the area of the circle radius $3 / 2$. Hence $\left(x_{1}{ }^{2}+x_{2}{ }^{2}+\ldots+x_{1997}{ }^{2}\right) / 4 \leq 9 / 4$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given 1997 points inside a circle of radius 1, one of them the center of the circle. For each point take the distance to the closest (distinct) point. Show that the sum of the squares of the resulting distances is at most 9 .
|
Let the points be $\mathrm{P}_{\mathrm{i}}$ for $\mathrm{i}=1,2, \ldots$, 1997. Take $\mathrm{P}_{1}$ to be the center of the given unit circle. Let $x_{i}$ be the distance from $P_{i}$ to the closest of the other 1996 points. Let $C_{i}$ be the circle center $P_{i}$ radius $\mathrm{x}_{\mathrm{i}} / 2$. Then $\mathrm{C}_{\mathrm{i}}$ and $\mathrm{C}_{\mathrm{j}}$ cannot overlap by more than one point because $\mathrm{x}_{\mathrm{i}}$ and $\mathrm{x}_{\mathrm{j}} \leq \mathrm{P}_{\mathrm{i}} \mathrm{P}_{\mathrm{j}}$. Also $\mathrm{x}_{\mathrm{i}} \leq 1$, since $\mathrm{P}_{1} \mathrm{P}_{\mathrm{i}} \leq 1$. Thus $\mathrm{C}_{\mathrm{i}}$ is entirely contained in the circle center $\mathrm{P}_{1}$ radius $3 / 2$. Since the circles $\mathrm{C}_{\mathrm{i}}$ do not overlap, their total area cannot exceed the area of the circle radius $3 / 2$. Hence $\left(x_{1}{ }^{2}+x_{2}{ }^{2}+\ldots+x_{1997}{ }^{2}\right) / 4 \leq 9 / 4$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B3",
"solution_match": "\n## Solution"
}
|
f0574263-1b4f-50be-a33a-848a04dc90df
| 604,855
|
The incircle of the triangle $\mathrm{ABC}$ touches $\mathrm{BC}, \mathrm{CA}, \mathrm{AB}$ at $\mathrm{D}, \mathrm{E}, \mathrm{F}$ respectively. $\mathrm{AD}$ meets the circle again at $\mathrm{Q}$. Show that the line $\mathrm{EQ}$ passes through the midpoint of $\mathrm{AF}$ iff $\mathrm{AC}=\mathrm{BC}$.
|
$\angle \mathrm{AQM}=\angle \mathrm{EQD}($ opposite angle $)=\angle \mathrm{EDC}(\mathrm{CD}$ tangent to circle $\mathrm{EQD})=\left(180^{\circ}-\angle \mathrm{C}\right) / 2=$ $\angle \mathrm{A} / 2+\angle \mathrm{B} / 2(*)$.
$\mathrm{MF}^{2}=\mathrm{MQ} \cdot \mathrm{ME}$ (MF tangent to circle $\mathrm{FQE}$ ). So $\mathrm{AM}=\mathrm{AF}$ is equivalent to $\mathrm{AM}^{2}=\mathrm{MQ} \cdot \mathrm{ME}$ or $\mathrm{AM} / \mathrm{MQ}=\mathrm{ME} / \mathrm{AM}$. But since triangles $\mathrm{AMQ}$ and EMA have a common angle $\mathrm{M}, \mathrm{AM} / \mathrm{MQ}=$ $\mathrm{ME} / \mathrm{AM}$ iff they are similar, and hence iff $\angle \mathrm{AQM}=\angle \mathrm{A}$. Using $(*) \mathrm{AM}=\mathrm{AF}$ iff $\angle \mathrm{A}=\angle \mathrm{B}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The incircle of the triangle $\mathrm{ABC}$ touches $\mathrm{BC}, \mathrm{CA}, \mathrm{AB}$ at $\mathrm{D}, \mathrm{E}, \mathrm{F}$ respectively. $\mathrm{AD}$ meets the circle again at $\mathrm{Q}$. Show that the line $\mathrm{EQ}$ passes through the midpoint of $\mathrm{AF}$ iff $\mathrm{AC}=\mathrm{BC}$.
|

$\angle \mathrm{AQM}=\angle \mathrm{EQD}($ opposite angle $)=\angle \mathrm{EDC}(\mathrm{CD}$ tangent to circle $\mathrm{EQD})=\left(180^{\circ}-\angle \mathrm{C}\right) / 2=$ $\angle \mathrm{A} / 2+\angle \mathrm{B} / 2(*)$.
$\mathrm{MF}^{2}=\mathrm{MQ} \cdot \mathrm{ME}$ (MF tangent to circle $\mathrm{FQE}$ ). So $\mathrm{AM}=\mathrm{AF}$ is equivalent to $\mathrm{AM}^{2}=\mathrm{MQ} \cdot \mathrm{ME}$ or $\mathrm{AM} / \mathrm{MQ}=\mathrm{ME} / \mathrm{AM}$. But since triangles $\mathrm{AMQ}$ and EMA have a common angle $\mathrm{M}, \mathrm{AM} / \mathrm{MQ}=$ $\mathrm{ME} / \mathrm{AM}$ iff they are similar, and hence iff $\angle \mathrm{AQM}=\angle \mathrm{A}$. Using $(*) \mathrm{AM}=\mathrm{AF}$ iff $\angle \mathrm{A}=\angle \mathrm{B}$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A2",
"solution_match": "\n## Solution"
}
|
9d5aee90-ec0a-5f4b-8f88-3ac689a8a923
| 604,881
|
Given two circles $\mathrm{C}$ and $\mathrm{C}^{\prime}$ we say that $\mathrm{C}$ bisects $\mathrm{C}^{\prime}$ if their common chord is a diameter of $\mathrm{C}^{\prime}$. Show that for any two circles which are not concentric, there are infinitely many circles which bisect them both. Find the locus of the centers of the bisecting circles.
|
Let $\mathrm{C}, \mathrm{C}^{\prime}$ have center $\mathrm{O}, \mathrm{O}^{\prime}$ respectively and radius $\mathrm{r}, \mathrm{r}^{\prime}$ respectively. Let a circle center $\mathrm{P}$ bisect $C$. Suppose it meets $C$ at $A$ and $B$. Then $A B$ is perpendicular to $O P$ and is a diameter of C. Hence $\mathrm{PA}^{2}=\mathrm{OP}^{2}+\mathrm{r}^{2}$. Conversely, the circle center $\mathrm{P}$, radius $\sqrt{ }\left(\mathrm{OP}^{2}+\mathrm{r}^{2}\right)$ bisects $\mathrm{C}$. So $\mathrm{P}$ will bisect $\mathrm{C}$ and $\mathrm{C}^{\prime}$ iff $\mathrm{OP}^{2}+\mathrm{r}^{2}=\mathrm{OP}^{\prime 2}+\mathrm{r}^{\prime 2}$.
It is well-known that the locus of points $\mathrm{P}^{\prime}$ with equal tangents to $\mathrm{C}$ and $\mathrm{C}^{\prime}$ is the radical axis. Call the radical axis $\mathrm{R}$. For a point $\mathrm{P}^{\prime}$ on the radical axis we have $\mathrm{P}^{\prime} \mathrm{O}^{2}-\mathrm{r}^{2}=\mathrm{P}^{\prime} \mathrm{O}^{\prime 2}-\mathrm{r}^{\prime 2}$. If we reflect $\mathrm{P}^{\prime}$ in the perpendicular bisector of $\mathrm{OO}^{\prime}$ to get $\mathrm{P}$, then $\mathrm{PO}=\mathrm{P}^{\prime} \mathrm{O}^{\prime}$ and $\mathrm{PO}^{\prime}=\mathrm{P}^{\prime} \mathrm{O}$, so $\mathrm{PO}^{\prime 2}$ $-r^{2}=\mathrm{PO}^{2-r^{2}}$ and hence $\mathrm{PO}^{2}+\mathrm{r}^{2}$. Call the reflection of the $\mathrm{R}$ in the perpendicular bisector of OO' the line $\mathrm{R}^{\prime}$. We have established that points on $\mathrm{R}^{\prime}$ form part of the locus. Conversely, if $\mathrm{P}^{\prime}$ is such that there is a circle center $\mathrm{P}^{\prime}$ bisecting both circles, then $\mathrm{OP}^{\prime 2}+\mathrm{r}^{2}=\mathrm{O}^{\prime} \mathrm{P}^{\prime 2}+\mathrm{r}^{\prime 2}$, so if $\mathrm{P}$ is the reflection of $\mathrm{P}^{\prime}$ then $\mathrm{OP}^{2}-\mathrm{r}^{2}=\mathrm{O}^{2}-\mathrm{r}^{\mathrm{r}^{2}}$ and hence $\mathrm{P}$ lies on the radical axis R. Hence $\mathrm{P}^{\prime}$ must lie on $\mathrm{R}^{\prime}$.
We have $\mathrm{PT}^{2}=\mathrm{PO}^{2}-\mathrm{r}^{2}=\mathrm{PX}^{2}+\mathrm{OX}^{2}-\mathrm{r}^{2}$, and similarly $\mathrm{PT}^{\prime 2}=\mathrm{PX}^{2}+\mathrm{O}^{\prime} \mathrm{X}^{2}-\mathrm{r}^{\prime 2}$. So $\mathrm{PT}=\mathrm{PT}^{\prime}$ iff $O X^{2}-r^{2}=O^{\prime} X^{2}-r^{\prime 2}$. There is evidently a unique point $X$ for which that is true, so the locus of such $\mathrm{P}$ is the line through $\mathrm{X}$ perpendicular to $\mathrm{OO}^{\prime}$
If the circles intersect, then the point $\mathrm{X}$ evidently lies on the line joining the two common points, because $O X^{2}-r^{2}=-X Y^{2}=O^{\prime} X^{2}-r^{\prime 2}$. In any case the midpoint of each common tangent evidently lies on the line, so that provides a way of constructing it.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given two circles $\mathrm{C}$ and $\mathrm{C}^{\prime}$ we say that $\mathrm{C}$ bisects $\mathrm{C}^{\prime}$ if their common chord is a diameter of $\mathrm{C}^{\prime}$. Show that for any two circles which are not concentric, there are infinitely many circles which bisect them both. Find the locus of the centers of the bisecting circles.
|
Let $\mathrm{C}, \mathrm{C}^{\prime}$ have center $\mathrm{O}, \mathrm{O}^{\prime}$ respectively and radius $\mathrm{r}, \mathrm{r}^{\prime}$ respectively. Let a circle center $\mathrm{P}$ bisect $C$. Suppose it meets $C$ at $A$ and $B$. Then $A B$ is perpendicular to $O P$ and is a diameter of C. Hence $\mathrm{PA}^{2}=\mathrm{OP}^{2}+\mathrm{r}^{2}$. Conversely, the circle center $\mathrm{P}$, radius $\sqrt{ }\left(\mathrm{OP}^{2}+\mathrm{r}^{2}\right)$ bisects $\mathrm{C}$. So $\mathrm{P}$ will bisect $\mathrm{C}$ and $\mathrm{C}^{\prime}$ iff $\mathrm{OP}^{2}+\mathrm{r}^{2}=\mathrm{OP}^{\prime 2}+\mathrm{r}^{\prime 2}$.
It is well-known that the locus of points $\mathrm{P}^{\prime}$ with equal tangents to $\mathrm{C}$ and $\mathrm{C}^{\prime}$ is the radical axis. Call the radical axis $\mathrm{R}$. For a point $\mathrm{P}^{\prime}$ on the radical axis we have $\mathrm{P}^{\prime} \mathrm{O}^{2}-\mathrm{r}^{2}=\mathrm{P}^{\prime} \mathrm{O}^{\prime 2}-\mathrm{r}^{\prime 2}$. If we reflect $\mathrm{P}^{\prime}$ in the perpendicular bisector of $\mathrm{OO}^{\prime}$ to get $\mathrm{P}$, then $\mathrm{PO}=\mathrm{P}^{\prime} \mathrm{O}^{\prime}$ and $\mathrm{PO}^{\prime}=\mathrm{P}^{\prime} \mathrm{O}$, so $\mathrm{PO}^{\prime 2}$ $-r^{2}=\mathrm{PO}^{2-r^{2}}$ and hence $\mathrm{PO}^{2}+\mathrm{r}^{2}$. Call the reflection of the $\mathrm{R}$ in the perpendicular bisector of OO' the line $\mathrm{R}^{\prime}$. We have established that points on $\mathrm{R}^{\prime}$ form part of the locus. Conversely, if $\mathrm{P}^{\prime}$ is such that there is a circle center $\mathrm{P}^{\prime}$ bisecting both circles, then $\mathrm{OP}^{\prime 2}+\mathrm{r}^{2}=\mathrm{O}^{\prime} \mathrm{P}^{\prime 2}+\mathrm{r}^{\prime 2}$, so if $\mathrm{P}$ is the reflection of $\mathrm{P}^{\prime}$ then $\mathrm{OP}^{2}-\mathrm{r}^{2}=\mathrm{O}^{2}-\mathrm{r}^{\mathrm{r}^{2}}$ and hence $\mathrm{P}$ lies on the radical axis R. Hence $\mathrm{P}^{\prime}$ must lie on $\mathrm{R}^{\prime}$.

We have $\mathrm{PT}^{2}=\mathrm{PO}^{2}-\mathrm{r}^{2}=\mathrm{PX}^{2}+\mathrm{OX}^{2}-\mathrm{r}^{2}$, and similarly $\mathrm{PT}^{\prime 2}=\mathrm{PX}^{2}+\mathrm{O}^{\prime} \mathrm{X}^{2}-\mathrm{r}^{\prime 2}$. So $\mathrm{PT}=\mathrm{PT}^{\prime}$ iff $O X^{2}-r^{2}=O^{\prime} X^{2}-r^{\prime 2}$. There is evidently a unique point $X$ for which that is true, so the locus of such $\mathrm{P}$ is the line through $\mathrm{X}$ perpendicular to $\mathrm{OO}^{\prime}$

If the circles intersect, then the point $\mathrm{X}$ evidently lies on the line joining the two common points, because $O X^{2}-r^{2}=-X Y^{2}=O^{\prime} X^{2}-r^{\prime 2}$. In any case the midpoint of each common tangent evidently lies on the line, so that provides a way of constructing it.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A2",
"solution_match": "\n## Solution"
}
|
631ec592-f781-55f4-9363-1123fe3fb61a
| 604,958
|
Show that any integer greater than 10 whose digits are all members of $\{1,3,7,9\}$ has a prime factor $\geq 11$.
|
Such a number cannot be divisible by 2 (or its last digit would be even) or by 5 (or its last digit would be 0 or 5). So if the result is false then the number must be of the form $3^{\mathrm{m}} 7^{\mathrm{n}}$ for non-negative integers $\mathrm{m}, \mathrm{n}$. But we claim that a number of this form must have even 10s digit.
It is easy to prove the claim by induction. It is true for 3 and 7 (the digit is 0 in both cases). But if we multiply such a number by 3 or 7 , then the new 10 s digit has the same parity as the carry from the units digit. But multiplying 1,3,7, 9 by 3 gives a carry of $0,0,2,6$ respectively, which is always even, and multiplying by 7 gives a carry of $0,2,4,6$, which is also always even. So the new number also has an even 10 s digit.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that any integer greater than 10 whose digits are all members of $\{1,3,7,9\}$ has a prime factor $\geq 11$.
|
Such a number cannot be divisible by 2 (or its last digit would be even) or by 5 (or its last digit would be 0 or 5). So if the result is false then the number must be of the form $3^{\mathrm{m}} 7^{\mathrm{n}}$ for non-negative integers $\mathrm{m}, \mathrm{n}$. But we claim that a number of this form must have even 10s digit.
It is easy to prove the claim by induction. It is true for 3 and 7 (the digit is 0 in both cases). But if we multiply such a number by 3 or 7 , then the new 10 s digit has the same parity as the carry from the units digit. But multiplying 1,3,7, 9 by 3 gives a carry of $0,0,2,6$ respectively, which is always even, and multiplying by 7 gives a carry of $0,2,4,6$, which is also always even. So the new number also has an even 10 s digit.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B1",
"solution_match": "\n## Solution"
}
|
2980fb84-f3a6-5967-a941-c290a9236528
| 604,980
|
Label the vertices of a regular $n$-gon from 1 to $n>3$. Draw all the diagonals. Show that if $n$ is odd then we can label each side and diagonal with a number from 1 to $n$ different from the labels of its endpoints so that at each vertex the sides and diagonals all have different labels.
|
Labeling the diagonal/side between $\mathrm{i}$ and $\mathrm{j}$ as $\mathrm{i}+\mathrm{j}$ (reduced if necessary mod $\mathrm{n}$ ) almost works. The labels for all the lines at a given vertex will be different. But the line between i and $n$ will have label i, the same as one endpoint. However, we are not using the label 2i for the lines from vertex i. So for the line between $i$ and $n$ we use $2 i$ instead of $i+n$. The only points that need checking are (1) whether a line from $\mathrm{i}$ to $\mathrm{n}$ has a label different from $\mathrm{n}$, and (2) whether all the lines at $\mathrm{n}$ have different labels. Both points are ok because $\mathrm{n}$ is odd.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Label the vertices of a regular $n$-gon from 1 to $n>3$. Draw all the diagonals. Show that if $n$ is odd then we can label each side and diagonal with a number from 1 to $n$ different from the labels of its endpoints so that at each vertex the sides and diagonals all have different labels.
|
Labeling the diagonal/side between $\mathrm{i}$ and $\mathrm{j}$ as $\mathrm{i}+\mathrm{j}$ (reduced if necessary mod $\mathrm{n}$ ) almost works. The labels for all the lines at a given vertex will be different. But the line between i and $n$ will have label i, the same as one endpoint. However, we are not using the label 2i for the lines from vertex i. So for the line between $i$ and $n$ we use $2 i$ instead of $i+n$. The only points that need checking are (1) whether a line from $\mathrm{i}$ to $\mathrm{n}$ has a label different from $\mathrm{n}$, and (2) whether all the lines at $\mathrm{n}$ have different labels. Both points are ok because $\mathrm{n}$ is odd.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A1",
"solution_match": "\n## Solution"
}
|
fab0e8e0-c159-54b6-9b0f-5d091c460af4
| 605,015
|
Two circles $\mathrm{C}$ and $\mathrm{C}^{\prime}$ have centers $\mathrm{O}$ and $\mathrm{O}^{\prime}$ and meet at $\mathrm{M}$ and $\mathrm{N}$. The common tangent closer to $\mathrm{M}$ touches $\mathrm{C}$ at $\mathrm{A}$ and $\mathrm{C}^{\prime}$ at $\mathrm{B}$. The line through $\mathrm{B}$ perpendicular to $\mathrm{AM}$ meets the line $\mathrm{OO}^{\prime}$ at D. BO'B' is a diameter of C'. Show that M, D and B' are collinear.
|
A neat coordinate solution by Massaki Yamamoto (a competitor) is as follows.
Take $A B$ as the $x$-axis and the perpendicular line through $M$ as the $y$-axis. Choose the unit of length so that $\mathrm{M}$ has coordinates $(0,1)$. Let $\mathrm{A}$ be $(-\mathrm{m}, 0)$ and $\mathrm{B}$ be $(\mathrm{n}, 0)$. Then considering the right-angled triangle $O^{\prime} M K$, where $K$ is $(n, 1)$ we find that $O^{\prime}$ is $\left(n,\left(n^{2}+1\right) / 2\right)$. Similarly, $O$ is $\left.\left(-\mathrm{m},\left(\mathrm{m}^{2}+1\right) / 2\right)\right)$.
The gradient of the lie AM is $1 / \mathrm{m}$, so the gradient of the line $\mathrm{BD}$ is $-\mathrm{m}$ and hence its equation is $m x+y=m n$. The gradient of the line OO' is $(n-m) / 2$, so its equation is $2 y-x(n-m)=m n+1$. These intersect at $\left((m n-1) /(m+n),\left(m n^{2}+m\right) /(m+n)\right)$. B' is $\left(n, n^{2}+1\right)$. It is now easy to check that the lines MB' and MD both have gradient $\mathrm{n}$, so $\mathrm{M}, \mathrm{D}, \mathrm{B}^{\prime}$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Two circles $\mathrm{C}$ and $\mathrm{C}^{\prime}$ have centers $\mathrm{O}$ and $\mathrm{O}^{\prime}$ and meet at $\mathrm{M}$ and $\mathrm{N}$. The common tangent closer to $\mathrm{M}$ touches $\mathrm{C}$ at $\mathrm{A}$ and $\mathrm{C}^{\prime}$ at $\mathrm{B}$. The line through $\mathrm{B}$ perpendicular to $\mathrm{AM}$ meets the line $\mathrm{OO}^{\prime}$ at D. BO'B' is a diameter of C'. Show that M, D and B' are collinear.
|

A neat coordinate solution by Massaki Yamamoto (a competitor) is as follows.
Take $A B$ as the $x$-axis and the perpendicular line through $M$ as the $y$-axis. Choose the unit of length so that $\mathrm{M}$ has coordinates $(0,1)$. Let $\mathrm{A}$ be $(-\mathrm{m}, 0)$ and $\mathrm{B}$ be $(\mathrm{n}, 0)$. Then considering the right-angled triangle $O^{\prime} M K$, where $K$ is $(n, 1)$ we find that $O^{\prime}$ is $\left(n,\left(n^{2}+1\right) / 2\right)$. Similarly, $O$ is $\left.\left(-\mathrm{m},\left(\mathrm{m}^{2}+1\right) / 2\right)\right)$.
The gradient of the lie AM is $1 / \mathrm{m}$, so the gradient of the line $\mathrm{BD}$ is $-\mathrm{m}$ and hence its equation is $m x+y=m n$. The gradient of the line OO' is $(n-m) / 2$, so its equation is $2 y-x(n-m)=m n+1$. These intersect at $\left((m n-1) /(m+n),\left(m n^{2}+m\right) /(m+n)\right)$. B' is $\left(n, n^{2}+1\right)$. It is now easy to check that the lines MB' and MD both have gradient $\mathrm{n}$, so $\mathrm{M}, \mathrm{D}, \mathrm{B}^{\prime}$ are collinear.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A2",
"solution_match": "\n## Solution"
}
|
995d72eb-14af-5209-8984-b5bc5188a313
| 605,024
|
Show that there are arbitrarily large numbers $n$ such that: (1) all its digits are 2 or more; and (2) the product of any four of its digits divides $n$.
|
$3232=16 \times 202$ and $10000=16 \times 625$. So any number with 3232 as its last 4 digits is divisible by 16 . So consider $\mathrm{N}=22223232$. Its sum of digits is 18 , so it is divisible by 9 . Hence it is divisible by $9 \cdot 16=144$. But any four digits have at most four $2 \mathrm{~s}$ and at most two 3s, so the product of any four digits divides 144 and hence $\mathrm{N}$. But now we can extend $\mathrm{N}$ by inserting an additional $9 \mathrm{~m} 2 \mathrm{~s}$ at the front. Its digit sum is increased by $18 \mathrm{~m}$, so it remains divisible by 144 and it is still divisible by the product of any four digits.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that there are arbitrarily large numbers $n$ such that: (1) all its digits are 2 or more; and (2) the product of any four of its digits divides $n$.
|
$3232=16 \times 202$ and $10000=16 \times 625$. So any number with 3232 as its last 4 digits is divisible by 16 . So consider $\mathrm{N}=22223232$. Its sum of digits is 18 , so it is divisible by 9 . Hence it is divisible by $9 \cdot 16=144$. But any four digits have at most four $2 \mathrm{~s}$ and at most two 3s, so the product of any four digits divides 144 and hence $\mathrm{N}$. But now we can extend $\mathrm{N}$ by inserting an additional $9 \mathrm{~m} 2 \mathrm{~s}$ at the front. Its digit sum is increased by $18 \mathrm{~m}$, so it remains divisible by 144 and it is still divisible by the product of any four digits.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A1",
"solution_match": "\n## Solution"
}
|
98fd938c-d864-5c8a-bae9-0923d220db05
| 605,080
|
Given a set of 9 points in the plane, no three collinear, show that for each point $\mathrm{P}$ in the set, the number of triangles containing $\mathrm{P}$ formed from the other 8 points in the set must be even.
|
Join each pair of points, thus dividing the plane into polygonal regions. If a point $\mathrm{P}$ moves around within one of the regions then the number of triangles it belongs to does not change. But if it crosses one of the lines then it leaves some triangles and enters others. Suppose the line is part of the segment joining the points $\mathrm{Q}$ and $\mathrm{R}$ of the set. Then it can only enter or leave a triangle QRX for some $\mathrm{X}$ in the set. Suppose $\mathrm{x}$ points in the set lie on the same side of the line $\mathrm{QR}$ as $\mathrm{P}$. Then there are 6 - $\mathrm{x}$ points on the other side of the line $\mathrm{QR}$. So $\mathrm{P}$ leaves $\mathrm{x}$ triangles and enters $6-\mathrm{x}$. Thus the net change is even. Thus if we move $\mathrm{P}$ until it is in the outer infinite region (outside the convex hull of the other 8 points), then we change the number of triangles by an even number. But in the outside region it belongs to no triangles.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Given a set of 9 points in the plane, no three collinear, show that for each point $\mathrm{P}$ in the set, the number of triangles containing $\mathrm{P}$ formed from the other 8 points in the set must be even.
|
Join each pair of points, thus dividing the plane into polygonal regions. If a point $\mathrm{P}$ moves around within one of the regions then the number of triangles it belongs to does not change. But if it crosses one of the lines then it leaves some triangles and enters others. Suppose the line is part of the segment joining the points $\mathrm{Q}$ and $\mathrm{R}$ of the set. Then it can only enter or leave a triangle QRX for some $\mathrm{X}$ in the set. Suppose $\mathrm{x}$ points in the set lie on the same side of the line $\mathrm{QR}$ as $\mathrm{P}$. Then there are 6 - $\mathrm{x}$ points on the other side of the line $\mathrm{QR}$. So $\mathrm{P}$ leaves $\mathrm{x}$ triangles and enters $6-\mathrm{x}$. Thus the net change is even. Thus if we move $\mathrm{P}$ until it is in the outer infinite region (outside the convex hull of the other 8 points), then we change the number of triangles by an even number. But in the outside region it belongs to no triangles.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A2",
"solution_match": "\n## Solution"
}
|
edd2bdd5-8b7e-51b6-b57a-2ec2054be926
| 605,127
|
$\mathrm{ABC}$ is a triangle. $\mathrm{BD}$ is the an angle bisector. $\mathrm{E}, \mathrm{F}$ are the feet of the perpendiculars from $\mathrm{A}$, $C$ respectively to the line $B D . M$ is the foot of the perpendicular from $D$ to the line $B C$. Show that $\angle \mathrm{DME}=\angle \mathrm{DMF}$.
|
Let $\mathrm{H}$ be the foot of the perpendicular from $\mathrm{D}$ to $\mathrm{AB} . \angle \mathrm{AHD}=\angle \mathrm{AED}=90^{\circ}$, so $\mathrm{AHED}$ is cyclic. Hence $\angle \mathrm{DAE}=\angle \mathrm{DHE}$. But $\mathrm{M}$ is the reflection of $\mathrm{H}$ is the line $\mathrm{BD}$, so $\angle \mathrm{DME}=$ $\angle \mathrm{DAE}$.
$\mathrm{AE}$ is parallel to $\mathrm{CD}$, so $\angle \mathrm{DAE}=\angle \mathrm{DCF}$. $\angle \mathrm{DFC}=\angle \mathrm{DMC}$, so $\mathrm{DMCF}$ is cyclic. Hence $\angle \mathrm{DCF}$ $=\angle \mathrm{DMF}$. Hence $\angle \mathrm{DME}=\angle \mathrm{DMF}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$\mathrm{ABC}$ is a triangle. $\mathrm{BD}$ is the an angle bisector. $\mathrm{E}, \mathrm{F}$ are the feet of the perpendiculars from $\mathrm{A}$, $C$ respectively to the line $B D . M$ is the foot of the perpendicular from $D$ to the line $B C$. Show that $\angle \mathrm{DME}=\angle \mathrm{DMF}$.
|

Let $\mathrm{H}$ be the foot of the perpendicular from $\mathrm{D}$ to $\mathrm{AB} . \angle \mathrm{AHD}=\angle \mathrm{AED}=90^{\circ}$, so $\mathrm{AHED}$ is cyclic. Hence $\angle \mathrm{DAE}=\angle \mathrm{DHE}$. But $\mathrm{M}$ is the reflection of $\mathrm{H}$ is the line $\mathrm{BD}$, so $\angle \mathrm{DME}=$ $\angle \mathrm{DAE}$.
$\mathrm{AE}$ is parallel to $\mathrm{CD}$, so $\angle \mathrm{DAE}=\angle \mathrm{DCF}$. $\angle \mathrm{DFC}=\angle \mathrm{DMC}$, so $\mathrm{DMCF}$ is cyclic. Hence $\angle \mathrm{DCF}$ $=\angle \mathrm{DMF}$. Hence $\angle \mathrm{DME}=\angle \mathrm{DMF}$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B1",
"solution_match": "\n## Solution"
}
|
4f3645df-8e71-58cc-a734-19cf6bd67340
| 605,147
|
The sequence $a_{n}$ is defined as follows: $a_{1}=56, a_{n+1}=a_{n}-1 / a_{n}$. Show that $a_{n}<0$ for some $n$ such that $0<\mathrm{n}<2002$.
|
Note that whilst $a_{n}$ remains positive we have $a_{1}>a_{2}>a_{3}>\ldots>a_{n}$. Hence if $a_{m}$ and $a_{m+n}$ are in this part of the sequence, then $a_{m+1}=a_{m}-1 / a_{m}, a_{m+2}=a_{m+1}-1 / a_{m+1}<a_{m+1}-1 / a_{m}=a_{m}-2 / a_{m}$. By a trivial induction $\mathrm{a}_{\mathrm{m}+\mathrm{n}}<\mathrm{a}_{\mathrm{m}}-\mathrm{n} / \mathrm{a}_{\mathrm{m}}$.
If we use one step then we need $56^{2}=3136$ terms to get $a_{1+3136}<56-56^{2} / 56=0$, which is not good enough. So we try several steps.
Thus suppose that $\mathrm{a}_{\mathrm{n}}>0$ for all $\mathrm{n}<=2002$. Then we get successively:
$a_{337}<56-336 / 56=50$
$a_{837}<50-500 / 50=40$
$a_{1237}<40-400 / 40=30$
$a_{1537}<30-300 / 30=20$
$\mathrm{a}_{1737}<20-200 / 20=10$
$\mathrm{a}_{1837}<10-100 / 10=0$.
Contradiction. So we must have $\mathrm{a}_{\mathrm{n}}<0$ for some $\mathrm{n}<2002$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
The sequence $a_{n}$ is defined as follows: $a_{1}=56, a_{n+1}=a_{n}-1 / a_{n}$. Show that $a_{n}<0$ for some $n$ such that $0<\mathrm{n}<2002$.
|
Note that whilst $a_{n}$ remains positive we have $a_{1}>a_{2}>a_{3}>\ldots>a_{n}$. Hence if $a_{m}$ and $a_{m+n}$ are in this part of the sequence, then $a_{m+1}=a_{m}-1 / a_{m}, a_{m+2}=a_{m+1}-1 / a_{m+1}<a_{m+1}-1 / a_{m}=a_{m}-2 / a_{m}$. By a trivial induction $\mathrm{a}_{\mathrm{m}+\mathrm{n}}<\mathrm{a}_{\mathrm{m}}-\mathrm{n} / \mathrm{a}_{\mathrm{m}}$.
If we use one step then we need $56^{2}=3136$ terms to get $a_{1+3136}<56-56^{2} / 56=0$, which is not good enough. So we try several steps.
Thus suppose that $\mathrm{a}_{\mathrm{n}}>0$ for all $\mathrm{n}<=2002$. Then we get successively:
$a_{337}<56-336 / 56=50$
$a_{837}<50-500 / 50=40$
$a_{1237}<40-400 / 40=30$
$a_{1537}<30-300 / 30=20$
$\mathrm{a}_{1737}<20-200 / 20=10$
$\mathrm{a}_{1837}<10-100 / 10=0$.
Contradiction. So we must have $\mathrm{a}_{\mathrm{n}}<0$ for some $\mathrm{n}<2002$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B2",
"solution_match": "\n## Solution"
}
|
1dac256f-facb-5adc-8823-d4f068290745
| 605,156
|
A game is played on a 2001 x 2001 board as follows. The first player's piece is the policeman, the second player's piece is the robber. Each piece can move one square south, one square east or one square northwest. In addition, the policeman (but not the robber) can move from the bottom right to the top left square in a single move. The policeman starts in the central square, and the robber starts one square diagonally northeast of the policeman. If the policeman moves onto the same square as the robber, then the robber is captured and the first player wins. However, the robber may move onto the same square as the policeman without being captured (and play continues). Show that the robber can avoid capture for at least 10000 moves, but that the policeman can ultimately capture the robber.
|
Color the squares with three colors as follows:
```
0<ccccccccoc
1cccccccccoc
2cccccccccccollo
```
```
\(0 \begin{array}{llllllllll}0 & 1 & 2 & 0 & 1 & 2 & 0 & \ldots & 2\end{array}\)
\(\begin{array}{llllllllll}1 & 2 & 0 & 1 & 2 & 0 & 1 & \cdots & 0\end{array}\)
. .
\(\begin{array}{lllllllll}2 & 0 & 1 & 2 & 0 & 1 & 2 & \cdots & 1\end{array}\)
```
The middle square is color 2 (moving 999+1 squares E from the top left increases the color by 1, then moving $999+1 \mathrm{~S}$ increases it by another 1) and the square immediately $\mathrm{NE}$ of it is also 2. So both $\mathrm{P}$ and $\mathrm{R}$ start on color 2 . Note that any move increases the color by 1 mod 3 , except for P's special move which changes the color from 1 to 0 .
Until $\mathrm{P}$ has made this move, after each move of $\mathrm{P}, \mathrm{P}$ 's color is always 1 more than R's color $(\bmod 3)$, so $\mathrm{P}$ cannot win (irrespective of the moves made by either player). Immediately after he makes the special move for the first time, $\mathrm{P}$ is on color 0 and $\mathrm{R}$ is on color 1 , so immediately after his move P's color is now 1 less than R's color mod 3. Again P cannot win. But after P has made the special move for the second time, P's color is the same as R's (mod 3 ) immediately after P's move.
Note that it takes P at least 2001 moves to complete his special move for the first time and at least 6002 moves (in total) to complete his special move for the second time. This solves the first part of the question. Suppose R just moves down to the bottom right and then moves in small circles (one move NW, one move S, one move E) waiting for P. It takes P at least 6002 +3999 (moving from top left to the capture square, one square short of the bottom right) $=$ 10001 to capture him, so R makes at least 10000 moves before being captured.
We claim that $\mathrm{P}$ wins if he can get into any of the positions shown below relative to $\mathrm{R}$, with $\mathrm{R}$ to move $(*)$ :
```
X P X X X
P \(\quad \mathrm{x} \quad \mathrm{X} \quad \mathrm{P} \quad \mathrm{x}\)
\(x \quad x \quad R \quad x \quad x\)
X \(\quad \mathrm{P} \quad \mathrm{x} \quad \mathrm{X} \quad \mathrm{P}\)
x \(x\) x \(\quad \mathrm{x}\)
```
If follows that $\mathrm{P}$ can also win from the four positions below $(* *)$ :
```
X X X P X X X
x \(\quad x \quad x \quad x \quad x \quad x \quad x\)
X \(x\) x \(x\) x \(x\) x
P X X \(\quad\) R \(\quad \mathrm{x}\) X \(\quad\) P
x \(\quad \mathrm{x} \quad \mathrm{x} \quad \mathrm{x}\) x \(\quad \mathrm{x} \quad \mathrm{x}\)
x \(\quad x \quad x \quad x \quad x \quad x \quad x\)
x \(\quad x \quad x \quad P \quad x \quad x \quad x\)
```
For in each case at least one of R's possible moves allow $\mathrm{P}$ to move immediately into one of the winning positions at $(*)$. But $\mathrm{R}$ can only make the other moves a limited number of times before running into the border. [That is obvious if the other two moves are $\mathrm{E}$ and $\mathrm{S}$. If they are NW and E, then every NW move takes R closer to the top border, but his total number of E moves can never exceed his total number of NW moves by more than 2000 because of the right border. Similarly, for NW and S.]
Now let $\mathrm{d}$ be the number of rows plus the number of columns that $\mathrm{R}$ and $\mathrm{P}$ are apart. It is easy to check that the positions in $(*)$ and $(* *)$ represent the only possibilities for $\mathrm{d}=2$ and 3 . We show that $\mathrm{P}$ can always get to $\mathrm{d}=2$ or 3 . For $\mathrm{P}$ can always copy R's move, so he can certainly move so that $\mathrm{d}$ never increases. But one of R's moves will always allow $\mathrm{P}$ to decrease $\mathrm{d}$ by 1 or 2 . There are three cases to consider:
Case 1. If $\mathrm{P}$ is east of $\mathrm{R}$ and $\mathrm{R}$ moves $\mathrm{E}$, then $\mathrm{P}$ moving $\mathrm{NW}$ will decrease $\mathrm{d}$ by 1 or 2 . That is not possible if $\mathrm{P}$ is in the top row, but then moving $\mathrm{S}$ will decrease $\mathrm{d}$ by 2 unless $\mathrm{R}$ is also in the top row. If both are in the top row, then P moves S. Now after R's next move, P moves NW which reduces $\mathrm{d}$ by 2 .
Case 2. If $\mathrm{P}$ is south of $\mathrm{R}$ and $\mathrm{R}$ moves $\mathrm{S}$, then a similar argument, shows that $\mathrm{P}$ can always decrease $\mathrm{d}$ by 1 or 2 in one or two moves.
Case 3. If $\mathrm{P}$ is not south or east or $\mathrm{R}$, and $\mathrm{R}$ moves $\mathrm{NW}$, then $\mathrm{P}$ can always decrease $\mathrm{d}$ by 1 or 2 by moving $\mathrm{S}$ or $\mathrm{E}$.
But repeated decreases by 1 or 2 must bring $\mathrm{d}$ ultimately to 2 or 3 and hence to one of $(*)$ or $(* *)$. So $\mathrm{P}$ can always win.
It remains to prove the claim that (*) are winning positions. The reason is that in each case $\mathrm{R}$ has one move blocked off, so must make one of the other two. P then copies R's move, so next turn $\mathrm{R}$ has the same move blocked off. Repeated use of the other two moves will bring him ultimately to one of the sides.
We start with the easiest case: in the two following positions. $\mathrm{R}$ cannot move to $\mathrm{z}$, so he must move east or south on each move. Hence he will (after at most 4000 moves) reach the bottom right corner. He then loses moving out of it.
```
X P X
P z x
x X R
```
The other cases of $(*)$ are slightly more complicated. Starting from either of the two positions below, we show that $\mathrm{R}$ must eventually reach the extreme left column.
```
w \(\quad x \quad P \quad x\)
\(x \quad R \quad z \quad x\)
x y x P
```
$\mathrm{R}$ cannot move to $\mathrm{z}$, so he can only make $\mathrm{NW}$ and $\mathrm{S}$ moves. But his total number of $\mathrm{S}$ moves can never exceed his total number of NW moves by more than 2000 because he cannot move off the bottom of the board, so he must eventually reach the extreme left column. [If he reaches the bottom row at $\mathrm{y}$, then $\mathrm{P}$ can always move to $\mathrm{z}$ to preserve the configuration. If $\mathrm{R}$ reaches the top row by moving to $\mathrm{w}$, then $\mathrm{P}$ can always move to $\mathrm{z}$ to preserve the configuration.]
Having reached the extreme left column he is forced to move south. Eventually moving to y will take him to the corner. $\mathrm{P}$ then moves to $\mathrm{z}$ and $\mathrm{R}$ is captured on his next move.
The final case to consider is the two positions below. $\mathrm{R}$ cannot move to $\mathrm{z}$, so must move $\mathrm{E}$ or $\mathrm{NW}$. A similar argument to the previous case shows that he must eventually reach the top row. Having reached it at w, P moves to z. So R is forced to move right along the top row. When he reaches the corner at $\mathrm{y}, \mathrm{P}$ moves to $\mathrm{z}$ and $\mathrm{R}$ is captured when he moves out of the corner.
```
W x x
x R y
P z x
X X P
```
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A game is played on a 2001 x 2001 board as follows. The first player's piece is the policeman, the second player's piece is the robber. Each piece can move one square south, one square east or one square northwest. In addition, the policeman (but not the robber) can move from the bottom right to the top left square in a single move. The policeman starts in the central square, and the robber starts one square diagonally northeast of the policeman. If the policeman moves onto the same square as the robber, then the robber is captured and the first player wins. However, the robber may move onto the same square as the policeman without being captured (and play continues). Show that the robber can avoid capture for at least 10000 moves, but that the policeman can ultimately capture the robber.
|
Color the squares with three colors as follows:
```
0<ccccccccoc
1cccccccccoc
2cccccccccccollo
```
```
\(0 \begin{array}{llllllllll}0 & 1 & 2 & 0 & 1 & 2 & 0 & \ldots & 2\end{array}\)
\(\begin{array}{llllllllll}1 & 2 & 0 & 1 & 2 & 0 & 1 & \cdots & 0\end{array}\)
. .
\(\begin{array}{lllllllll}2 & 0 & 1 & 2 & 0 & 1 & 2 & \cdots & 1\end{array}\)
```
The middle square is color 2 (moving 999+1 squares E from the top left increases the color by 1, then moving $999+1 \mathrm{~S}$ increases it by another 1) and the square immediately $\mathrm{NE}$ of it is also 2. So both $\mathrm{P}$ and $\mathrm{R}$ start on color 2 . Note that any move increases the color by 1 mod 3 , except for P's special move which changes the color from 1 to 0 .
Until $\mathrm{P}$ has made this move, after each move of $\mathrm{P}, \mathrm{P}$ 's color is always 1 more than R's color $(\bmod 3)$, so $\mathrm{P}$ cannot win (irrespective of the moves made by either player). Immediately after he makes the special move for the first time, $\mathrm{P}$ is on color 0 and $\mathrm{R}$ is on color 1 , so immediately after his move P's color is now 1 less than R's color mod 3. Again P cannot win. But after P has made the special move for the second time, P's color is the same as R's (mod 3 ) immediately after P's move.
Note that it takes P at least 2001 moves to complete his special move for the first time and at least 6002 moves (in total) to complete his special move for the second time. This solves the first part of the question. Suppose R just moves down to the bottom right and then moves in small circles (one move NW, one move S, one move E) waiting for P. It takes P at least 6002 +3999 (moving from top left to the capture square, one square short of the bottom right) $=$ 10001 to capture him, so R makes at least 10000 moves before being captured.
We claim that $\mathrm{P}$ wins if he can get into any of the positions shown below relative to $\mathrm{R}$, with $\mathrm{R}$ to move $(*)$ :
```
X P X X X
P \(\quad \mathrm{x} \quad \mathrm{X} \quad \mathrm{P} \quad \mathrm{x}\)
\(x \quad x \quad R \quad x \quad x\)
X \(\quad \mathrm{P} \quad \mathrm{x} \quad \mathrm{X} \quad \mathrm{P}\)
x \(x\) x \(\quad \mathrm{x}\)
```
If follows that $\mathrm{P}$ can also win from the four positions below $(* *)$ :
```
X X X P X X X
x \(\quad x \quad x \quad x \quad x \quad x \quad x\)
X \(x\) x \(x\) x \(x\) x
P X X \(\quad\) R \(\quad \mathrm{x}\) X \(\quad\) P
x \(\quad \mathrm{x} \quad \mathrm{x} \quad \mathrm{x}\) x \(\quad \mathrm{x} \quad \mathrm{x}\)
x \(\quad x \quad x \quad x \quad x \quad x \quad x\)
x \(\quad x \quad x \quad P \quad x \quad x \quad x\)
```
For in each case at least one of R's possible moves allow $\mathrm{P}$ to move immediately into one of the winning positions at $(*)$. But $\mathrm{R}$ can only make the other moves a limited number of times before running into the border. [That is obvious if the other two moves are $\mathrm{E}$ and $\mathrm{S}$. If they are NW and E, then every NW move takes R closer to the top border, but his total number of E moves can never exceed his total number of NW moves by more than 2000 because of the right border. Similarly, for NW and S.]
Now let $\mathrm{d}$ be the number of rows plus the number of columns that $\mathrm{R}$ and $\mathrm{P}$ are apart. It is easy to check that the positions in $(*)$ and $(* *)$ represent the only possibilities for $\mathrm{d}=2$ and 3 . We show that $\mathrm{P}$ can always get to $\mathrm{d}=2$ or 3 . For $\mathrm{P}$ can always copy R's move, so he can certainly move so that $\mathrm{d}$ never increases. But one of R's moves will always allow $\mathrm{P}$ to decrease $\mathrm{d}$ by 1 or 2 . There are three cases to consider:
Case 1. If $\mathrm{P}$ is east of $\mathrm{R}$ and $\mathrm{R}$ moves $\mathrm{E}$, then $\mathrm{P}$ moving $\mathrm{NW}$ will decrease $\mathrm{d}$ by 1 or 2 . That is not possible if $\mathrm{P}$ is in the top row, but then moving $\mathrm{S}$ will decrease $\mathrm{d}$ by 2 unless $\mathrm{R}$ is also in the top row. If both are in the top row, then P moves S. Now after R's next move, P moves NW which reduces $\mathrm{d}$ by 2 .
Case 2. If $\mathrm{P}$ is south of $\mathrm{R}$ and $\mathrm{R}$ moves $\mathrm{S}$, then a similar argument, shows that $\mathrm{P}$ can always decrease $\mathrm{d}$ by 1 or 2 in one or two moves.
Case 3. If $\mathrm{P}$ is not south or east or $\mathrm{R}$, and $\mathrm{R}$ moves $\mathrm{NW}$, then $\mathrm{P}$ can always decrease $\mathrm{d}$ by 1 or 2 by moving $\mathrm{S}$ or $\mathrm{E}$.
But repeated decreases by 1 or 2 must bring $\mathrm{d}$ ultimately to 2 or 3 and hence to one of $(*)$ or $(* *)$. So $\mathrm{P}$ can always win.
It remains to prove the claim that (*) are winning positions. The reason is that in each case $\mathrm{R}$ has one move blocked off, so must make one of the other two. P then copies R's move, so next turn $\mathrm{R}$ has the same move blocked off. Repeated use of the other two moves will bring him ultimately to one of the sides.
We start with the easiest case: in the two following positions. $\mathrm{R}$ cannot move to $\mathrm{z}$, so he must move east or south on each move. Hence he will (after at most 4000 moves) reach the bottom right corner. He then loses moving out of it.
```
X P X
P z x
x X R
```
The other cases of $(*)$ are slightly more complicated. Starting from either of the two positions below, we show that $\mathrm{R}$ must eventually reach the extreme left column.
```
w \(\quad x \quad P \quad x\)
\(x \quad R \quad z \quad x\)
x y x P
```
$\mathrm{R}$ cannot move to $\mathrm{z}$, so he can only make $\mathrm{NW}$ and $\mathrm{S}$ moves. But his total number of $\mathrm{S}$ moves can never exceed his total number of NW moves by more than 2000 because he cannot move off the bottom of the board, so he must eventually reach the extreme left column. [If he reaches the bottom row at $\mathrm{y}$, then $\mathrm{P}$ can always move to $\mathrm{z}$ to preserve the configuration. If $\mathrm{R}$ reaches the top row by moving to $\mathrm{w}$, then $\mathrm{P}$ can always move to $\mathrm{z}$ to preserve the configuration.]
Having reached the extreme left column he is forced to move south. Eventually moving to y will take him to the corner. $\mathrm{P}$ then moves to $\mathrm{z}$ and $\mathrm{R}$ is captured on his next move.
The final case to consider is the two positions below. $\mathrm{R}$ cannot move to $\mathrm{z}$, so must move $\mathrm{E}$ or $\mathrm{NW}$. A similar argument to the previous case shows that he must eventually reach the top row. Having reached it at w, P moves to z. So R is forced to move right along the top row. When he reaches the corner at $\mathrm{y}, \mathrm{P}$ moves to $\mathrm{z}$ and $\mathrm{R}$ is captured when he moves out of the corner.
```
W x x
x R y
P z x
X X P
```
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B3",
"solution_match": "\n## Solution"
}
|
09751054-5b5b-5d3d-9512-1875640b602f
| 605,174
|
$\mathrm{C}$ is a point on the semicircle with diameter $\mathrm{AB}$. D is a point on the $\operatorname{arc} \mathrm{BC} . \mathrm{M}, \mathrm{P}, \mathrm{N}$ are the midpoints of AC, CD and BD. The circumcenters of ACP and BDP are O, O'. Show that MN and $\mathrm{OO}^{\prime}$ are parallel.
|
Let the center of the circle be $X$ and the radius $r$. Let $\angle A X M=\theta, \angle B X N=\varphi$. Note that $O$ is the intersection of $\mathrm{XM}$ and the perpendicular to $\mathrm{CD}$ at $\mathrm{Q}$, the midpoint of $\mathrm{CP}$. We have $\mathrm{XM}=$ r $\cos \theta$. Let $\mathrm{CD}$ and $\mathrm{XM}$ meet at $\mathrm{Y}$. Then $\angle \mathrm{PYX}=90^{\circ}-\angle \mathrm{PXY}=90^{\circ}-\angle \mathrm{PXC}-\angle \mathrm{CXM}=\theta+$ $\varphi-\varphi=\theta$. Hence $O X=P Q \sec \varphi$, so $O X / X M=P Q /(r \cos \theta \cos \varphi)$. Similarly, $O^{\prime} X / O N=P Q /(r$ $\cos \theta \cos \varphi)$, so OO' and MN are parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$\mathrm{C}$ is a point on the semicircle with diameter $\mathrm{AB}$. D is a point on the $\operatorname{arc} \mathrm{BC} . \mathrm{M}, \mathrm{P}, \mathrm{N}$ are the midpoints of AC, CD and BD. The circumcenters of ACP and BDP are O, O'. Show that MN and $\mathrm{OO}^{\prime}$ are parallel.
|

Let the center of the circle be $X$ and the radius $r$. Let $\angle A X M=\theta, \angle B X N=\varphi$. Note that $O$ is the intersection of $\mathrm{XM}$ and the perpendicular to $\mathrm{CD}$ at $\mathrm{Q}$, the midpoint of $\mathrm{CP}$. We have $\mathrm{XM}=$ r $\cos \theta$. Let $\mathrm{CD}$ and $\mathrm{XM}$ meet at $\mathrm{Y}$. Then $\angle \mathrm{PYX}=90^{\circ}-\angle \mathrm{PXY}=90^{\circ}-\angle \mathrm{PXC}-\angle \mathrm{CXM}=\theta+$ $\varphi-\varphi=\theta$. Hence $O X=P Q \sec \varphi$, so $O X / X M=P Q /(r \cos \theta \cos \varphi)$. Similarly, $O^{\prime} X / O N=P Q /(r$ $\cos \theta \cos \varphi)$, so OO' and MN are parallel.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A2",
"solution_match": "\n## Solution"
}
|
98bb33db-2cbb-5f43-8e3c-17773e96e7cb
| 605,198
|
Pablo was trying to solve the following problem: find the sequence $\mathrm{x}_{0}, \mathrm{x}_{1}, \mathrm{x}_{2}, \ldots, \mathrm{x}_{2003}$ which satisfies $\mathrm{x}_{0}=1,0 \leq \mathrm{x}_{\mathrm{i}} \leq 2 \mathrm{x}_{\mathrm{i}-1}$ for $1 \leq \mathrm{i} \leq 2003$ and which maximises $\mathrm{S}$. Unfortunately he could not remember the expression for $\mathrm{S}$, but he knew that it had the form $\mathrm{S}= \pm \mathrm{x}_{1} \pm \mathrm{x}_{2} \pm \ldots \pm \mathrm{x}_{2002}$ $+\mathrm{x}_{2003}$. Show that he can still solve the problem.
|
For any combination of signs the maximum is obtained by taking all $\mathrm{x}_{\mathrm{i}}$ as large as possible. Suppose we have a different set of $\mathrm{x}_{\mathrm{i}}$. Then for some $\mathrm{k}$ we must have $\mathrm{x}_{\mathrm{k}}<2 \mathrm{x}_{\mathrm{k}-1}$ and $\mathrm{x}_{\mathrm{i}}=2 \mathrm{x}_{\mathrm{i}-1}$ for all $\mathrm{i}>\mathrm{k}$. Suppose $2 \mathrm{x}^{\mathrm{k}-1}-\mathrm{x}^{k}=\mathrm{h}>0$. Then we can increase $\mathrm{x}_{\mathrm{k}}$ by $\mathrm{h}, \mathrm{x}_{\mathrm{k}+1}$ by $2 \mathrm{~h}, \mathrm{x}_{\mathrm{k}+2}$ by $4 \mathrm{~h}$, ... So the sum will be increased by $\mathrm{h}\left( \pm 1 \pm 2 \pm \ldots \pm 2^{\mathrm{m}-1}+2^{\mathrm{m}}\right)$ for some $\mathrm{m} \geq 0$. But $\pm 1 \pm 2 \pm$ $\ldots \pm 2^{\mathrm{m}-1} \geq-\left(1+2+\ldots+2^{\mathrm{m}-1}\right)=-2^{\mathrm{m}}+1$, so the overall sum will be increased by at least 1 . So the set of $x_{i}$ was not maximal.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Pablo was trying to solve the following problem: find the sequence $\mathrm{x}_{0}, \mathrm{x}_{1}, \mathrm{x}_{2}, \ldots, \mathrm{x}_{2003}$ which satisfies $\mathrm{x}_{0}=1,0 \leq \mathrm{x}_{\mathrm{i}} \leq 2 \mathrm{x}_{\mathrm{i}-1}$ for $1 \leq \mathrm{i} \leq 2003$ and which maximises $\mathrm{S}$. Unfortunately he could not remember the expression for $\mathrm{S}$, but he knew that it had the form $\mathrm{S}= \pm \mathrm{x}_{1} \pm \mathrm{x}_{2} \pm \ldots \pm \mathrm{x}_{2002}$ $+\mathrm{x}_{2003}$. Show that he can still solve the problem.
|
For any combination of signs the maximum is obtained by taking all $\mathrm{x}_{\mathrm{i}}$ as large as possible. Suppose we have a different set of $\mathrm{x}_{\mathrm{i}}$. Then for some $\mathrm{k}$ we must have $\mathrm{x}_{\mathrm{k}}<2 \mathrm{x}_{\mathrm{k}-1}$ and $\mathrm{x}_{\mathrm{i}}=2 \mathrm{x}_{\mathrm{i}-1}$ for all $\mathrm{i}>\mathrm{k}$. Suppose $2 \mathrm{x}^{\mathrm{k}-1}-\mathrm{x}^{k}=\mathrm{h}>0$. Then we can increase $\mathrm{x}_{\mathrm{k}}$ by $\mathrm{h}, \mathrm{x}_{\mathrm{k}+1}$ by $2 \mathrm{~h}, \mathrm{x}_{\mathrm{k}+2}$ by $4 \mathrm{~h}$, ... So the sum will be increased by $\mathrm{h}\left( \pm 1 \pm 2 \pm \ldots \pm 2^{\mathrm{m}-1}+2^{\mathrm{m}}\right)$ for some $\mathrm{m} \geq 0$. But $\pm 1 \pm 2 \pm$ $\ldots \pm 2^{\mathrm{m}-1} \geq-\left(1+2+\ldots+2^{\mathrm{m}-1}\right)=-2^{\mathrm{m}}+1$, so the overall sum will be increased by at least 1 . So the set of $x_{i}$ was not maximal.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A3",
"solution_match": "\n## Solution"
}
|
6aa917be-7e58-518a-9598-4d2a7e03f124
| 605,210
|
$\mathrm{ABCD}$ is a square. $\mathrm{P}, \mathrm{Q}$ are points on the sides $\mathrm{BC}, \mathrm{CD}$ respectively, distinct from the endpoints such that $\mathrm{BP}=\mathrm{CQ}$. $\mathrm{X}, \mathrm{Y}$ are points on $\mathrm{AP}, \mathrm{AQ}$ respectively. Show that there is a triangle with side lengths $B X, X Y, Y D$.
|
We have $\mathrm{DY}<\mathrm{BY} \leq \mathrm{BX}+\mathrm{XY}$ (this is almost obvious, but to prove formally use the cosine formula for BAY and DAY and notice that $\angle \mathrm{BAY}>\angle \mathrm{DAY}$ ). Similarly, $\mathrm{BX}<\mathrm{DX} \leq \mathrm{DY}+$ YX. So it remains to show that $X Y<B X+D Y$.
Take $\mathrm{Q}^{\prime}$ on the extension of $\mathrm{BC}$ so that $\mathrm{BQ}^{\prime}=\mathrm{DQ}$, as shown in the diagram. Take $\mathrm{Y}^{\prime}$ on $\mathrm{AQ}^{\prime}$ so that $\mathrm{AY}^{\prime}=\mathrm{AY}$. Then $\mathrm{XY}^{\prime} \leq \mathrm{BX}+\mathrm{BY}^{\prime}=\mathrm{BX}+\mathrm{DY}$. Now we claim that $\angle \mathrm{PAQ}^{\prime}>\angle \mathrm{PAQ}$, so it follows by the same observation as above that $\mathrm{XY}^{\prime}>\mathrm{XY}$. But the claim is almost obvious. Note that $\mathrm{PQ}^{\prime}=\mathrm{AB}$
So take $\mathrm{P}^{\prime}$ on $\mathrm{AD}$ with $\angle \mathrm{P}^{\prime} \mathrm{PQ} \mathrm{P}^{\prime}=90^{\circ}$. Then $\mathrm{A}$ lies inside the circle $\mathrm{P}^{\prime} \mathrm{PQ}^{\prime}$, so extend $\mathrm{PA}$ to meet it again at $\mathrm{A}^{\prime}$. Then $\angle \mathrm{PA}^{\prime} \mathrm{Q}^{\prime}=\angle \mathrm{PP}^{\prime} \mathrm{Q}^{\prime}=45^{\circ}$, so $\angle \mathrm{PAQ}^{\prime}=\angle \mathrm{PA}^{\prime} \mathrm{Q}^{\prime}+\angle \mathrm{AQ}^{\prime} \mathrm{Q}^{\prime}>45^{\circ}$. But $\angle \mathrm{PAQ}^{\prime}+\angle \mathrm{PAQ}=90^{\circ}$, so $\angle \mathrm{PAQ}^{\prime}>\angle \mathrm{PAQ}$ as claimed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$\mathrm{ABCD}$ is a square. $\mathrm{P}, \mathrm{Q}$ are points on the sides $\mathrm{BC}, \mathrm{CD}$ respectively, distinct from the endpoints such that $\mathrm{BP}=\mathrm{CQ}$. $\mathrm{X}, \mathrm{Y}$ are points on $\mathrm{AP}, \mathrm{AQ}$ respectively. Show that there is a triangle with side lengths $B X, X Y, Y D$.
|

We have $\mathrm{DY}<\mathrm{BY} \leq \mathrm{BX}+\mathrm{XY}$ (this is almost obvious, but to prove formally use the cosine formula for BAY and DAY and notice that $\angle \mathrm{BAY}>\angle \mathrm{DAY}$ ). Similarly, $\mathrm{BX}<\mathrm{DX} \leq \mathrm{DY}+$ YX. So it remains to show that $X Y<B X+D Y$.
Take $\mathrm{Q}^{\prime}$ on the extension of $\mathrm{BC}$ so that $\mathrm{BQ}^{\prime}=\mathrm{DQ}$, as shown in the diagram. Take $\mathrm{Y}^{\prime}$ on $\mathrm{AQ}^{\prime}$ so that $\mathrm{AY}^{\prime}=\mathrm{AY}$. Then $\mathrm{XY}^{\prime} \leq \mathrm{BX}+\mathrm{BY}^{\prime}=\mathrm{BX}+\mathrm{DY}$. Now we claim that $\angle \mathrm{PAQ}^{\prime}>\angle \mathrm{PAQ}$, so it follows by the same observation as above that $\mathrm{XY}^{\prime}>\mathrm{XY}$. But the claim is almost obvious. Note that $\mathrm{PQ}^{\prime}=\mathrm{AB}$

So take $\mathrm{P}^{\prime}$ on $\mathrm{AD}$ with $\angle \mathrm{P}^{\prime} \mathrm{PQ} \mathrm{P}^{\prime}=90^{\circ}$. Then $\mathrm{A}$ lies inside the circle $\mathrm{P}^{\prime} \mathrm{PQ}^{\prime}$, so extend $\mathrm{PA}$ to meet it again at $\mathrm{A}^{\prime}$. Then $\angle \mathrm{PA}^{\prime} \mathrm{Q}^{\prime}=\angle \mathrm{PP}^{\prime} \mathrm{Q}^{\prime}=45^{\circ}$, so $\angle \mathrm{PAQ}^{\prime}=\angle \mathrm{PA}^{\prime} \mathrm{Q}^{\prime}+\angle \mathrm{AQ}^{\prime} \mathrm{Q}^{\prime}>45^{\circ}$. But $\angle \mathrm{PAQ}^{\prime}+\angle \mathrm{PAQ}=90^{\circ}$, so $\angle \mathrm{PAQ}^{\prime}>\angle \mathrm{PAQ}$ as claimed.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B2",
"solution_match": "\n## Solution"
}
|
0626e09c-1ad6-5a90-aac4-3ab2a9ed926a
| 605,235
|
The sequences $\mathrm{a}_{0}, \mathrm{a}_{1}, \mathrm{a}_{2}, \ldots$ and $\mathrm{b}_{0}, \mathrm{~b}_{1}, \mathrm{~b}_{2}, \ldots$ are defined by $\mathrm{a}_{0}=1, \mathrm{~b}_{0}=4, \mathrm{a}_{\mathrm{n}+1}=\mathrm{a}_{\mathrm{n}}{ }^{2001}+\mathrm{b}_{\mathrm{n}}$, $b_{n+1}=b_{n}^{2001}+a_{n}$. Show that no member of either sequence is divisible by 2003.
|
2003 is prime, so $\mathrm{a}^{2002}=1 \bmod 2003$ for any a not divisible by 2003. Thus $a_{n+1}=a_{n}^{-1}+b_{n}$ $\bmod 2003, b_{n+1}=b_{n}^{-1}+a_{n} \bmod 2003$. Put $c_{n}=a_{n} b_{n}$. Then $c_{n+1}=c_{n}+1 / c_{n}+2=\left(c_{n}+1\right)_{2} / c_{n}$ $\bmod 2003$. So if $\mathrm{c}_{\mathrm{n}} \neq 0 \bmod 2003$, then $\mathrm{c}_{\mathrm{n}+1} \neq 0 \bmod 2003$ unless $\mathrm{c}_{\mathrm{n}}=-1 \bmod 2003$. Then if $c_{n+1}=-1 \bmod 2003$, we must have $\left(c_{n}{ }^{2}+3 c_{n}+1\right) / c_{n}=0 \bmod 2003$, so $c_{n}{ }^{2}+3 c_{n}+1=0 \bmod$ 2003. Note that $c_{0}=4$. So it is sufficient to show that there are no solutions to $x^{2}+3 x+1=0$ $\bmod 2003$, or equivalently to $(x-1000)^{2}=1000^{2}-1=502 \bmod 2003$. In other words, we have to show that 502 is a quadratic non-residue mod 2003.
The easiest way to do that is to use the law of quadratic reciprocity, but that is almost certainly outside the syllabus. We note that 4. $502=5 \bmod 2003$, so 502 is a square iff 5 is a square. It is sufficient to show that $5^{1001}=-1 \bmod 2003$, for then if we had $x^{2}=5$, we would have $\mathrm{x}^{2002}=-1 \bmod 2003$, whereas we know that $\mathrm{x}^{2002}=1 \bmod 2003$. We note that $1001=$ 7. 11. 13. We start by showing that $5^{7}=8 \bmod 2003$. We have $5^{5}=3125=1122 \bmod 2003$, so $5^{6}=5610=1604 \bmod 2003$, so $5^{7}=8020=8 \bmod 2003$.
We calculate successively $2^{11}=2048=45 \bmod 2003$, so $2^{22}=2025=22 \bmod 2003$. Multiplying by 22 is relatively easy, so $2^{44}=484,2^{66}=10648=633,2^{88}=13926=-95,2^{110}$ $=-2090=-87,2^{132}=-1914=89,2^{143}=4005=-1$ all $\bmod 2003$. Hence $8^{11 \cdot 13}=-1 \bmod 2003$, so $5^{1001}=-1 \bmod 2003$, as required, and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
The sequences $\mathrm{a}_{0}, \mathrm{a}_{1}, \mathrm{a}_{2}, \ldots$ and $\mathrm{b}_{0}, \mathrm{~b}_{1}, \mathrm{~b}_{2}, \ldots$ are defined by $\mathrm{a}_{0}=1, \mathrm{~b}_{0}=4, \mathrm{a}_{\mathrm{n}+1}=\mathrm{a}_{\mathrm{n}}{ }^{2001}+\mathrm{b}_{\mathrm{n}}$, $b_{n+1}=b_{n}^{2001}+a_{n}$. Show that no member of either sequence is divisible by 2003.
|
2003 is prime, so $\mathrm{a}^{2002}=1 \bmod 2003$ for any a not divisible by 2003. Thus $a_{n+1}=a_{n}^{-1}+b_{n}$ $\bmod 2003, b_{n+1}=b_{n}^{-1}+a_{n} \bmod 2003$. Put $c_{n}=a_{n} b_{n}$. Then $c_{n+1}=c_{n}+1 / c_{n}+2=\left(c_{n}+1\right)_{2} / c_{n}$ $\bmod 2003$. So if $\mathrm{c}_{\mathrm{n}} \neq 0 \bmod 2003$, then $\mathrm{c}_{\mathrm{n}+1} \neq 0 \bmod 2003$ unless $\mathrm{c}_{\mathrm{n}}=-1 \bmod 2003$. Then if $c_{n+1}=-1 \bmod 2003$, we must have $\left(c_{n}{ }^{2}+3 c_{n}+1\right) / c_{n}=0 \bmod 2003$, so $c_{n}{ }^{2}+3 c_{n}+1=0 \bmod$ 2003. Note that $c_{0}=4$. So it is sufficient to show that there are no solutions to $x^{2}+3 x+1=0$ $\bmod 2003$, or equivalently to $(x-1000)^{2}=1000^{2}-1=502 \bmod 2003$. In other words, we have to show that 502 is a quadratic non-residue mod 2003.
The easiest way to do that is to use the law of quadratic reciprocity, but that is almost certainly outside the syllabus. We note that 4. $502=5 \bmod 2003$, so 502 is a square iff 5 is a square. It is sufficient to show that $5^{1001}=-1 \bmod 2003$, for then if we had $x^{2}=5$, we would have $\mathrm{x}^{2002}=-1 \bmod 2003$, whereas we know that $\mathrm{x}^{2002}=1 \bmod 2003$. We note that $1001=$ 7. 11. 13. We start by showing that $5^{7}=8 \bmod 2003$. We have $5^{5}=3125=1122 \bmod 2003$, so $5^{6}=5610=1604 \bmod 2003$, so $5^{7}=8020=8 \bmod 2003$.
We calculate successively $2^{11}=2048=45 \bmod 2003$, so $2^{22}=2025=22 \bmod 2003$. Multiplying by 22 is relatively easy, so $2^{44}=484,2^{66}=10648=633,2^{88}=13926=-95,2^{110}$ $=-2090=-87,2^{132}=-1914=89,2^{143}=4005=-1$ all $\bmod 2003$. Hence $8^{11 \cdot 13}=-1 \bmod 2003$, so $5^{1001}=-1 \bmod 2003$, as required, and we are done.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B3",
"solution_match": "\n## Solution"
}
|
6b8b3e9f-7376-5a20-b7cd-de4dfbfb3fca
| 605,247
|
Let $A B C$ be an acute scalene triangle with circumcenter $O$. Let $D$ be the foot of the altitude from $A$ to the side $B C$. The lines $B C$ and $A O$ intersect at $E$. Let $s$ be the line through $E$ perpendicular to $A O$. The line $s$ intersects $A B$ and $A C$ at $K$ and $L$, respectively. Denote by $\omega$ the circumcircle of triangle $A K L$. Line $A D$ intersects $\omega$ again at $X$.
Prove that $\omega$ and the circumcircles of triangles $A B C$ and $D E X$ have a common point.
|
Let us denote angles of triangle $A B C$ with $\alpha, \beta, \gamma$ in a standard way. By basic anglechasing we have
$$
\angle B A D=90^{\circ}-\beta=\angle O A C \text { and } \angle C A D=\angle B A O=90^{\circ}-\gamma
$$
Using the fact that lines $A E$ and $A X$ are isogonal with respect to $\angle K A L$ we can conclude that $X$ is an $A$-antipode on $\omega$. (This fact can be purely angle-chased: we have
$$
\angle K A X+\angle A X K=\angle K A X+\angle A L K=90^{\circ}-\beta+\beta=90^{\circ}
$$
which implies $\angle A K X=90^{\circ}$ ). Now let $F$ be the projection of $X$ on the line $A E$. Using that $A X$ is a diameter of $\omega$ and $\angle E D X=90^{\circ}$ it's clear that $F$ is the intersection point of $\omega$ and the circumcircle of triangle $D E X$. Now it suffices to show that $A B F C$ is cyclic. We have $\angle K L F=\angle K A F=90^{\circ}-\gamma$ and from $\angle F E L=90^{\circ}$ we have that $\angle E F L=\gamma=\angle E C L$ so quadrilateral $E F C L$ is cyclic. Next, we have
$$
\angle A F C=\angle E F C=180^{\circ}-\angle E L C=\angle E L A=\beta
$$
(where last equality holds because of $\angle A E L=90^{\circ}$ and $\angle E A L=90^{\circ}-\beta$ ).
Solution 2. We have $\angle B A D=90^{\circ}-\beta=\angle O A C$ and that $A X$ is the diameter of $\omega$. Also we note that
$$
\angle A L K=\beta, \angle K L C=180^{\circ}-\beta=\angle K B C
$$
so $B K C L$ is cyclic. Let $A O$ intersect circumcircle of $A B C$ again at $A^{\prime}$. We will show that $A^{\prime}$ is the desired concurrence point. Obviously $A A^{\prime}$ is the diameter of circumcircle of triangle $A B C$ so $\angle A^{\prime} C A=90^{\circ}$ which implies that $A^{\prime} C L E$ is cyclic. From power of point $E$ we have that $E K \cdot E L=E B \cdot E C=E A \cdot E A^{\prime}$ so we can conclude that $A^{\prime} \in \omega$. Now using the fact that $A X$ is a diameter of $\omega$ implies $\angle A X A^{\prime}=90^{\circ}$ we have that $D X A^{\prime} E$ is cyclic because of $\angle E D X=90^{\circ}$ which finishes the proof. $\square$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute scalene triangle with circumcenter $O$. Let $D$ be the foot of the altitude from $A$ to the side $B C$. The lines $B C$ and $A O$ intersect at $E$. Let $s$ be the line through $E$ perpendicular to $A O$. The line $s$ intersects $A B$ and $A C$ at $K$ and $L$, respectively. Denote by $\omega$ the circumcircle of triangle $A K L$. Line $A D$ intersects $\omega$ again at $X$.
Prove that $\omega$ and the circumcircles of triangles $A B C$ and $D E X$ have a common point.
|

Let us denote angles of triangle $A B C$ with $\alpha, \beta, \gamma$ in a standard way. By basic anglechasing we have
$$
\angle B A D=90^{\circ}-\beta=\angle O A C \text { and } \angle C A D=\angle B A O=90^{\circ}-\gamma
$$
Using the fact that lines $A E$ and $A X$ are isogonal with respect to $\angle K A L$ we can conclude that $X$ is an $A$-antipode on $\omega$. (This fact can be purely angle-chased: we have
$$
\angle K A X+\angle A X K=\angle K A X+\angle A L K=90^{\circ}-\beta+\beta=90^{\circ}
$$
which implies $\angle A K X=90^{\circ}$ ). Now let $F$ be the projection of $X$ on the line $A E$. Using that $A X$ is a diameter of $\omega$ and $\angle E D X=90^{\circ}$ it's clear that $F$ is the intersection point of $\omega$ and the circumcircle of triangle $D E X$. Now it suffices to show that $A B F C$ is cyclic. We have $\angle K L F=\angle K A F=90^{\circ}-\gamma$ and from $\angle F E L=90^{\circ}$ we have that $\angle E F L=\gamma=\angle E C L$ so quadrilateral $E F C L$ is cyclic. Next, we have
$$
\angle A F C=\angle E F C=180^{\circ}-\angle E L C=\angle E L A=\beta
$$
(where last equality holds because of $\angle A E L=90^{\circ}$ and $\angle E A L=90^{\circ}-\beta$ ).

Solution 2. We have $\angle B A D=90^{\circ}-\beta=\angle O A C$ and that $A X$ is the diameter of $\omega$. Also we note that
$$
\angle A L K=\beta, \angle K L C=180^{\circ}-\beta=\angle K B C
$$
so $B K C L$ is cyclic. Let $A O$ intersect circumcircle of $A B C$ again at $A^{\prime}$. We will show that $A^{\prime}$ is the desired concurrence point. Obviously $A A^{\prime}$ is the diameter of circumcircle of triangle $A B C$ so $\angle A^{\prime} C A=90^{\circ}$ which implies that $A^{\prime} C L E$ is cyclic. From power of point $E$ we have that $E K \cdot E L=E B \cdot E C=E A \cdot E A^{\prime}$ so we can conclude that $A^{\prime} \in \omega$. Now using the fact that $A X$ is a diameter of $\omega$ implies $\angle A X A^{\prime}=90^{\circ}$ we have that $D X A^{\prime} E$ is cyclic because of $\angle E D X=90^{\circ}$ which finishes the proof. $\square$
|
{
"resource_path": "JBMO/segmented/en-official/en-2021_jbmo_problems_and_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "## Solution."
}
|
8763c16c-5774-5bf9-9985-dc0e1df316c6
| 605,285
|
The real numbers $a, b, c, d$ satisfy simultaneously the equations
$$
a b c-d=1, b c d-a=2, c d a-b=3, d a b-c=-6
$$
Prove that $a+b+c+d \neq 0$.
|
Suppose that $a+b+c+d=0$. Then
$$
a b c+b c d+c d a+d a b=0
$$
If $a b c d=0$, then one of numbers, say $d$, must be 0 . In this case $a b c=0$, and so at least two of the numbers $a, b, c, d$ will be equal to 0 , making one of the given equations impossible. Hence $a b c d \neq 0$ and, from (1),
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}=0
$$
implying
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}
$$
It follows that $(a+b)(b+c)(c+a)=0$, which is impossible (for instance, if $a+b=0$, then adding the second and third given equations would lead to $0=2+3$, a contradiction). Thus $a+b+c+d \neq 0$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
The real numbers $a, b, c, d$ satisfy simultaneously the equations
$$
a b c-d=1, b c d-a=2, c d a-b=3, d a b-c=-6
$$
Prove that $a+b+c+d \neq 0$.
|
Suppose that $a+b+c+d=0$. Then
$$
a b c+b c d+c d a+d a b=0
$$
If $a b c d=0$, then one of numbers, say $d$, must be 0 . In this case $a b c=0$, and so at least two of the numbers $a, b, c, d$ will be equal to 0 , making one of the given equations impossible. Hence $a b c d \neq 0$ and, from (1),
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}=0
$$
implying
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}
$$
It follows that $(a+b)(b+c)(c+a)=0$, which is impossible (for instance, if $a+b=0$, then adding the second and third given equations would lead to $0=2+3$, a contradiction). Thus $a+b+c+d \neq 0$.
|
{
"resource_path": "JBMO/segmented/en-official/en-jbmo-2010-solutions.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
e8903db6-68a8-5b57-85da-352997aeda4f
| 605,287
|
Let $A B C$ be an acute triangle such that $A H=H D$, where $H$ is the orthocenter of $A B C$ and $D \in B C$ is the foot of the altitude from the vertex $A$. Let $\ell$ denote the line through $H$ which is tangent to the circumcircle of the triangle $B H C$. Let $S$ and $T$ be the intersection points of $\ell$ with $A B$ and $A C$, respectively. Denote the midpoints of $B H$ and $C H$ by $M$ and $N$, respectively. Prove that the lines $S M$ and $T N$ are parallel.
|
1. In order to prove that $S M$ and $T N$ are parallel, it suffices to prove that both of them are perpendicular to $S T$. Due to symmetry, we will provide a detailed proof of $S M \perp S T$, whereas the proof of $T N \perp S T$ is analogous. In this solution we will use the following notation: $\angle B A C=\alpha, \angle A B C=\beta, \angle A C B=\gamma$.
We first observe that, due to the tangency condition, we have
$$
\angle S H B=\angle H C B=90^{\circ}-\beta
$$
Combining the above with
$$
\angle S B H=\angle A B H=90^{\circ}-\alpha
$$
we get
$$
\angle B S H=180^{\circ}-\left(90^{\circ}-\beta\right)-\left(90^{\circ}-\alpha\right)=\alpha+\beta=180^{\circ}-\gamma
$$
from which it follows that $\angle A S T=\gamma$.
Since $A H=H D, H$ is the midpoint of $A D$. If $K$ denotes the midpoint of $A B$, we have that $K H$ and $B C$ are parallel. Since $M$ is the midpoint of $B H$, the lines $K M$ and $A D$ are parallel, from which it follows that $K M$ is perpendicular to $B C$. As $K H$ and $B C$ are parallel, we have that $K M$ is perpendicular to $K H$ so $\angle M K H=90^{\circ}$. Using the parallel lines $K H$ and $B C$ we also have
$$
\angle K H M=\angle K H B=\angle H B C
$$
Now,
$$
\angle H M K=90^{\circ}-\angle K H M=90^{\circ}-\angle H B C=90^{\circ}-\left(90^{\circ}-\gamma\right)=\gamma=\angle A S T=\angle K S H
$$
so the quadrilateral $M S K H$ is cyclic, which implies that $\angle M S H=\angle M K H=90^{\circ}$. In other words, the lines $S M$ and $S T$ are perpendicular, which completes our proof.
Solution 2. We will refer to the same figure as in the first solution. Since $C H$ is tangent to the circumcircle of triangle $B H C$, we have
$$
\angle S H B=\angle H C B=90^{\circ}-\angle A B C=\angle H A B
$$
From the above it follows that triangles $A H B$ and $H S B$ are similar. If $K$ denotes the midpoint of $A B$, then triangles $A H K$ and $H S M$ are also similar. Now, observe that $H$ and $K$ are respectively the midpoints of $A D$ and $A B$, which implies that $H K \| D B$, so
$$
\angle A H K=\angle A D B=90^{\circ}
$$
Now, from the last observation and the similarity of triangles $A H K$ and $H S M$, it follows that
$$
\angle H S M=\angle A H K=90^{\circ}
$$
Due to symmetry, analogously as above, we can prove that $\angle H T N=90^{\circ}$, implying that both $S M$ and $T N$ are perpendicular to $T S$, hence they are parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle such that $A H=H D$, where $H$ is the orthocenter of $A B C$ and $D \in B C$ is the foot of the altitude from the vertex $A$. Let $\ell$ denote the line through $H$ which is tangent to the circumcircle of the triangle $B H C$. Let $S$ and $T$ be the intersection points of $\ell$ with $A B$ and $A C$, respectively. Denote the midpoints of $B H$ and $C H$ by $M$ and $N$, respectively. Prove that the lines $S M$ and $T N$ are parallel.
|
1. In order to prove that $S M$ and $T N$ are parallel, it suffices to prove that both of them are perpendicular to $S T$. Due to symmetry, we will provide a detailed proof of $S M \perp S T$, whereas the proof of $T N \perp S T$ is analogous. In this solution we will use the following notation: $\angle B A C=\alpha, \angle A B C=\beta, \angle A C B=\gamma$.

We first observe that, due to the tangency condition, we have
$$
\angle S H B=\angle H C B=90^{\circ}-\beta
$$
Combining the above with
$$
\angle S B H=\angle A B H=90^{\circ}-\alpha
$$
we get
$$
\angle B S H=180^{\circ}-\left(90^{\circ}-\beta\right)-\left(90^{\circ}-\alpha\right)=\alpha+\beta=180^{\circ}-\gamma
$$
from which it follows that $\angle A S T=\gamma$.
Since $A H=H D, H$ is the midpoint of $A D$. If $K$ denotes the midpoint of $A B$, we have that $K H$ and $B C$ are parallel. Since $M$ is the midpoint of $B H$, the lines $K M$ and $A D$ are parallel, from which it follows that $K M$ is perpendicular to $B C$. As $K H$ and $B C$ are parallel, we have that $K M$ is perpendicular to $K H$ so $\angle M K H=90^{\circ}$. Using the parallel lines $K H$ and $B C$ we also have
$$
\angle K H M=\angle K H B=\angle H B C
$$
Now,
$$
\angle H M K=90^{\circ}-\angle K H M=90^{\circ}-\angle H B C=90^{\circ}-\left(90^{\circ}-\gamma\right)=\gamma=\angle A S T=\angle K S H
$$
so the quadrilateral $M S K H$ is cyclic, which implies that $\angle M S H=\angle M K H=90^{\circ}$. In other words, the lines $S M$ and $S T$ are perpendicular, which completes our proof.
Solution 2. We will refer to the same figure as in the first solution. Since $C H$ is tangent to the circumcircle of triangle $B H C$, we have
$$
\angle S H B=\angle H C B=90^{\circ}-\angle A B C=\angle H A B
$$
From the above it follows that triangles $A H B$ and $H S B$ are similar. If $K$ denotes the midpoint of $A B$, then triangles $A H K$ and $H S M$ are also similar. Now, observe that $H$ and $K$ are respectively the midpoints of $A D$ and $A B$, which implies that $H K \| D B$, so
$$
\angle A H K=\angle A D B=90^{\circ}
$$
Now, from the last observation and the similarity of triangles $A H K$ and $H S M$, it follows that
$$
\angle H S M=\angle A H K=90^{\circ}
$$
Due to symmetry, analogously as above, we can prove that $\angle H T N=90^{\circ}$, implying that both $S M$ and $T N$ are perpendicular to $T S$, hence they are parallel.
|
{
"resource_path": "JBMO/segmented/en-official/en-jbmo-2022-solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution "
}
|
63e6ca01-0a77-5a2c-aacc-9428c7631944
| 605,343
|
A trapezoid $A B C D(A B \| C D, A B>C D)$ is circumscribed. The incircle of the triangle $A B C$ touches the lines $A B$ and $A C$ at the points $M$ and $N$, respectively. Prove that the incenter of the trapezoid $A B C D$ lies on the line $M N$.
|
Version 1. Let $I$ be the incenter of triangle $A B C$ and $R$ be the common point of the lines $B I$ and $M N$. Since
$$
m(\widehat{A N M})=90^{\circ}-\frac{1}{2} m(\widehat{M A N}) \quad \text { and } \quad m(\widehat{B I C})=90^{\circ}+\frac{1}{2} m(\widehat{M A N})
$$
the quadrilateral $I R N C$ is cyclic.
It follows that $m(\widehat{B R C})=90^{\circ}$ and therefore
$$
m(\widehat{B C R})=90^{\circ}-m(\widehat{C B R})=90^{\circ}-\frac{1}{2}\left(180^{\circ}-m(\widehat{B C D})\right)=\frac{1}{2} m(\widehat{B C D})
$$
So, $(C R$ is the angle bisector of $\widehat{D C B}$ and $R$ is the incenter of the trapezoid.
Version 2. If $R$ is the incentre of the trapezoid $A B C D$, then $B, I$ and $R$ are collinear,
and $m(\widehat{B R C})=90^{\circ}$.
The quadrilateral $I R N C$ is cyclic.
Then $m(\widehat{M N C})=90^{\circ}+\frac{1}{2} \cdot m(\widehat{B A C})$
and $m(\widehat{R N C})=m(\widehat{B I C})=90^{\circ}+\frac{1}{2} \cdot m(\widehat{B A C})$,
so that $m(\widehat{M N C})=m(\widehat{R N C})$ and the points $M, R$ and $N$ are collinear.
Version 3. If $R$ is the incentre of the trapezoid $A B C D$, let $M^{\prime} \in(A B)$ and $N^{\prime} \in(A C)$ be the unique points, such that $R \in M^{\prime} N^{\prime}$ and $\left(A M^{\prime}\right) \equiv\left(A N^{\prime}\right)$.
Let $S$ be the intersection point of $C R$ and $A B$. Then $C R=R S$.
Consider $K \in A C$ such that $S K \| M^{\prime} N^{\prime}$. Then $N^{\prime}$ is the midpoint of $(C K)$.
We deduce
$$
A N^{\prime}=\frac{A K+A C}{2}=\frac{A S+A C}{2}=\frac{A B-B S+A C}{2}=\frac{A B+A C-B C}{2}=A N
$$
We conclude that $N=N^{\prime}$, hence $M=M^{\prime}$, and $R, M, N$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A trapezoid $A B C D(A B \| C D, A B>C D)$ is circumscribed. The incircle of the triangle $A B C$ touches the lines $A B$ and $A C$ at the points $M$ and $N$, respectively. Prove that the incenter of the trapezoid $A B C D$ lies on the line $M N$.

|
Version 1. Let $I$ be the incenter of triangle $A B C$ and $R$ be the common point of the lines $B I$ and $M N$. Since
$$
m(\widehat{A N M})=90^{\circ}-\frac{1}{2} m(\widehat{M A N}) \quad \text { and } \quad m(\widehat{B I C})=90^{\circ}+\frac{1}{2} m(\widehat{M A N})
$$
the quadrilateral $I R N C$ is cyclic.
It follows that $m(\widehat{B R C})=90^{\circ}$ and therefore
$$
m(\widehat{B C R})=90^{\circ}-m(\widehat{C B R})=90^{\circ}-\frac{1}{2}\left(180^{\circ}-m(\widehat{B C D})\right)=\frac{1}{2} m(\widehat{B C D})
$$
So, $(C R$ is the angle bisector of $\widehat{D C B}$ and $R$ is the incenter of the trapezoid.
Version 2. If $R$ is the incentre of the trapezoid $A B C D$, then $B, I$ and $R$ are collinear,
and $m(\widehat{B R C})=90^{\circ}$.
The quadrilateral $I R N C$ is cyclic.
Then $m(\widehat{M N C})=90^{\circ}+\frac{1}{2} \cdot m(\widehat{B A C})$
and $m(\widehat{R N C})=m(\widehat{B I C})=90^{\circ}+\frac{1}{2} \cdot m(\widehat{B A C})$,
so that $m(\widehat{M N C})=m(\widehat{R N C})$ and the points $M, R$ and $N$ are collinear.
Version 3. If $R$ is the incentre of the trapezoid $A B C D$, let $M^{\prime} \in(A B)$ and $N^{\prime} \in(A C)$ be the unique points, such that $R \in M^{\prime} N^{\prime}$ and $\left(A M^{\prime}\right) \equiv\left(A N^{\prime}\right)$.
Let $S$ be the intersection point of $C R$ and $A B$. Then $C R=R S$.
Consider $K \in A C$ such that $S K \| M^{\prime} N^{\prime}$. Then $N^{\prime}$ is the midpoint of $(C K)$.
We deduce
$$
A N^{\prime}=\frac{A K+A C}{2}=\frac{A S+A C}{2}=\frac{A B-B S+A C}{2}=\frac{A B+A C-B C}{2}=A N
$$
We conclude that $N=N^{\prime}$, hence $M=M^{\prime}$, and $R, M, N$ are collinear.
|
{
"resource_path": "JBMO/segmented/en-official/en-jbmo_2016_paper_eng.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "## Solution."
}
|
1a9f073a-c35c-5134-af03-ed940d1aa2e0
| 605,420
|
Let $a, b$ and $c$ be positive real numbers. Prove that
$$
\frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+\frac{8}{(c+a)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3}
$$
|
Since $2 a b \leq a^{2}+b^{2}$, it follows that $(a+b)^{2} \leq 2\left(a^{2}+b^{2}\right)$
and $4 a b c \leq 2 c\left(a^{2}+b^{2}\right)$, for any positive reals $a, b, c$.
Adding these inequalities, we find
$$
(a+b)^{2}+4 a b c \leq 2\left(a^{2}+b^{2}\right)(c+1)
$$
so that
$$
\frac{8}{(a+b)^{2}+4 a b c} \geq \frac{4}{\left(a^{2}+b^{2}\right)(c+1)}
$$
Using the AM-GM inequality, we have
$$
\frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq 2 \sqrt{\frac{2}{c+1}}=\frac{4}{\sqrt{2(c+1)}}
$$
respectively
$$
\frac{c+3}{8}=\frac{(c+1)+2}{8} \geq \frac{\sqrt{2(c+1)}}{4}
$$
We conclude that
$$
\frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq \frac{8}{c+3}
$$
and finally
$$
\frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(a+c)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$ and $c$ be positive real numbers. Prove that
$$
\frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+\frac{8}{(c+a)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3}
$$
|
Since $2 a b \leq a^{2}+b^{2}$, it follows that $(a+b)^{2} \leq 2\left(a^{2}+b^{2}\right)$
and $4 a b c \leq 2 c\left(a^{2}+b^{2}\right)$, for any positive reals $a, b, c$.
Adding these inequalities, we find
$$
(a+b)^{2}+4 a b c \leq 2\left(a^{2}+b^{2}\right)(c+1)
$$
so that
$$
\frac{8}{(a+b)^{2}+4 a b c} \geq \frac{4}{\left(a^{2}+b^{2}\right)(c+1)}
$$
Using the AM-GM inequality, we have
$$
\frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq 2 \sqrt{\frac{2}{c+1}}=\frac{4}{\sqrt{2(c+1)}}
$$
respectively
$$
\frac{c+3}{8}=\frac{(c+1)+2}{8} \geq \frac{\sqrt{2(c+1)}}{4}
$$
We conclude that
$$
\frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq \frac{8}{c+3}
$$
and finally
$$
\frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(a+c)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3}
$$
|
{
"resource_path": "JBMO/segmented/en-official/en-jbmo_2016_paper_eng.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
0b9b2693-2b1c-5377-a62a-aec889dd1157
| 605,430
|
Let $x, y, z$ be positive integers such that $x \neq y \neq z \neq x$. Prove that
$$
(x+y+z)(x y+y z+z x-2) \geq 9 x y z
$$
When does the equality hold?
|
Since $x, y, z$ are distinct positive integers, the required inequality is symmetric and WLOG we can suppose that $x \geq y+1 \geq z+2$. We consider 2 possible cases:
Case 1. $y \geq z+2$. Since $x \geq y+1 \geq z+3$ it follows that
$$
(x-y)^{2} \geq 1, \quad(y-z)^{2} \geq 4, \quad(x-z)^{2} \geq 9
$$
which are equivalent to
$$
x^{2}+y^{2} \geq 2 x y+1, \quad y^{2}+z^{2} \geq 2 y z+4, \quad x^{2}+z^{2} \geq 2 x z+9
$$
or otherwise
$$
z x^{2}+z y^{2} \geq 2 x y z+z, \quad x y^{2}+x z^{2} \geq 2 x y z+4 x, \quad y x^{2}+y z^{2} \geq 2 x y z+9 y
$$
Adding up the last three inequalities we have
$$
x y(x+y)+y z(y+z)+z x(z+x) \geq 6 x y z+4 x+9 y+z
$$
which implies that $(x+y+z)(x y+y z+z x-2) \geq 9 x y z+2 x+7 y-z$.
Since $x \geq z+3$ it follows that $2 x+7 y-z \geq 0$ and our inequality follows.
Case 2. $y=z+1$. Since $x \geq y+1=z+2$ it follows that $x \geq z+2$, and replacing $y=z+1$ in the required inequality we have to prove
$$
(x+z+1+z)(x(z+1)+(z+1) z+z x-2) \geq 9 x(z+1) z
$$
which is equivalent to
$$
(x+2 z+1)\left(z^{2}+2 z x+z+x-2\right)-9 x(z+1) z \geq 0
$$
Doing easy algebraic manipulations, this is equivalent to prove
$$
(x-z-2)(x-z+1)(2 z+1) \geq 0
$$
which is satisfied since $x \geq z+2$.
The equality is achieved only in the Case 2 for $x=z+2$, so we have equality when $(x, y, z)=$ $(k+2, k+1, k)$ and all the permutations for any positive integer $k$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y, z$ be positive integers such that $x \neq y \neq z \neq x$. Prove that
$$
(x+y+z)(x y+y z+z x-2) \geq 9 x y z
$$
When does the equality hold?
|
Since $x, y, z$ are distinct positive integers, the required inequality is symmetric and WLOG we can suppose that $x \geq y+1 \geq z+2$. We consider 2 possible cases:
Case 1. $y \geq z+2$. Since $x \geq y+1 \geq z+3$ it follows that
$$
(x-y)^{2} \geq 1, \quad(y-z)^{2} \geq 4, \quad(x-z)^{2} \geq 9
$$
which are equivalent to
$$
x^{2}+y^{2} \geq 2 x y+1, \quad y^{2}+z^{2} \geq 2 y z+4, \quad x^{2}+z^{2} \geq 2 x z+9
$$
or otherwise
$$
z x^{2}+z y^{2} \geq 2 x y z+z, \quad x y^{2}+x z^{2} \geq 2 x y z+4 x, \quad y x^{2}+y z^{2} \geq 2 x y z+9 y
$$
Adding up the last three inequalities we have
$$
x y(x+y)+y z(y+z)+z x(z+x) \geq 6 x y z+4 x+9 y+z
$$
which implies that $(x+y+z)(x y+y z+z x-2) \geq 9 x y z+2 x+7 y-z$.
Since $x \geq z+3$ it follows that $2 x+7 y-z \geq 0$ and our inequality follows.
Case 2. $y=z+1$. Since $x \geq y+1=z+2$ it follows that $x \geq z+2$, and replacing $y=z+1$ in the required inequality we have to prove
$$
(x+z+1+z)(x(z+1)+(z+1) z+z x-2) \geq 9 x(z+1) z
$$
which is equivalent to
$$
(x+2 z+1)\left(z^{2}+2 z x+z+x-2\right)-9 x(z+1) z \geq 0
$$
Doing easy algebraic manipulations, this is equivalent to prove
$$
(x-z-2)(x-z+1)(2 z+1) \geq 0
$$
which is satisfied since $x \geq z+2$.
The equality is achieved only in the Case 2 for $x=z+2$, so we have equality when $(x, y, z)=$ $(k+2, k+1, k)$ and all the permutations for any positive integer $k$.
|
{
"resource_path": "JBMO/segmented/en-official/en-jbmo_2017_english_solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
53523e95-d32b-5dcd-950d-adf99238ee69
| 605,466
|
Let $A B C$ be an acute triangle such that $A B \neq A C$, with circumcircle $\Gamma$ and circumcenter $O$. Let $M$ be the midpoint of $B C$ and $D$ be a point on $\Gamma$ such that $A D \perp B C$. Let $T$ be a point such that $B D C T$ is a parallelogram and $Q$ a point on the same side of $B C$ as $A$ such that
$$
\angle B Q M=\angle B C A \quad \text { and } \quad \angle C Q M=\angle C B A
$$
Let the line $A O$ intersect $\Gamma$ at $E,(E \neq A)$ and let the circumcircle of $\triangle E T Q$ intersect $\Gamma$ at point $X \neq E$. Prove that the points $A, M$, and $X$ are collinear.
|
Let $X^{\prime}$ be symmetric point to $Q$ in line $B C$. Now since $\angle C B A=\angle C Q M=\angle C X^{\prime} M$, $\angle B C A=\angle B Q M=\angle B X^{\prime} M$, we have
$$
\angle B X^{\prime} C=\angle B X^{\prime} M+\angle C X^{\prime} M=\angle C B A+\angle B C A=180^{\circ}-\angle B A C
$$
we have that $X^{\prime} \in \Gamma$. Now since $\angle A X^{\prime} B=\angle A C B=\angle M X^{\prime} B$ we have that $A, M, X^{\prime}$ are collinear. Note that since
$$
\angle D C B=\angle D A B=90^{\circ}-\angle A B C=\angle O A C=\angle E A C
$$
we get that $D B C E$ is an isosceles trapezoid.
Since $B D C T$ is a parallelogram we have $M T=M D$, with $M, D, T$ being collinear, $B D=C T$, and since $B D E C$ is an isosceles trapezoid we have $B D=C E$ and $M E=M D$. Since
$$
\angle B T C=\angle B D C=\angle B E D, \quad C E=B D=C T \quad \text { and } \quad M E=M T
$$
we have that $E$ and $T$ are symmetric with respect to the line $B C$. Now since $Q$ and $X^{\prime}$ are symmetric with respect to the line $B C$ as well, this means that $Q X^{\prime} E T$ is an isosceles trapezoid which means that $Q, X^{\prime}, E, T$ are concyclic. Since $X^{\prime} \in \Gamma$ this means that $X \equiv X^{\prime}$ and therefore $A, M, X$ are collinear.
Alternative solution. Denote by $H$ the orthocenter of $\triangle A B C$. We use the following well known properties:
(i) Point $D$ is the symmetric point of $H$ with respect to $B C$. Indeed, if $H_{1}$ is the symmetric point of $H$ with respect to $B C$ then $\angle B H_{1} C+\angle B A C=180^{\circ}$ and therefore $H_{1} \equiv D$.
(ii) The symmetric point of $H$ with respect to $M$ is the point $E$. Indeed, if $H_{2}$ is the symmetric point of $H$ with respect to $M$ then $B H_{2} C H$ is parallelogram, $\angle B H_{2} C+\angle B A C=180^{\circ}$ and since $E B \| C H$ we have $\angle E B A=90^{\circ}$.
Since $D E T H$ is a parallelogram and $M H=M D$ we have that $D E T H$ is a rectangle. Therefore $M T=M E$ and $T E \perp B C$ implying that $T$ and $E$ are symmetric with respect to $B C$. Denote by $Q^{\prime}$ the symmetric point of $Q$ with respect to $B C$. Then $Q^{\prime} E T Q$ is isosceles trapezoid, so $Q^{\prime}$ is a point on the circumcircle of $\triangle E T Q$. Moreover $\angle B Q^{\prime} C+\angle B A C=180^{\circ}$ and we conclude that $Q^{\prime} \in \Gamma$. Therefore $Q^{\prime} \equiv X$.
It remains to observe that $\angle C X M=\angle C Q M=\angle C B A$ and $\angle C X A=\angle C B A$ and we infer that $X, M$ and $A$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle such that $A B \neq A C$, with circumcircle $\Gamma$ and circumcenter $O$. Let $M$ be the midpoint of $B C$ and $D$ be a point on $\Gamma$ such that $A D \perp B C$. Let $T$ be a point such that $B D C T$ is a parallelogram and $Q$ a point on the same side of $B C$ as $A$ such that
$$
\angle B Q M=\angle B C A \quad \text { and } \quad \angle C Q M=\angle C B A
$$
Let the line $A O$ intersect $\Gamma$ at $E,(E \neq A)$ and let the circumcircle of $\triangle E T Q$ intersect $\Gamma$ at point $X \neq E$. Prove that the points $A, M$, and $X$ are collinear.
|
Let $X^{\prime}$ be symmetric point to $Q$ in line $B C$. Now since $\angle C B A=\angle C Q M=\angle C X^{\prime} M$, $\angle B C A=\angle B Q M=\angle B X^{\prime} M$, we have
$$
\angle B X^{\prime} C=\angle B X^{\prime} M+\angle C X^{\prime} M=\angle C B A+\angle B C A=180^{\circ}-\angle B A C
$$
we have that $X^{\prime} \in \Gamma$. Now since $\angle A X^{\prime} B=\angle A C B=\angle M X^{\prime} B$ we have that $A, M, X^{\prime}$ are collinear. Note that since
$$
\angle D C B=\angle D A B=90^{\circ}-\angle A B C=\angle O A C=\angle E A C
$$
we get that $D B C E$ is an isosceles trapezoid.

Since $B D C T$ is a parallelogram we have $M T=M D$, with $M, D, T$ being collinear, $B D=C T$, and since $B D E C$ is an isosceles trapezoid we have $B D=C E$ and $M E=M D$. Since
$$
\angle B T C=\angle B D C=\angle B E D, \quad C E=B D=C T \quad \text { and } \quad M E=M T
$$
we have that $E$ and $T$ are symmetric with respect to the line $B C$. Now since $Q$ and $X^{\prime}$ are symmetric with respect to the line $B C$ as well, this means that $Q X^{\prime} E T$ is an isosceles trapezoid which means that $Q, X^{\prime}, E, T$ are concyclic. Since $X^{\prime} \in \Gamma$ this means that $X \equiv X^{\prime}$ and therefore $A, M, X$ are collinear.
Alternative solution. Denote by $H$ the orthocenter of $\triangle A B C$. We use the following well known properties:
(i) Point $D$ is the symmetric point of $H$ with respect to $B C$. Indeed, if $H_{1}$ is the symmetric point of $H$ with respect to $B C$ then $\angle B H_{1} C+\angle B A C=180^{\circ}$ and therefore $H_{1} \equiv D$.
(ii) The symmetric point of $H$ with respect to $M$ is the point $E$. Indeed, if $H_{2}$ is the symmetric point of $H$ with respect to $M$ then $B H_{2} C H$ is parallelogram, $\angle B H_{2} C+\angle B A C=180^{\circ}$ and since $E B \| C H$ we have $\angle E B A=90^{\circ}$.
Since $D E T H$ is a parallelogram and $M H=M D$ we have that $D E T H$ is a rectangle. Therefore $M T=M E$ and $T E \perp B C$ implying that $T$ and $E$ are symmetric with respect to $B C$. Denote by $Q^{\prime}$ the symmetric point of $Q$ with respect to $B C$. Then $Q^{\prime} E T Q$ is isosceles trapezoid, so $Q^{\prime}$ is a point on the circumcircle of $\triangle E T Q$. Moreover $\angle B Q^{\prime} C+\angle B A C=180^{\circ}$ and we conclude that $Q^{\prime} \in \Gamma$. Therefore $Q^{\prime} \equiv X$.
It remains to observe that $\angle C X M=\angle C Q M=\angle C B A$ and $\angle C X A=\angle C B A$ and we infer that $X, M$ and $A$ are collinear.
|
{
"resource_path": "JBMO/segmented/en-official/en-jbmo_2017_english_solutions.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
419ec2f3-4eef-5d34-97a2-082a2b8e6336
| 605,474
|
Let $A B C$ be an acute triangle, $A^{\prime}, B^{\prime}$ and $C^{\prime}$ be the reflections of the vertices $A, B$ and $C$ with respect to $B C, C A$, and $A B$, respectively, and let the circumcircles of triangles $A B B^{\prime}$ and $A C C^{\prime}$ meet again at $A_{1}$. Points $B_{1}$ and $C_{1}$ are defined similarly. Prove that the lines $A A_{1}, B B_{1}$ and $C C_{1}$ have a common point.
|
Let $O_{1}, O_{2}$ and $O$ be the circumcenters of triangles $A B B^{\prime}, A C C^{\prime}$ and $A B C$ respectively. As $A B$ is the perpendicular bisector of the line segment $C C^{\prime}, O_{2}$ is the intersection of the perpendicular bisector of $A C$ with $A B$. Similarly, $O_{1}$ is the intersection of the perpendicular bisector of $A B$ with $A C$. It follows that $O$ is the orthocenter of triangle $A O_{1} O_{2}$. This means that $A O$ is perpendicular to $O_{1} O_{2}$. On the other hand, the segment $A A_{1}$ is the common chord of the two circles, thus it is perpendicular to $O_{1} O_{2}$. As a result, $A A_{1}$ passes through $O$. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent at $O$.
Comment by PSC. We present here a different approach.
We first prove that $A_{1}, B$ and $C^{\prime}$ are collinear. Indeed, since $\angle B A B^{\prime}=\angle C A C^{\prime}=2 \angle B A C$, then from the circles $\left(A B B^{\prime}\right),\left(A C C^{\prime}\right)$ we get
$$
\angle A A_{1} B=\frac{\angle B A_{1} B^{\prime}}{2}=\frac{180^{\circ}-\angle B A B^{\prime}}{2}=90^{\circ}-\angle B A C=\angle A A_{1} C^{\prime}
$$
It follows that
$$
\angle A_{1} A C=\angle A_{1} C^{\prime} C=\angle B C^{\prime} C=90^{\circ}-\angle A B C
$$
On the other hand, if $O$ is the circumcenter of $A B C$, then
$$
\angle O A C=90^{\circ}-\angle A B C \text {. }
$$
From (1) and (2) we conclude that $A_{1}, A$ and $O$ are collinear. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent in $O$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle, $A^{\prime}, B^{\prime}$ and $C^{\prime}$ be the reflections of the vertices $A, B$ and $C$ with respect to $B C, C A$, and $A B$, respectively, and let the circumcircles of triangles $A B B^{\prime}$ and $A C C^{\prime}$ meet again at $A_{1}$. Points $B_{1}$ and $C_{1}$ are defined similarly. Prove that the lines $A A_{1}, B B_{1}$ and $C C_{1}$ have a common point.
|
Let $O_{1}, O_{2}$ and $O$ be the circumcenters of triangles $A B B^{\prime}, A C C^{\prime}$ and $A B C$ respectively. As $A B$ is the perpendicular bisector of the line segment $C C^{\prime}, O_{2}$ is the intersection of the perpendicular bisector of $A C$ with $A B$. Similarly, $O_{1}$ is the intersection of the perpendicular bisector of $A B$ with $A C$. It follows that $O$ is the orthocenter of triangle $A O_{1} O_{2}$. This means that $A O$ is perpendicular to $O_{1} O_{2}$. On the other hand, the segment $A A_{1}$ is the common chord of the two circles, thus it is perpendicular to $O_{1} O_{2}$. As a result, $A A_{1}$ passes through $O$. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent at $O$.

Comment by PSC. We present here a different approach.
We first prove that $A_{1}, B$ and $C^{\prime}$ are collinear. Indeed, since $\angle B A B^{\prime}=\angle C A C^{\prime}=2 \angle B A C$, then from the circles $\left(A B B^{\prime}\right),\left(A C C^{\prime}\right)$ we get
$$
\angle A A_{1} B=\frac{\angle B A_{1} B^{\prime}}{2}=\frac{180^{\circ}-\angle B A B^{\prime}}{2}=90^{\circ}-\angle B A C=\angle A A_{1} C^{\prime}
$$
It follows that
$$
\angle A_{1} A C=\angle A_{1} C^{\prime} C=\angle B C^{\prime} C=90^{\circ}-\angle A B C
$$
On the other hand, if $O$ is the circumcenter of $A B C$, then
$$
\angle O A C=90^{\circ}-\angle A B C \text {. }
$$
From (1) and (2) we conclude that $A_{1}, A$ and $O$ are collinear. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent in $O$.
|
{
"resource_path": "JBMO/segmented/en-official/en-jbmo_2018_solutions.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
aaf6ab3f-c375-5d7f-93c0-2455958a11e5
| 605,522
|
Let $\triangle A B C$ be a right-angled triangle with $\angle B A C=90^{\circ}$ and let $E$ be the foot of the perpendicular from $A$ on $B C$. Let $Z \neq A$ be a point on the line $A B$ with $A B=B Z$. Let (c) be the circumcircle of the triangle $\triangle A E Z$. Let $D$ be the second point of intersection of $(c)$ with $Z C$ and let $F$ be the antidiametric point of $D$ with respect to (c). Let $P$ be the point of intersection of the lines $F E$ and $C Z$. If the tangent to (c) at $Z$ meets $P A$ at $T$, prove that the points $T, E, B, Z$ are concyclic.
|
We will first show that $P A$ is tangent to $(c)$ at $A$.
Since $E, D, Z, A$ are concyclic, then $\angle E D C=\angle E A Z=\angle E A B$. Since also the triangles $\triangle A B C$ and $\triangle E B A$ are similar, then $\angle E A B=\angle B C A$, therefore $\angle E D C=\angle B C A$.
Since $\angle F E D=90^{\circ}$, then $\angle P E D=90^{\circ}$ and so
$$
\angle E P D=90^{\circ}-\angle E D C=90^{\circ}-\angle B C A=\angle E A C
$$
Therefore the points $E, A, C, P$ are concyclic. It follows that $\angle C P A=90^{\circ}$ and therefore the triangle $\angle P A Z$ is right-angled. Since also $B$ is the midpoint of $A Z$, then $P B=A B=B Z$ and so $\angle Z P B=$ $\angle P Z B$.
Furthermore, $\angle E P D=\angle E A C=\angle C B A=\angle E B A$ from which it follows that the points $P, E, B, Z$ are also concyclic.
Now observe that
$$
\angle P A E=\angle P C E=\angle Z P B-\angle P B E=\angle P Z B-\angle P Z E=\angle E Z B
$$
Therefore $P A$ is tangent to $(c)$ at $A$ as claimed.
It now follows that $T A=T Z$. Therefore
$$
\begin{aligned}
\angle P T Z & =180^{\circ}-2(\angle T A B)=180^{\circ}-2(\angle P A E+\angle E A B)=180^{\circ}-2(\angle E C P+\angle A C B) \\
& =180^{\circ}-2\left(90^{\circ}-\angle P Z B\right)=2(\angle P Z B)=\angle P Z B+\angle B P Z=\angle P B A .
\end{aligned}
$$
Thus $T, P, B, Z$ are concyclic, and since $P, E, B, Z$ are also concyclic then $T, E, B, Z$ are concyclic as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\triangle A B C$ be a right-angled triangle with $\angle B A C=90^{\circ}$ and let $E$ be the foot of the perpendicular from $A$ on $B C$. Let $Z \neq A$ be a point on the line $A B$ with $A B=B Z$. Let (c) be the circumcircle of the triangle $\triangle A E Z$. Let $D$ be the second point of intersection of $(c)$ with $Z C$ and let $F$ be the antidiametric point of $D$ with respect to (c). Let $P$ be the point of intersection of the lines $F E$ and $C Z$. If the tangent to (c) at $Z$ meets $P A$ at $T$, prove that the points $T, E, B, Z$ are concyclic.
|
We will first show that $P A$ is tangent to $(c)$ at $A$.
Since $E, D, Z, A$ are concyclic, then $\angle E D C=\angle E A Z=\angle E A B$. Since also the triangles $\triangle A B C$ and $\triangle E B A$ are similar, then $\angle E A B=\angle B C A$, therefore $\angle E D C=\angle B C A$.
Since $\angle F E D=90^{\circ}$, then $\angle P E D=90^{\circ}$ and so
$$
\angle E P D=90^{\circ}-\angle E D C=90^{\circ}-\angle B C A=\angle E A C
$$
Therefore the points $E, A, C, P$ are concyclic. It follows that $\angle C P A=90^{\circ}$ and therefore the triangle $\angle P A Z$ is right-angled. Since also $B$ is the midpoint of $A Z$, then $P B=A B=B Z$ and so $\angle Z P B=$ $\angle P Z B$.

Furthermore, $\angle E P D=\angle E A C=\angle C B A=\angle E B A$ from which it follows that the points $P, E, B, Z$ are also concyclic.
Now observe that
$$
\angle P A E=\angle P C E=\angle Z P B-\angle P B E=\angle P Z B-\angle P Z E=\angle E Z B
$$
Therefore $P A$ is tangent to $(c)$ at $A$ as claimed.
It now follows that $T A=T Z$. Therefore
$$
\begin{aligned}
\angle P T Z & =180^{\circ}-2(\angle T A B)=180^{\circ}-2(\angle P A E+\angle E A B)=180^{\circ}-2(\angle E C P+\angle A C B) \\
& =180^{\circ}-2\left(90^{\circ}-\angle P Z B\right)=2(\angle P Z B)=\angle P Z B+\angle B P Z=\angle P B A .
\end{aligned}
$$
Thus $T, P, B, Z$ are concyclic, and since $P, E, B, Z$ are also concyclic then $T, E, B, Z$ are concyclic as required.
|
{
"resource_path": "JBMO/segmented/en-official/en-jbmo_2020_solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
bd0b8b37-d20e-5f51-af6b-00ddb14b1c96
| 605,543
|
Prove that for all non-negative real numbers $x, y, z$, not all equal to 0 , the following inequality holds
$$
\frac{2 x^{2}-x+y+z}{x+y^{2}+z^{2}}+\frac{2 y^{2}+x-y+z}{x^{2}+y+z^{2}}+\frac{2 z^{2}+x+y-z}{x^{2}+y^{2}+z} \geqslant 3
$$
Determine all the triples $(x, y, z)$ for which the equality holds.
|
Let us first write the expression $L$ on the left hand side in the following way
$$
\begin{aligned}
L & =\left(\frac{2 x^{2}-x+y+z}{x+y^{2}+z^{2}}+2\right)+\left(\frac{2 y^{2}+x-y+z}{x^{2}+y+z^{2}}+2\right)+\left(\frac{2 z^{2}+x+y-z}{x^{2}+y^{2}+z}+2\right)-6 \\
& =\left(2 x^{2}+2 y^{2}+2 z^{2}+x+y+z\right)\left(\frac{1}{x+y^{2}+z^{2}}+\frac{1}{x^{2}+y+z^{2}}+\frac{1}{x^{2}+y^{2}+z}\right)-6
\end{aligned}
$$
If we introduce the notation $A=x+y^{2}+z^{2}, B=x^{2}+y+z^{2}, C=x^{2}+y^{2}+z$, then the previous relation becomes
$$
L=(A+B+C)\left(\frac{1}{A}+\frac{1}{B}+\frac{1}{C}\right)-6
$$
Using the arithmetic-harmonic mean inequality or Cauchy-Schwartz inequality for positive real numbers $A, B, C$, we easily obtain
$$
(A+B+C)\left(\frac{1}{A}+\frac{1}{B}+\frac{1}{C}\right) \geqslant 9
$$
so it holds $L \geqslant 3$.
The equality occurs if and only if $A=B=C$, which is equivalent to the system of equations
$$
x^{2}-y^{2}=x-y, \quad y^{2}-z^{2}=y-z, \quad x^{2}-z^{2}=x-z
$$
It follows easily that the only solutions of this system are
$(x, y, z) \in\{(t, t, t) \mid t>0\} \cup\{(t, t, 1-t) \mid t \in[0,1]\} \cup\{(t, 1-t, t) \mid t \in[0,1]\} \cup\{(1-t, t, t) \mid t \in[0,1]\}$.
PSC Remark We feel the equality case needs more explanations in order to have a complete solution, our suggestion follows:
Clearly if $x, y, z$ are all equal and not 0 satisfy the condition. Now suppose that not all of them are equal it means we can't simultaneously have $x+y=y+z=z+x=1$ otherwise we would have all $x, y, z$ equal to $\frac{1}{2}$ which we already discussed. We can suppose now that $x=y$ and $y+z=z+x=1$ where we get $z=1-x$. So, all triples which satisfy the equality are $(x, y, z)=(a, a, a),(b, b, 1-b)$ and all permutations for any $a>0$ and $b \in[0,1]$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for all non-negative real numbers $x, y, z$, not all equal to 0 , the following inequality holds
$$
\frac{2 x^{2}-x+y+z}{x+y^{2}+z^{2}}+\frac{2 y^{2}+x-y+z}{x^{2}+y+z^{2}}+\frac{2 z^{2}+x+y-z}{x^{2}+y^{2}+z} \geqslant 3
$$
Determine all the triples $(x, y, z)$ for which the equality holds.
|
Let us first write the expression $L$ on the left hand side in the following way
$$
\begin{aligned}
L & =\left(\frac{2 x^{2}-x+y+z}{x+y^{2}+z^{2}}+2\right)+\left(\frac{2 y^{2}+x-y+z}{x^{2}+y+z^{2}}+2\right)+\left(\frac{2 z^{2}+x+y-z}{x^{2}+y^{2}+z}+2\right)-6 \\
& =\left(2 x^{2}+2 y^{2}+2 z^{2}+x+y+z\right)\left(\frac{1}{x+y^{2}+z^{2}}+\frac{1}{x^{2}+y+z^{2}}+\frac{1}{x^{2}+y^{2}+z}\right)-6
\end{aligned}
$$
If we introduce the notation $A=x+y^{2}+z^{2}, B=x^{2}+y+z^{2}, C=x^{2}+y^{2}+z$, then the previous relation becomes
$$
L=(A+B+C)\left(\frac{1}{A}+\frac{1}{B}+\frac{1}{C}\right)-6
$$
Using the arithmetic-harmonic mean inequality or Cauchy-Schwartz inequality for positive real numbers $A, B, C$, we easily obtain
$$
(A+B+C)\left(\frac{1}{A}+\frac{1}{B}+\frac{1}{C}\right) \geqslant 9
$$
so it holds $L \geqslant 3$.
The equality occurs if and only if $A=B=C$, which is equivalent to the system of equations
$$
x^{2}-y^{2}=x-y, \quad y^{2}-z^{2}=y-z, \quad x^{2}-z^{2}=x-z
$$
It follows easily that the only solutions of this system are
$(x, y, z) \in\{(t, t, t) \mid t>0\} \cup\{(t, t, 1-t) \mid t \in[0,1]\} \cup\{(t, 1-t, t) \mid t \in[0,1]\} \cup\{(1-t, t, t) \mid t \in[0,1]\}$.
PSC Remark We feel the equality case needs more explanations in order to have a complete solution, our suggestion follows:
Clearly if $x, y, z$ are all equal and not 0 satisfy the condition. Now suppose that not all of them are equal it means we can't simultaneously have $x+y=y+z=z+x=1$ otherwise we would have all $x, y, z$ equal to $\frac{1}{2}$ which we already discussed. We can suppose now that $x=y$ and $y+z=z+x=1$ where we get $z=1-x$. So, all triples which satisfy the equality are $(x, y, z)=(a, a, a),(b, b, 1-b)$ and all permutations for any $a>0$ and $b \in[0,1]$
|
{
"resource_path": "JBMO/segmented/en-official/en-jbmo_2023_final_paper_-_with_solutions_1.jsonl",
"problem_match": "## Problem 2.",
"solution_match": "\nSolution."
}
|
c51d32df-91ff-59ab-8133-2be046401763
| 605,588
|
Let $A B C$ be an acute triangle with circumcenter $O$. Let $D$ be the foot of the altitude from $A$ to $B C$ and let $M$ be the midpoint of $O D$. The points $O_{b}$ and $O_{c}$ are the circumcenters of triangles $A O C$ and $A O B$, respectively. If $A O=A D$, prove that the points $A, O_{b}, M$ and $O_{c}$ are concyclic.
|
Note that $A B=A C$ cannot hold since $A O=A D$ would imply that $O$ is the midpoint of $B C$, which is not possible for an acute triangle. So we may assume without loss of generality that $A B<A C$.
Let $M_{b}$ and $M_{c}$ be the midpoints of $A C$ and $A B$, respectively. Since $\angle A M_{b} O=\angle A M_{c} O=$ $90^{\circ}=\angle A M O$ (the latter since $A O=A D$ ), the pentagon $A M_{b} O M M_{c}$ is cyclic.
Next, notice that $A M$ is the perpendicular bisector of $O D, O_{b} O_{c}$ is the perpendicular bisector of $A O$ and $M_{b} M_{c}$ is the perpendicular bisector of $A D$. Hence these three lines are concurrent - denote their common point by $T$.
The quadrilateral $A O_{b} M O_{C}$ is cyclic if and only if $A T \cdot T M=O_{b} T \cdot O_{c} T$. From the cyclic $A M_{b} M M_{c}$ we have $A T \cdot T M=M_{b} T \cdot M_{c} T$. Hence it now suffices to argue $M_{b} T \cdot M_{c} T=O_{b} T \cdot O_{c} T$ - or equivalently, that $M_{b}, M_{c}, O_{b}$ and $O_{c}$ are concyclic.
We assume that $\angle A O B<90^{\circ}$ and $\angle A O C>90^{\circ}$ so that $O_{c}$ is in the interior of triangle $A O B$ and $O_{b}$ in external to the triangles $A O C$ (the other cases are analogous and if $\angle A O B=90^{\circ}$ or $\angle A O C=90^{\circ}$, then $M_{b} \equiv O_{b}$ or $M_{c} \equiv O_{c}$ and we are automatically done). We have
$$
\angle M_{c} M_{b} O_{b}=90^{\circ}+\angle A M_{b} M_{c}=90^{\circ}+\angle A C B
$$
as well as (since $O_{c} O_{b}$ is a perpendicular bisector of $A O$ and hence bisects $\angle A O_{C} O$ )
$$
\angle M_{c} O_{c} O_{b}=180^{\circ}-\angle O O_{c} O_{b}=90^{\circ}+\frac{\angle A O_{c} M_{c}}{2}
$$
$$
=90^{\circ}+\frac{\angle A O_{c} B}{4}=90^{\circ}+\frac{\angle A O B}{2}=90^{\circ}+\angle A C B
$$
and therefore $O_{b} M_{b} O_{c} M_{c}$ is cyclic, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with circumcenter $O$. Let $D$ be the foot of the altitude from $A$ to $B C$ and let $M$ be the midpoint of $O D$. The points $O_{b}$ and $O_{c}$ are the circumcenters of triangles $A O C$ and $A O B$, respectively. If $A O=A D$, prove that the points $A, O_{b}, M$ and $O_{c}$ are concyclic.
|

Note that $A B=A C$ cannot hold since $A O=A D$ would imply that $O$ is the midpoint of $B C$, which is not possible for an acute triangle. So we may assume without loss of generality that $A B<A C$.
Let $M_{b}$ and $M_{c}$ be the midpoints of $A C$ and $A B$, respectively. Since $\angle A M_{b} O=\angle A M_{c} O=$ $90^{\circ}=\angle A M O$ (the latter since $A O=A D$ ), the pentagon $A M_{b} O M M_{c}$ is cyclic.
Next, notice that $A M$ is the perpendicular bisector of $O D, O_{b} O_{c}$ is the perpendicular bisector of $A O$ and $M_{b} M_{c}$ is the perpendicular bisector of $A D$. Hence these three lines are concurrent - denote their common point by $T$.
The quadrilateral $A O_{b} M O_{C}$ is cyclic if and only if $A T \cdot T M=O_{b} T \cdot O_{c} T$. From the cyclic $A M_{b} M M_{c}$ we have $A T \cdot T M=M_{b} T \cdot M_{c} T$. Hence it now suffices to argue $M_{b} T \cdot M_{c} T=O_{b} T \cdot O_{c} T$ - or equivalently, that $M_{b}, M_{c}, O_{b}$ and $O_{c}$ are concyclic.
We assume that $\angle A O B<90^{\circ}$ and $\angle A O C>90^{\circ}$ so that $O_{c}$ is in the interior of triangle $A O B$ and $O_{b}$ in external to the triangles $A O C$ (the other cases are analogous and if $\angle A O B=90^{\circ}$ or $\angle A O C=90^{\circ}$, then $M_{b} \equiv O_{b}$ or $M_{c} \equiv O_{c}$ and we are automatically done). We have
$$
\angle M_{c} M_{b} O_{b}=90^{\circ}+\angle A M_{b} M_{c}=90^{\circ}+\angle A C B
$$
as well as (since $O_{c} O_{b}$ is a perpendicular bisector of $A O$ and hence bisects $\angle A O_{C} O$ )
$$
\angle M_{c} O_{c} O_{b}=180^{\circ}-\angle O O_{c} O_{b}=90^{\circ}+\frac{\angle A O_{c} M_{c}}{2}
$$
$$
=90^{\circ}+\frac{\angle A O_{c} B}{4}=90^{\circ}+\frac{\angle A O B}{2}=90^{\circ}+\angle A C B
$$
and therefore $O_{b} M_{b} O_{c} M_{c}$ is cyclic, as desired.
|
{
"resource_path": "JBMO/segmented/en-official/en-jbmo_2023_final_paper_-_with_solutions_1.jsonl",
"problem_match": "## Problem 4.",
"solution_match": "## Solution."
}
|
d9061dbc-027d-580f-81da-8c05211dbb75
| 605,601
|
Let $a, b$ be two distinct real numbers and let $c$ be a positive real number such that
$$
a^{4}-2019 a=b^{4}-2019 b=c .
$$
Prove that $-\sqrt{c}<a b<0$.
|
Firstly, we see that
$$
2019(a-b)=a^{4}-b^{4}=(a-b)(a+b)\left(a^{2}+b^{2}\right)
$$
Since $a \neq b$, we get $(a+b)\left(a^{2}+b^{2}\right)=2019$, so $a+b \neq 0$. Thus
$$
\begin{aligned}
2 c & =a^{4}-2019 a+b^{4}-2019 b \\
& =a^{4}+b^{4}-2019(a+b) \\
& =a^{4}+b^{4}-(a+b)^{2}\left(a^{2}+b^{2}\right) \\
& =-2 a b\left(a^{2}+a b+b^{2}\right)
\end{aligned}
$$
Hence $a b\left(a^{2}+a b+b^{2}\right)=-c<0$. Note that
$$
a^{2}+a b+b^{2}=\frac{1}{2}\left(a^{2}+b^{2}+(a+b)^{2}\right)>0
$$
thus $a b<0$. Finally, $a^{2}+a b+b^{2}=(a+b)^{2}-a b>-a b$ (the equality does not occur since $a+b \neq 0$ ). So
$$
-c=a b\left(a^{2}+a b+b^{2}\right)<-(a b)^{2} \Longrightarrow(a b)^{2}<c \Rightarrow-\sqrt{c}<a b<\sqrt{c}
$$
Therefore, we have $-\sqrt{c}<a b<0$.
Remark. We can get $c=-a b\left(a^{2}+a b+b^{2}\right)$ in several other ways. For example using that,
$$
(a-b) c=a\left(b^{4}-2019 b\right)-b\left(a^{4}-2019 a\right)=a b\left(b^{3}-a^{3}\right)=a b(b-a)\left(a^{2}+a b+b^{2}\right)
$$
We can also divide $f(x)=x^{4}-2019 x-c$ by $(x-a)(x-b)$ and look at the constant term of the remainder.
Alternative Solution. By Descartes' Rule of Signs, the polynomial $p(x)=x^{4}-2019 x-c$ has exactly one positive root and exactly one negative root. So $a, b$ must be its two real roots. Since one of them is positive and the other is negative, then $a b<0$. Let $r \pm i s$ be the two non-real roots of $p(x)$.
By Vieta, we have
$$
\begin{gathered}
a b\left(r^{2}+s^{2}\right)=-c, \\
a+b+2 r=0 \\
a b+2 a r+2 b r+r^{2}+s^{2}=0 .
\end{gathered}
$$
Using (2) and (3), we have
$$
r^{2}+s^{2}=-2 r(a+b)-a b=(a+b)^{2}-a b \geqslant-a b
$$
If in the last inequality we actually have an equality, then $a+b=0$. Then (2) gives $r=0$ and (3) gives $s^{2}=-a b$. Thus the roots of $p(x)$ are $a,-a, i a,-i a$. This would give that $p(x)=x^{4}+a^{4}$, a contradiction.
So the inequality in (4) is strict and now from (1) we get
$$
c=-\left(r^{2}+s^{2}\right) a b>(a b)^{2}
$$
which gives that $a b>-\sqrt{c}$.
Remark. One can get that $x^{4}-2019 x-c$ has only two real roots by showing (e.g. by calculus) that it is initially decreasing and then increasing.
Also, instead of Vieta one can also proceed by factorising the polynomial as:
$$
x^{4}-2019 x-c=\left(x^{2}-(a+b) x+a b\right)\left(x^{2}+(a+b) x-\frac{c}{a b}\right) .
$$
Since the second quadratic has no real roots, its discriminant is negative which gives that $c>(a b)^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a, b$ be two distinct real numbers and let $c$ be a positive real number such that
$$
a^{4}-2019 a=b^{4}-2019 b=c .
$$
Prove that $-\sqrt{c}<a b<0$.
|
Firstly, we see that
$$
2019(a-b)=a^{4}-b^{4}=(a-b)(a+b)\left(a^{2}+b^{2}\right)
$$
Since $a \neq b$, we get $(a+b)\left(a^{2}+b^{2}\right)=2019$, so $a+b \neq 0$. Thus
$$
\begin{aligned}
2 c & =a^{4}-2019 a+b^{4}-2019 b \\
& =a^{4}+b^{4}-2019(a+b) \\
& =a^{4}+b^{4}-(a+b)^{2}\left(a^{2}+b^{2}\right) \\
& =-2 a b\left(a^{2}+a b+b^{2}\right)
\end{aligned}
$$
Hence $a b\left(a^{2}+a b+b^{2}\right)=-c<0$. Note that
$$
a^{2}+a b+b^{2}=\frac{1}{2}\left(a^{2}+b^{2}+(a+b)^{2}\right)>0
$$
thus $a b<0$. Finally, $a^{2}+a b+b^{2}=(a+b)^{2}-a b>-a b$ (the equality does not occur since $a+b \neq 0$ ). So
$$
-c=a b\left(a^{2}+a b+b^{2}\right)<-(a b)^{2} \Longrightarrow(a b)^{2}<c \Rightarrow-\sqrt{c}<a b<\sqrt{c}
$$
Therefore, we have $-\sqrt{c}<a b<0$.
Remark. We can get $c=-a b\left(a^{2}+a b+b^{2}\right)$ in several other ways. For example using that,
$$
(a-b) c=a\left(b^{4}-2019 b\right)-b\left(a^{4}-2019 a\right)=a b\left(b^{3}-a^{3}\right)=a b(b-a)\left(a^{2}+a b+b^{2}\right)
$$
We can also divide $f(x)=x^{4}-2019 x-c$ by $(x-a)(x-b)$ and look at the constant term of the remainder.
Alternative Solution. By Descartes' Rule of Signs, the polynomial $p(x)=x^{4}-2019 x-c$ has exactly one positive root and exactly one negative root. So $a, b$ must be its two real roots. Since one of them is positive and the other is negative, then $a b<0$. Let $r \pm i s$ be the two non-real roots of $p(x)$.
By Vieta, we have
$$
\begin{gathered}
a b\left(r^{2}+s^{2}\right)=-c, \\
a+b+2 r=0 \\
a b+2 a r+2 b r+r^{2}+s^{2}=0 .
\end{gathered}
$$
Using (2) and (3), we have
$$
r^{2}+s^{2}=-2 r(a+b)-a b=(a+b)^{2}-a b \geqslant-a b
$$
If in the last inequality we actually have an equality, then $a+b=0$. Then (2) gives $r=0$ and (3) gives $s^{2}=-a b$. Thus the roots of $p(x)$ are $a,-a, i a,-i a$. This would give that $p(x)=x^{4}+a^{4}$, a contradiction.
So the inequality in (4) is strict and now from (1) we get
$$
c=-\left(r^{2}+s^{2}\right) a b>(a b)^{2}
$$
which gives that $a b>-\sqrt{c}$.
Remark. One can get that $x^{4}-2019 x-c$ has only two real roots by showing (e.g. by calculus) that it is initially decreasing and then increasing.
Also, instead of Vieta one can also proceed by factorising the polynomial as:
$$
x^{4}-2019 x-c=\left(x^{2}-(a+b) x+a b\right)\left(x^{2}+(a+b) x-\frac{c}{a b}\right) .
$$
Since the second quadratic has no real roots, its discriminant is negative which gives that $c>(a b)^{2}$.
|
{
"resource_path": "JBMO/segmented/en-official/en-optimizedjbmo_2019_problems_and_solutions_english.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
965e479d-7ae5-52d9-9c66-c020b044aab7
| 605,619
|
Triangle $A B C$ is such that $A B<A C$. The perpendicular bisector of side $B C$ intersects lines $A B$ and $A C$ at points $P$ and $Q$, respectively. Let $H$ be the orthocentre of triangle $A B C$, and let $M$ and $N$ be the midpoints of segments $B C$ and $P Q$, respectively. Prove that lines $H M$ and $A N$ meet on the circumcircle of $A B C$.
|
We have
$$
\angle A P Q=\angle B P M=90^{\circ}-\angle M B P=90^{\circ}-\angle C B A=\angle H C B
$$
and
$$
\angle A Q P=\angle M Q C=90^{\circ}-\angle Q C M=90^{\circ}-\angle A C B=\angle C B H
$$
From these two equalities, we see that the triangles $A P Q$ and $H C B$ are similar. Moreover, since $M$ and $N$ are the midpoints of the segments $B C$ and $P Q$ respectively, then the triangles $A Q N$ and $H B M$ are also similar. Therefore, we have $\angle A N Q=\angle H M B$.
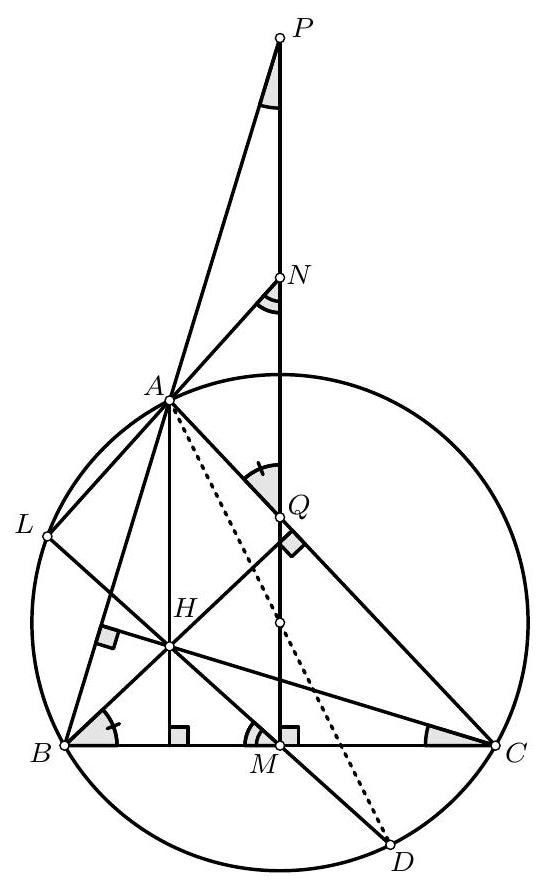
Let $L$ be the intersection of $A N$ and $H M$. We have
$$
\angle M L N=180^{\circ}-\angle L N M-\angle N M L=180^{\circ}-\angle L M B-\angle N M L=180^{\circ}-\angle N M B=90^{\circ} .
$$
Now let $D$ be the point on the circumcircle of $A B C$ diametrically oposite to $A$. It is known that $D$ is also the relfection of point $H$ over the point $M$. Therefore, we have that $D$ belongs on $M H$ and that $\angle D L A=\angle M L A=\angle M L N=90^{\circ}$. But, as $D A$ is the diameter of the circumcirle of $A B C$, the condition that $\angle D L A=90^{\circ}$ is enough to conclude that $L$ belongs on the circumcircle of $A B C$.
Remark. There is a spiral similarity mapping $A Q P$ to $H B C$. Since the similarity maps $A N$ to $H M$, it also maps $A H$ to $N M$, and since these two lines are parallel, the centre of the similarity is $L=A N \cap H M$. Since the similarity maps $B C$ to $Q P$, its centre belongs on the circumcircle of $B C X$, where $X=B Q \cap P C$. But $X$ is the reflection of $A$ on $Q M$ and so it must belong on the circumcircle of $A B C$. Hence so must $L$.
Remark. Students have also submitted correct proofs using radical axes, harmonic quadruples, coordinate geometry and complex numbers.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangle $A B C$ is such that $A B<A C$. The perpendicular bisector of side $B C$ intersects lines $A B$ and $A C$ at points $P$ and $Q$, respectively. Let $H$ be the orthocentre of triangle $A B C$, and let $M$ and $N$ be the midpoints of segments $B C$ and $P Q$, respectively. Prove that lines $H M$ and $A N$ meet on the circumcircle of $A B C$.
|
We have
$$
\angle A P Q=\angle B P M=90^{\circ}-\angle M B P=90^{\circ}-\angle C B A=\angle H C B
$$
and
$$
\angle A Q P=\angle M Q C=90^{\circ}-\angle Q C M=90^{\circ}-\angle A C B=\angle C B H
$$
From these two equalities, we see that the triangles $A P Q$ and $H C B$ are similar. Moreover, since $M$ and $N$ are the midpoints of the segments $B C$ and $P Q$ respectively, then the triangles $A Q N$ and $H B M$ are also similar. Therefore, we have $\angle A N Q=\angle H M B$.

Let $L$ be the intersection of $A N$ and $H M$. We have
$$
\angle M L N=180^{\circ}-\angle L N M-\angle N M L=180^{\circ}-\angle L M B-\angle N M L=180^{\circ}-\angle N M B=90^{\circ} .
$$
Now let $D$ be the point on the circumcircle of $A B C$ diametrically oposite to $A$. It is known that $D$ is also the relfection of point $H$ over the point $M$. Therefore, we have that $D$ belongs on $M H$ and that $\angle D L A=\angle M L A=\angle M L N=90^{\circ}$. But, as $D A$ is the diameter of the circumcirle of $A B C$, the condition that $\angle D L A=90^{\circ}$ is enough to conclude that $L$ belongs on the circumcircle of $A B C$.
Remark. There is a spiral similarity mapping $A Q P$ to $H B C$. Since the similarity maps $A N$ to $H M$, it also maps $A H$ to $N M$, and since these two lines are parallel, the centre of the similarity is $L=A N \cap H M$. Since the similarity maps $B C$ to $Q P$, its centre belongs on the circumcircle of $B C X$, where $X=B Q \cap P C$. But $X$ is the reflection of $A$ on $Q M$ and so it must belong on the circumcircle of $A B C$. Hence so must $L$.
Remark. Students have also submitted correct proofs using radical axes, harmonic quadruples, coordinate geometry and complex numbers.
|
{
"resource_path": "JBMO/segmented/en-official/en-optimizedjbmo_2019_problems_and_solutions_english.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
d92ffb9d-abb7-5027-9c6c-739b4adc6548
| 605,629
|
Let $\triangle A B C$ be an acute triangle. The lines $l_{1}, l_{2}$ are perpendicular to $A B$ at the points $A, B$ respectively. The perpendicular lines from the midpoint $M$ of $A B$ to the sides of the triangle $A C, B C$ intersect the lines $l_{1}, l_{2}$ at the points $E, F$, respectively. If $D$ is the intersection point of $E F$ and $M C$, prove that
$$
\angle A D B=\angle E M F
$$
|
Let $H, G$ be the points of intersection of $M E, M F$ with $A C, B C$ respectively. From the similarity of triangles $\triangle M H A$ and $\triangle M A E$ we get $\frac{M H}{M A}=\frac{M A}{M E}$, thus
$$
M A^{2}=M H \cdot M E
$$
Similarly, from the similarity of triangles $\triangle M B G$ and $\triangle M F B$ we get $\frac{M B}{M F}=\frac{M G}{M B}$, thus
$$
M B^{2}=M F \cdot M G
$$
Since $M A=M B$, from (1), (2), we conclude that the points $E, H, G, F$ are concyclic.
Therefore, we get that $\angle F E H=\angle F E M=\angle H G M$. Also, the quadrilateral $C H M G$ is cyclic, so $\angle C M H=\angle H G C$. We have
$$
\angle F E H+\angle C M H=\angle H G M+\angle H G C=90^{\circ}
$$
thus $C M \perp E F$. Now, from the cyclic quadrilaterals $F D M B$ and $E A M D$, we get that $\angle D F M=\angle D B M$ and $\angle D E M=\angle D A M$. Therefore, the triangles $\triangle E M F$ and $\triangle A D B$ are similar, so $\angle A D B=\angle E M F$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\triangle A B C$ be an acute triangle. The lines $l_{1}, l_{2}$ are perpendicular to $A B$ at the points $A, B$ respectively. The perpendicular lines from the midpoint $M$ of $A B$ to the sides of the triangle $A C, B C$ intersect the lines $l_{1}, l_{2}$ at the points $E, F$, respectively. If $D$ is the intersection point of $E F$ and $M C$, prove that
$$
\angle A D B=\angle E M F
$$
|
Let $H, G$ be the points of intersection of $M E, M F$ with $A C, B C$ respectively. From the similarity of triangles $\triangle M H A$ and $\triangle M A E$ we get $\frac{M H}{M A}=\frac{M A}{M E}$, thus
$$
M A^{2}=M H \cdot M E
$$
Similarly, from the similarity of triangles $\triangle M B G$ and $\triangle M F B$ we get $\frac{M B}{M F}=\frac{M G}{M B}$, thus
$$
M B^{2}=M F \cdot M G
$$
Since $M A=M B$, from (1), (2), we conclude that the points $E, H, G, F$ are concyclic.

Therefore, we get that $\angle F E H=\angle F E M=\angle H G M$. Also, the quadrilateral $C H M G$ is cyclic, so $\angle C M H=\angle H G C$. We have
$$
\angle F E H+\angle C M H=\angle H G M+\angle H G C=90^{\circ}
$$
thus $C M \perp E F$. Now, from the cyclic quadrilaterals $F D M B$ and $E A M D$, we get that $\angle D F M=\angle D B M$ and $\angle D E M=\angle D A M$. Therefore, the triangles $\triangle E M F$ and $\triangle A D B$ are similar, so $\angle A D B=\angle E M F$.
|
{
"resource_path": "JBMO/segmented/en-official/en-solutions-english-jbmo2015.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "## Solution:"
}
|
3d2fbc4b-d597-56ec-886d-8fd69d653a92
| 605,680
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq 3(a+b+c+1)
$$
When does equality hold?
|
Solution 2. From QM-AM we obtain
$$
\begin{gathered}
\sqrt{\frac{\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2}}{3}} \geq \frac{a+\frac{1}{b}+b+\frac{1}{c}+c+\frac{1}{a}}{3} \Leftrightarrow \\
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2}
\end{gathered} \Leftrightarrow \frac{\left(a+\frac{1}{b}+b+\frac{1}{c}+c+\frac{1}{a}\right)^{2}}{3}(1)
$$
From AM-GM we have $\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geq 3 \sqrt[3]{\frac{1}{a b c}}=3$, and substituting in (1) we get
$$
\begin{aligned}
& \left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq \frac{\left(a+\frac{1}{b}+b+\frac{1}{c}+c+\frac{1}{a}\right)^{2}}{3} \geq \frac{(a+b+c+3)^{2}}{3}= \\
& =\frac{(a+b+c)(a+b+c)+6(a+b+c)+9}{3} \geq \frac{(a+b+c) 3 \sqrt[3]{a b c}+6(a+b+c)+9}{3}= \\
& =\frac{9(a+b+c)+9}{3}=3(a+b+c+1) .
\end{aligned}
$$
The equality holds if and only if $a=b=c=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq 3(a+b+c+1)
$$
When does equality hold?
|
Solution 2. From QM-AM we obtain
$$
\begin{gathered}
\sqrt{\frac{\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2}}{3}} \geq \frac{a+\frac{1}{b}+b+\frac{1}{c}+c+\frac{1}{a}}{3} \Leftrightarrow \\
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2}
\end{gathered} \Leftrightarrow \frac{\left(a+\frac{1}{b}+b+\frac{1}{c}+c+\frac{1}{a}\right)^{2}}{3}(1)
$$
From AM-GM we have $\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geq 3 \sqrt[3]{\frac{1}{a b c}}=3$, and substituting in (1) we get
$$
\begin{aligned}
& \left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq \frac{\left(a+\frac{1}{b}+b+\frac{1}{c}+c+\frac{1}{a}\right)^{2}}{3} \geq \frac{(a+b+c+3)^{2}}{3}= \\
& =\frac{(a+b+c)(a+b+c)+6(a+b+c)+9}{3} \geq \frac{(a+b+c) 3 \sqrt[3]{a b c}+6(a+b+c)+9}{3}= \\
& =\frac{9(a+b+c)+9}{3}=3(a+b+c+1) .
\end{aligned}
$$
The equality holds if and only if $a=b=c=1$.
|
{
"resource_path": "JBMO/segmented/en-official/en-solutions_en-jbmo2014.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution "
}
|
14c80bca-0c2f-522a-b02c-b07e38894a67
| 605,720
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq 3(a+b+c+1)
$$
When does equality hold?
|
## Solution 3.
By using $x^{2}+y^{2}+z^{2} \geq x y+y z+z x$
$$
\begin{aligned}
& \left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2}=a^{2}+b^{2}+c^{2}+\frac{1}{b^{2}}+\frac{1}{c^{2}}+\frac{1}{a^{2}}+\frac{2 a}{b}+\frac{2 b}{c}+\frac{2 c}{a} \geq \\
& \geq a b+a c+b c+\frac{1}{b c}+\frac{1}{c a}+\frac{1}{a b}+\frac{2 a}{b}+\frac{2 b}{c}+\frac{2 c}{a}
\end{aligned}
$$
Clearly
$$
\begin{gathered}
\frac{1}{b c}+\frac{1}{c a}+\frac{1}{a b}=\frac{a b c}{b c}+\frac{a b c}{c a}+\frac{a b c}{a b}=a+b+c \\
a b+\frac{a}{b}+b c+\frac{b}{c}+c a+\frac{c}{a} \geq 2 a+2 b+2 c \\
\frac{a}{b}+\frac{b}{c}+\frac{c}{a} \geq 3 \sqrt[3]{\frac{a}{b} \cdot \frac{b}{c} \cdot \frac{c}{a}}=3
\end{gathered}
$$
Hence
$$
\begin{aligned}
& \left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq\left(a b+\frac{a}{b}\right)+\left(a c+\frac{c}{a}\right)+\left(b c+\frac{b}{c}\right)+a+b+c+\frac{a}{b}+\frac{b}{c}+\frac{c}{a} \geq \\
& \geq 2 a+2 b+2 c+a+b+c+3=3(a+b+c+1)
\end{aligned}
$$
The equality holds if and only if $a=b=c=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq 3(a+b+c+1)
$$
When does equality hold?
|
## Solution 3.
By using $x^{2}+y^{2}+z^{2} \geq x y+y z+z x$
$$
\begin{aligned}
& \left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2}=a^{2}+b^{2}+c^{2}+\frac{1}{b^{2}}+\frac{1}{c^{2}}+\frac{1}{a^{2}}+\frac{2 a}{b}+\frac{2 b}{c}+\frac{2 c}{a} \geq \\
& \geq a b+a c+b c+\frac{1}{b c}+\frac{1}{c a}+\frac{1}{a b}+\frac{2 a}{b}+\frac{2 b}{c}+\frac{2 c}{a}
\end{aligned}
$$
Clearly
$$
\begin{gathered}
\frac{1}{b c}+\frac{1}{c a}+\frac{1}{a b}=\frac{a b c}{b c}+\frac{a b c}{c a}+\frac{a b c}{a b}=a+b+c \\
a b+\frac{a}{b}+b c+\frac{b}{c}+c a+\frac{c}{a} \geq 2 a+2 b+2 c \\
\frac{a}{b}+\frac{b}{c}+\frac{c}{a} \geq 3 \sqrt[3]{\frac{a}{b} \cdot \frac{b}{c} \cdot \frac{c}{a}}=3
\end{gathered}
$$
Hence
$$
\begin{aligned}
& \left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq\left(a b+\frac{a}{b}\right)+\left(a c+\frac{c}{a}\right)+\left(b c+\frac{b}{c}\right)+a+b+c+\frac{a}{b}+\frac{b}{c}+\frac{c}{a} \geq \\
& \geq 2 a+2 b+2 c+a+b+c+3=3(a+b+c+1)
\end{aligned}
$$
The equality holds if and only if $a=b=c=1$.
|
{
"resource_path": "JBMO/segmented/en-official/en-solutions_en-jbmo2014.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution "
}
|
14c80bca-0c2f-522a-b02c-b07e38894a67
| 605,720
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq 3(a+b+c+1)
$$
When does equality hold?
|
Solution 4. $a=\frac{x}{y}, b=\frac{y}{z}, c=\frac{z}{x}$
$$
\begin{aligned}
& \left(\frac{x}{y}+\frac{z}{y}\right)^{2}+\left(\frac{y}{z}+\frac{x}{z}\right)^{2}+\left(\frac{z}{x}+\frac{y}{x}\right)^{2} \geq 3\left(\frac{x}{y}+\frac{y}{z}+\frac{z}{x}+1\right) \\
& (x+z)^{2} x^{2} z^{2}+(y+x)^{2} y^{2} x^{2}+(z+y)^{2} z^{2} y^{2} \geq 3 x y z\left(x^{2} z+y^{2} x+z^{2} y+x y z\right) \\
& x^{4} z^{2}+2 x^{3} z^{3}+x^{2} z^{4}+x^{2} y^{4}+2 x^{3} y^{3}+x^{4} y^{2}+y^{2} z^{4}+2 y^{3} z^{3}+y^{4} z^{2} \geq 3 x^{3} y z^{2}+3 x^{2} y^{3} z+3 x y^{2} z^{3}+3 x^{2} y^{2} z^{2} \\
& \text { 1) } x^{3} y^{3}+y^{3} z^{3}+z^{3} x^{3} \geq 3 x^{2} y^{2} z^{2} \\
& \text { 2) } x^{4} z^{2}+z^{4} x^{2}+x^{3} y^{3} \geq 3 x^{3} z^{2} y \\
& \text { 3) } x^{4} y^{2}+y^{4} x^{2}+y^{3} z^{3} \geq 3 y^{3} x^{2} z \\
& \text { 4) } z^{4} y^{2}+y^{4} z^{2}+x^{3} z^{3} \geq 3 z^{3} y^{2} x
\end{aligned}
$$
Equality holds when $x=y=z$, i.e., $a=b=c=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq 3(a+b+c+1)
$$
When does equality hold?
|
Solution 4. $a=\frac{x}{y}, b=\frac{y}{z}, c=\frac{z}{x}$
$$
\begin{aligned}
& \left(\frac{x}{y}+\frac{z}{y}\right)^{2}+\left(\frac{y}{z}+\frac{x}{z}\right)^{2}+\left(\frac{z}{x}+\frac{y}{x}\right)^{2} \geq 3\left(\frac{x}{y}+\frac{y}{z}+\frac{z}{x}+1\right) \\
& (x+z)^{2} x^{2} z^{2}+(y+x)^{2} y^{2} x^{2}+(z+y)^{2} z^{2} y^{2} \geq 3 x y z\left(x^{2} z+y^{2} x+z^{2} y+x y z\right) \\
& x^{4} z^{2}+2 x^{3} z^{3}+x^{2} z^{4}+x^{2} y^{4}+2 x^{3} y^{3}+x^{4} y^{2}+y^{2} z^{4}+2 y^{3} z^{3}+y^{4} z^{2} \geq 3 x^{3} y z^{2}+3 x^{2} y^{3} z+3 x y^{2} z^{3}+3 x^{2} y^{2} z^{2} \\
& \text { 1) } x^{3} y^{3}+y^{3} z^{3}+z^{3} x^{3} \geq 3 x^{2} y^{2} z^{2} \\
& \text { 2) } x^{4} z^{2}+z^{4} x^{2}+x^{3} y^{3} \geq 3 x^{3} z^{2} y \\
& \text { 3) } x^{4} y^{2}+y^{4} x^{2}+y^{3} z^{3} \geq 3 y^{3} x^{2} z \\
& \text { 4) } z^{4} y^{2}+y^{4} z^{2}+x^{3} z^{3} \geq 3 z^{3} y^{2} x
\end{aligned}
$$
Equality holds when $x=y=z$, i.e., $a=b=c=1$.
|
{
"resource_path": "JBMO/segmented/en-official/en-solutions_en-jbmo2014.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution "
}
|
14c80bca-0c2f-522a-b02c-b07e38894a67
| 605,720
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq 3(a+b+c+1)
$$
When does equality hold?
|
Solution 5. $\sum_{\text {cyc }}\left(a+\frac{1}{b}\right)^{2} \geq 3 \sum_{c y c} a+3$
$$
\begin{aligned}
& \Leftrightarrow 2 \sum_{\text {cyc }} \frac{a}{b}+\sum_{\text {cyc }}\left(a^{2}+\frac{1}{a^{2}}-3 a-1\right) \geq 0 \\
& 2 \sum_{\text {cyc }} \frac{a}{b} \geq 6 \sqrt[3]{\frac{a}{b} \frac{b}{c} \frac{c}{a}}=6
\end{aligned}
$$
$$
\begin{aligned}
& \forall a>0, a^{2}+\frac{1}{a^{2}}-3 a \geq \frac{3}{a}-4 \\
& \Leftrightarrow a^{4}-3 a^{3}+4 a^{2}-3 a+1 \geq 0 \\
& \Leftrightarrow(a-1)^{2}\left(a^{2}-a+1\right) \geq 0 \\
& \sum_{\text {cyc }}\left(a^{2}+\frac{1}{a^{2}}-3 a-1\right) \geq 3 \sum_{\text {cyc }} \frac{1}{a}-15 \geq 9 \sqrt[3]{\frac{1}{a b c}}-15=-6
\end{aligned}
$$
Using (1) and (2) we obtain
$2 \sum_{\text {cyc }} \frac{a}{b}+\sum\left(a^{2}+\frac{1}{a^{2}}-3 a-1\right) \geq 6-6=0$
Equality holds when $a=b=c=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq 3(a+b+c+1)
$$
When does equality hold?
|
Solution 5. $\sum_{\text {cyc }}\left(a+\frac{1}{b}\right)^{2} \geq 3 \sum_{c y c} a+3$
$$
\begin{aligned}
& \Leftrightarrow 2 \sum_{\text {cyc }} \frac{a}{b}+\sum_{\text {cyc }}\left(a^{2}+\frac{1}{a^{2}}-3 a-1\right) \geq 0 \\
& 2 \sum_{\text {cyc }} \frac{a}{b} \geq 6 \sqrt[3]{\frac{a}{b} \frac{b}{c} \frac{c}{a}}=6
\end{aligned}
$$
$$
\begin{aligned}
& \forall a>0, a^{2}+\frac{1}{a^{2}}-3 a \geq \frac{3}{a}-4 \\
& \Leftrightarrow a^{4}-3 a^{3}+4 a^{2}-3 a+1 \geq 0 \\
& \Leftrightarrow(a-1)^{2}\left(a^{2}-a+1\right) \geq 0 \\
& \sum_{\text {cyc }}\left(a^{2}+\frac{1}{a^{2}}-3 a-1\right) \geq 3 \sum_{\text {cyc }} \frac{1}{a}-15 \geq 9 \sqrt[3]{\frac{1}{a b c}}-15=-6
\end{aligned}
$$
Using (1) and (2) we obtain
$2 \sum_{\text {cyc }} \frac{a}{b}+\sum\left(a^{2}+\frac{1}{a^{2}}-3 a-1\right) \geq 6-6=0$
Equality holds when $a=b=c=1$.
|
{
"resource_path": "JBMO/segmented/en-official/en-solutions_en-jbmo2014.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution "
}
|
14c80bca-0c2f-522a-b02c-b07e38894a67
| 605,720
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that:
$\left(a^{5}+a^{4}+a^{3}+a^{2}+a+1\right)\left(b^{5}+b^{4}+b^{3}+b^{2}+b+1\right)\left(c^{5}+c^{4}+c^{3}+c^{2}+c+1\right) \geq 8\left(a^{2}+a+1\right)\left(b^{2}+b+1\right)\left(c^{2}+c+1\right)$.
|
We have $x^{5}+x^{4}+x^{3}+x^{2}+x+1=\left(x^{3}+1\right)\left(x^{2}+x+1\right)$ for all $x \in \mathbb{R}_{+}$.
Take $S=\left(a^{2}+a+1\right)\left(b^{2}+b+1\right)\left(c^{2}+c+1\right)$.
The inequality becomes $S\left(a^{3}+1\right)\left(b^{3}+1\right)\left(c^{3}+1\right) \geq 8 S$.
It remains to prove that $\left(a^{3}+1\right)\left(b^{3}+1\right)\left(c^{3}+1\right) \geq 8$.
By $A M-G M$ we have $x^{3}+1 \geq 2 \sqrt{x^{3}}$ for all $x \in \mathbb{R}_{+}$.
So $\left(a^{3}+1\right)\left(b^{3}+1\right)\left(c^{3}+1\right) \geq 2^{3} \cdot \sqrt{a^{3} b^{3} c^{3}}=8$ and we are done.
Equality holds when $a=b=c=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that:
$\left(a^{5}+a^{4}+a^{3}+a^{2}+a+1\right)\left(b^{5}+b^{4}+b^{3}+b^{2}+b+1\right)\left(c^{5}+c^{4}+c^{3}+c^{2}+c+1\right) \geq 8\left(a^{2}+a+1\right)\left(b^{2}+b+1\right)\left(c^{2}+c+1\right)$.
|
We have $x^{5}+x^{4}+x^{3}+x^{2}+x+1=\left(x^{3}+1\right)\left(x^{2}+x+1\right)$ for all $x \in \mathbb{R}_{+}$.
Take $S=\left(a^{2}+a+1\right)\left(b^{2}+b+1\right)\left(c^{2}+c+1\right)$.
The inequality becomes $S\left(a^{3}+1\right)\left(b^{3}+1\right)\left(c^{3}+1\right) \geq 8 S$.
It remains to prove that $\left(a^{3}+1\right)\left(b^{3}+1\right)\left(c^{3}+1\right) \geq 8$.
By $A M-G M$ we have $x^{3}+1 \geq 2 \sqrt{x^{3}}$ for all $x \in \mathbb{R}_{+}$.
So $\left(a^{3}+1\right)\left(b^{3}+1\right)\left(c^{3}+1\right) \geq 2^{3} \cdot \sqrt{a^{3} b^{3} c^{3}}=8$ and we are done.
Equality holds when $a=b=c=1$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-alg-20111.jsonl",
"problem_match": "\nA1 ",
"solution_match": "## Solution"
}
|
6d555ac2-a240-5c11-a571-f2d9fe41e499
| 605,765
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.