problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Show that for any positive real numbers $a, b, c$ such that $a+b+c=a b+b c+c a$, the following inequality holds
$$
3+\sqrt[3]{\frac{a^{3}+1}{2}}+\sqrt[3]{\frac{b^{3}+1}{2}}+\sqrt[3]{\frac{c^{3}+1}{2}} \leqslant 2(a+b+c)
$$
|
Using the condition we have
$$
a^{2}-a+1=a^{2}-a+1+a b+b c+c a-a-b-c=(c+a-1)(a+b-1)
$$
Hence we have
$$
\sqrt[3]{\frac{a^{3}+1}{2}}=\sqrt[3]{\frac{(a+1)\left(a^{2}-a+1\right)}{2}}=\sqrt[3]{\left(\frac{a+1}{2}\right)(c+a-1)(a+b-1)}
$$
Using the last equality together with the AM-GM Inequality, we have
$$
\begin{aligned}
\sum_{\mathrm{cyc}} \sqrt[3]{\frac{a^{3}+1}{2}} & =\sum_{\mathrm{cyc}} \sqrt[3]{\left(\frac{a+1}{2}\right)(c+a-1)(a+b-1)} \\
& \leqslant \sum_{\mathrm{cyc}} \frac{\frac{a+1}{2}+c+a-1+a+b-1}{3} \\
& =\sum_{c y c} \frac{5 a+2 b+2 c-3}{6} \\
& =\frac{3(a+b+c-1)}{2}
\end{aligned}
$$
Hence it is enough to prove that
$$
3+\frac{3(a+b+c-1)}{2} \leqslant 2(a+b+c)
$$
or equivalently, that $a+b+c \geqslant 3$. From a well- known inequality and the condition, we have
$$
(a+b+c)^{2} \geqslant 3(a b+b c+c a)=3(a+b+c)
$$
thus $a+b+c \geqslant 3$ as desired.
Alternative Proof by PSC. Since $f(x)=\sqrt[3]{x}$ is concave for $x \geqslant 0$, by Jensen's Inequality we have
$$
\sqrt[3]{\frac{a^{3}+1}{2}}+\sqrt[3]{\frac{b^{3}+1}{2}}+\sqrt[3]{\frac{c^{3}+1}{2}} \leqslant 3 \sqrt[3]{\frac{a^{3}+b^{3}+c^{3}+3}{6}}
$$
So it is enough to prove that
$$
\sqrt[3]{\frac{a^{3}+b^{3}+c^{3}+3}{6}} \leqslant \frac{2(a+b+c)-3}{3}
$$
We now write $s=a+b+c=a b+b c+c a$ and $p=a b c$. We have
$$
a^{2}+b^{2}+c^{2}=(a+b+c)^{2}-2(a b+b c+c a)=s^{2}-2 s
$$
and
$$
r=a^{2} b+a b^{2}+b^{2} c+b c^{2}+c^{2} a+c a^{2}=(a b+b c+c a)(a+b+c)-3 a b c=s^{2}-3 p
$$
Thus,
$$
a^{3}+b^{3}+c^{3}=(a+b+c)^{3}-3 r-6 a b c=s^{3}-3 s^{2}+3 p
$$
So to prove (1), it is enough to show that
$$
\frac{s^{3}-3 s^{2}+3 p+3}{6} \leqslant \frac{(2 s-3)^{3}}{27}
$$
Expanding, this is equivalent to
$$
7 s^{3}-45 s^{2}+108 s-27 p-81 \geqslant 0
$$
By the AM-GM Inequality we have $s^{3} \geqslant 27 p$. So it is enough to prove that $p(s) \geqslant 0$, where
$$
p(s)=6 s^{3}-45 s^{2}+108 s-81=3(s-3)^{2}(2 s-3)
$$
It is easy to show that $s \geqslant 3$ (e.g. as in the first solution) so $p(s) \geqslant 0$ as required.
## COMBINATORICS
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Show that for any positive real numbers $a, b, c$ such that $a+b+c=a b+b c+c a$, the following inequality holds
$$
3+\sqrt[3]{\frac{a^{3}+1}{2}}+\sqrt[3]{\frac{b^{3}+1}{2}}+\sqrt[3]{\frac{c^{3}+1}{2}} \leqslant 2(a+b+c)
$$
|
Using the condition we have
$$
a^{2}-a+1=a^{2}-a+1+a b+b c+c a-a-b-c=(c+a-1)(a+b-1)
$$
Hence we have
$$
\sqrt[3]{\frac{a^{3}+1}{2}}=\sqrt[3]{\frac{(a+1)\left(a^{2}-a+1\right)}{2}}=\sqrt[3]{\left(\frac{a+1}{2}\right)(c+a-1)(a+b-1)}
$$
Using the last equality together with the AM-GM Inequality, we have
$$
\begin{aligned}
\sum_{\mathrm{cyc}} \sqrt[3]{\frac{a^{3}+1}{2}} & =\sum_{\mathrm{cyc}} \sqrt[3]{\left(\frac{a+1}{2}\right)(c+a-1)(a+b-1)} \\
& \leqslant \sum_{\mathrm{cyc}} \frac{\frac{a+1}{2}+c+a-1+a+b-1}{3} \\
& =\sum_{c y c} \frac{5 a+2 b+2 c-3}{6} \\
& =\frac{3(a+b+c-1)}{2}
\end{aligned}
$$
Hence it is enough to prove that
$$
3+\frac{3(a+b+c-1)}{2} \leqslant 2(a+b+c)
$$
or equivalently, that $a+b+c \geqslant 3$. From a well- known inequality and the condition, we have
$$
(a+b+c)^{2} \geqslant 3(a b+b c+c a)=3(a+b+c)
$$
thus $a+b+c \geqslant 3$ as desired.
Alternative Proof by PSC. Since $f(x)=\sqrt[3]{x}$ is concave for $x \geqslant 0$, by Jensen's Inequality we have
$$
\sqrt[3]{\frac{a^{3}+1}{2}}+\sqrt[3]{\frac{b^{3}+1}{2}}+\sqrt[3]{\frac{c^{3}+1}{2}} \leqslant 3 \sqrt[3]{\frac{a^{3}+b^{3}+c^{3}+3}{6}}
$$
So it is enough to prove that
$$
\sqrt[3]{\frac{a^{3}+b^{3}+c^{3}+3}{6}} \leqslant \frac{2(a+b+c)-3}{3}
$$
We now write $s=a+b+c=a b+b c+c a$ and $p=a b c$. We have
$$
a^{2}+b^{2}+c^{2}=(a+b+c)^{2}-2(a b+b c+c a)=s^{2}-2 s
$$
and
$$
r=a^{2} b+a b^{2}+b^{2} c+b c^{2}+c^{2} a+c a^{2}=(a b+b c+c a)(a+b+c)-3 a b c=s^{2}-3 p
$$
Thus,
$$
a^{3}+b^{3}+c^{3}=(a+b+c)^{3}-3 r-6 a b c=s^{3}-3 s^{2}+3 p
$$
So to prove (1), it is enough to show that
$$
\frac{s^{3}-3 s^{2}+3 p+3}{6} \leqslant \frac{(2 s-3)^{3}}{27}
$$
Expanding, this is equivalent to
$$
7 s^{3}-45 s^{2}+108 s-27 p-81 \geqslant 0
$$
By the AM-GM Inequality we have $s^{3} \geqslant 27 p$. So it is enough to prove that $p(s) \geqslant 0$, where
$$
p(s)=6 s^{3}-45 s^{2}+108 s-81=3(s-3)^{2}(2 s-3)
$$
It is easy to show that $s \geqslant 3$ (e.g. as in the first solution) so $p(s) \geqslant 0$ as required.
## COMBINATORICS
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nA7.",
"solution_match": "\nSolution."
}
|
ab4fbe61-8b5e-5c94-8d3f-a8ad26729916
| 605,998
|
Let $S$ be a set of 100 positive integers having the following property:
"Among every four numbers of $S$, there is a number which divides each of the other three or there is a number which is equal to the sum of the other three."
Prove that the set $S$ contains a number which divides each of the other 99 numbers of $S$.
|
Alternative Solution by PSC. Order the elements of $S$ as $x_{1}<x_{2}<\cdots<x_{100}$.
For $2 \leqslant k \leqslant 97$, looking at the quadruples $\left(x_{1}, x_{k}, x_{k+1}, x_{k+2}\right)$ and $\left(x_{1}, x_{k}, x_{k+1}, x_{k+3}\right)$, we get that $x_{1} \mid x_{k}$ as alternatively, we would have $x_{k+2}=x_{1}+x_{k}+x_{k+1}=x_{k+3}$, a contradiction.
For $5 \leqslant k \leqslant 100$, looking at the quadruples $\left(x_{1}, x_{k-2}, x_{k-1}, x_{k}\right)$ and $\left(x_{1}, x_{k-3}, x_{k-1}, x_{k}\right)$ we get that $x_{1} \mid x_{k}$ as alternatively, we would have $x_{k}=x_{1}+x_{k-2}+x_{k-1}=x_{1}+x_{k-3}+x_{k-1}$, a contradiction.
So $x_{1}$ divides all other elements of $S$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $S$ be a set of 100 positive integers having the following property:
"Among every four numbers of $S$, there is a number which divides each of the other three or there is a number which is equal to the sum of the other three."
Prove that the set $S$ contains a number which divides each of the other 99 numbers of $S$.
|
Alternative Solution by PSC. Order the elements of $S$ as $x_{1}<x_{2}<\cdots<x_{100}$.
For $2 \leqslant k \leqslant 97$, looking at the quadruples $\left(x_{1}, x_{k}, x_{k+1}, x_{k+2}\right)$ and $\left(x_{1}, x_{k}, x_{k+1}, x_{k+3}\right)$, we get that $x_{1} \mid x_{k}$ as alternatively, we would have $x_{k+2}=x_{1}+x_{k}+x_{k+1}=x_{k+3}$, a contradiction.
For $5 \leqslant k \leqslant 100$, looking at the quadruples $\left(x_{1}, x_{k-2}, x_{k-1}, x_{k}\right)$ and $\left(x_{1}, x_{k-3}, x_{k-1}, x_{k}\right)$ we get that $x_{1} \mid x_{k}$ as alternatively, we would have $x_{k}=x_{1}+x_{k-2}+x_{k-1}=x_{1}+x_{k-3}+x_{k-1}$, a contradiction.
So $x_{1}$ divides all other elements of $S$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nC1.",
"solution_match": "\nSolution."
}
|
c728280c-e222-543c-ada1-42ad3d97e3a6
| 606,005
|
Let $S$ be a set of 100 positive integers having the following property:
"Among every four numbers of $S$, there is a number which divides each of the other three or there is a number which is equal to the sum of the other three."
Prove that the set $S$ contains a number which divides each of the other 99 numbers of $S$.
|
Alternative Solution by PSC. The condition that one element is the sum of the other three cannot be satisfied by all quadruples. So we have four elements such that one divides the other three. Suppose inductively that we have a subset $S^{\prime}$ of $S$ with $\left|S^{\prime}\right|=k \geqslant 4$ such that there is $x \in S^{\prime}$ with $x \mid y$ for every $y \in S^{\prime}$. Pick $s \in S \backslash S^{\prime}$ and $y, z \in S^{\prime}$ different from $x$. Considering $(s, x, y, z)$ either $s \mid x$, or $x \mid s$ or one of the four is a sum of the other three. In the last case we have $s= \pm x \pm y \pm z$ and so $x \mid s$. In any case either $x$ or $s$ divides all elements of $S^{\prime} \cup\{s\}$.
Remark by PSC. The last solution shows that the condition that the elements of $S$ are positive can be ignored.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $S$ be a set of 100 positive integers having the following property:
"Among every four numbers of $S$, there is a number which divides each of the other three or there is a number which is equal to the sum of the other three."
Prove that the set $S$ contains a number which divides each of the other 99 numbers of $S$.
|
Alternative Solution by PSC. The condition that one element is the sum of the other three cannot be satisfied by all quadruples. So we have four elements such that one divides the other three. Suppose inductively that we have a subset $S^{\prime}$ of $S$ with $\left|S^{\prime}\right|=k \geqslant 4$ such that there is $x \in S^{\prime}$ with $x \mid y$ for every $y \in S^{\prime}$. Pick $s \in S \backslash S^{\prime}$ and $y, z \in S^{\prime}$ different from $x$. Considering $(s, x, y, z)$ either $s \mid x$, or $x \mid s$ or one of the four is a sum of the other three. In the last case we have $s= \pm x \pm y \pm z$ and so $x \mid s$. In any case either $x$ or $s$ divides all elements of $S^{\prime} \cup\{s\}$.
Remark by PSC. The last solution shows that the condition that the elements of $S$ are positive can be ignored.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nC1.",
"solution_match": "\nSolution."
}
|
c728280c-e222-543c-ada1-42ad3d97e3a6
| 606,005
|
In a certain city there are $n$ straight streets, such that every two streets intersect, and no three streets pass through the same intersection. The City Council wants to organize the city by designating the main and the side street on every intersection. Prove that this can be done in such way that if one goes along one of the streets, from its beginning to its end, the intersections where this street is the main street, and the ones where it is not, will apear in alternating order.
|
Pick any street $s$ and organize the intersections along $s$ such that the intersections of the two types alternate, as in the statement of the problem.
On every other street $s_{1}$, exactly one intersection has been organized, namely the one where $s_{1}$ intersects $s$. Call this intersection $I_{1}$. We want to organize the intersections along $s_{1}$ such that they alternate between the two types. Note that, as $I_{1}$ is already organized, we have exactly one way to organize the remaining intersections along $s_{1}$.
For every street $s_{1} \neq s$, we can apply the procedure described above. Now, we only need to show that every intersection not on $s$ is well-organized. More precisely, this means that for every two streets $s_{1}, s_{2} \neq s$ intersecting at $s_{1} \cap s_{2}=A, s_{1}$ is the main street on $A$ if and only if $s_{2}$ is the side street on $A$.
Consider also the intersections $I_{1}=s_{1} \cap s$ and $I_{2}=s_{2} \cap s$. Now, we will define the "role" of the street $t$ at the intersection $X$ as "main" if this street $t$ is the main street on $X$, and "side" otherwise. We will prove that the roles of $s_{1}$ and $s_{2}$ at $A$ are different.
Consider the path $A \rightarrow I_{1} \rightarrow I_{2} \rightarrow A$. Let the number of intersections between $A$ and $I_{1}$ be $u_{1}$, the number of these between $A$ and $I_{2}$ be $u_{2}$, and the number of these between $I_{1}$ and $I_{2}$ be $v$. Now, if we go from $A$ to $I_{1}$, we will change our role $u_{1}+1$ times, as we will encounter $u_{1}+1$ new intersections. Then, we will change our street from $s_{1}$ to $s$, changing our role once more. Then, on the segment $I_{1} \rightarrow I_{2}$, we have $v+1$ new role changes, and after that one more when we change our street from $s_{1}$ to $s_{2}$. The journey from $I_{2}$ to $A$ will induce $u_{2}+1$ new role changes, so in total we have changed our role $u_{1}+1+1+v+1+1+u_{2}+1=u_{1}+v+u_{2}+5$, As we try to show that roles of $s_{1}$ and $s_{2}$ differ, we need to show that the number of role changes is odd, i.e. that $u_{1}+v+u_{2}+5$ is odd.
Obviously, this claim is equivalent to $2 \mid u_{1}+v+u_{2}$. But $u_{1}, v$ and $u_{2}$ count the number of intersections of the triangle $A I_{1} I_{2}$ with streets other than $s, s_{1}, s_{2}$. Since every street other than $s, s_{1}, s_{2}$ intersects the sides of $A I_{1} I_{2}$ in exactly two points, the total number of intersections is even. As a consequence, $2 \mid u_{1}+v+u_{2}$ as required.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In a certain city there are $n$ straight streets, such that every two streets intersect, and no three streets pass through the same intersection. The City Council wants to organize the city by designating the main and the side street on every intersection. Prove that this can be done in such way that if one goes along one of the streets, from its beginning to its end, the intersections where this street is the main street, and the ones where it is not, will apear in alternating order.
|
Pick any street $s$ and organize the intersections along $s$ such that the intersections of the two types alternate, as in the statement of the problem.
On every other street $s_{1}$, exactly one intersection has been organized, namely the one where $s_{1}$ intersects $s$. Call this intersection $I_{1}$. We want to organize the intersections along $s_{1}$ such that they alternate between the two types. Note that, as $I_{1}$ is already organized, we have exactly one way to organize the remaining intersections along $s_{1}$.
For every street $s_{1} \neq s$, we can apply the procedure described above. Now, we only need to show that every intersection not on $s$ is well-organized. More precisely, this means that for every two streets $s_{1}, s_{2} \neq s$ intersecting at $s_{1} \cap s_{2}=A, s_{1}$ is the main street on $A$ if and only if $s_{2}$ is the side street on $A$.
Consider also the intersections $I_{1}=s_{1} \cap s$ and $I_{2}=s_{2} \cap s$. Now, we will define the "role" of the street $t$ at the intersection $X$ as "main" if this street $t$ is the main street on $X$, and "side" otherwise. We will prove that the roles of $s_{1}$ and $s_{2}$ at $A$ are different.
Consider the path $A \rightarrow I_{1} \rightarrow I_{2} \rightarrow A$. Let the number of intersections between $A$ and $I_{1}$ be $u_{1}$, the number of these between $A$ and $I_{2}$ be $u_{2}$, and the number of these between $I_{1}$ and $I_{2}$ be $v$. Now, if we go from $A$ to $I_{1}$, we will change our role $u_{1}+1$ times, as we will encounter $u_{1}+1$ new intersections. Then, we will change our street from $s_{1}$ to $s$, changing our role once more. Then, on the segment $I_{1} \rightarrow I_{2}$, we have $v+1$ new role changes, and after that one more when we change our street from $s_{1}$ to $s_{2}$. The journey from $I_{2}$ to $A$ will induce $u_{2}+1$ new role changes, so in total we have changed our role $u_{1}+1+1+v+1+1+u_{2}+1=u_{1}+v+u_{2}+5$, As we try to show that roles of $s_{1}$ and $s_{2}$ differ, we need to show that the number of role changes is odd, i.e. that $u_{1}+v+u_{2}+5$ is odd.
Obviously, this claim is equivalent to $2 \mid u_{1}+v+u_{2}$. But $u_{1}, v$ and $u_{2}$ count the number of intersections of the triangle $A I_{1} I_{2}$ with streets other than $s, s_{1}, s_{2}$. Since every street other than $s, s_{1}, s_{2}$ intersects the sides of $A I_{1} I_{2}$ in exactly two points, the total number of intersections is even. As a consequence, $2 \mid u_{1}+v+u_{2}$ as required.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nC2.",
"solution_match": "\nSolution."
}
|
12f38ff0-6ae5-5030-a039-fe70d1c05ff4
| 606,019
|
Let $A B C$ be a right-angled triangle with $\hat{A}=90^{\circ}$ and $\hat{B}=30^{\circ}$. The perpendicular at the midpoint $M$ of $B C$ meets the bisector $B K$ of the angle $\hat{B}$ at the point $E$. The perpendicular bisector of $E K$ meets $A B$ at $D$. Prove that $K D$ is perpendicular to $D E$.
|
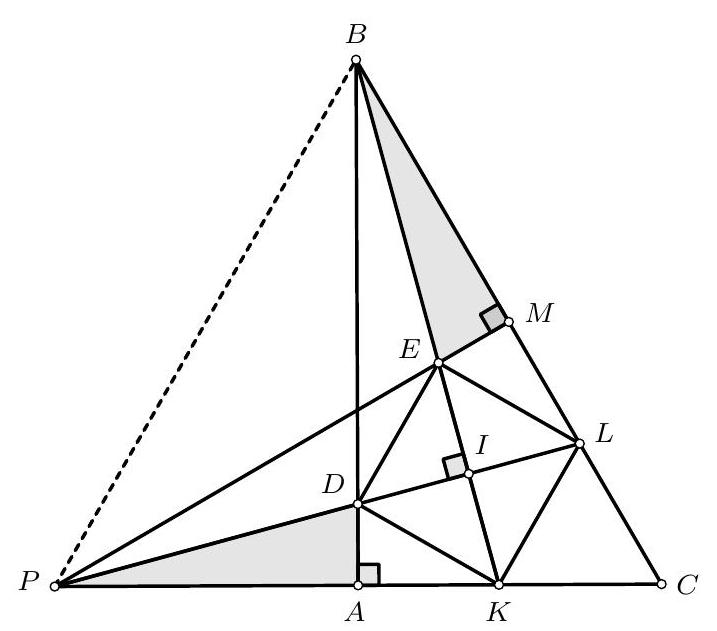
Alternative Solution by PSC. Let $P$ be the point of intersection of $E M$ with $A C$. The triangles $A B C$ and $M P C$ are equal since they have equal angles and $M C=\frac{B C}{2}=A C$. They also share the angle $\hat{C}$, so they must have identical incenter.
Let $I$ be the midpoint of $E K$. We have $\angle P E I=\angle B E M=75^{\circ}=\angle E K P$. So the triangle $P E K$ is isosceles and therefore $P I$ is a bisector of $\angle C P M$. So the incenter of $M P C$ belongs on $P I$. Since it shares the same incentre with $A B C$, then $I$ is the common incenter. We can now finish the proof as in the first solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a right-angled triangle with $\hat{A}=90^{\circ}$ and $\hat{B}=30^{\circ}$. The perpendicular at the midpoint $M$ of $B C$ meets the bisector $B K$ of the angle $\hat{B}$ at the point $E$. The perpendicular bisector of $E K$ meets $A B$ at $D$. Prove that $K D$ is perpendicular to $D E$.
|
Alternative Solution by PSC. Let $P$ be the point of intersection of $E M$ with $A C$. The triangles $A B C$ and $M P C$ are equal since they have equal angles and $M C=\frac{B C}{2}=A C$. They also share the angle $\hat{C}$, so they must have identical incenter.
Let $I$ be the midpoint of $E K$. We have $\angle P E I=\angle B E M=75^{\circ}=\angle E K P$. So the triangle $P E K$ is isosceles and therefore $P I$ is a bisector of $\angle C P M$. So the incenter of $M P C$ belongs on $P I$. Since it shares the same incentre with $A B C$, then $I$ is the common incenter. We can now finish the proof as in the first solution.

|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nG1.",
"solution_match": "\nSolution."
}
|
f150d7c8-4adb-5347-bdeb-5966ee8ecfda
| 606,052
|
Let $A B C$ be a right-angled triangle with $\hat{A}=90^{\circ}$ and $\hat{B}=30^{\circ}$. The perpendicular at the midpoint $M$ of $B C$ meets the bisector $B K$ of the angle $\hat{B}$ at the point $E$. The perpendicular bisector of $E K$ meets $A B$ at $D$. Prove that $K D$ is perpendicular to $D E$.
|
Alternative Solution by PSC. Let $P$ be the point of intersection of $E M$ with $A C$ and let $I$ be the midpoint of $E K$. Then the triangle $P B C$ is equilateral. We also have $\angle P E I=\angle B E M=75^{\circ}$ and $\angle P K E=75^{\circ}$, so $P E K$ is isosceles. We also have $P I \perp E K$ and $D I \perp E K$, so the points $P, D, I$ are collinear.
Furthermore, $\angle P B I=\angle B P I=45^{\circ}$, and therefore $B I=P I$.
We have $\angle D P A=\angle E B M=15^{\circ}$ and also $B M=\frac{A B}{2}=A C=P A$. So the right-angled triangles $P D A$ and $B E M$ are equal. Thus $P D=B E$.
So
$$
E I=B I-B E=P I-P D=D I
$$
Therefore $\angle D E I=\angle I D E=45^{\circ}$. Since $D E=D K$, we also have $\angle D E I=\angle D K I=$ $\angle K D I=45^{\circ}$. So finally, $\angle E D K=90^{\circ}$.
Coordinate Geometry Solution by PSC. We may assume that $A=(0,0), B=$ $(0, \sqrt{3})$ and $C=(1,0)$. Since $m_{B C}=-\sqrt{3}$, then $m_{E M}=\frac{\sqrt{3}}{3}$. Since also $M=\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$, then the equation of $E M$ is $y=\frac{\sqrt{3}}{3} x+\frac{\sqrt{3}}{3}$. The slope of $B K$ is
$$
m_{B K}=\tan \left(105^{\circ}\right)=\frac{\tan \left(60^{\circ}\right)+\tan \left(45^{\circ}\right)}{1-\tan \left(60^{\circ}\right) \tan \left(45^{\circ}\right)}=-(2+\sqrt{3})
$$
So the equation of $B K$ is $y=-(2+\sqrt{3}) x+\sqrt{3}$ which gives $K=(2 \sqrt{3}-3,0)$ and $E=(2-\sqrt{3}, \sqrt{3}-1)$. Letting $I$ be the midpoint of $E K$ we get $I=\left(\frac{\sqrt{3}-1}{2}, \frac{\sqrt{3}-1}{2}\right)$. Thus $I$ is equidistant from the sides $A B, A C$, so $A I$ is the bisector of $\hat{A}$, and thus $I$ is the incenter of triangle $A B C$. We can now finish the proof as in the first solution.
Metric Solution by PSC. We can assume that $A C=1$. Then $A B=\sqrt{3}$ and $B C=2$. So $B M=M C=1$. From triangle $B E M$ we get $B E=E C=\sec \left(15^{\circ}\right)$ and $E M=\tan \left(15^{\circ}\right)$. From triangle $B A K$ we get $B K=\sqrt{3} \sec \left(15^{\circ}\right)$. So $E K=B K-B E=$ $(\sqrt{3}-1) \sec \left(15^{\circ}\right)$. Thus, if $N$ is the midpoint of $E K$, then $E N=N K=\frac{\sqrt{3}-1}{2} \sec \left(15^{\circ}\right)$ and $B N=B E+E N=\frac{\sqrt{3}+1}{2} \sec \left(15^{\circ}\right)$. From triangle $B D N$ we get $D N=B N \tan \left(15^{\circ}\right)=$ $\frac{\sqrt{3}+1}{2} \tan \left(15^{\circ}\right) \sec \left(15^{\circ}\right)$. It is easy to check that $\tan \left(15^{\circ}\right)=2-\sqrt{3}$. Thus $D N=$ $\frac{\sqrt{3}-1}{2} \sec \left(15^{\circ}\right)=E N$. So $D N=E N=E K$ and therefore $\angle E D N=\angle K D N=45^{\circ}$ and $\angle K D E=90^{\circ}$ as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a right-angled triangle with $\hat{A}=90^{\circ}$ and $\hat{B}=30^{\circ}$. The perpendicular at the midpoint $M$ of $B C$ meets the bisector $B K$ of the angle $\hat{B}$ at the point $E$. The perpendicular bisector of $E K$ meets $A B$ at $D$. Prove that $K D$ is perpendicular to $D E$.
|
Alternative Solution by PSC. Let $P$ be the point of intersection of $E M$ with $A C$ and let $I$ be the midpoint of $E K$. Then the triangle $P B C$ is equilateral. We also have $\angle P E I=\angle B E M=75^{\circ}$ and $\angle P K E=75^{\circ}$, so $P E K$ is isosceles. We also have $P I \perp E K$ and $D I \perp E K$, so the points $P, D, I$ are collinear.
Furthermore, $\angle P B I=\angle B P I=45^{\circ}$, and therefore $B I=P I$.
We have $\angle D P A=\angle E B M=15^{\circ}$ and also $B M=\frac{A B}{2}=A C=P A$. So the right-angled triangles $P D A$ and $B E M$ are equal. Thus $P D=B E$.
So
$$
E I=B I-B E=P I-P D=D I
$$
Therefore $\angle D E I=\angle I D E=45^{\circ}$. Since $D E=D K$, we also have $\angle D E I=\angle D K I=$ $\angle K D I=45^{\circ}$. So finally, $\angle E D K=90^{\circ}$.
Coordinate Geometry Solution by PSC. We may assume that $A=(0,0), B=$ $(0, \sqrt{3})$ and $C=(1,0)$. Since $m_{B C}=-\sqrt{3}$, then $m_{E M}=\frac{\sqrt{3}}{3}$. Since also $M=\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$, then the equation of $E M$ is $y=\frac{\sqrt{3}}{3} x+\frac{\sqrt{3}}{3}$. The slope of $B K$ is
$$
m_{B K}=\tan \left(105^{\circ}\right)=\frac{\tan \left(60^{\circ}\right)+\tan \left(45^{\circ}\right)}{1-\tan \left(60^{\circ}\right) \tan \left(45^{\circ}\right)}=-(2+\sqrt{3})
$$
So the equation of $B K$ is $y=-(2+\sqrt{3}) x+\sqrt{3}$ which gives $K=(2 \sqrt{3}-3,0)$ and $E=(2-\sqrt{3}, \sqrt{3}-1)$. Letting $I$ be the midpoint of $E K$ we get $I=\left(\frac{\sqrt{3}-1}{2}, \frac{\sqrt{3}-1}{2}\right)$. Thus $I$ is equidistant from the sides $A B, A C$, so $A I$ is the bisector of $\hat{A}$, and thus $I$ is the incenter of triangle $A B C$. We can now finish the proof as in the first solution.
Metric Solution by PSC. We can assume that $A C=1$. Then $A B=\sqrt{3}$ and $B C=2$. So $B M=M C=1$. From triangle $B E M$ we get $B E=E C=\sec \left(15^{\circ}\right)$ and $E M=\tan \left(15^{\circ}\right)$. From triangle $B A K$ we get $B K=\sqrt{3} \sec \left(15^{\circ}\right)$. So $E K=B K-B E=$ $(\sqrt{3}-1) \sec \left(15^{\circ}\right)$. Thus, if $N$ is the midpoint of $E K$, then $E N=N K=\frac{\sqrt{3}-1}{2} \sec \left(15^{\circ}\right)$ and $B N=B E+E N=\frac{\sqrt{3}+1}{2} \sec \left(15^{\circ}\right)$. From triangle $B D N$ we get $D N=B N \tan \left(15^{\circ}\right)=$ $\frac{\sqrt{3}+1}{2} \tan \left(15^{\circ}\right) \sec \left(15^{\circ}\right)$. It is easy to check that $\tan \left(15^{\circ}\right)=2-\sqrt{3}$. Thus $D N=$ $\frac{\sqrt{3}-1}{2} \sec \left(15^{\circ}\right)=E N$. So $D N=E N=E K$ and therefore $\angle E D N=\angle K D N=45^{\circ}$ and $\angle K D E=90^{\circ}$ as required.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nG1.",
"solution_match": "\nSolution."
}
|
f150d7c8-4adb-5347-bdeb-5966ee8ecfda
| 606,052
|
Let $A B C$ be a triangle and let $\omega$ be its circumcircle. Let $\ell_{B}$ and $\ell_{C}$ be two parallel lines passing through $B$ and $C$ respectively. The lines $\ell_{B}$ and $\ell_{C}$ intersect with $\omega$ for the second time at the points $D$ and $E$ respectively, with $D$ belonging on the arc $A B$, and $E$ on the arc $A C$. Suppose that $D A$ intersects $\ell_{C}$ at $F$, and $E A$ intersects $\ell_{B}$ at $G$. If $O, O_{1}$ and $O_{2}$ are the circumcenters of the triangles $A B C, A D G$ and $A E F$ respectively, and $P$ is the center of the circumcircle of the triangle $O O_{1} O_{2}$, prove that $O P$ is parallel to $\ell_{B}$ and $\ell_{C}$.
|
Alternative Solution by PSC. Let us write $\alpha, \beta, \gamma$ for the angles of $A B C$. Since $A D B C$ is cyclic, we have $\angle G D A=180^{\circ}-\angle B D A=\gamma$. Similarly, we have
$$
\angle G A D=180^{\circ}-\angle D A E=\angle E B D=\angle B E C=\angle B A C=\alpha
$$
where we have also used the fact that $\ell_{B}$ and $\ell_{C}$ are parallel.
Thus, the triangles $A B C$ and $A G D$ are similar. Analogously, $A E F$ is also similar to them.
Since $A D$ is a common chord of $\omega$ and $\omega_{1}$ then $A D$ is perpendicular to $O O_{1}$. Thus,
$$
\angle O O_{1} A=\frac{1}{2} \angle D O_{1} A=\angle D G A=\beta
$$
Similarly, we have $\angle O O_{2} A=\gamma$. Since $O_{1}, A, O_{2}$ are collinear (as in the first solution) we get that $O O_{1} O_{2}$ is also similar to $A B C$. Their circumcentres are $P$ and $O$ respectively, thus $\angle P O O_{1}=\angle O A B=90^{\circ}-\gamma$.
Since $O O_{1}$ is perpendicular to $A D$, letting $X$ be the point of intersection of $O O_{1}$ with $G D$, we get that $\angle D X O_{1}=90^{\circ}-\gamma$. Thus $O P$ is parallel to $\ell_{B}$ and therefore to $\ell_{C}$ as well.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and let $\omega$ be its circumcircle. Let $\ell_{B}$ and $\ell_{C}$ be two parallel lines passing through $B$ and $C$ respectively. The lines $\ell_{B}$ and $\ell_{C}$ intersect with $\omega$ for the second time at the points $D$ and $E$ respectively, with $D$ belonging on the arc $A B$, and $E$ on the arc $A C$. Suppose that $D A$ intersects $\ell_{C}$ at $F$, and $E A$ intersects $\ell_{B}$ at $G$. If $O, O_{1}$ and $O_{2}$ are the circumcenters of the triangles $A B C, A D G$ and $A E F$ respectively, and $P$ is the center of the circumcircle of the triangle $O O_{1} O_{2}$, prove that $O P$ is parallel to $\ell_{B}$ and $\ell_{C}$.
|
Alternative Solution by PSC. Let us write $\alpha, \beta, \gamma$ for the angles of $A B C$. Since $A D B C$ is cyclic, we have $\angle G D A=180^{\circ}-\angle B D A=\gamma$. Similarly, we have
$$
\angle G A D=180^{\circ}-\angle D A E=\angle E B D=\angle B E C=\angle B A C=\alpha
$$
where we have also used the fact that $\ell_{B}$ and $\ell_{C}$ are parallel.
Thus, the triangles $A B C$ and $A G D$ are similar. Analogously, $A E F$ is also similar to them.
Since $A D$ is a common chord of $\omega$ and $\omega_{1}$ then $A D$ is perpendicular to $O O_{1}$. Thus,
$$
\angle O O_{1} A=\frac{1}{2} \angle D O_{1} A=\angle D G A=\beta
$$
Similarly, we have $\angle O O_{2} A=\gamma$. Since $O_{1}, A, O_{2}$ are collinear (as in the first solution) we get that $O O_{1} O_{2}$ is also similar to $A B C$. Their circumcentres are $P$ and $O$ respectively, thus $\angle P O O_{1}=\angle O A B=90^{\circ}-\gamma$.
Since $O O_{1}$ is perpendicular to $A D$, letting $X$ be the point of intersection of $O O_{1}$ with $G D$, we get that $\angle D X O_{1}=90^{\circ}-\gamma$. Thus $O P$ is parallel to $\ell_{B}$ and therefore to $\ell_{C}$ as well.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nG2.",
"solution_match": "\nSolution."
}
|
6a7d7a71-573c-5f13-9c40-ca6d29d7cf56
| 606,067
|
Let $A B C$ be a triangle and let $\omega$ be its circumcircle. Let $\ell_{B}$ and $\ell_{C}$ be two parallel lines passing through $B$ and $C$ respectively. The lines $\ell_{B}$ and $\ell_{C}$ intersect with $\omega$ for the second time at the points $D$ and $E$ respectively, with $D$ belonging on the arc $A B$, and $E$ on the arc $A C$. Suppose that $D A$ intersects $\ell_{C}$ at $F$, and $E A$ intersects $\ell_{B}$ at $G$. If $O, O_{1}$ and $O_{2}$ are the circumcenters of the triangles $A B C, A D G$ and $A E F$ respectively, and $P$ is the center of the circumcircle of the triangle $O O_{1} O_{2}$, prove that $O P$ is parallel to $\ell_{B}$ and $\ell_{C}$.
|
## Alternative Solution by PSC.
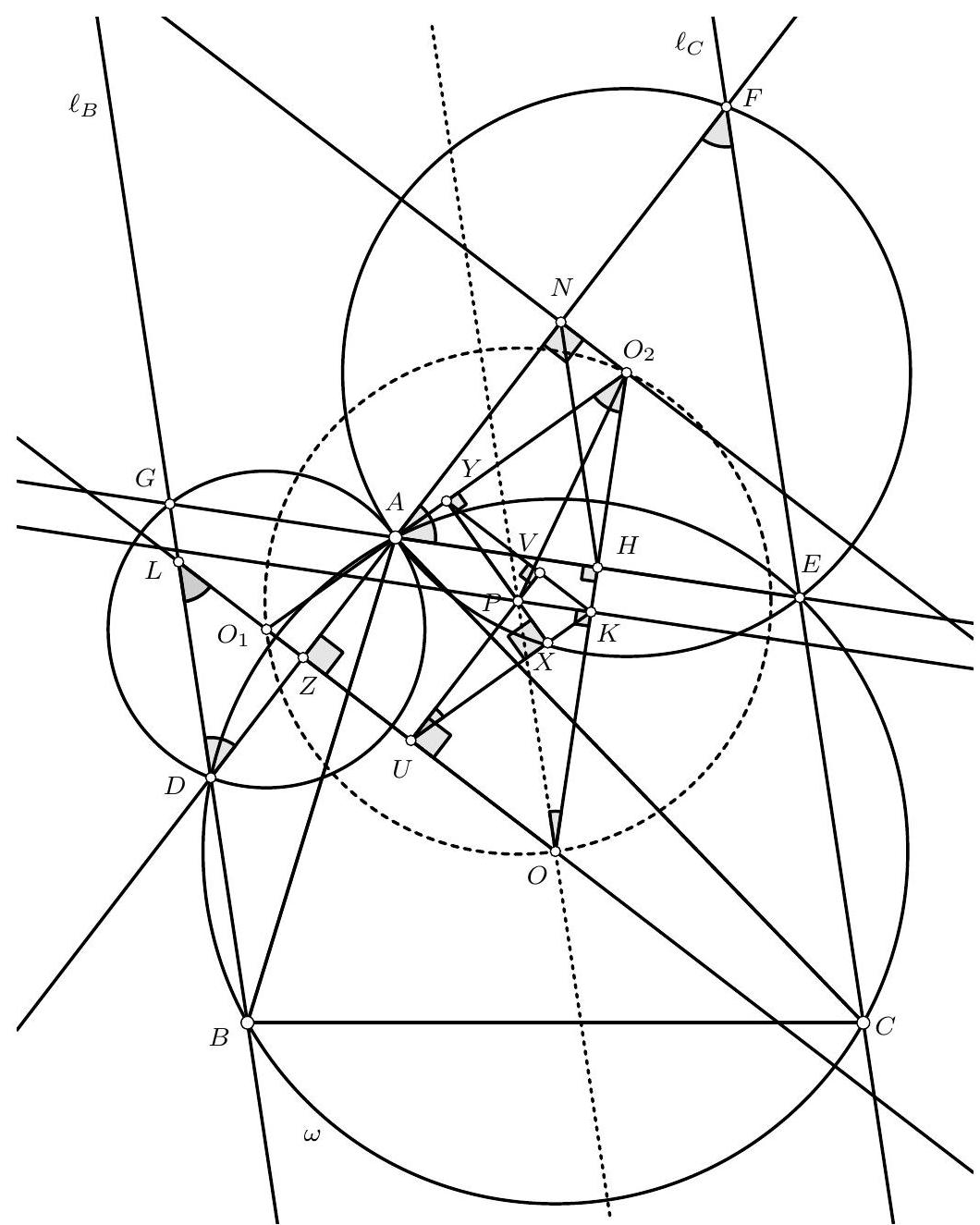
Let $L$ and $Z$ be the points of intesecrion of $O O_{1}$ with $\ell_{b}$ and $D A$ respectively. Since $L Z$ is perpendicular on $D A$, and since $\ell_{b}$ is parallel to $\ell_{c}$, then
$$
\angle D L O=90^{\circ}-\angle L D Z=90^{\circ}-\angle D F E=90^{\circ}-\angle A F E
$$
Since $A E$ is a common chord of $\omega$ and $\omega_{2}$, then it is perpendicular to $\mathrm{OO}_{2}$. So letting $H$ be their point of intersection, we get
$$
\angle D L O=90^{\circ}-\angle A F E=90^{\circ}-\angle A O_{2} H=\angle O_{2} A H
$$
Let $K, Y, U$ be the projections of $P$ onto $O O_{2}, O_{1} O_{2}$ and $O O_{1}$ respectively. Then $Y K U O_{1}$ is a parallelogram and so the extensions of $P Y$ and $P U$ meet the segments $U K$ and $K Y$ at points $X, V$ such that $Y X \perp K U$ and $U V \perp K Y$.
Since the points $O_{1}, A, O_{2}$ are collinear, we have
$$
\angle F A O_{2}=O_{1} A Z=90^{\circ}-\angle A O_{1} Z=90^{\circ}-\angle Y K U=\angle P U K=\angle P O K=\angle P O K
$$
where the last equality follows since $P U O K$ is cyclic.
Since $A Z O H$ is also cyclic, we have $\angle F A H=\angle O_{1} O O_{2}$. From this, together with (1) and (2) we get
$$
\angle D L O=\angle O_{2} A H=\angle F A H-\angle F A O_{2}=\angle O_{1} O O_{2}-\angle P O K=\angle U O P=\angle L O P
$$
Therefore $O P$ is parallel to $\ell_{B}$ and $\ell_{C}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and let $\omega$ be its circumcircle. Let $\ell_{B}$ and $\ell_{C}$ be two parallel lines passing through $B$ and $C$ respectively. The lines $\ell_{B}$ and $\ell_{C}$ intersect with $\omega$ for the second time at the points $D$ and $E$ respectively, with $D$ belonging on the arc $A B$, and $E$ on the arc $A C$. Suppose that $D A$ intersects $\ell_{C}$ at $F$, and $E A$ intersects $\ell_{B}$ at $G$. If $O, O_{1}$ and $O_{2}$ are the circumcenters of the triangles $A B C, A D G$ and $A E F$ respectively, and $P$ is the center of the circumcircle of the triangle $O O_{1} O_{2}$, prove that $O P$ is parallel to $\ell_{B}$ and $\ell_{C}$.
|
## Alternative Solution by PSC.

Let $L$ and $Z$ be the points of intesecrion of $O O_{1}$ with $\ell_{b}$ and $D A$ respectively. Since $L Z$ is perpendicular on $D A$, and since $\ell_{b}$ is parallel to $\ell_{c}$, then
$$
\angle D L O=90^{\circ}-\angle L D Z=90^{\circ}-\angle D F E=90^{\circ}-\angle A F E
$$
Since $A E$ is a common chord of $\omega$ and $\omega_{2}$, then it is perpendicular to $\mathrm{OO}_{2}$. So letting $H$ be their point of intersection, we get
$$
\angle D L O=90^{\circ}-\angle A F E=90^{\circ}-\angle A O_{2} H=\angle O_{2} A H
$$
Let $K, Y, U$ be the projections of $P$ onto $O O_{2}, O_{1} O_{2}$ and $O O_{1}$ respectively. Then $Y K U O_{1}$ is a parallelogram and so the extensions of $P Y$ and $P U$ meet the segments $U K$ and $K Y$ at points $X, V$ such that $Y X \perp K U$ and $U V \perp K Y$.
Since the points $O_{1}, A, O_{2}$ are collinear, we have
$$
\angle F A O_{2}=O_{1} A Z=90^{\circ}-\angle A O_{1} Z=90^{\circ}-\angle Y K U=\angle P U K=\angle P O K=\angle P O K
$$
where the last equality follows since $P U O K$ is cyclic.
Since $A Z O H$ is also cyclic, we have $\angle F A H=\angle O_{1} O O_{2}$. From this, together with (1) and (2) we get
$$
\angle D L O=\angle O_{2} A H=\angle F A H-\angle F A O_{2}=\angle O_{1} O O_{2}-\angle P O K=\angle U O P=\angle L O P
$$
Therefore $O P$ is parallel to $\ell_{B}$ and $\ell_{C}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nG2.",
"solution_match": "\nSolution."
}
|
6a7d7a71-573c-5f13-9c40-ca6d29d7cf56
| 606,067
|
Let $A B C$ be a triangle with incenter $I$. The points $D$ and $E$ lie on the segments $C A$ and $B C$ respectively, such that $C D=C E$. Let $F$ be a point on the segment $C D$. Prove that the quadrilateral $A B E F$ is circumscribable if and only if the quadrilateral $D I E F$ is cyclic.
|
Since $C D=C E$ it means that $E$ is the reflection of $D$ on the bisector of $\angle A C B$, i.e. the line $C I$. Let $G$ be the reflection of $F$ on $C I$. Then $G$ lies on the segment $C E$, the segment $E G$ is the reflection of the segment $D F$ on the line $C I$. Also, the quadraliteral $D E G F$ is cyclic since $\angle D F E=\angle E G D$.
Suppose that the quadrilateral $A B E F$ is circumscribable. Since $\angle F A I=\angle B A I$ and $\angle E B I=\angle A B I$, then $I$ is the centre of its inscribed circle. Then $\angle D F I=\angle E F I$ and since segment $E G$ is the reflection of segment $D F$ on the line $C I$, we have $\angle E F I=$ $\angle D G I$. So $\angle D F I=\angle D G I$ which means that quadrilateral $D I G F$ is cyclic. Since the quadrilateral $D E G F$ is also cyclic, we have that the quadrilateral $D I E F$ is cyclic.
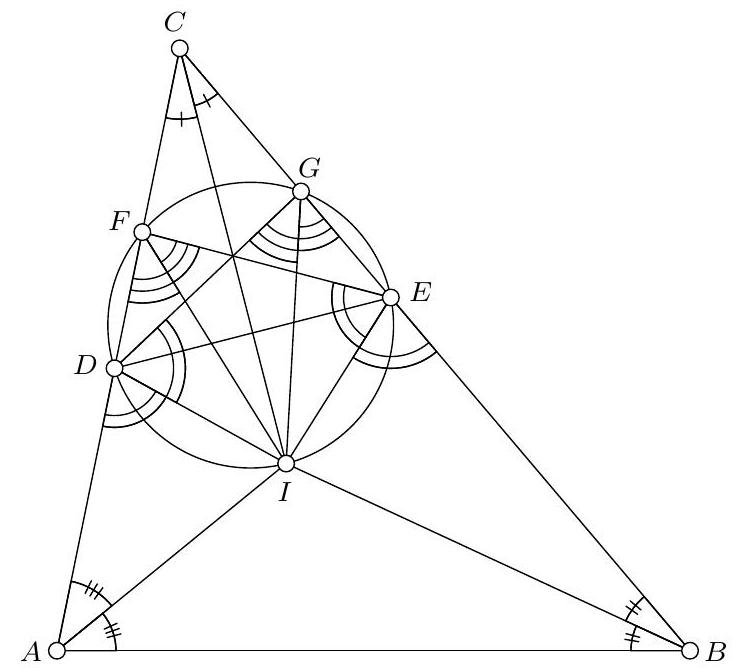
Suppose that the quadrilateral $D I E F$ is cyclic. Since quadrilateral $D E G F$ is also cyclic, we have that the pentagon $D I E G F$ is cyclic. So $\angle I E B=180^{\circ}-\angle I E G=\angle I D G$ and since segment $E G$ is the reflection of segment $D F$ on the line $C I$, we have $\angle I D G=$ $\angle I E F$. Hence $\angle I E B=\angle I E F$, which means that $E I$ is the angle bisector of $\angle B E F$. Since $\angle I F A=\angle I F D=\angle I G D$ and since the segment $E G$ is the reflection of segment $D F$ on the line $C I$, we have $\angle I G D=\angle I F E$, hence $\angle I F A=\angle I F E$, which means that $F I$ is the angle bisector of $\angle E F A$. We also know that $A I$ and $B I$ are the angle bisectors of $\angle F A B$ and $\angle A B E$. So all angle bisectors of the quadrilateral $A B E F$ intersect at $I$, which means that it is circumscribable.
Comment by PSC. There is no need for introducing the point $G$. One can show that triangles $C I D$ and $C I E$ are equal and also that the triangles $C D M$ and $C E M$ are equal, where $M$ is the midpoint of $D E$. From these, one can deduce that $\angle C D I=\angle C E I$ and $\angle I D E=\angle I E D$ and proceed with similar reasoning as in the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$. The points $D$ and $E$ lie on the segments $C A$ and $B C$ respectively, such that $C D=C E$. Let $F$ be a point on the segment $C D$. Prove that the quadrilateral $A B E F$ is circumscribable if and only if the quadrilateral $D I E F$ is cyclic.
|
Since $C D=C E$ it means that $E$ is the reflection of $D$ on the bisector of $\angle A C B$, i.e. the line $C I$. Let $G$ be the reflection of $F$ on $C I$. Then $G$ lies on the segment $C E$, the segment $E G$ is the reflection of the segment $D F$ on the line $C I$. Also, the quadraliteral $D E G F$ is cyclic since $\angle D F E=\angle E G D$.
Suppose that the quadrilateral $A B E F$ is circumscribable. Since $\angle F A I=\angle B A I$ and $\angle E B I=\angle A B I$, then $I$ is the centre of its inscribed circle. Then $\angle D F I=\angle E F I$ and since segment $E G$ is the reflection of segment $D F$ on the line $C I$, we have $\angle E F I=$ $\angle D G I$. So $\angle D F I=\angle D G I$ which means that quadrilateral $D I G F$ is cyclic. Since the quadrilateral $D E G F$ is also cyclic, we have that the quadrilateral $D I E F$ is cyclic.

Suppose that the quadrilateral $D I E F$ is cyclic. Since quadrilateral $D E G F$ is also cyclic, we have that the pentagon $D I E G F$ is cyclic. So $\angle I E B=180^{\circ}-\angle I E G=\angle I D G$ and since segment $E G$ is the reflection of segment $D F$ on the line $C I$, we have $\angle I D G=$ $\angle I E F$. Hence $\angle I E B=\angle I E F$, which means that $E I$ is the angle bisector of $\angle B E F$. Since $\angle I F A=\angle I F D=\angle I G D$ and since the segment $E G$ is the reflection of segment $D F$ on the line $C I$, we have $\angle I G D=\angle I F E$, hence $\angle I F A=\angle I F E$, which means that $F I$ is the angle bisector of $\angle E F A$. We also know that $A I$ and $B I$ are the angle bisectors of $\angle F A B$ and $\angle A B E$. So all angle bisectors of the quadrilateral $A B E F$ intersect at $I$, which means that it is circumscribable.
Comment by PSC. There is no need for introducing the point $G$. One can show that triangles $C I D$ and $C I E$ are equal and also that the triangles $C D M$ and $C E M$ are equal, where $M$ is the midpoint of $D E$. From these, one can deduce that $\angle C D I=\angle C E I$ and $\angle I D E=\angle I E D$ and proceed with similar reasoning as in the solution.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nG3.",
"solution_match": "\nSolution."
}
|
1c7ad48a-ce4c-5bae-ad9c-0c59c8748d12
| 606,083
|
Let $A B C$ be a triangle such that $A B \neq A C$, and let the perpendicular bisector of the side $B C$ intersect lines $A B$ and $A C$ at points $P$ and $Q$, respectively. If $H$ is the orthocenter of the triangle $A B C$, and $M$ and $N$ are the midpoints of the segments $B C$ and $P Q$ respectively, prove that $H M$ and $A N$ meet on the circumcircle of $A B C$.
|
We have
$$
\angle A P Q=\angle B P M=90^{\circ}-\angle M B P=90^{\circ}-\angle C B A=\angle H C B
$$
and
$$
\angle A Q P=\angle M Q C=90^{\circ}-\angle Q C M=90^{\circ}-\angle A C B=\angle C B H
$$
From these two equalities, we see that the triangles $A P Q$ and $H C B$ are similar. Moreover, since $M$ and $N$ are the midpoints of the segments $B C$ and $P Q$ respectively, then the triangles $A Q N$ and $H B M$ are also similar. Therefore, we have $\angle A N Q=\angle H M B$.
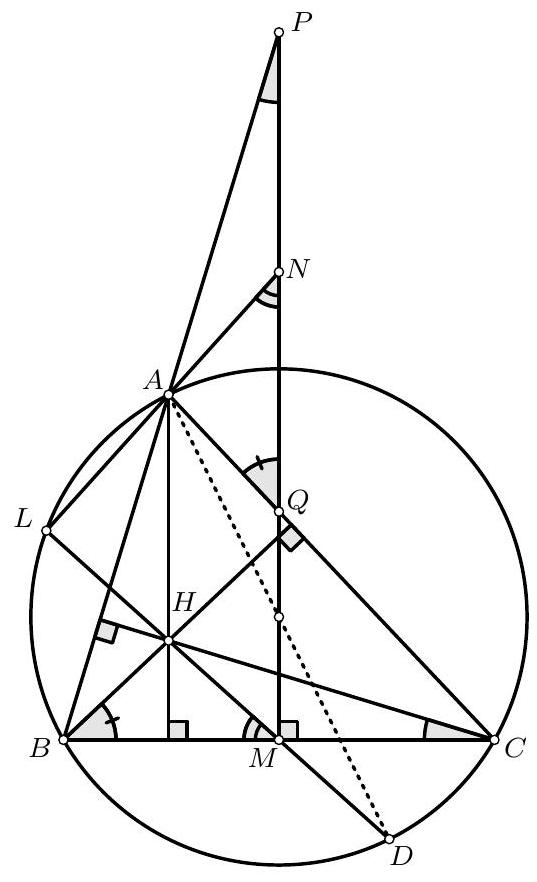
Let $L$ be the intersection of $A N$ and $H M$. We have
$\angle M L N=180^{\circ}-\angle L N M-\angle N M L=180^{\circ}-\angle L M B-\angle N M L=180^{\circ}-\angle N M B=90^{\circ}$.
Now let $D$ be the point on the circumcircle of $A B C$ diametrically oposite to $A$. It is known that $D$ is also the relfection of point $H$ over the point $M$. Therefore, we have that $D$ belongs on $M H$ and that $\angle D L A=\angle M L A=\angle M L N=90^{\circ}$. But, as $D A$ is the diameter of the circumcirle of $A B C$, the condition that $\angle D L A=90^{\circ}$ is enough to conclude that $L$ belongs on the circumcircle of $A B C$.
Remark by PSC. There is a spiral similarity mapping $A Q P$ to $H B C$. Since the similarity maps $A N$ to $H M$, it also maps $A H$ to $N M$, and since these two lines are parallel, the centre of the similarity is $L=A N \cap H M$. Since the similarity maps $B C$ to $Q P$, its centre belongs on the circumcircle of $B C X$, where $X=B Q \cap P C$. But $X$ is the reflection of $A$ on $Q M$ and so it must belong on the circumcircle of $A B C$. Hence so must $L$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle such that $A B \neq A C$, and let the perpendicular bisector of the side $B C$ intersect lines $A B$ and $A C$ at points $P$ and $Q$, respectively. If $H$ is the orthocenter of the triangle $A B C$, and $M$ and $N$ are the midpoints of the segments $B C$ and $P Q$ respectively, prove that $H M$ and $A N$ meet on the circumcircle of $A B C$.
|
We have
$$
\angle A P Q=\angle B P M=90^{\circ}-\angle M B P=90^{\circ}-\angle C B A=\angle H C B
$$
and
$$
\angle A Q P=\angle M Q C=90^{\circ}-\angle Q C M=90^{\circ}-\angle A C B=\angle C B H
$$
From these two equalities, we see that the triangles $A P Q$ and $H C B$ are similar. Moreover, since $M$ and $N$ are the midpoints of the segments $B C$ and $P Q$ respectively, then the triangles $A Q N$ and $H B M$ are also similar. Therefore, we have $\angle A N Q=\angle H M B$.

Let $L$ be the intersection of $A N$ and $H M$. We have
$\angle M L N=180^{\circ}-\angle L N M-\angle N M L=180^{\circ}-\angle L M B-\angle N M L=180^{\circ}-\angle N M B=90^{\circ}$.
Now let $D$ be the point on the circumcircle of $A B C$ diametrically oposite to $A$. It is known that $D$ is also the relfection of point $H$ over the point $M$. Therefore, we have that $D$ belongs on $M H$ and that $\angle D L A=\angle M L A=\angle M L N=90^{\circ}$. But, as $D A$ is the diameter of the circumcirle of $A B C$, the condition that $\angle D L A=90^{\circ}$ is enough to conclude that $L$ belongs on the circumcircle of $A B C$.
Remark by PSC. There is a spiral similarity mapping $A Q P$ to $H B C$. Since the similarity maps $A N$ to $H M$, it also maps $A H$ to $N M$, and since these two lines are parallel, the centre of the similarity is $L=A N \cap H M$. Since the similarity maps $B C$ to $Q P$, its centre belongs on the circumcircle of $B C X$, where $X=B Q \cap P C$. But $X$ is the reflection of $A$ on $Q M$ and so it must belong on the circumcircle of $A B C$. Hence so must $L$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nG4.",
"solution_match": "\nSolution."
}
|
8f4db640-220c-5ee1-800d-549b2f2d2003
| 606,094
|
Let $P$ be a point in the interior of a triangle $A B C$. The lines $A P, B P$ and $C P$ intersect again the circumcircles of the triangles $P B C, P C A$, and $P A B$ at $D, E$ and $F$ respectively. Prove that $P$ is the orthocenter of the triangle $D E F$ if and only if $P$ is the incenter of the triangle $A B C$.
|
If $P$ is the incenter of $A B C$, then $\angle B P D=\angle A B P+\angle B A P=\frac{\hat{A}+\hat{B}}{2}$, and $\angle B D P=\angle B C P=\frac{\hat{C}}{2}$. From triangle $B D P$, it follows that $\angle P B D=90^{\circ}$, i.e. that $E B$ is one of the altitudes of the triangle $D E F$. Similarly, $A D$ and $C F$ are altitudes, which means that $P$ is the orhocenter of $D E F$.
Notice that $A P$ separates $B$ from $C, B$ from $E$ and $C$ from $F$. Therefore $A P$ separates $E$ from $F$, which means that $P$ belongs to the interior of $\angle E D F$. It follows that $P \in$ $\operatorname{Int}(\triangle D E F)$.
If $P$ is the orthocenter of $D E F$, then clearly $D E F$ must be acute. Let $A^{\prime} \in E F, B^{\prime} \in D F$ and $C^{\prime} \in D E$ be the feet of the altitudes. Then the quadrilaterals $B^{\prime} P A^{\prime} F, C^{\prime} P B^{\prime} D$, and $A^{\prime} P C^{\prime} E$ are cyclic, which means that $\angle B^{\prime} F A^{\prime}=180^{\circ}-\angle B^{\prime} P A^{\prime}=180^{\circ}-\angle B P A=$ $\angle B F A$. Similarly, one obtains that $\angle C^{\prime} D B^{\prime}=\angle C D B$, and $\angle A^{\prime} E C^{\prime}=\angle A E C$.
- If $B \in \operatorname{Ext}(\triangle F P D)$, then $A \in \operatorname{Int}(\triangle E P F), C \in \operatorname{Ext}(\triangle D P E)$, and thus $B \in$ $\operatorname{Int}(\triangle F P D)$, contradiction.
- If $B \in \operatorname{Int}(\triangle F P D)$, then $A \in \operatorname{Ext}(\triangle E P F), C \in \operatorname{Int}(\triangle D P E)$, and thus $B \in$ $\operatorname{Ext}(\triangle F P D)$, contradiction.
This leaves us with $B \in F D$. Then we must have $A \in E F, C \in D E$, which means that $A=A^{\prime}, B=B^{\prime}, C=C^{\prime}$. Thus $A B C$ is the orthic triangle of triangle $D E F$ and it is well known that the orthocenter of an acute triangle $D E F$ is the incenter of its orthic triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point in the interior of a triangle $A B C$. The lines $A P, B P$ and $C P$ intersect again the circumcircles of the triangles $P B C, P C A$, and $P A B$ at $D, E$ and $F$ respectively. Prove that $P$ is the orthocenter of the triangle $D E F$ if and only if $P$ is the incenter of the triangle $A B C$.
|
If $P$ is the incenter of $A B C$, then $\angle B P D=\angle A B P+\angle B A P=\frac{\hat{A}+\hat{B}}{2}$, and $\angle B D P=\angle B C P=\frac{\hat{C}}{2}$. From triangle $B D P$, it follows that $\angle P B D=90^{\circ}$, i.e. that $E B$ is one of the altitudes of the triangle $D E F$. Similarly, $A D$ and $C F$ are altitudes, which means that $P$ is the orhocenter of $D E F$.

Notice that $A P$ separates $B$ from $C, B$ from $E$ and $C$ from $F$. Therefore $A P$ separates $E$ from $F$, which means that $P$ belongs to the interior of $\angle E D F$. It follows that $P \in$ $\operatorname{Int}(\triangle D E F)$.
If $P$ is the orthocenter of $D E F$, then clearly $D E F$ must be acute. Let $A^{\prime} \in E F, B^{\prime} \in D F$ and $C^{\prime} \in D E$ be the feet of the altitudes. Then the quadrilaterals $B^{\prime} P A^{\prime} F, C^{\prime} P B^{\prime} D$, and $A^{\prime} P C^{\prime} E$ are cyclic, which means that $\angle B^{\prime} F A^{\prime}=180^{\circ}-\angle B^{\prime} P A^{\prime}=180^{\circ}-\angle B P A=$ $\angle B F A$. Similarly, one obtains that $\angle C^{\prime} D B^{\prime}=\angle C D B$, and $\angle A^{\prime} E C^{\prime}=\angle A E C$.
- If $B \in \operatorname{Ext}(\triangle F P D)$, then $A \in \operatorname{Int}(\triangle E P F), C \in \operatorname{Ext}(\triangle D P E)$, and thus $B \in$ $\operatorname{Int}(\triangle F P D)$, contradiction.
- If $B \in \operatorname{Int}(\triangle F P D)$, then $A \in \operatorname{Ext}(\triangle E P F), C \in \operatorname{Int}(\triangle D P E)$, and thus $B \in$ $\operatorname{Ext}(\triangle F P D)$, contradiction.
This leaves us with $B \in F D$. Then we must have $A \in E F, C \in D E$, which means that $A=A^{\prime}, B=B^{\prime}, C=C^{\prime}$. Thus $A B C$ is the orthic triangle of triangle $D E F$ and it is well known that the orthocenter of an acute triangle $D E F$ is the incenter of its orthic triangle.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nG5.",
"solution_match": "\nSolution."
}
|
548cec89-70c9-5399-b394-f4b9375ba747
| 606,103
|
Let $A B C$ be a non-isosceles triangle with incenter $I$. Let $D$ be a point on the segment $B C$ such that the circumcircle of $B I D$ intersects the segment $A B$ at $E \neq B$, and the circumcircle of $C I D$ intersects the segment $A C$ at $F \neq C$. The circumcircle of $D E F$ intersects $A B$ and $A C$ at the second points $M$ and $N$ respectively. Let $P$ be the point of intersection of $I B$ and $D E$, and let $Q$ be the point of intersection of $I C$ and $D F$. Prove that the three lines $E N, F M$ and $P Q$ are parallel.
|
Since $B D I E$ is cyclic, and $B I$ is the bisector of $\angle D B E$, then $I D=I E$. Similarly, $I D=I F$, so $I$ is the circumcenter of the triangle $D E F$. We also have
$$
\angle I E A=\angle I D B=\angle I F C
$$
which implies that $A E I F$ is cyclic. We can assume that $A, E, M$ and $A, N, F$ are collinear in that order. Then $\angle I E M=\angle I F N$. Since also $I M=I E=I N=I F$, the two isosceles triangles $I E M$ and $I N F$ are congruent, thus $E M=F N$ and therefore $E N$ is parallel to $F M$. From that, we can also see that the two triangles $I E A$ and $I N A$ are congruent, which implies that $A I$ is the perpendicular bisector of $E N$ and $M F$.
Note that $\angle I D P=\angle I D E=\angle I B E=\angle I B D$, so the triangles $I P D$ and $I D B$ are similar, which implies that $\frac{I D}{I B}=\frac{I P}{I D}$ and $I P \cdot I B=I D^{2}$. Similarly, we have $I Q \cdot I C=I D^{2}$, thus $I P \cdot I B=I Q \cdot I C$. This implies that $B P Q C$ is cyclic, which leads to
$$
\angle I P Q=\angle I C B=\frac{\hat{C}}{2}
$$
But $\angle A I B=90^{\circ}+\frac{\hat{C}}{2}$, so $A I$ is perpendicular to $P Q$. Hence, $P Q$ is parallel to $E N$ and FM.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a non-isosceles triangle with incenter $I$. Let $D$ be a point on the segment $B C$ such that the circumcircle of $B I D$ intersects the segment $A B$ at $E \neq B$, and the circumcircle of $C I D$ intersects the segment $A C$ at $F \neq C$. The circumcircle of $D E F$ intersects $A B$ and $A C$ at the second points $M$ and $N$ respectively. Let $P$ be the point of intersection of $I B$ and $D E$, and let $Q$ be the point of intersection of $I C$ and $D F$. Prove that the three lines $E N, F M$ and $P Q$ are parallel.
|
Since $B D I E$ is cyclic, and $B I$ is the bisector of $\angle D B E$, then $I D=I E$. Similarly, $I D=I F$, so $I$ is the circumcenter of the triangle $D E F$. We also have
$$
\angle I E A=\angle I D B=\angle I F C
$$
which implies that $A E I F$ is cyclic. We can assume that $A, E, M$ and $A, N, F$ are collinear in that order. Then $\angle I E M=\angle I F N$. Since also $I M=I E=I N=I F$, the two isosceles triangles $I E M$ and $I N F$ are congruent, thus $E M=F N$ and therefore $E N$ is parallel to $F M$. From that, we can also see that the two triangles $I E A$ and $I N A$ are congruent, which implies that $A I$ is the perpendicular bisector of $E N$ and $M F$.
Note that $\angle I D P=\angle I D E=\angle I B E=\angle I B D$, so the triangles $I P D$ and $I D B$ are similar, which implies that $\frac{I D}{I B}=\frac{I P}{I D}$ and $I P \cdot I B=I D^{2}$. Similarly, we have $I Q \cdot I C=I D^{2}$, thus $I P \cdot I B=I Q \cdot I C$. This implies that $B P Q C$ is cyclic, which leads to
$$
\angle I P Q=\angle I C B=\frac{\hat{C}}{2}
$$
But $\angle A I B=90^{\circ}+\frac{\hat{C}}{2}$, so $A I$ is perpendicular to $P Q$. Hence, $P Q$ is parallel to $E N$ and FM.

|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nG6.",
"solution_match": "\nSolution."
}
|
a803a4db-80a4-5f23-be31-9e3aac5b37a1
| 606,111
|
Let $A B C$ be a right-angled triangle with $\hat{A}=90^{\circ}$. Let $K$ be the midpoint of $B C$, and let $A K L M$ be a parallelogram with centre $C$. Let $T$ be the intersection of the line $A C$ and the perpendicular bisector of $B M$. Let $\omega_{1}$ be the circle with centre $C$ and radius $C A$ and let $\omega_{2}$ be the circle with centre $T$ and radius $T B$. Prove that one of the points of intersection of $\omega_{1}$ and $\omega_{2}$ is on the line $L M$.
|
Let $M^{\prime}$ be the symmetric point of $M$ with respect to $T$. Observe that $T$ is equidistant from $B$ and $M$, therefore $M$ belongs on $\omega_{2}$ and $M^{\prime} M$ is a diameter of $\omega_{2}$. It suffices to prove that $M^{\prime} A$ is perpendicular to $L M$, or equivalently, to $A K$. To see this, let $S$ be the point of intersection of $M^{\prime} A$ with $L M$. We will then have $\angle M^{\prime} S M=90^{\circ}$ which shows that $S$ belongs on $\omega_{2}$ as $M^{\prime} M$ is a diameter of $\omega_{2}$. We also have that $S$ belongs on $\omega_{1}$ as $A L$ is diameter of $\omega_{1}$.
Since $T$ and $C$ are the midpoints of $M^{\prime} M$ and $K M$ respectively, then $T C$ is parallel to $M^{\prime} K$ and so $M^{\prime} K$ is perpendicular to $A B$. Since $K A=K B$, then $K M^{\prime}$ is the perpendicular bisector of $A B$. But then the triangles $K B M^{\prime}$ and $K A M^{\prime}$ are equal, showing that $\angle M^{\prime} A K=\angle M^{\prime} B K=\angle M^{\prime} B M=90^{\circ}$ as required.
Alternative Solution by Proposers. Since $C A=C L$, then $L$ belongs on $\omega_{1}$. Let $S$ be the other point of intersection of $\omega_{1}$ with the line $L M$. We need to show that $S$ belongs on $\omega_{2}$. Since $T B=T M$ ( $T$ is on the perpendicular bisector of $B M$ ) it is enough to show that $T S=T M$.
Let $N, T^{\prime}$ be points on the lines $A L$ and $L M$ respectively, such that $M N \perp L M$ and $T T^{\prime} \perp L M$. It is enough to prove that $T^{\prime}$ is the midpoint of $S M$. Since $A L$ is diameter of $\omega_{1}$ we have that $A S \perp L S$. Thus, it is enough to show that $T$ is the midpoint of $A N$. We have
$$
A T=\frac{A N}{2} \Leftrightarrow A C-C T=\frac{A L-L N}{2} \Leftrightarrow 2 A C-2 C T=A L-L N \Leftrightarrow L N=2 C T
$$
as $A L=2 A C$. So it suffices to prove that $L N=2 C T$.
Let $D$ be the midpoint of $B M$. Since $B K=K C=C M$, then $D$ is also the midpont of $K C$. The triangles $L M N$ and $C T D$ are similar since they are right-angled with
$\angle T C D=\angle C A K=\angle M L N$. (AK=KC and $A K$ is parallel to $L M$.) So we have
$$
\frac{L N}{C T}=\frac{L M}{C D}=\frac{A K}{C D}=\frac{C K}{C D}=2
$$
as required.
## NUMBER THEORY
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a right-angled triangle with $\hat{A}=90^{\circ}$. Let $K$ be the midpoint of $B C$, and let $A K L M$ be a parallelogram with centre $C$. Let $T$ be the intersection of the line $A C$ and the perpendicular bisector of $B M$. Let $\omega_{1}$ be the circle with centre $C$ and radius $C A$ and let $\omega_{2}$ be the circle with centre $T$ and radius $T B$. Prove that one of the points of intersection of $\omega_{1}$ and $\omega_{2}$ is on the line $L M$.
|
Let $M^{\prime}$ be the symmetric point of $M$ with respect to $T$. Observe that $T$ is equidistant from $B$ and $M$, therefore $M$ belongs on $\omega_{2}$ and $M^{\prime} M$ is a diameter of $\omega_{2}$. It suffices to prove that $M^{\prime} A$ is perpendicular to $L M$, or equivalently, to $A K$. To see this, let $S$ be the point of intersection of $M^{\prime} A$ with $L M$. We will then have $\angle M^{\prime} S M=90^{\circ}$ which shows that $S$ belongs on $\omega_{2}$ as $M^{\prime} M$ is a diameter of $\omega_{2}$. We also have that $S$ belongs on $\omega_{1}$ as $A L$ is diameter of $\omega_{1}$.
Since $T$ and $C$ are the midpoints of $M^{\prime} M$ and $K M$ respectively, then $T C$ is parallel to $M^{\prime} K$ and so $M^{\prime} K$ is perpendicular to $A B$. Since $K A=K B$, then $K M^{\prime}$ is the perpendicular bisector of $A B$. But then the triangles $K B M^{\prime}$ and $K A M^{\prime}$ are equal, showing that $\angle M^{\prime} A K=\angle M^{\prime} B K=\angle M^{\prime} B M=90^{\circ}$ as required.

Alternative Solution by Proposers. Since $C A=C L$, then $L$ belongs on $\omega_{1}$. Let $S$ be the other point of intersection of $\omega_{1}$ with the line $L M$. We need to show that $S$ belongs on $\omega_{2}$. Since $T B=T M$ ( $T$ is on the perpendicular bisector of $B M$ ) it is enough to show that $T S=T M$.
Let $N, T^{\prime}$ be points on the lines $A L$ and $L M$ respectively, such that $M N \perp L M$ and $T T^{\prime} \perp L M$. It is enough to prove that $T^{\prime}$ is the midpoint of $S M$. Since $A L$ is diameter of $\omega_{1}$ we have that $A S \perp L S$. Thus, it is enough to show that $T$ is the midpoint of $A N$. We have
$$
A T=\frac{A N}{2} \Leftrightarrow A C-C T=\frac{A L-L N}{2} \Leftrightarrow 2 A C-2 C T=A L-L N \Leftrightarrow L N=2 C T
$$
as $A L=2 A C$. So it suffices to prove that $L N=2 C T$.
Let $D$ be the midpoint of $B M$. Since $B K=K C=C M$, then $D$ is also the midpont of $K C$. The triangles $L M N$ and $C T D$ are similar since they are right-angled with
$\angle T C D=\angle C A K=\angle M L N$. (AK=KC and $A K$ is parallel to $L M$.) So we have
$$
\frac{L N}{C T}=\frac{L M}{C D}=\frac{A K}{C D}=\frac{C K}{C D}=2
$$
as required.
## NUMBER THEORY
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nG7.",
"solution_match": "\nSolution."
}
|
95d2732c-1fd7-574e-89df-a0f035e30660
| 606,122
|
Viktor and Natalia bought 2020 buckets of ice-cream and want to organize a degustation schedule with 2020 rounds such that:
- In every round, each one of them tries 1 ice-cream, and those 2 ice-creams tried in a single round are different from each other.
- At the end of the 2020 rounds, each one of them has tried each ice-cream exactly once.
We will call a degustation schedule fair if the number of ice-creams that were tried by Viktor before Natalia is equal to the number of ice creams tried by Natalia before Viktor.
Prove that the number of fair schedules is strictly larger than $2020!\left(2^{1010}+(1010!)^{2}\right)$.
|
If we fix the order in which Natalia tries the ice-creams, we may consider 2 types of fair schedules:
1) Her last 1010 ice-creams get assigned as Viktor's first 1010 ice-creams, and vice versa: Viktor's first 1010 ice-creams are assigned as Natalia's last 1010 ice-creams. This generates (1010!) $)^{2}$ distinct fair schedules by permuting the ice-creams within each group.
2) We divide all ice-creams into disjoint groups of 4 , and in each group we swap the first 2 ice-creams with the last 2 , which gives us $\left((2!)^{2}\right)^{504}=2^{1010}$ distinct schedules.
Now, to make the inequality strict, we consider 1 more schedule like 2 ), but with groups of 2 ice-creams instead of 4 .
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Viktor and Natalia bought 2020 buckets of ice-cream and want to organize a degustation schedule with 2020 rounds such that:
- In every round, each one of them tries 1 ice-cream, and those 2 ice-creams tried in a single round are different from each other.
- At the end of the 2020 rounds, each one of them has tried each ice-cream exactly once.
We will call a degustation schedule fair if the number of ice-creams that were tried by Viktor before Natalia is equal to the number of ice creams tried by Natalia before Viktor.
Prove that the number of fair schedules is strictly larger than $2020!\left(2^{1010}+(1010!)^{2}\right)$.
|
If we fix the order in which Natalia tries the ice-creams, we may consider 2 types of fair schedules:
1) Her last 1010 ice-creams get assigned as Viktor's first 1010 ice-creams, and vice versa: Viktor's first 1010 ice-creams are assigned as Natalia's last 1010 ice-creams. This generates (1010!) $)^{2}$ distinct fair schedules by permuting the ice-creams within each group.
2) We divide all ice-creams into disjoint groups of 4 , and in each group we swap the first 2 ice-creams with the last 2 , which gives us $\left((2!)^{2}\right)^{504}=2^{1010}$ distinct schedules.
Now, to make the inequality strict, we consider 1 more schedule like 2 ), but with groups of 2 ice-creams instead of 4 .
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2020.jsonl",
"problem_match": "\nC 2.",
"solution_match": "\nSolution."
}
|
65f8f715-cece-5f11-8366-e57615e0b989
| 604,184
|
Problem: Let $\triangle A B C$ be a right-angled triangle with $\angle B A C=90^{\circ}$, and let $E$ be the foot of the perpendicular from $A$ on $B C$. Let $Z \neq A$ be a point on the line $A B$ with $A B=B Z$. Let (c), $\left(c_{1}\right)$ be the circmucircles of the triangles $\triangle A E Z$ and $\triangle B E Z$, respectively. Let ( $c_{2}$ ) be an arbitrary circle passing through the points $A$ and $E$. Suppose $\left(c_{1}\right)$ meets the line $C Z$ again at the point $F$, and meets $\left(c_{2}\right)$ again at the point $N$. If $P$ is the other point of intesection of $\left(c_{2}\right)$ with $A F$, prove that the points $N, B, P$ are collinear.
|
Since the triangles $\triangle A E B$ and $\triangle C A B$ are similar, then
$$
\frac{A B}{E B}=\frac{C B}{A B}
$$
Since $A B=B Z$ we get
$$
\frac{B Z}{E B}=\frac{C B}{B Z}
$$
from which it follows that the triangles $\triangle Z B E$ and $\triangle C B Z$ are also similar. Since $F E B Z$ is cyclic,
then $\angle B E Z=\angle B F Z$. So by the similarity of triangles $\triangle Z B E$ and $\triangle C B Z$ we get
$$
\angle B F Z=\angle B E Z=\angle B Z C=\angle B Z F
$$
and therefore the triangle $\triangle B F Z$ is isosceles. Since $B F=B Z=A B$, then the triangle $\triangle A F Z$ is right-angled with $\angle A F Z=90^{\circ}$.
It now follows that the points $A, E, F, C$ are concyclic. Since $A, P, E, N$ are also concyclic, then
$$
\angle E N P=\angle E A P=\angle E A F=\angle E C F=\angle B C Z=\angle B Z E,
$$
where in the last equality we used again the similarity of the triangles $\triangle Z B E$ and $\triangle C B Z$. Since $N, B, E, Z$ are concyclic, then $\angle E N P=\angle B Z E=\angle E N B$, from which it follows that the points $N, B, P$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Problem: Let $\triangle A B C$ be a right-angled triangle with $\angle B A C=90^{\circ}$, and let $E$ be the foot of the perpendicular from $A$ on $B C$. Let $Z \neq A$ be a point on the line $A B$ with $A B=B Z$. Let (c), $\left(c_{1}\right)$ be the circmucircles of the triangles $\triangle A E Z$ and $\triangle B E Z$, respectively. Let ( $c_{2}$ ) be an arbitrary circle passing through the points $A$ and $E$. Suppose $\left(c_{1}\right)$ meets the line $C Z$ again at the point $F$, and meets $\left(c_{2}\right)$ again at the point $N$. If $P$ is the other point of intesection of $\left(c_{2}\right)$ with $A F$, prove that the points $N, B, P$ are collinear.
|
Since the triangles $\triangle A E B$ and $\triangle C A B$ are similar, then
$$
\frac{A B}{E B}=\frac{C B}{A B}
$$
Since $A B=B Z$ we get
$$
\frac{B Z}{E B}=\frac{C B}{B Z}
$$
from which it follows that the triangles $\triangle Z B E$ and $\triangle C B Z$ are also similar. Since $F E B Z$ is cyclic,
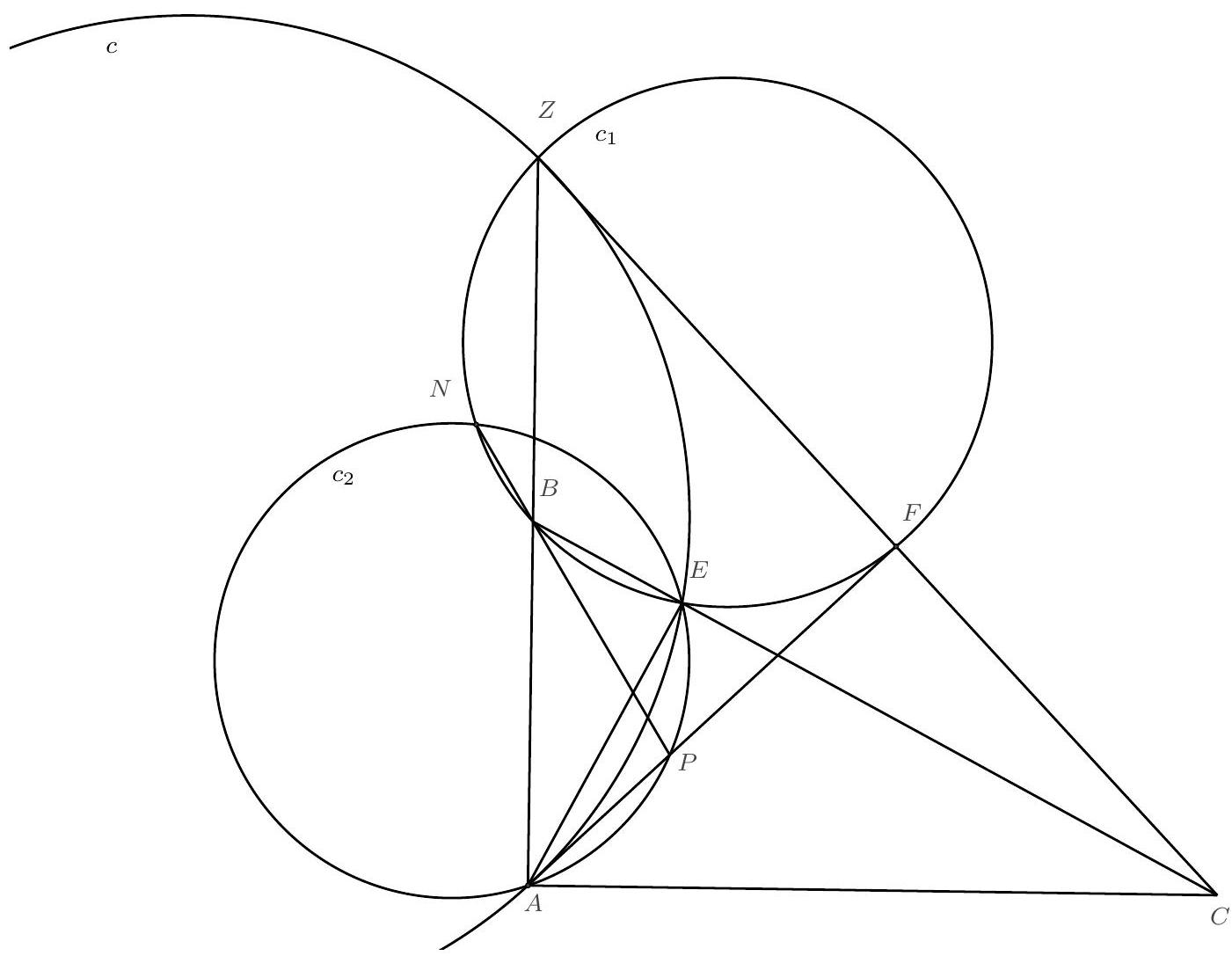
then $\angle B E Z=\angle B F Z$. So by the similarity of triangles $\triangle Z B E$ and $\triangle C B Z$ we get
$$
\angle B F Z=\angle B E Z=\angle B Z C=\angle B Z F
$$
and therefore the triangle $\triangle B F Z$ is isosceles. Since $B F=B Z=A B$, then the triangle $\triangle A F Z$ is right-angled with $\angle A F Z=90^{\circ}$.
It now follows that the points $A, E, F, C$ are concyclic. Since $A, P, E, N$ are also concyclic, then
$$
\angle E N P=\angle E A P=\angle E A F=\angle E C F=\angle B C Z=\angle B Z E,
$$
where in the last equality we used again the similarity of the triangles $\triangle Z B E$ and $\triangle C B Z$. Since $N, B, E, Z$ are concyclic, then $\angle E N P=\angle B Z E=\angle E N B$, from which it follows that the points $N, B, P$ are collinear.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2020.jsonl",
"problem_match": "\nG 2.",
"solution_match": "\nSolution."
}
|
60974c8c-fca3-5d43-96bb-83abb7c925d6
| 604,253
|
Let $\triangle A B C$ be a right-angled triangle with $\angle B A C=90^{\circ}$ and let $E$ be the foot of the perpendicular from $A$ on $B C$. Let $Z \neq A$ be a point on the line $A B$ with $A B=B Z$. Let (c) be the circumcircle of the triangle $\triangle A E Z$. Let $D$ be the second point of intersection of $(c)$ with $Z C$ and let $F$ be the antidiametric point of $D$ with respect to $(c)$. Let $P$ be the point of intersection of the lines $F E$ and $C Z$. If the tangent to $(c)$ at $Z$ meets $P A$ at $T$, prove that the points $T, E, B, Z$ are concyclic.
|
We will first show that $P A$ is tangent to $(c)$ at $A$.
Since $E, D, Z, A$ are concyclic, then $\angle E D C=\angle E A Z=\angle E A B$. Since also the triangles $\triangle A B C$ and $\triangle E B A$ are similar, then $\angle E A B=\angle B C A$, therefore $\angle E D C=\angle B C A$.
Since $\angle F E D=90^{\circ}$, then $\angle P E D=90^{\circ}$ and so
$$
\angle E P D=90^{\circ}-\angle E D C=90^{\circ}-\angle B C A=\angle E A C
$$
Therefore the points $E, A, C, P$ are concyclic. It follows that $\angle C P A=90^{\circ}$ and therefore the triangle $\angle P A Z$ is right-angled. Since also $B$ is the midpoint of $A Z$, then $P B=A B=B Z$ and so $\angle Z P B=$ $\angle P Z B$.
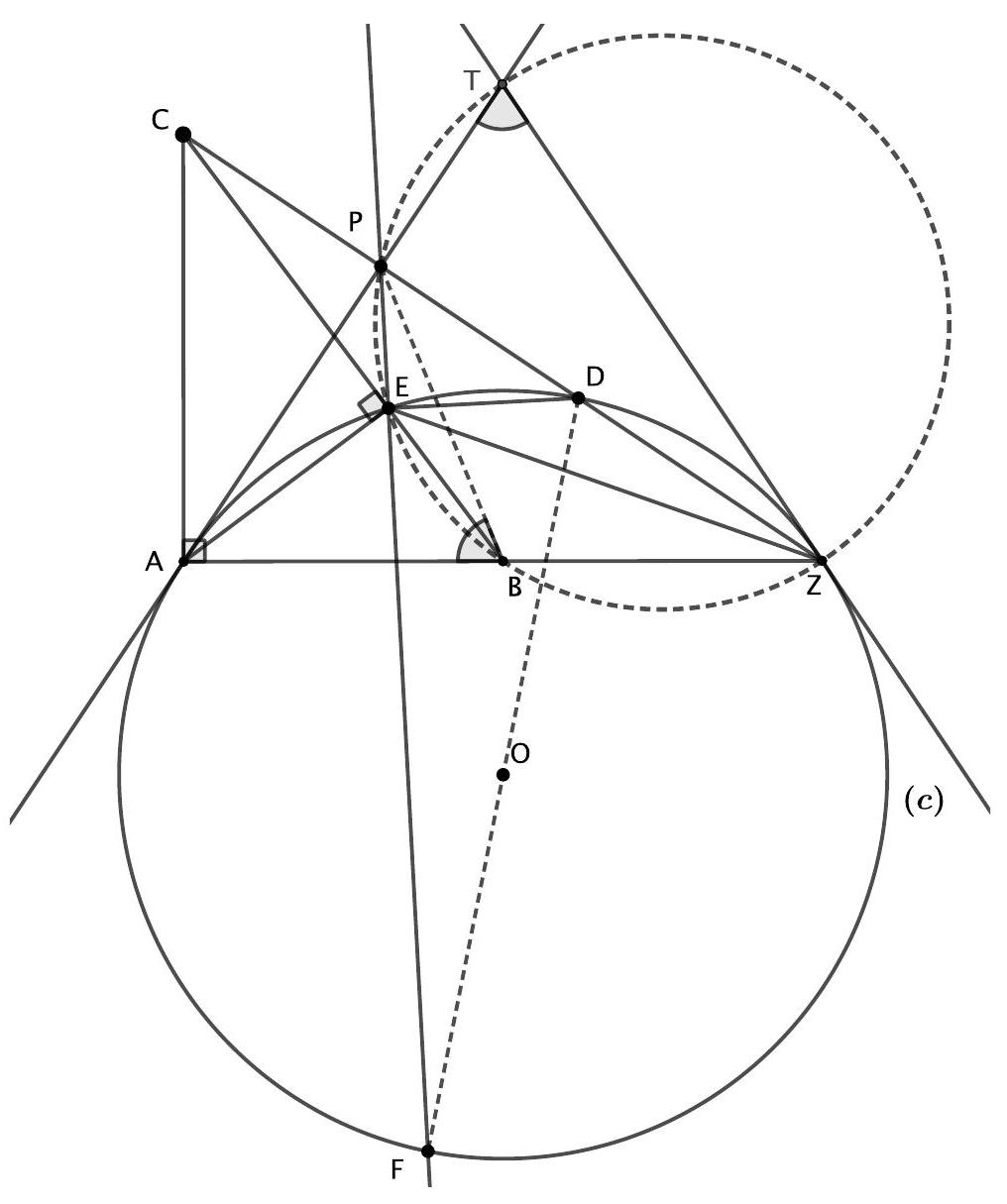
Furthermore, $\angle E P D=\angle E A C=\angle C B A=\angle E B A$ from which it follows that the points $P, E, B, Z$ are also concyclic.
Now observe that
$$
\angle P A E=\angle P C E=\angle Z P B-\angle P B E=\angle P Z B-\angle P Z E=\angle E Z B
$$
Therefore $P A$ is tangent to $(c)$ at $A$ as claimed.
It now follows that $T A=T Z$. Therefore
$$
\begin{aligned}
\angle P T Z & =180^{\circ}-2(\angle T A B)=180^{\circ}-2(\angle P A E+\angle E A B)=180^{\circ}-2(\angle E C P+\angle A C B) \\
& =180^{\circ}-2\left(90^{\circ}-\angle P Z B\right)=2(\angle P Z B)=\angle P Z B+\angle B P Z=\angle P B A .
\end{aligned}
$$
Thus $T, P, B, Z$ are concyclic, and since $P, E, B, Z$ are also concyclic then $T, E, B, Z$ are concyclic as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\triangle A B C$ be a right-angled triangle with $\angle B A C=90^{\circ}$ and let $E$ be the foot of the perpendicular from $A$ on $B C$. Let $Z \neq A$ be a point on the line $A B$ with $A B=B Z$. Let (c) be the circumcircle of the triangle $\triangle A E Z$. Let $D$ be the second point of intersection of $(c)$ with $Z C$ and let $F$ be the antidiametric point of $D$ with respect to $(c)$. Let $P$ be the point of intersection of the lines $F E$ and $C Z$. If the tangent to $(c)$ at $Z$ meets $P A$ at $T$, prove that the points $T, E, B, Z$ are concyclic.
|
We will first show that $P A$ is tangent to $(c)$ at $A$.
Since $E, D, Z, A$ are concyclic, then $\angle E D C=\angle E A Z=\angle E A B$. Since also the triangles $\triangle A B C$ and $\triangle E B A$ are similar, then $\angle E A B=\angle B C A$, therefore $\angle E D C=\angle B C A$.
Since $\angle F E D=90^{\circ}$, then $\angle P E D=90^{\circ}$ and so
$$
\angle E P D=90^{\circ}-\angle E D C=90^{\circ}-\angle B C A=\angle E A C
$$
Therefore the points $E, A, C, P$ are concyclic. It follows that $\angle C P A=90^{\circ}$ and therefore the triangle $\angle P A Z$ is right-angled. Since also $B$ is the midpoint of $A Z$, then $P B=A B=B Z$ and so $\angle Z P B=$ $\angle P Z B$.

Furthermore, $\angle E P D=\angle E A C=\angle C B A=\angle E B A$ from which it follows that the points $P, E, B, Z$ are also concyclic.
Now observe that
$$
\angle P A E=\angle P C E=\angle Z P B-\angle P B E=\angle P Z B-\angle P Z E=\angle E Z B
$$
Therefore $P A$ is tangent to $(c)$ at $A$ as claimed.
It now follows that $T A=T Z$. Therefore
$$
\begin{aligned}
\angle P T Z & =180^{\circ}-2(\angle T A B)=180^{\circ}-2(\angle P A E+\angle E A B)=180^{\circ}-2(\angle E C P+\angle A C B) \\
& =180^{\circ}-2\left(90^{\circ}-\angle P Z B\right)=2(\angle P Z B)=\angle P Z B+\angle B P Z=\angle P B A .
\end{aligned}
$$
Thus $T, P, B, Z$ are concyclic, and since $P, E, B, Z$ are also concyclic then $T, E, B, Z$ are concyclic as required.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2020.jsonl",
"problem_match": "\nG 3.",
"solution_match": "\nSolution."
}
|
2fd6f8f6-5dba-5346-97a0-b145de618bd3
| 604,267
|
The positive integer $k$ and the set $A$ of different integers from 1 to $3 k$ inclusive are such that there are no distinct $a, b, c$ in $A$ satisfying $2 b=a+c$. The numbers from $A$ in the interval $[1, k]$ will be called small; those in $[k+1,2 k]$ - medium and those in $[2 k+1,3 k]$ - large. Is it always true that there are no positive integers $x$ and $d$ such that if $x, x+d$ and $x+2 d$ are divided by $3 k$ then the remainders belong to $A$ and those of $x$ and $x+d$ are different and are:
a) small?
b) medium?
c) large?
(In this problem we assume that if a multiple of $3 k$ is divided by $3 k$ then the remainder is $3 k$ rather than 0. )
|
Solution. A counterexample for a) is $k=3, A=\{1,2,9\}, x=2$ and $d=8$. A counterexample for c) is $k=3, A=\{1,8,9\}, x=8$ and $d=1$.
We will prove that b) is true.
Suppose the contrary and let $x, d$ have the above properties. We can assume $0<d<3 k, 0<x \leq 3 k$ (since for $d=3 k$ the remainders for $x$ and $x+d$ are equal). Hence $0<x+d<6 k$ and there are two cases:
- If $x+d>3 k$, then since the remainder for $x+d$ is medium we have $4 k<x+d \leq 5 k$. This means that the remainder of $x+d$ when it is divided by $3 k$ is
$$
x+d-3 k
$$
Since $x$ is medium we have $x \leq 2 k$ so $d=(x+d)-x>2 k$. Therefore $6 k=4 k+2 k<(x+d)+d<$ $8 k$. This means that the remainder of $x+2 d$ when it is divided by $3 k$ is
$$
x+2 d-6 k \text {. }
$$
Thus the remainders $(x+2 d-6 k),(x+d-3 k)$ and $x$ are in $[1,3 k]$, they belong to $A$ and
$$
2(x+d-3 k)=(x+2 d-6 k)+x
$$
a contradiction.
- If $x+d \leq 3 k$ then as $x+d$ is medium we have $k<x+d \leq 2 k$. From the limitations on $x$, we have $x>k$ so $d=(x+d)-x<k$. Hence $0 \leq x+2 d=(x+d)+d<3 k$. Thus the remainders $x, x+d$ and $x+2 d$ are in $A$ and
$$
2(x+d)=(x+2 d)+x
$$
a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
The positive integer $k$ and the set $A$ of different integers from 1 to $3 k$ inclusive are such that there are no distinct $a, b, c$ in $A$ satisfying $2 b=a+c$. The numbers from $A$ in the interval $[1, k]$ will be called small; those in $[k+1,2 k]$ - medium and those in $[2 k+1,3 k]$ - large. Is it always true that there are no positive integers $x$ and $d$ such that if $x, x+d$ and $x+2 d$ are divided by $3 k$ then the remainders belong to $A$ and those of $x$ and $x+d$ are different and are:
a) small?
b) medium?
c) large?
(In this problem we assume that if a multiple of $3 k$ is divided by $3 k$ then the remainder is $3 k$ rather than 0. )
|
Solution. A counterexample for a) is $k=3, A=\{1,2,9\}, x=2$ and $d=8$. A counterexample for c) is $k=3, A=\{1,8,9\}, x=8$ and $d=1$.
We will prove that b) is true.
Suppose the contrary and let $x, d$ have the above properties. We can assume $0<d<3 k, 0<x \leq 3 k$ (since for $d=3 k$ the remainders for $x$ and $x+d$ are equal). Hence $0<x+d<6 k$ and there are two cases:
- If $x+d>3 k$, then since the remainder for $x+d$ is medium we have $4 k<x+d \leq 5 k$. This means that the remainder of $x+d$ when it is divided by $3 k$ is
$$
x+d-3 k
$$
Since $x$ is medium we have $x \leq 2 k$ so $d=(x+d)-x>2 k$. Therefore $6 k=4 k+2 k<(x+d)+d<$ $8 k$. This means that the remainder of $x+2 d$ when it is divided by $3 k$ is
$$
x+2 d-6 k \text {. }
$$
Thus the remainders $(x+2 d-6 k),(x+d-3 k)$ and $x$ are in $[1,3 k]$, they belong to $A$ and
$$
2(x+d-3 k)=(x+2 d-6 k)+x
$$
a contradiction.
- If $x+d \leq 3 k$ then as $x+d$ is medium we have $k<x+d \leq 2 k$. From the limitations on $x$, we have $x>k$ so $d=(x+d)-x<k$. Hence $0 \leq x+2 d=(x+d)+d<3 k$. Thus the remainders $x, x+d$ and $x+2 d$ are in $A$ and
$$
2(x+d)=(x+2 d)+x
$$
a contradiction.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2020.jsonl",
"problem_match": "\nNT 5.",
"solution_match": "## Solution."
}
|
bd91f50b-4b04-5353-a6cf-1aca9f6b1e89
| 604,323
|
Prove that there doesn't exist any prime $p$ such that every power of $p$ is a palindrome (palindrome is a number that is read the same from the left as it is from the right; in particular, number that ends in one or more zeros cannot be a palindrome).
|
Note that by criterion for divisibility by 11 and the definition of a palindrome we have that every palindrome that has even number of digits is divisible by 11 .
Since $11^{5}=161051$ is not a palindrome and since 11 cannot divide $p^{k}$ for any prime other than 11 we are now left to prove that no prime whose all powers have odd number of digits exists.
Assume the contrary. It means that the difference between the numbers of digits of $p^{m}$ and $p^{m+1}$ is even number. We will prove that for every natural $m$, the difference is the same even number.
If we assume not, that means that the difference for some $m_{1}$ has at least 2 digits more than the difference for some $m_{2}$. We will prove that this is impossible.
Let $p^{m_{1}}=10^{t_{1}} \cdot a_{1}, p^{m_{2}}=10^{t_{2}} \cdot a_{2}$ and $p=10^{h} \cdot z$, where
$$
1<a_{1}, a_{2}, z<10
$$
This implies that
$$
1<a_{1} \cdot z, a_{2} \cdot z<100
$$
which further implies that multiplying these powers of $p$ by $p$ can increase their number of digits by either $h$ or $h+1$.
This is a contradiction. Call the difference between numbers of digits of consecutive powers $d$. Number $p$ clearly cannot be equal to $10^{d}$ for $d \geq 1$ because 10 is divisible by two primes, but for $d=0$, we would have that 1 is a prime which is not true.
Case 1. $p>10^{d}$. Let $p=10^{d} \cdot a$, for some real number $a$ greater than 1. (1)
From the definition of $d$ we also see that $a$ is smaller than 10. (2)
From (1) we see that powering $a$ gives us arbitrarily large numbers and from (2) we conclude that there is some natural power of $a$, call it $b$, greater than 1 , such that
$$
10<a^{b}<100
$$
It is clear that $p^{b}$ has exactly $(b-1) d+1$ digits more than $p$ has, which is an odd number, but sum of even numbers is even.
Case 2. $p<10^{d}$. Let $p=\frac{10^{d}}{a}$, for some real number $a$ greater than 1. (1) From the definition of $d$ we also see that $a$ is smaller than 10. (2)
From (1) we see that powering $a$ gives us arbitrarily large numbers and from (2) we conclude that there is some natural power of $a$, call it $b$, greater than 1 , such that
$$
10<a^{b}<100
$$
It is clear that $p^{b}$ has exactly $(b-1) d-1$ digits more than $p$ has, which is an odd number, but sum of even numbers is even.
We have now arrived at the desired contradiction for both cases and have thus finished the proof.
Alternative solution. Note that the sequence $\left\{p^{n}\right\}$ is periodic $(\bmod 10)$. Let the period be $d$. Also, let $p^{d}=g$.
Since all powers of $p$ are palindromes, all powers of $g$ are as well. Since $\left\{g^{n}\right\}$ is constant (mod 10), the leftmost digit of each power of $g$ is equal to some $f$.
We will prove that the difference between numbers of digits of $g^{m}$ and $g^{m+1}$ is equal to some $r$ for every natural number $m$.
This is true due to size reasons. Namely, to add exactly $k$ digits, and yet to have the same leftmost digit, we need to multiply the number by at least $5 \cdot 10^{k-1}$ (if $k=0$ then it's 1 ) and by at most $2 \cdot 10^{k}$ (values depend on the leftmost digit, it can easily be seen that leftmost digit being 1 yields the extremal values). Notice that
$$
2 \cdot 10^{k}<5 \cdot 10^{k+1-1}
$$
Since this inequality has clearly shown that the interval of multipliers which add exactly $k$ digits and leave the leftmost digit the same is disjunct from the same kind of interval for $k+1$ digits, which implies that no number can belong to both intervals, we have successfully proven the claim.
Clearly, $g$ cannot be equal to $10^{r}$ for $r \geq 1$ because a palindrome cannot be divisible by 10 , but for $r=0$ we again cannot have the equality because 1 is not a natural power of a prime.
Case 1. $g>10^{r}$. Let $g=10^{r} \cdot a$, where $a$ is a real number, $10>a>1$. (1) Here, $a$ is less than 10 because if it was not, multiplying by $g$ would add at least $r+1$ digits, which is impossible.
From (1) we see that powering $a$ gives us arbitrarily large numbers and that there is some natural power of $a$, call it $b$, greater than 1 , such that
$$
10<a^{b}<100
$$
Pick smallest such $b$.
Now we easily see that the difference between numbers of digits of numbers $g^{b-1}$ and $g^{b}$ is exactly $r+1$.
Case 2. $g<10^{r}$. Let $g=\frac{10^{r}}{a}$, where $a$ is a real number, $10>a>1$. (2) Here, $a$ is less than 10 because if it was not, multiplying by $g$ would add at most $r-1$ digits, which is impossible.
From (2) we see that powering $a$ gives us arbitrarily large numbers and that there is some natural power of $a$, call it $b$, greater than 1 , such that
$$
10<a^{b}<100
$$
Pick smallest such $b$.
Now we easily see that the difference between numbers of digits of numbers $g^{b-1}$ and $g^{b}$ is exactly $r-1$.
We have arrived at the desired contradiction for both cases and have thus finished the proof.
Comment. In both solutions, after introducing $a$, there are multiple ways to finish the problem. In particular, solution 1 and solution 2 could be finished in the same way, but distinct finishes were purposely offered. Third, maybe even the most intuitive finishing argument, could be using non-exact size arguments; namely, just the fact that powers of $a$ grow arbitrarily large is enough to reach the contradiction.
Alternative problem. Find all positive integers $n$ such that every power of $n$ is a palindrome (palindrome is a number that is read the same from the left as it is from the right; in particular, number that ends in one or more zeros cannot be a palindrome).
Suggested difficulty for this problem is hard. Noting why solution 2 doesn't work for $n=1$ (because
$g$ now could be equal to 1 ) and saying that $n=1$ actually works are all necessary modifications to solution 2 to make it work for the alternative problem as well.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there doesn't exist any prime $p$ such that every power of $p$ is a palindrome (palindrome is a number that is read the same from the left as it is from the right; in particular, number that ends in one or more zeros cannot be a palindrome).
|
Note that by criterion for divisibility by 11 and the definition of a palindrome we have that every palindrome that has even number of digits is divisible by 11 .
Since $11^{5}=161051$ is not a palindrome and since 11 cannot divide $p^{k}$ for any prime other than 11 we are now left to prove that no prime whose all powers have odd number of digits exists.
Assume the contrary. It means that the difference between the numbers of digits of $p^{m}$ and $p^{m+1}$ is even number. We will prove that for every natural $m$, the difference is the same even number.
If we assume not, that means that the difference for some $m_{1}$ has at least 2 digits more than the difference for some $m_{2}$. We will prove that this is impossible.
Let $p^{m_{1}}=10^{t_{1}} \cdot a_{1}, p^{m_{2}}=10^{t_{2}} \cdot a_{2}$ and $p=10^{h} \cdot z$, where
$$
1<a_{1}, a_{2}, z<10
$$
This implies that
$$
1<a_{1} \cdot z, a_{2} \cdot z<100
$$
which further implies that multiplying these powers of $p$ by $p$ can increase their number of digits by either $h$ or $h+1$.
This is a contradiction. Call the difference between numbers of digits of consecutive powers $d$. Number $p$ clearly cannot be equal to $10^{d}$ for $d \geq 1$ because 10 is divisible by two primes, but for $d=0$, we would have that 1 is a prime which is not true.
Case 1. $p>10^{d}$. Let $p=10^{d} \cdot a$, for some real number $a$ greater than 1. (1)
From the definition of $d$ we also see that $a$ is smaller than 10. (2)
From (1) we see that powering $a$ gives us arbitrarily large numbers and from (2) we conclude that there is some natural power of $a$, call it $b$, greater than 1 , such that
$$
10<a^{b}<100
$$
It is clear that $p^{b}$ has exactly $(b-1) d+1$ digits more than $p$ has, which is an odd number, but sum of even numbers is even.
Case 2. $p<10^{d}$. Let $p=\frac{10^{d}}{a}$, for some real number $a$ greater than 1. (1) From the definition of $d$ we also see that $a$ is smaller than 10. (2)
From (1) we see that powering $a$ gives us arbitrarily large numbers and from (2) we conclude that there is some natural power of $a$, call it $b$, greater than 1 , such that
$$
10<a^{b}<100
$$
It is clear that $p^{b}$ has exactly $(b-1) d-1$ digits more than $p$ has, which is an odd number, but sum of even numbers is even.
We have now arrived at the desired contradiction for both cases and have thus finished the proof.
Alternative solution. Note that the sequence $\left\{p^{n}\right\}$ is periodic $(\bmod 10)$. Let the period be $d$. Also, let $p^{d}=g$.
Since all powers of $p$ are palindromes, all powers of $g$ are as well. Since $\left\{g^{n}\right\}$ is constant (mod 10), the leftmost digit of each power of $g$ is equal to some $f$.
We will prove that the difference between numbers of digits of $g^{m}$ and $g^{m+1}$ is equal to some $r$ for every natural number $m$.
This is true due to size reasons. Namely, to add exactly $k$ digits, and yet to have the same leftmost digit, we need to multiply the number by at least $5 \cdot 10^{k-1}$ (if $k=0$ then it's 1 ) and by at most $2 \cdot 10^{k}$ (values depend on the leftmost digit, it can easily be seen that leftmost digit being 1 yields the extremal values). Notice that
$$
2 \cdot 10^{k}<5 \cdot 10^{k+1-1}
$$
Since this inequality has clearly shown that the interval of multipliers which add exactly $k$ digits and leave the leftmost digit the same is disjunct from the same kind of interval for $k+1$ digits, which implies that no number can belong to both intervals, we have successfully proven the claim.
Clearly, $g$ cannot be equal to $10^{r}$ for $r \geq 1$ because a palindrome cannot be divisible by 10 , but for $r=0$ we again cannot have the equality because 1 is not a natural power of a prime.
Case 1. $g>10^{r}$. Let $g=10^{r} \cdot a$, where $a$ is a real number, $10>a>1$. (1) Here, $a$ is less than 10 because if it was not, multiplying by $g$ would add at least $r+1$ digits, which is impossible.
From (1) we see that powering $a$ gives us arbitrarily large numbers and that there is some natural power of $a$, call it $b$, greater than 1 , such that
$$
10<a^{b}<100
$$
Pick smallest such $b$.
Now we easily see that the difference between numbers of digits of numbers $g^{b-1}$ and $g^{b}$ is exactly $r+1$.
Case 2. $g<10^{r}$. Let $g=\frac{10^{r}}{a}$, where $a$ is a real number, $10>a>1$. (2) Here, $a$ is less than 10 because if it was not, multiplying by $g$ would add at most $r-1$ digits, which is impossible.
From (2) we see that powering $a$ gives us arbitrarily large numbers and that there is some natural power of $a$, call it $b$, greater than 1 , such that
$$
10<a^{b}<100
$$
Pick smallest such $b$.
Now we easily see that the difference between numbers of digits of numbers $g^{b-1}$ and $g^{b}$ is exactly $r-1$.
We have arrived at the desired contradiction for both cases and have thus finished the proof.
Comment. In both solutions, after introducing $a$, there are multiple ways to finish the problem. In particular, solution 1 and solution 2 could be finished in the same way, but distinct finishes were purposely offered. Third, maybe even the most intuitive finishing argument, could be using non-exact size arguments; namely, just the fact that powers of $a$ grow arbitrarily large is enough to reach the contradiction.
Alternative problem. Find all positive integers $n$ such that every power of $n$ is a palindrome (palindrome is a number that is read the same from the left as it is from the right; in particular, number that ends in one or more zeros cannot be a palindrome).
Suggested difficulty for this problem is hard. Noting why solution 2 doesn't work for $n=1$ (because
$g$ now could be equal to 1 ) and saying that $n=1$ actually works are all necessary modifications to solution 2 to make it work for the alternative problem as well.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2020.jsonl",
"problem_match": "\nNT 7.",
"solution_match": "\nSolution."
}
|
35920816-27ce-5e35-b420-b32f5d545790
| 604,345
|
Let $a, b, c$ be positive real numbers such that abc $=1$. Show that
$$
\frac{1}{a^{3}+b c}+\frac{1}{b^{3}+c a}+\frac{1}{c^{3}+a b} \leq \frac{(a b+b c+c a)^{2}}{6}
$$
so
|
By the AM-GM inequality we have $a^{3}+b c \geq 2 \sqrt{a^{3} b c}=2 \sqrt{a^{2}(a b c)}=2 a$ and
$$
\frac{1}{a^{3}+b c} \leq \frac{1}{2 a}
$$
Similarly; $\frac{1}{b^{3}+c a} \leq \frac{1}{2 b} \cdot \frac{1}{c^{3}+a b} \leq \frac{1}{2 c}$ and then
$$
\frac{1}{a^{3}+b c}+\frac{1}{b^{3}+c a}+\frac{1}{c^{3}+a b} \leq \frac{1}{2 a}+\frac{1}{2 b}+\frac{1}{2 c}=\frac{1}{2} \frac{a b+b c+c a}{a b c} \leq \frac{(a b+b c+c a)^{2}}{6}
$$
Therefore it is enongil to prove $\frac{(a h+b c+c a)^{2}}{6} \leq \frac{(a b+b c+c a)^{2}}{6}$. This mequalits is trivially shomn to be equivalent to $3 \leq a b+b c+c a$ which is true because of the AM-GM inequalit: $3=\sqrt[3]{(a b c)^{2}} \leq a b+b c+c a$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that abc $=1$. Show that
$$
\frac{1}{a^{3}+b c}+\frac{1}{b^{3}+c a}+\frac{1}{c^{3}+a b} \leq \frac{(a b+b c+c a)^{2}}{6}
$$
so
|
By the AM-GM inequality we have $a^{3}+b c \geq 2 \sqrt{a^{3} b c}=2 \sqrt{a^{2}(a b c)}=2 a$ and
$$
\frac{1}{a^{3}+b c} \leq \frac{1}{2 a}
$$
Similarly; $\frac{1}{b^{3}+c a} \leq \frac{1}{2 b} \cdot \frac{1}{c^{3}+a b} \leq \frac{1}{2 c}$ and then
$$
\frac{1}{a^{3}+b c}+\frac{1}{b^{3}+c a}+\frac{1}{c^{3}+a b} \leq \frac{1}{2 a}+\frac{1}{2 b}+\frac{1}{2 c}=\frac{1}{2} \frac{a b+b c+c a}{a b c} \leq \frac{(a b+b c+c a)^{2}}{6}
$$
Therefore it is enongil to prove $\frac{(a h+b c+c a)^{2}}{6} \leq \frac{(a b+b c+c a)^{2}}{6}$. This mequalits is trivially shomn to be equivalent to $3 \leq a b+b c+c a$ which is true because of the AM-GM inequalit: $3=\sqrt[3]{(a b c)^{2}} \leq a b+b c+c a$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2012.jsonl",
"problem_match": "\nA2.",
"solution_match": "\nSolution."
}
|
cc09e359-b763-5d39-a799-f36ac8043a4a
| 604,442
|
Let $a . b$ c ce positue real numbers such that $a+b+c=a^{2}+b^{2}+c^{2}$. Shou that
$$
\frac{a^{2}}{a^{2}+a b}+\frac{b^{2}}{b^{2}+b c}+\frac{c^{2}}{c^{2}+c a} \geq \frac{a+b+c}{2}
$$
|
By the Cauchy-Schwarz inequality it is
$$
\begin{aligned}
& \left(\frac{a^{2}}{a^{2}+a b}+\frac{b^{2}}{b^{2}+b c}+\frac{c^{2}}{c^{2}+c a}\right)\left(\left(a^{2}+a b\right)+\left(b^{2}+b c\right)+\left(c^{2}+c a\right)\right) \geq(a+b+c)^{2} \\
\Rightarrow & \frac{a^{2}}{a^{2}+a b}+\frac{b^{2}}{b^{2}+b c}+\frac{c^{2}}{c^{2}+c a} \geq \frac{(a+b+c)^{2}}{a^{2}+b^{2}+c^{2}+a b+b c+c a}
\end{aligned}
$$
So in is enough to prove $\frac{(a+b+c)^{2}}{a^{2}+b^{2}+c^{2}+a b+b c+c a} \geq \frac{a+b+c}{2}$, that is to prove
$$
2(a+b+c) \geq a^{2}+b^{2}+c^{2}+a b+b c+c a
$$
Substituting $a^{2}+b^{2}+c^{2}$ for $a+b+c$ into the left hand side we wish equivalently to prove
$$
a^{2}+b^{2}+c^{2} \geq a b+b c+c a
$$
But the $a^{2}+b^{2} \geq 2 a b, b^{2}+c^{2} \geq 2 b c, c^{2}+a^{2} \geq 2 c a$ which by addition imply the desired inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a . b$ c ce positue real numbers such that $a+b+c=a^{2}+b^{2}+c^{2}$. Shou that
$$
\frac{a^{2}}{a^{2}+a b}+\frac{b^{2}}{b^{2}+b c}+\frac{c^{2}}{c^{2}+c a} \geq \frac{a+b+c}{2}
$$
|
By the Cauchy-Schwarz inequality it is
$$
\begin{aligned}
& \left(\frac{a^{2}}{a^{2}+a b}+\frac{b^{2}}{b^{2}+b c}+\frac{c^{2}}{c^{2}+c a}\right)\left(\left(a^{2}+a b\right)+\left(b^{2}+b c\right)+\left(c^{2}+c a\right)\right) \geq(a+b+c)^{2} \\
\Rightarrow & \frac{a^{2}}{a^{2}+a b}+\frac{b^{2}}{b^{2}+b c}+\frac{c^{2}}{c^{2}+c a} \geq \frac{(a+b+c)^{2}}{a^{2}+b^{2}+c^{2}+a b+b c+c a}
\end{aligned}
$$
So in is enough to prove $\frac{(a+b+c)^{2}}{a^{2}+b^{2}+c^{2}+a b+b c+c a} \geq \frac{a+b+c}{2}$, that is to prove
$$
2(a+b+c) \geq a^{2}+b^{2}+c^{2}+a b+b c+c a
$$
Substituting $a^{2}+b^{2}+c^{2}$ for $a+b+c$ into the left hand side we wish equivalently to prove
$$
a^{2}+b^{2}+c^{2} \geq a b+b c+c a
$$
But the $a^{2}+b^{2} \geq 2 a b, b^{2}+c^{2} \geq 2 b c, c^{2}+a^{2} \geq 2 c a$ which by addition imply the desired inequality.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2012.jsonl",
"problem_match": "\nA3.",
"solution_match": "\nSolution."
}
|
ff7993c8-590f-57a0-934e-c5d3a2618e87
| 604,456
|
MKCD
Let $x, y, z$ be positive real numbers that satisfy the equality $x^{2}+y^{2}+z^{2}=3$. Prove that
$$
\frac{x^{2}+y z}{x^{2}+y z+1}+\frac{y^{2}+z x}{y^{2}+z x+1}+\frac{z^{2}+x y}{z^{2}+x y+1} \leq 2
$$
|
We have
$$
\begin{aligned}
& \frac{x^{2}+y z}{x^{2}+y z+1}+\frac{y^{2}+z x}{y^{2}+z x+1}+\frac{z^{2}+x y}{z^{2}+x y+1} \leq 2 \Leftrightarrow \\
& \frac{x^{2}+y z+1}{x^{2}+y z+1}+\frac{y^{2}+z x+1}{y^{2}+z x+1}+\frac{z^{2}+x y+1}{z^{2}+x y+1} \leq 2+\frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \Leftrightarrow \\
& 3 \leq 2+\frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \Leftrightarrow \\
& 1 \leq \frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \\
& \frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \geq \frac{9}{x^{2}+y z+1+y^{2}+z x+1+z^{2}+x y+1}= \\
& \frac{9}{x^{2}+y^{2}+z^{2}+x y+y z+z x+3} \geq \frac{9}{2 x^{2}+y^{2}+z^{2}+3}=1
\end{aligned}
$$
The first inequality: AM-GM inequality (also can be achieved with Cauchy-BunjakowskiSchwarz inequality). The second inequality: $x y+y z+z x £ x^{2}+y^{2}+z^{2}$ (there are more ways to prove it, AM-GM, full squares etc.)
## GEOMETRY
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
MKCD
Let $x, y, z$ be positive real numbers that satisfy the equality $x^{2}+y^{2}+z^{2}=3$. Prove that
$$
\frac{x^{2}+y z}{x^{2}+y z+1}+\frac{y^{2}+z x}{y^{2}+z x+1}+\frac{z^{2}+x y}{z^{2}+x y+1} \leq 2
$$
|
We have
$$
\begin{aligned}
& \frac{x^{2}+y z}{x^{2}+y z+1}+\frac{y^{2}+z x}{y^{2}+z x+1}+\frac{z^{2}+x y}{z^{2}+x y+1} \leq 2 \Leftrightarrow \\
& \frac{x^{2}+y z+1}{x^{2}+y z+1}+\frac{y^{2}+z x+1}{y^{2}+z x+1}+\frac{z^{2}+x y+1}{z^{2}+x y+1} \leq 2+\frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \Leftrightarrow \\
& 3 \leq 2+\frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \Leftrightarrow \\
& 1 \leq \frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \\
& \frac{1}{x^{2}+y z+1}+\frac{1}{y^{2}+z x+1}+\frac{1}{z^{2}+x y+1} \geq \frac{9}{x^{2}+y z+1+y^{2}+z x+1+z^{2}+x y+1}= \\
& \frac{9}{x^{2}+y^{2}+z^{2}+x y+y z+z x+3} \geq \frac{9}{2 x^{2}+y^{2}+z^{2}+3}=1
\end{aligned}
$$
The first inequality: AM-GM inequality (also can be achieved with Cauchy-BunjakowskiSchwarz inequality). The second inequality: $x y+y z+z x £ x^{2}+y^{2}+z^{2}$ (there are more ways to prove it, AM-GM, full squares etc.)
## GEOMETRY
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2015.jsonl",
"problem_match": "## A5 ",
"solution_match": "## Solution:"
}
|
9db4f18d-06d4-5ab8-b231-bd75e3868238
| 604,728
|
MNE
Around the triangle $A B C$ the circle is circumscribed, and at the vertex $C$ tangent $t$ to this circle is drawn. The line $p$ which is parallel to this tangent intersects the lines $B C$ and $A C$ at the points $D$ and $E$, respectively. Prove that the points $A, B, D, E$ belong to the same circle.
|
Let $O$ be the center of a circumscribed circle $k$ of the triangle $A B C$, and let $F$ and $G$ be the points of intersection of the line $C O$ with the line $p$ and the circle $k$, respectively (see Figure). From $p \| t$ it follows that $p \perp C O$. Furthermore, $\angle A B C=\angle A G C$, because these angles are peripheral over the same chord. The quadrilateral $A G F E$ has two right angles at the vertices $A$ and $F$, and hence, $\angle A E D+\angle A B D=\angle A E F+\angle A G F=180^{\circ}$. Hence, the quadrilateral $A B D E$ is cyclic, as asserted.
Figure
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
MNE
Around the triangle $A B C$ the circle is circumscribed, and at the vertex $C$ tangent $t$ to this circle is drawn. The line $p$ which is parallel to this tangent intersects the lines $B C$ and $A C$ at the points $D$ and $E$, respectively. Prove that the points $A, B, D, E$ belong to the same circle.
|
Let $O$ be the center of a circumscribed circle $k$ of the triangle $A B C$, and let $F$ and $G$ be the points of intersection of the line $C O$ with the line $p$ and the circle $k$, respectively (see Figure). From $p \| t$ it follows that $p \perp C O$. Furthermore, $\angle A B C=\angle A G C$, because these angles are peripheral over the same chord. The quadrilateral $A G F E$ has two right angles at the vertices $A$ and $F$, and hence, $\angle A E D+\angle A B D=\angle A E F+\angle A G F=180^{\circ}$. Hence, the quadrilateral $A B D E$ is cyclic, as asserted.

Figure
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2015.jsonl",
"problem_match": "## G1 ",
"solution_match": "## Solution:"
}
|
eea77bb8-c3a8-5391-aae3-404e7409eb8e
| 604,741
|
MLD
The point $P$ is outside of the circle $\Omega$. Two tangent lines, passing from the point $P$, touch the circle $\Omega$ at the points $A$ and $B$. The median $A M, M \in(B P)$, intersects the circle $\Omega$ at the point $C$ and the line $P C$ intersects again the circle $\Omega$ at the point $D$. Prove that the lines $A D$ and $B P$ are parallel.
|
Since $\angle B A C=\angle B A M=\angle M B C$, we have $\triangle M A B \cong \triangle M B C$.
We obtain $\frac{M A}{M B}=\frac{M B}{M C}=\frac{A B}{B C}$. The equality $\quad M B=M P$ implies $\frac{M A}{M P}=\frac{M P}{M C}$ and $\angle P M C \equiv \angle P M A$ gives the relation $\triangle P M A \cong \triangle C M P$. It follows that $\angle B P D \equiv \angle M P C \equiv \angle M A P \equiv \angle C A P \equiv \angle C D A \equiv \angle P D A$. So, the lines $A D$ and $B P$ are parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
MLD
The point $P$ is outside of the circle $\Omega$. Two tangent lines, passing from the point $P$, touch the circle $\Omega$ at the points $A$ and $B$. The median $A M, M \in(B P)$, intersects the circle $\Omega$ at the point $C$ and the line $P C$ intersects again the circle $\Omega$ at the point $D$. Prove that the lines $A D$ and $B P$ are parallel.
|
Since $\angle B A C=\angle B A M=\angle M B C$, we have $\triangle M A B \cong \triangle M B C$.

We obtain $\frac{M A}{M B}=\frac{M B}{M C}=\frac{A B}{B C}$. The equality $\quad M B=M P$ implies $\frac{M A}{M P}=\frac{M P}{M C}$ and $\angle P M C \equiv \angle P M A$ gives the relation $\triangle P M A \cong \triangle C M P$. It follows that $\angle B P D \equiv \angle M P C \equiv \angle M A P \equiv \angle C A P \equiv \angle C D A \equiv \angle P D A$. So, the lines $A D$ and $B P$ are parallel.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2015.jsonl",
"problem_match": "## G2 ",
"solution_match": "## Solution:"
}
|
af462bac-31fa-5697-9787-dc9628f80ebd
| 604,754
|
GRE
Let $c \equiv c(O, K)$ be a circle with center $O$ and radius $R$ and $A, B$ be two points on it, not belonging to the same diameter. The bisector of the angle $A \hat{B} O$ intersects the circle $c$ at point $C$, the circumcircle of the triangle $A O B$, say ${ }^{c_{1}}$ at point $K$ and the circumcircle of the triangle $A O C$, say ${ }^{c_{2}}$, at point $L$. Prove that the point $K$ is the circumcenter of the triangle $A O C$ and the point $L$ is the incenter of the triangle $A O B$.
|
The segments $O B, O C$ are equal, as radii of the circle ${ }^{c}$. Hence $O B C$ is an isosceles triangle and
$$
\hat{B}_{1}=\hat{C}_{1}=\hat{x}
$$
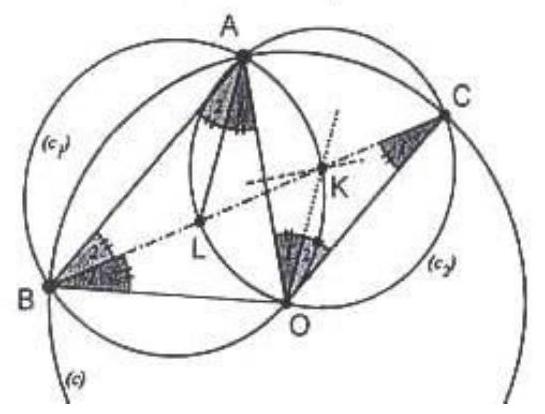
The chord $B C$ is the bisector of the angle $O \hat{B} A$, and hence
$$
\hat{B}_{1}=\hat{B}_{2}=\hat{x}
$$
The angles $\hat{B}_{2}$ and $\hat{O}_{1}$ are inscribed to the same arc $O K$ of the circle ${ }^{c_{1}}$ and hence
$$
\hat{B}_{2}=\hat{\mathrm{O}}_{1}=\hat{x}
$$
The segments $K O, K C$ are equal, as radii of the circle ${ }^{c_{2}}$. Hence the triangle $K O C$ is isosceles and so
$$
\hat{O}_{2}=\hat{C}_{1}=\hat{x}
$$
From equalities $(1),(2),(3)$ we conclude that
$$
\hat{O}_{1}=\hat{O}_{2}=\hat{x}
$$
and so $O K$ is the bisector, and hence perpendicular bisector of the isosceles triangle $O A C$. The point $K$ is the middle of the arc $O K$ (since $B K$ bisects the angle $O \hat{B} A$ ). Hence the perpendicular bisector of the chord $A O$ of the circle ${ }^{c_{1}}$ is passing through point $K$. It means that $K$ is the circumcenter of the triangle $O A C$.
From equalities (1),(2),(3) we conclude that $\hat{B}_{2}=\hat{C}_{1}=\hat{x}$ and so $A B / / O C \Rightarrow O \hat{A} B=A \hat{O} C$, that is $\hat{A}_{1}+\hat{A}_{2}=\hat{O}_{1}+\hat{O}_{2}$ and since $\hat{O}_{1}=\hat{O}_{2}=\hat{x}$, we conclude that
$$
\hat{A}_{1}+\hat{A}_{2}=2 \hat{O}_{1}=2 \hat{x}
$$
The angles $\hat{A}_{I}$ and $\hat{C}_{I}$ are inscribed into the circle ${ }^{c_{2}}$ and correspond to the same arc $O L$. Hence
$$
\hat{A}_{I}=\hat{C}_{1}=\hat{x}
$$
From (5) and (6) we have $\hat{A}_{1}=\hat{A}_{2}$, i.e. $A L$ is the bisector of the angle $B \hat{A} O$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
GRE
Let $c \equiv c(O, K)$ be a circle with center $O$ and radius $R$ and $A, B$ be two points on it, not belonging to the same diameter. The bisector of the angle $A \hat{B} O$ intersects the circle $c$ at point $C$, the circumcircle of the triangle $A O B$, say ${ }^{c_{1}}$ at point $K$ and the circumcircle of the triangle $A O C$, say ${ }^{c_{2}}$, at point $L$. Prove that the point $K$ is the circumcenter of the triangle $A O C$ and the point $L$ is the incenter of the triangle $A O B$.
|
The segments $O B, O C$ are equal, as radii of the circle ${ }^{c}$. Hence $O B C$ is an isosceles triangle and
$$
\hat{B}_{1}=\hat{C}_{1}=\hat{x}
$$

The chord $B C$ is the bisector of the angle $O \hat{B} A$, and hence
$$
\hat{B}_{1}=\hat{B}_{2}=\hat{x}
$$
The angles $\hat{B}_{2}$ and $\hat{O}_{1}$ are inscribed to the same arc $O K$ of the circle ${ }^{c_{1}}$ and hence
$$
\hat{B}_{2}=\hat{\mathrm{O}}_{1}=\hat{x}
$$
The segments $K O, K C$ are equal, as radii of the circle ${ }^{c_{2}}$. Hence the triangle $K O C$ is isosceles and so
$$
\hat{O}_{2}=\hat{C}_{1}=\hat{x}
$$
From equalities $(1),(2),(3)$ we conclude that
$$
\hat{O}_{1}=\hat{O}_{2}=\hat{x}
$$
and so $O K$ is the bisector, and hence perpendicular bisector of the isosceles triangle $O A C$. The point $K$ is the middle of the arc $O K$ (since $B K$ bisects the angle $O \hat{B} A$ ). Hence the perpendicular bisector of the chord $A O$ of the circle ${ }^{c_{1}}$ is passing through point $K$. It means that $K$ is the circumcenter of the triangle $O A C$.
From equalities (1),(2),(3) we conclude that $\hat{B}_{2}=\hat{C}_{1}=\hat{x}$ and so $A B / / O C \Rightarrow O \hat{A} B=A \hat{O} C$, that is $\hat{A}_{1}+\hat{A}_{2}=\hat{O}_{1}+\hat{O}_{2}$ and since $\hat{O}_{1}=\hat{O}_{2}=\hat{x}$, we conclude that
$$
\hat{A}_{1}+\hat{A}_{2}=2 \hat{O}_{1}=2 \hat{x}
$$
The angles $\hat{A}_{I}$ and $\hat{C}_{I}$ are inscribed into the circle ${ }^{c_{2}}$ and correspond to the same arc $O L$. Hence
$$
\hat{A}_{I}=\hat{C}_{1}=\hat{x}
$$
From (5) and (6) we have $\hat{A}_{1}=\hat{A}_{2}$, i.e. $A L$ is the bisector of the angle $B \hat{A} O$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2015.jsonl",
"problem_match": "## G3 ",
"solution_match": "## Solution:"
}
|
f9110015-a3bc-5931-b38b-e61c04184e33
| 604,768
|
CYP
Let $\triangle A B C$ be an acute triangle. The lines $\left(\varepsilon_{1}\right),\left(\varepsilon_{2}\right)$ are perpendicular to $A B$ at the points $A$, $B$, respectively. The perpendicular lines from the midpoint $M$ of $A B$ to the sides of the triangle $A C_{;} B C$ intersect the lines $\left(\varepsilon_{1}\right),\left(\xi_{2}\right)$ at the points $E, F$, respectively. If $I$ is the intersection point of $E F, M C$, prove that
$$
\angle A I B=\angle E M F=\angle C A B+\angle C B A
$$
|
Let $H, G$ be the points of intersection of $M E, M F$, with $A C, B C$ respectively. From the similarity of triangles $\triangle M H A$ and $\triangle M A E$ we get
$$
\frac{M H}{M A}=\frac{M A}{M E}
$$
thus, $M A^{2}=M H \cdot M E$
Similarly, from the similarity of triangles $\triangle M B G$ and $\triangle M F B$ we get
$$
\frac{M B}{M F}=\frac{M G}{M B}
$$
thus, $M B^{2}=M F \cdot M G$
Since $M A=M B$, from (1), (2), we have that the points $E, H, G, F$ are concyclic.
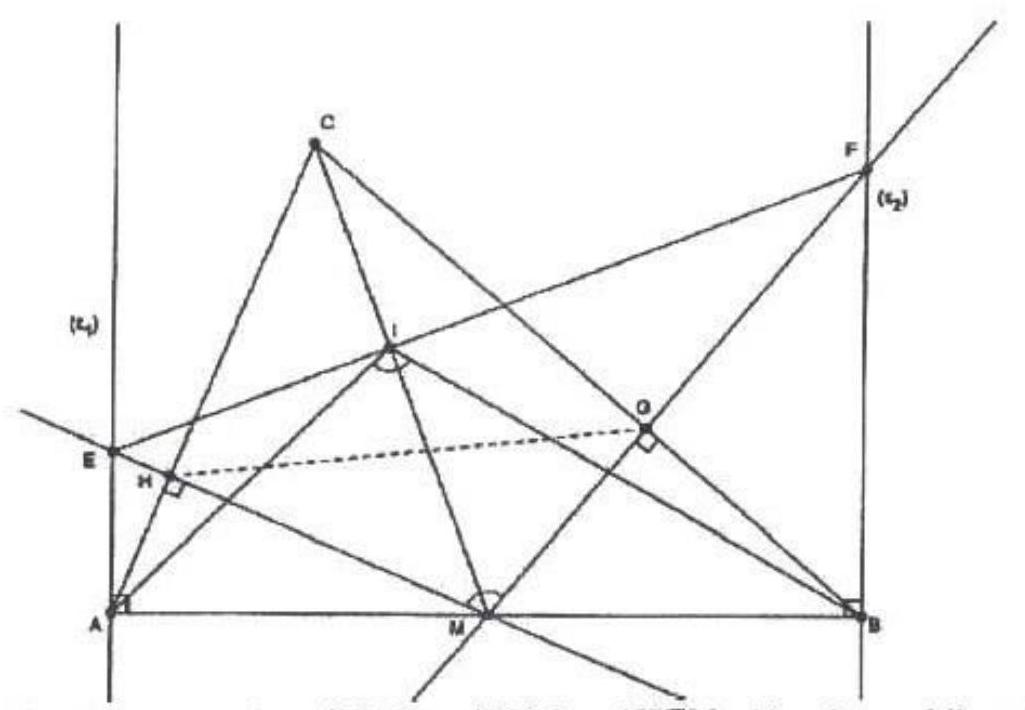
Therefore, we get that $\angle F E H=\angle F E M=\angle H G M$. Also, the quadrilateral $C H M G$ is cyclic, so $\angle C M H=\angle H G C$. We have
$$
\angle F E H+\angle C M H=\angle H G M+\angle H G C=90^{\circ}
$$
Thus $C M \perp E F$. Now, from the cyclic quadrilaterals $F I M B$ and EIMA, we get that
$\angle I F M=\angle I B M$ and $\angle I E M=\angle I A M$. Therefore, the triangles $\triangle E M F$ and $\triangle A I B$ are similar, so $\angle A J B=\angle E M F$. Finally
$$
\angle A I B=\angle A I M+\angle M I B=\angle A E M+\angle M F B=\angle C A B+\angle C B A
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
CYP
Let $\triangle A B C$ be an acute triangle. The lines $\left(\varepsilon_{1}\right),\left(\varepsilon_{2}\right)$ are perpendicular to $A B$ at the points $A$, $B$, respectively. The perpendicular lines from the midpoint $M$ of $A B$ to the sides of the triangle $A C_{;} B C$ intersect the lines $\left(\varepsilon_{1}\right),\left(\xi_{2}\right)$ at the points $E, F$, respectively. If $I$ is the intersection point of $E F, M C$, prove that
$$
\angle A I B=\angle E M F=\angle C A B+\angle C B A
$$
|
Let $H, G$ be the points of intersection of $M E, M F$, with $A C, B C$ respectively. From the similarity of triangles $\triangle M H A$ and $\triangle M A E$ we get
$$
\frac{M H}{M A}=\frac{M A}{M E}
$$
thus, $M A^{2}=M H \cdot M E$
Similarly, from the similarity of triangles $\triangle M B G$ and $\triangle M F B$ we get
$$
\frac{M B}{M F}=\frac{M G}{M B}
$$
thus, $M B^{2}=M F \cdot M G$
Since $M A=M B$, from (1), (2), we have that the points $E, H, G, F$ are concyclic.

Therefore, we get that $\angle F E H=\angle F E M=\angle H G M$. Also, the quadrilateral $C H M G$ is cyclic, so $\angle C M H=\angle H G C$. We have
$$
\angle F E H+\angle C M H=\angle H G M+\angle H G C=90^{\circ}
$$
Thus $C M \perp E F$. Now, from the cyclic quadrilaterals $F I M B$ and EIMA, we get that
$\angle I F M=\angle I B M$ and $\angle I E M=\angle I A M$. Therefore, the triangles $\triangle E M F$ and $\triangle A I B$ are similar, so $\angle A J B=\angle E M F$. Finally
$$
\angle A I B=\angle A I M+\angle M I B=\angle A E M+\angle M F B=\angle C A B+\angle C B A
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2015.jsonl",
"problem_match": "\nG4",
"solution_match": "## Solution:"
}
|
1547d3a6-177d-5bc5-8b80-f72749ff62a4
| 604,782
|
ROU
Let $A B C$ be an acute triangle with $A B \neq A C$. The incircle $\omega$ of the triangle touches the sides $B C, C A$ and $A B$ at $D, E$ and $F$, respectively. The perpendicular line erected at $C$ onto $B C$ meets $E F$ at $M$, and similarly, the perpendicular line erected at $B$ onto $B C$ meets $E F$ at $N$. The line $D M$ meets $\omega$ again in $P$, and the line $D N$ meets $\omega$ again at $Q$. Prove that $D P=D Q$.
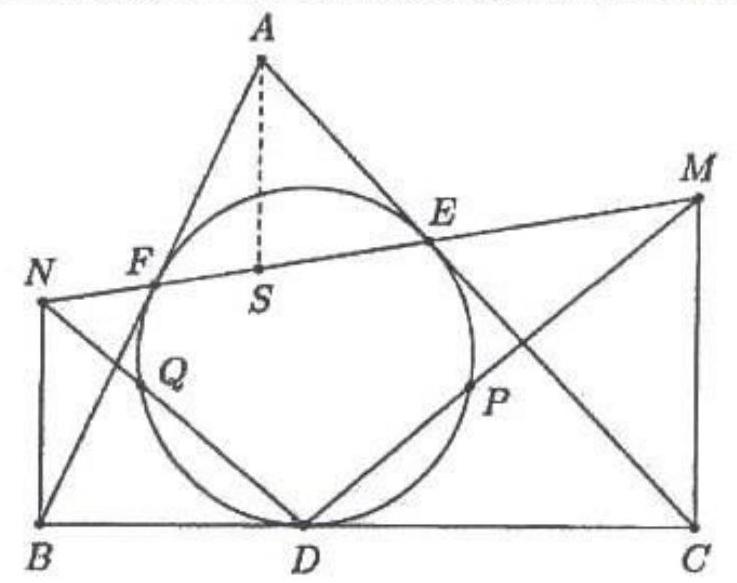
|
## Proof 1.1.
Let $\{T\}=E F \cap B C$. Applying Menelaus' theorem to the triangle $A B C$ and the transversal line $E-F-T$ we obtain $\frac{T B}{T C} \cdot \frac{E C}{E A} \cdot \frac{F A}{F B}=1$, i.e. $\frac{T B}{T C} \cdot \frac{s-c}{s-a} \cdot \frac{s-a}{s-b}=1$, or $\frac{T B}{T C}=\frac{s-b}{s-c}$, where the notations are the usual ones.
This means that triangles $T B N$ and $T C M$ are similar, therefore $\frac{T B}{T C}=\frac{B N}{C M}$. From the above it follows $\frac{B N}{C M}=\frac{s-b}{s-c}, \frac{B D}{C D}=\frac{s-b}{s-c}$, and $\angle D B N=\angle D C M=90^{\circ}$, which means that triangles $B D N$ and $C D M$ are similar, hence angles $B D N$ and $C D M$ are equal. This leads to the arcs $D Q$ and $D P$ being equal, and finally to $D P=D Q$.
## Proof 1.2.
Let $S$ be the meeting point of the altitude from $A$ with the line $E F$. Lines $B N, A S, C M$ are parallel, therefore triangles $B N F$ and $A S F$ are similar, as are triangles $A S E$ and $C M E$. We obtain $\frac{B N}{A S}=\frac{B F}{F A}$ and $\frac{A S}{C M}=\frac{A E}{E C}$.
Multiplying the two relations, we obtain $\frac{B N}{C M}=\frac{B F}{F A} \cdot \frac{A E}{E C}=\frac{B F}{E C}=\frac{B D}{D C}$ (we have used that $A E=A F, B F=B D$ and $C E=C D)$.
It follows that the right triangles $B D N$ and $C D M$ are similar (SAS), which leads to the same ending as in the first proof.
## NUMBER THEORY
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
ROU
Let $A B C$ be an acute triangle with $A B \neq A C$. The incircle $\omega$ of the triangle touches the sides $B C, C A$ and $A B$ at $D, E$ and $F$, respectively. The perpendicular line erected at $C$ onto $B C$ meets $E F$ at $M$, and similarly, the perpendicular line erected at $B$ onto $B C$ meets $E F$ at $N$. The line $D M$ meets $\omega$ again in $P$, and the line $D N$ meets $\omega$ again at $Q$. Prove that $D P=D Q$.

|
## Proof 1.1.
Let $\{T\}=E F \cap B C$. Applying Menelaus' theorem to the triangle $A B C$ and the transversal line $E-F-T$ we obtain $\frac{T B}{T C} \cdot \frac{E C}{E A} \cdot \frac{F A}{F B}=1$, i.e. $\frac{T B}{T C} \cdot \frac{s-c}{s-a} \cdot \frac{s-a}{s-b}=1$, or $\frac{T B}{T C}=\frac{s-b}{s-c}$, where the notations are the usual ones.
This means that triangles $T B N$ and $T C M$ are similar, therefore $\frac{T B}{T C}=\frac{B N}{C M}$. From the above it follows $\frac{B N}{C M}=\frac{s-b}{s-c}, \frac{B D}{C D}=\frac{s-b}{s-c}$, and $\angle D B N=\angle D C M=90^{\circ}$, which means that triangles $B D N$ and $C D M$ are similar, hence angles $B D N$ and $C D M$ are equal. This leads to the arcs $D Q$ and $D P$ being equal, and finally to $D P=D Q$.
## Proof 1.2.
Let $S$ be the meeting point of the altitude from $A$ with the line $E F$. Lines $B N, A S, C M$ are parallel, therefore triangles $B N F$ and $A S F$ are similar, as are triangles $A S E$ and $C M E$. We obtain $\frac{B N}{A S}=\frac{B F}{F A}$ and $\frac{A S}{C M}=\frac{A E}{E C}$.
Multiplying the two relations, we obtain $\frac{B N}{C M}=\frac{B F}{F A} \cdot \frac{A E}{E C}=\frac{B F}{E C}=\frac{B D}{D C}$ (we have used that $A E=A F, B F=B D$ and $C E=C D)$.
It follows that the right triangles $B D N$ and $C D M$ are similar (SAS), which leads to the same ending as in the first proof.
## NUMBER THEORY
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2015.jsonl",
"problem_match": "\nG5 ",
"solution_match": "## Solution:"
}
|
91afff1b-4a8d-5583-a097-d6538eeba9aa
| 604,796
|
BUL
A positive integer is called a repunit, if it is written only by ones. The repunit with $n$ digits will be denoted by $\underbrace{11 \ldots 1}_{n}$. Prove that:
a) the repunit $\underbrace{11 \ldots 1}_{n}$ is divisible by 37 if and only if $n$ is divisible by 3 ;
b) there exists a positive integer $k$ such that the repunit $\underbrace{11 \ldots 1}_{n}$ is divisible by 41 if and only if $n$ is divisible by $k$.
|
a) Let $n=3 m+r$, where $m$ and $r$ are non-negative integers and $r<3$.
Denote by $\underbrace{00 \ldots 0}_{p}$ a recording with $p$ zeroes and $\underbrace{a b c a b c \ldots a b c}_{p x a b c c}$ recording with $p$ times $a b c$. We
have: $\quad \underbrace{11 \ldots 1}_{n}=\underbrace{11 \ldots 1}_{3 m+r}=\underbrace{11 \ldots 1}_{3 m} \cdot \underbrace{00 \ldots 0}_{r}+\underbrace{11 \ldots 1}_{\tau}=111 \cdot \underbrace{100100 \ldots 100100 \ldots 0}_{(m-1) \times 100}+\underbrace{11 \ldots 1}_{r}$.
Since $111=37.3$, the numbers $\underbrace{11 \ldots 1}_{n}$ and $\underbrace{11 \ldots 1}_{r}$ are equal modulo 37 . On the other hand the numbers 1 and 11 are not divisible by 37 . We conclude that $\underbrace{11 \ldots 1}_{n}$ is divisible by 37 if only if $r=0$, i.e. if and only if $n$ is divisible by 3 .
b) Using the idea from a), we look for a repunit, which is divisible by 41 . Obviously, 1 and 11 are not divisible by 41 , while the residues of 111 and 1111 are 29 and 4 , respectively. We have $11111=41 \cdot 271$. Since 11111 is a repunit with 5 digits, it follows in the same way as in a) that $\underbrace{1}_{11 \ldots 1}$ is divisible by 41 if and only if $n$ is divisible by 5 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
BUL
A positive integer is called a repunit, if it is written only by ones. The repunit with $n$ digits will be denoted by $\underbrace{11 \ldots 1}_{n}$. Prove that:
a) the repunit $\underbrace{11 \ldots 1}_{n}$ is divisible by 37 if and only if $n$ is divisible by 3 ;
b) there exists a positive integer $k$ such that the repunit $\underbrace{11 \ldots 1}_{n}$ is divisible by 41 if and only if $n$ is divisible by $k$.
|
a) Let $n=3 m+r$, where $m$ and $r$ are non-negative integers and $r<3$.
Denote by $\underbrace{00 \ldots 0}_{p}$ a recording with $p$ zeroes and $\underbrace{a b c a b c \ldots a b c}_{p x a b c c}$ recording with $p$ times $a b c$. We
have: $\quad \underbrace{11 \ldots 1}_{n}=\underbrace{11 \ldots 1}_{3 m+r}=\underbrace{11 \ldots 1}_{3 m} \cdot \underbrace{00 \ldots 0}_{r}+\underbrace{11 \ldots 1}_{\tau}=111 \cdot \underbrace{100100 \ldots 100100 \ldots 0}_{(m-1) \times 100}+\underbrace{11 \ldots 1}_{r}$.
Since $111=37.3$, the numbers $\underbrace{11 \ldots 1}_{n}$ and $\underbrace{11 \ldots 1}_{r}$ are equal modulo 37 . On the other hand the numbers 1 and 11 are not divisible by 37 . We conclude that $\underbrace{11 \ldots 1}_{n}$ is divisible by 37 if only if $r=0$, i.e. if and only if $n$ is divisible by 3 .
b) Using the idea from a), we look for a repunit, which is divisible by 41 . Obviously, 1 and 11 are not divisible by 41 , while the residues of 111 and 1111 are 29 and 4 , respectively. We have $11111=41 \cdot 271$. Since 11111 is a repunit with 5 digits, it follows in the same way as in a) that $\underbrace{1}_{11 \ldots 1}$ is divisible by 41 if and only if $n$ is divisible by 5 .
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2015.jsonl",
"problem_match": "\nNT2 ",
"solution_match": "## Solution:"
}
|
cc96f680-3122-5bd5-87df-d72e411dd675
| 604,826
|
ALB
a) Show that the product of all differences of possible couples of six given positive integers is divisible by 960 (original from Albania).
b) Show that the product of all differences of possible couples of six given positive integers. is divisible by 34560 (modified by problem selecting committee).
|
a) Since we have six numbers then at least two of them have a same residue when divided by 3 , so at least one of the differences in our product is divisible by 3 .
Since we have six numbers then at least two of them have a same residuc when divided by 5 , so at least one of the differences in our product is divisible by 5 .
We may have:
a) six numbers with the same parity
b) five numbers with the same parity
c) four numbers with the same parity
d) three numbers with the same parity
There are $C_{6}^{2}=15$ different pairs, so there are 15 different differences in this product.
a) The six numbers have the same parity; then each difference is divisible by 2 , therefore our product is divisible by $2^{15}$.
b) If we have five numbers with the same parity, then the couples that have their difference odd are formed by taking one number from these five numbers, and the second will be the sixth one. Then $C_{5}^{1}=15=5$ differences are odd. So $15-5=10$ differences are even, so product is divisible by $2^{10}$.
c) If we have four numbers with the same parity, then the couples that have their difference odd are formed by taking one number from these four numbers, and the second will be from the two others numbers. Then $2 \cdot C_{4}^{1}=8$ differences are odd. So $15-8=7$ differences are even, so our product is divisible by $2^{7}$.
d) If we have three numbers with the same parity, then the couples that have their difference odd are formed by taking one from each triple. Then $C_{3}^{1} \cdot C_{3}^{1}=9$ differences are odd, therefore $15-9=6$ differences are even, so our product is divisible by $2^{6}$.
Thus, our production is divisible by $2^{6} \cdot 3 \cdot 5=960$.
b) Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}$ be these numbers. Since we have six numbers then at least two of them when divided by 5 have the same residue, so at least one of these differences in our product is divisible by 5 .
Since we have six numbers, and we have three possible residues at the division by 3 , then at least three of them replies the residue of previous numbers, so at least three of these differences in our product are divisible by 3 .
Since we have six numbers, and we have two possible residues at the division by 2 , then at least four of them replies the residue of previous numbers, and two of them replies replied residues, so at least six of these differences in our product are divisible by 2 .
Since we have six numbers, and we have four possible residues at the division by 4 , then at least two of them replies the residue of previous numbers, so at least two of these differences in our product are divisible by 4 . That means that two of these differences are divisible by 4 and moreover four of them are divisible by 2 .
Thus, our production is divisible by $2^{4} \cdot 4^{2} \cdot 3^{3} \cdot 5=34560$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
ALB
a) Show that the product of all differences of possible couples of six given positive integers is divisible by 960 (original from Albania).
b) Show that the product of all differences of possible couples of six given positive integers. is divisible by 34560 (modified by problem selecting committee).
|
a) Since we have six numbers then at least two of them have a same residue when divided by 3 , so at least one of the differences in our product is divisible by 3 .
Since we have six numbers then at least two of them have a same residuc when divided by 5 , so at least one of the differences in our product is divisible by 5 .
We may have:
a) six numbers with the same parity
b) five numbers with the same parity
c) four numbers with the same parity
d) three numbers with the same parity
There are $C_{6}^{2}=15$ different pairs, so there are 15 different differences in this product.
a) The six numbers have the same parity; then each difference is divisible by 2 , therefore our product is divisible by $2^{15}$.
b) If we have five numbers with the same parity, then the couples that have their difference odd are formed by taking one number from these five numbers, and the second will be the sixth one. Then $C_{5}^{1}=15=5$ differences are odd. So $15-5=10$ differences are even, so product is divisible by $2^{10}$.
c) If we have four numbers with the same parity, then the couples that have their difference odd are formed by taking one number from these four numbers, and the second will be from the two others numbers. Then $2 \cdot C_{4}^{1}=8$ differences are odd. So $15-8=7$ differences are even, so our product is divisible by $2^{7}$.
d) If we have three numbers with the same parity, then the couples that have their difference odd are formed by taking one from each triple. Then $C_{3}^{1} \cdot C_{3}^{1}=9$ differences are odd, therefore $15-9=6$ differences are even, so our product is divisible by $2^{6}$.
Thus, our production is divisible by $2^{6} \cdot 3 \cdot 5=960$.
b) Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}$ be these numbers. Since we have six numbers then at least two of them when divided by 5 have the same residue, so at least one of these differences in our product is divisible by 5 .
Since we have six numbers, and we have three possible residues at the division by 3 , then at least three of them replies the residue of previous numbers, so at least three of these differences in our product are divisible by 3 .
Since we have six numbers, and we have two possible residues at the division by 2 , then at least four of them replies the residue of previous numbers, and two of them replies replied residues, so at least six of these differences in our product are divisible by 2 .
Since we have six numbers, and we have four possible residues at the division by 4 , then at least two of them replies the residue of previous numbers, so at least two of these differences in our product are divisible by 4 . That means that two of these differences are divisible by 4 and moreover four of them are divisible by 2 .
Thus, our production is divisible by $2^{4} \cdot 4^{2} \cdot 3^{3} \cdot 5=34560$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2015.jsonl",
"problem_match": "## NT3 ",
"solution_match": "## Solution:"
}
|
8ba77af6-ae4e-5558-8869-b930f4abfd0e
| 604,837
|
Let $x, y$ and $z$ be positive numbers. Prove that
$$
\frac{x}{\sqrt{\sqrt[4]{y}+\sqrt[4]{z}}}+\frac{y}{\sqrt{\sqrt[4]{z}+\sqrt[4]{x}}}+\frac{z}{\sqrt{\sqrt[4]{x}+\sqrt[4]{y}}} \geq \frac{\sqrt[4]{(\sqrt{x}+\sqrt{y}+\sqrt{z})^{7}}}{\sqrt{2 \sqrt{27}}}
$$
|
Replacing $x=a^{2}, y=b^{2}, z=c^{2}$, where $a, b, c$ are positive numbers, our inequality is equivalent to
$$
\frac{a^{2}}{\sqrt{\sqrt{b}+\sqrt{c}}}+\frac{b^{2}}{\sqrt{\sqrt{c}+\sqrt{a}}}+\frac{c^{2}}{\sqrt{\sqrt{a}+\sqrt{b}}} \geq \frac{\sqrt[4]{(a+b+c)^{7}}}{\sqrt{2 \sqrt{27}}}
$$
Using the Cauchy-Schwarz inequality for the left hand side we get
$$
\frac{a^{2}}{\sqrt{\sqrt{b}+\sqrt{c}}}+\frac{b^{2}}{\sqrt{\sqrt{c}+\sqrt{a}}}+\frac{c^{2}}{\sqrt{\sqrt{a}+\sqrt{b}}} \geq \frac{(a+b+c)^{2}}{\sqrt{\sqrt{b}+\sqrt{c}}+\sqrt{\sqrt{c}+\sqrt{a}}+\sqrt{\sqrt{a}+\sqrt{b}}}
$$
Using Cauchy-Schwarz inequality for three positive numbers $\alpha . \beta . \uparrow$, we have
$$
\sqrt{\alpha}+\sqrt{\beta}+\sqrt{\gamma} \leq \sqrt{3(\alpha+\beta+\gamma)}
$$
Using this result twice, we have
$$
\begin{aligned}
\sqrt{\sqrt{b}+\sqrt{c}}+\sqrt{\sqrt{c}+\sqrt{a}}+\sqrt{\sqrt{a}+\sqrt{b}} & \leq \sqrt{6(\sqrt{a}+\sqrt{b}+\sqrt{c})} \\
& \leq \sqrt{6 \sqrt{3(a+b+c)}}
\end{aligned}
$$
Combining (1) and (2) we get the desired result.
Alternative solution by PSC. We will use Hölder's inequality in the form
$$
\begin{aligned}
& \left(a_{11}+a_{12}+a_{13}\right)\left(a_{21}+a_{22}+a_{23}\right)\left(a_{31}+a_{32}+a_{33}\right)\left(a_{41}+a_{42}+a_{43}\right) \\
& \quad \geq\left(\left(a_{11} a_{21} a_{31} a_{41}\right)^{1 / 4}+\left(a_{12} a_{22} a_{32} a_{42}\right)^{1 / 4}+\left(a_{13} a_{23} a_{33} a_{43}\right)^{1 / 4}\right)^{4}
\end{aligned}
$$
where $a_{i j}$ are positive numbers. Using this appropriately we get
$$
\begin{aligned}
&(1+1+1)((\sqrt{b}+\sqrt{c})+(\sqrt{c}+\sqrt{a})+(\sqrt{a}+\sqrt{b}))\left(\frac{a^{2}}{\sqrt{\sqrt{b}+\sqrt{c}}}+\frac{b^{2}}{\sqrt{\sqrt{c}+\sqrt{a}}}+\frac{c^{2}}{\sqrt{\sqrt{a}+\sqrt{b}}}\right)^{2} \\
& \geq(a+b+c)^{4}
\end{aligned}
$$
By the Cauchy-Schwarz inequality we have
$$
(\sqrt{b}+\sqrt{c})+(\sqrt{c}+\sqrt{a})+(\sqrt{a}+\sqrt{b})=2(\sqrt{a}+\sqrt{b}+\sqrt{c}) \leq 2 \sqrt{3(a+b+c)}
$$
Combining these two inequalities we get the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ and $z$ be positive numbers. Prove that
$$
\frac{x}{\sqrt{\sqrt[4]{y}+\sqrt[4]{z}}}+\frac{y}{\sqrt{\sqrt[4]{z}+\sqrt[4]{x}}}+\frac{z}{\sqrt{\sqrt[4]{x}+\sqrt[4]{y}}} \geq \frac{\sqrt[4]{(\sqrt{x}+\sqrt{y}+\sqrt{z})^{7}}}{\sqrt{2 \sqrt{27}}}
$$
|
Replacing $x=a^{2}, y=b^{2}, z=c^{2}$, where $a, b, c$ are positive numbers, our inequality is equivalent to
$$
\frac{a^{2}}{\sqrt{\sqrt{b}+\sqrt{c}}}+\frac{b^{2}}{\sqrt{\sqrt{c}+\sqrt{a}}}+\frac{c^{2}}{\sqrt{\sqrt{a}+\sqrt{b}}} \geq \frac{\sqrt[4]{(a+b+c)^{7}}}{\sqrt{2 \sqrt{27}}}
$$
Using the Cauchy-Schwarz inequality for the left hand side we get
$$
\frac{a^{2}}{\sqrt{\sqrt{b}+\sqrt{c}}}+\frac{b^{2}}{\sqrt{\sqrt{c}+\sqrt{a}}}+\frac{c^{2}}{\sqrt{\sqrt{a}+\sqrt{b}}} \geq \frac{(a+b+c)^{2}}{\sqrt{\sqrt{b}+\sqrt{c}}+\sqrt{\sqrt{c}+\sqrt{a}}+\sqrt{\sqrt{a}+\sqrt{b}}}
$$
Using Cauchy-Schwarz inequality for three positive numbers $\alpha . \beta . \uparrow$, we have
$$
\sqrt{\alpha}+\sqrt{\beta}+\sqrt{\gamma} \leq \sqrt{3(\alpha+\beta+\gamma)}
$$
Using this result twice, we have
$$
\begin{aligned}
\sqrt{\sqrt{b}+\sqrt{c}}+\sqrt{\sqrt{c}+\sqrt{a}}+\sqrt{\sqrt{a}+\sqrt{b}} & \leq \sqrt{6(\sqrt{a}+\sqrt{b}+\sqrt{c})} \\
& \leq \sqrt{6 \sqrt{3(a+b+c)}}
\end{aligned}
$$
Combining (1) and (2) we get the desired result.
Alternative solution by PSC. We will use Hölder's inequality in the form
$$
\begin{aligned}
& \left(a_{11}+a_{12}+a_{13}\right)\left(a_{21}+a_{22}+a_{23}\right)\left(a_{31}+a_{32}+a_{33}\right)\left(a_{41}+a_{42}+a_{43}\right) \\
& \quad \geq\left(\left(a_{11} a_{21} a_{31} a_{41}\right)^{1 / 4}+\left(a_{12} a_{22} a_{32} a_{42}\right)^{1 / 4}+\left(a_{13} a_{23} a_{33} a_{43}\right)^{1 / 4}\right)^{4}
\end{aligned}
$$
where $a_{i j}$ are positive numbers. Using this appropriately we get
$$
\begin{aligned}
&(1+1+1)((\sqrt{b}+\sqrt{c})+(\sqrt{c}+\sqrt{a})+(\sqrt{a}+\sqrt{b}))\left(\frac{a^{2}}{\sqrt{\sqrt{b}+\sqrt{c}}}+\frac{b^{2}}{\sqrt{\sqrt{c}+\sqrt{a}}}+\frac{c^{2}}{\sqrt{\sqrt{a}+\sqrt{b}}}\right)^{2} \\
& \geq(a+b+c)^{4}
\end{aligned}
$$
By the Cauchy-Schwarz inequality we have
$$
(\sqrt{b}+\sqrt{c})+(\sqrt{c}+\sqrt{a})+(\sqrt{a}+\sqrt{b})=2(\sqrt{a}+\sqrt{b}+\sqrt{c}) \leq 2 \sqrt{3(a+b+c)}
$$
Combining these two inequalities we get the desired result.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nA 1.",
"solution_match": "\nSolution."
}
|
b4f07074-17c9-57d6-97e7-adb53fc8f3a8
| 604,913
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{1}{a b(b+1)(c+1)}+\frac{1}{b c(c+1)(a+1)}+\frac{1}{c a(a+1)(b+1)} \geq \frac{3}{(1+a b c)^{2}}
$$
|
The required inequality is equivalent to
$$
\frac{c(a+1)+a(b+1)+b(c+1)}{a b c(a+1)(b+1)(c+1)} \geq \frac{3}{(1+a b c)^{2}}
$$
or equivalently to,
$$
(1+a b c)^{2}(a b+b c+c a+a+b+c) \geq 3 a b c(a b+b c+c a+a+b+c+a b c+1)
$$
Let $m=a+b+c, n=a b+b c+c a$ and $x^{3}=a b c$, then the above can be rewritten as
$$
(m+n)\left(1+x^{3}\right)^{2} \geq 3 x^{3}\left(x^{3}+m+n+1\right)
$$
or
$$
(m+n)\left(x^{6}-x^{3}+1\right) \geq 3 x^{3}\left(x^{3}+1\right)
$$
By the AM-GM inequality we have $m \geq 3 x$ and $n \geq 3 x^{2}$, hence $m+n \geq 3 x(x+1)$. It is sufficient to prove that
$$
\begin{aligned}
x(x+1)\left(x^{6}-x^{3}+1\right) & \geq x^{3}(x+1)\left(x^{2}-x+1\right) \\
3\left(x^{6}-x^{3}+1\right) & \geq x^{2}\left(x^{2}-x+1\right) \\
\left(x^{2}-1\right)^{2} & \geq 0
\end{aligned}
$$
which is true.
Alternative solution by PSC. We present here an approach without fully expanding.
Let $a b c=k^{3}$ and set $a=k \frac{x}{y}, b=k \frac{y}{z}, c=k \frac{z}{x}$, where $k, x, y, z>0$. Then, the inequality can be rewritten as
$$
\frac{z^{2}}{(k y+z)(k z+x)}+\frac{x^{2}}{(k z+x)(k x+y)}+\frac{y^{2}}{(k x+y)(k y+z)} \geq \frac{3 k^{2}}{\left(1+k^{3}\right)^{2}}
$$
Using the Cauchy-Schwarz inequality we have that
$$
\sum_{\text {cyclic }} \frac{z^{2}}{(k y+z)(k z+x)} \geq \frac{(x+y+z)^{2}}{(k y+z)(k z+x)+(k z+x)(k x+y)+(k x+y)(k y+z)}
$$
therefore it suffices to prove that
$$
\frac{(x+y+z)^{2}}{(k y+z)(k z+x)+(k z+x)(k x+y)+(k x+y)(k y+z)} \geq \frac{3 k^{2}}{\left(1+k^{3}\right)^{2}}
$$
or
$$
\left(\left(1+k^{3}\right)^{2}-3 k^{3}\right)\left(x^{2}+y^{2}+z^{2}\right) \geq\left(3 k^{2}\left(k^{2}+k+1\right)-2\left(1+k^{3}\right)^{2}\right)(x y+y z+z x)
$$
Since $x^{2}+y^{2}+z^{2} \geq x y+y z+z x$ and $\left(1+k^{3}\right)^{2}-3 k^{3}>0$, it is enough to prove that
$$
\left(1+k^{3}\right)^{2}-3 k^{3} \geq 3 k^{2}\left(k^{2}+k+1\right)-2\left(1+k^{3}\right)^{2}
$$
or
$$
(k-1)^{2}\left(k^{2}+1\right)(k+1)^{2} \geq 0
$$
which is true.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{1}{a b(b+1)(c+1)}+\frac{1}{b c(c+1)(a+1)}+\frac{1}{c a(a+1)(b+1)} \geq \frac{3}{(1+a b c)^{2}}
$$
|
The required inequality is equivalent to
$$
\frac{c(a+1)+a(b+1)+b(c+1)}{a b c(a+1)(b+1)(c+1)} \geq \frac{3}{(1+a b c)^{2}}
$$
or equivalently to,
$$
(1+a b c)^{2}(a b+b c+c a+a+b+c) \geq 3 a b c(a b+b c+c a+a+b+c+a b c+1)
$$
Let $m=a+b+c, n=a b+b c+c a$ and $x^{3}=a b c$, then the above can be rewritten as
$$
(m+n)\left(1+x^{3}\right)^{2} \geq 3 x^{3}\left(x^{3}+m+n+1\right)
$$
or
$$
(m+n)\left(x^{6}-x^{3}+1\right) \geq 3 x^{3}\left(x^{3}+1\right)
$$
By the AM-GM inequality we have $m \geq 3 x$ and $n \geq 3 x^{2}$, hence $m+n \geq 3 x(x+1)$. It is sufficient to prove that
$$
\begin{aligned}
x(x+1)\left(x^{6}-x^{3}+1\right) & \geq x^{3}(x+1)\left(x^{2}-x+1\right) \\
3\left(x^{6}-x^{3}+1\right) & \geq x^{2}\left(x^{2}-x+1\right) \\
\left(x^{2}-1\right)^{2} & \geq 0
\end{aligned}
$$
which is true.
Alternative solution by PSC. We present here an approach without fully expanding.
Let $a b c=k^{3}$ and set $a=k \frac{x}{y}, b=k \frac{y}{z}, c=k \frac{z}{x}$, where $k, x, y, z>0$. Then, the inequality can be rewritten as
$$
\frac{z^{2}}{(k y+z)(k z+x)}+\frac{x^{2}}{(k z+x)(k x+y)}+\frac{y^{2}}{(k x+y)(k y+z)} \geq \frac{3 k^{2}}{\left(1+k^{3}\right)^{2}}
$$
Using the Cauchy-Schwarz inequality we have that
$$
\sum_{\text {cyclic }} \frac{z^{2}}{(k y+z)(k z+x)} \geq \frac{(x+y+z)^{2}}{(k y+z)(k z+x)+(k z+x)(k x+y)+(k x+y)(k y+z)}
$$
therefore it suffices to prove that
$$
\frac{(x+y+z)^{2}}{(k y+z)(k z+x)+(k z+x)(k x+y)+(k x+y)(k y+z)} \geq \frac{3 k^{2}}{\left(1+k^{3}\right)^{2}}
$$
or
$$
\left(\left(1+k^{3}\right)^{2}-3 k^{3}\right)\left(x^{2}+y^{2}+z^{2}\right) \geq\left(3 k^{2}\left(k^{2}+k+1\right)-2\left(1+k^{3}\right)^{2}\right)(x y+y z+z x)
$$
Since $x^{2}+y^{2}+z^{2} \geq x y+y z+z x$ and $\left(1+k^{3}\right)^{2}-3 k^{3}>0$, it is enough to prove that
$$
\left(1+k^{3}\right)^{2}-3 k^{3} \geq 3 k^{2}\left(k^{2}+k+1\right)-2\left(1+k^{3}\right)^{2}
$$
or
$$
(k-1)^{2}\left(k^{2}+1\right)(k+1)^{2} \geq 0
$$
which is true.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nA 3.",
"solution_match": "\nSolution."
}
|
9006e4ed-ecda-5262-99b4-960f0d853c57
| 604,938
|
Let $H$ be the orthocentre of an acute triangle $A B C$ with $B C>A C$, inscribed in a circle $\Gamma$. The circle with centre $C$ and radius $C B$ intersects $\Gamma$ at the point $D$, which is on the arc $A B$ not containing $C$. The circle with centre $C$ and radius $C A$ intersects the segment $C D$ at the point $K$. The line parallel to $B D$ through $K$, intersects $A B$ at point $L$. If $M$ is the midpoint of $A B$ and $N$ is the foot of the perpendicular from $H$ to $C L$, prove that the line $M N$ bisects the segment $C H$.
|
We use standard notation for the angles of triangle $A B C$. Let $P$ be the midpoint of $C H$ and $O$ the centre of $\Gamma$. As
$$
\alpha=\angle B A C=\angle B D C=\angle D K L
$$
the quadrilateral $A C K L$ is cyclic. From the relation $C B=C D$ we get $\angle B C D=180^{\circ}-2 \alpha$, so
$$
\angle A C K=\gamma+2 \alpha-180^{\circ}
$$
where $\gamma=\angle A C B$. From the relation $C K=C A$ we get
$$
\angle A L C=\angle A K C=180^{\circ}-\alpha-\frac{\gamma}{2}
$$
and thus from the triangle $A C L$ we obtain
$$
\angle A C L=180^{\circ}-\alpha-\angle A L C=\frac{\gamma}{2}
$$
which means that $C L$ is the angle bisector of $\angle A C B$, thus $\angle A C L=\angle B C L$. Moreover, from the fact that $C H \perp A B$ and the isosceles triangle $B O C$ has $\angle B O C=2 \alpha$, we get $\angle A C H=\angle B C O=90^{\circ}-\alpha$. It follows that,
$$
\angle N P H=2 \angle N C H=\angle O C H
$$
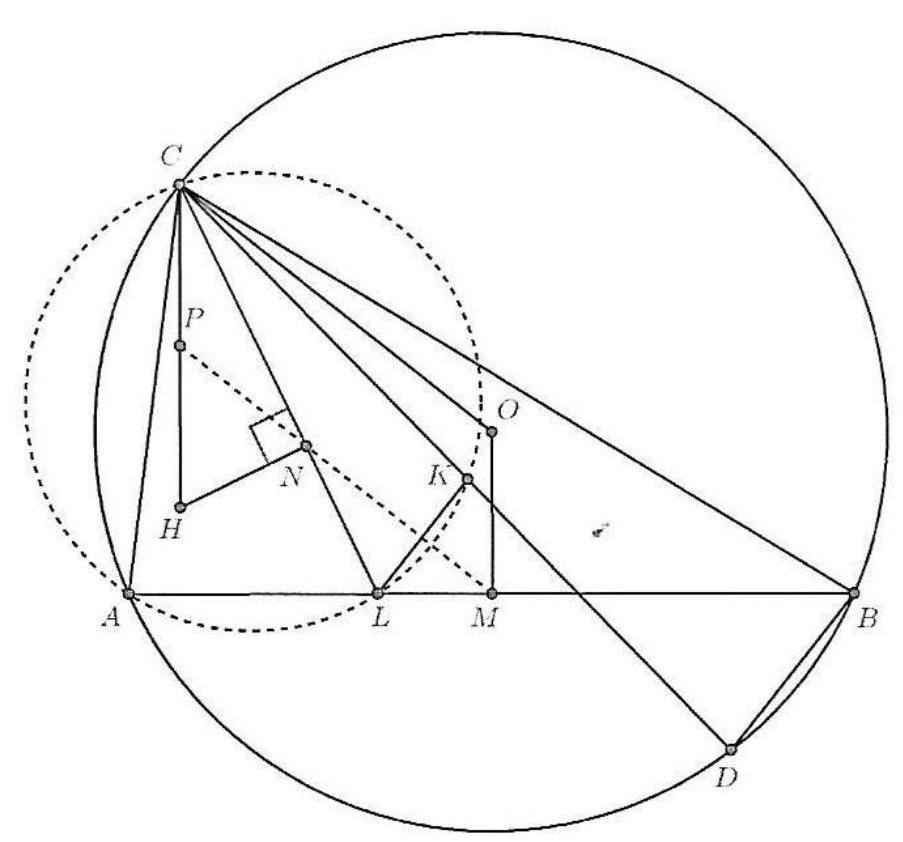
On the other hand, it is known that $2 C P=C H=2 O M$ and $C P \| O M$, so $C P M O$ is a parallelogram and
$$
\angle M P H=\angle O C H
$$
Now from (3) and (4) we obtain that
$$
\angle M P H=\angle N P H,
$$
which means that the points $M, N, P$ are collinear.
## Alternative formulation of the statement by PSC.
Let $H$ be the orthocentre of an acute triangle $A B C$ with $B C>A C$, inscribed in a circle $\Gamma$. A point $D$ on $\Gamma$, which is on the arc $A B$ not containing $C$, is chosen such that $C B=C D$. A point $K$ is chosen on the segment $C D$ such that $C A=C K$. The line parallel to $B D$ through $K$, intersects $A B$ at point $L$. If $M$ is the midpoint of $A B$ and $N$ is the foot of the perpendicular from $H$ to $C L$, prove that the line $M N$ bisects the segment $C H$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $H$ be the orthocentre of an acute triangle $A B C$ with $B C>A C$, inscribed in a circle $\Gamma$. The circle with centre $C$ and radius $C B$ intersects $\Gamma$ at the point $D$, which is on the arc $A B$ not containing $C$. The circle with centre $C$ and radius $C A$ intersects the segment $C D$ at the point $K$. The line parallel to $B D$ through $K$, intersects $A B$ at point $L$. If $M$ is the midpoint of $A B$ and $N$ is the foot of the perpendicular from $H$ to $C L$, prove that the line $M N$ bisects the segment $C H$.
|
We use standard notation for the angles of triangle $A B C$. Let $P$ be the midpoint of $C H$ and $O$ the centre of $\Gamma$. As
$$
\alpha=\angle B A C=\angle B D C=\angle D K L
$$
the quadrilateral $A C K L$ is cyclic. From the relation $C B=C D$ we get $\angle B C D=180^{\circ}-2 \alpha$, so
$$
\angle A C K=\gamma+2 \alpha-180^{\circ}
$$
where $\gamma=\angle A C B$. From the relation $C K=C A$ we get
$$
\angle A L C=\angle A K C=180^{\circ}-\alpha-\frac{\gamma}{2}
$$
and thus from the triangle $A C L$ we obtain
$$
\angle A C L=180^{\circ}-\alpha-\angle A L C=\frac{\gamma}{2}
$$
which means that $C L$ is the angle bisector of $\angle A C B$, thus $\angle A C L=\angle B C L$. Moreover, from the fact that $C H \perp A B$ and the isosceles triangle $B O C$ has $\angle B O C=2 \alpha$, we get $\angle A C H=\angle B C O=90^{\circ}-\alpha$. It follows that,
$$
\angle N P H=2 \angle N C H=\angle O C H
$$

On the other hand, it is known that $2 C P=C H=2 O M$ and $C P \| O M$, so $C P M O$ is a parallelogram and
$$
\angle M P H=\angle O C H
$$
Now from (3) and (4) we obtain that
$$
\angle M P H=\angle N P H,
$$
which means that the points $M, N, P$ are collinear.
## Alternative formulation of the statement by PSC.
Let $H$ be the orthocentre of an acute triangle $A B C$ with $B C>A C$, inscribed in a circle $\Gamma$. A point $D$ on $\Gamma$, which is on the arc $A B$ not containing $C$, is chosen such that $C B=C D$. A point $K$ is chosen on the segment $C D$ such that $C A=C K$. The line parallel to $B D$ through $K$, intersects $A B$ at point $L$. If $M$ is the midpoint of $A B$ and $N$ is the foot of the perpendicular from $H$ to $C L$, prove that the line $M N$ bisects the segment $C H$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nG 1.",
"solution_match": "\nSolution."
}
|
47ffa21c-38a3-5589-9d3d-f1727320be95
| 605,029
|
Let $A B C$ be a right angled triangle with $\angle A=90^{\circ}$ and $A D$ its altitude. We draw parallel lines from $D$ to the vertical sides of the triangle and we call $E, Z$ their points of intersection with $A B$ and $A C$ respectively. The parallel line from $C$ to $E Z$ intersects the line $A B$ at the point $N$ Let $A^{\prime}$ be the symmetric of $A$ with respect to the line $E Z$ and $I, K$ the projections of $A^{\prime}$ onto $A B$ and $A C$ respectively. If $T$ is the point of intersection of the lines $I K$ and $D E$, prove that $\angle N A^{\prime} T=\angle A D T$.
|
Suppose that the line $A A^{\prime}$ intersects the lines $E Z, B C$ and $C N$ at the points $L, M$, $F$ respectively. The line $I K$ being diagonal of the rectangle $K A^{\prime} I A$ passes through $L$, which by construction of $A^{\prime}$, is the middle of the other diagonal $A A^{\prime}$. The triangles $Z A L, A L E$ are similar, so $\angle Z A L=\angle A E Z$. By the similarity of the triangles $A B C, D A B$, we get $\angle A C B=\angle B A D$. We have also that $\angle A E Z=\angle B A D$, therefore
$$
\angle Z A L=\angle C A M=\angle A C B=\angle A C M
$$
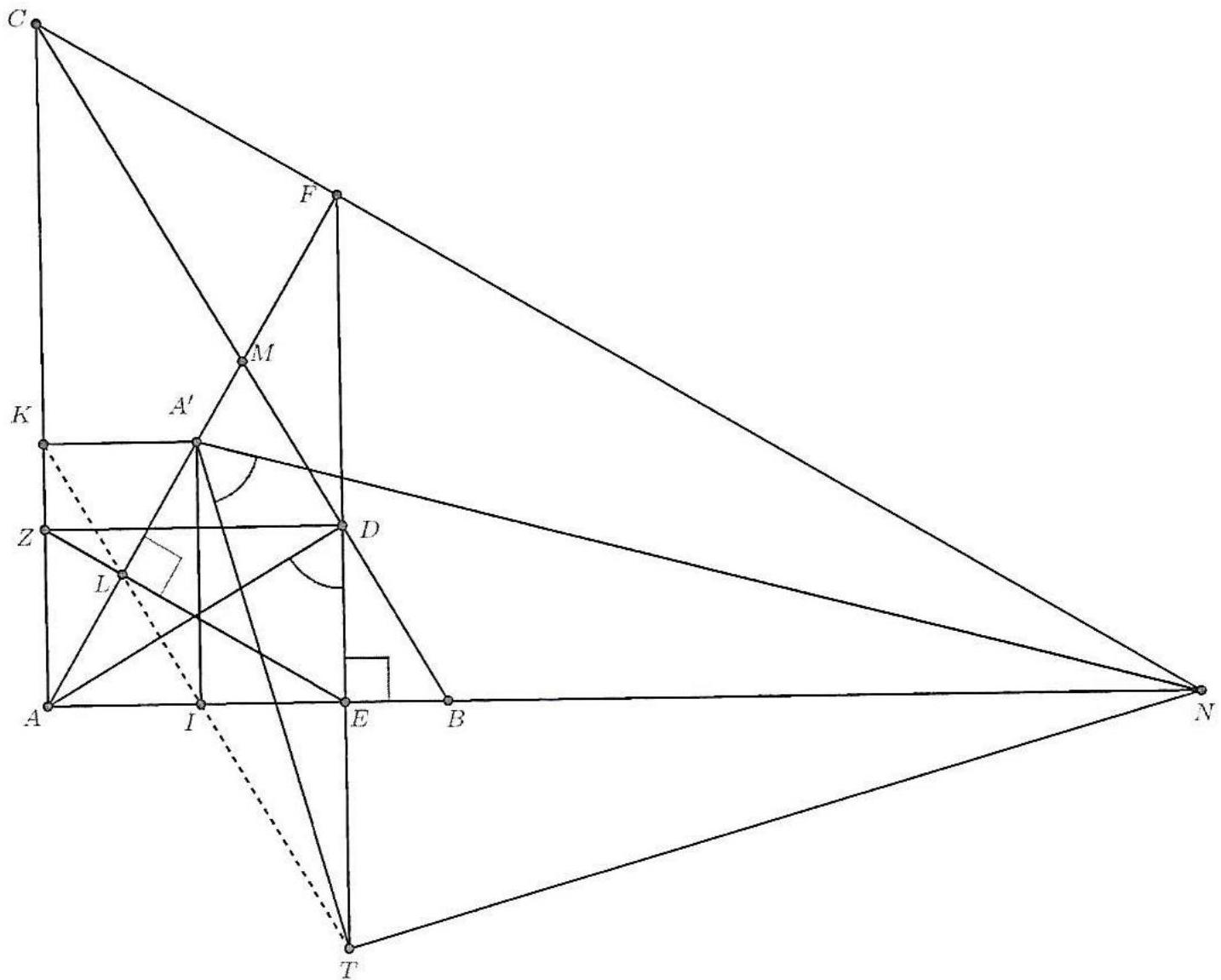
Since $A F \perp C N$, we have that the right triangles $A F C$ and $C D A$ are equal. Thus the altitudes from the vertices $F, D$ of the triangles $A F C, C D A$ respectively are equal. It follows that $F D \| A C$ and since $D E \| A C$ we get that the points $E, D, F$ are collinear.
In the triangle $L F T$ we have, $A^{\prime} I \| F T$ and $\angle L A^{\prime} I=\angle L I A^{\prime}$, so $\angle L F T=\angle L T F$. Therefore the points $F, A^{\prime}, I, T$ belong to the same circle. Also, $\angle A^{\prime} I N=\angle A^{\prime} F N=90^{\circ}$ so the quadrilateral $I A^{\prime} F N$ is cyclic. Thus, the points $F, A^{\prime}, I, T, N$ all lie on a circle. From the above, we infer that
$$
\angle N A^{\prime} T=\angle T F N=\angle A C F=\angle F E Z=\angle A D T \text {. }
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a right angled triangle with $\angle A=90^{\circ}$ and $A D$ its altitude. We draw parallel lines from $D$ to the vertical sides of the triangle and we call $E, Z$ their points of intersection with $A B$ and $A C$ respectively. The parallel line from $C$ to $E Z$ intersects the line $A B$ at the point $N$ Let $A^{\prime}$ be the symmetric of $A$ with respect to the line $E Z$ and $I, K$ the projections of $A^{\prime}$ onto $A B$ and $A C$ respectively. If $T$ is the point of intersection of the lines $I K$ and $D E$, prove that $\angle N A^{\prime} T=\angle A D T$.
|
Suppose that the line $A A^{\prime}$ intersects the lines $E Z, B C$ and $C N$ at the points $L, M$, $F$ respectively. The line $I K$ being diagonal of the rectangle $K A^{\prime} I A$ passes through $L$, which by construction of $A^{\prime}$, is the middle of the other diagonal $A A^{\prime}$. The triangles $Z A L, A L E$ are similar, so $\angle Z A L=\angle A E Z$. By the similarity of the triangles $A B C, D A B$, we get $\angle A C B=\angle B A D$. We have also that $\angle A E Z=\angle B A D$, therefore
$$
\angle Z A L=\angle C A M=\angle A C B=\angle A C M
$$

Since $A F \perp C N$, we have that the right triangles $A F C$ and $C D A$ are equal. Thus the altitudes from the vertices $F, D$ of the triangles $A F C, C D A$ respectively are equal. It follows that $F D \| A C$ and since $D E \| A C$ we get that the points $E, D, F$ are collinear.
In the triangle $L F T$ we have, $A^{\prime} I \| F T$ and $\angle L A^{\prime} I=\angle L I A^{\prime}$, so $\angle L F T=\angle L T F$. Therefore the points $F, A^{\prime}, I, T$ belong to the same circle. Also, $\angle A^{\prime} I N=\angle A^{\prime} F N=90^{\circ}$ so the quadrilateral $I A^{\prime} F N$ is cyclic. Thus, the points $F, A^{\prime}, I, T, N$ all lie on a circle. From the above, we infer that
$$
\angle N A^{\prime} T=\angle T F N=\angle A C F=\angle F E Z=\angle A D T \text {. }
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nG 2.",
"solution_match": "\nSolution."
}
|
4f9a9e7f-a892-5c5e-a642-295fab83f08e
| 605,035
|
Let $A B C$ be an acute triangle, $A^{\prime}, B^{\prime}, C^{\prime}$ the reflexions of the vertices $A, B$ and $C$ with respect to $B C, C A$, and $A B$, respectively, and let the circumcircles of triangles $A B B^{\prime}$ and $A C C^{\prime}$ meet again at $A_{1}$. Points $B_{1}$ and $C_{1}$ are defined similarly. Prove that the lines $A A_{1}, B B_{1}$, and $C C_{1}$ have a common point.
|
Let $O_{1}, O_{2}$ and $O$ be the circumcenters of triangles $A B B^{\prime}, A C C^{\prime}$ and $A B C$ respectively. As $A B$ is the perpendicular bisector of the line segment $C C^{\prime}, O_{2}$ is the intersection of the perpendicular bisector of $A C$ with $A B$. Similarly, $O_{1}$ is the intersection of the perpendicular bisector of $A B$ with $A C$. It follows that $O$ is the orthocenter of triangle $A O_{1} O_{2}$. This means that $A O$ is perpendicular to $O_{1} O_{2}$. On the other hand, the segment $A A_{1}$ is the common chord of the two circles, thus it is perpendicular to $O_{1} O_{2}$. As a result, $A A_{1}$ passes through $O$. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent at $O$.
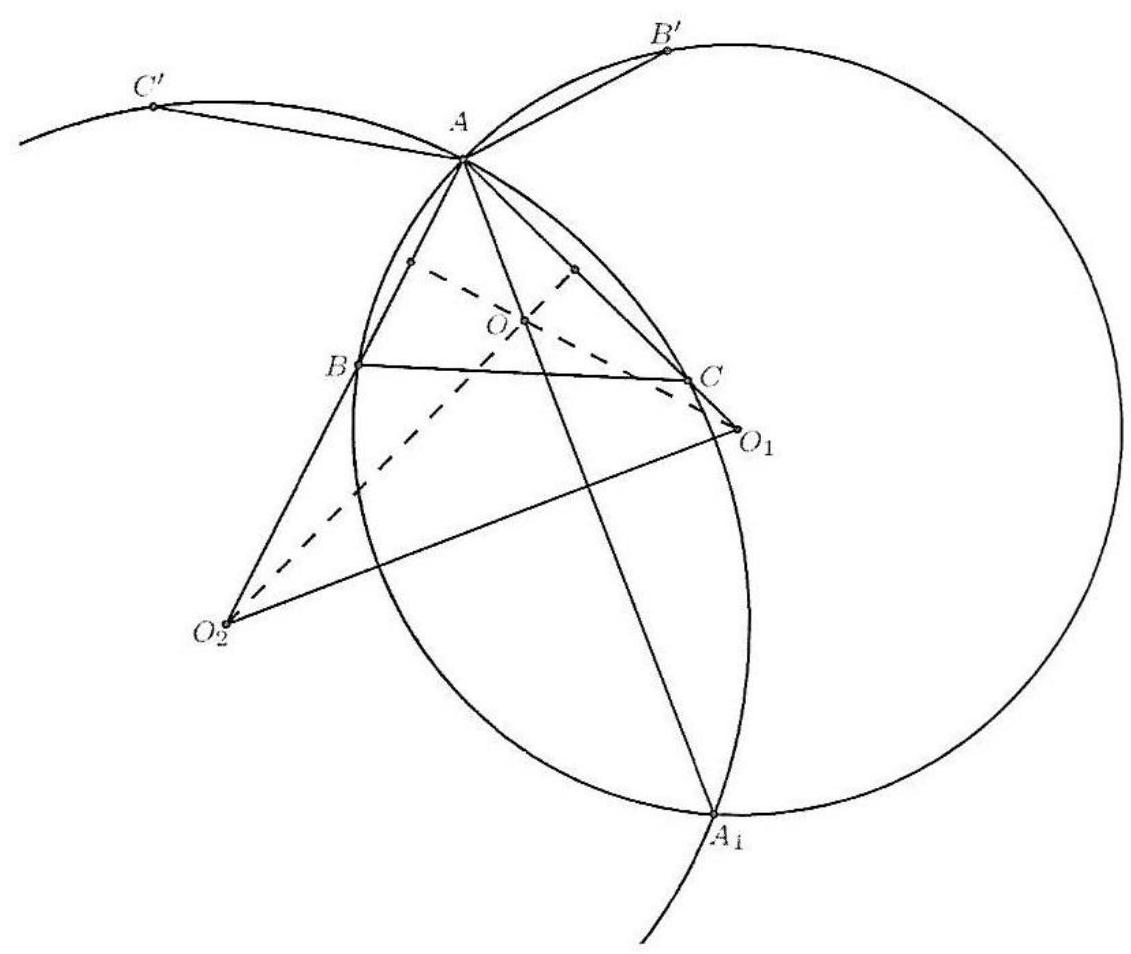
Comment by PSC. We present here a different approach.
We first prove that $A_{1}, B$ and $C^{\prime}$ are collinear. Indeed, since $\angle B A B^{\prime}=\angle C A C^{\prime}=2 \angle B A C$, then from the circles $\left(A B B^{\prime}\right),\left(A C C^{\prime}\right)$ we get
$$
\angle A A_{1} B=90^{\circ}-\angle B A C=\angle A A_{1} C^{\prime}
$$
It follows that
$$
\angle A_{1} A C=\angle A_{1} C^{\prime} C=\angle B C^{\prime} C=90^{\circ}-\angle A B C
$$
On the other hand, if $O$ is the circumcenter of $A B C$, then
$$
\angle O A C=90^{\circ}-\angle A B C
$$
From (1) and (2) we conclude that $A_{1}, A$ and $O$ are collinear. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent in $O$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle, $A^{\prime}, B^{\prime}, C^{\prime}$ the reflexions of the vertices $A, B$ and $C$ with respect to $B C, C A$, and $A B$, respectively, and let the circumcircles of triangles $A B B^{\prime}$ and $A C C^{\prime}$ meet again at $A_{1}$. Points $B_{1}$ and $C_{1}$ are defined similarly. Prove that the lines $A A_{1}, B B_{1}$, and $C C_{1}$ have a common point.
|
Let $O_{1}, O_{2}$ and $O$ be the circumcenters of triangles $A B B^{\prime}, A C C^{\prime}$ and $A B C$ respectively. As $A B$ is the perpendicular bisector of the line segment $C C^{\prime}, O_{2}$ is the intersection of the perpendicular bisector of $A C$ with $A B$. Similarly, $O_{1}$ is the intersection of the perpendicular bisector of $A B$ with $A C$. It follows that $O$ is the orthocenter of triangle $A O_{1} O_{2}$. This means that $A O$ is perpendicular to $O_{1} O_{2}$. On the other hand, the segment $A A_{1}$ is the common chord of the two circles, thus it is perpendicular to $O_{1} O_{2}$. As a result, $A A_{1}$ passes through $O$. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent at $O$.

Comment by PSC. We present here a different approach.
We first prove that $A_{1}, B$ and $C^{\prime}$ are collinear. Indeed, since $\angle B A B^{\prime}=\angle C A C^{\prime}=2 \angle B A C$, then from the circles $\left(A B B^{\prime}\right),\left(A C C^{\prime}\right)$ we get
$$
\angle A A_{1} B=90^{\circ}-\angle B A C=\angle A A_{1} C^{\prime}
$$
It follows that
$$
\angle A_{1} A C=\angle A_{1} C^{\prime} C=\angle B C^{\prime} C=90^{\circ}-\angle A B C
$$
On the other hand, if $O$ is the circumcenter of $A B C$, then
$$
\angle O A C=90^{\circ}-\angle A B C
$$
From (1) and (2) we conclude that $A_{1}, A$ and $O$ are collinear. Similarly, $B B_{1}$ and $C C_{1}$ pass through $O$, so the three lines are concurrent in $O$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nG 3.",
"solution_match": "\nSolution."
}
|
5bb916c8-d311-57e5-9795-e402a22f33cf
| 605,053
|
Let $A B C$ be a triangle with side-lengths $a, b, c$, inscribed in a circle with radius $R$ and let $I$ be it's incenter. Let $P_{1}, P_{2}$ and $P_{3}$ be the areas of the triangles $A B I, B C I$ and $C A I$, respectively. Prove that
$$
\frac{R^{4}}{P_{1}^{2}}+\frac{R^{4}}{P_{2}^{2}}+\frac{R^{4}}{P_{3}^{2}} \geq 16
$$
|
Let $r$ be the radius of the inscribed circle of the triangle $A B C$. We have that
$$
P_{1}=\frac{r c}{2}, \quad P_{2}=\frac{r a}{2}, \quad P_{3}=\frac{r b}{2}
$$
It follows that
$$
\frac{1}{P_{1}^{2}}+\frac{1}{P_{2}^{2}}+\frac{1}{P_{3}^{2}}=\frac{4}{r^{2}}\left(\frac{1}{c^{2}}+\frac{1}{a^{2}}+\frac{1}{b^{2}}\right)
$$
From Leibniz's relation we have that if $H$ is the orthocenter, then
$$
O H^{2}=9 R^{2}-a^{2}-b^{2}-c^{2}
$$
It follows that
$$
9 R^{2} \geq a^{2}+b^{2}+c^{2}
$$
Therefore, using the AM-HM inequality and then (1), we get
$$
\frac{1}{c^{2}}+\frac{1}{a^{2}}+\frac{1}{b^{2}} \geq \frac{9}{a^{2}+b^{2}+c^{2}} \geq \frac{1}{R^{2}}
$$
Finally, using Euler's inequality, namely that $R \geq 2 r$, we get
$$
\frac{1}{P_{1}^{2}}+\frac{1}{P_{2}^{2}}+\frac{1}{P_{3}^{2}} \geq \frac{4}{r^{2} R^{2}} \geq \frac{16}{R^{4}}
$$
Comment by PSC. We can avoid using Leibniz's relation as follows: as in the above solution we have that
$$
\frac{1}{P_{1}^{2}}+\frac{1}{P_{2}^{2}}+\frac{1}{P_{3}^{2}}=\frac{4}{r^{2}}\left(\frac{1}{c^{2}}+\frac{1}{a^{2}}+\frac{1}{b^{2}}\right)
$$
Let $a+b+c=2 \tau, E=(A B C)$ and using the inequality $x^{2}+y^{2}+z^{2} \geq x y+y z+z x$ we get
$$
\begin{aligned}
\frac{1}{c^{2}}+\frac{1}{a^{2}}+\frac{1}{b^{2}} & \geq \frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a}=\frac{2 \tau}{a b c} \\
& =\frac{\tau}{2 R E}=\frac{1}{2 R r}
\end{aligned}
$$
where we used the area formulas $E=\frac{a b c}{4 R}=\tau r$. Finally, using Euler's inequality, namely that $R \geq 2 r$, we get
$$
\frac{1}{P_{1}^{2}}+\frac{1}{P_{2}^{2}}+\frac{1}{P_{3}^{2}} \geq \frac{2}{r^{3} R} \geq \frac{16}{R^{4}}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $A B C$ be a triangle with side-lengths $a, b, c$, inscribed in a circle with radius $R$ and let $I$ be it's incenter. Let $P_{1}, P_{2}$ and $P_{3}$ be the areas of the triangles $A B I, B C I$ and $C A I$, respectively. Prove that
$$
\frac{R^{4}}{P_{1}^{2}}+\frac{R^{4}}{P_{2}^{2}}+\frac{R^{4}}{P_{3}^{2}} \geq 16
$$
|
Let $r$ be the radius of the inscribed circle of the triangle $A B C$. We have that
$$
P_{1}=\frac{r c}{2}, \quad P_{2}=\frac{r a}{2}, \quad P_{3}=\frac{r b}{2}
$$
It follows that
$$
\frac{1}{P_{1}^{2}}+\frac{1}{P_{2}^{2}}+\frac{1}{P_{3}^{2}}=\frac{4}{r^{2}}\left(\frac{1}{c^{2}}+\frac{1}{a^{2}}+\frac{1}{b^{2}}\right)
$$
From Leibniz's relation we have that if $H$ is the orthocenter, then
$$
O H^{2}=9 R^{2}-a^{2}-b^{2}-c^{2}
$$
It follows that
$$
9 R^{2} \geq a^{2}+b^{2}+c^{2}
$$
Therefore, using the AM-HM inequality and then (1), we get
$$
\frac{1}{c^{2}}+\frac{1}{a^{2}}+\frac{1}{b^{2}} \geq \frac{9}{a^{2}+b^{2}+c^{2}} \geq \frac{1}{R^{2}}
$$
Finally, using Euler's inequality, namely that $R \geq 2 r$, we get
$$
\frac{1}{P_{1}^{2}}+\frac{1}{P_{2}^{2}}+\frac{1}{P_{3}^{2}} \geq \frac{4}{r^{2} R^{2}} \geq \frac{16}{R^{4}}
$$
Comment by PSC. We can avoid using Leibniz's relation as follows: as in the above solution we have that
$$
\frac{1}{P_{1}^{2}}+\frac{1}{P_{2}^{2}}+\frac{1}{P_{3}^{2}}=\frac{4}{r^{2}}\left(\frac{1}{c^{2}}+\frac{1}{a^{2}}+\frac{1}{b^{2}}\right)
$$
Let $a+b+c=2 \tau, E=(A B C)$ and using the inequality $x^{2}+y^{2}+z^{2} \geq x y+y z+z x$ we get
$$
\begin{aligned}
\frac{1}{c^{2}}+\frac{1}{a^{2}}+\frac{1}{b^{2}} & \geq \frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a}=\frac{2 \tau}{a b c} \\
& =\frac{\tau}{2 R E}=\frac{1}{2 R r}
\end{aligned}
$$
where we used the area formulas $E=\frac{a b c}{4 R}=\tau r$. Finally, using Euler's inequality, namely that $R \geq 2 r$, we get
$$
\frac{1}{P_{1}^{2}}+\frac{1}{P_{2}^{2}}+\frac{1}{P_{3}^{2}} \geq \frac{2}{r^{3} R} \geq \frac{16}{R^{4}}
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nG 4.",
"solution_match": "\nSolution."
}
|
163e8b46-490c-55e8-8dca-fbd755e9f5bb
| 605,060
|
Given a rectangle $A B C D$ such that $A B=b>2 a=B C$, let $E$ be the midpoint of $A D$. On a line parallel to $A B$ through point $E$, a point $G$ is chosen such that the area of $G C E$ is
$$
(G C E)=\frac{1}{2}\left(\frac{a^{3}}{b}+a b\right)
$$
Point $H$ is the foot of the perpendicular from $E$ to $G D$ and a point $I$ is taken on the diagonal $A C$ such that the triangles $A C E$ and $A E I$ are similar. The lines $B H$ and $I E$ intersect at $K$ and the lines $C A$ and $E H$ intersect at $J$. Prove that $K J \perp A B$.
|
Let $L$ be the foot of the perpendicular from $G$ to $E C$ and let $Q$ the point of intersection of the lines $E G$ and $B C$. Then,
$$
(G C E)=\frac{1}{2} E C \cdot G L=\frac{1}{2} \sqrt{a^{2}+b^{2}} \cdot G L
$$
So, $G L=\frac{a}{b} \sqrt{a^{2}+b^{2}}$.
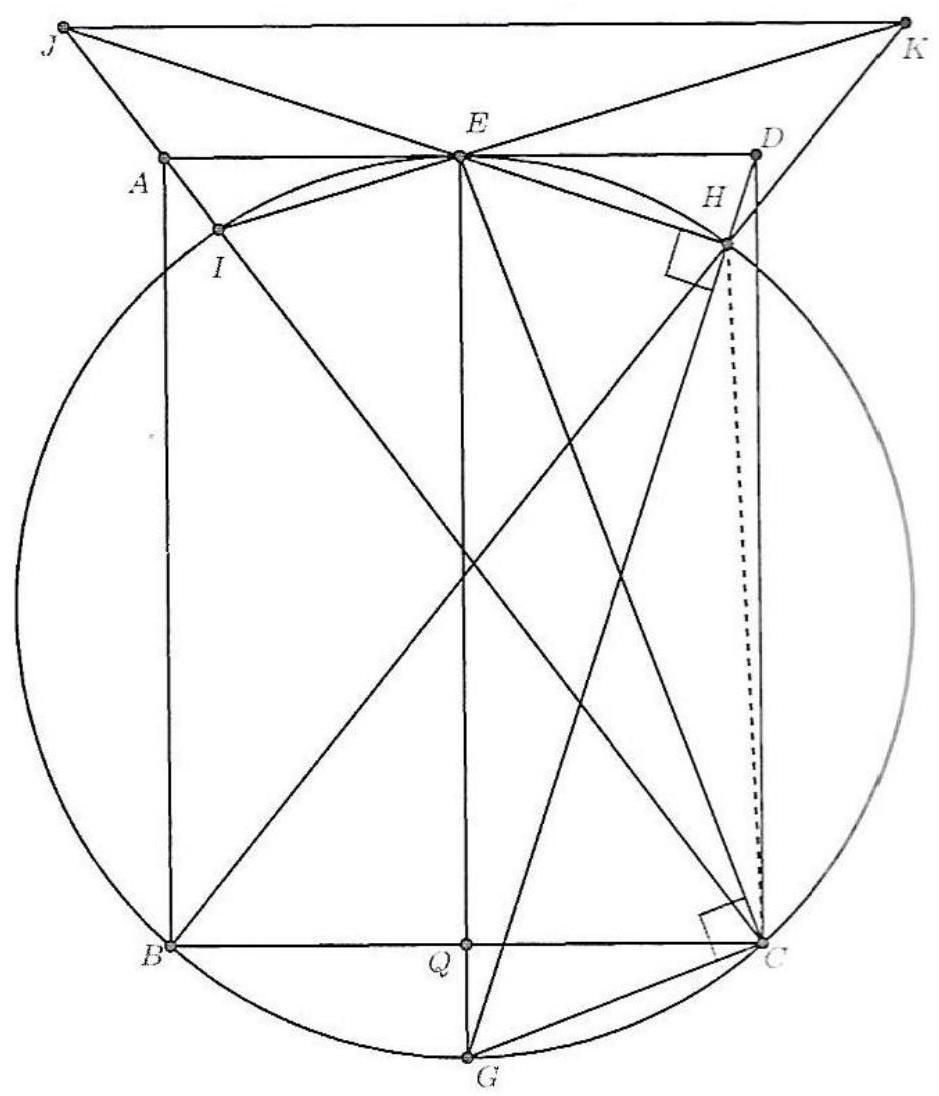
Observing that the triangles $Q C E$ and $E L G$ are similar, we have $\frac{a}{b}=\frac{G L}{E L}$, which implies that $E L=\sqrt{a^{2}+b^{2}}$, or in other words $L \equiv C$.
Consider the circumcircle $\omega$ of the triangle $E B C$. Since
$$
\angle E B G=\angle E C G=\angle E H G=90^{\circ}
$$
the points $H$ and $G$ lie on $\omega$.
From the given similarity of the triangles $A C E$ and $A E I$, we have that
$$
\angle A I E=\angle A E C=90^{\circ}+\angle G E C=90^{\circ}+\angle G H C=\angle E H C
$$
therefore $E H C I$ is cyclic, thus $I$ lies on $\omega$.
Since $E B=E C$, we get that $\angle E I C=\angle E H B$, thus $\angle J I E=\angle E H K$. We conclude that $J I H K$ is cyclic, therefore
$$
\angle J K H=\angle H I C=\angle H B C
$$
It follows that $K J \| B C$, so $K J \perp A B$.
Comment. The proposer suggests a different way to finish the proof after proving that $I$ lies on $\omega$ : We apply Pascal's Theorem to the degenerated hexagon $E E H B C I$. Since $B C$ and $E E$ intersect at infinity, this implies that $K J$, which is the line through the intersections of the other two opposite pairs of sides of the hexagon, has to go through this point at infinity, thus it is parallel to $B C$, and so $K J \perp A B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a rectangle $A B C D$ such that $A B=b>2 a=B C$, let $E$ be the midpoint of $A D$. On a line parallel to $A B$ through point $E$, a point $G$ is chosen such that the area of $G C E$ is
$$
(G C E)=\frac{1}{2}\left(\frac{a^{3}}{b}+a b\right)
$$
Point $H$ is the foot of the perpendicular from $E$ to $G D$ and a point $I$ is taken on the diagonal $A C$ such that the triangles $A C E$ and $A E I$ are similar. The lines $B H$ and $I E$ intersect at $K$ and the lines $C A$ and $E H$ intersect at $J$. Prove that $K J \perp A B$.
|
Let $L$ be the foot of the perpendicular from $G$ to $E C$ and let $Q$ the point of intersection of the lines $E G$ and $B C$. Then,
$$
(G C E)=\frac{1}{2} E C \cdot G L=\frac{1}{2} \sqrt{a^{2}+b^{2}} \cdot G L
$$
So, $G L=\frac{a}{b} \sqrt{a^{2}+b^{2}}$.

Observing that the triangles $Q C E$ and $E L G$ are similar, we have $\frac{a}{b}=\frac{G L}{E L}$, which implies that $E L=\sqrt{a^{2}+b^{2}}$, or in other words $L \equiv C$.
Consider the circumcircle $\omega$ of the triangle $E B C$. Since
$$
\angle E B G=\angle E C G=\angle E H G=90^{\circ}
$$
the points $H$ and $G$ lie on $\omega$.
From the given similarity of the triangles $A C E$ and $A E I$, we have that
$$
\angle A I E=\angle A E C=90^{\circ}+\angle G E C=90^{\circ}+\angle G H C=\angle E H C
$$
therefore $E H C I$ is cyclic, thus $I$ lies on $\omega$.
Since $E B=E C$, we get that $\angle E I C=\angle E H B$, thus $\angle J I E=\angle E H K$. We conclude that $J I H K$ is cyclic, therefore
$$
\angle J K H=\angle H I C=\angle H B C
$$
It follows that $K J \| B C$, so $K J \perp A B$.
Comment. The proposer suggests a different way to finish the proof after proving that $I$ lies on $\omega$ : We apply Pascal's Theorem to the degenerated hexagon $E E H B C I$. Since $B C$ and $E E$ intersect at infinity, this implies that $K J$, which is the line through the intersections of the other two opposite pairs of sides of the hexagon, has to go through this point at infinity, thus it is parallel to $B C$, and so $K J \perp A B$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nG 5.",
"solution_match": "\nSolution."
}
|
8001bcc2-35e6-5d9a-8020-c4dcf96cb350
| 605,073
|
Let $X Y$ be a chord of a circle $\Omega$, with center $O$, which is not a diameter. Let $P, Q$ be two distinct points inside the segment $X Y$, where $Q$ lies between $P$ and $X$. Let $\ell$ the perpendicular line dropped from $P$ to the diameter which passes through $Q$. Let $M$ be the intersection point of $\ell$ and $\Omega$, which is closer to $P$. Prove that
$$
M P \cdot X Y \geq 2 \cdot Q X \cdot P Y
$$
|
by PSC. At first, we will allow $P$ and $Q$ to coincide, and we will prove the inequality in this case. Let the perpendicular from $Q$ to $O Q$ meet $\Omega$ at $B$ and $C$. Then, we have that $Q B=Q C$. We will show that
$$
B Q \cdot X Y \geq 2 Q X \cdot Q Y
$$
By the power of a point Theorem we have that
$$
Q X \cdot Q Y=Q B \cdot Q C=Q B^{2}
$$
therefore it is enough to prove that $X Y \geq 2 B Q$ or $X Y \geq B C$. Let $T$ be the foot of the perpendicular from $O$ to $X Y$. Then, from the right-angled triangle $O T Q$ we have that $O T \leq O Q$, so the distance from $O$ to the chord $X Y$ is smaller or equal to the distance from $O$ to the chord $B C$. This means that $X Y \geq B C$, so (1) holds.
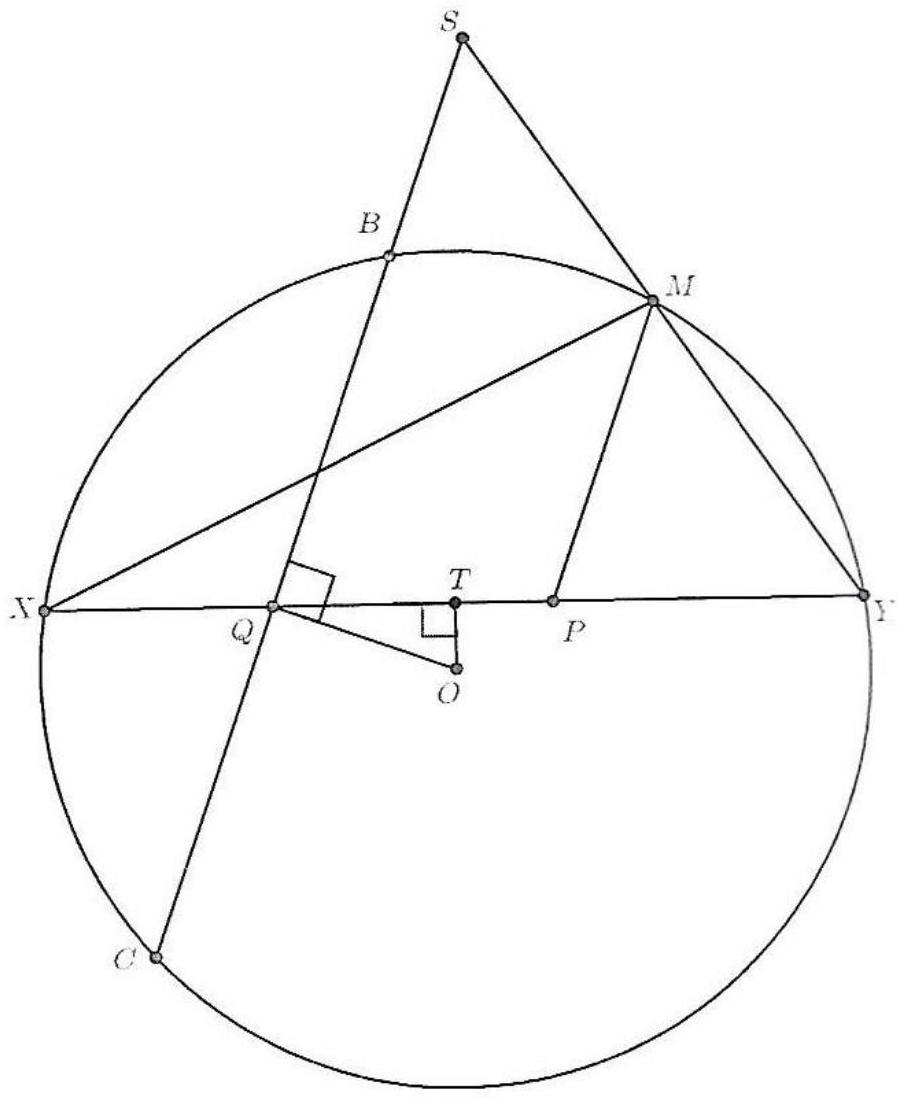
Back to the initial problem, we have to prove that
$$
M P \cdot X Y \geq 2 Q X \cdot P Y \Longleftrightarrow \frac{X Y}{2 Q X} \geq \frac{P Y}{P M}
$$
By (1) we have that
$$
\frac{X Y}{2 Q X} \geq \frac{Q Y}{Q B}
$$
so it is enough to prove that
$$
\frac{Q Y}{Q B} \geq \frac{P Y}{P M}
$$
If $C B$ meets $Y M$ at $S$, then from $M P \| Q S$ we get
$$
\frac{Q Y}{Q B} \geq \frac{Q Y}{Q S}=\frac{P Y}{P M}
$$
which is the desired.
Comment. The proposer's solution uses analytic geometry and it is the following.
We will show that $(Q M-Q P) \cdot X Y \geq 2 \cdot Q X \cdot P Y$. Since $M P \geq Q M-Q P$, our inequality follows directly. Let $A$ the intersection point of $\ell$ with the diameter which passes through $Q$. Like in the following picture, choose a coordinative system centered at $O$ and such that $Q=(a, 0), A=(c, 0)$, $P=(c, h)$ and denote the lengths $Q X=x, P Q=t, P Y=y, O P=d, Q M=z$.
Let $\lambda_{Q}=r^{2}-a^{2}$ and $\lambda_{P}=r^{2}-d^{2}$ respectively the power of $Q$ and $P$ qith respect to our circle $\Omega$. We will show that:
$$
(z-t)(t+x+y) \geq 2 x y
$$
Adding and multiplying respectively the relations $x(t+y)=\lambda_{Q}$ and $y(t+x)=\lambda_{P}$, we will have
$$
t(x+y)+2 x y=\lambda_{P}+\lambda_{Q}
$$
and
$$
x y(t+x)(t+y)=\lambda_{P} \lambda_{Q}
$$
Using these two equations, it's easy to deduce that:
$$
(x y)^{2}-x y\left(t^{2}+\lambda_{P}+\lambda_{Q}\right)+\lambda_{P} \lambda_{Q}=0
$$
So, $w_{1}=x y$ is a zero of the second degree polynomial:
$$
p(w)=w^{2}-w\left(t^{2}+\lambda_{P}+\lambda_{Q}\right)+\lambda_{P} \lambda_{Q}
$$
But $w_{1}=x y<x(t+y)=\lambda_{Q}$ and
$$
\begin{aligned}
p\left(\lambda_{Q}\right) & =\left(r^{2}-a^{2}\right)^{2}-\left(r^{2}-a^{2}\right)\left(t^{2}+\lambda_{P}+\lambda_{Q}\right)+\lambda_{P} \lambda_{Q} \\
& =\left(r^{2}-a^{2}\right)^{2}-\left(r^{2}-a^{2}\right)\left(t^{2}+r^{2}-d^{2}+r^{2}-a^{2}\right)+\left(r^{2}-d^{2}\right)\left(r^{2}-a^{2}\right) \\
& =\left(r^{2}-a^{2}\right)^{2}-\left(r^{2}-a^{2}\right) t^{2}-\left(r^{2}-d^{2}\right)\left(r^{2}-a^{2}\right)-\left(r^{2}-a^{2}\right)^{4}+\left(r^{2}-d^{2}\right)\left(r^{2}-a^{2}\right) \\
& =-t^{2}\left(r^{2}-a^{2}\right)=-t^{2} \lambda_{Q}<0
\end{aligned}
$$
This implies that $\lambda_{Q}$ lies (strictly) between the two (positive) zeros $w_{1}, w_{2}$ of $p(w)$ and $w_{1}=x y$ is the smaller one.
After using (2) and (3), inequality (1) can be rewritten as:
$$
(x y)^{2} \leq\left(\frac{z-t}{z+t}\right) \lambda_{P} \lambda_{Q}
$$
In order to show this, it is enough to show that
$$
p\left(\sqrt{\frac{z-t}{z+t} \lambda_{P} \lambda_{Q}}\right) \leq 0
$$
because this will imply $\sqrt{\frac{z-t}{z+t} \lambda_{P} \lambda_{Q}} \in\left[w_{1}, w_{2}\right]$. After some manipulations, inequality (6) can be equivalently transformed to:
$$
4 z^{2} \lambda_{P} \lambda_{Q} \leq\left(z^{2}-t^{2}\right)\left(t^{2}+\lambda_{P}+\lambda_{Q}\right)^{2}
$$
Since $z^{2}-t^{2}=r^{2}-d^{2}=\lambda_{P}$, this is equivalent to:
$$
4 z^{2} \lambda_{Q} \leq\left(t^{2}+\lambda_{P}+\lambda_{Q}\right)^{2}
$$
But $t^{2}=(a-c)^{2}+h^{2}=a^{2}+d^{2}-2 a c, z^{2}=t^{2}+r^{2}-d^{2}=a^{2}-2 a c+r^{2}$ and $t^{2}+\lambda_{P}+\lambda_{Q}=\ldots=2\left(r^{2}-a c\right)$. Hence, (8) is equivalent with:
$$
\left(a^{2}-2 a c+r^{2}\right)\left(r^{2}-a^{2}\right) \leq\left(r^{2}-a c\right)^{2} \Leftrightarrow \cdots \Leftrightarrow 0 \leq a^{2}(a-c)^{2}
$$
which is clearly true.
## NUMBER THEORY
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $X Y$ be a chord of a circle $\Omega$, with center $O$, which is not a diameter. Let $P, Q$ be two distinct points inside the segment $X Y$, where $Q$ lies between $P$ and $X$. Let $\ell$ the perpendicular line dropped from $P$ to the diameter which passes through $Q$. Let $M$ be the intersection point of $\ell$ and $\Omega$, which is closer to $P$. Prove that
$$
M P \cdot X Y \geq 2 \cdot Q X \cdot P Y
$$
|
by PSC. At first, we will allow $P$ and $Q$ to coincide, and we will prove the inequality in this case. Let the perpendicular from $Q$ to $O Q$ meet $\Omega$ at $B$ and $C$. Then, we have that $Q B=Q C$. We will show that
$$
B Q \cdot X Y \geq 2 Q X \cdot Q Y
$$
By the power of a point Theorem we have that
$$
Q X \cdot Q Y=Q B \cdot Q C=Q B^{2}
$$
therefore it is enough to prove that $X Y \geq 2 B Q$ or $X Y \geq B C$. Let $T$ be the foot of the perpendicular from $O$ to $X Y$. Then, from the right-angled triangle $O T Q$ we have that $O T \leq O Q$, so the distance from $O$ to the chord $X Y$ is smaller or equal to the distance from $O$ to the chord $B C$. This means that $X Y \geq B C$, so (1) holds.

Back to the initial problem, we have to prove that
$$
M P \cdot X Y \geq 2 Q X \cdot P Y \Longleftrightarrow \frac{X Y}{2 Q X} \geq \frac{P Y}{P M}
$$
By (1) we have that
$$
\frac{X Y}{2 Q X} \geq \frac{Q Y}{Q B}
$$
so it is enough to prove that
$$
\frac{Q Y}{Q B} \geq \frac{P Y}{P M}
$$
If $C B$ meets $Y M$ at $S$, then from $M P \| Q S$ we get
$$
\frac{Q Y}{Q B} \geq \frac{Q Y}{Q S}=\frac{P Y}{P M}
$$
which is the desired.
Comment. The proposer's solution uses analytic geometry and it is the following.
We will show that $(Q M-Q P) \cdot X Y \geq 2 \cdot Q X \cdot P Y$. Since $M P \geq Q M-Q P$, our inequality follows directly. Let $A$ the intersection point of $\ell$ with the diameter which passes through $Q$. Like in the following picture, choose a coordinative system centered at $O$ and such that $Q=(a, 0), A=(c, 0)$, $P=(c, h)$ and denote the lengths $Q X=x, P Q=t, P Y=y, O P=d, Q M=z$.
Let $\lambda_{Q}=r^{2}-a^{2}$ and $\lambda_{P}=r^{2}-d^{2}$ respectively the power of $Q$ and $P$ qith respect to our circle $\Omega$. We will show that:
$$
(z-t)(t+x+y) \geq 2 x y
$$

Adding and multiplying respectively the relations $x(t+y)=\lambda_{Q}$ and $y(t+x)=\lambda_{P}$, we will have
$$
t(x+y)+2 x y=\lambda_{P}+\lambda_{Q}
$$
and
$$
x y(t+x)(t+y)=\lambda_{P} \lambda_{Q}
$$
Using these two equations, it's easy to deduce that:
$$
(x y)^{2}-x y\left(t^{2}+\lambda_{P}+\lambda_{Q}\right)+\lambda_{P} \lambda_{Q}=0
$$
So, $w_{1}=x y$ is a zero of the second degree polynomial:
$$
p(w)=w^{2}-w\left(t^{2}+\lambda_{P}+\lambda_{Q}\right)+\lambda_{P} \lambda_{Q}
$$
But $w_{1}=x y<x(t+y)=\lambda_{Q}$ and
$$
\begin{aligned}
p\left(\lambda_{Q}\right) & =\left(r^{2}-a^{2}\right)^{2}-\left(r^{2}-a^{2}\right)\left(t^{2}+\lambda_{P}+\lambda_{Q}\right)+\lambda_{P} \lambda_{Q} \\
& =\left(r^{2}-a^{2}\right)^{2}-\left(r^{2}-a^{2}\right)\left(t^{2}+r^{2}-d^{2}+r^{2}-a^{2}\right)+\left(r^{2}-d^{2}\right)\left(r^{2}-a^{2}\right) \\
& =\left(r^{2}-a^{2}\right)^{2}-\left(r^{2}-a^{2}\right) t^{2}-\left(r^{2}-d^{2}\right)\left(r^{2}-a^{2}\right)-\left(r^{2}-a^{2}\right)^{4}+\left(r^{2}-d^{2}\right)\left(r^{2}-a^{2}\right) \\
& =-t^{2}\left(r^{2}-a^{2}\right)=-t^{2} \lambda_{Q}<0
\end{aligned}
$$
This implies that $\lambda_{Q}$ lies (strictly) between the two (positive) zeros $w_{1}, w_{2}$ of $p(w)$ and $w_{1}=x y$ is the smaller one.
After using (2) and (3), inequality (1) can be rewritten as:
$$
(x y)^{2} \leq\left(\frac{z-t}{z+t}\right) \lambda_{P} \lambda_{Q}
$$
In order to show this, it is enough to show that
$$
p\left(\sqrt{\frac{z-t}{z+t} \lambda_{P} \lambda_{Q}}\right) \leq 0
$$
because this will imply $\sqrt{\frac{z-t}{z+t} \lambda_{P} \lambda_{Q}} \in\left[w_{1}, w_{2}\right]$. After some manipulations, inequality (6) can be equivalently transformed to:
$$
4 z^{2} \lambda_{P} \lambda_{Q} \leq\left(z^{2}-t^{2}\right)\left(t^{2}+\lambda_{P}+\lambda_{Q}\right)^{2}
$$
Since $z^{2}-t^{2}=r^{2}-d^{2}=\lambda_{P}$, this is equivalent to:
$$
4 z^{2} \lambda_{Q} \leq\left(t^{2}+\lambda_{P}+\lambda_{Q}\right)^{2}
$$
But $t^{2}=(a-c)^{2}+h^{2}=a^{2}+d^{2}-2 a c, z^{2}=t^{2}+r^{2}-d^{2}=a^{2}-2 a c+r^{2}$ and $t^{2}+\lambda_{P}+\lambda_{Q}=\ldots=2\left(r^{2}-a c\right)$. Hence, (8) is equivalent with:
$$
\left(a^{2}-2 a c+r^{2}\right)\left(r^{2}-a^{2}\right) \leq\left(r^{2}-a c\right)^{2} \Leftrightarrow \cdots \Leftrightarrow 0 \leq a^{2}(a-c)^{2}
$$
which is clearly true.
## NUMBER THEORY
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nG 6.",
"solution_match": "\nSolution "
}
|
90e649e5-cb5a-5613-a4e1-fa9b438afb17
| 605,086
|
Show that there exist infinitely many positive integers $n$ such that
$$
\frac{4^{n}+2^{n}+1}{n^{2}+n+1}
$$
is an integer.
|
Let $f(n)=n^{2}+n+1$. Note that
$$
f\left(n^{2}\right)=n^{4}+n^{2}+1=\left(n^{2}+n+1\right)\left(n^{2}-n+1\right)
$$
This means that $f(n) \mid f\left(n^{2}\right)$ for every positive integer $n$. By induction on $k$, one can easily see that $f(n) \mid f\left(n^{2^{k}}\right)$ for every positive integers $n$ and $k$. Note that the required condition is equivalent to $f(n) \mid f\left(2^{n}\right)$. From the discussion above, if there exists a positive integer $n$ so that $2^{n}$ can be written as $n^{2^{k}}$, for some positive integer $k$, then $f(n) \mid f\left(2^{n}\right)$. If we choose $n=2^{2^{m}}$ and $k=2^{m}-m$ for some positive integer $m$, then $2^{n}=n^{2^{k}}$ and since there are infinitely many positive integers of the form $n=2^{2^{m}}$, we have the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that there exist infinitely many positive integers $n$ such that
$$
\frac{4^{n}+2^{n}+1}{n^{2}+n+1}
$$
is an integer.
|
Let $f(n)=n^{2}+n+1$. Note that
$$
f\left(n^{2}\right)=n^{4}+n^{2}+1=\left(n^{2}+n+1\right)\left(n^{2}-n+1\right)
$$
This means that $f(n) \mid f\left(n^{2}\right)$ for every positive integer $n$. By induction on $k$, one can easily see that $f(n) \mid f\left(n^{2^{k}}\right)$ for every positive integers $n$ and $k$. Note that the required condition is equivalent to $f(n) \mid f\left(2^{n}\right)$. From the discussion above, if there exists a positive integer $n$ so that $2^{n}$ can be written as $n^{2^{k}}$, for some positive integer $k$, then $f(n) \mid f\left(2^{n}\right)$. If we choose $n=2^{2^{m}}$ and $k=2^{m}-m$ for some positive integer $m$, then $2^{n}=n^{2^{k}}$ and since there are infinitely many positive integers of the form $n=2^{2^{m}}$, we have the desired result.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nNT 4.",
"solution_match": "\nSolution."
}
|
525fdfcb-447d-55b1-ad07-65cff18c607a
| 605,133
|
Given positive real numbers $a, b, c$, prove that
$$
\frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(a+c)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3}
$$
|
Since $2 a b \leq a^{2}+b^{2}$, it follows that $(a+b)^{2} \leq 2\left(a^{2}+b^{2}\right)$ and $4 a b c \leq 2 c\left(a^{2}+b^{2}\right)$, for any positive reals $a, b, c$. Adding these inequalities, we find
$$
(a+b)^{2}+4 a b c \leq 2\left(a^{2}+b^{2}\right)(c+1)
$$
so that
$$
\frac{8}{(a+b)^{2}+4 a b c} \geq \frac{4}{\left(a^{2}+b^{2}\right)(c+1)}
$$
Using the AM-GM inequality, we have
$$
\frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq 2 \sqrt{\frac{2}{c+1}}=\frac{4}{\sqrt{2(c+1)}}
$$
respectively
$$
\frac{c+3}{8}=\frac{(c+1)+2}{8} \geq \frac{\sqrt{2(c+1)}}{4}
$$
We conclude that
$$
\frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq \frac{8}{c+3}
$$
and finally
$\frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(a+c)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Given positive real numbers $a, b, c$, prove that
$$
\frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(a+c)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3}
$$
|
Since $2 a b \leq a^{2}+b^{2}$, it follows that $(a+b)^{2} \leq 2\left(a^{2}+b^{2}\right)$ and $4 a b c \leq 2 c\left(a^{2}+b^{2}\right)$, for any positive reals $a, b, c$. Adding these inequalities, we find
$$
(a+b)^{2}+4 a b c \leq 2\left(a^{2}+b^{2}\right)(c+1)
$$
so that
$$
\frac{8}{(a+b)^{2}+4 a b c} \geq \frac{4}{\left(a^{2}+b^{2}\right)(c+1)}
$$
Using the AM-GM inequality, we have
$$
\frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq 2 \sqrt{\frac{2}{c+1}}=\frac{4}{\sqrt{2(c+1)}}
$$
respectively
$$
\frac{c+3}{8}=\frac{(c+1)+2}{8} \geq \frac{\sqrt{2(c+1)}}{4}
$$
We conclude that
$$
\frac{4}{\left(a^{2}+b^{2}\right)(c+1)}+\frac{a^{2}+b^{2}}{2} \geq \frac{8}{c+3}
$$
and finally
$\frac{8}{(a+b)^{2}+4 a b c}+\frac{8}{(a+c)^{2}+4 a b c}+\frac{8}{(b+c)^{2}+4 a b c}+a^{2}+b^{2}+c^{2} \geq \frac{8}{a+3}+\frac{8}{b+3}+\frac{8}{c+3}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nA2.",
"solution_match": "\nSolution."
}
|
1abc063c-fde4-5b60-bec5-2209ba38e487
| 605,153
|
If $x, y, z$ are non-negative real numbers such that $x^{2}+y^{2}+z^{2}=x+y+z$, then show that:
$$
\frac{x+1}{\sqrt{x^{5}+x+1}}+\frac{y+1}{\sqrt{y^{5}+y+1}}+\frac{z+1}{\sqrt{z^{5}+z+1}} \geq 3
$$
When does the equality hold?
|
First we factor $x^{5}+x+1$ as follows:
$$
\begin{aligned}
x^{5}+x+1 & =x^{5}-x^{2}+x^{2}+x+1=x^{2}\left(x^{3}-1\right)+x^{2}+x+1=x^{2}(x-1)\left(x^{2}+x+1\right)+x^{2}+x+1 \\
& =\left(x^{2}+x+1\right)\left(x^{2}(x-1)+1\right)=\left(x^{2}+x+1\right)\left(x^{3}-x^{2}+1\right)
\end{aligned}
$$
Using the $A M-G M$ inequality, we have
$$
\sqrt{x^{5}+x+1}=\sqrt{\left(x^{2}+x+1\right)\left(x^{3}-x^{2}+1\right)} \leq \frac{x^{2}+x+1+x^{3}-x^{2}+1}{2}=\frac{x^{3}+x+2}{2}
$$
and since
$x^{3}+x+2=x^{3}+1+x+1=(x+1)\left(x^{2}-x+1\right)+x+1=(x+1)\left(x^{2}-x+1+1\right)=(x+1)\left(x^{2}-x+2\right)$,
then
$$
\sqrt{x^{5}+x+1} \leq \frac{(x+1)\left(x^{2}-x+2\right)}{2}
$$
Using $x^{2}-x+2=\left(x-\frac{1}{2}\right)^{2}+\frac{7}{4}>0$, we obtain $\frac{x+1}{\sqrt{x^{5}+x+1}} \geq \frac{2}{x^{2}-x+2}$ Applying the CauchySchwarz inequality and the given condition, we get
$$
\sum_{c y c} \frac{x+1}{\sqrt{x^{5}+x+1}} \geq \sum_{c y c} \frac{2}{x^{2}-x+2} \geq \frac{18}{\sum_{c y c}\left(x^{2}-x+2\right)}=\frac{18}{6}=3
$$
which is the desired result.
For the equality both conditions: $x^{2}-x+2=y^{2}-y+2=z^{2}-z+2$ (equality in CBS) and $x^{3}-x^{2}+1=x^{2}+x+1$ (equality in AM-GM) have to be satisfied.
By using the given condition it follows that $x^{2}-x+2+y^{2}-y+2+z^{2}-z+2=6$, hence $3\left(x^{2}-x+2\right)=6$, implying $x=0$ or $x=1$. Of these, only $x=0$ satisfies the second condition. We conclude that equality can only hold for $x=y=z=0$.
It is an immediate check that indeed for these values equality holds.
## Alternative solution
Let us present an heuristic argument to reach the key inequality $\frac{x+1}{\sqrt{x^{5}+x+1}} \geq \frac{2}{x^{2}-x+2}$.
In order to exploit the condition $x^{2}+y^{2}+z^{2}=x+y+z$ when applying CBS in Engel form, we are looking for $\alpha, \beta, \gamma>0$ such that
$$
\frac{x+1}{\sqrt{x^{5}+x+1}} \geq \frac{\gamma}{\alpha\left(x^{2}-x\right)+\beta}
$$
After squaring and cancelling the denominators, we get
$$
(x+1)^{2}\left(\alpha\left(x^{2}-x\right)+\beta\right)^{2} \geq \gamma^{2}\left(x^{5}+x+1\right)
$$
for all $x \geq 0$, and, after some manipulations, we reach to $f(x) \geq 0$ for all $x \geq 0$, where $f(x)=\alpha^{2} x^{6}-\gamma^{2} x^{5}+\left(2 \alpha \beta-2 \alpha^{2}\right) x^{4}+2 \alpha \beta x^{3}+(\alpha-\beta)^{2} x^{2}+\left(2 \beta^{2}-2 \alpha \beta-\gamma^{2}\right) x+\beta^{2}-\gamma^{2}$.
As we are expecting the equality to hold for $x=0$, we naturally impose the condition that $f$ has 0 as a double root. This implies $\beta^{2}-\gamma^{2}=0$ and $2 \beta^{2}-2 \alpha \beta-\gamma^{2}=0$, that is, $\beta=\gamma$ and $\gamma=2 \alpha$.
Thus the inequality $f(x) \geq 0$ becomes
$$
\alpha^{2} x^{6}-4 \alpha^{2} x^{5}+2 \alpha^{2} x^{4}+4 \alpha^{2} x^{3}+\alpha^{2} x^{2} \geq 0, \forall x \geq 0
$$
that is,
$$
\alpha^{2} x^{2}\left(x^{2}-2 x-1\right)^{2} \geq 0 \forall x \geq 0
$$
which is obviously true.
Therefore, the inequality $\frac{x+1}{\sqrt{x^{5}+x+1}} \geq \frac{2}{x^{2}-x+2}$ holds for all $x \geq 0$ and now we can continue as in the first solution.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
If $x, y, z$ are non-negative real numbers such that $x^{2}+y^{2}+z^{2}=x+y+z$, then show that:
$$
\frac{x+1}{\sqrt{x^{5}+x+1}}+\frac{y+1}{\sqrt{y^{5}+y+1}}+\frac{z+1}{\sqrt{z^{5}+z+1}} \geq 3
$$
When does the equality hold?
|
First we factor $x^{5}+x+1$ as follows:
$$
\begin{aligned}
x^{5}+x+1 & =x^{5}-x^{2}+x^{2}+x+1=x^{2}\left(x^{3}-1\right)+x^{2}+x+1=x^{2}(x-1)\left(x^{2}+x+1\right)+x^{2}+x+1 \\
& =\left(x^{2}+x+1\right)\left(x^{2}(x-1)+1\right)=\left(x^{2}+x+1\right)\left(x^{3}-x^{2}+1\right)
\end{aligned}
$$
Using the $A M-G M$ inequality, we have
$$
\sqrt{x^{5}+x+1}=\sqrt{\left(x^{2}+x+1\right)\left(x^{3}-x^{2}+1\right)} \leq \frac{x^{2}+x+1+x^{3}-x^{2}+1}{2}=\frac{x^{3}+x+2}{2}
$$
and since
$x^{3}+x+2=x^{3}+1+x+1=(x+1)\left(x^{2}-x+1\right)+x+1=(x+1)\left(x^{2}-x+1+1\right)=(x+1)\left(x^{2}-x+2\right)$,
then
$$
\sqrt{x^{5}+x+1} \leq \frac{(x+1)\left(x^{2}-x+2\right)}{2}
$$
Using $x^{2}-x+2=\left(x-\frac{1}{2}\right)^{2}+\frac{7}{4}>0$, we obtain $\frac{x+1}{\sqrt{x^{5}+x+1}} \geq \frac{2}{x^{2}-x+2}$ Applying the CauchySchwarz inequality and the given condition, we get
$$
\sum_{c y c} \frac{x+1}{\sqrt{x^{5}+x+1}} \geq \sum_{c y c} \frac{2}{x^{2}-x+2} \geq \frac{18}{\sum_{c y c}\left(x^{2}-x+2\right)}=\frac{18}{6}=3
$$
which is the desired result.
For the equality both conditions: $x^{2}-x+2=y^{2}-y+2=z^{2}-z+2$ (equality in CBS) and $x^{3}-x^{2}+1=x^{2}+x+1$ (equality in AM-GM) have to be satisfied.
By using the given condition it follows that $x^{2}-x+2+y^{2}-y+2+z^{2}-z+2=6$, hence $3\left(x^{2}-x+2\right)=6$, implying $x=0$ or $x=1$. Of these, only $x=0$ satisfies the second condition. We conclude that equality can only hold for $x=y=z=0$.
It is an immediate check that indeed for these values equality holds.
## Alternative solution
Let us present an heuristic argument to reach the key inequality $\frac{x+1}{\sqrt{x^{5}+x+1}} \geq \frac{2}{x^{2}-x+2}$.
In order to exploit the condition $x^{2}+y^{2}+z^{2}=x+y+z$ when applying CBS in Engel form, we are looking for $\alpha, \beta, \gamma>0$ such that
$$
\frac{x+1}{\sqrt{x^{5}+x+1}} \geq \frac{\gamma}{\alpha\left(x^{2}-x\right)+\beta}
$$
After squaring and cancelling the denominators, we get
$$
(x+1)^{2}\left(\alpha\left(x^{2}-x\right)+\beta\right)^{2} \geq \gamma^{2}\left(x^{5}+x+1\right)
$$
for all $x \geq 0$, and, after some manipulations, we reach to $f(x) \geq 0$ for all $x \geq 0$, where $f(x)=\alpha^{2} x^{6}-\gamma^{2} x^{5}+\left(2 \alpha \beta-2 \alpha^{2}\right) x^{4}+2 \alpha \beta x^{3}+(\alpha-\beta)^{2} x^{2}+\left(2 \beta^{2}-2 \alpha \beta-\gamma^{2}\right) x+\beta^{2}-\gamma^{2}$.
As we are expecting the equality to hold for $x=0$, we naturally impose the condition that $f$ has 0 as a double root. This implies $\beta^{2}-\gamma^{2}=0$ and $2 \beta^{2}-2 \alpha \beta-\gamma^{2}=0$, that is, $\beta=\gamma$ and $\gamma=2 \alpha$.
Thus the inequality $f(x) \geq 0$ becomes
$$
\alpha^{2} x^{6}-4 \alpha^{2} x^{5}+2 \alpha^{2} x^{4}+4 \alpha^{2} x^{3}+\alpha^{2} x^{2} \geq 0, \forall x \geq 0
$$
that is,
$$
\alpha^{2} x^{2}\left(x^{2}-2 x-1\right)^{2} \geq 0 \forall x \geq 0
$$
which is obviously true.
Therefore, the inequality $\frac{x+1}{\sqrt{x^{5}+x+1}} \geq \frac{2}{x^{2}-x+2}$ holds for all $x \geq 0$ and now we can continue as in the first solution.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nA4.",
"solution_match": "\nSolution."
}
|
b5cb1dd3-342a-5019-b16d-34f5e3df055b
| 605,184
|
Let $x, y, z$ be positive real numbers such that $x+y+z=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}$.
a) Prove the inequality
$$
x+y+z \geq \sqrt{\frac{x y+1}{2}}+\sqrt{\frac{y z+1}{2}}+\sqrt{\frac{z x+1}{2}}
$$
b) (Added by the problem selecting committee) When does the equality hold?
|
a) We rewrite the inequality as
$$
(\sqrt{x y+1}+\sqrt{y z+1}+\sqrt{z x+1})^{2} \leq 2 \cdot(x+y+z)^{2}
$$
and note that, from CBS,
$$
\text { LHS } \leq\left(\frac{x y+1}{x}+\frac{y z+1}{y}+\frac{z x+1}{z}\right)(x+y+z)
$$
But
$$
\frac{x y+1}{x}+\frac{y z+1}{y}+\frac{z x+1}{z}=x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=2(x+y+z)
$$
which proves (1).
b) The equality occurs when we have equality in CBS, i.e. when
$$
\frac{x y+1}{x^{2}}=\frac{y z+1}{y^{2}}=\frac{z x+1}{z^{2}}\left(=\frac{x y+y z+z x+3}{x^{2}+y^{2}+z^{2}}\right)
$$
Since we can also write
$$
(\sqrt{x y+1}+\sqrt{y z+1}+\sqrt{z x+1})^{2} \leq\left(\frac{x y+1}{y}+\frac{y z+1}{z}+\frac{z x+1}{x}\right)(y+z+x)=2(x+y+z)^{2}
$$
the equality implies also
$$
\frac{x y+1}{y^{2}}=\frac{y z+1}{z^{2}}=\frac{z x+1}{x^{2}}\left(=\frac{x y+y z+z x+3}{x^{2}+y^{2}+z^{2}}\right)
$$
But then $x=y=z$, and since $x+y+z=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}$, we conclude that $x=\frac{1}{x}=1=y=z$.
Alternative solution to $b$ ): The equality condition
$$
\frac{x y+1}{x^{2}}=\frac{y z+1}{y^{2}}=\frac{z x+1}{z^{2}}
$$
can be rewritten as
$$
\frac{y+\frac{1}{x}}{x}=\frac{z+\frac{1}{y}}{y}=\frac{x+\frac{1}{z}}{z}=\frac{x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}{x+y+z}=2
$$
and thus we obtain the system:
$$
\left\{\begin{array}{l}
y=2 x-\frac{1}{x} \\
z=2 y-\frac{1}{y} \\
x=2 z-\frac{1}{z}
\end{array}\right.
$$
We show that $x=y=z$. Indeed, if for example $x>y$, then $2 x-\frac{1}{x}>2 y-\frac{1}{y}$, that is, $y>z$ and $z=2 y-\frac{1}{y}>2 z-\frac{1}{z}=x$, and we obtain the contradiction $x>y>z>x$. Similarly, if $x<y$, we obtain $x<y<z<x$.
Hence, the numbers are equal, and as above we get $x=y=z=1$.
## Chapter 2
## Combinatorics
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y, z$ be positive real numbers such that $x+y+z=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}$.
a) Prove the inequality
$$
x+y+z \geq \sqrt{\frac{x y+1}{2}}+\sqrt{\frac{y z+1}{2}}+\sqrt{\frac{z x+1}{2}}
$$
b) (Added by the problem selecting committee) When does the equality hold?
|
a) We rewrite the inequality as
$$
(\sqrt{x y+1}+\sqrt{y z+1}+\sqrt{z x+1})^{2} \leq 2 \cdot(x+y+z)^{2}
$$
and note that, from CBS,
$$
\text { LHS } \leq\left(\frac{x y+1}{x}+\frac{y z+1}{y}+\frac{z x+1}{z}\right)(x+y+z)
$$
But
$$
\frac{x y+1}{x}+\frac{y z+1}{y}+\frac{z x+1}{z}=x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=2(x+y+z)
$$
which proves (1).
b) The equality occurs when we have equality in CBS, i.e. when
$$
\frac{x y+1}{x^{2}}=\frac{y z+1}{y^{2}}=\frac{z x+1}{z^{2}}\left(=\frac{x y+y z+z x+3}{x^{2}+y^{2}+z^{2}}\right)
$$
Since we can also write
$$
(\sqrt{x y+1}+\sqrt{y z+1}+\sqrt{z x+1})^{2} \leq\left(\frac{x y+1}{y}+\frac{y z+1}{z}+\frac{z x+1}{x}\right)(y+z+x)=2(x+y+z)^{2}
$$
the equality implies also
$$
\frac{x y+1}{y^{2}}=\frac{y z+1}{z^{2}}=\frac{z x+1}{x^{2}}\left(=\frac{x y+y z+z x+3}{x^{2}+y^{2}+z^{2}}\right)
$$
But then $x=y=z$, and since $x+y+z=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}$, we conclude that $x=\frac{1}{x}=1=y=z$.
Alternative solution to $b$ ): The equality condition
$$
\frac{x y+1}{x^{2}}=\frac{y z+1}{y^{2}}=\frac{z x+1}{z^{2}}
$$
can be rewritten as
$$
\frac{y+\frac{1}{x}}{x}=\frac{z+\frac{1}{y}}{y}=\frac{x+\frac{1}{z}}{z}=\frac{x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}{x+y+z}=2
$$
and thus we obtain the system:
$$
\left\{\begin{array}{l}
y=2 x-\frac{1}{x} \\
z=2 y-\frac{1}{y} \\
x=2 z-\frac{1}{z}
\end{array}\right.
$$
We show that $x=y=z$. Indeed, if for example $x>y$, then $2 x-\frac{1}{x}>2 y-\frac{1}{y}$, that is, $y>z$ and $z=2 y-\frac{1}{y}>2 z-\frac{1}{z}=x$, and we obtain the contradiction $x>y>z>x$. Similarly, if $x<y$, we obtain $x<y<z<x$.
Hence, the numbers are equal, and as above we get $x=y=z=1$.
## Chapter 2
## Combinatorics
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nA5.",
"solution_match": "## Solution."
}
|
e9840442-b2e8-5230-abed-fe853e267fe0
| 605,196
|
Let $A B C$ be an acute angled triangle, let $O$ be its circumcentre, and let $D, E, F$ be points on the sides $B C, A C, A B$, respectively. The circle $\left(c_{1}\right)$ of radius $F A$, centred at $F$, crosses the segment $(O A)$ at $A^{\prime}$ and the circumcircle (c) of the triangle $A B C$ again at $K$. Similarly, the circle $\left(c_{2}\right)$ of radius $D B$, centred at $D$, crosses the segment $(O B)$ at $B^{\prime}$ and the circle (c) again at $L$. Finally, the circle $\left(c_{3}\right)$ of radius $E C$, centred at $E$, crosses the segment $(O C)$ at $C^{\prime}$ and the circle (c) again at $M$. Prove that the quadrilaterals $B K F A^{\prime}$, $C L D B^{\prime}$ and $A M E C^{\prime}$ are all cyclic, and their circumcircles share a common point.
|
We will prove that the quadrilateral $B K F A^{\prime}$ is cyclic and its circumcircle passes through the center $O$ of the circle (c).
The triangle $A F K$ is isosceles, so $m(\widehat{K F B})=2 m(\widehat{K A B})=m(\widehat{K O B})$. It follows that the quadrilateral $B K F O$ is cyclic.
The triangles $O F K$ and $O F A$ are congruent (S.S.S.), hence $m(\widehat{O K F})=m(\widehat{O A F})$. The triangle $F A A^{\prime}$ is isosceles, so $m\left(\widehat{F A^{\prime} A}\right)=m(\widehat{O A F})$. Therefore $m\left(\widehat{F A^{\prime} A}\right)=m(\widehat{O K F})$, so the quadrilateral $O K F A^{\prime}$ is cyclic.
(1) and (2) prove the initial claim.
Along the same lines, we can prove that the points $C, D, L, B^{\prime}, O$ and $A, M, E, C^{\prime}, O$ are concylic, respectively, so their circumcircles also pass through $O$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute angled triangle, let $O$ be its circumcentre, and let $D, E, F$ be points on the sides $B C, A C, A B$, respectively. The circle $\left(c_{1}\right)$ of radius $F A$, centred at $F$, crosses the segment $(O A)$ at $A^{\prime}$ and the circumcircle (c) of the triangle $A B C$ again at $K$. Similarly, the circle $\left(c_{2}\right)$ of radius $D B$, centred at $D$, crosses the segment $(O B)$ at $B^{\prime}$ and the circle (c) again at $L$. Finally, the circle $\left(c_{3}\right)$ of radius $E C$, centred at $E$, crosses the segment $(O C)$ at $C^{\prime}$ and the circle (c) again at $M$. Prove that the quadrilaterals $B K F A^{\prime}$, $C L D B^{\prime}$ and $A M E C^{\prime}$ are all cyclic, and their circumcircles share a common point.

|
We will prove that the quadrilateral $B K F A^{\prime}$ is cyclic and its circumcircle passes through the center $O$ of the circle (c).
The triangle $A F K$ is isosceles, so $m(\widehat{K F B})=2 m(\widehat{K A B})=m(\widehat{K O B})$. It follows that the quadrilateral $B K F O$ is cyclic.
The triangles $O F K$ and $O F A$ are congruent (S.S.S.), hence $m(\widehat{O K F})=m(\widehat{O A F})$. The triangle $F A A^{\prime}$ is isosceles, so $m\left(\widehat{F A^{\prime} A}\right)=m(\widehat{O A F})$. Therefore $m\left(\widehat{F A^{\prime} A}\right)=m(\widehat{O K F})$, so the quadrilateral $O K F A^{\prime}$ is cyclic.
(1) and (2) prove the initial claim.
Along the same lines, we can prove that the points $C, D, L, B^{\prime}, O$ and $A, M, E, C^{\prime}, O$ are concylic, respectively, so their circumcircles also pass through $O$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nG1.",
"solution_match": "\nSolution."
}
|
eabfac71-f498-5c23-a787-77f01dc74bc5
| 605,254
|
Let $A B C$ be a triangle with $m(\widehat{B A C})=60^{\circ}$. Let $D$ and $E$ be the feet of the perpendiculars from $A$ to the external angle bisectors of $\widehat{A B C}$ and $\widehat{A C B}$, respectively. Let $O$ be the circumcenter of the triangle $A B C$. Prove that the circumcircles of the triangles $\triangle A D E$ and $\triangle B O C$ are tangent to each other.
|
Let $X$ be the intersection of the lines $B D$ and $C E$.
We will prove that $X$ lies on the circumcircles of both triangles $\triangle A D E$ and $\triangle B O C$ and then we will prove that the centers of these circles and the point $X$ are collinear, which is enough for proving that the circles are tangent to each other.
In this proof we will use the notation $(M N P)$ to denote the circumcircle of the triangle $\triangle M N P$.
Obviously, the quadrilateral $A D X E$ is cyclic, and the circle $(D A E)$ has $[A X]$ as diameter. (1)
Let $I$ be the incenter of triangle $A B C$. So, the point $I$ lies on the segment $[A X]$ (2), and the quadrilateral $X B I C$ is cyclic because $I C \perp X C$ and $I B \perp X B$. So, the circle (BIC) has $[I X]$ as diameter.
Finally, $m(\widehat{B I C})=90^{\circ}+\frac{1}{2} m(\widehat{B A C})=120^{\circ}$ and $m(\widehat{B O C})=2 m(\widehat{B A C})=120^{\circ}$.
So, the quadrilateral $B O I C$ is cyclic and the circle $(B O C)$ has $[I X]$ as diameter. (3)
(1), (2), (3) imply the conclusion.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $m(\widehat{B A C})=60^{\circ}$. Let $D$ and $E$ be the feet of the perpendiculars from $A$ to the external angle bisectors of $\widehat{A B C}$ and $\widehat{A C B}$, respectively. Let $O$ be the circumcenter of the triangle $A B C$. Prove that the circumcircles of the triangles $\triangle A D E$ and $\triangle B O C$ are tangent to each other.

|
Let $X$ be the intersection of the lines $B D$ and $C E$.
We will prove that $X$ lies on the circumcircles of both triangles $\triangle A D E$ and $\triangle B O C$ and then we will prove that the centers of these circles and the point $X$ are collinear, which is enough for proving that the circles are tangent to each other.
In this proof we will use the notation $(M N P)$ to denote the circumcircle of the triangle $\triangle M N P$.
Obviously, the quadrilateral $A D X E$ is cyclic, and the circle $(D A E)$ has $[A X]$ as diameter. (1)
Let $I$ be the incenter of triangle $A B C$. So, the point $I$ lies on the segment $[A X]$ (2), and the quadrilateral $X B I C$ is cyclic because $I C \perp X C$ and $I B \perp X B$. So, the circle (BIC) has $[I X]$ as diameter.
Finally, $m(\widehat{B I C})=90^{\circ}+\frac{1}{2} m(\widehat{B A C})=120^{\circ}$ and $m(\widehat{B O C})=2 m(\widehat{B A C})=120^{\circ}$.
So, the quadrilateral $B O I C$ is cyclic and the circle $(B O C)$ has $[I X]$ as diameter. (3)
(1), (2), (3) imply the conclusion.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nG2.",
"solution_match": "\nSolution."
}
|
a7100722-cd32-57f7-962f-8b3284902110
| 605,268
|
A trapezoid $A B C D(A B \| C D, A B>C D)$ is circumscribed. The incircle of triangle $A B C$ touches the lines $A B$ and $A C$ at $M$ and $N$, respectively. Prove that the incenter of the trapezoid lies on the line $M N$.
|
Let $I$ be the incenter of triangle $A B C$ and $R$ be the common point of the lines $B I$ and $M N$. Since
$$
m(\widehat{A N M})=90^{\circ}-\frac{1}{2} m(\widehat{M A N}) \quad \text { and } \quad m(\widehat{B I C})=90^{\circ}+\frac{1}{2} m(\widehat{M A N})
$$
the quadrilateral $I R N C$ is cyclic.
It follows that $m(\widehat{B R C})=90^{\circ}$ and therefore
$$
m(\widehat{B C R})=90^{\circ}-m(\widehat{C B R})=90^{\circ}-\frac{1}{2}\left(180^{\circ}-m(\widehat{B C D})\right)=\frac{1}{2} m(\widehat{B C D})
$$
So, $(C R$ is the angle bisector of $\widehat{D C B}$ and $R$ is the incenter of the trapezoid.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A trapezoid $A B C D(A B \| C D, A B>C D)$ is circumscribed. The incircle of triangle $A B C$ touches the lines $A B$ and $A C$ at $M$ and $N$, respectively. Prove that the incenter of the trapezoid lies on the line $M N$.

|
Let $I$ be the incenter of triangle $A B C$ and $R$ be the common point of the lines $B I$ and $M N$. Since
$$
m(\widehat{A N M})=90^{\circ}-\frac{1}{2} m(\widehat{M A N}) \quad \text { and } \quad m(\widehat{B I C})=90^{\circ}+\frac{1}{2} m(\widehat{M A N})
$$
the quadrilateral $I R N C$ is cyclic.
It follows that $m(\widehat{B R C})=90^{\circ}$ and therefore
$$
m(\widehat{B C R})=90^{\circ}-m(\widehat{C B R})=90^{\circ}-\frac{1}{2}\left(180^{\circ}-m(\widehat{B C D})\right)=\frac{1}{2} m(\widehat{B C D})
$$
So, $(C R$ is the angle bisector of $\widehat{D C B}$ and $R$ is the incenter of the trapezoid.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nG3.",
"solution_match": "\nSolution."
}
|
bfc8b476-1b98-5c5e-806a-fe903cdcfa56
| 605,279
|
Let $A B C$ be an acute angled triangle whose shortest side is $[B C]$. Consider a variable point $P$ on the side $[B C]$, and let $D$ and $E$ be points on $(A B]$ and $(A C]$, respectively, such that $B D=B P$ and $C P=C E$. Prove that, as $P$ traces $[B C]$, the circumcircle of the triangle $A D E$ passes through a fixed point.
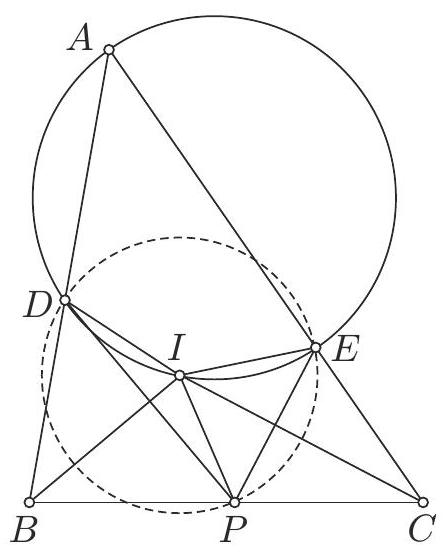
|
We claim that the fixed point is the center of the incircle of $A B C$.
Let $I$ be the center of the incircle of $A B C$. Since $B D=B P$ and $[B I$ is the bisector of $\widehat{D B P}$, the line $B I$ is the perpendicular bisector of $[D P]$. This yields $D I=P I$. Analogously we get $E I=P I$. So, the point $I$ is the circumcenter of the triangle $D E P$.
This means $m(\widehat{D I E})=2 m(\widehat{D P E})$.
On the other hand
$$
\begin{aligned}
m(\widehat{D P E}) & =180^{\circ}-m(\widehat{D P B})-m(\widehat{E P C}) \\
& =180^{\circ}-\left(90^{\circ}-\frac{1}{2} m(\widehat{D B P})\right)-\left(90^{\circ}-\frac{1}{2} m(\widehat{E C P})\right) \\
& =90^{\circ}-\frac{1}{2} m(\widehat{B A C})
\end{aligned}
$$
So, $m(\widehat{D I E})=2 m(\widehat{D P E})=180^{\circ}-m(\widehat{D A E})$, which means that the points $A, D, E$ and $I$ are cocyclic.
Remark. The fact that the incentre $I$ of the triangle $A B C$ is the required fixed point could be guessed by considering the two extremal positions of $P$. Thus, if $P=B$, then $D=D_{B}=B$ as well, and $C E=C E_{B}=B C$, so $m(\angle A E B)=m(\angle C)+m(\angle E B C)=$ $m(\angle C)+\frac{180^{\circ}-m(\angle C)}{2}=90^{\circ}+\frac{m(\angle C)}{2}=m(\angle A I B)$. Hence the points $A, E=E_{B}, I, D_{B}=B$ are cocyclic. Similarly, letting $P=C$, the points $A, D=D_{C}, I, E_{C}=C$ are cocyclic. Consequently, the circles $A D_{B} E_{B}$ and $A D_{C} E_{C}$ meet again at $I$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute angled triangle whose shortest side is $[B C]$. Consider a variable point $P$ on the side $[B C]$, and let $D$ and $E$ be points on $(A B]$ and $(A C]$, respectively, such that $B D=B P$ and $C P=C E$. Prove that, as $P$ traces $[B C]$, the circumcircle of the triangle $A D E$ passes through a fixed point.

|
We claim that the fixed point is the center of the incircle of $A B C$.
Let $I$ be the center of the incircle of $A B C$. Since $B D=B P$ and $[B I$ is the bisector of $\widehat{D B P}$, the line $B I$ is the perpendicular bisector of $[D P]$. This yields $D I=P I$. Analogously we get $E I=P I$. So, the point $I$ is the circumcenter of the triangle $D E P$.
This means $m(\widehat{D I E})=2 m(\widehat{D P E})$.
On the other hand
$$
\begin{aligned}
m(\widehat{D P E}) & =180^{\circ}-m(\widehat{D P B})-m(\widehat{E P C}) \\
& =180^{\circ}-\left(90^{\circ}-\frac{1}{2} m(\widehat{D B P})\right)-\left(90^{\circ}-\frac{1}{2} m(\widehat{E C P})\right) \\
& =90^{\circ}-\frac{1}{2} m(\widehat{B A C})
\end{aligned}
$$
So, $m(\widehat{D I E})=2 m(\widehat{D P E})=180^{\circ}-m(\widehat{D A E})$, which means that the points $A, D, E$ and $I$ are cocyclic.
Remark. The fact that the incentre $I$ of the triangle $A B C$ is the required fixed point could be guessed by considering the two extremal positions of $P$. Thus, if $P=B$, then $D=D_{B}=B$ as well, and $C E=C E_{B}=B C$, so $m(\angle A E B)=m(\angle C)+m(\angle E B C)=$ $m(\angle C)+\frac{180^{\circ}-m(\angle C)}{2}=90^{\circ}+\frac{m(\angle C)}{2}=m(\angle A I B)$. Hence the points $A, E=E_{B}, I, D_{B}=B$ are cocyclic. Similarly, letting $P=C$, the points $A, D=D_{C}, I, E_{C}=C$ are cocyclic. Consequently, the circles $A D_{B} E_{B}$ and $A D_{C} E_{C}$ meet again at $I$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nG4.",
"solution_match": "\nSolution."
}
|
b966e54d-8d77-54e5-ad74-4a38e3548cb2
| 605,289
|
Let $A B C$ be an acute angled triangle with orthocenter $H$ and circumcenter $O$. Assume the circumcenter $X$ of $B H C$ lies on the circumcircle of $A B C$. Reflect $O$ across $X$ to obtain $O^{\prime}$, and let the lines $X H$ and $O^{\prime} A$ meet at $K$. Let $L, M$ and $N$ be the midpoints of $[X B],[X C]$ and $[B C]$, respectively. Prove that the points $K, L, M$ and $N$ are cocyclic.
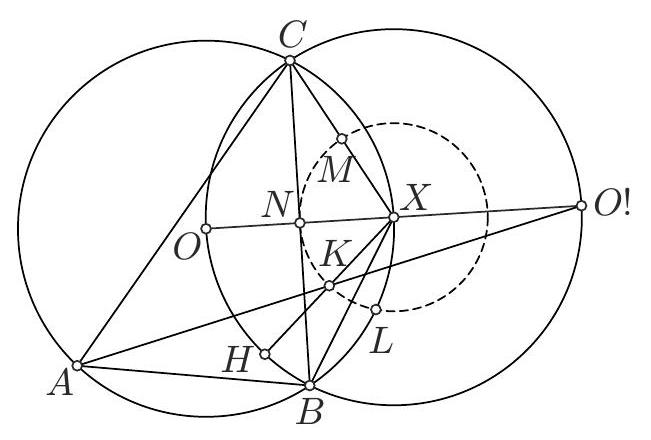
|
The circumcircles of $A B C$ and $B H C$ have the same radius. So, $X B=$ $X C=X H=X O=r$ (where $r$ is the radius of the circle $A B C$ ) and $O^{\prime}$ lies on $C(X, r)$. We conclude that $O X$ is the perpendicular bisector for $[B C]$. So, $B O X$ and $C O X$ are equilateral triangles.
It is known that $A H=2 O N=r$. So, $A H O^{\prime} X$ is parallelogram, and $X K=K H=r / 2$. Finally, $X L=X K=X N=X M=r / 2$. So, $K, L, M$ and $N$ lie on the circle $c(X, r / 2)$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute angled triangle with orthocenter $H$ and circumcenter $O$. Assume the circumcenter $X$ of $B H C$ lies on the circumcircle of $A B C$. Reflect $O$ across $X$ to obtain $O^{\prime}$, and let the lines $X H$ and $O^{\prime} A$ meet at $K$. Let $L, M$ and $N$ be the midpoints of $[X B],[X C]$ and $[B C]$, respectively. Prove that the points $K, L, M$ and $N$ are cocyclic.

|
The circumcircles of $A B C$ and $B H C$ have the same radius. So, $X B=$ $X C=X H=X O=r$ (where $r$ is the radius of the circle $A B C$ ) and $O^{\prime}$ lies on $C(X, r)$. We conclude that $O X$ is the perpendicular bisector for $[B C]$. So, $B O X$ and $C O X$ are equilateral triangles.
It is known that $A H=2 O N=r$. So, $A H O^{\prime} X$ is parallelogram, and $X K=K H=r / 2$. Finally, $X L=X K=X N=X M=r / 2$. So, $K, L, M$ and $N$ lie on the circle $c(X, r / 2)$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nG5.",
"solution_match": "\nSolution."
}
|
c4062c39-3eb8-5a2e-8876-ba4d21be52a9
| 605,300
|
Given an acute triangle $A B C$, erect triangles $A B D$ and $A C E$ externally, so that $m(\widehat{A D B})=m(\widehat{A E C})=90^{\circ}$ and $\widehat{B A D} \equiv \widehat{C A E}$. Let $A_{1} \in B C, B_{1} \in A C$ and $C_{1} \in A B$ be the feet of the altitudes of the triangle $A B C$, and let $K$ and $L$ be the midpoints of $\left[B C_{1}\right]$ and $\left[C B_{1}\right]$, respectively. Prove that the circumcenters of the triangles $A K L, A_{1} B_{1} C_{1}$ and $D E A_{1}$ are collinear.
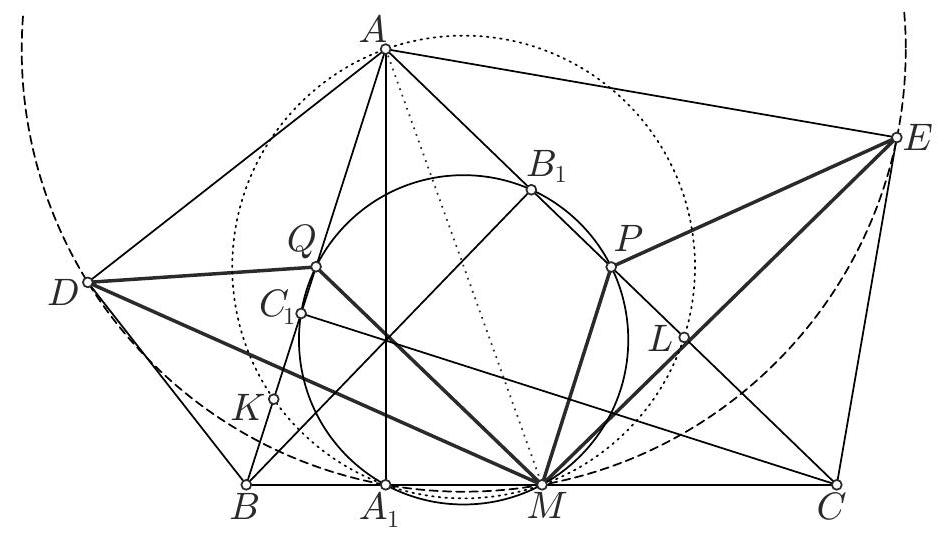
|
Let $M, P$ and $Q$ be the midpoints of $[B C],[C A]$ and $[A B]$, respectively.
The circumcircle of the triangle $A_{1} B_{1} C_{1}$ is the Euler's circle. So, the point $M$ lies on this circle.
It is enough to prove now that $\left[A_{1} M\right]$ is a common chord of the three circles $\left(A_{1} B_{1} C_{1}\right)$, $(A K L)$ and $\left(D E A_{1}\right)$.
The segments $[M K]$ and $[M L]$ are midlines for the triangles $B C C_{1}$ and $B C B_{1}$ respectively, hence $M K \| C C_{1} \perp A B$ and $M L \| B B_{1} \perp A C$. So, the circle $(A K L)$ has diameter $[A M]$ and therefore passes through $M$.
Finally, we prove that the quadrilateral $D A_{1} M E$ is cyclic.
From the cyclic quadrilaterals $A D B A_{1}$ and $A E C A_{1}, \widehat{A A_{1} D} \equiv \widehat{A B D}$ and $\widehat{A A_{1} E} \equiv \widehat{A C E} \equiv$ $\widehat{A B D}$, so $m\left(\widehat{D A_{1} E}\right)=2 m(\widehat{A B D})=180^{\circ}-2 m(\widehat{D A B})$.
We notice now that $D Q=A B / 2=M P, Q M=A C / 2=P E$ and
$$
\begin{aligned}
& m(\widehat{D Q M})=m(\widehat{D Q B})+m(\widehat{B Q M})=2 m(\widehat{D A B})+m(\widehat{B A C}) \\
& m(\widehat{E P M})=m(\widehat{E P C})+m(\widehat{C P M})=2 m(\widehat{E A C})+m(\widehat{C A B})
\end{aligned}
$$
so $\triangle M P E \equiv \triangle D Q M$ (S.A.S.). This leads to $m(\widehat{D M E})=m(\widehat{D M Q})+m(Q M P)+$ $m(P M E)=m(\widehat{D M Q})+m(B Q M)+m(Q D M)=180^{\circ}-m(\widehat{D Q B})=180^{\circ}-2 m(\widehat{D A B})$. Since $m\left(\widehat{D A_{1} E}\right)=m(\widehat{D M E})$, the quadrilateral $D A_{1} M E$ is cyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given an acute triangle $A B C$, erect triangles $A B D$ and $A C E$ externally, so that $m(\widehat{A D B})=m(\widehat{A E C})=90^{\circ}$ and $\widehat{B A D} \equiv \widehat{C A E}$. Let $A_{1} \in B C, B_{1} \in A C$ and $C_{1} \in A B$ be the feet of the altitudes of the triangle $A B C$, and let $K$ and $L$ be the midpoints of $\left[B C_{1}\right]$ and $\left[C B_{1}\right]$, respectively. Prove that the circumcenters of the triangles $A K L, A_{1} B_{1} C_{1}$ and $D E A_{1}$ are collinear.

|
Let $M, P$ and $Q$ be the midpoints of $[B C],[C A]$ and $[A B]$, respectively.
The circumcircle of the triangle $A_{1} B_{1} C_{1}$ is the Euler's circle. So, the point $M$ lies on this circle.
It is enough to prove now that $\left[A_{1} M\right]$ is a common chord of the three circles $\left(A_{1} B_{1} C_{1}\right)$, $(A K L)$ and $\left(D E A_{1}\right)$.
The segments $[M K]$ and $[M L]$ are midlines for the triangles $B C C_{1}$ and $B C B_{1}$ respectively, hence $M K \| C C_{1} \perp A B$ and $M L \| B B_{1} \perp A C$. So, the circle $(A K L)$ has diameter $[A M]$ and therefore passes through $M$.
Finally, we prove that the quadrilateral $D A_{1} M E$ is cyclic.
From the cyclic quadrilaterals $A D B A_{1}$ and $A E C A_{1}, \widehat{A A_{1} D} \equiv \widehat{A B D}$ and $\widehat{A A_{1} E} \equiv \widehat{A C E} \equiv$ $\widehat{A B D}$, so $m\left(\widehat{D A_{1} E}\right)=2 m(\widehat{A B D})=180^{\circ}-2 m(\widehat{D A B})$.
We notice now that $D Q=A B / 2=M P, Q M=A C / 2=P E$ and
$$
\begin{aligned}
& m(\widehat{D Q M})=m(\widehat{D Q B})+m(\widehat{B Q M})=2 m(\widehat{D A B})+m(\widehat{B A C}) \\
& m(\widehat{E P M})=m(\widehat{E P C})+m(\widehat{C P M})=2 m(\widehat{E A C})+m(\widehat{C A B})
\end{aligned}
$$
so $\triangle M P E \equiv \triangle D Q M$ (S.A.S.). This leads to $m(\widehat{D M E})=m(\widehat{D M Q})+m(Q M P)+$ $m(P M E)=m(\widehat{D M Q})+m(B Q M)+m(Q D M)=180^{\circ}-m(\widehat{D Q B})=180^{\circ}-2 m(\widehat{D A B})$. Since $m\left(\widehat{D A_{1} E}\right)=m(\widehat{D M E})$, the quadrilateral $D A_{1} M E$ is cyclic.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nG6.",
"solution_match": "\nSolution."
}
|
74ccd9ae-751a-51c8-98e8-0771bf99b91e
| 605,309
|
Let $[A B]$ be a chord of a circle $(c)$ centered at $O$, and let $K$ be a point on the segment $(A B)$ such that $A K<B K$. Two circles through $K$, internally tangent to (c) at $A$ and $B$, respectively, meet again at $L$. Let $P$ be one of the points of intersection of the line $K L$ and the circle (c), and let the lines $A B$ and $L O$ meet at $M$. Prove that the line $M P$ is tangent to the circle $(c)$.
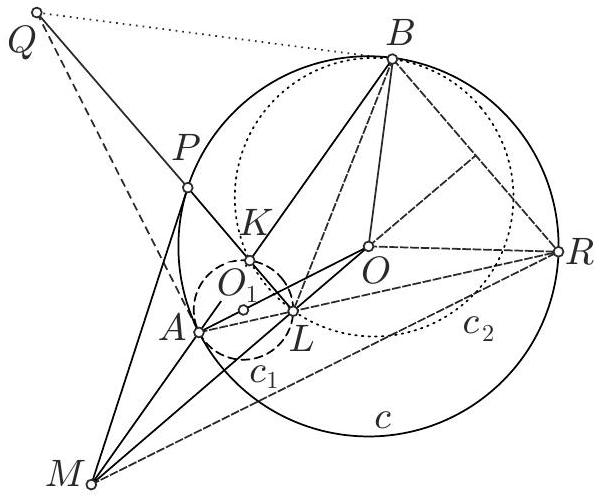
|
Let $\left(c_{1}\right)$ and $\left(c_{2}\right)$ be circles through $K$, internally tangent to (c) at $A$ and $B$, respectively, and meeting again at $L$, and let the common tangent to $\left(c_{1}\right)$ and $(c)$ meet the common tangent to $\left(c_{2}\right)$ and $(c)$ at $Q$. Then the point $Q$ is the radical center of the circles $\left(c_{1}\right),\left(c_{2}\right)$ and $(c)$, and the line $K L$ passes through $Q$.
We have $m(\widehat{Q L B})=m(\widehat{Q B K})=m(\widehat{Q B A})=\frac{1}{2} m(\overparen{B A})=m(\widehat{Q O B})$. So, the quadrilateral $O B Q L$ is cyclic. We conclude that $m(\widehat{Q L O})=90^{\circ}$ and the points $O, B, Q, A$ and $L$ are cocyclic on a circle $(k)$.
In the sequel, we will denote $\mathcal{P}_{\omega}(X)$ the power of the point $X$ with respect of the circle $\omega$. The first continuation.
From $M O^{2}-O P^{2}=\mathcal{P}_{c}(M)=M A \cdot M B=\mathcal{P}_{k}(M)=M L \cdot M O=(M O-O L) \cdot M O=$ $M O^{2}-O L \cdot M O$ follows that $O P^{2}=O L \cdot O M$. Since $P L \perp O M$, this shows that the triangle $M P O$ is right at point $P$. Thus, the line $M P$ is tangent to the circle (c).
The second continuation.
Let $R \in(c)$ be so that $B R \perp M O$. The triangle $L B R$ is isosceles with $L B=L R$, so $\widehat{O L R} \equiv \widehat{O L B} \equiv \widehat{O Q B} \equiv \widehat{O Q A} \equiv \widehat{M L A}$. We conclude that the points $A, L$ and $R$ are collinear.
Now $m(\widehat{A M R})+m(\widehat{A O R})=m(\widehat{A M R})+2 m(\widehat{A B R})=m(\widehat{A M R})+m(\widehat{A B R})+m(\widehat{M R B})=$ $180^{\circ}$, since the triangle $M B R$ is isosceles. So, the quadrilateral $M A O R$ is cyclic.
This yields $L M \cdot L O=-\mathcal{P}_{(\text {MAOR })}(L)=L A \cdot L R=-\mathcal{P}_{c}(L)=L P^{2}$, which as above, shows that $O P \perp P M$.
The third continuation.
$\widehat{K L A} \equiv \widehat{K A Q} \equiv \widehat{K L B}$ and $m(\widehat{M L K})=90^{\circ}$ show that $[L K$ and $[L M$ are the internal and external bisectors af the angle $\widehat{A L B}$, so $(M, K)$ and $(A, B)$ are harmonic conjugates. So, $L K$ is the polar line of $M$ in the circle $(c)$.
## Chapter 4
## Number Theory
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $[A B]$ be a chord of a circle $(c)$ centered at $O$, and let $K$ be a point on the segment $(A B)$ such that $A K<B K$. Two circles through $K$, internally tangent to (c) at $A$ and $B$, respectively, meet again at $L$. Let $P$ be one of the points of intersection of the line $K L$ and the circle (c), and let the lines $A B$ and $L O$ meet at $M$. Prove that the line $M P$ is tangent to the circle $(c)$.

|
Let $\left(c_{1}\right)$ and $\left(c_{2}\right)$ be circles through $K$, internally tangent to (c) at $A$ and $B$, respectively, and meeting again at $L$, and let the common tangent to $\left(c_{1}\right)$ and $(c)$ meet the common tangent to $\left(c_{2}\right)$ and $(c)$ at $Q$. Then the point $Q$ is the radical center of the circles $\left(c_{1}\right),\left(c_{2}\right)$ and $(c)$, and the line $K L$ passes through $Q$.
We have $m(\widehat{Q L B})=m(\widehat{Q B K})=m(\widehat{Q B A})=\frac{1}{2} m(\overparen{B A})=m(\widehat{Q O B})$. So, the quadrilateral $O B Q L$ is cyclic. We conclude that $m(\widehat{Q L O})=90^{\circ}$ and the points $O, B, Q, A$ and $L$ are cocyclic on a circle $(k)$.
In the sequel, we will denote $\mathcal{P}_{\omega}(X)$ the power of the point $X$ with respect of the circle $\omega$. The first continuation.
From $M O^{2}-O P^{2}=\mathcal{P}_{c}(M)=M A \cdot M B=\mathcal{P}_{k}(M)=M L \cdot M O=(M O-O L) \cdot M O=$ $M O^{2}-O L \cdot M O$ follows that $O P^{2}=O L \cdot O M$. Since $P L \perp O M$, this shows that the triangle $M P O$ is right at point $P$. Thus, the line $M P$ is tangent to the circle (c).
The second continuation.
Let $R \in(c)$ be so that $B R \perp M O$. The triangle $L B R$ is isosceles with $L B=L R$, so $\widehat{O L R} \equiv \widehat{O L B} \equiv \widehat{O Q B} \equiv \widehat{O Q A} \equiv \widehat{M L A}$. We conclude that the points $A, L$ and $R$ are collinear.
Now $m(\widehat{A M R})+m(\widehat{A O R})=m(\widehat{A M R})+2 m(\widehat{A B R})=m(\widehat{A M R})+m(\widehat{A B R})+m(\widehat{M R B})=$ $180^{\circ}$, since the triangle $M B R$ is isosceles. So, the quadrilateral $M A O R$ is cyclic.
This yields $L M \cdot L O=-\mathcal{P}_{(\text {MAOR })}(L)=L A \cdot L R=-\mathcal{P}_{c}(L)=L P^{2}$, which as above, shows that $O P \perp P M$.
The third continuation.
$\widehat{K L A} \equiv \widehat{K A Q} \equiv \widehat{K L B}$ and $m(\widehat{M L K})=90^{\circ}$ show that $[L K$ and $[L M$ are the internal and external bisectors af the angle $\widehat{A L B}$, so $(M, K)$ and $(A, B)$ are harmonic conjugates. So, $L K$ is the polar line of $M$ in the circle $(c)$.
## Chapter 4
## Number Theory
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nG7.",
"solution_match": "\nSolution."
}
|
d43da6b5-f19a-5fac-bb09-41fc305b57ee
| 605,322
|
Nine journalists from different countries attend a press conference. None of these speaks more than three languages, and each pair of the journalists share a common language. Show that there are at least five journalists sharing a common language.
|
Assume the journalists are $J_{1}, J_{2}, \ldots, J_{9}$. Assume that no five of them have a common language. Assume the languages $J_{1}$ speaks are $L_{1}, L_{2}$, and $L_{3}$. Group $J_{2}, J_{3}$, $\ldots, J_{9}$ according to the language they speak with $J_{1}$. No group can have more than three members. So either there are three groups of three members each, or two groups with three members and one with two. Consider the first alternative. We may assume that $J_{1}$ speaks $L_{1}$ with $J_{2}, J_{3}$, and $J_{4}, L_{2}$ with $J_{5}, J_{6}$, and $J_{7}$, and $L_{3}$ with $J_{8}, J_{9}$, and $J_{2}$. Now $J_{2}$ speaks $L_{1}$ with $J_{1}, J_{3}$, and $J_{4}, L_{3}$ with $J_{1}, J_{8}$, and $J_{9}$. $J_{2}$ must speak a fourth language, $L_{4}$, with $J_{5}, J_{6}$, and $J_{7}$. But now $J_{5}$ speaks both $L_{2}$ and $L_{4}$ with $J_{2}, J_{6}$, and $J_{7}$. So $J_{5}$ has to use his third language with $J_{1}, J_{4}, J_{8}$, and $J_{9}$. This contradicts the assumption we made. So we now may assume that $J_{1}$ speaks $L_{3}$ only with $J_{8}$ and $J_{9}$. As $J_{1}$ is not special, we conclude that for each journalist $J_{k}$, the remaining eight are divided into three mutually exclusive language groups, one of which has only two members. Now $J_{2}$ uses $L_{1}$ with three others, and there has to be another language he also speaks with three others. If this were $L_{2}$ or $L_{3}$, a group of five would arise (including $J_{1}$ ). So $J_{2}$ speaks $L_{4}$ with three among $J_{5}, \ldots, J_{9}$. Either two of these three are among $J_{5}, J_{6}$, and $J_{7}$, or among $J_{8}, J_{9}$. Both alternatives lead to a contradiction to the already proved fact that no pair of journalists speaks two languages together. The proof is complete.
Figure 1.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Nine journalists from different countries attend a press conference. None of these speaks more than three languages, and each pair of the journalists share a common language. Show that there are at least five journalists sharing a common language.
|
Assume the journalists are $J_{1}, J_{2}, \ldots, J_{9}$. Assume that no five of them have a common language. Assume the languages $J_{1}$ speaks are $L_{1}, L_{2}$, and $L_{3}$. Group $J_{2}, J_{3}$, $\ldots, J_{9}$ according to the language they speak with $J_{1}$. No group can have more than three members. So either there are three groups of three members each, or two groups with three members and one with two. Consider the first alternative. We may assume that $J_{1}$ speaks $L_{1}$ with $J_{2}, J_{3}$, and $J_{4}, L_{2}$ with $J_{5}, J_{6}$, and $J_{7}$, and $L_{3}$ with $J_{8}, J_{9}$, and $J_{2}$. Now $J_{2}$ speaks $L_{1}$ with $J_{1}, J_{3}$, and $J_{4}, L_{3}$ with $J_{1}, J_{8}$, and $J_{9}$. $J_{2}$ must speak a fourth language, $L_{4}$, with $J_{5}, J_{6}$, and $J_{7}$. But now $J_{5}$ speaks both $L_{2}$ and $L_{4}$ with $J_{2}, J_{6}$, and $J_{7}$. So $J_{5}$ has to use his third language with $J_{1}, J_{4}, J_{8}$, and $J_{9}$. This contradicts the assumption we made. So we now may assume that $J_{1}$ speaks $L_{3}$ only with $J_{8}$ and $J_{9}$. As $J_{1}$ is not special, we conclude that for each journalist $J_{k}$, the remaining eight are divided into three mutually exclusive language groups, one of which has only two members. Now $J_{2}$ uses $L_{1}$ with three others, and there has to be another language he also speaks with three others. If this were $L_{2}$ or $L_{3}$, a group of five would arise (including $J_{1}$ ). So $J_{2}$ speaks $L_{4}$ with three among $J_{5}, \ldots, J_{9}$. Either two of these three are among $J_{5}, J_{6}$, and $J_{7}$, or among $J_{8}, J_{9}$. Both alternatives lead to a contradiction to the already proved fact that no pair of journalists speaks two languages together. The proof is complete.

Figure 1.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n87.1. ",
"solution_match": "\nSolution. "
}
|
7398370e-9b2e-55b4-a257-f8fcdd93c1dd
| 607,920
|
Let $A B C D$ be a parallelogram in the plane. We draw two circles of radius $R$, one through the points $A$ and $B$, the other through $B$ and $C$. Let $E$ be the other point of
intersection of the circles. We assume that $E$ is not a vertex of the parallelogram. Show that the circle passing through $A, D$, and $E$ also has radius $R$.
|
(See Figure 1.) Let $F$ and $G$ be the centers of the two circles of radius $R$ passing through $A$ and $B$; and $B$ and $C$, respectively. Let $O$ be the point for which the the rectangle $A B G O$ is a parallelogram. Then $\angle O A D=\angle G B C$, and the triangles $O A D$ and $G B C$ are congruent (sas). Since $G B=G C=R$, we have $O A=O D=R$. The quadrangle $E F B G$ is a rhombus. So $E F\|G B\| O A$. Moreover, $E F=O A=R$, which means that $A F E O$ is a parallelogram. But this implies $O E=A F=R$. So $A, D$, and $E$ all are on the circle of radius $R$ centered at $O$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram in the plane. We draw two circles of radius $R$, one through the points $A$ and $B$, the other through $B$ and $C$. Let $E$ be the other point of
intersection of the circles. We assume that $E$ is not a vertex of the parallelogram. Show that the circle passing through $A, D$, and $E$ also has radius $R$.
|
(See Figure 1.) Let $F$ and $G$ be the centers of the two circles of radius $R$ passing through $A$ and $B$; and $B$ and $C$, respectively. Let $O$ be the point for which the the rectangle $A B G O$ is a parallelogram. Then $\angle O A D=\angle G B C$, and the triangles $O A D$ and $G B C$ are congruent (sas). Since $G B=G C=R$, we have $O A=O D=R$. The quadrangle $E F B G$ is a rhombus. So $E F\|G B\| O A$. Moreover, $E F=O A=R$, which means that $A F E O$ is a parallelogram. But this implies $O E=A F=R$. So $A, D$, and $E$ all are on the circle of radius $R$ centered at $O$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n87.2. ",
"solution_match": "\nSolution. "
}
|
95342cc4-01f0-527c-9483-159dffb29ba9
| 607,921
|
Let $a, b$, and $c$ be positive real numbers. Prove:
$$
\frac{a}{b}+\frac{b}{c}+\frac{c}{a} \leq \frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}
$$
|
The arithmetic-geometric inequality yields
$$
3=3 \sqrt[3]{\frac{a^{2}}{b^{2}} \cdot \frac{b^{2}}{c^{2}} \cdot \frac{c^{2}}{a^{2}}} \leq \frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}
$$
or
$$
\sqrt{3} \leq \sqrt{\frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}}
$$
On the other hand, the Cauchy-Schwarz inequality implies
$$
\begin{aligned}
\frac{a}{b}+\frac{b}{c}+ & \frac{c}{a} \leq \sqrt{1^{2}+1^{2}+1^{2}} \sqrt{\frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}} \\
& =\sqrt{3} \sqrt{\frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}}
\end{aligned}
$$
We arrive at the inequality of the problem by combining (1) and (2).
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be positive real numbers. Prove:
$$
\frac{a}{b}+\frac{b}{c}+\frac{c}{a} \leq \frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}
$$
|
The arithmetic-geometric inequality yields
$$
3=3 \sqrt[3]{\frac{a^{2}}{b^{2}} \cdot \frac{b^{2}}{c^{2}} \cdot \frac{c^{2}}{a^{2}}} \leq \frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}
$$
or
$$
\sqrt{3} \leq \sqrt{\frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}}
$$
On the other hand, the Cauchy-Schwarz inequality implies
$$
\begin{aligned}
\frac{a}{b}+\frac{b}{c}+ & \frac{c}{a} \leq \sqrt{1^{2}+1^{2}+1^{2}} \sqrt{\frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}} \\
& =\sqrt{3} \sqrt{\frac{a^{2}}{b^{2}}+\frac{b^{2}}{c^{2}}+\frac{c^{2}}{a^{2}}}
\end{aligned}
$$
We arrive at the inequality of the problem by combining (1) and (2).
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n87.4. ",
"solution_match": "\nSolution. "
}
|
452bb14f-18f8-546b-9c49-5a6786c8596a
| 607,923
|
Let $a, b$, and $c$ be non-zero real numbers and let $a \geq b \geq c$. Prove the inequality
$$
\frac{a^{3}-c^{3}}{3} \geq a b c\left(\frac{a-b}{c}+\frac{b-c}{a}\right)
$$
When does equality hold?
|
Since $c-b \leq 0 \leq a-b$, we have $(a-b)^{3} \geq(c-b)^{3}$, or
$$
a^{3}-3 a^{2} b+3 a b^{2}-b^{3} \geq c^{3}-3 b c^{2}+3 b^{2} c-b^{3}
$$
On simplifying this, we immediately have
$$
\frac{1}{3}\left(a^{3}-c^{3}\right) \geq a^{2} b-a b^{2}+b^{2} c-b c^{2}=a b c\left(\frac{a-b}{c}+\frac{b-c}{a}\right)
$$
A sufficient condition for equality is $a=c$. If $a>c$, then $(a-b)^{3}>(c-b)^{3}$, which makes the proved inequality a strict one. So $a=c$ is a necessary condition for equality, too.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be non-zero real numbers and let $a \geq b \geq c$. Prove the inequality
$$
\frac{a^{3}-c^{3}}{3} \geq a b c\left(\frac{a-b}{c}+\frac{b-c}{a}\right)
$$
When does equality hold?
|
Since $c-b \leq 0 \leq a-b$, we have $(a-b)^{3} \geq(c-b)^{3}$, or
$$
a^{3}-3 a^{2} b+3 a b^{2}-b^{3} \geq c^{3}-3 b c^{2}+3 b^{2} c-b^{3}
$$
On simplifying this, we immediately have
$$
\frac{1}{3}\left(a^{3}-c^{3}\right) \geq a^{2} b-a b^{2}+b^{2} c-b c^{2}=a b c\left(\frac{a-b}{c}+\frac{b-c}{a}\right)
$$
A sufficient condition for equality is $a=c$. If $a>c$, then $(a-b)^{3}>(c-b)^{3}$, which makes the proved inequality a strict one. So $a=c$ is a necessary condition for equality, too.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n88.2. ",
"solution_match": "\nSolution. "
}
|
28dc9b96-05c1-5f47-8b17-263e1612f5da
| 607,925
|
Two concentric spheres have radii $r$ and $R, r<R$. We try to select points $A, B$ and $C$ on the surface of the larger sphere such that all sides of the triangle $A B C$ would be tangent to the surface of the smaller sphere. Show that the points can be selected if and only if $R \leq 2 r$.
|
Assume $A, B$, and $C$ lie on the surface $\Gamma$ of a sphere of radius $R$ and center $O$, and $A B, B C$, and $C A$ touch the surface $\gamma$ of a sphere of radius $r$ and center $O$. The circumscribed and inscribed circles of $A B C$ then are intersections of the plane $A B C$ with $\Gamma$ and $\gamma$, respectively. The centers of these circles both are the foot $D$ of the perpendicular dropped from $O$ to the plane $A B C$. This point lies both on the angle bisectors of the triangle $A B C$ and on the perpendicular bisectors of its sides. So these lines are the same, which means that the triangle $A B C$ is equilateral, and the center of the circles is the common point of intersection of the medians of $A B C$. This again implies that the radii of the two circles are $2 r_{1}$ and $r_{1}$ for some real number $r_{1}$. Let $O D=d$. Then $2 r_{1}=\sqrt{R^{2}-d^{2}}$ and $r_{1}=\sqrt{r^{2}-d^{2}}$. Squaring, we get $R^{2}-d^{2}=4 r^{2}-4 d^{2}, 4 r^{2}-R^{2}=3 d^{2} \geq 0$, and $2 r \geq R$. On the other hand, assume $2 r \geq R$. Consider a plane at the distance
$$
d=\sqrt{\frac{4 r^{2}-R^{2}}{3}}
$$
from the common center of the two spheres. The plane cuts the surfaces of the spheres along concentric circles of radii
$$
r_{1}=\sqrt{\frac{R^{2}-r^{2}}{3}}, \quad R_{1}=2 \sqrt{\frac{R^{2}-r^{2}}{3}}
$$
The points $A, B$, and $C$ can now be chosen on the latter circle in such a way that $A B C$ is equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Two concentric spheres have radii $r$ and $R, r<R$. We try to select points $A, B$ and $C$ on the surface of the larger sphere such that all sides of the triangle $A B C$ would be tangent to the surface of the smaller sphere. Show that the points can be selected if and only if $R \leq 2 r$.
|
Assume $A, B$, and $C$ lie on the surface $\Gamma$ of a sphere of radius $R$ and center $O$, and $A B, B C$, and $C A$ touch the surface $\gamma$ of a sphere of radius $r$ and center $O$. The circumscribed and inscribed circles of $A B C$ then are intersections of the plane $A B C$ with $\Gamma$ and $\gamma$, respectively. The centers of these circles both are the foot $D$ of the perpendicular dropped from $O$ to the plane $A B C$. This point lies both on the angle bisectors of the triangle $A B C$ and on the perpendicular bisectors of its sides. So these lines are the same, which means that the triangle $A B C$ is equilateral, and the center of the circles is the common point of intersection of the medians of $A B C$. This again implies that the radii of the two circles are $2 r_{1}$ and $r_{1}$ for some real number $r_{1}$. Let $O D=d$. Then $2 r_{1}=\sqrt{R^{2}-d^{2}}$ and $r_{1}=\sqrt{r^{2}-d^{2}}$. Squaring, we get $R^{2}-d^{2}=4 r^{2}-4 d^{2}, 4 r^{2}-R^{2}=3 d^{2} \geq 0$, and $2 r \geq R$. On the other hand, assume $2 r \geq R$. Consider a plane at the distance
$$
d=\sqrt{\frac{4 r^{2}-R^{2}}{3}}
$$
from the common center of the two spheres. The plane cuts the surfaces of the spheres along concentric circles of radii
$$
r_{1}=\sqrt{\frac{R^{2}-r^{2}}{3}}, \quad R_{1}=2 \sqrt{\frac{R^{2}-r^{2}}{3}}
$$
The points $A, B$, and $C$ can now be chosen on the latter circle in such a way that $A B C$ is equilateral.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n88.3. ",
"solution_match": "\nSolution. "
}
|
eed456b3-48c9-5562-b103-253b5eda767f
| 607,926
|
Let $S$ be the set of all points $t$ in the closed interval $[-1,1]$ such that for the sequence $x_{0}, x_{1}, x_{2}, \ldots$ defined by the equations $x_{0}=t, x_{n+1}=2 x_{n}^{2}-1$, there exists a positive integer $N$ such that $x_{n}=1$ for all $n \geq N$. Show that the set $S$ has infinitely many elements.
|
All numbers in the sequence $\left\{x_{n}\right\}$ lie in the interval $[-1,1]$. For each $n$ we can pick an $\alpha_{n}$ such that $x_{n}=\cos \alpha_{n}$. If $x_{n}=\cos \alpha_{n}$, then $x_{n+1}=2 \cos ^{2} \alpha_{n}-1=\cos \left(2 \alpha_{n}\right)$. The nuber $\alpha_{n+1}$ can be chosen as $2 \alpha_{n}$, and by induction, $\alpha_{n}$ can be chosen as $2^{n} \alpha_{0}$. Now $x_{n}=1$ if and only if $\alpha_{n}=2 k \pi$ for some integer $k$. Take $S^{\prime}=\left\{\cos \left(2^{-m} \pi\right) \mid m \in \mathbb{N}\right\}$. Since every $\alpha_{0}=2^{-m} \pi$ multiplied by a sufficiently large power of 2 is a multiple of $2 \pi$, it follows from what was said above that $S^{\prime} \subset S$. Since $S^{\prime}$ is infinite, so is $S$.
89.4 For which positive integers $n$ is the following statement true: if $a_{1}, a_{2}, \ldots, a_{n}$ are positive integers, $a_{k} \leq n$ for all $k$ and $\sum_{k=1}^{n} a_{k}=2 n$, then it is always possible to choose $a_{i_{1}}, a_{i_{2}}, \ldots, a_{i_{j}}$ in such a way that the indices $i_{1}, i_{2}, \ldots, i_{j}$ are different numbers, and $\sum_{k=1}^{j} a_{i_{k}}=n$ ?
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $S$ be the set of all points $t$ in the closed interval $[-1,1]$ such that for the sequence $x_{0}, x_{1}, x_{2}, \ldots$ defined by the equations $x_{0}=t, x_{n+1}=2 x_{n}^{2}-1$, there exists a positive integer $N$ such that $x_{n}=1$ for all $n \geq N$. Show that the set $S$ has infinitely many elements.
|
All numbers in the sequence $\left\{x_{n}\right\}$ lie in the interval $[-1,1]$. For each $n$ we can pick an $\alpha_{n}$ such that $x_{n}=\cos \alpha_{n}$. If $x_{n}=\cos \alpha_{n}$, then $x_{n+1}=2 \cos ^{2} \alpha_{n}-1=\cos \left(2 \alpha_{n}\right)$. The nuber $\alpha_{n+1}$ can be chosen as $2 \alpha_{n}$, and by induction, $\alpha_{n}$ can be chosen as $2^{n} \alpha_{0}$. Now $x_{n}=1$ if and only if $\alpha_{n}=2 k \pi$ for some integer $k$. Take $S^{\prime}=\left\{\cos \left(2^{-m} \pi\right) \mid m \in \mathbb{N}\right\}$. Since every $\alpha_{0}=2^{-m} \pi$ multiplied by a sufficiently large power of 2 is a multiple of $2 \pi$, it follows from what was said above that $S^{\prime} \subset S$. Since $S^{\prime}$ is infinite, so is $S$.
89.4 For which positive integers $n$ is the following statement true: if $a_{1}, a_{2}, \ldots, a_{n}$ are positive integers, $a_{k} \leq n$ for all $k$ and $\sum_{k=1}^{n} a_{k}=2 n$, then it is always possible to choose $a_{i_{1}}, a_{i_{2}}, \ldots, a_{i_{j}}$ in such a way that the indices $i_{1}, i_{2}, \ldots, i_{j}$ are different numbers, and $\sum_{k=1}^{j} a_{i_{k}}=n$ ?
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n89.3. ",
"solution_match": "\nSolution. "
}
|
08cde141-2a4a-5d95-9cc9-20803a7b5fd5
| 607,928
|
Let $m, n$, and $p$ be odd positive integers. Prove that the number
$$
\sum_{k=1}^{(n-1)^{p}} k^{m}
$$
is divisible by $n$.
|
Since $n$ is odd, the sum has an even number of terms. So we can write it as
$$
\sum_{k=1}^{\frac{1}{2}(n-1)^{p}}\left(k^{m}+\left((n-1)^{p}-k+1\right)^{m}\right)
$$
Because $m$ is odd, each term in the sum has $k+(n-1)^{p}-k+1=(n-1)^{p}+1$ as a factor. As $p$ is odd, too, $(n-1)^{p}+1=(n-1)^{p}+1^{p}$ has $(n-1)+1=n$ as a factor. So each term in the sum (1) is divisible by $n$, and so is the sum.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $m, n$, and $p$ be odd positive integers. Prove that the number
$$
\sum_{k=1}^{(n-1)^{p}} k^{m}
$$
is divisible by $n$.
|
Since $n$ is odd, the sum has an even number of terms. So we can write it as
$$
\sum_{k=1}^{\frac{1}{2}(n-1)^{p}}\left(k^{m}+\left((n-1)^{p}-k+1\right)^{m}\right)
$$
Because $m$ is odd, each term in the sum has $k+(n-1)^{p}-k+1=(n-1)^{p}+1$ as a factor. As $p$ is odd, too, $(n-1)^{p}+1=(n-1)^{p}+1^{p}$ has $(n-1)+1=n$ as a factor. So each term in the sum (1) is divisible by $n$, and so is the sum.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n90.1. ",
"solution_match": "\nSolution. "
}
|
2da19163-10a8-5363-a3d8-c93b0e9e4f0e
| 607,929
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be real numbers. Prove
$$
\sqrt[3]{a_{1}^{3}+a_{2}^{3}+\ldots+a_{n}^{3}} \leq \sqrt{a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}}
$$
When does equality hold in (1)?
|
If $0 \leq x \leq 1$, then $x^{3 / 2} \leq x$, and equality holds if and only if $x=0$ or $x=1$. - The inequality is true as an equality, if all the $a_{k}$ 's are zeroes. Assume that at least one of the numbers $a_{k}$ is non-zero. Set
$$
x_{k}=\frac{a_{k}^{2}}{\sum_{j=1}^{n} a_{j}^{2}}
$$
Then $0 \leq x_{k} \leq 1$, and by the remark above,
$$
\sum_{k=1}^{n}\left(\frac{a_{k}^{2}}{\sum_{j=1}^{n} a_{j}^{2}}\right)^{3 / 2} \leq \sum_{k=1}^{n} \frac{a_{k}^{2}}{\sum_{j=1}^{n} a_{j}^{2}}=1
$$
So
$$
\sum_{k=1}^{n} a_{k}^{3} \leq\left(\sum_{j_{1}}^{n} a_{j}^{2}\right)^{3 / 2}
$$
which is what was supposed to be proved. For equality, exactly on $x_{k}$ has to be one and the rest have to be zeroes, which is equivalent to having exactly one of the $a_{k}$ 's positive and the rest zeroes.
Figure 2.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be real numbers. Prove
$$
\sqrt[3]{a_{1}^{3}+a_{2}^{3}+\ldots+a_{n}^{3}} \leq \sqrt{a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}}
$$
When does equality hold in (1)?
|
If $0 \leq x \leq 1$, then $x^{3 / 2} \leq x$, and equality holds if and only if $x=0$ or $x=1$. - The inequality is true as an equality, if all the $a_{k}$ 's are zeroes. Assume that at least one of the numbers $a_{k}$ is non-zero. Set
$$
x_{k}=\frac{a_{k}^{2}}{\sum_{j=1}^{n} a_{j}^{2}}
$$
Then $0 \leq x_{k} \leq 1$, and by the remark above,
$$
\sum_{k=1}^{n}\left(\frac{a_{k}^{2}}{\sum_{j=1}^{n} a_{j}^{2}}\right)^{3 / 2} \leq \sum_{k=1}^{n} \frac{a_{k}^{2}}{\sum_{j=1}^{n} a_{j}^{2}}=1
$$
So
$$
\sum_{k=1}^{n} a_{k}^{3} \leq\left(\sum_{j_{1}}^{n} a_{j}^{2}\right)^{3 / 2}
$$
which is what was supposed to be proved. For equality, exactly on $x_{k}$ has to be one and the rest have to be zeroes, which is equivalent to having exactly one of the $a_{k}$ 's positive and the rest zeroes.

Figure 2.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n90.2. ",
"solution_match": "\nSolution. "
}
|
657c487f-9f88-50a4-96f9-31d19d0777dc
| 607,930
|
It is possible to perform three operations $f, g$, and $h$ for positive integers: $f(n)=$ $10 n, g(n)=10 n+4$, and $h(2 n)=n$; in other words, one may write 0 or 4 in the end of the number and one may divide an even number by 2. Prove: every positive integer can be constructed starting from 4 and performing a finite number of the operations $f, g$, and $h$ in some order.
|
All odd numbers $n$ are of the form $h(2 n)$. All we need is to show that every even number can be obtained fron 4 by using the operations $f, g$, and $h$. To this end, we show that a suitably chosen sequence of inverse operations $F=f^{-1}, G=g^{-1}$, and $H=h^{-1}$ produces a smaller even number or the number 4 from every positive even integer. The operation $F$ can be applied to numbers ending in a zero, the operation $G$ can be applied to numbers ending in 4 , and $H(n)=2 n$. We obtain
$$
\begin{gathered}
H(F(10 n))=2 n \\
G(H(10 n+2))=2 n, \quad n \geq 1 \\
H(2)=4 \\
H(G(10 n+4))=2 n \\
G(H(H(10 n+6)))=4 n+2 \\
G(H(H(H(10 n+8))))=8 n+6
\end{gathered}
$$
After a finite number of these steps, we arrive at 4 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
It is possible to perform three operations $f, g$, and $h$ for positive integers: $f(n)=$ $10 n, g(n)=10 n+4$, and $h(2 n)=n$; in other words, one may write 0 or 4 in the end of the number and one may divide an even number by 2. Prove: every positive integer can be constructed starting from 4 and performing a finite number of the operations $f, g$, and $h$ in some order.
|
All odd numbers $n$ are of the form $h(2 n)$. All we need is to show that every even number can be obtained fron 4 by using the operations $f, g$, and $h$. To this end, we show that a suitably chosen sequence of inverse operations $F=f^{-1}, G=g^{-1}$, and $H=h^{-1}$ produces a smaller even number or the number 4 from every positive even integer. The operation $F$ can be applied to numbers ending in a zero, the operation $G$ can be applied to numbers ending in 4 , and $H(n)=2 n$. We obtain
$$
\begin{gathered}
H(F(10 n))=2 n \\
G(H(10 n+2))=2 n, \quad n \geq 1 \\
H(2)=4 \\
H(G(10 n+4))=2 n \\
G(H(H(10 n+6)))=4 n+2 \\
G(H(H(H(10 n+8))))=8 n+6
\end{gathered}
$$
After a finite number of these steps, we arrive at 4 .
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n90.4. ",
"solution_match": "\nSolution. "
}
|
57d8f7a9-a797-5ef2-994d-32cce59d8950
| 607,932
|
Let $f(x)$ be a polynomial with integer coefficients. We assume that there exists a positive integer $k$ and $k$ consecutive integers $n, n+1, \ldots, n+k-1$ so that none of the numbers $f(n), f(n+1), \ldots, f(n+k-1)$ is divisible by $k$. Show that the zeroes of $f(x)$ are not integers.
|
Let $f(x)=a_{0} x^{d}+a_{1} x^{d-1}+\cdots+a_{d}$. Assume that $f$ has a zero $m$ which is an integer. Then $f(x)=(x-m) g(x)$, where $g$ is a polynomial. If $g(x)=b_{0} x^{d-1}+b_{1} x^{d-2}+$ $\cdots+b_{d-1}$, then $a_{0}=b_{0}$, and $a_{k}=b_{k}-m b_{k-1}, 1 \leq k \leq d-1$. So $b_{0}$ is an integer, and by induction all $b_{k}$ 's are integers. Because $f(j)$ is not divisible by $k$ for $k$ consequtive values of $j$, no one of the $k$ consequtive integers $j-m, j=n, n+1, \ldots, n+k-1$, is divisible by $k$. But this is a contradiction, since exactly one of $k$ consequtive integers is divisible by $k$. So $f$ cannot have an integral zero.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f(x)$ be a polynomial with integer coefficients. We assume that there exists a positive integer $k$ and $k$ consecutive integers $n, n+1, \ldots, n+k-1$ so that none of the numbers $f(n), f(n+1), \ldots, f(n+k-1)$ is divisible by $k$. Show that the zeroes of $f(x)$ are not integers.
|
Let $f(x)=a_{0} x^{d}+a_{1} x^{d-1}+\cdots+a_{d}$. Assume that $f$ has a zero $m$ which is an integer. Then $f(x)=(x-m) g(x)$, where $g$ is a polynomial. If $g(x)=b_{0} x^{d-1}+b_{1} x^{d-2}+$ $\cdots+b_{d-1}$, then $a_{0}=b_{0}$, and $a_{k}=b_{k}-m b_{k-1}, 1 \leq k \leq d-1$. So $b_{0}$ is an integer, and by induction all $b_{k}$ 's are integers. Because $f(j)$ is not divisible by $k$ for $k$ consequtive values of $j$, no one of the $k$ consequtive integers $j-m, j=n, n+1, \ldots, n+k-1$, is divisible by $k$. But this is a contradiction, since exactly one of $k$ consequtive integers is divisible by $k$. So $f$ cannot have an integral zero.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n91.4. ",
"solution_match": "\nSolution. "
}
|
d62a1f86-ab62-52eb-9c98-436a6a588aef
| 607,936
|
Let $n>1$ be an integer and let $a_{1}, a_{2}, \ldots, a_{n}$ be $n$ different integers. Show that the polynomial
$$
f(x)=\left(x-a_{1}\right)\left(x-a_{2}\right) \cdots\left(x-a_{n}\right)-1
$$
is not divisible by any polynomial with integer coefficients and of degree greater than zero but less than $n$ and such that the highest power of $x$ has coefficient 1.
|
Suppose $g(x)$ is a polynomial of degree $m$, where $1 \leq m<n$, with integer coefficients and leading coefficient 1 , such that
$$
f(x)=g(x) h(x)
$$
whre $h(x)$ is a polynomial. Let
$$
\begin{aligned}
& g(x)=x^{m}+b_{m-1} x^{m-1}+\cdots+b_{1} x+b_{0} \\
& h(x)=x^{n-m}+c_{n-m-1} x^{n-m-1}+\cdots+c_{1} x+c_{0}
\end{aligned}
$$
We show that the coefficients of $h(x)$ are integers. If they are not, there is a greatest index $j=k$ such that $c_{k}$ is not an integer. But then the coefficient of $f$ multiplying $x^{k+m}-$ which is an integer - would be $c_{k}+b_{m-1} c_{k+1}+b_{m-2} c_{k+2}+\ldots b_{k-m}$. All terms except the first one in this sum are integers, so the sum cannot be an integer. A contradiction. So $h(x)$ is a polynomial with integral coefficients. Now
$$
f\left(a_{i}\right)=g\left(a_{i}\right) h\left(a_{i}\right)=-1
$$
for $i=1,2, \ldots, n$, and $g\left(a_{i}\right)$ and $h\left(a_{i}\right)$ are integers. This is only possible, if $g\left(a_{i}\right)=$ $-f\left(a_{i}\right)= \pm 1$ and $g\left(a_{i}\right)+h\left(a_{i}\right)=0$ for $i=1,2, \ldots, n$. So the polynomial $g(x)+h(x)$ has at least $n$ zeroes. But the degree of $g(x)+h(x)$ is less than $n$. So $g(x)=-h(x)$ for all $x$, and $f(x)=-g(x)^{2}$. This is impossible, however, because $f(x) \rightarrow+\infty$, as $x \rightarrow+\infty$. This contradiction proves the claim.
Figure 4 .
92.3 Prove that among all triangles with inradius 1, the equilateral one has the smallest perimeter.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n>1$ be an integer and let $a_{1}, a_{2}, \ldots, a_{n}$ be $n$ different integers. Show that the polynomial
$$
f(x)=\left(x-a_{1}\right)\left(x-a_{2}\right) \cdots\left(x-a_{n}\right)-1
$$
is not divisible by any polynomial with integer coefficients and of degree greater than zero but less than $n$ and such that the highest power of $x$ has coefficient 1.
|
Suppose $g(x)$ is a polynomial of degree $m$, where $1 \leq m<n$, with integer coefficients and leading coefficient 1 , such that
$$
f(x)=g(x) h(x)
$$
whre $h(x)$ is a polynomial. Let
$$
\begin{aligned}
& g(x)=x^{m}+b_{m-1} x^{m-1}+\cdots+b_{1} x+b_{0} \\
& h(x)=x^{n-m}+c_{n-m-1} x^{n-m-1}+\cdots+c_{1} x+c_{0}
\end{aligned}
$$
We show that the coefficients of $h(x)$ are integers. If they are not, there is a greatest index $j=k$ such that $c_{k}$ is not an integer. But then the coefficient of $f$ multiplying $x^{k+m}-$ which is an integer - would be $c_{k}+b_{m-1} c_{k+1}+b_{m-2} c_{k+2}+\ldots b_{k-m}$. All terms except the first one in this sum are integers, so the sum cannot be an integer. A contradiction. So $h(x)$ is a polynomial with integral coefficients. Now
$$
f\left(a_{i}\right)=g\left(a_{i}\right) h\left(a_{i}\right)=-1
$$
for $i=1,2, \ldots, n$, and $g\left(a_{i}\right)$ and $h\left(a_{i}\right)$ are integers. This is only possible, if $g\left(a_{i}\right)=$ $-f\left(a_{i}\right)= \pm 1$ and $g\left(a_{i}\right)+h\left(a_{i}\right)=0$ for $i=1,2, \ldots, n$. So the polynomial $g(x)+h(x)$ has at least $n$ zeroes. But the degree of $g(x)+h(x)$ is less than $n$. So $g(x)=-h(x)$ for all $x$, and $f(x)=-g(x)^{2}$. This is impossible, however, because $f(x) \rightarrow+\infty$, as $x \rightarrow+\infty$. This contradiction proves the claim.

Figure 4 .
92.3 Prove that among all triangles with inradius 1, the equilateral one has the smallest perimeter.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n92.2. ",
"solution_match": "\nSolution. "
}
|
254feee7-ede0-5d7a-aee7-d7d5ce4d2106
| 607,938
|
Let $O$ be an interior point in the equilateral triangle $A B C$, of side length $a$. The lines $A O, B O$, and $C O$ intersect the sides of the triangle in the points $A_{1}, B_{1}$, and $C_{1}$. Show that
$$
\left|O A_{1}\right|+\left|O B_{1}\right|+\left|O C_{1}\right|<a
$$
|
Let $H_{A}, H_{B}$, and $H_{C}$ be the orthogonal projections of $O$ on $B C, C A$, and $A B$, respectively. Because $60^{\circ}<\angle O A_{1} B<120^{\circ}$,
$$
\left|O H_{A}\right|=\left|O A_{1}\right| \sin \left(\angle O A_{1} B\right)>\left|O A_{1}\right| \frac{\sqrt{3}}{2}
$$
In the same way,
$$
\left|O H_{B}\right|>\left|O B_{1}\right| \frac{\sqrt{3}}{2} \quad \text { and } \quad\left|O H_{C}\right|>\left|O C_{1}\right| \frac{\sqrt{3}}{2}
$$
The area of $A B C$ is $a^{2} \frac{\sqrt{3}}{4}$ but also $\frac{a}{2}\left(O H_{A}+O H_{B}+O H_{C}\right)$ (as the sum of the areas of the three triangles with common vertex $O$ which together comprise $A B C$ ). So
$$
\left|O H_{A}\right|+\left|O H_{B}\right|+\left|O H_{C}\right|=a \frac{\sqrt{3}}{2}
$$
and the claim follows at once.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $O$ be an interior point in the equilateral triangle $A B C$, of side length $a$. The lines $A O, B O$, and $C O$ intersect the sides of the triangle in the points $A_{1}, B_{1}$, and $C_{1}$. Show that
$$
\left|O A_{1}\right|+\left|O B_{1}\right|+\left|O C_{1}\right|<a
$$
|
Let $H_{A}, H_{B}$, and $H_{C}$ be the orthogonal projections of $O$ on $B C, C A$, and $A B$, respectively. Because $60^{\circ}<\angle O A_{1} B<120^{\circ}$,
$$
\left|O H_{A}\right|=\left|O A_{1}\right| \sin \left(\angle O A_{1} B\right)>\left|O A_{1}\right| \frac{\sqrt{3}}{2}
$$
In the same way,
$$
\left|O H_{B}\right|>\left|O B_{1}\right| \frac{\sqrt{3}}{2} \quad \text { and } \quad\left|O H_{C}\right|>\left|O C_{1}\right| \frac{\sqrt{3}}{2}
$$
The area of $A B C$ is $a^{2} \frac{\sqrt{3}}{4}$ but also $\frac{a}{2}\left(O H_{A}+O H_{B}+O H_{C}\right)$ (as the sum of the areas of the three triangles with common vertex $O$ which together comprise $A B C$ ). So
$$
\left|O H_{A}\right|+\left|O H_{B}\right|+\left|O H_{C}\right|=a \frac{\sqrt{3}}{2}
$$
and the claim follows at once.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n94.1. ",
"solution_match": "\nSolution. "
}
|
636d1322-ed38-5945-8c32-fbfb7c4d2a30
| 607,944
|
A piece of paper is the square $A B C D$. We fold it by placing the vertex $D$ on the point $H$ of the side $B C$. We assume that $A D$ moves onto the segment $G H$ and that $H G$ intersects $A B$ at $E$. Prove that the perimeter of the triangle $E B H$ is one half of the perimeter of the square.
Figure 6 .
|
(See Figure 6.) The fold gives rise to an isosceles trapezium $A D H G$. Because of symmetry, the distance of the vertex $D$ from the side $G H$ equals the distance of the vertex
$H$ from side $A D$; the latter distance is the side length $a$ of the square. The line $G H$ thus is tangent to the circle with center $D$ and radius $a$. The lines $A B$ and $B C$ are tangent to the same circle. If the point common to $G H$ and the circle is $F$, then $A E=E F$ and $F H=H C$. This implies $A B+B C=A E+E B+B H+H C=E F+E B+B H+H F=E H+E B+B H$, which is equivalent to what we were asked to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A piece of paper is the square $A B C D$. We fold it by placing the vertex $D$ on the point $H$ of the side $B C$. We assume that $A D$ moves onto the segment $G H$ and that $H G$ intersects $A B$ at $E$. Prove that the perimeter of the triangle $E B H$ is one half of the perimeter of the square.

Figure 6 .
|
(See Figure 6.) The fold gives rise to an isosceles trapezium $A D H G$. Because of symmetry, the distance of the vertex $D$ from the side $G H$ equals the distance of the vertex
$H$ from side $A D$; the latter distance is the side length $a$ of the square. The line $G H$ thus is tangent to the circle with center $D$ and radius $a$. The lines $A B$ and $B C$ are tangent to the same circle. If the point common to $G H$ and the circle is $F$, then $A E=E F$ and $F H=H C$. This implies $A B+B C=A E+E B+B H+H C=E F+E B+B H+H F=E H+E B+B H$, which is equivalent to what we were asked to prove.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n94.3. ",
"solution_match": "\nSolution. "
}
|
f05d9f45-d224-568c-80bc-a322d6803147
| 607,946
|
Let $A B$ be a diameter of a circle with centre $O$. We choose a point $C$ on the circumference of the circle such that $O C$ and $A B$ are perpendicular to each other. Let $P$ be an arbitrary point on the (smaller) arc $B C$ and let the lines $C P$ and $A B$ meet at $Q$. We choose $R$ on $A P$ so that $R Q$ and $A B$ are perpendicular to each other. Show that $|B Q|=|Q R|$.
Figure 7 .
|
(See Figure 7.) Draw $P B$. By the Theorem of Thales, $\angle R P B=\angle A P B=$ $90^{\circ}$. So $P$ and $Q$ both lie on the circle with diameter $R B$. Because $\angle A O C=90^{\circ}$, $\angle R P Q=\angle C P A=45^{\circ}$. Then $\angle R B Q=45^{\circ}$, too, and $R B Q$ is an isosceles right triangle, or $|B Q|=|Q R|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B$ be a diameter of a circle with centre $O$. We choose a point $C$ on the circumference of the circle such that $O C$ and $A B$ are perpendicular to each other. Let $P$ be an arbitrary point on the (smaller) arc $B C$ and let the lines $C P$ and $A B$ meet at $Q$. We choose $R$ on $A P$ so that $R Q$ and $A B$ are perpendicular to each other. Show that $|B Q|=|Q R|$.

Figure 7 .
|
(See Figure 7.) Draw $P B$. By the Theorem of Thales, $\angle R P B=\angle A P B=$ $90^{\circ}$. So $P$ and $Q$ both lie on the circle with diameter $R B$. Because $\angle A O C=90^{\circ}$, $\angle R P Q=\angle C P A=45^{\circ}$. Then $\angle R B Q=45^{\circ}$, too, and $R B Q$ is an isosceles right triangle, or $|B Q|=|Q R|$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n95.1. ",
"solution_match": "\nSolution 1. "
}
|
caab7da2-4217-5d10-990a-1b885fe94aac
| 607,948
|
Let $A B$ be a diameter of a circle with centre $O$. We choose a point $C$ on the circumference of the circle such that $O C$ and $A B$ are perpendicular to each other. Let $P$ be an arbitrary point on the (smaller) arc $B C$ and let the lines $C P$ and $A B$ meet at $Q$. We choose $R$ on $A P$ so that $R Q$ and $A B$ are perpendicular to each other. Show that $|B Q|=|Q R|$.

Figure 7 .
|
Set $O=(0,0), A=(-1,0), B=(1,0), C=(0,1)$, and $P=(t, u)$, where $t>0, u>0$, and $t^{2}+u^{2}=1$. The equation of line $C P$ is $y-1=\frac{u-1}{t} x$. So $Q=\left(\frac{t}{1-u}, 0\right)$ and $|B Q|=\frac{t}{1-u}-1=\frac{t+u-1}{1-u}$. On the other hand, the equation of line $A P$ is $y=\frac{u}{t+1}(x+1)$. The $y$ coordinate of $R$ and also $|Q R|$ is $\frac{u}{t+1}\left(\frac{t}{1-u}+1\right)=$ $\frac{u t+u-u^{2}}{(t+1)(1-u)}=\frac{u t+u-1+t^{2}}{(t+1)(1-u)}=\frac{u+t-1}{1-u}$. The claim has been proved.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B$ be a diameter of a circle with centre $O$. We choose a point $C$ on the circumference of the circle such that $O C$ and $A B$ are perpendicular to each other. Let $P$ be an arbitrary point on the (smaller) arc $B C$ and let the lines $C P$ and $A B$ meet at $Q$. We choose $R$ on $A P$ so that $R Q$ and $A B$ are perpendicular to each other. Show that $|B Q|=|Q R|$.

Figure 7 .
|
Set $O=(0,0), A=(-1,0), B=(1,0), C=(0,1)$, and $P=(t, u)$, where $t>0, u>0$, and $t^{2}+u^{2}=1$. The equation of line $C P$ is $y-1=\frac{u-1}{t} x$. So $Q=\left(\frac{t}{1-u}, 0\right)$ and $|B Q|=\frac{t}{1-u}-1=\frac{t+u-1}{1-u}$. On the other hand, the equation of line $A P$ is $y=\frac{u}{t+1}(x+1)$. The $y$ coordinate of $R$ and also $|Q R|$ is $\frac{u}{t+1}\left(\frac{t}{1-u}+1\right)=$ $\frac{u t+u-u^{2}}{(t+1)(1-u)}=\frac{u t+u-1+t^{2}}{(t+1)(1-u)}=\frac{u+t-1}{1-u}$. The claim has been proved.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n95.1. ",
"solution_match": "\nSolution 2. "
}
|
caab7da2-4217-5d10-990a-1b885fe94aac
| 607,948
|
Let $n \geq 2$ and let $x_{1}, x_{2}, \ldots x_{n}$ be real numbers satisfying $x_{1}+x_{2}+\ldots+x_{n} \geq 0$ and $x_{1}^{2}+x_{2}^{2}+\ldots+x_{n}^{2}=1$. Let $M=\max \left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$. Show that
$$
M \geq \frac{1}{\sqrt{n(n-1)}}
$$
When does equality hold in (1)?
|
Denote by $I$ the set of indices $i$ for which $x_{i} \geq 0$, and by $J$ the set of indices $j$ for which $x_{j}<0$. Let us assume $M<\frac{1}{\sqrt{n(n-1)}}$. Then $I \neq\{1,2, \ldots, n\}$, since otherwise we would have $\left|x_{i}\right|=x_{i} \leq \frac{1}{\sqrt{n(n-1)}}$ for every $i$, and $\sum_{i=1}^{n} x_{i}^{2}<\frac{1}{n-1} \leq 1$. So $\sum_{i \in I} x_{i}^{2}<(n-1) \cdot \frac{1}{n(n-1)}=\frac{1}{n}$, and $\sum_{i \in I} x_{i}<(n-1) \frac{1}{\sqrt{n(n-1)}}=\sqrt{\frac{n-1}{n}}$. Because
$$
0 \leq \sum_{i=1}^{n} x_{i}=\sum_{i \in I} x_{i}-\sum_{i \in J}\left|x_{i}\right|
$$
we must have $\sum_{i \in J}\left|x_{i}\right| \leq \sum_{i \in I} x_{i}<\sqrt{\frac{n-1}{n}}$ and $\sum_{i \in J} x_{i}^{2} \leq\left(\sum_{i \in J}\left|x_{i}\right|\right)^{2}<\frac{n-1}{n}$. But then
$$
\sum_{i=1}^{n} x_{i}^{2}=\sum_{i \in I} x_{i}^{2}+\sum_{i \in J} x_{i}^{2}<\frac{1}{n}+\frac{n-1}{n}=1
$$
and we have a contradiction. - To see that equality $M=\frac{1}{\sqrt{n(n-1)}}$ is possible, we choose $x_{i}=\frac{1}{\sqrt{n(n-1)}}, i=1,2, \ldots, n-1$, and $x_{n}=-\sqrt{\frac{n-1}{n}}$. Now
$$
\sum_{i=1}^{n} x_{i}=(n-1) \frac{1}{\sqrt{n(n-1)}}-\sqrt{\frac{n-1}{n}}=0
$$
and
$$
\sum_{i=1}^{n} x_{i}^{2}=(n-1) \cdot \frac{1}{n(n-1)}+\frac{n-1}{n}=1
$$
We still have to show that equality can be obtained only in this case. Assume $x_{i}=$ $\frac{1}{\sqrt{n(n-1)}}$, for $i=1, \ldots, p, x_{i} \geq 0$, for $i \leq q$, and $x_{i}<0$, kun $q+1 \leq i \leq n$. As before we get
$$
\sum_{i=1}^{q} x_{i} \leq \frac{q}{\sqrt{n(n-1)}}, \quad \sum_{i=q+1}^{n}\left|x_{i}\right| \leq \frac{q}{\sqrt{n(n-1)}}
$$
and
$$
\sum_{i=q+1}^{n} x_{i}^{2} \leq \frac{q^{2}}{n(n-1)}
$$
so
$$
\sum_{i=1}^{n} x_{i}^{2} \leq \frac{q+q^{2}}{n^{2}-n}
$$
It is easy to see that $q^{2}+q<n^{2}+n$, for $n \geq 2$ and $q \leq n-2$, but $(n-1)^{2}+(n-1)=n^{2}-n$. Consequently, a necessary condition for $M=\frac{1}{\sqrt{n(n-1)}}$ is that the sequence only has one negative member. But if among the positive members there is at least one smaller than $M$ we have
$$
\sum_{i=1}^{n}<\frac{q+q^{2}}{n(n-1)}
$$
so the conditions of the problem are not satisfied. So there is equality if and only if $n-1$ of the numbers $x_{i}$ equal $\frac{1}{\sqrt{n(n-1)}}$, and the last one is $\frac{1-n}{\sqrt{n(n-1)}}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geq 2$ and let $x_{1}, x_{2}, \ldots x_{n}$ be real numbers satisfying $x_{1}+x_{2}+\ldots+x_{n} \geq 0$ and $x_{1}^{2}+x_{2}^{2}+\ldots+x_{n}^{2}=1$. Let $M=\max \left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$. Show that
$$
M \geq \frac{1}{\sqrt{n(n-1)}}
$$
When does equality hold in (1)?
|
Denote by $I$ the set of indices $i$ for which $x_{i} \geq 0$, and by $J$ the set of indices $j$ for which $x_{j}<0$. Let us assume $M<\frac{1}{\sqrt{n(n-1)}}$. Then $I \neq\{1,2, \ldots, n\}$, since otherwise we would have $\left|x_{i}\right|=x_{i} \leq \frac{1}{\sqrt{n(n-1)}}$ for every $i$, and $\sum_{i=1}^{n} x_{i}^{2}<\frac{1}{n-1} \leq 1$. So $\sum_{i \in I} x_{i}^{2}<(n-1) \cdot \frac{1}{n(n-1)}=\frac{1}{n}$, and $\sum_{i \in I} x_{i}<(n-1) \frac{1}{\sqrt{n(n-1)}}=\sqrt{\frac{n-1}{n}}$. Because
$$
0 \leq \sum_{i=1}^{n} x_{i}=\sum_{i \in I} x_{i}-\sum_{i \in J}\left|x_{i}\right|
$$
we must have $\sum_{i \in J}\left|x_{i}\right| \leq \sum_{i \in I} x_{i}<\sqrt{\frac{n-1}{n}}$ and $\sum_{i \in J} x_{i}^{2} \leq\left(\sum_{i \in J}\left|x_{i}\right|\right)^{2}<\frac{n-1}{n}$. But then
$$
\sum_{i=1}^{n} x_{i}^{2}=\sum_{i \in I} x_{i}^{2}+\sum_{i \in J} x_{i}^{2}<\frac{1}{n}+\frac{n-1}{n}=1
$$
and we have a contradiction. - To see that equality $M=\frac{1}{\sqrt{n(n-1)}}$ is possible, we choose $x_{i}=\frac{1}{\sqrt{n(n-1)}}, i=1,2, \ldots, n-1$, and $x_{n}=-\sqrt{\frac{n-1}{n}}$. Now
$$
\sum_{i=1}^{n} x_{i}=(n-1) \frac{1}{\sqrt{n(n-1)}}-\sqrt{\frac{n-1}{n}}=0
$$
and
$$
\sum_{i=1}^{n} x_{i}^{2}=(n-1) \cdot \frac{1}{n(n-1)}+\frac{n-1}{n}=1
$$
We still have to show that equality can be obtained only in this case. Assume $x_{i}=$ $\frac{1}{\sqrt{n(n-1)}}$, for $i=1, \ldots, p, x_{i} \geq 0$, for $i \leq q$, and $x_{i}<0$, kun $q+1 \leq i \leq n$. As before we get
$$
\sum_{i=1}^{q} x_{i} \leq \frac{q}{\sqrt{n(n-1)}}, \quad \sum_{i=q+1}^{n}\left|x_{i}\right| \leq \frac{q}{\sqrt{n(n-1)}}
$$
and
$$
\sum_{i=q+1}^{n} x_{i}^{2} \leq \frac{q^{2}}{n(n-1)}
$$
so
$$
\sum_{i=1}^{n} x_{i}^{2} \leq \frac{q+q^{2}}{n^{2}-n}
$$
It is easy to see that $q^{2}+q<n^{2}+n$, for $n \geq 2$ and $q \leq n-2$, but $(n-1)^{2}+(n-1)=n^{2}-n$. Consequently, a necessary condition for $M=\frac{1}{\sqrt{n(n-1)}}$ is that the sequence only has one negative member. But if among the positive members there is at least one smaller than $M$ we have
$$
\sum_{i=1}^{n}<\frac{q+q^{2}}{n(n-1)}
$$
so the conditions of the problem are not satisfied. So there is equality if and only if $n-1$ of the numbers $x_{i}$ equal $\frac{1}{\sqrt{n(n-1)}}$, and the last one is $\frac{1-n}{\sqrt{n(n-1)}}$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n95.3. ",
"solution_match": "\nSolution. "
}
|
b5c92774-a105-5399-9127-545791e56913
| 607,950
|
Show that there exist infinitely many mutually non-congruent triangles $T$, satisfying
(i) The side lengths of $T$ are consecutive integers.
(ii) The area of $T$ is an integer.
|
Let $n \geq 3$, and let $n-1, n, n+1$ be the side lengths of the triangle. The semiperimeter of the triangle then equals on $\frac{3 n}{2}$. By Heron's formula, the area of the triangle is
$$
\begin{gathered}
T=\sqrt{\frac{3 n}{2} \cdot\left(\frac{3 n}{2}-n+1\right)\left(\frac{3 n}{2}-n\right)\left(\frac{3 n}{2}-n-1\right)} \\
=\frac{n}{2} \sqrt{\frac{3}{4}\left(n^{2}-4\right)} .
\end{gathered}
$$
If $n=4$, then $T=6$. So at least one triangle of the kind required exists. We prove that we always can form new triangles of the required kind from ones already known to exist. Let $n$ be even, $n \geq 4$, and let $\frac{3}{4}\left(n^{2}-4\right)$ be a square number. Set $m=n^{2}-2$. Then $m>n$, $m$ is even, and $m^{2}-4=(m+2)(m-2)=n^{2}\left(n^{2}-4\right)$. So $\frac{3}{4}\left(m^{2}-4\right)=n^{2} \cdot \frac{3}{4}\left(n^{2}-4\right)$ is a square number. Also, $T=\frac{m}{2} \sqrt{\frac{3}{4}\left(m^{2}-4\right)}$ is an integer. The argument is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Show that there exist infinitely many mutually non-congruent triangles $T$, satisfying
(i) The side lengths of $T$ are consecutive integers.
(ii) The area of $T$ is an integer.
|
Let $n \geq 3$, and let $n-1, n, n+1$ be the side lengths of the triangle. The semiperimeter of the triangle then equals on $\frac{3 n}{2}$. By Heron's formula, the area of the triangle is
$$
\begin{gathered}
T=\sqrt{\frac{3 n}{2} \cdot\left(\frac{3 n}{2}-n+1\right)\left(\frac{3 n}{2}-n\right)\left(\frac{3 n}{2}-n-1\right)} \\
=\frac{n}{2} \sqrt{\frac{3}{4}\left(n^{2}-4\right)} .
\end{gathered}
$$
If $n=4$, then $T=6$. So at least one triangle of the kind required exists. We prove that we always can form new triangles of the required kind from ones already known to exist. Let $n$ be even, $n \geq 4$, and let $\frac{3}{4}\left(n^{2}-4\right)$ be a square number. Set $m=n^{2}-2$. Then $m>n$, $m$ is even, and $m^{2}-4=(m+2)(m-2)=n^{2}\left(n^{2}-4\right)$. So $\frac{3}{4}\left(m^{2}-4\right)=n^{2} \cdot \frac{3}{4}\left(n^{2}-4\right)$ is a square number. Also, $T=\frac{m}{2} \sqrt{\frac{3}{4}\left(m^{2}-4\right)}$ is an integer. The argument is complete.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n95.4. ",
"solution_match": "\nSolution. "
}
|
98d32099-5cbc-5fbb-89d4-c16b4801e2e9
| 607,951
|
Show that there exists an integer divisible by 1996 such that the sum of the its decimal digits is 1996 .
|
The sum of the digits of 1996 is 25 and the sum of the digits of $2 \cdot 1996=3992$ is 23 . Because $1996=78 \cdot 25+46$, the number obtained by writing 781996 's and two 3992 in succession satisfies the condition of the problem. - As $3 \cdot 1996=5998$, the sum of the digits of 5988 is 30 , and $1996=65 \cdot 30+46$, the number $39923992 \underbrace{5988 \ldots 5988}_{65 \text { times }}$ also can be be given as an answer, indeed a better one, as it is much smaller than the first suggestion.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that there exists an integer divisible by 1996 such that the sum of the its decimal digits is 1996 .
|
The sum of the digits of 1996 is 25 and the sum of the digits of $2 \cdot 1996=3992$ is 23 . Because $1996=78 \cdot 25+46$, the number obtained by writing 781996 's and two 3992 in succession satisfies the condition of the problem. - As $3 \cdot 1996=5998$, the sum of the digits of 5988 is 30 , and $1996=65 \cdot 30+46$, the number $39923992 \underbrace{5988 \ldots 5988}_{65 \text { times }}$ also can be be given as an answer, indeed a better one, as it is much smaller than the first suggestion.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n96.1. ",
"solution_match": "\nSolution. "
}
|
a6416400-1c99-5919-9041-5b6e711b6164
| 607,952
|
The circle whose diameter is the altitude dropped from the vertex $A$ of the triangle $A B C$ intersects the sides $A B$ and $A C$ at $D$ and $E$, respectively $(A \neq D, A \neq E)$. Show that the circumcentre of $A B C$ lies on the altitude dropped from the vertex $A$ of the triangle $A D E$, or on its extension.
Figure 8.
|
(See Figure 8.) Let $A F$ be the altitude of $A B C$. We may assume that $\angle A C B$ is sharp. From the right triangles $A C F$ and $A F E$ we obtain $\angle A F E=\angle A C F . \angle A D E$ and $\angle A F E$ subtend the same arc, so they are equal. Thus $\angle A C B=\angle A D E$, and the triangles $A B C$ and $A E D$ are similar. Denote by $P$ and $Q$ the circumcenters of $A B C$ and $A E D$, respectively. Then $\angle B A P=\angle E A Q$. If $A G$ is the altitude of $A E D$, then $\angle D A G=\angle C A F$. But this implies $\angle B A P=\angle D A G$, which means that $P$ is on the altitude $A G$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The circle whose diameter is the altitude dropped from the vertex $A$ of the triangle $A B C$ intersects the sides $A B$ and $A C$ at $D$ and $E$, respectively $(A \neq D, A \neq E)$. Show that the circumcentre of $A B C$ lies on the altitude dropped from the vertex $A$ of the triangle $A D E$, or on its extension.

Figure 8.
|
(See Figure 8.) Let $A F$ be the altitude of $A B C$. We may assume that $\angle A C B$ is sharp. From the right triangles $A C F$ and $A F E$ we obtain $\angle A F E=\angle A C F . \angle A D E$ and $\angle A F E$ subtend the same arc, so they are equal. Thus $\angle A C B=\angle A D E$, and the triangles $A B C$ and $A E D$ are similar. Denote by $P$ and $Q$ the circumcenters of $A B C$ and $A E D$, respectively. Then $\angle B A P=\angle E A Q$. If $A G$ is the altitude of $A E D$, then $\angle D A G=\angle C A F$. But this implies $\angle B A P=\angle D A G$, which means that $P$ is on the altitude $A G$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n96.3. ",
"solution_match": "\nSolution. "
}
|
1d88efb3-429d-5ff0-b95c-a81a6b716ec6
| 607,954
|
Let $A B C D$ be a convex quadrilateral. We assume that there exists a point $P$ inside the quadrilateral such that the areas of the triangles $A B P, B C P, C D P$, and $D A P$ are equal. Show that at least one of the diagonals of the quadrilateral bisects the other diagonal.
Figure 9.
|
(See Figure 9.) We first assume that $P$ does not lie on the diagonal $A C$ and the line $B P$ meets the diagonal $A C$ at $M$. Let $S$ and $T$ be the feet of the perpendiculars from $A$ and $C$ on the line $B P$. The triangles $A P B$ and $C B P$ have equal area. Thus $A S=C T$. If $S \neq T$, then the right trianges $A S M$ and $C T M$ are congruent, and $A M=C M$. If, on the other hand, $S=T$, the $A C \perp P B$ and $S=M=T$, and again $A M=C M$. In both cases $M$ is the midpoint of the diagonal $A C$. We prove exactly in the same way that the line $D P$ meets $A C$ at the midpoint of $A C$, i.e. at $M$. So $B, M$, and $P$, and also $D, M$, and $P$ are collinear. So $M$ is on the line $D B$, which means that $B D$ divides the diagonal $A C$ in two equal parts.
We then assume that $P$ lies on the diagonal $A C$. Then $P$ is the midpoint of $A C$. If $P$ is not on the diagonal $B D$, we argue as before that $A C$ divides $B D$ in two equal parts. If $P$ lies also on the diagonal $B D$, it has to be the common midpoint of the diagonals.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral. We assume that there exists a point $P$ inside the quadrilateral such that the areas of the triangles $A B P, B C P, C D P$, and $D A P$ are equal. Show that at least one of the diagonals of the quadrilateral bisects the other diagonal.

Figure 9.
|
(See Figure 9.) We first assume that $P$ does not lie on the diagonal $A C$ and the line $B P$ meets the diagonal $A C$ at $M$. Let $S$ and $T$ be the feet of the perpendiculars from $A$ and $C$ on the line $B P$. The triangles $A P B$ and $C B P$ have equal area. Thus $A S=C T$. If $S \neq T$, then the right trianges $A S M$ and $C T M$ are congruent, and $A M=C M$. If, on the other hand, $S=T$, the $A C \perp P B$ and $S=M=T$, and again $A M=C M$. In both cases $M$ is the midpoint of the diagonal $A C$. We prove exactly in the same way that the line $D P$ meets $A C$ at the midpoint of $A C$, i.e. at $M$. So $B, M$, and $P$, and also $D, M$, and $P$ are collinear. So $M$ is on the line $D B$, which means that $B D$ divides the diagonal $A C$ in two equal parts.
We then assume that $P$ lies on the diagonal $A C$. Then $P$ is the midpoint of $A C$. If $P$ is not on the diagonal $B D$, we argue as before that $A C$ divides $B D$ in two equal parts. If $P$ lies also on the diagonal $B D$, it has to be the common midpoint of the diagonals.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n97.2. ",
"solution_match": "\nSolution. "
}
|
5828a72a-6398-5476-8808-bcae54f25042
| 607,957
|
Let $f$ be a function defined in the set $\{0,1,2, \ldots\}$ of non-negative integers, satisfying $f(2 x)=2 f(x), f(4 x+1)=4 f(x)+3$, and $f(4 x-1)=2 f(2 x-1)-1$. Show that $f$ is an injection, i.e. if $f(x)=f(y)$, then $x=y$.
|
If $x$ is even, then $f(x)$ is even, and if $x$ is odd, then $f(x)$ is odd. Moreover, if $x \equiv 1 \bmod 4$, then $f(x) \equiv 3 \bmod 4$, and if $x \equiv 3 \bmod 4$, then $f(x) \equiv 1 \bmod 4$. Clearly $f(0)=0, f(1)=3, f(2)=6$, and $f(3)=5$. So at least $f$ restricted to the set $\{0,1,2,3\}$ ia an injection. We prove that $f(x)=f(y) \Longrightarrow x=y$, for $x, y<k$ implies $f(x)=f(y) \Longrightarrow x=y$, for $x, y<2 k$. So assume $x$ and $y$ are smaller than $2 k$ and $f(x)=f(y)$. If $f(x)$ is even, then $x=2 t, y=2 u$, and $2 f(t)=2 f(u)$. As $t$ and $u$ are less than $k$, we have $t=u$, and $x=y$. Assume $f(x) \equiv 1 \bmod 4$. Then $x \equiv 3 \bmod 4 ;$ $x=4 u-1$, and $f(x)=2 f(2 u-1)-1$. Also $y=4 t-1$ and $f(y)=2 f(2 t-1)-1$. Moreover, $2 u-1<\frac{1}{2}(4 u-1)<k$ and $2 t-1<k$, so $2 u-1=2 t-1, u=t$, and $x=y$. If, finally, $f(x) \equiv 3 \bmod 4$, then $x=4 u+1, y=4 t+1, u<k, t<k, 4 f(u)+3=4 f(t)+3, u=t$, and $x=y$. Since for all $x$ and $y$ there is an $n$ such that the larger one of the numbers $x$ and $y$ is $<2^{n} \cdot 3$, the induction argument above shows that $f(x)=f(y) \Rightarrow x=y$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f$ be a function defined in the set $\{0,1,2, \ldots\}$ of non-negative integers, satisfying $f(2 x)=2 f(x), f(4 x+1)=4 f(x)+3$, and $f(4 x-1)=2 f(2 x-1)-1$. Show that $f$ is an injection, i.e. if $f(x)=f(y)$, then $x=y$.
|
If $x$ is even, then $f(x)$ is even, and if $x$ is odd, then $f(x)$ is odd. Moreover, if $x \equiv 1 \bmod 4$, then $f(x) \equiv 3 \bmod 4$, and if $x \equiv 3 \bmod 4$, then $f(x) \equiv 1 \bmod 4$. Clearly $f(0)=0, f(1)=3, f(2)=6$, and $f(3)=5$. So at least $f$ restricted to the set $\{0,1,2,3\}$ ia an injection. We prove that $f(x)=f(y) \Longrightarrow x=y$, for $x, y<k$ implies $f(x)=f(y) \Longrightarrow x=y$, for $x, y<2 k$. So assume $x$ and $y$ are smaller than $2 k$ and $f(x)=f(y)$. If $f(x)$ is even, then $x=2 t, y=2 u$, and $2 f(t)=2 f(u)$. As $t$ and $u$ are less than $k$, we have $t=u$, and $x=y$. Assume $f(x) \equiv 1 \bmod 4$. Then $x \equiv 3 \bmod 4 ;$ $x=4 u-1$, and $f(x)=2 f(2 u-1)-1$. Also $y=4 t-1$ and $f(y)=2 f(2 t-1)-1$. Moreover, $2 u-1<\frac{1}{2}(4 u-1)<k$ and $2 t-1<k$, so $2 u-1=2 t-1, u=t$, and $x=y$. If, finally, $f(x) \equiv 3 \bmod 4$, then $x=4 u+1, y=4 t+1, u<k, t<k, 4 f(u)+3=4 f(t)+3, u=t$, and $x=y$. Since for all $x$ and $y$ there is an $n$ such that the larger one of the numbers $x$ and $y$ is $<2^{n} \cdot 3$, the induction argument above shows that $f(x)=f(y) \Rightarrow x=y$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n97.4. ",
"solution_match": "\nSolution. "
}
|
c9068a50-81af-5efc-a9b6-21053def76c4
| 607,959
|
Let $C_{1}$ and $C_{2}$ be two circles intersecting at $A$ and $B$. Let $S$ and $T$ be the centres of $C_{1}$ and $C_{2}$, respectively. Let $P$ be a point on the segment $A B$ such that $|A P| \neq|B P|$ and $P \neq A, P \neq B$. We draw a line perpendicular to $S P$ through $P$ and denote by $C$ and $D$ the points at which this line intersects $C_{1}$. We likewise draw a line perpendicular to TP through $P$ and denote by $E$ and $F$ the points at which this line intersects $C_{2}$. Show that $C, D, E$, and $F$ are the vertices of a rectangle.
|
(See Figure 10.) The power of the point $P$ with respect to the circles $C_{1}$ and $C_{2}$ is $P A \cdot P B=P C \cdot P D=P E \cdot P F$. Since $S P$ is perpendicular to the chord $C D, P$
Figure 10 .
has to be the midpoint of $C D$. So $P C=P D$. In a similar manner, we obtain $P E=P F$. Alltogether $P C=P D=P E=P F=\sqrt{P A \cdot P B}$. Consequently the points $C, D, E$, and $F$ all lie on a circle withe center $P$, and $C D$ and $E F$ as diameters. By Thales' theorem, the angles $\angle E C F, \angle C F D$ etc. are right angles. So $C D E F$ is a rectangle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $C_{1}$ and $C_{2}$ be two circles intersecting at $A$ and $B$. Let $S$ and $T$ be the centres of $C_{1}$ and $C_{2}$, respectively. Let $P$ be a point on the segment $A B$ such that $|A P| \neq|B P|$ and $P \neq A, P \neq B$. We draw a line perpendicular to $S P$ through $P$ and denote by $C$ and $D$ the points at which this line intersects $C_{1}$. We likewise draw a line perpendicular to TP through $P$ and denote by $E$ and $F$ the points at which this line intersects $C_{2}$. Show that $C, D, E$, and $F$ are the vertices of a rectangle.
|
(See Figure 10.) The power of the point $P$ with respect to the circles $C_{1}$ and $C_{2}$ is $P A \cdot P B=P C \cdot P D=P E \cdot P F$. Since $S P$ is perpendicular to the chord $C D, P$

Figure 10 .
has to be the midpoint of $C D$. So $P C=P D$. In a similar manner, we obtain $P E=P F$. Alltogether $P C=P D=P E=P F=\sqrt{P A \cdot P B}$. Consequently the points $C, D, E$, and $F$ all lie on a circle withe center $P$, and $C D$ and $E F$ as diameters. By Thales' theorem, the angles $\angle E C F, \angle C F D$ etc. are right angles. So $C D E F$ is a rectangle.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n98.2. ",
"solution_match": "\nSolution. "
}
|
acf9b4df-281e-5cfd-8999-af8b0872c6e6
| 607,961
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers and $n \geq 1$. Show that
$$
\begin{aligned}
& n\left(\frac{1}{a_{1}}+\cdots+\frac{1}{a_{n}}\right) \\
& \quad \geq\left(\frac{1}{1+a_{1}}+\cdots+\frac{1}{1+a_{n}}\right)\left(n+\frac{1}{a_{1}}+\cdots+\frac{1}{a_{n}}\right)
\end{aligned}
$$
When does equality hold?
|
The inequality of the problem can be written as
$$
\frac{1}{1+a_{1}}+\cdots+\frac{1}{1+a_{n}} \leq \frac{n\left(\frac{1}{a_{1}}+\cdots+\frac{1}{a_{n}}\right)}{n+\frac{1}{a_{1}}+\cdots+\frac{1}{a_{n}}}
$$
A small manipulation of the right hand side brings the inequality to the equivalent form
$$
\frac{1}{\frac{1}{a_{1}^{-1}}+1}+\cdots+\frac{1}{\frac{1}{a_{n}^{-1}}+1} \leq \frac{n}{\frac{1}{\frac{a_{1}^{-1}+\cdots+a_{n}^{-1}}{n}}+1}
$$
Consider the function
$$
f(x)=\frac{1}{\frac{1}{x}+1}=\frac{x}{1+x}
$$
We see that it is concave, i.e.
$$
t f(x)+(1-t) f(y)<f(t x+(1-t) y)
$$
for all $t \in(0,1)$. In fact, the inequality
$$
t \frac{x}{1+x}+(1-t) \frac{y}{1+y}<\frac{t x+(1-t) y}{1+t x+(1-t) y}
$$
can be written as
$$
t^{2}(x-y)^{2}<t(x-y)^{2}
$$
and because $0<t<1$, it is true. [Another standard way to see this is to compute
$$
f^{\prime}(x)=\frac{1}{(1+x)^{2}}, \quad f^{\prime \prime}(x)=-\frac{2}{(1+x)^{3}}<0
$$
A function with a positive second derivative is concave.] For any concave function $f$, the inequality
$$
\frac{1}{n}\left(f\left(x_{1}\right)+f\left(x_{2}\right)+\cdots+f\left(x_{n}\right)\right) \leq f\left(\frac{x_{1}+\cdots+x_{n}}{n}\right)
$$
holds, with equality only for $x_{1}=x_{2}=\ldots=x_{n}$. So (1) is true, and equality holds only if all $a_{i}$ 's are equal.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers and $n \geq 1$. Show that
$$
\begin{aligned}
& n\left(\frac{1}{a_{1}}+\cdots+\frac{1}{a_{n}}\right) \\
& \quad \geq\left(\frac{1}{1+a_{1}}+\cdots+\frac{1}{1+a_{n}}\right)\left(n+\frac{1}{a_{1}}+\cdots+\frac{1}{a_{n}}\right)
\end{aligned}
$$
When does equality hold?
|
The inequality of the problem can be written as
$$
\frac{1}{1+a_{1}}+\cdots+\frac{1}{1+a_{n}} \leq \frac{n\left(\frac{1}{a_{1}}+\cdots+\frac{1}{a_{n}}\right)}{n+\frac{1}{a_{1}}+\cdots+\frac{1}{a_{n}}}
$$
A small manipulation of the right hand side brings the inequality to the equivalent form
$$
\frac{1}{\frac{1}{a_{1}^{-1}}+1}+\cdots+\frac{1}{\frac{1}{a_{n}^{-1}}+1} \leq \frac{n}{\frac{1}{\frac{a_{1}^{-1}+\cdots+a_{n}^{-1}}{n}}+1}
$$
Consider the function
$$
f(x)=\frac{1}{\frac{1}{x}+1}=\frac{x}{1+x}
$$
We see that it is concave, i.e.
$$
t f(x)+(1-t) f(y)<f(t x+(1-t) y)
$$
for all $t \in(0,1)$. In fact, the inequality
$$
t \frac{x}{1+x}+(1-t) \frac{y}{1+y}<\frac{t x+(1-t) y}{1+t x+(1-t) y}
$$
can be written as
$$
t^{2}(x-y)^{2}<t(x-y)^{2}
$$
and because $0<t<1$, it is true. [Another standard way to see this is to compute
$$
f^{\prime}(x)=\frac{1}{(1+x)^{2}}, \quad f^{\prime \prime}(x)=-\frac{2}{(1+x)^{3}}<0
$$
A function with a positive second derivative is concave.] For any concave function $f$, the inequality
$$
\frac{1}{n}\left(f\left(x_{1}\right)+f\left(x_{2}\right)+\cdots+f\left(x_{n}\right)\right) \leq f\left(\frac{x_{1}+\cdots+x_{n}}{n}\right)
$$
holds, with equality only for $x_{1}=x_{2}=\ldots=x_{n}$. So (1) is true, and equality holds only if all $a_{i}$ 's are equal.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n99.4. ",
"solution_match": "\nSolution. "
}
|
4a1058fd-d3ce-5fbb-b920-fc0fcf5baf55
| 607,967
|
In the triangle $A B C$, the bisector of angle $B$ meets $A C$ at $D$ and the bisector of angle $C$ meets $A B$ at $E$. The bisectors meet each other at $O$. Furthermore, $O D=O E$. Prove that either $A B C$ is isosceles or $\angle B A C=60^{\circ}$.
|
(See Figure 11.) Consider the triangles $A O E$ and $A O D$. They have two equal pairs of sides and the angles facing one of these pairs are equal. Then either $A O E$ and $A O D$ are congruent or $\angle A E O=180^{\circ}-\angle A D O$. In the first case, $\angle B E O=\angle C D O$, and
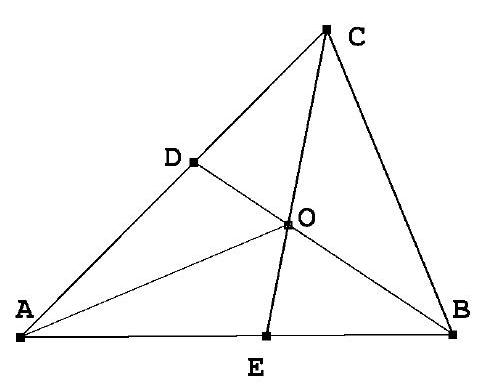
Figure 11.
the triangles $E B O$ and $D C O$ are congruent. Then $A B=A C$, and $A B C$ is isosceles. In the second case, denote the angles of $A B C$ by $2 \alpha, 2 \beta$, and $2 \gamma$, and the angle $A E O$ by $\delta$. By the theorem on the adjacent angle of an angle of a triangle, $\angle B O E=\angle D O C=\beta+\gamma$, $\delta=2 \beta+\gamma$, and $180^{\circ}-\delta=\beta+2 \gamma$. Adding these equations yields $3(\beta+\gamma)=180^{\circ}$ eli $\beta+\gamma=60^{\circ}$. Combining this with $2(\alpha+\beta+\gamma)=180^{\circ}$, we obtain $2 \alpha=60^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In the triangle $A B C$, the bisector of angle $B$ meets $A C$ at $D$ and the bisector of angle $C$ meets $A B$ at $E$. The bisectors meet each other at $O$. Furthermore, $O D=O E$. Prove that either $A B C$ is isosceles or $\angle B A C=60^{\circ}$.
|
(See Figure 11.) Consider the triangles $A O E$ and $A O D$. They have two equal pairs of sides and the angles facing one of these pairs are equal. Then either $A O E$ and $A O D$ are congruent or $\angle A E O=180^{\circ}-\angle A D O$. In the first case, $\angle B E O=\angle C D O$, and

Figure 11.
the triangles $E B O$ and $D C O$ are congruent. Then $A B=A C$, and $A B C$ is isosceles. In the second case, denote the angles of $A B C$ by $2 \alpha, 2 \beta$, and $2 \gamma$, and the angle $A E O$ by $\delta$. By the theorem on the adjacent angle of an angle of a triangle, $\angle B O E=\angle D O C=\beta+\gamma$, $\delta=2 \beta+\gamma$, and $180^{\circ}-\delta=\beta+2 \gamma$. Adding these equations yields $3(\beta+\gamma)=180^{\circ}$ eli $\beta+\gamma=60^{\circ}$. Combining this with $2(\alpha+\beta+\gamma)=180^{\circ}$, we obtain $2 \alpha=60^{\circ}$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n00.3. ",
"solution_match": "\nSolution. "
}
|
87dfd25a-8c74-5308-820e-21db8e59015e
| 607,970
|
Let $A$ be a finite collection of squares in the coordinate plane such that the vertices of all squares that belong to $A$ are $(m, n),(m+1, n),(m, n+1)$, and $(m+1, n+1)$ for some integers $m$ and $n$. Show that there exists a subcollection $B$ of $A$ such that $B$ contains at least $25 \%$ of the squares in $A$, but no two of the squares in $B$ have a common vertex.
|
Divide the plane into two sets by painting the strips of squares parallel to the $y$ axis alternately red and green. Denote the sets of red and green squares by $R$ and $G$, respectively. Of the sets $A \cap R$ and $A \cap G$ at least one contains at least one half of the squares in $A$. Denote this set by $A_{1}$. Next partition the strips of squares which contain squares of $A_{1}$ into two sets $E$ and $F$ so that each set contains every second square of $A_{1}$ on each strip. Now neither of the dets $E$ and $F$ has a common point with a square in the same set. On the other hand, at least one of the sets $E \cap A_{1}, F \cap A_{1}$ contains at least one half of the squares in $A_{1}$ and thus at least one quarter of the sets in $A$. This set is good for the required set $B$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $A$ be a finite collection of squares in the coordinate plane such that the vertices of all squares that belong to $A$ are $(m, n),(m+1, n),(m, n+1)$, and $(m+1, n+1)$ for some integers $m$ and $n$. Show that there exists a subcollection $B$ of $A$ such that $B$ contains at least $25 \%$ of the squares in $A$, but no two of the squares in $B$ have a common vertex.
|
Divide the plane into two sets by painting the strips of squares parallel to the $y$ axis alternately red and green. Denote the sets of red and green squares by $R$ and $G$, respectively. Of the sets $A \cap R$ and $A \cap G$ at least one contains at least one half of the squares in $A$. Denote this set by $A_{1}$. Next partition the strips of squares which contain squares of $A_{1}$ into two sets $E$ and $F$ so that each set contains every second square of $A_{1}$ on each strip. Now neither of the dets $E$ and $F$ has a common point with a square in the same set. On the other hand, at least one of the sets $E \cap A_{1}, F \cap A_{1}$ contains at least one half of the squares in $A_{1}$ and thus at least one quarter of the sets in $A$. This set is good for the required set $B$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n01.1. ",
"solution_match": "\nSolution. "
}
|
88b12633-c9e6-525c-b806-f556deb17a90
| 607,972
|
Let $f$ be a bounded real function defined for all real numbers and satisfying for all real numbers $x$ the condition
$$
f\left(x+\frac{1}{3}\right)+f\left(x+\frac{1}{2}\right)=f(x)+f\left(x+\frac{5}{6}\right)
$$
Show that $f$ is periodic. (A function $f$ is bounded, if there exists a number $L$ such that $|f(x)|<L$ for all real numbers $x$. A function $f$ is periodic, if there exists a positive number $k$ such that $f(x+k)=f(x)$ for all real numbers $x$.)
|
Let $g(6 x)=f(x)$. Then $g$ is bounded, and
$$
\begin{gathered}
g(t+2)=f\left(\frac{t}{6}+\frac{1}{3}\right), \quad g(t+3)=f\left(\frac{t}{6}+\frac{1}{2}\right) \\
g(t+5)=f\left(\frac{t}{6}+\frac{5}{6}\right), \quad g(t+2)+g(t+3)=g(t)+g(t+5) \\
g(t+5)-g(t+3)=g(t+2)-g(t)
\end{gathered}
$$
for all real numbers $t$. But then
$$
\begin{gathered}
g(t+12)-g(6) \\
=g(t+12)-g(t+10)+g(t+10)-g(t+8)+g(t+8)-g(t+6) \\
=g(t+9)-g(t+7)+g(t+7)-g(t+5)+g(t+5)-g(t+3) \\
=g(t+6)-g(t+4)+g(t+4)-g(t+2)+g(t+2)-g(t) \\
=g(t+6)-g(t)
\end{gathered}
$$
By induction, then $g(t+6 n)-g(t)=n(g(t+6)-g(0))$ for all positive integers $n$. Unless $g(t+6)-g(t)=0$ for all real $t, g$ cannot be bounded. So $g$ has to be periodic with 6 as a period, whence $f$ is periodic, with 1 as a period.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f$ be a bounded real function defined for all real numbers and satisfying for all real numbers $x$ the condition
$$
f\left(x+\frac{1}{3}\right)+f\left(x+\frac{1}{2}\right)=f(x)+f\left(x+\frac{5}{6}\right)
$$
Show that $f$ is periodic. (A function $f$ is bounded, if there exists a number $L$ such that $|f(x)|<L$ for all real numbers $x$. A function $f$ is periodic, if there exists a positive number $k$ such that $f(x+k)=f(x)$ for all real numbers $x$.)
|
Let $g(6 x)=f(x)$. Then $g$ is bounded, and
$$
\begin{gathered}
g(t+2)=f\left(\frac{t}{6}+\frac{1}{3}\right), \quad g(t+3)=f\left(\frac{t}{6}+\frac{1}{2}\right) \\
g(t+5)=f\left(\frac{t}{6}+\frac{5}{6}\right), \quad g(t+2)+g(t+3)=g(t)+g(t+5) \\
g(t+5)-g(t+3)=g(t+2)-g(t)
\end{gathered}
$$
for all real numbers $t$. But then
$$
\begin{gathered}
g(t+12)-g(6) \\
=g(t+12)-g(t+10)+g(t+10)-g(t+8)+g(t+8)-g(t+6) \\
=g(t+9)-g(t+7)+g(t+7)-g(t+5)+g(t+5)-g(t+3) \\
=g(t+6)-g(t+4)+g(t+4)-g(t+2)+g(t+2)-g(t) \\
=g(t+6)-g(t)
\end{gathered}
$$
By induction, then $g(t+6 n)-g(t)=n(g(t+6)-g(0))$ for all positive integers $n$. Unless $g(t+6)-g(t)=0$ for all real $t, g$ cannot be bounded. So $g$ has to be periodic with 6 as a period, whence $f$ is periodic, with 1 as a period.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n01.2. ",
"solution_match": "\nSolution. "
}
|
dc47e110-b673-5ef5-9671-5bd60a885eae
| 607,973
|
Let $A B C D E F$ be a convex hexagon, in which each of the diagonals $A D, B E$, and $C F$ divides the hexagon in two quadrilaterals of equal area. Show that $A D, B E$, and $C F$ are concurrent.
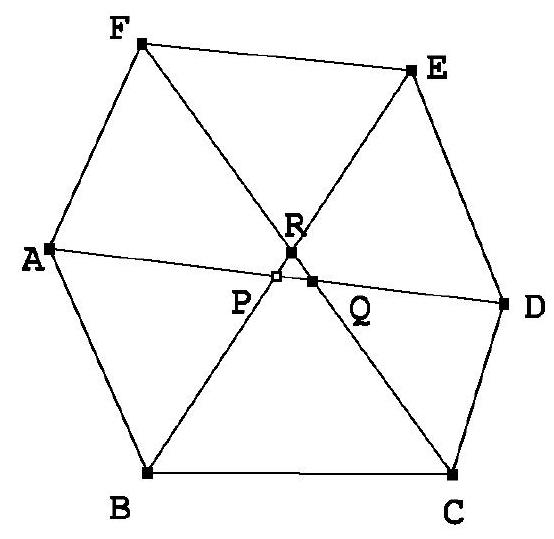
Figure 12.
|
(See Figure 12.) Denote the area of a figure by $|\cdot|$. Let $A D$ and $B E$ intersect at $P, A D$ and $C F$ at $Q$, and $B E$ and $C F$ at $R$. Assume that $P, Q$, and $R$ are different. We may assume that $P$ lies between $B$ and $R$, and $Q$ lies between $C$ and $R$. Both $|A B P|$ and $|D E P|$ differ from $\frac{1}{2}|A B C D E F|$ by $|B C D P|$. Thus $A B P$ and $D E P$ have equal area. Since $\angle A P B=\angle D P E$, we have $A P \cdot B P=D P \cdot E P=(D Q+Q P)(E R+R P)$. Likewise $C Q \cdot D Q=(A P+P Q)(F R+R Q)$ and $E R \cdot F R=(C Q+Q R)(B P+P R)$. When we multiply the three previous equalities, we obtain $A P \cdot B P \cdot C Q \cdot D Q \cdot E R \cdot F R=$ $D Q \cdot E R \cdot A P \cdot F R \cdot C Q \cdot B P+$ positive terms containing $P Q, Q R$, and $P R$. This is a contradiction. So $P, Q$ and $R$ must coincide.
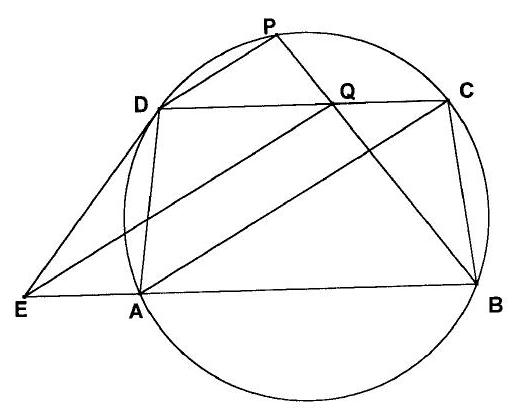
Figure 13.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E F$ be a convex hexagon, in which each of the diagonals $A D, B E$, and $C F$ divides the hexagon in two quadrilaterals of equal area. Show that $A D, B E$, and $C F$ are concurrent.

Figure 12.
|
(See Figure 12.) Denote the area of a figure by $|\cdot|$. Let $A D$ and $B E$ intersect at $P, A D$ and $C F$ at $Q$, and $B E$ and $C F$ at $R$. Assume that $P, Q$, and $R$ are different. We may assume that $P$ lies between $B$ and $R$, and $Q$ lies between $C$ and $R$. Both $|A B P|$ and $|D E P|$ differ from $\frac{1}{2}|A B C D E F|$ by $|B C D P|$. Thus $A B P$ and $D E P$ have equal area. Since $\angle A P B=\angle D P E$, we have $A P \cdot B P=D P \cdot E P=(D Q+Q P)(E R+R P)$. Likewise $C Q \cdot D Q=(A P+P Q)(F R+R Q)$ and $E R \cdot F R=(C Q+Q R)(B P+P R)$. When we multiply the three previous equalities, we obtain $A P \cdot B P \cdot C Q \cdot D Q \cdot E R \cdot F R=$ $D Q \cdot E R \cdot A P \cdot F R \cdot C Q \cdot B P+$ positive terms containing $P Q, Q R$, and $P R$. This is a contradiction. So $P, Q$ and $R$ must coincide.

Figure 13.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n01.4. ",
"solution_match": "\nSolution. "
}
|
57519c0d-61e1-594b-b69e-d33867771592
| 607,975
|
Let $a_{1}, a_{2}, \ldots, a_{n}$, and $b_{1}, b_{2}, \ldots, b_{n}$ be real numbers, and let $a_{1}, a_{2}, \ldots, a_{n}$ be all different.. Show that if all the products
$$
\left(a_{i}+b_{1}\right)\left(a_{i}+b_{2}\right) \cdots\left(a_{i}+b_{n}\right)
$$
$i=1,2, \ldots, n$, are equal, then the products
$$
\left(a_{1}+b_{j}\right)\left(a_{2}+b_{j}\right) \cdots\left(a_{n}+b_{j}\right)
$$
$j=1,2, \ldots, n$, are equal, too.
|
Let $P(x)=\left(x+b_{1}\right)\left(x+b_{2}\right) \cdots\left(x+b_{n}\right)$. Let $P\left(a_{1}\right)=P\left(a_{2}\right)=\ldots=P\left(a_{n}\right)=d$. Thus $a_{1}, a_{2}, \ldots, a_{n}$ are the roots of the $n$ :th degree polynomial equation $P(x)-d=0$. Then $P(x)-d=c\left(x-a_{1}\right)\left(x-a_{2}\right) \cdots\left(x-a_{n}\right)$. Clearly the $n$ :th degree terms of $P(x)$ and $P(x)-d$ are equal. So $c=1$. But $P\left(-b_{j}\right)=0$ for each $b_{j}$. Thus for every $j$,
$$
\begin{gathered}
-d=\left(-b_{j}-a_{1}\right)\left(-b_{j}-a_{2}\right) \cdots\left(-b_{j}-a_{n}\right) \\
=(-1)^{n}\left(a_{1}+b_{j}\right)\left(a_{2}+b_{j}\right) \cdots\left(a_{n}+b_{j}\right)
\end{gathered}
$$
and the claim follows.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a_{1}, a_{2}, \ldots, a_{n}$, and $b_{1}, b_{2}, \ldots, b_{n}$ be real numbers, and let $a_{1}, a_{2}, \ldots, a_{n}$ be all different.. Show that if all the products
$$
\left(a_{i}+b_{1}\right)\left(a_{i}+b_{2}\right) \cdots\left(a_{i}+b_{n}\right)
$$
$i=1,2, \ldots, n$, are equal, then the products
$$
\left(a_{1}+b_{j}\right)\left(a_{2}+b_{j}\right) \cdots\left(a_{n}+b_{j}\right)
$$
$j=1,2, \ldots, n$, are equal, too.
|
Let $P(x)=\left(x+b_{1}\right)\left(x+b_{2}\right) \cdots\left(x+b_{n}\right)$. Let $P\left(a_{1}\right)=P\left(a_{2}\right)=\ldots=P\left(a_{n}\right)=d$. Thus $a_{1}, a_{2}, \ldots, a_{n}$ are the roots of the $n$ :th degree polynomial equation $P(x)-d=0$. Then $P(x)-d=c\left(x-a_{1}\right)\left(x-a_{2}\right) \cdots\left(x-a_{n}\right)$. Clearly the $n$ :th degree terms of $P(x)$ and $P(x)-d$ are equal. So $c=1$. But $P\left(-b_{j}\right)=0$ for each $b_{j}$. Thus for every $j$,
$$
\begin{gathered}
-d=\left(-b_{j}-a_{1}\right)\left(-b_{j}-a_{2}\right) \cdots\left(-b_{j}-a_{n}\right) \\
=(-1)^{n}\left(a_{1}+b_{j}\right)\left(a_{2}+b_{j}\right) \cdots\left(a_{n}+b_{j}\right)
\end{gathered}
$$
and the claim follows.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n02.3. ",
"solution_match": "\nSolution. "
}
|
9c25ef68-d23e-5afe-b0b9-429b1f8bfc78
| 607,978
|
Stones are placed on the squares of a chessboard having 10 rows and 14 columns. There is an odd number of stones on each row and each column. The squares are coloured black and white in the usual fashion. Show that the number of stones on black squares is even. Note that there can be more than one stone on a square.
|
Changing the order of rows or columns does not influence the number of stones on a row, on a column or on black squares. Thus we can order the rows and columns in such a way that the $5 \times 7$ rectangles in the upper left and lower right corner are black and the other two $5 \times 7$ rectangles are white. If the number of stones on black squares would be odd, then one of the black rectangles would have an odd number of stones while the number of stones on the other would be even. Since the number of stones is even, one of the white rectangles would have an odd number of stones and the other an even number. But this would imply either a set of five rows or a set of seven columns with an even number of stones. But this is not possible, because every row and column has an odd number of stones. So the number of stones on black squares has to be even.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Stones are placed on the squares of a chessboard having 10 rows and 14 columns. There is an odd number of stones on each row and each column. The squares are coloured black and white in the usual fashion. Show that the number of stones on black squares is even. Note that there can be more than one stone on a square.
|
Changing the order of rows or columns does not influence the number of stones on a row, on a column or on black squares. Thus we can order the rows and columns in such a way that the $5 \times 7$ rectangles in the upper left and lower right corner are black and the other two $5 \times 7$ rectangles are white. If the number of stones on black squares would be odd, then one of the black rectangles would have an odd number of stones while the number of stones on the other would be even. Since the number of stones is even, one of the white rectangles would have an odd number of stones and the other an even number. But this would imply either a set of five rows or a set of seven columns with an even number of stones. But this is not possible, because every row and column has an odd number of stones. So the number of stones on black squares has to be even.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n03.1. ",
"solution_match": "\nSolution. "
}
|
f446553f-dc87-5994-981a-9591153a3320
| 607,980
|
The point $D$ inside the equilateral triangle $\triangle A B C$ satisfies $\angle A D C=150^{\circ}$. Prove that a triangle with side lengths $|A D|,|B D|,|C D|$ is necessarily a right-angled triangle.
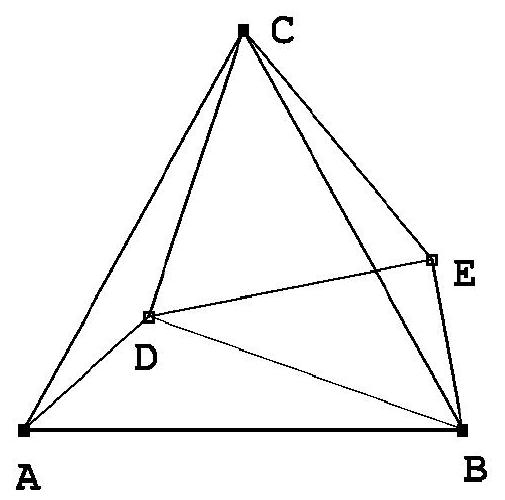
Figure 14 .
|
(See Figure 14.) We rotate the figure counterclockwise $60^{\circ}$ around $C$. Because $A B C$ is an equilateral triangle, $\angle B A C=60^{\circ}$, so $A$ is mapped on $B$. Assume $D$ maps to $E$. The properties of rotation imply $A D=B E$ and $\angle B E C=150^{\circ}$. Because the triangle $D E C$ is equilateral, $D E=D C$ and $\angle D E C=60^{\circ}$. But then $\angle D E B=150^{\circ}-60^{\circ}=90^{\circ}$. So segments having the lengths as specified in the problem indeed are sides of a right triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The point $D$ inside the equilateral triangle $\triangle A B C$ satisfies $\angle A D C=150^{\circ}$. Prove that a triangle with side lengths $|A D|,|B D|,|C D|$ is necessarily a right-angled triangle.

Figure 14 .
|
(See Figure 14.) We rotate the figure counterclockwise $60^{\circ}$ around $C$. Because $A B C$ is an equilateral triangle, $\angle B A C=60^{\circ}$, so $A$ is mapped on $B$. Assume $D$ maps to $E$. The properties of rotation imply $A D=B E$ and $\angle B E C=150^{\circ}$. Because the triangle $D E C$ is equilateral, $D E=D C$ and $\angle D E C=60^{\circ}$. But then $\angle D E B=150^{\circ}-60^{\circ}=90^{\circ}$. So segments having the lengths as specified in the problem indeed are sides of a right triangle.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n03.3. ",
"solution_match": "\nSolution. "
}
|
28047723-de00-58ce-ac41-8d14d0b61fe8
| 607,982
|
Let $f_{1}=0, f_{2}=1$, and $f_{n+2}=f_{n+1}+f_{n}$, for $n=1$, 2, ..., be the Fibonacci sequence. Show that there exists a strictly increasing infinite arithmetic sequence none of whose numbers belongs to the Fibonacci sequence. [A sequence is arithmetic, if the difference of any of its consecutive terms is a constant.]
|
The Fibonacci sequence modulo any integer $n>1$ is periodic. (Pairs of residues are a finite set, so some pair appears twice in the sequence, and the sequence from the second appearance of the pair onwards is a copy of the sequence from the first pair onwards.) There are integers for which the Fibonacci residue sequence does not contain all possible residues. For instance modulo 11 the sequence is $0,1,1,2,3,5,8,2,10,1$, $0,1,1, \ldots$ Wee see that the number 4 is missing. It follows that no integer of the form $4+11 k$ appears in the Fibonacci sequence. But here we have an arithmetic sequence of the kind required.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f_{1}=0, f_{2}=1$, and $f_{n+2}=f_{n+1}+f_{n}$, for $n=1$, 2, ..., be the Fibonacci sequence. Show that there exists a strictly increasing infinite arithmetic sequence none of whose numbers belongs to the Fibonacci sequence. [A sequence is arithmetic, if the difference of any of its consecutive terms is a constant.]
|
The Fibonacci sequence modulo any integer $n>1$ is periodic. (Pairs of residues are a finite set, so some pair appears twice in the sequence, and the sequence from the second appearance of the pair onwards is a copy of the sequence from the first pair onwards.) There are integers for which the Fibonacci residue sequence does not contain all possible residues. For instance modulo 11 the sequence is $0,1,1,2,3,5,8,2,10,1$, $0,1,1, \ldots$ Wee see that the number 4 is missing. It follows that no integer of the form $4+11 k$ appears in the Fibonacci sequence. But here we have an arithmetic sequence of the kind required.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n04.2. ",
"solution_match": "\nSolution. "
}
|
09883491-f4ef-5360-8f23-aee5c4713001
| 607,985
|
Let $x_{11}, x_{21}, \ldots, x_{n 1}, n>2$, be a sequence of integers. We assume that all of the numbers $x_{i 1}$ are not equal. Assuming that the numbers $x_{1 k}, x_{2 k}, \ldots, x_{n k}$ have been defined, we set
$$
\begin{aligned}
x_{i, k+1} & =\frac{1}{2}\left(x_{i k}+x_{i+1, k}\right), i=1,2, \ldots, n-1 \\
x_{n, k+1} & =\frac{1}{2}\left(x_{n k}+x_{1 k}\right)
\end{aligned}
$$
Show that for $n$ odd, $x_{j k}$ is not an integer for some $j, k$. Does the same conclusion hold for $n$ even?
|
We compute the first index modulo $n$, i.e. $x_{1 k}=x_{n+1, k}$. Let $M_{k}=\max _{j} x_{j k}$ and $m_{k}=\min _{j} x_{j k}$. Evidently $\left(M_{k}\right)$ is a non-increasing and $\left(m_{k}\right)$ a non-decreasing sequence, and $M_{k+1}=M_{k}$ is possible only if $x_{j k}=x_{j+1, k}=M_{k}$ for some $j$. If exactly $p$
consequtive numbers $x_{j k}$ equal $M_{k}$, then exactly $p-1$ consequtive numbers $x_{j, k+1}$ equal $M_{k+1}$ which is equal to $M_{k}$. So after a finite number of steps we arrive at the situation $M_{k+1}<M_{k}$. In a corresponding manner we see that $m_{k+1}>m_{k}$ for some $k$ 's. If all the numbers in all the sequences are integers, then all $m_{k}$ 's and $M_{k}$ 's are integers. So after a finite number of steps $m_{k}=M_{k}$, and all numbers $x_{j k}$ are equal. Then $x_{1, k-1}+x_{2, k-1}=x_{2, k-1}+x_{3, k-1}=\cdots=x_{n-1, k-1}+x_{n, k-1}=x_{n, k-1}+x_{1, k-1}$. If $n$ is odd, then $x_{1, k-1}=x_{3, k-1}=\cdots=x_{n, k-1}$ and $x_{1, k-1}=x_{n-1, k-1}=\cdots=x_{2, k-1}$. But then we could show in a similar way that all numbers $x_{j, k-2}$ are equal and finally that all numbers $x_{j, 1}$ are equal, contrary to the assumption. If $n$ is even, then all $x_{i, k}$ 's can be integers. Take, for instance, $x_{1,1}=x_{3,1}=\cdots=x_{n-1,1}=0, x_{2,1}=x_{4,1}=\cdots=x_{n, 1}=2$. Then every $x_{j, k}=1, k \geq 2$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $x_{11}, x_{21}, \ldots, x_{n 1}, n>2$, be a sequence of integers. We assume that all of the numbers $x_{i 1}$ are not equal. Assuming that the numbers $x_{1 k}, x_{2 k}, \ldots, x_{n k}$ have been defined, we set
$$
\begin{aligned}
x_{i, k+1} & =\frac{1}{2}\left(x_{i k}+x_{i+1, k}\right), i=1,2, \ldots, n-1 \\
x_{n, k+1} & =\frac{1}{2}\left(x_{n k}+x_{1 k}\right)
\end{aligned}
$$
Show that for $n$ odd, $x_{j k}$ is not an integer for some $j, k$. Does the same conclusion hold for $n$ even?
|
We compute the first index modulo $n$, i.e. $x_{1 k}=x_{n+1, k}$. Let $M_{k}=\max _{j} x_{j k}$ and $m_{k}=\min _{j} x_{j k}$. Evidently $\left(M_{k}\right)$ is a non-increasing and $\left(m_{k}\right)$ a non-decreasing sequence, and $M_{k+1}=M_{k}$ is possible only if $x_{j k}=x_{j+1, k}=M_{k}$ for some $j$. If exactly $p$
consequtive numbers $x_{j k}$ equal $M_{k}$, then exactly $p-1$ consequtive numbers $x_{j, k+1}$ equal $M_{k+1}$ which is equal to $M_{k}$. So after a finite number of steps we arrive at the situation $M_{k+1}<M_{k}$. In a corresponding manner we see that $m_{k+1}>m_{k}$ for some $k$ 's. If all the numbers in all the sequences are integers, then all $m_{k}$ 's and $M_{k}$ 's are integers. So after a finite number of steps $m_{k}=M_{k}$, and all numbers $x_{j k}$ are equal. Then $x_{1, k-1}+x_{2, k-1}=x_{2, k-1}+x_{3, k-1}=\cdots=x_{n-1, k-1}+x_{n, k-1}=x_{n, k-1}+x_{1, k-1}$. If $n$ is odd, then $x_{1, k-1}=x_{3, k-1}=\cdots=x_{n, k-1}$ and $x_{1, k-1}=x_{n-1, k-1}=\cdots=x_{2, k-1}$. But then we could show in a similar way that all numbers $x_{j, k-2}$ are equal and finally that all numbers $x_{j, 1}$ are equal, contrary to the assumption. If $n$ is even, then all $x_{i, k}$ 's can be integers. Take, for instance, $x_{1,1}=x_{3,1}=\cdots=x_{n-1,1}=0, x_{2,1}=x_{4,1}=\cdots=x_{n, 1}=2$. Then every $x_{j, k}=1, k \geq 2$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n04.3. ",
"solution_match": "\nSolution. "
}
|
fb33ec37-72c1-5e11-8fa7-1cd72eef3f1b
| 607,986
|
Let $a, b$, and $c$ be the side lengths of a triangle and let $R$ be its circumradius. Show that
$$
\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a} \geq \frac{1}{R^{2}}
$$
|
By the well-known (Euler) theorem, the inradius $r$ and circumradius $R$ of any triangle satisfy $2 r \leq R$. (In fact, $R(R-2 r)=d^{2}$, where $d$ is the distance between the incenter and circumcenter.) The area $S$ of a triangle can be written as
$$
A=\frac{r}{2}(a+b+c)
$$
and, by the sine theorem, as
$$
A=\frac{1}{2} a b \sin \gamma=\frac{1}{4} \frac{a b c}{R}
$$
Combining these, we obtain
$$
\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a}=\frac{a+b+c}{a b c}=\frac{2 A}{r} \cdot \frac{1}{4 R A}=\frac{1}{2 r R} \geq \frac{1}{R^{2}}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be the side lengths of a triangle and let $R$ be its circumradius. Show that
$$
\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a} \geq \frac{1}{R^{2}}
$$
|
By the well-known (Euler) theorem, the inradius $r$ and circumradius $R$ of any triangle satisfy $2 r \leq R$. (In fact, $R(R-2 r)=d^{2}$, where $d$ is the distance between the incenter and circumcenter.) The area $S$ of a triangle can be written as
$$
A=\frac{r}{2}(a+b+c)
$$
and, by the sine theorem, as
$$
A=\frac{1}{2} a b \sin \gamma=\frac{1}{4} \frac{a b c}{R}
$$
Combining these, we obtain
$$
\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a}=\frac{a+b+c}{a b c}=\frac{2 A}{r} \cdot \frac{1}{4 R A}=\frac{1}{2 r R} \geq \frac{1}{R^{2}}
$$
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n04.4. ",
"solution_match": "\nSolution 1. "
}
|
a1adb1e2-1a4f-53ee-b85e-3b449ed351ff
| 607,987
|
Let $a, b$, and $c$ be the side lengths of a triangle and let $R$ be its circumradius. Show that
$$
\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a} \geq \frac{1}{R^{2}}
$$
|
Assume $a \leq b \leq c$. Then $b=a+x$ and $c=a+x+y, x \geq 0, y \geq 0$. Now $a b c-(a+b-c)(a-b+c)(-a+b+c)=a(a+x)(a+x+y)-(a-y)(a+2 x+y)(a+y)=a x^{2}+$ $a x y+a y^{2}+2 x y^{2}+y^{3} \geq 0$. So $a b c(a+b+c) \geq(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=16 A^{2}$, where the last inequality is implied by Heron's formula. When we substitute $A=\frac{a b c}{4 R}$ (see Solution 1) we obtain, after simplification,
$$
a+b+c \geq \frac{a b c}{R^{2}}
$$
which is equivalent to the claim.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be the side lengths of a triangle and let $R$ be its circumradius. Show that
$$
\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a} \geq \frac{1}{R^{2}}
$$
|
Assume $a \leq b \leq c$. Then $b=a+x$ and $c=a+x+y, x \geq 0, y \geq 0$. Now $a b c-(a+b-c)(a-b+c)(-a+b+c)=a(a+x)(a+x+y)-(a-y)(a+2 x+y)(a+y)=a x^{2}+$ $a x y+a y^{2}+2 x y^{2}+y^{3} \geq 0$. So $a b c(a+b+c) \geq(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=16 A^{2}$, where the last inequality is implied by Heron's formula. When we substitute $A=\frac{a b c}{4 R}$ (see Solution 1) we obtain, after simplification,
$$
a+b+c \geq \frac{a b c}{R^{2}}
$$
which is equivalent to the claim.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n04.4. ",
"solution_match": "\nSolution 2. "
}
|
a1adb1e2-1a4f-53ee-b85e-3b449ed351ff
| 607,987
|
Let $a, b$, and $c$ be positive real numbers. Prove that
$$
\frac{2 a^{2}}{b+c}+\frac{2 b^{2}}{c+a}+\frac{2 c^{2}}{a+b} \geq a+b+c
$$
|
Use brute force. Removing the denominators and brackets and combining simililar terms yields the equivalent inequality
$$
\begin{gathered}
0 \leq 2 a^{4}+2 b^{4}+2 c^{4}+a^{3} b+a^{3} c+a b^{3}+b^{3} c+a c^{3}+b c^{3} \\
-2 a^{2} b^{2}-2 b^{2} c^{2}-2 a^{2} c^{2}-2 a b c^{2}-2 a b^{2} c-2 a^{2} b c \\
=a^{4}+b^{4}-2 a^{2} b^{2}+b^{4}+c^{4}-2 b^{2} c^{2}+c^{4}+a^{4}-2 a^{2} c^{2} \\
+a b\left(a^{2}+b^{2}-2 c^{2}\right)+b c\left(b^{2}+c^{2}-2 a^{2}\right)+c a\left(c^{2}+a^{2}-2 b^{2}\right) \\
=\left(a^{2}-b^{2}\right)^{2}+\left(b^{2}-c^{2}\right)^{2}+\left(c^{2}-a^{2}\right)^{2} \\
+a b(a-b)^{2}+b c(b-c)^{2}+c a(c-a)^{2} \\
+a b\left(2 a b-2 c^{2}\right)+b c\left(2 b c-2 a^{2}\right)+c a\left(2 c a-2 b^{2}\right)
\end{gathered}
$$
The six first terms on the right hand side are non-negative and the last three can be written as
$$
\begin{gathered}
2 a^{2} b^{2}-2 a b c^{2}+2 b^{2} c^{2}-2 a^{2} b c+2 c^{2} a^{2}-2 a b^{2} c \\
=a^{2}\left(b^{2}+c^{2}-2 b c\right)+b^{2}\left(a^{2}+c^{2}-2 a c\right)+c^{2}\left(a^{2}+b^{2}-2 a b\right) \\
=a^{2}(b-c)^{2}+b^{2}(c-a)^{2}+c^{2}(a-b)^{2} \geq 0
\end{gathered}
$$
So the original inequality is true.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be positive real numbers. Prove that
$$
\frac{2 a^{2}}{b+c}+\frac{2 b^{2}}{c+a}+\frac{2 c^{2}}{a+b} \geq a+b+c
$$
|
Use brute force. Removing the denominators and brackets and combining simililar terms yields the equivalent inequality
$$
\begin{gathered}
0 \leq 2 a^{4}+2 b^{4}+2 c^{4}+a^{3} b+a^{3} c+a b^{3}+b^{3} c+a c^{3}+b c^{3} \\
-2 a^{2} b^{2}-2 b^{2} c^{2}-2 a^{2} c^{2}-2 a b c^{2}-2 a b^{2} c-2 a^{2} b c \\
=a^{4}+b^{4}-2 a^{2} b^{2}+b^{4}+c^{4}-2 b^{2} c^{2}+c^{4}+a^{4}-2 a^{2} c^{2} \\
+a b\left(a^{2}+b^{2}-2 c^{2}\right)+b c\left(b^{2}+c^{2}-2 a^{2}\right)+c a\left(c^{2}+a^{2}-2 b^{2}\right) \\
=\left(a^{2}-b^{2}\right)^{2}+\left(b^{2}-c^{2}\right)^{2}+\left(c^{2}-a^{2}\right)^{2} \\
+a b(a-b)^{2}+b c(b-c)^{2}+c a(c-a)^{2} \\
+a b\left(2 a b-2 c^{2}\right)+b c\left(2 b c-2 a^{2}\right)+c a\left(2 c a-2 b^{2}\right)
\end{gathered}
$$
The six first terms on the right hand side are non-negative and the last three can be written as
$$
\begin{gathered}
2 a^{2} b^{2}-2 a b c^{2}+2 b^{2} c^{2}-2 a^{2} b c+2 c^{2} a^{2}-2 a b^{2} c \\
=a^{2}\left(b^{2}+c^{2}-2 b c\right)+b^{2}\left(a^{2}+c^{2}-2 a c\right)+c^{2}\left(a^{2}+b^{2}-2 a b\right) \\
=a^{2}(b-c)^{2}+b^{2}(c-a)^{2}+c^{2}(a-b)^{2} \geq 0
\end{gathered}
$$
So the original inequality is true.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n05.2. ",
"solution_match": "\nSolution 1. "
}
|
7ebb150b-baeb-54e6-a8be-8a1255d511a4
| 607,989
|
Let $a, b$, and $c$ be positive real numbers. Prove that
$$
\frac{2 a^{2}}{b+c}+\frac{2 b^{2}}{c+a}+\frac{2 c^{2}}{a+b} \geq a+b+c
$$
|
The inequality is equivalent to
$$
\begin{gathered}
2\left(a^{2}(a+b)(a+c)+b^{2}(b+c)(b+a)+c^{2}(c+a)(c+b)\right) \\
\geq(a+b+c)(a+b)(b+c)(c+a)
\end{gathered}
$$
The left hand side can be factored as $2(a+b+c)\left(a^{3}+b^{3}+c^{3}+a b c\right)$. Because $a+b+c$ is positive, the inequality is equivalent to
$$
2\left(a^{3}+b^{3}+c^{3}+a b c\right) \geq(a+b)(b+c)(c+a)
$$
After expanding the right hand side and subtracting $2 a b c$, we get the inequality
$$
2\left(a^{3}+b^{3}+c^{3}\right) \geq\left(a^{2} b+b^{2} c+c^{2} a\right)+\left(a^{2} c+b^{2} a+c^{2} b\right)
$$
still equivalent to the original one. But we now have two instances of the well-known inequality $x^{3}+y^{3}+z^{3} \geq x^{2} y+y^{2} z+z^{2} x$ or $x^{2}(x-y)+y^{2}(y-z)+z^{2}(z-x) \geq 0$. [Proof: We may assume $x \geq y, x \geq z$. If $y \geq z$, write $z-x=z-y+y-z$ to obtain the equivalent and true inequality $\left(y^{2}-z^{2}\right)(y-z)+\left(x^{2}-z^{2}\right)(x-y) \geq 0$, if $z \geq y$, similarly write $x-y=x-z+z-y$, and get $\left(x^{2}-z^{2}\right)(x-z)+\left(x^{2}-y^{2}\right)(z-y) \geq 0$.]
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be positive real numbers. Prove that
$$
\frac{2 a^{2}}{b+c}+\frac{2 b^{2}}{c+a}+\frac{2 c^{2}}{a+b} \geq a+b+c
$$
|
The inequality is equivalent to
$$
\begin{gathered}
2\left(a^{2}(a+b)(a+c)+b^{2}(b+c)(b+a)+c^{2}(c+a)(c+b)\right) \\
\geq(a+b+c)(a+b)(b+c)(c+a)
\end{gathered}
$$
The left hand side can be factored as $2(a+b+c)\left(a^{3}+b^{3}+c^{3}+a b c\right)$. Because $a+b+c$ is positive, the inequality is equivalent to
$$
2\left(a^{3}+b^{3}+c^{3}+a b c\right) \geq(a+b)(b+c)(c+a)
$$
After expanding the right hand side and subtracting $2 a b c$, we get the inequality
$$
2\left(a^{3}+b^{3}+c^{3}\right) \geq\left(a^{2} b+b^{2} c+c^{2} a\right)+\left(a^{2} c+b^{2} a+c^{2} b\right)
$$
still equivalent to the original one. But we now have two instances of the well-known inequality $x^{3}+y^{3}+z^{3} \geq x^{2} y+y^{2} z+z^{2} x$ or $x^{2}(x-y)+y^{2}(y-z)+z^{2}(z-x) \geq 0$. [Proof: We may assume $x \geq y, x \geq z$. If $y \geq z$, write $z-x=z-y+y-z$ to obtain the equivalent and true inequality $\left(y^{2}-z^{2}\right)(y-z)+\left(x^{2}-z^{2}\right)(x-y) \geq 0$, if $z \geq y$, similarly write $x-y=x-z+z-y$, and get $\left(x^{2}-z^{2}\right)(x-z)+\left(x^{2}-y^{2}\right)(z-y) \geq 0$.]
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n05.2. ",
"solution_match": "\nSolution 2. "
}
|
7ebb150b-baeb-54e6-a8be-8a1255d511a4
| 607,989
|
Let $a, b$, and $c$ be positive real numbers. Prove that
$$
\frac{2 a^{2}}{b+c}+\frac{2 b^{2}}{c+a}+\frac{2 c^{2}}{a+b} \geq a+b+c
$$
|
The original inequality is symmetric in $a, b, c$. So we may assume $a \geq b \geq c$, which implies
$$
\frac{1}{b+c} \geq \frac{1}{c+a} \geq \frac{1}{a+b}
$$
The power mean inequality gives
$$
\frac{a^{2}+b^{2}+c^{2}}{3} \geq\left(\frac{a+b+c}{3}\right)^{2}
$$
We combine this and the Chebyshev inequality to obtain
$$
\begin{gathered}
\frac{2 a^{2}}{b+c}+\frac{2 b^{2}}{c+a}+\frac{2 c^{2}}{a+b} \\
\geq \frac{2}{3}\left(a^{2}+b^{2}+c^{2}\right)\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right) \\
\geq \frac{2}{9}(a+b+c)^{2}\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right)
\end{gathered}
$$
To complete the proof, we have to show that
$$
2(a+b+c)\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right) \geq 9
$$
But this is equivalent to the harmonic-arithmetic mean inequality
$$
\frac{3}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}} \leq \frac{x+y+z}{3}
$$
with $x=a+b, y=b+c, z=c+a$.
05.3 There are 2005 young people sitting around a (large!) round table. Of these at most 668 are boys. We say that a girl $G$ is in a strong position, if, counting from $G$ to either direction at any length, the number of girls is always strictly larger than the number of boys. (G herself is included in the count.) Prove that in any arrangement, there always is a girl in a strong position.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be positive real numbers. Prove that
$$
\frac{2 a^{2}}{b+c}+\frac{2 b^{2}}{c+a}+\frac{2 c^{2}}{a+b} \geq a+b+c
$$
|
The original inequality is symmetric in $a, b, c$. So we may assume $a \geq b \geq c$, which implies
$$
\frac{1}{b+c} \geq \frac{1}{c+a} \geq \frac{1}{a+b}
$$
The power mean inequality gives
$$
\frac{a^{2}+b^{2}+c^{2}}{3} \geq\left(\frac{a+b+c}{3}\right)^{2}
$$
We combine this and the Chebyshev inequality to obtain
$$
\begin{gathered}
\frac{2 a^{2}}{b+c}+\frac{2 b^{2}}{c+a}+\frac{2 c^{2}}{a+b} \\
\geq \frac{2}{3}\left(a^{2}+b^{2}+c^{2}\right)\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right) \\
\geq \frac{2}{9}(a+b+c)^{2}\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right)
\end{gathered}
$$
To complete the proof, we have to show that
$$
2(a+b+c)\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right) \geq 9
$$
But this is equivalent to the harmonic-arithmetic mean inequality
$$
\frac{3}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}} \leq \frac{x+y+z}{3}
$$
with $x=a+b, y=b+c, z=c+a$.
05.3 There are 2005 young people sitting around a (large!) round table. Of these at most 668 are boys. We say that a girl $G$ is in a strong position, if, counting from $G$ to either direction at any length, the number of girls is always strictly larger than the number of boys. (G herself is included in the count.) Prove that in any arrangement, there always is a girl in a strong position.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n05.2. ",
"solution_match": "\nSolution 3. "
}
|
7ebb150b-baeb-54e6-a8be-8a1255d511a4
| 607,989
|
The circle $\mathcal{C}_{1}$ is inside the circle $\mathcal{C}_{2}$, and the circles touch each other at $A$. A line through $A$ intersects $\mathcal{C}_{1}$ also at $B$ and $\mathcal{C}_{2}$ also at $C$. The tangent to $\mathcal{C}_{1}$ at $B$ intersects $\mathcal{C}_{2}$ at $D$ and $E$. The tangents of $\mathcal{C}_{1}$ passing through $C$ touch $\mathcal{C}_{1}$ at $F$ and $G$. Prove that $D$, $E, F$, and $G$ are concyclic.
Figure 15.
|
(See Figure 15.) Draw the tangent $\mathrm{CH}$ to $\mathcal{C}_{2}$ at $C$. By the theorem of the angle between a tangent and chord, the angles $A B H$ and $A C H$ both equal the angle at $A$ between $B A$ and the common tangent of the circles at $A$. But this means that the angles $A B H$ and $A C H$ are equal, and $C H \| B E$. So $C$ is the midpoint of the arc $D E$. This again implies the equality of the angles $C E B$ and $B A E$, as well as $C E=C D$. So the triangles $A E C, C E B$, having also a common angle $E C B$, are similar. So
$$
\frac{C B}{C E}=\frac{C E}{A C}
$$
and $C B \cdot A C=C E^{2}=C D^{2}$. But by the power of a point theorem, $C B \cdot C A=C G^{2}=C F^{2}$. We have in fact proved $C D=C E=C F=C G$, so the four points are indeed concyclic.
06.1 Let $B$ and $C$ be points on two fixed rays emanating from a point $A$ such that $A B+A C$ is constant. Prove that there exists a point $D \neq A$ such that the circumcircles of the triangels $A B C$ pass through $D$ for every choice of $B$ and $C$.
Figure 16 .
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The circle $\mathcal{C}_{1}$ is inside the circle $\mathcal{C}_{2}$, and the circles touch each other at $A$. A line through $A$ intersects $\mathcal{C}_{1}$ also at $B$ and $\mathcal{C}_{2}$ also at $C$. The tangent to $\mathcal{C}_{1}$ at $B$ intersects $\mathcal{C}_{2}$ at $D$ and $E$. The tangents of $\mathcal{C}_{1}$ passing through $C$ touch $\mathcal{C}_{1}$ at $F$ and $G$. Prove that $D$, $E, F$, and $G$ are concyclic.

Figure 15.
|
(See Figure 15.) Draw the tangent $\mathrm{CH}$ to $\mathcal{C}_{2}$ at $C$. By the theorem of the angle between a tangent and chord, the angles $A B H$ and $A C H$ both equal the angle at $A$ between $B A$ and the common tangent of the circles at $A$. But this means that the angles $A B H$ and $A C H$ are equal, and $C H \| B E$. So $C$ is the midpoint of the arc $D E$. This again implies the equality of the angles $C E B$ and $B A E$, as well as $C E=C D$. So the triangles $A E C, C E B$, having also a common angle $E C B$, are similar. So
$$
\frac{C B}{C E}=\frac{C E}{A C}
$$
and $C B \cdot A C=C E^{2}=C D^{2}$. But by the power of a point theorem, $C B \cdot C A=C G^{2}=C F^{2}$. We have in fact proved $C D=C E=C F=C G$, so the four points are indeed concyclic.
06.1 Let $B$ and $C$ be points on two fixed rays emanating from a point $A$ such that $A B+A C$ is constant. Prove that there exists a point $D \neq A$ such that the circumcircles of the triangels $A B C$ pass through $D$ for every choice of $B$ and $C$.

Figure 16 .
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n05.4. ",
"solution_match": "\nSolution. "
}
|
e66ab9a1-9e37-5453-883f-063b7994d6e0
| 607,990
|
The squares of a $100 \times 100$ chessboard are painted with 100 different colours. Each square has only one colour and every colour is used exactly 100 times. Show that there exists a row or a column on the chessboard in which at least 10 colours are used.
|
Denote by $R_{i}$ the number of colours used to colour the squares of the $i$ 'th row and let $C_{j}$ be the number of colours used to colour the squares of the $j$ 'th column. Let $r_{k}$ be the number of rows on which colour $k$ appears and let $c_{k}$ be the number of columns on which colour $k$ appears. By the arithmetic-geometric inequality, $r_{k}+c_{k} \geq 2 \sqrt{r_{k} c_{k}}$. Since colour $k$ appears at most $c_{k}$ times on each of the $r_{k}$ columns on which it can be found, $c_{k} r_{k}$ must be at least the total number of occurences of colour $k$, which equals 100 . So $r_{k}+c_{k} \geq 20$. In the sum $\sum_{i=1}^{100} R_{i}$, each colour $k$ contributes $r_{k}$ times and in the sum $\sum_{j=1}^{100} C_{j}$ each colour $k$ contributes $c_{k}$ times. Hence
$$
\sum_{i=1}^{100} R_{i}+\sum_{j=1}^{100} C_{j}=\sum_{k=1}^{100} r_{k}+\sum_{k=1}^{100} c_{k}=\sum_{k=1}^{100}\left(r_{k}+c_{k}\right) \geq 2000
$$
But if the sum of 200 positive integers is at least 2000, at least one of the summands is at least 10. The claim has been proved.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The squares of a $100 \times 100$ chessboard are painted with 100 different colours. Each square has only one colour and every colour is used exactly 100 times. Show that there exists a row or a column on the chessboard in which at least 10 colours are used.
|
Denote by $R_{i}$ the number of colours used to colour the squares of the $i$ 'th row and let $C_{j}$ be the number of colours used to colour the squares of the $j$ 'th column. Let $r_{k}$ be the number of rows on which colour $k$ appears and let $c_{k}$ be the number of columns on which colour $k$ appears. By the arithmetic-geometric inequality, $r_{k}+c_{k} \geq 2 \sqrt{r_{k} c_{k}}$. Since colour $k$ appears at most $c_{k}$ times on each of the $r_{k}$ columns on which it can be found, $c_{k} r_{k}$ must be at least the total number of occurences of colour $k$, which equals 100 . So $r_{k}+c_{k} \geq 20$. In the sum $\sum_{i=1}^{100} R_{i}$, each colour $k$ contributes $r_{k}$ times and in the sum $\sum_{j=1}^{100} C_{j}$ each colour $k$ contributes $c_{k}$ times. Hence
$$
\sum_{i=1}^{100} R_{i}+\sum_{j=1}^{100} C_{j}=\sum_{k=1}^{100} r_{k}+\sum_{k=1}^{100} c_{k}=\sum_{k=1}^{100}\left(r_{k}+c_{k}\right) \geq 2000
$$
But if the sum of 200 positive integers is at least 2000, at least one of the summands is at least 10. The claim has been proved.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n06.4. ",
"solution_match": "\nSolution. "
}
|
468695b6-5363-584d-9b15-8089294fb20d
| 607,993
|
A triangle, a line and three rectangles, with one side parallel to the given line, are given in such a way that the rectangles completely cover the sides of the triangle. Prove that the rectangles must completely cover the interior of the triangle.
|
Take any point $P$ inside the triangle and draw through $P$ the line parallel to the given line as well as the line perpendicular to it. These lines meet the sides of the triangle in four points. Of these four, two must be in one of the three rectangles. Now if the two points are on the same line, then the whole segment between them, $P$ included, is in the same rectangle. If the two points, say $Q$ and $R$, are on perpendicular lines, the perpendicular segments $R P$ and $P Q$ are also in the same rectangle. So in any case, $P$ is in one of the rectangles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A triangle, a line and three rectangles, with one side parallel to the given line, are given in such a way that the rectangles completely cover the sides of the triangle. Prove that the rectangles must completely cover the interior of the triangle.
|
Take any point $P$ inside the triangle and draw through $P$ the line parallel to the given line as well as the line perpendicular to it. These lines meet the sides of the triangle in four points. Of these four, two must be in one of the three rectangles. Now if the two points are on the same line, then the whole segment between them, $P$ included, is in the same rectangle. If the two points, say $Q$ and $R$, are on perpendicular lines, the perpendicular segments $R P$ and $P Q$ are also in the same rectangle. So in any case, $P$ is in one of the rectangles.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n07.2. ",
"solution_match": "\nSolution. "
}
|
678b8b80-540c-54fe-aa9c-6257a21106e6
| 607,995
|
A line through a point $A$ intersects a circle in two points, $B$ and $C$, in such a way that $B$ lies between $A$ and $C$. From the point $A$ draw the two tangents to the circle, meeting the circle at points $S$ and $T$. Let $P$ be the intersection of the lines $S T$ and AC. Show that $A P / P C=2 \cdot A B / B C$.
|
First we show that if we fix the points $A, B$ and $C$ but vary the circle, then the point $P$ stays fixed. To that end, suppose we have two different circles through $B$ and $C$. Draw the tangents from $A$ to one circle, meeting the circle at points $S_{1}$ and $T_{1}$, and the tangents to the other circle, meeting that circle at points $S_{2}$ and $T_{2}$. Then, according to the power of a point theorem
$$
A S_{1}^{2}=A T_{1}^{2}=A B \cdot A C=A S_{2}^{2}=A T_{2}^{2}
$$
This implies that all the tangent points $S_{1}, T_{1}, S_{2}$ and $T_{2}$ lie on the same circle with center $A$. Let $Q$ be the intersection of $S_{1} T_{1}$ and $S_{2} T_{2}$. Then by applying again the theorem of a power of a point but now with respect to the circle with center A, we have that $Q S_{1} \cdot Q T_{1}=Q S_{2} \cdot Q T_{2}$. But this in turn means that the point $Q$ has the same power with respect to the two circles we started with, and hence lies on the radical axis of those two circles, that is, the line $B C$ (the radical axis is the locus of points of equal power with respect to two given circles). So $Q$ is the intersection of $A C$ and both $S_{1} T_{1}$ and $S_{2} T_{2}$, which proves that the intersection point defined in the problem is the same for both circles.
Since the location of $P$ is independent of the circle through $B$ and $C$ we can, without loss of generality, choose the circle with $B C$ as diameter. Let $O$ be the center of this circle, $R$ its radius, $d=A O$, and $r=P O$. Then the triangles $A S O$ and $S P O$ are similar, so $O S / A O=P O / O S$, that is, $R / d=r / R$, or $R^{2}=d r$. Then finally we have
$$
\frac{A P}{P C}=\frac{d-r}{R+r}=\frac{d^{2}-d r}{d R+d r}=\frac{d^{2}-{ }^{R} 2}{d r+r^{2}}=\frac{d-R}{R}=2 \cdot \frac{d-R}{2 R}=2 \cdot \frac{A B}{B C}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A line through a point $A$ intersects a circle in two points, $B$ and $C$, in such a way that $B$ lies between $A$ and $C$. From the point $A$ draw the two tangents to the circle, meeting the circle at points $S$ and $T$. Let $P$ be the intersection of the lines $S T$ and AC. Show that $A P / P C=2 \cdot A B / B C$.
|
First we show that if we fix the points $A, B$ and $C$ but vary the circle, then the point $P$ stays fixed. To that end, suppose we have two different circles through $B$ and $C$. Draw the tangents from $A$ to one circle, meeting the circle at points $S_{1}$ and $T_{1}$, and the tangents to the other circle, meeting that circle at points $S_{2}$ and $T_{2}$. Then, according to the power of a point theorem
$$
A S_{1}^{2}=A T_{1}^{2}=A B \cdot A C=A S_{2}^{2}=A T_{2}^{2}
$$

This implies that all the tangent points $S_{1}, T_{1}, S_{2}$ and $T_{2}$ lie on the same circle with center $A$. Let $Q$ be the intersection of $S_{1} T_{1}$ and $S_{2} T_{2}$. Then by applying again the theorem of a power of a point but now with respect to the circle with center A, we have that $Q S_{1} \cdot Q T_{1}=Q S_{2} \cdot Q T_{2}$. But this in turn means that the point $Q$ has the same power with respect to the two circles we started with, and hence lies on the radical axis of those two circles, that is, the line $B C$ (the radical axis is the locus of points of equal power with respect to two given circles). So $Q$ is the intersection of $A C$ and both $S_{1} T_{1}$ and $S_{2} T_{2}$, which proves that the intersection point defined in the problem is the same for both circles.
Since the location of $P$ is independent of the circle through $B$ and $C$ we can, without loss of generality, choose the circle with $B C$ as diameter. Let $O$ be the center of this circle, $R$ its radius, $d=A O$, and $r=P O$. Then the triangles $A S O$ and $S P O$ are similar, so $O S / A O=P O / O S$, that is, $R / d=r / R$, or $R^{2}=d r$. Then finally we have
$$
\frac{A P}{P C}=\frac{d-r}{R+r}=\frac{d^{2}-d r}{d R+d r}=\frac{d^{2}-{ }^{R} 2}{d r+r^{2}}=\frac{d-R}{R}=2 \cdot \frac{d-R}{2 R}=2 \cdot \frac{A B}{B C}
$$
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n07.4. ",
"solution_match": "\nSolution. "
}
|
6f23532d-7246-5747-9a41-f0a9ea54b53c
| 607,997
|
In a triangle $A B C$ assume $A B=A C$, and let $D$ and $E$ be points on the extension of segment $B A$ beyond $A$ and on the segment $B C$, respectively, such that the lines $C D$ and $A E$ are parallel. Prove that $C D \geq \frac{4 h}{B C} C E$, where $h$ is the height from $A$ in triangle ABC. When does equality hold?
|
Because $A E \| D C$, the triangles $A B E$ and $D B C$ are similar. So
$$
C D=\frac{B C}{B E} \cdot A E
$$
$\mathrm{ja}$
$$
C D=\frac{A E \cdot B C}{B E \cdot C E} \cdot C E
$$
Let $A F$ be an altitude of $A B C$. Then $A E \geq A F=h$, and equality holds if and only if $E=F$. Because $A B C$ is isosceles, $F$ is the midpoint of $B C$. The arithmetic-geometric mean inequality yields
$$
B E \cdot C E \leq\left(\frac{B E+E C}{2}\right)^{2}=\left(\frac{B C}{2}\right)^{2}
$$
and equality holds if and only if $E$ is the midpoint of $B C$ i.e. $E=F$. The conclusion folows when these estimates are inserted in (1); furthermore, equality is equivalent to $E=F$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a triangle $A B C$ assume $A B=A C$, and let $D$ and $E$ be points on the extension of segment $B A$ beyond $A$ and on the segment $B C$, respectively, such that the lines $C D$ and $A E$ are parallel. Prove that $C D \geq \frac{4 h}{B C} C E$, where $h$ is the height from $A$ in triangle ABC. When does equality hold?
|
Because $A E \| D C$, the triangles $A B E$ and $D B C$ are similar. So
$$
C D=\frac{B C}{B E} \cdot A E
$$
$\mathrm{ja}$
$$
C D=\frac{A E \cdot B C}{B E \cdot C E} \cdot C E
$$

Let $A F$ be an altitude of $A B C$. Then $A E \geq A F=h$, and equality holds if and only if $E=F$. Because $A B C$ is isosceles, $F$ is the midpoint of $B C$. The arithmetic-geometric mean inequality yields
$$
B E \cdot C E \leq\left(\frac{B E+E C}{2}\right)^{2}=\left(\frac{B C}{2}\right)^{2}
$$
and equality holds if and only if $E$ is the midpoint of $B C$ i.e. $E=F$. The conclusion folows when these estimates are inserted in (1); furthermore, equality is equivalent to $E=F$
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n11.2. ",
"solution_match": "\nSolution. "
}
|
4bc4139a-2909-59d1-bfd5-57fbdbad6ec4
| 608,011
|
Show that for any integer $n \geq 2$ the sum of the fractions $\frac{1}{a b}$, where $a$ and $b$ are relatively prime positive integers such that $a<b \leq n$ and $a+b>n$, equals $\frac{1}{2}$.
|
We prove this by induction. First observe that the statement holds for $n=2$, because $a=1$ and $b=2$ are the only numbers which satisfy the conditions. Next we show that increasing $n$ by 1 does not change the sum, so it remains equal to $\frac{1}{2}$. To that end it suffices to show that the sum of the terms removed from the sum equals the sum of the new terms added. All the terms in the sum for $n-1$ remain in the sum for $n$ except the fractions $\frac{1}{a b}$ with $a$ and $b$ relatively prime, $0<a<b \leq_{n}$ and $a+b=n$. On the other hand the new fractions added to the sum for $n$ have the form $\frac{1}{a n}$ with $0<a<n$. So it suffices to show
$$
\sum_{\substack{0<a<n / 2 \\(a, n-a)=1}} \frac{1}{n(a-n)}=\sum_{\substack{0<a<n \\(a, n)=1}} \frac{1}{a n}
$$
(We denote the greatest common factor of $x$ and $y$ by $(x, y)$.) Since $(a, n)=(n-a, n)$, the terms in the sum on the right hand side can be grouped into pairs
$$
\frac{1}{a n}+\frac{1}{(n-a) n}=\frac{(n-a)+a}{a(n-a) n}=\frac{1}{a(n-a)}
$$
No term is left out because if $\mathrm{n}$ is even and greater than 2 then $(n / 2, n)=\frac{n}{2}>1$. So the right hand side is given by
$$
\sum_{\substack{0<a<n \\(a, n)=1}} \frac{1}{a n}=\sum_{\substack{0<a<n / 2 \\(a, n)=1}} \frac{1}{a(n-a)}=\sum_{\substack{0<a<n / 2 \\(a, n-a)=1}} \frac{1}{a(n-a)}
$$
which is what we had to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that for any integer $n \geq 2$ the sum of the fractions $\frac{1}{a b}$, where $a$ and $b$ are relatively prime positive integers such that $a<b \leq n$ and $a+b>n$, equals $\frac{1}{2}$.
|
We prove this by induction. First observe that the statement holds for $n=2$, because $a=1$ and $b=2$ are the only numbers which satisfy the conditions. Next we show that increasing $n$ by 1 does not change the sum, so it remains equal to $\frac{1}{2}$. To that end it suffices to show that the sum of the terms removed from the sum equals the sum of the new terms added. All the terms in the sum for $n-1$ remain in the sum for $n$ except the fractions $\frac{1}{a b}$ with $a$ and $b$ relatively prime, $0<a<b \leq_{n}$ and $a+b=n$. On the other hand the new fractions added to the sum for $n$ have the form $\frac{1}{a n}$ with $0<a<n$. So it suffices to show
$$
\sum_{\substack{0<a<n / 2 \\(a, n-a)=1}} \frac{1}{n(a-n)}=\sum_{\substack{0<a<n \\(a, n)=1}} \frac{1}{a n}
$$
(We denote the greatest common factor of $x$ and $y$ by $(x, y)$.) Since $(a, n)=(n-a, n)$, the terms in the sum on the right hand side can be grouped into pairs
$$
\frac{1}{a n}+\frac{1}{(n-a) n}=\frac{(n-a)+a}{a(n-a) n}=\frac{1}{a(n-a)}
$$
No term is left out because if $\mathrm{n}$ is even and greater than 2 then $(n / 2, n)=\frac{n}{2}>1$. So the right hand side is given by
$$
\sum_{\substack{0<a<n \\(a, n)=1}} \frac{1}{a n}=\sum_{\substack{0<a<n / 2 \\(a, n)=1}} \frac{1}{a(n-a)}=\sum_{\substack{0<a<n / 2 \\(a, n-a)=1}} \frac{1}{a(n-a)}
$$
which is what we had to prove.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n11.4. ",
"solution_match": "\nSolution. "
}
|
948817ce-b2f2-5b31-a06a-8fd58b7585c6
| 608,013
|
Given a triangle $A B C$, let $P$ lie on the circumcircle of the triangle and be the midpoint of the arc $B C$ which does not contain $A$. Draw a straight line $l$ through $P$ so that $l$ is parallel to $A B$. Denote by $k$ the circle which passes through $B$, and is tangent to $l$ at the point $P$. Let $Q$ be the second point of intersection of $k$ and the line $A B$ (if there is no second point of intersection, choose $Q=B)$. Prove that $A Q=A C$.
|
Again we consider the case when $Q$ is between $A$ and $B$. We shall use trigonometry. As above, we have $\angle A B P=\beta+\frac{\alpha}{2}$, and thus
$$
Q B=2 P B \cos \left(\beta+\frac{\alpha}{2}\right)=2 P B \cos \left(\pi-\frac{\alpha}{2}-\gamma\right)
$$
and
$$
A Q=2 R \sin \gamma-4 R \sin \frac{\alpha}{2} \cos \left(\pi-\frac{\alpha}{2}-\gamma\right)
$$
Since $A C=2 R \cos \beta$, it remains to prove that
$$
\sin \beta=\sin \gamma+2 \sin \frac{\alpha}{2} \cos \left(\frac{\alpha}{2}+\gamma\right)
$$
which is easy, using standard trigonometry.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$, let $P$ lie on the circumcircle of the triangle and be the midpoint of the arc $B C$ which does not contain $A$. Draw a straight line $l$ through $P$ so that $l$ is parallel to $A B$. Denote by $k$ the circle which passes through $B$, and is tangent to $l$ at the point $P$. Let $Q$ be the second point of intersection of $k$ and the line $A B$ (if there is no second point of intersection, choose $Q=B)$. Prove that $A Q=A C$.
|
Again we consider the case when $Q$ is between $A$ and $B$. We shall use trigonometry. As above, we have $\angle A B P=\beta+\frac{\alpha}{2}$, and thus
$$
Q B=2 P B \cos \left(\beta+\frac{\alpha}{2}\right)=2 P B \cos \left(\pi-\frac{\alpha}{2}-\gamma\right)
$$
and
$$
A Q=2 R \sin \gamma-4 R \sin \frac{\alpha}{2} \cos \left(\pi-\frac{\alpha}{2}-\gamma\right)
$$
Since $A C=2 R \cos \beta$, it remains to prove that
$$
\sin \beta=\sin \gamma+2 \sin \frac{\alpha}{2} \cos \left(\frac{\alpha}{2}+\gamma\right)
$$
which is easy, using standard trigonometry.
|
{
"resource_path": "Nordic_MO/segmented/en-2012-sol.jsonl",
"problem_match": "\n\nProblem 2.",
"solution_match": "\n\nSolution II."
}
|
9b7800aa-279e-5e03-a1b0-ff8bb99a1f77
| 608,015
|
Define a sequence $\left(n_{k}\right)_{k \geq 0}$ by $n_{0}=n_{1}=1$, and $n_{2 k}=n_{k}+n_{k-1}$ and $n_{2 k+1}=n_{k}$ for $k \geq 1$. Let further $q_{k}=n_{k} / n_{k-1}$ for each $k \geq 1$. Show that every positive rational number is present exactly once in the sequence $\left(q_{k}\right)_{k \geq 1}$.
|
Clearly, all the numbers $n_{k}$ are positive integers. Moreover,
$$
q_{2 k}=\frac{n_{2 k}}{n_{2 k-1}}=\frac{n_{k}+n_{k-1}}{n_{k-1}}=q_{k}+1
$$
and similarly,
$$
\frac{1}{q_{2 k+1}}=\frac{n_{2 k}}{n_{2 k+1}}=\frac{n_{k}+n_{k-1}}{n_{k}}=\frac{1}{q_{k}}+1
$$
In particular, $q_{k}>1$ when $k$ is even, and $q_{k}<1$ when $k \geq 3$ is odd.
We will show the following by induction on $t=2,3,4, \ldots$ :
Claim: Every rational number $r / s$ where $r$, s are positive integers with $\operatorname{gcd}(r, s)=$ 1 and $r+s \leq t$ occurs precisely once among the numbers $q_{k}$.
The claim is clearly true for $t=2$, since then $r / s=1 / 1=1$ is the only possibility, and $q_{1}$ is the only occurrence of 1 in the sequence.
Now, assume that $u \geq 3$ and that the claim holds for $t=u-1$. Let $r$ and $s$ be positive integers with $\operatorname{gcd}(r, s)=1$ and $r+s=u$.
First, assume that $r>s$. We know that $r / s=q_{m}$ is only possible if $m$ is even. But
$$
\frac{r}{s}=q_{2 k} \Leftrightarrow \frac{r-s}{s}=q_{k}
$$
by (1), and moreover, the latter equality holds for precisely one $k$ according to the induction hypothesis, since $\operatorname{gcd}(r-s, s)=1$ and $(r-s)+s=r \leq t$.
Next, assume that $r<s$. We know that $r / s=q_{m}$ is only possible if $m$ is odd. But
$$
\frac{r}{s}=q_{2 k+1} \Leftrightarrow \frac{s}{r}=\frac{1}{q_{2 k+1}} \Leftrightarrow \frac{s-r}{r}=\frac{1}{q_{k}}
$$
by (2), and moreover, the latter equality holds for precisely one $k$ according to the induction hypothesis, since $\operatorname{gcd}(s-r, r)=1$ and $(s-r)+r=s \leq t$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Define a sequence $\left(n_{k}\right)_{k \geq 0}$ by $n_{0}=n_{1}=1$, and $n_{2 k}=n_{k}+n_{k-1}$ and $n_{2 k+1}=n_{k}$ for $k \geq 1$. Let further $q_{k}=n_{k} / n_{k-1}$ for each $k \geq 1$. Show that every positive rational number is present exactly once in the sequence $\left(q_{k}\right)_{k \geq 1}$.
|
Clearly, all the numbers $n_{k}$ are positive integers. Moreover,
$$
q_{2 k}=\frac{n_{2 k}}{n_{2 k-1}}=\frac{n_{k}+n_{k-1}}{n_{k-1}}=q_{k}+1
$$
and similarly,
$$
\frac{1}{q_{2 k+1}}=\frac{n_{2 k}}{n_{2 k+1}}=\frac{n_{k}+n_{k-1}}{n_{k}}=\frac{1}{q_{k}}+1
$$
In particular, $q_{k}>1$ when $k$ is even, and $q_{k}<1$ when $k \geq 3$ is odd.
We will show the following by induction on $t=2,3,4, \ldots$ :
Claim: Every rational number $r / s$ where $r$, s are positive integers with $\operatorname{gcd}(r, s)=$ 1 and $r+s \leq t$ occurs precisely once among the numbers $q_{k}$.
The claim is clearly true for $t=2$, since then $r / s=1 / 1=1$ is the only possibility, and $q_{1}$ is the only occurrence of 1 in the sequence.
Now, assume that $u \geq 3$ and that the claim holds for $t=u-1$. Let $r$ and $s$ be positive integers with $\operatorname{gcd}(r, s)=1$ and $r+s=u$.
First, assume that $r>s$. We know that $r / s=q_{m}$ is only possible if $m$ is even. But
$$
\frac{r}{s}=q_{2 k} \Leftrightarrow \frac{r-s}{s}=q_{k}
$$
by (1), and moreover, the latter equality holds for precisely one $k$ according to the induction hypothesis, since $\operatorname{gcd}(r-s, s)=1$ and $(r-s)+s=r \leq t$.
Next, assume that $r<s$. We know that $r / s=q_{m}$ is only possible if $m$ is odd. But
$$
\frac{r}{s}=q_{2 k+1} \Leftrightarrow \frac{s}{r}=\frac{1}{q_{2 k+1}} \Leftrightarrow \frac{s-r}{r}=\frac{1}{q_{k}}
$$
by (2), and moreover, the latter equality holds for precisely one $k$ according to the induction hypothesis, since $\operatorname{gcd}(s-r, r)=1$ and $(s-r)+r=s \leq t$.
|
{
"resource_path": "Nordic_MO/segmented/en-2013-sol.jsonl",
"problem_match": "\n\nProblem 3.",
"solution_match": "\n\nSolution."
}
|
3c72a700-7d19-5ad1-9348-16eee35849a5
| 608,020
|
Let $A B C$ be an acute angled triangle, and $H$ a point in its interior. Let the reflections of $H$ through the sides $A B$ and $A C$ be called $H_{c}$ and $H_{b}$, respectively, and let the reflections of $H$ through the midpoints of these same sides be called $H_{c}^{\prime}$ and $H_{b}^{\prime}$, respectively. Show that the four points $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ are concyclic if and only if at least two of them coincide or $H$ lies on the altitude from $A$ in triangle $A B C$.
|
If at least two of the four points $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ coincide, all four are obviously concyclic. Therefore we may assume that these four points are distinct.
Let $P_{b}$ denote the midpoint of segment $H H_{b}, P_{b}^{\prime}$ the midpoint of segment $H H_{b}^{\prime}, P_{c}$ the midpoint of segment $H H_{c}$, and $P_{c}^{\prime}$ the midpoint of segment $H H_{c}^{\prime}$.
The triangle $H H_{b} H_{b}^{\prime}$ being right-angled in $H_{b}$, it follows that the perpendicular bisector $\ell_{b}$ of the side $H_{b} H_{b}^{\prime}$ goes through the point $P_{b}^{\prime}$. Since the segments $P_{b} P_{b}^{\prime}$ and $H_{b} H_{b}^{\prime}$ are parallel and $P_{b}^{\prime}$ is the midpoint of the side $A C$, we then conclude that $\ell_{b}$ also goes through the circumcentre $O$ of triangle $A B C$.
Similarly the perpendicular bisector $\ell_{c}$ of the segment $H_{c} H_{c}^{\prime}$ also goes through $O$. Hence the four points $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ are concyclic if and only if also the perpendicular bisector $\ell$ of the segment $H_{b}^{\prime} H_{c}^{\prime}$ goes through the point $O$. Since $H_{b}^{\prime} H_{c}^{\prime}\left\|P_{b}^{\prime} P_{c}^{\prime}\right\| B C$, this is the case if and only if $\ell$ is the perpendicular bisector $m$ of the segment $B C$.
Let $k$ denote the perpendicular bisector of the segment $P_{b}^{\prime} P_{c}^{\prime}$. Since the lines $\ell$ and $m$ are obtained from $k$ by similarities of ratio 2 and centres $H$ and $A$, respectively, they coincide if and only if $H A$ is parallel to $m$. Thus $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ are concyclic if and only if $H$ lies on the altitude from $A$ in triangle $A B C$.
Click here to experiment with the figure in GeoGebra.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute angled triangle, and $H$ a point in its interior. Let the reflections of $H$ through the sides $A B$ and $A C$ be called $H_{c}$ and $H_{b}$, respectively, and let the reflections of $H$ through the midpoints of these same sides be called $H_{c}^{\prime}$ and $H_{b}^{\prime}$, respectively. Show that the four points $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ are concyclic if and only if at least two of them coincide or $H$ lies on the altitude from $A$ in triangle $A B C$.
|
If at least two of the four points $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ coincide, all four are obviously concyclic. Therefore we may assume that these four points are distinct.
Let $P_{b}$ denote the midpoint of segment $H H_{b}, P_{b}^{\prime}$ the midpoint of segment $H H_{b}^{\prime}, P_{c}$ the midpoint of segment $H H_{c}$, and $P_{c}^{\prime}$ the midpoint of segment $H H_{c}^{\prime}$.
The triangle $H H_{b} H_{b}^{\prime}$ being right-angled in $H_{b}$, it follows that the perpendicular bisector $\ell_{b}$ of the side $H_{b} H_{b}^{\prime}$ goes through the point $P_{b}^{\prime}$. Since the segments $P_{b} P_{b}^{\prime}$ and $H_{b} H_{b}^{\prime}$ are parallel and $P_{b}^{\prime}$ is the midpoint of the side $A C$, we then conclude that $\ell_{b}$ also goes through the circumcentre $O$ of triangle $A B C$.
Similarly the perpendicular bisector $\ell_{c}$ of the segment $H_{c} H_{c}^{\prime}$ also goes through $O$. Hence the four points $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ are concyclic if and only if also the perpendicular bisector $\ell$ of the segment $H_{b}^{\prime} H_{c}^{\prime}$ goes through the point $O$. Since $H_{b}^{\prime} H_{c}^{\prime}\left\|P_{b}^{\prime} P_{c}^{\prime}\right\| B C$, this is the case if and only if $\ell$ is the perpendicular bisector $m$ of the segment $B C$.
Let $k$ denote the perpendicular bisector of the segment $P_{b}^{\prime} P_{c}^{\prime}$. Since the lines $\ell$ and $m$ are obtained from $k$ by similarities of ratio 2 and centres $H$ and $A$, respectively, they coincide if and only if $H A$ is parallel to $m$. Thus $H_{b}, H_{b}^{\prime}, H_{c}$, and $H_{c}^{\prime}$ are concyclic if and only if $H$ lies on the altitude from $A$ in triangle $A B C$.

Click here to experiment with the figure in GeoGebra.
|
{
"resource_path": "Nordic_MO/segmented/en-2013-sol.jsonl",
"problem_match": "\n\nProblem 4.",
"solution_match": "\n\nSolution."
}
|
9643bad9-74cc-579c-ad68-a950b6654465
| 608,021
|
Let $A B C$ be a triangle and $\Gamma$ the circle with diameter $A B$. The bisectors of $\angle B A C$ and $\angle A B C$ intersect $\Gamma$ (also) at $D$ and $E$, respectively. The incircle of $A B C$ meets $B C$ and $A C$ at $F$ and $G$, respectively. Prove that $D, E, F$ and $G$ are collinear.
|
Let the line $E D$ meet $A C$ at $G^{\prime}$ and $B C$ at $F^{\prime} . A D$ and $B E$ intersect at $I$, the incenter of $A B C$. As angles subtending the same arc $\widehat{B D}$, $\angle D A B=\angle D E B=\angle G^{\prime} E I$. But $\angle D A B=\angle C A D=$ $\angle G^{\prime} A I$. This means that $E, A, I$ and $G^{\prime}$ are concyclic, and $\angle A E I=\angle A G^{\prime} I$ as angles subtending the same chord $A I$. But $A B$ is a diameter of $\Gamma$, and so $\angle A E B=$ $\angle A E I$ is a right angle. So $I G^{\prime} \perp A C$, or $G^{\prime}$ is the foot of the perpendicular from $I$ to $A C$. This implies $G^{\prime}=G$. In a similar manner we prove that $F^{\prime}=F$, and the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and $\Gamma$ the circle with diameter $A B$. The bisectors of $\angle B A C$ and $\angle A B C$ intersect $\Gamma$ (also) at $D$ and $E$, respectively. The incircle of $A B C$ meets $B C$ and $A C$ at $F$ and $G$, respectively. Prove that $D, E, F$ and $G$ are collinear.
|
Let the line $E D$ meet $A C$ at $G^{\prime}$ and $B C$ at $F^{\prime} . A D$ and $B E$ intersect at $I$, the incenter of $A B C$. As angles subtending the same arc $\widehat{B D}$, $\angle D A B=\angle D E B=\angle G^{\prime} E I$. But $\angle D A B=\angle C A D=$ $\angle G^{\prime} A I$. This means that $E, A, I$ and $G^{\prime}$ are concyclic, and $\angle A E I=\angle A G^{\prime} I$ as angles subtending the same chord $A I$. But $A B$ is a diameter of $\Gamma$, and so $\angle A E B=$ $\angle A E I$ is a right angle. So $I G^{\prime} \perp A C$, or $G^{\prime}$ is the foot of the perpendicular from $I$ to $A C$. This implies $G^{\prime}=G$. In a similar manner we prove that $F^{\prime}=F$, and the proof is complete.

|
{
"resource_path": "Nordic_MO/segmented/en-2015-sol.jsonl",
"problem_match": "\n## Problem 1.",
"solution_match": "\n\nSolution 1."
}
|
54c03a07-3c28-5341-bf0f-c452d9492b13
| 608,026
|
Let $A B C$ be a triangle and $\Gamma$ the circle with diameter $A B$. The bisectors of $\angle B A C$ and $\angle A B C$ intersect $\Gamma$ (also) at $D$ and $E$, respectively. The incircle of $A B C$ meets $B C$ and $A C$ at $F$ and $G$, respectively. Prove that $D, E, F$ and $G$ are collinear.
|
(Read the attached figure so that $F^{\prime}$ and $G^{\prime}$ are as $F$ and $G$ in the problem text.) The angles $\angle A E I=\angle A E B$ and $\angle A G I$ are right angles. This means that $A I G E$ is a cyclic quadrilateral. But then $\angle B E G=\angle I E G=\angle I A G=\angle D A C=\angle D A B=\angle B E D$, implying that $G$ and $D$ are on the same line through $E$. The same argument shows $F$ and $E$ are on the same line through $D$. So the points $G$ and $F$ are on the line $E D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and $\Gamma$ the circle with diameter $A B$. The bisectors of $\angle B A C$ and $\angle A B C$ intersect $\Gamma$ (also) at $D$ and $E$, respectively. The incircle of $A B C$ meets $B C$ and $A C$ at $F$ and $G$, respectively. Prove that $D, E, F$ and $G$ are collinear.
|
(Read the attached figure so that $F^{\prime}$ and $G^{\prime}$ are as $F$ and $G$ in the problem text.) The angles $\angle A E I=\angle A E B$ and $\angle A G I$ are right angles. This means that $A I G E$ is a cyclic quadrilateral. But then $\angle B E G=\angle I E G=\angle I A G=\angle D A C=\angle D A B=\angle B E D$, implying that $G$ and $D$ are on the same line through $E$. The same argument shows $F$ and $E$ are on the same line through $D$. So the points $G$ and $F$ are on the line $E D$.
|
{
"resource_path": "Nordic_MO/segmented/en-2015-sol.jsonl",
"problem_match": "\n## Problem 1.",
"solution_match": "\n\nSolution 2."
}
|
54c03a07-3c28-5341-bf0f-c452d9492b13
| 608,026
|
Let $n>1$ and $p(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0}$ be a polynomial with $n$ real roots (counted with multiplicity). Let the polynomial $q$ be defined by
$$
q(x)=\prod_{j=1}^{2015} p(x+j)
$$
We know that $p(2015)=2015$. Prove that $q$ has at least 1970 different roots $r_{1}, \ldots, r_{1970}$ such that $\left|r_{j}\right|<2015$ for all $j=1, \ldots, 1970$.
|
Let $h_{j}(x)=p(x+j)$. Consider $h_{2015}$. Like $p$, it has $n$ real roots $s_{1}, s_{2}, \ldots, s_{n}$, and $h_{2015}(0)=p(2015)=2015$. By Viète, the product $\left|s_{1} s_{2} \cdots s_{n}\right|$ equals 2015. Since $n \geq 2$, there is at least one $s_{j}$ such that $\left|s_{j}\right| \leq \sqrt{2015}<\sqrt{2025}=45$. Denote this $s_{j}$ by $m$. Now for all $j=0,1, \ldots, 2014, h_{2015-j}(m+j)=p(m+j+2015-j)=p(m+2015)=$ $h_{2015}(m)=0$. So $m, m+1, \ldots, m+2014$ are all roots of $q$. Since $0 \leq|m|<45$, the condition $|m+j|<2015$ is satisfied by at least 1970 different $j, 0 \leq j \leq 2014$, and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n>1$ and $p(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0}$ be a polynomial with $n$ real roots (counted with multiplicity). Let the polynomial $q$ be defined by
$$
q(x)=\prod_{j=1}^{2015} p(x+j)
$$
We know that $p(2015)=2015$. Prove that $q$ has at least 1970 different roots $r_{1}, \ldots, r_{1970}$ such that $\left|r_{j}\right|<2015$ for all $j=1, \ldots, 1970$.
|
Let $h_{j}(x)=p(x+j)$. Consider $h_{2015}$. Like $p$, it has $n$ real roots $s_{1}, s_{2}, \ldots, s_{n}$, and $h_{2015}(0)=p(2015)=2015$. By Viète, the product $\left|s_{1} s_{2} \cdots s_{n}\right|$ equals 2015. Since $n \geq 2$, there is at least one $s_{j}$ such that $\left|s_{j}\right| \leq \sqrt{2015}<\sqrt{2025}=45$. Denote this $s_{j}$ by $m$. Now for all $j=0,1, \ldots, 2014, h_{2015-j}(m+j)=p(m+j+2015-j)=p(m+2015)=$ $h_{2015}(m)=0$. So $m, m+1, \ldots, m+2014$ are all roots of $q$. Since $0 \leq|m|<45$, the condition $|m+j|<2015$ is satisfied by at least 1970 different $j, 0 \leq j \leq 2014$, and we are done.
|
{
"resource_path": "Nordic_MO/segmented/en-2015-sol.jsonl",
"problem_match": "\n## Problem 3.",
"solution_match": "\n\nSolution."
}
|
76ec71aa-6b43-53e4-ba88-82befa6fa1af
| 608,028
|
Let $n$ be a positive integer. Show that there exist positive integers $a$ and $b$ such that:
$$
\frac{a^{2}+a+1}{b^{2}+b+1}=n^{2}+n+1
$$
|
Let $P(x)=x^{2}+x+1$. We have $P(n) P(n+1)=\left(n^{2}+n+1\right)\left(n^{2}+3 n+3\right)=$ $n^{4}+4 n^{3}+7 n^{2}+6 n+3$. Also, $P\left((n+1)^{2}\right)=n^{4}+4 n^{3}+7 n^{2}+6 n+3$. By choosing $a=(n+1)^{2}$ and $b=n+1$ we get $P(a) / P(b)=P(n)$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer. Show that there exist positive integers $a$ and $b$ such that:
$$
\frac{a^{2}+a+1}{b^{2}+b+1}=n^{2}+n+1
$$
|
Let $P(x)=x^{2}+x+1$. We have $P(n) P(n+1)=\left(n^{2}+n+1\right)\left(n^{2}+3 n+3\right)=$ $n^{4}+4 n^{3}+7 n^{2}+6 n+3$. Also, $P\left((n+1)^{2}\right)=n^{4}+4 n^{3}+7 n^{2}+6 n+3$. By choosing $a=(n+1)^{2}$ and $b=n+1$ we get $P(a) / P(b)=P(n)$ as desired.
|
{
"resource_path": "Nordic_MO/segmented/en-2017-sol.jsonl",
"problem_match": "\n\nProblem 1",
"solution_match": "\n\nSolution 1"
}
|
04a4830a-0df6-5c09-b3b1-fe92b3e4c9bb
| 608,034
|
Let $a, b, \alpha, \beta$ be real numbers such that $0 \leq a, b \leq 1$, and $0 \leq \alpha, \beta \leq \frac{\pi}{2}$. Show that if
$$
a b \cos (\alpha-\beta) \leq \sqrt{\left(1-a^{2}\right)\left(1-b^{2}\right)}
$$
then
$$
a \cos \alpha+b \sin \beta \leq 1+a b \sin (\beta-\alpha)
$$
|
The condition can be rewritten as
$$
a b \cos (\alpha-\beta)=a b \cos \alpha \cos \beta+a b \sin \alpha \sin \beta \leq \sqrt{\left(1-a^{2}\right)\left(1-b^{2}\right)}
$$
Set $x=a \cos \alpha, y=b \sin \beta, z=b \cos \beta, t=a \sin \alpha$. We can now rewrite the condition as
$$
x z+y t \leq \sqrt{\left(1-x^{2}-t^{2}\right)\left(1-y^{2}-z^{2}\right)}
$$
whereas the inequality we need to prove now looks like
$$
x+y \leq 1+x y-z t
$$
Since $x, y, z, t \geq 0$, and $1+x y-z t=1+a b \sin (\beta-\alpha) \geq 0$, we can square both sides of both inequalities, and get equivalent ones. After a couple of cancelations the condition yields
$$
2 x y z t \leq 1-x^{2}-y^{2}-z^{2}-t^{2}+x^{2} y^{2}+z^{2} t^{2}
$$
so that
$$
x^{2}+y^{2}+z^{2}+t^{2} \leq(x y-z t)^{2}+1
$$
which is equivalent to
$$
x^{2}+y^{2}+z^{2}+t^{2}+2 x y-2 z t \leq(1+x y-z t)^{2}
$$
or
$$
(x+y)^{2}+(z-t)^{2} \leq(1+x y-z t)^{2}
$$
Since $(x+y)^{2} \leq(x+y)^{2}+(z-t)^{2}$, the desired inequality follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, \alpha, \beta$ be real numbers such that $0 \leq a, b \leq 1$, and $0 \leq \alpha, \beta \leq \frac{\pi}{2}$. Show that if
$$
a b \cos (\alpha-\beta) \leq \sqrt{\left(1-a^{2}\right)\left(1-b^{2}\right)}
$$
then
$$
a \cos \alpha+b \sin \beta \leq 1+a b \sin (\beta-\alpha)
$$
|
The condition can be rewritten as
$$
a b \cos (\alpha-\beta)=a b \cos \alpha \cos \beta+a b \sin \alpha \sin \beta \leq \sqrt{\left(1-a^{2}\right)\left(1-b^{2}\right)}
$$
Set $x=a \cos \alpha, y=b \sin \beta, z=b \cos \beta, t=a \sin \alpha$. We can now rewrite the condition as
$$
x z+y t \leq \sqrt{\left(1-x^{2}-t^{2}\right)\left(1-y^{2}-z^{2}\right)}
$$
whereas the inequality we need to prove now looks like
$$
x+y \leq 1+x y-z t
$$
Since $x, y, z, t \geq 0$, and $1+x y-z t=1+a b \sin (\beta-\alpha) \geq 0$, we can square both sides of both inequalities, and get equivalent ones. After a couple of cancelations the condition yields
$$
2 x y z t \leq 1-x^{2}-y^{2}-z^{2}-t^{2}+x^{2} y^{2}+z^{2} t^{2}
$$
so that
$$
x^{2}+y^{2}+z^{2}+t^{2} \leq(x y-z t)^{2}+1
$$
which is equivalent to
$$
x^{2}+y^{2}+z^{2}+t^{2}+2 x y-2 z t \leq(1+x y-z t)^{2}
$$
or
$$
(x+y)^{2}+(z-t)^{2} \leq(1+x y-z t)^{2}
$$
Since $(x+y)^{2} \leq(x+y)^{2}+(z-t)^{2}$, the desired inequality follows.
|
{
"resource_path": "Nordic_MO/segmented/en-2017-sol.jsonl",
"problem_match": "\n\nProblem 2",
"solution_match": "\n\nSolution 2"
}
|
9acc88c2-8051-51da-b4c4-0eab550e3624
| 608,035
|
Let $M$ and $N$ be the midpoints of the sides $A C$ and $A B$, respectively, of an acute triangle $A B C, A B \neq A C$. Let $\omega_{B}$ be the circle centered at $M$ passing through $B$, and let $\omega_{C}$ be the circle centered at $N$ passing through $C$. Let the point $D$ be such that $A B C D$ is an isosceles trapezoid with $A D$ parallel to $B C$. Assume that $\omega_{B}$ and $\omega_{C}$ intersect in two distinct points $P$ and $Q$. Show that $D$ lies on the line $P Q$.
|
Let $E$ be such that $A B E C$ is a parallelogram with $A B \| C E$ and $A C \| B E$, and let $\omega$ be the circumscribed circle of $\triangle A B C$ with centre $O$.
It is known that the radical axis of two circles is perpendicular to the line connecting the two centres. Since $B E \perp M O$ and $C E \perp N O$, this means that $B E$ and $C E$ are the radical axes of $\omega$ and $\omega_{B}$, and of $\omega$ and $\omega_{C}$, respectively, so $E$ is the radical centre of $\omega$, $\omega_{B}$, and $\omega_{C}$.
Now as $B E=A C=B D$ and $C E=A B=C D$ we find that $B C$ is the perpendicular bisector of $D E$. Most importantly we have $D E \perp B C$. Denote by $t$ the radical axis of $\omega_{B}$ and $\omega_{C}$, i.e. $t=P Q$. Then since $t \perp M N$ we find that $t$ and $D E$ are parallel. Therefore since $E$ lies on $t$ we get that $D$ also lies on $t$.
Alternative solution Reflect $B$ across $M$ to a point $B^{\prime}$ forming a parallelogram $A B C B^{\prime}$. Then $B^{\prime}$ lies on $\omega_{B}$ diagonally opposite $B$, and since $A B^{\prime} \| B C$ it lies on $A D$. Similarly reflect $C$ across $N$ to a point $C^{\prime}$, which satisfies analogous properties. Note that $C B^{\prime}=A B=C D$, so we find that triangle $C D B^{\prime}$ and similarly triangle $B D C^{\prime}$ are isosceles.
Let $B^{\prime \prime}$ and $C^{\prime \prime}$ be the orthogonal projections of $B$ and $C$ onto $A D$. Since $B B^{\prime}$ is a diameter of $\omega_{B}$ we get that $B^{\prime \prime}$ lies on $\omega_{B}$, and similarly $C^{\prime \prime}$ lies on $\omega_{C}$. Moreover $B B^{\prime \prime}$ is an altitude of the isosceles triangle $B D C^{\prime}$ with $B D=B C^{\prime}$, hence it coincides with the median from $B$, so $B^{\prime \prime}$ is in fact the midpoint of $D C^{\prime}$. Similarly $C^{\prime \prime}$ is the midpoint of $D B^{\prime}$. From this we get
$$
2=\frac{D C^{\prime}}{D B^{\prime \prime}}=\frac{D B^{\prime}}{D C^{\prime \prime}}
$$
which rearranges as $D C^{\prime} \cdot D C^{\prime \prime}=D B^{\prime} \cdot D B^{\prime \prime}$. This means that $D$ has same the power with respect to $\omega_{B}$ and $\omega_{C}$, hence it lies on their radical axis $P Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $M$ and $N$ be the midpoints of the sides $A C$ and $A B$, respectively, of an acute triangle $A B C, A B \neq A C$. Let $\omega_{B}$ be the circle centered at $M$ passing through $B$, and let $\omega_{C}$ be the circle centered at $N$ passing through $C$. Let the point $D$ be such that $A B C D$ is an isosceles trapezoid with $A D$ parallel to $B C$. Assume that $\omega_{B}$ and $\omega_{C}$ intersect in two distinct points $P$ and $Q$. Show that $D$ lies on the line $P Q$.
|
Let $E$ be such that $A B E C$ is a parallelogram with $A B \| C E$ and $A C \| B E$, and let $\omega$ be the circumscribed circle of $\triangle A B C$ with centre $O$.
It is known that the radical axis of two circles is perpendicular to the line connecting the two centres. Since $B E \perp M O$ and $C E \perp N O$, this means that $B E$ and $C E$ are the radical axes of $\omega$ and $\omega_{B}$, and of $\omega$ and $\omega_{C}$, respectively, so $E$ is the radical centre of $\omega$, $\omega_{B}$, and $\omega_{C}$.

Now as $B E=A C=B D$ and $C E=A B=C D$ we find that $B C$ is the perpendicular bisector of $D E$. Most importantly we have $D E \perp B C$. Denote by $t$ the radical axis of $\omega_{B}$ and $\omega_{C}$, i.e. $t=P Q$. Then since $t \perp M N$ we find that $t$ and $D E$ are parallel. Therefore since $E$ lies on $t$ we get that $D$ also lies on $t$.
Alternative solution Reflect $B$ across $M$ to a point $B^{\prime}$ forming a parallelogram $A B C B^{\prime}$. Then $B^{\prime}$ lies on $\omega_{B}$ diagonally opposite $B$, and since $A B^{\prime} \| B C$ it lies on $A D$. Similarly reflect $C$ across $N$ to a point $C^{\prime}$, which satisfies analogous properties. Note that $C B^{\prime}=A B=C D$, so we find that triangle $C D B^{\prime}$ and similarly triangle $B D C^{\prime}$ are isosceles.
Let $B^{\prime \prime}$ and $C^{\prime \prime}$ be the orthogonal projections of $B$ and $C$ onto $A D$. Since $B B^{\prime}$ is a diameter of $\omega_{B}$ we get that $B^{\prime \prime}$ lies on $\omega_{B}$, and similarly $C^{\prime \prime}$ lies on $\omega_{C}$. Moreover $B B^{\prime \prime}$ is an altitude of the isosceles triangle $B D C^{\prime}$ with $B D=B C^{\prime}$, hence it coincides with the median from $B$, so $B^{\prime \prime}$ is in fact the midpoint of $D C^{\prime}$. Similarly $C^{\prime \prime}$ is the midpoint of $D B^{\prime}$. From this we get
$$
2=\frac{D C^{\prime}}{D B^{\prime \prime}}=\frac{D B^{\prime}}{D C^{\prime \prime}}
$$
which rearranges as $D C^{\prime} \cdot D C^{\prime \prime}=D B^{\prime} \cdot D B^{\prime \prime}$. This means that $D$ has same the power with respect to $\omega_{B}$ and $\omega_{C}$, hence it lies on their radical axis $P Q$.
|
{
"resource_path": "Nordic_MO/segmented/en-2017-sol.jsonl",
"problem_match": "\n\nProblem 3",
"solution_match": "\n\nSolution 3"
}
|
33dbedbf-1787-5fb2-8644-aeafb3c5ffd4
| 608,036
|
Let $n$ be an integer with $n \geq 3$ and assume that $2 n$ vertices of a regular $(4 n+1)$-gon are coloured. Show that there must exist three of the coloured vertices forming an isosceles triangle.
|
Assume that it is possible to color $2 n$ of the vertices of a $4 n+1$-gon such that there are no three colored vertices forming an isosceles triangle. Enumerate the vertices consecutively as $H_{-2 n}, H_{-2 n+1}, \ldots, H_{0}, H_{1}, H_{2}, \ldots, H_{2 n}$ and consider first the case where there are two colored neighboring vertices. Assume wlog that the vertices $H_{0}$ and $H_{1}$ are colored. Then at most one of the vertices $H_{-i}$ and $H_{i}$ are colored for all $i=1,2, \ldots, 2 n$ since these form an isosceles triangle with $H_{0}$. Similarly at most one of $H_{-i}$ and $H_{i+2}$ are colored for all $i=1,2, \ldots, 2 n-2$, and at most one of $H_{-(2 n-1)}$ and $H_{-2 n}$ are colored since these form an isosceles triangles with $H_{1}$. The three vertices $H_{0}, H_{1}, H_{i}, i=2,-1,-2 n$ also form isoceles triangles and hence $H_{-1}, H_{2}, H_{-2 n}$ are not colored. It follows that no consecutive vertices in the two strings
$$
\begin{array}{r}
H_{-2}-H_{4}-H_{-4}-H_{6}-\ldots-H_{2 n-2}-H_{-(2 n-2)}-H_{2 n} \\
H_{3}-H_{-3}-H_{5}-H_{-5}-\ldots-H_{2 n-1}-H_{-(2 n-1)}
\end{array}
$$
are colored. Since each string contains an even amount of vertices, at most half of each string are colored and this is obtained only when every second vertex is colored in each string. By counting we see that each string contains $2 n-2$ vertices and we conclude that every second vertex is colored in each string. Because $n \geq 3$ at least one of the isoceles
triangles $H_{0} H_{-2} H_{-4}, H_{1} H_{3} H_{5}$ or $H_{2 n-2} H_{2 n} H_{-(2 n-1)}$ must be colored. Hence there are no colored neighboring vertices.
If there are no colored neighboring vertices we can assume wlog that $H_{i}$ is colored for all odd $i$, but then $H_{1} H_{3} H_{5}$ is an isosceles colored triangle. Hence we have a contradiction, showing that there must neccesarily exists 3 colored vertices forming an isosceles triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be an integer with $n \geq 3$ and assume that $2 n$ vertices of a regular $(4 n+1)$-gon are coloured. Show that there must exist three of the coloured vertices forming an isosceles triangle.
|
Assume that it is possible to color $2 n$ of the vertices of a $4 n+1$-gon such that there are no three colored vertices forming an isosceles triangle. Enumerate the vertices consecutively as $H_{-2 n}, H_{-2 n+1}, \ldots, H_{0}, H_{1}, H_{2}, \ldots, H_{2 n}$ and consider first the case where there are two colored neighboring vertices. Assume wlog that the vertices $H_{0}$ and $H_{1}$ are colored. Then at most one of the vertices $H_{-i}$ and $H_{i}$ are colored for all $i=1,2, \ldots, 2 n$ since these form an isosceles triangle with $H_{0}$. Similarly at most one of $H_{-i}$ and $H_{i+2}$ are colored for all $i=1,2, \ldots, 2 n-2$, and at most one of $H_{-(2 n-1)}$ and $H_{-2 n}$ are colored since these form an isosceles triangles with $H_{1}$. The three vertices $H_{0}, H_{1}, H_{i}, i=2,-1,-2 n$ also form isoceles triangles and hence $H_{-1}, H_{2}, H_{-2 n}$ are not colored. It follows that no consecutive vertices in the two strings
$$
\begin{array}{r}
H_{-2}-H_{4}-H_{-4}-H_{6}-\ldots-H_{2 n-2}-H_{-(2 n-2)}-H_{2 n} \\
H_{3}-H_{-3}-H_{5}-H_{-5}-\ldots-H_{2 n-1}-H_{-(2 n-1)}
\end{array}
$$
are colored. Since each string contains an even amount of vertices, at most half of each string are colored and this is obtained only when every second vertex is colored in each string. By counting we see that each string contains $2 n-2$ vertices and we conclude that every second vertex is colored in each string. Because $n \geq 3$ at least one of the isoceles
triangles $H_{0} H_{-2} H_{-4}, H_{1} H_{3} H_{5}$ or $H_{2 n-2} H_{2 n} H_{-(2 n-1)}$ must be colored. Hence there are no colored neighboring vertices.
If there are no colored neighboring vertices we can assume wlog that $H_{i}$ is colored for all odd $i$, but then $H_{1} H_{3} H_{5}$ is an isosceles colored triangle. Hence we have a contradiction, showing that there must neccesarily exists 3 colored vertices forming an isosceles triangle.
|
{
"resource_path": "Nordic_MO/segmented/en-2019-sol.jsonl",
"problem_match": "\n\nProblem 4",
"solution_match": "\n\nSolution 4"
}
|
0c1c222b-42b8-5482-b662-16834c116234
| 608,038
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.