problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $x, y, z$ be positive real numbers. Prove that:
$$
\frac{x+2 y}{z+2 x+3 y}+\frac{y+2 z}{x+2 y+3 z}+\frac{z+2 x}{y+2 z+3 x} \leq \frac{3}{2}
$$
|
Notice that $\sum_{c y c} \frac{x+2 y}{z+2 x+3 y}=\sum_{c y c}\left(1-\frac{x+y+z}{z+2 x+3 y}\right)=3-(x+y+z) \sum_{c y c} \frac{1}{z+2 x+3 y}$.
We have to proof that $3-(x+y+z) \sum_{c y c} \frac{1}{z+2 x+3 y} \leq \frac{3}{2}$ or $\frac{3}{2(x+y+z)} \leq \sum_{c y c} \frac{1}{z+2 x+3 y}$.
By Cauchy-Schwarz we obtain $\sum_{\text {cyc }} \frac{1}{z+2 x+3 y} \geq \frac{(1+1+1)^{2}}{\sum_{\text {cyc }}(z+2 x+3 y)}=\frac{3}{2(x+y+z)}$.
## Solution 2
Because the inequality is homogenous, we can take $x+y+z=1$.
Denote $x+2 y=a, y+2 z=b, z+2 x=c$. Hence, $a+b+c=3(x+y+z)=3$.
We have $(k-1)^{2} \geq 0 \Leftrightarrow(k+1)^{2} \geq 4 k \Leftrightarrow \frac{k+1}{4} \geq \frac{k}{k+1}$ for all $k>0$.
Hence $\sum_{\text {cyc }} \frac{x+2 y}{z+2 x+3 y}=\sum \frac{a}{1+a} \leq \sum \frac{a+1}{4}=\frac{a+b+c+3}{4}=\frac{3}{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y, z$ be positive real numbers. Prove that:
$$
\frac{x+2 y}{z+2 x+3 y}+\frac{y+2 z}{x+2 y+3 z}+\frac{z+2 x}{y+2 z+3 x} \leq \frac{3}{2}
$$
|
Notice that $\sum_{c y c} \frac{x+2 y}{z+2 x+3 y}=\sum_{c y c}\left(1-\frac{x+y+z}{z+2 x+3 y}\right)=3-(x+y+z) \sum_{c y c} \frac{1}{z+2 x+3 y}$.
We have to proof that $3-(x+y+z) \sum_{c y c} \frac{1}{z+2 x+3 y} \leq \frac{3}{2}$ or $\frac{3}{2(x+y+z)} \leq \sum_{c y c} \frac{1}{z+2 x+3 y}$.
By Cauchy-Schwarz we obtain $\sum_{\text {cyc }} \frac{1}{z+2 x+3 y} \geq \frac{(1+1+1)^{2}}{\sum_{\text {cyc }}(z+2 x+3 y)}=\frac{3}{2(x+y+z)}$.
## Solution 2
Because the inequality is homogenous, we can take $x+y+z=1$.
Denote $x+2 y=a, y+2 z=b, z+2 x=c$. Hence, $a+b+c=3(x+y+z)=3$.
We have $(k-1)^{2} \geq 0 \Leftrightarrow(k+1)^{2} \geq 4 k \Leftrightarrow \frac{k+1}{4} \geq \frac{k}{k+1}$ for all $k>0$.
Hence $\sum_{\text {cyc }} \frac{x+2 y}{z+2 x+3 y}=\sum \frac{a}{1+a} \leq \sum \frac{a+1}{4}=\frac{a+b+c+3}{4}=\frac{3}{2}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-alg-20111.jsonl",
"problem_match": "\nA2 ",
"solution_match": "## Solution 1"
}
|
b7dc794e-d831-5fd1-bd82-613117777a67
| 605,774
|
Let $a, b$ be positive real numbers. Prove that $\sqrt{\frac{a^{2}+a b+b^{2}}{3}}+\sqrt{a b} \leq a+b$.
|
Applying $x+y \leq \sqrt{2\left(x^{2}+y^{2}\right)}$ for $x=\sqrt{\frac{a^{2}+a b+b^{2}}{3}}$ and $y=\sqrt{a b}$, we will obtain $\sqrt{\frac{a^{2}+a b+b^{2}}{3}}+\sqrt{a b} \leq \sqrt{\frac{2 a^{2}+2 a b+2 b^{2}+6 a b}{3}} \leq \sqrt{\frac{3\left(a^{2}+b^{2}+2 a b\right)}{3}}=a+b$.
## Solution 2
The inequality is equivalent to $\frac{a^{2}+a b+b^{2}}{3}+\frac{3 a b}{3}+2 \sqrt{\frac{a b\left(a^{2}+a b+b^{2}\right)}{3}} \leq \frac{3 a^{2}+6 a b+3 b^{2}}{3}$. This can be rewritten as $2 \sqrt{\frac{a b\left(a^{2}+a b+b^{2}\right)}{3}} \leq \frac{2\left(a^{2}+a b+b^{2}\right)}{3}$ or $\sqrt{a b} \leq \sqrt{\frac{a^{2}+a b+b^{2}}{3}}$ which is obviously true since $a^{2}+b^{2}+a b \geq 2 a b+a b=3 a b$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$ be positive real numbers. Prove that $\sqrt{\frac{a^{2}+a b+b^{2}}{3}}+\sqrt{a b} \leq a+b$.
|
Applying $x+y \leq \sqrt{2\left(x^{2}+y^{2}\right)}$ for $x=\sqrt{\frac{a^{2}+a b+b^{2}}{3}}$ and $y=\sqrt{a b}$, we will obtain $\sqrt{\frac{a^{2}+a b+b^{2}}{3}}+\sqrt{a b} \leq \sqrt{\frac{2 a^{2}+2 a b+2 b^{2}+6 a b}{3}} \leq \sqrt{\frac{3\left(a^{2}+b^{2}+2 a b\right)}{3}}=a+b$.
## Solution 2
The inequality is equivalent to $\frac{a^{2}+a b+b^{2}}{3}+\frac{3 a b}{3}+2 \sqrt{\frac{a b\left(a^{2}+a b+b^{2}\right)}{3}} \leq \frac{3 a^{2}+6 a b+3 b^{2}}{3}$. This can be rewritten as $2 \sqrt{\frac{a b\left(a^{2}+a b+b^{2}\right)}{3}} \leq \frac{2\left(a^{2}+a b+b^{2}\right)}{3}$ or $\sqrt{a b} \leq \sqrt{\frac{a^{2}+a b+b^{2}}{3}}$ which is obviously true since $a^{2}+b^{2}+a b \geq 2 a b+a b=3 a b$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-alg-20111.jsonl",
"problem_match": "\nA3 ",
"solution_match": "\nSolution 1"
}
|
c75af119-20c0-527a-8588-f25d765a2fa0
| 605,787
|
Let $x_{i}>1$, for all $i \in\{1,2,3, \ldots, 2011\}$. Prove the inequality $\sum_{i=1}^{2011} \frac{x_{i}^{2}}{x_{i+1}-1} \geq 8044$ where $x_{2012}=x_{1}$. When does equality hold?
|
Realize that $\left(x_{i}-2\right)^{2} \geq 0 \Leftrightarrow x_{i}^{2} \geq 4\left(x_{i}-1\right)$. So we get:
$\frac{x_{1}^{2}}{x_{2}-1}+\frac{x_{2}^{2}}{x_{3}-1}+\ldots+\frac{x_{2011}^{2}}{x_{1}-1} \geq 4\left(\frac{x_{1}-1}{x_{2}-1}+\frac{x_{2}-1}{x_{3}-1}+\ldots+\frac{x_{2011}-1}{x_{1}-1}\right)$. By $A M-G M$ :
$\frac{x_{1}-1}{x_{2}-1}+\frac{x_{2}-1}{x_{3}-1}+\ldots+\frac{x_{2011}-1}{x_{1}-1} \geq 2011 \cdot \sqrt[2011]{\frac{x_{1}-1}{x_{2}-1} \cdot \frac{x_{2}-1}{x_{3}-1} \cdot \ldots \cdot \frac{x_{2011}-1}{x_{1}-1}}=2011$
Finally, we obtain that $\frac{x_{1}^{2}}{x_{2}-1}+\frac{x_{2}^{2}}{x_{3}-1}+\ldots+\frac{x_{2011}^{2}}{x_{1}-1} \geq 8044$.
Equality holds when $\left(x_{i}-2\right)^{2}=0,(\forall) i=\overline{1,2011}$, or $x_{1}=x_{2}=\ldots=x_{2011}=2$.
## Solution 2
All the denominators are greater than 0 , so by Cauchy - Schwar $z$ we have:
$\frac{x_{1}^{2}}{x_{2}-1}+\frac{x_{2}^{2}}{x_{3}-1}+\ldots+\frac{x_{2011}^{2}}{x_{1}-1} \geq \frac{\left(x_{1}+x_{2}+\ldots+x_{2011}\right)^{2}}{x_{1}+x_{2}+\ldots+x_{2011}-2011}$. It remains to prove that $\frac{\left(x_{1}+x_{2}+\ldots+x_{2011}\right)^{2}}{x_{1}+x_{2}+\ldots+x_{2011}-2011} \geq 8044$ or $\left(\sum_{i=1}^{2011} x_{i}\right)^{2}+4 \cdot 2011^{2} \geq 4 \cdot 2011 \cdot \sum_{i=1}^{2011} x_{i}$ which is obviously true by $A M-G M$ for $\left(\sum_{i=1}^{2011} x_{i}\right)^{2}$ and $4 \cdot 2011^{2}$.
Equality holds when $x_{1}+x_{2}+\ldots+x_{2011}=4022$ and $\frac{x_{1}}{x_{2}-1}=\frac{x_{2}}{x_{3}-1}=\ldots=\frac{x_{2011}}{x_{1}-1}$ or $x_{i}^{2}-x_{i}=x_{i-1} x_{i+1}-x_{i-1},(\forall) i=\overline{1,2011} \Rightarrow \sum_{i=1}^{2011} x_{i}^{2}=\sum_{i=1}^{2011} x_{i} x_{i+2}$ where $x_{2012}=x_{1}$ and $x_{2013}=x_{2}$. This means that $x_{1}=x_{2}=\ldots=x_{2011}$.
So equality holds when $x_{1}=x_{2}=\ldots=x_{2011}=2$ since $x_{1}+x_{2}+\ldots+x_{2011}=4022$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x_{i}>1$, for all $i \in\{1,2,3, \ldots, 2011\}$. Prove the inequality $\sum_{i=1}^{2011} \frac{x_{i}^{2}}{x_{i+1}-1} \geq 8044$ where $x_{2012}=x_{1}$. When does equality hold?
|
Realize that $\left(x_{i}-2\right)^{2} \geq 0 \Leftrightarrow x_{i}^{2} \geq 4\left(x_{i}-1\right)$. So we get:
$\frac{x_{1}^{2}}{x_{2}-1}+\frac{x_{2}^{2}}{x_{3}-1}+\ldots+\frac{x_{2011}^{2}}{x_{1}-1} \geq 4\left(\frac{x_{1}-1}{x_{2}-1}+\frac{x_{2}-1}{x_{3}-1}+\ldots+\frac{x_{2011}-1}{x_{1}-1}\right)$. By $A M-G M$ :
$\frac{x_{1}-1}{x_{2}-1}+\frac{x_{2}-1}{x_{3}-1}+\ldots+\frac{x_{2011}-1}{x_{1}-1} \geq 2011 \cdot \sqrt[2011]{\frac{x_{1}-1}{x_{2}-1} \cdot \frac{x_{2}-1}{x_{3}-1} \cdot \ldots \cdot \frac{x_{2011}-1}{x_{1}-1}}=2011$
Finally, we obtain that $\frac{x_{1}^{2}}{x_{2}-1}+\frac{x_{2}^{2}}{x_{3}-1}+\ldots+\frac{x_{2011}^{2}}{x_{1}-1} \geq 8044$.
Equality holds when $\left(x_{i}-2\right)^{2}=0,(\forall) i=\overline{1,2011}$, or $x_{1}=x_{2}=\ldots=x_{2011}=2$.
## Solution 2
All the denominators are greater than 0 , so by Cauchy - Schwar $z$ we have:
$\frac{x_{1}^{2}}{x_{2}-1}+\frac{x_{2}^{2}}{x_{3}-1}+\ldots+\frac{x_{2011}^{2}}{x_{1}-1} \geq \frac{\left(x_{1}+x_{2}+\ldots+x_{2011}\right)^{2}}{x_{1}+x_{2}+\ldots+x_{2011}-2011}$. It remains to prove that $\frac{\left(x_{1}+x_{2}+\ldots+x_{2011}\right)^{2}}{x_{1}+x_{2}+\ldots+x_{2011}-2011} \geq 8044$ or $\left(\sum_{i=1}^{2011} x_{i}\right)^{2}+4 \cdot 2011^{2} \geq 4 \cdot 2011 \cdot \sum_{i=1}^{2011} x_{i}$ which is obviously true by $A M-G M$ for $\left(\sum_{i=1}^{2011} x_{i}\right)^{2}$ and $4 \cdot 2011^{2}$.
Equality holds when $x_{1}+x_{2}+\ldots+x_{2011}=4022$ and $\frac{x_{1}}{x_{2}-1}=\frac{x_{2}}{x_{3}-1}=\ldots=\frac{x_{2011}}{x_{1}-1}$ or $x_{i}^{2}-x_{i}=x_{i-1} x_{i+1}-x_{i-1},(\forall) i=\overline{1,2011} \Rightarrow \sum_{i=1}^{2011} x_{i}^{2}=\sum_{i=1}^{2011} x_{i} x_{i+2}$ where $x_{2012}=x_{1}$ and $x_{2013}=x_{2}$. This means that $x_{1}=x_{2}=\ldots=x_{2011}$.
So equality holds when $x_{1}=x_{2}=\ldots=x_{2011}=2$ since $x_{1}+x_{2}+\ldots+x_{2011}=4022$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-alg-20111.jsonl",
"problem_match": "\nA6 ",
"solution_match": "## Solution 1"
}
|
fca810a1-07fe-5d0c-a1ed-1c23e67eab2e
| 605,815
|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers satisfying $\sum_{k=1}^{n-1} \min \left(x_{k} ; x_{k+1}\right)=\min \left(x_{1}, x_{n}\right)$.
Prove that $\sum_{k=2}^{n-1} x_{k} \geq 0$.
|
Case I. If $\min \left(x_{1}, x_{n}\right)=x_{1}$, we know that $x_{k} \geq \min \left(x_{k} ; x_{k+1}\right)$ for all $k \in\{1,2,3, \ldots, n-1\}$. So $x_{1}+x_{2}+\ldots+x_{n-1} \geq \sum_{k=1}^{n-1} \min \left(x_{k} ; x_{k+1}\right)=\min \left(x_{1}, x_{n}\right)=x_{1}$, hence $\sum_{k=2}^{n-1} x_{k} \geq 0$.
Case II. If $\min \left(x_{1}, x_{n}\right)=x_{n}$, we know that $x_{k} \geq \min \left(x_{k-1} ; x_{k}\right)$ for all $k \in\{2,3,4, \ldots, n\}$. So $x_{2}+x_{3}+\ldots+x_{n} \geq \sum_{k=1}^{n-1} \min \left(x_{k} ; x_{k+1}\right)=\min \left(x_{1}, x_{n}\right)=x_{n}$, hence $\sum_{k=2}^{n-1} x_{k} \geq 0$.
## Solution 2
Since $\min (a, b)=\frac{1}{2}(a+b-|a-b|)$, after substitutions, we will have:
$$
\begin{aligned}
\sum_{k=1}^{n-1} \frac{1}{2}\left(x_{k}+x_{k+1}-\left|x_{k}-x_{k+1}\right|\right) & =\frac{1}{2}\left(x_{1}+x_{n}-\left|x_{1}-x_{n}\right|\right) \Leftrightarrow \ldots \\
2\left(x_{2}+x_{3}+\ldots+x_{n-1}\right)+\left|x_{1}-x_{n}\right| & =\left|x_{1}-x_{2}\right|+\left|x_{2}-x_{3}\right|+\ldots+\left|x_{n-1}-x_{n}\right|
\end{aligned}
$$
As $\left|x_{1}-x_{2}\right|+\left|x_{2}-x_{3}\right|+\ldots+\left|x_{n-1}-x_{n}\right| \geq\left|x_{1}-x_{2}+x_{2}-x_{3}+\ldots+x_{n-1}-x_{n}\right|=\left|x_{1}-x_{n}\right|$, we obtain the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers satisfying $\sum_{k=1}^{n-1} \min \left(x_{k} ; x_{k+1}\right)=\min \left(x_{1}, x_{n}\right)$.
Prove that $\sum_{k=2}^{n-1} x_{k} \geq 0$.
|
Case I. If $\min \left(x_{1}, x_{n}\right)=x_{1}$, we know that $x_{k} \geq \min \left(x_{k} ; x_{k+1}\right)$ for all $k \in\{1,2,3, \ldots, n-1\}$. So $x_{1}+x_{2}+\ldots+x_{n-1} \geq \sum_{k=1}^{n-1} \min \left(x_{k} ; x_{k+1}\right)=\min \left(x_{1}, x_{n}\right)=x_{1}$, hence $\sum_{k=2}^{n-1} x_{k} \geq 0$.
Case II. If $\min \left(x_{1}, x_{n}\right)=x_{n}$, we know that $x_{k} \geq \min \left(x_{k-1} ; x_{k}\right)$ for all $k \in\{2,3,4, \ldots, n\}$. So $x_{2}+x_{3}+\ldots+x_{n} \geq \sum_{k=1}^{n-1} \min \left(x_{k} ; x_{k+1}\right)=\min \left(x_{1}, x_{n}\right)=x_{n}$, hence $\sum_{k=2}^{n-1} x_{k} \geq 0$.
## Solution 2
Since $\min (a, b)=\frac{1}{2}(a+b-|a-b|)$, after substitutions, we will have:
$$
\begin{aligned}
\sum_{k=1}^{n-1} \frac{1}{2}\left(x_{k}+x_{k+1}-\left|x_{k}-x_{k+1}\right|\right) & =\frac{1}{2}\left(x_{1}+x_{n}-\left|x_{1}-x_{n}\right|\right) \Leftrightarrow \ldots \\
2\left(x_{2}+x_{3}+\ldots+x_{n-1}\right)+\left|x_{1}-x_{n}\right| & =\left|x_{1}-x_{2}\right|+\left|x_{2}-x_{3}\right|+\ldots+\left|x_{n-1}-x_{n}\right|
\end{aligned}
$$
As $\left|x_{1}-x_{2}\right|+\left|x_{2}-x_{3}\right|+\ldots+\left|x_{n-1}-x_{n}\right| \geq\left|x_{1}-x_{2}+x_{2}-x_{3}+\ldots+x_{n-1}-x_{n}\right|=\left|x_{1}-x_{n}\right|$, we obtain the desired result.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-alg-20111.jsonl",
"problem_match": "\nA9 ",
"solution_match": "## Solution 1"
}
|
585f2765-2b24-5c0a-bbae-ebeeed6c1a07
| 605,844
|
Inside of a square whose side length is 1 there are a few circles such that the sum of their circumferences is equal to 10 . Show that there exists a line that meets alt least four of these circles.
|
Find projections of all given circles on one of the sides of the square. The projection of each circle is a segment whose length is equal to the length of a diameter of this circle. Since the sum of the lengths of all circles' diameters is equal to $10 / \pi$, it follows that the sum of the lengths of all mentioned projections is equal to $10 / \pi>3$. Because the side of the square is equal to 1 , we conclude that at least one point is covered with at least four of these projections. Hence, a perpendicular line to the projection side passing through this point meets at least four of the given circles, so this is a line with the desired property.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Inside of a square whose side length is 1 there are a few circles such that the sum of their circumferences is equal to 10 . Show that there exists a line that meets alt least four of these circles.
|
Find projections of all given circles on one of the sides of the square. The projection of each circle is a segment whose length is equal to the length of a diameter of this circle. Since the sum of the lengths of all circles' diameters is equal to $10 / \pi$, it follows that the sum of the lengths of all mentioned projections is equal to $10 / \pi>3$. Because the side of the square is equal to 1 , we conclude that at least one point is covered with at least four of these projections. Hence, a perpendicular line to the projection side passing through this point meets at least four of the given circles, so this is a line with the desired property.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-combi-2011.jsonl",
"problem_match": "\nC1 ",
"solution_match": "\nSolution"
}
|
214174d3-46fc-530e-9da5-800cd5bac322
| 605,856
|
Determine the polygons with $n$ sides $(n \geq 4)$, not necessarily convex, which satisfy the property that the reflection of every vertex of polygon with respect to every diagonal of the polygon does not fall outside the polygon.
Note: Each segment joining two non-neighboring vertices of the polygon is a diagonal. The reflection is considered with respect to the support line of the diagonal.
|
A polygon with this property has to be convex, otherwise we consider an edge of the convex hull of this set of vertices which is not an edge of this polygon. All the others vertices are situated in one of the half-planes determined by the support-line of this edge, therefore the reflections of the others vertices falls outside the polygon.
Now we choose a diagonal. It divides the polygon into two parts, $P 1$ and $P 2$. The reflection of $P 1$ falls into the interior of $P 2$ and viceversa. As a consequence, the diagonal is a symmetry axis for the polygon. Then every diagonal of the polygon bisects the angles of the polygon and this means that there are 4 vertices and the polygon is a rhombus. Each rhombus satisfies the desired condition.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Determine the polygons with $n$ sides $(n \geq 4)$, not necessarily convex, which satisfy the property that the reflection of every vertex of polygon with respect to every diagonal of the polygon does not fall outside the polygon.
Note: Each segment joining two non-neighboring vertices of the polygon is a diagonal. The reflection is considered with respect to the support line of the diagonal.
|
A polygon with this property has to be convex, otherwise we consider an edge of the convex hull of this set of vertices which is not an edge of this polygon. All the others vertices are situated in one of the half-planes determined by the support-line of this edge, therefore the reflections of the others vertices falls outside the polygon.
Now we choose a diagonal. It divides the polygon into two parts, $P 1$ and $P 2$. The reflection of $P 1$ falls into the interior of $P 2$ and viceversa. As a consequence, the diagonal is a symmetry axis for the polygon. Then every diagonal of the polygon bisects the angles of the polygon and this means that there are 4 vertices and the polygon is a rhombus. Each rhombus satisfies the desired condition.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-combi-2011.jsonl",
"problem_match": "\nC8 ",
"solution_match": "## Solution"
}
|
ec207dbf-601a-5521-acc5-fd4ff9ad4324
| 605,930
|
Decide if it is possible to consider 2011 points in a plane such that the distance between every two of these points is different from 1 and each unit circle centered at one of these points leaves exactly 1005 points outside the circle.
|
NO. If such a configuration existed, the number of segments starting from each of the 2011 points towards the other one and having length less than 1 would be 1005 . Since each segment is counted twice, their total number would be $1005 \cdot 2011 / 2$ which is not an integer, contradiction!
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Decide if it is possible to consider 2011 points in a plane such that the distance between every two of these points is different from 1 and each unit circle centered at one of these points leaves exactly 1005 points outside the circle.
|
NO. If such a configuration existed, the number of segments starting from each of the 2011 points towards the other one and having length less than 1 would be 1005 . Since each segment is counted twice, their total number would be $1005 \cdot 2011 / 2$ which is not an integer, contradiction!
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-combi-2011.jsonl",
"problem_match": "\nC9 ",
"solution_match": "## Solution"
}
|
bdec69b4-7e5d-5f79-8e5a-729e96e85b69
| 605,938
|
Let $A B C$ be an isosceles triangle with $A B=A C$. On the extension of the side $[C A]$ we consider the point $D$ such that $A D<A C$. The perpendicular bisector of the segment $[B D]$ meets the internal and the external bisectors of the angle $\widehat{B A C}$ at the points $E$ and $Z$, respectively. Prove that the points $A, E, D, Z$ are concyclic.
|
## Solution 2
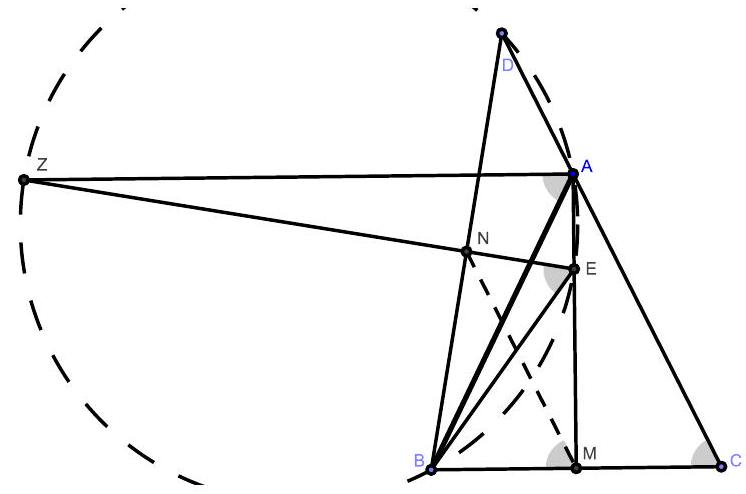
In $\triangle A B D$ the ray $[A Z$ bisects the angle $\widehat{D A B}$ and the line $Z E$ is the perpendicular bisector of the side $[B D]$. Hence $Z$ belongs to the circumcircle of $\triangle A B D$.
Therefore the points $A, B, D, Z$ are concyclic.
Let $M$ and $N$ be the midpoints of the sides $[B C]$ and $[D B]$, respectively. Then $N \in Z E$ and $M \in A E$. Next, $[M N]$ is a midline in $\triangle B C D$, so $M N \| C D \Rightarrow \widehat{N M B} \equiv \widehat{A C B}$.
But $[A Z$ is the external bisector of the angle $\widehat{B A C}$ of $\triangle A B C$, hence $\widehat{B A Z} \equiv \widehat{A C B}$. Therefore, $\widehat{N M B} \equiv \widehat{B A Z}$. In the quadrilateral $B M E N$ we have $\widehat{B N E}=\widehat{B M E}=90^{\circ}$, so $B M E N$ is cyclic $\Rightarrow \widehat{N M B} \equiv \widehat{B E Z}$, hence $\widehat{B A Z} \equiv \widehat{B E Z} \Rightarrow A E B Z$ is cyclic.
Therefore, since $A, B, D, Z$ are also concyclic, we conclude that $A E Z D$ is cyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an isosceles triangle with $A B=A C$. On the extension of the side $[C A]$ we consider the point $D$ such that $A D<A C$. The perpendicular bisector of the segment $[B D]$ meets the internal and the external bisectors of the angle $\widehat{B A C}$ at the points $E$ and $Z$, respectively. Prove that the points $A, E, D, Z$ are concyclic.
|
## Solution 2

In $\triangle A B D$ the ray $[A Z$ bisects the angle $\widehat{D A B}$ and the line $Z E$ is the perpendicular bisector of the side $[B D]$. Hence $Z$ belongs to the circumcircle of $\triangle A B D$.
Therefore the points $A, B, D, Z$ are concyclic.
Let $M$ and $N$ be the midpoints of the sides $[B C]$ and $[D B]$, respectively. Then $N \in Z E$ and $M \in A E$. Next, $[M N]$ is a midline in $\triangle B C D$, so $M N \| C D \Rightarrow \widehat{N M B} \equiv \widehat{A C B}$.
But $[A Z$ is the external bisector of the angle $\widehat{B A C}$ of $\triangle A B C$, hence $\widehat{B A Z} \equiv \widehat{A C B}$. Therefore, $\widehat{N M B} \equiv \widehat{B A Z}$. In the quadrilateral $B M E N$ we have $\widehat{B N E}=\widehat{B M E}=90^{\circ}$, so $B M E N$ is cyclic $\Rightarrow \widehat{N M B} \equiv \widehat{B E Z}$, hence $\widehat{B A Z} \equiv \widehat{B E Z} \Rightarrow A E B Z$ is cyclic.
Therefore, since $A, B, D, Z$ are also concyclic, we conclude that $A E Z D$ is cyclic.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-geome-2011.jsonl",
"problem_match": "\nG1 ",
"solution_match": "\nSolution 1"
}
|
89eb8c7c-020d-587c-93af-81a552cf0169
| 605,948
|
Let $A B C$ be an isosceles triangle with $A B=A C$. On the extension of the side $[C A]$ we consider the point $D$ such that $A D<A C$. The perpendicular bisector of the segment $[B D]$ meets the internal and the external bisectors of the angle $\widehat{B A C}$ at the points $E$ and $Z$, respectively. Prove that the points $A, E, D, Z$ are concyclic.
|
## Solution 3
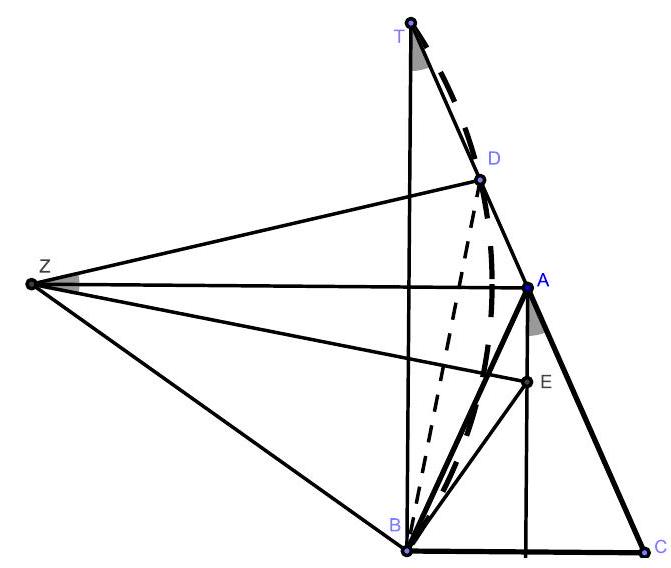
Let $T$ be the symmetric of $B$ with respect to the axis $A Z$. Obviously $T \in A D$. Since $A E$ and $B T$ are both perpendiculars to $A Z$, they are parallel, so $\widehat{B A C} \equiv \widehat{B T A}$. (1)
Since $Z B=Z T=Z D$, the point $Z$ is the circumcenter of $\triangle B D T$.
Therefore $\widehat{B T A}=\widehat{B Z D} / 2=\widehat{E Z D}$.
From (1) and (2) we conclude that $\widehat{E A C} \equiv \widehat{E Z D}$, which gives that $A E D Z$ is cyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an isosceles triangle with $A B=A C$. On the extension of the side $[C A]$ we consider the point $D$ such that $A D<A C$. The perpendicular bisector of the segment $[B D]$ meets the internal and the external bisectors of the angle $\widehat{B A C}$ at the points $E$ and $Z$, respectively. Prove that the points $A, E, D, Z$ are concyclic.
|
## Solution 3

Let $T$ be the symmetric of $B$ with respect to the axis $A Z$. Obviously $T \in A D$. Since $A E$ and $B T$ are both perpendiculars to $A Z$, they are parallel, so $\widehat{B A C} \equiv \widehat{B T A}$. (1)
Since $Z B=Z T=Z D$, the point $Z$ is the circumcenter of $\triangle B D T$.
Therefore $\widehat{B T A}=\widehat{B Z D} / 2=\widehat{E Z D}$.
From (1) and (2) we conclude that $\widehat{E A C} \equiv \widehat{E Z D}$, which gives that $A E D Z$ is cyclic.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-geome-2011.jsonl",
"problem_match": "\nG1 ",
"solution_match": "\nSolution 1"
}
|
89eb8c7c-020d-587c-93af-81a552cf0169
| 605,948
|
Let $A B C D$ be a convex quadrilateral, $E$ and $F$ points on the sides $A B$ and $C D$, respectively, such that $\frac{A B}{A E}=\frac{C D}{D F}=n$. Denote by $S$ the area of the quadrilateral $A E F D$. Prove that $S \leq \frac{A B \cdot C D+n(n-1) \cdot D A^{2}+n \cdot A D \cdot B C}{2 n^{2}}$.
|
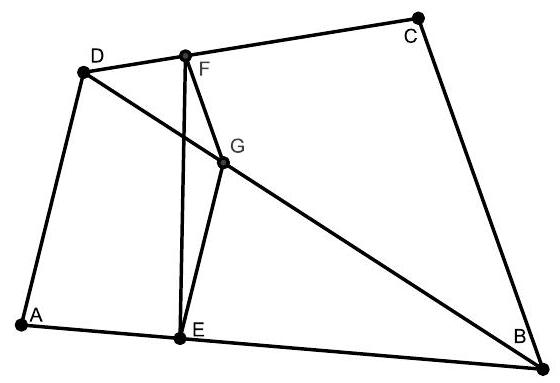
By Ptolemy's Inequality in $A E F D$, we get $S=\frac{A F \cdot D E \cdot \sin (\widehat{A F, D E})}{2} \leq \frac{A F \cdot D E}{2} \leq$ $\frac{A E \cdot D F+A D \cdot E F}{2}=\frac{A B \cdot C D+n^{2} \cdot D A \cdot E F}{2 n^{2}}$.
Let $G$ be a point on diagonal $B D$ such that $\frac{D B}{D G}=n$. By Thales's Theorem we get $G E=\frac{(n-1) A D}{n}$ and $G F=\frac{B C}{n}$. Applying the inequality of triangle in $\triangle E G F$ we get $E F \leq E G+G F=\frac{(n-1) A D+B C}{n}$. Now, we get:
$S \leq \frac{A B \cdot C D+n^{2} A D \cdot E F}{2 n^{2}} \leq \frac{A B \cdot C D+n(n-1) \cdot D A^{2}+n \cdot A D \cdot B C}{2 n^{2}}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral, $E$ and $F$ points on the sides $A B$ and $C D$, respectively, such that $\frac{A B}{A E}=\frac{C D}{D F}=n$. Denote by $S$ the area of the quadrilateral $A E F D$. Prove that $S \leq \frac{A B \cdot C D+n(n-1) \cdot D A^{2}+n \cdot A D \cdot B C}{2 n^{2}}$.
|

By Ptolemy's Inequality in $A E F D$, we get $S=\frac{A F \cdot D E \cdot \sin (\widehat{A F, D E})}{2} \leq \frac{A F \cdot D E}{2} \leq$ $\frac{A E \cdot D F+A D \cdot E F}{2}=\frac{A B \cdot C D+n^{2} \cdot D A \cdot E F}{2 n^{2}}$.
Let $G$ be a point on diagonal $B D$ such that $\frac{D B}{D G}=n$. By Thales's Theorem we get $G E=\frac{(n-1) A D}{n}$ and $G F=\frac{B C}{n}$. Applying the inequality of triangle in $\triangle E G F$ we get $E F \leq E G+G F=\frac{(n-1) A D+B C}{n}$. Now, we get:
$S \leq \frac{A B \cdot C D+n^{2} A D \cdot E F}{2 n^{2}} \leq \frac{A B \cdot C D+n(n-1) \cdot D A^{2}+n \cdot A D \cdot B C}{2 n^{2}}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-geome-2011.jsonl",
"problem_match": "\nG6 ",
"solution_match": "## Solution"
}
|
82a6867a-7f7a-53c5-951f-42d3b2cf4159
| 606,002
|
Let $a, b, c$ be lengths of triangle sides, $p=\frac{a}{b}+\frac{b}{c}+\frac{c}{a}$ and $q=\frac{a}{c}+\frac{c}{b}+\frac{b}{a}$.
Prove that $|p-q|<1$.
|
One has
$$
\begin{aligned}
a b c|p-q| & =a b c\left|\frac{c-b}{a}+\frac{a-c}{b}+\frac{b-a}{c}\right| \\
& =\left|b c^{2}-b^{2} c+a^{2} c-a c^{2}+a b^{2}-a^{2} b\right|= \\
& =\left|a b c-a c^{2}-a^{2} b+a^{2} c-b^{2} c+b c^{2}+a b^{2}-a b c\right|= \\
& =\left|(b-c)\left(a c-a^{2}-b c+a b\right)\right|= \\
& =|(b-c)(c-a)(a-b)| .
\end{aligned}
$$
Since $|b-c|<a,|c-a|<b$ and $|a-b|<c$ we infere
$$
|(b-c)(c-a)(a-b)|<a b c
$$
and
$$
|p-q|=\frac{|(b-c)(c-a)(a-b)|}{a b c}<1
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be lengths of triangle sides, $p=\frac{a}{b}+\frac{b}{c}+\frac{c}{a}$ and $q=\frac{a}{c}+\frac{c}{b}+\frac{b}{a}$.
Prove that $|p-q|<1$.
|
One has
$$
\begin{aligned}
a b c|p-q| & =a b c\left|\frac{c-b}{a}+\frac{a-c}{b}+\frac{b-a}{c}\right| \\
& =\left|b c^{2}-b^{2} c+a^{2} c-a c^{2}+a b^{2}-a^{2} b\right|= \\
& =\left|a b c-a c^{2}-a^{2} b+a^{2} c-b^{2} c+b c^{2}+a b^{2}-a b c\right|= \\
& =\left|(b-c)\left(a c-a^{2}-b c+a b\right)\right|= \\
& =|(b-c)(c-a)(a-b)| .
\end{aligned}
$$
Since $|b-c|<a,|c-a|<b$ and $|a-b|<c$ we infere
$$
|(b-c)(c-a)(a-b)|<a b c
$$
and
$$
|p-q|=\frac{|(b-c)(c-a)(a-b)|}{a b c}<1
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2003_shl.jsonl",
"problem_match": "\nALG 2.",
"solution_match": "\nSolution:"
}
|
cd8c746f-11ee-5edb-bcc7-2432dc350a34
| 606,017
|
Let $a, b, c$ be real numbers such that $a^{2}+b^{2}+c^{2}=1$. Prove that. $P=a b+b c+c a-2(a+b+c) \geq-\frac{5}{2}$. Are there values of $a, b, c$, such that $P=-\frac{5}{2}$.
|
We have $a b+b c+c a=\frac{(a+b+c)^{2}-c^{2}-b^{2}-a^{2}}{2}=\frac{(a+b+c)^{2}-1}{2}$.
If put $t=a+b+c$ we obtain
$$
P=\frac{t^{2}-1}{2}-2 t=\frac{t^{2}-4 t-1}{2}=\frac{(t-2)^{2}-5}{2} \geq-\frac{5}{2}
$$
Obviously $P=-\frac{5}{2}$ when $t=2$, i.e. $a+b+c=2$, or $c=2-a-b$. Substitute in $a^{2}+b^{2}+c^{2}=1$ and obtain $2 a^{2}+2(b-2) a+2 b^{2}-4 b+3=0$. Sinse this quadratic equation has solutions it follows that $(b-2)^{2}-2\left(2 b^{2}-3 b+3\right) \geq 0$, from where
$$
-3 b^{2}+4 b-6 \geq 0
$$
or
$$
3 b^{2}-4 b+6 \leq 0
$$
But $3 b^{2}-4 b+6=3\left(b-\frac{2}{3}\right)^{2}+\frac{14}{3}>0$. The contradiction shows that $P=-\frac{5}{2}$.
Comment: By the Cauchy Schwarz inequality $|t| \leq \sqrt{3}$, so the smallest value of $P$ is attained at $t=\sqrt{3}$ and equals $1-2 \sqrt{3} \approx-2.46$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be real numbers such that $a^{2}+b^{2}+c^{2}=1$. Prove that. $P=a b+b c+c a-2(a+b+c) \geq-\frac{5}{2}$. Are there values of $a, b, c$, such that $P=-\frac{5}{2}$.
|
We have $a b+b c+c a=\frac{(a+b+c)^{2}-c^{2}-b^{2}-a^{2}}{2}=\frac{(a+b+c)^{2}-1}{2}$.
If put $t=a+b+c$ we obtain
$$
P=\frac{t^{2}-1}{2}-2 t=\frac{t^{2}-4 t-1}{2}=\frac{(t-2)^{2}-5}{2} \geq-\frac{5}{2}
$$
Obviously $P=-\frac{5}{2}$ when $t=2$, i.e. $a+b+c=2$, or $c=2-a-b$. Substitute in $a^{2}+b^{2}+c^{2}=1$ and obtain $2 a^{2}+2(b-2) a+2 b^{2}-4 b+3=0$. Sinse this quadratic equation has solutions it follows that $(b-2)^{2}-2\left(2 b^{2}-3 b+3\right) \geq 0$, from where
$$
-3 b^{2}+4 b-6 \geq 0
$$
or
$$
3 b^{2}-4 b+6 \leq 0
$$
But $3 b^{2}-4 b+6=3\left(b-\frac{2}{3}\right)^{2}+\frac{14}{3}>0$. The contradiction shows that $P=-\frac{5}{2}$.
Comment: By the Cauchy Schwarz inequality $|t| \leq \sqrt{3}$, so the smallest value of $P$ is attained at $t=\sqrt{3}$ and equals $1-2 \sqrt{3} \approx-2.46$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2003_shl.jsonl",
"problem_match": "\nALG 3:",
"solution_match": "\nSolution:"
}
|
16791a9d-1aca-5258-af69-b8d97b9bbb4c
| 606,026
|
. Let $a, b, c$ be positive numbers such that $a b+b c+c a=3$. Prove that
$$
a+b+c \geq a b c+2
$$
|
Eliminating $c$ gives
$$
a+b+c-a b c=a+b+(1-a b) c=a+b+\frac{(1-a b)(3-a b)}{a+b}
$$
Put $x=\sqrt{a b}$. Then $a+b \geq 2 x$, and since $1<x^{2}<3, \frac{(1-a b)(3-a b)}{a+b} \geq \frac{\left(1-x^{2}\right)\left(3-x^{2}\right)}{2 x}$.
It then suffices to prove that
$$
2 x+\frac{\left(1-x^{2}\right)\left(3-x^{2}\right)}{2 x} \geq 2
$$
This iast inequality follows from the arithrnelic-geomeric means inequadily
$$
2 x+\frac{\left(1-x^{2}\right)\left(3-x^{2}\right)}{2 x}=\frac{3+x^{4}}{2 x}=\frac{1}{2 x}+\frac{1}{2 x}+\frac{1}{2 x}+\frac{x^{3}}{2} \geq 4\left(\frac{1}{-16}\right)^{\frac{1}{4}}=2
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
. Let $a, b, c$ be positive numbers such that $a b+b c+c a=3$. Prove that
$$
a+b+c \geq a b c+2
$$
|
Eliminating $c$ gives
$$
a+b+c-a b c=a+b+(1-a b) c=a+b+\frac{(1-a b)(3-a b)}{a+b}
$$
Put $x=\sqrt{a b}$. Then $a+b \geq 2 x$, and since $1<x^{2}<3, \frac{(1-a b)(3-a b)}{a+b} \geq \frac{\left(1-x^{2}\right)\left(3-x^{2}\right)}{2 x}$.
It then suffices to prove that
$$
2 x+\frac{\left(1-x^{2}\right)\left(3-x^{2}\right)}{2 x} \geq 2
$$
This iast inequality follows from the arithrnelic-geomeric means inequadily
$$
2 x+\frac{\left(1-x^{2}\right)\left(3-x^{2}\right)}{2 x}=\frac{3+x^{4}}{2 x}=\frac{1}{2 x}+\frac{1}{2 x}+\frac{1}{2 x}+\frac{x^{3}}{2} \geq 4\left(\frac{1}{-16}\right)^{\frac{1}{4}}=2
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2003_shl.jsonl",
"problem_match": "\nALG 6'",
"solution_match": "\nSolution."
}
|
c2ce0366-1ec5-5396-b69d-a4c7877b35ae
| 606,059
|
.
Let $x, y, z$ be real numbers greater than -1 . Prove that
$$
\frac{1+x^{2}}{1+y+z^{2}}+\frac{1+y^{2}}{1+z+x^{2}}+\frac{1+z^{2}}{1+x+y^{2}} \geq 2
$$
|
We have $y \leq \frac{1+y^{2}}{2}$, hence $\quad$
$$
\frac{1+x^{2}}{1+y+z^{2}} \geq \frac{1+x^{2}}{1+z^{2}+\frac{1+\dot{y}^{2}}{2}}
$$
and the similar inequalities.
Setting $a=1+x^{2}, b=1+y^{2}, c=1+z^{2}$, it sufices to prove that
$$
\frac{a}{2 c+b}+\frac{b}{2 a+c}+\frac{c}{2 b+a} \geq 1
$$
for all $a, b, c \geq 0$.
Put $A=2 c+b, B=2 a+c, C=2 b+a$. Then
$$
a=\frac{C+4 B-2 A}{9}, b=\frac{A+4 C-2 B}{9}, c=\frac{B+4 A-2 C}{9}
$$
and (1) rewrites as
$$
\frac{C+4 B-2 A}{A}+\frac{A+4 C-2 B}{B}+\frac{B+4 A-2 C}{C} \geq 9
$$
and consequently
$$
\frac{C}{A}+\frac{A}{B}+\frac{B}{C}+4\left(\frac{B}{A}+\frac{C}{B}+\frac{A}{C}\right) \geq 15
$$
As $A, B, C>0$, by $A M-G M$ inequality we have
$$
\frac{A}{B}+\frac{B}{C}+\frac{C}{A} \geq 3 \sqrt[3]{\frac{A}{B} \cdot \frac{B}{C} \cdot \frac{C}{A}}
$$
and
$$
\frac{B}{A}+\frac{C}{B}+\frac{A}{C} \geq 3
$$
and we are done.
Alternative solution for inequality (1).
By the Cauchy-Schwarz inequality,
$$
\frac{a}{2 c+b}+\frac{b}{2 a+c}+\frac{c}{2 b+a}=\frac{a^{2}}{2 a c+a b}+\frac{b^{2}}{2 a b+c b}+\frac{c^{2}}{2 b c+a c} \geq \frac{(a+b+c)^{2}}{3(a b+b c+c a)} \geq 1
$$
The last inequality reduces immediately to the obvious $a^{2}+b^{2}+c^{2} \geq a b+b c+c a$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
.
Let $x, y, z$ be real numbers greater than -1 . Prove that
$$
\frac{1+x^{2}}{1+y+z^{2}}+\frac{1+y^{2}}{1+z+x^{2}}+\frac{1+z^{2}}{1+x+y^{2}} \geq 2
$$
|
We have $y \leq \frac{1+y^{2}}{2}$, hence $\quad$
$$
\frac{1+x^{2}}{1+y+z^{2}} \geq \frac{1+x^{2}}{1+z^{2}+\frac{1+\dot{y}^{2}}{2}}
$$
and the similar inequalities.
Setting $a=1+x^{2}, b=1+y^{2}, c=1+z^{2}$, it sufices to prove that
$$
\frac{a}{2 c+b}+\frac{b}{2 a+c}+\frac{c}{2 b+a} \geq 1
$$
for all $a, b, c \geq 0$.
Put $A=2 c+b, B=2 a+c, C=2 b+a$. Then
$$
a=\frac{C+4 B-2 A}{9}, b=\frac{A+4 C-2 B}{9}, c=\frac{B+4 A-2 C}{9}
$$
and (1) rewrites as
$$
\frac{C+4 B-2 A}{A}+\frac{A+4 C-2 B}{B}+\frac{B+4 A-2 C}{C} \geq 9
$$
and consequently
$$
\frac{C}{A}+\frac{A}{B}+\frac{B}{C}+4\left(\frac{B}{A}+\frac{C}{B}+\frac{A}{C}\right) \geq 15
$$
As $A, B, C>0$, by $A M-G M$ inequality we have
$$
\frac{A}{B}+\frac{B}{C}+\frac{C}{A} \geq 3 \sqrt[3]{\frac{A}{B} \cdot \frac{B}{C} \cdot \frac{C}{A}}
$$
and
$$
\frac{B}{A}+\frac{C}{B}+\frac{A}{C} \geq 3
$$
and we are done.
Alternative solution for inequality (1).
By the Cauchy-Schwarz inequality,
$$
\frac{a}{2 c+b}+\frac{b}{2 a+c}+\frac{c}{2 b+a}=\frac{a^{2}}{2 a c+a b}+\frac{b^{2}}{2 a b+c b}+\frac{c^{2}}{2 b c+a c} \geq \frac{(a+b+c)^{2}}{3(a b+b c+c a)} \geq 1
$$
The last inequality reduces immediately to the obvious $a^{2}+b^{2}+c^{2} \geq a b+b c+c a$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2003_shl.jsonl",
"problem_match": "\nALG 7 ",
"solution_match": "\nSolution."
}
|
5de282a1-3143-52c3-988a-413a7420cf43
| 606,066
|
Prove that there exist two sets $A=\{x, y, z\}$ and $B=\{m, n, p\}$ of positive integers greater than 2003 such that the sets have no common elements and the equalities $x+y+z=m+n+p$ and $x^{2}+y^{2}+z^{2}=m^{2}+n^{2}+p^{2}$ hold.
|
Let $A B C$ be a triangle with $B C=a, A C=b, A B=c$ and $a<b<c$. Denote by $m_{a}, m_{b}, m_{c}$ the lengths of medianes drawing from the vertices $A, B, C$ respectively. Using the formulas
$$
4 m_{a}^{2}=2\left(b^{2}+c^{2}\right)-a^{2}, 4 m_{b}^{2}=2\left(a^{2}+c^{2}\right)-b^{2}, 4 m_{c}^{2}=2\left(a^{2}+b^{2}\right)-c^{2}
$$
we obtain the relations
$$
\begin{gathered}
4 m_{a}^{2}+4 m_{b}^{2}+4 m_{c}^{2}=3 a^{2}+3 b^{2}+3 c^{2} \\
\left(4 m_{a}^{2}\right)^{2}+\left(4 m_{b}^{2}\right)^{2}+\left(4 m_{c}^{2}\right)^{2}=\left(2 b^{2}+2 c^{2}-a^{2}\right)^{2}+ \\
\left(2 a^{2}+2 c^{2}-b^{2}\right)^{2}+\left(2 a^{2}+2 b^{2}-c^{2}\right)^{2}=9 a^{4}+9 b^{4}+9 c^{4}= \\
\left(3 a^{2}\right)^{2}+\left(3 b^{2}\right)^{2}+\left(3 c^{2}\right)^{2}
\end{gathered}
$$
We put $A=\left\{4 m_{a}^{2}, 4 m_{b}^{2}, 4 m_{c}^{2}\right\}$ and $B=\left\{3 a^{2}, 3 b^{2}, 3 c^{2}\right\}$. Let $k \geq 1$ be a positive integer. Let $a=k+1, b=k+2$ and $c=k+3$. Because
$$
a+b=(k+1)+(k+2)=2 k+3>k+3=c
$$
a triangle with such length sides there exist. After the simple calculations we have
$$
\begin{gathered}
A=\left\{3(k+1)^{2}-2,3(k+2)^{2}+4,3(k+3)^{2}-2\right\} \\
B=\left\{3(k+1)^{2}, 3(k+2)^{2}, 3(k+3)^{2}\right\}
\end{gathered}
$$
It easy to prove that
$$
\begin{gathered}
x+y+z=m+n+p=3\left[(k+1)^{2}+(k+2)^{2}+(k+3)^{2}\right] \\
x^{2}+y^{2}+z^{2}=m^{2}+n^{2}+p^{2}=9\left[(k+1)^{4}+(k+2)^{4}+(k+3)^{4}\right]
\end{gathered}
$$
$>$ From the inequality $3(k+1)^{2}-2>2003$ we obtain $k \geq 25$. For $k=25$ we have an example of two sets
$$
A=\{2026,2191,2350\}, \quad B=\{2028,2187,2352\}
$$
with desired properties.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there exist two sets $A=\{x, y, z\}$ and $B=\{m, n, p\}$ of positive integers greater than 2003 such that the sets have no common elements and the equalities $x+y+z=m+n+p$ and $x^{2}+y^{2}+z^{2}=m^{2}+n^{2}+p^{2}$ hold.
|
Let $A B C$ be a triangle with $B C=a, A C=b, A B=c$ and $a<b<c$. Denote by $m_{a}, m_{b}, m_{c}$ the lengths of medianes drawing from the vertices $A, B, C$ respectively. Using the formulas
$$
4 m_{a}^{2}=2\left(b^{2}+c^{2}\right)-a^{2}, 4 m_{b}^{2}=2\left(a^{2}+c^{2}\right)-b^{2}, 4 m_{c}^{2}=2\left(a^{2}+b^{2}\right)-c^{2}
$$
we obtain the relations
$$
\begin{gathered}
4 m_{a}^{2}+4 m_{b}^{2}+4 m_{c}^{2}=3 a^{2}+3 b^{2}+3 c^{2} \\
\left(4 m_{a}^{2}\right)^{2}+\left(4 m_{b}^{2}\right)^{2}+\left(4 m_{c}^{2}\right)^{2}=\left(2 b^{2}+2 c^{2}-a^{2}\right)^{2}+ \\
\left(2 a^{2}+2 c^{2}-b^{2}\right)^{2}+\left(2 a^{2}+2 b^{2}-c^{2}\right)^{2}=9 a^{4}+9 b^{4}+9 c^{4}= \\
\left(3 a^{2}\right)^{2}+\left(3 b^{2}\right)^{2}+\left(3 c^{2}\right)^{2}
\end{gathered}
$$
We put $A=\left\{4 m_{a}^{2}, 4 m_{b}^{2}, 4 m_{c}^{2}\right\}$ and $B=\left\{3 a^{2}, 3 b^{2}, 3 c^{2}\right\}$. Let $k \geq 1$ be a positive integer. Let $a=k+1, b=k+2$ and $c=k+3$. Because
$$
a+b=(k+1)+(k+2)=2 k+3>k+3=c
$$
a triangle with such length sides there exist. After the simple calculations we have
$$
\begin{gathered}
A=\left\{3(k+1)^{2}-2,3(k+2)^{2}+4,3(k+3)^{2}-2\right\} \\
B=\left\{3(k+1)^{2}, 3(k+2)^{2}, 3(k+3)^{2}\right\}
\end{gathered}
$$
It easy to prove that
$$
\begin{gathered}
x+y+z=m+n+p=3\left[(k+1)^{2}+(k+2)^{2}+(k+3)^{2}\right] \\
x^{2}+y^{2}+z^{2}=m^{2}+n^{2}+p^{2}=9\left[(k+1)^{4}+(k+2)^{4}+(k+3)^{4}\right]
\end{gathered}
$$
$>$ From the inequality $3(k+1)^{2}-2>2003$ we obtain $k \geq 25$. For $k=25$ we have an example of two sets
$$
A=\{2026,2191,2350\}, \quad B=\{2028,2187,2352\}
$$
with desired properties.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2003_shl.jsonl",
"problem_match": "\nALG 8.",
"solution_match": "\nSolution."
}
|
83065352-fc49-55f6-956c-2f82564df1bc
| 606,072
|
If $m$ is a number from the set $\{1,2,3,4\}$ and each point of the plane is painted in red or blue, prove that in the plane there exists at least an equilateral triangle with the vertices of the same colour and with length side $m$.
|
Suppose that in the plane there no exists an equilateral triangle with the vertices of the same colour and length side $m=1,2,3,4$.
First assertion: we shall prove that in the plane there no exists a segment with the length 2 such that the ends and the midpint of this segment have the same colour. Suppose that the segment $X Y$ with length 2 have the midpoint $T$ such that the points $X, Y, T$ have the same colour (for example, red). We construct the equilateral triangle. $X Y Z$. Hence, the point $Z$ is blue. Let $U$ and $V$ be the midpoints of the segments $X Z$ and $Y Z$ respectively. So, the points $U$ and $V$ are blue. We obtain a contradiction, because the equilateral triangle $U V Z$ have three blue vertices.
Second assertion: in the same way we prove that in the plane there no exists a segment with the length 4 such that the ends and the midpoint of this segment have the same colour.
Consider the equilateral triangle $A B C$ with length side 4 and divide it into 16 equilateral triangles with length sides 1. L $0: D$ be the midpoint of the segment $A B$. The vertices $A, B, C$ don't have the same colour. WLOG we suppose that $A$ and $B$ are red and $C$ is blue. So, the point $D$ is blue too. We shall investigate the following cases:
a) The midpoints $E$ and $F$ of the sides $A C$ and, respectively, $B C$ are red. From the first assertion it follows that the midpoints $M$ and $N$ of the segments $A E$ and, respectively, $B F$ are blue. Hence, the equilateral triangle $M N C$ have three blue vertices, a contradiction.
b) Let $E$ is red and $F$ is blue. The second one position of $E$ and $F$ is simmetrical. If $P, K, L$ are the midpoints of the segments $C F, A D, B D$ respectively, then by first assertion $P$ is red, $M$ is blue and $N$ is red. This imply that $K$ and $L$ are blue. So, the segment $K L$ with length 2 has the blue ends and blue midpoint, a contradiction.
c) If $E$ and $F$ are blue, then the equilateral triangle $E F C$ has three blue vertices, a contradiction.
Hence, in the plane there exists at least an equilateral triangle with the vertices of the same colour and with length side $m$, where $m \in\{1,2,3,4\}$.
Comment: The formuation of the problem suggests that one has to find 4 triangles, one for each $m$ from the set $\{1,2,3,4\}$ whereas the solution is for one $m$. A better formulation is:
Each point of the plane is painted in red or blue. Prove that in the plane there exists at least an equilateral triangle with the vertices of the same colour and with length side $m$, where $m$ is some number from the set $\{1,2,3,4\}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
If $m$ is a number from the set $\{1,2,3,4\}$ and each point of the plane is painted in red or blue, prove that in the plane there exists at least an equilateral triangle with the vertices of the same colour and with length side $m$.
|
Suppose that in the plane there no exists an equilateral triangle with the vertices of the same colour and length side $m=1,2,3,4$.
First assertion: we shall prove that in the plane there no exists a segment with the length 2 such that the ends and the midpint of this segment have the same colour. Suppose that the segment $X Y$ with length 2 have the midpoint $T$ such that the points $X, Y, T$ have the same colour (for example, red). We construct the equilateral triangle. $X Y Z$. Hence, the point $Z$ is blue. Let $U$ and $V$ be the midpoints of the segments $X Z$ and $Y Z$ respectively. So, the points $U$ and $V$ are blue. We obtain a contradiction, because the equilateral triangle $U V Z$ have three blue vertices.
Second assertion: in the same way we prove that in the plane there no exists a segment with the length 4 such that the ends and the midpoint of this segment have the same colour.
Consider the equilateral triangle $A B C$ with length side 4 and divide it into 16 equilateral triangles with length sides 1. L $0: D$ be the midpoint of the segment $A B$. The vertices $A, B, C$ don't have the same colour. WLOG we suppose that $A$ and $B$ are red and $C$ is blue. So, the point $D$ is blue too. We shall investigate the following cases:
a) The midpoints $E$ and $F$ of the sides $A C$ and, respectively, $B C$ are red. From the first assertion it follows that the midpoints $M$ and $N$ of the segments $A E$ and, respectively, $B F$ are blue. Hence, the equilateral triangle $M N C$ have three blue vertices, a contradiction.
b) Let $E$ is red and $F$ is blue. The second one position of $E$ and $F$ is simmetrical. If $P, K, L$ are the midpoints of the segments $C F, A D, B D$ respectively, then by first assertion $P$ is red, $M$ is blue and $N$ is red. This imply that $K$ and $L$ are blue. So, the segment $K L$ with length 2 has the blue ends and blue midpoint, a contradiction.
c) If $E$ and $F$ are blue, then the equilateral triangle $E F C$ has three blue vertices, a contradiction.
Hence, in the plane there exists at least an equilateral triangle with the vertices of the same colour and with length side $m$, where $m \in\{1,2,3,4\}$.
Comment: The formuation of the problem suggests that one has to find 4 triangles, one for each $m$ from the set $\{1,2,3,4\}$ whereas the solution is for one $m$. A better formulation is:
Each point of the plane is painted in red or blue. Prove that in the plane there exists at least an equilateral triangle with the vertices of the same colour and with length side $m$, where $m$ is some number from the set $\{1,2,3,4\}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2003_shl.jsonl",
"problem_match": "\nCOM 5.",
"solution_match": "\nSolution."
}
|
c1caa336-eb66-50f6-9355-9b03e9c557c9
| 606,112
|
Let $G$ be the centroid of the the triangle $A B C$. Reflect point $A$ across $C$ at $A^{\prime}$. Prove that $G, B, C, A^{\prime}$ are on the same circle if and only if $G A$ is perpendicular to $G C$.
|
Observe first that $G A \perp G C$ if and only if $5 A C^{2}=A B^{2}+B C^{2}$. Indeed,
$$
G A \perp G C \Leftrightarrow \frac{4}{9} m_{a}^{2}+\frac{4}{9} m_{c}^{2}=b^{2} \Leftrightarrow 5 b^{2}=a^{2}+c^{2}
$$
Moreover,
$$
G B^{2}=\frac{4}{9} m_{b}^{2}=\frac{2 a^{2}+2 c^{2}-b^{2}}{9}=\frac{9 b^{2}}{9}=b^{2}
$$
hence $G B=A C=C A^{\prime}$ (1). Let $C^{\prime}$ be the intersection point of the lines $G C$ and $A B$. Then $C C^{\prime}$ is the middle line of the triangle $A B A^{\prime}$, hence $G C \| B A^{\prime}$. Consequently, $G C A^{\prime} B$ is a trapezoid. From (1) we find that $G C A^{\prime} B$ is isosceles, thus cyclic, as needed.
Conversely, since $G C A^{\prime} B$ is a cyclic trapezoid, then it is also isosceles. Thus $C A^{\prime}=$ $G B$, which leads to (1).
Comment: An alternate proof is as follows:
Let $M$ be the midpoint of $A C$. Then the triangles $M C G$ and $M A^{\prime} B$ are similar. So $G C$ is parallel to $A^{\prime} B$.
$G A \perp G C$ if and only if $G M=M C$. By the above similarity, this happen if and only if $A^{\prime} C=G B$; if and only if the trapezoid is cyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $G$ be the centroid of the the triangle $A B C$. Reflect point $A$ across $C$ at $A^{\prime}$. Prove that $G, B, C, A^{\prime}$ are on the same circle if and only if $G A$ is perpendicular to $G C$.
|
Observe first that $G A \perp G C$ if and only if $5 A C^{2}=A B^{2}+B C^{2}$. Indeed,
$$
G A \perp G C \Leftrightarrow \frac{4}{9} m_{a}^{2}+\frac{4}{9} m_{c}^{2}=b^{2} \Leftrightarrow 5 b^{2}=a^{2}+c^{2}
$$
Moreover,
$$
G B^{2}=\frac{4}{9} m_{b}^{2}=\frac{2 a^{2}+2 c^{2}-b^{2}}{9}=\frac{9 b^{2}}{9}=b^{2}
$$
hence $G B=A C=C A^{\prime}$ (1). Let $C^{\prime}$ be the intersection point of the lines $G C$ and $A B$. Then $C C^{\prime}$ is the middle line of the triangle $A B A^{\prime}$, hence $G C \| B A^{\prime}$. Consequently, $G C A^{\prime} B$ is a trapezoid. From (1) we find that $G C A^{\prime} B$ is isosceles, thus cyclic, as needed.
Conversely, since $G C A^{\prime} B$ is a cyclic trapezoid, then it is also isosceles. Thus $C A^{\prime}=$ $G B$, which leads to (1).
Comment: An alternate proof is as follows:
Let $M$ be the midpoint of $A C$. Then the triangles $M C G$ and $M A^{\prime} B$ are similar. So $G C$ is parallel to $A^{\prime} B$.
$G A \perp G C$ if and only if $G M=M C$. By the above similarity, this happen if and only if $A^{\prime} C=G B$; if and only if the trapezoid is cyclic.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2003_shl.jsonl",
"problem_match": "## GEO 3.",
"solution_match": "\nSolution."
}
|
a460212b-515c-55b0-9c97-cbd8da35ccbe
| 606,146
|
Let three congruent circles intersect in one point $M$ and $A_{1}, A_{2}$ and $A_{3}$ be the other intersection points for those circles. Prove that $M$ is a.orthocenter for a triangle $A_{1} A_{2} A_{3}$.
|
The quadrilaterals $\mathrm{O}_{3} M O_{2} A_{1}, \mathrm{O}_{3} M O_{1} A_{2}$ and $O_{1} M O_{2} A_{3}$ are rombes. Therefore, $O_{2} A_{1} \| M O_{3}$ and $M O_{3} \| O_{1} A_{2}$, which imply $O_{2} A_{1} \| O_{1} A_{2}$. Because $O_{2} A_{1}=O_{3}{ }^{*} M=O_{1} A_{2}$ the quadrilateral $O_{2} A_{1} A_{2} O_{1}$ is parallelogram and then $A_{1} A_{2} \| O_{1} O_{2}$ and $A_{1} A_{2}=O_{1} O_{2}$. Similary, $A_{2} A_{3} \| O_{2} O_{3}$ and $A_{2} A_{3}=O_{2} O_{3} ; A_{3} A_{1} \| O_{3} O_{1}$ and $A_{3} A_{1}=O_{3} O_{1}$. The triangles $A_{1} A_{2} A_{3}$ and $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$ are congruent.
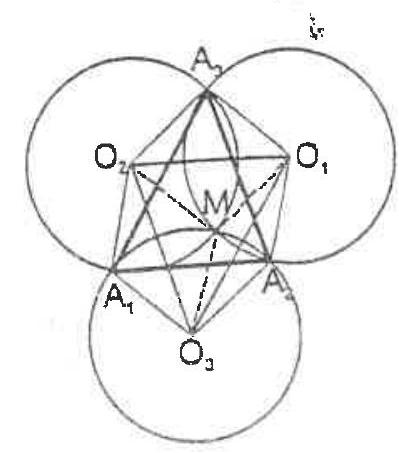
Since $A_{3} M \perp O_{1} O_{2}$ and $O_{1} O_{2} \| A_{1} A_{2}$ we infere $A_{3} M \perp A_{1} A_{2}$. Similary, $A_{2} M \perp A_{1} A_{3}$ and $A_{1} M \perp A_{2} A_{3}$. Thus, $M$ is the orthocenter for the triangle $A_{1} A_{2} A_{3}$.
## GEO.6.
Consider an isosceles triangle $A B C$ with $A B=A C$. A semicircle of diameter $E F$, lying on the side $B C$, is tangent to the lines $A B$ and $A C$ at $M$ and $N$, respectively. The line $A E$ intersects again the semicircle at point $P$.
Prove that the line PF passes through the midpoint of the chord $M N$.
Solution. Let $O$ be the center of the semicircle and let $R$ be the midpoint of $M N$. It is obvious that $M N$ is perpendicular to $A O$ at point $R$. Since $\angle A N O$ is right, then from the leg theorem we have $A N^{2}=A R \cdot A O$. From the powen of a point theorem,
$$
A P \cdot A E=A N^{2}=A M^{2}=A R \cdot A O
$$
Using the same theorem we infer that points $P, R, O$ and $E$ are concyclic, hence $\angle R P E$ is right. As $\angle F P E$ is also a right angle, the conclusion follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let three congruent circles intersect in one point $M$ and $A_{1}, A_{2}$ and $A_{3}$ be the other intersection points for those circles. Prove that $M$ is a.orthocenter for a triangle $A_{1} A_{2} A_{3}$.
|
The quadrilaterals $\mathrm{O}_{3} M O_{2} A_{1}, \mathrm{O}_{3} M O_{1} A_{2}$ and $O_{1} M O_{2} A_{3}$ are rombes. Therefore, $O_{2} A_{1} \| M O_{3}$ and $M O_{3} \| O_{1} A_{2}$, which imply $O_{2} A_{1} \| O_{1} A_{2}$. Because $O_{2} A_{1}=O_{3}{ }^{*} M=O_{1} A_{2}$ the quadrilateral $O_{2} A_{1} A_{2} O_{1}$ is parallelogram and then $A_{1} A_{2} \| O_{1} O_{2}$ and $A_{1} A_{2}=O_{1} O_{2}$. Similary, $A_{2} A_{3} \| O_{2} O_{3}$ and $A_{2} A_{3}=O_{2} O_{3} ; A_{3} A_{1} \| O_{3} O_{1}$ and $A_{3} A_{1}=O_{3} O_{1}$. The triangles $A_{1} A_{2} A_{3}$ and $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$ are congruent.

Since $A_{3} M \perp O_{1} O_{2}$ and $O_{1} O_{2} \| A_{1} A_{2}$ we infere $A_{3} M \perp A_{1} A_{2}$. Similary, $A_{2} M \perp A_{1} A_{3}$ and $A_{1} M \perp A_{2} A_{3}$. Thus, $M$ is the orthocenter for the triangle $A_{1} A_{2} A_{3}$.
## GEO.6.
Consider an isosceles triangle $A B C$ with $A B=A C$. A semicircle of diameter $E F$, lying on the side $B C$, is tangent to the lines $A B$ and $A C$ at $M$ and $N$, respectively. The line $A E$ intersects again the semicircle at point $P$.
Prove that the line PF passes through the midpoint of the chord $M N$.
Solution. Let $O$ be the center of the semicircle and let $R$ be the midpoint of $M N$. It is obvious that $M N$ is perpendicular to $A O$ at point $R$. Since $\angle A N O$ is right, then from the leg theorem we have $A N^{2}=A R \cdot A O$. From the powen of a point theorem,
$$
A P \cdot A E=A N^{2}=A M^{2}=A R \cdot A O
$$
Using the same theorem we infer that points $P, R, O$ and $E$ are concyclic, hence $\angle R P E$ is right. As $\angle F P E$ is also a right angle, the conclusion follows.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2003_shl.jsonl",
"problem_match": "\nGEO 5.",
"solution_match": "\nSolution:"
}
|
50686ff7-b4f5-5851-a2aa-913e9e39f599
| 606,155
|
Through a interior point of a triangle, three lines parallel to the sides of the triangle are constructed. In that way the triangle is divided on six figures, areas equal $a, b, c, \alpha, \beta, \gamma$ (see the picture).
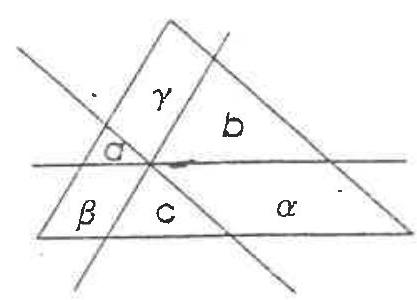
Prove that
$$
\frac{a}{\alpha}+\frac{b}{\beta}+\frac{c}{\gamma} \geqslant \frac{3}{2}
$$
|
We will prove the inequality in two steps. First one is the following
Lemma: Let $A B C$ be a triangle, $E$ arbitrary point on the side $A C$. Parallel lines to $A B$ and $B C$, drown through $E$ meet sides $B C$ and $A B$ in points $F$. and $D$ respectively. Then: $P_{B D E F}=2 \sqrt{P_{A D E} \cdot P_{E F C}}$ ( $P_{X}$ is area for the figure $X)$.
The triangles $A D E$ and $E F C$ are similar. Then:
$$
\frac{P_{B D E F}}{2 P_{A D E}}=\frac{P_{B D E}}{P_{A D E}}=\frac{B D}{A D}=\frac{E F}{A D}=\frac{\sqrt{P_{E F C}}}{\sqrt{P_{A D E}}}
$$
Hence, $P_{B D E F}=2 \sqrt{P_{A D E} \cdot P_{E F C}}$.
Using this lemma one has $\alpha=2 \sqrt{b c}, \beta=2 \sqrt{a c}, \gamma=2 \sqrt{a b}$. The GML-AM mean inequality provides
$$
\frac{a}{\alpha}+\frac{b}{\beta}+\frac{c}{\gamma} \geqslant 3 \sqrt[3]{\frac{a b c}{\alpha \beta \gamma}}=3 \sqrt[3]{\frac{a b c}{2^{3} \sqrt{a^{2} b^{2} c^{2}}}}=\frac{3}{2}
$$
BULGARIA
| Leader: | Chavdar Lozanov |
| :--- | :--- |
| Deputy Leader: | Ivan Tonov |
| Contestants: | Asparuh Vladislavov Hriston |
| | Tzvetelina Kirilova Tzeneva |
| | Vladislav Vladilenon Petkov |
| | Alexander Sotirov Bikov |
| | Deyan Stanislavov Simeonov |
| | Anton Sotirov Bikov |
## CYPRUS
| Leader: | Efthyvoulos Liasides |
| :--- | :--- |
| Deputy Leader: | Andreas Savvides |
| Contestants: | Marina Kouyiali |
| | Yiannis loannides |
| | Anastasia Solea |
| | Nansia Drakou |
| | Michalis Rossides |
| | Domna Fanidou |
| Observer: | Myrianthi Savvidou |
FORMER YUGOSLAV
REPUBLIC of MACEDONIA
| Leader: | Slavica Grkovska |
| :--- | :--- |
| Deputy Leader: | Misko Mitkovski |
| Contestants: | Aleksandar lliovski |
| | Viktor Simjanovski |
| | Maja Tasevska |
| | Tanja Velkova |
| | Matej Dobrevski |
| | Oliver Metodijev |
## GREECE
Leader: Anargyros Felouris
Deputy Leader: Ageliki Vlachou
Contestants: Theodosios Douvropoulos
Marina lliopoulou
Faethontas Karagiannopoulos
Stefanos Kasselakis
Fragiskos Koufogiannis
Efrosyni Sarla
ROMANIA
| Leader: | Dan Branzei |
| :--- | :--- |
| Deputy Leader: | Dinu Serbanescu |
| Contestants: | Dragos Michnea |
| | Adrian Zahariuc |
| | Cristian Talau |
| | Beniämin Bogosel |
| | Sebastian Dumitrescu |
| | Lucian Turea |
## TURKEY
Leader:
Halil Ibrahim Karakaş
\&Deputy Leader: Duru Türkoğlu
Contestants: Sait Tunç
Anmet Kabakulak
Türkü Çobanoğlu
Burak Sağlam
Ibrahim Çimentepe
Hale Nur Kazaçeşme
## YUGOSLAVIA
(SERBIA and MONTENEGRO)
| Leader: | Branislav Popovic |
| :--- | :--- |
| Deputy Leader: | Marija Stanic |
| Contestants: | Radojevic Mladen |
| | Jevremovic Marko |
| | Djoric Milos |
| | Lukic Dragan |
| | Andric Jelena |
| | Pajovic Jelena |
## TURKEY-B
## Leader:
Deputy Leader: Contestants:
Ahmet Karahan
Deniz Ahçihoca ..... Havva Yeşildağl|
Çağıl Şentip
Buse Uslu
Ali Yilmaz
Demirhan Çetereisi
Yakup Yildirim
## REPUBLIC of MOLDOVA
| Leader: | Ion Goian |
| :--- | :--- |
| Deputy Leader: | Ana Costas |
| Contestants: | lurie Boreico |
| | Andrei Frimu |
| | Mihaela Rusu |
| | Vladimir Vanovschi |
| | Da Vier: |
| | Alexandru Zamorzaev |
1.Prove that $7^{n}-1$ is not divisible by $6^{n}-1$ for any positive integer $n$.
2. 2003 denars were divided in several bags and the bags were placed in several pockets. The number of bags is greater than the number of denars in each pocket. Is it true that the number of pockets is greater than the number of denars in one of the bags?
3. In the triangle $\mathrm{ABC}, R$ and $r$ are the radii of the circumcircle and the incircle, respectively; $a$ is the longest side and $h$ is the shortest altitude. Prove that $R / r>a / h$.
4. Prove that for all positive numbers $x, y, z$ such that $x+y+z=1$ the following inequality holds
$$
\frac{x^{2}}{1+y}+\frac{y^{2}}{1+z}+\frac{z^{2}}{1+x} \leq 1
$$
5.Is it possible to cover a $2003 \times 2003$ board with $1 \times 2$ dominoes placed horizontally and $1 \times 3$ threeminoes placed vertically?
## THE 47-th MATHEMATIAL OLYMPIAD OF REPUBLIC OF MOLDOVA Chişinău, March 9-12, 2003
7.1 Let $m>n$ be pozitive integers. For every positive integers $k$ we define the number $a_{k}=(\sqrt{5}+2)^{k}+$ $(\sqrt{5}-2)^{k}$. Show that $a_{m+n}+a_{m-n}=a_{m} \cdot a_{n}$.
T. Fild all five digits numbers $\overline{a b c d e}$, written in decimal system, if it is known that $\overline{a b} c d e-\overline{e b c d a}=69993$, $\overline{b c d}-\overline{d c b}=792, \overline{b c}-\overline{c b}=72$.
7.3 In the triangle $A B C$ with semiperemeter $p$ the points $M, N$ and $P$ lie on the sides $(B C),(C A)$ and - (AB) respectively. Show that $p<A M+B N+C P<3 p$.
7.4 Let $a$ and $b$ be positive integer such, that $a+b \leq 10$. Find all pairs $(a, b)$ such, that the fraction $(2 n+a) /(5 n+b)$ are irreducible for every natural number $n$.
7.5 A given rectangular table has at least one column and at least one line. He is full completed by the first positive integers, written consecutively from the left to the right and begining to the first line. It is known, that the number 170 is written on the middle line and in the same column with him on the last line is written the number 329 . How much numbers are written in the given table.
7.6 Prove that for every positive integer $n$ the number $a=(2 n+1)^{5}-2 n-1$ is divisible by 240 .
7.7 In the square $A B C D$ the point $N$ is the middle point of the side $[A B]$ and the point $M$ lies on the diagonal $(A C)$ so that $A C=4 C M$. Prove that the angle $D M N$ is right.
7.8 The real numbers $x_{1}, x_{2}, \ldots, x_{2003}$ satisfy the relations $x_{1} / 1=x_{2} / 2=x_{3} / 3=\ldots=x_{2003} / 2003$ and $\sqrt{1^{2}+2^{2}+\ldots+2003^{2}}+\sqrt{x_{1}^{2}+x_{2}^{2}+\ldots+x_{2003}^{2}}=\sqrt{\left(1+x_{1}\right)^{2}+\left(2+x_{2}\right)^{2}+\ldots+\left(2003+x_{2003}\right)^{2}}$. Prove that $x_{i} \geq 0$ for every $i=1,2, \ldots, 2003$.
8.1 Calculate the sum
$$
\frac{2^{4}+2^{2}+1}{2^{7}-2}+\frac{3^{4}+3^{2}+1}{3^{7}-3}+\ldots+\frac{2003^{4}+2003^{2}+1}{2003^{7}-2003}+\frac{1}{2 \cdot 2003 \cdot 2004}
$$
8.2 Let $[A B]$ be a segment and $\sigma$ be one of the halfplane, determined by the straight line $A B$. The segments $[A P]$ and $[B Q]$ with integer lengths are situated in $\sigma$ and are perpendicular to the straight line $A B$. The intersection point $M$ of the straight lines $A Q$ and $B P$ is distanced at 8 units to the straight line $A B$. Find the lengths of the segments $[A P]$ and $[B Q]$, if it is known that the triangle $B Q M$ has a greatest area.
8.3 Let $A B C$ be an acuteangled triangle such that $m(\angle A C B) \neq 45^{\circ}$. The points $M$ and $N$ are the feets of the altitudes, drawn from the vertices $A$ and $B$ respectively. The points $P$ and $Q$ lyes on the halfstraight lines ( $M A$ and ( $N B$ respectively so that $M P=M B$ and $N Q=N A$. Prove that the straight lines $P Q$ and $M N$ are parallel.
8.4 The equation $x^{13}-x^{11}+x^{9}-x^{7}+x^{5}-x^{3}+x-2=0$ has a real solution $x_{0}$. Show that $\left[x_{0}^{14}\right]=3$, where $[a]$ is a integral part of the real number $a$.
8.5 Prove that every positive integer number $n \geq 3$ can be written as a sum of at least two consecutive positive integers if and only if he is not a power of the number 2 .
8.6 The prime number $p$ has the following property: the remainder $r$ of the division of $p$ by 210 is a composite number which can be represented us a sum of two perfect squares. Find the number $r$.
8.7 Through the arbitrary point of the triangle $A B C$ construct (explain the steps of the construction) a straight, line which divides the triangle $A B C$ in two parts so that the ratio of they areas is equal to $3 / 4$.
8.8 Let $x$ be a real number. Find the smallest value of the expression $\sqrt{x^{2}+2 x+4}+\sqrt{x^{2}-\sqrt{3} x+1}$.
9.1 In the space a geometrical configuration, which include $n(n \geq 3)$ distinct points, is given. A point $A$ of this configuration has the following properties: if $A$ is excluded from the configuration, then among the remaining points there are no colinear points; after the elimination of $A$ from the configuration the number of all straight lines, that were constructed through any 2 points of the configuration, is lowered by $1 / 15$ part. Find the value of $n$.
9.2 Let $x^{2}+b x+c=0$ be the equation, where $b$ and $c$ are two consecutive triangular numbers and $c>b \geq$ 10. Prove that this equation has two irrational solutions. (The number $m$ is triangular, if $m=n(n-1) / 2$ for certain positive integer $n \geq 1$ ).
9.3 The distinct points $M$ and $N$ lie on the hypotenuse ( $A C)$ of the right isosceles triangle $A B C$ so that $M \in(A N)$ and $M N^{2}=A M^{2}+C N^{2}$. Prove that $m(\angle M B N)=45^{\circ}$.
9.4 Find all the functions $f: N^{*} \rightarrow N^{*}$ which verify the relation $f(2 x+3 y)=2 f(x)+3 f(y)+4$ for every positive integers $x, y \geq 1$.
9.5 The numbers $a_{1}, a_{2}, \ldots, a_{n}$ are the first $n$ positive integers with the property that the number $8 a_{k}+1$ is a perfect square for every $k=1,2, \ldots, n$. Find the sum $S_{n}=a_{1}+a_{2}+\ldots+a_{n}$.
9.6 Find all real solutions of the equation $x^{4}+7 x^{3}+6 x^{2}+5 \sqrt{2003} x-2003=0$.
9.7 The side lengths of the triangle $A B C$ satisfy the relations $a>b \geq 2 c$. Prove that the altitudes of the triangle $A B C$ can not be the sides of any triangle.
9.8 The base of a pyramid is a convex polygon with 9 sides. All the lateral edges of the pyramid and all the liagunads ui the base are coloured in a random way in red or blue. Pröve that there exist at least three vertices of the pyramid which belong to a triangle with the sides coloured in the same colour.
10.1 Find all prime numbers $a, b$ and $c$ for which the equality $(a-2)!+2 b!=22 c-1$ holds.
10.2 Solve the system $x+y+z+t=6, \sqrt{1-x^{2}}+\sqrt{4-y^{2}}+\sqrt{9-z^{2}}+\sqrt{16-t^{2}}=8$.
10.3 In the scalen triangle $A B C$ the points $A_{1}$ and $B_{1}$ are the bissectrices feets, drawing from the vertices $A$ and $B$ respectively. The straight line $A_{1} B_{1}$ intersect the line $A B$ at the point $D$. Prove that one of the angles $\angle A C D$ or $\angle B C D$ is obtuze and $m(\angle A C D)+m(\angle B C D)=180^{\circ}$.
10.4 Let $a>1$ be not integer number and $a \neq \sqrt[2]{q}$ for every positive integers $p \geq 2$ and $q \geq 1$, $k=\left[\log _{a} n\right] \geq 1$, where $[x]$ is the integral part of the real number $x$. Prove that for every positive integer $n \geq 1$ the equality
$$
\left[\log _{a} 2\right]+\left[\log _{a} 3\right]+\ldots+\left[\log _{a} n\right]+[a]+\left[a^{2}\right]+\ldots+\left[a^{k}\right]=n k
$$
holds.
10.5 The rational numbers $p, q, r$ satisfy the relation $p q+p r+q r=1$. Prove that the number $\left(1+p^{2}\right)\left(1+q^{3}\right)\left(1+r^{2}\right)$ is a square of any rational number.
10.6 Let $n \geq 1$ be a positive integer. For every $k=1,2, \ldots, n$ the functions $f_{k}: R \rightarrow R, f_{k}(x)=$ $a_{k} x^{2}+b_{k} x+c_{k}$ with $a_{k} \neq 0$ are given. Find the greatest possible number of parts of the rectangular plane $x O y$ which can be obtained by the intersection of the graphs of the functions $f_{k}(k=1,2, \ldots, n)$.
10.7 The circle with the center $O$ is tangent to the sides $[A B],[B C],[C D]$ and $[D A]$ of the convex quadrilateral $A B C D$ at the points $M, N, \mathcal{K}$ and $L$ respectively. The straight lines $M N$ and $A C$ are parallel and the straight line $M K$ intersect the line $L N$ at the point $P$. Prove that the points $A, M, P, O$ and $L$ are concyclic.
10.8 Find all integers $n$ for which the number $\log _{2 n-1}\left(n^{2}+2\right)$ is rational.
11.1 Let $a, b, c, d \geq 1$ be arbitrary positive numbers. Prove that the equations system $a x-y z=$ $c, \quad b x-y t=-d$. has at least a solution $(x, y, z, t)$ in positive integers.
11.2 The sequences $\left(a_{n}\right)_{n \geq 0}$ and $\left(b_{n}\right)_{n \geq 0}$ satisfy the conditions $(1+\sqrt{3})^{2 n+1}=a_{n}+b_{n} \sqrt{3}$ and $a_{n}, b_{n} \in Z$. Find the recurrent relation for each of the sequences $\left(a_{n}\right)$ and $\left(b_{n}\right)$.
11.3 The triangle $A B C$ is rightangled in $A, A C=b, A B=c$ and $B C=a$. The halfstraight line ( $A z$ is perpendicular to the plane $(A B C), M \in(A z$ so that $\alpha, \beta, \gamma$ are the mesures of the angles, formed by the edges $M B, M C$ and the plane ( $M B C$ ) with the plane ( $A B C$ ) respectively. In the set of the triangular pyramids MABC on consider the pyramids with the volumes $V_{1}$ and $V_{2}$ which satisfy the relations $\alpha+\beta+\gamma=\pi$ and $\alpha+\beta+\gamma=\pi / 2$ respectively. Prove the equality $\left(V_{1} / V_{2}\right)^{2}=(a+b+c)(1 / a+1 / b+1 / c)$.
11.4 Find all the functions $f:[0 ;+\infty) \rightarrow[0 ;+\infty)$ which satisfy the conditions: : $f(x f(y)) \cdot f(y)=$ $f(x+y)$ for every $x, y \in[0 ;+\infty) ; f(2)=0 ; f(x) \neq 0$ for every $x \in[0 ; 2)$.
11.5 Let $0<a<b$ be real positive numbers. Prove that the equation $[(a+b) / 2]^{x+y}=a^{x} b^{y}$ has at least a solution in the set $(a ; b) \times(a ; b)$.
11.6 Each of the plane angles of the vertex $V$ of the tetrahedron $V A B C$ has the measure equal to $60^{\circ}$. Prove that $V A+V B+V C \leq A B+B C+C A$. When the equality holds?
11.7 The plane $\alpha$ is tangent in the points $A_{3}, A_{2}$ and $A_{3}$ to three spheres with different radii $R_{1}, R_{2}$ and $R_{3}$ respectively, situated in the same halfspace two by two exteriorly. The plane $\beta$ is parallel to the plane $\alpha$ and intersect all three spheres so that the circles $D_{1}, D_{2}$ and $D_{3}$ are obtained. Find the distance between the planes $\alpha$ and $\beta$ so that the sum of the volumes $V_{1}, V_{2}$ and $V_{3}$ of the cones with the bases $D_{1}, D_{2}, D_{3}$ and the vertices $A_{1}, A_{2}, A_{3}$ respectively, will be the greatest.
11.8 For every positive integer $n \geq 1$ wie define the matrix $A_{n}=\left(a_{i j}\right)_{1 \leq i, j \leq n}$, where $a_{i j}=$ $\max (i, j) / \min (i, j), \quad 1 \leq i, j \leq n$. Calculate the determinant of the matrix $A_{n}$.
12.1 Prove that $\lim _{n \rightarrow+\infty} \ln \left(1+2 e+4 e^{4}+6 e^{9}+\ldots+2 n e^{n^{2}}\right) / n^{2}=1$.
12.2 For every positive integer $n \geq 2$ the affirmation $P_{n}^{\prime}$ : "If the derivative $P^{\prime}(X)$ of a polynomial $P(X)$ * of degree $n$ with real coefficients has $n-1$ real distinct roots, then there exists a real constant $C$ such that the equation $P(x)=C$ has $n$ real distinct solutions" is considered. Prove that $P_{4}$ is true. Is the affirmation $P_{5}$ true? Prove the answer.
12.3 In the circle with radius $R$ the distinct chords $[A B]$ and $[C D]$ are concurrent and form an acute angle with mesure $\alpha$. Prove that $A B+C D>2 R \sin \alpha$.
12.4 The real numbers $\alpha, \beta, \gamma$ satisfy the relations $\sin \alpha+\sin \beta+\sin \gamma=0$ and $\cos \alpha+\cos \beta+\cos \gamma=0$. Find all positive integers $n \geq 0$ for-which $\sin (n \alpha+\pi / 4)+\sin (n \beta+\pi / 4)+\sin (n \gamma+\pi / 4)=0$.
12.5 For every positive integer $n \geq 1$ we define the polynomial $P(X)=X^{2 n}-X^{2 n-1}+\ldots-X+1$, Find the remainder of the division of the polynomial $P\left(X^{2 n+1}\right)$ by the polynomial $P(X)$.
12.6 Fie $n \in N$. Find all the primitives of the function
$$
f: R \rightarrow R, \quad f(x)=\frac{x^{3}-9 x^{2}+29 x-33}{\left(x^{2}-6 x+10\right)^{n}}
$$
12.7 In a rectangular system $x O y$ the graph of the function $f: R \rightarrow R, f(x)=x^{2}$ is drawn. The ordered triple $B, A, C$ has distinct points on the parabola, the point $D \in(B C)$ such that the straight line $A D$ is parallel to the axis $O y$ and the triangles $B A D$ and $C A D$ have the areas $s_{1}$ and $s_{2}$ respectively. Find the length of the segment $[A D]$.
12.8 Let $\left(F_{n}\right)_{n \in N^{*}}$ be the Fibonacci sequence so that: $F_{1}=1, F_{2}=1, F_{n+1}=F_{n}+F_{n-1}$ for every positive integer $n \geq 2$. Shown that $F_{n}<3^{n / 2}$ and calculate the limit $\lim _{n \rightarrow \infty}\left(F_{1} / 2+F_{2} / 2^{2}+\ldots+F_{n} / 2^{n}\right)$.
## The first selection test for IMO 2003 and BMO 2003, March 12, 2003
B1. Each side of the arbitrary triangle is divided into 2002 congruent segments. After that each interior division point of the side is joined with opposite vertex. Prove that the number of obtained regions of the triangle is divisible by 6 .
B2. The positive real numbers $x, y$ and $z$ satisfy the relation $x+y+z \geq 1$. Prove the inequality
$$
\frac{x \sqrt{x}}{y+z}+\frac{y \sqrt{y}}{x+z}+\frac{z \sqrt{z}}{x+y} \geq \frac{\sqrt{3}}{2}
$$
B3. The quadrilateral $A B C D$ is inscribed in the circle with center $O$, the points $M$ and $N$ are the middle points of the diagonals $[A C]$ and $[B D]$ respectively and $P$ is the intersection point of the diagonals. It is known that the points $O, M, N$ si $P$ are distinct. Prove that the points $O, M, B$ and $D$ are concyclic if and only if the points $O, N, A$ and $C$ are concyclic.
B4. Prove that the equation $1 / a+1 / b+1 / c+1 /(a b c) \doteq 12 /(a+b+c)$ has many solutions $(a, b, c)$ in strictly positive integers.
## The second selection test for IMO 2003, March 22, 2003
B5. Let $n \geq 1$ be positive integer. Find all polynomials of degree $2 n$ with real coefficients
$$
P(X)=X^{2 n}+(2 n-10) X^{2 n-1}+a_{2} X^{2 n-2}+\ldots+a_{2 n-2} X^{2}+(2 n-10) X+1
$$
-if it is known that they have positive real roots.
B6. The triangle $A B C$ has the semiperimeter $p$, the circumradius $R$, the inradius $r$ and $l_{a,}, l_{b}, l_{c}$ are the lengths of internal bissecticies, drawing from the vertices $A, B$ and $C$ respectively. Prove the inequality $l_{a} l_{b}+l_{b} l_{c}+l_{c} l_{a} \leq p \sqrt{3 r^{2}+12 R r}$.
B7. The points $M$ and $N$ are the tangent points of the sides $[A B]$ and $[A C]$ of the triangle $A B C$ to the incircle with the center $I$. The internal bissectrices, drawn from the vertices $B$ and $C$, intersect the straight line $M N$ at points $P$ and $Q$ respectively. If $F$ is the intersection point of the swtraight lines $C P$ and $B Q$, then prove that the straight lines $F I$ and $B C$ are perpendicular.
B8. Let $n \geq 4$ be the positive integer. On the checkmate table with dimensions $n \times n$ we put the coins. One consider the diagonal of the table each diagonal with at least two unit squares. What is the smallest number of coins put on the table so that on the each horizontal, each vertical and each diagonal there exists att least one coin. Prove the answer.
## The third selection test for IMO 2003, March 23, 2003
B9. Let $n \geq 1$ be positive integer. A permutation $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of the numbers $(1,2, \ldots, n)$ is called quadratique if among the numbers $a_{1}, a_{1}+a_{2}, \ldots, a_{1}+a_{2}+\ldots+a_{n}$ there exist at least a perfect square. Find the greatest number $n$, which is less than 2003 , such that every permutation of the numbers $(1,2, \ldots, n)$ will be quadratique.
B10. The real numbers $a_{1}, a_{2}, \ldots, a_{2003}$ satisfy simultaneousiy the relations: $a_{i} \geq 0$ for all $i=$ $1,2, \ldots, 2003 ; \quad a_{1}+a_{2}+\ldots+a_{2003}=2 ; \quad a_{1} a_{2}+a_{2} a_{3}+\ldots+a_{2003} a_{1}=1$. Find the smallest value of the sum $a_{1}^{2}+a_{2}^{2}+\ldots+a_{2003}^{2}$.
B11. The arbitrary point $M$ on the plane of the triangle $A B C$ does not belong on the straight lines $A B, B C$ and $A C$. If $S_{1}, S_{2}$ and $S_{3}$ are the areas of the triangles $A M B, B M C$ and $A M C$ respectively, find the geometrical locus of the points $M$ which satisfy the relation $\left(M A^{2}+M B^{2}+M C^{2}\right)^{2}=16\left(S_{1}^{2}+S_{2}^{2}+S_{3}^{2}\right)$.
812. Let $n \geq 1$ be a positive integer. A square table of dimensions $n \times n$ is full arbitrarly completed $\because$ the numb so, shat every number appear exactly conce the table. from cack fine one select the smallest number and the greatest of them is denote by $x$. From each column one select the greatest number and the smallest of them is denote by $y$. The table is called equilibrated if $x=y$. How match equilibrated tables there exist?
## The first selection test for JBMO 2003, April 12, 2003
JB1. Let $n \geq 2003$ be a positive integer such that the number $1+2003 n$ is a perfect square. Prove that the number $n+1$ is equal to the sum of 2003 positive perfect squares.
JB2. The positive real numbers $a, b, c$ satisfy the relation $a^{2}+b^{2}+c^{2}=3 a b c$. Prove the inequality
$$
\frac{a}{b^{2} c^{2}}+\frac{b}{c^{2} a^{2}}+\frac{c}{a^{2} b^{2}} \geq \frac{9}{a+b+c}
$$
JB3. The quadrilateral $A B C D$ with perpendicular diagonals is inscribed in the circle with center $O$, the points $M$ and $N$ are the middle points of the sides $[B C]$ and $[C D]$ respectively. Find the value of the ratio of areas of the figures $O M C N$ and $A B C D$.
JB4. Let $m$ and $n$ be the arbitrary digits of the decimal system and $a, b, c$ be the positive distinct integers of the form $2^{m} \cdot 5^{n}$. Find the number of the equations $a x^{2}-2 b x+c=0$, if it is known that each equation has a single real solution.
## The second selection test for JMBO 2003, April 13, 2003
JB5. Prove that each positive integer is equal to a difference of two positive integers with the same number of the prime divisors.
JB6. The real numbers $x$ and $y$ satisfy the equalities
$$
\sqrt{3 x}\left(1+\frac{1}{x+y}\right)=2, \quad \sqrt{7 y}\left(1-\frac{1}{x+y}\right)=4 \sqrt{2}
$$
Find the numerical value of the ratio $y / x$.
$J B 7$. The triangle $A B C$ is isosceles with $A B=B C$. The point $F$ on the side $[B C]$ and the point $D$ on the side $[A C]$ are the feets of the internal bissectrix drawn from $A$ and altitude drawn from $B$ respectively so that $A F=2 B D$. Find the measure of the angle $A B C$.
JB8. In the rectangular coordinate system every point with integer coordinates is called laticeal point. Let $P_{n}(n, n+5)$ be a laticeal point and denote by $f(n)$ the number of laticeal points on the open segment $\left(O P_{n}\right)$, where the point $O(0,0)$ is the coordinates system origine. Calculate the number $f(1)+f(2)+$ $f(3)+\ldots+f(2002)+f(2003)$.
7 th Junior Balkan Mathematical O-lympiad
$20-25$ Jun e, 20.03 I $\mathrm{m}$ i r $\quad$. $\quad$ u rke y
## English Version
1. Let $n$ be a positive integer. A number $A$ consists of $2 n$ digits, each of which is 4 ; and a number $B$ consists of $n$ digits, each of which is 8 . Prove that $A+2 B+4$ is a perfect square.
\&
2. Suppose there are $n$ points in a plane no three of which are collinear with the following property:
If we label these points as $A_{1}, A_{2}, \ldots, A_{n}$ in any way whatsoever, the broken line $A_{1} A_{2} \ldots A_{n}$ does not intersect itself.
Find the maximal value that $n$ can have.
3. Let $k$ be the circumcircle of the triangle $A B C$. Consider the arcs $\overparen{A B}, \widehat{B C}, \widetilde{C A}$ such that $C \notin \widetilde{A B}, A \notin \widetilde{B C}, B \notin \widetilde{C A}$. Let $D, E$ and $F$ be the midpoints of the arcs $\widehat{B C}, \overparen{C A}, \overparen{A B}$, respectively. Let $G$ and $H$ be the points of intersection of $D E$ with $C B$ and $C A$; let $I$ and $J$ be the points of intersection of $D F$ with $B C$ and $B A$, respectively. Denote the midpoints of $G H$ and $I J$ by $M$ and $N$, respectively.
a) Find the angles of the triangle $D M N$ in terms of the angles of the triangle $A B C$.
b) If $O$ is the circumcentre of the triangle $D M N$ and $P$ is the intersection point of $A D$ and $E F$, prove that $O, P, M$ and $N$ lie on the same circle.
4. Let $x, y, z$ be real numbers greater than -1 . Prove that
$$
\frac{1+x^{2}}{1+y+z^{2}}+\frac{1+y^{2}}{1+z+x^{2}}+\frac{1+z^{2}}{1+x+y^{2}} \geq 2
$$
## Romanian Version
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Through a interior point of a triangle, three lines parallel to the sides of the triangle are constructed. In that way the triangle is divided on six figures, areas equal $a, b, c, \alpha, \beta, \gamma$ (see the picture).

Prove that
$$
\frac{a}{\alpha}+\frac{b}{\beta}+\frac{c}{\gamma} \geqslant \frac{3}{2}
$$
|
We will prove the inequality in two steps. First one is the following
Lemma: Let $A B C$ be a triangle, $E$ arbitrary point on the side $A C$. Parallel lines to $A B$ and $B C$, drown through $E$ meet sides $B C$ and $A B$ in points $F$. and $D$ respectively. Then: $P_{B D E F}=2 \sqrt{P_{A D E} \cdot P_{E F C}}$ ( $P_{X}$ is area for the figure $X)$.

The triangles $A D E$ and $E F C$ are similar. Then:
$$
\frac{P_{B D E F}}{2 P_{A D E}}=\frac{P_{B D E}}{P_{A D E}}=\frac{B D}{A D}=\frac{E F}{A D}=\frac{\sqrt{P_{E F C}}}{\sqrt{P_{A D E}}}
$$
Hence, $P_{B D E F}=2 \sqrt{P_{A D E} \cdot P_{E F C}}$.
Using this lemma one has $\alpha=2 \sqrt{b c}, \beta=2 \sqrt{a c}, \gamma=2 \sqrt{a b}$. The GML-AM mean inequality provides
$$
\frac{a}{\alpha}+\frac{b}{\beta}+\frac{c}{\gamma} \geqslant 3 \sqrt[3]{\frac{a b c}{\alpha \beta \gamma}}=3 \sqrt[3]{\frac{a b c}{2^{3} \sqrt{a^{2} b^{2} c^{2}}}}=\frac{3}{2}
$$
BULGARIA
| Leader: | Chavdar Lozanov |
| :--- | :--- |
| Deputy Leader: | Ivan Tonov |
| Contestants: | Asparuh Vladislavov Hriston |
| | Tzvetelina Kirilova Tzeneva |
| | Vladislav Vladilenon Petkov |
| | Alexander Sotirov Bikov |
| | Deyan Stanislavov Simeonov |
| | Anton Sotirov Bikov |
## CYPRUS
| Leader: | Efthyvoulos Liasides |
| :--- | :--- |
| Deputy Leader: | Andreas Savvides |
| Contestants: | Marina Kouyiali |
| | Yiannis loannides |
| | Anastasia Solea |
| | Nansia Drakou |
| | Michalis Rossides |
| | Domna Fanidou |
| Observer: | Myrianthi Savvidou |
FORMER YUGOSLAV
REPUBLIC of MACEDONIA
| Leader: | Slavica Grkovska |
| :--- | :--- |
| Deputy Leader: | Misko Mitkovski |
| Contestants: | Aleksandar lliovski |
| | Viktor Simjanovski |
| | Maja Tasevska |
| | Tanja Velkova |
| | Matej Dobrevski |
| | Oliver Metodijev |
## GREECE
Leader: Anargyros Felouris
Deputy Leader: Ageliki Vlachou
Contestants: Theodosios Douvropoulos
Marina lliopoulou
Faethontas Karagiannopoulos
Stefanos Kasselakis
Fragiskos Koufogiannis
Efrosyni Sarla
ROMANIA
| Leader: | Dan Branzei |
| :--- | :--- |
| Deputy Leader: | Dinu Serbanescu |
| Contestants: | Dragos Michnea |
| | Adrian Zahariuc |
| | Cristian Talau |
| | Beniämin Bogosel |
| | Sebastian Dumitrescu |
| | Lucian Turea |
## TURKEY
Leader:
Halil Ibrahim Karakaş
\&Deputy Leader: Duru Türkoğlu
Contestants: Sait Tunç
Anmet Kabakulak
Türkü Çobanoğlu
Burak Sağlam
Ibrahim Çimentepe
Hale Nur Kazaçeşme
## YUGOSLAVIA
(SERBIA and MONTENEGRO)
| Leader: | Branislav Popovic |
| :--- | :--- |
| Deputy Leader: | Marija Stanic |
| Contestants: | Radojevic Mladen |
| | Jevremovic Marko |
| | Djoric Milos |
| | Lukic Dragan |
| | Andric Jelena |
| | Pajovic Jelena |
## TURKEY-B
## Leader:
Deputy Leader: Contestants:
Ahmet Karahan
Deniz Ahçihoca ..... Havva Yeşildağl|
Çağıl Şentip
Buse Uslu
Ali Yilmaz
Demirhan Çetereisi
Yakup Yildirim
## REPUBLIC of MOLDOVA
| Leader: | Ion Goian |
| :--- | :--- |
| Deputy Leader: | Ana Costas |
| Contestants: | lurie Boreico |
| | Andrei Frimu |
| | Mihaela Rusu |
| | Vladimir Vanovschi |
| | Da Vier: |
| | Alexandru Zamorzaev |
1.Prove that $7^{n}-1$ is not divisible by $6^{n}-1$ for any positive integer $n$.
2. 2003 denars were divided in several bags and the bags were placed in several pockets. The number of bags is greater than the number of denars in each pocket. Is it true that the number of pockets is greater than the number of denars in one of the bags?
3. In the triangle $\mathrm{ABC}, R$ and $r$ are the radii of the circumcircle and the incircle, respectively; $a$ is the longest side and $h$ is the shortest altitude. Prove that $R / r>a / h$.
4. Prove that for all positive numbers $x, y, z$ such that $x+y+z=1$ the following inequality holds
$$
\frac{x^{2}}{1+y}+\frac{y^{2}}{1+z}+\frac{z^{2}}{1+x} \leq 1
$$
5.Is it possible to cover a $2003 \times 2003$ board with $1 \times 2$ dominoes placed horizontally and $1 \times 3$ threeminoes placed vertically?
## THE 47-th MATHEMATIAL OLYMPIAD OF REPUBLIC OF MOLDOVA Chişinău, March 9-12, 2003
7.1 Let $m>n$ be pozitive integers. For every positive integers $k$ we define the number $a_{k}=(\sqrt{5}+2)^{k}+$ $(\sqrt{5}-2)^{k}$. Show that $a_{m+n}+a_{m-n}=a_{m} \cdot a_{n}$.
T. Fild all five digits numbers $\overline{a b c d e}$, written in decimal system, if it is known that $\overline{a b} c d e-\overline{e b c d a}=69993$, $\overline{b c d}-\overline{d c b}=792, \overline{b c}-\overline{c b}=72$.
7.3 In the triangle $A B C$ with semiperemeter $p$ the points $M, N$ and $P$ lie on the sides $(B C),(C A)$ and - (AB) respectively. Show that $p<A M+B N+C P<3 p$.
7.4 Let $a$ and $b$ be positive integer such, that $a+b \leq 10$. Find all pairs $(a, b)$ such, that the fraction $(2 n+a) /(5 n+b)$ are irreducible for every natural number $n$.
7.5 A given rectangular table has at least one column and at least one line. He is full completed by the first positive integers, written consecutively from the left to the right and begining to the first line. It is known, that the number 170 is written on the middle line and in the same column with him on the last line is written the number 329 . How much numbers are written in the given table.
7.6 Prove that for every positive integer $n$ the number $a=(2 n+1)^{5}-2 n-1$ is divisible by 240 .
7.7 In the square $A B C D$ the point $N$ is the middle point of the side $[A B]$ and the point $M$ lies on the diagonal $(A C)$ so that $A C=4 C M$. Prove that the angle $D M N$ is right.
7.8 The real numbers $x_{1}, x_{2}, \ldots, x_{2003}$ satisfy the relations $x_{1} / 1=x_{2} / 2=x_{3} / 3=\ldots=x_{2003} / 2003$ and $\sqrt{1^{2}+2^{2}+\ldots+2003^{2}}+\sqrt{x_{1}^{2}+x_{2}^{2}+\ldots+x_{2003}^{2}}=\sqrt{\left(1+x_{1}\right)^{2}+\left(2+x_{2}\right)^{2}+\ldots+\left(2003+x_{2003}\right)^{2}}$. Prove that $x_{i} \geq 0$ for every $i=1,2, \ldots, 2003$.
8.1 Calculate the sum
$$
\frac{2^{4}+2^{2}+1}{2^{7}-2}+\frac{3^{4}+3^{2}+1}{3^{7}-3}+\ldots+\frac{2003^{4}+2003^{2}+1}{2003^{7}-2003}+\frac{1}{2 \cdot 2003 \cdot 2004}
$$
8.2 Let $[A B]$ be a segment and $\sigma$ be one of the halfplane, determined by the straight line $A B$. The segments $[A P]$ and $[B Q]$ with integer lengths are situated in $\sigma$ and are perpendicular to the straight line $A B$. The intersection point $M$ of the straight lines $A Q$ and $B P$ is distanced at 8 units to the straight line $A B$. Find the lengths of the segments $[A P]$ and $[B Q]$, if it is known that the triangle $B Q M$ has a greatest area.
8.3 Let $A B C$ be an acuteangled triangle such that $m(\angle A C B) \neq 45^{\circ}$. The points $M$ and $N$ are the feets of the altitudes, drawn from the vertices $A$ and $B$ respectively. The points $P$ and $Q$ lyes on the halfstraight lines ( $M A$ and ( $N B$ respectively so that $M P=M B$ and $N Q=N A$. Prove that the straight lines $P Q$ and $M N$ are parallel.
8.4 The equation $x^{13}-x^{11}+x^{9}-x^{7}+x^{5}-x^{3}+x-2=0$ has a real solution $x_{0}$. Show that $\left[x_{0}^{14}\right]=3$, where $[a]$ is a integral part of the real number $a$.
8.5 Prove that every positive integer number $n \geq 3$ can be written as a sum of at least two consecutive positive integers if and only if he is not a power of the number 2 .
8.6 The prime number $p$ has the following property: the remainder $r$ of the division of $p$ by 210 is a composite number which can be represented us a sum of two perfect squares. Find the number $r$.
8.7 Through the arbitrary point of the triangle $A B C$ construct (explain the steps of the construction) a straight, line which divides the triangle $A B C$ in two parts so that the ratio of they areas is equal to $3 / 4$.
8.8 Let $x$ be a real number. Find the smallest value of the expression $\sqrt{x^{2}+2 x+4}+\sqrt{x^{2}-\sqrt{3} x+1}$.
9.1 In the space a geometrical configuration, which include $n(n \geq 3)$ distinct points, is given. A point $A$ of this configuration has the following properties: if $A$ is excluded from the configuration, then among the remaining points there are no colinear points; after the elimination of $A$ from the configuration the number of all straight lines, that were constructed through any 2 points of the configuration, is lowered by $1 / 15$ part. Find the value of $n$.
9.2 Let $x^{2}+b x+c=0$ be the equation, where $b$ and $c$ are two consecutive triangular numbers and $c>b \geq$ 10. Prove that this equation has two irrational solutions. (The number $m$ is triangular, if $m=n(n-1) / 2$ for certain positive integer $n \geq 1$ ).
9.3 The distinct points $M$ and $N$ lie on the hypotenuse ( $A C)$ of the right isosceles triangle $A B C$ so that $M \in(A N)$ and $M N^{2}=A M^{2}+C N^{2}$. Prove that $m(\angle M B N)=45^{\circ}$.
9.4 Find all the functions $f: N^{*} \rightarrow N^{*}$ which verify the relation $f(2 x+3 y)=2 f(x)+3 f(y)+4$ for every positive integers $x, y \geq 1$.
9.5 The numbers $a_{1}, a_{2}, \ldots, a_{n}$ are the first $n$ positive integers with the property that the number $8 a_{k}+1$ is a perfect square for every $k=1,2, \ldots, n$. Find the sum $S_{n}=a_{1}+a_{2}+\ldots+a_{n}$.
9.6 Find all real solutions of the equation $x^{4}+7 x^{3}+6 x^{2}+5 \sqrt{2003} x-2003=0$.
9.7 The side lengths of the triangle $A B C$ satisfy the relations $a>b \geq 2 c$. Prove that the altitudes of the triangle $A B C$ can not be the sides of any triangle.
9.8 The base of a pyramid is a convex polygon with 9 sides. All the lateral edges of the pyramid and all the liagunads ui the base are coloured in a random way in red or blue. Pröve that there exist at least three vertices of the pyramid which belong to a triangle with the sides coloured in the same colour.
10.1 Find all prime numbers $a, b$ and $c$ for which the equality $(a-2)!+2 b!=22 c-1$ holds.
10.2 Solve the system $x+y+z+t=6, \sqrt{1-x^{2}}+\sqrt{4-y^{2}}+\sqrt{9-z^{2}}+\sqrt{16-t^{2}}=8$.
10.3 In the scalen triangle $A B C$ the points $A_{1}$ and $B_{1}$ are the bissectrices feets, drawing from the vertices $A$ and $B$ respectively. The straight line $A_{1} B_{1}$ intersect the line $A B$ at the point $D$. Prove that one of the angles $\angle A C D$ or $\angle B C D$ is obtuze and $m(\angle A C D)+m(\angle B C D)=180^{\circ}$.
10.4 Let $a>1$ be not integer number and $a \neq \sqrt[2]{q}$ for every positive integers $p \geq 2$ and $q \geq 1$, $k=\left[\log _{a} n\right] \geq 1$, where $[x]$ is the integral part of the real number $x$. Prove that for every positive integer $n \geq 1$ the equality
$$
\left[\log _{a} 2\right]+\left[\log _{a} 3\right]+\ldots+\left[\log _{a} n\right]+[a]+\left[a^{2}\right]+\ldots+\left[a^{k}\right]=n k
$$
holds.
10.5 The rational numbers $p, q, r$ satisfy the relation $p q+p r+q r=1$. Prove that the number $\left(1+p^{2}\right)\left(1+q^{3}\right)\left(1+r^{2}\right)$ is a square of any rational number.
10.6 Let $n \geq 1$ be a positive integer. For every $k=1,2, \ldots, n$ the functions $f_{k}: R \rightarrow R, f_{k}(x)=$ $a_{k} x^{2}+b_{k} x+c_{k}$ with $a_{k} \neq 0$ are given. Find the greatest possible number of parts of the rectangular plane $x O y$ which can be obtained by the intersection of the graphs of the functions $f_{k}(k=1,2, \ldots, n)$.
10.7 The circle with the center $O$ is tangent to the sides $[A B],[B C],[C D]$ and $[D A]$ of the convex quadrilateral $A B C D$ at the points $M, N, \mathcal{K}$ and $L$ respectively. The straight lines $M N$ and $A C$ are parallel and the straight line $M K$ intersect the line $L N$ at the point $P$. Prove that the points $A, M, P, O$ and $L$ are concyclic.
10.8 Find all integers $n$ for which the number $\log _{2 n-1}\left(n^{2}+2\right)$ is rational.
11.1 Let $a, b, c, d \geq 1$ be arbitrary positive numbers. Prove that the equations system $a x-y z=$ $c, \quad b x-y t=-d$. has at least a solution $(x, y, z, t)$ in positive integers.
11.2 The sequences $\left(a_{n}\right)_{n \geq 0}$ and $\left(b_{n}\right)_{n \geq 0}$ satisfy the conditions $(1+\sqrt{3})^{2 n+1}=a_{n}+b_{n} \sqrt{3}$ and $a_{n}, b_{n} \in Z$. Find the recurrent relation for each of the sequences $\left(a_{n}\right)$ and $\left(b_{n}\right)$.
11.3 The triangle $A B C$ is rightangled in $A, A C=b, A B=c$ and $B C=a$. The halfstraight line ( $A z$ is perpendicular to the plane $(A B C), M \in(A z$ so that $\alpha, \beta, \gamma$ are the mesures of the angles, formed by the edges $M B, M C$ and the plane ( $M B C$ ) with the plane ( $A B C$ ) respectively. In the set of the triangular pyramids MABC on consider the pyramids with the volumes $V_{1}$ and $V_{2}$ which satisfy the relations $\alpha+\beta+\gamma=\pi$ and $\alpha+\beta+\gamma=\pi / 2$ respectively. Prove the equality $\left(V_{1} / V_{2}\right)^{2}=(a+b+c)(1 / a+1 / b+1 / c)$.
11.4 Find all the functions $f:[0 ;+\infty) \rightarrow[0 ;+\infty)$ which satisfy the conditions: : $f(x f(y)) \cdot f(y)=$ $f(x+y)$ for every $x, y \in[0 ;+\infty) ; f(2)=0 ; f(x) \neq 0$ for every $x \in[0 ; 2)$.
11.5 Let $0<a<b$ be real positive numbers. Prove that the equation $[(a+b) / 2]^{x+y}=a^{x} b^{y}$ has at least a solution in the set $(a ; b) \times(a ; b)$.
11.6 Each of the plane angles of the vertex $V$ of the tetrahedron $V A B C$ has the measure equal to $60^{\circ}$. Prove that $V A+V B+V C \leq A B+B C+C A$. When the equality holds?
11.7 The plane $\alpha$ is tangent in the points $A_{3}, A_{2}$ and $A_{3}$ to three spheres with different radii $R_{1}, R_{2}$ and $R_{3}$ respectively, situated in the same halfspace two by two exteriorly. The plane $\beta$ is parallel to the plane $\alpha$ and intersect all three spheres so that the circles $D_{1}, D_{2}$ and $D_{3}$ are obtained. Find the distance between the planes $\alpha$ and $\beta$ so that the sum of the volumes $V_{1}, V_{2}$ and $V_{3}$ of the cones with the bases $D_{1}, D_{2}, D_{3}$ and the vertices $A_{1}, A_{2}, A_{3}$ respectively, will be the greatest.
11.8 For every positive integer $n \geq 1$ wie define the matrix $A_{n}=\left(a_{i j}\right)_{1 \leq i, j \leq n}$, where $a_{i j}=$ $\max (i, j) / \min (i, j), \quad 1 \leq i, j \leq n$. Calculate the determinant of the matrix $A_{n}$.
12.1 Prove that $\lim _{n \rightarrow+\infty} \ln \left(1+2 e+4 e^{4}+6 e^{9}+\ldots+2 n e^{n^{2}}\right) / n^{2}=1$.
12.2 For every positive integer $n \geq 2$ the affirmation $P_{n}^{\prime}$ : "If the derivative $P^{\prime}(X)$ of a polynomial $P(X)$ * of degree $n$ with real coefficients has $n-1$ real distinct roots, then there exists a real constant $C$ such that the equation $P(x)=C$ has $n$ real distinct solutions" is considered. Prove that $P_{4}$ is true. Is the affirmation $P_{5}$ true? Prove the answer.
12.3 In the circle with radius $R$ the distinct chords $[A B]$ and $[C D]$ are concurrent and form an acute angle with mesure $\alpha$. Prove that $A B+C D>2 R \sin \alpha$.
12.4 The real numbers $\alpha, \beta, \gamma$ satisfy the relations $\sin \alpha+\sin \beta+\sin \gamma=0$ and $\cos \alpha+\cos \beta+\cos \gamma=0$. Find all positive integers $n \geq 0$ for-which $\sin (n \alpha+\pi / 4)+\sin (n \beta+\pi / 4)+\sin (n \gamma+\pi / 4)=0$.
12.5 For every positive integer $n \geq 1$ we define the polynomial $P(X)=X^{2 n}-X^{2 n-1}+\ldots-X+1$, Find the remainder of the division of the polynomial $P\left(X^{2 n+1}\right)$ by the polynomial $P(X)$.
12.6 Fie $n \in N$. Find all the primitives of the function
$$
f: R \rightarrow R, \quad f(x)=\frac{x^{3}-9 x^{2}+29 x-33}{\left(x^{2}-6 x+10\right)^{n}}
$$
12.7 In a rectangular system $x O y$ the graph of the function $f: R \rightarrow R, f(x)=x^{2}$ is drawn. The ordered triple $B, A, C$ has distinct points on the parabola, the point $D \in(B C)$ such that the straight line $A D$ is parallel to the axis $O y$ and the triangles $B A D$ and $C A D$ have the areas $s_{1}$ and $s_{2}$ respectively. Find the length of the segment $[A D]$.
12.8 Let $\left(F_{n}\right)_{n \in N^{*}}$ be the Fibonacci sequence so that: $F_{1}=1, F_{2}=1, F_{n+1}=F_{n}+F_{n-1}$ for every positive integer $n \geq 2$. Shown that $F_{n}<3^{n / 2}$ and calculate the limit $\lim _{n \rightarrow \infty}\left(F_{1} / 2+F_{2} / 2^{2}+\ldots+F_{n} / 2^{n}\right)$.
## The first selection test for IMO 2003 and BMO 2003, March 12, 2003
B1. Each side of the arbitrary triangle is divided into 2002 congruent segments. After that each interior division point of the side is joined with opposite vertex. Prove that the number of obtained regions of the triangle is divisible by 6 .
B2. The positive real numbers $x, y$ and $z$ satisfy the relation $x+y+z \geq 1$. Prove the inequality
$$
\frac{x \sqrt{x}}{y+z}+\frac{y \sqrt{y}}{x+z}+\frac{z \sqrt{z}}{x+y} \geq \frac{\sqrt{3}}{2}
$$
B3. The quadrilateral $A B C D$ is inscribed in the circle with center $O$, the points $M$ and $N$ are the middle points of the diagonals $[A C]$ and $[B D]$ respectively and $P$ is the intersection point of the diagonals. It is known that the points $O, M, N$ si $P$ are distinct. Prove that the points $O, M, B$ and $D$ are concyclic if and only if the points $O, N, A$ and $C$ are concyclic.
B4. Prove that the equation $1 / a+1 / b+1 / c+1 /(a b c) \doteq 12 /(a+b+c)$ has many solutions $(a, b, c)$ in strictly positive integers.
## The second selection test for IMO 2003, March 22, 2003
B5. Let $n \geq 1$ be positive integer. Find all polynomials of degree $2 n$ with real coefficients
$$
P(X)=X^{2 n}+(2 n-10) X^{2 n-1}+a_{2} X^{2 n-2}+\ldots+a_{2 n-2} X^{2}+(2 n-10) X+1
$$
-if it is known that they have positive real roots.
B6. The triangle $A B C$ has the semiperimeter $p$, the circumradius $R$, the inradius $r$ and $l_{a,}, l_{b}, l_{c}$ are the lengths of internal bissecticies, drawing from the vertices $A, B$ and $C$ respectively. Prove the inequality $l_{a} l_{b}+l_{b} l_{c}+l_{c} l_{a} \leq p \sqrt{3 r^{2}+12 R r}$.
B7. The points $M$ and $N$ are the tangent points of the sides $[A B]$ and $[A C]$ of the triangle $A B C$ to the incircle with the center $I$. The internal bissectrices, drawn from the vertices $B$ and $C$, intersect the straight line $M N$ at points $P$ and $Q$ respectively. If $F$ is the intersection point of the swtraight lines $C P$ and $B Q$, then prove that the straight lines $F I$ and $B C$ are perpendicular.
B8. Let $n \geq 4$ be the positive integer. On the checkmate table with dimensions $n \times n$ we put the coins. One consider the diagonal of the table each diagonal with at least two unit squares. What is the smallest number of coins put on the table so that on the each horizontal, each vertical and each diagonal there exists att least one coin. Prove the answer.
## The third selection test for IMO 2003, March 23, 2003
B9. Let $n \geq 1$ be positive integer. A permutation $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of the numbers $(1,2, \ldots, n)$ is called quadratique if among the numbers $a_{1}, a_{1}+a_{2}, \ldots, a_{1}+a_{2}+\ldots+a_{n}$ there exist at least a perfect square. Find the greatest number $n$, which is less than 2003 , such that every permutation of the numbers $(1,2, \ldots, n)$ will be quadratique.
B10. The real numbers $a_{1}, a_{2}, \ldots, a_{2003}$ satisfy simultaneousiy the relations: $a_{i} \geq 0$ for all $i=$ $1,2, \ldots, 2003 ; \quad a_{1}+a_{2}+\ldots+a_{2003}=2 ; \quad a_{1} a_{2}+a_{2} a_{3}+\ldots+a_{2003} a_{1}=1$. Find the smallest value of the sum $a_{1}^{2}+a_{2}^{2}+\ldots+a_{2003}^{2}$.
B11. The arbitrary point $M$ on the plane of the triangle $A B C$ does not belong on the straight lines $A B, B C$ and $A C$. If $S_{1}, S_{2}$ and $S_{3}$ are the areas of the triangles $A M B, B M C$ and $A M C$ respectively, find the geometrical locus of the points $M$ which satisfy the relation $\left(M A^{2}+M B^{2}+M C^{2}\right)^{2}=16\left(S_{1}^{2}+S_{2}^{2}+S_{3}^{2}\right)$.
812. Let $n \geq 1$ be a positive integer. A square table of dimensions $n \times n$ is full arbitrarly completed $\because$ the numb so, shat every number appear exactly conce the table. from cack fine one select the smallest number and the greatest of them is denote by $x$. From each column one select the greatest number and the smallest of them is denote by $y$. The table is called equilibrated if $x=y$. How match equilibrated tables there exist?
## The first selection test for JBMO 2003, April 12, 2003
JB1. Let $n \geq 2003$ be a positive integer such that the number $1+2003 n$ is a perfect square. Prove that the number $n+1$ is equal to the sum of 2003 positive perfect squares.
JB2. The positive real numbers $a, b, c$ satisfy the relation $a^{2}+b^{2}+c^{2}=3 a b c$. Prove the inequality
$$
\frac{a}{b^{2} c^{2}}+\frac{b}{c^{2} a^{2}}+\frac{c}{a^{2} b^{2}} \geq \frac{9}{a+b+c}
$$
JB3. The quadrilateral $A B C D$ with perpendicular diagonals is inscribed in the circle with center $O$, the points $M$ and $N$ are the middle points of the sides $[B C]$ and $[C D]$ respectively. Find the value of the ratio of areas of the figures $O M C N$ and $A B C D$.
JB4. Let $m$ and $n$ be the arbitrary digits of the decimal system and $a, b, c$ be the positive distinct integers of the form $2^{m} \cdot 5^{n}$. Find the number of the equations $a x^{2}-2 b x+c=0$, if it is known that each equation has a single real solution.
## The second selection test for JMBO 2003, April 13, 2003
JB5. Prove that each positive integer is equal to a difference of two positive integers with the same number of the prime divisors.
JB6. The real numbers $x$ and $y$ satisfy the equalities
$$
\sqrt{3 x}\left(1+\frac{1}{x+y}\right)=2, \quad \sqrt{7 y}\left(1-\frac{1}{x+y}\right)=4 \sqrt{2}
$$
Find the numerical value of the ratio $y / x$.
$J B 7$. The triangle $A B C$ is isosceles with $A B=B C$. The point $F$ on the side $[B C]$ and the point $D$ on the side $[A C]$ are the feets of the internal bissectrix drawn from $A$ and altitude drawn from $B$ respectively so that $A F=2 B D$. Find the measure of the angle $A B C$.
JB8. In the rectangular coordinate system every point with integer coordinates is called laticeal point. Let $P_{n}(n, n+5)$ be a laticeal point and denote by $f(n)$ the number of laticeal points on the open segment $\left(O P_{n}\right)$, where the point $O(0,0)$ is the coordinates system origine. Calculate the number $f(1)+f(2)+$ $f(3)+\ldots+f(2002)+f(2003)$.
7 th Junior Balkan Mathematical O-lympiad
$20-25$ Jun e, 20.03 I $\mathrm{m}$ i r $\quad$. $\quad$ u rke y
## English Version
1. Let $n$ be a positive integer. A number $A$ consists of $2 n$ digits, each of which is 4 ; and a number $B$ consists of $n$ digits, each of which is 8 . Prove that $A+2 B+4$ is a perfect square.
\&
2. Suppose there are $n$ points in a plane no three of which are collinear with the following property:
If we label these points as $A_{1}, A_{2}, \ldots, A_{n}$ in any way whatsoever, the broken line $A_{1} A_{2} \ldots A_{n}$ does not intersect itself.
Find the maximal value that $n$ can have.
3. Let $k$ be the circumcircle of the triangle $A B C$. Consider the arcs $\overparen{A B}, \widehat{B C}, \widetilde{C A}$ such that $C \notin \widetilde{A B}, A \notin \widetilde{B C}, B \notin \widetilde{C A}$. Let $D, E$ and $F$ be the midpoints of the arcs $\widehat{B C}, \overparen{C A}, \overparen{A B}$, respectively. Let $G$ and $H$ be the points of intersection of $D E$ with $C B$ and $C A$; let $I$ and $J$ be the points of intersection of $D F$ with $B C$ and $B A$, respectively. Denote the midpoints of $G H$ and $I J$ by $M$ and $N$, respectively.
a) Find the angles of the triangle $D M N$ in terms of the angles of the triangle $A B C$.
b) If $O$ is the circumcentre of the triangle $D M N$ and $P$ is the intersection point of $A D$ and $E F$, prove that $O, P, M$ and $N$ lie on the same circle.
4. Let $x, y, z$ be real numbers greater than -1 . Prove that
$$
\frac{1+x^{2}}{1+y+z^{2}}+\frac{1+y^{2}}{1+z+x^{2}}+\frac{1+z^{2}}{1+x+y^{2}} \geq 2
$$
## Romanian Version
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2003_shl.jsonl",
"problem_match": "\nGEO 7.",
"solution_match": "\nSolution:"
}
|
c45612e6-12f5-56e7-bfe6-75ad3e04a15d
| 606,167
|
If the positive integers $x$ and $y$ are such that both $3 x+4 y$ and $4 x+3 y$ are perfect squares, prove that both $x$ and $y$ are multiples of 7 .
|
Let
$$
3 x+4 y=m^{2}, \quad 4 x+3 y=n^{2}
$$
Then
$$
7(x+y)=m^{2}+n^{2} \Rightarrow 7 \mid m^{2}+n^{2}
$$
Considering $m=7 k+r, \quad r \in\{0,1,2,3,4,5,6\}$ we find that $m^{2} \equiv u(\bmod 7), \quad u \in$ $\{0,1,2,4\}$ and similarly $n^{2} \equiv v(\bmod 7), \quad v \in\{0,1,2,4\}$. Therefore we have either $m^{2}+n^{2} \equiv 0 \quad(\bmod 7)$, when $u=v=0$, or $m^{2}+n^{2} \equiv w(\bmod 7), w \in\{1,2,3,4,5,6\}$. However, from (2) we have that $m^{2}+n^{2} \equiv 0(\bmod \tau)$ and hence $u=v=0$ and
$$
m^{2}+n^{2} \equiv 0 \quad\left(\bmod \tau^{2}\right) \Rightarrow 7(x+y) \equiv 0 \quad\left(\bmod \tau^{2}\right)
$$
and cousequently
$$
x+y \equiv 0 \quad(\bmod 7)
$$
Moreover. from (1) we have $x-y=n^{2}-m^{2}$ and $n^{2}-m^{2} \equiv 0\left(\bmod i^{2}\right)$ (since $\left.u=c=0\right)$, so
$$
x-y \equiv 0 \quad(\bmod 7) .
$$
From (3) and (4) we have tliat $x+y=7 k, x-y=7 l$, where $k$ and $l$ are positive incegers. Hence
$$
2 x=7(k+l), 2 y=7(k-l)
$$
where $k+l$ and $k-l$ are positive integers. It follows that $i \mid 2 x$ and $i \mid 2 y$, and finally $\pi \mid x$ and i|y.
## ALGEBRA
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
If the positive integers $x$ and $y$ are such that both $3 x+4 y$ and $4 x+3 y$ are perfect squares, prove that both $x$ and $y$ are multiples of 7 .
|
Let
$$
3 x+4 y=m^{2}, \quad 4 x+3 y=n^{2}
$$
Then
$$
7(x+y)=m^{2}+n^{2} \Rightarrow 7 \mid m^{2}+n^{2}
$$
Considering $m=7 k+r, \quad r \in\{0,1,2,3,4,5,6\}$ we find that $m^{2} \equiv u(\bmod 7), \quad u \in$ $\{0,1,2,4\}$ and similarly $n^{2} \equiv v(\bmod 7), \quad v \in\{0,1,2,4\}$. Therefore we have either $m^{2}+n^{2} \equiv 0 \quad(\bmod 7)$, when $u=v=0$, or $m^{2}+n^{2} \equiv w(\bmod 7), w \in\{1,2,3,4,5,6\}$. However, from (2) we have that $m^{2}+n^{2} \equiv 0(\bmod \tau)$ and hence $u=v=0$ and
$$
m^{2}+n^{2} \equiv 0 \quad\left(\bmod \tau^{2}\right) \Rightarrow 7(x+y) \equiv 0 \quad\left(\bmod \tau^{2}\right)
$$
and cousequently
$$
x+y \equiv 0 \quad(\bmod 7)
$$
Moreover. from (1) we have $x-y=n^{2}-m^{2}$ and $n^{2}-m^{2} \equiv 0\left(\bmod i^{2}\right)$ (since $\left.u=c=0\right)$, so
$$
x-y \equiv 0 \quad(\bmod 7) .
$$
From (3) and (4) we have tliat $x+y=7 k, x-y=7 l$, where $k$ and $l$ are positive incegers. Hence
$$
2 x=7(k+l), 2 y=7(k-l)
$$
where $k+l$ and $k-l$ are positive integers. It follows that $i \mid 2 x$ and $i \mid 2 y$, and finally $\pi \mid x$ and i|y.
## ALGEBRA
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2004_shl.jsonl",
"problem_match": "\nNT4.",
"solution_match": "\nSolution."
}
|
6801c12d-ddfd-5cd5-9dc5-9f48864efefc
| 606,224
|
Prove that
$$
(1+a b c)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \geq 3+a+b+c
$$
for any real numbers $a, b, c \geq 1$.
|
The inequality rewrites as
$$
\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)+(b c+a c+a b) \geq 3+a+b+c
$$
or
$$
\left(\frac{\frac{1}{a}+\frac{1}{b}}{2}+\frac{\frac{1}{b}+\frac{1}{c}}{2}+\frac{\frac{1}{a}+\frac{1}{c}}{2}\right)+(b c+a c+a b) \geq 3+a+b+c
$$
which is equivalent to
$$
\frac{(2 a b-(a+b))(a b-1)}{2 a b}+\frac{(2 b c-(b+c))(b c-1)}{2 b c}+\frac{(2 c a-(c+a))(c a-1)}{2 c a} \geq 0
$$
The last inequality is true due to the obvious relations
$$
2 x y-(x+y)=x(y-1)+y(x-1) \geq 0
$$
for any two real numbers $x, y \geq 1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that
$$
(1+a b c)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \geq 3+a+b+c
$$
for any real numbers $a, b, c \geq 1$.
|
The inequality rewrites as
$$
\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)+(b c+a c+a b) \geq 3+a+b+c
$$
or
$$
\left(\frac{\frac{1}{a}+\frac{1}{b}}{2}+\frac{\frac{1}{b}+\frac{1}{c}}{2}+\frac{\frac{1}{a}+\frac{1}{c}}{2}\right)+(b c+a c+a b) \geq 3+a+b+c
$$
which is equivalent to
$$
\frac{(2 a b-(a+b))(a b-1)}{2 a b}+\frac{(2 b c-(b+c))(b c-1)}{2 b c}+\frac{(2 c a-(c+a))(c a-1)}{2 c a} \geq 0
$$
The last inequality is true due to the obvious relations
$$
2 x y-(x+y)=x(y-1)+y(x-1) \geq 0
$$
for any two real numbers $x, y \geq 1$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2004_shl.jsonl",
"problem_match": "\nA1.",
"solution_match": "\nSolution."
}
|
72782f96-1023-51ba-8085-bcad669bf33e
| 606,235
|
Prove that, for all real numbers $x, y, z$ :
$$
\frac{x^{2}-y^{2}}{2 x^{2}+1}+\frac{y^{2}-z^{2}}{2 y^{2}+1}+\frac{z^{2}-x^{2}}{2 z^{2}+1} \leq(x+y+z)^{2}
$$
When the equality holds?
|
For $x=y=z=0$ the equality is valid.
Since $(x+y+z)^{2} \geq 0$ it is enongh to prove that
$$
\frac{x^{2}-y^{2}}{2 x^{2}+1}+\frac{y^{2}-z^{2}}{2 y^{2}+1}+\frac{z^{2}-x^{2}}{2 z^{2}+1} \leq 0
$$
which is equivalent to the inequality
$$
\frac{x^{2}-y^{2}}{x^{2}+\frac{1}{2}}+\frac{y^{2}-z^{2}}{y^{2}+\frac{1}{2}}+\frac{z^{2}-x^{2}}{z^{2}+\frac{1}{2}} \leq 0
$$
Dellote
$$
a=x^{2}+\frac{1}{2}, b=y^{2}+\frac{1}{2}, c=z^{2}+\frac{1}{2}
$$
Then (1) is equivalent to
$$
\frac{a-b}{a}+\frac{b-c}{b}+\frac{c-a}{c} \leq 0
$$
From very well known $A G$ inequality follows that
$$
a^{2} b+b^{2} c+c^{2} a \geq 3 a b c
$$
Fron the equivalencies
$$
a^{2} b+b^{2} c+c^{2} a \geq 3 a b c \Leftrightarrow \frac{a}{c}+\frac{b}{a}+\frac{c}{b} \geq-3 \Leftrightarrow \frac{a-b}{a}+\frac{b-c}{b}+\frac{c-a}{c} \leq 0
$$
follows thait the inequality (2) is valid, for positive real numbers $a, b, c$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that, for all real numbers $x, y, z$ :
$$
\frac{x^{2}-y^{2}}{2 x^{2}+1}+\frac{y^{2}-z^{2}}{2 y^{2}+1}+\frac{z^{2}-x^{2}}{2 z^{2}+1} \leq(x+y+z)^{2}
$$
When the equality holds?
|
For $x=y=z=0$ the equality is valid.
Since $(x+y+z)^{2} \geq 0$ it is enongh to prove that
$$
\frac{x^{2}-y^{2}}{2 x^{2}+1}+\frac{y^{2}-z^{2}}{2 y^{2}+1}+\frac{z^{2}-x^{2}}{2 z^{2}+1} \leq 0
$$
which is equivalent to the inequality
$$
\frac{x^{2}-y^{2}}{x^{2}+\frac{1}{2}}+\frac{y^{2}-z^{2}}{y^{2}+\frac{1}{2}}+\frac{z^{2}-x^{2}}{z^{2}+\frac{1}{2}} \leq 0
$$
Dellote
$$
a=x^{2}+\frac{1}{2}, b=y^{2}+\frac{1}{2}, c=z^{2}+\frac{1}{2}
$$
Then (1) is equivalent to
$$
\frac{a-b}{a}+\frac{b-c}{b}+\frac{c-a}{c} \leq 0
$$
From very well known $A G$ inequality follows that
$$
a^{2} b+b^{2} c+c^{2} a \geq 3 a b c
$$
Fron the equivalencies
$$
a^{2} b+b^{2} c+c^{2} a \geq 3 a b c \Leftrightarrow \frac{a}{c}+\frac{b}{a}+\frac{c}{b} \geq-3 \Leftrightarrow \frac{a-b}{a}+\frac{b-c}{b}+\frac{c-a}{c} \leq 0
$$
follows thait the inequality (2) is valid, for positive real numbers $a, b, c$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2004_shl.jsonl",
"problem_match": "\nA2.",
"solution_match": "\nSolution."
}
|
ac0a9c5b-8df4-50ae-a27c-cb63d79bfce0
| 606,244
|
Prove that for all real $x, y$
$$
\frac{x+y}{x^{2}-x y+y^{2}} \leq \frac{2 \sqrt{2}}{\sqrt{x^{2}+y^{2}}}
$$
|
The inequality rewrites as
$$
\frac{x+y}{x^{2}-x y+y^{2}} \leq \frac{\sqrt{2\left(x^{2}+y^{2}\right)}}{\frac{x^{2}+y^{2}}{2}}
$$
Now it is enough to prove the next two simple inequalities:
$$
x+y \leq \sqrt{2\left(x^{2}+y^{2}\right)}, \quad x^{2}-x y+y^{2} \geq \frac{x^{2}+y^{2}}{2}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for all real $x, y$
$$
\frac{x+y}{x^{2}-x y+y^{2}} \leq \frac{2 \sqrt{2}}{\sqrt{x^{2}+y^{2}}}
$$
|
The inequality rewrites as
$$
\frac{x+y}{x^{2}-x y+y^{2}} \leq \frac{\sqrt{2\left(x^{2}+y^{2}\right)}}{\frac{x^{2}+y^{2}}{2}}
$$
Now it is enough to prove the next two simple inequalities:
$$
x+y \leq \sqrt{2\left(x^{2}+y^{2}\right)}, \quad x^{2}-x y+y^{2} \geq \frac{x^{2}+y^{2}}{2}
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2004_shl.jsonl",
"problem_match": "\nA3.",
"solution_match": "\nSolution."
}
|
11dce336-5df0-523f-9dba-99c7c30f03c4
| 606,254
|
Prove that if $0<\frac{a}{b}<b<2 a$ then
$$
\frac{2 a b-a^{2}}{7 a b-3 b^{2}-2 a^{2}}+\frac{2 a b-b^{2}}{7 a b-3 a^{2}-2 b^{2}} \geq 1+\frac{1}{4}\left(\frac{a}{b}-\frac{b}{a}\right)^{2}
$$
|
If we denote
$$
u=2-\frac{a}{b}, \quad v=2-\frac{b}{a}
$$
then the inequality rewrites as
$$
\begin{aligned}
& \frac{u}{v+u v}+\frac{v}{u+u v} \geq 1+\frac{1}{4}(u-u)^{2} \\
& \frac{(u-v)^{2}+u v(1-u v)}{u v(u v+u+v+1)} \geq \frac{(u-u)^{2}}{4}
\end{aligned}
$$
$\mathrm{Or}$
Since $u>0, v>0, u+v \leq 2, u v \leq 1, u v(u+v+u v+1) \leq 4$, the result is clear.
## GEOMETRY
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that if $0<\frac{a}{b}<b<2 a$ then
$$
\frac{2 a b-a^{2}}{7 a b-3 b^{2}-2 a^{2}}+\frac{2 a b-b^{2}}{7 a b-3 a^{2}-2 b^{2}} \geq 1+\frac{1}{4}\left(\frac{a}{b}-\frac{b}{a}\right)^{2}
$$
|
If we denote
$$
u=2-\frac{a}{b}, \quad v=2-\frac{b}{a}
$$
then the inequality rewrites as
$$
\begin{aligned}
& \frac{u}{v+u v}+\frac{v}{u+u v} \geq 1+\frac{1}{4}(u-u)^{2} \\
& \frac{(u-v)^{2}+u v(1-u v)}{u v(u v+u+v+1)} \geq \frac{(u-u)^{2}}{4}
\end{aligned}
$$
$\mathrm{Or}$
Since $u>0, v>0, u+v \leq 2, u v \leq 1, u v(u+v+u v+1) \leq 4$, the result is clear.
## GEOMETRY
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2004_shl.jsonl",
"problem_match": "\nA4.",
"solution_match": "\nSolution."
}
|
b0229e77-c25c-552f-836b-5f9f02351e36
| 606,259
|
Two circles $k_{1}$ and $k_{2}$ intersect a.t points $A$ and $B$. A circle $k_{3}$ centered at $A$ meet $k_{1}$ at $M$ and $P$ and $k_{2}$ at $N$ and $Q$, such that $N$ and $Q$ are on different sides of $M P$ and $A B>A M$.
Prove rhat the angles $\angle M B Q$ and $\angle N B P$ are equal.
|
As $A M=A P$, we have
$$
\angle M B A=\frac{1}{2} \operatorname{arcAM}=\frac{1}{2} \operatorname{arc} A P=\angle A B P
$$
and likewise
$$
\angle Q B A=\frac{1}{2} \operatorname{arc} A Q=\frac{1}{2} \operatorname{arc} c A N=\angle A B N
$$
Summing these equalities yields $\angle M B Q=\angle N B P$ as needed.
Q2. Let $E$ and $F$ be two distinct points inside of a parallelogram $A B C D$. Find the maximum number of triangles with the same area and having the vertices in three of the following five points: $A, B, C, D, E, F$.
Solution. We shall use the following two well known results:
Lemma 1. Let $A, B, C, D$ be four points lying in the same plane such that the line $A B$ do not intersect the segment $C D$ (in particular $\triangle B C D$ is a convex quadrilateral). If $[A B C]=[A B D]$, then $A B \| C D$.
Lemma 2. Let $X$ be a point inside of a parallelogram $A B C D$. Then $[A C X]<[A B C]$ and $[B D X]<[4 B D]$. (Here and below the notation $[S]$ stands for the area of the surface of $S$.
With the points $A, B, C, D, E, F$ we can form 20 triangles. We will show that at most ten of them can have the same area. In that sense three cases may occur.
Gase 1. EF is parallel with one side of the parallelogram $\triangle B C D$.
We can assume that $E F \|: A D, E$ lies inside of the triangle $A B F$ and $F$ lies inside of thr hiangle $C D E$. With the points $A, B, C, D, E$ we can form ten pairs of triangles als follows:
$(\triangle .4 D E, \triangle A E F) ;(\triangle . A D F, \triangle D E F) ;(\triangle B C E, \triangle B E F) ;(\triangle B C F, \triangle C E F) ;(\triangle C D E, \triangle C D F):$
$(\triangle A B E: \triangle A B F) ;(\triangle A D C ; \triangle A C E) ;(\triangle A B C, \triangle . A C F) ;(\triangle A B D, \triangle B D E) ;(\triangle C B D . \triangle B D F)$.
Using Lemmas $1-2$ one can easily prove that any two triangles that belong to the same pair have distinct area, so there exists at most ten triangles having the same area.
Case 2. $E F$ is parallel with a diagonal of the paralellogram $\triangle B C D$.
Let us assume $E F \| A C$ and that $E, F$ lie inside of the triangle $A B C$. We consider the following pairs of triangles:
$(\triangle A B D, \triangle B D E) ;(\triangle A B C, \triangle B C F) ;(\triangle A C D, \triangle B C E) ;(\triangle A B F, \triangle A B E) ;(\triangle B E F, \triangle D E F) ;$
$(\triangle A E F, \triangle A C E) ;(\triangle C E F, \triangle A C F) ;(\triangle A D E ; \triangle A D F) ;(\triangle D C E, \triangle D C F) ;(\triangle C B D, \triangle B D F)$.
With the same idea as above we deduce that any two triangles that belong to the same pair have distinct area and the conclusion follows.
We also note that if $E$ and $F$ lie on $A C$ then only 16 of 20 triangles are nondegenerate. In this case we consider the following pairs:
$$
\begin{aligned}
& (\triangle A B E, \triangle A B F) ;(\triangle A B C, \triangle B C F) ;(\triangle B C E, \triangle B E F) ;(\triangle A D E, \triangle A D F) \\
& (\triangle A C D, \triangle D C F) ;(\triangle C D E, \triangle E D F) ;(\triangle B D E, \triangle A B D) ;(\triangle B D F, \triangle B D C)
\end{aligned}
$$
Case 3. $E F$ is not parallel with any side or diagonal of $\triangle B C D$.
We claim that at most two of the triangles $A E F, B E F, C E F, D E F$ can have the same area. Indeed, supposing the contrary, we may have $[A E F]=[B E F]=[C E F]$. We remark first that $A, B, C$ do not belong to $E F$ (elsewhere, exactly one of the above triangles is degenerate, contradiction!). Hence at least two of the points $A, B, C$ belong to the same side of the line $E F$. Using now Lemma 1 we get that $E F$ is parallel with $A B$ or $B C$ or $A C$. This is clearly a contradiction and our claim follows. With the remaining 16 triangles we form 8 pairs as follows:
$(\triangle A B D, \triangle B D E) ;(\triangle C D B, \triangle B D F) ;(\triangle A D C, \triangle A C E) ;(\triangle A B C, \triangle A C F) ;$
$(\triangle A B E, \triangle A B F) ;(\triangle B C E, \triangle B C F) ;(\triangle A D E, \triangle A D F) ;(\triangle D C E, \triangle D C F)$.
With the same arguments as above, we get at most ten triangles with the same area.
To conclude the proof, it remains only to give an example of points $E, F$ inside of the parallelogram $A B C D$ such that exactly ten of the triangles that can be formed with the vetices $A, B, C, D, E, F$ have the same area.
Denote $A C \cap B D=\{O\}$ and let $M, N$ be the midpoints of $A B$ and $C D$ respectively Consider $E$ and $F$ the midpoints of $M O$ and $N O$. Then $O, M, N, E, F$ are collinear and $M E=E O=F O=N F$. Since $E$ and $F$ are the centroids of the triangles $A B F$ and $C D E$ we get $[A B E]=[A E F]=[B E F]$ and $[C E F]=[D E F]=[C D F]$. On the other hand, taking into account that $A E C F$ and $B E D F$ are parallelograms we deduce $[4 E F]=[C E F]=[4 C E]=[A C F]$ and $[B E F]=[D E F]=[B D E]=[B D F]$. From the above equalities we conclude that the triangles
## $\triangle A B E, \triangle C D F E, \triangle A C E, \triangle A C F, \triangle B D E, \triangle B D F, \triangle A E F, \triangle B E F, \triangle C E F, \triangle D E F$
have the same area. This finishes our proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Two circles $k_{1}$ and $k_{2}$ intersect a.t points $A$ and $B$. A circle $k_{3}$ centered at $A$ meet $k_{1}$ at $M$ and $P$ and $k_{2}$ at $N$ and $Q$, such that $N$ and $Q$ are on different sides of $M P$ and $A B>A M$.
Prove rhat the angles $\angle M B Q$ and $\angle N B P$ are equal.
|
As $A M=A P$, we have
$$
\angle M B A=\frac{1}{2} \operatorname{arcAM}=\frac{1}{2} \operatorname{arc} A P=\angle A B P
$$
and likewise
$$
\angle Q B A=\frac{1}{2} \operatorname{arc} A Q=\frac{1}{2} \operatorname{arc} c A N=\angle A B N
$$
Summing these equalities yields $\angle M B Q=\angle N B P$ as needed.
Q2. Let $E$ and $F$ be two distinct points inside of a parallelogram $A B C D$. Find the maximum number of triangles with the same area and having the vertices in three of the following five points: $A, B, C, D, E, F$.
Solution. We shall use the following two well known results:
Lemma 1. Let $A, B, C, D$ be four points lying in the same plane such that the line $A B$ do not intersect the segment $C D$ (in particular $\triangle B C D$ is a convex quadrilateral). If $[A B C]=[A B D]$, then $A B \| C D$.
Lemma 2. Let $X$ be a point inside of a parallelogram $A B C D$. Then $[A C X]<[A B C]$ and $[B D X]<[4 B D]$. (Here and below the notation $[S]$ stands for the area of the surface of $S$.
With the points $A, B, C, D, E, F$ we can form 20 triangles. We will show that at most ten of them can have the same area. In that sense three cases may occur.
Gase 1. EF is parallel with one side of the parallelogram $\triangle B C D$.
We can assume that $E F \|: A D, E$ lies inside of the triangle $A B F$ and $F$ lies inside of thr hiangle $C D E$. With the points $A, B, C, D, E$ we can form ten pairs of triangles als follows:
$(\triangle .4 D E, \triangle A E F) ;(\triangle . A D F, \triangle D E F) ;(\triangle B C E, \triangle B E F) ;(\triangle B C F, \triangle C E F) ;(\triangle C D E, \triangle C D F):$
$(\triangle A B E: \triangle A B F) ;(\triangle A D C ; \triangle A C E) ;(\triangle A B C, \triangle . A C F) ;(\triangle A B D, \triangle B D E) ;(\triangle C B D . \triangle B D F)$.
Using Lemmas $1-2$ one can easily prove that any two triangles that belong to the same pair have distinct area, so there exists at most ten triangles having the same area.
Case 2. $E F$ is parallel with a diagonal of the paralellogram $\triangle B C D$.
Let us assume $E F \| A C$ and that $E, F$ lie inside of the triangle $A B C$. We consider the following pairs of triangles:
$(\triangle A B D, \triangle B D E) ;(\triangle A B C, \triangle B C F) ;(\triangle A C D, \triangle B C E) ;(\triangle A B F, \triangle A B E) ;(\triangle B E F, \triangle D E F) ;$
$(\triangle A E F, \triangle A C E) ;(\triangle C E F, \triangle A C F) ;(\triangle A D E ; \triangle A D F) ;(\triangle D C E, \triangle D C F) ;(\triangle C B D, \triangle B D F)$.
With the same idea as above we deduce that any two triangles that belong to the same pair have distinct area and the conclusion follows.
We also note that if $E$ and $F$ lie on $A C$ then only 16 of 20 triangles are nondegenerate. In this case we consider the following pairs:
$$
\begin{aligned}
& (\triangle A B E, \triangle A B F) ;(\triangle A B C, \triangle B C F) ;(\triangle B C E, \triangle B E F) ;(\triangle A D E, \triangle A D F) \\
& (\triangle A C D, \triangle D C F) ;(\triangle C D E, \triangle E D F) ;(\triangle B D E, \triangle A B D) ;(\triangle B D F, \triangle B D C)
\end{aligned}
$$
Case 3. $E F$ is not parallel with any side or diagonal of $\triangle B C D$.
We claim that at most two of the triangles $A E F, B E F, C E F, D E F$ can have the same area. Indeed, supposing the contrary, we may have $[A E F]=[B E F]=[C E F]$. We remark first that $A, B, C$ do not belong to $E F$ (elsewhere, exactly one of the above triangles is degenerate, contradiction!). Hence at least two of the points $A, B, C$ belong to the same side of the line $E F$. Using now Lemma 1 we get that $E F$ is parallel with $A B$ or $B C$ or $A C$. This is clearly a contradiction and our claim follows. With the remaining 16 triangles we form 8 pairs as follows:
$(\triangle A B D, \triangle B D E) ;(\triangle C D B, \triangle B D F) ;(\triangle A D C, \triangle A C E) ;(\triangle A B C, \triangle A C F) ;$
$(\triangle A B E, \triangle A B F) ;(\triangle B C E, \triangle B C F) ;(\triangle A D E, \triangle A D F) ;(\triangle D C E, \triangle D C F)$.
With the same arguments as above, we get at most ten triangles with the same area.
To conclude the proof, it remains only to give an example of points $E, F$ inside of the parallelogram $A B C D$ such that exactly ten of the triangles that can be formed with the vetices $A, B, C, D, E, F$ have the same area.
Denote $A C \cap B D=\{O\}$ and let $M, N$ be the midpoints of $A B$ and $C D$ respectively Consider $E$ and $F$ the midpoints of $M O$ and $N O$. Then $O, M, N, E, F$ are collinear and $M E=E O=F O=N F$. Since $E$ and $F$ are the centroids of the triangles $A B F$ and $C D E$ we get $[A B E]=[A E F]=[B E F]$ and $[C E F]=[D E F]=[C D F]$. On the other hand, taking into account that $A E C F$ and $B E D F$ are parallelograms we deduce $[4 E F]=[C E F]=[4 C E]=[A C F]$ and $[B E F]=[D E F]=[B D E]=[B D F]$. From the above equalities we conclude that the triangles
## $\triangle A B E, \triangle C D F E, \triangle A C E, \triangle A C F, \triangle B D E, \triangle B D F, \triangle A E F, \triangle B E F, \triangle C E F, \triangle D E F$
have the same area. This finishes our proof.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2004_shl.jsonl",
"problem_match": "\nG1.",
"solution_match": "\nSolution "
}
|
2440d23e-85ea-5d6b-adab-c06b29e88c43
| 606,265
|
Let $A B C$ be a triangle with $\angle C=90^{\circ}$ and $D \in C .4, E \in C^{\prime} B$, and $k_{1}, k_{2}, k_{3}, k_{4}$ semicircles with diameters $C A, C B, C D, C E$ respectively, which have common part with the triangle $A B C$. Let also,
$$
k_{1} \cap k_{2}=\{C, K\}, k_{3} \cap k_{4}=\{C, M\}, k_{2} \cap k_{3}=\{C, L\}, k_{1} \cap k_{4}=\{C, N\}
$$
Prove that $K, L, M$ and $N$ are cocyclic points.
|
The points $K, L, M, N$ belong to the segments $A B, B D, D E, E A$ respectively, where $C K \perp A B, C L \perp B D, C M \perp D E, C N \perp A E$. Then quadrilaterals $C D L M$ and $C E N M$ are inscribed. Let $\angle C A E=\varphi, \angle D C L=\theta$. Then $\angle E M N=\angle E C N=\varphi$ and $\angle D M L=\angle D C L=\theta$. So $\angle D M L+\angle E M N=\varphi+\theta$ and therefore $\angle L M N=180^{\circ}-\varphi-\theta$. The quadrilaterals $C B K L$ and $C A K N$ are also inscribed and hence $\angle L K C=\angle L B C=\theta$, $\angle C K N=\angle C A N=\varphi$, and so $\angle L K N=\varphi+\theta$, while $\angle L M N=180^{\circ}-\varphi-\theta$, which means that $K L M N$ is inscribed.
Note that $K L M N$ is convex because $L, N$ lie in the interior of the convex quadrilateral $A D E B$.
## COMBINATORICS
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle C=90^{\circ}$ and $D \in C .4, E \in C^{\prime} B$, and $k_{1}, k_{2}, k_{3}, k_{4}$ semicircles with diameters $C A, C B, C D, C E$ respectively, which have common part with the triangle $A B C$. Let also,
$$
k_{1} \cap k_{2}=\{C, K\}, k_{3} \cap k_{4}=\{C, M\}, k_{2} \cap k_{3}=\{C, L\}, k_{1} \cap k_{4}=\{C, N\}
$$
Prove that $K, L, M$ and $N$ are cocyclic points.
|
The points $K, L, M, N$ belong to the segments $A B, B D, D E, E A$ respectively, where $C K \perp A B, C L \perp B D, C M \perp D E, C N \perp A E$. Then quadrilaterals $C D L M$ and $C E N M$ are inscribed. Let $\angle C A E=\varphi, \angle D C L=\theta$. Then $\angle E M N=\angle E C N=\varphi$ and $\angle D M L=\angle D C L=\theta$. So $\angle D M L+\angle E M N=\varphi+\theta$ and therefore $\angle L M N=180^{\circ}-\varphi-\theta$. The quadrilaterals $C B K L$ and $C A K N$ are also inscribed and hence $\angle L K C=\angle L B C=\theta$, $\angle C K N=\angle C A N=\varphi$, and so $\angle L K N=\varphi+\theta$, while $\angle L M N=180^{\circ}-\varphi-\theta$, which means that $K L M N$ is inscribed.
Note that $K L M N$ is convex because $L, N$ lie in the interior of the convex quadrilateral $A D E B$.

## COMBINATORICS
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2004_shl.jsonl",
"problem_match": "\nG5.",
"solution_match": "\nSolution."
}
|
1fbbf4bd-31b8-5c02-b9b4-c5283b7127f5
| 606,280
|
Let $a, b, c, d, e$ be real numbers such that $a+b+c+d+e=0$. Let, also $A=a b+b c+c d+d e+e a$ and $B=a c+c e+e b+b d+d a$.
Show that
$$
2005 A+B \leq 0 \text { or } \quad A+2005 B \leq 0
$$
|
We have
$$
0=(a+b+c+d+e)^{2}=a^{2}+b^{2}+c^{2}+d^{2}+e^{2}+2 A+2 B
$$
This implies that
$$
A+B \leq 0 \text { or } 2006(\dot{A}+B)=(2005 A+B)+(A+2005 B) \leq 0
$$
This implies the conclusion.
## Alternative solution
We haye
$$
\begin{aligned}
2 A+2 B & =a(b+c+d+e)+b(c+d+e+a)+c(d+e+a+b) \\
& +d(e+a+b+c)+e(a+b+c+d) \\
& =-a^{2}-b^{2}-c^{2}-d^{2}-e^{2} \leq 0
\end{aligned}
$$
Therefore we have $A+B \leq 0$, etc.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c, d, e$ be real numbers such that $a+b+c+d+e=0$. Let, also $A=a b+b c+c d+d e+e a$ and $B=a c+c e+e b+b d+d a$.
Show that
$$
2005 A+B \leq 0 \text { or } \quad A+2005 B \leq 0
$$
|
We have
$$
0=(a+b+c+d+e)^{2}=a^{2}+b^{2}+c^{2}+d^{2}+e^{2}+2 A+2 B
$$
This implies that
$$
A+B \leq 0 \text { or } 2006(\dot{A}+B)=(2005 A+B)+(A+2005 B) \leq 0
$$
This implies the conclusion.
## Alternative solution
We haye
$$
\begin{aligned}
2 A+2 B & =a(b+c+d+e)+b(c+d+e+a)+c(d+e+a+b) \\
& +d(e+a+b+c)+e(a+b+c+d) \\
& =-a^{2}-b^{2}-c^{2}-d^{2}-e^{2} \leq 0
\end{aligned}
$$
Therefore we have $A+B \leq 0$, etc.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2005_shl.jsonl",
"problem_match": "\nA1.",
"solution_match": "## Solution"
}
|
b450657c-f9fb-5bfa-9d97-2a689c521b30
| 604,174
|
Let $A B C D$ be an isosceles trapezoid with $A B=A D=B C, A B / / D C, A B>D C$. Let $E$ be the point of intersection of the diagonals $A C$ and $B D$ and $N$ be the symmetric point of $\mathrm{B}$ with respect to the line $\mathrm{AC}$. Prove that quadrilateral $A N D E$ is cyclic.
|
Let $\omega$ be a circle passing through the points $A, N, D$ and let $M$ the point where $\omega$ intersects $B D$ for the second time. The quadrilateral $A N D M$ is cyclic and it follows that
$$
\angle N D M+\angle N A M=\angle N D M+\angle B D C=180^{\circ}
$$
and
Figure 1
$$
\angle N A M=\angle B D C
$$
Now we have
$$
\angle B D C=\angle A C D=\angle N A C
$$
and
$$
\angle N A M=\angle N A C
$$
So the points $A, M, C$ are collinear and $M \equiv E$.
## Alternative solution
In this solution we do not need the circle passing through the points $A, N$ and $D$.
Because of the given symmetry we have
$$
\angle A N E=\angle A B D
$$
and from the equality $\mathrm{AD}=\mathrm{AB}$ the triangle $\mathrm{ABD}$ is isosceles with
$$
\angle A B D=\angle A D E
$$
From (1) and (2) we get that $\angle A N E=\angle A D E$, which means that the quadrilateral $A N D E$ is cyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be an isosceles trapezoid with $A B=A D=B C, A B / / D C, A B>D C$. Let $E$ be the point of intersection of the diagonals $A C$ and $B D$ and $N$ be the symmetric point of $\mathrm{B}$ with respect to the line $\mathrm{AC}$. Prove that quadrilateral $A N D E$ is cyclic.
|
Let $\omega$ be a circle passing through the points $A, N, D$ and let $M$ the point where $\omega$ intersects $B D$ for the second time. The quadrilateral $A N D M$ is cyclic and it follows that
$$
\angle N D M+\angle N A M=\angle N D M+\angle B D C=180^{\circ}
$$
and

Figure 1
$$
\angle N A M=\angle B D C
$$
Now we have
$$
\angle B D C=\angle A C D=\angle N A C
$$
and
$$
\angle N A M=\angle N A C
$$
So the points $A, M, C$ are collinear and $M \equiv E$.
## Alternative solution
In this solution we do not need the circle passing through the points $A, N$ and $D$.
Because of the given symmetry we have
$$
\angle A N E=\angle A B D
$$
and from the equality $\mathrm{AD}=\mathrm{AB}$ the triangle $\mathrm{ABD}$ is isosceles with
$$
\angle A B D=\angle A D E
$$
From (1) and (2) we get that $\angle A N E=\angle A D E$, which means that the quadrilateral $A N D E$ is cyclic.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2005_shl.jsonl",
"problem_match": "\nG1.",
"solution_match": "## Solution"
}
|
d32de329-2155-5f5f-8ba4-143e6e448d35
| 604,247
|
Let $A B C$ be a triangle inscribed in a circle $K$. The tangent from $A$ to the circle meets the line $B C$ at point $P$. Let $M$ be the midpoint of the line segment $A P$ and let $R$ be the intersection point of the circle $K$ with the line $B M$. The line $P R$ meets again the circle $K$ at the point $S$. Prove that the lines $A P$ and $C S$ are parallel.
|
Figure 2
Assume that point $C$ lies on the line segment $B P$. By the Power of Point theorem we have $M A^{2}=M R \cdot M B$ and so $M P^{2}=M R \cdot M B$. The last equality implies that the triangles $M R$ and $M P B$ are similar. Hence $\angle M P R=\angle M B P$ and since $\angle P S C=\angle M B P$, the claim is proved.
Slight changes are to be made if the point $B$ lies on the line segment $P C$.
Figure 3
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle inscribed in a circle $K$. The tangent from $A$ to the circle meets the line $B C$ at point $P$. Let $M$ be the midpoint of the line segment $A P$ and let $R$ be the intersection point of the circle $K$ with the line $B M$. The line $P R$ meets again the circle $K$ at the point $S$. Prove that the lines $A P$ and $C S$ are parallel.
|

Figure 2
Assume that point $C$ lies on the line segment $B P$. By the Power of Point theorem we have $M A^{2}=M R \cdot M B$ and so $M P^{2}=M R \cdot M B$. The last equality implies that the triangles $M R$ and $M P B$ are similar. Hence $\angle M P R=\angle M B P$ and since $\angle P S C=\angle M B P$, the claim is proved.
Slight changes are to be made if the point $B$ lies on the line segment $P C$.

Figure 3
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2005_shl.jsonl",
"problem_match": "\nG2.",
"solution_match": "## Solution"
}
|
36ea7b23-8d03-5f82-8e34-7dbe3376dcb9
| 604,258
|
Let $\mathrm{ABC}$ be an isosceles triangle such that $A B=A C$ and $\angle \frac{A}{2}<\angle B$. On the extension of the altitude $\mathrm{AM}$ we get the points $\mathrm{D}$ and $\mathrm{Z}$ such that $\angle C B D=\angle A$ and $\angle Z B A=90^{\circ}$. $\mathrm{E}$ is the foot of the perpendicular from $\mathrm{M}$ to the altitude $\mathrm{BF}$ and $\mathrm{K}$ is the foot of the perpendicular from $\mathrm{Z}$ to $\mathrm{AE}$. Prove that $\angle K D Z=\angle K B D=\angle K Z B$.
|
The points $A, B, K, Z$ and $C$ are co-cyclic.
Because ME//AC so we have
$$
\angle K E M=\angle E A C=\angle M B K
$$
Therefore the points $B, K, M$ and $E$ are co-cyclic. Now, we have
$$
\begin{aligned}
& \angle A B F=\angle A B C-\angle F B C \\
& =\angle A K C-\angle E K M=\angle M K C
\end{aligned}
$$
Also, we have
$$
\begin{aligned}
& \angle A B F=90^{\circ}-\angle B A F=90^{\circ}-\angle M B D \\
& =\angle B D M=\angle M D C
\end{aligned}
$$
From (1) and (2) we get $\angle M K C=\angle M D C$ and so the points $M, K, D$ and $C$ are co-cyclic.
Consequently,
$$
\angle K D M=\angle K C M=\angle B A K=\angle B Z K \text {, }
$$
and because the line $\mathrm{BD}$ is tangent to the circumcircle of triangle $A B C$, we have
$$
\angle K B D=\angle B A K
$$
Figure 5
Finally, we have
$$
\angle K D Z=\angle K B D=\angle K Z B
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\mathrm{ABC}$ be an isosceles triangle such that $A B=A C$ and $\angle \frac{A}{2}<\angle B$. On the extension of the altitude $\mathrm{AM}$ we get the points $\mathrm{D}$ and $\mathrm{Z}$ such that $\angle C B D=\angle A$ and $\angle Z B A=90^{\circ}$. $\mathrm{E}$ is the foot of the perpendicular from $\mathrm{M}$ to the altitude $\mathrm{BF}$ and $\mathrm{K}$ is the foot of the perpendicular from $\mathrm{Z}$ to $\mathrm{AE}$. Prove that $\angle K D Z=\angle K B D=\angle K Z B$.
|
The points $A, B, K, Z$ and $C$ are co-cyclic.
Because ME//AC so we have
$$
\angle K E M=\angle E A C=\angle M B K
$$
Therefore the points $B, K, M$ and $E$ are co-cyclic. Now, we have
$$
\begin{aligned}
& \angle A B F=\angle A B C-\angle F B C \\
& =\angle A K C-\angle E K M=\angle M K C
\end{aligned}
$$
Also, we have
$$
\begin{aligned}
& \angle A B F=90^{\circ}-\angle B A F=90^{\circ}-\angle M B D \\
& =\angle B D M=\angle M D C
\end{aligned}
$$
From (1) and (2) we get $\angle M K C=\angle M D C$ and so the points $M, K, D$ and $C$ are co-cyclic.
Consequently,
$$
\angle K D M=\angle K C M=\angle B A K=\angle B Z K \text {, }
$$
and because the line $\mathrm{BD}$ is tangent to the circumcircle of triangle $A B C$, we have
$$
\angle K B D=\angle B A K
$$

Figure 5
Finally, we have
$$
\angle K D Z=\angle K B D=\angle K Z B
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2005_shl.jsonl",
"problem_match": "\nG4.",
"solution_match": "## Solution"
}
|
a6e18c24-9d83-5c11-aac8-47e33577435d
| 604,280
|
Let $A B C D$ be a parallelogram, $\mathrm{P}$ a point on $C D$, and $Q$ a point on $A B$. Let also $M=A P \cap D Q, \quad N=B P \cap C Q, K=M N \cap A D$, and $L=M N \cap B C$. Show that $B L=D K$.
|
Let $O$ be the intersection of the diagonals. Let $P_{1}$ be on $A B$ such that $P P_{1} / / A D$, and let $Q_{1}$ be on $C D$ such that $\mathrm{Q} Q_{1} / / A D$. Let $\sigma$ be the central symmetry with center $\mathrm{O}$. Let $\left.P^{\prime}=\sigma(P), Q^{\prime}=\sigma(Q), P_{1}^{\prime}=\sigma\left(P_{1}\right)\right)$ and, (figure 1).
Let $M_{1}=A Q_{1} \cap D P_{1}, N_{1}=B Q_{1} \cap C P_{1}, N^{\prime}=A Q^{\prime} \cap D P^{\prime}$ and $M^{\prime}=B Q^{\prime} \cap C P^{\prime}$.
Then: $M^{\prime}=\sigma(M), N^{\prime}=\sigma(N), M_{1}^{\prime}=\sigma\left(M_{1}\right)$ and $N_{1}^{\prime}=\sigma\left(N_{1}\right)$.
Since $A P$ and $D P_{1}$ are the diagonals of the parallelogram $A P_{1} P D, C P_{1}$ and $B P$ are the diagonals of the parallelogram $P_{1} B C P$, and $A Q_{1}$ and $D O$ are the diagonals of the parallelogram $A Q Q_{1} D$, it follows that the points $U, V, W$ (figure 2) are collinear and they lie on the line passing through the midpoints $R$ of $A D$ and $Z$ of $B C$. The diagonals AM and $D M_{1}$ the quadrilateral $A M_{1} M D$ intersect at $U$ and the diagonals $A M_{1}$ and - $D M$ intersect at $W$. Since the midpoint of $A D$ is on the line $U W$, it follows that the quadrilateral $A M_{1} M D$ is a trapezoid. Hence, $M M_{1}$ is parallel to $A D$ and the midpoint $S$ of $M M_{1}$ lies on the line $U W$, (figure 2).
Figure 11
Similarly $M^{\prime} M_{1}^{\prime}$ is parallel to $A D$ and its midpoint lies on $U W$. So $M_{1} M^{\prime} M_{1}^{\prime} M$ is a parallelogram whose diagonals intersect at $\mathrm{O}$.
Similarly, $N_{1}^{\prime} N N_{1} N^{\prime}$ is a parallelogram whose diagonals intersect at $O$.
All these imply that $M, N, M^{\prime}, N^{\prime}$ and $O$ are collinear, i.e. $O$ lies on the line $K L$. This implies that $K=\sigma(L)$, and since $D=\sigma(B)$, the conclusion follows.
Figure 12
## Alternative solution
Let the line ( $\varepsilon$ ) through the points $\mathrm{M}, \mathrm{N}$ intersect the lines $\mathrm{DC}, \mathrm{AB}$ at points $\mathrm{T}_{1}, \mathrm{~T}_{2}$ respectively. Applying Menelaus Theorem to the triangles DQC, APB with intersecting line $(\varepsilon)$ in both cases we get:
$$
\frac{M D}{M Q} \frac{N Q}{N C} \frac{T_{1} C}{T_{1} D}=1 \text { and } \frac{M P}{M A} \frac{N B}{N P} \frac{T_{2} A}{T_{2} B}=1
$$
But it is true that $\frac{\mathrm{MD}}{\mathrm{MQ}}=\frac{\mathrm{MP}}{\mathrm{MA}}$ and $\frac{\mathrm{NQ}}{\mathrm{NC}}=\frac{\mathrm{NB}}{\mathrm{NP}}$.
It follows that $\frac{T_{1} C}{T_{1} D}=\frac{T_{2} A}{T_{2} B}$ i.e. $\frac{T_{1} D+D C}{T_{1} D}=\frac{T_{2} B+B A}{T_{2} B}$ hence $T_{1} D=T_{2} B$ (since
$\mathrm{DC}=\mathrm{BA})$.
Then of course by the similarity of the triangles $\mathrm{T}_{1} \mathrm{DK}$ and $\mathrm{T}_{2} \mathrm{BL}$ we get the desired equality $\mathrm{DK} \cdot \mathrm{BL}$.
Figure 13
## Number Theory
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram, $\mathrm{P}$ a point on $C D$, and $Q$ a point on $A B$. Let also $M=A P \cap D Q, \quad N=B P \cap C Q, K=M N \cap A D$, and $L=M N \cap B C$. Show that $B L=D K$.
|
Let $O$ be the intersection of the diagonals. Let $P_{1}$ be on $A B$ such that $P P_{1} / / A D$, and let $Q_{1}$ be on $C D$ such that $\mathrm{Q} Q_{1} / / A D$. Let $\sigma$ be the central symmetry with center $\mathrm{O}$. Let $\left.P^{\prime}=\sigma(P), Q^{\prime}=\sigma(Q), P_{1}^{\prime}=\sigma\left(P_{1}\right)\right)$ and, (figure 1).
Let $M_{1}=A Q_{1} \cap D P_{1}, N_{1}=B Q_{1} \cap C P_{1}, N^{\prime}=A Q^{\prime} \cap D P^{\prime}$ and $M^{\prime}=B Q^{\prime} \cap C P^{\prime}$.
Then: $M^{\prime}=\sigma(M), N^{\prime}=\sigma(N), M_{1}^{\prime}=\sigma\left(M_{1}\right)$ and $N_{1}^{\prime}=\sigma\left(N_{1}\right)$.
Since $A P$ and $D P_{1}$ are the diagonals of the parallelogram $A P_{1} P D, C P_{1}$ and $B P$ are the diagonals of the parallelogram $P_{1} B C P$, and $A Q_{1}$ and $D O$ are the diagonals of the parallelogram $A Q Q_{1} D$, it follows that the points $U, V, W$ (figure 2) are collinear and they lie on the line passing through the midpoints $R$ of $A D$ and $Z$ of $B C$. The diagonals AM and $D M_{1}$ the quadrilateral $A M_{1} M D$ intersect at $U$ and the diagonals $A M_{1}$ and - $D M$ intersect at $W$. Since the midpoint of $A D$ is on the line $U W$, it follows that the quadrilateral $A M_{1} M D$ is a trapezoid. Hence, $M M_{1}$ is parallel to $A D$ and the midpoint $S$ of $M M_{1}$ lies on the line $U W$, (figure 2).

Figure 11
Similarly $M^{\prime} M_{1}^{\prime}$ is parallel to $A D$ and its midpoint lies on $U W$. So $M_{1} M^{\prime} M_{1}^{\prime} M$ is a parallelogram whose diagonals intersect at $\mathrm{O}$.
Similarly, $N_{1}^{\prime} N N_{1} N^{\prime}$ is a parallelogram whose diagonals intersect at $O$.
All these imply that $M, N, M^{\prime}, N^{\prime}$ and $O$ are collinear, i.e. $O$ lies on the line $K L$. This implies that $K=\sigma(L)$, and since $D=\sigma(B)$, the conclusion follows.

Figure 12
## Alternative solution
Let the line ( $\varepsilon$ ) through the points $\mathrm{M}, \mathrm{N}$ intersect the lines $\mathrm{DC}, \mathrm{AB}$ at points $\mathrm{T}_{1}, \mathrm{~T}_{2}$ respectively. Applying Menelaus Theorem to the triangles DQC, APB with intersecting line $(\varepsilon)$ in both cases we get:
$$
\frac{M D}{M Q} \frac{N Q}{N C} \frac{T_{1} C}{T_{1} D}=1 \text { and } \frac{M P}{M A} \frac{N B}{N P} \frac{T_{2} A}{T_{2} B}=1
$$
But it is true that $\frac{\mathrm{MD}}{\mathrm{MQ}}=\frac{\mathrm{MP}}{\mathrm{MA}}$ and $\frac{\mathrm{NQ}}{\mathrm{NC}}=\frac{\mathrm{NB}}{\mathrm{NP}}$.
It follows that $\frac{T_{1} C}{T_{1} D}=\frac{T_{2} A}{T_{2} B}$ i.e. $\frac{T_{1} D+D C}{T_{1} D}=\frac{T_{2} B+B A}{T_{2} B}$ hence $T_{1} D=T_{2} B$ (since
$\mathrm{DC}=\mathrm{BA})$.
Then of course by the similarity of the triangles $\mathrm{T}_{1} \mathrm{DK}$ and $\mathrm{T}_{2} \mathrm{BL}$ we get the desired equality $\mathrm{DK} \cdot \mathrm{BL}$.

Figure 13
## Number Theory
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2005_shl.jsonl",
"problem_match": "\nG7.",
"solution_match": "## Solution"
}
|
a7a3cd4f-1176-5052-9a19-3bbc030cdd9c
| 604,326
|
Let $p$ be an odd prime. Prove that $p$ divides the integer
$$
\frac{2^{p!}-1}{2^{k}-1}
$$
for all integers $k=1,2, \ldots, p$.
|
At first, note that $\frac{2^{p!}-1}{2^{k}-1}$ is indeed an integer.
We start with the case $\mathrm{k}=\mathrm{p}$. Since $p \mid 2^{p}-2$, then $p / 22^{p}-1$ and so it suffices to prove that $p \mid 2^{(p)!}-1$. This is obvious as $p \mid 2^{p-1}-1$ and $\left(2^{p-1}-1\right) \mid 2^{(p)!}-1$.
If $\mathrm{k}=1,2, \ldots, \mathrm{p}-1$, let $m=\frac{(p-1)!}{k} \in \mathbb{N}$ and observe that $p!=k m p$. Consider $a \in \mathbb{N}$ so that $p^{a} \mid 2^{k}-1$ and observe that it suffices to prove $p^{a+1} \mid 2^{p!}-1$. The case $a=0$ is solved as the case $k=p$. If else, write $2^{k}=1+p^{a} \cdot l, l \in \mathbb{N}$ and rising at the power mp gives
$$
2^{p!}=\left(1+p^{a} \cdot l\right)^{m p}=1+m p \cdot p^{a} \cdot l+M p^{2 a}
$$
where $M n$ stands for a multiply of $\mathrm{n}$. Now it is clear that $p^{a+1} \mid 2^{p!}-1$, as claimed.
Comment. The case $\mathrm{k}=\mathrm{p}$ can be included in the case $a=0$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be an odd prime. Prove that $p$ divides the integer
$$
\frac{2^{p!}-1}{2^{k}-1}
$$
for all integers $k=1,2, \ldots, p$.
|
At first, note that $\frac{2^{p!}-1}{2^{k}-1}$ is indeed an integer.
We start with the case $\mathrm{k}=\mathrm{p}$. Since $p \mid 2^{p}-2$, then $p / 22^{p}-1$ and so it suffices to prove that $p \mid 2^{(p)!}-1$. This is obvious as $p \mid 2^{p-1}-1$ and $\left(2^{p-1}-1\right) \mid 2^{(p)!}-1$.
If $\mathrm{k}=1,2, \ldots, \mathrm{p}-1$, let $m=\frac{(p-1)!}{k} \in \mathbb{N}$ and observe that $p!=k m p$. Consider $a \in \mathbb{N}$ so that $p^{a} \mid 2^{k}-1$ and observe that it suffices to prove $p^{a+1} \mid 2^{p!}-1$. The case $a=0$ is solved as the case $k=p$. If else, write $2^{k}=1+p^{a} \cdot l, l \in \mathbb{N}$ and rising at the power mp gives
$$
2^{p!}=\left(1+p^{a} \cdot l\right)^{m p}=1+m p \cdot p^{a} \cdot l+M p^{2 a}
$$
where $M n$ stands for a multiply of $\mathrm{n}$. Now it is clear that $p^{a+1} \mid 2^{p!}-1$, as claimed.
Comment. The case $\mathrm{k}=\mathrm{p}$ can be included in the case $a=0$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2005_shl.jsonl",
"problem_match": "\nNT3.",
"solution_match": "## Solution"
}
|
5d451955-dd90-5f4b-b762-eeca8856e7e3
| 604,365
|
Let $p$ be a prime number and let $a$ be an integer. Show that if $n^{2}-5$ is not divisible by $p$ for any integer $n$, there exist infinitely many integers $m$ so that $p$ divides $m^{5}+a$.
|
We start with a simple fact:
Lemma: If $b$ is an integer not divisible by $p$ then there is an integer $s$ so that $s b$ has the remainder $l$ when divided by $p$.
For a proof, just note that numbers $b, 2 b, \ldots,(p-1) b$ have distinct non-zero remainders when divided by $p$, and hence one of them is equal to 1 .
We prove that if $x, y=0,1,2, \ldots, p-1$ and $\mathrm{p}$ divides $x^{5}-y^{5}$, then $x=y$.
Indeed, assume that $x \neq y$. If $x=0$, then $p \mid y^{5}$ and so $y=0$, a contradiction.
To this point we have $x, y \neq 0$. Since
$$
p \mid(x-y)\left(x^{4}+x^{3} y+x^{2} y^{2}+x y^{3}+y^{4}\right) \text { and } p /(x-y)
$$
we have
$$
\begin{aligned}
& p l\left(x^{2}+y^{2}\right)^{2}+x y\left(x^{2}+y^{2}\right)-x^{2} y^{2} \text {, and so } \\
& p \|\left(2\left(x^{2}+y^{2}\right)+x y\right)^{2}-5 x^{2} y^{2}
\end{aligned}
$$
As $p / x y$, from the lemma we find an integer $s$ so that $s x y=k p+1, k \in \mathbb{N}$. Then
$$
p \mid\left[s\left(2 x^{2}+2 y^{2}+x y\right)\right]^{2}-5\left(k^{2} p^{2}+2 k p+1\right)
$$
and so $p \mid z^{2}-5$, where $z=s\left(2 x^{2}+2 y^{2}+x y\right)$, a contradiction.
Consequeatly $r=y$.
Since we have proved that numbers $0^{5}, 1^{5}, \ldots,(p-1)^{5}$ have distinct remainders when divided by $p$, the same goes for the numbers $0^{5}+a, 1^{5}+a, \ldots,(p-1)^{5}+a$ and the conclusion can be reached easily.
## Comments
1. For beauty we may choose $a=-2$ or any other value.
2. Moreover, we may ask only for one value of $m$, instead of "infinitely many".
3. A simple version will be to ask for a proof that the numbers $0^{5}, 1^{5}, \ldots,(p-1)^{5}$ have distinct remainders when divided by $p$.
## Combinatorics
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be a prime number and let $a$ be an integer. Show that if $n^{2}-5$ is not divisible by $p$ for any integer $n$, there exist infinitely many integers $m$ so that $p$ divides $m^{5}+a$.
|
We start with a simple fact:
Lemma: If $b$ is an integer not divisible by $p$ then there is an integer $s$ so that $s b$ has the remainder $l$ when divided by $p$.
For a proof, just note that numbers $b, 2 b, \ldots,(p-1) b$ have distinct non-zero remainders when divided by $p$, and hence one of them is equal to 1 .
We prove that if $x, y=0,1,2, \ldots, p-1$ and $\mathrm{p}$ divides $x^{5}-y^{5}$, then $x=y$.
Indeed, assume that $x \neq y$. If $x=0$, then $p \mid y^{5}$ and so $y=0$, a contradiction.
To this point we have $x, y \neq 0$. Since
$$
p \mid(x-y)\left(x^{4}+x^{3} y+x^{2} y^{2}+x y^{3}+y^{4}\right) \text { and } p /(x-y)
$$
we have
$$
\begin{aligned}
& p l\left(x^{2}+y^{2}\right)^{2}+x y\left(x^{2}+y^{2}\right)-x^{2} y^{2} \text {, and so } \\
& p \|\left(2\left(x^{2}+y^{2}\right)+x y\right)^{2}-5 x^{2} y^{2}
\end{aligned}
$$
As $p / x y$, from the lemma we find an integer $s$ so that $s x y=k p+1, k \in \mathbb{N}$. Then
$$
p \mid\left[s\left(2 x^{2}+2 y^{2}+x y\right)\right]^{2}-5\left(k^{2} p^{2}+2 k p+1\right)
$$
and so $p \mid z^{2}-5$, where $z=s\left(2 x^{2}+2 y^{2}+x y\right)$, a contradiction.
Consequeatly $r=y$.
Since we have proved that numbers $0^{5}, 1^{5}, \ldots,(p-1)^{5}$ have distinct remainders when divided by $p$, the same goes for the numbers $0^{5}+a, 1^{5}+a, \ldots,(p-1)^{5}+a$ and the conclusion can be reached easily.
## Comments
1. For beauty we may choose $a=-2$ or any other value.
2. Moreover, we may ask only for one value of $m$, instead of "infinitely many".
3. A simple version will be to ask for a proof that the numbers $0^{5}, 1^{5}, \ldots,(p-1)^{5}$ have distinct remainders when divided by $p$.
## Combinatorics
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2005_shl.jsonl",
"problem_match": "\nNT5.",
"solution_match": "## Solution"
}
|
d68a435e-b91b-5ac7-8342-88510c5833d3
| 604,386
|
A triangle with area 2003 is divided into non-overlapping small triangles. The number of all the vertices of all those triangles is 2005 . Show that at mest one of the smaller triangles has area less or equal to 1.
|
Since all the vertices are 2005 , and the vertices of the big triangle are among them, it follows that the number of the small triangles is at least 2003. So, it follows that at least one of the small triangles has area at most 1
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A triangle with area 2003 is divided into non-overlapping small triangles. The number of all the vertices of all those triangles is 2005 . Show that at mest one of the smaller triangles has area less or equal to 1.
|
Since all the vertices are 2005 , and the vertices of the big triangle are among them, it follows that the number of the small triangles is at least 2003. So, it follows that at least one of the small triangles has area at most 1
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2005_shl.jsonl",
"problem_match": "\nC1.",
"solution_match": "## Solution"
}
|
33816caa-3f9f-5dcb-88be-ae104857eb8b
| 604,396
|
Let $a$ be a real positive number such that $a^{3}=6(a+1)$. Prove that the equation $x^{2}+a x+a^{2}-6=0$ has no solution in the set of the real number.
|
The discriminant of the equation is $\Delta=3\left(8-a^{2}\right)$. If we accept that $\Delta \geq 0$, then $a \leq 2 \sqrt{2}$ and $\frac{1}{a} \geq \frac{\sqrt{2}}{4}$, from where $a^{2} \geq 6+6 \cdot \frac{\sqrt{2}}{4}=6+\frac{6}{a} \geq 6+\frac{3 \sqrt{2}}{2}>8$ (contradiction).
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a$ be a real positive number such that $a^{3}=6(a+1)$. Prove that the equation $x^{2}+a x+a^{2}-6=0$ has no solution in the set of the real number.
|
The discriminant of the equation is $\Delta=3\left(8-a^{2}\right)$. If we accept that $\Delta \geq 0$, then $a \leq 2 \sqrt{2}$ and $\frac{1}{a} \geq \frac{\sqrt{2}}{4}$, from where $a^{2} \geq 6+6 \cdot \frac{\sqrt{2}}{4}=6+\frac{6}{a} \geq 6+\frac{3 \sqrt{2}}{2}>8$ (contradiction).
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2007_shl.jsonl",
"problem_match": "\nA1 ",
"solution_match": "## Solution"
}
|
a00c4596-9083-56c8-8ff5-c8f4d69544e7
| 604,432
|
Prove that $\frac{a^{2}-b c}{2 a^{2}+b c}+\frac{b^{2}-c a}{2 b^{2}+c a}+\frac{c^{2}-a b}{2 c^{2}+a b} \leq 0$ for any real positive numbers $a, b, c$.
|
The inequality rewrites as $\sum \frac{2 a^{2}+b c-3 b c}{2 a^{2}+b c} \leq 0$, or $3-3 \sum \frac{b c}{2 a^{2}+b c} \leq 0$ in other words $\sum \frac{b c}{2 a^{2}+b c} \geq 1$.
Using Cauchy-Schwarz inequality we have
$$
\sum \frac{b c}{2 a^{2}+b c}=\sum \frac{b^{2} c^{2}}{2 a^{2} b c+b^{2} c^{2}} \geq \frac{\left(\sum b c\right)^{2}}{2 a b c(a+b+c)+\sum b^{2} c^{2}}=1
$$
as claimed.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that $\frac{a^{2}-b c}{2 a^{2}+b c}+\frac{b^{2}-c a}{2 b^{2}+c a}+\frac{c^{2}-a b}{2 c^{2}+a b} \leq 0$ for any real positive numbers $a, b, c$.
|
The inequality rewrites as $\sum \frac{2 a^{2}+b c-3 b c}{2 a^{2}+b c} \leq 0$, or $3-3 \sum \frac{b c}{2 a^{2}+b c} \leq 0$ in other words $\sum \frac{b c}{2 a^{2}+b c} \geq 1$.
Using Cauchy-Schwarz inequality we have
$$
\sum \frac{b c}{2 a^{2}+b c}=\sum \frac{b^{2} c^{2}}{2 a^{2} b c+b^{2} c^{2}} \geq \frac{\left(\sum b c\right)^{2}}{2 a b c(a+b+c)+\sum b^{2} c^{2}}=1
$$
as claimed.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2007_shl.jsonl",
"problem_match": "\nA2 ",
"solution_match": "## Solution"
}
|
149dda45-9084-5ef5-a823-4ba72739e8f1
| 604,445
|
Let $A$ be a set of positive integers containing the number 1 and at least one more element. Given that for any two different elements $m, n$ of $A$ the number $\frac{m+1}{(m+1, n+1)}$ is also an element of $A$, prove that $A$ coincides with the set of positive integers.
|
Let $a>1$ be lowest number in $A \backslash\{1\}$. For $m=a, n=1$ one gets $y=\frac{a+1}{(2, a+1)} \in A$. Since $(2, a+1)$ is either 1 or 2 , then $y=a+1$ or $y=\frac{a+1}{2}$.
But $1<\frac{a+1}{2}<a$, hence $y=a+1$. Applying the given property for $m=a+1, n=a$ one has $\frac{a+2}{(a+2, a+1)}=a+2 \in A$, and inductively $t \in A$ for all integers $t \geq a$.
Furthermore, take $m=2 a-1, n=3 a-1$ (now in $A!$ ); as $(m+1, n+1)=(2 a, 3 a)=a$ one obtains $\frac{2 a}{a}=2 \in A$, so $a=2$, by the definition of $a$.
The conclusion follows immediately.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $A$ be a set of positive integers containing the number 1 and at least one more element. Given that for any two different elements $m, n$ of $A$ the number $\frac{m+1}{(m+1, n+1)}$ is also an element of $A$, prove that $A$ coincides with the set of positive integers.
|
Let $a>1$ be lowest number in $A \backslash\{1\}$. For $m=a, n=1$ one gets $y=\frac{a+1}{(2, a+1)} \in A$. Since $(2, a+1)$ is either 1 or 2 , then $y=a+1$ or $y=\frac{a+1}{2}$.
But $1<\frac{a+1}{2}<a$, hence $y=a+1$. Applying the given property for $m=a+1, n=a$ one has $\frac{a+2}{(a+2, a+1)}=a+2 \in A$, and inductively $t \in A$ for all integers $t \geq a$.
Furthermore, take $m=2 a-1, n=3 a-1$ (now in $A!$ ); as $(m+1, n+1)=(2 a, 3 a)=a$ one obtains $\frac{2 a}{a}=2 \in A$, so $a=2$, by the definition of $a$.
The conclusion follows immediately.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2007_shl.jsonl",
"problem_match": "\nA3 ",
"solution_match": "## Solution"
}
|
ecc37940-4f94-588f-a75f-c7e5e4fc3ccc
| 604,458
|
Let $a$ and $b$ be positive integers bigger than 2. Prove that there exists a positive integer $k$ and a sequence $n_{1}, n_{2}, \ldots, n_{k}$ consisting of positive integers, such that $n_{1}=a$, $n_{k}=b$, and $\left(n_{i}+n_{i+1}\right) \mid n_{i} n_{i+1}$ for all $i=1,2, \ldots, k-1$.
|
We write $a \Leftrightarrow b$ if the required sequence exists. It is clear that $\Leftrightarrow$ is equivalence relation, i.e. $a \Leftrightarrow a,(a \Leftrightarrow b$ implies $b \Rightarrow a)$ and $(a \Leftrightarrow b, b \Leftrightarrow c$ imply $a \Leftrightarrow c$ ).
We shall prove that for every $a \geq 3$, ( $a-$ an integer), $a \Leftrightarrow 3$.
If $a=2^{s} t$, where $t>1$ is an odd number, we take the sequence
$$
2^{s} t, 2^{s}\left(t^{2}-t\right), 2^{s}\left(t^{2}+t\right), 2^{s}(t+1)=2^{s+1} \cdot \frac{t+1}{2}
$$
Since $\frac{t+1}{2}<t$ after a finite number of steps we shall get a power of 2 . On the other side, if $s>1$ we have $2^{s}, 3 \cdot 2^{s}, 3 \cdot 2^{s-1}, 3 \cdot 2^{s-2}, \ldots, 3$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be positive integers bigger than 2. Prove that there exists a positive integer $k$ and a sequence $n_{1}, n_{2}, \ldots, n_{k}$ consisting of positive integers, such that $n_{1}=a$, $n_{k}=b$, and $\left(n_{i}+n_{i+1}\right) \mid n_{i} n_{i+1}$ for all $i=1,2, \ldots, k-1$.
|
We write $a \Leftrightarrow b$ if the required sequence exists. It is clear that $\Leftrightarrow$ is equivalence relation, i.e. $a \Leftrightarrow a,(a \Leftrightarrow b$ implies $b \Rightarrow a)$ and $(a \Leftrightarrow b, b \Leftrightarrow c$ imply $a \Leftrightarrow c$ ).
We shall prove that for every $a \geq 3$, ( $a-$ an integer), $a \Leftrightarrow 3$.
If $a=2^{s} t$, where $t>1$ is an odd number, we take the sequence
$$
2^{s} t, 2^{s}\left(t^{2}-t\right), 2^{s}\left(t^{2}+t\right), 2^{s}(t+1)=2^{s+1} \cdot \frac{t+1}{2}
$$
Since $\frac{t+1}{2}<t$ after a finite number of steps we shall get a power of 2 . On the other side, if $s>1$ we have $2^{s}, 3 \cdot 2^{s}, 3 \cdot 2^{s-1}, 3 \cdot 2^{s-2}, \ldots, 3$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2007_shl.jsonl",
"problem_match": "\nA4 ",
"solution_match": "## Solution"
}
|
a6a4feb4-7964-527e-8cff-625bbd0322c7
| 604,468
|
The real numbers $x, y, z, m, n$ are positive, such that $m+n \geq 2$. Prove that
$$
\begin{gathered}
x \sqrt{y z(x+m y)(x+n z)}+y \sqrt{x z(y+m x)(y+n z)}+z \sqrt{x y(z+m x)(x+n y)} \leq \\
\frac{3(m+n)}{8}(x+y)(y+z)(z+x) .
\end{gathered}
$$
|
Using the AM-GM inequality we have
$$
\begin{aligned}
& \sqrt{y z(x+m y)(x+n z)}=\sqrt{(x z+m y z)(x y+n y z)} \leq \frac{x y+x z+(m+n) y z}{2} \\
& \sqrt{x z(y+m x)(y+n z)}=\sqrt{(y z+m x z)(x y+n x z)} \leq \frac{x y+y z+(m+n) x z}{2} \\
& \sqrt{x y(z+m x)(z+n y)}=\sqrt{(y z+m x y)(x z+n x y)} \leq \frac{x z+y z+(m+n) x y}{2}
\end{aligned}
$$
Thus it is enough to prove that
$$
\begin{aligned}
x[x y+x z+(m+n) y z] & +y[x y+y z+(m+n) x z]+z[x y+y z+(m+n) x z] \leq \\
\leq & \frac{3(m+n)}{4}(x+y)(y+z)(z+x),
\end{aligned}
$$
or
$$
4[A+3(m+n) B] \leq 3(m+n)(A+2 B) \Leftrightarrow 6(m+n) B \leq[3(m+n)-4] A
$$
where $A=x^{2} y+x^{2} z+x y^{2}+y^{2} z+x z^{2}+y z^{2}, B=x y z$.
Because $m+n \geq 2$ we obtain the inequality $m+n \leq 3(m+n)-4$. From AMGM inequality it follows that $6 B \leq A$. From the last two inequalities we deduce that $6(m+n) B \leq[3(m+n)-4] A$. The inequality is proved.
Equality holds when $m=n=1$ and $x=y=z$.
### 2.2 Combinatorics
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
The real numbers $x, y, z, m, n$ are positive, such that $m+n \geq 2$. Prove that
$$
\begin{gathered}
x \sqrt{y z(x+m y)(x+n z)}+y \sqrt{x z(y+m x)(y+n z)}+z \sqrt{x y(z+m x)(x+n y)} \leq \\
\frac{3(m+n)}{8}(x+y)(y+z)(z+x) .
\end{gathered}
$$
|
Using the AM-GM inequality we have
$$
\begin{aligned}
& \sqrt{y z(x+m y)(x+n z)}=\sqrt{(x z+m y z)(x y+n y z)} \leq \frac{x y+x z+(m+n) y z}{2} \\
& \sqrt{x z(y+m x)(y+n z)}=\sqrt{(y z+m x z)(x y+n x z)} \leq \frac{x y+y z+(m+n) x z}{2} \\
& \sqrt{x y(z+m x)(z+n y)}=\sqrt{(y z+m x y)(x z+n x y)} \leq \frac{x z+y z+(m+n) x y}{2}
\end{aligned}
$$
Thus it is enough to prove that
$$
\begin{aligned}
x[x y+x z+(m+n) y z] & +y[x y+y z+(m+n) x z]+z[x y+y z+(m+n) x z] \leq \\
\leq & \frac{3(m+n)}{4}(x+y)(y+z)(z+x),
\end{aligned}
$$
or
$$
4[A+3(m+n) B] \leq 3(m+n)(A+2 B) \Leftrightarrow 6(m+n) B \leq[3(m+n)-4] A
$$
where $A=x^{2} y+x^{2} z+x y^{2}+y^{2} z+x z^{2}+y z^{2}, B=x y z$.
Because $m+n \geq 2$ we obtain the inequality $m+n \leq 3(m+n)-4$. From AMGM inequality it follows that $6 B \leq A$. From the last two inequalities we deduce that $6(m+n) B \leq[3(m+n)-4] A$. The inequality is proved.
Equality holds when $m=n=1$ and $x=y=z$.
### 2.2 Combinatorics
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2007_shl.jsonl",
"problem_match": "\nA5 ",
"solution_match": "## Solution"
}
|
3d83425a-5973-5968-9de6-5a0c5e88ceeb
| 604,479
|
We call a tiling of an $m \times n$ rectangle with corners (see figure below) "regular" if there is no sub-rectangle which is tiled with corners. Prove that if for some $m$ and $n$ there exists a "regular" tiling of the $m \times n$ rectangular then there exists a "regular" tiling also for the $2 m \times 2 n$ rectangle.
|
A corner-shaped tile consists of 3 squares. Let us call "center of the tile" the square that has two neighboring squares. Notice that in a "regular" tiling, the squares situated in the corners of the rectangle have to be covered by the "center" of a tile, otherwise a $2 \times 3$ (or $3 \times 2$ ) rectangle tiled with two tiles would form.
Consider a $2 m \times 2 n$ rectangle, divide it into four $m \times n$ rectangles by drawing its midlines, then do a "regular" tiling for each of these rectangles. In the center of the $2 m \times 2 n$ rectangle we will necessarily obtain the following configuration:

Now simply change the position of these four tiles into:
It is easy to see that this tiling is "regular".
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
We call a tiling of an $m \times n$ rectangle with corners (see figure below) "regular" if there is no sub-rectangle which is tiled with corners. Prove that if for some $m$ and $n$ there exists a "regular" tiling of the $m \times n$ rectangular then there exists a "regular" tiling also for the $2 m \times 2 n$ rectangle.

|
A corner-shaped tile consists of 3 squares. Let us call "center of the tile" the square that has two neighboring squares. Notice that in a "regular" tiling, the squares situated in the corners of the rectangle have to be covered by the "center" of a tile, otherwise a $2 \times 3$ (or $3 \times 2$ ) rectangle tiled with two tiles would form.
Consider a $2 m \times 2 n$ rectangle, divide it into four $m \times n$ rectangles by drawing its midlines, then do a "regular" tiling for each of these rectangles. In the center of the $2 m \times 2 n$ rectangle we will necessarily obtain the following configuration:

Now simply change the position of these four tiles into:

It is easy to see that this tiling is "regular".
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2007_shl.jsonl",
"problem_match": "\nC1 ",
"solution_match": "## Solution"
}
|
464c491c-7dbb-5c1c-a4eb-1e3bf40ba7fa
| 604,494
|
Let $M$ be an interior point of the triangle $A B C$ with angles $\varangle B A C=70^{\circ}$ and $\varangle A B C=80^{\circ}$. If $\varangle A C M=10^{\circ}$ and $\varangle C B M=20^{\circ}$, prove that $A B=M C$.
|
Let $O$ be the circumcenter of the triangle $A B C$. Because the triangle $A B C$ is acute, $O$ is in the interior of $\triangle A B C$. Now we have that $\varangle A O C=2 \varangle A B C=160^{\circ}$, so $\varangle A C O=10^{\circ}$ and $\varangle B O C=2 \varangle B A C=140^{\circ}$, so $\varangle C B O=20^{\circ}$. Therefore $O \equiv M$, thus $M A=$ $M B=M C$. Because $\varangle A B O=80^{\circ}-20^{\circ}=60^{\circ}$, the triangle $A B M$ is equilateral and so $A B=M B=M C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $M$ be an interior point of the triangle $A B C$ with angles $\varangle B A C=70^{\circ}$ and $\varangle A B C=80^{\circ}$. If $\varangle A C M=10^{\circ}$ and $\varangle C B M=20^{\circ}$, prove that $A B=M C$.
|
Let $O$ be the circumcenter of the triangle $A B C$. Because the triangle $A B C$ is acute, $O$ is in the interior of $\triangle A B C$. Now we have that $\varangle A O C=2 \varangle A B C=160^{\circ}$, so $\varangle A C O=10^{\circ}$ and $\varangle B O C=2 \varangle B A C=140^{\circ}$, so $\varangle C B O=20^{\circ}$. Therefore $O \equiv M$, thus $M A=$ $M B=M C$. Because $\varangle A B O=80^{\circ}-20^{\circ}=60^{\circ}$, the triangle $A B M$ is equilateral and so $A B=M B=M C$.

|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2007_shl.jsonl",
"problem_match": "\nG1 ",
"solution_match": "## Solution"
}
|
ea735a46-48b2-597a-a798-af8cdd0e2f05
| 604,529
|
Let $S$ be a point inside $\varangle p O q$, and let $k$ be a circle which contains $S$ and touches the legs $O p$ and $O q$ in points $P$ and $Q$ respectively. Straight line $s$ parallel to $O p$ from $S$ intersects $O q$ in a point $R$. Let $T$ be the point of intersection of the ray $(P S$ and circumscribed circle of $\triangle S Q R$ and $T \neq S$. Prove that $O T \| S Q$ and $O T$ is a tangent of the circumscribed circle of $\triangle S Q R$.
|
Let $\varangle O P S=\varphi_{1}$ and $\varangle O Q S=\varphi_{2}$. We have that $\varangle O P S=\varangle P Q S=\varphi_{1}$ and $\varangle O Q S=$ $\varangle Q P S=\varphi_{2}$ (tangents to circle $k$ ).
Because $R S \| O P$ we have $\varangle O P S=\varangle R S T=\varphi_{1}$ and $\varangle R Q T=\varangle R S T=\varphi_{1}$ (cyclic quadrilateral $R S Q T$ ). So, we have as follows $\varangle O P T=\varphi_{1}=\varangle R Q T=\varangle O Q T$, which implies that the quadrilateral $O P Q T$ is cyclic. From that we directly obtain $\varangle Q O T=$ $\varangle Q P T=\varphi_{2}=\varangle O Q S$, so $O T \| S Q$. From the cyclic quadrilateral $O P Q T$ by easy calculation we get
$$
\varangle O T R=\varangle O T P-\varangle R T S=\varangle O Q P-\varangle R Q S=\left(\varphi_{1}+\varphi_{2}\right)-\varphi_{2}=\varphi_{1}=\varangle R Q T
$$
Thus, $O T$ is a tangent to the circumscribed circle of $\triangle S Q R$.
### 2.4 Number Theory
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $S$ be a point inside $\varangle p O q$, and let $k$ be a circle which contains $S$ and touches the legs $O p$ and $O q$ in points $P$ and $Q$ respectively. Straight line $s$ parallel to $O p$ from $S$ intersects $O q$ in a point $R$. Let $T$ be the point of intersection of the ray $(P S$ and circumscribed circle of $\triangle S Q R$ and $T \neq S$. Prove that $O T \| S Q$ and $O T$ is a tangent of the circumscribed circle of $\triangle S Q R$.
|
Let $\varangle O P S=\varphi_{1}$ and $\varangle O Q S=\varphi_{2}$. We have that $\varangle O P S=\varangle P Q S=\varphi_{1}$ and $\varangle O Q S=$ $\varangle Q P S=\varphi_{2}$ (tangents to circle $k$ ).
Because $R S \| O P$ we have $\varangle O P S=\varangle R S T=\varphi_{1}$ and $\varangle R Q T=\varangle R S T=\varphi_{1}$ (cyclic quadrilateral $R S Q T$ ). So, we have as follows $\varangle O P T=\varphi_{1}=\varangle R Q T=\varangle O Q T$, which implies that the quadrilateral $O P Q T$ is cyclic. From that we directly obtain $\varangle Q O T=$ $\varangle Q P T=\varphi_{2}=\varangle O Q S$, so $O T \| S Q$. From the cyclic quadrilateral $O P Q T$ by easy calculation we get
$$
\varangle O T R=\varangle O T P-\varangle R T S=\varangle O Q P-\varangle R Q S=\left(\varphi_{1}+\varphi_{2}\right)-\varphi_{2}=\varphi_{1}=\varangle R Q T
$$
Thus, $O T$ is a tangent to the circumscribed circle of $\triangle S Q R$.

### 2.4 Number Theory
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2007_shl.jsonl",
"problem_match": "\nG4 ",
"solution_match": "## Solution"
}
|
93ae6f3c-b67d-54fe-8676-f288cb790122
| 604,563
|
Prove that the equation $x^{2006}-4 y^{2006}-2006=4 y^{2007}+2007 y$ has no solution in the set of the positive integers.
|
We assume the contrary is true. So there are $x$ and $y$ that satisfy the equation. Hence we have
$$
\begin{gathered}
x^{2006}=4 y^{2007}+4 y^{2006}+2007 y+2006 \\
x^{2006}+1=4 y^{2006}(y+1)+2007(y+1) \\
x^{2006}+1=\left(4 y^{2006}+2007\right)(y+1)
\end{gathered}
$$
But $4 y^{2006}+2007 \equiv 3(\bmod 4)$, so $x^{2006}+1$ will have at least one prime divisor of the type $4 k+3$. It is known (and easily obtainable by using Fermat's Little Theorem) that this is impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that the equation $x^{2006}-4 y^{2006}-2006=4 y^{2007}+2007 y$ has no solution in the set of the positive integers.
|
We assume the contrary is true. So there are $x$ and $y$ that satisfy the equation. Hence we have
$$
\begin{gathered}
x^{2006}=4 y^{2007}+4 y^{2006}+2007 y+2006 \\
x^{2006}+1=4 y^{2006}(y+1)+2007(y+1) \\
x^{2006}+1=\left(4 y^{2006}+2007\right)(y+1)
\end{gathered}
$$
But $4 y^{2006}+2007 \equiv 3(\bmod 4)$, so $x^{2006}+1$ will have at least one prime divisor of the type $4 k+3$. It is known (and easily obtainable by using Fermat's Little Theorem) that this is impossible.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2007_shl.jsonl",
"problem_match": "\nNT2 ",
"solution_match": "## Solution"
}
|
9fbf350a-4724-58cc-bdb4-b5b4aeb5a8b6
| 604,582
|
Let $n>1$ be a positive integer and $p$ a prime number such that $n \mid(p-1)$ and $p \mid\left(n^{6}-1\right)$. Prove that at least one of the numbers $p-n$ and $p+n$ is a perfect square.
|
Since $n \mid p-1$, then $p=1+n a$, where $a \geq 1$ is an integer. From the condition $p \mid n^{6}-1$, it follows that $p|n-1, p| n+1, p \mid n^{2}+n+1$ or $p \mid n^{2}-n+1$.
- Let $p \mid n-1$. Then $n \geq p+1>n$ which is impossible.
- Let $p \mid n+1$. Then $n+1 \geq p=1+n a$ which is possible only when $a=1$ and $p=n+1$, i.e. $p-n=1=1^{2}$.
- Let $p \mid n^{2}+n+1$, i.e. $n^{2}+n+1=p b$, where $b \geq 1$ is an integer.
The equality $p=1+n a$ implies $n \mid b-1$, from where $b=1+n c, c \geq 0$ is an integer. We have
$$
n^{2}+n+1=p b=(1+n a)(1+n c)=1+(a+c) n+a c n^{2} \text { or } n+1=a c n+a+c
$$
If $a c \geq 1$ then $a+c \geq 2$, which is impossible. If $a c=0$ then $c=0$ and $a=n+1$. Thus we obtain $p=n^{2}+n+1$ from where $p+n=n^{2}+2 n+1=(n+1)^{2}$.
- Let $p \mid n^{2}-n+1$, i.e. $n^{2}-n+1=p b$ and analogously $b=1+n c$. So
$$
n^{2}-n+1=p b=(1+n a)(1+n c)=1+(a+c) n+a c n^{2} \text { or } n-1=a c n+a+c
$$
Similarly, we have $c=0, a=n-1$ and $p=n^{2}-n+1$ from where $p-n=n^{2}-2 n+1=$ $(n-1)^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n>1$ be a positive integer and $p$ a prime number such that $n \mid(p-1)$ and $p \mid\left(n^{6}-1\right)$. Prove that at least one of the numbers $p-n$ and $p+n$ is a perfect square.
|
Since $n \mid p-1$, then $p=1+n a$, where $a \geq 1$ is an integer. From the condition $p \mid n^{6}-1$, it follows that $p|n-1, p| n+1, p \mid n^{2}+n+1$ or $p \mid n^{2}-n+1$.
- Let $p \mid n-1$. Then $n \geq p+1>n$ which is impossible.
- Let $p \mid n+1$. Then $n+1 \geq p=1+n a$ which is possible only when $a=1$ and $p=n+1$, i.e. $p-n=1=1^{2}$.
- Let $p \mid n^{2}+n+1$, i.e. $n^{2}+n+1=p b$, where $b \geq 1$ is an integer.
The equality $p=1+n a$ implies $n \mid b-1$, from where $b=1+n c, c \geq 0$ is an integer. We have
$$
n^{2}+n+1=p b=(1+n a)(1+n c)=1+(a+c) n+a c n^{2} \text { or } n+1=a c n+a+c
$$
If $a c \geq 1$ then $a+c \geq 2$, which is impossible. If $a c=0$ then $c=0$ and $a=n+1$. Thus we obtain $p=n^{2}+n+1$ from where $p+n=n^{2}+2 n+1=(n+1)^{2}$.
- Let $p \mid n^{2}-n+1$, i.e. $n^{2}-n+1=p b$ and analogously $b=1+n c$. So
$$
n^{2}-n+1=p b=(1+n a)(1+n c)=1+(a+c) n+a c n^{2} \text { or } n-1=a c n+a+c
$$
Similarly, we have $c=0, a=n-1$ and $p=n^{2}-n+1$ from where $p-n=n^{2}-2 n+1=$ $(n-1)^{2}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2007_shl.jsonl",
"problem_match": "\nNT3 ",
"solution_match": "## Solution"
}
|
bb077656-a136-564d-88d9-5f2e8e7dc80b
| 604,596
|
Let $a, b$ be two co-prime positive integers. A number is called good if it can be written in the form $a x+b y$ for non-negative integers $x, y$. Define the function $f: \mathbb{Z} \rightarrow \mathbb{Z}$ as $f(n)=n-n_{a}-n_{b}$, where $s_{t}$ represents the remainder of $s$ upon division by $t$. Show that an integer $n$ is good if and only if the infinite sequence $n, f(n), f(f(n)), \ldots$ contains only non-negative integers.
|
If $n$ is good then $n=a x+b y$ also $n_{a}=(b y)_{a}$ and $n_{b}=(a x)_{b}$ so
$$
f(n)=a x-(a x)_{b}+b y-(b y)_{a}=b y^{\prime}+a x^{\prime}
$$
is also good, thus the sequence contains only good numbers which are non-negative.
Now we have to prove that if the sequence contains only non-negative integers then $n$ is good. Because the sequence is non-increasing then the sequence will become constant from some point onwards. But $f(k)=k$ implies that $k$ is a multiple of $a b$ thus some term of the sequence is good. We are done if we prove the following:
Lemma: $f(n)$ is good implies $n$ is good.
Proof of Lemma: $n=2 n-n_{a}-n_{b}-f(n)=a x^{\prime}+b y^{\prime}-a x-b y=a\left(x^{\prime}-x\right)+b\left(y^{\prime}-y\right)$ and $x^{\prime} \geq x$ because $n \geq f(n) \Rightarrow n-n_{a} \geq f(n)-f(n)_{a} \Rightarrow a x^{\prime} \geq a x+b y-(b y)_{a} \geq a x$. Similarly $y^{\prime} \geq y$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a, b$ be two co-prime positive integers. A number is called good if it can be written in the form $a x+b y$ for non-negative integers $x, y$. Define the function $f: \mathbb{Z} \rightarrow \mathbb{Z}$ as $f(n)=n-n_{a}-n_{b}$, where $s_{t}$ represents the remainder of $s$ upon division by $t$. Show that an integer $n$ is good if and only if the infinite sequence $n, f(n), f(f(n)), \ldots$ contains only non-negative integers.
|
If $n$ is good then $n=a x+b y$ also $n_{a}=(b y)_{a}$ and $n_{b}=(a x)_{b}$ so
$$
f(n)=a x-(a x)_{b}+b y-(b y)_{a}=b y^{\prime}+a x^{\prime}
$$
is also good, thus the sequence contains only good numbers which are non-negative.
Now we have to prove that if the sequence contains only non-negative integers then $n$ is good. Because the sequence is non-increasing then the sequence will become constant from some point onwards. But $f(k)=k$ implies that $k$ is a multiple of $a b$ thus some term of the sequence is good. We are done if we prove the following:
Lemma: $f(n)$ is good implies $n$ is good.
Proof of Lemma: $n=2 n-n_{a}-n_{b}-f(n)=a x^{\prime}+b y^{\prime}-a x-b y=a\left(x^{\prime}-x\right)+b\left(y^{\prime}-y\right)$ and $x^{\prime} \geq x$ because $n \geq f(n) \Rightarrow n-n_{a} \geq f(n)-f(n)_{a} \Rightarrow a x^{\prime} \geq a x+b y-(b y)_{a} \geq a x$. Similarly $y^{\prime} \geq y$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2007_shl.jsonl",
"problem_match": "\nNT4 ",
"solution_match": "## Solution"
}
|
52f362dd-ff6d-5613-ba46-5b0903abb7cf
| 604,611
|
Let $p$ be a prime number. Show that $7 p+3^{p}-4$ is not a perfect square.
|
Assume that for a prime number $p$ greater than $3, m=7 p+3^{p}-4$ is a perfect square. Let $m=n^{2}$ for some $n \in \mathbb{Z}$. By Fermat's Little Theorem,
$$
m=7 p+3^{p}-4 \equiv 3-4 \equiv-1 \quad(\bmod p)
$$
If $p=4 k+3, k \in \mathbb{Z}$, then again by Fermat's Little Theorem
$$
-1 \equiv m^{2 k+1} \equiv n^{4 k+2} \equiv n^{p-1} \equiv 1 \quad(\bmod p), \text { but } p>3
$$
a contradiction. So $p \equiv 1(\bmod 4)$.
Therefore $m=7 p+3^{p}-4 \equiv 3-1 \equiv 2(\bmod 4)$. But this is a contradiction since 2 is not perfect square in $(\bmod 4)$. For $p=2$ we have $m=19$ and for $p=3$ we have $m=44$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be a prime number. Show that $7 p+3^{p}-4$ is not a perfect square.
|
Assume that for a prime number $p$ greater than $3, m=7 p+3^{p}-4$ is a perfect square. Let $m=n^{2}$ for some $n \in \mathbb{Z}$. By Fermat's Little Theorem,
$$
m=7 p+3^{p}-4 \equiv 3-4 \equiv-1 \quad(\bmod p)
$$
If $p=4 k+3, k \in \mathbb{Z}$, then again by Fermat's Little Theorem
$$
-1 \equiv m^{2 k+1} \equiv n^{4 k+2} \equiv n^{p-1} \equiv 1 \quad(\bmod p), \text { but } p>3
$$
a contradiction. So $p \equiv 1(\bmod 4)$.
Therefore $m=7 p+3^{p}-4 \equiv 3-1 \equiv 2(\bmod 4)$. But this is a contradiction since 2 is not perfect square in $(\bmod 4)$. For $p=2$ we have $m=19$ and for $p=3$ we have $m=44$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2007_shl.jsonl",
"problem_match": "\nNT5 ",
"solution_match": "## Solution"
}
|
6112a377-7d27-58bc-8b84-3f1a5d37edaf
| 604,624
|
If the real numbers $a, b, c, d$ are such that $0<a, b, c, d<1$, show that
$$
1+a b+b c+c d+d a+a c+b d>a+b+c+d
$$
|
If $1 \geq a+b+c$ then we write the given inequality equivalently as
$$
\begin{gathered}
1-(a+b+c)+d[(a+b+c)-1]+a b+b c+c a>0 \\
\Leftrightarrow[1-(a+b+c)](1-d)+a b+b c+c a>0
\end{gathered}
$$
which is of course true.
If instead $a+b+c>1$, then $d(a+b+c)>d$ i.e.
$$
d a+d b+d c>d
$$
We are going to prove that also
$$
1+a b+b c+c a>a+b+c
$$
thus adding (1) and (2) together we'll get the desired result in this case too.
For the truth of $(2)$ :
If $1 \geq a+b$, then we rewrite (2) equivalently as
$$
\begin{gathered}
1-(a+b)+c[(a+b)-1]+a b>0 \\
\quad \Leftrightarrow[1-(a+b)](1-c)+a b>0
\end{gathered}
$$
which is of course true.
If instead $a+b>1$, then $c(a+b)>c$, i.e.
$$
c a+c b>c
$$
But it is also true that
$$
1+a b>a+b
$$
because this is equivalent to $(1-a)+b(a-1)>0$, i.e. to $(1-a)(1-b)>0$ which holds. Adding (3) and (4) together we get the truth of (2) in this case too and we are done. You can instead consider the following generalization:
Exercise. If for the real numbers $x_{1}, x_{2}, \ldots, x_{n}$ it is $0<x_{i}<1$, for any $i$, show that
$$
1+\sum_{1 \leq i<j \leq n} x_{i} x_{j}>\sum_{i=1}^{n} x_{i}
$$
## Solution
We'll prove it by induction.
For $n=1$ the desired result becomes $1>x_{1}$ which is true.
Let the result be true for some natural number $n \geq 1$.
We'll prove it to be true for $n+1$ as well, and we'll be done.
So let $x_{1}, x_{2}, \ldots, x_{n}, x_{n+1}$ be $n+1$ given real numbers with $0<x_{i}<1$, for any $i$. We wish to show that
$$
1+\sum_{1 \leq i<j \leq n+1} x_{i} x_{j}>x_{1}+x_{2}+\ldots+x_{n}+x_{n+1}
$$
If $1 \geq x_{1}+x_{2}+\ldots+x_{n}$ then we rewrite (5) equivalently as
$$
1-\left(x_{1}+x_{2}+\ldots+x_{n}\right)+x_{n+1}\left(x_{1}+x_{2}+\ldots+x_{n}-1\right)+\sum_{1 \leq i<j \leq n} x_{i} x_{j}>0
$$
This is also written as
$$
\left(1-x_{n+1}\right)\left[1-\left(x_{1}+x_{2}+\ldots+x_{n}\right)\right]+\sum_{1 \leq i<j \leq n} x_{i} x_{j}>0
$$
which is clearly true.
If instead $x_{1}+x_{2}+\ldots+x_{n}>1$ then $x_{n+1}\left(x_{1}+x_{2}+\ldots+x_{n}\right)>x_{n+1}$, i.e.
$$
x_{n+1} x_{1}+x_{n+1} x_{2}+\ldots+x_{n+1} x_{n}>x_{n+1}
$$
By the induction hypothesis applied to the $n$ real numbers $x_{1}, x_{2}, \ldots, x_{n}$ we also know that
$$
1+\sum_{1 \leq i<j \leq n} x_{i} x_{j}>\sum_{i=1}^{n} x_{i}
$$
Adding (6) and (7) together we get the validity of (5) in this case too, and we are done.
You can even consider the following variation:
Exercise. If the real numbers $x_{1}, x_{2}, \ldots, x_{2008}$ are such that $0<x_{i}<1$, for any $i$, show that
$$
1+\sum_{1 \leq i<j \leq 2008} x_{i} x_{j}>\sum_{i=1}^{2008} x_{i}
$$
Remark: Inequality (2) follows directly from $(1-a)(1-b)(1-c)>0 \Leftrightarrow 1-a-b-c+$ $a b+b c+c a>a b c>0$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
If the real numbers $a, b, c, d$ are such that $0<a, b, c, d<1$, show that
$$
1+a b+b c+c d+d a+a c+b d>a+b+c+d
$$
|
If $1 \geq a+b+c$ then we write the given inequality equivalently as
$$
\begin{gathered}
1-(a+b+c)+d[(a+b+c)-1]+a b+b c+c a>0 \\
\Leftrightarrow[1-(a+b+c)](1-d)+a b+b c+c a>0
\end{gathered}
$$
which is of course true.
If instead $a+b+c>1$, then $d(a+b+c)>d$ i.e.
$$
d a+d b+d c>d
$$
We are going to prove that also
$$
1+a b+b c+c a>a+b+c
$$
thus adding (1) and (2) together we'll get the desired result in this case too.
For the truth of $(2)$ :
If $1 \geq a+b$, then we rewrite (2) equivalently as
$$
\begin{gathered}
1-(a+b)+c[(a+b)-1]+a b>0 \\
\quad \Leftrightarrow[1-(a+b)](1-c)+a b>0
\end{gathered}
$$
which is of course true.
If instead $a+b>1$, then $c(a+b)>c$, i.e.
$$
c a+c b>c
$$
But it is also true that
$$
1+a b>a+b
$$
because this is equivalent to $(1-a)+b(a-1)>0$, i.e. to $(1-a)(1-b)>0$ which holds. Adding (3) and (4) together we get the truth of (2) in this case too and we are done. You can instead consider the following generalization:
Exercise. If for the real numbers $x_{1}, x_{2}, \ldots, x_{n}$ it is $0<x_{i}<1$, for any $i$, show that
$$
1+\sum_{1 \leq i<j \leq n} x_{i} x_{j}>\sum_{i=1}^{n} x_{i}
$$
## Solution
We'll prove it by induction.
For $n=1$ the desired result becomes $1>x_{1}$ which is true.
Let the result be true for some natural number $n \geq 1$.
We'll prove it to be true for $n+1$ as well, and we'll be done.
So let $x_{1}, x_{2}, \ldots, x_{n}, x_{n+1}$ be $n+1$ given real numbers with $0<x_{i}<1$, for any $i$. We wish to show that
$$
1+\sum_{1 \leq i<j \leq n+1} x_{i} x_{j}>x_{1}+x_{2}+\ldots+x_{n}+x_{n+1}
$$
If $1 \geq x_{1}+x_{2}+\ldots+x_{n}$ then we rewrite (5) equivalently as
$$
1-\left(x_{1}+x_{2}+\ldots+x_{n}\right)+x_{n+1}\left(x_{1}+x_{2}+\ldots+x_{n}-1\right)+\sum_{1 \leq i<j \leq n} x_{i} x_{j}>0
$$
This is also written as
$$
\left(1-x_{n+1}\right)\left[1-\left(x_{1}+x_{2}+\ldots+x_{n}\right)\right]+\sum_{1 \leq i<j \leq n} x_{i} x_{j}>0
$$
which is clearly true.
If instead $x_{1}+x_{2}+\ldots+x_{n}>1$ then $x_{n+1}\left(x_{1}+x_{2}+\ldots+x_{n}\right)>x_{n+1}$, i.e.
$$
x_{n+1} x_{1}+x_{n+1} x_{2}+\ldots+x_{n+1} x_{n}>x_{n+1}
$$
By the induction hypothesis applied to the $n$ real numbers $x_{1}, x_{2}, \ldots, x_{n}$ we also know that
$$
1+\sum_{1 \leq i<j \leq n} x_{i} x_{j}>\sum_{i=1}^{n} x_{i}
$$
Adding (6) and (7) together we get the validity of (5) in this case too, and we are done.
You can even consider the following variation:
Exercise. If the real numbers $x_{1}, x_{2}, \ldots, x_{2008}$ are such that $0<x_{i}<1$, for any $i$, show that
$$
1+\sum_{1 \leq i<j \leq 2008} x_{i} x_{j}>\sum_{i=1}^{2008} x_{i}
$$
Remark: Inequality (2) follows directly from $(1-a)(1-b)(1-c)>0 \Leftrightarrow 1-a-b-c+$ $a b+b c+c a>a b c>0$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nA6 ",
"solution_match": "## Solution"
}
|
5f2e06a9-27a1-5845-95a8-e70091b5d6b9
| 604,693
|
Let $a, b$ and $c$ be a positive real numbers such that $a b c=1$. Prove the inequality
$$
\left(a b+b c+\frac{1}{c a}\right)\left(b c+c a+\frac{1}{a b}\right)\left(c a+a b+\frac{1}{b c}\right) \geq(1+2 a)(1+2 b)(1+2 c)
$$
|
By Cauchy-Schwarz inequality and $a b c=1$ we get
$$
\begin{gathered}
\sqrt{\left(b c+c a+\frac{1}{a b}\right)\left(a b+b c+\frac{1}{c a}\right)}=\sqrt{\left(b c+c a+\frac{1}{a b}\right)\left(\frac{1}{c a}+a b+b c\right)} \geq \\
\left(\sqrt{a b} \cdot \sqrt{\frac{1}{a b}}+\sqrt{b c} \cdot \sqrt{b c}+\sqrt{\frac{1}{c a}} \cdot \sqrt{c a}\right)=(2+b c)=(2 a b c+b c)=b c(1+2 a)
\end{gathered}
$$
Analogously we get $\sqrt{\left(b c+c a+\frac{1}{a b}\right)\left(c a+a b+\frac{1}{b c}\right)} \geq c a(1+2 b)$ and
$\sqrt{\left(c a+a b+\frac{1}{b c}\right)\left(a b+b c+\frac{1}{c a}\right)} \geq a b(1+2 a)$.
Multiplying these three inequalities we get:
$$
\left(a b+b c+\frac{1}{c a}\right)\left(b c+c a+\frac{1}{a b}\right)\left(c a+a b+\frac{1}{b c}\right) \geq a^{2} b^{2} c^{2}(1+2 a)(1+2 b)(1+2 c)=
$$
$(1+2 a)(1+2 b)(1+2 c)$ because $a b c=1$.
Equality holds if and only if $a=b=c=1$.
## Solution 2
Using $a b c=1$ we get
$$
\begin{gathered}
\left(a b+b c+\frac{1}{c a}\right)\left(b c+c a+\frac{1}{a b}\right)\left(c a+a b+\frac{1}{b c}\right)= \\
=\left(\frac{1}{c}+\frac{1}{a}+b\right)\left(\frac{1}{a}+\frac{1}{b}+c\right)\left(\frac{1}{b}+\frac{1}{c}+a\right)= \\
=\frac{(a+c+a b c)}{a c} \cdot \frac{(b+a+a b c)}{a b} \cdot \frac{(b+c+a b c)}{b c}=(a+b+1)(b+c+1)(c+a+1)
\end{gathered}
$$
Thus, we need to prove
$$
(a+b+1)(b+c+1)(c+a+1) \geq(1+2 a)(1+2 b)(1+2 c)
$$
After multiplication and using the fact $a b c=1$ we have to prove
$$
\begin{gathered}
a^{2} b+a^{2} c+b^{2} c+b^{2} a+c^{2} a+c^{2} b+3(a b+b c+c a)+2(a+b+c)+a^{2}+b^{2}+c^{2}+3 \geq \\
\geq 4(a b+b c+c a)+2(a+b+c)+9
\end{gathered}
$$
So we need to prove
$$
a^{2} b+a^{2} c+b^{2} c+b^{2} a+c^{2} a+c^{2} b+a^{2}+b^{2}+c^{2} \geq a b+b c+c a+6
$$
This follows from the well-known (AM-GM inequality) inequalities
$$
a^{2}+b^{2}+c^{2} \geq a b+b c+c a
$$
and
$$
a^{2} b+a^{2} c+b^{2} c+b^{2} a+c^{2} a+c^{2} b \geq 6 a b c=6
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$ and $c$ be a positive real numbers such that $a b c=1$. Prove the inequality
$$
\left(a b+b c+\frac{1}{c a}\right)\left(b c+c a+\frac{1}{a b}\right)\left(c a+a b+\frac{1}{b c}\right) \geq(1+2 a)(1+2 b)(1+2 c)
$$
|
By Cauchy-Schwarz inequality and $a b c=1$ we get
$$
\begin{gathered}
\sqrt{\left(b c+c a+\frac{1}{a b}\right)\left(a b+b c+\frac{1}{c a}\right)}=\sqrt{\left(b c+c a+\frac{1}{a b}\right)\left(\frac{1}{c a}+a b+b c\right)} \geq \\
\left(\sqrt{a b} \cdot \sqrt{\frac{1}{a b}}+\sqrt{b c} \cdot \sqrt{b c}+\sqrt{\frac{1}{c a}} \cdot \sqrt{c a}\right)=(2+b c)=(2 a b c+b c)=b c(1+2 a)
\end{gathered}
$$
Analogously we get $\sqrt{\left(b c+c a+\frac{1}{a b}\right)\left(c a+a b+\frac{1}{b c}\right)} \geq c a(1+2 b)$ and
$\sqrt{\left(c a+a b+\frac{1}{b c}\right)\left(a b+b c+\frac{1}{c a}\right)} \geq a b(1+2 a)$.
Multiplying these three inequalities we get:
$$
\left(a b+b c+\frac{1}{c a}\right)\left(b c+c a+\frac{1}{a b}\right)\left(c a+a b+\frac{1}{b c}\right) \geq a^{2} b^{2} c^{2}(1+2 a)(1+2 b)(1+2 c)=
$$
$(1+2 a)(1+2 b)(1+2 c)$ because $a b c=1$.
Equality holds if and only if $a=b=c=1$.
## Solution 2
Using $a b c=1$ we get
$$
\begin{gathered}
\left(a b+b c+\frac{1}{c a}\right)\left(b c+c a+\frac{1}{a b}\right)\left(c a+a b+\frac{1}{b c}\right)= \\
=\left(\frac{1}{c}+\frac{1}{a}+b\right)\left(\frac{1}{a}+\frac{1}{b}+c\right)\left(\frac{1}{b}+\frac{1}{c}+a\right)= \\
=\frac{(a+c+a b c)}{a c} \cdot \frac{(b+a+a b c)}{a b} \cdot \frac{(b+c+a b c)}{b c}=(a+b+1)(b+c+1)(c+a+1)
\end{gathered}
$$
Thus, we need to prove
$$
(a+b+1)(b+c+1)(c+a+1) \geq(1+2 a)(1+2 b)(1+2 c)
$$
After multiplication and using the fact $a b c=1$ we have to prove
$$
\begin{gathered}
a^{2} b+a^{2} c+b^{2} c+b^{2} a+c^{2} a+c^{2} b+3(a b+b c+c a)+2(a+b+c)+a^{2}+b^{2}+c^{2}+3 \geq \\
\geq 4(a b+b c+c a)+2(a+b+c)+9
\end{gathered}
$$
So we need to prove
$$
a^{2} b+a^{2} c+b^{2} c+b^{2} a+c^{2} a+c^{2} b+a^{2}+b^{2}+c^{2} \geq a b+b c+c a+6
$$
This follows from the well-known (AM-GM inequality) inequalities
$$
a^{2}+b^{2}+c^{2} \geq a b+b c+c a
$$
and
$$
a^{2} b+a^{2} c+b^{2} c+b^{2} a+c^{2} a+c^{2} b \geq 6 a b c=6
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nA7 ",
"solution_match": "## Solution 1"
}
|
3ce88902-df34-58fa-95eb-c8836f2dfcfa
| 604,707
|
Show that
$$
(x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right) \geq 4\left(\frac{x}{x y+1}+\frac{y}{y z+1}+\frac{z}{z x+1}\right)^{2}
$$
for any real positive numbers $x, y$ and $z$.
|
The idea is to split the inequality in two, showing that
$$
\left(\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{z}}+\sqrt{\frac{z}{x}}\right)^{2}
$$
can be intercalated between the left-hand side and the right-hand side. Indeed, using the Cauchy-Schwarz inequality one has
$$
(x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right) \geq\left(\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{z}}+\sqrt{\frac{z}{x}}\right)^{2}
$$
On the other hand, as
$$
\sqrt{\frac{x}{y}} \geq \frac{2 x}{x y+1} \Leftrightarrow(\sqrt{x y}-1)^{2} \geq 0
$$
by summation one has
$$
\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{z}}+\sqrt{\frac{z}{x}} \geq \frac{2 x}{x y+1}+\frac{2 y}{y z+1}+\frac{2 z}{z x+1}
$$
The rest is obvious.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Show that
$$
(x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right) \geq 4\left(\frac{x}{x y+1}+\frac{y}{y z+1}+\frac{z}{z x+1}\right)^{2}
$$
for any real positive numbers $x, y$ and $z$.
|
The idea is to split the inequality in two, showing that
$$
\left(\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{z}}+\sqrt{\frac{z}{x}}\right)^{2}
$$
can be intercalated between the left-hand side and the right-hand side. Indeed, using the Cauchy-Schwarz inequality one has
$$
(x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right) \geq\left(\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{z}}+\sqrt{\frac{z}{x}}\right)^{2}
$$
On the other hand, as
$$
\sqrt{\frac{x}{y}} \geq \frac{2 x}{x y+1} \Leftrightarrow(\sqrt{x y}-1)^{2} \geq 0
$$
by summation one has
$$
\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{z}}+\sqrt{\frac{z}{x}} \geq \frac{2 x}{x y+1}+\frac{2 y}{y z+1}+\frac{2 z}{z x+1}
$$
The rest is obvious.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nA8 ",
"solution_match": "## Solution"
}
|
1e039154-4643-5d05-b9dd-2204d4d78d83
| 604,719
|
On a $5 \times 5$ board, $n$ white markers are positioned, each marker in a distinct $1 \times 1$ square. A smart child got an assignment to recolor in black as many markers as possible, in the following manner: a white marker is taken from the board; it is colored in black, and then put back on the board on an empty square such that none of the neighboring squares contains a white marker (two squares are called neighboring if they contain a common side). If it is possible for the child to succeed in coloring all the markers black, we say that the initial positioning of the markers was good.
a) Prove that if $n=20$, then a good initial positioning exists.
b) Prove that if $n=21$, then a good initial positioning does not exist.
|
a) Position 20 white markers on the board such that the left-most column is empty. This
positioning is good because the coloring can be realized column by column, starting with the second (from left), then the third, and so on, so that the white marker on position $(i, j)$ after the coloring is put on position $(i, j-1)$.
b) Suppose there exists a good positioning with 21 white markers on the board i.e. there exists a re-coloring of them all, one by one. In any moment when there are 21 markers on the board, there must be at least one column completely filled with markers, and there must be at least one row completely filled with markers. So, there exists a "cross" of markers on the board. At the initial position, each such cross is completely white, at the final position each such cross is completely black, and at every moment when there are 21 markers on the board, each such cross is monochromatic. But this cannot be, since every two crosses have at least two common squares and therefore it is not possible for a white cross to vanish and for a black cross to appear by re-coloring of only one marker. Contradiction!
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On a $5 \times 5$ board, $n$ white markers are positioned, each marker in a distinct $1 \times 1$ square. A smart child got an assignment to recolor in black as many markers as possible, in the following manner: a white marker is taken from the board; it is colored in black, and then put back on the board on an empty square such that none of the neighboring squares contains a white marker (two squares are called neighboring if they contain a common side). If it is possible for the child to succeed in coloring all the markers black, we say that the initial positioning of the markers was good.
a) Prove that if $n=20$, then a good initial positioning exists.
b) Prove that if $n=21$, then a good initial positioning does not exist.
|
a) Position 20 white markers on the board such that the left-most column is empty. This
positioning is good because the coloring can be realized column by column, starting with the second (from left), then the third, and so on, so that the white marker on position $(i, j)$ after the coloring is put on position $(i, j-1)$.
b) Suppose there exists a good positioning with 21 white markers on the board i.e. there exists a re-coloring of them all, one by one. In any moment when there are 21 markers on the board, there must be at least one column completely filled with markers, and there must be at least one row completely filled with markers. So, there exists a "cross" of markers on the board. At the initial position, each such cross is completely white, at the final position each such cross is completely black, and at every moment when there are 21 markers on the board, each such cross is monochromatic. But this cannot be, since every two crosses have at least two common squares and therefore it is not possible for a white cross to vanish and for a black cross to appear by re-coloring of only one marker. Contradiction!
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nC1 ",
"solution_match": "\nSolution"
}
|
98ce9130-ae92-5596-b21e-e5dedd5c0d19
| 604,744
|
Integers $1,2, \ldots, 2 n$ are arbitrarily assigned to boxes labeled with numbers $1,2, \ldots, 2 n$. Now, we add the number assigned to the box to the number on the box label. Show that two such sums give the same remainder modulo $2 n$.
|
Let us assume that all sums give different remainder modulo $2 n$, and let $S$ denote the value of their sum.
For our assumption,
$$
S \equiv 0+1+\ldots+2 n-1=\frac{(2 n-1) 2 n}{2}=(2 n-1) n \equiv n \quad(\bmod 2 n)
$$
But, if we sum, breaking all sums into its components, we derive
$$
S \equiv 2(1+\ldots+2 n)=2 \cdot \frac{2 n(2 n+1)}{2}=2 n(2 n+1) \equiv 0 \quad(\bmod 2 n)
$$
From the last two conclusions we derive $n \equiv 0(\bmod 2 n)$. Contradiction.
Therefore, there are two sums with the same remainder modulo $2 n$.
Remark: The result is no longer true if one replaces $2 n$ by $2 n+1$. Indeed, one could assign the number $k$ to the box labeled $k$, thus obtaining the sums $2 k, k=\overline{1,2 n+1}$. Two such numbers give different remainders when divided by $2 n+1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Integers $1,2, \ldots, 2 n$ are arbitrarily assigned to boxes labeled with numbers $1,2, \ldots, 2 n$. Now, we add the number assigned to the box to the number on the box label. Show that two such sums give the same remainder modulo $2 n$.
|
Let us assume that all sums give different remainder modulo $2 n$, and let $S$ denote the value of their sum.
For our assumption,
$$
S \equiv 0+1+\ldots+2 n-1=\frac{(2 n-1) 2 n}{2}=(2 n-1) n \equiv n \quad(\bmod 2 n)
$$
But, if we sum, breaking all sums into its components, we derive
$$
S \equiv 2(1+\ldots+2 n)=2 \cdot \frac{2 n(2 n+1)}{2}=2 n(2 n+1) \equiv 0 \quad(\bmod 2 n)
$$
From the last two conclusions we derive $n \equiv 0(\bmod 2 n)$. Contradiction.
Therefore, there are two sums with the same remainder modulo $2 n$.
Remark: The result is no longer true if one replaces $2 n$ by $2 n+1$. Indeed, one could assign the number $k$ to the box labeled $k$, thus obtaining the sums $2 k, k=\overline{1,2 n+1}$. Two such numbers give different remainders when divided by $2 n+1$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nC3 ",
"solution_match": "## Solution"
}
|
6f676cd3-7212-5a4d-a07d-32fb7b19e7f5
| 604,774
|
Two perpendicular chords of a circle, $A M, B N$, which intersect at point $K$, define on the circle four arcs with pairwise different length, with $A B$ being the smallest of them.
We draw the chords $A D, B C$ with $A D \| B C$ and $C, D$ different from $N, M$. If $L$ is the point of intersection of $D N, M C$ and $T$ the point of intersection of $D C, K L$, prove that $\angle K T C=\angle K N L$.
|
First we prove that $N L \perp M C$. The arguments depend slightly on the position of $D$. The other cases are similar.
From the cyclic quadrilaterals $A D C M$ and $D N B C$ we have:
$$
\varangle D C L=\varangle D A M \text { and } \varangle C D L=\varangle C B N \text {. }
$$
So we obtain
$$
\varangle D C L+\varangle C D L=\varangle D A M+\varangle C B N .
$$
And because $A D \| B C$, if $Z$ the point of intersection of $A M, B C$ then $\varangle D A M=\varangle B Z A$, and we have
$$
\varangle D C L+\varangle C D L=\varangle B Z A+\varangle C B N=90^{\circ}
$$
Let $P$ the point of intersection of $K L, A C$, then $N P \perp A C$, because the line $K P L$ is a Simson line of the point $N$ with respect to the triangle $A C M$.
From the cyclic quadrilaterals $N P C L$ and $A N D C$ we obtain:
$$
\varangle C P L=\varangle C N L \text { and } \varangle C N L=\varangle C A D \text {, }
$$
so $\varangle C P L=\varangle C A D$, that is $K L\|A D\| B C$ therefore $\varangle K T C=\varangle A D C$ (1).
But $\varangle A D C=\varangle A N C=\varangle A N K+\varangle K N C=\varangle C N L+\varangle K N C$, so
$$
\varangle A D C=\varangle K N L
$$
From (1) and (2) we obtain the result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Two perpendicular chords of a circle, $A M, B N$, which intersect at point $K$, define on the circle four arcs with pairwise different length, with $A B$ being the smallest of them.
We draw the chords $A D, B C$ with $A D \| B C$ and $C, D$ different from $N, M$. If $L$ is the point of intersection of $D N, M C$ and $T$ the point of intersection of $D C, K L$, prove that $\angle K T C=\angle K N L$.
|
First we prove that $N L \perp M C$. The arguments depend slightly on the position of $D$. The other cases are similar.
From the cyclic quadrilaterals $A D C M$ and $D N B C$ we have:
$$
\varangle D C L=\varangle D A M \text { and } \varangle C D L=\varangle C B N \text {. }
$$
So we obtain
$$
\varangle D C L+\varangle C D L=\varangle D A M+\varangle C B N .
$$
And because $A D \| B C$, if $Z$ the point of intersection of $A M, B C$ then $\varangle D A M=\varangle B Z A$, and we have
$$
\varangle D C L+\varangle C D L=\varangle B Z A+\varangle C B N=90^{\circ}
$$
Let $P$ the point of intersection of $K L, A C$, then $N P \perp A C$, because the line $K P L$ is a Simson line of the point $N$ with respect to the triangle $A C M$.
From the cyclic quadrilaterals $N P C L$ and $A N D C$ we obtain:
$$
\varangle C P L=\varangle C N L \text { and } \varangle C N L=\varangle C A D \text {, }
$$
so $\varangle C P L=\varangle C A D$, that is $K L\|A D\| B C$ therefore $\varangle K T C=\varangle A D C$ (1).
But $\varangle A D C=\varangle A N C=\varangle A N K+\varangle K N C=\varangle C N L+\varangle K N C$, so
$$
\varangle A D C=\varangle K N L
$$
From (1) and (2) we obtain the result.

|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nG1 ",
"solution_match": "## Solution"
}
|
77b70d91-a274-5cff-b4ec-96e4dd25d803
| 604,800
|
For a fixed triangle $A B C$ we choose a point $M$ on the ray $C A$ (after $A$ ), a point $N$ on the ray $A B$ (after $B$ ) and a point $P$ on the ray $B C$ (after $C$ ) in a way such that $A M-B C=B N-A C=C P-A B$. Prove that the angles of triangle $M N P$ do not depend on the choice of $M, N, P$.
|
Consider the points $M^{\prime}$ on the ray $B A$ (after $A$ ), $N^{\prime}$ on the ray $C B$ (after $B$ ) and $P^{\prime}$ on the ray $A C$ (after $C$ ), so that $A M=A M^{\prime}, B N=B N^{\prime}, C P=C P^{\prime}$. Since $A M-B C=B N-A C=B N^{\prime}-A C$, we get $C M=A C+A M=B C+B N^{\prime}=C N^{\prime}$. Thus triangle $M C N^{\prime}$ is isosceles, so the perpendicular bisector of $\left[M N^{\prime}\right]$ bisects angle $A C B$ and hence passes through the incenter $I$ of triangle $A B C$. Arguing similarly, we may conclude that $I$ lies also on the perpendicular bisectors of $\left[N P^{\prime}\right]$ and $\left[P M^{\prime}\right]$. On the other side, $I$ clearly lies on the perpendicular bisectors of $\left[M M^{\prime}\right],\left[N N^{\prime}\right]$ and $\left[P P^{\prime}\right]$. Thus the hexagon $M^{\prime} M N^{\prime} N P^{\prime} P$ is cyclic. Then angle $P M N$ equals angle $P N^{\prime} N$, which measures $90^{\circ}-\frac{\beta}{2}$ (the angles of triangle $A B C$ are $\alpha, \beta, \gamma$ ). In the same way angle $M N P$ measures $90^{\circ}-\frac{\gamma}{2}$ and angle $M P N$ measures $90^{\circ}-\frac{\alpha}{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
For a fixed triangle $A B C$ we choose a point $M$ on the ray $C A$ (after $A$ ), a point $N$ on the ray $A B$ (after $B$ ) and a point $P$ on the ray $B C$ (after $C$ ) in a way such that $A M-B C=B N-A C=C P-A B$. Prove that the angles of triangle $M N P$ do not depend on the choice of $M, N, P$.
|
Consider the points $M^{\prime}$ on the ray $B A$ (after $A$ ), $N^{\prime}$ on the ray $C B$ (after $B$ ) and $P^{\prime}$ on the ray $A C$ (after $C$ ), so that $A M=A M^{\prime}, B N=B N^{\prime}, C P=C P^{\prime}$. Since $A M-B C=B N-A C=B N^{\prime}-A C$, we get $C M=A C+A M=B C+B N^{\prime}=C N^{\prime}$. Thus triangle $M C N^{\prime}$ is isosceles, so the perpendicular bisector of $\left[M N^{\prime}\right]$ bisects angle $A C B$ and hence passes through the incenter $I$ of triangle $A B C$. Arguing similarly, we may conclude that $I$ lies also on the perpendicular bisectors of $\left[N P^{\prime}\right]$ and $\left[P M^{\prime}\right]$. On the other side, $I$ clearly lies on the perpendicular bisectors of $\left[M M^{\prime}\right],\left[N N^{\prime}\right]$ and $\left[P P^{\prime}\right]$. Thus the hexagon $M^{\prime} M N^{\prime} N P^{\prime} P$ is cyclic. Then angle $P M N$ equals angle $P N^{\prime} N$, which measures $90^{\circ}-\frac{\beta}{2}$ (the angles of triangle $A B C$ are $\alpha, \beta, \gamma$ ). In the same way angle $M N P$ measures $90^{\circ}-\frac{\gamma}{2}$ and angle $M P N$ measures $90^{\circ}-\frac{\alpha}{2}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nG2 ",
"solution_match": "## Solution"
}
|
88619ecd-2359-56d7-84e9-7b29a880cb98
| 604,815
|
Let $A B C$ be a triangle, $(B C<A B)$. The line $\ell$ passing trough the vertices $C$ and orthogonal to the angle bisector $B E$ of $\angle B$, meets $B E$ and the median $B D$ of the side $A C$ at points $F$ and $G$, respectively. Prove that segment $D F$ bisect the segment $E G$.
|
Let $C F \cap A B=\{K\}$ and $D F \cap B C=\{M\}$. Since $B F \perp K C$ and $B F$ is angle bisector of $\varangle K B C$, we have that $\triangle K B C$ is isosceles i.e. $B K=B C$, also $F$ is midpoint of $K C$. Hence $D F$ is midline for $\triangle A C K$ i.e. $D F \| A K$, from where it is clear that $M$ is a midpoint of $B C$.
We will prove that $G E \| B C$. It is sufficient to show $\frac{B G}{G D}=\frac{C E}{E D}$. From $D F \| A K$ and $D F=\frac{A K}{2}$ we have
$$
\frac{B G}{G D}=\frac{B K}{D F}=\frac{2 B K}{A K}
$$
Also
$$
\begin{gathered}
\frac{C E}{D E}=\frac{C D-D E}{D E}=\frac{C D}{D E}-1=\frac{A D}{D E}-1=\frac{A E-D E}{D E}-1=\frac{A E}{D E}-2= \\
=\frac{A B}{D F}-2=\frac{A K+B K}{\frac{A K}{2}}-2=2+2 \frac{B K}{A K}-2=\frac{2 B K}{A K}
\end{gathered}
$$
From (1) and (2) we have $\frac{B G}{G D}=\frac{C E}{E D}$, so $G E \| B C$, as $M$ is the midpoint of $B C$, it follows that the segment $D F$, bisects the segment $G E$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle, $(B C<A B)$. The line $\ell$ passing trough the vertices $C$ and orthogonal to the angle bisector $B E$ of $\angle B$, meets $B E$ and the median $B D$ of the side $A C$ at points $F$ and $G$, respectively. Prove that segment $D F$ bisect the segment $E G$.

|
Let $C F \cap A B=\{K\}$ and $D F \cap B C=\{M\}$. Since $B F \perp K C$ and $B F$ is angle bisector of $\varangle K B C$, we have that $\triangle K B C$ is isosceles i.e. $B K=B C$, also $F$ is midpoint of $K C$. Hence $D F$ is midline for $\triangle A C K$ i.e. $D F \| A K$, from where it is clear that $M$ is a midpoint of $B C$.
We will prove that $G E \| B C$. It is sufficient to show $\frac{B G}{G D}=\frac{C E}{E D}$. From $D F \| A K$ and $D F=\frac{A K}{2}$ we have
$$
\frac{B G}{G D}=\frac{B K}{D F}=\frac{2 B K}{A K}
$$
Also
$$
\begin{gathered}
\frac{C E}{D E}=\frac{C D-D E}{D E}=\frac{C D}{D E}-1=\frac{A D}{D E}-1=\frac{A E-D E}{D E}-1=\frac{A E}{D E}-2= \\
=\frac{A B}{D F}-2=\frac{A K+B K}{\frac{A K}{2}}-2=2+2 \frac{B K}{A K}-2=\frac{2 B K}{A K}
\end{gathered}
$$
From (1) and (2) we have $\frac{B G}{G D}=\frac{C E}{E D}$, so $G E \| B C$, as $M$ is the midpoint of $B C$, it follows that the segment $D F$, bisects the segment $G E$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nG4 ",
"solution_match": "## Solution"
}
|
8f3f82b0-194d-5453-83d2-7e92868579ac
| 604,838
|
The side lengths of a parallelogram are $a, b$ and diagonals have lengths $x$ and $y$, Knowing that $a b=\frac{x y}{2}$, show that
$$
a=\frac{x}{\sqrt{2}}, b=\frac{y}{\sqrt{2}} \text { or } a=\frac{y}{\sqrt{2}}, b=\frac{x}{\sqrt{2}}
$$
|
## Solution 2.
Let us consider a parallelogram $A B C D$, with $A B=a, B C=b, A C=x, B D=y$, $\widehat{B O C}=\theta$, and let us produce the line $A D$ towards $D$ and consider $M \in(A D$ so that $A D=D M$. Then $B C M D$ is a parallelogram, so $C M=B D=y$.
Observe also that $(A B C D)=2(A C D)=(A C M)$ which is written equivalently as
$$
C B \cdot C D \cdot \sin C=\frac{A C \cdot C M \cdot \sin \theta}{2} \text { i.e. } a b \sin C=\frac{x y \sin \theta}{2}
$$
Because of the given relation $a b=\frac{x y}{2}$ the last relation becomes $\sin C=\sin \theta$, i.e.
$$
\theta=\widehat{C} \text { or } \theta=180^{\circ}-\widehat{C}=\widehat{B}
$$
If $\theta=\widehat{C}$, then the triangles $A C M$ and $B C D$ are similar because their angles at $C$ are equal, as well as their angles at $B, M$ (remember $B C M D$ is a parallelogram).
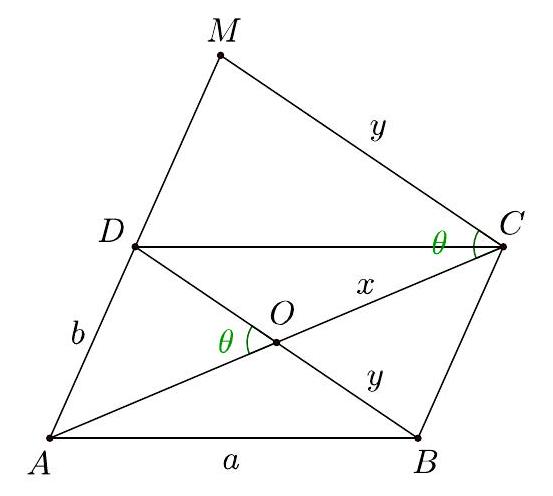
Then
$$
\frac{b}{y}=\frac{a}{x}=\frac{y}{2 b} \Rightarrow\left(b=\frac{y}{2}, a=\frac{x}{2}\right)
$$
If $\theta=\widehat{B}$, then similarly we prove that the triangles $A C M$ and $A C D$ are similar, which then implies
$$
\frac{a}{y}=\frac{b}{x}=\frac{x}{2 b} \Rightarrow\left(a=\frac{y}{2}, b=\frac{x}{2}\right)
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The side lengths of a parallelogram are $a, b$ and diagonals have lengths $x$ and $y$, Knowing that $a b=\frac{x y}{2}$, show that
$$
a=\frac{x}{\sqrt{2}}, b=\frac{y}{\sqrt{2}} \text { or } a=\frac{y}{\sqrt{2}}, b=\frac{x}{\sqrt{2}}
$$
|
## Solution 2.
Let us consider a parallelogram $A B C D$, with $A B=a, B C=b, A C=x, B D=y$, $\widehat{B O C}=\theta$, and let us produce the line $A D$ towards $D$ and consider $M \in(A D$ so that $A D=D M$. Then $B C M D$ is a parallelogram, so $C M=B D=y$.
Observe also that $(A B C D)=2(A C D)=(A C M)$ which is written equivalently as
$$
C B \cdot C D \cdot \sin C=\frac{A C \cdot C M \cdot \sin \theta}{2} \text { i.e. } a b \sin C=\frac{x y \sin \theta}{2}
$$
Because of the given relation $a b=\frac{x y}{2}$ the last relation becomes $\sin C=\sin \theta$, i.e.
$$
\theta=\widehat{C} \text { or } \theta=180^{\circ}-\widehat{C}=\widehat{B}
$$
If $\theta=\widehat{C}$, then the triangles $A C M$ and $B C D$ are similar because their angles at $C$ are equal, as well as their angles at $B, M$ (remember $B C M D$ is a parallelogram).

Then
$$
\frac{b}{y}=\frac{a}{x}=\frac{y}{2 b} \Rightarrow\left(b=\frac{y}{2}, a=\frac{x}{2}\right)
$$
If $\theta=\widehat{B}$, then similarly we prove that the triangles $A C M$ and $A C D$ are similar, which then implies
$$
\frac{a}{y}=\frac{b}{x}=\frac{x}{2 b} \Rightarrow\left(a=\frac{y}{2}, b=\frac{x}{2}\right)
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nG8 ",
"solution_match": "## Solution 1."
}
|
e296a7b2-0350-53fc-a132-502e03e7ec97
| 604,898
|
The side lengths of a parallelogram are $a, b$ and diagonals have lengths $x$ and $y$, Knowing that $a b=\frac{x y}{2}$, show that
$$
a=\frac{x}{\sqrt{2}}, b=\frac{y}{\sqrt{2}} \text { or } a=\frac{y}{\sqrt{2}}, b=\frac{x}{\sqrt{2}}
$$
|
## Solution 3 .
The Parallelogram Law states that, in any parallelogram, the sum of the squares of its diagonals is equal to the sum of the squares of its sides.
In our case, this translates to $x^{2}+y^{2}=2\left(a^{2}+b^{2}\right)$. First adding $2 x y=4 a b$, then subtracting the same equality, yields $(x+y)^{2}=2(a+b)^{2}$ and $(x-y)^{2}=2(a-b)^{2}$. It follows that $x+y=a \sqrt{2}+b \sqrt{2}$ and either $x-y=a \sqrt{2}-b \sqrt{2}$, or $x-y=b \sqrt{2}-a \sqrt{2}$. In the first case one obtains $x=a \sqrt{2}, y=b \sqrt{2}$, in the latter case, $x=b \sqrt{2}, y=a \sqrt{2}$.
For the proof of the Parallelogram Law, simply apply the Law of cosines in triangles $A B C$ and $A B D$ and use the fact that $\cos (\varangle A B C)=-\cos (\varangle B A D)$. Adding the two relations gives the desired condition.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The side lengths of a parallelogram are $a, b$ and diagonals have lengths $x$ and $y$, Knowing that $a b=\frac{x y}{2}$, show that
$$
a=\frac{x}{\sqrt{2}}, b=\frac{y}{\sqrt{2}} \text { or } a=\frac{y}{\sqrt{2}}, b=\frac{x}{\sqrt{2}}
$$
|
## Solution 3 .
The Parallelogram Law states that, in any parallelogram, the sum of the squares of its diagonals is equal to the sum of the squares of its sides.
In our case, this translates to $x^{2}+y^{2}=2\left(a^{2}+b^{2}\right)$. First adding $2 x y=4 a b$, then subtracting the same equality, yields $(x+y)^{2}=2(a+b)^{2}$ and $(x-y)^{2}=2(a-b)^{2}$. It follows that $x+y=a \sqrt{2}+b \sqrt{2}$ and either $x-y=a \sqrt{2}-b \sqrt{2}$, or $x-y=b \sqrt{2}-a \sqrt{2}$. In the first case one obtains $x=a \sqrt{2}, y=b \sqrt{2}$, in the latter case, $x=b \sqrt{2}, y=a \sqrt{2}$.
For the proof of the Parallelogram Law, simply apply the Law of cosines in triangles $A B C$ and $A B D$ and use the fact that $\cos (\varangle A B C)=-\cos (\varangle B A D)$. Adding the two relations gives the desired condition.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nG8 ",
"solution_match": "## Solution 1."
}
|
e296a7b2-0350-53fc-a132-502e03e7ec97
| 604,898
|
Let $O$ be a point inside the parallelogram $A B C D$ such that
$$
\angle A O B+\angle C O D=\angle B O C+\angle C O D
$$
Prove that there exists a circle $k$ tangent to the circumscribed circles of the triangles $\triangle A O B, \triangle B O C, \triangle C O D$ and $\triangle D O A$.
|
From given condition it is clear that $\varangle A O B+\varangle C O D=\varangle B O C+\varangle A O D=180^{\circ}$.
Let $E$ be a point such that $A E=D O$ and $B E=C E$. Clearly, $\triangle A E B \equiv \triangle D O C$ and from that $A E \| D O$ and $B E \| C O$. Also, $\varangle A E B=\varangle C O D$ so $\varangle A O B+\varangle A E B=$ $\varangle A O B+\varangle C O D=180^{\circ}$. Thus, the quadrilateral $A O B E$ is cyclic.
So $\triangle A O B$ and $\triangle A E B$ the same circumcircle, therefor the circumcircles of the triangles $\triangle A O B$ and $\triangle C O D$ have the same radius.
Also, $A E \| D O$ and $A E=D O$ gives $A E O D$ is parallelogram and $\triangle A O D \equiv \triangle O A E$. So $\triangle A O B, \triangle C O D$ and $\triangle D O A$ has the same radius of their circumcircle (the radius of the cyclic quadrilateral $A E B O)$. Analogously, triangles $\triangle A O B, \triangle B O C, \triangle C O D$ and $\triangle D O A$ has same radius $R$.
Obviously, the circle with center $O$ and radius $2 R$ is externally tangent to each of these circles, so this will be the circle $k$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $O$ be a point inside the parallelogram $A B C D$ such that
$$
\angle A O B+\angle C O D=\angle B O C+\angle C O D
$$
Prove that there exists a circle $k$ tangent to the circumscribed circles of the triangles $\triangle A O B, \triangle B O C, \triangle C O D$ and $\triangle D O A$.

|
From given condition it is clear that $\varangle A O B+\varangle C O D=\varangle B O C+\varangle A O D=180^{\circ}$.
Let $E$ be a point such that $A E=D O$ and $B E=C E$. Clearly, $\triangle A E B \equiv \triangle D O C$ and from that $A E \| D O$ and $B E \| C O$. Also, $\varangle A E B=\varangle C O D$ so $\varangle A O B+\varangle A E B=$ $\varangle A O B+\varangle C O D=180^{\circ}$. Thus, the quadrilateral $A O B E$ is cyclic.
So $\triangle A O B$ and $\triangle A E B$ the same circumcircle, therefor the circumcircles of the triangles $\triangle A O B$ and $\triangle C O D$ have the same radius.
Also, $A E \| D O$ and $A E=D O$ gives $A E O D$ is parallelogram and $\triangle A O D \equiv \triangle O A E$. So $\triangle A O B, \triangle C O D$ and $\triangle D O A$ has the same radius of their circumcircle (the radius of the cyclic quadrilateral $A E B O)$. Analogously, triangles $\triangle A O B, \triangle B O C, \triangle C O D$ and $\triangle D O A$ has same radius $R$.
Obviously, the circle with center $O$ and radius $2 R$ is externally tangent to each of these circles, so this will be the circle $k$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nG9 ",
"solution_match": "## Solution"
}
|
5a9c5e5f-b3cf-5fee-b154-9a298c8a58be
| 604,920
|
Let $\Gamma$ be a circle of center $O$, and $\delta$ be a line in the plane of $\Gamma$, not intersecting it. Denote by $A$ the foot of the perpendicular from $O$ onto $\delta$, and let $M$ be a (variable) point on $\Gamma$. Denote by $\gamma$ the circle of diameter $A M$, by $X$ the (other than $M$ ) intersection point of $\gamma$ and $\Gamma$, and by $Y$ the (other than $A$ ) intersection point of $\gamma$ and $\delta$. Prove that the line $X Y$ passes through a fixed point.
|
Consider the line $\rho$ tangent to $\gamma$ at $A$, and take the points $\{K\}=A M \cap X Y,\{L\}=$ $\rho \cap X M$, and $\{F\}=O A \cap X Y$.
(Remark: Moving $M$ into its reflection with respect to the line $O A$ will move $X Y$ into its reflection with respect to $O A$. These old and the new $X Y$ meet on $O A$, hence it should be clear that the fixed point mult be $F$.)
Since $\varangle L M A=\varangle F Y A$ and $\varangle Y A F=\varangle L A M=90^{\circ}$, it follows that triangles $F A Y$ and $L A M$ are similar, therefore $\varangle A F Y=\varangle A L M$, hence the quadrilateral $A L X F$ is cyclic. But then $\varangle A F L=\varangle A X L=90^{\circ}$, so $L F \perp A F$, hence $L F \| \delta$.
Now, $\rho$ is the radical axis of circles $\gamma$ and $A$ (consider $A$ as a circle of center $A$ and radius 0 ), while $X M$ is the radical axis of circles $\gamma$ and $\Gamma$, so $L$ is the radical center of the three circle, which means that $L$ lies on the radical axis of circles $\Gamma$ and $A$. From $L F \perp O A$, where $O A$ is the line of the centers of the circles $A$ and $\Gamma$, and $F \in X Y$, it follows that $F$ is (the) fixed point of $X Y$.
(The degenerate two cases when $M \in O A$, where $X \equiv M$ and $Y \equiv A$, also trivially satisfy the conclusion, as then $F \in A M)$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma$ be a circle of center $O$, and $\delta$ be a line in the plane of $\Gamma$, not intersecting it. Denote by $A$ the foot of the perpendicular from $O$ onto $\delta$, and let $M$ be a (variable) point on $\Gamma$. Denote by $\gamma$ the circle of diameter $A M$, by $X$ the (other than $M$ ) intersection point of $\gamma$ and $\Gamma$, and by $Y$ the (other than $A$ ) intersection point of $\gamma$ and $\delta$. Prove that the line $X Y$ passes through a fixed point.
|
Consider the line $\rho$ tangent to $\gamma$ at $A$, and take the points $\{K\}=A M \cap X Y,\{L\}=$ $\rho \cap X M$, and $\{F\}=O A \cap X Y$.
(Remark: Moving $M$ into its reflection with respect to the line $O A$ will move $X Y$ into its reflection with respect to $O A$. These old and the new $X Y$ meet on $O A$, hence it should be clear that the fixed point mult be $F$.)
Since $\varangle L M A=\varangle F Y A$ and $\varangle Y A F=\varangle L A M=90^{\circ}$, it follows that triangles $F A Y$ and $L A M$ are similar, therefore $\varangle A F Y=\varangle A L M$, hence the quadrilateral $A L X F$ is cyclic. But then $\varangle A F L=\varangle A X L=90^{\circ}$, so $L F \perp A F$, hence $L F \| \delta$.
Now, $\rho$ is the radical axis of circles $\gamma$ and $A$ (consider $A$ as a circle of center $A$ and radius 0 ), while $X M$ is the radical axis of circles $\gamma$ and $\Gamma$, so $L$ is the radical center of the three circle, which means that $L$ lies on the radical axis of circles $\Gamma$ and $A$. From $L F \perp O A$, where $O A$ is the line of the centers of the circles $A$ and $\Gamma$, and $F \in X Y$, it follows that $F$ is (the) fixed point of $X Y$.
(The degenerate two cases when $M \in O A$, where $X \equiv M$ and $Y \equiv A$, also trivially satisfy the conclusion, as then $F \in A M)$.

|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nG10 ",
"solution_match": "## Solution"
}
|
82ec2368-d119-523e-87cb-e5217c1ce27e
| 604,931
|
Consider $A B C$ an acute-angled triangle with $A B \neq A C$. Denote by $M$ the midpoint of $B C$, by $D, E$ the feet of the altitudes from $B, C$ respectively and let $P$ be the intersection point of the lines $D E$ and $B C$. The perpendicular from $M$ to $A C$ meets the perpendicular from $C$ to $B C$ at point $R$. Prove that lines $P R$ and $A M$ are perpendicular.
|
Let $F$ be the foot of the altitude from $A$ and let $S$ be the intersection point of $A M$ and $R C$. As $P C$ is an altitude of the triangle $P R S$, the claim is equivalent to $R M \perp P S$, since the latter implies that $M$ is the orthocenter of $P R S$. Due to $R M \perp A C$, we need to prove that $A C \| P S$, in other words
$$
\frac{M C}{M P}=\frac{M A}{M S}
$$
Notice that $A F \| C S$, so $\frac{M A}{M S}=\frac{M F}{M C}$. Now the claim is reduced to proving $M C^{2}=$ $M F \cdot M P$, a well-known result considering that $A F$ is the polar line of $P$ with respect to circle of radius $M C$ centered at $M$.
The "elementary proof" on the latter result may be obtained as follows: $\frac{P B}{P C}=\frac{F B}{F C}$, using, for instance, Menelaus and Ceva theorems with respect to $A B C$. Cross-multiplying one gets $(P M-x)(F M+x)=(x-F M)(P M+x)$
- $x$ stands for the length of $M C$ - and then $P M \cdot F M=x^{2}$.
Comment. The proof above holds for both cases $A B<A C$ and $A B>A C$; it is for the committee to decide if a contestant is supposed to (even) mention this.
### 2.4 Number Theory
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider $A B C$ an acute-angled triangle with $A B \neq A C$. Denote by $M$ the midpoint of $B C$, by $D, E$ the feet of the altitudes from $B, C$ respectively and let $P$ be the intersection point of the lines $D E$ and $B C$. The perpendicular from $M$ to $A C$ meets the perpendicular from $C$ to $B C$ at point $R$. Prove that lines $P R$ and $A M$ are perpendicular.
|
Let $F$ be the foot of the altitude from $A$ and let $S$ be the intersection point of $A M$ and $R C$. As $P C$ is an altitude of the triangle $P R S$, the claim is equivalent to $R M \perp P S$, since the latter implies that $M$ is the orthocenter of $P R S$. Due to $R M \perp A C$, we need to prove that $A C \| P S$, in other words
$$
\frac{M C}{M P}=\frac{M A}{M S}
$$
Notice that $A F \| C S$, so $\frac{M A}{M S}=\frac{M F}{M C}$. Now the claim is reduced to proving $M C^{2}=$ $M F \cdot M P$, a well-known result considering that $A F$ is the polar line of $P$ with respect to circle of radius $M C$ centered at $M$.
The "elementary proof" on the latter result may be obtained as follows: $\frac{P B}{P C}=\frac{F B}{F C}$, using, for instance, Menelaus and Ceva theorems with respect to $A B C$. Cross-multiplying one gets $(P M-x)(F M+x)=(x-F M)(P M+x)$
- $x$ stands for the length of $M C$ - and then $P M \cdot F M=x^{2}$.

Comment. The proof above holds for both cases $A B<A C$ and $A B>A C$; it is for the committee to decide if a contestant is supposed to (even) mention this.
### 2.4 Number Theory
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nG11 ",
"solution_match": "\nSolution"
}
|
47d90b39-8b49-5918-a4ef-b5fab082e719
| 604,944
|
Let $n \geq 2$ be a fixed positive integer. An integer will be called " $n$-free" if it is not a multiple of an $n$-th power of a prime. Let $M$ be an infinite set of rational numbers, such that the product of every $n$ elements of $M$ is an $n$-free integer. Prove that $M$ contains only integers.
|
We first prove that $M$ can contain only a finite number of non-integers. Suppose that there are infinitely many of them: $\frac{p_{1}}{q_{1}}, \frac{p_{2}}{q_{2}}, \ldots, \frac{p_{k}}{q_{k}}, \ldots$, with $\left(p_{k}, q_{k}\right)=1$ and $q_{k}>1$ for each $k$. Let $\frac{p}{q}=\frac{p_{1} p_{2} \ldots p_{n-1}}{q_{1} q_{2} \ldots q_{n-1}}$, where $(p, q)=1$. For each $i \geq n$, the number $\frac{p}{q} \cdot \frac{p_{i}}{q_{i}}$ is an integer, so $q_{i}$ is a divisor of $p$ (as $q_{i}$ and $p_{i}$ are coprime). But $p$ has a finite set of divisors, so there are $n$ numbers of $M$ with equal denominators. Their product cannot be an integer, a contradiction.
Now suppose that $M$ contains a fraction $\frac{a}{b}$ in lowest terms with $b>1$. Take a prime divisor $p$ of $b$. If we take any $n-1$ integers from $M$, their product with $\frac{a}{b}$ is an integer, so some of them is a multiple of $p$. Therefore there are infinitely many multiples of $p$ in $M$, and the product of $n$ of them is not $n$-free, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n \geq 2$ be a fixed positive integer. An integer will be called " $n$-free" if it is not a multiple of an $n$-th power of a prime. Let $M$ be an infinite set of rational numbers, such that the product of every $n$ elements of $M$ is an $n$-free integer. Prove that $M$ contains only integers.
|
We first prove that $M$ can contain only a finite number of non-integers. Suppose that there are infinitely many of them: $\frac{p_{1}}{q_{1}}, \frac{p_{2}}{q_{2}}, \ldots, \frac{p_{k}}{q_{k}}, \ldots$, with $\left(p_{k}, q_{k}\right)=1$ and $q_{k}>1$ for each $k$. Let $\frac{p}{q}=\frac{p_{1} p_{2} \ldots p_{n-1}}{q_{1} q_{2} \ldots q_{n-1}}$, where $(p, q)=1$. For each $i \geq n$, the number $\frac{p}{q} \cdot \frac{p_{i}}{q_{i}}$ is an integer, so $q_{i}$ is a divisor of $p$ (as $q_{i}$ and $p_{i}$ are coprime). But $p$ has a finite set of divisors, so there are $n$ numbers of $M$ with equal denominators. Their product cannot be an integer, a contradiction.
Now suppose that $M$ contains a fraction $\frac{a}{b}$ in lowest terms with $b>1$. Take a prime divisor $p$ of $b$. If we take any $n-1$ integers from $M$, their product with $\frac{a}{b}$ is an integer, so some of them is a multiple of $p$. Therefore there are infinitely many multiples of $p$ in $M$, and the product of $n$ of them is not $n$-free, a contradiction.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nNT2 ",
"solution_match": "## Solution"
}
|
0366ee18-9e22-5c3e-85c6-bec6c06e7408
| 604,966
|
Prove that $2^{n}+3^{n}$ is not a perfect cube for any positive integer $n$.
|
If $n=1$ then $2^{1}+3^{1}=5$ is not perfect cube.
Perfect cube gives residues $-1,0$ and 1 modulo 9 . If $2^{n}+3^{n}$ is a perfect cube, then $n$ must be divisible with 3 (congruence $2^{n}+3^{n}=x^{3}$ modulo 9 ).
If $n=3 k$ then $2^{3 k}+3^{2 k}>\left(3^{k}\right)^{3}$. Also, $\left(3^{k}+1\right)^{3}=3^{3 k}+3 \cdot 3^{2 k}+3 \cdot 3^{k}+1>3^{3 k}+3^{2 k}=$ $3^{3 k}+9^{k}>3^{3 k}+8^{k}=3^{3 k}+2^{3 k}$. But, $3^{k}$ and $3^{k}+1$ are two consecutive integers so $2^{3 k}+3^{3 k}$ is not a perfect cube.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that $2^{n}+3^{n}$ is not a perfect cube for any positive integer $n$.
|
If $n=1$ then $2^{1}+3^{1}=5$ is not perfect cube.
Perfect cube gives residues $-1,0$ and 1 modulo 9 . If $2^{n}+3^{n}$ is a perfect cube, then $n$ must be divisible with 3 (congruence $2^{n}+3^{n}=x^{3}$ modulo 9 ).
If $n=3 k$ then $2^{3 k}+3^{2 k}>\left(3^{k}\right)^{3}$. Also, $\left(3^{k}+1\right)^{3}=3^{3 k}+3 \cdot 3^{2 k}+3 \cdot 3^{k}+1>3^{3 k}+3^{2 k}=$ $3^{3 k}+9^{k}>3^{3 k}+8^{k}=3^{3 k}+2^{3 k}$. But, $3^{k}$ and $3^{k}+1$ are two consecutive integers so $2^{3 k}+3^{3 k}$ is not a perfect cube.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nNT10 ",
"solution_match": "## Solution"
}
|
04f3d032-d13d-5519-89b9-3467ac868fb5
| 605,043
|
Real numbers $x, y, z$ satisfy
$$
0<x, y, z<1
$$
and
$$
x y z=(1-x)(1-y)(1-z) .
$$
Show that
$$
\frac{1}{4} \leq \max \{(1-x) y,(1-y) z,(1-z) x\}
$$
|
It is clear that $a(1-a) \leq \frac{1}{4}$ for any real numbers $a$ (equivalent to $0<(2 a-1)^{2}$ ). Thus,
$$
\begin{gathered}
x y z=(1-x)(1-y)(1-z) \\
(x y z)^{2}=[x(1-x)][y(1-y)][z(1-z)] \leq \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4}=\frac{1}{4^{3}} \\
x y z \leq \frac{1}{2^{3}}
\end{gathered}
$$
It implies that at least one of $x, y, z$ is at less or equal to $\frac{1}{2}$. Let us say that $x \leq \frac{1}{2}$, and notice that $1-x \geq \frac{1}{2}$.
Assume contrary to required result, that we have
$$
\frac{1}{4}>\max \{(1-x) y,(1-y) x,(1-z) x\}
$$
Now
$$
(1-x) y<\frac{1}{4}, \quad(1-y) z<\frac{1}{4}, \quad(1-z) x<\frac{1}{4}
$$
From here we deduce:
$$
y<\frac{1}{4} \cdot \frac{1}{1-x} \leq \frac{1}{4} \cdot 2=\frac{1}{2}
$$
Notice that $1-y>\frac{1}{2}$.
Using same reasoning we conclude:
$$
z<\frac{1}{2}, \quad 1-z>\frac{1}{2}
$$
Using these facts we derive:
$$
\frac{1}{8}=\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2}>x y z=(1-x)(1-y)(1-z)>\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2}=\frac{1}{8}
$$
Contradiction!
Remark: The exercise along with its proof generalizes for any given (finite) number of numbers, and you can consider this new form in place of the proposed one:
Exercise: If for the real numbers $x_{1}, x_{2}, \ldots, x_{n}, 0<x_{i}<1$, for all indices $i$, and
$$
x_{1} x_{2} \ldots x_{n}=\left(1-x_{1}\right)\left(1-x_{2}\right) \ldots\left(1-x_{n}\right)
$$
show that
$$
\frac{1}{4} \leq \max _{1 \leq i \leq n}\left(1-x_{i}\right) x_{i+1}
$$
(where $x_{n+1}=x_{1}$ ).
Or you can consider the following variation:
Exercise: If for the real numbers $x_{1}, x_{2}, \ldots, x_{2009}, 0<x_{i}<1$, for all indices $i$, and
$$
x_{1} x_{2} \ldots x_{2009}=\left(1-x_{1}\right)\left(1-x_{2}\right) \ldots\left(1-x_{2009}\right)
$$
show that
$$
\frac{1}{4} \leq \max _{1 \leq i \leq 2009}\left(1-x_{i}\right) x_{i+1}
$$
(where $x_{2010}=x_{1}$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Real numbers $x, y, z$ satisfy
$$
0<x, y, z<1
$$
and
$$
x y z=(1-x)(1-y)(1-z) .
$$
Show that
$$
\frac{1}{4} \leq \max \{(1-x) y,(1-y) z,(1-z) x\}
$$
|
It is clear that $a(1-a) \leq \frac{1}{4}$ for any real numbers $a$ (equivalent to $0<(2 a-1)^{2}$ ). Thus,
$$
\begin{gathered}
x y z=(1-x)(1-y)(1-z) \\
(x y z)^{2}=[x(1-x)][y(1-y)][z(1-z)] \leq \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4}=\frac{1}{4^{3}} \\
x y z \leq \frac{1}{2^{3}}
\end{gathered}
$$
It implies that at least one of $x, y, z$ is at less or equal to $\frac{1}{2}$. Let us say that $x \leq \frac{1}{2}$, and notice that $1-x \geq \frac{1}{2}$.
Assume contrary to required result, that we have
$$
\frac{1}{4}>\max \{(1-x) y,(1-y) x,(1-z) x\}
$$
Now
$$
(1-x) y<\frac{1}{4}, \quad(1-y) z<\frac{1}{4}, \quad(1-z) x<\frac{1}{4}
$$
From here we deduce:
$$
y<\frac{1}{4} \cdot \frac{1}{1-x} \leq \frac{1}{4} \cdot 2=\frac{1}{2}
$$
Notice that $1-y>\frac{1}{2}$.
Using same reasoning we conclude:
$$
z<\frac{1}{2}, \quad 1-z>\frac{1}{2}
$$
Using these facts we derive:
$$
\frac{1}{8}=\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2}>x y z=(1-x)(1-y)(1-z)>\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2}=\frac{1}{8}
$$
Contradiction!
Remark: The exercise along with its proof generalizes for any given (finite) number of numbers, and you can consider this new form in place of the proposed one:
Exercise: If for the real numbers $x_{1}, x_{2}, \ldots, x_{n}, 0<x_{i}<1$, for all indices $i$, and
$$
x_{1} x_{2} \ldots x_{n}=\left(1-x_{1}\right)\left(1-x_{2}\right) \ldots\left(1-x_{n}\right)
$$
show that
$$
\frac{1}{4} \leq \max _{1 \leq i \leq n}\left(1-x_{i}\right) x_{i+1}
$$
(where $x_{n+1}=x_{1}$ ).
Or you can consider the following variation:
Exercise: If for the real numbers $x_{1}, x_{2}, \ldots, x_{2009}, 0<x_{i}<1$, for all indices $i$, and
$$
x_{1} x_{2} \ldots x_{2009}=\left(1-x_{1}\right)\left(1-x_{2}\right) \ldots\left(1-x_{2009}\right)
$$
show that
$$
\frac{1}{4} \leq \max _{1 \leq i \leq 2009}\left(1-x_{i}\right) x_{i+1}
$$
(where $x_{2010}=x_{1}$ ).
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2009_shl.jsonl",
"problem_match": "\nA4 ",
"solution_match": "\nSolution:"
}
|
db84b241-1f1e-5a2c-a467-0431500c42cb
| 605,121
|
Let $x, y, z$ be positive real numbers. Prove that:
$$
\left(x^{2}+y+1\right)\left(x^{2}+z+1\right)\left(y^{2}+z+1\right)\left(y^{2}+x+1\right)\left(z^{2}+x+1\right)\left(z^{2}+y+1\right) \geq(x+y+z)^{6}
$$
|
I: Applying Cauchy-Schwarz's inequality:
$$
\left(x^{2}+y+1\right)\left(z^{2}+y+1\right)=\left(x^{2}+y+1\right)\left(1+y+z^{2}\right) \geq(x+y+z)^{2}
$$
Using the same reasoning we deduce:
$$
\left(x^{2}+z+1\right)\left(y^{2}+z+1\right) \geq(x+y+z)^{2}
$$
and
$$
\left(y^{2}+x+1\right)\left(z^{2}+x+1\right) \geq(x+y+z)^{2}
$$
Multiplying these three inequalities we get the desired result.
Solution II: We have
$$
\begin{gathered}
\left(x^{2}+y+1\right)\left(z^{2}+y+1\right) \geq(x+y+z)^{2} \Leftrightarrow \\
x^{2} z^{2}+x^{2} y+x^{2}+y z^{2}+y^{2}+y+z^{2}+y+1 \geq x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x \Leftrightarrow \\
\left(x^{2} z^{2}-2 z x+1\right)+\left(x^{2} y-2 x y+y\right)+\left(y z^{2}-2 y z+y\right) \geq 0 \Leftrightarrow \\
(x z-1)^{2}+y(x-1)^{2}+y(z-1)^{2} \geq 0
\end{gathered}
$$
which is correct.
Using the same reasoning we get:
$$
\begin{aligned}
& \left(x^{2}+z+1\right)\left(y^{2}+z+1\right) \geq(x+y+z)^{2} \\
& \left(y^{2}+x+1\right)\left(z^{2}+x+1\right) \geq(x+y+z)^{2}
\end{aligned}
$$
Multiplying these three inequalities we get the desired result. Equality is attained at $x=y=z=1$.
### 2.2 Combinatorics
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y, z$ be positive real numbers. Prove that:
$$
\left(x^{2}+y+1\right)\left(x^{2}+z+1\right)\left(y^{2}+z+1\right)\left(y^{2}+x+1\right)\left(z^{2}+x+1\right)\left(z^{2}+y+1\right) \geq(x+y+z)^{6}
$$
|
I: Applying Cauchy-Schwarz's inequality:
$$
\left(x^{2}+y+1\right)\left(z^{2}+y+1\right)=\left(x^{2}+y+1\right)\left(1+y+z^{2}\right) \geq(x+y+z)^{2}
$$
Using the same reasoning we deduce:
$$
\left(x^{2}+z+1\right)\left(y^{2}+z+1\right) \geq(x+y+z)^{2}
$$
and
$$
\left(y^{2}+x+1\right)\left(z^{2}+x+1\right) \geq(x+y+z)^{2}
$$
Multiplying these three inequalities we get the desired result.
Solution II: We have
$$
\begin{gathered}
\left(x^{2}+y+1\right)\left(z^{2}+y+1\right) \geq(x+y+z)^{2} \Leftrightarrow \\
x^{2} z^{2}+x^{2} y+x^{2}+y z^{2}+y^{2}+y+z^{2}+y+1 \geq x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x \Leftrightarrow \\
\left(x^{2} z^{2}-2 z x+1\right)+\left(x^{2} y-2 x y+y\right)+\left(y z^{2}-2 y z+y\right) \geq 0 \Leftrightarrow \\
(x z-1)^{2}+y(x-1)^{2}+y(z-1)^{2} \geq 0
\end{gathered}
$$
which is correct.
Using the same reasoning we get:
$$
\begin{aligned}
& \left(x^{2}+z+1\right)\left(y^{2}+z+1\right) \geq(x+y+z)^{2} \\
& \left(y^{2}+x+1\right)\left(z^{2}+x+1\right) \geq(x+y+z)^{2}
\end{aligned}
$$
Multiplying these three inequalities we get the desired result. Equality is attained at $x=y=z=1$.
### 2.2 Combinatorics
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2009_shl.jsonl",
"problem_match": "\nA5 ",
"solution_match": "\nSolution "
}
|
cce5756e-4cc1-592a-81c7-04083dce4abc
| 605,129
|
Let $A B C D$ be a parallelogram with $A C>B D$, and let $O$ be the point of intersection of $A C$ and $B D$. The circle with center at $O$ and radius $O A$ intersects the extensions of $A D$ and $A B$ at points $G$ and $L$, respectively. Let $Z$ be intersection point of lines $B D$ and $G L$. Prove that $\angle Z C A=90^{\circ}$.
|
From the point $L$ we draw a parallel line to $B D$ that intersects lines $A C$ and $A G$ at points $N$ and $R$ respectively. Since $D O=O B$, we have that $N R=N L$, and point $N$ is the midpoint of segment $L R$.
Let $K$ be the midpoint of $G L$. Now, $N K \| R G$, and
$$
\angle A G L=\angle N K L=\angle A C L
$$
Therefore, from the cyclic quadrilateral $N K C L$ we deduce:
$$
\angle K C N=\angle K L N
$$
Now, since $L R \| D Z$, we have
$$
\angle K L N=\angle K Z O
$$
It implies that quadrilateral $O K C Z$ is cyclic, and
$$
\angle O K Z=\angle O C Z
$$
Since $O K \perp G L$, we derive that $\angle Z C A=90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram with $A C>B D$, and let $O$ be the point of intersection of $A C$ and $B D$. The circle with center at $O$ and radius $O A$ intersects the extensions of $A D$ and $A B$ at points $G$ and $L$, respectively. Let $Z$ be intersection point of lines $B D$ and $G L$. Prove that $\angle Z C A=90^{\circ}$.
|
From the point $L$ we draw a parallel line to $B D$ that intersects lines $A C$ and $A G$ at points $N$ and $R$ respectively. Since $D O=O B$, we have that $N R=N L$, and point $N$ is the midpoint of segment $L R$.
Let $K$ be the midpoint of $G L$. Now, $N K \| R G$, and
$$
\angle A G L=\angle N K L=\angle A C L
$$
Therefore, from the cyclic quadrilateral $N K C L$ we deduce:
$$
\angle K C N=\angle K L N
$$
Now, since $L R \| D Z$, we have
$$
\angle K L N=\angle K Z O
$$

It implies that quadrilateral $O K C Z$ is cyclic, and
$$
\angle O K Z=\angle O C Z
$$
Since $O K \perp G L$, we derive that $\angle Z C A=90^{\circ}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2009_shl.jsonl",
"problem_match": "\nG1 ",
"solution_match": "## Solution:"
}
|
9ab12718-8a9b-51e1-ae62-13da832842be
| 605,183
|
A parallelogram $A B C D$ with obtuse angle $\angle A B C$ is given. After rotating the triangle $A C D$ around the vertex $C$, we get a triangle $C D^{\prime} A^{\prime}$, such that points $B, C$ and $D^{\prime}$ are collinear. The extension of the median of triangle $C D^{\prime} A^{\prime}$ that passes through $D^{\prime}$ intersects the straight line $B D$ at point $P$. Prove that $P C$ is the bisector of the angle $\angle B P D^{\prime}$.
|
Let $A C \cap B D=\{X\}$ and $P D^{\prime} \cap C A^{\prime}=\{Y\}$. Because $A X=C X$ and $C Y=Y A^{\prime}$, we deduce:
$$
\triangle A B C \cong \triangle C D A \cong \triangle C D^{\prime} A^{\prime} \Rightarrow \triangle A B X \cong \triangle C D^{\prime} Y, \triangle B C X \cong \triangle D^{\prime} A^{\prime} Y
$$
It follows that
$$
\angle A B X=\angle C D^{\prime} Y
$$
Let $M$ and $N$ be orthogonal projections of the point $C$ on the straight lines $P D^{\prime}$ and $B P$, respectively, and $Q$ is the orthogonal projection of the point $A$ on the straight line $B P$. Because $C D^{\prime}=A B$, we have that $\triangle A B Q \cong \triangle C D^{\prime} M$.
We conclude that $C M=A Q$. But, $A X=C X$ and $\triangle A Q X \cong \triangle C N X$. So, $C M=C N$ and $P C$ is the bisector of the angle $\angle B P D^{\prime}$.
Much shortened: $\triangle C D^{\prime} Y \equiv \triangle C D X$ means their altitudes from $C$ are also equal, i.e. $C M=C N$ and the conclusion.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A parallelogram $A B C D$ with obtuse angle $\angle A B C$ is given. After rotating the triangle $A C D$ around the vertex $C$, we get a triangle $C D^{\prime} A^{\prime}$, such that points $B, C$ and $D^{\prime}$ are collinear. The extension of the median of triangle $C D^{\prime} A^{\prime}$ that passes through $D^{\prime}$ intersects the straight line $B D$ at point $P$. Prove that $P C$ is the bisector of the angle $\angle B P D^{\prime}$.
|
Let $A C \cap B D=\{X\}$ and $P D^{\prime} \cap C A^{\prime}=\{Y\}$. Because $A X=C X$ and $C Y=Y A^{\prime}$, we deduce:
$$
\triangle A B C \cong \triangle C D A \cong \triangle C D^{\prime} A^{\prime} \Rightarrow \triangle A B X \cong \triangle C D^{\prime} Y, \triangle B C X \cong \triangle D^{\prime} A^{\prime} Y
$$
It follows that
$$
\angle A B X=\angle C D^{\prime} Y
$$
Let $M$ and $N$ be orthogonal projections of the point $C$ on the straight lines $P D^{\prime}$ and $B P$, respectively, and $Q$ is the orthogonal projection of the point $A$ on the straight line $B P$. Because $C D^{\prime}=A B$, we have that $\triangle A B Q \cong \triangle C D^{\prime} M$.
We conclude that $C M=A Q$. But, $A X=C X$ and $\triangle A Q X \cong \triangle C N X$. So, $C M=C N$ and $P C$ is the bisector of the angle $\angle B P D^{\prime}$.

Much shortened: $\triangle C D^{\prime} Y \equiv \triangle C D X$ means their altitudes from $C$ are also equal, i.e. $C M=C N$ and the conclusion.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2009_shl.jsonl",
"problem_match": "\nG3 ",
"solution_match": "\nSolution:"
}
|
60e87e7b-e82b-5400-b738-fa1aafb6f77e
| 605,205
|
Let $A B C D E$ be a convex pentagon such that $A B+C D=B C+D E$ and let $k$ be a semicircle with center on side $A E$ that touches the sides $A B, B C, C D$ and $D E$ of the pentagon, respectively, at points $P, Q, R$ and $S$ (different from the vertices of the pentagon). Prove that $P S \| A E$.
|
Let $O$ be center of $k$. We deduce that $B P=B Q, C Q=C R, D R=D S$, since those are tangents to the circle $k$. Using the condition $A B+C D=B C+D E$, we derive:
$$
A P+B P+C R+D R=B Q+C Q+D S+E S
$$
From here we have $A P=E S$.
Thus,
$$
\triangle A P O \cong \triangle E S O\left(A P=E S, \angle A P O=\angle E S O=90^{\circ}, P O=S O\right)
$$
This implies
$$
\angle O P S=\angle O S P
$$
Therefore,
$$
\angle A P S=\angle A P O+\angle O P S=90^{\circ}+\angle O P S=90^{\circ}+\angle O S P=\angle P S E
$$
Now, from quadrilateral $A P S E$ we deduce:
$$
2 \angle E A P+2 \angle A P S=\angle E A P+\angle A P S+\angle P S E+\angle S E A=360^{\circ}
$$
So,
$$
\angle E A P+\angle A P S=180^{\circ}
$$
and $A P S E$ is isosceles trapezoid. Therefore, $A E \| P S$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E$ be a convex pentagon such that $A B+C D=B C+D E$ and let $k$ be a semicircle with center on side $A E$ that touches the sides $A B, B C, C D$ and $D E$ of the pentagon, respectively, at points $P, Q, R$ and $S$ (different from the vertices of the pentagon). Prove that $P S \| A E$.
|
Let $O$ be center of $k$. We deduce that $B P=B Q, C Q=C R, D R=D S$, since those are tangents to the circle $k$. Using the condition $A B+C D=B C+D E$, we derive:
$$
A P+B P+C R+D R=B Q+C Q+D S+E S
$$
From here we have $A P=E S$.
Thus,
$$
\triangle A P O \cong \triangle E S O\left(A P=E S, \angle A P O=\angle E S O=90^{\circ}, P O=S O\right)
$$
This implies
$$
\angle O P S=\angle O S P
$$
Therefore,
$$
\angle A P S=\angle A P O+\angle O P S=90^{\circ}+\angle O P S=90^{\circ}+\angle O S P=\angle P S E
$$
Now, from quadrilateral $A P S E$ we deduce:
$$
2 \angle E A P+2 \angle A P S=\angle E A P+\angle A P S+\angle P S E+\angle S E A=360^{\circ}
$$
So,
$$
\angle E A P+\angle A P S=180^{\circ}
$$
and $A P S E$ is isosceles trapezoid. Therefore, $A E \| P S$.

|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2009_shl.jsonl",
"problem_match": "\nG4 ",
"solution_match": "\nSolution:"
}
|
d3be572c-3aa7-52a9-ab73-f144a5d5a844
| 605,218
|
Let $A, B, C$ and $O$ be four points in the plane, such that $\angle A B C>90^{\circ}$ and $O A=$ $O B=O C$. Define the point $D \in A B$ and the line $\ell$ such that $D \in \ell, A C \perp D C$ and $\ell \perp A O$. Line $\ell$ cuts $A C$ at $E$ and the circumcircle of $\triangle A B C$ at $F$. Prove that the circumcircles of triangles $B E F$ and $C F D$ are tangent at $F$.
|
Let $\ell \cap A C=\{K\}$ and define $G$ to be the mirror image of the point $A$ with respect to $O$. Then $A G$ is a diameter of the circumcircle of the triangle $A B C$, therefore $A C \perp C G$. On the other hand we have $A C \perp D C$, and it implies that points $D, C, G$ are collinear.
Moreover, as $A E \perp D G$ and $D E \perp A G$, we obtain that $E$ is the orthocenter of triangle $A D G$ and $G E \perp A D$. As $A G$ is a diameter, we have $A B \perp B G$, and since $A D \perp G E$, the points $E, G$, and $B$ are collinear.
Notice that
$$
\angle C A G=90^{\circ}-\angle A G C=\angle K D C
$$
and
$$
\angle C A G=\angle G F C
$$
since both subtend the same arc.
Hence,
$$
\angle F D G=\angle G F C
$$
Therefore, $G F$ is tangent to the circumcircle of the triangle $C D F$ at point $F$.
We claim that line $G F$ is also tangent to the circumcircle of triangle $B E F$ at point $F$, which concludes the proof.
The claim is equivalent to $\angle G B F=\angle E F G$. Denote by $F^{\prime}$ the second intersection point - other than $F$ - of line $\ell$ with the circumcircle of triangle $A B C$. Observe that $\angle G B F=\angle G F^{\prime} F$, because both angles subtend the same arc, and $\angle F F^{\prime} G=\angle E F G$, since $A G$ is the perpendicular bisector of the chord $F F^{\prime}$, and we are done.
### 2.4 Number Theory
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A, B, C$ and $O$ be four points in the plane, such that $\angle A B C>90^{\circ}$ and $O A=$ $O B=O C$. Define the point $D \in A B$ and the line $\ell$ such that $D \in \ell, A C \perp D C$ and $\ell \perp A O$. Line $\ell$ cuts $A C$ at $E$ and the circumcircle of $\triangle A B C$ at $F$. Prove that the circumcircles of triangles $B E F$ and $C F D$ are tangent at $F$.
|
Let $\ell \cap A C=\{K\}$ and define $G$ to be the mirror image of the point $A$ with respect to $O$. Then $A G$ is a diameter of the circumcircle of the triangle $A B C$, therefore $A C \perp C G$. On the other hand we have $A C \perp D C$, and it implies that points $D, C, G$ are collinear.
Moreover, as $A E \perp D G$ and $D E \perp A G$, we obtain that $E$ is the orthocenter of triangle $A D G$ and $G E \perp A D$. As $A G$ is a diameter, we have $A B \perp B G$, and since $A D \perp G E$, the points $E, G$, and $B$ are collinear.

Notice that
$$
\angle C A G=90^{\circ}-\angle A G C=\angle K D C
$$
and
$$
\angle C A G=\angle G F C
$$
since both subtend the same arc.
Hence,
$$
\angle F D G=\angle G F C
$$
Therefore, $G F$ is tangent to the circumcircle of the triangle $C D F$ at point $F$.
We claim that line $G F$ is also tangent to the circumcircle of triangle $B E F$ at point $F$, which concludes the proof.
The claim is equivalent to $\angle G B F=\angle E F G$. Denote by $F^{\prime}$ the second intersection point - other than $F$ - of line $\ell$ with the circumcircle of triangle $A B C$. Observe that $\angle G B F=\angle G F^{\prime} F$, because both angles subtend the same arc, and $\angle F F^{\prime} G=\angle E F G$, since $A G$ is the perpendicular bisector of the chord $F F^{\prime}$, and we are done.
### 2.4 Number Theory
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2009_shl.jsonl",
"problem_match": "\nG5 ",
"solution_match": "\nSolution:"
}
|
538d7668-c9e4-5ea3-9418-20161e3efb2a
| 605,231
|
The real numbers $a, b, c, d$ satisfy simultaneously the equations
$$
a b c-d=1, b c d-a=2, c d a-b=3, d a b-c=-6
$$
Prove that $a+b+c+d \neq 0$.
|
Suppose that $a+b+c+d=0$. Then
$$
a b c+b c d+c d a+d a b=0
$$
If $a b c d=0$, then one of numbers, say $d$, must be 0 . In this case $a b c=0$, and so at least two of the numbers $a, b, c, d$ will be equal to 0 , making one of the given equations impossible. Hence $a b c d \neq 0$ and, from (1),
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}=0
$$
implying
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}
$$
It follows that $(a+b)(b+c)(c+a)=0$, which is impossible (for instance, if $a+b=0$, then adding the second and third given equations would lead to $0=2+3$, a contradiction). Thus $a+b+c+d \neq 0$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
The real numbers $a, b, c, d$ satisfy simultaneously the equations
$$
a b c-d=1, b c d-a=2, c d a-b=3, d a b-c=-6
$$
Prove that $a+b+c+d \neq 0$.
|
Suppose that $a+b+c+d=0$. Then
$$
a b c+b c d+c d a+d a b=0
$$
If $a b c d=0$, then one of numbers, say $d$, must be 0 . In this case $a b c=0$, and so at least two of the numbers $a, b, c, d$ will be equal to 0 , making one of the given equations impossible. Hence $a b c d \neq 0$ and, from (1),
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}=0
$$
implying
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}
$$
It follows that $(a+b)(b+c)(c+a)=0$, which is impossible (for instance, if $a+b=0$, then adding the second and third given equations would lead to $0=2+3$, a contradiction). Thus $a+b+c+d \neq 0$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2010_shl.jsonl",
"problem_match": "\nProblem A1.",
"solution_match": "\nSolution."
}
|
e8903db6-68a8-5b57-85da-352997aeda4f
| 605,287
|
Let $a, b, c$ be positive real numbers such that $a b c(a+b+c)=3$. Prove the inequality
$$
(a+b)(b+c)(c+a) \geq 8
$$
and determine all cases when equality holds.
|
We have
$A=(a+b)(b+c)(c+a)=\left(a b+a c+b^{2}+b c\right)(c+a)=(b(a+b+c)+a c)(c+a)$,
so by the given condition
$$
A=\left(\frac{3}{a c}+a c\right)(c+a)=\left(\frac{1}{a c}+\frac{1}{a c}+\frac{1}{a c}+a c\right)(c+a)
$$
Aplying the AM-GM inequality for four and two terms respectively, we get
$$
A \geq 4 \sqrt[4]{\frac{a c}{(a c)^{3}}} \cdot 2 \sqrt{a c}=8
$$
From the last part, it is easy to see that inequality holds when $a=c$ and $\frac{1}{a c}=a c$, i.e. $a=b=c=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c(a+b+c)=3$. Prove the inequality
$$
(a+b)(b+c)(c+a) \geq 8
$$
and determine all cases when equality holds.
|
We have
$A=(a+b)(b+c)(c+a)=\left(a b+a c+b^{2}+b c\right)(c+a)=(b(a+b+c)+a c)(c+a)$,
so by the given condition
$$
A=\left(\frac{3}{a c}+a c\right)(c+a)=\left(\frac{1}{a c}+\frac{1}{a c}+\frac{1}{a c}+a c\right)(c+a)
$$
Aplying the AM-GM inequality for four and two terms respectively, we get
$$
A \geq 4 \sqrt[4]{\frac{a c}{(a c)^{3}}} \cdot 2 \sqrt{a c}=8
$$
From the last part, it is easy to see that inequality holds when $a=c$ and $\frac{1}{a c}=a c$, i.e. $a=b=c=1$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2010_shl.jsonl",
"problem_match": "\nProblem A4.",
"solution_match": "\nSolution."
}
|
16c711f3-a21d-5db9-b8ff-e76d9c63e89a
| 605,320
|
The real positive numbers $x, y, z$ satisfy the relations $x \leq 2$, $y \leq 3, x+y+z=11$. Prove that $\sqrt{x y z} \leq 6$.
|
For $x=2, y=3$ and $z=6$ the equality holds.
After the substitutions $x=2-u, y=3-v$ with $u \in[0,2), v \in[0,3)$, we obtain that $z=6+u+v$ and the required inequality becomes
$$
(2-u)(3-v)(6+u+v) \leqslant 36
$$
We shall need the following lemma.
Lemma. If real numbers $a$ and $b$ satisfy the relations $0<b \leq a$, then for every real number $y \in[0, b)$ the inequality
$$
\frac{a}{a+y} \geqslant \frac{b-y}{b}
$$
holds.
Proof of the lemma. The inequality (2) is equivalent to
$$
a b \geq a b-a y+b y-y^{2} \Leftrightarrow y^{2}+(a-b) y \geq 0
$$
The last inequality is true, because $a \geq b>0$ and $y \geq 0$.
The equality in (2) holds if $y=0$. The lemma is proved.
By using the lemma we can write the following inequalities:
$$
\begin{gathered}
\frac{6}{6+u} \geqslant \frac{2-u}{2} \\
\frac{6}{6+v} \geqslant \frac{3-v}{3} \\
\frac{6+u}{6+u+v} \geqslant \frac{6}{6+v}
\end{gathered}
$$
By multiplying the inequalities (3), (4) and (5) we obtain:
$$
\begin{gathered}
\frac{6 \cdot 6 \cdot(6+u)}{(6+u)(6+v)(6+u+v)} \geqslant \frac{6(2-u)(3-v)}{2 \cdot 3(6+v)} \Leftrightarrow \\
(2-u)(3-v)(6+u+v) \leqslant 2 \cdot 3 \cdot 6=36 \Leftrightarrow \quad(1)
\end{gathered}
$$
By virtue of lemma, the equality holds if and only if $u=v=0$.
Alternative solution. With the same substitutions write the inequality as
$$
(6-u-v)(6+u+v)+(u v-2 u-v)(6+u+v) \leq 36
$$
As the first product on the lefthand side is $36-(u+v)^{2} \leq 36$, it is enough to prove that the second product is nonpositive. This comes easily from $|u-1| \leq 1$, $|v-2| \leq 2$ and $u v-2 u-v=(u-1)(v-2)-2$, which implies $u v-v-2 u \leq 0$.
## Geometry
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
The real positive numbers $x, y, z$ satisfy the relations $x \leq 2$, $y \leq 3, x+y+z=11$. Prove that $\sqrt{x y z} \leq 6$.
|
For $x=2, y=3$ and $z=6$ the equality holds.
After the substitutions $x=2-u, y=3-v$ with $u \in[0,2), v \in[0,3)$, we obtain that $z=6+u+v$ and the required inequality becomes
$$
(2-u)(3-v)(6+u+v) \leqslant 36
$$
We shall need the following lemma.
Lemma. If real numbers $a$ and $b$ satisfy the relations $0<b \leq a$, then for every real number $y \in[0, b)$ the inequality
$$
\frac{a}{a+y} \geqslant \frac{b-y}{b}
$$
holds.
Proof of the lemma. The inequality (2) is equivalent to
$$
a b \geq a b-a y+b y-y^{2} \Leftrightarrow y^{2}+(a-b) y \geq 0
$$
The last inequality is true, because $a \geq b>0$ and $y \geq 0$.
The equality in (2) holds if $y=0$. The lemma is proved.
By using the lemma we can write the following inequalities:
$$
\begin{gathered}
\frac{6}{6+u} \geqslant \frac{2-u}{2} \\
\frac{6}{6+v} \geqslant \frac{3-v}{3} \\
\frac{6+u}{6+u+v} \geqslant \frac{6}{6+v}
\end{gathered}
$$
By multiplying the inequalities (3), (4) and (5) we obtain:
$$
\begin{gathered}
\frac{6 \cdot 6 \cdot(6+u)}{(6+u)(6+v)(6+u+v)} \geqslant \frac{6(2-u)(3-v)}{2 \cdot 3(6+v)} \Leftrightarrow \\
(2-u)(3-v)(6+u+v) \leqslant 2 \cdot 3 \cdot 6=36 \Leftrightarrow \quad(1)
\end{gathered}
$$
By virtue of lemma, the equality holds if and only if $u=v=0$.
Alternative solution. With the same substitutions write the inequality as
$$
(6-u-v)(6+u+v)+(u v-2 u-v)(6+u+v) \leq 36
$$
As the first product on the lefthand side is $36-(u+v)^{2} \leq 36$, it is enough to prove that the second product is nonpositive. This comes easily from $|u-1| \leq 1$, $|v-2| \leq 2$ and $u v-2 u-v=(u-1)(v-2)-2$, which implies $u v-v-2 u \leq 0$.
## Geometry
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2010_shl.jsonl",
"problem_match": "\nProblem A5.",
"solution_match": "\nSolution."
}
|
d809415a-24c6-575d-81cb-d67fb8916186
| 605,327
|
Consider a triangle $A B C$ with $\angle A C B=90^{\circ}$. Let $F$ be the foot of the altitude from $C$. Circle $\omega$ touches the line segment $F B$ at point $P$, the altitude $C F$ at point $Q$ and the circumcircle of $A B C$ at point $R$. Prove that points $A, Q, R$ are collinear and $A P=A C$.
|
Let $M$ be the midpoint of $A B$ and let $N$ be the center of $\omega$. Then $M$ is the circumcenter of triangle $A B C$, so points $M, N$ and $R$ are collinear. From $Q N \| A M$ we get $\angle A M R=\angle Q N R$. Besides that, triangles $A M R$ and $Q N R$ are isosceles, therefore $\angle M R A=\angle N R Q$; thus points $A, Q, R$ are collinear.
Right angled triangles $A F Q$ and $A R B$ are similar, which implies $\frac{A Q}{A B}=\frac{A F}{A R}$, that is $A Q \cdot A R=A F \cdot A B$. The power of point $A$ with respect to $\omega$ gives $A Q \cdot A R=A P^{2}$. Also, from similar triangles $A B C$ and $A C F$ we get $A F \cdot A B=$ $A C^{2}$. Now, the claim follows from $A C^{2}=A F \cdot A B=A Q \cdot A R=A P^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider a triangle $A B C$ with $\angle A C B=90^{\circ}$. Let $F$ be the foot of the altitude from $C$. Circle $\omega$ touches the line segment $F B$ at point $P$, the altitude $C F$ at point $Q$ and the circumcircle of $A B C$ at point $R$. Prove that points $A, Q, R$ are collinear and $A P=A C$.

|
Let $M$ be the midpoint of $A B$ and let $N$ be the center of $\omega$. Then $M$ is the circumcenter of triangle $A B C$, so points $M, N$ and $R$ are collinear. From $Q N \| A M$ we get $\angle A M R=\angle Q N R$. Besides that, triangles $A M R$ and $Q N R$ are isosceles, therefore $\angle M R A=\angle N R Q$; thus points $A, Q, R$ are collinear.
Right angled triangles $A F Q$ and $A R B$ are similar, which implies $\frac{A Q}{A B}=\frac{A F}{A R}$, that is $A Q \cdot A R=A F \cdot A B$. The power of point $A$ with respect to $\omega$ gives $A Q \cdot A R=A P^{2}$. Also, from similar triangles $A B C$ and $A C F$ we get $A F \cdot A B=$ $A C^{2}$. Now, the claim follows from $A C^{2}=A F \cdot A B=A Q \cdot A R=A P^{2}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2010_shl.jsonl",
"problem_match": "\nProblem G1.",
"solution_match": "\nSolution."
}
|
7c64d4f6-7a8f-52a4-a524-e822c3424e83
| 605,339
|
Let $A B C$ be an acute-angled triangle. A circle $\omega_{1}\left(O_{1}, R_{1}\right)$ passes through points $B$ and $C$ and meets the sides $A B$ and $A C$ at points $D$ and $E$, respectively. Let $\omega_{2}\left(O_{2}, R_{2}\right)$ be the circumcircle of the triangle $A D E$. Prove that $O_{1} O_{2}$ is equal to the circumradius of the triangle $A B C$.
|
Recall that, in every triangle, the altitude and the diameter of the circumcircle drawn from the same vertex are isogonal. The proof offers no difficulty, being a simple angle chasing around the circumcircle of the triangle.
Let $O$ be the circumcenter of the triangle $A B C$. From the above, one has $\angle O A E=90^{\circ}-B$. On the other hand $\angle D E A=B$, for $B C D E$ is cyclic. Thus $A O \perp D E$, implying that in the triangle $A D E$ cevians $A O$ and $A O_{2}$ are isogonal. So, since $A O$ is a radius of the circumcircle of triangle $A B C$, one obtains that $A O_{2}$ is an altitude in this triangle.
Moreover, since $O O_{1}$ is the perpendicular bisector of the line segment $B C$, one has $O O_{1} \perp B C$, and furthermore $A O_{2} \| O O_{1}$.
Chord $D E$ is common to $\omega_{1}$ and $\omega_{2}$, hence $O_{1} O_{2} \perp D E$. It follows that $A O \|$ $O_{1} O_{2}$, so $A O O_{1} O_{2}$ is a parallelogram. The conclusion is now obvious.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle. A circle $\omega_{1}\left(O_{1}, R_{1}\right)$ passes through points $B$ and $C$ and meets the sides $A B$ and $A C$ at points $D$ and $E$, respectively. Let $\omega_{2}\left(O_{2}, R_{2}\right)$ be the circumcircle of the triangle $A D E$. Prove that $O_{1} O_{2}$ is equal to the circumradius of the triangle $A B C$.

|
Recall that, in every triangle, the altitude and the diameter of the circumcircle drawn from the same vertex are isogonal. The proof offers no difficulty, being a simple angle chasing around the circumcircle of the triangle.
Let $O$ be the circumcenter of the triangle $A B C$. From the above, one has $\angle O A E=90^{\circ}-B$. On the other hand $\angle D E A=B$, for $B C D E$ is cyclic. Thus $A O \perp D E$, implying that in the triangle $A D E$ cevians $A O$ and $A O_{2}$ are isogonal. So, since $A O$ is a radius of the circumcircle of triangle $A B C$, one obtains that $A O_{2}$ is an altitude in this triangle.
Moreover, since $O O_{1}$ is the perpendicular bisector of the line segment $B C$, one has $O O_{1} \perp B C$, and furthermore $A O_{2} \| O O_{1}$.
Chord $D E$ is common to $\omega_{1}$ and $\omega_{2}$, hence $O_{1} O_{2} \perp D E$. It follows that $A O \|$ $O_{1} O_{2}$, so $A O O_{1} O_{2}$ is a parallelogram. The conclusion is now obvious.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2010_shl.jsonl",
"problem_match": "\nProblem G3.",
"solution_match": "\nSolution."
}
|
b39e1b8f-d2f6-508b-9b93-c33c13571ce3
| 605,358
|
Show that
$$
\left(a+2 b+\frac{2}{a+1}\right)\left(b+2 a+\frac{2}{b+1}\right) \geq 16
$$
for all positive real numbers $a, b$ satisfying $a b \geq 1$.
|
Solution 3. We have
$$
\begin{aligned}
\left(a+2 b+\frac{2}{a+1}\right)\left(b+2 a+\frac{2}{b+1}\right) & =\left((a+b)+b+\frac{2}{a+1}\right)\left((a+b)+a+\frac{2}{b+1}\right) \\
& \geq\left(a+b+\sqrt{a b}+\frac{2}{\sqrt{(a+1)(b+1)}}\right)^{2}
\end{aligned}
$$
by the Cauchy-Schwarz Inequality.
On the other hand,
$$
\frac{2}{\sqrt{(a+1)(b+1)}} \geq \frac{4}{a+b+2}
$$
by the AM-GM Inequality and
$$
a+b+\sqrt{a b}+\frac{2}{\sqrt{(a+1)(b+1)}} \geq a+b+1+\frac{4}{a+b+2}=\frac{(a+b+1)(a+b-2)}{a+b+2}+4 \geq 4
$$
as $a+b \geq 2 \sqrt{a b} \geq 2$, finishing the proof.
Q1. Find the largest number of distinct integers that can be chosen from the set $\{1,2, \ldots, 2013\}$ so that the difference of no two of them is equal to 17 .
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Show that
$$
\left(a+2 b+\frac{2}{a+1}\right)\left(b+2 a+\frac{2}{b+1}\right) \geq 16
$$
for all positive real numbers $a, b$ satisfying $a b \geq 1$.
|
Solution 3. We have
$$
\begin{aligned}
\left(a+2 b+\frac{2}{a+1}\right)\left(b+2 a+\frac{2}{b+1}\right) & =\left((a+b)+b+\frac{2}{a+1}\right)\left((a+b)+a+\frac{2}{b+1}\right) \\
& \geq\left(a+b+\sqrt{a b}+\frac{2}{\sqrt{(a+1)(b+1)}}\right)^{2}
\end{aligned}
$$
by the Cauchy-Schwarz Inequality.
On the other hand,
$$
\frac{2}{\sqrt{(a+1)(b+1)}} \geq \frac{4}{a+b+2}
$$
by the AM-GM Inequality and
$$
a+b+\sqrt{a b}+\frac{2}{\sqrt{(a+1)(b+1)}} \geq a+b+1+\frac{4}{a+b+2}=\frac{(a+b+1)(a+b-2)}{a+b+2}+4 \geq 4
$$
as $a+b \geq 2 \sqrt{a b} \geq 2$, finishing the proof.
Q1. Find the largest number of distinct integers that can be chosen from the set $\{1,2, \ldots, 2013\}$ so that the difference of no two of them is equal to 17 .
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2013.jsonl",
"problem_match": "\nA3.",
"solution_match": "\nSolution 1."
}
|
9088756f-c65d-5c10-9a55-cfd3c58ec130
| 605,437
|
Let $A B$ be a diameter of a circle $\omega$ with center $O$ and $O C$ be a radius of $\omega$ which is perpendicular to $A B$. Let $M$ be a point on the line segment $O C$. Let $N$ be the second point of intersection of the line $A M$ with $\omega$, and let $P$ be the point of intersection of the lines tangent to $\omega$ at $N$ and at $B$. Show that the points $M, O, P, N$ are concyclic.
|
Since the lines $P N$ and $B P$ are tangent to $\omega, N P=P B$ and $O P$ is the bisector of $\angle N O B$. Therefore the lines $O P$ and $N B$ are perpendicular. Since $\angle A N B=90^{\circ}$, it follows that the lines $A N$ and $O P$ are parallel. As $M O$ and $P B$ are also parallel and $A O=O B$, the triangles $A M O$ and $O P B$ are congruent and $M O=P B$. Hence $M O=N P$. Therefore $M O P N$ is an isosceles trapezoid and therefore cyclic. Hence the points $M, O, P, N$ are concyclic.
8.2. $\omega_{1}$ and $\omega_{2}$ are two circles that are externally tangent to each other at the point $M$ and internally tangent to a circle $\omega_{3}$ at the points $K$ and $L$, respectively. Let $A$ and $B$ be the two points where the common tangent line at $M$ to $\omega_{1}$ and $\omega_{2}$ intersects $\omega_{3}$. Show that if $\angle K A B=\angle L A B$ then the line segment $A B$ is a diameter of $\omega_{3}$.
Solution. Let $C$ be the intersection point of the tangent lines to the circles $\omega_{1}$ at $K$ and $\omega_{2}$ at $L$. Point $C$ lies on the radical axis of circles $\omega_{1}$ and $\omega_{3}$, and also on the radical axis of the circles $\omega_{2}$ and $\omega_{3}$. Therefore $C$ lies on the radical axis of the circles $\omega_{1}$ and $\omega_{2}$ too. Therefore the points $A, B, C$ are collinear.
Since $\angle K A B=\angle L A B$, the chords $K B$ and $B L$ have the same length. As we also have $C K=C L$, the triangles $K B C$ and $L B C$ are congruent. In particular, $\angle K B A=\angle L B A$. Therefore, $\angle B K A=180^{\circ}-(\angle A B K+\angle B A K)=180^{\circ}-(\angle L B K+\angle L A K) / 2=180^{\circ}-90^{\circ}=$ $90^{\circ}$, and $A B$ is a diameter.
Comment. The original problem proposal gives $\angle K A B=\angle L A B=15^{\circ}$ and asks the measures of the angles of the quadrilateral $A K B L$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B$ be a diameter of a circle $\omega$ with center $O$ and $O C$ be a radius of $\omega$ which is perpendicular to $A B$. Let $M$ be a point on the line segment $O C$. Let $N$ be the second point of intersection of the line $A M$ with $\omega$, and let $P$ be the point of intersection of the lines tangent to $\omega$ at $N$ and at $B$. Show that the points $M, O, P, N$ are concyclic.
|
Since the lines $P N$ and $B P$ are tangent to $\omega, N P=P B$ and $O P$ is the bisector of $\angle N O B$. Therefore the lines $O P$ and $N B$ are perpendicular. Since $\angle A N B=90^{\circ}$, it follows that the lines $A N$ and $O P$ are parallel. As $M O$ and $P B$ are also parallel and $A O=O B$, the triangles $A M O$ and $O P B$ are congruent and $M O=P B$. Hence $M O=N P$. Therefore $M O P N$ is an isosceles trapezoid and therefore cyclic. Hence the points $M, O, P, N$ are concyclic.

8.2. $\omega_{1}$ and $\omega_{2}$ are two circles that are externally tangent to each other at the point $M$ and internally tangent to a circle $\omega_{3}$ at the points $K$ and $L$, respectively. Let $A$ and $B$ be the two points where the common tangent line at $M$ to $\omega_{1}$ and $\omega_{2}$ intersects $\omega_{3}$. Show that if $\angle K A B=\angle L A B$ then the line segment $A B$ is a diameter of $\omega_{3}$.
Solution. Let $C$ be the intersection point of the tangent lines to the circles $\omega_{1}$ at $K$ and $\omega_{2}$ at $L$. Point $C$ lies on the radical axis of circles $\omega_{1}$ and $\omega_{3}$, and also on the radical axis of the circles $\omega_{2}$ and $\omega_{3}$. Therefore $C$ lies on the radical axis of the circles $\omega_{1}$ and $\omega_{2}$ too. Therefore the points $A, B, C$ are collinear.
Since $\angle K A B=\angle L A B$, the chords $K B$ and $B L$ have the same length. As we also have $C K=C L$, the triangles $K B C$ and $L B C$ are congruent. In particular, $\angle K B A=\angle L B A$. Therefore, $\angle B K A=180^{\circ}-(\angle A B K+\angle B A K)=180^{\circ}-(\angle L B K+\angle L A K) / 2=180^{\circ}-90^{\circ}=$ $90^{\circ}$, and $A B$ is a diameter.

Comment. The original problem proposal gives $\angle K A B=\angle L A B=15^{\circ}$ and asks the measures of the angles of the quadrilateral $A K B L$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2013.jsonl",
"problem_match": "\nG1.",
"solution_match": "\nSolution."
}
|
70a5a047-7036-5dd6-b3e6-21629045c4d4
| 605,501
|
Let $D$ be a point on the side $B C$ of an acute triangle $A B C$ such that $\angle B A D=\angle C A O$ where $O$ is the center of the circumcircle $\omega$ of the triangle $A B C$. Let $E$ be the second point of intersection of $\omega$ and the line $A D$. Let $M, N, P$ be the midpoints of the line segments $B E, O D, A C$, respectively. Show that $M, N, P$ are collinear.
|
We will show that $M O P D$ is a parallelogram. From this it follows that $M, N$, $P$ are collinear.
Since $\angle B A D=\angle C A O=90^{\circ}-\angle A B C, D$ is the foot of the perpendicular from $A$ to side $B C$. Since $M$ is the midpoint of the line segment $B E$, we have $B M=M E=M D$ and hence $\angle M D E=\angle M E D=\angle A C B$.
Let the line $M D$ intersect the line $A C$ at $D_{1}$. Since $\angle A D D_{1}=\angle M D E=\angle A C D, M D$ is perpendicular to $A C$. On the other hand, since $O$ is the center of the circumcircle of triangle $A B C$ and $P$ is the midpoint of the side $A C, O P$ is perpendicular to $A C$. Therefore $M D$ and $O P$ are parallel.
Similarly, since $P$ is the midpoint of the side $A C$, we have $A P=P C=D P$ and hence $\angle P D C=\angle A C B$. Let the line $P D$ intersect the line $B E$ at $D_{2}$. Since $\angle B D D_{2}=\angle P D C=$ $\angle A C B=\angle B E D$, we conclude that $P D$ is perpendicular to $B E$. Since $M$ is the midpoint of the line segment $B E, O M$ is perpendicular to $B E$ and hence $O M$ and $P D$ are parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $D$ be a point on the side $B C$ of an acute triangle $A B C$ such that $\angle B A D=\angle C A O$ where $O$ is the center of the circumcircle $\omega$ of the triangle $A B C$. Let $E$ be the second point of intersection of $\omega$ and the line $A D$. Let $M, N, P$ be the midpoints of the line segments $B E, O D, A C$, respectively. Show that $M, N, P$ are collinear.
|
We will show that $M O P D$ is a parallelogram. From this it follows that $M, N$, $P$ are collinear.
Since $\angle B A D=\angle C A O=90^{\circ}-\angle A B C, D$ is the foot of the perpendicular from $A$ to side $B C$. Since $M$ is the midpoint of the line segment $B E$, we have $B M=M E=M D$ and hence $\angle M D E=\angle M E D=\angle A C B$.
Let the line $M D$ intersect the line $A C$ at $D_{1}$. Since $\angle A D D_{1}=\angle M D E=\angle A C D, M D$ is perpendicular to $A C$. On the other hand, since $O$ is the center of the circumcircle of triangle $A B C$ and $P$ is the midpoint of the side $A C, O P$ is perpendicular to $A C$. Therefore $M D$ and $O P$ are parallel.
Similarly, since $P$ is the midpoint of the side $A C$, we have $A P=P C=D P$ and hence $\angle P D C=\angle A C B$. Let the line $P D$ intersect the line $B E$ at $D_{2}$. Since $\angle B D D_{2}=\angle P D C=$ $\angle A C B=\angle B E D$, we conclude that $P D$ is perpendicular to $B E$. Since $M$ is the midpoint of the line segment $B E, O M$ is perpendicular to $B E$ and hence $O M$ and $P D$ are parallel.

|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2013.jsonl",
"problem_match": "\nG3.",
"solution_match": "\nSolution."
}
|
f6f8202e-32bf-5335-86d4-8f3e5fe5f931
| 605,513
|
Let $I$ be the incenter and $A B$ the shortest side of a triangle $A B C$. The circle with center $I$ and passing through $C$ intersects the ray $A B$ at the point $P$ and the ray $B A$ at the point $Q$. Let $D$ be the point where the excircle of the triangle $A B C$ belonging to angle $A$ touches the side $B C$, and let $E$ be the symmetric of the point $C$ with respect to $D$. Show that the lines $P E$ and $C Q$ are perpendicular.
|
First we will show that points $P$ and $Q$ are not on the line segment $A B$.
Assume that $Q$ is on the line segment $A B$. Since $C I=Q I$ and $\angle I B Q=\angle I B C$, either the triangles $C B I$ and $Q B I$ are congruent or $\angle I C B+\angle I Q B=180^{\circ}$. In the first case, we have $B C=B Q$ which contradicts $A B$ being the shortest side.
In the second case, we have $\angle I Q A=\angle I C B=\angle I C A$ and the triangles $I A C$ and $I A Q$ are congruent. Hence this time we have $A C=A Q$, contradicting $A B$ being the shortest side.
Case 1
Now we will show that the lines $P E$ and $C Q$ are perpendicular.
Since $\angle I Q B \leq \angle I A B=(\angle C A B) / 2<90^{\circ}$ and $\angle I C B=(\angle A C B) / 2<90^{\circ}$, the triangles $C B I$ and $Q B I$ are congruent. Hence $B C=B Q$ and $\angle C Q P=\angle C Q B=90^{\circ}-(\angle A B C) / 2$. Similarly, we have $A C=A P$ and hence $B P=A C-A B$.
On the other hand, as $D E=C D$ and $C D+A C=u$, where $u$ denotes the semiperimeter of the triangle $A B C$, we have $B E=B C-2(u-A C)=A C-A B$. Therefore $B P=B E$ and $\angle Q P E=(\angle A B C) / 2$.
Hence, $\angle C Q P+\angle Q P E=90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ be the incenter and $A B$ the shortest side of a triangle $A B C$. The circle with center $I$ and passing through $C$ intersects the ray $A B$ at the point $P$ and the ray $B A$ at the point $Q$. Let $D$ be the point where the excircle of the triangle $A B C$ belonging to angle $A$ touches the side $B C$, and let $E$ be the symmetric of the point $C$ with respect to $D$. Show that the lines $P E$ and $C Q$ are perpendicular.
|
First we will show that points $P$ and $Q$ are not on the line segment $A B$.
Assume that $Q$ is on the line segment $A B$. Since $C I=Q I$ and $\angle I B Q=\angle I B C$, either the triangles $C B I$ and $Q B I$ are congruent or $\angle I C B+\angle I Q B=180^{\circ}$. In the first case, we have $B C=B Q$ which contradicts $A B$ being the shortest side.
In the second case, we have $\angle I Q A=\angle I C B=\angle I C A$ and the triangles $I A C$ and $I A Q$ are congruent. Hence this time we have $A C=A Q$, contradicting $A B$ being the shortest side.

Case 1

Now we will show that the lines $P E$ and $C Q$ are perpendicular.
Since $\angle I Q B \leq \angle I A B=(\angle C A B) / 2<90^{\circ}$ and $\angle I C B=(\angle A C B) / 2<90^{\circ}$, the triangles $C B I$ and $Q B I$ are congruent. Hence $B C=B Q$ and $\angle C Q P=\angle C Q B=90^{\circ}-(\angle A B C) / 2$. Similarly, we have $A C=A P$ and hence $B P=A C-A B$.
On the other hand, as $D E=C D$ and $C D+A C=u$, where $u$ denotes the semiperimeter of the triangle $A B C$, we have $B E=B C-2(u-A C)=A C-A B$. Therefore $B P=B E$ and $\angle Q P E=(\angle A B C) / 2$.
Hence, $\angle C Q P+\angle Q P E=90^{\circ}$.

|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2013.jsonl",
"problem_match": "\nG4.",
"solution_match": "\nSolution."
}
|
e325aa90-2e24-5169-9043-e1f414797d09
| 605,523
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that:
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq 3(a+b+c+1)
$$
When does equality hold?
|
By using AM-GM $\left(x^{2}+y^{2}+z^{2} \geq x y+y z+z x\right)$ we have
$$
\begin{aligned}
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} & \geq\left(a+\frac{1}{b}\right)\left(b+\frac{1}{c}\right)+\left(b+\frac{1}{c}\right)\left(c+\frac{1}{a}\right)+\left(c+\frac{1}{a}\right)\left(a+\frac{1}{b}\right) \\
& =\left(a b+1+\frac{a}{c}+a\right)+\left(b c+1+\frac{b}{a}+b\right)+\left(c a+1+\frac{c}{b}+c\right) \\
& =a b+b c+c a+\frac{a}{c}+\frac{c}{b}+\frac{b}{a}+3+a+b+c
\end{aligned}
$$
Notice that by AM-GM we have $a b+\frac{b}{a} \geq 2 b, b c+\frac{c}{b} \geq 2 c$, and $c a+\frac{a}{c} \geq 2 a$.
Thus,
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq\left(a b+\frac{b}{a}\right)+\left(b c+\frac{c}{b}\right)+\left(c a+\frac{a}{c}\right)+3+a+b+c \geq 3(a+b+c+1)
$$
The equality holds if and only if $a=b=c=1$.
Solution2. From QM-AM we obtain
$$
\begin{aligned}
& \sqrt{\frac{\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2}}{3}} \geq \frac{a+\frac{1}{b}+b+\frac{1}{c}+c+\frac{1}{a}}{3} \Leftrightarrow \\
& \left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq \frac{\left(a+\frac{1}{b}+b+\frac{1}{c}+c+\frac{1}{a}\right)^{2}}{3}
\end{aligned}
$$
From AM-GM we have $\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geq 3 \sqrt[3]{\frac{1}{a b c}}=3$, and substituting in (1) we get
$$
\begin{aligned}
&\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq \frac{\left(a+\frac{1}{b}+b+\frac{1}{c}+c+\frac{1}{a}\right)^{2}}{3} \geq \frac{(a+b+c+3)^{2}}{3}= \\
&=\frac{(a+b+c)(a+b+c)+6(a+b+c)+9}{3} \geq \frac{(a+b+c) 3 \sqrt[3]{a b c}+6(a+b+c)+9}{3}= \\
&=\frac{9(a+b+c)+9}{3}=3(a+b+c+1)
\end{aligned}
$$
The equality holds if and only if $a=b=c=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that:
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq 3(a+b+c+1)
$$
When does equality hold?
|
By using AM-GM $\left(x^{2}+y^{2}+z^{2} \geq x y+y z+z x\right)$ we have
$$
\begin{aligned}
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} & \geq\left(a+\frac{1}{b}\right)\left(b+\frac{1}{c}\right)+\left(b+\frac{1}{c}\right)\left(c+\frac{1}{a}\right)+\left(c+\frac{1}{a}\right)\left(a+\frac{1}{b}\right) \\
& =\left(a b+1+\frac{a}{c}+a\right)+\left(b c+1+\frac{b}{a}+b\right)+\left(c a+1+\frac{c}{b}+c\right) \\
& =a b+b c+c a+\frac{a}{c}+\frac{c}{b}+\frac{b}{a}+3+a+b+c
\end{aligned}
$$
Notice that by AM-GM we have $a b+\frac{b}{a} \geq 2 b, b c+\frac{c}{b} \geq 2 c$, and $c a+\frac{a}{c} \geq 2 a$.
Thus,
$$
\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq\left(a b+\frac{b}{a}\right)+\left(b c+\frac{c}{b}\right)+\left(c a+\frac{a}{c}\right)+3+a+b+c \geq 3(a+b+c+1)
$$
The equality holds if and only if $a=b=c=1$.
Solution2. From QM-AM we obtain
$$
\begin{aligned}
& \sqrt{\frac{\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2}}{3}} \geq \frac{a+\frac{1}{b}+b+\frac{1}{c}+c+\frac{1}{a}}{3} \Leftrightarrow \\
& \left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq \frac{\left(a+\frac{1}{b}+b+\frac{1}{c}+c+\frac{1}{a}\right)^{2}}{3}
\end{aligned}
$$
From AM-GM we have $\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geq 3 \sqrt[3]{\frac{1}{a b c}}=3$, and substituting in (1) we get
$$
\begin{aligned}
&\left(a+\frac{1}{b}\right)^{2}+\left(b+\frac{1}{c}\right)^{2}+\left(c+\frac{1}{a}\right)^{2} \geq \frac{\left(a+\frac{1}{b}+b+\frac{1}{c}+c+\frac{1}{a}\right)^{2}}{3} \geq \frac{(a+b+c+3)^{2}}{3}= \\
&=\frac{(a+b+c)(a+b+c)+6(a+b+c)+9}{3} \geq \frac{(a+b+c) 3 \sqrt[3]{a b c}+6(a+b+c)+9}{3}= \\
&=\frac{9(a+b+c)+9}{3}=3(a+b+c+1)
\end{aligned}
$$
The equality holds if and only if $a=b=c=1$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## A3",
"solution_match": "\nSolution1."
}
|
9eecb30a-ba1f-5696-9557-492c8c9a7513
| 605,599
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\left(\left(3 a^{2}+1\right)^{2}+2\left(1+\frac{3}{b}\right)^{2}\right)\left(\left(3 b^{2}+1\right)^{2}+2\left(1+\frac{3}{c}\right)^{2}\right)\left(\left(3 c^{2}+1\right)^{2}+2\left(1+\frac{3}{a}\right)^{2}\right) \geq 48^{3}
$$
When does equality hold?
|
Let $x$ be a positive real number. By AM-GM we have $\frac{1+x+x+x}{4} \geq x^{\frac{3}{4}}$, or equivalently $1+3 x \geq 4 x^{\frac{3}{4}}$. Using this inequality we obtain:
$$
\left(3 a^{2}+1\right)^{2} \geq 16 a^{3} \text { and } 2\left(1+\frac{3}{b}\right)^{2} \geq 32 b^{-\frac{3}{2}}
$$
Moreover, by inequality of arithmetic and geometric means we have
$$
f(a, b)=\left(3 a^{2}+1\right)^{2}+2\left(1+\frac{3}{b}\right)^{2} \geq 16 a^{3}+32 b^{-\frac{3}{2}}=16\left(a^{3}+b^{-\frac{3}{2}}+b^{-\frac{3}{2}}\right) \geq 48 \frac{a}{b}
$$
Therefore, we obtain
$$
f(a, b) f(b, c) f(c, a) \geq 48 \cdot \frac{a}{b} \cdot 48 \cdot \frac{b}{c} \cdot 48 \cdot \frac{c}{a}=48^{3}
$$
Equality holds only when $a=b=c=1$.
## 1 IH $^{\text {th J.M. }} 2014$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\left(\left(3 a^{2}+1\right)^{2}+2\left(1+\frac{3}{b}\right)^{2}\right)\left(\left(3 b^{2}+1\right)^{2}+2\left(1+\frac{3}{c}\right)^{2}\right)\left(\left(3 c^{2}+1\right)^{2}+2\left(1+\frac{3}{a}\right)^{2}\right) \geq 48^{3}
$$
When does equality hold?
|
Let $x$ be a positive real number. By AM-GM we have $\frac{1+x+x+x}{4} \geq x^{\frac{3}{4}}$, or equivalently $1+3 x \geq 4 x^{\frac{3}{4}}$. Using this inequality we obtain:
$$
\left(3 a^{2}+1\right)^{2} \geq 16 a^{3} \text { and } 2\left(1+\frac{3}{b}\right)^{2} \geq 32 b^{-\frac{3}{2}}
$$
Moreover, by inequality of arithmetic and geometric means we have
$$
f(a, b)=\left(3 a^{2}+1\right)^{2}+2\left(1+\frac{3}{b}\right)^{2} \geq 16 a^{3}+32 b^{-\frac{3}{2}}=16\left(a^{3}+b^{-\frac{3}{2}}+b^{-\frac{3}{2}}\right) \geq 48 \frac{a}{b}
$$
Therefore, we obtain
$$
f(a, b) f(b, c) f(c, a) \geq 48 \cdot \frac{a}{b} \cdot 48 \cdot \frac{b}{c} \cdot 48 \cdot \frac{c}{a}=48^{3}
$$
Equality holds only when $a=b=c=1$.
## 1 IH $^{\text {th J.M. }} 2014$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## A6",
"solution_match": "\nSolution."
}
|
ac8acafb-f794-5bee-bd30-9ba9c936e2ea
| 605,631
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove the inequality
$$
\frac{1}{x(a y+b)}+\frac{1}{y(a z+b)}+\frac{1}{z(a x+b)} \geq 3 \text {, if: }
$$
a) $a=0$ and $b=1$;
b) $a=1$ and $b=0$;
c) $a+b=1$ for $a, b>0$
When does the equality hold true?
|
a) The inequality reduces to $\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq 3$, which follows directly from the AM-GM inequality.
Equality holds only when $x=y=z=1$.
b) Here the inequality reduces to $\frac{1}{x y}+\frac{1}{y z}+\frac{1}{z x} \geq 3$, i.e. $x+y+z \geq 3$, which also follows from the AM-GM inequality.
Equality holds only when $x=y=z=1$.
c) Let $m, n$ and $p$ be such that $x=\frac{m}{n}, y=\frac{n}{p}$ и $z=\frac{p}{m}$. The inequality reduces to
$$
\frac{n p}{a m n+b m p}+\frac{p m}{a n p+b n m}+\frac{m n}{a p m+b p n} \geq 3
$$
By substituting $u=n p, v=p m$ and $w=m n$, (1) becomes
$$
\frac{u}{a w+b v}+\frac{v}{a u+b w}+\frac{w}{a v+b u} \geq 3
$$
The last inequality is equivalent to
$$
\frac{u^{2}}{a u w+b u v}+\frac{v^{2}}{a u v+b v w}+\frac{w^{2}}{a v w+b u w} \geq 3
$$
Cauchy-Schwarz Inequality implies
$$
\frac{u^{2}}{a u w+b u v}+\frac{v^{2}}{a u v+b v w}+\frac{w^{2}}{a v w+b u w} \geq \frac{(u+v+w)^{2}}{a u w+b u v+a u v+b v w+a v w+b u w}=\frac{(u+v+w)^{2}}{u w+v u+w v}
$$
Thus, the problem simplifies to $(u+v+w)^{2} \geq 3(u w+v u+w v)$, which is equivalent to $(u-v)^{2}+(v-w)^{2}+(w-u)^{2} \geq 0$.
Equality holds only when $u=v=w$, that is only for $x=y=z=1$.
Remark. The problem can be reformulated:
Let $a, b, x, y$ and $z$ be nonnegative real numbers such that $x y z=1$ and $a+b=1$. Prove the inequality
$$
\frac{1}{x(a y+b)}+\frac{1}{y(a z+b)}+\frac{1}{z(a x+b)} \geq 3
$$
When does the equality hold true?
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove the inequality
$$
\frac{1}{x(a y+b)}+\frac{1}{y(a z+b)}+\frac{1}{z(a x+b)} \geq 3 \text {, if: }
$$
a) $a=0$ and $b=1$;
b) $a=1$ and $b=0$;
c) $a+b=1$ for $a, b>0$
When does the equality hold true?
|
a) The inequality reduces to $\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq 3$, which follows directly from the AM-GM inequality.
Equality holds only when $x=y=z=1$.
b) Here the inequality reduces to $\frac{1}{x y}+\frac{1}{y z}+\frac{1}{z x} \geq 3$, i.e. $x+y+z \geq 3$, which also follows from the AM-GM inequality.
Equality holds only when $x=y=z=1$.
c) Let $m, n$ and $p$ be such that $x=\frac{m}{n}, y=\frac{n}{p}$ и $z=\frac{p}{m}$. The inequality reduces to
$$
\frac{n p}{a m n+b m p}+\frac{p m}{a n p+b n m}+\frac{m n}{a p m+b p n} \geq 3
$$
By substituting $u=n p, v=p m$ and $w=m n$, (1) becomes
$$
\frac{u}{a w+b v}+\frac{v}{a u+b w}+\frac{w}{a v+b u} \geq 3
$$
The last inequality is equivalent to
$$
\frac{u^{2}}{a u w+b u v}+\frac{v^{2}}{a u v+b v w}+\frac{w^{2}}{a v w+b u w} \geq 3
$$
Cauchy-Schwarz Inequality implies
$$
\frac{u^{2}}{a u w+b u v}+\frac{v^{2}}{a u v+b v w}+\frac{w^{2}}{a v w+b u w} \geq \frac{(u+v+w)^{2}}{a u w+b u v+a u v+b v w+a v w+b u w}=\frac{(u+v+w)^{2}}{u w+v u+w v}
$$
Thus, the problem simplifies to $(u+v+w)^{2} \geq 3(u w+v u+w v)$, which is equivalent to $(u-v)^{2}+(v-w)^{2}+(w-u)^{2} \geq 0$.
Equality holds only when $u=v=w$, that is only for $x=y=z=1$.
Remark. The problem can be reformulated:
Let $a, b, x, y$ and $z$ be nonnegative real numbers such that $x y z=1$ and $a+b=1$. Prove the inequality
$$
\frac{1}{x(a y+b)}+\frac{1}{y(a z+b)}+\frac{1}{z(a x+b)} \geq 3
$$
When does the equality hold true?
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## A8",
"solution_match": "\nSolution."
}
|
2311460f-0fb2-573d-b88c-8d6f94af5922
| 605,640
|
Let $n$ be a positive integer, and let $x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{n}$ be positive real numbers such that $x_{1}+\ldots+x_{n}=y_{1}+\ldots+y_{n}=1$. Show that
$$
\left|x_{1}-y_{1}\right|+\ldots\left|x_{n}-y_{n}\right| \leq 2-\min _{1 \leq i \leq n} \frac{x_{i}}{y_{i}}-\min _{1 \leq i \leq n} \frac{y_{i}}{x_{i}}
$$
|
Up to reordering the real numbers $x_{i}$ and $y_{i}$, we may assume that $\frac{x_{1}}{y_{1}} \leq \ldots \leq \frac{x_{n}}{y_{n}}$. Let $A=\frac{x_{1}}{y_{1}}$ and $B=\frac{x_{n}}{y_{n}}$, and $\mathrm{S}=\left|x_{1}-y_{1}\right|+\ldots\left|x_{n}-y_{n}\right|$. Our aim is to prove that $S \leq 2-A-\frac{1}{B}$.
First, note that we cannot have $A>1$, since that would imply $x_{i}>y_{i}$ for all $i \leq n$, hence $x_{1}+\ldots+x_{n}>y_{1}+\ldots+y_{n}$. Similarly, we cannot have $B<1$, since that would imply $x_{i}<y_{i}$ for all $i \leq n$, hence $x_{1}+\ldots+x_{n}<y_{1}+\ldots+y_{n}$.
If $n=1$, then $x_{1}=y_{1}=A=B=1$ and $S=0$, hence $S \leq 2-A-\frac{1}{B}$. For $n \geq 2$ let $1 \leq k<n$ be some integer such that $\frac{x_{k}}{y_{k}} \leq 1 \leq \frac{x_{k+1}}{y_{k+1}}$. We define the positive real numbers $X_{1}=x_{1}+\ldots+x_{k}$, $X_{2}=x_{k+1}+\ldots+x_{n}, Y_{1}=y_{1}+\ldots+y_{k}, Y_{2}=y_{k+1}+\ldots+y_{n}$. Note that $Y_{1} \geq X_{1} \geq A Y_{1}$ and $Y_{2} \leq X_{2} \leq B Y_{2}$. Thus, $A \leq \frac{X_{1}}{Y_{1}} \leq 1 \leq \frac{X_{2}}{Y_{2}} \leq B$. In addition, $S=Y_{1}-X_{1}+X_{2}-Y_{2}$.
From $0<X_{2}, Y_{1} \leq 1,0 \leq Y_{1}-X_{1}$ and $0 \leq X_{2}-Y_{2}$, follows
$$
S=Y_{1}-X_{1}+X_{2}-Y_{2}=\frac{Y_{1}-X_{1}}{Y_{1}}+\frac{X_{2}-Y_{2}}{X_{2}}=2-\frac{X_{1}}{Y_{1}}-\frac{Y_{2}}{X_{2}} \leq 2-A-\frac{1}{B}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be a positive integer, and let $x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{n}$ be positive real numbers such that $x_{1}+\ldots+x_{n}=y_{1}+\ldots+y_{n}=1$. Show that
$$
\left|x_{1}-y_{1}\right|+\ldots\left|x_{n}-y_{n}\right| \leq 2-\min _{1 \leq i \leq n} \frac{x_{i}}{y_{i}}-\min _{1 \leq i \leq n} \frac{y_{i}}{x_{i}}
$$
|
Up to reordering the real numbers $x_{i}$ and $y_{i}$, we may assume that $\frac{x_{1}}{y_{1}} \leq \ldots \leq \frac{x_{n}}{y_{n}}$. Let $A=\frac{x_{1}}{y_{1}}$ and $B=\frac{x_{n}}{y_{n}}$, and $\mathrm{S}=\left|x_{1}-y_{1}\right|+\ldots\left|x_{n}-y_{n}\right|$. Our aim is to prove that $S \leq 2-A-\frac{1}{B}$.
First, note that we cannot have $A>1$, since that would imply $x_{i}>y_{i}$ for all $i \leq n$, hence $x_{1}+\ldots+x_{n}>y_{1}+\ldots+y_{n}$. Similarly, we cannot have $B<1$, since that would imply $x_{i}<y_{i}$ for all $i \leq n$, hence $x_{1}+\ldots+x_{n}<y_{1}+\ldots+y_{n}$.
If $n=1$, then $x_{1}=y_{1}=A=B=1$ and $S=0$, hence $S \leq 2-A-\frac{1}{B}$. For $n \geq 2$ let $1 \leq k<n$ be some integer such that $\frac{x_{k}}{y_{k}} \leq 1 \leq \frac{x_{k+1}}{y_{k+1}}$. We define the positive real numbers $X_{1}=x_{1}+\ldots+x_{k}$, $X_{2}=x_{k+1}+\ldots+x_{n}, Y_{1}=y_{1}+\ldots+y_{k}, Y_{2}=y_{k+1}+\ldots+y_{n}$. Note that $Y_{1} \geq X_{1} \geq A Y_{1}$ and $Y_{2} \leq X_{2} \leq B Y_{2}$. Thus, $A \leq \frac{X_{1}}{Y_{1}} \leq 1 \leq \frac{X_{2}}{Y_{2}} \leq B$. In addition, $S=Y_{1}-X_{1}+X_{2}-Y_{2}$.
From $0<X_{2}, Y_{1} \leq 1,0 \leq Y_{1}-X_{1}$ and $0 \leq X_{2}-Y_{2}$, follows
$$
S=Y_{1}-X_{1}+X_{2}-Y_{2}=\frac{Y_{1}-X_{1}}{Y_{1}}+\frac{X_{2}-Y_{2}}{X_{2}}=2-\frac{X_{1}}{Y_{1}}-\frac{Y_{2}}{X_{2}} \leq 2-A-\frac{1}{B}
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## A9",
"solution_match": "\nSolution."
}
|
a0799aa7-f6cb-5bab-9889-bed985357b9e
| 605,650
|
Several (at least two) segments are drawn on a board. Select two of them, and let $a$ and $b$ be their lengths. Delete the selected segments and draw a segment of length $\frac{a b}{a+b}$. Continue this procedure until only one segment remains on the board. Prove:
a) the length of the last remaining segment does not depend on the order of the deletions.
b) for every positive integer $n$, the initial segments on the board can be chosen with distinct integer lengths, such that the last remaining segment has length $n$.
|
a) Observe that $\frac{1}{\frac{a b}{a+b}}=\frac{1}{a}+\frac{1}{b}$. Thus, if the lengths of the initial segments on the board were $a_{1}, a_{2}, \ldots, a_{n}$, and $c$ is the length of the last remaining segment, then $\frac{1}{c}=\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n}}$ , proving a).
b) From a) and the equation $\frac{1}{n}=\frac{1}{2 n}+\frac{1}{3 n}+\frac{1}{6 n}$ it follows that if the lengths of the starting segments are $2 n, 3 n$ and $6 n$, then the length of the last remaining segment is $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Several (at least two) segments are drawn on a board. Select two of them, and let $a$ and $b$ be their lengths. Delete the selected segments and draw a segment of length $\frac{a b}{a+b}$. Continue this procedure until only one segment remains on the board. Prove:
a) the length of the last remaining segment does not depend on the order of the deletions.
b) for every positive integer $n$, the initial segments on the board can be chosen with distinct integer lengths, such that the last remaining segment has length $n$.
|
a) Observe that $\frac{1}{\frac{a b}{a+b}}=\frac{1}{a}+\frac{1}{b}$. Thus, if the lengths of the initial segments on the board were $a_{1}, a_{2}, \ldots, a_{n}$, and $c$ is the length of the last remaining segment, then $\frac{1}{c}=\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n}}$ , proving a).
b) From a) and the equation $\frac{1}{n}=\frac{1}{2 n}+\frac{1}{3 n}+\frac{1}{6 n}$ it follows that if the lengths of the starting segments are $2 n, 3 n$ and $6 n$, then the length of the last remaining segment is $n$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## C1",
"solution_match": "\nSolution."
}
|
8c053955-b017-5670-8e09-4bea431bb598
| 605,660
|
Let $A B C$ be an acute triangle with $\overline{A B}<\overline{A C}<\overline{B C}$ and $c(O, R)$ be its circumcircle. Denote with $D$ and $E$ be the points diametrically opposite to the points $B$ and $C$, respectively. The circle $c_{1}(A, \overline{A E})$ intersects $\overline{A C}$ at point $K$, the circle $c_{2}(A, \overline{A D})$ intersects $B A$ at point $L(A$ lies between $B$ and $L$ ). Prove that the lines $E K$ and $D L$ meet on the circle $c$.
|
Let $\mathrm{M}$ be the point of intersection of the line $D L$ with the circle $c(O, R)$ (we choose $M \equiv D$ if $L D$ is tangent to $c$ and $M$ to be the second intersecting point otherwise). It is
sufficient to prove that the points $E, K$ and $M$ are collinear.
We have that $\measuredangle E A C=90^{\circ}$ (since $E C$ is diameter of the circle $c$ ). The triangle $A E K$ is right-angled and isosceles ( $\overline{A E}$ and $\overline{A K}$ are radii of the circle $c_{1}$ ). Therefore
$$
\measuredangle \mathrm{AEK}=\measuredangle \mathrm{AKE}=45^{\circ} \text {. }
$$
Similarly, we obtain that $\measuredangle B A D=90^{\circ}=\measuredangle D A L$. Since $\overline{A D}=\overline{A L}$ the triangle $A D L$ is right-angled and isosceles, we have
$$
\measuredangle \mathrm{ADL}=\measuredangle \mathrm{A} L D=45^{\circ} .
$$
If $M$ is between $D$ and $L$, then $\measuredangle \mathrm{ADM}=\measuredangle A E M$, because they are inscribed in the circle $c(O, R)$ and they correspond to the same arch $\overparen{A M}$. Hence $\measuredangle \mathrm{AEK}=\measuredangle \mathrm{AEM}=45^{\circ}$ i.e. the points $E, K, M$ are collinear.
If $D$ is between $M$ and $L$, then $\measuredangle \mathrm{ADM}+\measuredangle A E M=180^{\circ}$ as opposite angles in cyclic quadrilateral. Hence $\measuredangle \mathrm{AEK}=\measuredangle \mathrm{AEM}=45^{\circ}$ i.e. the points $E, K, M$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $\overline{A B}<\overline{A C}<\overline{B C}$ and $c(O, R)$ be its circumcircle. Denote with $D$ and $E$ be the points diametrically opposite to the points $B$ and $C$, respectively. The circle $c_{1}(A, \overline{A E})$ intersects $\overline{A C}$ at point $K$, the circle $c_{2}(A, \overline{A D})$ intersects $B A$ at point $L(A$ lies between $B$ and $L$ ). Prove that the lines $E K$ and $D L$ meet on the circle $c$.
|
Let $\mathrm{M}$ be the point of intersection of the line $D L$ with the circle $c(O, R)$ (we choose $M \equiv D$ if $L D$ is tangent to $c$ and $M$ to be the second intersecting point otherwise). It is

sufficient to prove that the points $E, K$ and $M$ are collinear.
We have that $\measuredangle E A C=90^{\circ}$ (since $E C$ is diameter of the circle $c$ ). The triangle $A E K$ is right-angled and isosceles ( $\overline{A E}$ and $\overline{A K}$ are radii of the circle $c_{1}$ ). Therefore
$$
\measuredangle \mathrm{AEK}=\measuredangle \mathrm{AKE}=45^{\circ} \text {. }
$$
Similarly, we obtain that $\measuredangle B A D=90^{\circ}=\measuredangle D A L$. Since $\overline{A D}=\overline{A L}$ the triangle $A D L$ is right-angled and isosceles, we have
$$
\measuredangle \mathrm{ADL}=\measuredangle \mathrm{A} L D=45^{\circ} .
$$
If $M$ is between $D$ and $L$, then $\measuredangle \mathrm{ADM}=\measuredangle A E M$, because they are inscribed in the circle $c(O, R)$ and they correspond to the same arch $\overparen{A M}$. Hence $\measuredangle \mathrm{AEK}=\measuredangle \mathrm{AEM}=45^{\circ}$ i.e. the points $E, K, M$ are collinear.
If $D$ is between $M$ and $L$, then $\measuredangle \mathrm{ADM}+\measuredangle A E M=180^{\circ}$ as opposite angles in cyclic quadrilateral. Hence $\measuredangle \mathrm{AEK}=\measuredangle \mathrm{AEM}=45^{\circ}$ i.e. the points $E, K, M$ are collinear.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## G2",
"solution_match": "\nSolution."
}
|
0989ccb4-f556-5ca1-a78d-450eec012782
| 605,703
|
Let $A B C$ be a triangle such that $\overline{A B} \neq \overline{A C}$. Let $M$ be a midpoint of $\overline{B C}, H$ the orthocenter of $A B C, O_{1}$ the midpoint of $\overline{A H}$ and $O_{2}$ the circumcenter of $B C H$. Prove that $O_{1} A M O_{2}$ is a parallelogram.
|
Let $O_{2}^{\prime}$ be the point such that $O_{1} A M O_{2}^{\prime}$ is a parallelogram. Note that $\overrightarrow{M O_{2}}=\overrightarrow{A O_{1}}=\overrightarrow{O_{1} H}$. Therefore, $O_{1} H O_{2}^{\prime} M$ is a parallelogram and $\overrightarrow{M O_{1}}=\overrightarrow{O_{2} H}$.
Since $M$ is the midpoint of $\overline{B C}$ and $O_{1}$ is the midpoint of $\overline{A H}$, it follows that $4 \overrightarrow{M O_{1}}=\overrightarrow{B A}+\overrightarrow{B H}+\overrightarrow{C A}+\overrightarrow{C H}=2(\overrightarrow{C A}+\overrightarrow{B H})$. Moreover, let $B^{\prime}$ be the midpoint of $\overrightarrow{B H}$. Then,
$$
\begin{aligned}
2 \overrightarrow{O_{2}^{\prime B}} \cdot \overrightarrow{B H} & =\left(\overline{O_{2}^{\prime H}}+\overline{O_{2}^{\prime B}}\right) \cdot \overrightarrow{B H}=\left(2 \overline{O_{2}^{\prime} H}+\overrightarrow{H B}\right) \cdot \overrightarrow{B H}= \\
& =\left(2 \overline{M O_{1}}+\overline{H B}\right) \cdot \overline{B H}=(\overline{C A}+\overrightarrow{B H}+\overrightarrow{H B}) \cdot \overrightarrow{B H}=\overline{C A} \cdot \overrightarrow{B H}=0 .
\end{aligned}
$$
By $\vec{a} \cdot \vec{b}$ we denote the inner product of the vectors $\vec{a}$ and $\vec{b}$.
Therefore, $O_{2}^{\prime}$ lies on the perpendicular bisector of $\overline{B H}$. Since $B$ and $C$ play symmetric roles, $\mathrm{O}_{2}^{\prime}$ also lies on the perpendicular bisector of $\overline{\mathrm{CH}}$, hence $\mathrm{O}_{2}^{\prime}$ is the circumcenter of $\triangle B C H$ and $\mathrm{O}_{2}=\mathrm{O}_{2}^{\prime}$.
Note: The condition $\overline{A B} \neq \overline{A C}$ just aims at ensuring that the parallelogram $O_{1} A N O_{2}$ is not degenerate, hence at helping students to focus on the "general" case.
Solution2. We use the following two well-known facts:
$\sigma_{B C}(H)$ lies on the circumcircle of $\triangle A B C$.
$\overrightarrow{A H}=-2 \overrightarrow{M O}$, where $O$ is the circumcenter of $\triangle A B C$.
The statement " $\mathrm{O}_{1} A M O_{2}$ is parallelogram" is equivalent to " $\sigma_{B C}\left(O_{2}\right)=O$ ". The later is true because the circumcircles of $\triangle A B C$ and $\triangle B C H$ are symmetrical with respect to $B C$, from (1).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle such that $\overline{A B} \neq \overline{A C}$. Let $M$ be a midpoint of $\overline{B C}, H$ the orthocenter of $A B C, O_{1}$ the midpoint of $\overline{A H}$ and $O_{2}$ the circumcenter of $B C H$. Prove that $O_{1} A M O_{2}$ is a parallelogram.
|
Let $O_{2}^{\prime}$ be the point such that $O_{1} A M O_{2}^{\prime}$ is a parallelogram. Note that $\overrightarrow{M O_{2}}=\overrightarrow{A O_{1}}=\overrightarrow{O_{1} H}$. Therefore, $O_{1} H O_{2}^{\prime} M$ is a parallelogram and $\overrightarrow{M O_{1}}=\overrightarrow{O_{2} H}$.
Since $M$ is the midpoint of $\overline{B C}$ and $O_{1}$ is the midpoint of $\overline{A H}$, it follows that $4 \overrightarrow{M O_{1}}=\overrightarrow{B A}+\overrightarrow{B H}+\overrightarrow{C A}+\overrightarrow{C H}=2(\overrightarrow{C A}+\overrightarrow{B H})$. Moreover, let $B^{\prime}$ be the midpoint of $\overrightarrow{B H}$. Then,
$$
\begin{aligned}
2 \overrightarrow{O_{2}^{\prime B}} \cdot \overrightarrow{B H} & =\left(\overline{O_{2}^{\prime H}}+\overline{O_{2}^{\prime B}}\right) \cdot \overrightarrow{B H}=\left(2 \overline{O_{2}^{\prime} H}+\overrightarrow{H B}\right) \cdot \overrightarrow{B H}= \\
& =\left(2 \overline{M O_{1}}+\overline{H B}\right) \cdot \overline{B H}=(\overline{C A}+\overrightarrow{B H}+\overrightarrow{H B}) \cdot \overrightarrow{B H}=\overline{C A} \cdot \overrightarrow{B H}=0 .
\end{aligned}
$$
By $\vec{a} \cdot \vec{b}$ we denote the inner product of the vectors $\vec{a}$ and $\vec{b}$.
Therefore, $O_{2}^{\prime}$ lies on the perpendicular bisector of $\overline{B H}$. Since $B$ and $C$ play symmetric roles, $\mathrm{O}_{2}^{\prime}$ also lies on the perpendicular bisector of $\overline{\mathrm{CH}}$, hence $\mathrm{O}_{2}^{\prime}$ is the circumcenter of $\triangle B C H$ and $\mathrm{O}_{2}=\mathrm{O}_{2}^{\prime}$.
Note: The condition $\overline{A B} \neq \overline{A C}$ just aims at ensuring that the parallelogram $O_{1} A N O_{2}$ is not degenerate, hence at helping students to focus on the "general" case.
Solution2. We use the following two well-known facts:
$\sigma_{B C}(H)$ lies on the circumcircle of $\triangle A B C$.
$\overrightarrow{A H}=-2 \overrightarrow{M O}$, where $O$ is the circumcenter of $\triangle A B C$.
The statement " $\mathrm{O}_{1} A M O_{2}$ is parallelogram" is equivalent to " $\sigma_{B C}\left(O_{2}\right)=O$ ". The later is true because the circumcircles of $\triangle A B C$ and $\triangle B C H$ are symmetrical with respect to $B C$, from (1).
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## G4",
"solution_match": "\nSolution1."
}
|
eefdc942-aeb1-5541-8eea-843eb037d95d
| 605,719
|
Let $A B C$ be a triangle with $\overline{A B} \neq \overline{B C}$, and let $B D$ be the internal bisector of $\measuredangle A B C(D \in A C)$. Denote the midpoint of the arc $A C$ which contains point BbyM. The circumcircle of the triangle $B D M$ intersects the segment $A B$ at point $K \neq B$, and let $J$ be the reflection of $A$ with respect to $K$. If $D J \cap A M=\{O\}$, prove that the points $J, B, M, O$ belong to the same circle.
|
Let the circumcircle of the triangle $B D M$ intersect the line segment $B C$ at point $L \neq B$. From $\measuredangle C B D=\measuredangle D B A$ we have $\overline{D L}=\overline{D K}$. Since $\measuredangle L C M=\measuredangle B C M=\measuredangle B A M=\measuredangle K A M, \overline{M C}=\overline{M A}$ and
$$
\measuredangle L M C=\measuredangle L M K-\measuredangle C M K=\measuredangle L B K-\measuredangle C M K=\measuredangle C B A-\measuredangle C M K=\measuredangle C M A-\measuredangle C M K=\measuredangle K M A,
$$
it follows that triangles $M L C$ and $M K A$ are congruent, which implies $\overline{C L}=\overline{A K}=\overline{K J}$. Furthermore, $\measuredangle C L D=180^{\circ}-\measuredangle B L D=\measuredangle D K B=\measuredangle D K J$ and $\overline{D L}=\overline{D K}$, it follows that triangles $D C L$ and $D J K$ are congruent. Hence, $\angle D C L=\angle D J K=\measuredangle B J O$. Then
$$
\measuredangle B J O+\measuredangle B M O=\angle D C L+\angle B M A=\angle B C A+180^{\circ}-\angle B C A=180^{\circ}
$$
so the points $J, B, M, O$ belong to the same circle, q.e.d.
## Solution2.
Since $\overline{M C}=\overline{M A}$ and $\measuredangle C M A=\measuredangle C B A$, we have $\measuredangle A C M=\measuredangle C A M=90^{\circ}-\frac{\measuredangle C B A}{2}$. It follows that $\measuredangle M B D=\measuredangle M B A+\measuredangle A B D=\measuredangle A C M+\measuredangle A B D=90^{\circ}-\frac{\measuredangle C B A}{2}+\frac{\measuredangle C B A}{2}=90^{\circ}$. Denote the midpoint of $\overline{A C}$ by $N$. Since $\measuredangle D N M=\measuredangle C N M=90^{\circ}, N$ belongs to the circumcircle of the triangle $B D M$. Since $N K$ is the midline of the triangle $A C J$ and $N K \| C J$, we have
$$
\measuredangle B J C=\measuredangle B K N=180^{\circ}-\measuredangle N D B=\measuredangle C D B
$$
Hence, the quadrilateral $C D J B$ is cyclic (this can also be obtained from the power of a point theorem, because $\overline{A N} \cdot \overline{A D}=\overline{A K} \cdot \overline{A B}$ implies $\overline{A C} \cdot \overline{A D}=\overline{A J} \cdot \overline{A B}$ ), and
$$
\measuredangle B J O=\measuredangle 180^{\circ}-\measuredangle B J D=\angle B C D=\angle B C A=180^{\circ}-\angle B M A=180^{\circ}-\measuredangle B M O
$$
so the points $J, B, M, O$ belong to the same circle, q.e.d.
Remark. If $J$ is between $A$ and $K$ the solution can be easily adapted.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\overline{A B} \neq \overline{B C}$, and let $B D$ be the internal bisector of $\measuredangle A B C(D \in A C)$. Denote the midpoint of the arc $A C$ which contains point BbyM. The circumcircle of the triangle $B D M$ intersects the segment $A B$ at point $K \neq B$, and let $J$ be the reflection of $A$ with respect to $K$. If $D J \cap A M=\{O\}$, prove that the points $J, B, M, O$ belong to the same circle.
|

Let the circumcircle of the triangle $B D M$ intersect the line segment $B C$ at point $L \neq B$. From $\measuredangle C B D=\measuredangle D B A$ we have $\overline{D L}=\overline{D K}$. Since $\measuredangle L C M=\measuredangle B C M=\measuredangle B A M=\measuredangle K A M, \overline{M C}=\overline{M A}$ and
$$
\measuredangle L M C=\measuredangle L M K-\measuredangle C M K=\measuredangle L B K-\measuredangle C M K=\measuredangle C B A-\measuredangle C M K=\measuredangle C M A-\measuredangle C M K=\measuredangle K M A,
$$
it follows that triangles $M L C$ and $M K A$ are congruent, which implies $\overline{C L}=\overline{A K}=\overline{K J}$. Furthermore, $\measuredangle C L D=180^{\circ}-\measuredangle B L D=\measuredangle D K B=\measuredangle D K J$ and $\overline{D L}=\overline{D K}$, it follows that triangles $D C L$ and $D J K$ are congruent. Hence, $\angle D C L=\angle D J K=\measuredangle B J O$. Then
$$
\measuredangle B J O+\measuredangle B M O=\angle D C L+\angle B M A=\angle B C A+180^{\circ}-\angle B C A=180^{\circ}
$$
so the points $J, B, M, O$ belong to the same circle, q.e.d.
## Solution2.

Since $\overline{M C}=\overline{M A}$ and $\measuredangle C M A=\measuredangle C B A$, we have $\measuredangle A C M=\measuredangle C A M=90^{\circ}-\frac{\measuredangle C B A}{2}$. It follows that $\measuredangle M B D=\measuredangle M B A+\measuredangle A B D=\measuredangle A C M+\measuredangle A B D=90^{\circ}-\frac{\measuredangle C B A}{2}+\frac{\measuredangle C B A}{2}=90^{\circ}$. Denote the midpoint of $\overline{A C}$ by $N$. Since $\measuredangle D N M=\measuredangle C N M=90^{\circ}, N$ belongs to the circumcircle of the triangle $B D M$. Since $N K$ is the midline of the triangle $A C J$ and $N K \| C J$, we have
$$
\measuredangle B J C=\measuredangle B K N=180^{\circ}-\measuredangle N D B=\measuredangle C D B
$$
Hence, the quadrilateral $C D J B$ is cyclic (this can also be obtained from the power of a point theorem, because $\overline{A N} \cdot \overline{A D}=\overline{A K} \cdot \overline{A B}$ implies $\overline{A C} \cdot \overline{A D}=\overline{A J} \cdot \overline{A B}$ ), and
$$
\measuredangle B J O=\measuredangle 180^{\circ}-\measuredangle B J D=\angle B C D=\angle B C A=180^{\circ}-\angle B M A=180^{\circ}-\measuredangle B M O
$$
so the points $J, B, M, O$ belong to the same circle, q.e.d.
Remark. If $J$ is between $A$ and $K$ the solution can be easily adapted.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## G5",
"solution_match": "## Solution1."
}
|
6eb3724f-b022-5c23-a078-64185fd109eb
| 605,727
|
Let $A B C D$ be a quadrilateral whose sides $A B$ and $C D$ are not parallel, and let $O$ be the intersection of its diagonals. Denote with $H_{1}$ and $H_{2}$ the orthocenters of the triangles $O A B$ and OCD, respectively. If $M$ and $N$ are the midpoints of the segments $\overline{A B}$ and $\overline{C D}$, respectively, prove that the lines $M N$ and $\mathrm{H}_{1} \mathrm{H}_{2}$ are parallel if and only if $\overline{A C}=\overline{B D}$.
|
Let $A^{\prime}$ and $B^{\prime}$ be the feet of the altitudes drawn from $A$ and $B$ respectively in the triangle $A O B$, and $C^{\prime}$ and $D^{\prime}$ are the feet of the altitudes drawn from $C$ and $D$ in the triangle $C O D$. Obviously, $A^{\prime}$ and $D^{\prime}$ belong to the circle $c_{1}$ of diameter $\overline{A D}$, while $B^{\prime}$ and $C^{\prime}$ belong to the circle $c_{2}$ of diameter $\overline{B C}$.
It is easy to see that triangles $H_{1} A B$ and $H_{1} B^{\prime} A^{\prime}$ are similar. It follows that $\overline{H_{1} A} \cdot \overline{H_{1} A^{\prime}}=\overline{H_{1} B} \cdot \overline{H_{1} B^{\prime}}$. (Alternatively, one could notice that the quadrilateral $A B A^{\prime} B^{\prime}$ is cyclic and obtain the previous relation by writing the power of $H_{1}$ with respect to its circumcircle.) It
follows that $H_{1}$ has the same power with respect to circles $c_{1}$ and $c_{2}$. Thus, $H_{1}$ (and similarly, $\mathrm{H}_{2}$ ) is on the radical axis of the two circles.
The radical axis being perpendicular to the line joining the centers of the two circles, one concludes that $\mathrm{H}_{1} \mathrm{H}_{2}$ is perpendicular to $P Q$, where $P$ and $Q$ are the midpoints of the sides $\overline{A D}$ and $\overline{B C}$, respectively. ( $P$ and $Q$ are the centers of circles $c_{1}$ and $c_{2}$.)
The condition $H_{1} H_{2} \| M N$ is equivalent to $M N \perp P Q$. As $M P N Q$ is a parallelogram, we conclude that $H_{1} H_{2} \| M N \Leftrightarrow M N \perp P Q \Leftrightarrow M P N Q$ a rhombus $\Leftrightarrow \overline{M P}=\overline{M Q} \Leftrightarrow \overline{A C}=\overline{B D}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral whose sides $A B$ and $C D$ are not parallel, and let $O$ be the intersection of its diagonals. Denote with $H_{1}$ and $H_{2}$ the orthocenters of the triangles $O A B$ and OCD, respectively. If $M$ and $N$ are the midpoints of the segments $\overline{A B}$ and $\overline{C D}$, respectively, prove that the lines $M N$ and $\mathrm{H}_{1} \mathrm{H}_{2}$ are parallel if and only if $\overline{A C}=\overline{B D}$.
|

Let $A^{\prime}$ and $B^{\prime}$ be the feet of the altitudes drawn from $A$ and $B$ respectively in the triangle $A O B$, and $C^{\prime}$ and $D^{\prime}$ are the feet of the altitudes drawn from $C$ and $D$ in the triangle $C O D$. Obviously, $A^{\prime}$ and $D^{\prime}$ belong to the circle $c_{1}$ of diameter $\overline{A D}$, while $B^{\prime}$ and $C^{\prime}$ belong to the circle $c_{2}$ of diameter $\overline{B C}$.
It is easy to see that triangles $H_{1} A B$ and $H_{1} B^{\prime} A^{\prime}$ are similar. It follows that $\overline{H_{1} A} \cdot \overline{H_{1} A^{\prime}}=\overline{H_{1} B} \cdot \overline{H_{1} B^{\prime}}$. (Alternatively, one could notice that the quadrilateral $A B A^{\prime} B^{\prime}$ is cyclic and obtain the previous relation by writing the power of $H_{1}$ with respect to its circumcircle.) It
follows that $H_{1}$ has the same power with respect to circles $c_{1}$ and $c_{2}$. Thus, $H_{1}$ (and similarly, $\mathrm{H}_{2}$ ) is on the radical axis of the two circles.
The radical axis being perpendicular to the line joining the centers of the two circles, one concludes that $\mathrm{H}_{1} \mathrm{H}_{2}$ is perpendicular to $P Q$, where $P$ and $Q$ are the midpoints of the sides $\overline{A D}$ and $\overline{B C}$, respectively. ( $P$ and $Q$ are the centers of circles $c_{1}$ and $c_{2}$.)
The condition $H_{1} H_{2} \| M N$ is equivalent to $M N \perp P Q$. As $M P N Q$ is a parallelogram, we conclude that $H_{1} H_{2} \| M N \Leftrightarrow M N \perp P Q \Leftrightarrow M P N Q$ a rhombus $\Leftrightarrow \overline{M P}=\overline{M Q} \Leftrightarrow \overline{A C}=\overline{B D}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## G6",
"solution_match": "## Solution."
}
|
7f4fa619-ee2b-58a6-a703-8085786d811b
| 605,734
|
Prove there are no integers $a$ and $b$ satisfying the following conditions:
i) $16 a-9 b$ is a prime number
ii) $\quad a b$ is a perfect square
iii) $a+b$ is a perfect square
|
Suppose $a$ and $b$ be integers satisfying the given conditions. Let $p$ be a prime number, $n$ and $m$ be integers. Then we can write the conditions as follows:
$$
\begin{aligned}
& 16 a-9 b=p \\
& a b=n^{2} \\
& a+b=m^{2}
\end{aligned}
$$
Moreover, let $d=g d c(a, b)$ and $a=d x, b=d y$ for some relatively prime integers $x$ and $y$. Obviously $a \neq 0$ and $b \neq 0, a$ and $b$ are positive (by (2) and (3)).
From (2) follows that $x$ and $y$ are perfect squares, say $x=l^{2}$ and $y=s^{2}$.
From (1), $d \mid p$ and hence $d=p$ or $d=1$. If $d=p$, then $16 x-9 y=1$, and we obtain $x=9 k+4$, $y=16 k+7$ for some nonnegative integer $k$. But then $s^{2}=y \equiv 3(\bmod 4)$, which is a contradiction.
If $d=1$ then $16 l^{2}-9 s^{2}=p \Rightarrow(4 l-3 s)(4 l+3 s)=p \Rightarrow(4 l+3 s=p \wedge 4 l-3 s=1)$.
By adding the last two equations we get $8 l=p+1$ and by subtracting them we get $6 s=p-1$. Therefore $p=24 t+7$ for some integer $t$ and $a=(3 t+1)^{2}$ and $b=(4 t+1)^{2}$ satisfy the conditions (1) and (2). By (3) we have $m^{2}=(3 t+1)^{2}+(4 t+1)^{2}=25 t^{2}+14 t+2$, or equivalently $25 m^{2}=(25 t+7)^{2}+1$.
Since the difference between two nonzero perfect square cannot be 1 , we have a contradiction. As a result there is no solution.
## NS
Find all nonnegative integers $x, y, z$ such that
$$
2013^{x}+2014^{y}=2015^{z}
$$
Solution. Clearly, $y>0$, and $z>0$. If $x=0$ and $y=1$, then $z=1$ and $(x, y, z)=(0,1,1)$ is a solution. If $x=0$ and $y \geq 2$, then modulo 4 we have $1+0 \equiv(-1)^{z}$, hence $z$ is even $\left(z=2 z_{1}\right.$ for some integer $\left.z_{1}\right)$. Then $2^{y} 1007^{y}=\left(2015^{z_{1}}-1\right)\left(2015^{z_{1}}+1\right)$, and since $\operatorname{gcd}\left(1007,2015^{z_{1}}+1\right)=1$ we obtain $2 \cdot 1007^{y} \mid 2015^{z_{1}}-1$ and $2015^{z_{1}}+1 \mid 2^{y-1}$. From this we get $2015^{z_{1}}+1 \leq 2^{y-1}<2 \cdot 1007^{y} \leq 2015^{z_{1}}-1$, which is impossible.
Now for $x>0$, modulo 3 we get $0+1 \equiv(-1)^{z}$, hence $z$ must be even $\left(z=2 z_{1}\right.$ for some integer $z_{1}$ ). Modulo 2014 we get $(-1)^{x}+0 \equiv 1$, thus $x$ must be even $\left(x=2 x_{1}\right.$ for some integer $\left.x_{1}\right)$. We transform the equation to $2^{y} 1007^{y}=\left(2015^{z_{1}}-2013^{x_{1}}\right)\left(2015^{z_{1}}+2013^{x_{1}}\right)$ and since $\operatorname{gcd}\left(2015^{z_{1}}-2013^{x_{1}}, 2015^{z_{1}}+2013^{x_{1}}\right)=2,1007^{y}$ divides $2015^{z_{1}}-2013^{x_{1}}$ or $2015^{z_{1}}+2013^{x_{1}}$ but not both. If $1007^{y} \mid 2015^{z_{1}}-2013^{x_{1}}$, then $2015^{z_{1}}+2013^{x_{1}} \leq 2^{y}<1007^{y} \leq 2015^{z_{1}}-2013^{x_{1}}$, which is impossible. Hence $1007 \mid 2015^{z_{1}}+2013^{x_{1}}$, and from $2015^{z_{1}}+2013^{x_{1}} \equiv 1+(-1)^{x_{1}}(\bmod 1007), x_{1}$ is odd $\left(x=2 x_{1}=4 x_{2}+2\right.$ for some integer $\left.x_{2}\right)$.
Now modulo 5 we get $-1+(-1)^{y} \equiv(-2)^{4 x_{2}+2}+(-1)^{y} \equiv 0$, hence $y$ must be even $\left(y=2 y_{1}\right.$ for some integer $y_{1}$ ). Finally modulo 31 , we have $(-2)^{4 x_{2}+2}+(-1)^{2 y_{1}} \equiv 0$ or $4^{2 x_{2}+1} \equiv-1$. This is impossible since the reminders of the powers of 4 modulo 31 are 1, 2, 4, 8 and 16 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove there are no integers $a$ and $b$ satisfying the following conditions:
i) $16 a-9 b$ is a prime number
ii) $\quad a b$ is a perfect square
iii) $a+b$ is a perfect square
|
Suppose $a$ and $b$ be integers satisfying the given conditions. Let $p$ be a prime number, $n$ and $m$ be integers. Then we can write the conditions as follows:
$$
\begin{aligned}
& 16 a-9 b=p \\
& a b=n^{2} \\
& a+b=m^{2}
\end{aligned}
$$
Moreover, let $d=g d c(a, b)$ and $a=d x, b=d y$ for some relatively prime integers $x$ and $y$. Obviously $a \neq 0$ and $b \neq 0, a$ and $b$ are positive (by (2) and (3)).
From (2) follows that $x$ and $y$ are perfect squares, say $x=l^{2}$ and $y=s^{2}$.
From (1), $d \mid p$ and hence $d=p$ or $d=1$. If $d=p$, then $16 x-9 y=1$, and we obtain $x=9 k+4$, $y=16 k+7$ for some nonnegative integer $k$. But then $s^{2}=y \equiv 3(\bmod 4)$, which is a contradiction.
If $d=1$ then $16 l^{2}-9 s^{2}=p \Rightarrow(4 l-3 s)(4 l+3 s)=p \Rightarrow(4 l+3 s=p \wedge 4 l-3 s=1)$.
By adding the last two equations we get $8 l=p+1$ and by subtracting them we get $6 s=p-1$. Therefore $p=24 t+7$ for some integer $t$ and $a=(3 t+1)^{2}$ and $b=(4 t+1)^{2}$ satisfy the conditions (1) and (2). By (3) we have $m^{2}=(3 t+1)^{2}+(4 t+1)^{2}=25 t^{2}+14 t+2$, or equivalently $25 m^{2}=(25 t+7)^{2}+1$.
Since the difference between two nonzero perfect square cannot be 1 , we have a contradiction. As a result there is no solution.
## NS
Find all nonnegative integers $x, y, z$ such that
$$
2013^{x}+2014^{y}=2015^{z}
$$
Solution. Clearly, $y>0$, and $z>0$. If $x=0$ and $y=1$, then $z=1$ and $(x, y, z)=(0,1,1)$ is a solution. If $x=0$ and $y \geq 2$, then modulo 4 we have $1+0 \equiv(-1)^{z}$, hence $z$ is even $\left(z=2 z_{1}\right.$ for some integer $\left.z_{1}\right)$. Then $2^{y} 1007^{y}=\left(2015^{z_{1}}-1\right)\left(2015^{z_{1}}+1\right)$, and since $\operatorname{gcd}\left(1007,2015^{z_{1}}+1\right)=1$ we obtain $2 \cdot 1007^{y} \mid 2015^{z_{1}}-1$ and $2015^{z_{1}}+1 \mid 2^{y-1}$. From this we get $2015^{z_{1}}+1 \leq 2^{y-1}<2 \cdot 1007^{y} \leq 2015^{z_{1}}-1$, which is impossible.
Now for $x>0$, modulo 3 we get $0+1 \equiv(-1)^{z}$, hence $z$ must be even $\left(z=2 z_{1}\right.$ for some integer $z_{1}$ ). Modulo 2014 we get $(-1)^{x}+0 \equiv 1$, thus $x$ must be even $\left(x=2 x_{1}\right.$ for some integer $\left.x_{1}\right)$. We transform the equation to $2^{y} 1007^{y}=\left(2015^{z_{1}}-2013^{x_{1}}\right)\left(2015^{z_{1}}+2013^{x_{1}}\right)$ and since $\operatorname{gcd}\left(2015^{z_{1}}-2013^{x_{1}}, 2015^{z_{1}}+2013^{x_{1}}\right)=2,1007^{y}$ divides $2015^{z_{1}}-2013^{x_{1}}$ or $2015^{z_{1}}+2013^{x_{1}}$ but not both. If $1007^{y} \mid 2015^{z_{1}}-2013^{x_{1}}$, then $2015^{z_{1}}+2013^{x_{1}} \leq 2^{y}<1007^{y} \leq 2015^{z_{1}}-2013^{x_{1}}$, which is impossible. Hence $1007 \mid 2015^{z_{1}}+2013^{x_{1}}$, and from $2015^{z_{1}}+2013^{x_{1}} \equiv 1+(-1)^{x_{1}}(\bmod 1007), x_{1}$ is odd $\left(x=2 x_{1}=4 x_{2}+2\right.$ for some integer $\left.x_{2}\right)$.
Now modulo 5 we get $-1+(-1)^{y} \equiv(-2)^{4 x_{2}+2}+(-1)^{y} \equiv 0$, hence $y$ must be even $\left(y=2 y_{1}\right.$ for some integer $y_{1}$ ). Finally modulo 31 , we have $(-2)^{4 x_{2}+2}+(-1)^{2 y_{1}} \equiv 0$ or $4^{2 x_{2}+1} \equiv-1$. This is impossible since the reminders of the powers of 4 modulo 31 are 1, 2, 4, 8 and 16 .
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "\nN4",
"solution_match": "\nSolution."
}
|
79ac64dc-2c25-5b74-a662-b720ec3a11ec
| 605,760
|
Let $a, b, c$ be positive real numbers such that $a+b+c+a b+b c+c a+a b c=7$. Prove that
$$
\sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} \geq 6
$$
|
First we see that $x^{2}+y^{2}+1 \geq x y+x+y$. Indeed, this is equivalent to
$$
(x-y)^{2}+(x-1)^{2}+(y-1)^{2} \geq 0
$$
Therefore
$$
\begin{aligned}
& \sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} \\
\geq & \sqrt{a b+a+b+1}+\sqrt{b c+b+c+1}+\sqrt{c a+c+a+1} \\
= & \sqrt{(a+1)(b+1)}+\sqrt{(b+1)(a+1)}+\sqrt{(c+1)(a+1)}
\end{aligned}
$$
It follows from the AM-GM inequality that
$$
\begin{aligned}
& \sqrt{(a+1)(b+1)}+\sqrt{(b+1)(a+1)}+\sqrt{(c+1)(a+1)} \\
\geq & 3 \sqrt[3]{\sqrt{(a+1)(b+1)} \cdot \sqrt{(b+1)(a+1)} \cdot \sqrt{(c+1)(a+1)}} \\
= & 3 \sqrt[3]{(a+1)(b+1)(c+1)}
\end{aligned}
$$
On the other hand, the given condition is equivalent to $(a+1)(b+1)(c+1)=8$ and we get the desired inequality.
Obviously, equality is attained if and only if $a=b=c=1$.
Remark. The condition of positivity of $a, b, c$ is superfluous and the equality $\cdots=7$ can be replaced by the inequality $\cdots \geq 7$. Indeed, the above proof and the triangle inequality imply that
$$
\begin{aligned}
\sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} & \geq 3 \sqrt[3]{(|a|+1)(|b|+1)(|c|+1)} \\
& \geq 3 \sqrt[3]{|a+1| \cdot|b+1| \cdot|c+1|} \geq 6
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a+b+c+a b+b c+c a+a b c=7$. Prove that
$$
\sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} \geq 6
$$
|
First we see that $x^{2}+y^{2}+1 \geq x y+x+y$. Indeed, this is equivalent to
$$
(x-y)^{2}+(x-1)^{2}+(y-1)^{2} \geq 0
$$
Therefore
$$
\begin{aligned}
& \sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} \\
\geq & \sqrt{a b+a+b+1}+\sqrt{b c+b+c+1}+\sqrt{c a+c+a+1} \\
= & \sqrt{(a+1)(b+1)}+\sqrt{(b+1)(a+1)}+\sqrt{(c+1)(a+1)}
\end{aligned}
$$
It follows from the AM-GM inequality that
$$
\begin{aligned}
& \sqrt{(a+1)(b+1)}+\sqrt{(b+1)(a+1)}+\sqrt{(c+1)(a+1)} \\
\geq & 3 \sqrt[3]{\sqrt{(a+1)(b+1)} \cdot \sqrt{(b+1)(a+1)} \cdot \sqrt{(c+1)(a+1)}} \\
= & 3 \sqrt[3]{(a+1)(b+1)(c+1)}
\end{aligned}
$$
On the other hand, the given condition is equivalent to $(a+1)(b+1)(c+1)=8$ and we get the desired inequality.
Obviously, equality is attained if and only if $a=b=c=1$.
Remark. The condition of positivity of $a, b, c$ is superfluous and the equality $\cdots=7$ can be replaced by the inequality $\cdots \geq 7$. Indeed, the above proof and the triangle inequality imply that
$$
\begin{aligned}
\sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} & \geq 3 \sqrt[3]{(|a|+1)(|b|+1)(|c|+1)} \\
& \geq 3 \sqrt[3]{|a+1| \cdot|b+1| \cdot|c+1|} \geq 6
\end{aligned}
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2017_short_list.jsonl",
"problem_match": "\nA1.",
"solution_match": "\nSolution."
}
|
36da045a-2a1f-51a9-b459-319c7bed33a8
| 605,779
|
Let $a, b, c, d$ be real numbers such that $0 \leq a \leq b \leq c \leq d$. Prove the inequality
$$
a b^{3}+b c^{3}+c d^{3}+d a^{3} \geq a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}
$$
|
The inequality is equivalent to
$$
\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)^{2} \geq\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\right)^{2}
$$
By the Cauchy-Schwarz inequality,
$$
\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\right) \geq\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\right)^{2}
$$
Hence it is sufficient to prove that
$$
\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)^{2} \geq\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\right)
$$
i.e. to prove $a b^{3}+b c^{3}+c d^{3}+d a^{3} \geq a^{3} b+b^{3} c+c^{3} d+d^{3} a$.
This inequality can be written successively
$$
a\left(b^{3}-d^{3}\right)+b\left(c^{3}-a^{3}\right)+c\left(d^{3}-b^{3}\right)+d\left(a^{3}-c^{3}\right) \geq 0
$$
or
$$
(a-c)\left(b^{3}-d^{3}\right)-(b-d)\left(a^{3}-c^{3}\right) \geq 0
$$
which comes down to
$$
(a-c)(b-d)\left(b^{2}+b d+d^{2}-a^{2}-a c-c^{2}\right) \geq 0
$$
The last inequality is true because $a-c \leq 0, b-d \leq 0$, and $\left(b^{2}-a^{2}\right)+(b d-a c)+\left(d^{2}-c^{2}\right) \geq 0$ as a sum of three non-negative numbers.
The last inequality is satisfied with equality whence $a=b$ and $c=d$. Combining this with the equality cases in the Cauchy-Schwarz inequality we obtain the equality cases for the initial inequality: $a=b=c=d$.
Remark. Instead of using the Cauchy-Schwarz inequality, once the inequality $a b^{3}+b c^{3}+c d^{3}+$ $d a^{3} \geq a^{3} b+b^{3} c+c^{3} d+d^{3} a$ is established, we have $2\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right) \geq\left(a b^{3}+b c^{3}+c d^{3}+\right.$ $\left.d a^{3}\right)+\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\right)=\left(a b^{3}+a^{3} b\right)+\left(b c^{3}+b^{3} c\right)+\left(c d^{3}+c^{3} d\right)+\left(d a^{3}+d^{3} a\right) \stackrel{A M-G M}{\geq}$ $2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} d^{2}+2 d^{2} a^{2}$ which gives the conclusion.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c, d$ be real numbers such that $0 \leq a \leq b \leq c \leq d$. Prove the inequality
$$
a b^{3}+b c^{3}+c d^{3}+d a^{3} \geq a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}
$$
|
The inequality is equivalent to
$$
\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)^{2} \geq\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\right)^{2}
$$
By the Cauchy-Schwarz inequality,
$$
\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\right) \geq\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\right)^{2}
$$
Hence it is sufficient to prove that
$$
\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)^{2} \geq\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right)\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\right)
$$
i.e. to prove $a b^{3}+b c^{3}+c d^{3}+d a^{3} \geq a^{3} b+b^{3} c+c^{3} d+d^{3} a$.
This inequality can be written successively
$$
a\left(b^{3}-d^{3}\right)+b\left(c^{3}-a^{3}\right)+c\left(d^{3}-b^{3}\right)+d\left(a^{3}-c^{3}\right) \geq 0
$$
or
$$
(a-c)\left(b^{3}-d^{3}\right)-(b-d)\left(a^{3}-c^{3}\right) \geq 0
$$
which comes down to
$$
(a-c)(b-d)\left(b^{2}+b d+d^{2}-a^{2}-a c-c^{2}\right) \geq 0
$$
The last inequality is true because $a-c \leq 0, b-d \leq 0$, and $\left(b^{2}-a^{2}\right)+(b d-a c)+\left(d^{2}-c^{2}\right) \geq 0$ as a sum of three non-negative numbers.
The last inequality is satisfied with equality whence $a=b$ and $c=d$. Combining this with the equality cases in the Cauchy-Schwarz inequality we obtain the equality cases for the initial inequality: $a=b=c=d$.
Remark. Instead of using the Cauchy-Schwarz inequality, once the inequality $a b^{3}+b c^{3}+c d^{3}+$ $d a^{3} \geq a^{3} b+b^{3} c+c^{3} d+d^{3} a$ is established, we have $2\left(a b^{3}+b c^{3}+c d^{3}+d a^{3}\right) \geq\left(a b^{3}+b c^{3}+c d^{3}+\right.$ $\left.d a^{3}\right)+\left(a^{3} b+b^{3} c+c^{3} d+d^{3} a\right)=\left(a b^{3}+a^{3} b\right)+\left(b c^{3}+b^{3} c\right)+\left(c d^{3}+c^{3} d\right)+\left(d a^{3}+d^{3} a\right) \stackrel{A M-G M}{\geq}$ $2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} d^{2}+2 d^{2} a^{2}$ which gives the conclusion.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2017_short_list.jsonl",
"problem_match": "\nA3.",
"solution_match": "\nSolution."
}
|
965489cb-c880-5f7c-8dea-041165cdfcac
| 605,800
|
Let $x, y, z$ be three distinct positive integers. Prove that
$$
(x+y+z)(x y+y z+z x-2) \geq 9 x y z
$$
When does the equality hold?
|
Since $x, y, z$ are distinct positive integers, the required inequality is symmetric and WLOG we can suppose that $x \geq y+1 \geq z+2$. We consider 2 possible cases:
Case 1. $y \geq z+2$. Since $x \geq y+1 \geq z+3$ it follows that
$$
(x-y)^{2} \geq 1, \quad(y-z)^{2} \geq 4, \quad(x-z)^{2} \geq 9
$$
which are equivalent to
$$
x^{2}+y^{2} \geq 2 x y+1, \quad y^{2}+z^{2} \geq 2 y z+4, \quad x^{2}+z^{2} \geq 2 x z+9
$$
or otherwise
$$
z x^{2}+z y^{2} \geq 2 x y z+z, \quad x y^{2}+x z^{2} \geq 2 x y z+4 x, \quad y x^{2}+y z^{2} \geq 2 x y z+9 y
$$
Adding up the last three inequalities we have
$$
x y(x+y)+y z(y+z)+z x(z+x) \geq 6 x y z+4 x+9 y+z
$$
which implies that $(x+y+z)(x y+y z+z x-2) \geq 9 x y z+2 x+7 y-z$.
Since $x \geq z+3$ it follows that $2 x+7 y-z \geq 0$ and our inequality follows.
Case 2. $y=z+1$. Since $x \geq y+1=z+2$ it follows that $x \geq z+2$, and replacing $y=z+1$ in the required inequality we have to prove
$$
(x+z+1+z)(x(z+1)+(z+1) z+z x-2) \geq 9 x(z+1) z
$$
which is equivalent to
$$
(x+2 z+1)\left(z^{2}+2 z x+z+x-2\right)-9 x(z+1) z \geq 0
$$
Doing easy algebraic manipulations, this is equivalent to prove
$$
(x-z-2)(x-z+1)(2 z+1) \geq 0
$$
which is satisfied since $x \geq z+2$.
The equality is achieved only in the Case 2 for $x=z+2$, so we have equality when $(x, y, z)=$ $(k+2, k+1, k)$ and all the permutations for any positive integer $k$.
## Combinatorics
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y, z$ be three distinct positive integers. Prove that
$$
(x+y+z)(x y+y z+z x-2) \geq 9 x y z
$$
When does the equality hold?
|
Since $x, y, z$ are distinct positive integers, the required inequality is symmetric and WLOG we can suppose that $x \geq y+1 \geq z+2$. We consider 2 possible cases:
Case 1. $y \geq z+2$. Since $x \geq y+1 \geq z+3$ it follows that
$$
(x-y)^{2} \geq 1, \quad(y-z)^{2} \geq 4, \quad(x-z)^{2} \geq 9
$$
which are equivalent to
$$
x^{2}+y^{2} \geq 2 x y+1, \quad y^{2}+z^{2} \geq 2 y z+4, \quad x^{2}+z^{2} \geq 2 x z+9
$$
or otherwise
$$
z x^{2}+z y^{2} \geq 2 x y z+z, \quad x y^{2}+x z^{2} \geq 2 x y z+4 x, \quad y x^{2}+y z^{2} \geq 2 x y z+9 y
$$
Adding up the last three inequalities we have
$$
x y(x+y)+y z(y+z)+z x(z+x) \geq 6 x y z+4 x+9 y+z
$$
which implies that $(x+y+z)(x y+y z+z x-2) \geq 9 x y z+2 x+7 y-z$.
Since $x \geq z+3$ it follows that $2 x+7 y-z \geq 0$ and our inequality follows.
Case 2. $y=z+1$. Since $x \geq y+1=z+2$ it follows that $x \geq z+2$, and replacing $y=z+1$ in the required inequality we have to prove
$$
(x+z+1+z)(x(z+1)+(z+1) z+z x-2) \geq 9 x(z+1) z
$$
which is equivalent to
$$
(x+2 z+1)\left(z^{2}+2 z x+z+x-2\right)-9 x(z+1) z \geq 0
$$
Doing easy algebraic manipulations, this is equivalent to prove
$$
(x-z-2)(x-z+1)(2 z+1) \geq 0
$$
which is satisfied since $x \geq z+2$.
The equality is achieved only in the Case 2 for $x=z+2$, so we have equality when $(x, y, z)=$ $(k+2, k+1, k)$ and all the permutations for any positive integer $k$.
## Combinatorics
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2017_short_list.jsonl",
"problem_match": "\nA4.",
"solution_match": "\nSolution."
}
|
e587ca83-7628-504d-ad36-201c52fd886e
| 605,808
|
Given a parallelogram $A B C D$. The line perpendicular to $A C$ passing through $C$ and the line perpendicular to $B D$ passing through $A$ intersect at point $P$. The circle centered at point $P$ and radius $P C$ intersects the line $B C$ at point $X,(X \neq C)$ and the line $D C$ at point $Y$, $(Y \neq C)$. Prove that the line $A X$ passes through the point $Y$.
|
Denote the feet of the perpendiculars from $P$ to the lines $B C$ and $D C$ by $M$ and $N$ respectively and let $O=A C \cap B D$. Since the points $O, M$ and $N$ are midpoints of $C A, C X$ and $C Y$ respectively it suffices to prove that $M, N$ and $O$ are collinear. According to Menelaus's theorem for $\triangle B C D$ and points $M, N$ and $O$ we have to prove that
$$
\frac{B M}{M C} \cdot \frac{C N}{N D} \cdot \frac{D O}{O B}=1
$$
Since $D O=O B$ the above simplifies to $\frac{B M}{C M}=\frac{D N}{C N}$. It follows from $B M=B C+C M$ and $D N=D C-C N=A B-C N$ that the last equality is equivalent to:
$$
\frac{B C}{C M}+2=\frac{A B}{C N}
$$
Denote by $S$ the foot of the perpendicular from $B$ to $A C$. Since $\Varangle B C S=\Varangle C P M=\varphi$ and $\Varangle B A C=\Varangle A C D=\Varangle C P N=\psi$ we conclude that $\triangle C B S \sim \triangle P C M$ and $\triangle A B S \sim \triangle P C N$. Therefore
$$
\frac{C M}{B S}=\frac{C P}{B C} \text { and } \frac{C N}{B S}=\frac{C P}{A B}
$$
and thus,
$$
C M=\frac{C P . B S}{B C} \text { and } C N=\frac{C P . B S}{A B}
$$
Now equality (1) becomes $A B^{2}-B C^{2}=2 C P . B S$. It follows from
$$
A B^{2}-B C^{2}=A S^{2}-C S^{2}=(A S-C S)(A S+C S)=2 O S . A C
$$
that
$$
D C^{2}-B C^{2}=2 C P \cdot B S \Longleftrightarrow 2 O S \cdot A C=2 C P . B S \Longleftrightarrow O S \cdot A C=C P \cdot B S .
$$
Since $\Varangle A C P=\Varangle B S O=90^{\circ}$ and $\Varangle C A P=\Varangle S B O$ we conclude that $\triangle A C P \sim \triangle B S O$. This implies $O S . A C=C P . B S$, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a parallelogram $A B C D$. The line perpendicular to $A C$ passing through $C$ and the line perpendicular to $B D$ passing through $A$ intersect at point $P$. The circle centered at point $P$ and radius $P C$ intersects the line $B C$ at point $X,(X \neq C)$ and the line $D C$ at point $Y$, $(Y \neq C)$. Prove that the line $A X$ passes through the point $Y$.
|
Denote the feet of the perpendiculars from $P$ to the lines $B C$ and $D C$ by $M$ and $N$ respectively and let $O=A C \cap B D$. Since the points $O, M$ and $N$ are midpoints of $C A, C X$ and $C Y$ respectively it suffices to prove that $M, N$ and $O$ are collinear. According to Menelaus's theorem for $\triangle B C D$ and points $M, N$ and $O$ we have to prove that

$$
\frac{B M}{M C} \cdot \frac{C N}{N D} \cdot \frac{D O}{O B}=1
$$
Since $D O=O B$ the above simplifies to $\frac{B M}{C M}=\frac{D N}{C N}$. It follows from $B M=B C+C M$ and $D N=D C-C N=A B-C N$ that the last equality is equivalent to:
$$
\frac{B C}{C M}+2=\frac{A B}{C N}
$$
Denote by $S$ the foot of the perpendicular from $B$ to $A C$. Since $\Varangle B C S=\Varangle C P M=\varphi$ and $\Varangle B A C=\Varangle A C D=\Varangle C P N=\psi$ we conclude that $\triangle C B S \sim \triangle P C M$ and $\triangle A B S \sim \triangle P C N$. Therefore
$$
\frac{C M}{B S}=\frac{C P}{B C} \text { and } \frac{C N}{B S}=\frac{C P}{A B}
$$
and thus,
$$
C M=\frac{C P . B S}{B C} \text { and } C N=\frac{C P . B S}{A B}
$$
Now equality (1) becomes $A B^{2}-B C^{2}=2 C P . B S$. It follows from
$$
A B^{2}-B C^{2}=A S^{2}-C S^{2}=(A S-C S)(A S+C S)=2 O S . A C
$$
that
$$
D C^{2}-B C^{2}=2 C P \cdot B S \Longleftrightarrow 2 O S \cdot A C=2 C P . B S \Longleftrightarrow O S \cdot A C=C P \cdot B S .
$$
Since $\Varangle A C P=\Varangle B S O=90^{\circ}$ and $\Varangle C A P=\Varangle S B O$ we conclude that $\triangle A C P \sim \triangle B S O$. This implies $O S . A C=C P . B S$, which completes the proof.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2017_short_list.jsonl",
"problem_match": "\nG1.",
"solution_match": "\nSolution."
}
|
4b43a956-0507-5cc0-9d22-9fe2d3d2f167
| 605,847
|
Let $A B C$ be an acute triangle such that $A B$ is the shortest side of the triangle. Let $D$ be the midpoint of the side $A B$ and $P$ be an interior point of the triangle such that
$$
\Varangle C A P=\Varangle C B P=\Varangle A C B
$$
Denote by $M$ and $N$ the feet of the perpendiculars from $P$ to $B C$ and $A C$, respectively. Let $p$ be the line through $M$ parallel to $A C$ and $q$ be the line through $N$ parallel to $B C$. If $p$ and $q$ intersect at $K$ prove that $D$ is the circumcenter of triangle $M N K$.
|
If $\gamma=\Varangle A C B$ then $\Varangle C A P=\Varangle C B P=\Varangle A C B=\gamma$. Let $E=K N \cap A P$ and $F=K M \cap B P$. We show that points $E$ and $F$ are midpoints of $A P$ and $B P$, respectively.
Indeed, consider the triangle $A E N$. Since $K N \| B C$, we have $\Varangle E N A=\Varangle B C A=\gamma$. Moreover $\Varangle E A N=\gamma$ giving that triangle $A E N$ is isosceles, i.e. $A E=E N$. Next, consider the triangle $E N P$. Since $\Varangle E N A=\gamma$ we find that
$$
\Varangle P N E=90^{\circ}-\Varangle E N A=90^{\circ}-\gamma
$$
Now $\Varangle E P N=90^{\circ}-\gamma$ implies that the triangle $E N P$ is isosceles triangle, i.e. $E N=E P$.
Since $A E=E N=E P$ point $E$ is the midpoint of $A P$ and analogously, $F$ is the midpoint of $B P$. Moreover, $D$ is also midpoint of $A B$ and we conclude that $D F P E$ is parallelogram.
It follows from $D E \| A P$ and $K E \| B C$ that $\Varangle D E K=\Varangle C B P=\gamma$ and analogously $\Varangle D F K=\gamma$.
We conclude that $\triangle E D N \cong \triangle F M D(E D=F P=F M, E N=E P=F D$ and $\Varangle D E N=$ $\left.\Varangle M F D=180^{\circ}-\gamma\right)$ and thus $N D=M D$. Therefore $D$ is a point on the perpendicular bisector of $M N$. Further,
$$
\begin{aligned}
\Varangle F D E & =\Varangle F P E=360^{\circ}-\Varangle B P M-\Varangle M P N-\Varangle N P A= \\
& =360^{\circ}-\left(90^{\circ}-\gamma\right)-\left(180^{\circ}-\gamma\right)-\left(90^{\circ}-\gamma\right)=3 \gamma
\end{aligned}
$$
It follows that
$$
\begin{aligned}
\Varangle M D N & =\Varangle F D E-\Varangle F D M-\Varangle E D N=\Varangle F D E-\Varangle E N D-\Varangle E D N= \\
& =\Varangle F D E-(\Varangle E N D+\Varangle E D N)=3 \gamma-\gamma=2 \gamma .
\end{aligned}
$$
Fianlly, $K M C N$ is parallelogram, i.e. $\Varangle M K N=\Varangle M C N=\gamma$. Therefore $D$ is a point on the perpendicular bisector of $M N$ and $\Varangle M D N=2 \Varangle M K N$, so $D$ is the circumcenter of $\triangle M N K$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle such that $A B$ is the shortest side of the triangle. Let $D$ be the midpoint of the side $A B$ and $P$ be an interior point of the triangle such that
$$
\Varangle C A P=\Varangle C B P=\Varangle A C B
$$
Denote by $M$ and $N$ the feet of the perpendiculars from $P$ to $B C$ and $A C$, respectively. Let $p$ be the line through $M$ parallel to $A C$ and $q$ be the line through $N$ parallel to $B C$. If $p$ and $q$ intersect at $K$ prove that $D$ is the circumcenter of triangle $M N K$.
|
If $\gamma=\Varangle A C B$ then $\Varangle C A P=\Varangle C B P=\Varangle A C B=\gamma$. Let $E=K N \cap A P$ and $F=K M \cap B P$. We show that points $E$ and $F$ are midpoints of $A P$ and $B P$, respectively.

Indeed, consider the triangle $A E N$. Since $K N \| B C$, we have $\Varangle E N A=\Varangle B C A=\gamma$. Moreover $\Varangle E A N=\gamma$ giving that triangle $A E N$ is isosceles, i.e. $A E=E N$. Next, consider the triangle $E N P$. Since $\Varangle E N A=\gamma$ we find that
$$
\Varangle P N E=90^{\circ}-\Varangle E N A=90^{\circ}-\gamma
$$
Now $\Varangle E P N=90^{\circ}-\gamma$ implies that the triangle $E N P$ is isosceles triangle, i.e. $E N=E P$.
Since $A E=E N=E P$ point $E$ is the midpoint of $A P$ and analogously, $F$ is the midpoint of $B P$. Moreover, $D$ is also midpoint of $A B$ and we conclude that $D F P E$ is parallelogram.
It follows from $D E \| A P$ and $K E \| B C$ that $\Varangle D E K=\Varangle C B P=\gamma$ and analogously $\Varangle D F K=\gamma$.
We conclude that $\triangle E D N \cong \triangle F M D(E D=F P=F M, E N=E P=F D$ and $\Varangle D E N=$ $\left.\Varangle M F D=180^{\circ}-\gamma\right)$ and thus $N D=M D$. Therefore $D$ is a point on the perpendicular bisector of $M N$. Further,
$$
\begin{aligned}
\Varangle F D E & =\Varangle F P E=360^{\circ}-\Varangle B P M-\Varangle M P N-\Varangle N P A= \\
& =360^{\circ}-\left(90^{\circ}-\gamma\right)-\left(180^{\circ}-\gamma\right)-\left(90^{\circ}-\gamma\right)=3 \gamma
\end{aligned}
$$
It follows that
$$
\begin{aligned}
\Varangle M D N & =\Varangle F D E-\Varangle F D M-\Varangle E D N=\Varangle F D E-\Varangle E N D-\Varangle E D N= \\
& =\Varangle F D E-(\Varangle E N D+\Varangle E D N)=3 \gamma-\gamma=2 \gamma .
\end{aligned}
$$
Fianlly, $K M C N$ is parallelogram, i.e. $\Varangle M K N=\Varangle M C N=\gamma$. Therefore $D$ is a point on the perpendicular bisector of $M N$ and $\Varangle M D N=2 \Varangle M K N$, so $D$ is the circumcenter of $\triangle M N K$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2017_short_list.jsonl",
"problem_match": "\nG2.",
"solution_match": "\nSolution."
}
|
2ecdcace-1a6f-580a-86c7-21dd1018d830
| 605,858
|
Consider triangle $A B C$ such that $A B \leq A C$. Point $D$ on the arc $B C$ of the circumcirle of $A B C$ not containing point $A$ and point $E$ on side $B C$ are such that
$$
\Varangle B A D=\Varangle C A E<\frac{1}{2} \Varangle B A C .
$$
Let $S$ be the midpoint of segment $A D$. If $\Varangle A D E=\Varangle A B C-\Varangle A C B$ prove that
$$
\Varangle B S C=2 \Varangle B A C
$$
|
Let the tangent to the circumcircle of $\triangle A B C$ at point $A$ intersect line $B C$ at $T$. Since $A B \leq A C$ we get that $B$ lies between $T$ and $C$. Since $\Varangle B A T=\Varangle A C B$ and $\Varangle A B T=\Varangle 180^{\circ}-\Varangle A B C$ we get $\Varangle E T A=\Varangle B T A=\Varangle A B C-\Varangle A C B=\Varangle A D E$ which gives that $A, E, D, T$ are concyclic. Since
$$
\Varangle T D B+\Varangle B C A=\Varangle T D B+\Varangle B D A=\Varangle T D A=\Varangle A E T=\Varangle A C B+\Varangle E A C
$$
this means $\Varangle T D B=\Varangle E A C=\Varangle D A B$ which means that $T D$ is tangent to the circumcircle of $\triangle A B C$ at point $D$.
Using similar triangles $T A B$ and $T C A$ we get
$$
\frac{A B}{A C}=\frac{T A}{T C}
$$
Using similar triangles $T B D$ and $T D C$ we get
$$
\frac{B D}{C D}=\frac{T D}{T C}
$$
Using the fact that $T A=T D$ with (1) and (2) we get
$$
\frac{A B}{A C}=\frac{B D}{C D}
$$
Now since $\Varangle D A B=\Varangle C A E$ and $\Varangle B D A=\Varangle E C A$ we get that the triangles $D A B$ and $C A E$ are similar. Analogously, we get that triangles $C A D$ and $E A B$ are similar. These similarities give us
$$
\frac{D B}{C E}=\frac{A B}{A E} \quad \text { and } \quad \frac{C D}{E B}=\frac{C A}{E A}
$$
which, when combined with (3) give us $B E=C E$ giving $E$ is the midpoint of side $B C$.
Using the fact that triangles $D A B$ and $C A E$ are similar with the fact that $E$ is the midpoint of $B C$ we get:
$$
\frac{2 D S}{C A}=\frac{D A}{C A}=\frac{D B}{C E}=\frac{D B}{\frac{C B}{2}}=\frac{2 D B}{C B}
$$
implying that
$$
\frac{D S}{D B}=\frac{C A}{C B}
$$
Since $\Varangle S D B=\Varangle A D B=\Varangle A C B$ we get from (4) that the triangles $S D B$ and $A C B$ are similar, giving us $\Varangle B S D=\Varangle B A C$. Analogously we get $\triangle S D C$ and $\triangle A B C$ are similar we get $\Varangle C S D=\Varangle C A B$. Combining the last two equalities we get
$$
2 \Varangle B A C=\Varangle B A C+\Varangle C A B=\Varangle C S D+\Varangle B S D=\Varangle C S B
$$
This completes the proof.
## Alternative solution (PSC).
Lemma 1. A point $P$ is such that $\Varangle P X Y=\Varangle P Y Z$ and $\Varangle P Z Y=\Varangle P Y X$. If $R$ is the midpoint of $X Z$ then $\Varangle X Y P=\Varangle Z Y R$.
Proof. We consider the case when $P$ is inside the triangle $X Y Z$ (the other case is treated in similar way). Let $Q$ be the conjugate of $P$ in $\triangle X Y Z$ and let $Y Q$ intersects $X Z$ at $S$.
Then $\Varangle Q X Z=\Varangle Q Y X$ and $\Varangle Q Z X=\Varangle Q Y Z$ and therefore $\triangle S X Y \sim \triangle S Q X$ and $\triangle S Z Y \sim$ $\triangle S Q Z$. Thus $S X^{2}=S Q . S Y=S Z^{2}$ and we conclude that $S \equiv R$. This completes the proof of the Lemma.
For $\triangle D C A$ we have $\Varangle C D E=\Varangle E C A$ and $\Varangle E A C=\Varangle E C D$. By the Lemma 1 for $\triangle D C A$ and point $E$ we have that $\Varangle S C A=\Varangle D C E$. Therefore
$$
\Varangle D S C=\Varangle S A C+\Varangle S C A=\Varangle S A C+\Varangle D C E=\Varangle S A C+\Varangle B A D=\Varangle B A C .
$$
By analogy, Lemma 1 applied for $\triangle B D A$ and point $E$ gives $\Varangle B S D=\Varangle B A C$. Thus, $\Varangle B S C=$ $2 \Varangle B A C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider triangle $A B C$ such that $A B \leq A C$. Point $D$ on the arc $B C$ of the circumcirle of $A B C$ not containing point $A$ and point $E$ on side $B C$ are such that
$$
\Varangle B A D=\Varangle C A E<\frac{1}{2} \Varangle B A C .
$$
Let $S$ be the midpoint of segment $A D$. If $\Varangle A D E=\Varangle A B C-\Varangle A C B$ prove that
$$
\Varangle B S C=2 \Varangle B A C
$$
|
Let the tangent to the circumcircle of $\triangle A B C$ at point $A$ intersect line $B C$ at $T$. Since $A B \leq A C$ we get that $B$ lies between $T$ and $C$. Since $\Varangle B A T=\Varangle A C B$ and $\Varangle A B T=\Varangle 180^{\circ}-\Varangle A B C$ we get $\Varangle E T A=\Varangle B T A=\Varangle A B C-\Varangle A C B=\Varangle A D E$ which gives that $A, E, D, T$ are concyclic. Since
$$
\Varangle T D B+\Varangle B C A=\Varangle T D B+\Varangle B D A=\Varangle T D A=\Varangle A E T=\Varangle A C B+\Varangle E A C
$$
this means $\Varangle T D B=\Varangle E A C=\Varangle D A B$ which means that $T D$ is tangent to the circumcircle of $\triangle A B C$ at point $D$.

Using similar triangles $T A B$ and $T C A$ we get
$$
\frac{A B}{A C}=\frac{T A}{T C}
$$
Using similar triangles $T B D$ and $T D C$ we get
$$
\frac{B D}{C D}=\frac{T D}{T C}
$$
Using the fact that $T A=T D$ with (1) and (2) we get
$$
\frac{A B}{A C}=\frac{B D}{C D}
$$
Now since $\Varangle D A B=\Varangle C A E$ and $\Varangle B D A=\Varangle E C A$ we get that the triangles $D A B$ and $C A E$ are similar. Analogously, we get that triangles $C A D$ and $E A B$ are similar. These similarities give us
$$
\frac{D B}{C E}=\frac{A B}{A E} \quad \text { and } \quad \frac{C D}{E B}=\frac{C A}{E A}
$$
which, when combined with (3) give us $B E=C E$ giving $E$ is the midpoint of side $B C$.
Using the fact that triangles $D A B$ and $C A E$ are similar with the fact that $E$ is the midpoint of $B C$ we get:
$$
\frac{2 D S}{C A}=\frac{D A}{C A}=\frac{D B}{C E}=\frac{D B}{\frac{C B}{2}}=\frac{2 D B}{C B}
$$
implying that
$$
\frac{D S}{D B}=\frac{C A}{C B}
$$
Since $\Varangle S D B=\Varangle A D B=\Varangle A C B$ we get from (4) that the triangles $S D B$ and $A C B$ are similar, giving us $\Varangle B S D=\Varangle B A C$. Analogously we get $\triangle S D C$ and $\triangle A B C$ are similar we get $\Varangle C S D=\Varangle C A B$. Combining the last two equalities we get
$$
2 \Varangle B A C=\Varangle B A C+\Varangle C A B=\Varangle C S D+\Varangle B S D=\Varangle C S B
$$
This completes the proof.
## Alternative solution (PSC).
Lemma 1. A point $P$ is such that $\Varangle P X Y=\Varangle P Y Z$ and $\Varangle P Z Y=\Varangle P Y X$. If $R$ is the midpoint of $X Z$ then $\Varangle X Y P=\Varangle Z Y R$.
Proof. We consider the case when $P$ is inside the triangle $X Y Z$ (the other case is treated in similar way). Let $Q$ be the conjugate of $P$ in $\triangle X Y Z$ and let $Y Q$ intersects $X Z$ at $S$.

Then $\Varangle Q X Z=\Varangle Q Y X$ and $\Varangle Q Z X=\Varangle Q Y Z$ and therefore $\triangle S X Y \sim \triangle S Q X$ and $\triangle S Z Y \sim$ $\triangle S Q Z$. Thus $S X^{2}=S Q . S Y=S Z^{2}$ and we conclude that $S \equiv R$. This completes the proof of the Lemma.
For $\triangle D C A$ we have $\Varangle C D E=\Varangle E C A$ and $\Varangle E A C=\Varangle E C D$. By the Lemma 1 for $\triangle D C A$ and point $E$ we have that $\Varangle S C A=\Varangle D C E$. Therefore
$$
\Varangle D S C=\Varangle S A C+\Varangle S C A=\Varangle S A C+\Varangle D C E=\Varangle S A C+\Varangle B A D=\Varangle B A C .
$$
By analogy, Lemma 1 applied for $\triangle B D A$ and point $E$ gives $\Varangle B S D=\Varangle B A C$. Thus, $\Varangle B S C=$ $2 \Varangle B A C$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2017_short_list.jsonl",
"problem_match": "\nProblem G3.",
"solution_match": "\nSolution."
}
|
c8c51719-ae34-573f-9331-1566c99ec5e2
| 605,873
|
Let $A B C$ be a scalene triangle with circumcircle $\Gamma$ and circumcenter $O$. Let $M$ be the midpoint of $B C$ and $D$ be a point on $\Gamma$ such that $A D \perp B C$. Let $T$ be a point such that $B D C T$ is a parallelogram and $Q$ a point on the same side of $B C$ as $A$ such that
$$
\Varangle B Q M=\Varangle B C A \quad \text { and } \quad \Varangle C Q M=\Varangle C B A
$$
Let $A O$ intersect $\Gamma$ again at $E$ and let the circumcircle of $E T Q$ intersect $\Gamma$ at point $X \neq E$. Prove that the points $A, M$, and $X$ are collinear.
|
Let $X^{\prime}$ be symmetric point to $Q$ in line $B C$. Now since $\Varangle C B A=\Varangle C Q M=$ $\Varangle C X^{\prime} M, \Varangle B C A=\Varangle B Q M=\Varangle B X^{\prime} M$, we have
$$
\Varangle B X^{\prime} C=\Varangle B X^{\prime} M+\Varangle C X^{\prime} M=\Varangle C B A+\Varangle B C A=180^{\circ}-\Varangle B A C
$$
we have that $X^{\prime} \in \Gamma$. Now since $\Varangle A X^{\prime} B=\Varangle A C B=\Varangle M X^{\prime} B$ we have that $A, M, X^{\prime}$ are collinear. Note that since
$$
\Varangle D C B=\Varangle D A B=90^{\circ}-\Varangle A B C=\Varangle O A C=\Varangle E A C
$$
we get that $D B C E$ is an isosceles trapezoid.
Since $B D C T$ is a parallelogram we have $M T=M D$, with $M, D, T$ being collinear, $B D=C T$, and since $B D E C$ is an isosceles trapezoid we have $B D=C E$ and $M E=M D$. Since
$$
\Varangle B T C=\Varangle B D C=\Varangle B E D, \quad C E=B D=C T \quad \text { and } \quad M E=M T
$$
we have that $E$ and $T$ are symmetric with respect to the line $B C$. Now since $Q$ and $X^{\prime}$ are symmetric with respect to the line $B C$ as well, this means that $Q X^{\prime} E T$ is an isosceles trapezoid which means that $Q, X^{\prime}, E, T$ are concyclic. Since $X^{\prime} \in \Gamma$ this means that $X \equiv X^{\prime}$ and therefore $A, M, X$ are collinear.
Alternative solution (PSC). Denote by $H$ the orthocenter of $\triangle A B C$. We use the following well known properties:
(i) Point $D$ is the symmetric point of $H$ with respect to $B C$. Indeed, if $H_{1}$ is the symmetric point of $H$ with respect to $B C$ then $\Varangle B H_{1} C+\Varangle B A C=180^{\circ}$ and therefore $H_{1} \equiv D$.
(ii) The symmetric point of $H$ with respect to $M$ is the point $E$. Indeed, if $H_{2}$ is the symmetric point of $H$ with respect to $M$ then $B H_{2} C H$ is parallelogram, $\Varangle B H_{2} C+\Varangle B A C=180^{\circ}$ and since $E B \| C H$ we have $\Varangle E B A=90^{\circ}$.
Since $D E T H$ is a parallelogram and $M H=M D$ we have that $D E T H$ is a rectangle. Therefore $M T=M E$ and $T E \perp B C$ implying that $T$ and $E$ are symmetric with respect to $B C$. Denote by $Q^{\prime}$ the symmetric point of $Q$ with respect to $B C$. Then $Q^{\prime} E T Q$ is isosceles trapezoid, so $Q^{\prime}$ is a point on the circumcircle of $\triangle E T Q$. Moreover $\Varangle B Q^{\prime} C+\Varangle B A C=180^{\circ}$ and we conclude that $Q^{\prime} \in \Gamma$. Therefore $Q^{\prime} \equiv X$.
It remains to observe that $\Varangle C X M=\Varangle C Q M=\Varangle C B A$ and $\Varangle C X A=\Varangle C B A$ and we infer that $X, M$ and $A$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle with circumcircle $\Gamma$ and circumcenter $O$. Let $M$ be the midpoint of $B C$ and $D$ be a point on $\Gamma$ such that $A D \perp B C$. Let $T$ be a point such that $B D C T$ is a parallelogram and $Q$ a point on the same side of $B C$ as $A$ such that
$$
\Varangle B Q M=\Varangle B C A \quad \text { and } \quad \Varangle C Q M=\Varangle C B A
$$
Let $A O$ intersect $\Gamma$ again at $E$ and let the circumcircle of $E T Q$ intersect $\Gamma$ at point $X \neq E$. Prove that the points $A, M$, and $X$ are collinear.
|
Let $X^{\prime}$ be symmetric point to $Q$ in line $B C$. Now since $\Varangle C B A=\Varangle C Q M=$ $\Varangle C X^{\prime} M, \Varangle B C A=\Varangle B Q M=\Varangle B X^{\prime} M$, we have
$$
\Varangle B X^{\prime} C=\Varangle B X^{\prime} M+\Varangle C X^{\prime} M=\Varangle C B A+\Varangle B C A=180^{\circ}-\Varangle B A C
$$
we have that $X^{\prime} \in \Gamma$. Now since $\Varangle A X^{\prime} B=\Varangle A C B=\Varangle M X^{\prime} B$ we have that $A, M, X^{\prime}$ are collinear. Note that since
$$
\Varangle D C B=\Varangle D A B=90^{\circ}-\Varangle A B C=\Varangle O A C=\Varangle E A C
$$
we get that $D B C E$ is an isosceles trapezoid.

Since $B D C T$ is a parallelogram we have $M T=M D$, with $M, D, T$ being collinear, $B D=C T$, and since $B D E C$ is an isosceles trapezoid we have $B D=C E$ and $M E=M D$. Since
$$
\Varangle B T C=\Varangle B D C=\Varangle B E D, \quad C E=B D=C T \quad \text { and } \quad M E=M T
$$
we have that $E$ and $T$ are symmetric with respect to the line $B C$. Now since $Q$ and $X^{\prime}$ are symmetric with respect to the line $B C$ as well, this means that $Q X^{\prime} E T$ is an isosceles trapezoid which means that $Q, X^{\prime}, E, T$ are concyclic. Since $X^{\prime} \in \Gamma$ this means that $X \equiv X^{\prime}$ and therefore $A, M, X$ are collinear.
Alternative solution (PSC). Denote by $H$ the orthocenter of $\triangle A B C$. We use the following well known properties:
(i) Point $D$ is the symmetric point of $H$ with respect to $B C$. Indeed, if $H_{1}$ is the symmetric point of $H$ with respect to $B C$ then $\Varangle B H_{1} C+\Varangle B A C=180^{\circ}$ and therefore $H_{1} \equiv D$.
(ii) The symmetric point of $H$ with respect to $M$ is the point $E$. Indeed, if $H_{2}$ is the symmetric point of $H$ with respect to $M$ then $B H_{2} C H$ is parallelogram, $\Varangle B H_{2} C+\Varangle B A C=180^{\circ}$ and since $E B \| C H$ we have $\Varangle E B A=90^{\circ}$.
Since $D E T H$ is a parallelogram and $M H=M D$ we have that $D E T H$ is a rectangle. Therefore $M T=M E$ and $T E \perp B C$ implying that $T$ and $E$ are symmetric with respect to $B C$. Denote by $Q^{\prime}$ the symmetric point of $Q$ with respect to $B C$. Then $Q^{\prime} E T Q$ is isosceles trapezoid, so $Q^{\prime}$ is a point on the circumcircle of $\triangle E T Q$. Moreover $\Varangle B Q^{\prime} C+\Varangle B A C=180^{\circ}$ and we conclude that $Q^{\prime} \in \Gamma$. Therefore $Q^{\prime} \equiv X$.
It remains to observe that $\Varangle C X M=\Varangle C Q M=\Varangle C B A$ and $\Varangle C X A=\Varangle C B A$ and we infer that $X, M$ and $A$ are collinear.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2017_short_list.jsonl",
"problem_match": "\nProblem G4.",
"solution_match": "\nSolution."
}
|
c595c84c-907a-5232-9cf7-0a732dfaa7da
| 605,879
|
A point $P$ lies in the interior of the triangle $A B C$. The lines $A P, B P$, and $C P$ intersect $B C, C A$, and $A B$ at points $D, E$, and $F$, respectively. Prove that if two of the quadrilaterals $A B D E, B C E F, C A F D, A E P F, B F P D$, and $C D P E$ are concyclic, then all six are concyclic.
|
We first prove the following lemma:
Lemma 1. Let $A B C D$ be a convex quadrilateral and let $A B \cap C D=E$ and $B C \cap D A=F$. Then the circumcircles of triangles $A B F, C D F, B C E$ and $D A E$ all pass through a common point $P$. This point lies on line $E F$ if and only if $A B C D$ in concyclic.
Proof. Let the circumcircles of $A B F$ and $B C F$ intersect at $P \neq B$. We have
$$
\begin{aligned}
\Varangle F P C & =\Varangle F P B+\Varangle B P C=\Varangle B A D+\Varangle B E C=\Varangle E A D+\Varangle A E D= \\
& =180^{\circ}-\Varangle A D E=180^{\circ}-\Varangle F D C
\end{aligned}
$$
which gives us $F, P, C$ and $D$ are concyclic. Similarly we have
$$
\begin{aligned}
\Varangle A P E & =\Varangle A P B+\Varangle B P E=\Varangle A F B+\Varangle B C D=\Varangle D F C+\Varangle F C D= \\
& =180^{\circ}-\Varangle F D C=180^{\circ}-\Varangle A D E
\end{aligned}
$$
which gives us $E, P, A$ and $D$ are concyclic. Since $\Varangle F P E=\Varangle F P B+\Varangle E P B=\Varangle B A D+$ $\Varangle B C D$ we get that $\Varangle F P E=180^{\circ}$ if and only if $\Varangle B A D+\Varangle B C D=180^{\circ}$ which completes the lemma. We now divide the problem into cases:
Case 1: $A E P F$ and $B F E C$ are concyclic. Here we get that
$$
180^{\circ}=\Varangle A E P+\Varangle A F P=360^{\circ}-\Varangle C E B-\Varangle B F C=360^{\circ}-2 \Varangle C E B
$$
and here we get that $\Varangle C E B=\Varangle C F B=90^{\circ}$, from here it follows that $P$ is the ortocenter of $\triangle A B C$ and that gives us $\Varangle A D B=\Varangle A D C=90^{\circ}$. Now the quadrilaterals $C E P D$ and $B D P F$ are concyclic because
$$
\Varangle C E P=\Varangle C D P=\Varangle P D B=\Varangle P F B=90^{\circ} .
$$
Quadrilaterals $A C D F$ and $A B D E$ are concyclic because
$$
\Varangle A E B=\Varangle A D B=\Varangle A D C=\Varangle A F C=90^{\circ}
$$
Case 2: $A E P F$ and $C E P D$ are concyclic. Now by lemma 1 applied to the quadrilateral $A E P F$ we get that the circumcircles of $C E P, C A F, B P F$ and $B E A$ intersect at a point on $B C$. Since $D \in B C$ and $C E P D$ is concyclic we get that $D$ is the desired point and it follows that $B D P F, B A E D, C A F D$ are all concylic and now we can finish same as Case 1 since $A E D B$ and $C E P D$ are concyclic.
Case 3: $A E P F$ and $A E D B$ are concyclic. We apply lemma 1 as in Case 2 on the quadrilateral $A E P F$. From the lemma we get that $B D P F, C E P D$ and $C A F D$ are concylic and we finish off the same as in Case 1.
Case 4: $A C D F$ and $A B D E$ are concyclic. We apply lemma 1 on the quadrilateral $A E P F$ and get that the circumcircles of $A C F, E C P, P F B$ and $B A E$ intersect at one point. Since this point is $D$ (because $A C D F$ and $A B D E$ are concyclic) we get that $A E P F, C E P D$ and $B F P D$ are concylic. We now finish off as in Case 1. These four cases prove the problem statement.
Remark. A more natural approach is to solve each of the four cases by simple angle chasing.
## Number Theory
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A point $P$ lies in the interior of the triangle $A B C$. The lines $A P, B P$, and $C P$ intersect $B C, C A$, and $A B$ at points $D, E$, and $F$, respectively. Prove that if two of the quadrilaterals $A B D E, B C E F, C A F D, A E P F, B F P D$, and $C D P E$ are concyclic, then all six are concyclic.
|
We first prove the following lemma:
Lemma 1. Let $A B C D$ be a convex quadrilateral and let $A B \cap C D=E$ and $B C \cap D A=F$. Then the circumcircles of triangles $A B F, C D F, B C E$ and $D A E$ all pass through a common point $P$. This point lies on line $E F$ if and only if $A B C D$ in concyclic.
Proof. Let the circumcircles of $A B F$ and $B C F$ intersect at $P \neq B$. We have
$$
\begin{aligned}
\Varangle F P C & =\Varangle F P B+\Varangle B P C=\Varangle B A D+\Varangle B E C=\Varangle E A D+\Varangle A E D= \\
& =180^{\circ}-\Varangle A D E=180^{\circ}-\Varangle F D C
\end{aligned}
$$
which gives us $F, P, C$ and $D$ are concyclic. Similarly we have
$$
\begin{aligned}
\Varangle A P E & =\Varangle A P B+\Varangle B P E=\Varangle A F B+\Varangle B C D=\Varangle D F C+\Varangle F C D= \\
& =180^{\circ}-\Varangle F D C=180^{\circ}-\Varangle A D E
\end{aligned}
$$
which gives us $E, P, A$ and $D$ are concyclic. Since $\Varangle F P E=\Varangle F P B+\Varangle E P B=\Varangle B A D+$ $\Varangle B C D$ we get that $\Varangle F P E=180^{\circ}$ if and only if $\Varangle B A D+\Varangle B C D=180^{\circ}$ which completes the lemma. We now divide the problem into cases:
Case 1: $A E P F$ and $B F E C$ are concyclic. Here we get that
$$
180^{\circ}=\Varangle A E P+\Varangle A F P=360^{\circ}-\Varangle C E B-\Varangle B F C=360^{\circ}-2 \Varangle C E B
$$
and here we get that $\Varangle C E B=\Varangle C F B=90^{\circ}$, from here it follows that $P$ is the ortocenter of $\triangle A B C$ and that gives us $\Varangle A D B=\Varangle A D C=90^{\circ}$. Now the quadrilaterals $C E P D$ and $B D P F$ are concyclic because
$$
\Varangle C E P=\Varangle C D P=\Varangle P D B=\Varangle P F B=90^{\circ} .
$$
Quadrilaterals $A C D F$ and $A B D E$ are concyclic because
$$
\Varangle A E B=\Varangle A D B=\Varangle A D C=\Varangle A F C=90^{\circ}
$$
Case 2: $A E P F$ and $C E P D$ are concyclic. Now by lemma 1 applied to the quadrilateral $A E P F$ we get that the circumcircles of $C E P, C A F, B P F$ and $B E A$ intersect at a point on $B C$. Since $D \in B C$ and $C E P D$ is concyclic we get that $D$ is the desired point and it follows that $B D P F, B A E D, C A F D$ are all concylic and now we can finish same as Case 1 since $A E D B$ and $C E P D$ are concyclic.
Case 3: $A E P F$ and $A E D B$ are concyclic. We apply lemma 1 as in Case 2 on the quadrilateral $A E P F$. From the lemma we get that $B D P F, C E P D$ and $C A F D$ are concylic and we finish off the same as in Case 1.
Case 4: $A C D F$ and $A B D E$ are concyclic. We apply lemma 1 on the quadrilateral $A E P F$ and get that the circumcircles of $A C F, E C P, P F B$ and $B A E$ intersect at one point. Since this point is $D$ (because $A C D F$ and $A B D E$ are concyclic) we get that $A E P F, C E P D$ and $B F P D$ are concylic. We now finish off as in Case 1. These four cases prove the problem statement.
Remark. A more natural approach is to solve each of the four cases by simple angle chasing.
## Number Theory
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2017_short_list.jsonl",
"problem_match": "\nProblem G5.",
"solution_match": "\nSolution."
}
|
7a2bde0e-d1f9-5581-83f5-36978922536a
| 605,892
|
Real numbers $a$ and $b$ satisfy $a^{3}+b^{3}-6 a b=-11$. Prove that $-\frac{7}{3}<a+b<-2$.
|
Using the identity
$$
x^{3}+y^{3}+z^{3}-3 x y z=\frac{1}{2}(x+y+z)\left((x-y)^{2}+(y-z)^{2}+(z-x)^{2}\right)
$$
we get
$$
-3=a^{3}+b^{3}+2^{3}-6 a b=\frac{1}{2}(a+b+2)\left((a-b)^{2}+(a-2)^{2}+(b-2)^{2}\right)
$$
Since $S=(a-b)^{2}+(a-2)^{2}+(b-2)^{2}$ must be positive, we conclude that $a+b+2<0$, i.e. that $a+b<-2$. Now $S$ can be bounded by
$$
S \geqslant(a-2)^{2}+(b-2)^{2}=a^{2}+b^{2}-4(a+b)+8 \geqslant \frac{(a+b)^{2}}{2}-4(a+b)+8>18
$$
Here, we have used the fact that $a+b<-2$, which we have proved earlier. Since $a+b+2$ is negative, it immediately implies that $a+b+2<-\frac{2 \cdot 3}{18}=-\frac{1}{3}$, i.e. $a+b<-\frac{7}{3}$ which we wanted.
Alternative Solution by PSC. Writing $s=a+b$ and $p=a b$ we have
$$
a^{3}+b^{3}-6 a b=(a+b)\left(a^{2}-a b+b^{2}\right)-6 a b=s\left(s^{2}-3 p\right)-6 p=s^{3}-3 p s-6 p
$$
This gives $3 p(s+2)=s^{3}+11$. Thus $s \neq-2$ and using the fact that $s^{2} \geqslant 4 p$ we get
$$
p=\frac{s^{3}+11}{3(s+2)} \leqslant \frac{s^{2}}{4}
$$
If $s>-2$, then (1) gives $s^{3}-6 s^{2}+44 \leqslant 0$. This is impossible as
$$
s^{3}-6 s^{2}+44=(s+2)(s-4)^{2}+8>0
$$
So $s<-2$. Then from (1) we get $s^{3}-6 s^{2}+44 \geqslant 0$. If $s<-\frac{7}{3}$ this is again impossible as $s^{3}-6 s^{2}=s^{2}(s-6)<-\frac{49}{9} \cdot \frac{25}{3}<-44$. (Since $49 \cdot 25=1225>1188=44 \cdot 27$.) So $-\frac{7}{3}<s<-2$ as required.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Real numbers $a$ and $b$ satisfy $a^{3}+b^{3}-6 a b=-11$. Prove that $-\frac{7}{3}<a+b<-2$.
|
Using the identity
$$
x^{3}+y^{3}+z^{3}-3 x y z=\frac{1}{2}(x+y+z)\left((x-y)^{2}+(y-z)^{2}+(z-x)^{2}\right)
$$
we get
$$
-3=a^{3}+b^{3}+2^{3}-6 a b=\frac{1}{2}(a+b+2)\left((a-b)^{2}+(a-2)^{2}+(b-2)^{2}\right)
$$
Since $S=(a-b)^{2}+(a-2)^{2}+(b-2)^{2}$ must be positive, we conclude that $a+b+2<0$, i.e. that $a+b<-2$. Now $S$ can be bounded by
$$
S \geqslant(a-2)^{2}+(b-2)^{2}=a^{2}+b^{2}-4(a+b)+8 \geqslant \frac{(a+b)^{2}}{2}-4(a+b)+8>18
$$
Here, we have used the fact that $a+b<-2$, which we have proved earlier. Since $a+b+2$ is negative, it immediately implies that $a+b+2<-\frac{2 \cdot 3}{18}=-\frac{1}{3}$, i.e. $a+b<-\frac{7}{3}$ which we wanted.
Alternative Solution by PSC. Writing $s=a+b$ and $p=a b$ we have
$$
a^{3}+b^{3}-6 a b=(a+b)\left(a^{2}-a b+b^{2}\right)-6 a b=s\left(s^{2}-3 p\right)-6 p=s^{3}-3 p s-6 p
$$
This gives $3 p(s+2)=s^{3}+11$. Thus $s \neq-2$ and using the fact that $s^{2} \geqslant 4 p$ we get
$$
p=\frac{s^{3}+11}{3(s+2)} \leqslant \frac{s^{2}}{4}
$$
If $s>-2$, then (1) gives $s^{3}-6 s^{2}+44 \leqslant 0$. This is impossible as
$$
s^{3}-6 s^{2}+44=(s+2)(s-4)^{2}+8>0
$$
So $s<-2$. Then from (1) we get $s^{3}-6 s^{2}+44 \geqslant 0$. If $s<-\frac{7}{3}$ this is again impossible as $s^{3}-6 s^{2}=s^{2}(s-6)<-\frac{49}{9} \cdot \frac{25}{3}<-44$. (Since $49 \cdot 25=1225>1188=44 \cdot 27$.) So $-\frac{7}{3}<s<-2$ as required.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nA1.",
"solution_match": "\nSolution."
}
|
ae9ff2a1-3478-5948-b926-e07c014a5581
| 605,936
|
Let $a, b, c$ be positive real numbers such that $a b c=\frac{2}{3}$. Prove that
$$
\frac{a b}{a+b}+\frac{b c}{b+c}+\frac{c a}{c+a} \geqslant \frac{a+b+c}{a^{3}+b^{3}+c^{3}}
$$
|
Alternative Solution by PSC. By the Power Mean Inequality we have
$$
\frac{a^{3}+b^{3}+c^{3}}{3} \geqslant\left(\frac{a+b+c}{3}\right)^{3}
$$
So it is enough to prove that
$$
(a+b+c)^{2}\left(\frac{a b}{a+b}+\frac{b c}{b+c}+\frac{c a}{c+a}\right) \geqslant 9
$$
or equivalently, that
$$
(a+b+c)^{2}\left(\frac{1}{a c+b c}+\frac{1}{b a+c a}+\frac{1}{c b+a b}\right) \geqslant \frac{27}{2}
$$
Since $(a+b+c)^{2} \geqslant 3(a b+b c+c a)=\frac{3}{2}((a c+b c)+(b a+c a)+(c b+a c))$, then (5) follows by the Cauchy-Schwarz Inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c=\frac{2}{3}$. Prove that
$$
\frac{a b}{a+b}+\frac{b c}{b+c}+\frac{c a}{c+a} \geqslant \frac{a+b+c}{a^{3}+b^{3}+c^{3}}
$$
|
Alternative Solution by PSC. By the Power Mean Inequality we have
$$
\frac{a^{3}+b^{3}+c^{3}}{3} \geqslant\left(\frac{a+b+c}{3}\right)^{3}
$$
So it is enough to prove that
$$
(a+b+c)^{2}\left(\frac{a b}{a+b}+\frac{b c}{b+c}+\frac{c a}{c+a}\right) \geqslant 9
$$
or equivalently, that
$$
(a+b+c)^{2}\left(\frac{1}{a c+b c}+\frac{1}{b a+c a}+\frac{1}{c b+a b}\right) \geqslant \frac{27}{2}
$$
Since $(a+b+c)^{2} \geqslant 3(a b+b c+c a)=\frac{3}{2}((a c+b c)+(b a+c a)+(c b+a c))$, then (5) follows by the Cauchy-Schwarz Inequality.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nA2.",
"solution_match": "\nSolution."
}
|
6450c8f3-c247-5fb6-8680-d7d138a1929d
| 605,946
|
Let $a, b, c$ be positive real numbers such that $a b c=\frac{2}{3}$. Prove that
$$
\frac{a b}{a+b}+\frac{b c}{b+c}+\frac{c a}{c+a} \geqslant \frac{a+b+c}{a^{3}+b^{3}+c^{3}}
$$
|
## Alternative Solution by PSC. We have
$$
\left(a^{3}+b^{3}+c^{3}\right) \frac{a b}{a+b}=a b\left(a^{2}-a b+b^{2}\right)+\frac{a b c^{3}}{a+b} \geqslant a^{2} b^{2}+\frac{2}{3} \frac{c^{2}}{a+b}
$$
So the required inequality follows from
$$
\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}\right)+\frac{2}{3}\left(\frac{a^{2}}{b+c}+\frac{b^{2}}{c+a}+\frac{c^{2}}{a+b}\right) \geqslant a+b+c
$$
By applying the AM-GM Inequality three times we get
$$
a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2} \geqslant a b c(a+b+c)=\frac{2}{3}(a+b+c)
$$
By the Cauchy-Schwarz Inequality we also have
$$
((b+c)+(c+a)+(a+b))\left(\frac{a^{2}}{b+c}+\frac{b^{2}}{c+a}+\frac{c^{2}}{a+b}\right) \geqslant(a+b+c)^{2}
$$
which gives
$$
\frac{a^{2}}{b+c}+\frac{b^{2}}{c+a}+\frac{c^{2}}{a+b} \geqslant \frac{a+b+c}{2}
$$
Combining (7) and (8) we get (6) as required.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c=\frac{2}{3}$. Prove that
$$
\frac{a b}{a+b}+\frac{b c}{b+c}+\frac{c a}{c+a} \geqslant \frac{a+b+c}{a^{3}+b^{3}+c^{3}}
$$
|
## Alternative Solution by PSC. We have
$$
\left(a^{3}+b^{3}+c^{3}\right) \frac{a b}{a+b}=a b\left(a^{2}-a b+b^{2}\right)+\frac{a b c^{3}}{a+b} \geqslant a^{2} b^{2}+\frac{2}{3} \frac{c^{2}}{a+b}
$$
So the required inequality follows from
$$
\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2}\right)+\frac{2}{3}\left(\frac{a^{2}}{b+c}+\frac{b^{2}}{c+a}+\frac{c^{2}}{a+b}\right) \geqslant a+b+c
$$
By applying the AM-GM Inequality three times we get
$$
a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2} \geqslant a b c(a+b+c)=\frac{2}{3}(a+b+c)
$$
By the Cauchy-Schwarz Inequality we also have
$$
((b+c)+(c+a)+(a+b))\left(\frac{a^{2}}{b+c}+\frac{b^{2}}{c+a}+\frac{c^{2}}{a+b}\right) \geqslant(a+b+c)^{2}
$$
which gives
$$
\frac{a^{2}}{b+c}+\frac{b^{2}}{c+a}+\frac{c^{2}}{a+b} \geqslant \frac{a+b+c}{2}
$$
Combining (7) and (8) we get (6) as required.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nA2.",
"solution_match": "\nSolution."
}
|
6450c8f3-c247-5fb6-8680-d7d138a1929d
| 605,946
|
Let $a, b$ be two distinct real numbers and let $c$ be a positive real number such that
$$
a^{4}-2019 a=b^{4}-2019 b=c
$$
Prove that $-\sqrt{c}<a b<0$.
|
Firstly, we see that
$$
2019(a-b)=a^{4}-b^{4}=(a-b)(a+b)\left(a^{2}+b^{2}\right)
$$
Since $a \neq b$, we get $(a+b)\left(a^{2}+b^{2}\right)=2019$, so $a+b \neq 0$. Thus
$$
\begin{aligned}
2 c & =a^{4}-2019 a+b^{4}-2019 b \\
& =a^{4}+b^{4}-2019(a+b) \\
& =a^{4}+b^{4}-(a+b)^{2}\left(a^{2}+b^{2}\right) \\
& =-2 a b\left(a^{2}+a b+b^{2}\right)
\end{aligned}
$$
Hence $a b\left(a^{2}+a b+b^{2}\right)=-c<0$. Note that
$$
a^{2}+a b+b^{2}=\frac{1}{2}\left(a^{2}+b^{2}+(a+b)^{2}\right) \geqslant 0
$$
thus $a b<0$. Finally, $a^{2}+a b+b^{2}=(a+b)^{2}-a b>-a b$ (the equality does not occur since $a+b \neq 0)$. So
$$
-c=a b\left(a^{2}+a b+b^{2}\right)<-(a b)^{2} \Longrightarrow(a b)^{2}<c \Rightarrow-\sqrt{c}<a b<\sqrt{c}
$$
Therefore, we have $-\sqrt{c}<a b<0$.
Alternative Solution by PSC. By Descartes' Rule of Signs, the polynomial $p(x)=$ $x^{4}-2019 x-c$ has exactly one positive root and exactly one negative root. So $a, b$ must be its two real roots. Since one of them is positive and the other is negative, then $a b<0$. Let $r \pm i s$ be the two non-real roots of $p(x)$.
By Vieta, we have
$$
\begin{gathered}
a b\left(r^{2}+s^{2}\right)=-c \\
a+b+2 r=0 \\
a b+2 a r+2 b r+r^{2}+s^{2}=0
\end{gathered}
$$
Using (2) and (3), we have
$$
r^{2}+s^{2}=-2 r(a+b)-a b=(a+b)^{2}-a b \geqslant-a b
$$
If in the last inequality we actually have an equality, then $a+b=0$. Then (2) gives $r=0$ and (3) gives $s^{2}=-a b$. Thus the roots of $p(x)$ are $a,-a, i a,-i a$. This would give that $p(x)=x^{4}+a^{4}$, a contradiction.
So the inequality in (4) is strict and now from (1) we get
$$
c=-\left(r^{2}+s^{2}\right) a b>(a b)^{2}
$$
which gives that $a b>-\sqrt{c}$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a, b$ be two distinct real numbers and let $c$ be a positive real number such that
$$
a^{4}-2019 a=b^{4}-2019 b=c
$$
Prove that $-\sqrt{c}<a b<0$.
|
Firstly, we see that
$$
2019(a-b)=a^{4}-b^{4}=(a-b)(a+b)\left(a^{2}+b^{2}\right)
$$
Since $a \neq b$, we get $(a+b)\left(a^{2}+b^{2}\right)=2019$, so $a+b \neq 0$. Thus
$$
\begin{aligned}
2 c & =a^{4}-2019 a+b^{4}-2019 b \\
& =a^{4}+b^{4}-2019(a+b) \\
& =a^{4}+b^{4}-(a+b)^{2}\left(a^{2}+b^{2}\right) \\
& =-2 a b\left(a^{2}+a b+b^{2}\right)
\end{aligned}
$$
Hence $a b\left(a^{2}+a b+b^{2}\right)=-c<0$. Note that
$$
a^{2}+a b+b^{2}=\frac{1}{2}\left(a^{2}+b^{2}+(a+b)^{2}\right) \geqslant 0
$$
thus $a b<0$. Finally, $a^{2}+a b+b^{2}=(a+b)^{2}-a b>-a b$ (the equality does not occur since $a+b \neq 0)$. So
$$
-c=a b\left(a^{2}+a b+b^{2}\right)<-(a b)^{2} \Longrightarrow(a b)^{2}<c \Rightarrow-\sqrt{c}<a b<\sqrt{c}
$$
Therefore, we have $-\sqrt{c}<a b<0$.
Alternative Solution by PSC. By Descartes' Rule of Signs, the polynomial $p(x)=$ $x^{4}-2019 x-c$ has exactly one positive root and exactly one negative root. So $a, b$ must be its two real roots. Since one of them is positive and the other is negative, then $a b<0$. Let $r \pm i s$ be the two non-real roots of $p(x)$.
By Vieta, we have
$$
\begin{gathered}
a b\left(r^{2}+s^{2}\right)=-c \\
a+b+2 r=0 \\
a b+2 a r+2 b r+r^{2}+s^{2}=0
\end{gathered}
$$
Using (2) and (3), we have
$$
r^{2}+s^{2}=-2 r(a+b)-a b=(a+b)^{2}-a b \geqslant-a b
$$
If in the last inequality we actually have an equality, then $a+b=0$. Then (2) gives $r=0$ and (3) gives $s^{2}=-a b$. Thus the roots of $p(x)$ are $a,-a, i a,-i a$. This would give that $p(x)=x^{4}+a^{4}$, a contradiction.
So the inequality in (4) is strict and now from (1) we get
$$
c=-\left(r^{2}+s^{2}\right) a b>(a b)^{2}
$$
which gives that $a b>-\sqrt{c}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nA4.",
"solution_match": "\nSolution."
}
|
9306f294-9f3f-5fae-99f3-af285a061b4c
| 605,971
|
Let $a, b, c, d$ be positive real numbers such that $a b c d=1$. Prove the inequality
$$
\frac{1}{a^{3}+b+c+d}+\frac{1}{a+b^{3}+c+d}+\frac{1}{a+b+c^{3}+d}+\frac{1}{a+b+c+d^{3}} \leqslant \frac{a+b+c+d}{4}
$$
|
From the Cauchy-Schwarz Inequality, we obtain
$$
(a+b+c+d)^{2} \leqslant\left(a^{3}+b+c+d\right)\left(\frac{1}{a}+b+c+d\right)
$$
Using this, together with the other three analogous inequalities, we get
$$
\begin{aligned}
\frac{1}{a^{3}+b+c+d}+\frac{1}{a+b^{3}+c+d}+\frac{1}{a+b+c^{3}+d} & +\frac{1}{a+b+c+d^{3}} \\
& \leqslant \frac{3(a+b+c+d)+\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}\right)}{(a+b+c+d)^{2}}
\end{aligned}
$$
So it suffices to prove that
$$
(a+b+c+d)^{3} \geqslant 12(a+b+c+d)+4\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}\right)
$$
or equivalently, that
$$
\begin{aligned}
& \left(a^{3}+b^{3}+c^{3}+d^{3}\right)+3 \sum a^{2} b+6(a b c+a b d+a c d+b c d) \\
& \quad \geqslant 12(a+b+c+d)+4(a b c+a b d+a c d+b c d)
\end{aligned}
$$
(Here, the sum is over all possible $x^{2} y$ with $x, y \in\{a, b, c, d\}$ and $x \neq y$.) From the AM-GM Inequality we have
$a^{3}+a^{2} b+a^{2} b+a^{2} c+a^{2} c+a^{2} d+a^{2} d+b^{2} a+c^{2} a+d^{2} a+b c d+b c d \geqslant 12 \sqrt[12]{a^{18} b^{6} c^{6} d^{6}}=12 a$.
Similarly, we get three more inequalities. Adding them together gives the inequality we wanted. Equality holds if and only if $a=b=c=d=1$.
Remark by PSC. Alternatively, we can finish off the proof by using the following two inequalities: Firstly, we have $a+b+c+d \geqslant 4 \sqrt[4]{a b c d}=4$ by the AM-GM Inequality, giving
$$
\frac{3}{4}(a+b+c+d)^{3} \geqslant 12(a+b+c+d)
$$
Secondly, by Mclaurin's Inequality, we have
$$
\left(\frac{a+b+c+d}{4}\right)^{3} \geqslant \frac{b c d+a c d+a b d+a b c}{4}
$$
giving
$$
\frac{1}{4}(a+b+c+d)^{3} \geqslant 4(b c d+a c d+a b d+a b c)
$$
Adding those inequlities we get the required result.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c, d$ be positive real numbers such that $a b c d=1$. Prove the inequality
$$
\frac{1}{a^{3}+b+c+d}+\frac{1}{a+b^{3}+c+d}+\frac{1}{a+b+c^{3}+d}+\frac{1}{a+b+c+d^{3}} \leqslant \frac{a+b+c+d}{4}
$$
|
From the Cauchy-Schwarz Inequality, we obtain
$$
(a+b+c+d)^{2} \leqslant\left(a^{3}+b+c+d\right)\left(\frac{1}{a}+b+c+d\right)
$$
Using this, together with the other three analogous inequalities, we get
$$
\begin{aligned}
\frac{1}{a^{3}+b+c+d}+\frac{1}{a+b^{3}+c+d}+\frac{1}{a+b+c^{3}+d} & +\frac{1}{a+b+c+d^{3}} \\
& \leqslant \frac{3(a+b+c+d)+\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}\right)}{(a+b+c+d)^{2}}
\end{aligned}
$$
So it suffices to prove that
$$
(a+b+c+d)^{3} \geqslant 12(a+b+c+d)+4\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}\right)
$$
or equivalently, that
$$
\begin{aligned}
& \left(a^{3}+b^{3}+c^{3}+d^{3}\right)+3 \sum a^{2} b+6(a b c+a b d+a c d+b c d) \\
& \quad \geqslant 12(a+b+c+d)+4(a b c+a b d+a c d+b c d)
\end{aligned}
$$
(Here, the sum is over all possible $x^{2} y$ with $x, y \in\{a, b, c, d\}$ and $x \neq y$.) From the AM-GM Inequality we have
$a^{3}+a^{2} b+a^{2} b+a^{2} c+a^{2} c+a^{2} d+a^{2} d+b^{2} a+c^{2} a+d^{2} a+b c d+b c d \geqslant 12 \sqrt[12]{a^{18} b^{6} c^{6} d^{6}}=12 a$.
Similarly, we get three more inequalities. Adding them together gives the inequality we wanted. Equality holds if and only if $a=b=c=d=1$.
Remark by PSC. Alternatively, we can finish off the proof by using the following two inequalities: Firstly, we have $a+b+c+d \geqslant 4 \sqrt[4]{a b c d}=4$ by the AM-GM Inequality, giving
$$
\frac{3}{4}(a+b+c+d)^{3} \geqslant 12(a+b+c+d)
$$
Secondly, by Mclaurin's Inequality, we have
$$
\left(\frac{a+b+c+d}{4}\right)^{3} \geqslant \frac{b c d+a c d+a b d+a b c}{4}
$$
giving
$$
\frac{1}{4}(a+b+c+d)^{3} \geqslant 4(b c d+a c d+a b d+a b c)
$$
Adding those inequlities we get the required result.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nA5.",
"solution_match": "\nSolution."
}
|
dbdc507a-866f-5394-b702-d92f47d35cb2
| 605,980
|
Let $a, b, c$ be positive real numbers. Prove the inequality
$$
\left(a^{2}+a c+c^{2}\right)\left(\frac{1}{a+b+c}+\frac{1}{a+c}\right)+b^{2}\left(\frac{1}{b+c}+\frac{1}{a+b}\right)>a+b+c
$$
|
By the Cauchy-Schwarz Inequality, we have
$$
\frac{1}{a+b+c}+\frac{1}{a+c} \geqslant \frac{4}{2 a+b+2 c}
$$
and
$$
\frac{1}{b+c}+\frac{1}{a+b} \geqslant \frac{4}{a+2 b+c}
$$
Since
$$
a^{2}+a c+c^{2}=\frac{3}{4}(a+c)^{2}+\frac{1}{4}(a-c)^{2} \geqslant \frac{3}{4}(a+c)^{2}
$$
then, writing $L$ for the Left Hand Side of the required inequality, we get
$$
L \geqslant \frac{3(a+c)^{2}}{2 a+b+2 c}+\frac{4 b^{2}}{a+2 b+c}
$$
Using again the Cauchy-Schwarz Inequality, we have:
$$
L \geqslant \frac{(\sqrt{3}(a+c)+2 b)^{2}}{3 a+3 b+3 c}>\frac{(\sqrt{3}(a+c)+\sqrt{3} b)^{2}}{3 a+3 b+3 c}=a+b+c
$$
Alternative Question by Proposers. Let $a, b, c$ be positive real numbers. Prove the inequality
$$
\frac{a^{2}}{a+c}+\frac{b^{2}}{b+c}>\frac{a b-c^{2}}{a+b+c}+\frac{a b}{a+b}
$$
Note that both this inequality and the original one are equivalent to
$$
\left(c+\frac{a^{2}}{a+c}\right)+\left(a-\frac{a b-c^{2}}{a+b+c}\right)+\frac{b^{2}}{b+c}+\left(b-\frac{a b}{a+b}\right)>a+b+c
$$
Alternative Solution by PSC. The required inequality is equivalent to
$$
\left[\frac{b^{2}}{a+b}-(b-a)\right]+\frac{b^{2}}{b+c}+\left[\frac{a^{2}+a c+c^{2}}{a+c}-a\right]+\left[\frac{a^{2}+a c+c^{2}}{a+b+c}-(a+c)\right]>0
$$
or equivalently, to
$$
\frac{a^{2}}{a+b}+\frac{b^{2}}{b+c}+\frac{c^{2}}{c+a}>\frac{a b+b c+c a}{a+b+c}
$$
However, by the Cauchy-Schwarz Inequality we have
$$
\frac{a^{2}}{a+b}+\frac{b^{2}}{b+c}+\frac{c^{2}}{c+a} \geqslant \frac{(a+b+c)^{2}}{2(a+b+c)} \geqslant \frac{3(a b+b c+c a)}{2(a+b+c)}>\frac{a b+b c+c a}{a+b+c}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers. Prove the inequality
$$
\left(a^{2}+a c+c^{2}\right)\left(\frac{1}{a+b+c}+\frac{1}{a+c}\right)+b^{2}\left(\frac{1}{b+c}+\frac{1}{a+b}\right)>a+b+c
$$
|
By the Cauchy-Schwarz Inequality, we have
$$
\frac{1}{a+b+c}+\frac{1}{a+c} \geqslant \frac{4}{2 a+b+2 c}
$$
and
$$
\frac{1}{b+c}+\frac{1}{a+b} \geqslant \frac{4}{a+2 b+c}
$$
Since
$$
a^{2}+a c+c^{2}=\frac{3}{4}(a+c)^{2}+\frac{1}{4}(a-c)^{2} \geqslant \frac{3}{4}(a+c)^{2}
$$
then, writing $L$ for the Left Hand Side of the required inequality, we get
$$
L \geqslant \frac{3(a+c)^{2}}{2 a+b+2 c}+\frac{4 b^{2}}{a+2 b+c}
$$
Using again the Cauchy-Schwarz Inequality, we have:
$$
L \geqslant \frac{(\sqrt{3}(a+c)+2 b)^{2}}{3 a+3 b+3 c}>\frac{(\sqrt{3}(a+c)+\sqrt{3} b)^{2}}{3 a+3 b+3 c}=a+b+c
$$
Alternative Question by Proposers. Let $a, b, c$ be positive real numbers. Prove the inequality
$$
\frac{a^{2}}{a+c}+\frac{b^{2}}{b+c}>\frac{a b-c^{2}}{a+b+c}+\frac{a b}{a+b}
$$
Note that both this inequality and the original one are equivalent to
$$
\left(c+\frac{a^{2}}{a+c}\right)+\left(a-\frac{a b-c^{2}}{a+b+c}\right)+\frac{b^{2}}{b+c}+\left(b-\frac{a b}{a+b}\right)>a+b+c
$$
Alternative Solution by PSC. The required inequality is equivalent to
$$
\left[\frac{b^{2}}{a+b}-(b-a)\right]+\frac{b^{2}}{b+c}+\left[\frac{a^{2}+a c+c^{2}}{a+c}-a\right]+\left[\frac{a^{2}+a c+c^{2}}{a+b+c}-(a+c)\right]>0
$$
or equivalently, to
$$
\frac{a^{2}}{a+b}+\frac{b^{2}}{b+c}+\frac{c^{2}}{c+a}>\frac{a b+b c+c a}{a+b+c}
$$
However, by the Cauchy-Schwarz Inequality we have
$$
\frac{a^{2}}{a+b}+\frac{b^{2}}{b+c}+\frac{c^{2}}{c+a} \geqslant \frac{(a+b+c)^{2}}{2(a+b+c)} \geqslant \frac{3(a b+b c+c a)}{2(a+b+c)}>\frac{a b+b c+c a}{a+b+c}
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nA6.",
"solution_match": "\nSolution."
}
|
22bc3fcb-c49d-58de-b29d-fdf04b9bf077
| 605,989
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.