code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # The Development of Python HDBSCAN Compared to the Reference Implementation in Java
#
# ### Or, why I still use Python for high performance scientific computing
#
# Python is a great high level language for easily expressing ideas, but people don't tend to think of it as a high performance language; for that you would want a compiled language -- ideally C or C++ but Java would do. This notebook started out as a simple benchmarking of the hdbscan clustering library written in Python against the reference implementation written in Java. It still does that, but it has expanded into an explanation of why I choose to use Python for performance critical scientific computing code.
# ## Some quick background
#
# In 2013 Campello, Moulavi and Sander published a paper on a new clustering algorithm that they called HDBSCAN. In mid-2014 I was doing some general research on the current state of clustering, particularly with regard to exploratory data analysis. At the time DBSCAN or OPTICS appeared to be the most promising algorithm available. A colleague ran across the HDBSCAN paper in her literature survey, and suggested we look into how well it performed. We spent an afternoon learning the algorithm and coding it up and found that it gave remarkably good results for the range of test data we had. Things stayed in that state for some time, with the intention being to use a good HDBSCAN implementation when one became available. By early 2015 our needs for clustering grew and, having no good implementation of HDBSCAN to hand, I set about writing our own. Since the first version, coded up in an afternoon, had been in python I stuck with that choice -- but obviously performance might be an issue. In July 2015, after our implementation was well underway Campello, Moulavi and Sander published a new HDBSCAN paper, and released Java code to peform HDBSCAN clustering. Since one of our goals had been to get good scaling it became necessary to see how our python version compared to the high performance reference implementation in Java.
#
# This is the story of how our codebase evolved and was optimized, and how it compares with the Java version at different stages of that journey.
#
# To make the comparisons we'll need data on runtimes of both algorithms, ranging over dataset size, and dataset dimension. To save time and space I've done that work in [another notebook](http://nbviewer.jupyter.org/github/scikit-learn-contrib/hdbscan/blob/master/notebooks/Performance%20data%20generation%20.ipynb) and will just load the data in here.
import pandas as pd
import numpy as np
reference_timing_series = pd.read_csv('reference_impl_external_timings.csv',
index_col=(0,1), names=('dim', 'size', 'time'))['time']
hdbscan_v01_timing_series = pd.read_csv('hdbscan01_timings.csv',
index_col=(0,1), names=('dim', 'size', 'time'))['time']
hdbscan_v03_timing_series = pd.read_csv('hdbscan03_timings.csv',
index_col=(0,1), names=('dim', 'size', 'time'))['time']
hdbscan_v04_timing_series = pd.read_csv('hdbscan04_timings.csv',
index_col=(0,1), names=('dim', 'size', 'time'))['time']
hdbscan_v05_timing_series = pd.read_csv('hdbscan05_timings.csv',
index_col=(0,1), names=('dim', 'size', 'time'))['time']
hdbscan_v06_timing_series = pd.read_csv('hdbscan06_timings.csv',
index_col=(0,1), names=('dim', 'size', 'time'))['time']
# ## Why I chose Python: Easy development
#
# The very first implementation of HDBSCAN that we did was coded up in an afternoon, and that code was in python. Why? There were a few reasons; the test data for clustering was already loaded in a notebook (we were using sklearn for testing many of the different clustering algorithms available); the notebook interface itself was very useful for the sort of iterative "what did we get at the end of this step" coding that occurs when you are both learning and coding a new algorithm at the same time; most of all though, python made the development *easy*. As a high level language, python simply made development that much easier by getting out of the way -- instead of battling with the language we could focus on battling with our understanding of the algorithm.
#
# Easy development comes at a cost of course. That initial experimental implementation was terribly slow, taking thirty seconds or more to cluster only a few thousand points. That was to be expected to some extent: we were still learning and understanding the algorithm, and hence implemented things in a very literal and naive way. The benefit was in being able to get a working implementation put together well enough to test of real data and see the results -- because it was the remarkable promise of those results that made us pick HDBSCAN as the ideal clustering algorithm for exploratory data analysis.
# ## Why I chose Python: Great libraries
#
# When push came to shove and it was decided that we needed to just write and implementation of HDBSCAN, I stuck with python. This was done despite the fact that the initial naive implementation was essentially abandoned, and a fresh start made. What motivated the decision this time? The many great libraries available for python. For a start there is [numpy](http://www.numpy.org) which provides access to highly optimized numerical array operations -- if you can phrase things in vectorized `numpy` operations then things will run fast, and the library is sufficiently flexible and expressive that it is usually not hard to phrase your problem that way. Next there is [scipy](http://www.scipy.org) and the excellent [sklearn](http://scikit-learn.org/stable/) libraries. By inhertiting from the `sklearn` estimator and cluster base classes (and making use of associated sklearn functions) the initial implementation supported input validation and conversion for a wide variety of input formats, a huge range of distance functions, and a standardised calling API all for practically free. In the early development stages I also benefitted from the power of libraries like [pandas](http://pandas.pydata.org) and [networkx](https://networkx.github.io) which provided easy and efficient access to database-like functionality and graphs and graph analytics.
#
# When you combine that with easy checking and comparison with the naive implementation within the original clustering evaluation notebooks it just made a great deal of sense. With powerful and optimized libraries like `numpy` and `sklearn` doing the heavy lifting and a less naive implementation, hopefully performance wouldn't suffer too much...
# We can compare that initial implementation with the reference implementation. First we need to load some plotting libraries so we can visualize the results.
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_context('poster')
# %matplotlib inline
# Next we'll join together the reference timings with v0.1 hdbscan library timings, keeping track of which implementation is which, so that we can fit tidily into the `seaborn` library's `lmplot` routine.
# +
reference_series = pd.DataFrame(reference_timing_series.copy()).reset_index()
reference_series['implementation'] = 'Reference Implemetation'
hdbscan_series = pd.DataFrame(hdbscan_v01_timing_series.copy()).reset_index()
hdbscan_series['implementation'] = 'hdbscan library'
hdbscan_series.columns = ('dim', 'size', 'time', 'implementation')
combined_data = pd.concat([reference_series, hdbscan_series])
combined_data['log(time)'] = np.log10(combined_data.time)
combined_data['log(size)'] = np.log10(combined_data['size'])
# -
# And now we plot the results. First we plot the raw timings ranging over increasing dataset sizes, using a different plot for datasets of different dimensions. Below that we have the log/log plots of the same.
#
# (Double click on plots to make them larger)
base_plot = sns.lmplot(x='size', y='time', hue='implementation', col='dim',
data=combined_data.reset_index(), order=2, size=5)
base_plot.set_xticklabels(np.arange(8)*20000, rotation=75)
log_plot = sns.lmplot(x='log(size)', y='log(time)', hue='implementation', col='dim',
data=combined_data.reset_index(), size=5)
# The result is perhaps a little surprising if you haven't worked with `numpy` that much: the python code doesn't scale as well the Java code, but it is not all that far off -- in fact when working with 25 or 50 dimensional data it is actually faster!
# ## Why I chose Python: Cython for bottlenecks
#
# At this point in development I was still unaware of the reference implementation, and was comapring performance with other clustering algorithms such as single linkage, DBSCAN, and K-Means. From that point of view the hdbscan library still performed very poorly, and certainly didn't scale out to the size of datasets I potentially wanted to cluster. That meant it was time to roll up my sleeves and see if I could wring some further optimizations out. This is where the next win for python came: the easy gradient toward C. While `numpy` provided easy python access to fast routines written in C, not everything sat entirely within `numpy`. On the other hand [Cython](http://cython.org) provided an easy way to take my existing working python implementation and simply decorate it with C type information to allow the Cython compiler to generate efficient C code from my python. This allowed me get fast performance without having to rewrite anything -- I could modify the existing python code and be sure everything was still working (by running in the now familiar cluster testing notebooks). Better still, I only needed to spend effort on those parts of the code that were significant bottlenecks, everything else could simply remain as it was (the Cython compiler will happily work with pure undecorated python code).
#
# I should point out that I could equally well have done similar things using [Numba](http://numba.pydata.org), but I had more familiarity with Cython at the time and it fit in better with `sklearn` practice and dependencies.
#
# So, how did performance look at around this point? Let's have a look...
# +
reference_series = pd.DataFrame(reference_timing_series.copy()).reset_index()
reference_series['implementation'] = 'Reference Implemetation'
hdbscan_series = pd.DataFrame(hdbscan_v03_timing_series.copy()).reset_index()
hdbscan_series['implementation'] = 'hdbscan library'
hdbscan_series.columns = ('dim', 'size', 'time', 'implementation')
combined_data = pd.concat([reference_series, hdbscan_series])
combined_data['log(time)'] = np.log10(combined_data.time)
combined_data['log(size)'] = np.log10(combined_data['size'])
# -
base_plot = sns.lmplot(x='size', y='time', hue='implementation', col='dim',
data=combined_data.reset_index(), order=2, size=5)
base_plot.set_xticklabels(np.arange(8)*20000, rotation=75)
log_plot = sns.lmplot(x='log(size)', y='log(time)', hue='implementation', col='dim',
data=combined_data.reset_index(), size=5)
# With a little optimization via Cython, the 0.3 version of hdbscan was now outperforming the reference implementation in Java! In fact in dimension 2 the hdbscan library is getting close to being an order of magnitude faster. It would seem that python isn't such a poor choice for performant code after all ...
# ## Why I chose Python: Because ultimately algorithms matter more
#
# While I had been busy optimizing code, I had also been doing research on the side. The core of the HDBSCAN algorithm relied on a modified single linkage algorithm, which in turn relied on something akin to a minimum spanning tree algorithm. The optimal algorithm for that, according to the literature, is Prims algorithm. The catch is that this is an optimal choice for graphs where the number of edges is usually some (small) constant multiple of the number of vertices. The graph problem for HDBSCAN is a weighted complete graph with $N^2$ edges! That means that in practice we are stuck with an $O(N^2)$ algorithm. Other people, however, had been looking at what can be done when dealing with minimum spanning trees in the pathological case of complete graphs, and as long as you can embed your points into a metric space it turns out that there are other options. A paper by March, Ram and Gray described an algorithm using kd-trees that had $O(N \log N)$ complexity for small dimensional data.
#
# Faced with the difference between $O(N^2)$ and $O(N\log N)$ for large $N$ the choice of development language becomes much less significant -- what matters more is getting that $O(N\log N)$ algorithm implemented. Fortunately python made that easy. As in the case of the first naive versions of HDBSCAN, the notebook provided an excellent interface for exploratory interactive development while learning the algorithm. As in step two, great libraries made a difference: `sklearn` comes equipped with high performance implementations of kd-trees and ball trees that I could simpy make use of. Finally, as in step three, once I had a decent algorithm, I could turn to Cython to tighten up the bottlenecks and make it fast.
#
# What sort of performance did we achieve with new algorithms?
# +
reference_series = pd.DataFrame(reference_timing_series.copy()).reset_index()
reference_series['implementation'] = 'Reference Implemetation'
hdbscan_series = pd.DataFrame(hdbscan_v04_timing_series.copy()).reset_index()
hdbscan_series['implementation'] = 'hdbscan library'
hdbscan_series.columns = ('dim', 'size', 'time', 'implementation')
combined_data = pd.concat([reference_series, hdbscan_series])
combined_data['log(time)'] = np.log10(combined_data.time)
combined_data['log(size)'] = np.log10(combined_data['size'])
# -
base_plot = sns.lmplot(x='size', y='time', hue='implementation', col='dim',
data=combined_data.reset_index(), order=2, size=5)
base_plot.set_xticklabels(np.arange(8)*20000, rotation=75)
log_plot = sns.lmplot(x='log(size)', y='log(time)', hue='implementation', col='dim',
data=combined_data.reset_index(), size=5)
# Now we are really starting to really separate out from the reference implementation. Only in the higher dimensional cases can you even see separation between the hdbscan library line and the x-axis. In the log/log plots we can see the difference really show, especially in low dimensions. The $O(N\log N)$ performance isn't showing up there though, so obviously we may still have some work to do.
# ## Why I chose Python: Because it makes optimization easy
#
# The 0.4 release was a huge step forward in performance, but the $O(N\log N)$ scaling I was expecting to see (at least for low dimensions) wasn't apparent. Now the problem became tracking down where exactly time was being spent that perhaps it shouldn't be. Again python provided some nice benefits here. I was already doing my testing and benchmarking in the notebook (for the sake of plotting the benchmarks if nothing else). Merely adding `%prun` or `%lprun` to the top of cells got me profiling and even line level profiling information quickly and easily. From there it was easy to see that portions of code I had previously left written in very simple naive forms because they had negligible impact on performance were now, suddenly, a bottleneck. Going back to Cython, and particularly making use of [reports](http://docs.cython.org/src/quickstart/cythonize.html?highlight=html%20report#determining-where-to-add-types) produced by `cython -a` which provide excellent information about how your python code is being converted to C, it was not hard to speed up these routines. The result was the 0.5 release with performance below:
# +
reference_series = pd.DataFrame(reference_timing_series.copy()).reset_index()
reference_series['implementation'] = 'Reference Implemetation'
hdbscan_series = pd.DataFrame(hdbscan_v05_timing_series.copy()).reset_index()
hdbscan_series['implementation'] = 'hdbscan library'
hdbscan_series.columns = ('dim', 'size', 'time', 'implementation')
combined_data = pd.concat([reference_series, hdbscan_series])
combined_data['log(time)'] = np.log10(combined_data.time)
combined_data['log(size)'] = np.log10(combined_data['size'])
# -
base_plot = sns.lmplot(x='size', y='time', hue='implementation', col='dim',
data=combined_data.reset_index(), order=2, size=5)
base_plot.set_xticklabels(np.arange(8)*20000, rotation=75)
log_plot = sns.lmplot(x='log(size)', y='log(time)', hue='implementation', col='dim',
data=combined_data.reset_index(), size=5)
# Now we can see a real difference in slopes in the log/log plot, with the implementation performance diverging in log scale for large dataset sizes (particularly in dimension 2). By the time we are dealing with datasets of size $10^5$ the python implementation is *two orders of magnitude faster* in dimension two! And that is only going to get better for the python implementation as we scale to larger and larger data sizes.
#
# But there's still more -- there are still performance gains to be had for the python implementation, some to be delivered in the 0.6 release.
# +
reference_series = pd.DataFrame(reference_timing_series.copy()).reset_index()
reference_series['implementation'] = 'Reference Implemetation'
hdbscan_series = pd.DataFrame(hdbscan_v06_timing_series.copy()).reset_index()
hdbscan_series['implementation'] = 'hdbscan library'
hdbscan_series.columns = ('dim', 'size', 'time', 'implementation')
combined_data = pd.concat([reference_series, hdbscan_series])
combined_data['log(time)'] = np.log10(combined_data.time)
combined_data['log(size)'] = np.log10(combined_data['size'])
# -
base_plot = sns.lmplot(x='size', y='time', hue='implementation', col='dim',
data=combined_data.reset_index(), order=2, size=5)
base_plot.set_xticklabels(np.arange(8)*20000, rotation=75)
log_plot = sns.lmplot(x='log(size)', y='log(time)', hue='implementation', col='dim',
data=combined_data.reset_index(), size=5)
# ## Conclusions
#
# So how did we fare developing a high performance clustering algorithm in python? Python certainly made the development process easy, not just in terms of initial code, but through great libraries, and by making optimization easy. The end result is an implementation several orders of magnitude faster than the current reference implementation in Java. So really, despite expectations, python didn't make things slow; quite the contrary. The lesson here is an old one from Knuth that I'm sure you already knew: *"premature optimization is root of all evil"*. Choosing a language "for performance" before you even know your algorithm well, and what parts of it will really be bottlenecks, is optimizing prematurely. Why not develop in a language that makes the first version easy to implement, and provides plenty of powerful tools for optimization later when you understand where and how you need it? And that's why I use python for high performance scientific computing.
|
notebooks/Python vs Java.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:simulate_expression_compendia]
# language: python
# name: conda-env-simulate_expression_compendia-py
# ---
# # Create pseudo experiments using simulated compendia
#
# This notebook is a continuation of ```generate_E_GEOD_51409_template_experiment.ipynb```. This notebook generates new pseudo-experiments using the experiment-preserving approach from the experiment level simulation. In this simulation we are preserving the experiment type but not the actual experiment so the relationship between samples within an experiment are preserved but the genes that are expressed will be different (see module ```simulate_compendium``` in ```functions/generate_data_parallel.py```).
# +
# %load_ext autoreload
# %autoreload 2
import os
from pathlib import Path
import sys
import ast
import pandas as pd
import numpy as np
import seaborn as sns
import random
import glob
from sklearn import preprocessing
from ponyo import utils, generate_labeled_data
import warnings
warnings.filterwarnings(action='ignore')
from numpy.random import seed
randomState = 123
seed(randomState)
# -
# Read in config variables
config_file = os.path.abspath(os.path.join(os.getcwd(),"../configs", "config_Pa_experiment_limma.tsv"))
params = utils.read_config(config_file)
# Load parameters
num_runs = 100
dataset_name = params["dataset_name"]
num_simulated_experiments = params["num_simulated_experiments"]
NN_architecture = params["NN_architecture"]
local_dir = params["local_dir"]
# +
# Input files
base_dir = os.path.abspath(
os.path.join(
os.getcwd(), "../")) # base dir on repo
# Load experiment id file
# Contains ALL experiment ids
experiment_ids_file = os.path.join(
base_dir,
dataset_name,
"data",
"metadata",
"experiment_ids.txt")
normalized_data_file = os.path.join(
base_dir,
dataset_name,
"data",
"input",
"train_set_normalized.pcl")
original_data_file = os.path.join(
local_dir,
"pseudo_experiment",
"Pa_compendium_02.22.2014.pcl")
mapping_file = os.path.join(
base_dir,
dataset_name,
"data",
"metadata",
"sample_annotations.tsv")
# -
# ## Generate simulated data with labels
#
# Simulate a compendia by experiment and label each new sample with the experiment id that it originated from
# +
# Load experiment id file
# Contains ALL experiment ids
base_dir = os.path.abspath(
os.path.join(
os.getcwd(), "../")) # base dir on repo
experiment_ids_file = os.path.join(
base_dir,
dataset_name,
"data",
"metadata",
"experiment_ids.txt")
# -
# Generate simulated data
simulated_labeled_data_file = os.path.join(
local_dir,
"pseudo_experiment",
"simulated_data_labeled.txt.xz")
if not Path(simulated_labeled_data_file).exists():
generate_labeled_data.simulate_compendium_labeled(experiment_ids_file,
num_simulated_experiments,
normalized_data_file,
NN_architecture,
dataset_name,
local_dir,
base_dir)
# ## Process data
# Load simulated data
simulated_data_file = os.path.join(
local_dir,
"pseudo_experiment",
"simulated_data_labeled.txt.xz")
# +
# Read data
original_data = pd.read_table(
original_data_file,
header=0,
sep='\t',
index_col=0).T
simulated_data = pd.read_table(
simulated_data_file,
header=0,
sep='\t',
index_col=0)
print(original_data.shape)
print(simulated_data.shape)
# -
original_data.head(5)
simulated_data.head(5)
# +
# 0-1 normalize per gene
scaler = preprocessing.MinMaxScaler()
original_data_scaled = scaler.fit_transform(original_data)
original_data_scaled_df = pd.DataFrame(original_data_scaled,
columns=original_data.columns,
index=original_data.index)
original_data_scaled_df.head(5)
# +
# Re-scale simulated data back into the same range as the original data
simulated_data_numeric = simulated_data.drop(columns=['experiment_id'])
simulated_data_scaled = scaler.inverse_transform(simulated_data_numeric)
simulated_data_scaled_df = pd.DataFrame(simulated_data_scaled,
columns=simulated_data_numeric.columns,
index=simulated_data_numeric.index)
simulated_data_scaled_df['experiment_id'] = simulated_data['experiment_id']
simulated_data_scaled_df.head(5)
# +
# Read in metadata
metadata = pd.read_table(
mapping_file,
header=0,
sep='\t',
index_col=0)
metadata.head()
# -
map_experiment_sample = metadata[['sample_name', 'ml_data_source']]
map_experiment_sample.head()
map_sample_description = metadata[['ml_data_source', 'description']]
map_sample_description.set_index('ml_data_source', inplace=True)
map_sample_description.head()
# # Template experiment E-GEOD-21704
#
# This experiment measures the transcriptome of WT and ndk1 mutant *P. aeruginosa* in the presence of exposure to H_2O_2 and polymorphonuclear neutrophils (PMNs), which kill *P. aeruginosa*.
#
# More information can be found on the [corresponding array express site](https://www.ebi.ac.uk/arrayexpress/experiments/E-GEOD-21704/)
#
# Since this experiment contains multiple different comparisons, to show the consistency between the orginal and the simulated experiment, we performed a hierarchal clustering of the expression data.
# Get experiment id
experiment_id = 'E-GEOD-21704'
# +
# Output files
heatmap_original_file = os.path.join(
base_dir,
"Pseudomonas",
"results",
"DE_heatmap_original_"+experiment_id+"_example.svg")
heatmap_simulated_file = os.path.join(
base_dir,
"Pseudomonas",
"results",
"DE_heatmap_simulated_"+experiment_id+"_example.svg")
# +
# Get original samples associated with experiment_id
selected_mapping = map_experiment_sample.loc[experiment_id]
original_selected_sample_ids = list(selected_mapping['ml_data_source'].values)
selected_original_data = original_data.loc[original_selected_sample_ids]
# Map numeric sample ids to descriptive ids
desc_id = list(map_sample_description.loc[list(selected_original_data.index)]['description'])
selected_original_data.index = desc_id
# downsample columns
random_subset_genes = random.sample(selected_original_data.columns.tolist(), 50)
selected_original_data = selected_original_data.loc[:,random_subset_genes]
selected_original_data.head(5)
# -
# Want to get simulated samples associated with experiment_id
# Since we sampled experiments with replacement, we want to find the first set of samples matching the experiment id
match_experiment_id = ''
for experiment_name in simulated_data_scaled_df['experiment_id'].values:
if experiment_name.split("_")[0] == experiment_id:
match_experiment_id = experiment_name
# +
# Get simulated samples associated with experiment_id
selected_simulated_data = simulated_data_scaled_df[simulated_data_scaled_df['experiment_id'] == match_experiment_id]
# Map sample ids from original data to simulated data
selected_simulated_data.index = original_selected_sample_ids
selected_simulated_data = selected_simulated_data.drop(columns=['experiment_id'])
selected_simulated_data.index = desc_id
selected_simulated_data = selected_simulated_data.loc[:,random_subset_genes]
selected_simulated_data.head(5)
# -
# Plot original data
sns.set(style="ticks", context="talk")
sns.set(font='sans-serif', font_scale=1.5)
f = sns.clustermap(selected_original_data.T, cmap="viridis")
f.fig.suptitle('Original experiment')
f.savefig(heatmap_original_file)
# Plot simulated data
sns.set(style="ticks", context="talk")
sns.set(font='sans-serif', font_scale=1.5)
f = sns.clustermap(selected_simulated_data.T, cmap="viridis")
f.fig.suptitle('Experiment-level simulated experiment')
f.savefig(heatmap_simulated_file)
# # Template experiment E-GEOD-10030
#
# This experiment measures the transcriptome of biofilm grown on human cells and planktonic *P. aeruginosa* after treated with Tobramycin, an antibiotic.
#
# More information can be found on the [corresponding array express site](https://www.ebi.ac.uk/arrayexpress/experiments/E-GEOD-10030/)
#
# Since this experiment contains multiple different comparisons, to show the consistency between the orginal and the simulated experiment, we performed a hierarchal clustering of the expression data.
# Get experiment id
experiment_id = 'E-GEOD-10030'
# +
# Output files
heatmap_original_file = os.path.join(
base_dir,
"Pseudomonas",
"results",
"DE_heatmap_original_"+experiment_id+"_example.svg")
heatmap_simulated_file = os.path.join(
base_dir,
"Pseudomonas",
"results",
"DE_heatmap_simulated_"+experiment_id+"_example.svg")
# +
# Get original samples associated with experiment_id
selected_mapping = map_experiment_sample.loc[experiment_id]
original_selected_sample_ids = list(selected_mapping['ml_data_source'].values)
selected_original_data = original_data.loc[original_selected_sample_ids]
# Map numeric sample ids to descriptive ids
uniq_desc = map_sample_description.loc[list(selected_original_data.index)].drop_duplicates()
desc_id = list(uniq_desc['description'])
selected_original_data.index = desc_id
# downsample columns
random_subset_genes = random.sample(selected_original_data.columns.tolist(), 50)
selected_original_data = selected_original_data.loc[:,random_subset_genes]
selected_original_data.head(5)
# -
# Want to get simulated samples associated with experiment_id
# Since we sampled experiments with replacement, we want to find the first set of samples matching the experiment id
match_experiment_id = ''
for experiment_name in simulated_data_scaled_df['experiment_id'].values:
if experiment_name.split("_")[0] == experiment_id:
match_experiment_id = experiment_name
# +
# Get simulated samples associated with experiment_id
selected_simulated_data = simulated_data_scaled_df[simulated_data_scaled_df['experiment_id'] == match_experiment_id]
# Map sample ids from original data to simulated data
selected_simulated_data.index = original_selected_sample_ids
selected_simulated_data = selected_simulated_data.drop(columns=['experiment_id'])
selected_simulated_data.index = desc_id
selected_simulated_data = selected_simulated_data.loc[:,random_subset_genes]
selected_simulated_data.head(5)
# -
# Plot original data
sns.set(style="ticks", context="talk")
sns.set(font='sans-serif', font_scale=1.5)
f = sns.clustermap(selected_original_data.T, cmap="viridis")
f.fig.suptitle('Original experiment')
f.savefig(heatmap_original_file)
# Plot simulated data
sns.set(style="ticks", context="talk")
sns.set(font='sans-serif', font_scale=1.5)
f = sns.clustermap(selected_simulated_data.T, cmap="viridis")
f.fig.suptitle('Experiment-level simulated experiment')
f.savefig(heatmap_simulated_file)
|
Pseudo_experiments/generate_additional_template_experiments.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # DataKind Red Cross Project Phase 2
# ## Home Fire Risk Data Model
# 10/28/2019
# Tasks:
# 1. <b>Home Fire County Assessment</b>: Score and rank order counties based on highest fire rates per-capita using NFIRS Data (aggregate) and SVI population estimates
# 2. <b>Home Fire Census Tract Assessment</b>: Score and rank order census tracts based on highest fire rates per-capita using NFIRS Data (aggregate) and SVI population estimates
# 3. <b>Home Fire Severity Assessment (county)</b>: Score and rank order counties based on rates of severe fires per-capita using NFIRS Data (aggregate) and SVI population estimates.
# 4. <b>Home Fire Severity Assessment (census tract)</b>Score and rank order census tracts based on rates of severe fires per-capita using NFIRS Data (aggregate) and SVI population estimates
# 5. <b>Home Fire Predictablility Assessment</b>: Using Census Tract Fire Severity Assesment bin Data at 3-month 6-month or 1-year intervals and train simple linear/logistic regression model
# +
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
pd.set_option('display.max_columns',500)
sns.set()
# -
# # Data Import and Cleaning
# ## NFIRS Data
# First, make sure that I import the dataset correctly and get the column dtypes correct so that data isn't lost (for id numbers with leading zeros for example)
# +
nfirs_path = '../data/raw/NFIRS_2009_2016_Combined_Census_Tract.csv'
cols_to_use = ['state','fdid','city','zip5','inc_date','oth_inj','oth_death','prop_loss',
'cont_loss','tot_loss','GEOID']
col_dtypes = {'GEOID':str}
nfirs = pd.read_csv(nfirs_path,
dtype = col_dtypes,
usecols = cols_to_use,
encoding='latin-1')
nfirs['inc_date'] = pd.to_datetime(nfirs['inc_date'], infer_datetime_format=True)
# -
# Fix the tot_loss column which had incorrect data for 2015. Since tot_loss = prop_loss + cont_loss, it was easy enough to recalculate those values
nfirs['tot_loss'] = nfirs['prop_loss'] + nfirs['cont_loss']
# Add the severe fire column to the dataset
sev_fire_mask = (nfirs['oth_death'] > 0) | (nfirs['oth_inj'] > 0) | (nfirs['tot_loss'] >= 10000)
nfirs['severe_fire'] = 'not_sev_fire'
nfirs.loc[sev_fire_mask,'severe_fire'] = 'sev_fire'
nfirs.sample(5)
# ## Fix GEOIDs (add leading zeros to correct columns)
# It seems that a lot of the GEOIDs are missing the leading 0. For now I'm just going to add a leading 0 if the GEOID length is 10.
nfirs['GEOID'].str.len().value_counts()
nfirs['GEOID'] = (nfirs['GEOID'].str[:-2]
.str.zfill(11))
nfirs.head()
# Add a year column to be used to groupby in addition to GEOID
nfirs['year'] = nfirs['inc_date'].dt.year
# ## SVI Data
# +
svi2016_path = '../data/raw/SVI2016_US.csv'
svi2016_top = pd.read_csv(svi2016_path,nrows=1000)
svi_col_dtypes = {'ST':str,'STCNTY':str,'FIPS':str}
svi2016 = pd.read_csv(svi2016_path,
index_col=0,
dtype = svi_col_dtypes)
# -
svi2016.head(3)
# # Tasks 1 & 3
#
# - Task 1: <b>Home Fire County Assessment</b>: Score and rank order counties based on highest fire rates per-capita using NFIRS Data (aggregate) and SVI population estimates
# - Task 3: <b>Home Fire Severity Assessment (county)</b>: Score and rank order counties based on rates of severe fires per-capita using NFIRS Data (aggregate) and SVI population estimates.
# +
# add the state+county unique identifier column to nfirs
nfirs['STCNTY'] = nfirs['GEOID'].str[:5]
# Do frequency counts based on the year & the number of severe vs non-severe fires
nfirs_counties = pd.crosstab(nfirs['STCNTY'],[nfirs['year'],nfirs['severe_fire']])
# Iterate through years and calculate the total number of fires
for year in [2009,2010,2011,2012,2013,2014,2015,2016]:
nfirs_counties[(year,'tot_fires')] = nfirs_counties[(year,'not_sev_fire')] + nfirs_counties[(year,'sev_fire')]
# Sort the columns
nfirs_counties = nfirs_counties[sorted(nfirs_counties.columns)]
# aggregate svi data by county
svi2016_counties = svi2016.groupby('STCNTY').agg({'E_TOTPOP':'sum'})
# add nfirs data to svi data and insure it's a one-to-one merge
nfirs_svi_counties = svi2016_counties.merge(nfirs_counties,how='left',left_index=True,right_index=True, validate='one_to_one')
nfirs_svi_counties_rates = nfirs_svi_counties[['E_TOTPOP']].copy()
# Calculate the per capita fire rates
for year in [2009,2010,2011,2012,2013,2014,2015,2016]:
nfirs_svi_counties_rates[str(year) + '_tot_fire_rate_per_cap'] = nfirs_svi_counties[(year,'tot_fires')] / nfirs_svi_counties['E_TOTPOP']
nfirs_svi_counties_rates[str(year) + '_sev_fire_rate_per_cap'] = nfirs_svi_counties[(year,'sev_fire')] / nfirs_svi_counties['E_TOTPOP']
# Add the county and state columns to the dataset
nfirs_svi_counties_rates = nfirs_svi_counties_rates.merge(svi2016[['COUNTY','ST_ABBR','STCNTY']].drop_duplicates(subset='STCNTY'),how='left',left_index=True,right_on='STCNTY')
nfirs_svi_counties_rates = nfirs_svi_counties_rates.set_index('STCNTY')
# create list of severe columns & total columns
sev_cols = nfirs_svi_counties_rates.columns[nfirs_svi_counties_rates.columns.str.contains('sev_')]
tot_cols = nfirs_svi_counties_rates.columns[nfirs_svi_counties_rates.columns.str.contains('tot_')]
# calculate mean and standard deviation from 2009-2016
nfirs_svi_counties_rates['avg_sev_fire_rate_per_cap'] = nfirs_svi_counties_rates[sev_cols].mean(axis=1)
nfirs_svi_counties_rates['std_sev_fire_rate_per_cap'] = nfirs_svi_counties_rates[sev_cols].std(axis=1)
nfirs_svi_counties_rates['avg_tot_fire_rate_per_cap'] = nfirs_svi_counties_rates[tot_cols].mean(axis=1)
nfirs_svi_counties_rates['std_tot_fire_rate_per_cap'] = nfirs_svi_counties_rates[tot_cols].std(axis=1)
# Rearrange columns
first_cols = ['ST_ABBR','COUNTY','E_TOTPOP','avg_tot_fire_rate_per_cap','std_tot_fire_rate_per_cap',
'avg_sev_fire_rate_per_cap','std_sev_fire_rate_per_cap']
cols = list(nfirs_svi_counties_rates.columns)
cols = first_cols + [col for col in cols if col not in first_cols]
nfirs_svi_counties_rates = nfirs_svi_counties_rates[cols]
# -
nfirs_svi_counties_rates.head()
# ### Save fire rates by county
nfirs_svi_counties_rates.to_csv('../data/processed/Per_capita_fire_rates_by_county.csv')
# # Tasks 2 & 4
#
# - Task 2: <b>Home Fire Census Tract Assessment</b>: Score and rank order census tracts based on highest fire rates per-capita using NFIRS Data (aggregate) and SVI population estimates
# - Task 4: <b>Home Fire Severity Assessment (census tract)</b>Score and rank order census tracts based on rates of severe fires per-capita using NFIRS Data (aggregate) and SVI population
# +
# Do frequency counts based on the year & the number of severe vs non-severe fires
nfirs_tracts = pd.crosstab(nfirs['GEOID'],[nfirs['year'],nfirs['severe_fire']])
# Iterate through years and calculate the total number of fires
for year in nfirs['year'].unique():
nfirs_tracts[(year,'tot_fires')] = nfirs_tracts[(year,'not_sev_fire')] + nfirs_tracts[(year,'sev_fire')]
# Sort the columns
nfirs_tracts = nfirs_tracts[sorted(nfirs_tracts.columns)]
# data already aggregated by census tract, so simply select the columns to merge
svi2016_tracts = svi2016[['FIPS','ST_ABBR','COUNTY','LOCATION','E_TOTPOP']].set_index('FIPS')
# add nfirs data to svi data and insure it's a one-to-one merge
nfirs_svi_tracts = svi2016_tracts.merge(nfirs_tracts,how='left',left_index=True,right_index=True, validate='one_to_one')
nfirs_svi_tracts_rates = nfirs_svi_tracts[['ST_ABBR','COUNTY','LOCATION','E_TOTPOP']].copy()
# Calculate the per capita fire rates
for year in [2009,2010,2011,2012,2013,2014,2015,2016]:
nfirs_svi_tracts_rates[str(year) + '_tot_fire_rate_per_cap'] = nfirs_svi_tracts[(year,'tot_fires')] / nfirs_svi_tracts['E_TOTPOP']
nfirs_svi_tracts_rates[str(year) + '_sev_fire_rate_per_cap'] = nfirs_svi_tracts[(year,'sev_fire')] / nfirs_svi_tracts['E_TOTPOP']
nfirs_svi_tracts_rates.index.name = 'GEOID'
# create list of severe columns & total columns
sev_cols = nfirs_svi_tracts_rates.columns[nfirs_svi_tracts_rates.columns.str.contains('sev_')]
tot_cols = nfirs_svi_tracts_rates.columns[nfirs_svi_tracts_rates.columns.str.contains('tot_')]
# calculate mean and standard deviation from 2009-2016
nfirs_svi_tracts_rates['avg_sev_fire_rate_per_cap'] = nfirs_svi_tracts_rates[sev_cols].mean(axis=1)
nfirs_svi_tracts_rates['std_sev_fire_rate_per_cap'] = nfirs_svi_tracts_rates[sev_cols].std(axis=1)
nfirs_svi_tracts_rates['avg_tot_fire_rate_per_cap'] = nfirs_svi_tracts_rates[tot_cols].mean(axis=1)
nfirs_svi_tracts_rates['std_tot_fire_rate_per_cap'] = nfirs_svi_tracts_rates[tot_cols].std(axis=1)
# Rearrange columns
first_cols = ['ST_ABBR','COUNTY','E_TOTPOP','LOCATION','avg_tot_fire_rate_per_cap','std_tot_fire_rate_per_cap',
'avg_sev_fire_rate_per_cap','std_sev_fire_rate_per_cap']
cols = list(nfirs_svi_tracts_rates.columns)
cols = first_cols + [col for col in cols if col not in first_cols]
nfirs_svi_tracts_rates = nfirs_svi_tracts_rates[cols]
# -
nfirs_svi_tracts_rates.sample(5)
# ### Save fire rates by census_tract
nfirs_svi_tracts_rates.to_csv('../data/processed/Per_capita_fire_rates_by_census_tract.csv')
# + [markdown] toc-hr-collapsed=false
# # Task 5
# - Task 5: <b>Home Fire Predictablility Assessment</b>: Using Census Tract Fire Severity Assesment bin Data at 3-month 6-month or 1-year intervals and train simple linear/logistic regression model
# -
# 1 year intervals will be used to capture the temporal aspect of the data, which occurs at one year intervals (most fires occur during the winter months)
# ## Plotting correlation coefficients
def plot_correlation_matrix_heat_map(df,label,qty_fields=10):
df = pd.concat([df[label],df.drop(label,axis=1)],axis=1)
correlation_matrix = df.corr()
index = correlation_matrix.sort_values(label, ascending=False).index
correlation_matrix = correlation_matrix[index].sort_values(label,ascending=False)
fig,ax = plt.subplots()
fig.set_size_inches((10,10))
sns.heatmap(correlation_matrix.iloc[:qty_fields,:qty_fields],annot=True,fmt='.2f',ax=ax)
return(fig,ax)
# ### County correlation heat maps
plot_correlation_matrix_heat_map(nfirs_svi_counties_rates[tot_cols],'2016_tot_fire_rate_per_cap')
plot_correlation_matrix_heat_map(nfirs_svi_counties_rates[sev_cols],'2016_sev_fire_rate_per_cap')
# ### Census tract correlation heat maps
plot_correlation_matrix_heat_map(nfirs_svi_tracts_rates[tot_cols],'2016_tot_fire_rate_per_cap')
# ## Linear Regression Model
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.linear_model import LinearRegression
# I'll use the yearly aggregated rates to create a simple linear regression algorithm to predict the rate for 2016 by census tract
def null_counts(df):
null_df = pd.DataFrame(df.isnull().sum(),columns=['null_count'])
null_df['null_fraction'] = null_df['null_count'] / df.shape[0]
null_df = null_df.sort_values('null_count',ascending=False)
return null_df
null_counts(nfirs_svi_tracts_rates)
tot_cols
# +
label = '2016_tot_fire_rate_per_cap'
# features = tot_cols.drop(label)
features = ['2014_tot_fire_rate_per_cap','2015_tot_fire_rate_per_cap']
X_train, X_test, y_train, y_test = train_test_split(nfirs_svi_tracts_rates.dropna()[features],nfirs_svi_tracts_rates.dropna()[label],train_size=.8,random_state=1)
# -
X_train2, X_test2, y_train2, y_test2 = train_test_split(X_train,y_train,random_state=1)
lr = LinearRegression()
lr.fit(X_train2,y_train2)
lr.score(X_train2,y_train2)
lr = LinearRegression()
cross_val_score(lr,X_train,y_train,cv=10)
nfirs_svi_tracts_rates.sample(5,random_state=1)
|
notebooks/thw_per_capita_fire_rate_analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Molecular Dynamics (MD)
#
# ## Objective:
# Perform some basic molecular dynamics (MD) simulations on a simple polymer model, perform some initial tests, and then after equilibrating the system, compute the self-diffusion coefficient for several different chain lengths.
#
# __Due date__: As assigned in class
#
# ## Overview:
# One simple model of a polymer is just a chain of Lennard-Jones atoms. Here we will simulate such chains, interacting according to the potential (in dimensionless form):
#
# \begin{equation}
# U^* = \sum \limits_{i<j \mathrm{,\ ij\ not\ bonded}} 4\left( r_{ij}^{-12} - r_{ij}^{-6}\right) + \sum \limits_{i<j\mathrm{,\ ij\ bonded}} \frac{k}{2} \left( r_{ij} - r_0\right)^2
# \end{equation}
#
# (Note that, as in the Energy Minimization assignment, we are using the dimensionless form, so that all of the constants are hidden in the units.)
#
# Here, atoms have Lennard-Jones attractions and repulsions, and bonds between atoms along the polymer chain(s) are represented by simple harmonic springs. There are no torsional or angle potentials, and no electrostatic interactions. However, this simple model does share basic elements with the models we still use today for proteins and small molecules -- specifically, our classical MD models today begin with the potential above and add additional terms.
# Simple systems like this polymer model have been thoroughly studied as models of polyatomic molecules, and as models of short polymers. It is relatively easy to derive or determine scaling laws for various physical properties as a function of polymer length in such systems. One such study, by <NAME>., [ Fluid Phase Equilibria 221: 25 (2004) ](https://doi.org/10.1016/j.fluid.2004.04.007) evaluated the self-diffusion coefficient for chains of different lengths. (The self-diffusion coefficient measures diffusive motion of something in a solution consisting of itself, for example the self-diffusion coefficient of water in water describes how mobile a water molecule is in pure water.)
# Here, you will use some Python and Fortran libraries to set up some initial test simulations and make a plot relating to equilibration. Following that, you will compute the self-diffusion coefficient as directed below, making contact with the data of Reis et al.
#
# Most of the functions you will need have already been written for you and are provided here. Most of this assignment will involve using them to conduct a simulation. In addition to the paper mentioned, you will need `mdlib.f90` and `MD_functions.py`. As in the Energy Minimization assignment you did previously, you will need to compile `mdlib.f90` into a .so file suitable for use within Python.
#
# ## Background/settings:
# ### Introduction of our variables:
# Here, the potential energy will be as given above. Again, note that we are working in dimensionless form.
#
# We will simulate a system with a total of N monomers, some of which will be linked to form polymers. Each polymer will consist of M monomers, so that if $N_{poly}$ is the number of polymers, $N = M\times N_{poly}$. That is to say, we have $N_{poly}$ polymers each consisting of $M$ linked monomers in a chain, for a total of $N$ particles.
#
# As usual, our system will have a density, $\rho$, which is N/V. We will work with a particular temperature, $T$, and cutoff distance, $R_c$, beyond which Lennard-Jones interactions will not be included. Additionally, we need to specify a bond strength and equilibrium separation, $k$ and $r_0$, respectively. And we will take timesteps $\Delta t$ using the velocity Verlet integrator.
#
# ### Settings to use (unless otherwise noted)
#
# Unless otherwise noted, here you should use the following settings:
# * $k = 3000$ (spring constant)
# * $r_0 = 1$ (preferred bond length)
# * $N = 240$ (number of particles)
# * $\rho = N/V = 0.8$ so that $L$, the box size, is $(N/\rho)^{1/3}$
# * Use $L$ as the box size in your code
# * $\Delta t = 0.001$ (timestep)
# * $T = 1.0$ (temperature)
# * $R_c = 2.5$ (call this Cut in your code)
#
# Our use of the dimensionless form here includes setting all particle masses to 1. Because of this, forces and accelerations are the same thing. Additionally, units can be dropped, and the Boltzmann constant is equal to 1 in these units.
#
#
# ### What's provided
#
# In this case, mdlib provides almost the same CalcEnergy and CalcEnergyForces routines you used in the previous assignment (for energy minimizations). Additionally, it provides a VVIntegrate function to actually use the integrator (Velocity Verlet) to take a timestep. You should look through the Fortran code to make sure you understand what is being done and see how it connects to what we covered in lecture.
#
# The Python syntax for using VVintegrate looks like:
#
# `Pos, Vel, Accel, KEnergy, PEnergy = mdlib.vvintegrate( Pos, Vel, Accel, M, L, Cut, dt )`
#
# This takes a single timestep (covering time dt) and returns the position, velocity, acceleration, kinetic energy, and potential energy.
#
# Likewise, mdlib provides functions for calculating the potential energy, or the potential energy and forces, as:
# `PEnergy = mdlib.calcenergy(Pos, M, L, Cut)`
# and
# `PE, Forces = mdlib.calcenergyforces(Pos, M, L, Cut, Forces)`
#
# ## Your assignment
# All, or almost all, of the functions you will need to complete this assignment are described below. But before getting to the description, I want to explain the assignment.
#
# ### Part A: Develop a simple molecular dynamics code and examine potential energy versus time for several values of M
# Edit the supplied code below (or MD.py if you prefer to work with the plain text; note that I have also provided MD_functions.py which is utilized by this notebook which provides only the functions you need and not a template for the code you need to write, since this is below) to develop a simple molecular dynamics code. Most of the functions you need are already provided (see documentation below, or in MD_functions.py). But, you do need to fill in the core of two functions:
#
# * InitVelocities(N,T): Should take N, a number of particles and a target temperature and return a velocity array (‘Vel’) which is Nx3 with mean velocity corresponding to the correct average temperature. You may wish to do this by assigning random velocities and rescaling (see below).
#
# * RescaleVelocities(Vel, T): Re-center the velocities to zero net momentum to remove any overall translational motion (i.e., subtract off the average velocity from all particles) and then re-scale the velocities to maintain the correct temperature. This can be done by noting that the average kinetic energy of the system is related in a simple way to the effective temperature:
#
# \begin{equation}
# \frac{1}{2}\sum \limits_i m_i v_i^2 = \frac{3}{2} N k_B T
# \end{equation}
#
# The left-hand term is the kinetic energy, and here can be simplified by noting all of the masses in the system are defined to be 1. The right hand term involves the Boltzmann constant, the number of particles in the system, and the instantaneous temperature.
#
# So, you can compute the effective temperature of your system, and translate this into a scaling factor which you can use to multiply (scale) all velocities in the system to ensure you get the correct average temperature (see http://www.pages.drexel.edu/~cfa22/msim/node33.html). **Specifically, following the Drexel page (eq. 177), compute a (scalar) constant by which you will multiply all of the velocities to ensure that the effective temperature is at the correct target value after rescaling.** To do this calculation you will need to compute the kinetic energy, which involves the sum above.
#
# Remove translational motion, rescale the velocities, and have your function return the updated velocity array.
# Once the above two functions are written, finishing write a simple MD code using the available functions to:
# * Initially place atoms on a cubic lattice with the correct box size
# * Energy-minimize the initial configuration using the conjugate-gradient energy minimizer; this will help ensure the simulation doesn’t “explode” (a highly technical term meaning “crash”) when you begin MD
# * Assign initial velocities and compute forces (accelerations)
# * Use the velocity Verlet integrator to perform a molecular dynamics run. Rescale atomic velocities every **RescaleFreq** integration steps to achieve the target temperature T. ( You can test whether you should rescale the velocities using the modulo (remainder) operator, for example $i % RescaleFreq == 0$)
# * You might want to use RescaleFreq = 100 (for extra credit, you can try several values of RescaleFreq and explain the differences in fluctuations in the potential energy versus time that you see)
#
# Use the settings given above for $N$, $\rho$, $T$, the timestep, and the cutoff distance.
#
# Perform simulations for $M = 2, 4, 6, 8, 12,$ and $16$ and store the total energies versus time out to 2,000 timesteps. (Remember, $M$ controls the number of particles per polymer; you are keeping the same total number of particles in the system and changing the size of the polymers). On a single graph, plot the potential energy versus time for each of these cases (each in a different color). Turn in this graph.
#
# Note also you can visualize, if desired, using the Python module for writing to PDB files which you saw in the Energy Minimization exercise.
#
#
# ### Part B: Extend your code to compute the self-diffusion coefficient as a function of chain length
#
# Modify your MD code from above to perform a series of steps that will allow you to compute the self-diffusion coefficient as a function of chain length and determine how diffusion of polymers depends on the size of the polymer. To compute the self-diffusion coefficient, you will simply need to monitor the motion of each polymer in time.
#
# Here, you will first perform two equilibrations at constant temperature using velocity rescaling . The first will allow the system to reach the desired temperature and forget about its initial configuration (remember, it was started on a lattice). The second will allow you to compute the average total energy of the system. Then, you will fix the total energy at this value and perform a production simulation.
#
# Here’s what you should do:
# * Following initial preparation (like above), first perform equilibration for NStepsEquil1 using velocity rescaling to target temperature T every RescaleFreq steps, using whatever value of RescaleFreq you used previously (NOT every step!)
# * Perform a second equilibration for `NStepsEquil2` timesteps using velocity rescaling at the same frequency, storing energies while you do this.
# * Compute the average total energy over this second equilibration and rescale the velocities to start the final phase with the correct total energy. In other words, the total energy at the end of equilibration will be slightly above or below the average; you should find the kinetic energy you need to have to get the correct total energy, and rescale the velocities to get this kinetic energy. After this you will be doing no more velocity rescaling. (Hint: You can do this final rescaling easily by computing a scaling factor, and you will probably not be using the rescaling code you use to maintain the temperature during equilibration.)
# * Copy the initial positions of the particles into a reference array for computing the mean squared displacement, for example using `Pos0 = Pos.copy()`
# * Perform a production run for `NStepsProd` integration steps with constant energy (NVE) rather than velocity rescaling. Periodically record the time and mean squared displacement of the atoms from their initial positions. (You will need to write a small bit of code to compute mean squared displacements, but it shouldn’t take more than a couple of lines; you may send it to me to check if you are concerned about it). The mean squared displacement is given by
# \begin{equation}
# \left<\left| \mathbf{r}-\mathbf{r_0} \right|^2 \right>
# \end{equation}
#
# where the $\mathbf{r}$'s are the current and initial positions of the object in question so the mean squared
# displacement measures the square of the distance traveled for the object.
#
# * Compute the self-diffusion coefficient, $D$. The mean squared displacement relates to the self-diffusion coefficient, $D$, in this way:
# \begin{equation}
# \left< \left| \mathbf{r} - \mathbf{r_0}\right| \right>^2 = 6 D t
# \end{equation}
#
# Here $D$ is the self-diffusion coefficient and t is the elapsed time. That is, the expected squared distance traveled (mean squared displacement) grows linearly with the elapsed time.
#
# For settings, use NStepsEquil1 = 10,000 = NStepsEquil2 and NStepsProd = 100,000. (Note: You should probably do a “dry run” first with shorter simulations to ensure everything is working, as 100,000 steps might take an hour or more to run).
#
# * Perform these runs for $M = 2, 4, 6, 8, 12,$ and $16$, storing results for each.
# * Plot the mean-squared displacement versus time for each M on the same graph.
# * Compute the diffusion coefficient for each $M$ from the slope of each graph and plot these fits on the same graph. You can do a linear least-squares fit easily in Numpy.
#
# `Slope, Intercept = np.polyfit( xvals, yvals, 1)`
#
# Plot the diffusion coefficient versus $M$ and try and see if it follows any obvious scaling law. It should decrease with increasing $M$, but with what power? (You may want to refer to the Reis et al. paper).
#
# ### What to turn in:
# * Your plot of the potential energy versus time for each $M$ in Part A
# * Mean-squared displacement versus time, and fit, for each $M$ in Part B, all on one plot
# * The diffusion coefficient versus $M$ in Part B
# * Your code for at least Part B
# * Any comments you have - do you think you got it right? Why or why not? What was confusing/helpful? What would you do if you had more time?
# * Clearly label axes and curves on your plots!
#
# You can send your comments/discussion as an e-mail, and the rest of the items as attachments.
#
# ### What’s provided for you:
# In this case, most of what you need is provided in the importable module `MD_functions.py` (which you can view with your favorite text editor, like `vi` or Atom), except for the functions for initial velocities and velocity rescaling -- in those cases, the shells are present below and you need to write the core (which will be very brief!). **However, you will also need to insert the code for the `ConjugateGradient` function in `MD_functions.py`** from your work you did in the Energy Minimization assignment. If you did not do this, or did not get it correct (or if you are not certain if you did), you will need to e-mail <NAME> for solutions.
#
# From the Fortran library `mdlib` (which you will compile as usual via `f2py -c -m mdlib mdlib.f90`), the only new function you need is Velocity Verlet. In `MD_functions.py`, the following tools are available (this shows their documentation, not the details of the code, but you should only need to read the documentation in order to be able to use them. NOTE: No modification of these functions is needed; you only need to use them. You will only need to write `InitVelocities` and `RescaleVelocities` as described above, plus provide your previous code for `ConjugateGradient`:
#
#
# Help on module MD:
#
# NAME
#
# MD - #MD exercise template for PharmSci 175/275
#
#
# FUNCTIONS
#
# FUNCTIONS
#
# ConjugateGradient(Pos, dx, EFracTolLS, EFracTolCG, M, L, Cut)
# Performs a conjugate gradient search.
# Input:
# Pos: starting positions, (N,3) array
# dx: initial step amount
# EFracTolLS: fractional energy tolerance for line search
# EFracTolCG: fractional energy tolerance for conjugate gradient
# M: Monomers per polymer
# L: Box size
# Cut: Cutoff
# Output:
# PEnergy: value of potential energy at minimum
# Pos: minimum energy (N,3) position array
#
# InitPositions(N, L)
# Returns an array of initial positions of each atom,
# placed on a cubic lattice for convenience.
# Input:
# N: number of atoms
# L: box length
# Output:
# Pos: (N,3) array of positions
#
# InitVelocities(N, T)
# Returns an initial random velocity set.
# Input:
# N: number of atoms
# T: target temperature
# Output:
# Vel: (N,3) array of atomic velocities
#
# InstTemp(Vel)
# Returns the instantaneous temperature.
# Input:
# Vel: (N,3) array of atomic velocities
# Output:
# Tinst: float
#
# InstTemp(Vel):
# Returns the instantaneous temperature.
# Input:
# Vel: (N,3) array of atomic velocities
# Output:
# Tinst: float
#
# RescaleVelocities(Vel, T)
# Rescales velocities in the system to the target temperature.
# Input:
# Vel: (N,3) array of atomic velocities
# T: target temperature
# Output:
# Vel: same as above
#
# LineSearch(Pos, Dir, dx, EFracTol, M, L, Cut, Accel=1.5, MaxInc=10.0,
# MaxIter=10000)
# Performs a line search along direction Dir.
# Input:
# Pos: starting positions, (N,3) array
# Dir: (N,3) array of gradient direction
# dx: initial step amount
# EFracTol: fractional energy tolerance
# M: Monomers per polymer
# L: Box size
# Cut: Cutoff
# Accel: acceleration factor
# MaxInc: the maximum increase in energy for bracketing
# MaxIter: maximum number of iteration steps
# Output:
# PEnergy: value of potential energy at minimum along Dir
# Pos: minimum energy (N,3) position array along Dir
#
#
# ## Here, you should actually write your functions:
# +
import mdlib
from MD_functions import *
def InitVelocities(N, T):
"""Returns an initial random velocity set.
Input:
N: number of atoms
T: target temperature
Output:
Vel: (N,3) array of atomic velocities
"""
#WRITE THIS CODE
#THEN RETURN THE NEW VELOCITIES
return Vel
def RescaleVelocities(Vel, T):
"""Rescales velocities in the system to the target temperature.
Input:
Vel: (N,3) numpy array of atomic velocities
T: target temperature
Output:
Vel: same as above
"""
#WRITE THIS CODE
#recenter to zero net momentum (assuming all masses same)
#find the total kinetic energy
#find velocity scale factor from ratios of kinetic energy
#Update velocities
#NOW RETURN THE NEW VELOCITIES
return Vel
# -
# ## Now use your functions, coupled with those provided, to code up your assignment:
# +
#PART A:
#Define box size and other settings
k=3000
r0=1
N=240
rho=0.8 #Solve to find L
#Set L
dt=0.001
T=1.0
Cut=2.5
RescaleFreq = 100 #See note above - may want to try several values
#Define your M value(s)
#Initially place atoms on a cubic lattice
#Energy-minimize the initial configuration using the conjugate-gradient energy minimizer
#Assign initial velocities and compute forces (accelerations)
#Use the velocity Verlet integrator to perform a molecular dynamics run, rescaling velocities when appropriate
# +
#PART B:
#Additionally:
NStepsEquil1 = 10000
NStepsEquil2 = 10000
NStepsProd = 100000
#Set up as in A
#Equilibrate for NStepsEquil1 with velocity rescaling every RescaleFreq steps, discarding energies
#Equilibrate for NStepsEquil2 with velocity rescaling, storing energies
#Stop and average the energy. Rescale the velocities so the current (end-of-equilibration) energy matches the average
#Store the particle positions so you can later compute the mean squared displacement
#Run for NStepsProd at constant energy (NVE) recording time and mean squared displacement periodically
#Compute diffusion coefficient for each M using a fit to the mean squared displacement
#Plot mean squared displacement for each M
#Plot diffusion coefficient as a function of M
# -
# ## Follow-up:
# The thermostat used here is not in general recommended, for reasons we will discuss in class. To understand one such reason, please read the “flying ice cube” paper referenced here: J Comp Chem 19:726-740 (1998) <http://onlinelibrary.wiley.com/doi/10.1002/(SICI)1096-987X(199805)19:7%3C726::AID-JCC4%3E3.0.CO;2-S/full>
|
uci-pharmsci/assignments/MD/MD.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# [[source]](../api/alibi.explainers.shap_wrappers.rst)
# # Tree SHAP
# <div class="alert alert-info">
# To enable SHAP support, you may need to run
#
# ```bash
# pip install alibi[shap]
# ```
#
# </div>
# ## Overview
# The tree SHAP (**SH**apley **A**dditive ex**P**lanations) algorithm is based on the paper [From local explanations to global understanding with explainable AI for trees](https://www.nature.com/articles/s42256-019-0138-9) by Lundberg et al. and builds on the open source [shap library](https://github.com/slundberg/shap) from the paper's first author.
#
#
# The algorithm provides human interpretable explanations suitable for regression and classification of models with tree structure applied to tabular data. This method is a member of the *additive feature attribution methods* class; feature attribution refers to the fact that the change of an outcome to be explained (e.g., a class probability in a classification problem) with respect to a *baseline* (e.g., average prediction probability for that class in the training set) can be attributed in different proportions to the model input features.
#
# A simple illustration of the explanation process is shown in Figure 1. Here we see depicted a tree-based model which takes as an input features such as `Age`, `BMI` or `Blood pressure` and outputs `Mortality risk score`, a continuous value. Let's assume that we aim to explain the difference between and observed outcome and no risk, corresponding to a base value of `0.0`. Using the Tree SHAP algorithm, we attribute the `4.0` difference to the input features. Because the sum of the attribute values equals `output - base value`, this method is _additive_. We can see for example that the `Sex` feature contributes negatively to this prediction whereas the remainder of the features have a positive contribution (i.e., increase the mortality risk). For explaining this particular data point, the `Blood Pressure` feature seems to have the largest effect, and corresponds to an increase in the mortality risk. See our example on how to perform explanations with this algorithm and visualise the results using the `shap` library visualisations [here](../examples/interventional_tree_shap_adult_xgb.ipynb) and [here](../examples/path_dependent_tree_shap_adult_xgb.ipynb).
# 
# Figure 1: Cartoon ilustration of explanation models with Tree SHAP.
#
# Image Credit: <NAME> (see source [here](https://www.nature.com/articles/s42256-019-0138-9))
# ## Usage
# In order to compute the shap values , the following arguments can optionally be set when calling the `explain` method:
#
# - `interactions`: set to `True` to decompose the shap value of every feature for every example into a main effect and interaction effects
#
# - `approximate`: set to `True` to calculate an approximation to shap values (see our [example](../examples/path_dependent_tree_shap_adult_xgb.ipynb))
#
# - `check_additivity`: if the explainer is initialised with `model_output = raw` and this option is `True` the explainer checks that the sum of the shap values is equal to model output - expected value
#
# - `tree_limit`: it an `int` is passed, an ensemble formed of only `tree_limit` trees is explained
#
# If the dataset contains categorical variables that have been encoded before being passed to the explainer and a single shap value is desired for each categorical variable, the the following options should be specified:
#
#
# - `summarise_result`: set to `True`
#
# - `cat_var_start_idx`: a sequence of integers containing the column indices where categorical variables start. If the feature matrix contains a categorical feature starting at index 0 and one at index 10, then `cat_var_start_idx=[0, 10]`
#
# - `cat_vars_enc_dim`: a list containing the dimension of the encoded categorical variables. The number of columns specified in this list is summed for each categorical variable starting with the corresponding index in `cat_var_start_idx`. So if `cat_var_start_idx=[0, 10]` and `cat_vars_enc_dim=[3, 5]`, then the columns with indices `0, 1` and `2` and `10, 11, 12, 13` and `14` will be combined to return one shap value for each categorical variable, as opposed to `3` and `5`.
#
# ### Path-dependent feature perturbation algorithm
# #### Initialiastion and fit
# The explainer is initialised with the following agruments:
#
# - a model, which could be an `sklearn`, `xgboost`, `catboost` or `lightgbm` model. Note that some of the models in these packages or models trained with specific objectives may not be supported. In particular, passing raw strings as categorical levels for `catboost` and `lightgbm` is not supported
#
# - `model_output` should always default to `raw` for this algorithm
#
# - optionally, set `task` to `'classification'` or `'regression'` to indicate the type of prediction the model makes. If set to `regression` the `prediction` field of the response is empty
#
# - optionally, a list of feature names via `feature_names`. This is used to provide information about feature importances in the response
#
# - optionally, a dictionary, `category_names`, that maps the columns of the categorical variables to a list of strings representing the names of the categories. This may be used for visualisation in the future.
#
# ```python
# from alibi.explainers import TreeShap
#
# explainer = TreeShap(
# model,
# feature_names=['size', 'age'],
# categorical_names={0: ['S', 'M', 'L', 'XL', 'XXL']}
# )
# ```
#
# For this algorithm, fit is called with no arguments:
#
# ```python
# explainer.fit()
# ```
# #### Explanation
# To explain an instance `X`, we simply pass it to the explain method:
#
# ```python
# explanation = explainer.explain(X)
# ```
# The returned explanation object has the following fields:
#
# * `explanation.meta`:
#
# ```python
# {'name': 'TreeShap',
# 'type': ['whitebox'],
# 'task': 'classification',
# 'explanations': ['local', 'global'],
# 'params': {'summarise_background': False, 'algorithm': 'tree_path_dependent' ,'kwargs': {}}
# }
# ```
#
# This field contains metadata such as the explainer name and type as well as the type of explanations this method can generate. In this case, the `params` attribute shows the Tree SHAP variant that will be used to explain the model in the `algorithm` attribute.
#
# * `explanation.data`:
#
# ```python
# data={'shap_values': [
# array([[ 5.0661433e-01, 2.7620478e-02],
# [-4.1725192e+00, 4.4859368e-03],
# [ 4.1338313e-01, -5.5618007e-02]],
# dtype=float32)
# ],
# 'shap_interaction_values': [array([], dtype=float64)],
# 'expected_value': array([-0.06472124]),
# 'model_output': 'raw',
# 'categorical_names': {0: ['S', 'M', 'L', 'XL', 'XXL']},
# 'feature_names': ['size', 'age'],
# 'raw': {
# 'raw_prediction': array([-0.73818872, -8.8434663 , -3.24204564]),
# 'loss': [],
# 'prediction': array([0, 0, 0]),
# 'instances': array([[0, 23],
# [4, 55],
# [2, 43]]),
# 'labels': array([], dtype=float64),
# 'importances': {
# '0': {
# 'ranked_effect': array([1.6975055 , 1.3598266], dtype=float32),
# 'names': [
# 'size',
# 'age',
# ]
# },
# 'aggregated': {
# 'ranked_effect': array([1.6975055 , 1.3598266], dtype=float32),
# 'names': [
# 'size',
# 'age',
# ]
# }
# }
# }
# }
# ```
# This field contains:
#
# * `shap_values`: a list of length equal to the number of model outputs, where each entry is an array of dimension samples x features of shap values. For the example above , 3 instances with 2 features has been explained so the shap values for each class are of dimension 3 x 2
#
# * `shap_interaction_values`: an empty list since this `interactions` was set to `False` in the explain call
#
# * `expected_value`: an array containing expected value for each model output
#
# * `model_output`: `raw` indicates that the model raw output was explained, the only option for the path dependent algorithm
#
# * `feature_names`: a list with the feature names
#
# * `categorical_names`: a mapping of the categorical variables (represented by indices in the shap_values columns) to the description of the category
#
# * `raw`: this field contains:
#
# * `raw_prediction`: a samples x n_outputs array of predictions for each instance to be explained.
#
# * `prediction`: an array containing the index of the maximum value in the `raw_prediction` array
#
# * `instances`: a samples x n_features array of instances which have been explained
#
# * `labels`: an array containing the labels for the instances to be explained
#
# * `importances`: a dictionary where each entry is a dictionary containing the sorted average magnitude of the shap value (ranked_effect) along with a list of feature names corresponding to the re-ordered shap values (names). There are n_outputs + 1 keys, corresponding to n_outputs and the aggregated output (obtained by summing all the arrays in shap_values)
#
#
# Please see our examples on how to visualise these outputs using the shap library visualisations library visualisations [here](../examples/interventional_tree_shap_adult_xgb.ipynb) and [here](../examples/path_dependent_tree_shap_adult_xgb.ipynb).
# #### Shapley interaction values
# ##### Initialisation and fit
# Shapley interaction values can only be calculated using the path-dependent feature perturbation algorithm in this release, so no arguments are passed to the `fit` method:
#
# ```python
# explainer = TreeShap(
# model,
# model_output='raw',
# )
#
# explainer.fit()
# ```
# ##### Explanation
# To obtain the Shapley interaction values, the `explain` method is called with the option `interactions=True`:
#
# ```python
# explanation = explainer.explain(X, interactions=True)
# ```
#
# The explanation contains a list with the shap interaction values for each model output in the `shap_interaction_values` field of the `data` property.
# ### Interventional feature perturbation algorithm
# #### Explaining model output
# ##### Initialiastion and fit
# ```python
# explainer = TreeShap(
# model,
# model_output='raw',
# )
#
# explainer.fit(X_reference)
# ```
# Model output can be set to `model_output='probability'` to explain models which return probabilities. Note that this requires the model to be trained with specific objectives. Please the footnote to our path-dependent feature perturbation [example](../examples/path_dependent_tree_shap_adult_xgb.ipynb) for an example of how to set the model training objective in order to explain probability outputs.
# ##### Explanation
# To explain instances in `X`, the explainer is called as follows:
# ```python
# explanation = explainer.explain(X)
# ```
# #### Explaining loss functions
# ##### Initialisation and fit
# To explain loss function, the following configuration and fit steps are necessary:
#
# ```python
# explainer = TreeShap(
# model,
# model_output='log_loss',
# )
#
# explainer.fit(X_reference)
# ```
#
# Only square loss regression objectives and cross-entropy classification objectives are supported in this release.
# ##### Explanation
# Note that the labels need to be passed to the `explain` method in order to obtain the explanation:
#
# ```python
# explanation = explainer.explain(X, y)
# ```
# ### Miscellaneous
#
# #### Runtime considerations
# ##### Adjusting the size of the reference dataset
# The algorithm automatically warns the user if a background dataset size of more than `1000` samples is passed. If the runtime of an explanation with the original dataset is too large, then the algorithm can automatically subsample the background dataset during the `fit` step. This can be achieve by specifying the fit step as
#
# ```python
# explainer.fit(
# X_reference,
# summarise_background=True,
# n_background_samples=300,
# )
# ```
#
# or
# ```python
# explainer.fit(
# X_reference,
# summarise_background='auto'
# )
# ```
#
# The `auto` option will select `1000` examples, whereas using the boolean argument allows the user to directly control the size of the reference set. If categorical variables are specified, the algorithm uses subsampling of the data. Otherwise, a kmeans clustering algorithm is used to select the background dataset.
#
# As describe above, the explanations are performed with respect to the expected output over this dataset so the shap values will be affected by the dataset selection. We recommend experimenting with various ways to choose the background dataset before deploying explanations.
# ## Theoretical overview
#
# Recall that, for a model $f$, the Kernel SHAP algorithm [[1]](#References) explains a certain outcome with respect to a chosen reference (or an expected value) by estimating the shap values of each feature $i$ from $\{1, ..., M\}$, as follows:
#
# - enumerate all subsets $S$ of the set $F \setminus \{i\}$
#
# - for each $S \subseteq F \setminus \{i\}$, compute the contribution of feature $i$ as $C(i|S) = f(S \cup \{i\}) - f(S)$
#
# - compute the shap value according to
#
# $$
# \phi_i := \frac{1}{M} \sum \limits_{{S \subseteq F \setminus \{i\}}} \frac{1}{ M - 1 \choose |S|} C(i|S).
# \tag{1}
# $$
#
#
# Since most models do not accept arbitrary patterns of missing values at inference time, $f(S)$ needs to be approximated. The original formulation of the Kernel Shap algorithm [[1]](#References) proposes to compute $f(S)$ as the _observational conditional expectation_
#
# $$
# f(S) := \mathbb{E}\left[f(\mathbf{x}_{S}, \mathbf{X}_{\bar{S}} | \mathbf{X}_S = \mathbf{x}_S) \right]
# \tag{2}
# $$
#
# where the expectation is taken over a *background dataset*, $\mathcal{D}$, after conditioning. Computing this expectation involves drawing sufficiently many samples from $\mathbf{X}_{\bar{S}}$ for every sample from $\mathbf{X}_S$, which is expensive. Instead, $(2)$ is approximated by
#
# $$
# f(S) := \mathbb{E} \left[f(\mathbf{x}_{S}, \mathbf{X}_{\bar{S}})\right]
# $$
#
# where features in a subset $S$ are fixed and features in $\bar{S}$ are sampled from the background dataset. This quantity is referred to as _marginal_ or *interventional conditional expectation*, to emphasise that setting features in $S$ to the values $\mathbf{x}_{S}$ can be viewed as an intervention on the instance to be explained.
#
# As described in [[2]](#References), if estimating impact of a feature $i$ on the function value by $\mathbb{E} \left[ f | X_i = x_i \right]$, one should bear in mind that observing $X_i = x_i$ changes the distribution of the features $X_{j \neq i}$ if these variables are correlated. Hence, if the conditional expectation if used to estimate $f(S)$, the Shapley values might not be accurate since they also depend on the remaining variables, effect which becomes important if there are strong correlations amongst the independent variables. Furthermore, the authors show that estimating $f(S)$ using the conditional expectation violates the *sensitivity principle*, according to which the Shapley value of a redundant variable should be 0. On the other hand, the intervention breaks the dependencies, ensuring that the sensitivity holds. One potential drawback of this method is that setting a subset of values to certain values without regard to the values of the features in the complement (i.e., $\bar{S}$) can generate instances that are outside the training data distribution, which will affect the model prediction and hence the contributions.
#
# The following sections detail how these methods work and how, unlike Kernel SHAP, compute the exact shap values in polynomial time. The algorithm estimating contributions using interventional expectations is presented, with the remaining sections being dedicated to presenting an approximate algorithm for evaluating the interventional expectation that does not require a background dataset and Shapley interaction values.
#
# <a id='source_1'></a>
#
#
# ### Interventional feature perturbation
# <a id='interventional'></a>
#
# The interventional feature perturbation algorithm provides an efficient way to calculate the expectation $f(S) := \mathbb{E} \left[f(\mathbf{x}_{S}, \mathbf{X}_{\bar{S}})\right]$ for all possible subsets $S$, and to combine these values according to equation $(1)$ in order to obtain the Shapley value. Intuitively, one can proceed as follows:
#
# - choose a background sample $r \in \mathcal{D}$
#
# - for each feature $i$, enumerate all subsets $S \subseteq F \setminus \{i\}$
#
# - for each such subset, $S$, compute $f(S)$ by traversing the tree with a _hybrid sample_ where the features in $\bar{S}$ are replaced by their corresponding values in $r$
#
# - combine results according to equation $(1)$
#
# If $R$ samples from the background distribution are used, then the complexity of this algorithm is $O(RM2^M)$ since we perform $2^M$ enumerations for each of the $M$ features, $R$ times. The key insight into this algorithm is that multiple hybrid samples will end up traversing identical paths and that this can be avoided if the shap values' calculation is reformulated as a summation over the paths in the tree (see [[4]](#References) for a proof):
#
# $$
# \phi_i = \sum_{P}\phi_{i}^P
# $$
#
# where the summation is over paths $P$ in the tree descending from $i$. The value and sign of the contribution of each path descending through a node depends on whether the split from the node is due to a foreground or a background feature, as explained in the practical example below.
#
# <a id='source_4'></a>
#
# #### Computing contributions with interventional Tree SHAP: a practical example.
# 
# Figure 2: Ilustration of the feature contribution and expected value estimation process using interventional perturbation Tree SHAP. The positive and the negative contributions of a node are represented in <span style="color:green">green</span> and <span style="color:red">red</span>, respectively.
# In the figure above, the paths followed due the instance to be explained $x$ are coloured in red, paths followed due to the background sample in red, and common paths in yellow.
#
# The instance to be explained is perturbed using a reference sample by the values of the features $F1$, $F3$ and $F5$ in $x$ with the corresponding values in $r$. This process gives the name of the algorithm since following the paths indicated by the background sample is akin to intervening on the instance to be explained with features from the background sample. Therefore, one defines the set $F$ in the previous section as $F = \{ j: x_{j} \neq r_{j}\}$ for this case. Note that these are the only features for which one can estimate a contribution given this background sample; the same path is followed for features $F2$ and $F4$ for both the original and the perturbed sample, so these features do not contribute to explain the difference between the observed outcome ($v_6$) and the outcome that would have been observed if the tree had been traversed according to the reference $(v_{10})$.
#
#
# Considering the structure of the tree for the given $x$ and $r$ together with equation $(1)$ reveals that the left subtree can be traversed to compute the negative terms in the summation whereas the right subtree will provide positive terms. This is because the nodes in the left subtree can only be reached if $F1$ takes the value from the background sample, that is, only $F1$ is missing. Because $F2$ and $F4$ do not contribute to explaining $f(x) - f(r)$, the negative contribution of the left subtree will be equal to the negative contribution of node $8$. This node sums two negative components: one when the downstream feature $F5$ is also missing (corresponding to evaluating $f$ at $S = \varnothing$) and one when $F5$ is present (corresponding to evaluating $f$ at $S=\{F5\}$). These negative values are weighted according to the combinatorial factor in equation $(1)$. By a similar reasoning, the nodes in the right subtree are reached only if $F1$ is present and they provide the positive terms for the shap value computation. Note that the combinatorial factor in $(1)$ should be evaluated with $|S| \gets |S| - 1$ for positive contributions since $|S|$ is increased by $1$ because of the feature whose contribution is calculated is present in the right subtree.
#
# A similar reasoning is applied to compute the contributions of the downstream nodes. For example, to estimate the contribution of $F5$, one considers a set $S = \varnothing$ and observes the value of node $10$, and weighs that with the combinatorial factor from equation $(1)$ where $M-1 = 1$ and $|S|=0$ (because there are no features present on the path) and a positive contribution from node $9$ weighted by the same combinatorial factor (because $S = \{F5\}$ so $|S| - 1 = 0$).
#
# To summarise, the efficient algorithm relies on the following key ideas:
#
# - each node in the tree is assigned a positive contribution reflecting membership of the splitting feature in a subset $S$ and a negative contribution to indicate the feature is missing ($i\in \bar{S}$)
#
# - the positive and negative contributions of a node can be computed by summing the positive and negative contributions of the children nodes, in keeping with the fact that the Shapley value can be computed by summing a contribution from each path the feature is on
#
# - to compute the contribution of a feature at a node, one adds a positive contribution from the node reached by splitting on the feature from the instance to be explained and a negative contribution from the node reached by splitting on the feature in the background sample
#
# - features for which the instance to be explained and the reference follow the same path are assigned $0$ contribution.
#
# #### Explaining loss functions
# One advantage of the interventional approach is that it allows to approximately transform the shap values to account for nonlinear transformation of outputs, such as the loss function. Recall that given $\phi_i, ..., \phi_M$ the local accuracy property guarantees that given $\phi_0 = \mathbb{E}[f(x)]$
#
# $$
# f(x) = \phi_0 + \sum \limits_{i=1}^M \phi_i.
# \tag{3}
# $$
#
# Hence, in order to account for the effect of the nonlinear transformation $h$, one has to find the functions $g_0, ..., g_M$ such that
#
# $$
# h(f(x)) = g(\phi_0) + \sum \limits_{i=1}^M g_i(\phi_i)
# \tag{4}
# $$
#
# For simplicity, let $y=h(x)$. Then using a first-order Taylor series expansion around $\mathbb{E}[y]$ one obtains
#
# $$
# h(y) \approx h(\mathbb{E}[y]) + \frac{\partial h(y) }{\partial y} \Bigr|_{y=\mathbb{E}[y]}(y - \mathbb{E}[y]).
# \tag{5}
# $$
#
# Substituting $(3)$ in $(5)$ and comparing coefficients with $(4)$ yields
#
# $$
# \begin{split}
# g_0 & \approx & \; h(\mathbb{E}[y]) \\
# g_i &\approx & \; \phi_i \frac{\partial h(y) }{\partial y} \Bigr|_{y=\mathbb{E}[y]} .
# \end{split}
# $$
#
# Hence, an approximate correction is given by simply scaling the shap values using the gradient of the nonlinear function. Note that in practice one may take the Taylor series expansion at a reference point $r$ from the background dataset and average over the entire background dataset to compute the scaling factor. This introduces an additional source of noise since $h(\mathbb{E}[y]) = \mathbb{E}[h(y)]$ only when $h$ is linear.
# #### Computational complexity
# For a single foreground and background sample and a single tree, the algorithm runs in $O(LD)$ time. Thus, using $R$ background samples and a model containing $T$ trees, yields a complexity of $O(TRLD)$.
# ### Path dependent feature perturbation
# <a id='path_dependent'></a>
# Another way to approximate equation $(2)$ to compute $f(S)$ given an instance $x$ and a set of missing features $\bar{S}$ is to recursively follow the decision path through the tree and:
#
# - return the node value if a split on a feature $i \in S$ is performed
#
# - take a weighted average of the values returned by children if $i \in \bar{S}$, where the weighing factor is equal to the proportion of training examples flowing down each branch. This proportion is a property of each node, sometimes referred to as _weight_ or _cover_ and measures how important is that node with regard to classifying the training data.
#
# Therefore, in the path-dependent perturbation method, we compute the expectations with respect to the training data distribution by weighting the leaf values according to the proportion of the training examples that flow to that leaf.
#
# To avoid repeating the above recursion $M2^M$ times, one first notices that for a single decision tree, applying a perturbation would result in the sample ending up in a different leaf. Therefore, following each path from the root to a leaf in the tree is equivalent to perturbing subsets of features of varying cardinalities. Consequently, each leaf will contain a certain proportion of all possible subsets $S \subseteq F$. Therefore, to compute the shap values, the following quantities are computed at each leaf, *for every feature $i$ on the path leading to that leaf*:
#
# - the proportion of subsets $S$ at the leaf that contain $i$ and the proportion of subsets $S$ that do not contain $i$
#
# - for each cardinality, the proportion of the sets of that cardinality contained at the leaf. Tracking each cardinality as opposed to a single count of subsets falling into a given leaf is necessary since it allows to apply the weighting factor in equation (1), which depends on the subset size, $|S|$.
#
# This intuition can be summarised as follows:
# $$
# \phi_i := \sum \limits_{j=1}^L \sum \limits_{P \in {S_j}} \frac {w(|P|, j)}{ M_j {M_j - 1 \choose |P|}} (p_o^{i,j} - p_z^{i, j}) v_j
# \tag{6}
# $$
#
# where $S_j$ is the set of present feature subsets at leaf $j$, $M_j$ is the length of the path and $w(|P|, j)$ is the proportion of all subsets of cardinality $P$ at leaf $j$, $p_o^{i, j}$ and $p_z^{i, j}$ represent the fractions of subsets that contain or do not contain feature $i$ respectively.
# #### Computational complexity
# Using the above quantities, one can compute the _contribution_ of each leaf to the Shapley value of every feature. This algorithm has complexity $O(TLD^2)$ for an ensemble of trees where $L$ is the number of leaves, $T$ the number of trees in the ensemble and $D$ the maximum tree depth. If the tree is balanced, then $D=\log L$ and the complexity of our algorithm is $O(TL\log^2L)$
# #### Expected value for the path-dependent perturbation algorithm
# Note that although a background dataset is not provided, the expected value is computed using the node cover information, stored at each node. The computation proceeds recursively, starting at the root. The contribution of a node to the expected value of the tree is a function of the expected values of the children and is computed as follows:
#
# $$
# c_j = \frac{c_{r(j)}r_{r(j)} + c_{l(j)}r_{l(j)}}{r_j}
# $$
#
# where $j$ denotes the node index, $c_j$ denotes the node expected value, $r_j$ is the cover of the $j$th node and $r(j)$ and $l(j)$ represent the indices of the right and left children, respectively. The expected value used by the tree is simply $c_{root}$. Note that for tree ensembles, the expected values of the ensemble members is weighted according to the tree weight and the weighted expected values of all trees are summed to obtain a single value.
#
# The cover depends on the objective function and the model chosen. For example, in a gradient boosted tree trained with squared loss objective, $r_j$ is simply the number of training examples flowing through $j$. For an arbitrary objective, this is the sum of the Hessian of the loss function evaluated at each point flowing through $j$, as explained [here](../examples/xgboost_model_fitting_adult.ipynb).
# ### Shapley interaction values
# While the Shapley values provide a solution to the problem of allocating a function variation to the input features, in practice it might be of interest to understand how the importance of a feature depends on the other features. The Shapley interaction values can solve this problem, by allocating the change in the function amongst the individual features (*main effects*) and all pairs of features (*interaction effects*). Thus, they are defined as
#
# $$
# \Phi_{i, j}(f, x) = \sum_{S \subseteq {F \setminus \{i, j\}}} \frac{1}{2|S| { M-1 \choose |S| - 1}} \nabla_{ij}(f, x, S), \; i \neq j
# \tag{7}
# $$
#
# and
#
# $$
# \nabla_{ij}(f, x, S) = \underbrace{f_{x}(S \cup \{i, j\}) - f_x(S \cup \{j\})}_{j \; present} - \underbrace{[f_x(S \cup \{i\}) - f_x(S)]}_{j \; not \; present}.
# \tag{8}
# $$
#
# Therefore, the interaction of features $i$ and $j$ can be computed by taking the difference between the shap values of $i$ when $j$ is present and when $j$ is not present. The main effects are defined as
#
# $$
# \Phi_{i,i}(f, x) = \phi_i(f, x) - \sum_{i \neq j} \Phi_{i, j}(f, x),
# $$
#
# Setting $\Phi_{0, 0} = f_x(\varnothing)$ yields the local accuracy property for Shapley interaction values:
#
# $$f(x) = \sum \limits_{i=0}^M \sum \limits_{j=0}^M \Phi_{i, j}.(f, x) $$.
#
# The interaction is split equally between feature $i$ and $j$, which is why the division by two appears in equation $(7)$. The total interaction effect is defined as $\Phi_{i, j}(f, x) + \Phi_{j, i}(f,x)$.
# #### Computational complexity
# According to equation $(8)$, the interaction values can be computed by applying either the interventional or path-dependent feature perturbation algorithm twice: once by fixing the value of feature $j$ to $x_j$ and computing the shapley value for feature $i$ in this configuration, and once by fixing $x_j$ to a "missing" value and performing the same computation. Thus, the interaction values can be computed in $O(TMLD^2)$ with the path-dependent perturbation algorithm and $O(TMLDR)$ with the interventional feature perturbation algorithm.
#
# ### Comparison to other methods
# Tree-based models are widely used in areas where model interpretability is of interest because node-level statistics gathered from the training data can be used to provide insights into the behaviour of the model across the training dataset, providing a _global explanation_ technique. As shown in our [example](../examples/path_dependent_tree_shap_adult_xgb.ipynb), considering different statistics gives rise to different importance rankings. As discussed in [[1]](#References) and [[3]](#References), depending on the statistic chosen, feature importances derived from trees are not *consistent*, meaning that a model where a feature is known to have a bigger impact might fail to have a larger importance. As such, feature importances cannot be compared across models. In contrast, both the path-dependent and interventional perturbation algorithms tackle this limitation.
#
# In contrast to feature importances derived from tree statistics, the Tree SHAP algorithms can also provide local explanations, allowing the identification of features that are globally "not important", but can affect specific outcomes significantly, as might be the case in healthcare applications. Additionally, it provides a means to succinctly summarise the effect magnitude and direction (positive or negative) across potentially large samples. Finally, as shown in [[1]](#References) (see [here](https://static-content.springer.com/esm/art%3A10.1038%2Fs42256-019-0138-9/MediaObjects/42256_2019_138_MOESM1_ESM.pdf), p. 26), averaging the instance-level shap values importance to derive a global score for each feature can result in improvements in feature selection tasks.
#
# Another method to derive instance-level explanations for tree-based model has been proposed by Sabaas [here](https://github.com/andosa/treeinterpreter). This feature attribution method is similar in spirit to Shapley value, but does not account for the effect of variable order as explained [here](https://static-content.springer.com/esm/art%3A10.1038%2Fs42256-019-0138-9/MediaObjects/42256_2019_138_MOESM1_ESM.pdf) (pp. 10-11) as well as not satisfying consistency ([[3]](#References)).
#
# Finally, both Tree SHAP algorithms exploit model structure to provide exact Shapley values computation albeit using different estimates for the effect of missing features, achieving explanations in low-order polynomial time. The KernelShap method relies on post-hoc (black-box) function modelling and approximations to approximate the same quantities and given enough samples has been shown to to the exact values (see experiments [here](https://static-content.springer.com/esm/art%3A10.1038%2Fs42256-019-0138-9/MediaObjects/42256_2019_138_MOESM1_ESM.pdf) and our [example](../examples/interventional_tree_shap_adult_xgb.ipynb)). Our Kernel SHAP [documentation](KernelSHAP.ipynb) provides comparisons of feature attribution methods based on Shapley values with other algorithms such as LIME and [anchors](Anchors.ipynb).
#
# <a id='source_3'></a>
#
# ## References
# <a id='References'></a>
#
# [[1]](#source_1) <NAME>. and <NAME>., 2017. A unified approach to interpreting model predictions. In Advances in neural information processing systems (pp. 4765-4774).
#
# [[2]](#source_2) <NAME>., <NAME>. and <NAME>., 2019. Feature relevance quantification in explainable AI: A causality problem. arXiv preprint arXiv:1910.13413.
#
# [[3]](#source_3) <NAME>., <NAME>. and <NAME>., 2018. Consistent individualized feature attribution for tree ensembles. arXiv preprint arXiv:1802.03888.
#
# [[4]](#source_4) <NAME>., <NAME>. and <NAME>., 2018. Understanding Shapley value explanation algorithms for trees. Under review for publication in Distill, draft available [here](https://hughchen.github.io/its_blog/index.html).
# ## Examples
# ### Path-dependent Feature Perturbation Tree SHAP
# [Explaing tree models with path-dependent feature perturbation Tree SHAP](../examples/path_dependent_tree_shap_adult_xgb.nblink)
#
#
# ### Interventional Feature Perturbation Tree SHAP
# [Explaing tree models with path-dependent feature perturbation Tree SHAP](../examples/interventional_tree_shap_adult_xgb.nblink)
|
doc/source/methods/TreeSHAP.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Working with Scikit-learn pipelines
#
# Nearest neighbor search is a fundamental building block of many machine learning algorithms, including in supervised learning with kNN-classifiers and kNN-regressors, and unsupervised learning with manifold learning, and clustering. It would be useful to be able to bring the speed of PyNNDescent's approximate nearest neighbor search to bear on these problems without having to re-implement everything from scratch. Fortunately Scikit-learn has done most of the work for us with their [KNeighborsTransformer](https://scikit-learn.org/stable/modules/neighbors.html#neighbors-transformer), which provides a means to insert nearest neighbor computations into sklearn pipelines, and feed the results to many of their models that make use of nearest neighbor computations. It is worth reading through the documentation they have, because we are going to use PyNNDescent as a drop in replacement.
#
# To make this as simple as possible PyNNDescent implements a class ``PyNNDescentTransformer`` that acts as a ``KNeighborsTransformer`` and can be dropped into all the same pipelines. Let's see an example of this working ...
# +
from sklearn.manifold import Isomap, TSNE
from sklearn.neighbors import KNeighborsTransformer
from pynndescent import PyNNDescentTransformer
from sklearn.pipeline import make_pipeline
from sklearn.datasets import fetch_openml
from sklearn.utils import shuffle
import seaborn as sns
# -
# As usual we will need some data to play with. In this case let's use a random subsample of MNIST digits.
def load_mnist(n_samples):
"""Load MNIST, shuffle the data, and return only n_samples."""
mnist = fetch_openml("mnist_784")
X, y = shuffle(mnist.data, mnist.target, random_state=2)
return X[:n_samples] / 255, y[:n_samples]
data, target = load_mnist(10000)
# Now we need to make a pipeline that feeds the nearest neighbor results into a downstream task. To demonstrate how this can work we'll try manifold learning. First we will try out [Isomap](https://en.wikipedia.org/wiki/Isomap) and then [t-SNE](https://en.wikipedia.org/wiki/T-distributed_stochastic_neighbor_embedding). In both cases we can provide a "precomputed" distance matrix, and if it is a sparse matrix (as output by ``KNeighborsTransformer``) then any entry not explicitly provided as a non-zero element of the matrix will be ignored (or treated as an effectively infinite distance). To make the whole thing work we simple make an sklearn pipeline (and could easily include pre-processing steps such as categorical encoding, or data scaling and standardisation as earlier steps if we wished) that first uses the ``KNeighborsTransformer`` to process the raw data into a nearest neighbor graph, and then passes that on to either ``Isomap`` or ``TSNE``. For comparison we'll drop in a ``PyNNDescentTransformer`` instead and see how that effects the results.
sklearn_isomap = make_pipeline(
KNeighborsTransformer(n_neighbors=15),
Isomap(metric='precomputed')
)
pynnd_isomap = make_pipeline(
PyNNDescentTransformer(n_neighbors=15),
Isomap(metric='precomputed')
)
sklearn_tsne = make_pipeline(
KNeighborsTransformer(n_neighbors=92),
TSNE(metric='precomputed', random_state=42)
)
pynnd_tsne = make_pipeline(
PyNNDescentTransformer(n_neighbors=92, early_termination_value=0.05),
TSNE(metric='precomputed', random_state=42)
)
# First let's try Isomap. The algorithm first constructs a k-nearest-neighbor graph (which our transformers will handle in the pipeline), then measures distances between points as path lengths in that graph. Finally it performs an eigendecomposition of the resulting distance matrix. We can do much to speed up the later two steps, which are still non-trivial, but hopefully we can get some speedup by substituting in the approximate nearest neighbor computation.
# %%time
sklearn_iso_map = sklearn_isomap.fit_transform(data)
# %%time
pynnd_iso_map = pynnd_isomap.fit_transform(data)
# A two-times speedup is not bad, especially since we only accelerated one component of the full algorithm. It is quite good considering it was simply a matter of dropping a different class into a pipeline. More importantly as we scale to larger amounts of data the nearest neighbor search comes to dominate the over algorithm run-time, so we can expect to only get better speedups for more data. We can plot the results to ensure we are getting qualitatively the same thing.
sns.scatterplot(x=sklearn_iso_map.T[0], y=sklearn_iso_map.T[1], hue=target, palette="Spectral", size=1);
sns.scatterplot(x=pynnd_iso_map.T[0], y=pynnd_iso_map.T[1], hue=target, palette="Spectral", size=1);
# Now let's try t-SNE. This algorithm requires nearest neighbors as a first step, and then the second major part, in terms of computation time, is the optimization of a layout of a modified k-neighbor graph. We can hope for some improvement in the first part, which usually accounts for around half the overall run-time for small data (and comes to consume a majority of the run-time for large datasets).
# %%time
sklearn_tsne_map = sklearn_tsne.fit_transform(data)
# %%time
pynnd_tsne_map = pynnd_tsne.fit_transform(data)
# Again we have an approximate two-times speedup. Again this was achieved by simply substituting a different class into the pipeline (although in the case we tweaked the ``early_termination_value`` so it would stop *sooner*). Again we can look at the qualitative results and see that we are getting something very similar.
sns.scatterplot(x=sklearn_tsne_map.T[0], y=sklearn_tsne_map.T[1], hue=target, palette="Spectral", size=1);
sns.scatterplot(x=pynnd_tsne_map.T[0], y=pynnd_tsne_map.T[1], hue=target, palette="Spectral", size=1);
# So the results, in both cases, look pretty good, and we did get a good speed-up. A question remains -- how fast was he nearest neighbor component, and how accurate was it? We can write a simple function to measure the neighbor accuracy: compute the average percentage intersection in the neighbor sets of each sample point. Then let's just run the transformers and compare the times as well as computing the actual percentage accuracy.
# +
import numba
import numpy as np
@numba.njit()
def arr_intersect(ar1, ar2):
aux = np.sort(np.concatenate((ar1, ar2)))
return aux[:-1][aux[:-1] == aux[1:]]
@numba.njit()
def neighbor_accuracy_numba(n1_indptr, n1_indices, n2_indptr, n2_indices):
result = 0.0
for i in range(n1_indptr.shape[0] - 1):
indices1 = n1_indices[n1_indptr[i]:n1_indptr[i+1]]
indices2 = n2_indices[n2_indptr[i]:n2_indptr[i+1]]
n_correct = np.float64(arr_intersect(indices1, indices2).shape[0])
result += n_correct / indices1.shape[0]
return result / (n1_indptr.shape[0] - 1)
def neighbor_accuracy(neighbors1, neighbors2):
return neighbor_accuracy_numba(
neighbors1.indptr, neighbors1.indices, neighbors2.indptr, neighbors2.indices
)
# +
# %time true_neighbors = KNeighborsTransformer(n_neighbors=15).fit_transform(data)
# %time pynnd_neighbors = PyNNDescentTransformer(n_neighbors=15).fit_transform(data)
print(f"Neighbor accuracy is {neighbor_accuracy(true_neighbors, pynnd_neighbors) * 100.0}%")
# -
# So for the Isomap case we went from taking over one and half minutes down to less then a second. While doing so we still achieved over 99% accuracy in the nearest neighbors. This seems like a good tradeoff.
#
# By constrast t-SNE requires a much larger number of neighbors (approximately three times the desired perplexity value, which defaults to 30 in sklearn's implementation). This is a little more of a challenge so we might expect it to take longer.
# +
# %time true_neighbors = KNeighborsTransformer(n_neighbors=92).fit_transform(data)
# %time pynnd_neighbors = PyNNDescentTransformer(n_neighbors=92, early_termination_value=0.05).fit_transform(data)
print(f"Neighbor accuracy is {neighbor_accuracy(true_neighbors, pynnd_neighbors) * 100.0}%")
# -
# We see that the ``KNeighborsTransformer`` takes the same amount of time for this -- this is because it is making the choice, given the dataset size and dimensionality, to compute nearest neighbors by effectively computing the full distance matrix. That means regardless of how many neighbors we ask for it will take a largely constant amount of time.
#
# In constrast we see that the ``PyNNDescentTransformer`` is having to work harder, taking almost eight seconds (still a lot better than one and half minutes!). The increased ``early_termination_value`` (the default is 0.001) stops the computation early, but even with this we are still getting over 99.9% accuracy! Certainly the minute and a half saved in computation time at this step is worth the drop of 0.033% accuracy in nearest neighbors. And these differences in computation time will only increase as dataset sizes get larger.
|
doc/pynndescent_in_pipelines.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 0.6.0
# language: julia
# name: julia-0.6
# ---
# # nash test
# Giving some parameter values
alpha = 0.5;
beta = -0.7;
delta = -0.3;
lambda = 0.5
function nash(row)
if row[4] <= -alpha*row[1]-beta*row[2]
if row[5] <= -alpha*row[1]-beta*row[3]
return [0,0, 1]
else
return [0,1, 2]
end
elseif -alpha*row[1]-beta*row[2] <= row[4] <= -alpha*row[1]-beta*row[2] -delta
if row[5] <= -alpha*row[1]-beta*row[3]
return [1,0, 3]
elseif -alpha*row[1]-beta*row[3] <= row[5] <= -alpha*row[1]-beta*row[3] -delta
if rand() < lambda
return [0,1,2]
else
return [1,0,3]
end
elseif -alpha*row[1]-beta*row[3] -delta <= row[5]
return [0,1,2]
end
elseif -alpha*row[1]-beta*row[2] -delta <= row[ 4]
if row[5] <= -alpha*row[1]-beta*row[3] -delta
return [1,0,3]
else
return [1,1,4]
end
end
end
function dg(random::Int64, Num_Market::Int64)
srand(random)
data = zeros(Num_Market, 8)
data[:, 1] = rand(Num_Market, 1)
data[:, 2:3] = rand(Num_Market, 2)
data[:, 4:5] = randn(Num_Market, 2)
for i in 1:Num_Market
data[i, 6:8] = nash(data[i, :])
end
return data
end
seed = 123
Num_market = 100000
data = dg(seed, Num_market);
using DataFrames
df = DataFrame(Pop = data[:, 1], Dist1 = data[:, 2], Dist2 = data[:, 3], eps1 = data[:, 4],
eps2 = data[:, 5], Ent1 = data[:, 6], Ent2 = data[:, 7], Equi = data[:, 8])
writetable("data.csv", df)
|
entry_game.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#
# # ULMFiT for Airline Tweet Sentiment Analysis
# This notebook demonstrates how to apply a supervised ULMFiT model to "Twitter US Airline Sentiment" dataset available at https://www.kaggle.com/crowdflower/twitter-airline-sentiment#Tweets.csv
# ## Environment Setup
# +
# # ! conda create -n fastai
# # ! conda activate fastai
# # ! conda install jupyter notebook
# # ! conda install pytorch torchvision cudatoolkit=10.0 -c pytorch
# # ! conda install nltk
# # ! conda install pandas
# +
"""
Authour: <NAME>
Email: <EMAIL>
License: Apache License 2.0
"""
import re
import os
from functools import partial
from collections import Counter
import string
import pandas as pd
import nltk
from nltk.corpus import wordnet
from fastai.text import *
# -
# ## Pre-processing Data
# In this step, we'll pre-process the data for feeding into the model. I am jumping directly to pre-processing, before Exploratory Data Analysis (EDA) for brevity. To ensure better model performce, we must perform EDA to unerstand the data prior to moving on to the model.
#
# For pre-processing I am using a subset of techniques discussed in the paper titled "A Comparison of Pre-processing Techniques for Twitter Sentiment Analysis". The code is available at https://github.com/Deffro/text-preprocessing-techniques. I am using the provided code with some minor modifications.
# Import tweets from csv file and view the first few lines
df = pd.read_csv('Tweets.csv', sep=',')
df.head()
# get the feature names
features = df.columns.tolist()
print(features)
# Number of tweets and features
df.shape
# We have 14,640 tweets in the dataset and a number of features. Since I am using ULMFiT, I will only use the text (or their contexual embeddings) as features for fine-tuning the language model and the supervised text classifier.
#
#
# ### Pre-processing techniques
# I am using the following tweet pre-processing techniques.
# 1. Remove unicode strings
# 2. Replace urls with empty string
# 3. Replace user mentions with empty string
# 4. Replace hashtags
# 5. Replace slang and abbreviations
# 6. Replace contractions
# 7. Remove numbers
# 8. Remove punctuation marks and special characters
# 9. Replace emoticons
# 10. Lowercase text
# 11. Replace negations
#
# I have tested, but omitted the spell correction feature, since the implementation is not very efficient and takes too long. For the same reeason, I have not applied stopword removal here.
# +
# A subset of techniques for tweet pre-processing
# Originally published by <NAME> at
# https://github.com/Deffro/text-preprocessing-techniques
def removeUnicode(text):
""" Removes unicode strings like "\u002c" and "x96" """
text = re.sub(r'(\\u[0-9A-Fa-f]+)',r'', text)
text = re.sub(r'[^\x00-\x7f]',r'',text)
return text
def replaceURL(text):
""" Replaces url address with "url" """
# text = re.sub('((www\.[^\s]+)|(https?://[^\s]+))','url',text)
text = re.sub('((www\.[^\s]+)|(https?://[^\s]+))','',text)
text = re.sub(r'#([^\s]+)', r'\1', text)
return text
def replaceAtUser(text):
""" Replaces "@user" with "atUser" """
# text = re.sub('@[^\s]+','atUser',text)
text = re.sub('@[^\s]+','',text)
return text
def removeHashtagInFrontOfWord(text):
""" Removes hastag in front of a word """
text = re.sub(r'#([^\s]+)', r'\1', text)
return text
def removeNumbers(text):
""" Removes integers """
text = ''.join([i for i in text if not i.isdigit()])
return text
def removeEmoticons(text):
""" Removes emoticons from text """
text = re.sub(':\)|;\)|:-\)|\(-:|:-D|=D|:P|xD|X-p|\^\^|:-*|\^\.\^|\^\-\^|\^\_\^|\,-\)|\)-:|:\'\(|:\(|:-\(|:\S|T\.T|\.\_\.|:<|:-\S|:-<|\*\-\*|:O|=O|=\-O|O\.o|XO|O\_O|:-\@|=/|:/|X\-\(|>\.<|>=\(|D:', '', text)
return text
""" Creates a dictionary with slangs and their equivalents and replaces them """
with open('slang.txt', encoding='utf8', errors='ignore') as file:
slang_map = dict(map(str.strip, line.partition('\t')[::2])
for line in file if line.strip())
slang_words = sorted(slang_map, key=len, reverse=True) # longest first for regex
regex = re.compile(r"\b({})\b".format("|".join(map(re.escape, slang_words))))
replaceSlang = partial(regex.sub, lambda m: slang_map[m.group(1)])
def replaceElongated(word):
""" Replaces an elongated word with its basic form, unless the word exists in the lexicon """
repeat_regexp = re.compile(r'(\w*)(\w)\2(\w*)')
repl = r'\1\2\3'
if wordnet.synsets(word):
return word
repl_word = repeat_regexp.sub(repl, word)
if repl_word != word:
return replaceElongated(repl_word)
else:
return repl_word
""" Replaces contractions from a string to their equivalents """
contraction_patterns = [ (r'won\'t', 'will not'), (r'can\'t', 'cannot'), (r'i\'m', 'i am'), (r'ain\'t', 'is not'), (r'(\w+)\'ll', '\g<1> will'), (r'(\w+)n\'t', '\g<1> not'),
(r'(\w+)\'ve', '\g<1> have'), (r'(\w+)\'s', '\g<1> is'), (r'(\w+)\'re', '\g<1> are'), (r'(\w+)\'d', '\g<1> would'), (r'&', 'and'), (r'dammit', 'damn it'), (r'dont', 'do not'), (r'wont', 'will not') ]
def replaceContraction(text):
patterns = [(re.compile(regex), repl) for (regex, repl) in contraction_patterns]
for (pattern, repl) in patterns:
(text, count) = re.subn(pattern, repl, text)
return text
def lowercase(text):
""" Make all characters lowercase """
return text.lower()
# +
### Spell Correction begin ###
""" Spell Correction http://norvig.com/spell-correct.html """
def words(text): return re.findall(r'\w+', text.lower())
WORDS = Counter(words(open('corporaForSpellCorrection.txt').read()))
def P(word, N=sum(WORDS.values())):
"""P robability of `word`. """
return WORDS[word] / N
def spellCorrection(word):
""" Most probable spelling correction for word. """
return max(candidates(word), key=P)
def candidates(word):
""" Generate possible spelling corrections for word. """
return (known([word]) or known(edits1(word)) or known(edits2(word)) or [word])
def known(words):
""" The subset of `words` that appear in the dictionary of WORDS. """
return set(w for w in words if w in WORDS)
def edits1(word):
""" All edits that are one edit away from `word`. """
letters = 'abcdefghijklmnopqrstuvwxyz'
splits = [(word[:i], word[i:]) for i in range(len(word) + 1)]
deletes = [L + R[1:] for L, R in splits if R]
transposes = [L + R[1] + R[0] + R[2:] for L, R in splits if len(R)>1]
replaces = [L + c + R[1:] for L, R in splits if R for c in letters]
inserts = [L + c + R for L, R in splits for c in letters]
return set(deletes + transposes + replaces + inserts)
def edits2(word):
""" All edits that are two edits away from `word`. """
return (e2 for e1 in edits1(word) for e2 in edits1(e1))
### Spell Correction End ###
# +
## Replace Negations Begin ###
def replace(word, pos=None):
""" Creates a set of all antonyms for the word and if there is only one antonym, it returns it """
antonyms = set()
for syn in wordnet.synsets(word, pos=pos):
for lemma in syn.lemmas():
for antonym in lemma.antonyms():
antonyms.add(antonym.name())
if len(antonyms) == 1:
return antonyms.pop()
else:
return None
def replaceNegations(text):
""" Finds "not" and antonym for the next word and if found, replaces not and the next word with the antonym """
i, l = 0, len(text)
words = []
while i < l:
word = text[i]
if word == 'not' and i+1 < l:
ant = replace(text[i+1])
if ant:
words.append(ant)
i += 2
continue
words.append(word)
i += 1
return words
### Replace Negations End ###
# +
# Some more methods for pre-processing
# Author: <NAME>
def removeSpecialCharacters(text):
""" Removes puncatuations from text """
# translator = str.maketrans('', '', string.punctuation)
# return text.translate(translator)
return re.sub(r'[^\w\s]',' ',text)
def replaceNegationsText(text):
""" Replace negations from the entire text string (not a single token) """
tokens = nltk.word_tokenize(text)
tokens = replaceNegations(tokens) # Technique 6: finds "not" and antonym
# for the next word and if found, replaces not
# and the next word with the antonym
onlyOneSentence = " ".join(tokens) # form again the sentence from the list of tokens
return onlyOneSentence
def spellCorrectionText(text):
""" Correct misspelled words in entire text """
onlyOneSentenceTokens = [] # tokens of one sentence each time
tokens = nltk.word_tokenize(text)
for token in tokens:
final_word = spellCorrection(token)
onlyOneSentenceTokens.append(final_word)
return " ".join(onlyOneSentenceTokens)
# -
# Pre-processing techniques applied sequentially
df.text = df.text.apply(removeUnicode) # Remove Unicode characters
df.text = df.text.apply(lowercase) # Lowercase the text
df.text = df.text.apply(replaceURL) # Replace URLs with empty string
df.text = df.text.apply(replaceAtUser) # Replace @user with empty string
df.text = df.text.apply(removeHashtagInFrontOfWord) # Remove hashtags
df.text = df.text.apply(replaceSlang) # Replace slang and abbreviations
df.text = df.text.apply(replaceContraction) # Replace contractions with equivalent words
df.text = df.text.apply(removeNumbers) # Remove numbers from text
df.text = df.text.apply(removeEmoticons) # Remove emoticons from text
df.text = df.text.apply(removeSpecialCharacters) # Remove special characters
df.text = df.text.apply(replaceNegationsText) # Replace negations with antonyms
# Create new dataframe with text and labels
df = df[['airline_sentiment', 'text']]
df = df.rename(columns={'airline_sentiment':'labels'})
df.head()
# +
# Change labels into integers
# df.loc[df['labels'] == 'positive', 'labels'] = 0
# df.loc[df['labels'] == 'neutral', 'labels'] = 1
# df.loc[df['labels'] == 'negative', 'labels'] = 2
# -
# Divide data into training and test sets
test_df = df.sample(frac=0.2) # Randomly select 20% as test set
train_df = df.drop(test_df.index) # Keep the rest as training set
# Print the number of samples in each set
print('Trainset-sample size: {} \nTestset-sample size: {}'.\
format(train_df.shape[0], test_df.shape[0]))
# Now that we have splitted the data into training and test at 80-20 ratio, we should verify if both datasets contain similar distribution of sentiments.
# +
def column_value_counts(df, target_column, new_column):
'''
Get value counts of each categorical variable. Store this data in
a dataframe. Also add a column with relative percentage of each
categorical variable.
:param df: A Pandas dataframe
:param target_column: Name of the column in the original dataframe (string)
:param new_column: Name of the new column where the frequency counts are stored
:type df: pandas.core.frame.DataFrame
:type target_column: str
:type new_column: str
:return: A Pandas dataframe containing the frequency counts
:rtype: pandas.core.frame.DataFrame
'''
df_value_counts = df[target_column].value_counts()
df = pd.DataFrame(df_value_counts)
df.columns = [new_column]
df[new_column+'_%'] = 100*df[new_column] / df[new_column].sum()
return df
# Get frequency distribution of labels in each set
df_train = column_value_counts(train_df, 'labels', 'Train')
df_test = column_value_counts(test_df, 'labels', 'Test')
label_count = pd.concat([df_train, df_test], axis=1) # Merge dataframes by index
label_count = label_count.fillna(0) # Replace Nan with 0 (zero)
label_count = label_count.round(2) # Rounding decimals to two digits after .
print(pronoun_count.sort_values(by=['Train'], ascending=False))
# -
# The above table shows that in both sets the distribution of negative, postitive and neutral tweets are similar. Hence, we can now save this for future use.
# Save training and test sets into CSV files
train_df.to_csv('train.csv', header=False, index=False, encoding='utf-8')
test_df.to_csv('test.csv', header=False, index=False, encoding='utf-8')
# ## Language Model and Supervised Classifier
# To complete this part, I have taken help from three different sources.
# - https://docs.fast.ai/text.html#Fine-tuning-a-language-model
# - https://www.analyticsvidhya.com/blog/2018/11/tutorial-text-classification-ulmfit-fastai-library/
# - https://github.com/estorrs/twitter-celebrity-tweet-sentiment/blob/master/celebrity-twitter-sentiment.ipynb
#
# I have used fastai version 1.0 for this demo. The last example above is based on version 0.7. However, it helped me understand some of the issues related to retraining the ULMFiT model for a new dataset.
# Before we can proceed with retraing and fine-tuning the language model on our dataset, we need to download the ULMFiT pretrained models weights on WikiPedia using the following command.
# +
# # ! wget -nH -r -np -P http://files.fast.ai/models/wt103/
# -
# We would also use the LSTM model weights pre-trained on the same dataset.
# +
# # ! wget -nH -r -np -P http://files.fast.ai/models/wt103_v1/lstm_wt103.pth
# # ! wget -nH -r -np -P http://files.fast.ai/models/wt103_v1/itos_wt103.pkl
# -
# Now that we have downloaded the pretrained models, we can reload the training and test sets.
# +
# Load training set in Pandas dataframe
train_df = pd.read_csv('train.csv', header=None, encoding='latin-1')
# Load test set in Pandas dataframe
val_df = pd.read_csv('test.csv', header=None, encoding='latin-1')
# -
# Now that we have both the pretrained model and the datasets, we can prepare the data for our language model and classifier model. Notice that we would need two different data objects. Fast.ai DataBunch class in version 1.0 has made it really easy to read preapre the data for training the models. The basic ppre-processing tasks are handle internally by the DataBunch class.
# +
# Prepare data for language model
data_lm = TextLMDataBunch.from_df(train_df = train_df, valid_df = test_df, path = "")
# Prepare data for classifier model
# I am using a batch size of 16
data_clas = TextClasDataBunch.from_df(path = "", train_df = train_df, valid_df = test_df,
vocab=data_lm.train_ds.vocab, bs=16)
# -
# ### Language model
# Since we have the data ready, we can now re-train and fine-tune the language model. The AWD_LSTM model automatically use the pretrained weights. Probably this is why, the LSTM model provides the best downstream performance. I'll be using the LSTM model to train and fine-tune my model with the pre-trained weights.
# Initialize the learner object with the AWD_LSTM model
# I am using 50% dropout
learn = language_model_learner(data_lm, arch=AWD_LSTM,
pretrained_fnames=['lstm_wt103', 'itos_wt103'], drop_mult=0.5)
# Fast.ai provides two different methods to train the model - fit() and fit_one_cycle(). I have tested both. For re-training and fine-tuning I'll stick to fit_one_cycle(). To know more about these you can read - https://arxiv.org/abs/1803.09820
# train the learner object with learning rate = 1e-2
learn.fit_one_cycle(1, 1e-2)
#learn.fit(10)
# Let's start our fine-tuning process now. I'll use gradual unfreezing of the last layers before fine-tuning all layers.
# unfreeze the last layer
learn.freeze_to(-1)
learn.fit_one_cycle(1, 1e-2)
# unfreeze one more layer
learn.freeze_to(-2)
learn.fit_one_cycle(1, 1e-2)
# unfreeze one more layer
learn.freeze_to(-3)
learn.fit_one_cycle(1, 1e-2)
# unfreeze all layers
learn.unfreeze()
learn.fit_one_cycle(1, 1e-2)
# We are done with the fine-tuning for now. We can now save the model for future use.
# Save the language model
learn.save_encoder('tweet_lm')
# ### Classifier model
# We have fine-tuned the language model. Now we can use the model to build our sentiment classifier. I am using a LSTM based classifier. However, we could have also gone for the RNN classifier. In that case, we would need to train our language model differently.
# Initialize classifier model using the fine-tuned language model
# I am using the AWD_LSTM model with 50% dropout
learn_c = text_classifier_learner(data_clas, arch=AWD_LSTM, drop_mult=0.5)
learn_c.load_encoder('tweet_lm')
# Now we go through a similar process of re-training and fine-tuning for the classifier model, as compared to the language model.
learn_c.fit_one_cycle(1, 1e-2)
learn_c.freeze_to(-1)
learn_c.fit_one_cycle(1, slice(5e-3/2., 5e-3))
learn_c.unfreeze()
learn_c.fit_one_cycle(1, slice(2e-3/100, 2e-3))
# Our classifier model is now trained. We can now use the model to predict the classes. For a single tweet we need to use the predict() method. For batch prediction, we would need to use the get_preds() method.
# Example of prediction on a single tweet
learn_c.predict('your ticket prices are bad')
# Example of batch prediction on the validation set
# It ouputs class probabilities, which we would need to process
# to get the final class value
learn_c.get_preds(ds_type=DatasetType.Valid)
# ## Remarks
# The classifier model was able to achieve around 80% accuracy. This result can be improved by applying the following.
# - We should test how different pre-processing techniques affects the accuracy.
# - I have noticed that gradual unfreezing improves accuracy by a significant amount. This should be explored futher.
# - However, I have not touched two other prominent features of ULMFiT - discriminative fine-tuning and slanted triangular learning rates. I believe, the language and classifier models can be improved a lot by trying out these two.
# ### END
|
ULMFiT for Airline Tweet Sentiment Analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="aCZBFzjClURz" colab_type="text"
# # Train a basic TensorFlow Lite for Microcontrollers model
#
# This notebook demonstrates the process of training a 2.5 kB model using TensorFlow and converting it for use with TensorFlow Lite for Microcontrollers.
#
# Deep learning networks learn to model patterns in underlying data. Here, we're going to train a network to model data generated by a [sine](https://en.wikipedia.org/wiki/Sine) function. This will result in a model that can take a value, `x`, and predict its sine, `y`.
#
# The model created in this notebook is used in the [hello_world](https://github.com/tensorflow/tensorflow/tree/master/tensorflow/lite/micro/examples/hello_world) example for [TensorFlow Lite for MicroControllers](https://www.tensorflow.org/lite/microcontrollers/overview).
#
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/hello_world/train/train_hello_world_model.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/hello_world/train/train_hello_world_model.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# </table>
# + [markdown] id="0Cz6uV1zU_hV" colab_type="text"
# **Training is much faster using GPU acceleration.** Before you proceed, ensure you are using a GPU runtime by going to **Runtime -> Change runtime type** and set **Hardware accelerator: GPU**.
# + [markdown] id="_UQblnrLd_ET" colab_type="text"
# ## Configure Defaults
# + id="5PYwRFppd-WB" colab_type="code" colab={}
# Define paths to model files
import os
MODELS_DIR = 'models/'
os.mkdir(MODELS_DIR)
MODEL_TF = MODELS_DIR + 'model.pb'
MODEL_NO_QUANT_TFLITE = MODELS_DIR + 'model_no_quant.tflite'
MODEL_TFLITE = MODELS_DIR + 'model.tflite'
MODEL_TFLITE_MICRO = MODELS_DIR + 'model.cc'
# + [markdown] id="dh4AXGuHWeu1" colab_type="text"
# ## Setup Environment
#
# Install Dependencies
# + colab_type="code" outputId="e5cbcfca-b6a5-4a61-ac95-1a8d3fd5411b" id="cr1VLfotanf6" colab={"base_uri": "https://localhost:8080/", "height": 85}
# ! pip install -q tensorflow==2
# + [markdown] id="6rLYpvtg9P4o" colab_type="text"
# Set Seed for Repeatable Results
# + id="EIH9NN1c9PJn" colab_type="code" colab={}
# Set a "seed" value, so we get the same random numbers each time we run this
# notebook for reproducible results.
# Numpy is a math library
import numpy as np
np.random.seed(1) # numpy seed
# TensorFlow is an open source machine learning library
import tensorflow as tf
tf.random.set_seed(1) # tensorflow global random seed
# + [markdown] id="tx9lOPWh9grN" colab_type="text"
# Import Dependencies
# + id="53PBJBv1jEtJ" colab_type="code" colab={}
# Keras is TensorFlow's high-level API for deep learning
from tensorflow import keras
# Matplotlib is a graphing library
import matplotlib.pyplot as plt
# Math is Python's math library
import math
# + [markdown] id="p-PuBEb6CMeo" colab_type="text"
# ## Dataset
# + [markdown] id="7gB0-dlNmLT-" colab_type="text"
# ### 1. Generate Data
#
# The code in the following cell will generate a set of random `x` values, calculate their sine values, and display them on a graph.
# + id="uKjg7QeMDsDx" colab_type="code" outputId="0afa45df-3766-467c-c92f-2428aa04f22b" colab={"base_uri": "https://localhost:8080/", "height": 265}
# Number of sample datapoints
SAMPLES = 1000
# Generate a uniformly distributed set of random numbers in the range from
# 0 to 2π, which covers a complete sine wave oscillation
x_values = np.random.uniform(
low=0, high=2*math.pi, size=SAMPLES).astype(np.float32)
# Shuffle the values to guarantee they're not in order
np.random.shuffle(x_values)
# Calculate the corresponding sine values
y_values = np.sin(x_values).astype(np.float32)
# Plot our data. The 'b.' argument tells the library to print blue dots.
plt.plot(x_values, y_values, 'b.')
plt.show()
# + [markdown] id="iWOlC7W_FYvA" colab_type="text"
# ### 2. Add Noise
# Since it was generated directly by the sine function, our data fits a nice, smooth curve.
#
# However, machine learning models are good at extracting underlying meaning from messy, real world data. To demonstrate this, we can add some noise to our data to approximate something more life-like.
#
# In the following cell, we'll add some random noise to each value, then draw a new graph:
# + id="i0FJe3Y-Gkac" colab_type="code" outputId="38886dba-5757-4c7e-bcd6-32c1eb82863e" colab={"base_uri": "https://localhost:8080/", "height": 265}
# Add a small random number to each y value
y_values += 0.1 * np.random.randn(*y_values.shape)
# Plot our data
plt.plot(x_values, y_values, 'b.')
plt.show()
# + [markdown] id="Up8Xk_pMH4Rt" colab_type="text"
# ### 3. Split the Data
# We now have a noisy dataset that approximates real world data. We'll be using this to train our model.
#
# To evaluate the accuracy of the model we train, we'll need to compare its predictions to real data and check how well they match up. This evaluation happens during training (where it is referred to as validation) and after training (referred to as testing) It's important in both cases that we use fresh data that was not already used to train the model.
#
# The data is split as follows:
# 1. Training: 60%
# 2. Validation: 20%
# 3. Testing: 20%
#
# The following code will split our data and then plots each set as a different color:
#
# + id="nNYko5L1keqZ" colab_type="code" outputId="a016bf4f-60a9-4c3f-9954-71218f7f4a25" colab={"base_uri": "https://localhost:8080/", "height": 265}
# We'll use 60% of our data for training and 20% for testing. The remaining 20%
# will be used for validation. Calculate the indices of each section.
TRAIN_SPLIT = int(0.6 * SAMPLES)
TEST_SPLIT = int(0.2 * SAMPLES + TRAIN_SPLIT)
# Use np.split to chop our data into three parts.
# The second argument to np.split is an array of indices where the data will be
# split. We provide two indices, so the data will be divided into three chunks.
x_train, x_test, x_validate = np.split(x_values, [TRAIN_SPLIT, TEST_SPLIT])
y_train, y_test, y_validate = np.split(y_values, [TRAIN_SPLIT, TEST_SPLIT])
# Double check that our splits add up correctly
assert (x_train.size + x_validate.size + x_test.size) == SAMPLES
# Plot the data in each partition in different colors:
plt.plot(x_train, y_train, 'b.', label="Train")
plt.plot(x_test, y_test, 'r.', label="Test")
plt.plot(x_validate, y_validate, 'y.', label="Validate")
plt.legend()
plt.show()
# + [markdown] id="Wfdelu1TmgPk" colab_type="text"
# ## Training
# + [markdown] id="t5McVnHmNiDw" colab_type="text"
# ### 1. Design the Model
# We're going to build a simple neural network model that will take an input value (in this case, `x`) and use it to predict a numeric output value (the sine of `x`). This type of problem is called a _regression_. It will use _layers_ of _neurons_ to attempt to learn any patterns underlying the training data, so it can make predictions.
#
# To begin with, we'll define two layers. The first layer takes a single input (our `x` value) and runs it through 8 neurons. Based on this input, each neuron will become _activated_ to a certain degree based on its internal state (its _weight_ and _bias_ values). A neuron's degree of activation is expressed as a number.
#
# The activation numbers from our first layer will be fed as inputs to our second layer, which is a single neuron. It will apply its own weights and bias to these inputs and calculate its own activation, which will be output as our `y` value.
#
# **Note:** To learn more about how neural networks function, you can explore the [Learn TensorFlow](https://codelabs.developers.google.com/codelabs/tensorflow-lab1-helloworld) codelabs.
#
# The code in the following cell defines our model using [Keras](https://www.tensorflow.org/guide/keras), TensorFlow's high-level API for creating deep learning networks. Once the network is defined, we _compile_ it, specifying parameters that determine how it will be trained:
# + id="gD60bE8cXQId" colab_type="code" colab={}
# We'll use Keras to create a simple model architecture
model_1 = tf.keras.Sequential()
# First layer takes a scalar input and feeds it through 8 "neurons". The
# neurons decide whether to activate based on the 'relu' activation function.
model_1.add(keras.layers.Dense(8, activation='relu', input_shape=(1,)))
# Final layer is a single neuron, since we want to output a single value
model_1.add(keras.layers.Dense(1))
# Compile the model using a standard optimizer and loss function for regression
model_1.compile(optimizer='adam', loss='mse', metrics=['mae'])
# + [markdown] id="O0idLyRLQeGj" colab_type="text"
# ### 2. Train the Model
# Once we've defined the model, we can use our data to _train_ it. Training involves passing an `x` value into the neural network, checking how far the network's output deviates from the expected `y` value, and adjusting the neurons' weights and biases so that the output is more likely to be correct the next time.
#
# Training runs this process on the full dataset multiple times, and each full run-through is known as an _epoch_. The number of epochs to run during training is a parameter we can set.
#
# During each epoch, data is run through the network in multiple _batches_. Each batch, several pieces of data are passed into the network, producing output values. These outputs' correctness is measured in aggregate and the network's weights and biases are adjusted accordingly, once per batch. The _batch size_ is also a parameter we can set.
#
# The code in the following cell uses the `x` and `y` values from our training data to train the model. It runs for 500 _epochs_, with 64 pieces of data in each _batch_. We also pass in some data for _validation_. As you will see when you run the cell, training can take a while to complete:
#
#
# + id="p8hQKr4cVOdE" colab_type="code" outputId="5e9fcc84-1733-4786-8fde-ce47a510cde6" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# Train the model on our training data while validating on our validation set
history_1 = model_1.fit(x_train, y_train, epochs=500, batch_size=64,
validation_data=(x_validate, y_validate))
# + [markdown] id="cRE8KpEqVfaS" colab_type="text"
# ### 3. Plot Metrics
# + [markdown] id="SDsjqfjFm7Fz" colab_type="text"
# **1. Mean Squared Error**
#
# During training, the model's performance is constantly being measured against both our training data and the validation data that we set aside earlier. Training produces a log of data that tells us how the model's performance changed over the course of the training process.
#
# The following cells will display some of that data in a graphical form:
# + id="CmvA-ksoln8r" colab_type="code" outputId="2796d3ca-deb7-4cf9-cc01-78df3cacf12a" colab={"base_uri": "https://localhost:8080/", "height": 295}
# Draw a graph of the loss, which is the distance between
# the predicted and actual values during training and validation.
loss = history_1.history['loss']
val_loss = history_1.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.plot(epochs, loss, 'g.', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
# + [markdown] id="iOFBSbPcYCN4" colab_type="text"
# The graph shows the _loss_ (or the difference between the model's predictions and the actual data) for each epoch. There are several ways to calculate loss, and the method we have used is _mean squared error_. There is a distinct loss value given for the training and the validation data.
#
# As we can see, the amount of loss rapidly decreases over the first 25 epochs, before flattening out. This means that the model is improving and producing more accurate predictions!
#
# Our goal is to stop training when either the model is no longer improving, or when the _training loss_ is less than the _validation loss_, which would mean that the model has learned to predict the training data so well that it can no longer generalize to new data.
#
# To make the flatter part of the graph more readable, let's skip the first 50 epochs:
# + id="Zo0RYroFZYIV" colab_type="code" outputId="5844429f-cb52-41e0-c41c-52485efcd0ac" colab={"base_uri": "https://localhost:8080/", "height": 295}
# Exclude the first few epochs so the graph is easier to read
SKIP = 50
plt.plot(epochs[SKIP:], loss[SKIP:], 'g.', label='Training loss')
plt.plot(epochs[SKIP:], val_loss[SKIP:], 'b.', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
# + [markdown] id="W4EQD-Bb8hLM" colab_type="text"
# From the plot, we can see that loss continues to reduce until around 500 epochs, at which point it is mostly stable. This means that there's no need to train our network beyond 500 epochs.
#
# However, we can also see that the lowest loss value is still around 0.155. This means that our network's predictions are off by an average of ~15%. In addition, the validation loss values jump around a lot, and is sometimes even higher.
#
# **2. Mean Absolute Error**
#
# To gain more insight into our model's performance we can plot some more data. This time, we'll plot the _mean absolute error_, which is another way of measuring how far the network's predictions are from the actual numbers:
# + id="Md9E_azmpkZU" colab_type="code" outputId="90fff6f3-8dc1-42ec-a0e2-f2434c790a3d" colab={"base_uri": "https://localhost:8080/", "height": 295}
plt.clf()
# Draw a graph of mean absolute error, which is another way of
# measuring the amount of error in the prediction.
mae = history_1.history['mae']
val_mae = history_1.history['val_mae']
plt.plot(epochs[SKIP:], mae[SKIP:], 'g.', label='Training MAE')
plt.plot(epochs[SKIP:], val_mae[SKIP:], 'b.', label='Validation MAE')
plt.title('Training and validation mean absolute error')
plt.xlabel('Epochs')
plt.ylabel('MAE')
plt.legend()
plt.show()
# + [markdown] id="ctawd0CXAVEw" colab_type="text"
# This graph of _mean absolute error_ tells another story. We can see that training data shows consistently lower error than validation data, which means that the network may have _overfit_, or learned the training data so rigidly that it can't make effective predictions about new data.
#
# In addition, the mean absolute error values are quite high, ~0.305 at best, which means some of the model's predictions are at least 30% off. A 30% error means we are very far from accurately modelling the sine wave function.
#
# **3. Actual vs Predicted Outputs**
#
# To get more insight into what is happening, we can plot our network's predictions for the training data against the expected values:
# + id="i13eVIT3B9Mj" colab_type="code" outputId="372e169f-f97d-47ee-e64c-162b8ba4e38c" colab={"base_uri": "https://localhost:8080/", "height": 281}
# Use the model to make predictions from our validation data
predictions = model_1.predict(x_train)
# Plot the predictions along with to the test data
plt.clf()
plt.title('Training data predicted vs actual values')
plt.plot(x_test, y_test, 'b.', label='Actual')
plt.plot(x_train, predictions, 'r.', label='Predicted')
plt.legend()
plt.show()
# + [markdown] id="Wokallj1D21L" colab_type="text"
# Oh dear! The graph makes it clear that our network has learned to approximate the sine function in a very limited way. From `0 <= x <= 1.1` the line mostly fits, but for the rest of our `x` values it is a rough approximation at best.
#
# The rigidity of this fit suggests that the model does not have enough capacity to learn the full complexity of the sine wave function, so it's only able to approximate it in an overly simplistic way. By making our model bigger, we should be able to improve its performance.
# + [markdown] id="T7sL-hWtoAZC" colab_type="text"
# ## Training a Larger Model
# + [markdown] id="aQd0JSdOoAbw" colab_type="text"
# ### 1. Design the Model
# To make our model bigger, let's add an additional layer of neurons. The following cell redefines our model in the same way as earlier, but with 16 neurons in the first layer and an additional layer of 16 neurons in the middle:
# + id="oW0xus6AF-4o" colab_type="code" colab={}
model_2 = tf.keras.Sequential()
# First layer takes a scalar input and feeds it through 16 "neurons". The
# neurons decide whether to activate based on the 'relu' activation function.
model_2.add(keras.layers.Dense(16, activation='relu', input_shape=(1,)))
# The new second layer may help the network learn more complex representations
model_2.add(keras.layers.Dense(16, activation='relu'))
# Final layer is a single neuron, since we want to output a single value
model_2.add(keras.layers.Dense(1))
# Compile the model using a standard optimizer and loss function for regression
model_2.compile(optimizer='adam', loss='mse', metrics=['mae'])
# + [markdown] id="Dv2SC409Grap" colab_type="text"
# ### 2. Train the Model ###
#
# We'll now train the new model.
# + id="DPAUrdkmGq1M" colab_type="code" outputId="64730ff7-488e-4b74-d5a1-49a1b733e9e5" colab={"base_uri": "https://localhost:8080/", "height": 1000}
history_2 = model_2.fit(x_train, y_train, epochs=500, batch_size=64,
validation_data=(x_validate, y_validate))
# + [markdown] id="Mc_CQu2_IvOP" colab_type="text"
# ### 3. Plot Metrics
# Each training epoch, the model prints out its loss and mean absolute error for training and validation. You can read this in the output above (note that your exact numbers may differ):
#
# ```
# Epoch 500/500
# 600/600 [==============================] - 0s 51us/sample - loss: 0.0118 - mae: 0.0873 - val_loss: 0.0105 - val_mae: 0.0832
# ```
#
# You can see that we've already got a huge improvement - validation loss has dropped from 0.15 to 0.01, and validation MAE has dropped from 0.33 to 0.08.
#
# The following cell will print the same graphs we used to evaluate our original model, but showing our new training history:
# + id="SYHGswAJJgrC" colab_type="code" outputId="bdc6e8f7-480d-4d3e-c20b-94776722360f" colab={"base_uri": "https://localhost:8080/", "height": 851}
# Draw a graph of the loss, which is the distance between
# the predicted and actual values during training and validation.
loss = history_2.history['loss']
val_loss = history_2.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.plot(epochs, loss, 'g.', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
# Exclude the first few epochs so the graph is easier to read
SKIP = 100
plt.clf()
plt.plot(epochs[SKIP:], loss[SKIP:], 'g.', label='Training loss')
plt.plot(epochs[SKIP:], val_loss[SKIP:], 'b.', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
plt.clf()
# Draw a graph of mean absolute error, which is another way of
# measuring the amount of error in the prediction.
mae = history_2.history['mae']
val_mae = history_2.history['val_mae']
plt.plot(epochs[SKIP:], mae[SKIP:], 'g.', label='Training MAE')
plt.plot(epochs[SKIP:], val_mae[SKIP:], 'b.', label='Validation MAE')
plt.title('Training and validation mean absolute error')
plt.xlabel('Epochs')
plt.ylabel('MAE')
plt.legend()
plt.show()
# + [markdown] id="f86dWOyZKmN9" colab_type="text"
# Great results! From these graphs, we can see several exciting things:
#
# * Our network has reached its peak accuracy much more quickly (within 200 epochs instead of 500)
# * The overall loss and MAE are much better than our previous network
# * Metrics are better for validation than training, which means the network is not overfitting
#
# The reason the metrics for validation are better than those for training is that validation metrics are calculated at the end of each epoch, while training metrics are calculated throughout the epoch, so validation happens on a model that has been trained slightly longer.
#
# This all means our network seems to be performing well! To confirm, let's check its predictions against the test dataset we set aside earlier:
#
# + id="lZfztKKyhLxX" colab_type="code" outputId="7ed4e1c5-4d19-4d10-cd65-0cae30486734" colab={"base_uri": "https://localhost:8080/", "height": 318}
# Calculate and print the loss on our test dataset
loss = model_2.evaluate(x_test, y_test)
# Make predictions based on our test dataset
predictions = model_2.predict(x_test)
# Graph the predictions against the actual values
plt.clf()
plt.title('Comparison of predictions and actual values')
plt.plot(x_test, y_test, 'b.', label='Actual')
plt.plot(x_test, predictions, 'r.', label='Predicted')
plt.legend()
plt.show()
# + [markdown] id="3h7IcvuOOS4J" colab_type="text"
# Much better! The evaluation metrics we printed show that the model has a low loss and MAE on the test data, and the predictions line up visually with our data fairly well.
#
# The model isn't perfect; its predictions don't form a smooth sine curve. For instance, the line is almost straight when `x` is between 4.2 and 5.2. If we wanted to go further, we could try further increasing the capacity of the model, perhaps using some techniques to defend from overfitting.
#
# However, an important part of machine learning is knowing when to quit, and this model is good enough for our use case - which is to make some LEDs blink in a pleasing pattern.
#
# ## Generate a TensorFlow Lite Model
# + [markdown] id="sHe-Wv47rhm8" colab_type="text"
# ### 1. Generate Models with or without Quantization
# We now have an acceptably accurate model. We'll use the [TensorFlow Lite Converter](https://www.tensorflow.org/lite/convert) to convert the model into a special, space-efficient format for use on memory-constrained devices.
#
# Since this model is going to be deployed on a microcontroller, we want it to be as tiny as possible! One technique for reducing the size of models is called [quantization](https://www.tensorflow.org/lite/performance/post_training_quantization) while converting the model. It reduces the precision of the model's weights, and possibly the activations (output of each layer) as well, which saves memory, often without much impact on accuracy. Quantized models also run faster, since the calculations required are simpler.
#
# *Note: Currently, TFLite Converter produces TFlite models with float interfaces (input and output ops are always float). This is a blocker for users who require TFlite models with pure int8 or uint8 inputs/outputs. Refer to https://github.com/tensorflow/tensorflow/issues/38285*
#
# In the following cell, we'll convert the model twice: once with quantization, once without.
# + id="1muAoUm8lSXL" colab_type="code" outputId="5ff328ef-73c5-45cd-e339-da52696b00e3" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Convert the model to the TensorFlow Lite format without quantization
converter = tf.lite.TFLiteConverter.from_keras_model(model_2)
model_no_quant_tflite = converter.convert()
# # Save the model to disk
open(MODEL_NO_QUANT_TFLITE, "wb").write(model_no_quant_tflite)
# Convert the model to the TensorFlow Lite format with quantization
def representative_dataset():
for i in range(500):
yield([x_train[i].reshape(1, 1)])
# Set the optimization flag.
converter.optimizations = [tf.lite.Optimize.DEFAULT]
# Enforce full-int8 quantization (except inputs/outputs which are always float)
converter.target_spec.supported_ops = [tf.lite.OpsSet.TFLITE_BUILTINS_INT8]
# Provide a representative dataset to ensure we quantize correctly.
converter.representative_dataset = representative_dataset
model_tflite = converter.convert()
# Save the model to disk
open(MODEL_TFLITE, "wb").write(model_tflite)
# + [markdown] id="8X1yO3h5pYbt" colab_type="text"
# ### 2. Compare Model Sizes
# + id="jAIe0dK3pXU8" colab_type="code" outputId="ce15b7eb-f857-4cb0-ba70-5a67ce04566b" colab={"base_uri": "https://localhost:8080/", "height": 68}
import os
model_no_quant_size = os.path.getsize(MODEL_NO_QUANT_TFLITE)
print("Model is %d bytes" % model_no_quant_size)
model_size = os.path.getsize(MODEL_TFLITE)
print("Quantized model is %d bytes" % model_size)
difference = model_no_quant_size - model_size
print("Difference is %d bytes" % difference)
# + [markdown] id="cR2OuokFpkEM" colab_type="text"
# Our quantized model is only 224 bytes smaller than the original version, which only a tiny reduction in size! At around 2.5 kilobytes, this model is already so small that the weights make up only a small fraction of the overall size, meaning quantization has little effect.
#
# More complex models have many more weights, meaning the space saving from quantization will be much higher, approaching 4x for most sophisticated models.
#
# Regardless, our quantized model will take less time to execute than the original version, which is important on a tiny microcontroller!
# + [markdown] id="L_vE-ZDkHVxe" colab_type="text"
# ### 3. Test the Models
#
# To prove these models are still accurate after conversion and quantization, we'll use both of them to make predictions and compare these against our test results:
# + id="-J7IKlXiYVPz" colab_type="code" outputId="87d2fd39-4ddc-4f73-e164-e0089a5cfb59" colab={"base_uri": "https://localhost:8080/", "height": 281}
# Instantiate an interpreter for each model
model_no_quant = tf.lite.Interpreter(MODEL_NO_QUANT_TFLITE)
model = tf.lite.Interpreter(MODEL_TFLITE)
# Allocate memory for each model
model_no_quant.allocate_tensors()
model.allocate_tensors()
# Get the input and output tensors so we can feed in values and get the results
model_no_quant_input = model_no_quant.tensor(model_no_quant.get_input_details()[0]["index"])
model_no_quant_output = model_no_quant.tensor(model_no_quant.get_output_details()[0]["index"])
model_input = model.tensor(model.get_input_details()[0]["index"])
model_output = model.tensor(model.get_output_details()[0]["index"])
# Create arrays to store the results
model_no_quant_predictions = np.empty(x_test.size)
model_predictions = np.empty(x_test.size)
# Run each model's interpreter for each value and store the results in arrays
for i in range(x_test.size):
model_no_quant_input().fill(x_test[i])
model_no_quant.invoke()
model_no_quant_predictions[i] = model_no_quant_output()[0]
model_input().fill(x_test[i])
model.invoke()
model_predictions[i] = model_output()[0]
# See how they line up with the data
plt.clf()
plt.title('Comparison of various models against actual values')
plt.plot(x_test, y_test, 'bo', label='Actual predictions')
plt.plot(x_test, predictions, 'ro', label='Original predictions')
plt.plot(x_test, model_no_quant_predictions, 'bx', label='Lite predictions')
plt.plot(x_test, model_predictions, 'gx', label='Lite quantized predictions')
plt.legend()
plt.show()
# + [markdown] id="jWxvLGexKv0D" colab_type="text"
# We can see from the graph that the predictions for the original model, the converted model, and the quantized model are all close enough to be indistinguishable. This means that our quantized model is ready to use!
# + [markdown] id="HPSFmDL7pv2L" colab_type="text"
# ## Generate a TensorFlow Lite for Microcontrollers Model
# Convert the TensorFlow Lite quantized model into a C source file that can be loaded by TensorFlow Lite for Microcontrollers.
# + id="j1FB4ieeg0lw" colab_type="code" outputId="a2ba48f0-c440-409a-dad0-747a22ac3a64" colab={"base_uri": "https://localhost:8080/", "height": 476}
# Install xxd if it is not available
# !apt-get update && apt-get -qq install xxd
# Convert to a C source file
# !xxd -i {MODEL_TFLITE} > {MODEL_TFLITE_MICRO}
# Update variable names
REPLACE_TEXT = MODEL_TFLITE.replace('/', '_').replace('.', '_')
# !sed -i 's/'{REPLACE_TEXT}'/g_model/g' {MODEL_TFLITE_MICRO}
# + [markdown] id="JvRy0ZyMhQOX" colab_type="text"
# ## Deploy to a Microcontroller
#
# Follow the instructions in the [hello_world](https://github.com/tensorflow/tensorflow/tree/master/tensorflow/lite/micro/examples/hello_world) README.md for [TensorFlow Lite for MicroControllers](https://www.tensorflow.org/lite/microcontrollers/overview) to deploy this model on a specific microcontroller.
#
# **Reference Model:** If you have not modified this notebook, you can follow the instructions as is, to deploy the model. Refer to the [`hello_world/train/models`](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/hello_world/train/models) directory to access the models generated in this notebook.
#
# **New Model:** If you have generated a new model, then update the values assigned to the variables defined in [`hello_world/model.cc`](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/hello_world/model.cc) with values displayed after running the following cell.
# + id="l4-WhtGpvb-E" colab_type="code" outputId="ba008623-d568-43b1-a824-68adbe811567" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# Print the C source file
# !cat {MODEL_TFLITE_MICRO}
|
tensorflow/lite/micro/examples/hello_world/train/train_hello_world_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # A Cantera Simulation with Reaction Sensitivity: Comparison with Native RMG Sensitivity Analysis and CHEMKIN Sensitivity Analysis
#
#
# Note that this requires Cantera with SUNDIALS installed for sensitivity support. If you are using Anaconda,
# Cantera version >= 2.3.0 is required
import cantera
print cantera.__version__ # Check Cantera version
# +
import shutil
from IPython.display import display, Image
from rmgpy.chemkin import loadChemkinFile
from rmgpy.species import Species
from rmgpy.tools.canteraModel import Cantera, getRMGSpeciesFromUserSpecies
from rmgpy.tools.plot import SimulationPlot, ReactionSensitivityPlot, parseCSVData
from rmgpy.tools.simulate import run_simulation
# -
# Load the species and reaction from the RMG-generated chemkin file `chem_annotated.inp` and `species_dictionary.txt` file found in your `chemkin` folder after running a job.
speciesList, reactionList = loadChemkinFile('./data/ethane_model/chem_annotated.inp',
'./data/ethane_model/species_dictionary.txt',
'./data/ethane_model/tran.dat')
# Set the reaction conditions
# +
# Find the species: ethane and methane
user_ethane = Species().fromSMILES('CC')
user_methane = Species().fromSMILES('C')
speciesDict = getRMGSpeciesFromUserSpecies([user_ethane, user_methane], speciesList)
ethane = speciesDict[user_ethane]
methane = speciesDict[user_methane]
sensitiveSpecies = [ethane, methane]
#reactorTypeList = ['IdealGasReactor']
reactorTypeList = ['IdealGasConstPressureTemperatureReactor']
molFracList=[{ethane: 1}]
Tlist = ([1300], 'K')
Plist = ([1], 'bar')
reactionTimeList = ([0.5], 'ms')
# +
# Create cantera object, loading in the species and reactions
job = Cantera(speciesList=speciesList, reactionList=reactionList, outputDirectory='temp', sensitiveSpecies=sensitiveSpecies)
# The cantera file must be created from an associated chemkin file
# We can either load the Model from the initialized set of rmg species and reactions
job.loadModel()
# Or load it from a chemkin file by uncommenting the following line:
#job.loadChemkinModel('data/minimal_model/chem_annotated.inp',transportFile='data/minimal_model/tran.dat')
# Generate the conditions based on the settings we declared earlier
job.generateConditions(reactorTypeList, reactionTimeList, molFracList, Tlist, Plist)
# +
# Simulate and plot
alldata = job.simulate()
job.plot(alldata)
# Show the plots in the ipython notebook
for i, condition in enumerate(job.conditions):
print 'Cantera Simulation: Condition {0} Species Mole Fractions'.format(i+1)
display(Image(filename="temp/{0}_mole_fractions.png".format(i+1)))
print 'Cantera Simulation: Condition {0} Ethane Reaction Sensitivity'.format(i+1)
display(Image(filename="temp/{0}_ethane(1)_sensitivity.png".format(i+1)))
# +
# Copy example input file to temp folder
shutil.copy('./data/ethane_model/input.py', './temp')
# We can run the same simulation using RMG's native solver
run_simulation(
'./temp/input.py',
'./data/ethane_model/chem_annotated.inp',
'./data/ethane_model/species_dictionary.txt',
)
# +
print 'RMG Native Simulation: Species Mole Fractions'
display(Image(filename="./temp/solver/simulation_1_27.png"))
print 'RMG Native Simulation: Ethane Reaction Sensitivity'
display(Image(filename="./temp/solver/sensitivity_1_SPC_1_reactions.png"))
# +
# Let's also compare against the same simulation and sensitivity analysis that was conducted in CHEMKIN
# and saved as a .csv file
time, dataList = parseCSVData('./data/ethane_model/chemkin_mole_fractions.csv')
SimulationPlot(xVar=time, yVar=dataList, numSpecies=10).plot('./temp/chemkin_mole_fractions.png')
print 'CHEMKIN Simulation: Species Mole Fractions'
display(Image(filename="./temp/chemkin_mole_fractions.png"))
time, dataList = parseCSVData('./data/ethane_model/chemkin_sensitivity_ethane.csv')
ReactionSensitivityPlot(xVar=time, yVar=dataList, numReactions=10).barplot('./temp/chemkin_sensitivity_ethane.png')
print 'CHEMKIN Simulation: Ethane Reaction Sensitivity'
display(Image(filename="./temp/chemkin_sensitivity_ethane.png"))
# -
|
ipython/canteraSensitivityComparison.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # pytf Examples
#
# The first section demonstrates the use of FilterBank.
#
# The second section demonstrates the use of Spectrogram.
# +
import numpy as np
from pytf import FilterBank, Spectrogram
import matplotlib.pyplot as plt
from mspacman.generator.noise import (white, pink) # I can't share this repository yet until my paper is published.
# So in order to make this example to work on your local machine, try generating your own test signal.
# +
tdur = 10
fs = 2**14
nsamp = fs * tdur
# Generate a time domain signal
t = np.linspace(0, tdur, nsamp)
sig = white(nsamp, mean=0, std=1) + pink(nsamp, mean=0, std=1)
# Convert generated signal to frequency domain
sigF = np.fft.fft(sig, axis=-1)
w = np.fft.fftfreq(sigF.size) * fs
sigF = np.fft.fftshift(sigF)
w = np.fft.fftshift(w)
# -
# # FilterBank Example
# Initialize the filter bank class
fb = FilterBank(nch=1, nsamp=nsamp, binsize=2**10, decimate_by=1, \
bandwidth=100, center_freqs=np.array([50]), freq_bands=None, order=2**10, sample_rate=fs, \
hilbert=False, domain='time', nprocs=1, mprocs=False,
logger=None)
x = fb.analysis(sig, window='hanning')
_w = np.fft.fftshift(np.fft.fftfreq(fb._filts.size)) * fs
X = np.fft.fft(x, axis=-1)
X = np.fft.fftshift(X)
# +
plt.figure(figsize=(12, 3))
plt.subplot(121)
plt.plot(t*1000, sig.flatten())
plt.plot(t*1000, x.flatten(), c='k')
plt.xlim([0, 1000])
plt.xlabel('Time [ms]')
plt.grid('on')
plt.subplot(122)
plt.plot(w, np.abs(sigF.flatten()) / np.abs(sigF).max())
plt.plot(w, np.abs(X.flatten()) / np.abs(sigF).max(), c='k', alpha=.5)
plt.xlim([0, 500])
plt.ylim([0, 1.25])
plt.xlabel('Frequencies [Hz]')
plt.grid('on')
# -
# ## Notes:
# Notice the slight scaling issue in the low frequencies. This is because that filter bank (at the moment) filters all signals using only one bandpass filter. A typical application of filtering from 0-100 Hz should be done in lowpass filter, but that would introduce additional complexity in the implementation and will be overlooked for now.
# # Spectrogram Example
spec = Spectrogram(nch=1, nsamp=nsamp, sample_rate=fs, binsize=2**9, hopsize=None, overlap_factor=.5)
X_ = spec.analysis(sig)
spec.plot_spectra(ch=None, axs=None, tlim=None, flim=(0, 5000), figsize=(8, 6), norm='db',
title=None, label=False, xlabel=True, ylabel=True,
fontsize={'ticks': 15, 'axis': 15, 'title': 20})
# ## Notes:
# Play around with binsize argument to notice the changes in frequency resolution vs time resolution.
|
examples/.ipynb_checkpoints/pytf_examples-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Hierarchical Indexing
#
# Up to this point we've been focused primarily on one-dimensional and two-dimensional data, stored in Pandas `Series` and `DataFrame` objects, respectively. Often it is useful to go beyond this and store higher-dimensional data-that is, data indexing by more than one or two keys. While Pandas does provide `Panel` and `Panel4D` objects that natevely handle three-dimensional nd four-dimensional data, a far more common pattern in practice is to make use of *hierarchical indexing* (also known as *multi-indexing*) to incorporate multiple index *levels* within a single index. In this way, higher-dimensional data can be compactly represented within the familiar one-dimesional `Series` and two-dimensional `DataFrame` objects.
#
# In this section, we'll explore the direct creation of `MultiIndex` objects, considerations when indexing, slicing, and computing statistics across multiply indexed data, and useful routines for converting between simple and hierarchically indexed representations of your data.
#
# We begin with the standard imports:
import numpy as np
import pandas as pd
# ## A Multiply Indexed Series
#
# Let's start by considering how we might represent two-dimensional data within a one-dimensional `Series`. For concreteness, we will consider a series of data where each point has a character and numerical key.
# ### The bad way
#
# Suppose you wuoul like to track data about states from two different years. Using the Pandas tools we've already covered, you might be tempted to simply use Python tuples as keys:
# +
index = [('California', 2000), ('California', 2010),
('New York', 2000), ('New York', 2010),
('Texas', 2000), ('Texas', 2010)]
populations = [33871648, 37253956,
18976457, 19378102,
20851820, 25145561]
pop = pd.Series(populations, index=index)
pop
# -
# With this indexing Scheme, you can straightforwardly index or slice the series based on this multiple index:
pop[('California', 2010):('Texas', 2000)]
# But the convenience ends there. For example, if you need to select all values from 2010, you'll need to do some messy (and potentially slow) munging to make it happen:
pop[[i for i in pop.index if i[1] == 2010]]
# This produces the desired result, but is not as clean(or as efficient for large datasets) as the slicing syntax we've grown to love in Pandas.
# ### The Better Way: Pandas MultiIndex
#
# Fortunately, Pandas provides a better way. Our tuple-based indexing is essentially a rudimentary multi-index, and the Pandas `MultiIndex` type gives us the type of operations we wish to have. We can create a multi-index from the tuples as follows:
index = pd.MultiIndex.from_tuples(index)
index
# Notice that the `MultiIndex` contains multiple `levels` of indexing-in this case, the state names and the years, as well as multiple *labels* for each data point which encode these levels.
#
# If we re-index our series with this `MiltiIndex`, we see the hierarchical representation of the data:
pop = pop.reindex(index)
pop
# Here the first two columns of the `Series` representation show the multiple index values, while the third column shows the data. Notice that some entries are missing in the first column: in this multi-index represenattion, any blank entry indicates the same value as the line above it.
#
# Now to access all data for which the second index is 2010, we can simply use the Pandas slicing notation:
pop[:, 2010]
# The result is a singly index array with jsut he keys we´re interested in. This syntax is much convenient (and the operation is much more efficient) than the home-spun tuple-based multi-indexing solution that we started with. We'll now further discuss this sort of indexing operation on hierarchically indexed data.
# ### MultiIndex as extra dimension
#
# You might notice something else here: we could easily have stored the same data using a simple `DataFrame` with index and column labels. In fact, Pandas is built with this equivalence in mind. The `unstack()` method will quickly convert a multiply indexed `Series` into a conventionally indexed `DataFrame`:
pop_df = pop.unstack()
pop_df
# Naturally, the `stack()` method provides the opposite operation:
pop_df.stack()
# Seeing this, you migth wonder why would we would obther with hierarchical idnexing at all. The reason is simple: just as we were able to use multi-indexing to represent two-dimensional data within a one-dimensional `Series`, we can also use it to represent data of three or more dimensions in a `Series` or `DataFrame`. Each extra level in a multi-index represents an extra dimension of data; taking advantage of this property gives us much more flexibility in the types of data we can represent. Concretely, we might want ot add another column of demographic data for each state at each year(say, population under 18); with a `MultiIndex` this is as easy as adding another column to the `DataFrame`:
pop_df = pd.DataFrame({'total': pop, 'under18': [9267089, 9284094,
4687374, 4318033,
5906301, 6879014]})
pop_df
# In addition, all the ufuncs and other functionality work with hierarchical indices as well. Here we compute the fraction of people under 18 by year, given the above data:
f_u18 = pop_df['under18'] / pop_df['total']
f_u18.unstack()
# This allows us to easily and quickly manipulate and explore even high-dimensional data.
# ## Methods of MultiIndex Creation
#
# The most straightforward way to construct a multiply indexed `Series` or `DataFrame` is to simply pass a list of two or more index arrays to the constructor. For example:
df = pd.DataFrame(np.random.rand(4, 2),
index=[['a', 'a', 'b', 'b'], [1, 2, 1, 2]],
columns=['data1', 'data2'])
df
# The work of creatin the `MultiIndex` is done in the background.
#
# Similarly, if you pass a dictionary with appropriate tuples as keys, Pandas will automatically recognize this and use a `MultiIndex` by default:
# +
data = {('California', 2000): 33871648,
('California', 2010): 3725956,
('Texas', 2000): 20851820,
('Texas', 2010): 25145561,
('New York', 2000): 18976457,
('New York', 2010): 19378102}
pd.Series(data)
# -
# Nevertheless, it is sometimes useful to explicitly create a `MultiIndex`; we'll see a couple of these methods here.
# ### Explicit MultiIndex constructors
#
# For more flexibility in how the index is constructed, you can isntead use the class method constructors available in the `pd.MultiIndex`. For example, as we did before, you can construct the `MultiIndex` from a simple list of arrays giving the index values within each level:
#
pd.MultiIndex.from_arrays([['a', 'a', 'b', 'b'], [1, 2, 1, 2]])
# You can construct it from a list of tuples giving the multiple index values of each point:
pd.MultiIndex.from_tuples([('a', 1), ('a', 2), ('b', 1), ('b', 2)])
# You can even construct it from a Cartesian product of single indices:
pd.MultiIndex.from_product([['a', 'b'], [1, 2]])
# Similarly, you can construct the `MultiIndex` directly using its internal encoding by passing `levels`(a list of lists containig available index values for each level) and `labels` (a list of lists that reference these labels):
pd.MultiIndex(levels=[['a', 'b'], [1, 2]], labels=[[0, 0, 1, 1], [0, 1, 0, 1]])
# Any of these objects can be passed as the `index` argument when creating a `Series` or `DataFrame`, or be passed to the `reindex` method of an existing `Series` or `DataFrame`.
# ### MultiIndex level names
#
# Sometimes it is convenient to name the levels of the `MultiIndex`. This can be accomplished by passing the `names` argument to any of the above `MultiIndex` constructores, or by setting the `names` attribute of the index after the fact:
pop.index.names = ['state', 'year']
pop
# With more involved datasets, this can be a useful way to keep track of the meaning of various index values.
# ### MultiIndex for columns
#
# In a `DataFrame`, the rows and columns are completely symmetric, and just as the rows can have multiple levels of indices, the columns can have multiple levels as well. Consider the following, which is a mock-up of some(somewhat realistic) medical data:
# +
# hierarchical indices and columns
index = pd.MultiIndex.from_product([[2013,2014], [1, 2]],
names=['year', 'visit'])
columns = pd.MultiIndex.from_product([['Bob', 'Guido', 'Sue'], ['HR', 'Temp']],
names=['subject', 'type'])
# mock some data
data = np.round(np.random.rand(4, 6), 1)
data[:, ::2] *= 10
data += 37
# create the DataFrame
health_data = pd.DataFrame(data, index=index, columns=columns)
health_data
# -
# Here we see where the multi-indexing for both rows and columns can come in *very* handy. this is fundamentally four-dimensional data, where the dimensions are the subject, the measurement type, the year, nad the visit number. With this in place we can, for example, index the top-level column by the peron's name and get a full `DataFrame` containing just that person's information:
health_data['Guido']
# For more complicated records containing multiple labeled measurements across multiple times for many subcjets(people, countrie, cities, etc.) use of hierarchical rows and columns canbe extremely convenient!
# ## Indexing and Slicing a MultiIndex
#
# Indexing and slicing on a `MultiIndex` is designed to be intuitive, and it helps if you think about the indices as added dimensions. We'll first look at indexing multiply indexed `Series`, and then multiply-indexed `DataFrames`s.
# ### Multiply indexed Series
#
# Consider the multiply indexed `Series` of state populations we saw earlier:
pop
# We can access single elements by indexing with multiple terms:
pop['California', 2000]
# The `MultiIndex` also supports *partial indexing*, or indexing just one of the levels in the index. The result is another `Series`, with the lower-level indices maintained:
pop['California']
# Partial slicing is available as well, as long as the `MultiIndex` is sorted
pop.loc['California':'New York']
# With sorted indices, partial indexing can be performed on lower levels by passing an empty slicei nthe first index:
pop[:, 2000]
# Other types of indexing and selection work as well; for example, selection based on Boolean mask:
pop[pop > 22000000]
# Selection based on fancy indexing also works:
pop[['California', 'Texas']]
# ### Multiply indexed DataFrames
# A multiply indexed `DataFrame` behaves in a similar manner. Consider our toy medical `DataFrame` from before:
health_data
# Remember that columns are primary in a `DataFrame`, and the syntax used for multiply index `Series` applies to the columns. For example, we can recover Guido's heart rate data with a simple operation:
health_data['Guido', 'HR']
# Also, as with the single-index case, we can sue the `loc`, `iloc`, and `ix` indexers. For example:
health_data.iloc[:2, :2]
# These indexers provide an array-like view of the underlying two-dimensional data, but each individual index in `loc` or `iloc` can be passed a tuple of multiple indices.
#
# For example:
health_data.loc[:, ('Bob', 'HR')]
# Working with slieces within these index tuples is not especially convenient; trying to create a slice within a tuple with lead to a syntax error:
health_data.loc[(:, 1), (:, 'HR')]
# You could get around this by building the desired slice explicitly using Python's buil-in `slice()` function, but a better way in this context is to use an `IndexSlice` object, which Pandas provides for precisely this situation. For example:
idx = pd.IndexSlice
health_data.loc[idx[:, 1], idx[:, 'HR']]
# There are so many ways to interact with data in multiply indexed `Series` and `Dataframe`s, and as with many tools int his book the best way to become familiar with the mis to try them out.
# ## Rearranging Multi-Indices
# One of the keys to working with multiply indexed data is knowing how to effectively transform the data. There are a umber of operations that will preserve all the information in the dataset, but rearrange it for the purposes of various computations. We say a brief example of this in the `stack()` and `unstack()` methods, but there are many more ways to finaly control the rearrangement of data between hierarchical indices and columns, and we'll explore them here.
# ### Sorted and unsorted indices
# Earlier, we briefly mentioned a caveat, but we should emphasize it more here. *Many of the `MultiIndex` slicing operatiosn will fail if the index is not sorted.* Let's take a look at this here.
#
# We'll start by creating some simple multiply indexed data where the indices are *not lexographically sorted:*
index = pd.MultiIndex.from_product([['a', 'c', 'b'], [1, 2]])
data = pd.Series(np.random.rand(6), index=index)
data.index.names = ['char', 'int']
data
# If we try to take a partia lslice of this index, it will result in an error:
try:
data['a':'b']
except KeyError as e:
print(type(e))
print(e)
# Although it is not entirely clear from the error message, this is the result of the MultiIndex not being sorted. For various reasons, partial slices and other similar operations require the levels in the `MultiIndex` to be in sorted (i.e, lexographical) order. Pandas provides a number of convenience routines to perform this type of sorting; examples are the `sort_index()` and `sortlevel()` methods of the `DataFrame`. We'll use the simplest, `sort_index()`, here:
data = data.sort_index()
data
# With the index sorted in this way, partial slicing will work as expected:
data['a':'b']
# ### Stacking and untacking indices
#
# As we saw briefly before, it is possible to convert a dataset from a stacked multi-index to a simple two-dimensional representatnion, optionally specifying the level to use:
pop
pop.unstack(level=0)
pop.unstack(level=1)
# The opposite of `unstack()` is `stack()`, which here can be used to recover the original series:
pop.unstack().stack()
# ### Index setting and resetting
# Another way to rearrange hierarchical data is to turn the index lables into columns;
# this can be accomplished with the `reset_index` method. Calling this on the population dictionary will result in a `DataFrame` with a *state* and *year* column holding the information that was formerly in the index. For clarity, we can optionally specify the name of the data for the column representation:
pop_flat = pop.reset_index(name='population')
pop_flat
# Often when workign with data in the real world, the raw input data looks like this and it's useful to build a `MultiIndex` from the column values. This can be done with the `set_index` method of the `DataFrame`, which returns a multiply indexed `DataFrame`:
pop_flat.set_index(['state', 'year'])
# In practice I find this type of reindexing to be one of the more useful patterns when encountering real-world datasets.
# ## Data aggregations on Multi-Indices
#
# We've previously seen that Pandas has built-in data aggregation methods, such as `mean()`, `sum()`, and `max()`. For hierarchically indexed data, these can be passed a `level` parameter that controls which subset of the data the aggregate is computed on.
#
# For example, let's return to our health data:
health_data
# Perhaps we'd like to average-out the measurements in the two visits each year. We can do this by naming the index level we'd like to explore, in this case the year:
data_mean = health_data.mean(level='year')
data_mean
# By further making use of the `axis` keyword, we can take the mean among levels on the columns as well:
data_mean.mean(axis=1, level='type')
# Thus in two lines, we've been able to find the average heart rate and temperature measured among all subjects in all visits each year. This syntax is actually a short cut to the `GroupBy` functionality.
# ## Aside: Panel Data
#
# Pandas has a few other fundamental data structures that we have not yet discussed, namely the `pd.Panel` and `pd.Panel4D` objects. These can be thought of, respectively, as theree-dimensional and four-dimensional generalizatiosn of the (one-dimensional) `Series` and (two-dimensional) `DataFrame` structures. Once you are familiar with indexing and manipulation of data in `Series` and `DataFrame`, `Panel` and `Panel4D` are relatively straightforward to use. In particular, the `ix`, `loc` and `iloc` indexers discussed extend readily to these higher-dimensional structures.
#
# In majority of cases that multi-indexing is a more useful and conceptually simpler representation for higher-dimensional data. Additionally, panel data is fundamentally a dense data representation, while multi-indexing is fundamentally a sparse data representation. As the number of dimensions increases, the dense representation can become very inefficient for the majority of real-world datasets. For the occasional specialized application, however, these structures can e useful.
|
pandas/hierarchical_indexing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from causalinfo import *
# You only need this if you want to draw pretty pictures of the Networksa
from nxpd import draw, nxpdParams
nxpdParams['show'] = 'ipynb'
switch = Variable("S", 2)
dial = Variable("D", 10)
audio = Variable("A", 10+1) # 10 + silence
def radio(switch, dial, audio):
if switch == 0:
audio[0] = 1.0
else:
audio[dial+1] = 1.0
r_eq = Equation('Radio', [switch, dial], [audio], radio)
r_eq
radio_c = CausalGraph([r_eq])
draw(radio_c.full_network)
radio_dist = JointDist({switch: [.1, .9], dial: [1.0/10] * 10})
radio_dist
radio_c.generate_joint(radio_dist)#.mutual_info(audio, dial)
|
notebooks/radio.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import glob, os
os.environ["CUDA_VISIBLE_DEVICES"]="1"
# +
from __future__ import print_function
import tensorflow as tf
from keras.layers import Flatten, Dense, Reshape
from keras.layers import Input,InputLayer, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D
from keras.layers import AveragePooling2D, MaxPooling2D, Dropout
from keras.models import Sequential,Model
from keras.optimizers import SGD
from keras.callbacks import ModelCheckpoint,LearningRateScheduler
from keras.callbacks import ModelCheckpoint
from keras import losses
from keras.datasets import mnist
from keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D
from keras.models import Model
from keras import backend as K
from keras import models
from keras import layers
import keras
from sklearn.utils import shuffle
from sklearn import preprocessing
import scipy.io
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import pandas as pd
import sys
from sklearn.manifold import TSNE
from sklearn.utils import shuffle
from sklearn import preprocessing
import scipy.io
from mpl_toolkits.mplot3d import Axes3D
#from keract import get_activations
import numpy as np
import pandas as pd
from tensorflow import keras
from keras.layers import Conv2D,MaxPool2D,Dense,Dropout,Flatten
from keras.models import Sequential
from keras.preprocessing.image import ImageDataGenerator
from keras import regularizers
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D, BatchNormalization
from keras import optimizers
import keras
from keras.layers import Dense, Conv2D, BatchNormalization, Activation
from keras.layers import AveragePooling2D, Input, Flatten
from keras.optimizers import Adam
from keras.callbacks import ModelCheckpoint, LearningRateScheduler
from keras.callbacks import ReduceLROnPlateau
from keras.preprocessing.image import ImageDataGenerator
from keras.regularizers import l2
from keras import backend as K
from keras.models import Model
from keras.datasets import cifar10
from keras import losses
import numpy as np
import os, glob
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
from sklearn.metrics import confusion_matrix
# +
def pairwise_dist(A):
# Taken frmo https://stackoverflow.com/questions/37009647/compute-pairwise-distance-in-a-batch-without-replicating-tensor-in-tensorflow
r = tf.reduce_sum(A*A, 1)
r = tf.reshape(r, [-1, 1])
D = tf.maximum(r - 2*tf.matmul(A, tf.transpose(A)) + tf.transpose(r), 1e-7)
D = tf.sqrt(D)
return D
def dist_corr(X, Y):
n = tf.cast(tf.shape(X)[0], tf.float32)
a = pairwise_dist(X)
b = pairwise_dist(Y)
A = a - tf.reduce_mean(a, axis=1) - tf.expand_dims(tf.reduce_mean(a, axis=0), axis=1) + tf.reduce_mean(a)
B = b - tf.reduce_mean(b, axis=1) - tf.expand_dims(tf.reduce_mean(b, axis=0), axis=1) + tf.reduce_mean(b)
dCovXY = tf.sqrt(tf.reduce_sum(A*B) / (n ** 2))
dVarXX = tf.sqrt(tf.reduce_sum(A*A) / (n ** 2))
dVarYY = tf.sqrt(tf.reduce_sum(B*B) / (n ** 2))
dCorXY = dCovXY / tf.sqrt(dVarXX * dVarYY)
return dCorXY
def custom_loss1(y_true,y_pred):
dcor = dist_corr(y_true,y_pred)
return dcor
def custom_loss2(y_true,y_pred):
recon_loss = losses.categorical_crossentropy(y_true, y_pred)
return recon_loss
# -
def parse_filepath(filepath):
try:
path, filename = os.path.split(filepath)
filename, ext = os.path.splitext(filename)
age, gender, race, _ = filename.split("_")
return int(age), ID_GENDER_MAP[int(gender)], ID_RACE_MAP[int(race)]
except Exception as e:
print(filepath)
return None, None, None
# +
DATA_DIR = "./UTKFace/"
TRAIN_TEST_SPLIT = 0.7
IM_WIDTH = IM_HEIGHT = 198
ID_GENDER_MAP = {0: 'male', 1: 'female'}
GENDER_ID_MAP = dict((g, i) for i, g in ID_GENDER_MAP.items())
ID_RACE_MAP = {0: 'white', 1: 'black', 2: 'asian', 3: 'indian', 4: 'others'}
RACE_ID_MAP = dict((r, i) for i, r in ID_RACE_MAP.items())
# +
def parse_filepath(filepath):
try:
path, filename = os.path.split(filepath)
filename, ext = os.path.splitext(filename)
age, gender, race, _ = filename.split("_")
return int(age), ID_GENDER_MAP[int(gender)], ID_RACE_MAP[int(race)]
except Exception as e:
print(filepath)
return None, None, None
files = glob.glob(os.path.join(DATA_DIR, "*.jpg"))
attributes = list(map(parse_filepath, files))
df = pd.DataFrame(attributes)
df['file'] = files
df.columns = ['age', 'gender', 'race', 'file']
df = df.dropna()
df = df[(df['age'] > 10) & (df['age'] < 65)]
df.head()
# +
p = np.random.RandomState(10).permutation(len(df))
print(p)
train_up_to = int(len(df) * TRAIN_TEST_SPLIT)
train_idx = p[:train_up_to]
test_idx = p[train_up_to:]
# split train_idx further into training and validation set
train_up_to = int(train_up_to * 0.7)
train_idx, valid_idx = train_idx[:train_up_to], train_idx[train_up_to:]
df['gender_id'] = df['gender'].map(lambda gender: GENDER_ID_MAP[gender])
df['race_id'] = df['race'].map(lambda race: RACE_ID_MAP[race])
max_age = df['age'].max()
len(train_idx), len(valid_idx), len(test_idx), max_age
# +
from keras.utils import to_categorical
from PIL import Image
def get_data_generator(df, indices, for_training, batch_size=16):
images, ages, races, genders = [], [], [], []
while True:
for i in indices:
r = df.iloc[i]
file, age, race, gender = r['file'], r['age'], r['race_id'], r['gender_id']
im = Image.open(file)
im = im.resize((IM_WIDTH, IM_HEIGHT))
im = np.array(im) / 255.0
images.append(im)
ages.append(age / max_age)
races.append(to_categorical(race, len(RACE_ID_MAP)))
genders.append(to_categorical(gender, 2))
if len(images) >= batch_size:
images = np.array(images)
#flattened_images = np.reshape(images, (-1, IM_HEIGHT * IM_WIDTH * 3))
yield images, [np.array(races), np.array(ages), np.array(genders)]
images, ages, races, genders = [], [], [], []
if not for_training:
break
# +
from __future__ import print_function
import keras
from keras.layers import Dense, Conv2D, BatchNormalization, Activation
from keras.layers import AveragePooling2D, Input, Flatten
from keras.optimizers import Adam
from keras.callbacks import ModelCheckpoint, LearningRateScheduler
from keras.callbacks import ReduceLROnPlateau
from keras.preprocessing.image import ImageDataGenerator
from keras.regularizers import l2
from keras import backend as K
from keras.models import Model
from keras import losses
import numpy as np
import os
# Training parameters
batch_size = 32 # orig paper trained all networks with batch_size=128
epochs = 200
data_augmentation = False
# Subtracting pixel mean improves accuracy
subtract_pixel_mean = False
# Model parameter
# ----------------------------------------------------------------------------
# | | 200-epoch | Orig Paper| 200-epoch | Orig Paper| sec/epoch
# Model | n | ResNet v1 | ResNet v1 | ResNet v2 | ResNet v2 | GTX1080Ti
# |v1(v2)| %Accuracy | %Accuracy | %Accuracy | %Accuracy | v1 (v2)
# ----------------------------------------------------------------------------
# ResNet20 | 3 (2)| 92.16 | 91.25 | ----- | ----- | 35 (---)
# ResNet32 | 5(NA)| 92.46 | 92.49 | NA | NA | 50 ( NA)
# ResNet44 | 7(NA)| 92.50 | 92.83 | NA | NA | 70 ( NA)
# ResNet56 | 9 (6)| 92.71 | 93.03 | 93.01 | NA | 90 (100)
# ResNet110 |18(12)| 92.65 | 93.39+-.16| 93.15 | 93.63 | 165(180)
# ResNet164 |27(18)| ----- | 94.07 | ----- | 94.54 | ---(---)
# ResNet1001| (111)| ----- | 92.39 | ----- | 95.08+-.14| ---(---)
# ---------------------------------------------------------------------------
n = 3
# Model version
# Orig paper: version = 1 (ResNet v1), Improved ResNet: version = 2 (ResNet v2)
version = 2
# Computed depth from supplied model parameter n
if version == 1:
depth = n * 6 + 2
elif version == 2:
depth = n * 9 + 2
# Model name, depth and version
model_type = 'ResNet%dv%d' % (depth, version)
input_shape = (IM_HEIGHT, IM_WIDTH, 3)
def lr_schedule(epoch):
"""Learning Rate Schedule
Learning rate is scheduled to be reduced after 80, 120, 160, 180 epochs.
Called automatically every epoch as part of callbacks during training.
# Arguments
epoch (int): The number of epochs
# Returns
lr (float32): learning rate
"""
lr = 1e-3
if epoch > 180:
lr *= 0.5e-3
elif epoch > 160:
lr *= 1e-3
elif epoch > 120:
lr *= 1e-2
elif epoch > 80:
lr *= 1e-1
print('Learning rate: ', lr)
return lr
def resnet_layer(inputs,
num_filters=16,
kernel_size=3,
strides=1,
activation='relu',
batch_normalization=True,
conv_first=True):
"""2D Convolution-Batch Normalization-Activation stack builder
# Arguments
inputs (tensor): input tensor from input image or previous layer
num_filters (int): Conv2D number of filters
kernel_size (int): Conv2D square kernel dimensions
strides (int): Conv2D square stride dimensions
activation (string): activation name
batch_normalization (bool): whether to include batch normalization
conv_first (bool): conv-bn-activation (True) or
bn-activation-conv (False)
# Returns
x (tensor): tensor as input to the next layer
"""
conv = Conv2D(num_filters,
kernel_size=kernel_size,
strides=strides,
padding='same',
kernel_initializer='he_normal',
kernel_regularizer=l2(1e-4))
x = inputs
if conv_first:
x = conv(x)
if batch_normalization:
x = BatchNormalization()(x)
if activation is not None:
x = Activation(activation)(x)
else:
if batch_normalization:
x = BatchNormalization()(x)
if activation is not None:
x = Activation(activation)(x)
x = conv(x)
return x
def resnet_v2(input_shape, depth, num_classes=10):
#def custom_loss1(y_true,y_pred):
# dcor = 1 * distance_correlation(y_true,splitLayer)
# return dcor
#def custom_loss2(y_true,y_pred):
# recon_loss = losses.categorical_crossentropy(y_true, y_pred)
# return recon_loss
"""ResNet Version 2 Model builder [b]
Stacks of (1 x 1)-(3 x 3)-(1 x 1) BN-ReLU-Conv2D or also known as
bottleneck layer
First shortcut connection per layer is 1 x 1 Conv2D.
Second and onwards shortcut connection is identity.
At the beginning of each stage, the feature map size is halved (downsampled)
by a convolutional layer with strides=2, while the number of filter maps is
doubled. Within each stage, the layers have the same number filters and the
same filter map sizes.
Features maps sizes:
Experiment for UTKFace -
fmap initial size -
conv1: 198x198x3
conv2: 99x99x3
conv3: 49x49x16
conv4: 24x24x64
stage 0: 24x24x64
stage 1: 12x12x128
stage 2: 6x6x256
# Arguments
input_shape (tensor): shape of input image tensor
depth (int): number of core convolutional layers
num_classes (int): number of classes (CIFAR10 has 10)
# Returns
model (Model): Keras model instance
"""
if (depth - 2) % 9 != 0:
raise ValueError('depth should be 9n+2 (eg 56 or 110 in [b])')
# Start model definition.
num_filters_in = 16
num_res_blocks = int((depth - 2) / 9)
inputs = Input(shape=input_shape)
conv1 = Conv2D(3,
kernel_size=5,
strides=2,
padding='valid',
kernel_initializer='he_normal',
kernel_regularizer=l2(1e-4))
conv2 = Conv2D(3,
kernel_size=5,
strides=2,
padding='same',
kernel_initializer='he_normal',
kernel_regularizer=l2(1e-4))
conv3 = Conv2D(16,
kernel_size=3,
strides=2,
padding='same',
kernel_initializer='he_normal',
kernel_regularizer=l2(1e-4))
conv4 = Conv2D(filters = 64,
kernel_size=3,
strides=2,
padding='same',
kernel_initializer='he_normal',
kernel_regularizer=l2(1e-4))
z1 = conv1(inputs)
#before_flatten_dims = z1.get_shape().as_list()[1:]
#before_flatten_dims[0] = -1
#print(before_flatten_dims)
#split_layer = Flatten(name='split_layer')(z1)
#reshaped = Reshape(before_flatten_dims)(split_layer)
#print(reshaped)
z2 = conv2(z1)
z3 = conv3(z2)
z4 = conv4(z3)
#print(z3)
# v2 performs Conv2D with BN-ReLU on input before splitting into 2 paths
x = resnet_layer(inputs=z3,
num_filters=num_filters_in,
conv_first=True)
#print(x)
# Instantiate the stack of residual units
for stage in range(3):
for res_block in range(num_res_blocks):
activation = 'relu'
batch_normalization = True
strides = 1
if stage == 0:
num_filters_out = num_filters_in * 4
if res_block == 0: # first layer and first stage
activation = None
batch_normalization = False
else:
num_filters_out = num_filters_in * 2
if res_block == 0: # first layer but not first stage
strides = 2 # downsample
# bottleneck residual unit
y = resnet_layer(inputs=x,
num_filters=num_filters_in,
kernel_size=1,
strides=strides,
activation=activation,
batch_normalization=batch_normalization,
conv_first=False)
y = resnet_layer(inputs=y,
num_filters=num_filters_in,
conv_first=False)
y = resnet_layer(inputs=y,
num_filters=num_filters_out,
kernel_size=1,
conv_first=False)
if res_block == 0:
# linear projection residual shortcut connection to match
# changed dims
x = resnet_layer(inputs=x,
num_filters=num_filters_out,
kernel_size=1,
strides=strides,
activation=None,
batch_normalization=False)
if stage == 2 and res_block == 2:
before_flatten_dims = x.get_shape().as_list()[1:]
split_layer = Flatten(name='split_layer')(x)
x = Reshape(before_flatten_dims)(split_layer)
x = keras.layers.add([x, y])
num_filters_in = num_filters_out
print(x)
# Add classifier on top.
# v2 has BN-ReLU before Pooling
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = AveragePooling2D(pool_size=6)(x)
x = Flatten()(x)
x = Dense(100,
activation='relu',
kernel_initializer='he_normal')(x)
# for race prediction
# race = Dense(units=128, activation='relu')(x)
# race_output = Dense(units=len(RACE_ID_MAP), activation='softmax', name='race_output')(race)
age = Dense(units=128, activation='relu')(x)
age_output = Dense(units=1, activation='sigmoid', name='age_output')(age)
# for gender prediction
gender = Dense(units=128, activation='relu')(x)
gender_output = Dense(units=len(GENDER_ID_MAP), activation='softmax', name='gender_output')(gender)
# Instantiate model.
model = Model(inputs=inputs, outputs=[split_layer, age_output, gender_output])
return model
if version == 2:
model = resnet_v2(input_shape=input_shape, depth=depth)
else:
model = resnet_v1(input_shape=input_shape, depth=depth)
# + jupyter={"source_hidden": true}
alpha1, alpha2 = 0.9999, 0.0001
experiment_name = "{}-{}-UTKFace-age-attribute".format(alpha1, alpha2)
model.compile(loss={'age_output': 'mse', 'gender_output': 'categorical_crossentropy',
'split_layer': custom_loss1},
loss_weights={'split_layer':alpha1, 'age_output':alpha2, 'gender_output':alpha2},
optimizer=Adam(lr=lr_schedule(0)),
metrics={'age_output': 'mae', 'gender_output': 'accuracy'})
# Prepare model model saving directory.
#filepath = os.path.join(save_dir, model_name)
lr_scheduler = LearningRateScheduler(lr_schedule)
lr_reducer = ReduceLROnPlateau(factor=np.sqrt(0.1),
cooldown=0,
patience=5,
min_lr=0.5e-6)
#callbacks = [checkpoint, lr_reducer, lr_scheduler]
from keras.callbacks import ModelCheckpoint
train_gen = get_data_generator(df, train_idx, for_training=True, batch_size=batch_size)
valid_gen = get_data_generator(df, valid_idx, for_training=True, batch_size=batch_size)
callbacks = [
ModelCheckpoint("./saved_models/{}_{}_age_attribute_model.h5".format(alpha1,alpha2), monitor='val_loss'),
lr_reducer, lr_scheduler
]
history = model.fit_generator(train_gen,
steps_per_epoch=len(train_idx)//batch_size,
epochs=200,
callbacks=callbacks,
validation_data=valid_gen,
validation_steps=len(valid_idx)//batch_size,
verbose=2)
# +
def plot_train_history(history):
fig, axes = plt.subplots(1, 4, figsize=(20, 5))
"""axes[0].plot(history.history['race_output_accuracy'], label='Race Train accuracy')
axes[0].plot(history.history['val_race_output_accuracy'], label='Race Val accuracy')
axes[0].set_xlabel('Epochs')
axes[0].legend()"""
axes[1].plot(history.history['gender_output_accuracy'], label='Gender Train accuracy')
axes[1].plot(history.history['val_gender_output_accuracy'], label='Gener Val accuracy')
axes[1].set_xlabel('Epochs')
axes[1].legend()
"""
axes[2].plot(history.history['age_output_mae'], label='Age Train MAE')
axes[2].plot(history.history['val_age_output_mae'], label='Age Val MAE')
axes[2].set_xlabel('Epochs')
axes[2].legend()"""
axes[2].plot(history.history['split_layer_loss'], label='Split Layer loss')
axes[2].plot(history.history['val_split_layer_loss'], label='Split Val loss')
axes[2].set_xlabel('Epochs')
axes[2].legend()
axes[3].plot(history.history['loss'], label='Training loss')
axes[3].plot(history.history['val_loss'], label='Validation loss')
axes[3].set_xlabel('Epochs')
axes[3].legend()
plot_train_history(history)
# -
len(train_idx)
len(valid_idx)
# +
#import keras
#import keras_resnet.models
#shape, classes = (32, 32, 3), 10
#x = keras.layers.Input(shape)
#model = keras_resnet.models.ResNet50(x, classes=classes)
#model.compile("adam", "categorical_crossentropy", ["accuracy"])
#(training_x, training_y), (_, _) = keras.datasets.cifar10.load_data()
#training_y = keras.utils.np_utils.to_categorical(training_y)
#model.fit(training_x, training_y)
#model.layers.pop()
#model.summary()
# -
from keras.models import load_model
#alpha1, alpha2 = 0.2, 4.0
model = load_model('./saved_models/{}_{}_weighted_VGG_model.h5'.format(alpha1, alpha2),
custom_objects={'custom_loss1': custom_loss1})
test_gen = get_data_generator(df, test_idx, for_training=False, batch_size=128)
dict(zip(model.metrics_names, model.evaluate_generator(test_gen, steps=len(test_idx)//128)))
test_gen = get_data_generator(df, test_idx, for_training=False, batch_size=128)
dict(zip(model.metrics_names, model.evaluate_generator(test_gen, steps=len(test_idx)//128)))
# +
Z_HEIGHT = Z_WIDTH = 7
x_test_encoded = np.random.randn(0, Z_HEIGHT, Z_WIDTH, 256)
x_raw = np.random.randn(0, IM_HEIGHT, IM_WIDTH, 3)
test_gen = get_data_generator(df, test_idx, for_training=False, batch_size=128)
labels = [np.zeros((0, 5)), np.zeros((0,)), np.zeros((0, 2))]
for test_data_batch in test_gen:
labels[0] = np.concatenate((labels[0], test_data_batch[1][0]))
labels[1] = np.concatenate((labels[1], test_data_batch[1][1]))
labels[2] = np.concatenate((labels[2], test_data_batch[1][2]))
test_prediction = model.predict(test_data_batch[0])
x_raw = np.concatenate((x_raw, test_data_batch[0]))
x_test_encoded = np.concatenate((x_test_encoded, test_prediction[0].reshape(-1, Z_HEIGHT, Z_WIDTH, 256)))
# +
#test raw vs smash
n = 20
plt.figure(figsize=(40, 5))
for i in range(10,20):
# display original
ax = plt.subplot(2, n, i)
plt.imshow(x_raw[i])
#plt.imshow((x_test[i] * 255).astype(np.int64))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
ax = plt.subplot(2, n, i + n)
plt.imshow(x_test_encoded[i].reshape(Z_HEIGHT, Z_WIDTH, 3))
#plt.imshow((x_test_encoded[0][i].reshape(32, 32, 3) * 255).astype(np.int64))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
# -
labels[1][26]
import os
experiment_name = "UTKFace_race_0.9999_0.0001_2_2".format(alpha1, alpha2)
out_dir = './datasets/{}/output/'.format(experiment_name)
inp_dir = './datasets/{}/input/'.format(experiment_name)
os.makedirs(out_dir)
os.makedirs(inp_dir)
for i in range(x_raw.shape[0]):
#np.save('rawCifar10_baseline/'+str(i), x_test[i],allow_pickle = True)
#np.save('noSmashCifar10_baseline/'+str(i), x_test_encoded[0][i].reshape(32, 32, 3),allow_pickle = True)
np.save('{}/{}_{}_{}'.format(out_dir, i, labels[0][i].argmax(),
labels[2][i].argmax()), x_test_encoded[i].reshape(7, 7, 256), allow_pickle = True)
np.save('{}/{}'.format(inp_dir, i), x_raw[i].reshape(IM_HEIGHT, IM_WIDTH, 3), allow_pickle = True)
#matplotlib.image.imsave('rawCifar10/'+str(i)+'.png', x_test[i])
#matplotlib.image.imsave('smashCifar10/'+str(i)+'.png', x_test_encoded[0][i].reshape(32, 32, 3))
# +
import pickle
with open('./saved_models/{}'.format(experiment_name), 'wb') as file_pi:
pickle.dump(history.history, file_pi)
# +
#train raw vs smash
n = 10
plt.figure(figsize=(20, 4))
for i in range(1,n):
# display original
ax = plt.subplot(2, n, i)
plt.imshow(x_train[i])
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
ax = plt.subplot(2, n, i + n)
plt.imshow(x_train_encoded[0][i].reshape(32, 32, 3))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
# +
#Uncomment and use below to get activations. Also try to get for particual layer at a time via book, instead of enumerating all.
#from keract import get_activations
#activations = get_activations(model, x_test[1:2])
#from keract import display_activations
#display_activations(activations, cmap="gray", save=False)
# -
x_test_encoded[0][1].shape
x_testRaw.shape
print(experiment_name)
labels[0][0]
|
noPeekUTKFace-attribute-Copy1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # freud.environment.EnvironmentCluster
# The `freud.environment.EnvironmentCluster` class finds and clusters local environments, as determined by the vectors pointing to neighbor particles. Neighbors can be defined by a cutoff distance or a number of nearest-neighbors, and the resulting `freud.locality.NeighborList` is used to enumerate a set of vectors, defining an "environment." These environments are compared with the environments of neighboring particles to form spatial clusters, which usually correspond to grains, droplets, or crystalline domains of a system. `EnvironmentCluster` has several parameters that alter its behavior, please see the documentation or helper functions below for descriptions of these parameters.
#
# In this example, we cluster the local environments of hexagons. Clusters with 5 or fewer particles are colored dark gray.
# +
from collections import Counter
import freud
import matplotlib.pyplot as plt
import numpy as np
def get_cluster_arr(
system, num_neighbors, threshold, registration=False, global_search=False
):
"""Computes clusters of particles' local environments.
Args:
system:
Any object that is a valid argument to
:class:`freud.locality.NeighborQuery.from_system`.
num_neighbors (int):
Number of neighbors to consider in every particle's local environment.
threshold (float):
Maximum magnitude of the vector difference between two vectors,
below which we call them matching.
global_search (bool):
If True, do an exhaustive search wherein the environments of
every single pair of particles in the simulation are compared.
If False, only compare the environments of neighboring particles.
registration (bool):
Controls whether we first use brute force registration to
orient the second set of vectors such that it minimizes the
RMSD between the two sets.
Returns:
tuple(np.ndarray, dict): array of cluster indices for every particle
and a dictionary mapping from cluster_index keys to vector_array)
pairs giving all vectors associated with each environment.
"""
# Perform the env-matching calcuation
neighbors = {"num_neighbors": num_neighbors}
match = freud.environment.EnvironmentCluster()
match.compute(
system,
threshold,
neighbors=neighbors,
registration=registration,
global_search=global_search,
)
return match.cluster_idx, match.cluster_environments
def color_by_clust(
cluster_index_arr,
no_color_thresh=1,
no_color="#333333",
cmap=plt.get_cmap("viridis"),
):
"""Takes a cluster_index_array for every particle and returns a
dictionary of (cluster index, hexcolor) color pairs.
Args:
cluster_index_arr (numpy.ndarray):
The array of cluster indices, one per particle.
no_color_thresh (int):
Clusters with this number of particles or fewer will be
colored with no_color.
no_color (color):
What we color particles whose cluster size is below no_color_thresh.
cmap (color map):
The color map we use to color all particles whose
cluster size is above no_color_thresh.
"""
# Count to find most common clusters
cluster_counts = Counter(cluster_index_arr)
# Re-label the cluster indices by size
color_count = 0
color_dict = {
cluster[0]: counter
for cluster, counter in zip(
cluster_counts.most_common(), range(len(cluster_counts))
)
}
# Don't show colors for clusters below the threshold
for cluster_id in cluster_counts:
if cluster_counts[cluster_id] <= no_color_thresh:
color_dict[cluster_id] = -1
OP_arr = np.linspace(0.0, 1.0, max(color_dict.values()) + 1)
# Get hex colors for all clusters of size greater than no_color_thresh
for old_cluster_index, new_cluster_index in color_dict.items():
if new_cluster_index == -1:
color_dict[old_cluster_index] = no_color
else:
color_dict[old_cluster_index] = cmap(OP_arr[new_cluster_index])
return color_dict
# -
# We load the simulation data and call the analysis functions defined above. Notice that we use 6 nearest neighbors, since our system is made of hexagons that tend to cluster with 6 neighbors.
# +
ex_data = np.load("data/MatchEnv_Hexagons.npz")
box = ex_data["box"]
positions = ex_data["positions"]
orientations = ex_data["orientations"]
aq = freud.AABBQuery(box, positions)
cluster_index_arr, cluster_envs = get_cluster_arr(
aq, num_neighbors=6, threshold=0.2, registration=False, global_search=False
)
color_dict = color_by_clust(cluster_index_arr, no_color_thresh=5)
colors = [color_dict[i] for i in cluster_index_arr]
# -
# Below, we plot the resulting clusters. The colors correspond to the cluster size.
plt.figure(figsize=(12, 12), facecolor="white")
aq.plot(ax=plt.gca(), c=colors, s=20)
plt.title("Clusters Colored by Particle Local Environment")
plt.show()
|
module_intros/environment.EnvironmentCluster.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="ZiwRJ15WOLnD" colab_type="text"
# #Question 2
#
# + id="-_NNjZXxOPiQ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="f61c54a0-e9ac-4731-92b0-035eecfd45a8"
lst = list(range(1,1000+1))
# Generator to generate armstrong number
def armstrong(lst):
for num in lst:
s = 0
temp = num
while temp > 0:
d = temp % 10
s += d ** 3
temp //= 10
if num == s:
yield num
print(list(armstrong(lst)))
|
Day 9/Day9_Question2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Question 1:
# + active=""
# Define a class with a generator which can iterate the numbers, which are divisible by
# 7, between a given range 0 and n.
# -
# Answer :
class div_by_7:
def __init__(self,n):
self.n = n
def genrator(self):
for i in range(self.n + 1):
if i%7 == 0:
yield i
n = 100 # from 0 to n
d7 = div_by_7(n)
for i in d7.genrator():print(i)
# Question 2:
# + active=""
# Write a program to compute the frequency of the words from the input. The output
# should output after sorting the key alphanumerically.
# Suppose the following input is supplied to the program:
# New to Python or choosing between Python 2 and Python 3? Read Python 2 or
# Python 3.
# Then, the output should be:
# 2:2
# 3.:1
# 3?:1
# New:1
# Python:5
# Read:1
# and:1
# between:1
# choosing:1
# or:2
# to:1
# -
# Answer :
# +
print("Enter the words")
words = input().split()
count_ = {}
for i in words:
if i in count_.keys():
count_[i] += 1
else:
count_[i] = 1
sort_dic = dict(sorted(count_.items(),key=lambda x : x[0]))
for i,k in sort_dic.items(): print(i,":",k)
# -
# Question 3:
# + active=""
# Define a class Person and its two child classes: Male and Female. All classes have a
# method "getGender" which can print "Male" for Male class and "Female" for Female
# class.
# -
# Answer :
# +
class Person:
def __init__(self,gender):
self.gender = gender
def getGender(self):
print(self.gender)
class Male(Person):
def getGender(self):
print("Male")
class Female(Person):
def getGender(self):
print("Female")
# -
p = Person("Male")
p.getGender()
m = Male("Male")
m.getGender()
f = Female("Male")
f.getGender()
# Question 4:
# + active=""
# Please write a program to generate all sentences where subject is in ["I", "You"] and
# verb is in ["Play", "Love"] and the object is in ["Hockey","Football"].
# -
# Answer :
# +
sub = ["I", "You"]
verb = ["Play", "Love"]
obj = ["Hockey","Football"]
sen = []
for i in sub:
for j in verb:
for k in obj:
sen.append(i+" "+j.lower()+" "+k.lower()+".")
for i in sen:print(i)
# -
# Question 5:
# + active=""
# Please write a program to compress and decompress the string "hello world!hello
# world!hello world!hello world!".
# -
# Answer :
import gzip
text="Hello world"
comp=gzip.compress(text.encode())
print("Compressed: ", comp)
decomp=gzip.decompress(comp)
print("Decompressed: ", decomp.decode())
# Question 6:
# + active=""
# Please write a binary search function which searches an item in a sorted list. The
# function should return the index of element to be searched in the list.
# -
# Answer :
def BinarySearch(arr, x):
lb = 0
ub = len(arr) - 1
mid = 0
while lb <= ub:
mid = (ub + lb) // 2
if arr[mid] < x:
lb = mid + 1
elif arr[mid] > x:
ub = mid - 1
else:
return f"{x} is present at index {mid}"
return f"{x} is not present in this array."
sl = [1,5,9,56,78,80,96,99,110,124,144]# sorted list
print(BinarySearch(sl,78))
print(BinarySearch(sl,90))
print(BinarySearch(sl,124))
|
Python Programming Basic Assignment/Assignment_14.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import io
import detectron2
# import some common detectron2 utilities
from detectron2.engine import DefaultPredictor
from detectron2.config import get_cfg
from detectron2.utils.visualizer import Visualizer
from detectron2.data import MetadataCatalog
# import some common libraries
import numpy as np
import cv2
import torch
# Show the image in ipynb
from IPython.display import clear_output, Image, display
import PIL.Image
def showarray(a, fmt='jpeg'):
a = np.uint8(np.clip(a, 0, 255))
f = io.BytesIO()
PIL.Image.fromarray(a).save(f, fmt)
display(Image(data=f.getvalue()))
# +
# Load VG Classes
data_path = 'data/genome/1600-400-20'
vg_classes = []
with open(os.path.join(data_path, 'objects_vocab.txt')) as f:
for object in f.readlines():
vg_classes.append(object.split(',')[0].lower().strip())
vg_attrs = []
with open(os.path.join(data_path, 'attributes_vocab.txt')) as f:
for object in f.readlines():
vg_attrs.append(object.split(',')[0].lower().strip())
MetadataCatalog.get("vg").thing_classes = vg_classes
MetadataCatalog.get("vg").attr_classes = vg_attrs
# -
cfg = get_cfg()
cfg.merge_from_file("../configs/VG-Detection/faster_rcnn_R_101_C4_attr_caffemaxpool.yaml")
cfg.MODEL.RPN.POST_NMS_TOPK_TEST = 300
cfg.MODEL.ROI_HEADS.NMS_THRESH_TEST = 0.6
cfg.MODEL.ROI_HEADS.SCORE_THRESH_TEST = 0.2
# VG Weight
cfg.MODEL.WEIGHTS = "http://nlp.cs.unc.edu/models/faster_rcnn_from_caffe_attr.pkl"
predictor = DefaultPredictor(cfg)
im = cv2.imread("data/images/input.jpg")
im_rgb = cv2.cvtColor(im, cv2.COLOR_BGR2RGB)
showarray(im_rgb)
# +
NUM_OBJECTS = 36
from torch import nn
from detectron2.modeling.postprocessing import detector_postprocess
from detectron2.modeling.roi_heads.fast_rcnn import FastRCNNOutputLayers, FastRCNNOutputs, fast_rcnn_inference_single_image
from detectron2.structures.boxes import Boxes
from detectron2.structures.instances import Instances
def doit(raw_image, raw_boxes):
# Process Boxes
raw_boxes = Boxes(torch.from_numpy(raw_boxes).cuda())
with torch.no_grad():
raw_height, raw_width = raw_image.shape[:2]
print("Original image size: ", (raw_height, raw_width))
# Preprocessing
image = predictor.transform_gen.get_transform(raw_image).apply_image(raw_image)
print("Transformed image size: ", image.shape[:2])
# Scale the box
new_height, new_width = image.shape[:2]
scale_x = 1. * new_width / raw_width
scale_y = 1. * new_height / raw_height
#print(scale_x, scale_y)
boxes = raw_boxes.clone()
boxes.scale(scale_x=scale_x, scale_y=scale_y)
# ----
image = torch.as_tensor(image.astype("float32").transpose(2, 0, 1))
inputs = [{"image": image, "height": raw_height, "width": raw_width}]
images = predictor.model.preprocess_image(inputs)
# Run Backbone Res1-Res4
features = predictor.model.backbone(images.tensor)
# Run RoI head for each proposal (RoI Pooling + Res5)
proposal_boxes = [boxes]
features = [features[f] for f in predictor.model.roi_heads.in_features]
box_features = predictor.model.roi_heads._shared_roi_transform(
features, proposal_boxes
)
feature_pooled = box_features.mean(dim=[2, 3]) # pooled to 1x1
print('Pooled features size:', feature_pooled.shape)
# Predict classes pred_class_logits, pred_proposal_deltas = predictor.model.roi_heads.box_predictor(feature_pooled) and boxes for each proposal.
pred_class_logits, pred_attr_logits, pred_proposal_deltas = predictor.model.roi_heads.box_predictor(feature_pooled)
pred_class_prob = nn.functional.softmax(pred_class_logits, -1)
pred_scores, pred_classes = pred_class_prob[..., :-1].max(-1)
attr_prob = pred_attr_logits[..., :-1].softmax(-1)
max_attr_prob, max_attr_label = attr_prob.max(-1)
# Detectron2 Formatting (for visualization only)
roi_features = feature_pooled
instances = Instances(
image_size=(raw_height, raw_width),
pred_boxes=raw_boxes,
scores=pred_scores,
pred_classes=pred_classes,
attr_scores = max_attr_prob,
attr_classes = max_attr_label
)
return instances, roi_features
given_boxes = np.array(
[[1.7333e+02, 2.1515e+02, 4.8672e+02, 4.7373e+02],
[1.2166e+02, 2.0614e+02, 3.4905e+02, 4.8000e+02],
[5.8896e+02, 0.0000e+00, 6.3909e+02, 3.6998e+02],
[6.0792e+02, 9.0849e+01, 6.3765e+02, 4.2150e+02],
[2.8171e+02, 1.6275e+02, 3.2904e+02, 1.9557e+02],
[1.5337e+02, 9.6636e+01, 3.9307e+02, 4.5865e+02],
[3.9510e+00, 3.0141e-01, 1.7087e+02, 3.7003e+02],
[2.0478e+02, 0.0000e+00, 3.0078e+02, 2.7645e+02],
[3.8164e+02, 3.1898e+02, 6.1028e+02, 4.2289e+02],
[4.2380e+02, 2.7979e+02, 6.3800e+02, 3.9043e+02],
[5.3907e+01, 2.1506e+01, 1.2955e+02, 3.8665e+02],
[2.1639e+02, 3.3180e+02, 4.9085e+02, 4.7821e+02],
[4.5419e+01, 3.1766e+02, 5.8115e+02, 4.7680e+02],
[5.2262e+01, 1.5123e+02, 4.9093e+02, 4.3199e+02],
[3.4266e+02, 4.8674e+01, 6.3398e+02, 3.8901e+02],
[2.4584e+02, 1.8033e+02, 3.4975e+02, 4.0818e+02],
[1.7189e+02, 1.6335e+02, 6.3919e+02, 4.1045e+02],
[1.9629e+01, 0.0000e+00, 5.6497e+02, 1.5761e+02],
[3.9222e+02, 0.0000e+00, 6.3402e+02, 2.7783e+02],
[3.6025e+01, 0.0000e+00, 5.5431e+02, 2.8221e+02],
[1.5994e+02, 1.5115e+00, 3.5376e+02, 3.1772e+02],
[2.9326e+02, 1.4786e+02, 3.2540e+02, 1.8938e+02],
[0.0000e+00, 3.6491e+02, 4.3185e+02, 4.7849e+02],
[1.9907e+01, 4.2409e+02, 4.5854e+02, 4.7957e+02],
[4.9555e+00, 8.1566e+01, 2.3710e+02, 4.5235e+02],
[5.5625e+02, 2.7353e+02, 6.0216e+02, 3.7322e+02],
[9.2086e+01, 2.8328e+02, 3.2548e+02, 4.4708e+02],
[1.7761e+02, 3.6624e+02, 4.5720e+02, 4.6956e+02],
[1.7253e+02, 3.7161e+02, 6.4000e+02, 4.7876e+02],
[2.7954e+02, 2.0651e+02, 3.4036e+02, 3.1626e+02],
[1.9732e+02, 3.8317e+01, 6.4000e+02, 3.2455e+02],
[2.7082e+02, 1.1922e+00, 5.8803e+02, 3.0338e+02],
[6.5850e+00, 1.8703e+02, 3.0191e+02, 4.7954e+02],
[0.0000e+00, 0.0000e+00, 2.2748e+02, 2.3305e+02],
[2.4732e-01, 3.3860e+02, 3.1494e+02, 4.7737e+02],
[2.0554e+02, 1.9619e+00, 6.4000e+02, 2.7667e+02]]
)
instances, features = doit(im, given_boxes)
print("Classes", instances.pred_classes)
# -
# Show the boxes, labels, and features
pred = instances.to('cpu')
v = Visualizer(im[:, :, :], MetadataCatalog.get("vg"), scale=1.2)
v = v.draw_instance_predictions(pred)
showarray(v.get_image()[:, :, ::-1])
print('instances:\n', instances)
print()
print('boxes:\n', instances.pred_boxes)
print()
print('Shape of features:\n', features.shape)
# Verify the correspondence of RoI features
pred_class_logits, _, pred_proposal_deltas = predictor.model.roi_heads.box_predictor(features)
pred_class_probs = torch.nn.functional.softmax(pred_class_logits, -1)[:, :-1]
max_probs, max_classes = pred_class_probs.max(-1)
print("%d objects are different, it is because the classes-aware NMS process" % (NUM_OBJECTS - torch.eq(instances.pred_classes, max_classes).sum().item()))
print("The total difference of score is %0.4f" % (instances.scores - max_probs).abs().sum().item())
|
demo/demo_feature_extraction_attr_given_box.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="ecRT5851lqEB"
# The **variance inflation factor** (VIF) quantifies the extent of correlation between one predictor and the other predictors in a model. It is used for diagnosing collinearity/multicollinearity. Higher values signify that it is difficult to impossible to assess accurately the contribution of predictors to a model.
#
# $$VIF = \frac {1} {1 - R^2}$$
#
# The higher the value, the greater the correlation of the variable with other variables.
#
#
# + colab={"base_uri": "https://localhost:8080/"} id="hMQhqmP7k5TU" outputId="e202fca9-98c2-40be-b110-a57f971ac073"
import numpy as np
import pandas as pd
import statsmodels.api as sm
import warnings
from pandas import DataFrame,Series
from scipy import stats
from sklearn.datasets import load_boston
warnings.filterwarnings('ignore')
# + colab={"base_uri": "https://localhost:8080/"} id="IW_vUNvok5T1" outputId="9a0199f0-ab83-4759-c7bc-6f24e11bc75e"
boston = load_boston()
print (boston.DESCR)
# + id="k_QwmSDCk5T8"
X = boston["data"]
Y = boston["target"]
names = list(boston["feature_names"])
# + id="1e_jPjcYk5Ud"
inp_df = pd.DataFrame(X, columns=names)
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="PjFDHCtRk5Uf" outputId="176766c7-8131-48f2-9d3f-072b3bdfe1f8"
inp_df.head()
# + colab={"base_uri": "https://localhost:8080/"} id="J6n_18jUk5Ui" outputId="40283e33-8247-4d53-80ae-7062dc8c5d63"
for i in range(0, len(names)):
y = inp_df.loc[:, inp_df.columns == names[i]]
x = inp_df.loc[:, inp_df.columns != names[i]]
model = sm.OLS(y, x)
results = model.fit()
rsq = results.rsquared
vif = round(1 / (1 - rsq), 2)
print(
"R Square value of {} column is {} keeping all other columns as features".format(
names[i], (round(rsq, 2))
)
)
print(
"Variance Inflation Factor of {} column is {} \n".format(
names[i], vif)
)
|
08. Regression/09. Variance Inflation Factor for Multicolinearity.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# This is a small example of how to wrangle data.
# +
import pandas as pd
import matplotlib as plt
# %matplotlib inline
# -
# Continents-Countries List
Continent_Country_File = pd.read_csv('Countries-Continents-csv.csv')
Continent_Country_File = Continent_Country_File[['Country','Continent']]
Continent_Country_File = Continent_Country_File.apply(lambda x: x.astype(str).str.upper())
Continent_Country_File = Continent_Country_File.sort_values(by =['Country'])
Continent_Country_File['Country'].replace(['KOREA, NORTH', 'KOREA, SOUTH' ], ['KOREA, DEM. PEOPLE’S REP.', 'KOREA, REP.'], inplace=True)
Continent_Country_File.to_csv("FR2.csv")
Continent_Country_File.head()
# Fertility Rate Data from 1960 - 2015
Fert_Rate_File1 = pd.ExcelFile('API_SP.DYN.TFRT.IN_DS2_en_excel_v2.xls')
Fert_Rate_File1 = Fert_Rate_File1.parse("Data")
Fert_Rate_File1.columns = ['Country', 'Country Code', 'Indicator Name', 'Indicator Code', '1960', '1961', '1962', '1963',
'1964', '1965','1966','1967', '1968', '1969', '1970', '1971', '1972', '1973', '1974', '1975', '1976',
'1977', '1978', '1979', '1980', '1981', '1982', '1983', '1984', '1985', '1986', '1987', '1988', '1989',
'1990', '1991', '1992', '1993', '1994', '1995', '1996', '1997', '1998', '1999', '2000', '2001', '2002',
'2003', '2004', '2005', '2006', '2007', '2008', '2009', '2010', '2011', '2012', '2013', '2014', '2015',
'2016']
Fert_Rate_File1 = Fert_Rate_File1[['Country', '2008', '2010', '2012', '2014']]
Fert_Rate_File1 = Fert_Rate_File1.fillna(0)
Fert_Rate_File1 = Fert_Rate_File1.apply(lambda x: x.astype(str).str.upper())
Fert_Rate_File1[['2008', '2010', '2012', '2014']] = Fert_Rate_File1[['2008', '2010', '2012', '2014']].apply(pd.to_numeric, errors='ignore')
Fert_Rate_File1.head()
# Fertility Rate Data for 2016
Fert_Rate_File2 = pd.read_csv('Global Fertility Rate.csv')
Fert_Rate_File2.columns = ['Rank','Country','2016', 'DoI']
Fert_Rate_File2 = Fert_Rate_File2[['Country','2016', 'Rank']]
Fert_Rate_File2 = Fert_Rate_File2.fillna(0)
Fert_Rate_File2 = Fert_Rate_File2.apply(lambda x: x.astype(str).str.upper())
Fert_Rate_File2[['2016']] = Fert_Rate_File2[['2016']].apply(pd.to_numeric, errors='ignore')
Fert_Rate_File2.head()
# Final Fertility Rate Data from 2008-2016
Fert_Rate_File2['Country'].replace(['RUSSIA', 'KOREA, NORTH', 'KOREA, SOUTH' ], ['RUSSIAN FEDERATION', 'KOREA, DEM. PEOPLE’S REP.', 'KOREA, REP.'], inplace=True)
Fert_Rate_File = Fert_Rate_File1.merge (Fert_Rate_File2, on='Country', how='outer')
Fert_Rate_File.head()
Continents_Merged = Fert_Rate_File.merge (Continent_Country_File, on='Country', how='outer')
Continents_Merged[['2008', '2010', '2012', '2014', '2016']] = Continents_Merged[['2008', '2010', '2012', '2014', '2016']].apply(pd.to_numeric, errors='ignore')
Continents_Merged.to_csv("CC_GFR.csv")
Continents_Merged.head()
# GDP data
GDP_File = pd.read_csv('API_NY.GDP.MKTP.KD.ZG_DS2_en_csv_v2.csv')
GDP_File.columns = ['Country', 'Country Code', 'Indicator Name', 'Indicator Code', '1960', '1961', '1962', '1963',
'1964', '1965','1966','1967', '1968', '1969', '1970', '1971', '1972', '1973', '1974', '1975', '1976',
'1977', '1978', '1979', '1980', '1981', '1982', '1983', '1984', '1985', '1986', '1987', '1988', '1989',
'1990', '1991', '1992', '1993', '1994', '1995', '1996', '1997', '1998', '1999', '2000', '2001', '2002',
'2003', '2004', '2005', '2006', '2007', '2008', '2009', '2010', '2011', '2012', '2013', '2014', '2015',
'2016']
GDP_File = GDP_File[['Country', '2008', '2010', '2012', '2014']]
GDP_File = GDP_File.fillna(0)
GDP_File = GDP_File.apply(lambda x: x.astype(str).str.upper())
GDP_File[['2008', '2010', '2012', '2014']] = GDP_File[['2008', '2010', '2012', '2014']].apply(pd.to_numeric, errors='ignore')
GDP_File.to_csv("GDP_File.csv")
GDP_File.head()
# Urbanization Data
Urb_File = pd.read_csv('API_SP.URB.TOTL.IN.ZS_DS2_en_csv_v2.csv')
Urb_File.columns = ['Country', 'Country Code', 'Indicator Name', 'Indicator Code', '1960', '1961', '1962', '1963',
'1964', '1965','1966','1967', '1968', '1969', '1970', '1971', '1972', '1973', '1974', '1975', '1976',
'1977', '1978', '1979', '1980', '1981', '1982', '1983', '1984', '1985', '1986', '1987', '1988', '1989',
'1990', '1991', '1992', '1993', '1994', '1995', '1996', '1997', '1998', '1999', '2000', '2001', '2002',
'2003', '2004', '2005', '2006', '2007', '2008', '2009', '2010', '2011', '2012', '2013', '2014', '2015',
'2016']
Urb_File = Urb_File[['Country', '2008', '2010', '2012', '2014']]
Urb_File = Urb_File.fillna(0)
Urb_File = Urb_File.apply(lambda x: x.astype(str).str.upper())
Urb_File[['2008', '2010', '2012', '2014']] = Urb_File[['2008', '2010', '2012', '2014']].apply(pd.to_numeric, errors='ignore')
Urb_File.to_csv("Urb_File.csv")
Urb_File.head()
# Female Literacy Data
Female_Literacy_File = pd.ExcelFile('LiteracyRatesFemales.xlsx')
Female_Literacy_File = Female_Literacy_File.parse("Sheet1")
Female_Literacy_File.columns = ['Rank','Country','2016', 'DoI']
Female_Literacy_File = Female_Literacy_File[['Country','2016']]
Female_Literacy_File = Female_Literacy_File.fillna(0)
Female_Literacy_File = Female_Literacy_File.apply(lambda x: x.astype(str).str.upper())
Female_Literacy_File[['2016']] = Female_Literacy_File[['2016']].apply(pd.to_numeric, errors='ignore')
Female_Literacy_File['Country'].replace(['RUSSIA', 'KOREA (NORTH)'], ['RUSSIAN FEDERATION', 'KOREA, DEM. PEOPLE’S REP.'], inplace=True)
Female_Literacy_File.loc[len(Female_Literacy_File)]=['JAPAN',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['AUSTRALIA',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['KOREA, REP.',0]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['UNITED STATES',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['UNITED KINGDOM',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['CANADA',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['BARBADOS',99.7]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['BELGIUM',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['DENMARK',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['FRANCE',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['GERMANY',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['IRELAND',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['MONACO',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['NETHERLANDS',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['NEW ZEALAND',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['NORWAY',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['SWEDEN',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['SWITZERLAND',99]
Female_Literacy_File.loc[len(Female_Literacy_File)]=['MARSHALL ISLANDS',98]
Female_Literacy_File.to_csv("Female_Literacy_File.csv")
Female_Literacy_File.head()
|
Global Fertility Data Files.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Visualizing image data with astropy.visualization
#
# In the previous tutorials, when we have made plots of the image data, the axes have showed pixel coordinates. However, you may want to show the world coordinates, and optionally a coordinate grid on the image. The [astropy.visualization](http://docs.astropy.org/en/stable/visualization/index.html) sub-module provides a way to do this that integrates with Matplotlib ([astropy.visualization.wcsaxes](http://docs.astropy.org/en/stable/visualization/wcsaxes/index.html)). In addition, the [APLpy](https://aplpy.github.io/) package provides a user-friendly way of making these kinds of plots (and is now built on top of astropy.visualization.wcsaxes). In this tutorial we will take a look at both options.
#
# <section class="objectives panel panel-warning">
# <div class="panel-heading">
# <h2><span class="fa fa-certificate"></span> Objectives</h2>
# </div>
#
#
# <div class="panel-body">
#
# <ul>
# <li>Make an image plot with Matplotlib with world coordinates shown</li>
# <li>Customize the ticks, tick labels, and axis labels</li>
# <li>Overplot data (points and contours) on top of the image</li>
# <li>Overplot different coordinate systems</li>
# <li>Normalizing and stretching image data</li>
# <li>Using APLpy for quick plots</li>
# </ul>
#
# </div>
#
# </section>
#
# ## Documentation
#
# This notebook only shows a subset of the functionality in astropy.visualization and APLpy. For more information about the features presented below as well as other available features, you can read the
# [astropy.visualization](http://docs.astropy.org/en/stable/visualization/index.html) and the [APLpy](https://aplpy.github.io/) documentation.
# %matplotlib inline
import matplotlib.pyplot as plt
plt.rc('image', origin='lower')
plt.rc('figure', figsize=(10, 6))
# ## Making a simple plot
#
# We start off by loading in the GAIA source density image from previous tutorials:
from astropy.io import fits
hdulist = fits.open('data/LMCDensFits1k.fits')
# and we extract the WCS from the header:
from astropy.wcs import WCS
wcs = WCS(hdulist[0].header)
# We can now use Matplotlib as normal but passing the ``projection=`` keyword argument to the ``subplot`` function:
ax = plt.subplot(projection=wcs)
ax.imshow(hdulist[0].data)
ax.grid()
# As you can see, this automatically shows the longitude and latitude on the axes and calling ``grid`` shows the curved grid of the celestial sphere!
#
# ## Customizing ticks and labels
#
# When using a WCS projection, controlling the ticks, tick labels, and axis labels is a little different to normal Matplotlib - this is because there is now not a one to one correspondance between world coordinates and pixel axes, so talking about the 'x' or 'y' ticks does not make sense in some cases, and instead we should talk about e.g. longitude and latitude ticks.
#
# Once you have a plot initialized, you can access the ``ax.coords`` property which gives you access to ways of controlling each world coordinate. You can either index this by an integer for the index of the world coordinate:
lon = ax.coords[0]
lat = ax.coords[1]
# or, in the case of common coordinate systems, by their name:
lon = ax.coords['glon']
lat = ax.coords['glat']
# The object you have for each coordinate can then be used to customize it, for example to set the axis labels:
lon.set_axislabel('Galactic Longitude')
lat.set_axislabel('Galactic Latitude')
ax.figure
# The tick label format:
lon.set_major_formatter('dd:mm:ss.s')
lat.set_major_formatter('dd:mm')
ax.figure
# The tick spacing or the number of ticks:
from astropy import units as u
lon.set_ticks(spacing=4. * u.deg)
lat.set_ticks(number=10)
ax.figure
# Since the world axes are not necessarily tied to a single pixel axis, it is possible to show each coordinate on any of the axes:
lon.set_ticks_position('bt')
lon.set_ticklabel_position('bt')
lon.set_axislabel_position('bt')
lat.set_ticks_position('lr')
lat.set_ticklabel_position('lr')
lat.set_axislabel_position('lr')
ax.figure
# ## Overlaying markers and contours
#
# By default, the normal Matplotlib methods on axes should work, and assume pixel coordinates:
ax = plt.subplot(projection=wcs)
ax.imshow(hdulist[0].data)
ax.plot([300, 350, 400], [200, 250, 300], 'wo')
ax.figure
# However, most Matplotlib methods can take a ``transform=`` option which allows us to plot data in various coordinate systems. For example, to plot markers in Galactic coordinates, we can do:
ax.plot([279, 278, 277], [-30, -31, -32], 'o', color='orange', transform=ax.get_transform('world'))
ax.figure
# In this case we used ``'world'`` but we could also have explicitly said ``'galactic'`` or plotted markers in e.g. ``'fk5'``. You can also pass astropy coordinate frames to this if needed.
#
# To overplot contours, you can use a similar approach, but in this case ``get_transform`` should be given the WCS object for the contour map. We can try this out by using an IRAS 100 micron map of the LMC:
hdulist_iras = fits.open('data/ISSA_100_LMC.fits')
wcs_iras = WCS(hdulist_iras[0].header)
ax = plt.subplot(projection=wcs)
ax.imshow(hdulist[0].data)
ax.contour(hdulist_iras[0].data, transform=ax.get_transform(wcs_iras),
colors='white', levels=[50, 100, 250, 500])
# ## Overlaying a different coordinate grid
#
# Another useful feature is the ability to overplot different coordinate systems - for example in the above case we can add an RA/Dec grid and ticks for reference:
# +
ax = plt.subplot(projection=wcs)
ax.imshow(hdulist[0].data)
lon, lat = ax.coords
lon.set_axislabel('Galactic Longitude')
lat.set_axislabel('Galactic Longitude')
ra, dec = ax.get_coords_overlay('icrs')
dec.set_axislabel('Declination')
dec.set_ticks_position('t')
dec.set_ticklabel_position('t')
dec.set_axislabel_position('t')
ra.set_axislabel('Right Ascension')
ra.set_ticks_position('r')
ra.set_ticklabel_position('r')
ra.set_axislabel_position('r')
lon.grid(color='white')
lat.grid(color='yellow')
ra.grid(color='green')
dec.grid(color='cyan')
# -
# ## Normalizing and stretching data
#
# Another set of functionality in the [astropy.visualization](http://docs.astropy.org/en/stable/visualization/) sub-package are classes and functions to help with normalizing and stretching data. The easiest way to use this is to use the [simple_norm()](http://docs.astropy.org/en/stable/api/astropy.visualization.mpl_normalize.simple_norm.html#astropy.visualization.mpl_normalize.simple_norm) function:
from astropy.visualization import simple_norm
sqrt_norm = simple_norm(hdulist[0].data, stretch='sqrt', percent=99.5)
plt.imshow(hdulist[0].data, norm=sqrt_norm)
#
# <section class="challenge panel panel-success">
# <div class="panel-heading">
# <h2><span class="fa fa-pencil"></span> Challenge</h2>
# </div>
#
#
# <div class="panel-body">
#
# <ol>
# <li>Make a figure of the IRAS data used above, with the GAIA source density map shown as a contour (note that you might need to smooth the GAIA source density image - check the <a href="https://docs.scipy.org/doc/scipy/reference/ndimage.html">scipy.ndimage</a> module for some useful functions!)</li>
# <li>Add the positions of the GAIA sources from the table used in previous tutorials to the image</li>
# <li>If you have FITS images available, try this out with your own data!</li>
# </ol>
#
# </div>
#
# </section>
#
# +
#1
from scipy.ndimage import gaussian_filter
ax = plt.subplot(projection=wcs_iras)
ax.imshow(hdulist_iras[0].data, vmax=100)
ax.contour(gaussian_filter(hdulist[0].data, 3), transform=ax.get_transform(wcs),
colors='white')
ax.set_xlim(-0.5, 499.5)
ax.set_ylim(-0.5, 499.5)
#2
from astropy.table import Table
psc = Table.read('data/gaia_lmc_psc.fits')
ax.plot(psc['ra'], psc['dec'], 'w.', transform=ax.get_transform('icrs'), alpha=0.3)
# -
# ## Using APLpy
#
# APLpy is a relatively old Python package that has recently been re-worked to be a wrapper around astropy.visualization. It makes it very easy to make simple plots, although it does not allow full customization to the extent that wcsaxes does. For example, we can make a plot similar to the one in the solution above by doing:
import aplpy
fig = aplpy.FITSFigure('data/ISSA_100_LMC.fits')
fig.show_colorscale()
fig.show_contour('data/LMCDensFits1k.fits', smooth=3, colors='white')
# Note that you can get to the underlying WCSAxes axes object by doing:
fig.ax
# The documentation for APLpy can be found at https://aplpy.readthedocs.io/en/stable/
# <center><i>This notebook was written by <a href="https://aperiosoftware.com/">Aperio Software Ltd.</a> © 2019, and is licensed under a <a href="https://creativecommons.org/licenses/by/4.0/">Creative Commons Attribution 4.0 International License (CC BY 4.0)</a></i></center>
#
# 
|
instructor/08-wcsaxes_instructor.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Example notebook usage of DESI tile picker
# +
import tilepicker
from astropy.io import fits
tiles = fits.getdata('tiles.fits')
# -
tilepicker.plot_visibility(tiles, airmass=1.5)
|
TilePicker.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.5 64-bit
# metadata:
# interpreter:
# hash: d8b274d99e8fb8d9facd229017fb192c20e27208913b8ae525f29c1e2086d313
# name: python3
# ---
# +
# #!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
Standard main script for the shunt connection procedure.
Copyright 2021 Christian Doppler Laboratory for Embedded Machine Learning
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
"""
# Built-in/Generic Imports
import configparser
from pathlib import Path
import sys
# Libs
import numpy as np
from tensorflow import keras
from keras_applications import correct_pad
# Own modules
import shunt_connector
__author__ = '<NAME>'
__copyright__ = 'Copyright 2021, Christian Doppler Laboratory for ' \
'Embedded Machine Learning'
__credits__ = ['']
__license__ = 'Apache 2.0'
__version__ = '1.0.0'
__maintainer__ = '<NAME>'
__email__ = '<EMAIL>'
__status__ = 'Release'
#-------------------------------------------------------------------------------------------------------------
# PARAMS
s_and_e_location = 'mnv3'
#s_and_e_location = 'en-de'
s_and_e_ratio = 0.25
# +
config_path = Path("config", "standard.cfg")
config = configparser.ConfigParser()
config.read(config_path)
connector = shunt_connector.ShuntConnector(config)
connector.create_dataset()
connector.create_original_model()
# +
# Firstly, calculate properties like input & output shapes, stride layers, and dilation rates
input_shape = connector.original_model.get_layer(index=connector.shunt_params['locations'][0]).input_shape[1:]
if isinstance(input_shape, list):
input_shape = input_shape[0][1:]
output_shape = connector.original_model.get_layer(index=connector.shunt_params['locations'][1]).output_shape[1:]
if isinstance(output_shape, list):
output_shape = output_shape[0][1:]
num_stride_layers = np.round(np.log2(input_shape[1] / output_shape[1]))
dilation_rates = shunt_connector.shunt.find_dilation_rates.find_input_output_dilation_rates(connector.original_model, connector.shunt_params['locations'])
# The predefined s_and_e blocks from MobileNetV3 are used. They are implemented in the keras_application module.
with connector.activate_distribution_scope():
# shunt model
input_net = keras.layers.Input(shape=input_shape)
x = input_net
x = keras.layers.Conv2D(192,
kernel_size=(1,1),
strides=(1,1),
padding='same',
use_bias=False,
activation=None,
name="shunt_conv_1",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(4e-5))(x)
x = keras.layers.BatchNormalization(epsilon=1e-3,
momentum=0.999,
name="shunt_batch_norm_1")(x)
x = keras.layers.ReLU(6., name="shunt_relu_1")(x)
if num_stride_layers > 0:
x = keras.layers.DepthwiseConv2D(kernel_size=(3,3),
strides=(2,2),
padding='same',
use_bias=False,
activation=None,
name="shunt_depth_conv_1",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(4e-5))(x)
else:
x = keras.layers.DepthwiseConv2D(kernel_size=(3,3),
strides=(1,1),
dilation_rate=(dilation_rates[0],dilation_rates[0]),
padding='same',
use_bias=False,
activation=None,
name="shunt_depth_conv_1",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(4e-5))(x)
x = keras.layers.BatchNormalization(epsilon=1e-3,
momentum=0.999,
name="shunt_batch_norm_2")(x)
x = keras.layers.ReLU(6., name="shunt_relu_2")(x)
if s_and_e_location == 'mnv3':
x = shunt_connector.models.mobile_net_v3._se_block(x, filters=192, se_ratio=s_and_e_ratio, prefix="shunt_1/")
x = keras.layers.Conv2D(64,
kernel_size=(1,1),
strides=(1,1),
padding='same',
use_bias=False,
activation=None,
name="shunt_conv_2",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(4e-5))(x)
x = keras.layers.BatchNormalization(epsilon=1e-3,
momentum=0.999,
name="shunt_batch_norm_3")(x)
if s_and_e_location == 'en_de':
x = shunt_connector.models.mobile_net_v3._se_block(x, filters=64, se_ratio=s_and_e_ratio, prefix="shunt_1/")
x = keras.layers.Conv2D(192,
kernel_size=(1,1),
strides=(1,1),
padding='same',
use_bias=False,
activation=None,
name="shunt_conv_3",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(4e-5))(x)
x = keras.layers.BatchNormalization(epsilon=1e-3,
momentum=0.999,
name="shunt_batch_norm_4")(x)
x = keras.layers.ReLU(6., name="shunt_relu_3")(x)
if num_stride_layers > 1:
x = keras.layers.DepthwiseConv2D(kernel_size=(3,3),
strides=(2,2),
padding='same',
use_bias=False,
activation=None,
name="shunt_depth_conv_2",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(4e-5))(x)
else:
x = keras.layers.DepthwiseConv2D(kernel_size=(3,3),
strides=(1,1),
dilation_rate=(dilation_rates[1],dilation_rates[1]),
padding='same',
use_bias=False,
activation=None,
name="shunt_depth_conv_2",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(4e-5))(x)
x = keras.layers.BatchNormalization(epsilon=1e-3,
momentum=0.999,
name="shunt_batch_norm_5")(x)
x = keras.layers.ReLU(6., name="shunt_relu_4")(x)
if s_and_e_location == 'mnv3':
x = shunt_connector.models.mobile_net_v3._se_block(x, filters=192, se_ratio=s_and_e_ratio, prefix="shunt_2/")
x = keras.layers.Conv2D(output_shape[-1],
kernel_size=(1,1),
strides=(1,1),
padding='same',
use_bias=False,
activation=None,
name="shunt_conv_4",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(4e-5))(x)
x = keras.layers.BatchNormalization(epsilon=1e-3,
momentum=0.999,
name="shunt_batch_norm_6")(x)
shunt_model = keras.models.Model(inputs=input_net, outputs=x, name='shunt')
connector.set_shunt_model(shunt_model)
connector.print_summary()
|
shunt_connector/examples/create_s_and_e_shunt_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # 数组与字符串的转换
# ## tostring 方法
import numpy as np
a = np.array([[1,2],
[3,4]],
dtype = np.uint8)
# 转化为字符串:
a.tostring()
# 我们可以使用不同的顺序来转换字符串:
a.tostring(order='F')
# 这里使用了**Fortran**的格式,按照列来读数据。
# ## fromstring 函数
# 可以使用 `fromstring` 函数从字符串中读出数据,不过要指定类型:
s = a.tostring()
a = np.fromstring(s,
dtype=np.uint8)
a
# 此时,返回的数组是一维的,需要重新设定维度:
a.shape = 2,2
a
# 对于文本文件,推荐使用
# - `loadtxt`
# - `genfromtxt`
# - `savetxt`
#
# 对于二进制文本文件,推荐使用
# - `save`
# - `load`
# - `savez`
|
04. Python Numpy/09 data to & from string.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: python3.7.4
# language: python
# name: python3.7.4
# ---
# # BinaryBrain のシステム操作
#
# ## 概要
# BinaryBrain のシステム操作についての説明です。
# +
import numpy as np
import binarybrain as bb
# -
# ## バージョン番号取得
bb.get_version_string()
# ## OpenMP 利用
#
# OpenMPで使用するスレッド数を制限できます。
bb.omp_set_num_threads(4)
# ## CUDA 利用
#
# CUDAを利用できる環境でビルドに成功していればGPUが利用可能です。
# ### GPUの情報取得
# GPUが利用可能な状態か調べる
print(bb.is_device_available())
# 利用可能なGPUの個数
device_count = bb.get_device_count()
print('利用可能なGPUは %d 個' % device_count)
# GPUの情報表示
for i in range(device_count):
print('------------------------------------------')
print('GPU[%d]\n'%i)
print(bb.get_device_properties_string(i))
# ### GPUの選択
# set_device()で利用するGPUボードを切り替えできます
# 利用するGPUの選択
bb.set_device(0)
# ### GPUを使用しない
# set_host_only() で GPU を利用せずにホストCPUでのみ計算するように指定することができます。
# GPUを使用しない場合
bb.set_host_only(True)
print(bb.is_device_available())
# GPUを使用しない場合
bb.set_host_only(False)
print(bb.is_device_available())
|
samples/python/introduction/binarybrain_system.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Import modules
import pylab
import numpy as np
x = np.linspace(-1,1,100)
signal = 2 + x + 2*x*x
noise = np.random.normal(0,0.1,100)
y = signal+noise
x_train = x[0:80]
y_train = y[0:80]
train_rmse= []
test_rmse = []
degree = 80
lambda_reg_values = np.linspace(0.01,0.99,100)
for lambda_reg in lambda_reg_values:
x_train = np.column_stack([np.power(x[0:80],i) for i in range(degree)])
model = np.dot(
np.dot(
np.linalg.inv(
np.dot(
x_train.transpose(), x_train
) + lambda_reg * np.identity(degree)
), x_train.transpose()
),
y_train
)
predicted = np.dot(model, [np.power(x,i) for i in range(degree)])
train_rmse.append(
np.sqrt(
np.sum(
np.dot(
y[0:80]-predicted[0:80],
y_train - predicted[0:80])
)
)
)
test_rmse.append(
np.sqrt(
np.sum(
np.dot(
y[80:]-predicted[80:],
y[80:]-predicted[80:]
)
)
)
)
pylab.plot(lambda_reg_values,train_rmse)
pylab.plot(lambda_reg_values,test_rmse)
pylab.xlabel(r"$\lambda$")
pylab.ylabel("RMSE")
pylab.legend(["Train","Test"],loc=2)
|
Regularization.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [Root]
# language: python
# name: Python [Root]
# ---
import pandas as pd
from pandas import Series, DataFrame
titanic_df = pd.read_csv('train.csv')
titanic_df.head()
titanic_df.info()
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
sns.factorplot('Sex',data=titanic_df,
kind='count')
sns.factorplot('Sex',data=titanic_df,hue='Pclass',kind='count')
sns.factorplot('Pclass',data=titanic_df,hue='Sex',kind='count')
def male_female_child(passenger):
age,sex = passenger
if age < 16:
return 'child'
else:
return sex
titanic_df['person'] = titanic_df[['Age', 'Sex']].apply(male_female_child,axis=1)
titanic_df[0:10]
sns.factorplot('Pclass',data=titanic_df,hue='person',kind='count')
titanic_df['Age'].hist(bins=70)
titanic_df['Age'].mean()
titanic_df['person'].value_counts()
titanic_df['Sex'].value_counts()
# +
fig = sns.FacetGrid(titanic_df,hue='Sex',aspect=4)
fig.map(sns.kdeplot,'Age',shade=True)
oldest = titanic_df['Age'].max()
fig.set(xlim=(0,oldest))
fig.add_legend()
# +
fig = sns.FacetGrid(titanic_df,hue='person',aspect=4)
fig.map(sns.kdeplot,'Age',shade=True)
oldest = titanic_df['Age'].max()
fig.set(xlim=(0,oldest))
fig.add_legend()
# +
fig = sns.FacetGrid(titanic_df,hue='Pclass',aspect=4)
fig.map(sns.kdeplot,'Age',shade=True)
oldest = titanic_df['Age'].max()
fig.set(xlim=(0,oldest))
fig.add_legend()
# -
titanic_df.head()
deck = titanic_df['Cabin'].dropna()
deck.head()
# +
levels = []
for level in deck:
levels.append(level[0])
cabin_df = DataFrame(levels)
cabin_df.columns = ['Cabin']
sns.factorplot('Cabin',data=cabin_df,palette='winter_d',kind='count')
# -
cabin_df = cabin_df[cabin_df.Cabin !='T']
sns.factorplot('Cabin',data=cabin_df,palette='summer',kind='count')
titanic_df.head()
sns.factorplot('Embarked',data=titanic_df,hue='Pclass',kind='count',x_order=['C','Q','S'])
titanic_df.head()
titanic_df['Alone'] = titanic_df.SibSp + titanic_df.Parch
titanic_df['Alone']
# +
titanic_df['Alone'].loc[titanic_df['Alone'] >0] = 'With family'
titanic_df['Alone'].loc[titanic_df['Alone'] == 0] = 'Alone'
# +
titanic_df['Survivor'] = titanic_df.Survived.map({0:'no',1:'yes'})
sns.factorplot('Survivor', data=titanic_df,kind='count')
# -
sns.factorplot('Pclass','Survived',hue='person',data=titanic_df)
sns.lmplot('Age','Survived',data=titanic_df)
sns.lmplot('Age','Survived',hue='Pclass'
,data=titanic_df)
|
Titanic_udemy walk thur.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import numpy as np
import pandas as pd
#plotting
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
#getting data
from pydob.exploratory import (
get_issuance_rates_df,
get_issuance_num_df,
get_issuance_rates_type_df,
applications_year,
permits_year,
savefig,
get_year_counts,
get_dataset_type_df,
permits_now_year
)
from pydob.settings import nt_style, nt_blue, nt_black
# -
# %matplotlib inline
plt.style.use(nt_style)
# # 1. Applications and permits relations
# # Applications and permits trend, pct change
permits_now_year = permits_now_year()
permits_now_year.columns = ['permits_now']
applications_year= applications_year()
permits_year = permits_year()
table_to_plot = applications_year.join(permits_year).join(permits_now_year)
table_to_plot.columns = ['applications','permits','permits_now']
table_to_plot = table_to_plot.loc[2000:2019]
permit_applic_rate_assum = table_to_plot.loc[2016].permits / table_to_plot.loc[2016].applications
# +
table_to_plot.permits_now = table_to_plot.permits_now.fillna(0)
table_to_plot['permits_total'] = table_to_plot.permits+table_to_plot.permits_now
table_to_plot.loc[2017,'applications'] = table_to_plot.loc[2017,'permits_total']/permit_applic_rate_assum
table_to_plot.loc[2018,'applications'] = table_to_plot.loc[2018,'permits_total']/permit_applic_rate_assum
table_to_plot.loc[2019,'applications'] = table_to_plot.loc[2019,'permits_total']/permit_applic_rate_assum
table_to_plot.drop(columns=['permits_now','permits'],inplace=True)
# -
table_to_plot
# +
fig, ax = plt.subplots()
table_to_plot_normed = table_to_plot / table_to_plot.iloc[0]
table_to_plot_normed = (table_to_plot_normed - 1) * 100
ax = table_to_plot_normed['applications'].loc[:2016].plot(alpha = .5,
label = 'Applications',
color = nt_blue)
ax = table_to_plot_normed['applications'].loc[2016:].plot(alpha = .5,
label = '_',
color = nt_blue,
linestyle = '--')
ax.plot(table_to_plot_normed.index,
table_to_plot_normed.permits_total,
color = nt_blue,
alpha = 1,
label = "Permits")
l = ax.legend(loc='center left',
bbox_to_anchor=(0.255, -0.125),
fancybox=True,
shadow=False,
ncol=4)
xlabs = ax.xaxis.set_major_formatter(ticker.FormatStrFormatter('%d'))
ylabs = ax.yaxis.set_major_formatter(ticker.FormatStrFormatter('%s%%'))
plt.title("Growth in Yearly Figures: Applications and Permits")
ylab = ax.set_ylabel("Since Year 2000 (%)")
xlab = ax.set_xlabel(None)
g = plt.grid(axis="y")
ax.spines["top"].set_visible(True)
ax.spines["right"].set_visible(True)
savefig("percent_change_appli_permits.png", fig, bottom=.125)
# -
table_to_plot_normed
# # Application Issuance Rate Analysis <a class="anchor" id="step3"></a>
# +
# preparing table
acceptance_rates = get_issuance_rates_df()
acceptance_rates = acceptance_rates * 100
acceptance_nums =get_issuance_num_df()
acceptance_nums = acceptance_nums / 1000
acceptance_rates = acceptance_rates.rename("acceptance_rate").to_frame()
acceptance_nums = acceptance_nums.rename(columns={"approved": "acceptance_num"})
# -
acceptance_to_plot = acceptance_rates.join(acceptance_nums)
# ## Adding DoB NOW permits to the table
# +
permits_now_year_counts = get_year_counts(index_col='job_filing_number',
year_col='issued_date_year',
dataset_name='permits_now')
permits_now_year_counts.columns = ['approved_counts']
# -
permits_now_year_counts = permits_now_year_counts/1000
acceptance_to_plot = acceptance_to_plot.join(permits_now_year_counts)
acceptance_to_plot.columns = ['acceptance_rate','acceptance_num','permit_now']
acceptance_to_plot = acceptance_to_plot.loc[:2019]
acceptance_to_plot.loc[2017, 'acceptance_rate']= acceptance_to_plot.acceptance_rate.loc[2016:2016].values
acceptance_to_plot.loc[2018, 'acceptance_rate'] = acceptance_to_plot.acceptance_rate.loc[2016:2016].values
acceptance_to_plot.loc[2019, 'acceptance_rate'] = acceptance_to_plot.acceptance_rate.loc[2016:2016].values
# **notes**
# - add number of permits issued as per DoB NOW (for 2017 - 2029)
# - let's assume a constant issuance rate (whatever it was for 2016)
# - and then get applications from $\large \frac {issued}{rate}$
# +
# ploting
fig, ax = plt.subplots()
# ax2 = ax.twinx()
ax.bar(acceptance_to_plot.index,
acceptance_to_plot["acceptance_num"],
color=nt_blue,
label='Number of Issuances (k)',
alpha = 0.5)
ax.bar(acceptance_to_plot.index,
acceptance_to_plot["permit_now"],
bottom=acceptance_to_plot.acceptance_num,
color=nt_blue,
alpha = 0.35,
edgecolor='white',
label = 'Number of DoB NOW Issuances (k)')
ax.plot(acceptance_to_plot.index[:17],
acceptance_to_plot["acceptance_rate"].loc[:2016],
color=nt_blue,
label='Issuance Rate (%)')
ax.plot(acceptance_to_plot.index[16:],
acceptance_to_plot["acceptance_rate"].loc[2016:],
linestyle = '--',
color=nt_blue,
label='Esimated Issuance Rate (%)')
# xaxis labeling
ax.set_xticklabels(acceptance_to_plot.index,rotation=30)
ax.set_xticks(acceptance_to_plot.index )
# l = ax.legend()
# l2 = ax2.legend(loc = "upper left")
ax.legend(loc='center left',
bbox_to_anchor=(0.065, -0.175),
fancybox=True,
shadow=False,
ncol=2)
# limiting yaxis
ylim = ax.set_ylim([50, 110])
ylab = ax.set_ylabel(None)
# ylim2 = ax.set_ylim([70, 92])
# ylab2 = ax.set_ylabel("Number Accepted (K)", rotation=270, labelpad=22.5)
# formating grid line
ax.grid(axis="y", color=nt_black, linestyle="--", linewidth=1)
t = plt.title("Permit Application Issuances, Yearly")
ax.spines["top"].set_visible(True)
ax.spines["right"].set_visible(True)
savefig("permit_issuance_rates.png", fig, bottom=0.2)
# -
acceptance_to_plot_total = acceptance_to_plot
acceptance_to_plot_total.permit_now.fillna(0, inplace =True)
acceptance_to_plot_total['permits_total'] = acceptance_to_plot_total.acceptance_num \
+ acceptance_to_plot_total.permit_now
acceptance_to_plot_total['application_num'] = acceptance_to_plot_total.permits_total /(
acceptance_to_plot_total.acceptance_rate
/100
)
acceptance_to_plot_total.application_num/acceptance_to_plot_total.application_num.iloc[0]-1
acceptance_to_plot.loc[2016:, "application_num"] = acceptance_to_plot.loc[
2016:, "permits_total"
] / (acceptance_to_plot.loc[
2016:, "acceptance_rate"
] / 100)
acceptance_to_plot
# ## Acceptance Rates for Top Application Categories
#
# - nice chart, but may exclude
# - some categories disappear / are merged in an un-clean way over time
# - this complicates taking a time-series view at the category level
acceptance_rates_categories = get_issuance_rates_type_df()
acceptance_rates_categories= acceptance_rates_categories.loc[2010:].to_frame()
acceptance_rates_categories.columns = ["acceptance_rate"]
acceptance_rates_categories_top3 =acceptance_rates_categories.groupby(level='pre_filing_date_year')\
.apply(lambda x: x.nlargest(3,columns = ['acceptance_rate']))\
.reset_index(level =0, drop = True)
acceptance_rates_categories_top3= acceptance_rates_categories_top3.loc[2010:2018]
acceptance_colors= ['#006ead',
'#008ad9',
'#32a1e0',
'#7fc4ec',
'#b2dbf3',
'#e5f3fb',
'#ffffff']
# +
to_plot = acceptance_rates_categories_top3.unstack()
to_plot.columns = to_plot.columns.droplevel()
ax =to_plot.plot(kind = "bar",
width = 1,
color=acceptance_colors,
stacked = False,
ylim=[0.7,1.1],
edgecolor = nt_black)
# Put a legend to the right of the current axis
plt.legend(loc='center left',
bbox_to_anchor=(-0.1, -0.2),
fancybox=True,
shadow=True,
ncol=7)
ylab = ax.set_ylabel("Acceptance Rate")
xlab = ax.set_xlabel(None)
xticklabels = to_plot.index
ax.set_xticklabels(xticklabels, rotation = 30)
title = plt.title("Issuance Rate, by Category")
# -
#
# Expected values are:
#
# - A1 = Alteration Type I, A major alteration that will change the use, egress, or occupancy of the building.
#
# - A2 = Alteration Type II, An application with multiple types of work that do not affect the use, egress, or occupancy of the building.
#
# - A3 = Alteration Type III, One type of minor work that doesn't affect the use, egress, or occupancy of the building.
#
# - NB = New Building, An application to build a new structure. “NB” cannot be selected if any existing building elements are to remain—for example a part of an old foundation, a portion of a façade that will be incorporated into the construction, etc.
#
# - DM = Demolition, An application to fully or partially demolish an existing building.
#
# - PA = A Place of Assembly (PA) Certificate of Operation is required for premises where 75 or more members of the public gather indoors
#
# - SC = Subdivision Condominiums, The division of a tax lot into several smaller tax lots allowing each condominium to have its own tax lot.
#
# - SI = Subdivision Improved, An improved subdivision is when one lot is being broken into several smaller lots. The Department of Finance must assign new lot numbers to subdivisions.
|
notebooks/applications_and_premits.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import fastbook
fastbook.setup_book()
from fastbook import *
from fastai.vision.widgets import *
learn_inf = load_learner(Path('./bears.pkl'))
out_pl = widgets.Output()
lbl_pred = widgets.Label()
btn_upload = widgets.FileUpload()
def classify(change):
img = PILImage.create(btn_upload.data[-1])
out_pl.clear_output()
with out_pl: display(img.to_thumb(128,128))
pred,pred_idx,probs = learn_inf.predict(img)
lbl_pred.value = f'Prediction: {pred}; Probability: {probs[pred_idx]:.04f}'
btn_upload.observe(classify, names='data')
VBox([widgets.Label('Select your bear!'), btn_upload, out_pl, lbl_pred])
|
bear_classifier.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Copyright (c) 2020, salesforce.com, inc.
# All rights reserved.
# SPDX-License-Identifier: BSD-3-Clause
# For full license text, see the LICENSE file in the repo root or https://opensource.org/licenses/BSD-3-Clause
# ### Colab
#
# Try this notebook on [Colab](http://colab.research.google.com/github/salesforce/ai-economist/blob/master/tutorials/economic_simulation_advanced.ipynb).
# # The Structure of Foundation + How to Extend It
#
# In this tutorial, we will explain the low-level compositional structure of Foundation, the economic simulation. Its architecture stems from three main design goals:
#
# 1. Flexibility: e.g., it should be easy to create worlds with or without income taxes.
# 2. Extensibility: adding new entities and components should follow an easy and transparent process.
# 3. Simplicity: avoid deep class hierarchies.
#
# To support these goals, Foundation modularizes the pieces of the simulation as much as possible. Below, we explain what these pieces actually are and how simulation environments are built from them. Understanding this structure will undoubtedly be useful when extending Foundation.
#
# Foundation builds economic simulations using Scenario classes. Scenarios compose the simulation's constituent classes into an actual simulation environment. The majority of this tutorial is used to introduce the semantics of each such class type:
#
# 1. Scenario
# 2. World
# - Maps
# 3. Entities
# - Resources
# - Landmarks
# - Endogenous
# 4. Agents
# 5. Components
#
#
# To conclude the tutorial, we will focus on how to extend the economic simulation:
#
# 6. How the simulation pieces interact
# 7. Exercise: creating a new Component
# 8. Helpful tips
# ### Before we jump into the details...
# ... let's revisit some basics (covered in detail [here](https://github.com/salesforce/ai-economist/blob/master/tutorials/economic_simulation_basic.ipynb)).
#
# Simulation environments exist as Python objects and are interacted with through a gym-style API:
# ```python
# env = Scenario(...)
# obs = env.reset()
# obs, rew, done, info = env.step(actions) # w/ actions <-- policy(obs)
# ```
# An environment is responsible for providing some *observations* based on the world & agent states and updating these states based on the *actions* taken by the agents and the dynamics of the environment.
#
# These dynamics are encapsulated in **Scenario** and **Component** classes, and most extensions of the simulation framework will likely focus on those classes. As a general description...
# - A **Scenario** provides the backbone of the environment:
# - it sets up the world and the agents,
# - adds some passive dynamics,
# - supplies some observations,
# - and generates rewards.
# - **Components** are how agents interact with the environment:
# - they add actions,
# - mediate the effect of whatever actions they add,
# - and provide relevant observations.
#
# (now for the details!)
# ## Dependencies
#
# You can install the ai-economist package using the pip package manager:
# +
import os, signal, sys, time
IN_COLAB = 'google.colab' in sys.modules
if IN_COLAB:
# !pip install ai-economist
# Restart the Python runtime to automatically use the installed packages
print("\n\nRestarting the Python runtime! Please (re-)run the cells below.")
time.sleep(1)
os.kill(os.getpid(), signal.SIGKILL)
else:
# !pip install ai-economist
# -
from ai_economist import foundation
# ## Registry
#
# The Registry class enables conveniently creating classes, such as Scenarios and Resources, using their names (as a string). Each class can be added to the Registry using the *add()* method and can be retrieved using their *name* property.
#
# For example, the *make_env_instance* convenience method used below, can create a basic ```"layout_from_file/simple_wood_and_stone"``` Scenario by first retrieving the associated Class from the registry:
from ai_economist.foundation.base.base_env import BaseEnvironment, scenario_registry
test_env_cls = scenario_registry.get("layout_from_file/simple_wood_and_stone")
test_env_cls.name
# To add a new class to a Registry, you can use a decorator as follows:
@scenario_registry.add
class NewEnvironment(BaseEnvironment):
name = "NewEnvironment"
new_env_cls = scenario_registry.get("NewEnvironment")
new_env_cls.name
# These are the Scenario classes registered in scenario_registry
print(scenario_registry.entries)
# There is a separate registry for each type of environment component. The ```foundation``` package exposes them as follows:
# Scenarios:
print(foundation.scenarios.entries)
# Entities (landmarks, resources, endogenous):
print(foundation.landmarks.entries)
print(foundation.resources.entries)
print(foundation.endogenous.entries)
# Agents:
print(foundation.agents.entries)
# Components:
print(foundation.components.entries)
# # 1. Scenarios
#
# As discussed in [the basics tutorial](https://github.com/salesforce/ai-economist/blob/master/tutorials/economic_simulation_basic.ipynb), the Scenario class implements an economic simulation with multiple agents and (optionally) a social planner.
#
# We will create the same environment instance used in that tutorial, using the configuration below. This configuration defines a simulation with four agents in a world of 15 by 15 cells. Each Agent can:
#
# - gather collectible Resources (through the Gather Component),
# - build Houses (through the Build Component), and
# - trade collectible Resources (through the ContinuousDoubleAuction Component).
# +
# Define the configuration of the environment that will be built
env_config = {
# ===== STANDARD ARGUMENTS ======
'n_agents': 4, # Number of non-planner agents
'world_size': [15, 15], # [Height, Width] of the env world
'episode_length': 1000, # Number of timesteps per episode
# In multi-action-mode, the policy selects an action for each action subspace (defined in component code)
# Otherwise, the policy selects only 1 action
'multi_action_mode_agents': False,
'multi_action_mode_planner': True,
# When flattening observations, concatenate scalar & vector observations before output
# Otherwise, return observations with minimal processing
'flatten_observations': False,
# When Flattening masks, concatenate each action subspace mask into a single array
# Note: flatten_masks = True is recommended for masking action logits
'flatten_masks': True,
# ===== COMPONENTS =====
# Which components to use (specified as list of {"component_name": {component_kwargs}} dictionaries)
# "component_name" refers to the component class's name in the Component Registry
# {component_kwargs} is a dictionary of kwargs passed to the component class
# The order in which components reset, step, and generate obs follows their listed order below
'components': [
# (1) Building houses
{'Build': {}},
# (2) Trading collectible resources
{'ContinuousDoubleAuction': {'max_num_orders': 5}},
# (3) Movement and resource collection
{'Gather': {}},
],
# ===== SCENARIO =====
# Which scenario class to use (specified by the class's name in the Scenario Registry)
'scenario_name': 'uniform/simple_wood_and_stone',
# (optional) kwargs of the chosen scenario class
'starting_agent_coin': 10,
'starting_stone_coverage': 0.10,
'starting_wood_coverage': 0.10,
}
# -
# This configuration dictionary lists the used Components, each can be configured through a dictionary of Component-specific settings.
#
# Creating a Scenario can be done using a convenience method:
env = foundation.make_env_instance(**env_config)
obs = env.reset()
# In the above code, ```env``` is an instance of the Scenario class stored in ```scenario_registry``` as ```"uniform/simple_wood_and_stone"```
uniform_cls = scenario_registry.get(env_config['scenario_name'])
isinstance(env, uniform_cls)
# This Scenario class (and all Scenario classes) are subclasses of ```BaseEnvironment``` (meaning ```env``` is also an instance of ```BaseEnvironment```).
isinstance(env, BaseEnvironment)
# **Why this structure?** The ```env``` object is responsible for a lot! It organizes all the pieces (the world, agents, and components) into a coherent environment with a simple and consistent API. It also implements some of the behavior of the environment itself: the passive (not action-dependent) dynamics of the world, baseline observations, and rewards.
#
# That first domain of functionality is implemented in the ```BaseEnvironment``` code and the second domain of functionality (the "behavior") is implemented separately by each Scenario class via the following methods:
# ```python
# from ai_economist.foundation.base.base_env import BaseEnvironment, scenario_registry
#
# @scenario_registry.add
# class EmptyScenario(BaseEnvironment):
# name = "Empty"
# required_entities = []
#
# def reset_layout(self):
# """Resets the state of the world object (self.world)."""
# pass
#
# def reset_agent_states(self):
# """Resets the state of the agent objects (self.world.agents & self.world.planner)."""
# pass
#
# def scenario_step(self):
# """Implements the passive dynamics of the environment."""
# pass
#
# def generate_observations(self):
# """Yields some basic observations about the world/agent states."""
# pass
#
# def compute_reward(self):
# """Determines the reward each agent receives at the end of each timestep."""
# pass
# ```
#
# The expected behaviors of these methods are described extensively in the internal documentation of ```BaseEnvironment```, where they are defined as abstract methods (see [foundation/base/base_env.py](https://github.com/salesforce/ai-economist/blob/master/ai_economist/foundation/base/base_env.py)).
# ```env```, which is an instance of the ```"uniform/simple_wood_and_stone"``` Scenario class, has the following behavior:
# - **reset_layout**: Samples a new spatial layout of Stone and Wood source tiles in the world.
# - **reset_agent_states**: Resets agent inventories and their starting locations in the world.
# - **scenario_step**: Stochastically re-spawns Stone and Wood at empty source tiles.
# - **generate_observations**: Generates observations related to inventory and the spatial state of the world.
# - **compute_reward**: Marginal utility for each agent in ```env.world.agents```; marginal social welfare for ```env.world.planner```.
#
# Check out [the code for this Scenario class](https://github.com/salesforce/ai-economist/blob/master/ai_economist/foundation/scenarios/simple_wood_and_stone/dynamic_layout.py) to see how this behavior is implemented.
#
# **Note**: This example refers to some concepts we haven't introduced yet (source tiles, inventories, etc.). We'll cover those in the sections below!
# # 2. World and Maps
#
# Above, we saw how a Scenario class resets the spatial state of the world, but **where is this spatial state represented?**
#
# Each Scenario will include an instance of the **World** class ```env.world``` to wrap agent instances (more on that below) and an instance of the **Maps** class ```env.world.maps```. **The Maps class stores and manipulates the spatial state of the environment**, such as the locations of Agents and other Entities.
#
# Both classes (World and Maps) are implemented in [foundation/base/world.py](https://github.com/salesforce/ai-economist/blob/master/ai_economist/foundation/base/world.py).
#
# The **maps** object ```env.world.maps``` holds a 2-dimensional NumPy array that records the location of Entities in the world.
# For each key, the maps object has a [Height, Width] array for the spatial layout of that Entity in the world.
env.world.maps.keys()
# For instance, we can visualize where the Stone is in the world:
# Note: this map has the same size as our world (15 by 15)
env.world.maps.get("Stone")
# The **world** object ```env.world``` provides some tools for interfacing with **maps**.
#
# To see which Resources are in a certain cell, you can use the convenience method *location_resources*:
env.world.location_resources(0, 0)
# To see which Landmarks are in a certain cell, you can use the convenience method *location_landmarks*:
env.world.location_landmarks(0, 0)
# # 3. Entities
#
# Agents in the economic simulation can interact with Entities. There are 3 groups of Entities, each with their own semantics:
#
# - **Landmarks** show up in the spatial world
# - **Resources** show up in agent inventories and (optionally) also the spatial world
# - **Endogenous** entities represent abstract quantities (like effort) that agents can only observe about themselves
#
# You can find their definitions in [foundation/entities](https://github.com/salesforce/ai-economist/blob/master/ai_economist/foundation/entities). Again, we will use convenient Registries to retrieve the various classes.
# ## Landmarks
#
# Landmarks represent entities that exist exclusively in the spatial world, for example a block of Water that agents can't move over.
#
# In the current implementation, there are three types of Landmarks: House, Water and SourceBlock. SourceBlocks are special Landmarks from which Resources can spawn.
house = foundation.landmarks.get("House")
water = foundation.landmarks.get("Water")
source_block_wood = foundation.landmarks.get("WoodSourceBlock")
# For each Landmark, the class defines:
#
# - its name,
# - its color,
# - whether the Landmark is ownable by an Agent (e.g., Houses), and
# - whether it's solid (e.g., Water).
#
# An agent cannot occupy the same location as a solid landmark (e.g. Water) unless it owns that landmark (e.g. a House).
[k for k in dir(house) if k[0] != "_"]
# **Note**: The simulation does *not* instantiate a separate Python instance of a Landmark for each occurrence of a Landmark in the world! Rather, each Landmark class defines the abstract properties of any instance of that Landmark.
#
# ```env.world.maps``` keeps track of where all the units of a Landmark are using a 2-dimensional NumPy array, as illustrated above.
# ## Resources
#
# Resources are another important type of Entity in the world. Resources are semantically different from Landmarks, because Resources can be traded, collected, and converted into other Entities (e.g., Wood and Stone are used to build a House).
#
# In particular, Resources are the entities in the world that an agent can own as part of its **inventory**:
env.get_agent(agent_idx=0).inventory
# A Resource has three main attributes:
# - its name,
# - its color (convenient for visualization),
# - and whether it's collectible.
#
# For example, we can see that Wood is collectible.
# +
wood = foundation.resources.get("Wood")
wood.name, wood.collectible, wood.color
# -
# On the other hand, Coin is *not* collectible (but can be owned).
# +
coin = foundation.resources.get("Coin")
coin.collectible
# -
# Note that collectible Resources (Wood & Stone) get a special Landmark type (source blocks), which both show up in the Map, whereas non-collectible Resources (Coin) only exist as part of the inventory.
#
# In other words, **collectible Resources start as part of the spatial world but can be moved into an agent's inventory.**
#
# ```env.world.maps``` keeps track of where all the units of a **collectible** Resource are using a 2-dimensional NumPy array, as illustrated above.
# ## Endogenous Entities
#
# Certain semantic concepts do not have a physical realization, but are important because they determine, e.g., an Agent's utility. The main example is Labor.
#
# The definition of Labor is rather simple, it only defines the name.
# +
labor = foundation.endogenous.get("Labor")
[k for k in dir(labor) if k[0] != "_"]
# -
# Endogenous entities, like Resources, can be accumulated, **but their quantities are stored outside of the inventory**. (This is done to make it easier to separate Resources and Endogenous entities when generating observations.)
agent0 = env.get_agent(agent_idx=0)
print(agent0.inventory)
print(agent0.endogenous)
# # 4. Agents
#
# ```env.world``` also wraps **agent** instances. There will be ```env.n_agents``` "mobile" agents + 1 "planner" agent. Each such agent is represented as a separate Python object:
#
# The ```env.n_agents``` "mobile" agents (representing individual workers in the economy):
env.world.agents
# The "planner" agent (representing a Social Planner that sets, for example, tax policy)
env.world.planner
# Agents can be easily accessed:
agent0 = env.get_agent(agent_idx=0) # Mobile agents are numerically indexed
agent1 = env.get_agent(agent_idx=1)
planner = env.get_agent(agent_idx='p') # The planner agent always uses index 'p'
# Each agent instance maintains the state of the agent
agent0.state
agent1.state
planner.state
# # 5. Components
#
# Up to this point, we have learned about how the state of the world is represented in the **world** object: with spatial state represented by ```env.world.maps```, and agent states represented in ```env.world.agents``` and ```env.world.planner```.
#
# We have also learned how custom **Scenario** classes define methods for resetting these states and rules for passive dynamics (in our working example, resource regeneration).
#
# **How then do agents actually _interact_ with the environment?**
#
# **Components** are used to flexibly extend the behavior of a Scenario by encapsulating specific interactions/dynamics. They enable a plug-and-play approach to building economic simulations.
#
# This structure also vastly simplifies the process of extending the simulation framework through the addition of new Component classes.
# ### Let's revisit our working example to better understand how Components work...
#
# ... recall the ```'components'``` argument set in the environment configuration we used to build ```env```:
env_config['components']
# This argument tells the Scenario class which Component classes to make use of. Notice that ```env``` has created an instance of each such class:
env._components
# which are better accessed via...
build = env.get_component("Build")
# ```build``` is an instance of the Component class ```Build```
isinstance(build, foundation.components.get("Build"))
# All Component classes are subclasses of ```BaseComponent``` (so ```build``` is also an instance of ```BaseComponent```)
from ai_economist.foundation.base.base_component import BaseComponent
isinstance(build, BaseComponent)
# **Why this structure?** Building Component classes (such as ```Build```) on top of ```BaseComponent``` enforces consistent semantics for defining the behavior of the Component and allowing a Scenario to make use of it. Each Component class must implement the following abstract methods:
#
# ```python
# from foundation.base.base_component import BaseComponent, component_registry
#
# @component_registry.add
# class EmptyComponent(BaseComponent):
# name = "Empty"
# required_entities = []
#
# def get_n_agent_actions(self, agent_cls_name):
# """Returns the actions that agents with type agent_cls_name can take through this component."""
# pass
#
# def get_additional_state_fields(self, agent_cls_name):
# """Returns a dictionary to be be added to the state dictionary of agents with type agent_cls_name."""
# pass
#
# def component_step(self):
# """Implements the (passive and active) dynamics that this Component adds to the environment."""
# pass
#
# def generate_observations(self):
# """Yields observations."""
# pass
#
# def generate_masks(self):
# """Specifies which of the Component actions are valid given the current state."""
# pass
# ```
#
# The expected behaviors of these methods are described extensively in the internal documentation of ```BaseComponent```, where they are defined as abstract methods (see [foundation/base/base_component.py](https://github.com/salesforce/ai-economist/blob/master/ai_economist/foundation/base/base_component.py)).
# As an example, the ```Build``` Component class implements the following behavior:
# - **get_n_agent_actions**: returns 1 action that mobile agents can take (to build a house).
# - **get_additional_state_fields**: returns mobile agents' state dictionary, which includes payment-per-house info.
# - **component_step**: For each agent that takes the build action, place an agent-owned house landmark at the agent's location and update its state (remove Stone & Wood used for building, add Coin income, add Labor cost).
# - **generate_observations**: Generates observations related to the payment-per-house state info.
# - **generate_masks**: Mask the build action for agents that are on non-empty map cells or do not have the resources to build.
#
# Check out [the code for the Build Component class](https://github.com/salesforce/ai-economist/blob/master/ai_economist/foundation/components/build.py) to see how this behavior is implemented.
# As an additional example, the ```Gather``` Component class implements the following behavior:
# - **get_n_agent_actions**: returns 4 actions that mobile agents can take (move up, down, left, and right).
# - **get_additional_state_fields**: returns mobile agents' state dictionary, which includes probability of collecting bonus resources.
# - **component_step**: For each agent that takes a move action: update its location, if the new location has a Resource, move it from the spatial world to the agent's inventory, add Labor cost(s) associated with moving and collecting.
# - **generate_observations**: Generates observations related to the bonus probability state info.
# - **generate_masks**: For each agent, mask whichever move actions would move it to a location it is not allowed to occupy.
#
# Check out [the code for the Gather Component class](https://github.com/salesforce/ai-economist/blob/master/ai_economist/foundation/components/move.py) to see how this behavior is implemented.
# When the agent objects are created, each one registers the actions afforded to it by the ```env``` components. As described: ```Build``` adds 1 action and ```Gather``` adds 4. ```ContinuousDoubleAuction``` (which implements trading) is more complex: it adds several action sets for buying and selling Wood and Stone (each action in a set corresponds to a different price level).
#
# More concretely, the ```ContinuousDoubleAuction``` Component class implements the following behavior:
# - **get_n_agent_actions**: (For mobile agents) returns a *pair* action action sets (for buying and selling) for each *collectible* resource; each action set adds M+1 actions, where M is the maximum trading price.
# - **get_additional_state_fields**: Doesn't add any state fields.
# - **component_step**: For each agent that takes a buy/sell action: create an order in the associated resource market and add a small Labor cost; match orders and execute trades, which moves Coin and the resource between inventories; update the order books, removing expired orders.
# - **generate_observations**: For each agent, generates observations related to price levels of past successful trades, current available orders, and the agent's own outstanding orders.
# - **generate_masks**: For each agent, mask any buying actions that it does not have enough Coin to fulfill and mask any selling actions that it does not have the resources to fulfill.
#
# Check out [the code for the ContinuousDoubleAuction Component class](https://github.com/salesforce/ai-economist/blob/master/ai_economist/foundation/components/continuous_double_auction.py) to see how this behavior is implemented.
# After setting up the environment, the agents have registered the following actions:
agent0.action_dim
# Right now, the planner has not registered any actions because none of the 3 Components add any planner actions.
planner.action_dim
# In particular, we did not include a Taxation Component in ```env_config['components']```, which would introduce actions for the planner.
# +
from copy import deepcopy
tax_config = deepcopy(env_config)
tax_config['components'].append({"PeriodicBracketTax": {}})
tax_env = foundation.make_env_instance(**tax_config)
tax_env._components
# -
# Same as with the other env (PeriodicBracketTax doesn't add actions for this agent type)
tax_env.get_agent(agent_idx=0).action_dim
# Now the planner has actions (PeriodicBracketTax creates an action set for the planner for each tax bracket)
tax_env.get_agent(agent_idx='p').action_dim
# # Extending the Economic Simulation
#
# Having introduced the constituent parts of the simulation, we now focus on how to extend it.
# # 6. How the Simulation Pieces Interact
#
# Before we can dive into actually writing new code, we still need to understand how the simulation pieces interact to build a coherent environment with a consistent and simple API.
#
# In particular, let's look at how the environment sets itself up when an environment instance is created and what happens under the hood when stepping through the simulation.
#
# The underlying design follows the principle of *encapsulation* by making it easy to create new simulation classes, such as Entities, Scenarios, and Components, without having to re-write existing code.
# ### Set up
#
# Earlier, when we looked at ```env.world.maps```, we saw that it already had populated a handful of maps, ones for Wood, Stone, their associated SourceBlocks, and Houses.
#
# Also, when we looked at some of the ```env.world.agents```, we saw that their states were already populated, for example with inventories referencing Resources such as Wood, Stone, and Coin.
#
# **Where did that come from?**
#
# Each Scenario and Component must declare the entities that it will interact with in the attribute ```required_entities```. For example:
#
# ```python
# @scenario_registry.add
# class Uniform(BaseEnvironment):
# name = "uniform/simple_stone_and_wood"
# required_entities = ["Stone", "Wood"]
# ...
# ```
#
# or
#
# ```python
# @component_registry.add
# class Build(BaseComponent):
# name = "Build"
# required_entities = ["Stone", "Wood", "House"]
# ...
# ```
#
# When ```env``` gets created (as part of ```BaseEnvironment.__init__```), the following happens:
#
# 1. It looks at the ```required_entities``` of the Scenario class and the included Component classes and it determines which Resources, Landmarks, and Endogenous entities need to be part of the game.
# - By default, Coin and Labor are always included, even if they are not mentioned in the Scenario's or Components' ```required_entities```.
#
#
# 2. It constructs a world object ```env.world```, which involves creating partially-initialized agent objects for each agent in the environment and creating the maps object ```env.world.maps```.
# - The world object is told which Resources and Landmarks to include and this gets passed to the maps object. The maps object creates a map for these and uses their class properties to preserve semantics: for example, the maps object maintain a separate map indicating ownership for ownable Landmarks, like Houses.
# - Agent objects are also told which Resources and Endogenous entities are in use. The ```inventory```, ```escrow```, and ```endogenous``` portions of their state dictionaries are configured accordingly.
#
#
# 3. It creates an instance of each of the included Component classes (using, for each, any paired keyword arguments).
#
#
# 4. It finishes initializing the agent objects by allowing each one to register the actions defined by the different component objects.
# ### Stepping
#
# Outside of initialization, the logic for integrating Scenarios with Components is fairly straightforward.
#
# When calling ```env.step(actions)``` (the main method for interacting with the environment), the following happens:
# 1. The environment interprets ```actions```, which updates each agent objects' ```agent.action``` to represent which action the agent is taking for each of the action sets (0 denotes NO-OP, meaning no action).
#
#
# 2. The environment performs the ```component_step``` method for each of the component objects. Inside ```component_step```, agent method ```agent.get_component_action(self.name, [action_set_name])``` can be used to query the action(s) ```agent``` chose.
#
#
# 3. The environment performs the ```scenario_step``` of its own Scenario class.
#
#
# 4. For each agent, ```agent.action``` is reset to all NO-OPs.
#
#
# 5. The environment collects observations from its own ```generate_observations``` method and those of each of the component objects, and it combines and formats them into a single observations dictionary.
#
#
# 6. The environment collects action masks using the ```generate_masks``` method of each of the component objects, and it combines and formats them before packaging them as ```'action_masks'``` in each agent's observations.
#
#
#
#
# A similar logic is applied for ```env.reset()```, in which:
# 1. ```env.reset_starting_layout``` and ```env.reset_agent_states``` (which are defined by the Scenario class) are first called.
#
#
# 2. Each component object's ```reset``` method is called.
#
#
# 3. Finally, ```env.additional_reset_steps``` is called (which is also defined by the Scenario class).
# # 7. Exercise: Creating a New BuyWidgetFromVirtualStore Component
#
# Let's put all these concepts together and introduce a new Resource entity, a Widget, and implement a simple Component in which agents can buy Widgets from an external source, like an online store, for a fixed price of 5 Coin. The store randomly adds a single Widget to its inventory each step.
# ### Adding "Widget" as a new Resource entity
#
# In order to add a new Resource entity that other Scenario and Component classes can reference, we simply need to define a new Resource class and put it in the appropriate registry. Let's do this directly in code:
# +
from ai_economist.foundation.entities.resources import Resource, resource_registry
@resource_registry.add
class Widget(Resource):
name = "Widget"
color = [1, 1, 1]
collectible = False # <--- Goes in agent inventory, but not in the world
# -
# That's it. It's that easy.
# ### Component Initialization
#
# Let's start with the initialization of the Component. We'll define a customizable ```widget_refresh_rate``` which determines how likely the store will add a new Widget unit to its inventory each step. Additionally, we'll use a fixed price of 5 Coin per Widget, and initialize the store's inventory to 0.
#
# ```python
# @component_registry.add
# class BuyWidgetFromVirtualStore(BaseComponent):
# name = "BuyWidgetFromVirtualStore"
# required_entities = ["Coin", "Widget"] # <--- We can now look up "Widget" in the resource registry
# agent_subclasses = ["BasicMobileAgent"]
#
# def __init__(
# self,
# *base_component_args,
# widget_refresh_rate=0.1,
# **base_component_kwargs
# ):
# super().__init__(*base_component_args, **base_component_kwargs)
# self.widget_refresh_rate = widget_refresh_rate
# self.available_widget_units = 0
# self.widget_price = 5
# ```
#
# Note that we define the Component's name as a string ```BuyWidgetFromVirtualStore```, and decorate the Component with the ```add``` method from the component registry. This allows us to create the Component by using the ```get``` method on ```component_registry```.
#
# We also declare the ```required_entities``` as ```Coin``` and ```Widget```. This instructs ```BaseEnvironment``` to include these entity types in the environment when ```BuyWidgetFromVirtualStore``` is used as a component.
# ### Reset
#
# Sometimes, a Component wants to expose part of the state it manages as a part of the agents' state. ```get_additional_state_fields``` is used to set that up and reset the associated state when a new episode starts. Here, we won't use that functionality so we return an empty dictionary, which is interpreted as *no additional state fields*.
#
# ```python
# def get_additional_state_fields(self, agent_cls_name):
# return {}
# ```
#
# When a new episode starts (whenever the ```BaseEnvironment``` resets), the store should have 0 Widgets. We can use ```additional_reset_steps``` to implement this behavior.
#
# ```python
# def additional_reset_steps(self):
# self.available_wood_units = 0
# ```
# ### Actions
#
# Each agent can choose to *buy* a Widget or not each step. Hence, we add an extra action to the action space of a ```BasicMobileAgent```. Other agent types (like planners) do not get an extra action: if ```get_n_actions``` returns ```None```, it is interpreted as *no action added*. **Note**: the simulation framework only supports discrete action types for now.
#
# ```python
# def get_n_actions(self, agent_cls_name):
# # This component adds 1 binary action that mobile agents can take: buy widget (or not).
# if agent_cls_name == "BasicMobileAgent":
# return 1 # Buy or not.
#
# return None
# ```
# ### Action Masks
#
# Whether or not an agent can buy depends on:
#
# - Does the agent have at least ```self.widget_price``` Coin? We check this by looking at ```agent.state["inventory"]["Coin"]```.
# - Does the store have at least 1 Widget in store?
#
# Because a BasicMobileAgent has 1 extra discrete action, the mask is simply a single bit, stored in a NumPy array.
#
# **Note: ```world.agents``` loops over ```BasicMobileAgent```s only! It does not include the planner agent!**
#
# ```python
# def generate_masks(self, completions=0):
# masks = {}
# # Mobile agents' buy action is masked if they cannot build with their
# # current coin or if no widgets are available.
# for agent in self.world.agents:
# masks[agent.idx] = np.array([
# agent.state["inventory"]["Coin"] >= self.widget_price and self.available_widget_units > 0
# ])
#
# return masks
# ```
# ### Step
#
# The main logic of this Component is defined in ```component_step```. Two pieces of logic are defined:
#
# 1. The store randomly adds a unit of Wood to its inventory.
# 2. Agents buy orders are executed in random order (to break ties if, say, there's only 1 Widget but 2 agents try to buy it).
#
# ```python
# def component_step(self):
# # Maybe add a Widget to store's inventory.
# if random.random() < self.widget_refresh_rate:
# self.available_widget_units += 1
#
# # Agents can buy 1 unit of Wood, in random order.
# for agent in self.world.get_random_order_agents():
#
# action = agent.get_component_action(self.name)
#
# if action == 0: # NO-OP. Agent is not interacting with this component.
# continue
#
# if action == 1: # Agent wants to buy. Execute a purchase if possible.
# if self.available_widget_units > 0 and agent.state["inventory"]["Coin"] >= self.widget_price:
# # Remove the purchase price from the agent's inventory
# agent.state["inventory"]["Coin"] -= self.widget_price
# # Add a Widget to the agent's inventory
# agent.state["inventory"]["Widget"] += 1
# # Remove the Widget from the market
# self.available_widget_units -= 1
#
# else: # We only declared 1 action for this agent type, so action > 1 is an error.
# raise ValueError
# ```
#
# **Note how the step logic supports action=0 and action=1.** action=0 denotes ``NO-OP`` (no operation). **All Components are expected to obey this semantic.** The action added by this Component starts (and in this case ends) with action=1.
# ### Observations
#
# The store is quite transparent: each ```BasicMobileAgent``` can observe how likely it is that the store will add new a new Widget unit, what the store's current inventory looks like, and what the price is.
#
# The observation that a Component generates should be structured as a dictionary, keyed by each agent's ```id``` and each value being a dictionary.
#
# ```python
# def generate_observations(self):
# obs_dict = dict()
# for agent in self.world.agents:
# obs_dict[agent.idx] = {
# "widget_refresh_rate": self.widget_refresh_rate,
# "available_widget_units": self.available_widget_units,
# "widget_price": self.widget_price
# }
#
# return obs_dict
# ```
# ### Final Component
#
# Let's combine this into actual code so we can create the new Component class and have it available in the component registry:
# +
import numpy as np
from ai_economist.foundation.base.base_component import BaseComponent, component_registry
@component_registry.add
class BuyWidgetFromVirtualStore(BaseComponent):
name = "BuyWidgetFromVirtualStore"
required_entities = ["Coin", "Widget"] # <--- We can now look up "Widget" in the resource registry
agent_subclasses = ["BasicMobileAgent"]
def __init__(
self,
*base_component_args,
widget_refresh_rate=0.1,
**base_component_kwargs
):
super().__init__(*base_component_args, **base_component_kwargs)
self.widget_refresh_rate = widget_refresh_rate
self.available_widget_units = 0
self.widget_price = 5
def get_additional_state_fields(self, agent_cls_name):
return {}
def additional_reset_steps(self):
self.available_wood_units = 0
def get_n_actions(self, agent_cls_name):
if agent_cls_name == "BasicMobileAgent":
return 1
return None
def generate_masks(self, completions=0):
masks = {}
for agent in self.world.agents:
masks[agent.idx] = np.array([
agent.state["inventory"]["Coin"] >= self.widget_price and self.available_widget_units > 0
])
return masks
def component_step(self):
if random.random() < self.widget_refresh_rate:
self.available_widget_units += 1
for agent in self.world.get_random_order_agents():
action = agent.get_component_action(self.name)
if action == 0: # NO-OP. Agent is not interacting with this component.
continue
if action == 1: # Agent wants to buy. Execute a purchase if possible.
if self.available_widget_units > 0 and agent.state["inventory"]["Coin"] >= self.widget_price:
agent.state["inventory"]["Coin"] -= self.widget_price
agent.state["inventory"]["Widget"] += 1
self.available_widget_units -= 1
else: # We only declared 1 action for this agent type, so action > 1 is an error.
raise ValueError
def generate_observations(self):
obs_dict = dict()
for agent in self.world.agents:
obs_dict[agent.idx] = {
"widget_refresh_rate": self.widget_refresh_rate,
"available_widget_units": self.available_widget_units,
"widget_price": self.widget_price
}
return obs_dict
# -
# ### Create a new environment instance that uses the new Component
#
# To add the ```BuyWoodFromVirtualStore``` to the Scenario, modify the ```env_config``` as follows:
# +
new_env_config = deepcopy(env_config)
# Compared to env_config, new_env_config simply adds our new Component
new_env_config['components'] = [
# (1) Building houses
{'Build': {}},
# (2) Trading collectible resources
{'ContinuousDoubleAuction': {'max_num_orders': 5}},
# (3) Movement and resource collection
{'Gather': {}},
# (4) Let each mobile agent buy widgets from a virtual store.
{'BuyWidgetFromVirtualStore': {'widget_refresh_rate': 0.1}}, # <--- This.
]
# -
# And there you have it!
new_env = foundation.make_env_instance(**new_env_config)
obs = new_env.reset()
# Let's compare ```env``` and ```new_env```!
env.resources
new_env.resources
# Notice how ```new_env``` now includes ```'Widget'``` as a Resource in the environment. This is because ```BuyWidgetFromVirtualStore.required_entities``` includes ```'Widget'```!
#
# This difference also shows up in the agent states -- specifically, the inventory:
old_agent0 = env.get_agent(agent_idx=0)
new_agent0 = new_env.get_agent(agent_idx=0)
# Inventory includes Coin, Stone, and Wood...
old_agent0.state
# Inventory includes Coin, Stone, Wood and Widget!
new_agent0.state
# Mobile agents in ```new_env``` should also have an extra action set:
old_agent0.action_dim
new_agent0.action_dim
new_agent0.get_component_action('BuyWidgetFromVirtualStore')
# And, with that, ```BuyWidgetFromVirtualStore``` is a brand new Component, ready to go. Pretty cool, huh?!
#
# If you're interested in learning more about how to extend the simulation by adding new classes, we encourage you to check out the existing implementations provided in the code and to refer back to the documentation in the base classes on which everything is built!
# ### One last thing (because it's cool)...
# Once we included our new Component, Widgets automatically became part of the agents' inventory space. That's because we defined the Widget entity as a Resource class.
#
# However, Widgets are not part of the spatial map. That's because we defined ```Widget.collectible = False```.
# No Widget map:
new_env.world.maps.keys()
# Let's re-define the Widget Resource class, but with ```Widget.collectible = True```, which will give it the same semantics as Wood and Stone.
# +
from ai_economist.foundation.entities.landmarks import Landmark, landmark_registry
@resource_registry.add
class Widget(Resource):
name = "Widget"
color = [1, 1, 1]
collectible = True # <--- Goes in agent inventory, AND in the world
# Since we're doing this in a notebook, we need to manually add a Source Block Landmark for Widgets.
# If we defined the Widget class in /foundation/entities/resources.py,
# this class construction would happen automatically.
@landmark_registry.add
class SourceBlock(Landmark):
"""Special Landmark for generating collectible resources. Not ownable. Not solid."""
name = "{}SourceBlock".format(Widget.name)
color = np.array(Widget.color)
ownable = False
solid = False
# -
# Now that we've given Widget new semantics, let's make another environment object and look at the map keys
# +
new_env_with_collectible_widgets = foundation.make_env_instance(**new_env_config)
new_env_with_collectible_widgets.world.maps.keys()
# -
# Cool! Spatial maps for ```'Widget'``` and ```'WidgetSourceBlock'``` are automatically created because we've defined Widget as something that should be collectible from the spatial world.
#
# The Component ```BuyWidgetFromVirtualStore``` will still work just the same -- no need to re-write that. However, the two new maps will always be empty because our Scenario class only handles populating/regenerating Wood and Stone.
#
# That's fine. After all, this was just to demonstrate the plug-and-play design of the simulation framework!
# # 8. Helpful Tips
# ### Components can be passive.
#
# If you wish to introduce a dynamic to the environment that doesn't depend on agent actions, you can do so through a Component class. Components don't need to add actions and the ```component_step``` doesn't need to depend on actions. An example is found in the [WealthRedistribution](https://github.com/salesforce/ai-economist/blob/master/ai_economist/foundation/components/redistribution.py) class.
# ### Components can be stateful.
#
# In the actual environment, components are Python objects, so you might as well use them that way. A simple demonstration of this is actually found in the example Component above (```BuyWidgetFromVirtualStore```). Notice how the class has a ```available_widget_units``` attribute, which it creates during ```__init___```, updates during ```component_step```, and resets in ```additional_reset_steps```.
#
# Conceptually, ```BuyWidgetFromVirtualStore.available_widget_units``` is just as much a part of the environment state as, say, ```new_agent0.state```. You should feel free to take advantage of the object-oriented design. Just make sure to properly reset internally managed states in ```additional_reset_steps```!
# ### Components can add multiple action sets per agent.
#
# Components can create many sets of actions. For example (for mobile agents):
# - ```BuyWidgetFromVirtualStore``` adds 1 action set with only 1 action.
# - ```Gather``` adds 1 action set with 4 actions.
# - ```ContinuousDoubleAuction``` adds 2\*N action sets each with M+1 actions, where N is the number of collectible Resources and M is the maximum buying/selling price.
#
# In that last example ```ContinuousDoubleAuction``` (which implements trading) the structure of the action sets it creates depend on the choice of maximum buying/selling price (an argument to the class) as well as the collectible Resources in the environment.
#
# That might seem complicated but it's simpler than it sounds. Check out [the actual code](https://github.com/salesforce/ai-economist/blob/master/ai_economist/foundation/components/continuous_double_auction.py) for a useful example. In particular, look at the ```__init__``` and ```get_n_agent_actions``` to see how the action sets are set up and look at ```component_step``` to see how the step method makes use of them.
# ### Only *you* can ensure NO-OP semantics.
#
# Smokey the Bear famously said, "Only *you* can prevent forest fires." While that hazard doesn't apply here, the sense of responsibility is just the same:
# **If ```agent.get_component_action(...)``` returns 0, that means NO-OP!**
#
# If you look through [the implemented Components](https://github.com/salesforce/ai-economist/blob/master/ai_economist/foundation/components), you'll notice throughout the ```component_step``` methods something along the lines of:
# ```python
# for agent in self.world.agents:
# action = agent.get_component_action(self.name)
#
# # NO-OP! Agent is NOT interacting with this component.
# if action == 0:
# continue # Move on to the next agent
#
# # Agent is interacting with this component
# else:
# ... # Do something
# ```
#
# Referring back to our ```BuyWidgetFromVirtualStore``` example, notice how it adds 1 action for mobile agents. When an agent actually takes that action we would see ```agent.get_component_action('BuyWidgetFromVirtualStore')``` returns 1. Not 0! If the agent chose an action belonging to another component (say, took a movement action), then we would see ```agent.get_component_action('BuyWidgetFromVirtualStore')``` returns 0, and it would be up to ```BuyWidgetFromVirtualStore``` to treat that like the NO-OP that it is.
#
# **When you implement a new Component class, it is up to you to ensure that NO-OP semantics are preserved!**
# ### Environments come with a couple tools for logging.
#
# There are 2 main types of logs that ```BaseEnvironment``` supports: metrics and dense logs.
#
# **Metrics** are used to summarize an episode. Scenarios and Components each have a method for producing a metrics dictionary, which adds a tool to generate a readout on what happened. At the end of the episode, any such metrics are combined into a single metrics dictionary which is accessible through ```env.metrics```.
#
# **Dense logs** offer a timestep-by-timestep breakdown of how an episode played out. By default, ```BaseEnvironment``` includes world state, agent state, and action info for each timestep. Components can contribute their own dense logs, which get added to the final log at the end of the episode.
#
# Because they can be time consuming to create, dense logs are not (by default) generated during every episode. You can use the ```BaseEnvironment``` argument ```dense_log_frequency``` to set how often they are created. If, for example, you use ```dense_log_frequency=20```, then the environment will create dense logs during episodes where the number of total episode completions is a multiple of 20 (that is, every 20 episodes). If you don't want to wait, you can use ```env.reset(force_dense_logging=True)``` to tell the environment to create a dense log for the upcoming episode.
# ### Have fun!
# And congratulate yourself on making it to the end of the advanced tutorial :)
#
# If you really want to go for the extra credit, check out [optimal_taxation_theory_and_simulation.ipynb](https://github.com/salesforce/ai-economist/blob/master/tutorials/optimal_taxation_theory_and_simulation.ipynb), our final tutorial which walks through how Foundation is used to study the problem of optimal taxation!
|
tutorials/economic_simulation_advanced.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# installing packages (if they do not exist)
# !conda install --yes numpy=1.18.5
# !conda install --yes pandas=1.2.0
# !conda install --yes scikit-learn=0.23.2
# !conda install --yes matplotlib=3.2.2
# !conda install --yes seaborn=0.10.1
import numpy as np
import pandas as pd
import time
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
import string
from sklearn.model_selection import KFold, StratifiedKFold
from decimal import *
from sklearn.metrics import roc_auc_score
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.naive_bayes import GaussianNB, MultinomialNB
from sklearn import svm
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
# ## Functions For Data Preparation
# +
# The following functions may be used in case we need to do a data transformation into categorical data.
def gas_bining(org_df):
df = org_df.copy()
df['gas_used'] = pd.cut(df['gas_used'], bins=[i * 100000 for i in range(0, 20)], labels=list(string.ascii_uppercase[:19]))
return df
def transform_balance_delta(org_df):
df = org_df.copy()
for i in range(0, df.shape[0]):
if int(df.at[i, 'victim_balance_delta']) == 0:
df.at[i, 'victim_balance_delta'] = 'zero'
elif int(df.at[i, 'victim_balance_delta']) > 0:
df.at[i, 'victim_balance_delta'] = 'positive'
elif int(df.at[i, 'victim_balance_delta']) < 0:
df.at[i, 'victim_balance_delta'] = 'negative'
if int(df.at[i, 'attacker_balance_delta']) == 0:
df.at[i, 'attacker_balance_delta'] = 'zero'
elif int(df.at[i, 'attacker_balance_delta']) > 0:
df.at[i, 'attacker_balance_delta'] = 'positive'
elif int(df.at[i, 'attacker_balance_delta']) < 0:
df.at[i, 'attacker_balance_delta'] = 'negative'
return df
def call_stack_depth_bining(org_df):
df = org_df.copy()
df['call_stack_depth'] = pd.cut(df['call_stack_depth'], bins=[i for i in range(0, 20)], labels=list(string.ascii_uppercase[:19]))
return df
def replace_labels_col(org_df):
df = org_df.copy()
harmful = list()
labels = list(df['label'])
for label in labels:
if label == 'safe':
harmful.append(False)
elif label == 'vul':
harmful.append(True)
return harmful
# +
# Helper functions
def get_ys_from_prediction(prediction_df):
df = prediction_df.copy()
ys = list()
col_list = df.columns
for index, row in df.iterrows():
max_prob = row.max()
for col in col_list:
if row[col] == max_prob:
predicted = col
break
ys.append(predicted)
return ys
def get_fn_fp(y_pred, test_labels):
fp, fn, tp, tn = 0, 0, 0, 0
y_pred_list = list(y_pred)
for i in range(0, len(y_pred_list)):
if y_pred_list[i] != test_labels[i]:
if (y_pred_list[i] == "vul" and test_labels[i] == "safe"):
fp += 1
if (y_pred_list[i] == 'safe' and test_labels[i] == 'vul'):
fn += 1
else:
if (y_pred_list[i] == 'vul' and test_labels[i] == 'vul'):
tp += 1
if (y_pred_list[i] == 'safe' and test_labels[i] == 'safe'):
tn += 1
fnr = fn / (fn + tp)
fpr = fp / (fp + tn)
return (fnr, fpr)
# -
# ## Defining a constant list of random seeds for numpy
# ## Defining our Classifiers
# +
# Our implementation of a Random Forest with Bagging based on sikitlearn
class RandomForest:
def __init__(self):
self.column_filter = None
self.imputation = None
self.one_hot = None
self.labels = None
self.model = None
# HELPER
self.no_trees = None
# DEBUG
self.tree_predictions_list = None
def fit(self, df, no_trees=100):
self.no_trees = no_trees
df = df.copy()
# initializing our random forest as a list of all our generated trees:
self.model = list()
y = df['label'].values
df.drop(columns=['label'], inplace=True)
#df, self.one_hot = create_one_hot(df)
#df, self.column_filter = create_column_filter(df)
#df, self.imputation = create_imputation(df)
x = df.values
# total number of features:
F_size = len(df.columns)
# just to use later!
df_with_classes = df.copy()
df_with_classes['label'] = pd.Series(y, index=df_with_classes.index)
def select_with_replacement(trees_i):
'''
This function will return a newly selected with replacement sample.
'''
np.random.seed(random_seeds[trees_i])
sample = pd.DataFrame(columns = df_with_classes.columns)
np.random.seed(random_seeds[trees_i])
selections = np.random.choice(df_with_classes.shape[0], df_with_classes.shape[0], replace=True)
for selection in selections:
sample = sample.append(df_with_classes.iloc[selection])
return sample
for trees_i in range(0, no_trees):
sample_df = select_with_replacement(trees_i)
y = sample_df['label'].values
sample_df.drop(columns=['label'], inplace=True)
x = sample_df.values
self.model.append(DecisionTreeClassifier(max_features='log2'))
self.model[-1].fit(x, y)
print('tree # {} is built,'.format(trees_i))
# I used these lines to get insight into how are my decision trees doing (commented)
'''
tree_desc = tree.export_graphviz(self.model[-1], out_file='1_forest/{}.dot'.format(trees_i), feature_names=list(sample_df.columns))
dot_data = tree.export_graphviz(self.model[-1], feature_names=list(sample_df.columns), class_names=[str(c) for c in self.model[-1].classes_], filled=True, rounded=True)
graph = graphviz.Source(dot_data)
graph.render('1_forest/{}.gv'.format(trees_i), view=False)
'''
def predict(self, df):
test_df = df.copy()
#test_df = apply_one_hot(test_df, self.one_hot)
#test_df = apply_column_filter(test_df, self.column_filter)
#test_df = apply_imputation(test_df, self.imputation)
test_x = test_df.values
# let's add all predictions from all trees to a single list so that we can use it later!
# each index in this list denotes the prediction of a tree
tree_predictions_list = list()
for dt in self.model:
tree_predictions = dt.predict_proba(test_x)
tree_predictions_list.append(tree_predictions)
self.tree_predictions_list = tree_predictions_list
predictions = pd.DataFrame(columns=['safe' ,'vul'])
# averaging for each instance:
for instance_index in range(0, len(test_x)):
total_negative = 0
total_positive = 0
for model_index in range(0, self.no_trees):
total_negative += tree_predictions_list[model_index][instance_index][0]
total_positive += tree_predictions_list[model_index][instance_index][1]
predictions = predictions.append({
'safe': Decimal(total_negative) / Decimal(self.no_trees),
'vul': Decimal(total_positive) / Decimal(self.no_trees)
}, ignore_index=True)
return predictions
def accuracy(original_df, correctlabels):
df = original_df.copy()
'''
Assumption: I assume that the accuracy is ratio `number of data instances
correctly classified / total no of data instances`
Furthermore, for an instance that does not have a label with highest probability,
I will choose the first label in column orders as the predicted label for that instance.
'''
cor_pred = list() # correct predictions list
inc_pred = list() # incorrect predictions list
col_list = df.columns
for index, row in df.iterrows():
max_prob = row.max()
for col in col_list:
if row[col] == max_prob:
predicted = col
break
correct = correctlabels[index]
if correct == predicted:
cor_pred.append(index)
else:
inc_pred.append(index)
return len(cor_pred)/ len(correctlabels)
# -
# ## Loading the data
# +
df = pd.read_csv('data/transactions2.csv')
# The following dictionary will be used to hold the performance measurements of our classifiers
perfs_dict = {
'nb': {
},
'lr': {
},
'knn': {
},
'svm': {
},
'rf': {
},
'nn': {
}
}
display(df)
# -
random_seeds = [31403, 31429, 31579, 31523, 31679, 31693, 31589, 31697, 32099, 31871, 31683, 32063, 31403, 32365, 32313, 32363, 32811, 31794, 32195, 31612, 32083, 32579, 32679, 32990, 33347, 32128, 32703, 32132, 31459, 32911, 32003, 33821, 33803, 33086, 34633, 33363, 32735, 31884, 33797, 33548, 34683, 34314, 31907, 31747, 34703, 35318, 31863, 31638, 33707, 33559, 35103, 35891, 35615, 35590, 36101, 33713, 35547, 35393, 31693, 33409, 33743, 32074, 32767, 35183, 35499, 37773, 34175, 38036, 35211, 32783, 35183, 33533, 36659, 37170, 33623, 35153, 37939, 34329, 34835, 32588, 34683, 35453, 32469, 38624, 35771, 36928, 32693, 34883, 34747, 37633, 34913, 36681, 32507, 33542, 37137, 34823, 34187, 34895, 41007, 40016]
# ## Heatmap correlation matrix
# +
new_df = df.copy()
new_df.drop(columns = ['Unnamed: 0', 'tx_hash'], inplace=True)
new_df['victim_balance_delta'] = pd.to_numeric(new_df['victim_balance_delta'], errors='coerce')
new_df['attacker_balance_delta'] = pd.to_numeric(new_df['attacker_balance_delta'], errors='coerce')
labels = list(new_df['label'])
labels_num = list()
for index in range(0, len(labels)):
if labels[index] == 'safe':
labels_num.append(0)
else:
labels_num.append(1)
new_df['labels'] = pd.to_numeric(labels_num)
corr_matrix = new_df.corr()
matrix = np.triu(new_df.corr())
plt.figure(figsize=(6, 4))
heatmap = sns.heatmap(corr_matrix, annot = True, cbar_kws= {'orientation': 'vertical'}, cmap='BrBG')
plt.xticks(rotation=25, ha='right')
plt.savefig('new-figures/heatmap.pdf', dpi=300, bbox_inches='tight')
# -
# ## Applying the classifiers
# +
# Random Forest
rf = RandomForest()
# trying to scale the data
scaler = StandardScaler()
kf = StratifiedKFold(n_splits=5, shuffle=True)
labels = list(df['label'])
# split into input (X) and output (Y) variables
#X = dataset[:,0:60].astype(float)
#Y = dataset[:,60]
new_df = df.copy()
new_df.drop(columns=["Unnamed: 0"], inplace=True)
new_df.drop(columns=["label"], inplace=True)
new_df.drop(columns=["tx_hash"], inplace=True)
#uncomment the next line to get rid of the 'call stack depth' feature
#new_df.drop(columns=["call_stack_depth"], inplace=True)
scaler = StandardScaler()
scaler.fit(new_df)
new_df = scaler.transform(new_df)
#X = new_df.to_numpy()
X = np.copy(new_df)
Y = np.array(list(df['label']))
accuracies = list()
fn_list = list()
fp_list = list()
recall_list = list()
f1_list = list()
for i in range(0, 10):
for train_indices, test_indices in kf.split(df, labels):
'''
train_indices = pd.read_csv("data/processing_steps/train_indices_{}.csv".format(counter))
test_indices = pd.read_csv("data/processing_steps/test_indices_{}.csv".format(counter))
train_indices.drop(columns=["Unnamed: 0"], inplace=True)
test_indices.drop(columns=["Unnamed: 0"], inplace=True)
train_indices = train_indices['0'].to_numpy()
test_indices = test_indices['0'].to_numpy()
'''
print("TRAIN:", train_indices, "\nTEST:", test_indices)
train_df = df.loc[train_indices, :].copy()
test_df = df.loc[test_indices, :].copy()
train_df.drop(columns=['tx_hash'], inplace=True)
train_df.drop(columns=['Unnamed: 0'], inplace=True)
test_df.drop(columns=['tx_hash'], inplace=True)
test_df.drop(columns=['Unnamed: 0'], inplace=True)
test_labels = list(test_df['label'])
test_df.drop(columns=['label'], inplace=True)
train_labels = list(train_df['label'])
train_df.drop(columns=['label'], inplace=True)
# scaling:
scaler.fit(train_df)
train_ndarray = scaler.transform(train_df)
test_ndarray = scaler.transform(test_df)
# let's add the labels to the train_df after scalling, the fit function in our Random Forest classifier needs them:
train_df = pd.DataFrame(train_ndarray)
train_df['label'] = train_labels
test_df = pd.DataFrame(test_ndarray)
rf.fit(train_df, no_trees=100)
predictions = rf.predict(test_df)
y_pred = get_ys_from_prediction(predictions)
print(classification_report(test_labels, y_pred))
#print(test_labels)
#print(y_pred)
# classification report (cr)
cr = classification_report(test_labels, y_pred, output_dict=True)
recall_list.append(cr['vul']['recall'])
f1_list.append(cr['vul']['f1-score'])
ac = metrics.accuracy_score(test_labels, y_pred)
accuracies.append(ac)
# obtain fp and fn
fn, fp = get_fn_fp(y_pred, test_labels)
print('fn is: {0}, fp is: {1}'.format(fn, fp))
fp_list.append(fp)
fn_list.append(fn)
ac = metrics.accuracy_score(test_labels, y_pred)
#ac = accuracy(predictions, labels)
accuracies.append(ac)
print("\nAccuracy of prediction is: {}".format(ac))
print("========================================================")
print("========================================================")
print("*********************************************************")
print("\nAverage accuracy: {}".format(sum(accuracies) / len(accuracies)))
perfs_dict['rf']['fp'] = sum(fp_list) / len(fp_list)
perfs_dict['rf']['fn'] = sum(fn_list) / len(fn_list)
perfs_dict['rf']['ac'] = sum(accuracies) / len(accuracies)
perfs_dict['rf']['f1'] = sum(f1_list) / len(f1_list)
perfs_dict['rf']['recall'] = sum(recall_list) / len(recall_list)
print('---------------------------------------------------------')
print(perfs_dict)
# +
# Logistic Regression
# trying to scale the data
scaler = StandardScaler()
kf = StratifiedKFold(n_splits=5, shuffle=True)
labels = list(df['label'])
# split into input (X) and output (Y) variables
#X = dataset[:,0:60].astype(float)
#Y = dataset[:,60]
new_df = df.copy()
new_df.drop(columns=["Unnamed: 0"], inplace=True)
new_df.drop(columns=["label"], inplace=True)
new_df.drop(columns=["tx_hash"], inplace=True)
#uncomment the next line to get rid of the 'call stack depth' feature
#new_df.drop(columns=["call_stack_depth"], inplace=True)
scaler = StandardScaler()
scaler.fit(new_df)
new_df = scaler.transform(new_df)
#X = new_df.to_numpy()
X = np.copy(new_df)
Y = np.array(list(df['label']))
accuracies = list()
fn_list = list()
fp_list = list()
recall_list = list()
f1_list = list()
for i in range(0, 10):
for train_indices, test_indices in kf.split(X, Y):
'''
train_indices = pd.read_csv("data/processing_steps/train_indices_{}.csv".format(counter))
test_indices = pd.read_csv("data/processing_steps/test_indices_{}.csv".format(counter))
train_indices.drop(columns=["Unnamed: 0"], inplace=True)
test_indices.drop(columns=["Unnamed: 0"], inplace=True)
train_indices = train_indices['0'].to_numpy()
test_indices = test_indices['0'].to_numpy()
print("TRAIN:", train_indices, "\nTEST:", test_indices)
counter += 1
train_df = df.loc[train_indices, :].copy()
test_df = df.loc[test_indices, :].copy()
train_df.drop(columns=['tx_hash'], inplace=True)
train_df.drop(columns=['Unnamed: 0'], inplace=True)
test_df.drop(columns=['tx_hash'], inplace=True)
test_df.drop(columns=['Unnamed: 0'], inplace=True)
train_labels = list(train_df['label'])
train_df.drop(columns=['label'], inplace=True)
test_labels = list(test_df['label'])
test_df.drop(columns=['label'], inplace=True)
# scaling:
scaler.fit(train_df)
train_df = scaler.transform(train_df)
test_df = scaler.transform(test_df)
'''
# training
logreg = LogisticRegression()
logreg.fit(X[train_indices], Y[train_indices])
# prediction
y_pred=logreg.predict(X[test_indices])
print(classification_report(Y[test_indices], y_pred))
# classification report (cr)
cr = classification_report(Y[test_indices], y_pred, output_dict=True)
recall_list.append(cr['vul']['recall'])
f1_list.append(cr['vul']['f1-score'])
ac = metrics.accuracy_score(Y[test_indices], y_pred)
accuracies.append(ac)
# obtain fp and fn
fn, fp = get_fn_fp(y_pred, Y[test_indices])
print('fn is: {0}, fp is: {1}'.format(fn, fp))
fp_list.append(fp)
fn_list.append(fn)
print("\nAccuracy of prediction is: {}".format(ac))
print("========================================================")
print("========================================================")
print("*********************************************************")
print("\nAverage accuracy: {}".format(sum(accuracies) / len(accuracies)))
perfs_dict['lr']['fp'] = sum(fp_list) / len(fn_list)
perfs_dict['lr']['fn'] = sum(fn_list) / len(fn_list)
perfs_dict['lr']['ac'] = sum(accuracies) / len(accuracies)
perfs_dict['lr']['f1'] = sum(f1_list) / len(f1_list)
perfs_dict['lr']['recall'] = sum(recall_list) / len(recall_list)
print('---------------------------------------------------------')
print(perfs_dict)
# +
# K-Nearest Neighbors
# trying to scale the data
scaler = StandardScaler()
kf = StratifiedKFold(n_splits=5, shuffle=True)
labels = list(df['label'])
# split into input (X) and output (Y) variables
#X = dataset[:,0:60].astype(float)
#Y = dataset[:,60]
new_df = df.copy()
new_df.drop(columns=["Unnamed: 0"], inplace=True)
new_df.drop(columns=["label"], inplace=True)
new_df.drop(columns=["tx_hash"], inplace=True)
#uncomment the next line to get rid of the 'call stack depth' feature
#new_df.drop(columns=["call_stack_depth"], inplace=True)
scaler = StandardScaler()
scaler.fit(new_df)
new_df = scaler.transform(new_df)
#X = new_df.to_numpy()
X = np.copy(new_df)
Y = np.array(list(df['label']))
accuracies = list()
fn_list = list()
fp_list = list()
recall_list = list()
f1_list = list()
for i in range(0, 10):
for train_indices, test_indices in kf.split(X, Y):
'''
train_indices = pd.read_csv("data/processing_steps/train_indices_{}.csv".format(counter))
test_indices = pd.read_csv("data/processing_steps/test_indices_{}.csv".format(counter))
train_indices.drop(columns=["Unnamed: 0"], inplace=True)
test_indices.drop(columns=["Unnamed: 0"], inplace=True)
train_indices = train_indices['0'].to_numpy()
test_indices = test_indices['0'].to_numpy()
print("TRAIN:", train_indices, "\nTEST:", test_indices)
counter += 1
train_df = df.loc[train_indices, :].copy()
test_df = df.loc[test_indices, :].copy()
train_df.drop(columns=['tx_hash'], inplace=True)
train_df.drop(columns=['Unnamed: 0'], inplace=True)
test_df.drop(columns=['tx_hash'], inplace=True)
test_df.drop(columns=['Unnamed: 0'], inplace=True)
train_labels = list(train_df['label'])
train_df.drop(columns=['label'], inplace=True)
test_labels = list(test_df['label'])
test_df.drop(columns=['label'], inplace=True)
# scaling:
scaler.fit(train_df)
train_df = scaler.transform(train_df)
test_df = scaler.transform(test_df)
'''
classifier = KNeighborsClassifier(n_neighbors=5)
# training
classifier.fit(X[train_indices], Y[train_indices])
# prediction
y_pred = classifier.predict(X[test_indices])
print(classification_report(Y[test_indices], y_pred))
# classification report (cr)
cr = classification_report(Y[test_indices], y_pred, output_dict=True)
recall_list.append(cr['vul']['recall'])
f1_list.append(cr['vul']['f1-score'])
ac = metrics.accuracy_score(Y[test_indices], y_pred)
accuracies.append(ac)
# obtain fp and fn
fn, fp = get_fn_fp(y_pred, test_labels)
print('fn is: {0}, fp is: {1}'.format(fn, fp))
fp_list.append(fp)
fn_list.append(fn)
# measuring performance
ac = metrics.accuracy_score(Y[test_indices], y_pred)
accuracies.append(ac)
print("\nAccuracy of prediction is: {}".format(ac))
print("========================================================")
print("========================================================")
print("*********************************************************")
print("\nAverage accuracy: {}".format(sum(accuracies) / len(accuracies)))
perfs_dict['knn']['fp'] = sum(fp_list) / len(fp_list)
perfs_dict['knn']['fn'] = sum(fn_list) / len(fp_list)
perfs_dict['knn']['ac'] = sum(accuracies) / len(accuracies)
perfs_dict['knn']['f1'] = sum(f1_list) / len(f1_list)
perfs_dict['knn']['recall'] = sum(recall_list) / len(recall_list)
print('---------------------------------------------------------')
print(perfs_dict)
# +
# Naive Bayes Classifier
# trying to scale the data
scaler = StandardScaler()
kf = StratifiedKFold(n_splits=5, shuffle=True)
labels = list(df['label'])
# split into input (X) and output (Y) variables
#X = dataset[:,0:60].astype(float)
#Y = dataset[:,60]
new_df = df.copy()
new_df.drop(columns=["Unnamed: 0"], inplace=True)
new_df.drop(columns=["label"], inplace=True)
new_df.drop(columns=["tx_hash"], inplace=True)
#uncomment the next line to get rid of the 'call stack depth' feature
#new_df.drop(columns=["call_stack_depth"], inplace=True)
scaler = StandardScaler()
scaler.fit(new_df)
new_df = scaler.transform(new_df)
#X = new_df.to_numpy()
X = np.copy(new_df)
Y = np.array(list(df['label']))
accuracies = list()
fn_list = list()
fp_list = list()
recall_list = list()
f1_list = list()
for i in range(0, 10):
for train_indices, test_indices in kf.split(X, Y):
'''
train_indices = pd.read_csv("data/processing_steps/train_indices_{}.csv".format(counter))
test_indices = pd.read_csv("data/processing_steps/test_indices_{}.csv".format(counter))
train_indices.drop(columns=["Unnamed: 0"], inplace=True)
test_indices.drop(columns=["Unnamed: 0"], inplace=True)
train_indices = train_indices['0'].to_numpy()
test_indices = test_indices['0'].to_numpy()
print("TRAIN:", train_indices, "\nTEST:", test_indices)
counter += 1
train_df = df.loc[train_indices, :].copy()
test_df = df.loc[test_indices, :].copy()
train_df.drop(columns=['tx_hash'], inplace=True)
train_df.drop(columns=['Unnamed: 0'], inplace=True)
test_df.drop(columns=['tx_hash'], inplace=True)
test_df.drop(columns=['Unnamed: 0'], inplace=True)
train_labels = list(train_df['label'])
train_df.drop(columns=['label'], inplace=True)
test_labels = list(test_df['label'])
test_df.drop(columns=['label'], inplace=True)
# scaling:
scaler.fit(train_df)
#train_df = scaler.transform(train_df)
#test_df = scaler.transform(test_df)
'''
# Gaussian Naive Bayes classier:
gnb = GaussianNB()
# training
gnb.fit(X[train_indices, :], Y[train_indices])
# prediction
y_pred = gnb.predict(X[test_indices])
print(classification_report(Y[test_indices], y_pred))
# classification report (cr)
cr = classification_report(Y[test_indices], y_pred, output_dict=True)
recall_list.append(cr['vul']['recall'])
f1_list.append(cr['vul']['f1-score'])
ac = metrics.accuracy_score(Y[test_indices], y_pred)
accuracies.append(ac)
# obtain fp and fn
fn, fp = get_fn_fp(y_pred, Y[test_indices])
print('fn is: {0}, fp is: {1}'.format(fn, fp))
fp_list.append(fp)
fn_list.append(fn)
# measuring performance
ac = metrics.accuracy_score(Y[test_indices], y_pred)
accuracies.append(ac)
print("\nAccuracy of prediction is: {}".format(ac))
print("========================================================")
print("========================================================")
print("*********************************************************")
print("\nAverage accuracy: {}".format(sum(accuracies) / len(accuracies)))
perfs_dict['nb']['fp'] = sum(fp_list) / len(fp_list)
perfs_dict['nb']['fn'] = sum(fn_list) / len(fn_list)
perfs_dict['nb']['ac'] = sum(accuracies) / len(accuracies)
perfs_dict['nb']['f1'] = sum(f1_list) / len(f1_list)
perfs_dict['nb']['recall'] = sum(recall_list) / len(recall_list)
print('---------------------------------------------------------')
print(perfs_dict)
# +
# SVM Classifier
# trying to scale the data
scaler = StandardScaler()
kf = StratifiedKFold(n_splits=5, shuffle=True)
labels = list(df['label'])
# split into input (X) and output (Y) variables
#X = dataset[:,0:60].astype(float)
#Y = dataset[:,60]
new_df = df.copy()
new_df.drop(columns=["Unnamed: 0"], inplace=True)
new_df.drop(columns=["label"], inplace=True)
new_df.drop(columns=["tx_hash"], inplace=True)
#uncomment the next line to get rid of the 'call stack depth' feature
#new_df.drop(columns=["call_stack_depth"], inplace=True)
scaler = StandardScaler()
scaler.fit(new_df)
new_df = scaler.transform(new_df)
#X = new_df.to_numpy()
X = np.copy(new_df)
Y = np.array(list(df['label']))
accuracies = list()
fn_list = list()
fp_list = list()
recall_list = list()
f1_list = list()
for i in range(0, 10):
for train_indices, test_indices in kf.split(X, Y):
'''
train_indices = pd.read_csv("data/processing_steps/train_indices_{}.csv".format(counter))
test_indices = pd.read_csv("data/processing_steps/test_indices_{}.csv".format(counter))
train_indices.drop(columns=["Unnamed: 0"], inplace=True)
test_indices.drop(columns=["Unnamed: 0"], inplace=True)
train_indices = train_indices['0'].to_numpy()
test_indices = test_indices['0'].to_numpy()
print("TRAIN:", train_indices, "\nTEST:", test_indices)
counter += 1
'''
train_df = df.loc[train_indices, :].copy()
test_df = df.loc[test_indices, :].copy()
train_df.drop(columns=['tx_hash'], inplace=True)
train_df.drop(columns=['Unnamed: 0'], inplace=True)
test_df.drop(columns=['tx_hash'], inplace=True)
test_df.drop(columns=['Unnamed: 0'], inplace=True)
train_labels = list(train_df['label'])
train_df.drop(columns=['label'], inplace=True)
test_labels = list(test_df['label'])
test_df.drop(columns=['label'], inplace=True)
# SVM classier:
clf = svm.SVC(kernel='linear')
# training
clf.fit(X[train_indices, :], Y[train_indices])
# prediction
y_pred = clf.predict(X[test_indices, :])
print(classification_report(Y[test_indices], y_pred))
# classification report (cr)
cr = classification_report(Y[test_indices], y_pred, output_dict=True)
recall_list.append(cr['vul']['recall'])
f1_list.append(cr['vul']['f1-score'])
ac = metrics.accuracy_score(test_labels, y_pred)
accuracies.append(ac)
# obtain fp and fn
fn, fp = get_fn_fp(y_pred, test_labels)
print('fn is: {0}, fp is: {1}'.format(fn, fp))
fp_list.append(fp)
fn_list.append(fn)
# measuring performance
ac = metrics.accuracy_score(test_labels, y_pred)
accuracies.append(ac)
print("\nAccuracy of prediction is: {}".format(ac))
print("========================================================")
print("========================================================")
print("*********************************************************")
print("\nAverage accuracy: {}".format(sum(accuracies) / len(accuracies)))
perfs_dict['svm']['fp'] = sum(fp_list) / len(fp_list)
perfs_dict['svm']['fn'] = sum(fn_list) / len(fn_list)
perfs_dict['svm']['ac'] = sum(accuracies) / len(accuracies)
perfs_dict['svm']['f1'] = sum(f1_list) / len(f1_list)
perfs_dict['svm']['recall'] = sum(recall_list) / len(recall_list)
print('---------------------------------------------------------')
print(perfs_dict)
# -
# # Trying the neural network classifiers
# !pip3 install keras
# +
import pandas
from keras.models import Sequential
from keras.layers import Dense
from keras.wrappers.scikit_learn import KerasClassifier
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import StratifiedKFold
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
# split into input (X) and output (Y) variables
#X = dataset[:,0:60].astype(float)
#Y = dataset[:,60]
new_df = df.copy()
new_df.drop(columns=["Unnamed: 0"], inplace=True)
new_df.drop(columns=["label"], inplace=True)
new_df.drop(columns=["tx_hash"], inplace=True)
#uncomment the next line to get rid of the 'call stack depth' feature
#new_df.drop(columns=["call_stack_depth"], inplace=True)
scaler = StandardScaler()
scaler.fit(new_df)
new_df = scaler.transform(new_df)
#X = new_df.to_numpy()
X = np.copy(new_df)
Y = np.array(list(df['label']))
# encode class values as integers
encoder = LabelEncoder()
encoder.fit(Y)
encoded_Y = encoder.transform(Y)
# baseline model
def create_baseline():
# create model
model = Sequential()
model.add(Dense(10, input_dim=4, activation='relu'))
model.add(Dense(5, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
# Compile model
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
return model
# evaluate model with standardized dataset
estimator = KerasClassifier(build_fn=create_baseline, epochs=100, batch_size=5, verbose=0)
kfold = StratifiedKFold(n_splits=10, shuffle=True)
accuracies = list()
fn_list = list()
fp_list = list()
recall_list = list()
f1_list = list()
counter = 0
for i in range(0, 10):
for train_indices, test_indices in kfold.split(X, Y):
'''
train_indices = pd.read_csv("data/processing_steps/train_indices_{}.csv".format(counter))
test_indices = pd.read_csv("data/processing_steps/test_indices_{}.csv".format(counter))
train_indices.drop(columns=["Unnamed: 0"], inplace=True)
test_indices.drop(columns=["Unnamed: 0"], inplace=True)
train_indices = train_indices['0'].to_numpy()
test_indices = test_indices['0'].to_numpy()
print("TRAIN:", train_indices, "\nTEST:", test_indices)
counter += 1
train_df = df.loc[train_indices, :].copy()
test_df = df.loc[test_indices, :].copy()
train_df.drop(columns=['tx_hash'], inplace=True)
train_df.drop(columns=['Unnamed: 0'], inplace=True)
test_df.drop(columns=['tx_hash'], inplace=True)
test_df.drop(columns=['Unnamed: 0'], inplace=True)
train_labels = list(train_df['label'])
train_df.drop(columns=['label'], inplace=True)
test_labels = list(test_df['label'])
test_df.drop(columns=['label'], inplace=True)
'''
'''
# scaling:
scaler.fit(train_df)
#train_df = scaler.transform(train_df)
#test_df = scaler.transform(test_df)
'''
# training
estimator.fit(X[train_indices, :], Y[train_indices])
# prediction
y_pred = estimator.predict(X[test_indices])
print(classification_report(Y[test_indices], y_pred))
# classification report (cr)
cr = classification_report(Y[test_indices], y_pred, output_dict=True)
recall_list.append(cr['vul']['recall'])
f1_list.append(cr['vul']['f1-score'])
ac = metrics.accuracy_score(Y[test_indices], y_pred)
accuracies.append(ac)
# obtain fp and fn
fn, fp = get_fn_fp(y_pred, list(Y[test_indices]))
print('fn is: {0}, fp is: {1}'.format(fn, fp))
fp_list.append(fp)
fn_list.append(fn)
# measuring performance
ac = metrics.accuracy_score(Y[test_indices], y_pred)
accuracies.append(ac)
print("\nAccuracy of prediction is: {}".format(ac))
print("========================================================")
print("========================================================")
print("*********************************************************")
print("\nAverage accuracy: {}".format(sum(accuracies) / len(accuracies)))
perfs_dict['nn']['fp'] = sum(fp_list) / len(fp_list)
perfs_dict['nn']['fn'] = sum(fn_list) / len(fn_list)
perfs_dict['nn']['ac'] = sum(accuracies) / len(accuracies)
perfs_dict['nn']['f1'] = sum(f1_list) / len(f1_list)
perfs_dict['nn']['recall'] = sum(recall_list) / len(recall_list)
print('---------------------------------------------------------')
print(perfs_dict)
# +
fp_ = list()
fn_ = list()
f1_ = list()
ac_ = list()
recall_ = list()
for classifier, classifier_dict in perfs_dict.items():
fp_.append(round(classifier_dict['fp'] * 100, 2))
fn_.append(round(classifier_dict['fn'] * 100, 2))
f1_.append(round(classifier_dict['f1'], 2))
ac_.append(round(classifier_dict['ac'], 2))
recall_.append(round(classifier_dict['recall'], 2))
labels = ['NB', 'LR', 'K-NN', 'SVM', 'RF', 'NN']
x = np.arange(len(labels)) # the label locations
width = 0.35 # the width of the bars
fig, ax = plt.subplots()
rects1 = ax.bar(x - width/2, fp_, width, label='FPR', color='mediumseagreen')
rects2 = ax.bar(x + width/2, fn_, width, label='FNR')
# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_ylabel('Percentage')
#ax.set_title('Number of False Positive and False Negative')
ax.set_xticks(x)
ax.set_xticklabels(labels)
ax.legend()
def autolabel(rects):
"""Attach a text label above each bar in *rects*, displaying its height."""
for rect in rects:
height = rect.get_height()
ax.annotate('{}'.format(height),
xy=(rect.get_x() + rect.get_width() / 2, height),
xytext=(0, 0), # 3 points vertical offset
textcoords="offset points",
ha='center', va='bottom')
autolabel(rects1)
autolabel(rects2)
plt.rcParams["figure.figsize"] = (6, 4)
fig.tight_layout()
plt.savefig('new-figures/fpr_fnr.pdf')
plt.show()
# +
# Ploting the f1_score, accuracy, and recall
labels = ['NB', 'LR', 'K-NN', 'SVM', 'RF', 'NN']
x = np.arange(len(labels)) # the label locations
width = 0.25 # the width of the bars
fig, ax = plt.subplots()
rects1 = ax.bar(x - width/2, ac_, width, label='Accuracy', color='mediumseagreen')
rects2 = ax.bar(x + width/2, f1_, width, label='F1 Score')
rects3 = ax.bar(x + 3*width/2, recall_, width, label='Recall')
ax.set_ylim(bottom=0.60)
# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_ylabel('Score')
#ax.set_title('Number of False Positive and False Negative')
ax.set_xticks(x)
ax.set_xticklabels(labels)
ax.legend(fontsize=9)
ax.legend(loc='l', bbox_to_anchor=(0.55,0.77))
def autolabel(rects, rect_num=None):
"""Attach a text label above each bar in *rects*, displaying its height."""
for rect in rects:
height = rect.get_height()
xytext=(0, 0)
ax.annotate('{}'.format(height),
xy=(rect.get_x() + rect.get_width() / 2, height),
xytext=xytext, # 3 points vertical offset
textcoords="offset points",
ha='center', va='bottom', rotation=35)
autolabel(rects1)
autolabel(rects2, rect_num=2)
autolabel(rects3)
fig.tight_layout()
plt.savefig('new-figures/ac_f1_recall.pdf')
plt.show()
# -
print(perfs_dict)
|
detector/dynamit-v-1.1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # MCMC sampling using the emcee package
#
# ## Introduction
#
# The goal of Markov Chain Monte Carlo (MCMC) algorithms is to approximate the posterior distribution of your model parameters by random sampling in a probabilistic space. For most readers this sentence was probably not very helpful so here we'll start straight with and example but you should read the more detailed mathematical approaches of the method [here](https://www.pas.rochester.edu/~sybenzvi/courses/phy403/2015s/p403_17_mcmc.pdf) and [here](https://github.com/jakevdp/BayesianAstronomy/blob/master/03-Bayesian-Modeling-With-MCMC.ipynb).
#
# ### How does it work ?
#
# The idea is that we use a number of walkers that will sample the posterior distribution (i.e. sample the Likelihood profile).
#
# The goal is to produce a "chain", i.e. a list of $\theta$ values, where each $\theta$ is a vector of parameters for your model.<br>
# If you start far away from the truth value, the chain will take some time to converge until it reaches a stationary state. Once it has reached this stage, each successive elements of the chain are samples of the target posterior distribution.<br>
# This means that, once we have obtained the chain of samples, we have everything we need. We can compute the distribution of each parameter by simply approximating it with the histogram of the samples projected into the parameter space. This will provide the errors and correlations between parameters.
#
#
# Now let's try to put a picture on the ideas described above. With this notebook, we have simulated and carried out a MCMC analysis for a source with the following parameters:<br>
# $Index=2.0$, $Norm=5\times10^{-12}$ cm$^{-2}$ s$^{-1}$ TeV$^{-1}$, $Lambda =(1/Ecut) = 0.02$ TeV$^{-1}$ (50 TeV) for 20 hours.
#
# The results that you can get from a MCMC analysis will look like this :
#
# <img src="../../images/gammapy_mcmc.png" width="800">
#
# On the first two top panels, we show the pseudo-random walk of one walker from an offset starting value to see it evolve to a better solution.
# In the bottom right panel, we show the trace of each 16 walkers for 500 runs (the chain described previsouly). For the first 100 runs, the parameter evolve towards a solution (can be viewed as a fitting step). Then they explore the local minimum for 400 runs which will be used to estimate the parameters correlations and errors.
# The choice of the Nburn value (when walkers have reached a stationary stage) can be done by eye but you can also look at the autocorrelation time.
#
# ### Why should I use it ?
#
# When it comes to evaluate errors and investigate parameter correlation, one typically estimate the Likelihood in a gridded search (2D Likelihood profiles). Each point of the grid implies a new model fitting. If we use 10 steps for each parameters, we will need to carry out 100 fitting procedures.
#
# Now let's say that I have a model with $N$ parameters, we need to carry out that gridded analysis $N*(N-1)$ times.
# So for 5 free parameters you need 20 gridded search, resulting in 2000 individual fit.
# Clearly this strategy doesn't scale well to high-dimensional models.
#
# Just for fun: if each fit procedure takes 10s, we're talking about 5h of computing time to estimate the correlation plots.
#
# There are many MCMC packages in the python ecosystem but here we will focus on [emcee](https://emcee.readthedocs.io), a lightweight Python package. A description is provided here : [Foreman-Mackey, <NAME> (2012)](https://arxiv.org/abs/1202.3665).
# +
# %matplotlib inline
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
# -
import numpy as np
import astropy.units as u
from astropy.coordinates import SkyCoord
from gammapy.irf import load_cta_irfs
from gammapy.maps import WcsGeom, MapAxis
from gammapy.modeling.models import (
ExpCutoffPowerLawSpectralModel,
GaussianSpatialModel,
SkyModel,
Models,
FoVBackgroundModel,
)
from gammapy.datasets import MapDataset
from gammapy.makers import MapDatasetMaker
from gammapy.data import Observation
from gammapy.modeling.sampling import (
run_mcmc,
par_to_model,
plot_corner,
plot_trace,
)
from gammapy.modeling import Fit
# +
import logging
logging.basicConfig(level=logging.INFO)
# -
# ## Simulate an observation
#
# Here we will start by simulating an observation using the `simulate_dataset` method.
# +
irfs = load_cta_irfs(
"$GAMMAPY_DATA/cta-1dc/caldb/data/cta/1dc/bcf/South_z20_50h/irf_file.fits"
)
observation = Observation.create(
pointing=SkyCoord(0 * u.deg, 0 * u.deg, frame="galactic"),
livetime=20 * u.h,
irfs=irfs,
)
# +
# Define map geometry
axis = MapAxis.from_edges(
np.logspace(-1, 2, 15), unit="TeV", name="energy", interp="log"
)
geom = WcsGeom.create(
skydir=(0, 0), binsz=0.05, width=(2, 2), frame="galactic", axes=[axis]
)
empty_dataset = MapDataset.create(geom=geom, name="dataset-mcmc")
maker = MapDatasetMaker(selection=["background", "edisp", "psf", "exposure"])
dataset = maker.run(empty_dataset, observation)
# +
# Define sky model to simulate the data
spatial_model = GaussianSpatialModel(
lon_0="0 deg", lat_0="0 deg", sigma="0.2 deg", frame="galactic"
)
spectral_model = ExpCutoffPowerLawSpectralModel(
index=2,
amplitude="3e-12 cm-2 s-1 TeV-1",
reference="1 TeV",
lambda_="0.05 TeV-1",
)
sky_model_simu = SkyModel(
spatial_model=spatial_model, spectral_model=spectral_model, name="source"
)
bkg_model = FoVBackgroundModel(dataset_name="dataset-mcmc")
models = Models([sky_model_simu, bkg_model])
print(models)
# -
dataset.models = models
dataset.fake()
dataset.counts.sum_over_axes().plot(add_cbar=True);
# +
# If you want to fit the data for comparison with MCMC later
# fit = Fit(dataset, optimize_opts={"print_level": 1})
# result = fit.run()
# -
# ## Estimate parameter correlations with MCMC
#
# Now let's analyse the simulated data.
# Here we just fit it again with the same model we had before as a starting point.
# The data that would be needed are the following:
# - counts cube, psf cube, exposure cube and background model
#
# Luckily all those maps are already in the Dataset object.
#
# We will need to define a Likelihood function and define priors on parameters.<br>
# Here we will assume a uniform prior reading the min, max parameters from the sky model.
# ### Define priors
#
# This steps is a bit manual for the moment until we find a better API to define priors.<br>
# Note the you **need** to define priors for each parameter otherwise your walkers can explore uncharted territories (e.g. negative norms).
print(dataset)
# +
# Define the free parameters and min, max values
parameters = dataset.models.parameters
parameters["sigma"].frozen = True
parameters["lon_0"].frozen = True
parameters["lat_0"].frozen = True
parameters["amplitude"].frozen = False
parameters["index"].frozen = False
parameters["lambda_"].frozen = False
parameters["norm"].frozen = True
parameters["tilt"].frozen = True
parameters["norm"].min = 0.5
parameters["norm"].max = 2
parameters["index"].min = 1
parameters["index"].max = 5
parameters["lambda_"].min = 1e-3
parameters["lambda_"].max = 1
parameters["amplitude"].min = 0.01 * parameters["amplitude"].value
parameters["amplitude"].max = 100 * parameters["amplitude"].value
parameters["sigma"].min = 0.05
parameters["sigma"].max = 1
# Setting amplitude init values a bit offset to see evolution
# Here starting close to the real value
parameters["index"].value = 2.0
parameters["amplitude"].value = 3.2e-12
parameters["lambda_"].value = 0.05
print(dataset.models)
print("stat =", dataset.stat_sum())
# -
# %%time
# Now let's define a function to init parameters and run the MCMC with emcee
# Depending on your number of walkers, Nrun and dimensionality, this can take a while (> minutes)
sampler = run_mcmc(dataset, nwalkers=6, nrun=150) # to speedup the notebook
# sampler=run_mcmc(dataset,nwalkers=12,nrun=1000) # more accurate contours
# ## Plot the results
#
# The MCMC will return a sampler object containing the trace of all walkers.<br>
# The most important part is the chain attribute which is an array of shape:<br>
# _(nwalkers, nrun, nfreeparam)_
#
# The chain is then used to plot the trace of the walkers and estimate the burnin period (the time for the walkers to reach a stationary stage).
plot_trace(sampler, dataset)
# + nbsphinx-thumbnail={"tooltip": "Use Markov Chain Monte Carlo (MCMC) algorithms for modeling and fitting."}
plot_corner(sampler, dataset, nburn=50)
# -
# ## Plot the model dispersion
#
# Using the samples from the chain after the burn period, we can plot the different models compared to the truth model. To do this we need to the spectral models for each parameter state in the sample.
# +
emin, emax = [0.1, 100] * u.TeV
nburn = 50
fig, ax = plt.subplots(1, 1, figsize=(12, 6))
for nwalk in range(0, 6):
for n in range(nburn, nburn + 100):
pars = sampler.chain[nwalk, n, :]
# set model parameters
par_to_model(dataset, pars)
spectral_model = dataset.models["source"].spectral_model
spectral_model.plot(
energy_bounds=(emin, emax),
ax=ax,
energy_power=2,
alpha=0.02,
color="grey",
)
sky_model_simu.spectral_model.plot(
energy_bounds=(emin, emax), energy_power=2, ax=ax, color="red"
);
# -
# ## Fun Zone
#
# Now that you have the sampler chain, you have in your hands the entire history of each walkers in the N-Dimensional parameter space. <br>
# You can for example trace the steps of each walker in any parameter space.
# +
# Here we plot the trace of one walker in a given parameter space
parx, pary = 0, 1
plt.plot(sampler.chain[0, :, parx], sampler.chain[0, :, pary], "ko", ms=1)
plt.plot(
sampler.chain[0, :, parx],
sampler.chain[0, :, pary],
ls=":",
color="grey",
alpha=0.5,
)
plt.xlabel("Index")
plt.ylabel("Amplitude");
# -
# ## PeVatrons in CTA ?
#
# Now it's your turn to play with this MCMC notebook. For example to test the CTA performance to measure a cutoff at very high energies (100 TeV ?).
#
# After defining your Skymodel it can be as simple as this :
# +
# dataset = simulate_dataset(model, geom, pointing, irfs)
# sampler = run_mcmc(dataset)
# plot_trace(sampler, dataset)
# plot_corner(sampler, dataset, nburn=200)
|
docs/tutorials/analysis/3D/mcmc_sampling.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Import libraries you'll need
from urbansim_templates import modelmanager as mm
from urbansim_templates.models import LargeMultinomialLogitStep
import orca
import os; os.chdir('../')
import warnings; warnings.simplefilter('ignore')
# ### Load data and pre-defined model steps
from scripts import datasources
from scripts import models
from scripts import variables
# ### Generate accessibility variables
orca.run(['initialize_network_small', 'network_aggregations_small'])
orca.run(['initialize_network_walk', 'network_aggregations_walk'])
# ### List the tables and columns you can now use for model estimation
for table_name in orca.list_tables():
print(table_name.upper())
print(orca.get_table(table_name).to_frame().columns.tolist())
print()
# ### List the pre-defined merge relationships between tables
orca.list_broadcasts()
# ### View the contents of a single table
orca.get_table('buildings').to_frame().describe()
|
fall-2018-models/notebooks/generic_modeling_template.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import scipy as sp
import scipy.stats
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
import sklearn as sk
import requests
import time
from sklearn.model_selection import train_test_split
from sklearn import linear_model
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
from sklearn import preprocessing
from sklearn.ensemble import RandomForestRegressor
from sklearn.preprocessing import RobustScaler
# 정제된 데이터가져오기
df = pd.read_csv("df1.csv", encoding='utf-8')
df.head(10)
# 시군구 데이터 가져오기
cgoongoo=pd.read_csv("cgoongoo1.csv", encoding='utf-8')
cgoongoo.head()
# 시군구와 정제된 데이터 머지
df1=pd.merge(df, cgoongoo, on=['district'])
df1.head()
df1.columns
df1.drop(['year','quarter','district'],axis=1,inplace=True)
# 비율을 값으로 바꾸기
df2=df1.copy()
df2.drop(['prop_2030s','prop_06_11','prop_11_14','prop_14_17', 'prop_17_21', 'prop_21_24','sales_female_ratio',
'sales_weekday_ratio'],axis=1,inplace=True)
df3= df1[['prop_2030s','prop_06_11','prop_11_14','prop_14_17', 'prop_17_21', 'prop_21_24','sales_female_ratio',
'sales_weekday_ratio']]
df3['prop_2030s'] = df3['prop_2030s']*df1['sales']
df3['prop_06_11'] = df3['prop_06_11']*df1['sales']
df3['prop_11_14'] = df3['prop_11_14']*df1['sales']
df3['prop_14_17'] = df3['prop_14_17']*df1['sales']
df3['prop_17_21'] = df3['prop_17_21']*df1['sales']
df3['prop_21_24'] = df3['prop_21_24']*df1['sales']
df3['sales_female_ratio'] = df3['sales_female_ratio']*df1['sales']
df3['sales_weekday_ratio'] = df3['sales_weekday_ratio']*df1['sales']
df3.head()
#데이터 콘캣
df4= pd.concat([df2,df3], axis=1)
df4.head()
# 같은 시군구 코드와 서비스코드 특성 합치기
df5=df4.groupby(['cgoongoo', 'code']).sum()
# df5.reset_index(inplace=True)
# +
# df5.drop(['level_0','index'],axis=1,inplace=True)
# -
df5.head()
df6=df5[df5.columns[2:]]
df6
# RobustScaling
rb = RobustScaler()
rb.fit(df6)
X_robust_scaled = rb.transform(df6)
dfX=pd.DataFrame(X_robust_scaled, columns= df6.columns)
dfX.head()
dfX.columns
dfX2=dfX.copy()
dfX2.drop(['sales'],axis=1,inplace=True)
dfX2.columns
# 서비스 코드 , 상권코드 콘캣
result=pd.concat([df5[['cgoongoo','code']],dfX], axis=1)
result
#서비스코드 더미화
result2 = pd.get_dummies(result)
result2.columns
result3 = pd.get_dummies(result2['cgoongoo'], prefix='d')
result3.columns
result4 = pd.concat([result2,result3] ,axis=1)
result4.head()
result4.drop(['cgoongoo','sales'],axis=1,inplace=True )
result4.columns
import numpy as np
np.log(df5['sales'])
# +
# OLS
import statsmodels.api as sm
X= result4
y= np.log(df5['sales'])
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
df_train=pd.concat([y_train, X_train], axis=1)
model= sm.OLS.from_formula("sales ~ "+" + ".join(df_train.columns[1:]), data=df_train)
result = model.fit()
print(result.summary())
# +
# 모델 생성
lm = linear_model.LinearRegression()
# 학습
lm.fit(X_train, y_train)
# 예측
pred_y = lm.predict(X_train)
print("정확도 : ", str(round(lm.score(X_test, y_test), 4) * 100) + "%")
# -
# LASSO 모형
#importing libraries
import seaborn as sns
import statsmodels.api as sm
# %matplotlib inline
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.feature_selection import RFE
from sklearn.linear_model import RidgeCV, LassoCV, Ridge, Lasso
reg = LassoCV()
reg.fit(X, y)
print("Best alpha using built-in LassoCV: %f" % reg.alpha_)
print("Best score using built-in LassoCV: %f" %reg.score(X,y))
coef = pd.Series(reg.coef_, index = X.columns)
print("Lasso picked " + str(sum(coef != 0)) + " variables and eliminated the other " + str(sum(coef == 0)) + " variables")
|
dayoung_trial1/cgoongoo(groupby and get dummies).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Puzzle 1: Calculate the highest possible amp signal
# ### Unique phase setting between 0 and 4 for any amp --> what is the highest signal?
import numpy as np
from copy import deepcopy
# ## Load input
with open('./input7.txt', 'r') as file:
software = file.readlines()
# #### Convert data to list of integers
software = list(map(int, software[0].split(',')))
# ## Calculation
def intcode_computer(inputs, data):
i = 0
run = True
while run is True:
if len(str(data[i])) < 5:
add = (5-len(str(data[i])))*'0'
data[i] = '{0}{1}'.format(add, str(data[i]))
optcode = data[i][-2:]
mode1 = data[i][-3]
mode2 = data[i][-4]
mode3 = data[i][-5]
if mode1 == '0' and optcode != '99':
param1 = int(data[data[i+1]])
else:
param1 = int(data[i+1])
if optcode == '01':
if mode2 == '0':
param2 = int(data[data[i+2]])
else:
param2 = int(data[i+2])
data[data[i+3]] = param1 + param2
i += 4
if optcode == '02':
if mode2 == '0':
param2 = int(data[data[i+2]])
else:
param2 = int(data[i+2])
data[data[i+3]] = param1 * param2
i += 4
if optcode == '03':
data[data[i+1]] = inputs[0]
del inputs[0]
i += 2
if optcode == '04':
if mode1 == '0':
out = data[data[i+1]]
# print(data[data[i+1]])
else:
out = data[data[i+1]]
# print(data[i+1])
i += 2
if optcode == '05':
if mode2 == '0':
param2 = int(data[data[i+2]])
else:
param2 = int(data[i+2])
if param1 != 0:
i = param2
else:
i += 3
if optcode == '06':
if mode2 == '0':
param2 = int(data[data[i+2]])
else:
param2 = int(data[i+2])
if param1 == 0:
i = param2
else:
i += 3
if optcode == '07':
if mode2 == '0':
param2 = int(data[data[i+2]])
else:
param2 = int(data[i+2])
if param1 < param2:
data[data[i+3]] = 1
else:
data[data[i+3]] = 0
i += 4
if optcode == '08':
if mode2 == '0':
param2 = int(data[data[i+2]])
else:
param2 = int(data[i+2])
if param1 == param2:
data[data[i+3]] = 1
else:
data[data[i+3]] = 0
i += 4
if optcode == '99':
run = False
return out
# +
best_output = 0
for pA in range(0, 5):
outA = intcode_computer([pA, 0], deepcopy(software))
for pB in range(0, 5):
if pA == pB:
outB = False
else:
outB = intcode_computer([pB, outA], deepcopy(software))
for pC in range(0, 5):
if pC in [pA, pB] or outB == False:
outC = False
else:
outC = intcode_computer([pC, outB], deepcopy(software))
for pD in range(0, 5):
if pD in [pA, pB, pC] or outC == False or outB == False:
outD = False
else:
outD = intcode_computer([pD, outC], deepcopy(software))
for pE in range(0, 5):
if pE in [pA, pB, pC, pD] or outD == False or outC == False or outB == False:
outE = 0
else:
outE = intcode_computer([pE, outD], deepcopy(software))
if outE > best_output:
best_output = outE
best_combination = [pA, pB, pC, pD, pE]
# -
print('The highest signal is {0}.'.format(best_output))
# # Puzzle 2: Calculate the highest possible amp signal using a feedback loop
# ### phase settings from 5 to 9
class intcode_computer(object):
def __init__(self, phase, data):
self.phase = phase
self.data = data
self.inputs = [phase]
self.i = 0
def step(self, amp_in):
self.inputs.append(amp_in)
self.run = True
self.done = False
self.out = 0
while self.run is True:
if len(str(self.data[self.i])) < 5:
add = (5-len(str(self.data[self.i])))*'0'
self.data[self.i] = '{0}{1}'.format(add, str(self.data[self.i]))
optcode = self.data[self.i][-2:]
mode1 = self.data[self.i][-3]
mode2 = self.data[self.i][-4]
mode3 = self.data[self.i][-5]
if mode1 == '0' and optcode != '99':
param1 = int(self.data[self.data[self.i+1]])
else:
if optcode != '99':
param1 = int(self.data[self.i+1])
if optcode == '01':
if mode2 == '0':
param2 = int(self.data[self.data[self.i+2]])
else:
param2 = int(self.data[self.i+2])
self.data[self.data[self.i+3]] = param1 + param2
self.i += 4
if optcode == '02':
if mode2 == '0':
param2 = int(self.data[self.data[self.i+2]])
else:
param2 = int(self.data[self.i+2])
self.data[self.data[self.i+3]] = param1 * param2
self.i += 4
if optcode == '03':
if len(self.inputs) > 0:
self.data[self.data[self.i+1]] = self.inputs[0]
del self.inputs[0]
self.i += 2
else:
self.run = False
# print('Amp waits for input')
break
if optcode == '04':
if mode1 == '0':
self.out = self.data[self.data[self.i+1]]
else:
self.out = self.data[self.data[self.i+1]]
self.i += 2
if optcode == '05':
if mode2 == '0':
param2 = int(self.data[self.data[self.i+2]])
else:
param2 = int(self.data[self.i+2])
if param1 != 0:
self.i = param2
else:
self.i += 3
if optcode == '06':
if mode2 == '0':
param2 = int(self.data[self.data[self.i+2]])
else:
param2 = int(self.data[self.i+2])
if param1 == 0:
self.i = param2
else:
self.i += 3
if optcode == '07':
if mode2 == '0':
param2 = int(self.data[self.data[self.i+2]])
else:
param2 = int(self.data[self.i+2])
if param1 < param2:
self.data[self.data[self.i+3]] = 1
else:
self.data[self.data[self.i+3]] = 0
self.i += 4
if optcode == '08':
if mode2 == '0':
param2 = int(self.data[self.data[self.i+2]])
else:
param2 = int(self.data[self.i+2])
if param1 == param2:
self.data[self.data[self.i+3]] = 1
else:
self.data[self.data[self.i+3]] = 0
self.i += 4
if optcode == '99':
self.run = False
self.i += 1
self.done = True
return self.out, self.done
# #### generate all possible phase settings
from itertools import permutations
phase_settings = list(permutations(range(5, 10)))
# +
best_output = 0
for phase in phase_settings:
done = [False]*5
outE = 0
ampA = intcode_computer(phase[0], deepcopy(software))
ampB = intcode_computer(phase[1], deepcopy(software))
ampC = intcode_computer(phase[2], deepcopy(software))
ampD = intcode_computer(phase[3], deepcopy(software))
ampE = intcode_computer(phase[4], deepcopy(software))
while True not in done:
outA, done[0] = ampA.step(outE)
outB, done[1] = ampB.step(outA)
outC, done[2] = ampC.step(outB)
outD, done[3] = ampD.step(outC)
outE, done[4] = ampE.step(outD)
if True in done and outE > best_output:
best_output = outE
print('The value of the highest possible amp signal is {0}.'.format(best_output))
# -
|
day7/Script7.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.9.5 64-bit (''origin'': conda)'
# name: python395jvsc74a57bd04e62c5f72907caf2f8e50c4e1b95548d48fade11eacc296cd4faa51b1d77304e
# ---
# +
import sys
import numpy as np
import matplotlib.pyplot as plt
import empymod
sys.path.append('../')
import emulatte.forward as fwd
# VMD
emsrc_name = 'VMD'
# 層厚
thicks = [60, 60] #空気層+2層
# 比抵抗
res = [2e14, 1, 10, 100] #空気層+2層
# 送信座標
sc = [10, 0, -30]
# 受信座標
rc = [30, 50, 150]
# 測定周波数
time = np.logspace(-6, 1, 500)
# 地下の物性値
props = {'res' : res}
# 物理空間モデルの呼び出し
model = fwd.model(thicks)
# 物性値の割り当て
model.set_properties(**props)
# 送信ソースの呼び出しと設定
emsrc = fwd.transmitter(emsrc_name, time, moment=1)
# 送信ソースの設置と受信座標の設定
model.locate(emsrc, sc, rc)
# 電磁応答の取得
EMF = model.emulate(hankel_filter='werthmuller201',
td_transform='FFT', time_diff=True)
# 成分抽出
hz = EMF['h_z'][:-1]
dtime = time[:-1]
# 描画
fig = plt.figure(figsize=(8,5), facecolor='w')
ax = fig.add_subplot(111)
ax.plot(dtime, hz, "C0-", label='real')
ax.plot(dtime, -hz, "C0--")
ax.grid(which='major', c='#ccc')
#ax.grid(which='minor', c='#eee')
plt.tick_params(which='both', direction='in')
ax.set_yscale('log')
ax.set_xscale('log')
ax.set_xlabel('Frequency [Hz]')
ax.set_ylabel('$dH_z/dt$ [A/m-t]')
ax.set_title(emsrc_name+' Frequency Domain')
ax.legend()
# plt.savefig(emsrc_name+'_FD.png')
# +
import sys
import numpy as np
import matplotlib.pyplot as plt
import empymod
sys.path.append('../')
import emulatte.forward as fwd
# VMD
emsrc_name = 'CircularLoop'
# 層厚
thicks = [100, 100] #空気層+2層
# 比抵抗
res = [2e14, 1, 10, 100] #空気層+2層
# 送信座標
sc = [0, 0, -5]
# 受信座標
rc = [0, 0, -10]
# 測定周波数
time = np.logspace(-6, -3, 500)
# 地下の物性値
props = {'res' : res}
# 物理空間モデルの呼び出し
model = fwd.model(thicks)
# 物性値の割り当て
model.set_properties(**props)
# 送信ソースの呼び出しと設定
emsrc = fwd.transmitter(emsrc_name, time, current=300, radius=2, turns=5)
# 送信ソースの設置と受信座標の設定
model.locate(emsrc, sc, rc)
# 電磁応答の取得
EMF = model.emulate(hankel_filter='werthmuller201', td_transform='FFT', time_diff=False)
# 成分抽出
hz = EMF['h_z'][:-1]
dtime = time[:-1]
# 描画
fig = plt.figure(figsize=(8,5), facecolor='w')
ax = fig.add_subplot(111)
ax.plot(dtime, hz, "C0-", label='real')
#ax.plot(dtime, -hz, "C0--")
ax.grid(which='major', c='#ccc')
#ax.grid(which='minor', c='#eee')
plt.tick_params(which='both', direction='in')
#ax.set_yscale('log')
ax.set_xscale('log')
ax.set_xlabel('Frequency [Hz]')
ax.set_ylabel('$dH_z/dt$ [A/m-t]')
ax.set_title(emsrc_name+' Frequency Domain')
ax.legend()
# plt.savefig(emsrc_name+'_FD.png')
# +
import sys
import numpy as np
import matplotlib.pyplot as plt
import empymod
sys.path.append('../')
import emulatte.forward as fwd
# VMD
emsrc_name = 'CircularLoop'
# 層厚
thicks = [100, 100] #空気層+2層
# 比抵抗
res = [2e14, 1, 10, 100] #空気層+2層
# 送信座標
sc = [0, 0, -5]
# 受信座標
rc = [0, 0, -10]
# 測定周波数
time = np.logspace(-6, -3, 500)
# 地下の物性値
props = {'res' : res}
# 物理空間モデルの呼び出し
model = fwd.model(thicks)
# 物性値の割り当て
model.set_properties(**props)
# 送信ソースの呼び出しと設定
emsrc = fwd.transmitter(emsrc_name, time, current=300, radius=2, turns=5)
# 送信ソースの設置と受信座標の設定
model.locate(emsrc, sc, rc)
# 電磁応答の取得
EMF = model.emulate(hankel_filter='werthmuller201', td_transform='FFT', time_diff=True)
# 成分抽出
hz = EMF['h_z'][:-1]
dtime = time[:-1]
# 描画
fig = plt.figure(figsize=(8,5), facecolor='w')
ax = fig.add_subplot(111)
ax.plot(dtime, hz, "C0-", label='real')
#ax.plot(dtime, -hz, "C0--")
ax.grid(which='major', c='#ccc')
#ax.grid(which='minor', c='#eee')
plt.tick_params(which='both', direction='in')
#ax.set_yscale('log')
ax.set_xscale('log')
ax.set_xlabel('Frequency [Hz]')
ax.set_ylabel('$dH_z/dt$ [A/m-t]')
ax.set_title(emsrc_name+' Frequency Domain')
ax.legend()
# plt.savefig(emsrc_name+'_FD.png')
|
test/TDALL.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Objetos
# ## Em python tudo é objeto
# criando uma lista
list_num = ['Data', 'Science', 'Academy', 'Nota', 10, 10]
# é um objeto uma instância da classe lista
type(list_num)
# contando quantas vezes apareçe o item 10 na lista
print(list_num.count(10))
# usamos a função type para ver o tipo do objeto em python
print(type(10))
print(type([]))
print(type(()))
print(type({}))
print(type('a'))
# +
# criando um novo tipo de objeto chamado carro
# especificação macro, uma ideia daquilo que ele vai criar em cada classe
# e depois coloca o código necessário
class Carro(object):
pass # pass classe não tem nenhum atributo ou método
# intância do Carro()
palio = Carro()
print(type(palio)) # saida uma classe principla Carro()
# -
# criando uma classe
class Estudante():
def __init__(self, nome, idade, nota):
self.nome = nome
self.idade = idade
self.nota = nota
# criando uma instância do Classe Estudante
carlos = Estudante(nome = '<NAME>', idade = 39, nota = 7.5)
# Atributo da classe estudante, utilizado cada objeto criado apartir desta classe
print(carlos.nome)
print(carlos.idade)
print(carlos.nota)
# criando uma classe
class Funcionario:
def __init__(self, nome, salario):
self.nome = nome
self.salario = salario
def list_func(self):
print(f'O nome do funcionário é {self.nome} e seu salário de {self.salario:.3}')
# instânciando um objeto da classe Funcionário
marcio = Funcionario(nome = 'Marcio', salario = 1.250)
# chamando a função list_func
print(marcio.list_func())
# manipulando atributos em python [has, to have, tem][attr, atributo]
print('****************** Usando atributos *******************')
# tem um atributo, retorna True
hasattr(marcio, 'nome')
# set verifica se ele tem um atributo salário e defina um novo valor 1.800
setattr(marcio, 'salario', 1.800)
# tem um atributo
hasattr(marcio, 'salario')
# obter o atributo
getattr(marcio, 'nome')
# deletando um atributo
delattr(marcio, 'salario')
# tem um atributo
hasattr(marcio, 'salario')
# ## Uma forma de você operar com funções especiais atributos em python
# ## Fim
|
Cap05/objetos.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **Reminder:**
# <ul>
# <li>The laminar flow creates less skin friction drag than the turbulent flow, but is less stable
# <li>
# Friction Drag is created in the boundary layer due to the viscosity of the fluid and the resulting friction against the surface of the structure.
# </ul>
from IPython.core.display import HTML
HTML("""
<script type="text/x-mathjax-config">
MathJax.Hub.Config({
"HTML-CSS": {
availableFonts: ["TeX"],
preferredFont: "TeX",
webFont: "TeX"
}
});
</script>
<script type="text/javascript" src="path-to-MathJax/MathJax.js">
</script>
<style>
div.cell { /* Tunes the space between cells */
margin-top:1em;
margin-bottom:1em;
margin-right:0em;
margin-left:0em;
}
div.text_cell_render h1 { /* Main titles bigger, centered */
font-size: 2.0em;
line-height:1.4em;
text-align:center;
}
div.text_cell_render h2 { /* Parts names nearer from text */
margin-bottom: 0em;
}
div.text_cell_render { /* Customize text cells */
font-size:3.9em;
line-height:2em;
padding-left:3em;
padding-right:3em;
}
.MathJax { font-size: 1.6em !important; }
.container { width:80% !important; }
.output_png {
display: flex;
align-items: center;
text-align: center;
}
.output {
display: flex;
align-items: center;
}
</style>
""")
# ### Summary
# <p>
# <big>
# Skin friction drag reduction of surfaces with sinusoidal riblet (*wrinkled texture*) aligned in the flow direction and the effect of surface texture on the evolution of a laminar boundary layer flow has been studied numerically (using OpenFOAM). The parameter space unedr study includes:
# <ul>
# <li>wavelength to plate length ratios($\frac{\lambda}{L}$)
# <li>aspect ratios $\frac{2A}{\lambda}$ where $A$ is the amplitude of the sine function
# <li>Inlet velocity (plug flow)</li>
# </ul>
#
#
# <p>
# Their results show that:
# <ul>
# <li>The riblets are able to retard the viscous flow inside the groovesin the laminar regime by creating a cushion of stagnant fluid. that The high-speed fluid above can partially slide over this stagnant fluid and thus reducing the shear stress inside the grooves and total viscous drag on the plate.
# <br><br>
# <li> The optimal riblet aspect ratio for drag reduction has been found by assessing the variation of boundary layer thickness, local average shear stress distribution, and total drag force with the aspect ratio of the riblets as well as the length of the plate.
# </ul>
# </big>
# **Parameter space to investigate the effect of geometry on drag reduction:**
# $$
# \begin{array}{c}
# \lambda=200 \ \mu m \cr
# 0 < \frac{L}{\lambda} < 191 \cr
# AR = 0.48, 0.72, 0.95, 1.43, 1.91 \cr
# h \ (\text{height of the domain}) = 1 \ m \ (\text{constant}) \cr
# Re_L < 5 \times 10^5
# \end{array}
# $$
# <big>The **Reynolds number** that characterizes the relative importance of inertial and viscous effects **is defined using the flow direction as the length scale** plus **the maximum velocity of the free stream ($W_{\infty}$)** along the plate (determined after simulation).m
# $$
# Re_z = \frac{W_{\infty}z}{\nu}\text{, where} \ \ \nu=\frac{\mu}{\rho}
# $$
# ### Boundary conditions
# <img src="images/BC.png" alt="Drawing" style="width: 1450px;"/>
# ### Definition of the coefficient of drag ($C_D$)
#
# $$
# C_D=\frac{D}{\frac{1}{2}\rho W_{\infty}^2 A_w}=\frac{1}{\frac{1}{2}\rho W_{\infty}^2 A_w}\int_{A_w}(\tau_w \cdot n_w) \cdot \textbf{e}_z \ d A_w
# $$
# where $D$ is the total drag force on the wall and $A_w$ is the wetted area.
# The drag coefficient on the wrinkled plate ($AR = 1.9$) is substantially lower than the flat plate, however, it should be noted that this drag coefficient **has been normalized by the total wetted area of the plate** and ***DOES NOT explicitly display the increase in the surface area due to the presence of the riblets.***
# **Benchmarked their theory with flat plate boundary layer (Blasius)** for friction coefficient ($C_f(z)=\frac{\tau_{yz}(y=0,\ z)}{\frac{1}{2}\rho W_{\infty}^2}=\frac{0.664}{\sqrt{Re_z}}$)
# ### Peak versus groove velocity profile and boundary layer
# <img src="images/peak_vs_groove_1.png" alt="Drawing" style="width: 1500px;"/>
# <img src="images/peak_vs_groove_2.png" alt="Drawing" style="width: 1500px;"/>
# <big>***The velocity contours at the peak appear very similar to the flat plate boundary layer***
#
# ***Groove velocity profiles depicts a thicker boundary layer for which most of the region inside the groove has velocities lower than 25% of the free-stream velocity.***
# # Simulation Setup
# Figure below shows the schematic of the fluid-structure-interaction (FSI) problem:
# <img src="im/schematic.png" alt="Drawing" style="width: 550px;"/>
# Model parameters in the problem are:
# <li>Beam height (𝐿)
# <li>Beam thickness (2a)
# <li>Beam spacing (𝛿)
# <li>Beam angle (𝜃)
# <li>Beam stiffness (𝐸)
# <li>Number of beams (𝑁)
# <li>Wall velocity (𝑣)
# <li>Channel height (𝐻)
# <li>Viscosity (𝜂)
#
#
|
notebook/shabnam.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import forge
from puzzle.puzzlepedia import puzzlepedia
puzzle = puzzlepedia.parse("""
name in {Beth, Charles, David, Frank, Jessica, Karen, Taylor}
room in {small, large, left_small, left_large}
crime in {innocent*6, guilty}
#1 Background.
#2 Background.
#3 Guilty suspect is lying.
#4 Background.
#5 Background.
#6 Murder happened at 11am.
#7
small != guilty
large != guilty
#8 Background.
#9
if Beth == innocent:
Charles == large
David == large
Jessica == left_large
Taylor == left_large
# Beth seems to be in the small room.
Beth.small or Beth.left_small
#10
if Charles == innocent:
Beth.small | Frank.small | Karen.small
#11
if David == innocent:
Beth.left_small | Frank.left_small | Karen.left_small
#12
if Frank == innocent:
Karen.small | Beth.left_small
#13
if Karen == innocent:
Beth.small | Frank.left_small
#14
if Jessica == innocent:
if Frank == innocent: Karen == innocent
if Karen == innocent: Frank == innocent
#15
if Taylor == innocent:
Frank.small | Karen.left_small
""")
# -
|
src/puzzle/examples/mim/p9_2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.8 ('base')
# language: python
# name: python3
# ---
# # JOINING IMAGES
# +
import cv2
import numpy as np
img = cv2.imread('resources/trust.png')
imgHor = np.hstack((img, img))
imgVar = np.vstack((img, img))
cv2.imshow('Horizontal', imgHor)
cv2.imshow('Vertical', imgVar)
cv2.waitKey(0)
# -
# # Function to reduce the size of images and to stack them
# +
import cv2
import numpy as np
def stackImages(scale, imgArray):
rows = len(imgArray)
cols = len(imgArray[0])
rowsAvailable = isinstance(imgArray[0], list)
width = imgArray[0][0].shape[1]
height = imgArray[0][0].shape[0]
if rowsAvailable:
for x in range (0, rows):
for y in range (0, cols):
if imgArray[x][y].shape[:2] == imgArray[0][0].shape[:2]:
imgArray[x][y] = cv2.resize(imgArray[x][y], (0,0), None, scale, scale)
else:
imgArray[x][y] = cv2.resize(imgArray[x][y], (imgArray[0][0].shape[1], imgArray[0][0].shape[0]), None, scale, scale)
if len(imgArray[x][y].shape) == 2:imgArray[x][y]= cv2.cvtColor(imgArray[x][y], cv2.COLOR_GRAY2BGR)
imageBlank = np.zeros((height, width, 3), np.uint8)
hor = [imageBlank]*rows
hor_con = [imageBlank]*rows
for x in range(0, rows):
hor[x] = np.hstack(imgArray[x])
ver = np.vstack(hor)
else:
for x in range(0, rows):
if imgArray[x].shape[:2] == imgArray[0].shape[:2]:
imgArray[x] = cv2.resize(imgArray[x], (0,0), None, scale, scale)
else:
imgArray[x] = cv2.resize(imgArray[x], (imgArray[0].shape[1], imgArray[0].shape[0]), None, scale, scale)
if len(imgArray[x].shape) == 2: imgArray[x] = cv2.cvtColor(imgArray[x], cv2.COLOR_GRAY2BGR)
hor = np.hstack(imgArray)
ver = hor
return ver
img = cv2.imread('resources/trust.png')
imgStack = stackImages(0.5, ([img,img,img]))
cv2.imshow('ImageStack', imgStack)
cv2.waitKey(0)
# -
|
basics5.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# #### New to Plotly?
# Plotly's Python library is free and open source! [Get started](https://plotly.com/python/getting-started/) by dowloading the client and [reading the primer](https://plotly.com/python/getting-started/).
# <br>You can set up Plotly to work in [online](https://plotly.com/python/getting-started/#initialization-for-online-plotting) or [offline](https://plotly.com/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plotly.com/python/getting-started/#start-plotting-online).
# <br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
# #### Imports
# The tutorial below imports [NumPy](http://www.numpy.org/), [Pandas](https://plotly.com/pandas/intro-to-pandas-tutorial/), and [SciPy](https://www.scipy.org/).
# +
import plotly.plotly as py
import plotly.graph_objs as go
from plotly.tools import FigureFactory as FF
import numpy as np
import pandas as pd
import scipy
# -
# #### Tips
# Interpolation refers to the process of generating data points between already existing data points. Extrapolation is the process of generating points outside a given set of known data points.
# <br/>(_inter_ and _extra_ are derived from Latin words meaning 'between' and 'outside' respectively)
# #### Interpolation and Extrapolation
# Interpolate and Extrapolate for a set of points and generate the curve of best fit that intersects all the points.
# +
points = np.array([(1, 1), (2, 4), (3, 1), (9, 3)])
x = points[:,0]
y = points[:,1]
z = np.polyfit(x, y, 3)
f = np.poly1d(z)
x_new = np.linspace(0, 10, 50)
y_new = f(x_new)
trace1 = go.Scatter(
x=x,
y=y,
mode='markers',
name='Data',
marker=dict(
size=12
)
)
trace2 = go.Scatter(
x=x_new,
y=y_new,
mode='lines',
name='Fit'
)
annotation = go.Annotation(
x=6,
y=-4.5,
text='$0.43X^3 - 0.56X^2 + 16.78X + 10.61$',
showarrow=False
)
layout = go.Layout(
title='Polynomial Fit in Python',
annotations=[annotation]
)
data = [trace1, trace2]
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='interpolation-and-extrapolation')
# -
# #### Interpolation and Extrapolation of Y From X
# Interpolation and Extrapolation of (x, y) points with pre-existant points and an array of specific x values.
# +
points = np.array([(1, 1), (2, 4), (3, 1), (9, 3)])
# get x and y vectors
x = points[:,0]
y = points[:,1]
# calculate polynomial
z = np.polyfit(x, y, 3)
f = np.poly1d(z)
# other x values
other_x = np.array([1.2, 1.34, 1.57, 1.7, 3.6, 3.8, 3.9, 4.0, 5.4, 6.6, 7.2, 7.3, 7.7, 8, 8.9, 9.1, 9.3])
other_y = f(other_x)
# calculate new x's and y's
x_new = np.linspace(0, 10, 50)
y_new = f(x_new)
# Creating the dataset, and generating the plot
trace1 = go.Scatter(
x=x,
y=y,
mode='markers',
name='Data',
marker=dict(
size=12
)
)
trace2 = go.Scatter(
x=other_x,
y=other_y,
name='Interpolated/Extrapolated Data',
mode='markers',
marker=dict(
symbol='square-open',
size=12
)
)
layout = go.Layout(
title='Interpolation and Extrapolation of Y From X',
)
data2 = [trace1, trace2]
fig2 = go.Figure(data=data2, layout=layout)
py.iplot(fig2, filename='interpolation-and-extrapolation-of-y-from-x')
# +
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
# ! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'python_Interpolation_and_Extrapolation_in_1D.ipynb', 'python/interpolation-and-extrapolation-in-1d/', 'Interpolation and Extrapolation in 1D | plotly',
'Learn how to interpolation and extrapolate data in one dimension',
title='Interpolation and Extrapolation in 1D in Python. | plotly',
name='Interpolation and Extrapolation in 1D',
language='python',
page_type='example_index', has_thumbnail='false', display_as='mathematics', order=3,
ipynb= '~notebook_demo/106')
# -
|
_posts/python-v3/mathematics/interpolation-and-extrapolation-in-1d/python_Interpolation_and_Extrapolation_in_1D.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (system-wide)
# language: python
# metadata:
# cocalc:
# description: Python 3 programming language
# priority: 100
# url: https://www.python.org/
# name: python3
# ---
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
# %matplotlib inline
import warnings
warnings.filterwarnings('ignore')
dataset = pd.read_csv("census_data.csv")
rows_columns=dataset.shape
rows_columns
dataset[' annual-income'].fillna(method='ffill',inplace=True)
dataset[' annual-income']
dataset[' sex'].fillna(method='ffill',inplace=True)
dataset[' sex']
dataset[' workclass'].fillna(method='ffill',inplace=True)
dataset[' workclass']
dataset.isnull().sum()
dataset.dropna(inplace=True)
dataset.isnull().sum()
dataset.shape
dataset.drop_duplicates(subset=None, inplace=True)
dataset.shape
dataset.drop(dataset[dataset['age'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' workclass'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' fnlwgt'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' education'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' education-num'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' marital-status'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' occupation'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' relationship'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' race'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' sex'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' native-country'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' capital-gain'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' capital-loss'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' hours-per-week'] == ' ?'].index, inplace = True)
dataset.shape
dataset.drop(dataset[dataset[' annual-income'] == ' ?'].index, inplace = True)
dataset.shape
dataset=dataset.sample(700,replace=False,axis=0)
dataset.shape
import pandas as pd
import numpy as np
df = pd.DataFrame(dataset)
x_data= df[[' hours-per-week',' education-num',' capital-gain',' capital-loss']]
x_data= x_data.apply(lambda x:(x -x.min(axis=0)) / (x.max(axis=0)-x.min(axis=0)))
print(x_data.head(50))
fig,ax=plt.subplots(figsize=(18,5))
df=pd.DataFrame(dataset)
ax.bar(df[' workclass'],df[' fnlwgt'])
df.boxplot(by =' occupation', column =[' hours-per-week'], grid = False, figsize=(25,10))
plt.hist(df['age'])
plt.show()
# +
import pandas as pd
from scipy import stats
from statsmodels.stats import weightstats as stests
df = pd.DataFrame(dataset)
ztest,pval=stests.ztest(df[' hours-per-week'],x2=None,alternative='two-sided',value=40)
print(float(pval))
if(pval<0.05):
print("reject null hypothesis")
else:
print("failed to reject null hypothesis")
# -
x1=df[' education-num']
x2=df[' hours-per-week']
plt.scatter(x1,x2)
plt.xlabel('Age')
plt.ylabel('Hours-per-week')
plt.title('Comparison between the level of education of a person and the hours worked per week')
#Pearson Correlation
from scipy.stats import pearsonr
corr,p_value=pearsonr(x1,x2)
print(corr)#weak correlation
#Kendall Correlation
from scipy.stats import kendalltau
tau, p_value=kendalltau(x1,x2,initial_lexsort=True)
print(tau)
#Spearman
from scipy.stats import spearmanr
rho,p_value=spearmanr(x1,x2)
print(rho)
from statistics import mean
m = (((mean(x1)*mean(x2)) - mean(x1*x2)) /
((mean(x1)*mean(x1)) - mean(x1*x1)))
print(m)
b = mean(x2) - m*mean(x1)
print(b)
regression_line = [(m*x)+b for x in x1]
plt.scatter(x1,x2)
plt.plot(x1, regression_line)
plt.show()
|
dataset3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Unsupervised Transformations for Data Exploration/Visualization:
# - Principle Component Analysis (PCA)
# - Non-negative Matrix Factorization (NMF)
# - t-SNE manifold learning
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
from scipy import stats
import warnings
warnings.filterwarnings("ignore")
# +
df=pd.read_csv('C:/Users/rhash/Documents/Datasets/pima-indian-diabetes/indians-diabetes.csv')
df.columns=['NP', 'GC', 'BP', 'ST', 'I', 'BMI', 'PF', 'Age', 'Class']
# -
print(df.head(), "\n")
df.info()
df['ST'].replace(0, df[df['ST']!=0]['ST'].mean(), inplace=True)
df['GC'].replace(0, df[df['GC']!=0]['GC'].mean(), inplace=True)
df['BP'].replace(0, df[df['BP']!=0]['BP'].mean(), inplace=True)
df['BMI'].replace(0, df[df['BMI']!=0]['BMI'].mean(), inplace=True)
df['I'].replace(0, df[df['I']!=0]['I'].mean(), inplace=True)
X=df[['NP', 'GC', 'BP', 'ST', 'I', 'BMI', 'PF', 'Age']]
y=df['Class']
# +
from sklearn.preprocessing import MinMaxScaler, StandardScaler
scaler=StandardScaler()
X_scaled=scaler.fit_transform(X)
# +
# PCA: _________________
from sklearn.decomposition import PCA
pca=PCA(n_components=3, whiten=True, random_state=42)
pca.fit(X_scaled)
X_pca=pca.transform(X_scaled)
# +
colors = ["orangered", "blue"]
plt.figure(figsize=(10, 10))
plt.xlim(X_pca[:, 0].min(), X_pca[:, 0].max())
plt.ylim(X_pca[:, 1].min(), X_pca[:, 1].max())
for i in range(len(X_scaled)):
# actually plot the digits as text instead of using scatter
plt.text(X_pca[i, 0], X_pca[i, 1], str(y[i]), color = colors[y[i]],
fontdict={'weight': 'bold', 'size': 12})
plt.xlabel("First principal component")
plt.ylabel("Second principal component")
# -
X_pca.shape
df_pca=pd.concat((pd.DataFrame(X_pca), y) , axis=1)
df_pca.columns=['X_1', 'X_2', 'X_3', 'Target']
sns.pairplot(df_pca, hue='Target')
plt.matshow(pca.components_, cmap='viridis' )
plt.yticks([0,1,2], ['1st component', '2nd component', '3rd component'])
plt.colorbar()
plt.xticks(range(len(df.columns[:-1])), df.columns[:-1], rotation=60, ha='left')
plt.xlabel('Feature')
plt.ylabel('Principle components')
X_back=pca.inverse_transform(X_pca)
# +
# Manifold Learning with t-SNE ____________________________________________________
from sklearn.manifold import TSNE
tsne = TSNE(random_state=123)
scaler=MinMaxScaler()
X_scaled=scaler.fit_transform(X)
# use fit_transform instead of fit, as TSNE has no transform method
X_tsne = tsne.fit_transform(X_scaled)
# -
X_tsne.shape
# +
colors = ["orangered", "blue"]
plt.figure(figsize=(10, 10))
plt.xlim(X_tsne[:, 0].min(), X_tsne[:, 0].max())
plt.ylim(X_tsne[:, 1].min(), X_tsne[:, 1].max())
for i in range(len(X_scaled)):
# actually plot the digits as text instead of using scatter
plt.text(X_tsne[i, 0], X_tsne[i, 1], str(y[i]), color = colors[y[i]], fontdict={'weight': 'bold', 'size': 12})
plt.xlabel("t-SNE feature 1")
plt.ylabel("t-SNE feature 2")
|
Projects in Python with Scikit-Learn- XGBoost- Pandas- Statsmodels- etc./Diabetes dataset (transformation with PCA, NMF, t-SNE manifold learning).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # MNIST Image Classification with TensorFlow
#
# This notebook demonstrates how to implement a simple linear image model on [MNIST](http://yann.lecun.com/exdb/mnist/) using the [tf.keras API](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras). It builds the foundation for this <a href="https://github.com/GoogleCloudPlatform/training-data-analyst/blob/master/courses/machine_learning/deepdive2/image_classification/labs/2_mnist_models.ipynb">companion notebook</a>, which explores tackling the same problem with other types of models such as DNN and CNN.
#
# ## Learning Objectives
# 1. Know how to read and display image data
# 2. Know how to find incorrect predictions to analyze the model
# 3. Visually see how computers see images
# !sudo chown -R jupyter:jupyter /home/jupyter/training-data-analyst
# +
import os
import shutil
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.callbacks import ModelCheckpoint, TensorBoard
from tensorflow.keras.layers import Dense, Flatten, Softmax
print(tf.__version__)
# -
# ## Exploring the data
#
# The MNIST dataset is already included in tensorflow through the keras datasets module. Let's load it and get a sense of the data.
# + jupyter={"outputs_hidden": false}
mnist = tf.keras.datasets.mnist.load_data()
(x_train, y_train), (x_test, y_test) = mnist
# + jupyter={"outputs_hidden": false}
HEIGHT, WIDTH = x_train[0].shape
NCLASSES = tf.size(tf.unique(y_train).y)
print("Image height x width is", HEIGHT, "x", WIDTH)
tf.print("There are", NCLASSES, "classes")
# -
# Each image is 28 x 28 pixels and represents a digit from 0 to 9. These images are black and white, so each pixel is a value from 0 (white) to 255 (black). Raw numbers can be hard to interpret sometimes, so we can plot the values to see the handwritten digit as an image.
# + jupyter={"outputs_hidden": false}
IMGNO = 12
# Uncomment to see raw numerical values.
# print(x_test[IMGNO])
plt.imshow(x_test[IMGNO].reshape(HEIGHT, WIDTH));
print("The label for image number", IMGNO, "is", y_test[IMGNO])
# -
# ## Define the model
# Let's start with a very simple linear classifier. This was the first method to be tried on MNIST in 1998, and scored an 88% accuracy. Quite ground breaking at the time!
# We can build our linear classifier using the [tf.keras API](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras), so we don't have to define or initialize our weights and biases. This happens automatically for us in the background. We can also add a softmax layer to transform the logits into probabilities. Finally, we can compile the model using categorical cross entropy in order to strongly penalize high probability predictions that were incorrect.
#
# When building more complex models such as DNNs and CNNs our code will be more readable by using the [tf.keras API](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras). Let's get one working so we can test it and use it as a benchmark.
def linear_model():
# TODO: Build a sequential model and compile it.
return model
# ## Write Input Functions
#
# As usual, we need to specify input functions for training and evaluating. We'll scale each pixel value so it's a decimal value between 0 and 1 as a way of normalizing the data.
#
# **TODO 1**: Define the scale function below and build the dataset
# + jupyter={"outputs_hidden": false}
BUFFER_SIZE = 5000
BATCH_SIZE = 100
def scale(image, label):
# TODO
def load_dataset(training=True):
"""Loads MNIST dataset into a tf.data.Dataset"""
(x_train, y_train), (x_test, y_test) = mnist
x = x_train if training else x_test
y = y_train if training else y_test
# TODO: a) one-hot encode labels, apply `scale` function, and create dataset.
# One-hot encode the classes
if training:
# TODO
return dataset
# +
def create_shape_test(training):
dataset = load_dataset(training=training)
data_iter = dataset.__iter__()
(images, labels) = data_iter.get_next()
expected_image_shape = (BATCH_SIZE, HEIGHT, WIDTH)
expected_label_ndim = 2
assert(images.shape == expected_image_shape)
assert(labels.numpy().ndim == expected_label_ndim)
test_name = 'training' if training else 'eval'
print("Test for", test_name, "passed!")
create_shape_test(True)
create_shape_test(False)
# -
# Time to train the model! The original MNIST linear classifier had an error rate of 12%. Let's use that to sanity check that our model is learning.
# +
NUM_EPOCHS = 10
STEPS_PER_EPOCH = 100
model = linear_model()
train_data = load_dataset()
validation_data = load_dataset(training=False)
OUTDIR = "mnist_linear/"
checkpoint_callback = ModelCheckpoint(
OUTDIR, save_weights_only=True, verbose=1)
tensorboard_callback = TensorBoard(log_dir=OUTDIR)
history = model.fit(
# TODO: specify training/eval data, # epochs, steps per epoch.
verbose=2,
callbacks=[checkpoint_callback, tensorboard_callback]
)
# +
BENCHMARK_ERROR = .12
BENCHMARK_ACCURACY = 1 - BENCHMARK_ERROR
accuracy = history.history['accuracy']
val_accuracy = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
assert(accuracy[-1] > BENCHMARK_ACCURACY)
assert(val_accuracy[-1] > BENCHMARK_ACCURACY)
print("Test to beat benchmark accuracy passed!")
assert(accuracy[0] < accuracy[1])
assert(accuracy[1] < accuracy[-1])
assert(val_accuracy[0] < val_accuracy[1])
assert(val_accuracy[1] < val_accuracy[-1])
print("Test model accuracy is improving passed!")
assert(loss[0] > loss[1])
assert(loss[1] > loss[-1])
assert(val_loss[0] > val_loss[1])
assert(val_loss[1] > val_loss[-1])
print("Test loss is decreasing passed!")
# -
# ## Evaluating Predictions
# Were you able to get an accuracy of over 90%? Not bad for a linear estimator! Let's make some predictions and see if we can find where the model has trouble. Change the range of values below to find incorrect predictions, and plot the corresponding images. What would you have guessed for these images?
#
# **TODO 2**: Change the range below to find an incorrect prediction
# +
image_numbers = range(0, 10, 1) # Change me, please.
def load_prediction_dataset():
dataset = (x_test[image_numbers], y_test[image_numbers])
dataset = tf.data.Dataset.from_tensor_slices(dataset)
dataset = dataset.map(scale).batch(len(image_numbers))
return dataset
predicted_results = model.predict(load_prediction_dataset())
for index, prediction in enumerate(predicted_results):
predicted_value = np.argmax(prediction)
actual_value = y_test[image_numbers[index]]
if actual_value != predicted_value:
print("image number: " + str(image_numbers[index]))
print("the prediction was " + str(predicted_value))
print("the actual label is " + str(actual_value))
print("")
# -
bad_image_number = 8
plt.imshow(x_test[bad_image_number].reshape(HEIGHT, WIDTH));
# It's understandable why the poor computer would have some trouble. Some of these images are difficult for even humans to read. In fact, we can see what the computer thinks each digit looks like.
#
# Each of the 10 neurons in the dense layer of our model has 785 weights feeding into it. That's 1 weight for every pixel in the image + 1 for a bias term. These weights are flattened feeding into the model, but we can reshape them back into the original image dimensions to see what the computer sees.
#
# **TODO 3**: Reshape the layer weights to be the shape of an input image and plot.
# +
DIGIT = 0 # Change me to be an integer from 0 to 9.
LAYER = 1 # Layer 0 flattens image, so no weights
WEIGHT_TYPE = 0 # 0 for variable weights, 1 for biases
dense_layer_weights = model.layers[LAYER].get_weights()
digit_weights = dense_layer_weights[WEIGHT_TYPE][:, DIGIT]
plt.imshow(digit_weights.reshape((HEIGHT, WIDTH)))
# -
# Did you recognize the digit the computer was trying to learn? Pretty trippy, isn't it! Even with a simple "brain", the computer can form an idea of what a digit should be. The human brain, however, uses [layers and layers of calculations for image recognition](https://www.salk.edu/news-release/brain-recognizes-eye-sees/). Ready for the next challenge? <a href="https://github.com/GoogleCloudPlatform/training-data-analyst/blob/master/courses/machine_learning/images/mnist_linear.ipynb">Click here</a> to super charge our models with human-like vision.
# ## Bonus Exercise
#
# Want to push your understanding further? Instead of using Keras' built in layers, try repeating the above exercise with your own [custom layers](https://www.tensorflow.org/tutorials/eager/custom_layers).
# Copyright 2020 Google Inc.
# Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
|
courses/machine_learning/deepdive2/image_classification/labs/1_mnist_linear.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Boundary Modeling
#
# The following notebook is comprised of 7 primary steps:
# 1. Initialize required packages, directories and parameters
# 2. Load and inspect the domain indicator data
# 3. Calculate and model the boundary indicator variogram
# 4. Calculate and model the Gaussian variogram that yields the indicator variogram when truncated
# 5. Model the distance function
# 6. Simulate boundary realizations, through truncation of simulated distance function deviates
# 7. Save project setting and clean the output files
# ## 1. Initialize required packages and parameters
import pygeostat as gs
import numpy as np
import os
import pandas as pd
import matplotlib.pyplot as plt
# ### Project settings
# Load the previously set Matplotlib and Pygeostat settings.
# +
#path to GSLIB executables
exe_dir="../pygeostat/executable/"
gs.Parameters['data.griddef'] = gs.GridDef('''
120 5.0 10.0
110 1205.0 10.0
1 0.5 1.0''')
gs.Parameters['data.catdict'] = {1: 'Inside', 0: 'Outside'}
# Data values
gs.Parameters['data.tmin'] = -998
gs.Parameters['data.null'] = -999
# Color map settings
gs.Parameters['plotting.cmap'] = 'bwr'
gs.Parameters['plotting.cmap_cat'] = 'bwr'
# Number of realizations
nreal = 100
gs.Parameters['data.nreal'] = nreal
# Parallel Processing threads
gs.Parameters['config.nprocess'] = 4
# Pot Style settings
gs.PlotStyle['legend.fontsize'] = 12
gs.PlotStyle['font.size'] = 11
# -
# ### Directories
# Create the output directory
outdir = 'Output/'
gs.mkdir(outdir)
# ## 2. Load and Inspect the Boundary Data
#
# Note that content in this section was explained in the introduction notebooks. Only new concepts are generally annotated in detail.
#
# ### Load the data and note its attributes
dat = gs.ExampleData('reservoir_boundary', cat='Domain Indicator')
dat.info
# ### Data content and summary statistics
print(dat.describe())
dat.head()
# ### Map of the indicator
gs.location_plot(dat)
# ## 3. Calculate and Model the Indicator Variogram
#
# The indicator variogram is calculated and modeled, since this is required input to calculation of the Gaussian variogram model in the next section (used for distance function $df$ modeling).
#
# ### Apply the variogram object for convenience
# Variogram calculation, modeling, plotting and checking are readily accomplished with the variogram object, although unprovided parameters are inferred.
# +
# get the proportions
proportion = sum(dat['Domain Indicator'])/len(dat)
print('Proportion of inside data: %.3f'%(proportion))
variance = proportion - proportion**2
# -
# Perform data spacing analysis
dat.spacing(n_nearest=1)
lag_length = dat['Data Spacing (m)'].values.mean()
print('average data spacing in XY plane: {:.3f} {}'.format(lag_length,
gs.Parameters['plotting.unit']))
mean_range = (np.ptp(dat[dat.x].values) + np.ptp(dat[dat.y].values)) * 0.5
n_lag = np.ceil((mean_range * 0.5) / lag_length)
lag_tol = lag_length * 0.6
var_calc = gs.Program(program=exe_dir+'varcalc')
# +
parstr = """ Parameters for VARCALC
**********************
START OF PARAMETERS:
{file} -file with data
2 3 0 - columns for X, Y, Z coordinates
1 4 - number of variables,column numbers (position used for tail,head variables below)
{t_min} 1.0e21 - trimming limits
{n_directions} -number of directions
0.0 90 1000 0.0 22.5 1000 0.0 -Dir 01: azm,azmtol,bandhorz,dip,diptol,bandvert,tilt
{n_lag} {lag_length} {lag_tol} - number of lags,lag distance,lag tolerance
{output} -file for experimental variogram points output.
0 -legacy output (0=no, 1=write out gamv2004 format)
1 -run checks for common errors
1 -standardize sills? (0=no, 1=yes)
1 -number of variogram types
1 1 10 1 {variance} -tail variable, head variable, variogram type (and cutoff/category), sill
"""
n_directions = 1
varcalc_outfl = os.path.join(outdir, 'varcalc.out')
var_calc.run(parstr=parstr.format(file=dat.flname,
n_directions = n_directions,
t_min = gs.Parameters['data.tmin'],
n_lag=n_lag,
lag_length = lag_length,
lag_tol = lag_tol,
variance = variance,
output=varcalc_outfl),
liveoutput=True)
# -
varfl = gs.DataFile(varcalc_outfl)
varfl.head()
var_model = gs.Program(program=exe_dir+'varmodel')
# +
parstr = """ Parameters for VARMODEL
***********************
START OF PARAMETERS:
{varmodel_outfl} -file for modeled variogram points output
1 -number of directions to model points along
0.0 0.0 100 6 - azm, dip, npoints, point separation
2 0.05 -nst, nugget effect
1 ? 0.0 0.0 0.0 -it,cc,azm,dip,tilt (ang1,ang2,ang3)
? ? ? -a_hmax, a_hmin, a_vert (ranges)
1 ? 0.0 0.0 0.0 -it,cc,azm,dip,tilt (ang1,ang2,ang3)
? ? ? -a_hmax, a_hmin, a_vert (ranges)
1 100000 -fit model (0=no, 1=yes), maximum iterations
1.0 - variogram sill (can be fit, but not recommended in most cases)
1 - number of experimental files to use
{varcalc_outfl} - experimental output file 1
1 1 - # of variograms (<=0 for all), variogram #s
1 0 10 - # pairs weighting, inverse distance weighting, min pairs
0 10.0 - fix Hmax/Vert anis. (0=no, 1=yes)
0 1.0 - fix Hmin/Hmax anis. (0=no, 1=yes)
{varmodelfit_outfl} - file to save fit variogram model
"""
varmodel_outfl = os.path.join(outdir, 'varmodel.out')
varmodelfit_outfl = os.path.join(outdir, 'varmodelfit.out')
var_model.run(parstr=parstr.format(varmodel_outfl= varmodel_outfl,
varmodelfit_outfl = varmodelfit_outfl,
varcalc_outfl = varcalc_outfl), liveoutput=False, quiet=True)
# -
varmdl = gs.DataFile(varmodel_outfl)
varmdl.head()
ax = gs.variogram_plot(varfl, index=1, color='b', grid=True, label = 'Indicator Variogram (Experimental)')
gs.variogram_plot(varmdl, index=1, ax=ax, color='b', experimental=False, label = 'Indicator Variogram (Model)')
_ = ax.legend(fontsize=12)
# ## 4. Calculate and model the Gaussian Variogram
#
# The Gaussian variogram that yields the indicator variogram after truncation of a Gaussian random field is calculated. This Gaussian variogram is modeled and input to $df$ modeing.
# #### Calculate the Gaussian variogram
# The bigaus2 program applies the Gaussian integration method, given the indicator variogram and the proportion of the indicator.
bigaus2 = gs.Program(exe_dir+'bigaus2')
# +
parstr = """ Parameters for BIGAUS2
**********************
START OF PARAMETERS:
1 -input mode (1) model or (2) variogram file
nofile.out -file for input variogram
{proportion} -threshold/proportion
2 -calculation mode (1) NS->Ind or (2) Ind->NS
{outfl} -file for output of variograms
1 -number of thresholds
{proportion} -threshold cdf values
1 {n_lag} -number of directions and lags
0 0.0 {lag_length} -azm(1), dip(1), lag(1)
{varstr}
"""
with open(varmodelfit_outfl, 'r') as f:
varmodel_ = f.readlines()
varstr = ''''''
for line in varmodel_:
varstr += line
pars = dict(proportion=proportion,
lag_length=lag_length,
n_lag=n_lag,
outfl= os.path.join(outdir, 'bigaus2.out'),
varstr=varstr)
bigaus2.run(parstr=parstr.format(**pars), nogetarg=True)
# -
# ### Data manipulation to handle an odd data format
# The bigaus2 program outputs an odd (legacyish) variogram format, which must be translated to the standard Variogram format.
# Read in the data before demonstrating its present form
expvargs = gs.readvarg(os.path.join(outdir, 'bigaus2.out'), 'all')
expvargs.head()
varclac_gaussian = gs.DataFile(data = varfl.data[:-1].copy(), flname=os.path.join(outdir,'gaussian_exp_variogram.out'))
varclac_gaussian['Lag Distance'] = expvargs['Distance']
varclac_gaussian['Variogram Value'] = expvargs['Value']
varclac_gaussian.write_file(varclac_gaussian.flname)
varclac_gaussian.head()
# ### Gaussian variogram modeling
# This model is input to distance function estimation.
# +
parstr = """ Parameters for VARMODEL
***********************
START OF PARAMETERS:
{varmodel_outfl} -file for modeled variogram points output
1 -number of directions to model points along
0.0 0.0 100 6 - azm, dip, npoints, point separation
2 0.01 -nst, nugget effect
3 ? 0.0 0.0 0.0 -it,cc,azm,dip,tilt (ang1,ang2,ang3)
? ? ? -a_hmax, a_hmin, a_vert (ranges)
3 ? 0.0 0.0 0.0 -it,cc,azm,dip,tilt (ang1,ang2,ang3)
? ? ? -a_hmax, a_hmin, a_vert (ranges)
1 100000 -fit model (0=no, 1=yes), maximum iterations
1.0 - variogram sill (can be fit, but not recommended in most cases)
1 - number of experimental files to use
{varcalc_outfl} - experimental output file 1
1 1 - # of variograms (<=0 for all), variogram #s
1 0 10 - # pairs weighting, inverse distance weighting, min pairs
0 10.0 - fix Hmax/Vert anis. (0=no, 1=yes)
0 1.0 - fix Hmin/Hmax anis. (0=no, 1=yes)
{varmodelfit_outfl} - file to save fit variogram model
"""
varmodel_outfl_g = os.path.join(outdir, 'varmodel_g.out')
varmodelfit_outfl_g = os.path.join(outdir, 'varmodelfit_g.out')
var_model.run(parstr=parstr.format(varmodel_outfl= varmodel_outfl_g,
varmodelfit_outfl = varmodelfit_outfl_g,
varcalc_outfl = varclac_gaussian.flname), liveoutput=True, quiet=False)
# -
varmdl_g = gs.DataFile(varmodel_outfl_g)
varmdl_g.head()
# +
fig, axes = plt.subplots(1, 2, figsize= (15,4))
ax = axes[0]
ax = gs.variogram_plot(varfl, index=1, ax=ax, color='b', grid=True, label = 'Indicator Variogram (Experimental)')
gs.variogram_plot(varmdl, index=1, ax=ax, color='b', experimental=False, label = 'Indicator Variogram (Model)')
_ = ax.legend(fontsize=12)
ax = axes[1]
gs.variogram_plot(varclac_gaussian, index=1, ax=ax, color='g', grid=True, label = 'Gaussian Variogram (Experimental)')
gs.variogram_plot(varmdl_g, index=1, ax=ax, color='g', experimental=False, label = 'Gaussian Variogram (Model)')
_ = ax.legend(fontsize=12)
# -
# ## 5. Distance Function $df$ Modeling
#
# The $df$ is calculated at the data locations, before being estimated at the grid locations. The $c$ parameter is applied to the $df$ calculation, defining the bandwidth of uncertainty that will be simulated in the next section.
#
# ### Determine the $c$ parameter
# Normally the optimal $c$ would be calculated using a jackknife study, but it is simply provided here.
selected_c = 200
# ### Calculate the $df$ at the data locations
# +
dfcalc = gs.Program(exe_dir+'dfcalc')
# Print the columns for populating the parameter file without variables
print(dat.columns)
# -
parstr = """ Parameters for DFCalc
*********************
START OF PARAMETERS:
{datafl} -file with input data
1 2 3 0 4 -column for DH,X,Y,Z,Ind
1 -in code: indicator for inside domain
0.0 0.0 0.0 -angles for anisotropy ellipsoid
1.0 1.0 -first and second anisotropy ratios (typically <=1)
0 -proportion of drillholes to remove
696969 -random number seed
{c} -C
{outfl} -file for distance function output
'nofile.out' -file for excluded drillholes output
"""
pars = dict(datafl=dat.flname, c=selected_c,
outfl=os.path.join(outdir,'df_calc.out'))
dfcalc.run(parstr=parstr.format(**pars))
# ### Manipulate the $df$ data before plotting
# A standard naming convention of the distance function variable is used for convenience in the workflow, motivating the manipulation.
# +
# Load the data and note the abbreviated name of the distance function
dat_df = gs.DataFile(os.path.join(outdir,'df_calc.out'), notvariables='Ind', griddef=gs.Parameters['data.griddef'])
print('Initial distance Function variable name = ', dat_df.variables)
# Set a standard distance function name
dfvar = 'Distance Function'
dat_df.rename({dat_df.variables:dfvar})
print('Distance Function variable name = ', dat_df.variables)
# -
# Set symmetric color limits for the distance function
df_vlim = (-350, 350)
gs.location_plot(dat_df, vlim=df_vlim, cbar_label='m')
# ### Estimate the $df$ across the grid
# Kriging is performed with a large number of data to provide a smooth and conditionally unbiased estimate. Global kriging would also be appropriate.
kd3dn = gs.Program(exe_dir+'kt3dn')
varmodelfit_outfl_g
# +
parstr = """ Parameters for KT3DN
********************
START OF PARAMETERS:
{input_file} -file with data
1 2 3 0 6 0 - columns for DH,X,Y,Z,var,sec var
-998.0 1.0e21 - trimming limits
0 -option: 0=grid, 1=cross, 2=jackknife
xvk.dat -file with jackknife data
1 2 0 3 0 - columns for X,Y,Z,vr and sec var
nofile.out -data spacing analysis output file (see note)
0 15.0 - number to search (0 for no dataspacing analysis, rec. 10 or 20) and composite length
0 100 0 -debugging level: 0,3,5,10; max data for GSKV;output total weight of each data?(0=no,1=yes)
{out_sum} -file for debugging output (see note)
{out_grid} -file for kriged output (see GSB note)
{gridstr}
1 1 1 -x,y and z block discretization
1 100 100 1 -min, max data for kriging,upper max for ASO,ASO incr
0 0 -max per octant, max per drillhole (0-> not used)
700.0 700.0 500.0 -maximum search radii
0.0 0.0 0.0 -angles for search ellipsoid
1 -0=SK,1=OK,2=LVM(resid),3=LVM((1-w)*m(u))),4=colo,5=exdrift,6=ICCK
0.0 0.6 0.8 1.6 - mean (if 0,4,5,6), corr. (if 4 or 6), var. reduction factor (if 4)
0 0 0 0 0 0 0 0 0 -drift: x,y,z,xx,yy,zz,xy,xz,zy
0 -0, variable; 1, estimate trend
extdrift.out -gridded file with drift/mean
4 - column number in gridded file
keyout.out -gridded file with keyout (see note)
0 1 - column (0 if no keyout) and value to keep
{varmodelstr}
"""
with open(varmodelfit_outfl_g, 'r') as f:
varmodel_ = f.readlines()
varstr = ''''''
for line in varmodel_:
varstr += line
pars = dict(input_file=os.path.join(outdir,'df_calc.out'),
out_grid=os.path.join(outdir,'kt3dn_df.out'),
out_sum=os.path.join(outdir,'kt3dn_sum.out'),
gridstr=gs.Parameters['data.griddef'], varmodelstr=varstr)
kd3dn.run(parstr=parstr.format(**pars))
# -
# ### Manipulate and plot the $df$ estimate
# pixelplt selects pointvar as the color of the overlain dat_df point data since its name matches the column name of est_df.
# +
est_df = gs.DataFile(os.path.join(outdir,'kt3dn_df.out'))
# Drop the variance since we won't be using it,
# allowing for specification of the column to be avoided
est_df.drop('EstimationVariance')
# Rename to the standard distance function name for convenience
est_df.rename({est_df.variables:dfvar})
est_df.describe()
# +
# Generate a figure object
fig, axes = gs.subplots(1, 2, figsize=(10, 8),cbar_mode='each',
axes_pad=0.8, cbar_pad=0.1)
# Location map of indicator data for comparison
gs.location_plot(dat, ax=axes[0])
# Map of distance function data and estimate
gs.slice_plot(est_df, pointdata=dat_df,
pointkws={'edgecolors':'k', 's':25},
cbar_label='Distance Function (m)', vlim=df_vlim, ax=axes[1])
# -
# ## 6. Boundary Simulation
#
# This section is subdivided into 4 sub-sections:
# 1. Boot starp a value between -c and c using a uniform distribution
# 2. Transform this Gaussian deviate into $df$ deviates with a range of $[−C, C]$
# 3. Add the $df$ deviates to the $df$ estimate, yielding a $df$ realization
# 4. Truncate the realization at $df=0$ , generating a realization of the domain indicator
# +
# Required package for this calculation
from scipy.stats import norm
# Create a directory for the output
domaindir = os.path.join(outdir, 'Domains/')
gs.mkdir(domaindir)
for real in range(nreal):
# Transform the Gaussian deviates to probabilities
sim = np.random.rand()
# Transform the probabilities to distance function deviates
sim = 2 *selected_c * sim - selected_c
# Initialize the final realization as the distance function estimate
df = est_df[dfvar].values
idx = np.logical_and(est_df[dfvar].values>selected_c, est_df[dfvar].values<selected_c)
# Add the distance function deviates to the distance function estimate,
# yielding a distance function realization
df[idx] = df[idx] + sim
# If the distance function is greater than 0, the simulated indicator is 1
sim = (df <= 0).astype(int)
# Convert the Numpy array to a Pandas DataFrame, which is required
# for initializing a DataFile (aside from the demonstrated flname approach).
# The DataFile is then written out
sim = pd.DataFrame(data=sim, columns=[dat.cat])
sim = gs.DataFile(data=sim)
sim.write_file(domaindir+'real{}.out'.format(real+1))
# -
# ### Plot the realizations
fig, axes = gs.subplots(2, 3, figsize=(15, 8), cbar_mode='single')
for real, ax in enumerate(axes):
sim = gs.DataFile(domaindir+'real{}.out'.format(real+1))
gs.slice_plot(sim, title='Realization {}'.format(real+1),
pointdata=dat,
pointkws={'edgecolors':'k', 's':25},
vlim=(0, 1), ax=ax)
# ## 7. Save project settings and clean the output directory
gs.Parameters.save('Parameters.json')
gs.rmdir(outdir) #command to delete generated data file
gs.rmfile('temp')
|
examples/BoundaryModeling.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv("./data/cleaned-data.csv")
df["Week"] = pd.to_datetime(df["Created Date"]).dt.week
df.groupby('Week')['Unique Key'].nunique().plot(kind='bar')
plt.savefig("./tex/pictures/bar.png")
plt.show()
df_bronx = df.query('Borough=="BRONX"')
df_manhattan = df.query('Borough=="MANHATTAN"')
values_manhattan = list(df_manhattan.groupby('Week')['Unique Key'].nunique())#.plot(kind='bar')
values_bronx =list(df_bronx.groupby('Week')['Unique Key'].nunique())
# +
ax = plt.subplot(111)
ax.bar(np.arange(13,33)-0.3, values_manhattan, width=0.3, color='b', align='center', label='Manhattan')
ax.bar(np.arange(13,34), values_bronx, width=0.3, color='g', align='center', label='Bronx')
plt.xlabel('Week')
plt.legend()
plt.savefig('./tex/pictures/comp_bronx_manhattan.png')
plt.show()
# -
|
Analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ls
# cd Desktop/tensorflow-self-driven-car/
# ls
# cd ..
# cd track/
# ls
import os
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import keras
from keras.models import Sequential
from keras.optimizers import Adam
from keras.layers import Convolution2D, MaxPooling2D, Dropout, Flatten, Dense
from sklearn.utils import shuffle
from sklearn.model_selection import train_test_split
import cv2
import pandas as pd
import ntpath
import random
# +
datadir = 'C:/Users/user/Desktop/track'
columns = ['center', 'left', 'right', 'steering', 'throttle', 'reverse', 'speed']
data = pd.read_csv(os.path.join(datadir, 'driving_log.csv'), names = columns)
pd.set_option('display.max_colwidth', -1)
data.head()
# -
def path_leaf(path):
head, tail = ntpath.split(path)
return tail
data['center'] = data['center'].apply(path_leaf)
data['left'] = data['left'].apply(path_leaf)
data['right'] = data['right'].apply(path_leaf)
data.head()
num_bins = 25
samples_per_bin = 200
hist, bins = np.histogram(data['steering'], num_bins)
center = (bins[:-1]+ bins[1:]) * 0.5
plt.bar(center, hist, width=0.05)
plt.plot((np.min(data['steering']), np.max(data['steering'])), (samples_per_bin, samples_per_bin))
# +
print('total data:', len(data))
remove_list = []
for j in range(num_bins):
list_ = []
for i in range(len(data['steering'])):
if data['steering'][i] >= bins[j] and data['steering'][i] <= bins[j+1]:
list_.append(i)
list_ = shuffle(list_)
list_ = list_[samples_per_bin:]
remove_list.extend(list_)
print('removed:', len(remove_list))
data.drop(data.index[remove_list], inplace=True)
print('remaining:', len(data))
hist, _ = np.histogram(data['steering'], (num_bins))
plt.bar(center, hist, width=0.05)
plt.plot((np.min(data['steering']), np.max(data['steering'])), (samples_per_bin, samples_per_bin))
# -
print(data.iloc[1])
def load_img_steering(datadir, df):
image_path = []
steering = []
for i in range(len(data)):
indexed_data = data.iloc[i]
center, left, right = indexed_data[0], indexed_data[1], indexed_data[2]
image_path.append(os.path.join(datadir, center.strip()))
steering.append(float(indexed_data[3]))
image_paths = np.asarray(image_path)
steering = np.asarray(steering)
return image_paths, steering
image_paths, steering = load_img_steering(datadir + '\IMG', data)
x_train, x_valid, y_train, y_valid = train_test_split(image_paths, steering, test_size=0.2, random_state=6)
print('Traning Samples: {}\nValid Samples: {}'.format(len(x_train), len(x_valid)))
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].hist(y_train, bins = num_bins, width=0.05, color='blue')
axes[0].set_title('Traning set')
axes[1].hist(y_valid, bins=num_bins, width=0.05, color='red')
axes[1].set_title('Validation set')
def img_preprocess(img):
img = mpimg.imread(img)
img = img[60:135,:,:]
img = cv2.cvtColor(img, cv2.COLOR_RGB2YUV)
img = cv2.GaussianBlur(img, (3, 3), 0)
img = cv2.resize(img, (200,66))
img = img/255
return img
# +
image = image_paths[100]
original_image = mpimg.imread(image)
preprocessed_image = img_preprocess(image)
fig, axs = plt.subplots(1, 2, figsize=(15, 10))
fig.tight_layout()
axs[0].imshow(original_image)
axs[0].set_title('Original Image')
axs[1].imshow(preprocessed_image)
axs[1].set_title('Preprocessed Image')
# -
x_train = np.array(list(map(img_preprocess, x_train)))
x_valid = np.array(list(map(img_preprocess, x_valid)))
plt.imshow(x_train[random.randint(0, len(x_train)-1)])
plt.axis('off')
print(x_train.shape)
# +
def nvidia_model():
model = Sequential()
model.add(Convolution2D(24, 5, 5, subsample=(2, 2), input_shape=(66, 200, 3), activation='relu'))
model.add(Convolution2D(36, 5, 5, subsample=(2, 2), activation='elu'))
model.add(Convolution2D(48, 5, 5, subsample=(2, 2), activation='elu'))
model.add(Convolution2D(64, 3, 3, activation='elu'))
model.add(Convolution2D(64, 3, 3, activation='elu'))
model.add(Dropout(0.5))
model.add(Flatten())
model.add(Dense(100, activation='elu'))
model.add(Dropout(0.5))
model.add(Dense(50, activation='elu'))
model.add(Dropout(0.5))
model.add(Dense(10, activation='elu'))
model.add(Dropout(0.5))
model.add(Dense(1))
optimizer = Adam(lr=1e-3)
model.compile(loss='mse', optimizer=optimizer)
return model
# -
model = nvidia_model()
print(model.summary())
history = model.fit(x_train, y_train, epochs=30, validation_data=(x_valid, y_valid), batch_size=100, verbose=1, shuffle=1)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.legend(['training', 'validation'])
plt.title('Loss')
plt.xlabel('Epoch')
model.save('model.h5')
from google.colab import files
files.download('model.h5')
|
Behavioural Cloning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Black Scholes Exercise 3: Numexpr implementation
#
# - Use numexpr
# - Use cProfile and Line Profiler to look for bottlenecks and hotspots in the code
# +
# Boilerplate for the example
import cProfile
import pstats
import numpy as np
try:
import numpy.random_intel as rnd
except:
import numpy.random as rnd
# make xrange available in python 3
try:
xrange
except NameError:
xrange = range
SEED = 7777777
S0L = 10.0
S0H = 50.0
XL = 10.0
XH = 50.0
TL = 1.0
TH = 2.0
RISK_FREE = 0.1
VOLATILITY = 0.2
TEST_ARRAY_LENGTH = 1024
###############################################
def gen_data(nopt):
return (
rnd.uniform(S0L, S0H, nopt),
rnd.uniform(XL, XH, nopt),
rnd.uniform(TL, TH, nopt),
)
nopt=100000
price, strike, t = gen_data(nopt)
call = np.zeros(nopt, dtype=np.float64)
put = -np.ones(nopt, dtype=np.float64)
# -
# # The numexpr Black Scholes algorithm
#
# How does this differ from the NumPy and Naive variants?
# +
import numexpr as ne
def black_scholes (nopt, price, strike, t, rate, vol ):
mr = -rate
sig_sig_two = vol * vol * 2
P = price
S = strike
T = t
a = ne.evaluate("log(P / S) ")
b = ne.evaluate("T * mr ")
z = ne.evaluate("T * sig_sig_two ")
c = ne.evaluate("0.25 * z ")
y = ne.evaluate("1/sqrt(z) ")
w1 = ne.evaluate("(a - b + c) * y ")
w2 = ne.evaluate("(a - b - c) * y ")
d1 = ne.evaluate("0.5 + 0.5 * erf(w1) ")
d2 = ne.evaluate("0.5 + 0.5 * erf(w2) ")
Se = ne.evaluate("exp(b) * S ")
call = ne.evaluate("P * d1 - Se * d2 ")
# TODO convert put = call - P + Se to numexpr
return call, put
ne.set_num_threads(ne.detect_number_of_cores())
ne.set_vml_accuracy_mode('high')
# -
# ## Run timeit, cProfile, and/or VTune to see what is happening
# ## Crunching the commands down
#
# What is different in this variant of Black Scholes?
# +
def black_scholes(price, strike, t, rate, vol ):
mr = -rate
sig_sig_two = vol * vol * 2
P = price
S = strike
T = t
call = ne.evaluate("P * (0.5 + 0.5 * erf((log(P / S) - T * mr + 0.25 * T * sig_sig_two) * 1/sqrt(T * sig_sig_two))) - S * exp(T * mr) * (0.5 + 0.5 * erf((log(P / S) - T * mr - 0.25 * T * sig_sig_two) * 1/sqrt(T * sig_sig_two))) ")
put = ne.evaluate("call - P + S * exp(T * mr) ")
# TODO compute put using numexpr
# Note: there is no variable "Se"
return call, put
ne.set_num_threads(ne.detect_number_of_cores())
ne.set_vml_accuracy_mode('high')
# -
# ## Run timeit, cProfile, and/or VTune to see what is happening
|
3_BlackScholes_numexpr.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.6 64-bit (''Pythonic'': pipenv)'
# name: python38664bitpythonicpipenv6de764fe9a9949f68e00c05971b5099c
# ---
# # Python sqlite3
# ```
# Commit : DB에 영구적으로 쓰는 것
# Rollback : Data가 수정되기 전으로 되돌리는 것
# Sqlite3 Data Type : TEXT, NUMERIC, INTEGER, REAL, BLOB
# ```
# 1. DB 생성
# 2. 데이터 삽입
# 3. 데이터 삭제
# 4. 데이터 조회
# 5. 데이터 수정
# ## [1. DB 생성]
# + tags=[]
import sqlite3
# sqlite3 버전 확인
print('sqlite3.version : ', sqlite3.version)
# + tags=[]
import datetime
# 현재 날짜 생성
now = datetime.datetime.now()
print('현재 시간 : ', now)
now_format = now.strftime('%Y년 %m월 %d일 %H시 %M분 %S초')
print('현재 시간 : ', now_format)
# + tags=[]
from pathlib import Path
import sqlite3
# 현재 디렉터리 경로
dir_path = str(Path('__file__').resolve().parent)
# DB 생성 & Auto Commit(isolation_level=None)
connect = sqlite3.connect(dir_path + '/database.db', isolation_level=None)
# Cursor
cursor = connect.cursor()
print(type(cursor))
# 테이블 생성
cursor.execute("CREATE TABLE IF NOT EXISTS users(id INTEGER PRIMARY KEY, username TEXT, email TEXT, register TEXT)")
# 접속 해제
connect.close()
# -
# ## [2. 데이터 삽입]
# + tags=[]
from pathlib import Path
import sqlite3
import datetime
now = datetime.datetime.now().strftime('%Y년 %m월 %d일 %H시 %M분 %S초')
dir_path = str(Path('__file__').resolve().parent)
connect = sqlite3.connect(dir_path + '/database.db', isolation_level=None)
cursor = connect.cursor()
cursor.execute("CREATE TABLE IF NOT EXISTS users(id INTEGER PRIMARY KEY, username TEXT, email TEXT, regdate TEXT)")
# 데이터 삽입
cursor.execute("INSERT INTO users VALUES(1, 'joy', '<EMAIL>', ?)", (now,))
cursor.execute("INSERT INTO users(id, username, email, regdate) VALUES(?, ?, ?, ?)", (2, 'amamov', '<EMAIL>', now))
# 다량의 데이터 삽입(튜플, 리스트)
userlist = (
(3, 'yoon', '<EMAIL>', now),
(4, 'sang', '<EMAIL>', now),
(5, 'wow', '<EMAIL>', now),
)
cursor.executemany("INSERT INTO users(id, username, email, regdate) VALUES(?, ?, ?, ?)", userlist)
# 접속 해제
connect.close()
# -
# ## [3. 데이터 삭제]
# +
from pathlib import Path
import sqlite3
import datetime
now = datetime.datetime.now().strftime('%Y년 %m월 %d일 %H시 %M분 %S초')
dir_path = str(Path('__file__').resolve().parent)
connect = sqlite3.connect(dir_path + '/database.db', isolation_level=None)
cursor = connect.cursor()
# 데이터 모두 삭제
cursor.execute("DELETE FROM users")
# 접속 해제
connect.close()
# + tags=[]
from pathlib import Path
import sqlite3
import datetime
now = datetime.datetime.now().strftime('%Y년 %m월 %d일 %H시 %M분 %S초')
dir_path = str(Path('__file__').resolve().parent)
connect = sqlite3.connect(dir_path + '/database.db', isolation_level=None)
cursor = connect.cursor()
# 테이블을 삭제 후 삭제한 row의 개수를 반환
print('users db deleted : ', cursor.execute("DELETE FROM users").rowcount)
# rollback (참고)
# connect.rollback()
# 접속 해제
connect.close()
# +
from pathlib import Path
import sqlite3
dir_path = str(Path('__file__').resolve().parent)
connect = sqlite3.connect(dir_path + '/database.db', isolation_level=None)
cursor = connect.cursor()
id_3 = (3,)
# 데이터 조건 삭제
cursor.execute("DELETE FROM users WHERE id=?", id_3)
cursor.execute("SELECT * FROM users")
print(cursor.fetchall())
# + tags=[]
from pathlib import Path
import sqlite3
dir_path = str(Path('__file__').resolve().parent)
connect = sqlite3.connect(dir_path + '/database.db', isolation_level=None)
cursor = connect.cursor()
id_1_5 = (3, 5)
# 데이터 조건 삭제
cursor.execute("DELETE FROM users WHERE id IN(?, ?)", id_1_5)
cursor.execute("SELECT * FROM users")
print(cursor.fetchall())
# -
# ## [4. 데이터 조회]
# + tags=[]
from pathlib import Path
import sqlite3
dir_path = str(Path('__file__').resolve().parent)
connect = sqlite3.connect(dir_path + '/database.db', isolation_level=None)
cursor = connect.cursor()
# users의 모든 데이터 조회
cursor.execute("SELECT * FROM users")
first_row = cursor.fetchone()
print('first_row ->', first_row)
size_three_row = cursor.fetchmany(size=3)
print('size_three_row ->', size_three_row)
all_rows = cursor.fetchall()
print('all ->', all_rows)
# + tags=[]
from pathlib import Path
import sqlite3
dir_path = str(Path('__file__').resolve().parent)
connect = sqlite3.connect(dir_path + '/database.db', isolation_level=None)
cursor = connect.cursor()
# users의 모든 데이터 조회
cursor.execute("SELECT * FROM users")
all_rows = cursor.fetchall()
for row in all_rows:
print('row ->', row)
# + tags=[]
from pathlib import Path
import sqlite3
dir_path = str(Path('__file__').resolve().parent)
connect = sqlite3.connect(dir_path + '/database.db', isolation_level=None)
cursor = connect.cursor()
id_3 = (3,)
# 데이터 조건 조회
cursor.execute("SELECT * FROM users WHERE id=?", id_3)
print(cursor.fetchone())
# + tags=[]
from pathlib import Path
import sqlite3
dir_path = str(Path('__file__').resolve().parent)
connect = sqlite3.connect(dir_path + '/database.db', isolation_level=None)
cursor = connect.cursor()
id_1_5 = (1, 5)
# 데이터 조건 조회
cursor.execute("SELECT * FROM users WHERE id IN(?, ?)", id_1_5)
print(cursor.fetchall())
# -
# ## [Dump 출력]
# + tags=[]
from pathlib import Path
import sqlite3
dir_path = str(Path('__file__').resolve().parent)
connect = sqlite3.connect(dir_path + '/database.db', isolation_level=None)
cursor = connect.cursor()
with connect:
with open(dir_path + '/test_files/dump.sql', 'w') as file:
for line in connect.iterdump():
file.write('%s\n' % line)
print('Dump Print Complete!')
# -
# ## [5. 데이터 수정]
# + tags=[]
from pathlib import Path
import sqlite3
dir_path = str(Path('__file__').resolve().parent)
connect = sqlite3.connect(dir_path + '/database.db', isolation_level=None)
cursor = connect.cursor()
cursor.execute("UPDATE users SET username = ? WHERE id = ?", ('joyjoy', 2))
cursor.execute("SELECT * FROM users")
print(cursor.fetchall())
# -
|
04_data_handle/02_sqlite3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Multiclass classifier
#
# Classify articles from a Reuters dataset having 46 different categories
# ### Import libraries
# +
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras import models, layers, optimizers, losses, metrics
from tensorflow.keras.datasets import reuters
from tensorflow.keras.utils import to_categorical
# -
# ### Get datasets
# +
LIMIT_WORD = 10000
(train_data, train_labels), (test_data, test_labels) = reuters.load_data(num_words=LIMIT_WORD)
# -
# ### Data exploring (convert sequences to original review)
def convert_to_english(sequence):
word_index = reuters.get_word_index()
reverse_word_index = dict(
[(value, key) for (key, value) in word_index.items()]
)
decoded_review = " ".join(
[reverse_word_index.get(i - 3, '?') for i in sequence]
)
return decoded_review
print(convert_to_english(train_data[0]))
# ### Pre-process the data (convert sequences into tensors)
def vectorize_sequences(sequences, dimension=LIMIT_WORD):
results = np.zeros((len(sequences), dimension))
for i, sequence in enumerate(sequences):
results[i, sequence] = 1
return results
# #### Vectorize examples
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)
x_train[0]
# #### One-hot encoding of labels (categorical encoding)
one_hot_train_labels = to_categorical(train_labels)
one_hot_test_labels = to_categorical(test_labels)
one_hot_train_labels[0]
# ### Building the network
#
# #### Architecture
#
# - 2 intermediate Dense layers with 16 hidden unites per each (relu actovation function)
# - 1 output layer (with sigmoid activation function)
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(LIMIT_WORD,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))
# #### Compile
#
# **Loss function:** _binary crossentropy_
# **Optimizer:** _rmsprop_
model.compile(
optimizer=optimizers.RMSprop(lr=0.001),
loss=losses.categorical_crossentropy,
metrics=[metrics.categorical_accuracy]
)
# #### Training
# - Define validation data
# - Define epochs and batch size
# - Fit the model
x_val = x_train[:1000]
partial_x_train = x_train[1000:]
y_val = one_hot_train_labels[:1000]
partial_y_train = one_hot_train_labels[1000:]
history = model.fit(
partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val, y_val)
)
# ### Plot results
#
# #### Training and validation loss
# +
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
acc = history_dict['categorical_accuracy']
epochs = range(1, len(acc) + 1)
plt.plot(epochs, loss_values, 'bo', label='Training loss')
plt.plot(epochs, val_loss_values, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show
# -
history_dict.keys()
# #### Training and validation accuracy
# +
plt.clf()
acc_values = history_dict['categorical_accuracy']
val_acc_values = history_dict['val_categorical_accuracy']
plt.plot(epochs, acc_values, 'bo', label='Training accuracy')
plt.plot(epochs, val_acc_values, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show
# -
# The graphs show that the model starts overfitting after ~10 epochs. Let's train it again with better hyperparameters
# +
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(LIMIT_WORD,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))
model.compile(
optimizer=optimizers.RMSprop(lr=0.001),
loss=losses.categorical_crossentropy,
metrics=[metrics.categorical_accuracy]
)
model.fit(
partial_x_train,
partial_y_train,
epochs=10,
batch_size=512,
validation_data=(x_val, y_val)
)
results = model.evaluate(x_test, one_hot_test_labels)
# -
print(results)
model.predict(x_test)
# With this approach we obtained an accuracy of ~80%.
|
notebooks/chapter_03/02 - Multiclass classifier.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/yanpaing-DL/TensorFlow-Beginner/blob/main/coding-exercise/week4/part2/Augmentation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="PhLkFlLy66Tn"
# # Loading dataset and make a directory
# + id="R9POLi3FAn7o"
# Downloading dataset
# !wget --no-check-certificate \
# https://storage.googleapis.com/laurencemoroney-blog.appspot.com/horse-or-human.zip \
# -O /tmp/horse-or-human.zip
# !wget --no-check-certificate \
# https://storage.googleapis.com/laurencemoroney-blog.appspot.com/validation-horse-or-human.zip \
# -O /tmp/validation-horse-or-human.zip
# + id="usfHyYjwBtRX"
# Unzipping zip file and extract
import os
import zipfile
local_zip = '/tmp/horse-or-human.zip' # create a directory
zip_ref = zipfile.ZipFile(local_zip, 'r') # read zipfile
zip_ref.extractall('/tmp/horse-or-human') # extract all data from zipfile
local_zip = '/tmp/validation-horse-or-human.zip' # create a directory
zip_ref = zipfile.ZipFile(local_zip, 'r') # read zipfile
zip_ref.extractall('/tmp/validation-horse-or-human') # extract all data from zipfile
zip_ref.close()
# + id="Uof22I6vJE87" outputId="f4be2467-c967-492e-d8fb-44fbf98ab594" colab={"base_uri": "https://localhost:8080/", "height": 391}
# join path with os module
train_horse_dir = os.path.join('/tmp/horse-or-human/horses')
train_human_dir = os.path.join('/tmp/horse-or-human/humans')
validation_horse_dir = os.path.join('/tmp/validation-horse-or-human/horses')
validation_human_dir = os.path.join('/tmp/validation-horse-or-human/humans')
# + [markdown] id="px4JgamaB-Fq"
# # Build Model
# + id="qmciCo3ONy-Q"
import tensorflow as tf
model = tf.keras.models.Sequential([
# Note the input shape is the desired size of the image 300x300 with 3 bytes color
# This is the first convolution
tf.keras.layers.Conv2D(16, (3,3), activation='relu', input_shape=(300, 300, 3)),
tf.keras.layers.MaxPooling2D(2, 2),
# The second convolution
tf.keras.layers.Conv2D(32, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# The third convolution
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# The fourth convolution
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# The fifth convolution
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# Flatten the results to feed into a DNN
tf.keras.layers.Flatten(),
# 512 neuron hidden layer
tf.keras.layers.Dense(512, activation='relu'),
# Only 1 output neuron. It will contain a value from 0-1 where 0 for 1 class ('horses') and 1 for the other ('humans')
tf.keras.layers.Dense(1, activation='sigmoid')
])
# + [markdown] id="_UYmABJv9CJ7"
# # Optimization
# + id="moeO4Y-IN5rH"
from tensorflow.keras.optimizers import RMSprop
model.compile(loss='binary_crossentropy',
optimizer=RMSprop(lr=1e-4),
metrics=['accuracy'])
# + [markdown] id="rfwRLsuN9KpE"
# # Data preprocessing with ImageDataGenerator
# + id="o08RVXGzOE2C" outputId="a6775eff-80fe-411a-eff2-52db71c9b674" colab={"base_uri": "https://localhost:8080/", "height": 51}
from tensorflow.keras.preprocessing.image import ImageDataGenerator
# All images will be rescaled by 1./255
train_datagen = ImageDataGenerator(
rescale=1./255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
validation_datagen = ImageDataGenerator(rescale=1/255)
# Flow training images in batches of 128 using train_datagen generator
train_generator = train_datagen.flow_from_directory(
'/tmp/horse-or-human/', # This is the source directory for training images
target_size=(300, 300), # All images will be resized to 150x150
batch_size=128,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
# Flow training images in batches of 128 using train_datagen generator
validation_generator = validation_datagen.flow_from_directory(
'/tmp/validation-horse-or-human/', # This is the source directory for training images
target_size=(300, 300), # All images will be resized to 150x150
batch_size=32,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
# + [markdown] id="GYgSkSif9SZq"
# # Model training
# + id="NTMQkxuyOJVe" outputId="2c8a34e7-8237-43a5-d90f-bb9b71c13410" colab={"base_uri": "https://localhost:8080/", "height": 1000}
history = model.fit(
train_generator,
steps_per_epoch=8,
epochs=100,
verbose=1,
validation_data = validation_generator,
validation_steps=8)
# + [markdown] id="gUaeE0Mp9bkH"
# # Check in Model Accuracy
# + id="iJG43x5pXZm8" outputId="21be5ebf-94bd-4fe9-e1a9-f90ab3d53ecb" colab={"base_uri": "https://localhost:8080/", "height": 545}
import matplotlib.pyplot as plt
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'r', label='Training accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.figure()
plt.plot(epochs, loss, 'r', label='Training Loss')
plt.plot(epochs, val_loss, 'b', label='Validation Loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
|
coding-exercise/week4/part2/Augmentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Advanced Lane Finding Project
#
# The goals / steps of this project are the following:
#
# * Compute the camera calibration matrix and distortion coefficients given a set of chessboard images.
# * Apply a distortion correction to raw images.
# * Use color transforms, gradients, etc., to create a thresholded binary image.
# * Apply a perspective transform to rectify binary image ("birds-eye view").
# * Detect lane pixels and fit to find the lane boundary.
# * Determine the curvature of the lane and vehicle position with respect to center.
# * Warp the detected lane boundaries back onto the original image.
# * Output visual display of the lane boundaries and numerical estimation of lane curvature and vehicle position.
#
# ---
# ## First, I'll compute the camera calibration using chessboard images
# +
import numpy as np
import cv2
import glob
import matplotlib.pyplot as plt
# %matplotlib qt
# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((6*9,3), np.float32)
objp[:,:2] = np.mgrid[0:9,0:6].T.reshape(-1,2)
# Arrays to store object points and image points from all the images.
objpoints = [] # 3d points in real world space
imgpoints = [] # 2d points in image plane.
# Make a list of calibration images
images = glob.glob('../camera_cal/calibration*.jpg')
# Step through the list and search for chessboard corners
for fname in images:
img = cv2.imread(fname)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# Find the chessboard corners
ret, corners = cv2.findChessboardCorners(gray, (9,6),None)
# If found, add object points, image points
if ret == True:
objpoints.append(objp)
imgpoints.append(corners)
# Draw and display the corners
#img = cv2.drawChessboardCorners(img, (9,6), corners, ret)
#cv2.imshow('img',img)
#cv2.waitKey(500)
#cv2.destroyAllWindows()
# -
# ## And so on and so forth...
# +
import numpy as np
import cv2
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import os
import pickle
# Import everything needed to edit/save/watch video clips
from moviepy.editor import VideoFileClip
from IPython.display import HTML
from PIL import Image, ImageFont, ImageDraw
#output of camera calibration
mtx = None
dist = None
first_frame = False
left_fit,right_fit = None,None
def convertImage(images,convertion_type):
converted_images = []
#This will return an image with only one color channel
if(images is not None) and (len(images) > 0) and (convertion_type is not None):
if (type(images) is list):
for image_item in images:
converted_image = cv2.cvtColor(image_item,convertion_type)
converted_images.append(converted_image)
else:
converted_images = cv2.cvtColor(images,convertion_type)
return converted_images
def weighted_img(img, initial_img, α=0.8, β=1., γ=0.):
"""
`img` is the output of the hough_lines(), An image with lines drawn on it.
Should be a blank image (all black) with lines drawn on it.
`initial_img` should be the image before any processing.
The result image is computed as follows:
initial_img * α + img * β + γ
NOTE: initial_img and img must be the same shape!
"""
return cv2.addWeighted(initial_img, α, img, β, γ)
def readImages(folder_name):
#the list that will contain all calibraion images
images_list = []
#select the source folder for calibration images
images_names = os.listdir(str(folder_name))
for cal_image_name in images_names:
#Create relative path of the image
image_full_name = str(folder_name)+str("/")+str(cal_image_name)
#read the image
image = cv2.imread(image_full_name)
images_list.append(image)
return images_names,images_list
def saveImage(save_path,image_name,image_file):
if(image_name is not None) and (save_path is not None) and (len(image_name) > 0) and (len(image_file) > 0) :
#saving files
name_of_file = image_name+"_output.jpg"
completeName = os.path.join(save_path, name_of_file)
#x= cv2.imwrite(save_path+name_of_file,image_file)
cv2.imwrite(completeName,image_file,[int(cv2.IMWRITE_PNG_COMPRESSION), 9])
#x= cv2.imwrite("./output_images/"+name_of_file,image_file,[int(cv2.IMWRITE_PNG_COMPRESSION), 9])
#cv2.imwrite("./output_images/"+img ,output)
# Used for duébugging to make sure that the output is written
#return x
# +
#Used for debugging to check if the files are exist
import os
os.listdir("test_images/")
# -
for img in os.listdir("test_images/"):
print("test_images/"+img)
#= mpimg.imread('test_images/solidWhiteCurve.jpg')
image = mpimg.imread("test_images/"+img)
#output = Lane_Detction(image)
#"imwrite" always re-encode image data (with some parameters which is not same
#as for original image, so image quality may be reduced).
#x= cv2.imwrite("./output_images/"+img ,image)
#x=saveImage ("./output_images/",img , image )
# Used for duébugging to make sure that the output is written
#print(x)
# +
def findChessboardCorners(gray_cal_images,nx,ny,images_names,images):
objpoints = [] #3D points in real world space
imgpoints = [] #2D points in image plan
# prepare object points like (0,0,0),(1,0,0),(2,0,0).....(8,5,0)
objp = np.zeros((6*9,3),np.float32)
objp[:,:2] = np.mgrid[0:9,0:6].T.reshape(-1,2)
image_index = 0
for gray_cal_image in gray_cal_images:
#find chessboard corners in the image
ret, corners = cv2.findChessboardCorners(gray_cal_image, (nx, ny), None)
#Check if the function worked properly
if ret == True:
objpoints.append(objp)
imgpoints.append(corners)
# Use CV2 library for drawing and displaying the corners
img = cv2.drawChessboardCorners(images[image_index], (nx, ny), corners, ret)
saveImage("./output_images/calibration_output/",images_names[image_index][:-4],img)
image_index = image_index + 1
return objpoints,imgpoints
def checkCalibrationData():
#Check if the file exist
exists = os.path.isfile('Calibration_data.p')
return exists
def readCalibrationData():
# Read in the saved objpoints and imgpoints
dist_pickle = pickle.load( open( "Calibration_data.p", "rb" ) )
mtx = dist_pickle["mtx"]
dist = dist_pickle["dist"]
return mtx,dist
def SaveCalibrationData(mtx,dist):
dist_pickle = {}
if(mtx is not None) and (dist is not None):
dist_pickle["mtx"] = mtx
dist_pickle["dist"] = dist
pickle.dump(dist_pickle,open("Calibration_data.p","wb"))
def calibrateCamera(nx,ny):
mtx = None
dist = None
camera_cal_exist = False
camera_cal_exist = checkCalibrationData()
if(camera_cal_exist is True):
mtx,dist = readCalibrationData()
if(camera_cal_exist is False) or (mtx is None) or (dist is None):
#read calibration images
cal_images_names,cal_images = readImages("camera_cal")
gray_cal_images = convertImage(cal_images,cv2.COLOR_BGR2GRAY)
if (gray_cal_images is not None) and (len(gray_cal_images) > 0):
# Find the chessboard corners
objpoints,imgpoints = findChessboardCorners(gray_cal_images,nx,ny,cal_images_names,cal_images)
#imgpoints = np.array(imgpoints).astype('float32')
img_size = (cal_images[0].shape[1],cal_images[0].shape[0])
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints,imgpoints,img_size, None, None)
#save the calibration
SaveCalibrationData(mtx,dist)
return mtx, dist
def calibrateCamera_trial(nx,ny):
mtx = None
dist = None
#read calibration images
cal_images_names,cal_images = readImages("camera_cal")
#Please note we are using COLOR_BGR2GRAY because we used cv2.imread at reaing
gray_cal_images = convertImage(cal_images,cv2.COLOR_BGR2GRAY)
# Find the chessboard corners
objpoints,imgpoints = findChessboardCorners(gray_cal_images,nx,ny,cal_images_names,cal_images)
#imgpoints = np.array(imgpoints).astype('float32')
img_size = (cal_images[0].shape[1],cal_images[0].shape[0])
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints,imgpoints,img_size, None, None)
return mtx, dist
def measureCurvaturePixels(left_fit,right_fit,ploty):
# Calculates the curvature of polynomial functions in pixels.
# Define y-value where we want radius of curvature
# We'll choose the maximum y-value, corresponding to the bottom of the image
y_eval = np.max(ploty)
# Calculation of R_curve (radius of curvature)
left_curverad = ((1 + (2*left_fit[0]*y_eval + left_fit[1])**2)**1.5) / np.absolute(2*left_fit[0])
right_curverad = ((1 + (2*right_fit[0]*y_eval + right_fit[1])**2)**1.5) / np.absolute(2*right_fit[0])
return left_curverad, right_curverad
def undistortImage(image,mtx,dist,save_image,save_path,image_name):
undistorted_image = cv2.undistort(image, mtx, dist,None)
#save the undistorted image
if(save_image is True):
saveImage("./output_images/undistortion_output",image_name,undistorted_image)
return undistorted_image
#Test the function and plot the image
#caibrate the camera
#nx and ny are the numer of intersections between white and black
image_trial = cv2.imread('test_images/test2.jpg')
nx_trial = 9
ny_trial = 6
mtx_trial, dist_trial = calibrateCamera_trial(nx_trial,ny_trial)
undistorted_image_trial = undistortImage(image_trial,mtx_trial,dist_trial,None,None,None)
plt.imshow(undistorted_image_trial)
# -
gray_image_trial = convertImage(undistorted_image_trial,cv2.COLOR_BGR2GRAY)
plt.imshow(gray_image_trial)
# +
def absSobelThresh(gray_image,sobel_kernel,orientaion):
#Calculate the derivative in the xx direction (the 1, 0 at the end denotes xx direction)
if orientaion == 'x':
sobelx = cv2.Sobel(gray_image,cv2.CV_64F,1,0,ksize = sobel_kernel)
abs_sobel_thresh = np.absolute(sobelx)
elif orientaion == 'y':
sobely = cv2.Sobel(gray_image,cv2.CV_64F,0,1,ksize = sobel_kernel)
abs_sobel_thresh = np.absolute(sobely)
else:
abs_sobel_thresh = None
return abs_sobel_thresh
def createBinaryImage(gradient,min_threshold,max_threshold):
#create zeros vector with the size of gradient
grad_binary_image = np.zeros_like(gradient)
#set the pixels that more than min threshold and less than max_threshold with 1
grad_binary_image[(gradient >= min_threshold) & (gradient <= max_threshold)] = 1
return grad_binary_image
def magnitudeThresh(gray_image,abs_sobelx,abs_sobely,mag_thresh_min,mag_thresh_max):
# Calculate the gradient magnitude
gradmag = np.sqrt(abs_sobelx**2,abs_sobely**2)
#Convert the absolute value image to 8-bit
scaled_gradmag = np.uint8(255 * gradmag/np.max(gradmag))
mag_binary_image = createBinaryImage(scaled_gradmag,mag_thresh_min,mag_thresh_max)
return mag_binary_image
def dirThreshold(gray_image,abs_sobelx,abs_sobely,dir_min_threshold,dir_max_threshold):
# Calculate gradient direction
# Apply threshold
graddir = np.arctan2(abs_sobely,abs_sobelx)
dir_binary_image = createBinaryImage(graddir,dir_min_threshold,dir_max_threshold)
return dir_binary_image
def combineMagDirThresholds(mag_binary_image,dir_binary_image,abs_sobelx,abs_sobely):
combined_binary_image = np.zeros_like(dir_binary_image)
combined_binary_image[(abs_sobelx == 1) & (abs_sobely == 1) | ((mag_binary_image == 1) & (dir_binary_image == 1))] = 1
return combined_binary_image
def applyMagDirThresholds(gray_image,sobel_kernel,mag_min_thresh,mag_max_thresh,dir_min_thresh,dir_max_thresh,save_image,save_path,image_name):
#apply Sobel threshold
abs_sobelx = absSobelThresh(gray_image,sobel_kernel,'x')
abs_sobely = absSobelThresh(gray_image,sobel_kernel,'y')
#apply magnitude Threshold
mag_threshold_binary_image = magnitudeThresh(gray_image,abs_sobelx,abs_sobely,mag_min_thresh,mag_max_thresh)
#apply direction threshold
dir_threshold_binary_image = dirThreshold(gray_image,abs_sobelx,abs_sobely,dir_min_thresh,dir_max_thresh)
#combine the magnitude and direction thresholds into 1 threshold
combined_mag_dir_binary_image = combineMagDirThresholds(mag_threshold_binary_image,dir_threshold_binary_image,dir_min_thresh,dir_max_thresh)
#save the undistorted image
if(save_image is True):
mag_dir_example_image = combined_mag_dir_binary_image *255
saveImage("./output_images/gradient/mag_dir",image_name,mag_dir_example_image)
return combined_mag_dir_binary_image
def applyColorThreshold(original_image,s_min_threshold,s_max_threshold):
hls_image = convertImage(original_image,cv2.COLOR_BGR2HLS)
s_channel_image = hls_image[:,:,2]
color_gradient_binary_output = createBinaryImage(s_channel_image,s_min_threshold,s_max_threshold)
return color_gradient_binary_output
def applyDifferentGradients(image,gray_image,save_image,save_path,image_name):
combined_mag_dir_binary_image = applyMagDirThresholds(gray_image,3,30,100,0,np.pi/2,save_image,save_path,image_name)
color_threshold_binary_image = applyColorThreshold(image,170,255)
combined_mag_dir_color_image = np.zeros_like(combined_mag_dir_binary_image)
combined_mag_dir_color_image[(combined_mag_dir_binary_image == 1) | (color_threshold_binary_image == 1)] = 1
if(save_image is True):
all_gradients_example = combined_mag_dir_color_image*255
saveImage(str(save_path)+"/gradient/color_mag_dir",image_name,all_gradients_example)
return combined_mag_dir_color_image
#apply gradients
combined_mag_dir_color_image_trial = applyDifferentGradients(image_trial,gray_image_trial,None,None,None)
plt.imshow(combined_mag_dir_color_image_trial)
# +
def GetBirdEyeView(gradient_binary_image,save_image,save_path,image_name):
h, w = gradient_binary_image.shape[:2]
# This should be chosen to present the result at the proper aspect ratio
# My choice of 100 pixels is not exact, but close enough for our purpose here
# offset for dst points
offset = 100
src = np.float32([[w, h-10], # br
[0, h-10], # bl
[(w/2) - offset, (h/2) + offset], # tl
[(w/2) + offset, (h/2) + offset] ]) # tr
dst = np.float32([[w, h], # br
[0, h], # bl
[0, 0], # tl
[w, 0] ]) # tr
M = cv2.getPerspectiveTransform(src, dst)
Minv = cv2.getPerspectiveTransform(dst,src)
Bird_eye_view_binary = cv2.warpPerspective(gradient_binary_image, M, (w, h), flags=cv2.INTER_LINEAR)
if(save_image is True):
bird_eye_example = Bird_eye_view_binary*255
saveImage(str(save_path)+"/bird_eye_output",image_name,bird_eye_example)
return Bird_eye_view_binary,Minv
bird_eye_binary_image_trial,Minv_trial = GetBirdEyeView(combined_mag_dir_color_image_trial,None,None,None)
plt.imshow(bird_eye_binary_image_trial)
# +
def getHist(binary_warped_image):
height = binary_warped_image.shape[0]
# Lane lines are likely to be mostly vertical nearest to the car
bottom_half = binary_warped_image[height//2:,:]
# i.e. the highest areas of vertical lines should be larger values
histogram = np.sum(bottom_half,axis = 0)
return histogram
def findLanesPixels(binary_warped,nwindows,margin,minpix):
#get the histogram of the image
histogram = getHist(binary_warped)
#get the height
image_height = binary_warped.shape[0]
# Create an output image to draw on and visualize the result
out_img = np.dstack((binary_warped, binary_warped, binary_warped))*255
# Find the peak of the left and right halves of the histogram
# These will be the starting point for the left and right lines
midpoint = np.int(image_height//2)
right_side_values = histogram[midpoint:]
left_side_values = histogram[:midpoint]
#find the index where there is maximum pixel value starting from beginning to the mid point
leftx_base = np.argmax(left_side_values)
#find the index where there is maximum pixel value starting from the mid point till the end of histogram
rightx_base = np.argmax(right_side_values) + midpoint
# Set height of windows - based on nwindows above and image shape
window_height = np.int(image_height//nwindows)
# Identify the x and y positions of all nonzero pixels in the image
nonzero = binary_warped.nonzero()
#get the coulmn indicies that doesn't contain zeros
nonzeroy = np.array(nonzero[0])
#get the row indicies that doesn't contain zeros
nonzerox = np.array(nonzero[1])
# Current positions to be updated later for each window in nwindows
leftx_current = leftx_base
rightx_current = rightx_base
# Create empty lists to receive left and right lane pixel indices
left_lane_inds = []
right_lane_inds = []
# Step through the windows one by one
for window in range(nwindows):
# Identify window boundaries in x and y (and right and left)
win_y_low = image_height - (window+1)*window_height #720 - 80
win_y_high = image_height - window*window_height #720
#Find the four below boundaries of the window
win_xleft_low = leftx_current - margin
win_xleft_high = leftx_current + margin
win_xright_low = rightx_current - margin
win_xright_high = rightx_current + margin
# Draw the window on left line
#cv2.rectangle(out_img,(win_xleft_low,win_y_low),(win_xleft_high,win_y_high),(0,255,0), 2)
#draw the window on the right line
#cv2.rectangle(out_img,(win_xright_low,win_y_low),(win_xright_high,win_y_high),(0,255,0), 2)
#Identifying the nonzero pixels in x and y within the window
#mark the left pixels that are within the valid range
good_left = ((nonzeroy >= win_y_low) & (nonzeroy < win_y_high) &
(nonzerox >= win_xleft_low) & (nonzerox < win_xleft_high))
#Get the y indicies that contains True values
good_left_inds = good_left.nonzero()[0]
#Mark the left pixels that are within the valid range
good_right = ((nonzeroy >= win_y_low) & (nonzeroy < win_y_high) &
(nonzerox >= win_xright_low) & (nonzerox < win_xright_high))
#Getting the y indicies that contains True values
good_right_inds = good_right.nonzero()[0]
# Append these indices to the lists
left_lane_inds.append(good_left_inds)
right_lane_inds.append(good_right_inds)
# If you found > minpix pixels, recenter next window on their mean position
if len(good_left_inds) > minpix:
#get the indicies values of the wraped image
good_left_indicies_wraped = nonzerox[good_left_inds]
#get the middle index of them
leftx_current = np.int(np.mean(good_left_indicies_wraped))
if len(good_right_inds) > minpix:
#get the indicies values of the wraped image
good_right_indicies_wraped = nonzerox[good_right_inds]
#get the middle index of them
rightx_current = np.int(np.mean(good_right_indicies_wraped))
# Concatenate the arrays of indices (previously was a list of lists of pixels)
try:
#convert multiple lists into 1 big array
left_lane_inds = np.concatenate(left_lane_inds)
right_lane_inds = np.concatenate(right_lane_inds)
except ValueError:
# Avoids an error if the above is not implemented fully
pass
# Extract left and right line pixel positions
leftx = nonzerox[left_lane_inds]
lefty = nonzeroy[left_lane_inds]
rightx = nonzerox[right_lane_inds]
righty = nonzeroy[right_lane_inds]
return leftx, lefty, rightx, righty, out_img
def fitPolynomial(binary_warped_img_shape, leftx, lefty, rightx, righty):
left_fit = np.polyfit(lefty, leftx, 2)
right_fit = np.polyfit(righty, rightx, 2)
# Generate x and y values for plotting
ploty = np.linspace(0, binary_warped_img_shape[0]-1, binary_warped_img_shape[0])
#Calc both polynomials using ploty, left_fit and right_fit ###
left_fitx = left_fit[0]*ploty**2 + left_fit[1]*ploty + left_fit[2]
right_fitx = right_fit[0]*ploty**2 + right_fit[1]*ploty + right_fit[2]
return left_fit,right_fit,left_fitx, right_fitx, ploty
def fitCurvatureUsingSlidingWindow(binary_warped_image,nwindows,margin,minpix):
# Find our lane pixels first
leftx, lefty, rightx, righty, out_img = findLanesPixels(binary_warped_image,nwindows,margin,minpix)
# Fit a second order polynomial to each using `np.polyfit`
left_fit,right_fit,left_fitx, right_fitx, ploty = fitPolynomial(binary_warped_image.shape, leftx, lefty, rightx, righty)
## Visualization ##
# Colors in the left and right lane regions
out_img[lefty, leftx] = [255, 0, 0]
out_img[righty, rightx] = [0, 0, 255]
return left_fit,right_fit,ploty,left_fitx,right_fitx,out_img
def fitCurvatureUsingPreviousPoly(binary_warped,left_fit,right_fit):
# HYPERPARAMETER
# Choose the width of the margin around the previous polynomial to search
# The quiz grader expects 100 here, but feel free to tune on your own!
margin = 100
# Grab activated pixels
nonzero = binary_warped.nonzero()
nonzeroy = np.array(nonzero[0])
nonzerox = np.array(nonzero[1])
### Set the area of search based on activated x-values ###
### within the +/- margin of our polynomial function ###
### Hint: consider the window areas for the similarly named variables ###
### in the previous quiz, but change the windows to our new search area ###
left_lane_inds = ((nonzerox > (left_fit[0]*(nonzeroy**2) + left_fit[1]*nonzeroy +
left_fit[2] - margin)) & (nonzerox < (left_fit[0]*(nonzeroy**2) +
left_fit[1]*nonzeroy + left_fit[2] + margin)))
right_lane_inds = ((nonzerox > (right_fit[0]*(nonzeroy**2) + right_fit[1]*nonzeroy +
right_fit[2] - margin)) & (nonzerox < (right_fit[0]*(nonzeroy**2) +
right_fit[1]*nonzeroy + right_fit[2] + margin)))
# Again, extract left and right line pixel positions
leftx = nonzerox[left_lane_inds]
lefty = nonzeroy[left_lane_inds]
rightx = nonzerox[right_lane_inds]
righty = nonzeroy[right_lane_inds]
# Fit new polynomials
left_fit,right_fit,left_fitx, right_fitx, ploty = fitPolynomial(binary_warped.shape, leftx, lefty, rightx, righty)
## Visualization ##
# Create an image to draw on and an image to show the selection window
out_img = np.dstack((binary_warped, binary_warped, binary_warped))*255
window_img = np.zeros_like(out_img)
# Color in left and right line pixels
out_img[nonzeroy[left_lane_inds], nonzerox[left_lane_inds]] = [255, 0, 0]
out_img[nonzeroy[right_lane_inds], nonzerox[right_lane_inds]] = [0, 0, 255]
# Generate a polygon to illustrate the search window area
# And recast the x and y points into usable format for cv2.fillPoly()
left_line_window1 = np.array([np.transpose(np.vstack([left_fitx-margin, ploty]))])
left_line_window2 = np.array([np.flipud(np.transpose(np.vstack([left_fitx+margin,
ploty])))])
left_line_pts = np.hstack((left_line_window1, left_line_window2))
right_line_window1 = np.array([np.transpose(np.vstack([right_fitx-margin, ploty]))])
right_line_window2 = np.array([np.flipud(np.transpose(np.vstack([right_fitx+margin,
ploty])))])
right_line_pts = np.hstack((right_line_window1, right_line_window2))
# Draw the lane onto the warped blank image
cv2.fillPoly(window_img, np.int_([left_line_pts]), (0,255, 0))
cv2.fillPoly(window_img, np.int_([right_line_pts]), (0,255, 0))
curved_binary_image = cv2.addWeighted(out_img, 1, window_img, 0.3, 0)
return left_fit,right_fit,ploty,left_fitx,right_fitx,curved_binary_image
def findCurvatures(bird_eye_binary_image,nwindows,margin,minpix):
global left_fit,right_fit
global first_frame
if first_frame is True:
left_fit,right_fit,ploty,left_fitx,right_fitx,curved_binary_image = fitCurvatureUsingSlidingWindow(bird_eye_binary_image,nwindows,margin,minpix)
first_frame = False
else:
left_fit,right_fit,ploty,left_fitx,right_fitx,curved_binary_image = fitCurvatureUsingPreviousPoly(bird_eye_binary_image,left_fit,right_fit)
return ploty,left_fitx,right_fitx,curved_binary_image
# HYPERPARAMETERS
# Choose the number of sliding windows
nwindows_trial = 9
# Set the width of the windows +/- margin
margin_trial = 100
# Set minimum number of pixels found to recenter window
minpix_trial = 50
global first_frame
first_frame = True
ploty_trial,left_fitx_trial,right_fitx_trial,curved_binary_image_trial = findCurvatures(bird_eye_binary_image_trial,nwindows_trial,margin_trial,minpix_trial)
plt.imshow(curved_binary_image_trial)
first_frame = True
# +
def insertAreaBetweenLanes(left_fitx,right_fitx,ploty,road_warp):
# Recast the x and y points into usable format for cv2.fillPoly()
pts_left = np.array([np.transpose(np.vstack([left_fitx, ploty]))])
pts_right = np.array([np.flipud(np.transpose(np.vstack([right_fitx, ploty])))])
pts = np.hstack((pts_left, pts_right))
# Draw the lane onto the warped blank image
cv2.fillPoly(road_warp,np.int_([pts]),(0,255, 0))
def alignLanesWithImage(road_warp,Minv,curved_binary_image,image):
restored_curved_binary_image = cv2.warpPerspective(road_warp,Minv,(curved_binary_image.shape[1],curved_binary_image.shape[0]))
restored_curved_binary_image = restored_curved_binary_image.astype(np.uint8)
final_image = weighted_img(restored_curved_binary_image,image, 0.8, 1, 0)
return final_image
def insertLanesAreaonImage(image,undistorted_image,curved_binary_image,left_fitx,right_fitx,ploty,Minv):
# Create an image to draw the lines on
road_warp = np.zeros_like(undistorted_image,dtype=np.uint8)
#Draw the green area between lanes
insertAreaBetweenLanes(left_fitx,right_fitx,ploty,road_warp)
lanes_inserted_image = alignLanesWithImage(road_warp,Minv,curved_binary_image,image)
return lanes_inserted_image
lanes_inserted_image_trial = insertLanesAreaonImage(image_trial,undistorted_image_trial,curved_binary_image_trial,left_fitx_trial,right_fitx_trial,ploty_trial,Minv_trial)
plt.imshow(lanes_inserted_image_trial)
# +
def measureCurvatureReal(ploty, left_fit_cr, right_fit_cr):
'''
Calculates the curvature of polynomial functions in meters.
'''
# Define conversions in x and y from pixels space to meters
ym_per_pix = 30/720 # meters per pixel in y dimension
xm_per_pix = 3.7/700 # meters per pixel in x dimension
# Define y-value where we want radius of curvature
# We'll choose the maximum y-value, corresponding to the bottom of the image
y_eval = np.max(ploty)
# Calculation of R_curve (radius of curvature)
left_curverad = ((1 + (2*left_fit_cr[0]*y_eval*ym_per_pix + left_fit_cr[1])**2)**1.5) / np.absolute(2*left_fit_cr[0])
right_curverad = ((1 + (2*right_fit_cr[0]*y_eval*ym_per_pix + right_fit_cr[1])**2)**1.5) / np.absolute(2*right_fit_cr[0])
return left_curverad, right_curverad
def putRadiusAndOffset(image,radius,offset):
font = cv2.FONT_HERSHEY_SIMPLEX
cv2.putText(image, "Curvature radius:"+str(radius),(np.int_(image.shape[0]/5),np.int_(image.shape[1]/7)),font,1.0,(255,255,255))
cv2.putText(image, "Offset from center:"+str(offset),(np.int_(image.shape[0]/5),np.int_(image.shape[1]/9)),font,1.0,(255,255,255))
return image
global left_fit,right_fit
left_curverad_real_trial, right_curverad_real_trial = measureCurvatureReal(ploty_trial,left_fit,right_fit)
radius_trial = np.int_(np.mean([left_curverad_real_trial,right_curverad_real_trial]))
offset_trial = radius_trial - 3.7
final_image_trial = putRadiusAndOffset(lanes_inserted_image_trial,radius_trial,offset_trial)
plt.imshow(final_image_trial)
# +
def processImage(image,save_image = False,save_path = None,full_image_name = None):
global mtx,dist
final_image = None
if save_image is True:
#remove the extention part
image_name = full_image_name[:-4]
else:
image_name = None
undistorted_image = undistortImage(image,mtx,dist,save_image,save_path,image_name)
gray_image = convertImage(undistorted_image,cv2.COLOR_BGR2GRAY)
#apply gradients
combined_mag_dir_color_image = applyDifferentGradients(image,gray_image,save_image,save_path,image_name)
#transform binary image to bird view image
bird_eye_binary_image,Minv = GetBirdEyeView(combined_mag_dir_color_image,save_image,save_path,image_name)
# HYPERPARAMETERS
# Choose the number of sliding windows
nwindows = 9
# Set the width of the windows +/- margin
margin = 100
# Set minimum number of pixels found to recenter window
minpix = 50
ploty,left_fitx,right_fitx,curved_binary_image = findCurvatures(bird_eye_binary_image,nwindows,margin,minpix)
lanes_inserted_image = insertLanesAreaonImage(image,undistorted_image,curved_binary_image,left_fitx,right_fitx,ploty,Minv)
left_curverad_real, right_curverad_real = measureCurvatureReal(ploty,left_fit,right_fit)
radius = np.int_(np.mean([left_curverad_real,right_curverad_real]))
offset = radius - 3.7
final_image = putRadiusAndOffset(lanes_inserted_image,radius,offset)
if(save_image is True):
saveImage(str(save_path)+"/final_image",image_name+"binary_",curved_binary_image)
saveImage(str(save_path)+"/final_image",image_name,final_image)
return final_image
def ProcessTestImages(test_images_list,test_images_names):
final_processed_images = []
#global first_frame
if(test_images_list is not None) and (len(test_images_list) > 0):
for test_image_name,test_image in zip(test_images_names,test_images_list):
first_frame = True
final_image = processImage(test_image,True,"output_images",test_image_name)
final_processed_images.append(final_image)
return final_processed_images
def processTestVideos(videos_path):
#convert video to images
test_images_list = None
global first_frame
#select the source folder for calibration images
videos_names = os.listdir(str(videos_path))
for video_name in videos_names:
clip = VideoFileClip(str(videos_path)+"/"+str(video_name))
first_frame = True
white_clip = clip.fl_image(processImage) #NOTE: this function expects color images!!
white_clip.write_videofile("test_videos_output/"+str(video_name), audio=False)
def pipeline():
global mtx,dist
#caibrate the camera
#nx and ny are the numer of intersections between white and black
nx = 9
ny = 6
mtx, dist = calibrateCamera(nx,ny)
test_images_names,test_images_list = readImages("test_images")
ProcessTestImages(test_images_list,test_images_names)
#print(test_images_list)
processTestVideos("test_videos")
pipeline()
# -
|
P2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="PWC1w1-0xJlE" colab={"base_uri": "https://localhost:8080/"} outputId="daf529df-8ec8-488d-da5c-27bfc575f9de"
from google.colab import drive
drive.mount('/content/drive')
# + id="KsbddzBi8gMQ" colab={"base_uri": "https://localhost:8080/"} outputId="906104ba-14e9-4e66-a4e2-12cfea2de7a2"
# ! git clone https://github.com/ifp-uiuc/do-neural-networks-learn-faus-iccvw-2015.git
# + id="J76fXHTw-FCU"
# ! rm -rf ck+ && mkdir ck+
# ! unzip -q '/content/drive/MyDrive/Facial Emotion Recognition Project/Dataset/CK+/extended-cohn-kanade-images.zip' -d /content/ck+
# ! unzip -q '/content/drive/MyDrive/Facial Emotion Recognition Project/Dataset/CK+/FACS_labels.zip' -d /content/ck+
# ! unzip -q '/content/drive/MyDrive/Facial Emotion Recognition Project/Dataset/CK+/Emotion_labels.zip' -d /content/ck+
# ! mv '/content/ck+/Emotion'{,_labels}
# + id="cJgl4RTOzaSu"
# These folders give some processing issue, so we delete them
# ! rm -rf ck+/cohn-kanade-images/S5*
# + id="hNFoCurh6_j7"
# ! sed -i 's/96/48/g' do-neural-networks-learn-faus-iccvw-2015/data_scripts/make_ck_plus_dataset.py
# + id="I9IUoYiGyyOx" colab={"base_uri": "https://localhost:8080/"} outputId="176c3fb9-98d9-42a6-dda5-27065c4dbd7c"
# ! rm -rf ck-output && mkdir ck-output
# keep only the first and last three images in each sequence
# ! python2 do-neural-networks-learn-faus-iccvw-2015/data_scripts/make_ck_plus_dataset.py --input_path /content/ck+/ --save_path /content/ck-output
# + id="ssPdIwrJGVSv"
def reindex_labels(y8):
y = np.zeros(y8.shape, dtype=np.int8)
label_mapping = {0:6, 2:-1, 1:0, 3:1, 4:2, 5:3, 6:4, 7:5}
for i in range(0,len(y8)):
y[i] = label_mapping[y8[i]]
return y
# + id="WNnIXqDyDL60" colab={"base_uri": "https://localhost:8080/"} outputId="da281b4a-7825-4704-aec4-1c6cb05f5f6f"
y8[y8==2]
# + id="7thKHuzr4enP"
import numpy as np
X = np.load('/content/ck-output/npy_files/X.npy')
y8 = np.load('/content/ck-output/npy_files/y.npy')
y = reindex_labels(y8)
# + id="Oz92dXgDABoj" colab={"base_uri": "https://localhost:8080/"} outputId="983b3241-119e-4f8a-f47b-ac642698248f"
#y8[y8==0]
y[y==6]
# + id="GSH3CX8IE5yj" colab={"base_uri": "https://localhost:8080/", "height": 299} outputId="c7f1d99a-1618-4949-823b-c70709560f04"
import matplotlib.pyplot as plt
emotions = {0:'angry', 1:'disgust', 2:'fear', 3:'happy', 4:'sad', 5:'surprise', 6:'neutral'}
for i in range(0,10):
plt.xlabel(emotions[y[i]])
plt.imshow(X[i].reshape(48,48),cmap='gray')
plt.figure()
break
# + id="ZvgocTG4KF1v"
# ! rm -rf ck-images && mkdir ck-images
from os import mkdir
for emotion in emotions:
mkdir(f'/content/ck-images/' + f'{emotion} ' + f'{emotions[emotion]}')
# + id="ojFKvNRXFA5G"
from PIL import Image
count = 0
for i in range(0,X.shape[0]):
if y[i] == -1:
continue
count_string = str(count).zfill(7)
fname = '/content/ck-images/' + f'{y[i]} ' + f'{emotions[y[i]]}/' + f'{emotions[y[i]]}-{count_string}.png'
img = Image.fromarray(X[i].reshape(48,48))
img.save(fname)
count += 1
# + id="b-lZOMv4JCPC" colab={"base_uri": "https://localhost:8080/"} outputId="85c54d61-2c9b-4dc1-d9f0-10fa30471a50"
# ! cd ck-images && zip -r ck-plus.zip *
# + id="pCsREeBHK2N7"
# ! mv ck-images/ck-plus.zip '/content/drive/MyDrive/Facial Emotion Recognition Project/Dataset/CK+'
|
dataset/ck_plus_to_png.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Synthetic Control
# -------------------
# > The model extends the traditional linear panel data (difference-in-differences) framework, allowing that **the effects of unobserved variables on the outcome vary with time**. (Abadie & Diamond & Hainmueller (2010))
#
# -> This is the key differnce to the difference-in-difference design. However, it is important to clarify that this statement refers to **!time-constant!** unobserved confounders. Now, the intuition that reproducing well a long time-series of pre-treatment outcomes of the eventually treated unit with a weighted average of the donor pool also picks up the effect of **unobserved confounders**. Then, because these are time-constant, their time-varying effect after treatment is also incporporated.
#
# Consider the following factor model:
#
# \begin{align*}
# Y^N_{it} = \delta_t + \mathbb{\theta}_t Z_{i} + \lambda_t \mu_i + \epsilon_{it}
# \end{align*}
#
# If $\lambda_t = \lambda$, i.e. $\lambda_t$ is constant over time, then we are back in the standard setting.
# # References
#
# * **<NAME>. (2021)**. [Using synthetic controls: feasibility, data requirements, and methodological aspects](https://www.aeaweb.org/articles?id=10.1257/jel.20191450), *Journal of Economic Literature*, 59(2), 391-425.
#
# * **<NAME>., <NAME>., & <NAME>. (2010)**. [Synthetic control methods for comparative casecStudies: cstimating the effect of california’s tobacco control program](https://economics.mit.edu/files/11859), *Journal of the American Statistical Association*, 105(490), 493-505.
#
#
# * **<NAME>., & <NAME>. (2018)**. [Synthetic control method: inference, sensitivity analysis and confidence sets](https://www.degruyter.com/document/doi/10.1515/jci-2016-0026/html), Journal of Causal Inference, 6(2), 2-26.
|
lectures/synthethic-control/notebook.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + pycharm={}
import os
import pandas as pd
from sklearn.model_selection import StratifiedShuffleSplit
from dimensionality_reduction import reduce_dimension
import load_database
from algorithms import *
# + pycharm={}
import warnings
warnings.filterwarnings('ignore')
# + pycharm={}
database_name = os.environ['DATABASE']
n_components = int(os.environ['N_COMPONENTS'])
dimensionality_algorithm = os.environ['DIMENSIONALITY_ALGORITHM']
# -
result_path = 'results/%s_%s_%s.csv' %(database_name, n_components, dimensionality_algorithm)
X, y = load_database.load(database_name)
X = reduce_dimension(dimensionality_algorithm, X, n_components) if n_components else X
# + pycharm={}
X.shape
# -
results = {}
# + pycharm={}
sss = StratifiedShuffleSplit(n_splits=1, test_size=0.2)
for train_index, test_index in sss.split(X, y):
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'ada_boost')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'bagging')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'extra_trees')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'random_forest')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'logistic_regression')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'passive_aggressive')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'ridge')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'sgd')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'bernoulli')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'gaussian')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'k_neighbors')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'nearest_centroid')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'mlp')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'linear_svc')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'decision_tree')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'extra_tree')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'gradient_boosting')
results.update(result)
# + pycharm={}
result = train_test(X_train, y_train, X_test, y_test, 'hist_gradient_boosting')
results.update(result)
# + pycharm={}
df = pd.DataFrame.from_records(results)
# + pycharm={}
df
# + pycharm={}
df.to_csv(result_path)
|
outputs/wine/64_nmf.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Coding Conventions
# Let's import first the context for this chapter.
from context import *
# ## One code, many layouts:
#
# Consider the following fragment of python:
#
#
#
# +
import species
def AddToReaction(name, reaction):
reaction.append(species.Species(name))
# -
#
#
#
# this could also have been written:
#
#
#
# +
from species import Species
def add_to_reaction(a_name, a_reaction):
l_species = Species(a_name)
a_reaction.append(l_species)
# -
# ## So many choices
#
# * Layout
# * Naming
# * Syntax choices
#
# ## Layout
reaction = {
"reactants": ["H", "H", "O"],
"products": ["H2O"]
}
#
#
#
#
reaction2 = {
"reactants":
[
"H",
"H",
"O"
],
"products":
[
"H2O"
]
}
# ## Layout choices
#
# * Brace style
# * Line length
# * Indentation
# * Whitespace/Tabs
#
# Inconsistency will produce a mess in your code! Some choices will make your code harder to read, whereas others may affect the code. For example, if you copy/paste code with tabs in a place that's using spaces, they may appear OK in your screen but it will fail when running it.
# ## Naming Conventions
# [Camel case](https://en.wikipedia.org/wiki/Camel_case) is used in the following example, where class name is in UpperCamel, functions in lowerCamel and underscore_separation for variables names:
class ClassName:
def methodName(variable_name):
instance_variable = variable_name
# This example uses `underscore_separation` for all the names:
class class_name:
def method_name(a_variable):
m_instance_variable = a_variable
# The usual Python convention (see [PEP8](https://www.python.org/dev/peps/pep-0008)) is UpperCamel for class names, and underscore_separation for function and variable names:
class ClassName:
def method_name(variable_name):
instance_variable = variable_name
# However, particular projects may have their own conventions (and you will even find Python standard libraries that don't follow these conventions).
# ## Hungarian Notation
#
# Prefix denotes *type*:
#
#
#
fNumber = float(sEntry) + iOffset
# So in the example above we know that we are creating a `f`loat number as a composition of a `s`tring entry and an `i`nteger offset.
#
# People may find this useful in languages like Python where the type is intrinsic in the variable.
number = float(entry) + offset
#
# ## Newlines
#
# * Newlines make code easier to read
# * Newlines make less code fit on a screen
#
# Use newlines to describe your code's *rhythm*.
#
# ## Syntax Choices
# The following two snippets do the same, but the second is separated into more steps, making it more readable.
anothervariable += 1
if (variable == anothervariable) and flag1 or flag2:
do_something()
anothervariable = anothervariable + 1
variable_equality = variable == anothervariable
if (variable_equality and flag1) or flag2:
do_something()
# We create extra variables as an intermediate step. Don't worry about the performance now, the compiler will do the right thing.
#
# What about operator precedence? Being explicit helps to remind yourself what you are doing.
#
# * Explicit operator precedence
# * Compound expressions
# * Package import choices
#
# ## Coding Conventions
#
# You should try to have an agreed policy for your team for these matters.
#
# If your language sponsor has a standard policy, use that. For example:
#
# - **Python**: [PEP8](https://www.python.org/dev/peps/pep-0008/)
# - **R**: [Google's guide for R](https://google.github.io/styleguide/Rguide.xml), [tidyverse style guide](https://style.tidyverse.org/)
# - **C++**: [Google's style guide](https://google.github.io/styleguide/cppguide.html), [Mozilla's](https://developer.mozilla.org/en-US/docs/Mozilla/Developer_guide/Coding_Style)
# - **Julia**: [Official style guide](https://docs.julialang.org/en/v1/manual/style-guide/index.html)
#
# ## Lint
#
# There are automated tools which enforce coding conventions and check for common mistakes.
#
# These are called *linters*:
#
# E.g. `pip install` [pycodestyle](https://pypi.org/project/pycodestyle/)
#
#
#
# + language="bash"
# pycodestyle species.py
# -
#
#
#
# It is a good idea to run a linter before every commit, or include it in your CI tests.
#
#
# There are other tools that help with linting that are worth mentioning.
# With `pylint` you can also get other useful information about the quality of your code:
#
# `pip install` [pylint](https://www.pylint.org/)
#
# + language="bash"
# pylint species.py || echo "Note the linting failures"
# -
# and with [black](https://black.readthedocs.io/) you can fix all the errors at once.
# ```bash
# black species.py
# ```
# These linters can be configured to choose which points to flag and which to ignore.
#
# Do not blindly believe all these automated tools! Style guides are **guides** not **rules**.
# Finally, there are tools like [editorconfig](https://editorconfig.org/) to help sharing the conventions used within a project, where each contributor uses different IDEs and tools. There are also bots like [pep8speaks](https://pep8speaks.com/) that comments on contributors' pull requests suggesting what to change to follow the conventions for the project.
#
|
module07_construction_and_design/07_01_coding_conventions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import tensorflow as tf
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
import os
import math
# +
train_dir = 'F:/Desktop/TF图集/flower_train_1/output/'
L1 = []
L2 = []
L3 = []
L4 = []
L5 = []
label_1 = []
label_2 = []
label_3 = []
label_4 = []
label_5 = []
# +
#获取(处理后64x64)图片路径
#ratio,测试集比率
def get_files(file_dir, ratio):
for file in os.listdir(file_dir + '/1'):
L1.append(file_dir + '/1/' +file)
label_1.append(0)
for file in os.listdir(file_dir + '/2'):
L2.append(file_dir + '/2/' +file)
label_2.append(1)
for file in os.listdir(file_dir + '/3'):
L3.append(file_dir + '/3/' +file)
label_3.append(2)
for file in os.listdir(file_dir + '/4'):
L4.append(file_dir + '/4/' +file)
label_4.append(3)
for file in os.listdir(file_dir + '/5'):
L5.append(file_dir + '/5/' +file)
label_5.append(4)
#hstack 水平叠堆数组
#均在数组中使用hstack
image_list = np.hstack((L1, L2, L3, L4, L5))
label_list = np.hstack((label_1, label_2, label_3, label_4, label_5))
#shuffle 打乱顺序
order1 = np.array([image_list, label_list])
#transpose 转置
order2 = order1.transpose()
np.random.shuffle(order2)
# print(order1)
# print(order2)
# print(disorder)
#disorder转list
image_list_turn = list(order2[:,0])
label_list_turn = list(order2[:,1])
#划分list为test & train
n_sample = len(label_list_turn)
n_test = int(math.ceil(n_sample * ratio))
n_train = n_sample - n_test
train_images = image_list_turn[0:n_train]
train_labels = label_list_turn[0:n_train]
train_labels = [int(float(i)) for i in train_labels]
test_images = image_list_turn[n_train:-1]
test_labels = label_list_turn[n_train:-1]
test_labels = [int(float(i)) for i in test_labels]
return train_images, train_labels, test_images, test_labels
# -
def get_one_image(train):
n = len(train)
ind = np.random.randint(1, n) #1到n的随机数
img_dir = train[ind] #选择图片
print('dir' + img_dir)
img = Image.open(img_dir)
plt.imshow(img)
img2 = img.resize([64, 64])
img3 = np.array(img2)
return img3
# +
def inference(images, batch_size, n_classes):
#一个简单的卷积神经网络,卷积+池化层x2,全连接层x2,最后一个softmax层做分类。
#卷积层1
#64个3x3的卷积核(3通道),padding=’SAME’,表示padding后卷积的图与原图尺寸一致,激活函数relu()
with tf.variable_scope('conv1') as scope:
weights = tf.Variable(tf.truncated_normal(shape=[3,3,3,64], stddev = 1.0, dtype = tf.float32),
name = 'weights', dtype = tf.float32)
biases = tf.Variable(tf.constant(value = 0.1, dtype = tf.float32, shape = [64]),
name = 'biases', dtype = tf.float32)
conv = tf.nn.conv2d(images, weights, strides=[1,1,1,1], padding='SAME')
pre_activation = tf.nn.bias_add(conv, biases)
conv1 = tf.nn.relu(pre_activation, name= scope.name)
#池化层1
#3x3最大池化,步长strides为2,池化后执行lrn()操作,局部响应归一化,对训练有利。
with tf.variable_scope('pooling1_lrn') as scope:
pool1 = tf.nn.max_pool(conv1, ksize=[1,3,3,1],strides=[1,2,2,1],padding='SAME', name='pooling1')
norm1 = tf.nn.lrn(pool1, depth_radius=4, bias=1.0, alpha=0.001/9.0, beta=0.75, name='norm1')
#卷积层2
#16个3x3的卷积核(16通道),padding=’SAME’,表示padding后卷积的图与原图尺寸一致,激活函数relu()
with tf.variable_scope('conv2') as scope:
weights = tf.Variable(tf.truncated_normal(shape=[3,3,64,16], stddev = 0.1, dtype = tf.float32),
name = 'weights', dtype = tf.float32)
biases = tf.Variable(tf.constant(value = 0.1, dtype = tf.float32, shape = [16]),
name = 'biases', dtype = tf.float32)
conv = tf.nn.conv2d(norm1, weights, strides = [1,1,1,1],padding='SAME')
pre_activation = tf.nn.bias_add(conv, biases)
conv2 = tf.nn.relu(pre_activation, name='conv2')
#池化层2
#3x3最大池化,步长strides为2,池化后执行lrn()操作,
#pool2 and norm2
with tf.variable_scope('pooling2_lrn') as scope:
norm2 = tf.nn.lrn(conv2, depth_radius=4, bias=1.0, alpha=0.001/9.0,beta=0.75,name='norm2')
pool2 = tf.nn.max_pool(norm2, ksize=[1,3,3,1], strides=[1,1,1,1],padding='SAME',name='pooling2')
#全连接层3
#128个神经元,将之前pool层的输出reshape成一行,激活函数relu()
with tf.variable_scope('local3') as scope:
reshape = tf.reshape(pool2, shape=[batch_size, -1])
dim = reshape.get_shape()[1].value
weights = tf.Variable(tf.truncated_normal(shape=[dim,128], stddev = 0.005, dtype = tf.float32),
name = 'weights', dtype = tf.float32)
biases = tf.Variable(tf.constant(value = 0.1, dtype = tf.float32, shape = [128]),
name = 'biases', dtype=tf.float32)
local3 = tf.nn.relu(tf.matmul(reshape/2, weights) + biases, name=scope.name)
#全连接层4
#128个神经元,激活函数relu()
with tf.variable_scope('local4') as scope:
weights = tf.Variable(tf.truncated_normal(shape=[128,128], stddev = 0.005, dtype = tf.float32),
name = 'weights',dtype = tf.float32)
biases = tf.Variable(tf.constant(value = 0.1, dtype = tf.float32, shape = [128]),
name = 'biases', dtype = tf.float32)
local4 = tf.nn.relu(tf.matmul(local3, weights) + biases, name='local4')
#dropout层
# with tf.variable_scope('dropout') as scope:
# drop_out = tf.nn.dropout(local4, 0.8)
#Softmax回归层
#将前面的FC层输出,做一个线性回归,计算出每一类的得分,在这里是2类,所以这个层输出的是两个得分。
with tf.variable_scope('softmax_linear') as scope:
weights = tf.Variable(tf.truncated_normal(shape=[128, n_classes], stddev = 0.005, dtype = tf.float32),
name = 'softmax_linear', dtype = tf.float32)
biases = tf.Variable(tf.constant(value = 0.1, dtype = tf.float32, shape = [n_classes]),
name = 'biases', dtype = tf.float32)
softmax_linear = tf.add(tf.matmul(local4, weights), biases, name='softmax_linear')
return softmax_linear
#-----------------------------------------------------------------------------
#loss计算
#传入参数:logits,网络计算输出值。labels,真实值,在这里是0或者1
#返回参数:loss,损失值
def losses(logits, labels):
with tf.variable_scope('loss') as scope:
cross_entropy =tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits, labels=labels, name='xentropy_per_example')
loss = tf.reduce_mean(cross_entropy, name='loss')
tf.summary.scalar(scope.name+'/loss', loss)
return loss
#--------------------------------------------------------------------------
#loss损失值优化
#输入参数:loss。learning_rate,学习速率。
#返回参数:train_op,训练op,这个参数要输入sess.run中让模型去训练。
def trainning(loss, learning_rate):
with tf.name_scope('optimizer'):
optimizer = tf.train.AdamOptimizer(learning_rate= learning_rate)
global_step = tf.Variable(0, name='global_step', trainable=False)
train_op = optimizer.minimize(loss, global_step= global_step)
return train_op
#-----------------------------------------------------------------------
#评价/准确率计算
#输入参数:logits,网络计算值。labels,标签,也就是真实值,在这里是0或者1。
#返回参数:accuracy,当前step的平均准确率,也就是在这些batch中多少张图片被正确分类了。
def evaluation(logits, labels):
with tf.variable_scope('accuracy') as scope:
correct = tf.nn.in_top_k(logits, labels, 1)
correct = tf.cast(correct, tf.float16)
accuracy = tf.reduce_mean(correct)
tf.summary.scalar(scope.name+'/accuracy', accuracy)
return accuracy
# -
#测试图片
def evaluate_one_image(image_array):
with tf.Graph().as_default():
BATCH_SIZE = 1
N_CLASSES = 5
img = tf.cast(image_array, tf.float32)
img = tf.image.per_image_standardization(img)
img = tf.reshape(img, [1, 64, 64, 3])
logit = inference(img, BATCH_SIZE, N_CLASSES)
logit = tf.nn.softmax(logit)
x = tf.placeholder(tf.float32, shape=[64, 64, 3])
logs_train_dir = 'F:/Desktop/TF图集/flower_train_1/log/'
saver = tf.train.Saver()
with tf.Session() as sess:
print("Reading checkpoints...")
ckpt = tf.train.get_checkpoint_state(logs_train_dir)
if ckpt and ckpt.model_checkpoint_path:
global_step = ckpt.model_checkpoint_path.split('/')[-1].split('-')[-1]
saver.restore(sess, ckpt.model_checkpoint_path)
print("加载成功,global_step = %s" % global_step)
else:
print("未找到checkpoint文件")
prediction = sess.run(logit, feed_dict = {x: image_array})
max_index = np.argmax(prediction)
if max_index == 0:
print('This is a 1 with possibility %.6f' %prediction[:, 0])
elif max_index==1:
print('This is a 2 with possibility %.6f' %prediction[:, 1])
elif max_index==2:
print('This is a 3 with possibility %.6f' %prediction[:, 2])
elif max_index==3:
print('This is a 4 with possibility %.6f' %prediction[:, 3])
elif max_index==4:
print('This is a 5 with possibility %.6f' %prediction[:, 4])
else:
print('NNNNNNG')
if __name__ == '__main__':
train_dir = 'F:/Desktop/TF图集/flower_train_1/output/'
train, train_label, test, test_label = get_files(train_dir, 0.3)
img = get_one_image(test)
evaluate_one_image(img)
|
my_3_test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
df = pd.read_csv(r'Data/uniprot_ACC.tsv', header=None, delimiter="\t")
#print(df)
df.columns=['Epitope', 'ACC']
ACC=list(df.ACC)
print(len(set(ACC)))
cleanedList = [x for x in ACC if str(x) != 'nan']
# +
#ACC=['P40925', 'P40926', 'O43175', 'Q9UM73', 'P97793', 'P36956', 'A2AQ07']
ACC=' '.join(cleanedList)
ACC
# +
import urllib.parse
import urllib.request
url = 'https://www.uniprot.org/uploadlists/'
params = {
'from': 'ACC+ID',
'to': 'GENENAME',
'format': 'tab',
'query': ACC
}
data = urllib.parse.urlencode(params)
data = data.encode('utf-8')
req = urllib.request.Request(url, data)
with urllib.request.urlopen(req) as f:
response = f.read()
print(response.decode('utf-8'))
# +
from pandas.compat import StringIO
df1=response.decode('utf-8')
df1=pd.read_csv(StringIO(df1), delimiter='\t')
df1.columns=['ACC', 'Gene']
output=pd.merge(df, df1, how='inner', on='ACC')
output
# -
output.to_csv(r'acc_gene.csv', sep=',', encoding='utf-8', index=False, header=True)
df
|
ACC_2_GENE.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="BlmQIFSLZDdc"
# #[How to run Object Detection and Segmentation on a Video Fast for Free](https://www.dlology.com/blog/how-to-run-object-detection-and-segmentation-on-video-fast-for-free/)
#
# ## Confirm TensorFlow can see the GPU
#
# Simply select "GPU" in the Accelerator drop-down in Notebook Settings (either through the Edit menu or the command palette at cmd/ctrl-shift-P).
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="3IEVK-KFxi5Z" outputId="4508e71b-234b-4107-9244-595c700a672a"
import tensorflow as tf
DEVICE = "/Gpu:0"
#("Num GPUs Available: ", len(tf.config.experimental.list_physical_devices(device_type='GPU')))
# + [markdown] colab_type="text" id="G4QlSH4BAmvF"
# ## Install pycocotools
# + colab={"base_uri": "https://localhost:8080/", "height": 102} colab_type="code" id="6Jkma4_y0Gn8" outputId="f1907582-f8a8-40b9-9961-61bacbe426cf"
# !pip install Cython
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="tT7xOQD5pS5G" outputId="bb2ccb63-12eb-4abc-bc73-985292ffc205"
# !ls
# + colab={"base_uri": "https://localhost:8080/", "height": 102} colab_type="code" id="1efXeBhJ0MIi" outputId="b02c2fbc-b7c2-4a96-bf66-dc03e6e1cc21"
# !git clone https://github.com/waleedka/coco
# + colab={"base_uri": "https://localhost:8080/", "height": 1499} colab_type="code" id="85CxqaK8yHEV" outputId="b4c62948-a471-45d4-c109-9483e259658e"
# !pip install -U setuptools
# !pip install -U wheel
# !make install -C coco/PythonAPI
# + [markdown] colab_type="text" id="DswpLud4A0jf"
# ## Git Clone the code
# + colab={"base_uri": "https://localhost:8080/", "height": 102} colab_type="code" id="-MrtCPbyzb12" outputId="4ef7404d-f079-485a-ead9-1bc42f7a58e0"
# !git clone https://github.com/matterport/Mask_RCNN
# + [markdown] colab_type="text" id="UZd4msdzA5HT"
# # # ## cd to the code directory and optionally download the weights file
# + colab={"base_uri": "https://localhost:8080/", "height": 309} colab_type="code" id="zuWUMbul22-u" outputId="6f575416-2bd9-40d2-ecb0-2d368fde6668"
import os
os.chdir('./Mask_RCNN')
# !git checkout 555126ee899a144ceff09e90b5b2cf46c321200c
# !wget https://github.com/matterport/Mask_RCNN/releases/download/v2.0/mask_rcnn_coco.h5
# + colab={"base_uri": "https://localhost:8080/", "height": 102} colab_type="code" id="F_bTpx1X9Yjq" outputId="b5685224-4cdb-4e00-d610-ab594591acc9"
# !ls
# + [markdown] colab_type="text" id="QHLQOznQ-WSC"
# # Mask R-CNN Demo
#
# A quick intro to using the pre-trained model to detect and segment objects.
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="NInWHdIE2GpR" outputId="101eaafe-264a-45e7-e7b9-e55943ba6f07"
import os
import sys
import random
import math
import numpy as np
import skimage.io
import matplotlib
import matplotlib.pyplot as plt
import coco
import utils
import model as modellib
import visualize
# %matplotlib inline
# Root directory of the project
ROOT_DIR = os.getcwd()
# Directory to save logs and trained model
MODEL_DIR = os.path.join(ROOT_DIR, "logs")
# Local path to trained weights file
COCO_MODEL_PATH = os.path.join(ROOT_DIR, "mask_rcnn_coco.h5")
# Download COCO trained weights from Releases if needed
if not os.path.exists(COCO_MODEL_PATH):
utils.download_trained_weights(COCO_MODEL_PATH)
# Directory of images to run detection on
IMAGE_DIR = os.path.join(ROOT_DIR, "images")
# + [markdown] colab_type="text" id="04kWKli09fpq"
# ## Configurations
#
# We'll be using a model trained on the MS-COCO dataset. The configurations of this model are in the ```CocoConfig``` class in ```coco.py```.
#
# For inferencing, modify the configurations a bit to fit the task. To do so, sub-class the ```CocoConfig``` class and override the attributes you need to change.
# + colab={"base_uri": "https://localhost:8080/", "height": 816} colab_type="code" id="Rymd_7lP9gCC" outputId="5cef988c-2097-485a-8e4e-54113531d18c"
class InferenceConfig(coco.CocoConfig):
# Set batch size to 1 since we'll be running inference on
# one image at a time. Batch size = GPU_COUNT * IMAGES_PER_GPU
GPU_COUNT = 1
IMAGES_PER_GPU = 1
config = InferenceConfig()
config.display()
# + [markdown] colab_type="text" id="m5PVECAQ9kkn"
# ## Create Model and Load Trained Weights
# + colab={} colab_type="code" id="M3wcuq8-9g7X"
# Create model object in inference mode.
model = tf.keras.models.load_model('my_model.h5')
= modellib.MaskRCNN(mode="inference", model_dir=MODEL_DIR, config=config)
# Load weights trained on MS-COCO
model.load_weights(COCO_MODEL_PATH, by_name=True)
# + [markdown] colab_type="text" id="alMRDVDo9qGB"
# ## Class Names
#
# The model classifies objects and returns class IDs, which are integer value that identify each class. Some datasets assign integer values to their classes and some don't. For example, in the MS-COCO dataset, the 'person' class is 1 and 'teddy bear' is 88. The IDs are often sequential, but not always. The COCO dataset, for example, has classes associated with class IDs 70 and 72, but not 71.
#
# To improve consistency, and to support training on data from multiple sources at the same time, our ```Dataset``` class assigns it's own sequential integer IDs to each class. For example, if you load the COCO dataset using our ```Dataset``` class, the 'person' class would get class ID = 1 (just like COCO) and the 'teddy bear' class is 78 (different from COCO). Keep that in mind when mapping class IDs to class names.
#
# To get the list of class names, you'd load the dataset and then use the ```class_names``` property like this.
# ```
# # Load COCO dataset
# dataset = coco.CocoDataset()
# dataset.load_coco(COCO_DIR, "train")
# dataset.prepare()
#
# # Print class names
# print(dataset.class_names)
# ```
#
# We don't want to require you to download the COCO dataset just to run this demo, so we're including the list of class names below. The index of the class name in the list represent its ID (first class is 0, second is 1, third is 2, ...etc.)
# + colab={} colab_type="code" id="p4BA4vKD9mbQ"
# COCO Class names
# Index of the class in the list is its ID. For example, to get ID of
# the teddy bear class, use: class_names.index('teddy bear')
class_names = ['BG', 'person', 'bicycle', 'car', 'motorcycle', 'airplane',
'bus', 'train', 'truck', 'boat', 'traffic light',
'fire hydrant', 'stop sign', 'parking meter', 'bench', 'bird',
'cat', 'dog', 'horse', 'sheep', 'cow', 'elephant', 'bear',
'zebra', 'giraffe', 'backpack', 'umbrella', 'handbag', 'tie',
'suitcase', 'frisbee', 'skis', 'snowboard', 'sports ball',
'kite', 'baseball bat', 'baseball glove', 'skateboard',
'surfboard', 'tennis racket', 'bottle', 'wine glass', 'cup',
'fork', 'knife', 'spoon', 'bowl', 'banana', 'apple',
'sandwich', 'orange', 'broccoli', 'carrot', 'hot dog', 'pizza',
'donut', 'cake', 'chair', 'couch', 'potted plant', 'bed',
'dining table', 'toilet', 'tv', 'laptop', 'mouse', 'remote',
'keyboard', 'cell phone', 'microwave', 'oven', 'toaster',
'sink', 'refrigerator', 'book', 'clock', 'vase', 'scissors',
'teddy bear', 'hair drier', 'toothbrush']
# + [markdown] colab_type="text" id="g8IqukPA9vC0"
# ## Run Object Detection
# + colab={"base_uri": "https://localhost:8080/", "height": 823} colab_type="code" id="NYCQe9ex9oj3" outputId="4631e1ce-bf96-4983-8758-9c2a3dbe6b44"
# Load a random image from the images folder
file_names = next(os.walk(IMAGE_DIR))[2]
image = skimage.io.imread(os.path.join(IMAGE_DIR, random.choice(file_names)))
# Run detection
results = model.detect([image], verbose=1)
# Visualize results
r = results[0]
visualize.display_instances(image, r['rois'], r['masks'], r['class_ids'],
class_names, r['scores'])
# + colab={"base_uri": "https://localhost:8080/", "height": 764} colab_type="code" id="1mrNkY5a9xS3" outputId="9dea48db-d7ad-474b-d89c-c8afb181e1ad"
# Load a random image from the images folder
file_names = next(os.walk(IMAGE_DIR))[2]
image = skimage.io.imread(os.path.join(IMAGE_DIR, '8734543718_37f6b8bd45_z.jpg'))
# Run detection
results = model.detect([image], verbose=1)
# Visualize results
r = results[0]
visualize.display_instances(image, r['rois'], r['masks'], r['class_ids'],
class_names, r['scores'])
# + [markdown] colab_type="text" id="aRuz2KLuHOMA"
# ## Custom image
# You can upload an image to a third party website like
#
# * [imgbb](https://imgbb.com/)
# * [GitHub](https://github.com) repo raw image
#
# Then download the image url here with `wget`.
#
# We will also introduce using Google drive with Colab in the later section.
# + colab={"base_uri": "https://localhost:8080/", "height": 221} colab_type="code" id="lg47GK_9C4mb" outputId="e885133a-7900-4cd1-896a-5254e2d409e3"
# !wget https://preview.ibb.co/cubifS/sh_expo.jpg -P ./images
# + colab={"base_uri": "https://localhost:8080/", "height": 880} colab_type="code" id="QowhnmS2EqxU" outputId="d79c94db-2a57-4fd5-8727-b63b994909e4"
# Load a random image from the images folder
file_names = next(os.walk(IMAGE_DIR))[2]
image = skimage.io.imread(os.path.join(IMAGE_DIR, 'sh_expo.jpg'))
# Run detection
results = model.detect([image], verbose=1)
# Visualize results
r = results[0]
visualize.display_instances(image, r['rois'], r['masks'], r['class_ids'],
class_names, r['scores'])
# + [markdown] colab_type="text" id="A6IPpQ5R2R-e"
# ## Process Video
# Download the video mp4 file.
# + colab={"base_uri": "https://localhost:8080/", "height": 309} colab_type="code" id="QSxgxJGyGBuf" outputId="9de3007a-d9f5-4194-8f64-51d7c516456b"
# !mkdir videos
# !wget https://github.com/Tony607/blog_statics/releases/download/v1.0/trailer1.mp4 -P ./videos
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="BrYJWnZpr2Pm" outputId="e66439bd-7954-434d-9d7e-ae3a97343d58"
# !ls ./videos
# + colab={"base_uri": "https://localhost:8080/", "height": 32881} colab_type="code" id="z0o6sUx0sD3S" outputId="c8f6a690-0d08-4e48-cc5d-2a7e081ccd1c"
import cv2
import numpy as np
def random_colors(N):
np.random.seed(1)
colors = [tuple(255 * np.random.rand(3)) for _ in range(N)]
return colors
def apply_mask(image, mask, color, alpha=0.5):
"""apply mask to image"""
for n, c in enumerate(color):
image[:, :, n] = np.where(
mask == 1,
image[:, :, n] * (1 - alpha) + alpha * c,
image[:, :, n]
)
return image
def display_instances(image, boxes, masks, ids, names, scores):
"""
take the image and results and apply the mask, box, and Label
"""
n_instances = boxes.shape[0]
colors = random_colors(n_instances)
if not n_instances:
print('NO INSTANCES TO DISPLAY')
else:
assert boxes.shape[0] == masks.shape[-1] == ids.shape[0]
for i, color in enumerate(colors):
if not np.any(boxes[i]):
continue
y1, x1, y2, x2 = boxes[i]
label = names[ids[i]]
score = scores[i] if scores is not None else None
caption = '{} {:.2f}'.format(label, score) if score else label
mask = masks[:, :, i]
image = apply_mask(image, mask, color)
image = cv2.rectangle(image, (x1, y1), (x2, y2), color, 2)
image = cv2.putText(
image, caption, (x1, y1), cv2.FONT_HERSHEY_COMPLEX, 0.7, color, 2
)
return image
if __name__ == '__main__':
"""
test everything
"""
import os
import sys
import coco
import utils
import model as modellib
# We use a K80 GPU with 24GB memory, which can fit 3 images.
batch_size = 3
ROOT_DIR = os.getcwd()
MODEL_DIR = os.path.join(ROOT_DIR, "logs")
VIDEO_DIR = os.path.join(ROOT_DIR, "videos")
VIDEO_SAVE_DIR = os.path.join(VIDEO_DIR, "save")
COCO_MODEL_PATH = os.path.join(ROOT_DIR, "mask_rcnn_coco.h5")
if not os.path.exists(COCO_MODEL_PATH):
utils.download_trained_weights(COCO_MODEL_PATH)
class InferenceConfig(coco.CocoConfig):
GPU_COUNT = 1
IMAGES_PER_GPU = batch_size
config = InferenceConfig()
config.display()
model = modellib.MaskRCNN(
mode="inference", model_dir=MODEL_DIR, config=config
)
model.load_weights(COCO_MODEL_PATH, by_name=True)
class_names = [
'BG', 'person', 'bicycle', 'car', 'motorcycle', 'airplane',
'bus', 'train', 'truck', 'boat', 'traffic light',
'fire hydrant', 'stop sign', 'parking meter', 'bench', 'bird',
'cat', 'dog', 'horse', 'sheep', 'cow', 'elephant', 'bear',
'zebra', 'giraffe', 'backpack', 'umbrella', 'handbag', 'tie',
'suitcase', 'frisbee', 'skis', 'snowboard', 'sports ball',
'kite', 'baseball bat', 'baseball glove', 'skateboard',
'surfboard', 'tennis racket', 'bottle', 'wine glass', 'cup',
'fork', 'knife', 'spoon', 'bowl', 'banana', 'apple',
'sandwich', 'orange', 'broccoli', 'carrot', 'hot dog', 'pizza',
'donut', 'cake', 'chair', 'couch', 'potted plant', 'bed',
'dining table', 'toilet', 'tv', 'laptop', 'mouse', 'remote',
'keyboard', 'cell phone', 'microwave', 'oven', 'toaster',
'sink', 'refrigerator', 'book', 'clock', 'vase', 'scissors',
'teddy bear', 'hair drier', 'toothbrush'
]
capture = cv2.VideoCapture(os.path.join(VIDEO_DIR, 'trailer1.mp4'))
try:
if not os.path.exists(VIDEO_SAVE_DIR):
os.makedirs(VIDEO_SAVE_DIR)
except OSError:
print ('Error: Creating directory of data')
frames = []
frame_count = 0
# these 2 lines can be removed if you dont have a 1080p camera.
capture.set(cv2.CAP_PROP_FRAME_WIDTH, 1920)
capture.set(cv2.CAP_PROP_FRAME_HEIGHT, 1080)
while True:
ret, frame = capture.read()
# Bail out when the video file ends
if not ret:
break
# Save each frame of the video to a list
frame_count += 1
frames.append(frame)
print('frame_count :{0}'.format(frame_count))
if len(frames) == batch_size:
results = model.detect(frames, verbose=0)
print('Predicted')
for i, item in enumerate(zip(frames, results)):
frame = item[0]
r = item[1]
frame = display_instances(
frame, r['rois'], r['masks'], r['class_ids'], class_names, r['scores']
)
name = '{0}.jpg'.format(frame_count + i - batch_size)
name = os.path.join(VIDEO_SAVE_DIR, name)
cv2.imwrite(name, frame)
print('writing to file:{0}'.format(name))
# Clear the frames array to start the next batch
frames = []
capture.release()
# + colab={"base_uri": "https://localhost:8080/", "height": 1496} colab_type="code" id="OKvhT2uCsIl5" outputId="45533f85-556a-427f-eb22-d66a59d82c36"
# !ls ./videos/save
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="VWDC3g8OARuc" outputId="7fc1c66a-7748-4d2e-e82f-4e026fc1168b"
video = cv2.VideoCapture(os.path.join(VIDEO_DIR, 'trailer1.mp4'));
# Find OpenCV version
(major_ver, minor_ver, subminor_ver) = (cv2.__version__).split('.')
if int(major_ver) < 3 :
fps = video.get(cv2.cv.CV_CAP_PROP_FPS)
print("Frames per second using video.get(cv2.cv.CV_CAP_PROP_FPS): {0}".format(fps))
else :
fps = video.get(cv2.CAP_PROP_FPS)
print("Frames per second using video.get(cv2.CAP_PROP_FPS) : {0}".format(fps))
video.release();
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="ObiV83ORsg6o" outputId="b47631cf-c3c8-44c4-db08-bbd17d6185ca"
def make_video(outvid, images=None, fps=30, size=None,
is_color=True, format="FMP4"):
"""
Create a video from a list of images.
@param outvid output video
@param images list of images to use in the video
@param fps frame per second
@param size size of each frame
@param is_color color
@param format see http://www.fourcc.org/codecs.php
@return see http://opencv-python-tutroals.readthedocs.org/en/latest/py_tutorials/py_gui/py_video_display/py_video_display.html
The function relies on http://opencv-python-tutroals.readthedocs.org/en/latest/.
By default, the video will have the size of the first image.
It will resize every image to this size before adding them to the video.
"""
from cv2 import VideoWriter, VideoWriter_fourcc, imread, resize
fourcc = VideoWriter_fourcc(*format)
vid = None
for image in images:
if not os.path.exists(image):
raise FileNotFoundError(image)
img = imread(image)
if vid is None:
if size is None:
size = img.shape[1], img.shape[0]
vid = VideoWriter(outvid, fourcc, float(fps), size, is_color)
if size[0] != img.shape[1] and size[1] != img.shape[0]:
img = resize(img, size)
vid.write(img)
vid.release()
return vid
import glob
import os
# Directory of images to run detection on
ROOT_DIR = os.getcwd()
VIDEO_DIR = os.path.join(ROOT_DIR, "videos")
VIDEO_SAVE_DIR = os.path.join(VIDEO_DIR, "save")
images = list(glob.iglob(os.path.join(VIDEO_SAVE_DIR, '*.*')))
# Sort the images by integer index
images = sorted(images, key=lambda x: float(os.path.split(x)[1][:-3]))
outvid = os.path.join(VIDEO_DIR, "out.mp4")
make_video(outvid, images, fps=30)
# + colab={"base_uri": "https://localhost:8080/", "height": 119} colab_type="code" id="S1KYLXXD0YKd" outputId="5773eafc-c446-4fa3-824f-dd1a33c2b051"
# !ls -alh ./videos/
# + colab={} colab_type="code" id="T6vgRRXH0hwa"
# + [markdown] colab_type="text" id="MD-3Z88I6lng"
# ### Downlod the output video to our local machine
# + colab={} colab_type="code" id="ScC6ZUJq1Pc_"
from google.colab import files
files.download('videos/out.mp4')
# + colab={"base_uri": "https://localhost:8080/", "height": 102} colab_type="code" id="d7kJVPEl5NYO" outputId="5e64939f-6daa-40bf-9799-4fdb169512a6"
# !ls
# + colab={} colab_type="code" id="IZNNEa_SuoFn"
|
Notebook/Mask_R_CNN_Demo (2).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc" style="margin-top: 1em;"><ul class="toc-item"><li><span><a href="#Tutorial:-The-Greek-Syntax-Package" data-toc-modified-id="Tutorial:-The-Greek-Syntax-Package-1"><span class="toc-item-num">1 </span>Tutorial: The Greek Syntax Package</a></span><ul class="toc-item"><li><span><a href="#Queries-using-Lowfat-and-Jupyter-Notebooks" data-toc-modified-id="Queries-using-Lowfat-and-Jupyter-Notebooks-1.1"><span class="toc-item-num">1.1 </span>Queries using Lowfat and Jupyter Notebooks</a></span></li><li><span><a href="#Installing-and-Running-the-Greek-Syntax-Package-with-Docker" data-toc-modified-id="Installing-and-Running-the-Greek-Syntax-Package-with-Docker-1.2"><span class="toc-item-num">1.2 </span>Installing and Running the Greek Syntax Package with Docker</a></span></li><li><span><a href="#Opening-the-Database" data-toc-modified-id="Opening-the-Database-1.3"><span class="toc-item-num">1.3 </span>Opening the Database</a></span></li><li><span><a href="#Don't-Try-to-Return-the-Whole-Database" data-toc-modified-id="Don't-Try-to-Return-the-Whole-Database-1.4"><span class="toc-item-num">1.4 </span>Don't Try to Return the Whole Database</a></span></li><li><span><a href="#References:-Book,-Chapter,-Verse,-Word" data-toc-modified-id="References:-Book,-Chapter,-Verse,-Word-1.5"><span class="toc-item-num">1.5 </span>References: Book, Chapter, Verse, Word</a></span><ul class="toc-item"><li><span><a href="#The-milestone()-function" data-toc-modified-id="The-milestone()-function-1.5.1"><span class="toc-item-num">1.5.1 </span>The milestone() function</a></span></li></ul></li><li><span><a href="#Displaying-Results" data-toc-modified-id="Displaying-Results-1.6"><span class="toc-item-num">1.6 </span>Displaying Results</a></span></li><li><span><a href="#Words,-Lemmas,-and-Morphology" data-toc-modified-id="Words,-Lemmas,-and-Morphology-1.7"><span class="toc-item-num">1.7 </span>Words, Lemmas, and Morphology</a></span></li><li><span><a href="#Syntax" data-toc-modified-id="Syntax-1.8"><span class="toc-item-num">1.8 </span>Syntax</a></span></li><li><span><a href="#Next-Steps" data-toc-modified-id="Next-Steps-1.9"><span class="toc-item-num">1.9 </span>Next Steps</a></span></li></ul></li></ul></div>
# -
# # Tutorial: The Greek Syntax Package
#
# ## Queries using Lowfat and Jupyter Notebooks
# <blockquote>**Important**: If you are reading this in GitHub the results are not shown. Please view it using this link: <a href="http://jonathanrobie.biblicalhumanities.org/assets/greeksyntax-tutorial.html">Tutorial: Greek Syntax Queries using Lowfat and Jupyter Notebooks</a>.</blockquote>
# This tutorial illustrates some of the kinds of queries that can be done using the <a href="https://github.com/biblicalhumanities/greek-new-testament/tree/master/syntax-trees/nestle1904-lowfat">Nestle 1904 Lowfat Syntax Trees</a> and <a href="https://jupyter.org/">Jupyter notebooks</a>. It is aimed at someone who knows Greek fairly well but may not have experience with query languages or programming. It uses the [Greek Syntax Package](https://github.com/biblicalhumanities/greek-syntax/), written to simplify the task of writing queries for this environment, which also provides a database in a Docker image.
#
# Jupyter notebooks allow headings, text, and query results to appear together. This document is a Jupyter notebook. If you have properly installed the software, you can run the queries in this notebook and see the results, or modify the queries to see different results.
#
# ## Installing and Running the Greek Syntax Package with Docker
#
# To run this notebook live, you must first install the Greek Syntax Package and run it with Docker. Follow the instructions here:
#
# [The Greek Syntax Jupyter Notebook Environment](https://github.com/biblicalhumanities/greek-syntax/blob/master/README.md)
#
# ## Opening the Database
#
# The following code imports the functions we need and opens the database:
# +
from greeksyntax.lowfat import *
q = lowfat("nestle1904lowfat")
# -
# Let's make sure that we have successfully opened the database using a simple query:
q.xquery("count(//book)")
# If the query works, you are up and running. Let's get on with the tutorial.
# ## Don't Try to Return the Whole Database
# You should be aware that there are limits on the amount of data Jupyter allows a query to return. Queries can return large results, even entire books, but there are limits. If your query returns too much data, you will see the following error:
# This query attempts to return every word in the Greek New Testament. Jupyter returns an error.
q.xquery("//w")
# The solution is to write a more specific query. You will see how to do that in the following sections.
# ## References: Book, Chapter, Verse, Word
#
# Let's start by looking up specific texts using references.
#
# The following query returns Mathew 5:6. If you hover a mouse over a word in the query results, it displays morphological information about the word and a contextualized English gloss:
q.find(milestone("Matt.5.6"))
# The Greek Syntax Package uses OSIS references, extended to support individual words. The following forms of references are supported:
#
# - Book: "Matt"
# - Chapter: "Matt.5"
# - Verse: "Matt.5.6"
# - Word: "Matt.5.6!10"
#
# Try modifying the query below to refer to other texts, then execute the cell to see the result.
q.find(milestone("Matt.5.6!10"))
# ### The milestone() function
#
# The `milestone()` function creates a query that searches for data using an OSIS reference. This function saves you the trouble of thinking about the exact structure of the XML every time you want to look up a reference.
#
# For books, chapters, and verses, it returns sentences. Try executing the following query to see the query it creates.
milestone("Matt.5.6")
# XQuery and XPath are compositional languages. The `find()` method takes a query that returns text containg words in the lowfat format and returns the corresponding text in a readable format.
q.find(milestone("Matt.5.6"))
# While convenient and readable, the `find()` method does not show you the XML that corresponds to the query. You can see the raw results of the query using the `xquery()` method. Note the `<milestone/>` element near the beginning. Try this with other references.
q.xquery(milestone("Matt.5.6"))
# Words do not contain milestones, the reference for a word is an attribute, e.g.
#
# ```
# <w role="p" class="adj" osisId="Matt.5.6!1" n="400050060010010" lemma="μακάριος" normalized="μακάριοι" strong="3107" number="plural" gender="masculine" case="nominative" head="true" gloss="Blessed [are]">μακάριοι</w>
# ```
#
# Let's take a look at how the `milestone()` function works for words.
milestone("Matt.5.6!1")
q.find(milestone("Matt.5.6!1"))
q.xquery(milestone("Matt.5.6!1"))
# You can use the `interlinear()` function to show a table with contextualized glosses and morphology for a given word or verse:
# ## Displaying Results
#
# The following methods show results in different formats:
#
# - `find()` - display a result as readable text.
# - `highlight()` - display a result as readable text, highlighting 'hits' (this is discussed in the next section)
# - `xquery()` - display a result as raw XML
# - `interlinear()` - display the words in a result as a tabular interlinear
# - `boxwood()` - display the syntactic structure of a result
#
# Let's try using the same query with each of these displays except highlight, which we discuss in the next section. Here is the query we will use:
milestone("Matt.5.6")
# To avoid typing that in each query, let's assign it to a variable:
ref = milestone("Matt.5.6")
# Now let's show the results of this query in various formats.
q.find(ref)
q.boxwood(ref)
q.xquery(ref)
# ## Words, Lemmas, and Morphology
# Many queries are based on the characteristics of individual words. Let's look at the structure of a word in our representation. First, let's look up an individual word the way we did previously:
q.find(milestone("Matt.5.6!1"))
# In this tutorial, most results are presented as readable text, but words have a rich structure that contains a great deal of information. Let's use the `xquery()` function to see the raw structure of that same word:
q.xquery(milestone("Matt.5.6!1"))
# We can use this information to look for specific characteristics of words. Let's take a look at the individual parts of this:
#
# - `<w>` - Each word is wrapped in a `w` element. You can count the words in the Greek New Testament with this query: `count(//w)`.
# - `xmlns:xi="http://www.w3.org/2001/XInclude"` is just noise for our purposes. Ignore it. It comes from including individual books into a master file using XInclude.
# - `class="verb"` - this word is a verb. You can count the verbs in the Greek New Testament with this query: `count(//w[@class='verb'])`, which counts the `w` elements that have `class` attributes with the value `verb`.
# - `role` - the grammatical role of the word within its clause, in this case `p` means `predicate`. Not all words have roles - sometimes the role is given to a group of words rather than individual words, and some words like conjunctions do not have clausal roles. You can count individual words that occur as predicates using this query: `count(//w[@role='p'])`.
# - `osisId` - the milestone for the individual word. You can find this word using the following query: `//w[@osisId='Matt.5.6!1']`.
# - `n` - an integer that can be used to sort words into sentence order.
# - `lemma` - the dictionary form of the word. You can look up other instances of this word with this query: `//w[@lemma='μακάριος']`.
# - `normalized` - a "normalized" form of the word that ignores changes in accent due to phonological context such as position in the sentence or the presence of clitics. You can look up other instances of this normalized form with this query: `//w[@normalized='μακάριοι']`.
# - `strong` - a Strong's number.
# - `number`, `gender`, `case`, etc - morphology of the word. You can look up other adjectives that are plural, masculine, and nominative using this query: `//w[@class='adj' and @number='plural' and @gender='masculine' and @case='nominative']`.
# - `gloss` - an English gloss, contextualized.
#
# For more documentation on this format, see [the Lowfat documentation](https://github.com/biblicalhumanities/greek-new-testament/tree/master/syntax-trees/nestle1904-lowfat).
#
# You can play with the queries shown above by creating new cells with the + button in the menu bar and putting your conditions in a string like this:
query = "//w[@class='adj' and @number='plural' and @gender='masculine' and @case='nominative']"
# We can search for all instances by calling `q.find()` like this:
#
# `q.find(query)`
#
# To search for instances in a given scope, we can use the `milestone()` function to specify the scope like this:
#
# `q.find(milestone("Matt.5") + query)`
#
# Let's look for instances of this in Matthew 5.
q.find(milestone("Matt.5") + query)
# The `highlight()` function gives more useful output for queries like this, showing the result highlighted in context of the original sentence. Let's use `highlight()` instead of `find()`, using the same query.
q.highlight(milestone("Matt.5") + query)
# A similar function, `sentence()`, shows the matching item after the sentence. This can be useful for posting to some online forums that strip formatting.
q.sentence(milestone("Matt.5") + query)
# We can search for results in a set of scopes by specifying each one in the same cell. Let's look for instances of our query in Luke 1 and Acts 1:
q.highlight(milestone("Luke.1") + query)
q.highlight(milestone("Acts.1") + query)
# ## Syntax
#
# Syntax is largely about exploring relationships within a clause. The `@role` attribute identifies these relationships. Clauses can contain other clauses and phrases in complex recursive structures.
#
# Groups of words are found in `<wg>` elements ("word group"). A clause is identified by the attribute `class='cl'`. Like words, word groups can have `role` attributes that identify their role in a clause.
#
# Let's look for clauses that function as objects of other clauses.
q.highlight(milestone("Matt.1") + "//wg[@class='cl' and @role='o']")
# Queries can combine conditions on individual words and conditions on word groups. Let's modify that query to show only clauses that contain participles and function as objects of other clauses. We will use `role='v'` rather than `class='verb` so that we find only clauses in which the participle governs the clause.
q.highlight(milestone("Acts") + "//wg[@class='cl' and @role='o' and w[@role='v' and @mood='participle']]")
# Word groups can also represent phrases of various kinds (see [this documentation](https://github.com/biblicalhumanities/greek-new-testament/tree/master/syntax-trees/nestle1904-lowfat)).
#
# Let's look for prepositional phrases that contain the word πίστις:
q.highlight(milestone("Acts") + "//wg[@class='pp' and .//w[@lemma='πίστις']]")
# And let's narrow that to prepostitional phrases where the preposition is ἐν. But let's also broaden the scope, looking for all instances in the Greek New Testament instead of specifying a milestone.
q.highlight("//wg[@class='pp' and w[@lemma='ἐν'] and .//w[@lemma='πίστις']]")
# Now let's narrow these results further, showing only phrases where πίστις occurs in the same word group as ἐν or the word group immediately below it.
q.highlight("//wg[@class='pp' and w[@lemma='ἐν'] and (w, wg/w)[@lemma='πίστις']]")
# ## Next Steps
#
# This is only an introductory tutorial showing a small number of queries. It is meant to whet your appetite, to inspire you to think of queries that will teach you about aspects of biblical Greek you are interested in.
#
# I plan to follow this up with more Jupyter notebooks, illustrating specific questions I would like to explore. I also expect to add more resources to the `greeksyntax` package. If you want to follow this work, I encourage you to [follow my blog](http://jonathanrobie.biblicalhumanities.org/).
|
notebooks/Greek Syntax Tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <table width="100%"> <tr>
# <td style="background-color:#ffffff;">
# <a href="http://qworld.lu.lv" target="_blank"><img src="..\images\qworld.jpg" width="35%" align="left"> </a></td>
# <td style="background-color:#ffffff;vertical-align:bottom;text-align:right;">
# prepared by <NAME> (<a href="http://qworld.lu.lv/index.php/qlatvia/" target="_blank">QLatvia</a>)
# </td>
# </tr></table>
# <table width="100%"><tr><td style="color:#bbbbbb;background-color:#ffffff;font-size:11px;font-style:italic;text-align:right;">This cell contains some macros. If there is a problem with displaying mathematical formulas, please run this cell to load these macros. </td></tr></table>
# $ \newcommand{\bra}[1]{\langle #1|} $
# $ \newcommand{\ket}[1]{|#1\rangle} $
# $ \newcommand{\braket}[2]{\langle #1|#2\rangle} $
# $ \newcommand{\dot}[2]{ #1 \cdot #2} $
# $ \newcommand{\biginner}[2]{\left\langle #1,#2\right\rangle} $
# $ \newcommand{\mymatrix}[2]{\left( \begin{array}{#1} #2\end{array} \right)} $
# $ \newcommand{\myvector}[1]{\mymatrix{c}{#1}} $
# $ \newcommand{\myrvector}[1]{\mymatrix{r}{#1}} $
# $ \newcommand{\mypar}[1]{\left( #1 \right)} $
# $ \newcommand{\mybigpar}[1]{ \Big( #1 \Big)} $
# $ \newcommand{\sqrttwo}{\frac{1}{\sqrt{2}}} $
# $ \newcommand{\dsqrttwo}{\dfrac{1}{\sqrt{2}}} $
# $ \newcommand{\onehalf}{\frac{1}{2}} $
# $ \newcommand{\donehalf}{\dfrac{1}{2}} $
# $ \newcommand{\hadamard}{ \mymatrix{rr}{ \sqrttwo & \sqrttwo \\ \sqrttwo & -\sqrttwo }} $
# $ \newcommand{\vzero}{\myvector{1\\0}} $
# $ \newcommand{\vone}{\myvector{0\\1}} $
# $ \newcommand{\vhadamardzero}{\myvector{ \sqrttwo \\ \sqrttwo } } $
# $ \newcommand{\vhadamardone}{ \myrvector{ \sqrttwo \\ -\sqrttwo } } $
# $ \newcommand{\myarray}[2]{ \begin{array}{#1}#2\end{array}} $
# $ \newcommand{\X}{ \mymatrix{cc}{0 & 1 \\ 1 & 0} } $
# $ \newcommand{\Z}{ \mymatrix{rr}{1 & 0 \\ 0 & -1} } $
# $ \newcommand{\Htwo}{ \mymatrix{rrrr}{ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} } } $
# $ \newcommand{\CNOT}{ \mymatrix{cccc}{1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0} } $
# $ \newcommand{\norm}[1]{ \left\lVert #1 \right\rVert } $
# <h2>Vectors: Dot (Scalar) Product</h2>
#
# Two vectors can be multiplied with each other in different ways.
#
# One of the very basic methods is <i>dot product</i>.
#
# It is also called <i>scalar product</i>, because the result is a <i>scalar value</i>, e.g., a real number.
#
# Consider the following two vectors:
# $$
# u = \myrvector{-3 \\ -2 \\ 0 \\ -1 \\ 4} \mbox{ and } v = \myrvector{-1\\ -1 \\2 \\ -3 \\ 5}.
# $$
#
# The dot product of $ u $ and $ v $, denoted by $ \dot{u}{v}$, can be defined algorithmically.
#
# <u>Pairwise multiplication</u>: the values in the same positions are multiplied with each other.
#
# <u>Summation of all pairwise multiplications</u>: Then we sum all the results obtained from the pairwise multiplications.
#
# We write its Python code below.
# +
# let's define both vectors
u = [-3,-2,0,-1,4]
v = [-1,-1,2,-3,5]
uv = 0; # summation is initially zero
for i in range(len(u)): # iteratively access every pair with the same indices
print("pairwise multiplication of the entries with index",i,"is",u[i]*v[i])
uv = uv + u[i]*v[i] # i-th entries are multiplied and then added to summation
print() # print an empty line
print("The dot product of",u,'and',v,'is',uv)
# -
# The pairwise multiplications of entries are
# <ul>
# <li> $ (-3)\cdot(-1) = 3 $, </li>
# <li> $ (-2)\cdot(-1) = 2 $, </li>
# <li> $ 0\cdot 2 = 0 $, </li>
# <li> $ (-1)\cdot(-3) = 3 $, and, </li>
# <li> $ 4 \cdot 5 = 20 $. </li>
# </ul>
#
# Thus the summation of all pairwise multiplications of entries is $ 3+2+0+3+20 = 28 $.
#
# <b>Remark that the dimensions of the given vectors must be the same. Otherwise, the dot product is not defined.</b>
# <h3> Task 1 </h3>
#
# Find the dot product of the following vectors in Python:
#
# $$
# v = \myrvector{-3 \\ 4 \\ -5 \\ 6} ~~~~\mbox{and}~~~~ u = \myrvector{4 \\ 3 \\ 6 \\ 5}.
# $$
#
# Your outcome should be $0$.
#
# your solution is here
#
# <a href="Math24_Dot_Product_Solutions.ipynb#task1">click for our solution</a>
# <h3> Task 2 </h3>
#
# Let $ u = \myrvector{ -3 \\ -4 } $ be a 2 dimensional vector.
#
# Find $ \dot{u}{u} $ in Python.
#
# your solution is here
#
# <a href="Math24_Dot_Product_Solutions.ipynb#task2">click for our solution</a>
# <h3> Notes:</h3>
#
# As may be observed from Task 2, the <b>length</b> of a vector can be calculated by using its <b>dot product</b> with itself.
#
# $$ \norm{u} = \sqrt{\dot{u}{u}}. $$
#
# $ \dot{u}{u} $ is $25$, and so $ \norm{u} = \sqrt{25} = 5 $.
#
# $ \dot{u}{u} $ automatically accumulates the contribution of each entry to the length.
# <h3> Orthogonal (perpendicular) vectors </h3>
#
# For simplicity, we consider 2-dimensional vectors.
#
# The following two vectors are perpendicular (orthogonal) to each other.
#
# The angle between them is $ 90 $ degrees.
#
# <img src="../images/vector_-4_-5-small.jpg" width="40%">
#
# +
# let's find the dot product of v and u
v = [-4,0]
u = [0,-5]
result = 0;
for i in range(2):
result = result + v[i]*u[i]
print("the dot product of u and v is",result)
# -
# Now, let's check the dot product of the following two vectors:
#
# <img src="../images/length_v_u.jpg" width="40%">
# +
# we can use the same code
v = [-4,3]
u = [-3,-4]
result = 0;
for i in range(2):
result = result + v[i]*u[i]
print("the dot product of u and v is",result)
# -
# The dot product of new $ u $ and $ v $ is also $0$.
#
# This is not surprising, because the vectors $u$ and $v$ (in both cases) are orthogonal to each other.
#
# <h3>Fact:</h3>
# <ul>
# <li>The dot product of two orthogonal (perpendicular) vectors is zero.</li>
# <li>If the dot product of two vectors is zero, then they are orthogonal to each other.</li>
# </ul>
#
# <i> This fact is important, because, as we will see later, orthogonal vectors (states) can be distinguished perfectly. </i>
# <h3> Task 3 </h3>
#
# Verify that (i) $ u $ is orthogonal to $ -v $, (ii) $ -u $ is orthogonal to $ v $, and (iii) $ -u $ is orthogonal to $ -v $.
#
# <img src="../images/inner_v_u_-v_-u.jpg" width="40%">
# +
# you may consider to write a function in Python for dot product
#
# your solution is here
#
# -
# <a href="Math24_Dot_Product_Solutions.ipynb#task3">click for our solution</a>
# <h3> Task 4 </h3>
#
# Find the dot product of $ v $ and $ u $ in Python.
#
# $$
# v = \myrvector{-1 \\ 2 \\ -3 \\ 4} ~~~~\mbox{and}~~~~ u = \myrvector{-2 \\ -1 \\ 5 \\ 2}.
# $$
#
# Find the dot product of $ -2v $ and $ 3u $ in Python.
#
# Compare both results.
#
# your solution is here
#
# <a href="Math24_Dot_Product_Solutions.ipynb#task4">click for our solution</a>
|
math/Math24_Dot_Product.ipynb
|
/ ---
/ jupyter:
/ jupytext:
/ text_representation:
/ extension: .q
/ format_name: light
/ format_version: '1.5'
/ jupytext_version: 1.14.4
/ kernelspec:
/ display_name: SQL
/ language: sql
/ name: SQL
/ ---
/ + [markdown] azdata_cell_guid="412dfc1e-a714-4f01-aeb5-ef0dde626c7d"
/ # SQL Server 2019 Data Virtualization - Using Polybase to query Azure SQL Database
/ This notebook contains an example of how to use external tables to query data in Azure SQL Database without moving data. You may need to change identity, secret, connection, database, schema, and remote table names to work with your Azure SQL Database.
/
/ This notebook also assumes you are using SQL Server 2019 Release Candidate or later and that the Polybase feature has been installed and enabled.
/
/ This notebook uses the sample WideWorldImporters sample database but can be used with any user database.
/ + [markdown] azdata_cell_guid="cd8d3616-4164-4a3c-9cbc-36dc2b82e34a"
/ ## Step 0: Create a database in Azure SQL, table, and add data
/
/ Create a database in Azure SQL called **wwiazure**. Execute the following T-SQL to create a table and insert a row in the database
/
/ ```sql
/ DROP TABLE IF EXISTS [ModernStockItems]
/ GO
/ CREATE TABLE [ModernStockItems](
/ [StockItemID] [int] NOT NULL,
/ [StockItemName] [nvarchar](100) COLLATE Latin1_General_100_CI_AS NOT NULL,
/ [SupplierID] [int] NOT NULL,
/ [ColorID] [int] NULL,
/ [UnitPackageID] [int] NOT NULL,
/ [OuterPackageID] [int] NOT NULL,
/ [Brand] [nvarchar](50) COLLATE Latin1_General_100_CI_AS NULL,
/ [Size] [nvarchar](20) COLLATE Latin1_General_100_CI_AS NULL,
/ [LeadTimeDays] [int] NOT NULL,
/ [QuantityPerOuter] [int] NOT NULL,
/ [IsChillerStock] [bit] NOT NULL,
/ [Barcode] [nvarchar](50) COLLATE Latin1_General_100_CI_AS NULL,
/ [TaxRate] [decimal](18, 3) NOT NULL,
/ [UnitPrice] [decimal](18, 2) NOT NULL,
/ [RecommendedRetailPrice] [decimal](18, 2) NULL,
/ [TypicalWeightPerUnit] [decimal](18, 3) NOT NULL,
/ [LastEditedBy] [int] NOT NULL,
/ CONSTRAINT [PK_Warehouse_StockItems] PRIMARY KEY CLUSTERED
/ (
/ [StockItemID] ASC
/ )
/ )
/ GO
/ -- Now insert some data. We don't coordinate with unique keys in WWI on SQL Server
/ -- so pick numbers way larger than exist in the current StockItems in WWI which is only 227
/ INSERT INTO ModernStockItems VALUES
/ (100000,
/ 'Dallas Cowboys Jersey',
/ 5,
/ 4, -- Blue
/ 4, -- Box
/ 4, -- Bob
/ 'Under Armour',
/ 'L',
/ 30,
/ 1,
/ 0,
/ '123456789',
/ 2.0,
/ 50,
/ 75,
/ 2.0,
/ 1
/ )
/ GO```
/
/ + [markdown] azdata_cell_guid="36f8b63f-f989-47fd-905f-7c5707e0f7fd"
/ ## Step 1: Create a master key
/ Create a master key to encrypt the database credential
/ + azdata_cell_guid="19a32a92-ec3f-49ae-aa3c-ea50a8a914b2"
USE [WideWorldImporters]
GO
CREATE MASTER KEY ENCRYPTION BY PASSWORD = '<password>'
GO
/ + [markdown] azdata_cell_guid="91f196a7-67f4-43cd-b7a7-943474c788b9"
/ ## Step 2: Create a database credential.
/ The database credential contains the IDENTITY (login) and SECRET (password) of the remote Azure SQL Database server or Managed Instance. Change this to the login and password for your server.
/ + azdata_cell_guid="b2f1ec1e-6d76-4510-85fb-1a14c1989490"
CREATE DATABASE SCOPED CREDENTIAL AzureSQLDatabaseCredentials
WITH IDENTITY = '<login>', SECRET = '<password>'
GO
/ + [markdown] azdata_cell_guid="4e9960e4-dc9a-47ab-8da1-468762a1b7ef"
/ ## Step 3: Create an EXTERNAL DATA SOURCE
/ The EXTERNAL DATA SOURCE indicates what type of data source, the connection "string", where PUSHDOWN predicates should be used (if possible), and the name of the database credential.
/
/ The LOCATION syntax is <datasourcetype>:<connection string>.
/
/ datasourcetype can be sqlserver, oracle, teradata, mongodb, or odbc (Windows only)
/ The connection string depends on the datasourcetype
/
/ For this example, put in the name of the Azure SQL Server database server or Managed instance
/ + azdata_cell_guid="821a3725-a003-4f16-9c6e-a71df376eca3"
CREATE EXTERNAL DATA SOURCE AzureSQLDatabase
WITH (
LOCATION = 'sqlserver://<server name>.database.windows.net',
PUSHDOWN = ON,
CREDENTIAL = AzureSQLDatabaseCredentials
)
GO
/ + [markdown] azdata_cell_guid="479ab414-46f8-4844-967f-3bc958505ada"
/ ## Step 4: Create a schema for the EXTERNAL TABLE
/ Schemas provide convenient methods to secure and organize objects
/ + azdata_cell_guid="3f8b9e0f-2cf3-4226-87c4-eee30f3a23ed"
CREATE SCHEMA azuresqldb
GO
/ + [markdown] azdata_cell_guid="f0224273-4579-4c7c-bdca-e8cacf7aa3d1"
/ ## Step 5: Create an EXTERNAL TABLE
/ An external table provides metadata so SQL Server knows how to map columns to the remote table. The name of the table for the external table can be your choice. But the columns must be specified with the same name as they are defined in the remote table. Furthermore, local data types must be compatible with the remote table.
/
/ The WITH clause specifies a LOCATION. This LOCATION is different than the EXTERNAL DATA SOURCE. This LOCATION indicates the [database].[schema].[table] of the remote table. The DATA_SOURCE clauses is the name of the EXTERNAL DATA SOURCE you created earlier.
/ + azdata_cell_guid="54154846-4eb6-445a-980b-17c2beaca255"
CREATE EXTERNAL TABLE azuresqldb.ModernStockItems
(
[StockItemID] [int] NOT NULL,
[StockItemName] [nvarchar](100) COLLATE Latin1_General_100_CI_AS NOT NULL,
[SupplierID] [int] NOT NULL,
[ColorID] [int] NULL,
[UnitPackageID] [int] NOT NULL,
[OuterPackageID] [int] NOT NULL,
[Brand] [nvarchar](50) COLLATE Latin1_General_100_CI_AS NULL,
[Size] [nvarchar](20) COLLATE Latin1_General_100_CI_AS NULL,
[LeadTimeDays] [int] NOT NULL,
[QuantityPerOuter] [int] NOT NULL,
[IsChillerStock] [bit] NOT NULL,
[Barcode] [nvarchar](50) COLLATE Latin1_General_100_CI_AS NULL,
[TaxRate] [decimal](18, 3) NOT NULL,
[UnitPrice] [decimal](18, 2) NOT NULL,
[RecommendedRetailPrice] [decimal](18, 2) NULL,
[TypicalWeightPerUnit] [decimal](18, 3) NOT NULL,
[LastEditedBy] [int] NOT NULL
)
WITH (
LOCATION='wwiazure.dbo.ModernStockItems',
DATA_SOURCE=AzureSQLDatabase
)
GO
/ + [markdown] azdata_cell_guid="8be4b3b9-2284-45cb-9941-aadbb1d56ab1"
/ ## Step 6: Create statistics
/ SQL Server allows you to store local statistics about specific columns from the remote table. This can help the query processing to make more efficient plan decisions.
/ + azdata_cell_guid="1fe5ec9e-4b71-4598-a7f0-7d5631977e06"
CREATE STATISTICS ModernStockItemsStats ON azuresqldb.ModernStockItems ([StockItemID]) WITH FULLSCAN
GO
/ + [markdown] azdata_cell_guid="2a56ae08-7d9b-49a6-b248-21fc58f4f3c9"
/ ## Step 7: Try to scan the remote table
/ Run a simple query on the EXTERNAL TABLE to scan all rows.
/ + azdata_cell_guid="bb682367-ef18-4de6-9b97-6f663bd6df19"
SELECT * FROM azuresqldb.ModernStockItems
GO
/ + [markdown] azdata_cell_guid="539c8798-1cfe-4892-911d-48a28b3b8db3"
/ ## Step 8: Query the remote table with a WHERE clause
/ Even though the table may be small SQL Server will "push" the WHERE clause filter to the remote table
/ + azdata_cell_guid="62972697-b63b-40af-9431-c413fc001996"
SELECT * FROM azuresqldb.ModernStockItems WHERE StockItemID = 100000
GO
/ + [markdown] azdata_cell_guid="2c39cabc-ccc7-465f-aae0-ff02b46824d6"
/ ## Step 9: Join with local SQL Server tables
/ Use a UNION to find all stockitems for a specific supplier both locally and in the Azure table
/ + azdata_cell_guid="bc07b1da-2ff8-4712-8685-40d5aef896a3"
SELECT msi.StockItemName, msi.Brand, c.ColorName
FROM azuresqldb.ModernStockItems msi
JOIN [Purchasing].[Suppliers] s
ON msi.SupplierID = s.SupplierID
and s.SupplierName = 'Graphic Design Institute'
JOIN [Warehouse].[Colors] c
ON msi.ColorID = c.ColorID
UNION
SELECT si.StockItemName, si.Brand, c.ColorName
FROM [Warehouse].[StockItems] si
JOIN [Purchasing].[Suppliers] s
ON si.SupplierID = s.SupplierID
and s.SupplierName = 'Graphic Design Institute'
JOIN [Warehouse].[Colors] c
ON si.ColorID = c.ColorID
GO
/ + [markdown] azdata_cell_guid="914d355e-03f8-4317-b246-324b80f159a5"
/
|
sql2019workshop/sql2019wks/08_DataVirtualization/sqldatahub/azuredb/azuredbexternaltable.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **This notebook implements a one-dimensional GAN which generates the output of a cubic function**
# The function below generates n samples of the cubic function, the domain of the function is chosen to be n random integers in the range -0.5 to 0.5. The function returns a two dimensional vector(inputs in the first column and outputs in the second) and a one dimensional vector of class labels( in this case, 1)
import numpy as np
def generate_real_samples(n):
'''generate n real samples with class labels'''
x1 = np.random.rand(n) - 0.5 #generate a random number between [-0.5,0.5]
x2 = x1**3 #generate outputs
x1 = x1.reshape(n, 1)
x2 = x2.reshape(n, 1)
X = np.hstack((x1, x2)) #stack layers
y = np.ones((n, 1)) #generate class label
return X,y
# The function below defines the discriminator model, it is one of the two components of a GAN. It's job is to classify whether the numbers generated by the generator model are real or fake( ie: if they are the output to our function or not).
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
from keras.models import Sequential
from keras.layers import Dense, LeakyReLU
from keras.utils import plot_model
import matplotlib.pyplot as plt
def define_discriminator(inputs = 2):
''' function to return the compiled discriminator model'''
model = Sequential()
model.add(Dense(25, activation = 'relu', kernel_initializer = 'he_uniform', input_dim = inputs))
model.add(LeakyReLU(alpha = 0.01))
model.add(Dense(15, activation = 'relu', kernel_initializer = 'he_uniform'))
model.add(LeakyReLU(alpha = 0.01))
model.add(Dense(5, activation = 'relu', kernel_initializer = 'he_uniform'))
model.add(LeakyReLU(alpha = 0.01))
model.add(Dense(1, activation = 'sigmoid'))
model.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])
return model
discriminator_model = define_discriminator()
discriminator_model.summary()
plot_model(discriminator_model, to_file = 'discriminator_model.png', show_shapes = True, show_layer_names = True)
# -
# The function below makes up the second component of a GAN. It takes an input point from a latent space and generate a vector with two dimensions(like the X vector returned by the generate_real_samples function)
# <br>
# A latent variable is a hidden variable, and the space it belongs to is called the latent space. We can arbitrarily assign a size to our latent space(here it is 5). The points in the latent space are meaningless until the generator model begins learning and starts assigning meaning to the points in the space. After training, the points in the latent space correspond to the generated samples.
# Note that the generator model isn't compiled here, it's because it is fit indirectly.
def define_generator(latent_dim, outputs = 2):
model = Sequential()
model.add(Dense(25, activation = 'relu', kernel_initializer= 'he_uniform', input_dim = latent_dim))
model.add(LeakyReLU(alpha = 0.01))
model.add(Dense(15, activation = 'relu', kernel_initializer = 'he_uniform'))
model.add(LeakyReLU(alpha = 0.01))
model.add(Dense(outputs, activation = 'linear'))
return model
latent_dim = 5
generator_model = define_generator(latent_dim)
generator_model.summary()
plot_model(generator_model, to_file = 'generator_model.png', show_shapes = True, show_layer_names = True)
# The function generates_latent_points generates n points in the latent space. The generate_fake_samples function uses the generator model to generate 'fake' samples.
# +
def generate_latent_points(latent_dim, n):
'''generate points in latent space as input for the generator'''
x_input = np.random.rand(latent_dim*n) #generate points in latent space
x_input = x_input.reshape(n,latent_dim) #reshape
return x_input
def generate_fake_samples(generator, latent_dim, n):
x_input = generate_latent_points(latent_dim, n) #genarate points in latent space
x = generator.predict(x_input) #predict outputs
y = np.zeros((n, 1))
return x, y
# -
# As of now, the fake samples produced by the generator is garbage because we haven't trained it yet. It is supposed to closely follow our function after training.
X, _ = generate_fake_samples(generator_model, latent_dim, 100)
plt.scatter(X[:,0], X[:,1])
plt.show()
# The function below combines the generator and discriminator models. The layers of the discriminator model are made non-trainable( because we do not want to update it's weights during the training of the generator). Here, the discriminator's only job is to classify real and fake samples.
def define_gan(generator, discriminator):
'''define the combined generator and discriminator model'''
discriminator.trainable = False
model = Sequential()
model.add(generator)
model.add(discriminator)
model.compile(optimizer = 'adam', loss = 'binary_crossentropy')
return model
gan_model = define_gan(generator_model, discriminator_model)
gan_model.summary()
plot_model(gan_model, to_file = 'gan_model.png', show_layer_names = True, show_shapes = True)
# We want the discriminator model to believe that the samples generated by the generator are real, so we label them as '1'(real). In the ideal case, the discriminator is fooled about half of the times into believing that the samples generated by the generator are real.
# The train_gan function simultaneously trains the discriminator and the GAN.
def train_gan(g_model,d_model,gan_model,latent_dim, num_epochs = 10000,num_eval = 2000, batch_size = 128):
''' function to train gan model'''
half_batch = int(batch_size/2)
#run epochs
for i in range(num_epochs):
X_real, y_real = generate_real_samples(half_batch) #generate real examples
d_model.train_on_batch(X_real, y_real) # train on real data
X_fake, y_fake = generate_fake_samples(g_model, latent_dim, half_batch) #generate fake samples
d_model.train_on_batch(X_fake, y_fake) #train on fake data
#prepare points in latent space as input for the generator
x_gan = generate_latent_points(latent_dim, batch_size)
y_gan = np.ones((batch_size, 1)) #generate fake labels for gan
gan_model.train_on_batch(x_gan, y_gan)
if (i+1) % num_eval == 0:
summarize_performance(i + 1, g_model, d_model, latent_dim)
# The function defined below is called every two thousand epochs to summarize the performance of the training.
def summarize_performance(epoch, generator, discriminator, latent_dim, n = 100):
'''evaluate the discriminator and plot real and fake samples'''
x_real, y_real = generate_real_samples(n) #generate real samples
_, acc_real = discriminator.evaluate(x_real, y_real, verbose = 1)
x_fake, y_fake = generate_fake_samples(generator, latent_dim, n)
_, acc_fake = discriminator.evaluate(x_fake, y_fake, verbose = 1)
print('Epoch: ' + str(epoch) + ' Real Acc.: ' + str(acc_real) + ' Fake Acc.: '+ str(acc_fake))
plt.scatter(x_real[:,0], x_real[:,1], color = 'red')
plt.scatter(x_fake[:,0], x_fake[:,1], color = 'blue')
plt.show()
train_gan(generator_model, discriminator_model, gan_model, latent_dim)
# References:
# 1. <a href = 'https://machinelearningmastery.com/how-to-develop-a-generative-adversarial-network-for-a-1-dimensional-function-from-scratch-in-keras/' >This </a> blog article.
# 2. The GAN paper by <NAME>: https://arxiv.org/pdf/1406.2661.pdf
# Improvements and further insights possible:
# 1. Try deeper layers in discriminator and generator models.
# 2. Try experimenting with different activation functions and learning rates
# 3. Try out more functions!
|
1d-gan.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "subslide"}
# # The merge function
#
# -
# ## Always use how, indicator, on
# + slideshow={"slide_type": "subslide"}
import pandas as pd
left_df = pd.DataFrame({
'firm': ['Accenture','Citi','GS'],
'varA': ['A1', 'A2', 'A3']})
right_df = pd.DataFrame({
'firm': ['GS','Chase','WF'],
'varB': ['B1', 'B2', 'B3'],
'varc': ['C1', 'C2', 'C3']})
# -
left_df
# + [markdown] slideshow={"slide_type": "subslide"}
# Let use shift+tab to talk about the parameters.
#
# Put your cursor in the merge function below and hit shift tab
# -
right_df
left_df.merge(right_df, how='inner').shape[0]
left_df.merge(right_df, how='left')
left_df.merge(right_df, how='right')
left_df.merge(right_df, how='outer')
left_df.merge(right_df, how='cross')
# The main parameters:
# - right
# - how
# - on and its variants
# - indicator
# - validate
# ## Part 1
#
# _Prof: Leave the "how" slide on the board_
#
# Some work with the mechanics:
#
# - Q0 Merge both datasets above with each possible value of `how`. How many observations result from each of the four merges?
left_df.merge(right_df, how='inner').shape[0]
left_df.merge(right_df, how='left').shape[0]
left_df.merge(right_df, how='right').shape[0]
left_df.merge(right_df, how='outer').shape[0]
left_df.merge(right_df, how='cross').shape[0]
# - Q1 Compare `left_df.merge(right_df)` and `pd.merge(left_df, right_df)`. Are they the same or different? What do we learn from this?
left_df.merge(right_df)
pd.merge(left_df, right_df)
# ### They are the same
# - df.merge calls pd.merge
# - https://morioh.com/p/a26b95f657d6
# - Q2 Successfully do an outer merge between `left_df` and `ChosenOne`. Then try to do an outer merge between `left_df` and `CurryForThree` (both are defined below)
# - Q3 Do an outer merge with `left_df` and `right_df` and output the source of each observation by using the "indicate" option.
a_bad_name = left_df.merge(right_df, how='outer', indicator=True)
a_bad_name['_merge'].value_counts() #always do this
# # Using Validate
left_df.merge(right_df, how='outer', indicator=True, validate='1:1')
left_df.merge(right_df, how='outer', indicator=True, validate='1:m')
left_df.merge(right_df, how='outer', indicator=True, validate='m:1')
left_df.merge(right_df, how='outer', indicator=True, validate='m:m')
# - Q4 Repeat the outer merge we just did, but four times: try each possible value of "validate"
# +
ChosenOne = pd.DataFrame({
'tic': ['GS','GS','GS'],
'varB': ['B1', 'B2', 'B3'],
'varc': ['C1', 'C2', 'C3']})
CurryForThree = pd.DataFrame({
'var1': ['GS','GS','GS'],
'varD': ['D1', 'D2', 'D3'],
'varE': ['E1', 'E2', 'E3']}).set_index('var1')
# -
#left_df.merge(ChosenOne, how='outer', left_on=('firm'), right_on=('tic'))
left_df.merge(ChosenOne,
how = 'outer'
)
left_df.merge(CurryForThree,
how='outer',
left_on=('firm'),
right_index=True)
# ## Part 2
#
# - Q5: [Guess what category of join](https://ledatascifi.github.io/ledatascifi-2022/content/03/05b_merging.html#categories-of-joins) each of the following merges are?
# 1. `left_df` and `right_df` (you already know from Q4)
# 1:1
# #### `left_df` and `ChosenOne` 1:m because Chosen one is all GS
#left_df.merge(ChosenOne, how='outer', left_on=('firm'), right_on=('tic'))
left_df.merge(ChosenOne,
how = 'inner',
left_on = 'firm',
right_on='tic',
validate='1:m')
# 1:M can expand the dataset
# 1. `CurryForThree` and `left_df` M:1
#left_df.merge(ChosenOne, how='outer', left_on=('firm'), right_on=('tic'))
CurryForThree.merge(left_df,
how = 'left',
right_on='firm',
left_index=True)
# m:1 dataset can't expand
# m:1 + left --> dataset will stay the same length
# 1. `ChosenOne` and `CurryForThree` M:M
# - Q6: Do each of those four merge with `how='inner'` as an option. What is the length of each resulting dataframe?
# - Q7: Do an outer merge of `left_df` and `ChosenOne`. How many observations are in the resulting data, and why is it different than we foudn in Q6?
# - Q8: Merge these next two datasets with `how='inner'` as an option. What s the length of the resulting dataframe and do you think it's right?
# +
poppop = pd.DataFrame({
'tic': ['TSLA','TSLA','GM'],
'varB': ['2016', '2017', '2018'],
'varc': ['C1', 'C2', 'C3']})
CurryForThree = pd.DataFrame({
'var1': ['F','TSLA','TSLA'],
'varD': ['2016', '2017', '2018'],
'varE': ['E1', 'E2', 'E3']}).set_index('var1')
# +
# You can merge on multiple variables
# If varB and varD were named the same thing it would only appear once
poppop.merge(CurryForThree,
left_on = ['tic','varB'],
right_on = ['var1','varD'])
# -
poppop
CurryForThree
# ## Part 3 - Collecting tips
#
# You should, after class, collect tips about
# - The most common use of merging and safeguards you can use
# - When should you create variables - before or after a merge?
# - Best practices for merging
# +
import pandas as pd
import numpy as np
df = pd.DataFrame({"A":[12, 4, 5, None, 1],
"B":[None, 2, 54, 3, None],
"C":[20, 16, None, 3, 8],
"D":[14, 3, None, None, 6]})
_df1 = df.copy()
_df1['firm'] = 1
_df1['date'] = _df1.index
_df2 = df.copy()
_df2['firm'] = 2
_df2['date'] = _df2.index
df2 = _df1.append(_df2)
# -
df
## Q1
df.fillna(-1)
## Q2
df['B'] = df['B'].fillna(-1)
df
# +
## Q3
##for col in df:
##df[col] = df[col].fillna(df[col].mean())
#Better way
df.fillna(df.mean())
df
|
handouts/Merging exercises.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:py37]
# language: python
# name: conda-env-py37-py
# ---
# + [markdown] colab_type="text" id="GlK6GW-xK88A"
# # **Thinking in tensors, writing in PyTorch**
# Hands-on course by [<NAME>](https://p.migdal.pl). This notebook prepared by [<NAME>](https://github.com/werkaaa). Version for ML in PL 2019 workshop.
#
# ## ConvNets: Convolutions
#
# <a href="https://colab.research.google.com/github/stared/thinking-in-tensors-writing-in-pytorch/blob/master/convnets/Convolutions.ipynb" target="_parent">
# <img src="https://colab.research.google.com/assets/colab-badge.svg"/>
# </a>
#
# 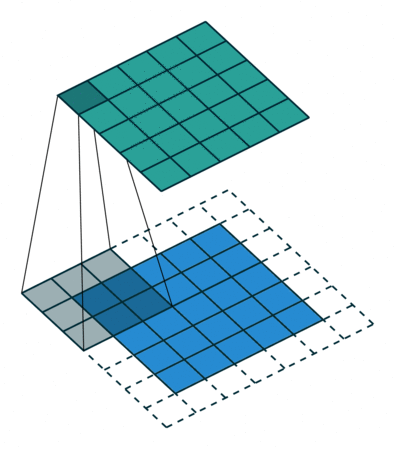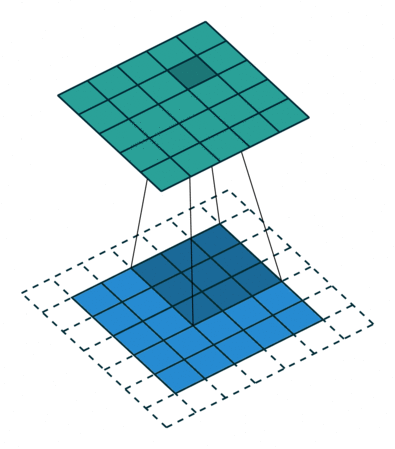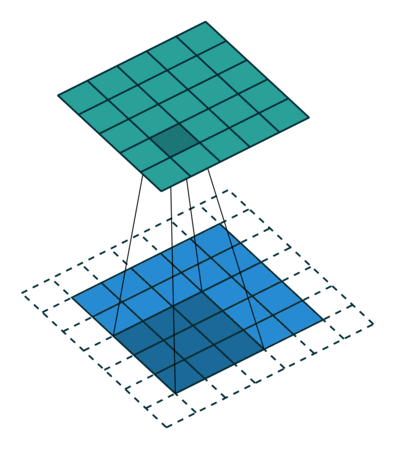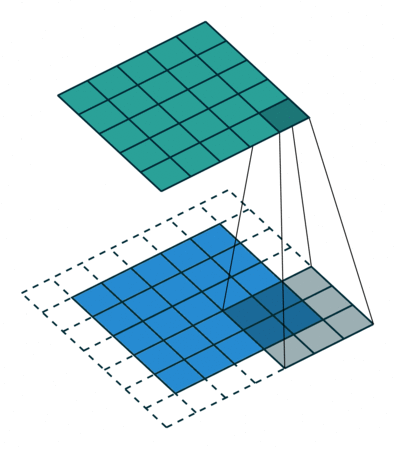
#
# (image source: [Convolution arithmetic](https://github.com/vdumoulin/conv_arithmetic))
#
# Convolution (properly cross-correlation) is an operation on kernel and input data. It consists of following steps:
# * Place the kernel above the input data
# * Perform an elementwise multiplication between kernel elements and overlaping input elements and sum the products
# * Repeat for all pixels of the input data
#
# Each convolution layer produces new channels based on those which preceded it. First, we start with 3 channels for red, green and blue (RGB) components. Next, channels get more and more abstract.
#
# While producing new channels with representations of various properties of the image, we also reduce the resolution, usually using pooling layers.
#
# See also:
# * [Image Kernels - visually explained](http://setosa.io/ev/image-kernels/)
# * [How neural networks build up their understanding of images](https://distill.pub/2017/feature-visualization/) by <NAME> et al at Distill
# * [Convolutional Neural Networks by <NAME>](http://cs231n.github.io/convolutional-networks/) for in-depth explanation of convolutions and other accompanying blocks
# * [CNNs, Part 1: An Introduction to Convolutional Neural Networks](https://victorzhou.com/blog/intro-to-cnns-part-1/) by <NAME>
# * [How do Convolutional Neural Networks work?](http://brohrer.github.io/how_convolutional_neural_networks_work.html)
# -
#Downgrading matplotlib, so seaborn works correctly. Use only in Colab.
# !pip install matplotlib==3.1.0 --quiet
# + colab={"base_uri": "https://localhost:8080/", "height": 147} colab_type="code" id="nbAxaziqsXao" outputId="24d446a4-7fb3-44f8-ffc2-deccb4e72079"
import torch
from torch import utils
from torchvision import transforms
import torchvision
from PIL import Image
import requests
from io import BytesIO
import torch.nn.functional as F
import matplotlib.pyplot as plt
import seaborn as sns
# + [markdown] colab_type="text" id="aRSdW_kWRhoQ"
# ## Tic-tac-toe
# + [markdown] colab_type="text" id="R_epEqwgFjvZ"
# Firstly, we will play with an one-channel tic-tac-toe board. Let's look at 6 kernels which will try to detect 6 particular patterns at the tic-tac-toe bord.
# + colab={} colab_type="code" id="Rhl8Qf5FbG0m"
class Tic_tac_toe():
def __init__(self, width, height):
self.width = width
self.height = height
self.board = torch.zeros(4*width+3, 4*height+3)
def place_X(self, x, y):
x_pos = 4*x + 3
y_pos = 4*y + 3
dx = [-1, 1, 1, -1]
dy = [-1, 1, -1, 1]
for i, j in zip(dx, dy):
self.board[y_pos+i][x_pos+j] = 1.0
self.board[y_pos][x_pos] = 1.0
def place_O(self, x, y):
x_pos = 4*x + 3
y_pos = 4*y + 3
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
for i, j in zip(dx, dy):
self.board[y_pos+i][x_pos+j] = 1.0
def fill_up(self, X, O):
for (x, y) in X:
self.place_X(x, y)
for (x, y) in O:
self.place_O(x, y)
def __str__(self):
return str(self.board)
def draw(self):
plt.imshow(self.board, cmap="gray")
plt.show()
# + [markdown] colab_type="text" id="WWfKPTcXsqj-"
# Create a tic-tac-toe board of preferred size and place marks on it.
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 265} colab_type="code" id="ziD6_IYlQHEb" outputId="897f5f51-730a-45e0-9204-20fef46275f0"
#@title Create a tic-tac-toe board
width = 5 # @param {type:"integer"}
height = 5 # @param {type:"integer"}
place_X = [(4, 0), (3, 1), (2, 2), (1, 3), (0, 4)] # @param {}
place_O = [(0, 0), (0, 1), (1, 0), (2, 1), (3, 2), (4, 3)] # @param {}
tic_tac_toe = Tic_tac_toe(5, 5)
tic_tac_toe.fill_up(X=place_X, O=place_O)
board = tic_tac_toe.board
tic_tac_toe.draw()
# + colab={} colab_type="code" id="_b6K4DNnLC4F"
def visualize_kernels(kernels, s=3, annot=True, l=0):
columns = len(kernels)
fig, axs = plt.subplots(1, columns, figsize=(s*columns, s))
j = 0
for k in kernels.keys():
ax = axs[j]
ax.set_title(k)
sns.heatmap(kernels[k].squeeze(dim=0).squeeze(
dim=0), ax=ax, annot=annot, cbar=False, linewidths=l, cmap="YlGnBu", fmt=".1f")
ax.axis('off')
j = j+1
# + [markdown] colab_type="text" id="pgFqnbGst-ET"
# Now, let's look at 2 kernels, which will help us with the analisis of the board.
# + colab={"base_uri": "https://localhost:8080/", "height": 210} colab_type="code" id="oCFa57cn0TBx" outputId="5d0df772-3690-49a1-b2e0-d213bda89e37"
x_o_kernels = {
'x': torch.tensor([[[[1.0, 0.0, 1.0],
[0.0, 1.0, 0.0],
[1.0, 0.0, 1.0]]]]),
'o': torch.tensor([[[[0.0, 1.0, 0.0],
[1.0, 0.0, 1.0],
[0.0, 1.0, 0.0]]]])
}
visualize_kernels(x_o_kernels, l=.5)
# + [markdown] colab_type="text" id="H-9B2478ulOo"
# Firstly, we apply the **x** kernel and **o** kernel to the input image respectively. As you can see, places where crosses and circles were located have now the biggest values.
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 591} colab_type="code" id="wJXIR4vKYCZw" outputId="29f9d80e-9862-4622-dcdb-152670bf1201"
#@title Specify bias and activation function:
bias = 0 # @param {type:"slider", min:-5, max:5, step:0.5}
activation_function = "Identity" # @param ["Identity", "ReLU", "Sigmoid"]
functions = {'Identity': lambda x: x,
'ReLU': torch.relu,
'Sigmoid': torch.sigmoid}
activation = functions[activation_function]
layer1 = {k+' kernel': activation(torch.conv2d(board.unsqueeze(dim=0).unsqueeze(dim=0), v)+bias)
for (k, v) in x_o_kernels.items()}
visualize_kernels(layer1, s=10)
# + [markdown] colab_type="text" id="Aa2naWWl9byA"
# Try changing the bias value, so places where crosses and circles were located are more visible. You can also add the activation function.
# + [markdown] colab_type="text" id="5Co0I2b7wEUs"
# To make it even more clear, let's apply max pooling operation. Out of every four pixels we will choose one with the greatest value.
#
#
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 373} colab_type="code" id="cjQrxWDzZ4w7" outputId="579565c5-ab78-4bbf-f86b-cc1000a94785"
#@title Specify pooling:
pooling_kernel_size = 2 # @param {type:"number"}
pooling_type = "max-pooling" # @param ["max-pooling", "avg-pooling"]
types = {'avg-pooling': F.avg_pool2d, 'max-pooling': F.max_pool2d}
pooling = types[pooling_type]
layer1_pooling = {k+'+'+pooling_type: pooling(v, pooling_kernel_size)
for (k, v) in layer1.items()}
visualize_kernels(layer1_pooling, s=6)
# + [markdown] colab_type="text" id="X9jwCpZUyQhd"
# Sometimes, we don't have to use max pooling of size 2 here. You can try to use average pooling here or choose a different size of the kernel.
# + [markdown] colab_type="text" id="G5tVUmnI2572"
# Finally, we can use 4 more kernels to find lines of croses and circles.
# + colab={"base_uri": "https://localhost:8080/", "height": 210} colab_type="code" id="ocwcmwEXOExe" outputId="4bc4b488-f7c7-4028-da5e-34f42073c17b"
line_kernels = {
'vertical': torch.tensor([[[[0.0, 1.0, 0.0],
[0.0, 1.0, 0.0],
[0.0, 1.0, 0.0]]]]),
'horizontal': torch.tensor([[[[0.0, 0.0, 0.0],
[1.0, 1.0, 1.0],
[0.0, 0.0, 0.0]]]]),
'diagonal_1': torch.tensor([[[[0.0, 0.0, 1.0],
[0.0, 1.0, 0.0],
[1.0, 0.0, 0.0]]]]),
'diagonal_2': torch.tensor([[[[1.0, 0.0, 0.0],
[0.0, 1.0, 0.0],
[0.0, 0.0, 1.0]]]])
}
visualize_kernels(line_kernels, l=.5)
# + [markdown] colab_type="text" id="kXw1fpGqRD-8"
# Let's use remaining kernels combined with max pooling and ReLU to see, where whole lines of crosses and circles were located.
# + colab={"base_uri": "https://localhost:8080/", "height": 512} colab_type="code" id="qNBGTaCZ2R2q" outputId="60a85b0e-b5f1-4752-8bf8-08e4c289e837"
layer1_ = list(layer1_pooling.values())
layer2_x = {k+' x': torch.conv2d(layer1_[0], v)
for (k, v) in line_kernels.items()}
layer2_o = {k+' o': torch.conv2d(layer1_[1], v)
for (k, v) in line_kernels.items()}
visualize_kernels(layer2_x, s=4)
visualize_kernels(layer2_o, s=4)
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 512} colab_type="code" id="2G5P9UkZzRYo" outputId="05eddafd-c107-43ab-85bf-823b09560e3c"
# @title Specify second layer parameters:
pooling_kernel_size = 2 # @param {type:"number"}
pooling_type = "max-pooling" # @param ["max-pooling", "avg-pooling"]
types = {'avg-pooling': F.avg_pool2d, 'max-pooling': F.max_pool2d}
pooling = types[pooling_type]
bias = 0 # @param {type:"slider", min:-5, max:5, step:0.5}
activation_function = "Identity" # @param ["Identity", "ReLU", "Sigmoid"]
functions = {'Identity': lambda x: x,
'ReLU': torch.relu,
'Sigmoid': torch.sigmoid}
activation = functions[activation_function]
layer2_x_activation = {k+'+activation': pooling(activation(
v+bias), pooling_kernel_size) for (k, v) in layer2_x.items()}
layer2_o_activation = {k+'+activation': pooling(activation(
v+bias), pooling_kernel_size) for (k, v) in layer2_o.items()}
visualize_kernels(layer2_x_activation, s=4)
visualize_kernels(layer2_o_activation, s=4)
# + [markdown] colab_type="text" id="whCON0Eo3hc7"
# ## Bigger picture
# -
# On bigger scale, pattern recognition is nicely visible on edge detection by so called Sobel kernels.
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 285} colab_type="code" id="4V6mTGNtSS9R" outputId="65375500-27b9-4e63-eb0d-752592ab64c5"
#@markdown ### Enter a path with the photo:
#"https://upload.wikimedia.org/wikipedia/commons/thumb/9/96/Common_zebra_1.jpg/250px-Common_zebra_1.jpg"
# @param {type:"string"}
file_path = "https://upload.wikimedia.org/wikipedia/commons/thumb/9/96/Common_zebra_1.jpg/250px-Common_zebra_1.jpg"
if ":" in file_path:
response = requests.get(file_path)
img = Image.open(BytesIO(response.content))
else:
img = Image.open(file_path)
transform = transforms.Compose([
transforms.Resize((64, 64)),
transforms.Grayscale(),
transforms.ToTensor()])
img_tensor = transform(img)
plt.imshow(img_tensor.squeeze(dim=0), cmap="gray")
# + colab={} colab_type="code" id="ng0LoK2QWCIe"
sobel_vertical_kernel = torch.tensor([[[[-1.0, 0.0, 1.0],
[-2.0, 0.0, 2.0],
[-1.0, 0.0, 1.0]]]])
sobel_horizontal_kernel = torch.tensor([[[[-1.0, -2.0, -1.0],
[0.0, 0.0, 0.0],
[1.0, 2.0, 1.0]]]])
# + colab={"base_uri": "https://localhost:8080/", "height": 268} colab_type="code" id="d9yahXnUWwFq" outputId="49753f4d-2f66-48bf-c94a-5f48f4410e0d"
zebra_with_sobel_vertical = torch.conv2d(
img_tensor.unsqueeze(dim=0), sobel_vertical_kernel)
plt.imshow(zebra_with_sobel_vertical.squeeze(
dim=0).squeeze(dim=0), cmap="gray")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 268} colab_type="code" id="6UlzwvhqYg44" outputId="3300644c-83f8-4ff0-b349-a5b002fc9c4a"
zebra_with_sobel_horizontal = torch.conv2d(
img_tensor.unsqueeze(dim=0), sobel_horizontal_kernel)
plt.imshow(zebra_with_sobel_horizontal.squeeze(
dim=0).squeeze(dim=0), cmap="gray")
plt.show()
# -
# You can try and experiment with your own images.
|
convnets/Convolutions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# !pip install SciPy
# Scipy - To perform Mathematical, Scientific and Engineering Computations.
#
# <h3>SciPy Sub-packages</h3>
#
# <table class="table table-bordered">
# <tbody><tr>
# <td style="text-align:center" width="40%"><a href="https://docs.scipy.org/doc/scipy/reference/cluster.html#module-scipy.cluster" target="_blank" rel="nofollow">scipy.cluster</a></td>
# <td>Vector quantization / Kmeans</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/constants.html#module-scipy.constants" target="_blank" rel="nofollow">scipy.constants</a></td>
# <td>Physical and mathematical constants</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/fftpack.html#module-scipy.fftpack" target="_blank" rel="nofollow">scipy.fftpack</a></td>
# <td>Fourier transform</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/integrate.html#module-scipy.integrate" target="_blank" rel="nofollow">scipy.integrate</a></td>
# <td>Integration routines</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/interpolate.html#module-scipy.interpolate" target="_blank" rel="nofollow">scipy.interpolate</a></td>
# <td>Interpolation</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/io.html#module-scipy.io" target="_blank" rel="nofollow">scipy.io</a></td>
# <td>Data input and output</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/linalg.html#module-scipy.linalg" target="_blank" rel="nofollow">scipy.linalg</a></td>
# <td>Linear algebra routines</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/ndimage.html#module-scipy.ndimage" target="_blank" rel="nofollow">scipy.ndimage</a></td>
# <td>n-dimensional image package</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/odr.html#module-scipy.odr" target="_blank" rel="nofollow">scipy.odr</a></td>
# <td>Orthogonal distance regression</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/optimize.html#module-scipy.optimize" target="_blank" rel="nofollow">scipy.optimize</a></td>
# <td>Optimization</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/signal.html#module-scipy.signal" target="_blank" rel="nofollow">scipy.signal</a></td>
# <td>Signal processing</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/sparse.html#module-scipy.sparse" target="_blank" rel="nofollow">scipy.sparse</a></td>
# <td>Sparse matrices</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/spatial.html#module-scipy.spatial" target="_blank" rel="nofollow">scipy.spatial</a></td>
# <td>Spatial data structures and algorithms</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/special.html#module-scipy.special" target="_blank" rel="nofollow">scipy.special</a></td>
# <td>Any special mathematical functions</td>
# </tr>
# <tr>
# <td style="text-align:center"><a href="https://docs.scipy.org/doc/scipy/reference/stats.html#module-scipy.stats" target="_blank" rel="nofollow">scipy.stats</a></td>
# <td>Statistics</td>
# </tr>
# </tbody></table>
# By default, all the NumPy functions have been available through the SciPy namespace
# <h3>SciPy - Cluster</h3>
#
#
# K-means clustering is a method for finding clusters and cluster centers in a set of unlabelled data. Intuitively, we might think of a cluster as – comprising of a group of data points, whose inter-point distances are small compared with the distances to points outside of the cluster. Given an initial set of K centers, the K-means algorithm iterates the following two steps −
#
# For each center, the subset of training points (its cluster) that is closer to it is identified than any other center.
#
# The mean of each feature for the data points in each cluster are computed, and this mean vector becomes the new center for that cluster.
#
# These two steps are iterated until the centers no longer move or the assignments no longer change. Then, a new point x can be assigned to the cluster of the closest prototype.
from scipy.cluster.vq import kmeans,vq,whiten
import numpy as np
# creating random data
testdata = ((np.random.rand(1000,3)) * 10)+1
# print(testdata)
# <b>Whiten the data</b>
#
# Normalize a group of observations on a per feature basis. Before running K-Means, it is beneficial to rescale each feature dimension of the observation set with whitening. Each feature is divided by its standard deviation across all observations to give it unit variance.
#
testdata = whiten(testdata)
# <b>Compute K-Means with Three Clusters</b>
centroids,_ = kmeans(testdata,3)
print(centroids)
# The vq function compares each observation vector in the ‘M’ by ‘N’ obs array with the centroids and assigns the observation to the closest cluster. It returns the cluster of each observation and the distortion.
# +
clx,_ = vq(testdata,centroids)
print((clx))
# to check the frequency of each occurences
# unique_elements, counts_elements = np.unique(clx, return_counts=True)
# print(np.asarray((unique_elements, counts_elements)))
# -
# <h3>SciPy - FFTpack</h3>
#
#
# Fourier Transformation is computed on a time domain signal to check its behavior in the frequency domain. Fourier transformation finds its application in disciplines such as signal and noise processing, image processing, audio signal processing, etc.
# +
from scipy.fftpack import fft,ifft
x = np.array([1.0, 2.0, 1.0, -1.0, 1.5, 1.0, 1.0])
y = fft(x)
print(y,end="\n\n")
yinv = ifft(y)
print (yinv)
# -
# <h3>SciPy - Integrate</h3>
#
# <table class="table table-bordered">
# <tbody><tr>
# <th style="text-align:center;" width="12%">Sr No.</th>
# <th style="text-align:center;">Function & Description</th>
# </tr>
# <tr>
# <td class="ts">1</td>
# <td><p><b>quad</b></p>
# <p>Single integration</p></td>
# </tr>
# <tr>
# <td class="ts">2</td>
# <td><p><b>dblquad</b></p>
# <p>Double integration</p></td>
# </tr>
# <tr>
# <td class="ts">3</td>
# <td><p><b>tplquad</b></p>
# <p>Triple integration</p></td>
# </tr>
# <tr>
# <td class="ts">4</td>
# <td><p><b>nquad</b></p>
# <p><i>n</i>-fold multiple integration</p></td>
# </tr>
# <tr>
# <td class="ts">5</td>
# <td><p><b>fixed_quad</b></p>
# <p>Gaussian quadrature, order n</p></td>
# </tr>
#
# </tbody></table>
# +
import scipy.integrate
f= lambda x:x**2
i = scipy.integrate.quad(f, 0, 1)
print(i)
# the first number is the value of integral and
# the second value is the estimate of the absolute error in the value of integral.
# -
# <h3>SciPy - Interpolate</h3>
#
# Interpolation is the process of finding a value between two points on a line or a curve.
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.linspace(0, 4, 15)
y = np.cos(x**2/3+4)
print (x)
print(y)
plt.plot(x, y, "o")
plt.show()
# <b>1-D Interpolation</b>
#
#
# The interp1d class in the scipy.interpolate is a convenient method to create a function based on fixed data points, which can be evaluated anywhere within the domain defined by the given data using linear interpolation.
#
# ------
#
# Using the interp1d function, we created two functions f1 and f2. These functions, for a given input x returns y. The third variable kind represents the type of the interpolation technique. 'Linear', 'Nearest', 'Zero', 'Slinear', 'Quadratic', 'Cubic' are a few techniques of interpolation.
#
#
# +
f1 = interpolate.interp1d(x, y,kind = 'linear')
f2 = interpolate.interp1d(x, y, kind = 'cubic')
plt.plot(x, y, 'o', x, f1(x), '-',x, f2(x), '--')
plt.legend(['data', 'linear', 'cubic','nearest'], loc = 'best')
plt.show()
# -
# <h3>SciPy - Input And Output</h3>
#
# MATLAB:
#
# <table class="table table-bordered">
# <tbody><tr>
# <th width="12%">Sr. No.</th>
# <th style="text-align:center;">Function & Description</th>
# </tr>
# <tr>
# <td class="ts">1</td>
# <td><p><b>loadmat</b></p>
# <p>Loads a MATLAB file<br>Syntax : mat_file_content = scipy.io.loadmat(‘filename.mat’)
#
# </p></td>
# </tr>
# <tr>
# <td class="ts">2</td>
# <td><p><b>savemat</b></p>
# <p>Saves a MATLAB file<br>Syntax : scipy.io.savemat('filename.mat', {'vect':nparray})</p></td>
# </tr>
# <tr>
# <td class="ts">3</td>
# <td><p><b>whosmat</b></p><p>Lists variables inside a MATLAB file</p></td>
# </tr>
# </tbody></table>
# <h3>SciPy - Ndimage</h3>
#
#
#
# <b>Opening and Writing to Image Files</b>
#
# !pip install imageio
# +
import imageio
from scipy import ndimage
import matplotlib.pyplot as plt
f = imageio.imread('face.png')
plt.imshow(f)
plt.show()
lx, ly,lz = f.shape
print(lx," ",ly,' ',lz)
print(f.shape)
crop_face = f[200:500,200:800,:]
plt.imshow(crop_face)
plt.show()
blurred_face = ndimage.gaussian_filter(f, sigma=3)
plt.imshow(blurred_face)
plt.show()
# -
# <b>Edge Detection
# +
import scipy.ndimage
# im = np.zeros((256, 256))
# im[64:-64, 64:-64] = 1
# im[90:-90,90:-90] = 2
# im[80:-80,80:-80] = 5
# im[70:-70,70:-70] = 4
# im[100:-9,0:-60] = 6
im = np.random.rand(256,256)
im[64:-64, 64:-64] = 1
# im[90:-90,90:-90] = 2
im[80:-80,80:-80] = 5
# im[70:-70,70:-70] = 4
im[100:-9,0:-60] = 6
plt.imshow(im)
plt.show()
im = ndimage.gaussian_filter(im, 5)
plt.imshow(im)
plt.show()
sx = ndimage.sobel(im, axis = 0, mode = 'constant')
sy = ndimage.sobel(im, axis = 1, mode = 'constant')
sob = np.hypot(sx, sy)
plt.imshow(sob)
plt.show()
# -
# <h3>SciPy - Optimize</h3>
#
#
# The scipy.optimize package provides several commonly used optimization algorithms. This module contains the following aspects −
#
# Unconstrained and constrained minimization of multivariate scalar functions (minimize()) using a variety of algorithms (e.g. BFGS, Nelder-Mead simplex, Newton Conjugate Gradient, COBYLA or SLSQP)
#
# Global (brute-force) optimization routines (e.g., anneal(), basinhopping())
#
# Least-squares minimization (leastsq()) and curve fitting (curve_fit()) algorithms
#
# Scalar univariate functions minimizers (minimize_scalar()) and root finders (newton())
#
# Multivariate equation system solvers (root()) using a variety of algorithms (e.g. hybrid Powell, Levenberg-Marquardt or large-scale methods such as Newton-Krylov)
# <b>Unconstrained And Constrained minimization of multivariate scalar functions</b>
#
# Type of solver. Should be one of
#
# ‘Nelder-Mead’
#
# ‘Powell’
#
# ‘CG’
#
# ‘BFGS’
#
# ‘Newton-CG’
#
# ‘L-BFGS-B’
#
# ‘TNC’
#
# ‘COBYLA’
#
# ‘SLSQP’
#
# ‘trust-constr’
#
# ‘dogleg’
#
# ‘trust-ncg’
#
# ‘trust-exact’
#
# ‘trust-krylov’
#
# +
from scipy.optimize import minimize,rosen
# rosen is a func to be minimised.
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
print(rosen(x0))
res = minimize(rosen, x0, method='nelder-mead')
print(res.x)
# -
# rosen function :
#
# <img src= "https://upload.wikimedia.org/wikipedia/commons/thumb/3/32/Rosenbrock_function.svg/2880px-Rosenbrock_function.svg.png">
# <b>Least Squares</b>
#
# Solve a nonlinear least-squares problem with bounds on the variables. Given the residuals f(x) (an m-dimensional real function of n real variables) and the loss function rho(s) (a scalar function), least_squares find a local minimum of the cost function F(x).
# +
from scipy.optimize import least_squares
# definition of the rosenbrock function
def fun_rosenbrock(x):
return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])
x = np.array([2, 2])
res = least_squares(fun_rosenbrock, x)
print (res)
# -
# ------------
# Notice that, we only provide the vector of the residuals. The algorithm constructs the cost function as a sum of squares of the residuals, which gives the Rosenbrock function. The exact minimum is at x = [1.0,1.0].
# <h3>SciPy - Stats</h3>
#
# All of the statistics functions are located in the sub-package scipy.stats and a fairly complete listing of these functions can be obtained using info(stats) function. A list of random variables available can also be obtained from the docstring for the stats sub-package. This module contains a large number of probability distributions as well as a growing library of statistical functions.
#
# https://www.tutorialspoint.com/scipy/scipy_stats.htm
# <h3>SciPy - CSGraph</h3>
#
# CSGraph stands for Compressed Sparse Graph, which focuses on Fast graph algorithms based on sparse matrix representations.
#
# https://www.tutorialspoint.com/scipy/scipy_csgraph.htm
|
Scipy/Everything in SciPy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # User's Guide, Chapter 13: More Music21Object Attributes and Properties
#
# At this point you know how to find a `Music21Object`, how to name them and group them (with `.id` and `.groups`) and how to position them in Streams (with `.offset`, `.priority`, `.classSortOrder` and the `.activeSite`). This section gets first into some more advanced things that Music21Objects have, then some more fun things.
# ### Sites and the storing of elements
#
# All `Music21Objects` (i.e., elements) have a `.sites` property which is a :class:`~music21.sites.Sites` object which holds information about all the places the `Music21Object` is stored in. At its simplest, it's something that can be iterated over:
# +
from music21 import *
n = note.Note()
s1 = stream.Stream(id='s1')
s2 = stream.Stream(id='s2')
s1.insert(10, n)
s2.insert(20, n)
for s in n.sites:
print(s, s.elementOffset(n))
# -
# Note that the order of the Streams in `.sites` is guaranteed to be the order in which the note was inserted into the site.
#
# There's a lot more that `.sites` can do, but primarily for developers. We will get back to sites later.
# ### Derivations
#
# We will talk about derivations more in a future chapter, but we alluded to them in the Example in chapter 10, so let's say a few words about this advanced feature. A :class:`~music21.derivation.Derivation` object is a pointer to an object that this object is derived from in some way. They've gone their separate ways to an extent, but may want to talk to each other later. A `Music21Object` starts out with no useful Derivation:
c = note.Note('C4')
c.derivation
# But we can create new notes from it and they're not totally connected, but show their connection through `.derivation`:
f = c.transpose('P4')
f
f.derivation
# Now `c` has a life of its own from `f`. We can add a sharp to C and the transpose relationship of F to C does not affect it:
c.pitch.accidental = pitch.Accidental('sharp')
(c, f)
# But if `f` wants to do something to `c`, it can by changing itself and every element of its `.derivation.chain()`:
# +
f.notehead = 'diamond'
for n in f.derivation.chain():
n.notehead = 'diamond'
(f.notehead, c.notehead)
# -
# While `f` can search upwards in its `.derivation.chain()` and find `c`, `c` cannot find `f` in its derivation; it is a connection that is designed to be one-way only.
#
# Setting derivations can be done manually, but it's an advanced enough topic that we will get to it later.
# ### Context attributes
#
# Several attributes of `Music21Objects` only work after the object has been placed inside a Stream that has certain features of their own.
#
# An easy one to understand is `.measureNumber` which finds the `.number` value of the measure that an object is placed in:
n = note.Note('C')
m = stream.Measure()
m.number = 7
m.append(n)
n.measureNumber
# This works even if a note is inside a voice inside a measure:
v = stream.Voice()
n2 = note.Note('D')
v.append(n2)
m.insert(0, v)
n2.measureNumber
# Without a context, you'll get None
n3 = note.Note()
n3.measureNumber is None
# The second context attribute is, appropriately, called `.seconds`. It requires a tempo.MetronomeMark() to be placed into the Stream before the object and will calculate how many seconds the object (note, etc.) lasts at that tempo:
m.insert(0, tempo.MetronomeMark('Allegro', 120))
print (n.quarterLength, n.seconds)
# Unlike `.measureNumber` and the rest of the attributes we will see below, you can change `.seconds` to reflect exact timing you might have from audio or MIDI data.
n.seconds = 0.6
n.seconds
# An object with no tempo information in its surrounding context returns the special `nan` meaning "not a number" for `.seconds`
n3 = note.Note('E')
n3.seconds
# So use `math.isnan()` to catch this:
# +
from math import isnan
for el in (n, n2, n3):
seconds = el.seconds
if isnan(seconds):
seconds = 'No information'
print(el.step, seconds)
# + [markdown] sphinx_links={"any": true}
# The last three context attributes, `.beat`, `.beatStr` (beat string), and `.beatStrength`, all require :class:`~music21.meter.TimeSignature` contexts or they return `nan` or "nan". Since they're the topic of :ref:`our next chapter<usersGuide_14_timeSignatures>` we'll put them off until then.
#
# Most `Music21Objects` such as `Notes` have many additional attributes, but these are all the ones that are common to every object that can go in a `Stream` (after all, what would `.step` mean for a :class:`~music21.tempo.MetronomeMark`?)
# + active=""
# .. note::
#
# You may find other attributes on your base.Music21Object, especially if you are running
# an older version of `music21`. They are all deprecated most have been removed in
# v3 or v6; programmers are advised to stick to the safe list of attributes described here.
#
# Before v6.2, `.seconds` without a TimeSignature in contexts raised an exception.
# -
# ## Methods on `Music21Objects`
#
# Attributes and properties are aspects of an object that are lightweight and have no configuration options, so they are accessed without `()`. Methods tend to do more work and have more options, so they will always be called with `()` signs.
#
# Unlike attributes, where we have documented all of them, only a subset of the methods on `Music21Objects` are listed below. All of them can be found in the documentation to :class:`~music21.base.Music21Object`, but many of them have obscure uses and might be moved later to not clutter up what is really important! And those are...
# ### .getOffsetBySite and .setOffsetBySite
#
# These methods work as the `.offset` attribute but can work on any site where the object is a part of.
n = note.Note()
s1 = stream.Stream(id='s1')
s1.insert(10, n)
s2 = stream.Stream(id='s2')
s2.insert(20, n)
n.getOffsetBySite(s1)
n.setOffsetBySite(s1, 15.0)
n.getOffsetBySite(s1)
# There is one extra possible attribute on `.getOffsetBySite`, "returnSpecial=True" which will say whether or not an element has a shifting offset. Right barlines have one:
s3 = stream.Measure()
n3 = note.Note(type='whole')
s3.append(n3)
rb = bar.Barline()
s3.rightBarline = rb
rb.getOffsetBySite(s3)
rb.getOffsetBySite(s3, returnSpecial=True)
# And in fact if we change the duration of `n3` the position of the barline will shift along with it:
n3.duration.type = 'half'
rb.getOffsetBySite(s3)
# ### getContextByClass()
#
# This is an extremely powerful tool -- you might not use it often, but be assured that `music21` is using it on your behalf all the time when sophisticated analysis is involved. It finds the active element matching a certain class preceeding the element. Let me demonstrate:
bach = corpus.parse('bwv66.6')
lastNote = bach.recurse().getElementsByClass(note.Note).last()
lastNote
# What part is it in?
lastNote.getContextByClass(stream.Part)
# What was the Key at that moment?
lastNote.getContextByClass(key.KeySignature)
# What is the TimeSignature at that moment?
lastNote.getContextByClass(meter.TimeSignature)
# Why is this such a sophisticated method? It knows about the differences in different types of Streams. If the key signature changes in a different part then it doesn't affect the notes of the current part, but if it changes in a previous measure in the same part, then that matters. Furthermore, the caching mechanism via something called `Timespans` is amazingly fast, so that running through an entire score getting the context for each object doesn't take long at all.
#
# We demonstrate here on an early 15th-century Mass piece that uses four different time singatures:
# +
gloria = corpus.parse('luca/gloria')
soprano = gloria.parts[0]
lastTimeSignature = None
for n in soprano.recurse().getElementsByClass(note.Note):
thisTimeSignature = n.getContextByClass(meter.TimeSignature)
if thisTimeSignature is not lastTimeSignature:
lastTimeSignature = thisTimeSignature
print(thisTimeSignature, n.measureNumber)
# -
# As you might expect, the `.measureNumber` routine uses `.getContextByClass(stream.Measure)` internally. What is also interesting is that `.getContextByClass` is smart enough to search out derivation chains to find what it is looking for. For instance, this flat stream has only notes, no time signatures. But it can still find each note's time signature and measure number context.
#
# Here we will use the string `('TimeSignature')` form of getContextByClass instead of the class name `(meter.TimeSignature)`
lastTimeSignature = None
for n in soprano.flatten().notes:
thisTimeSignature = n.getContextByClass('TimeSignature')
if thisTimeSignature is not lastTimeSignature:
lastTimeSignature = thisTimeSignature
print(thisTimeSignature, n.measureNumber)
# Internally `.getContextByClass` uses another `Music21Object` method called `.contextSites()` which is a generator that tells the system where to search next:
for cs in lastNote.contextSites():
print(cs)
# `.contextSites` returns a "ContextTuple" which is a lightweight namedtuple that has three attributes, `site`, `offset`, and `recurseType`.
#
# The first ContextTuple says that first the elements of `site`: Measure 9 should be searched, beginning at `offset` 2.0 and (because `recurseType` is elementsFirst) working backwards to the beginning of the measure, then if the matching context isn't found, the measure will be flattened (in case there are other voices in the measure) and anything from before offset 2.0 of that flattened stream will be searched.
#
# If that fails, then the Bass part as a whole will be searched, with all elements flattened, beginning at offset 35 and working backwards. That way if the context is in another measure it will be found.
#
# Then if that fails, it will look at the score as a whole, beginning at offset 35 and working backwards, but only looking at things that are at the score level, not looking at elements within other parts. There may be scores where for instance, expressive markings appear at the Score level. This will find them.
#
# Related to `.getContextByClass()` is `.getAllContextsByClass()` which is a generator that returns each preceeding context.
# + active=""
# .. note::
#
# Two known bugs that we hope to get fixed soon: if there are two or more
# contexts at the same offset, `.getAllContextsByClass()` will skip over
# all but one of them. Using `Music21Object` as a class list can create infinite loops.
# +
lastGloriaNote = soprano.recurse().notes.last()
for ts in lastGloriaNote.getAllContextsByClass(meter.TimeSignature):
print(ts, ts.measureNumber)
# -
# Similar to `.getContextByClass()` are the `.next(class)` and `.previous(class)` methods which move to the next or previous element of the same class at the same (or a higher) hierarchical level. They're designed to be really easy to use, but so far, I've failed at achieving that. Hopefully in the next few versions I'll be able to demonstrate in practice how these commands were designed to work. For now, I'd suggest avoiding them.
#
# ### Splitting methods
#
# `Music21` has three methods on `Music21Object`s for splitting them. Eventually the plan is to unite them into a single `.split()` method, but we're not there yet.
#
# The three methods are:
#
# * `.splitAtQuarterLength` -- splits an object into two objects at the given quarter length
# * `.splitByQuarterLengths` -- splits an object into two or more objects according to a list of quarter lengths
# * `.splitAtDurations` -- takes an object with a complex duration (such as 5.0 quarters) and splits it into notatable units.
#
# These all work rather similarly. Behind their seeming simplicity are a host of complex musical decisions that are being made. Take this rather complex note (we're introducing `expressions` and `articulations` softly here, so that you don't need to wait for :ref:`Chapter 32<usersGuide_32_articulations>` to encounter them):
n = note.Note('C#5')
n.duration.type = 'whole'
n.articulations = [articulations.Staccato(), articulations.Accent()]
n.lyric = 'hi!'
n.expressions = [expressions.Mordent(), expressions.Trill(), expressions.Fermata()]
n.show()
# Now let's split this note just before beat 4:
splitTuple = n.splitAtQuarterLength(3.0)
s = stream.Stream()
s.append(splitTuple)
s.show()
# Notice the choices that `music21` made -- the two notes are tied, the lyrics are sung at the beginning, the accent and mordent appear at the beginning of the note while the staccato and fermata(!) appear on the second note, while trill mark gets put onto the first note only. This is part of the "batteries included" `music21` approach -- try to do something musically smart in most cases. In fact, it's even a bit smarter -- the `splitTuple` knows that there's something called a TrillExtension spanner in it which should be put into the Stream:
splitTuple.spannerList
for thisSpanner in splitTuple.spannerList:
s.insert(0, thisSpanner)
s.show()
# + [markdown] sphinx_links={"any": true}
# ### Showing and Writing
#
# The two last methods are almost certainly the most important: `.show()` and `.write()`. We've been using `.show()` throughout the User's Guide, so it's familiar. It usually takes a single argument which is the format (default is `'musicxml'` except on IPython where it is `'musicxml.png'`. `.write()` by contrast writes out the file to disk. The first argument is again the format. The second argument, optional, is the filename with path. If omitted then a temporary file is written (and the filename is returned).
#
# We'll see enough about `.show()` and `.write()` later, so that's enough for now on this long chapter. Let's return to the `.beat` related function in :ref:`Chapter 14, Time Signatures <usersGuide_14_timeSignatures>`.
|
documentation/source/usersGuide/usersGuide_13_music21object2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#importing libraries
import numpy as np
import pandas as pd
from pandas import DataFrame,read_csv
import matplotlib.pyplot as plt
# %matplotlib inline
# +
#Passing Los Angeles temperature csv file into a DataFrame
file=r'LA.csv'
LA = pd.read_csv(file)
#Adding the moving averages for Los Angeles Temperatures
LA['moving_temp'] = LA.avg_temp.rolling(window=20).mean()
LA
# -
#Creating a line chart for LA Temperatures in moving avg
plt.plot(LA.year,LA.moving_temp)
plt.title('Los Angeles Temperatures Moving Averages')
plt.ylabel('Temperatures')
plt.xlabel('Year')
plt.show()
# +
#Passing global temperature csv file into a DataFrame
file=r'global.csv'
globaltemp = pd.read_csv(file)
#Adding the moving averages for global temperatures
globaltemp['moving_temp'] = globaltemp.avg_temp.rolling(window=20).mean()
globaltemp
# -
#Creating a line chart of the global temperatures dataFrame
plt.plot(globaltemp.year,globaltemp.moving_temp)
plt.title('Global Temperatures Moving Averages')
plt.ylabel('Temperatures')
plt.xlabel('Year')
plt.show()
# +
#Creating a line chart using LA & global dataFrames in the same plot
fig, ax = plt.subplots()
ax2 = ax.twinx()
LA.plot(x='year', y='moving_temp', ax=ax, color='purple', ls='--')
globaltemp.plot(x='year', y='moving_temp', ax=ax2, color='green')
ax2.legend().set_visible(False)
ax.legend().set_visible(False)
ax2.set_ylabel('Global Temperatures',color='green',fontsize=14)
ax.set_ylabel('LA Temperatures',color='purple', fontsize=14)
# -
# **OBSERVATIONS:**
#
# 1.) Whereas global temperatures were tracked and recorded in as early as 1750, records of Los Angeles temperatures did not begin until 1849.
#
# 2.) Both global and Los Angeles temperatures increased over time.
#
# 3.) Whereas there was a significant drop of temperatures in Los Angeles between the period of1900-1950, the temperatures globally remained more or less the same, albeit still trending upwards.
#
# 4.) Whereas the temperatures in Los Angeles dropped sharply in the 1870s, there was a subtle uptick globally.
|
Weather-Dataset.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import re
import datetime
import pandas as pd
import numpy as np
from datetime import datetime as dt
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib.patches as mpatches
from matplotlib import ticker
# %matplotlib inline
data_dir = '/Users/boyuliu/pyprojects/Joann/Joann-Thailand-Project/notebooks/datasets/new_dataset/'
grid_search_dir = '/Users/boyuliu/Dropbox (MIT)/Boyu-Joann/Intermediate output/outputs/grid_search/'
wv_data_file = data_dir + 'regression_data_wv_cases1_causal_ma_detrend_20210301.csv'
residual_data = grid_search_dir + 'residual_over_time_02192021.csv'
df = pd.read_csv(wv_data_file)
print(df.shape)
df.head()
# -
print(df.province.nunique())
df.province.unique()
df.year_week.min(), df.year_week.max()
def week_num_to_date(w):
# return date of the first day of week
return dt.strptime(w + '-1', "%Y-%W-%w").date().isoformat()
# +
weekly_ts = df.groupby('year_week').sum()['total_demand'].values
num_weeks = df.year_week.nunique()
xtick_locs = range(0, num_weeks, 20)
weeks = sorted(df.year_week.unique().tolist())
weeks_label = [week_num_to_date(weeks[i]) for i in xtick_locs]
fig, ax = plt.subplots(1,1, figsize = (12, 8))
plt.plot(weekly_ts, color='lightskyblue')
plt.xticks(ticks=xtick_locs, labels=weeks_label, rotation='45')
plt.xlabel('Week', fontsize=15, fontweight='black', color = '#333F4B')
plt.title('Aggregate labor shortage for Burmese workers in Thailand',
fontsize=15, fontweight='black', color = '#333F4B')
plt.ylabel('Aggregate labor shortage', fontsize=15, fontweight='black', color = '#333F4B')
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_smart_bounds(True)
ax.spines['bottom'].set_smart_bounds(True)
ax.get_yaxis().set_major_formatter(
ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
plt.savefig('../../../plots/paper/aggregate_demand_ts.jpg')
plt.show()
# -
# need to remove these weeks from analysis data
[weeks[i] for i in range(num_weeks) if weekly_ts[i]==0]
# +
weekly_shock_ts = df.groupby('year_week').mean()['demand_shock'].values
std_demand_shock = df.groupby('year_week').std()['demand_shock'].values
num_weeks = df.year_week.nunique()
xtick_locs = range(0, num_weeks, 20)
weeks = sorted(df.year_week.unique().tolist())
weeks_label = [week_num_to_date(weeks[i]) for i in xtick_locs]
fig, ax = plt.subplots(1,1, figsize = (12, 8))
plt.plot(weekly_shock_ts, 'o', color='royalblue', label='average')
plt.errorbar(range(0, num_weeks), weekly_shock_ts, yerr=std_demand_shock, fmt='o', alpha=0.7,
color='lightskyblue', label='s.d.')
plt.xticks(ticks=xtick_locs, labels=weeks_label, rotation='45')
plt.xlabel('Week', fontsize=15, fontweight='black', color = '#333F4B')
plt.title('Labor shortage shocks for Burmese workers in Thai provinces',
fontsize=15, fontweight='black', color = '#333F4B')
plt.ylabel('Average labor shortage shock', fontsize=15, fontweight='black', color = '#333F4B')
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_smart_bounds(True)
ax.spines['bottom'].set_smart_bounds(True)
ax.get_yaxis().set_major_formatter(
ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
plt.legend()
plt.savefig('../../../plots/paper/demand_shocks_ts.jpg')
plt.show()
# +
#### OLD data including 2017
# data_dir = '/Users/boyuliu/pyprojects/Joann/Joann-Thailand-Project/notebooks/datasets/new_dataset/'
# raw_demand_3yrs = pd.read_csv(data_dir + 'raw_demand_3yrs.csv')
# weekly_ts = raw_demand_3yrs.groupby('year_week').sum()['total'].values
# num_weeks = raw_demand_3yrs.year_week.nunique()
# xtick_locs = range(0, num_weeks, 20)
# weeks = sorted(raw_demand_3yrs.year_week.unique().tolist())
# weeks_label = [week_num_to_date(weeks[i]) for i in xtick_locs]
# fig, ax = plt.subplots(1,1, figsize = (12, 8))
# plt.plot(weekly_ts, color='lightskyblue')
# plt.xticks(ticks=xtick_locs, labels=weeks_label, rotation='45')
# plt.xlabel('Week', fontsize=15, fontweight='black', color = '#333F4B')
# plt.title('Aggregate excess demand for Burmese workers in Thailand',
# fontsize=15, fontweight='black', color = '#333F4B')
# plt.ylabel('Aggregate excess demand', fontsize=15, fontweight='black', color = '#333F4B')
# ax.spines['top'].set_color('none')
# ax.spines['right'].set_color('none')
# ax.spines['left'].set_smart_bounds(True)
# ax.spines['bottom'].set_smart_bounds(True)
# ax.get_yaxis().set_major_formatter(
# ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
# plt.savefig('../../../plots/paper/aggregate_demand_ts.jpg')
# plt.show()
# +
plotdata = df
weekly_ts = plotdata.groupby('year_week').mean()['total_demand'].values
std_demand = plotdata.groupby('year_week').std()['total_demand'].values
num_weeks = plotdata.year_week.nunique()
xtick_locs = range(0, num_weeks, 20)
weeks = sorted(plotdata.year_week.unique().tolist())
weeks_label = [week_num_to_date(weeks[i]) for i in xtick_locs]
fig, ax = plt.subplots(1,1, figsize = (12, 8))
plt.plot(range(0, num_weeks), weekly_ts, 'o', color='royalblue', label='average')
plt.errorbar(range(0, num_weeks), weekly_ts, yerr=std_demand, fmt='o', alpha=0.7,
color='lightskyblue', label='s.d.')
plt.xticks(ticks=xtick_locs, labels=weeks_label, rotation='45')
plt.xlabel('Week', fontsize=15, fontweight='black', color = '#333F4B')
plt.title('Distribution of labor shortage for Burmese workers in Thailand',
fontsize=15, fontweight='black', color = '#333F4B')
plt.ylabel('Labor shortage', fontsize=15, fontweight='black', color = '#333F4B')
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_smart_bounds(True)
ax.spines['bottom'].set_smart_bounds(True)
plt.legend()
ax.get_yaxis().set_major_formatter(
ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
plt.savefig('../../../plots/paper/demand_mean_and_std.jpg')
plt.show()
# +
num_weeks = df.year_week.nunique()
xtick_locs = range(0, num_weeks, 20)
weeks = sorted(df.year_week.unique().tolist())
weeks_label = [week_num_to_date(weeks[i]) for i in xtick_locs]
fig, ax = plt.subplots(1,1, figsize = (12, 8))
plt.plot(df.groupby('year_week').sum()['wv_count'].values, color='lightskyblue')
plt.xticks(ticks=xtick_locs, labels=weeks_label, rotation='45')
plt.xlabel('Week', fontsize=15, fontweight='black', color = '#333F4B')
plt.ylabel('Aggregate # worker voice observations', fontsize=15, fontweight='black', color = '#333F4B')
plt.title('Aggregate worker voice records in Thailand', fontsize=15, fontweight='black', color = '#333F4B')
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_smart_bounds(True)
ax.spines['bottom'].set_smart_bounds(True)
plt.savefig('../../../plots/paper/wv_count_ts.jpg')
plt.show()
# -
df['wv_count'].sum()/num_weeks
# +
weekly_ts = df.groupby('year_week').mean()['total_demand'].values
std_demand = df.groupby('year_week').std()['total_demand'].values
xtick_locs = range(0, num_weeks, 20)
weeks = sorted(df.year_week.unique().tolist())
weeks_label = [week_num_to_date(weeks[i]) for i in xtick_locs]
fig, ax = plt.subplots(1,1, figsize = (12, 8))
plt.plot(range(0, num_weeks), weekly_ts, 'o', color='royalblue', label='average')
plt.errorbar(range(0, num_weeks), weekly_ts, yerr=std_demand, fmt='o', alpha=0.7,
color='lightskyblue', label='s.d.')
plt.xticks(ticks=xtick_locs, labels=weeks_label, rotation='45')
plt.xlabel('Week', fontsize=15, fontweight='black', color = '#333F4B')
plt.title('Distribution of excess demand for Burmese workers in Thailand',
fontsize=15, fontweight='black', color = '#333F4B')
plt.ylabel('Excess demand', fontsize=15, fontweight='black', color = '#333F4B')
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_smart_bounds(True)
ax.spines['bottom'].set_smart_bounds(True)
plt.legend()
ax.get_yaxis().set_major_formatter(
ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
# plt.savefig('../../../plots/paper/demand_mean_and_std.jpg')
plt.show()
# -
df.head()
# +
df['abuse'] = df['perc_abuse'] * df['wv_count']
ave_abuse = df.groupby('year_week').sum()['abuse'].values / df.groupby('year_week').sum()['wv_count'].values
std_abuse = df.groupby('year_week').std()['perc_abuse']
weekly_ts = df.groupby('year_week').sum()['total_demand'].values
# xtick_locs = range(0, 141, 20)
weeks = sorted(df.year_week.unique().tolist())
weeks_label = [week_num_to_date(weeks[i]) for i in xtick_locs]
fig, ax = plt.subplots(1,1, figsize = (12, 8))
# plt.plot(range(0, 145), ave_abuse)
plt.plot(range(0, num_weeks), ave_abuse, 'o', color='royalblue', label='average')
plt.errorbar(range(0, num_weeks), ave_abuse, yerr=std_abuse, fmt='o', alpha=0.7,
color='lightskyblue', label='s.d.')
plt.xticks(ticks=xtick_locs, labels=weeks_label, rotation='45')
plt.xlabel('Week', fontsize=15, fontweight='black', color = '#333F4B')
plt.ylabel('% abuse', fontsize=15, fontweight='black', color = '#333F4B')
plt.title('Percentage labor abuse in Thailand', fontsize=15, fontweight='black', color = '#333F4B')
plt.legend()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_smart_bounds(True)
ax.spines['bottom'].set_smart_bounds(True)
plt.savefig('../../../plots/paper/ave_perc_abuse_ts.jpg')
plt.show()
# +
boxplot_data = df.sort_values('year_week')[['year_week','total_demand']]
y_weeks = boxplot_data.year_week.unique()
boxplot_data_l = []
for w in y_weeks:
boxplot_data_l.append(boxplot_data[(boxplot_data.year_week==w)&(boxplot_data.total_demand>0)].total_demand.values)
fig, ax = plt.subplots(1,1, figsize = (21, 14))
# plt.plot(weekly_ts)
plt.boxplot(boxplot_data_l, showfliers=False)
plt.xticks(ticks=xtick_locs, labels=weeks_label, rotation='45')
plt.xlabel('Week', fontsize=15, fontweight='black', color = '#333F4B')
plt.title('Distribution of MOU demand of each province of Thailand',
fontsize=15, fontweight='black', color = '#333F4B')
plt.ylabel('MOU Demand', fontsize=15, fontweight='black', color = '#333F4B')
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_smart_bounds(True)
ax.spines['bottom'].set_smart_bounds(True)
# plt.savefig('../../plots/paper/aggregate_demand_boxplot.jpg')
plt.show()
# -
df.year_week.max(), df.year_week.min()
# +
fig, ax1 = plt.subplots(1,1, figsize = (12, 8))
color = 'tab:blue'
weekly_ts = df.groupby('year_week').sum()['total_demand'].values
plt.plot(weekly_ts, color=color)
ax1.set_ylabel('Total MOU Demand')
ax2 = ax1.twinx()
color = 'tab:orange'
plt.plot(ave_abuse*100, color=color)
ax2.set_ylabel('Pertange Labor Abuse (%)')
blue_patch = mpatches.Patch(color='tab:blue', label='Total MOU Demand')
orange_patch = mpatches.Patch(color='tab:orange', label='Pertange Labor Abuse')
# plt.rcParams["legend.fontsize"] = 24
plt.legend(handles=[blue_patch, orange_patch])
plt.xticks(ticks=xtick_locs, labels=weeks_label, rotation='45')
plt.xlabel('Week')
plt.title('Aggregate MOU demand and labor abuse in entire Thailand each week from 2018 Jan. to 2020 Feb.')
fig.tight_layout()
# plt.savefig('../plots/paper/demand_and_abuse_ts.jpg')
plt.show()
# -
# # plot effect dissipation
df = pd.read_csv('/Users/boyuliu/Dropbox (MIT)/Boyu-Joann/Intermediate output/outputs/final_result/for_plot.csv')
df.head()
t_val = 1.644854
df['beta'] = 100*df['beta']
df['std'] = 100*df['std']
df['lower_CI'] = df['beta'] - t_val * df['std']
df['upper_CI'] = df['beta'] + t_val * df['std']
df.head()
df=df.sort_values('lag', ascending=False)
df
# +
fig, ax = plt.subplots(1,1, figsize = (12, 8))
# g = sns.lineplot(x="lag", y="beta", data=df)
plt.plot(range(1,5), df.beta, c='deepskyblue')
plt.xticks(range(1,5), df.lag.values)
# axis = df.plot(y='beta', kind='line', color='deepskyblue')
# _ = axis.set_xticklabels(df['lag'])
plt.hlines(0, 1, 4, colors='red', linestyles='dotted')
plt.fill_between(range(1,5), df.lower_CI.values, df.upper_CI.values, alpha=0.4, color='skyblue')
plt.xlabel('Demand shock lags (week)', fontsize=15, fontweight='black', color = '#333F4B')
plt.ylabel('Effect (% abuse)', fontsize=15, fontweight='black', color = '#333F4B')
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_smart_bounds(True)
ax.spines['bottom'].set_smart_bounds(True)
plt.savefig('../../../plots/paper/effect_dissipation.jpg')
plt.show()
# -
|
notebooks/analysis_w_2020/Make plots for paper.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#MIT License
#Copyright (c) [2021] [<NAME>]
#Permission is hereby granted, free of charge, to any person obtaining a copy
#of this software and associated documentation files (the "Software"), to deal
#in the Software without restriction, including without limitation the rights
#to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
#copies of the Software, and to permit persons to whom the Software is
#furnished to do so, subject to the following conditions:
#The above copyright notice and this permission notice shall be included in all
#copies or substantial portions of the Software.
#THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
#IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
#FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
#AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
#LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
#OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
#SOFTWARE.
# +
#I. SETUP AND DATA PREPROCESSING
#Import libraries
import pandas as pd
import numpy as np
from sklearn.preprocessing import Normalizer
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.neural_network import MLPClassifier
from sklearn.pipeline import make_pipeline
from sklearn.svm import SVC
from sklearn.svm import LinearSVC
from sklearn.linear_model import SGDClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from dtaidistance import dtw
from dtaidistance import dtw_visualisation as dtwvis
import tensorflow as tf
from tensorflow import keras
from keras.wrappers.scikit_learn import KerasClassifier
from keras.models import Sequential
from keras.layers import Dense, LSTM, Activation, Embedding, Flatten, LeakyReLU, BatchNormalization, Dropout
from keras.activations import relu, tanh, softmax
from sklearn.model_selection import GridSearchCV
import matplotlib as mpl
import matplotlib.pyplot as plt
# %matplotlib inline
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
import IPython
np.random.seed(7)
# -
#Import dataset und split train/test
data_raw = pd.read_excel('',0)
print('Shape of the Dataset: ',data_raw.shape)
data_raw.head()
# +
#Define matrices from raw data
data = data_raw.iloc[:,9:28]
projects = data_raw.iloc[:,2:3]
classes = data_raw.iloc[:,6:7]
#Join matrices:
data_projects = pd.concat([projects, data], axis=1)
classes_projects = pd.concat([projects, classes], axis=1)
data_projects
# +
#Reforming input features:
#Create the basic lines for each vehicle project and reset the indices
for j in range (0, 302):
exec(f'row_{j}=data_projects.iloc[(0+(j*195)):(1+(j*195)),0:20]')
exec(f'row_{j}=row_{j}.reset_index(drop=True)')
#Add all features sorted by time stamps to the basic lines per vehicle project
for i in range (1, 194):
add_i=data_projects.iloc[(i+(j*195)):((i+1)+(j*195)),1:20]
add_i=add_i.reset_index(drop=True)
exec(f'row_{j}=pd.concat([row_{j}, add_i], axis=1)')
exec(f'print(row_{j})')
#Now append all rows to each other, so that a matrix "data_transformed" is created.
data_transformed = {} #Create dictionairy
data_transformed = pd.DataFrame(data_transformed) #Transform dictionairy into DataFrame
for j in range (0, 302):
exec(f'data_transformed = data_transformed.append(row_{j})')
print("Shape: ",data_transformed.shape)
data_transformed.head()
# +
#Reforming output feature
#Create the basic lines for each vehicle project and reset the indices
for j in range (0, 302):
exec(f'row_{j}=classes.iloc[(0+(j*195)):(1+(j*195)),0:20]')
exec(f'row_{j}=row_{j}.reset_index(drop=True)')
#Now again append all rows to each other, so that a matrix data_transformed is created.
classes_transformed = {} #Create dictionairy
classes_transformed = pd.DataFrame(classes_transformed) #Transform dictionairy into DataFrame
for j in range (0, 302):
exec(f'classes_transformed = classes_transformed.append(row_{j})')
print("Shape: ",classes_transformed.shape)
classes_transformed.head()
# +
#Here you can define which part of the data will be used: First Third: 0:99 | Second Third: 99:200 | Third Third 200:301
#Define X
X = data_transformed.iloc[:,1:3687]
#Normalize input data
scaler = Normalizer().fit(X) #Define model
normalizedX = scaler.transform(X) #Normalize data
X = normalizedX #Transform into normal X
#Define y
y = classes_transformed.iloc[0:99,0:1]
#Split data in train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7, shuffle=True, random_state=42)
#Convert in numpy array for efficiency reasons
X_train=np.array(X_train)
y_train=np.array(y_train)
X_test=np.array(X_test)
y_test=np.array(y_test)
#Transfer the line names of X_test into an additional variable, so that the projects can be assigned to the classifications later on
Projekte = data_transformed.iloc[0:99,0:1]
Ypsilon = classes_transformed.iloc[0:99,0:1]
#Split data in train and test sets
Projekte_train, Projekte_test, Ypsilon_train, Ypsilon_test = train_test_split(Projekte, Ypsilon, train_size=0.7, shuffle=True, random_state=42)
#print(Projekte_test)
# +
#Visualization:
print(data_projects.shape)
#Call the function and parameterise the variables:
for i in range(0, 302):
plt.figure(figsize=(14, 6), dpi=100) #Definiere die Größe des Diagramms
plt.plot(data_projects.iloc[(i*195):((i*195)+194),19:20], color='grey') #https://matplotlib.org/2.1.1/api/_as_gen/matplotlib.pyplot.plot.html
plt.xlabel("time",fontsize=12, color='black')
plt.ylabel("Number of errors",fontsize=12, color='black')
plt.title("Error graph by projects",fontsize=14, color='black')
plt.show()
# +
#II. APPLIED MULTIVARIATE CLASSIFICATION
#1 Ada Boost Classifier
#Initialize the model:
clf_1 = AdaBoostClassifier(n_estimators=400)
param_grid = {'algorithm': ["SAMME", "SAMME.R"], 'random_state': [0,"None"]}
clf_1 = GridSearchCV(clf_1, param_grid, cv=5, verbose=1)
#Train the model:
clf_1.fit(X_train, y_train)
#Print best parameters:
print("Best parameters: ",clf_1.best_params_,"\n")
#Calculate confusion matrix:
pred_y = clf_1.predict(X_test)
y_pred = (pred_y > 0.5)
tp, fp, fn, tn = confusion_matrix(y_test, y_pred).ravel()
print("True Positives (TP) : ",tp,"\nFalse Positives (FP): ",fp,"\nFalse Negatives (FN): ",fn,"\nTrue Negatives (TN) : ",tn,"\n")
#Show Confusion Matrix:
url = 'https://glassboxmedicine.files.wordpress.com/2019/02/confusion-matrix.png'
IPython.display.Image(url, width = 800)
#Calculate scores:
score = accuracy_score(y_test, y_pred) #In multilabel classification, this function computes subset accuracy: the set of labels predicted for a sample must exactly match the corresponding set of labels in y_true.
print("Accuracy Score: ",score*100,"%\n")
precision = tp/(tp+fp)
print("Precision: ",precision*100,"%")
recall = tp/(tp+fn)
print("Recall: ",recall*100,"%")
f_one = 2*(precision*recall)/(precision+recall)
print("F1-Score: ",f_one*100,"%")
#Assignment of project names to classifications
tp_Projekte=[]
fp_Projekte=[]
fn_Projekte=[]
tn_Projekte=[]
for j in range(0,len(pred_y)):
if pred_y[j]+y_test[j]==0:
#print('True Positive')
tp_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==2:
#print('True Negative')
tn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==0:
#print("False Negativ")
fn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==1:
#print("False Positive")
fp_Projekte.append(Projekte_test.iloc[j])
print("\n\nThe following projects are classified as True Positive: \n",tp_Projekte)
print("\n\nThe following projects are classified as False Positive: \n",fp_Projekte)
print("\n\nThe following projects are classified as False Negative: \n",fn_Projekte)
print("\n\nThe following projects are classified as True Negative: \n",tn_Projekte)
# +
#2 Decision Tree Classifier
#Initialize the model:
clf_2 = DecisionTreeClassifier(random_state=0)
param_grid = {'criterion': ["gini", "entropy"], 'splitter': ["best", "random"], 'max_features': ["None", "int", "float", "auto", "sqrt", "log2"]}
clf_2 = GridSearchCV(clf_2, param_grid, cv=5, verbose=1)
#Train the model:
clf_2.fit(X_train, y_train)
#Print best parameters:
print("Best parameters: ",clf_2.best_params_,"\n")
#Calculate confusion matrix:
pred_y = clf_2.predict(X_test)
y_pred = (pred_y > 0.5)
tp, fp, fn, tn = confusion_matrix(y_test, y_pred).ravel()
print("True Positives (TP) : ",tp,"\nFalse Positives (FP): ",fp,"\nFalse Negatives (FN): ",fn,"\nTrue Negatives (TN) : ",tn,"\n")
#Show Confusion Matrix:
url = 'https://glassboxmedicine.files.wordpress.com/2019/02/confusion-matrix.png'
IPython.display.Image(url, width = 800)
#Calculate scores:
score = accuracy_score(y_test, y_pred) #In multilabel classification, this function computes subset accuracy: the set of labels predicted for a sample must exactly match the corresponding set of labels in y_true.
print("Accuracy Score: ",score*100,"%\n")
precision = tp/(tp+fp)
print("Precision: ",precision*100,"%")
recall = tp/(tp+fn)
print("Recall: ",recall*100,"%")
f_one = 2*(precision*recall)/(precision+recall)
print("F1-Score: ",f_one*100,"%")
#Assignment of project names to classifications
tp_Projekte=[]
fp_Projekte=[]
fn_Projekte=[]
tn_Projekte=[]
for j in range(0,len(pred_y)):
if pred_y[j]+y_test[j]==0:
#print('True Positive')
tp_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==2:
#print('True Negative')
tn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==0:
#print("False Negativ")
fn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==1:
#print("False Positive")
fp_Projekte.append(Projekte_test.iloc[j])
print("\n\nThe following projects are classified as True Positive: \n",tp_Projekte)
print("\n\nThe following projects are classified as False Positive: \n",fp_Projekte)
print("\n\nThe following projects are classified as False Negative: \n",fn_Projekte)
print("\n\nThe following projects are classified as True Negative: \n",tn_Projekte)
# +
#3 Discriminant Analysis
#Initialize the model:
clf_3 = QuadraticDiscriminantAnalysis()
param_grid = {'reg_param':[0.0, 0.1, 0.5, 1], 'store_covariance': ["True", "False"], 'tol': [0.001, 0.0001, 0.00001]}
clf_3 = GridSearchCV(clf_3, param_grid, cv=5, verbose=1)
#Train the model:
clf_3.fit(X_train, y_train)
#Print best parameters:
print("Best parameters: ",clf_3.best_params_,"\n")
#Calculate confusion matrix:
pred_y = clf_3.predict(X_test)
y_pred = (pred_y > 0.5)
tp, fp, fn, tn = confusion_matrix(y_test, y_pred).ravel()
print("True Positives (TP) : ",tp,"\nFalse Positives (FP): ",fp,"\nFalse Negatives (FN): ",fn,"\nTrue Negatives (TN) : ",tn,"\n")
#Show Confusion Matrix:
url = 'https://glassboxmedicine.files.wordpress.com/2019/02/confusion-matrix.png'
IPython.display.Image(url, width = 800)
#Calculate scores:
score = accuracy_score(y_test, y_pred) #In multilabel classification, this function computes subset accuracy: the set of labels predicted for a sample must exactly match the corresponding set of labels in y_true.
print("Accuracy Score: ",score*100,"%\n")
precision = tp/(tp+fp)
print("Precision: ",precision*100,"%")
recall = tp/(tp+fn)
print("Recall: ",recall*100,"%")
f_one = 2*(precision*recall)/(precision+recall)
print("F1-Score: ",f_one*100,"%")
#Assignment of project names to classifications
tp_Projekte=[]
fp_Projekte=[]
fn_Projekte=[]
tn_Projekte=[]
for j in range(0,len(pred_y)):
if pred_y[j]+y_test[j]==0:
#print('True Positive')
tp_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==2:
#print('True Negative')
tn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==0:
#print("False Negativ")
fn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==1:
#print("False Positive")
fp_Projekte.append(Projekte_test.iloc[j])
print("\n\nThe following projects are classified as True Positive: \n",tp_Projekte)
print("\n\nThe following projects are classified as False Positive: \n",fp_Projekte)
print("\n\nThe following projects are classified as False Negative: \n",fn_Projekte)
print("\n\nThe following projects are classified as True Negative: \n",tn_Projekte)
# +
#4 Gaussian Process Classifier
#Initialize the model:
clf_4 = GaussianProcessClassifier(random_state=0, n_jobs=-1) #Initialisiere das Modell
param_grid = {'n_restarts_optimizer': np.arange(0,11), 'max_iter_predict': [50, 100, 200, 400]}
clf_4= GridSearchCV(clf_4, param_grid, cv=5, verbose=1)
#Train the model:
clf_4.fit(X_train, y_train)
#Print best parameters:
print("Best parameters: ",clf_4.best_params_,"\n")
#Calculate confusion matrix:
pred_y = clf_4.predict(X_test)
y_pred = (pred_y > 0.5)
tp, fp, fn, tn = confusion_matrix(y_test, y_pred).ravel()
print("True Positives (TP) : ",tp,"\nFalse Positives (FP): ",fp,"\nFalse Negatives (FN): ",fn,"\nTrue Negatives (TN) : ",tn,"\n")
#Show Confusion Matrix:
url = 'https://glassboxmedicine.files.wordpress.com/2019/02/confusion-matrix.png'
IPython.display.Image(url, width = 800)
#Calculate scores:
score = accuracy_score(y_test, y_pred) #In multilabel classification, this function computes subset accuracy: the set of labels predicted for a sample must exactly match the corresponding set of labels in y_true.
print("Accuracy Score: ",score*100,"%\n")
precision = tp/(tp+fp)
print("Precision: ",precision*100,"%")
recall = tp/(tp+fn)
print("Recall: ",recall*100,"%")
f_one = 2*(precision*recall)/(precision+recall)
print("F1-Score: ",f_one*100,"%")
#Assignment of project names to classifications
tp_Projekte=[]
fp_Projekte=[]
fn_Projekte=[]
tn_Projekte=[]
for j in range(0,len(pred_y)):
if pred_y[j]+y_test[j]==0:
#print('True Positive')
tp_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==2:
#print('True Negative')
tn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==0:
#print("False Negativ")
fn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==1:
#print("False Positive")
fp_Projekte.append(Projekte_test.iloc[j])
print("\n\nThe following projects are classified as True Positive: \n",tp_Projekte)
print("\n\nThe following projects are classified as False Positive: \n",fp_Projekte)
print("\n\nThe following projects are classified as False Negative: \n",fn_Projekte)
print("\n\nThe following projects are classified as True Negative: \n",tn_Projekte)
# +
#5. Multi Layer Perceptron Classifier
#Initialize the model:
clf_5 = MLPClassifier(random_state=1, max_iter=1000, verbose=1) #Initialisiere das Modell
#param_grid = {'hidden_layer_sizes': [50, 100, 200, 400], 'activation': ["identity", "logistic", "tanh", "relu"], 'solver': ["lbfgs", "sgd", "adam"]}
param_grid = {'hidden_layer_sizes': [6, 7, 8, 9, 10], 'activation': ["logistic", "tanh", "relu"], 'solver': ["adam"]}
clf_5 = GridSearchCV(clf_5, param_grid, cv=5, verbose=1)
#Train the model:
clf_5.fit(X_train, y_train)
#Print best parameters:
print("Best parameters: ",clf_5.best_params_,"\n")
#Calculate confusion matrix:
pred_y = clf_5.predict(X_test)
y_pred = (pred_y > 0.5)
tp, fp, fn, tn = confusion_matrix(y_test, y_pred).ravel()
print("True Positives (TP) : ",tp,"\nFalse Positives (FP): ",fp,"\nFalse Negatives (FN): ",fn,"\nTrue Negatives (TN) : ",tn,"\n")
#Show Confusion Matrix:
url = 'https://glassboxmedicine.files.wordpress.com/2019/02/confusion-matrix.png'
IPython.display.Image(url, width = 800)
#Calculate scores:
score = accuracy_score(y_test, y_pred) #In multilabel classification, this function computes subset accuracy: the set of labels predicted for a sample must exactly match the corresponding set of labels in y_true.
print("Accuracy Score: ",score*100,"%\n")
precision = tp/(tp+fp)
print("Precision: ",precision*100,"%")
recall = tp/(tp+fn)
print("Recall: ",recall*100,"%")
f_one = 2*(precision*recall)/(precision+recall)
print("F1-Score: ",f_one*100,"%")
#Assignment of project names to classifications
tp_Projekte=[]
fp_Projekte=[]
fn_Projekte=[]
tn_Projekte=[]
for j in range(0,len(pred_y)):
if pred_y[j]+y_test[j]==0:
#print('True Positive')
tp_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==2:
#print('True Negative')
tn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==0:
#print("False Negativ")
fn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==1:
#print("False Positive")
fp_Projekte.append(Projekte_test.iloc[j])
print("\n\nThe following projects are classified as True Positive: \n",tp_Projekte)
print("\n\nThe following projects are classified as False Positive: \n",fp_Projekte)
print("\n\nThe following projects are classified as False Negative: \n",fn_Projekte)
print("\n\nThe following projects are classified as True Negative: \n",tn_Projekte)
# +
#6. Support Vector Machine
#Initialize the model:
clf_6 = SVC() #Initialisiere das Modell
param_grid = {'C': np.arange(1, 10), 'kernel': ["linear", "poly", "rbf", "sigmoid"], 'degree': np.arange(1, 10), 'gamma': ["scale", "auto"]}
clf_6 = GridSearchCV(clf_6, param_grid, cv=5, verbose=1)
#Train the model:
clf_6.fit(X_train, y_train)
#Print best parameters:
print("Best parameters: ",clf_6.best_params_,"\n")
#Calculate confusion matrix:
pred_y = clf_6.predict(X_test)
y_pred = (pred_y > 0.5)
tp, fp, fn, tn = confusion_matrix(y_test, y_pred).ravel()
print("True Positives (TP) : ",tp,"\nFalse Positives (FP): ",fp,"\nFalse Negatives (FN): ",fn,"\nTrue Negatives (TN) : ",tn,"\n")
#Show Confusion Matrix:
url = 'https://glassboxmedicine.files.wordpress.com/2019/02/confusion-matrix.png'
IPython.display.Image(url, width = 800)
#Calculate scores:
score = accuracy_score(y_test, y_pred) #In multilabel classification, this function computes subset accuracy: the set of labels predicted for a sample must exactly match the corresponding set of labels in y_true.
print("Accuracy Score: ",score*100,"%\n")
precision = tp/(tp+fp)
print("Precision: ",precision*100,"%")
recall = tp/(tp+fn)
print("Recall: ",recall*100,"%")
f_one = 2*(precision*recall)/(precision+recall)
print("F1-Score: ",f_one*100,"%")
#Assignment of project names to classifications
tp_Projekte=[]
fp_Projekte=[]
fn_Projekte=[]
tn_Projekte=[]
for j in range(0,len(pred_y)):
if pred_y[j]+y_test[j]==0:
#print('True Positive')
tp_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==2:
#print('True Negative')
tn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==0:
#print("False Negativ")
fn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==1:
#print("False Positive")
fp_Projekte.append(Projekte_test.iloc[j])
print("\n\nThe following projects are classified as True Positive: \n",tp_Projekte)
print("\n\nThe following projects are classified as False Positive: \n",fp_Projekte)
print("\n\nThe following projects are classified as False Negative: \n",fn_Projekte)
print("\n\nThe following projects are classified as True Negative: \n",tn_Projekte)
# +
#7. Linear Support Vector Machine
#Initialize the model:
clf_7 = LinearSVC() #Initialisiere das Modell
param_grid = {'penalty': ["l1", "l2"], 'C': np.arange(1, 10)}
clf_7 = GridSearchCV(clf_7, param_grid, cv=5, verbose=1)
#Train the model:
clf_7.fit(X_train, y_train)
#Print best parameters:
print("Best parameters: ",clf_7.best_params_,"\n")
#Calculate confusion matrix:
pred_y = clf_7.predict(X_test)
y_pred = (pred_y > 0.5)
tp, fp, fn, tn = confusion_matrix(y_test, y_pred).ravel()
print("True Positives (TP) : ",tp,"\nFalse Positives (FP): ",fp,"\nFalse Negatives (FN): ",fn,"\nTrue Negatives (TN) : ",tn,"\n")
#Show Confusion Matrix:
url = 'https://glassboxmedicine.files.wordpress.com/2019/02/confusion-matrix.png'
IPython.display.Image(url, width = 800)
#Calculate scores:
score = accuracy_score(y_test, y_pred) #In multilabel classification, this function computes subset accuracy: the set of labels predicted for a sample must exactly match the corresponding set of labels in y_true.
print("Accuracy Score: ",score*100,"%\n")
precision = tp/(tp+fp)
print("Precision: ",precision*100,"%")
recall = tp/(tp+fn)
print("Recall: ",recall*100,"%")
f_one = 2*(precision*recall)/(precision+recall)
print("F1-Score: ",f_one*100,"%")
#Assignment of project names to classifications
tp_Projekte=[]
fp_Projekte=[]
fn_Projekte=[]
tn_Projekte=[]
for j in range(0,len(pred_y)):
if pred_y[j]+y_test[j]==0:
#print('True Positive')
tp_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==2:
#print('True Negative')
tn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==0:
#print("False Negativ")
fn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==1:
#print("False Positive")
fp_Projekte.append(Projekte_test.iloc[j])
print("\n\nThe following projects are classified as True Positive: \n",tp_Projekte)
print("\n\nThe following projects are classified as False Positive: \n",fp_Projekte)
print("\n\nThe following projects are classified as False Negative: \n",fn_Projekte)
print("\n\nThe following projects are classified as True Negative: \n",tn_Projekte)
# +
#8. Stochastic Gradient Descent Linear Support Vector Machine
#Initialize the model:
clf_8 = SGDClassifier(learning_rate="invscaling", eta0=0.1, shuffle=True, n_jobs=-1) #Initialisiere das Modell
param_grid = {'loss': ["hinge", "log", "modified_huber", "squared_hinge", "perceptron", "squared_loss", "huber", "epsilon_insensitive", "squared_epsilon_insensitive"], 'penalty': ["l1", "l2"], 'alpha': [0.00001, 0.0001, 0.001, 0.1]}
clf_8 = GridSearchCV(clf_8, param_grid, cv=5, verbose=1)
#Train the model:
clf_8.fit(X_train, y_train)
#Print best parameters:
print("Best parameters: ",clf_8.best_params_,"\n")
#Calculate confusion matrix:
pred_y = clf_8.predict(X_test)
y_pred = (pred_y > 0.5)
tp, fp, fn, tn = confusion_matrix(y_test, y_pred).ravel()
print("True Positives (TP) : ",tp,"\nFalse Positives (FP): ",fp,"\nFalse Negatives (FN): ",fn,"\nTrue Negatives (TN) : ",tn,"\n")
#Show Confusion Matrix:
url = 'https://glassboxmedicine.files.wordpress.com/2019/02/confusion-matrix.png'
IPython.display.Image(url, width = 800)
#Calculate scores:
score = accuracy_score(y_test, y_pred) #In multilabel classification, this function computes subset accuracy: the set of labels predicted for a sample must exactly match the corresponding set of labels in y_true.
print("Accuracy Score: ",score*100,"%\n")
precision = tp/(tp+fp)
print("Precision: ",precision*100,"%")
recall = tp/(tp+fn)
print("Recall: ",recall*100,"%")
f_one = 2*(precision*recall)/(precision+recall)
print("F1-Score: ",f_one*100,"%")
#Assignment of project names to classifications
tp_Projekte=[]
fp_Projekte=[]
fn_Projekte=[]
tn_Projekte=[]
for j in range(0,len(pred_y)):
if pred_y[j]+y_test[j]==0:
#print('True Positive')
tp_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==2:
#print('True Negative')
tn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==0:
#print("False Negativ")
fn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==1:
#print("False Positive")
fp_Projekte.append(Projekte_test.iloc[j])
print("\n\nThe following projects are classified as True Positive: \n",tp_Projekte)
print("\n\nThe following projects are classified as False Positive: \n",fp_Projekte)
print("\n\nThe following projects are classified as False Negative: \n",fn_Projekte)
print("\n\nThe following projects are classified as True Negative: \n",tn_Projekte)
# +
#9. Random Forest Classifier
#Initialize the model:
clf_9 = RandomForestClassifier(max_depth=2, random_state=0, n_jobs=-1)
param_grid = {'n_estimators': [50, 100, 200, 400], 'criterion': ["gini", "entropy"], 'max_features': ["auto", "sqrt", "log2", "int", "float"]}
clf_9 = GridSearchCV(clf_9, param_grid, cv=5, verbose=1)
#Train the model:
clf_9.fit(X_train, y_train)
#Print best parameters:
print("Best parameters: ",clf_9.best_params_,"\n")
#Calculate confusion matrix:
pred_y = clf_9.predict(X_test)
y_pred = (pred_y > 0.5)
tp, fp, fn, tn = confusion_matrix(y_test, y_pred).ravel()
print("True Positives (TP) : ",tp,"\nFalse Positives (FP): ",fp,"\nFalse Negatives (FN): ",fn,"\nTrue Negatives (TN) : ",tn,"\n")
#Show Confusion Matrix:
url = 'https://glassboxmedicine.files.wordpress.com/2019/02/confusion-matrix.png'
IPython.display.Image(url, width = 800)
#Calculate scores:
score = accuracy_score(y_test, y_pred) #In multilabel classification, this function computes subset accuracy: the set of labels predicted for a sample must exactly match the corresponding set of labels in y_true.
print("Accuracy Score: ",score*100,"%\n")
precision = tp/(tp+fp)
print("Precision: ",precision*100,"%")
recall = tp/(tp+fn)
print("Recall: ",recall*100,"%")
f_one = 2*(precision*recall)/(precision+recall)
print("F1-Score: ",f_one*100,"%")
#Assignment of project names to classifications
tp_Projekte=[]
fp_Projekte=[]
fn_Projekte=[]
tn_Projekte=[]
for j in range(0,len(pred_y)):
if pred_y[j]+y_test[j]==0:
#print('True Positive')
tp_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==2:
#print('True Negative')
tn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==0:
#print("False Negativ")
fn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==1:
#print("False Positive")
fp_Projekte.append(Projekte_test.iloc[j])
print("\n\nThe following projects are classified as True Positive: \n",tp_Projekte)
print("\n\nThe following projects are classified as False Positive: \n",fp_Projekte)
print("\n\nThe following projects are classified as False Negative: \n",fn_Projekte)
print("\n\nThe following projects are classified as True Negative: \n",tn_Projekte)
# +
#10. K Nearest Neighbors Classifier
#Definition of DTW function (Source: https://gist.github.com/nikolasrieble)
def DTW(a, b):
an = a.size
bn = b.size
pointwise_distance = distance.cdist(a.reshape(-1,1),b.reshape(-1,1))
cumdist = np.matrix(np.ones((an+1,bn+1)) * np.inf)
cumdist[0,0] = 0
for ai in range(an):
for bi in range(bn):
minimum_cost = np.min([cumdist[ai, bi+1],
cumdist[ai+1, bi],
cumdist[ai, bi]])
cumdist[ai+1, bi+1] = pointwise_distance[ai,bi] + minimum_cost
return cumdist[an, bn]
#Initialize the model:
clf_10 = KNeighborsClassifier(n_jobs=-1) #Initialisiere das Modell
param_grid = {'n_neighbors': np.arange(1, 6), 'weights': ["uniform", "distance"], 'leaf_size': [15,30,45], 'metric': [DTW, "minkowski"], 'p': np.arange(1,3)}
clf_10 = GridSearchCV(clf_10, param_grid, cv=5, verbose=1)
#Train the model:
clf_10.fit(X_train, y_train)
#Print best parameters:
print("Best parameters: ",clf_10.best_params_,"\n")
#Calculate confusion matrix:
pred_y = clf_10.predict(X_test)
y_pred = (pred_y > 0.5)
tp, fp, fn, tn = confusion_matrix(y_test, y_pred).ravel()
print("True Positives (TP) : ",tp,"\nFalse Positives (FP): ",fp,"\nFalse Negatives (FN): ",fn,"\nTrue Negatives (TN) : ",tn,"\n")
#Show Confusion Matrix:
url = 'https://glassboxmedicine.files.wordpress.com/2019/02/confusion-matrix.png'
IPython.display.Image(url, width = 800)
#Calculate scores:
score = accuracy_score(y_test, y_pred) #In multilabel classification, this function computes subset accuracy: the set of labels predicted for a sample must exactly match the corresponding set of labels in y_true.
print("Accuracy Score: ",score*100,"%\n")
precision = tp/(tp+fp)
print("Precision: ",precision*100,"%")
recall = tp/(tp+fn)
print("Recall: ",recall*100,"%")
f_one = 2*(precision*recall)/(precision+recall)
print("F1-Score: ",f_one*100,"%")
#Assignment of project names to classifications
tp_Projekte=[]
fp_Projekte=[]
fn_Projekte=[]
tn_Projekte=[]
for j in range(0,len(pred_y)):
if pred_y[j]+y_test[j]==0:
#print('True Positive')
tp_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==2:
#print('True Negative')
tn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==0:
#print("False Negativ")
fn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==1:
#print("False Positive")
fp_Projekte.append(Projekte_test.iloc[j])
print("\n\nThe following projects are classified as True Positive: \n",tp_Projekte)
print("\n\nThe following projects are classified as False Positive: \n",fp_Projekte)
print("\n\nThe following projects are classified as False Negative: \n",fn_Projekte)
print("\n\nThe following projects are classified as True Negative: \n",tn_Projekte)
# +
#11. Long-Short-Time-Memory Network (Baseline)
#Define neural network model creation function
def create_model(layers, activation):
model = tf.keras.models.Sequential()
for i, nodes in enumerate(layers):
if i==0:
model.add(tf.keras.layers.Embedding(input_dim=X_train.shape[0], output_dim=X_train.shape[0]))
else:
model.add(tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(nodes, activation='relu', return_sequences=True)))
model.add(tf.keras.layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
return model
#Initialize model
clf_11 = KerasClassifier(build_fn=create_model, verbose=1)
reduce_lr = keras.callbacks.ReduceLROnPlateau(monitor='loss', factor=0.5, patience=50, min_lr=0.001) #https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/ReduceLROnPlateau
#Define parameter spaces
layers = [(100, 100, 100, 100)]
activations = ['relu']
#Create parameter grid:
param_grid = dict(layers=layers, activation=activations, batch_size=[32], epochs=[50])
clf_11 = GridSearchCV(estimator=clf_11, param_grid=param_grid, cv=5)
hist = clf_11.fit(X_train, y_train, validation_data=(X_test, y_test), verbose=1, callbacks=[reduce_lr])
#Print best parameters:
print("Best parameters: ",hist.best_params_)
#Calculate confusion matrix
#Predict y:
pred_y = clf_11.predict(X_test)
#print('pred_y Shape:', pred_y.shape) #Print Shape of pred_y (for debuging)
#Reshape pred_y to 2D:
pred_y = pred_y[:,0:1]
#print('pred_y Shape:', pred_y.shape) #Print Shape of pred_y (for debuging)
pred_y = np.reshape(pred_y,(30,1))
#print('pred_y Shape:', pred_y.shape) #Print Shape of pred_y (for debuging)
y_pred = (pred_y > 0.5)
#Calculate confusion matrix:
cm = confusion_matrix(y_test, y_pred)
tp, fp, fn, tn = confusion_matrix(y_test, y_pred).ravel()
print("True Positives (TP) : ",tp,"\nFalse Positives (FP): ",fp,"\nFalse Negatives (FN): ",fn,"\nTrue Negatives (TN) : ",tn,"\n")
#Show Confusion Matrix:
url = 'https://glassboxmedicine.files.wordpress.com/2019/02/confusion-matrix.png'
IPython.display.Image(url, width = 800)
#Calculate scores:
score = accuracy_score(y_test, y_pred) #In multilabel classification, this function computes subset accuracy: the set of labels predicted for a sample must exactly match the corresponding set of labels in y_true.
print("Accuracy Score: ",score*100,"%\n")
precision = tp/(tp+fp)
print("Precision: ",precision*100,"%")
recall = tp/(tp+fn)
print("Recall: ",recall*100,"%")
f_one = 2*(precision*recall)/(precision+recall)
print("F1-Score: ",f_one*100,"%")
#Assignment of project names to classifications
tp_Projekte=[]
fp_Projekte=[]
fn_Projekte=[]
tn_Projekte=[]
for j in range(0,len(pred_y)):
if pred_y[j]+y_test[j]==0:
#print('True Positive')
tp_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==2:
#print('True Negative')
tn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==0:
#print("False Negativ")
fn_Projekte.append(Projekte_test.iloc[j])
elif pred_y[j]+y_test[j]==1 and pred_y[j]==1:
#print("False Positive")
fp_Projekte.append(Projekte_test.iloc[j])
print("\n\nThe following projects are classified as True Positive: \n",tp_Projekte)
print("\n\nThe following projects are classified as False Positive: \n",fp_Projekte)
print("\n\nThe following projects are classified as False Negative: \n",fn_Projekte)
print("\n\nThe following projects are classified as True Negative: \n",tn_Projekte)
|
carclass_v11e_20210205_OB.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # More Control Flow
# ### RECAP
# Ex.1 Write a program that asks the user if he/she likes python. Print “awesome” if the answer is ‘yes’ and print “wrong answer, try again” if the answer is ‘no’!
answer = input("Do you like python?")
if answer == 'yes':
print("awesome")
elif answer == 'no':
print('wrong answer')
else:
print("please choose between 'yes' and 'no' ")
# Ex.2 Write a program that requires the user to input a letter, if the letter is ‘a’ or ‘A’, print ‘awesome’, otherwise print “I was thinking about ‘a’/ ‘A’ ”
answer = input('enter a letter')
if answer == 'a':
print('awesome')
elif answer == 'A':
print('awesome')
else:
print(" I was thinking about 'a'/ 'A' ")
answer = input('enter a letter')
if answer =='a' or answer == 'A':
print('Awesome')
else:
print(" I was thinking about 'a'/ 'A' ")
# Ex.3 Let the user choose from a, b, c and print the letter the user chose. For example, if the user choose letter a, the program should print: you chose a. if the user input an invalid letter, print: the letter is invalid. Write this program using if-else statement. (hint: you might want to add elif in there)
answer = input('choose a letter from a, b ,c')
if answer == 'a':
print("you choose 'a'")
elif answer == 'b':
print("you choose 'b'")
elif answer == 'c':
print("you choose 'c'")
else:
print('the letter is invalid')
# ### Little Interactive Programs
# #### 1. Return the length of the input string, if input == quit, break
while True:
string = input('Enter something: ')
if string == 'quit':
break
print('The length of the string is', len(string))
# #### 2. Return the length of an input string, if input == quit, break. If length of the input string is less than 3, give a feedback and continue
while True:
string = input('Enter something: ')
if string == 'quit':
break
if len(string) < 3:
print('Too short')
continue
print('The length of the string is', len(string))
# #### Guessing number
number = 23
chance = 10
while True:
guess = int(input('Enter an integer:'))
if guess > 100 or guess < 1:
print("Please enter a number between 1 and 100")
continue
elif guess == number:
print('Congrats, you win')
break
chance = chance - 1
print('Chances remaining:', chance)
if chance < 1:
print('You have used up your chances, the correct number is', number)
break
elif guess < number:
print('No, it is a litte higher than that.')
else:
print('No, it is a litte lower than that.')
# ## FOR LOOP
# A **for loop** is used for iterating over a sequence (that is either a list, a tuple, a dictrionary, a set, or a string)
fruit = ['apple', 'banana', 'cherry']
for fruits in fruit:
print(fruits)
# <img src="../forLoop.jpg">
# #### Looping through a string
string = 'banana'
for letter in string:
print(letter)
for letter in 'banana':
print(letter)
# #### break statement
fruit = ['apple', 'banana', 'cherry']
for x in fruit:
print(x)
if x == 'banana':
break
for x in fruit:
if x == 'banana':
break
print(x)
# ### continue statement
fruit = ['apple', 'banana', 'cherry']
for x in fruit:
if x == 'banana':
continue
print(x)
# ### range() function
# To loop through a set of code a specified number of times, we can use the **range()** function, the **range()** function returns a sequence of numbers, starting from 0 by default, and increment by 1 by default, and ends at a specified number.
list(range(6))
for x in range(6):
print(x)
for x in range(2,6):
print(x)
for x in range(2,21,2):
print(x)
music = ['pop', 'rock','jazz']
for x in range(len(music)):
print(music[x])
music = ['pop', 'rock','jazz']
list(range(len(music)))
# ### Nested Loops
# +
adj = ['red', 'big','tasty']
fruits = ['apple', 'banana','cherry']
for x in adj:
for y in fruits:
print(x,y)
# -
guessing_word()
def guessing_word():
word = 'candy'
running = True
count = 0
while running:
guess = int(input("Enter an integer:"))
if guess == len(word):
print('Yes, the word contains',len(word),'letters')
while True:
guess_letter = input('Enter a letter:')
if guess_letter in word:
print('Yes, the word contains', guess_letter)
count = count+1
if count >= len(word)/2:
final_guess = input('Do you want to guess what the word is? (y/n) \n')
if final_guess == 'y':
final_guess_word = input('What the word?\n')
if final_guess_word == word:
print('Congratulations, you are correct!')
break
else:
print('No, the word is not',final_guess_word)
else:
print('Keep guessing letters\n')
else:
print('No,', guess_letter,'is not in the word')
running = False
elif guess < len(word):
print("No, it is a litter higher than that.")
else:
print("No, it is a litter lower than that.")
|
Python_Class/Class_4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <p class='cooltitle' style="font-size:35px; text-align:center;" >Neuronal Models</p>
# <br><br>
#
# Hudgkin & Huxley's model (1952) seen in the previous chapter has a very high biological plausibility, it takes into account a lot of underlying phenomena. Unfortunately, this can be very complex at certain times and it is accompanied by a very high implementation cost (in TFLOPS). <br>
# Putting aside that biologically realistic model, there are a lot of other neuronal models that try to simplify or simply not take into account neither the geometry of the neuron nor some of its underlying mechanisms.
#
# In 1962, **<NAME>** tried to introduce some simplifications to the 4 nonlinear differential equations systems in H&H model, reducing it to a 2 state variable system; keeping in tact the spike generation behavior after a stimulus and yet reducing the model complexity; although not being biologically as plausible as the H&H model.
#
# Years later in 1983, and building upon the Fitzugh - Nagumo Model, **Hindmarsh and Rose** proposed a dynamical system of 3 coupled differential equations, accounting for the extra chaotic dynamics of membrane voltage while still being simpler than H&H model.
#
# In this notebook, we're going to start with a simple introduction to qualitative approach of differential equations and dynamical systems by studying a unidimensional neuronal dynamical system **The $I_{Kir}$ model**, and then we can move on to simulating those 2 models : **The Fitzugh-Nagumo model** and **the Hindmarsh-Rose model**
# + [markdown] toc=true
# <h1>Table of contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#The-uni-dimensional-$I_{Kir}$-model" data-toc-modified-id="The-uni-dimensional-$I_{Kir}$-model-1"><span class="toc-item-num">1 </span>The uni-dimensional $I_{Kir}$ model</a></span></li><li><span><a href="#The--Fitzugh-Nagumo-Model" data-toc-modified-id="The--Fitzugh-Nagumo-Model-2"><span class="toc-item-num">2 </span>The Fitzugh-Nagumo Model</a></span></li><li><span><a href="#The-Hindmarsh-Rose-Model" data-toc-modified-id="The-Hindmarsh-Rose-Model-3"><span class="toc-item-num">3 </span>The Hindmarsh-Rose Model</a></span></li></ul></div>
# -
# Let's start by importing some libraries and functions that will serve our purpose.
# + hide_input=false
import numpy as np
import matplotlib.pyplot as plt
from celluloid import Camera
from scipy.optimize import bisect
from scipy.integrate import solve_ivp
from mpl_toolkits.mplot3d import Axes3D
# -
# # The uni-dimensional $I_{Kir}$ model
#
#
# - A uni-dimensional dynamical system like :
# $$\dot V = F(V)$$
# <br>
#
# > Describes how the rate of change $\frac{dV}{dt}$ depends on the variable $V$ itself, if $F(V) > 0$ increases, so does V and vice versa.
#
# - The equilibrium of the system is the state of the system $V$ for which $F(V) = 0$, we consider the equilibrium to be stable when $F(V)$ changes the sign of $V$ so when $F'(V) < 0$, the equilibrium will be unstable when $F'(V) > 0$
#
# - The phase portrait is a representation of the trajectories of the dynamical system in the phase plane.
#
# - A bifurcation is considered a qualitative change in the phase portrait of the system (its equilibria).
#
# - The inward rectifying potassium channel model $I_{Kir}$ is described as a uni-dimensional dynamical system :
#
# <br>
#
# $$\large{\color{red}{C\dot{V} = I - g_L(V - E_L) - g_{Kir}h_\infty(V)(V - E_K)}}$$
#
# <br>
# $$\large{\color{red}{h_\infty(V) = \frac{1}{1 + e^{(\frac{V_{1/2} - V}{k})}}}}$$
#
#
#
# > With the following given parameters :
#
#
#
# <table style="width:90%;border: 1px solid black; border-collapse: collapse;">
# <tr>
# <th style="text-align:center; border-right:1px solid black; background-color: black;
# color: white">$\bf{C}$</th>
# <th style="text-align:center; border-right:1px solid black; background-color: black;
# color: white">$\bf{g_L}$</th>
# <th style="text-align:center; background-color: black;
# color: white ">$\bf{E_L}$</th>
# <th style="text-align:center; border-right:1px solid black; background-color: black;
# color: white">$\bf{g_K}$</th>
# <th style="text-align:center; border-right:1px solid black; background-color: black;
# color: white">$\bf{E_K}$</th>
# <th style="text-align:center; background-color: black;
# color: white ">$\bf{V_{1/2}}$</th>
# <th style="text-align:center; background-color: black;
# color: white ">$\bf{k}$</th>
# </tr>
# <tr>
# <td style="text-align:center;border-right:1px solid black;border-bottom: 1px solid black">$\bf{1}$</td>
# <td style="text-align:center;border-right:1px solid black;border-bottom: 1px solid black">$\bf{0.2}$</td>
# <td style="text-align:center; border-right:1px solid black;border-bottom: 1px solid black">$\bf{-50}$</td>
# <td style="text-align:center;border-right:1px solid black;border-bottom: 1px solid black">$\bf{2}$</td>
# <td style="text-align:center;border-right:1px solid black;border-bottom: 1px solid black">$\bf{-80}$</td>
# <td style="text-align:center; border-right:1px solid black;border-bottom: 1px solid black">$\bf{-76}$</td>
# <td style="text-align:center;border-right:1px solid black;border-bottom: 1px solid black">$\bf{-12}$</td>
# </tr>
# </table>
# **First off, let's take a look at the gating variable $h_\infty(V)$** and the **I-V** curves
# > Declaring the given parameters :
# + cell_style="center"
C ,g_L, E_L, g_K, E_K, V_half, k = 1, 0.2, -50, 2, -80, -76, -12
# -
# > Writing lambda functions to send back the gating variable and the currents of the model :
# + cell_style="center"
h_infty = lambda voltage: 1 / (1 + np.exp((V_half - voltage) / k))
leak = lambda voltage: g_L * (voltage - E_L)
kir = lambda voltage: g_K * h_infty(voltage) * (voltage - E_K)
# -
# > And now let's take a look at how they change between -200 and +100 mV
# + cell_style="center"
v = np.linspace(-200,100,100)
fig, ax = plt.subplots(1,2, figsize = (10,5), dpi = 150)
ax[0].plot(v, h_infty(v), 'r') #h_infty plot
ax[0].set_title("Graphical representation of $h_\infty(V)$")
ax[0].set_xlabel("Voltage in mV", position = (1.1,0))
ax[1].plot(v, leak(v), color = 'orange', label='$I_L$') #leak current
ax[1].plot(v, kir(v), 'b', label='$I_{Kir}$') #Kir current
ax[1].set_title("$I_V$ curves")
ax[1].legend()
plt.suptitle("$I_{Kir}$ model")
# -
# **Now let's take a look at the phase portrait while injecting a current $I = 6$**
#
# > We can start by writing a function for $\frac{dv}{dt}$
iinj = 6
def V_dot(voltage, inject):
return (inject - g_L * (voltage - E_L) - g_K * h_infty(voltage) *
(voltage - E_K)) / C
# > In order to find the equilibrium points for the system we must solve the equation while the derivative is 0.
# <br>We can use a function from scipy module to find the root of our function for a certain interval. <br>
# P.S : It might be interesting to plot our phase portrait before doing this step in order to approximate where our equlibrium points are.
# +
eq1 = bisect(
V_dot, -70, -60, iinj
) # Solve it for an interval [-70,-60], iinj = 6 is the injected current
eq2 = bisect(V_dot, -50, -40, iinj)
eq3 = bisect(V_dot, -40, -20, iinj)
eq_points = [eq1, eq2, eq3]
# -
# > To determine the equilibrium type we must see the sign of the slope of $\frac{dv}{dt}$, if it was negative, then the equilibrium will be stable, otherwise it will be unstable
# +
def eq_type(equilibrium, xdot, xdot_params):
for eq in equilibrium:
print('%s point is stable' %
eq) if xdot(eq, xdot_params) < 0 else print('%s point is unstable' %
eq)
eq_type(eq_points, V_dot, iinj)
# -
# > So we have 1 stable equilbrium and 2 unstable equilibria, let's now see the phase portrait between -75 and -10 mV
# +
volt = np.linspace(-75, -10, 200)
# Phase portrait
plt.figure(dpi=150)
plt.plot(volt, V_dot(volt, iinj), color="limegreen")
plt.axhline(y=0, color='black') # Horizontal line to see where dvdt = 0
for eq in eq_points: # Three vertical lines that pass through equilibrium
plt.axvline(x=eq, color='black')
# Equilibrium points
plt.plot(eq1, 0, 'ro', fillstyle='full', markersize=12, label="Stable")
plt.plot(eq3, 0, 'wo', markeredgecolor='red', markersize=12)
plt.plot(eq2, 0, 'wo', markeredgecolor='red', markersize=12, label="Unstable")
# Plotting to show stability
plt.arrow(-75, 0, dx=+8, dy=0, width=0.08, color='red', head_length=2)
plt.arrow(-50, 0, dx=-8, dy=0, width=0.08, color='red', head_length=2)
plt.arrow(-44, 0, dx=+8, dy=0, width=0.08, color='red', head_length=2)
plt.arrow(-22, 0, dx=-6, dy=0, width=0.08, color='red', head_length=2)
plt.ylim(-2, 2)
plt.xlim(-77, -20)
plt.title("Phase portrait of $I_{Kir}$ model for $I = 6$")
plt.xlabel("$V$")
plt.ylabel("$\dot{V}$", rotation=0)
plt.legend()
# -
# **Bifurcation diagram with $I$ as a bifurcation parameter**
#
# > We only saw the phase portrait for $I=6$, but we can consider $I$ as bifurcation parameter that'll qualitatively change the equilibria of the systems and induce a bifurcation. <br>
# Now it would be interesting to see the eqilibria points of the system in function of the injected current $I$.<br>
# While $\dot V = 0$, we can see that $I = I_{Kir} + I_L$
#
def injected(voltage):
return leak(voltage) + kir(voltage)
# > Now let's take a look at the bifurcation diagram
plt.figure(dpi=150)
plt.plot(injected(v), v, 'g')
plt.axvline(x=6, color='black',
label="Model while $I=6$") # See equilbria while I=6
plt.plot(iinj, eq1, 'ro', iinj, eq2, 'ro', iinj, eq3, 'ro')
plt.xlim(5, 7.5)
plt.ylim(-100, 0)
plt.xlabel("$I$")
plt.ylabel("$V$", rotation=0)
plt.title(
"Bifurcation diagram for $I_{Kir}$ model with $I$ as a control parameter")
plt.legend()
# <hr class="sep">
# + [markdown] cell_style="center"
# # The Fitzugh-Nagumo Model
# **Bi-dimensional dynamical systems**
#
#
# - A bi-dimensional dynamical system of differential equations :
#
# >$$\dot{x} = f(x,y)\ ,\ \dot{x} = \frac{\delta{f}}{\delta{x}}x + \frac{\delta{f}}{\delta{y}}y $$ <br>
# $$\dot{y} = g(x,y)\ , \ \dot{y} = \frac{\delta{g}}{\delta{x}}x + \frac{\delta{g}}{\delta{y}}y$$ <br>
# will describe the evolution of our two state variables $x$ and $y$, at most cases, our two variables are the membrane voltage and the recovery variable.
#
#
# - The group of points given by the equations $f(x,y) = 0$ and $g(x,y) = 0$ are the **$\bf{x-}$** and **$\bf{y-}$nullclines** respectively.
#
# - The points of intersection of our nullclines are the equilibria of the system.
# - An equilibrium is stable when the the neighbouring trajectories are attracted to it.
#
# -
# **The Fitzhugh-Nagumo equations describe a bi-dimensional dynamical system :**
# <br>
# <br>
# $$\large{\color{red}{\dot{v} = v - \frac{v^3}{3} - w + I}}$$
# <br>
# $$\large{\color{red}{\tau\dot{w} = v + a -b*w}}$$
#
#
# > With the following parameters :
#
# <table style="width:30%;border: 1px solid black; border-collapse: collapse;">
# <tr>
# <th style="text-align:center; border-right:1px solid black; background-color: black;
# color: white">$\bf{a}$</th>
# <th style="text-align:center; border-right:1px solid black; background-color: black;
# color: white">$\bf{b}$</th>
# <th style="text-align:center; background-color: black;
# color: white ">$\bf{\tau}$</th>
# </tr>
# <tr>
# <td style="text-align:center;border-right:1px solid black;border-bottom: 1px solid black">$\bf{0.7}$</td>
# <td style="text-align:center;border-right:1px solid black;border-bottom: 1px solid black">$\bf{0.8}$</td>
# <td style="text-align:center; border-right:1px solid black;border-bottom: 1px solid black">$\bf{13}$</td>
# </tr>
# </table>
#
#
# - At The equilibrium $\bf{(v^\ast,w^\ast)}$, the derivatives will be zero :
# $$v - \frac{v^3}{3} - w + I= 0$$
# $$v + a -b*w = 0$$
# <br>
#
# > which makes : $$w = v - \frac{v^3}{3} + I \ \ (V-nullcline)$$ <br>
# $$w = \frac{(v + a)}{b} \ \ (w-nullcline)$$
#
# <br>
# $$\Rightarrow\boxed{v - \frac{v^3}{3} + I - \frac{(v + a)}{b} = 0}$$
# <br>
#
# > This is the equation to be solved if we wanted to find the equilibrium (the intersection of the nullclines), we can use either NumPy or SymPy like we saw in other notebooks.
#
# > Like always, let's start by declaring the model's parameters
# + cell_style="center" hide_input=true
a, b, tau = 0.7, 0.8, 13 # The parameters of the model
# -
# > Now let's implement the equation to be solved
# + cell_style="center" hide_input=true
eq_equation = lambda v, I: v - (v**3 / 3) + I - ((v + a) / b)
def eq_coordinates(eq_equation, I):
"""This function sends back the equilibrium coordinates of The Fitzugh-Nagumo Model
for the equilibrium equation specified as the eq_equation.
"""
vstar = bisect(
eq_equation, -2, +2, I
) #solve eq_equation between -2 and +2 with bisect function from scipy
wstar = (vstar + a) / b
return vstar, wstar
# -
# > Next step would be to implement our model's nullclines and equations
# + cell_style="center" hide_input=true
def vnull(v, I):
"V-nullcline of the Fitzugh-Nagumo model"
return v - v**3 / 3 + I
def wnull(v, a, b):
"w-nullcline of the Fitzugh-Nagumo model"
return (v + a) / b
def vdot(v, w, I):
"""this function sends back the values of dvdt"""
return v - v**3 / 3 - w + I
def wdot(v, w):
"""this function sends back the values of dwdt"""
return (v + a - b * w) / tau
def fitz_nagu(t, z, I):
"""This function contains the equations of the model,
it will be used with scipy's solve_ivp function in order to solve the system
numerically starting from initial conditions."""
v, w = z
return np.array([vdot(v, w, I), wdot(v, w)])
# -
# > Now the system of equations can be solved numerically like we did with Hugkin and Huxley's model with scipy's solve_ivp. <br>
# It would be interesting to write a function that simulates the model for given initial conditions of $V$ , $w$ and $I$.
#
def simulate_fitz_nagu(V_init, w_init, I_init, Tmax):
# Determining equilibrium
v_star, w_star = eq_coordinates(eq_equation,
I=I_init)
# Solve the system
sol = solve_ivp(
lambda t, z: fitz_nagu(t, z, I=I_init), [0, Tmax],
(V_init, w_init
), t_eval=np.linspace(0, Tmax, 150)) # An anonymous function with fitz-nagu was used because solve_ip
# doesn't suppport specifiying other parameters for the function to be
# solved, this can be a work-around as it lets us specify I
tt, vt, wt = sol.t, sol.y[0], sol.y[
1] # Time, voltage and recovery variable
# Voltage and arrows
volt = np.linspace(-5, 5, 100) # Voltage array between -5 and +5 mV
x_arrs, y_arrs = np.meshgrid(np.linspace(-3, +3, 15),
np.linspace(-2, +2, 10))
# Figure and axes
fig, axes = plt.subplots(1, 2, figsize=(12, 5), dpi=150)
cam = Camera(fig)
# Animation
for i in range(len(tt)):
s1, = axes[0].plot(vt[:i], wt[:i], 'r')
ng1, = axes[0].plot(volt, vnull(volt, I=I_init), color="orange")
ng2, = axes[0].plot(volt, wnull(volt, a, b), 'b')
eq, = axes[0].plot(v_star, w_star, 'ko', label="Stable Node")
axes[0].quiver(x_arrs,y_arrs,vdot(x_arrs,y_arrs,I_init),wdot(\
x_arrs,y_arrs), color = 'green')
axes[0].legend(
[ng1, ng2, eq, s1],
['$V$-nullcline', '$w$-nullcline', 'Equilibrium', 'Solution'])
axes[0].set_ylim(-2, +2)
axes[0].set_xlim(-3, 3)
axes[0].set_ylabel('$w$', rotation=0)
axes[0].set_xlabel('$V$')
axes[0].set_title('Phase portrait')
vg, = axes[1].plot(tt[:i], vt[:i], color='orange')
wg, = axes[1].plot(tt[:i], wt[:i], 'b')
axes[1].legend([vg, wg], ['$V(t)$', '$w(t)$'])
axes[1].set_xlabel('Time')
axes[1].set_title('Numerical solution')
fig.suptitle(
"Fitzugh and Nagumo model Simulation, Initial conditions : $V$ = %s, $w$ = %s, $I$ = %s"
% (V_init, w_init, I_init))
cam.snap()
cam.animate(blit=False, interval=30,
repeat=True).save('fitz_nagu.mp4')
# > Let's take a look at the system while $I = 0.3$ and with the initial conditions are : $V =0, w=0$
simulate_fitz_nagu(V_init=0,w_init=0, I_init=0.3, Tmax=100)
# > Another simulation with : $V =-2, w=-1.5, I = 0.5$
simulate_fitz_nagu(V_init=-2,w_init=-1.5, I_init=0.5, Tmax=100)
# <hr class="sep">
# # The Hindmarsh-Rose Model
# <br>
#
# - This model was made to account for the bursting activity of certain neurons, it is made of 3 dimensionless state variables :
#
# > $x(t)$ The membrane potential <br>
# $y(t)$ which represents the spiking variable or the fast sodium and potassium currents<br>
# $z(t)$ is the bursting variable, it represents the slow ionic currents.<br>
#
# - The Model is expressed by the following equations :
#
# $$\large{\color {red} {\dot x = y + \phi(x) - z + I}}$$
# $$\large{\color {red} {\dot y = \psi(x) - y}}$$
# $$\large{\color {red} {\dot z = r(s(x - x_r)-z)}}$$
# <br><br>
#
# > with :
# <br>
# $$\large{\color {red} {\phi(x) = -ax^3 + bx^2}}$$
# $$\large{\color {red} {\psi(x) = c - dx^2}}$$
# <br>
# > And The parameters are :
# <table style="width:90%;border: 1px solid black; border-collapse: collapse;">
# <tr>
# <th style="text-align:center; border-right:1px solid black; background-color: black;
# color: white">$\bf{s}$</th>
# <th style="text-align:center; border-right:1px solid black; background-color: black;
# color: white">$\bf{x_r}$</th>
# <th style="text-align:center; background-color: black;
# color: white ">$\bf{a}$</th>
# <th style="text-align:center; border-right:1px solid black; background-color: black;
# color: white">$\bf{b}$</th>
# <th style="text-align:center; border-right:1px solid black; background-color: black;
# color: white">$\bf{c}$</th>
# <th style="text-align:center; background-color: black;
# color: white ">$\bf{d}$</th>
# <th style="text-align:center; background-color: black;
# color: white ">$\bf{I}$</th>
# <th style="text-align:center; background-color: black;
# color: white ">$\bf{r}$</th>
# </tr>
# <tr>
# <td style="text-align:center;border-right:1px solid black;border-bottom: 1px solid black">$\bf{4}$</td>
# <td style="text-align:center;border-right:1px solid black;border-bottom: 1px solid black">$\bf{\frac{-8}{5}}$</td>
# <td style="text-align:center; border-right:1px solid black;border-bottom: 1px solid black">$\bf{1}$</td>
# <td style="text-align:center;border-right:1px solid black;border-bottom: 1px solid black">$\bf{3}$</td>
# <td style="text-align:center;border-right:1px solid black;border-bottom: 1px solid black">$\bf{1}$</td>
# <td style="text-align:center;border-right:1px solid black;border-bottom: 1px solid black">$\bf{5}$</td>
# <td style="text-align:center; border-right:1px solid black;border-bottom: 1px solid black">$\bf{[-10,10]}$</td>
# <td style="text-align:center;border-right:1px solid black;border-bottom: 1px solid black">$\bf{10^{-3}}$</td>
# </tr>
# </table>
#
# **Let's do a numerical simulation of the system while using r as a bifurcation parameter**
# > In order to be able to change the values of r (or any other parameter) while solving the system, we can write a wrapper function around the equations function (that returns it); and then we can pass the wrapper function to solve_ivp.
def hind_rose(r , s = 4, xr = -8/5, a = 1, b = 3, c = 1, d = 5, I = 2) :
"""
Hindmarsh-Rose system (x,y,z)
r : bifurcation parameter
"""
def pre_hind_rose(t, vars) :
x, y, z = vars
return np.array([y - a*x**3 + b*x**2 - z + I,\
c - d*x**2 - y,\
r *(s*(x - xr) - z)])
return pre_hind_rose
# > Now we're going to write a function to simulate this model from chosen initial conditions, this function will be written while using r as a bifurcation parameter but it can be easily modified for it to suit the use of other parameters as control.
def simulate_hind_rose(x_init, y_init, z_init, r_param, Tmax):
# First off, let's solve the system from our initial conditions and our chose r value
sol = solve_ivp(hind_rose(r=r_param), [0, Tmax], (x_init, y_init, z_init), t_eval=np.linspace(0, Tmax, 500))
# Let's separate the solutions and the time vector
tt, tx, ty, tz = sol.t, sol.y[0], sol.y[1], sol.y[2]
# And now let's create the animation
fig = plt.figure(figsize=(12, 5), dpi=150)
cam = Camera(fig)
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122, projection='3d')
for i in range(len(tt)):
ax1.plot(tt[:i], tx[:i], 'r')
ax1.set_xlabel('t')
ax1.set_ylabel('$x$', rotation=0)
ax2.plot(tx[:i], ty[:i], tz[:i], 'b')
ax2.set_zlabel('$z$')
ax2.set_xlabel('$x$')
ax2.set_ylabel('$y$')
ax2.set_zlim(1.6,2.2)
fig.suptitle(
"Hindmarsh and Rose model Simulation, Initial conditions : $x$ = %s, $y$ = %s, $z$ = %s, $r$=%s"
% (x_init, y_init, z_init, r_param))
cam.snap()
cam.animate(blit=False, interval=40, repeat=True).save('HR.mp4')
# > Let's now simulate the model with $r=0.001$ and $x=-1.5, y=-10, z=2$
simulate_hind_rose(x_init=-1.5, y_init=-10, z_init=2, r_param=0.001, Tmax=1000)
# <hr class="sep">
|
Notebooks/4_Neuronal_Models.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_chainer_p36
# language: python
# name: conda_chainer_p36
# ---
# # Chainer の学習と推論を SageMaker で行う
#
# #### ノートブックに含まれる内容
#
# - Chainer の学習と推論を SageMaker で行うやりかた
#
# #### ノートブックで使われている手法の詳細
#
# - アルゴリズム: MNIST
# - データ: MLP
# +
import sagemaker
from sagemaker import get_execution_role
sagemaker_session = sagemaker.Session()
role = get_execution_role()
# -
# ## データのロード
#
# ここでは,`Chainer` でサポートされている関数を使って,MNIST データをダウンロードします.SageMaker の学習時につかうデータは,S3 に置く必要があります.ここでは,ローカルに落とした MNIST データを npz 形式で固めてから,SageMaker のラッパー関数を使って S3 にアップロードします.
#
# デフォルトでは SageMaker は `sagemaker-{region}-{your aws account number}` というバケットを使用します.当該バケットがない場合には,自動で新しく作成します.`upload_data()` メソッドの引数に bucket=XXXX という形でデータを配置するバケットを指定することが可能です
# +
import chainer
train, test = chainer.datasets.get_mnist()
# -
# 以下を実行する前に,**<span style="color: red;">2 箇所ある `notebook/chainer/XX/mnist` の XX を指定された適切な数字に変更</span>**してください.
# +
import os
import shutil
import numpy as np
train_images = np.array([data[0] for data in train])
train_labels = np.array([data[1] for data in train])
test_images = np.array([data[0] for data in test])
test_labels = np.array([data[1] for data in test])
try:
os.makedirs('/tmp/data/train')
os.makedirs('/tmp/data/test')
np.savez('/tmp/data/train/train.npz', images=train_images, labels=train_labels)
np.savez('/tmp/data/test/test.npz', images=test_images, labels=test_labels)
train_input = sagemaker_session.upload_data(
path=os.path.join('/tmp/data', 'train'),
key_prefix='notebook/chainer/XX/mnist')
test_input = sagemaker_session.upload_data(
path=os.path.join('/tmp/data', 'test'),
key_prefix='notebook/chainer/XX/mnist')
finally:
shutil.rmtree('/tmp/data')
# -
# ## Chainer を SageMaker で使う際のポイント
#
# 学習については,main 関数内にそのままモデルを記述するだけで大丈夫です.あとは SageMaker 側で学習ジョブを走らせる際に,main 関数内の学習処理が実行されます.ですので,既存の Chainer の実行スクリプトをほぼそのまま SageMaker に移植することができます.また,環境変数経由で入力データの場所や GPU の数などを取得することが可能です.これは `argparse` 経由で `main` 関数内で受け取ることができます.詳細は[こちら](https://github.com/aws/sagemaker-python-sdk/blob/master/src/sagemaker/chainer/README.rst)をご覧ください.
#
# また推論時の処理は,`model_fn` で学習済みモデルをロードする部分だけ記述する必要があります.その他オプションで,前処理,推論処理,後処理部分を `input_fn`, `predict_fn`, `output_fn` で書くこともできます.デフォルトでは,`application/x-npy` コンテントタイプで指定される,NumPy 配列を入力として受け取ります.
#
# !pygmentize 'chainer_mnist.py'
# ## モデルの学習を実行
#
# 以下のように,`Estimator` クラスの子クラスの `Chainer` オブジェクトを作成し,`fit()` メソッドで学習ジョブを実行します. `entry_point` で指定したローカルのスクリプトが,学習用のコンテナ内で実行されます.また合わせてローカルの `source_dir` を指定することで,依存するスクリプト群をコンテナにコピーして,学習時に使用することが可能です.
# +
import subprocess
from sagemaker.chainer.estimator import Chainer
instance_type = 'ml.m4.xlarge'
chainer_estimator = Chainer(entry_point='chainer_mnist.py', role=role,
train_instance_count=1, train_instance_type=instance_type,
hyperparameters={'epochs': 3, 'batch_size': 128})
chainer_estimator.fit({'train': train_input, 'test': test_input})
# -
# # モデルの推論を実行
#
#
# 推論を行うために,まず学習したモデルをデプロイします.`deploy()` メソッドでは,デプロイ先エンドポイントのインスタンス数,インスタンスタイプを指定します.こちらもインスタンスタイプを `local` にすることで,このインスタンス内にエンドポイントを作成します.
predictor = chainer_estimator.deploy(initial_instance_count=1, instance_type=instance_type)
# デプロイが終わったら,実際に手書き文字認識を行ってみましょう.
# +
import random
import matplotlib.pyplot as plt
num_samples = 5
indices = random.sample(range(test_images.shape[0] - 1), num_samples)
images, labels = test_images[indices], test_labels[indices]
for i in range(num_samples):
plt.subplot(1,num_samples,i+1)
plt.imshow(images[i].reshape(28, 28), cmap='gray')
plt.title(labels[i])
plt.axis('off')
# -
prediction = predictor.predict(images)
predicted_label = prediction.argmax(axis=1)
print('The predicted labels are: {}'.format(predicted_label))
from IPython.display import HTML
HTML(open("input.html").read())
# あとは,上のキャンバスに文字を書いて,実際に予測をしてみましょう.
image = np.array(data, dtype=np.float32)
prediction = predictor.predict(image)
predicted_label = prediction.argmax(axis=1)[0]
print('What you wrote is: {}'.format(predicted_label))
# ## エンドポイントの削除
#
# 全て終わったら,エンドポイントを削除します.
chainer_estimator.delete_endpoint()
|
supported_frameworks/chainer_mnist/chainer_mnist.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
arr = [-13, -3, -25, 20, -3, 16, -23, -12, -5, 22, 15, -9, 17]
def max_sum_contiguous_subarray(arr):
max_so_far = max(arr)
max_now = 0
f = 0
for i in arr:
if i<0 and f==0:
continue
f=1
max_now += i
if max_now>max_so_far:
max_so_far = max_now
if max_now<0:
max_now=0
return(max_so_far)
print(max_sum_contiguous_subarray(arr))
|
1. Largest Sum Contiguous SubArray.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/john77R/Machine_vision/blob/main/examples/vision/ipynb/video_classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="y0ZtUWSp377f"
# # Video Classification with a CNN-RNN Architecture
#
# **Author:** [<NAME>](https://twitter.com/RisingSayak)<br>
# **Date created:** 2021/05/28<br>
# **Last modified:** 2021/06/05<br>
# **Description:** Training a video classifier with transfer learning and a recurrent model on the UCF101 dataset.
# + [markdown] id="rm1xRBSe377l"
# This example demonstrates video classification, an important use-case with
# applications in recommendations, security, and so on.
# We will be using the [UCF101 dataset](https://www.crcv.ucf.edu/data/UCF101.php)
# to build our video classifier. The dataset consists of videos categorized into different
# actions, like cricket shot, punching, biking, etc. This dataset is commonly used to
# build action recognizers, which are an application of video classification.
#
# A video consists of an ordered sequence of frames. Each frame contains *spatial*
# information, and the sequence of those frames contains *temporal* information. To model
# both of these aspects, we use a hybrid architecture that consists of convolutions
# (for spatial processing) as well as recurrent layers (for temporal processing).
# Specifically, we'll use a Convolutional Neural Network (CNN) and a Recurrent Neural
# Network (RNN) consisting of [GRU layers](https://keras.io/api/layers/recurrent_layers/gru/).
# This kind of hybrid architecture is popularly known as a **CNN-RNN**.
#
# This example requires TensorFlow 2.5 or higher, as well as TensorFlow Docs, which can be
# installed using the following command:
# + id="yoFFuTNT377m"
# !pip install -q git+https://github.com/tensorflow/docs
# + [markdown] id="q4W_Z7Mo377o"
# ## Data collection
#
# In order to keep the runtime of this example relatively short, we will be using a
# subsampled version of the original UCF101 dataset. You can refer to
# [this notebook](https://colab.research.google.com/github/sayakpaul/Action-Recognition-in-TensorFlow/blob/main/Data_Preparation_UCF101.ipynb)
# to know how the subsampling was done.
# + id="qmJqiDE9377p"
# !wget -q https://git.io/JGc31 -O ucf101_top5.tar.gz
# !tar xf ucf101_top5.tar.gz
# + [markdown] id="oTQBFuhm377q"
# ## Setup
# + id="Jf9oes7m377r"
from tensorflow_docs.vis import embed
from tensorflow import keras
from imutils import paths
import matplotlib.pyplot as plt
import tensorflow as tf
import pandas as pd
import numpy as np
import imageio
import cv2
import os
# + [markdown] id="j5UzwcAQ377r"
# ## Define hyperparameters
# + id="9jkqBGor377s"
IMG_SIZE = 224
BATCH_SIZE = 64
EPOCHS = 10
MAX_SEQ_LENGTH = 20
NUM_FEATURES = 2048
# + [markdown] id="tJpGCS7-377s"
# ## Data preparation
# + id="rUb8aPOZ377t"
train_df = pd.read_csv("train.csv")
test_df = pd.read_csv("test.csv")
print(f"Total videos for training: {len(train_df)}")
print(f"Total videos for testing: {len(test_df)}")
train_df.sample(10)
# + [markdown] id="LDzrSoq7377t"
# One of the many challenges of training video classifiers is figuring out a way to feed
# the videos to a network. [This blog post](https://blog.coast.ai/five-video-classification-methods-implemented-in-keras-and-tensorflow-99cad29cc0b5)
# discusses five such methods. Since a video is an ordered sequence of frames, we could
# just extract the frames and put them in a 3D tensor. But the number of frames may differ
# from video to video which would prevent us from stacking them into batches
# (unless we use padding). As an alternative, we can **save video frames at a fixed
# interval until a maximum frame count is reached**. In this example we will do
# the following:
#
# 1. Capture the frames of a video.
# 2. Extract frames from the videos until a maximum frame count is reached.
# 3. In the case, where a video's frame count is lesser than the maximum frame count we
# will pad the video with zeros.
#
# Note that this workflow is identical to [problems involving texts sequences](https://developers.google.com/machine-learning/guides/text-classification/). Videos of the UCF101 dataset is [known](https://www.crcv.ucf.edu/papers/UCF101_CRCV-TR-12-01.pdf)
# to not contain extreme variations in objects and actions across frames. Because of this,
# it may be okay to only consider a few frames for the learning task. But this approach may
# not generalize well to other video classification problems. We will be using
# [OpenCV's `VideoCapture()` method](https://docs.opencv.org/master/dd/d43/tutorial_py_video_display.html)
# to read frames from videos.
# + id="FVfLVPgO377u"
# The following two methods are taken from this tutorial:
# https://www.tensorflow.org/hub/tutorials/action_recognition_with_tf_hub
def crop_center_square(frame):
y, x = frame.shape[0:2]
min_dim = min(y, x)
start_x = (x // 2) - (min_dim // 2)
start_y = (y // 2) - (min_dim // 2)
return frame[start_y : start_y + min_dim, start_x : start_x + min_dim]
def load_video(path, max_frames=0, resize=(IMG_SIZE, IMG_SIZE)):
cap = cv2.VideoCapture(path)
frames = []
try:
while True:
ret, frame = cap.read()
if not ret:
break
frame = crop_center_square(frame)
frame = cv2.resize(frame, resize)
frame = frame[:, :, [2, 1, 0]]
frames.append(frame)
if len(frames) == max_frames:
break
finally:
cap.release()
return np.array(frames)
# + [markdown] id="WkgdBvdl377v"
# We can use a pre-trained network to extract meaningful features from the extracted
# frames. The [`Keras Applications`](https://keras.io/api/applications/) module provides
# a number of state-of-the-art models pre-trained on the [ImageNet-1k dataset](http://image-net.org/).
# We will be using the [InceptionV3 model](https://arxiv.org/abs/1512.00567) for this purpose.
# + id="q21JxQi3377v"
def build_feature_extractor():
feature_extractor = keras.applications.InceptionV3(
weights="imagenet",
include_top=False,
pooling="avg",
input_shape=(IMG_SIZE, IMG_SIZE, 3),
)
preprocess_input = keras.applications.inception_v3.preprocess_input
inputs = keras.Input((IMG_SIZE, IMG_SIZE, 3))
preprocessed = preprocess_input(inputs)
outputs = feature_extractor(preprocessed)
return keras.Model(inputs, outputs, name="feature_extractor")
feature_extractor = build_feature_extractor()
# + [markdown] id="nQcarBgv377w"
# The labels of the videos are strings. Neural networks do not understand string values,
# so they must be converted to some numerical form before they are fed to the model. Here
# we will use the [`StringLookup`](https://keras.io/api/layers/preprocessing_layers/categorical/string_lookup)
# layer encode the class labels as integers.
# + id="uPklygoq377x"
label_processor = keras.layers.StringLookup(
num_oov_indices=0, vocabulary=np.unique(train_df["tag"])
)
print(label_processor.get_vocabulary())
# + [markdown] id="YgJeUvxK377x"
# Finally, we can put all the pieces together to create our data processing utility.
# + id="APcsl4d-377x"
def prepare_all_videos(df, root_dir):
num_samples = len(df)
video_paths = df["video_name"].values.tolist()
labels = df["tag"].values
labels = label_processor(labels[..., None]).numpy()
# `frame_masks` and `frame_features` are what we will feed to our sequence model.
# `frame_masks` will contain a bunch of booleans denoting if a timestep is
# masked with padding or not.
frame_masks = np.zeros(shape=(num_samples, MAX_SEQ_LENGTH), dtype="bool")
frame_features = np.zeros(
shape=(num_samples, MAX_SEQ_LENGTH, NUM_FEATURES), dtype="float32"
)
# For each video.
for idx, path in enumerate(video_paths):
# Gather all its frames and add a batch dimension.
frames = load_video(os.path.join(root_dir, path))
frames = frames[None, ...]
# Initialize placeholders to store the masks and features of the current video.
temp_frame_mask = np.zeros(shape=(1, MAX_SEQ_LENGTH,), dtype="bool")
temp_frame_features = np.zeros(
shape=(1, MAX_SEQ_LENGTH, NUM_FEATURES), dtype="float32"
)
# Extract features from the frames of the current video.
for i, batch in enumerate(frames):
video_length = batch.shape[0]
length = min(MAX_SEQ_LENGTH, video_length)
for j in range(length):
temp_frame_features[i, j, :] = feature_extractor.predict(
batch[None, j, :]
)
temp_frame_mask[i, :length] = 1 # 1 = not masked, 0 = masked
frame_features[idx,] = temp_frame_features.squeeze()
frame_masks[idx,] = temp_frame_mask.squeeze()
return (frame_features, frame_masks), labels
train_data, train_labels = prepare_all_videos(train_df, "train")
test_data, test_labels = prepare_all_videos(test_df, "test")
print(f"Frame features in train set: {train_data[0].shape}")
print(f"Frame masks in train set: {train_data[1].shape}")
# + [markdown] id="HC8IGBGu377y"
# The above code block will take ~20 minutes to execute depending on the machine it's being
# executed.
# + [markdown] id="SWbVbz3n377y"
# ## The sequence model
#
# Now, we can feed this data to a sequence model consisting of recurrent layers like `GRU`.
# + id="6nyZ2dPC377y"
# Utility for our sequence model.
def get_sequence_model():
class_vocab = label_processor.get_vocabulary()
frame_features_input = keras.Input((MAX_SEQ_LENGTH, NUM_FEATURES))
mask_input = keras.Input((MAX_SEQ_LENGTH,), dtype="bool")
# Refer to the following tutorial to understand the significance of using `mask`:
# https://keras.io/api/layers/recurrent_layers/gru/
x = keras.layers.GRU(16, return_sequences=True)(
frame_features_input, mask=mask_input
)
x = keras.layers.GRU(8)(x)
x = keras.layers.Dropout(0.4)(x)
x = keras.layers.Dense(8, activation="relu")(x)
output = keras.layers.Dense(len(class_vocab), activation="softmax")(x)
rnn_model = keras.Model([frame_features_input, mask_input], output)
rnn_model.compile(
loss="sparse_categorical_crossentropy", optimizer="adam", metrics=["accuracy"]
)
return rnn_model
# Utility for running experiments.
def run_experiment():
filepath = "/tmp/video_classifier"
checkpoint = keras.callbacks.ModelCheckpoint(
filepath, save_weights_only=True, save_best_only=True, verbose=1
)
seq_model = get_sequence_model()
history = seq_model.fit(
[train_data[0], train_data[1]],
train_labels,
validation_split=0.3,
epochs=EPOCHS,
callbacks=[checkpoint],
)
seq_model.load_weights(filepath)
_, accuracy = seq_model.evaluate([test_data[0], test_data[1]], test_labels)
print(f"Test accuracy: {round(accuracy * 100, 2)}%")
return history, seq_model
_, sequence_model = run_experiment()
# + [markdown] id="0PyrBBnB377z"
# **Note**: To keep the runtime of this example relatively short, we just used a few
# training examples. This number of training examples is low with respect to the sequence
# model being used that has 99,909 trainable parameters. You are encouraged to sample more
# data from the UCF101 dataset using [the notebook](https://colab.research.google.com/github/sayakpaul/Action-Recognition-in-TensorFlow/blob/main/Data_Preparation_UCF101.ipynb) mentioned above and train the same model.
# + [markdown] id="rs6ZMVo5377z"
# ## Inference
# + id="fWmrpOJO3770"
def prepare_single_video(frames):
frames = frames[None, ...]
frame_mask = np.zeros(shape=(1, MAX_SEQ_LENGTH,), dtype="bool")
frame_features = np.zeros(shape=(1, MAX_SEQ_LENGTH, NUM_FEATURES), dtype="float32")
for i, batch in enumerate(frames):
video_length = batch.shape[0]
length = min(MAX_SEQ_LENGTH, video_length)
for j in range(length):
frame_features[i, j, :] = feature_extractor.predict(batch[None, j, :])
frame_mask[i, :length] = 1 # 1 = not masked, 0 = masked
return frame_features, frame_mask
def sequence_prediction(path):
class_vocab = label_processor.get_vocabulary()
frames = load_video(os.path.join("test", path))
frame_features, frame_mask = prepare_single_video(frames)
probabilities = sequence_model.predict([frame_features, frame_mask])[0]
for i in np.argsort(probabilities)[::-1]:
print(f" {class_vocab[i]}: {probabilities[i] * 100:5.2f}%")
return frames
# This utility is for visualization.
# Referenced from:
# https://www.tensorflow.org/hub/tutorials/action_recognition_with_tf_hub
def to_gif(images):
converted_images = images.astype(np.uint8)
imageio.mimsave("animation.gif", converted_images, fps=10)
return embed.embed_file("animation.gif")
test_video = np.random.choice(test_df["video_name"].values.tolist())
print(f"Test video path: {test_video}")
test_frames = sequence_prediction(test_video)
to_gif(test_frames[:MAX_SEQ_LENGTH])
# + [markdown] id="T0GeOKFD3770"
# ## Next steps
#
# * In this example, we made use of transfer learning for extracting meaningful features
# from video frames. You could also fine-tune the pre-trained network to notice how that
# affects the end results.
# * For speed-accuracy trade-offs, you can try out other models present inside
# `tf.keras.applications`.
# * Try different combinations of `MAX_SEQ_LENGTH` to observe how that affects the
# performance.
# * Train on a higher number of classes and see if you are able to get good performance.
# * Following [this tutorial](https://www.tensorflow.org/hub/tutorials/action_recognition_with_tf_hub), try a
# [pre-trained action recognition model](https://arxiv.org/abs/1705.07750) from DeepMind.
# * Rolling-averaging can be useful technique for video classification and it can be
# combined with a standard image classification model to infer on videos.
# [This tutorial](https://www.pyimagesearch.com/2019/07/15/video-classification-with-keras-and-deep-learning/)
# will help understand how to use rolling-averaging with an image classifier.
# * When there are variations in between the frames of a video not all the frames might be
# equally important to decide its category. In those situations, putting a
# [self-attention layer](https://www.tensorflow.org/api_docs/python/tf/keras/layers/Attention) in the
# sequence model will likely yield better results.
# * Following [this book chapter](https://livebook.manning.com/book/deep-learning-with-python-second-edition/chapter-11),
# you can implement Transformers-based models for processing videos.
|
examples/vision/ipynb/video_classification.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_amazonei_mxnet_p36
# language: python
# name: conda_amazonei_mxnet_p36
# ---
# # Plagiarism Detection, Feature Engineering
#
# In this project, you will be tasked with building a plagiarism detector that examines an answer text file and performs binary classification; labeling that file as either plagiarized or not, depending on how similar that text file is to a provided, source text.
#
# Your first task will be to create some features that can then be used to train a classification model. This task will be broken down into a few discrete steps:
#
# * Clean and pre-process the data.
# * Define features for comparing the similarity of an answer text and a source text, and extract similarity features.
# * Select "good" features, by analyzing the correlations between different features.
# * Create train/test `.csv` files that hold the relevant features and class labels for train/test data points.
#
# In the _next_ notebook, Notebook 3, you'll use the features and `.csv` files you create in _this_ notebook to train a binary classification model in a SageMaker notebook instance.
#
# You'll be defining a few different similarity features, as outlined in [this paper](https://s3.amazonaws.com/video.udacity-data.com/topher/2019/January/5c412841_developing-a-corpus-of-plagiarised-short-answers/developing-a-corpus-of-plagiarised-short-answers.pdf), which should help you build a robust plagiarism detector!
#
# To complete this notebook, you'll have to complete all given exercises and answer all the questions in this notebook.
# > All your tasks will be clearly labeled **EXERCISE** and questions as **QUESTION**.
#
# It will be up to you to decide on the features to include in your final training and test data.
#
# ---
# ## Read in the Data
#
# The cell below will download the necessary, project data and extract the files into the folder `data/`.
#
# This data is a slightly modified version of a dataset created by <NAME> (Information Studies) and <NAME> (Computer Science), at the University of Sheffield. You can read all about the data collection and corpus, at [their university webpage](https://ir.shef.ac.uk/cloughie/resources/plagiarism_corpus.html).
#
# > **Citation for data**: <NAME>. and <NAME>. Developing A Corpus of Plagiarised Short Answers, Language Resources and Evaluation: Special Issue on Plagiarism and Authorship Analysis, In Press. [Download]
# +
# NOTE:
# you only need to run this cell if you have not yet downloaded the data
# otherwise you may skip this cell or comment it out
# !wget https://s3.amazonaws.com/video.udacity-data.com/topher/2019/January/5c4147f9_data/data.zip
# !unzip data
# -
# import libraries
import pandas as pd
import numpy as np
import os
# This plagiarism dataset is made of multiple text files; each of these files has characteristics that are is summarized in a `.csv` file named `file_information.csv`, which we can read in using `pandas`.
# +
csv_file = 'data/file_information.csv'
plagiarism_df = pd.read_csv(csv_file)
# print out the first few rows of data info
plagiarism_df.head()
# -
plagiarism_df.dtypes
# ## Types of Plagiarism
#
# Each text file is associated with one **Task** (task A-E) and one **Category** of plagiarism, which you can see in the above DataFrame.
#
# ### Tasks, A-E
#
# Each text file contains an answer to one short question; these questions are labeled as tasks A-E. For example, Task A asks the question: "What is inheritance in object oriented programming?"
#
# ### Categories of plagiarism
#
# Each text file has an associated plagiarism label/category:
#
# **1. Plagiarized categories: `cut`, `light`, and `heavy`.**
# * These categories represent different levels of plagiarized answer texts. `cut` answers copy directly from a source text, `light` answers are based on the source text but include some light rephrasing, and `heavy` answers are based on the source text, but *heavily* rephrased (and will likely be the most challenging kind of plagiarism to detect).
#
# **2. Non-plagiarized category: `non`.**
# * `non` indicates that an answer is not plagiarized; the Wikipedia source text is not used to create this answer.
#
# **3. Special, source text category: `orig`.**
# * This is a specific category for the original, Wikipedia source text. We will use these files only for comparison purposes.
# ---
# ## Pre-Process the Data
#
# In the next few cells, you'll be tasked with creating a new DataFrame of desired information about all of the files in the `data/` directory. This will prepare the data for feature extraction and for training a binary, plagiarism classifier.
# ### EXERCISE: Convert categorical to numerical data
#
# You'll notice that the `Category` column in the data, contains string or categorical values, and to prepare these for feature extraction, we'll want to convert these into numerical values. Additionally, our goal is to create a binary classifier and so we'll need a binary class label that indicates whether an answer text is plagiarized (1) or not (0). Complete the below function `numerical_dataframe` that reads in a `file_information.csv` file by name, and returns a *new* DataFrame with a numerical `Category` column and a new `Class` column that labels each answer as plagiarized or not.
#
# Your function should return a new DataFrame with the following properties:
#
# * 4 columns: `File`, `Task`, `Category`, `Class`. The `File` and `Task` columns can remain unchanged from the original `.csv` file.
# * Convert all `Category` labels to numerical labels according to the following rules (a higher value indicates a higher degree of plagiarism):
# * 0 = `non`
# * 1 = `heavy`
# * 2 = `light`
# * 3 = `cut`
# * -1 = `orig`, this is a special value that indicates an original file.
# * For the new `Class` column
# * Any answer text that is not plagiarized (`non`) should have the class label `0`.
# * Any plagiarized answer texts should have the class label `1`.
# * And any `orig` texts will have a special label `-1`.
#
# ### Expected output
#
# After running your function, you should get a DataFrame with rows that looks like the following:
# ```
#
# File Task Category Class
# 0 g0pA_taska.txt a 0 0
# 1 g0pA_taskb.txt b 3 1
# 2 g0pA_taskc.txt c 2 1
# 3 g0pA_taskd.txt d 1 1
# 4 g0pA_taske.txt e 0 0
# ...
# ...
# 99 orig_taske.txt e -1 -1
#
# ```
# +
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
mapping = {
'non' : 0,
'heavy' : 1,
'light' : 2,
'cut' : 3,
'orig' : -1,
}
classMapping = {
'non' : 0,
'heavy' : 1,
'light' : 1,
'cut' : 1,
'orig' : -1,
}
# Read in a csv file and return a transformed dataframe
def numerical_dataframe(csv_file='data/file_information.csv'):
'''Reads in a csv file which is assumed to have `File`, `Category` and `Task` columns.
This function does two things:
1) converts `Category` column values to numerical values
2) Adds a new, numerical `Class` label column.
The `Class` column will label plagiarized answers as 1 and non-plagiarized as 0.
Source texts have a special label, -1.
:param csv_file: The directory for the file_information.csv file
:return: A dataframe with numerical categories and a new `Class` label column'''
# your code here
df = pd.read_csv(csv_file)
df['Class'] = df['Category'].apply(lambda x: classMapping[x])
df['Category']= df['Category'].apply(lambda x: mapping[x])
return df
# -
# ### Test cells
#
# Below are a couple of test cells. The first is an informal test where you can check that your code is working as expected by calling your function and printing out the returned result.
#
# The **second** cell below is a more rigorous test cell. The goal of a cell like this is to ensure that your code is working as expected, and to form any variables that might be used in _later_ tests/code, in this case, the data frame, `transformed_df`.
#
# > The cells in this notebook should be run in chronological order (the order they appear in the notebook). This is especially important for test cells.
#
# Often, later cells rely on the functions, imports, or variables defined in earlier cells. For example, some tests rely on previous tests to work.
#
# These tests do not test all cases, but they are a great way to check that you are on the right track!
# +
# informal testing, print out the results of a called function
# create new `transformed_df`
transformed_df = numerical_dataframe(csv_file ='data/file_information.csv')
# check work
# check that all categories of plagiarism have a class label = 1
transformed_df.head(10)
# +
# test cell that creates `transformed_df`, if tests are passed
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
# importing tests
import problem_unittests as tests
# test numerical_dataframe function
tests.test_numerical_df(numerical_dataframe)
# if above test is passed, create NEW `transformed_df`
transformed_df = numerical_dataframe(csv_file ='data/file_information.csv')
# check work
print('\nExample data: ')
transformed_df.head()
# -
# ## Text Processing & Splitting Data
#
# Recall that the goal of this project is to build a plagiarism classifier. At it's heart, this task is a comparison text; one that looks at a given answer and a source text, compares them and predicts whether an answer has plagiarized from the source. To effectively do this comparison, and train a classifier we'll need to do a few more things: pre-process all of our text data and prepare the text files (in this case, the 95 answer files and 5 original source files) to be easily compared, and split our data into a `train` and `test` set that can be used to train a classifier and evaluate it, respectively.
#
# To this end, you've been provided code that adds additional information to your `transformed_df` from above. The next two cells need not be changed; they add two additional columns to the `transformed_df`:
#
# 1. A `Text` column; this holds all the lowercase text for a `File`, with extraneous punctuation removed.
# 2. A `Datatype` column; this is a string value `train`, `test`, or `orig` that labels a data point as part of our train or test set
#
# The details of how these additional columns are created can be found in the `helpers.py` file in the project directory. You're encouraged to read through that file to see exactly how text is processed and how data is split.
#
# Run the cells below to get a `complete_df` that has all the information you need to proceed with plagiarism detection and feature engineering.
# +
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
import helpers
# create a text column
text_df = helpers.create_text_column(transformed_df)
text_df.head()
# +
# after running the cell above
# check out the processed text for a single file, by row index
row_idx = 0 # feel free to change this index
sample_text = text_df.iloc[0]['Text']
print('Sample processed text:\n\n', sample_text)
# -
# ## Split data into training and test sets
#
# The next cell will add a `Datatype` column to a given DataFrame to indicate if the record is:
# * `train` - Training data, for model training.
# * `test` - Testing data, for model evaluation.
# * `orig` - The task's original answer from wikipedia.
#
# ### Stratified sampling
#
# The given code uses a helper function which you can view in the `helpers.py` file in the main project directory. This implements [stratified random sampling](https://en.wikipedia.org/wiki/Stratified_sampling) to randomly split data by task & plagiarism amount. Stratified sampling ensures that we get training and test data that is fairly evenly distributed across task & plagiarism combinations. Approximately 26% of the data is held out for testing and 74% of the data is used for training.
#
# The function **train_test_dataframe** takes in a DataFrame that it assumes has `Task` and `Category` columns, and, returns a modified frame that indicates which `Datatype` (train, test, or orig) a file falls into. This sampling will change slightly based on a passed in *random_seed*. Due to a small sample size, this stratified random sampling will provide more stable results for a binary plagiarism classifier. Stability here is smaller *variance* in the accuracy of classifier, given a random seed.
# +
random_seed = 1 # can change; set for reproducibility
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
import helpers
# create new df with Datatype (train, test, orig) column
# pass in `text_df` from above to create a complete dataframe, with all the information you need
complete_df = helpers.train_test_dataframe(text_df, random_seed=random_seed)
# check results
complete_df.head(10)
# -
# # Determining Plagiarism
#
# Now that you've prepared this data and created a `complete_df` of information, including the text and class associated with each file, you can move on to the task of extracting similarity features that will be useful for plagiarism classification.
#
# > Note: The following code exercises, assume that the `complete_df` as it exists now, will **not** have its existing columns modified.
#
# The `complete_df` should always include the columns: `['File', 'Task', 'Category', 'Class', 'Text', 'Datatype']`. You can add additional columns, and you can create any new DataFrames you need by copying the parts of the `complete_df` as long as you do not modify the existing values, directly.
#
# ---
#
# # Similarity Features
#
# One of the ways we might go about detecting plagiarism, is by computing **similarity features** that measure how similar a given answer text is as compared to the original wikipedia source text (for a specific task, a-e). The similarity features you will use are informed by [this paper on plagiarism detection](https://s3.amazonaws.com/video.udacity-data.com/topher/2019/January/5c412841_developing-a-corpus-of-plagiarised-short-answers/developing-a-corpus-of-plagiarised-short-answers.pdf).
# > In this paper, researchers created features called **containment** and **longest common subsequence**.
#
# Using these features as input, you will train a model to distinguish between plagiarized and not-plagiarized text files.
#
# ## Feature Engineering
#
# Let's talk a bit more about the features we want to include in a plagiarism detection model and how to calculate such features. In the following explanations, I'll refer to a submitted text file as a **Student Answer Text (A)** and the original, wikipedia source file (that we want to compare that answer to) as the **Wikipedia Source Text (S)**.
#
# ### Containment
#
# Your first task will be to create **containment features**. To understand containment, let's first revisit a definition of [n-grams](https://en.wikipedia.org/wiki/N-gram). An *n-gram* is a sequential word grouping. For example, in a line like "bayes rule gives us a way to combine prior knowledge with new information," a 1-gram is just one word, like "bayes." A 2-gram might be "bayes rule" and a 3-gram might be "combine prior knowledge."
#
# > Containment is defined as the **intersection** of the n-gram word count of the Wikipedia Source Text (S) with the n-gram word count of the Student Answer Text (S) *divided* by the n-gram word count of the Student Answer Text.
#
# $$ \frac{\sum{count(\text{ngram}_{A}) \cap count(\text{ngram}_{S})}}{\sum{count(\text{ngram}_{A})}} $$
#
# If the two texts have no n-grams in common, the containment will be 0, but if _all_ their n-grams intersect then the containment will be 1. Intuitively, you can see how having longer n-gram's in common, might be an indication of cut-and-paste plagiarism. In this project, it will be up to you to decide on the appropriate `n` or several `n`'s to use in your final model.
#
# ### EXERCISE: Create containment features
#
# Given the `complete_df` that you've created, you should have all the information you need to compare any Student Answer Text (A) with its appropriate Wikipedia Source Text (S). An answer for task A should be compared to the source text for task A, just as answers to tasks B, C, D, and E should be compared to the corresponding original source text.
#
# In this exercise, you'll complete the function, `calculate_containment` which calculates containment based upon the following parameters:
# * A given DataFrame, `df` (which is assumed to be the `complete_df` from above)
# * An `answer_filename`, such as 'g0pB_taskd.txt'
# * An n-gram length, `n`
#
# ### Containment calculation
#
# The general steps to complete this function are as follows:
# 1. From *all* of the text files in a given `df`, create an array of n-gram counts; it is suggested that you use a [CountVectorizer](https://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.CountVectorizer.html) for this purpose.
# 2. Get the processed answer and source texts for the given `answer_filename`.
# 3. Calculate the containment between an answer and source text according to the following equation.
#
# >$$ \frac{\sum{count(\text{ngram}_{A}) \cap count(\text{ngram}_{S})}}{\sum{count(\text{ngram}_{A})}} $$
#
# 4. Return that containment value.
#
# You are encouraged to write any helper functions that you need to complete the function below.
# +
from sklearn.feature_extraction.text import CountVectorizer
import helpers
# Calculate the ngram containment for one answer file/source file pair in a df
def calculate_containment(df, n, answer_filename):
'''Calculates the containment between a given answer text and its associated source text.
This function creates a count of ngrams (of a size, n) for each text file in our data.
Then calculates the containment by finding the ngram count for a given answer text,
and its associated source text, and calculating the normalized intersection of those counts.
:param df: A dataframe with columns,
'File', 'Task', 'Category', 'Class', 'Text', and 'Datatype'
:param n: An integer that defines the ngram size
:param answer_filename: A filename for an answer text in the df, ex. 'g0pB_taskd.txt'
:return: A single containment value that represents the similarity
between an answer text and its source text.
'''
task = answer_filename[len('g0pA_'):]
origFileName = 'orig_{}'.format(task)
answerText = helpers.read_and_process_file(answer_filename)
origText = df.loc[df['File'] == origFileName]['Text'].values[0]
cv = CountVectorizer(analyzer='word', ngram_range=(n,n))
ngrams = cv.fit_transform([answerText, origText])
ngram_array = ngrams.toarray()
intersection = 0
ngramACount = 0.0
for i in range(0, len(ngram_array[0])):
if ngram_array[0][i] != 0:
intersection = intersection + min(ngram_array[0][i], ngram_array[1][i])
ngramACount = ngramACount + ngram_array[0][i]
result = intersection / ngramACount
#print('{} {}: {} {} {}'.format(origFileName, n, intersection, ngramACount, result))
return result
# -
# ### Test cells
#
# After you've implemented the containment function, you can test out its behavior.
#
# The cell below iterates through the first few files, and calculates the original category _and_ containment values for a specified n and file.
#
# >If you've implemented this correctly, you should see that the non-plagiarized have low or close to 0 containment values and that plagiarized examples have higher containment values, closer to 1.
#
# Note what happens when you change the value of n. I recommend applying your code to multiple files and comparing the resultant containment values. You should see that the highest containment values correspond to files with the highest category (`cut`) of plagiarism level.
complete_df[complete_df['Class'] == -1].head()
complete_df.head()
# +
# select a value for n
n = 3
# indices for first few files
test_indices = range(5)
# iterate through files and calculate containment
category_vals = []
containment_vals = []
for i in test_indices:
# get level of plagiarism for a given file index
category_vals.append(complete_df.loc[i, 'Category'])
# calculate containment for given file and n
filename = complete_df.loc[i, 'File']
c = calculate_containment(complete_df, n, filename)
containment_vals.append(c)
# print out result, does it make sense?
print('Original category values: \n', category_vals)
print()
print(str(n)+'-gram containment values: \n', containment_vals)
# -
# run this test cell
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
# test containment calculation
# params: complete_df from before, and containment function
tests.test_containment(complete_df, calculate_containment)
complete_df.Datatype.unique()
# ### QUESTION 1: Why can we calculate containment features across *all* data (training & test), prior to splitting the DataFrame for modeling? That is, what about the containment calculation means that the test and training data do not influence each other?
# **Answer:** Each answer is compared with the corresponding 'orig' rows. 'orig' rows are not part of train and test sets. Hence the order in which we do the containment feature calucation does not matter.
#
# ---
# ## Longest Common Subsequence
#
# Containment a good way to find overlap in word usage between two documents; it may help identify cases of cut-and-paste as well as paraphrased levels of plagiarism. Since plagiarism is a fairly complex task with varying levels, it's often useful to include other measures of similarity. The paper also discusses a feature called **longest common subsequence**.
#
# > The longest common subsequence is the longest string of words (or letters) that are *the same* between the Wikipedia Source Text (S) and the Student Answer Text (A). This value is also normalized by dividing by the total number of words (or letters) in the Student Answer Text.
#
# In this exercise, we'll ask you to calculate the longest common subsequence of words between two texts.
#
# ### EXERCISE: Calculate the longest common subsequence
#
# Complete the function `lcs_norm_word`; this should calculate the *longest common subsequence* of words between a Student Answer Text and corresponding Wikipedia Source Text.
#
# It may be helpful to think of this in a concrete example. A Longest Common Subsequence (LCS) problem may look as follows:
# * Given two texts: text A (answer text) of length n, and string S (original source text) of length m. Our goal is to produce their longest common subsequence of words: the longest sequence of words that appear left-to-right in both texts (though the words don't have to be in continuous order).
# * Consider:
# * A = "i think pagerank is a link analysis algorithm used by google that uses a system of weights attached to each element of a hyperlinked set of documents"
# * S = "pagerank is a link analysis algorithm used by the google internet search engine that assigns a numerical weighting to each element of a hyperlinked set of documents"
#
# * In this case, we can see that the start of each sentence of fairly similar, having overlap in the sequence of words, "pagerank is a link analysis algorithm used by" before diverging slightly. Then we **continue moving left -to-right along both texts** until we see the next common sequence; in this case it is only one word, "google". Next we find "that" and "a" and finally the same ending "to each element of a hyperlinked set of documents".
# * Below, is a clear visual of how these sequences were found, sequentially, in each text.
#
# <img src='notebook_ims/common_subseq_words.png' width=40% />
#
# * Now, those words appear in left-to-right order in each document, sequentially, and even though there are some words in between, we count this as the longest common subsequence between the two texts.
# * If I count up each word that I found in common I get the value 20. **So, LCS has length 20**.
# * Next, to normalize this value, divide by the total length of the student answer; in this example that length is only 27. **So, the function `lcs_norm_word` should return the value `20/27` or about `0.7408`.**
#
# In this way, LCS is a great indicator of cut-and-paste plagiarism or if someone has referenced the same source text multiple times in an answer.
# ### LCS, dynamic programming
#
# If you read through the scenario above, you can see that this algorithm depends on looking at two texts and comparing them word by word. You can solve this problem in multiple ways. First, it may be useful to `.split()` each text into lists of comma separated words to compare. Then, you can iterate through each word in the texts and compare them, adding to your value for LCS as you go.
#
# The method I recommend for implementing an efficient LCS algorithm is: using a matrix and dynamic programming. **Dynamic programming** is all about breaking a larger problem into a smaller set of subproblems, and building up a complete result without having to repeat any subproblems.
#
# This approach assumes that you can split up a large LCS task into a combination of smaller LCS tasks. Let's look at a simple example that compares letters:
#
# * A = "ABCD"
# * S = "BD"
#
# We can see right away that the longest subsequence of _letters_ here is 2 (B and D are in sequence in both strings). And we can calculate this by looking at relationships between each letter in the two strings, A and S.
#
# Here, I have a matrix with the letters of A on top and the letters of S on the left side:
#
# <img src='notebook_ims/matrix_1.png' width=40% />
#
# This starts out as a matrix that has as many columns and rows as letters in the strings S and O **+1** additional row and column, filled with zeros on the top and left sides. So, in this case, instead of a 2x4 matrix it is a 3x5.
#
# Now, we can fill this matrix up by breaking it into smaller LCS problems. For example, let's first look at the shortest substrings: the starting letter of A and S. We'll first ask, what is the Longest Common Subsequence between these two letters "A" and "B"?
#
# **Here, the answer is zero and we fill in the corresponding grid cell with that value.**
#
# <img src='notebook_ims/matrix_2.png' width=30% />
#
# Then, we ask the next question, what is the LCS between "AB" and "B"?
#
# **Here, we have a match, and can fill in the appropriate value 1**.
#
# <img src='notebook_ims/matrix_3_match.png' width=25% />
#
# If we continue, we get to a final matrix that looks as follows, with a **2** in the bottom right corner.
#
# <img src='notebook_ims/matrix_6_complete.png' width=25% />
#
# The final LCS will be that value **2** *normalized* by the number of n-grams in A. So, our normalized value is 2/4 = **0.5**.
#
# ### The matrix rules
#
# One thing to notice here is that, you can efficiently fill up this matrix one cell at a time. Each grid cell only depends on the values in the grid cells that are directly on top and to the left of it, or on the diagonal/top-left. The rules are as follows:
# * Start with a matrix that has one extra row and column of zeros.
# * As you traverse your string:
# * If there is a match, fill that grid cell with the value to the top-left of that cell *plus* one. So, in our case, when we found a matching B-B, we added +1 to the value in the top-left of the matching cell, 0.
# * If there is not a match, take the *maximum* value from either directly to the left or the top cell, and carry that value over to the non-match cell.
#
# <img src='notebook_ims/matrix_rules.png' width=50% />
#
# After completely filling the matrix, **the bottom-right cell will hold the non-normalized LCS value**.
#
# This matrix treatment can be applied to a set of words instead of letters. Your function should apply this to the words in two texts and return the normalized LCS value.
import pprint as pp
# Compute the normalized LCS given an answer text and a source text
def lcs_norm_word(answer_text, source_text):
'''Computes the longest common subsequence of words in two texts; returns a normalized value.
:param answer_text: The pre-processed text for an answer text
:param source_text: The pre-processed text for an answer's associated source text
:return: A normalized LCS value'''
a = answer_text.split()
s = source_text.split()
dp = []
for i in range(len(a)):
dp.append(np.zeros(len(s)).tolist())
for row in range(0, len(dp)):
for col in range(0, len(dp[0])):
val = 0
c1 = a[row]
c2 = s[col]
if row == 0 and col == 0:
val = 1 if c1 == c2 else 0
elif row == 0:
val = 1 if c1 == c2 else dp[row][col-1]
elif col == 0:
val = 1 if c1 == c2 else dp[row-1][col]
else:
val = max(dp[row-1][col], dp[row][col-1])
if c1 == c2:
val = max(val, dp[row-1][col-1] + 1)
dp[row][col] = val
#for l in dp:
#print(l)
rows = len(dp)
cols = len(dp[0])
result = dp[rows-1][cols-1] / len(a)
#print(answer_text)
#print(source_text)
#print('{} {} {} {} '.format(rows, cols, dp[rows-1][cols-1], result))
return result
# ### Test cells
#
# Let's start by testing out your code on the example given in the initial description.
#
# In the below cell, we have specified strings A (answer text) and S (original source text). We know that these texts have 20 words in common and the submitted answer is 27 words long, so the normalized, longest common subsequence should be 20/27.
#
# +
# Run the test scenario from above
# does your function return the expected value?
A = "i think pagerank is a link analysis algorithm used by google that uses a system of weights attached to each element of a hyperlinked set of documents"
S = "pagerank is a link analysis algorithm used by the google internet search engine that assigns a numerical weighting to each element of a hyperlinked set of documents"
#A = "inheritance is a basic concept of object oriented programming where the basic idea is to create new classes that add extra detail to existing classes this is done by allowing the new classes to reuse the methods and variables of the existing classes and new methods and classes are added to specialise the new class inheritance models the is kind of relationship between entities or objects for example postgraduates and undergraduates are both kinds of student this kind of relationship can be visualised as a tree structure where student would be the more general root node and both postgraduate and undergraduate would be more specialised extensions of the student node or the child nodes in this relationship student would be known as the superclass or parent class whereas postgraduate would be known as the subclass or child class because the postgraduate class extends the student class inheritance can occur on several layers where if visualised would display a larger tree structure for example we could further extend the postgraduate node by adding two extra extended classes to it called msc student and phd student as both these types of student are kinds of postgraduate student this would mean that both the msc student and phd student classes would inherit methods and variables from both the postgraduate and student classes"
#S = "in object oriented programming inheritance is a way to form new classes instances of which are called objects using classes that have already been defined the inheritance concept was invented in 1967 for simula the new classes known as derived classes take over or inherit attributes and behavior of the pre existing classes which are referred to as base classes or ancestor classes it is intended to help reuse existing code with little or no modification inheritance provides the support for representation by categorization in computer languages categorization is a powerful mechanism number of information processing crucial to human learning by means of generalization what is known about specific entities is applied to a wider group given a belongs relation can be established and cognitive economy less information needs to be stored about each specific entity only its particularities inheritance is also sometimes called generalization because the is a relationships represent a hierarchy between classes of objects for instance a fruit is a generalization of apple orange mango and many others one can consider fruit to be an abstraction of apple orange etc conversely since apples are fruit i e an apple is a fruit apples may naturally inherit all the properties common to all fruit such as being a fleshy container for the seed of a plant an advantage of inheritance is that modules with sufficiently similar interfaces can share a lot of code reducing the complexity of the program inheritance therefore has another view a dual called polymorphism which describes many pieces of code being controlled by shared control code inheritance is typically accomplished either by overriding replacing one or more methods exposed by ancestor or by adding new methods to those exposed by an ancestor complex inheritance or inheritance used within a design that is not sufficiently mature may lead to the yo yo problem "
#A = "XMJYAUZ"
#S = "MZJAWXU"
# calculate LCS
lcs = lcs_norm_word(A, S)
print('LCS = ', lcs)
# expected value test
assert lcs==20/27., "Incorrect LCS value, expected about 0.7408, got "+str(lcs)
print('Test passed!')
# -
# This next cell runs a more rigorous test.
# run test cell
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
# test lcs implementation
# params: complete_df from before, and lcs_norm_word function
tests.test_lcs(complete_df, lcs_norm_word)
# Finally, take a look at a few resultant values for `lcs_norm_word`. Just like before, you should see that higher values correspond to higher levels of plagiarism.
# +
# test on your own
test_indices = range(5) # look at first few files
category_vals = []
lcs_norm_vals = []
# iterate through first few docs and calculate LCS
for i in test_indices:
category_vals.append(complete_df.loc[i, 'Category'])
# get texts to compare
answer_text = complete_df.loc[i, 'Text']
task = complete_df.loc[i, 'Task']
# we know that source texts have Class = -1
orig_rows = complete_df[(complete_df['Class'] == -1)]
orig_row = orig_rows[(orig_rows['Task'] == task)]
source_text = orig_row['Text'].values[0]
# calculate lcs
lcs_val = lcs_norm_word(answer_text, source_text)
lcs_norm_vals.append(lcs_val)
# print out result, does it make sense?
print('Original category values: \n', category_vals)
print()
print('Normalized LCS values: \n', lcs_norm_vals)
# -
# ---
# # Create All Features
#
# Now that you've completed the feature calculation functions, it's time to actually create multiple features and decide on which ones to use in your final model! In the below cells, you're provided two helper functions to help you create multiple features and store those in a DataFrame, `features_df`.
#
# ### Creating multiple containment features
#
# Your completed `calculate_containment` function will be called in the next cell, which defines the helper function `create_containment_features`.
#
# > This function returns a list of containment features, calculated for a given `n` and for *all* files in a df (assumed to the the `complete_df`).
#
# For our original files, the containment value is set to a special value, -1.
#
# This function gives you the ability to easily create several containment features, of different n-gram lengths, for each of our text files.
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
# Function returns a list of containment features, calculated for a given n
# Should return a list of length 100 for all files in a complete_df
def create_containment_features(df, n, column_name=None):
containment_values = []
if(column_name==None):
column_name = 'c_'+str(n) # c_1, c_2, .. c_n
# iterates through dataframe rows
for i in df.index:
file = df.loc[i, 'File']
# Computes features using calculate_containment function
if df.loc[i,'Category'] > -1:
c = calculate_containment(df, n, file)
containment_values.append(c)
# Sets value to -1 for original tasks
else:
containment_values.append(-1)
print(str(n)+'-gram containment features created!')
return containment_values
# ### Creating LCS features
#
# Below, your complete `lcs_norm_word` function is used to create a list of LCS features for all the answer files in a given DataFrame (again, this assumes you are passing in the `complete_df`. It assigns a special value for our original, source files, -1.
#
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
# Function creates lcs feature and add it to the dataframe
def create_lcs_features(df, column_name='lcs_word'):
lcs_values = []
# iterate through files in dataframe
for i in df.index:
# Computes LCS_norm words feature using function above for answer tasks
if df.loc[i,'Category'] > -1:
# get texts to compare
answer_text = df.loc[i, 'Text']
task = df.loc[i, 'Task']
# we know that source texts have Class = -1
orig_rows = df[(df['Class'] == -1)]
orig_row = orig_rows[(orig_rows['Task'] == task)]
source_text = orig_row['Text'].values[0]
# calculate lcs
lcs = lcs_norm_word(answer_text, source_text)
lcs_values.append(lcs)
# Sets to -1 for original tasks
else:
lcs_values.append(-1)
print('LCS features created!')
return lcs_values
# ## EXERCISE: Create a features DataFrame by selecting an `ngram_range`
#
# The paper suggests calculating the following features: containment *1-gram to 5-gram* and *longest common subsequence*.
# > In this exercise, you can choose to create even more features, for example from *1-gram to 7-gram* containment features and *longest common subsequence*.
#
# You'll want to create at least 6 features to choose from as you think about which to give to your final, classification model. Defining and comparing at least 6 different features allows you to discard any features that seem redundant, and choose to use the best features for your final model!
#
# In the below cell **define an n-gram range**; these will be the n's you use to create n-gram containment features. The rest of the feature creation code is provided.
# +
# Define an ngram range
ngram_range = range(1,15)
# The following code may take a minute to run, depending on your ngram_range
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
features_list = []
# Create features in a features_df
all_features = np.zeros((len(ngram_range)+1, len(complete_df)))
# Calculate features for containment for ngrams in range
i=0
for n in ngram_range:
column_name = 'c_'+str(n)
features_list.append(column_name)
# create containment features
all_features[i]=np.squeeze(create_containment_features(complete_df, n))
i+=1
# Calculate features for LCS_Norm Words
features_list.append('lcs_word')
all_features[i]= np.squeeze(create_lcs_features(complete_df))
# create a features dataframe
features_df = pd.DataFrame(np.transpose(all_features), columns=features_list)
# Print all features/columns
print()
print('Features: ', features_list)
print()
# -
# print some results
features_df.head(10)
# ## Correlated Features
#
# You should use feature correlation across the *entire* dataset to determine which features are ***too*** **highly-correlated** with each other to include both features in a single model. For this analysis, you can use the *entire* dataset due to the small sample size we have.
#
# All of our features try to measure the similarity between two texts. Since our features are designed to measure similarity, it is expected that these features will be highly-correlated. Many classification models, for example a Naive Bayes classifier, rely on the assumption that features are *not* highly correlated; highly-correlated features may over-inflate the importance of a single feature.
#
# So, you'll want to choose your features based on which pairings have the lowest correlation. These correlation values range between 0 and 1; from low to high correlation, and are displayed in a [correlation matrix](https://www.displayr.com/what-is-a-correlation-matrix/), below.
# +
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
# Create correlation matrix for just Features to determine different models to test
corr_matrix = features_df.corr().abs().round(2)
# display shows all of a dataframe
display(corr_matrix)
# -
# ## EXERCISE: Create selected train/test data
#
# Complete the `train_test_data` function below. This function should take in the following parameters:
# * `complete_df`: A DataFrame that contains all of our processed text data, file info, datatypes, and class labels
# * `features_df`: A DataFrame of all calculated features, such as containment for ngrams, n= 1-5, and lcs values for each text file listed in the `complete_df` (this was created in the above cells)
# * `selected_features`: A list of feature column names, ex. `['c_1', 'lcs_word']`, which will be used to select the final features in creating train/test sets of data.
#
# It should return two tuples:
# * `(train_x, train_y)`, selected training features and their corresponding class labels (0/1)
# * `(test_x, test_y)`, selected training features and their corresponding class labels (0/1)
#
# ** Note: x and y should be arrays of feature values and numerical class labels, respectively; not DataFrames.**
#
# Looking at the above correlation matrix, you should decide on a **cutoff** correlation value, less than 1.0, to determine which sets of features are *too* highly-correlated to be included in the final training and test data. If you cannot find features that are less correlated than some cutoff value, it is suggested that you increase the number of features (longer n-grams) to choose from or use *only one or two* features in your final model to avoid introducing highly-correlated features.
#
# Recall that the `complete_df` has a `Datatype` column that indicates whether data should be `train` or `test` data; this should help you split the data appropriately.
# Takes in dataframes and a list of selected features (column names)
# and returns (train_x, train_y), (test_x, test_y)
def train_test_data(complete_df, features_df, selected_features):
'''Gets selected training and test features from given dataframes, and
returns tuples for training and test features and their corresponding class labels.
:param complete_df: A dataframe with all of our processed text data, datatypes, and labels
:param features_df: A dataframe of all computed, similarity features
:param selected_features: An array of selected features that correspond to certain columns in `features_df`
:return: training and test features and labels: (train_x, train_y), (test_x, test_y)'''
print(selected_features)
combined = pd.concat([complete_df, features_df], axis=1, sort=False)
print(combined.columns)
# get the training features
train_x = combined.loc[combined['Datatype'] == 'train'][selected_features]
# And training class labels (0 or 1)
train_y = combined.loc[combined['Datatype'] == 'train']['Class']
# get the test features and labels
test_x_all_fields = combined.loc[combined['Datatype'] == 'test']
test_x = combined.loc[combined['Datatype'] == 'test'][selected_features]
test_y = combined.loc[combined['Datatype'] == 'test']['Class']
print(''.format(len(train_x), len(train_y), len(test_x), len(test_y)))
return (train_x.to_numpy(), train_y.to_numpy()), (test_x.to_numpy(), test_y.to_numpy()), test_x_all_fields
# ### Test cells
#
# Below, test out your implementation and create the final train/test data.
# +
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
test_selection = list(features_df)[:2] # first couple columns as a test
# test that the correct train/test data is created
(train_x, train_y), (test_x, test_y), test_x_df = train_test_data(complete_df, features_df, test_selection)
# params: generated train/test data
tests.test_data_split(train_x, train_y, test_x, test_y)
# -
# ## EXERCISE: Select "good" features
#
# If you passed the test above, you can create your own train/test data, below.
#
# Define a list of features you'd like to include in your final mode, `selected_features`; this is a list of the features names you want to include.
# +
# Select your list of features, this should be column names from features_df
# ex. ['c_1', 'lcs_word']
selected_features = ['c_1', 'c_4', 'lcs_word']
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
(train_x, train_y), (test_x, test_y), test_x_df = train_test_data(complete_df, features_df, selected_features)
# check that division of samples seems correct
# these should add up to 95 (100 - 5 original files)
print('Training size: ', len(train_x))
print('Test size: ', len(test_x))
print()
print('Training df sample: \n', train_x[:10])
# -
# ### Question 2: How did you decide on which features to include in your final model?
# **Answer:**
#
# 1. lcs_word need to be present since it is a very different feature, eventhough the feature has high correlation with other n-gram features.
#
#
# 2. c_1 has to be there since it captures the fact that documents with similar words are more likely be related to the same topic
#
# 3. Once c_1 is picked, the next feature which is less correlated than threshold .9 is c_4. Hence c_4 is picked.
#
# 4. c_4 is highly correlated to other longer n-grams. Hence those are not picked.
# ---
# ## Creating Final Data Files
#
# Now, you are almost ready to move on to training a model in SageMaker!
#
# You'll want to access your train and test data in SageMaker and upload it to S3. In this project, SageMaker will expect the following format for your train/test data:
# * Training and test data should be saved in one `.csv` file each, ex `train.csv` and `test.csv`
# * These files should have class labels in the first column and features in the rest of the columns
#
# This format follows the practice, outlined in the [SageMaker documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/cdf-training.html), which reads: "Amazon SageMaker requires that a CSV file doesn't have a header record and that the target variable [class label] is in the first column."
#
# ## EXERCISE: Create csv files
#
# Define a function that takes in x (features) and y (labels) and saves them to one `.csv` file at the path `data_dir/filename`.
#
# It may be useful to use pandas to merge your features and labels into one DataFrame and then convert that into a csv file. You can make sure to get rid of any incomplete rows, in a DataFrame, by using `dropna`.
def make_csv(x, y, filename, data_dir):
'''Merges features and labels and converts them into one csv file with labels in the first column.
:param x: Data features
:param y: Data labels
:param file_name: Name of csv file, ex. 'train.csv'
:param data_dir: The directory where files will be saved
'''
# make data dir, if it does not exist
if not os.path.exists(data_dir):
os.makedirs(data_dir)
combined = pd.concat([pd.DataFrame(y), pd.DataFrame(x)], axis=1, sort=False)
outFilename = os.path.join(data_dir, filename)
lenBeforeDropNull = combined.shape[0]
combined = combined.dropna()
print('Deleted {} rows'.format(lenBeforeDropNull - combined.shape[0]))
combined.to_csv(outFilename, index=False, header=False)
# nothing is returned, but a print statement indicates that the function has run
print('Path created: '+str(data_dir)+'/'+str(filename))
# ### Test cells
#
# Test that your code produces the correct format for a `.csv` file, given some text features and labels.
# +
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
fake_x = [ [0.39814815, 0.0001, 0.19178082],
[0.86936937, 0.44954128, 0.84649123],
[0.44086022, 0., 0.22395833] ]
fake_y = [0, 1, 1]
make_csv(fake_x, fake_y, filename='to_delete.csv', data_dir='test_csv')
# read in and test dimensions
fake_df = pd.read_csv('test_csv/to_delete.csv', header=None)
# check shape
assert fake_df.shape==(3, 4), \
'The file should have as many rows as data_points and as many columns as features+1 (for indices).'
# check that first column = labels
assert np.all(fake_df.iloc[:,0].values==fake_y), 'First column is not equal to the labels, fake_y.'
print('Tests passed!')
# -
# delete the test csv file, generated above
# ! rm -rf test_csv
# If you've passed the tests above, run the following cell to create `train.csv` and `test.csv` files in a directory that you specify! This will save the data in a local directory. Remember the name of this directory because you will reference it again when uploading this data to S3.
# +
# can change directory, if you want
data_dir = 'plagiarism_data'
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
make_csv(train_x, train_y, filename='train.csv', data_dir=data_dir)
make_csv(test_x, test_y, filename='test.csv', data_dir=data_dir)
# -
import os
test_x_df.to_csv(os.path.join(data_dir, "test_df.csv"), index=False, header=True)
# ## Up Next
#
# Now that you've done some feature engineering and created some training and test data, you are ready to train and deploy a plagiarism classification model. The next notebook will utilize SageMaker resources to train and test a model that you design.
|
Project_Plagiarism_Detection/2_Plagiarism_Feature_Engineering.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
from IPython import display
from matplotlib import pyplot as plt
# %matplotlib inline
import math, itertools
import tensorflow as tf
from scipy import special
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
# -
IMAGE_PIXELS = 28*28
NOISE_SIZE = 100
# +
def noise(n_rows, n_cols):
return np.random.normal(size=(n_rows, n_cols))
def xavier_init(size):
in_dim = size[0] if len(size) == 1 else size[1]
stddev = 1. / math.sqrt(float(in_dim))
return tf.random_uniform(shape=size, minval=-stddev, maxval=stddev)
# -
# ## Load Data
# No rescaling needed. MNIST data is in range [0, 1]
mnist = input_data.read_data_sets("tf_data/")
mnist_data = (mnist.train.images - .5 ) / .5
np.random.shuffle(mnist_data)
# ## Initialize Graph
# +
## Discriminator
# Input
X = tf.placeholder(tf.float32, shape=(None, IMAGE_PIXELS))
# Layer 1 Variables
D_W1 = tf.Variable(xavier_init([784, 1024]))
D_B1 = tf.Variable(xavier_init([1024]))
# Layer 2 Variables
D_W2 = tf.Variable(xavier_init([1024, 512]))
D_B2 = tf.Variable(xavier_init([512]))
# Layer 3 Variables
D_W3 = tf.Variable(xavier_init([512, 256]))
D_B3 = tf.Variable(xavier_init([256]))
# Out Layer Variables
D_W4 = tf.Variable(xavier_init([256, 1]))
D_B4 = tf.Variable(xavier_init([1]))
# Store Variables in list
D_var_list = [D_W1, D_B1, D_W2, D_B2, D_W3, D_B3, D_W4, D_B4]
# +
## Generator
# Input
Z = tf.placeholder(tf.float32, shape=(None, NOISE_SIZE))
# Layer 1 Variables
G_W1 = tf.Variable(xavier_init([100, 256]))
G_B1 = tf.Variable(xavier_init([256]))
# Layer 2 Variables
G_W2 = tf.Variable(xavier_init([256, 512]))
G_B2 = tf.Variable(xavier_init([512]))
# Layer 3 Variables
G_W3 = tf.Variable(xavier_init([512, 1024]))
G_B3 = tf.Variable(xavier_init([1024]))
# Out Layer Variables
G_W4 = tf.Variable(xavier_init([1024, 784]))
G_B4 = tf.Variable(xavier_init([784]))
# Store Variables in list
G_var_list = [G_W1, G_B1, G_W2, G_B2, G_W3, G_B3, G_W4, G_B4]
# +
def discriminator(x):
l1 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(x, D_W1) + D_B1, .2), .3)
l2 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(l1, D_W2) + D_B2, .2), .3)
l3 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(l2, D_W3) + D_B3, .2), .3)
out = tf.matmul(l3, D_W4) + D_B4
return out
def generator(z):
l1 = tf.nn.leaky_relu(tf.matmul(z, G_W1) + G_B1, .2)
l2 = tf.nn.leaky_relu(tf.matmul(l1, G_W2) + G_B2, .2)
l3 = tf.nn.leaky_relu(tf.matmul(l2, G_W3) + G_B3, .2)
out = tf.nn.tanh(tf.matmul(l3, G_W4) + G_B4)
return out
# +
G_sample = generator(Z)
D_real = discriminator(X)
D_fake = discriminator(G_sample)
# Losses
D_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_real, labels=tf.ones_like(D_real)))
D_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_fake, labels=tf.zeros_like(D_fake)))
D_loss = D_loss_real + D_loss_fake
G_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_fake, labels=tf.ones_like(D_fake)))
# Optimizers
D_opt = tf.train.AdamOptimizer(2e-4).minimize(D_loss, var_list=D_var_list)
G_opt = tf.train.AdamOptimizer(2e-4).minimize(G_loss, var_list=G_var_list)
# -
# ## Train
BATCH_SIZE = 100
NUM_EPOCHS = 200
# +
# create figure for plotting
size_figure_grid = int(math.sqrt(16))
fig, ax = plt.subplots(size_figure_grid, size_figure_grid, figsize=(6, 6))
for i, j in itertools.product(range(size_figure_grid), range(size_figure_grid)):
ax[i,j].get_xaxis().set_visible(False)
ax[i,j].get_yaxis().set_visible(False)
# Start interactive session
session = tf.InteractiveSession()
# Init Variables
tf.global_variables_initializer().run()
# Iterate through epochs
for epoch in range(NUM_EPOCHS):
for n_batch in range(mnist_data.shape[0] // BATCH_SIZE):
# Train Discriminator
X_batch = mnist_data[ (n_batch * BATCH_SIZE):(n_batch * BATCH_SIZE)+BATCH_SIZE]
feed_dict = {X: X_batch, Z: noise(BATCH_SIZE, NOISE_SIZE)}
_, D_loss_i, D_real_i, D_fake_i = session.run([D_opt, D_loss, D_real, D_fake], feed_dict=feed_dict)
# Train Generator
feed_dict = {Z: noise(BATCH_SIZE, NOISE_SIZE)}
_, G_loss_i, G_sample_i = session.run([G_opt, G_loss, G_sample], feed_dict=feed_dict)
if n_batch % 100 == 0:
display.clear_output(True)
for k in range(16):
i = k//4
j = k%4
ax[i,j].cla()
ax[i,j].imshow(G_sample_i[k,:].reshape(28, 28), cmap='Greys')
display.display(plt.gcf())
print('Epoch: {} Batch: {}'.format(epoch, n_batch))
print('Discriminator Loss: {:.4f}, Generator Loss: {:.4f}'.format(D_loss_i, G_loss_i))
print('D(x): {:.4f}, D(G(z)): {:.4f}'.format(
special.expit(D_real_i).mean(), special.expit(D_fake_i).mean()))
|
Online-Courses/gans/Vanilla GAN TensorFlow.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab={} colab_type="code" id="TC-6xmJavHcb"
import numpy as np
import pandas as pd
import itertools
import io
from sklearn.metrics import accuracy_score
from sklearn.svm import LinearSVC
from sklearn.preprocessing import scale
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import LabelEncoder
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
# + colab={"base_uri": "https://localhost:8080/", "height": 256} colab_type="code" id="91EIe5Dc5Z0L" outputId="52d199a7-ce23-4632-be98-c8c4d9b053e5"
#from google.colab import files
#uploaded = files.upload()
train_data = pd.read_csv('../data/train.csv')
test_data = pd.read_csv('../data/test.csv')
variabals = pd.read_csv('../data/VariableDescription.csv')
display(train_data.head())
# + colab={"base_uri": "https://localhost:8080/", "height": 318} colab_type="code" id="g3wVq5hDvlXy" outputId="6dd2b999-9844-4e32-f812-b42c28aca481"
train_x = train_data.dropna(axis=1)
le =LabelEncoder()
train_x=train_x.drop(columns=['EXE_EXERCI'],axis=1)
train_x['CTR_CATEGO_X']=le.fit_transform(train_x['CTR_CATEGO_X'])
train_x=train_x.drop(columns=['id'],axis=1)
display(train_x.head())
X=train_x.drop('target',1)
y=train_x['target']
cols =train_x.columns
print(cols)
scale = MinMaxScaler()
train_x=scale.fit_transform(train_x)
# + colab={"base_uri": "https://localhost:8080/", "height": 336} colab_type="code" id="RDHWcecmvned" outputId="63acdc1a-be7b-4d6e-e058-512f85af340f"
test_x = test_data.dropna(axis=1)
test_x['CTR_CATEGO_X']=le.fit_transform(test_x['CTR_CATEGO_X'])
test_x=test_x.drop(columns=['EXE_EXERCI'],axis=1)
test_x['CTR_CATEGO_X']=le.fit_transform(test_x['CTR_CATEGO_X'])
test_x=test_x.drop(columns=['id'],axis=1)
display(test_x.head())
train_x=scale.fit_transform(train_x)
# + colab={} colab_type="code" id="QWv3erF5Slwe"
# + colab={} colab_type="code" id="Ykjq6bo_v3fZ"
from sklearn.linear_model import LinearRegression
lr=LinearRegression()
pred = lr.fit(X, y).predict(test_x)
submission = pd.DataFrame(index=test_x.index,columns=['client_id','target'])
submission['client_id']=test_data['id']
submission['target']=pred
submission.to_csv('../data/submission_LR.csv',index=False)
# + [markdown] colab_type="text" id="vhXicmYYYs_W"
#
# + colab={"base_uri": "https://localhost:8080/", "height": 74} colab_type="code" id="GNrGEN1E6iO2" outputId="1d7f18f4-6c00-46a0-dfd1-d5d5f929c81b"
from sklearn.ensemble import RandomForestRegressor
my_model = RandomForestRegressor()
pred=my_model.fit(X, y).predict(test_x)
submission = pd.DataFrame(index=test_x.index,columns=['client_id','target'])
submission['client_id']=test_data['id']
submission['target']=pred
submission.to_csv('../data/submission_RF.csv',index=False)
# + colab={} colab_type="code" id="OuZaPyNCnJkZ"
|
app/AI_Hackathon.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="4Pjmz-RORV8E"
# # Train without labels
#
# _This notebook is part of a tutorial series on [txtai](https://github.com/neuml/txtai), an AI-powered semantic search platform._
#
# Almost all data available is unlabeled. Labeled data takes effort to manually review and/or takes time to collect. Zero-shot classification takes existing large language models and runs a similarity comparison between candidate text and a list of labels. This has been shown to perform surprisingly well.
#
# The problem with zero-shot classifiers is that they need to have a large number of parameters (400M+) to perform well against general tasks, which comes with sizable hardware requirements.
#
# This notebook explores using zero-shot classifiers to build training data for smaller models. A simple form of [knowledge distillation](https://en.wikipedia.org/wiki/Knowledge_distillation).
# + [markdown] id="Dk31rbYjSTYm"
# # Install dependencies
#
# Install `txtai` and all dependencies.
# + id="XMQuuun2R06J"
# %%capture
# !pip install git+https://github.com/neuml/txtai datasets pandas
# + [markdown] id="3PUe1OW8IZR5"
# # Apply zero-shot classifier to unlabeled text
#
# The following section takes a small 1000 record random sample of the sst2 dataset and applies a zero-shot classifer to the text. The labels are ignored. This dataset was chosen only to be able to evaluate the accuracy at then end.
# + id="GlrOnS4cmkih"
import random
from datasets import load_dataset
from txtai.pipeline import Labels
def batch(texts, size):
return [texts[x : x + size] for x in range(0, len(texts), size)]
# Set random seed for repeatable sampling
random.seed(42)
ds = load_dataset("glue", "sst2")
sentences = random.sample(ds["train"]["sentence"], 1000)
# Load a zero shot classifier - txtai provides this through the Labels pipeline
labels = Labels("microsoft/deberta-large-mnli")
train = []
# Zero-shot prediction using ["negative", "positive"] labels
for chunk in batch(sentences, 32):
train.extend([{"text": chunk[x], "label": label[0][0]} for x, label in enumerate(labels(chunk, ["negative", "positive"]))])
# + [markdown] id="TLsZmRpHJGav"
# Next, we'll use the training set we just built to train a smaller Electra model.
# + colab={"base_uri": "https://localhost:8080/", "height": 214} id="nAt42TIHnfTN" outputId="7080b21d-ecf4-459a-c818-11c748e28bb7"
from txtai.pipeline import HFTrainer
trainer = HFTrainer()
model, tokenizer = trainer("google/electra-base-discriminator", train, num_train_epochs=5)
# + [markdown] id="J9pugqJSJRn6"
# # Evaluating accuracy
#
# Recall the training set is only 1000 records. To be clear, training an Electra model against the full sst2 dataset would perform better than below. But for this exercise, we're are not using the training labels and simulating labeled data not being available.
#
# First, lets see what the baseline accuracy for the zero-shot model would be against the sst2 evaluation set. Reminder that this has not seen any of the sst2 training data.
#
# + colab={"base_uri": "https://localhost:8080/"} id="RbgIrkgMvJS4" outputId="69287790-e01c-4c17-dfd5-0dc6afd73c98"
labels = Labels("microsoft/deberta-large-mnli")
# + colab={"base_uri": "https://localhost:8080/"} id="-36UBMILpKYh" outputId="3a340b9f-57c5-4c4c-d975-0fcc47df4930"
results = [row["label"] == labels(row["sentence"], ["negative", "positive"])[0][0] for row in ds["validation"]]
sum(results) / len(ds["validation"])
# + [markdown] id="uJVnWHZZKFIN"
# 88.19% accuracy, not bad for a model that has not been trained on the dataset at all! Shows the power of zero-shot classification.
#
# Next, let's test our model trained on the 1000 zero-shot labeled records.
# + colab={"base_uri": "https://localhost:8080/"} id="Kr5IZqZtvXlP" outputId="1faeb0d6-349b-4982-e9e8-cdbbde9e9a09"
labels = Labels((model, tokenizer), dynamic=False)
results = [row["label"] == labels(row["sentence"])[0][0] for row in ds["validation"]]
sum(results) / len(ds["validation"])
# + [markdown] id="sDw-Zh43KVdX"
# 87.39% accuracy! Wouldn't get too carried away with the percentages but this at least nearly meets the accuracy of the zero-shot classifier.
#
# Now this model will be highly tuned for a specific task but it had the opportunity to learn from the combined 1000 records whereas the zero-shot classifier views each record independently. It's also much more performant.
# + [markdown] id="QEAwki2lLM2A"
# # Conclusion
#
# This notebook explored a method of building trained text classifiers without training data being available. Given the amount of resources needed to run large-scale zero-shot classifiers, this method is a simple way to build smaller models tuned for specific tasks. In this example, the zero-shot classifier has 400M parameters and the trained text classifier has 110M.
|
examples/17_Train_without_labels.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/hamletbatista/smx/blob/main/VueJs_Example.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="hikHa5IVxgiu"
# #Setup
# + id="tmjO7WoBsmGe"
# %%capture
# !wget https://bin.equinox.io/c/4VmDzA7iaHb/ngrok-stable-linux-amd64.zip && unzip ngrok-stable-linux-amd64.zip
# !apt-get install jq
# + id="fTtYWzjGwv5O" outputId="10ca9e75-b2c7-4e2b-9ad6-1036a811d5c2" colab={"base_uri": "https://localhost:8080/"}
# !node -v
# + id="H05HK-Mmw7Z5"
# + [markdown] id="Xjk5kSuyw-Ji"
# ###Start server
#
# ``%%bash --bg
# npm run dev``
#
# ###Start ngrok
#
# ``
# ./ngrok http 3000 > ngrok.log 2>&1 &
# ``
#
# ###Get ngrok URL
#
# ``
# # # !curl -s http://localhost:4040/api/tunnels | jq ".tunnels[0].public_url"
# ``
# + id="Kg2Tvvfoxbze"
# + [markdown] id="PiEiO_72xju4"
# #VueJs
#
# https://github.com/arijs/vue-next-example
#
# More examples here: https://awesome-vue.js.org/resources/examples.html
#
#
# + id="sJlSIrhq4q4p" outputId="23baedfe-e996-4b23-bb83-b7b203d70633" colab={"base_uri": "https://localhost:8080/"}
# !git clone https://github.com/snturk/covid19-vue-component
# + id="jELSvQ3s4tgJ" outputId="ba9823b6-e92b-4a58-d5dd-3759cdbf2704" colab={"base_uri": "https://localhost:8080/"}
# %cd covid19-vue-component
# + [markdown] id="cb5uTgtOLfaO"
# ##Vue Meta
#
# https://vue-meta.nuxtjs.org/
#
# ``npm install vue-meta --save
# ``
# + id="wnnHvBt1LwUL" outputId="5c4051ac-3d2b-46c2-d37f-8c3e7b669313" colab={"base_uri": "https://localhost:8080/"}
# !npm install vue-meta --save
# + id="GaUehqkbLxRf"
# + id="uE7sx3YqDZ0j" outputId="cd9c61d7-74bf-4b3c-fd11-6cfc06816c7e" colab={"base_uri": "https://localhost:8080/"}
# !npm install
# + id="vzVpVhusDbti"
# #!cat package.json
# + id="E5yRqamV1oXk" outputId="af3e9527-c526-43ea-bcc7-8eb6cf531274" colab={"base_uri": "https://localhost:8080/"}
# !../ngrok authtoken #INPUT ngrok auth token
# + id="2mkLiG_32ZKT"
#https://stackoverflow.com/questions/45425721/invalid-host-header-when-ngrok-tries-to-connect-to-react-dev-server
# !../ngrok http -hostname=rnd.ranksense.com --host-header=rewrite 8081 > ngrok.log 2>&1 &
# + id="8FqmUnrM25yg"
# #!pkill ngrok
# + id="KMSf7H3F9Zzr"
# !tail ngrok.log
# + id="FsSa24ps2i4E" outputId="1f1c1954-a0c5-49f2-db5b-7965fe811cdd" colab={"base_uri": "https://localhost:8080/"}
# !curl -s http://localhost:4040/api/tunnels | jq ".tunnels[0].public_url"
# + id="jA4EC0gt2PfV" outputId="c5af2ec9-a977-4510-be84-95dba225db07" colab={"base_uri": "https://localhost:8080/"}
# !npm run-script serve
# + id="lIyVS98q52v0"
|
VueJs_Example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Think Bayes
#
# Copyright 2018 <NAME>
#
# MIT License: https://opensource.org/licenses/MIT
# +
# Configure Jupyter so figures appear in the notebook
# %matplotlib inline
# Configure Jupyter to display the assigned value after an assignment
# %config InteractiveShell.ast_node_interactivity='last_expr_or_assign'
import numpy as np
import pandas as pd
# import classes from thinkbayes2
from thinkbayes2 import Pmf, Cdf, Suite, Joint
import thinkplot
# -
# ## The Space Shuttle problem
#
# Here's a problem from [Bayesian Methods for Hackers](http://nbviewer.jupyter.org/github/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers/blob/master/Chapter2_MorePyMC/Ch2_MorePyMC_PyMC2.ipynb)
#
# >On January 28, 1986, the twenty-fifth flight of the U.S. space shuttle program ended in disaster when one of the rocket boosters of the Shuttle Challenger exploded shortly after lift-off, killing all seven crew members. The presidential commission on the accident concluded that it was caused by the failure of an O-ring in a field joint on the rocket booster, and that this failure was due to a faulty design that made the O-ring unacceptably sensitive to a number of factors including outside temperature. Of the previous 24 flights, data were available on failures of O-rings on 23, (one was lost at sea), and these data were discussed on the evening preceding the Challenger launch, but unfortunately only the data corresponding to the 7 flights on which there was a damage incident were considered important and these were thought to show no obvious trend. The data are shown below (see [1](https://amstat.tandfonline.com/doi/abs/10.1080/01621459.1989.10478858)):
#
#
# +
# #!wget https://raw.githubusercontent.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers/master/Chapter2_MorePyMC/data/challenger_data.csv
# -
columns = ['Date', 'Temperature', 'Incident']
df = pd.read_csv('challenger_data.csv', parse_dates=[0])
df.drop(labels=[3, 24], inplace=True)
df
df['Incident'] = df['Damage Incident'].astype(float)
df
# +
import matplotlib.pyplot as plt
plt.scatter(df.Temperature, df.Incident, s=75, color="k",
alpha=0.5)
plt.yticks([0, 1])
plt.ylabel("Damage Incident?")
plt.xlabel("Outside temperature (Fahrenheit)")
plt.title("Defects of the Space Shuttle O-Rings vs temperature");
# -
# ### Grid algorithm
#
# We can solve the problem first using a grid algorithm, with parameters `b0` and `b1`, and
#
# $\mathrm{logit}(p) = b0 + b1 * T$
#
# and each datum being a temperature `T` and a boolean outcome `fail`, which is true is there was damage and false otherwise.
#
# Hint: the `expit` function from `scipy.special` computes the inverse of the `logit` function.
# +
from scipy.special import expit
class Logistic(Suite, Joint):
def Likelihood(self, data, hypo):
"""
data: T, fail
hypo: b0, b1
"""
T,fail=data;
b0,b1=hypo;
if fail:
return expit(b0+b1*t)
# +
# Solution goes here
# -
b0 = np.linspace(0, 50, 101);
b1 = np.linspace(-1, 1, 101);
from itertools import product
hypos = product(b0, b1)
suite = Logistic(hypos);
for data in zip(df.Temperature, df.Incident):
print(data)
suite.Update(data)
thinkplot.Pdf(suite.Marginal(0))
thinkplot.decorate(xlabel='Intercept',
ylabel='PMF',
title='Posterior marginal distribution')
thinkplot.Pdf(suite.Marginal(1))
thinkplot.decorate(xlabel='Log odds ratio',
ylabel='PMF',
title='Posterior marginal distribution')
# According to the posterior distribution, what was the probability of damage when the shuttle launched at 31 degF?
# +
# Solution goes here
# +
# Solution goes here
# -
# ### MCMC
#
# Implement this model using MCMC. As a starting place, you can use this example from [the PyMC3 docs](https://docs.pymc.io/notebooks/GLM-logistic.html#The-model).
#
# As a challege, try writing the model more explicitly, rather than using the GLM module.
import pymc3 as pm
# +
# Solution goes here
# -
pm.traceplot(trace);
# The posterior distributions for these parameters should be similar to what we got with the grid algorithm.
|
examples/.ipynb_checkpoints/shuttle-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="WiPP6XSlfDC_"
# <img align="right" style="max-width: 200px; height: auto" src="https://github.com/aarimond/CFDS-Notebooks/blob/master/lab_00/cfds_logo.png?raw=1">
#
# ### Lab 00 - "Testing the CFDS Lab Environment"
#
# Chartered Financial Data Scientist (CFDS), Autumn Term 2020
# + [markdown] id="N8w2cJiyfDDB"
# The lab environment of the **"Chartered Financial Data Scientist (CFDS)"** course is powered by Jupyter Notebooks (https://jupyter.org), which allow one to perform a great deal of data analysis and statistical validation. With this test notebook, we like to ensure that Jupyter Notebook and Python is appropriately set up, and you did install the first set of necessary Python libraries.
# + [markdown] id="058b9qpWfDDC"
# ### Test 1: Running Python
# + [markdown] id="h7jjeiAmfDDC"
# Let's run a simple addition to determine if Python is running correctly:
# + id="KJ_35S-cfDDC"
# run simple addition
1 + 1
# + [markdown] id="pmgxWIDVfDDD"
# ### Test 2: Importing Python Libraries
# + [markdown] id="XiFzMX62fDDD"
# Let's now import the needed python libraries to determine if they are setup correctly:
# + id="o6iVHEBVfDDD"
# import additional python libraries
import numpy
import scipy
import pandas
import pandas_datareader
import matplotlib
import seaborn
import sklearn
import torch
import torchvision
# + [markdown] id="_lUeBgS6fDDE"
# ### Test 3: Install additional Python Libraries
# + [markdown] id="cHKxt6RbfDDE"
# To import a library that's not in Google's Colaboratory by default, you can use `!pip install` or `!apt-get install`:
# + id="d6vg2sOAfDDE"
# !pip install ffn
# !pip install bt
# !pip install yfinance
# + [markdown] id="EcB9cFH-fDDF"
# Import the just installed libraries:
# + id="0q44kxMafDDF"
import ffn
import bt
import yfinance as yf
yf.pdr_override() # needed to access Yahoo Finance
# + [markdown] id="EWEMpTCSfDDF"
# If the code cell above executes without running into an error you should be good to go for the upcoming labs :) Happy coding!
|
lab_00/cfds_colab_00.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Example using random forest:
#
# In this example we use a pool of classifiers generated using the Random Forest method rather than Bagging. We also
# show how to change the size of the region of competence, used to estimate the local competence of the base classifiers.
#
# This demonstrates that the library accepts any kind of base classifiers as long as they implement the predict and
# predict proba functions. Moreover, any ensemble generation method such as Boosting or Rotation Trees can be used
# to generate a pool containing diverse base classifiers. We also included the performance of the RandomForest classifier
# as a baseline comparison.
#
# +
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
# Generate a classification dataset
data = load_breast_cancer()
X = data.data
y = data.target
# split the data into training and test data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
#Training a random forest classifier using the whole training data
RF = RandomForestClassifier()
RF.fit(X_train, y_train)
X_train, X_dsel, y_train, y_dsel = train_test_split(X, y, test_size=0.50)
# -
# ## Training a random forest to be used as the pool of classifiers.
#
# We set the maximum depth of each decision tree to 5 so that it can estimate posterior probabilities. Otherwise, sklearn generates decision tree in which each leaf contains only samples from a single class, attributing always probability 1 to the predicted class and 0 to all others. Some DS techinques such as the META-DES, requires good probabilities estimates to achieve a better performance.
pool_classifiers = RandomForestClassifier(max_depth=5)
pool_classifiers.fit(X_train, y_train)
# +
# Example of a dcs techniques
from deslib.dcs.ola import OLA
from deslib.dcs.mcb import MCB
# Example of a des techniques
from deslib.des.knora_e import KNORAE
from deslib.des.des_p import DESP
from deslib.des.knora_u import KNORAU
from deslib.des.meta_des import METADES
# Initialize a DS technique. Here we specify the size of the region of competence (5 neighbors)
knorau = KNORAU(pool_classifiers)
kne = KNORAE(pool_classifiers, k=5)
desp = DESP(pool_classifiers, k=5)
ola = OLA(pool_classifiers, k=5)
mcb = MCB(pool_classifiers, k=5)
meta = METADES(pool_classifiers, k=5)
# Fit the DS techniques
knorau.fit(X_dsel, y_dsel)
kne.fit(X_dsel, y_dsel)
desp.fit(X_dsel, y_dsel)
meta.fit(X_dsel, y_dsel)
ola.fit(X_dsel, y_dsel)
mcb.fit(X_dsel, y_dsel)
# -
# Calculate classification accuracy of each technique
print('Classification accuracy RF: ', RF.score(X_test, y_test))
print('Evaluating DS techniques:')
print('Classification accuracy KNORAU: ', knorau.score(X_test, y_test))
print('Classification accuracy KNORA-Eliminate: ', kne.score(X_test, y_test))
print('Classification accuracy DESP: ', desp.score(X_test, y_test))
print('Classification accuracy OLA: ', ola.score(X_test, y_test))
print('Classification accuracy MCB: ', mcb.score(X_test, y_test))
print('Classification accuracy META-DES: ', meta.score(X_test, y_test))
|
examples/Notebooks_examples/Example_random_forest.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/etatc/faces-autoencoder/blob/main/facesautoencoder.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + colab={"base_uri": "https://localhost:8080/"} id="Fy5bu0LNN3WW" outputId="0a043bd1-e23e-4a8e-b316-07b4558ad70e"
# !curl http://vis-www.cs.umass.edu/lfw/lfw.tgz -o data.tgz
# + id="3MkqXKOlOati"
# !tar -xvzf /content/data.tgz -C /content
# + id="qUt0dkrRrH93"
from PIL import Image
# + id="JcI0PyLkQM9Q"
from os import listdir
from os.path import isfile, join
mypath = '/content/lfw'
directories = listdir(mypath)
onlyfiles = []
for dir in directories:
path = '/content/lfw/' + dir
for f in listdir(path):
onlyfiles += [path + '/' + f]
# + colab={"base_uri": "https://localhost:8080/"} id="GTNs2i8hRM4e" outputId="b4813f11-8e4d-4a7f-8017-619a2d1959e3"
print(directories)
# + colab={"base_uri": "https://localhost:8080/"} id="ocZ-aEBKR3ss" outputId="5cdca2f3-24c9-4e4b-cb46-f814200373de"
print(onlyfiles[:50])
# + id="KwXqZX-SrM7K"
import numpy as np
resized = []
for pic in onlyfiles:
img = Image.open(pic)
img = img.resize((200, 200), Image.ANTIALIAS)
image = np.array(img)
resized += [image]
# + id="Mb-0AZMLW88W"
x_train = np.array(resized)
# + id="Co44cOFihtqw"
x_train = x_train.astype('float32') / 255.
# + colab={"base_uri": "https://localhost:8080/"} id="X7cBr3gBXQl3" outputId="b67fa895-9e1e-42dd-ec1f-45df3c225dca"
x_train.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="OZASzHuYodpu" outputId="62db1634-68af-426a-d6af-a9344111f9e3"
from matplotlib import image
from matplotlib import pyplot
pyplot.imshow(x_train[6900])
pyplot.show()
# + id="iKnGyKswsfuH"
from keras.layers import Conv2D, MaxPooling2D, Conv2DTranspose, BatchNormalization, Reshape, Input
from keras.models import Sequential, Model
import keras.models as model
from keras import backend as K
# + id="yv3AdJVXshgx"
def build_encoder(img_shape):
# The encoder
encoder = Sequential()
encoder.add(Conv2D(100, (3, 3), activation='relu', input_shape=(img_shape)))
encoder.add(MaxPooling2D((2, 2)))
encoder.add(Conv2D(50, (3, 3), activation='relu', padding='same'))
encoder.add(MaxPooling2D((2, 2), padding='same'))
encoder.add(Conv2D(25, (3, 3), activation='relu', padding='same'))
encoder.add(MaxPooling2D((2, 2), padding='same'))
encoded = encoder.layers[5].output
'''= K.function([encoder.layers[0].input],
[encoder.layers[3].output])
encoded = o([x])[0]
'''
return encoder, encoded
def build_decoder(img_shape):
# The decoder
decoder = Sequential()
decoder.add(Conv2DTranspose(25, (3, 3), strides=2, activation='relu', padding='same', input_shape=(img_shape)))
decoder.add(Conv2DTranspose(50, (3, 3), strides=2, activation='relu', padding='same'))
decoder.add(Conv2DTranspose(100, (3, 3), strides=2, activation='relu', padding='same'))
decoder.add(Conv2D(3, (3, 3), activation='sigmoid', padding='same'))
#decoder.add(Reshape((100, 100, 3)))
decoded = decoder.layers[2].output
return decoder, decoded
# + colab={"base_uri": "https://localhost:8080/"} id="8cK5xuo-smuC" outputId="cd863737-0ba9-4f4d-f748-b3e52a6d83ef"
img_shape = x_train.shape[1:]
encoder, encoded = build_encoder(img_shape)
decoder, decoded = build_decoder(encoded.shape[1:])
inp = Input(img_shape)
code = encoder(inp)
reconstruction = decoder(code)
autoencoder = Model(inp,reconstruction)
autoencoder.compile(optimizer='adam', loss='mse')
print(autoencoder.summary())
# + colab={"base_uri": "https://localhost:8080/", "height": 466} id="XRdO1nmPbPnu" outputId="851a66b0-3df3-4d7d-de1c-160b9b418ef4"
autoencoder.load_weights('autoencoderfaces200.h5')
# + colab={"base_uri": "https://localhost:8080/"} id="Sb_m28veXjjc" outputId="64a91337-50fa-43b7-e131-de747bce5cfb"
}\ shuffle=True,
validation_data=(x_train, x_train))
# + id="cMVo9N7EwNWK"
autoencoder.save(autoencodefaces200.h5)
|
facesautoencoder.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
@my_deco
def add(a, b):
return a + b
# +
# THink as this
def add(a, b):
return a + b
add = my_deco(add)
# +
# Three callable
@my_deco #First callable
def add(a, b): #second callable
return a + b
# third callable is what returns when we call add which is add = my_deco(add)
# +
# Defining a decorator
def my_deco(func):
def wrapper(*args, **kwargs):
return f"{func(*args, **kwargs)}!!!"
return wrapper # this will add to original function name which is add =
# -
# How does the wrapper has access to the outside function. this is because of LEGB rule which does the magic
# ##### Solution to problem, where we can use it
# Example 1: timing
# When we have an argument
@once(5)
def add(a, b):
return a + b
# +
#think of this as
add = once(5)add()
#we have foour callabale
# -
# Example - 4 Memoization
#
# cache the result of result
# #### Examle 5: Attributes
# 1. Decorator will help you to DRY up your callable
# 2. decorator will helps you to callable
# 3.
#
# https://sebastianraschka.com/Articles/2014_python_scope_and_namespaces.html
|
Decorator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # All Snippets (don´t run this notebook)
import sys
import os
import urllib, base64
import datetime as dt
import numpy as np
import pandas as pd
import json
from pandas.io.json import json_normalize
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
from matplotlib import cm
from matplotlib import colors as mcolors
import re
from decimal import Decimal
from datetime import timedelta
# # Files
# +
# Read JSON File
with open('../../data/dir1/file-name.json') as f:
content = json.load(f)
content['key']
# +
# Save JSON File
_notebook_folder = 'block-000'
_version = '1.0'
dirPath = '../../data/master/dir1/'
fileName = f'{_notebook_folder}-{_version}.json'
fullPath = dirPath + fileName
with open( fullPath, 'w') as outfile:
json.dump(data, outfile, indent=4)
# +
# Read CSV
_version = '1.0'
dirPath = '../../data/master/dir1/'
fileName = f'prefix__name-{_version}.csv'
fullPath = dirPath + fileName
plotDf = pd.read_csv( fullPath )
plotDf.head(10)
# -
# # Helpers
# +
# Loop
tasks = [1,2,3,4,0,1,2,0]
taskNoEmptys = [task for task in tasks if task > 0 ]
print( len(tasks),'>' , len(taskNoEmptys))
# +
# Exec
emptyList = []
for item in fullList:
resultItem = doSomething(item)
try:
result = doSomethingElse(resultItem)
emptyList.append( result )
except Exception as e:
print('ERROR in ',item, e)
emptyList[0]
# -
# # Javascript
# + language="javascript"
# // var nbPathParts = IPython.notebook.notebook_path.split('/')
# //var nbFolder = nbPathParts[ nbPathParts.length - 2]
# //IPython.notebook.kernel.execute('nb_name = "' + IPython.notebook.notebook_name + '"')
# //IPython.notebook.kernel.execute('nb_folder = "' + nbFolder + '"')
# -
# # Store
# Store Save
# %store myVariable
# +
# Store Read
# %store -r
# myVariable
# -
# # Dataframes
# +
# Parse
def parseJsonToDf( jsonPicEntry, idx ):
df = json_normalize( data=jsonTaskEntry['status'], meta=[ 'statusName','statusId','date','sprintDay',] )
# date = df.groupby('date').last().index[0]
# df['_task_idx'] = idx
# df['sp'] = jsonTaskEntry['sp']
# df['author'] = jsonTaskEntry['author']
# df['_plt_pos_X'] = df.sprintDay.astype('float')
# df['_plt_pos_x'] = df.groupby(['sprintDay','task']).cumcount()
# df['_plt_width'] = 1/df.groupby('date')['date'].transform('count').astype('int')
# df['_plt_division'] = df.groupby('date')['date'].transform('count').astype('int')
return df
dataFrames = [ parseJsonToDf(jsonItem, idx) for idx, jsonItem in enumerate(parseJSONFileContent) ]
# -
# Concat
dfAll = pd.concat(dataFrames).reset_index(drop=True)
# +
# Append
dfBuffer = pd.DataFrame(data=None, columns=dfTarget.columns, index=dfTarget.index).dropna()
listOfSeries = []
def addToList( valuesList ):
listOfSeries.append( pd.Series( valuesList, index=dfBuffer.columns ) )
def addRawToList( row ):
listOfSeries.append( row )
def addListToDfRows():
# print('##########', len(listOfSeries))
# Pass a list of series to the append() to add multiple rows
dfBuffer01 = dfBuffer.append(listOfSeries , ignore_index=True)
return dfBuffer01
## Test
# addToList( ['a', 1, 1, 1,0,'ABC',7,1,0.0,0,1.00,1] )
# newDF = addListToDfRows()
# newDF
# +
# Iterator ???
row_iterator = dfTarget.iterrows()
_, nrow = next(row_iterator) # take first item from row_iterator
for idx, row in row_iterator:
#print( row['columName'], row['date'] , nrow['date'] ) # issue with last sprint pics
nextPointer = datesList[0] if row['date'] < datesList[0] else row['date']
lastPointer = datesList[0] if nrow['date'] < datesList[0] else nrow['date']
lastDayStatus = diffDays(lastPointer, nextPointer )
if row['columName'] == nrow['columName'] and lastDayStatus > 1: # Create a needed row
#print('---- direfence', lastDayStatus)
for d in range(1,lastDayStatus):
ghostRow = nrow.copy()
ghostRow['_gen'] = 1
print( ghostRow )
addRawToList(ghostRow)
nrow = row
# +
# Sort
#.sort_values(by=['date', 'ref'], ascending=False).reset_index(drop=True)
# -
# Sort
dfFull = pd.concat([dfTarget,newDF])
dfFullSorted = dfFull.sort_values(by=['author','ref','sprintDay','status']).reset_index(drop=True)
# # Ressources
#
#
# - https://realpython.com/python-data-visualization-bokeh/
# - https://jakevdp.github.io/PythonDataScienceHandbook/04.09-text-and-annotation.html
# - https://stackoverflow.com/questions/47373762/pyplot-sorting-y-values-automatically
#
|
notebooks/sandbox/sandbox_all/sandbox_all.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/pkm29/Philosophy_Analysis/blob/master/Text_Generation_(LSTM).ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="q39DZaqcE-c3"
# # Text Generation by Analytics Vidhya
# source: https://www.analyticsvidhya.com/blog/2018/03/text-generation-using-python-nlp/
# + [markdown] colab_type="text" id="x21LvZU4E-c6"
# ## Importing Libraries
# + colab={} colab_type="code" id="o8A4nQ7GE-c7"
import numpy as np
import pandas as pd
import os
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Dropout
from keras.layers import LSTM
from keras.utils import np_utils
import tensorflow as tf
from tensorflow import keras
# #!pip install -U -q PyDrive
# + [markdown] colab_type="text" id="MvF_w3zQE-dB"
# ## Loading Data
# + colab={"base_uri": "https://localhost:8080/", "height": 221} colab_type="code" id="tLQkcNawE-dB" outputId="db02990b-71f4-4ae8-b747-aa4210bbe1d5"
try:
sent_df = pd.read_csv("sentiment_dataframe.csv")
except:
sent_df = pd.read_csv("https://github.com/pkm29/Philosophy_Analysis/raw/master/sentiment_dataframe.csv")
sent_df.head()
# + [markdown] colab_type="text" id="x76-1cowE-dF"
# chapter_text_num is NaN only for Preface, this is ok as this column was only created for graphical visualations. Basically just shortened chapter names to numbers.
# + [markdown] colab_type="text" id="leNyP1bDE-dG"
# ## Creating Word/Character Mappings
# + [markdown] colab_type="text" id="gAE8YfukE-dH"
# Here are some interesting pros and cons to word vs character mapping highlighted by this [lighttag.io blogpost](https://www.lighttag.io/blog/character-level-NLP/). <br>
# ### Advantages
# - Character mapping is more general when discerning syntax. With word mapping, words like 3/4", csv w/, or 50k need to be specified. A regular model usually has the 10-30k most frequent words in its vocabulary, and so "unusual" looking words are interpreted poorly. Character mapping sees the input "as-is" and each word is equally strange. This is beneficial for poorly spelled, user-generated text as this approach is more generalized and robust. <br>
# - Due to the smaller vocabulary of character level models, pretraining avoids softmax bottlenecking. Softmax bottlenecking occurs when probability calculations (matrix factorization problems) use such large matrices that the softmax calculations become too difficult to perform. This is a problem faced by recurrent neural networks (RNNs) in general because context of words are incredibly important, leading to much larger matrices, or more specifically, high-rank matrices. A well-known paper by <NAME> in 2018 explores this problem and solution [further](https://arxiv.org/pdf/1711.03953.pdf).
# + [markdown] colab_type="text" id="839De6RUE-dH"
# ### Disdvantages
# - Character mapping loses the semantic content of words, which is oftentimes useful for accuracy purposes.
# - Character mapping is sometimes more computationally expensive. While character mapping is generally characterized by lower computational costs than word mapping, working at the character level effectively multiplies the length of our sequence by the average number of characters per word. As a result, certain NLP architectures may be necessary to keep computational expenses low. (The lighttag article mentions convolutions or transformers as a way to nullify the cost of long sequences)
# - The output of character level models requires more work from the user to convert it into words and meaningful insights. Additionally, more work is needed to account for tokenization errors, as character level models split up words into individual charaters and during that process, may interpret words differently than we would like or have a preference for.
# + [markdown] colab_type="text" id="SMYZ9SgTE-dJ"
# ## Character Mapping Approach
# + [markdown] colab_type="text" id="zgDzlb6dE-dK"
# Below we can visualize what is inside of our character mapping. I noticed some weird errors of sentences composed of only numbers and went back to filter them out. Uncomment the last line "text" to display the entire text and char_to_n to view the character mapping, I have kept it commented as our notebook output will display the entire thing and be way too large. <br>
# In this iteration I use the entire book's text. Later on I will try variations such as training seperately on the two authors.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="aIF9d1T6E-dL" outputId="ebbd0c7e-fec4-4c7a-cfe7-ec68df50c332"
#Convert sentences back into book
join_with = " "
text = join_with.join(sent_df["sentence"][sent_df["chapter_author"] == "Aesthetic"])
text=text.lower()
characters = sorted(list(set(text)))
n_to_char = {n:char for n, char in enumerate(characters)}
char_to_n = {char:n for n, char in enumerate(characters)}
#text
char_to_n
# + [markdown] colab_type="text" id="f3vl1tUSE-dO"
# For the rest of this code I will be following Analytics Vidhya's blogpost by [<NAME>](https://www.analyticsvidhya.com/blog/2018/03/text-generation-using-python-nlp/) without including much explanatory text. His descriptions are great and I don't see a reason to copy and paste his explanations if they are already in the article. There are a couple of technical terms that I think are worth explaining further though.
# + [markdown] colab_type="text" id="FBJ1DXInE-dO"
# ## Data Preprocessing for LSTM Training Format
# + colab={} colab_type="code" id="BsJfaq3ZE-dP"
X = []
Y = []
length = len(text)
#seq_length = length of the sequence of characters that we want to consider before predicting a particular character.
seq_length = 100
for i in range(0, length-seq_length, 1):
sequence = text[i:i + seq_length]
label = text[i + seq_length]
X.append([char_to_n[char] for char in sequence])
Y.append(char_to_n[label])
# + colab={} colab_type="code" id="dMcy7_QcE-dS"
X_modified = np.reshape(X, (len(X), seq_length, 1))
X_modified = X_modified / float(len(characters))
Y_modified = np_utils.to_categorical(Y)
# + [markdown] colab_type="text" id="SfslzIp7E-dW"
# ## Modelling
# + colab={} colab_type="code" id="iBmsjQeaE-dX"
#sequential model with two LSTM layers having 400 units each
model = Sequential()
model.add(LSTM(700, input_shape=(X_modified.shape[1], X_modified.shape[2]), return_sequences=True))
#20% dropout layer to check for overfitting
model.add(Dropout(0.2))
model.add(LSTM(700, return_sequences=True))
model.add(Dropout(0.2))
model.add(LSTM(700))
model.add(Dropout(0.2))
model.add(Dense(Y_modified.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam')
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="7gatKifLE-db" outputId="4a488fff-dfe1-4961-e706-392c33d590a2"
model.fit(X_modified, Y_modified, epochs=24, batch_size=64)
#100 epochs, batch size 50, and 3 levels of 700 units and 20% dropout layer
model.save_weights('text_generator_e24_bs64_700_0.2_x3.h5')
from google.colab import files
files.download('text_generator_e24_bs64_700_0.2_x3.h5')
# + colab={} colab_type="code" id="s3InhHGP3Mzf"
files.download('text_generator_e24_bs64_700_0.2_x3.h5')
# + [markdown] colab_type="text" id="F8ZM1AbSE-dh"
# ## Generating Text
# + colab={} colab_type="code" id="JbA-QA81E-dh"
string_mapped = X[99]
full_string = [n_to_char[value] for value in string_mapped]
# generating characters
for i in range(seq_length):
x = np.reshape(string_mapped,(1,len(string_mapped), 1))
x = x / float(len(characters))
pred_index = np.argmax(model.predict(x, verbose=0))
seq = [n_to_char[value] for value in string_mapped]
string_mapped.append(pred_index)
string_mapped = string_mapped[1:len(string_mapped)]
# + colab={} colab_type="code" id="XNvkbTAlE-dl"
txt=""
for char in full_string:
txt = txt+char
txt
|
Text_Generation_(LSTM).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Consumer Loan Pricing
import loans
# The loans module contains the following functions *compute_annuity()* and *get_cashflow_schedule()* for pricing a basic consumer loan, plus a couple of utility functions. A functional programming approach is used over an object-oriented approach because simpler is always better, and for computing annuity and cashflow schedule, defining a class is not necessary. Using just pure functions, the risk of side effects from managing changing states is avoided and extension to concurrency is also straightforward.
help(loans.compute_annuity)
help(loans.get_cashflow_schedule)
# The *compute_annuity()* function takes in the APR, principal and number of terms, and returns the monthly annuity using the simple amortised loan equation. The *get_cashflow_schedule()* use *compute_annuity()* to generate a cashflow schedule and returns a Pandas dataframe containing the payment dates, the payment amounts, the principal and interest components of the payments, and the balance. Unfortunately, the current version of the *loans* module generates the cashflow schedule imperatively rather than declaratively, which is to do in the future.
#
# In both functions, all operations are done on the Python *decimal* type instead *float* due to the importance of computing precise values in financial applications. It should be noted that although the decimal type is rather slow in Python 2.7x, in Python 3 Decimal runs on a C backend so it should be much faster.
# Using a small SQL database, the functionality of the *loans* module is tested as follows. The SQL database is queried into a Pandas dataframe. To be done in the future is to write a Client class and use SQLAlchemy ORM to map the class to the database.
# +
import sqlite3 as lite
import pandas as pd
con = lite.connect('loans.db')
with con:
cur = con.cursor()
query = "SELECT * FROM Loans"
df = pd.read_sql(query,con)
# -
for idx,client in df.iterrows():
cashdf = loans.get_cashflow_schedule(client.APR,client.Principal,client.NumTerms,client.LentDate,client.RepaymentDate)
print('---------------------------------------')
print('Cashflow for ClientID '+client.ClientID)
print('---------------------------------------')
print(cashdf)
print('\n')
|
write_up.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
from matplotlib import style
import matplotlib.pyplot as plt
plt.style.use('ggplot')
import numpy as np
import pandas as pd
import datetime as dt
# ---
# # Reflect Tables into SQLAlchemy ORM
import sqlalchemy
from sqlalchemy.orm import Session
from sqlalchemy.ext.automap import automap_base
from sqlalchemy import create_engine, func, inspect
engine=create_engine('sqlite:///Resources/hawaii.sqlite')
Base=automap_base()
Base.prepare(engine, reflect=True)
Base.classes.keys()
Station=Base.classes.station
Measurement=Base.classes.measurement
session=Session(engine)
inspector=inspect(engine)
# ### Inspect Tables
# ---
# ##### Station Table
stations=engine.execute('SELECT * FROM Station')
print(stations.keys())
stations.fetchall()
columns=inspector.get_columns('Station')
for column in columns:
print(column['name'], column['type'])
# ---
# ##### Measurement Table
measurements=engine.execute('SELECT * FROM Measurement LIMIT 15')
print(measurements.keys())
measurements.fetchall()
columns=inspector.get_columns('Measurement')
for column in columns:
print(column['name'], column['type'])
# ---
# # Exploratory Climate Analysis
# ---
# ### - Precipitation Analysis
#
# Plot of the last 12 months of the precipitation data and its summary statistics.
# ---
# ##### The Latest Date in The Dataset
latest_date=(session.query(Measurement.date)
.order_by(Measurement.date.desc())
.first())
latest_date
# ##### The Date 1 Year Before The Latest Date in The Dataset
year_ago_date=dt.date(2017, 8, 23) - dt.timedelta(days=366)
print('Query Date:', year_ago_date)
# ##### Max Precipitation Scores For The Last Year in The Dataset
year_prcp=(session.query(Measurement.date,func.max(Measurement.prcp))
.filter(func.strftime('%Y-%m-%d',Measurement.date) > year_ago_date)
.group_by(Measurement.date)
.all())
year_prcp
# ##### Precipitation Query Results as Pandas DataFrame
prcp_df=pd.DataFrame(year_prcp, columns=['date', 'prcp'])
prcp_df.set_index('date',inplace=True)
prcp_df.head(10)
# ##### Precipitation DataFrame Sorted by Date
prcp_df.sort_values('date')
# ##### Daily Maximum Precipitation for One Year in Honolulu, Hawaii
# +
plt.rcParams['figure.figsize']=(15,7)
prcp_df.plot(linewidth=2,alpha=1,rot=0,
xticks=(0,60,120,180,240,300,365),
color='xkcd:deep aqua')
plt.xlim(-5,370)
plt.ylim(-0.4,7)
plt.yticks(size=14)
plt.xticks(fontsize=14)
plt.legend('',frameon=False)
plt.xlabel('Date',fontsize=16,color='black',labelpad=20)
plt.ylabel('Precipitation (in)',fontsize=16,color='black',labelpad=20)
plt.title('Daily Maximum Precipitation for One Year\nHonolulu, Hawaii',fontsize=20,pad=40)
plt.show()
# -
# ##### All Precipitation Scores For The Last Year in The Dataset
year_prcp_stats=(session.query(Measurement.date, Measurement.prcp)
.filter(Measurement.date > year_ago_date)
.all())
year_prcp_stats
year_prcp_stats_df=pd.DataFrame(year_prcp_stats, columns=['date', 'prcp'])
year_prcp_stats_df
year_prcp_stats_df.dropna()
# ##### Summary Statistics For The Precipitation Data
year_prcp_stats_df.describe()
# ---
# ### - Station Analysis
#
# Temperature observation data (TOBS) for the last 12 months and histogram plot for the station with the highest number of observations.
# ---
# ##### Number of Stations in The Dataset
total_stations=session.query(Station).count()
print(f'There are {total_stations} stations at Honolulu, Hawaii.')
# ##### Station Activity
station_activity=(session.query(Measurement.station,func.count(Measurement.station))
.group_by(Measurement.station)
.order_by(func.count(Measurement.station).desc())
.all())
station_activity
# ##### Min, Avg, and Max Temperature Records of The Most Active Station
# +
tobs=[Measurement.station,
func.min(Measurement.tobs),
func.max(Measurement.tobs),
func.avg(Measurement.tobs)]
most_active_st=(session.query(*tobs)
.filter(Measurement.station=='USC00519281')
.all())
most_active_st
most_active_st_temp=pd.DataFrame(most_active_st, columns=['station', 'min_temp',
'max_temp', 'avg_temp'])
most_active_st_temp.set_index('station', inplace=True)
most_active_st_temp
# -
# ##### Temperature Observations Between Aug 2016 and Aug 2017 at USC00519281 Station
year_tobs=(session.query(Measurement.date,(Measurement.tobs))
.filter(func.strftime(Measurement.date) > year_ago_date)
.filter(Measurement.station=='USC00519281')
.all())
year_tobs
# +
tobs_df=pd.DataFrame(year_tobs)
tobs_df.set_index('date',inplace=True)
plt.rcParams['figure.figsize']=(10,7)
plt.hist(tobs_df['tobs'],bins=12,alpha=0.6,edgecolor='xkcd:light gray',
linewidth=1,color='xkcd:deep aqua')
plt.title('Temperature Observation Aug 2016 - Aug 2017\nHonolulu, Hawaii',fontsize=20,pad=40)
plt.xlabel('Temperature (F)',fontsize=16,color='black',labelpad=20)
plt.ylabel('Frequency',fontsize=16,color='black',labelpad=20)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.ylim(0,70)
plt.show()
# -
# ---
# ## Bonus Challenge Assignment
# ---
# +
# This function called `calc_temps` will accept start date and end date in the format '%Y-%m-%d'
# and return the minimum, average, and maximum temperatures for that range of dates
def calc_temps(start_date, end_date):
"""TMIN, TAVG, and TMAX for a list of dates.
Args:
start_date (string): A date string in the format %Y-%m-%d
end_date (string): A date string in the format %Y-%m-%d
Returns:
TMIN, TAVE, and TMAX
"""
return session.query(func.min(Measurement.tobs),
func.avg(Measurement.tobs),
func.max(Measurement.tobs))
.filter(Measurement.date >= start_date)
.filter(Measurement.date <= end_date).all()
# function usage example
print(calc_temps('2012-02-28', '2012-03-05'))
# -
# ---
# ### - Temperature Analysis II
# ---
# ##### Min, Avg, and Max Temperature for The Trip Dates
# +
start_date='2017-08-05'
end_date='2017-08-15'
def calc_temps(start_date,end_date):
return (session.query(func.min(Measurement.tobs),
func.round(
func.avg(Measurement.tobs)),
func.max(Measurement.tobs))
.filter(Measurement.date >= start_date)
.filter(Measurement.date <= end_date)
.all())
trip_temp=calc_temps(start_date,end_date)
#print(trip_temp)
trip_temp_df=pd.DataFrame({'start_date': start_date,
'end_date': end_date,
'min_temp': [trip_temp[0][0]],
'avg_temp': [trip_temp[0][1]],
'max_temp': [trip_temp[0][2]]
})
trip_temp_df.set_index(['start_date','end_date'],inplace=True)
trip_temp_df
# -
# ##### Trip Average Temperature and Error Bar (YERR)
tavg = [int(result[1]) for result in trip_temp[::]]
tavg
# +
tmax_tmin=(session.query(func.max(Measurement.tobs) - func.min(Measurement.tobs))
.filter(Measurement.date >= start_date)
.filter(Measurement.date <= end_date)
.all())
ptp=list(np.ravel(tmax_tmin))
ptp
# +
plt.rcParams['figure.figsize']=(4,7)
tick_locations = [value for value in x_axis]
plt.bar(x_axis,tavg, color='xkcd:teal blue', alpha=0.3, width=0.1,align="center",yerr=ptp[0])
plt.xticks(tick_locations, [(f'From {start_date} To {end_date}')],fontsize=14,color='black')
plt.title('Trip Avg Temperature\nHonolulu, Hawaii',fontsize=20,pad=40)
plt.ylabel('Temperature (F)',fontsize=16,color='black',labelpad=20)
plt.yticks(fontsize=14)
plt.xlim(-0.1,0.1)
plt.ylim(-5,100)
plt.show()
# -
# ---
# ### - Daily Rainfall Estimate
# ---
# ##### Daily Total Rainfall by Station for The Trip Dates
total_prcp_by_st=(session.query(Measurement.station,Station.name,func.sum(Measurement.prcp),
Station.latitude,Station.longitude,Station.elevation)
.filter(Measurement.date >= start_date)
.filter(Measurement.date <= end_date)
.filter(Measurement.station == Station.station)
.group_by(Measurement.station)
.order_by(func.sum(Measurement.prcp)
.desc())
.all())
# +
print(f'Daily total rainfall estimates by station for dates between {start_date} and {end_date}.')
total_prcp_by_st_df=pd.DataFrame(total_prcp_by_st,
columns=['station','name',
'total_prcp','latitude',
'longitude','elevation'])
total_prcp_by_st_df
# -
# ---
# ### - Daily Temperature Normals
# ---
# +
# Create a query that will calculate the daily normals
# (i.e. the averages for tmin, tmax, and tavg for all historic data matching a specific month and day)
def daily_normals(date):
"""Daily Normals.
Args:
date (str): A date string in the format '%m-%d'
Returns:
A list of tuples containing the daily normals, tmin, tavg, and tmax
"""
sel = [func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)]
return session.query(*sel).filter(func.strftime("%m-%d", Measurement.date) == date).all()
daily_normals("01-01")
# -
# ##### Daily Temperature Normals For Trip Dates
# +
trip_dates=['08-05','08-06','08-07','08-08','08-09',
'08-10','08-11','08-12','08-13','08-14','08-15']
normals=[]
def daily_normals(date):
sel = [func.min(Measurement.tobs),
func.round(func.avg(Measurement.tobs),2),
func.max(Measurement.tobs)]
return session.query(*sel).filter(func.strftime("%m-%d", Measurement.date) == date).all()
for i in trip_dates:
normals.append(daily_normals(i)[0])
normals
# +
trip_daily_normals_df=pd.DataFrame(normals,columns=['min_temp','avg_temp','max_temp'],
index=trip_dates)
trip_daily_normals_df.index.name='date'
trip_daily_normals_df
# -
# ##### Trip Daily Temperature Normals Plot
# +
plt.rcParams['figure.figsize']=(11,7)
colors=['xkcd:green yellow','xkcd:very light blue','xkcd:deep aqua']
trip_daily_normals_df.plot.area(linewidth=5,stacked=False,rot=0,alpha=0.5,color=colors);
plt.ylim(-5,100)
plt.yticks(size=14)
plt.xticks(fontsize=14)
plt.xlabel('Date (mm-dd)',fontsize=16,color='black',labelpad=20)
plt.ylabel('Temperature (F)',fontsize=16,color='black',labelpad=20)
plt.title('Daily Temperature Normals\nHonolulu, Hawaii',fontsize=20,pad=40)
plt.gca().legend(loc='center left', bbox_to_anchor=(1.02, 0.91),shadow=True,borderpad=1);
# -
# ---
# ### - Temperature Analysis I
# ---
# +
from sqlalchemy.ext.declarative import declarative_base
from sqlalchemy import Column, Integer, String, Float
class HawaiiPrcpTobs(Base):
__tablename__ = 'prcptobs'
id = Column(Integer, primary_key = True)
station = Column(String)
date = Column(String)
prcp = Column(Float)
tobs = Column(Float)
# -
hm_df=pd.read_csv('Resources/hawaii_measurements.csv')
hm_df
engine=create_engine('sqlite:///hawaii_measurements.sqlite')
hm_df.to_sql('prcptobs', engine, if_exists='append', index=False)
Base.metadata.create_all(engine)
session=Session(bind=engine)
# ##### Testing Data
hm_df=engine.execute('SELECT * FROM prcptobs')
hm_df.fetchall()
print(hm_df.keys())
hm_df=engine.execute('SELECT station FROM prcptobs ORDER BY station')
hm_df.fetchall()
session.query(HawaiiPrcpTobs.station).group_by(HawaiiPrcpTobs.station).all()
session.query(HawaiiPrcpTobs.station,func.max(HawaiiPrcpTobs.tobs)).group_by(HawaiiPrcpTobs.station).all()
# ##### Average Temperature in June and December
from scipy import stats
from scipy import mean
avg_temp_j=(session.query(func.avg(HawaiiPrcpTobs.tobs))
.filter(func.strftime('%m',HawaiiPrcpTobs.date) == '06')
.all())
avg_temp_j
avg_temp_d=(session.query(func.avg(HawaiiPrcpTobs.tobs))
.filter(func.strftime('%m',HawaiiPrcpTobs.date) == '12')
.all())
avg_temp_d
# ##### June TOBS for All Years in The Data Set
june_temp=(session.query(HawaiiPrcpTobs.date,HawaiiPrcpTobs.tobs)
.filter(func.strftime('%m',HawaiiPrcpTobs.date) == '06')
.all())
june_temp
# ##### December TOBS for All Years in The Dataset
december_temp=(session.query(HawaiiPrcpTobs.date,HawaiiPrcpTobs.tobs)
.filter(func.strftime('%m',HawaiiPrcpTobs.date) == '12')
.all())
december_temp
# ##### Filtering Out Null Values From June and December TOBS Lists
# +
j_temp_list = []
for temp in june_temp:
if type(temp.tobs) == int:
j_temp_list.append(temp.tobs)
d_temp_list = []
for temp in december_temp:
if type(temp.tobs) == int:
d_temp_list.append(temp.tobs)
# -
# ##### Average Temperature in June at All Stations Across All Available Years in The Dataset
mean(j_temp_list)
# ##### Average Temperature in December at All Stations Across All Available Years in The Dataset
mean(d_temp_list)
# ##### Paired T-Test
# + Paired t-test is used to determine the difference in the June and December average temperature in Honolulu, Hawaii for a time period between 2010 and 2017. The paired t-test is used because the two compared samples of temperature observations are related to the same location and represent a difference between summer temperature (after a cold season is over) and winter temperature (after a worm season is over).
#
#
# + The null hypothesis in this case is that there is no statistically significant difference in the mean of June temperature and December temperature in Honolulu, Hawaii.
stats.ttest_rel(j_temp_list[0:200],d_temp_list[0:200])
# + The t-statistic value is 21.813, and along with a given degrees of freedom (199) this can be used to calculate a p-value.
#
#
# + The p-value in this case is 1.1468e-54, which is far less than the standard thresholds of 0.05 or 0.01, so the null hypothesis is rejected and it can be concluded that there is a statistically significant difference between the June temperature and the December temperature in Honolulu, Hawaii.
|
ClimateSQLAlchemy/ClimateAnalysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
from IPython.display import display
# read in data files
# item_df = pd.read_csv("kensho-derived-wikimedia-data/item.csv")
# item_aliases_df = pd.read_csv("kensho-derived-wikimedia-data/item_aliases.csv")
item_df = pd.read_csv("kensho-derived-wikimedia-data/items_filtered.csv")
item_aliases_df = pd.read_csv("kensho-derived-wikimedia-data/item_aliases_filtered.csv")
page_df = pd.read_csv("kensho-derived-wikimedia-data/page.csv")
# sampling data from item_df and item_aliases_df
item_df = item_df.dropna()
item_aliases_df = item_aliases_df.dropna()
sampled_items = item_df.sample(n = 10000, random_state=1)
sampled_item_aliases = item_aliases_df.sample(n = 10000, random_state=1)
sampled_items.head()
sampled_item_aliases.head()
page_df.head()
# +
# going through all the items and item_aliases
def get_item_target(name, df):
dataframe = df[df['en_label']==name]
final_view_df = pd.DataFrame(columns = df.columns)
item_ids = list(dataframe['item_id'])
views = []
for item_id in item_ids:
view_df = page_df[page_df['item_id'] == item_id]
final_view_df = pd.concat([final_view_df, view_df])
views = list(final_view_df['views'])
if len(views) != 0:
max_view = max(views)
target = list(final_view_df[final_view_df['views'] == max_view]['page_id'])[0]
return target
def get_alias_target(name, df):
dataframe = df[df['en_alias']==name]
final_view_df = pd.DataFrame(columns = df.columns)
item_ids = list(dataframe['item_id'])
views = []
for item_id in item_ids:
view_df = page_df[page_df['item_id'] == item_id]
final_view_df = pd.concat([final_view_df, view_df])
views = list(final_view_df['views'])
if len(views) != 0:
max_view = max(views)
target = list(final_view_df[final_view_df['views'] == max_view]['page_id'])[0]
return target
predicted_dict = {}
item_names = set(list(sampled_items['en_label'])+list(sampled_item_aliases['en_alias']))
for name in item_names:
if name in set(list(sampled_items['en_label'])):
target = get_item_target(name, sampled_items)
predicted_dict.update({name: target})
elif name in set(list(sampled_item_aliases['en_alias'])):
target = get_alias_target(name, sampled_item_aliases)
predicted_dict.update({name: target})
# -
predicted_df = pd.DataFrame(predicted_dict.items(), columns=['entity name', 'page id'])
predicted_df
# +
# examples
# sentence1 = "<NAME> (born 1957) is an American scientist, professor, and leading researcher in machine learning and artificial intelligence."
sentence = "Christmas Songs is the eighth full-length studio album and first Christmas album from Jars of Clay, that was released on October 16, 2007 through Gray Matters/Nettwerk."
candidates = ["<NAME>", "<NAME>", "<NAME>"]
pool = list(predicted_dict.keys())
for candidate in candidates:
if candidate in set(pool):
print(str(candidate)+":")
page_id = predicted_dict.get(candidate)
cand_df = page_df[page_df['page_id'] == page_id]
display(cand_df)
item_id = list(cand_df['item_id'])[0]
cand_item_df = item_df[item_df['item_id'] == item_id]
display(cand_item_df)
# -
# ### Test for Baseline Model
# readin test data
combined_entity_df = pd.read_csv("test_data/combined_entity.csv")
combined_entity_df.head()
combined_text_df = pd.read_csv("test_data/combined_text.csv")
combined_text_df.head()
single_entity_df = pd.read_csv("test_data/single_entity.csv")
single_entity_df.head()
# +
# random sampling from test data
sampled_entities = combined_entity_df.sample(n = 20000, random_state=1)
sampled_entities.head()
# -
data_array = item_df.to_numpy()
data_alias_array = item_aliases_df.to_numpy()
page_array = page_df.to_numpy()
# +
# test data
# change some dataframe into numpy arrays
def get_item_target(name):
data_array_indices = np.where(data_array[:,1]==name)[0]
item_ids = data_array[:,0][list(data_array_indices)]
views = []
for item_id in item_ids:
page_array_indices = np.where(page_array[:,1]==item_id)[0]
view_array = page_array[list(page_array_indices)]
views.append(view_array)
views = np.array(views)[0]
views = np.asarray(views)
num_views = list(views[:,3])
if len(num_views) != 0:
max_view = max(num_views)
max_view_idx = num_views.index(max_view)
target = views[max_view_idx][0]
return target
def get_alias_target(name):
data_array_indices = np.where(data_alias_array[:,1]==name)[0]
item_ids = data_alias_array[:,0][list(data_array_indices)]
views = []
for item_id in item_ids:
page_array_indices = np.where(page_array[:,1]==item_id)[0]
view_array = page_array[list(page_array_indices)]
views.append(view_array)
views = np.array(views)[0]
views = np.asarray(views)
num_views = list(views[:,3])
if len(num_views) != 0:
max_view = max(num_views)
max_view_idx = num_views.index(max_view)
target = views[max_view_idx][0]
return target
# +
total = 0
correct = 0
test_array = sampled_entities[['entity','page_id']].to_numpy()
item_names = list(item_df['en_label'])
alias_names = list(item_aliases_df['en_alias'])
# +
for i in range(len(test_array)):
if i%1000 == 0:
print(i)
name = test_array[i,0]
if name in item_names:
target = get_item_target(name)
if target == test_array[i,1]:
correct += 1
elif name in alias_names:
target = get_alias_target(name)
if target == test_array[i,1]:
correct += 1
total += 1
accuracy = correct/total
print("The accuracy rate for the baseline model is", accuracy)
# -
# example sentence
text_id = 3
sentence = list(combined_text_df[combined_text_df['text_id'] == text_id]['text'])[0]
candidate_entities = list(combined_entity_df[combined_entity_df['text_id'] == text_id]['entity'])
print(sentence)
print(candidate_entities)
# +
for candidate in candidate_entities:
if candidate in item_names:
target = get_item_target(candidate)
if target is not None:
print(str(candidate))
target_item = list(page_df[page_df['page_id'] == target]['item_id'])[0]
print("Predicted entity:")
display(item_df[item_df['item_id'] == target_item])
print("Actual entity:")
actual_pre = combined_entity_df[combined_entity_df['text_id'] == text_id]
actual = list(actual_pre[actual_pre['entity'] == candidate]['page_id'])[0]
actual_item = list(page_df[page_df['page_id'] == actual]['item_id'])[0]
display(item_df[item_df['item_id'] == actual_item])
elif candidate in alias_names:
target = get_alias_target(candidate)
if target is not None:
print(str(candidate))
target_item = list(page_df[page_df['page_id'] == target]['item_id'])[0]
print("Predicted entity:")
display(item_aliases_df[item_aliases_df['item_id'] == target_item])
print("Actual entity:")
actual_pre = combined_entity_df[combined_entity_df['text_id'] == text_id]
actual = list(actual_pre[actual_pre['entity'] == candidate]['page_id'])[0]
actual_item = list(page_df[page_df['page_id'] == actual]['item_id'])[0]
display(item_aliases_df[item_aliases_df['item_id'] == actual_item])
# +
# example sentence
text_id = 9
sentence = list(combined_text_df[combined_text_df['text_id'] == text_id]['text'])[0]
candidate_entities = list(combined_entity_df[combined_entity_df['text_id'] == text_id]['entity'])
print(sentence)
for candidate in candidate_entities:
if candidate in item_names:
target = get_item_target(candidate)
if target is not None:
print(str(candidate))
target_item = list(page_df[page_df['page_id'] == target]['item_id'])[0]
print("Predicted entity:")
display(item_df[item_df['item_id'] == target_item])
print("Actual entity:")
actual_pre = combined_entity_df[combined_entity_df['text_id'] == text_id]
actual = list(actual_pre[actual_pre['entity'] == candidate]['page_id'])[0]
actual_item = list(page_df[page_df['page_id'] == actual]['item_id'])[0]
display(item_df[item_df['item_id'] == actual_item])
elif candidate in alias_names:
target = get_alias_target(candidate)
if target is not None:
print(str(candidate))
target_item = list(page_df[page_df['page_id'] == target]['item_id'])[0]
print("Predicted entity:")
display(item_aliases_df[item_aliases_df['item_id'] == target_item])
print("Actual entity:")
actual_pre = combined_entity_df[combined_entity_df['text_id'] == text_id]
actual = list(actual_pre[actual_pre['entity'] == candidate]['page_id'])[0]
actual_item = list(page_df[page_df['page_id'] == actual]['item_id'])[0]
display(item_aliases_df[item_aliases_df['item_id'] == actual_item])
# -
|
baseline_model/baseline model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 任务2 数据清洗(2天)
# +
#coding:utf-8
#导入warnings包,利用过滤器来实现忽略警告语句。
import warnings
warnings.filterwarnings('ignore')
# GBDT
from sklearn.ensemble import GradientBoostingRegressor
# XGBoost
import xgboost as xgb
# LightGBM
import lightgbm as lgb
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import KFold
from sklearn.metrics import r2_score
from sklearn.preprocessing import LabelEncoder
import pickle
import multiprocessing
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
from sklearn.model_selection import StratifiedKFold
from sklearn.linear_model import ElasticNet, Lasso, BayesianRidge, LassoLarsIC,LinearRegression,LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import RobustScaler
from sklearn.model_selection import train_test_split
from sklearn.ensemble import IsolationForest
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
# -
#载入数据
data_train = pd.read_csv('./train_data.csv')
data_train['Type'] = 'Train'
data_test = pd.read_csv('./test_a.csv')
data_test['Type'] = 'Test'
data_all = pd.concat([data_train, data_test], ignore_index=True)
fea_cols = [col for col in data_train.columns]
# # 异常值处理
data_train.head(5)
print(fea_cols)
# **该数据集房屋面积特征有明显异常值**
sns.regplot(x=data_train['area'],y=data_train['tradeMoney'])
# **孤立森林:基于Ensemble的快速异常检测方法**
# +
# clean data
def IF_drop(train):
IForest = IsolationForest(contamination=0.01)
IForest.fit(train["tradeMoney"].values.reshape(-1,1))
y_pred = IForest.predict(train["tradeMoney"].values.reshape(-1,1))
drop_index = train.loc[y_pred==-1].index
print(len(drop_index))
print(drop_index)
train.drop(drop_index,inplace=True)
return train
data_train = IF_drop(data_train)
# data_train.head(5)
# -
def dropData(train):
# 丢弃部分异常值
train = train[train.area <= 200]
train = train[(train.tradeMoney <=16000) & (train.tradeMoney >=700)]
train.drop(train[(train['totalFloor'] == 0)].index, inplace=True)
sns.regplot(x=data_train['area'],y=data_train['tradeMoney'])
plt.show()
return train
#数据集异常值处理
data_train = dropData(data_train)
print('len(data_train):', len(data_train))
# 处理异常值后再次查看面积和租金分布图
plt.figure(figsize=(15,5))
sns.boxplot(data_train.area)
plt.show()
plt.figure(figsize=(15,5))
sns.boxplot(data_train.tradeMoney),
plt.show()
# # 缺失值处理、数据变换
# **缺失值的处理方式:**<br>
# - 删除带有缺失值的特征,最简单也最浪费信息的方式<br>
# - 用均值,众数或固定的数等填充,比1好,但仍不够好<br>
# - 考虑缺失的含义,把缺失值作为一种信息<br>
# - 用未缺失的数据训练模型,预测缺失的数据(分类型变量用分类算法,数值型变量用回归)<br>
# (tip:把训练集和测试集合并处理,减少代码量)
#
data_train.head(5)
# +
def preprocessingData(data):
# 填充缺失值
data['rentType'][data['rentType'] == '--'] = '未知方式'
# 转换object类型数据
columns = ['rentType', 'houseType', 'houseFloor', 'houseToward', 'houseDecoration', 'communityName', 'plate']
for feature in columns:
data[feature] = LabelEncoder().fit_transform(data[feature])
# 将buildYear列转换为整型数据
buildYearmean = pd.DataFrame(data[data['buildYear'] != '暂无信息']['buildYear'].mode())
data.loc[data[data['buildYear'] == '暂无信息'].index, 'buildYear'] = buildYearmean.iloc[0, 0]
data['buildYear'] = data['buildYear'].astype('int')
# 处理pv和uv的空值填充为平均值
data['pv'].fillna(data['pv'].mean(), inplace=True)
data['uv'].fillna(data['uv'].mean(), inplace=True)
data['pv'] = data['pv'].astype('int')
data['uv'] = data['uv'].astype('int')
# 分割交易时间
def month(x):
month = int(x.split('/')[1])
return month
def day(x):
day = int(x.split('/')[2])
return day
data['month'] = data['tradeTime'].apply(lambda x: month(x))
data['day'] = data['tradeTime'].apply(lambda x: day(x))
# 去掉部分特征:city=SH, ID唯一,
data.drop('city', axis=1, inplace=True)
data.drop('tradeTime', axis=1, inplace=True)
data.drop('ID', axis=1, inplace=True)
return data
data_train = preprocessingData(data_train)
data_train
# -
# # 深度清洗
data_train[data_train['region']=='RG00001']
# +
def cleanData(data):
data.drop(data[(data['region']=='RG00001') & (data['tradeMoney']<1000)&(data['area']>50)].index,inplace=True)
data.drop(data[(data['region']=='RG00001') & (data['tradeMoney']>25000)].index,inplace=True)
data.drop(data[(data['region']=='RG00001') & (data['area']>250)&(data['tradeMoney']<20000)].index,inplace=True)
data.drop(data[(data['region']=='RG00001') & (data['area']>400)&(data['tradeMoney']>50000)].index,inplace=True)
data.drop(data[(data['region']=='RG00001') & (data['area']>100)&(data['tradeMoney']<2000)].index,inplace=True)
data.drop(data[(data['region']=='RG00002') & (data['area']<100)&(data['tradeMoney']>60000)].index,inplace=True)
data.drop(data[(data['region']=='RG00003') & (data['area']<300)&(data['tradeMoney']>30000)].index,inplace=True)
data.drop(data[(data['region']=='RG00003') & (data['tradeMoney']<500)&(data['area']<50)].index,inplace=True)
data.drop(data[(data['region']=='RG00003') & (data['tradeMoney']<1500)&(data['area']>100)].index,inplace=True)
data.drop(data[(data['region']=='RG00003') & (data['tradeMoney']<2000)&(data['area']>300)].index,inplace=True)
data.drop(data[(data['region']=='RG00003') & (data['tradeMoney']>5000)&(data['area']<20)].index,inplace=True)
data.drop(data[(data['region']=='RG00003') & (data['area']>600)&(data['tradeMoney']>40000)].index,inplace=True)
data.drop(data[(data['region']=='RG00004') & (data['tradeMoney']<1000)&(data['area']>80)].index,inplace=True)
data.drop(data[(data['region']=='RG00006') & (data['tradeMoney']<200)].index,inplace=True)
data.drop(data[(data['region']=='RG00005') & (data['tradeMoney']<2000)&(data['area']>180)].index,inplace=True)
data.drop(data[(data['region']=='RG00005') & (data['tradeMoney']>50000)&(data['area']<200)].index,inplace=True)
data.drop(data[(data['region']=='RG00006') & (data['area']>200)&(data['tradeMoney']<2000)].index,inplace=True)
data.drop(data[(data['region']=='RG00007') & (data['area']>100)&(data['tradeMoney']<2500)].index,inplace=True)
data.drop(data[(data['region']=='RG00010') & (data['area']>200)&(data['tradeMoney']>25000)].index,inplace=True)
data.drop(data[(data['region']=='RG00010') & (data['area']>400)&(data['tradeMoney']<15000)].index,inplace=True)
data.drop(data[(data['region']=='RG00010') & (data['tradeMoney']<3000)&(data['area']>200)].index,inplace=True)
data.drop(data[(data['region']=='RG00010') & (data['tradeMoney']>7000)&(data['area']<75)].index,inplace=True)
data.drop(data[(data['region']=='RG00010') & (data['tradeMoney']>12500)&(data['area']<100)].index,inplace=True)
data.drop(data[(data['region']=='RG00004') & (data['area']>400)&(data['tradeMoney']>20000)].index,inplace=True)
data.drop(data[(data['region']=='RG00008') & (data['tradeMoney']<2000)&(data['area']>80)].index,inplace=True)
data.drop(data[(data['region']=='RG00009') & (data['tradeMoney']>40000)].index,inplace=True)
data.drop(data[(data['region']=='RG00009') & (data['area']>300)].index,inplace=True)
data.drop(data[(data['region']=='RG00009') & (data['area']>100)&(data['tradeMoney']<2000)].index,inplace=True)
data.drop(data[(data['region']=='RG00011') & (data['tradeMoney']<10000)&(data['area']>390)].index,inplace=True)
data.drop(data[(data['region']=='RG00012') & (data['area']>120)&(data['tradeMoney']<5000)].index,inplace=True)
data.drop(data[(data['region']=='RG00013') & (data['area']<100)&(data['tradeMoney']>40000)].index,inplace=True)
data.drop(data[(data['region']=='RG00013') & (data['area']>400)&(data['tradeMoney']>50000)].index,inplace=True)
data.drop(data[(data['region']=='RG00013') & (data['area']>80)&(data['tradeMoney']<2000)].index,inplace=True)
data.drop(data[(data['region']=='RG00014') & (data['area']>300)&(data['tradeMoney']>40000)].index,inplace=True)
data.drop(data[(data['region']=='RG00014') & (data['tradeMoney']<1300)&(data['area']>80)].index,inplace=True)
data.drop(data[(data['region']=='RG00014') & (data['tradeMoney']<8000)&(data['area']>200)].index,inplace=True)
data.drop(data[(data['region']=='RG00014') & (data['tradeMoney']<1000)&(data['area']>20)].index,inplace=True)
data.drop(data[(data['region']=='RG00014') & (data['tradeMoney']>25000)&(data['area']>200)].index,inplace=True)
data.drop(data[(data['region']=='RG00014') & (data['tradeMoney']<20000)&(data['area']>250)].index,inplace=True)
data.drop(data[(data['region']=='RG00005') & (data['tradeMoney']>30000)&(data['area']<100)].index,inplace=True)
data.drop(data[(data['region']=='RG00005') & (data['tradeMoney']<50000)&(data['area']>600)].index,inplace=True)
data.drop(data[(data['region']=='RG00005') & (data['tradeMoney']>50000)&(data['area']>350)].index,inplace=True)
data.drop(data[(data['region']=='RG00006') & (data['tradeMoney']>4000)&(data['area']<100)].index,inplace=True)
data.drop(data[(data['region']=='RG00006') & (data['tradeMoney']<600)&(data['area']>100)].index,inplace=True)
data.drop(data[(data['region']=='RG00006') & (data['area']>165)].index,inplace=True)
data.drop(data[(data['region']=='RG00012') & (data['tradeMoney']<800)&(data['area']<30)].index,inplace=True)
data.drop(data[(data['region']=='RG00007') & (data['tradeMoney']<1100)&(data['area']>50)].index,inplace=True)
data.drop(data[(data['region']=='RG00004') & (data['tradeMoney']>8000)&(data['area']<80)].index,inplace=True)
data.loc[(data['region']=='RG00002')&(data['area']>50)&(data['rentType']=='合租'),'rentType']='整租'
data.loc[(data['region']=='RG00014')&(data['rentType']=='合租')&(data['area']>60),'rentType']='整租'
data.drop(data[(data['region']=='RG00008')&(data['tradeMoney']>15000)&(data['area']<110)].index,inplace=True)
data.drop(data[(data['region']=='RG00008')&(data['tradeMoney']>20000)&(data['area']>110)].index,inplace=True)
data.drop(data[(data['region']=='RG00008')&(data['tradeMoney']<1500)&(data['area']<50)].index,inplace=True)
data.drop(data[(data['region']=='RG00008')&(data['rentType']=='合租')&(data['area']>50)].index,inplace=True)
data.drop(data[(data['region']=='RG00015') ].index,inplace=True)
data.reset_index(drop=True, inplace=True)
data['region'] = LabelEncoder().fit_transform(data['region'])
return data
data_train = cleanData(data_train)
data_train
# -
|
2_Clearing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # if, else, elif
if 1 == 1:
print('Hey, one is equal to one. what is going on ? ')
# +
a = 10
if a > 5:
print('Whoo')
print('and whooo')
# -
a = 20
if a > 10:
print('Big number')
else:
print('The number is small')
# +
a = int(input('Give me a number'))
if a < 10:
print('low')
elif a < 20:
print('mid')
else:
print('high')
# -
a = input()
a
type(a)
a = int(a)
type(a)
a
# +
a = 5
if a <2:
print(1)
if a < 7:
print(2)
# -
|
07 - if else.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
# set the current working directory. This is required by isaac.
# This cell should only run once.
os.chdir("../../../")
os.getcwd()
# +
from IPython.display import display
import json
import numpy as np
from packages.pyalice import Application, Codelet
from packages.pyalice.gui.composite_widget import CompositeWidget
np.set_printoptions(precision=3)
# -
# A Python codelet for joint control through widget
class JointControl(Codelet):
def start(self):
self.rx = self.isaac_proto_rx("CompositeProto", "state")
self.tx = self.isaac_proto_tx("CompositeProto", "command")
self._widget = CompositeWidget(self.config.joints, self.config.measure, self.config.limits)
if self._widget is None:
report_failure("Cannot create valid widget")
return
display(self._widget.panel)
self.tick_periodically(0.1)
def tick(self):
state_msg = self.rx.message
if state_msg is None:
return
self._widget.composite = state_msg
self.tx._msg = self._widget.composite
if self.tx._msg is not None:
self.tx.publish()
# UR10 with LQR planner in Omniverse Isaac Sim
# ======
#
# Open the ur10_playground stage in Kit, start Robot Engine Bridge and hit Play before continuing
# set kinematic file and get list of joints
kinematic_file = "apps/assets/kinematic_trees/ur10.kinematic.json"
joints = []
with open(kinematic_file,'r') as fd:
kt = json.load(fd)
for link in kt['links']:
if 'motor' in link and link['motor']['type'] != 'constant':
joints.append(link['name'])
print(joints)
# +
app = Application(name="simple_joint_control_lqr_ur10_sim")
# load subgraphs
app.load(filename="packages/planner/apps/multi_joint_lqr_control.subgraph.json", prefix="lqr")
app.load(filename="packages/navsim/apps/navsim_tcp.subgraph.json", prefix="simulation")
# edges
simulation_node = app.nodes["simulation.interface"]
lqr_interface = app.nodes["lqr.subgraph"]["interface"]
app.connect(simulation_node["output"], "joint_state", lqr_interface, "joint_state")
app.connect(lqr_interface, "joint_command", simulation_node["input"], "joint_position")
# configs
app.nodes["lqr.kinematic_tree"]["KinematicTree"].config.kinematic_file = kinematic_file
lqr_planner = app.nodes["lqr.local_plan"]["MultiJointLqrPlanner"]
lqr_planner.config.speed_min = [-1.0] * len(joints)
lqr_planner.config.speed_max = [1.0] * len(joints)
lqr_planner.config.acceleration_min = [-1.0] * len(joints)
lqr_planner.config.acceleration_max = [1.0] * len(joints)
# add pycodelet JointControl for arm control
joint_commander = app.add("command_generator").add(JointControl)
joint_commander.config.joints = joints
joint_commander.config.limits = [[-2*np.pi, 2*np.pi]] * len(joints)
joint_commander.config.measure = "position"
app.connect(joint_commander, "command", lqr_interface, "joint_target")
app.connect(simulation_node["output"], "joint_state", joint_commander, "state")
# add pycodelet JointControl for finger control
finger_commander = app.add("finger_generator").add(JointControl)
finger_commander.config.joints = ["gripper"]
finger_commander.config.limits = [[0.0, 1.0]] * len(finger_commander.config.joints)
finger_commander.config.measure = "none"
app.connect(finger_commander, "command", simulation_node["input"], "io_command")
app.connect(simulation_node["output"], "io_state", finger_commander, "state")
app.start()
# -
# stop Isaac app
app.stop()
# UR10 with RMP planner in Omniverse Isaac Sim
# ======
#
# Open the ur10_playground stage in Kit, start Robot Engine Bridge and hit Play before continuing
# set kinematic file and get list of joints
kinematic_file = "apps/assets/kinematic_trees/ur10.kinematic.json"
joints = []
with open(kinematic_file,'r') as fd:
kt = json.load(fd)
for link in kt['links']:
if 'motor' in link and link['motor']['type'] != 'constant':
joints.append(link['name'])
print(joints)
# +
app = Application(name="simple_joint_control_rmp_ur10_sim")
# load subgraphs
app.load(filename="packages/planner/apps/multi_joint_rmp_control.subgraph.json", prefix="rmp")
app.load(filename="packages/navsim/apps/navsim_tcp.subgraph.json", prefix="simulation")
# edges
simulation_node = app.nodes["simulation.interface"]
rmp_interface = app.nodes["rmp.subgraph"]["interface"]
app.connect(simulation_node["output"], "joint_state", rmp_interface, "joint_state")
app.connect(rmp_interface, "joint_command", simulation_node["input"], "joint_position")
# configs
app.nodes["rmp.kinematic_tree"]["KinematicTree"].config.kinematic_file = kinematic_file
rmp_planner = app.nodes["rmp.local_plan"]["MultiJointRmpPlanner"]
rmp_planner.config.rmpflow_config_file = "apps/assets/lula_assets/ur10_rmpflow_config.yaml"
rmp_planner.config.robot_description_file = "apps/assets/lula_assets/ur10_robot_description.yaml"
rmp_planner.config.robot_urdf = "apps/assets/lula_assets/ur10_robot.urdf"
rmp_planner.config.end_effector_frame = "tool"
# add pycodelet JointPositionControl
widget_node = app.add("command_generator")
joint_commander = widget_node.add(JointControl)
joint_commander.config.joints = joints
joint_commander.config.limits = [[-2*np.pi, 2*np.pi]] * len(joints)
joint_commander.config.measure = "position"
app.connect(joint_commander, "command", rmp_interface, "joint_target")
app.connect(simulation_node["output"], "joint_state", joint_commander, "state")
app.start()
# -
# stop Isaac app
app.stop()
# Kinova Jaco (gen2, 7 joints) Hardware
# ======
#
# Install the KinoveJaco SDK in /opt/JACO2SDK (tested with v1.4.2) and connect to workstation via USB. Make sure the USB port has write permission
kinematic_file = "apps/assets/kinematic_trees/kinova.kinematic.json"
joints = []
with open(kinematic_file,'r') as fd:
kt = json.load(fd)
for link in kt['links']:
if 'motor' in link and link['motor']['type'] != 'constant':
joints.append(link['name'])
print(joints)
# +
app = Application(name="simple_joint_control_kinova_real")
# load lqr subgraphcs
app.load(filename="packages/planner/apps/multi_joint_lqr_control.subgraph.json", prefix="lqr")
lqr_interface = app.nodes["lqr.subgraph"]["interface"]
# add kinova driver codelet
app.load_module("kinova_jaco")
driver = app.add("driver").add(app.registry.isaac.kinova_jaco.KinovaJaco)
# edges
app.connect(driver, "arm_state", lqr_interface, "joint_state")
app.connect(lqr_interface, "joint_command", driver, "arm_command")
# configs
app.nodes["lqr.kinematic_tree"]["KinematicTree"].config.kinematic_file = kinematic_file
lqr_planner = app.nodes["lqr.local_plan"]["MultiJointLqrPlanner"]
lqr_planner.config.speed_min = [-0.5] * len(joints)
lqr_planner.config.speed_max = [0.5] * len(joints)
lqr_planner.config.acceleration_min = [-0.5] * len(joints)
lqr_planner.config.acceleration_max = [0.5] * len(joints)
app.nodes["lqr.controller"]["MultiJointController"].config.control_mode = "speed"
driver.config.kinematic_tree = "lqr.kinematic_tree"
driver.config.kinova_jaco_sdk_path = "/opt/JACO2SDK/API/"
driver.config.tick_period = "10ms"
driver.config.control_mode = "joint velocity"
# add pycodelet JointControl for arm control
joint_commander = app.add("command_generator").add(JointControl)
joint_commander.config.joints = joints
joint_commander.config.limits = [[-2*np.pi, 2*np.pi]] * len(joints)
joint_commander.config.measure = "position"
app.connect(joint_commander, "command", lqr_interface, "joint_target")
app.connect(driver, "arm_state", joint_commander, "state")
# add pycodelet JointControl for finger control
finger_commander = app.add("finger_generator").add(JointControl)
finger_commander.config.joints = ["finger1", "finger2", "finger3"]
finger_commander.config.limits = [[0.0, 1.0]] * len(finger_commander.config.joints)
finger_commander.config.measure = "none"
app.connect(finger_commander, "command", driver, "finger_command")
app.connect(driver, "finger_state", finger_commander, "state")
app.start()
# -
app.stop()
|
sdk/apps/samples/manipulation/simple_joint_control.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/pantelis/PRML/blob/master/notebooks/ch01_Introduction.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="ceRmVgOq6XmY"
# # 1. Introduction
# + [markdown] id="Wj_RTULpriir"
# <table class="tfo-notebook-buttons" align="left">
#
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/pantelis/PRML/blob/master/notebooks/ch01_Introduction.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# </table>
# + id="TMxmVuag7eyA" outputId="e7a14285-f2ef-4457-e802-f2f488679beb" colab={"base_uri": "https://localhost:8080/", "height": 34}
from google.colab import drive
drive.mount('/content/drive')
# + id="F3rYRMAD6ynO"
# You need to adjust the directory names below for your own account
# e.g. you may elect to create ms-notebooks dir or not
# Execute this cell once
# 1. Download the repo and set it as the current directory
# %cd /content/drive/My Drive/Colab Notebooks/ml-notebooks
# !git clone https://github.com/pantelis/PRML
# %cd /content/drive/My Drive/Colab Notebooks/ml-notebooks/PRML
# 2. install the project/module
# !python setup.py install
# + id="iv9ADzLqiNsU" outputId="4be99758-4704-43df-cfca-5b190e0f7043" colab={"base_uri": "https://localhost:8080/", "height": 34}
# 3. Add the project directory to the path
# %cd /content/drive/My Drive/Colab Notebooks/ml-notebooks/PRML
import os, sys
sys.path.append(os.getcwd())
# + id="qwxjFZSR_vuX"
# Import seaborn
import seaborn as sns
# Apply the default theme
sns.set_theme()
# + id="pxBLdL3r6XmZ"
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
from prml.preprocess import PolynomialFeature
from prml.linear import (
LinearRegression,
RidgeRegression,
BayesianRegression
)
np.random.seed(1234)
# + [markdown] id="TWjYKLNc6Xmd"
# ## 1.1. Example: Polynomial Curve Fitting
# + [markdown] id="6XPE-VC_-OYK"
# The cell below defines $p_{data}(y|x)$ and generates the $\hat p_{data}(y|x)$
# + id="Tj4RTV3X6Xmd" outputId="0baceadf-7645-418a-c6eb-2a06134b4c00" colab={"base_uri": "https://localhost:8080/", "height": 285}
def create_toy_data(func, sample_size, std):
x = np.linspace(0, 1, sample_size) # p(x)
y = func(x) + np.random.normal(scale=std, size=x.shape)
return x, y
def func(x):
return np.sin(2 * np.pi * x)
x_train, y_train = create_toy_data(func, 10, 0.25)
x_test = np.linspace(0, 1, 100)
y_test = func(x_test)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.legend()
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()
# + id="diJlsNGo6Xmg" outputId="f13b190d-24bd-4904-b9e7-fb3240dabe70" colab={"base_uri": "https://localhost:8080/", "height": 442}
plt.subplots(figsize=(20, 10))
for i, degree in enumerate([0, 1, 3, 9]):
plt.subplot(2, 2, i + 1)
feature = PolynomialFeature(degree)
X_train = feature.transform(x_train)
X_test = feature.transform(x_test)
model = LinearRegression()
model.fit(X_train, y_train)
y = model.predict(X_test)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, y, c="r", label="hypothesis")
plt.ylim(-1.5, 1.5)
plt.annotate("M={}".format(degree), xy=(-0.15, 1))
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.legend(bbox_to_anchor=(1.05, 0.64), loc=2, borderaxespad=0.)
plt.show()
# + id="nfpg434z6Xmj" outputId="596e2af7-bb0c-4f96-dfcd-b5ab841107eb" colab={"base_uri": "https://localhost:8080/", "height": 285}
def rmse(a, b):
return np.sqrt(np.mean(np.square(a - b)))
training_errors = []
test_errors = []
for i in range(10):
feature = PolynomialFeature(i)
X_train = feature.transform(x_train)
X_test = feature.transform(x_test)
model = LinearRegression()
model.fit(X_train, y_train)
y = model.predict(X_test)
training_errors.append(rmse(model.predict(X_train), y_train))
test_errors.append(rmse(model.predict(X_test), y_test + np.random.normal(scale=0.25, size=len(y_test))))
plt.plot(training_errors, 'o-', mfc="none", mec="b", ms=10, c="b", label="Training")
plt.plot(test_errors, 'o-', mfc="none", mec="r", ms=10, c="r", label="Test")
plt.legend()
plt.xlabel("model capacity (degree)")
plt.ylabel("RMSE")
plt.show()
# + [markdown] id="PTOLlihm6Xml"
# #### Regularization
# + id="18aoGaUg6Xml" outputId="f144ee73-3e4c-4986-d1ac-2c9a61d9b337" colab={"base_uri": "https://localhost:8080/", "height": 289}
feature = PolynomialFeature(9)
X_train = feature.transform(x_train)
X_test = feature.transform(x_test)
model = RidgeRegression(alpha=1e-3)
model.fit(X_train, y_train)
y = model.predict(X_test)
#y = model.predict(X_test)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, y, c="r", label="hypothesis")
plt.ylim(-1.5, 1.5)
plt.legend()
plt.annotate("M=9", xy=(-0.15, 1))
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()
# + [markdown] id="kfmJy1-96Xmo"
# ### 1.2.6 Bayesian curve fitting
# + id="GFCXxwiz6Xmo" outputId="85c564ea-96a2-4c9a-da36-b245f8dccfb2" colab={"base_uri": "https://localhost:8080/", "height": 289}
model = BayesianRegression(alpha=2e-3, beta=2)
model.fit(X_train, y_train)
y, y_err = model.predict(X_test, return_std=True)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, y, c="r", label="mean")
plt.fill_between(x_test, y - y_err, y + y_err, color="pink", label="std.", alpha=0.5)
plt.xlim(-0.1, 1.1)
plt.ylim(-1.5, 1.5)
plt.annotate("M=9", xy=(0.8, 1))
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.legend(bbox_to_anchor=(1.05, 1.), loc=2, borderaxespad=0.)
plt.show()
# + id="i4VIskNS6Xmt"
|
notebooks/ch01_Introduction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Graphical Causal Models
#
#
# ## Thinking About Causality
#
# Have you ever noticed how those cooks in YouTube videos are excellent at describing food? "Reduce the sauce until it reaches a velvety consistency". If you are just starting to learn how to cook, you have no idea what this even means. Just give me the time I should leave this thing on the stove! With causality, it's the same thing. If you walk into a bar and hear folks discussing causality (probably a bar next to an economics department), you will hear them say how the confounding of income made it challenging to identify the imigration effect on that neighborhood, so they had to use an instrumental variable. And by now, you might not understand what they are talking about. But I'll fix at least some of this problem right now.
#
# Graphical models is the language of causality. Is what you use not only to talk with other brave and true causality aficionados, but it is also something you use to make your own thoughts clearer.
#
# As a starting point, let's take conditional independence of the potential outcomes, for example. This is one of the main assumptions that we require to be true when doing causal inference:
#
# $
# (Y_0, Y_1) \perp T | X
# $
#
# Conditional Independence makes it possible for us to measure an effect on the outcome that is solely due to the treatment, and not any other variable lurking around. The classic example of this is the effect of a medicine on an ill patient. If only severely ill patients get the drug, it might even look like giving the drug decreases the patients' health. That is because the effect of the severity is getting mixed up with the effect of the drug. If, however, we break down the patients by severe and not severe cases and analyse the drug impact in each subgroup, we will get a more clear picture of what the true effect is. This breaking down the population by its features is what we call controlling for or conditioning on X. By conditioning on the severe cases, the treatment mechanism becomes as good as random. Patients within the severe group may or may not receive the drug only due to chance, not due a high severity anymore, since all patients are the same on this dimension. And if treatment is as if randomly assigned within groups, the treatment becomes conditionally independent of the potential outcomes.
#
# Independence and conditional independence are central to causal inference. Yet, it can be quite challenging to wrap our head around them. But this can change if we use the right language to describe this problem. Here is where **causal graphical models** comes in. A causal graphical model is a way to represent how causality works in terms of what causes what.
#
# A graphical model looks like this
# + tags=["hide-input"]
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import graphviz as gr
from matplotlib import style
import seaborn as sns
from matplotlib import pyplot as plt
style.use("fivethirtyeight")
# + tags=["hide-input"]
g = gr.Digraph()
g.edge("Z", "X")
g.edge("U", "X")
g.edge("U", "Y")
g.edge("medicine", "survived")
g.edge("severeness", "survived")
g.edge("severeness", "medicine")
g
# -
# Each node is a random variable. We use arrows, or edges, to show if a variable causes another. In the first graphical model above we are saying that Z causes X and that U causes X and Y. To give a more concrete example, we can translate our thoughts about the impact of the medicine on patient survival as the second graph above. Severeness causes both medicine and survival and medicine also causes survival. As we will see, this causal graphical models language will help us make our thinking about causality more clear, as it makes it explicit our beliefs about how the world works.
#
# ## Crash Course in Graphical Models
#
# There are [whole semesters on graphical models](https://www.coursera.org/specializations/probabilistic-graphical-models). But, for our purpose, it is just (very) important that we understand what kind of independence and conditional independence assumptions a graphical model entails. As we shall see, independence flows through a graphical model like water flows through a stream. We can stop this flow or we can enable it, depending on how we treat the variables in it. To understand this, let's examine some common graphical structures and examples. They will be quite simple, but they are the sufficient building blocks to understand everything about independence and conditional independence on graphical models.
#
# First, look at this very simple graph. A causes B, B causes C. Or X causes Y which causes Z.
# + tags=["hide-input"]
g = gr.Digraph()
g.edge("A", "B")
g.edge("B", "C")
g.edge("X", "Y")
g.edge("Y", "Z")
g.node("Y", "Y", color="red")
g.edge("causal knowledge", "solve problems")
g.edge("solve problems", "job promotion")
g
# -
# In the first graph, dependence flows in the direction of the arrows. To give a more concrete example, let's say that knowing about causal inference is the only way to solve business problems and solving those problems is the only way to get a job promotion. So causal knowledge causes problem solving which causes job promotion. We can say here that job promotion is dependent on causal knowledge. The greater the causal knowledge, the greater your chances of getting a promotion. Notice that dependence is symmetric, although it is a little less intuitive. The greater your chances of promotion, the greater the chance you have causal knowledge, otherwise it would be difficult to get a promotion.
#
# Now, let's say I condition on the intermediary variable. In this case, the dependence is blocked. So, X and Z are independent given Y. By the same token, in our example, if I know that you are good at solving problems, knowing that you know causal inference doesn't give any further information about your chances of getting a job promotion. In mathematical terms, \\(E[Promotion|Solve \ problems, Causal \ knowledge]=E[Promotion|Solve \ problems]\\). The inverse is also true, once I know how good you are at solving problems, knowing about your job promotion status gives me no further information about how likely you are to know causal inference.
#
# As a general rule, the dependence flow in the direct path from A to B is blocked when we condition on an intermediary variable C. Or,
#
# $A \not\!\perp\!\!\!\perp B$
#
# and
#
# $
# A \!\perp\!\!\!\perp B | C
# $
#
# Now, let's consider a fork structure. In this case, the same variable causes two other variables down the graph. In this case, the dependence flows backward through the arrows and we have what it is called a **backdoor path**. We can close the backdoor path and shut down dependence by conditioning on the common cause.
# + tags=["hide-input"]
g = gr.Digraph()
g.edge("C", "A")
g.edge("C", "B")
g.edge("X", "Y")
g.edge("X", "Z")
g.node("X", "X", color="red")
g.edge("statistics", "causal inference")
g.edge("statistics", "machine learning")
g
# -
# As an example, let's say your knowledge of statistics causes you to know more of causal inference and machine learning. If I don't know your level of statistical knowledge, then knowing that you are good at causal inference makes it more likely that you are also good at machine learning. That is because even if I don't know your level of statistical knowledge, I can infer it from your causal inference knowledge: if you are good at causal inference you are probably good at statistics, which also makes it more likely that you are good at machine learning.
#
# Now, if I condition on your knowledge about statistics, then how much you know about machine learning becomes independent of how much you know about causal inference. You see, knowing your level of statistics already gives me all the information I need to infer the level of your machine learning skills. Knowing your level of causal inference will give no further information in this case.
#
# As a general rule, two variables that share a common cause are dependent, but independent when we condition on the common cause. Or
#
# $A \not\!\perp\!\!\!\perp B$
#
# and
#
# $
# A \!\perp\!\!\!\perp B | C
# $
#
# The only structure that is missing is the collider. A collider is when two arrows collide on a single variable. We can say that in this case if both variables share a common effect.
# + tags=["hide-input"]
g = gr.Digraph()
g.edge("B", "C")
g.edge("A", "C")
g.edge("Y", "X")
g.edge("Z", "X")
g.node("X", "X", color="red")
g.edge("statistics", "job promotion")
g.edge("flatter", "job promotion")
g
# -
# As an example, consider that there are two ways to get a job promotion. You can either be good at statistics or flatter your boss. If I don't condition on your job promotion, that is, I know nothing if you will or won't get it, then your level of statistics and flattering are independent. In other words, knowing how good you are at statistics tells me nothing about how good you are at flattering your boss. On the other hand, if you did get a job promotion, suddenly, knowing your level of statistics tells me about your level of flattering. If you are bad at statistics and you did get a promotion, it becomes more likely that you know how to flatter, otherwise you wouldn't get a promotion. Conversely, if you are bad at flattering, it must be the case that you are good at statistics. This phenomenon is sometimes called **explaining away**, because one cause already explains the effect, making the other cause less likely.
#
# As a general rule, conditioning on a collider opens the dependence path. Not conditioning on it leaves it closed. Or
#
# $A \!\perp\!\!\!\perp B$
#
# and
#
# $
# A \not\!\perp\!\!\!\perp B | C
# $
#
# Knowing the three structures, we can derive an even more general rule. A path is blocked if and only if:
# 1. It contains a non collider that has been conditioned on
# 2. It contains a collider that has not been conditioned on and has no descendants that have been conditioned on.
#
# Here is a cheat sheet about how dependence flows in a graph. I've taken from a [Stanford presentation](http://ai.stanford.edu/~paskin/gm-short-course/lec2.pdf) by <NAME>.
# 
#
# As a final example, try to figure out some independence and dependence relationship in the following causal graph.
# 1. Is \\(D \perp C\\)?
# 2. Is \\(D \perp C| A \\) ?
# 3. Is \\(D \perp C| G \\) ?
# 4. Is \\(A \perp F \\) ?
# 5. Is \\(A \perp F|E \\) ?
# 6. Is \\(A \perp F|E,C \\) ?
# + tags=["hide-input"]
g = gr.Digraph()
g.edge("C", "A")
g.edge("C", "B")
g.edge("D", "A")
g.edge("B", "E")
g.edge("F", "E")
g.edge("A", "G")
g
# -
# **Answers**:
# 1. \\(D \perp C\\). It contains a collider that it has **not** been conditioned on.
# 2. \\(D \not\perp C| A \\). It contains a collider that it has been conditioned on.
# 3. \\(D \not\perp C| G \\). It contains the descendent of a collider that has been conditioned on. You can see G as some kind of proxy for A here.
# 4. \\(A \perp F \\). It contains a collider, B->E<-F, that it has **not** been conditioned on.
# 5. \\(A \not\perp F|E \\). It contains a collider, B->E<-F, that it has been conditioned on.
# 6. \\(A \perp F|E, C \\). It contains a collider, B->E<-F, that it has been conditioned on, but it contains a non collider that has been conditioned on. Conditioning on E opens the path, but conditioning on C closes it again.
#
# Knowing about causal graphical models enables us to understand the problems that arise in causal inference. As we've seen, the problem always boils down to bias.
#
# $
# E[Y|T=1] - E[Y|T=0] = \underbrace{E[Y_1 - Y_0|T=1]}_{ATET} + \underbrace{\{ E[Y_0|T=1] - E[Y_0|T=0] \}}_{BIAS}
# $
#
# Graphical models allow us to diagnose which bias we are dealing with and what are the tools we need to correct for them.
#
# ## Confounding Bias
#
# 
#
# The first big cause of bias is confounding. It happens when the treatment and the outcome shares a common cause. For example, let's say that the treatment is education and the outcome is income. It is hard to know the causal effect of education on the wage because both share a common cause: intelligence. So we could make the argument that more educated people earn more money simply because they are more intelligent, not because they have more education. In order to identify the causal effect, we need to close all backdoor paths between the treatment and the outcome. If we do so, the only effect that will be left is the direct effect T->Y. In our example, if we control for intelligence, that is, we compare people with the same level of intelligence but different levels of education, the difference in the outcome will be only due to the difference in education, since intelligence will be the same for everyone. In order to fix confounding bias, we need to control all common causes of the treatment and the outcome.
# + tags=["hide-input"]
g = gr.Digraph()
g.edge("X", "T")
g.edge("X", "Y")
g.edge("T", "Y")
g.edge("Inteligence", "Educ"),
g.edge("Inteligence", "Wage"),
g.edge("Educ", "Wage")
g
# -
# Unfortunately, it is not always possible to control for all common causes. Sometimes, there are unknown causes or known causes that we can't measure. The case of intelligence is one of the latter. Despite all the effort, scientists haven't yet figured out how to measure intelligence well. I'll use U to denote unmeasured variables here. Now, assume for a moment that intelligence can't affect your education directly. It just affects how well you do on the SATs, but it is the SATs that determine your level of education, since it opens the possibility of a good college. Even if we can't control for the unmeasurable intelligence, we can control for SAT and close that backdoor path.
# + tags=["hide-input"]
g = gr.Digraph()
g.edge("X1", "T")
g.edge("T", "Y")
g.edge("X2", "T")
g.edge("X1", "Y")
g.edge("U", "X2")
g.edge("U", "Y")
g.edge("Family Income", "Educ")
g.edge("Educ", "Wage")
g.edge("SAT", "Educ")
g.edge("Family Income", "Wage")
g.edge("Inteligence", "SAT")
g.edge("Inteligence", "Wage")
g
# -
# In the following graph, conditioning on X1 and X2, or, SAT and family income, is sufficient to close all backdoor paths between the treatment and the outcome. In other words, \\((Y_0, Y_1) \perp T | X1, X2\\). So even if we can't measure all common causes, we can still attain conditional independence if we control for measurable variables that mediate the effect of the unmeasured on the treatment.
#
# But what if that is not the case? What if the unmeasured variable causes the treatment and the outcome directly? In the following example, intelligence causes education and income directly. So there is confounding on the relationship between the treatment education and the outcome wage. In this case, we can't control the confounder, because it is unmeasurable. However, we have other measured variables that can act as a proxy for the confounder. Those variables are not in the backdoor path, but controlling for them will help lower the bias (but it won't eliminate it). Those variables are sometimes referred to as surrogate confounders.
#
# In our example, we can't measure intelligence, but we can measure some causes of it, like the father's and mother's education, and some effects of it, like IQ or SAT score. Controlling for those surrogate variables is not sufficient to eliminate bias, but it sure helps.
# + tags=["hide-input"]
g = gr.Digraph()
g.edge("X", "U")
g.edge("U", "T")
g.edge("T", "Y")
g.edge("U", "Y")
g.edge("Inteligence", "QI")
g.edge("Inteligence", "SAT")
g.edge("Father's Educ", "Inteligence")
g.edge("Mother's Educ", "Inteligence")
g.edge("Inteligence", "Educ")
g.edge("Educ", "Wage")
g.edge("Inteligence", "Wage")
g
# -
# ## Selection Bias
#
# You might think that it is a good idea to add everything you can measure to your model just to be sure you don't have confounding bias. Well, think again.
#
# 
#
# The second big source of bias is what we will call selection bias. If confounding bias happens when we don't control for a common cause, selection bias is more related to effects. One word of caution here, economists tend to refer to all sorts of bias as selection bias. Here, I think the distinction between it and confounding bias is very helpful, so I'll stick to it.
#
# More often than not, selection bias arises when we control for more variables that we should. It might be the case that the treatment and the potential outcome are marginally independent, but become dependent once we condition on a collider.
#
# Imagine that with the help of some miracle you are finally able to randomize education in order to measure its effect on wage. But just to be sure you won't have confounding, you control for a lot of variables. Among them, you control for investments. But investment is not a common cause of education and wage. Instead, it is a consequence of both. More educated people both earn more and invest more. Also, those who earn more invest more. Since investment is a collider, by conditioning on it, you are opening a second path between the treatment and the outcome, which will make it harder to measure the direct effect. One way to think about this is that by controlling investments, you are looking at small groups of the population where investment is the same and then finding the effect of education on those groups. But by doing so, you are also indirectly and inadvertently not allowing wages to change much. As a result, you won't be able to see how education changes wage, because you are not allowing wages to change as it should.
# + tags=["hide-input"]
g = gr.Digraph()
g.edge("T", "X")
g.edge("T", "Y")
g.edge("Y", "X")
g.node("X", "X", color="red")
g.edge("Educ", "Investments")
g.edge("Educ", "Wage")
g.edge("Wage", "Investments")
g
# -
# To demonstrate why this is the case, imagine that investments and education takes only 2 values. Either people invest or not. They are either educated or not. Initially, when we don't control for investments, the bias term is zero \\(E[Y_0|T=1] - E[Y_0|T=0] = 0\\) because the education was randomised. This means that the wage people would have in the case they didn't receive education \\(Wage_0\\) is the same if they do or don't receive the education treatment. But what happens if we condition on investments?
#
# Looking at those that invest, we probably have the case that \\(E[Y_0|T=0, I=1] > E[Y_0|T=1, I=1]\\). In words, among those that invest, those that manage to do so even without education are more independent of education to achieve high earnings. For this reason, the wage those people have, \\(Wage_0|T=0\\), is probably higher than the wage the educated group would have in the case that they didn't had education, \\(Wage_0|T=1\\). A similar reasoning can be applied to those that don't invest, where we also probably have \\(E[Y_0|T=0, I=0] > E[Y_0|T=1, I=0]\\). Those that don't invest even with education, probably would have a lower wage, had they not got the education, than those that didn't invest but also didn't have education.
#
# To use a purely graphical argument, if someone invests, knowing that they have high education explains away the second cause which is wage. Conditioned on investing, higher education is associated with low wages and we have a negative bias \\(E[Y_0|T=0, I=i] > E[Y_0|T=1, I=i]\\).
#
# Just as a side note, all of this we've discussed is also true if we condition on any descendent of a common effect.
# + tags=["hide-input"]
g = gr.Digraph()
g.edge("T", "X")
g.edge("T", "Y")
g.edge("Y", "X")
g.edge("X", "S")
g.node("S", "S", color="red")
g
# -
# A similar thing happens when we condition on a mediator of the treatment. A mediator is a variable between the treatment and the outcome. It, well, mediates the causal effect. For example, suppose again you are able to randomize education. But, just to be sure, you decide to control whether or not the person had a white collar job. Once again, this conditioning biasses the causal effect estimation. This time, not because it opens a front door path with a collider, but because it closes one of the channels through which the treatment operates. In our example, getting a white collar job is one way that more education leads to higher pay. By controlling it, we close this channel and leave open only the direct effect of education on wage.
# + tags=["hide-input"]
g = gr.Digraph()
g.edge("T", "X")
g.edge("T", "Y")
g.edge("X", "Y")
g.node("X", "X", color="red")
g.edge("educ", "white collar")
g.edge("educ", "wage")
g.edge("white collar", "wage")
g
# + [markdown] tags=["hide-input"]
# To give a potential outcome argument, we know that, due to randomisation, the bias is zero \\(E[Y_0|T=0] - E[Y_0|T=1] = 0\\). However, if we condition on the white collar individuals, we have that \\(E[Y_0|T=0, WC=1] > E[Y_0|T=1, WC=1]\\). That is because those that manage to get a white collar job even without education are probably more hard working than those that required the help of education to get the same job. With the same reasoning, \\(E[Y_0|T=0, WC=0] > E[Y_0|T=1, WC=0]\\) because those that didn't get a white collar job even with education are probably less hard working than those that didn't, but also didn't have any education.
#
# In our case, conditioning on the mediator induces a negative bias. It makes the effect of education seem lower than it actually is. This is the case because the causal effect is positive. If the effect were negative, conditioning on a mediator would have a positive bias. In all cases, this sort of conditioning makes the effect look weaker than it is.
#
# To put it in a more prosaic way, suppose that you have to choose between two candidates for a job at your company. Both have equally impressive professional achievements, but one does not have a higher education degree. Which one should you choose? Of course, you should go with the one without the higher education, because he managed to achieve the same things as the other one but had the odds stacked against him.
#
# 
#
# ## Key Ideas
#
# We've studied graphical models as a language to better understand and express causality ideas. We did a quick summary on the rules of conditional independence on a graph. This helped us then explore three structures that can lead to bias.
#
# The first one was confounding, which happens when treatment and outcome have a common cause that we don't account or control for. The second is selection bias due to conditioning on a common effect. This excessive controlling can lead to bias even if the treatment was randomly assigned. The third structure is also a form of selection bias, this time due to excessive controlling of mediator variables. Selection bias can often be fixed by simply doing nothing, which is why it is so dangerous. Since we are biased to action, we tend to see ideas that control for things as clever, when they can be doing more harm than good.
#
# ## References
#
# I like to think of this entire book as a tribute to <NAME>, <NAME> and <NAME> for their amazing Econometrics class. Most of the ideas here are taken from their classes at the American Economic Association. Watching them is what is keeping me sane during this tough year of 2020.
# * [Cross-Section Econometrics](https://www.aeaweb.org/conference/cont-ed/2017-webcasts)
# * [Mastering Mostly Harmless Econometrics](https://www.aeaweb.org/conference/cont-ed/2020-webcasts)
#
# I'll also like to reference the amazing books from Angrist. They have shown me that Econometrics, or 'Metrics as they call it, is not only extremely useful but also profoundly fun.
#
# * [Mostly Harmless Econometrics](https://www.mostlyharmlesseconometrics.com/)
# * [Mastering 'Metrics](https://www.masteringmetrics.com/)
#
# My final reference is <NAME> and <NAME>' book. It has been my trustworthy companion in the most thorny causal questions I had to answer.
#
# * [Causal Inference Book](https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/)
#
#
# 
#
# ## Contribute
#
# Causal Inference for the Brave and True is an open-source material on causal inference, the statistics of science. It uses only free software, based in Python. Its goal is to be accessible monetarily and intellectually.
# If you found this book valuable and you want to support it, please go to [Patreon](https://www.patreon.com/causal_inference_for_the_brave_and_true). If you are not ready to contribute financially, you can also help by fixing typos, suggesting edits or giving feedback on passages you didn't understand. Just go to the book's repository and [open an issue](https://github.com/matheusfacure/python-causality-handbook/issues). Finally, if you liked this content, please share it with others who might find it useful and give it a [star on GitHub](https://github.com/matheusfacure/python-causality-handbook/stargazers).
# -
|
causal-inference-for-the-brave-and-true/04-Graphical-Causal-Models.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # NumPy Fundamentals
# ### 1. Run the following cells:
import numpy as np
array_1D = np.array([10,11,12,13, 14])
array_1D
array_2D = np.array([[20,30,40,50,60], [43,54,65,76,87], [11,22,33,44,55]])
array_2D
array_3D = np.array([[[1,2,3,4,5], [11,21,31,41,51]], [[11,12,13,14,15], [51,52,53,54,5]]])
array_3D
# ### 2. Display the first element (not necessarily individual element) for each of the 3 arrays we defined above.
array_1D = np.array([10,11,12,13, 14])
# ### 3. Call the first individual element of the each of the 3 arrays.
# ### 4. Uses negative indices to display the last element of each array.
# ### 5. Set the penultimate (second-to-last) <i> individual </i> element of each array equal to 10. Then display the variables to check your work.
# (<b>Hint</b>: If it's the penultimate individual element of the 2-D/3-D array, it needs to be in the last row of the 2-D array)
# ### 6. Set the last column of the 2-D array to 100. Then display the variables to check your work.
# ### 7. Set all the values of the 3-D array to 1000. Then display the variables to check your work.
# ### 8. Run the next 3 cells to re-define the 3 arrays, since we altered their contents.
array_1D = np.array([10,11,12,13,14])
array_1D
array_2D = np.array([[20,30,40,50,60], [43,54,65,76,87], [11,22,33,44,55]])
array_2D
array_3D = np.array([[[1,2,3,4,5], [11,21,31,41,51]], [[11,12,13,14,15], [51,52,53,54,5]]])
array_3D
# ### 9. Add 2 to every element of the 3 arrays without overwriting their values.
# ### 10. Multiply the values of each array by 100 without overwriting their values.
# ### 11. Add up <i>array_1D</i> and the first row of <i>array_2D</i>
# ### 12. Find the product of <i>array_1D</i> and the first row of <i>array_2D</i>
# ### 13. Find the product of the first row of <i>array_2D</i> and the first row of the first array of <i> array_3D </i>
# ### 14. Subtract <i> array_1D </i> from the first row of <i>array_2D</i>
# ### 15. Subtract the first row of <i>array_2D</i> from <i> array_1D </i>
# ### 16. Alter the code in the next 3 cells to re-define the 3 arrays as the following datatypes:
# A) array_1D -> NumPy Strings
# B) array_2D -> Complex Numbers
# C) array_3D -> 64-bit Floats
#
# (<b>Hint</b>: The datatypes are the following: <i>np.str</i>, <i>np.complex</i>, <i>np.float64</i>)
array_1D = np.array([10,11,12,13,14])
array_1D
array_2D = np.array([[20,30,40,50,60], [43,54,65,76,87], [11,22,33,44,55]])
array_2D
array_3D = np.array([[[1,2,3,4,5], [11,21,31,41,51]], [[11,12,13,14,15], [51,52,53,54,5]]])
array_3D
# ### 17. Now run the next 3 cells to re-define the 3 arrays as 32-bit floats, since we want to run some more computations on them
array_1D = np.array([10,11,12,13,14], dtype = np.float32)
array_1D
array_2D = np.array([[20,30,40,50,60], [43,54,65,76,87], [11,22,33,44,55]], dtype = np.float32)
array_2D
array_3D = np.array([[[1,2,3,4,5], [11,21,31,41,51]], [[11,12,13,14,15], [51,52,53,54,5]]], dtype = np.float32)
array_3D
# ### 18. Use broadcasting to subtract <i>array_1D</i> from every row of <i> array_2D </i>
# (<b>Hint</b>: You **don't** need a function to do this.)
# ### 19. Use broadcasting to divide all rows of <i>array_3D</i> by <i> array_1D </i>
# ### 19. Use broadcasting to find the product of all rows of <i>array_3D</i> and the last row of <i> array_2D </i>
# ### 20. Since these products are all integers, let's cast them as such
# (<b>Hint</b>: You can use the np.array() function here)
# ### 21. Let's use axis argument of the np.mean() function to find the mean for every column of the 2-D array
# ### 22. Let's use axis argument of the np.mean() function to find the mean for every column of the 3-D array
# (<b>Hint</b>: Make sure you define the correct axis.)
|
.ipynb_checkpoints/NumPy-Fundamentals-Exercise-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: TFA-GAMMA
# language: python
# name: tf-max-tfa-gamma
# ---
# + [markdown] id="cQ0KLSD0cxSw"
# # DCASE-2021 Audio Subnetwork
# + [markdown] id="_HegByO_cxSz"
# Author: <NAME>
#
# + id="wR2B5EtFcxSz"
# Import necessary standard packages
import tensorflow as tf
import numpy as np
import pandas as pd
from pathlib import Path
import matplotlib.pyplot as plt
#import tensorflow_addons as tfa
# + id="QWgw824wcxS0" outputId="c49b5a2c-e4c9-4414-c2cf-e6279c85cac1"
tf.version.VERSION
# + [markdown] id="5Xss3nXzcxS1"
# ## Input Data
# + [markdown] id="ElCr0orjcxS1"
# Specify path to folder containing the video dataset and the output path for the tfrecords:
# + id="fomAiOFscxS1" outputId="386dab06-c93a-4732-c3c5-8097b0cd6962"
# TFRecords folder
main_dir = '.\\tfrecords_gamma'
root_path = Path(main_dir)
# Train Fold
train_fold_path = '.\\dataset\\evaluation_setup\\fold1_train.csv'
traindf = pd.read_csv(train_fold_path, sep='\t', lineterminator='\r')
trainlist = traindf[traindf.columns[1]].tolist()
trainfiles = [Path(f).with_suffix('.tfrecords').name for f in trainlist]
# Validation Fold
val_fold_path = '.\\dataset\\evaluation_setup\\fold1_test.csv'
valdf = pd.read_csv(val_fold_path, sep='\t', lineterminator='\r')
vallist = valdf[valdf.columns[1]].tolist()
valfiles = [Path(f).with_suffix('.tfrecords').name for f in vallist]
len(trainfiles), len(valfiles)
# + [markdown] id="huDvG5tTcxS2"
# Get class weights:
# + id="0GARU3dtcxS2"
def get_label(filepath):
'''Receives a path to a video and returns its label
'''
scn_dict = {'airport': 0, 'shopping_mall': 1, 'metro_station': 2,
'street_pedestrian': 3, 'public_square': 4, 'street_traffic': 5,
'tram': 6, 'bus': 7, 'metro': 8, 'park': 9}
fileid = Path(filepath).name
scn_id = fileid.split('-')[0]
label = scn_dict[scn_id]
return label
# Get labels
train_labels = [get_label(f) for f in trainfiles]
val_labels = [get_label(f) for f in valfiles]
trainfiles = [main_dir + '\\' + str(label) + '\\' + f for f,label in zip(trainfiles,train_labels)]
valfiles = [main_dir + '\\' + str(label) + '\\' + f for f,label in zip(valfiles,val_labels)]
N_val = len(valfiles)
# Get number of examples per class
num_class_ex = []
for i in range(10):
num_class_ex.append(train_labels.count(i))
# Get class weights
N_train = len(train_labels)
num_classes = 10
class_weights = []
for i in range(num_classes):
weight = ( 1 / num_class_ex[i]) * N_train / num_classes
class_weights.append(weight)
keylst = np.arange(0,len(class_weights))
class_weights = {keylst[i]: class_weights[i] for i in range(0, len(class_weights))}
# + [markdown] id="qtkmYVlFcxS2"
# ### Parsing function
# + id="cUb9YHl_cxS2"
def parse_sequence(sequence_example, avmode = 'audiovideo'):
"""this function is the sequence parser for the created TFRecords file"""
sequence_features = {'VideoFrames': tf.io.FixedLenSequenceFeature([], dtype=tf.string),
'Labels': tf.io.FixedLenSequenceFeature([], dtype=tf.int64)}
context_features = {'AudioFrames': tf.io.FixedLenFeature((96000,), dtype=tf.float32),
'length': tf.io.FixedLenFeature([], dtype=tf.int64)}
context, sequence = tf.io.parse_single_sequence_example(
sequence_example, context_features=context_features, sequence_features=sequence_features)
# get features context
seq_length = tf.cast(context['length'], dtype = tf.int32)
# decode video and audio
video = tf.io.decode_raw(sequence['VideoFrames'], tf.uint8)
video = tf.reshape(video, shape=(seq_length, 224, 224, 3))
audio = tf.cast(context['AudioFrames'], tf.float32)
audio = tf.reshape(audio, shape=(64, 500, 3))
label = tf.cast(sequence['Labels'], dtype = tf.int32)
if avmode == 'audio':
return audio, label
elif avmode == 'video':
return video, label
elif avmode == 'audiovideo':
return video, audio, label
# + [markdown] id="KC55t-F_cxS3"
# Check parsing function:
# + id="y-r_Mg0qcxS3" outputId="22a5b9e1-d6fd-4d62-a279-cad126981fa7"
# Check parsing function
filesds = tf.data.Dataset.from_tensor_slices(trainfiles)
dataset = tf.data.TFRecordDataset(filesds)
dataset = dataset.map(lambda tf_file: parse_sequence(tf_file,'audio'), num_parallel_calls=4)
datait = iter(dataset)
example = datait.get_next()
print(example[0].shape, example[1].shape)
# + id="dglweANEcxS4" outputId="f7f02aae-b60c-414b-a908-9b8f9cfc69f7"
plt.figure(figsize=(12,1.5));
plt.imshow(example[0][:,:,0]);
plt.colorbar();
# + [markdown] id="o6ZLZzQIcxS4"
# ## Augmentation
# + id="sAm33QFbcxS4"
def sample_beta_distribution(size, concentration_0=0.2, concentration_1=0.2):
gamma_1_sample = tf.random.gamma(shape=[size], alpha=concentration_1)
gamma_2_sample = tf.random.gamma(shape=[size], alpha=concentration_0)
return gamma_1_sample / (gamma_1_sample + gamma_2_sample)
def mix_up(ds_one, ds_two, alpha=0.2):
# Unpack two datasets
images_one, labels_one = ds_one
images_two, labels_two = ds_two
batch_size = tf.shape(images_one)[0]
# Sample lambda and reshape it to do the mixup
l = sample_beta_distribution(batch_size, alpha, alpha)
x_l = tf.reshape(l, (batch_size, 1, 1, 1))
y_l = tf.reshape(l, (batch_size, 1))
# Perform mixup on both images and labels by combining a pair of images/labels
# (one from each dataset) into one image/label
images = images_one * x_l + images_two * (1 - x_l)
labels = labels_one * y_l + labels_two * (1 - y_l)
return (images, labels)
# + [markdown] id="YwJSGaCfcxS4"
# ## Pipeline
# + [markdown] id="f_D2CHjQcxS5"
# Useful functions for the pipeline
# + id="RNYmzbahcxS5"
def random_cut_gamma(audio, cut_length):
"""Selects randomly a segment of size cut_length from the input audio acroos dimension 0"""
seq_length = tf.shape(audio)[0]
min_v = 0
max_v = seq_length - cut_length
rnum = tf.random.uniform([1], minval=min_v, maxval=max_v, dtype=tf.dtypes.int32)
audio = audio[:,rnum[0]:rnum[0]+cut_length,:]
return audio
def normalize_sp(sp):
sp = sp - tf.math.reduce_min(sp)
sp = sp / tf.math.reduce_max(sp)
sp = 2*(sp-0.5)
return sp
def process_ds_audio_train(audio,label):
audio = random_cut_gamma(audio, 50)
audio = normalize_sp(audio)
# process label, get one label per example
label = label[0]
label = tf.one_hot(label,10)
return audio, label
def process_ds_audio_val(audio,label):
audio = tf.transpose(audio,(1,0,2))
audio = tf.reshape(audio, shape=(10,50,64,3))
audio =tf.map_fn(fn=lambda t: normalize_sp(t) , elems=audio)
audio = tf.transpose(audio,(0,2,1,3))
# process label, get ten labels per example
label = label[0:10]
label = tf.one_hot(label,10)
return audio, label
# + id="aCV7OV4jcxS5" outputId="74e2e5ca-ee34-4825-d75a-ade26c9a9e60"
train_batch_size = 32
# Create two differente datasets that are mixed with mix-up
train_ds_one = tf.data.Dataset.from_tensor_slices(trainfiles)
train_ds_one = train_ds_one.shuffle(N_train)
train_ds_one = train_ds_one.repeat()
train_ds_one = tf.data.TFRecordDataset(train_ds_one)
train_ds_one = train_ds_one.map(lambda tf_file: parse_sequence(tf_file,'audio'), num_parallel_calls=4)
train_ds_one = train_ds_one.map(lambda audio, label: process_ds_audio_train(audio, label), num_parallel_calls=4)
train_ds_one = train_ds_one.batch(train_batch_size)
train_ds_two = tf.data.Dataset.from_tensor_slices(trainfiles)
train_ds_two = train_ds_two.shuffle(N_train)
train_ds_two = train_ds_two.repeat()
train_ds_two = tf.data.TFRecordDataset(train_ds_two)
train_ds_two = train_ds_two.map(lambda tf_file: parse_sequence(tf_file,'audio'), num_parallel_calls=4)
train_ds_two = train_ds_two.map(lambda audio, label: process_ds_audio_train(audio, label), num_parallel_calls=4)
train_ds_two = train_ds_two.batch(train_batch_size)
train_ds = tf.data.Dataset.zip((train_ds_one, train_ds_two))
# Mix-up
trainds = train_ds.map(
lambda ds_one, ds_two: mix_up(ds_one, ds_two, alpha=0.4), num_parallel_calls=4
)
valds = tf.data.Dataset.from_tensor_slices(valfiles)
valds = tf.data.TFRecordDataset(valds)
valds = valds.map(lambda tf_file: parse_sequence(tf_file,'audio'), num_parallel_calls=4)
valds = valds.map(lambda audio, label: process_ds_audio_val(audio, label), num_parallel_calls=4)
datait = iter(valds)
example = datait.get_next()
print(example[0].shape, example[1].shape)
# + id="vvpUC77WcxS5" outputId="308a27a6-fa09-4fed-d2d3-a3855b177bf3"
plt.imshow(example[0][0,:,:,0]);
plt.colorbar();
# + [markdown] id="5ydt03crcxS5"
# ## Squeeze-Excite Network (without TD)
# + id="62pYrNDJcxS6" outputId="6a4459f1-24ca-4b36-d503-7d1f419dcfdf"
from tensorflow.keras.layers import (Conv2D, Dense, Permute, GlobalAveragePooling2D, GlobalMaxPooling2D,
Reshape, BatchNormalization, ELU, Lambda, Input, MaxPooling2D, Activation,
Dropout, add, multiply)
import tensorflow.keras.backend as k
from tensorflow.keras.models import Model
import tensorflow as tf
from tensorflow.keras.regularizers import l2
regularization = l2(0.0001)
def construct_asc_network_csse(include_classification=True, nclasses=10, **parameters):
"""
Args:
include_classification (bool): include classification layer
**parameters (dict): setting use to construct the network presented in
(https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=9118879)
"""
nfilters = parameters['nfilters']
pooling = parameters['pooling']
dropout = parameters['dropout']
top_flatten = parameters['top_flatten']
ratio = parameters['ratio']
pre_act = parameters['pre_act']
spectrogram_dim = parameters['spectrogram_dim']
verbose = parameters['verbose']
inp = Input(shape=spectrogram_dim)
for i in range(0, len(nfilters)):
if i == 0:
x = conv_standard_post(inp, nfilters[i], ratio, pre_act=pre_act)
else:
x = conv_standard_post(x, nfilters[i], ratio, pre_act=pre_act)
x = MaxPooling2D(pool_size=pooling[i])(x)
x = Dropout(rate=dropout[i])(x)
if top_flatten == 'avg':
x = GlobalAveragePooling2D()(x)
elif top_flatten == 'max':
x = GlobalMaxPooling2D()(x)
if include_classification:
x = Dense(units=nclasses, activation='softmax', name='SP_Pred')(x)
model = Model(inputs=inp, outputs=x)
if verbose:
print(model.summary())
return model
def conv_standard_post(inp, nfilters, ratio, pre_act=False):
"""
Block presented in (https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=9118879)
Args:
inp (tensor): input to the block
nfilters (int): number of filters of a specific block
ratio (int): ratio used in the channel excitation
pre_act (bool): presented in this work, use a pre-activation residual block
Returns:
"""
x1 = inp
if pre_act:
x = BatchNormalization()(inp)
x = ELU()(x)
x = Conv2D(nfilters, 3, padding='same')(x)
x = BatchNormalization()(x)
x = Conv2D(nfilters, 3, padding='same')(x)
else:
x = Conv2D(nfilters, 3, padding='same')(inp)
x = BatchNormalization()(x)
x = ELU()(x)
x = Conv2D(nfilters, 3, padding='same')(x)
x = BatchNormalization()(x)
# shortcut
x1 = Conv2D(nfilters, 1, padding='same')(x1)
x1 = BatchNormalization()(x1)
x = module_addition(x, x1)
x = ELU()(x)
x = channel_spatial_squeeze_excite(x, ratio=ratio)
x = module_addition(x, x1)
return x
def channel_spatial_squeeze_excite(input_tensor, ratio=16):
""" Create a spatial squeeze-excite block
Args:
input_tensor: input Keras tensor
ratio: number of output filters
Returns: a Keras tensor
References
- [Squeeze and Excitation Networks](https://arxiv.org/abs/1709.01507)
- [Concurrent Spatial and Channel Squeeze & Excitation in Fully Convolutional Networks]
(https://arxiv.org/abs/1803.02579)
"""
cse = squeeze_excite_block(input_tensor, ratio)
sse = spatial_squeeze_excite_block(input_tensor)
x = add([cse, sse])
return x
def squeeze_excite_block(input_tensor, ratio=16):
""" Create a channel-wise squeeze-excite block
Args:
input_tensor: input Keras tensor
ratio: number of output filters
Returns: a Keras tensor
References
- [Squeeze and Excitation Networks](https://arxiv.org/abs/1709.01507)
"""
init = input_tensor
channel_axis = 1 if k.image_data_format() == "channels_first" else -1
filters = _tensor_shape(init)[channel_axis]
se_shape = (1, 1, filters)
se = GlobalAveragePooling2D()(init)
se = Reshape(se_shape)(se)
se = Dense(filters // ratio, activation='relu', kernel_initializer='he_normal', use_bias=False)(se)
se = Dense(filters, activation='sigmoid', kernel_initializer='he_normal', use_bias=False)(se)
if k.image_data_format() == 'channels_first':
se = Permute((3, 1, 2))(se)
x = multiply([init, se])
return x
def spatial_squeeze_excite_block(input_tensor):
""" Create a spatial squeeze-excite block
Args:
input_tensor (): input Keras tensor
Returns: a Keras tensor
References
- [Concurrent Spatial and Channel Squeeze & Excitation in Fully Convolutional Networks]
(https://arxiv.org/abs/1803.02579)
"""
se = Conv2D(1, (1, 1), activation='sigmoid', use_bias=False,
kernel_initializer='he_normal')(input_tensor)
x = multiply([input_tensor, se])
return x
def module_addition(inp1, inp2):
"""
Module of addition of two tensors with same H and W, but can have different channels
If number of channels of the second tensor is the half of the other, this dimension is repeated
Args:
inp1 (tensor): one branch of the addition module
inp2 (tensor): other branch of the addition module
Returns:
"""
if k.int_shape(inp1)[3] != k.int_shape(inp2)[3]:
x = add(
[inp1, Lambda(lambda y: k.repeat_elements(y, rep=int(k.int_shape(inp1)[3] // k.int_shape(inp2)[3]),
axis=3))(inp2)])
else:
x = add([inp1, inp2])
return x
def _tensor_shape(tensor):
"""
Obtain shape in order to use channel excitation
Args:
tensor (tensor): input tensor
Returns:
"""
return tensor.get_shape()
audio_network_settings = {
'nfilters': (32, 64, 128),
#'pooling': [(2, 1), (2, 1), (2, 1)],
'pooling': [(1, 2), (1, 2), (1, 1)],
'dropout': [0.0, 0.0, 0.0],
'top_flatten': 'avg',
'ratio': 2,
'pre_act': False,
'spectrogram_dim': (64, 50, 3),
'verbose': True
}
audio_model = construct_asc_network_csse(include_classification=True, **audio_network_settings)
# + [markdown] id="3qIVTptWcxS7"
# ## Compile and Train
# + id="oMb5GXnQcxS9"
learning_rate = 0.001
opt = tf.keras.optimizers.Adam(learning_rate = learning_rate)
audio_model.compile(
loss = {'SP_Pred': 'categorical_crossentropy'},
optimizer=opt,
metrics = {'SP_Pred': 'accuracy'},
)
from tensorflow.keras.callbacks import CSVLogger, ModelCheckpoint, EarlyStopping, ReduceLROnPlateau
import os
callbacks = []
ckpt_dir = 'WHERE_TO_STORE\checkpoints_audio'
model_name = 'audio_final'
callbacks.append(
ModelCheckpoint(
filepath=os.path.join(ckpt_dir, '%s-{epoch:02d}-{val_accuracy:.2f}.hdf5' % model_name),
monitor="val_accuracy",
mode="max",
save_best_only=True,
save_weights_only=True,
verbose=True,
)
)
callbacks.append(
EarlyStopping(
monitor="val_loss",
patience=80,
)
)
callbacks.append(
ReduceLROnPlateau(
monitor="val_loss",
factor=0.5,
patience=15,
verbose=True,
)
)
callbacks.append(
CSVLogger(
filename = os.path.join(ckpt_dir, '%s.csv' % model_name),
append = False,
)
)
# + id="ZXP3MicwcxS9"
# Train model
history = audio_model.fit(
trainds,
epochs=200,
steps_per_epoch= int(N_train/train_batch_size), # Set according to number of examples and training batch size
validation_data = valds,
validation_steps = int(N_val),
callbacks=callbacks, # Include list of callbacks
#class_weight = class_weights,
)
# + id="bRmoU4TDcxS9"
plt.figure(figsize=(16,5))
plt.subplot(1,2,1)
# summarize history for accuracy
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.subplot(1,2,2)
# summarize history for loss
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
|
train_audio.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Ruby 2.7.1
# language: ruby
# name: ruby
# ---
# +
$LOAD_PATH << File.dirname(__FILE__) + "/../lib"
require 'toji'
require './example_core'
require 'rbplotly'
cal = Example::Calendar.load_yaml_file("calendar.yaml")
cal.products.each {|product|
puts "%s %s" % [product.serial_num, product.description]
product.recipe.table.tap {|t|
t.layout.height = 350
}.show
}
cal.table.tap {|t|
t.layout.height = 1000
}.show
nil
# -
|
example/calendar_file.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1 align="center"> Circuit Analysis Using Sympy</h1>
# <h2 align="center"> Assignment 7</h2>
# <h3 align="center"> <NAME>,EE17B109</h3>
# <h4 align="center">March 16,2019 </h4>
# # Introduction
# In this assignment, we use Sympy to analytically solve a matrix equation governing an analog circuit. We look at two circuits, an active low pass filter and an active high pass filter. We create matrices using node equations for the circuits in sympy, and then solve the equations analytically. We then convert the resulting sympy solution into a numpy function which can be called. We then use the signals toolbox we studied in the last assignment to understand the responses of the two circuits to various inputs.
# Importing required packages
# +
from sympy import *
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as sp
from pylab import *
from IPython.display import *
# -
# # Low pass Filter
#
# 
#
# where G =1.586 and R1 = R2 = 10kΩ and C1=C2=10pF. This gives a 3dB Butter-worth filter with cutoff frequency of 1/2πMHz.
#
# Circuit Equations are as follows:
# $$V_{m}=\frac{V_{o}}{G}$$
# $$ V_{p} =V_{1} \frac{1}{1+s R_{2}C_{2}}$$
# $$ V_{o} = G(V_{p} - V_{m})$$
# $$\frac{V_{i}-V_{1}}{R_{1}} + \frac{V_{p}-V_{1}}{R_{2}} + s C_{1}(V_{0}-V_{1}) = 0$$
# Solving the above equations with approxmtion gives
#
# $$ V_{o} \approx \frac{V_{i}}{s R_{1} C_{1}}$$
#
# We would like to solve this in Python and also get (and plot) the exact result. For this we need the sympy module.
# To solve the equtions exactly we use matrix method of solving:
#
init_printing()
R1,R2,C1,C2,G = symbols("R1 R2 C1 C2 G")
V1,Vp,Vm,Vo,Vi = symbols("V1 Vp Vm Vo Vi")
s = symbols("s")
A = Matrix([[0,0,1,-1/G],
[-1/(1+s*R2*C2),1,0,0],
[0,-G,G,1],
[-1/R1-1/R2-s*C1,1/R2,0,s*C1]])
M = Matrix([V1,Vp,Vm,Vo])
b = Matrix([0,0,0,Vi/R1])
display(Eq(MatMul(A,M),b))
# Solving the above matrix yield exact result
# Function defining low pass filter:
def lowpass(R1=10**4,R2=10**4,C1=10**-11,C2=10**-11,G=1.586,Vi=1):
s=symbols("s")
A=Matrix([[0,0,1,-1/G],
[-1/(1+s*R2*C2),1,0,0],
[0,-G,G,1],
[-1/R1-1/R2-s*C1,1/R2,0,s*C1]])
b=Matrix([0,0,0,Vi/R1])
V = A.inv()*b
return(A,b,V)
# Function which can take input in laplace domain or time domain and give the output of low pass filter:
def low_pass_output(laplace_fn = None,time_fn=None,t=np.linspace(0,1e-5,1e5),C=10**-11):
A,b,V = lowpass(C1=C,C2=C)
v_low_pass = V[-1]
temp = expand(simplify(v_low_pass))
n,d = fraction(temp)
n,d = Poly(n,s),Poly(d,s)
num,den = n.all_coeffs(),d.all_coeffs()
H_v_low_pass = sp.lti([-float(f) for f in num],[float(f) for f in den])
if laplace_fn !=None:
temp = expand(simplify(laplace_fn))
n,d = fraction(temp)
n,d = Poly(n,s),Poly(d,s)
num,den = n.all_coeffs(),d.all_coeffs()
lap = sp.lti([float(f) for f in num],[float(f) for f in den])
t,u = sp.impulse(lap,None,t)
else:
u = time_fn
t,V_out,svec = sp.lsim(H_v_low_pass,u,t)
return (t,V_out)
# # High pass filter
# 
# values you can use are R1=R3=10kΩ, C1=C2=1nF, and G=1.586
#
# Circuit Equations are as follows:
# $$V_{n}=\frac{V_{o}}{G}$$
# $$ V_{p} =V_{1} \frac{s R_{3}C_{2}}{1+s R_{3}C_{2}}$$
# $$ V_{o} = G(V_{p} - V_{n})$$
# $$(V_{1}-V_{i})sC_{1} + \frac{(V_{1}-V_{o})}{R_{1}} + (V_{i}-V_{p})sC_{2} = 0 $$
# +
R1, R3, C1, C2, G, Vi = symbols('R_1 R_3 C_1 C_2 G V_i')
V1,Vn,Vp,Vo = symbols('V_1 V_n V_p V_o')
x=Matrix([V1,Vn,Vp,Vo])
A=Matrix([[0,-1,0,1/G],
[s*C2*R3/(s*C2*R3+1),0,-1,0],
[0,G,-G,1],
[-s*C2-1/R1-s*C1,0,s*C2,1/R1]])
b=Matrix([0,0,0,-Vi*s*C1])
init_printing
display(Eq(MatMul(A,x),b))
# -
# Function defining high pass filter:
def highpass(R1=10**4,R3=10**4,C1=10**-9,C2=10**-9,G=1.586,Vi=1):
s= symbols("s")
A=Matrix([[0,-1,0,1/G],
[s*C2*R3/(s*C2*R3+1),0,-1,0],
[0,G,-G,1],
[-s*C2-1/R1-s*C1,0,s*C2,1/R1]])
b=Matrix([0,0,0,-Vi*s*C1])
V =A.inv() * b
return (A,b,V)
# Function which can take input in laplace domain or time domain and give the output of high pass filter:
# +
def high_pass_output(laplace_fn = None,time_fn=None,t=np.linspace(0,1e-4,1e5),C=10**-11):
A,b,V = highpass(C1=C,C2=C)
v_high_pass = V[-1]
temp = expand(simplify(v_high_pass))
n,d = fraction(temp)
n,d = Poly(n,s),Poly(d,s)
num,den = n.all_coeffs(),d.all_coeffs()
H_v_high_pass = sp.lti([float(f) for f in num],[float(f) for f in den])
if laplace_fn !=None:
temp = expand(simplify(laplace_fn))
n,d = fraction(temp)
n,d = Poly(n,s),Poly(d,s)
num,den = n.all_coeffs(),d.all_coeffs()
lap = sp.lti([float(f) for f in num],[float(f) for f in den])
t,u = sp.impulse(lap,None,t)
else:
u = time_fn
t,V_out,svec = sp.lsim(H_v_high_pass,u,t)
return (t,V_out)
# -
# # Question1
# Step Response for low pass filter
t,V_low_step = low_pass_output(laplace_fn=1/s)
plt.plot(t,V_low_step)
plt.grid(True)
plt.xlabel("t ------>",size=14)
plt.ylabel(r"$Step\ Response\ V_{o}(t)$",size=14)
plt.title("Step Response When Capacitance = 10pF in low pass filter")
plt.show()
# Step response is starting from zero and reaching 0.793 at steady state.This is because DC gain oftransfer function is 0.793.Initial value is 0 because AC gain of low pass filter is zero(impulse can be assumed as High frequency signal and we know low pass filter dosen't pass high frequency signal).
# # Question2
# Finding Output when input signal is $$(sin(2000πt)+cos(2×106πt))u_{o}(t)$$
t = np.linspace(0,1e-3,1e5)
plt.plot(t,np.sin(2000*np.pi*t)+np.cos(2e6*np.pi*t))
plt.grid(True)
plt.xlabel("t ------>",size=14)
plt.ylabel(r"$V_{i}(t)$",size=14)
plt.title("Mixed frequency input")
plt.show()
# Band is high frequency wave and envolope is the low frequency wave
# +
t = linspace(0,1e-5,1e5)
t,vout = low_pass_output(time_fn=np.sin(2000*np.pi*t)+np.cos(2e6*np.pi*t),t=t,C=10**-9)
# -
plt.plot(t,vout)
plt.grid(True)
plt.xlabel("t ------>",size=14)
plt.ylabel(r"$V_{o}(t)$",size=14)
plt.title("Output for mixed frequency Sinusoid in lowpass filter in transient time")
plt.show()
# From above we can clearly see that Output is superposition of High Amplitude low frequency wave and Low amplitude High frquency wave(Since Low pass filter attenuates the High frequencies)
# +
t = linspace(0,1e-5,1e5)
t,vout = high_pass_output(time_fn=np.sin(2000*np.pi*t)+np.cos(2e6*np.pi*t),t=t,C=10**-9)
# -
plt.plot(t,vout)
plt.grid(True)
plt.xlabel("t ------>",size=14)
plt.ylabel(r"$V_{o}(t)$",size=14)
plt.title("Output for mixed frequency Sinusoid in High pass filter in transient time")
plt.show()
# The plot which is appearing to be band(closely placed lines) is superposition of High Amplitude High frequency wave and Low amplitude Low frquency wave(Since High pass filter attenuates the Low frequencies) which inturn appears to be non distorted sine wave.
# +
t = linspace(0,1e-3,1e5)
t,vout = low_pass_output(time_fn=np.sin(2000*np.pi*t)+np.cos(2e6*np.pi*t),t=t,C=10**-9)
# -
plt.plot(t,vout)
plt.grid(True)
plt.xlabel("t ------>",size=14)
plt.ylabel(r"$V_{o}(t)$",size=14)
plt.title("Output for mixed frequency Sinusoid in lowpass filter in steady time")
plt.show()
# From graph we can see frequency is close to 1000Hz(which is low frquency input)
# +
t = linspace(0,1e-4,1e5)
t,vout = high_pass_output(time_fn=np.sin(2000*np.pi*t)+np.cos(2e6*np.pi*t),t=t,C=10**-9)
# -
plt.plot(t,vout)
plt.grid(True)
plt.xlabel("t ------>",size=14)
plt.ylabel(r"$V_{o}(t)$",size=14)
plt.title("Output for mixed frequency Sinusoid in High pass filter in steay time")
plt.show()
# From graph we can see frequency is close to 1000KHz(which is high frquency input)
# # Question 3,4
# Damped Sinusoid -----> $exp(-300t)sin(10^{6}t)$
# +
t = linspace(0,1e-3,1e6)
f = np.exp(-3000*t) * np.sin(10**6 *t)
# -
plt.title("High frequency damped sinusoid")
plt.xlabel("$t$")
plt.ylabel("$v_i(t)$",size=20)
plt.plot(t,f)
plt.grid()
plt.show()
# +
t = linspace(0,1e-3,1e6)
t,vout = high_pass_output(time_fn=f,t=t,C=10**-9)
# -
plt.plot(t,vout)
plt.grid(True)
plt.xlabel("t ------>",size=14)
plt.ylabel(r"$V_{o}(t)$",size=14)
plt.title("Output for High frequency damped input in High pass filter")
plt.show()
# From above graph we can clearly see that High pass filter passed high frequency sinusoid with out attenuating much.(Since property of high pass filter)
# +
t = linspace(0,1e-3,1e6)
t,vout = low_pass_output(time_fn=f,t=t,C=10**-9)
# -
plt.plot(t,vout)
plt.grid(True)
plt.xlabel("t ------>",size=14)
plt.ylabel(r"$V_{o}(t)$",size=14)
plt.title("Output for High frequency damped input in low pass filter")
plt.show()
# From above graph Low pass filter quickly attenuated the High frequency Sinusoid and gives distorted Output
# # Question 5
t,V_high_step = high_pass_output(laplace_fn=1/s,C=10**-9)
plt.plot(t,V_high_step)
plt.grid(True)
plt.xlabel("t ------>",size=14)
plt.ylabel(r"$Step\ Response\ V_{o}(t)$",size=14)
plt.title("Step Response When Capacitance = 1nF in high pass filter")
plt.show()
# Step response here saturates at zero and this is because DC gain of High pass filter is 0. We can clearly see from graph that it starts from 0.793 and this because AC gain of transfer function at high frequencies is 0.793(Step can assumed as infinite frequency signal and we know high pass filter only allows high frequency signals)
#
# step response overshoots the steady state value of 0, reaches an
# extremum, then settles back to 0, unlike the response of the low pass filter which steadily
# approaches the steady state value with no extrema. This occurs because of the presence of
# zeros at the origin in the transfer function of the high pass filter(which imply that the DC
# gain is 0). Since the steady state value of the step response is 0, the total signed area under
# the curve of the impulse response must also be 0. This means that the impulse response must
# equal zero at one or more time instants. Since the impulse response is the derivative of the
# step response, this therefore means that the step response must have at least one extremum.
# This explains the behaviour of the step response of the high pass filter.
# # Conclusions:
# The low pass filter responds by letting the low frequency sinusoid pass through without
# much additional attenuation. The output decays as the input also decays.
#
# The high pass filter responds by quickly attenuating the input. Notice that the time scales
# show that the high pass filter response is orders of magnitudes faster than the low pass
# response. This is because the input frequency is below the cutoff frequency, so the output
# goes to 0 very fast.
#
# In conclusion, the sympy module has allowed us to analyse quite complicated circuits by
# analytically solving their node equations. We then interpreted the solutions by plotting time
# domain responses using the signals toolbox. Thus, sympy combined with the scipy.signal
# module is a very useful toolbox for analyzing complicated systems like the active filters in
# this assignment.
|
week7/week7.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: py36
# language: python
# name: py36
# ---
# ## [Troisi06](https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.96.086601)
# Charge-Transport Regime of Crystalline Organic Semiconductors: Diffusion Limited by Thermal Off-Diagonal Electronic Disorder. <NAME> and <NAME>. *Phys. Rev. Lett.* **2006**, *96*, 086601
# +
import os
for env in ["MKL_NUM_THREADS", "NUMEXPR_NUM_THREADS", "OMP_NUM_THREADS"]:
os.environ[env] = "1"
del env
import numpy as np
import scipy.sparse
import tqdm
from matplotlib import pyplot as plt
# +
cm_inv_convertor = 4.5563e-6 # a.u. / cm-1
amu_convertor = 1823 # a.u. / amu
A_convertor = 1.88973 # a.u. / A
ps_convertor = 41341 # a.u. / ps
K_convertor = 1.38064881e-23 / 4.3597447222071e-18
m = 250 * amu_convertor
K = 14500 * amu_convertor / ps_convertor ** 2
# N = 600 in the paper
N = 100
tau = 300 * cm_inv_convertor
alpha = 995 * cm_inv_convertor / A_convertor
dt = 0.025e-3 * ps_convertor
T = 300 * K_convertor
# +
trajectories = []
# 125 trajctories in the paper
for trajectory_idx in range(1):
u = np.random.normal(0, np.sqrt(T/K), N)
v = np.random.normal(0, np.sqrt(T/m), N)
def periodic_diag(d):
H = scipy.sparse.diags(d[:-1], offsets=1) + scipy.sparse.diags(d[:-1], offsets=-1) \
+ scipy.sparse.diags([d[-1]], offsets=len(d)-1) + scipy.sparse.diags([d[-1]], offsets=1-len(d))
return H
diag_elems = -tau + alpha * (np.roll(u, -1) - u)
H = periodic_diag(diag_elems)
evals, evecs = np.linalg.eigh(H.toarray())
prop = np.exp(-evals/T)
prop /= prop.sum()
init_idx = np.random.choice(np.arange(N), p=prop)
C = evecs[:, init_idx].reshape(N)
C_p1 = np.roll(C, -1)
C_m1 = np.roll(C, 1)
a = ( -K * u - alpha * (-C.conj() * C_p1 - C_p1.conj() * C + C_m1.conj() * C + C.conj() * C_m1) ) / m
new_u = u + v * dt + 1/2 * a * dt**2
deriv_diag_elems = alpha * (np.roll(v, -1) - v)
H_deriv = periodic_diag(deriv_diag_elems)
new_C = C - 1j * H * dt @ C - 1/2 * 1j * ( H @ (-1j * H @ C) + H_deriv @ C) * dt**2
stored_C = [C]
# 600e3 steps in the paper
for i in tqdm.tqdm(range(1, int(100e3))):
old_u, old_C = u, C
u, C = new_u, new_C
C_p1 = np.roll(C, -1)
C_m1 = np.roll(C, 1)
v = (u - old_u) / dt
a = (-K * u - alpha * (-C.conj() * C_p1 - C_p1.conj() * C + C_m1.conj() * C + C.conj() * C_m1)) / m
new_u = 2 * u - old_u + a * dt ** 2
diag_elems = -tau + alpha * (np.roll(u, -1) - u)
H = periodic_diag(diag_elems)
deriv_diag_elems = alpha * (np.roll(v, -1) - v)
H_deriv = periodic_diag(deriv_diag_elems)
HC = H @ C
new_C = C - 1j * HC * dt - 1 / 2 * 1j * (H @ (-1j * HC) + H_deriv @ C) * dt ** 2
if i % 1000 == 999:
stored_C.append(C)
trajectories.append(stored_C)
# -
occus = [(np.array(stored_C).conj() * stored_C) for stored_C in trajectories]
occu = occus[0]
occu = np.roll(occu, N//2 - occu[0].argmax())
r2 = np.arange(N) ** 2 @ occu.T - (np.arange(N) @ occu.T) **2
plt.plot(r2)
|
notebooks/Troisi06.ipynb
|