code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Day 04
import numpy as np
from aocd.models import Puzzle
# ## Data
puzzle = Puzzle(year=2021, day=4)
data = puzzle.input_data.split('\n')
draws = np.array(data[0].split(','), dtype=int)
boards = np.zeros((len(data[1:])//6, 5, 5))
for b in range(boards.shape[0]):
boards[b, :, :] = np.array([data[6*b+i].split() for i in range(2, 7)], dtype=float)
# ## Part One
# +
for d in draws:
boards[boards == d] = np.nan
test = [np.all(np.isnan(boards), 1), np.all(np.isnan(boards), 2)]
if np.any(test):
board = np.where(np.sum(test, axis=(0, 2)))[0][0]
break
d, board
# -
answer_a = int(np.nansum(boards[board, :, :]))*d
answer_a
puzzle.answer_a = answer_a
# ## Part Two
# +
for d in draws:
boards[boards == d] = np.nan
test = [np.all(np.isnan(boards), 1), np.all(np.isnan(boards), 2)]
ind = np.where(np.sum(test, axis=(0, 2)))[0]
if ind.size < boards.shape[0]:
old = ind
else:
board = np.where(~np.in1d(ind, old))[0][0]
break
d, board
# -
answer_b = int(np.nansum(boards[board, :, :]))*d
answer_b
puzzle.answer_b = answer_b
import scooby
scooby.Report('aocd')
|
2021/Day-04.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Matplotlib Subplots
#
# The `plt.subplots()` function creates a `Figure` and a Numpy array of `Subplot`/`Axes` objects which you store in `fig` and `axes` respectively.
#
# Specify the number of rows and columns you want with the `nrows` and `ncols` arguments.
#
# ```python
# fig, axes = plt.subplots(nrows=3, ncols=1)
# ```
#
# This creates a `Figure` and `Subplots` in a 3x1 grid. The Numpy array `axes` has shape `(nrows, ncols)` the same shape as the grid, in this case `(3,)` (it's a 1D array since one of `nrows` or `ncols` is 1). Access each `Subplot` using Numpy slice notation and call the `plot()` method to plot a line graph.
#
# Once all `Subplots` have been plotted, call `plt.tight_layout()` to ensure no parts of the plots overlap. Finally, call `plt.show()` to display your plot.
# +
# Import necessary modules and (optionally) set Seaborn style
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
# Generate data to plot
linear = [x for x in range(5)]
square = [x**2 for x in range(5)]
cube = [x**3 for x in range(5)]
# Generate Figure object and Axes object with shape 3x1
fig, axes = plt.subplots(nrows=3, ncols=1)
# Access first Subplot and plot linear numbers
axes[0].plot(linear)
# Access second Subplot and plot square numbers
axes[1].plot(square)
# Access third Subplot and plot cube numbers
axes[2].plot(cube)
plt.tight_layout()
plt.show()
# -
# ## Matplotlib Figures and Axes
#
# Up until now, you have probably made all your plots with the functions in `matplotlib.pyplot` i.e. all the functions that start with `plt.`.
#
# These work nicely when you draw one plot at a time. But to draw multiple plots on one `Figure`, you need to learn the underlying classes in matplotlib.
#
# Let's look at an image that explains the main classes from the [AnatomyOfMatplotlib](https://github.com/matplotlib/AnatomyOfMatplotlib) tutorial:
# <div>
# <img src="Figures/figure_axes_axis_labeled.png" width=500 align="left" />
# </div>
# To quote AnatomyOfMatplotlib:
#
# > The ``Figure`` is the top-level container in this hierarchy. It is the overall window/page that everything is drawn on. You can have multiple independent figures and ``Figure``s can contain multiple ``Axes``.
# >
# > Most plotting ocurs on an ``Axes``. The axes is effectively the area that we plot data on and any ticks/labels/etc associated with it. Usually we'll set up an Axes with a call to ``subplots`` (which places Axes on a regular grid), so in most cases, ``Axes`` and ``Subplot`` are synonymous.
# >
# > Each ``Axes`` has an ``XAxis`` and a ``YAxis``. These contain the ticks, tick locations, labels, etc. In this tutorial, we'll mostly control ticks, tick labels, and data limits through other mechanisms, so we won't touch the individual ``Axis`` part of things all that much. However, it is worth mentioning here to explain where the term ``Axes`` comes from.
#
# The typical variable names for each object are:
# * `Figure` - `fig` or `f`,
# * `Axes` (plural) - `axes` or `axs`,
# * `Axes` (singular) - `ax` or `a`
#
# The word `Axes` refers to the area you plot on and is synonymous with `Subplot`. However, you can have multiple `Axes` (`Subplots`) on a `Figure`. In speech and writing use the same word for the singular and plural form. In your code, you should make a distinction between each - you plot on a singular `Axes` but will store all the `Axes` in a Numpy array.
#
# An `Axis` refers to the `XAxis` or `YAxis` - the part that gets ticks and labels.
#
# The `pyplot` module implicitly works on one `Figure` and one `Axes` at a time. When we work with `Subplots`, we work with multiple `Axes` on one `Figure`. So, it makes sense to plot with respect to the `Axes` and it is much easier to keep track of everything.
#
# The main differences between using `Axes` methods and `pyplot` are:
# 1. Always create a `Figure` and `Axes` objects on the first line
# 2. To plot, write `ax.plot()` instead of `plt.plot()`.
#
# Once you get the hang of this, you won't want to go back to using `pyplot`. It's much easier to create interesting and engaging plots this way. In fact, this is why most [StackOverflow answers](https://stackoverflow.com/questions/tagged/matplotlib) are written with this syntax.
#
# All of the functions in `pyplot` have a corresponding method that you can call on `Axes` objects, so you don't have to learn any new functions.
#
# Let's get to it.
# ## Matplotlib Subplots Example
#
# The `plt.subplots()` function creates a `Figure` and a Numpy array of `Subplots`/`Axes` objects which we store in `fig` and `axes` respectively.
#
# Specify the number of rows and columns you want with the `nrows` and `ncols` arguments.
#
# ```python
# fig, axes = plt.subplots(nrows=3, ncols=1)
# ```
#
# This creates a `Figure` and `Subplots` in a 3x1 grid. The Numpy array `axes` is the same shape as the grid, in this case `(3,)`. Access each `Subplot` using Numpy slice notation and call the `plot()` method to plot a line graph.
#
# Once all `Subplots` have been plotted, call `plt.tight_layout()` to ensure no parts of the plots overlap. Finally, call `plt.show()` to display your plot.
# +
fig, axes = plt.subplots(nrows=2, ncols=2)
plt.tight_layout()
plt.show()
# -
# The most important arguments for `plt.subplots()` are similar to the [matplotlib subplot](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.subplot.html) function but can be specified with keywords. Plus, there are more powerful ones which we will discuss later.
#
# To create a `Figure` with one `Axes` object, call it without any arguments
#
# ```python
# fig, ax = plt.subplots()
# ```
#
# Note: this is implicitly called whenever you use the `pyplot` module. All 'normal' plots contain one `Figure` and one `Axes`.
#
# In advanced blog posts and StackOverflow answers, you will see a line similar to this at the top of the code. It is much more Pythonic to create your plots with respect to a `Figure` and `Axes`.
#
# To create a `Grid` of subplots, specify `nrows` and `ncols` - the number of rows and columns respectively
#
# ```python
# fig, axes = plt.subplots(nrows=2, ncols=2)
# ```
#
# The variable `axes` is a numpy array with shape `(nrows, ncols)`. Note that it is in the plural form to indicate it contains more than one `Axes` object. Another common name is `axs`. Choose whichever you prefer. If you call `plt.subplots()` without an argument name the variable `ax` as there is only one `Axes` object returned.
#
# I will select each `Axes` object with slicing notation and plot using the appropriate methods. Since I am using Numpy slicing, the index of the first `Axes` is 0, not 1.
# +
# Create Figure and 2x2 gris of Axes objects
fig, axes = plt.subplots(nrows=2, ncols=2)
# Generate data to plot.
data = np.array([1, 2, 3, 4, 5])
# Access Axes object with Numpy slicing then plot different distributions
axes[0, 0].plot(data)
axes[0, 1].plot(data**2)
axes[1, 0].plot(data**3)
axes[1, 1].plot(np.log(data))
plt.tight_layout()
plt.show()
# -
# First I import the necessary modules, then create the `Figure` and `Axes` objects using `plt.subplots()`. The `Axes` object is a Numpy array with shape `(2, 2)` and I access each subplot via Numpy slicing before doing a line plot of the data. Then, I call `plt.tight_layout()` to ensure the axis labels don't overlap with the plots themselves. Finally, I call `plt.show()` as you do at the end of all matplotlib plots.
# ## Matplotlib Subplots Title
#
# To add an overall title to the `Figure`, use `plt.suptitle()`.
#
# To add a title to each `Axes`, you have two methods to choose from:
# 1. `ax.set_title('bar')`
# 2. `ax.set(title='bar')`
#
# In general, you can set anything you want on an `Axes` using either of these methods. I recommend using `ax.set()` because you can pass *any* setter function to it as a keyword argument. This is faster to type, takes up fewer lines of code and is easier to read.
#
# Let's set the title, xlabel and ylabel for two `Subplots` using both methods for comparison
# +
# Unpack the Axes object in one line instead of using slice notation
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2)
# First plot - 3 lines
ax1.set_title('many')
ax1.set_xlabel('lines')
ax1.set_ylabel('of code')
# Second plot - 1 line
ax2.set(title='one', xlabel='line', ylabel='of code')
# Overall title
plt.suptitle('My Lovely Plot')
plt.tight_layout()
plt.show()
# -
# Clearly using `ax.set()` is the better choice.
#
# Note that I unpacked the `Axes` object into individual variables on the first line. You can do this instead of Numpy slicing if you prefer. It is easy to do with 1D arrays. Once you create grids with multiple rows and columns, it's easier to read if you don't unpack them.
# ## Matplotlib Subplots Share X Axis
#
# To share the x axis for subplots in matplotlib, set `sharex=True` in your `plt.subplots()` call.
# +
# Generate data
data = [0, 1, 2, 3, 4, 5]
# 3x1 grid that shares the x axis
fig, axes = plt.subplots(nrows=3, ncols=1, sharex=True)
# 3 different plots
axes[0].plot(data)
axes[1].plot(np.sqrt(data))
axes[2].plot(np.exp(data))
plt.tight_layout()
plt.show()
# -
# Here I created 3 line plots that show the linear, square root and exponential of the numbers 0-5.
#
# As I used the same numbers, it makes sense to share the x-axis.
# <div>
# <img src="Figures/sharex=False.png" width=400 align="left" />
# </div>
# Here I wrote the same code but set `sharex=False` (the default behavior). Now there are unnecessary axis labels on the top 2 plots.
#
# You can also share the y axis for plots by setting `sharey=True` in your `plt.subplots()` call.
# ## Matplotlib Subplots Legend
#
# To add a legend to each `Axes`, you must
# 1. Label it using the `label` keyword
# 2. Call `ax.legend()` on the `Axes` you want the legend to appear
#
# Let's look at the same plot as above but add a legend to each `Axes`.
# +
# Generate data, 3x1 plot with shared XAxis
data = [0, 1, 2, 3, 4, 5]
fig, axes = plt.subplots(nrows=3, ncols=1, sharex=True)
# Plot the distributions and label each Axes
axes[0].plot(data, label='Linear')
axes[1].plot(np.sqrt(data), label='Square Root')
axes[2].plot(np.exp(data), label='Exponential')
# Add a legend to each Axes with default values
for ax in axes:
ax.legend()
plt.tight_layout()
plt.show()
# -
# The legend now tells you which function has been applied to the data. I used a for loop to call `ax.legend()` on each of the `Axes`. I could have done it manually instead by writing:
#
# ```python
# axes[0].legend()
# axes[1].legend()
# axes[2].legend()
# ```
#
# Instead of having 3 legends, let's just add one legend to the `Figure` that describes each line. Note that you need to change the color of each line, otherwise the legend will show three blue lines.
#
# The [matplotlib legend](https://matplotlib.org/3.1.1/api/_as_gen/matplotlib.pyplot.legend.html) function takes 2 arguments
#
# ```python
# ax.legend(handles, labels)
# ```
#
# * `handles` - the lines/plots you want to add to the legend (list)
# * `labels` - the labels you want to give each line (list)
#
# Get the `handles` by storing the output of you `ax.plot()` calls in a list. You need to create the list of `labels` yourself. Then call `legend()` on the `Axes` you want to add the legend to.
# +
# Generate data and 3x1 grid with a shared x axis
data = [0, 1, 2, 3, 4, 5]
fig, axes = plt.subplots(nrows=3, ncols=1, sharex=True)
# Store the output of our plot calls to use as handles
# Plot returns a list of length 1, so unpack it using a comma
linear, = axes[0].plot(data, 'b')
sqrt, = axes[1].plot(np.sqrt(data), 'r')
exp, = axes[2].plot(np.exp(data), 'g')
# Create handles and labels for the legend
handles = [linear, sqrt, exp]
labels = ['Linear', 'Square Root', 'Exponential']
# Draw legend on first Axes
axes[0].legend(handles, labels)
plt.tight_layout()
plt.show()
# -
# First I generated the data and a 3x1 grid. Then I made three `ax.plot()` calls and applied different functions to the data.
#
# Note that `ax.plot()` returns a `list` of `matplotlib.line.Line2D` objects. You have to pass these `Line2D` objects to `ax.legend()` and so need to unpack them first.
#
# Standard unpacking syntax in Python is:
#
# ```python
# a, b = [1, 2]
# # a = 1, b = 2
# ```
#
# However, each `ax.plot()` call returns a list of length 1. To unpack these lists, write
#
# ```python
# x, = [5]
# # x = 5
# ```
#
# If you just wrote `x = [5]` then `x` would be a list and not the object inside the list.
#
# After the `plot()` calls, I created 2 lists of `handles` and `labels` which I passed to `axes[0].legend()` to draw it on the first plot.
# <div>
# <img src="Figures/legendmiddle.png" width=400 align="left" />
# </div>
# In the above plot, I changed the`legend` call to `axes[1].legend(handles, labels)` to plot it on the second (middle) `Axes`.
# ## Matplotlib Subplots Size
#
# You have total control over the size of subplots in matplotlib.
#
# You can either change the size of the entire `Figure` or the size of the `Subplots` themselves.
#
# First, let's look at changing the `Figure`.
#
# ### Matplotlib Figure Size
#
# If you are happy with the size of your subplots but you want the final image to be larger/smaller, change the `Figure`.
#
# If you've read my article on the matplotlib subplot function, you know to use the `plt.figure()` function to to change the `Figure`. Fortunately, any arguments passed to `plt.subplots()` are also passed to `plt.figure()`. So, you don't have to add any extra lines of code, just keyword arguments.
#
# Let's change the size of the `Figure`.
# Create 2x1 grid - 3 inches wide, 6 inches long
fig, axes = plt.subplots(nrows=2, ncols=1, figsize=(3, 6))
plt.show()
# I created a 2x1 plot and set the `Figure` size with the `figsize` argument. It accepts a tuple of 2 numbers - the `(width, height)` of the image in inches.
#
# So, I created a plot 3 inches wide and 6 inches long - `figsize=(3, 6)`.
# 2x1 grid - twice as long as it is wide
fig, axes = plt.subplots(nrows=2, ncols=1, figsize=plt.figaspect(2))
plt.show()
# You can set a more general `Figure` size with the [matplotlib figaspect](https://matplotlib.org/3.1.0/api/_as_gen/matplotlib.figure.figaspect.html) function. It lets you set the aspect ratio (height/width) of the `Figure`.
#
# Above, I created a `Figure` twice as long as it is wide by setting `figsize=plt.figaspect(2)`.
#
# Note: Remember the aspect ratio (height/width) formula by recalling that `height` comes first in the alphabet before `width`.
# ## Matplotlib Subplots Different Sizes
#
# If you have used `plt.subplot()` before, you'll know that the grids you create are limited. Each `Subplot` must be part of a regular grid i.e. of the form `1/x` for some integer `x`. If you create a 2x1 grid, you have 2 rows and each row takes up 1/2 of the space. If you create a 3x2 grid, you have 6 subplots and each takes up 1/6 of the space.
#
# Using `plt.subplots()` you can create a 2x1 plot with 2 rows that take up any fraction of space you want.
#
# Let's make a 2x1 plot where the top row takes up 1/3 of the space and the bottom takes up 2/3.
#
# You do this by specifying the `gridspec_kw` argument and passing a dictionary of values. The main arguments we are interested in are `width_ratios` and `height_ratios`. They accept lists that specify the width ratios of columns and height ratios of the rows. In this example the top row is `1/3` of the `Figure` and the bottom is `2/3`. Thus the height ratio is `1:2` or `[1, 2]` as a list.
# +
# 2 x1 grid where top is 1/3 the size and bottom is 2/3 the size
fig, axes = plt.subplots(nrows=2, ncols=1,
gridspec_kw={'height_ratios': [1, 2]})
plt.tight_layout()
plt.show()
# -
# The only difference between this and a regular 2x1 `plt.subplots()` call is the `gridspec_kw` argument. It accepts a dictionary of values. These are passed to the [matplotlib GridSpec](https://matplotlib.org/api/_as_gen/matplotlib.gridspec.GridSpec.html#matplotlib.gridspec.GridSpec) constructor (the underlying class that creates the grid).
#
# Let's create a 2x2 plot with the same `[1, 2]` height ratios but let's make the left hand column take up 3/4 of the space.
# +
# Heights: Top row is 1/3, bottom is 2/3 --> [1, 2]
# Widths : Left column is 3/4, right is 1/4 --> [3, 1]
ratios = {'height_ratios': [1, 2],
'width_ratios': [3, 1]}
fig, axes = plt.subplots(nrows=2, ncols=2, gridspec_kw=ratios)
plt.tight_layout()
plt.show()
# -
# Everything is the same as the previous plot but now we have a 2x2 grid and have specified `width_ratios`. Since the left column takes up `3/4` of the space and the right takes up `1/4` the ratios are `[3, 1]`.
#
# ## Matplotlib Subplots Size
#
# In the previous examples, there were white lines that cross over each other to separate the `Subplots` into a clear grid. But sometimes you will not have that to guide you. To create a more complex plot, you have to manually add `Subplots` to the grid.
#
# You could do this using the `plt.subplot()` function. But since we are focusing on `Figure` and `Axes` notation in this article, I'll show you how to do it another way.
#
# You need to use the `fig.add_subplot()` method and it has the same notation as [`plt.subplot()`](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.subplot.html). Since it is a `Figure` method, you first need to create one with the `plt.figure()` function.
fig = plt.figure()
# The hardest part of creating a `Figure` with different sized `Subplots` in matplotlib is figuring out what fraction of space each `Subplot` takes up.
#
# So, it's a good idea to know what you are aiming for before you start. You could sketch it on paper or draw shapes in PowerPoint. Once you've done this, everything else is much easier.
#
# I'm going to create this shape.
# <div>
# <img src="Figures/labelled_subplot.png" width=400 align="left" />
# </div>
# I've labeled the fraction each `Subplot` takes up as we need this for our `fig.add_subplot()` calls.
#
# I'll create the biggest `Subplot` first and the others in descending order.
# <div>
# <img src="Figures/2s.png" width=400 align="left" />
# </div>
# The right hand side is half of the plot. It is one of two plots on a `Figure` with 1 row and 2 columns. To select it with `fig.add_subplot()`, you need to set `index=2`.
#
# Remember that indexing starts from 1 for the functions `plt.subplot()` and `fig.add_subplot()`.
#
# In the image, the blue numbers are the index values each `Subplot` has.
#
# ```python
# ax1 = fig.add_subplot(122)
# ```
#
# As you are working with `Axes` objects, you need to store the result of `fig.add_subplot()` so that you can plot on it afterwards.
# <div>
# <img src="Figures/4s.png" width=400 align="left" />
# </div>
# Now, select the bottom left `Subplot` in a a 2x2 grid i.e. `index=3`
#
# ```python
# ax2 = fig.add_subplot(223)
# ```
# <div>
# <img src="Figures/8s.png" width=400 align="left" />
# </div>
# Lastly, select the top two `Subplots` on the left hand side of a 4x2 grid i.e. `index=1` and `index=3`.
#
# ```python
# ax3 = fig.add_subplot(423)
# ax4 = fig.add_subplot(421)
# ```
#
# When you put this altogether you get
# +
# Initialise Figure
fig = plt.figure()
# Add 4 Axes objects of the size we want
ax1 = fig.add_subplot(122)
ax2 = fig.add_subplot(223)
ax3 = fig.add_subplot(423)
ax4 = fig.add_subplot(421)
plt.tight_layout(pad=0.1)
plt.show()
# -
# Perfect! Breaking the `Subplots` down into their individual parts and knowing the shape you want, makes everything easier.
#
# Now, let's do something you can't do with `plt.subplot()`. Let's have 2 plots on the left hand side with the bottom plot twice the height as the top plot.
# <div>
# <img src="Figures/halves and thirds.png" width=400 align="left" />
# </div>
# Like with the above plot, the right hand side is half of a plot with 1 row and 2 columns. It is `index=2`.
#
# So, the first two lines are the same as the previous plot
#
# ```python
# fig = plt.figure()
# ax1 = fig.add_subplot(122)
# ```
# <div>
# <img src="Figures/toplefta.png" width=400 align="left" />
# </div>
# The top left takes up `1/3` of the space of the left-hand half of the plot. Thus, it takes up `1/3 x 1/2 = 1/6` of the total plot. So, it is `index=1` of a 3x2 grid.
#
# ```python
# ax2 = fig.add_subplot(321)
# ```
# <div>
# <img src="Figures/bottom2a.png" width=400 align="left" />
# </div>
# The final subplot takes up 2/3 of the remaining space i.e. `index=3` and `index=5` of a 3x2 grid. But you can't add both of these indexes as that would add two `Subplots` to the `Figure`. You need a way to add one `Subplot` that *spans* two rows.
#
# You need the [matplotlib subplot2grid](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.subplot2grid.html#matplotlib.pyplot.subplot2grid) function - `plt.subplot2grid()`. It returns an `Axes` object and adds it to the current `Figure`.
#
# Here are the most important arguments:
#
# ```python
# ax = plt.subplot2grid(shape, loc, rowspan, colspan)
# ```
#
# * `shape` - tuple of 2 integers - the *shape* of the overall grid e.g. (3, 2) has 3 rows and 2 columns.
# * `loc` - tuple of 2 integers - the *location* to place the `Subplot` in the grid. It uses 0-based indexing so (0, 0) is first row, first column and (1, 2) is second row, third column.
# * `rowspan` - integer, default 1- number of rows for the `Subplot` to span to the right
# * `colspan` - integer, default 1 - number of columns for the `Subplot` to span down
# <div>
# <img src="Figures/mid.png" width=400 align="left" />
# </div>
# From those definitions, you need to select the middle left `Subplot` and set `rowspan=2` so that it spans down 2 rows.
# <div>
# <img src="Figures/midextend.png" width=400 align="left" />
# </div>
# Thus, the arguments you need for `subplot2grid` are:
# * `shape=(3, 2)` - 3x2 grid
# * `loc=(1, 0)` - second row, first colunn (0-based indexing)
# * `rowspan=2` - span down 2 rows
#
# This gives
#
# ```python
# ax3 = plt.subplot2grid(shape=(3, 2), loc=(1, 0), rowspan=2)
# ```
#
# Sidenote: why matplotlib chose 0-based indexing for `loc` when *everything else* uses 1-based indexing is a mystery to me. One way to remember it is that `loc` is similar to `locating`. This is like slicing Numpy arrays which use 0-indexing. Also, if you use `GridSpec`, you will often use Numpy slicing to choose the number of rows and columns that `Axes` span.
#
# Putting this together, you get
# +
fig = plt.figure()
ax1 = fig.add_subplot(122)
ax2 = fig.add_subplot(321)
ax3 = plt.subplot2grid(shape=(3, 2), loc=(1, 0), rowspan=2)
plt.tight_layout()
plt.show()
# -
# ## Matplotlib Subplots_Adjust
#
# If you aren't happy with the spacing between plots that `plt.tight_layout()` provides, manually adjust the spacing with the [matplotlib subplots_adjust](https://matplotlib.org/devdocs/api/_as_gen/matplotlib.pyplot.subplots_adjust.html) function.
#
# It takes 6 optional, self explanatory arguments. Each is a float in the range [0.0, 1.0] and is a fraction of the font size:
# * `left`, `right`, `bottom` and `top` is the spacing on each side of the `Suplots`
# * `wspace` - the **width** between `Subplots`
# * `hspace` - the **height** between `Subplots`
#
# Let's compare `tight_layout` with `subplots_adjust`.
# +
fig, axes = plt.subplots(nrows=2, ncols=2, sharex=True, sharey=True)
plt.tight_layout()
plt.show()
# -
# Here is a 2x2 grid with `plt.tight_layout()`. I've set `sharex` and `sharey` to `True` to remove unnecessary axis labels.
# +
fig, axes = plt.subplots(nrows=2, ncols=2, sharex=True, sharey=True)
plt.subplots_adjust(wspace=0.05, hspace=0.05)
plt.show()
# -
# Now I've decreased the height and width between `Subplots` to `0.05` and there is hardly any space between them.
#
# To avoid loads of similar examples, I recommend you play around with the arguments to get a feel for how this function works.
# ## Matplotlib Subplots Colorbar
#
# Adding a colorbar to each `Axes` is similar to adding a legend. You store the `ax.plot()` call in a variable and pass it to `fig.colorbar()`.
#
# Colorbars are `Figure` methods since they are placed on the `Figure` itself and not the `Axes`. Yet, they do take up space from the `Axes` they are placed on.
#
# Let's look at an example.
# +
# Generate two 10x10 arrays of random numbers in the range [0.0, 1.0]
data1 = np.random.random((10, 10))
data2 = np.random.random((10, 10))
# Initialise Figure and Axes objects with 1 row and 2 columns
# Constrained_layout=True is better than plt.tight_layout()
# Make twice as wide as it is long with figaspect
fig, axes = plt.subplots(nrows=1, ncols=2, constrained_layout=True,
figsize=plt.figaspect(1/2))
pcm1 = axes[0].pcolormesh(data1, cmap='Blues')
# Place first colorbar on first column - index 0
fig.colorbar(pcm1, ax=axes[0])
pcm2 = axes[1].pcolormesh(data2, cmap='Greens')
# Place second colorbar on second column - index 1
fig.colorbar(pcm2, ax=axes[1])
plt.show()
# -
# First, I generated two 10x10 arrays of random numbers in the range [0.0, 1.0] using the `np.random.random()` function. Then I initialized the 1x2 grid with `plt.subplots()`.
#
# The keyword argument `constrained_layout=True` achieves a similar result to calling `plt.tight_layout()`. However, `tight_layout` only checks for tick labels, axis labels and titles. Thus, it ignores colorbars and legends and often produces bad looking plots. Fortunately, `constrained_layout` takes colorbars and legends into account. Thus, it should be your go-to when automatically adjusting these types of plots.
#
# Finally, I set `figsize=plt.figaspect(1/2)` to ensure the plots aren't too squashed together.
#
# After that, I plotted the first heatmap, colored it blue and saved it in the variable `pcm1`. I passed that to `fig.colorbar()` and placed it on the first column - `axes[0]` with the `ax` keyword argument. It's a similar story for the second heatmap.
#
# The more `Axes` you have, the fancier you can be with [placing colorbars in matplotlib](https://matplotlib.org/3.1.1/gallery/subplots_axes_and_figures/colorbar_placement.html). Now, let's look at a 2x2 example with 4 `Subplots` but only 2 colorbars.
# +
# Set seed to reproduce results
np.random.seed(1)
# Generate 4 samples of the same data set using a list comprehension
# and assignment unpacking
data1, data2, data3, data4 = [np.random.random((10, 10)) for _ in range(4)]
# 2x2 grid with constrained layout
fig, axes = plt.subplots(nrows=2, ncols=2, constrained_layout=True)
# First column heatmaps with same colormap
pcm1 = axes[0, 0].pcolormesh(data1, cmap='Blues')
pcm2 = axes[1, 0].pcolormesh(data2, cmap='Blues')
# First column colorbar - slicing selects all rows, first column
fig.colorbar(pcm1, ax=axes[:, 0])
# Second column heatmaps with same colormap
pcm3 = axes[0, 1].pcolormesh(data3+1, cmap='Greens')
pcm4 = axes[1, 1].pcolormesh(data4+1, cmap='Greens')
# Second column colorbar - slicing selects all rows, second column
# Half the size of the first colorbar
fig.colorbar(pcm3, ax=axes[:, 1], shrink=0.5)
plt.show()
# -
# If you pass a list of `Axes` to `ax`, matplotlib places the colorbar along those `Axes`. Moreover, you can specify where the colorbar is with the `location` keyword argument. It accepts the strings `'bottom'`, `'left'`, `'right'`, `'top'` or `'center'`.
#
# The code is similar to the 1x2 plot I made above. First, I set the seed to 1 so that you can reproduce the results - you will soon plot this again with the colorbars in different places.
#
# I used a list comprehension to generate 4 samples of the same dataset. Then I created a 2x2 grid with `plt.subplots()` and set `constrained_layout=True` to ensure nothing overlaps.
#
# Then I made the plots for the first column - `axes[0, 0]` and `axes[1, 0]` - and saved their output. I passed one of them to `fig.colorbar()`. It doesn't matter which one of `pcm1` or `pcm2` I pass since they are just different samples of the same dataset. I set `ax=axes[:, 0]` using Numpy slicing notation, that is all rows `:` and the first column `0`.
#
# It's a similar process for the second column but I added 1 to `data3` and `data4` to give a range of numbers in [1.0, 2.0] instead. Lastly, I set `shrink=0.5` to make the colorbar half its default size.
#
# Now, let's plot the same data with the same colors on each row rather than on each column.
# +
# Same as above
np.random.seed(1)
data1, data2, data3, data4 = [np.random.random((10, 10)) for _ in range(4)]
fig, axes = plt.subplots(nrows=2, ncols=2, constrained_layout=True)
# First row heatmaps with same colormap
pcm1 = axes[0, 0].pcolormesh(data1, cmap='Blues')
pcm2 = axes[0, 1].pcolormesh(data2, cmap='Blues')
# First row colorbar - placed on first row, all columns
fig.colorbar(pcm1, ax=axes[0, :], shrink=0.8)
# Second row heatmaps with same colormap
pcm3 = axes[1, 0].pcolormesh(data3+1, cmap='Greens')
pcm4 = axes[1, 1].pcolormesh(data4+1, cmap='Greens')
# Second row colorbar - placed on second row, all columns
fig.colorbar(pcm3, ax=axes[1, :], shrink=0.8)
plt.show()
# -
# This code is similar to the one above but the plots of the same color are on the same row rather than the same column. I also shrank the colorbars to 80% of their default size by setting `shrink=0.8`.
#
# Finally, let's set the blue colorbar to be on the bottom of the heatmaps.
# <div>
# <img src="Figures/bottomcolorbar.png" width=400 align="left" />
# </div>
# You can change the location of the colorbars with the `location` keyword argument in `fig.colorbar()`. The only difference between this plot and the one above is this line
#
# ```python
# fig.colorbar(pcm1, ax=axes[0, :], shrink=0.8, location='bottom')
# ```
#
# If you increase the `figsize` argument, this plot will look much better - at the moment it's quite cramped.
#
# I recommend you play around with matplotlib colorbar placement. You have total control over how many colorbars you put on the `Figure`, their location and how many rows and columns they span. These are some basic ideas but check out the docs to see more examples of how you can [place colorbars in matplotlib](https://matplotlib.org/3.1.1/gallery/subplots_axes_and_figures/colorbar_placement.html).
# ## Matplotlib Subplot Grid
#
# I've spoken about [`GridSpec`](https://matplotlib.org/api/_as_gen/matplotlib.gridspec.GridSpec.html) a few times in this article. It is the underlying class that *specifies the geometry of the grid that a subplot can be placed in*.
#
# You can create any shape you want using `plt.subplots()` and `plt.subplot2grid()`. But some of the more complex shapes are easier to create using `GridSpec`. If you want to become a total pro with matplotlib, check out the docs and look out for my article discussing it in future.
# ## Summary
#
# You can now create *any* shape you can imagine in matplotlib. Congratulations! This is a huge achievement. Don't worry if you didn't fully understand everything the first time around. I recommend you bookmark this article and revisit it from time to time.
#
# You've learned the underlying classes in matplotlib: `Figure`, `Axes`, `XAxis` and `YAxis` and how to plot with respect to them. You can write shorter, more readable code by using these methods and `ax.set()` to add titles, xlabels and many other things to each `Axes`. You can create more professional looking plots by sharing the x-axis and y-axis and add legends anywhere you like.
#
# You can create `Figures` of any size that include `Subplots` of any size - you're no longer restricted to those that take up `1/x`th of the plot. You know that to make the best plots, you should plan ahead and figure out the shape you are aiming for.
#
# You know when to use `plt.tight_layout()` (ticks, labels and titles) and `constrained_layout=True` (legends and colorbars) and how to manually adjust spacing between plots with `plt.subplots_adjust()`.
#
# Finally, you can add colorbars to as many `Axes` as you want and place them wherever you'd like.
#
# You've done everything now. All that is left is to practice these plots so that you can quickly create amazing plots whenever you want.
|
subplots/plt.subplots.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.3 32-bit
# name: python383jvsc74a57bd003e80f00e8a0b9204e9c928296cca598eb1fee14ca0655e081f97bf8e0459b57
# ---
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# %matplotlib inline
import numpy as np
pd.options.mode.chained_assignment = None
class_df.columns
relevant_cols = ["What's your hometown?", 'How did you make friends/meet people during online school?']
hometown_campus = class_df[relevant_cols]
hometown_campus.head(10)
hometown_campus.loc[hometown_campus['How did you make friends/meet people during online school?'].isna() == True, :]
# +
def count_home_people(row):
# print(row)
try:
if 'I lived on campus' in row['How did you make friends/meet people during online school?']:
row['home'] = 0
else:
row['home'] = 1
except:
# field is NaN
row['home'] = 0
return row
home_df = hometown_campus.apply(count_home_people, axis=1)
home_df.head(10)
# -
# get the total num of home people
home_df.loc[home_df['home'] == 1, :].count()
# +
hometown_campus['How did you make friends/meet people during online school?'] = hometown_campus['How did you make friends/meet people during online school?'].str.split(';')
hometown_campus = (hometown_campus
.set_index(["What's your hometown?"])['How did you make friends/meet people during online school?']
.apply(pd.Series)
.stack()
.reset_index()
.drop('level_1', axis=1)
.rename(columns={0:'How did you make friends/meet people during online school?'}))
hometown_campus.head(20)
# -
# filtering for people who lived on campus
hometown_campus = hometown_campus[hometown_campus['How did you make friends/meet people during online school?'] == 'I lived on campus']
hometown_campus
hometown_campus['Number of people'] = hometown_campus.groupby(["What's your hometown?"])['How did you make friends/meet people during online school?'].transform('count')
hometown_campus
# index = ['Peel Region', 'Toronto Region', 'USA', 'Durham Region', 'International', 'Halton Region', 'British Columbia', 'Kitchener/Waterloo Region', 'Ottawa–Gatineau Region', 'York Region']
hometown_campus = hometown_campus.drop_duplicates(subset=["What's your hometown?", 'How did you make friends/meet people during online school?', 'Number of people'], keep='first')
hometown_campus
hometown_campus.reset_index(inplace=True, drop=True)
hometown_campus
hometown_campus.loc[10] = ['Stayed Home', 'NA', 70]
hometown_campus = hometown_campus.sort_values(by='Number of people')
hometown_campus
total_respondants = hometown_campus['Number of people'].sum()
hometown_campus['Percentage of People'] = (hometown_campus['Number of people'] / total_respondants) * 100
hometown_campus
plt.figure(figsize=(24,10))
plt.title("Hometown VS Living On Campus", fontsize=16, y=1.02)
sns.set_style('darkgrid')
sns.set_theme(palette="colorblind")
ax = sns.barplot(x=hometown_campus["What's your hometown?"], y=hometown_campus["Percentage of People"], data=hometown_campus)
# ax.set(ylim=(0, 75))
plt.xlabel("Hometown", labelpad=15)
plt.ylabel("Percentage of people", labelpad=15)
|
Lifestyle/.ipynb_checkpoints/moving_on_campus_v_where_you_are_from-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# Analytics Expression Language Example
# %matplotlib inline
import xarray as xr
from datetime import datetime
from datacube.api import API
from datacube.ndexpr import NDexpr
# +
# Instantiating API and NDexpr
g = API()
nd = NDexpr()
# +
# construct data request parameters for band_30 and band_40
data_request_descriptor = {
'platform': 'LANDSAT_5',
'product': 'ledaps',
'variables': ('red', 'nir'),
'dimensions': {
'x': {
'range': (79,79.1)
},
'y': {
'range': (30,30.1)
},
'time': {
'range': (datetime(1995, 1, 1), datetime(1995, 12, 31))
}
}
}
# Retrieving data from API
d1 = g.get_data(data_request_descriptor)
# construct data request parameters for PQ
pq_request_descriptor = {
'platform': 'LANDSAT_5',
'product': 'pqa',
'variables': ('pixelquality'),
'dimensions': {
'x': {
'range': (79,79.1)
},
'y': {
'range': (30,30.1)
},
'time': {
'range': (datetime(1995, 1, 1), datetime(1995, 12, 31))
}
}
}
# Retrieving data from API
d2 = g.get_data(pq_request_descriptor)
# +
# The following 3 lines shouldn't be done like this
# Currently done like this for the sake of the example.
b30 = d1['arrays']['red']
b40 = d1['arrays']['nir']
#pq = d2['arrays']['pixelquality']
# +
# NDexpr demo begins here
# perform ndvi as expressed in this language.
ndvi = nd.evaluate('((b40 - b30) / (b40 + b30))')
# perform mask on ndvi as expressed in this language.
#masked_ndvi = nd.evaluate('ndvi{(pq == 32767) | (pq == 16383) | (pq == 2457)}')
# -
print(ndvi)
ndvi.plot()
print(masked_ndvi)
# +
# currently dimensions are integer indices, later will be labels when
# Data Access API Interface has been finalised.
reduction_on_dim0 = nd.evaluate('median(masked_ndvi, 0)')
print(reduction_on_dim0)
# -
reduction_on_dim01 = nd.evaluate('median(masked_ndvi, 0, 1)')
print(reduction_on_dim01)
reduction_on_dim012 = nd.evaluate('median(masked_ndvi, 0, 1, 2)')
print(reduction_on_dim012)
|
examples/notebooks/analytics_execution_engine/analytics_expression_language_example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# orphan: true
# ---
# # Working with Components
#
# - [Declaring Continuous Variables](continuous_variables.ipynb)
# - [ExplicitComponent](explicit_component.ipynb)
# - [ImplicitComponent](implicit_component.ipynb)
# - [Distributed Components](distributed_components.ipynb)
# - [IndepVarComp](indepvarcomp.ipynb)
# - [Specifying Units for Variables](units.ipynb)
# - [Scaling Variables](scaling.ipynb)
# - [Discrete Variables](discrete_variables.ipynb)
# - [Component Options and Arguments](options.ipynb)
|
openmdao/docs/openmdao_book/features/core_features/working_with_components/main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Question 1
developer = ['python', 'LetsUpgrade', 'Githup']
developer.append("YouTube")
developer
# # Question 2
# +
users = {
"name": "aswin",
"email": "<EMAIL>",
"age": 23
}
users.clear()
print(users)
# -
# # Question 3
# +
coding = {"python", "java", "c++"}
coding.add("javaScript")
print(coding)
# -
# # Question 4
# +
tuples = (1, 3, 7,5,9,9, 8, 7, 5,9, 4,9, 6, 8, 5)
numbers = tuples.count(9)
print(numbers)
# -
# # Question 5
# +
letsUpgrade = "aswin rao LetsUpgrade Learner."
cap = letsUpgrade.capitalize()
print (cap)
|
Day-2 Python batch-7.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import datetime as dt
from rpy2.robjects.packages import importr
from rpy2.robjects import r
from rpy2.robjects import pandas2ri
pandas2ri.activate()
# %matplotlib inline
# -
charlotte_rainfall = pd.read_csv('./charlotte_2_rg_2011.csv', header = None)
charlotte_rainfall.columns = ["year","month","day", "hour", "min", "Rainfall_1", "Rainfall_2"]
charlotte_rainfall.loc[:,'dt'] = pd.to_datetime(dict(year=charlotte_rainfall['year'], month=charlotte_rainfall['month'], day=charlotte_rainfall['day'], hour=charlotte_rainfall['hour'], minute=charlotte_rainfall['min']))
charlotte_rainfall.index=charlotte_rainfall['dt']
charlotte_rainfall.drop('year', 1, inplace=True)
charlotte_rainfall.drop('month', 1, inplace=True)
charlotte_rainfall.drop('day', 1, inplace=True)
charlotte_rainfall.drop('hour', 1, inplace=True)
charlotte_rainfall.drop('min', 1, inplace=True)
charlotte_rainfall.drop('dt', 1, inplace=True)
# +
charlotte_rainfall["Rainfall_1"] = charlotte_rainfall["Rainfall_1"].replace(-99, np.nan)
fig = plt.figure(figsize=(10,5))
plt.subplot(121)
plt.plot(charlotte_rainfall.index, charlotte_rainfall["Rainfall_1"])
plt.ylabel('mm/15min')
fig.autofmt_xdate()
charlotte_rainfall["Rainfall_2"] = charlotte_rainfall["Rainfall_2"].replace(-99, np.nan)
plt.subplot(122)
plt.plot(charlotte_rainfall.index, charlotte_rainfall["Rainfall_2"])
plt.ylabel('mm/15min')
fig.autofmt_xdate()
# -
# #### Accumulate 24h
charlotte_24h_rainfall = pd.DataFrame()
charlotte_24h_rainfall['mean_rain_1'] = charlotte_rainfall.Rainfall_1.resample('D').mean()
charlotte_24h_rainfall['accum_rain_1'] = charlotte_rainfall.Rainfall_1.resample('D').sum()
charlotte_24h_rainfall['mean_rain_2'] = charlotte_rainfall.Rainfall_2.resample('D').mean()
charlotte_24h_rainfall['accum_rain_2'] = charlotte_rainfall.Rainfall_2.resample('D').sum()
# #### Select only dates with rainfall
# +
mask = (charlotte_24h_rainfall.accum_rain_1 == 0) | (charlotte_24h_rainfall.accum_rain_2 == 0)
charlotte_24h_rainfall = charlotte_24h_rainfall.loc[~mask]
mask = (np.isnan(charlotte_24h_rainfall.accum_rain_1)) | (np.isnan(charlotte_24h_rainfall.accum_rain_2))
charlotte_24h_rainfall = charlotte_24h_rainfall.loc[~mask]
# Do the same with 15 min data
mask = (charlotte_rainfall.Rainfall_1 == 0) | (charlotte_rainfall.Rainfall_2 == 0)
charlotte_rainfall = charlotte_rainfall.loc[~mask]
mask = (np.isnan(charlotte_rainfall.Rainfall_1)) | (np.isnan(charlotte_rainfall.Rainfall_2))
charlotte_rainfall = charlotte_rainfall.loc[~mask]
# +
fig = plt.figure(figsize=(10,5))
plt.subplot(121)
plt.plot(charlotte_24h_rainfall.index, charlotte_24h_rainfall['accum_rain_1'])
plt.ylabel('mm/24h')
fig.autofmt_xdate()
plt.subplot(122)
plt.plot(charlotte_24h_rainfall.index, charlotte_24h_rainfall['accum_rain_2'])
plt.ylabel('mm/24h')
fig.autofmt_xdate()
fig = plt.figure(figsize=(10,5))
plt.subplot(121)
plt.plot(charlotte_rainfall.index, charlotte_rainfall['Rainfall_1'])
plt.ylabel('mm/15min')
fig.autofmt_xdate()
plt.subplot(122)
plt.plot(charlotte_rainfall.index, charlotte_rainfall['Rainfall_2'])
plt.ylabel('mm/15min')
fig.autofmt_xdate()
# -
# #### Use seconds as x and zeros as y
# +
charlotte_24h_rainfall['seconds'] = charlotte_24h_rainfall.index.astype(np.int64) // 10 ** 9 - ( charlotte_24h_rainfall.index.astype(np.int64)[0] // 10 ** 9)
charlotte_24h_rainfall['zeros'] = np.zeros((len(charlotte_24h_rainfall.accum_rain_1), 1), dtype=np.int8)
charlotte_rainfall['seconds'] = charlotte_rainfall.index.astype(np.int64) // 10 ** 9 - ( charlotte_rainfall.index.astype(np.int64)[0] // 10 ** 9)
charlotte_rainfall['zeros'] = np.zeros((len(charlotte_rainfall.Rainfall_1), 1), dtype=np.int8)
# +
sp = importr('sp')
gstat = importr('gstat')
intamap = importr('intamap')
r('jet.colors <- c("#00007F","blue","#007FFF","cyan","#7FFF7F","yellow","#FF7F00","red","#7F0000")')
r('col.palette <- colorRampPalette(jet.colors)')
# -
# ### Respect the time (in seconds)
# +
#charlotte_rainfall['seconds'] = charlotte_24h_rainfall.index.astype(np.int64) // 10 ** 9 - ( charlotte_24h_rainfall.index.astype(np.int64)[0] // 10 ** 9)
rain1 = charlotte_rainfall[['Rainfall_1', 'seconds', 'zeros']]
rain2 = charlotte_rainfall[['Rainfall_2', 'seconds', 'zeros']]
r_df = pandas2ri.py2ri(rain1)
r.assign('mydata', r_df)
r_df2 = pandas2ri.py2ri(rain2)
r.assign('mydata2', r_df2)
r('''
mydata <- data.frame(mydata)
coordinates(mydata) <- ~seconds+zeros
mydata2 <- data.frame(mydata2)
coordinates(mydata2) <- ~seconds+zeros
''')
p_myiso = r('myiso <- variogram(Rainfall_1~1,mydata,width=900,cutoff=86400)')
p_myiso2 = r('myiso2 <- variogram(Rainfall_2~1,mydata2,width=900,cutoff=86400)')
plt.figure(figsize=(10,5))
plt.subplot(121)
plt.plot(p_myiso['dist'], p_myiso['gamma'], '-o')
plt.subplot(122)
plt.plot(p_myiso2['dist'], p_myiso2['gamma'], '-o')
# +
charlotte_24h_rainfall['seconds'] = charlotte_24h_rainfall.index.astype(np.int64) // 10 ** 9 - ( charlotte_24h_rainfall.index.astype(np.int64)[0] // 10 ** 9)
rain1 = charlotte_24h_rainfall[['accum_rain_1', 'seconds', 'zeros']]
rain2 = charlotte_24h_rainfall[['accum_rain_2', 'seconds', 'zeros']]
r_df = pandas2ri.py2ri(rain1)
r.assign('mydata', r_df)
r_df2 = pandas2ri.py2ri(rain2)
r.assign('mydata2', r_df2)
r('''
mydata <- data.frame(mydata)
coordinates(mydata) <- ~seconds+zeros
mydata2 <- data.frame(mydata2)
coordinates(mydata2) <- ~seconds+zeros
''')
p_myiso = r('myiso <- variogram(accum_rain_1~1,mydata,width=172800,cutoff=8640000)')
p_myiso2 = r('myiso2 <- variogram(accum_rain_2~1,mydata2,width=172800,cutoff=8640000)')
plt.figure(figsize=(10,5))
plt.subplot(121)
plt.plot(p_myiso['dist'], p_myiso['gamma'], '-o')
plt.subplot(122)
plt.plot(p_myiso2['dist'], p_myiso2['gamma'], '-o')
# -
# ### Ignore the observation time and just ascend it...
# +
charlotte_24h_rainfall['seconds'] = np.arange(0,len(charlotte_24h_rainfall.accum_rain_1), 1)
rain1 = charlotte_24h_rainfall[['accum_rain_1', 'seconds', 'zeros']]
rain2 = charlotte_24h_rainfall[['accum_rain_2', 'seconds', 'zeros']]
r_df = pandas2ri.py2ri(rain1)
r.assign('mydata', r_df)
r_df2 = pandas2ri.py2ri(rain2)
r.assign('mydata2', r_df2)
r('''
mydata <- data.frame(mydata)
coordinates(mydata) <- ~seconds+zeros
mydata2 <- data.frame(mydata2)
coordinates(mydata2) <- ~seconds+zeros
''')
p_myiso = r('myiso <- variogram(accum_rain_1~1,mydata,width=5,cutoff=200)')
p_myiso2 = r('myiso2 <- variogram(accum_rain_2~1,mydata2,width=5,cutoff=200)')
plt.figure(figsize=(10,5))
plt.subplot(121)
plt.plot(p_myiso['dist'], p_myiso['gamma'], '-o')
plt.subplot(122)
plt.plot(p_myiso2['dist'], p_myiso2['gamma'], '-o')
# -
# ## Select rainfall on 5th August (15 min sampling)
event_rain = charlotte_rainfall.loc['2011-08-05 00:00:00':'2011-08-05 23:59:59']
event_rain_1 = event_rain.Rainfall_1
event_rain_2 = event_rain.Rainfall_2
event_rain_2.index = event_rain_2.index + dt.timedelta(hours=72)
my_event = event_rain_1.append(event_rain_2)
my_event = pd.DataFrame(my_event)
my_event.columns = ['R']
my_event['zeros'] = np.zeros((len(my_event.R), 1), dtype=np.int8)
# ## Taking time into account (but the time gap of 72h won't be seen with the current cutoff)
# +
my_event['seconds'] = my_event.index.astype(np.int64) // 10 ** 9 - ( my_event.index.astype(np.int64)[0] // 10 ** 9)
r_df = pandas2ri.py2ri(my_event)
r.assign('mydata_event', r_df)
r('''
mydata_event <- data.frame(mydata_event)
coordinates(mydata_event) <- ~seconds+zeros
''')
p_myiso = r('myiso_event <- variogram(R~1,mydata_event,width=1800,cutoff=90000)')
plt.plot(p_myiso['dist'], p_myiso['gamma'], '-o')
# -
# #### Ignore time
# +
my_event['seconds'] = np.arange(0,len(my_event.R), 1)
r_df = pandas2ri.py2ri(my_event)
r.assign('mydata_event', r_df)
r('''
mydata_event <- data.frame(mydata_event)
coordinates(mydata_event) <- ~seconds+zeros
''')
p_myiso = r('myiso_event <- variogram(R~1,mydata_event,width=2,cutoff=100)')
plt.plot(p_myiso['dist'], p_myiso['gamma'], '-o')
# -
from pandas.plotting import autocorrelation_plot
autocorrelation_plot(my_event.R)
autocorrelation_plot(rain1)
autocorrelation_plot(rain2)
|
week_7_temporal_variogram.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # **Bias-Variance Tradeoff**
# Source: [https://github.com/d-insight/code-bank.git](https://github.com/d-insight/code-bank.git)
# License: [MIT License](https://opensource.org/licenses/MIT). See open source [license](LICENSE) in the Code Bank repository.
# -------------
# ## Overview
# This project explores how __Bias__ and __Variance__ change as a linear regression is expanded with additional polynomial terms.
#
# First we define a __Data Generating Process__ (DGP) as a sigmoid function; then draw repeated samples from the DGP to allow for random variation; and finally we show the degree of __Bias__ and __Variance__ of the model at a given value of X. At the end of the project we can copare how the model performs at different levels of the polynomial expansion.
# -------------
# ## **Part 0**: Setup
# ### Import Packages
# +
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from IPython.display import clear_output
import math
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
# %matplotlib inline
# -
# ### Define Constants
X0 = 4 # value of the arbitrary point where bias will be measured
NOISE = 0.2 # offset for draw from uniform distribution
FONTSIZE = 18
OFFSET = 0.1 # plot offset on x and y axes
DRAWS = 100 # number of draws
# ### Helper Functions
#
# We will help you get started by defining some helper functions" for you to use, that just work. There is nothing for you to do in this section, and you don't need to worry about the internal aspects of each function, other than to just understand at a high level what each function returns or accomplishes.
# __Data Generating Function__:
# We define the true data generating function (DGP) for this example to be a logistic sigmoid function. The sigmoid function *without* any noise is the true function that we aim to recover. A sigmoid function is defined as: $sigmoid(x) = \frac{1}{1+e^{-x}}$
def sigmoid(x):
y = 1 / (1 + math.exp(-x))
return y
# __Custom Plotting Function__:
# The following function will plot the data and the given model predictions. This custom functioin simply "wraps" a basic matplotlib plotting function, but it does so in a standardized way that fits the needs of this project.
def myPlot(X, y, y_DGP, y_pred, draw, symbol = 'o'):
font = {'size' : FONTSIZE}
matplotlib.rc('font', **font)
plt.figure(figsize=(16, 12))
plt.plot(X, y, symbol, markersize=12, linewidth=3, label='Sampled data')
plt.plot(X, y_DGP, markersize=12, linewidth=3, label='Ground truth')
plt.ylim(0 - OFFSET, 1 + OFFSET)
plt.xlim(min(X) - OFFSET, max(X) + OFFSET)
plt.hlines(0, xmin = min(X), xmax = max(X), colors='black', linewidth=3)
plt.hlines(1, xmin = min(X), xmax = max(X), colors='black', linewidth=3)
if type(y_pred) == float:
plt.hlines(y_pred, xmin = min(X), xmax = max(X), colors='red', label='Latest estimate', linewidth=3)
if type(y_pred) == np.ndarray:
plt.plot(X, y_pred, '-', markersize = 12, linewidth=3, color = 'red', label='Latest estimate')
plt.ylabel('y')
plt.xlabel('X')
plt.title('Draw: {}'.format(draw))
plt.legend()
return plt
# __Test above two functions to see them in action__...
X = list(range(-50, 50))
X = [i/10 for i in X if i%2 == 0]
y_DGP = [sigmoid(i) for i in X]
y = [i + np.random.uniform(-NOISE, +NOISE) for i in y_DGP]
myPlot(X, y, y_DGP, None, 0)
plt.show()
# ## **Part 1**: Model 1 - The Mean
#
# The simplest model of all predicts the mean of the outcome variable. The model has a high bias, but a low variance.
#
# We will now resample from DGP and measure bias/variance at an arbitrary point to demonstrate this point.
# Initialize
estimates = []
draw = 0
# __Q 1: Draw data, estimate model, plot the result__:
# Repeatedly execute the following block of code to draw a new sample, estimate the model, and inspect the variance and the bias at an arbitrary point X0.
# +
# Draw sample
draw += 1
y_DGP = [sigmoid(i) for i in X]
y = [i + np.random.uniform(-NOISE, +NOISE) for i in y_DGP]
# CODE HERE
# Estimate: compute the mean of y
y_pred = None
# Assert OK to proceed
assert y_pred is not None, 'HINT: you need to complete the code to proceed.'
estimates.append(y_pred)
# Plot
p = myPlot(X, y, y_DGP, y_pred, draw) # Plot data
for est in estimates[:-1]: # Plot estimates
p.hlines(est, xmin = min(X), xmax = max(X), colors='gray', linestyle='dashed', linewidth=2)
p.show()
# -
# __Q 2: Summarize Bias and Variance at X0__
# Draw from the DGP and compute the difference to the prediction
biases = []
for draw in range(DRAWS):
biases.append(y_pred - sigmoid(X0))
print('Mean Bias at point X0: {}'.format(round(abs(np.mean(biases)), 4)))
print('Variance at point X0: {}'.format(round(np.var(biases), 4)))
# ## **Part 2**: Model 2 - A Line
#
# The next most complicated model predicts a linear relationship between X and the outcome variable Y. The model still has moderate bias, but somewhat lower variance.
#
# We will now resample from DGP and measure bias/variance at an arbitrary point to demonstrate this point.
# Initialize
estimates = []
draw = 0
# __Q 1: Draw data, estimate model, plot the result__:
# Repeatedly execute the following block of code to draw a new sample, estimate the model, and inspect the variance and the bias at an arbitrary point X0.
# +
# Draw sample
draw += 1
y_DGP = [sigmoid(i) for i in X]
y = [i + np.random.uniform(-NOISE, +NOISE) for i in y_DGP]
# CODE HERE
# Estimate: fit a LinearRegression() model
model = None
# Assert OK to proceed
assert model is not None, 'HINT: you need to complete the code to proceed.'
y_pred = model.predict(np.array(X).reshape(-1, 1))
estimates.append(y_pred)
# Plot
p = myPlot(X, y, y_DGP, y_pred, draw) # Plot data
for est in estimates[:-1]: # Plot estimates
plt.plot(X, est, '-', markersize = 12, linewidth=2, color = 'gray', linestyle='dashed')
p.show()
# -
# __Q 2: Summarize Bias and Variance at X0__
# Draw from the DGP and compute the difference to the prediction
biases = []
for draw in range(DRAWS):
y = [i + np.random.uniform(-NOISE, +NOISE) for i in y_DGP]
model = LinearRegression().fit(np.array(X).reshape(-1, 1), y)
y_pred = model.predict(np.array(X).reshape(-1, 1))
biases.append(y_pred[X.index(X0)] - sigmoid(X0))
print('Mean Bias at point X0: {}'.format(round(abs(np.mean(biases)), 4)))
print('Variance at point X0: {}'.format(round(np.var(biases), 4)))
# ## **Part 3**: Model 3 - A Higher Order Polynomial Regression
#
# We can expand the predictor space for X with higher order polynomials (X*X, X*X*X, etc...) to allow for non-linearities in the relationshio between X and Y. These modeled will bring down bias, but increase variance as each model chases the randomness of sampling variation.
#
# We will now resample from DGP and measure bias/variance at an arbitrary point to demonstrate this point.
# +
# Initialize
estimates = []
draw = 0
degree = 4 # Set the polynomial basis expansion (try 20)
# -
# __Q 1: Draw data, estimate model, plot the result__:
# Repeatedly execute the following block of code to draw a new sample, estimate the model, and inspect the variance and the bias at an arbitrary point X0.
# +
# Draw sample
draw += 1
y_DGP = [sigmoid(i) for i in X]
y = [i + np.random.uniform(-NOISE, +NOISE) for i in y_DGP]
# Generate a polynomial "basis expansion" -- new feature variables to add into the regression
polynomial = PolynomialFeatures(degree=degree, include_bias=True)
X_ = polynomial.fit_transform(np.array(X).reshape(-1, 1))
# Estimate
model = LinearRegression().fit(X_, y)
# CODE HERE
# Use the fitted model to predict values for X_
y_pred = None
# Assert OK to proceed
assert y_pred is not None, 'HINT: you need to complete the code to proceed.'
# Smooth estimation line so we can see the prediction better
X_smooth = list(range(-500, 491, 1))
X_smooth = [i/100 for i in X_smooth]
y_polynomial = [sigmoid(i) for i in X_smooth]
X_polynomial = polynomial.transform(np.array(X_smooth).reshape(-1, 1)) # fit on only 10 datapoints
y_polynomial_pred = model.predict(X_polynomial)
estimates.append(y_polynomial_pred)
# Plot
p = myPlot(X, y, y_DGP, y_pred, draw) # Plot data
for est in estimates[:-1]: # Plot estimates
p.plot(X_smooth, est, '-', markersize = 12, linewidth=2, color = 'gray', linestyle='dashed')
p.show()
# -
# __Q 2: Summarize Bias and Variance at X0__
# Draw from the DGP and compute the difference to the prediction
biases = []
for draw in range(DRAWS):
y = [i + np.random.uniform(-NOISE, +NOISE) for i in y_DGP]
model = LinearRegression().fit(X_, y)
y_pred = model.predict(np.array(X_))
biases.append(y_pred[X.index(X0)] - sigmoid(X0))
print('Mean Bias at point X0: {}'.format(round(abs(np.mean(biases)), 4)))
print('Variance at point X0: {}'.format(round(np.var(biases), 4)))
# ## **Part 4, Bonus**: Bias and variance across the domain of X
#
# We demonstrated the average bias and variance at one point, X0, which was arbitrarily set to a point defined by the constant X0. To get a complete and reliable assessment of bias and variance for the model _overall_, however, one would have to average bias and variance across the domain of possible levels of X.
# Can you copy and adapt the code above to loop the tested point X0 across the domain of X? You might want to step across the range in steps of 0.1; you will need to average across the averages you are already doing; and for greater reliability, you should complete 1000 draws at each point.
|
_development/projects/bias-variance/bias-variance.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] tags=["hide"]
# # Notebook Utils
#
# This notebook contains helper functions and classes for use with OpenVINO Notebooks. The code is synchronized with the `notebook_utils.py` file in the same directory as this notebook.
#
# There are five categories:
#
# - [Files](#Files)
# - [Images](#Images)
# - [Videos](#Videos)
# - [Visualization](#Visualization)
# - [OpenVINO Tools](#OpenVINO-Tools)
# - [Checks and Alerts](#Checks-and-Alerts)
#
# Each category contains a test cell that also shows how to use the functions in the section.
# +
import os
import shutil
import socket
import threading
import time
import urllib
import urllib.parse
import urllib.request
from os import PathLike
from pathlib import Path
from typing import Callable, List, NamedTuple, Optional, Tuple
import cv2
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import openvino.inference_engine
from async_pipeline import AsyncPipeline
from IPython.display import HTML, Image, Markdown, clear_output, display
from matplotlib.lines import Line2D
from models import model
from openvino.inference_engine import IECore
from tqdm.notebook import tqdm_notebook
# -
# ## Files
#
# Load an image, download a file, download an IR model, and create a progress bar to show download progress.
# +
def load_image(path: str) -> np.ndarray:
"""
Loads an image from `path` and returns it as BGR numpy array. `path`
should point to an image file, either a local filename or a url. The image is
not stored to the filesystem. Use the `download_file` function to download and
store an image.
:param path: Local path name or URL to image.
:return: image as BGR numpy array
"""
if path.startswith("http"):
# Set User-Agent to Mozilla because some websites block
# requests with User-Agent Python
request = urllib.request.Request(path, headers={"User-Agent": "Mozilla/5.0"})
response = urllib.request.urlopen(request)
array = np.asarray(bytearray(response.read()), dtype="uint8")
image = cv2.imdecode(array, -1) # Loads the image as BGR
else:
image = cv2.imread(path)
return image
class DownloadProgressBar(tqdm_notebook):
"""
TQDM Progress bar for downloading files with urllib.request.urlretrieve
"""
def update_to(self, block_num: int, block_size: int, total_size: int):
downloaded = block_num * block_size
if downloaded <= total_size:
self.update(downloaded - self.n)
def download_file(
url: PathLike,
filename: PathLike = None,
directory: PathLike = None,
show_progress: bool = True,
silent: bool = False,
timeout: int = 10,
) -> str:
"""
Download a file from a url and save it to the local filesystem. The file is saved to the
current directory by default, or to `directory` if specified. If a filename is not given,
the filename of the URL will be used.
:param url: URL that points to the file to download
:param filename: Name of the local file to save. Should point to the name of the file only,
not the full path. If None the filename from the url will be used
:param directory: Directory to save the file to. Will be created if it doesn't exist
If None the file will be saved to the current working directory
:param show_progress: If True, show an TQDM ProgressBar
:param silent: If True, do not print a message if the file already exists
:param timeout: Number of seconds before cancelling the connection attempt
:return: path to downloaded file
"""
try:
opener = urllib.request.build_opener()
opener.addheaders = [("User-agent", "Mozilla/5.0")]
urllib.request.install_opener(opener)
urlobject = urllib.request.urlopen(url, timeout=timeout)
if filename is None:
filename = urlobject.info().get_filename() or Path(urllib.parse.urlparse(url).path).name
except urllib.error.HTTPError as e:
raise Exception(f"File downloading failed with error: {e.code} {e.msg}") from None
except urllib.error.URLError as error:
if isinstance(error.reason, socket.timeout):
raise Exception(
"Connection timed out. If you access the internet through a proxy server, please "
"make sure the proxy is set in the shell from where you launched Jupyter. If your "
"internet connection is slow, you can call `download_file(url, timeout=30)` to "
"wait for 30 seconds before raising this error."
) from None
else:
raise
filename = Path(filename)
if len(filename.parts) > 1:
raise ValueError(
"`filename` should refer to the name of the file, excluding the directory. "
"Use the `directory` parameter to specify a target directory for the downloaded file."
)
# create the directory if it does not exist, and add the directory to the filename
if directory is not None:
directory = Path(directory)
directory.mkdir(parents=True, exist_ok=True)
filename = directory / Path(filename)
# download the file if it does not exist, or if it exists with an incorrect file size
urlobject_size = int(urlobject.info().get("Content-Length", 0))
if not filename.exists() or (os.stat(filename).st_size != urlobject_size):
progress_callback = DownloadProgressBar(
total=urlobject_size,
unit="B",
unit_scale=True,
unit_divisor=1024,
desc=str(filename),
disable=not show_progress,
)
urllib.request.urlretrieve(url, filename, reporthook=progress_callback.update_to)
if os.stat(filename).st_size >= urlobject_size:
progress_callback.update(urlobject_size - progress_callback.n)
progress_callback.refresh()
else:
if not silent:
print(f"'{filename}' already exists.")
return filename.resolve()
def download_ir_model(model_xml_url: str, destination_folder: PathLike = None) -> PathLike:
"""
Download IR model from `model_xml_url`. Downloads model xml and bin file; the weights file is
assumed to exist at the same location and name as model_xml_url with a ".bin" extension.
:param model_xml_url: URL to model xml file to download
:param destination_folder: Directory where downloaded model xml and bin are saved. If None, model
files are saved to the current directory
:return: path to downloaded xml model file
"""
model_bin_url = model_xml_url[:-4] + ".bin"
model_xml_path = download_file(model_xml_url, directory=destination_folder, show_progress=False)
download_file(model_bin_url, directory=destination_folder)
return model_xml_path
# + [markdown] tags=["hide"]
# ### Test File Functions
# + tags=["hide"]
model_url = "https://github.com/openvinotoolkit/openvino_notebooks/raw/main/notebooks/002-openvino-api/model/segmentation.xml"
download_ir_model(model_url, "model")
assert os.path.exists("model/segmentation.xml")
assert os.path.exists("model/segmentation.bin")
# + tags=["hide"]
url = "https://github.com/intel-iot-devkit/safety-gear-detector-python/raw/master/resources/Safety_Full_Hat_and_Vest.mp4"
if os.path.exists(os.path.basename(url)):
os.remove(os.path.basename(url))
video_file = download_file(url)
print(video_file)
assert Path(video_file).exists()
# + tags=["hide"]
url = "https://raw.githubusercontent.com/openvinotoolkit/openvino_notebooks/main/README.md"
filename = "openvino_notebooks_readme.md"
if os.path.exists(filename):
os.remove(filename)
readme_file = download_file(url, filename=filename)
print(readme_file)
assert Path(readme_file).exists()
# + tags=["hide"]
url = "https://raw.githubusercontent.com/openvinotoolkit/openvino_notebooks/main/README.md"
filename = "openvino_notebooks_readme.md"
directory = "temp"
video_file = download_file(
url, filename=filename, directory=directory, show_progress=False, silent=True
)
print(readme_file)
assert Path(readme_file).exists()
shutil.rmtree("temp")
# -
# ## Images
# ### Convert Pixel Data
#
# Normalize image pixel values between 0 and 1, and convert images to RGB and BGR.
# +
def normalize_minmax(data):
"""
Normalizes the values in `data` between 0 and 1
"""
if data.max() == data.min():
raise ValueError(
"Normalization is not possible because all elements of"
f"`data` have the same value: {data.max()}."
)
return (data - data.min()) / (data.max() - data.min())
def to_rgb(image_data: np.ndarray) -> np.ndarray:
"""
Convert image_data from BGR to RGB
"""
return cv2.cvtColor(image_data, cv2.COLOR_BGR2RGB)
def to_bgr(image_data: np.ndarray) -> np.ndarray:
"""
Convert image_data from RGB to BGR
"""
return cv2.cvtColor(image_data, cv2.COLOR_RGB2BGR)
# + [markdown] tags=["hide"]
# ### Test Data Conversion Functions
# + tags=["hide"]
test_array = np.random.randint(0, 255, (100, 100, 3))
normalized_array = normalize_minmax(test_array)
assert normalized_array.min() == 0
assert normalized_array.max() == 1
# + tags=["hide"]
bgr_array = np.ones((100, 100, 3), dtype=np.uint8)
bgr_array[:, :, 0] = 0
bgr_array[:, :, 1] = 1
bgr_array[:, :, 2] = 2
rgb_array = to_rgb(bgr_array)
assert np.all(bgr_array[:, :, 0] == rgb_array[:, :, 2])
bgr_array_converted = to_bgr(rgb_array)
assert np.all(bgr_array_converted == bgr_array)
# -
# ## Videos
# ### Video Player
#
# Custom video player to fulfill FPS requirements. You can set target FPS and output size, flip the video horizontally or skip first N frames.
# + pycharm={"name": "#%% \n"}
class VideoPlayer:
"""
Custom video player to fulfill FPS requirements. You can set target FPS and output size,
flip the video horizontally or skip first N frames.
:param source: Video source. It could be either camera device or video file.
:param size: Output frame size.
:param flip: Flip source horizontally.
:param fps: Target FPS.
:param skip_first_frames: Skip first N frames.
"""
def __init__(self, source, size=None, flip=False, fps=None, skip_first_frames=0):
self.__cap = cv2.VideoCapture(source)
if not self.__cap.isOpened():
raise RuntimeError(
f"Cannot open {'camera' if isinstance(source, int) else ''} {source}"
)
# skip first N frames
self.__cap.set(cv2.CAP_PROP_POS_FRAMES, skip_first_frames)
# fps of input file
self.__input_fps = self.__cap.get(cv2.CAP_PROP_FPS)
if self.__input_fps <= 0:
self.__input_fps = 60
# target fps given by user
self.__output_fps = fps if fps is not None else self.__input_fps
self.__flip = flip
self.__size = None
self.__interpolation = None
if size is not None:
self.__size = size
# AREA better for shrinking, LINEAR better for enlarging
self.__interpolation = (
cv2.INTER_AREA
if size[0] < self.__cap.get(cv2.CAP_PROP_FRAME_WIDTH)
else cv2.INTER_LINEAR
)
# first frame
_, self.__frame = self.__cap.read()
self.__lock = threading.Lock()
self.__thread = None
self.__stop = False
"""
Start playing.
"""
def start(self):
self.__stop = False
self.__thread = threading.Thread(target=self.__run, daemon=True)
self.__thread.start()
"""
Stop playing and release resources.
"""
def stop(self):
self.__stop = True
if self.__thread is not None:
self.__thread.join()
self.__cap.release()
def __run(self):
prev_time = 0
while not self.__stop:
t1 = time.time()
ret, frame = self.__cap.read()
if not ret:
break
# fulfill target fps
if 1 / self.__output_fps < time.time() - prev_time:
prev_time = time.time()
# replace by current frame
with self.__lock:
self.__frame = frame
t2 = time.time()
# time to wait [s] to fulfill input fps
wait_time = 1 / self.__input_fps - (t2 - t1)
# wait until
time.sleep(max(0, wait_time))
self.__frame = None
"""
Get current frame.
"""
def next(self):
with self.__lock:
if self.__frame is None:
return None
# need to copy frame, because can be cached and reused if fps is low
frame = self.__frame.copy()
if self.__size is not None:
frame = cv2.resize(frame, self.__size, interpolation=self.__interpolation)
if self.__flip:
frame = cv2.flip(frame, 1)
return frame
# + [markdown] tags=["hide"]
# ### Test Video Player
# + tags=["hide"]
video = "../201-vision-monodepth/data/Coco Walking in Berkeley.mp4"
player = VideoPlayer(video, fps=15, skip_first_frames=10)
player.start()
for i in range(50):
frame = player.next()
_, encoded_img = cv2.imencode(".jpg", frame, params=[cv2.IMWRITE_JPEG_QUALITY, 90])
img = Image(data=encoded_img)
clear_output(wait=True)
display(img)
player.stop()
print("Finished")
# -
# ## Visualization
# ### Segmentation
#
# Define a SegmentationMap NamedTuple that keeps the labels and colormap for a segmentation project/dataset. Create CityScapesSegmentation and BinarySegmentation SegmentationMaps. Create a function to convert a segmentation map to an RGB image with a colormap, and to show the segmentation result as an overlay over the original image.
class Label(NamedTuple):
index: int
color: Tuple
name: Optional[str] = None
class SegmentationMap(NamedTuple):
labels: List
def get_colormap(self):
return np.array([label.color for label in self.labels])
def get_labels(self):
labelnames = [label.name for label in self.labels]
if any(labelnames):
return labelnames
else:
return None
# +
cityscape_labels = [
Label(index=0, color=(128, 64, 128), name="road"),
Label(index=1, color=(244, 35, 232), name="sidewalk"),
Label(index=2, color=(70, 70, 70), name="building"),
Label(index=3, color=(102, 102, 156), name="wall"),
Label(index=4, color=(190, 153, 153), name="fence"),
Label(index=5, color=(153, 153, 153), name="pole"),
Label(index=6, color=(250, 170, 30), name="traffic light"),
Label(index=7, color=(220, 220, 0), name="traffic sign"),
Label(index=8, color=(107, 142, 35), name="vegetation"),
Label(index=9, color=(152, 251, 152), name="terrain"),
Label(index=10, color=(70, 130, 180), name="sky"),
Label(index=11, color=(220, 20, 60), name="person"),
Label(index=12, color=(255, 0, 0), name="rider"),
Label(index=13, color=(0, 0, 142), name="car"),
Label(index=14, color=(0, 0, 70), name="truck"),
Label(index=15, color=(0, 60, 100), name="bus"),
Label(index=16, color=(0, 80, 100), name="train"),
Label(index=17, color=(0, 0, 230), name="motorcycle"),
Label(index=18, color=(119, 11, 32), name="bicycle"),
Label(index=19, color=(255, 255, 255), name="background"),
]
CityScapesSegmentation = SegmentationMap(cityscape_labels)
binary_labels = [
Label(index=0, color=(255, 255, 255), name="background"),
Label(index=1, color=(0, 0, 0), name="foreground"),
]
BinarySegmentation = SegmentationMap(binary_labels)
# + tags=[]
def segmentation_map_to_image(
result: np.ndarray, colormap: np.ndarray, remove_holes: bool = False
) -> np.ndarray:
"""
Convert network result of floating point numbers to an RGB image with
integer values from 0-255 by applying a colormap.
:param result: A single network result after converting to pixel values in H,W or 1,H,W shape.
:param colormap: A numpy array of shape (num_classes, 3) with an RGB value per class.
:param remove_holes: If True, remove holes in the segmentation result.
:return: An RGB image where each pixel is an int8 value according to colormap.
"""
if len(result.shape) != 2 and result.shape[0] != 1:
raise ValueError(
f"Expected result with shape (H,W) or (1,H,W), got result with shape {result.shape}"
)
if len(np.unique(result)) > colormap.shape[0]:
raise ValueError(
f"Expected max {colormap[0]} classes in result, got {len(np.unique(result))} "
"different output values. Please make sure to convert the network output to "
"pixel values before calling this function."
)
elif result.shape[0] == 1:
result = result.squeeze(0)
result = result.astype(np.uint8)
contour_mode = cv2.RETR_EXTERNAL if remove_holes else cv2.RETR_TREE
mask = np.zeros((result.shape[0], result.shape[1], 3), dtype=np.uint8)
for label_index, color in enumerate(colormap):
label_index_map = result == label_index
label_index_map = label_index_map.astype(np.uint8) * 255
contours, hierarchies = cv2.findContours(
label_index_map, contour_mode, cv2.CHAIN_APPROX_SIMPLE
)
cv2.drawContours(
mask,
contours,
contourIdx=-1,
color=color.tolist(),
thickness=cv2.FILLED,
)
return mask
def segmentation_map_to_overlay(image, result, alpha, colormap, remove_holes=False) -> np.ndarray:
"""
Returns a new image where a segmentation mask (created with colormap) is overlayed on
the source image.
:param image: Source image.
:param result: A single network result after converting to pixel values in H,W or 1,H,W shape.
:param alpha: Alpha transparency value for the overlay image.
:param colormap: A numpy array of shape (num_classes, 3) with an RGB value per class.
:param remove_holes: If True, remove holes in the segmentation result.
:return: An RGP image with segmentation mask overlayed on the source image.
"""
if len(image.shape) == 2:
image = np.repeat(np.expand_dims(image, -1), 3, 2)
mask = segmentation_map_to_image(result, colormap, remove_holes)
image_height, image_width = image.shape[:2]
mask = cv2.resize(src=mask, dsize=(image_width, image_height))
return cv2.addWeighted(mask, alpha, image, 1 - alpha, 0)
# -
# ### Network Results
#
# Show network result image, optionally together with the source image and a legend with labels.
# + tags=[]
def viz_result_image(
result_image: np.ndarray,
source_image: np.ndarray = None,
source_title: str = None,
result_title: str = None,
labels: List[Label] = None,
resize: bool = False,
bgr_to_rgb: bool = False,
hide_axes: bool = False,
) -> matplotlib.figure.Figure:
"""
Show result image, optionally together with source images, and a legend with labels.
:param result_image: Numpy array of RGB result image.
:param source_image: Numpy array of source image. If provided this image will be shown
next to the result image. source_image is expected to be in RGB format.
Set bgr_to_rgb to True if source_image is in BGR format.
:param source_title: Title to display for the source image.
:param result_title: Title to display for the result image.
:param labels: List of labels. If provided, a legend will be shown with the given labels.
:param resize: If true, resize the result image to the same shape as the source image.
:param bgr_to_rgb: If true, convert the source image from BGR to RGB. Use this option if
source_image is a BGR image.
:param hide_axes: If true, do not show matplotlib axes.
:return: Matplotlib figure with result image
"""
if bgr_to_rgb:
source_image = to_rgb(source_image)
if resize:
result_image = cv2.resize(result_image, (source_image.shape[1], source_image.shape[0]))
num_images = 1 if source_image is None else 2
fig, ax = plt.subplots(1, num_images, figsize=(16, 8), squeeze=False)
if source_image is not None:
ax[0, 0].imshow(source_image)
ax[0, 0].set_title(source_title)
ax[0, num_images - 1].imshow(result_image)
ax[0, num_images - 1].set_title(result_title)
if hide_axes:
for a in ax.ravel():
a.axis("off")
if labels:
colors = labels.get_colormap()
lines = [
Line2D(
[0],
[0],
color=[item / 255 for item in c.tolist()],
linewidth=3,
linestyle="-",
)
for c in colors
]
plt.legend(
lines,
labels.get_labels(),
bbox_to_anchor=(1, 1),
loc="upper left",
prop={"size": 12},
)
plt.close(fig)
return fig
# + [markdown] tags=["hide"]
# ### Test Visualization Functions
# + tags=["hide"]
testimage = np.zeros((100, 100, 3), dtype=np.uint8)
testimage[30:80, 30:80, :] = [0, 255, 0]
testimage[0:10, 0:10, :] = 100
testimage[40:60, 40:60, :] = 128
testimage[testimage == 0] = 128
testmask1 = np.zeros((testimage.shape[:2]))
testmask1[30:80, 30:80] = 1
testmask1[40:50, 40:50] = 0
testmask1[0:15, 0:10] = 2
result_image_overlay = segmentation_map_to_overlay(
image=testimage,
result=testmask1,
alpha=0.6,
colormap=np.array([[0, 0, 0], [255, 0, 0], [255, 255, 0]]),
)
result_image = segmentation_map_to_image(testmask1, CityScapesSegmentation.get_colormap())
result_image_no_holes = segmentation_map_to_image(
testmask1, CityScapesSegmentation.get_colormap(), remove_holes=True
)
resized_result_image = cv2.resize(result_image, (50, 50))
overlay_result_image = segmentation_map_to_overlay(
testimage, testmask1, 0.6, CityScapesSegmentation.get_colormap(), remove_holes=False
)
fig1 = viz_result_image(result_image, testimage)
fig2 = viz_result_image(result_image_no_holes, testimage, labels=CityScapesSegmentation)
fig3 = viz_result_image(
resized_result_image,
testimage,
source_title="Source Image",
result_title="Resized Result Image",
resize=True,
)
fig4 = viz_result_image(
overlay_result_image,
labels=CityScapesSegmentation,
result_title="Image with Result Overlay",
)
display(fig1, fig2, fig3, fig4)
# -
# ### Live Inference
# +
def showarray(frame: np.ndarray, display_handle=None):
"""
Display array `frame`. Replace information at `display_handle` with `frame`
encoded as jpeg image. `frame` is expected to have data in BGR order.
Create a display_handle with: `display_handle = display(display_id=True)`
"""
_, frame = cv2.imencode(ext=".jpeg", img=frame)
if display_handle is None:
display_handle = display(Image(data=frame.tobytes()), display_id=True)
else:
display_handle.update(Image(data=frame.tobytes()))
return display_handle
def show_live_inference(
ie, image_paths: List, model: model.Model, device: str, reader: Optional[Callable] = None
):
"""
Do inference of images listed in `image_paths` on `model` on the given `device` and show
the results in real time in a Jupyter Notebook
:param image_paths: List of image filenames to load
:param model: Model instance for inference
:param device: Name of device to perform inference on. For example: "CPU"
:param reader: Image reader. Should return a numpy array with image data.
If None, cv2.imread will be used, with the cv2.IMREAD_UNCHANGED flag
"""
display_handle = None
next_frame_id = 0
next_frame_id_to_show = 0
input_layer = next(iter(model.net.input_info))
# Create asynchronous pipeline and print time it takes to load the model
load_start_time = time.perf_counter()
pipeline = AsyncPipeline(
ie=ie, model=model, plugin_config={}, device=device, max_num_requests=0
)
load_end_time = time.perf_counter()
# Perform asynchronous inference
start_time = time.perf_counter()
while next_frame_id < len(image_paths) - 1:
results = pipeline.get_result(next_frame_id_to_show)
if results:
# Show next result from async pipeline
result, meta = results
display_handle = showarray(result, display_handle)
next_frame_id_to_show += 1
if pipeline.is_ready():
# Submit new image to async pipeline
image_path = image_paths[next_frame_id]
if reader is None:
image = cv2.imread(filename=str(image_path), flags=cv2.IMREAD_UNCHANGED)
else:
image = reader(str(image_path))
pipeline.submit_data(
inputs={input_layer: image}, id=next_frame_id, meta={"frame": image}
)
del image
next_frame_id += 1
else:
# If the pipeline is not ready yet and there are no results: wait
pipeline.await_any()
pipeline.await_all()
# Show all frames that are in the pipeline after all images have been submitted
while pipeline.has_completed_request():
results = pipeline.get_result(next_frame_id_to_show)
if results:
result, meta = results
display_handle = showarray(result, display_handle)
next_frame_id_to_show += 1
end_time = time.perf_counter()
duration = end_time - start_time
fps = len(image_paths) / duration
print(f"Loaded model to {device} in {load_end_time-load_start_time:.2f} seconds.")
print(f"Total time for {next_frame_id} frames: {duration:.2f} seconds, fps:{fps:.2f}")
del pipeline.exec_net
del pipeline
# + [markdown] tags=["hide"]
# #### Test Live Inference
# + tags=["hide"]
# Test binary segmentation
from models.custom_segmentation import SegmentationModel
image_paths = sorted(list(Path("../111-detection-quantization/data").glob("*.jpg")))
ie = IECore()
segmentation_model = SegmentationModel(
ie,
Path("model/segmentation.xml"),
sigmoid=False,
colormap=np.array([[0, 0, 0], [0, 0, 255]]),
rgb=True,
rotate_and_flip=False,
)
show_live_inference(
ie=ie,
image_paths=image_paths,
model=segmentation_model,
device="CPU",
reader=lambda x: cv2.cvtColor(cv2.imread(x), cv2.COLOR_BGR2RGB),
)
# + tags=["hide"]
# Test multiclass segmentation with different input shape
# This requires running the 102 notebook first, to generate the Fastseg model
fastseg_path = Path("../102-pytorch-onnx-to-openvino/model/fastseg1024.xml")
image_path = "../102-pytorch-onnx-to-openvino/data/street.jpg"
if fastseg_path.exists():
image_paths = [
image_path,
] * 5
ie = IECore()
CityScapesSegmentation = SegmentationMap(cityscape_labels)
segmentation_model = SegmentationModel(
ie,
fastseg_path,
sigmoid=False,
argmax=True,
colormap=CityScapesSegmentation.get_colormap(),
rgb=True,
)
show_live_inference(ie=ie, image_paths=image_paths, model=segmentation_model, device="CPU")
# + [markdown] tags=[]
# ## OpenVINO Tools
# -
def benchmark_model(
model_path: PathLike,
device: str = "CPU",
seconds: int = 60,
api: str = "async",
batch: int = 1,
cache_dir: PathLike = "model_cache",
):
"""
Benchmark model `model_path` with `benchmark_app`. Returns the output of `benchmark_app`
without logging info, and information about the device
:param model_path: path to IR model xml file, or ONNX model
:param device: device to benchmark on. For example, "CPU" or "MULTI:CPU,GPU"
:param seconds: number of seconds to run benchmark_app
:param api: API. Possible options: sync or async
:param batch: Batch size
:param cache_dir: Directory that contains model/kernel cache files
"""
ie = IECore()
model_path = Path(model_path)
if ("GPU" in device) and ("GPU" not in ie.available_devices):
raise ValueError(
f"A GPU device is not available. Available devices are: {ie.available_devices}"
)
else:
benchmark_command = f"benchmark_app -m {model_path} -d {device} -t {seconds} -api {api} -b {batch} -cdir {cache_dir}"
display(
Markdown(
f"**Benchmark {model_path.name} with {device} for {seconds} seconds with {api} inference**"
)
)
display(Markdown(f"Benchmark command: `{benchmark_command}`"))
benchmark_output = get_ipython().run_line_magic("sx", "$benchmark_command")
benchmark_result = [
line
for line in benchmark_output
if not (line.startswith(r"[") or line.startswith(" ") or line == "")
]
print("\n".join(benchmark_result))
print()
if "MULTI" in device:
devices = device.replace("MULTI:", "").split(",")
for single_device in devices:
device_name = ie.get_metric(
device_name=single_device, metric_name="FULL_DEVICE_NAME"
)
print(f"{single_device} device: {device_name}")
else:
print(f"Device: {ie.get_metric(device_name=device, metric_name='FULL_DEVICE_NAME')}")
# + [markdown] tags=["hide"]
# ### Test OpenVINO Tools
#
# + tags=["hide"]
ie = IECore()
model_url = "https://github.com/openvinotoolkit/openvino_notebooks/raw/main/notebooks/002-openvino-api/model/segmentation.xml"
model_path = download_ir_model(model_url, "model")
device = "MULTI:CPU,GPU" if "GPU" in ie.available_devices else "CPU"
display(Markdown(device))
benchmark_model(model_path=model_path, device=device, seconds=5)
# -
# ## Checks and Alerts
#
# Create an alert class to show stylized info/error/warning messages and a `check_device` function that checks whether a given device is available.
# +
class NotebookAlert(Exception):
def __init__(self, message: str, alert_class: str):
"""
Show an alert box with the given message.
:param message: The message to display.
:param alert_class: The class for styling the message. Options: info, warning, success, danger.
"""
self.message = message
self.alert_class = alert_class
self.show_message()
def show_message(self):
display(HTML(f"""<div class="alert alert-{self.alert_class}">{self.message}"""))
class DeviceNotFoundAlert(NotebookAlert):
def __init__(self, device: str):
"""
Show a warning message about an unavailable device. This class does not check whether or
not the device is available, use the `check_device` function to check this. `check_device`
also shows the warning if the device is not found.
:param device: The unavailable device.
:return: A formatted alert box with the message that `device` is not available, and a list
of devices that are available.
"""
ie = IECore()
supported_devices = ie.available_devices
self.message = (
f"Running this cell requires a {device} device, "
"which is not available on this system. "
)
self.alert_class = "warning"
if len(supported_devices) == 1:
self.message += f"The following device is available: {ie.available_devices[0]}"
else:
self.message += (
"The following devices are available: " f"{', '.join(ie.available_devices)}"
)
super().__init__(self.message, self.alert_class)
def check_device(device: str) -> bool:
"""
Check if the specified device is available on the system.
:param device: Device to check. e.g. CPU, GPU
:return: True if the device is available, False if not. If the device is not available,
a DeviceNotFoundAlert will be shown.
"""
ie = IECore()
if device not in ie.available_devices:
DeviceNotFoundAlert(device)
return False
else:
return True
def check_openvino_version(version: str) -> bool:
"""
Check if the specified OpenVINO version is installed.
:param version: the OpenVINO version to check. Example: 2021.4
:return: True if the version is installed, False if not. If the version is not installed,
an alert message will be shown.
"""
installed_version = openvino.inference_engine.get_version()
if version not in installed_version:
NotebookAlert(
f"This notebook requires OpenVINO {version}. "
f"The version on your system is: <i>{installed_version}</i>.<br>"
"Please run <span style='font-family:monospace'>pip install --upgrade -r requirements.txt</span> "
"in the openvino_env environment to install this version. "
"See the <a href='https://github.com/openvinotoolkit/openvino_notebooks'>"
"OpenVINO Notebooks README</a> for detailed instructions",
alert_class="danger",
)
return False
else:
return True
# + [markdown] tags=["hide"]
# ### Test Alerts
# + tags=["hide"]
NotebookAlert(message="Hello, world!", alert_class="info")
DeviceNotFoundAlert("GPU");
# + tags=["hide"]
assert check_device("CPU")
# + tags=["hide"]
if check_device("HELLOWORLD"):
print("Hello World device found.")
# + tags=["hide"]
check_openvino_version("2022.1");
|
notebooks/utils/notebook_utils.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ___
#
# <a href='http://www.pieriandata.com'> <img src='../../Pierian_Data_Logo.png' /></a>
# ___
# # SF Salaries Exercise - Solutions
#
# Welcome to a quick exercise for you to practice your pandas skills! We will be using the [SF Salaries Dataset](https://www.kaggle.com/kaggle/sf-salaries) from Kaggle! Just follow along and complete the tasks outlined in bold below. The tasks will get harder and harder as you go along.
# ** Import pandas as pd.**
import pandas as pd
# ** Read Salaries.csv as a dataframe called sal.**
sal = pd.read_csv('Salaries.csv')
# ** Check the head of the DataFrame. **
sal.head()
# ** Use the .info() method to find out how many entries there are.**
sal.info() # 148654 Entries
# **What is the average BasePay ?**
sal['BasePay'].mean()
# ** What is the highest amount of OvertimePay in the dataset ? **
sal['OvertimePay'].max()
# ** What is the job title of JOSEPH DRISCOLL ? Note: Use all caps, otherwise you may get an answer that doesn't match up (there is also a lowercase Joseph Driscoll). **
sal[sal['EmployeeName']=='<NAME>']['JobTitle']
# ** How much does <NAME>ISCOLL make (including benefits)? **
sal[sal['EmployeeName']=='<NAME>']['TotalPayBenefits']
# ** What is the name of highest paid person (including benefits)?**
sal[sal['TotalPayBenefits']== sal['TotalPayBenefits'].max()] #['EmployeeName']
# or
# sal.loc[sal['TotalPayBenefits'].idxmax()]
# ** What is the name of lowest paid person (including benefits)? Do you notice something strange about how much he or she is paid?**
# +
sal[sal['TotalPayBenefits']== sal['TotalPayBenefits'].min()] #['EmployeeName']
# or
# sal.loc[sal['TotalPayBenefits'].idxmax()]['EmployeeName']
## ITS NEGATIVE!! VERY STRANGE
# -
# ** What was the average (mean) BasePay of all employees per year? (2011-2014) ? **
sal.groupby('Year').mean()['BasePay']
# ** How many unique job titles are there? **
sal['JobTitle'].nunique()
# ** What are the top 5 most common jobs? **
sal['JobTitle'].value_counts().head(5)
# ** How many Job Titles were represented by only one person in 2013? (e.g. Job Titles with only one occurence in 2013?) **
sum(sal[sal['Year']==2013]['JobTitle'].value_counts() == 1) # pretty tricky way to do this...
# ** How many people have the word Chief in their job title? (This is pretty tricky) **
def chief_string(title):
if 'chief' in title.lower():
return True
else:
return False
sum(sal['JobTitle'].apply(lambda x: chief_string(x)))
# ** Bonus: Is there a correlation between length of the Job Title string and Salary? **
sal['title_len'] = sal['JobTitle'].apply(len)
sal[['title_len','TotalPayBenefits']].corr() # No correlation.
# # Great Job!
|
res/Python-for-Data-Analysis/Pandas/Pandas Exercises/SF Salaries Exercise- Solutions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <a href="https://githubtocolab.com/giswqs/geemap/blob/master/examples/notebooks/59_whitebox.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab"/></a>
#
# Uncomment the following line to install [geemap](https://geemap.org) if needed.
# +
# # !pip install geemap
# +
import subprocess
try:
import whiteboxgui
except ImportError:
print('Installing whiteboxgui ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'whiteboxgui'])
# -
import geemap
import whiteboxgui
Map = geemap.Map()
Map
whiteboxgui.show()
whiteboxgui.show(tree=True)
|
examples/notebooks/59_whitebox.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # World Wide Products Inc.
# __Problem Statement__: Build the forecasting models to determine the demand of a particular product
# __Dataset__: Data set contains the product demands for encoded products
# <br>
# Source: https://www.kaggle.com/felixzhao/productdemandforecasting
# __Reference__: http://dacatay.com/data-science/part-4-time-series-prediction-arima-python/
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
import warnings
import itertools
import numpy as np
import math
warnings.filterwarnings("ignore") # specify to ignore warning messages
# ## Data Extraction and Feature Engineering
demand = pd.read_csv('../data/external/Historical Product Demand.csv', low_memory=False)
list(demand)
demand.head()
demand.Product_Code.unique()
# +
## Which product has maximum demand?
# -
demand.groupby("Product_Code").sum().sort_values("Order_Demand", ascending=False).head(1)
# +
## Which warehouse has maximum demand?
# -
demand.groupby("Warehouse").sum().sort_values("Order_Demand", ascending=False).head(1)
# +
## Which product category has maximum demand?
# -
demand.groupby("Product_Category").sum().sort_values("Order_Demand", ascending=False).head(1)
# +
##Picking the product with most order demand
# -
product = demand.loc[demand['Product_Code'] == 'Product_1359']
product['Date'].min(), product['Date'].max()
product.head()
product.info()
product = product.drop(columns=['Warehouse','Product_Category','Product_Code'])
product.head()
productnew = product.copy()
productnew.info()
productnew.head()
productnew['Date'] = pd.to_datetime(productnew['Date'])
productnew = productnew.set_index('Date')
productnew = productnew.apply(pd.to_numeric, errors='ignore')
# Day with the highest demand
productnew.loc[productnew['Order_Demand'].idxmax()]
productnew = productnew.infer_objects()
productnew.dtypes
productnew.Order_Demand = productnew.Order_Demand.astype(float)
productnew.dtypes
productnew.index
y = productnew['Order_Demand'].resample('MS').mean()
y.head()
y_train = y[:'2016']
y_test = y['2017':]
y.plot(figsize=(15, 6))
plt.show()
# ## Time Series using Arima
# +
# define the p, d and q parameters to take any value between 0 and 2
p = d = q = range(0, 3)
# generate all different combinations of p, d and q triplets
pdq = list(itertools.product(p, d, q))
# generate all different combinations of seasonal p, q and q triplets
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
# +
# To find the best fitting model we iteratively create a SARIMAX model
# with a given parameter constellation and fit the data to it. For each
# of these models we compute the Akaike Information Criterion (AIC)
# and eventually choose the model for which the fitted data results in the lowest AIC.
# +
best_aic = np.inf
best_pdq = None
best_seasonal_pdq = None
tmp_model = None
best_mdl = None
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
tmp_mdl = sm.tsa.statespace.SARIMAX(y_train,
order = param,
seasonal_order = param_seasonal,
enforce_stationarity=True,
enforce_invertibility=True)
res = tmp_mdl.fit()
if res.aic < best_aic:
best_aic = res.aic
best_pdq = param
best_seasonal_pdq = param_seasonal
best_mdl = tmp_mdl
except:
continue
print("Best SARIMAX{}x{}12 model - AIC:{}".format(best_pdq, best_seasonal_pdq, best_aic))
# +
# The SARIMAX model will be trained on the training data y_train
# -
mod = sm.tsa.statespace.SARIMAX(y_train,
order=(1, 1, 1),
seasonal_order=(1, 1, 0, 12),
enforce_stationarity=False,
enforce_invertibility=False)
results = mod.fit()
print(results.summary().tables[1])
# print statistics
print(res.aic)
print(res.summary())
res.plot_diagnostics(figsize=(16, 10))
plt.tight_layout()
plt.show()
# +
# in-sample-prediction and confidence bounds
pred = res.get_prediction(start=pd.to_datetime('2017-01-01'),end=pd.to_datetime('2018-01-01'),
dynamic=True)
pred_ci = pred.conf_int()
# plot in-sample-prediction
ax = y['2012':].plot(label='Observed');
pred.predicted_mean.plot(ax=ax, label='One-step Ahead Prediction', alpha=.7, figsize=(14, 7));
# draw confidence bound
ax.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], color='k', alpha=.2);
# style the plot
ax.fill_betweenx(ax.get_ylim(), pd.to_datetime('2012-10-01'), y.index[-1], alpha=.15, zorder=-1);
ax.set_xlabel('Date')
ax.set_ylabel('Product_1359 Demand')
plt.legend(loc='upper left')
plt.show()
# +
y_hat = pred.predicted_mean
y_true = y['2012-10-01':]
# compute the mean square error
mse = ((y_hat - y_true) ** 2).mean()
print('Prediction quality: {:.2f} MSE ({:.2f} RMSE)'.format(mse, math.sqrt(mse)))
# -
plt.plot(y_true, label='Observed')
plt.plot(y_hat, label='Out-of-Sample Forecast')
ax.set_xlabel('Date')
ax.set_ylabel('Product_1359 Demand')
plt.legend(loc='upper left');
plt.show()
# +
mod = sm.tsa.statespace.SARIMAX(y,
order=(1, 1, 1),
seasonal_order=(1, 1, 0, 12),
enforce_stationarity=False,
enforce_invertibility=False)
res = mod.fit()
# get forecast 120 steps ahead in future
pred_uc = res.get_forecast(steps=120)
# get confidence intervals of forecasts
pred_ci = pred_uc.conf_int()
ax = y.plot(label='Observed', figsize=(16, 8));
pred_uc.predicted_mean.plot(ax=ax, label='Forecast');
ax.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], alpha=.25);
ax.set_xlabel('Date');
ax.set_ylabel('Product_1359 Demand');
plt.legend(loc='upper left')
plt.show()
# -
|
notebooks/WorldWide Products Arima.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Transformer Network Application: Named-Entity Recognition
#
# Welcome to Week 4's first ungraded lab. In this notebook you'll explore one application of the transformer architecture that you built in the previous assignment.
#
# **After this assignment you'll be able to**:
#
# * Use tokenizers and pre-trained models from the HuggingFace Library.
# * Fine-tune a pre-trained transformer model for Named-Entity Recognition
# ## Table of Contents
#
# - [Packages](#0)
# - [1 - Named-Entity Recogniton to Process Resumes](#1)
# - [1.1 - Data Cleaning](#1-1)
# - [1.2 - Padding and Generating Tags](#1-2)
# - [1.3 - Tokenize and Align Labels with 🤗 Library](#1-3)
# - [Exercise 1 - tokenize_and_align_labels](#ex-1)
# - [1.4 - Optimization](#1-4)
# <a name='0'></a>
# ## Packages
#
# Run the following cell to load the packages you'll need.
import pandas as pd
import tensorflow as tf
import json
import random
import logging
import re
# <a name='1'></a>
# ## 1 - Named-Entity Recogniton to Process Resumes
#
# When faced with a large amount of unstructured text data, named-entity recognition (NER) can help you detect and classify important information in your dataset. For instance, in the running example "Jane vists Africa in September", NER would help you detect "Jane", "Africa", and "September" as named-entities and classify them as person, location, and time.
#
# * You will use a variation of the Transformer model you built in the last assignment to process a large dataset of resumes.
# * You will find and classify relavent information such as the companies the applicant worked at, skills, type of degree, etc.
# <a name='1-1'></a>
# ### 1.1 - Dataset Cleaning
#
# In this assignment you will optimize a Transformer model on a dataset of resumes. Take a look at how the data you will be working with are structured.
df_data = pd.read_json("ner.json", lines=True)
df_data = df_data.drop(['extras'], axis=1)
df_data['content'] = df_data['content'].str.replace("\n", " ")
df_data.head()
df_data.iloc[0]['annotation']
def mergeIntervals(intervals):
sorted_by_lower_bound = sorted(intervals, key=lambda tup: tup[0])
merged = []
for higher in sorted_by_lower_bound:
if not merged:
merged.append(higher)
else:
lower = merged[-1]
if higher[0] <= lower[1]:
if lower[2] is higher[2]:
upper_bound = max(lower[1], higher[1])
merged[-1] = (lower[0], upper_bound, lower[2])
else:
if lower[1] > higher[1]:
merged[-1] = lower
else:
merged[-1] = (lower[0], higher[1], higher[2])
else:
merged.append(higher)
return merged
def get_entities(df):
entities = []
for i in range(len(df)):
entity = []
for annot in df['annotation'][i]:
try:
ent = annot['label'][0]
start = annot['points'][0]['start']
end = annot['points'][0]['end'] + 1
entity.append((start, end, ent))
except:
pass
entity = mergeIntervals(entity)
entities.append(entity)
return entities
df_data['entities'] = get_entities(df_data)
df_data.head()
# +
def convert_dataturks_to_spacy(dataturks_JSON_FilePath):
try:
training_data = []
lines=[]
with open(dataturks_JSON_FilePath, 'r') as f:
lines = f.readlines()
for line in lines:
data = json.loads(line)
text = data['content'].replace("\n", " ")
entities = []
data_annotations = data['annotation']
if data_annotations is not None:
for annotation in data_annotations:
#only a single point in text annotation.
point = annotation['points'][0]
labels = annotation['label']
# handle both list of labels or a single label.
if not isinstance(labels, list):
labels = [labels]
for label in labels:
point_start = point['start']
point_end = point['end']
point_text = point['text']
lstrip_diff = len(point_text) - len(point_text.lstrip())
rstrip_diff = len(point_text) - len(point_text.rstrip())
if lstrip_diff != 0:
point_start = point_start + lstrip_diff
if rstrip_diff != 0:
point_end = point_end - rstrip_diff
entities.append((point_start, point_end + 1 , label))
training_data.append((text, {"entities" : entities}))
return training_data
except Exception as e:
logging.exception("Unable to process " + dataturks_JSON_FilePath + "\n" + "error = " + str(e))
return None
def trim_entity_spans(data: list) -> list:
"""Removes leading and trailing white spaces from entity spans.
Args:
data (list): The data to be cleaned in spaCy JSON format.
Returns:
list: The cleaned data.
"""
invalid_span_tokens = re.compile(r'\s')
cleaned_data = []
for text, annotations in data:
entities = annotations['entities']
valid_entities = []
for start, end, label in entities:
valid_start = start
valid_end = end
while valid_start < len(text) and invalid_span_tokens.match(
text[valid_start]):
valid_start += 1
while valid_end > 1 and invalid_span_tokens.match(
text[valid_end - 1]):
valid_end -= 1
valid_entities.append([valid_start, valid_end, label])
cleaned_data.append([text, {'entities': valid_entities}])
return cleaned_data
# -
data = trim_entity_spans(convert_dataturks_to_spacy("ner.json"))
from tqdm.notebook import tqdm
def clean_dataset(data):
cleanedDF = pd.DataFrame(columns=["setences_cleaned"])
sum1 = 0
for i in tqdm(range(len(data))):
start = 0
emptyList = ["Empty"] * len(data[i][0].split())
numberOfWords = 0
lenOfString = len(data[i][0])
strData = data[i][0]
strDictData = data[i][1]
lastIndexOfSpace = strData.rfind(' ')
for i in range(lenOfString):
if (strData[i]==" " and strData[i+1]!=" "):
for k,v in strDictData.items():
for j in range(len(v)):
entList = v[len(v)-j-1]
if (start>=int(entList[0]) and i<=int(entList[1])):
emptyList[numberOfWords] = entList[2]
break
else:
continue
start = i + 1
numberOfWords += 1
if (i == lastIndexOfSpace):
for j in range(len(v)):
entList = v[len(v)-j-1]
if (lastIndexOfSpace>=int(entList[0]) and lenOfString<=int(entList[1])):
emptyList[numberOfWords] = entList[2]
numberOfWords += 1
cleanedDF = cleanedDF.append(pd.Series([emptyList], index=cleanedDF.columns ), ignore_index=True )
sum1 = sum1 + numberOfWords
return cleanedDF
cleanedDF = clean_dataset(data)
# Take a look at your cleaned dataset and the categories the named-entities are matched to, or 'tags'.
cleanedDF.head()
# <a name='1-2'></a>
# ### 1.2 - Padding and Generating Tags
#
# Now, it is time to generate a list of unique tags you will match the named-entities to.
unique_tags = set(cleanedDF['setences_cleaned'].explode().unique())#pd.unique(cleanedDF['setences_cleaned'])#set(tag for doc in cleanedDF['setences_cleaned'].values.tolist() for tag in doc)
tag2id = {tag: id for id, tag in enumerate(unique_tags)}
id2tag = {id: tag for tag, id in tag2id.items()}
unique_tags
# Next, you will create an array of tags from your cleaned dataset. Oftentimes your input sequence will exceed the maximum length of a sequence your network can process. In this case, your sequence will be cut off, and you need to append zeroes onto the end of the shortened sequences using this [Keras padding API](https://www.tensorflow.org/api_docs/python/tf/keras/preprocessing/sequence/pad_sequences).
from tensorflow.keras.preprocessing.sequence import pad_sequences
# +
MAX_LEN = 512
labels = cleanedDF['setences_cleaned'].values.tolist()
tags = pad_sequences([[tag2id.get(l) for l in lab] for lab in labels],
maxlen=MAX_LEN, value=tag2id["Empty"], padding="post",
dtype="long", truncating="post")
# -
tags
# <a name='1-3'></a>
# ### 1.3 - Tokenize and Align Labels with 🤗 Library
#
# Before feeding the texts to a Transformer model, you will need to tokenize your input using a [🤗 Transformer tokenizer](https://huggingface.co/transformers/main_classes/tokenizer.html). It is crucial that the tokenizer you use must match the Transformer model type you are using! In this exercise, you will use the 🤗 [DistilBERT fast tokenizer](https://huggingface.co/transformers/model_doc/distilbert.html), which standardizes the length of your sequence to 512 and pads with zeros. Notice this matches the maximu length you used when creating tags.
from transformers import DistilBertTokenizerFast #, TFDistilBertModel
tokenizer = DistilBertTokenizerFast.from_pretrained('tokenizer/')
# Transformer models are often trained by tokenizers that split words into subwords. For instance, the word 'Africa' might get split into multiple subtokens. This can create some misalignment between the list of tags for the dataset and the list of labels generated by the tokenizer, since the tokenizer can split one word into several, or add special tokens. Before processing, it is important that you align the lists of tags and the list of labels generated by the selected tokenizer with a `tokenize_and_align_labels()` function.
#
# <a name='ex-1'></a>
# ### Exercise 1 - tokenize_and_align_labels
#
# Implement `tokenize_and_align_labels()`. The function should perform the following:
# * The tokenizer cuts sequences that exceed the maximum size allowed by your model with the parameter `truncation=True`
# * Aligns the list of tags and labels with the tokenizer `word_ids` method returns a list that maps the subtokens to the original word in the sentence and special tokens to `None`.
# * Set the labels of all the special tokens (`None`) to -100 to prevent them from affecting the loss function.
# * Label of the first subtoken of a word and set the label for the following subtokens to -100.
label_all_tokens = True
def tokenize_and_align_labels(tokenizer, examples, tags):
tokenized_inputs = tokenizer(examples, truncation=True, is_split_into_words=False, padding='max_length', max_length=512)
labels = []
for i, label in enumerate(tags):
word_ids = tokenized_inputs.word_ids(batch_index=i)
previous_word_idx = None
label_ids = []
for word_idx in word_ids:
# Special tokens have a word id that is None. We set the label to -100 so they are automatically
# ignored in the loss function.
if word_idx is None:
label_ids.append(-100)
# We set the label for the first token of each word.
elif word_idx != previous_word_idx:
label_ids.append(label[word_idx])
# For the other tokens in a word, we set the label to either the current label or -100, depending on
# the label_all_tokens flag.
else:
label_ids.append(label[word_idx] if label_all_tokens else -100)
previous_word_idx = word_idx
labels.append(label_ids)
tokenized_inputs["labels"] = labels
return tokenized_inputs
# Now that you have tokenized inputs, you can create train and test datasets!
test = tokenize_and_align_labels(tokenizer, df_data['content'].values.tolist(), tags)
train_dataset = tf.data.Dataset.from_tensor_slices((
test['input_ids'],
test['labels']
))
test['labels'][0]
# <a name='1-4'></a>
# ### 1.4 - Optimization
#
# Fantastic! Now you can finally feed your data into into a pretrained 🤗 model. You will optimize a DistilBERT model, which matches the tokenizer you used to preprocess your data. Try playing around with the different hyperparamters to improve your results!
# +
from transformers import TFDistilBertForTokenClassification
model = TFDistilBertForTokenClassification.from_pretrained('model/', num_labels=len(unique_tags))
# -
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-5)
model.compile(optimizer=optimizer, loss=model.compute_loss, metrics=['accuracy']) # can also use any keras loss fn
model.fit(train_dataset.shuffle(1000).batch(16),
epochs=3,
batch_size=16)
# ### Congratulations!
#
# #### Here's what you should remember
#
# - Named-entity recognition (NER) detects and classifies named-entities, and can help process resumes, customer reviews, browsing histories, etc.
# - You must preprocess text data with the corresponding tokenizer to the pretrained model before feeding your input into your Transformer model
|
M5_Sequence_Models/Week4/codes/Transformer_application_Named_Entity_Recognition.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="fJAD-U9MZp35" colab_type="code" outputId="faca1b0b-8c23-4a42-d0a4-766765607fd6" colab={"base_uri": "https://localhost:8080/", "height": 374}
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
df = pd.read_excel(
'https://github.com/pierretd/investor-classifier/blob/master/Part%202/investor_data.xlsx?raw=true'
)
df.sample(5)
# + id="m1hQT2-ShGlN" colab_type="code" outputId="e43d6324-e1e4-4e49-8435-924c546dca61" colab={"base_uri": "https://localhost:8080/", "height": 410}
df = pd.read_excel('https://github.com/pierretd/investor-classifier/blob/master/Part%202/investor_data.xlsx?raw=true', sheetname='investor_data')
df.sample(5)
# + id="OoSaMsSrhPXI" colab_type="code" outputId="c058c306-42a0-4e09-8b5a-61ffe2051631" colab={"base_uri": "https://localhost:8080/", "height": 374}
df = pd.read_excel('https://github.com/pierretd/investor-classifier/blob/master/Part%202/investor_data.xlsx?raw=true', sheet_name='investor_data')
df.sample(5)
# + id="7_nsA3fxsta2" colab_type="code" colab={}
rvlvr = df.copy(deep=True) # Syndicated Revolver = rlvlr
# + id="DdSg0RrMs9__" colab_type="code" outputId="09e8c54b-0fb2-4198-b168-4fa85bb7afa4" colab={"base_uri": "https://localhost:8080/", "height": 35}
print('Syndicated Revolver data set has {} features and {} degrees of freedom.'.format(df.shape[1], df.shape[0]))
# + id="V3_P2hAltUar" colab_type="code" outputId="8a969a20-386a-4874-a32b-faa160a65545" colab={"base_uri": "https://localhost:8080/", "height": 308}
rvlvr.info()
# + id="Kg0UjT1AtrBw" colab_type="code" outputId="a2c6af4d-8f5d-40d3-fe89-400078e48937" colab={"base_uri": "https://localhost:8080/", "height": 145}
rvlvr.select_dtypes(float).nunique()
# + id="xaPDUfVKuIzz" colab_type="code" outputId="e73f960f-c3f5-4237-b341-db6a1bdebc5a" colab={"base_uri": "https://localhost:8080/", "height": 288}
df.describe()
# + id="SLLei2Iit_XY" colab_type="code" outputId="213de988-7624-428b-a98b-84f81269ca43" colab={"base_uri": "https://localhost:8080/", "height": 126}
rvlvr.select_dtypes(object).nunique()
# + id="-puGJIBcudUs" colab_type="code" outputId="00de06cc-94be-4c5a-d731-cb99497f5f36" colab={"base_uri": "https://localhost:8080/", "height": 72}
rvlvr.lender.unique()
# + id="QzvQpzKyu_Xl" colab_type="code" outputId="eafafaa4-0bcf-4cd4-ce4f-51a5084ad838" colab={"base_uri": "https://localhost:8080/", "height": 35}
rvlvr.commit.unique()
# + id="8tbaLOqTvYLs" colab_type="code" colab={}
mapping = {'Commit':1, 'Decline':0}
rvlvr['commit'] = rvlvr['commit'].replace(mapping).astype(np.float64)
# + id="WJpVelnhu6zc" colab_type="code" outputId="5859aab6-0993-447c-cd5f-124e3b090147" colab={"base_uri": "https://localhost:8080/", "height": 35}
rvlvr.commit.unique()
# + id="TPP3sgvgvC7T" colab_type="code" outputId="efc735d9-c372-4cd0-8047-deb2f50b5b54" colab={"base_uri": "https://localhost:8080/", "height": 35}
rvlvr.prior_tier.unique()
# + id="TaO5hPRTvGHi" colab_type="code" outputId="28792c15-1f13-4a4e-8c7a-b5cf7fe5838b" colab={"base_uri": "https://localhost:8080/", "height": 35}
df.invite_tier.unique()
# + colab_type="code" id="v9-QNwRbwQ0d" colab={}
mapping2 = {'Bookrunner':1, 'Participant':0}
rvlvr['prior_tier'] = rvlvr['prior_tier'].replace(mapping2).astype(np.float64)
rvlvr['invite_tier'] = rvlvr['invite_tier'].replace(mapping2).astype(np.float64)
# + colab_type="code" outputId="160a8b71-6add-4276-aa7d-98f268a3914b" id="yaDrT6xAwxZj" colab={"base_uri": "https://localhost:8080/", "height": 35}
rvlvr.prior_tier.unique()
# + colab_type="code" outputId="8d7eed00-f093-4d4e-fb53-19ef70be4ba0" id="nJ0Og6R6wxZl" colab={"base_uri": "https://localhost:8080/", "height": 35}
rvlvr.invite_tier.unique()
# + id="HxS7tdmcxBqu" colab_type="code" outputId="93a85b91-3fc4-45d8-f23d-346a06fabff2" colab={"base_uri": "https://localhost:8080/", "height": 35}
rvlvr.int_rate.unique()
# + id="m-y0lGB_TJqQ" colab_type="code" colab={}
mapping3 = {'Above':2, 'Below':0, 'Market': 1}
rvlvr['int_rate'] = rvlvr['int_rate'].replace(mapping3).astype(np.float64)
# + id="77ek0UgH2xjB" colab_type="code" outputId="e7b00c3f-0dea-4ec5-dde4-1bc646a71647" colab={"base_uri": "https://localhost:8080/", "height": 35}
rvlvr.int_rate.unique()
# + _uuid="a2a2a5ae0cd320e261942a76cc14b778271ba30a" id="B-dDT7m5Ve5l" colab_type="code" outputId="6b4f9e97-c8f7-4f38-aeb3-ed49edae755b" colab={"base_uri": "https://localhost:8080/", "height": 391}
rvlvr.head()
# + id="EEY91MTv4DEc" colab_type="code" outputId="1bbf7ab9-6ff7-4fb5-9a35-754b9f47f91b" colab={"base_uri": "https://localhost:8080/", "height": 35}
rvlvr.shape
# + id="DXtVMEi9yQz8" colab_type="code" outputId="0cbae339-6936-4615-ea89-af91fe0bf1a7" colab={"base_uri": "https://localhost:8080/", "height": 368}
rvlvr.corr()
# + id="yzlqhwtztTi7" colab_type="code" outputId="2dc7e787-2430-475d-f2e8-0e5786bd7d46" colab={"base_uri": "https://localhost:8080/", "height": 820}
def correlation_heat(rvlvr):
_ , ax = plt.subplots(figsize =(14, 12))
colormap = sns.diverging_palette(220, 10, as_cmap = True)
_ = sns.heatmap(
df.corr(),
cmap = colormap,
square=True,
cbar_kws={'shrink':.9 },
ax=ax,
annot=True,
linewidths=0.1,vmax=1.0, linecolor='white',
annot_kws={'fontsize':12 }
)
plt.title('Pearson Correlation of Features', y=1.05, size=15)
correlation_heat(rvlvr[["commit", "deal_size", "invite", "rating",
"int_rate", "covenants" ,"total_fees", "prior_tier",
"invite_tier"
]])
# + id="YEFouHBUZp3-" colab_type="code" outputId="84eaf2df-6d0f-4fe6-a0ba-50ac43967b49" colab={"base_uri": "https://localhost:8080/", "height": 653}
plt.style.use('fivethirtyeight')
df.hist(figsize=(10,10));
plt.show();
# + id="8hOsk3VMZp4C" colab_type="code" outputId="d9ade758-9806-4c91-a684-f1de7af4ab97" colab={"base_uri": "https://localhost:8080/", "height": 535}
df = df[df.total_fees>0]
df.hist(figsize=(8,8))
plt.show();
# + id="FNRAqFajZp4G" colab_type="code" outputId="d6ac64a3-857c-4cb5-845c-2cd85aa456b7" colab={"base_uri": "https://localhost:8080/", "height": 445}
sns.countplot(y='commit', data=df)
plt.show()
# + id="qu63PUSsZp4K" colab_type="code" outputId="9157920e-e946-4b33-e7d5-d1c2f6a59fda" colab={"base_uri": "https://localhost:8080/", "height": 369}
df.groupby('invite_tier').commit.value_counts().plot(kind='barh')
plt.show()
|
Part 2/InvestorClassifierPart2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from rdkit import Chem
import pyaniasetools as pya
from ase_interface import ANIENS,ensemblemolecule
import hdnntools as hdt
import numpy as np
# %matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
import ase
from ase.optimize import BFGS, LBFGS
import time
# +
nets = dict()
ntdir = '/home/jsmith48/scratch/ANI-2x_retrain/ani-2x-1/'
#ntdir = '/home/jsmith48/scratch/transfer_learning/train_ens_DFTTZ/'
nets['ANI-2x']= {'cns' : ntdir + 'rHCNOSFCl-4.6R_16-3.1A_a4-8.params',
'sae' : ntdir + 'sae_linfit.dat',
'nnf' : ntdir + 'train',
'Nn' : 8}
# -
ens = ensemblemolecule(nets['ANI-2x']['cns'], nets['ANI-2x']['sae'], nets['ANI-2x']['nnf'], nets['ANI-2x']['Nn'], 1)
# +
mol = Chem.MolFromMolFile('/home/jsmith48/scratch/ANI-2x_retrain/dhl_test/thienyl-pyridine-2-2.mol', removeHs=False)
ts = pya.ani_tortion_scanner(ens, fmax=0.001, printer=True)
torsions = {'Phi':[6, 2, 8, 16]}
st = time.time()
p,e,s = ts.scan_tortion(mol, torsions, 10.0, 37)
print(time.time()-st)
# -
plt.errorbar(p,e-e.min(),yerr=s)
plt.show()
X_tmp, S = pya.__convert_rdkitconfs_to_nparr__(mol)
print(idx)
hdt.writexyzfile('/home/jsmith48/scratch/ANI-2x_retrain/dhl_test/test_dhl.xyz',ts.X,list(S))
# +
from scipy.ndimage import zoom
n_zoom = 8
data_x = zoom(p[:,:,0],n_zoom,order=1)
data_y = zoom(p[:,:,1],n_zoom,order=1)
data_z = zoom(e-e.min(),n_zoom,order=1)
fig = plt.figure(figsize=(18,12))
plt.style.use('seaborn-white')
contours = plt.contour(data_x, data_y, data_z, 30, colors='black')
plt.clabel(contours, inline=True, fontsize=12)
im1 = plt.imshow(data_z.T, extent=[data_x.min(), data_x.max(), data_y.min(), data_y.max()], origin='lower',
cmap='nipy_spectral', alpha=1.0, interpolation='gaussian')
print(im1)
plt.xlabel('Phi',fontsize=22)
plt.ylabel('Psi',fontsize=22)
plt.colorbar()
plt.axis(aspect='image');
# +
n_zoom = 20
data_x = zoom(p[:,:,0],n_zoom,order=1)
data_y = zoom(p[:,:,1],n_zoom,order=1)
data_z = zoom(s,n_zoom,order=1)
fig = plt.figure(figsize=(18,12))
plt.style.use('seaborn-white')
contours = plt.contour(data_x, data_y, data_z, 10, colors='black')
plt.clabel(contours, inline=True, fontsize=12)
im1 = plt.imshow(data_z.T, extent=[data_x.min(), data_x.max(), data_y.min(), data_y.max()], origin='lower',
cmap='nipy_spectral', alpha=1.0, interpolation='gaussian')
print(im1)
plt.colorbar()
plt.axis(aspect='image');
# -
def get_angle_pos(find_idx,rho):
ids = []
for i,ps in enumerate(rho):
for j,pe in enumerate(ps):
if np.allclose(np.array(find_idx),pe):
ids.append((i,j))
return ids
pos1 = get_angle_pos([-90.0,60.0],p)
pos2 = get_angle_pos([-150.0,150.0],p)
pos3 = get_angle_pos([60.0,-90.0],p)
print(pos1+pos2+pos3)
E = []
D = []
for ind in pos1+pos2+pos3:
ase_mol = pya.__convert_rdkitmol_to_aseatoms__(mol)
ase_mol.set_positions(ts.X[ind])
ase_mol.set_calculator(ANIENS(ens))
dyn = LBFGS(ase_mol, logfile='out.log')
dyn.run(fmax=0.0005)
E.append(ase_mol.get_potential_energy())
D.append(np.array([ase_mol.get_dihedral(torsions['Phi'])*180.0/np.pi,ase_mol.get_dihedral(torsions['Psi'])*180.0/np.pi]))
E = np.array(E)
D = np.stack(D)
print(E)
print(D)
hdt.evtokcal*(E-E.min())
D[np.where(D>180.0)] = D[np.where(D>180.0)]-360.0
D
|
notebooks/dihedral_test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# <img src="http://imgur.com/1ZcRyrc.png" style="float: left; margin: 20px; height: 55px">
#
#
# # Building a "Slack" Chatbot
#
# _Authors: <NAME>(SF) _
#
# 
#
# ---
#
# <a id="learning-objectives"></a>
# ### Learning Objectives
# *After this lesson, you will be able to:*
# - Setup a Slack application from their developer portal
# - Understand the basic "slackclient" API
# - Events
# - Messages
# - Users
# - Getting your bot to respond to basic queries
#
# # 1.1 Slack Bot Integration
#
# Create a new "bot" here:
# [New Bot](https://my.slack.com/services/new/bot)
# ## 1.2 Give your bot a name
# 
# ## 1.3 Customize your bot
# 
#
# At this point you can customize the name, the avatar, and even description. Make note of the API Token becuase we will need it later when we setup the Docker container. You will plug this info into your Dockerfile in the near future.
# # 2.1 Build your slackbot Docker container
#
# Edit the Dockerfile in this repo, and plug in your bot's API Token from 1.3, and also give it the same name.
# ## 2.2 Run the build
# The following will create a Docker container for the bot to run in:
#
# ```bash
# docker build -t slackbot .
# ```
#
# This will create a Docker container called "slackbot".
#
# > As a future point of refernece, you can extend the packages using the requirements.txt for anything you may want to add to the container in terms of Python packages (ie: Pandas, sklearn, Keras, etc).
# ## 2.3 Run your first bot!!
#
# Your bot will run in the background and it will reload whenever you make updates to run.py, which is the main file that handles all of the logic for how your bot can respond to messages.
#
# <style>
# @-webkit-keyframes blinker {
# from {opacity: 1.0;}
# to {opacity: 0.0;}
# }
# .blink{
# text-decoration: blink;
# -webkit-animation-name: blinker;
# -webkit-animation-duration: 0.6s;
# -webkit-animation-iteration-count:infinite;
# -webkit-animation-timing-function:ease-in-out;
# -webkit-animation-direction: alternate;
# }
# </style>
#
# >### Docker Command
# >```bash
# docker run -v `pwd`:"/usr/src/app" slackbot python -u run.py
# ```
# > _ctrl-c terminates your bot._
# >
# > **<span style="color: red;" class="blink"><blink>As tempting as it may be, reframe from inviting your bot to our DSI channel. This could quickly get annoying. We can play with our bots using private messages at first then we may invite it to a botnet channel in the near future.</blink></span>**
# ### Troubleshooting
#
# - **Not seeing your bot?** Double check that you have a bot setup at all.
# - **Error on connection?** Check your API key and bot name matches the configured bot from previous steps.
#
# If you're not sure where to find your bot, check out [https://ga-students.slack.com/apps/manage/custom-integrations](https://ga-students.slack.com/apps/manage/custom-integrations) under "bots".
# ## Slackclient API
#
# Slackclient is the official client authored by Slack itself. The documents are really quite good and you can view them here: [Slackclient API Documentation](http://slackapi.github.io/python-slackclient/).
#
# ### What can you do with this API?
#
# - Send messages
# - Mine channel data
# - List/Join/Create channels automatically
# - Connect any of the above features to anything Python can do!
# - Check the weather
# - Email someone
# - ML Process / AI
#
# In your console, you will see a real-time interaction between your Python script and the Slack service itself. Each one of these messages is being handled by a function called `handle_message()`. Each one of these message types can be looked at and responded by either writing Python code that runs another API call to send a message, or anything that Python can do. For instance, a message can be sent to someone after their status has changed from "active" to "away" such as "HEY COME BACK HERE! WE'RE NOT DONE YET!?".
# ## From here we will talk about the code a little bit.
# Open your editors and look at the file `run.py`.
# ### What does our bot do currently?
#
# Our bot will patiently wait for someone to say "hi", then respond with a random response. There are a few qualifiers that the bot is programmed to observe. For one, it will not respond to anything unless the method `is_for_me()` returns `True`.
#
# ### Have a look at the method `is_for_me()`. Can you think of why it might be important to use this method?
# # Independent Practice
#
# We are going to make our bots sassy. They will respond when the sentiment of anything anyone directs at them is negative. We will use basic "TextBlob" packages for this.
# ### 1. Add the packages "textblob" to a new line of your requirements.txt file, then rebuild your Docker container.
# We only really install "slackclient" into our environment. You can probably figure out how to add the line from here if you really wanted. Otherwise just edit the requirements.txt file and add the line "textblob" to the end of it. Rebuild your container. Restart your bot.
#
# > Don't forget to import the appropriate modules into `run.py` to use TextBlob!
# !cat Docker/requirements.txt
# ### 2. Research how to use "textblob" using the power of your mind.
# http://textblob.readthedocs.io/en/dev/quickstart.html
# ### 3. Implement a method that will check the sentiment of any message directed at your bot.
#
# - If the sentiment polarity is > -.5, have your bot respond with "That's harsh {username}!".
# - If the sentiment polarity is < .5, have your bot respond with "How nice {username}!".
# - All other responses reply with the polarity to check it.
# ## BONUS 4. Install wordnet and have to bot respond with word defintions.
#
# Read up on this in the TextBlob documenation quickstart. When your bot is addressed in a channel with "@botname define regression", have it respond with the given definitions found from the Wordnet object.
#
# - Check to see if the word "define" is pressent in the message directed at your bot
# - Somehow capture the word(s) after the word "define"
# - Look it up using the Wordnet method in Textblob
# - Have it respond to the channel (NOT in our DSI channel please! Test in the channel dsi-botnet).
#
# > Hint:`python -m nltk.downloader wordnet`
# >
# > Somehow, install Wordnet to your container and/or rebuild your Docker container to do this.
# ### Where to go from here.
#
# #### LSTM
# - https://github.com/fchollet/keras/blob/master/examples/lstm_text_generation.py
# - https://machinelearningmastery.com/text-generation-lstm-recurrent-neural-networks-python-keras/
#
# #### Dynamic Memory Network Reponse
# - https://www.youtube.com/watch?v=t5qgjJIBy9g
# - https://github.com/llSourcell/How_to_make_a_chatbot
# - https://github.com/ethancaballero/Improved-Dynamic-Memory-Networks-DMN-plus
#
# #### Seq2Seq
# - [End-to-end Adversarial Learning for Generative Conversational Agents](https://arxiv.org/abs/1711.10122v2)
# - https://github.com/oswaldoludwig/Seq2seq-Chatbot-for-Keras
|
Deployment/.ipynb_checkpoints/chatbots-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Case Study
# For this case study, we will use the Car Seats dataset to predict the sales of car seats in US. The goal is to show how decision trees can model a regression problem (predicting sales).
# +
# importing libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
# %matplotlib inline
import warnings
warnings.filterwarnings('ignore')
from sklearn import tree
import graphviz
from sklearn import metrics
from sklearn.model_selection import cross_val_score, train_test_split
from sklearn.ensemble import BaggingRegressor, RandomForestRegressor
# +
# load and display dataset
carseats_df = pd.read_csv('Carseats.csv')
carseats_df.head()
# -
# ## Data Cleaning
# Real world datasets are always messy (far messier that the one used for this case study). Before we do any analysis, we should do some data cleaning to ensure that the data is ready for analysis.
# Some of the cleaning steps are
# - Checking for missing values
# - Checking for ourliers and using an appropriate strategy to handle them
# - Encode any string variables with floats so that the algorithms can use those variables
#
# In this case, there is an unnecessary 'Unnamed: 0' column. We need to get rid of this.
# +
carseats_df = carseats_df.drop('Unnamed: 0', axis=1)
carseats_df.head()
# -
# ### Missing values
# Check for missing values
carseats_df.isnull().sum()
# ### Check feature types
# Check if there are any features that have values other floats. These features will need to be encoded so that they can used appropriately in ML algorithms
carseats_df.info()
# Looks like we have three features, ShelveLoc, Urban and US, which take on non-float values (shown by the category 'object'). Let's check what are the unique values for each of these features
cat_cols = ['ShelveLoc', 'Urban', 'US']
for col in cat_cols:
print('{}: {}'.format(col, carseats_df[col].unique()))
# ## Feature Encoding
# We need to encode the categorical features to some floats. The simplest form of encoding is called 'One-hot encoding'. One-hot encoding is a process by which categorical variables are converted into a form that could be provided to ML algorithms to do a better job in prediction.
#
# The figure below explains the difference between label encoding and one-hot encoding.
# 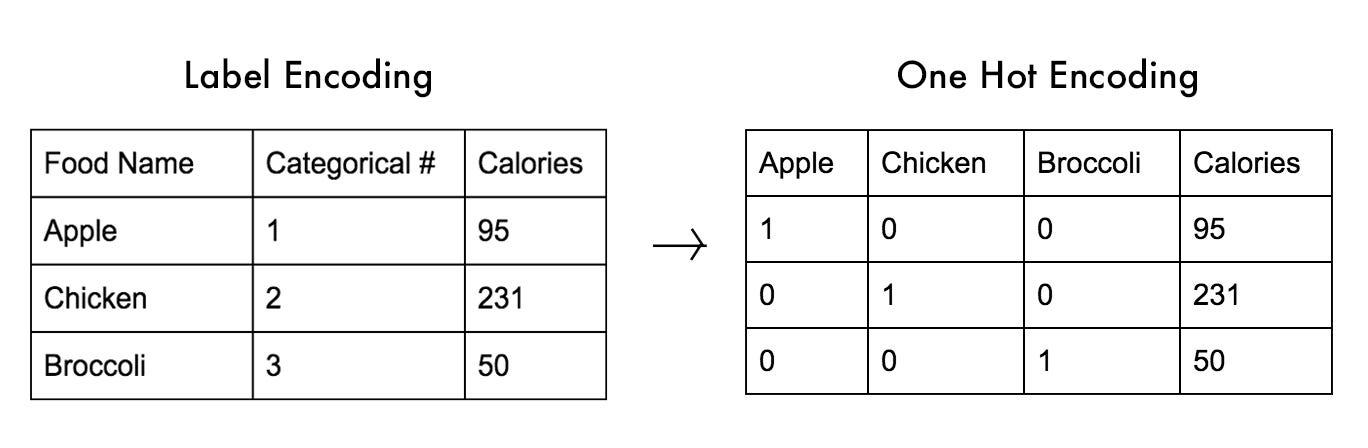
# +
X = carseats_df.drop(['Sales'], axis = 1)
y = carseats_df['Sales']
# this step does the feture encoding for us
X = pd.get_dummies(X)
X.head()
# -
# ### Train-test split
# Reserve 30% of the data for testing
# +
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
print('Train features shape: {}'.format(X_train.shape))
print('Train labels shape: {}'.format(y_train.shape))
print('Test features shape: {}'.format(X_test.shape))
print('Test labels shape: {}'.format(y_test.shape))
# -
# ### Machine Learning
# Fit a Decision Tree model with max_depth = 5 and test MSE and RMSE on the test set
# +
# Fit Sklearn's tree regressor
clf = tree.DecisionTreeRegressor(max_depth=5).fit(X_train, y_train)
# Measure test set MSE
y_pred = clf.predict(X_test)
mse = metrics.mean_squared_error(y_test, y_pred)
# Get proportion of correct classifications on test set
print('Test MSE: {}'.format(np.around(mse, 3)))
print('Test RMSE: {}'.format(np.around(np.sqrt(mse), 3)))
# -
# ### Improving MSE
# We can use cross-validation to optimize the max_depth hyperparameter. Remember that setting this too low results in underfitting and setting this too high results in overfitting.
#
# We will use 10-fold cv on the training set to choose the best value of this hyperparameter. Then we will use the best value to make predictions on the test dataset
# +
cv_folds = 10
tuning_param = 'max_depth'
columns=[tuning_param, 'RMSE']
results = []
for m in np.arange(2, 50):
regr = tree.DecisionTreeRegressor(max_depth=m)
scores = cross_val_score(regr, X_train, y_train, cv=cv_folds, scoring='neg_mean_squared_error')
rmses = np.sqrt(np.absolute(scores))
rmse = np.mean(rmses)
results += [[m, rmse]]
# Plot classification accuracy for each max_depth cv result
plot_df = pd.DataFrame(np.asarray(results), columns=columns).set_index(tuning_param)
plt.figure(figsize=(10,10))
sns.lineplot(data=plot_df)
plt.ylabel('RMSE')
plt.show();
# Show chosen model
chosen = plot_df[plot_df['RMSE'] == plot_df['RMSE'].min()]
print(chosen)
# Use chosen model for test prediction
regr = tree.DecisionTreeRegressor(max_depth=int(chosen.index[0])).fit(X_train, y_train)
y_pred = regr.predict(X_test)
mse = metrics.mean_squared_error(y_test, y_pred)
print('Test MSE : {}'.format(np.around(mse, 3)))
print('Test RMSE: {}'.format(np.around(np.sqrt(mse), 3)))
# -
# ### Bagging
# A single decision tree is almost always avoided due to its tendency to overfit. As we learned in the class, a better approach is to use a Bagging strategy. In this case, we create 10 bootstrap samples and fit 10 decision trees on them. Their predictions are averaged to determine the final prediction.
#
# Let's check if this improves our MSE.
# +
# Bagging with 10 trees
max_features = X.shape[1]
regr = RandomForestRegressor(max_features=max_features, random_state=0, n_estimators=10)
regr.fit(X_train, y_train)
y_pred = regr.predict(X_test)
mse = metrics.mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
print('Test MSE : {}'.format(np.around(mse, 3)))
print('Test RMSE: {}'.format(np.around(rmse, 3)))
# -
# We can see that our MSE is lower on the test set with a bagging approach
# ## Variable Importance plots
# Tree models provide us the ability to look at different features and their importance when fitting the training dataset. We can use these importance plots to see which features are contributing towards the training data fit. This interpretability is very useful as it helps us in explaining the model to a business audience.
#
# We can also use these plots to choose the top-X features and use them to refit the model.
# +
plot_df = pd.DataFrame({'feature': X.columns, 'importance': regr.feature_importances_})
plt.figure(figsize=(10,10))
sns.barplot(x='importance', y='feature', data=plot_df.sort_values('importance', ascending=False),
color='b')
plt.xticks(rotation=90);
# -
# #### Remove Variables with Least Importance
# We can refit the training data with a bagging strategy by dropping the 'Urban' and 'US' variables. If we do not see a significant increase in MSE after dropping features, we can exclude those features.
#
# In this case, this leads to a better MSE (not always the case in every dataset)
# +
X = carseats_df.drop(['Sales', 'Urban', 'US'], axis = 1)
y = carseats_df['Sales']
# this step does the feture encoding for us
X = pd.get_dummies(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Bagging with 10 trees
max_features = X.shape[1]
regr = RandomForestRegressor(max_features=max_features, random_state=0, n_estimators=10)
regr.fit(X_train, y_train)
y_pred = regr.predict(X_test)
mse = metrics.mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
print('Test MSE : {}'.format(np.around(mse, 3)))
print('Test RMSE: {}'.format(np.around(rmse, 3)))
# -
# # Exercise
# Visualize the fitted tree using [sklearn.tree](https://scikit-learn.org/stable/modules/generated/sklearn.tree.plot_tree.html) library
|
module02/lessons/Lesson02_CaseStudy.ipynb
|
# # Regularization of linear regression model
#
# In this notebook, we will see the limitations of linear regression models and
# the advantage of using regularized models instead.
#
# Besides, we will also present the preprocessing required when dealing
# with regularized models, furthermore when the regularization parameter
# needs to be tuned.
#
# We will start by highlighting the over-fitting issue that can arise with
# a simple linear regression model.
#
# ## Effect of regularization
#
# We will first load the California housing dataset.
# <div class="admonition note alert alert-info">
# <p class="first admonition-title" style="font-weight: bold;">Note</p>
# <p class="last">If you want a deeper overview regarding this dataset, you can refer to the
# Appendix - Datasets description section at the end of this MOOC.</p>
# </div>
# +
from sklearn.datasets import fetch_california_housing
data, target = fetch_california_housing(as_frame=True, return_X_y=True)
target *= 100 # rescale the target in k$
data.head()
# -
# In one of the previous notebook, we showed that linear models could be used
# even in settings where `data` and `target` are not linearly linked.
#
# We showed that one can use the `PolynomialFeatures` transformer to create
# additional features encoding non-linear interactions between features.
#
# Here, we will use this transformer to augment the feature space.
# Subsequently, we will train a linear regression model. We will use the
# out-of-sample test set to evaluate the generalization capabilities of our
# model.
# +
from sklearn.model_selection import cross_validate
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
linear_regression = make_pipeline(PolynomialFeatures(degree=2),
LinearRegression())
cv_results = cross_validate(linear_regression, data, target,
cv=10, scoring="neg_mean_squared_error",
return_train_score=True,
return_estimator=True)
# -
# We can compare the mean squared error on the training and testing set to
# assess the generalization performance of our model.
train_error = -cv_results["train_score"]
print(f"Mean squared error of linear regression model on the train set:\n"
f"{train_error.mean():.3f} +/- {train_error.std():.3f}")
test_error = -cv_results["test_score"]
print(f"Mean squared error of linear regression model on the test set:\n"
f"{test_error.mean():.3f} +/- {test_error.std():.3f}")
# The score on the training set is much better. This generalization performance
# gap between the training and testing score is an indication that our model
# overfitted our training set.
#
# Indeed, this is one of the danger when augmenting the number of features
# with a `PolynomialFeatures` transformer. Our model will focus on some
# specific features. We can check the weights of the model to have a
# confirmation. Let's create a dataframe: the columns will contain the name
# of the feature while the line the coefficients values stored by each model
# during the cross-validation.
#
# Since we used a `PolynomialFeatures` to augment the data, we will create
# feature names representative of the feature combination. Scikit-learn
# provides a `get_feature_names` method for this purpose. First, let's get
# the first fitted model from the cross-validation.
model_first_fold = cv_results["estimator"][0]
# Now, we can access to the fitted `PolynomialFeatures` to generate the feature
# names
feature_names = model_first_fold[0].get_feature_names(
input_features=data.columns)
feature_names
# Finally, we can create the dataframe containing all the information.
# +
import pandas as pd
coefs = [est[-1].coef_ for est in cv_results["estimator"]]
weights_linear_regression = pd.DataFrame(coefs, columns=feature_names)
# -
# Now, let's use a box plot to see the coefficients variations.
# +
import matplotlib.pyplot as plt
color = {"whiskers": "black", "medians": "black", "caps": "black"}
weights_linear_regression.plot.box(color=color, vert=False, figsize=(6, 16))
_ = plt.title("Linear regression coefficients")
# -
# We can force the linear regression model to consider all features in a more
# homogeneous manner. In fact, we could force large positive or negative weight
# to shrink toward zero. This is known as regularization. We will use a ridge
# model which enforces such behavior.
# +
from sklearn.linear_model import Ridge
ridge = make_pipeline(PolynomialFeatures(degree=2),
Ridge(alpha=100))
cv_results = cross_validate(ridge, data, target,
cv=10, scoring="neg_mean_squared_error",
return_train_score=True,
return_estimator=True)
# -
train_error = -cv_results["train_score"]
print(f"Mean squared error of linear regression model on the train set:\n"
f"{train_error.mean():.3f} +/- {train_error.std():.3f}")
test_error = -cv_results["test_score"]
print(f"Mean squared error of linear regression model on the test set:\n"
f"{test_error.mean():.3f} +/- {test_error.std():.3f}")
# We see that the training and testing scores are much closer, indicating that
# our model is less overfitting. We can compare the values of the weights of
# ridge with the un-regularized linear regression.
coefs = [est[-1].coef_ for est in cv_results["estimator"]]
weights_ridge = pd.DataFrame(coefs, columns=feature_names)
weights_ridge.plot.box(color=color, vert=False, figsize=(6, 16))
_ = plt.title("Ridge weights")
# By comparing the magnitude of the weights on this plot compared to the
# previous plot, we see that the magnitude of the weights are shrunk towards
# zero in comparison with the linear regression model.
#
# However, in this example, we omitted two important aspects: (i) the need to
# scale the data and (ii) the need to search for the best regularization
# parameter.
#
# ## Scale your data!
#
# Regularization will add constraints on weights of the model. We saw in the
# previous example that a ridge model will enforce that all weights have a
# similar magnitude. Indeed, the larger alpha is, the larger this enforcement
# will be.
#
# This procedure should make us think about feature rescaling. Let's consider
# the case where features have an identical data dispersion: if two features
# are found equally important by the model, they will be affected similarly by
# regularization strength.
#
# Now, let's consider the scenario where features have completely different
# data dispersion (for instance age in years and annual revenue in dollars).
# If two features are as important, our model will boost the weights of
# features with small dispersion and reduce the weights of features with
# high dispersion.
#
# We recall that regularization forces weights to be closer. Therefore, we get
# an intuition that if we want to use regularization, dealing with rescaled
# data would make it easier to find an optimal regularization parameter and
# thus an adequate model.
#
# As a side note, some solvers based on gradient computation are expecting such
# rescaled data. Unscaled data will be detrimental when computing the optimal
# weights. Therefore, when working with a linear model and numerical data, it
# is generally good practice to scale the data.
#
# Thus, we will add a `StandardScaler` in the machine learning pipeline. This
# scaler will be placed just before the regressor.
# +
from sklearn.preprocessing import StandardScaler
ridge = make_pipeline(PolynomialFeatures(degree=2), StandardScaler(),
Ridge(alpha=0.5))
cv_results = cross_validate(ridge, data, target,
cv=10, scoring="neg_mean_squared_error",
return_train_score=True,
return_estimator=True)
# -
train_error = -cv_results["train_score"]
print(f"Mean squared error of linear regression model on the train set:\n"
f"{train_error.mean():.3f} +/- {train_error.std():.3f}")
test_error = -cv_results["test_score"]
print(f"Mean squared error of linear regression model on the test set:\n"
f"{test_error.mean():.3f} +/- {test_error.std():.3f}")
# We observe that scaling data has a positive impact on the test score and that
# the test score is closer to the train score. It means that our model is less
# overfitted and that we are getting closer to the best generalization sweet
# spot.
#
# Let's have an additional look to the different weights.
coefs = [est[-1].coef_ for est in cv_results["estimator"]]
weights_ridge = pd.DataFrame(coefs, columns=feature_names)
weights_ridge.plot.box(color=color, vert=False, figsize=(6, 16))
_ = plt.title("Ridge weights with data scaling")
# Compare to the previous plots, we see that now all weight manitudes are
# closer and that all weights are more equally contributing.
#
# In the previous analysis, we did not study if the parameter `alpha` will have
# an effect on the performance. We chose the parameter beforehand and fix it
# for the analysis.
#
# In the next section, we will check the impact of this hyperparameter and how
# it should be tuned.
#
# ## Fine tuning the regularization parameter
#
# As mentioned, the regularization parameter needs to be tuned on each dataset.
# The default parameter will not lead to the optimal model. Therefore, we need
# to tune the `alpha` parameter.
#
# Model hyperparameter tuning should be done with care. Indeed, we want to
# find an optimal parameter that maximizes some metrics. Thus, it requires both
# a training set and testing set.
#
# However, this testing set should be different from the out-of-sample testing
# set that we used to evaluate our model: if we use the same one, we are using
# an `alpha` which was optimized for this testing set and it breaks the
# out-of-sample rule.
#
# Therefore, we should include search of the hyperparameter `alpha` within the
# cross-validation. As we saw in previous notebooks, we could use a
# grid-search. However, some predictor in scikit-learn are available with
# an integrated hyperparameter search, more efficient than using a grid-search.
# The name of these predictors finishes by `CV`. In the case of `Ridge`,
# scikit-learn provides a `RidgeCV` regressor.
#
# Therefore, we can use this predictor as the last step of the pipeline.
# Including the pipeline a cross-validation allows to make a nested
# cross-validation: the inner cross-validation will search for the best
# alpha, while the outer cross-validation will give an estimate of the
# testing score.
# +
import numpy as np
from sklearn.linear_model import RidgeCV
alphas = np.logspace(-2, 0, num=20)
ridge = make_pipeline(PolynomialFeatures(degree=2), StandardScaler(),
RidgeCV(alphas=alphas, store_cv_values=True))
# +
from sklearn.model_selection import ShuffleSplit
cv = ShuffleSplit(n_splits=5, random_state=1)
cv_results = cross_validate(ridge, data, target,
cv=cv, scoring="neg_mean_squared_error",
return_train_score=True,
return_estimator=True, n_jobs=2)
# -
train_error = -cv_results["train_score"]
print(f"Mean squared error of linear regression model on the train set:\n"
f"{train_error.mean():.3f} +/- {train_error.std():.3f}")
test_error = -cv_results["test_score"]
print(f"Mean squared error of linear regression model on the test set:\n"
f"{test_error.mean():.3f} +/- {test_error.std():.3f}")
# By optimizing `alpha`, we see that the training and testing scores are close.
# It indicates that our model is not overfitting.
#
# When fitting the ridge regressor, we also requested to store the error found
# during cross-validation (by setting the parameter `store_cv_values=True`).
# We will plot the mean squared error for the different `alphas` regularization
# strength that we tried.
mse_alphas = [est[-1].cv_values_.mean(axis=0)
for est in cv_results["estimator"]]
cv_alphas = pd.DataFrame(mse_alphas, columns=alphas)
cv_alphas
cv_alphas.mean(axis=0).plot(marker="+")
plt.ylabel("Mean squared error\n (lower is better)")
plt.xlabel("alpha")
_ = plt.title("Error obtained by cross-validation")
# As we can see, regularization is just like salt in cooking: one must balance
# its amount to get the best generalization performance. We can check if the best
# `alpha` found is stable across the cross-validation fold.
best_alphas = [est[-1].alpha_ for est in cv_results["estimator"]]
best_alphas
# In this notebook, you learned about the concept of regularization and
# the importance of preprocessing and parameter tuning.
|
notebooks/linear_models_regularization.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.7 (tensorflow)
# language: python
# name: tensorflow
# ---
# <a href="https://colab.research.google.com/github/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_11_03_embedding.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#
# # T81-558: Applications of Deep Neural Networks
# **Module 11: Natural Language Processing and Speech Recognition**
# * Instructor: [<NAME>](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
# * For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# # Module 11 Material
#
# * Part 11.1: Getting Started with Spacy in Python [[Video]](https://www.youtube.com/watch?v=A5BtU9vXzu8&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_11_01_spacy.ipynb)
# * Part 11.2: Word2Vec and Text Classification [[Video]](https://www.youtube.com/watch?v=nWxtRlpObIs&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_11_02_word2vec.ipynb)
# * **Part 11.3: What are Embedding Layers in Keras** [[Video]](https://www.youtube.com/watch?v=OuNH5kT-aD0&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_11_03_embedding.ipynb)
# * Part 11.4: Natural Language Processing with Spacy and Keras [[Video]](https://www.youtube.com/watch?v=BKgwjhao5DU&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_11_04_text_nlp.ipynb)
# * Part 11.5: Learning English from Scratch with Keras and TensorFlow [[Video]](https://www.youtube.com/watch?v=Y1khuuSjZzc&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN&index=58) [[Notebook]](t81_558_class_11_05_english_scratch.ipynb)
# # Google CoLab Instructions
#
# The following code ensures that Google CoLab is running the correct version of TensorFlow.
try:
# %tensorflow_version 2.x
COLAB = True
print("Note: using Google CoLab")
except:
print("Note: not using Google CoLab")
COLAB = False
# # Part 11.3: What are Embedding Layers in Keras
#
# [Embedding Layers](https://keras.io/layers/embeddings/) are a handy feature of Keras that allows the program to automatically insert additional information into the data flow of your neural network. In the previous section, you saw that Word2Vec could expand words to a 300 dimension vector. An embedding layer would allow you to insert these 300-dimension vectors in the place of word-indexes automatically.
#
# Programmers often use embedding layers with Natural Language Processing (NLP); however, they can be used in any instance where you wish to insert a lengthier vector in an index value place. In some ways, you can think of an embedding layer as dimension expansion. However, the hope is that these additional dimensions provide more information to the model and provide a better score.
#
# ### Simple Embedding Layer Example
#
# * **input_dim** = How large is the vocabulary? How many categories are you encoding? This parameter is the number of items in your "lookup table."
# * **output_dim** = How many numbers in the vector that you wish to return.
# * **input_length** = How many items are in the input feature vector that you need to transform?
#
# Now we create a neural network with a vocabulary size of 10, which will reduce those values between 0-9 to 4 number vectors. Each feature vector coming in will have two such features. This neural network does nothing more than pass the embedding on to the output. But it does let us see what the embedding is doing.
# +
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Embedding
import numpy as np
model = Sequential()
embedding_layer = Embedding(input_dim=10, output_dim=4, input_length=2)
model.add(embedding_layer)
model.compile('adam', 'mse')
# -
# Let's take a look at the structure of this neural network so that we can see what is happening inside it.
model.summary()
# For this neural network, which is just an embedding layer, the input is a vector of size 2. These two inputs are integer numbers from 0 to 9 (corresponding to the requested input_dim quantity of 10 values). Looking at the summary above, we see that the embedding layer has 40 parameters. This value comes from the embedded lookup table that contains four amounts (output_dim) for each of the 10 (input_dim) possible integer values for the two inputs. The output is 2 (input_length) length 4 (output_dim) vectors, resulting in a total output size of 8, which corresponds to the Output Shape given in the summary above.
#
# Now, let us query the neural network with two rows. The input is two integer values, as was specified when we created the neural network.
# +
input_data = np.array([
[1,2]
])
pred = model.predict(input_data)
print(input_data.shape)
print(pred)
# -
# Here we see two length-4 vectors that Keras looked up for each of the input integers. Recall that Python arrays are zero-based. Keras replaced the value of 1 with the second row of the 10 x 4 lookup matrix. Similarly, Keras replaced the value of 2 by the third row of the lookup matrix. The following code displays the lookup matrix in its entirety. The embedding layer performs no mathematical operations other than inserting the correct row from the lookup table.
embedding_layer.get_weights()
# The values above are random parameters that Keras generated as starting points. Generally, we will either transfer an embedding or train these random values into something useful. The next section demonstrates how to embed a hand-coded embedding.
#
# ### Transferring An Embedding
#
# Now, we see how to hard-code an embedding lookup that performs a simple one-hot encoding. One-hot encoding would transform the input integer values of 0, 1, and 2 to the vectors $[1,0,0]$, $[0,1,0]$, and $[0,0,1]$ respectively. The following code replaced the random lookup values in the embedding layer with this one-hot coding inspired lookup table.
# +
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Embedding
import numpy as np
embedding_lookup = np.array([
[1,0,0],
[0,1,0],
[0,0,1]
])
model = Sequential()
embedding_layer = Embedding(input_dim=3, output_dim=3, input_length=2)
model.add(embedding_layer)
model.compile('adam', 'mse')
embedding_layer.set_weights([embedding_lookup])
# -
# We have the following parameters to the Embedding layer:
#
# * input_dim=3 - There are three different integer categorical values allowed.
# * output_dim=3 - Per one-hot encoding, three columns represent a categorical value with three possible values.
# * input_length=2 - The input vector has two of these categorical values.
#
# Now we query the neural network with two categorical values to see the lookup performed.
# +
input_data = np.array([
[0,1]
])
pred = model.predict(input_data)
print(input_data.shape)
print(pred)
# -
# The given output shows that we provided the program with two rows from the one-hot encoding table. This encoding is a correct one-hot encoding for the values 0 and 1, where there are up to 3 unique values possible.
#
# The next section demonstrates how to train this embedding lookup table.
#
# ### Training an Embedding
#
# First, we make use of the following imports.
from numpy import array
from tensorflow.keras.preprocessing.text import one_hot
from tensorflow.keras.preprocessing.sequence import pad_sequences
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Flatten, Embedding, Dense
# We create a neural network that classifies restaurant reviews according to positive or negative. This neural network can accept strings as input, such as given here. This code also includes positive or negative labels for each review.
# +
# Define 10 resturant reviews.
reviews = [
'Never coming back!',
'Horrible service',
'Rude waitress',
'Cold food.',
'Horrible food!',
'Awesome',
'Awesome service!',
'Rocks!',
'poor work',
'Couldn\'t have done better']
# Define labels (1=negative, 0=positive)
labels = array([1,1,1,1,1,0,0,0,0,0])
# -
# Notice that the second to the last label is incorrect. Errors such as this are not too out of the ordinary, as most training data could have some noise.
#
# We define a vocabulary size of 50 words. Though we do not have 50 words, it is okay to use a value larger than needed. If there are more than 50 words, the least frequently used words in the training set are automatically dropped by the embedding layer during training. For input, we one-hot encode the strings. Note that we use the TensorFlow one-hot encoding method here, rather than Scikit-Learn. Scikit-learn would expand these strings to the 0's and 1's as we would typically see for dummy variables. TensorFlow translates all of the words to index values and replaces each word with that index.
VOCAB_SIZE = 50
encoded_reviews = [one_hot(d, VOCAB_SIZE) for d in reviews]
print(f"Encoded reviews: {encoded_reviews}")
# The program one-hot encodes these reviews to word indexes; however, their lengths are different. We pad these reviews to 4 words and truncate any words beyond the fourth word.
# +
MAX_LENGTH = 4
padded_reviews = pad_sequences(encoded_reviews, maxlen=MAX_LENGTH, \
padding='post')
print(padded_reviews)
# -
# Each review is padded by appending zeros at the end, as specified by the padding=post setting.
#
# Next, we create a neural network to learn to classify these reviews.
# +
model = Sequential()
embedding_layer = Embedding(VOCAB_SIZE, 8, input_length=MAX_LENGTH)
model.add(embedding_layer)
model.add(Flatten())
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['acc'])
print(model.summary())
# -
# This network accepts four integer inputs that specify the indexes of a padded movie review. The first embedding layer converts these four indexes into four vectors of length 8. These vectors come from the lookup table that contains 50 (VOCAB_SIZE) rows of vectors of length 8. This encoding is evident by the 400 (8 times 50) parameters in the embedding layer. The size of the output from the embedding layer is 32 (4 words expressed as 8-number embedded vectors). A single output neuron is connected to the embedding layer by 33 weights (32 from the embedding layer and a single bias neuron). Because this is a single-class classification network, we use the sigmoid activation function and binary_crossentropy.
#
# The program now trains the neural network. Both the embedding lookup and dense 33 weights are updated to produce a better score.
# fit the model
model.fit(padded_reviews, labels, epochs=100, verbose=0)
# We can see the learned embeddings. Think of each word's vector as a location in 8 dimension space where words associated with positive reviews are close to other words with positive reviews. Similarly, training places negative reviews close to each other. In addition to the training setting these embeddings, the 33 weights between the embedding layer and output neuron similarly learn to transform these embeddings into an actual prediction. You can see these embeddings here.
print(embedding_layer.get_weights()[0].shape)
print(embedding_layer.get_weights())
# We can now evaluate this neural network's accuracy, including both the embeddings and the learned dense layer.
loss, accuracy = model.evaluate(padded_reviews, labels, verbose=0)
print(f'Accuracy: {accuracy}')
# The accuracy is a perfect 1.0, indicating there is likely overfitting. For a more complex data set, it would be good to use early stopping to not overfit.
print(f'Log-loss: {loss}')
# However, the loss is not perfect, meaning that even though the predicted probabilities indicated a correct prediction in every case, the program did not achieve absolute confidence in each correct answer. The lack of confidence was likely due to the small amount of noise (previously discussed) in the data set. Additionally, the fact that some words appeared in both positive and negative reviews contributed to this lack of absolute certainty.
|
t81_558_class_11_03_embedding.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_python3
# language: python
# name: conda_python3
# ---
print('hello' in "hello world")
print('hello,world'.split())
print('test '.strip())
url = 'http://ia-340-gp32-2020-fall.s3-website-us-east-1.amazonaws.com/'
# +
import urllib.request
response = urllib.request.urlopen(url)
html_data=response.read()
print(html_data.decode('utf-8'))
# -
# !pip install beautifulsoup4
from bs4 import BeautifulSoup
soup = BeautifulSoup(html_data,'html.parser')
print(soup)
for div in soup.find_all('div',class_='div_style'):
for li in div.find_all('li'):
print(li)
for p in soup.find_all('p'):
if 'instuctor' in p.text:
print(p.text.split('1')[1])
for p in soup.find_all('p'):
for a in p.find_all('a'):
print(a['href'])
|
lec6.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Pandas Tutorial
import pandas as pd
games = pd.read_csv("vgsalesGlobale.csv", index_col = "Name")
games.head()
games.tail(10)
len(games)
games.shape
games.dtypes
games.iloc[299]
games.loc["Super Mario Bros."]
games.head()
games.sort_values(by = "Year").head()
games.sort_values(by = "Year", ascending=False).head()
games.sort_values(by = ["Year", "Genre"], ascending=False).head()
games.sort_index().head()
games["Publisher"].head(10)
games[games["Genre"] =="Action"]
games_by_genre = games["Genre"] =="Action"
games[games_by_genre]
games_in_2010 = games["Year"] == 2010
games[games_by_genre & games_in_2010]
games[games_by_genre | games_in_2010]
after_2015 = games["Year"] > 2015
games[after_2015]
mid_2000s = games["Year"].between(2000, 2010)
games[mid_2000s]
sport_in_title = games.index.str.lower().str.contains("sport")
games[sport_in_title]
games["Global_Sales"].mean()
genres = games.groupby("Genre")
genres["Global_Sales"].sum()
genres["Global_Sales"].sum().sort_values(ascending = False)
|
jupyter/pandas-tut/29-Pandas_Tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Using the DBSCAN algorithm to cluster localizations.
#
# This notebook demonstrates how to cluster localizations using the DBSCAN algorithm. It also demonstrates how to work with the clustered data.
#
# Note:
# * The algorithm works in 2D or 3D, but in this example we just do 2D clustering.
#
# References:
# * [DBSCAN (Wikipedia)](https://en.wikipedia.org/wiki/DBSCAN).
# * [Ester et al, Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, 1996](http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.121.9220).
# ### Configuration
#
# Create an empty directory somewhere on your computer and tell Python to go to that directory.
# +
import matplotlib
import matplotlib.pyplot as pyplot
import numpy
import os
os.chdir("/home/hbabcock/Data/storm_analysis/jy_testing/")
print(os.getcwd())
numpy.random.seed(1)
# -
# ### Generate data to cluster
#
# In this example we are just going to generate the clustering data synthetically.
# +
import storm_analysis.jupyter_examples.clustering_data as clusteringData
clusteringData.makeClusters("clusters.hdf5", 40, 1000, 20000)
# +
# Make an image from the data.
import storm_analysis.sa_utilities.hdf5_to_image as h5_image
sr_im = h5_image.render2DImage("clusters.hdf5", scale = 2, sigma = 1)
fig = pyplot.figure(figsize = (9, 6))
pyplot.imshow(sr_im, cmap = "gray")
pyplot.show()
# -
# ### Cluster the data
#
# Note:
# * The results of the clustering are saved in the HDF5 that contained the tracks / localizations.
# * Clustering is done on tracks if they are available, otherwise it is done on the localizations.
# +
import storm_analysis.dbscan.dbscan_analysis as dbscanAnalysis
# The second parameter is the DBSCAN eps value in nanometers.
# The third parameter is the DBSCAN mc value.
dbscanAnalysis.findClusters("clusters.hdf5", 100.0, 50)
# -
# ### RGB image of the clustering results
# +
import storm_analysis.dbscan.cluster_images as clusterImages
[rgb_im, sum_im, num_clusters] = clusterImages.clusterImages("clusters.hdf5", 10, 3, scale = 2,
show_unclustered = True)
fig = pyplot.figure(figsize = (9, 6))
pyplot.imshow(rgb_im, cmap = "gray")
pyplot.show()
# -
# ### Create a file with some statistics for each cluster
# +
stats_name = dbscanAnalysis.clusterStats("clusters.hdf5", 10)
print()
print("Cluster statistics:")
with open(stats_name) as fp:
for line in fp:
print(line.strip())
# -
# ### Working with HDF5 clusters files
# +
import storm_analysis.dbscan.clusters_sa_h5py as clSAH5Py
# The SAH5Clusters object is a sub-class of the SAH5Py object, so it provides all
# the methods of SAH5Py object in addition to a few of it's own.
#
with clSAH5Py.SAH5Clusters("clusters.hdf5") as cl_h5:
# Get clustering program information.
print("Analysis info", cl_h5.getClusteringInfo())
# Get the number of clusters.
print("Total clusters", cl_h5.getNClusters())
# This is the recommended way to iterate over all the clusters. Like the tracks
# and localizations iterators you can specify which fields you want if you don't
# want to get them all.
#
print()
for index, cluster in cl_h5.clustersIterator(min_size = 100):
print("cluster {0:0d} <x> = {1:.3f}".format(index, numpy.mean(cluster['x'])))
if (index >= 5):
break
# Note that if you only need the fields that are stored with each cluster this
# iteration can be much faster. This is because the other fields have to be
# looked up from each localization/track that is in the cluster.
# These are the fields that are stored with each cluster.
print()
print("Cluster fields:", cl_h5.getClustersFields())
# This should be noticeably faster. As 'x' is available in the cluster so we
# don't have to go the through the tracks to get it.
print()
for index, cluster in cl_h5.clustersIterator(min_size = 100, fields = ['x']):
print("cluster {0:0d} <x> = {1:.3f}".format(index, numpy.mean(cluster['x'])))
if (index >= 5):
break
# -
|
jupyter_notebooks/dbscan_clustering.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import jax.numpy as jnp
from jax import random,grad
from jax.scipy.stats import norm
from AutoKSD import KSD
key = random.PRNGKey(0)
# +
## Define the kernel function
rbf=lambda x,y:jnp.exp(-1*jnp.sum((x-y)**2))
## Define the score function of p
p_score=grad(lambda x:norm.logpdf(x,loc=0., scale=1.).sum())
## Initialize the KSD
ksd=KSD(rbf,p_score)
## Samples from q
q_samples=random.normal(key,[100,2])
## Compute statsitics
# %time print(ksd.U_stats(q_samples))
# %time print(ksd.V_stats(q_samples))
|
demo_KSD.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/jwkanggist/EverybodyTensorflow2.0/blob/master/lab13_cnn_pool.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="tnKobaptb6XG" colab_type="text"
# # LAB13 Pooling over CNN
# Pooling 함수를 사용해서 필터링 해보자
# + id="AamVQqD1b2-_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="e88f210a-ea05-4190-9de7-4ea4d9fb031b"
# preprocessor parts
from __future__ import absolute_import, division, print_function, unicode_literals
# Install TensorFlow
try:
# # %tensorflow_version only exists in Colab.
# %tensorflow_version 2.x
except Exception:
pass
import tensorflow.compat.v1 as tfv1
tfv1.disable_eager_execution()
from tensorflow.keras.callbacks import TensorBoard
from sklearn.datasets import load_sample_image
import numpy as np
import pandas as pd
from matplotlib import cm
from matplotlib import gridspec
import matplotlib.pyplot as plt
from datetime import datetime
# + id="79gPevV-dZIy" colab_type="code" colab={}
# load images
china = load_sample_image("china.jpg")
flower = load_sample_image("flower.jpg")
dataset = np.array([china,flower],dtype=np.float32)
# load images data set size
batch_size,height, width, channels = dataset.shape
# + id="vmr69YS3diXD" colab_type="code" colab={}
# Creat a graph with with input X plus a convolutional layer
# applying the 2 filter defined above
X = tfv1.placeholder(tfv1.float32, shape=[None, height, width, channels],name='input')
stride = 4
tile_size = 4
# prediction CNN with two filters and input X
# X is the input mini-batch
# 4 X 4 tiny kernel is used for max pooling: ksize=[batch_size=1,height=4,width=4,channels=1]
# padding = 'VAILD', which means the conv layer does not use zero padding
pooling_output = tfv1.nn.max_pool(X,ksize=[1,tile_size,tile_size,1],strides=[1,stride,stride,1],padding='VALID')
with tfv1.Session() as sess:
output = sess.run(pooling_output,feed_dict= {X:dataset})
# + id="L6kWtpKLfw08" colab_type="code" outputId="fc577785-3644-475a-c5f0-285731521f92" colab={"base_uri": "https://localhost:8080/", "height": 786}
hfig = plt.figure(1,figsize=(5,15))
plt.subplot(4,2,1)
plt.imshow(china)
plt.title('The original china')
plt.subplot(4,2,2)
plt.imshow(flower)
plt.title('The original flower')
plt.subplot(4,2,3)
plt.imshow(output[0,:,:,0], cmap='gray')
plt.title('R')
plt.subplot(4,2,4)
plt.imshow(output[1,:,:,0], cmap='gray')
plt.title('R')
plt.subplot(4,2,5)
plt.imshow(output[0,:,:,1], cmap='gray')
plt.title('G')
plt.subplot(4,2,6)
plt.imshow(output[1,:,:,1], cmap='gray')
plt.title('G')
plt.subplot(4,2,7)
plt.imshow(output[0,:,:,2], cmap='gray')
plt.title('B')
plt.subplot(4,2,8)
plt.imshow(output[1,:,:,2], cmap='gray')
plt.title('B')
plt.show()
|
lab13_cnn_pool.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="40HCfCO9DEHp" colab_type="text"
#
# # Rain In Australia
#
# + [markdown] id="YP32YwqUDEH5" colab_type="text"
# Rains are essential part of our lives. Clouds give the gift of rains to humans. Weather department tries to forecast when will it rain. So,try to predict whether it will rain in Australia tomorrow or not.
# + [markdown] id="EWPpV-rVDEID" colab_type="text"
# Hence, in this kernel,we are going to implement Decision Tree Classifier with Python and Scikit-Learn and build a classifier to predict whether or not it will rain tomorrow in Australia.lets train a binary classification model using Decision Tree Classifier.
# + [markdown] id="aycO_jwuDEIK" colab_type="text"
# ## Import libraries
# Lets import all the libraries that we'll need during this project.
# + id="8DP0mv0VDEIS" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 74} outputId="21a77cc9-2da9-42bb-cf86-825be4ce9545"
import numpy as np # linear algebra
import pandas as pd # data processing,
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
# + [markdown] id="ViKbZahcDEJP" colab_type="text"
# ## Import dataset
# The next step is to import the dataset.
# + id="oiW0d6iBDEJX" colab_type="code" colab={}
data = '../weatherAUS.csv'
df = pd.read_csv(data)
# + [markdown] id="hx93hKjYDEJz" colab_type="text"
# ## Data Analysis
#
# - We have imported the data.
# - Now, its time to explore the data to gain insights about it.
# + id="t_7-HRFTDEJ9" colab_type="code" colab={}
# View dimensions of dataset
# + [markdown] id="3WJdqorFDEKf" colab_type="text"
# We can see how many instances and variables are there in the data set.
# + id="slFOIxh6DEKq" colab_type="code" colab={} outputId="07bd542a-ee3a-4989-9233-eb36098de68e"
# Preview the dataset
df.head()
# + [markdown] id="mshZxh8XDELF" colab_type="text"
# ### View column names <a class="anchor" id="4.3"></a>
# + id="KPxBg8TLDELM" colab_type="code" colab={} outputId="e9d89466-67f1-4d93-c956-00f099138100"
col_names = df.columns
col_names
# + [markdown] id="aPn0oCO9DELt" colab_type="text"
# ### Drop RISK_MM variable <a class="anchor" id="4.4"></a>
#
# It is given in the dataset description, that we should drop the `RISK_MM` feature variable from the dataset description. So, we
# should drop it as follows-
# + id="JrXEDM5oDELx" colab_type="code" colab={}
df.drop(['RISK_MM'], axis=1, inplace=True)
# + id="4pRGbu2pDEMV" colab_type="code" colab={}
# View summary of dataset
# + [markdown] id="EcjnFWF3HnZ6" colab_type="text"
# ### Explore RainTomorrow target variable
# + id="OOkmv7xpG3fN" colab_type="code" colab={}
# Explore RainTomorrow target variable
# + id="Sp6WtaAPG_51" colab_type="code" colab={}
# Check for missing values in RainTomorrow
# + id="Mt6JeX02DEOX" colab_type="code" colab={}
# View number of unique values
# + [markdown] id="XTG8tlIgDEOx" colab_type="text"
# We can see that the number of unique values in `RainTomorrow` variable.
# + [markdown] id="Z9r-4IOMDEP_" colab_type="text"
# #### View percentage of frequency distribution of values
# + id="mH_m06ntDEQC" colab_type="code" colab={}
# View percentage of frequency distribution of values
# + id="sZazq6TvDEQh" colab_type="code" colab={}
#Visualize frequency distribution of RainTomorrow variable
# + [markdown] id="BdVa6GIUDERV" colab_type="text"
# ### Explore Categorical Variables <a class="anchor" id="6.2"></a>
# + id="JbXRnENIDERX" colab_type="code" colab={}
# find categorical variables
# + id="otc4DGtUDERu" colab_type="code" colab={}
# view the categorical variables
# + [markdown] id="I4KSLajDDEV6" colab_type="text"
# ### Explore `Location` variable
#
#
#
# + id="PJbccrE7DEV9" colab_type="code" colab={}
# print number of labels in Location variable
# + id="6hTf_eEDDEWN" colab_type="code" colab={}
# check labels in location variable
# + id="54D1lL9VDEWf" colab_type="code" colab={}
# check frequency distribution of values in Location variable
# + id="4mEA97AtDEW1" colab_type="code" colab={}
# let's do One Hot Encoding of Location variable
# get k-1 dummy variables after One Hot Encoding
# preview the dataset with head() method
# + [markdown] id="MgLQL6uLDEXI" colab_type="text"
# ### Explore `WindGustDir` variable
# + id="29mK557EDEXL" colab_type="code" colab={}
# print number of labels in WindGustDir variable
# + id="qdNJVtl2DEXj" colab_type="code" colab={}
# check labels in WindGustDir variable
# + id="uLFIPpeXDEXy" colab_type="code" colab={}
# check frequency distribution of values in WindGustDir variable
# + id="E0WFrLbIDEX_" colab_type="code" colab={}
# let's do One Hot Encoding of WindGustDir variable
# get k-1 dummy variables after One Hot Encoding
# also add an additional dummy variable to indicate there was missing data
# preview the dataset with head() method
# + id="LFbxFBgcDEYN" colab_type="code" colab={}
# sum the number of 1s per boolean variable over the rows of the dataset
# it will tell us how many observations we have for each category
# + [markdown] id="vj4Uyl3qDEYh" colab_type="text"
# ### Explore `WindDir9am` variable
# + id="P-DW_s99DEYk" colab_type="code" colab={}
# print number of labels in WindDir9am variable
# + id="-WMs5YNBDEY1" colab_type="code" colab={}
# check labels in WindDir9am variable
# + id="-p7fPdnMDEY_" colab_type="code" colab={}
# check frequency distribution of values in WindDir9am variable
# + id="BRC8Laa6DEZL" colab_type="code" colab={}
# let's do One Hot Encoding of WindDir9am variable
# get k-1 dummy variables after One Hot Encoding
# also add an additional dummy variable to indicate there was missing data
# preview the dataset with head() method
# + id="1cVO_q8ADEZd" colab_type="code" colab={}
# sum the number of 1s per boolean variable over the rows of the dataset
# it will tell us how many observations we have for each category
# + [markdown] id="6fhdzZJUDEZ7" colab_type="text"
# ### Explore `WindDir3pm` variable
# + id="bJZ-mNImDEZ-" colab_type="code" colab={}
# print number of labels in WindDir3pm variable
# + id="wKdgT9iWDEaL" colab_type="code" colab={}
# check labels in WindDir3pm variable
# + id="nO2NQBsCDEaV" colab_type="code" colab={}
# check frequency distribution of values in WindDir3pm variable
# + id="bVAqcYqODEag" colab_type="code" colab={}
# let's do One Hot Encoding of WindDir3pm variable
# get k-1 dummy variables after One Hot Encoding
# also add an additional dummy variable to indicate there was missing data
# preview the dataset with head() method
# + id="FeKWT0QtDEaw" colab_type="code" colab={}
# sum the number of 1s per boolean variable over the rows of the dataset
# it will tell us how many observations we have for each category
# + [markdown] id="y-Rk4-DeDEa_" colab_type="text"
# ### Explore `RainToday` variable
# + id="cKP-VsRgDEbB" colab_type="code" colab={}
# print number of labels in RainToday variable
# + id="sIYtYdzFDEbL" colab_type="code" colab={}
# check labels in WindGustDir variable
# + id="SjrYBTuhDEbU" colab_type="code" colab={}
# check frequency distribution of values in WindGustDir variable
# + id="cxK-5wlODEbc" colab_type="code" colab={}
# let's do One Hot Encoding of RainToday variable
# get k-1 dummy variables after One Hot Encoding
# also add an additional dummy variable to indicate there was missing data
# preview the dataset with head() method
# + id="A5fybCpKDEbl" colab_type="code" colab={}
# sum the number of 1s per boolean variable over the rows of the dataset
# it will tell us how many observations we have for each category
# + [markdown] id="V-rG7ZPWDEby" colab_type="text"
# ### Explore Numerical Variables <a class="anchor" id="6.5"></a>
# + id="Z49HBp6sDEb2" colab_type="code" colab={}
# find numerical variables
# + id="g9ED6ScBDEcB" colab_type="code" colab={}
# view the numerical variables
# + [markdown] id="XUtNv8-fDEcQ" colab_type="text"
# ### Explore problems within numerical variables
#
# + id="Pmg0l1wmDEca" colab_type="code" colab={}
# check missing values in numerical variables
# + id="VVsKxecPDEcu" colab_type="code" colab={}
# view summary statistics in numerical variables
# + id="4SYeTrFvDEc4" colab_type="code" colab={}
# draw boxplots to visualize outliers
# + [markdown] id="USAFjKm2DEdB" colab_type="text"
# The above boxplots will confirm number of outliers in these variables.
# + [markdown] id="gsPYRjqxDEdC" colab_type="text"
# ### Check the distribution of variables
#
#
# - Now,plot the histograms to check distributions to find out if they are normal or skewed.
#
# - If the variable follows normal distribution, then do `Extreme Value Analysis` otherwise if they are skewed, find IQR (Interquantile range).
# + id="AVeTeXgzDEdD" colab_type="code" colab={}
# plot histogram to check distribution
# + [markdown] id="Sq_5G43cDEdQ" colab_type="text"
# We can see that all the four variables are skewed. So, I will use interquantile range to find outliers.
# + id="y_8jB5xkDEdT" colab_type="code" colab={}
# find outliers for Rainfall variable
# + id="eTGEj90EDEdc" colab_type="code" colab={}
# find outliers for Evaporation variable
# + id="kp4gkzk0DEdv" colab_type="code" colab={}
# find outliers for WindSpeed3pm variable
# + [markdown] id="OAFLTZwmDEd4" colab_type="text"
# ## Multivariate Analysis
#
#
# - An important step in EDA is to discover patterns and relationships between variables in the dataset.
#
# - use heat map and pair plot to discover the patterns and relationships in the dataset.
#
# + id="ss_I2QQmDEd6" colab_type="code" colab={}
# check correlation between them
# + id="KDYKH1riDEeD" colab_type="code" colab={}
# Plot heatmap for correlation
# + [markdown] id="uvMTeCe8DEey" colab_type="text"
# ## Declare features and target variable
# + id="DPoi_aw3DEe0" colab_type="code" colab={}
# code here
# + [markdown] id="navyBRnhDEfE" colab_type="text"
# ## Split data into separate training and test set
# + id="n7uQZQ8ZDEfJ" colab_type="code" colab={}
# split X and y into training and testing sets
from sklearn.model_selection import train_test_split
# + id="p5YtW8PeDEfT" colab_type="code" colab={}
# check the shape of X_train and X_test
# + [markdown] id="0TyDD9C7DEle" colab_type="text"
# ## Model training
# + id="7YewhSRiDElf" colab_type="code" colab={}
# train a logistic regression model on the training set
from sklearn.linear_model import LogisticRegression
# instantiate the model
# fit the model
# + [markdown] id="ECkHHJ1KDElq" colab_type="text"
# ## Predict results
# + id="_E52HZJ5DElr" colab_type="code" colab={}
# code here
# + [markdown] id="F-mDrYBDDEmD" colab_type="text"
# ## Check accuracy score
# + id="8XzUTi4CDEmF" colab_type="code" colab={}
from sklearn.metrics import accuracy_score
# + [markdown] id="o0B7fqJrDEmh" colab_type="text"
# ### Check for overfitting and underfitting <a class="anchor" id="14.2"></a>
# + id="2E-nMGfxDEmi" colab_type="code" colab={}
# print the scores on training and test set
# + [markdown] id="8jcYBKaFDEnf" colab_type="text"
# ## Confusion matrix
#
#
# + id="Cz3yxqebDEnh" colab_type="code" colab={}
# Print the Confusion Matrix and slice it into four pieces
from sklearn.metrics import confusion_matrix
# + id="9G_d5H9tDEno" colab_type="code" colab={}
# visualize confusion matrix with seaborn heatmap
# + [markdown] id="bjj3d1F_DErx" colab_type="text"
# ## k-Fold Cross Validation
# + id="SfvaV46IDEry" colab_type="code" colab={}
# Apply 5-Fold Cross Validation
# + id="cUcvkUiDDEr5" colab_type="code" colab={}
# compute Average cross-validation score
# + [markdown] id="EldU-G8SDEsX" colab_type="text"
# Now try to use different classification algorithm and compare them.
|
Rain_in_Australia/Rain_in_Australia_template.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # Sympy
# +
import sympy as sp
# See: http://docs.sympy.org/latest/tutorial/printing.html
sp.init_printing()
# -
# ## Live shell
# http://live.sympy.org/
# ## Make symbols
# Make one symbol:
x = sp.symbols("x")
# Make several symbols at once:
x, y, z = sp.symbols("x y z")
# ## Substitute
# See: http://docs.sympy.org/latest/tutorial/basic_operations.html#substitution
x = sp.symbols("x")
expr = sp.cos(x) + 1
expr.subs(x, 0)
# ## Simplify
# See: http://docs.sympy.org/latest/tutorial/simplification.html#simplify
x = sp.symbols("x")
sp.simplify((x**3 + x**2 - x - 1)/(x**2 + 2*x + 1))
sp.simplify(sp.exp(sp.I * sp.pi) + sp.exp(sp.I * sp.pi))
# ## Factor
# See: http://docs.sympy.org/latest/tutorial/simplification.html#factor
x = sp.symbols("x")
sp.factor(x**3 - x**2 + x - 1)
# ## Expand
# See: http://docs.sympy.org/latest/tutorial/simplification.html#expand
x = sp.symbols("x")
sp.expand((x - 1)*(x**2 + 1))
# ## Solve
# See: http://docs.sympy.org/latest/tutorial/solvers.html
x = sp.symbols("x")
eq = sp.Eq(x**2, 1)
sp.solveset(eq, x)
# ## Derivatives
# See: http://docs.sympy.org/latest/tutorial/calculus.html#derivatives
x, y, z = sp.symbols("x y z")
# ### Create an unevaluated derivative
sp.Derivative(sp.cos(x), x)
# ### Evaluate an unevaluated derivative
diff = sp.Derivative(sp.cos(x), x)
diff
diff.doit()
# ### Directly compute an integral
sp.diff(sp.cos(x), x)
# ### Print the equation
expr = sp.exp(x*y*z)
diff = sp.Derivative(expr, x, y, y, z, z, z, z)
sp.Eq(diff, diff.doit())
# ### First derivatives
diff = sp.Derivative(sp.cos(x), x)
sp.Eq(diff, diff.doit())
diff = sp.Derivative(3*sp.cos(x)**2, x)
sp.Eq(diff, diff.doit())
diff = sp.Derivative(sp.exp(x**2), x)
sp.Eq(diff, diff.doit())
# ### Second derivatives
diff = sp.Derivative(x**4, x, 2)
sp.Eq(diff, diff.doit())
# or
diff = sp.Derivative(x**4, x, x)
sp.Eq(diff, diff.doit())
# ### Third derivatives
diff = sp.Derivative(x**4, x, 3)
sp.Eq(diff, diff.doit())
# or
diff = sp.Derivative(x**4, x, x, x)
sp.Eq(diff, diff.doit())
# ### Derivatives with respect to several variables at once
diff = sp.Derivative(sp.exp(x*y), x, y)
sp.Eq(diff, diff.doit())
# ### Multiple derivatives with respect to several variables at once
diff = sp.Derivative(sp.exp(x*y*z), x, y, y, z, z, z, z)
sp.Eq(diff, diff.doit())
# ## Integrals
# See: http://docs.sympy.org/latest/tutorial/calculus.html#integrals
x, y, z = sp.symbols("x y z")
# ### Create an unevaluated derivative
sp.Integral(sp.cos(x), x)
# ### Evaluate an unevaluated derivative
integ = sp.Integral(sp.cos(x), x)
integ
integ.doit()
# ### Directly compute an integral
sp.integrate(sp.cos(x), x)
# ### Print the equation
integ = sp.Integral(sp.cos(x), x)
sp.Eq(integ, integ.doit())
# ### Create an indefinite integral (i.e. an antiderivative or primitive)
integ = sp.Integral(sp.cos(x), x)
sp.Eq(integ, integ.doit())
# ### Create a definite integral
# `sp.oo` means infinity.
integ = sp.Integral(sp.cos(x), (x, -sp.oo, sp.oo))
sp.Eq(integ, integ.doit())
integ = sp.Integral(sp.cos(x), (x, -sp.pi, sp.pi))
sp.Eq(integ, integ.doit())
integ = sp.Integral(sp.exp(-x), (x, 0, sp.oo))
sp.Eq(integ, integ.doit())
# ### Multiple integrals
integ = sp.Integral(sp.cos(x), (x, -sp.oo, sp.oo), (x, -sp.oo, sp.oo))
sp.Eq(integ, integ.doit())
# ### Multiple variables integrals
integ = sp.Integral(sp.cos(x**2 + y**2), (x, -sp.oo, sp.oo), (y, -sp.oo, sp.oo))
sp.Eq(integ, integ.doit())
# ## Limits
# See: http://docs.sympy.org/latest/tutorial/calculus.html#limits
# ## Series expansion
# See: http://docs.sympy.org/latest/tutorial/calculus.html#series-expansion
# ## Finite differences
# See: http://docs.sympy.org/latest/tutorial/calculus.html#finite-differences
|
nb_dev_python/python_sympy_calculus_en.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/butchland/fastai_xla_extensions/blob/master/explore_nbs/AWD_LSTM_small_patched_GPU_butch_colab.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="0lsfWpbs6kll" colab_type="text"
#
# + id="BWVEfK55QSGr" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 52} outputId="fa194398-b2c7-48c6-d280-c601abc3060d"
# !curl -s https://course.fast.ai/setup/colab | bash
# + id="qrBMcV2MQSwJ" colab_type="code" colab={}
# from google.colab import drive
# drive.mount('/content/drive')
# + [markdown] id="6MxdCtAZQzOP" colab_type="text"
#
# + id="S3nXsaoGbQhu" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 54} outputId="3623ca72-3998-45b8-b820-5caaefdc02ec"
# !pip install git+https://github.com/butchland/my_timesaver_utils > /dev/null
# + id="BmWqY8o5PD2J" colab_type="code" colab={}
# # !pip install git+https://github.com/butchland/fastai_xla_extensions > /dev/null
# + id="BacUuFcoPD2U" colab_type="code" colab={}
# !pip install fastai2 > /dev/null
# + id="HLmFvS5tPD18" colab_type="code" colab={}
# VERSION = "20200707" #@param ["1.5" ,"20200325", "20200515", "20200707","nightly"]
# # !curl https://raw.githubusercontent.com/pytorch/xla/master/contrib/scripts/env-setup.py -o pytorch-xla-env-setup.py > /dev/null
# # !python pytorch-xla-env-setup.py --version $VERSION > /dev/null
# + id="fodwDNw9TiQg" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 104} outputId="20d98d49-be27-471b-c1b6-0778314a2cdb"
# !pip freeze | grep torch
# !pip freeze | grep fastai2
# !pip freeze | grep fastai_xla_extensions
# + [markdown] id="XXbkRNRS9-bZ" colab_type="text"
#
# + id="7-Fk2RFQPD2c" colab_type="code" colab={}
# import fastai_xla_extensions.core
# + id="4AOfeagHROQv" colab_type="code" colab={}
from fastai2.text.all import *
# + id="rtvw_m5vbdHz" colab_type="code" colab={}
from my_timesaver_utils.profiling_callback import *
# + id="dFOnSIShUGMP" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="693e7075-ff5d-4a32-a388-ef96963cc375"
default_device()
# + id="krSFy5j4PD2i" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 17} outputId="6d7c58a9-8cd7-49e6-f304-d94aa95429e1"
path = untar_data(URLs.IMDB_SAMPLE)
# + id="DiHIusqbPD2q" colab_type="code" colab={}
#hide
Path.BASE_PATH = path
# + id="5nN21fyPPD2x" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="249d5ec1-4d5c-439d-c7fb-ed1fcc8aa0f8"
path.ls()
# + id="j72_QpMFeSyR" colab_type="code" colab={}
df = pd.read_csv(path/'texts.csv')
# + id="ff_5BncUX9Bp" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 17} outputId="62de7f02-f8f4-414e-9d3b-bec02b9c8d28"
dls = TextDataLoaders.from_df(df,path=path, text_col='text', label_col='label', valid_col='is_valid')
# + id="8Hxazu6PbC8D" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="9f58ff59-0418-44af-c48f-5404a5b4ba2c"
dls.device
# + id="h-DN_ZQRYOq3" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 17} outputId="66e8ef74-b2c3-457e-f403-fdf3cb148e45"
learner = text_classifier_learner(dls, AWD_LSTM, drop_mult=0.5, metrics=accuracy)
# + id="slrc-jQTYncD" colab_type="code" colab={}
learner.to_my_profile(); learner.my_profile.clear_stats()
# + id="BYr1SM5mYbyr" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 112} outputId="b3b9b0e0-715f-4b30-c824-6852ae5eff3d"
learner.fit(2, 1e-2)
# + id="5ypFiKs6bRv-" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 243} outputId="d6df82a1-ef29-4273-b6d8-e4432861b640"
learner.my_profile.print_stats()
# + [markdown] id="ItpV8J8EPx5y" colab_type="text"
#
# + colab_type="code" id="yqGXawGjPzDT" colab={}
train_pred_stats = learner.my_profile.get_stats('train_pred')
train_step_stats = learner.my_profile.get_stats('train_step')
train_batch_stats = learner.my_profile.get_stats('train_batch')
valid_batch_stats = learner.my_profile.get_stats('valid_batch')
train_stats = learner.my_profile.get_stats('train')
valid_stats = learner.my_profile.get_stats('valid')
epoch_stats = learner.my_profile.get_stats('epoch')
fit_stats = learner.my_profile.get_stats('fit')
# + id="mnyQLMTpKTAz" colab_type="code" colab={}
# %matplotlib inline
# + id="e4JhAtZCKPip" colab_type="code" colab={}
def show_stats(data,title):
fig = plt.figure()
fig.suptitle(title, fontsize=20)
plt.xlabel('batches', fontsize=18)
plt.ylabel('secs', fontsize=16)
plt.plot(data,);
# + id="yauor8HqMOa2" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 316} outputId="71198d93-daf2-4bb3-89e2-9548a60ccf43"
show_stats(train_pred_stats[2],'train_pred')
# + id="_YaWcTKAMaeS" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 316} outputId="5a83b102-8502-4215-81e1-c8115882ac41"
show_stats(train_step_stats[2],'train_step')
# + id="6cVjc_2RMnhQ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 615} outputId="14021a5b-f404-4d65-ef02-a14b6abe4d1e"
show_stats(train_batch_stats[2],'train_batch')
show_stats(valid_batch_stats[2],'valid_batch')
# + id="6SowUp7tNWcF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="02a5b415-cdc0-47ed-83d1-2e9c79284c22"
show_stats(train_stats[2],'train')
show_stats(valid_stats[2],'valid')
show_stats(epoch_stats[2],'epoch')
show_stats(fit_stats[2],'fit')
# + id="QdUXmoQQPO0c" colab_type="code" colab={}
# + id="WN72s1NFPwy_" colab_type="code" colab={}
# + id="03_LiRy584gW" colab_type="code" colab={}
|
explore_nbs/AWD_LSTM_small_patched_GPU_butch_colab.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.8 64-bit (''pyisalie'': conda)'
# name: python3
# ---
# # Hessian-based toolbox for more reliable and interpretable machines learning physics
# The aim of this Jupyter Notebook is to give a ready-to-use code of the Hessian-based toolbox which increases the reliability and interpretability of pre-trained ML models. We described this toolbox in the paper 'Hessian-based toolbox for more reliable and interpretable machines learning physics' by <NAME>, <NAME>, <NAME>, <NAME>, and <NAME> (collaboration of ICFO, Spain and University of Warsaw, Poland) available at [arXiv](https://arxiv.org/abs/?). We will analyze here the CNN trained to recognize phases in the 1D spinless Fermi-Hubbard model.
#
# The scope of the notebook is the following:
#
# 1. Loading a data set (in our case, the transition line of the 1D spinless Fermi-Hubbard, marked with (1) in the figure below)
#
# 2. Loading a trained ML model and the Hessian of the training loss function at the model parameters corresponding to the training loss landscape minimum. You can calculate the Hessian with [this notebook](https://doi.org/10.5281/zenodo.3759432).
#
# 3. Calculation of [influence functions](http://proceedings.mlr.press/v70/koh17a.html), [RelatIFs](https://proceedings.mlr.press/v108/barshan20a), [Resampling Uncertainty Estimation (RUE)](https://proceedings.mlr.press/v89/schulam19a), and [Extrapolation Score with Local Ensembles (LEs)](https://openreview.net/forum?id=BJl6bANtwH).
#
# 4. Produce figures
#
# <img src="./phase_diagram.png" width=800/>
# ## Note!
# All interpretability and reliability methods, implemented here, are contributions of other amazing people. We implement them here in PyTorch and we calculate them exactly, but there are ways of approximating the Hessian and approximating the toolbox. See our paper and papers cited above to find out!
# ## Part 1: Load data
#
# We have computed the ground states of the 1D spinless Fermi-Hubbard model for $V_2/J=0$ and between 0-40 $V_1/J$. You can reproduce these data using [this notebook](https://doi.org/10.5281/zenodo.3759432). We have 1000 training, 200 validation, and 50 test examples.
# +
import torch
import numpy as np
from data_loader import Downloader
training_set_size = 1000
batch_size = training_set_size
test_set_size = 50 #45 or 50
chosen_test_examples = np.arange(test_set_size)
input_size = 924 # Fock basis size for 12-site problem
data_name = 'CDW_ED_size12_full'
CDW_data = Downloader(data_name, batch_size)
train_loader = CDW_data.train_loader()
test_loader = CDW_data.test_loader(batch_size=test_set_size)
print("Data loaded.")
# -
# ## Part 2: Load trained model and its Hessian
# We trained our CNN with SGD with momentum and with decreasing learning rate, with $L_2$ regularization. The architecture is the following (length scale doesn't apply):
#
# <img src="./CNN_architecture.png" width=800/>
# +
from architectures import CNN1D_tiny_ED
num_classes = 2
folder_model = "./model"
model_name = "Conv1D_original_l005_12site"
λ = 0.05 # Regularization
model = CNN1D_tiny_ED(num_classes)
model.load_state_dict(torch.load(folder_model + '/' + model_name + '.pt', map_location=torch.device('cpu')))
# +
# Compute traditional test loss (using known ground-truth labels) and 'minimal' test loss (when ground-truth labels are unavailable, needed for extrapolation score)
# Save also two last neurons' outputs
import torch.nn as nn
from torch.nn import CrossEntropyLoss
criterion = nn.CrossEntropyLoss(reduction='none')
model.eval()
for eigenvectors, labels in test_loader:
eigenvectors = eigenvectors.reshape(-1, 1, input_size) #(test_set_size, 25, 50)
outputs = model(eigenvectors)
neuron_0 = outputs[:,0].data
neuron_1 = outputs[:,1].data
_, predicted = torch.max(outputs.data, 1)
original_test_loss = criterion(outputs, labels)
minimal_test_loss = criterion(outputs, predicted)
correct = (predicted == labels).sum().item()
incorrect_mask = (predicted != labels).detach().numpy()
# We manually add L2 regularization
if λ != 0:
l2_reg = 0.0
for param in model.parameters():
l2_reg += torch.norm(param)**2
original_test_loss += 1/training_set_size * λ/2 * l2_reg
minimal_test_loss += 1/training_set_size * λ/2 * l2_reg
model_accuracy = correct / len(labels)
print("Accuracy of the model on the", len(labels), "test images:", 100 * model_accuracy, "%")
misclassified_array = np.arange(test_set_size)[incorrect_mask]
print("Misclassified examples: ", misclassified_array)
# -
# Load the exact hessian
hessian = np.load(folder_model + '/' + model_name + '_hessian.npy')
# ## Part 3: Use the Hessian-based toolbox
# We compute here:
# - [influence functions](http://proceedings.mlr.press/v70/koh17a.html)
# - [RelatIFs](https://proceedings.mlr.press/v108/barshan20a)
# - [Resampling Uncertainty Estimation (RUE)](https://proceedings.mlr.press/v89/schulam19a)
# - [Extrapolation Score with Local Ensembles (LEs)](https://openreview.net/forum?id=BJl6bANtwH)
# +
from influence_function import exact_influence_functions
folder = "./toolbox_output"
folder_influence = folder + "/influence"
damping = 0.2 # needs to be larger than absolute value of the largest negative eigenvalue of the Hessian
# Influence functions and RelatIFs
exact_influence_functions(input_size, train_loader, test_loader, model, λ, hessian, damping, folder_influence, chosen_test_examples = chosen_test_examples)
# +
from rue import calculateRUE
# RUE. "True" RUE is a version with ground-truth labels, "minimal" RUE is a version when we don't provide ground-truth labels, so we assume all predicted labels are correct.
# We do that to mimic a real-life scenario where we don't know the true labels.
folder_rue = folder + "./RUE"
rue_number_of_repetitions = 50 # how many repetitions of the bootstrap sampling do we do?
true_rue, minimal_rue = calculateRUE(input_size, train_loader, test_loader, model, λ, hessian, 1.0 + damping, number_of_repetitions = rue_number_of_repetitions, chosen_test_examples = chosen_test_examples)
np.savetxt(folder_rue + '/true_RUE.txt', true_rue)
np.savetxt(folder_rue + '/minimal_RUE.txt', minimal_rue)
# +
from lees import calculateLEES
lees_tresholds = [1, 0.1, 0.01, 0.001] # to find optimal number of eigenvectors corresponding to positive eigenvalues, which we get rid of
folder_lees = folder + "./LEs"
# Compute extrapolation score via local ensemble for both ground-truth and minimal version
various_min_lees = []
various_true_lees = []
ms = []
for treshold in lees_tresholds:
# Version with test loss computed by assuming that predicted labels are true labels
print("Minimal version of LEs")
min_lees, m = calculateLEES(input_size, test_loader, model, λ, hessian, treshold, MINIMAL_VERSION = True, chosen_test_examples = chosen_test_examples)
various_min_lees = np.append(various_min_lees, min_lees, axis=0)
ms = np.append(ms, m) # only once, they're independent of a version
np.savetxt(folder_lees + '/LEES_t' + str(treshold) + '_minver.txt', min_lees)
# Version with ground-truth labels available
print("Now true version of LEs")
true_lees, m = calculateLEES(input_size, test_loader, model, λ, hessian, treshold, MINIMAL_VERSION = False, chosen_test_examples = chosen_test_examples)
various_true_lees = np.append(various_true_lees, true_lees, axis=0)
np.savetxt(folder_lees + '/LEES_t' + str(treshold) + '_truever.txt', true_lees)
np.save(folder_lees + '/LEES_ms', ms)
# -
# ## Part 4: Let's make plots!
# +
from utility_plots import make_IF_analysis
folder_figure = folder + "/figures"
U_array = np.concatenate((np.linspace(0, 1, 500), np.linspace(1.01, 40, 500))) # interactions V_1 / J for which training points where calculated
U_testarray = np.concatenate((np.linspace(0.01, 0.999, 20), np.linspace(1.02, 2, 10), np.geomspace(2.066, 39, 20))) # interactions V_1 / J for which test points where calculated
test_order_parameters = np.array([2.13535619e-07, 2.30400170e-07, 2.48600148e-07, 2.68252485e-07, 2.89489252e-07, 3.12459487e-07, 3.37331205e-07, 3.64293650e-07, 3.93559760e-07, 4.25368908e-07, 4.59989898e-07, 4.97724255e-07, 5.38909797e-07, 5.83924505e-07, 6.33190669e-07, 6.87179309e-07, 7.46414828e-07, 8.11479867e-07, 8.83020302e-07, 9.61750320e-07, 9.95724383e-07, 1.19490140e-06, 1.43923798e-06, 1.73911456e-06, 2.10677157e-06, 2.55641407e-06, 3.10427868e-06, 3.76867765e-06, 4.57004190e-06, 5.53098407e-06, 6.20153402e-06, 1.10660053e-05, 2.07024188e-05, 4.01604972e-05, 8.00898654e-05, 1.63111549e-04, 3.37516091e-04, 7.06781356e-04, 1.49327368e-03, 3.17585576e-03, 6.78731763e-03, 1.45570573e-02, 3.12947590e-02, 6.73145077e-02, 1.44066125e-01, 2.99967069e-01, 5.61992278e-01, 8.26284042e-01, 9.53248223e-01, 9.88994793e-01])
# Basic influence functions and RelatIF plots (x test_set_size)
print('Plotting influence functions...')
# This is the mask of training data, generated by the Downloader, when shuffling training data (once)
# Now we can recover which training point corresponds to which interaction V_1 / J.
# You may not need it in your dataset, if you designed a cleverer way of tracking the features of training data!
mask = np.load(folder_model + '/' + data_name + '_mask.npy')
make_IF_analysis(chosen_test_examples, mask, folder_influence, 'exact_influence', U_array, U_testarray, test_order_parameters, misclassified_array, "original_12site", folder_figure, model_accuracy)
print('Plotting RelatIFs...')
make_IF_analysis(chosen_test_examples, mask, folder_influence, 'exact_RelatIF', U_array, U_testarray, test_order_parameters, misclassified_array, "original_12site", folder_figure, model_accuracy)
# -
from utility_plots import make_RUE_plot
# Plot for real/minimal test loss and RUE (as a percentage of test loss)
print("Plotting RUE with real/minimal test loss...")
make_RUE_plot(minimal_rue, minimal_test_loss, chosen_test_examples, U_array, U_testarray, test_order_parameters, 'min_version', folder_figure, model_accuracy, LOSS_PERCENTAGE=False)
make_RUE_plot(true_rue, original_test_loss, chosen_test_examples, U_array, U_testarray, test_order_parameters, 'true_version', folder_figure, model_accuracy, LOSS_PERCENTAGE=False)
from utility_plots import make_LEES_plot
# Plot for various overlapped LEES + real/minimal scaled test loss + scaled neuron output + RUE (NOT as a percentage of test loss)
print("Plotting LEES for different tresholds with real/minimal test loss, neurons' outputs, and RUE...")
make_LEES_plot(various_min_lees, ms, minimal_test_loss, minimal_rue, chosen_test_examples, U_array, U_testarray, test_order_parameters, 'min_version', folder_figure, model_accuracy)
make_LEES_plot(various_true_lees, ms, original_test_loss, true_rue, chosen_test_examples, U_array, U_testarray, test_order_parameters, 'true_version', folder_figure, model_accuracy)
from utility_plots import make_neurons_outputs_plot
# Plot for neurons' outputs
make_neurons_outputs_plot([neuron_0, neuron_1], chosen_test_examples, U_array, U_testarray, test_order_parameters, "original_12site", folder_figure, model_accuracy)
|
Hessian-based_notebook.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Soft Computing
#
# ## Vežba 2 - OCR (Optical Character Recognition)
# Cilj ovih vežbi je implementacija sistema za optičko prepoznavanje karaktera (OCR).<br>
# Za rad sa neuronskim mrežama koristićemo <a href="https://keras.io/">Keras</a> biblioteku.
# ### Tok aktivnosti implementacije OCR-a
# Tok aktivnosti predstavlja korake koje je potrebno izvršiti prilikom implementacije OCR-a.
# <img src="images/tok_aktivnosti.png"/>
# ### Početak implementacije
#
# Skup paketa/biblioteka sa prethodnih vežbi smo proširili Keras bibliotekom za rad sa neuronskim mrežama.
import numpy as np
import cv2 # OpenCV
import matplotlib
import matplotlib.pyplot as plt
import collections
# iscrtavanje slika u notebook-u
# %matplotlib inline
# prikaz vecih slika
matplotlib.rcParams['figure.figsize'] = 16,12
# keras
from keras.models import Sequential
from keras.layers.core import Dense, Activation
from keras.optimizers import SGD
# ### Koraci [1, 3]
#
# Ovi koraci su detaljno objašnjeni na prethodnim vežbama.
# +
def load_image(path):
return cv2.cvtColor(cv2.imread(path), cv2.COLOR_BGR2RGB)
def image_gray(image):
return cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)
def image_bin(image_gs):
height, width = image_gs.shape[0:2]
image_binary = np.ndarray((height, width), dtype=np.uint8)
ret, image_bin = cv2.threshold(image_gs, 127, 255, cv2.THRESH_BINARY)
return image_bin
def invert(image):
return 255-image
def display_image(image, color=False):
if color:
plt.imshow(image)
else:
plt.imshow(image, 'gray')
def dilate(image):
kernel = np.ones((3, 3)) # strukturni element 3x3 blok
return cv2.dilate(image, kernel, iterations=1)
def erode(image):
kernel = np.ones((3, 3)) # strukturni element 3x3 blok
return cv2.erode(image, kernel, iterations=1)
# -
# Prilikom implementacije koraka [4, 9] oslonićemo se na slike vezane za **Primer 1**:
# * treniranje: **images/brojevi.png**
# * testiranje: **images/test.png**
# ### Korak 4 - Izdvajanje regiona od interesa
#
# U ovom koraku potrebno je izdvojiti samo regione (konture) od interesa. Potrebno je označiti regione od interesa na slici i napraviti listu slika od regiona koja će kasnije biti ulaz za neuronsku mrežu.
#
# Kako bi svi regioni koje ćemo koristiti za neuronsku mrežu biti iste veličine, implementiraćemo metodu za promenu veličine slike na 28 x 28.
def resize_region(region):
return cv2.resize(region, (28, 28), interpolation=cv2.INTER_NEAREST)
# test za proveru rada
test_resize_img = load_image('images/test_resize.png')
test_resize_ref = (28, 28)
test_resize_res = resize_region(test_resize_img).shape[0:2]
print("Test resize passsed: ", test_resize_res == test_resize_ref)
# Metoda za označavanje regiona od interesa treba da označi regione od interesa na originalnoj slici i za svaki region napravi posebnu sliku dimenzija 28 x 28. Kao povratnu vrednost vraća originalnu sliku na kojoj su obeleženi regioni i niz slika koje predstavljaju regione sortirane po rastućoj vrednosti **X** ose.
#
# Za potrebe označavanja regiona iskoristićemo **boundingRect**, a za obeležavanje regiona **rectangle** metodu OpenCV-ja.
def select_roi(image_orig, image_bin):
contours, hierarchy = cv2.findContours(image_bin.copy(), cv2.RETR_LIST, cv2.CHAIN_APPROX_SIMPLE)
sorted_regions = [] # lista sortiranih regiona po X osi
regions_array = []
for contour in contours:
x, y, w, h = cv2.boundingRect(contour) # koordinate i velicina granicnog pravougaonika
area = cv2.contourArea(contour)
if area > 100 and h < 100 and h > 15 and w > 20:
# kopirati [y:y+h+1, x:x+w+1] sa binarne slike i smestiti u novu sliku
# oznaciti region pravougaonikom na originalnoj slici sa rectangle funkcijom
region = image_bin[y:y+h+1, x:x+w+1]
regions_array.append([resize_region(region), (x, y, w, h)])
cv2.rectangle(image_orig, (x, y), (x + w, y + h), (0, 255, 0), 2)
regions_array = sorted(regions_array, key=lambda x: x[1][0])
sorted_regions = [region[0] for region in regions_array]
return image_orig, sorted_regions
# ### Korak 5 - Priprema podataka za obučavanje
#
# Regioni od interesa su predstavljeni vektorom čiji su elementi matrice dimenzija 28 x 28. Elementi matrica su vrednosti 0 ili 255. Potrebno je skalirati vrednosti elemenata matrice na opseg [0, 1], kako bi se pogodio linearni deo sigmoid funkcije i smanjilo vreme obučavanja. Nakon skaliranja, matrice je potrebno transformisati u vektor od 784 elementa.
def scale_to_range(image):
return image/255
# test za proveru
test_scale_matrix = np.array([[0, 255], [51, 153]], dtype='float')
test_scale_ref = np.array([[0., 1.], [0.2, 0.6]], dtype='float')
test_scale_res = scale_to_range(test_scale_matrix)
print("Test scale passed: ", np.array_equal(test_scale_res, test_scale_ref))
def matrix_to_vector(image):
return image.flatten()
test_mtv = np.ndarray((28, 28))
test_mtv_ref = (784, )
test_mtv_res = matrix_to_vector(test_mtv).shape
print("Test matrix to vector passed: ", test_mtv_res == test_mtv_ref)
def prepare_for_ann(regions):
ready_for_ann = []
for region in regions:
scale = scale_to_range(region)
ready_for_ann.append(matrix_to_vector(scale))
return ready_for_ann
# Potrebno je konvertovati alfabet u niz pogodan za obučavanje neuronske mreže, odnosno niz čiji su svi elementi 0 osim elemenata čiji je indeks jednak indeksu elementa iz alfabeta za koji formiramo niz.
#
# Primeri:
# <ul>
# <li>Prvi element alfabeta: [1, 0, 0, 0, 0, 0, 0, 0, 0, 0],</li>
# <li>Drugi element alfabeta: [0, 1, 0, 0, 0, 0, 0, 0, 0, 0] itd.</li>
# </ul>
def convert_output(alphabet):
nn_outputs = []
for index in range(len(alphabet)):
output = np.zeros(len(alphabet))
output[index] = 1
nn_outputs.append(output)
return np.array(nn_outputs)
# test konverzije
test_convert_alphabet = [0, 1, 2]
test_convert_ref = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]], dtype='float')
test_convert_res = convert_output(test_convert_alphabet).astype('float')
print("Test convert output: ", np.array_equal(test_convert_res, test_convert_ref))
# ### Koraci [6, 7]
#
# Veštačka neuronska mreža se sastoji od 784 ulazna neurona, 128 neurona u skrivenom sloju i 10 neurona na izlazu.
#
# Zašto baš 784 neurona na ulazu i 10 neurona na izlazu?
#
# Regione smo transformisali prvo na matricu dimenzija 28 x 28, a zatim u vektor od 784 elementa. Broj neurona na izlazu je posledica broja znakova u alfabetu.
#
# <img src="images/neuronska_mreza.png" />
def create_ann(output_size):
ann = Sequential()
ann.add(Dense(128, input_dim=784, activation='sigmoid'))
ann.add(Dense(output_size, activation='sigmoid'))
return ann
def train_ann(ann, X_train, y_train, epochs):
X_train = np.array(X_train, np.float32) # dati ulaz
y_train = np.array(y_train, np.float32) # zeljeni izlazi na date ulaze
print("\nTraining started...")
sgd = SGD(lr=0.01, momentum=0.9)
ann.compile(loss='mean_squared_error', optimizer=sgd)
ann.fit(X_train, y_train, epochs=epochs, batch_size=1, verbose=0, shuffle=False)
print("\nTraining completed...")
return ann
# ### Korak 8 - Određivanje pobedničkog neurona
#
# Pobednički neuron je neuron čija je aktivaciona vrednost najveća.
def winner(output):
return max(enumerate(output), key=lambda x: x[1])[0]
# test winner
test_winner_output = [0., 0.2, 0.3, 0.95]
test_winner_ref = 3
test_winner_res = winner(test_winner_output)
print("Test winner passed: ", test_winner_res == test_winner_ref)
# ### Korak 9 - Prikaz rezultata
#
# Prikaz rezultata prepoznavanja - za svaki rezultat je potrebno pronaći indeks pobedničkog neurona koji ujedno predstavlja i indeks prepoznatog elementa u alfabetu. Karakter se dodaje u rezultujuću listu.
def display_result(outputs, alphabet):
result = []
for output in outputs:
result.append(alphabet[winner(output)])
return result
# ### Primer 1
#
# `Implementirati sistem koji će vršiti optičko prepoznavanje brojeva. Sistem obučiti na **images/brojevi.png**, a testirati na **images/test.png**.`
# Za početak, učitavamo sliku za obučavanje veštačke neuronske mreže i transformišemo je u binarni oblik. Nakon toga označavamo regione od interesa i prikazujemo ih na originalnoj slici.
image_color = load_image('images/brojevi.png')
img = image_bin(image_gray(image_color))
img_bin = erode(dilate(img))
selected_regions, numbers = select_roi(image_color.copy(), img_bin)
display_image(selected_regions)
# Zatim definišemo alfabet i vršimo treniranje veštačke neuronske mreže.
# +
alphabet = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
inputs = prepare_for_ann(numbers)
outputs = convert_output(alphabet)
ann = create_ann(output_size=10)
ann = train_ann(ann, inputs, outputs, epochs=2000)
# -
# Verifikujemo obučenost neuronske mreže uz pomoć trećeg i četvrtog ulaznog vektora (brojevi 2 i 3).
result = ann.predict(np.array(inputs[2:4], np.float32))
print(result)
print("\n")
print(display_result(result, alphabet))
# Nakon verifikacije obučenosti neuronske mreže, prelazimo na testiranje.
#
# Potrebno je da:
# * učitamo sliku za testiranje
# * transformišemo je u oblik pogodan za ulaz u neuronsku mrežu (na isti način kao što smo to uradili kod treniranja)
# * prikažemo rezultate predikcije
test_color = load_image('images/test.png')
test = image_bin(image_gray(test_color))
test_bin = erode(dilate(test))
selected_test, test_numbers = select_roi(test_color.copy(), test_bin)
display_image(selected_test)
test_inputs = prepare_for_ann(test_numbers)
result = ann.predict(np.array(test_inputs, np.float32))
print(display_result(result, alphabet))
# ### Primer 2
#
# `Implementirati sistem koji će vršiti optičko prepoznavanje slova. Sistem obučiti na **images/alphabet.png**, a testirati na **images/lorem_ipsum.png**.`
# ### K - Means
# Kada je reč o čitanju stvarnog teksta, deo problema predstavlja i određivanje granica između reči i redova u tekstu. Kao rešenje moguće je koristiti K-Means algoritam i klasterizovati razmak između regiona u dva klastera:
# * Razmak između slova u reči i
# * Razmak između reči.
#
# Koristićemo <a href="http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html">scikit-learn</a> implementaciju K-Means algoritma.
from sklearn.cluster import KMeans
# Potrebno je prvo modifikovati metodu za određivanje regiona od interesa tako da vraća i vrednosti rastojanja po X osi, između svih regiona.
def select_roi_with_distances(image_orig, image_bin):
contours, hierarchy = cv2.findContours(image_bin.copy(), cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
regions_array = []
for contour in contours:
x, y, w, h = cv2.boundingRect(contour)
region = image_bin[y:y+h+1, x:x+w+1]
regions_array.append([resize_region(region), (x, y, w, h)])
cv2.rectangle(image_orig, (x, y), (x+w, y+h), (0, 255, 0), 2)
regions_array = sorted(regions_array, key=lambda x: x[1][0])
sorted_regions = [region[0] for region in regions_array]
sorted_rectangles = [region[1] for region in regions_array]
region_distances = []
# izdvojiti sortirane parametre opisujucih pravougaonika
# izracunati rastojanja izmedju svih susednih regiona po X osi i dodati ih u niz rastojanja
for index in range(0, len(sorted_rectangles) - 1):
current = sorted_rectangles[index]
next_rect = sorted_rectangles[index + 1]
distance = next_rect[0] - (current[0] + current[2]) # x_next - (x_current + w_current)
region_distances.append(distance)
return image_orig, sorted_regions, region_distances
# Zatim se vrši modifikacija metode za prikaz rezultata, tako da formira string sa razmacima između reči. Metodi je neophodno proslediti obučen KMeans objekat kako bi odredila koja grupa rastojanja predstavlja razmak između reči, a koja između slova, i na osnovu toga formirala string od elemenata pronađenih sa slike.
def display_result_with_spaces(outputs, alphabet, k_means):
# odredjivanje indeksa grupe koja odgovara rastojanju izmedju reci
w_space_group = max(enumerate(k_means.cluster_centers_), key=lambda x: x[1])[0]
result = alphabet[winner(outputs[0])]
# iterativno dodavanje prepoznatih elemenata
# dodavanje space karaktera ako je rastojanje izmedju dva slova odgovara rastojanju izmedju reci
for idx, output in enumerate(outputs[1:, :]):
if k_means.labels_[idx] == w_space_group:
result += ' '
result += alphabet[winner(output)]
return result
# Nakon što smo modifikovali pomoćne metode, prelazimo na obučavanje veštačke neuronske mreže.
#
# Prvo učitavamo sliku za obučavanje i prikazujemo naše regione od interesa.
image_color = load_image('images/alphabet.png')
img = image_bin(image_gray(image_color))
selected_regions, letters, region_distances = select_roi_with_distances(image_color.copy(), img)
print("Broj prepoznatih regiona: ", len(letters))
display_image(selected_regions)
# Zatim definišemo alfabet i vršimo treniranje veštačke neuronske mreže
alphabet = ['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z']
inputs = prepare_for_ann(letters)
outputs = convert_output(alphabet)
ann = create_ann(output_size=26)
ann = train_ann(ann, inputs, outputs, epochs=2000)
# Vršimo testiranje obučene veštačke neuronske mreže tako što ćemo:
# * učitati sliku za testiranje
# * odrediti regione od interesa i rastojanja među njima
# * iskoristiti K-Means za grupisanje rastojanja u dve grupe (rastojanja između reči i rastojanja između slova)
# * prikazati rezultate predikcije.
# +
image_color = load_image('images/lorem_ipsum.png')
img = image_bin(image_gray(image_color))
selected_regions, letters, distances = select_roi_with_distances(image_color.copy(), img)
print("Broj prepoznatih regiona: ", len(letters))
display_image(selected_regions)
# neophodno je da u K-Means algoritam bude prosledjena matrica u kojoj vrste odredjuju elemente
distances = np.array(distances).reshape(len(distances), 1)
k_means = KMeans(n_clusters=2)
k_means.fit(distances)
# -
inputs = prepare_for_ann(letters)
results = ann.predict(np.array(inputs, np.float32))
print(display_result_with_spaces(results, alphabet, k_means))
# ## Kompleksniji OCR
#
# OCR sistemi vrše optičko prepoznavanje tekstualnih sadržaja sa fotografija, gde je fotografija ulazni parametar sistema. Performanse sistema će u mnogome zavisiti od pretpostavke o ulaznoj fotografiji. Pošto se takva fotografija pravi u realnom okruženju, normalno je za očekivati dosta spoljnih uticaja. Ukoliko pretpostavimo da ulazna fotografija neće biti pod uticajem određenog broja faktora iz okruženja sistem može da se pojednostavi. Recimo, kamere u industrijskim pogonima prave fotografije u okruženju u kome se nivo osvetljenja može kontrolisati, uređaj za fotografisanje je uvek isti i pravi fotografije koje su "sličnog" oblika.
#
# Do sada smo OCR sistem implementirali uz pretpostavku da je fotografija idealna i da je tekstualni sadržaj na njoj prost. Međutim, to najčešće nije slučaj. Ulazna fotografija će obično izgledati ovako:
#
# <img src="images/cifre.jpg"/>
# ### Obrada digitalne slike
#
# Obrada digitalne slike predstavlja prvi skup aktivnosti OCR sistemu. Cilj ovog skupa aktivnosti jeste prilagođavanje ulazne fotografije da bi se nad njom mogla vršiti analiza sadržaja. Obrada digitalne slike može biti dosta složen proces, pošto bi on trebao biti u stanju da obradi bilo kakvu ulaznu fotografiju. Proces analize digitalne slike će biti mnogo jednostavniji ukoliko se fotografija prethodno dobro obradi i ukloni većina šuma.
# #### Neuniformna osvetljenost fotografije
#
# Cilj segmentacije jeste klasifikovanje piksela fotografije u one koji pripadaju sadržaju i one koji pripadaju pozadini. Do sada smo za segmentaciju koristili metode bazirane na računanju praga - **threshold**. Ukoliko se za celu fotografiju pronađe jedan prag segmentacije, problem se javlja ako su delovi fotografije osetno manje ili više osvetljeni od ostatka fotografije. Ovaj problem se može rešiti uz korišćenje adaptivnog threshold-a. Na taj način se može rešiti problem neuniformna osvetljenosti fotografije.
image_color = load_image('images/cifre2.jpg')
img = image_bin(image_gray(image_color))
display_image(img)
# #### Šum na fotografiji nakon segmentacije
#
# Proces segmentacije će pokušati da klasifikuje piksele tako da ih obeleži da pripadaju sadržaju ili pozadini, ali ne mora da znači da će u tome biti 100% uspešan. Na fotografiji koja je rezultat procesa segmentacije može postojati šum koji može znatno otežati analizu ovakve fotografije u narednim koracima OCR-a. Zbog toga je takav šum potrebno ukloniti u što većoj meri u ranim fazama.
# ### Analiza digitalne slike
#
# Analiza digitalne slike počinje kreiranjem skupa regiona(kontura) sa binarne slike. Takav skup regiona je potrebno analizirati i izvršiti njihovo prepoznavanje. Problem predstavlja činjenica da region ne mora izgledati uvek isto, iako predstavlja isti karakter. Jedan primer takve situacije jeste rotacija.
# #### Zarotirani simboli na fotografiji
#
# Svaki region se skalira na dimenzije 28 x 28 i formira matricu, a nakon toga se pretvara u vektor od 784 elementa. Očigledno je da će takva matrica izgledati drugačije ukoliko je region zarotiran, što će rezultovati činjenicom da ćemo na ulaz neuronske mreže dovesti ulazni vektor koji će jako loše opisivati region koji bi on trebalo da predstavlja. Posledica će biti loša predikcija od strane veštačke neuronske mreže. Zbog toga je regione potrebno zarotirati tako da se oni postave u prirodan položaj.
# Tačke regiona je potrebno rotirati oko tačke **(c<sub>x</sub>, c<sub>y</sub>)** za zadati ugao **$\alpha = \pi / 2 - |\theta|$** gde su **c<sub>x</sub>, c<sub>y</sub> i $\theta$** parametri dobijeni iz osobina regiona. Na ovaj način treba da se dobiju slike regiona koje su "relativno" vertikalne.
# Formula za rotiranje tačke sa koordinatama **(x,y)** za ugao **$\alpha$** oko tačke sa koordinatama **(c<sub>x</sub>, c<sub>y</sub>)**:
# <img src="images/rotacija.jpg"/>
# #### Simboli koji se sastoje iz više regiona
#
# Činjenica da se jedan simbol ne mora sastojati iz samo jednog regiona nama može predstavljati problem (npr: i, ž, ć...). Zbog toga je potrebno izvršiti spajanje kukica i kvačica u okolini simbola pre slanja podataka na predikciju neuronskoj mreži.
#
# <img src="images/slovo.jpg"/>
# Nakon spajanja kukica i kvačica na red dolazi skaliranje regiona na dimenzije 28 x 28. Region je sada niz tačaka čije su koordinate apsolutne koordinate na fotografiji sa koje su regioni preuzeti. Kako bi se isekao pravougaonik oko regiona potrebno je proći kroz sve tačke regiona i koordinate svake od njih prebaciti iz apsolutnih u relativne koordinate u odnosu na poziciju tačke unutar regiona.
# ## Zadaci
# ### Zadatak 1 - Kalkulator
#
# Implementirati OCR za kalkulator. Obučiti sistem na **images/kalkulator_alfabet.png**. Testirati na:
# * **images/sabiranje.png**
# * **images/oduzimanje.png**
# * **images/slozen_izraz.png**
# ### Zadatak 2 - Redovi
#
# Implementirati OCR koji će moći čitati tekst sa više redova. Obučiti sistem na **images/alphabet.png**. Testirati na: **images/redovi.png**.
# ### Zadatak 3 - Kukice
#
# Implementirati OCR koji će moći čitati simbole koji se sastoje iz više regiona. Obučiti sistem na **images/obucavanje.jpg**. Testirati na **images/testiranje.jpg**.
|
v2-ocr/sc-siit-v2-ocr.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %pylab inline
import pandas as pd
from scipy import stats
import statsmodels.api as sm
import matplotlib.pyplot as plt
import warnings
from itertools import product
#import progressbar
from multiprocessing import Pool
def invboxcox(y,lmbda):
if lmbda == 0:
return(np.exp(y))
else:
return(np.exp(np.log(lmbda*y+1)/lmbda))
# -
# index_col говорим, что индексом будет являться столбец datetime
# parse_dates говорим, что столбец datetime является датой
data = pd.read_csv('../data/raw/bike_sharing_demand.csv', index_col=['datetime'], parse_dates=['datetime'], dayfirst=True)
data.head(5)
# data[['count']]
newdata = data[['count']]
newdata.head(5)
# ## Визуальный анализ ряда
plt.figure(figsize=(15,7))
# почему не сработало newdata.count.plot() ??
newdata.plot()
plt.ylabel('Количество великов')
newdata.plot(figsize=(12,6))
# замечаем, что в каждом месяце отсутствуют данные позднее 19го числа
# тут мы оставляем только месяц март
newdata_march = newdata[(newdata.index >= '2011-03-01 00:00:00') & (newdata.index <= '2011-03-19 23:00:00')]
newdata_march.dtypes # типы данных столбцов
# меняем имя столбеца count на quantity так как count оказалось зарезервированным
newdata_march=newdata_march.rename(columns = {'count':'quantity'})
newdata_march.dtypes
newdata_march.plot(figsize=(15,4))
plt.figure(figsize=(15,7))
sm.tsa.seasonal_decompose(newdata_march.quantity, freq=24, model='additive').plot()
# plt.show() # почему-то удаляется 2-я копия графика после этой строки
# удаляется верхняя копия, если после строки seasonal_decompose есть ещё какая-то строка, например как щас print
print("Критерий Дики-Фуллера: p=%f" % sm.tsa.stattools.adfuller(newdata_march.quantity)[1])
# ## Стабилизация дисперсии
# Сделаем преобразование Бокса-Кокса для стабилизации дисперсии:
# создаем столбец 'boxcox'
newdata_march['boxcox'], lmbda = stats.boxcox(newdata_march.quantity)
plt.figure(figsize(15,4))
newdata_march.boxcox.plot()
plt.ylabel('Transformed wages data')
print("Оптимальный параметр преобразования Бокса-Кокса: %f" % lmbda)
# ## Выбор порядка дифференцирования
# В данных есть тренд и сезонность. Попробуем провести сезонное дифференцирование.
newdata_march.head(5)
sm.tsa.seasonal_decompose(newdata_march.quantity, freq=24, model='additive').plot()
plt.show()
# создаем столбец 'bc_diff_24 '
# дифференцируем из каждого значение вычитаем значение через 24 строки, т.е. через сутки
# del newdata_march['bc_diff_24']
newdata_march['bc_diff_24'] = newdata_march.boxcox - newdata_march.boxcox.shift(24)
plt.figure(figsize=(15,7))
sm.tsa.seasonal_decompose(newdata_march.bc_diff_24[24:], freq=24, model='additive').plot();
print("Критерий Дики-Фуллера: p=%f" % sm.tsa.stattools.adfuller(newdata_march.bc_diff_24[24:])[1])
# создаем столбец 'bc_diff_24_1 '
# del newdata_march['bc_diff_24_1']
newdata_march['bc_diff_24_1'] = newdata_march.bc_diff_24 - newdata_march.bc_diff_24.shift(1)
plt.figure(figsize=(15,7))
sm.tsa.seasonal_decompose(newdata_march.bc_diff_24[24: ], freq=25, model='additive').plot();
print("Критерий Дики-Фуллера: p=%f" % sm.tsa.stattools.adfuller(newdata_march.bc_diff_24[25: ])[1])
# ## Выбор начальных приближений для p,q,P,Q
# Посмотрим на ACF и PACF полученного ряда:
plt.figure(figsize(15,8))
ax = plt.subplot(211)
sm.graphics.tsa.plot_acf(newdata_march.bc_diff_24[25: ].values.squeeze(), lags=48, ax=ax)
pylab.show()
ax = plt.subplot(212)
sm.graphics.tsa.plot_pacf(newdata_march.bc_diff_24[25: ].values.squeeze(), lags=48, ax=ax)
pylab.show()
# Начальные приближения: Q=0, q=0, P=0, p=0
# ## Обучение и сравнение моделей-кандидатов, выбор победителя
# Пусть будет некий trade-off между вычислительной сложностью и начальным приближением.
ps=range(0,5)
d=1
qs=range(0,2)
Ps=range(0,2)
D=1
Qs=range(0,2)
parametrs = product(ps,qs,Ps,Qs)
parameters_list=list(parametrs)
len(parameters_list)
# +
# %%time
results = []
best_aic = float("inf")
warnings.filterwarnings('ignore')
for param in parameters_list:
# try except нужен, потому что на некоторых наборах параметров модель не обучается
try:
model=sm.tsa.statespace.SARIMAX(newdata_march.boxcox, order=(param[0], d, param[1]),
seasonal_order=(param[2], D, param[3], 24)).fit(disp=-1)
# выводим параметры, на которых модель не обучается и переходим к следующему набору
except:
print ('wrong parameters: ', param)
continue
aic = model.aic
# сохраняем лучшую модель, aic, параметры
if aic < best_aic:
best_model = model
best_aic = aic
best_param = param
results.append([param,model.aic])
warnings.filterwarnings('default')
# -
result_table = pd.DataFrame(results)
result_table.columns = ['parametrs','aic']
print (result_table.sort_values(by='aic',ascending=[True]).head())
print (best_model.summary())
# +
plt.figure(figsize(15,8))
plt.subplot(211)
best_model.resid[13: ].plot()
plt.ylabel(u'Residuals')
ax = plt.subplot(212)
sm.graphics.tsa.plot_acf(best_model.resid[13: ].values.squeeze(), lags=48, ax=ax)
print("<NAME>: p=%f" % stats.ttest_1samp(best_model.resid[13: ], 0)[1])
print("<NAME>: p=%f" % sm.tsa.stattools.adfuller(best_model.resid[13:])[1])
# -
# отдельно напоминаем обратного кокса
def invboxcox(y,lmbda):
if lmbda == 0:
return(np.exp(y))
else:
return(np.exp(np.log(lmbda*y+1)/lmbda))
newdata_march['model'] = invboxcox(best_model.fittedvalues, lmbda)
plt.figure(figsize(15,7))
newdata_march.quantity.plot()
newdata_march.model[25: ].plot(color='r')
plt.ylabel('Количество велосипедов')
pylab.show()
newdata_march.tail()
newdata_march.describe()
# +
# строим прогноз
newdata_march2=newdata_march[['quantity']]
# тут выбираем момент начала прогноза
date_list = [datetime.datetime.strptime("2011-03-20","%Y-%m-%d")+relativedelta(hour=x) for x in range(0,24)]
future = pd.DataFrame(index=date_list, columns=newdata_march2.columns)
# -
newdata_march2 = pd.concat([newdata_march2,future])
newdata_march2.loc[date_list, 'forecast'] = invboxcox(best_model.predict(start=447, end=447+23).values, lmbda)
newdata_march2.tail(25)
# +
plt.figure(figsize(20,7))
newdata_march2.quantity.plot()
newdata_march2.forecast.plot(color='r')
plt.ylabel('Количество велосипедов')
pylab.show()
# -
|
notebooks/Anton_full_stack.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import matplotlib.pyplot as plt
import imripy.merger_system as ms
from imripy import halo
from imripy import inspiral
from imripy import waveform
from imripy import detector
# +
m1 = 10.*ms.solar_mass_to_pc
m2 = 10.*ms.solar_mass_to_pc
D = 5e8
sp_0 = ms.SystemProp(m1, m2, halo.ConstHalo(0.), D=D, inclination_angle=np.pi/2., pericenter_angle=np.pi/4.)
# +
# first, compare to Maggiore 2007
a0 = 500.* sp_0.r_isco()
afin = 1.*sp_0.r_isco()
e0 = 0.9
ev_0 = inspiral.Classic.Evolve(sp_0, a0, e_0=e0, a_fin=afin)
# +
def g(e):
return e**(12./19.)/(1. - e**2) * (1. + 121./304. * e**2)**(870./2299.)
plt.figure(figsize=(16,10))
plt.plot(ev_0.e, ev_0.a, label='numeric')
plt.plot(ev_0.e, a0 * g(ev_0.e)/g(e0), label='analytic', linestyle='--')
plt.xlabel('e'); plt.ylabel('a')
plt.yscale('log')
plt.grid(); plt.legend()
# -
# Now compare to 1807.07163
a0 = 20.*sp_0.r_isco()
e0 = 0.6
#t, a, e = inspiral.Classic.evolve_elliptic_binary(sp_0, a0, e0, a_fin = 1e-1*sp_0.r_isco(), acc=1e-12)
ev = inspiral.Classic.Evolve(sp_0, a0, e_0=e0, opt=inspiral.Classic.EvolutionOptions(accuracy=1e-12))
# +
fig, (ax_a, ax_e) = plt.subplots(2, 1, figsize=(8,10))
ax_a.plot(ev.t/ms.year_to_pc, ev.a)
ax_e.plot(ev.t/ms.year_to_pc, ev.e)
ax_a.grid(); ax_a.set_xscale('log'); ax_a.set_ylabel('y')
ax_e.grid(); ax_e.set_xscale('log'); ax_e.set_ylabel('e'); ax_e.set_xlabel('t / yr')
# +
n_comp = 20
wfs = [waveform.h_n(n, sp_0, ev, acc=1e-13) for n in range(1, n_comp+1)]
# +
n_disp = 5
plt.figure(figsize=(10, 8))
for i in range( min(len(wfs), n_disp)):
plt.plot(wfs[i][0]/ms.hz_to_invpc, np.abs(wfs[i][1]), label=r"$|h^{(" + str(i+1) + ")}_+|$")
f_gw = np.geomspace(np.min(wfs[0][0]), np.max(wfs[n_disp][0]), 5000)
h_plus_tot = np.sum([ np.interp(f_gw, wf[0], wf[1], left=0., right=0.) * np.exp(1.j * np.interp(f_gw, wf[0], wf[3], left=0., right=0.)) for wf in wfs ], axis=0)
h_cross_tot = np.sum([ np.interp(f_gw, wf[0], wf[2], left=0., right=0.) * np.exp(1.j * np.interp(f_gw, wf[0], wf[3], left=0., right=0.)) for wf in wfs ], axis=0)
plt.plot(f_gw/ms.hz_to_invpc, np.abs(h_plus_tot), label=r"$|h^{SPA}_+|$")
plt.xlim(left=np.min(wfs[0][0])/ms.hz_to_invpc, right=np.max(wfs[n_disp][0])*1e-1/ms.hz_to_invpc)
#plt.xscale('log')
plt.xlabel('f / Hz');
plt.grid(); plt.legend();
# +
plt.figure(figsize=(10, 8))
plt.loglog(f_gw/ms.hz_to_invpc, 2.*f_gw*np.abs(h_plus_tot), label=r"$|h^{SPA}_+|$")
#plt.loglog(f_gw, 2.*f_gw*np.abs(h_2_cross), label=r"$|h^{(2)}_x|$")
f = np.geomspace(detector.Lisa().Bandwith()[0], detector.Lisa().Bandwith()[1], 100)
plt.plot(f/ms.hz_to_invpc, detector.Lisa().NoiseStrain(f), label='LISA')
plt.ylim(1e-22, 2e-18)
#plt.xlim(detector.Lisa().Bandwith()[0]/ms.hz_to_invpc, detector.Lisa().Bandwith()[1]/ms.hz_to_invpc, )
plt.xlabel('f / Hz'); plt.ylabel('characteristic strain')
plt.grid(); plt.legend();
# +
t_plot = np.linspace(np.min(ev.t) if ev.t[0] > 0. else ev.t[1]*1e-1, np.max(ev.t), 500)
f_plot = np.linspace(np.min(f_gw), np.max(f_gw)/50., 200)
t_plot, f_plot = np.meshgrid(t_plot, f_plot)
h_plus_plot = np.zeros(shape=np.shape(t_plot))
h_cross_plot = np.zeros(shape=np.shape(t_plot))
for i in range(len(t_plot[0])):
for wf in wfs:
#print(t_plot[i,0])
f = np.interp(t_plot[0, i], ev.t, wf[0], left=0., right=0.)
index_f = (np.abs(f_plot[:, i] - f)).argmin()
#print(f, f_plot[i], index_f)
h_plus_plot[index_f, i] = np.abs(np.interp(f_plot[index_f, i], wf[0], wf[1]))
h_cross_plot[index_f, i] = np.abs(np.interp(f_plot[index_f, i], wf[0], wf[2]))
h_plus_plot = h_plus_plot/np.max(h_plus_plot)
plt.figure(figsize=(10, 8))
#plt.xscale('log'); plt.yscale('log')
plt.contourf( t_plot/ms.s_to_pc, f_plot/ms.hz_to_invpc, h_plus_plot, cmap=plt.get_cmap("YlOrRd"))
plt.figure(figsize=(10, 8))
#plt.xscale('log'); plt.yscale('log')
plt.contourf( t_plot/ms.s_to_pc, f_plot/ms.hz_to_invpc, h_cross_plot, cmap=plt.get_cmap("YlOrRd"))
plt.show()
# -
# Now compare eccentricity and circular implementation for consistency
from scipy.interpolate import interp1d
D = 1e3
m1 = 1e3 * ms.solar_mass_to_pc
m2 = 1e0 * ms.solar_mass_to_pc
sp_dm = ms.SystemProp(m1, m2, halo.Spike(226.*ms.solar_mass_to_pc, 0.54, 7./3.), D=D, inclination_angle=np.pi/3.)
# +
a0 = 100.*sp_dm.r_isco()
e0 = 0.001
afin= 1.*sp_dm.r_isco()
ev_circ = inspiral.Classic.Evolve(sp_dm, a0, a_fin=afin, opt=inspiral.Classic.EvolutionOptions(accuracy=1e-12))
ev_ecc = inspiral.Classic.Evolve(sp_dm, a0, e_0=e0, a_fin=afin, opt=inspiral.Classic.EvolutionOptions(accuracy=1e-12))
# -
plt.figure(figsize=(16, 10))
plt.loglog(ev_ecc.t, ev_ecc.a, label='$a_{ecc}$')
plt.loglog(ev_circ.t, ev_circ.a, label='$a_{circ}$')
plt.loglog(ev_circ.t, np.abs(ev_circ.a - interp1d(ev_ecc.t, ev_ecc.a, kind='cubic', bounds_error=False, fill_value=(0.,0.))(ev_circ.t))/ev_circ.a
, label=r'$|\Delta a|/a_{circ}$')
plt.loglog(ev_ecc.t, ev_ecc.e, label='$e_{ecc}$')
plt.xlabel('t')
plt.grid(); plt.legend()
f_gw_circ, h_plus_circ, h_cross_circ, Psi_circ, _, Phi_circ, __ = waveform.h_2(sp_dm, ev_circ, dbg=True)
f_gw_ecc, h_plus_ecc, h_cross_ecc, Psi_ecc, Phi_ecc, _ = waveform.h_n(2, sp_dm, ev_ecc, dbg=True)
# +
plt.figure(figsize=(16, 10))
plt.loglog(f_gw_circ/ms.hz_to_invpc, h_plus_circ, label="$h_{+}^{circ}$")
plt.loglog(f_gw_ecc/ms.hz_to_invpc, np.abs(h_plus_ecc), linestyle="--", label="$h_{+}^{ecc}$")
plt.loglog(f_gw_circ/ms.hz_to_invpc, h_cross_circ, label="$h_{x}^{circ}$")
plt.loglog(f_gw_ecc/ms.hz_to_invpc, np.abs(h_cross_ecc), linestyle="--", label="$h_{x}^{ecc}$")
plt.grid(); plt.legend()
# +
plt.figure(figsize=(16,10))
plt.loglog(f_gw_ecc/ms.hz_to_invpc, Phi_ecc, label='$\Phi_{ecc}$')
plt.loglog(f_gw_circ/ms.hz_to_invpc, Phi_circ, label='$\Phi_{circ}$')
plt.loglog(f_gw_circ/ms.hz_to_invpc, np.abs(Phi_circ
- interp1d(f_gw_ecc, Phi_ecc, kind='cubic', fill_value=(0.,0.), bounds_error=False)(f_gw_circ))
, label='$|\Delta\Phi|$' )
plt.legend(); plt.grid()
# -
|
tests/test_eccentricity.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import copy
import matplotlib
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import random, os, pathlib
import torch
import torch.nn as nn
import torch.nn.functional as F
# +
def smooth_l1(x, beta=1):
mask = x<beta
y = torch.empty_like(x)
y[mask] = 0.5*(x[mask]**2)/beta
y[~mask] = torch.abs(x[~mask])-0.5*beta
return y
def get_gp(cond):
a=-20
intolerables = F.softplus(cond-0.01, beta=-20)*5
# intolerables = torch.clamp(F.softplus(cond-0.01, beta=-20), -1, 1)
# intolerables = F.softplus(F.softplus(cond-0.1, beta=-20)+2, beta=10)-2
# self.gp = (self.smooth_l1(intolerables*5)).mean()*self.lamda
return intolerables
# return smooth_l1(intolerables)
# self.gp = (self.smooth_l1(intolerables*5)).mean()*self.lamda
def get_gs(cond):
linear_mask = cond>0.14845
a = 20.
gclipper = -((1.05*(cond-1))**4)+1
gclipper = torch.log(torch.exp(a*gclipper)+1)/a
gc2 = 3*cond-0.0844560006
gclipper[linear_mask] = gc2[linear_mask]
return gclipper
def get_gs2(cond):
linear_mask = cond>0.08497
a = 20.
gclipper = -((1.05*(cond-1))**4)+1
gclipper = torch.log(torch.exp(a*gclipper)+1)/a
gc2 = 20.833544724 * (x**2)
gclipper[linear_mask] = gc2[linear_mask]
return gclipper
# +
x = torch.linspace(-1.3, 0.7, 200)
gp = get_gp(x)
gs = get_gs(x)
# %matplotlib inline
# plt.axis('equal')
plt.figure(figsize=(4,3))
plt.plot(x, gp, lw=2, label='gradient penalty')
plt.plot(x, gs, lw=2, label='output-gradient clipper')
plt.hlines(0, -2, 2)
plt.vlines(0, -5, 2)
plt.xlim(-0.7, 0.7)
plt.ylim(-3, 2)
# plt.xlim(-0.5, 0.5)
# plt.ylim(-0.5, 0.5)
plt.xlabel("x")
plt.ylabel("y")
plt.grid()
plt.legend()
plt.savefig("./invex_out/gc_gp.pdf", bbox_inches='tight')
# -
plt.plot(x, F.sigmoid(4*x))
|
04.0_Penalty and clipping function.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import math
def hello(name):
print('Hello {0}'.format(name))
your_name = 'Jyupter'
hello(your_name)
math.sqrt(2)
# -
|
HelloJupyter.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Raian-Rahman/Data-Mining-Implementation/blob/main/FP_Growth_Impelementation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="vr52Q4kc32r4"
# #### Mounting drive
# + colab={"base_uri": "https://localhost:8080/"} id="fHToR32t3wIO" outputId="3583d163-f8b7-4642-b959-316247af62f8"
from google.colab import drive
drive.mount('/content/drive')
# + id="8kJ5SetR362I"
import numpy as np
import pandas as pd
import time
from itertools import chain, combinations
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="l-oe4AIE4Mmf" outputId="9f831f99-e895-4376-9069-e83ada0a22fd"
df = pd.read_csv('/content/drive/MyDrive/Data Mining Assignment/shortened_dataset.csv')
df = df[:500]
df.head()
# + id="Ywlvi_zH8PRe"
def preprocess_data(df):
item_LUT = dict()
item_index = 1
transaction = dict()
for index in df.index:
product_id = df['products'][index]
product_id = product_id.strip('][').split(', ')
# print(product_id)
item_list = list()
for item in product_id:
if item_LUT.get(item,-100) == -100:
#its not on the list
item_LUT[item] = item_index
item_index+=1
item_list.append(item_LUT[item])
transaction[item_index] = item_list
item_index+=1
processed_transaction = []
for key in transaction.keys():
row = dict()
row['order_id'] = key
row['products'] = transaction[key]
processed_transaction.append(row)
all_transaction = dict()
for item in processed_transaction:
# print(item['products'])
itemss = set(item['products'])
all_transaction[item['order_id']] = itemss
all_transaction
return all_transaction
# + [markdown] id="g7VufQBl4hU2"
# ### Coding FP-Growth
# + id="67uqpw6Y7JrF"
## all Possible Combination
def generate_subsets(iterable):
s = list(iterable)
return list(chain.from_iterable(combinations(s, r) for r in range(1,len(s)+1)))
# + id="qFIw5mJc4cOO"
class Node:
def __init__(self, item):
self.item = item
self.branch = dict()
self.frequency = 0
def addBranch(self, node):
if node == None:
return
self.branch[node.item]=node
# + id="HYvXspj94kk2"
class FP_Growth:
def __init__(self, transactions: dict, min_sup = 2):
self.transactions = transactions.copy()
self.runTime = 0
self.uniqe_items = set()
self.supportCount = dict()
self.root = Node('NULL')
self.min_sup = min_sup
self.conditionalPatterBase = dict()
self.conditionalFPTree = dict()
self.frequentPatterns = dict()
def __generateSupportCount__(self):
for itemSet in self.transactions.values():
for item in itemSet:
if self.supportCount.get(item)==None:
self.supportCount[item]=0
self.supportCount[item]+=1
self.supportCount = dict(sorted(list(self.supportCount.items()), key = lambda item: (-1*item[1],item)))
def __sortitemSets__(self):
for key in self.transactions.keys():
itemSet = self.transactions[key]
itemSet = sorted(itemSet, key= lambda item: (-1*self.supportCount[item],item))
self.transactions[key] = itemSet
def __generateUniqeItemList__(self):
for itemSet in self.transactions.values():
for item in itemSet:
self.uniqe_items.add(item)
self.uniqe_items = set(sorted(self.uniqe_items))
def __addItemSetToTree__(self, nextNode, itemSet):
nextNode.frequency+=1
if len(itemSet)==0:
return nextNode
item = itemSet.pop(0)
# print(item)
if nextNode.branch.get(item)==None:
nextNode.addBranch(self.__addItemSetToTree__(Node(item),itemSet))
else:
nextNode.addBranch(self.__addItemSetToTree__(nextNode.branch[item],itemSet))
#print("[Ret]", nextNode.branch)
return nextNode
def __buildTree__(self):
self.__generateSupportCount__()
self.__sortitemSets__()
for itemSet in self.transactions.values():
self.root = self.__addItemSetToTree__( self.root, itemSet.copy())
def showTreeTravers(self, node):
if(node == None):
return
print("Enter",node.item,node.frequency)
for next in node.branch.keys():
self.showTreeTravers(node.branch[next])
print("exit", node.item, node.frequency)
def __generatePattern__(self, path, node):
if node == None:
return
for next in node.branch.keys():
newPath = path.copy()
newPath.append(next)
self.__generatePattern__(newPath.copy(),node.branch[next])
if len(path) > 0:
path.pop()
if self.conditionalPatterBase.get(node.item)==None:
self.conditionalPatterBase[node.item]=[]
self.conditionalPatterBase[node.item].append((tuple(path.copy()),node.frequency))
def __generateConditionalFPTree__(self):
for item, frqPat in list(self.conditionalPatterBase.items()):
prefix = dict()
occurence = dict()
sortedFrqPat = sorted(list(frqPat))
sortedFrqPat.append(('!!##',0))
#print(item, sortedFrqPat)
for idx in range(len(sortedFrqPat)-1):
pat, frq = sortedFrqPat[idx]
nextPat, nextFrq = sortedFrqPat[idx+1]
for it in pat:
if occurence.get(it)==None:
occurence[it]=0
occurence[it]+=frq
if len(pat) > len(nextPat) or (len(pat) <= len(nextPat) and pat != nextPat[:len(pat)]):
prefix[pat]=occurence.copy()
# print(pat)
occurence = dict()
for x in prefix.values():
if self.conditionalFPTree.get(item)==None:
self.conditionalFPTree[item]=[]
self.conditionalFPTree[item].append(list(x.items()))
def generateFrequentPatterns(self):
self.__init__(self.transactions,self.min_sup)
self.frequentPatterns = dict()
startTime = time.time()
self.__generateUniqeItemList__()
self.__buildTree__()
self.__generatePattern__([],self.root)
self.__generateConditionalFPTree__()
for item, fpTree in self.conditionalFPTree.items():
for itemset in fpTree:
allSubSet = generate_subsets(itemset)
for subset in allSubSet:
frqSet = []
mnFrq = 1e18
for it,frq in subset:
mnFrq = min(mnFrq,frq)
frqSet.append(it)
frqSet.append(item)
frqSet = sorted(frqSet)
if self.frequentPatterns.get(tuple(frqSet))==None:
self.frequentPatterns[tuple(frqSet)]=0
self.frequentPatterns[tuple(frqSet)]+=mnFrq
fqPat = list(self.frequentPatterns.keys())
for pat in fqPat:
if self.frequentPatterns[pat]<self.min_sup:
del self.frequentPatterns[pat]
patternSet = set()
for item in self.frequentPatterns.items():
patternSet.add(item)
self.frequentPatterns = sorted(patternSet)
self.runTime+=time.time()-startTime
# + id="BIchs31z4swH"
import time
def test_fp_growth(transaction_list):
time_list = list()
for i in range(10,250,10):
tic = time.time()
print('*'*160)
print(f'CALCULATING FOR SUPPORT COUNT: {i}')
fp = FP_Growth(preprocess_data(transaction_list),min_sup=i)
fp.generateFrequentPatterns()
# print(fp.supportCount)
# print(fp.conditionalPatterBase)
# print(fp.conditionalFPTree)
fp.showTreeTravers(fp.root)
fp.generateFrequentPatterns()
fp.showTreeTravers(fp.root)
fp.generateFrequentPatterns()
print("Frequent Patterns by FP_Growth:")
for pat in fp.frequentPatterns:
print(pat)
print('*'*160)
print('\n'*5)
tac = time.time()
time_list.append((i,tac-tic))
print(time_list)
return time_list
# variable = test_apriori(transaction_list)
# fp = FP_Growth(preprocess_data(df),min_sup=2)
# fp.generateFrequentPatterns()
# print(fp.supportCount)
# print(fp.conditionalPatterBase)
# print(fp.conditionalFPTree)
# fp.showTreeTravers(fp.root)
# fp.generateFrequentPatterns()
# print("Frequent Patterns by FP_Growth:")
# for pat in fp.frequentPatterns:
# print(pat)
# + id="nebZgxFr8nKe" colab={"base_uri": "https://localhost:8080/"} outputId="7af3be2b-66e8-4c2b-ab77-5652d65831b3"
variable1 = test_fp_growth(df)
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="-TsrZdyqyzi3" outputId="40e3e783-5613-4049-dff8-f5db30e0f503"
df2 = pd.read_csv('/content/drive/MyDrive/Data Mining Assignment/shortened_dataset_2.csv')
df2 = df[:1000]
df2.head()
# + colab={"base_uri": "https://localhost:8080/"} id="bzcEexjZ-ckm" outputId="5b0ac7a2-50e0-4b57-9ecd-1498252c0e7c"
variable2 = test_fp_growth(df)
# + id="5PVJdlpydsAd"
import matplotlib.pyplot as plt
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="psecZ1GkATCs" outputId="5983cfcd-2503-48d3-9931-7f47f9dcbbe0"
def show_plot(time_list, time_list2):
X1 = list()
Y1 = list()
for item in time_list:
X1.append(item[0])
Y1.append(item[1])
X2 = list()
Y2 = list()
for item in time_list2:
X2.append(item[0])
Y2.append(item[1])
plt.plot(X1,Y1, 'r-*', label = 'On Market Basket')
plt.plot(X2,Y2, 'g-*', label = 'On French Dataset')
plt.plot()
plt.xlim(0,300)
plt.ylim(100,200)
plt.xlabel('MINIMUM SUPPORT COUNT')
plt.ylabel('TIME TAKEN')
plt.legend()
plt.title(f"Apriori Running Time")
show_plot(variable1, variable2)
# plt.plot(variable[1][:], range(10,250,10))
# + id="HqP9KSDEcv7G"
|
FP_Growth_Impelementation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R [conda env:cell-painting-vae-figures] *
# language: R
# name: conda-env-cell-painting-vae-figures-r
# ---
suppressPackageStartupMessages(library(dplyr))
suppressPackageStartupMessages(library(ggplot2))
# +
file_extensions <- c(".png", ".pdf")
plot_theme <- theme(
title = element_text(size = 9),
axis.title = element_text(size = 9),
legend.text = element_text(size = 7),
legend.title = element_text(size = 9),
legend.key.size = unit(0.5, "cm"),
strip.text = element_text(size = 10),
strip.background = element_rect(colour="black", fill="#fdfff4")
)
# +
# Load data
file <- file.path("data", "lsa_distribution_full_results.tsv.gz")
lsa_cols <- readr::cols(
input_data_type_full = readr::col_character(),
dist = readr::col_double(),
input_data_type = readr::col_character(),
shuffled = readr::col_character(),
assay = readr::col_character(),
data_level = readr::col_character(),
model = readr::col_character()
)
lsa_df <- readr::read_tsv(file, col_types = lsa_cols)
lsa_df$model <- factor(lsa_df$model, levels = c("Complete", "PCA", "vanilla", "beta", "mmd"))
lsa_df$model <- dplyr::recode(lsa_df$model, "vanilla" = "Vanilla VAE", "beta" = "Beta VAE", "mmd" = "MMD VAE")
print(dim(lsa_df))
head(lsa_df, 3)
# -
panel_a_gg <- (
ggplot(
lsa_df %>%
dplyr::filter(assay == 'cell-painting', data_level == 'level5'),
aes(y = dist, x = model, color = shuffled)
)
+ geom_point(size = 0.2, alpha = 0.5, position = position_jitterdodge())
+ geom_boxplot(aes(middle = mean(dist)), size = 0.2, alpha = 0.8, outlier.alpha = 0)
+ theme_bw()
+ plot_theme
+ ylab("L2 distance between\nreal 'A|B' and predicted 'A|B'")
+ xlab("")
+ scale_color_manual(
"Data",
values = c("Shuffled" = "#E66100", "Unshuffled" = "#5D3A9B"),
labels = c("Shuffled" = "Shuffled", "Unshuffled" = "Real")
)
+ ggtitle("Cell Painting - Level 5")
)
panel_b_gg <- (
ggplot(
lsa_df %>%
dplyr::filter(assay == 'cell-painting', data_level == 'level4'),
aes(y = dist, x = model, color = shuffled)
)
+ geom_point(size = 0.2, alpha = 0.5, position = position_jitterdodge())
+ geom_boxplot(aes(middle = mean(dist)), size = 0.2, alpha = 0.8, outlier.alpha = 0)
+ theme_bw()
+ plot_theme
+ ylab("L2 distance between\nreal 'A|B' and predicted 'A|B'")
+ xlab("")
+ scale_color_manual(
"Data",
values = c("Shuffled" = "#E66100", "Unshuffled" = "#5D3A9B"),
labels = c("Shuffled" = "Shuffled", "Unshuffled" = "Real")
)
+ ggtitle("Cell Painting - Level 4")
)
panel_c_gg <- (
ggplot(
lsa_df %>%
dplyr::filter(assay == 'L1000', data_level == 'level5'),
aes(y = dist, x = model, color = shuffled)
)
+ geom_point(size = 0.2, alpha = 0.5, position = position_jitterdodge())
+ geom_boxplot(aes(middle = mean(dist)), size = 0.2, alpha = 0.8, outlier.alpha = 0)
+ theme_bw()
+ plot_theme
+ ylab("L2 distance between\nreal 'A|B' and predicted 'A|B'")
+ xlab("Models")
+ scale_color_manual(
"Data",
values = c("Shuffled" = "#E66100", "Unshuffled" = "#5D3A9B"),
labels = c("Shuffled" = "Shuffled", "Unshuffled" = "Real")
)
+ ggtitle("L1000 - Level 5")
)
# Get legend
sup_fig_legend <- cowplot::get_legend(panel_a_gg)
# +
# Combine figure together
sup_fig_gg <- (
cowplot::plot_grid(
cowplot::plot_grid(
panel_a_gg + theme(legend.position = "none"),
panel_b_gg + theme(legend.position = "none"),
panel_c_gg + theme(legend.position = "none"),
labels = c("a", "b", "c"),
nrow = 3
),
sup_fig_legend,
rel_widths = c(1, 0.2),
ncol = 2
)
)
sup_fig_gg
# -
# Save figure
output_file_base <- file.path("output", "sup_fig_lsa_distributions")
for (file_extension in file_extensions) {
output_file <- paste0(output_file_base, file_extension)
cowplot::save_plot(output_file, sup_fig_gg, dpi = 500, base_width = 6, base_height = 8)
}
|
figures/supfig_full_lsa_distribution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Model project - Externalities and Pigou taxes
# Our model project consists of a microeconomic model describing the inefficiencies of pollution from production from a social economic point of view. We introduce a demand and a supply function, but the production of the suppliers is associated with a negative externality cost.
#
# We apply model analysis methods to find the market and social equlibria output and prices, where we include graphs to illustrate these equlibria. As a method to solve this social inefficiency from the market powers, we introduce a Pigou tax and calculate the optimal size of this.
# **1: Setup**
# +
#Importing the relevant packages
import sympy as sm
from sympy import *
import numpy as np
import scipy as sp
from scipy import optimize
import matplotlib.pyplot as plt
import ipywidgets as widgets
from ipywidgets import interact, fixed
sm.init_printing(use_unicode=True) #This code enables pretty printing for the mathematical symbols we will use
# -
#Defining the relevant variables and parameters from our model with the sympy symbols function
xd = sm.symbols('x_d') #The amount of goods demanded by consumers
xs = sm.symbols('x_s') #The amount of goods supplied by suppliers
A = sm.symbols('A') #The price consumers are willing to pay if they can only get an infinitely small amount of goods (assumed declining willingess to pay)
B = sm.symbols('B') #The price the suppliers are willing to sell for if they can only sell an infinitely small amount of goods
p = sm.symbols('p') #The price of goods
alpha = sm.symbols('alpha') #A measure of the consumers' sensitivity to changes in prices
beta = sm.symbols('beta') #A measure of the suppliers' sensitivity to changes in prices
delta = sm.symbols('\delta') #An abritrarily chosen multiplier that creates the negative externality through production
x = sm.symbols('x') #The quantity of the goods traded
xc = sm.symbols('xc') #Used for plotting x
deltax = sm.symbols('deltax') #Used for plotting delta
#Checking whether the variables and parameters are correctly defined
xd, xs, A, B, p, alpha, beta, delta, x
# **2: The Model**
# To set up our model, we firstly introduce the following demand and supply functions from the consumers and suppliers of the economy respectively including the negative externality function. It is a simple economy-setup with only one representative consumer, one representative supplier and a single type of good. The agents seek to trade based on the following equations. The producers and the consumers does not care about the negative externality and therefore this doesn't impact their trading behaviour. The equations are as follows:
#
# Demand: $x_{d}=\frac{A-p}{a}$
#
# Supply: $x_{s}=\frac{B+p}{\beta}$
#
# Negative externality: $C_E(x)=(\delta x)^2$
#
# Firstly, we define the demand, supply and negative externality cost functions as follows:
demand = (A-p)/alpha
supply = (B+p)/beta
externality = (delta*x)**2
demand, supply, externality #Prints the three definitions
# Firstly, from the demand and supply functions we can calculate the market price for the good by setting the two equal to each other and solving for $p$. This yields:
#Setting demand and supply equal to each other and solving for p
Marketprice = sm.solve(sm.Eq(demand,supply),p) #We use the sympy .Eq function to set the two equal to each other
#and use the sympy solve function to solve for p in this equation. Marketprice)
Marketprice
# From this result we see that the price - intuitively - is positively dependent on the consumers' initial valuation of the goods and negatively of the producers' initial valuation. This result can be inserted in either the demand or the supply function to obtain the amount of traded goods in equilibrium where supply equals demand.
#Finding the equilibrium output by inserting the marketprice into the demand function
Marketoutput = demand.subs(p, Marketprice[0])
#We use the .subs method to insert the marketprice result from before instead of p in the demand function.
#As the marketprice expression is defined as a list-type, we include the index [0] to refer to the expression herein.
sm.simplify(Marketoutput) #This function simplifies the marketoutput expression.
#We can check whether we get the same result by inserting the market price equilibrium into the supply function
CheckMarketoutput = supply.subs(p, Marketprice[0]) #Same calculation procedure as in code cell above.
sm.simplify(CheckMarketoutput)
# Luckily, we find that the two results are identical, which shows that the found price should be correct.
# From the marketoutput expression we once again see, that more goods are traded if consumers are willing to pay high prices for initial goods (through A) and suppliers are willing to supply them cheaply (through B). We also see that it depends negatively on the price sensitiviy of both the agents.
# Unfortunately, the production from the suppliers also create a negative externality due to pollution or some other externality. This is assumed to have a convex negative impact on society. This convex function can be seen from the graphical depiction below, where we as an example have set $\delta=1$.
#We impose an externality cost of production due to emission
delta = 1
xc = np.linspace(0,2)
ExternalityCost = (delta*xc)**2
plt.plot(xc,ExternalityCost)
plt.xlabel("Quantity")
plt.ylabel("Costs from externality")
plt.title("The convex cost function of the externality")
plt.show
# In order to find the social optimal quantity produces and the associated price, we start by calculating the marginal cost of the externality below. From this the convex nature of the externality is once again evident. We get:
#Finding the marginal externality cost by differentiating w.r.t. x
MarginalExternalityCost = sm.diff(externality, x) #Using the sympy function "diff" to differentiate externality wrt.x
MarginalExternalityCost #Printing the result
# We now also need to find the inverse supply function, which shall be added to the marginal externality cost to give us the social marginal cost of production.
#Private marginal cost (the inverse supply function)
PrivateMarginalCost = sm.solve(sm.Eq(supply,x),p) #We set the supply expression equal to x and solve for p.
PrivateMarginalCost
#Social marginal cost is the sum of the private marginal cost and the marginal externality cost
SocialMarginalCost = PrivateMarginalCost[0] + MarginalExternalityCost
SocialMarginalCost
# Seen above is the social marginal cost function, which takes the negative effects of the externality into account and adds it to the supply function. As $\delta>0$, the social marginal cost will be larger than the private cost from the suppliers. The social marginal cost curve will thus have a steeper slope than the supply curve.
# To now finally find the socially optimal amount of traded goods and the associated price, we start by finding the inverse demand function:
#Inverse demand curve
InverseDemand = sm.solve(sm.Eq(demand,x),p)
InverseDemand
# And we now set this inverse demand function equal to the social marginal cost and solve for $x$ to find the optimal amount of traded goods:
#Finding the social optimal output by setting the demand function equal to the social marginal cost
SocialOptimal = sm.solve(sm.Eq(InverseDemand[0], SocialMarginalCost), x)
SocialOptimal
# Now to finally find the optimal price, we insert this expression into the demand function:
SocialOptimalPrice = sm.solve(sm.Eq(demand,SocialOptimal[0]),p)
SocialOptimalPrice
# Which is the optimal price when considering the externality.
# **3: Graphing the economy**
# To give a graphical overview of the economy, we plot a graph below, where it is possible to change the value of the parameter $\delta$ to give an insight in how the social cost and thereby the optimum depend greatly on this parameter.
def PlotGraph(A, alpha, beta, B, delta):
#This function is able to plot the graphs of the demand, supply and SMC-functions with different parameter values.
x = np.linspace(0,200) #Here we choose over which span the x quantity runs in the graph.
d = A-alpha*x #Defining the demand function
s = beta*x-B #Defining the supply function
smc = x*(beta+2*delta**2)-B #Defining the social marginal cost function
plt.xlabel("Quantity") #Labelling x-axis
plt.ylabel("Price") #Labelling y-axis
plt.grid() #Putting a grid in the background of the graph
plt.title("Supply, demand and social marginal cost") #Adding title to graph
plt.plot(x, d, label="D") #Plotting and labelling demand function
plt.plot(x, s, label="S") #Plotting and labelling supply function
plt.plot(x, smc, label="SMC") #Plotting and labelling SMC function
plt.legend(loc="upper right") #Choosing to put label names in upper right corner.
widgets.interact(PlotGraph,A=widgets.fixed(800), alpha=widgets.fixed(4),
delta=widgets.FloatSlider(description="$\delta$", min=0.0, max=2 , step=0.05, value=1),
B=widgets.fixed(0), beta=widgets.fixed(2))
#These lines of code use the graphing function "PlotGraph" and adds a Floatslider, so the user can adjust
#the value of the delta parameter.
# From this graph we clearly see that when $\delta$ increases the socially optimal price also increases and thereby the quantity traded will be reduced. When $\delta$ on the other hand reaches zero, the SMC and supply curve will be identical - so in the lack of externalities the social optimum will also be the market optimum.
#
# In this example, when externalities are present this is however not the case as neither the consumers nor the producers cares about the externality. To take this into account and reach the social optimum, we will now look at the effects of introducing a Pigou tax.
# **4: Pigou taxes**
# A Pigou tax is a tax that aims at correcting ineffecient market outcomes as with the current example. The tax will aim at increasing the price level of the specific good with the externality and thus, hopefully, affect the trading behaviour so the externality is reduced optimally. The optimal size of the Pigouvian tax is the difference between what the consumers are willing to pay and what the suppliers are willing to sell their goods for at the socially optimal traded quantity.
#
# We have already found the price level for the consumers in the social optimum, and now only need to find the price at which the suppliers are willing to sell at the social optimum. These two prices are:
#Inserting the social optimal output into the supply function
SocialOptimalSupply = sm.solve(sm.Eq(SocialOptimal[0], supply), p)
SocialOptimalSupply,SocialOptimalPrice
# And now we simply subtract the two from each other to get:
#The optimal pigou tax is the difference between the demand and supply
PigouTax = SocialOptimalPrice[0] - SocialOptimalSupply[0]
sm.simplify(PigouTax)
# Which is then the optimal size of the Pigouvian tax, that can bring the two agents of the economy to trade the desired level of goods from a social point of view. We will quickly have a graphical look at how the size of this tax is affected by the size of $\delta$ as this is not necessarily clear from the expression above:
# +
#First we choose the parameter values for the graphing example below
A = 800
B = 0
alpha = 4
beta = 2
deltax = np.linspace(0,8) #Choosing the span in which delta should be plotted on the graph
Pigoutax = (2*deltax**2*(A+B))/(2*deltax**2+alpha+beta) #Defining the function for the Pigouvian tax
plt.plot(deltax,Pigoutax) #Plotting the graph and adding labels and titles.
plt.xlabel("Delta")
plt.ylabel("Pigou")
plt.title("Pigoutax")
plt.show
# -
# As before we have arbitrarily set the parameter values - specifically $A=800, B=0, \alpha=4$ and $\beta=2$. We see that as $\delta$ increases so does the optimal size of the Pigouvian tax. The optimal size is concave wrt. the size of $\delta$ and converges towards the size of A, which is the highest possible amount a consumer will be willing to pay for an infinitely small amount of goods.
#
# **5: Solving the model numerically**
# We will now solve the model numerically, where we assign arbitrary value to the parameters of the model and calculate the equilibrium outcomes with and without externalities. We recall that the equlibria are given as:
#
# Private market equilibrium price: $p^{opt}=\frac{A \beta-B \alpha}{\alpha+\beta}$
#
# Private market equilibrium output: $x^{opt}=\frac{A+B}{\alpha+\beta}$
#
# Social market equilibrium price: $p^{soc}=\frac{2A\delta^2+A\beta-B\alpha}{2\delta^2+\alpha+\beta}$
#
# Social market equilibrium price: $x^{soc}=\frac{A+B}{2\delta^2+\alpha+\beta}$
#
# We will continue to use the parameter values that we used in the graphs above, that is: $A=800$, $B=0$, $\alpha=4$, $\beta=2$, $\delta=1$
# +
#We find the market equilibria with and without the externality included given the chosen parameter values
MarketEquilibriumPrice_num = optimize.fsolve(lambda p: (A*beta-B*alpha)/(alpha+beta)-p,0)
MarketEquilibriumOutput_num = optimize.fsolve(lambda x: (A+B)/(alpha+beta)-x,0)
SocialEquilibriumPrice_num = optimize.fsolve(lambda p: (2*A*delta**2+A*beta-B*alpha)/(2*delta**2+alpha+beta)-p,0)
SocialEquilibriumOutput_num = optimize.fsolve(lambda x: (A+B)/(2*delta**2+alpha+beta)-x,0)
print(f'The equilibrium price in the economy without externality costs is: {MarketEquilibriumPrice_num}')
print(f'The equilibrium output in the economy without externality costs is: {MarketEquilibriumOutput_num}')
print(f'The equilibrium price in the economy with externality costs is: {SocialEquilibriumPrice_num}')
print(f'The equilibrium output in the economy with externality costs is: {SocialEquilibriumOutput_num}')
# -
# Thus, we have now numerically solved the equilibria with and without the negative externality cost. We know from the graph, that when we included this externality, the prices would increase and the output decrease. We now see that including the externality cost raises the equilibrium price from 267 to 400, while the output falls from 133 to 100.
#
# As a method to correct this market inefficiency, we introduced a Pigouvian tax to reach this social market equilibrium. Given the chosen parameter values, we can find this optimal size:
PigouTax_num = optimize.fsolve(lambda t: (2*delta**2*(A+B))/(2*delta**2+alpha+beta)-t,0)
print(f'The optimal size of the Pigouvian tax in the economy is: {PigouTax_num}')
# This optimal size of the tax means that there is a difference of 200 between the price that the buyer pays and the price that the seller receives for one unit of the good. Thus, when the buyer pays 400 for one unit of the good, the seller only receives 200. The remaining 200 goes to the government.
# **6: Conclusion**
# This model project has showed us how the presence of externalities in a market can cause differences between the market optimum and the social optimum. The larger the externality cost, the larger the difference between these two optimums will be. This is a very relevant insight as many parts of the real world economy are faced with similar issues, where many agents' behavior and incentives contradicts with what the society desires as a whole.
#
# In the second part of the project, we introduced an instrument to fix potential market inefficiencies and lead the agents in the market towards the social optimum of goods traded. Of course this is a simple microeconomic setup, and in the real world it is impossible to identify the optimal size of the Pigouvian tax, as the exact desires and incentives from the agents of the economy are unknown. However, this tax is an effective way to reduce market inefficiencies, though it is impossible to get rid of all of them.
#
# In the third and final part of the project, we solved the model numerically where we signed arbitrary values to the parameters of the model. Unsurprisingly, we found the output equilibrium to decrease and the price equilibrium to increase, when we included the negative externality in the model - which was similar to what we found from the graphical inspection. It's important to note that we have chosen the parameter values arbitrarily and changes to any of the variables will affect the equilibria.
|
1312/modelproject/Model-project.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## algorithm
fac = lambda i, *j: i and fac(*divmod(i, len(j) + 1), *j) or j or (i,)
dec = lambda i, k=0, *j: j and dec(i * len(j) + i + k, *j) or i
# ## run
for i in range(0, 11):
f = fac(i ** 3)
d = dec(*f)
print(d, '<->', ' '.join(map(str, f)))
fac(6281)
dec(*(1, 1, 4, 1, 2, 2, 1, 0))
|
100days/day 47 - factoradic.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Extract Precisions with tabular
# This notebook requires [tabula-py](https://pypi.org/project/tabula-py/) and Java to be installed.
#
# It uses tabular to extract the RV precision from the appendix table of the previous paper [docs/Figueira_etal_2016.pdf](https://github.com/jason-neal/eniric/blob/master/docs/Figueira_etal_2016.pdf).
#
# +
import sys
import pandas as pd
import tabula
from tabula import read_pdf
# Tabular needs java 6 or 7!
# This is a hack may not work everywhere.
# I included it because my system java is version 9.
# You will need to point to own location of java.
# https://stackoverflow.com/questions/31414041/how-to-prepend-a-path-to-sys-path-in-python
# May need to manually prepend java location
# using export to PATH before launching jupyter
sys.path = ["/opt/java/jre1.7.0_79/bin"] + sys.path
# -
# Specify paper
paper = "../Figueira_etal_2016.pdf"
pages = [15, 16, 17]
# Read in the table from the pdf
df = read_pdf(paper, pages=pages, guess=True)
# There is an extra line of headings which need removed.
# There is also a couple more futher in the data from
# the top of each table as it spans 3 pages.
df.head()
# Remove mistakenly added title rows
# Easily done beacuse they do not start with "M"
df = df[df.Simulation.str.startswith("M")]
df.head()
# Format the column names
print(df.columns)
df.columns = df.columns.str.replace(" ", "_")
df.columns = df.columns.str.replace("σ", "")
df.columns = df.columns.str.replace("(", "")
df.columns = df.columns.str.replace(")", "")
df.columns = df.columns.str.replace(".", "")
df.columns
# +
# Turing RV precision values to floats
print("Before:\n", df.dtypes)
df["RV_Cond_1"] = df.RV_Cond_1.astype(float)
df["RV_Cond_2"] = df.RV_Cond_2.astype(float)
df["RV_Cond_3"] = df.RV_Cond_3.astype(float)
print("\nAfter:\n", df.dtypes)
# -
# Add units to headers to save
hdr = df.columns
new_header = [
hdr[0],
hdr[1] + "[m/s]",
hdr[2] + "[m/s]",
hdr[3] + "[m/s]",
] # Adjust header to save results
new_header
# +
# Save Results to file
f = "../../data/precision_figueira_2016.dat"
df.to_csv(f, mode="w", sep="\t", float_format="%6.2f", header=new_header, index=False)
# +
# Check read in
newdf = pd.read_csv(f, sep="\t")
newdf.head()
# -
# This has successfully imported the precision value from the Figueira et al. (2016) appendix.
|
docs/Notebooks/Extract-paper-precisions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Candlestick Shooting Star
# https://www.investopedia.com/terms/s/shootingstar.asp
# + outputHidden=false inputHidden=false
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import talib
import warnings
warnings.filterwarnings("ignore")
# yahoo finance is used to fetch data
import yfinance as yf
yf.pdr_override()
# + outputHidden=false inputHidden=false
# input
symbol = 'AMD'
start = '2020-01-01'
end = '2021-10-22'
# Read data
df = yf.download(symbol,start,end)
# View Columns
df.head()
# -
# ## Candlestick with Shooting Star
# + outputHidden=false inputHidden=false
from matplotlib import dates as mdates
import datetime as dt
dfc = df.copy()
dfc['VolumePositive'] = dfc['Open'] < dfc['Adj Close']
#dfc = dfc.dropna()
dfc = dfc.reset_index()
dfc['Date'] = pd.to_datetime(dfc['Date'])
dfc['Date'] = dfc['Date'].apply(mdates.date2num)
dfc.head()
# + outputHidden=false inputHidden=false
from mplfinance.original_flavor import candlestick_ohlc
fig = plt.figure(figsize=(14,10))
ax = plt.subplot(2, 1, 1)
candlestick_ohlc(ax,dfc.values, width=0.5, colorup='g', colordown='r', alpha=1.0)
ax.xaxis_date()
ax.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
ax.grid(True, which='both')
ax.minorticks_on()
axv = ax.twinx()
colors = dfc.VolumePositive.map({True: 'g', False: 'r'})
axv.bar(dfc.Date, dfc['Volume'], color=colors, alpha=0.4)
axv.axes.yaxis.set_ticklabels([])
axv.set_ylim(0, 3*df.Volume.max())
ax.set_title('Stock '+ symbol +' Closing Price')
ax.set_ylabel('Price')
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}}
shooting_star = talib.CDLSHOOTINGSTAR(df['Open'], df['High'], df['Low'], df['Close'])
shooting_star = shooting_star[shooting_star != 0]
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}}
df['shooting_star'] = talib.CDLSHOOTINGSTAR(df['Open'], df['High'], df['Low'], df['Close'])
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}}
df.loc[df['shooting_star'] !=0]
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}}
df['Adj Close'].loc[df['shooting_star'] !=0]
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}}
df['shooting_star'].loc[df['shooting_star'] !=0].index
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}}
shooting_star
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}}
shooting_star.index
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}}
df
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}}
fig = plt.figure(figsize=(20,16))
ax = plt.subplot(2, 1, 1)
candlestick_ohlc(ax,dfc.values, width=0.5, colorup='g', colordown='r', alpha=1.0)
ax.xaxis_date()
ax.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
ax.grid(True, which='both')
ax.minorticks_on()
axv = ax.twinx()
ax.plot_date(df['Adj Close'].loc[df['shooting_star'] !=0].index, df['Adj Close'].loc[df['shooting_star'] !=0],
'Dc', # marker style 'o', color 'g'
fillstyle='none', # circle is not filled (with color)
ms=10.0)
colors = dfc.VolumePositive.map({True: 'g', False: 'r'})
axv.bar(dfc.Date, dfc['Volume'], color=colors, alpha=0.4)
axv.axes.yaxis.set_ticklabels([])
axv.set_ylim(0, 3*df.Volume.max())
ax.set_title('Stock '+ symbol +' Closing Price')
ax.set_ylabel('Price')
# + [markdown] nteract={"transient": {"deleting": false}}
# ## Plot Certain dates
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}}
df = df['2021-08-01':'2021-08-30']
dfc = df.copy()
dfc['VolumePositive'] = dfc['Open'] < dfc['Adj Close']
#dfc = dfc.dropna()
dfc = dfc.reset_index()
dfc['Date'] = pd.to_datetime(dfc['Date'])
dfc['Date'] = dfc['Date'].apply(mdates.date2num)
dfc.head()
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}}
fig = plt.figure(figsize=(20,16))
ax = plt.subplot(2, 1, 1)
ax.set_facecolor('black')
candlestick_ohlc(ax,dfc.values, width=0.5, colorup='azure', colordown='yellow', alpha=1.0)
ax.xaxis_date()
ax.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
#ax.grid(True, which='both')
#ax.minorticks_on()
axv = ax.twinx()
ax.plot_date(df['Adj Close'].loc[df['shooting_star'] !=0].index, df['Adj Close'].loc[df['shooting_star'] !=0],
'*y', # marker style 'o', color 'g'
fillstyle='none', # circle is not filled (with color)
ms=25.0)
colors = dfc.VolumePositive.map({True: 'snow', False: 'lemonchiffon'})
axv.bar(dfc.Date, dfc['Volume'], color=colors, alpha=0.4)
axv.axes.yaxis.set_ticklabels([])
axv.set_ylim(0, 3*df.Volume.max())
ax.set_title('Stock '+ symbol +' Closing Price')
ax.set_ylabel('Price')
# + [markdown] nteract={"transient": {"deleting": false}}
# # Highlight Candlestick
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}}
from matplotlib.dates import date2num
from datetime import datetime
fig = plt.figure(figsize=(20,16))
ax = plt.subplot(2, 1, 1)
candlestick_ohlc(ax,dfc.values, width=0.5, colorup='g', colordown='r', alpha=1.0)
ax.xaxis_date()
ax.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
#ax.grid(True, which='both')
#ax.minorticks_on()
axv = ax.twinx()
ax.axvspan(date2num(datetime(2021,8,19)), date2num(datetime(2021,8,21)),
label="Shooting Star",color="yellow", alpha=0.3)
ax.legend()
colors = dfc.VolumePositive.map({True: 'g', False: 'r'})
axv.bar(dfc.Date, dfc['Volume'], color=colors, alpha=0.4)
axv.axes.yaxis.set_ticklabels([])
axv.set_ylim(0, 3*df.Volume.max())
ax.set_title('Stock '+ symbol +' Closing Price')
ax.set_ylabel('Price')
|
Python_Stock/Candlestick_Patterns/Candlestick_Shooting_Star.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## 1. Setup
# +
import matplotlib.pyplot as plt
import numpy as np
import os
import skimage
import warnings
from dataset_utils import *
from preprocessing import load_patches, merge_patches, get_img_shapes
from preprocessing import merge_patches_and_save, merge_patches_and_save_all
from vis_utils import grid_vis_for_crop_and_merge
# +
# %matplotlib inline
# %load_ext autoreload
# %autoreload 2
warnings.filterwarnings('ignore')
# -
ICOSEG_SUBSET_80_PATH = '../datasets/icoseg/subset_80'
# ## 2. Load patches and merge (for 1 image)
# +
img_name = '2805945719_a77fcbd727'
img_patches_path = f'{ICOSEG_SUBSET_80_PATH}/val/val_img_patches'
mask_patches_path = f'{ICOSEG_SUBSET_80_PATH}/val/val_mask_patches'
img = skimage.io.imread(f'{ICOSEG_SUBSET_80_PATH}/images/{img_name}.jpg')
img_h, img_w = img.shape[:2]
print(f'real img_h, img_w: {img_h}, {img_w}')
# load_patches
img_patches = load_patches(img_name, img_patches_path)
print('img_patches')
print(img_patches.shape, img_patches.dtype,
img_patches.min(), img_patches.max(), '\n')
mask_patches = load_patches(img_name, mask_patches_path)
print('mask_patches')
print(mask_patches.shape, mask_patches.dtype,
mask_patches.min(), mask_patches.max(), '\n')
# merge_patches
img_from_patches = merge_patches(img_patches, img_h=img_h, img_w=img_w)
print('img_from_patches')
print(img_from_patches.shape, img_from_patches.dtype,
img_from_patches.min(), img_from_patches.max())
mask_from_patches = merge_patches(mask_patches, img_h=img_h, img_w=img_w)
print('mask_from_patches')
print(mask_from_patches.shape, mask_from_patches.dtype,
mask_from_patches.min(), mask_from_patches.max())
# grid_vis
grid_vis_for_crop_and_merge(img_from_patches, img_patches,
mask_from_patches, mask_patches)
# -
# ## 3. Merge patches and save (for images from a dataset split)
# +
_, _, val, val_img_names, _, _ = load_icoseg_subset_80_with_img_names()
val_images, val_masks = val
val_img_shapes = get_img_shapes(val_images)
img_patches_path = f'{ICOSEG_SUBSET_80_PATH}/val/val_img_patches'
img_save_path = f'{ICOSEG_SUBSET_80_PATH}/val/val_img_from_patches'
mask_patches_path = f'{ICOSEG_SUBSET_80_PATH}/val/val_mask_patches'
mask_save_path = f'{ICOSEG_SUBSET_80_PATH}/val/val_mask_from_patches'
merge_patches_and_save(val_img_shapes, val_img_names, img_patches_path,
img_save_path, img_format='png')
merge_patches_and_save(val_img_shapes, val_img_names, mask_patches_path,
mask_save_path, img_format='png')
# -
# ## 4. Merge patches and save all (for all dataset splits)
# %%time
merge_patches_and_save_all(load_icoseg_subset_80_with_img_names(),
dataset_path=ICOSEG_SUBSET_80_PATH,
img_format='png')
|
2018-2019/project/utils/merge_patches_and_save_all.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Abhipsakumaripriyadarshinee/predictionusingsupervisedML/blob/main/sfml.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="BQZ5qGhkocmj"
#
# Author: <NAME>
#
# THE SPARK FOUNDATION INTERNSHIP
#
# GRIPMAY21
#
# Task1: Prediction using Supervised ML
#
# Problem Statement: Predict the percentage of an student based on the no of study hours.
#
# I will be performing the following steps:-
#
# Data reading and understanding
# Exploratory Data Analysis
# Building a Simple Regression Model
# Model Evaluation and Prediction
# Simple Linear Regression
# In this regression task we will predict the percentage of marks that a student is expected to score based upon the number of hours they studied. This is a simple linear regression task as it involves just two variables.
# + [markdown] id="lC87yLlIpEe5"
# **Simple Linear Regression**
#
# In this regression task we will predict the percentage of marks that a student is expected to score based upon the number of hours they studied. This is a simple linear regression task as it involves just two variables.
#
#
# + id="vdwpI06vmqIi"
# Importing all libraries required in this notebook
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
from sklearn import metrics
# %matplotlib inline
# + [markdown] id="FBtsyXMboZ8h"
#
# + colab={"base_uri": "https://localhost:8080/", "height": 804} id="Sk5vzxqLm7Nc" outputId="240dfcdd-b901-446a-a7a3-4325996523a5"
# Reading data from remote link
s_data = pd.read_csv("http://bit.ly/w-data")
print("Data imported successfully")
s_data.head(25)
# + colab={"base_uri": "https://localhost:8080/"} id="V0-cejBNnAfy" outputId="e42d34c9-8ec0-469f-e180-15c9b84dbcf3"
s_data.isnull == True
# + [markdown] id="FCeOJjkVpqbz"
# There are no NULL values in the Dataset so, plot the data points on 2-D graph and see if we can find any relationship between the data.
#
# **Exploratory Data Analysis**
#
# Let's plot our data points on 2-D graph to eyeball our dataset and see if we can manually find any relationship between the data
# + colab={"base_uri": "https://localhost:8080/", "height": 305} id="oc_9QRnMnFY7" outputId="47110073-6113-4a86-a236-2c38fb3c7f67"
# Plotting the distribution of scores
sns.set_style('darkgrid')
sns.scatterplot(y = s_data['Scores'], x = s_data['Hours'])
plt.title('Score vs Hours', size = 20)
plt.xlabel('Hours Studied', size=15)
plt.ylabel('Percentage Scores', size=15)
plt.show()
# + [markdown] id="a6lF73jKqN9v"
# From the graph above, we can clearly see that there is a positive linear relation between the number of hours studied and percentage of score.
#
# **Plotting Regression line:**
#
#
#
#
# + colab={"base_uri": "https://localhost:8080/", "height": 355} id="BfYjOvr7nLVa" outputId="213ff076-8ae4-4c6e-f333-cc5aa1899d63"
sns.regplot(x = s_data['Hours'], y = s_data['Scores'])
plt.title('Regression Line', size = 20)
plt.xlabel('Hours Studied', size=15)
plt.ylabel('Percentage Scores', size=15)
plt.show()
print(s_data.corr())
# + [markdown] id="Svujv_uTqwmV"
# **Preparing the data:**
#
# The next step is to divide the data into "attributes" (inputs) and "labels" (outputs).
# + id="B1LK77AjnQxR"
X = s_data.iloc[:, :-1].values
y = s_data.iloc[:, 1].values
# + [markdown] id="Owd7HMLWq_FK"
# **Splitting the data:**
#
# Now that we have our attributes and labels, the next step is to split this data into training and test sets.
# + id="pb6q-gGNnWcT"
#splitting our data into training and testing sets
train_X, test_X, train_y, test_y = train_test_split(X, y, random_state = 0)
# + [markdown] id="MQ5huj8UrILH"
# **Training the Algorithm:**
#
# We have split our data into training and testing sets, and now is finally the time to train our algorithm.
# + colab={"base_uri": "https://localhost:8080/"} id="shFkWlUgnbOa" outputId="1d7de0d1-e4e6-41f6-a9fb-285d3d4e8dd2"
regression = LinearRegression()
regression.fit(train_X, train_y)
print("Training Complete.")
print("Model Trained.")
# + [markdown] id="glh3r8KwrQ3Z"
# **Predicting the Percentage:**
#
# Now that we have trained our algorithm, it's time to make some predictions.
# + colab={"base_uri": "https://localhost:8080/", "height": 254} id="h_wG5-0Ynf_p" outputId="38c2bb93-ebda-4a5a-ad3c-9e64471244bc"
pred_y = regression.predict(test_X)
prediction = pd.DataFrame({'Hours': [i[0] for i in test_X], 'Predicted Marks': [k for k in pred_y]})
prediction
# + [markdown] id="nxop5LFYrbaa"
# **Comparing the Actual and Predicted Marks:**
# + colab={"base_uri": "https://localhost:8080/", "height": 254} id="EFSiz-4KnkuH" outputId="62f79bd3-20bc-4011-8061-12b559634ccb"
# Comparing Actual vs Predicted
df = pd.DataFrame({'Actual': test_y, 'Predicted' : pred_y})
df
# + [markdown] id="OT1BfmkIril4"
# **Plotting Actual and Predicted Marks:**
# + colab={"base_uri": "https://localhost:8080/", "height": 303} id="v8-oPsCXnpP3" outputId="279350b2-df31-4001-f908-e4f0be349347"
plt.scatter(x=test_X, y=test_y, color='Red')
plt.plot(test_X, pred_y, color='Black')
plt.title('Actual vs Predicted', size=20)
plt.ylabel('Marks Percentage', size=12)
plt.xlabel('Hours Studied', size=12)
plt.show()
# + [markdown] id="ekwg9ohtrr8m"
# **Predicting the score if studied for 9.25 hours/day:**
# + colab={"base_uri": "https://localhost:8080/"} id="I0eZgnXrnzz1" outputId="b6df5571-75f4-4be6-80da-1745309494dc"
hours = [9.25]
answer = regression.predict([hours])
print("Score = {}".format(round(answer[0],3)))
# + [markdown] id="be6Pf95Urw15"
# According to linear regression model, predicted score if a student studies for 9.25 hrs/ day is 93.893
#
# Evaluating the model:
#
# The final step is to evaluate the performance of algorithm using mean square error.
# + colab={"base_uri": "https://localhost:8080/"} id="gSY79tYwn031" outputId="48ed7b40-0725-46c9-fa9b-d5ddc8be568c"
#mean absolute error to evaluate performance of the algorithm
print('Mean Absolute Error:', metrics.mean_absolute_error(test_y, pred_y))
|
sfml.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Ensemble Study
#
# In this notebook we study the features of annotated hypergraphs in reference to an ensemble of hypergraphs generated from a null model.
# +
# # !pip install seaborn --user --quiet
# %matplotlib inline
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pylab as plt
# -
def read_results(path):
"""Read results from a directory."""
original = pd.read_csv(f'{path}/original.csv', index_col=0, header=None)[1]
role_preserving_ensemble = pd.read_csv(f'{path}/role_preserving_ensemble.csv', index_col=False, header=0)
role_destroying_ensemble = pd.read_csv(f'{path}/role_destroying_ensemble.csv', index_col=False, header=0)
return original, role_preserving_ensemble, role_destroying_ensemble
original, preserving_ensemble, destroying_ensemble = read_results('../results/enron_r/')
results = read_results('../results/enron_r')
# +
def get_min_max(a, b):
"""Get bounds for two series"""
lower = min(a.min(), b.min())
upper = max(a.max(), b.max())
return lower, upper
def plot_feature(feature, original, role_preserving_ensemble, role_destroying_ensemble, num_bins=20, **fig_kwargs):
"""Plot a feature"""
fig = plt.figure(**fig_kwargs)
ax = fig.add_subplot(111)
ymax=0
# lower, upper = get_min_max(role_preserving_ensemble[feature],role_destroying_ensemble[feature])
# bins = np.linspace(lower, upper, num_bins)
lower, upper = get_min_max(role_preserving_ensemble[feature],role_preserving_ensemble[feature])
bins = np.linspace(lower, upper, num_bins)
y,binEdges=np.histogram(role_preserving_ensemble[feature], bins=bins)
bincenters = 0.5*(binEdges[1:]+binEdges[:-1])
rp = ax.plot(bincenters,y,'-o', color='r', label='Role Preserving Ensemble')
ymax=max(ymax,max(y))
lower, upper = get_min_max(role_destroying_ensemble[feature],role_destroying_ensemble[feature])
bins = np.linspace(lower, upper, num_bins)
y,binEdges=np.histogram(role_destroying_ensemble[feature], bins=bins)
bincenters = 0.5*(binEdges[1:]+binEdges[:-1])
rd = ax.plot(bincenters,y,'-o', color='b', label='Role Destroying Ensemble')
ymax=max(ymax,max(y))
line = ax.vlines(original[feature],0.0,ymax, label='Data')
ax.legend(loc='best')
return fig, ax, (line, rp, rd)
# +
def get_features_for_dataset(dataset, features):
"""
"""
original, preserving_ensemble, destroying_ensemble = read_results(f'../results/{dataset}/')
all_features = []
for feature in features:
rp = preserving_ensemble[feature]
rd = destroying_ensemble[feature]
og = pd.Series(original[feature])
combined = pd.DataFrame(pd.concat([rp,rd,og], axis=0))
combined.columns = [feature]
all_features.append(combined)
combined = pd.concat(all_features, axis=1)
combined['model'] = pd.Series(data=(['RP']*len(rp) + ['RD']*len(rd) + ['OG']), index=combined.index)
return combined
def get_datasets_for_feature(feature, datasets):
"""
"""
if isinstance(feature,str):
feature = [feature]
all_data = []
for feature in feature:
for data in datasets:
# original, preserving_ensemble, destroying_ensemble = read_results(f'../results/{data}/')
# rp = preserving_ensemble[feature].head(500) # ANDY QUICK FIX
# rd = destroying_ensemble[feature].head(500) # ANDY QUICK FIX
# og = pd.Series(original[feature])
# combined = pd.DataFrame(pd.concat([rp,rd,og], axis=0))
# combined.columns = [data]
original, preserving_ensemble, destroying_ensemble = read_results(f'../results/{data}/')
rp = preserving_ensemble[feature].head(500) # ANDY QUICK FIX
rd = destroying_ensemble[feature].head(500) # ANDY QUICK FIX
og = pd.Series(original[feature])
og = pd.DataFrame(og).T
combined = pd.concat([og,rp,rd],
keys=['Original','Role-preserving','Non-role-preserving'],
names=['ensemble','sample'])
combined = combined.stack()
combined.index.names = ['ensemble','sample','feature']
combined = combined.reset_index()
combined = combined.rename({0:'value'}, axis=1)
combined['data'] = data
combined['feature'] = feature
all_data.append(combined)
combined = pd.concat(all_data, axis=0)
# combined['model'] = pd.Series(data=(['RP']*len(rp) + ['RD']*len(rd) + ['OG']), index=combined.index)
return combined
# -
combined = get_datasets_for_feature(feature='neighbourhood_role_entropy',
datasets=['enron_r','stack_overflow_r','math_overflow_r',
'scopus_multilayer_r','movielens_r', 'twitter_r'])
# #### Figure 3
with plt.style.context("seaborn-whitegrid", {'font.size':14}):
fontsize=14
sax = sns.catplot(data=combined,
kind='box',
hue='ensemble',
y='value',
x='feature',
col='data',
fliersize=2,
linewidth=1.5,
notch=False,
legend=False,
sharey=False,
legend_out=True,
height=4,
aspect=0.4,
);
fig = plt.gcf()
for ix, ax in enumerate(fig.axes):
ax.set_xlabel(None);
ax.set_xticklabels([None]);
ax.set_title(ax.title.get_text().split('=')[-1].strip().strip('r').strip('_').replace('_','-'))
if ix==0:
ax.set_ylabel('Neighbourhood Role Entropy', fontsize=fontsize);
ax.legend(ncol=3, bbox_to_anchor=(10,0))
fig.savefig('../fig/ensemble_local_role_entropy.pdf', bbox_inches='tight')
# #### Figure 4
combined = get_datasets_for_feature(feature=['neighbourhood_role_entropy', 'weighted_degree_entropy',
'weighted_pagerank_entropy', 'node_role_entropy', 'connected_components',
'weighted_eigenvector_entropy'],
datasets=['enron_r','stack_overflow_r','math_overflow_r',
'scopus_multilayer_r','movielens_r', 'twitter_r'])
with plt.style.context("seaborn-whitegrid", {'font.size':14}):
fontsize=14
sax = sns.catplot(data=combined,
kind='box',
hue='ensemble',
y='value',
x='x',
col='data',
row='feature',
fliersize=2,
linewidth=1.5,
notch=False,
legend=False,
sharey=False,
legend_out=True,
height=3.5,
aspect=0.5,
);
n_features = combined.feature.nunique()
fig = plt.gcf()
for ix, ax in enumerate(fig.axes):
ax.set_xlabel(None);
ax.set_xticklabels([None]);
long_title = ax.get_title()
feature = long_title.split('|')[0].split('=')[-1].strip().replace('_', ' ').title()
dataset = long_title.split('|')[-1].split('=')[-1].strip().replace('_', '-').strip('r').strip('-')
if (ix % n_features) == 0:
ax.set_ylabel(feature)
if ix < n_features:
ax.set_title(dataset)
else:
ax.set_title(None)
if ix==0:
ax.legend(loc='lower center', ncol=3, bbox_to_anchor=(4,-5.6))
fig.savefig('../fig/ensemble_all_features.pdf', bbox_inches='tight')
# ### Tables
# +
def get_statistics(feature, original, role_preserving_ensemble, role_destroying_ensemble):
"""Get the statistics for a specific feature of a specific dataset. """
data = original[feature]
pres = role_preserving_ensemble[feature]
pres_mean, pres_std = pres.mean(), pres.std()
if np.isclose(pres_std,0.0):
pres_z = 0
else:
pres_z = (data - pres_mean)/pres_std # Not using abs to detect under or over rep.
dest = role_destroying_ensemble[feature]
dest_mean, dest_std = dest.mean(), dest.std()
if np.isclose(dest_std,0.0):
dest_z = 0
else:
dest_z = (data - dest_mean)/dest_std
return pd.DataFrame({'Role Preserving Ensemble': {'data':data, 'mean':pres_mean, 'std':pres_std, 'z':pres_z},
'Role Destroying Ensemble': {'data':data, 'mean':dest_mean, 'std':dest_std, 'z':dest_z}})
def statistics_table(data_list, feature_list=None):
"""Returns a complete statistical summary of the data analysis."""
# Currently needs generalising if it goes into the main package.
data_tables = []
for dataset in data_list:
results = read_results(f'../results/{dataset}')
feature_tables = []
if feature_list is None: feature_list = results[0].index
for feature in feature_list:
feature_tables.append(get_statistics(feature, *results))
feature_table = pd.concat(feature_tables, keys=feature_list, names=['feature'])
data_tables.append(feature_table)
complete_table = pd.concat(data_tables, keys=data_list, names=['data'])
return complete_table
# +
DATASETS = ['enron', 'enron_r',
'math_overflow', 'math_overflow_r',
'scopus_multilayer', 'scopus_multilayer_r',
'stack_overflow', 'stack_overflow_r',
'movielens', 'movielens_r',
'twitter', 'twitter_r'
]
stats = statistics_table(DATASETS)
def color_significance(val):
"""
Color values which are statistically significant.
"""
if val > 2:
color='red'
elif val < -2:
color='blue'
else:
color='black'
return 'color: %s' % color
# -
stats.xs('z', level=2).style.applymap(color_significance)
# +
def format_and_color(x, color=True):
""" Converts to 2 d.p. and colours red if greater than two sigma, blue less than two sigma. """
number = '{:.2f}'.format(x)
if color:
if x > 2:
return r'\textcolor{red}{%s}' % number
elif x < -2:
return r'\textcolor{blue}{%s}' % number
else:
return number
else:
return number
def produce_latex_table(statistics, datasets, feature_map=None, data_map=None, as_tex=True):
"""
Produce the table in Latex format to be used in the manuscript.
"""
if feature_map is None:
pass
comb = pd.concat([statistics.xs('mean', level=2), statistics.xs('z', level=2)], axis=1, names=['mean', 'z'])
comb.columns = pd.MultiIndex(levels=[['rp', 'rd'], ['mean', 'z']], codes=[[0,1,0,1], [0,0,1,1]])
comb = comb.loc[datasets,:].reset_index(drop=False)
if feature_map is not None:
comb['feature'] = comb.feature.apply(lambda x: feature_map[x])
if data_map is not None:
comb['data'] = comb.data.apply(lambda x: data_map[x])
comb = comb.set_index(['data','feature'])
# Construct the original dataframe.
originals = []
for data in datasets:
original, _, _ = read_results(f'../results/{data}/')
original = pd.DataFrame(original)
original['data'] = data
originals.append(original)
originals = pd.concat(originals)
originals = originals.reset_index(drop=False)
originals.columns = ['feature','original','data']
originals = originals.set_index(['data','feature'])
originals.columns = pd.MultiIndex(levels=[[''],['original']], codes=[[0],[0]])
comb = pd.merge(left=originals, right=comb, left_index=True, right_index=True).sort_index().sort_index(axis=1)
if as_tex:
return comb.to_latex(formatters={('rp','z'): lambda x: format_and_color(x),
('rd','z'): lambda x: format_and_color(x),
('rp','mean'): lambda x: '{:0.2f}'.format(x),
('rd','mean'): lambda x: '{:0.2f}'.format(x),
('','original'): lambda x: '{:0.2f}'.format(x)},
escape=False)
return comb.style.applymap(color_significance, subset=[('rp','z'),('rd','z')])
# -
produce_latex_table(stats, datasets=['enron_r', 'stack_overflow_r'], as_tex=False)
print(produce_latex_table(stats, datasets=['enron_r', 'stack_overflow_r']))
|
analysis/ensemble_study.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 
# Machine Learning and Statistics 2021
#
#
# **Author:** <NAME>
#
#
# **Lecturer:** <NAME>
#
#
# **Student ID:** <EMAIL>
# # Assessment Outline
#
# Include a Jupyter notebook called scipy-stats.ipynb that contains the following:
#
# 10% A clear and concise overview of the scipy.stats Python library.
#
# 20% An example hypothesis test using ANOVA. You should find a data set on which
# it is appropriate to use ANOVA, ensure the assumptions underlying ANOVA are met, and then perform and display the results of your ANOVA using scipy.stats.
#
# 10% Appropriate plots and other visualisations to enhance your notebook for viewers.
# # Preliminaries
#
# In order to effectively answer the Problem Statement various relevant libraries must be imported. For this we will import Numpy as it contains essential libraries namely the numpy.random library. Matplotlib.plyplot and Seaborn libraries will be utilised to assist in the visualisation of numbers to user friendly graphs.
# +
# Import the the necessary libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
from scipy.stats import norm
from scipy.stats import uniform
from scipy.stats import binom
from scipy import stats
from scipy.stats import levene
from scipy.stats import bartlett
from statsmodels.formula.api import ols
from scipy.stats import f, norm
# -
# The magic inline command will be utilised in order to ensure the correct display of the plots within the Jupyter Notebook. This will allow the plots to be rendered inline within the Notebook [1].
# Magic command used to visualise plots in Jupyter
# %matplotlib inline
# # Overview of Scipy-Stats
#
# All of the statistics functions are located in the sub-package scipy.stats and a fairly complete listing of these functions can be obtained using info(stats) function. A list of random variables available can also be obtained from the docstring for the stats sub-package. This module contains a large number of probability distributions as well as a growing library of statistical functions.
#
# Statistics is a very large area, and there are topics that are out of scope for SciPy and are covered by other packages. Some of the most important ones are:
#
# * statsmodels: regression, linear models, time series analysis, extensions to topics also covered by scipy.stats.
#
# * Pandas: tabular data, time series functionality, interfaces to other statistical languages.
#
# * PyMC3: Bayesian statistical modeling, probabilistic machine learning.
#
# * scikit-learn: classification, regression, model selection.
#
# * Seaborn: statistical data visualization.
#
# * rpy2: Python to R bridge.
#
#
# Each univariate distribution has its own subclass:
#
# * **rv_continuous:** A generic continuous random variable class meant for subclassing
# <br>
#
# * **rv_discrete:** A generic discrete random variable class meant for subclassing
# <br>
#
# * **rv_histogram:** Generates a distribution given by a histogram
# <br>
# <center> Normal Continuous Random Variable <center/>
#
# <br>
#
# A probability distribution in which the random variable X can take any value is continuous random variable. The location (loc) keyword specifies the mean. The scale (scale) keyword specifies the standard deviation.
#
# As an instance of the rv_continuous class, norm object inherits from it a collection of generic methods and completes them with details specific for this particular distribution.
#
# To compute the CDF at a number of points, we can pass a list or a NumPy array. Let us consider the following example.
#
#
#
# Cumulative Distribution Function (CDF)
norm.cdf(np.array([1,-1., 0, 1, 3, 4, -2, 6]))
# to find the median we can simply use the Percent Point Function (PPF)
# ppf
norm.ppf(0.5)
# to generate random variates use the following
norm.rvs(size = 5)
# <br> <br> <br>
# <center> Uniform Distribution <center/>
# A uniform distribution can be generated using the uniform function.
#
#
uniform.cdf([0, 1, 2, 3, 4], loc = 0, scale = 4)
s = uniform.cdf([0, 1, 2, 3, 4], loc = 0, scale = 4)
s
count, bins, ignored = plt.hist(s, 10, density=True)
plt.plot(bins, np.ones_like(bins))
plt.show()
# <br> <br> <br>
# <center> Discrete Distribution <center/>
# **Binomial Distribution:** As an instance of the rv_discrete class, the "binom object" inherits from it a collection of generic methods and completes them with details specific for this particular distribution.
#
#
# +
n = 6
p = 0.6
# defining list of r values
r_values = list(range(n + 1))
# list of pmf values
dist = [binom.pmf(r, n, p) for r in r_values ]
# plotting the graph
plt.bar(r_values, dist)
plt.show()
# -
# <br><br><br>
# <center> Descriptive Statistics <center/>
#
# The basic stats such as Min, Max, Mean and Variance takes the NumPy array as input and returns the respective results. A few basic statistical functions available in the scipy.stats package are described in the following table.
#
#
# 
# create np array for use by discriptive methods
np.arange(10)
x= np.arange(10)
x
print(x.min()) # equivalent to np.min(x)
-3.78975572422 # random
print(x.max()) # equivalent to np.max(x)
5.26327732981 # random
print(x.mean()) # equivalent to np.mean(x)
0.0140610663985 # random
print(x.var()) # equivalent to np.var(x))
1.28899386208 # random
# <br><br><br>
# <center> T-test <center/>
# **ttest_1samp** is used to calculate the T-test for the mean of ONE group of scores. This is a two-sided test for the null hypothesis that the expected value (mean) of a sample of independent observations ‘a’ is equal to the given population mean, popmean.
#
rvs = stats.norm.rvs(loc = 5, scale = 10, size = (50,2))
stats.ttest_1samp(rvs,5.0)
# +
# sample one
rvs1 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
# sample two
rvs2 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
# -
# show output
stats.ttest_ind(rvs1,rvs2)
# p-value is a measure of the probability that an observed difference could have occurred just by random chance.
# The lower the p-value, the greater the statistical significance of the observed difference.
# A p-value less than 0.05 (typically ≤ 0.05) is statistically significant. It indicates strong evidence against the null hypothesis, as there is less than a 5%
#
# **Therefore, we reject the null hypothesis, and accept the alternative hypothesis**
#
# However in this example it is 77%
#
#
# There are certain conditions that need to be met in order for the T-test results to be considered reliable [1]:
#
# 1. Dependent variables should be measured on a continuous scale
# 2. Independent variable should consist of two categorical, independent groups
# 3. Independence of observations should exist
# 4. There should be no significant outliers.
# 5. Dependent variables should be approximately normally distributed for each group of the independent variables.
#
# <center> Summary Statistics <center/>
# the summary statistics focuses on descriptive statistical sub-functions. The min, max, mean values from the input NumPy arrays are evaulated. popular funcations are:
#
# * describe() - it returns descriptive stats of the arrays.
# * bootstrap() - Compute a two-sided bootstrap confidence interval of a statistic.
# * gmean()- it returns the geometric mean along a specific axis of an array.
# * hmean() - it returns the harmonic mean along a specific axis of an array.
# * sem() - it returns the standard error mean of the mean.
# * kurtosis() - it returns the kurtosis value of an array.
# * mode() - it returns the mode of an array.
# * mvsdist()- Frozen distributions for mean, variance, and standard deviation of data.
# * skew() - it is to perform the skew test on an array.
# * zscore() - it returns the z-score relative to the mean and standard deviation values.
# * variation()- Compute the coefficient of variation.
# <center> Frequency statistics <center/>
#
# Examples:
#
# * cumfreq()- Return a cumulative frequency histogram, using the histogram function.
#
# * itemfreq()-itemfreq is deprecated! itemfreq is deprecated and will be removed in a future version.
#
# * percentileofscore()-Compute the percentile rank of a score relative to a list of scores.
#
# * scoreatpercentile()-Calculate the score at a given percentile of the input sequence.
#
# * relfreq()- Return a relative frequency histogram, using the histogram function.
#
# * binned_statistic()-Compute a binned statistic for one or more sets of data.
#
# * binned_statistic_2d()-Compute a bidimensional binned statistic for one or more sets of data.
#
# * binned_statistic_dd()-Compute a multidimensional binned statistic for a set of data.
# <Center> Statistical distances <Center>
#
# Examples:
#
# * wasserstein_distance()-Compute the first Wasserstein distance between two 1D distributions.
#
# * energy_distance-() Compute the energy distance between two 1D distributions.
# <Center> Random variate generation / CDF Inversion <Center>
#
# Examples:
#
# * rvs_ratio_uniforms()-Generate random samples from a probability density function using the ratio-of-uniforms method.
#
# * NumericalInverseHermite()- A Hermite spline fast numerical inverse of a probability distribution.
# <Center> Circular statistical functions <Center>
#
# Examples:
#
# * circmean()- Compute the circular mean for samples in a range.
#
# * circvar()- Compute the circular variance for samples assumed to be in a range.
#
#
# <Center> Contingency table functions <Center>
#
# Examples:
# * chi2_contingency()- Chi-square test of independence of variables in a contingency table.
#
# * contingency.crosstab()-Return table of counts for each possible unique combination in *args.
#
# * contingency.expected_freq()- Compute the expected frequencies from a contingency table.
#
#
#
#
# <center> Plot-tests <center/>
#
# Examples:
# * ppcc_max()- Calculate the shape parameter that maximizes the PPCC.
#
# * ppcc_plot()- Calculate and optionally plot probability plot correlation coefficient.
#
# * probplot()- Calculate quantiles for a probability plot, and optionally show the plot.
#
# * boxcox_normplot()- Compute parameters for a Box-Cox normality plot, optionally show it.
#
#
# <center> Univariate and multivariate kernel density estimation <center/>
#
# * gaussian_kde()- Representation of a kernel-density estimate using Gaussian kernels
# <center> Warnings used in scipy.stats <center>
#
# Examples:
# * F_onewayConstantInputWarning()- Warning generated by f_oneway when an input is constant, e.g.
#
# * \F_onewayBadInputSizesWarning- Warning generated by f_oneway when an input has length 0, or if all the inputs have length 1.
#
# * PearsonRConstantInputWarning()- Warning generated by pearsonr when an input is constant.
#
# * PearsonRNearConstantInputWarning()-Warning generated by pearsonr when an input is nearly constant.
#
# * SpearmanRConstantInputWarning()- Warning generated by spearmanr when an input is constant.
# <center/> Quasi-Monte Carlo <center/>
# In Monte Carlo (MC) sampling the sample averages of random quantities are used
# to estimate the corresponding expectations. The justification is through the law of
# large numbers. In quasi-Monte Carlo (QMC) sampling we are able to get a law
# of large numbers with deterministic inputs instead of random ones. Naturally we
# seek deterministic inputs that make the answer converge as quickly as possible. In
# particular it is common for QMC to produce much more accurate answers than MC
# does. Keller was an early proponent of QMC methods for computer graphics.
# This module provides Quasi-Monte Carlo generators and associated helper functions[3].
#
#
#
# # Anova
# The one-way analysis of variance (ANOVA) is used to determine whether there are any statistically significant differences between the means of three or more independent (unrelated) groups. This example will provide a brief introduction to the one-way ANOVA and the underlying assumptions of the test [13, 14].
#
#
# **Overview:** Essentially the one-way ANOVA compares the means between the groups you are interested in and determines whether any of those means are statistically significantly different from each other. Specifically, it tests the null hypothesis [6].
#
#
#
#
# **when should you use it:** Use a one-way ANOVA when you have collected data about one categorical independent variable and one quantitative dependent variable. The independent variable should have at least three levels (i.e. at least three different groups or categories). ANOVA tells you if the dependent variable changes according to the level of the independent variable [7].
#
#
# **Assumptions:** Assumptions of ANOVA
# The assumptions of the ANOVA test are the same as the general assumptions for any parametric test:
#
# 1. **Assumption One- Independence of observations:** the data were collected using statistically-valid methods, and there are no hidden relationships among observations. If your data fail to meet this assumption because you have a confounding variable that you need to control for statistically, use an ANOVA with blocking variables [15].
#
#
# 2. **Assumption Two- Normally-distributed** response variable: The values of the dependent variable follow a normal distribution [12].
#
#
# 3. **Assumption Three- Homogeneity of variance:** The variation within each group being compared is similar for every group. If the variances are different among the groups, then ANOVA probably isn’t the right fit for the data [8].
#
#
#
# # Types of ANOVA Tests
#
#
# * One-Way ANOVA: A one-way ANOVA has just one independent variable: For example, differences in Corona cases can be assessed by Country, and a Country can have 2 or more different categories to compare [9].
#
#
#
#
# * Two-Way ANOVA: A two-way ANOVA (also called factorial ANOVA) refers to an ANOVA using two independent variables Expanding the example above, a two-way ANOVA can examine differences in Corona cases (the dependent variable) by Age group (independent variable 1) and Gender (independent variable 2). Two-way ANOVA can be used to examine the interaction between the two independent variables. Interactions indicate that differences are not uniform across all categories of the independent variables For example, Old Age Group may have higher Corona cases overall compared to the Young Age group, but this difference could be greater (or less) in Asian countries compared to European countries [10].
#
#
#
# * N-Way ANOVA: A researcher can also use more than two independent variables, and this is an n-way ANOVA (with n being the number of independent variables you have), aka MANOVA Test. For example, potential differences in Corona cases can be examined by Country, Gender, Age group, Ethnicity, etc, simultaneously. An ANOVA will give you a single (univariate) f-value while a MANOVA will give you a multivariate F-value [11].
#
#
#
#
# 
#
# <center>Background to Data and Example Problem<center/>
#
# In order to demonstrate ANOVA a fake data set was created using **numpy.random.normal** where three fake normal distribution groups was create.
# In the example, forty randomly selected students were selected from three different countries Ireland (IRL), Northern Ireland (NI), and France (FRA) and entered a spelling competition. They all got their results back with means of IRL=74, NI=88 and FRA=85. For this example, we want to see if we can find a **statically significant difference** amongst these student groups regarding the mean score or was it by pure chance that we happen to select better or worse students at spelling for certain countries.
#
# set the seed for random data
np.random.seed(99)
# use numpy to generate random data for student exam results in 3 countries
IRL = np.random.normal(loc=74,scale=4,size=40)
NI = np.random.normal(loc=88,scale=4,size=40)
FRA = np.random.normal(loc=84,scale=4,size=40)
# for loop used to round the mean of the numbers
# print scores
print("----------------------")
print("Mean Score Data")
print("----------------------")
for i in range(3):
print(['IRL: ','NI: ','FRA: '][i],[IRL,NI,FRA][i].mean().round(1))
print("----------------------")
# Create a list for IRL and put list into a dataframe representing each student group
list_IRL = []
for i in range(40): list_IRL.append('IRL')
# use lambda function and store in dataframe
df_IRL = pd.DataFrame(data={'Country':list_IRL,'Results':list(map(lambda x: x.round(1), IRL))})
# Create a list for NI and put list into a dataframe representing each student group
list_NI = []
for i in range(40): list_NI.append('NI')
# use lambda function and store in dataframe
df_NI = pd.DataFrame(data={'Country':list_NI,'Results':list(map(lambda x: x.round(1), NI))})
# Create a list for FRA and put list into a dataframe representing each student group
list_FRA = []
for i in range(40): list_FRA.append('FRA')
# use lambda function and store in dataframe
df_FRA = pd.DataFrame(data={'Country':list_FRA,'Results':list(map(lambda x: x.round(1), FRA))})
# merge the data frames into one for easier viewing by appending to IRL dataframe
df_students = df_IRL.append([df_NI,df_FRA],ignore_index=True)
df_students
# describe data
df_students.describe()
# see data info
df_students.info()
# Visualise the DataFrame to view the data
sns.displot(df_students,x='Results',hue='Country',kind='kde',height=5,aspect=2)
sns.displot(df_students,x='Results',hue='Country',multiple='dodge',height=5,aspect=2)
# <br><br><br>
# # Assumption One- Independent Observations
# the assumption of independent observations in this instance is based on the knowledge of the author of the data and its source. To ensure that the data is independent the author must ensure no cross contamination of data. For example, if some students represented IRL and NI at the same time then the data would be skewed, and the assumption of independent observations would be void. However, in this case we can say that we meet the requirements of **Assumption One** and can conduct our ANOVA test.
#
# <br>
# # Assumption Two- Normality
# Chen and Shapiro (1995) introduced a test for normality that compares the spacings between order statistics with the spacings between their expected values under
# normality.
#
# The **def shapiro_test(x)** function will return two values in a list. The first value is the t-stat of the test, and the second value is the p-value. You can use the p-value to make a judgement about the normality of the data. If the p-value is less than or equal to 0.05, you can safely reject the null hypothesis of normality and assume that the data are non-normally distributed [5].
# +
# Normality test using shapiro_test function [4]
print("-----------------------")
print("RESULTS")
def shapiro_test(x):
a = 0.05
test = stats.shapiro(x)
if test.pvalue <= 0.05: # P-value of significance [16]
return f'The distribution departed from normality significantly, W= {round(test.statistic,2)}, P-value= {round(test.pvalue,2)}'
else:
return f"Shapiro Wilk Test did not show non-normality, W= {round(test.statistic,2)}, P-value= {round(test.pvalue,2)}. No evidence to REJECT the null hypothesis of normality."
# display results from shapiro test
for i in range(3):
print("-------------------------")
print("Shapiro Wilk Test Results")
print("-------------------------")
print(["For IRL: ","For NI: ","For FRA: "][i], shapiro_test([IRL,NI,FRA][i]))
print('\n')
# -
# # Assumption Three- Homogeneity
# We can use **Bartlett’s Test** or **Levene Test**
# <br>
#
# <center> Bartlett’s test <center/>
# <br>
#
#
# Bartlett’s test was introduced in 1937 by <NAME> (1910–2002) and is an inferential procedure used to assess the equality of variance in different populations. Bartlett’s test of homogeneity of variance is based on a chi-square statistic with (k − 1) degrees of freedom, where k is the number of categories (or groups) in the independent variable. In other words, Bartlett’s test is used to test if k populations have equal variances [17.]
#
#
# Example, if we wish to conduct the following hypothesis:
# 
# The test statistic has the following expression:
# 
# where N corresponds to the sum of all sample sizes. It is asymptotically distributed as a χ2 distribution with (k − 1) degrees of freedom. The null hypothesis of equal population variances is rejected if test statistics is larger than the critical value. One may also use online tools to perform this test, under condition that each sample contains at least five observations [17].
# <center> Levene Test <center/>
# The Levene’s test uses an F-test to test the null hypothesis that the variance is equal across groups. A p value less than .05 indicates a violation of the assumption. If a violation occurs, it is likely that conducting the non-parametric equivalent of the analysis is more appropriate [18]. For Levene’s test of the homogeneity of group variances, the residuals eij of the group means from the cell means are calculated as follows [19]:
# 
# An ANOVA is then conducted on the absolute value of the residuals. If the group variances are equal, then the average size of the residual should be the same across all groups.
#
#
# Initial look at the variances between countries
[round(np.var(x, ddof=1),3) for x in [IRL,NI,FRA]]
# Bartlett Test [20]
alpha = 0.05
stat, p_bartlet = bartlett(IRL,NI,FRA)
if p_bartlet <= alpha:
print(p_bartlet,": SMALL P-value indicates data of NOT EQUAL variances")
else:
print(p_bartlet, ": LARGE P-value indicates data of EQUAL variances")
# Levene's Test [21]
alpha = 0.05
w_stats, p_value =levene(IRL,NI,FRA, center ='mean')
if p_value > alpha :
print("We DO NOT REJECT the null hypothesis")
else:
print("REJECT the Null Hypothesis")
# # Null and Alternative Hypothesis
#
#
# <center>Null Hypothesis<center/>
# This is the default hypothesis against the initial assumptions which would suggest that NO statistically significant difference exists between the data groups. For example, there is no statistically significant difference between the means of IRL and FRA data.
#
# Therefore H0 is equal to the following:
#
# **H0:** There is no statistically significant difference between the groups of students in IRL, NI and FRA data.
#
# <center>Alternative Hypothesis<center/>
# The alternative hypothesis states the assumption. For example, the mean data in NI is statistically significantly different than the mean data in IRL.
#
# Therefore H1 is equal to the following:
#
# **H1:** There is a statistically significant difference between the data of the students in NI and IRL. This difference is based upon their country.
#
# # Alpha Value, F-Critical value, and P-Value
# <center>Alpha Value<center>
# Setting up alpha value, 0.05α level is appropriate
alpha = 0.05
# Alpha value can be dependent on the nature of the study, however for the most part a value of 0.05 is used. This number reflects the probability of obtaining results as extreme as what you obtained in your sample if the null hypothesis was true [23].
# <center> F-Critical Value <center/>
# The F-Critical value is a specific value you compare your F-Value to. In general, if your calculated F-Value in a test is larger than your F-Critical value, you can reject the null hypothesis. However, the statistic is only one measure of significance in an F-Test. To get the F-Critical value we require the following:
#
# * Alpha level DF1 = K-1, DF2 = N-K (DFN- Degrees of Freedom Nominator).
# * K= number of groups
# * N= number of observations
# * F distribution table
# dfn= number of degrees of freedom numerator [29]
# dfd= number of degrees of freedom deminator [29]
dfn = len([IRL,NI,FRA])-1
dfd = len(df_students) - len([IRL,NI,FRA])
f_crit = f.ppf(1-alpha,dfn,dfd)
print("----------------")
print("F-Critical")
print("----------------")
print(f_crit)
print("----------------")
# fit student data [24]
anova = ols('Results~Country',data=df_students).fit()
anova
# Statsmodels allows users to fit statistical models using R-style formulas. Internally, statsmodels uses the patsy package to convert formulas and data to the matrices that are used in model fitting [24].
# <br><br><br> <center> Variance Between Groups <center/>
# The variance between groups describes how much the means of each group vary from the overall mean. Here is its mathematical formula [25]:
# 
# Visualise overall mean and see how it varies in comparasion to the group means
# print overall mean
print("-----------------------")
print("Overall Mean",round(df_students.Results.mean(),2))
# loop over dataframe and retrun mean for all studnets in each country and print
print("-----------------------")
for i in df_students.Country.unique():
print(f'{i} Mean : ',round(df_students[df_students.Country == i].Results.mean(),2))
print("-----------------------")
# dist plot
sns.displot(df_students,x='Results',hue='Country',kind='kde',height=5,aspect=2)
# +
# dist plot
sns.displot(df_students,x='Results',hue='Country',kind='kde',height=5,aspect=2)
# plot vertical line along the mean and dash it
plt.axvline(x=df_students[df_students.Country == 'NI'].Results.mean(),ymin=0,ymax=0.65,linestyle="--",label='NI mean',color='orange')
plt.axvline(x=df_students[df_students.Country == 'FRA'].Results.mean(),ymin=0,ymax=0.81,linestyle="--",label='FRA mean',color='g')
plt.axvline(x=df_students[df_students.Country == 'IRL'].Results.mean(),ymin=0,ymax=0.95,linestyle="--",label='IRL mean',color='steelblue')
# show image
plt.legend()
plt.show()
# +
# dist plot
sns.displot(df_students,x='Results',hue='Country',kind='kde',height=10,aspect=2)
# plot vertical line along the mean and dash it
plt.axvline(x=df_students[df_students.Country == 'NI'].Results.mean(),ymin=0,ymax=0.65,linestyle="--",label='NI mean',color='orange')
plt.axvline(x=df_students[df_students.Country == 'FRA'].Results.mean(),ymin=0,ymax=0.81,linestyle="--",label='FRA mean',color='g')
plt.axvline(x=df_students[df_students.Country == 'IRL'].Results.mean(),ymin=0,ymax=0.95,linestyle="--",label='IRL mean',color='steelblue')
# plot thick red line for overall average mean
plt.axvline(x=df_students.Results.mean(),ymin=0,ymax=0.95,label='overall mean',color='r')
# plot horizontal line along top of mean and dash it FRA
plt.axhline(y=0.032,xmin=0.50,xmax=0.56,color='g',label='Mean Difference FRA',linestyle='-.')
# plot horizontal line along top of mean and dash it IRL
plt.axhline(y=0.0375,xmin=0.332,xmax=0.513,color='steelblue',label='Mean Difference IRL',linestyle='-.')
# plot horizontal line along top of mean and dash it NI
plt.axhline(y=0.026,xmin=0.51,xmax=0.62,color='orange',label='Mean Difference NI',linestyle='-.')
# show image
plt.legend()
plt.show()
# -
# <br><br><br>
# <center> Calculate the SSb <center/>
# +
# Calculate overal mean and store in variable
overal_mean = sum(df_students.Results/len(df_students))
# Calculate sums of squared mean differences for each observation in each group
ssb = []
# for loop over data frame
for i in df_students.Country.unique():
# store group mean in a variable
group_mean = df_students[df_students.Country == i].Results.mean()
# store the squared difference in mean between groups (get rid of negative figures)
sqr_mean_diff = (group_mean-overal_mean)**2
# store the sum of the squared in a variable
sum_sqr = len(df_students[df_students.Country == i])*sqr_mean_diff
# append them
ssb.append(sum_sqr)
# Sum of group variability of each group and store in a variable
SSb = sum(ssb)
print("----------------------")
print("Sum of Squares Between")
print("----------------------")
print(SSb)
print("----------------------")
# -
# Now we can find the Mean Square Between MSb as we have the SSb. SSb/(K-1)
# <center> Calculate the MSb <center/>
# Calculate MSb (Explained Variance)
# K is number of observations
k = len(df_students.Country.unique())
MSb = SSb/(k-1)
print("----------------------")
print("Mean Square Between")
print("----------------------")
print(MSb)
print("----------------------")
# # Difference in Mean Differences
#
#
# <center> Mean Difference Between IRL, FRA and NI <center/>
# The formula for variance within groups is:
# 
# The formula to calculate the sum of the squared differences of each observation and group mean (SSw). Then divid by the degrees of freedom within each group (N-K number of groups) is below:
# <br><br><br>
# +
# Display Variance of means
sns.catplot(y="Country", x="Results", data=df_students,height=5,aspect=2)
plt.axvline(x=df_students.Results.mean(),color='r')
plt.axvline(x=df_students[df_students.Country == 'FRA'].Results.mean(),color='g',linestyle='-.')
plt.axvline(x=df_students[df_students.Country == 'IRL'].Results.mean(),color='steelblue',linestyle='-.')
plt.axvline(x=df_students[df_students.Country == 'NI'].Results.mean(),color='orange',linestyle='-.')
plt.show()
# +
# Calculate sum of the squared differences between the observations and its group variance for each group
sum_sqr_diff = []
# for loop over dataframe
print("-----------------------")
print("RESULTS")
print("-----------------------")
for i in df_students.Country.unique():
# put group mean in a variable
group_mean = df_students[df_students.Country == i].Results.mean()
# put sum squared in a variable
sum_sqr = sum(list(map(lambda x: (x-group_mean)**2, df_students[df_students.Country == i].Results)))
# append sum_squared
sum_sqr_diff.append(sum_sqr)
print(i,": "+str(sum_sqr))
# Sum them together and put in variable (SSw= sum of squares within )
print("-----------------------")
SSw = sum(sum_sqr_diff)
print("SSw: " + str(SSw))
print("-----------------------")
# -
# <center>Mean Sum of Squares Within (MSw) <center/>
# Calculate MSw (Unexplained Variance) [26]
N = len(df_students)
MSw = SSw/(N-k)
print("MSw: ",MSw)
# <center>ANOVA Table<center/>
# +
# SSb= 4497.354500000003
# SSw= 1808.4067499999996
# MSw= 15.456467948717945
# MSb= 2248.6772500000015
# -
# set anova table variable to equal data from above calculations
anova_table = pd.DataFrame({"Variation Source": ["Between Groups","Erro Residual","Total"], # rows
"Sums of Squares":[round(SSb,2),round(SSw,2),round(SSb+SSw,2)], # columns
"Degrees of Freedom":[k-1,N-k,N-1], # columns
"Mean Squares":[round(MSb,2),round(MSw,2),""]}) # columns
anova_table.set_index("Variation Source",inplace=True) # index
anova_table
# <center>F-Statistic<center/>
# F-tests are named after its test statistic, F, which was named in honor of <NAME>. The F-statistic is simply a ratio of two variances. Variances are a measure of dispersion, or how far the data are scattered from the mean. Larger values represent greater dispersion [28].
#
# F-statistics are based on the ratio of mean squares. The term “mean squares” may sound confusing but it is simply an estimate of population variance that accounts for the degrees of freedom (DF) used to calculate that estimate.
# [27].
#
# **F = variation between sample means / variation within the samples**
#
#
# use F-stat formula above
f_stat = MSb/MSw
f_stat
# <center>P-Value in F-Test<center/>
# +
# store the data variables
rv = f(dfn=k-1, dfd=N-k)
x = np.linspace(rv.ppf(0.0001),rv.ppf(0.9999),100)
y = rv.pdf(x)
# plot title and axvline
plt.title("F-distribution for K-1=2 and N-K=117 ")
plt.xlim(0,10)
plt.axvline(x=f_crit,color='r',ymax=0.9,linestyle='-.',label='F-critic')
# plot information
plt.ylabel("P-values")
plt.xlabel("F-values")
plt.legend()
plt.plot(x,y, 'b--')
# +
#How much we are far from the
plt.figure(figsize=(18,4))
from scipy.stats import f, norm
rv = f(dfn=k-1, dfd=N-k)
x = np.linspace(rv.ppf(0.0001),rv.ppf(0.9999),100)
y = rv.pdf(x)
plt.title("F-distribution for K-1=2 and N-K=117 ")
plt.xlim(0,180)
plt.axvline(x=f_crit,color='r',ymax=0.90,linestyle='-.',label='F-critic')
plt.axvline(x=f_stat,color='b',ymax=0.90,linestyle='-.',label='F-statistic')
plt.ylabel("P-values")
plt.xlabel("F-values")
plt.legend()
plt.plot(x,y, 'b--')
# -
# Find the P-value
p_value = f.sf(f_stat, dfn, dfd) #find p-value of F test statistic
p_value
# Reject the null Hypothesis
if (f_stat > f_crit) & (p_value<alpha):
print(f"We reject H0 because f-statisitic {f_stat} > f-critical {f_crit} and p-value {p_value} < alpha {alpha}",
"\nWe have significant evidence at 0.05 level the student groups are belong to different populations.")
# add in new values to ANOVA table
anova_table["F"] =[f_stat,"",""]
anova_table['P-Value'] = [str(p_value),"",""]
anova_table
# # H0: is REJECTED
#
# We reject H0 because:
# * **F-Statistic 145.48 > **F-Critical 3.07** and:
# * **P-Value 1.850026150119184e-32 < alpha 0.05**.
#
# Therefore we have significcant evidence at the alpha 0.05 figure that the spelling results of students from IRL, NI and FRA groups belong to different populations.
# # References
#
# [1]. SPSS Tutorials - SPSS Shapiro-Wilk Test – Quick Tutorial with Example [online] available: https://www.sps s-tutorials.com/spss-shapiro-wilk-test-for-normality/
#
# [2]. Docs.scipy [online] available: https://docs.scipy.org/doc/scipy/reference/stats.html
#
# [3]. Quasi-Monte Carlo[online] available: https://artowen.su.domains/reports/siggraph03.pdf
#
# [4]. Methods for Normality Test with Application in Python [online] available: https://towardsdatascience.com/methods-for-normality-test-with-application-in-python-bb91b49ed0f5
#
# [5]. Statistical tests for normality [online] available: https://campus.datacamp.com/courses/introduction-to-portfolio-risk-management-in-python/univariate-investment-risk-and-returns?ex=12
#
# [6]. Statistical-guide [online] available: https://statistics.laerd.com/statistical-guides/one-way-anova-statistical-guide.php
#
# [7]. One-way-anova [online] available:
# https://www.scribbr.com/statistics/one-way-anova/
#
# [8]. Checking_ANOVA_assumptions [online] available: https://yieldingresults.org/wp-content/uploads/2015/03/Checking_ANOVA_assumptions.html
#
# [9]. One-way-anova-using-spss-statistics [online] available: https://statistics.laerd.com/spss-tutorials/one-way-anova-using-spss-statistics.php
#
# [10]. Statology [online] available: https://www.statology.org/two-way-anova/
#
# [11]. Pythonfordatascience [online] available: https://www.pythonfordatascience.org/factorial-anova-python/
#
# [12]. theanalysisfactor [online] available: https://www.theanalysisfactor.com/checking-normality-anova-model/
#
# [13]. <NAME>., 2017. Understanding one-way ANOVA using conceptual figures. Korean journal of anesthesiology, 70(1), p.22.
#
# [14]. <NAME>. and <NAME>., 2009. One-way anova. In R through excel (pp. 165-191). Springer, New York, NY.
#
# [15]. <NAME>. and <NAME>., 1987. The effects of violations of independence assumptions in the one-way ANOVA. The American Statistician, 41(2), pp.123-129.
#
# [16]. <NAME>. and <NAME>., 2020. Statistical significance: p value, 0.05 threshold, and applications to radiomics—reasons for a conservative approach. European radiology experimental, 4(1), pp.1-8.
#
# [17]. <NAME>. and <NAME>., 2011. Bartlett's Test. [online] available: https://www.researchgate.net/profile/Dr-Hossein-Arsham/publication/344731676_BARTLETT'S_TEST/links/5f8ce5cb299bf1b53e324a18/BARTLETTS-TEST.pdf
#
# [18]. The Assumption of Homogeneity of Variance [online] available https://www.statisticssolutions.com/the-assumption-of-homogeneity-of-variance/
#
# [19]. Levene’s Test [online] available: https://www.real-statistics.com/one-way-analysis-of-variance-anova/homogeneity-variances/levenes-test/
#
# [20]. How to Perform Bartlett’s Test in Python (Step-by-Step) [online] available: https://www.statology.org/bartletts-test-python/
#
# [21]. Levene’s test [online] available: https://www.geeksforgeeks.org/levenes-test/
#
# [23]. HYPOTHESIS TESTING [online] available:
# https://www.westga.edu/academics/research/vrc/assets/docs/HypothesisTesting_HANDOUT.pdf
#
# [24]. Formulas: Fitting models using R-style formulas [online] available:
# https://www.statsmodels.org/dev/examples/notebooks/generated/formulas.html
#
# [25]. Sum of squares between-groups [online] available: http://web.pdx.edu/~newsomj/uvclass/ho_ANOVA.pdf
#
# [26]. Oneway Analysis of Variance[online] available: https://www.lboro.ac.uk/media/media/schoolanddepartments/mlsc/downloads/1_5_OnewayANOVA.pdf
#
# [27]. Understanding Analysis of Variance (ANOVA) and the F-test [online] available: https://blog.minitab.com/en/adventures-in-statistics-2/understanding-analysis-of-variance-anova-and-the-f-test
#
# [28]. Statistics How To, F Statistic / F Value: Simple Definition and Interpretation [online] available: https://www.statisticshowto.com/probability-and-statistics/f-statistic-value-test/
#
# [29].Critical Value and P V Value (SCIPY) with Python [online] available: https://www.programmerall.com/article/91001524204/
#
|
Scipy-stats.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
import numpy as np
# set up orthographic map projection with
# perspective of satellite looking down at 50N, 100W.
# use low resolution coastlines.
map = Basemap(projection='ortho',lat_0=45,lon_0=-100,resolution='l')
# draw coastlines, country boundaries, fill continents.
map.drawcoastlines(linewidth=0.25)
map.drawcountries(linewidth=0.25)
map.fillcontinents(color='coral',lake_color='aqua')
# draw the edge of the map projection region (the projection limb)
map.drawmapboundary(fill_color='aqua')
# draw lat/lon grid lines every 30 degrees.
map.drawmeridians(np.arange(0,360,30))
map.drawparallels(np.arange(-90,90,30))
# make up some data on a regular lat/lon grid.
nlats = 73; nlons = 145; delta = 2.*np.pi/(nlons-1)
lats = (0.5*np.pi-delta*np.indices((nlats,nlons))[0,:,:])
lons = (delta*np.indices((nlats,nlons))[1,:,:])
wave = 0.75*(np.sin(2.*lats)**8*np.cos(4.*lons))
mean = 0.5*np.cos(2.*lats)*((np.sin(2.*lats))**2 + 2.)
# compute native map projection coordinates of lat/lon grid.
x, y = map(lons*180./np.pi, lats*180./np.pi)
# contour data over the map.
cs = map.contour(x,y,wave+mean,15,linewidths=1.5)
plt.title('contour lines over filled continent background')
plt.show()
|
pyfund/8 - Modulos Python para analise de dados/Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="Mm9l9wSh1dke" colab_type="text"
# <h1><center>Hyperparameter optimization in machine learning models</center></h1><br>
#
# Machine learning involves predicting and classifying data and to do so you employ various machine learning models according to the dataset. Machine learning models are parameterized so that their behavior can be tuned for a given problem. These models can have many parameters and finding the best combination of parameters can be treated as a search problem. But this very term called parameter may appear unfamiliar to you if you are new to applied machine learning. But don’t worry! You will get to know about it in the very first place of this blog and you will also discover what is the difference between a parameter and a hyperparameter of a machine learning model. This blog consists of following sections:<br>
# - What are a parameter and a hyperparameter in a machine learning model?
# - Why hyperparameter optimization / tuning is vital in order to enhance your model’s performance?
# - Two simple strategies to optimize / tune the hyperparameters
# - A simple case study in Python with the two strategies
#
# Let’s straight jump into the first section!
#
# <h3>What is a parameter in a machine learning learning model?</h3>
# A model parameter is a configuration variable that is internal to the model and whose value can be estimated from the given data.
# <ul>
# <li> They are required by the model when making predictions.
# <li>Their values define the skill of the model on your problem.
# <li>They are estimated or learned from data.
# <li>They are often not set manually by the practitioner.
# <li>They are often saved as part of the learned model.
# </ul>
# So your main take away from the above points should be parameters are key to machine learning algorithms. Also, they are the part of the model that is learned from historical training data. Let’s dig it a bit deeper.
# Think of the function parameters that you use while programming in general. You may pass a parameter to a function. In this case, a parameter is a function argument that could have one of a range of values. In machine learning, the specific model you are using is the function and requires parameters in order to make a prediction on new data.
# Whether a model has a fixed or variable number of parameters determines whether it may be referred to as <i>“parametric”</i> or <i>“nonparametric“</i>.
# <br><br>
# Some examples of model parameters include:
# <ul>
# <li> The weights in an artificial neural network.
# <li>The support vectors in a support vector machine.
# <li>The coefficients in a linear regression or logistic regression.
# </ul>
# <br><h3>
# What is a hyperparameter in a machine learning learning model?</h3>
# A model hyperparameter is a configuration that is external to the model and whose value cannot be estimated from data.
# <ul>
# <li>They are often used in processes to help estimate model parameters.
# <li>They are often specified by the practitioner.
# <li>They can often be set using heuristics.
# <li>They are often tuned for a given predictive modeling problem.
# </ul>
#
# You cannot know the best value for a model hyperparameter on a given problem. You may use rules of thumb, copy values used on other problems, or search for the best value by trial and error.
# When a machine learning algorithm is tuned for a specific problem then essentially you are tuning the hyperparameters of the model in order to discover the parameters of the model that result in the most skillful predictions.
# <br><br>
# According to a very popular book called “Applied Predictive Modelling” -
# “<i>Many models have important parameters which cannot be directly estimated from the data. For example, in the K-nearest neighbor classification model … This type of model parameter is referred to as a tuning parameter because there is no analytical formula available to calculate an appropriate value.</i>”
# <br><br>
# Model hyperparameters are often referred to as model parameters which can make things confusing. A good rule of thumb to overcome this confusion is as follows:
# “<i>If you have to specify a model parameter manually then it is probably a model hyperparameter. </i>”
# Some examples of model hyperparameters include:
# <ul>
# <li>The learning rate for training a neural network.
# <li>The C and sigma hyperparameters for support vector machines.
# <li>The k in k-nearest neighbors.
# </ul>
#
# In the next section, you will discover the importance of the right set of hyperparameter values in a machine learning model.
#
# <h3>Importance of the right set of hyperparameter values in a machine learning model:</h3>
#
# The best way to think about hyperparameters is like the settings of an algorithm that can be adjusted to optimize performance, just as you might turn the knobs of an AM radio to get a clear signal. When creating a machine learning model, you'll be presented with design choices as to how to define your model architecture. Often times, you don't immediately know what the optimal model architecture should be for a given model, and thus you'd like to be able to explore a range of possibilities. In a true machine learning fashion, you’ll ideally ask the machine to perform this exploration and select the optimal model architecture automatically.
#
# You will see in the case study section how the right choice of hyperparameter values affect the performance of a machine learning model. In this context, choosing the right set of values is typically known as “<i>Hyperparameter optimization</i>” or “<i>Hyperparameter tuning</i>”.
#
# <h3>Two simple strategies to optimize / tune the hyperparameters:</h3>
# Models can have many hyperparameters and finding the best combination of parameters can be treated as a search problem.
#
# Although there are a number of hyperparameter optimization / tuning algorithms now, but this post discusses two simple strategies: 1. grid search and 2. Random Search.
#
# <h3>Grid searching of hyperparameters:</h3>
# Grid search is an approach to hyperparameter tuning that will methodically build and evaluate a model for each combination of algorithm parameters specified in a grid.
#
# Let’s consider the following example:
#
# Suppose, a machine learning model X takes hyperparameters a<sub>1</sub>, a<sub>2</sub> and a<sub>3</sub>. In <i>grid searching</i>, you first define the range of values for each of the hyperparameters a<sub>1</sub>, a<sub>2</sub> and a<sub>3</sub>. You can think of this as an array of values for each of the hyperparameters. Now the <i>grid search</i> technique will construct many versions of X with all the possible combinations of hyperparameter (a<sub>1</sub>, a<sub>2</sub> and a<sub>3</sub>) values that you defined in the first place. This range of hyperparameter values is referred to as <b><i>grid</i></b>.
# <br><br>
# Suppose, you defined the grid as:<br>
# a<sub>1</sub> = [0,1,2,3,4,5]<br>
# a<sub>2</sub> = [10,20,30,40,5,60]<br>
# a<sub>3</sub> = [105,105,110,115,120,125]
#
# <br><br>Note that, the array of values of that you are defining for the hyperparameters has to be legitimate in a sense that you cannot supply <i>Floating</i> type values to the array if the hyperparameter only takes <i>Integer</i> values.
#
# <br><br>Now, <i>grid search</i> will begin its process of constructing several versions of X with the grid that you just defined.
#
# <br><br>It will start with the combination of [0,10,105] and it will end with [5,60,125]. It will go through all the intermediate combinations between these two which makes <i>grid search computationally very expensive</i>.
#
# Let’s take a look at the other search technique Random search:
#
#
# <h3>Random searching of hyperparameters:</h3>
# The idea of random searching of hyperparameters was proposed by <NAME> & <NAME>. You can check the original paper [here](http://www.jmlr.org/papers/volume13/bergstra12a/bergstra12a.pdf).
#
# <br><br>Random search differs from grid search. In that you longer provide a discrete set of values to explore for each hyperparameter; rather, you provide a statistical distribution for each hyperparameter from which values may be randomly sampled.
#
# <br><br>Before going any further, let’s understand what distribution and sampling mean:
#
# <br><br>In Statistics, by distribution, it is essentially meant an arrangement of values of a variable showing their observed or theoretical frequency of occurrence.
#
# <br><br>On the other hand, Sampling is a term used in statistics. It is the process of choosing a representative sample from a target population and collecting data from that sample in order to understand something about the population as a whole.
#
# <br><br>Now let's again get back to the concept of random <i>search</i>.
#
# <br><br>You’ll define a sampling distribution for each hyperparameter. You can also define how many iterations you’d like to build when searching for the optimal model. For each iteration, the hyperparameter values of the model will be set by sampling the defined distributions.
# One of the main theoretical backings to motivate the use of random search in place of grid search is the fact that for most cases, hyperparameters are not equally important. According to the original paper:
#
# <br><br>“<i>….for most data sets only a few of the hyper-parameters really matter, but that different hyper-parameters are important on different data sets. This phenomenon makes grid search a poor choice for configuring algorithms for new datasets</i>.”
#
# <br><br>In the following figure, we're searching over a hyperparameter space where the one hyperparameter has significantly more influence on optimizing the model score - the distributions shown on each axis represent the model's score. In each case, we're evaluating nine different models. The grid search strategy blatantly misses the optimal model and spends redundant time exploring the unimportant parameter. During this grid search, we isolated each hyperparameter and searched for the best possible value while holding all other hyperparameters constant. For cases where the hyperparameter being studied has little effect on the resulting model score, this results in wasted effort. Conversely, the random search has much improved exploratory power and can focus on finding the optimal value for the important hyperparameter.
# <br>
# 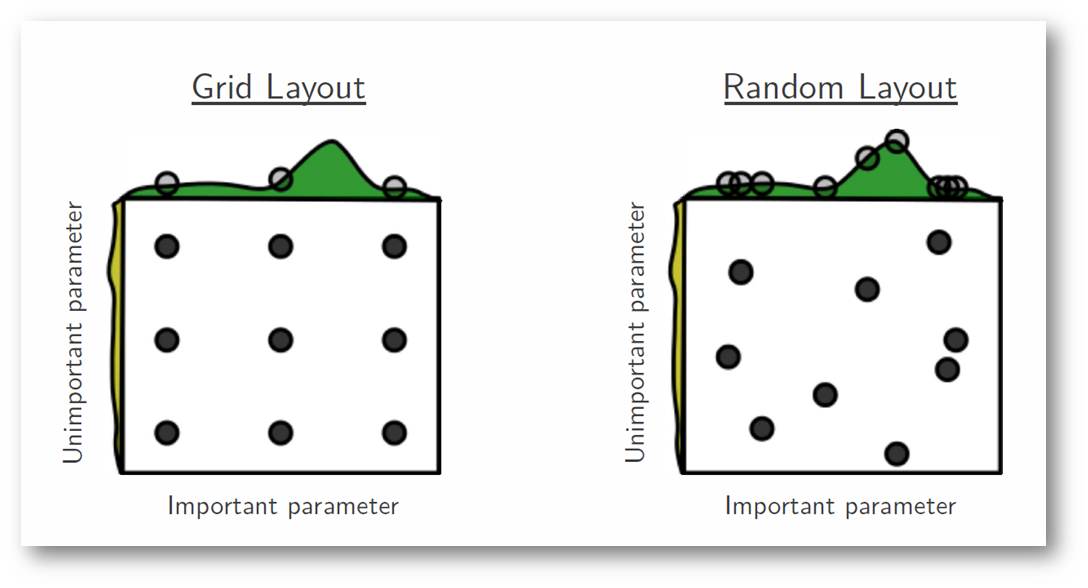
#
# <br>In the following sections, you will see <i>grid search</i> and <i>random search</i> in action with Python. You will also be able to decide which is better in terms of the effectiveness and efficiency.
#
# <h3>Case study in Python:</h3>
#
# Hyperparameter tuning is a final step in the process of applied machine learning before presenting results.
#
# <br>You will use the Pima Indian diabetes dataset. The dataset corresponds to a <i>classification</i> problem on which you need to make predictions on the basis of whether a person is to suffer diabetes given the 8 features in the dataset. You can find the complete description of the dataset <a href = "https://www.kaggle.com/uciml/pima-indians-diabetes-database" target = "_blank">here</a>.
#
# <br>There are a total of 768 observations in the dataset. Your first task is to load the dataset so that you can proceed. But before that let's import the dependencies you are gonna need.
#
#
# + id="m3dG8tS5KEd5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 37} outputId="4dda28f8-b20d-4f93-f1d8-43c17c95eec8"
# Dependencies
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
# + [markdown] id="KpOOBrat_5iw" colab_type="text"
# Now that the depedencies are imported, let's load Pima Indians dataset into a Dataframe object with the famous Pandas library.
# + id="J7QUYQ8xCU-G" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 17} outputId="232dd49b-f13f-4582-a779-0801951f31ca"
data = pd.read_csv("diabetes.csv") # Make sure the .csv file and the notebook are residing on the same directory otherwise supply an absolute path of the .csv file
# + [markdown] id="emLYRbUqBKvD" colab_type="text"
# The dataset is successfully loaded into the Dataframe object <i>data</i>. Now, let's take a look at the data.
# + id="ZYhWvSajBUMG" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="4e99c562-3471-4bfd-a001-a2f13e1d9106"
data.head()
# + [markdown] id="IMIJVoIWCfmx" colab_type="text"
# So you can 8 different features labeled into the outcomes of 1 and 0 where 1 stands for the observation has diabetes and 0 denotes the observation does not have diabetes. The dataset is known to have missing values. Specifically, there are missing observations for some columns that are marked as a zero value.
# We can corroborate this by the definition of those columns and the domain knowledge that a zero value is invalid for those measures, e.g. a zero for body mass index or blood pressure is invalid.
#
# (Missing value creates a lot of problems when you try to build a machine learning model. In this case, you will use a Logistic Regression classifier for predicting the patients having diabetes or not. Now, Logistic Regression cannot handle the problems of missing values. )
#
# (If you want a quick refresher on Logistic Regression you can refer [here]("https://www.analyticsvidhya.com/blog/2015/10/basics-logistic-regression/").)
#
#
# Let's get some statistics about the data with Pandas' <i>describe()</i> utility.
# + id="cugDDfSGDXJ9" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 297} outputId="b28824ba-ff96-4230-cd0c-0aafe6dde59c"
data.describe()
# + [markdown] id="a2rROKC2DnEl" colab_type="text"
# This is useful.
#
# We can see that there are columns that have a minimum value of zero (0). On some columns, a value of zero does not make sense and indicates an invalid or missing value.
#
# Specifically, the following columns have an invalid zero minimum value:
#
# - Plasma glucose concentration
# - Diastolic blood pressure
# - Triceps skinfold thickness
# - 2-Hour serum insulin
# - Body mass index
#
# Now you need to identify and mark values as missing. Let’s confirm this by looking at the raw data, the example prints the first 20 rows of data.
# + id="BxNdJX_9D9c6" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 669} outputId="2aa757ac-6f1a-45d7-c7f1-9594051f2d75"
data.head(20)
# + [markdown] id="EzaKGLl7HYVM" colab_type="text"
# You are able to see 0 in several columns right?
#
# You can get a count of the number of missing values in each of these columns. You can do this by marking all of the values in the subset of the DataFrame you are interested in that have zero values as True. you can then count the number of true values in each column. For this, you will have to reimport the data without the column names.
# + id="1D_U2SA2HrHa" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 119} outputId="97c42054-bf32-4fcf-d0dc-d0ff7255617e"
data = pd.read_csv("https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv",header=None)
print((data[[1,2,3,4,5]] == 0).sum())
# + [markdown] id="jcUzTwAsJibb" colab_type="text"
# You can see that columns 1,2 and 5 have just a few zero values, whereas columns 3 and 4 show a lot more, nearly half of the rows. Column 0 has several missing values although but that is natural. Column 8 denotes the target variable so, '0's in it is natural.
#
# This highlights that different “missing value” strategies may be needed for different columns, e.g. to ensure that there are still a sufficient number of records left to train a predictive model.
#
# In Python, specifically Pandas, NumPy and Scikit-Learn, you mark missing values as NaN.
#
# Values with a NaN value are ignored from operations like sum, count, etc.
#
# You can mark values as NaN easily with the Pandas DataFrame by using the replace() function on a subset of the columns you are interested in.
#
# After you have marked the missing values, you can use the isnull() function to mark all of the NaN values in the dataset as True and get a count of the missing values for each column.
# + id="NBgFyTm6LPxL" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 187} outputId="e33006de-42f4-4084-80dd-319029aeed72"
# Mark zero values as missing or NaN
data[[1,2,3,4,5]] = data[[1,2,3,4,5]].replace(0, np.NaN)
# Count the number of NaN values in each column
print(data.isnull().sum())
# + [markdown] id="Ds1xbgmILlyL" colab_type="text"
# You can see that the columns 1:5 have the same number of missing values as zero values identified above. This is a sign that you have marked the identified missing values correctly.
#
# This is a useful summary. But you'd like to look at the actual data though, to confirm that you have not fooled yourselves.
#
# Below is the same example, except you print the first 5 rows of data.
# + id="hqbxzeG4MF96" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="b589b8d4-4708-4a68-b61c-0d9a7c449fca"
data.head()
# + [markdown] id="SctCA6siMOlP" colab_type="text"
# It is clear from the raw data that marking the missing values had the intended effect. Now, you will impute the missing values. Imputing refers to using a model to replace missing values. Although there are several solutions for imputing missing values, you will use mean imputation which means replacing the missing values in a column with the mean of that particular column. Let's do this with Pandas' fillna() utility.
# + id="tJxr8YeUNFbv" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 187} outputId="9bb380ef-a8c7-4060-8689-545e476a6cc5"
# Fill missing values with mean column values
data.fillna(data.mean(), inplace=True)
# Count the number of NaN values in each column
print(data.isnull().sum())
# + [markdown] id="OxS-o2DWNMgK" colab_type="text"
# Cheers! You have now handled the missing value problem. Now let's use this data to build a Logistic Regression model using scikit-learn.
#
# First, you will see the model with some random hyperparameter values. Then you will build two other Logistic Regression models with two different strategies - Grid search and Random search.
# + id="y98ByclGNzl8" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 37} outputId="f2b57c71-35fe-4aaf-cec6-b34d0b234b1e"
# Split dataset into inputs and outputs
values = data.values
X = values[:,0:8]
y = values[:,8]
# + id="N1PE1xG0NL2p" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 37} outputId="9963679c-3a2f-4193-d4e2-5e7fe0ccdb85"
# Initiate the LR model with random hyperparameters
lr = LogisticRegression(penalty='l1',dual=False,max_iter=110)
# + [markdown] id="CMQ4vu-kcGC7" colab_type="text"
# You have created the Logistic Regression model with some random hyperparameter values. The hyperparameters that you used are:
#
# - penalty : Used to specify the norm used in the penalization (regularization).
# - dual : Dual or primal formulation. Dual formulation is only implemented for l2 penalty with liblinear solver. Prefer dual=False when n_samples > n_features.
# - max_iter : Maximum number of iterations taken to converge.
#
# Later in the case study, you will optimize / tune these hyperparameters so see the change in the results.
# + id="aCATaREfc7fx" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 85} outputId="95655950-a482-43cb-e821-82ec7bb28d47"
# Pass data to the LR model
lr.fit(X,y)
# + [markdown] id="LHEaVhWNdf0F" colab_type="text"
# It's time to check the accuracy score.
# + id="yIQAU1QhdjKl" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="acb22e4f-5fec-490e-8f68-dbef2848bdf2"
lr.score(X,y)
# + [markdown] id="V0MReWlwdqy1" colab_type="text"
# In the above step, you applied your LR model to the same data and evaluated its score. But there is always a need to validate the stability of your machine learning model. You just can’t fit the model to your training data and hope it would accurately work for the real data it has never seen before. You need some kind of assurance that your model has got most of the patterns from the data correct.
#
# Well, Cross-validation is there for rescue. I will not go into the details of it as it is out of the scope of this blog. But [this post](https://towardsdatascience.com/cross-validation-in-machine-learning-72924a69872f) does a very fine job.
# + id="WsLC5IA0eh1C" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 37} outputId="a398d155-b424-45c0-df7a-16f8725e9739"
# You will need the following dependencies for applying Cross validation and evaluating the cross-validated score
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
# + id="IVeN9Q0Reyll" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 37} outputId="859dfec8-c6f8-4ffe-cf48-33955c9d1413"
# Build the k-fold cross-validator
kfold = KFold(n_splits=3, random_state=7)
# + [markdown] id="Vr6FuZMgfJPK" colab_type="text"
# You supplied n_splits as 3, which essentially makes it a 3-fold cross-validation. You also supplied random_state as 7. This is just to reproduce the results. You could have supplied any integer value as well. Now, let's apply this.
# + id="JwIdjnu-ff0E" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="4c7b72ef-42a9-4d9d-f4ad-d9bfe86b4579"
result = cross_val_score(lr, X, y, cv=kfold, scoring='accuracy')
print(result.mean())
# + [markdown] id="LpiBngxMfq-v" colab_type="text"
# You can see there's a slight decrease in the score. Anyway, you can do better with hyperparameter tuning / optimization.
#
# Let's build another LR model, but this time its hyperparameter will be tuned. You will first do this grid search.
#
# Let's first import the dependencies you will need. Scikit-learn provides a utility called GridSearchCV for this.
#
# + id="YNPwvG2bih7X" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 37} outputId="b40e64cf-da1c-43d0-fa2c-d48d82868b09"
from sklearn.model_selection import GridSearchCV
# + [markdown] id="r1BQAKzKikpY" colab_type="text"
# Let's define the grid values of the hyperparameters that you used above.
# + id="Ji0gj2NViplU" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 37} outputId="545cb729-beac-4afe-9a65-709ea8b14519"
dual=[True,False]
max_iter=[100,110,120,130,140]
param_grid = dict(dual=dual,max_iter=max_iter)
# + [markdown] id="lgm36qbMjA2h" colab_type="text"
# You have defined the grid. Let's run the grid search over them and see the results with execution time.
# + id="-cmhYe_XjTba" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="d129f990-e1b1-4378-9535-0f6874ff3389"
import time
lr = LogisticRegression(penalty='l2')
grid = GridSearchCV(estimator=lr, param_grid=param_grid, cv = 3, n_jobs=-1)
start_time = time.time()
grid_result = grid.fit(X, y)
# Summarize results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
print("Execution time: " + str((time.time() - start_time)) + ' ms')
# + [markdown] id="yqwtvSvolbQH" colab_type="text"
# You can define larger grid of hyperparameter as well and apply grid search.
# + id="pJIE_abtlZpj" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 37} outputId="a75ae47d-024b-43a5-ef11-6e45753aa58b"
dual=[True,False]
max_iter=[100,110,120,130,140]
C = [1.0,1.5,2.0,2.5]
param_grid = dict(dual=dual,max_iter=max_iter,C=C)
# + id="pJzPF7qumjEK" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="e8f95529-c93c-4a2c-cfe7-a6d9600ccf71"
lr = LogisticRegression(penalty='l2')
grid = GridSearchCV(estimator=lr, param_grid=param_grid, cv = 3, n_jobs=-1)
start_time = time.time()
grid_result = grid.fit(X, y)
# Summarize results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
print("Execution time: " + str((time.time() - start_time)) + ' ms')
# + [markdown] id="pEhvPmi2n2vi" colab_type="text"
# You can see an increase in the accuracy score but there is a sufficient amount of increase in the execution time as well. The larger the grid the more execution time.
#
# Let's run everything again but this time with random search. Scikit-learn provides RandomSearchCV to do that. As usual, you will have to import the necessary dependencies for that.
# + id="35J5Dg6qpcEW" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 37} outputId="f5bc7aaf-2897-40a2-83ec-d5b7b22b913c"
from sklearn.model_selection import RandomizedSearchCV
# + id="h_9o6xtJpnfX" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="cf12067d-5aef-42a4-9a44-f4a0ce5a6979"
random = RandomizedSearchCV(estimator=lr, param_distributions=param_grid, cv = 3, n_jobs=-1)
start_time = time.time()
random_result = random.fit(X, y)
# Summarize results
print("Best: %f using %s" % (random_result.best_score_, random_result.best_params_))
print("Execution time: " + str((time.time() - start_time)) + ' ms')
# + [markdown] id="DBWaPj77qQbV" colab_type="text"
# Woah! Random search yielded same accuracy but in a much lesser time.
#
# That is all for the case study part. Now, let's wrap things up!
# + [markdown] id="R74Je7-QqeNv" colab_type="text"
# <h3>Conclusion and further reading:</h3>
# In this tutorial, you learned about parameters and hyperparameters of a machine learning model and their differences as well. You also got to know about what role hyperparameter optimization plays in building efficient machine learning models. You built a simple Logistic Regression classifier in Python with the help of scikit-learn.
#
# You tuned the hyperparameters with grid search and random search and saw which one performs better.
#
# Besides, you saw small data preprocessing steps (like handling missing values) that are required before you feed your data into the machine learning model. You covered Cross-validation as well.
#
# That is a lot to take in and all of them are equally important in your data science journey. I will leave you with some further readings that you can do.
#
# <b>Further readings: </b>
#
# - [Problems in hyperparameter optimization](https://blog.sigopt.com/posts/common-problems-in-hyperparameter-optimization)
# - [Hyperparameter optimization with soft computing techniques](https://papers.nips.cc/paper/4443-algorithms-for-hyper-parameter-optimization.pdf)
#
# For the ones who are a bit more advanced, I would highly recommend reading this paper for effectively optimizing the hyperparameters of neural networks. [link](https://arxiv.org/abs/1803.09820)
|
DataCamp Hyperparameter Optimization blog/Hyperparameter_optimization_in_machine_learning_models.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os.path as op
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
plt.style.use('ggplot')
import bids as sb
data_path = op.join(sb.__path__[0], 'data')
ortho_x, ortho_y, ortho_n = sb.transform_data(op.join(data_path, 'ortho.csv'))
para_x, para_y, para_n = sb.transform_data(op.join(data_path, 'para.csv'))
model = sb.Model()
ortho_fit = model.fit(ortho_x, ortho_y)
para_fit = model.fit(para_x, para_y)
ortho_fit.params
para_fit.params
# +
fig, ax = plt.subplots(1)
x_predict = np.linspace(0, 1, 100)
for x, y, n in zip(ortho_x, ortho_y, ortho_n):
ax.plot(x, y, 'bo', markersize=n)
ax.plot(x_predict, ortho_fit.predict(x_predict), 'b')
for x,y,n in zip(para_x, para_y, para_n):
ax.plot(x, y, 'go', markersize=n)
ax.plot(x_predict, para_fit.predict(x_predict), 'g')
ax.set_xlabel('Contrast in interval 1')
ax.set_ylabel("Proportion answers '1'")
ax.set_ylim([-0.1, 1.1])
ax.set_xlim([-0.1, 1.1])
fig.set_size_inches([8,8])
# -
|
scripts/Figure1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.9.1 64-bit (''mypython'': conda)'
# language: python
# name: python3
# ---
# # Targets with low accuracy
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
pd.options.display.float_format = '{:.3f}'.format
plt.rcParams["figure.dpi"] = 150
sns.set(style='darkgrid')
from IPython.display import display
import warnings
warnings.simplefilter('ignore', UserWarning)
from pathlib import Path
plt.rcParams['font.family'] = 'Times New Roman'
plt.rcParams['mathtext.fontset'] = 'stix'
plt.rcParams["font.size"] = 15
plt.rcParams['figure.figsize'] = (6, 4)
from scipy import stats
data_dir = Path('../../../../../data/')
dataset_dir = data_dir / 'out' / 'dataset'
subset_name = 'target_subset_' + Path('.').resolve().parent.name
score_dir = dataset_dir / 'score' / 'subsets' / subset_name
assert score_dir.exists()
fig_dir = score_dir / 'fig' / 'accuracy'
fig_dir.mkdir(parents=True, exist_ok=True)
target_list = data_dir / 'interim' / f'{subset_name}.csv'
assert target_list.exists()
label_path = score_dir / 'label.csv'
label_df = pd.read_csv(label_path, index_col=0)
af2_resolved_path = score_dir / 'af2_confidence_resolved.csv.gz'
af2_resolved_df = pd.read_csv(af2_resolved_path, index_col=0)
label_df = pd.merge(label_df, af2_resolved_df, on=['Target', 'Model'])
target_df = pd.read_csv(target_list, index_col=0)
df = pd.merge(label_df, target_df, left_on='Target', right_on='id', how='left')
df
# ## Targets with low maximum GDT_TS
label = 'GDT_TS'
target_num = 20
gdtts_max_df = df.groupby('Target').apply(lambda x: x.loc[x[label].idxmax()]).sort_values(label)
display(gdtts_max_df.head(target_num))
sample_targets_low_max_gdtts = gdtts_max_df.head(target_num).index.to_list()
data = df.groupby('Target').filter(lambda x: x.name in sample_targets_low_max_gdtts)
method = 'pLDDT_resolved'
label = 'GDT_TS'
x, y = label, method
sns.relplot(data=data, x=x, y=y, kind='scatter', col='Target', col_wrap=5, col_order=sample_targets_low_max_gdtts, s=15)
data = df.groupby('Target').filter(lambda x: x.name in sample_targets_low_max_gdtts)
method = 'pTM_resolved'
label = 'GDT_TS'
x, y = label, method
sns.relplot(data=data, x=x, y=y, kind='scatter', col='Target', col_wrap=5, col_order=sample_targets_low_max_gdtts, s=15)
# ## Targets with a low GDT_TS model
label = 'GDT_TS'
target_num = 20
gdtts_min_df = df.groupby('Target').apply(lambda x: x.loc[x[label].idxmin()]).sort_values(label)
display(gdtts_min_df.head(target_num))
sample_targets_with_low_gdtts = gdtts_min_df.head(target_num).index.to_list()
set(sample_targets_with_low_gdtts) - set(sample_targets_low_max_gdtts)
# ## Targets with low GDT_TS and high mean-LDDT
df.query('GDT_TS < 0.6 and Mean_LDDT > 0.8')['Target'].unique()
|
src/notebooks/datasets/how_eq_random_num_500_seed_0/accuracy/targets_low_accuracy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Import Libraries
import requests
import json
import pandas as pd
import time
import datetime
# ## Configuration
# +
baseURL = 'http://ec2-18-235-248-253.compute-1.amazonaws.com:2990/jira/rest/'
loginAPI = 'auth/1/session'
userAPI = 'api/2/user?username=alexA'
issuePickerAPI = 'api/2/issue/picker?currentJQL=assignee%3Dadmin'
biExportAPI = 'getbusinessintelligenceexport/1.0/message'
loginUserName = 'admin'
loginPassWord = '<PASSWORD>'
analysisStartDate = '01-FEB-19'
analysisEndDate = '31-FEB-19'
exportDirectory = './downloads/'
# -
# ## Login to Jira
# +
loginURL = baseURL + loginAPI
loginData = {"username": loginUserName, "password": loginPassWord}
loginResponse = requests.post(loginURL, json=loginData)
if loginResponse.status_code != 200:
raise Exception('POST ' + loginURL + ' {}'.format(loginResonse.status_code))
else:
myJSessionID = loginResponse.cookies['JSESSIONID']
print('JSESSIONID: ' + myJSessionID)
# -
# ## Request Data
# +
url = baseURL + userAPI
url = baseURL + issuePickerAPI
url = baseURL + biExportAPI + "?startDate=" + analysisStartDate + "&endDate=" + analysisEndDate
myCookie = dict(JSESSIONID=myJSessionID)
resp = requests.get(url, cookies=myCookie)
if resp.status_code != 200:
raise Exception('GET ' + url + ' {}'.format(resp.status_code))
else:
#print("resp: {}".format(resp.json()))
myRecords = resp.json()["records"]
#print("myRecords: " + json.dumps(myRecords))
# -
# ## Save to File
df = pd.read_json(json.dumps(myRecords), orient='records')
myTimeStamp = datetime.datetime.fromtimestamp(time.time()).strftime('%Y-%m-%d_%H-%M-%S')
df.to_csv(exportDirectory + "records_" + myTimeStamp + ".csv")
|
PythonApiClient/PythonApiClient.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "-"}
# # Cyberinfrastructure Exploration
#
# In this segment you will take a few minutes to explore how you can get involved in cyberinfastructure as you build your own cyber literacy.
#
# While this might sound daunting, luckily there are a number of cyberinfrastructure projects that are ready to help you at any stage. From the very beginner to the very advanced!
#
# + hide_input=true init_cell=true slideshow={"slide_type": "skip"} tags=["Hide"]
# This code cell starts the necessary setup for Hour of CI lesson notebooks.
# First, it enables users to hide and unhide code by producing a 'Toggle raw code' button below.
# Second, it imports the hourofci package, which is necessary for lessons and interactive Jupyter Widgets.
# Third, it helps hide/control other aspects of Jupyter Notebooks to improve the user experience
# This is an initialization cell
# It is not displayed because the Slide Type is 'Skip'
from IPython.display import HTML, IFrame, Javascript, display
from ipywidgets import interactive
import ipywidgets as widgets
from ipywidgets import Layout
import getpass # This library allows us to get the username (User agent string)
# import package for hourofci project
import sys
sys.path.append('../../supplementary') # relative path (may change depending on the location of the lesson notebook)
import hourofci
# Retreive the user agent string, it will be passed to the hourofci submit button
agent_js = """
IPython.notebook.kernel.execute("user_agent = " + "'" + navigator.userAgent + "'");
"""
Javascript(agent_js)
# load javascript to initialize/hide cells, get user agent string, and hide output indicator
# hide code by introducing a toggle button "Toggle raw code"
HTML('''
<script type="text/javascript" src=\"../../supplementary/js/custom.js\"></script>
<input id="toggle_code" type="button" value="Toggle raw code">
''')
# -
# ## 1. You are using Cyberinfrastructure right now!
#
# The Hour of CI project uses Jetstream - a cloud-based, on-demand, 24/7 system that includes discipline-specific apps to host these lessons. Learn more about Jetstream by visiting their website: https://www.jetstream-cloud.org/. Jetstream is part of XSEDE, which is one of the world's most advanced cyberinfrastructure! You will explore some XSEDE resources below. You are also using Jupyter Notebooks (this exploration and this entire lesson was constructed in Jupyter Notebooks), which are part of cyberinfrastructure. To learn more about notebooks visit their website: https://jupyter.org/. So you are now officially a cyberinfrastructure user.
# ## 2. Science Gateways Community Institute (SGCI)
#
# The SGCI "connect people and resources to accelerate discovery by empowering the science gateway community." They help researchers build their own science gateways for their own domains. They host a list of existing science gateways that users (like you!) can use to move their own research forward. They offere Student-focused programsn ad training for all levels of professionals.
#
# Spend 5 minutes exploring at least one SGCI resource:
#
# 1. **<a href="https://catalog.sciencegateways.org/">Gateway Catalog</a>** - A list of over 500 Science Gateways. Maybe one can help you move your science forward.
# 2. **<a href="https://sciencegateways.org/consulting">Consulting Services</a>** - A list of services SGCI provides researchers interested in answering questions or helping them build their own science gateways.
# 3. **<a href="https://sciencegateways.org/where-to-begin">Where to begin</a>** - If you are not sure where to go. Go here. This page points you to information whether you are new to science gateways or are ready to build your own.
#
#
# ## 3. The Extreme Science and Engineering Discovery Environment (XSEDE)
#
# You have already heard a little bit about XSEDE. Now you can a closer look at XSEDE yourself. XSEDE offers resources, expertise, and training to help you move your science forward.
#
# Spend 5 minutes exploring XSEDE resources:
#
# 1. **<a href="https://www.xsede.org/for-users/getting-started">Getting Started using XSEDE</a>** - This page will provide resources how to get started using XSEDE resources. If you are ready to try CI for yourself. This is the place for you.
# 1. **<a href="https://portal.xsede.org/training/overview">XSEDE Training</a>** - If you want to learn more about XSEDE, programming, visualizing data, analyzing data, etc. Then take a look at XSEDE Training. They offer live and recorded training classes including New User Training.
# 1. **<a href="https://www.xsede.org/community-engagement/campus-champions">Champions</a>** - Campus Champions, Domain Champions, and Student Champions are people who are ready to help you learn more about and use cyberinfrastructure. Take a look at the current <a href="https://www.xsede.org/web/site/community-engagement/campus-champions/current">Campus Champions page</a> that includes more than 700 champions at over 300 institutions across the US - you may just have a cyberinfrastructure expert at your institution ready to help. You can also look for <a href="https://www.xsede.org/community-engagement/campus-champions/domain-champions">Domain Champions here</a>. If you have a question, then a champion is the perfect person to ask!
# 1. **<a href="http://computationalscience.org/xsede-empower">XSEDE Empower</a>** - XSEDE EMPOWER ( Expert Mentoring Producing Opportunities for Work, Education, and Research ) aims to expand the community by recruiting and enabling a diverse group of students who have the skills — or are interested in acquiring the skills — to participate in the actual work of XSEDE. If you are an undergraduate student and are interested, then take a look at this excellent program. If you are a graduate student or professional, take a look at some of the other programs hosted by XSEDE, SGCI, and other CI projects that may provide training and opportunities for you as well.
#
# ## 4. Tell us what you have learned so far
#
# ### Congratulations! You have finished an Hour of CI!
#
# But, before you go ...
#
# 1. Please fill out a very brief questionnaire to tell us what you have learned so far and to provide feedback to help us improve the Hour of CI lessons. It is fast and your feedback is very important to let us know what you learned and how we can improve the lessons in the future.
# 2. If you would like a certificate, then please type your name below and click "Create Certificate" and you will be presented with a PDF certificate.
#
#
# <font size="+1"><a style="background-color:blue;color:white;padding:12px;margin:10px;font-weight:bold;" href="https://forms.gle/JUUBm76rLB8iYppN7">Tell us what you learned and provide feedback</a></font>
#
#
# + hide_input=true slideshow={"slide_type": "-"} tags=["Hide", "Init"]
# This code cell loads the Interact Textbox that will ask users for their name
# Once they click "Create Certificate" then it will add their name to the certificate template
# And present them a PDF certificate
from PIL import Image
from PIL import ImageFont
from PIL import ImageDraw
from ipywidgets import interact
def make_cert(learner_name):
cert_filename = 'hourofci_certificate.pdf'
img = Image.open("../../supplementary/hci-certificate-template.jpg")
draw = ImageDraw.Draw(img)
cert_font = ImageFont.load_default()
cert_font = ImageFont.truetype('times.ttf', 150)
w,h = cert_font.getsize(learner_name)
draw.text( xy = (1650-w/2,1100-h/2), text = learner_name, fill=(0,0,0),font=cert_font)
img.save(cert_filename, "PDF", resolution=100.0)
return cert_filename
interact_cert=interact.options(manual=True, manual_name="Create Certificate")
@interact_cert(name="Your Name")
def f(name):
print("Congratulations",name)
filename = make_cert(name)
print("Download your certificate by clicking the link below.")
# -
# <font size="+1"><a style="background-color:blue;color:white;padding:12px;margin:10px;font-weight:bold;" href="hourofci_certificate.pdf?download=1" download="hourofci_certificate.pdf">Download your certificate</a></font>
|
beginner-lessons/cyberinfrastructure/cyberinfrastructure-exploration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="mUaJMUDUezt1" colab_type="text"
# # Self DCGAN Keras TPU
#
# <table class="tfo-notebook-buttons" align="left" >
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/HighCWu/SelfGAN/blob/master/implementations/dcgan/self_dcgan_keras_tpu.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/HighCWu/SelfGAN/blob/master/implementations/dcgan/self_dcgan_keras_tpu.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# </table>
# + id="_sFEKpmpesjv" colab_type="code" colab={}
# ! pip install 'tensorflow>1.12,<2.0' -q
# + [markdown] id="LHK5Y87sVWAa" colab_type="text"
# ## Datasets
# + id="yg6TxwMvVVKo" colab_type="code" colab={}
import h5py
import sys
import time
import numpy as np
import tensorflow as tf
import threading
import glob
import random
import os
import numpy as np
from PIL import Image
from tensorflow.python.keras.utils import Sequence
from tensorflow.python.keras.utils.data_utils import OrderedEnqueuer
class ImageDataset:
def __init__(self, root):
self.files = sorted(glob.glob(root + '/**/*.*', recursive=True))
def __getitem__(self, index):
img = Image.open(self.files[index % len(self.files)]).convert('RGB' if channels==3 else 'L')
w, h = img.size
img = img.resize((img_rows, img_cols), Image.LANCZOS)
img = np.asarray(img)
img = img/255*2 - 1
if channels==1:
img = img.reshape(img.shape+(1,))
return img
def __len__(self):
return len(self.files)
class DataLoader:
def __init__(self, dataset, batch_size, workers=1, max_queue_size=10, cache_filepath='tmp/cache.h5', pool_size=64000):
self.idx = 0
bsz = batch_size
batch_pool = pool_size // bsz
self.length = batch_pool
os.makedirs(os.path.dirname(cache_filepath), exist_ok=True)
cache_file = h5py.File(cache_filepath, 'w')
counter = {'i': 0, 'full': False}
def data_reader(counter, cache_file):
idx = 0
while True:
try:
X=[]
for i in range(bsz):
x = dataset[idx]
X.append(x)
idx = (idx + 1) % len(dataset)
if not counter['full']:
cache_file.create_dataset('x/{}'.format(counter['i']), data=X)
else:
cache_file['x/{}'.format(counter['i'])][...] = X
counter['i'] = (counter['i']+1)%(batch_pool)
if counter['i'] == 0:
counter['full'] = True
time.sleep(0.5)
except Exception as e:
raise e
dt = threading.Thread(target=data_reader, args=(counter, cache_file))
dt.start()
while counter['i'] < 100:
sys.stdout.flush()
print('\rWaiting for enough cache.%d/100'%counter['i'], end='')
print('')
class generator(Sequence):
def __len__(_self):
return self.length
def __getitem__(_self, index):
return cache_file['x/{}'.format(index % (counter['i'] if not counter['full'] else batch_pool))].value.astype('float')
enqueuer = OrderedEnqueuer(
generator(),
use_multiprocessing=False,
shuffle=False)
enqueuer.start(workers=workers, max_queue_size=max_queue_size)
self.o_g = enqueuer.get()
def __iter__(self):
self.idx = -1
return self
def __next__(self):
self.idx += 1
if self.idx >= self.length:
raise StopIteration()
return next(self.o_g)
def __len__(self):
return self.length
# + [markdown] id="LIQn0pnWfvoj" colab_type="text"
# ## Prepare
# + id="psbNazmKfpFj" colab_type="code" colab={}
from tensorflow import keras
from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import Input, Dense, Reshape, Flatten, Dropout, Lambda
from tensorflow.keras.layers import BatchNormalization, Activation, ZeroPadding2D
from tensorflow.python.keras.layers.advanced_activations import LeakyReLU
from tensorflow.python.keras.layers.convolutional import UpSampling2D, Conv2D
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.optimizers import Adam
import tensorflow as tf
import tensorflow.keras.backend as K
import matplotlib.pyplot as plt
import os
import sys
import numpy as np
os.makedirs('images', exist_ok=True)
os.makedirs('data/bedroom', exist_ok=True)
data_use = 'mnist' #@param ["bedroom", "mnist"] {allow-input: false}
if data_use=='mnist':
img_rows = 28
img_cols = 28
channels = 1
else:
img_rows = 64
img_cols = 64
channels = 3
img_shape = (img_rows, img_cols, channels)
latent_dim = 100
batch_size = 64
sample_interval = 200
epochs = 200
# + id="r6j3-fn2VJ2U" colab_type="code" colab={}
import os, zipfile
from google.colab import files
if data_use == 'bedroom':
print('Please upload your kaggle api json.')
files.upload()
# ! mkdir /root/.kaggle
# ! mv ./kaggle.json /root/.kaggle
# ! chmod 600 /root/.kaggle/kaggle.json
# ! kaggle datasets download -d jhoward/lsun_bedroom
out_fname = 'lsun_bedroom.zip'
zip_ref = zipfile.ZipFile(out_fname)
zip_ref.extractall('./')
zip_ref.close()
os.remove(out_fname)
out_fname = 'sample.zip'
zip_ref = zipfile.ZipFile(out_fname)
zip_ref.extractall('data/bedroom/')
zip_ref.close()
os.remove(out_fname)
# + id="nDkhsw7vMBNh" colab_type="code" colab={}
# UpSample on TPU
from tensorflow.python.keras.engine.base_layer import InputSpec
from tensorflow.python.keras.utils import get_custom_objects
from tensorflow.python.keras.utils import conv_utils
def _blur2d(x, f=[1,2,1], normalize=True, flip=False, stride=1):
assert x.shape.ndims == 4 and all(dim.value is not None for dim in x.shape[1:])
assert isinstance(stride, int) and stride >= 1
# Finalize filter kernel.
f = np.array(f, dtype=np.float32)
if f.ndim == 1:
f = f[:, np.newaxis] * f[np.newaxis, :]
assert f.ndim == 2
if normalize:
f /= np.sum(f)
if flip:
f = f[::-1, ::-1]
f = f[:, :, np.newaxis, np.newaxis]
f = np.tile(f, [1, 1, int(x.shape[1]), 1])
# No-op => early exit.
if f.shape == (1, 1) and f[0,0] == 1:
return x
# Convolve using depthwise_conv2d.
orig_dtype = x.dtype
x = tf.cast(x, tf.float32) # tf.nn.depthwise_conv2d() doesn't support fp16
f = tf.constant(f, dtype=x.dtype, name='filter')
strides = [1, 1, stride, stride]
x = tf.nn.depthwise_conv2d(x, f, strides=strides, padding='SAME', data_format='NCHW')
x = tf.cast(x, orig_dtype)
return x
def _upscale2d(x, factor=2, gain=1):
assert x.shape.ndims == 4 and all(dim.value is not None for dim in x.shape[1:])
assert isinstance(factor, int) and factor >= 1
# Apply gain.
if gain != 1:
x *= gain
# No-op => early exit.
if factor == 1:
return x
# Upscale using tf.tile().
s = x.shape
x = tf.reshape(x, [-1, s[1], s[2], 1, s[3], 1])
x = tf.tile(x, [1, 1, 1, factor, 1, factor])
x = tf.reshape(x, [-1, s[1], s[2] * factor, s[3] * factor])
return x
def _downscale2d(x, factor=2, gain=1):
assert x.shape.ndims == 4 and all(dim.value is not None for dim in x.shape[1:])
assert isinstance(factor, int) and factor >= 1
# 2x2, float32 => downscale using _blur2d().
if factor == 2 and x.dtype == tf.float32:
f = [np.sqrt(gain) / factor] * factor
return _blur2d(x, f=f, normalize=False, stride=factor)
# Apply gain.
if gain != 1:
x *= gain
# No-op => early exit.
if factor == 1:
return x
# Large factor => downscale using tf.nn.avg_pool().
# NOTE: Requires tf_config['graph_options.place_pruned_graph']=True to work.
ksize = [1, 1, factor, factor]
return tf.nn.avg_pool(x, ksize=ksize, strides=ksize, padding='VALID', data_format='NCHW')
def upscale2d(x, factor=2):
with tf.variable_scope('Upscale2D'):
@tf.custom_gradient
def func(x):
y = _upscale2d(x, factor)
@tf.custom_gradient
def grad(dy):
dx = _downscale2d(dy, factor, gain=factor**2)
return dx, lambda ddx: _upscale2d(ddx, factor)
return y, grad
return func(x)
class UpSampling2D(keras.layers.Layer):
"""Upsampling layer for 2D inputs.
Repeats the rows and columns of the data
by size[0] and size[1] respectively.
Arguments:
size: int, or tuple of 2 integers.
The upsampling factors for rows and columns.
data_format: A string,
one of `channels_last` (default) or `channels_first`.
The ordering of the dimensions in the inputs.
`channels_last` corresponds to inputs with shape
`(batch, height, width, channels)` while `channels_first`
corresponds to inputs with shape
`(batch, channels, height, width)`.
It defaults to the `image_data_format` value found in your
Keras config file at `~/.keras/keras.json`.
If you never set it, then it will be "channels_last".
Input shape:
4D tensor with shape:
- If `data_format` is `"channels_last"`:
`(batch, rows, cols, channels)`
- If `data_format` is `"channels_first"`:
`(batch, channels, rows, cols)`
Output shape:
4D tensor with shape:
- If `data_format` is `"channels_last"`:
`(batch, upsampled_rows, upsampled_cols, channels)`
- If `data_format` is `"channels_first"`:
`(batch, channels, upsampled_rows, upsampled_cols)`
"""
def __init__(self, size=(2, 2), data_format=None, **kwargs):
super(UpSampling2D, self).__init__(**kwargs)
self.data_format = conv_utils.normalize_data_format(data_format)
self.size = conv_utils.normalize_tuple(size, 2, 'size')
self.input_spec = InputSpec(ndim=4)
def call(self, inputs):
if self.data_format == 'channels_first':
return upscale2d(inputs, self.size[0])
else:
T = tf.transpose(inputs, [0,3,1,2])
up_T = upscale2d(T, self.size[0])
return tf.transpose(up_T, [0,2,3,1])
def get_config(self):
config = {'size': self.size, 'data_format': self.data_format}
base_config = super(UpSampling2D, self).get_config()
return dict(list(base_config.items()) + list(config.items()))
get_custom_objects().update({'UpSampling2D': UpSampling2D})
# + id="QjDp0s5ZgqlN" colab_type="code" colab={}
class Generator:
def __init__(self):
self.layers = []
model = self.layers
model.append(Dense(128 * img_rows * img_cols // (4**2), activation="relu", input_dim=latent_dim))
model.append(Reshape((img_rows//4, img_cols//4, 128)))
model.append(UpSampling2D())
model.append(Conv2D(128, kernel_size=3, padding="same"))
model.append(BatchNormalization(momentum=0.8))
model.append(Activation("relu"))
model.append(UpSampling2D())
model.append(Conv2D(64, kernel_size=3, padding="same"))
model.append(BatchNormalization(momentum=0.8))
model.append(Activation("relu"))
model.append(Conv2D(channels, kernel_size=3, padding="same"))
model.append(Activation("tanh", name='output'))
def __call__(self, x):
y = x
for layer in self.layers:
y = layer(y)
return y
class Discriminator:
def __init__(self):
self.layers = []
model = self.layers
model.append(Conv2D(32, kernel_size=3, strides=2, input_shape=img_shape, padding="same"))
model.append(LeakyReLU(alpha=0.2))
model.append(Dropout(0.25))
model.append(Conv2D(64, kernel_size=3, strides=2, padding="same"))
model.append(ZeroPadding2D(padding=((0,1),(0,1))))
model.append(BatchNormalization(momentum=0.8))
model.append(LeakyReLU(alpha=0.2))
model.append(Dropout(0.25))
model.append(Conv2D(128, kernel_size=3, strides=2, padding="same"))
model.append(BatchNormalization(momentum=0.8))
model.append(LeakyReLU(alpha=0.2))
model.append(Dropout(0.25))
model.append(Conv2D(256, kernel_size=3, strides=1, padding="same"))
model.append(BatchNormalization(momentum=0.8))
model.append(LeakyReLU(alpha=0.2))
model.append(Dropout(0.25))
model.append(Flatten())
model.append(Dense(1, activation='sigmoid'))
def __call__(self, x):
y = x
for layer in self.layers:
y = layer(y)
return y
def SelfGAN():
generator = Generator()
discriminator = Discriminator()
real_img = Input(shape=img_shape)
fake_img = Input(shape=img_shape)
noise = Input(shape=(latent_dim,))
gen_img = generator(noise)
validity_gen = discriminator(gen_img)
validity_real = discriminator(real_img)
validity_fake = discriminator(fake_img)
# compute loss
adversarial_loss = Lambda(lambda x: keras.losses.binary_crossentropy(x[0], x[1]))
valid = Input(shape=(1,))
fake = Input(shape=(1,))
gen_loss = adversarial_loss([validity_gen, valid])
real_loss = adversarial_loss([validity_real, valid])
fake_loss = adversarial_loss([validity_fake, fake])
gen_loss = Lambda(lambda x: x*1.0, name='gen_loss')(gen_loss)
real_loss = Lambda(lambda x: x*1.0, name='real_loss')(real_loss)
fake_loss = Lambda(lambda x: x*1.0, name='fake_loss')(fake_loss)
v_g = Lambda(lambda x: 1 - K.mean(x))(validity_gen)
v_r = Lambda(lambda x: 1 - K.mean(x))(validity_real)
v_f = Lambda(lambda x: K.mean(x))(validity_fake)
v_sum = Lambda(lambda x: x[0]+x[1]+x[2])([v_g,v_r,v_f])
s_loss = Lambda(lambda x: x[2]*x[1]/x[0] \
+ x[4]*x[3]/x[0] \
+ x[6]*x[5]/x[0])([v_sum, v_r, real_loss, v_g, gen_loss, v_f, fake_loss])
return Model([noise, real_img, fake_img, valid, fake], [s_loss])
def sample_images(model, epoch):
r = 5
c = 5
noise = np.random.normal(0, 1, (batch_size, latent_dim))
gen_imgs = model.predict([noise, last_imgs, last_imgs, valid, fake])[-1][:r*c]
# Rescale images 0 - 1
gen_imgs = 0.5 * gen_imgs + 0.5
fig, axs = plt.subplots(r, c)
cnt = 0
for i in range(r):
for j in range(c):
if channels==1:
axs[i,j].imshow(gen_imgs[cnt, :,:,0], cmap='gray')
else:
axs[i,j].imshow(gen_imgs[cnt, :,:,:])
axs[i,j].axis('off')
cnt += 1
fig.savefig("images/%d.png" % epoch)
plt.close()
# + id="lipEQUtOX_UA" colab_type="code" colab={}
# Function override
from tensorflow.contrib.tpu.python.tpu.keras_support import TPUFunction
from tensorflow.keras.models import Model
from tensorflow.python.estimator import model_fn as model_fn_lib
ModeKeys = model_fn_lib.ModeKeys
def extra_outputs(self):
outputs = []
for layer in self.layers:
if 'loss' in layer.name:
outputs.append(layer.output)
for layer in self.layers:
if 'output' in layer.name:
outputs.append(layer.output)
return outputs
def _make_predict_function(self):
if not hasattr(self, 'predict_function'):
self.predict_function = None
if self.predict_function is None:
inputs = self._feed_inputs
# Gets network outputs. Does not update weights.
# Does update the network states.
kwargs = getattr(self, '_function_kwargs', {})
with K.name_scope(ModeKeys.PREDICT):
self.predict_function = K.function(
inputs,
self.outputs+extra_outputs(self),
updates=self.state_updates,
name='predict_function',
**kwargs)
def _make_fit_function(self):
metrics_tensors = [
self._all_stateful_metrics_tensors[m] for m in self.metrics_names[1:]
]
self._make_train_function_helper(
'_fit_function', [self.total_loss] + metrics_tensors + extra_outputs(self))
Model._make_predict_function = _make_predict_function
Model._make_fit_function = _make_fit_function
def _process_outputs(self, outfeed_outputs):
"""Processes the outputs of a model function execution.
Args:
outfeed_outputs: The sharded outputs of the TPU computation.
Returns:
The aggregated outputs of the TPU computation to be used in the rest of
the model execution.
"""
# TODO(xiejw): Decide how to reduce outputs, or discard all but first.
if self.execution_mode == ModeKeys.PREDICT:
outputs = [[] for _ in range(len(self._outfeed_spec))]
outputs_per_replica = len(self._outfeed_spec)
for i in range(self._tpu_assignment.num_towers):
output_group = outfeed_outputs[i * outputs_per_replica:(i + 1) *
outputs_per_replica]
for j in range(outputs_per_replica):
outputs[j].append(output_group[j])
return [np.concatenate(group) for group in outputs]
else:
outputs = [[] for _ in range(len(self._outfeed_spec))]
outputs_per_replica = len(self._outfeed_spec)
for i in range(self._tpu_assignment.num_towers):
output_group = outfeed_outputs[i * outputs_per_replica:(i + 1) *
outputs_per_replica]
for j in range(outputs_per_replica):
outputs[j].append(output_group[j])
ret = []
for group in outputs:
if len(group[0].shape) > 0:
ret.append(np.concatenate(group))
else:
ret.append(group[0])
return ret
TPUFunction._process_outputs = _process_outputs
# + id="F8kXVRyfpz2I" colab_type="code" colab={}
tf.keras.backend.clear_session()
optimizer = Adam(0.0002, 0.5)
model = SelfGAN()
model.compile(loss='mae',optimizer=optimizer)
TPU_WORKER = 'grpc://' + os.environ['COLAB_TPU_ADDR']
model = tf.contrib.tpu.keras_to_tpu_model(
model,
strategy=tf.contrib.tpu.TPUDistributionStrategy(
tf.contrib.cluster_resolver.TPUClusterResolver(TPU_WORKER)))
def initialize_uninitialized_variables():
sess = K.get_session()
uninitialized_variables = set([i.decode('ascii') for i in sess.run(tf.report_uninitialized_variables())])
init_op = tf.variables_initializer(
[v for v in tf.global_variables() if v.name.split(':')[0] in uninitialized_variables]
)
sess.run(init_op)
initialize_uninitialized_variables()
# Adversarial ground truths
valid = np.ones((batch_size, 1))
fake = np.zeros((batch_size, 1))
last_imgs = np.zeros((batch_size,)+img_shape)
s_loss_zeros = np.zeros((batch_size,))
# + id="ly2F41ptrog1" colab_type="code" colab={}
# Init tpu model
noise = np.random.normal(0, 1, (batch_size, latent_dim))
train_outputs = model.train_on_batch([noise, last_imgs, last_imgs, valid, fake], [s_loss_zeros])
predict_output = model.predict([noise, last_imgs, last_imgs, valid, fake])
dataLoader = DataLoader(ImageDataset('data/bedroom') if data_use == 'bedroom' else
mnist.load_data()[0][0].reshape((-1,28,28,1))/127.5-1, batch_size)
# + id="hVjnI8dKspOQ" colab_type="code" colab={}
for epoch in range(epochs):
for i, imgs in enumerate(dataLoader):
# ---------------------
# Train Discriminator
# ---------------------
noise = np.random.normal(0, 1, (batch_size, latent_dim))
# Generate a batch of new images
outputs = model.train_on_batch([noise, imgs, last_imgs, valid, fake], [s_loss_zeros])
s_loss = outputs[0]/8
gen_loss = np.mean(outputs[2])/(batch_size/8)
real_loss = np.mean(outputs[1])/(batch_size/8)
fake_loss = np.mean(outputs[3])/(batch_size/8)
last_imgs = outputs[-1]
# Plot the progress
if i % 25 == 0:
sys.stdout.flush()
print ("\r[Epoch %d/%d] [Batch %d/%d] [S loss: %f G loss: %f R loss: %f F loss: %f]" % (epoch, epochs, i,
len(dataLoader), s_loss,
gen_loss, real_loss, fake_loss),end='')
# If at save interval => save generated image samples
if (epoch*len(dataLoader) + i) % sample_interval == 0:
sample_images(model, epoch*len(dataLoader) + i)
|
implementations/dcgan/self_dcgan_keras_tpu.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Метрики качества бинарной классификации
#
# <NAME> (<EMAIL>)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Обнаружение мошеннических транзакций
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Загрузка данных
# На основе [Machine Learning for Credit Card Fraud Detection](https://fraud-detection-handbook.github.io/fraud-detection-handbook/Foreword.html)
# + slideshow={"slide_type": "skip"}
# Initialization: Load shared functions and simulated data
# Load shared functions
if not os.path.exists("shared_functions.py"):
# !curl -O https://raw.githubusercontent.com/Fraud-Detection-Handbook/fraud-detection-handbook/main/Chapter_References/shared_functions.py
# %run shared_functions.py
# Get simulated data from Github repository
if not os.path.exists("simulated-data-transformed"):
# !git clone https://github.com/Fraud-Detection-Handbook/simulated-data-transformed
# +
DIR_INPUT='./simulated-data-transformed/data/'
BEGIN_DATE = "2018-05-01"
END_DATE = "2018-05-31"
print("Load files")
# %time transactions_df=read_from_files(DIR_INPUT, BEGIN_DATE, END_DATE)
print("{0} transactions loaded, containing {1} fraudulent transactions".format(len(transactions_df),transactions_df.TX_FRAUD.sum()))
# + slideshow={"slide_type": "subslide"}
transactions_df.head()
# + slideshow={"slide_type": "subslide"}
from sklearn.model_selection import train_test_split
output_feature="TX_FRAUD"
input_features=['TX_AMOUNT','TX_DURING_WEEKEND', 'TX_DURING_NIGHT', 'CUSTOMER_ID_NB_TX_1DAY_WINDOW',
'CUSTOMER_ID_AVG_AMOUNT_1DAY_WINDOW', 'CUSTOMER_ID_NB_TX_7DAY_WINDOW',
'CUSTOMER_ID_AVG_AMOUNT_7DAY_WINDOW', 'CUSTOMER_ID_NB_TX_30DAY_WINDOW',
'CUSTOMER_ID_AVG_AMOUNT_30DAY_WINDOW', 'TERMINAL_ID_NB_TX_1DAY_WINDOW',
'TERMINAL_ID_RISK_1DAY_WINDOW', 'TERMINAL_ID_NB_TX_7DAY_WINDOW',
'TERMINAL_ID_RISK_7DAY_WINDOW', 'TERMINAL_ID_NB_TX_30DAY_WINDOW',
'TERMINAL_ID_RISK_30DAY_WINDOW']
X = transactions_df[input_features]
y = transactions_df[output_feature]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# +
# %%time
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
knn_params = {
'n_neighbors': 5,
}
knn = KNeighborsClassifier(**knn_params).fit(X_train, y_train)
knn_y_pred = knn.predict(X_test)
knn_acc = accuracy_score(y_test, knn_y_pred)
print(f"Доля верных ответов для knn: {knn_acc:.4}")
# -
# ## Классификатор "болванчик"
#
# Этот классификатор просто предсказывает самый частый выходной класс (или случайный класс) без учета значений входных признаков.
#
# Данный тип классификаторов можно рассматривать в качестве простых базовых оценок для метрик классификации. Любой предложенный алгоритм должен показывать качество лучше, чем "болванчик"
# +
# %%time
from sklearn.dummy import DummyClassifier
dummy = DummyClassifier().fit(X_train, y_train)
dummy_y_pred = dummy.predict(X_test)
dummy_acc = accuracy_score(y_test, dummy_y_pred)
print(f"Доля верных ответов для dummy: {dummy_acc:.4}")
# -
# ### Дизбаланс классов
ax = sns.countplot(x=y)
ax.set_yscale('log')
total = len(y)
for p in ax.patches:
px = p.get_bbox().get_points()[:,0]
py = p.get_bbox().get_points()[1,1]
ax.annotate('{:.1f}%'.format(100.*py/total), (px.mean(), py),
ha='center', va='bottom') # set the alignment of the text
# ### Матрица ошибок бинарной классификации
# <img src="https://miro.medium.com/max/332/1*BTB9weIUfSsSRy5kvh_-uA.png" />
#
# $$
# Accuracy = \frac{TP + TN}{TP + TN + FP + FN}
# $$
# ### Матрица ошибок для "болванчика"
# +
from sklearn.metrics import plot_confusion_matrix
plot_confusion_matrix(dummy, X_test, y_test, cmap=plt.cm.Blues, labels=[1, 0], colorbar=False);
# -
# ### Матрица ошибок для kNN
plot_confusion_matrix(knn, X_test, y_test, cmap=plt.cm.Blues, labels=[1, 0], colorbar=False);
# ### Точность и полнота
#
# **Точность** (Precision) - Доля правильных ответов, среди всех _предсказаний_ позитивного класса
# $$
# P = \frac{TP}{TP + FP}
# $$
#
# **Полнота** (Recall) - доля правильных ответов среди всех _истинных_ примеров позитивного класса
# $$
# R = \frac{TP}{TP + FN}
# $$
# +
from sklearn.metrics import precision_score, recall_score
dummy_precision = precision_score(y_test, dummy_y_pred)
dummy_recall = recall_score(y_test, dummy_y_pred)
knn_precision = precision_score(y_test, knn_y_pred)
knn_recall = recall_score(y_test, knn_y_pred)
print(f"Dummy precision = {dummy_precision:.5}")
print(f"Dummy recall = {dummy_recall:.5}")
print("")
print(f"kNN precision = {knn_precision:.4}")
print(f"kNN recall = {knn_recall:.4}")
# -
# ### Сравнение классификаторов
# Обучим логистическую регрессию
# +
# %%time
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression().fit(X_train, y_train)
logreg_y_pred = logreg.predict(X_test)
# -
logreg_precision = precision_score(y_test, logreg_y_pred)
logreg_recall = recall_score(y_test, logreg_y_pred)
print(f"LogReg precision = {logreg_precision:.5}")
print(f"LogReg recall = {logreg_recall:.5}")
print("")
print(f"kNN precision = {knn_precision:.4}")
print(f"kNN recall = {knn_recall:.4}")
# ## F мера
#
# $F_1$ мера - гармоническое среднее между точностью и полнотой
# $$
# F_1 = \frac{2PR}{P+R}.
# $$
#
# $F_\beta$ - обобщенние $F$-меры, использующая коэффициент $\beta$ - степень важности полноты по сравнению с точностью.
# $$
# F_\beta = (1+\beta^2)\frac{PR}{\beta^2 P + R} = \frac{(1+\beta^2)TP}{(1+\beta^2)TP + \beta^2 FN + FP}.
# $$
# +
from sklearn.metrics import f1_score
knn_f1 = f1_score(y_test, knn_y_pred)
logreg_f1 = f1_score(y_test, logreg_y_pred)
print(f"LogReg F1 = {logreg_f1:.5}")
print(f"kNN F1 = {knn_f1:.5}")
# -
# ## PR (Precison Recall)-кривая
# Рассмотрим упрощенную задачу бинарной классификации, когда у нас есть всего 1 признак.
# +
sns.set()
from sklearn.datasets import make_classification
from sklearn.metrics import precision_recall_curve
from scipy.special import logit
def sinlge_dim_ex():
X, y = make_classification(
n_samples=100,
n_classes=2,
n_clusters_per_class=1,
n_features=1,
n_informative=1,
n_redundant=0,
n_repeated=0,
class_sep=0.4,
random_state=42,
)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
logreg = LogisticRegression().fit(X_train, y_train)
y_pred = logreg.predict_proba(X_test)[:, 1]
xx = np.linspace(min(X), max(X), 100)
yy = logreg.predict_proba(xx)[:, 1]
logreg.coef_
logreg.intercept_
pre, rec, thr = precision_recall_curve(y_test, y_pred)
X_test_sorted = np.sort(X_test, axis=0)
pre = list()
rec = list()
for x in X_test_sorted:
pre.append(precision_score(y_test, X_test >= x))
rec.append(recall_score(y_test, X_test >= x))
plt.figure(figsize=(16,9))
plt.scatter(x=X_test, y=np.zeros(len(X_test)), s=50, c=y_test, cmap=plt.cm.RdBu)
plt.plot(xx, yy, label='Logistic')
plt.step(X_test_sorted, pre, label='Precision', )
plt.step(X_test_sorted, rec, label='Recall')
idx_to_plot = [4, 10]
for idx in idx_to_plot:
plt.vlines(X_test_sorted[idx], ymin=0, ymax=1, linestyles='dashed')
plt.scatter(X_test_sorted[idx], logreg.predict_proba(X_test_sorted[idx].reshape(-1, 1))[0, 1], c='b')
plt.legend()
sinlge_dim_ex()
# +
from sklearn.metrics import plot_precision_recall_curve
plt.figure(figsize=(16, 9))
pr_disp = plot_precision_recall_curve(logreg, X_test, y_test, ax=plt.axes())
plot_precision_recall_curve(knn, X_test, y_test, ax=pr_disp.ax_);
# -
# ### ROC (Receiver Operating Characteristic)-кривая
# **True Positive Rate** (Recall) - доля верных ответов среди всех *истинных* объектов позитивного класса
# $$
# TPR = \frac{TP}{TP + FN}
# $$
# **False Positive Rate** - доля верных ответов среди всех *истинных* объектов негативного класса
# $$
# FPR = \frac{FP}{FP + TN}
# $$
# +
from sklearn.metrics import plot_roc_curve
plt.figure(figsize=(10, 8))
roc_disp = plot_roc_curve(logreg, X_test, y_test, ax=plt.axes())
plot_roc_curve(knn, X_test, y_test, ax=roc_disp.ax_)
roc_disp.ax_.plot([0, 1], [0, 1], 'k--');
# -
# ### Площадь под ROC-кривой
# ROC-AUC - ROC area under the curve
# +
from sklearn.metrics import roc_auc_score
knn_y_pred_proba = knn.predict_proba(X_test)[:, 1]
logreg_y_pred_proba = logreg.predict_proba(X_test)[:, 1]
knn_roc_auc = roc_auc_score(y_test, knn_y_pred_proba)
logreg_roc_auc = roc_auc_score(y_test, logreg_y_pred_proba)
print(f"kNN ROC-AUC = {knn_roc_auc:.5}")
print(f"LogReg ROC-AUC = {logreg_roc_auc:.5}")
# -
|
notebooks/Classification quality metrics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/mariel/Sisteme-Inteligente/blob/master/Decision_Tree.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="SIKEauTGZmW9" colab_type="code" colab={}
import pandas as pd
from sklearn.tree import DecisionTreeClassifier # Import Decision Tree Classifier
from sklearn.model_selection import train_test_split # Import train_test_split function
from sklearn import metrics #Import scikit-learn metrics module for accuracy calculation
# + id="SlZUO5AcZu7D" colab_type="code" colab={}
col_names = ['id',
'diagnosis',
'radius_mean',
'texture_mean',
'perimeter_mean',
'area_mean',
'smoothness_mean',
'compactness_mean',
'concavity_mean',
'concave points_mean',
'symmetry_mean',
'fractal_dimension_mean',
'radius_se',
'texture_se',
'perimeter_se',
'area_se',
'smoothness_se',
'compactness_se',
'concavity_se',
'concave points_se',
'symmetry_se',
'fractal_dimension_se',
'radius_worst',
'texture_worst',
'perimeter_worst',
'area_worst',
'smoothness_worst',
'compactness_worst',
'concavity_worst',
'concave points_worst',
'symmetry_worst',
'fractal_dimension_worst',
'wtf?!']
# load dataset
pima = pd.read_csv("/content/data.csv")
pima.columns = col_names
# + id="qv1G1eysaDQ3" colab_type="code" colab={}
pima.head()
# + id="IYr6zLwaaaSq" colab_type="code" colab={}
#split dataset in features and target variable
feature_cols = ['radius_mean',
'texture_mean',
'perimeter_mean',
'area_mean',
'smoothness_mean',
'compactness_mean',
'concavity_mean',
'concave points_mean',
'symmetry_mean',
'fractal_dimension_mean',
'radius_se',
'texture_se',
'perimeter_se',
'area_se',
'smoothness_se',
'compactness_se',
'concavity_se',
'concave points_se',
'symmetry_se',
'fractal_dimension_se',
'radius_worst',
'texture_worst',
'perimeter_worst',
'area_worst',
'smoothness_worst',
'compactness_worst',
'concavity_worst',
'concave points_worst',
'symmetry_worst',
'fractal_dimension_worst']
X = pima[feature_cols] # Features
y = pima.diagnosis # Target variable
# + id="pwwZcPwUb4y8" colab_type="code" colab={}
# Split dataset into training set and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1) # 70% training and 30% test
# + id="iWNfbrYrcFrJ" colab_type="code" colab={}
# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
# + id="thRjHu6acHiW" colab_type="code" colab={}
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['M','B'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('breastcancer.png')
Image(graph.create_png())
# + id="-eLvOqCjcScX" colab_type="code" colab={}
# Create Decision Tree classifer object
clf = DecisionTreeClassifier(criterion="entropy", max_depth=3)
# Train Decision Tree Classifer
clf = clf.fit(X_train,y_train)
#Predict the response for test dataset
y_pred = clf.predict(X_test)
# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
# + id="hVnbF4afcaB4" colab_type="code" colab={}
from sklearn.externals.six import StringIO
from IPython.display import Image
from sklearn.tree import export_graphviz
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True, rounded=True,
special_characters=True, feature_names = feature_cols,class_names=['M','B'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('breastcancer.png')
Image(graph.create_png())
|
Decision_Tree.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Question 1
def functionOne(argsFun):
def newFun():
num = int(input("Enter any Number - "))
argsFun(num)
return newFun
@functionOne
def fibonacci(n):
oldnum = 0
previousnum = 1
print('1')
for i in range(0,n):
newnum = previousnum +oldnum
oldnum = previousnum
previousnum = newnum
print(newnum)
fibonacci()
# # Question 2
file = open("Mrunal.txt","w")
file.write("Hey Mrunal! ")
file.close()
file = open("Mrunal.txt","r")
file.write("How are you?")
file.close()
try :
file = open("Mrunal.txt","r")
file.write("How are you?")
file.close()
print("Success")
except Exception as v:
print(v)
finally:
print("HEY Execute Later!")
|
Day 8 Assignment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Precomptued Analysis
#
# Use precomputed optimal angles to measure the expected value of $\langle C \rangle$ across a variety of problem types, sizes, $p$-depth, and random instances.
# ## Load in Raw Data
# Go through each record, load in supporting objects, flatten everything into records, and put into a massive dataframe.
# +
import recirq
import cirq
import numpy as np
import pandas as pd
from recirq.qaoa.experiments.precomputed_execution_tasks import \
DEFAULT_BASE_DIR, DEFAULT_PROBLEM_GENERATION_BASE_DIR, DEFAULT_PRECOMPUTATION_BASE_DIR
records = []
for record in recirq.iterload_records(dataset_id="2020-03-tutorial", base_dir=DEFAULT_BASE_DIR):
dc_task = record['task']
apre_task = dc_task.precomputation_task
pgen_task = apre_task.generation_task
problem = recirq.load(pgen_task, base_dir=DEFAULT_PROBLEM_GENERATION_BASE_DIR)['problem']
record['problem'] = problem.graph
record['problem_type'] = problem.__class__.__name__
record['optimum'] = recirq.load(apre_task, base_dir=DEFAULT_PRECOMPUTATION_BASE_DIR)['optimum']
record['bitstrings'] = record['bitstrings'].bits
recirq.flatten_dataclass_into_record(record, 'task')
recirq.flatten_dataclass_into_record(record, 'precomputation_task')
recirq.flatten_dataclass_into_record(record, 'generation_task')
recirq.flatten_dataclass_into_record(record, 'optimum')
records.append(record)
df_raw = pd.DataFrame(records)
df_raw['timestamp'] = pd.to_datetime(df_raw['timestamp'])
df_raw.head()
# -
# ## Narrow down to Relevant Data
# Drop unnecessary metadata and use bitstrings to compute the expected value of the energy. In general, it's better to save the raw data and lots of metadata so we can use it if it becomes necessary in the future.
# +
from recirq.qaoa.simulation import hamiltonian_objectives, hamiltonian_objective_avg_and_err
import cirq.google as cg
def compute_energy_w_err(row):
permutation = []
for i, q in enumerate(row['qubits']):
fi = row['final_qubits'].index(q)
permutation.append(fi)
energy, err = hamiltonian_objective_avg_and_err(row['bitstrings'], row['problem'], permutation)
return pd.Series([energy, err], index=['energy', 'err'])
# Start cleaning up the raw data
df = df_raw.copy()
# Don't need these columns for present analysis
df = df.drop(['gammas', 'betas', 'circuit', 'violation_indices',
'precomputation_task.dataset_id',
'generation_task.dataset_id',
'generation_task.device_name'], axis=1)
# p is specified twice (from a parameter and from optimum)
assert (df['optimum.p'] == df['p']).all()
df = df.drop('optimum.p', axis=1)
# Compute energies
df = df.join(df.apply(compute_energy_w_err, axis=1))
df = df.drop(['bitstrings', 'qubits', 'final_qubits', 'problem'], axis=1)
# Normalize
df['energy_ratio'] = df['energy'] / df['min_c']
df['err_ratio'] = df['err'] * np.abs(1/df['min_c'])
df['f_val_ratio'] = df['f_val'] / df['min_c']
df
# -
# ## Plots
# +
# %matplotlib inline
from matplotlib import pyplot as plt
import seaborn as sns
sns.set_style('ticks')
plt.rc('axes', labelsize=16, titlesize=16)
plt.rc('xtick', labelsize=14)
plt.rc('ytick', labelsize=14)
plt.rc('legend', fontsize=14, title_fontsize=16)
# theme colors
QBLUE = '#1967d2'
QRED = '#ea4335ff'
QGOLD = '#fbbc05ff'
QGREEN = '#34a853ff'
QGOLD2 = '#ffca28'
QBLUE2 = '#1e88e5'
# -
C = r'\langle C \rangle'
CMIN = r'C_\mathrm{min}'
COVERCMIN = f'${C}/{CMIN}$'
def percentile(n):
def percentile_(x):
return np.nanpercentile(x, n)
percentile_.__name__ = 'percentile_%s' % n
return percentile_
# ### Raw swarm plots of all data
# +
import numpy as np
from matplotlib import pyplot as plt
pretty_problem = {
'HardwareGridProblem': 'Hardware Grid',
'SKProblem': 'SK Model',
'ThreeRegularProblem': '3-Regular MaxCut'
}
for problem_type in ['HardwareGridProblem', 'SKProblem', 'ThreeRegularProblem']:
df1 = df
df1 = df1[df1['problem_type'] == problem_type]
for p in sorted(df1['p'].unique()):
dfb = df1
dfb = dfb[dfb['p'] == p]
dfb = dfb.sort_values(by='n_qubits')
plt.subplots(figsize=(7,5))
n_instances = dfb.groupby('n_qubits').count()['energy_ratio'].unique()
if len(n_instances) == 1:
n_instances = n_instances[0]
label = f'{n_instances}'
else:
label = f'{min(n_instances)} - {max(n_instances)}'
#sns.boxplot(dfb['n_qubits'], dfb['energy_ratio'], color=QBLUE, saturation=1)
#sns.boxplot(dfb['n_qubits'], dfb['f_val_ratio'], color=QGREEN, saturation=1)
sns.swarmplot(dfb['n_qubits'], dfb['energy_ratio'], color=QBLUE)
sns.swarmplot(dfb['n_qubits'], dfb['f_val_ratio'], color=QGREEN)
plt.axhline(1, color='grey', ls='-')
plt.axhline(0, color='grey', ls='-')
plt.title(f'{pretty_problem[problem_type]}, {label} instances, p={p}')
plt.xlabel('# Qubits')
plt.ylabel(COVERCMIN)
plt.tight_layout()
plt.show()
# -
# ### Compare SK and Hardware Grid vs. $n$
# +
pretty_problem = {
'HardwareGridProblem': 'Hardware Grid',
'SKProblem': 'SK Model',
'ThreeRegularProblem': '3-Regular MaxCut'
}
df1 = df
df1 = df1[
((df1['problem_type'] == 'SKProblem') & (df1['p'] == 3))
| ((df1['problem_type'] == 'HardwareGridProblem') & (df1['p'] == 3))
]
df1 = df1.sort_values(by='n_qubits')
MINQ = 3
df1 = df1[df1['n_qubits'] >= MINQ]
plt.subplots(figsize=(8, 6))
plt.xlim((8, 23))
# SK
dfb = df1
dfb = dfb[dfb['problem_type'] == 'SKProblem']
sns.swarmplot(dfb['n_qubits'], dfb['energy_ratio'], s=5, linewidth=0.5, edgecolor='k', color=QRED)
sns.swarmplot(dfb['n_qubits'], dfb['f_val_ratio'], s=5, linewidth=0.5, edgecolor='k', color=QRED,
marker='s')
dfg = dfb.groupby('n_qubits').mean().reset_index()
# --------
# Hardware
dfb = df1
dfb = dfb[dfb['problem_type'] == 'HardwareGridProblem']
sns.swarmplot(dfb['n_qubits'], dfb['energy_ratio'], s=5, linewidth=0.5, edgecolor='k', color=QBLUE)
sns.swarmplot(dfb['n_qubits'], dfb['f_val_ratio'], s=5, linewidth=0.5, edgecolor='k', color=QBLUE,
marker='s')
dfg = dfb.groupby('n_qubits').mean().reset_index()
# -------
plt.axhline(1, color='grey', ls='-')
plt.axhline(0, color='grey', ls='-')
plt.xlabel('# Qubits')
plt.ylabel(COVERCMIN)
from matplotlib.patches import Patch
from matplotlib.lines import Line2D
from matplotlib.legend_handler import HandlerTuple
lelements = [
Line2D([0], [0], color=QBLUE, marker='o', ms=7, ls='', ),
Line2D([0], [0], color=QRED, marker='o', ms=7, ls='', ),
Line2D([0], [0], color='k', marker='s', ms=7, ls='', markerfacecolor='none'),
Line2D([0], [0], color='k', marker='o', ms=7, ls='', markerfacecolor='none'),
]
plt.legend(lelements, ['Hardware Grid', 'SK Model', 'Noiseless', 'Experiment', ], loc='best',
title=f'p = 3',
handler_map={tuple: HandlerTuple(ndivide=None)}, framealpha=1.0)
plt.tight_layout()
plt.show()
# -
# ### Hardware Grid vs. $p$
# +
dfb = df
dfb = dfb[dfb['problem_type'] == 'HardwareGridProblem']
dfb = dfb[['p', 'instance_i', 'n_qubits', 'energy_ratio', 'f_val_ratio']]
P_LIMIT = max(dfb['p'])
def max_over_p(group):
i = group['energy_ratio'].idxmax()
return group.loc[i][['energy_ratio', 'p']]
def count_p(group):
new = {}
for i, c in enumerate(np.bincount(group['p'], minlength=P_LIMIT+1)):
if i == 0:
continue
new[f'p{i}'] = c
return pd.Series(new)
dfgy = dfb.groupby(['n_qubits', 'instance_i']).apply(max_over_p).reset_index()
dfgz = dfgy.groupby(['n_qubits']).apply(count_p).reset_index()
# In the paper, we restrict to n > 10
# dfgz = dfgz[dfgz['n_qubits'] > 10]
dfgz = dfgz.set_index('n_qubits').sum(axis=0)
dfgz /= (dfgz.sum())
dfgz
# +
dfb = df
dfb = dfb[dfb['problem_type'] == 'HardwareGridProblem']
dfb = dfb[['p', 'instance_i', 'n_qubits', 'energy_ratio', 'f_val_ratio']]
# In the paper, we restrict to n > 10
# dfb = dfb[dfb['n_qubits'] > 10]
dfg = dfb.groupby('p').agg(['median', percentile(25), percentile(75), 'mean', 'std']).reset_index()
plt.subplots(figsize=(5.5,4))
plt.errorbar(x=dfg['p'], y=dfg['f_val_ratio', 'mean'],
yerr=(dfg['f_val_ratio', 'std'],
dfg['f_val_ratio', 'std']),
fmt='o-',
capsize=7,
color=QGREEN,
label='Noiseless'
)
plt.errorbar(x=dfg['p'], y=dfg['energy_ratio', 'mean'],
yerr=(dfg['energy_ratio', 'std'],
dfg['energy_ratio', 'std']),
fmt='o-',
capsize=7,
color=QBLUE,
label='Experiment'
)
plt.xlabel('p')
plt.ylabel('Mean ' + COVERCMIN)
plt.ylim((0, 1))
plt.text(0.05, 0.9, r'Hardware Grid', fontsize=16, transform=plt.gca().transAxes, ha='left', va='bottom')
plt.legend(loc='center right')
ax2 = plt.gca().twinx() # instantiate a second axes that shares the same x-axis
dfgz_p = [int(s[1:]) for s in dfgz.index]
dfgz_y = dfgz.values
ax2.bar(dfgz_p, dfgz_y, color=QBLUE, width=0.9, lw=1, ec='k')
ax2.tick_params(axis='y')
ax2.set_ylim((0, 2))
ax2.set_yticks([0, 0.25, 0.50])
ax2.set_yticklabels(['0%', None, '50%'])
ax2.set_ylabel('Fraction best' + ' ' * 41, fontsize=14)
plt.tight_layout()
|
docs/qaoa/Precomputed-Analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Hello Node Kubernetes
#
# **Learning Objectives**
# * Create a Node.js server
# * Create a Docker container image
# * Create a container cluster and a Kubernetes pod
# * Scale up your services
# ## Overview
#
# The goal of this hands-on lab is for you to turn code that you have developed into a replicated application running on Kubernetes, which is running on Kubernetes Engine. For this lab the code will be a simple Hello World node.js app.
#
# Here's a diagram of the various parts in play in this lab, to help you understand how the pieces fit together with one another. Use this as a reference as you progress through the lab; it should all make sense by the time you get to the end (but feel free to ignore this for now).
#
# <img src='../assets/k8s_hellonode_overview.png' width='50%'>
# ## Create a Node.js server
#
# The file `./src/server.js` contains a simple Node.js server. Use `cat` to examine the contents of that file.
# !cat ./src/server.js
# Start the server by running `node server.js` in the cell below. Open a terminal and type
# ```bash
# curl http://localhost:8000
# ```
# to see what the server outputs.
# !node ./src/server.js
# You should see the output `"Hello World!"`. Once you've verfied this, interupt the above running cell by hitting the stop button.
# ## Create and build a Docker image
#
# Now we will create a docker image called `hello_node.docker` that will do the following:
#
# 1. Start from the node image found on the Docker hub by inhereting from `node:6.9.2`
# 2. Expose port 8000
# 3. Copy the `./src/server.js` file to the image
# 4. Start the node server as we previously did manually
#
# Save your Dockerfile in the folder labeled `dockerfiles`. Your finished Dockerfile should look something like this
#
#
# ```bash
# FROM node:6.9.2
#
# EXPOSE 8080
#
# COPY ./src/server.js .
#
# CMD node server.js
# ```
# Next, build the image in your project using `docker build`.
# +
import os
PROJECT_ID = "your-gcp-project-here" # REPLACE WITH YOUR PROJECT NAME
os.environ["PROJECT_ID"] = PROJECT_ID
# + language="bash"
# docker build -f dockerfiles/hello_node.docker -t gcr.io/${PROJECT_ID}/hello-node:v1 .
# -
# It'll take some time to download and extract everything, but you can see the progress bars as the image builds. Once complete, test the image locally by running a Docker container as a daemon on port 8000 from your newly-created container image.
#
# Run the container using `docker run`
# + language="bash"
# docker run -d -p 8000:8000 gcr.io/${PROJECT_ID}/hello-node:v1
# -
# Your output should look something like this:
# ```bash
# b16e5ccb74dc39b0b43a5b20df1c22ff8b41f64a43aef15e12cc9ac3b3f47cfd
# ```
# Right now, since you used the `--d` flag, the container process is running in the background. You can verify it's running using `curl` as before.
# !curl http://localhost:8000
# Now, stop running the container. Get the container id using `docker ps` and then terminate using `docker stop`
# !docker ps
# your container id will be different
# !docker stop b16e5ccb74dc
# Now that the image is working as intended, push it to the Google Container Registry, a private repository for your Docker images, accessible from your Google Cloud projects. First, configure docker uisng your local config file. The initial push may take a few minutes to complete. You'll see the progress bars as it builds.
# !gcloud auth configure-docker
# + language="bash"
# docker push gcr.io/${PROJECT_ID}/hello-node:v1
# -
# The container image will be listed in your Console. Select `Navigation` > `Container Registry`.
# ## Create a cluster on GKE
#
# Now you're ready to create your Kubernetes Engine cluster. A cluster consists of a Kubernetes master API server hosted by Google and a set of worker nodes. The worker nodes are Compute Engine virtual machines.
#
# Create a cluster with two n1-standard-1 nodes (this will take a few minutes to complete). You can safely ignore warnings that come up when the cluster builds.
#
# **Note**: You can also create this cluster through the Console by opening the Navigation menu and selecting `Kubernetes Engine` > `Kubernetes clusters` > `Create cluster`.
# !gcloud container clusters create hello-world \
# --num-nodes 2 \
# --machine-type n1-standard-1 \
# --zone us-central1-a
# ## Create a pod
#
# A Kubernetes pod is a group of containers tied together for administration and networking purposes. It can contain single or multiple containers. Here you'll use one container built with your `Node.js` image stored in your private container registry. It will serve content on port 8000.
#
# Create a pod with the `kubectl run` command.
# + language="bash"
# kubectl create deployment hello-node \
# --image=gcr.io/${PROJECT_ID}/hello-node:v1
# -
# As you can see, you've created a deployment object. Deployments are the recommended way to create and scale pods. Here, a new deployment manages a single pod replica running the `hello-node:v1` image.
#
# View the deployment using `kubectl get`
# !kubectl get deployments
# Similarly, view the pods created by the deployment by also using `kubectl get`
# !kubectl get pods
# Here are some other good kubectl commands you should know. They won't change the state of the cluster. Others can be found [here](https://kubernetes.io/docs/reference/kubectl/overview/).
# * `kubectl cluster-info`
# * `kubectl config view`
# * `kubectl get events`
# * `kubectl logs <pod-name>`
# ## Allow external traffic
#
# By default, the pod is only accessible by its internal IP within the cluster. In order to make the hello-node container accessible from outside the Kubernetes virtual network, you have to expose the pod as a Kubernetes service.
#
# You can expose the pod to the public internet with the `kubectl expose` command. The `--type="LoadBalancer"` flag is required for the creation of an externally accessible IP. This flag specifies that we are using the load-balancer provided by the underlying infrastructure (in this case the Compute Engine load balancer). Note that you expose the deployment, and not the pod, directly. This will cause the resulting service to load balance traffic across all pods managed by the deployment (in this case only 1 pod, but you will add more replicas later).
# !kubectl expose deployment hello-node --type="LoadBalancer" --port=8000
# The Kubernetes master creates the load balancer and related Compute Engine forwarding rules, target pools, and firewall rules to make the service fully accessible from outside of Google Cloud.
#
# To find the publicly-accessible IP address of the service, request kubectl to list all the cluster services.
# !kubectl get services
# There are 2 IP addresses listed for your `hello-node` service, both serving port 8000. The `CLUSTER-IP` is the internal IP that is only visible inside your cloud virtual network; the `EXTERNAL-IP` is the external load-balanced IP.
# You should now be able to reach the service by calling `curl http://<EXTERNAL_IP>:8000`.
# !curl http://192.168.3.11:8000
# At this point you've gained several features from moving to containers and Kubernetes - you do not need to specify on which host to run your workload and you also benefit from service monitoring and restart. Now see what else can be gained from your new Kubernetes infrastructure.
# ## Scale up your service
# One of the powerful features offered by Kubernetes is how easy it is to scale your application. Suppose you suddenly need more capacity. You can tell the replication controller to manage a new number of replicas for your pod:
# ```bash
# kubectl scale deployment hello-node --replicas=4
# ```
# Scale your `hello-node` application to have 6 replicas. Then use `kubectl get` to request a description of the updated deployment and list all the pods:
# !kubectl scale deployment hello-node --replicas=6
# !kubectl get deployment
# !kubectl get pods
# A declarative approach is being used here. Rather than starting or stopping new instances, you declare how many instances should be running at all times. Kubernetes reconciliation loops makes sure that reality matches what you requested and takes action if needed.
#
# Here's a diagram summarizing the state of your Kubernetes cluster:
#
# <img src='../assets/k8s_cluster.png' width='60%'>
# ## Roll out an upgrade to your service
# At some point the application that you've deployed to production will require bug fixes or additional features. Kubernetes helps you deploy a new version to production without impacting your users.
#
# First, modify the application by opening `server.js` so that the response is
# ```bash
# response.end("Hello Kubernetes World!");
# ```
# Now you can build and publish a new container image to the registry with an incremented tag (`v2` in this case).
#
# **Note**: Building and pushing this updated image should be quicker since caching is being taken advantage of.
# + language="bash"
# docker build -f dockerfiles/hello_node.docker -t gcr.io/${PROJECT_ID}/hello-node:v2 .
# -
# Kubernetes will smoothly update your replication controller to the new version of the application. In order to change the image label for your running container, you will edit the existing `hello-node` deployment and change the image from `gcr.io/PROJECT_ID/hello-node:v1` to `gcr.io/PROJECT_ID/hello-node:v2`.
#
# To do this, use the `kubectl edit` command. It opens a text editor displaying the full deployment yaml configuration. It isn't necessary to understand the full yaml config right now, just understand that by updating the `spec.template.spec.containers.image` field in the config you are telling the deployment to update the pods with the new image.
# Open a terminal and run the following command:
#
# ```bash
# kubectl edit deployment hello-node
# ```
#
# Look for `Spec` > `containers` > `image` and change the version number to `v2`. This is the output you should see:
#
# ```bash
# deployment.extensions/hello-node edited
# ```
#
# New pods will be created with the new image and the old pods will be deleted. Run `kubectl get deployments` to confirm.
#
# **Note**: You may need to rerun the above command as it provisions machines.
# !kubectl get deployments
# While this is happening, the users of your services shouldn't see any interruption. After a little while they'll start accessing the new version of your application. You can find more details on rolling updates in this documentation.
#
# Hopefully with these deployment, scaling, and updated features, once you've set up your Kubernetes Engine cluster, you'll agree that Kubernetes will help you focus on the application rather than the infrastructure.
# ## Cleanup
#
# Delete the cluster using `gcloud` to free up those resources. Use the `--quiet` flag if you are executing this in a notebook. Deleting the cluster can take a few minutes.
# !gcloud container clusters --quiet delete hello-world
# Copyright 2020 Google LLC Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at https://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
|
notebooks/docker_and_kubernetes/solutions/3_k8s_hello_node.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Asteroid detection
# <NAME>
# 19/02/2021
# The purpose of this notebook is to estimate how long ( in days ) an asteroid would be visible by a telescope given some parameters like minimum magnitude detectable which depends on the integration time, the detector size, the FOV...
#
# The final goal is to study the possibilty to find a strategy to be able to detected asteroids above 100m diameter with a 99.9% probability. That is why in this study we will often compute quantities for 100m asteroids because it represents the worst case ( less bright as they are the smallest asteroids we want to detect ).
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pyplot import colorbar, pcolor, show
from matplotlib import ticker,cm
import pandas as pd
import matplotlib as mpl
from scipy.integrate import quad
# +
###################
# Constants
###################
h = 6.62607004e-34 # Planck Constant
c = 299792458.0 # Speed of light
G = 6.67*10**(-11) # Gravitational constant
M = 1.989*10**(30) # Solar mass
# -
# #### Diameter, absolute magnitude and apparent magnitude
#
# First of all, it is important to find the link between the diameter and the Absolute Magnitude which is :
# \begin{align} D=\frac{1329km*10^{\frac{-H}{5}}}{\sqrt{p_v}}\end{align}
#
# With $D$ the diameter in km, $H$ the absolute magnitude and $p_v$ the geometric albedo.
#
# **Source** : *Physical properties of near-Earth asteroids from thermal infrared observations and thermal modeling
# / <NAME>*
# The absolute magnitude is measured by the telescope but the geometric albedo $p_v$ cannot be measured, that is why we decided to take $p_v$ between 0.03 and 0.15 as its distribution among C type asteroids ( which are the most abundant ) is :
from IPython.display import Image
Image("pv.png",width=300)
# +
def D_to_abs_mag(D,p_v):
'''
Parameters
----------
D : Diameter (km)
p_v : Geometric Albedo ( from 0.03 to 0.15 for NEO )
Returns
-------
H : Absolute Magnitude
'''
return -5*np.log10(np.sqrt(p_v)*D/1329)
def abs_mag_to_D(H,pv):
'''
Parameters
----------
H : Absolute Magnitude
pv : Geometric Albedo ( from 0.03 to 0.15 for NEO )
Returns
-------
H : Diameter in meter (m)
'''
return 1329*10**(-H/5)/(np.sqrt(pv))*10**3
# -
# Given two distances :
# - distance to the Sun $d_{sun}$ in UA
# - distance to the observer $d_{obs}$ in UA
#
# it is then possible to compute the apparent magnitude m from absolute magnitude H :
#
# \begin{align} m = H + 5log_{10}\left ( \frac{d_{sun}*d_{obs}}{1UA^2}\right ) -2.5log_{10}(q)\end{align}
#
# With q the phase angle, that we will assume to be $0.290+0.684*0.15$
#
# **Source :** *https://en.wikipedia.org/wiki/Absolute_magnitude*
def abs_mag_to_mag(H,d_sun_ast,d_obs_ast):
'''
Parameters
----------
H : Absolute Magnitude
d_sun_ast : distance bewteen Sun and NEO ( /!\ UA )
d_obs_ast : distance bewteen Satellite and NEO ( /!\ UA )
Returns
-------
m : Apparent Magnitude
'''
# Distance in UA
q=0.290+0.684*0.15
return H + 5*np.log10(d_sun_ast*d_obs_ast) - 2.5*np.log10(q)
# +
D_SUN = np.linspace(0.00001,6,1000) # in UA
D_OBS = np.linspace(0.00001,5,1000) # in UA
X, Y = np.meshgrid(D_SUN, D_OBS)
mag_abs=D_to_abs_mag(0.1,0.03) # absolute magnitude of a 100m diameter asteroid with pv = 0.03
mag_app = abs_mag_to_mag(mag_abs,X,Y)
fig, ax = plt.subplots()
plt.pcolor(X, Y, mag_app) # from magnitude 18 because if the asteroid is very close to the Sun and the observer
# the magnitude will be very low and it won't be easy to put very low and high magnitude
# on the same graph that is why there is green in the back left corner
level = [18,20,21,22,23,24,25,26,27,28,29,30,31,32,35,40]
cs = ax.contourf(X, Y, mag_app,level)
cbar = fig.colorbar(cs)
cbar.ax.set_ylabel('mag')
plt.xlabel('Distance to observer (UA)')
plt.ylabel('Distance to Sun (UA)')
plt.title('Magnitude for 100m diameter and 0.03 geometric albedo')
plt.show()
# -
# In order to be able to determine if an asteroid is detected or not it is then necessary to compute the flux of a given source with a certain magnitude m. We assume that a source of magnitude 0 has a flux of $3.6*10^6$ ph/s/cm². Moreover, we consider that the background has a magnitude of 22mag/arcsec² which will contribute to generate some noise.
# +
def compute_min_flux(M_min):
'''
Parameters
----------
M_min : Apparent Magnitude of source
Returns
-------
F : Flux in photon/cm2/s sent by a source with apparent magnitude M_min
'''
M_origine = 0
# Flux of origine in ph/s/cm-2.
F_origine = 3.6*10**(6)
Flux_min = F_origine*10**(2/5*(M_origine-M_min))
# Flux in photons/cm2/s
Flux_photons_cm_s = Flux_min
return Flux_photons_cm_s
def compute_F_background():
'''
Returns
-------
F_background : Flux from background considering it as an apparent magnitude
of 22mag/degree
'''
F_origine = 3.6*10**(6)
M_origine = 0
return F_origine*10**(2/5*(M_origine-22))
# -
# We then import data from a csv file on keplerian parameters of a sample of 1000 asteroids.
neos1000 = 'Atens_Apollos_sup100m_r.csv'
neos1000 = pd.read_csv(neos1000)
def compute_period_fromtraj(neo):
'''
Parameters
----------
neo : for a dataframe containing keplerian parameters of neo(s)
Returns
-------
T : orbital period using Kepler 3rd law T**2/a**3 = 4pi**2/MG
'''
M = 1.989*10**30 # Solar mass
G = 6.67*10**(-11)
a = neo['a']
if isinstance(a,float):
a_axe = np.sqrt(4*np.pi**2*(a*1.496*10**(11))**3/(G*M))
else:
a_axe = []
for i in range(len(neo)):
a_axe.append(np.sqrt(4*np.pi**2*(a[i]*1.496*10**(11))**3/(G*M)))
return a_axe
# #### Characteristics of asteroids sample
# In order to better understand the calculs that will be done further in this notebook it is important to have an idea of the parameters of the sample of 1000 asteroids.
# That is why we plot the histograms of semi major axis, exentricity and orbital period of the sample of 1000 asteroids.
# +
plt.hist(neos1000['a'],bins=50,facecolor='blue', alpha=0.5)
plt.xlabel('UA')
plt.ylabel('Frequency')
plt.title('Semi major axis histogram of some NEO')
plt.show()
plt.hist(neos1000['e'],bins=50,facecolor='blue', alpha=0.5)
plt.xlabel('Excentricity')
plt.ylabel('Frequency')
plt.title('Excentricty histogram of some NEO')
plt.show()
plt.hist(compute_period_fromtraj(neos1000),bins=50,facecolor='blue', alpha=0.5)
plt.xlabel('Period (years)')
plt.ylabel('Frequency')
plt.title('Period histogram of some NEO')
plt.show()
plt.hist(neos1000['i'],bins=50,facecolor='blue', alpha=0.5)
plt.xlabel('Inclinaison')
plt.ylabel('Frequency')
plt.title('Inclinaison histogram of some NEO')
plt.show()
# -
# Now that we better understand NEOs ( Near Earth Objects ) that we want to detect, it is important to think of a strategy to detect as much NEO as we can. In this study the goal was to be able to detect 99.9% of NEO with a diameter larger than 100m.
# #### SNR needed on telescope detectors
# In order to maximize the Signal to Noise Ratio on detectors we decided to fix some detectors characteristics :
# | Capacity | Size | IFOV | Dark Current |
# | :-: | :-: | :-: | :-:|
# | $75$*$10^3$ electrons | 10000*10000pix | 1.08 | 1 |
# For the instrument we have :
# | FOV | Diameter | Efficiency | Quantum Efficiency |
# | :-: | :-: | :-: | :-:|
# | 3°x3° | 1m | 0.8 | 0.9 |
# In order to compute the SNR the time allowed per sky portion need to be known. Our satellite will be on a Venus like orbit, in order to simplify the study, it has been decided that in 1 period ( 224.7 days ) all the sky must have been scanned and a guard angle of 90° must be left between the sun and the line of sight.
# +
def compute_scanning_time_m(time_to_scan_entier_sky,FOV):
'''
Parameters
----------
time_to_scan_entier_sky : time allowed to scan entierely the sky (days)
FOV : Field of view ( degree )
Returns
-------
Time allowed per image
'''
nb_pointing_horiz = 360/FOV
nb_pointing_vert = 180/FOV
return (time_to_scan_entier_sky / nb_pointing_horiz)/nb_pointing_vert
print('Time per sky portion (min):',compute_scanning_time_m(224.7,3)*60*24)
# -
# In order to respect the criterion : scan all the sky in 1 period, we have 44min94s per sky portion ( 3°x3°).
# With all these characteristics it is then possible to compute the signal to noise ratio :
# \begin{align} \frac{S}{N} = \frac{FA_{\epsilon}\sqrt{\tau}}{(\frac{N_R^2}{\tau}+FA_{\epsilon}+i_{DC}+F_{\beta}A_{\epsilon}\Omega)^{\frac{1}{2}}}\end{align}
#
# with :
# - $F$ = point source signal flux
# - $F_{\beta}$ = Background flux from sky
# - $\Omega$ = Pixel size
# - $\tau$ = Integration time
# - $i_{DC}$ = Dark current
# - $A_e=A\epsilon Q_e$
# - $Q_e$ = Quantum efficiency
# - $NR$ = Read out noise
#
# **Source** : *Notes for PHYS 134: Observational Astrophysics / <NAME> and <NAME>*
# We computed with an excel table that for 1 image the SNR needed to have 99.9% probability of detection is 9.6 and for 2 images the SNR needed is 6.1.
# As the SNR is related to the incoming flux, it is then possible to compute the minimum magnitude visible with our telescope in order to be capable of detecting an object with accuracy 99.9%. The aim is to maximize the limit detectable magnitude in order to be able to detect fainter objects. After an optimization study, on either doing lot of image with small integration time or longer but fewer images, the chosen strategy is the following :
Image("strategie.png",width=300)
# The limit magnitude detected is 25.27. That is to says, a 100m diameter asteroid would be visible under the dark curve which corresponds to apparent magnitude 25.21 :
# +
# 100m asteroid
D_SUN = np.linspace(0.00001,6,1000)
D_OBS = np.linspace(0.00001,5,1000)
X, Y = np.meshgrid(D_SUN, D_OBS)
mag_abs=D_to_abs_mag(0.1,0.03)
mag_app = abs_mag_to_mag(mag_abs,X,Y)
fig, ax = plt.subplots()
plt.pcolor(X, Y, mag_app)
level = [18,20,21,22,23,24,25,26,27,28,29,30,31,32,35,40]
cs = ax.contourf(X, Y, mag_app,level)
cs2 = ax.contour(cs,levels=[25.21],colors="black" )
cbar = fig.colorbar(cs)
cbar.ax.set_ylabel('mag')
plt.xlabel('Distance to observer (UA)')
plt.ylabel('Distance to Sun (UA)')
plt.title('Magnitude for 100m diameter and 0.03 geometric albedo')
plt.show()
# -
# #### Study of asteroid visibility windows
# Now that we have the limit magnitude detected it can be interessant to ask the question : How long asteroids are detectable ?
# In order to do this, we will use Kepler second law ( area law ). For a given radius of position on the ellipse we have :
# \begin{align} r = \frac{p}{1+ecos(\theta)}\end{align}
#
#
# The area of a section of an ellispe can be compute :
# \begin{align} A = \int_{\theta_1}^{\theta_2}\frac{1}{2}r^2d\theta\end{align}
#
Image("aire.png",width=300)
# In order to compute time spend by the asteroid in this area we use the 2nd Kepler law :
# \begin{align} \frac{dA}{dt}=\frac{C}{2}\end{align}
#
# With $C=r^2\theta = v_{perihelion}*r_{perihelion} = \sqrt{\mu a (1+e)(1-e)}$
def compute_period_fromtraj(neo):
'''
Parameters
----------
neo : for a dataframe containing keplerian parameters of neo(s)
Returns
-------
T : orbital period using Kepler 3rd law T**2/a**3 = 4pi**2/MG
'''
M = 1.989*10**30 # Solar mass
G = 6.67*10**(-11)
a = neo['a']
if isinstance(a,float):
a_axe = np.sqrt(4*np.pi**2*(a*1.496*10**(11))**3/(G*M))
else:
a_axe = []
for i in range(len(neo)):
a_axe.append(np.sqrt(4*np.pi**2*(a[i]*1.496*10**(11))**3/(G*M)))
return a_axe
def compute_b_from_ae(neo):
'''
Parameters
----------
neo : a dataframe containing keplerian parameters of neo(s)
Returns
-------
b : Semi minor axis ( same units as a, /!\ could be in UA )
'''
return neo['a']*np.sqrt(1-neo['e']**2)
def compute_theta_from_dist(dist,neo):
'''
Parameters
----------
dist : distance between NEO and Sun ( UA )
neo : a dataframe containing keplerian parameters of neo(s)
Returns
-------
theta : angle between apogee and actual position
'''
# dist en UA
dist = dist*1.496*10**(11) # in m
a = neo['a']*1.496*10**(11)
e = neo['e']
b = compute_b_from_ae(neo)*1.496*10**(11)
p = b**2/a
return np.arccos((dist-p)/(dist*e))
def compute_theta_from_dist(dist,neo):
'''
Parameters
----------
dist : distance between NEO and Sun ( UA )
neo : a dataframe containing keplerian parameters of neo(s)
Returns
-------
theta : angle between apogee and actual position
'''
# dist en UA
dist = dist*1.496*10**(11) # in m
a = neo['a']*1.496*10**(11)
e = neo['e']
b = compute_b_from_ae(neo)*1.496*10**(11)
p = b**2/a
return np.arccos((dist-p)/(dist*e))
def arealaw_constant(neo):
'''
Parameters
----------
neo : a dataframe containing keplerian parameters of neo(s)
Returns
-------
C : constant of the 2nd Kepler law ( area law )
'''
mu = G*M
a = neo['a']*1.496*10**(11)
e = neo['e']
return np.sqrt(mu*a*(1+e)*(1-e))
def r2(a,b,e,theta):
p = b**2/a
return 1/2*(p/(1-e*np.cos(theta)))**2
# ##### Link between Sun distance and satellite distance
# As mentionned before, in order to compute how much time an asteroid will stay in visible area ( in function of its diameter and orbit ) it is necessary to compute the distance from Sun at which it will become visible given the limit magnitude. But to deduce a distance from Sun it is necessary to have the distance from observer.
# We will then simplify the study. As mentionned before, we decided to consider a Venus like orbit ( $a = 0.7$ UA, e~0 ) for our satellite, considering that it is possible to detect the asteroid at $n$UA and as we want to keep a 90° angle with the Sun, we are in this configuration :
Image("dist_obs_max_min.png",width=300)
# That is to say that if an asteroid is visible at nUA from the Sun it is at a maximum distance $d_{max} = \sqrt{nUA^2-0.7^2}$ ( worst case ) from satellite and minimum distance of $d_{min}=nUA - 0.7$ ( best case ). With this simplification, it will be easier to compute the time of visible area for each asteroid. We will consider a best case, a worst case and an average case.
# It then now possible from the 1000neos catalogue to compute for each neo the distance from the Sun at which they are visible ( in the best case $ d_{min} $, worst case $d_{max}$ and average case $mean(d_{min},d_{max})$). Then it is possible to deduce with the area of an ellipse portion and 2nd kepler law the time spend for each asteroid in the visibility zone : distance from Sun for which the apparent magnitude is smaller than $25.21$.
def time_nUA_to_peri(dist,neo):
'''
Parameters
----------
neo : a dataframe containing keplerian parameters of neo(s)
dist [UA] : dist from Sun
Returns
-------
Compute time to go from dist UA to perihelion
'''
theta = compute_theta_from_dist(dist,neo)
a = neo['a']*1.496*10**(11)
e = neo['e']
b = compute_b_from_ae(neo)*1.496*10**(11)
if isinstance(a,float):
area, err = quad(lambda x : r2(a,b,e,x), np.pi, theta)
else:
area = np.zeros(len(neo['a']))
for i in range(len(neo['a'])):
area[i], err = quad(lambda x : r2(a[i],b[i],e[i],x), np.pi, theta[i])
C = arealaw_constant(neo)
period = compute_period_fromtraj(neo)
airetot = np.pi*a*b
return period - 2/C*(airetot - np.abs(area))
def dist_maxmin_nUAsun_kUAobs(distSUN,print_dist=False):
'''
We want to keep a 90 degree angle with the Sun, so if the asteroid is at
nUA from the Sun and is visible we can deduce the asteroid max distance to observer
and asteroid min distance to the observer
'''
dist_min = distSUN - 0.7
dist_max = np.sqrt(distSUN**2-0.7**2)
if print_dist :
print('Distance max to observer if {} to SUN : '.format(distSUN),dist_max)
print('Distance min to observer if {} to SUN : '.format(distSUN),dist_min)
return dist_min,dist_max
def time_inside_visible_area_astero(neo,magnitude_lim,case='best'):
'''
Parameters
----------
neo : a dataframe containing keplerian parameters of neo(s)
magnitude_lim : limite magnitude detectable by satellite
Returns
-------
Compute time inside visible area, different for each asteroide depending on size and keplerian parameters
'''
d_SUN = np.linspace(0.7,8,3000)
s = 0
visible_time = []
for k in range(len(neo['a'])):
neok = neo.iloc[k]
H = neok['H']
visible_dist = []
visible_dist_nb = 0
for i in range(len(d_SUN)):
# Compute visible distance
d_SUNi = d_SUN[i]
d_min , d_max = dist_maxmin_nUAsun_kUAobs(d_SUNi)
if case == 'best':
d_to_obs = d_min
if case == 'worst':
d_to_obs = d_max
if case == 'average':
d_to_obs = np.mean([d_min,d_max])
magapp = abs_mag_to_mag(H, d_SUNi, d_to_obs)
if ( magapp < magnitude_lim + 0.01 and magapp > magnitude_lim - 0.01):
visible_dist.append( d_SUNi )
if len(visible_dist) > 0 :
visible_dist_nb = np.max(visible_dist)
else :
print('## Either the asteroid is never visible ##')
print('/!\ Or the d spacing must be changed, or magnitude range comparision')
s = s+1
if visible_dist_nb != 0 :
if visible_dist_nb > neok['a']*(1+neok['e']):
a=0 # if visible distance > apogee
#visible_time.append(compute_period_fromtraj(neok)/(60*60*24))
else :
if abs_mag_to_D(H,0.03)<100:
a=0
else :
# 2*(Compute time to go from visible distance to perihelion)
visible_time.append(2*time_nUA_to_peri(visible_dist_nb,neok)/(60*60*24))
print(s)
return visible_time
case = 'best'
lim_mag = 25.21
visible_times = time_inside_visible_area_astero(neos1000,lim_mag,case)
plt.hist(visible_times,bins=80,range=[0,600],facecolor='blue', alpha=0.5)
plt.xlabel('Visible time distribution : m ={}, case={} '.format(lim_mag,case))
plt.ylabel('Frequency')
plt.title('Time ( Days )')
plt.show()
case = 'worst'
lim_mag = 25.21
visible_times = time_inside_visible_area_astero(neos1000,lim_mag,case)
plt.hist(visible_times,bins=80,range=[0,600],facecolor='blue', alpha=0.5)
plt.xlabel('Visible time distribution : m ={}, case={} '.format(lim_mag,case))
plt.ylabel('Frequency')
plt.title('Time ( Days )')
plt.show()
case = 'average'
lim_mag = 25.21
visible_times = time_inside_visible_area_astero(neos1000,lim_mag,case)
plt.hist(visible_times,bins=80,range=[0,600],facecolor='blue', alpha=0.5)
plt.xlabel('Visible time distribution : m ={}, case={} '.format(lim_mag,case))
plt.ylabel('Frequency')
plt.title('Time ( Days )')
plt.show()
# This visible time has to be compared with the satellite period 224.7days. The best case would be that visility time for asteroid is longer than satellite period ( 224.7days ) in order to be able to be sure to detect the asteroid 1 time at least in a period. But this is not the case that is why this study is completed by propagating orbits on CelestLab ( CNES ) in order to determine more precisely the probability to detect an asteroid with this strategy.
#
# #### If all the 1000ateroids where 100m diameter
# In order to complete the study we will assume that we are always in the worst case :
# - all the asteroid are 100m diameter and $p_v = 0.03$ ( worst case ) and $p_v=0.15$ ( best case )
# +
def time_inside_visible_area_100m_astero(neo,magnitude_lim):
''' /!\ Similar to previous function but here we assume each asteroid is 100m diameter ( in order to consider a worst case )
Parameters
----------
neo : a dataframe containing keplerian parameters of neo(s)
magnitude_lim : limite magnitude detectable by satellite
Returns
-------
Compute time inside visible area, different for each asteroide depending keplerian parameters
'''
d_SUN = np.linspace(0.1,8,3000)
dist = []
s = 0
visible_time_min = []
visible_time_max = []
pv_max = 0.15
pv_min = 0.03
D = 0.100
H_min = D_to_abs_mag(D,pv_min)
H_max = D_to_abs_mag(D,pv_max)
for k in range(len(neo['a'])):
neok = neo.iloc[k]
visible_dist_min = []
visible_dist_min_nb = 0
visible_dist_max = []
visible_dist_max_nb = 0
for i in range(len(d_SUN)):
d_SUNi = d_SUN[i]
d_min , d_max = dist_maxmin_nUAsun_kUAobs(d_SUNi)
magapp_min = abs_mag_to_mag(H_min, d_SUNi, d_min)
magapp_max = abs_mag_to_mag(H_max, d_SUNi, d_min)
if ( magapp_min < magnitude_lim + 0.01 and magapp_min > magnitude_lim - 0.01):
visible_dist_min.append( d_SUNi )
if ( magapp_max < magnitude_lim + 0.01 and magapp_max > magnitude_lim - 0.01):
visible_dist_max.append( d_SUNi )
if len(visible_dist_min) > 0 :
visible_dist_min_nb = np.max(visible_dist_min)
visible_dist_max_nb = np.max(visible_dist_max)
else :
print('## Either the asteroid is never visible ##')
print('/!\ Or the d spacing must be changed, or magnitude range comparision')
s = s+1
if visible_dist_min_nb != 0 :
if visible_dist_min_nb > neok['a']*(1+neok['e']):
a=0
#visible_time_min.append(compute_period_fromtraj(neok)/(60*60*24))
else :
visible_time_min.append(2*time_nUA_to_peri(visible_dist_min_nb,neok)/(60*60*24))
if visible_dist_max_nb != 0 :
if visible_dist_max_nb > neok['a']*(1+neok['e']):
a=0
#visible_time_max.append(compute_period_fromtraj(neok)/(60*60*24))
else :
visible_time_max.append(2*time_nUA_to_peri(visible_dist_max_nb,neok)/(60*60*24))
print(s)
return visible_time_min , visible_time_max
# +
lim_mag = 25.21
visible_times_100m_min,visible_times_100m_max = time_inside_visible_area_100m_astero(neos1000,lim_mag)
plt.hist(visible_times_100m_min,bins=80,range=[0,600],facecolor='blue', alpha=0.5)
plt.xlabel('Time (days)')
plt.ylabel('Frequency')
plt.title('Visible time distribution : m ={}, worst case pv=0.03 '.format(lim_mag))
plt.show()
# +
plt.hist(visible_times_100m_max,bins=80,range=[0,600],facecolor='blue', alpha=0.5)
plt.xlabel('Time (days)')
plt.ylabel('Frequency')
plt.title('Visible time distribution : m ={}, best case pv=0.15 '.format(lim_mag))
plt.show()
# -
# This approach has some limits, we can deduce here the detection probability of detecting a NEO or we cannot estimate how much before impact we can detect an asteroid. That is why we added to this study some orbit propagation on CelestLab.
# ## References
# Asteroid size :
# - *Multiple asteroid systems: Dimensions and thermal properties from Spitzer Space Telescope and ground-based observations / F. Marchis*
#
# Detection Probability :
# - *Survey Simulations of a new near-Earth asteroid detection systeme / <NAME>*
# - *Detection Systems, Institut d'Optique Graduate School / <NAME> and <NAME>*
# - *Notes for PHYS 134: Observational Astrophysics / <NAME> and <NAME>*
|
Asteroids.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Joins using pandas
# ## Introduction
# This Jupyter notebook explores SQL joins using Python.
# ## Left outer join
import pandas as pd
import numpy as np
department_data = {
'DepartmentID': [31, 33, 34, 35],
'DepartmentName': ['Sales', 'Engineering', 'Clerical', 'Marketing']
}
df_department = pd.DataFrame(department_data,
columns=['DepartmentID',
'DepartmentName'])
df_department
df_department.dtypes
employee_data = {
'LastName': ['Rafferty', 'Jones', 'Heisenberg', 'Robinson', 'Smith', 'Williams'],
'DepartmentID': [31, 33, 33, 34, 34, np.nan]
}
df_employee = pd.DataFrame(employee_data,
columns=['LastName',
'DepartmentID'])
df_employee['DepartmentID'] = df_employee['DepartmentID'].round().astype('Int64')
df_employee
df_employee.dtypes
# ## Previous example deprecated
left_table = pd.read_csv('left_table.csv')
left_table.head()
left_table.shape
left_table.insert(loc=2, column='Desk Location', value='')
left_table.head()
left_table.dtypes
left_table.head()
right_table = pd.read_csv('right_table.csv')
right_table.head()
right_table.dtypes
left_table['Desk Location'] = left_table[['Employee']]\
.merge(right_table[['Names', 'Desk Location']],\
left_on='Employee', \
right_on='Names', \
how='left')['Desk Location'].values
left_table.shape
left_table.head(10)
# Find employees not assigned a 'Desk Location'.
# Their name was misspelled or not entered in table_right.
left_table = left_table[['ID', \
'Employee', \
'Desk Location']]\
[left_table['Desk Location'].isnull()]
left_table.head(10)
left_table = left_table.dropna(subset=['Employee'])
left_table['ID'] = left_table['ID'].astype(int)
left_table.head()
left_table.to_csv('left_table_exceptions.csv')
# descriptive statistics
left_table['ID'].count()
|
joins_pandas.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Testinnsening av person skattemelding med næringspesifikasjon
# Denne demoen er ment for å vise hvordan flyten for et sluttbrukersystem kan hente et utkast, gjøre endringer, validere/kontrollere det mot Skatteetatens apier, for å sende det inn via Altinn3
# +
try:
from altinn3 import *
from skatteetaten_api import main_relay, base64_decode_response, decode_dokument
import requests
import base64
import xmltodict
import xml.dom.minidom
from pathlib import Path
except ImportError as e:
print("Mangler en avhengighet, installer dem via pip")
# !pip install python-jose
# !pip install xmltodict
# !pip install pathlib
import xmltodict
from skatteetaten_api import main_relay, base64_decode_response, decode_dokument
#hjelpe metode om du vil se en request printet som curl
def print_request_as_curl(r):
command = "curl -X {method} -H {headers} -d '{data}' '{uri}'"
method = r.request.method
uri = r.request.url
data = r.request.body
headers = ['"{0}: {1}"'.format(k, v) for k, v in r.request.headers.items()]
headers = " -H ".join(headers)
print(command.format(method=method, headers=headers, data=data, uri=uri))
# -
# ## Generer ID-porten token
# Tokenet er gyldig i 300 sekunder, rekjørt denne biten om du ikke har kommet frem til Altinn3 biten før 300 sekunder
idporten_header = main_relay()
# # Hent utkast og gjeldende
# Her legger vi inn fødselsnummeret vi logget oss inn med, Dersom du velger et annet fødselsnummer så må den du logget på med ha tilgang til skattemeldingen du ønsker å hente
#
# #### Parten nedenfor er brukt for internt test, pass på bruk deres egne testparter når dere tester
#
# 01014700230 har fått en myndighetsfastsetting
#
# Legg merke til `/api/skattemelding/v2/` biten av url'n er ny for 2021
# + pycharm={"name": "#%%\n"}
s = requests.Session()
s.headers = dict(idporten_header)
fnr="01014700230" #oppdater med test fødselsnummerene du har fått tildelt
# -
# ### Utkast
url_utkast = f'https://mp-test.sits.no/api/skattemelding/v2/utkast/2021/{fnr}'
r = s.get(url_utkast)
r
# ### Gjeldende
url_gjeldende = f'https://mp-test.sits.no/api/skattemelding/v2/2021/{fnr}'
r_gjeldende = s.get(url_gjeldende)
r_gjeldende
# #### Fastsatt
# Her får en _http 404_ om vedkommende ikke har noen fastsetting, rekjørt denne etter du har sendt inn og fått tilbakemdling i Altinn at den har blitt behandlet, du skal nå ha en fastsatt skattemelding om den har blitt sent inn som Komplett
url_fastsatt = f'https://mp-test.sits.no/api/skattemelding/v2/fastsatt/2021/{fnr}'
r_fastsatt = s.get(url_fastsatt)
r_fastsatt
# + [markdown] pycharm={"name": "#%% md\n"}
# ## Svar fra hent gjeldende
#
# ### Gjeldende dokument referanse:
# I responsen på alle api kallene, være seg utkast/fastsatt eller gjeldene, så følger det med en dokumentreferanse.
# For å kalle valider tjenesten, er en avhengig av å bruke korrekt referanse til gjeldende skattemelding.
#
# Cellen nedenfor henter ut gjeldende dokumentrefranse printer ut responsen fra hent gjeldende kallet
# + pycharm={"name": "#%%\n"}
sjekk_svar = r_gjeldende
sme_og_naering_respons = xmltodict.parse(sjekk_svar.text)
skattemelding_base64 = sme_og_naering_respons["skattemeldingOgNaeringsspesifikasjonforespoerselResponse"]["dokumenter"]["skattemeldingdokument"]
sme_base64 = skattemelding_base64["content"]
dokref = sme_og_naering_respons["skattemeldingOgNaeringsspesifikasjonforespoerselResponse"]["dokumenter"]['skattemeldingdokument']['id']
decoded_sme_xml = decode_dokument(skattemelding_base64)
sme_utkast = xml.dom.minidom.parseString(decoded_sme_xml["content"]).toprettyxml()
print(f"Responsen fra hent gjeldende ser slik ut, gjeldende dokumentrerefanse er {dokref}\n")
print(xml.dom.minidom.parseString(sjekk_svar.text).toprettyxml())
# +
with open("../../../src/resources/eksempler/v2/Naeringspesifikasjon-enk-v2.xml", 'r') as f:
naering_enk_xml = f.read()
innsendingstype = "ikkeKomplett"
naeringsspesifikasjoner_enk_b64 = base64.b64encode(naering_enk_xml.encode("utf-8"))
naeringsspesifikasjoner_enk_b64 = str(naeringsspesifikasjoner_enk_b64.decode("utf-8"))
skattemeldingPersonligSkattepliktig_base64=sme_base64 #bruker utkastet uten noen endringer
naeringsspesifikasjoner_base64=naeringsspesifikasjoner_enk_b64
dok_ref=dokref
valider_konvlutt_v2 = """
<?xml version="1.0" encoding="utf-8" ?>
<skattemeldingOgNaeringsspesifikasjonRequest xmlns="no:skatteetaten:fastsetting:formueinntekt:skattemeldingognaeringsspesifikasjon:request:v2">
<dokumenter>
<dokument>
<type>skattemeldingPersonlig</type>
<encoding>utf-8</encoding>
<content>{sme_base64}</content>
</dokument>
<dokument>
<type>naeringsspesifikasjon</type>
<encoding>utf-8</encoding>
<content>{naeringsspeifikasjon_base64}</content>
</dokument>
</dokumenter>
<dokumentreferanseTilGjeldendeDokument>
<dokumenttype>skattemeldingPersonlig</dokumenttype>
<dokumentidentifikator>{dok_ref}</dokumentidentifikator>
</dokumentreferanseTilGjeldendeDokument>
<inntektsaar>2021</inntektsaar>
<innsendingsinformasjon>
<innsendingstype>{innsendingstype}</innsendingstype>
<opprettetAv>TurboSkatt</opprettetAv>
</innsendingsinformasjon>
</skattemeldingOgNaeringsspesifikasjonRequest>
""".replace("\n","")
naering_enk = valider_konvlutt_v2.format(sme_base64=skattemeldingPersonligSkattepliktig_base64,
naeringsspeifikasjon_base64=naeringsspesifikasjoner_base64,
dok_ref=dok_ref,
innsendingstype=innsendingstype)
# + [markdown] pycharm={"name": "#%% md\n"}
# # Valider utkast sme med næringsopplysninger
# + pycharm={"name": "#%%\n"}
def valider_sme(payload):
url_valider = f'https://mp-test.sits.no/api/skattemelding/v2/valider/2021/{fnr}'
header = dict(idporten_header)
header["Content-Type"] = "application/xml"
return s.post(url_valider, headers=header, data=payload)
valider_respons = valider_sme(naering_enk)
resultatAvValidering = xmltodict.parse(valider_respons.text)["skattemeldingerOgNaeringsspesifikasjonResponse"]["resultatAvValidering"]
if valider_respons:
print(resultatAvValidering)
print()
print(xml.dom.minidom.parseString(valider_respons.text).toprettyxml())
else:
print(valider_respons.status_code, valider_respons.headers, valider_respons.text)
# + [markdown] pycharm={"name": "#%% md\n"}
# # Altinn 3
# + [markdown] pycharm={"name": "#%% md\n"}
# 1. Hent Altinn Token
# 2. Oppretter en ny instans av skjemaet
# 3. lasteropp metadata til skjemaet
# 4. last opp vedlegg til skattemeldingen
# 5. oppdater skattemelding xml med referanse til vedlegg_id fra altinn3.
# 6. laster opp skattemeldingen og næringsopplysninger som et vedlegg
# + pycharm={"name": "#%%\n"}
#1
altinn3_applikasjon = "skd/formueinntekt-skattemelding-v2"
altinn_header = hent_altinn_token(idporten_header)
#2
instans_data = opprett_ny_instans(altinn_header, fnr, appnavn=altinn3_applikasjon)
# -
# ### 3 Last opp metadata (skattemelding_V1)
# legg merke til `<innsendingstype>` er satt til `ikkeKomplett` i payloaden, og ikke i Altinn3 metadata
#
print(f"innsendingstypen er satt til: {innsendingstype}")
req_metadata = last_opp_metadata_json(instans_data, altinn_header, inntektsaar=2021, appnavn=altinn3_applikasjon)
req_metadata
# ## Last opp skattemelding
# ### Last først opp vedlegg som hører til skattemeldingen
# Eksemplet nedenfor gjelder kun generelle vedlegg for skattemeldingen,
#
# ```xml
# <vedlegg>
# <id>En unik id levert av altinn når du laster opp vedleggsfilen</id>
# <vedleggsfil>
# <opprinneligFilnavn><tekst>vedlegg_eksempel_sirius_stjerne.jpg</tekst></opprinneligFilnavn>
# <opprinneligFiltype><tekst>jpg</tekst></opprinneligFiltype>
# </vedleggsfil>
# <vedleggstype>dokumentertMarkedsverdi</vedleggstype>
# </vedlegg>
# ```
#
# men samme prinsippet gjelder for andre kort som kan ha vedlegg. Husk at rekkefølgen på xml elementene har noe å si for å få validert xml'n
# +
vedleggfil = "vedlegg_eksempel_sirius_stjerne.jpg"
opplasting_respons = last_opp_vedlegg(instans_data,
altinn_header,
vedleggfil,
content_type="image/jpeg",
data_type="skattemelding-vedlegg",
appnavn=altinn3_applikasjon)
vedlegg_id = opplasting_respons.json()["id"]
# Så må vi modifisere skattemeldingen slik at vi får med vedlegg idn inn skattemelding xml'n
with open("../../../src/resources/eksempler/v2/personligSkattemeldingV9EksempelVedlegg.xml") as f:
filnavn = Path(vedleggfil).name
filtype = "jpg"
partsnummer = xmltodict.parse(decoded_sme_xml["content"])["skattemelding"]["partsreferanse"]
sme_xml = f.read().format(partsnummer=partsnummer, vedlegg_id=vedlegg_id, filnavn=filnavn, filtype=filtype)
sme_xml_b64 = base64.b64encode(sme_xml.encode("utf-8"))
sme_xml_b64 = str(sme_xml_b64.decode("utf-8"))
#La oss validere at skattemeldingen fortsatt validerer mot valideringstjenesten
naering_enk_med_vedlegg = valider_konvlutt_v2.format(sme_base64=sme_xml_b64,
naeringsspeifikasjon_base64=naeringsspesifikasjoner_base64,
dok_ref=dok_ref,
innsendingstype=innsendingstype)
valider_respons = valider_sme(naering_enk)
resultat_av_validering_med_vedlegg = xmltodict.parse(valider_respons.text)["skattemeldingerOgNaeringsspesifikasjonResponse"]["resultatAvValidering"]
resultat_av_validering_med_vedlegg
# -
#Last opp skattemeldingen
req_send_inn = last_opp_skattedata(instans_data, altinn_header,
xml=naering_enk_med_vedlegg,
data_type="skattemeldingOgNaeringsspesifikasjon",
appnavn=altinn3_applikasjon)
req_send_inn
# ### Sett statusen klar til henting av skatteetaten.
req_bekreftelse = endre_prosess_status(instans_data, altinn_header, "next", appnavn=altinn3_applikasjon)
req_bekreftelse = endre_prosess_status(instans_data, altinn_header, "next", appnavn=altinn3_applikasjon)
req_bekreftelse
# ### Framtidig: Sjekk status på altinn3 instansen om skatteetaten har hentet instansen.
# ### Se innsending i Altinn
#
# Ta en slurk av kaffen og klapp deg selv på ryggen, du har nå sendt inn, la byråkratiet gjøre sin ting... og det tar litt tid. Pt så sjekker skatteeaten hos Altinn3 hvert 5 min om det har kommet noen nye innsendinger.
# # Ikke komplett skattemelding
# 1. Når du har fått svar i altinn innboksen, så kan du gå til
# https://skatt-ref.sits.no/web/skattemeldingen/2021
# 2. Her vil du se næringsinntekter overført fra skattemeldingen
# 3. Når du har sendt inn i SME så vil du kunne se i altinn instansen at den har blitt avsluttet
# 4. Kjør cellen nedenfor for å se at du har fått en ny fastsatt skattemelding og næringsopplysninger
#
# +
print("Resultat av hent fastsatt før fastsetting")
print(r_fastsatt.text)
print("Resultat av hent fastsatt etter fastsetting")
r_fastsatt2 = s.get(url_fastsatt)
r_fastsatt2.text
#r_fastsatt.elapsed.total_seconds()
|
docs/test/testinnsending/person-enk-med-vedlegg-2021.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Subsetting ICESat-2 Data with the NSIDC Subsetter
# ### How to Use the NSIDC Subsetter Example Notebook
# This notebook illustrates the use of icepyx for subsetting ICESat-2 data ordered through the NSIDC DAAC. We'll show how to find out what subsetting options are available and how to specify the subsetting options for your order.
#
# For more information on using icepyx to find, order, and download data, see our complimentary [ICESat-2_DAAC_DataAccess_Example Notebook](https://github.com/icesat2py/icepyx/blob/main/doc/examples/ICESat-2_DAAC_DataAccess_Example.ipynb).
#
# Questions? Be sure to check out the FAQs throughout this notebook, indicated as italic headings.
#
# #### Credits
# * notebook by: <NAME> and <NAME>
# * some source material: [NSIDC Data Access Notebook](https://github.com/ICESAT-2HackWeek/ICESat2_hackweek_tutorials/tree/main/03_NSIDCDataAccess_Steiker) by <NAME> and <NAME>
# ### _What is SUBSETTING anyway?_
#
# Anyone who's worked with geospatial data has probably encountered subsetting. Typically, we search for data wherever it is stored and download the chunks (aka granules, scenes, passes, swaths, etc.) that contain something we are interested in. Then, we have to extract from each chunk the pieces we actually want to analyze. Those pieces might be geospatial (i.e. an area of interest), temporal (i.e. certain months of a time series), and/or certain variables. This process of extracting the data we are going to use is called subsetting.
#
# In the case of ICESat-2 data coming from the NSIDC DAAC, we can do this subsetting step on the data prior to download, reducing our number of data processing steps and resulting in smaller, faster downloads and storage.
# ### Import packages, including icepyx
# +
import icepyx as ipx
import numpy as np
import xarray as xr
import pandas as pd
import h5py
import os,json
from pprint import pprint
# -
# ### Create a query object and log in to Earthdata
#
# For this example, we'll be working with a sea ice dataset (ATL09) for an area along West Greenland (Disko Bay).
region_a = ipx.Query('ATL09',[-55, 68, -48, 71],['2019-02-22','2019-02-28'], \
start_time='00:00:00', end_time='23:59:59')
region_a.earthdata_login('username','email')
# ### Discover Subsetting Options
#
# You can see what subsetting options are available for a given dataset by calling `show_custom_options()`. The options are presented as a series of headings followed by available values in square brackets. Headings are:
# * **Subsetting Options**: whether or not temporal and spatial subsetting are available for the dataset
# * **Data File Formats (Reformatting Options)**: return the data in a format other than the native hdf5 (submitted as a key=value kwarg to `order_granules(format='NetCDF4-CF')`)
# * **Data File (Reformatting) Options Supporting Reprojection**: return the data in a reprojected reference frame. These will be available for gridded ICESat-2 L3B datasets.
# * **Data File (Reformatting) Options NOT Supporting Reprojection**: data file formats that cannot be delivered with reprojection
# * **Data Variables (also Subsettable)**: a dictionary of variable name keys and the paths to those variables available in the dataset
region_a.show_custom_options(dictview=True)
# By default, spatial and temporal subsetting based on your initial inputs is applied to your order unless you specify `subset=False` to `order_granules()` or `download_granules()`. Additional subsetting options must be specified as keyword arguments to the order/download functions.
#
# Although some file format conversions and reprojections are possible using the `format`, `projection`,and `projection_parameters` keywords, the rest of this tutorial will focus on variable subsetting, which is provided with the `Coverage` keyword.
# ### _Why do I have to provide spatial bounds to icepyx even if I don't use them to subset my data order?_
#
# Because they're still needed for the granule level search. Spatial inputs are usually required for any data search, on any platform, even if your search parameters cover the entire globe.
#
# The spatial information you provide is used to search the data repository and determine which granules might contain data over your area of interest. When you use that spatial information for subsetting, it's actually asking the NSIDC subsetter to extract the appropriate data from each granule. Thus, even if you set `subset=False` and download entire granules, you still need to provide some inputs on what geographic area you'd like data for.
# ## About Data Variables in a query object
# There are two possible variable parameters associated with each ```query``` object.
# 1. `order_vars`, which is for interacting with variables during data querying, ordering, and downloading activities. `order_vars.wanted` holds the user's list to be submitted to the NSIDC subsetter and download a smaller, reproducible dataset.
# 2. `file_vars`, which is for interacting with variables associated with local files [not yet implemented].
#
# Each variables parameter (which is actually an associated Variables class object) has methods to:
# * get available variables, either available from the NSIDC or the file (`avail()` method/attribute).
# * append new variables to the wanted list (`append()` method).
# * remove variables from the wanted list (`remove()` method).
#
# Each variables instance also has a set of attributes, including `avail` and `wanted` to indicate the list of variables that is available (unmutable, or unchangeable, as it is based on the input dataset specifications or files) and the list of variables that the user would like extracted (updateable with the `append` and `remove` methods), respectively. We'll showcase the use of all of these methods and attributes below.
# ### ICESat-2 data variables
# ICESat-2 data is natively stored in a nested file format called hdf5. Much like a directory-file system on a computer, each variable (file) has a unique path through the heirarchy (directories) within the file. Thus, some variables (e.g. `'latitude'`, `'longitude'`) have multiple paths (one for each of the six beams in most datasets).
#
# To increase readability, some display options (2 and 3, below) show the 200+ variable + path combinations as a dictionary where the keys are variable names and the values are the paths to that variable.
#
# ### Determine what variables are available
# There are multiple ways to get a complete list of available variables.
#
# 1. `region_a.order_vars.avail`, a list of all valid path+variable strings
# 2. `region_a.show_custom_options(dictview=True)`, all available subsetting options
# 3. `region_a.order_vars.parse_var_list(region_a.order_vars.avail)`, a dictionary of variable:paths key:value pairs
region_a.order_vars.avail()
# By passing the boolean `options=True` to the `avail` method, you can obtain lists of unique possible variable inputs (var_list inputs) and path subdirectory inputs (keyword_list and beam_list inputs) for your dataset. These can be helpful for building your wanted variable list.
region_a.order_vars.avail(options=True)
# ### _Why not just download all the data and subset locally? What if I need more variables/granules?_
#
# Taking advantage of the NSIDC subsetter is a great way to reduce your download size and thus your download time and the amount of storage required, especially if you're storing your data locally during analysis. By downloading your data using `icepyx`, it is easy to go back and get additional data with the same, similar, or different parameters (e.g. you can keep the same spatial and temporal bounds but change the variable list). Related tools (e.g. [`captoolkit`](https://github.com/fspaolo/captoolkit)) will let you easily merge files if you're uncomfortable merging them during read-in for processing.
# ### Building your wanted variable list
#
# Now that you know which variables and path components are available for your dataset, you need to build a list of the ones you'd like included in your dataset. There are several options for generating your initial list as well as modifying it, giving the user complete control over the list submitted.
#
# The options for building your initial list are:
# 1. Use a default list for the dataset (not yet fully implemented across all datasets. Have a default variable list for your field/dataset? Submit a pull request or post it as an issue on GitHub!)
# 2. Provide a list of variable names
# 3. Provide a list of profiles/beams or other path keywords, where "keywords" are simply the unique subdirectory names contained in the full variable paths of the dataset. A full list of available keywords for the dataset is displayed in the error message upon entering `keyword_list=['']` into the `append` function (see below for an example) or by running `region_a.order_vars.avail(options=True)`, as above
#
# Note: all datasets have a short list of "mandatory" variables/paths (containing spacecraft orientation and time information needed to convert the data's `delta_time` to a readable datetime) that are automatically added to any built list. If you have any recommendations for other variables that should always be included (e.g. uncertainty information), please let us know!
#
# Examples of using each method to build and modify your wanted variable list are below.
region_a.order_vars.wanted
region_a.order_vars.append(defaults=True)
pprint(region_a.order_vars.wanted)
# The keywords available for this dataset are shown in the error message upon entering a blank keyword_list, as seen in the next cell.
region_a.order_vars.append(keyword_list=[''])
# ### Modifying your wanted variable list
#
# Generating and modifying your variable request list, which is stored in `region_a.order_vars.wanted`, is controlled by the `append` and `remove` functions that operate on `region_a.order_vars.wanted`. The input options to `append` are as follows (the full documentation for this function can be found by executing `help(region_a.order_vars.append)`).
# * `defaults` (default False) - include the default variable list for your dataset (not yet fully implemented for all datasets; please submit your default variable list for inclusion!)
# * `var_list` (default None) - list of variables (entered as strings)
# * `beam_list` (default None) - list of beams/profiles (entered as strings)
# * `keyword_list` (default None) - list of keywords (entered as strings); use `keyword_list=['']` to obtain a list of available keywords
#
# Similarly, the options for `remove` are:
# * `all` (default False) - reset `region_a.order_vars.wanted` to None
# * `var_list` (as above)
# * `beam_list` (as above)
# * `keyword_list` (as above)
region_a.order_vars.remove(all=True)
pprint(region_a.order_vars.wanted)
# ### Examples
# Below are a series of examples to show how you can use `append` and `remove` to modify your wanted variable list. For clarity, `region_a.order_vars.wanted` is cleared at the start of many examples. However, multiple `append` and `remove` commands can be called in succession to build your wanted variable list (see Examples 3+)
# #### Example 1: choose variables
# Add all `latitude` and `longitude` variables
region_a.order_vars.append(var_list=['latitude','longitude'])
pprint(region_a.order_vars.wanted)
# #### Example 2: specify beams/profiles and variable
# Add `latitude` for only `profile_1` and `profile_2`
region_a.order_vars.remove(all=True)
pprint(region_a.order_vars.wanted)
var_dict = region_a.order_vars.append(beam_list=['profile_1','profile_2'], var_list=['latitude'])
pprint(region_a.order_vars.wanted)
# #### Example 3: add/remove selected beams+variables
# Add `latitude` for `profile_3` and remove it for `profile_2`
region_a.order_vars.append(beam_list=['profile_3'],var_list=['latitude'])
region_a.order_vars.remove(beam_list=['profile_2'], var_list=['latitude'])
pprint(region_a.order_vars.wanted)
# #### Example 4: `keyword_list`
# Add `latitude` for all profiles and with keyword `low_rate`
region_a.order_vars.append(var_list=['latitude'],keyword_list=['low_rate'])
pprint(region_a.order_vars.wanted)
# #### Example 5: target a specific variable + path
# Remove `'profile_1/high_rate/latitude'` (but keep `'profile_3/high_rate/latitude'`)
region_a.order_vars.remove(beam_list=['profile_1'], var_list=['latitude'], keyword_list=['high_rate'])
pprint(region_a.order_vars.wanted)
# #### Example 6: add variables not specific to beams/profiles
# Add `rgt` under `orbit_info`.
region_a.order_vars.append(keyword_list=['orbit_info'],var_list=['rgt'])
pprint(region_a.order_vars.wanted)
# #### Example 7: add all variables+paths of a group
# In addition to adding specific variables and paths, we can filter all variables with a specific keyword as well. Here, we add all variables under `orbit_info`. Note that paths already in `region_a.order_vars.wanted`, such as `'orbit_info/rgt'`, are not duplicated.
region_a.order_vars.append(keyword_list=['orbit_info'])
pprint(region_a.order_vars.wanted)
# #### Example 8: add all possible values for variables+paths
# Append all `longitude` paths and all variables/paths with keyword `high_rate`.
# Simlarly to what is shown in Example 4, if you submit only one `append` call as `region_a.order_vars.append(var_list=['longitude'], keyword_list=['high_rate'])` rather than the two `append` calls shown below, you will only add the variable `longitude` and only paths containing `high_rate`, not ALL paths for `longitude` and ANY variables with `high_rate` in their path.
region_a.order_vars.append(var_list=['longitude'])
region_a.order_vars.append(keyword_list=['high_rate'])
pprint(region_a.order_vars.wanted)
# #### Example 9: remove all variables+paths associated with a beam
# Remove all paths for `profile_1` and `profile_3`
region_a.order_vars.remove(beam_list=['profile_1','profile_3'])
pprint(region_a.order_vars.wanted)
# #### Example 10: generate a default list for the rest of the tutorial
# Generate a reasonable variable list prior to download
region_a.order_vars.remove(all=True)
region_a.order_vars.append(defaults=True)
pprint(region_a.order_vars.wanted)
# ## Applying variable subsetting to your order and download
#
# In order to have your wanted variable list included with your order, you must pass it as a keyword argument to the `subsetparams()` attribute or the `order_granules()` or `download_granules()` (which calls `order_granules` under the hood if you have not already placed your order) functions.
region_a.subsetparams(Coverage=region_a.order_vars.wanted)
# Or, you can put the `Coverage` parameter directly into `order_granules`:
# `region_a.order_granules(Coverage=region_a.order_vars.wanted)`
#
# However, then you cannot view your subset parameters (`region_a.subsetparams`) prior to submitting your order.
region_a.order_granules()# <-- you do not need to include the 'Coverage' kwarg to
# order if you have already included it in a call to subsetparams
region_a.download_granules('/home/jovyan/icepyx/dev-notebooks/vardata') # <-- you do not need to include the 'Coverage' kwarg to
# download if you have already submitted it with your order
# ### _Why does the subsetter say no matching data was found?_
# Sometimes, chunks (granules) returned in our initial search end up not containing any data in our specified area of interest. This is because the initial search is completed using summary metadata for a chunk. You've likely encountered this before when viewing available imagery online: your spatial search turns up a bunch of images with only a few border or corner pixels, maybe even in no data regions, in your area of interest. Thus, when you go to extract the data from the area you want (i.e. spatially subset it), you don't get any usable data from that image.
# ## Check the variable list in your downloaded file
#
# Compare the available variables associated with the full dataset relative to those in your downloaded data file.
# put the full filepath to a data file here. You can get this in JupyterHub by navigating to the file,
# right clicking, and selecting copy path. Then you can paste the path in the quotes below.
fn = ''
# #### Check the downloaded dataset
# Get all `latitude` variables in your downloaded file:
# +
varname = 'latitude'
varlist = []
def IS2h5walk(vname, h5node):
if isinstance(h5node, h5py.Dataset):
varlist.append(vname)
return
with h5py.File(fn,'r') as h5pt:
h5pt.visititems(IS2h5walk)
for tvar in varlist:
vpath,vn = os.path.split(tvar)
if vn==varname: print(tvar)
# -
# #### Compare to the variable paths available in the original data
region_a.order_vars.parse_var_list(region_a.order_vars.avail)[0][varname]
|
examples/ICESat-2_DAAC_DataAccess2_Subsetting.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from sklearn.datasets import load_digits
digit=load_digits()
# Describe
dir(digit) # 0 to 9 umbers datasets
# Reading data
digit.DESCR
digit.target_names # Actual target, we want to recognize
# Features data
features=digit.data
# Labels ---means answer
label=digit.target
label[0:21]
# To show actual image
images=digit.images
images[0].shape
import matplotlib.pyplot as plt
plt.imshow(images[0])
|
Data_Processing/SVM_Digit.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="nCc3XZEyG3XV"
# Lambda School Data Science, Unit 2: Predictive Modeling
#
# # Kaggle Challenge, Module 4
#
# ## Assignment
# - [ ] If you haven't yet, [review requirements for your portfolio project](https://lambdaschool.github.io/ds/unit2), then submit your dataset.
# - [ ] Plot a confusion matrix for your Tanzania Waterpumps model.
# - [ ] Continue to participate in our Kaggle challenge. Every student should have made at least one submission that scores at least 60% accuracy (above the majority class baseline).
# - [ ] Submit your final predictions to our Kaggle competition. Optionally, go to **My Submissions**, and _"you may select up to 1 submission to be used to count towards your final leaderboard score."_
# - [ ] Commit your notebook to your fork of the GitHub repo.
# - [ ] Read [Maximizing Scarce Maintenance Resources with Data: Applying predictive modeling, precision at k, and clustering to optimize impact](https://towardsdatascience.com/maximizing-scarce-maintenance-resources-with-data-8f3491133050), by Lambda DS3 student <NAME>. His blog post extends the Tanzania Waterpumps scenario, far beyond what's in the lecture notebook.
#
#
# ## Stretch Goals
#
# ### Reading
# - [Attacking discrimination with smarter machine learning](https://research.google.com/bigpicture/attacking-discrimination-in-ml/), by Google Research, with interactive visualizations. _"A threshold classifier essentially makes a yes/no decision, putting things in one category or another. We look at how these classifiers work, ways they can potentially be unfair, and how you might turn an unfair classifier into a fairer one. As an illustrative example, we focus on loan granting scenarios where a bank may grant or deny a loan based on a single, automatically computed number such as a credit score."_
# - [Notebook about how to calculate expected value from a confusion matrix by treating it as a cost-benefit matrix](https://github.com/podopie/DAT18NYC/blob/master/classes/13-expected_value_cost_benefit_analysis.ipynb)
# - [Simple guide to confusion matrix terminology](https://www.dataschool.io/simple-guide-to-confusion-matrix-terminology/) by <NAME>, with video
# - [Visualizing Machine Learning Thresholds to Make Better Business Decisions](https://blog.insightdatascience.com/visualizing-machine-learning-thresholds-to-make-better-business-decisions-4ab07f823415)
#
#
# ### Doing
# - [ ] Share visualizations in our Slack channel!
# - [ ] RandomizedSearchCV / GridSearchCV, for model selection. (See below)
# - [ ] Stacking Ensemble. (See below)
# - [ ] More Categorical Encoding. (See below)
#
# ### RandomizedSearchCV / GridSearchCV, for model selection
#
# - _[Introduction to Machine Learning with Python](http://shop.oreilly.com/product/0636920030515.do)_ discusses options for "Grid-Searching Which Model To Use" in Chapter 6:
#
# > You can even go further in combining GridSearchCV and Pipeline: it is also possible to search over the actual steps being performed in the pipeline (say whether to use StandardScaler or MinMaxScaler). This leads to an even bigger search space and should be considered carefully. Trying all possible solutions is usually not a viable machine learning strategy. However, here is an example comparing a RandomForestClassifier and an SVC ...
#
# The example is shown in [the accompanying notebook](https://github.com/amueller/introduction_to_ml_with_python/blob/master/06-algorithm-chains-and-pipelines.ipynb), code cells 35-37. Could you apply this concept to your own pipelines?
#
# ### Stacking Ensemble
#
# Here's some code you can use to "stack" multiple submissions, which is another form of ensembling:
#
# ```python
# import pandas as pd
#
# # Filenames of your submissions you want to ensemble
# files = ['submission-01.csv', 'submission-02.csv', 'submission-03.csv']
#
# target = 'status_group'
# submissions = (pd.read_csv(file)[[target]] for file in files)
# ensemble = pd.concat(submissions, axis='columns')
# majority_vote = ensemble.mode(axis='columns')[0]
#
# sample_submission = pd.read_csv('sample_submission.csv')
# submission = sample_submission.copy()
# submission[target] = majority_vote
# submission.to_csv('my-ultimate-ensemble-submission.csv', index=False)
# ```
#
#
# ### More Categorical Encodings
#
# **1.** The article **[Categorical Features and Encoding in Decision Trees](https://medium.com/data-design/visiting-categorical-features-and-encoding-in-decision-trees-53400fa65931)** mentions 4 encodings:
#
# - **"Categorical Encoding":** This means using the raw categorical values as-is, not encoded. Scikit-learn doesn't support this, but some tree algorithm implementations do. For example, [Catboost](https://catboost.ai/), or R's [rpart](https://cran.r-project.org/web/packages/rpart/index.html) package.
# - **Numeric Encoding:** Synonymous with Label Encoding, or "Ordinal" Encoding with random order. We can use [category_encoders.OrdinalEncoder](https://contrib.scikit-learn.org/categorical-encoding/ordinal.html).
# - **One-Hot Encoding:** We can use [category_encoders.OneHotEncoder](http://contrib.scikit-learn.org/categorical-encoding/onehot.html).
# - **Binary Encoding:** We can use [category_encoders.BinaryEncoder](http://contrib.scikit-learn.org/categorical-encoding/binary.html).
#
#
# **2.** The short video
# **[Coursera — How to Win a Data Science Competition: Learn from Top Kagglers — Concept of mean encoding](https://www.coursera.org/lecture/competitive-data-science/concept-of-mean-encoding-b5Gxv)** introduces an interesting idea: use both X _and_ y to encode categoricals.
#
# Category Encoders has multiple implementations of this general concept:
#
# - [CatBoost Encoder](http://contrib.scikit-learn.org/categorical-encoding/catboost.html)
# - [James-Stein Encoder](http://contrib.scikit-learn.org/categorical-encoding/jamesstein.html)
# - [Leave One Out](http://contrib.scikit-learn.org/categorical-encoding/leaveoneout.html)
# - [M-estimate](http://contrib.scikit-learn.org/categorical-encoding/mestimate.html)
# - [Target Encoder](http://contrib.scikit-learn.org/categorical-encoding/targetencoder.html)
# - [Weight of Evidence](http://contrib.scikit-learn.org/categorical-encoding/woe.html)
#
# Category Encoder's mean encoding implementations work for regression problems or binary classification problems.
#
# For multi-class classification problems, you will need to temporarily reformulate it as binary classification. For example:
#
# ```python
# encoder = ce.TargetEncoder(min_samples_leaf=..., smoothing=...) # Both parameters > 1 to avoid overfitting
# X_train_encoded = encoder.fit_transform(X_train, y_train=='functional')
# X_val_encoded = encoder.transform(X_train, y_val=='functional')
# ```
#
# **3.** The **[dirty_cat](https://dirty-cat.github.io/stable/)** library has a Target Encoder implementation that works with multi-class classification.
#
# ```python
# dirty_cat.TargetEncoder(clf_type='multiclass-clf')
# ```
# It also implements an interesting idea called ["Similarity Encoder" for dirty categories](https://www.slideshare.net/GaelVaroquaux/machine-learning-on-non-curated-data-154905090).
#
# However, it seems like dirty_cat doesn't handle missing values or unknown categories as well as category_encoders does. And you may need to use it with one column at a time, instead of with your whole dataframe.
#
# **4. [Embeddings](https://www.kaggle.com/learn/embeddings)** can work well with sparse / high cardinality categoricals.
#
# _**I hope it’s not too frustrating or confusing that there’s not one “canonical” way to encode categorcals. It’s an active area of research and experimentation! Maybe you can make your own contributions!**_
# + colab={} colab_type="code" id="lsbRiKBoB5RE"
import os, sys
in_colab = 'google.colab' in sys.modules
# If you're in Colab...
if in_colab:
# Pull files from Github repo
os.chdir('/content')
# !git init .
# !git remote add origin https://github.com/LambdaSchool/DS-Unit-2-Kaggle-Challenge.git
# !git pull origin master
# Install required python packages
# !pip install -r requirements.txt
# Change into directory for module
os.chdir('module4')
# -
# import block
pd.set_option('display.max_columns', None)
import matplotlib.pyplot as plt
# %matplotlib inline
import seaborn as sns
plt.style.use('dark_background')
import numpy as np
from scipy.stats import randint, uniform
from sklearn.model_selection import train_test_split, GridSearchCV, RandomizedSearchCV
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.pipeline import make_pipeline
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.metrics import accuracy_score
import category_encoders as ce
# + colab={} colab_type="code" id="BVA1lph8CcNX"
import pandas as pd
# Merge train_features.csv & train_labels.csv
train = pd.merge(pd.read_csv('../data/tanzania/train_features.csv'),
pd.read_csv('../data/tanzania/train_labels.csv'))
# Read test_features.csv & sample_submission.csv
test = pd.read_csv('../data/tanzania/test_features.csv')
sample_submission = pd.read_csv('../data/tanzania/sample_submission.csv')
# Split train into train & val. Make val the same size as test.
target = 'status_group'
train, val = train_test_split(train, test_size=len(test),
stratify=train[target], random_state=42)
# -
# Cleaning/engineering function
def wrangler(X):
# Make a copy to avoid warning, prevent making changes from view.
X = X.copy()
# Replace near-zero latitudes with zero
X['latitude'] = X['latitude'].replace(-2e-08, 0)
# Replace near-zero longitudes with zero
X['longitude'] = X['longitude'].replace(-2e-08, 0)
# Swap zeros with nulls
cols_with_zeros = ['longitude', 'latitude', 'construction_year',
'gps_height', 'population']
zeros = [0, '0']
for col in cols_with_zeros:
X[col] = X[col].replace(zeros, np.nan)
X[col+'_MISSING'] = X[col].isna()
# clean text columns by lowercasing, swapping unknowns with NaNs and add a 'MISSING' column for each
textcols = ['installer','funder','wpt_name','basin','subvillage','region','lga','ward',
'scheme_management','scheme_name','extraction_type','extraction_type_group',
'extraction_type_class','management','management_group','payment','water_quality',
'quality_group','quantity','source','source_type','source_class','waterpoint_type',
'waterpoint_type_group']
unknowns = ['unknown', 'not known', 'none', 'nan', '-', '##',
'unknown installer']
for col in textcols:
X[col] = X[col].str.lower().str.replace(' ','').str.replace('.','').str.replace('-','')
X[col] = X[col].replace(unknowns, np.nan)
X[col+'_MISSING'] = X[col].isna()
# clean boolean columns by imputing the most common value and flagging missing vals
boolcols = ['public_meeting','permit']
for col in boolcols:
X[col+'_MISSING'] = X[col].isna()
# Drop recorded_by (never varies) and id (always varies, random)
unusable_variance = ['recorded_by', 'id','num_private','wpt_name']
X = X.drop(columns=unusable_variance)
# create a distance feature for population centers
X['dardistance'] = (((X['latitude']-(6.7924))**2)+((X['longitude']-(39.2083))**2))**0.5
X['mwanzadistance'] = (((X['latitude']-(2.5164))**2)+((X['longitude']-(32.9175))**2))**0.5
X['dodomadistance'] = (((X['latitude']-(6.1630))**2)+((X['longitude']-(35.7516))**2))**0.5
X['dardistance_MISSING'] = X['dardistance'].isnull()
X['mwanzadistance_MISSING'] = X['mwanzadistance'].isnull()
X['dodomadistance_MISSING'] = X['dodomadistance'].isnull()
# change date_recorded to datetime format
X['date_recorded'] = pd.to_datetime(X.date_recorded, infer_datetime_format=True)
X['date_recorded_MISSING'] = X['date_recorded'].isnull()
# Extract components from date_recorded, then drop the original column
X['year_recorded'] = X['date_recorded'].dt.year
X['month_recorded'] = X['date_recorded'].dt.month
X['day_recorded'] = X['date_recorded'].dt.day
X = X.drop(columns='date_recorded')
# make list of columns of numeric and categoric type
numericcolumns = X.select_dtypes(include = 'number').columns.tolist()
nonnumericcolumns = X.select_dtypes(exclude = 'number').columns.tolist()
# create 'structspect_interval' - number of years between construction and date recorded
X['structspect_interval'] = X['year_recorded'] - X['construction_year']
X['structspect_MISSING'] = X['structspect_interval'].isnull()
return X
# Clean and engineer all datasets
train = wrangler(train)
val = wrangler(val)
test = wrangler(test)
# Arrange data into X features matrix and y target vector
target = 'status_group'
X_train = train.drop(columns=target)
y_train = train[target]
X_val = val.drop(columns=target)
y_val = val[target]
X_test = test
# +
# fit it
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(),
RandomForestClassifier(n_estimators=129, max_depth=30, min_samples_leaf=2,
random_state=42, n_jobs=-1, min_samples_split=4)
)
pipeline.fit(X_train, y_train)
# -
y_pred = pipeline.predict(X_val)
print('Validation Accuracy', accuracy_score(y_val, y_pred))
# +
from sklearn.metrics import confusion_matrix
from sklearn.utils.multiclass import unique_labels
def plot_confusion_matrix(y_true, y_pred):
labels = unique_labels(y_pred)
columns = [f'Predicted {label}' for label in labels]
index = [f'Actual {label}' for label in labels]
table = pd.DataFrame(confusion_matrix(y_true, y_pred), columns=columns, index=index)
return sns.heatmap(table, annot=True, fmt='d')
plot_confusion_matrix(y_val, y_pred);
# -
|
module4/assignment_kaggle_challenge_4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import json
seeds = [0,2077,2434,314159,42]
d = {
"task": "Neighbor_Attack",
"model": "GAL",
"experiment": "gnn_type_layers",
"show_tqdm": 0,
"num_epochs": 25,
"batch_size": 8192,
"valid_freq": 1,
"embed_dim": 20,
"lr": 0.01,
"prefetch_to_gpu": 0,
"seed": 11,
"debug": 0,
"gnn_layers": 3,
"gnn_type": "ChebConv",
"finetune_epochs": 30,
"data_path" : "/",
"cutoff" : 0.8,
"lambda_reg": 0.5
}
for i in range(3):
for gt in ['ChebConv','GCNConv','GINConv','GATConv']:
for seed in seeds:
with open('neighbor_attack_adv_gnn_'+str(seed)+'_'+str(i)+gt+'.json', 'w') as outfile:
d['gnn_layers'] = i+1
d['gnn_type'] = gt
d['seed'] = seed
json.dump(d, outfile)
# -
|
Movielens_Wasserstein/config/Neighbor_Attack/gnn_type_layers/gen_json.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# <div class="contentcontainer med left" style="margin-left: -50px;">
# <dl class="dl-horizontal">
# <dt>Title</dt> <dd> BoundsY stream example</dd>
# <dt>Description</dt> <dd>A linked streams example demonstrating how to use BoundsY streams.</dd>
# <dt>Backends</dt> <dd> Bokeh</dd>
# <dt>Tags</dt> <dd> streams, linked, interactive</dd>
# </dl>
# </div>
import numpy as np
import holoviews as hv
from holoviews import streams
hv.extension('bokeh')
# +
# %%opts Curve[tools=['ybox_select']]
xs = np.linspace(0, 1, 200)
ys = xs*(1-xs)
curve = hv.Curve((xs,ys))
bounds_stream = streams.BoundsY(source=curve,boundsy=(0,0))
def make_area(boundsy):
return hv.Area((xs, np.minimum(ys, boundsy[0]), np.minimum(ys, boundsy[1])), vdims=['min','max'])
def make_items(boundsy):
times = ["{0:.2f}".format(x) for x in sorted(np.roots([-1,1,-boundsy[0]])) + sorted(np.roots([-1,1,-boundsy[1]]))]
return hv.ItemTable(sorted(zip(['1_entry', '2_exit', '1_exit', '2_entry'], times)))
curve * hv.DynamicMap(make_area, streams=[bounds_stream]) + hv.DynamicMap(make_items, streams=[bounds_stream])
# -
# <center><img src="https://assets.holoviews.org/gifs/examples/streams/bokeh/boundsy_selection.gif"></center>
|
examples/reference/streams/bokeh/BoundsY.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1>human organ classification </h1>
# <h2> C-NN model<h3> [transfer learn on MobileNetV2 model]</h3></h2>
# call to packages & libraries
# + pycharm={"name": "#%%\n"}
from tensorflow import keras
from datetime import datetime
from src.sup.evaluation import *
from src.sup.support import *
from src.sup.test_set_eval import *
from tensorflow.keras.optimizers import RMSprop,SGD,Adam
from tensorflow.keras.layers import Dense,BatchNormalization,Dropout
from tensorflow.keras.layers import Conv2D,MaxPool2D,Flatten
from tensorflow.keras.applications import MobileNetV2
from tensorflow.keras import Model
# + pycharm={"name": "#%%\n"}
model_name = "mobileNet_v2_transfer_learn_2.3"
# Load the TensorBoard notebook extension.
# %load_ext tensorboard
# call inline plt.
# + pycharm={"name": "#%%\n"}
# Clear any logs from previous runs
# !rm -rf ./logs/
# -
# callout dataset
# + pycharm={"name": "#%%\n"}
classes = ['Heart','Brain','Eye','Kidney','Skeleton','Other']
root_dir = '../../datasets/'
train_dir = os.path.join(root_dir,'train/')
validation_dir = os.path.join(root_dir,'validation/')
tr_heart_dir,tr_brain_dir,tr_eye_dir,tr_kidney_dir,tr_skull_dir,tr_other_dir = path_update(train_dir,classes)
vl_heart_dir,vl_brain_dir,vl_eye_dir,vl_kidney_dir,vl_skull_dir,vl_other_dir = path_update(validation_dir,classes)
# -
# take a glance at training dataset
# + pycharm={"name": "#%%\n"}
plot_sample_of_img(4,4,os.listdir(tr_heart_dir)+os.listdir(tr_eye_dir))
# -
# ImageGenator - autolabelling, and categorizing.
# + pycharm={"name": "#%%\n"}
train_gen_tmp = ImageDataGenerator(rescale=1./255,
width_shift_range=0.2,
height_shift_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
validation_gen_tmp = ImageDataGenerator(rescale=1/225.)
train_gen = train_gen_tmp.flow_from_directory(train_dir,
target_size=(224,224),
color_mode='rgb',
class_mode='categorical',
batch_size= 20,
shuffle=True,
seed=42)
validation_gen = validation_gen_tmp.flow_from_directory(validation_dir,
target_size=(224,224),
color_mode='rgb',
class_mode='categorical',
batch_size= 20,
shuffle=True,
seed=42)
STEP_SIZE_TRAIN=train_gen.n//train_gen.batch_size
STEP_SIZE_VALID=validation_gen.n//validation_gen.batch_size
clToInt_dict = train_gen.class_indices
clToInt_dict = dict((k,v) for v,k in clToInt_dict.items())
# -
# define the model
# + pycharm={"name": "#%%\n"}
weight_path = '../../h5_files/mobilenet_v2_weights_tf_dim_ordering_tf_kernels_1.0_224.h5'
pre_model = MobileNetV2(input_shape=(224,224,3),
weights = None,
include_top = True)
pre_model.load_weights(weight_path)
#model.summary()
for layer in pre_model.layers:
layer.trainable = False
conn_layer = pre_model.get_layer('block_12_add')
conn_output = conn_layer.output
x = Conv2D(128,(3,3),activation='relu')(conn_output)
x = MaxPool2D(2,2)(x)
x = Conv2D(256,(3,3),activation='relu')(x)
x = MaxPool2D(2,2)(x)
x = Flatten()(x)
#x = Dense(256,activation='relu')(x)
#x = Dropout(0.2)(x)
x = Dense(128,activation='relu')(x)
#x = Dropout(0.2)(x)
#x = BatchNormalization()(x)
x = Dense(6,activation='softmax')(x)
model = Model(pre_model.input,x)
model.summary()
# -
# compile the model
# + pycharm={"name": "#%%\n"}
model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
# -
# save the log
# + pycharm={"name": "#%%\n"}
# Define the Keras TensorBoard callback.
logdir="logs/fit/" + datetime.now().strftime("%Y%m%d-%H%M%S")+'/'
if not os.path.exists(logdir):
os.mkdir(logdir)
#print(datetime.now().strftime("%Y%m%d%H%M%S"))
tensorboard_callback = keras.callbacks.TensorBoard(log_dir=logdir, histogram_freq=1, profile_batch = 100000000)
# -
# fit & train the model.
# + pycharm={"name": "#%%\n"}
history = model.fit(train_gen,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=validation_gen,
validation_steps=STEP_SIZE_VALID,
epochs=14,
verbose=1,
callbacks= [tensorboard_callback])
# -
# visualize layer process in cnn
# + pycharm={"name": "#%%\n"}
#visualize_model(model,validation_dir+'/Brain/20.jpg')
# #!mkdir -p saved_model
model.save('saved_model/my_model/')
# -
# instant evaluation
# + pycharm={"name": "#%%\n"}
#call to the tensorboard
# #%tensorboard --logdir ./logs/fit/
#look at training model performance
acc_n_loss(history)
#model.evaluate_generator(validation_gen,
# steps=STEP_SIZE_VALID)
# -
# evaluate the model on test set.
#
# + pycharm={"name": "#%%\n"}
model_path = '../../h5_files/models/20200829133245mobileNet_v2_transfer_learn_2.2.h5'
model_weight_path = '../../h5_files/weights/20200829133245mobileNet_v2_transfer_learn_2.2.h5'
model = load_model(model_path)
model.load_weights(model_weight_path)
y_pred,y_test = test_eval(model)
plot_confusion_metrix(y_test,y_pred,classes)
ROC_classes(6,y_test,y_pred,classes)
# -
# save the model in .h5 file
# + pycharm={"name": "#%%\n"}
model_path,model_weight_path = save(model,datetime.now().strftime("%Y%m%d%H%M%S")+model_name+'.h5')
# -
# make prediction on random images
# + pycharm={"name": "#%%\n"}
model_path = '../../h5_files/models/20200829133245mobileNet_v2_transfer_learn_2.2.h5'
model_weight_path = '../../h5_files/weights/20200829133245mobileNet_v2_transfer_learn_2.2.h5'
img_path = '../../datasets/validation/../../datasets/validation/Brain/Capture.jpg'
#rnd_predict(model_path,model_weight_path,img_path,clToInt_dict)
visualize_model(model_path,model_weight_path,img_path)
# + pycharm={"name": "#%%\n"}
preds,testy = test_eval(model)
plot_confusion_metrix(testy,preds,classes)
ROC_classes(5,testy,preds,classes)
# + pycharm={"name": "#%%\n"}
from io import BytesIO
import dill,base64,tempfile
# + pycharm={"name": "#%%\n"}
#Saving Model as base64
model_json = model.to_json()
def Base64Converter(ObjectFile):
bytes_container = BytesIO()
dill.dump(ObjectFile, bytes_container)
bytes_container.seek(0)
bytes_file = bytes_container.read()
base64File = base64.b64encode(bytes_file)
return base64File
base64KModelJson = Base64Converter(model_json)
# + pycharm={"name": "#%%\n"}
import joblib
# + pycharm={"name": "#%%\n"}
joblib.dump(base64KModelJson,'../../h5_files/models/model.bytes')
# + pycharm={"name": "#%%\n"}
|
src/model/tl_mobliNet2_3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Global Root-zone moisture Analysis & Forecasting System (GRAFS)
#
# * **Products used:**
# [GRAFS](http://dap.nci.org.au/thredds/remoteCatalogService?catalog=http://dapds00.nci.org.au/thredds/catalog/ub8/global/GRAFS/catalog.xml),
# [ERA5](https://registry.opendata.aws/ecmwf-era5/)
#
# *Both datasets are external to the Digital Earth Africa platform.*
# + raw_mimetype="text/restructuredtext" active=""
# **Keywords**: :index:`data used; ERA5`, :index:`datasets; ERA5`, :index:`data used; GRAFS`, :index:`datasets; GRAFS`, :index:`soil moisture`, :index:`precipitation`
# -
# ## Background
#
# Soil moisture is a measure of water stored in the soil zone that is accessible to plant roots, making it a major contributing factor to plant health and crop yield.
#
# The Global Root-zone moisture Analysis & Forecasting System (GRAFS) is produced by the [ANU Centre for Water and Landscape Dynamics](https://www.wald.anu.edu.au/).
# The model estimates the surface (0-5 cm) and root-zone (0-1 m) soil moisture at 10 km spatial resolution globally, using the precipitation measured by the Global Precipitation Measurement (GPM) mission and through assimilation of the soil moisture product from the [Soil Moisture Active/Passive](https://smap.jpl.nasa.gov/mission/description/) (SMAP) mission.
#
# This product is regularly updated and made available through National Computational Infrastructure's open access THREDDS data server.
#
# For more information on this product, contact [<NAME>](mailto:<EMAIL>) and [<NAME>](mailto:<EMAIL>).
# ## Description
#
# This notebook demonstrates the following steps:
# 1. Retrieval of surface and root-zone wetness through NCI's THREDDS OPeNDAP service
# 2. Compare soil moisture to precipitation data from ERA5
#
# ***
# ## Getting started
#
# To run this analysis, run all the cells in the notebook, starting with the "Load packages" cell.
# ### Load packages
# Import Python packages that are used for the analysis.
# +
# %matplotlib inline
from matplotlib import pyplot as plt
import xarray as xr
import numpy as np
import datacube
from deafrica_tools.load_era5 import load_era5
# -
# ### Analysis parameters
#
# Define location and time period of interest.
# The time period is chosen to be less than a year to limit ERA5 data download.
# +
# Define the analysis region (Lat-Lon box)
# Il Ngwesi region of Kenya - Rhino Project
lat = (0.412, 0.266)
lon = (37.32, 37.40)
# High Energy Stereoscopic System site near Windhoek Namibia
#lat = (-23.28, -23.26)
#lon = (16.49, 16.51)
# Define the time window
time = '2018-07-01', '2019-05-31'
# -
# ## Retrieval of surface and root-zone wetness
#
# > `Surface wetness` is measured relative to wettest condition recorded for a location.
#
# > `Rootzone Soil Water Index` is derived from surface relative wetness
# +
# function to load soil moisture data
def load_soil_moisture(lat, lon, time, product = 'surface', grid = 'nearest'):
product_baseurl = 'http://dapds00.nci.org.au/thredds/dodsC/ub8/global/GRAFS/'
assert product in ['surface', 'rootzone'], 'product parameter must be surface or root-zone'
# lat, lon grid
if grid == 'nearest':
# select lat/lon range from data; snap to nearest grid
lat_range, lon_range = None, None
else:
# define a grid that covers the entire area of interest
lat_range = np.arange(np.max(np.ceil(np.array(lat)*10.+0.5)/10.-0.05), np.min(np.floor(np.array(lat)*10.-0.5)/10.+0.05)-0.05, -0.1)
lon_range = np.arange(np.min(np.floor(np.array(lon)*10.-0.5)/10.+0.05), np.max(np.ceil(np.array(lon)*10.+0.5)/10.-0.05)+0.05, 0.1)
# split time window into years
day_range = np.array(time).astype("M8[D]")
year_range = np.array(time).astype("M8[Y]")
if product == 'surface':
product_name = 'GRAFS_TopSoilRelativeWetness_'
else: product_name = 'GRAFS_RootzoneSoilWaterIndex_'
datasets = []
for year in np.arange(year_range[0], year_range[1]+1, np.timedelta64(1, 'Y')):
start = np.max([day_range[0], year.astype("M8[D]")])
end = np.min([day_range[1], (year+1).astype("M8[D]")-1])
product_url = product_baseurl + product_name +'%s.nc'%str(year)
print(product_url)
# data is loaded lazily through OPeNDAP
ds = xr.open_dataset(product_url)
if lat_range is None:
# select lat/lon range from data if not specified; snap to nearest grid
test = ds.sel(lat=lat, lon=lon, method='nearest')
lat_range = slice(test.lat.values[0], test.lat.values[1])
lon_range = slice(test.lon.values[0], test.lon.values[1])
# slice before return
ds = ds.sel(lat=lat_range, lon=lon_range, time=slice(start, end)).compute()
datasets.append(ds)
return xr.merge(datasets)
# -
# Retrieve surface soil moisture using query parameters
surface_wetness = load_soil_moisture(lat, lon, time, grid='nearest')
# retrieve rootzone soil moisture using query parameters
rootzone_wetness = load_soil_moisture(lat, lon, time, product='rootzone', grid='nearest')
# ### Plot surface and root-zone wetness over time
surface_wetness.relative_wetness.mean(['lat','lon']).plot(figsize=(16,8), label='surface');
rootzone_wetness.soil_water_index.mean(['lat','lon']).plot(label='root-zone');
plt.legend()
# ## Compare soil moisture to precipitation data from ERA5
#
# The first cell will load the precipitation parameter, `precipitation_amount_1hour_Accumulation`, from ERA5. Depending on the size of your query, this step can take a few minutes to complete. Data will be stored in the folder `era5`.
# +
# load precipitation data from ERA5
var_precipitation = 'precipitation_amount_1hour_Accumulation'
precipitation = load_era5(var_precipitation, lat, lon, time, reduce_func=np.sum)
# Convert from Meters (m) to Millimeters (mm)
precipitation[var_precipitation]=precipitation[var_precipitation]*1000
# -
# ### Plot soil moisture with precipitation
# +
# plot soil moisture with precipitation
fig, ax1 = plt.subplots(figsize=(16,8))
ax2 = ax1.twinx()
surface_wetness.relative_wetness.mean(['lat','lon']).plot(ax = ax1, label = 'surface wetness', color = 'blue');
rootzone_wetness.soil_water_index.mean(['lat','lon']).plot(ax = ax1, label = 'root-zone wetness', color = 'black');
precipitation[var_precipitation].mean(['lat','lon']).plot(ax = ax2, label = 'precipitation (mm)', color = 'orange');
ax1.legend()
ax2.legend()
# -
# ---
#
# ## Additional information
#
# **License:** The code in this notebook is licensed under the [Apache License, Version 2.0](https://www.apache.org/licenses/LICENSE-2.0).
# Digital Earth Africa data is licensed under the [Creative Commons by Attribution 4.0](https://creativecommons.org/licenses/by/4.0/) license.
#
# **Contact:** If you need assistance, please post a question on the [Open Data Cube Slack channel](http://slack.opendatacube.org/) or on the [GIS Stack Exchange](https://gis.stackexchange.com/questions/ask?tags=open-data-cube) using the `open-data-cube` tag (you can view previously asked questions [here](https://gis.stackexchange.com/questions/tagged/open-data-cube)).
# If you would like to report an issue with this notebook, you can file one on [Github](https://github.com/digitalearthafrica/deafrica-sandbox-notebooks).
#
# **Compatible datacube version:**
print(datacube.__version__)
# **Last Tested:**
# + raw_mimetype="text/restructuredtext"
from datetime import datetime
datetime.today().strftime('%Y-%m-%d')
|
Datasets/Soil_Moisture.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 8.1 FGSM 공격
#
# 정상 이미지에 노이즈를 더해 머신러닝 모델을 헷갈리게 하는 이미지가
# 바로 적대적 예제(Adversarial Example) 입니다.
# 이 프로젝트에선 Fast Gradient Sign Method, 즉 줄여서 FGSM이라는 방식으로
# 적대적 예제를 생성해 미리 학습이 완료된 딥러닝 모델을 공격해보도록 하겠습니다.
# +
import torch
import torch.nn.functional as F
import torchvision.models as models
import torchvision.transforms as transforms
from PIL import Image
import json
# -
import matplotlib.pyplot as plt
# ## 학습된 모델 불러오기
model = models.resnet101(pretrained=True)
model.eval()
print(model)
# ## 데이터셋 불러오기
CLASSES = json.load(open('./imagenet_samples/imagenet_classes.json'))
idx2class = [CLASSES[str(i)] for i in range(1000)]
# ## 이미지 불러오기
# 이미지 불러오기
img = Image.open('imagenet_samples/corgie.jpg')
# +
# 이미지를 텐서로 변환하기
img_transforms = transforms.Compose([
transforms.Resize((224, 224), Image.BICUBIC),
transforms.ToTensor(),
])
img_tensor = img_transforms(img)
img_tensor = img_tensor.unsqueeze(0)
print("이미지 텐서 모양:", img_tensor.size())
# +
# 시각화를 위해 넘파이 행렬 변환
original_img_view = img_tensor.squeeze(0).detach() # [1, 3, 244, 244] -> [3, 244, 244]
original_img_view = original_img_view.transpose(0,2).transpose(0,1).numpy()
# 텐서 시각화
plt.imshow(original_img_view)
# -
# ## 공격 전 성능 확인하기
#
# +
output = model(img_tensor)
prediction = output.max(1, keepdim=False)[1]
prediction_idx = prediction.item()
prediction_name = idx2class[prediction_idx]
print("예측된 레이블 번호:", prediction_idx)
print("레이블 이름:", prediction_name)
# -
# ## FGSM 공격 함수 정의
def fgsm_attack(image, epsilon, gradient):
# 기울기값의 원소의 sign 값을 구함
sign_gradient = gradient.sign()
# 이미지 각 픽셀의 값을 sign_gradient 방향으로 epsilon 만큼 조절
perturbed_image = image + epsilon * sign_gradient
# [0,1] 범위를 벗어나는 값을 조절
perturbed_image = torch.clamp(perturbed_image, 0, 1)
return perturbed_image
# ## 적대적 예제 생성
# +
# 이미지의 기울기값을 구하도록 설정
img_tensor.requires_grad_(True)
# 이미지를 모델에 통과시킴
output = model(img_tensor)
# 오차값 구하기 (레이블 263은 웰시코기)
loss = F.nll_loss(output, torch.tensor([263]))
# 기울기값 구하기
model.zero_grad()
loss.backward()
# 이미지의 기울기값을 추출
gradient = img_tensor.grad.data
# FGSM 공격으로 적대적 예제 생성
epsilon = 0.03
perturbed_data = fgsm_attack(img_tensor, epsilon, gradient)
# 생성된 적대적 예제를 모델에 통과시킴
output = model(perturbed_data)
# -
# ## 적대적 예제 성능 확인
# +
perturbed_prediction = output.max(1, keepdim=True)[1]
perturbed_prediction_idx = perturbed_prediction.item()
perturbed_prediction_name = idx2class[perturbed_prediction_idx]
print("예측된 레이블 번호:", perturbed_prediction_idx)
print("레이블 이름:", perturbed_prediction_name)
# +
# 시각화를 위해 넘파이 행렬 변환
perturbed_data_view = perturbed_data.squeeze(0).detach()
perturbed_data_view = perturbed_data_view.transpose(0,2).transpose(0,1).numpy()
plt.imshow(perturbed_data_view)
# -
# ## 원본과 적대적 예제 비교
# +
f, a = plt.subplots(1, 2, figsize=(10, 10))
# 원본
a[0].set_title(prediction_name)
a[0].imshow(original_img_view)
# 적대적 예제
a[1].set_title(perturbed_prediction_name)
a[1].imshow(perturbed_data_view)
plt.show()
|
08-Adversarial_Attack/fgsm_attack.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # CNN Models
# The goal of this note book is to build a Convolutional Neural Network model and compare the results.
# ## Libraries
# +
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
import numpy as np
from datetime import datetime
import random
from tensorflow.keras import models
from tensorflow.keras import layers
from tensorflow.keras.models import load_model
from tensorflow.keras import regularizers
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
from sklearn.metrics import confusion_matrix
import util as ut # Checking result
from malig_data import * #Accessing Data
# -
# ## CNN Model
# This CNN model is made with 4 hidden layers with few regularizer and dropout layers to prevent overfitting of the model since CNN tends to overfit.
def CNN_model(x, y, val_x, val_y, filepath, epochs=150, batch_size=32):
""" CNN model function that returns the model and the history.
x: train image
y: train target
val_x: test image
val_y: test target
filepath: where the model to be saved
epochs: default at 150
batch_size: default at 32"""
start_time = datetime.now()
random.seed(123)
cnn_model = models.Sequential()
cnn_model.add(layers.Conv2D(32, (3, 3), activation='relu',
input_shape=(64,64,3)))#1st Hidden Layer
cnn_model.add(layers.MaxPooling2D((2, 2))) #Maxpooling to 1st Layer
cnn_model.add(layers.Dropout(.3)) #Dropout layer to 1st layer
cnn_model.add(layers.Conv2D(32, (3, 3), activation='relu', kernel_regularizer = regularizers.l2(0.005)))#2nd Hidden Layer
cnn_model.add(layers.MaxPooling2D((2, 2))) #Maxpooling to 2nd Layer
cnn_model.add(layers.Dropout(.3)) #Dropout layer to 2nd layer
cnn_model.add(layers.Conv2D(64, (3, 3), activation='relu', kernel_regularizer = regularizers.l2(0.005)))#3rd Hidden Layer
cnn_model.add(layers.MaxPooling2D((2, 2))) #Maxpooling to 3rd Layer
cnn_model.add(layers.Dropout(.3)) #Dropout layer to 3rd layer
cnn_model.add(layers.Flatten()) #Flattening Layer
cnn_model.add(layers.Dense(64, activation='relu', kernel_regularizer = regularizers.l2(0.005)))#4th Hidden Layer
cnn_model.add(layers.Dense(1, activation='sigmoid')) #Output Layer
cnn_model.compile(loss='binary_crossentropy',
optimizer="adam", # For CNN model we will use 'adam' as an optimizer which is most commonly used optimizer
metrics=['accuracy'])
cnn_early_stopping = [EarlyStopping(monitor='val_loss', patience=50),
ModelCheckpoint(filepath=filepath,
monitor='val_loss',
save_best_only=True)]
cnn_history = cnn_model.fit(x, y,
epochs=epochs,
batch_size=batch_size,
validation_data=(val_x, val_y),
callbacks=cnn_early_stopping)
end_time = datetime.now()
print('Time elapsed', end_time - start_time)
return cnn_model, cnn_history
filepath = '../models/basic_cnn.h5'
basic_cnn_model, basic_cnn_history = CNN_model(train_images, train_y,
test_images, test_y,
filepath=filepath,
epochs=200,
batch_size=32)
# +
cnn_saved_model = load_model(filepath)
cnn_results_train = cnn_saved_model.evaluate(train_images, train_y)
print(f'Training Loss: {cnn_results_train[0]:.3} \nTraining Accuracy: {cnn_results_train[1]:.3}')
print('----------')
cnn_results_test = cnn_saved_model.evaluate(val_images, val_y)
print(f'Test Loss: {cnn_results_test[0]:.3} \nTest Accuracy: {cnn_results_test[1]:.3}')
# -
title = "../reports/Basic CNN Model: Iteration of Loss Graph"
ut.training_results_Loss(basic_cnn_history, title=title)
title = '../reports/Basic CNN Model: Iteration of Accuracy Graph'
ut.training_results_Accuracy(basic_cnn_history, title=title)
index=["Actual Malig", "Actual Benign"]
columns=["Predicted Malig", "Predicted Benign"]
basic_cnn_predictions = cnn_saved_model.predict_classes(val_images)
basic_cnn_cm = confusion_matrix(val_y, basic_cnn_predictions, labels=[0,1])
ut.cm_df(basic_cnn_cm, index, columns)
# Although result accuracy seems similar to Neural Network model, the perfomance graph is much more stable and we can predict that when the model is ran mutiple times, it will probably bring us similar results.
# ## Smote CNN Model
filepath = '../models/smote_cnn.h5'
smote_cnn_model, smote_cnn_history = CNN_model(smote_images, smote_labels,
test_images, test_y,
filepath=filepath,
epochs=200,
batch_size=32)
# +
smote_cnn_saved_model = load_model(filepath)
smote_cnn_results_train = smote_cnn_saved_model.evaluate(smote_images, smote_labels)
print(f'Training Loss: {smote_cnn_results_train[0]:.3} \nTraining Accuracy: {smote_cnn_results_train[1]:.3}')
print('----------')
smote_cnn_results_test = smote_cnn_saved_model.evaluate(val_images, val_y)
print(f'Test Loss: {smote_cnn_results_test[0]:.3} \nTest Accuracy: {smote_cnn_results_test[1]:.3}')
# -
title = "../reports/SMOTE CNN Model: Iteration of Loss Graph"
ut.training_results_Loss(smote_cnn_history, title=title)
title = '../reports/SMOTE CNN Model: Iteration of Accuracy Graph'
ut.training_results_Accuracy(smote_cnn_history, title=title)
smote_cnn_predictions = smote_cnn_saved_model.predict_classes(val_images)
smote_cnn_cm = confusion_matrix(val_y, smote_cnn_predictions, labels=[0,1])
ut.cm_df(smote_cnn_cm, index, columns)
# Although accuracy has gone down by 2%, more true positive (Malignant) is detected.
# ## Adasyn CNN Model
filepath = '../models/adasyn_cnn.h5'
adasyn_cnn_model, adasyn_cnn_history = CNN_model(adasyn_images, adasyn_labels,
test_images, test_y,
filepath=filepath,
epochs=200,
batch_size=32)
# +
adasyn_cnn_saved_model = load_model(filepath)
adasyn_cnn_results_train = adasyn_cnn_saved_model.evaluate(adasyn_images, adasyn_labels)
print(f'Training Loss: {adasyn_cnn_results_train[0]:.3} \nTraining Accuracy: {adasyn_cnn_results_train[1]:.3}')
print('----------')
adasyn_cnn_results_test = adasyn_cnn_saved_model.evaluate(val_images, val_y)
print(f'Test Loss: {adasyn_cnn_results_test[0]:.3} \nTest Accuracy: {adasyn_cnn_results_test[1]:.3}')
# -
title = "../reports/ADASYN CNN Model: Iteration of Loss Graph"
ut.training_results_Loss(adasyn_cnn_history, title=title)
title = '../reports/ADASYN CNN Model: Iteration of Accuracy Graph'
ut.training_results_Accuracy(adasyn_cnn_history, title=title)
adasyn_cnn_predictions = adasyn_cnn_saved_model.predict_classes(val_images)
adasyn_cnn_cm = confusion_matrix(val_y, adasyn_cnn_predictions, labels=[0,1])
ut.cm_df(adasyn_cnn_cm, index, columns)
# The overall accuracy of the model is at 94.6% which is the highest results in all models. The model is under trained and there is a potential to increase the accuracy.
# ## Conclusion
# Adasyn CNN model so far exhibits the highest accuracy and satisfying precesion and recall rates.
#
# Next, pretrained model will be tested.
|
notebooks/.ipynb_checkpoints/(4) CNN Models-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import loader_helper
import os
import numpy as np
import tqdm
import nibabel as nii
from scipy.ndimage import zoom
data_path = '/home/dlachinov/brats2019/data/Task01_BrainTumour/imagesTr'
annotation_path = '/home/dlachinov/brats2019/data/Task01_BrainTumour/labelsTr'
# +
files = [f for f in os.listdir(data_path) if os.path.isfile(os.path.join(data_path,f))]
files.sort()
print(len(files))
# -
data, annotation, affine = loader_helper.read_multimodal_decatlon(data_path, annotation_path, files[0])
def get_bbox(data):
bboxes = np.stack([loader_helper.bbox3(d) for d in data],axis=0)
return np.stack([np.min(bboxes[:,0],axis=0),np.max(bboxes[:,1],axis=0)],axis=0)
bboxes = []
affines = []
for f in tqdm.tqdm(files):
data, annotation, affine = loader_helper.read_multimodal_decatlon(data_path, annotation_path, f, False)
affines.append(affine)
bboxes.append(get_bbox(data))
bboxes = np.stack(bboxes,axis=0)
print(bboxes.shape)
sizes = [b[1] - b[0] for b in bboxes]
print(np.max(sizes,axis=0))
crop_size = [loader_helper.closest_to_k(i,16) for i in np.max(sizes,axis=0)]
print(crop_size)
# +
min = np.array([0,0,0])
max = np.array([240, 240, 155])
output_dir = '/home/dlachinov/brats2019/data/2018_deca_cropped'
crop_size = np.array(crop_size)
#resample_to_size = (64,64,64)
#scale_factor = np.array(crop_size) / np.array(resample_to_size)
for idx, f in enumerate(tqdm.tqdm(files)):
data, annotation, affine = loader_helper.read_multimodal_decatlon(data_path, annotation_path, f, True)
b = get_bbox(data)
size = b[1] - b[0]
output = np.zeros(shape=(data.shape[0],)+tuple(crop_size))
out_annotation = np.zeros(shape=tuple(crop_size))
diff = np.array(crop_size) - np.array(size)
low = diff // 2
high = low - diff
bbox = b - np.stack([low,high])
index_input_min = np.maximum(bbox[0],min)
index_input_max = np.minimum(bbox[1],max)
size = index_input_max - index_input_min
index_output_min = crop_size//2 - size//2
index_output_max = crop_size//2 + size - size//2
output[:,index_output_min[0]:index_output_max[0],index_output_min[1]:index_output_max[1],index_output_min[2]:index_output_max[2]] =\
data[:,index_input_min[0]:index_input_max[0],index_input_min[1]:index_input_max[1],index_input_min[2]:index_input_max[2]]
out_annotation[index_output_min[0]:index_output_max[0],index_output_min[1]:index_output_max[1],index_output_min[2]:index_output_max[2]] =\
annotation[index_input_min[0]:index_input_max[0],index_input_min[1]:index_input_max[1],index_input_min[2]:index_input_max[2]]
suffixes = ['_flair.nii.gz', '_t1.nii.gz','_t1ce.nii.gz','_t2.nii.gz']
os.makedirs(name=os.path.join(output_dir,f), exist_ok=True)
#affine = np.diag([affine[i,i]*scale_factor[i] for i in range(3)]+[1])
for jdx, d in enumerate(output):
#d = zoom(d, 1/scale_factor, order=3, mode='constant', cval=0)
output_header = nii.Nifti1Image(d.astype(np.float32), affine)
nii.save(output_header, os.path.join(output_dir,f,f+suffixes[jdx]))
#out_annotation = zoom(out_annotation, 1/scale_factor, order=0, mode='constant', cval=0)
out_annotation[out_annotation==4] = 3
out = np.zeros_like(out_annotation)
out[out_annotation==2] = 1
out[out_annotation==1] = 2
out[out_annotation==3] = 3
output_header = nii.Nifti1Image(out.astype(np.uint8), affine)
nii.save(output_header, os.path.join(output_dir,f,f+'_seg.nii.gz'))
# -
|
crop_data_decatlon.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ___
#
# <a href='http://www.pieriandata.com'> <img src='../Pierian_Data_Logo.png' /></a>
# ___
# # Matplotlib Exercises - Solutions
#
# Welcome to the exercises for reviewing matplotlib! Take your time with these, Matplotlib can be tricky to understand at first. These are relatively simple plots, but they can be hard if this is your first time with matplotlib, feel free to reference the solutions as you go along.
#
# Also don't worry if you find the matplotlib syntax frustrating, we actually won't be using it that often throughout the course, we will switch to using seaborn and pandas built-in visualization capabilities. But, those are built-off of matplotlib, which is why it is still important to get exposure to it!
#
# ** * NOTE: ALL THE COMMANDS FOR PLOTTING A FIGURE SHOULD ALL GO IN THE SAME CELL. SEPARATING THEM OUT INTO MULTIPLE CELLS MAY CAUSE NOTHING TO SHOW UP. * **
#
# # Exercises
#
# Follow the instructions to recreate the plots using this data:
#
# ## Data
import numpy as np
x = np.arange(0,100)
y = x*2
z = x**2
# ** Import matplotlib.pyplot as plt and set %matplotlib inline if you are using the jupyter notebook. What command do you use if you aren't using the jupyter notebook?**
import matplotlib.pyplot as plt
# %matplotlib inline
# plt.show() for non-notebook users
# ## Exercise 1
#
# ** Follow along with these steps: **
# * ** Create a figure object called fig using plt.figure() **
# * ** Use add_axes to add an axis to the figure canvas at [0,0,1,1]. Call this new axis ax. **
# * ** Plot (x,y) on that axes and set the labels and titles to match the plot below:**
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
ax.plot(x,y)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('title')
# ## Exercise 2
# ** Create a figure object and put two axes on it, ax1 and ax2. Located at [0,0,1,1] and [0.2,0.5,.2,.2] respectively.**
# +
fig = plt.figure()
ax1 = fig.add_axes([0,0,1,1])
ax2 = fig.add_axes([0.2,0.5,.2,.2])
# -
# ** Now plot (x,y) on both axes. And call your figure object to show it.**
# +
ax1.plot(x,y)
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax2.plot(x,y)
ax2.set_xlabel('x')
ax2.set_ylabel('y')
fig # Show figure object
# -
# ## Exercise 3
#
# ** Create the plot below by adding two axes to a figure object at [0,0,1,1] and [0.2,0.5,.4,.4]**
# +
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
ax2 = fig.add_axes([0.2,0.5,.4,.4])
# -
# ** Now use x,y, and z arrays to recreate the plot below. Notice the xlimits and y limits on the inserted plot:**
# +
ax.plot(x,z)
ax.set_xlabel('X')
ax.set_ylabel('Z')
ax2.plot(x,y)
ax2.set_xlabel('X')
ax2.set_ylabel('Y')
ax2.set_title('zoom')
ax2.set_xlim(20,22)
ax2.set_ylim(30,50)
fig
# -
# ## Exercise 4
#
# ** Use plt.subplots(nrows=1, ncols=2) to create the plot below.**
# Empty canvas of 1 by 2 subplots
fig, axes = plt.subplots(nrows=1, ncols=2)
# ** Now plot (x,y) and (x,z) on the axes. Play around with the linewidth and style**
axes[0].plot(x,y,color="blue", lw=3, ls='--')
axes[1].plot(x,z,color="red", lw=3, ls='-')
fig
# ** See if you can resize the plot by adding the figsize() argument in plt.subplots() are copying and pasting your previous code.**
# +
fig, axes = plt.subplots(nrows=1, ncols=2,figsize=(12,2))
axes[0].plot(x,y,color="blue", lw=5)
axes[0].set_xlabel('x')
axes[0].set_ylabel('y')
axes[1].plot(x,z,color="red", lw=3, ls='--')
axes[1].set_xlabel('x')
axes[1].set_ylabel('z')
# -
# # Great Job!
|
udemy_ml_bootcamp/Python-for-Data-Visualization/Matplotlib/Matplotlib Exercises - Solutions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
df = pd.read_csv('car.csv');
df
missing = df.experience.median()
df.experience = df.experience.fillna(missing)
df
# +
# import model
from sklearn.linear_model import LinearRegression
# instantiate
linreg = LinearRegression()
# -
linreg.fit(df[['speed' , 'car_age' , 'experience']] , df.risk)
linreg.predict([[160,10,5]])
x = df[['speed' , 'car_age' , 'experience']]
y = df[['risk']]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.30, random_state=1)
linreg.fit(X_train , y_train)
linreg.predict([[160,10,5]])
|
Machine Learning Models/Supervised Learning/Regression/Linear Regression1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Overview of the mapclassify API
#
# There are a number of ways to access the functionality in `mapclassify`
# We first load the example dataset that we have seen earlier.
from libpysal import examples
import geopandas as gpd
from mapclassify import classify
pth = examples.get_path('columbus.shp')
gdf = gpd.read_file(pth)
y = gdf.HOVAL
gdf.head()
# ## Original API (< 2.4.0)
#
# +
import mapclassify
bp = mapclassify.BoxPlot(y)
bp
# -
# ## Extended API (>= 2.40)
#
# Note the original API is still available so this extension keeps backwards compatibility.
bp = classify(y, 'box_plot')
bp
type(bp)
q5 = classify(y, 'quantiles', k=5)
q5
# ### Robustness of the `scheme` argument
classify(y, 'boxPlot')
classify(y, 'Boxplot')
classify(y, 'Box_plot')
# +
# classify?
# -
|
notebooks/06_api.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Quality control
# ## Goal
# Remove sequences and regions with low quality or potential adapter contamination from the raw sequence pool.
# ## Protocol
# We use [Atropos](https://github.com/jdidion/atropos) ([Didion et al., 2017](https://peerj.com/articles/3720/)) for quality control.
#
# The following command is adopted from Oecophylla, under [qc.rule](https://github.com/biocore/oecophylla/blob/7e2c8e030fb2e3943762156dd7d84fdf945dbc92/oecophylla/qc/qc.rule#L158).
#
# ```
# atropos --threads {threads} {params.atropos} --report-file {log} --report-formats txt -o {temp_dir}/{f_fp} -p {temp_dir}/{r_fp} -pe1 {input.forward} -pe2 {input.reverse}
# ```
#
# For parameters (`params.atropos`), we use the following:
# ```
# -a GATCGGAAGAGCACACGTCTGAACTCCAGTCAC
# -A GATCGGAAGAGCGTCGTGTAGGGAAAGGAGTGT
# -q 15 --minimum-length 100 --pair-filter any
# ```
# Note: the two sequences are adapters to be removed (assuming the library prep kit is Illumina TruSeq or compatible models such as Kapa HyperPlus, which we use).
#
# ## Benchmark
# The following benchmarks were obtained on 692 AGP shotgun samples, using 8 CPUs and 8 GB memory.
#
# Basically, the run time is linear to the sample size, while memory consumption is linear and trivial.
#
# For a typical dataset of 1 million sequences, this step will cost roughly 1 min 15 sec.
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import linregress
# %matplotlib inline
df = pd.read_table('support_files/benchmarks/atropos.tsv', index_col=0)
df.head()
df['mseqs'] = df['seqs'] / 1000000
df['mbram'] = df['max_rss'] / 1000
reg = linregress(df['mseqs'].values, df['s'].values)
reg
fig = plt.figure(figsize=(5, 5))
ax = plt.gca()
plt.plot(df['mseqs'], df['s'], 'o', markersize=4)
x0, x1 = plt.xlim()
y0 = x0 * reg.slope + reg.intercept
y1 = x1 * reg.slope + reg.intercept
plt.plot([x0, x1], [y0, y1], '--')
plt.text(0.1, 0.8, '$\it{y} = %.3g %+.3g \it{x}$\n$\it{R}^2 = %.3g$'
% (reg.intercept, reg.slope, reg.rvalue ** 2),
transform=ax.transAxes)
plt.xlabel('Million sequences')
plt.ylabel('Wall clock time (sec)');
reg = linregress(df['mseqs'].values, df['mbram'].values)
reg
fig = plt.figure(figsize=(5, 5))
ax = plt.gca()
plt.plot(df['mseqs'], df['mbram'], 'o', markersize=4)
x0, x1 = plt.xlim()
y0 = x0 * reg.slope + reg.intercept
y1 = x1 * reg.slope + reg.intercept
plt.plot([x0, x1], [y0, y1], '--')
plt.text(0.1, 0.8, '$\it{y} = %.3g %+.3g \it{x}$\n$\it{R}^2 = %.3g$'
% (reg.intercept, reg.slope, reg.rvalue ** 2),
transform=ax.transAxes)
plt.xlabel('Million sequences')
plt.ylabel('Maximum memory usage (MB)');
|
notebooks/quality_control.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# ### Question 1.
# Create a function to perform basic arithmetic operations that includes addition, subtraction, multiplication and division on a string number (e.g. '12 + 24' or '23 - 21' or '12 // 12' or '12 * 21').
#
# Here, we have 1 followed by a space, operator followed by another space and 2. For the challenge, we are going to have only two numbers between 1 valid operator. The return value should be a number. eval() is not allowed. In case of division, whenever the second number equals'0' return -1.
#
# For example:`'15 // 0' ➞ -1`
#
# Examples:
# * arithmetic_operation('12 + 12') ➞ 24 // 12 + 12 = 24
# * arithmetic_operation('12 - 12') ➞ 24 // 12 - 12 = 0
# * arithmetic_operation('12 * 12') ➞ 144 // 12 * 12 = 144
# * arithmetic_operation('12 // 0') ➞ -1 // 12 / 0 = -1
# +
def arithmetic_operation(string_input):
a, operator, b = string_input.split(" ")
if operator == "+":
return int(a)+int(b)
if operator == "-":
return int(a)-int(b)
if operator == "*":
return int(a)*int(b)
if operator == "//":
if b == '0':
return -1
else:
return int(a)//int(b)
print(arithmetic_operation('12 + 12'))
print(arithmetic_operation('12 - 12'))
print(arithmetic_operation('12 * 12'))
print(arithmetic_operation('12 // 0'))
# -
# ### Question 2
# Write a function that takes the coordinates of three points in the form of a 2d array and returns the perimeter of the triangle. The given points are the vertices of a triangle on a two-dimensional plane.
#
# Examples:
# * perimeter( [ [15, 7], [5, 22], [11, 1] ] ) ➞ 47.08
# * perimeter( [ [0, 0], [0, 1], [1, 0] ] ) ➞ 3.42
# * perimeter( [ [-10, -10], [10, 10 ], [-10, 10] ] ) ➞ 68.28
# +
import math
def perimeter(coordinates) -> float:
a, b, c = coordinates
ab = math.dist(a, b)
bc = math.dist(b, c)
ac = math.dist(a, c)
return round(ab + bc + ac, 2)
print(perimeter( [ [15, 7], [5, 22], [11, 1] ] ))
print(perimeter( [ [0, 0], [0, 1], [1, 0] ] ) )
print(perimeter( [ [-10, -10], [10, 10 ], [-10, 10] ] ) )
# -
# ### Question 3
# A city skyline can be represented as a 2-D list with 1s representing buildings. In the example below, the height of the tallest building is 4 (second-most right column).
#
# [[0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 1, 0],
# [0, 0, 1, 0, 1, 0],
# [0, 1, 1, 1, 1, 0],
# [1, 1, 1, 1, 1, 1]]
#
# Create a function that takes a skyline (2-D list of 0's and 1's) and returns the height of the tallest skyscraper.
#
# Examples
# * tallest_skyscraper([[0, 0, 0, 0], [0, 1, 0, 0], [0, 1, 1, 0], [1, 1, 1, 1]]) ➞ 3
# * tallest_skyscraper([ [0, 1, 0, 0], [0, 1, 0, 0], [0, 1, 1, 0], [1, 1, 1, 1]]) ➞ 4
# * tallest_skyscraper([ [0, 0, 0, 0], [0, 0, 0, 0], [1, 1, 1, 0], [1, 1, 1, 1]]) ➞ 2
# +
def tallest_skyscraper(array):
heights = []
sum = 0
for i in range(len(array[0])):
for j in range(len(array[0])):
sum = sum + array[j][i]
heights.append(sum)
sum = 0
# find index of highest number
return max(heights)
print(tallest_skyscraper([[0, 0, 0, 0], [0, 1, 0, 0], [0, 1, 1, 0], [1, 1, 1, 1]]))
print(tallest_skyscraper([ [0, 1, 0, 0], [0, 1, 0, 0], [0, 1, 1, 0], [1, 1, 1, 1]]))
print(tallest_skyscraper([ [0, 0, 0, 0], [0, 0, 0, 0], [1, 1, 1, 0], [1, 1, 1, 1]]))
# -
# ### Question 4
# A financial institution provides professional services to banks and claims charges from the customers based on the number of man-days provided. Internally, it has set a scheme to motivate and reward staff to meet and exceed targeted billable utilization and revenues by paying a bonus for each day claimed from customers in excess of a threshold target.
#
# This quarterly scheme is calculated with a threshold target of 32 days per quarter, and the incentive payment for each billable day in excess of such threshold target is shown as follows:
#
# Days Bonus
# * 0 to 32 days Zero
# * 33 to 40 days SGD\$325 per billable day
# * 41 to 48 days SGD\$550 per billable day
# * Greater than 48 days SGD$600 per billable day
#
# Please note that incentive payment is calculated progressively. As an example, if an employee reached total billable days of 45 in a quarter, his/her incentive payment is computed as follows:
#
# 32\**0 + 8\**325 + 5*550 = 5350
#
# Write a function to read the billable days of an employee and return the bonus
# he/she has obtained in that quarter.
#
# Examples
# * bonus(15) ➞ 0
# * bonus(37) ➞ 1625
# * bonus(50) ➞ 8200
# +
def bonus(days:int) -> int:
bonus = 0
if 0 <= days <= 32:
bonus = days * 0
if 33 <= days <= 40:
bonus = (days - 32) * 325
if 41 <= days <= 48:
rem = days - 40
bonus = rem * 550 + 8 * 325
if days > 48:
rem = days - 48
bonus = rem * 600 + 8 * 550 + 8 * 325
return bonus
print(bonus(15))
print(bonus(37))
print(bonus(50))
# -
# ### Question 5
# A number is said to be Disarium if the sum of its digits raised to their respective positions is the number itself. Create a function that determines whether a number is a Disarium or not.
#
# Examples
# * is_disarium(75) ➞ False # 7^1 + 5^2 = 7 + 25 = 32
# * is_disarium(135) ➞ True # 1^1 + 3^2 + 5^3 = 1 + 9 + 125 = 135
# * is_disarium(544) ➞ False
# * is_disarium(518) ➞ True
# * is_disarium(466) ➞ False
# * is_disarium(8) ➞ True
# +
def is_disarium(num):
sum = 0
tempNum = num
while(num>0):
dgcnt= len(str(num))
digit = num%10
sum= sum + digit**dgcnt
dgcnt-=1
num = num//10
if sum == tempNum:
return tempNum, True
else:
return tempNum, False
print(is_disarium(75))
print(is_disarium(135))
print(is_disarium(544))
print(is_disarium(518))
print(is_disarium(466))
print(is_disarium(8))
|
assignments/PythonAdvanceProgramming/Python_Advance_Programming_3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/songqsh/MA2210/blob/main/src/matrix.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="zvFu_ZEup6Nl"
# import packages
import numpy as np
import numpy.linalg as la
# + colab={"base_uri": "https://localhost:8080/"} id="yUeKOm6fqCVZ" outputId="b85c8b89-578d-4124-85ea-cd169c70bd08"
# matrix input
A = np.array([[2,3], [1, -5]])
B = np.array([[4,3,6], [1,-2,3.]])
print(A)
print(B)
# + colab={"base_uri": "https://localhost:8080/"} id="KuH3AHHKqaRr" outputId="6bb45dda-0cdb-4ce2-cd19-dbfc24c94942"
# transpose
print(A.T)
print(B.T)
# + colab={"base_uri": "https://localhost:8080/"} id="NlXSUcRfq5BR" outputId="a268b12c-47be-43da-e0fb-83a9444b28d8"
# matrix multiplication
print(B.T@A.T)
# + id="wYL07_OUrF0_"
|
src/matrix.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Managing flowsheets
# ### Retrieve any Unit, Stream or System object by ID
# `find` has access to Flowsheet objects where all BioSTEAM objects are registered. The main flowsheet defaults to the 'Default' flowsheet:
import biosteam as bst
bst.find
# Find a Unit object:
import thermosteam as tmo
chemicals = tmo.Chemicals(['Water', 'Ethanol'])
tmo.settings.set_thermo(chemicals)
unit = bst.units.Mixer('M1')
bst.find('M1')
# Find a Stream object:
bst.find('s1')
# All Unit objects can be viewed as a diagram:
bst.units.Mixer('M2')
bst.find.diagram()
# All Stream, Unit, and System objects are stored as Register objects in `find`:
bst.find.stream
bst.find.unit
bst.find.system
# Access items in a register:
bst.find.unit.M1
# ### Switch between flowsheets
# A new flowsheet may be created and set as the main flowsheet:
bst.find.set_flowsheet('new_flowsheet')
bst.find
# Now all new objects will be registered in the new flowsheet:
unit = bst.units.Mixer('M3')
bst.find.diagram()
# Note that objects in the original flowsheet are not defined anymore and searching them would raise an error:
bst.find('M1')
# All Flowsheet objects are added to the `flowsheet` registry. Switching between flowsheets is easy:
bst.find.set_flowsheet('default') # Switch back to default flowsheet
bst.find
# As an example, the `lipidcane` biorefinery defines its own flowsheet and leaves it as the main flowsheet when you import it:
from biorefineries.lipidcane import system
bst.find
bst.find.system.lipidcane_sys.diagram()
|
docs/tutorial/Managing flowsheets.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/pachterlab/kallistobustools/blob/master/notebooks/Introduction_single_cell_RNA_seq.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="a-eRv9kSISgz" colab_type="text"
# # An introduction to single-cell RNA-seq
#
# #### Written by <NAME>* and <NAME>*. Based on [material taught in Caltech course Bi/BE/CS183](https://figshare.com/articles/Introduction_to_single-cell_RNA-seq_technologies/7704659/1) by <NAME> and <NAME>, with contributions from <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME> and <NAME>.
#
# #### *Division of Biology and Biological Engineering, California Institute of Technology
# + [markdown] id="3QavWOXvopRl" colab_type="text"
# The rapid development of single-cell genomics methods starting in 2009 has created unprecedented opportunity for highly resolved measurements of cellular states. Among such methods, single-cell RNA-seq (scRNA-seq) is having a profound impact on biology. Here we introduce some of the key concepts of single-cell RNA-seq technologies, with a focus on droplet based methods.
#
# To learn how to pre-process and analyze single-cell RNA-seq explore the following Google Colab notebooks that explain how to go from reads to results:
#
# - Pre-processing and quality control [[Python](https://colab.research.google.com/github/pachterlab/kallistobustools/blob/master/notebooks/kb_intro_1_python.ipynb), [R](https://colab.research.google.com/github/pachterlab/kallistobustools/blob/master/notebooks/kb_intro_1_R.ipynb)]
# - Getting started with analysis [[Python](https://colab.research.google.com/github/pachterlab/kallistobustools/blob/master/notebooks/kb_intro_2_python.ipynb), [R](https://colab.research.google.com/github/pachterlab/kallistobustools/blob/master/notebooks/kb_intro_2_R.ipynb)]
# - Building and annotating an atlas [[Python](https://colab.research.google.com/github/pachterlab/kallistobustools/blob/master/notebooks/kb_analysis_0_python.ipynb), [R](https://colab.research.google.com/github/pachterlab/kallistobustools/blob/master/notebooks/kb_analysis_0_R.ipynb)]
#
# The [kallistobus.tools tutorials](https://www.kallistobus.tools/tutorials) site has a extensive list of tutorials and vignettes on single-cell RNA-seq.
# + [markdown] id="dkRGcW-wGqHd" colab_type="text"
# ## Setup
# + [markdown] id="FiBr3LBHpbM0" colab_type="text"
# This notebook is a "living document". It downloads data and performs computations. As such it requires the installation of some python packages, which are installed with the commands below. In addition to running on Google Colab, the notebook can be downloaded and run locally on any machine which has python3 installed.
# + id="eGxol-mbHc8f" colab_type="code" cellView="form" colab={}
#@title Install packages
# %%capture
# !pip install matplotlib
# !pip install scikit-learn
# !pip install numpy
# !pip install scipy
# !pip install anndata
import numpy as np
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import matplotlib.colors as mplcol
import matplotlib.font_manager
import matplotlib as mpl
import pandas as pd
import io
import anndata
from scipy.stats import binom
from scipy.stats import poisson
from scipy.sparse import csr_matrix
from scipy.io import mmread
from IPython.display import HTML
from mizani.breaks import date_breaks
from mizani.formatters import date_format
# Only pandas >= v0.25.0 supports column names with spaces in querys
import plotnine as p
import requests
import warnings
import colorsys
warnings.filterwarnings("ignore") # plotnine has a lot of MatplotlibDeprecationWarning's
import seaborn as sns
sns.set_context("notebook", font_scale=1.5, rc={"lines.linewidth": 2.5})
fsize=20
plt.rcParams.update({'font.size': fsize})
# %config InlineBackend.figure_format = 'retina'
# + [markdown] id="Is99Ot4xGlgl" colab_type="text"
# ## Motivation
# + [markdown] id="wdO6InfgIeHi" colab_type="text"
# The goal of single-cell transcriptomics is to measure the transcriptional states of large numbers of cells simultaneously. The input to a scRNA-seq method is a collection of cells, possibly from intact tissue, or in dissociated form. Formally, the desired output is a *transcripts x cells* or *genes x cells* matrix that describes, for each cell, the abundance of its constituent transcripts or genes. More generally, single-cell genomics methods seek to measure not just transcriptional state, but other modalities in cells, e.g. protein abundances, epigenetic states, cellular morphology, etc.
#
# The ideal single-cell technology should thus:
#
# - Be ***universal*** in terms of cell size, type and state.
# - Perform ***in situ*** measurements.
# - Have no ***minimum input*** requirements.
# - Assay every cell, i.e. have a 100% ***capture rate***.
# - Detect every transcript in every cell, i.e. have 100% ***sensitivity***.
# - Identify individual transcripts by their ***full-length sequence***.
# - Assign transcripts correctly to cells, e.g. no ***doublets***.
# - Be compatible with additional ***multimodal measurements***.
# - Be ***cost effective*** per cell.
# - Be ***easy to use***.
# - Be ***open source*** so that it is transparent, and results from it reproducible.
# + [markdown] id="G870xfWmrO-N" colab_type="text"
# There is no method satisfying all of these requirements, however progress has been rapid. The development of single-cell RNA-seq technologies and their adoption by biologists, has been remarkable. [Svensson et al. 2019](https://www.biorxiv.org/content/10.1101/742304v2) describes a database of articles which present single-cell RNA-seq experiments, and the graph below, rendered from the [current version of the database](https://docs.google.com/spreadsheets/d/1En7-UV0k0laDiIfjFkdn7dggyR7jIk3WH8QgXaMOZF0/edit#gid=0), makes clear the exponential growth in single-cell transcriptomics:
# + id="BgUXVOgAOPbV" colab_type="code" cellView="form" outputId="4b19e1b3-3f96-4116-a169-ba74056eb9f0" colab={"base_uri": "https://localhost:8080/", "height": 350}
#@title Growth of single-cell RNA-seq
df = pd.read_csv('http://nxn.se/single-cell-studies/data.tsv', sep='\t')
# converts string to date format, can only be run once!
df['Date'] = pd.to_datetime(df['Date'], format='%Y%m%d')
# converts string of reported cells total to float, can only be run once!
df['Reported cells total'] = df['Reported cells total'].str.replace(',', '').map(float)
# plot number of studies over time
fig, ax = plt.subplots(figsize=(12, 5))
papers = pd.read_csv('http://nxn.se/single-cell-studies/data.tsv', sep='\t')
papers['Datetime'] = pd.to_datetime(papers['Date'], format='%Y%m%d')
papers = papers.sort_values("Date")
papers["count"] = 1
x = papers.Datetime
y = papers["count"].groupby(papers.Datetime.dt.time).cumsum()
ax.plot(x, y, color="k")
ax.set_xlabel("Date")
ax.set_ylabel("Cumulative number of studies")
plt.show()
# + [markdown] id="635a5WEKsPxq" colab_type="text"
# There are many different scRNA-seq technologies in use and under development, but broadly they fall into a few categories
# - well-based methods (e.g. Fluidigm SMARTer C1, Smart-seq2)
# - droplet-based methods (e.g. Drop-seq, InDrops, 10X Genomics Chromium)
# - spatial transcriptomics approaches (e.g. MERFISH, SEQFISH)
#
# At the time of initial writing of this document (2019), droplet-based approaches have become popular due to their relative low-cost, easy of use, and scalability. This is evident in a breakdown of articles by technology used:
# + id="0M7wjAq7PaKK" colab_type="code" cellView="form" outputId="a8e458f0-33e5-4fbb-bb1e-8fbcfbbcea4c" colab={"base_uri": "https://localhost:8080/", "height": 304}
#@title Technologies used
def tidy_split(df, column, sep='|', keep=False):
indexes = list()
new_values = list()
df = df.dropna(subset=[column])
for i, presplit in enumerate(df[column].astype(str)):
values = presplit.split(sep)
if keep and len(values) > 1:
indexes.append(i)
new_values.append(presplit)
for value in values:
indexes.append(i)
new_values.append(value)
new_df = df.iloc[indexes, :].copy()
new_df[column] = new_values
return new_df
ts = pd.Timestamp
tdf = tidy_split(df, 'Technique', ' & ')
t_dict = {k: k for k in tdf['Technique'].value_counts().head(5).index}
tdf['Technique'] = tdf['Technique'].map(lambda s: t_dict.get(s, 'Other'))
techs = list(
tdf['Technique']
.value_counts()
.sort_index()
.index
.difference(['Other'])
)
techs.append('Other')
tdf['Technique'] = (
pd.Categorical(
tdf['Technique'],
categories=techs,
ordered=True
)
)
def desaturate(color, prop):
# Check inputs
# if not 0 <= prop <= 1:
# raise ValueError("prop must be between 0 and 1")
# Get rgb tuple rep
rgb = mplcol.colorConverter.to_rgb(color)
# Convert to hls
h, l, s = colorsys.rgb_to_hls(*rgb)
# Desaturate the saturation channel
# l *= prop
l = 0.8
# Convert back to rgb
new_color = colorsys.hls_to_rgb(h, l, s)
hex_color = '#{:02x}{:02x}{:02x}'.format(*map(lambda c: int(c * 255), new_color))
return hex_color
# lighten matplotlib default colors
clrs = list(map(lambda c: desaturate(c, 1.2), ['C0', 'C1', 'C2', 'C3', 'C4', 'black']))
#### Plot number of studies per month by technique
per_month = (
tdf
.groupby('Technique')
.resample('1M', on='Date')
.count()['DOI']
.reset_index()
)
p.options.figure_size = (9, 2)
fig = (
p.ggplot(
p.aes(x='Date', y='DOI', fill='Technique'),
data=per_month.query('Date > @ts("20130101T010101")')
)
+ p.geom_bar(stat='identity', color='grey')
+ p.theme_minimal(base_family='DejaVu Sans')
+ p.scale_x_datetime(
breaks=date_breaks('1 years'),
labels=date_format('%Y')
)
+ p.labs(y='Number of studies')
+ p.scale_fill_manual(clrs)
)
fig
# + [markdown] id="t0yOrA0lcZ3m" colab_type="text"
# We therefore restrict this exposition to droplet-based technologies.
# + [markdown] id="orVyX2Sms1r2" colab_type="text"
# ## Droplet-based methods
#
# Droplet based single-cell RNA-seq methods were popularized by a pair of papers published concurrently in 2015:
# - Macosko et al., [Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets](https://www.cell.com/fulltext/S0092-8674(15)00549-8), 2015. DOI:10.1016/j.cell.2015.05.002 - describes Drop-seq.
# - Klein et al., [Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells](https://www.cell.com/cell/fulltext/S0092-8674(15)00500-0), 2015. DOI:10.1016/j.cell.2015.04.044 - descibes inDrops.
#
# Both of the methods makes use of developments in microfluidics published in:
# - Song, <NAME>, [Reactions in droplets in microfluidic channels](https://onlinelibrary.wiley.com/doi/10.1002/anie.200601554), 2006. DOI:10.1002/anie.200601554
# - <NAME>, <NAME> Weitz, [Droplet microfluidics for high-throughput biological assays](https://pubs.rsc.org/en/content/articlelanding/2012/lc/c2lc21147e#!divAbstract), 2012. DOI:10.1039/C2LC21147E
# + [markdown] id="Admx-IUOihd5" colab_type="text"
# ### Overview
# An overview of how a droplet based scRNA-seq method works is illustrated in a figure from the Drop-seq [Macosko et al. 2015](https://www.cell.com/fulltext/S0092-8674(15)00549-8) paper:
#
# 
#
# A microfluidic device is used to generate an emulsion, which consists of aqueous droplets in oil. The droplets are used to encapsulate cells, beads and reagents. In other words, each droplet is a "mini laboratory" in which the RNA from a single-cell can be captured and prepared for identification. Thus, the consistuent parts are as follows:
#
# - an emulsion (white circles containing beads and cells on the right hand-side of the figure).
# - dissociated cells (depicted as odd-shaped colored objects in the figure).
# - beads (flowing in from the left hand side of the figure).
# + [markdown] id="a2MjWRbTyC64" colab_type="text"
# ### Emulsions
# The foundation of droplet based single-cell RNA-seq methods are *mono-dispersed emulsions*. Mono-dispersed refers to the requirements that droplets are of (near) uniform size. Mono-dispersed emulsions can be generated with a microfluidic device, as shown below. The droplets are being "pinched off" at the junction, and one can see a polystyrene bead being captured in one droplet, while others are empty.
#
# 
#
# The movie is from the [McCarolll Drop-seq tutorial](http://mccarrolllab.org/dropseq/) courtesy of <NAME>, <NAME>, <NAME>, <NAME> & <NAME> at the Centre for Hybrid Biodevices & Cancer Sciences Unit at the University of Southampton.
#
# + [markdown] id="zl3Lg2-GmAcO" colab_type="text"
# ### Beads
# 
#
# The figure above, reproduce from Klein et al. 2015, shows the procedure used to make hydrogel beads for inDrops. Every bead contains the same barcode sequence, while the barcode sequences on two different beads are distinct.
#
# The barcode and UMI structure for a variety of technologies is viewable in a [compilation](https://teichlab.github.io/scg_lib_structs/) by <NAME>.
# + [markdown] id="0DuvNIYWnX0h" colab_type="text"
# ### Single cell suspensions
#
# In order to assay the transcriptomes of individual cells with droplet-based single-cell RNA-seq technologies, it is necessary to first dissociate tissue. Procedures for tissue dissociation are varied, and highly dependent on the organism, type of tissue, and many other factors. Protocols may be be enzymatic, but can also utilize mechanical dissociators. The talk below provides an introduction to tissue handling and dissociation.
# + id="3-3BHYdCQF_1" colab_type="code" cellView="form" outputId="f911ea8e-33bd-4283-d3a1-b7ba99608600" colab={"base_uri": "https://localhost:8080/", "height": 517}
#@title Tissue handling and dissociation
from IPython.display import HTML
HTML('<iframe width="882" height="496" src="https://www.youtube.com/embed/ARozvI4AbS8" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>')
# + [markdown] id="w4e42XFNnitJ" colab_type="text"
# ## Statistics of beads & cells in droplets
# + [markdown] id="XUlfCNWEnwGb" colab_type="text"
# ### The binomial distribution
#
# An understanding of droplet-based single-cell RNA-seq requires consideration of the statistics describing the capture of cells and beads in droplets. Suppose that in an experiment multiple droplets have been formed, and focus on one of the droplets. Assume that the probability that any single one of $n$ cells were captured inside it is $p$. We can calculate the probability that $k$ cells have been captured in the droplet as follows:
#
# $$ \mathbb{P}({\mbox Droplet\ contains\ k\ cells}) = \binom{n}{k}p^k(1-p)^{n-k}.$$
#
# The expected number of cells in the droplet is
#
# $$\lambda := \sum_{k=0}^n k \binom{n}{k}p^k(1-p)^{n-k} = n \cdot p.$$
#
# We plot this distribution on number of cells in a droplet below. It is called the Binomial distribution and has two parameters: $n$ and $p$.
# + id="60yOhEjjEt5L" colab_type="code" outputId="847dc40b-f3c9-4675-f5e9-13b2dff1ec53" cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 295}
#@title Binomial distribution { run: "auto" }
n = 10#@param {type:"integer"}
p = 0.02 #@param {type:"slider", min:0, max:1, step:0.01}
fig, ax = plt.subplots(figsize=(7, 4))
s = 10
x = np.arange(s)
y = binom.pmf(x,n,p)
ax.bar(x, y, color="k", label="Binomial n, p = ({}, {})".format(n,p))
ax.set_xlabel("Number of Trials")
ax.set_ylabel("Probability")
ax.set_xticks(x)
ax.legend()
plt.show()
# + [markdown] id="NB6l2QKkD7CN" colab_type="text"
# With $n=10$ and $p=0.02$, it's quite probable that the droplet is empty, and while possible that it contains one cell, unlikely that it has 2 or more. This is a good regime for a single-cell experiment; we will see that it is problematic if two cells are captured in a single droplet. Empty droplets are not problematic in the sense that they will not lead to data, and can therefore be ignored.
# + [markdown] id="YV9gs9pVnz3v" colab_type="text"
# ### The Poisson distribution
#
# The Binomial distribution can be difficult to work with in practice. Suppose, for example, that $n=1000$ and $p=0.002$. Suppose that we are interested in the probability of seeing 431 cells in a droplet. This probability is given by
#
# $$\binom{1000}{421}0.02^{421}(1-0.02)^{1000-431},$$
#
# which is evidently a difficult number to calculate exactly.
#
# A practical alternative to the binmomial is the Poisson distribution. The Poisson distribution has one parameter, and its support is the non-negative integers. A random variable $X$ is Poisson distributed if
# $$\mathbb{P}(X=k)\quad = \quad \frac{e^{-\lambda}\lambda^k}{k!}.$$
#
# The Poisson limit theorem states that if $p_n$ is a sequence of real numbers in $[0,1]$ with the sequence $np_n$ converging to to a finite limit $\lambda$, then
# $${\mbox lim}_{n \rightarrow \infty} \binom{n}{k}p_n^{k}(1-p_n)^{n-k} = e^{-\lambda}\frac{\lambda^k}{k!}.$$
#
# Thus, the Poisson distribution serves as a useful, tractable distribution to work with in lieu of the Binomial distribution for large $n$ and small $p$.
#
# The histogram below can be used to explore the Poisson and its relationship to the binomial
# + id="1S6lZC1vEwEp" colab_type="code" outputId="8fd2c09e-d174-43d3-d21b-14cf2d829061" cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 295}
#@title Binomial - Poisson comparison { run: "auto" }
n = 10#@param {type:"integer"}
p = 0.02 #@param {type:"slider", min:0, max:1, step:0.01}
s = 10
lambda_param = n*p
fig, ax = plt.subplots(figsize=(14, 4), ncols=2)
x = np.arange(s)
y = poisson.pmf(x, lambda_param)
ax[0].bar(x, y, color="k", label="Binomial n, p = ({}, {})".format(n,p))
ax[0].set_xlabel("Number of Trials")
ax[0].set_ylabel("Probability")
ax[0].set_xticks(x)
ax[0].legend()
x = np.arange(s)
y = binom.pmf(x,n,p)
ax[1].bar(x, y, color="k", label="Poisson $\lambda$={}".format(lambda_param))
ax[1].set_xlabel("Number of Trials")
ax[1].set_ylabel("Probability")
ax[1].set_xticks(x)
ax[1].legend()
plt.show()
# + [markdown] id="aqFb3KJXEd0B" colab_type="text"
# We therefore posit that
#
# $$ \mathbb{P}({\mbox Droplet\ contains\ k\ cells}) = \frac{e^{-\lambda}\lambda^k}{k!}$$ and
# $$ \mathbb{P}({\mbox Droplet\ contains\ j\ beads}) = \frac{e^{-\mu}\mu^j}{j!}.$$
#
# + [markdown] id="24KZTXzjBjms" colab_type="text"
# ## Droplet tuning
# + [markdown] id="9kyEiovXBp7y" colab_type="text"
# ### Cell capture and bead overload
#
# The cell capture rate is the probability that a droplet has at least one bead, and is given by $1-e^{-\mu}$.
#
# The bead overload rate is the rate at which captured single cells are associated with two or more different barcodes, which will happen when multiple beads are loaded into a droplet with one cell. The probability this happens is $$\frac{1-e^{-\mu}-\mu e^{-\mu}}{1-e^{-\mu}}.$$
#
# This leads to a tradeoff, as shown below.
#
# + id="hH9_sNPGHPub" colab_type="code" outputId="164cfe21-ca1c-413c-e3e8-11987b540f9a" cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 350}
#@title Tradeoff { run: "auto" }
fig, ax = plt.subplots(figsize=(5,5))
mu = np.arange(0, 10, 0.1)
x = 1 - np.exp(-mu)
y = (1 - np.exp(-mu)-mu*np.exp(-mu))/(1-np.exp(-mu))
ax.plot(x, y, color='k')
ax.set_xlabel("Cell capture rate")
ax.set_ylabel("Bead overload rate")
plt.show()
# + [markdown] id="Rbk3eSzdB7YT" colab_type="text"
# ### Sub-Poisson loading
#
# In order to circumvent the limit posed by a Poisson process for beads in droplets, the inDrops method uses tightly packed hydrogel beads that can be injected into droplets without loss. This approach, which leads to "[sub-Poisson loading](https://liorpachter.wordpress.com/tag/hydrogel-beads/
# )" is also used by 10X Genomics, and allows for increased capture rate.
#
# The difference is shown in two videos from the [Abate lab](https://www.abatelab.org/) linked to below. The first video, shows beads loaded being loaded in droplets with Poisson statistics:
#
# + id="spD7H27UGrOI" colab_type="code" outputId="b1e97b6e-f6dc-4d3c-c457-22cc13891784" cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 408}
#@title Poisson loading
HTML('<iframe width="688" height="387" src="https://www.youtube.com/embed/usK71SG30t0?autoplay=1&loop=1&playlist=usK71SG30t0" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>')
# + [markdown] id="u8G-Hy19ey_h" colab_type="text"
# The next video shows sub-Poisson loading with hydrogel beads. In this case the flow rate has been set so that exactly two beads are situated in each droplet.
# + id="6VcOiEMvHQ8e" colab_type="code" outputId="ef42922a-7d08-404c-86f0-dea31a31aed7" cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 336}
#@title Sub-Poisson loading { run: "auto" }
HTML('<iframe width="560" height="315" src="https://www.youtube.com/embed/2q1Lt9DWmRQ?autoplay=1&loop=1&playlist=2q1Lt9DWmRQ" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>')
# + [markdown] id="YtgSRpk6egPt" colab_type="text"
# The following shows the types of beads used for different droplet-based scRNA-seq methods, and associated properties:
#
# Property | Drop-seq | inDrops | 10x genomics
# ---| --- | --- |---
# Bead material | Polystyrene | Hydrogel | Hydrogel
# Loading dynamics | Poisson | sub-Poisson | sub-Poisson
# Dissolvable | No | No | Yes
# Barcode release | No | UV release | Chemical release
# Customizable | Demonstrated | Not shown | Feasible
# Licensing | Open source | Open Source | Proprietary
# Availability | Beads are sold | Commercial | Commercial
#
# + [markdown] id="6giT7bPVDWfd" colab_type="text"
# ### Barcode collisions
#
# Barcode collisions arise when two cells are separately encapsulated with beads that happen to contain identical barcodes.
#
# For $n$ assayed cells with $m$ barcodes, the barcode collision rate is the expected proportion of assayed cells that did not receive a unique barcode, i.e.
#
# $$1-\frac{\mathbb{E}[\mbox{cells with a unique barcode}]}{\mbox{number of cells}}$$
#
# $$= 1-(1-\frac{1}{m})^{n-1} \approx 1-\left(\frac{1}{e}\right)^\frac{n}{m}.$$
#
# Avoiding barcode collisions requires high barcode diversity, i.e. a small ratio of $\frac{n}{m}$.
# + id="-HKF-6a4mFe3" colab_type="code" outputId="13feffb8-0f95-4e95-908c-7ff672a75171" cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 350}
#@title Diversity and collisions { run: "auto" }
fig, ax = plt.subplots(figsize=(5,5))
bc = np.arange(0, 1, 0.01)
x = bc
y = 1 - np.exp(-bc)
ax.plot(x, y, color='k')
ax.set_xlabel("n/m")
ax.set_ylabel("Barcode collision rate")
plt.show()
# + [markdown] id="NJhCCxyrDY0B" colab_type="text"
# ### Barcode diversity and length
# A 1% barcode collision rate requires a barcode diversity of ~1%, i.e. the number of barcodes should be 100 times the number of cells. The number of barcodes from a sequence of length $L$ is $4^L$. Therefore, to assay $n$ cells, the barcode sequence must be of length at least $log_4n+3\frac{1}{3}$. This is a minimum and does not account for the need to be robust to sequencing errors.
# + [markdown] id="79fq83bMDcop" colab_type="text"
# ### Technical doublets
# Technical doublets arise when two or more cells are captured in a droplet with a single bead. The technical doublet rate is therefore the probability of capturing two or more cells in a droplet given that at least one cell has been captured in a droplet:
#
# $\frac{1-e^{-\lambda}-\lambda e^{-\lambda}}{1-e^{-\lambda}}$.
#
# Note that "overloading" a droplet-based single-cell experiment by loading more cells while keeping flow rates constant will increase the number of technical doublets due to an effective increase in $\lambda$ and also the number of synthetic doublets due to an increase in barcode diversity.
#
# + [markdown] id="9G44HtjhDfCI" colab_type="text"
# #### The barnyard plot
#
# Technical doublet rates can be measured by experiments in which a mixture of cells from two different species are assayed together. For example, if mouse and human cells are pooled prior to single-cell RNA-seq, the resultant reads ought to be assignable to either human or mouse. If a droplet contained a "mixed" doublet, i.e. two cells one of which is from human and the other from mouse, it will generate reads some of which can be aligned to mouse, and some to human.
#
# An example from a 10X Genomics dataset ([5k 1:1 mixture of fresh frozen human (HEK293T) and mouse (NIH3T3) cells](https://support.10xgenomics.com/single-cell-gene-expression/datasets/3.0.2/5k_hgmm_v3_nextgem)) is shown in the plot below, which is called a *Barnyard plot* in Macosko et al. **2015**.
#
# + id="-83zHC4cAiNq" colab_type="code" cellView="both" colab={}
# %%capture
# Download a matrix of human and mouse
# !wget http://cf.10xgenomics.com/samples/cell-exp/3.0.0/hgmm_1k_v2/hgmm_1k_v2_filtered_feature_bc_matrix.tar.gz
# !tar -xvf hgmm_1k_v2_filtered_feature_bc_matrix.tar.gz
# + id="mCJ3ULcbjMBb" colab_type="code" cellView="form" outputId="d81331ab-ac0d-4744-e8e9-65bba2a70689" colab={"base_uri": "https://localhost:8080/", "height": 350}
#@title Human & mouse PBMCs
mtx = csr_matrix(mmread("/content/filtered_feature_bc_matrix/matrix.mtx.gz").T)
genes = pd.read_csv("/content/filtered_feature_bc_matrix/features.tsv.gz", header=None, names=["gene_id", "gene_name", "extra"], sep="\t")
cells = pd.read_csv("/content/filtered_feature_bc_matrix/barcodes.tsv.gz", header=None, names=["cell_barcode"], sep="\t")
adata = anndata.AnnData(X=mtx, var=genes, obs=cells)
adata.var["human"] = adata.var["gene_id"].str.contains("hg19").values
x = (mtx[:,adata.var["human"].values]).sum(axis=1)
y = (mtx[:,~adata.var["human"].values]).sum(axis=1)
fig, ax = plt.subplots(figsize=(5,5))
x = np.asarray(x).reshape(-1)
y = np.asarray(y).reshape(-1)
ax.scatter(x, y, color='k')
ax.set_xlabel("Human UMI counts per cell")
ax.set_ylabel("Mouse UMI counts per cell")
ax.xaxis.set_major_formatter(mpl.ticker.StrMethodFormatter('{x:,.0f}'))
ax.yaxis.set_major_formatter(mpl.ticker.StrMethodFormatter('{x:,.0f}'))
plt.show()
# + [markdown] id="4COS_Y_qj_P0" colab_type="text"
# THe plot shows that there are only 7 doublets out of 5,000 cells in this experiment. This is an unusually small number and atypical of most experiments, where doublet rates are between 5%--15% (see [DePasquale et al. 2018](https://www.biorxiv.org/content/10.1101/364810v1.abstract)); perhaps the 5k human mouse PBMC dataset data is articularly "clean" as it is an advertisement distributed by 10X Genomics.
# + [markdown] id="Do436tT4Dl3H" colab_type="text"
# #### Bloom's correction
#
# The 7 doublets identifiable by eye in the plot above are all *mixed doublets*, i.e. they contain one human and one mouse cell. However doublets may consist of two mouse cells, or two human cells. If the number of droplets containing at least one human cells is $n_1$, the number containing at least one mouse cell is $n_2$, and the number of mixed doublets is $n_{1,2}$, then an estimate for the actual doublet rate can be obtained from the calculation below ([Bloom 2018](https://peerj.com/articles/5578/)):
#
# Given $n_1, n_2$ and $n_{1,2}$ as described above (note that $n_1$ is the number of cells on the *x* axis + the number of mixed doublets and $n_2$ is the number of cells on the *y* axis + the number of mixed doublets), then in expectation
#
# $$\frac{n_1}{N} \cdot \frac{n_2}{N} = \frac{n_{1,2}}{N}, $$
#
# where $N$ is the total number of droplets. From this we see that
#
# $$ \hat{N} = \frac{n_1 \cdot n_2}{n_{1,2}}.$$
#
# This is the maximum likelihood [Lincoln-Petersen estimator](https://en.wikipedia.org/wiki/Mark_and_recapture) for population size from mark and recapture.
#
# Let $\mu_1$ nad $\mu_2$ be the Poisson rates for the respective types of cells, i.e. the average number of cells of each type per droplet. Then
#
# $$ \hat{\mu}_1 = -\mbox{ln } \left( \frac{N-n_1}{N} \right)$$ and
# $$ \hat{\mu}_2 = -\mbox{ln } \left( \frac{N-n_2}{N} \right).$$
#
# From this the doublet rate $D$ can be estimated as
#
# $$\hat{D} = 1 - \frac{(\mu_1+\mu_2)e^{-\mu_1+\mu_2}}{1-e^{-\mu_1-\mu_2}}.$$
#
# + [markdown] id="5s-AOvBWCEZu" colab_type="text"
# ### Biological doublets
#
# Biological doublets arise when two cells form a discrete unit that does not break apart during disruption to form a single-cell suspension. Note that biological doublets cannot be detected in barnyard plots.
#
# One approach to avoiding biological doublets is to perform single-nuclei RNA-seq. See, e.g. [Habib et al., 2017](https://www.nature.com/articles/nmeth.4407). However, biological doublets are not necessarily just a technical artifact to be avoided. [Halpern et al., 2018](https://www.nature.com/articles/nbt.4231) utilizes biological doublets of hepatocytes and liver endothelial cells to assign tissue coordinates to liver endothelial cells via imputation from their hepatocyte partners.
# + [markdown] id="O6WeiAjdDyFs" colab_type="text"
# ### Unique Molecular Identifiers
#
# The number of distinct UMIs on a bead in a droplet is at most $4^L$ where $L$ is the number of UMI bases. For example, for 10X Genomics v2 technology $L=10$ and for 10X Genomics v3 technology $L=12$. [Melsted, Booeshaghi et al. 2019](https://www.biorxiv.org/content/10.1101/673285v2) show how to estimate the number of the actual distinct UMIs on each bead for which data is obtained in a scRNA-seq experiment.
#
# + [markdown] id="tl2PVIfAEFj8" colab_type="text"
# ## Summary
#
# Selection of a single-cell RNA-seq method requires choosing among many tradeoffs that reflect the underlying technologies. The table below, from From [Zhang et al. 2019. DOI:10.1016/j.molcel.2018.10.020](https://www.sciencedirect.com/science/article/pii/S1097276518308803?via%3Dihub), summarizes the three most popular droplet-based single-cell RNA-seq assays:
#
# 
#
#
# + [markdown] id="iwsCMlv-qTgb" colab_type="text"
# The generation of single-cell RNA-seq data is just the first step in understanding the transcriptomes cells. To interpret the data reads must be aligned or pseudoaligned, UMIs counted, and large *cell x gene* matrices examined. The growth in single-cell RNA-seq analysis *tools* for these tasks has been breathtaking. The graph below, plotted from real-time data downloaded from the [scRNA-seq tools database](https://www.scrna-tools.org/tools), shows the number of tools published since 2016.
# + id="GkpGjR5BtCe1" colab_type="code" cellView="form" outputId="8cfba296-e7b5-4ad8-87a3-02c78c35996b" colab={"base_uri": "https://localhost:8080/", "height": 394}
#@title Growth of single-cell tools { run: "auto" }
tools = pd.read_csv('https://raw.githubusercontent.com/Oshlack/scRNA-tools/master/database/tools.tsv', sep='\t')
tools["Datetime"] = pd.to_datetime(tools["Added"])
tools = tools.sort_values("Added")
tools["count"] = 1
fig, ax = plt.subplots(figsize=(12, 5))
x = tools.Datetime
y = tools["count"].groupby(tools.Datetime.dt.time).cumsum()
ax.plot(x, y, color="k")
ax.set_xlabel("Date")
ax.set_ylabel("Number of tools")
ax.tick_params(axis='x', rotation=45)
plt.show()
# + [markdown] id="nehALDscrVkN" colab_type="text"
# In fact, the rate of growth of single-cell RNA-seq *tools* is similar to that of single-cell RNA-seq *studies*:
# + id="nJag_4YC4tsL" colab_type="code" cellView="form" outputId="3361c302-9ad8-4f8f-f63c-bf69b42a1a54" colab={"base_uri": "https://localhost:8080/", "height": 350}
#@title scRNA-seq tools vs. studies
date_papers = papers.groupby("Datetime")["count"].sum()
date_tools = tools.groupby("Datetime")["count"].sum()
dates = pd.date_range(start='7/26/2002', end='2/01/2020')
combined = pd.DataFrame(index=dates)
combined["tool_counts"] = combined.index.map(date_tools)
combined["paper_counts"] = combined.index.map(date_papers)
combined = combined.fillna(0)
combined["Datetime"] = combined.index.values
fig, ax = plt.subplots(figsize=(5,5))
x = combined["paper_counts"].groupby(combined.Datetime.dt.time).cumsum()
y = combined["tool_counts"].groupby(combined.Datetime.dt.time).cumsum()
ax.scatter(x, y, color="k")
lims = [np.min([ax.get_xlim(), ax.get_ylim()]), # min of both axes
np.max([ax.get_xlim(), ax.get_ylim()])] # max of both axes
ax.plot(lims, lims, 'k-', alpha=0.75, zorder=0)
ax.set_aspect('equal')
ax.set_xlim(lims)
ax.set_ylim(lims)
ax.set_xlabel("Cumulative Papers")
ax.set_ylabel("Cumulative Tools")
plt.show()
# + [markdown] id="Ds9wn5ORrmto" colab_type="text"
# Next step: to learn how to analyze single-cell RNA-seq data, visit the [kallistobus.tools site tutorials](https://www.kallistobus.tools/tutorials) site and explore the "Introduction 1: pre-processing and quality control" notebook in [Python](https://colab.research.google.com/github/pachterlab/kallistobustools/blob/master/notebooks/kb_intro_1_python.ipynb) or [R](https://colab.research.google.com/github/pachterlab/kallistobustools/blob/master/notebooks/kb_intro_1_R.ipynb).
# + [markdown] id="zsIQeTGUROkQ" colab_type="text"
# **Feedback**: please report any issues, or submit pull requests for improvements, in the [Github repository where this notebook is located](https://github.com/pachterlab/kallistobustools/blob/master/notebooks/Introduction_single_cell_RNA_seq.ipynb).
|
notebooks/Introduction_single_cell_RNA_seq.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <div class="alert alert-warning">
#
# <h3> Домашнее задание</h3>
#
# <p></p>
# Выполнять в отдельном файле!
#
# <ul>1. Для <b>своего</b> ряда (см. папку Данные на de.unecon) определите наилучшую адаптивную модель прогнозирования. Для этого загрузите данные и отобразите их на графике. Есть ли в ряде тренд, сезонность?</ul>
#
# <ul>2. С помощью библиотеки statsmodels обучите выбранную модель и постройте прогноз. Отобразите результат на графике.</ul>
#
# <ul>3. Вычислите среднеквадратичную ошибку для оценки качества аппроксимации.</ul>
# <p></p>
#
# </div>
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
# -
plt.rcParams["figure.figsize"] = (12,5)
prod = pd.read_csv('general-index-of-industrial-prod.csv',
index_col=0)[:-1]
prod.index = pd.to_datetime(prod.index, format='%Y-%m')
prod.columns = ['prod_index']
prod.head()
prod.plot()
# Явно есть годовая сезонность, но на всякий случай проверим автокоррелеяцию.
from statsmodels.graphics.tsaplots import plot_acf
fig, ax = plt.subplots(figsize=(12,5))
plot_acf(prod['prod_index'], lags=40, ax=ax)
plt.show()
# Есть пики автокорреляции в лагах, кратным 12, то есть существует годовая сезонность. Посмотрим на скользящее среднее, чтобы проверить, есть ли тренд.
prod['SME'] = prod.rolling(window=12).mean()
prod['prod_index'].plot()
prod['SME'].plot()
plt.show()
# Есть повышающийся тренд, скорее аддитивный, чем мультипликативный. Остаётся вопрос сезонности: непонятно, брать аддитивную сезонность или мультипликативную, поэтому проверим для обоих. Будем использовать метод Хольта-Уинтерса для аддитивного тренда, сначала с аддитивной сезонностью, потом с мультипликативной.
from statsmodels.tsa.holtwinters import ExponentialSmoothing
prod_model_seasonal_add = ExponentialSmoothing(endog=prod['prod_index'],
trend='add',
seasonal='add',
seasonal_periods=12,
freq='MS').fit()
alpha_seasonal_add = prod_model_seasonal_add.model.params['smoothing_level']
beta_seasonal_add = prod_model_seasonal_add.model.params['smoothing_trend']
gamma_seasonal_add = prod_model_seasonal_add.model.params['smoothing_seasonal']
prod['prod_index'].rename('Production index').plot(legend=True)
prod_model_seasonal_add.fittedvalues.rename(r'$\alpha=%.2f$' % alpha_seasonal_add + ', ' +
r'$\beta=%.2f$' % beta_seasonal_add + ', ' +
r'$\gamma=%.2f$' % gamma_seasonal_add).plot(legend=True)
plt.title('Сравнение начальных данных и модели с аддитивными трендом и сезонностью')
plt.show()
def MSE(actual, prediction):
return np.mean((actual - prediction)**2)
# Среднеквадратичная ошибка модели:
MSE(prod['prod_index'].values, prod_model_seasonal_add.fittedvalues.values)
prod_model_seasonal_mul = ExponentialSmoothing(endog=prod['prod_index'],
trend='add',
seasonal='mul',
seasonal_periods=12,
freq='MS').fit()
alpha_seasonal_mul = prod_model_seasonal_mul.model.params['smoothing_level']
beta_seasonal_mul = prod_model_seasonal_mul.model.params['smoothing_trend']
gamma_seasonal_mul = prod_model_seasonal_mul.model.params['smoothing_seasonal']
prod['prod_index'].rename('Production index').plot(legend=True)
prod_model_seasonal_mul.fittedvalues.rename(r'$\alpha=%.2f$' % alpha_seasonal_mul + ', ' +
r'$\beta=%.2f$' % beta_seasonal_mul + ', ' +
r'$\gamma=%.2f$' % gamma_seasonal_mul).plot(legend=True)
plt.title('Сравнение начальных данных и модели с аддитивным трендом и мультипликативной сезонностью')
plt.show()
# Среднеквадратичная ошибка модели:
MSE(prod['prod_index'].values, prod_model_seasonal_mul.fittedvalues.values)
prod['prod_index'].rename('Production index').plot(legend=True)
prod_model_seasonal_add.fittedvalues.rename(r'$\alpha=%.2f$' % alpha_seasonal_add + ', ' +
r'$\beta=%.2f$' % beta_seasonal_add + ', ' +
r'$\gamma=%.2f$' % gamma_seasonal_add + ', ' +
"seasonal='add'").plot(legend=True)
prod_model_seasonal_mul.fittedvalues.rename(r'$\alpha=%.2f$' % alpha_seasonal_mul + ', ' +
r'$\beta=%.2f$' % beta_seasonal_mul + ', ' +
r'$\gamma=%.2f$' % gamma_seasonal_mul + ', ' +
"seasonal='mul'").plot(legend=True)
plt.title('Сравнение начальных данных и двух моделей')
plt.show()
# <div class="alert alert-danger">
#
# Я не понимаю, почему получились некоторые значения параметров нулевые, но почему-то всё работает.
#
# </div>
# Поскольку среднеквадратичная ошибка получилась меньше у модели с мультипликативной сезонностью, будем использовать эту модель для построения прогноза на пять лет.
start = prod.index[-1] + pd.DateOffset(months=1)
end = start + pd.DateOffset(years=5)
start, end
prod['prod_index'].rename('Production index').plot(legend=True)
prod_model_seasonal_mul.predict(start=start, end=end).rename('Prediction').plot(legend=True)
|
Forecasting-Methods/Adaptive Methods HW/Adaptive Methods HW.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3-azureml
# kernelspec:
# display_name: Python 3.6 - AzureML
# language: python
# name: python3-azureml
# ---
# # Interpret Models
#
# You can use Azure Machine Learning to interpret a model by using an *explainer* that quantifies the amount of influence each feature contribues to the predicted label. There are many common explainers, each suitable for different kinds of modeling algorithm; but the basic approach to using them is the same.
#
# ## Install SDK packages
#
# In addition to the latest version of the **azureml-sdk** and **azureml-widgets** packages, you'll need the **azureml-explain-model** package to run the code in this notebook. You'll also use the Azure ML Interpretability library (**azureml-interpret**). You can use this to interpret many typical kinds of model, even if they haven't been trained in an Azure ML experiment or registered in an Azure ML workspace.
#
# Run the cell below to verify that these packages are installed.
# !pip show azureml-explain-model azureml-interpret
# ## Explain a model
#
# Let's start with a model that is trained outside of Azure Machine Learning - Run the cell below to train a decision tree classification model.
# + gather={"logged": 1633897014486}
import pandas as pd
import numpy as np
import joblib
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve
# load the diabetes dataset
print("Loading Data...")
data = pd.read_csv('data/diabetes.csv')
# Separate features and labels
features = ['Pregnancies','PlasmaGlucose','DiastolicBloodPressure','TricepsThickness','SerumInsulin','BMI','DiabetesPedigree','Age']
labels = ['not-diabetic', 'diabetic']
X, y = data[features].values, data['Diabetic'].values
# Split data into training set and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=0)
# Train a decision tree model
print('Training a decision tree model')
model = DecisionTreeClassifier().fit(X_train, y_train)
# calculate accuracy
y_hat = model.predict(X_test)
acc = np.average(y_hat == y_test)
print('Accuracy:', acc)
# calculate AUC
y_scores = model.predict_proba(X_test)
auc = roc_auc_score(y_test,y_scores[:,1])
print('AUC: ' + str(auc))
print('Model trained.')
# -
# The training process generated some model evaluation metrics based on a hold-back validation dataset, so you have an idea of how accurately it predicts; but how do the features in the data influence the prediction?
# ### Get an explainer for the model
#
# Let's get a suitable explainer for the model from the Azure ML interpretability library you installed earlier. There are many kinds of explainer. In this example you'll use a *Tabular Explainer*, which is a "black box" explainer that can be used to explain many kinds of model by invoking an appropriate [SHAP](https://github.com/slundberg/shap) model explainer.
# + gather={"logged": 1633898069403}
from interpret.ext.blackbox import TabularExplainer
# "features" and "classes" fields are optional
tab_explainer = TabularExplainer(model,
X_train,
features=features,
classes=labels)
print(tab_explainer, "ready!")
# -
# ### Get *global* feature importance
#
# The first thing to do is try to explain the model by evaluating the overall *feature importance* - in other words, quantifying the extent to which each feature influences the prediction based on the whole training dataset.
# + gather={"logged": 1633898099326}
# you can use the training data or the test data here
global_tab_explanation = tab_explainer.explain_global(X_train)
# Get the top features by importance
global_tab_feature_importance = global_tab_explanation.get_feature_importance_dict()
for feature, importance in global_tab_feature_importance.items():
print(feature,":", importance)
# -
# The feature importance is ranked, with the most important feature listed first.
#
# ### Get *local* feature importance
#
# So you have an overall view, but what about explaining individual observations? Let's generate *local* explanations for individual predictions, quantifying the extent to which each feature influenced the decision to predict each of the possible label values. In this case, it's a binary model, so there are two possible labels (non-diabetic and diabetic); and you can quantify the influence of each feature for each of these label values for individual observations in a dataset. You'll just evaluate the first two cases in the test dataset.
# + [markdown] nteract={"transient": {"deleting": false}}
#
# + gather={"logged": 1633898151460}
# Get the observations we want to explain (the first two)
X_explain = X_test[0:2]
# Get predictions
predictions = model.predict(X_explain)
# Get local explanations
local_tab_explanation = tab_explainer.explain_local(X_explain)
# Get feature names and importance for each possible label
local_tab_features = local_tab_explanation.get_ranked_local_names()
local_tab_importance = local_tab_explanation.get_ranked_local_values()
for l in range(len(local_tab_features)):
print('Support for', labels[l])
label = local_tab_features[l]
for o in range(len(label)):
print("\tObservation", o + 1)
feature_list = label[o]
total_support = 0
for f in range(len(feature_list)):
print("\t\t", feature_list[f], ':', local_tab_importance[l][o][f])
total_support += local_tab_importance[l][o][f]
print("\t\t ----------\n\t\t Total:", total_support, "Prediction:", labels[predictions[o]])
# -
# ## Adding explainability to a model training experiment
#
# As you've seen, you can generate explanations for models trained outside of Azure Machine Learning; but when you use experiments to train and register models in your Azure Machine Learning workspace, you can generate model explanations and log them.
#
# Run the code in the following cell to connect to your workspace.
#
# > **Note**: If you haven't already established an authenticated session with your Azure subscription, you'll be prompted to authenticate by clicking a link, entering an authentication code, and signing into Azure.
# + gather={"logged": 1633898361353}
import azureml.core
from azureml.core import Workspace
# Load the workspace from the saved config file
ws = Workspace.from_config()
print('Ready to use Azure ML {} to work with {}'.format(azureml.core.VERSION, ws.name))
# -
# ### Train and explain a model using an experiment
#
# OK, let's create an experiment and put the files it needs in a local folder - in this case we'll just use the same CSV file of diabetes data to train the model.
# + gather={"logged": 1633898463378}
import os, shutil
from azureml.core import Experiment
# Create a folder for the experiment files
experiment_folder = 'diabetes_train_and_explain'
os.makedirs(experiment_folder, exist_ok=True)
# Copy the data file into the experiment folder
shutil.copy('data/diabetes.csv', os.path.join(experiment_folder, "diabetes.csv"))
# -
# Now we'll create a training script that looks similar to any other Azure ML training script except that is includes the following features:
#
# - The same libraries to generate model explanations we used before are imported and used to generate a global explanation
# - The **ExplanationClient** library is used to upload the explanation to the experiment output
# +
# %%writefile $experiment_folder/diabetes_training.py
# Import libraries
import pandas as pd
import numpy as np
import joblib
import os
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve
# Import Azure ML run library
from azureml.core.run import Run
# Import libraries for model explanation
from azureml.interpret import ExplanationClient
from interpret.ext.blackbox import TabularExplainer
# Get the experiment run context
run = Run.get_context()
# load the diabetes dataset
print("Loading Data...")
data = pd.read_csv('diabetes.csv')
features = ['Pregnancies','PlasmaGlucose','DiastolicBloodPressure','TricepsThickness','SerumInsulin','BMI','DiabetesPedigree','Age']
labels = ['not-diabetic', 'diabetic']
# Separate features and labels
X, y = data[features].values, data['Diabetic'].values
# Split data into training set and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=0)
# Train a decision tree model
print('Training a decision tree model')
model = DecisionTreeClassifier().fit(X_train, y_train)
# calculate accuracy
y_hat = model.predict(X_test)
acc = np.average(y_hat == y_test)
run.log('Accuracy', np.float(acc))
# calculate AUC
y_scores = model.predict_proba(X_test)
auc = roc_auc_score(y_test,y_scores[:,1])
run.log('AUC', np.float(auc))
os.makedirs('outputs', exist_ok=True)
# note file saved in the outputs folder is automatically uploaded into experiment record
joblib.dump(value=model, filename='outputs/diabetes.pkl')
# Get explanation
explainer = TabularExplainer(model, X_train, features=features, classes=labels)
explanation = explainer.explain_global(X_test)
# Get an Explanation Client and upload the explanation
explain_client = ExplanationClient.from_run(run)
explain_client.upload_model_explanation(explanation, comment='Tabular Explanation')
# Complete the run
run.complete()
# -
# The experiment needs a Python environment in which to run the script, so we'll define a Conda specification for it. Note that the **azureml-interpret** library is included in the training environment so the script can create a **TabularExplainer** and use the **ExplainerClient** class.
# %%writefile $experiment_folder/interpret_env.yml
name: batch_environment
dependencies:
- python=3.6.2
- scikit-learn
- pandas
- pip
- pip:
- azureml-defaults
- azureml-interpret
# Now you can run the experiment.
# + gather={"logged": 1633898782161}
from azureml.core import Experiment, ScriptRunConfig, Environment
from azureml.widgets import RunDetails
# Create a Python environment for the experiment
explain_env = Environment.from_conda_specification("explain_env", experiment_folder + "/interpret_env.yml")
# Create a script config
script_config = ScriptRunConfig(source_directory=experiment_folder,
script='diabetes_training.py',
environment=explain_env)
# submit the experiment
experiment_name = 'mslearn-diabetes-explain'
experiment = Experiment(workspace=ws, name=experiment_name)
run = experiment.submit(config=script_config)
RunDetails(run).show()
run.wait_for_completion()
# -
# ## Retrieve the feature importance values
#
# With the experiment run completed, you can use the **ExplanationClient** class to retrieve the feature importance from the explanation registered for the run.
# + gather={"logged": 1633898875602}
from azureml.interpret import ExplanationClient
# Get the feature explanations
client = ExplanationClient.from_run(run)
engineered_explanations = client.download_model_explanation()
feature_importances = engineered_explanations.get_feature_importance_dict()
# Overall feature importance
print('Feature\tImportance')
for key, value in feature_importances.items():
print(key, '\t', value)
# -
# ## View the model explanation in Azure Machine Learning studio
#
# You can also click the **View run details** link in the Run Details widget to see the run in Azure Machine Learning studio, and view the **Explanations** tab. Then:
#
# 1. Select the explanation ID for your tabular explainer.
# 2. View the **Aggregate feature importance** chart, which shows the overall global feature importance.
# 3. View the **Individual feature importance** chart, which shows each data point from the test data.
# 4. Select an individual point to see the local feature importance for the individual prediction for the selected data point.
# 5. Use the **New Cohort** button to define a subset of the data with the following settings:
# - **Dataset cohort name**: Under 25s
# - **Select filter**: Dataset
# - Age less than 25 (Make sure you add this filter before saving the new cohort).
# 6. Create a second new cohort named **25 and over** with a filter on Age greater than or equal to 25.
# 6. Review the **Aggregate feature importance** visualization and compare the relative feature importance for the two cohorts you have defined. The ability to compare cohorts makes it possible to see how the features influence preedictions differently for multiple subsets of the data population.
#
#
# **More Information**: For more information about using explainers in Azure ML, see [the documentation](https://docs.microsoft.com/azure/machine-learning/how-to-machine-learning-interpretability).
|
14 - Interpret Models.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Rechneranwendungen in der Physik - Übung N.2 Taylorentwicklung der Kosinusfunktion
# Santiago.R <NAME>
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import math
import time
# Zur Approximation der Kosinusfunktion entwickeln wir die Taylorreihe für $f(x)=cos(x)$ um den Entwicklungspunkt $x_0=0$. Die Taylorreihe, die beliebige Funktionen mithilfe von Polynomen n-ter Ordnungen annähert, ist allgemein definiert als $T(x,x_0,n)=\sum_{k=0}^n \frac{f^{(k)}(x_0)}{k!}(x-x_0)^k$, d.h. also als Summe der Produkte von den k-ten Ableitungen am Entwicklungspunkt und den k-Potenzen der Variable $x$. Um diese Taylorreihe zu entwickeln müssen also die Ableitungen (oder die Werte der Differentialquotienten am Entwicklungspunkt) bis zur k-ten Ordnung aus der angenäherten Funktion entnommen werden. Diese ist die Kosinusfunktion und diese definieren wir also zunächst im Notebook mithilfe vom Modul Numpy als $y_1(x)=cos(x)$, weshalb folgt;
def y1(x):
return np.cos(x)
# Für die Ableitungen der Kosinusfunktion gilt aus der Lehre in der mathematischen Analyse $f'(x)=-sin(x)$, $f''(x)=-cos(x)$, $f'''(x)=sin(x)$ u.s.w. sodass gilt
# $
# f^{(k)}(x)=
# \begin{cases}
# (-1)^{i} sin(x) \ \ \ \ \ \ \ \ \ \ \forall k=2i-1 \ \ :i \in \mathbb{N} \\
# (-1)^j cos(x) \ \ \ \ \ \ \ \ \ \ \forall k=2j \ \ :j \in \mathbb{N} \\
# \end{cases}
# $, wobei aber alle Terme im ersten Fall mit $sin(x)$ für den Entwicklungspunkt $x_0=0$ entfallen aufgrund von $sin(0)=0$. Somit bleiben für die Taylorentwicklung der Kosinusfunktion um den Punkt $x_0=0$ nur die Terme von $f^{(k)}(x_0)=(-1)^k cos(x_0)= (-1)^k$ in der Summe s.d. für die Taylorreihe um $x_0=0$ folgt; $\ \ T_{(0)}(x,n)=\sum_{k=0}^n \frac{(-1)^{k}}{(2k)!}x^{2k}$
def T(x, n):
taylor = 0
for k in range(n+1):
taylor += ((-1)**k) * (x ** (2*k)) / (math.factorial(2 * k))
return taylor
# Diese Taylorreihe soll nun für $n=0,2,4...10$ entwickelt und die Laufzeiten $\Delta t$ der nummerischen Berechnungen für jede einzelne Taylorentwicklung angegeben werden. Anschließend werden die ausgewerteten Polynome mitsamt der eigentlichen Kosinusfunktion gemeinsam in einem Plot dargestellt.
x = np.linspace(0,20,num=20000)
n0=0
t0 = time.time()
plt.plot(x, T(x, n0),label=0)
Laufzeit0 = time.time()-t0
mylist=[]
for n in range(1,11,2):
t = time.time()
plt.plot(x, T(x, n),label=n+1)
Laufzeit = time.time()-t
mylist.append(Laufzeit)
plt.plot(x, y1(x), color="brown", linewidth=2.5, linestyle="--",label='cos(x)')
plt.legend(title="Ordnung n",loc='upper right')
plt.xlabel('X-Achse')
plt.ylabel('Y-Achse')
startx, endx = 0, 20
starty, endy = -1.5, 1.5
plt.axis([startx, endx, starty, endy])
plt.show()
s = set(mylist)
print('Die Laufzeit der Taylor-Entwicklung bis zur Ordnung n =', 0,'ist t =',round(Laufzeit0,3),'Sekunden')
for i in range(0,5,1):
print('Die Laufzeit der Taylor-Entwicklung bis zur Ordnung n =', 2+2*i,'ist t =',round(list(s)[i],3),'Sekunden')
|
Approximation der Kosinusfunktion/Approximation der Kosinusfunktion.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Python Classes
class A:
pass
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
p1 = Point(3, 4)
print(p1)
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
def __str__(self):
return 'x: {}, y:{}'.format(self.x, self.y)
def calc_dist(self, p2):
pass
# +
p1 = Point(3, 4)
print(p1)
p2 = Point(4, 7)
if p1 == p2:
pass
p1.calc_dist(p2)
# -
dir(tuple())
# +
class A: # super class
pass
class B(A): # B is a sub class of A
pass
# -
class Rectangle:
def __init__(self, length=4, width=3):
self.length = length
self.width = width
def __str__(self):
return 'length: {}, width:{}\narea: {}'.format(self.length,
self.width,
self.get_area())
def get_area(self):
return self.length * self.width
r1 = Rectangle()
print(r1)
r2 = Rectangle(6, 4)
print(r2)
r3 = Rectangle(width=3, length=10)
print(r3)
print(r3.get_area())
class Squar(Rectangle):
def __init__(self, x):
super().__init__(x, x)
s1 = Squar(3)
print(s1)
class A:
def __init__(self, a, b):
self.__a = a
self.b = b
def set_a(self, a):
self.__a = a
def get_a(self):
return self.__a
def __str__(self):
return 'a:{}, b:{}'.format(self.__a, self.b)
a1 = A(3, 2)
print(a1)
a1.b = 10
print(a1)
a1.a = 12
print(a1)
a1.set_a(12)
print(a1)
class Person:
def __init__(self, name, age):
self.name = name
self.age = age
def __str__(self):
return 'name: {}, age: {}'.format(self.name, self.age)
p1 = Person(name='Ahmed', age=12)
print(p1)
p1.name = 'Mohammed'
print(p1)
p1.age = -12
print(p1)
class Person:
def __init__(self, name, age):
self.name = name
#self.__age = age
self.set_age(age)
def __str__(self):
return 'name: {}, age: {}'.format(self.name, self.__age)
def set_age(self, age):
if age > 0:
self.__age = age
else:
age = None
p1 = Person(name='Ahmed', age=12)
print(p1)
p1.set_age(-20)
print(p1)
|
notebooks/Python_classes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Polynomial Linear regression
#
# y = b0 + b1*x1 + b2*x1^2 + .... + bn*x1^n
#
# Note: Linear beacuse we are takling of y in respect to bi(coefficients)
#
#
#
# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importing the dataset
dataset = pd.read_csv('./Position_Salaries.csv')
X = dataset.iloc[:, 1:2].values
y = dataset.iloc[:, 2].values
dataset.head(2)
plt.scatter(X, y, color="blue")
plt.xlabel("Level")
plt.ylabel("Salary")
plt.title("Non linear dependencies between level and salary")
# +
# Splitting the dataset into the Training set and Test set
"""
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
"""
# Feature Scaling
"""from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
X_train = sc_X.fit_transform(X_train)
X_test = sc_X.transform(X_test)
sc_y = StandardScaler()
y_train = sc_y.fit_transform(y_train)"""
# -
# # Fitting linear regression to the dataset
# +
from sklearn.linear_model import LinearRegression
linear_regressor = LinearRegression()
linear_regressor.fit(X, y)
# -
# # Fitting polynomial regression to the dataset
# +
from sklearn.preprocessing import PolynomialFeatures
poly_regressor = PolynomialFeatures(degree = 5)
x_poly = poly_regressor.fit_transform(X)
x_poly
# -
# x_poly = poly_regressor.fit_transform(X)
linear_regressor2 = LinearRegression()
linear_regressor2.fit(x_poly, y)
# # Visualizing the linear regression results
# +
plt.scatter(X, y, color = "red")
plt.plot(X, linear_regressor.predict(X), color = "blue")
plt.title("Truth or bluff Linear Regression")
plt.xlabel("Position Level")
plt.xlabel("Salary")
plt.show()
# -
# # Visualizing the Polynomial regression results
# +
plt.scatter(X, y, color = "red")
plt.plot(X, linear_regressor2.predict(poly_regressor.fit_transform(X)), color = "blue")
plt.title("Truth or bluff Polynomial Regression")
plt.xlabel("Position Level")
plt.xlabel("Salary")
plt.show()
# +
x_grid = np.arange(min(X), max(X), 0.25)
x_grid = x_grid.reshape((len(x_grid), 1))
plt.scatter(X, y, color = "red")
plt.plot(x_grid, linear_regressor2.predict(poly_regressor.fit_transform(x_grid)), color = "blue")
plt.title("Truth or bluff Polynomial Regression")
plt.xlabel("Position Level")
plt.xlabel("Salary")
plt.show()
# -
# # Prediction of new result - Linear
data = np.array([2.5, 3.5, 5.2, 7,8]).reshape(-1, 1)
linear_regressor.predict(data)
# # Prediction of new result - Polynomial
data = np.array([2.5, 3.5, 5.2, 7,8]).reshape(-1, 1)
linear_regressor2.predict(poly_regressor.fit_transform(data))
dataset
|
regression/polynomial/polynomial_regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/DanielMartinAlarcon/DS-Sprint-01-Dealing-With-Data/blob/master/module1-afirstlookatdata/ManifoldLearning.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="1QUBvAG0EdDv" colab_type="text"
# This example is based on the sklearn "[Manifold learning on Handwriting](http://scikit-learn.org/stable/auto_examples/manifold/plot_lle_digits.html)" example. Let's start by loading some libraries and data.
#
# This example was prepared by <NAME> and <NAME> for their
# "Machine learning for ART" workshop at Rhizomatiks Research in
# January, 2016.
# + id="irp5e_zTEdDw" colab_type="code" colab={}
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
from matplotlib import offsetbox
from sklearn import manifold, datasets, decomposition, ensemble, discriminant_analysis, random_projection
# %matplotlib inline
digits = datasets.load_digits(n_class=6)
X = digits.data
y = digits.target
n_samples, n_features = X.shape
n_neighbors = 30
# + [markdown] id="rXsMa3w-EdDz" colab_type="text"
# The data we loaded is a subset of MNIST, which contains 70k handwritten digits. We're only using around 1,000 digits. Here's what they look like:
# + id="MB3aQfdyEdDz" colab_type="code" colab={}
n_img_per_row = 32
img = np.zeros((10 * n_img_per_row, 10 * n_img_per_row))
for i in range(n_img_per_row):
ix = 10 * i + 1
for j in range(n_img_per_row):
iy = 10 * j + 1
img[ix:ix + 8, iy:iy + 8] = X[i * n_img_per_row + j].reshape((8, 8))
plt.figure(figsize=(5, 5))
plt.imshow(img, cmap=plt.cm.binary)
plt.xticks([])
plt.yticks([])
plt.show()
# + [markdown] id="7OI4jWrZEdD4" colab_type="text"
# Manifold learning is about discovering a low-dimensional structure (also called a projection, decomposition, manifold, or embedding) for high-dimensional data.
#
# Linear dimensionality reduction is the process of finding a projection. If your data existed in three dimensions and you wanted a two dimensional view, this would be similar to rotating or skewing the data until the shadow looked informative. PCA, LDA, and ICA find a rotation and skewing of the data that gives a good projection.
#
# Before we look at these projections, we need to define a helper function that will plot the results of our projection.
# + id="2YnC_PXVEdD5" colab_type="code" colab={}
def plot_embedding(X, y):
x_min, x_max = np.min(X, 0), np.max(X, 0)
X = (X - x_min) / (x_max - x_min)
plt.figure(figsize=(6, 6))
ax = plt.subplot(111)
for i in range(X.shape[0]):
plt.text(X[i, 0], X[i, 1], str(digits.target[i]),
color=plt.cm.Set1(y[i] / 10.),
fontdict={'size': 8})
if hasattr(offsetbox, 'AnnotationBbox'):
# only print thumbnails with matplotlib > 1.0
shown_images = np.array([[1., 1.]]) # just something big
for i in range(digits.data.shape[0]):
dist = np.sum((X[i] - shown_images) ** 2, 1)
if np.min(dist) < 4e-3:
# don't show points that are too close
continue
shown_images = np.r_[shown_images, [X[i]]]
imagebox = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(digits.images[i], cmap=plt.cm.gray_r),
X[i])
ax.add_artist(imagebox)
plt.xticks([]), plt.yticks([])
# + [markdown] id="THojTqSBEdD8" colab_type="text"
# Now we can find a projection and see what it looks like. The most common one is principle components analysis (PCA).
# + id="dGdSIae9EdD9" colab_type="code" colab={}
X_pca = decomposition.TruncatedSVD(n_components=2).fit_transform(X)
plot_embedding(X_pca, y)
# + [markdown] id="00Ezu7KoEdEA" colab_type="text"
# PCA is good at finding the main axes of variation in a dataset. Here it looks like it's separated the digits a little bit, but it's still hard to see the boundaries between them. One the other hand, linear discriminant analysis (LDA) will find a projection that maximally separates all the classes.
# + id="DsfR_5gjEdEB" colab_type="code" colab={}
X2 = X.copy()
X2.flat[::X.shape[1] + 1] += 0.01 # Make X invertible
X_lda = discriminant_analysis.LinearDiscriminantAnalysis(n_components=2).fit_transform(X2, y)
plot_embedding(X_lda, y)
# + [markdown] id="4omVLEfHEdEG" colab_type="text"
# LDA can have great results, but if you look at the code it says `fit_transform(X2, y)` while PCA says `fit_transform(X)`. This means for LDA you need labeled data (supervised learning), but for PCA you can use unlabaled data (unsupervised learning). Here's a picture explaining the difference:
#
# ### PCA
# [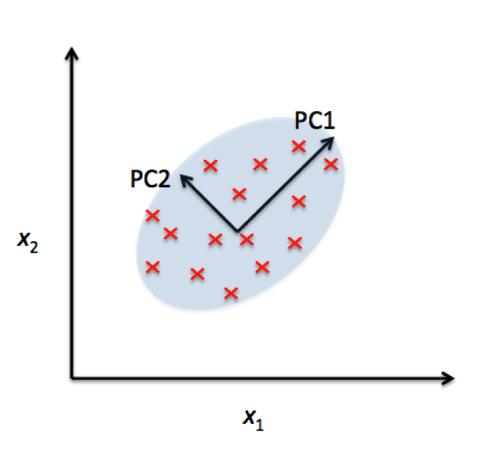](http://sebastianraschka.com/faq/docs/lda-vs-pca.html)
#
# ### LDA
# [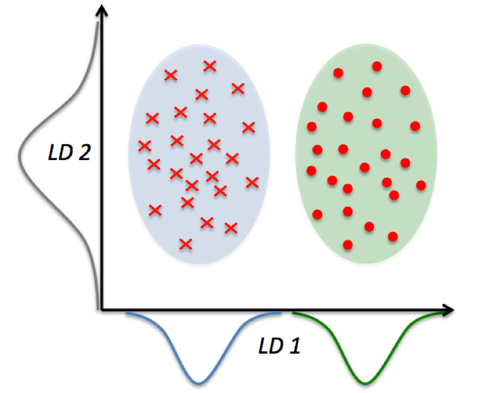](http://sebastianraschka.com/faq/docs/lda-vs-pca.html)
#
# Independent components analysis (ICA) is like PCA in that it can be run without labels (unsupervised). Instead of the directions of maximum variance, it finds the directions in which the data varies most independently.
#
# [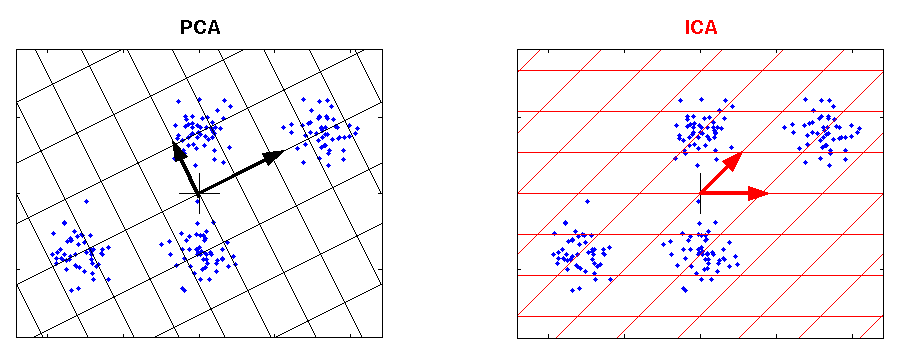](http://phdthesis-bioinformatics-maxplanckinstitute-molecularplantphys.matthias-scholz.de/#pca_ica_independent_component_analysis)
# [](http://gael-varoquaux.info/science/ica_vs_pca.html)
#
# Here's what ICA looks like on the digits dataset:
# + id="xM3O-egdEdEH" colab_type="code" colab={}
X_ica = decomposition.FastICA(n_components=2).fit_transform(X)
plot_embedding(X_ica, y)
# + [markdown] id="Qs4u2sxqEdEL" colab_type="text"
# The separation of the classes is closer to LDA than to PCA, but without any supervision. This isn't an inherent property of ICA or PCA, but it has more to do with the kind of data we're looking at.
#
# Besides these linear techniques, there are others called "nonlinear dimensionality reduction algorithms". Instead of imagining the projection like a shadow, imagine each point in high dimensional space like a particle get pushed and pulled independently. The goal is usually to end up with an embedding that keeps similar points close by, distant points far apart, and maintains some locally continuous behavior of variation.
#
# One of the most useful techniques for visualization purposes is called t-SNE ("tee snee"). A great paper showing comparisons is [here](https://lvdmaaten.github.io/publications/papers/JMLR_2008.pdf). For a visualization of t-SNE see this [great article by <NAME>](http://colah.github.io/posts/2014-10-Visualizing-MNIST/).
# + id="Bl0F4SUVEdEN" colab_type="code" colab={}
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
# %time X_tsne = tsne.fit_transform(X)
plot_embedding(X_tsne, y)
# + [markdown] id="H_R0HXpbEdET" colab_type="text"
# But there are many others with their own benefits and disavantages. For example, Isomap has a very impressive demo of being able to "unroll" an extruded spiral (called a "swiss roll"), and to project images of hands in two dimensions that capture the two ways the hand gestures vary.
#
# 
#
# 
# + id="3Q-6SMtaEdEU" colab_type="code" colab={}
# %time X_iso = manifold.Isomap(n_neighbors, n_components=2).fit_transform(X)
plot_embedding(X_iso, y)
# + [markdown] id="cp5dGuWFEdEY" colab_type="text"
# Some other algorithms are listed below.
# + id="xat9NJ6pEdEZ" colab_type="code" colab={}
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2, method='standard')
# %time X_lle = clf.fit_transform(X)
plot_embedding(X_lle, y)
# + id="a_5hFm26EdEc" colab_type="code" colab={}
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2, method='modified')
# %time X_mlle = clf.fit_transform(X)
plot_embedding(X_mlle, y)
# + id="pKo2kAo1EdEh" colab_type="code" colab={}
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2, method='hessian')
# %time X_hlle = clf.fit_transform(X)
plot_embedding(X_hlle, y)
# + id="i9GLggKOEdEl" colab_type="code" colab={}
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2, method='ltsa')
# %time X_ltsa = clf.fit_transform(X)
plot_embedding(X_ltsa, y)
# + id="8t9RqzGmEdEo" colab_type="code" colab={}
clf = manifold.MDS(n_components=2, n_init=1, max_iter=100)
# %time X_mds = clf.fit_transform(X)
plot_embedding(X_mds, y)
# + id="9WGx7IeBEdEu" colab_type="code" colab={}
hasher = ensemble.RandomTreesEmbedding(n_estimators=200, random_state=0, max_depth=5)
# %time X_transformed = hasher.fit_transform(X)
pca = decomposition.TruncatedSVD(n_components=2)
# %time X_reduced = pca.fit_transform(X_transformed)
plot_embedding(X_reduced, y)
# + id="lR5l7bVwEdEx" colab_type="code" colab={}
embedder = manifold.SpectralEmbedding(n_components=2, random_state=0, eigen_solver="arpack")
# %time X_se = embedder.fit_transform(X)
plot_embedding(X_se, y)
|
module1-afirstlookatdata/ManifoldLearning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: jax
# language: python
# name: jax
# ---
# ## Keras for Jax, 2022-1-10
# - Basic numpy works for Keras while jax Numpy does not work for JAX
from jax import grad, jit, pmap
import jax.numpy as jnp
import numpy as np
import tensorflow as tf
layer = tf.keras.layers.Dense(2)
x = np.zeros((10,2))
y = layer(x)
y
x = jnp.zeros((10,5))
x
layer(x)
y = tf.add(x,x)
y
grad(y, x)
grad(lambda x: x+x,x)
x = np.zeros((10,5))
L = lambda x: jnp.sum(2*x)
df = grad(L)
df(x)
x
f = lambda x: tf.reduce_sum(x)
df = grad(f)
x = np.ones((2,))
f(x)
# +
df(x)
# -
|
diffprog/jax_tf_dp/keras for jax.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import torch
import torch.nn as nn
class autoencoder(nn.Module):
def __init__(self):
super(Autoencoder, self).__init__()
self.encoder = nn.Sequential(
nn.Conv2d(1, 16, 3, stride=5, padding=1),
nn.ReLU(),
nn.Conv2d(16, 32, 3, stride=5, padding=1),
)
self.decoder = nn.Sequential(
nn.ConvTranspose2d(64, 32, 7),
nn.ReLU(),
nn.ConvTranspose2d(32, 16, 3, stride=2, padding=1, output_padding=1),
nn.ReLU(),
nn.ConvTranspose2d(16, 1, 3, stride=2, padding=1, output_padding=1),
nn.Sigmoid()
)
def forward(self, x):
x = self.encoder(x)
x = self.decoder(x)
return x
|
autoencer_torch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Data Extraction Notebook for :Savings from a battery and solar system during ERCOT 4CP events
#
# ## This notebook will connect to the database and extract the data live and put it into compressed zip files in this directory.
#
# We're going to look at if solar equipped homes stored all excess energy produced on the day of a 4CP event between 7AM until 4PM, then started discharging it from 4-5:30PM. How much energy would be stored up, and what would the potential savings of that be based on a cost of $55/kWh.
#
# <p>You'll need to modify the read_csv calls in that notebook to point at these instead of the ones we've extracted and prepared for you in the /shared/JupyterHub-Examples-Data/ directory on the JupyterHub server if you would like to use the ones exported by this notebook in the analysis notebook.</p>
import pandas as pd
import psycopg2
import sqlalchemy as sqla
import os
import sys
sys.path.insert(0,'..')
from config.read_config import get_database_config
sys.executable # shows you your path to the python you're using
# +
# read in db credentials from config/config.txt
# * make sure you add those to the config/config.txt file! *
database_config = get_database_config("../config/config.txt")
# -
# get our DB connection
engine = sqla.create_engine('postgresql://{}:{}@{}:{}/{}'.format(database_config['username'],
database_config['password'],
database_config['hostname'],
database_config['port'],
database_config['database']
))
# +
# Set the cost of a kWh in dollars
cost_kWh = 55
# These are the ERCOT 4CP events (start date/time and end date/time) for 2016 - 2019 acquired from
# http://mis.ercot.com/misapp/GetReports.do?reportTypeId=13037&reportTitle=Planned%20Service%20Four%20Coincident%20Peak%20Calculations&showHTMLView=&mimicKey
event_days = ['2019-06-19', '2019-07-30', '2019-08-12', '2019-09-06',
'2018-06-27', '2018-07-19', '2018-08-23', '2018-09-19',
'2017-06-23', '2017-07-28', '2017-08-16', '2017-09-20',
'2016-06-15', '2016-07-14', '2016-08-11', '2016-09-19'
]
# we're going to look at using 7AM to 4PM to charge the theoretical battery as the time the sun becomes available to the PV systems
# until the earliest possible time of a 4CP event (4PM), then discharge from 4PM - 5:30PM to cover any 4CP timeslots that have happened thus far
start_time = '07:00:00-05'
end_time = '16:00:00-05'
# these are the actual 4CP event start times and end times from 2016-2019 for reference
event_start_dates = ['2019-06-19 17:00:00-05', '2019-07-30 16:30:00-05', '2019-08-12 17:00:00-05', '2019-09-06 16:45:00-05',
'2018-06-27 17:00:00-05', '2018-07-19 17:00:00-05', '2018-08-23 16:45:00-05', '2018-09-19 16:30:00-05',
'2017-06-23 16:45:00-05', '2017-07-28 17:00:00-05', '2017-08-16 17:00:00-05', '2017-09-20 16:45:00-05',
'2016-06-15 17:00:00-05', '2016-07-14 16:00:00-05', '2016-08-11 16:30:00-05', '2016-09-19 16:15:00-05'
]
event_end_dates = ['2019-06-19 17:15:00-05', '2019-07-30 16:45:00-05', '2019-08-12 17:15:00-05', '2019-09-06 17:00:00-05',
'2018-06-27 17:15:00-05', '2018-07-19 17:15:00-05', '2018-08-23 17:00:00-05', '2018-09-19 16:45:00-05',
'2017-06-23 17:00:00-05', '2017-07-28 17:15:00-05', '2017-08-16 17:15:00-05', '2017-09-20 17:00:00-05',
'2016-06-15 17:15:00-05', '2016-07-14 16:15:00-05', '2016-08-11 16:45:00-05', '2016-09-19 16:30:00-05'
]
# +
# let's select homes that have solar and a high amount of data completeness
# we're also filtering out homes that have really large solar arrays (larger than 6.25)
# we're excluding dataids 5448, 2925 due to having a battery already
query = """
select dataid, pv, total_amount_of_pv
from other_datasets.metadata
where pv is not null
and grid is not null
and solar is not null
and total_amount_of_pv is not null
and total_amount_of_pv <= 6.25
and egauge_1min_min_time < '2016-06-15'
and egauge_1min_max_time > '2019-09-06'
and dataid not in (5448, 2925)
and (egauge_1min_data_availability like '%100%' or egauge_1min_data_availability like '99%' or egauge_1min_data_availability like '98%')
limit 25
"""
# create a Pandas dataframe with the data from the sql query
dataids = pd.read_sql_query(sqla.text(query), engine)
dataids.head(10)
# -
dataids.describe()
# extract the dataids
# grab dataids and convert them to a string to put into the SQL query
dataids_list = dataids['dataid'].tolist()
print("{} dataids selected listed here:".format(len(dataids_list)))
dataids_str = ','.join(list(map(str, dataids_list)))
dataids_str
# dataids_list
# +
# select the data for all of the events for all of these homes starting at 7AM and ending at 4PM
# the first date starting at midnight and ending at the end time of one of the 4CP events
first_start = event_days.pop(0)
energy_query = """
select dataid, localminute, solar, grid from electricity.eg_realpower_1min
where ((localminute >= '{} {}' and localminute <= '{} {}') """.format(first_start, start_time, first_start, end_time)
for day in event_days:
energy_query = energy_query + "OR (localminute >= '{} {}' and localminute <= '{} {}') ".format(day, start_time, day, end_time)
energy_query = energy_query + """ ) AND dataid in ({})""".format(dataids_str)
print("query is {}".format(energy_query))
df2 = pd.read_sql_query(sqla.text(energy_query), engine)
# -
df2.describe()
# +
# calculate usage as grid minus solar (which is actually grid + solar because solar is negative use)
# Calculate the difference with a lambda function and add it as a new column called 'usage'
# NOTE: This takes a while to run, after all it's running this lambda function on ~520k points
df2['usage'] = df2.apply(lambda row: row.solar + row.grid, axis=1)
df2.describe()
# -
# export homes to csv file
compression_opts = dict(method='zip',
archive_name='pv_storage_savings.zip')
df2.to_csv('pv_storage_savings.zip', index=False,
compression=compression_opts)
# +
# convert localminute to pandas datetime type
df2['datetime'] = pd.to_datetime(df2['localminute'])
# and set as index
df2 = df2.set_index('datetime')
# set local timezone
df2 = df2.tz_convert('US/Central')
df2
# +
# group by month and dataid and sum negative grid grouping into month by dataid giving us each home's accumulated negative grid
# (extra solar production) for that month's 4CP event day between 7AM and 4PM
df3 = df2.loc[df2['grid'] < 0].groupby([pd.Grouper(freq='M'), 'dataid']).sum()
df3
# +
# we're going to have a look at what happens when we average them all together by month
df4 = df3.reset_index()
df4 = df4.set_index('datetime')
df4 = df4.groupby([pd.Grouper(freq='M')]).mean()
# drop all rows that are all NaN
df4 = df4.dropna(thresh=3)
# drop all the dataids
df4 = df4.drop(columns=['dataid'])
# convert to KWh
df4 = df4.apply(lambda x : x / 60.0)
# this gives us the 16 event days averaged together per day
df4
# -
# let's put this all on a bar chart with a set of solar/grid/usage per day
ax = df4.plot.bar(rot=90, figsize=[60,30], fontsize=25, grid=True)
ax.set_xlabel('4CP Event Date', fontsize = 30)
ax.set_ylabel('kWh', fontsize = 30)
legend = ax.legend(loc=1, prop={'size': 50})
# +
# OK, back to the 3rd dataframe before we averaged them all together by month when we simply had grouped by month and dataid
# and taken a sum of the rows with negative grid
# let's drop the usage and solar columns now that we'll only be working with the grid column
df3 = df3.drop(columns=['solar','usage'])
df3.describe()
# -
# average that entire negative grid column
ave_neg = df3.mean()
ave_neg.grid
# convert summed up usage to give us kWh by dividing by 60 (one minute data / 60 because there are 60 minutes per hour)
kWh = ave_neg.grid / 60
kWh
# divide by 1.5 to calculate the kW discharged over the 1.5 hours of the time between 4PM and 5:30PM to cover the potential 4CP event.
kW = kWh / 1.5
kW
# At a rate of $550 / kW how much on average is saved per house if we store up all the solar produced starting at
# 7AM until 4PM and then discharge to cover the potential 4CP event that day from 4PM - 5:30 PM
value = abs(kW) * cost_kWh
print("Average $ saved per house if they charged their battery day of a 4CP event, then started discharging at 4PM would be ${}".format(str(round(value, 2))))
|
PV/Data-Extraction--PV-storage-savings-4CP.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <div align='left' style="width:400px;height:120px;overflow:hidden;">
# <img align='left' style='display: block;height: 92%' src='imgs/riotext.png' alt='RIO logo' title='RIO logo'/>
# </div>
# + [markdown] slideshow={"align_type": "Left", "slide_type": "-"}
# ## Machine Learning
#
# # 4. Artificial Neural Networks
#
# ### by [<NAME>](http://www.nayatsanchezpi.com) and [<NAME>](http://lmarti.com)
#
# $\renewcommand{\vec}[1]{\boldsymbol{#1}}$
# + [markdown] slideshow={"slide_type": "skip"}
# ### About the notebook/slides
#
# * The slides are _programmed_ as a [Jupyter](http://jupyter.org)/[IPython](https://ipython.org/) notebook.
# * **Feel free to try them and experiment on your own by launching the notebooks.**
#
# * You can run the notebook online: [](https://mybinder.org/v2/gh/rio-group/machine-learning-course/master)
# + [markdown] slideshow={"slide_type": "skip"}
# If you are using [nbviewer](http://nbviewer.jupyter.org) you can change to slides mode by clicking on the icon:
#
# <div class="container-fluid">
# <div class="row">
# <div class="col-md-3"><span/></div>
# <div class="col-md-6">
# <img src='imgs/view-as-slides.png'/>
# </div>
# <div class="col-md-3" align='center'><span/></div>
# </div>
# </div>
# + slideshow={"slide_type": "skip"}
import random, itertools
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from mpl_toolkits.mplot3d import Axes3D
# + slideshow={"slide_type": "skip"}
plt.rc('font', family='serif')
import seaborn
seaborn.set(style='whitegrid'); seaborn.set_context('talk')
# %matplotlib inline
# %config InlineBackend.figure_format = 'retina'
# + slideshow={"slide_type": "skip"}
random.seed(a=42)
# + slideshow={"slide_type": "skip"}
from ipywidgets import interact, interactive, fixed
import ipywidgets as widgets
# + slideshow={"slide_type": "skip"}
# tikzmagic extesion for figures
# !pip install git+git://github.com/mkrphys/ipython-tikzmagic.git
# %load_ext tikzmagic
# + [markdown] slideshow={"slide_type": "slide"}
# # Why to study bio-inspired methods
#
# * Nature is one of the best problem-solvers we know.
# * Evolutionary optimization.
# * Natural intelligence and artificial intelligence
# * Cellular automata
# * **Neural computation**
# * Evolutionary computation
# * Swarm intelligence
# * Artificial immune systems
# * Membrane computing
# * Amorphous computing
# + [markdown] slideshow={"slide_type": "slide"}
# ## Pigeons as art connoisseurs (Watanabe et al., 1995)
# * Pigeons were put in a Skinner box, and
# * presented with photos of paintings by Monet and Picasso.
# * They were rewarded if they recognized correctly the painter they were presented with.
# <hr/>
# <div class="container-fluid">
# <div class="row">
# <div class="col-md-4" align='center'>
# [Skinner box](https://en.wikipedia.org/wiki/Operant_conditioning_chamber)
# <img class='img-thumbnail' width='96%' src='imgs/05/pigeon.png'/>
# </div>
# <div class="col-md-4" align='center'>
# [Claude Monet](https://en.wikipedia.org/wiki/Claude_Monet)
# <img class='img-thumbnail' src='imgs/05/monet.jpg'/>
# </div>
# <div class="col-md-4" align='center'>
# [<NAME>](https://en.wikipedia.org/wiki/Pablo_Picasso)
# <img class='img-thumbnail' width='83%' src='imgs/05/picasso.jpg'/>
# </div>
# </div>
# </div>
# + [markdown] slideshow={"slide_type": "skip"}
# <small><NAME>., <NAME>., & <NAME>. (1995). Pigeons’ discrimination of paintings by Monet and Picasso. Journal of the Experimental Analysis of Behavior, 63(2), 165–174. http://doi.org/10.1901/jeab.1995.63-165</small>
# + [markdown] slideshow={"slide_type": "slide"}
# ## Results
#
# * Pigeons were capable of discriminate between painters with an accuracy of **95%** when confronted with paintings on the **training set**.
# * Surprinsingly, they scored a **85%** on paintings they had never seen during training (**validation set**).
# * They were not just learning exhaustively which painting belonged to each painter.
# * They were able to recognize **styles** or **patterns** and
# * to **generalize** from what they had seen before.
#
# > In AI, we have been trying to replicate this capacity (and many others) in a computer for about 60 years.
# + [markdown] slideshow={"slide_type": "slide"}
# # Artificial neural networks
#
# * Inspired (at different degrees) on the brain and the nervous system.
# * Massive parallelization of relatively simple processing units.
# * Simple principles lead to complex behaviours.
# * Capable of learn form data.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Creating [artificial neurons](https://en.wikipedia.org/wiki/Artificial_neuron)
#
# Artificial neurons are designed to mimic aspects of their biological counterparts.
# <hr/>
# <div class="container-fluid">
# <div class="row">
# <div class="col-md-4" align='center'>
# <img class='img-thumbnail' src='imgs/05/Complete_neuron_cell_diagram_en.svg'/>
# </div>
# <div class="col-md-8">
# <ul>
# <li>**Dendrites** – act as the input receptor, allowing the cell to receive signals from a large (>1000) number of neighboring neurons. Each dendrite is able to perform a "multiplication" by that dendrite's "weight value."
#
# <li>**Soma** – acts as a summation function. As positive and negative signals (exciting and inhibiting, respectively) arrive in the soma from the dendrites they are added together.
#
# <li>**Axon** – gets its signal from the summation behavior which occurs inside the soma. The opening to the axon samples the electrical potential inside the soma. Once the soma reaches a certain potential, the axon will transmit an all-in signal pulse down its length.
# <li>In this regard, the axon behaves as the ability for us to connect our artificial neuron to other artificial neurons.
# </ul>
# </div>
# </div>
# </div>
#
#
# + [markdown] slideshow={"slide_type": "skip"}
# #### Note:
#
# * Unlike most artificial neurons, biological neurons fire in discrete pulses.
# * Each time the electrical potential inside the soma reaches a certain threshold, a pulse is transmitted down the axon.
# * This pulsing can be translated into continuous values. The rate (activations per second, etc.) at which an axon fires converts directly into the rate at which neighboring cells get signal ions introduced into them.
# * The faster a biological neuron fires, the faster nearby neurons accumulate electrical potential (or lose electrical potential, depending on the "weighting" of the dendrite that connects to the neuron that fired).
# * It is this conversion that allows computer scientists and mathematicians to simulate biological neural networks using artificial neurons which can output distinct values (often from −1 to 1).
# + [markdown] slideshow={"slide_type": "slide"}
# The first artificial neuron was the **Threshold Logic Unit (TLU)**, proposed by McCulloch and Pitts (1943).
# * The model was specifically targeted as a computational model of the "nerve net" in the brain.
# * As a transfer function, it employed a threshold, equivalent to using the Heaviside step function.
# * A simple model was considered, with binary inputs and outputs, and
# * restrictions on the possible weights, and a more flexible threshold value.
#
# * Any Boolean function could be implemented by networks of such devices, what is easily seen from the fact that one can implement the `AND` and `OR` functions, and use them in the disjunctive or the conjunctive normal form.
# * Cyclic TLU networks, with feedbacks through neurons, could define dynamical systems with memory, but
# * most research concentrated (and still does) on strictly feed-forward networks because of the smaller difficulty they pose.
# + [markdown] slideshow={"slide_type": "skip"}
# <small><NAME>. and <NAME>. (1943). A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics, 5:115–133. http://link.springer.com/article/10.1007%2FBF02478259</small>
# + [markdown] slideshow={"slide_type": "slide"}
# ## Artificial neuron as a neuron abstraction
# -
# %tikz -s 700,400 -sc 1.0 -l shapes,calc,shapes,arrows -f png \input{imgs/05/neuron.tikz}
# + [markdown] slideshow={"slide_type": "fragment"}
# In general terms, an input $\vec{x}\in\mathbb{R}^n$ is multiplied by a weight vector $\vec{w}$ and added a bias $b$ producing the net activation, $\text{net}$. $\text{net}$ is passed to the *activation function* $f()$ that computed the neuron's output $\hat{y}$.
# $$
# \hat{y} = f\left(\text{net}\right)= f\left(\vec{w}\cdot\vec{x}+b\right) = f\left(\sum_{i=1}^{n}{w_i x_i + b}\right).
# $$
# + [markdown] slideshow={"slide_type": "skip"}
# **Note:** This is a rather simplistic approximation of natural neurons. See [Spiking Neural Networks](https://en.wikipedia.org/wiki/Spiking_neural_network) for a more biologically plausible representation.
# + [markdown] slideshow={"slide_type": "slide"}
# # The Perceptron
#
# The [Perceptron](https://en.wikipedia.org/wiki/Perceptron) and its learning algorithm pioneered the research in neurocomputing.
#
# * The perceptron is an algorithm for learning a linear binary classifier.
# * That is a function that maps its input $\vec{x}\in\mathbb{R}^n$ (a real-valued vector) to an output value $f(\vec{x})$ (a single binary value) as,
#
# $$
# f(\vec{x}) = \begin{cases}
# 1 & \text{if }\vec{w} \cdot \vec{x} + b > 0\,,\\
# 0 & \text{otherwise};
# \end{cases}
# $$
#
# where $\vec{w}$ is a vector of real-valued *weights*, $\vec{w} \cdot \vec{x}$ is the *dot product* $\sum_{i=1}^n w_i x_i$, and $b$ is known as the *bias*.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Perceptron learning
#
# Learning goes by calculating the prediction of the perceptron, $\hat{y}$, as
#
# $$\hat{y} = f\left(\vec{w}\cdot\vec{x} + b) = f( w_{1}x_{1} + w_2x_{2} + \cdots + w_nx_{n}+b\right)\,.$$
#
# After that, we update the weights and the bias using the perceptron rule:
#
# $$
# \begin{align*}
# w_i & = w_i + \alpha (y - \hat{y}) x_{i} \,,\ i=1,\ldots,n\,;\\
# b & = b + \alpha (y - \hat{y})\,.
# \end{align*}
# $$
#
# Here $\alpha\in\left(0,1\right]$ is known as the *learning rate*.
# + [markdown] slideshow={"slide_type": "slide"}
# ## <NAME>: The Perceptron implementation
#
# <hr/>
# <div class="container-fluid">
# <div class="col-md-1"> </div>
# <div class="row">
# <div class="col-md-4">
# <img src='imgs/04/mark1.png'/>
# </div>
# <div class="col-md-6">
# <ul><li>An array of cadmium sulfide photocells was used for capturing 20x20 (400) pixel images that were used as inputs.
# <li>A switchboard was used for manually selecting which input elements (pixels) were passed to the perceptrons.
# <li>They used potentiometers as variable weights.
# <li>Electric motors automatically modified the weights.</ul>
# </div>
# <div class="col-md-1"> </div>
# </div>
# </div>
# + [markdown] slideshow={"slide_type": "slide"}
# # Implementing the Perceptron
#
# We are going to start implementing a perceptron as a class.
# -
class Perceptron:
'A simple Perceptron implementation.'
def __init__(self, weights, bias, alpha=0.1):
self.weights = weights
self.bias = bias
self.alpha = alpha
def propagate(self, x):
return self.activation(self.net(x))
def activation(self, net):
if net > 0:
return 1
return 0
def net(self, x):
return np.dot(self.weights, x) + self.bias
def learn(self, x, y):
y_hat = self.propagate(x)
self.weights = [ w_i + self.alpha*x_i*(y-y_hat) for (w_i, x_i) in zip(self.weights, x)]
self.bias = self.bias + self.alpha*(y-y_hat)
return np.abs(y_hat - y)
# + [markdown] slideshow={"slide_type": "skip"}
# **Note**: Bear in mind that I have made the implementation as clear and easy to follow as possible and, therefore, I have sacrificed performance in the sake of clarity. There are many points where it can be improved.
# + [markdown] slideshow={"slide_type": "slide"}
# ### Testing our `Perceptron` class.
#
# After having the perceptron implementation ready we need an example data set.
#
# We are going to create a dataset containing random points in $\left[0,1\right]^2$.
# -
size = 50 # size of data set
data = pd.DataFrame(columns=('$x_1$', '$x_2$'),
data=np.random.uniform(size=(size,2)))
# + [markdown] slideshow={"slide_type": "slide"}
# So far, our data set looks like this (we are showning only the first ten elements):
# -
data.head(10)
# + [markdown] slideshow={"slide_type": "slide"}
# We need to add a *target* or *classification* attribute. In this example, we are going to make this target to be equal to one if the point lies in the upper-right triangle of the $\left[0,1\right]\times\left[0,1\right]$ square and zero otherwise:
#
# <div class="container-fluid">
# <div class="row">
# <div class="col-md-4"> </div>
# <div class="col-md-4">
# <img src='imgs/04/dataset.jpeg' alt='description of the data set' title='description of the data set'/>
# </div>
# <div class="col-md-4"> </div>
# </div>
# </div>
# + [markdown] slideshow={"slide_type": "slide"}
# We can formalize this condition as:
#
# $$
# y = \begin{cases}
# 1 & \ \text{if}\ x_1 + x_2 > 1\,,\\
# 0 & \ \text{otherwise}\,.
# \end{cases}
# $$
# + [markdown] slideshow={"slide_type": "fragment"}
# Lets code it...
# -
def condition(x):
return int(np.sum(x) > 1)
# + [markdown] slideshow={"slide_type": "fragment"}
# ...and apply it to the data set.
# -
data['y'] = data.apply(condition, axis=1)
# + [markdown] slideshow={"slide_type": "subslide"}
# The resulting data set looks like this:
# -
data.head(10)
# + [markdown] slideshow={"slide_type": "slide"}
# We can now take a better look at the data set in graphical form. Elements with $y=1$ are shown in green ($\color{green}{\bullet}$) and those with $y=0$ are shown in red ($\color{red}{\bullet}$):
# -
def plot_data(data, ax):
data[data.y==1].plot(kind='scatter',
x='$x_1$', y='$x_2$',
color='green', ax=ax)
data[data.y==0].plot(kind='scatter',
x='$x_1$', y='$x_2$',
color='red', ax=ax)
ax.set_xlim(-0.1,1.1); ax.set_ylim(-0.1,1.1)
# + slideshow={"slide_type": "slide"}
fig = plt.figure(figsize=(5,5))
plot_data(data, fig.gca())
# + [markdown] slideshow={"slide_type": "slide"}
# ## Iterating the data set
#
# Having the data set we can now code how the perceptron learns it by iterating throu it.
# -
def learn_data(perceptron, data):
'Returns the number of errors made.'
count = 0
for i, row in data.iterrows():
count += perceptron.learn(row[0:2], row[2])
return count
# + [markdown] slideshow={"slide_type": "slide"}
# ## Visualizing learning
#
# We need now to plot the decision boundary or threshold of the perceptron.
#
# To calculate it we start with the equation that describes the boundary,
# $$w_1x_1+w_2x_2 + b =0.$$
#
# From it we can obtain $x_2$ from a given $x_1$ applying a fairy simple math,
# $$x_2 = \frac{-w_1x_1-b}{w_2}.$$
# -
def threshold(perceptron, x_1):
return (-perceptron.weights[0] * x_1 - perceptron.bias) / perceptron.weights[1]
# + slideshow={"slide_type": "skip"}
def plot_perceptron_threshold(perceptron, ax):
xlim = ax.get_xlim(); ylim = ax.get_ylim()
x2s = [threshold(perceptron, x1) for x1 in xlim]
ax.plot(xlim, x2s)
ax.set_xlim(-0.1,1.1); ax.set_ylim(-0.1,1.1)
# + [markdown] slideshow={"slide_type": "skip"}
# A function that plots a perceptron as the threshold and the data set.
# + slideshow={"slide_type": "skip"}
def plot_all(perceptron, data, t, ax=None):
if ax==None:
fig = plt.figure(figsize=(5,4))
ax = fig.gca()
plot_data(data, ax)
plot_perceptron_threshold(perceptron, ax)
ax.set_title('$t='+str(t+1)+'$')
# + [markdown] slideshow={"slide_type": "slide"}
# ## Our perceptron in action
#
# All set now! Let's create a perceptron and train it.
#
# **Note**: Normally the initial weights and the bias should be set to *small* random values. I am setting them by hand to a value that I know that looks good in the examples.
# + slideshow={"slide_type": "fragment"}
perceptron = Perceptron([0.1,-0.1], 0.02)
# + slideshow={"slide_type": "slide"}
f, axarr = plt.subplots(3, 4, sharex=True, sharey=True, figsize=(9,7))
axs = list(itertools.chain.from_iterable(axarr))
for t in range(12):
plot_all(perceptron, data, t, ax=axs[t])
learn_data(perceptron, data)
f.tight_layout()
# -
# It is clear how the Perceptron threshold is progresively adjusted according to the data set.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Animating the Perceptron
#
# This results are better understood in animated from.
# + slideshow={"slide_type": "skip"}
from matplotlib import animation
from IPython.display import HTML
# + slideshow={"slide_type": "skip"}
def animate(frame_index, perceptron, data, ax):
ax.clear()
plot_data(data, ax=ax)
ax.set_title('$t='+str(frame_index)+'$')
if not frame_index:
return None
plot_perceptron_threshold(perceptron, ax=ax)
learn_data(perceptron, data)
return None
# -
fig = plt.figure(figsize=(4,4))
ax = fig.gca()
perceptron = Perceptron([0.1,-0.1], 0.02)
anim = animation.FuncAnimation(fig, lambda i: animate(i, perceptron, data, ax), frames=30, interval=600,
blit=False)
plt.tight_layout()
plt.close()
HTML(anim.to_html5_video())
# + [markdown] slideshow={"slide_type": "slide"}
# ## Self-study
#
# * Experiment with the learning rate ($\alpha$). How it impacts learning? Do you remember if we have seen another similar parameter in previous classes?
# * Create a new data set with a non-linear boundary. What happens now with our perceptron? How would you fix it?
# + [markdown] slideshow={"slide_type": "slide"}
# ## Suggested reading
#
# * <NAME>. and <NAME>. (1969). *Perceptrons*. Cambridge, MA: MIT Press.
# * <NAME>. (1990). *Perceptron-based learning algorithms*. IEEE Transactions on Neural Networks, vol. 1, no. 2, pp. 179–191.
# * <NAME> (1996). *A Sociological Study of the Official History of the Perceptrons Controversy*. Social Studies of Science 26 (3): 611–659. doi:10.1177/030631296026003005.
# + [markdown] slideshow={"slide_type": "slide"}
# ## The XOR issue
#
# Take a dataset that contains all the possible value combination of the logical XOR function:
# -
X = np.array([[0, 1], [1, 0], [0, 0], [1, 1]])
Y = np.array([1, 1, 0, 0])
N = Y.shape[0]
# The data set has ones (represented in black) when $x_1 = 1$ and $x_2 = 0$ or when $x_1 = 0$ and $x_2 = 1$, as defined for the XOR function.
# + slideshow={"slide_type": "slide"}
plt.scatter(X[:, 0], X[:, 1], c=Y, edgecolor='k', cmap=cm.gray_r, s=100)
plt.xlabel('$x_1$');plt.ylabel('$x_2$');
# -
# It is evident that a perceptron is unable to solve this simple problem as it is only able to separate the space by a hyperplane.
# + [markdown] slideshow={"slide_type": "slide"}
# To solve the XOR problem we need to stack perceptrons
# -
# %tikz -s 500,250 -sc 1.0 -l positioning -f svg \input{imgs/05/xor-nn.tikz}
# + [markdown] slideshow={"slide_type": "slide"}
# But, how can we train the weights from neurons 1 and 2?
# * This is known as a credit assignment problem.
# * Our current method for Perceptron learning determine how the weights of neurons 1 and 2 influence the error.
# * Let's visualize it.
# + [markdown] slideshow={"slide_type": "slide"}
# ### A "handcoded" XOR neural network
#
# Forward propagation for 2 inputs $(x_1, x_2)$, 2 hidden nodes, 1 output.
# * We will be extending the Perceptron activation as the logistic (*logit*) function
# $$\hat{y} = f(\text{net}) = \frac{1}{1+\exp{\left(-\text{net}\right)}}.$$
# -
def logit(a):
return 1.0 / (1+np.exp(-a))
# + slideshow={"slide_type": "slide"}
def fprop(x1, x2,
w1= 0.1, w2= 0.2, b1= 0.1,
w3=-0.2, w4= 0.2, b2=-0.1,
w5=-0.3, w6=-0.25, b3=0.2):
y_hat_1 = logit(b2 + w3*x1 + w4*x2) # N1
y_hat_2 = logit(b3 + w5*x1 + w6*x2) # N2
return logit(b1 + w1*y_hat_1 + w2*y_hat_2)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Error Surface of the XOR Problem
# -
@interact(i=(1,6), j=(1,6))
def error_plot(i=5, j=6):
W1, W2 = np.meshgrid(np.arange(-10, 10, 0.5), np.arange(-10, 10, 0.5))
E = np.sum([(fprop(X[n, 0], X[n, 1],
**{"w%d"%(i) : W1, "w%d"%(j) : W2})-Y[n])**2
for n in range(N)], axis=0)
ax = plt.figure(figsize=(7, 4.5)).add_subplot(111, projection="3d")
surf = ax.plot_surface(W1, W2, E, rstride=1, cstride=1, cmap=cm.viridis, lw=0.11, alpha=0.74)
plt.setp(ax, xlabel="$w_%d$" % (i), ylabel="$w_%d$" % (j), zlabel="$E()$");
plt.tight_layout()
plt.show()
# + [markdown] slideshow={"slide_type": "slide"}
# ## Local Minima
# -
@interact(i=(0,5), j=(0,5))
def errors_plot(i=0, j=1):
plt.figure(figsize=(12, 3))
W = np.arange(-10, 10, 0.25)
errors = [(fprop(X[n, 0], X[n, 1], **{"w%d"%(i+1) : W, "w%d"%(j+1) : W+2})-Y[n])**2 for n in range(N)]
plt.subplot(1, 2, 1)
for n in range(N):
plt.plot(W, errors[n], label="$E^{(%d)}$" % (n+1))
plt.setp(plt.gca(), xlabel="$w$", ylabel="$E$", title='Split errors');plt.legend(loc="best", frameon=True)
plt.subplot(1, 2, 2)
plt.plot(W, np.sum(errors, axis=0), label="$E(\cdot)$")
plt.setp(plt.gca(), xlabel="$w$", ylabel="$E$", title='Total error');plt.legend(loc="best", frameon=True);
plt.show()
# + [markdown] slideshow={"slide_type": "slide"}
# # The Multilayer Perceptron (MLP)
# -
# The composition of layers of perceptrons can capture complex relations between inputs and outputs in a hierarchical way.
# %tikz -s 600,400 -sc 1.0 -l positioning -f png \input{imgs/05/neural-network.tikz}
# ...but how can we adapt the weights of the neurons in the hidden layers?
# + [markdown] slideshow={"slide_type": "slide"}
# ## Improving the notation
# -
# In order to proceed we need to improve the notation we have been using. That for, for each layer $1\geq l\geq L$, the activations and outputs are calculated as:
#
# $$\text{net}^l_j = \sum_i w^l_{ji} x^l_i\,,$$
# $$y^l_j = f^l(\text{net}^l_j)\,,$$
#
# where:
#
# * $y^l_j$ is the $j$th output of layer $l$,
# * $x^l_i$ is the $i$th input to layer $l$,
# * $w^l_{ji}$ is the weight of the $j$-th neuron connected to input $i$,
# * $\text{net}^l_{j}$ is called net activation, and
# * $f^l(\cdot)$ is the activation function of layer $l$, e.g. $\tanh()$, in the hidden layers and the identity in the last layer (for regression)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Error function (SSE)
#
# * For $\Psi=\left\{\left<\vec{x}^{(1)},\vec{y}^{(1)}\right>,\ldots,\left<\vec{x}^{(k)},\vec{y}^{(k)}\right>,\ldots\left<\vec{x}^{(K)},\vec{y}^{(K)}\right>\right\}$:
#
# $$
# E =
# \frac{1}{2} \sum_{k=1}^{K}{\ell(\hat{\vec{y}}_j^{L}(\vec{x}^{(k)}), \vec{y}^{(k)})} =
# \frac{1}{2} \sum_{k=1}^{K} \sum_{j=1}^{m} \left( \hat{y}_j^{L}(\vec{x}^{(k)}) - y_j^{(k)} \right)^2\,.
# $$
# + [markdown] slideshow={"slide_type": "slide"}
# ## Training MLPs with Backpropagation
#
# * Backpropagation of errors is a procedure to compute the **gradient of the error function with respect to the weights** of a neural network.
# * We can use the gradient from backpropagation to apply **gradient descent**!
# + [markdown] slideshow={"slide_type": "slide"}
# #### A math flashback
#
# The **chain rule** can be applied in composite functions as,
# $$
# \left( f \circ g\right)'(x) = \left(f\left(g\left(x\right)\right)\right)'= f'\left(g(x)\right)g'(x).
# $$
# or, in Leibniz notation,
# $$
# \frac{\partial f\left(g\left(x\right)\right)}{\partial x} =
# \frac{\partial f\left(g\left(x\right)\right)}{\partial g\left(x\right)} \cdot
# \frac{\partial g\left(x\right)}{\partial x}
# $$
#
# The **total derivative** of $f(x_1,x_2,...x_n)$ on $x_i$ is
# $$
# \frac{\partial f}{\partial x_i}=
# \sum_{j=1}^n{\frac{\partial f}{\partial x_j}\cdot\frac{\partial x_j}{\partial x_i}}
# $$
# + [markdown] slideshow={"slide_type": "slide"}
# #### To apply gradient descent we need... to calculate the gradients
#
# Applying the chain rule,
# $$
# \frac{\partial \ell}{\partial w^l_{ji}}=
# \color{blue}{\overbrace{\frac{\partial \ell}{\partial \text{net}^l_j}}^{\delta^l_j}}
# \color{forestgreen}{\underbrace{\frac{\partial{\text{net}^l_j}}{\partial w^l_{ji}}}_{\frac{\partial\left(\sum_{i}w^l_{ji}x^l_i\right)}{\partial w^l_{ji}}=x^l_i}}
# $$
# hence we can write
# $$
# \frac{\partial \ell}{\partial w^l_{ji}}=
# \color{blue}{\delta^l_j}
# \color{forestgreen}{x^l_i}
# $$
# + [markdown] slideshow={"slide_type": "slide"}
# #### For the output layer ($l=L$)
# $$
# \delta^L_j = \frac{\partial \ell}{\partial \text{net}^L_j} =
# \color{red}{
# \overbrace{
# \frac{\partial \ell}{\partial\hat{y}^L_j}}^{\frac{\partial\left(\frac{1}{2}\sum_j{\left(y_j-\hat{y}^L_j\right)^2} \right)}
# {\partial\hat{y}^L_j}=\left(y_j-\hat{y}^L_j\right)}}
# \cdot
# \color{magenta}{
# \underbrace{\frac{\partial\hat{y}^L_j}{\text{net}^l_j}}_{f'(\text{net}_j^L)}}
# =\color{red}{\left(y_j-\hat{y}^L_j\right)}\color{magenta}{f'(\text{net}_j^L)}.
# $$
# therefore
# $$
# \frac{\partial \ell}{\partial w^L_{ji}}=
# \color{red}{\left(y_j-\hat{y}^L_j\right)}\color{magenta}{f'(\text{net}_j^L)}
# \color{forestgreen}{x^L_i}
# $$
# + [markdown] slideshow={"slide_type": "slide"}
# #### What about the hidden layers ($1\leq l<L$)?
#
# We can express the loss $\ell$ as a function of the activations of the subsequent layer,
#
# $$
# \ell = \ell\left(\text{net}^{l+1}_1,\ldots,\text{net}^{l+1}_K\right)\,,
# $$
#
# therefore, applying total derivatives,
#
# $$
# \frac{\partial \ell}{\partial\hat{y}^l_j} =
# \frac{\partial \ell\left(\text{net}^{l+1}_1,\ldots,\text{net}^{l+1}_K\right)}{\partial\hat{y}^l_j}\,.
# $$
# + [markdown] slideshow={"slide_type": "slide"}
# #### Applying total derivatives we get
#
# $$
# \frac{\partial \ell}{\partial\hat{y}^l_j} =
# \sum_{k}{
# \color{orange}{
# \overbrace{
# \frac{\partial \ell}{\partial\text{net}^{l+1}_k}}^{\delta^{l+1}_k}}
# \color{purple}{
# \underbrace{\frac{\partial \text{net}^{l+1}_{k}}{\partial\hat{y}^l_j}
# }_{\frac{\partial{\sum_{j}{w^{l+1}_{kj}\hat{y}^l_j}}}{\partial\hat{y}^l_j}=w^{l+1}_{kj}}}
# } =
# \sum_{k}{\color{orange}{\delta^{l+1}_k}\color{purple}{w^{l+1}_{kj}}}
# $$
# + [markdown] slideshow={"slide_type": "slide"}
# #### Back-propagating the errors to the hidden layer
#
# The $\delta$s of the subsequent layers are used to calculate the $\delta$s of the more internal ones.
#
# $$
# \delta^{l}_j =
# \frac{\partial\ell}{\partial\text{net}^l_j} =
# \overbrace{\frac{\partial\ell}{\partial\hat{y}^l_j}}^
# {\sum_{k}{
# \color{orange}{\delta^{l+1}_k}
# \color{purple}{w^{l+1}_{kj}}}}
# \color{forestgreen}{\underbrace{\frac{\partial\hat{y}^l_j}{\partial\text{net}^l_j}}_
# {f'(\text{net}^l_j)}}=
# \sum_{k}{\left(
# \color{orange}{\delta^{l+1}_k}
# \color{purple}{w^{l+1}_{kj}}
# \right)}\color{forestgreen}{f'(\text{net}^l_j)}
# $$
# + [markdown] slideshow={"align_type": "Left", "slide_type": "slide"}
# ## Backpropagation in brief
# + [markdown] slideshow={"align_type": "Left", "slide_type": "slide"}
# In each layer (we will omit the sample index $k$ and layer $l$)
#
# $$
# \delta_j =
# \begin{cases}
# \hat{y}_j - y_j & \text{in the output layer,}\\
# \\ f'(\text{net}_j) \sum_k \frac{\partial \ell}{\partial \hat{y}_k} & \text{otherwise.}
# \end{cases}
# $$
#
# $$\frac{\partial \ell}{\partial w_{ji}} = \delta_j x_i\,;\quad \frac{\partial \ell}{\partial x_i} = \delta_j w_{ji}\,.$$
#
# where
#
# * all nodes $k$ are in the layer after $j$;
# * $\text{net}_j$ is known from propagation: $\sum_i w_{ji} x_i$;
# * actually you do not have to save $a_j$ because $g'(a_j)$ usually can be computed from $y_j$, e.g.
# * identity function: $f'(\text{net}_j) = 1$,
# * $\tanh$: $f'(\text{net}_j) = 1 - y_j^2$;
# * $\frac{\partial \ell}{\partial w_{ji}}$ will be used to update the weight $w_{ji}$ in gradient descent;
# * $\frac{\partial \ell}{\partial x_i}$ will be passed to the previous layer to compute the deltas;
#
# **Do not forget to sum up the gradient with respect to the weights for each training example!**
# + [markdown] slideshow={"align_type": "Left", "slide_type": "slide"}
# ## Efficient Implementation for Fully Connected Layers
# + [markdown] slideshow={"align_type": "Left", "slide_type": "fragment"}
# * Make sure that you have an efficient **linear algebra library**.
# * Organize your data in matrices, i.e.
# * The matrix $\boldsymbol{X}$ contains an input vector in each row. Note that you must expand each row by the bias 1.
# * The matrix $\boldsymbol{T}$ contains an output (of the network) in each row.
# * Each layer should have the functions
# * `fprop(W, X, f) -> Y`
# * `backprop(W, X, f_derivative, Y, d_loss/dY) -> d_loss/dX, d_lossdW`
# + [markdown] slideshow={"slide_type": "slide"}
# <div class="container-fluid">
# <div class="row">
# <div class="col-md-3" align='center'>
# </div>
# <div class="col-md-6">
# <div class='well well-sm'>
# <img src='imgs/05/backprop.svg'/>
# </div>
# </div>
# <div class="col-md-3" align='center'>
# </div>
# </div>
# </div>
# + [markdown] slideshow={"align_type": "Left", "slide_type": "slide"}
# ## Efficient forward propagation
# + [markdown] slideshow={"align_type": "Left", "slide_type": "-"}
# In each layer
#
# $$\boldsymbol{NET} = \boldsymbol{X} \boldsymbol{W}^\intercal$$
# $$\boldsymbol{\hat{Y}} = f(\boldsymbol{NET})$$
#
# where
#
# * $\boldsymbol{Y} \in \mathbb{R}^{N \times J}$ contains an output vector in each row, i.e. $\boldsymbol{Y}_{kj} = y^{(k)}_j$
# * $\boldsymbol{X} \in \mathbb{R}^{N \times I}$ contains an input vector (the output of the previous layer) in each row, i.e. $\boldsymbol{X}_{ki} = x^{(k)}_i$
# * $\boldsymbol{W} \in \mathbb{R}^{J \times I}$ is the weight matrix of the layer, i.e. $\boldsymbol{W}_{ji}$ is the weight between input $i$ and output $j$.
# * $f$ is the activation function (implemented to work with matrices)
# * $I$ is the number of inputs, i.e. the number of outputs of the previous layer plus 1 (for the bias)
# * $J$ is the number of outputs
#
# **Make sure that you add the bias entry in each row before you pass $Y$ as input to the next layer!**
# + [markdown] slideshow={"slide_type": "slide"}
# Error function (SSE)
#
# $$E = \frac{1}{2} ||\boldsymbol{Y} - \boldsymbol{T}||_2^2$$
#
# where
#
# * $||\cdot||_2$ is the [Frobenius norm](http://en.wikipedia.org/wiki/Matrix_norm#Frobenius_norm).
# + [markdown] slideshow={"align_type": "Left", "slide_type": "slide"}
# # Efficient Backpropagation
# + [markdown] slideshow={"align_type": "Left", "slide_type": "-"}
# In each layer:
#
# $$\Delta = f'(\boldsymbol{NET}) \ast \frac{\partial \ell}{\partial \boldsymbol{Y}}\,,$$
# $$\frac{\partial \ell}{\partial \boldsymbol{W}} = \Delta^T \cdot \boldsymbol{X}\,,$$
# $$\frac{\partial \ell}{\partial \boldsymbol{X}} = \Delta \cdot \boldsymbol{W}\,.$$
#
# where:
#
# * $*$ is the [Hadamard product](http://en.wikipedia.org/wiki/Hadamard_product_%28matrices%29) or Schur product or entrywise product
# * $\frac{\partial \ell}{\partial \boldsymbol{Y}}$ contains derivatives of the error function with respect to the outputs ($\boldsymbol{Y} - \boldsymbol{T} = \frac{\partial \ell}{\partial \boldsymbol{Y}}$ in the last layer)
# * $\frac{\partial \ell}{\partial \boldsymbol{X}} \in \mathbb{R}^{N \times I}$ contains derivatives of the error function with respect to the inputs and will be passed to the previous layer
# * $\Delta \in \mathbb{R}^{N \times J}$ contains deltas: $\delta_j^{(n)} = \Delta_{jn}$
# * $g'$ is the derivative of $g$ and can be computed based only on $\boldsymbol{Y}$
# * $\frac{\partial \ell}{\partial \boldsymbol{W}} \in \mathbb{R}^{J \times I}$ contains the derivatives of the error function with respect to $\boldsymbol{W}$ and will be used to optimize the weights of the ANN
#
# **Make sure that you remove the bias entry in each row before you pass $\frac{\partial \ell}{\partial \boldsymbol{X}}$ to the previous layer!**
# + [markdown] slideshow={"slide_type": "slide"}
# ## Pseudocode of backpropagation
#
# ```pseudo
# initialize network weights (often small random values)
# do
# foreach training example, x
# prediction = neural-net-output(network, x) // forward pass
# actual = teacher-output(x)
# compute error (prediction - actual) at the output units
# compute deltas for all weights from hidden layer to output layer // backward pass
# compute deltas for all weights from input layer to hidden layer // backward pass continued
# update network weights // input layer not modified by error estimate
# until all examples classified correctly or another stopping criterion satisfied
# return the network
# ```
# + [markdown] slideshow={"align_type": "Left", "slide_type": "slide"}
# ## Tips for Your Implementations
# + [markdown] slideshow={"align_type": "Left", "slide_type": "fragment"}
# * Depending on the problem type you have to select different activation functions for the output layer.
# * Check your gradients with finite differences:
# $$\frac{\partial f}{\partial x} = \frac{f(x + \varepsilon) - f(x - \varepsilon)}{2 \varepsilon} + \mathcal{O}(\varepsilon^2)\,.$$
# + [markdown] slideshow={"align_type": "Left", "slide_type": "slide"}
# ### How to initialize weights $\boldsymbol{w}$?
# + slideshow={"align_type": "Left", "slide_type": "fragment"}
np.random.randn(10) * 0.05
# + [markdown] slideshow={"align_type": "Left", "slide_type": "fragment"}
# * Draw components of $\boldsymbol{w}$ iid (independent and identically distributed) from a Gaussian distribution with **small** standard deviation, e.g. 0.05.
# * Initialization with 0 will prevent the gradient from flowing back to the lower layers as
#
# $$\frac{\partial \ell}{\partial x_i} = \delta_j w_{ji}\,.$$
#
# * It has been shown that initialization of weights is a key to have good results. See:
# - <small><NAME>., & <NAME>. (2010). *Understanding the difficulty of training deep feedforward neural networks*. Proceedings of the 13th International Conference on Artificial Intelligence and Statistics (AISTATS), 9, 249–256. http://doi.org/10.1.1.207.2059</small>
# + slideshow={"slide_type": "subslide"}
def plot_afun(x, y, sp_idx, label=None):
"""Plot activation function."""
ax = plt.subplot(2, 4, sp_idx)
if label is not None:
plt.title(label)
plt.setp(ax, xlim=(np.min(x), np.max(x)), ylim=(np.min(y)-0.5, np.max(y)+0.5))
plt.plot(x, y)
# + slideshow={"align_type": "Left", "slide_type": "slide"}
plt.figure(figsize=(10, 4))
x = np.linspace(-5, 5, 100)
plot_afun(x, x, 1, label="Identity")
plot_afun(x, np.tanh(x), 2, label="tanh")
plot_afun(x, logit(x), 3, label="Logistic (logit)")
plot_afun(x, np.max((x, np.zeros_like(x)), axis=0), 4, label="Rectified \nLinear Unit (ReLU)")
plot_afun(x, np.ones_like(x), 5)
plot_afun(x, 1-np.tanh(x)**2, 6)
plot_afun(x, logit(x)*(1-logit(x)), 7)
plot_afun(x, np.max((np.sign(x), np.zeros_like(x)), axis=0), 8)
# + [markdown] slideshow={"align_type": "Left", "slide_type": "slide"}
# ## Derivatives of Activation Functions
# + [markdown] slideshow={"align_type": "Left", "slide_type": "fragment"}
# * Identity
#
# $$\hat{y} = f(\text{net}) = a;\quad f'(\text{net}) = 1\,.$$
# + [markdown] slideshow={"align_type": "Left", "slide_type": "fragment"}
# * Hyperbolic tangent
#
# $$\hat{y} = f(\text{net}) = \tanh(\text{net});\quad f'(\text{net}) = 1 - \tanh^2(\text{net}) = 1-\hat{y}^2\,.$$
# + [markdown] slideshow={"align_type": "Left", "slide_type": "fragment"}
# * Logistic function
#
# $$y = f(\text{net}) = \frac{1}{1+\exp{\left(-\text{net}\right)}}\,,$$
# $$f'(\text{net}) = f(\text{net}) (1 - f(\text{net})) = \hat{y} (1-\hat{y})\,.$$
# + [markdown] slideshow={"slide_type": "slide"}
# # Summarizing
#
# * We now know how to compute the $\frac{\partial\ell}{\partial w^l_{ji}}$ for all neurons.
# * For the neurons on the hidden layers we use the $\delta$s of the next layer.
# * We know how to updates the weights as:
# $$
# \Delta w^l_{ji}=-\eta\frac{\partial\ell}{w^l_{ji}}=-\eta\delta^l_j x^l_i.
# $$
# + [markdown] slideshow={"slide_type": "slide"}
# ## Difficulties
#
# * There are many **local minima**.
# * The optimization problem is **ill-conditioned**.
# * There are many **flat regions** (saddle points).
# * There is **no guarantee** to reach the global minimum.
# * Deep architectures suffer from the **vanishing gradient** problem.
# * Neural networks are *usually* considered to be the **blackest box** of all learning algorithms.
# * There are sooo many **hyperparameters** (number of layers/nodes, activation function, connectivity, weight initialization, loss function, regularization, ...).
# * Training neural networks has been regarded as **black magic** by many researchers.
# * And here is the grimoire: [Neural Networks: Tricks of the Trade](http://link.springer.com/book/10.1007%2F978-3-642-35289-8) (1st edition: 1998; 2nd edition: 2012).
#
# + [markdown] slideshow={"slide_type": "slide"}
# ## Theoretical features
#
# **Universal approximation theorem**:
#
# > A feed-forward network with **a single hidden** layer containing a finite number of neurons can approximate any continuous functions on compact subsets of $\mathbb{R}^n$, under mild assumptions on the activation function.
#
# Hornik showed in 1991 that it is not the specific choice of the activation function, but rather the multilayer feedforward architecture itself which gives neural networks the potential of being universal approximators.
#
# <small><NAME> (1991) Approximation Capabilities of Multilayer Feedforward Networks, Neural Networks, 4(2), 251–257</small>
# + [markdown] slideshow={"slide_type": "slide"}
# There have been three hypes around ANNs:
#
# * Perceptron (50s-XOR problem)
# * Backpropagation (80s-SVM)
# * Deep Learning (2006-now)
#
# And they work incredibly well in practice.
# + [markdown] slideshow={"slide_type": "slide"}
# ### But... why do neural nets work well in practice?
# * Universal function approximation property.
# * Stochastic gradient descent finds **sufficiently good** local minima.
# * We don't want to find the global minimum $\implies$ ** fights overfitting!**
# * Neural nets learn **feature hierarchies** to represent functions *efficiently*.
# * **features will be learned** automatically
# * allows learning of **hierarchical features** which is much more efficient than just one layer of abstraction
# * **multiclass classification** can be integrated with linear complexity (softmax activation function, cross-entropy error function)
# * it is a **parametric** model, it does not store any training data directly.
# + [markdown] slideshow={"slide_type": "slide"}
# ### Drawbacks
#
# * input has to be a **vector of real numbers**, e.g. text must be converted before classification
# * in general, the **optimization problem** is very difficult because it is **ill-conditioned** and **non-separable**
# * objective function is **not convex**, there are many local minima and flat regions
# * **black box**: in most cases it is very difficult to interpret the weights of a neural network although it is possible!
# * **catastrophic forgetting**: learning one instance can change the whole network
# + [markdown] slideshow={"slide_type": "skip"}
# <hr/>
# <div class="container-fluid">
# <div class="row">
# <div class="col-md-3" align='center'>
# <img align='center' alt="Creative Commons License" style="border-width:0" src="https://i.creativecommons.org/l/by-nc-sa/4.0/88x31.png"/>
# </div>
# <div class="col-md-9">
# This work is licensed under a [Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License](http://creativecommons.org/licenses/by-nc-sa/4.0/).
# </div>
# </div>
# </div>
# + slideshow={"slide_type": "skip"}
# %load_ext version_information
# %version_information scipy, numpy, matplotlib, sklearn
# + slideshow={"slide_type": "skip"}
# this code is here for cosmetic reasons
from IPython.core.display import HTML
from urllib.request import urlopen
HTML(urlopen('https://raw.githubusercontent.com/lmarti/jupyter_custom/master/custom.include').read().decode('utf-8'))
# -
# ---
|
04. Artificial neural networks.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# annwork
# #topic 6 - plots using matplotlib and seaborn
# EDA - Exploratory Data analysis
#
# +
import pandas as pd
import matplotlib.pyplot as plt
# +
## read the iris dataset
data = pd.read_csv("D:/py/iris.csv",header=0)
data
print(data.shape) # 150 rows and 5 columns
# -
## plot the entire dataset
data.plot()
## Line plot
data.plot(x='sepal_length',y='sepal_width') ## in this case, line plot is not of great use
plt.show()
# +
## scatter plot
data.plot(x='sepal_length',y='sepal_width', kind='scatter')
plt.xlabel('Sepal length in cm')
plt.ylabel('Sepal width in cm')
plt.show()
# -
## bar chart
data.plot(x='sepal_length', kind='bar')
plt.xlabel('Sepal length in cm')
plt.ylabel('Sepal width in cm')
plt.show()
## Box Plot
data.plot(kind='box') # for all the variables
data.plot(x='sepal_length',y='sepal_width', kind='box') ## for specific variables
plt.ylabel('Sepal width in cm')
plt.show()
##Histogram, calculates the frequncy and so y axis is not needed here
data.plot( kind='hist') # histogram for all the variables
data.plot(x='sepal_length',y='sepal_width', kind='hist') # histogram for specific variables
plt.xlabel('Sepal length in cm')
plt.show()
## bins - num of intervals
## range - min and max values
#normed - weather to normalize to one, normed is replaced with density
#cumulative - apply cdf
data.plot(y='sepal_length', kind='hist',bins=30,range=(4,12), density=True)
plt.xlabel('Sepal length in cm')
plt.show()
# +
## CDF
data.plot(y='sepal_length', kind='hist',bins=30,range=(4,12), density=True, cumulative=True)
plt.xlabel('Sepal length in cm')
plt.title("Cumulative distribution function - CDF")
plt.show()
# +
# Univariate Histograms
import matplotlib.pyplot as plt
import pandas
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = pandas.read_csv(url, names=names)
data.hist()
plt.show()
# +
#Density plot
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = pandas.read_csv(url, names=names)
data.plot(kind='density', subplots=True, layout=(3,3), sharex=False)
plt.show()
# +
# box plot
data.plot(kind='box', subplots=True, layout=(3,3), sharex=False, sharey=False)
plt.show()
# +
#Multivariant
# Correction Matrix Plot
import matplotlib.pyplot as plt
import pandas
import numpy
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = pandas.read_csv(url, names=names)
correlations = data.corr()
# plot correlation matrix
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(correlations, vmin=-1, vmax=1)
fig.colorbar(cax)
ticks = numpy.arange(0,9,1)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
ax.set_xticklabels(names)
ax.set_yticklabels(names)
plt.show()
# +
## scatter plot - multi variant
# Scatterplot Matrix
import matplotlib.pyplot as plt
import pandas
from pandas.plotting import scatter_matrix
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = pandas.read_csv(url, names=names)
scatter_matrix(data)
plt.show()
# +
#histogram
import seaborn as sns
print(data.head())
# Distribution Plot (a.k.a. Histogram)
sns.distplot(data.mass)
# +
## Histogram and distribution of data
# +
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
matplotlib.style.use('ggplot')
df = pd.DataFrame(np.random.randint(0,10,(20,4)),columns=list('abcd'))
df.hist(alpha=0.5, figsize=(16, 10))
# -
df.skew()
df.describe()
# Generate some data
np.random.seed(42) # To ensure we get the same data every time.
X = (np.random.randn(100,1) * 5 + 10)**2
print(X[:10])
import os # Library to do things on the filesystem
import pandas as pd # Super cool general purpose data handling library
import matplotlib.pyplot as plt # Standard plotting library
import numpy as np # General purpose math library
from IPython.display import display # A notebook function to display more complex data (like tables)
import scipy.stats as stats # Scipy again
# Print the mean and standard deviation
print("Raw: %0.3f +/- %0.3f" % (np.mean(X), np.std(X)))
## plot a histogram
df = pd.DataFrame(X) # Create a pandas DataFrame out of the numpy array
df.plot.hist(alpha=0.5, bins=15, grid=True, legend=None)
# Pandas helper function to plot a hist. Uses matplotlib under the hood.
plt.xlabel("Feature value")
plt.title("Histogram")
plt.show() ## data is right skewed where mean > median
# +
## apply log function to the data
df_exp = df.apply(np.log) # pd.DataFrame.apply accepts a function to apply to each column of the data
df_exp.plot.hist(alpha=0.5, bins=15, grid=True, legend=None)
plt.xlabel("Feature value")
plt.title("Histogram")
plt.show() # still data is left skewed
# -
## apply power
df_pow = df.apply(np.sqrt)
df_pow.plot.hist(alpha=0.5, bins=15, grid=True, legend=None)
plt.xlabel("Feature value")
plt.title("Histogram")
plt.show()
# +
param = stats.norm.fit(df_pow) # Fit a normal distribution to the data
x = np.linspace(0, 20, 100) # Linear spacing of 100 elements between 0 and 20.
pdf_fitted = stats.norm.pdf(x, *param) # Use the fitted paramters to create the y datapoints
# Plot the histogram again
df_pow.plot.hist(alpha=0.5, bins=15, grid=True, normed=True, legend=None)
# Plot some fancy text to show us what the paramters of the distribution are (mean and standard deviation)
plt.text(x=np.min(df_pow), y=0.1, s=r"$\mu=%0.1f$" % param[0] + "\n" + r"$\sigma=%0.1f$" % param[1], color='r')
# Plot a line of the fitted distribution over the top
plt.plot(x, pdf_fitted, color='b')
# Standard plot stuff
plt.xlabel("Feature value")
plt.title("Histogram with fitted normal distribution")
plt.show()
|
Statistics_All/1.Stats_EDA/3.Chart_types.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
text_file = open("../results_msst20/numa_affects/parallel/ar.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
ar_dram_wa = list()
ar_dram_stdev_wa = list()
ar_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ar_dram_wa_tmp.append(val)
ar_dram_wa.append(mean(ar_dram_wa_tmp))
ar_dram_stdev_wa.append(stdev(ar_dram_wa_tmp))
#print("dram wa_tmp:", ar_dram_wa_tmp)
ar_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", ar_dram_wa)
print("dram stdev wa:", ar_dram_stdev_wa)
#dram workload e
ar_dram_we = list()
ar_dram_stdev_we = list()
ar_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ar_dram_we_tmp.append(val)
ar_dram_we.append(mean(ar_dram_we_tmp))
ar_dram_stdev_we.append(stdev(ar_dram_we_tmp))
#print("dram we_tmp:", ar_dram_we_tmp)
ar_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", ar_dram_we)
print("dram stdev we:", ar_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
ar_vmem_wa = list()
ar_vmem_stdev_wa = list()
ar_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ar_vmem_wa_tmp.append(val)
ar_vmem_wa.append(mean(ar_vmem_wa_tmp))
ar_vmem_stdev_wa.append(stdev(ar_vmem_wa_tmp))
#print("vmem wa_tmp:", ar_vmem_wa_tmp)
ar_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", ar_vmem_wa)
print("vmem stdev wa:", ar_vmem_stdev_wa)
#vmem workload e
ar_vmem_we = list()
ar_vmem_stdev_we = list()
ar_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ar_vmem_we_tmp.append(val)
ar_vmem_we.append(mean(ar_vmem_we_tmp))
ar_vmem_stdev_we.append(stdev(ar_vmem_we_tmp))
#print("vmem we_tmp:", ar_vmem_we_tmp)
ar_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", ar_vmem_we)
print("vmem stdev we:", ar_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
ar_pmem_wa = list()
ar_pmem_stdev_wa = list()
ar_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ar_pmem_wa_tmp.append(val)
ar_pmem_wa.append(mean(ar_pmem_wa_tmp))
ar_pmem_stdev_wa.append(stdev(ar_pmem_wa_tmp))
#print("pmem wa_tmp:", ar_pmem_wa_tmp)
ar_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", ar_pmem_wa)
print("pmem stdev wa:", ar_pmem_stdev_wa)
#pmem workload e
ar_pmem_we = list()
ar_pmem_stdev_we = list()
ar_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ar_pmem_we_tmp.append(val)
ar_pmem_we.append(mean(ar_pmem_we_tmp))
ar_pmem_stdev_we.append(stdev(ar_pmem_we_tmp))
#print("pmem we_tmp:", ar_pmem_we_tmp)
ar_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", ar_pmem_we)
print("pmem stdev we:", ar_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
ar_pmem_tx_wa = list()
ar_pmem_tx_stdev_wa = list()
ar_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ar_pmem_tx_wa_tmp.append(val)
ar_pmem_tx_wa.append(mean(ar_pmem_tx_wa_tmp))
ar_pmem_tx_stdev_wa.append(stdev(ar_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", ar_pmem_tx_wa_tmp)
ar_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", ar_pmem_tx_wa)
print("pmem_tx stdev wa:", ar_pmem_stdev_wa)
#pmem_tx workload e
ar_pmem_tx_we = list()
ar_pmem_tx_stdev_we = list()
ar_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ar_pmem_tx_we_tmp.append(val)
ar_pmem_tx_we.append(mean(ar_pmem_tx_we_tmp))
ar_pmem_tx_stdev_we.append(stdev(ar_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", ar_pmem_tx_we_tmp)
ar_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", ar_pmem_tx_we)
print("pmem_tx stdev we:", ar_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
text_file = open("../results_msst20/device_characteristics/parallel/ar.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
numa_ar_dram_wa = list()
numa_ar_dram_stdev_wa = list()
numa_ar_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ar_dram_wa_tmp.append(val)
numa_ar_dram_wa.append(mean(numa_ar_dram_wa_tmp))
numa_ar_dram_stdev_wa.append(stdev(numa_ar_dram_wa_tmp))
#print("dram wa_tmp:", numa_ar_dram_wa_tmp)
numa_ar_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", numa_ar_dram_wa)
print("dram stdev wa:", numa_ar_dram_stdev_wa)
#dram workload e
numa_ar_dram_we = list()
numa_ar_dram_stdev_we = list()
numa_ar_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ar_dram_we_tmp.append(val)
numa_ar_dram_we.append(mean(numa_ar_dram_we_tmp))
numa_ar_dram_stdev_we.append(stdev(numa_ar_dram_we_tmp))
#print("dram we_tmp:", numa_ar_dram_we_tmp)
numa_ar_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", numa_ar_dram_we)
print("dram stdev we:", numa_ar_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
numa_ar_vmem_wa = list()
numa_ar_vmem_stdev_wa = list()
numa_ar_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ar_vmem_wa_tmp.append(val)
numa_ar_vmem_wa.append(mean(numa_ar_vmem_wa_tmp))
numa_ar_vmem_stdev_wa.append(stdev(numa_ar_vmem_wa_tmp))
#print("vmem wa_tmp:", numa_ar_vmem_wa_tmp)
numa_ar_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", numa_ar_vmem_wa)
print("vmem stdev wa:", numa_ar_vmem_stdev_wa)
#vmem workload e
numa_ar_vmem_we = list()
numa_ar_vmem_stdev_we = list()
numa_ar_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ar_vmem_we_tmp.append(val)
numa_ar_vmem_we.append(mean(numa_ar_vmem_we_tmp))
numa_ar_vmem_stdev_we.append(stdev(numa_ar_vmem_we_tmp))
#print("vmem we_tmp:", numa_ar_vmem_we_tmp)
numa_ar_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", numa_ar_vmem_we)
print("vmem stdev we:", numa_ar_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
numa_ar_pmem_wa = list()
numa_ar_pmem_stdev_wa = list()
numa_ar_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ar_pmem_wa_tmp.append(val)
numa_ar_pmem_wa.append(mean(numa_ar_pmem_wa_tmp))
numa_ar_pmem_stdev_wa.append(stdev(numa_ar_pmem_wa_tmp))
#print("pmem wa_tmp:", numa_ar_pmem_wa_tmp)
numa_ar_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", numa_ar_pmem_wa)
print("pmem stdev wa:", numa_ar_pmem_stdev_wa)
#pmem workload e
numa_ar_pmem_we = list()
numa_ar_pmem_stdev_we = list()
numa_ar_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ar_pmem_we_tmp.append(val)
numa_ar_pmem_we.append(mean(numa_ar_pmem_we_tmp))
numa_ar_pmem_stdev_we.append(stdev(numa_ar_pmem_we_tmp))
#print("pmem we_tmp:", numa_ar_pmem_we_tmp)
numa_ar_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", numa_ar_pmem_we)
print("pmem stdev we:", numa_ar_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
numa_ar_pmem_tx_wa = list()
numa_ar_pmem_tx_stdev_wa = list()
numa_ar_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ar_pmem_tx_wa_tmp.append(val)
numa_ar_pmem_tx_wa.append(mean(numa_ar_pmem_tx_wa_tmp))
numa_ar_pmem_tx_stdev_wa.append(stdev(numa_ar_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", numa_ar_pmem_tx_wa_tmp)
numa_ar_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", numa_ar_pmem_tx_wa)
print("pmem_tx stdev wa:", numa_ar_pmem_stdev_wa)
#pmem_tx workload e
numa_ar_pmem_tx_we = list()
numa_ar_pmem_tx_stdev_we = list()
numa_ar_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ar_pmem_tx_we_tmp.append(val)
numa_ar_pmem_tx_we.append(mean(numa_ar_pmem_tx_we_tmp))
numa_ar_pmem_tx_stdev_we.append(stdev(numa_ar_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", numa_ar_pmem_tx_we_tmp)
numa_ar_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", numa_ar_pmem_tx_we)
print("pmem_tx stdev we:", numa_ar_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
text_file = open("../results_msst20/numa_affects/parallel/ll.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
ll_dram_wa = list()
ll_dram_stdev_wa = list()
ll_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ll_dram_wa_tmp.append(val)
ll_dram_wa.append(mean(ll_dram_wa_tmp))
ll_dram_stdev_wa.append(stdev(ll_dram_wa_tmp))
#print("dram wa_tmp:", ll_dram_wa_tmp)
ll_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", ll_dram_wa)
print("dram stdev wa:", ll_dram_stdev_wa)
#dram workload e
ll_dram_we = list()
ll_dram_stdev_we = list()
ll_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ll_dram_we_tmp.append(val)
ll_dram_we.append(mean(ll_dram_we_tmp))
ll_dram_stdev_we.append(stdev(ll_dram_we_tmp))
#print("dram we_tmp:", ll_dram_we_tmp)
ll_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", ll_dram_we)
print("dram stdev we:", ll_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
ll_vmem_wa = list()
ll_vmem_stdev_wa = list()
ll_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ll_vmem_wa_tmp.append(val)
ll_vmem_wa.append(mean(ll_vmem_wa_tmp))
ll_vmem_stdev_wa.append(stdev(ll_vmem_wa_tmp))
#print("vmem wa_tmp:", ll_vmem_wa_tmp)
ll_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", ll_vmem_wa)
print("vmem stdev wa:", ll_vmem_stdev_wa)
#vmem workload e
ll_vmem_we = list()
ll_vmem_stdev_we = list()
ll_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ll_vmem_we_tmp.append(val)
ll_vmem_we.append(mean(ll_vmem_we_tmp))
ll_vmem_stdev_we.append(stdev(ll_vmem_we_tmp))
#print("vmem we_tmp:", ll_vmem_we_tmp)
ll_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", ll_vmem_we)
print("vmem stdev we:", ll_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
ll_pmem_wa = list()
ll_pmem_stdev_wa = list()
ll_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ll_pmem_wa_tmp.append(val)
ll_pmem_wa.append(mean(ll_pmem_wa_tmp))
ll_pmem_stdev_wa.append(stdev(ll_pmem_wa_tmp))
#print("pmem wa_tmp:", ll_pmem_wa_tmp)
ll_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", ll_pmem_wa)
print("pmem stdev wa:", ll_pmem_stdev_wa)
#pmem workload e
ll_pmem_we = list()
ll_pmem_stdev_we = list()
ll_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ll_pmem_we_tmp.append(val)
ll_pmem_we.append(mean(ll_pmem_we_tmp))
ll_pmem_stdev_we.append(stdev(ll_pmem_we_tmp))
#print("pmem we_tmp:", ll_pmem_we_tmp)
ll_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", ll_pmem_we)
print("pmem stdev we:", ll_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
ll_pmem_tx_wa = list()
ll_pmem_tx_stdev_wa = list()
ll_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ll_pmem_tx_wa_tmp.append(val)
ll_pmem_tx_wa.append(mean(ll_pmem_tx_wa_tmp))
ll_pmem_tx_stdev_wa.append(stdev(ll_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", ll_pmem_tx_wa_tmp)
ll_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", ll_pmem_tx_wa)
print("pmem_tx stdev wa:", ll_pmem_stdev_wa)
#pmem_tx workload e
ll_pmem_tx_we = list()
ll_pmem_tx_stdev_we = list()
ll_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ll_pmem_tx_we_tmp.append(val)
ll_pmem_tx_we.append(mean(ll_pmem_tx_we_tmp))
ll_pmem_tx_stdev_we.append(stdev(ll_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", ll_pmem_tx_we_tmp)
ll_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", ll_pmem_tx_we)
print("pmem_tx stdev we:", ll_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
text_file = open("../results_msst20/device_characteristics/parallel/ll.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
numa_ll_dram_wa = list()
numa_ll_dram_stdev_wa = list()
numa_ll_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ll_dram_wa_tmp.append(val)
numa_ll_dram_wa.append(mean(numa_ll_dram_wa_tmp))
numa_ll_dram_stdev_wa.append(stdev(numa_ll_dram_wa_tmp))
#print("dram wa_tmp:", numa_ll_dram_wa_tmp)
numa_ll_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", numa_ll_dram_wa)
print("dram stdev wa:", numa_ll_dram_stdev_wa)
#dram workload e
numa_ll_dram_we = list()
numa_ll_dram_stdev_we = list()
numa_ll_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ll_dram_we_tmp.append(val)
numa_ll_dram_we.append(mean(numa_ll_dram_we_tmp))
numa_ll_dram_stdev_we.append(stdev(numa_ll_dram_we_tmp))
#print("dram we_tmp:", numa_ll_dram_we_tmp)
numa_ll_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", numa_ll_dram_we)
print("dram stdev we:", numa_ll_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
numa_ll_vmem_wa = list()
numa_ll_vmem_stdev_wa = list()
numa_ll_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ll_vmem_wa_tmp.append(val)
numa_ll_vmem_wa.append(mean(numa_ll_vmem_wa_tmp))
numa_ll_vmem_stdev_wa.append(stdev(numa_ll_vmem_wa_tmp))
#print("vmem wa_tmp:", numa_ll_vmem_wa_tmp)
numa_ll_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", numa_ll_vmem_wa)
print("vmem stdev wa:", numa_ll_vmem_stdev_wa)
#vmem workload e
numa_ll_vmem_we = list()
numa_ll_vmem_stdev_we = list()
numa_ll_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ll_vmem_we_tmp.append(val)
numa_ll_vmem_we.append(mean(numa_ll_vmem_we_tmp))
numa_ll_vmem_stdev_we.append(stdev(numa_ll_vmem_we_tmp))
#print("vmem we_tmp:", numa_ll_vmem_we_tmp)
numa_ll_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", numa_ll_vmem_we)
print("vmem stdev we:", numa_ll_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
numa_ll_pmem_wa = list()
numa_ll_pmem_stdev_wa = list()
numa_ll_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ll_pmem_wa_tmp.append(val)
numa_ll_pmem_wa.append(mean(numa_ll_pmem_wa_tmp))
numa_ll_pmem_stdev_wa.append(stdev(numa_ll_pmem_wa_tmp))
#print("pmem wa_tmp:", numa_ll_pmem_wa_tmp)
numa_ll_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", numa_ll_pmem_wa)
print("pmem stdev wa:", numa_ll_pmem_stdev_wa)
#pmem workload e
numa_ll_pmem_we = list()
numa_ll_pmem_stdev_we = list()
numa_ll_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ll_pmem_we_tmp.append(val)
numa_ll_pmem_we.append(mean(numa_ll_pmem_we_tmp))
numa_ll_pmem_stdev_we.append(stdev(numa_ll_pmem_we_tmp))
#print("pmem we_tmp:", numa_ll_pmem_we_tmp)
numa_ll_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", numa_ll_pmem_we)
print("pmem stdev we:", numa_ll_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
numa_ll_pmem_tx_wa = list()
numa_ll_pmem_tx_stdev_wa = list()
numa_ll_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ll_pmem_tx_wa_tmp.append(val)
numa_ll_pmem_tx_wa.append(mean(numa_ll_pmem_tx_wa_tmp))
numa_ll_pmem_tx_stdev_wa.append(stdev(numa_ll_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", numa_ll_pmem_tx_wa_tmp)
numa_ll_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", numa_ll_pmem_tx_wa)
print("pmem_tx stdev wa:", numa_ll_pmem_stdev_wa)
#pmem_tx workload e
numa_ll_pmem_tx_we = list()
numa_ll_pmem_tx_stdev_we = list()
numa_ll_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ll_pmem_tx_we_tmp.append(val)
numa_ll_pmem_tx_we.append(mean(numa_ll_pmem_tx_we_tmp))
numa_ll_pmem_tx_stdev_we.append(stdev(numa_ll_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", numa_ll_pmem_tx_we_tmp)
numa_ll_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", numa_ll_pmem_tx_we)
print("pmem_tx stdev we:", numa_ll_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
text_file = open("../results_msst20/numa_affects/parallel/ht.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
ht_dram_wa = list()
ht_dram_stdev_wa = list()
ht_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ht_dram_wa_tmp.append(val)
ht_dram_wa.append(mean(ht_dram_wa_tmp))
ht_dram_stdev_wa.append(stdev(ht_dram_wa_tmp))
#print("dram wa_tmp:", ht_dram_wa_tmp)
ht_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", ht_dram_wa)
print("dram stdev wa:", ht_dram_stdev_wa)
#dram workload e
ht_dram_we = list()
ht_dram_stdev_we = list()
ht_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ht_dram_we_tmp.append(val)
ht_dram_we.append(mean(ht_dram_we_tmp))
ht_dram_stdev_we.append(stdev(ht_dram_we_tmp))
#print("dram we_tmp:", ht_dram_we_tmp)
ht_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", ht_dram_we)
print("dram stdev we:", ht_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
ht_vmem_wa = list()
ht_vmem_stdev_wa = list()
ht_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ht_vmem_wa_tmp.append(val)
ht_vmem_wa.append(mean(ht_vmem_wa_tmp))
ht_vmem_stdev_wa.append(stdev(ht_vmem_wa_tmp))
#print("vmem wa_tmp:", ht_vmem_wa_tmp)
ht_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", ht_vmem_wa)
print("vmem stdev wa:", ht_vmem_stdev_wa)
#vmem workload e
ht_vmem_we = list()
ht_vmem_stdev_we = list()
ht_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ht_vmem_we_tmp.append(val)
ht_vmem_we.append(mean(ht_vmem_we_tmp))
ht_vmem_stdev_we.append(stdev(ht_vmem_we_tmp))
#print("vmem we_tmp:", ht_vmem_we_tmp)
ht_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", ht_vmem_we)
print("vmem stdev we:", ht_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
ht_pmem_wa = list()
ht_pmem_stdev_wa = list()
ht_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ht_pmem_wa_tmp.append(val)
ht_pmem_wa.append(mean(ht_pmem_wa_tmp))
ht_pmem_stdev_wa.append(stdev(ht_pmem_wa_tmp))
#print("pmem wa_tmp:", ht_pmem_wa_tmp)
ht_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", ht_pmem_wa)
print("pmem stdev wa:", ht_pmem_stdev_wa)
#pmem workload e
ht_pmem_we = list()
ht_pmem_stdev_we = list()
ht_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ht_pmem_we_tmp.append(val)
ht_pmem_we.append(mean(ht_pmem_we_tmp))
ht_pmem_stdev_we.append(stdev(ht_pmem_we_tmp))
#print("pmem we_tmp:", ht_pmem_we_tmp)
ht_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", ht_pmem_we)
print("pmem stdev we:", ht_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
ht_pmem_tx_wa = list()
ht_pmem_tx_stdev_wa = list()
ht_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ht_pmem_tx_wa_tmp.append(val)
ht_pmem_tx_wa.append(mean(ht_pmem_tx_wa_tmp))
ht_pmem_tx_stdev_wa.append(stdev(ht_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", ht_pmem_tx_wa_tmp)
ht_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", ht_pmem_tx_wa)
print("pmem_tx stdev wa:", ht_pmem_stdev_wa)
#pmem_tx workload e
ht_pmem_tx_we = list()
ht_pmem_tx_stdev_we = list()
ht_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
ht_pmem_tx_we_tmp.append(val)
ht_pmem_tx_we.append(mean(ht_pmem_tx_we_tmp))
ht_pmem_tx_stdev_we.append(stdev(ht_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", ht_pmem_tx_we_tmp)
ht_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", ht_pmem_tx_we)
print("pmem_tx stdev we:", ht_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
text_file = open("../results_msst20/device_characteristics/parallel/ht.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
numa_ht_dram_wa = list()
numa_ht_dram_stdev_wa = list()
numa_ht_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ht_dram_wa_tmp.append(val)
numa_ht_dram_wa.append(mean(numa_ht_dram_wa_tmp))
numa_ht_dram_stdev_wa.append(stdev(numa_ht_dram_wa_tmp))
#print("dram wa_tmp:", numa_ht_dram_wa_tmp)
numa_ht_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", numa_ht_dram_wa)
print("dram stdev wa:", numa_ht_dram_stdev_wa)
#dram workload e
numa_ht_dram_we = list()
numa_ht_dram_stdev_we = list()
numa_ht_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ht_dram_we_tmp.append(val)
numa_ht_dram_we.append(mean(numa_ht_dram_we_tmp))
numa_ht_dram_stdev_we.append(stdev(numa_ht_dram_we_tmp))
#print("dram we_tmp:", numa_ht_dram_we_tmp)
numa_ht_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", numa_ht_dram_we)
print("dram stdev we:", numa_ht_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
numa_ht_vmem_wa = list()
numa_ht_vmem_stdev_wa = list()
numa_ht_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ht_vmem_wa_tmp.append(val)
numa_ht_vmem_wa.append(mean(numa_ht_vmem_wa_tmp))
numa_ht_vmem_stdev_wa.append(stdev(numa_ht_vmem_wa_tmp))
#print("vmem wa_tmp:", numa_ht_vmem_wa_tmp)
numa_ht_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", numa_ht_vmem_wa)
print("vmem stdev wa:", numa_ht_vmem_stdev_wa)
#vmem workload e
numa_ht_vmem_we = list()
numa_ht_vmem_stdev_we = list()
numa_ht_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ht_vmem_we_tmp.append(val)
numa_ht_vmem_we.append(mean(numa_ht_vmem_we_tmp))
numa_ht_vmem_stdev_we.append(stdev(numa_ht_vmem_we_tmp))
#print("vmem we_tmp:", numa_ht_vmem_we_tmp)
numa_ht_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", numa_ht_vmem_we)
print("vmem stdev we:", numa_ht_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
numa_ht_pmem_wa = list()
numa_ht_pmem_stdev_wa = list()
numa_ht_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ht_pmem_wa_tmp.append(val)
numa_ht_pmem_wa.append(mean(numa_ht_pmem_wa_tmp))
numa_ht_pmem_stdev_wa.append(stdev(numa_ht_pmem_wa_tmp))
#print("pmem wa_tmp:", numa_ht_pmem_wa_tmp)
numa_ht_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", numa_ht_pmem_wa)
print("pmem stdev wa:", numa_ht_pmem_stdev_wa)
#pmem workload e
numa_ht_pmem_we = list()
numa_ht_pmem_stdev_we = list()
numa_ht_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ht_pmem_we_tmp.append(val)
numa_ht_pmem_we.append(mean(numa_ht_pmem_we_tmp))
numa_ht_pmem_stdev_we.append(stdev(numa_ht_pmem_we_tmp))
#print("pmem we_tmp:", numa_ht_pmem_we_tmp)
numa_ht_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", numa_ht_pmem_we)
print("pmem stdev we:", numa_ht_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
numa_ht_pmem_tx_wa = list()
numa_ht_pmem_tx_stdev_wa = list()
numa_ht_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ht_pmem_tx_wa_tmp.append(val)
numa_ht_pmem_tx_wa.append(mean(numa_ht_pmem_tx_wa_tmp))
numa_ht_pmem_tx_stdev_wa.append(stdev(numa_ht_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", numa_ht_pmem_tx_wa_tmp)
numa_ht_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", numa_ht_pmem_tx_wa)
print("pmem_tx stdev wa:", numa_ht_pmem_stdev_wa)
#pmem_tx workload e
numa_ht_pmem_tx_we = list()
numa_ht_pmem_tx_stdev_we = list()
numa_ht_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_ht_pmem_tx_we_tmp.append(val)
numa_ht_pmem_tx_we.append(mean(numa_ht_pmem_tx_we_tmp))
numa_ht_pmem_tx_stdev_we.append(stdev(numa_ht_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", numa_ht_pmem_tx_we_tmp)
numa_ht_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", numa_ht_pmem_tx_we)
print("pmem_tx stdev we:", numa_ht_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
text_file = open("../results_msst20/numa_affects/parallel/bt.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
bt_dram_wa = list()
bt_dram_stdev_wa = list()
bt_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bt_dram_wa_tmp.append(val)
bt_dram_wa.append(mean(bt_dram_wa_tmp))
bt_dram_stdev_wa.append(stdev(bt_dram_wa_tmp))
#print("dram wa_tmp:", bt_dram_wa_tmp)
bt_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", bt_dram_wa)
print("dram stdev wa:", bt_dram_stdev_wa)
#dram workload e
bt_dram_we = list()
bt_dram_stdev_we = list()
bt_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bt_dram_we_tmp.append(val)
bt_dram_we.append(mean(bt_dram_we_tmp))
bt_dram_stdev_we.append(stdev(bt_dram_we_tmp))
#print("dram we_tmp:", bt_dram_we_tmp)
bt_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", bt_dram_we)
print("dram stdev we:", bt_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
bt_vmem_wa = list()
bt_vmem_stdev_wa = list()
bt_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bt_vmem_wa_tmp.append(val)
bt_vmem_wa.append(mean(bt_vmem_wa_tmp))
bt_vmem_stdev_wa.append(stdev(bt_vmem_wa_tmp))
#print("vmem wa_tmp:", bt_vmem_wa_tmp)
bt_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", bt_vmem_wa)
print("vmem stdev wa:", bt_vmem_stdev_wa)
#vmem workload e
bt_vmem_we = list()
bt_vmem_stdev_we = list()
bt_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bt_vmem_we_tmp.append(val)
bt_vmem_we.append(mean(bt_vmem_we_tmp))
bt_vmem_stdev_we.append(stdev(bt_vmem_we_tmp))
#print("vmem we_tmp:", bt_vmem_we_tmp)
bt_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", bt_vmem_we)
print("vmem stdev we:", bt_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
bt_pmem_wa = list()
bt_pmem_stdev_wa = list()
bt_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bt_pmem_wa_tmp.append(val)
bt_pmem_wa.append(mean(bt_pmem_wa_tmp))
bt_pmem_stdev_wa.append(stdev(bt_pmem_wa_tmp))
#print("pmem wa_tmp:", bt_pmem_wa_tmp)
bt_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", bt_pmem_wa)
print("pmem stdev wa:", bt_pmem_stdev_wa)
#pmem workload e
bt_pmem_we = list()
bt_pmem_stdev_we = list()
bt_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bt_pmem_we_tmp.append(val)
bt_pmem_we.append(mean(bt_pmem_we_tmp))
bt_pmem_stdev_we.append(stdev(bt_pmem_we_tmp))
#print("pmem we_tmp:", bt_pmem_we_tmp)
bt_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", bt_pmem_we)
print("pmem stdev we:", bt_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
bt_pmem_tx_wa = list()
bt_pmem_tx_stdev_wa = list()
bt_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bt_pmem_tx_wa_tmp.append(val)
bt_pmem_tx_wa.append(mean(bt_pmem_tx_wa_tmp))
bt_pmem_tx_stdev_wa.append(stdev(bt_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", bt_pmem_tx_wa_tmp)
bt_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", bt_pmem_tx_wa)
print("pmem_tx stdev wa:", bt_pmem_stdev_wa)
#pmem_tx workload e
bt_pmem_tx_we = list()
bt_pmem_tx_stdev_we = list()
bt_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bt_pmem_tx_we_tmp.append(val)
bt_pmem_tx_we.append(mean(bt_pmem_tx_we_tmp))
bt_pmem_tx_stdev_we.append(stdev(bt_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", bt_pmem_tx_we_tmp)
bt_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", bt_pmem_tx_we)
print("pmem_tx stdev we:", bt_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
text_file = open("../results_msst20/device_characteristics/parallel/bt.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
numa_bt_dram_wa = list()
numa_bt_dram_stdev_wa = list()
numa_bt_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bt_dram_wa_tmp.append(val)
numa_bt_dram_wa.append(mean(numa_bt_dram_wa_tmp))
numa_bt_dram_stdev_wa.append(stdev(numa_bt_dram_wa_tmp))
#print("dram wa_tmp:", numa_bt_dram_wa_tmp)
numa_bt_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", numa_bt_dram_wa)
print("dram stdev wa:", numa_bt_dram_stdev_wa)
#dram workload e
numa_bt_dram_we = list()
numa_bt_dram_stdev_we = list()
numa_bt_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bt_dram_we_tmp.append(val)
numa_bt_dram_we.append(mean(numa_bt_dram_we_tmp))
numa_bt_dram_stdev_we.append(stdev(numa_bt_dram_we_tmp))
#print("dram we_tmp:", numa_bt_dram_we_tmp)
numa_bt_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", numa_bt_dram_we)
print("dram stdev we:", numa_bt_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
numa_bt_vmem_wa = list()
numa_bt_vmem_stdev_wa = list()
numa_bt_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bt_vmem_wa_tmp.append(val)
numa_bt_vmem_wa.append(mean(numa_bt_vmem_wa_tmp))
numa_bt_vmem_stdev_wa.append(stdev(numa_bt_vmem_wa_tmp))
#print("vmem wa_tmp:", numa_bt_vmem_wa_tmp)
numa_bt_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", numa_bt_vmem_wa)
print("vmem stdev wa:", numa_bt_vmem_stdev_wa)
#vmem workload e
numa_bt_vmem_we = list()
numa_bt_vmem_stdev_we = list()
numa_bt_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bt_vmem_we_tmp.append(val)
numa_bt_vmem_we.append(mean(numa_bt_vmem_we_tmp))
numa_bt_vmem_stdev_we.append(stdev(numa_bt_vmem_we_tmp))
#print("vmem we_tmp:", numa_bt_vmem_we_tmp)
numa_bt_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", numa_bt_vmem_we)
print("vmem stdev we:", numa_bt_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
numa_bt_pmem_wa = list()
numa_bt_pmem_stdev_wa = list()
numa_bt_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bt_pmem_wa_tmp.append(val)
numa_bt_pmem_wa.append(mean(numa_bt_pmem_wa_tmp))
numa_bt_pmem_stdev_wa.append(stdev(numa_bt_pmem_wa_tmp))
#print("pmem wa_tmp:", numa_bt_pmem_wa_tmp)
numa_bt_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", numa_bt_pmem_wa)
print("pmem stdev wa:", numa_bt_pmem_stdev_wa)
#pmem workload e
numa_bt_pmem_we = list()
numa_bt_pmem_stdev_we = list()
numa_bt_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bt_pmem_we_tmp.append(val)
numa_bt_pmem_we.append(mean(numa_bt_pmem_we_tmp))
numa_bt_pmem_stdev_we.append(stdev(numa_bt_pmem_we_tmp))
#print("pmem we_tmp:", numa_bt_pmem_we_tmp)
numa_bt_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", numa_bt_pmem_we)
print("pmem stdev we:", numa_bt_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
numa_bt_pmem_tx_wa = list()
numa_bt_pmem_tx_stdev_wa = list()
numa_bt_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bt_pmem_tx_wa_tmp.append(val)
numa_bt_pmem_tx_wa.append(mean(numa_bt_pmem_tx_wa_tmp))
numa_bt_pmem_tx_stdev_wa.append(stdev(numa_bt_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", numa_bt_pmem_tx_wa_tmp)
numa_bt_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", numa_bt_pmem_tx_wa)
print("pmem_tx stdev wa:", numa_bt_pmem_stdev_wa)
#pmem_tx workload e
numa_bt_pmem_tx_we = list()
numa_bt_pmem_tx_stdev_we = list()
numa_bt_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bt_pmem_tx_we_tmp.append(val)
numa_bt_pmem_tx_we.append(mean(numa_bt_pmem_tx_we_tmp))
numa_bt_pmem_tx_stdev_we.append(stdev(numa_bt_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", numa_bt_pmem_tx_we_tmp)
numa_bt_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", numa_bt_pmem_tx_we)
print("pmem_tx stdev we:", numa_bt_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
text_file = open("../results_msst20/numa_affects/parallel/bp.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
bp_dram_wa = list()
bp_dram_stdev_wa = list()
bp_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bp_dram_wa_tmp.append(val)
bp_dram_wa.append(mean(bp_dram_wa_tmp))
bp_dram_stdev_wa.append(stdev(bp_dram_wa_tmp))
#print("dram wa_tmp:", bp_dram_wa_tmp)
bp_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", bp_dram_wa)
print("dram stdev wa:", bp_dram_stdev_wa)
#dram workload e
bp_dram_we = list()
bp_dram_stdev_we = list()
bp_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bp_dram_we_tmp.append(val)
bp_dram_we.append(mean(bp_dram_we_tmp))
bp_dram_stdev_we.append(stdev(bp_dram_we_tmp))
#print("dram we_tmp:", bp_dram_we_tmp)
bp_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", bp_dram_we)
print("dram stdev we:", bp_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
bp_vmem_wa = list()
bp_vmem_stdev_wa = list()
bp_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bp_vmem_wa_tmp.append(val)
bp_vmem_wa.append(mean(bp_vmem_wa_tmp))
bp_vmem_stdev_wa.append(stdev(bp_vmem_wa_tmp))
#print("vmem wa_tmp:", bp_vmem_wa_tmp)
bp_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", bp_vmem_wa)
print("vmem stdev wa:", bp_vmem_stdev_wa)
#vmem workload e
bp_vmem_we = list()
bp_vmem_stdev_we = list()
bp_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bp_vmem_we_tmp.append(val)
bp_vmem_we.append(mean(bp_vmem_we_tmp))
bp_vmem_stdev_we.append(stdev(bp_vmem_we_tmp))
#print("vmem we_tmp:", bp_vmem_we_tmp)
bp_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", bp_vmem_we)
print("vmem stdev we:", bp_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
bp_pmem_wa = list()
bp_pmem_stdev_wa = list()
bp_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bp_pmem_wa_tmp.append(val)
bp_pmem_wa.append(mean(bp_pmem_wa_tmp))
bp_pmem_stdev_wa.append(stdev(bp_pmem_wa_tmp))
#print("pmem wa_tmp:", bp_pmem_wa_tmp)
bp_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", bp_pmem_wa)
print("pmem stdev wa:", bp_pmem_stdev_wa)
#pmem workload e
bp_pmem_we = list()
bp_pmem_stdev_we = list()
bp_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bp_pmem_we_tmp.append(val)
bp_pmem_we.append(mean(bp_pmem_we_tmp))
bp_pmem_stdev_we.append(stdev(bp_pmem_we_tmp))
#print("pmem we_tmp:", bp_pmem_we_tmp)
bp_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", bp_pmem_we)
print("pmem stdev we:", bp_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
bp_pmem_tx_wa = list()
bp_pmem_tx_stdev_wa = list()
bp_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bp_pmem_tx_wa_tmp.append(val)
bp_pmem_tx_wa.append(mean(bp_pmem_tx_wa_tmp))
bp_pmem_tx_stdev_wa.append(stdev(bp_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", bp_pmem_tx_wa_tmp)
bp_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", bp_pmem_tx_wa)
print("pmem_tx stdev wa:", bp_pmem_stdev_wa)
#pmem_tx workload e
bp_pmem_tx_we = list()
bp_pmem_tx_stdev_we = list()
bp_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
bp_pmem_tx_we_tmp.append(val)
bp_pmem_tx_we.append(mean(bp_pmem_tx_we_tmp))
bp_pmem_tx_stdev_we.append(stdev(bp_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", bp_pmem_tx_we_tmp)
bp_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", bp_pmem_tx_we)
print("pmem_tx stdev we:", bp_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
text_file = open("../results_msst20/device_characteristics/parallel/bp.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
numa_bp_dram_wa = list()
numa_bp_dram_stdev_wa = list()
numa_bp_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bp_dram_wa_tmp.append(val)
numa_bp_dram_wa.append(mean(numa_bp_dram_wa_tmp))
numa_bp_dram_stdev_wa.append(stdev(numa_bp_dram_wa_tmp))
#print("dram wa_tmp:", numa_bp_dram_wa_tmp)
numa_bp_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", numa_bp_dram_wa)
print("dram stdev wa:", numa_bp_dram_stdev_wa)
#dram workload e
numa_bp_dram_we = list()
numa_bp_dram_stdev_we = list()
numa_bp_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bp_dram_we_tmp.append(val)
numa_bp_dram_we.append(mean(numa_bp_dram_we_tmp))
numa_bp_dram_stdev_we.append(stdev(numa_bp_dram_we_tmp))
#print("dram we_tmp:", numa_bp_dram_we_tmp)
numa_bp_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", numa_bp_dram_we)
print("dram stdev we:", numa_bp_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
numa_bp_vmem_wa = list()
numa_bp_vmem_stdev_wa = list()
numa_bp_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bp_vmem_wa_tmp.append(val)
numa_bp_vmem_wa.append(mean(numa_bp_vmem_wa_tmp))
numa_bp_vmem_stdev_wa.append(stdev(numa_bp_vmem_wa_tmp))
#print("vmem wa_tmp:", numa_bp_vmem_wa_tmp)
numa_bp_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", numa_bp_vmem_wa)
print("vmem stdev wa:", numa_bp_vmem_stdev_wa)
#vmem workload e
numa_bp_vmem_we = list()
numa_bp_vmem_stdev_we = list()
numa_bp_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bp_vmem_we_tmp.append(val)
numa_bp_vmem_we.append(mean(numa_bp_vmem_we_tmp))
numa_bp_vmem_stdev_we.append(stdev(numa_bp_vmem_we_tmp))
#print("vmem we_tmp:", numa_bp_vmem_we_tmp)
numa_bp_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", numa_bp_vmem_we)
print("vmem stdev we:", numa_bp_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
numa_bp_pmem_wa = list()
numa_bp_pmem_stdev_wa = list()
numa_bp_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bp_pmem_wa_tmp.append(val)
numa_bp_pmem_wa.append(mean(numa_bp_pmem_wa_tmp))
numa_bp_pmem_stdev_wa.append(stdev(numa_bp_pmem_wa_tmp))
#print("pmem wa_tmp:", numa_bp_pmem_wa_tmp)
numa_bp_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", numa_bp_pmem_wa)
print("pmem stdev wa:", numa_bp_pmem_stdev_wa)
#pmem workload e
numa_bp_pmem_we = list()
numa_bp_pmem_stdev_we = list()
numa_bp_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bp_pmem_we_tmp.append(val)
numa_bp_pmem_we.append(mean(numa_bp_pmem_we_tmp))
numa_bp_pmem_stdev_we.append(stdev(numa_bp_pmem_we_tmp))
#print("pmem we_tmp:", numa_bp_pmem_we_tmp)
numa_bp_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", numa_bp_pmem_we)
print("pmem stdev we:", numa_bp_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
numa_bp_pmem_tx_wa = list()
numa_bp_pmem_tx_stdev_wa = list()
numa_bp_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bp_pmem_tx_wa_tmp.append(val)
numa_bp_pmem_tx_wa.append(mean(numa_bp_pmem_tx_wa_tmp))
numa_bp_pmem_tx_stdev_wa.append(stdev(numa_bp_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", numa_bp_pmem_tx_wa_tmp)
numa_bp_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", numa_bp_pmem_tx_wa)
print("pmem_tx stdev wa:", numa_bp_pmem_stdev_wa)
#pmem_tx workload e
numa_bp_pmem_tx_we = list()
numa_bp_pmem_tx_stdev_we = list()
numa_bp_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_bp_pmem_tx_we_tmp.append(val)
numa_bp_pmem_tx_we.append(mean(numa_bp_pmem_tx_we_tmp))
numa_bp_pmem_tx_stdev_we.append(stdev(numa_bp_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", numa_bp_pmem_tx_we_tmp)
numa_bp_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", numa_bp_pmem_tx_we)
print("pmem_tx stdev we:", numa_bp_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
text_file = open("../results_msst20/numa_affects/parallel/sk.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
sk_dram_wa = list()
sk_dram_stdev_wa = list()
sk_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
sk_dram_wa_tmp.append(val)
sk_dram_wa.append(mean(sk_dram_wa_tmp))
sk_dram_stdev_wa.append(stdev(sk_dram_wa_tmp))
#print("dram wa_tmp:", sk_dram_wa_tmp)
sk_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", sk_dram_wa)
print("dram stdev wa:", sk_dram_stdev_wa)
#dram workload e
sk_dram_we = list()
sk_dram_stdev_we = list()
sk_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
sk_dram_we_tmp.append(val)
sk_dram_we.append(mean(sk_dram_we_tmp))
sk_dram_stdev_we.append(stdev(sk_dram_we_tmp))
#print("dram we_tmp:", sk_dram_we_tmp)
sk_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", sk_dram_we)
print("dram stdev we:", sk_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
sk_vmem_wa = list()
sk_vmem_stdev_wa = list()
sk_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
sk_vmem_wa_tmp.append(val)
sk_vmem_wa.append(mean(sk_vmem_wa_tmp))
sk_vmem_stdev_wa.append(stdev(sk_vmem_wa_tmp))
#print("vmem wa_tmp:", sk_vmem_wa_tmp)
sk_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", sk_vmem_wa)
print("vmem stdev wa:", sk_vmem_stdev_wa)
#vmem workload e
sk_vmem_we = list()
sk_vmem_stdev_we = list()
sk_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
sk_vmem_we_tmp.append(val)
sk_vmem_we.append(mean(sk_vmem_we_tmp))
sk_vmem_stdev_we.append(stdev(sk_vmem_we_tmp))
#print("vmem we_tmp:", sk_vmem_we_tmp)
sk_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", sk_vmem_we)
print("vmem stdev we:", sk_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
sk_pmem_wa = list()
sk_pmem_stdev_wa = list()
sk_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
sk_pmem_wa_tmp.append(val)
sk_pmem_wa.append(mean(sk_pmem_wa_tmp))
sk_pmem_stdev_wa.append(stdev(sk_pmem_wa_tmp))
#print("pmem wa_tmp:", sk_pmem_wa_tmp)
sk_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", sk_pmem_wa)
print("pmem stdev wa:", sk_pmem_stdev_wa)
#pmem workload e
sk_pmem_we = list()
sk_pmem_stdev_we = list()
sk_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
sk_pmem_we_tmp.append(val)
sk_pmem_we.append(mean(sk_pmem_we_tmp))
sk_pmem_stdev_we.append(stdev(sk_pmem_we_tmp))
#print("pmem we_tmp:", sk_pmem_we_tmp)
sk_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", sk_pmem_we)
print("pmem stdev we:", sk_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
sk_pmem_tx_wa = list()
sk_pmem_tx_stdev_wa = list()
sk_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
sk_pmem_tx_wa_tmp.append(val)
sk_pmem_tx_wa.append(mean(sk_pmem_tx_wa_tmp))
sk_pmem_tx_stdev_wa.append(stdev(sk_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", sk_pmem_tx_wa_tmp)
sk_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", sk_pmem_tx_wa)
print("pmem_tx stdev wa:", sk_pmem_stdev_wa)
#pmem_tx workload e
sk_pmem_tx_we = list()
sk_pmem_tx_stdev_we = list()
sk_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
sk_pmem_tx_we_tmp.append(val)
sk_pmem_tx_we.append(mean(sk_pmem_tx_we_tmp))
sk_pmem_tx_stdev_we.append(stdev(sk_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", sk_pmem_tx_we_tmp)
sk_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", sk_pmem_tx_we)
print("pmem_tx stdev we:", sk_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
text_file = open("../results_msst20/device_characteristics/parallel/sk.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
numa_sk_dram_wa = list()
numa_sk_dram_stdev_wa = list()
numa_sk_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_sk_dram_wa_tmp.append(val)
numa_sk_dram_wa.append(mean(numa_sk_dram_wa_tmp))
numa_sk_dram_stdev_wa.append(stdev(numa_sk_dram_wa_tmp))
#print("dram wa_tmp:", numa_sk_dram_wa_tmp)
numa_sk_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", numa_sk_dram_wa)
print("dram stdev wa:", numa_sk_dram_stdev_wa)
#dram workload e
numa_sk_dram_we = list()
numa_sk_dram_stdev_we = list()
numa_sk_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_sk_dram_we_tmp.append(val)
numa_sk_dram_we.append(mean(numa_sk_dram_we_tmp))
numa_sk_dram_stdev_we.append(stdev(numa_sk_dram_we_tmp))
#print("dram we_tmp:", numa_sk_dram_we_tmp)
numa_sk_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", numa_sk_dram_we)
print("dram stdev we:", numa_sk_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
numa_sk_vmem_wa = list()
numa_sk_vmem_stdev_wa = list()
numa_sk_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_sk_vmem_wa_tmp.append(val)
numa_sk_vmem_wa.append(mean(numa_sk_vmem_wa_tmp))
numa_sk_vmem_stdev_wa.append(stdev(numa_sk_vmem_wa_tmp))
#print("vmem wa_tmp:", numa_sk_vmem_wa_tmp)
numa_sk_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", numa_sk_vmem_wa)
print("vmem stdev wa:", numa_sk_vmem_stdev_wa)
#vmem workload e
numa_sk_vmem_we = list()
numa_sk_vmem_stdev_we = list()
numa_sk_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_sk_vmem_we_tmp.append(val)
numa_sk_vmem_we.append(mean(numa_sk_vmem_we_tmp))
numa_sk_vmem_stdev_we.append(stdev(numa_sk_vmem_we_tmp))
#print("vmem we_tmp:", numa_sk_vmem_we_tmp)
numa_sk_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", numa_sk_vmem_we)
print("vmem stdev we:", numa_sk_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
numa_sk_pmem_wa = list()
numa_sk_pmem_stdev_wa = list()
numa_sk_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_sk_pmem_wa_tmp.append(val)
numa_sk_pmem_wa.append(mean(numa_sk_pmem_wa_tmp))
numa_sk_pmem_stdev_wa.append(stdev(numa_sk_pmem_wa_tmp))
#print("pmem wa_tmp:", numa_sk_pmem_wa_tmp)
numa_sk_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", numa_sk_pmem_wa)
print("pmem stdev wa:", numa_sk_pmem_stdev_wa)
#pmem workload e
numa_sk_pmem_we = list()
numa_sk_pmem_stdev_we = list()
numa_sk_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_sk_pmem_we_tmp.append(val)
numa_sk_pmem_we.append(mean(numa_sk_pmem_we_tmp))
numa_sk_pmem_stdev_we.append(stdev(numa_sk_pmem_we_tmp))
#print("pmem we_tmp:", numa_sk_pmem_we_tmp)
numa_sk_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", numa_sk_pmem_we)
print("pmem stdev we:", numa_sk_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
numa_sk_pmem_tx_wa = list()
numa_sk_pmem_tx_stdev_wa = list()
numa_sk_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_sk_pmem_tx_wa_tmp.append(val)
numa_sk_pmem_tx_wa.append(mean(numa_sk_pmem_tx_wa_tmp))
numa_sk_pmem_tx_stdev_wa.append(stdev(numa_sk_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", numa_sk_pmem_tx_wa_tmp)
numa_sk_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", numa_sk_pmem_tx_wa)
print("pmem_tx stdev wa:", numa_sk_pmem_stdev_wa)
#pmem_tx workload e
numa_sk_pmem_tx_we = list()
numa_sk_pmem_tx_stdev_we = list()
numa_sk_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_sk_pmem_tx_we_tmp.append(val)
numa_sk_pmem_tx_we.append(mean(numa_sk_pmem_tx_we_tmp))
numa_sk_pmem_tx_stdev_we.append(stdev(numa_sk_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", numa_sk_pmem_tx_we_tmp)
numa_sk_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", numa_sk_pmem_tx_we)
print("pmem_tx stdev we:", numa_sk_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
text_file = open("../results_msst20/numa_affects/parallel/rb.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
rb_dram_wa = list()
rb_dram_stdev_wa = list()
rb_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
rb_dram_wa_tmp.append(val)
rb_dram_wa.append(mean(rb_dram_wa_tmp))
rb_dram_stdev_wa.append(stdev(rb_dram_wa_tmp))
#print("dram wa_tmp:", rb_dram_wa_tmp)
rb_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", rb_dram_wa)
print("dram stdev wa:", rb_dram_stdev_wa)
#dram workload e
rb_dram_we = list()
rb_dram_stdev_we = list()
rb_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
rb_dram_we_tmp.append(val)
rb_dram_we.append(mean(rb_dram_we_tmp))
rb_dram_stdev_we.append(stdev(rb_dram_we_tmp))
#print("dram we_tmp:", rb_dram_we_tmp)
rb_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", rb_dram_we)
print("dram stdev we:", rb_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
rb_vmem_wa = list()
rb_vmem_stdev_wa = list()
rb_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
rb_vmem_wa_tmp.append(val)
rb_vmem_wa.append(mean(rb_vmem_wa_tmp))
rb_vmem_stdev_wa.append(stdev(rb_vmem_wa_tmp))
#print("vmem wa_tmp:", rb_vmem_wa_tmp)
rb_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", rb_vmem_wa)
print("vmem stdev wa:", rb_vmem_stdev_wa)
#vmem workload e
rb_vmem_we = list()
rb_vmem_stdev_we = list()
rb_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
rb_vmem_we_tmp.append(val)
rb_vmem_we.append(mean(rb_vmem_we_tmp))
rb_vmem_stdev_we.append(stdev(rb_vmem_we_tmp))
#print("vmem we_tmp:", rb_vmem_we_tmp)
rb_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", rb_vmem_we)
print("vmem stdev we:", rb_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
rb_pmem_wa = list()
rb_pmem_stdev_wa = list()
rb_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
rb_pmem_wa_tmp.append(val)
rb_pmem_wa.append(mean(rb_pmem_wa_tmp))
rb_pmem_stdev_wa.append(stdev(rb_pmem_wa_tmp))
#print("pmem wa_tmp:", rb_pmem_wa_tmp)
rb_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", rb_pmem_wa)
print("pmem stdev wa:", rb_pmem_stdev_wa)
#pmem workload e
rb_pmem_we = list()
rb_pmem_stdev_we = list()
rb_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
rb_pmem_we_tmp.append(val)
rb_pmem_we.append(mean(rb_pmem_we_tmp))
rb_pmem_stdev_we.append(stdev(rb_pmem_we_tmp))
#print("pmem we_tmp:", rb_pmem_we_tmp)
rb_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", rb_pmem_we)
print("pmem stdev we:", rb_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
rb_pmem_tx_wa = list()
rb_pmem_tx_stdev_wa = list()
rb_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
rb_pmem_tx_wa_tmp.append(val)
rb_pmem_tx_wa.append(mean(rb_pmem_tx_wa_tmp))
rb_pmem_tx_stdev_wa.append(stdev(rb_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", rb_pmem_tx_wa_tmp)
rb_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", rb_pmem_tx_wa)
print("pmem_tx stdev wa:", rb_pmem_stdev_wa)
#pmem_tx workload e
rb_pmem_tx_we = list()
rb_pmem_tx_stdev_we = list()
rb_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
rb_pmem_tx_we_tmp.append(val)
rb_pmem_tx_we.append(mean(rb_pmem_tx_we_tmp))
rb_pmem_tx_stdev_we.append(stdev(rb_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", rb_pmem_tx_we_tmp)
rb_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", rb_pmem_tx_we)
print("pmem_tx stdev we:", rb_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
text_file = open("../results_msst20/device_characteristics/parallel/rb.out", "r")
lines = text_file.readlines()
print("# of lines: ", len(lines))
text_file.close()
# +
import numpy as np
from statistics import mean, stdev
line_it = 0
#dram workload a
numa_rb_dram_wa = list()
numa_rb_dram_stdev_wa = list()
numa_rb_dram_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_rb_dram_wa_tmp.append(val)
numa_rb_dram_wa.append(mean(numa_rb_dram_wa_tmp))
numa_rb_dram_stdev_wa.append(stdev(numa_rb_dram_wa_tmp))
#print("dram wa_tmp:", numa_rb_dram_wa_tmp)
numa_rb_dram_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean wa:", numa_rb_dram_wa)
print("dram stdev wa:", numa_rb_dram_stdev_wa)
#dram workload e
numa_rb_dram_we = list()
numa_rb_dram_stdev_we = list()
numa_rb_dram_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_rb_dram_we_tmp.append(val)
numa_rb_dram_we.append(mean(numa_rb_dram_we_tmp))
numa_rb_dram_stdev_we.append(stdev(numa_rb_dram_we_tmp))
#print("dram we_tmp:", numa_rb_dram_we_tmp)
numa_rb_dram_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("dram mean we:", numa_rb_dram_we)
print("dram stdev we:", numa_rb_dram_stdev_we)
print("######################[dram data loaded]######################")
#vmem workload a
numa_rb_vmem_wa = list()
numa_rb_vmem_stdev_wa = list()
numa_rb_vmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_rb_vmem_wa_tmp.append(val)
numa_rb_vmem_wa.append(mean(numa_rb_vmem_wa_tmp))
numa_rb_vmem_stdev_wa.append(stdev(numa_rb_vmem_wa_tmp))
#print("vmem wa_tmp:", numa_rb_vmem_wa_tmp)
numa_rb_vmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean wa:", numa_rb_vmem_wa)
print("vmem stdev wa:", numa_rb_vmem_stdev_wa)
#vmem workload e
numa_rb_vmem_we = list()
numa_rb_vmem_stdev_we = list()
numa_rb_vmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_rb_vmem_we_tmp.append(val)
numa_rb_vmem_we.append(mean(numa_rb_vmem_we_tmp))
numa_rb_vmem_stdev_we.append(stdev(numa_rb_vmem_we_tmp))
#print("vmem we_tmp:", numa_rb_vmem_we_tmp)
numa_rb_vmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("vmem mean we:", numa_rb_vmem_we)
print("vmem stdev we:", numa_rb_vmem_stdev_we)
print("######################[vmem data loaded]######################")
#pmem workload a
numa_rb_pmem_wa = list()
numa_rb_pmem_stdev_wa = list()
numa_rb_pmem_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_rb_pmem_wa_tmp.append(val)
numa_rb_pmem_wa.append(mean(numa_rb_pmem_wa_tmp))
numa_rb_pmem_stdev_wa.append(stdev(numa_rb_pmem_wa_tmp))
#print("pmem wa_tmp:", numa_rb_pmem_wa_tmp)
numa_rb_pmem_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean wa:", numa_rb_pmem_wa)
print("pmem stdev wa:", numa_rb_pmem_stdev_wa)
#pmem workload e
numa_rb_pmem_we = list()
numa_rb_pmem_stdev_we = list()
numa_rb_pmem_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_rb_pmem_we_tmp.append(val)
numa_rb_pmem_we.append(mean(numa_rb_pmem_we_tmp))
numa_rb_pmem_stdev_we.append(stdev(numa_rb_pmem_we_tmp))
#print("pmem we_tmp:", numa_rb_pmem_we_tmp)
numa_rb_pmem_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem mean we:", numa_rb_pmem_we)
print("pmem stdev we:", numa_rb_pmem_stdev_we)
print("######################[pmem data loaded]######################")
#pmem_tx workload a
numa_rb_pmem_tx_wa = list()
numa_rb_pmem_tx_stdev_wa = list()
numa_rb_pmem_tx_wa_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_rb_pmem_tx_wa_tmp.append(val)
numa_rb_pmem_tx_wa.append(mean(numa_rb_pmem_tx_wa_tmp))
numa_rb_pmem_tx_stdev_wa.append(stdev(numa_rb_pmem_tx_wa_tmp))
#print("pmem_tx wa_tmp:", numa_rb_pmem_tx_wa_tmp)
numa_rb_pmem_tx_wa_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean wa:", numa_rb_pmem_tx_wa)
print("pmem_tx stdev wa:", numa_rb_pmem_stdev_wa)
#pmem_tx workload e
numa_rb_pmem_tx_we = list()
numa_rb_pmem_tx_stdev_we = list()
numa_rb_pmem_tx_we_tmp = list()
while(1):
while(1):
line = lines[line_it]
line_it += 1
if line.startswith("*"): break
if line.startswith("storeds ../../../workloads/"):
val = float(line.split('\t')[-1].strip())
numa_rb_pmem_tx_we_tmp.append(val)
numa_rb_pmem_tx_we.append(mean(numa_rb_pmem_tx_we_tmp))
numa_rb_pmem_tx_stdev_we.append(stdev(numa_rb_pmem_tx_we_tmp))
#print("pmem_tx we_tmp:", numa_rb_pmem_tx_we_tmp)
numa_rb_pmem_tx_we_tmp.clear()
line = lines[line_it]
if line.startswith("~"):
line_it += 1
break
print("pmem_tx mean we:", numa_rb_pmem_tx_we)
print("pmem_tx stdev we:", numa_rb_pmem_stdev_we)
print("######################[pmem-tx data loaded]######################")
# +
# libraries
import numpy as np
import matplotlib
matplotlib.use("PDF")
import matplotlib.pyplot as plt
import matplotlib.backends as pdf_backend
from statistics import mean, stdev
pdf = pdf_backend.backend_pdf.PdfPages("msst20_eval_6.pdf")
plt.rcParams['ps.useafm'] = True
plt.rcParams['pdf.use14corefonts'] = True
plt.rcParams['text.usetex'] = True
# set width of bar
barWidth = 0.30
################### WA DATA ###################
wa_numa_ar_mean = [(numa_ar_dram_wa[0]), (numa_ar_vmem_wa[0]), (numa_ar_pmem_wa[0]), (numa_ar_pmem_tx_wa[0])]
wa_numa_ll_mean = [(numa_ll_dram_wa[0]), (numa_ll_vmem_wa[0]), (numa_ll_pmem_wa[0]), (numa_ll_pmem_tx_wa[0])]
wa_numa_ht_mean = [(numa_ht_dram_wa[0]), (numa_ht_vmem_wa[0]), (numa_ht_pmem_wa[0]), (numa_ht_pmem_tx_wa[0])]
wa_numa_bt_mean = [(numa_bt_dram_wa[0]), (numa_bt_vmem_wa[0]), (numa_bt_pmem_wa[0]), (numa_bt_pmem_tx_wa[0])]
wa_numa_bp_mean = [(numa_bp_dram_wa[0]), (numa_bp_vmem_wa[0]), (numa_bp_pmem_wa[0]), (numa_bp_pmem_tx_wa[0])]
wa_numa_sk_mean = [(numa_sk_dram_wa[0]), (numa_sk_vmem_wa[0]), (numa_sk_pmem_wa[0]), (numa_sk_pmem_tx_wa[0])]
wa_numa_rb_mean = [(numa_rb_dram_wa[0]), (numa_rb_vmem_wa[0]), (numa_rb_pmem_wa[0]), (numa_rb_pmem_tx_wa[0])]
wa_numa_ar_stdev = [(numa_ar_dram_stdev_wa[0]), (numa_ar_vmem_stdev_wa[0]), (numa_ar_pmem_stdev_wa[0]), (numa_ar_pmem_tx_stdev_wa[0])]
wa_numa_ll_stdev = [(numa_ll_dram_stdev_wa[0]), (numa_ll_vmem_stdev_wa[0]), (numa_ll_pmem_stdev_wa[0]), (numa_ll_pmem_tx_stdev_wa[0])]
wa_numa_ht_stdev = [(numa_ht_dram_stdev_wa[0]), (numa_ht_vmem_stdev_wa[0]), (numa_ht_pmem_stdev_wa[0]), (numa_ht_pmem_tx_stdev_wa[0])]
wa_numa_bt_stdev = [(numa_bt_dram_stdev_wa[0]), (numa_bt_vmem_stdev_wa[0]), (numa_bt_pmem_stdev_wa[0]), (numa_bt_pmem_tx_stdev_wa[0])]
wa_numa_bp_stdev = [(numa_bp_dram_stdev_wa[0]), (numa_bp_vmem_stdev_wa[0]), (numa_bp_pmem_stdev_wa[0]), (numa_bp_pmem_tx_stdev_wa[0])]
wa_numa_sk_stdev = [(numa_sk_dram_stdev_wa[0]), (numa_sk_vmem_stdev_wa[0]), (numa_sk_pmem_stdev_wa[0]), (numa_sk_pmem_tx_stdev_wa[0])]
wa_numa_rb_stdev = [(numa_rb_dram_stdev_wa[0]), (numa_rb_vmem_stdev_wa[0]), (numa_rb_pmem_stdev_wa[0]), (numa_rb_pmem_tx_stdev_wa[0])]
wa_non_numa_ar_mean = [(ar_dram_wa[0]), (ar_vmem_wa[0]), (ar_pmem_wa[0]), (ar_pmem_tx_wa[0])]
wa_non_numa_ll_mean = [(ll_dram_wa[0]), (ll_vmem_wa[0]), (ll_pmem_wa[0]), (ll_pmem_tx_wa[0])]
wa_non_numa_ht_mean = [(ht_dram_wa[0]), (ht_vmem_wa[0]), (ht_pmem_wa[0]), (ht_pmem_tx_wa[0])]
wa_non_numa_bt_mean = [(bt_dram_wa[0]), (bt_vmem_wa[0]), (bt_pmem_wa[0]), (bt_pmem_tx_wa[0])]
wa_non_numa_bp_mean = [(bp_dram_wa[0]), (bp_vmem_wa[0]), (bp_pmem_wa[0]), (bp_pmem_tx_wa[0])]
wa_non_numa_sk_mean = [(sk_dram_wa[0]), (sk_vmem_wa[0]), (sk_pmem_wa[0]), (sk_pmem_tx_wa[0])]
wa_non_numa_rb_mean = [(rb_dram_wa[0]), (rb_vmem_wa[0]), (rb_pmem_wa[0]), (rb_pmem_tx_wa[0])]
wa_non_numa_ar_stdev = [(ar_dram_stdev_wa[0]), (ar_vmem_stdev_wa[0]), (ar_pmem_stdev_wa[0]), (ar_pmem_tx_stdev_wa[0])]
wa_non_numa_ll_stdev = [(ll_dram_stdev_wa[0]), (ll_vmem_stdev_wa[0]), (ll_pmem_stdev_wa[0]), (ll_pmem_tx_stdev_wa[0])]
wa_non_numa_ht_stdev = [(ht_dram_stdev_wa[0]), (ht_vmem_stdev_wa[0]), (ht_pmem_stdev_wa[0]), (ht_pmem_tx_stdev_wa[0])]
wa_non_numa_bt_stdev = [(bt_dram_stdev_wa[0]), (bt_vmem_stdev_wa[0]), (bt_pmem_stdev_wa[0]), (bt_pmem_tx_stdev_wa[0])]
wa_non_numa_bp_stdev = [(bp_dram_stdev_wa[0]), (bp_vmem_stdev_wa[0]), (bp_pmem_stdev_wa[0]), (bp_pmem_tx_stdev_wa[0])]
wa_non_numa_sk_stdev = [(sk_dram_stdev_wa[0]), (sk_vmem_stdev_wa[0]), (sk_pmem_stdev_wa[0]), (sk_pmem_tx_stdev_wa[0])]
wa_non_numa_rb_stdev = [(rb_dram_stdev_wa[0]), (rb_vmem_stdev_wa[0]), (rb_pmem_stdev_wa[0]), (rb_pmem_tx_stdev_wa[0])]
################### WE DATA ###################
we_numa_ar_mean = [(numa_ar_dram_we[0]), (numa_ar_vmem_we[0]), (numa_ar_pmem_we[0]), (numa_ar_pmem_tx_we[0])]
we_numa_ll_mean = [(numa_ll_dram_we[0]), (numa_ll_vmem_we[0]), (numa_ll_pmem_we[0]), (numa_ll_pmem_tx_we[0])]
we_numa_ht_mean = [(numa_ht_dram_we[0]), (numa_ht_vmem_we[0]), (numa_ht_pmem_we[0]), (numa_ht_pmem_tx_we[0])]
we_numa_bt_mean = [(numa_bt_dram_we[0]), (numa_bt_vmem_we[0]), (numa_bt_pmem_we[0]), (numa_bt_pmem_tx_we[0])]
we_numa_bp_mean = [(numa_bp_dram_we[0]), (numa_bp_vmem_we[0]), (numa_bp_pmem_we[0]), (numa_bp_pmem_tx_we[0])]
we_numa_sk_mean = [(numa_sk_dram_we[0]), (numa_sk_vmem_we[0]), (numa_sk_pmem_we[0]), (numa_sk_pmem_tx_we[0])]
we_numa_rb_mean = [(numa_rb_dram_we[0]), (numa_rb_vmem_we[0]), (numa_rb_pmem_we[0]), (numa_rb_pmem_tx_we[0])]
we_numa_ar_stdev = [(numa_ar_dram_stdev_we[0]), (numa_ar_vmem_stdev_we[0]), (numa_ar_pmem_stdev_we[0]), (numa_ar_pmem_tx_stdev_we[0])]
we_numa_ll_stdev = [(numa_ll_dram_stdev_we[0]), (numa_ll_vmem_stdev_we[0]), (numa_ll_pmem_stdev_we[0]), (numa_ll_pmem_tx_stdev_we[0])]
we_numa_ht_stdev = [(numa_ht_dram_stdev_we[0]), (numa_ht_vmem_stdev_we[0]), (numa_ht_pmem_stdev_we[0]), (numa_ht_pmem_tx_stdev_we[0])]
we_numa_bt_stdev = [(numa_bt_dram_stdev_we[0]), (numa_bt_vmem_stdev_we[0]), (numa_bt_pmem_stdev_we[0]), (numa_bt_pmem_tx_stdev_we[0])]
we_numa_bp_stdev = [(numa_bp_dram_stdev_we[0]), (numa_bp_vmem_stdev_we[0]), (numa_bp_pmem_stdev_we[0]), (numa_bp_pmem_tx_stdev_we[0])]
we_numa_sk_stdev = [(numa_sk_dram_stdev_we[0]), (numa_sk_vmem_stdev_we[0]), (numa_sk_pmem_stdev_we[0]), (numa_sk_pmem_tx_stdev_we[0])]
we_numa_rb_stdev = [(numa_rb_dram_stdev_we[0]), (numa_rb_vmem_stdev_we[0]), (numa_rb_pmem_stdev_we[0]), (numa_rb_pmem_tx_stdev_we[0])]
we_non_numa_ar_mean = [(ar_dram_we[0]), (ar_vmem_we[0]), (ar_pmem_we[0]), (ar_pmem_tx_we[0])]
we_non_numa_ll_mean = [(ll_dram_we[0]), (ll_vmem_we[0]), (ll_pmem_we[0]), (ll_pmem_tx_we[0])]
we_non_numa_ht_mean = [(ht_dram_we[0]), (ht_vmem_we[0]), (ht_pmem_we[0]), (ht_pmem_tx_we[0])]
we_non_numa_bt_mean = [(bt_dram_we[0]), (bt_vmem_we[0]), (bt_pmem_we[0]), (bt_pmem_tx_we[0])]
we_non_numa_bp_mean = [(bp_dram_we[0]), (bp_vmem_we[0]), (bp_pmem_we[0]), (bp_pmem_tx_we[0])]
we_non_numa_sk_mean = [(sk_dram_we[0]), (sk_vmem_we[0]), (sk_pmem_we[0]), (sk_pmem_tx_we[0])]
we_non_numa_rb_mean = [(rb_dram_we[0]), (rb_vmem_we[0]), (rb_pmem_we[0]), (rb_pmem_tx_we[0])]
we_non_numa_ar_stdev = [(ar_dram_stdev_we[0]), (ar_vmem_stdev_we[0]), (ar_pmem_stdev_we[0]), (ar_pmem_tx_stdev_we[0])]
we_non_numa_ll_stdev = [(ll_dram_stdev_we[0]), (ll_vmem_stdev_we[0]), (ll_pmem_stdev_we[0]), (ll_pmem_tx_stdev_we[0])]
we_non_numa_ht_stdev = [(ht_dram_stdev_we[0]), (ht_vmem_stdev_we[0]), (ht_pmem_stdev_we[0]), (ht_pmem_tx_stdev_we[0])]
we_non_numa_bt_stdev = [(bt_dram_stdev_we[0]), (bt_vmem_stdev_we[0]), (bt_pmem_stdev_we[0]), (bt_pmem_tx_stdev_we[0])]
we_non_numa_bp_stdev = [(bp_dram_stdev_we[0]), (bp_vmem_stdev_we[0]), (bp_pmem_stdev_we[0]), (bp_pmem_tx_stdev_we[0])]
we_non_numa_sk_stdev = [(sk_dram_stdev_we[0]), (sk_vmem_stdev_we[0]), (sk_pmem_stdev_we[0]), (sk_pmem_tx_stdev_we[0])]
we_non_numa_rb_stdev = [(rb_dram_stdev_we[0]), (rb_vmem_stdev_we[0]), (rb_pmem_stdev_we[0]), (rb_pmem_tx_stdev_we[0])]
######################[plotting array graph]######################
plt.rcParams.update({'font.size': 16})
plt.rcParams["font.weight"] = "bold"
plt.rcParams["axes.labelweight"] = "bold"
plt.figure(figsize=(10,3))
##### WA
# Set position of bar on X axis
wa_numa_ar = np.arange(len(wa_numa_ar_mean))
wa_non_numa_ar = [x + barWidth for x in wa_numa_ar]
wa_ar_plt = plt.subplot(1, 2, 1)
# Make the plot
wa_numa_ar_bar = wa_ar_plt.bar(wa_numa_ar, wa_numa_ar_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=wa_numa_ar_stdev, capsize=3)
wa_non_numa_ar_bar = wa_ar_plt.bar(wa_non_numa_ar, wa_non_numa_ar_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=wa_non_numa_ar_stdev, capsize=3)
# Add xticks on the middle of the group bars
wa_ar_plt.set_title('100\% Write', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_ar_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_ar_mean))])
wa_ar_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_ar_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,12000])
# Add counts above the two bar graphs
for rect in wa_numa_ar_bar + wa_non_numa_ar_bar:
height = rect.get_height()
wa_ar_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### WE
# Set position of bar on X axis
we_numa_ar = np.arange(len(we_numa_ar_mean))
we_non_numa_ar = [x + barWidth for x in we_numa_ar]
we_ar_plt = plt.subplot(1, 2, 2)
# Make the plot
we_numa_ar_bar = we_ar_plt.bar(we_numa_ar, we_numa_ar_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=we_numa_ar_stdev, capsize=3)
we_non_numa_ar_bar = we_ar_plt.bar(we_non_numa_ar, we_non_numa_ar_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=we_non_numa_ar_stdev, capsize=3)
# Add xticks on the middle of the group bars
we_ar_plt.set_title('100\% Read', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_ar_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_ar_mean))])
we_ar_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_ar_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,12000])
# Add counts above the two bar graphs
for rect in we_numa_ar_bar + we_non_numa_ar_bar:
height = rect.get_height()
we_ar_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
plt.legend(ncol=2, bbox_to_anchor=(0.40, 1.60), fancybox=True, shadow=True, fontsize=14)
plt.suptitle('Array Benchmark', y=1.10)
pdf.savefig(bbox_inches = 'tight')
######################[plotted array graph]######################
######################[plotting linkedlist graph]######################
plt.rcParams.update({'font.size': 16})
plt.rcParams["font.weight"] = "bold"
plt.rcParams["axes.labelweight"] = "bold"
plt.figure(figsize=(10,3))
##### WA
# Set position of bar on X axis
wa_numa_ll = np.arange(len(wa_numa_ll_mean))
wa_non_numa_ll = [x + barWidth for x in wa_numa_ll]
wa_ll_plt = plt.subplot(1, 2, 1)
# Make the plot
wa_numa_ll_bar = wa_ll_plt.bar(wa_numa_ll, wa_numa_ll_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=wa_numa_ll_stdev, capsize=3)
wa_non_numa_ll_bar = wa_ll_plt.bar(wa_non_numa_ll, wa_non_numa_ll_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=wa_non_numa_ll_stdev, capsize=3)
# Add xticks on the middle of the group bars
wa_ll_plt.set_title('100\% Write', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_ll_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_ll_mean))])
wa_ll_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_ll_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,7500])
# Add counts above the two bar graphs
for rect in wa_numa_ll_bar + wa_non_numa_ll_bar:
height = rect.get_height()
wa_ll_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### WE
# Set position of bar on X axis
we_numa_ll = np.arange(len(we_numa_ll_mean))
we_non_numa_ll = [x + barWidth for x in we_numa_ll]
we_ll_plt = plt.subplot(1, 2, 2)
# Make the plot
we_numa_ll_bar = we_ll_plt.bar(we_numa_ll, we_numa_ll_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=we_numa_ll_stdev, capsize=3)
we_non_numa_ll_bar = we_ll_plt.bar(we_non_numa_ll, we_non_numa_ll_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=we_non_numa_ll_stdev, capsize=3)
# Add xticks on the middle of the group bars
we_ll_plt.set_title('100\% Read', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_ll_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_ll_mean))])
we_ll_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_ll_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,7500])
# Add counts above the two bar graphs
for rect in we_numa_ll_bar + we_non_numa_ll_bar:
height = rect.get_height()
we_ll_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
plt.legend(ncol=2, bbox_to_anchor=(0.40, 1.60), fancybox=True, shadow=True, fontsize=14)
plt.suptitle('Linkedlist Benchmark', y=1.10)
pdf.savefig(bbox_inches = 'tight')
######################[plotted linkedlist graph]######################
######################[plotting hashtable graph]######################
plt.rcParams.update({'font.size': 16})
plt.rcParams["font.weight"] = "bold"
plt.rcParams["axes.labelweight"] = "bold"
plt.figure(figsize=(10,3))
##### WA
# Set position of bar on X axis
wa_numa_ht = np.arange(len(wa_numa_ht_mean))
wa_non_numa_ht = [x + barWidth for x in wa_numa_ht]
wa_ht_plt = plt.subplot(1, 2, 1)
# Make the plot
wa_numa_ht_bar = wa_ht_plt.bar(wa_numa_ht, wa_numa_ht_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=wa_numa_ht_stdev, capsize=3)
wa_non_numa_ht_bar = wa_ht_plt.bar(wa_non_numa_ht, wa_non_numa_ht_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=wa_non_numa_ht_stdev, capsize=3)
# Add xticks on the middle of the group bars
wa_ht_plt.set_title('100\% Write', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_ht_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_ht_mean))])
wa_ht_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_ht_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,7500])
# Add counts above the two bar graphs
for rect in wa_numa_ht_bar + wa_non_numa_ht_bar:
height = rect.get_height()
wa_ht_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### WE
# Set position of bar on X axis
we_numa_ht = np.arange(len(we_numa_ht_mean))
we_non_numa_ht = [x + barWidth for x in we_numa_ht]
we_ht_plt = plt.subplot(1, 2, 2)
# Make the plot
we_numa_ht_bar = we_ht_plt.bar(we_numa_ht, we_numa_ht_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=we_numa_ht_stdev, capsize=3)
we_non_numa_ht_bar = we_ht_plt.bar(we_non_numa_ht, we_non_numa_ht_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=we_non_numa_ht_stdev, capsize=3)
# Add xticks on the middle of the group bars
we_ht_plt.set_title('100\% Read', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_ht_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_ht_mean))])
we_ht_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_ht_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,7500])
# Add counts above the two bar graphs
for rect in we_numa_ht_bar + we_non_numa_ht_bar:
height = rect.get_height()
we_ht_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
plt.legend(ncol=2, bbox_to_anchor=(0.40, 1.60), fancybox=True, shadow=True, fontsize=14)
plt.suptitle('Hashtable Benchmark', y=1.10)
pdf.savefig(bbox_inches = 'tight')
######################[plotted hashtable graph]######################
######################[plotting skiplist graph]######################
plt.rcParams.update({'font.size': 16})
plt.rcParams["font.weight"] = "bold"
plt.rcParams["axes.labelweight"] = "bold"
plt.figure(figsize=(10,3))
##### WA
# Set position of bar on X axis
wa_numa_sk = np.arange(len(wa_numa_sk_mean))
wa_non_numa_sk = [x + barWidth for x in wa_numa_sk]
wa_sk_plt = plt.subplot(1, 2, 1)
# Make the plot
wa_numa_sk_bar = wa_sk_plt.bar(wa_numa_sk, wa_numa_sk_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=wa_numa_sk_stdev, capsize=3)
wa_non_numa_sk_bar = wa_sk_plt.bar(wa_non_numa_sk, wa_non_numa_sk_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=wa_non_numa_sk_stdev, capsize=3)
# Add xticks on the middle of the group bars
wa_sk_plt.set_title('100\% Write', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_sk_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_sk_mean))])
wa_sk_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_sk_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,7500])
# Add counts above the two bar graphs
for rect in wa_numa_sk_bar + wa_non_numa_sk_bar:
height = rect.get_height()
wa_sk_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### WE
# Set position of bar on X axis
we_numa_sk = np.arange(len(we_numa_sk_mean))
we_non_numa_sk = [x + barWidth for x in we_numa_sk]
we_sk_plt = plt.subplot(1, 2, 2)
# Make the plot
we_numa_sk_bar = we_sk_plt.bar(we_numa_sk, we_numa_sk_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=we_numa_sk_stdev, capsize=3)
we_non_numa_sk_bar = we_sk_plt.bar(we_non_numa_sk, we_non_numa_sk_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=we_non_numa_sk_stdev, capsize=3)
# Add xticks on the middle of the group bars
we_sk_plt.set_title('100\% Read', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_sk_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_sk_mean))])
we_sk_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_sk_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,7500])
# Add counts above the two bar graphs
for rect in we_numa_sk_bar + we_non_numa_sk_bar:
height = rect.get_height()
we_sk_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
plt.legend(ncol=2, bbox_to_anchor=(0.40, 1.60), fancybox=True, shadow=True, fontsize=14)
plt.suptitle('Skiplist Benchmark', y=1.10)
pdf.savefig(bbox_inches = 'tight')
######################[plotted skiplist graph]######################
######################[plotting b-tree graph]######################
plt.rcParams.update({'font.size': 16})
plt.rcParams["font.weight"] = "bold"
plt.rcParams["axes.labelweight"] = "bold"
plt.figure(figsize=(10,3))
##### WA
# Set position of bar on X axis
wa_numa_bt = np.arange(len(wa_numa_bt_mean))
wa_non_numa_bt = [x + barWidth for x in wa_numa_bt]
wa_bt_plt = plt.subplot(1, 2, 1)
# Make the plot
wa_numa_bt_bar = wa_bt_plt.bar(wa_numa_bt, wa_numa_bt_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=wa_numa_bt_stdev, capsize=3)
wa_non_numa_bt_bar = wa_bt_plt.bar(wa_non_numa_bt, wa_non_numa_bt_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=wa_non_numa_bt_stdev, capsize=3)
# Add xticks on the middle of the group bars
wa_bt_plt.set_title('100\% Write', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_bt_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_bt_mean))])
wa_bt_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_bt_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,7500])
# Add counts above the two bar graphs
for rect in wa_numa_bt_bar + wa_non_numa_bt_bar:
height = rect.get_height()
wa_bt_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### WE
# Set position of bar on X axis
we_numa_bt = np.arange(len(we_numa_bt_mean))
we_non_numa_bt = [x + barWidth for x in we_numa_bt]
we_bt_plt = plt.subplot(1, 2, 2)
# Make the plot
we_numa_bt_bar = we_bt_plt.bar(we_numa_bt, we_numa_bt_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=we_numa_bt_stdev, capsize=3)
we_non_numa_bt_bar = we_bt_plt.bar(we_non_numa_bt, we_non_numa_bt_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=we_non_numa_bt_stdev, capsize=3)
# Add xticks on the middle of the group bars
we_bt_plt.set_title('100\% Read', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_bt_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_bt_mean))])
we_bt_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_bt_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,7500])
# Add counts above the two bar graphs
for rect in we_numa_bt_bar + we_non_numa_bt_bar:
height = rect.get_height()
we_bt_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
plt.legend(ncol=2, bbox_to_anchor=(0.40, 1.60), fancybox=True, shadow=True, fontsize=14)
plt.suptitle('B-Tree Benchmark', y=1.10)
pdf.savefig(bbox_inches = 'tight')
######################[plotted b-tree graph]######################
######################[plotting b+-tree graph]######################
plt.rcParams.update({'font.size': 16})
plt.rcParams["font.weight"] = "bold"
plt.rcParams["axes.labelweight"] = "bold"
plt.figure(figsize=(10,3))
##### WA
# Set position of bar on X axis
wa_numa_bp = np.arange(len(wa_numa_bp_mean))
wa_non_numa_bp = [x + barWidth for x in wa_numa_bp]
wa_bp_plt = plt.subplot(1, 2, 1)
# Make the plot
wa_numa_bp_bar = wa_bp_plt.bar(wa_numa_bp, wa_numa_bp_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=wa_numa_bp_stdev, capsize=3)
wa_non_numa_bp_bar = wa_bp_plt.bar(wa_non_numa_bp, wa_non_numa_bp_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=wa_non_numa_bp_stdev, capsize=3)
# Add xticks on the middle of the group bars
wa_bp_plt.set_title('100\% Write', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_bp_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_bp_mean))])
wa_bp_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_bp_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,7500])
# Add counts above the two bar graphs
for rect in wa_numa_bp_bar + wa_non_numa_bp_bar:
height = rect.get_height()
wa_bp_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### WE
# Set position of bar on X axis
we_numa_bp = np.arange(len(we_numa_bp_mean))
we_non_numa_bp = [x + barWidth for x in we_numa_bp]
we_bp_plt = plt.subplot(1, 2, 2)
# Make the plot
we_numa_bp_bar = we_bp_plt.bar(we_numa_bp, we_numa_bp_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=we_numa_bp_stdev, capsize=3)
we_non_numa_bp_bar = we_bp_plt.bar(we_non_numa_bp, we_non_numa_bp_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=we_non_numa_bp_stdev, capsize=3)
# Add xticks on the middle of the group bars
we_bp_plt.set_title('100\% Read', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_bp_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_bp_mean))])
we_bp_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_bp_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,7500])
# Add counts above the two bar graphs
for rect in we_numa_bp_bar + we_non_numa_bp_bar:
height = rect.get_height()
we_bp_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
plt.legend(ncol=2, bbox_to_anchor=(0.40, 1.60), fancybox=True, shadow=True, fontsize=14)
plt.suptitle('B+Tree Benchmark', y=1.10)
pdf.savefig(bbox_inches = 'tight')
######################[plotted b+-tree graph]######################
######################[plotting rb-tree graph]######################
plt.rcParams.update({'font.size': 16})
plt.rcParams["font.weight"] = "bold"
plt.rcParams["axes.labelweight"] = "bold"
plt.figure(figsize=(10,3))
##### WA
# Set position of bar on X axis
wa_numa_rb = np.arange(len(wa_numa_rb_mean))
wa_non_numa_rb = [x + barWidth for x in wa_numa_rb]
wa_rb_plt = plt.subplot(1, 2, 1)
# Make the plot
wa_numa_rb_bar = wa_rb_plt.bar(wa_numa_rb, wa_numa_rb_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=wa_numa_rb_stdev, capsize=3)
wa_non_numa_rb_bar = wa_rb_plt.bar(wa_non_numa_rb, wa_non_numa_rb_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=wa_non_numa_rb_stdev, capsize=3)
# Add xticks on the middle of the group bars
wa_rb_plt.set_title('100\% Write', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_rb_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_rb_mean))])
wa_rb_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_rb_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,7500])
# Add counts above the two bar graphs
for rect in wa_numa_rb_bar + wa_non_numa_rb_bar:
height = rect.get_height()
wa_rb_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### WE
# Set position of bar on X axis
we_numa_rb = np.arange(len(we_numa_rb_mean))
we_non_numa_rb = [x + barWidth for x in we_numa_rb]
we_rb_plt = plt.subplot(1, 2, 2)
# Make the plot
we_numa_rb_bar = we_rb_plt.bar(we_numa_rb, we_numa_rb_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='black', label='NUMA', yerr=we_numa_rb_stdev, capsize=3)
we_non_numa_rb_bar = we_rb_plt.bar(we_non_numa_rb, we_non_numa_rb_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='black', label='NON NUMA', yerr=we_non_numa_rb_stdev, capsize=3)
# Add xticks on the middle of the group bars
we_rb_plt.set_title('100\% Read', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_rb_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_rb_mean))])
we_rb_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_rb_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,7500])
# Add counts above the two bar graphs
for rect in we_numa_rb_bar + we_non_numa_rb_bar:
height = rect.get_height()
we_rb_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
plt.legend(ncol=2, bbox_to_anchor=(0.40, 1.60), fancybox=True, shadow=True, fontsize=14)
plt.suptitle('RB-Tree Benchmark', y=1.10)
pdf.savefig(bbox_inches = 'tight')
######################[plotted rb-tree graph]######################
pdf.close()
# +
# libraries
import numpy as np
import matplotlib
matplotlib.use("PDF")
import matplotlib.pyplot as plt
import matplotlib.backends as pdf_backend
from statistics import mean, stdev
pdf = pdf_backend.backend_pdf.PdfPages("msst20_eval_6_1.pdf")
plt.rcParams['ps.useafm'] = True
plt.rcParams['pdf.use14corefonts'] = True
plt.rcParams['text.usetex'] = True
# set width of bar
barWidth = 0.35
################### WA DATA ###################
wa_numa_ar_mean = [(numa_ar_dram_wa[0]), (numa_ar_vmem_wa[0]), (numa_ar_pmem_wa[0]), (numa_ar_pmem_tx_wa[0])]
wa_numa_ll_mean = [(numa_ll_dram_wa[0]), (numa_ll_vmem_wa[0]), (numa_ll_pmem_wa[0]), (numa_ll_pmem_tx_wa[0])]
wa_numa_ht_mean = [(numa_ht_dram_wa[0]), (numa_ht_vmem_wa[0]), (numa_ht_pmem_wa[0]), (numa_ht_pmem_tx_wa[0])]
wa_numa_bt_mean = [(numa_bt_dram_wa[0]), (numa_bt_vmem_wa[0]), (numa_bt_pmem_wa[0]), (numa_bt_pmem_tx_wa[0])]
wa_numa_bp_mean = [(numa_bp_dram_wa[0]), (numa_bp_vmem_wa[0]), (numa_bp_pmem_wa[0]), (numa_bp_pmem_tx_wa[0])]
wa_numa_sk_mean = [(numa_sk_dram_wa[0]), (numa_sk_vmem_wa[0]), (numa_sk_pmem_wa[0]), (numa_sk_pmem_tx_wa[0])]
wa_numa_rb_mean = [(numa_rb_dram_wa[0]), (numa_rb_vmem_wa[0]), (numa_rb_pmem_wa[0]), (numa_rb_pmem_tx_wa[0])]
wa_numa_ar_stdev = [(numa_ar_dram_stdev_wa[0]), (numa_ar_vmem_stdev_wa[0]), (numa_ar_pmem_stdev_wa[0]), (numa_ar_pmem_tx_stdev_wa[0])]
wa_numa_ll_stdev = [(numa_ll_dram_stdev_wa[0]), (numa_ll_vmem_stdev_wa[0]), (numa_ll_pmem_stdev_wa[0]), (numa_ll_pmem_tx_stdev_wa[0])]
wa_numa_ht_stdev = [(numa_ht_dram_stdev_wa[0]), (numa_ht_vmem_stdev_wa[0]), (numa_ht_pmem_stdev_wa[0]), (numa_ht_pmem_tx_stdev_wa[0])]
wa_numa_bt_stdev = [(numa_bt_dram_stdev_wa[0]), (numa_bt_vmem_stdev_wa[0]), (numa_bt_pmem_stdev_wa[0]), (numa_bt_pmem_tx_stdev_wa[0])]
wa_numa_bp_stdev = [(numa_bp_dram_stdev_wa[0]), (numa_bp_vmem_stdev_wa[0]), (numa_bp_pmem_stdev_wa[0]), (numa_bp_pmem_tx_stdev_wa[0])]
wa_numa_sk_stdev = [(numa_sk_dram_stdev_wa[0]), (numa_sk_vmem_stdev_wa[0]), (numa_sk_pmem_stdev_wa[0]), (numa_sk_pmem_tx_stdev_wa[0])]
wa_numa_rb_stdev = [(numa_rb_dram_stdev_wa[0]), (numa_rb_vmem_stdev_wa[0]), (numa_rb_pmem_stdev_wa[0]), (numa_rb_pmem_tx_stdev_wa[0])]
wa_non_numa_ar_mean = [(ar_dram_wa[0]), (ar_vmem_wa[0]), (ar_pmem_wa[0]), (ar_pmem_tx_wa[0])]
wa_non_numa_ll_mean = [(ll_dram_wa[0]), (ll_vmem_wa[0]), (ll_pmem_wa[0]), (ll_pmem_tx_wa[0])]
wa_non_numa_ht_mean = [(ht_dram_wa[0]), (ht_vmem_wa[0]), (ht_pmem_wa[0]), (ht_pmem_tx_wa[0])]
wa_non_numa_bt_mean = [(bt_dram_wa[0]), (bt_vmem_wa[0]), (bt_pmem_wa[0]), (bt_pmem_tx_wa[0])]
wa_non_numa_bp_mean = [(bp_dram_wa[0]), (bp_vmem_wa[0]), (bp_pmem_wa[0]), (bp_pmem_tx_wa[0])]
wa_non_numa_sk_mean = [(sk_dram_wa[0]), (sk_vmem_wa[0]), (sk_pmem_wa[0]), (sk_pmem_tx_wa[0])]
wa_non_numa_rb_mean = [(rb_dram_wa[0]), (rb_vmem_wa[0]), (rb_pmem_wa[0]), (rb_pmem_tx_wa[0])]
wa_non_numa_ar_stdev = [(ar_dram_stdev_wa[0]), (ar_vmem_stdev_wa[0]), (ar_pmem_stdev_wa[0]), (ar_pmem_tx_stdev_wa[0])]
wa_non_numa_ll_stdev = [(ll_dram_stdev_wa[0]), (ll_vmem_stdev_wa[0]), (ll_pmem_stdev_wa[0]), (ll_pmem_tx_stdev_wa[0])]
wa_non_numa_ht_stdev = [(ht_dram_stdev_wa[0]), (ht_vmem_stdev_wa[0]), (ht_pmem_stdev_wa[0]), (ht_pmem_tx_stdev_wa[0])]
wa_non_numa_bt_stdev = [(bt_dram_stdev_wa[0]), (bt_vmem_stdev_wa[0]), (bt_pmem_stdev_wa[0]), (bt_pmem_tx_stdev_wa[0])]
wa_non_numa_bp_stdev = [(bp_dram_stdev_wa[0]), (bp_vmem_stdev_wa[0]), (bp_pmem_stdev_wa[0]), (bp_pmem_tx_stdev_wa[0])]
wa_non_numa_sk_stdev = [(sk_dram_stdev_wa[0]), (sk_vmem_stdev_wa[0]), (sk_pmem_stdev_wa[0]), (sk_pmem_tx_stdev_wa[0])]
wa_non_numa_rb_stdev = [(rb_dram_stdev_wa[0]), (rb_vmem_stdev_wa[0]), (rb_pmem_stdev_wa[0]), (rb_pmem_tx_stdev_wa[0])]
################### WE DATA ###################
we_numa_ar_mean = [(numa_ar_dram_we[0]), (numa_ar_vmem_we[0]), (numa_ar_pmem_we[0]), (numa_ar_pmem_tx_we[0])]
we_numa_ll_mean = [(numa_ll_dram_we[0]), (numa_ll_vmem_we[0]), (numa_ll_pmem_we[0]), (numa_ll_pmem_tx_we[0])]
we_numa_ht_mean = [(numa_ht_dram_we[0]), (numa_ht_vmem_we[0]), (numa_ht_pmem_we[0]), (numa_ht_pmem_tx_we[0])]
we_numa_bt_mean = [(numa_bt_dram_we[0]), (numa_bt_vmem_we[0]), (numa_bt_pmem_we[0]), (numa_bt_pmem_tx_we[0])]
we_numa_bp_mean = [(numa_bp_dram_we[0]), (numa_bp_vmem_we[0]), (numa_bp_pmem_we[0]), (numa_bp_pmem_tx_we[0])]
we_numa_sk_mean = [(numa_sk_dram_we[0]), (numa_sk_vmem_we[0]), (numa_sk_pmem_we[0]), (numa_sk_pmem_tx_we[0])]
we_numa_rb_mean = [(numa_rb_dram_we[0]), (numa_rb_vmem_we[0]), (numa_rb_pmem_we[0]), (numa_rb_pmem_tx_we[0])]
we_numa_ar_stdev = [(numa_ar_dram_stdev_we[0]), (numa_ar_vmem_stdev_we[0]), (numa_ar_pmem_stdev_we[0]), (numa_ar_pmem_tx_stdev_we[0])]
we_numa_ll_stdev = [(numa_ll_dram_stdev_we[0]), (numa_ll_vmem_stdev_we[0]), (numa_ll_pmem_stdev_we[0]), (numa_ll_pmem_tx_stdev_we[0])]
we_numa_ht_stdev = [(numa_ht_dram_stdev_we[0]), (numa_ht_vmem_stdev_we[0]), (numa_ht_pmem_stdev_we[0]), (numa_ht_pmem_tx_stdev_we[0])]
we_numa_bt_stdev = [(numa_bt_dram_stdev_we[0]), (numa_bt_vmem_stdev_we[0]), (numa_bt_pmem_stdev_we[0]), (numa_bt_pmem_tx_stdev_we[0])]
we_numa_bp_stdev = [(numa_bp_dram_stdev_we[0]), (numa_bp_vmem_stdev_we[0]), (numa_bp_pmem_stdev_we[0]), (numa_bp_pmem_tx_stdev_we[0])]
we_numa_sk_stdev = [(numa_sk_dram_stdev_we[0]), (numa_sk_vmem_stdev_we[0]), (numa_sk_pmem_stdev_we[0]), (numa_sk_pmem_tx_stdev_we[0])]
we_numa_rb_stdev = [(numa_rb_dram_stdev_we[0]), (numa_rb_vmem_stdev_we[0]), (numa_rb_pmem_stdev_we[0]), (numa_rb_pmem_tx_stdev_we[0])]
we_non_numa_ar_mean = [(ar_dram_we[0]), (ar_vmem_we[0]), (ar_pmem_we[0]), (ar_pmem_tx_we[0])]
we_non_numa_ll_mean = [(ll_dram_we[0]), (ll_vmem_we[0]), (ll_pmem_we[0]), (ll_pmem_tx_we[0])]
we_non_numa_ht_mean = [(ht_dram_we[0]), (ht_vmem_we[0]), (ht_pmem_we[0]), (ht_pmem_tx_we[0])]
we_non_numa_bt_mean = [(bt_dram_we[0]), (bt_vmem_we[0]), (bt_pmem_we[0]), (bt_pmem_tx_we[0])]
we_non_numa_bp_mean = [(bp_dram_we[0]), (bp_vmem_we[0]), (bp_pmem_we[0]), (bp_pmem_tx_we[0])]
we_non_numa_sk_mean = [(sk_dram_we[0]), (sk_vmem_we[0]), (sk_pmem_we[0]), (sk_pmem_tx_we[0])]
we_non_numa_rb_mean = [(rb_dram_we[0]), (rb_vmem_we[0]), (rb_pmem_we[0]), (rb_pmem_tx_we[0])]
we_non_numa_ar_stdev = [(ar_dram_stdev_we[0]), (ar_vmem_stdev_we[0]), (ar_pmem_stdev_we[0]), (ar_pmem_tx_stdev_we[0])]
we_non_numa_ll_stdev = [(ll_dram_stdev_we[0]), (ll_vmem_stdev_we[0]), (ll_pmem_stdev_we[0]), (ll_pmem_tx_stdev_we[0])]
we_non_numa_ht_stdev = [(ht_dram_stdev_we[0]), (ht_vmem_stdev_we[0]), (ht_pmem_stdev_we[0]), (ht_pmem_tx_stdev_we[0])]
we_non_numa_bt_stdev = [(bt_dram_stdev_we[0]), (bt_vmem_stdev_we[0]), (bt_pmem_stdev_we[0]), (bt_pmem_tx_stdev_we[0])]
we_non_numa_bp_stdev = [(bp_dram_stdev_we[0]), (bp_vmem_stdev_we[0]), (bp_pmem_stdev_we[0]), (bp_pmem_tx_stdev_we[0])]
we_non_numa_sk_stdev = [(sk_dram_stdev_we[0]), (sk_vmem_stdev_we[0]), (sk_pmem_stdev_we[0]), (sk_pmem_tx_stdev_we[0])]
we_non_numa_rb_stdev = [(rb_dram_stdev_we[0]), (rb_vmem_stdev_we[0]), (rb_pmem_stdev_we[0]), (rb_pmem_tx_stdev_we[0])]
######################[plotting WA graph]######################
plt.rcParams.update({'font.size': 16})
plt.rcParams["font.weight"] = "bold"
plt.rcParams["axes.labelweight"] = "bold"
plt.rcParams['xtick.labelsize'] = 14
plt.figure(figsize=(30,3))
##### Array
# Set position of bar on X axis
wa_numa_ar = np.arange(len(wa_numa_ar_mean))
wa_non_numa_ar = [x + barWidth for x in wa_numa_ar]
wa_ar_plt = plt.subplot(1, 7, 1)
# Make the plot
wa_numa_ar_bar = wa_ar_plt.bar(wa_numa_ar, wa_numa_ar_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=wa_numa_ar_stdev, capsize=3, hatch="//")
wa_non_numa_ar_bar = wa_ar_plt.bar(wa_non_numa_ar, wa_non_numa_ar_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=wa_non_numa_ar_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
wa_ar_plt.set_title('ArrayList', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_ar_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_ar_mean))])
wa_ar_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_ar_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,6500])
# Add counts above the two bar graphs
for rect in wa_numa_ar_bar + wa_non_numa_ar_bar:
height = rect.get_height()
wa_ar_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### Linkedlist
# Set position of bar on X axis
wa_numa_ll = np.arange(len(wa_numa_ll_mean))
wa_non_numa_ll = [x + barWidth for x in wa_numa_ll]
wa_ll_plt = plt.subplot(1, 7, 2)
# Make the plot
wa_numa_ll_bar = wa_ll_plt.bar(wa_numa_ll, wa_numa_ll_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=wa_numa_ll_stdev, capsize=3, hatch="//")
wa_non_numa_ll_bar = wa_ll_plt.bar(wa_non_numa_ll, wa_non_numa_ll_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=wa_non_numa_ll_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
wa_ll_plt.set_title('LinkedList', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_ll_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_ll_mean))])
wa_ll_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_ll_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,5500])
# Add counts above the two bar graphs
for rect in wa_numa_ll_bar + wa_non_numa_ll_bar:
height = rect.get_height()
wa_ll_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### Hashtable
# Set position of bar on X axis
wa_numa_ht = np.arange(len(wa_numa_ht_mean))
wa_non_numa_ht = [x + barWidth for x in wa_numa_ht]
wa_ht_plt = plt.subplot(1, 7, 3)
# Make the plot
wa_numa_ht_bar = wa_ht_plt.bar(wa_numa_ht, wa_numa_ht_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=wa_numa_ht_stdev, capsize=3, hatch="//")
wa_non_numa_ht_bar = wa_ht_plt.bar(wa_non_numa_ht, wa_non_numa_ht_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=wa_non_numa_ht_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
wa_ht_plt.set_title('Hashtable', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_ht_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_ht_mean))])
wa_ht_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_ht_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,4500])
# Add counts above the two bar graphs
for rect in wa_numa_ht_bar + wa_non_numa_ht_bar:
height = rect.get_height()
wa_ht_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 50), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### Skiplist
# Set position of bar on X axis
wa_numa_sk = np.arange(len(wa_numa_sk_mean))
wa_non_numa_sk = [x + barWidth for x in wa_numa_sk]
wa_sk_plt = plt.subplot(1, 7, 4)
# Make the plot
wa_numa_sk_bar = wa_sk_plt.bar(wa_numa_sk, wa_numa_sk_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=wa_numa_sk_stdev, capsize=3, hatch="//")
wa_non_numa_sk_bar = wa_sk_plt.bar(wa_non_numa_sk, wa_non_numa_sk_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=wa_non_numa_sk_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
wa_sk_plt.set_title('Skiplist', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_sk_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_sk_mean))])
wa_sk_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_sk_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,1200])
# Add counts above the two bar graphs
for rect in wa_numa_sk_bar + wa_non_numa_sk_bar:
height = rect.get_height()
wa_sk_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 50), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### B-tree
# Set position of bar on X axis
wa_numa_bt = np.arange(len(wa_numa_bt_mean))
wa_non_numa_bt = [x + barWidth for x in wa_numa_bt]
wa_bt_plt = plt.subplot(1, 7, 5)
# Make the plot
wa_numa_bt_bar = wa_bt_plt.bar(wa_numa_bt, wa_numa_bt_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=wa_numa_bt_stdev, capsize=3, hatch="//")
wa_non_numa_bt_bar = wa_bt_plt.bar(wa_non_numa_bt, wa_non_numa_bt_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=wa_non_numa_bt_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
wa_bt_plt.set_title('B-Tree', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_bt_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_bt_mean))])
wa_bt_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_bt_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,2000])
# Add counts above the two bar graphs
for rect in wa_numa_bt_bar + wa_non_numa_bt_bar:
height = rect.get_height()
wa_bt_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 50), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### B+-tree
# Set position of bar on X axis
wa_numa_bp = np.arange(len(wa_numa_bp_mean))
wa_non_numa_bp = [x + barWidth for x in wa_numa_bp]
wa_bp_plt = plt.subplot(1, 7, 6)
# Make the plot
wa_numa_bp_bar = wa_bp_plt.bar(wa_numa_bp, wa_numa_bp_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=wa_numa_bp_stdev, capsize=3, hatch="//")
wa_non_numa_bp_bar = wa_bp_plt.bar(wa_non_numa_bp, wa_non_numa_bp_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=wa_non_numa_bp_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
wa_bp_plt.set_title('B+Tree', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_bp_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_bp_mean))])
wa_bp_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_bp_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,3000])
# Add counts above the two bar graphs
for rect in wa_numa_bp_bar + wa_non_numa_bp_bar:
height = rect.get_height()
wa_bp_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 50), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### RB-tree
# Set position of bar on X axis
wa_numa_rb = np.arange(len(wa_numa_rb_mean))
wa_non_numa_rb = [x + barWidth for x in wa_numa_rb]
wa_rb_plt = plt.subplot(1, 7, 7)
# Make the plot
wa_numa_rb_bar = wa_rb_plt.bar(wa_numa_rb, wa_numa_rb_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=wa_numa_rb_stdev, capsize=3, hatch="//")
wa_non_numa_rb_bar = wa_rb_plt.bar(wa_non_numa_rb, wa_non_numa_rb_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=wa_non_numa_rb_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
wa_rb_plt.set_title('RBTree', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
wa_rb_plt.set_xticks([r + 0.50*barWidth for r in range(len(wa_numa_rb_mean))])
wa_rb_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
wa_rb_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,2000])
# Add counts above the two bar graphs
for rect in wa_numa_rb_bar + wa_non_numa_rb_bar:
height = rect.get_height()
wa_rb_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 50), '%d' % int(height), ha='center', va='bottom', rotation=90)
plt.legend(ncol=4, bbox_to_anchor=(-2.25, 1.65), fancybox=True, shadow=True, fontsize=20)
plt.suptitle('(a) 100\% Write Workload', y=1.10)
pdf.savefig(bbox_inches = 'tight')
######################[plotting WE graph]######################
plt.rcParams.update({'font.size': 16})
plt.rcParams["font.weight"] = "bold"
plt.rcParams["axes.labelweight"] = "bold"
plt.rcParams['xtick.labelsize'] = 14
plt.figure(figsize=(30,3))
##### Array
# Set position of bar on X axis
we_numa_ar = np.arange(len(we_numa_ar_mean))
we_non_numa_ar = [x + barWidth for x in we_numa_ar]
we_ar_plt = plt.subplot(1, 7, 1)
# Make the plot
we_numa_ar_bar = we_ar_plt.bar(we_numa_ar, we_numa_ar_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=we_numa_ar_stdev, capsize=3, hatch="//")
we_non_numa_ar_bar = we_ar_plt.bar(we_non_numa_ar, we_non_numa_ar_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=we_non_numa_ar_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
we_ar_plt.set_title('ArrayList', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_ar_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_ar_mean))])
we_ar_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_ar_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,12000])
# Add counts above the two bar graphs
for rect in we_numa_ar_bar + we_non_numa_ar_bar:
height = rect.get_height()
we_ar_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### Linkedlist
# Set position of bar on X axis
we_numa_ll = np.arange(len(we_numa_ll_mean))
we_non_numa_ll = [x + barWidth for x in we_numa_ll]
we_ll_plt = plt.subplot(1, 7, 2)
# Make the plot
we_numa_ll_bar = we_ll_plt.bar(we_numa_ll, we_numa_ll_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=we_numa_ll_stdev, capsize=3, hatch="//")
we_non_numa_ll_bar = we_ll_plt.bar(we_non_numa_ll, we_non_numa_ll_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=we_non_numa_ll_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
we_ll_plt.set_title('LinkedList', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_ll_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_ll_mean))])
we_ll_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_ll_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,6000])
# Add counts above the two bar graphs
for rect in we_numa_ll_bar + we_non_numa_ll_bar:
height = rect.get_height()
we_ll_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### Hashtable
# Set position of bar on X axis
we_numa_ht = np.arange(len(we_numa_ht_mean))
we_non_numa_ht = [x + barWidth for x in we_numa_ht]
we_ht_plt = plt.subplot(1, 7, 3)
# Make the plot
we_numa_ht_bar = we_ht_plt.bar(we_numa_ht, we_numa_ht_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=we_numa_ht_stdev, capsize=3, hatch="//")
we_non_numa_ht_bar = we_ht_plt.bar(we_non_numa_ht, we_non_numa_ht_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=we_non_numa_ht_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
we_ht_plt.set_title('Hashtable', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_ht_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_ht_mean))])
we_ht_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_ht_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,6500])
# Add counts above the two bar graphs
for rect in we_numa_ht_bar + we_non_numa_ht_bar:
height = rect.get_height()
we_ht_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### Skiplist
# Set position of bar on X axis
we_numa_sk = np.arange(len(we_numa_sk_mean))
we_non_numa_sk = [x + barWidth for x in we_numa_sk]
we_sk_plt = plt.subplot(1, 7, 4)
# Make the plot
we_numa_sk_bar = we_sk_plt.bar(we_numa_sk, we_numa_sk_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=we_numa_sk_stdev, capsize=3, hatch="//")
we_non_numa_sk_bar = we_sk_plt.bar(we_non_numa_sk, we_non_numa_sk_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=we_non_numa_sk_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
we_sk_plt.set_title('Skiplist', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_sk_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_sk_mean))])
we_sk_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_sk_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,1500])
# Add counts above the two bar graphs
for rect in we_numa_sk_bar + we_non_numa_sk_bar:
height = rect.get_height()
we_sk_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### B-tree
# Set position of bar on X axis
we_numa_bt = np.arange(len(we_numa_bt_mean))
we_non_numa_bt = [x + barWidth for x in we_numa_bt]
we_bt_plt = plt.subplot(1, 7, 5)
# Make the plot
we_numa_bt_bar = we_bt_plt.bar(we_numa_bt, we_numa_bt_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=we_numa_bt_stdev, capsize=3, hatch="//")
we_non_numa_bt_bar = we_bt_plt.bar(we_non_numa_bt, we_non_numa_bt_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=we_non_numa_bt_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
we_bt_plt.set_title('B-Tree', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_bt_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_bt_mean))])
we_bt_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_bt_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,2500])
# Add counts above the two bar graphs
for rect in we_numa_bt_bar + we_non_numa_bt_bar:
height = rect.get_height()
we_bt_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### B+Tree
# Set position of bar on X axis
we_numa_bp = np.arange(len(we_numa_bp_mean))
we_non_numa_bp = [x + barWidth for x in we_numa_bp]
we_bp_plt = plt.subplot(1, 7, 6)
# Make the plot
we_numa_bp_bar = we_bp_plt.bar(we_numa_bp, we_numa_bp_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=we_numa_bp_stdev, capsize=3, hatch="//")
we_non_numa_bp_bar = we_bp_plt.bar(we_non_numa_bp, we_non_numa_bp_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=we_non_numa_bp_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
we_bp_plt.set_title('B+Tree', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_bp_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_bp_mean))])
we_bp_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_bp_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,4500])
# Add counts above the two bar graphs
for rect in we_numa_bp_bar + we_non_numa_bp_bar:
height = rect.get_height()
we_bp_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
##### RB-tree
# Set position of bar on X axis
we_numa_rb = np.arange(len(we_numa_rb_mean))
we_non_numa_rb = [x + barWidth for x in we_numa_rb]
we_rb_plt = plt.subplot(1, 7, 7)
# Make the plot
we_numa_rb_bar = we_rb_plt.bar(we_numa_rb, we_numa_rb_mean, color=(0.1, 0.45, 0.1), width=barWidth, edgecolor='white', label='LOCAL', yerr=we_numa_rb_stdev, capsize=3, hatch="//")
we_non_numa_rb_bar = we_rb_plt.bar(we_non_numa_rb, we_non_numa_rb_mean, color=(0.9, 0, 0), width=barWidth, edgecolor='white', label='NON LOCAL', yerr=we_non_numa_rb_stdev, capsize=3, hatch="--")
# Add xticks on the middle of the group bars
we_rb_plt.set_title('RBTree', fontweight='bold')
# ht_plt.xticks([r + 1.5*barWidth for r in range(len(ht_dram_mean))], ['0(R)/100(W)', '25(R)/75(W)', '50(R)/50(W)', '75(R)/25(W)', '100(R)/0(W)'])
we_rb_plt.set_xticks([r + 0.50*barWidth for r in range(len(we_numa_rb_mean))])
we_rb_plt.set_xticklabels(['DRAM', 'PMEM-\nVolatile', 'PMEM-\nPersist', 'PMEM-\nTrans'])
we_rb_plt.ticklabel_format(axis='y', style='sci', scilimits=(0, 0))
# Add ylim to [0-1200]
# plt.ylabel('throughput (KTPS)', fontweight='bold')
plt.ylim([0,2500])
# Add counts above the two bar graphs
for rect in we_numa_rb_bar + we_non_numa_rb_bar:
height = rect.get_height()
we_rb_plt.text(rect.get_x() + rect.get_width()/2.0, (height + 100), '%d' % int(height), ha='center', va='bottom', rotation=90)
# plt.legend(ncol=2, bbox_to_anchor=(-2.6, 1.60), fancybox=True, shadow=True, fontsize=16)
plt.suptitle('(b) 100\% Read Workload', y=1.10)
pdf.savefig(bbox_inches = 'tight')
pdf.close()
# +
#clear loaded array data
ar_dram_wa.clear()
ar_dram_wb.clear()
ar_dram_wc.clear()
ar_dram_wd.clear()
ar_dram_we.clear()
ar_pmem_wa.clear()
ar_pmem_wb.clear()
ar_pmem_wc.clear()
ar_pmem_wd.clear()
ar_pmem_we.clear()
ar_pmem_tx_wa.clear()
ar_pmem_tx_wb.clear()
ar_pmem_tx_wc.clear()
ar_pmem_tx_wd.clear()
ar_pmem_tx_we.clear()
#clear loaded hashtable data
ht_dram_wa.clear()
ht_dram_wb.clear()
ht_dram_wc.clear()
ht_dram_wd.clear()
ht_dram_we.clear()
ht_pmem_wa.clear()
ht_pmem_wb.clear()
ht_pmem_wc.clear()
ht_pmem_wd.clear()
ht_pmem_we.clear()
ht_pmem_tx_wa.clear()
ht_pmem_tx_wb.clear()
ht_pmem_tx_wc.clear()
ht_pmem_tx_wd.clear()
ht_pmem_tx_we.clear()
#clear loaded btree data
bt_dram_wa.clear()
bt_dram_wb.clear()
bt_dram_wc.clear()
bt_dram_wd.clear()
bt_dram_we.clear()
bt_pmem_wa.clear()
bt_pmem_wb.clear()
bt_pmem_wc.clear()
bt_pmem_wd.clear()
bt_pmem_we.clear()
bt_pmem_tx_wa.clear()
bt_pmem_tx_wb.clear()
bt_pmem_tx_wc.clear()
bt_pmem_tx_wd.clear()
bt_pmem_tx_we.clear()
#clear loaded bplus-tree data
bp_dram_wa.clear()
bp_dram_wb.clear()
bp_dram_wc.clear()
bp_dram_wd.clear()
bp_dram_we.clear()
bp_pmem_wa.clear()
bp_pmem_wb.clear()
bp_pmem_wc.clear()
bp_pmem_wd.clear()
bp_pmem_we.clear()
bp_pmem_tx_wa.clear()
bp_pmem_tx_wb.clear()
bp_pmem_tx_wc.clear()
bp_pmem_tx_wd.clear()
bp_pmem_tx_we.clear()
#clear loaded skiplist data
sk_dram_wa.clear()
sk_dram_wb.clear()
sk_dram_wc.clear()
sk_dram_wd.clear()
sk_dram_we.clear()
sk_pmem_wa.clear()
sk_pmem_wb.clear()
sk_pmem_wc.clear()
sk_pmem_wd.clear()
sk_pmem_we.clear()
sk_pmem_tx_wa.clear()
sk_pmem_tx_wb.clear()
sk_pmem_tx_wc.clear()
sk_pmem_tx_wd.clear()
sk_pmem_tx_we.clear()
#clear loaded rb-tree data
rb_dram_wa.clear()
rb_dram_wb.clear()
rb_dram_wc.clear()
rb_dram_wd.clear()
rb_dram_we.clear()
rb_pmem_wa.clear()
rb_pmem_wb.clear()
rb_pmem_wc.clear()
rb_pmem_wd.clear()
rb_pmem_we.clear()
rb_pmem_tx_wa.clear()
rb_pmem_tx_wb.clear()
rb_pmem_tx_wc.clear()
rb_pmem_tx_wd.clear()
rb_pmem_tx_we.clear()
|
workloads/plotting/0_msst20_single-numa.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: torch-1.0
# language: python
# name: torch-1.0
# ---
# #### Study notes for TorchVision
# This is the study notes from [https://pytorch.org/tutorials/beginner/finetuning_torchvision_models_tutorial.html]
#
# To increase the code reuse, I have moved the help functions into the "core" folder
#
from __future__ import print_function
from __future__ import division
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import torchvision
from torchvision import datasets, models, transforms
import matplotlib.pyplot as plt
import time
import os
import sys
import copy
print("PyTorch Version: ", torch.__version__)
print("Torchvision Version: ", torchvision.__version__)
# Eable local module access
module_path = os.path.abspath(os.path.join('.'))
if module_path not in sys.path:
sys.path.append(module_path)
print("Module Path: ", module_path)
# +
# Top level dta directory. Here we assume the format of the directory conforms
data_dir = "./data/hymenoptera_data"
from core.types import ModelName
# Models to choose from [resnet, alexnet, vgg, squeezenet, desenet, inception]
model_name = ModelName.Densenet
# Number of classes in the dataset
num_classes = 2
# Batch size for training (The larger, the better, but requires more memory)
batch_size = 8
# Number of epoches to train for
num_epoches = 15
# -
# Flag for feature extracting. When False, we finetune the whole model,
# when True, we only update the reshaped layer params
feature_extract = True
from core.utils import device
device = device
# Setup the loss function
criterion = nn.CrossEntropyLoss()
from core.network_initializer import initialize_model
img_model = initialize_model(
device=device,
model_name=model_name,
num_classes = num_classes,
feature_extract=feature_extract
)
model_ft = img_model.model_ft
input_size = img_model.input_size
# +
from core.param_optimizer import optimize_params
optimize_ft = optimize_params(
model=img_model,
feature_extract=feature_extract
)
# -
from core.data_loader import transform_data
data_loaders = transform_data(
data_dir = data_dir,
input_size=input_size,
batch_size=batch_size
)
# +
from core.model_trainer import ModelTrainer
trainer = ModelTrainer(
model=model_ft,
dataloaders=data_loaders,
optimizer=optimize_ft,
criterion=criterion,
number_epoches=num_epoches
)
good_model, acc_history = trainer.train()
# -
# ### COMPARISON WITH MODEL TRAINED FROM SCRATCH
#
# Just for fun, lets see how the model learns if we do not use transfer
# learning. The performance of fine-tuning vs. feature extracting depends
# largely on the dataset but in general both transfer learning methods
# produce favorable result in terms of traing time and overall accuracy
# versus a model trained from scratch
# +
scratch_img_model = initialize_model(
model_name=model_name,
num_classes=num_classes,
feature_extract=False,
use_pretrained=False,
device = device,
)
scratch_model_ft = scratch_img_model.model_ft
scratch_optimizer = optim.SGD(
scratch_model_ft.parameters(),
lr=0.001,
momentum=0.9
)
scratch_criterion=nn.CrossEntropyLoss()
scratch_trainer = ModelTrainer(
model=scratch_model_ft,
dataloaders=data_loaders,
criterion=scratch_criterion,
optimizer=scratch_optimizer,
number_epoches=num_epoches
)
good_scratch_model, scratch_acc_history = scratch_trainer.train()
ohist = []
shist = []
ohist = [h.cpu().numpy() for h in acc_history]
shist = [h.cpu().numpy() for h in scratch_acc_history]
plt.title("Validation Accuracy vs. Number of Training Epochs")
plt.xlabel("Training Epochs")
plt.ylabel("Validation Accuracy")
plt.plot(range(1,num_epoches+1),ohist,label="Pretrained")
plt.plot(range(1,num_epoches+1),shist,label="Scratch")
plt.ylim((0,1.))
plt.xticks(np.arange(1, num_epoches+1, 1.0))
plt.legend()
plt.show()
# -
|
torch-vision.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:envruntime2]
# language: python
# name: conda-env-envruntime2-py
# ---
# # Quantum Kernel Alignment with Qiskit Runtime
#
# <br>
#
# **Classification with Support Vector Machines**<br>
# Classification problems are widespread in machine learning applications. Examples include credit card risk, handwriting recognition, and medical diagnosis. One approach to tackling classification problems is the support vector machine (SVM) [1,2]. This supervised learning algorithm uses labeled data samples to train a model that can predict to which class a test sample belongs. It does this by finding a separating hyperplane maximizing the margin between data classes. Often, data is not linearly separable in the original space. In these cases, the kernel trick is used to implicitly encode a transformation of the data into a higher-dimensional feature space, through the inner product between pairs of data points, where the data may become separable.
#
# **Quantum Kernels**<br>
# Quantum computers can be used to encode classical data in a quantum-enhanced feature space. In 2019, IBM introduced an algorithm called the quantum kernel estimator (QKE) for computing quantum kernels [3]. This algorithm uses quantum circuits with data provided classically and offers an efficient way to evaluate inner products between data in a quantum feature space. For two data samples $\theta$ and $\theta'$, the kernel matrix is given as
#
# $$
# K(\theta, \theta') = \lvert\langle 0^n \rvert U^\dagger(\theta) U(\theta') \lvert 0^n \rangle \rvert^2,
# $$
#
# where $U(\theta)$ prepares the quantum feature state. Quantum kernels used in a classification framework inherit the convex optimization program of the SVM and avoid common limitations of variational quantum classifiers. A key observation of this paper was that a necessary condition for a computational advantage requires quantum circuits for the kernel that are hard to simulate classically. More recently, IBM proved that quantum kernels can offer superpolynomial speedups over any classical learner on a learning problem based on the hardness of the discrete logarithm problem [4]. This means that quantum kernels can someday offer quantum advantage on suitable problems.
#
#
# **Quantum Kernels that Exploit Structure in Data**<br>
# An important approach in the search for practical quantum advantage in machine learning is to identify quantum kernels for learning problems that have underlying structure in the data. We've taken a step in this direction in our recent paper [5], where we introduced a broad class of quantum kernels that exploit group structure in data. Examples of learning problems for data with group structure could include learning permutations or classifying translations. We call this new class of kernels _covariant quantum kernels_ as they are related to covariant quantum measurements. The quantum feature map is defined by a unitary representation $D(\theta)$ of a group $G$ for some element $\theta \in G$, and a fiducial reference state $\lvert\psi\rangle = V\lvert0^n\rangle$ prepared by a unitary circuit $V$. The kernel matrix is given as
#
# $$
# K(\theta, \theta') = \vert\langle 0^n \rvert V^\dagger D^\dagger(\theta) D(\theta') V \lvert 0^n \rangle \rvert^2. \qquad (1)
# $$
#
# In general, the choice of the fiducial state is not known _a priori_ and can significantly impact the performance of the classifier. Here, we use a method called quantum kernel alignment (QKA) to find a good fiducial state for a given group.
#
# **Aligning Quantum Kernels on a Dataset**<br>
# In practice, SVMs require a choice of the kernel function. Sometimes, symmetries in the data can inform this selection, other times it is chosen in an ad hoc manner. Kernel alignment is one approach to learning a kernel on a given dataset by iteratively adapting it to have high similarity to a target kernel informed from the underlying data distribution [6]. As a result, the SVM with an aligned kernel will likely generalize better to new data than with an unaligned kernel. Using this concept, we introduced in [5] an algorithm for quantum kernel alignment, which provides a way to learn a quantum kernel from a family of kernels. Specifically, the algorithm optimizes the parameters in a quantum circuit to maximize the alignment of a kernel while converging to the maximum SVM margin. In the context of covariant quantum kernels, we extend Eq. $(1)$ to
#
# $$
# K_\lambda(\theta,\theta') = \lvert\langle 0^n \rvert V^\dagger_\lambda D^\dagger(\theta) D(\theta') V_\lambda \lvert 0^n \rangle \rvert^2, \qquad (2)
# $$
#
# and use QKA to learn a good fiducial state parametrized by $\lambda$ for a given group.
#
#
# **Covariant Quantum Kernels on a Specific Learning Problem**<br>
# Let's try out QKA on a learning problem. In the following, we'll consider a binary classification problem we call _labeling cosets with error_ [5]. In this problem, we will use a group and a subgroup to form two cosets, which will represent our data classes. We take the group $G = SU(2)^{\otimes n}$ for $n$ qubits, which is the special unitary group of $2\times2$ matrices and has wide applicability in nature, for example, the Standard Model of particle physics and in many condensed matter systems. We take the graph-stabilizer subgroup $S_{\mathrm{graph}} \in G$ with $S_{\mathrm{graph}} = \langle \{ X_i \otimes_{k:(k,i) \in \mathcal{E}} Z_k \}_{i \in \mathcal{V}} \rangle$ for a graph $(\mathcal{E},\mathcal{V})$ with edges $\mathcal{E}$ and vertices $\mathcal{V}$. Note that the stabilizers fix a stabilizer state such that $D_s \lvert \psi\rangle = \lvert \psi\rangle$. This observation will be useful a bit later.
#
# To generate the dataset, we write the rotations of the group as $D(\theta_1, \theta_2, 0)=\exp(i \theta_1 X) \exp(i \theta_2 Z) \in SU(2)$, so that each qubit is parametrized by the first two Euler angles (the third we set to zero). Then, we draw randomly two sets of angles $\mathbf{\theta}_\pm \in [-\pi/4, \pi/4]^{2n}$ for the $n$-qubit problem. From these two sets, we construct a binary classification problem by forming two left-cosets (representing the two classes) with those angles, $C_\pm = D(\mathbf{\theta}_\pm) S_{\mathrm{graph}}$ where $D(\mathbf{\theta}_\pm) = \otimes_{k=1}^n D(\theta_\pm^{2k-1}, \theta_\pm^{2k}, 0)$. Note that the elements of the cosets can again be written in terms of Euler angles. We build training and testing sets by randomly drawing elements from $C_\pm$ such that the dataset has samples $i=1,...,m$ containing the first two Euler angles for each qubit $\mathbf{\theta}_{y_i} = (\theta_{y_i}^{1}, \theta_{y_i}^{2}, \theta_{y_i}^{3}, \theta_{y_i}^{4}, ..., \theta_{y_i}^{2n-1}, \theta_{y_i}^{2n})$ and labels $y_i \in \{-1,1\}$ that indicate to which coset a sample belongs.
#
# Next, we select a fiducial state. A natural candidate is the stabilizer state we encountered above. Why? Because this is a subgroup invariant state, $D_s\lvert\psi\rangle = \lvert\psi\rangle$, which causes the data for a given coset to be mapped to a unique state: $D(\mathbf{\theta}_\pm)D_s \lvert\psi\rangle = D(\mathbf{\theta}_\pm) \lvert\psi\rangle$. This means the classifier only needs to distinguish the _two_ states $D(\mathbf{\theta}_\pm) \lvert\psi\rangle \langle \psi\rvert D^\dagger(\mathbf{\theta}_\pm)$ for every element of the coset. In this tutorial, we will add a small Gaussian error with variance $0.01$ to the Euler angles of the dataset. This noise will perturb these two states, but if the variance is sufficiently small, we expect the states will still be classified correctly. Let's consider a parametrized version of the stabilizer state, associated with the coupling graph $(\mathcal{E},\mathcal{V})$ given by the device connectivity, as our fiducial state and then use kernel alignment to find its optimal parameters. Specifically, we'll replace the initial layers of Hadamards in the graph state with $y$-rotations by an angle $\lambda$,
#
# $$
# \lvert \psi_\lambda\rangle = V_\lambda \lvert 0^n\rangle = \prod_{(k,t) \in \mathcal{E}} CZ_{k,t} \prod_{k \in \mathcal{V}} \exp\left(i \frac{\lambda}{2} Y_k\right)\lvert 0^n\rangle,
# $$
#
# where $CZ=\mathrm{diag}(1,1,1,-1)$. Then, given two samples from our dataset, $\mathbf{\theta}$ and $\mathbf{\theta}'$, the kernel matrix is evaluated as in Eq. $(2)$. If we initialize the kernel with $\lambda \approx 0$, we expect the quantum kernel alignment algorithm to converge towards the optimal $\lambda = \pi/2$ and the classifier to yield 100\% test accuracy.
#
# Let's define two specific problem instances to test these ideas out. We'll be using the quantum device `ibmq_montreal`, with coupling map shown below:
#
# <br>
# <img src="images/chip.png" width="500">
# <br>
#
# We'll pick two different subgraphs, one for 7 qubits and one for 10, to define our problem instances. Using these subgraphs, we'll generate the corresponding datasets as described above, and then align the quantum kernel with QKA to learn a good fiducial state.
#
# <br>
# <img src="images/subgraphs.png" width="550">
# <br>
#
# **Speeding up Algorithms with Qiskit Runtime**<br>
# QKA is an iterative quantum-classical algorithm, in which quantum hardware is used to execute parametrized quantum circuits for evaluating the quantum kernel matrices with QKE, while a classical optimizer tunes the parameters of those circuits to maximize the alignment. Iterative algorithms of this type can be slow due to latency between the quantum and classical calculations. Qiskit Runtime is a new architecture that can speed up iterative algorithms like QKA by co-locating classical computations with the quantum hardware executions. In this tutorial, we'll use QKA with Qiskit Runtime to learn a good quantum kernel for the _labeling cosets with error_ problem defined above.
#
# <br>
#
# **References**<br>
# [1] <NAME>, <NAME>, and <NAME>, Proceedings of the Fifth Annual Workshop on Computational Learning Theory, COLT ’92 (Association for Computing Machinery, New York, NY, USA, 1992) pp. 144-152 [link](https://doi.org/10.1145/130385.130401) <br>
# [2] <NAME>, The Nature of Statistical Learning Theory, Information Science and Statistics (Springer New York, 2013) [link](https://books.google.com/books?id=EqgACAAAQBAJ) <br>
# [3] <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, and <NAME>, Nature 567, 209-212 (2019) [link](https://doi.org/10.1038/s41586-019-0980-2) <br>
# [4] <NAME>, <NAME>, and <NAME>, arXiv:2010.02174 (2020) [link](https://arxiv.org/abs/2010.02174) <br>
# [5] <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, arXiv:2105.03406 (2021) [link](https://arxiv.org/abs/2105.03406)<br>
# [6] <NAME>, <NAME>, <NAME>, and <NAME>, Advances in Neural Information Processing Systems 14 (2001) [link](https://proceedings.neurips.cc/paper/2001/file/1f71e393b3809197ed66df836fe833e5-Paper.pdf) <br>
#
# # Load your IBM Quantum account and get the quantum backend
#
# We'll be using the 27-qubit device `ibmq_montreal` for this tutorial.
# + slideshow={"slide_type": "fragment"}
import sys
sys.path.insert(0, '..') # Add qiskit_runtime directory to the path
from qiskit import IBMQ
IBMQ.load_account()
provider = IBMQ.get_provider(project='qiskit-runtime') # Change this to your provider.
backend = provider.get_backend('ibmq_montreal')
# -
# # Invoke the Quantum Kernel Alignment program
#
# Before executing the runtime program for QKA, we need to prepare the dataset and configure the input parameters for the algorithm.
#
# ### 1. Prepare the dataset
#
# First, we load the dataset from the `csv` file and then extract the labeled training and test samples. Here, we'll look at the 7-qubit problem, shown above in subfigure a). A second dataset is also available for the 10-qubit problem in b).
# +
import pandas as pd
df = pd.read_csv('../qiskit_runtime/qka/aux_file/dataset_graph7.csv',sep=',', header=None) # alterative problem: dataset_graph10.csv
data = df.values
# -
# Let's take a look at the data to see how it's formatted. Each row of the dataset contains a list of Euler angles, followed by the class label $\pm1$ in the last column. For an $n$-qubit problem, there are $2n$ features corresponding to the first two Euler angles for each qubit (recall discussion above). The rows alternate between class labels.
print(df.head(4))
# Now, let's explicitly construct the training and test samples (denoted `x`) and their labels (denoted `y`).
# +
import numpy as np
# choose number of training and test samples per class:
num_train = 10
num_test = 10
# extract training and test sets and sort them by class label
train = data[:2*num_train, :]
test = data[2*num_train:2*(num_train+num_test), :]
ind=np.argsort(train[:,-1])
x_train = train[ind][:,:-1]
y_train = train[ind][:,-1]
ind=np.argsort(test[:,-1])
x_test = test[ind][:,:-1]
y_test = test[ind][:,-1]
# -
# ### 2. Configure the QKA algorithm
#
# The first task is to set up the feature map and its entangler map, which specifies the arrangement of $CZ$ gates in the fiducial state. We will choose this to match the connectivity of the problem subgraph, pictured above. We also initialize the fiducial state parameter $\lambda$ with `initial_point`.
# +
from qiskit_runtime.qka import FeatureMap
d = np.shape(data)[1]-1 # feature dimension is twice the qubit number
em = [[0,2],[3,4],[2,5],[1,4],[2,3],[4,6]] # we'll match this to the 7-qubit graph
# em = [[0,1],[2,3],[4,5],[6,7],[8,9],[1,2],[3,4],[5,6],[7,8]] # we'll match this to the 10-qubit graph
fm = FeatureMap(feature_dimension=d, entangler_map=em) # define the feature map
initial_point = [0.1] # set the initial parameter for the feature map
# -
# Let's print out the circuit for the feature map (the circuit for the kernel will be a feature map for one data sample composed with an inverse feature map for a second sample). The first part of the feature map is the fiducial state, which is prepared with a layer of $y$ rotations followed by $CZ$s. Then, the last two layers of $z$ and $x$ rotations in the circuit denote the group representation $D(\theta)$ for a data sample $\theta$. Note that a single-qubit rotation is defined as $RP(\phi) = \exp(- i [\phi/2] P)$ for $P \in {X, Y, Z}$.
from qiskit.tools.visualization import circuit_drawer
circuit_drawer(fm.construct_circuit(x=x_train[0], parameters=initial_point),
output='text', fold=200)
# Next, we set the values for the SVM soft-margin penalty `C` and the number of SPSA iterations `maxiters` we use to align the quantum kernel.
# + slideshow={"slide_type": "fragment"}
C = 1 # SVM soft-margin penalty
maxiters = 10 # number of SPSA iterations
# -
# Finally, we decide how to map the virtual qubits of our problem graph to the physical qubits of the hardware. For example, in the 7-qubit problem, we can directly map the virtual qubits `[0, 1, 2, 3, 4, 5, 6]` to the physical qubits `[10, 11, 12, 13, 14, 15, 16]` of the device. This allows us to avoid introducing SWAP gates for qubits that are not connected, which can increase the circuit depth.
initial_layout = [10, 11, 12, 13, 14, 15, 16] # see figure above for the 7-qubit graph
# initial_layout = [9, 8, 11, 14, 16, 19, 22, 25, 24, 23] # see figure above for the 10-qubit graph
# ### 3. Set up and run the program
#
# We're almost ready to run the program. First, let's take a look at the program metadata, which includes a description of the input parameters and their default values.
print(provider.runtime.program('quantum-kernel-alignment'))
# We see that this program has several input parameters, which we'll configure below. To run the program, we'll set up its two main components: `inputs` (the input parameters from the program metadata) and `options` (the quantum backend). We'll also define a callback function so that the intermediate results of the algorithm will be printed as the program runs. Note that each step of the algorithm for the settings we've selected here takes approximately 11 minutes.
# + slideshow={"slide_type": "fragment"}
def interim_result_callback(job_id, interim_result):
print(f"interim result: {interim_result}\n")
# + slideshow={"slide_type": "slide"}
program_inputs = {
'feature_map': fm,
'data': x_train,
'labels': y_train,
'initial_kernel_parameters': initial_point,
'maxiters': maxiters,
'C': C,
'initial_layout': initial_layout
}
options = {'backend_name': backend.name()}
job = provider.runtime.run(program_id="quantum-kernel-alignment",
options=options,
inputs=program_inputs,
callback=interim_result_callback,
)
print(job.job_id())
result = job.result()
# -
# ### 4. Retrieve the results of the program
#
# Now that we've run the program, we can retrieve the output, which is the aligned kernel parameter and the aligned kernel matrix. Let's also plot this kernel matrix (we'll subtract off the diagonal to show the contrast between the remaining entries). The kernel matrix is expected to have a block-diagonal structure. This reflects the fact that the kernel maps the input data effectively to just two states (modulo the small noise we added to the data; recall the discussion above). That is, data in the same coset (same class label) have a larger overlap than do data from different cosets.
# +
print(f"aligned_kernel_parameters: {result['aligned_kernel_parameters']}")
from matplotlib import pyplot as plt
from pylab import cm
plt.rcParams['font.size'] = 20
plt.imshow(result['aligned_kernel_matrix']-np.identity(2*num_train), cmap=cm.get_cmap('bwr', 20))
plt.show()
# + [markdown] slideshow={"slide_type": "slide"}
# # Use the results of the program to test an SVM on new data
#
# Equipped with the aligned kernel and its optimized parameter, we can use the `sklearn` package to train an SVM and then evaluate its classification accuracy on new test points. Note that a second kernel matrix built from the test points is needed for the SVM decision function.
# + slideshow={"slide_type": "fragment"}
from qiskit_runtime.qka import KernelMatrix
from sklearn.svm import SVC
from sklearn import metrics
# train the SVM with the aligned kernel matrix:
kernel_aligned = result['aligned_kernel_matrix']
model = SVC(C=C, kernel='precomputed')
model.fit(X=kernel_aligned, y=y_train)
# test the SVM on new data:
km = KernelMatrix(feature_map=fm, backend=backend, initial_layout=initial_layout)
kernel_test = km.construct_kernel_matrix(x1_vec=x_test, x2_vec=x_train, parameters=result['aligned_kernel_parameters'])
labels_test = model.predict(X=kernel_test)
accuracy_test = metrics.balanced_accuracy_score(y_true=y_test, y_pred=labels_test)
print(f"accuracy test: {accuracy_test}")
# -
import qiskit.tools.jupyter
# %qiskit_version_table
# %qiskit_copyright
|
qiskit-runtime/tutorials/qka.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
from io import BytesIO
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
import cv2
import IPython.display
import operator
# -
def showimage(cimg):
if len(cimg.shape) == 2:
img = Image.fromarray(cimg)
else:
img = Image.fromarray(cv2.cvtColor(cimg, cv2.COLOR_BGR2RGB))
b = BytesIO()
img.save(b, format='png')
IPython.display.display(IPython.display.Image(data=b.getvalue(), format='png', embed=True))
# +
MIN_CONTOUR_AREA = 100
RESIZED_IMAGE_WIDTH = 20
RESIZED_IMAGE_HEIGHT = 30
# -
|
micro/Train.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.0 64-bit
# name: python390jvsc74a57bd063fd5069d213b44bf678585dea6b12cceca9941eaf7f819626cde1f2670de90d
# ---
# +
# importing libraries
from facenet_pytorch import MTCNN, InceptionResnetV1
import torch
from torchvision import datasets
from torch.utils.data import DataLoader
from PIL import Image
import cv2
import time
import os
import numpy as np
# -
# initializing MTCNN and InceptionResnetV1
# We use mtcnn0 to detect faces in our data,
mtcnn0 = MTCNN(image_size=240, margin=0, keep_all=False, min_face_size=40) # keep_all=False
# We use mtcnn to detect multiple faces in our cam
mtcnn = MTCNN(image_size=240, margin=0, keep_all=True, min_face_size=40) # keep_all=True
# This return a pretrained model that is vggface2
resnet = InceptionResnetV1(pretrained='vggface2').eval()
# + tags=["outputPrepend"]
# Read data from folder
dataset = datasets.ImageFolder('data2') # photos folder path
idx_to_class = {i:c for c,i in dataset.class_to_idx.items()} # accessing names of peoples from folder names
def collate_fn(x):
return x[0]
loader = DataLoader(dataset, collate_fn=collate_fn)
name_list = [] # list of names corrospoing to cropped photos
embedding_list = [] # list of embeding matrix after conversion from cropped faces to embedding matrix using resnet
for img, idx in loader:
print(img.size)
#Unlike other implementations, calling a facenet-pytorch MTCNN object directly with an image (i.e., using the forward method for those familiar with pytorch) will return torch tensors containing the detected face(s), rather than just the bounding boxes. This is to enable using the module easily as the first stage of a facial recognition pipeline, in which the faces are passed directly to an additional network or algorithm.
face, prob = mtcnn0(img, return_prob=True)
print("face: ",face," prob:",prob)
if face is not None and prob>0.92:
emb = resnet(face.unsqueeze(0))
embedding_list.append(emb.detach())
name_list.append(idx_to_class[idx])
# save data
data = [embedding_list, name_list]
torch.save(data, 'data.pt') # saving data.pt file
# +
# Using webcam recognize face
# loading data.pt file
load_data = torch.load('data.pt')
embedding_list = load_data[0]
name_list = load_data[1]
cam = cv2.VideoCapture("./personas.mp4")
while not cam.isOpened():
cam = cv2.VideoCapture("./personas.mp4")
cv2.waitKey(1000)
print ("Wait for the header")
post_frame = cam.get(cv2.CAP_PROP_POS_FRAMES)
while True:
ret, frame = cam.read()
if not ret:
print("fail to grab frame, try again")
# The next frame is not ready, so we try to read it again
cap.set(cv2.CV_CAP_PROP_POS_FRAMES, pos_frame-1)
print("frame is not ready")
# It is better to wait for a while for the next frame to be ready
cv2.waitKey(1000)
break
img = Image.fromarray(frame)
img_cropped_list, prob_list = mtcnn(img, return_prob=True)
if img_cropped_list is not None:
#return boxed faces
boxes, _ = mtcnn.detect(img)
for i, prob in enumerate(prob_list):
if prob>0.90:
emb = resnet(img_cropped_list[i].unsqueeze(0)).detach()
dist_list = [] # list of matched distances, minimum distance is used to identify the person
for idx, emb_db in enumerate(embedding_list):
dist = torch.dist(emb, emb_db).item()
dist_list.append(dist)
min_dist = min(dist_list) # get minumum dist value
min_dist_idx = dist_list.index(min_dist) # get minumum dist index
name = name_list[min_dist_idx] # get name corrosponding to minimum dist
box = boxes[i]
original_frame = frame.copy() # storing copy of frame before drawing on it
if min_dist<0.90:
#bgr
frame = cv2.putText(frame, str(name)+' '+str(min_dist), (box[0],box[1]), cv2.FONT_HERSHEY_SIMPLEX, 1, (63, 0, 252),1, cv2.LINE_AA)
#frame = cv2.putText(frame, 'Hola ' +name, (box[0],box[1]), cv2.FONT_HERSHEY_SIMPLEX, 1, (63, 0, 252),1, cv2.LINE_AA)
frame = cv2.rectangle(frame, (box[0].astype(int),box[1].astype(int)) , (box[2].astype(int),box[3].astype(int)), (13,214,53), 2)
cv2.imshow("IMG", frame)
if cv2.waitKey(10) == 27:
break
#if cam.get(cv2.CAP_PROP_POS_FRAMEScv2.CV_CAP_PRcv2.CAP_PROP_POS_FRAMESv2.CV_CAP_PROP_FRAME_COUNT):
# If the number of captured frames is equal to the total number of frames,
# # we stop
break
k = cv2.waitKey(1)
if k%256==27: # ESC
print('Esc pressed, closing...')
break
elif k%256==32: # space to save image
print('Enter your name :')
name = input()
# create directory if not exists
if not os.path.exists('data2/'+name):
os.mkdir('data2/'+name)
img_name = "data2/{}/{}.jpg".format(name, int(time.time()))
cv2.imwrite(img_name, original_frame)
print(" saved: {}".format(img_name))
cam.release()
cv2.destroyAllWindows()
# -
type(box[1].astype(int))
|
recFacesVideo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# ## Training Agents
# 1. Load required libraries:
from stable_baselines3.ppo import CnnPolicy
from stable_baselines3 import PPO
from pettingzoo.butterfly import pistonball_v5
import supersuit as ss
# 2. Initialize the PettingZoo environment:
env = pistonball_v5.parallel_env(n_pistons=20, time_penalty=-0.1,
continuous=True, random_drop=True,
random_rotate=True, ball_mass=0.75,
ball_friction=0.3, ball_elasticity=1.5,
max_cycles=125)
# 3. We wrap our environment in SuperSuit to remove the 3 color channels, as we only need grey scale for this task
env = ss.color_reduction_v0(env, mode='B')
# 4. We resize our input to 84x84 pixels
env = ss.resize_v0(env, x_size=84, y_size=84)
# 5. We stack the previous frames together to give information related to the balls movement
env = ss.frame_stack_v1(env, 4)
# 6. We convert the environments API which causes Stable Baselines to do parameter sharing of the policy network on a multiagent environment
env = ss.pettingzoo_env_to_vec_env_v1(env)
# 7. This step enables parallel training
# 8 threads on 4 cpus
env = ss.concat_vec_envs_v1(env, 8, num_cpus=4, base_class='stable_baselines3')
# 8. We can finally train our agent
# +
model = PPO(CnnPolicy, env, verbose=3, gamma=0.95, n_steps=256,
ent_coef=0.0905168, learning_rate=0.0006221, vf_coef=0.042202,
max_grad_norm=0.9, gae_lambda=0.99, n_epochs=5, clip_range=0.3,
batch_size=256)
model.learn(total_timesteps=2_000_000)
model.save('policy')
# -
# ## Watching Agents Play
# Now that the model is trained and saved, we can load the policy and watch it play!
# We reinstantiate the environment
env = pistonball_v5.env()
env = ss.color_reduction_v0(env, mode='B')
env = ss.resize_v0(env, x_size=84, y_size=84)
env = ss.frame_stack_v1(env, 4)
# Load the policy
model = PPO.load('policy')
# And finally we can use the policy and render this
env.reset()
for agent in env.agent_iter():
obs, reward, done, info = env.last()
act = model.predict(obs, deterministic=True)[0] if not done else None
env.step(act)
env.render()
# Finally, we close the environment.
env.close()
|
PettingZoo/Multi Agent Deep Reinforcement Learning in 15 Lines of Code.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import requests
from flask import json
post = requests.post(
'http://127.0.0.1:5000/api/test',
json = {
# "String":"test_string",
"Float":123.456,
}
)
print(post.content)
get = requests.get(
'http://127.0.0.1:5000/api/test',
)
print(json.loads(get.content))
|
test_openradiodata_api.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import binascii
def shift_left(k, nth_shifts):
s = ""
for i in range(nth_shifts):
for j in range(1,len(k)):
s = s + k[j]
s = s + k[0]
k = s
s = ""
return k
# calculating xor of two strings of binary number a and b
def xor(a, b):
ans = ""
for i in range(len(a)):
if a[i] == b[i]:
ans = ans + "0"
else:
ans = ans + "1"
return ans
def band(a, b):
ans = ""
for i in range(len(a)):
if a[i]==1 and b[i]==1:
ans = ans + "1"
else:
ans = ans + "0"
return ans
def hex2bin(s):
mp = {'0' : "0000",
'1' : "0001",
'2' : "0010",
'3' : "0011",
'4' : "0100",
'5' : "0101",
'6' : "0110",
'7' : "0111",
'8' : "1000",
'9' : "1001",
'A' : "1010",
'B' : "1011",
'C' : "1100",
'D' : "1101",
'E' : "1110",
'F' : "1111" }
bin = ""
for i in range(len(s)):
bin = bin + mp[s[i]]
return bin
# Binary to hexadecimal conversion
def bin2hex(s):
mp = {"0000" : '0',
"0001" : '1',
"0010" : '2',
"0011" : '3',
"0100" : '4',
"0101" : '5',
"0110" : '6',
"0111" : '7',
"1000" : '8',
"1001" : '9',
"1010" : 'A',
"1011" : 'B',
"1100" : 'C',
"1101" : 'D',
"1110" : 'E',
"1111" : 'F' }
hex = ""
for i in range(0,len(s),4):
ch = ""
ch = ch + s[i]
ch = ch + s[i + 1]
ch = ch + s[i + 2]
ch = ch + s[i + 3]
hex = hex + mp[ch]
return hex
#text=input("Enter the plain text:")
#key=input("Enter key:")
text="Two One Nine Two"
key="Thats my Kung Fu"
a=text.encode("utf-8").hex()
b=key.encode("utf-8").hex()
print("Plain text:"+a)
rc = {'1' : "00000001000000000000000000000000",
'2' : "00000010000000000000000000000000",
'3' : "00000100000000000000000000000000",
'4' : "00001000000000000000000000000000",
'5' : "00010000000000000000000000000000",
'6' : "00100000000000000000000000000000",
'7' : "01000000000000000000000000000000",
'8' : "10000000000000000000000000000000",
'9' : "00011011000000000000000000000000",
'10': "00110110000000000000000000000000"
}
sbox={'00':'63',
'01':'7C',
'02':'77',
'03':'7B',
'04':'F2',
'05':'6B',
'06':'6F',
'07':'C5',
'08':'30',
'09':'01',
'0A':'67',
'0B':'2B',
'0C':'FE',
'0D':'D7',
'0E':'AB',
'0F':'76',
'10':'CA',
'11':'82',
'12':'C9',
'13':'7D',
'14':'FA',
'15':'59',
'16':'47',
'17':'F0',
'18':'AD',
'19':'D4',
'1A':'A2',
'1B':'AF',
'1C':'9C',
'1D':'A4',
'1E':'72',
'1F':'C0',
'20':'B7',
'21':'FD',
'22':'93',
'23':'26',
'24':'36',
'25':'3F',
'26':'F7',
'27':'CC',
'28':'34',
'29':'A5',
'2A':'E5',
'2B':'F1',
'2C':'71',
'2D':'D8',
'2E':'31',
'2F':'15',
'30':'04',
'31':'C7',
'32':'23',
'33':'C3',
'34':'18',
'35':'96',
'36':'05',
'37':'9A',
'38':'07',
'39':'12',
'3A':'80',
'3B':'E2',
'3C':'EB',
'3D':'27',
'3E':'B2',
'3F':'75',
'40':'09',
'41':'83',
'42':'2C',
'43':'1A',
'44':'1B',
'45':'6E',
'46':'5A',
'47':'A0',
'48':'52',
'49':'3B',
'4A':'D6',
'4B':'B3',
'4C':'29',
'4D':'E3',
'4E':'2F',
'4F':'84',
'50':'53',
'51':'D1',
'52':'00',
'53':'ED',
'54':'20',
'55':'FC',
'56':'B1',
'57':'5B',
'58':'6A',
'59':'CB',
'5A':'BE',
'5B':'39',
'5C':'4A',
'5D':'4C',
'5E':'58',
'5F':'CF',
'60':'D0',
'61':'EF',
'62':'AA',
'63':'FB',
'64':'43',
'65':'4D',
'66':'33',
'67':'85',
'68':'45',
'69':'F9',
'6A':'02',
'6B':'7F',
'6C':'50',
'6D':'3C',
'6E':'9F',
'6F':'A8',
'70':'51',
'71':'A3',
'72':'40',
'73':'8F',
'74':'92',
'75':'9D',
'76':'38',
'77':'F5',
'78':'BC',
'79':'B6',
'7A':'DA',
'7B':'21',
'7C':'10',
'7D':'FF',
'7E':'F3',
'7F':'D2',
'80':'CD',
'81':'0C',
'82':'13',
'83':'EC',
'84':'5F',
'85':'97',
'86':'44',
'87':'17',
'88':'C4',
'89':'A7',
'8A':'7E',
'8B':'3D',
'8C':'64',
'8D':'5D',
'8E':'19',
'8F':'73',
'90':'60',
'91':'81',
'92':'4F',
'93':'DC',
'94':'22',
'95':'2A',
'96':'90',
'97':'88',
'98':'46',
'99':'EE',
'9A':'B8',
'9B':'14',
'9C':'DE',
'9D':'5E',
'9E':'0B',
'9F':'DB',
'A0':'E0',
'A1':'32',
'A2':'3A',
'A3':'0A',
'A4':'49',
'A5':'06',
'A6':'24',
'A7':'5C',
'A8':'C2',
'A9':'D3',
'AA':'AC',
'AB':'62',
'AC':'91',
'AD':'95',
'AE':'E4',
'AF':'79',
'B0':'E7',
'B1':'C8',
'B2':'37',
'B3':'6D',
'B4':'8D',
'B5':'D5',
'B6':'4E',
'B7':'A9',
'B8':'6C',
'B9':'56',
'BA':'F4',
'BB':'EA',
'BC':'65',
'BD':'7A',
'BE':'AE',
'BF':'08',
'C0':'BA',
'C1':'78',
'C2':'25',
'C3':'2E',
'C4':'1C',
'C5':'A6',
'C6':'B4',
'C7':'C6',
'C8':'E8',
'C9':'DD',
'CA':'74',
'CB':'1F',
'CC':'4B',
'CD':'BD',
'CE':'8B',
'CF':'8A',
'D0':'70',
'D1':'3E',
'D2':'B5',
'D3':'66',
'D4':'48',
'D5':'03',
'D6':'F6',
'D7':'0E',
'D8':'61',
'D9':'35',
'DA':'57',
'DB':'B9',
'DC':'86',
'DD':'C1',
'DE':'1D',
'DF':'9E',
'E0':'E1',
'E1':'F8',
'E2':'98',
'E3':'11',
'E4':'69',
'E5':'D9',
'E6':'8E',
'E7':'94',
'E8':'9B',
'E9':'1E',
'EA':'87',
'EB':'E9',
'EC':'CE',
'ED':'55',
'EE':'28',
'EF':'DF',
'F0':'8C',
'F1':'A1',
'F2':'89',
'F3':'0D',
'F4':'BF',
'F5':'E6',
'F6':'42',
'F7':'68',
'F8':'41',
'F9':'99',
'FA':'2D',
'FB':'0F',
'FC':'B0',
'FD':'54',
'FE':'BB',
'FF':'16'
}
k=[]
kh=[]
t=[]
rt=a.upper()
t.append(rt)
rk=b.upper()
kh.append(rk)
tm=[]
km=[]
for i in range(0,10):
w=[rk[i:i+8] for i in range(0, len(rk), 8)]
w0=[w[0][i:i+2] for i in range(0, len(w[0]), 2)]
w1=[w[1][i:i+2] for i in range(0, len(w[1]), 2)]
w2=[w[2][i:i+2] for i in range(0, len(w[2]), 2)]
ws=[w[3][i:i+2] for i in range(0, len(w[3]), 2)]
w3=shift_left(w[3],2)
w3=[w3[i:i+2] for i in range(0, len(w[3]), 2)]
s=[]
for j in range(0,len(w3)):
s.append(sbox[w3[j]])
s="".join(s)
s=hex2bin(s)
s=xor(s,rc[str(i+1)])
w4=bin2hex(xor(hex2bin(w[0]),s))
w5=bin2hex(xor(hex2bin(w4),hex2bin(w[1])))
w6=bin2hex(xor(hex2bin(w5),hex2bin(w[2])))
w7=bin2hex(xor(hex2bin(w6),hex2bin(w[3])))
rk=w4+w5+w6+w7
print("Round ",i+1," key:"+rk)
kh.append(rk)
t=[rt[i:i+8] for i in range(0, len(rt), 8)]
t0=[t[0][i:i+2] for i in range(0, len(t[0]), 2)]
t1=[t[1][i:i+2] for i in range(0, len(t[1]), 2)]
t2=[t[2][i:i+2] for i in range(0, len(t[2]), 2)]
t3=[t[3][i:i+2] for i in range(0, len(t[3]), 2)]
if i==0:
for c in range(0,4):
temp=[]
temp.append(t0[c])
temp.append(t1[c])
temp.append(t2[c])
temp.append(t3[c])
tm.append(temp)
for c in range(0,4):
temp=[]
temp.append(w0[c])
temp.append(w1[c])
temp.append(w2[c])
temp.append(ws[c])
km.append(temp)
arc=[]
for j in range(0,4):
temp=[]
for c in range(0,4):
temp.append(bin2hex(xor(hex2bin(tm[j][c]),hex2bin(km[j][c]))))
arc.append(temp)
#print("add",arc)
sm=[]
for j in range(0,4):
temp=[]
for c in range(0,4):
temp.append(sbox[arc[j][c]])
sm.append(temp)
#print("sbox",sm)
before_shift=[]
for j in range(0,4):
res=""
for c in range(0,4):
res+=sm[j][c]
before_shift.append(res)
#print("before shift",before_shift)
t4=shift_left(before_shift[0],0)
t5=shift_left(before_shift[1],2)
t6=shift_left(before_shift[2],4)
t7=shift_left(before_shift[3],6)
after_shift=[]
t4=[t4[i:i+2] for i in range(0, len(t4), 2)]
t5=[t5[i:i+2] for i in range(0, len(t5), 2)]
t6=[t6[i:i+2] for i in range(0, len(t6), 2)]
t7=[t7[i:i+2] for i in range(0, len(t7), 2)]
after_shift.append(t4)
after_shift.append(t5)
after_shift.append(t6)
after_shift.append(t7)
#print("After shift",after_shift)
if i!=9:
mix=[[2,3,1,1],[1,2,3,1],[1,1,2,3],[3,1,1,2]]
mc=[[0 for i in range(4)] for j in range(4)]
value=0
for j in range(0,4):
for c in range(0,4):
for l in range(0,4):
value=int(after_shift[l][c],16)
if mix[j][l]==3:
if value >=128:
mc[j][c]^=(((2)*value)^int(after_shift[l][c],16)^283)
else:
mc[j][c]^=(((2)*value)^int(after_shift[l][c],16))
elif mix[j][l]==2:
if value >=128:
mc[j][c]^=((2*value)^283)
else:
mc[j][c]^=(2*value)
else:
mc[j][c]^=(mix[j][l]*value)
for j in range(0,4):
for c in range(0,4):
mc[j][c]=str(format(mc[j][c],'02x')).upper()
#print("mix",mc)
x=[rk[i:i+8] for i in range(0, len(rk), 8)]
x0=[x[0][i:i+2] for i in range(0, len(x[0]), 2)]
x1=[x[1][i:i+2] for i in range(0, len(x[1]), 2)]
x2=[x[2][i:i+2] for i in range(0, len(x[2]), 2)]
xs=[x[3][i:i+2] for i in range(0, len(x[3]), 2)]
kx=[]
for c in range(0,4):
temp=[]
temp.append(x0[c])
temp.append(x1[c])
temp.append(x2[c])
temp.append(xs[c])
kx.append(temp)
#print(kx)
arc=[]
for j in range(0,4):
temp=[]
for c in range(0,4):
temp.append(bin2hex(xor(hex2bin(mc[j][c]),hex2bin(kx[j][c]))))
arc.append(temp)
res=""
for j in range(0,4):
for c in range(0,4):
res+=arc[j][c]
print("After Round",i+1,":",res)
if i==9:
x=[rk[i:i+8] for i in range(0, len(rk), 8)]
x0=[x[0][i:i+2] for i in range(0, len(x[0]), 2)]
x1=[x[1][i:i+2] for i in range(0, len(x[1]), 2)]
x2=[x[2][i:i+2] for i in range(0, len(x[2]), 2)]
xs=[x[3][i:i+2] for i in range(0, len(x[3]), 2)]
kx=[]
for c in range(0,4):
temp=[]
temp.append(x0[c])
temp.append(x1[c])
temp.append(x2[c])
temp.append(xs[c])
kx.append(temp)
arc=[]
for j in range(0,4):
temp=[]
for c in range(0,4):
temp.append(bin2hex(xor(hex2bin(after_shift[j][c]),hex2bin(kx[j][c]))))
arc.append(temp)
res=""
for j in range(0,4):
for c in range(0,4):
res+=arc[j][c]
print("cipher text",res)
# -
|
AES.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:525]
# language: python
# name: conda-env-525-py
# ---
# # Task 3
# # Imports
import numpy as np
import pandas as pd
from joblib import dump, load
import s3io
import s3fs
from sklearn.metrics import mean_squared_error
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
import tempfile
import boto3
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.rcParams.update({'font.size': 16, 'axes.labelweight': 'bold', 'figure.figsize': (8,6)})
# ## Part 1:
# Recall as a final goal of this project. We want to build and deploy ensemble machine learning models in the cloud, where features are outputs of different climate models and the target is the actual rainfall observation. In this milestone, you'll actually build these ensemble machine learning models in the cloud.
#
# **Your tasks:**
#
# 1. Read the data CSV from your s3 bucket.
# 2. Drop rows with nans.
# 3. Split the data into train (80%) and test (20%) portions with `random_state=123`.
# 4. Carry out EDA of your choice on the train split.
# 5. Train ensemble machine learning model using `RandomForestRegressor` and evaluate with metric of your choice (e.g., `RMSE`) by considering `Observed` as the target column.
# 6. Discuss your results. Are you getting better results with ensemble models compared to the individual climate models?
#
# > Recall that individual columns in the data are predictions of different climate models.
## You could download it from your bucket, or you can use the file that I have in my bucket.
## You should be able to access it from my bucket using your key and secret
aws_credentials ={"key": "": ""}
pandas_df = pd.read_csv("s3://mds-s3-student76/output/ml_data_SYD.csv", storage_options=aws_credentials, index_col=0, parse_dates=True)
pandas_df.head()
#Step 2 Remove NAs
pandas_df=pandas_df.dropna()
# Step 3: Split dataframe
train_df, test_df = train_test_split(pandas_df, test_size=0.2,random_state=123)
#Step 4: Carry EDA
train_df.describe()
train_df.info()
# Plot the last 100 years to observe the overall behaviour of the rainfall by month
(train_df.resample("M")
.mean().iloc[-1000:]
.plot.line(y = "observed_rainfall",
xlabel="time",
ylabel="Rainfall",
title = "Rainfall Time Series",
legend=False, figsize=(15,9)))
#Step 5: Train default random forest
X_train = train_df.drop(columns=["observed_rainfall"])
y_train = train_df["observed_rainfall"]
X_test = test_df.drop(columns=["observed_rainfall"])
y_test = test_df["observed_rainfall"]
model = RandomForestRegressor()
model.fit(X_train, y_train)
# +
#Step 6: Compare mean square error with individual models
y_predict = model.predict(X_train)
mse_dict = {}
mse_dict["Ensemble Model"] = mean_squared_error(y_train, y_predict, squared=False)
for rain_model in X_train.columns:
mse_dict[str(rain_model)] = mean_squared_error(y_train, X_train[rain_model], squared=False)
# -
pd.DataFrame(mse_dict, index=["MSE"]).transpose().sort_values(by=["MSE"])
# By comparing the mean squared error of each individual prediction model with the ensemble, it is possible to observe that the latter has the slightest error by almost 40% compared to the second-best choice KIOSK-ESM model.
# ## Part 2:
# ### Preparation for deploying model next week
# #### Complete task 4 from the milestone3 before coming here
# We’ve found ```n_estimators=50, max_depth=5``` to be the best hyperparameter settings with MLlib (from the task 4 from milestone3), here we then use the same hyperparameters to train a scikit-learn model.
model = RandomForestRegressor(n_estimators=50, max_depth=20)
model.fit(X_train, y_train)
print(f"Train RMSE: {mean_squared_error(y_train, model.predict(X_train), squared=False):.2f}")
print(f" Test RMSE: {mean_squared_error(y_test, model.predict(X_test), squared=False):.2f}")
# ***Upload model.joblib to s3. You choose how you want to upload it.***
# +
import tempfile
import boto3
import joblib
s3 = boto3.resource(
's3',
aws_access_key_id="",
aws_secret_access_key=""
)
model_filename = 'model.joblib'
# WRITE
with tempfile.TemporaryFile() as fp:
joblib.dump(model, fp)
fp.seek(0)
# use bucket_name and OutputFile - s3 location path in string format.
s3.Bucket('mds-s3-student76').put_object(Key= model_filename, Body=fp.read())
# -
|
notebooks/milestone_3_files/Milestone3-Task3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
## Brute-force Approach (Time: O(n^2); Space: O(1))
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
ptrA = headA
while ptrA:
ptrB = headB
while ptrB:
if ptrA == ptrB:
return ptrA
ptrB = ptrB.next
ptrA = ptrA.next
return None
# +
## Optimized Approach (Time: O(n); Space: O(1))
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
ptrA = headA
ptrB = headB
a = b = 0
while ptrA:
ptrA = ptrA.next
a += 1
while ptrB:
ptrB = ptrB.next
b += 1
if a > b:
diff = a - b
ptrA = headA
while diff > 0:
ptrA = ptrA.next
diff -= 1
ptrB = headB
else:
diff = b - a
ptrB = headB
while diff > 0:
ptrB = ptrB.next
diff -= 1
ptrA = headA
while ptrA != ptrB:
ptrA = ptrA.next
ptrB = ptrB.next
return ptrA
# +
## Further-Optimized Approach (Time: O(n); Space: O(1))
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
ptrA = headA
ptrB = headB
while ptrA is not ptrB:
if not ptrA:
ptrA = headB
else:
ptrA = ptrA.next
if not ptrB:
ptrB = headA
else:
ptrB = ptrB.next
return ptrA
|
Anjani/Leetcode/Linked List/Intersection of Two Linked Lists.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Test code for shifting images
#
# +
import matplotlib.pyplot as plt # import matplotlib
import numpy as np
def rgb2gray(a, method = "wgt"):
"""
Convert RGB array to grayscale
Input:
a - 3d array[ny,nx,3] representing RGB image
method - 'wgt' [default] - weighted or luminosity method
- 'avg' - average method
Returns:
gy - 2d array representing grayscale image
"""
ny, nx = a.shape[0],a.shape[1]
gy = np.zeros((ny ,nx))
if method == "avg":
rw, gw, bw = 1./3., 1./3., 1./3.
elif method == "wgt":
rw, gw, bw = 0.299,0.587,0.114
else:
rw, gw, bw = 1./3., 1./3., 1./3.
print ("bad value for method, using default")
gy = a[:,:,0]*rw+a[:,:,1]*gw+a[:,:,2]*bw
return gy
def jpg2a(fname):
"""
Read in image as grayscale
"""
im = plt.imread(fname)
img = rgb2gray(im)
return img
im1 = jpg2a('small1.jpg') # load image into np array
im2 = jpg2a('small1_shifted.jpg') # load image into np array
print(np.shape(im1))
# -
# #### Three Stooges method - adjust image visually; iterate until they agree
# pick some offsets to try
iy = -15
ix = -33
# plot section of image with some useful texture
plt.subplot(221)
plt.imshow(im1[300:380,600:680],cmap='Greys')
plt.title('Original')
plt.subplot(223)
plt.imshow(im2[300+iy:380+iy,600+ix:680+ix],cmap='Greys')
plt.title('Shifted')
plt.subplot(222)
plt.title('Difference')
plt.imshow(im1[300:380,600:680]-im2[300+iy:380+iy,600+ix:680+ix],cmap='Greys')
print(np.sum(im1[300:380,600:680]-im2[300+iy:380+iy,600+ix:680+ix]))
# #### One-liner in scikit-image
from skimage.feature import register_translation
# pixel precision first
shift, error, diffphase = register_translation(im1, im2)
print(shift, error, diffphase)
# Show the output of a cross-correlation to show what the algorithm is
# doing behind the scenes
image_product = np.fft.fft2(im1[300:380,600:680]) * np.fft.fft2(im2[300:380,600:680]).conj()
cc_image = np.fft.fftshift(np.fft.ifft2(image_product))
fig = plt.figure(figsize=(8, 3))
ax1 = plt.subplot(111)
ax1.imshow(cc_image.real)
ax1.set_title("Cross-correlation")
# #### Crappy example kind of showing how this works
# (Also, poor coding example)
# +
ny,nx = cc_image.shape
X,Y = np.meshgrid(range(0,ny),range(0,nx))
# X = range(0,nx)
# Y = range(0,ny)
from mpl_toolkits.mplot3d import Axes3D # <--- This is important for 3d plotting
from matplotlib import cm
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
surf = ax.plot_surface(X,Y,cc_image.real, cmap=cm.coolwarm,
linewidth=0, antialiased=True)
ax.view_init(elev=40., azim=-20)
# -
|
adjust_offset_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: PythonData
# language: python
# name: pythondata
# ---
# Import Splinter and BeautifulSoup
from splinter import Browser
from bs4 import BeautifulSoup as soup
from webdriver_manager.chrome import ChromeDriverManager
import pandas as pd
executable_path = {'executable_path': ChromeDriverManager().install()}
browser = Browser('chrome', **executable_path, headless=False)
# Visit the mars nasa news site
url = 'https://redplanetscience.com'
browser.visit(url)
# Optional delay for loading the page
browser.is_element_present_by_css('div.list_text', wait_time=1)
html = browser.html
news_soup = soup(html, 'html.parser')
# this is the parent element which holds all other elements
slide_elem = news_soup.select_one('div.list_text')
# looking for the content title
slide_elem.find('div', class_='content_title')
# Use the parent element to find the first `a` tag and save it as `news_title`
news_title = slide_elem.find('div', class_='content_title').get_text()
news_title
# Use the parent element to find the paragraph text
news_p = slide_elem.find('div', class_='article_teaser_body').get_text()
news_p
# ### Featured Images
# Visit URL
url = 'https://spaceimages-mars.com'
browser.visit(url)
# Find and click the full image button
full_image_elem = browser.find_by_tag('button')[1]
full_image_elem.click()
# Parse the resulting html with soup
html = browser.html
img_soup = soup(html, 'html.parser')
# Find the relative image url
img_url_rel = img_soup.find('img', class_='fancybox-image').get('src')
img_url_rel
# Use the base URL to create an absolute URL
img_url = f'https://spaceimages-mars.com/{img_url_rel}'
img_url
df = pd.read_html('https://galaxyfacts-mars.com')[0]
df.columns=['description', 'Mars', 'Earth']
df.set_index('description', inplace=True)
df
df.to_html()
browser.quit()
|
Mission_to_Mars.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# Memprediksi jenis kelamin dari nama bahasa Indonesia menggunakan Machine Learning
# -----
# ### Loading dataset
import pandas as pd # pandas is a dataframe library
df = pd.read_csv("./data/data-pemilih-kpu.csv", encoding = 'utf-8-sig')
#dimensi dataset terdiri dari 13137 baris dan 2 kolom
df.shape
#melihat 5 baris pertama dataset
df.head(5)
#melihat 5 baris terakhir dataset
df.tail(5)
# ### Cleansing dataset
# mengecek apakah ada data yang berisi null
df.isnull().values.any()
# mengecek jumlah baris data yang berisi null
len(df[pd.isnull(df).any(axis=1)])
# menghapus baris null dan recheck kembali
df = df.dropna(how='all')
len(df[pd.isnull(df).any(axis=1)])
# mengecek dimensi dataset
df.shape
# mengubah isi kolom jenis kelamin dari text menjadi integer (Laki-laki = 1; Perempuan= 0)
jk_map = {"Laki-Laki" : 1, "Perempuan" : 0}
df["jenis_kelamin"] = df["jenis_kelamin"].map(jk_map)
# cek kembali data apakah telah berubah
df.head(5)
# +
# Mengecek distribusi jenis kelamin pada dataset
num_obs = len(df)
num_true = len(df.loc[df['jenis_kelamin'] == 1])
num_false = len(df.loc[df['jenis_kelamin'] == 0])
print("Jumlah Pria: {0} ({1:2.2f}%)".format(num_true, (num_true/num_obs) * 100))
print("Jumlah Wanita: {0} ({1:2.2f}%)".format(num_false, (num_false/num_obs) * 100))
# -
# ### Split Dataset
# Dataset yang adalah akan dipecah menjadi dua bagian, 70% data akan digunakan sebagai data training untuk melatih mesin. Kemudian 30% sisanya akan digunakan sebagai data testing untuk mengevaluasi akurasi predisksi machine learning.
# +
from sklearn.model_selection import train_test_split
feature_col_names = ["nama"]
predicted_class_names = ["jenis_kelamin"]
X = df[feature_col_names].values
y = df[predicted_class_names].values
split_test_size = 0.30
text_train, text_test, y_train, y_test = train_test_split(X, y, test_size=split_test_size, stratify=y, random_state=42)
# -
# Dataset telah dipecah menjadi 2 bagian, mari kita cek distribusi nya.
print("Dataset Asli Pria : {0} ({1:0.2f}%)".format(len(df.loc[df['jenis_kelamin'] == 1]), (len(df.loc[df['jenis_kelamin'] == 1])/len(df.index)) * 100.0))
print("Dataset Asli Wanita : {0} ({1:0.2f}%)".format(len(df.loc[df['jenis_kelamin'] == 0]), (len(df.loc[df['jenis_kelamin'] == 0])/len(df.index)) * 100.0))
print("")
print("Dataset Training Pria : {0} ({1:0.2f}%)".format(len(y_train[y_train[:] == 1]), (len(y_train[y_train[:] == 1])/len(y_train) * 100.0)))
print("Dataset Training Wanita : {0} ({1:0.2f}%)".format(len(y_train[y_train[:] == 0]), (len(y_train[y_train[:] == 0])/len(y_train) * 100.0)))
print("")
print("Dataset Test Pria : {0} ({1:0.2f}%)".format(len(y_test[y_test[:] == 1]), (len(y_test[y_test[:] == 1])/len(y_test) * 100.0)))
print("Dataset Test Wanita : {0} ({1:0.2f}%)".format(len(y_test[y_test[:] == 0]), (len(y_test[y_test[:] == 0])/len(y_test) * 100.0)))
# Terlihat hasilnya, dataset yang telah dipecah dua tetap dapat mempertahankan persentase distribusi jenis kelamin seperti pada dataset asli.
# ### Features Extraction
# Proses features extraction, berpengaruh terhadap hasil akurasi yang didapatkan nantinya. Disini saya kan menggunakan metode simple yaitu [CountVectorizer](http://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.CountVectorizer.html) yang akan membuat matrix frekwensi kemunculan dari suatu karakter di tiap nama yang diberikan, dengan opsi analisa ngram_range 2 - 6 hanya di dalam satu kata saja.
# Misal <NAME>, menghasilkan n-gram :
# * mu
# * ham
# * mad
# * nur
# * dst
# +
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer(analyzer = 'char_wb', ngram_range=(2,6))
vectorizer.fit(text_train.ravel())
X_train = vectorizer.transform(text_train.ravel())
X_test = vectorizer.transform(text_test.ravel())
# -
# ### Logistic Regression
# Percobaan pertama menggunakan algoritma Logistic Regression. Data hasil feature extraction akan diinput sebagai data training.
# +
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression()
clf.fit(X_train, y_train.ravel())
# -
# Akurasi prediksi menggunakan data test yang didapat cukup lumayan berada pada tingkat **93.6%**
# +
# dataset training
print(clf.score(X_train, y_train))
# dataset test
print(clf.score(X_test, y_test))
# -
# #### Detail akurasi metriks
# +
from sklearn import metrics
clf_predict = clf.predict(X_test)
# training metrics
print("Accuracy: {0:.4f}".format(metrics.accuracy_score(y_test, clf_predict)))
print(metrics.confusion_matrix(y_test, clf_predict, labels=[1, 0]) )
print("")
print("Classification Report")
print(metrics.classification_report(y_test, clf_predict, labels=[1,0]))
# -
# #### Testing prediksi jenis kelamin
# +
jk_label = {1:"Laki-Laki", 0:"Perempuan"}
test_predict = vectorizer.transform(["<NAME>"])
res = clf.predict(test_predict)
print(jk_label[int(res)])
# -
# ### Menggunakan Pipeline
#
# Scikit memiliki fitur untuk memudahkan proses diatas dengan mengguanakan [Pipeline](scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html). Penulisan kode jadi lebih simple dan rapih, berikut konversi kode diatas jika menggunakan Pipeline
# +
from sklearn.pipeline import Pipeline
clf_lg = Pipeline([('vect', CountVectorizer(analyzer = 'char_wb', ngram_range=(2,6))),
('clf', LogisticRegression()),
])
_ = clf_lg.fit(text_train.ravel(), y_train.ravel())
predicted = clf_lg.predict(text_test.ravel())
np.mean(predicted == y_test.ravel())
# -
# Tingkat akurasi persis sama, dan lebih mudah dalam penulisan kode nya.
# Mari kita lakukan kembali testing prediksi jenis kelamin
result = clf_lg.predict(["<NAME>"])
print(jk_label[result[0]])
# ### Naive Bayes
#
# Algoritma berikutnya yang akan digunakan adalah [Naive Bayes](http://scikit-learn.org/stable/modules/naive_bayes.html). Lansung saja kita coba
# +
from sklearn.naive_bayes import MultinomialNB
clf_nb = Pipeline([('vect', CountVectorizer(analyzer = 'char_wb', ngram_range=(2,6))),
('clf', MultinomialNB()),
])
clf_nb = clf_nb.fit(text_train.ravel(), y_train.ravel())
predicted = clf_nb.predict(text_test.ravel())
np.mean(predicted == y_test.ravel())
# -
# Dengan algoritman Naive Bayes, tingkat akurasi yang didapatkan sedikit saja lebih rendah dari Logistic Regression yaitu **93.3%**. Mari kita lakukan kembali testing prediksi jenis kelamin
result = clf_nb.predict(["<NAME>"])
print(jk_label[result[0]])
# ### Random Forest
#
# Algoritma terakhir yang akan digunakan adalah [Random Forest](http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html). Lansung saja kita coba
# +
from sklearn.ensemble import RandomForestClassifier
clf_rf = Pipeline([('vect', CountVectorizer(analyzer = 'char_wb', ngram_range=(2,6))),
('clf', RandomForestClassifier(n_estimators=90, n_jobs=-1)),
])
clf_rf = clf_rf.fit(text_train.ravel(), y_train.ravel())
predicted = clf_rf.predict(text_test.ravel())
np.mean(predicted == y_test.ravel())
# -
# Dengan algoritman Random Forest, tingkat akurasi yang didapatkan lebih rendah dari dua algoritma sebelumnya, itu sebesar **93.12%**.
# Algoritma ini juga mempunyai kekurangan, yaitu performance yang yang lebih lambat.
# Ok, Mari kita lakukan kembali testing prediksi jenis kelamin
result = clf_rf.predict(["Yuni ahmad"])
print(jk_label[result[0]])
# ### Github Repository
#
# Saya telah membuat implementasi aplikasi prediksi jenis kelamin, silahkan cek di [github](https://github.com/irfani/Jenis-Kelamin).
|
Gender Prediction.ipynb
|