code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# # Logistic Regression 3-class Classifier
#
#
# Show below is a logistic-regression classifiers decision boundaries on the
# first two dimensions (sepal length and width) of the `iris
# <https://en.wikipedia.org/wiki/Iris_flower_data_set>`_ dataset. The datapoints
# are colored according to their labels.
#
#
#
# +
print(__doc__)
# Code source: <NAME>
# Modified for documentation by <NAME>
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2] # we only take the first two features.
Y = iris.target
logreg = LogisticRegression(C=1e5, solver='lbfgs', multi_class='multinomial')
# Create an instance of Logistic Regression Classifier and fit the data.
logreg.fit(X, Y)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = .02 # step size in the mesh
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = logreg.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(4, 3))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=Y, edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
plt.show()
# -
|
04 Lineal Regression/.ipynb_checkpoints/plot_iris_logistic-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# -*- coding: utf-8 -*-
########### Banco de dados aleatório usado para prática.
### By: <NAME>
### Data: 03/08/2020
### Algoritmo: KNN
### Base de dados: bank-full.csv
### Objetivo: baseado em um histórico de dados, predizer se um cliente irá ou não assinar um depósito a prazo.
### Base de dados para estudo fornecida por: archive.ics.uci.edu
### Você pode obter uma descrição sobre cada um dos atributos no arquivo 'descricao_bank_full' situado na pasta 00_daatasets
# +
import pandas as pd
dataset = pd.read_csv('../00_datasets/bank-full.csv')
# +
# atributos categóricos: [0, 1, 2, 3, 4, 6, 7, 8, 10, 15]
# -
previsores = dataset.iloc[ :, 0:16].values
classe = dataset.iloc[ :, 16 ].values
# +
from sklearn.preprocessing import LabelEncoder
label_encoder = LabelEncoder()
previsores[:, 0] = label_encoder.fit_transform(previsores[:, 0])
previsores[:, 1] = label_encoder.fit_transform(previsores[:, 1])
previsores[:, 2] = label_encoder.fit_transform(previsores[:, 2])
previsores[:, 3] = label_encoder.fit_transform(previsores[:, 3])
previsores[:, 4] = label_encoder.fit_transform(previsores[:, 4])
previsores[:, 6] = label_encoder.fit_transform(previsores[:, 6])
previsores[:, 7] = label_encoder.fit_transform(previsores[:, 7])
previsores[:, 8] = label_encoder.fit_transform(previsores[:, 8])
previsores[:, 10] = label_encoder.fit_transform(previsores[:, 10])
previsores[:, 15] = label_encoder.fit_transform(previsores[:, 15])
classe = label_encoder.fit_transform( classe )
# +
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
previsores = scaler.fit_transform(previsores)
# +
from sklearn.model_selection import train_test_split
previsores_treinamento, previsores_teste, classe_treinamento, classe_teste = train_test_split( previsores, classe, test_size=0.25, random_state=0 )
# +
from sklearn.neighbors import KNeighborsClassifier
classificador = KNeighborsClassifier( n_neighbors=5, metric='minkowski', p=2 )
classificador.fit( previsores_treinamento, classe_treinamento )
previsoes = classificador.predict( previsores_teste )
# +
from sklearn.metrics import accuracy_score
accuracy = accuracy_score( classe_teste, previsoes )
accuracy
# -
|
04_aprendizagem-baseada-em-instancias/KNN_bank_full.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python2
# ---
# +
import microdrop_sync.microdrop_sync as ms
import microdrop_sync.utils
reload(microdrop_sync.device)
reload(microdrop_sync.microdrop_sync)
reload(microdrop_sync.utils)
utils = microdrop_sync.utils.MicrodropUtils()
microdrop = ms.MicrodropSync()
device = microdrop.device
from pprint import PrettyPrinter
pp = PrettyPrinter()
# -
filelocation1 = "C:\Users\lucaszw\Desktop\Devices\90_pin_map.svg"
filelocation2 = "C:\Users\lucaszw\Desktop\Devices\pin_map.svg"
dmf_device1 = device.get_from_filelocation(filelocation1)
dmf_device2 = device.load_from_filelocation(filelocation2)
device.change_dmf_device(dmf_device1)
device.device_info_is_running()
device.stop_device_info_plugin()
device.start_device_info_plugin()
|
Device.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="PF219yewQCuv"
import pandas as pd
import numpy as np
import seaborn as sns
import scipy as sp
# + id="zSjmkZ8vQRIY"
dados = pd.read_csv('dados.csv')
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="Fnl9CST_QasK" outputId="7a44d884-c5b5-4501-da06-f12fcf99e94e"
dados.head()
# + id="ZUEPmANAQnyi"
sexo = {0: 'Masculino',
1: 'Feminino'}
cor = {0: 'Indígena',
2: 'Branca',
4: 'Preta',
6: 'Amarela',
8: 'Parda',
9: 'Sem declaração'}
estudo = {
1: 'Sem instrução',
2: '1 ano',
3: '2 anos',
4: '3 anos',
5: '4 anos',
6: '5 anos',
7: '6 anos',
8: '7 anos',
9: '8 anos',
10: '9 anos',
11: '10 anos',
12: '11 anos',
13: '12 anos',
14: '13 anos',
15: '14 anos',
16: '15 anos',
17: 'Não Determinando'
}
estados = {
11: 'Rondônia (RO)',
12: 'Acre (AC)',
13: 'Amazonas (AM)',
14: 'Roraima (RR)',
15: 'Pará (PA)',
16: 'Amapá (AP)',
17: 'Tocantins (TO)',
21: 'Maranhão (MA)',
22: 'Piauí (PI)',
23: 'Ceará (CE)',
24: 'Rio Grande do Norte (RN)',
25: 'Paraíba (PB)',
26: 'Pernambuco (PE)',
27: 'Alagoas (AL)',
28: 'Sergipe (SE)',
29: 'Bahia (BA)',
31: 'Minas Gerais (MG)',
32: 'Espírito Santo (ES)',
33: 'Rio de Janeiro (RJ)',
35: 'São Paulo (SP)',
41: 'Paraná (PR)',
42: 'Santa Catarina (SC)',
43: 'Rio Grande do Sul (RS)',
50: 'Mato Grosso do Sul (MS)',
51: 'Mato Grosso (MT)',
52: 'Goiás (GO)',
53: 'Distrito Federal (DF)'
}
# + [markdown] id="mkyCoffnQKet"
# #Distribuição de probabilidade
# + [markdown] id="DVl8TC6fRBQ3"
# ##Distribuição binomial
# + id="I62ZjsRnTStg"
from scipy.special import comb
# + colab={"base_uri": "https://localhost:8080/"} id="fef3kalGTcN3" outputId="53d56a80-412f-4494-deb8-4b57f0f9668a"
combinacoes = comb(60,6)
combinacoes
# + colab={"base_uri": "https://localhost:8080/"} id="B8vx85-tThjc" outputId="996c4901-901f-43ba-ed7f-ed67e11d08aa"
1/combinacoes*100
# + colab={"base_uri": "https://localhost:8080/"} id="SVN1mFdpT_Oq" outputId="f63f2d31-bae7-4ece-d3c6-90a9215ba19b"
comb(25,20)
# + colab={"base_uri": "https://localhost:8080/"} id="zQgTMJADUbyN" outputId="698d8bb2-125b-4612-cd92-5a80419df3f8"
1/comb(25,20)
# + colab={"base_uri": "https://localhost:8080/"} id="cCFgsINwUdUU" outputId="421b5233-7fa5-4e58-9393-ed52ec3614cb"
n = 10
n
# + colab={"base_uri": "https://localhost:8080/"} id="Dlc9MV9SVIzG" outputId="9e29f548-e60b-4a54-b7b8-08612e0fc7a2"
p = 1/3
p
# + colab={"base_uri": "https://localhost:8080/"} id="1lYyYtLmVc4i" outputId="30c25de4-42ff-4bfd-e542-d216b46416ff"
q = 1-p
q
# + colab={"base_uri": "https://localhost:8080/"} id="F-_dDaVSVfK6" outputId="ea37f872-944b-4e12-acc1-b0a8b1191cd8"
k = 5
k
# + colab={"base_uri": "https://localhost:8080/"} id="h7kpIttgVlIq" outputId="b21a86cd-f0c0-4544-8573-e419f56bcf6b"
prob = (comb(n, k) * (p**k) * (q ** (n - k)))
prob
# + id="VtDjS-YwWATl"
from scipy.stats import binom
# + colab={"base_uri": "https://localhost:8080/"} id="P53Df_qAWSok" outputId="60066e09-8a78-4aa7-f622-4b850a5ae023"
prob = binom.pmf(k,n,p)
print(f'{prob:.8f}')
# + colab={"base_uri": "https://localhost:8080/"} id="AphyFq5GWjEo" outputId="67be3870-6848-45db-a21b-c3abc9322976"
binom.pmf(5,n,p) + binom.pmf(6,n,p) + binom.pmf(7,n,p) + binom.pmf(8,n,p) + binom.pmf(9,n,p) + binom.pmf(10,n,p)
# + colab={"base_uri": "https://localhost:8080/"} id="Gc33z7DTWz_E" outputId="3139ac92-2bc2-4f18-a0b0-6e1ce47f3d13"
binom.pmf([5, 6, 7, 8, 9, 10], n, p).sum()
# + colab={"base_uri": "https://localhost:8080/"} id="d01Zu4l7XGvK" outputId="1dc6e140-227f-452b-8ba9-d870d9d15e7c"
1 - binom.cdf(4, n, p)
# + colab={"base_uri": "https://localhost:8080/"} id="zTWDpAcNXPnS" outputId="fdf8e6df-ad3d-4e00-f829-0dfa4e56cdc0"
binom.sf(4, n, p)
# + id="HGtC4eaJXdHy"
k = 2
n = 4
p = 1/2
# + colab={"base_uri": "https://localhost:8080/"} id="ERh5uVTZYIaV" outputId="b2392825-cf35-4871-d453-61090b60dd84"
binom.pmf(k, n, p)
# + id="4DbHA5gbYKQO"
k = 3
n = 10
p = 1/6
# + colab={"base_uri": "https://localhost:8080/"} id="09-jGyavY73O" outputId="f59ae2e0-c8a0-4c64-995e-138ecb6af6a0"
1-binom.cdf(k, n, p)
# + id="Jk_F8OjsY8ml"
#exemplo
p = 0.6
n = 12
k = 8
# + colab={"base_uri": "https://localhost:8080/"} id="3w7yOdTCgI9B" outputId="7fd8757a-3fbb-44fe-c11d-be9d63c74327"
prob = binom.pmf(k, n, p)
prob
# + colab={"base_uri": "https://localhost:8080/"} id="Gc89pqejgTCr" outputId="3b5f2c6f-a6d0-4277-d243-80d6ba205223"
n = 30 * prob
n
# + id="LoYDegoUghdS"
p = 0.22
n = 3
k = 2
# + colab={"base_uri": "https://localhost:8080/"} id="XIidc1fdg7XI" outputId="c9e09a71-b425-4939-8578-92f5af8cf7e9"
prob = binom.pmf(k, n, p)
prob
# + colab={"base_uri": "https://localhost:8080/"} id="CUDXHxhNg77n" outputId="033c3685-0380-4e71-8bd2-d3ac2125f06d"
50*prob
# + [markdown] id="3j4LSvjvh_MP"
# ##Distribuição de probabilidade Poisson
# + colab={"base_uri": "https://localhost:8080/"} id="UOrF7lCIhKll" outputId="f4c7c754-b437-4c88-9b37-0a2d54a4ecf1"
np.e
# + id="_T2TeYS3izZo"
media = 20
k = 15
# + colab={"base_uri": "https://localhost:8080/"} id="lrjRkUnQjgS1" outputId="3dffb9ac-0555-4e08-adfc-7c5297bd22c1"
prob = ((np.e**(-media)) * (media**k)) / np.math.factorial(k)
print(f'{prob:.8f}')
# + id="7BGN5WbOj4FH"
from scipy.stats import poisson
# + colab={"base_uri": "https://localhost:8080/"} id="x6VunZG3kFUL" outputId="2b0c5c53-8712-4e2d-f125-622c7773bff6"
prob = poisson.pmf(k, media)
prob
# + colab={"base_uri": "https://localhost:8080/"} id="ry18FVrMkJ4y" outputId="2f90171c-325e-4047-c13c-7a3f13791acb"
k = 25
media = 20
prob = poisson.pmf(k, media)
print(f'{prob*100:.2f}')
# + [markdown] id="YSlpHPM6k4vZ"
# ##Distribuição Normal
# + id="aGtsfefpkoIv"
from scipy.stats import norm
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="9b_fCLv3nNNm" outputId="f2718145-d0f6-49fa-c01f-868bae6aef72"
tabela_normal_padronizada = pd.DataFrame(
[],
index=[f"{i/100:.2f}" for i in range(0, 400, 10)],
columns=[f"{i/100:.2f}" for i in range(0, 10)]
)
for index in tabela_normal_padronizada.index:
for columns in tabela_normal_padronizada.columns:
Z = np.round(float(index) + float(columns), 2)
tabela_normal_padronizada.loc[index, columns] = f'{norm.cdf(Z):.4f}'
tabela_normal_padronizada.rename_axis('Z', axis=1, inplace=True)
tabela_normal_padronizada
# + id="6g3LcAtooxyp"
media = 1.70
dp = 0.1
x = 1.80
# + colab={"base_uri": "https://localhost:8080/"} id="BTXB7SUUTfth" outputId="92055d94-15e5-429a-f978-7b89d1f6448a"
Z = (x - media)/dp
Z
# + colab={"base_uri": "https://localhost:8080/"} id="sWOfTs6bTlwX" outputId="d56214c5-51fa-4eb8-f545-8df3f49d711b"
prob = 0.8413
prob
# + colab={"base_uri": "https://localhost:8080/"} id="GIF89WozT6Qp" outputId="46a1bc1f-6fa3-48bd-9d5a-9e1421f7ba64"
prob=norm.cdf(Z)
prob
# + colab={"base_uri": "https://localhost:8080/"} id="-CfjZqCbUKzf" outputId="c8a67076-6f59-464b-df99-74f305581a7c"
prob = norm.cdf((85-70)/5)
prob
# + colab={"base_uri": "https://localhost:8080/"} id="HTZJHFtCUniI" outputId="2d2d636c-b5e9-4719-99f6-e6e3db4fce36"
prob = norm.cdf((1.80-1.70)/0.1) - norm.cdf((1.60-1.70)/0.1)
prob
# + colab={"base_uri": "https://localhost:8080/"} id="YUL0AHnEVGuz" outputId="0c48e2ab-7e33-4db7-db6f-4ddecab5fe06"
prob = (norm.cdf((1.80-1.70)/0.1) - 0.5)*2
prob
# + colab={"base_uri": "https://localhost:8080/"} id="dyx1WDDgVwBQ" outputId="b5607dff-b7c3-48cc-a029-4cd51682bfbc"
prob = norm.cdf((1.80-1.70)/0.1) - (1 - norm.cdf((1.80-1.70)/0.1))
prob
# + colab={"base_uri": "https://localhost:8080/"} id="JXTvdMV7WY5g" outputId="701b6292-e434-45a7-d140-4bc0490eb989"
media = 300
dp = 50
x1 = 250
x2 = 350
prob = norm.cdf((x1-media)/dp) - (norm.cdf((x2-media)/dp))
prob*100
# + colab={"base_uri": "https://localhost:8080/"} id="kKfec8jWXMxx" outputId="30c9024d-d2e5-43c0-8ee3-35ce3b5a51ba"
media = 300
dp = 50
x1 = 400
x2 = 500
prob = norm.cdf((x1-media)/dp) - (norm.cdf((x2-media)/dp))
prob*100
# + colab={"base_uri": "https://localhost:8080/"} id="fVNe-1tRXFSU" outputId="fe3c0292-e792-4391-da37-af86fa31ebb2"
media = 1.70
dp = 0.1
x1 = 1.90
prob = 1- (norm.cdf((x1-media)/dp))
prob*100
# + colab={"base_uri": "https://localhost:8080/"} id="bjVjxz7EYZV0" outputId="77c9839c-37f6-4849-db75-4a2bd1d5f7d5"
media = 1.70
dp = 0.1
x1 = 1.90
prob = (norm.cdf(-(x1-media)/dp))
prob*100
# + colab={"base_uri": "https://localhost:8080/"} id="DGjwNXcxYbaL" outputId="caefe7a5-a789-4dd1-c9a5-3940dc404dab"
media = 720
dp = 30
x1 = 650
x2 = 750
x3 = 800
x4 = 700
prob = norm.cdf((x1-media)/dp) - (norm.cdf((x2-media)/dp))
prob*100
# + colab={"base_uri": "https://localhost:8080/"} id="8EZYtk20Y_gl" outputId="26254dd7-9467-46a0-ad7c-b6af1ff41d2f"
prob = (norm.cdf(-(x3-media)/dp))
prob*100
# + colab={"base_uri": "https://localhost:8080/"} id="HnOgB0moZNit" outputId="ae2a098a-0779-422a-e6b8-e1d877a83b00"
prob = (norm.cdf((x4-media)/dp))
prob*100
# + colab={"base_uri": "https://localhost:8080/"} id="TzCLDlpiZQ58" outputId="f23e6b02-8f59-428a-d638-ee89c60e57ea"
prob = norm.cdf(1.96)
prob
# + colab={"base_uri": "https://localhost:8080/"} id="LSURMz_GcKc7" outputId="3b205bed-36f5-4abb-b3a2-40ee0278ced5"
prob = 1-norm.cdf(2.15)
prob
# + colab={"base_uri": "https://localhost:8080/"} id="tRWdVpP5cTiw" outputId="d6fe8803-6cf2-467b-8c61-5b33796f84f5"
prob = norm.cdf(-0.78)
prob
# + colab={"base_uri": "https://localhost:8080/"} id="sfsmnD5-cdjl" outputId="8a997bb5-e093-4875-d74c-a60a3bcd8cea"
prob = 1-norm.cdf(0.59)
prob
# + [markdown] id="BQXyi-ZUcyGE"
# #Amostragem
# + [markdown] id="wt-5Pnedc3KI"
# ##Populacao e amostragem
# + colab={"base_uri": "https://localhost:8080/"} id="wgPDiprMch6V" outputId="d016c0b8-6a90-43f9-bae3-dca8ba1caa0e"
dados.shape[0]
# + colab={"base_uri": "https://localhost:8080/"} id="-_FP1H2Meai2" outputId="cab9a48b-cfcd-4639-c45d-46afd9e773a4"
dados.Renda.mean()
# + id="h3MnchT-hQy_"
amostra = dados.sample(n = 100, random_state=101)
# + colab={"base_uri": "https://localhost:8080/"} id="JU8NVfZlhh2i" outputId="707e7a23-a682-46fb-9963-9a7f1ace35cf"
amostra.shape[0]
# + colab={"base_uri": "https://localhost:8080/"} id="wf3XBGzRhjTo" outputId="b57cadf9-e64a-4fb1-dfd7-458befc6c8b9"
amostra.Renda.mean()
# + colab={"base_uri": "https://localhost:8080/"} id="9AhDiBx5hogZ" outputId="f00d5148-369b-48ac-a8a4-0f5fe6b339fd"
dados.Sexo.value_counts(normalize=True)
# + colab={"base_uri": "https://localhost:8080/"} id="vwSl__94h47c" outputId="4c72c0cf-4994-40fb-9446-a4be6f57daa2"
amostra.Sexo.value_counts(normalize=True)
# + [markdown] id="5TOHrVfpjS5y"
# #Estimação
# + [markdown] id="BMTZe6mbjVbx"
# ##Teorema do limíte central
# + id="WYGteoRBh7kJ"
n = 2000
total_amostras = 1500
# + id="RUHaZigUk0xu"
amostras = pd.DataFrame()
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="9LxXoIA2j6gY" outputId="64862f31-4032-42d8-a89c-14981a8c2e90"
for i in range(total_amostras):
_ = dados.Idade.sample(2000)
_.index = range(0, len(_))
amostras['Amostra_' + str(i)] = _
amostras
# + colab={"base_uri": "https://localhost:8080/"} id="9QtOjq3LkBqm" outputId="e9298834-ae28-4978-e742-57d9e4759d09"
amostras.mean()
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="LYQGMsowmyux" outputId="fd2a6d6d-5019-4740-f103-bb4d2196a6c4"
amostras.mean().hist()
# + colab={"base_uri": "https://localhost:8080/"} id="2F1iYeGhm63a" outputId="87cf2a37-8afc-4f51-e018-7efdaf7f5340"
dados.Idade.mean()
# + colab={"base_uri": "https://localhost:8080/"} id="HDm2p2k5m-Y6" outputId="01bcff7a-8242-4af7-a96b-1d382addf339"
amostras.mean().mean()
# + colab={"base_uri": "https://localhost:8080/"} id="s-6jx5mmnCrO" outputId="78ffa3e1-2069-40d0-83bd-19043afa7964"
amostras.mean().std()
# + colab={"base_uri": "https://localhost:8080/"} id="YGWXpqWfnJEO" outputId="917ffe57-f891-46fd-92e4-4391089c4511"
dados.Idade.std()
# + colab={"base_uri": "https://localhost:8080/"} id="5M59BfMrnQXA" outputId="96705507-8f73-488a-cc7d-7b33bf6b99d8"
dados.Idade.std()/np.sqrt(n)
# + [markdown] id="5F5rRjpnBZ_b"
# ##Intervalo de confiança
# + id="RczjjEMpnVhU"
media_amostral = 5050
significancia = 0.05
confiança = (1-significancia)
alpha = confiança/2+0.5
dp = 150
n=20
raiz_n = np.sqrt(n)
# + colab={"base_uri": "https://localhost:8080/"} id="AWPcSZzBDCqf" outputId="299bc89b-5516-4a6d-f9cc-9c90840c2d85"
z = norm.ppf(alpha)
round(z, 4)
# + id="ZGSxuXhuDxKz"
#calculo do erro amostras
sigma = dp/raiz_n
# + colab={"base_uri": "https://localhost:8080/"} id="99JB4YvsD4B9" outputId="0887f189-48ba-47c2-d4a6-d5e26715c9f3"
e = z * sigma
e
# + colab={"base_uri": "https://localhost:8080/"} id="4QHcgtuAD-oA" outputId="6091397e-02e0-4d52-80c0-b0e4a099a0c0"
e = norm.ppf((1-0.05)/2+0.5)*dp/np.sqrt(n)
round(e, 2) #gramas
# + colab={"base_uri": "https://localhost:8080/"} id="X-9LKab7EoZx" outputId="84daad32-f49e-488b-af2a-3f11ace601bf"
#Intervalo de confiança
intervalo = (
media_amostral - e,
media_amostral + e
)
intervalo
# + colab={"base_uri": "https://localhost:8080/"} id="NHfMfgRxFiUf" outputId="880787e8-e9af-429b-8e90-<KEY>"
intervalo = norm.interval(alpha = confiança, loc = media_amostral, scale = sigma)
intervalo
# + id="YhX4A-axGJ_l"
#exercício
media_amostral = ''
significancia = 0.05
confiança = (1-significancia)
alpha = confiança/2+0.5
dp = 6
n=50
raiz_n = np.sqrt(n)
# + colab={"base_uri": "https://localhost:8080/"} id="aqDB7ktmG3sX" outputId="fa6aacd9-1e2c-4861-e695-468bf3c4058f"
e = norm.ppf(alpha)*dp/np.sqrt(n)
round(e, 2) #gramas
# + id="vERiGQOFJoKR"
#exercício
media_amostral = 28
significancia = 1 - confiança
confiança = 0.9
alpha = confiança/2+0.5
dp = 11
n = 1976
raiz_n = np.sqrt(n)
sigma = dp/raiz_n
# + colab={"base_uri": "https://localhost:8080/"} id="AnmwxmS5KFn1" outputId="8392dcd8-8173-4104-ad2a-e0318606b429"
intervalo = norm.interval(alpha = confiança, loc = media_amostral, scale = sigma)
intervalo
# + [markdown] id="AmCqEq2BNGWK"
# ##Calculo do tamanho de amostra
# + id="6Y1EIfevNzYa"
confiança = 0.95
alpha = confiança/2+0.5
sigma = 3323.29 #desvio padrão populacional
e = 100
# + colab={"base_uri": "https://localhost:8080/"} id="HAD4yZsdKQFa" outputId="814eee0a-5714-4ef1-c494-3fb2368e2b78"
z = norm.ppf(alpha)
z
# + colab={"base_uri": "https://localhost:8080/"} id="QGCjW5NFOB7l" outputId="6a5b545a-96bb-492f-968e-59c59a34865d"
n = (norm.ppf(alpha)*((sigma)/(e)))**2
int(round(n))
# + id="dP3OnEdFOzcu"
#exercício
media_amostral = 45.50
significancia = 0.1
confianca = 1 - significancia
alpha = confianca/2+0.5
dp = 15 #pq é sigma?
n = ''
erro = 0.1
e= media_amostral * erro #erro diferencial
#raiz_n = np.sqrt(n)
#sigma = dp/raiz_n
# + colab={"base_uri": "https://localhost:8080/"} id="hdxr-WbyP16v" outputId="6efaff20-2f31-4a8f-9997-87d7a7007147"
n = (norm.ppf(alpha)*((dp)/(e)))**2
int(round(n))
# + colab={"base_uri": "https://localhost:8080/"} id="StEUtYPxRwd9" outputId="dfa45cd4-ef47-4988-d09e-082c3ebabb40"
media = 45.5
sigma = 15
significancia = 0.10
confianca = 1 - significancia
z = norm.ppf(0.5 + (confianca / 2))
erro_percentual = 0.10
e = media * erro_percentual
n = (z * (sigma / e)) ** 2
n.round()
# + [markdown] id="bz_WH1s2V9n0"
# ##Calculo da amostra para população finita
# + id="O5m49lJ1RttD"
N = 10000 #tamanho da população
significancia = 1 - confianca
confianca = 0.95
alpha = alpha = confianca/2+0.5
z = norm.ppf(alpha) #variavel normal padronizada
sigma = '' #desvio padrão populacional
s = 12 #desvio padrão amostral
e = 5 #erro diferencial
# + colab={"base_uri": "https://localhost:8080/"} id="Es5a5muGWy8R" outputId="1de13d85-3f34-4014-c69d-5a711de64eaf"
n = ((z**2)*(s**2)*(N)) / (((z**2)*(s**2))+((e**2)*(N-1)))
int(n.round())
# + id="xZeTljUXXjrJ"
N = 2000 #tamanho da população
significancia = 1 - confianca
confianca = 0.95
alpha = alpha = confianca/2+0.5
z = norm.ppf(alpha) #variavel normal padronizada
sigma = '' #desvio padrão populacional
s = 0.480 #desvio padrão amostral
e = 0.3 #erro diferencial
# + colab={"base_uri": "https://localhost:8080/"} id="R1nAziZ0Yh4M" outputId="1753f488-1b13-4e96-a7a4-1efeea5a0a1c"
n = ((z**2)*(s**2)*(N)) / (((z**2)*(s**2))+((e**2)*(N-1)))
int(n.round())
# + id="sbqtJkppYiNx"
renda_5mil = dados.query('Renda <=5000').Renda
# + id="09a0BcvGZpEm"
N = '' #tamanho da população
significancia = 1 - confianca
confianca = 0.95
alpha = alpha = confianca/2+0.5
z = norm.ppf(alpha) #variavel normal padronizada
sigma = renda_5mil.std() #desvio padrão populacional
media = renda_5mil.mean()
s = '' #desvio padrão amostral
e = 10 #erro diferencial
# + colab={"base_uri": "https://localhost:8080/"} id="eYY1OovIaROk" outputId="feff32b3-1177-43ba-ba69-ae4fcaf3c59a"
n = int((z * (sigma / e)) ** 2)
n
# + colab={"base_uri": "https://localhost:8080/"} id="O1CjcguPaR9Z" outputId="3d9c737d-7e2a-4bf8-d5ab-c7968e9b8ed7"
intervalo = norm.interval(alpha = confianca, loc = media, scale = sigma/np.sqrt(n))
intervalo
# + id="wg4S8owbazKl"
import matplotlib.pyplot as plt
# + id="rEBzQnu2bN3K"
tamanho_simulacao = 1000
medias = [renda_5mil.sample(n = n).mean() for i in range(1 , tamanho_simulacao)]
medias = pd.DataFrame(medias)
# + colab={"base_uri": "https://localhost:8080/", "height": 391} id="csV69Czebkwv" outputId="729db28f-9ead-4e6c-cf33-d072375f952e"
ax = medias.plot(style = '.')
ax.figure.set_size_inches(12,6)
ax.hlines(y= media, xmin=0, xmax=tamanho_simulacao, color='black', linestyles='dashed')
ax.hlines(y= intervalo[0], xmin=0, xmax=tamanho_simulacao, color='red', linestyles='dashed')
ax.hlines(y= intervalo[1], xmin=0, xmax=tamanho_simulacao, color='red', linestyles='dashed')
ax
# + [markdown] id="z4gDB_uFfTy0"
# ##Desafio
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="o5WhkbJxc5e9" outputId="5eb46b46-1077-4ed3-e45d-018be8460917"
dados.head()
# + id="n8Rmc-HSfYDj"
k = 7
n = 10
p = 0.7
# + colab={"base_uri": "https://localhost:8080/"} id="V8mYqKJnfy4o" outputId="1cbfc91f-1f56-4469-92d5-ce2e95ee8a0f"
prob = binom.pmf(k, n, p)
prob
# + colab={"base_uri": "https://localhost:8080/"} id="aGn2-8iAgPEW" outputId="f2e28a6f-9c66-4cc8-9248-760a521c92ac"
media = 100
#media = n * prob
n = media / prob
n
# + id="M3D6eO06g1CT"
dataset= dados.Renda.sample(n=200, random_state=101)
# + colab={"base_uri": "https://localhost:8080/"} id="vMMZcm1zhw27" outputId="7e6d57d8-ef22-49d1-9bbe-fccb7356fa66"
dataset.mean()
# + colab={"base_uri": "https://localhost:8080/"} id="5vkCLIvvh1c7" outputId="ff397ca5-f478-4625-8b86-457475d12c8b"
dataset.std()
# + id="rrQgHnykh3oU"
media_amostra = dataset.mean()
desvio_padrao_amostra = dataset.std()
recursos = 150000
custo_por_entrevista = 100
# + id="VK3fQoLSiQYL"
e = 0.1*media_amostra
# + id="XRtgikWh3ZeK"
z = norm.ppf((0.9/2)+0.5)
# + colab={"base_uri": "https://localhost:8080/"} id="Y0noJ8nl3mwa" outputId="ff45dfb4-9c97-4538-cc5b-287014ce5421"
n_90 = int((z * (desvio_padrao_amostra/ e))**2)
n_90
# + colab={"base_uri": "https://localhost:8080/"} id="BxzPDorL32zv" outputId="548b6e5f-744f-4f07-f7c7-66006739b186"
z = norm.ppf((0.95/2)+0.5)
n_95 = int((z * (desvio_padrao_amostra/ e))**2)
n_95
# + colab={"base_uri": "https://localhost:8080/"} id="qDviOZUZ4Dxc" outputId="5d62d38c-e1e3-4e07-be1b-28217d3a8dbe"
z = norm.ppf((0.99/2)+0.5)
n_99 = int((z * (desvio_padrao_amostra/ e))**2)
n_99
# + colab={"base_uri": "https://localhost:8080/"} id="Khq_UWD54HYu" outputId="623904a3-1403-46f7-a635-8f9921ac03d1"
print(f'O custo para a pesquisa com 90% de conficança é R${n_90*custo_por_entrevista:,.2f}')
print(f'O custo para a pesquisa com 95% de conficança é R${n_95*custo_por_entrevista:,.2f}')
print(f'O custo para a pesquisa com 99% de conficança é R${n_99*custo_por_entrevista:,.2f}')
# + colab={"base_uri": "https://localhost:8080/"} id="je_vO8Ws4bPg" outputId="f5624be6-5d7b-47b2-ea1a-9b419e87c12e"
intervalo = norm.interval(alpha = 0.95, loc = media_amostra, scale = desvio_padrao_amostra/np.sqrt(n_95))
intervalo
# + colab={"base_uri": "https://localhost:8080/"} id="FVRxRXYz47v5" outputId="2963181c-6ef5-4169-824a-f51152e6ac51"
n = recursos/custo_por_entrevista
n
# + colab={"base_uri": "https://localhost:8080/"} id="zkV1_3c05X3e" outputId="2cfe4e48-eb1d-474c-a914-f55b07e5bf01"
e = norm.ppf((1-0.05)/2+0.5)*desvio_padrao_amostra/np.sqrt(n)
round(e, 2)
# + colab={"base_uri": "https://localhost:8080/"} id="pGkoYT9H5y6k" outputId="168937be-50ca-425b-f7ee-827e0a1c48e0"
e_percentual = (e / media_amostra )*100
e_percentual
# + id="doYtDpgG6L2M"
e = 0.05*media_amostra
# + colab={"base_uri": "https://localhost:8080/"} id="dxCgVX8r6mn8" outputId="4a198412-801d-4195-ec2f-318e4cd5cf07"
z = norm.ppf((0.95/2)+0.5)
n_95 = int((z * (desvio_padrao_amostra/ e))**2)
n_95
# + colab={"base_uri": "https://localhost:8080/"} id="5kcThSVw6w71" outputId="a886e15b-2efc-469f-ae44-7da02d3f84ca"
custo = n_95*custo_por_entrevista
custo
# + id="MkaUh06b7Z8n"
|
alura_estatistica_probabilidade.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="vl-0acX6FBQu"
# # This notebook describes how the FruitNet was built and trained.
# *The source code for the FruitNet app is available [here](https://github.com/AlexanderKlanovets/fruitnet).*
#
# ## Installing and importing dependencies
#
# For this project, the following tools were used:
# - [Tensorflow 2](https://www.tensorflow.org/install) for building and training the model;
# - [Numpy](https://numpy.org/) for working with arrays;
# - [Matplotlib](https://matplotlib.org/) for visualizing the data.
#
# + id="yHwLm_tUIghQ"
# !pip install -q tf-nightly numpy matplotlib
# + id="OyA5UUZGIqHE"
import matplotlib.pyplot as plt
import numpy as np
import os
import tensorflow as tf
from tensorflow.keras.preprocessing import image_dataset_from_directory
from google.colab import drive
# -
# I've trained the model using Google Colab. The dataset was uploaded to my Google Drive and mounted it in Colab:
# + id="QB88VcquIzQa" outputId="623e3865-eaa2-4de0-c0fa-7c2e26a000c5" colab={"base_uri": "https://localhost:8080/", "height": 34}
drive.mount('/content/drive')
# + [markdown] id="8MJ3JNefIOvl"
# ## Data preprocessing
#
# The dataset used for model implementation is [Fruits fresh and rotten for classification](https://www.kaggle.com/sriramr/fruits-fresh-and-rotten-for-classification) provided by <NAME>.
#
# The following steps of the data preprocessing are:
# - data download;
# - data samples visualization;
# - creating training, validation and test sets from the initial dataset;
# - rescaling pixel values of the images in the datasets.
#
# ### Data download
# + id="tEXd71W0I9s1" outputId="6b1f2faa-30db-4074-8c2a-fd813dfa52b3" colab={"base_uri": "https://localhost:8080/", "height": 34}
PATH = '/content/drive/My Drive/Rotten fruits dataset/dataset'
train_dir = os.path.join(PATH, 'train')
validation_dir = os.path.join(PATH, 'test')
LABELS = ['fresh apple', 'fresh banana', 'fresh orange',
'rotten apple', 'rotten banana', 'rotten orange']
BATCH_SIZE = 32
EPOCHS = 20
IMG_SIZE = (160, 160)
train_dataset = image_dataset_from_directory(train_dir,
shuffle=True,
batch_size=BATCH_SIZE,
image_size=IMG_SIZE,
label_mode='categorical')
# + id="HFOfQHNCJV5A" outputId="e10200b8-ebf2-473d-8cb6-41cd672c714b" colab={"base_uri": "https://localhost:8080/", "height": 34}
validation_dataset = image_dataset_from_directory(validation_dir,
shuffle=True,
batch_size=BATCH_SIZE,
image_size=IMG_SIZE,
label_mode='categorical')
# + [markdown] id="ZWFhnx7RKZxH"
# ### Visualizing data samples
# + id="AZ76xNotJbMb" outputId="332b630e-53fd-4771-8d28-a939df1f0f0f" colab={"base_uri": "https://localhost:8080/", "height": 591}
class_names = train_dataset.class_names
plt.figure(figsize=(10, 10))
for images, labels in train_dataset.take(1):
for i in range(9):
ax = plt.subplot(3, 3, i + 1)
plt.imshow(images[i].numpy().astype("uint8"))
plt.title(class_names[labels[i]])
plt.axis("off")
# + [markdown] id="diITNkiBKv0q"
# ### Creating a test dataset
# + id="M2TyDNjfK2zM"
val_batches = tf.data.experimental.cardinality(validation_dataset)
test_dataset = validation_dataset.take(val_batches // 5)
validation_dataset = validation_dataset.skip(val_batches // 5)
# + id="KEmVVSDgLYun" outputId="36835509-2211-462d-8883-a8dd797b6a36" colab={"base_uri": "https://localhost:8080/", "height": 51}
val_batches_num = tf.data.experimental.cardinality(validation_dataset)
test_batches_num = tf.data.experimental.cardinality(test_dataset)
print('Number of validation batches: %d' % val_batches_num)
print('Number of test batches: %d' % test_batches_num)
# + [markdown] id="RnptH4tqK3cJ"
# ### Configuring the dataset for performance
# + id="s-ZUqyEoLb4D"
AUTOTUNE = tf.data.experimental.AUTOTUNE
train_dataset = train_dataset.prefetch(buffer_size=AUTOTUNE)
validation_dataset = validation_dataset.prefetch(buffer_size=AUTOTUNE)
test_dataset = test_dataset.prefetch(buffer_size=AUTOTUNE)
# + [markdown] id="pt2Bj_-9LX5D"
# ### Rescaling pixel values
# + id="mm-3yos4NPVx"
preprocess_input = tf.keras.applications.mobilenet_v2.preprocess_input
# + [markdown] id="nCHKbveML4P3"
# # Building the model
#
# I've used Google MobileNet V2 as a base model for this problem. Here I'm importing the model without the classification layers:
# + id="duN2bpaiLjD7"
IMG_SHAPE = IMG_SIZE + (3,)
base_model = tf.keras.applications.MobileNetV2(input_shape=IMG_SHAPE,
include_top=False,
weights='imagenet')
# -
# Freezing the convolutional base before appling the transfer learning:
# + id="h9ud0TPbLodM"
base_model.trainable = False
# + id="BFPrMm5bMuZF" outputId="aa206984-84d4-42d1-d339-963ed5b913af" colab={"base_uri": "https://localhost:8080/", "height": 34}
image_batch, label_batch = next(iter(train_dataset))
feature_batch = base_model(image_batch)
print(feature_batch.shape)
# + id="9hL9Til-Lo6q"
base_model.summary()
# -
# Converting the features from the convolutional layers to a vector. As I'm using 32-sized mini-batches for training, I get 32 vectors:
# + id="LO3B1nskL4c5" outputId="c9994309-b069-470e-9677-1c2ba6b53c98" colab={"base_uri": "https://localhost:8080/", "height": 34}
global_average_layer = tf.keras.layers.GlobalAveragePooling2D()
feature_batch_average = global_average_layer(feature_batch)
print(feature_batch_average.shape)
# -
# Adding a custom classification layer:
# + id="3lNWDZSCMJx1" outputId="3fd9b3ee-cc8f-4467-f0ac-1e23d77eb998" colab={"base_uri": "https://localhost:8080/", "height": 34}
prediction_layer = tf.keras.layers.Dense(6, activation='softmax')
prediction_batch = prediction_layer(feature_batch_average)
print(prediction_batch.shape)
# -
# Putting it all together:
# + id="NaihBAHeMbzh"
inputs = tf.keras.Input(shape=(160, 160, 3))
x = preprocess_input(inputs)
x = base_model(x, training=False)
x = global_average_layer(x)
x = tf.keras.layers.Dropout(0.2)(x)
outputs = prediction_layer(x)
model = tf.keras.Model(inputs, outputs)
# -
# ## Compling the model
# + id="WgxK0qkzNBkf"
base_learning_rate = 0.0001
model.compile(optimizer=tf.keras.optimizers.Adam(lr=base_learning_rate),
loss=tf.keras.losses.CategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
# + id="yh8uaKVjNiU1" outputId="f61790c1-c45a-4c11-df63-2a413047a9af" colab={"base_uri": "https://localhost:8080/", "height": 391}
model.summary()
# + id="oZuOdVLZNsfF" outputId="a7b2aa3d-0170-461e-8386-b92d75f33b36" colab={"base_uri": "https://localhost:8080/", "height": 34}
initial_epochs = 10
loss0, accuracy0 = model.evaluate(validation_dataset)
# + id="orhpJaCyjYS5" outputId="f5558db7-1cfd-437a-8706-d22a09fa5007" colab={"base_uri": "https://localhost:8080/", "height": 51}
print("initial loss: {:.2f}".format(loss0))
print("initial accuracy: {:.2f}".format(accuracy0))
# -
# ## Training the model
# + id="o7VZDjk4N5M0" outputId="c3b5381a-1987-499b-e2fc-4df6c2d1728a" colab={"base_uri": "https://localhost:8080/", "height": 697}
history = model.fit(train_dataset,
epochs=EPOCHS,
validation_data=validation_dataset)
# -
# ## Plotting the learning curves
# + id="MFrVzp2XN8rK" outputId="3280211d-f80b-4f0f-e7f7-c64ddc741e15" colab={"base_uri": "https://localhost:8080/", "height": 513}
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.figure(figsize=(8, 8))
plt.subplot(2, 1, 1)
plt.plot(acc, label='Training Accuracy')
plt.plot(val_acc, label='Validation Accuracy')
plt.legend(loc='lower right')
plt.ylabel('Accuracy')
plt.ylim([min(plt.ylim()),1])
plt.title('Training and Validation Accuracy')
plt.subplot(2, 1, 2)
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.legend(loc='upper right')
plt.ylabel('Cross Entropy')
plt.ylim([0,1.0])
plt.title('Training and Validation Loss')
plt.xlabel('epoch')
plt.show()
# + id="xDWFHPCh3ZtR"
model.save('fruit_classifier_v2_dropout.h5')
# -
# ## Checking the final accuracy:
# + id="bxSxLiCNLKvw" outputId="eb5ca7bf-0be8-4053-b4dd-159abf70ef2b" colab={"base_uri": "https://localhost:8080/", "height": 34}
loss_final, accuracy_final = model.evaluate(test_dataset)
# + id="j1qlecCHqv1m" outputId="39152040-583f-461e-f4ed-62435863fd7d" colab={"base_uri": "https://localhost:8080/", "height": 51}
print("Final loss: {:.2f}".format(loss_final))
print("Final accuracy: {:.2f}".format(accuracy_final))
|
notebooks/FruitNetTransferLearning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# <a href="https://colab.research.google.com/github/haribharadwaj/notebooks/blob/main/BME511/SystemIdentificationMAP.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# # ML vs. MAP estimation for system identification
# +
import numpy as np
import pylab as pl
# Setting it so figs will be a bit bigger
from matplotlib import pyplot as plt
plt.rcParams['figure.figsize'] = [5, 3.33]
plt.rcParams['figure.dpi'] = 120
# -
# ## ML filter (same on previous active filter code)
from scipy import linalg
def deconvML(x, y, p):
A = linalg.toeplitz(x[(p-1):], x[:p][::-1])
ysub = y[(p-1):]
h = np.dot(linalg.pinv(A), ysub)
return h
# ## Simulated test scenario
#
# ### Impulse response
# +
fs = 1024
t = np.arange(0, 2, 1./fs)
f = 10;
tau = 0.25/f;
h = np.sin(2 * np.pi * f * t) * np.exp(-t/tau)
pl.plot(t, h);
pl.xlabel('Time (s)')
pl.ylabel('h(t)')
pl.xlim([0, 0.4])
# -
# ### Create some inputs and outputs
# +
from scipy import signal
f2 = 5
tau2 = 0.25 / f2
h2 = np.sin(2 * np.pi * f2 * t) * np.exp(-t/tau2)
x = signal.lfilter(h2, 1, np.random.randn(t.shape[0]))
SNR = 100
y_temp = signal.lfilter(h, 1, x)
sigma_n = np.sqrt((y_temp ** 2).mean()) / SNR
y = y_temp + np.random.randn(t.shape[0]) * sigma_n
pl.subplot(211)
pl.plot(t, x)
pl.ylabel('x(t)')
pl.subplot(212)
pl.plot(t, y)
pl.xlabel('Time (s)')
pl.ylabel('y(t)')
# +
p = 500
hhat = deconvML(x, y, p)
tplot = np.arange(p) / fs
pl.plot(tplot, hhat)
pl.plot(tplot, h[:tplot.shape[0]], '--')
pl.xlabel('Time (s)')
pl.ylabel('System Function')
pl.legend(('$\widehat{h}(t)$', 'h(t)'))
pl.xlim([0, 0.4])
# -
# ## MAP filter estimate
def deconvMAP(x, y, p, lam):
A = linalg.toeplitz(x[(p-1):], x[:p][::-1])
ysub = y[(p-1):]
B = np.dot(A.T, A) + lam * np.eye(p)
h = np.dot(np.dot(linalg.inv(B), A.T), ysub)
return h
# +
p = 500
lam = 100 # Hyperparameter
hhat = deconvMAP(x, y, p, lam)
tplot = np.arange(p) / fs
pl.plot(tplot, hhat)
pl.plot(tplot, h[:tplot.shape[0]], '--')
pl.xlabel('Time (s)')
pl.ylabel('System Function')
pl.legend(('$\widehat{h}(t)$', 'h(t)'))
pl.xlim([0, 0.4])
# -
# ## L-curve for choosing hyperparameter(s): Bias-variance tradeoff in action
# +
lams = 10. ** np.arange(-5, 5, 0.1)
fit_error = np.zeros(lams.shape)
h_norm = np.zeros(lams.shape)
for k, lam in enumerate(lams):
hhat = deconvMAP(x, y, p, lam)
y_fitted = signal.lfilter(hhat, 1, x)
fit_error[k] = ((y - y_fitted) ** 2.).mean()
h_norm[k] = (hhat ** 2.).mean()
pl.loglog(h_norm, fit_error)
pl.xlabel('L2 norm of parameter estimate')
pl.ylabel('Squared-error of the fitted solution')
# -
pl.loglog(h_norm, lams)
pl.xlabel('L2 norm of parameter estimate')
pl.ylabel('$lambda$')
|
BME511/SystemIdentificationMAP.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Week 8: Reinforcement Learning for seq2seq
#
# This time we'll solve a problem of transribing hebrew words in english, also known as g2p (grapheme2phoneme)
#
# * word (sequence of letters in source language) -> translation (sequence of letters in target language)
#
# Unlike most deep learning researchers do, we won't only train it to maximize likelihood of correct translation, but also employ reinforcement learning to actually teach it to translate with as few errors as possible.
#
#
# ### About the task
#
# One notable property of Hebrew is that it's consonant language. That is, there are no wovels in the written language. One could represent wovels with diacritics above consonants, but you don't expect people to do that in everyay life.
#
# Therefore, some hebrew characters will correspond to several english letters and others - to none, so we should use encoder-decoder architecture to figure that out.
#
# 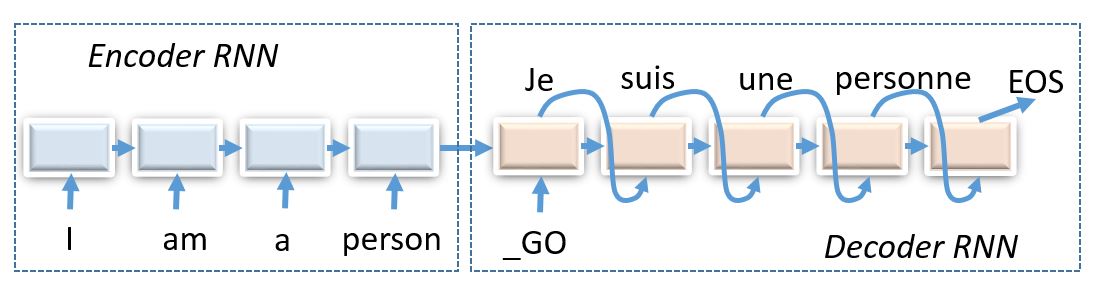
# _(img: esciencegroup.files.wordpress.com)_
#
# Encoder-decoder architectures are about converting anything to anything, including
# * Machine translation and spoken dialogue systems
# * [Image captioning](http://mscoco.org/dataset/#captions-challenge2015) and [image2latex](https://openai.com/requests-for-research/#im2latex) (convolutional encoder, recurrent decoder)
# * Generating [images by captions](https://arxiv.org/abs/1511.02793) (recurrent encoder, convolutional decoder)
# * Grapheme2phoneme - convert words to transcripts
#
# We chose simplified __Hebrew->English__ machine translation for words and short phrases (character-level), as it is relatively quick to train even without a gpu cluster.
# +
EASY_MODE = True #If True, only translates phrases shorter than 20 characters (way easier).
#Useful for initial coding.
#If false, works with all phrases (please switch to this mode for homework assignment)
MODE = "he-to-en" #way we translate. Either "he-to-en" or "en-to-he"
MAX_OUTPUT_LENGTH = 50 if not EASY_MODE else 20 #maximal length of _generated_ output, does not affect training
REPORT_FREQ = 100 #how often to evaluate validation score
# -
# ### Step 1: preprocessing
#
# We shall store dataset as a dictionary
# `{ word1:[translation1,translation2,...], word2:[...],...}`.
#
# This is mostly due to the fact that many words have several correct translations.
#
# We have implemented this thing for you so that you can focus on more interesting parts.
#
#
# __Attention python2 users!__ You may want to cast everything to unicode later during homework phase, just make sure you do it _everywhere_.
# +
import numpy as np
from collections import defaultdict
word_to_translation = defaultdict(list) #our dictionary
bos = '_'
eos = ';'
with open("main_dataset.txt") as fin:
for line in fin:
en,he = line[:-1].lower().replace(bos,' ').replace(eos,' ').split('\t')
word,trans = (he,en) if MODE=='he-to-en' else (en,he)
if len(word) < 3: continue
if EASY_MODE:
if max(len(word),len(trans))>20:
continue
word_to_translation[word].append(trans)
print ("size = ",len(word_to_translation))
# -
#get all unique lines in source language
all_words = np.array(list(word_to_translation.keys()))
# get all unique lines in translation language
all_translations = np.array([ts for all_ts in word_to_translation.values() for ts in all_ts])
# ### split the dataset
#
# We hold out 10% of all words to be used for validation.
#
from sklearn.model_selection import train_test_split
train_words,test_words = train_test_split(all_words,test_size=0.1,random_state=42)
# ### Building vocabularies
#
# We now need to build vocabularies that map strings to token ids and vice versa. We're gonna need these fellas when we feed training data into model or convert output matrices into english words.
from voc import Vocab
inp_voc = Vocab.from_lines(''.join(all_words), bos=bos, eos=eos, sep='')
out_voc = Vocab.from_lines(''.join(all_translations), bos=bos, eos=eos, sep='')
# +
# Here's how you cast lines into ids and backwards.
batch_lines = all_words[:5]
batch_ids = inp_voc.to_matrix(batch_lines)
batch_lines_restored = inp_voc.to_lines(batch_ids)
print("lines")
print(batch_lines)
print("\nwords to ids (0 = bos, 1 = eos):")
print(batch_ids)
print("\nback to words")
print(batch_lines_restored)
# -
# Draw word/translation length distributions to estimate the scope of the task.
# +
import matplotlib.pyplot as plt
# %matplotlib inline
plt.figure(figsize=[8,4])
plt.subplot(1,2,1)
plt.title("words")
plt.hist(list(map(len,all_words)),bins=20);
plt.subplot(1,2,2)
plt.title('translations')
plt.hist(list(map(len,all_translations)),bins=20);
# -
# ### Step 3: deploy encoder-decoder (1 point)
#
# __assignment starts here__
#
# Our architecture consists of two main blocks:
# * Encoder reads words character by character and outputs code vector (usually a function of last RNN state)
# * Decoder takes that code vector and produces translations character by character
#
# Than it gets fed into a model that follows this simple interface:
# * __`model.symbolic_translate(inp, **flags) -> out, logp`__ - takes symbolic int32 matrix of hebrew words, produces output tokens sampled from the model and output log-probabilities for all possible tokens at each tick.
# * __`model.symbolic_score(inp, out, **flags) -> logp`__ - takes symbolic int32 matrices of hebrew words and their english translations. Computes the log-probabilities of all possible english characters given english prefices and hebrew word.
# * __`model.weights`__ - weights from all model layers [a list of variables]
#
# That's all! It's as hard as it gets. With those two methods alone you can implement all kinds of prediction and training.
# +
import tensorflow as tf
tf.reset_default_graph()
s = tf.InteractiveSession()
# ^^^ if you get "variable *** already exists": re-run this cell again
# +
from basic_model_tf import BasicTranslationModel
model = BasicTranslationModel('model',inp_voc,out_voc,
emb_size=64, hid_size=128)
s.run(tf.global_variables_initializer())
# +
# Play around with symbolic_translate and symbolic_score
inp = tf.placeholder_with_default(np.random.randint(0,10,[3,5],dtype='int32'),[None,None])
out = tf.placeholder_with_default(np.random.randint(0,10,[3,5],dtype='int32'),[None,None])
# translate inp (with untrained model)
sampled_out, logp = model.symbolic_translate(inp, greedy=False)
print("\nSymbolic_translate output:\n",sampled_out,logp)
print("\nSample translations:\n", s.run(sampled_out))
# -
# score logp(out | inp) with untrained input
logp = model.symbolic_score(inp,out)
print("\nSymbolic_score output:\n",logp)
print("\nLog-probabilities (clipped):\n", s.run(logp)[:,:2,:5])
# +
# Prepare any operations you want here
input_sequence = tf.placeholder('int32', [None,None])
greedy_translations, logp = <build symbolic translations with greedy=True>
def translate(lines):
"""
You are given a list of input lines.
Make your neural network translate them.
:return: a list of output lines
"""
# Convert lines to a matrix of indices
lines_ix = <YOUR CODE>
# Compute translations in form of indices
trans_ix = s.run(greedy_translations, {<YOUR CODE - feed dict>})
# Convert translations back into strings
return out_voc.to_lines(trans_ix)
# +
print("Sample inputs:",all_words[:3])
print("Dummy translations:",translate(all_words[:3]))
assert isinstance(greedy_translations,tf.Tensor) and greedy_translations.dtype.is_integer, "trans must be a tensor of integers (token ids)"
assert translate(all_words[:3]) == translate(all_words[:3]), "make sure translation is deterministic (use greedy=True and disable any noise layers)"
assert type(translate(all_words[:3])) is list and (type(translate(all_words[:1])[0]) is str or type(translate(all_words[:1])[0]) is unicode), "translate(lines) must return a sequence of strings!"
print("Tests passed!")
# -
# ### Scoring function
#
# LogLikelihood is a poor estimator of model performance.
# * If we predict zero probability once, it shouldn't ruin entire model.
# * It is enough to learn just one translation if there are several correct ones.
# * What matters is how many mistakes model's gonna make when it translates!
#
# Therefore, we will use minimal Levenshtein distance. It measures how many characters do we need to add/remove/replace from model translation to make it perfect. Alternatively, one could use character-level BLEU/RougeL or other similar metrics.
#
# The catch here is that Levenshtein distance is not differentiable: it isn't even continuous. We can't train our neural network to maximize it by gradient descent.
# +
import editdistance # !pip install editdistance
def get_distance(word,trans):
"""
A function that takes word and predicted translation
and evaluates (Levenshtein's) edit distance to closest correct translation
"""
references = word_to_translation[word]
assert len(references)!=0,"wrong/unknown word"
return min(editdistance.eval(trans,ref) for ref in references)
def score(words, bsize=100):
"""a function that computes levenshtein distance for bsize random samples"""
assert isinstance(words,np.ndarray)
batch_words = np.random.choice(words,size=bsize,replace=False)
batch_trans = translate(batch_words)
distances = list(map(get_distance,batch_words,batch_trans))
return np.array(distances,dtype='float32')
# -
#should be around 5-50 and decrease rapidly after training :)
[score(test_words,10).mean() for _ in range(5)]
# ## Step 2: Supervised pre-training
#
# Here we define a function that trains our model through maximizing log-likelihood a.k.a. minimizing crossentropy.
# +
# import utility functions
from basic_model_tf import initialize_uninitialized, infer_length, infer_mask, select_values_over_last_axis
class supervised_training:
# variable for inputs and correct answers
input_sequence = tf.placeholder('int32',[None,None])
reference_answers = tf.placeholder('int32',[None,None])
# Compute log-probabilities of all possible tokens at each step. Use model interface.
logprobs_seq = <YOUR CODE>
# compute mean crossentropy
crossentropy = - select_values_over_last_axis(logprobs_seq,reference_answers)
mask = infer_mask(reference_answers, out_voc.eos_ix)
loss = tf.reduce_sum(crossentropy * mask)/tf.reduce_sum(mask)
# Build weights optimizer. Use model.weights to get all trainable params.
train_step = <YOUR CODE>
# intialize optimizer params while keeping model intact
initialize_uninitialized(s)
# -
# Actually run training on minibatches
import random
def sample_batch(words, word_to_translation, batch_size):
"""
sample random batch of words and random correct translation for each word
example usage:
batch_x,batch_y = sample_batch(train_words, word_to_translations,10)
"""
#choose words
batch_words = np.random.choice(words,size=batch_size)
#choose translations
batch_trans_candidates = list(map(word_to_translation.get,batch_words))
batch_trans = list(map(random.choice,batch_trans_candidates))
return inp_voc.to_matrix(batch_words), out_voc.to_matrix(batch_trans)
bx,by = sample_batch(train_words, word_to_translation, batch_size=3)
print("Source:")
print(bx)
print("Target:")
print(by)
# +
from IPython.display import clear_output
from tqdm import tqdm,trange #or use tqdm_notebook,tnrange
loss_history=[]
editdist_history = []
for i in trange(25000):
bx,by = sample_batch(train_words, word_to_translation, 32)
feed_dict = {
supervised_training.input_sequence:bx,
supervised_training.reference_answers:by
}
loss,_ = s.run([supervised_training.loss,supervised_training.train_step],feed_dict)
loss_history.append(loss)
if (i+1)%REPORT_FREQ==0:
clear_output(True)
current_scores = score(test_words)
editdist_history.append(current_scores.mean())
plt.figure(figsize=(12,4))
plt.subplot(131)
plt.title('train loss / traning time')
plt.plot(loss_history)
plt.grid()
plt.subplot(132)
plt.title('val score distribution')
plt.hist(current_scores, bins = 20)
plt.subplot(133)
plt.title('val score / traning time')
plt.plot(editdist_history)
plt.grid()
plt.show()
print("llh=%.3f, mean score=%.3f"%(np.mean(loss_history[-10:]),np.mean(editdist_history[-10:])))
# Note: it's okay if loss oscillates up and down as long as it gets better on average over long term (e.g. 5k batches)
# -
for word in train_words[:10]:
print("%s -> %s"%(word,translate([word])[0]))
# +
test_scores = []
for start_i in trange(0,len(test_words),32):
batch_words = test_words[start_i:start_i+32]
batch_trans = translate(batch_words)
distances = list(map(get_distance,batch_words,batch_trans))
test_scores.extend(distances)
print("Supervised test score:",np.mean(test_scores))
# -
# ## Preparing for reinforcement learning (2 points)
#
# First we need to define loss function as a custom tf operation.
#
# The simple way to do so is through `tensorflow.py_func` wrapper.
# ```
# def my_func(x):
# # x will be a numpy array with the contents of the placeholder below
# return np.sinh(x)
# inp = tf.placeholder(tf.float32)
# y = tf.py_func(my_func, [inp], tf.float32)
# ```
#
#
# __Your task__ is to implement `_compute_levenshtein` function that takes matrices of words and translations, along with input masks, then converts those to actual words and phonemes and computes min-levenshtein via __get_distance__ function above.
#
# +
def _compute_levenshtein(words_ix,trans_ix):
"""
A custom tensorflow operation that computes levenshtein loss for predicted trans.
Params:
- words_ix - a matrix of letter indices, shape=[batch_size,word_length]
- words_mask - a matrix of zeros/ones,
1 means "word is still not finished"
0 means "word has already finished and this is padding"
- trans_mask - a matrix of output letter indices, shape=[batch_size,translation_length]
- trans_mask - a matrix of zeros/ones, similar to words_mask but for trans_ix
Please implement the function and make sure it passes tests from the next cell.
"""
#convert words to strings
words = <restore words (a list of strings) from words_ix. Use vocab>
assert type(words) is list and type(words[0]) is str and len(words)==len(words_ix)
#convert translations to lists
translations = <restore trans (a list of lists of phonemes) from trans_ix
assert type(translations) is list and type(translations[0]) is str and len(translations)==len(trans_ix)
#computes levenstein distances. can be arbitrary python code.
distances = <apply get_distance to each pair of [words,translations]>
assert type(distances) in (list,tuple,np.ndarray) and len(distances) == len(words_ix)
distances = np.array(list(distances),dtype='float32')
return distances
def compute_levenshtein(words_ix,trans_ix):
out = tf.py_func(_compute_levenshtein,[words_ix,trans_ix,],tf.float32)
out.set_shape([None])
return tf.stop_gradient(out)
# -
# Simple test suite to make sure your implementation is correct. Hint: if you run into any bugs, feel free to use print from inside _compute_levenshtein.
# +
#test suite
#sample random batch of (words, correct trans, wrong trans)
batch_words = np.random.choice(train_words, size=100 )
batch_trans = list(map(random.choice,map(word_to_translation.get,batch_words )))
batch_trans_wrong = np.random.choice(all_translations,size=100)
batch_words_ix = tf.constant(inp_voc.to_matrix(batch_words))
batch_trans_ix = tf.constant(out_voc.to_matrix(batch_trans))
batch_trans_wrong_ix = tf.constant(out_voc.to_matrix(batch_trans_wrong))
# +
#assert compute_levenshtein is zero for ideal translations
correct_answers_score = compute_levenshtein(batch_words_ix ,batch_trans_ix).eval()
assert np.all(correct_answers_score==0),"a perfect translation got nonzero levenshtein score!"
print("Everything seems alright!")
# +
#assert compute_levenshtein matches actual scoring function
wrong_answers_score = compute_levenshtein(batch_words_ix,batch_trans_wrong_ix).eval()
true_wrong_answers_score = np.array(list(map(get_distance,batch_words,batch_trans_wrong)))
assert np.all(wrong_answers_score==true_wrong_answers_score),"for some word symbolic levenshtein is different from actual levenshtein distance"
print("Everything seems alright!")
# -
# Once you got it working...
#
#
# * You may now want to __remove/comment asserts__ from function code for a slight speed-up.
#
# * There's a more detailed tutorial on custom tensorflow ops: [`py_func`](https://www.tensorflow.org/api_docs/python/tf/py_func), [`low-level`](https://www.tensorflow.org/api_docs/python/tf/py_func).
# ## 3. Self-critical policy gradient (2 points)
#
# In this section you'll implement algorithm called self-critical sequence training (here's an [article](https://arxiv.org/abs/1612.00563)).
#
# The algorithm is a vanilla policy gradient with a special baseline.
#
# $$ \nabla J = E_{x \sim p(s)} E_{y \sim \pi(y|x)} \nabla log \pi(y|x) \cdot (R(x,y) - b(x)) $$
#
# Here reward R(x,y) is a __negative levenshtein distance__ (since we minimize it). The baseline __b(x)__ represents how well model fares on word __x__.
#
# In practice, this means that we compute baseline as a score of greedy translation, $b(x) = R(x,y_{greedy}(x)) $.
#
# Luckily, we already obtained the required outputs: `model.greedy_translations, model.greedy_mask` and we only need to compute levenshtein using `compute_levenshtein` function.
#
# +
class trainer:
input_sequence = tf.placeholder('int32',[None,None])
# use model to __sample__ symbolic translations given input_sequence
sample_translations, sample_logp = <YOUR CODE>
# use model to __greedy__ symbolic translations given input_sequence
greedy_translations, greedy_logp = <YOUR CODE>
rewards = - compute_levenshtein(input_sequence, sample_translations)
# compute __negative__ levenshtein for greedy mode
baseline = <YOUR CODE>
# compute advantage using rewards and baseline
advantage = <your code - compute advantage>
assert advantage.shape.ndims ==1, "advantage must be of shape [batch_size]"
# compute log_pi(a_t|s_t), shape = [batch, seq_length]
logprobs_phoneme = select_values_over_last_axis(sample_logp, sample_translations)
# Compute policy gradient
# or rather surrogate function who's gradient is policy gradient
J = logprobs_phoneme*advantage[:,None]
mask = infer_mask(sample_translations,out_voc.eos_ix)
loss = - tf.reduce_sum(J*mask) / tf.reduce_sum(mask)
# regularize with negative entropy. Don't forget the sign!
# note: for entropy you need probabilities for all tokens (sample_logp), not just phoneme_logprobs
entropy = <compute entropy matrix of shape [batch,seq_length], H=-sum(p*log_p), don't forget the sign!>
assert entropy.shape.ndims == 2, "please make sure elementwise entropy is of shape [batch,time]"
loss -= 0.01*tf.reduce_sum(entropy*mask) / tf.reduce_sum(mask)
# compute weight updates, clip by norm
grads = tf.gradients(loss,model.weights)
grads = tf.clip_by_global_norm(grads,50)[0]
train_step = tf.train.AdamOptimizer(learning_rate=1e-5).apply_gradients(zip(grads, model.weights,))
initialize_uninitialized()
# -
# # Policy gradient training
#
for i in trange(100000):
bx = sample_batch(train_words,word_to_translation,32)[0]
pseudo_loss,_ = s.run([trainer.loss, trainer.train_step],{trainer.input_sequence:bx})
loss_history.append(
pseudo_loss
)
if (i+1)%REPORT_FREQ==0:
clear_output(True)
current_scores = score(test_words)
editdist_history.append(current_scores.mean())
plt.figure(figsize=(8,4))
plt.subplot(121)
plt.title('val score distribution')
plt.hist(current_scores, bins = 20)
plt.subplot(122)
plt.title('val score / traning time')
plt.plot(editdist_history)
plt.grid()
plt.show()
print("J=%.3f, mean score=%.3f"%(np.mean(loss_history[-10:]),np.mean(editdist_history[-10:])))
model.translate("EXAMPLE;")
# ### Results
for word in train_words[:10]:
print("%s -> %s"%(word,translate([word])[0]))
# +
test_scores = []
for start_i in trange(0,len(test_words),32):
batch_words = test_words[start_i:start_i+32]
batch_trans = translate(batch_words)
distances = list(map(get_distance,batch_words,batch_trans))
test_scores.extend(distances)
print("Supervised test score:",np.mean(test_scores))
# ^^ If you get Out Of Memory, please replace this with batched computation
# -
# ## Step 6: Make it actually work (5++ pts)
#
# In this section we want you to finally __restart with EASY_MODE=False__ and experiment to find a good model/curriculum for that task.
#
# We recommend the following architecture
#
# ```
# encoder---decoder
#
# P(y|h)
# ^
# LSTM -> LSTM
# ^ ^
# LSTM -> LSTM
# ^ ^
# input y_prev
# ```
#
# with __both__ LSTMs having equal or more units than the default gru.
#
#
# It's okay to modify the code above without copy-pasting it.
#
# __Some tips:__
# * You will likely need to adjust pre-training time for such a network.
# * Supervised pre-training may benefit from clipping gradients somehow.
# * SCST may indulge a higher learning rate in some cases and changing entropy regularizer over time.
# * There's more than one way of sending information from encoder to decoder, especially if there's more than one layer:
# * __Vanilla:__ layer_i of encoder last state goes to layer_i of decoder initial state
# * __Intermediate layers:__ add dense (and possibly concat) layers between encoder last and decoder first.
# * __Every tick:__ feed encoder last state _on every iteration_ of decoder.
#
#
# * It's often useful to save pre-trained model parameters to not re-train it every time you want new policy gradient parameters.
# * When leaving training for nighttime, try setting REPORT_FREQ to a larger value (e.g. 500) not to waste time on it.
#
#
# * (advanced deep learning) It may be a good idea to first train on small phrases and then adapt to larger ones (a.k.a. training curriculum).
# * (advanced nlp) You may want to switch from raw utf8 to something like unicode or even syllables to make task easier.
# * (advanced nlp) Since hebrew words are written __with vowels omitted__, you may want to use a small Hebrew vowel markup dataset at `he-pron-wiktionary.txt`.
#
# __Formal criteria__:
#
# To get 5 points we want you to build an architecture that:
# * _doesn't consist of single GRU_
# * _works better_ than single GRU baseline.
# * We also want you to provide either learning curve or trained model, preferably both
# * ... and write a brief report or experiment log describing what you did and how it fared.
# ### Bonus hints: [here](https://github.com/yandexdataschool/Practical_RL/blob/master/week8_scst/bonus.ipynb)
assert not EASY_MODE, "make sure you set EASY_MODE = False at the top of the notebook."
# `[your report/log here or anywhere you please]`
# __Contributions:__ This notebook is brought to you by
# * Yandex [MT team](https://tech.yandex.com/translate/)
# * <NAME> ([DeniskaMazur](https://github.com/DeniskaMazur)), <NAME> ([Omrigan](https://github.com/Omrigan/)), <NAME> ([TixFeniks](https://github.com/tixfeniks)) and <NAME> ([justheuristic](https://github.com/justheuristic/))
# * Dataset is parsed from [Wiktionary](https://en.wiktionary.org), which is under CC-BY-SA and GFDL licenses.
#
|
Practical_RL/week8_scst/practice_tf.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Library imports
# +
#usual imports
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
#Outliers
from scipy import stats
# -
data = pd.read_csv('data/raw/Walmart_Store_sales.csv')
data.head()
print(f'There is {data.shape[0]} rows and {data.shape[1]} columns in this dataset')
print(f'Columns in this dataset {list(data.columns)}')
print(f'Overall missing values: \n{100*data.isnull().sum()/data.shape[0]}')
data.dtypes
data['Store'].value_counts()
# There is no missing values on the stores, we can convert it to an integer
data.dtypes
data['Store'] = data['Store'].astype(int)
data.head(1)
data['Holiday_Flag'].isnull().sum()
data[data['Holiday_Flag'].isnull()]
# # Re-assess Holiday_Flag column
# +
#Holidays = 27/08/2010 <NAME> Day in Texas will be transformed to 1 in Holiday_Flag
#The rest of the dates are not holidays according to the national register so we'll transform them to 0
# -
data.loc[data.Date == "27-08-2010", "Holiday_Flag"] = 1.0
data['Holiday_Flag'].isnull().sum()
data['Holiday_Flag'] = data['Holiday_Flag'].replace(np.nan, 1.0)
data['Holiday_Flag'].isnull().sum()
# +
days = data['Holiday_Flag'].value_counts()[0]
holidays = data['Holiday_Flag'].value_counts()[1]
print(f'There is {days} normal days in the dataset')
print(f'There is {holidays} holidays in the dataset')
# -
data = data.dropna(subset=['Weekly_Sales'])
# +
#Drop the nan values in Temperature/Fuel Price/CPI/Unemployment
# -
data = data.dropna(subset=['Temperature','Fuel_Price','CPI','Unemployment'])
data.describe()
# # Computing confidence interval taking 99,73%
y23 = [data.Temperature.mean()-3*data.Temperature.std(),data.Temperature.mean()+3*data.Temperature.std()]
y24 = [data.Fuel_Price.mean()-3*data.Fuel_Price.std(),data.Fuel_Price.mean()+3*data.Fuel_Price.std()]
y25 = [data.CPI.mean()-3*data.CPI.std(),data.CPI.mean()+3*data.CPI.std()]
y26 = [data.Unemployment.mean()-3*data.Unemployment.std(),data.Unemployment.mean()+3*data.Unemployment.std()]
print(f'Any values outside of this interval within Temperature will be removed {y23}')
print(f'Any values outside of this interval within Fuel price will be removed {y24}')
print(f'Any values outside of this interval within CPI will be removed {y25}')
print(f'Any values outside of this interval within Unemployment will be removed {y26}')
# +
#Therefore we have to focus on the outliers in unemployment
# -
data.drop(data[data.Unemployment > y26[1]].index, inplace=True)
data.describe()
print(f'After cleaning, there is only {data.shape[0]} rows left, we dropped {(100-((data.shape[0])/150)*100)}%')
data.head()
# ## EDA
store_sales = data.groupby('Store')['Weekly_Sales'].sum()
first_shop = store_sales.sort_values(ascending = False).index[0]
print(f'The shop n°{first_shop} sold the most over one week')
plt.figure(figsize = (10, 5))
g = sns.barplot(data = data, x = 'Store', y = 'Weekly_Sales', color = 'RED')
g.set_title("Weekly sales per store")
plt.show()
# +
#Even though the store #13 holds the record in the biggest weekly sale,
#it isn't the best performance overall, #4 seems to be performing better (We have to take into account its 10^6)
# -
data.corr()
plt.figure(figsize = (16,10))
sns.heatmap(data.corr(), cmap = 'Reds', annot = True)
plt.show()
# As we're speaking of sales, we can take into account two factors, the first would be the week aka date, when there are sales. The second factor could be the quarters as any financial firm would assess their performance.
#
# However, we dropped the date column, it could be a way of fine tuning our model, this could be explored in the future
#
data = data[['Store','Weekly_Sales','Holiday_Flag','Temperature','Fuel_Price','CPI','Unemployment']]
# +
#data.to_csv('./data/walmart_store_cleaned.csv', index = False)
|
03-Walmart Sales/walmart_store.ipynb
|
# Assignment: Linear regression on the Advertising data
# =====================================================
#
# **TODO**: Edit this cell to fill in your NYU Net ID and your name:
#
# - **Net ID**:
# - **Name**:
# To illustrate principles of linear regression, we are going to use some
# data from the textbook “An Introduction to Statistical Learning
# withApplications in R” (<NAME>, <NAME>, <NAME>,
# <NAME>) (available via NYU Library).
#
# The dataset is described as follows:
#
# > Suppose that we are statistical consultants hired by a client to
# > provide advice on how to improve sales of a particular product. The
# > `Advertising` data set consists of the sales of that product in 200
# > different markets, along with advertising budgets for the product in
# > each of those markets for three different media: TV, radio, and
# > newspaper.
# >
# > …
# >
# > It is not possible for our client to directly increase sales of the
# > product. On the other hand, they can control the advertising
# > expenditure in each of the three media. Therefore, if we determine
# > that there is an association between advertising and sales, then we
# > can instruct our client to adjust advertising budgets, thereby
# > indirectly increasing sales. In other words, our goal is to develop an
# > accurate model that can be used to predict sales on the basis of the
# > three media budgets.
#
# Sales are reported in thousands of units, and TV, radio, and newspaper
# budgets, are reported in thousands of dollars.
#
# For this assignment, you will fit a linear regression model to a small
# dataset. You will iteratively improve your linear regression model by
# examining the residuals at each stage, in order to identify problems
# with the model.
#
# Make sure to include your name and net ID in a text cell at the top of
# the notebook.
# +
from sklearn import metrics
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
# -
# ### 1. Read in and pre-process data
#
# In this section, you will read in the “Advertising” data, and make sure
# it is loaded correctly. Visually inspect the data using a pairplot, and
# note any meaningful observations. In particular, comment on which
# features appear to be correlated with product sales, and which features
# appear to be correlated with one another. Then, split the data into
# training data (70%) and test data (30%).
#
# **The code in this section is provided for you**. However, you should
# add a text cell at the end of this section, in which you write your
# comments and observations.
# #### Read in data
url = 'https://www.statlearning.com/s/Advertising.csv'
df = pd.read_csv(url, index_col=0)
df.head()
# Note that in this dataset, the first column in the data file is the row
# label; that’s why we use `index_col=0` in the `read_csv` command. If we
# would omit that argument, then we would have an additional (unnamed)
# column in the dataset, containing the row number.
#
# (You can try removing the `index_col` argument and re-running the cell
# above, to see the effect and to understand why we used this argument.)
# #### Visually inspect the data
sns.pairplot(df);
# The most important panels here are on the bottom row, where `sales` is
# on the vertical axis and the advertising budgets are on the horizontal
# axes.
# #### Split up data
#
# We will use 70% of the data for training and the remaining 30% to test
# the regression model.
train, test = train_test_split(df, test_size=0.3)
train.info()
test.info()
# ### 2. Fit simple linear regression models
#
# Use the training data to fit a simple linear regression to predict
# product sales, for each of three features: TV ad budget, radio ad
# budget, and newspaper ad budget. In other words, you will fit *three*
# regression models, with each model being trained on one feature. For
# each of the three regression models, create a plot of the training data
# and the regression line, with product sales ($y$) on the vertical axis
# and the feature on which the model was trained ($x$) on the horizontal
# axis.
#
# Also, for each regression model, print the intercept and coefficients,
# and compute the MSE and R2 on the training data, and MSE and R2 on the
# test data.
#
# Comment on the results. Which type of ad spending seems to be associated
# with the largest increase in product sales? Which regression model is
# most effective at predicting product sales?
#
# **The code in this section is provided for you**. However, you should
# add text cells in which you write your comments, observations, and
# answers to the questions.
# #### Fit a simple linear regression
reg_tv = LinearRegression().fit(train[['TV']], train['sales'])
reg_radio = LinearRegression().fit(train[['radio']], train['sales'])
reg_news = LinearRegression().fit(train[['newspaper']], train['sales'])
# #### Look at coefficients
print("TV : ", reg_tv.coef_[0], reg_tv.intercept_)
print("Radio : ", reg_radio.coef_[0], reg_radio.intercept_)
print("Newspaper: ", reg_news.coef_[0], reg_news.intercept_)
# #### Plot data and regression line
# +
fig = plt.figure(figsize=(12,3))
plt.subplot(1,3,1)
sns.scatterplot(data=train, x="TV", y="sales");
sns.lineplot(data=train, x="TV", y=reg_tv.predict(train[['TV']]), color='red');
plt.subplot(1,3,2)
sns.scatterplot(data=train, x="radio", y="sales");
sns.lineplot(data=train, x="radio", y=reg_radio.predict(train[['radio']]), color='red');
plt.subplot(1,3,3)
sns.scatterplot(data=train, x="newspaper", y="sales");
sns.lineplot(data=train, x="newspaper", y=reg_news.predict(train[['newspaper']]), color='red');
# -
# #### Compute R2, MSE for simple regression
y_pred_tr_tv = reg_tv.predict(train[['TV']])
y_pred_tr_radio = reg_radio.predict(train[['radio']])
y_pred_tr_news = reg_news.predict(train[['newspaper']])
r2_tr_tv = metrics.r2_score(train['sales'], y_pred_tr_tv)
r2_tr_radio = metrics.r2_score(train['sales'], y_pred_tr_radio)
r2_tr_news = metrics.r2_score(train['sales'], y_pred_tr_news)
print("TV : ", r2_tr_tv)
print("Radio : ", r2_tr_radio)
print("Newspaper: ", r2_tr_news)
mse_tr_tv = metrics.mean_squared_error(train['sales'], y_pred_tr_tv)
mse_tr_radio = metrics.mean_squared_error(train['sales'], y_pred_tr_radio)
mse_tr_news = metrics.mean_squared_error(train['sales'], y_pred_tr_news)
print("TV : ", mse_tr_tv)
print("Radio : ", mse_tr_radio)
print("Newspaper: ", mse_tr_news)
y_pred_ts_tv = reg_tv.predict(test[['TV']])
y_pred_ts_radio = reg_radio.predict(test[['radio']])
y_pred_ts_news = reg_news.predict(test[['newspaper']])
r2_ts_tv = metrics.r2_score(test['sales'], y_pred_ts_tv)
r2_ts_radio = metrics.r2_score(test['sales'], y_pred_ts_radio)
r2_ts_news = metrics.r2_score(test['sales'], y_pred_ts_news)
print("TV : ", r2_ts_tv)
print("Radio : ", r2_ts_radio)
print("Newspaper: ", r2_ts_news)
mse_ts_tv = metrics.mean_squared_error(test['sales'], y_pred_ts_tv)
mse_ts_radio = metrics.mean_squared_error(test['sales'], y_pred_ts_radio)
mse_ts_news = metrics.mean_squared_error(test['sales'], y_pred_ts_news)
print("TV : ", mse_ts_tv)
print("Radio : ", mse_ts_radio)
print("Newspaper: ", mse_ts_news)
# ### 3. Explore the residuals for the single linear regression models
#
# We know that computing MSE or R2 is not sufficient to diagnose a problem
# with a linear regression.
#
# Create some additional plots as described below to help you identify any
# problems with the regression. Use training data for all of the items
# below.
#
# For each of the three regression models,
#
# - Plot predicted sales ($\hat{y}$) on the vertical axis, and actual
# sales ($y$) on the horizontal axis. Make sure both axes use the same
# scale. Comment on your observations. What would you expect this plot
# to look like for a model that explains the data well?
# - Compute the residuals ($y - \hat{y}$). Note that some of these will
# be negative, and some will be positive. What is the mean residual
# for each of the regression models? What *should* be the mean
# residual for a fitted linear regression model? Explain your answer.
# - Plot the residuals ($y - \hat{y}$) on the vertical axis, and actual
# sales ($y$) on the horizontal axis. Use the same scale for all three
# subplots. Comment on your observations. Is there a pattern in the
# residuals (and if so, what might it indicate), or do they appear to
# have no pattern with respect to actual sales?
# - For each of the three regression models AND each of the three
# features, plot the residuals ($y - \hat{y}$) on the vertical axis,
# and the feature ($x$) on the horizontal axis. This plot will include
# nine subplots in total. Make sure to clearly label each axis, and
# also label each subplot with a title that indicates which regression
# model it uses. Is there a pattern in the residuals (and if so, what
# might it indicate), or do they appear to have no pattern with
# respect to each of the three features?
#
# **The code in this section is not provided for you**. You will need to
# write code, in addition to the text cells in which you write your
# comments, observations, and answers to the questions.
# ### 4. Try a multiple linear regression
#
# Next, fit a multiple linear regression to predict product sales, using
# all three features to train a single model: TV ad budget, radio ad
# budget, and newspaper ad budget.
#
# Print the intercept and coefficients, and compute the MSE and R2 on the
# training data, and MSE and R2 on the test data. Comment on the results.
# Make sure to explain any differences between the coefficients of the
# multiple regression model, and the coefficients of the three simple
# linear regression models. If they are different, why?
#
# **The code in the first part of this section is provided for you**.
# However, you should add text cells in which you write your comments,
# observations, and answers to the questions.
#
# Also repeat the analysis of part (3) for this regression model. Use
# training data for all of these items:
#
# - Plot predicted sales ($\hat{y}$) on the vertical axis, and actual
# sales ($y$) on the horizontal axis. Make sure both axes use the same
# scale. Comment on your observations. What would you expect this plot
# to look like for a model that explains the data well?
# - Compute the residuals ($y - \hat{y}$). What is the mean of the
# residuals? What *should* be the mean of the residuals for a fitted
# linear regression model? Explain your answer.
# - Plot the residuals ($y - \hat{y}$) on the vertical axis, and actual
# sales ($y$) on the horizontal axis. Comment on your observations. Is
# there a pattern in the residuals (and if so, what might it
# indicate), or do they appear to have no pattern with respect to
# actual sales?
# - For each of the three features, plot the residuals ($y - \hat{y}$)
# on the vertical axis, and the feature ($x$) on the horizontal axis.
# Make sure to clearly label each axis. Is there a pattern in the
# residuals (and if so, what might it indicate), or do they appear to
# have no pattern with respect to each of the three features?
#
# **The code in the last part of this section is not provided for you**.
# You will need to write code, in addition to the text cells in which you
# write your comments, observations, and answers to the questions.
# #### Fit a multiple linear regression
reg_multi = LinearRegression().fit(train[['TV', 'radio', 'newspaper']], train['sales'])
# #### Look at coefficients
print("Coefficients (TV, radio, newspaper):", reg_multi.coef_)
print("Intercept: ", reg_multi.intercept_)
# #### Compute R2, MSE for multiple regression
# +
y_pred_tr_multi = reg_multi.predict(train[['TV', 'radio', 'newspaper']])
r2_tr_multi = metrics.r2_score(train['sales'], y_pred_tr_multi)
mse_tr_multi = metrics.mean_squared_error(train['sales'], y_pred_tr_multi)
print("Multiple regression R2: ", r2_tr_multi)
print("Multiple regression MSE: ", mse_tr_multi)
# +
y_pred_ts_multi = reg_multi.predict(test[['TV', 'radio', 'newspaper']])
r2_ts_multi = metrics.r2_score(test['sales'], y_pred_ts_multi)
mse_ts_multi = metrics.mean_squared_error(test['sales'], y_pred_ts_multi)
print("Multiple regression R2: ", r2_ts_multi)
print("Multiple regression MSE: ", mse_ts_multi)
# -
# ### 5. Linear regression with interaction terms
#
# Our multiple linear regression includes additive effects of all three
# types of advertising media. However, it does not include *interaction*
# effects, in which combining different types of advertising media
# together results in a bigger boost in sales than just the additive
# effect of the individual media. The pattern in the residuals plots from
# parts (1) through (4) suggest that a model including an interaction
# effect may explain sales data better than a model including additive
# effects. Add four columns to your data frame:
#
# - `newspaper` $\times$ `radio`
# - `TV` $\times$ `radio`
# - `newspaper` $\times$ `TV`
# - `newspaper` $\times$ `radio` $\times$ `TV`
#
# Then, train a linear regression model on all seven features: the three
# types of ad budgets, and the four interaction effects. Repeat the
# analysis of part (4) for the model including interaction effects.
# Comment on the results. Are the interaction effects helpful for
# explaining the effect of ads on product sales? Are there any patterns
# evident in the residual plots that suggest further opportunities for
# improving the model?
#
# (If you think the results suggest further opportunities for improving
# the model, you are welcome to try and to comment on the results!)
#
# **The code in this section is not provided for you**. You will need to
# write code, in addition to the text cells in which you write your
# comments, observations, and answers to the questions.
|
notebooks/2-advertising-hw.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# # Predicting Survival on the Titanic
#
# **_Note! Work in Progress - This notebook is not yet finished_**
#
# An implementation in Python of the exploration of the Titanic dataset that closely follows the excellent *Exploring Survival on the Titanic* notebook by <NAME> found at https://www.kaggle.com/mrisdal/titanic/exploring-survival-on-the-titanic/notebook. Data preprocessing largely follows what she did though predictive modeling attempts to explore more models than just the random forest she used.
#
# As an aside, this also serves as an interesting look at how some of the tasks performed in her notebook might be done in Python and, in a way, shows both languages' relative strengths and weaknesses.
# Import necessary libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.cross_validation import train_test_split, cross_val_score
from sklearn import metrics
# ## The Dataset
train = pd.read_csv("train.csv", index_col='PassengerId')
test = pd.read_csv("test.csv", index_col='PassengerId')
train.head(3)
test.head(3)
# print(train.shape)
# print(test.shape)
print('Number of features: {}'.format(test.shape[1]))
print('Training samples: {}'.format(train.shape[0]))
print('Test samples: {}'.format(test.shape[0]))
print('Total number of samples: {}'.format(train.shape[0]+test.shape[0]))
# The data contains the following features:
#
# - PassengerId - a number describing a unique passenger
# - Survived - the binary dependent variable indicating whether a passenger survived (1) or died (0)
# - Pclass - the passenger's class, from first class (1) to third class (3)
# - Name
# - Sex
# - Age
# - SibSp - the number of siblings or spouses aboard
# - Parch - the number of parents or children aboard
# - Ticket - the ticket number
# - Fare - the fare that the passenger paid
# - Cabin - the cabin number the passenger stayed in
# - Embarked - the port where the passenger embarked, whether at Cherbourg (C), Queenstown (Q), or Southampton (S)
#
# It's time to explore the dataset to get a general idea of what it's like.
# ## Exploratory Data Analysis
#
# We first do some general overviews of the data via summary statistics and histograms before moving on to preprocessing.
# +
# First, combine datasets
total = pd.concat([train, test])
# View summary statistics
total.describe()
# -
# Most numerical data appear to be fairly complete, with the exception of fare (which only has one missing value) and age (which has 263 missing values). We can deal with the missing values later.
#
# Let's also visualize the data with histograms to see the general distribution of the data.
# Generate histograms
sns.set_color_codes('muted')
total.hist(color='g')
plt.tight_layout()
plt.show()
# A fairly obvious observation here is that the PassengerId variable is not very useful -- we should drop this column. The rest of the data is quite interesting, with most passengers being somewhat young (around 20 to 30 years of age) and most people traveling without too much family.
#
# Pclass serves as a proxy for the passengers' socioeconomic stata. Interestingly, the middle class appears to be the lowest in size, though not by much compared to upperclass passengers.
#
# Looking at the data, given that we don't have the ticket number does not appear to be too informative.
totalwithoutnas = total.dropna()
scattermatrix = sns.pairplot(totalwithoutnas)
plt.show()
# ## Data Preprocessing
#
# The first thing we should do is drop columns that will not be particularly helpful in our analysis. This includes the Ticket variable identified previously.
total.drop('Ticket', axis=1, inplace=True)
# ### Feature Engineering
#
# A number of the variables in the data present opportunities to be further generate meaningful features. One particular feature that appears to contain a lot of meaning is the names of the passengers. As in the notebook of Megan, we will be able to extract titles (which are indicative of both gender and marriage status) and families (given by shared surnames, under the assumption that incidences of unrelated people having the same surname are trivial).
# #### Surnames and Titles
# +
Surnames = pd.DataFrame(total['Name'].str.split(",").tolist(), columns=['Surname', 'Rest'])
Titles = pd.DataFrame(Surnames['Rest'].str.split(".").tolist(), columns=['Title', 'Rest1', 'Rest2'])
Surnames.drop('Rest',axis=1,inplace=True)
Titles = pd.DataFrame(Titles['Title'])
Surnames['Surname'].str.strip()
Titles['Title'].str.strip()
total['Surname'] = Surnames.set_index(np.arange(1,1310))
total['Title'] = Titles.set_index(np.arange(1,1310))
total.head()
# -
# Let's tabulate our titles against sex to see the frequency of the various titles.
pd.crosstab(total['Sex'], total['Title'])
# We see that with the exception of Master, Mr, Miss, and Mrs, the other titles are relatively rare. We can group rare titles together to simplify our analysis. Also note that Mlle and Ms are synonymous with Miss, and Mme is synonymous with Mrs.
# +
raretitles = ['Dona', 'Lady', 'the Countess','Capt', 'Col', 'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer']
total.ix[total['Title'].str.contains('Mlle|Ms|Miss'), 'Title'] = 'Miss'
total.ix[total['Title'].str.contains('Mme|Mrs'), 'Title'] = 'Mrs'
total.ix[total['Title'].str.contains('|'.join(raretitles)), 'Title'] = 'Rare Title'
pd.crosstab(total['Sex'], total['Title'])
# -
total['Surname'].nunique()
# We have 875 unique surnames.
# #### Family Sizes
# Family size may have an impact on survival. To this end, we create a family size attribute and plot the relationship.
# +
total['FamilySize'] = total['SibSp'] + total['Parch'] + 1
total['Family'] = total['Surname'] + "_" + total['FamilySize'].apply(str)
total.head(1)
# -
# Plot family size
famsizebarplot = sns.countplot(total['FamilySize'].loc[1:len(train.index)], hue=total['Survived'])
famsizebarplot.set_xlabel('Family Size')
plt.show()
# The chart above clearly shows an interesting phenomenon -- single people and families of over 4 people have a significantly lower chance of survival than those in small (2 to 4 person) families.
# +
# Categorize family size
total['FamSizeCat'] = 'small'
total.loc[(total['FamilySize'] == 1), 'FamSizeCat'] = 'singleton'
total.loc[(total['FamilySize'] > 4), 'FamSizeCat'] = 'large'
# Create mosaic plot
# To be done in the future using statsmodel
# -
# ### Dealing with Missing Values
# We first check columns with missing values.
total.isnull().sum()
# It appears that age, cabin, embarked, and fare have missing values. Let's first work on "Embarked" and "Fare" given that there are few enough NaN's for us to be able to manually work out what values they should have. For Cabin, given that there are 1309 samples and more than 75% of them are missing, we can probably just drop this column. It might have been useful given that location on the ship might influence their chance of survival, but data is too sparse on this particular attribute.
total[(total['Embarked'].isnull()) | (total['Fare'].isnull())]
# <NAME> and <NAME>, both shared the same cabin, both survived, both paid the same fare, and are both of the same class, interestingly enough. Mr. Storey is of the third class and embarked from Southampton.
#
# Visualizing the fares by embarkation location may shed some light on where the two first class ladies embarked.
sns.boxplot(x='Embarked',y='Fare',data=train.dropna(),hue='Pclass')
plt.tight_layout()
plt.show()
trainwithoutnas = train.dropna()
print("Mean fares for passengers traveling in first class:")
print(trainwithoutnas[trainwithoutnas['Pclass']==1].groupby('Embarked')['Fare'].mean())
print("\nMedian fares for passengers traveling in first class:")
print(trainwithoutnas[trainwithoutnas['Pclass']==1].groupby('Embarked')['Fare'].median())
# The closest value to the $80 fare paid by both ladies for first class is very close to the mean fare paid by first class passengers embarking from Southampton, but also aligns very nicely with the median fare paid by those embarking from Cherbourg. Perhaps a swarm plot will better show how passengers are distributed.
sns.swarmplot(x='Embarked',y='Fare',data=train.dropna(),hue='Pclass')
plt.show()
# This is a tough call. Looking at the spread of the points, however, it seems that those that embarked from Southampton generally paid lower fares. It appears that the mean fare paid by those from Cherbourg is pulled up by the extreme outliers that paid more than \$500 for their tickets, with a majority of first class passengers indeed paying around $80. As such, we classify the two ladies as having embarked from Cherbourg (C).
total.loc[(62,830), 'Embarked'] = "C"
total.loc[(62,830), 'Embarked']
# The swarm plot also shows that the passengers embarking from Southampton in third class have paid around the same fare. It would be reasonable to use the mean value of third class passengers from Southampton as his fare value.
total.loc[1044,'Fare'] = total[(total['Embarked']=="S") & (total['Pclass']==3)]['Fare'].mean()
total.loc[1044, ['Name','Fare']]
# We could do mice imputation similar to Megan's notebook via the fancyimpute package.
AgeHistogram = total['Age'].hist(bins=20, edgecolor="black")
AgeHistogram.set_xlabel("Age")
AgeHistogram.set_ylabel("Count")
AgeHistogram.set_title("Age (Prior to Missing Value Imputation)")
plt.show()
import fancyimpute
total.isnull().sum()
totalforMICE = total.drop(['Survived','Cabin','FamSizeCat','Family','Name','Surname'], axis=1)
# totalforMICE.fillna(np.nan)
totalforMICE['Sex'] = pd.get_dummies(totalforMICE['Sex'])['male']
dummycodedTitles = pd.get_dummies(totalforMICE['Title']).drop('Rare Title', axis=1)
totalforMICE = pd.merge(totalforMICE, dummycodedTitles, left_index=True, right_index=True, how='outer')
totalforMICE = totalforMICE.drop(['Title'],axis=1)
dummycodedEmbarked = pd.get_dummies(totalforMICE['Embarked'])[['C','Q']]
totalforMICE = totalforMICE.join(dummycodedEmbarked).drop(['Embarked'],axis=1)
dummycodedPclass = pd.get_dummies(totalforMICE['Pclass'], columns=[list("123")]).drop(3,axis=1)
totalforMICE = totalforMICE.join(dummycodedPclass).drop('Pclass',axis=1)
MICEdtotal = fancyimpute.MICE().complete(totalforMICE.values.astype(float))
MICEdtotal = pd.DataFrame(MICEdtotal, columns=totalforMICE.columns)
MICEdtotal.isnull().sum()
# We see that the MICE'd data has no more missing Age values. Plotting these values in the histogram:
MICEAgeHistogram = MICEdtotal['Age'].hist(bins=20, edgecolor="black")
MICEAgeHistogram.set_xlabel("Age")
MICEAgeHistogram.set_ylabel("Count")
MICEAgeHistogram.set_title("Age (After Missing Value Imputation)")
plt.show()
# +
AgeHists, AgeHistAxes = plt.subplots(nrows=1,ncols=2, figsize=(10,5), sharey=True)
AgeHistAxes[0].hist(total['Age'].dropna(), bins=20, edgecolor='black', normed=True)
AgeHistAxes[0].set_xlabel("Age")
AgeHistAxes[0].set_ylabel("Density")
AgeHistAxes[0].set_title("Age Density (Original Data)")
AgeHistAxes[1].hist(MICEdtotal['Age'], bins=20, edgecolor='black', normed=True)
AgeHistAxes[1].set_xlabel("Age")
AgeHistAxes[1].set_ylabel("Density")
AgeHistAxes[1].set_title("Age Density (After MICE)")
AgeHists.tight_layout()
AgeHists
# -
# Most age values were added around the 20 to 30 year-old age range, which makes sense given the distribution of the ages in the data that we had. Note that the fancyimpute version of MICE uses Bayesian Ridge Regression. The density is not perfectly preserved but is useful enough to proceed with the analysis.
#
# We use the new Age column with the imputed values for our analysis.
newtotal = total
newtotal['Age'] = MICEdtotal['Age']
# We can create some additional categorical columns based on our complete age feature -- whether the person is a child (18 or under) and whether a person is a mother (female, over 18, with children, and does not have the title "Miss").
AgeandSexHist = sns.FacetGrid(newtotal.iloc[0:891,:], col = 'Sex', hue='Survived', size=5)
# AgeandSexHist.map(sns.distplot, 'Age', kde=False, hist_kws={'edgecolor':'black','stacked':True})
AgeandSexHist.map(plt.hist, 'Age', alpha=0.5, bins=20)
AgeandSexHist.add_legend()
# plt.close('all')
plt.show(AgeandSexHist)
AgeandSexHist, AgeandSexHistAxes = plt.subplots(nrows=1,ncols=2, figsize=(10,5), sharey=True)
AgeandSexHistAxes[0].hist([newtotal.loc[0:891, 'Age'].loc[(newtotal['Sex']=='male') & (newtotal['Survived']==1)],
newtotal.loc[0:891, 'Age'].loc[(newtotal['Sex']=='male') & (newtotal['Survived']==0)]],stacked=True, edgecolor='black', label=['Survived','Did Not Survive'], bins=24)
AgeandSexHistAxes[1].hist([newtotal.loc[0:891, 'Age'].loc[(newtotal['Sex']=='female') & (newtotal['Survived']==1)],
newtotal.loc[0:891, 'Age'].loc[(newtotal['Sex']=='female') & (newtotal['Survived']==0)]],stacked=True, edgecolor='black', bins=24)
AgeandSexHistAxes[0].set_title('Survival By Age for Males')
AgeandSexHistAxes[1].set_title('Survival By Age for Females')
for i in range(2):
AgeandSexHistAxes[i].set_xlabel('Age')
AgeandSexHistAxes[0].set_ylabel('Count')
AgeandSexHistAxes[0].legend()
plt.show()
# +
# Create the 'Child' variable
newtotal['Child'] = 1
newtotal.loc[newtotal['Age']>=18, 'Child'] = 0
pd.crosstab(newtotal['Child'],newtotal['Survived'])
# +
# Create the 'Mother' variable
newtotal['Mother'] = 0
newtotal.loc[(newtotal['Sex']=='female') & (newtotal['Parch'] > 0) & (newtotal['Age']>18) & (newtotal['Title'] != "Miss"), 'Mother'] = 1
pd.crosstab(newtotal['Mother'], newtotal['Survived'])
# -
# Let's take a look at the dataset once again.
newtotal.head()
newtotal.shape
# We ensure that all important categorical variables are dummy coded.
dummycodedFamSizeCat = pd.get_dummies(newtotal['FamSizeCat']).drop('large',axis=1)
newtotal = newtotal.drop(['Title','Embarked','Pclass', 'Cabin', 'Name', 'Family', 'Surname'], axis=1)
newtotal['Sex'] = pd.get_dummies(newtotal['Sex'])['male']
newtotal = newtotal.join(dummycodedEmbarked)
newtotal = newtotal.join(dummycodedPclass)
newtotal = newtotal.join(dummycodedTitles)
newtotal = newtotal.join(dummycodedFamSizeCat)
newtotal.head()
# After we split the data back into training and test sets, our data set will be ready to use for modeling.
newtrain = newtotal.loc[:891,:]
newtest = newtotal.loc[892:,:]
# ## Modeling and Prediction
# **_Note! Work in Progress - This notebook is not yet finished_**
|
Predicting Survival on the Titanic.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.9.1 64-bit (''mypython'': conda)'
# name: python3
# ---
# # Analyze target statistics
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
pd.options.display.float_format = '{:.3f}'.format
plt.rcParams["figure.dpi"] = 150
sns.set(style='darkgrid')
from IPython.display import display
import warnings
warnings.simplefilter('ignore', UserWarning)
from pathlib import Path
# fig_dir = Path('../../fig')
plt.rcParams['font.family'] = 'Times New Roman'
plt.rcParams['mathtext.fontset'] = 'stix'
plt.rcParams["font.size"] = 15
# Read target csv
df = pd.read_csv('../../../data/interim/target_list.csv', index_col=0)
df
df['is_similar_AF2'] = ['True' if x == True else 'False' for x in df['is_similar_AF2']]
# Number of sequences included in the AF2 training data in the cluster
df['num_sequence_in_cluster_included_AF2'] = df['num_entry_in_cluster'] - df['num_entry_in_cluster_AF2_notInclude']
# ## Show target distribution
# Sequence length
plt.figure(figsize=(10, 6))
sns.boxplot(data=df, x='length')
plt.figure(figsize=(10, 6))
sns.boxplot(data=df, x='length', y='is_similar_AF2')
# Resolution
sns.boxplot(data=df, x='resolution')
plt.figure(figsize=(10, 6))
sns.boxplot(data=df, x='resolution', y='is_similar_AF2')
# Target number that have similar sequence to AF2 training dataset and not
plt.figure(figsize=(4, 3))
sns.countplot(data=df, x='is_similar_AF2')
plt.figure(figsize=(4, 3))
sns.distplot(df['num_entry_in_cluster'], kde=False, norm_hist=True)
plt.figure(figsize=(4, 3))
sns.distplot(df['num_sequence_in_cluster_included_AF2'], kde=False, norm_hist=True)
# ## Sampling targets
df['is_similar_AF2'].value_counts()
similar_df = df[df['is_similar_AF2'] == 'True']
non_similar_df = df[df['is_similar_AF2'] == 'False']
random_state = 0
target_num = 100
df_sample = df.sample(target_num, random_state=random_state)
display(df_sample)
df_sample['is_similar_AF2'].value_counts()
plt.figure(figsize=(10, 6))
sns.boxplot(data=df_sample, x='length')
plt.figure(figsize=(4, 3))
sns.distplot(df_sample['num_entry_in_cluster'], kde=False, norm_hist=True)
# Equalize the number of targets that have similar sequence to AF2 training data and have not.
similar_sample = similar_df.sample(target_num // 2, random_state=random_state)
non_similar_sample = non_similar_df.sample(target_num // 2, random_state=random_state)
df_eq_sample = pd.concat([similar_sample, non_similar_sample])
df_eq_sample
plt.figure(figsize=(10, 6))
sns.boxplot(data=df_eq_sample, x='length')
plt.figure(figsize=(4, 3))
sns.distplot(df_eq_sample['num_entry_in_cluster'], kde=False, norm_hist=True)
# sort by resolution and select top
df_res_top = df.sort_values(by='resolution').head(target_num)
df_res_top
plt.figure(figsize=(10, 6))
sns.boxplot(data=df_res_top, x='length')
sns.swarmplot(data=df_res_top, x='length')
sns.countplot(data=df_res_top, x='is_similar_AF2')
|
src/notebooks/targets/target_stat.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: nni-dev
# language: python
# name: nni-dev
# ---
# ## Connect and Manage an Exist Experiment
# ### 1. Connect Experiment
from nni.experiment import Experiment
experiment = Experiment.connect(8080)
# ### 2. Experiment View & Control
experiment.get_experiment_profile()
experiment.update_max_trial_number(200)
experiment.get_experiment_profile()
# ### 3. Stop Experiment
experiment.stop()
|
docs/zh_CN/Tutorial/python_api_connect.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import os
os.environ['PYSPARK_SUBMIT_ARGS'] = \
'--conf spark.cassandra.connection.host=cassandra --packages com.datastax.spark:spark-cassandra-connector_2.11:2.0.2 pyspark-shell'
from pyspark import SparkContext
from pyspark.sql import SQLContext
from pyspark.sql import functions as F
from pyspark.sql.types import *
sc = SparkContext(appName="WWM_Exercise_Lambda")
sc.setLogLevel("WARN")
sc.setCheckpointDir('checkpoint/')
sql = SQLContext(sc)
def usersWhoBoughtXAlsoBought(df):
productDf = df.select('user_id', 'product')
otherProductDf = productDf.toDF('user_id', 'other_product')
matchedProductsDf = productDf.join(otherProductDf, otherProductDf['user_id'] == productDf['user_id'], 'inner').\
filter("`product` != `other_product`").select('product','other_product').\
groupby('product','other_product').count().toDF("product","other_product","count")
return matchedProductsDf
def selectTopProducts(df):
df.registerTempTable("products")
topProductsDf = sql.sql("""
SELECT
*,
ROW_NUMBER() OVER(PARTITION BY product ORDER BY count DESC) rn
FROM products
""").where("rn <= 5").groupBy("product").agg(F.collect_list("other_product").alias("other_products"))
return topProductsDf
def processBatch():
allUserProductsDf = sql.read.format("org.apache.spark.sql.cassandra").\
options(table="all_user_products", keyspace="bdr").load().cache()
topDf = selectTopProducts(usersWhoBoughtXAlsoBought(allUserProductsDf))
topDf.show()
topDf.write.format("org.apache.spark.sql.cassandra").\
mode('append').options(table="top_other_products_batch", keyspace="bdr").save()
processBatch()
|
workshop/Lambda - Batch - Users who bought X also bought ....ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <div style="text-align: center;">
# <h2>INFSCI 2915 Foundations- Machine Learning - Spring 2018 </h2>
# <h1 style="font-size: 250%;">Assignment #1</h1>
# <h3>Issued Tuesday, 2/06/2018; Due Tuesday, 11:59pm, 2/13/2018</h3>
# <h3>Total points: 100 </h3>
# </div>
# Type in your information in the double quotes
firstName = "YUHAO"
lastName = "WU"
pittID = "yuw121"
# --
# <h3> Problem #1. K-nearest neighbors [20 points] </h3>
#
# The table below provides a training data set containing six observations, three predictors, and one qualitative response variable.
# Suppose we wish to use this data set to make a prediction for Y when X1 = X2 = X3 = 0 using K-nearest neighbors.
# |Obs.|X1|X2|X3|Y
# |--|-------------------------------|
# |1 |0|3|0|Green|
# |2 |2|0|0|Green|
# |3|0|1|3|Green|
# |4|0|1|2|Red|
# |5|-1|0|1|Red|
# |6|1|1|1|Green|
# <b>Problem #1-1.</b> Compute the Euclidean distance between each observation and the test point, X1 = X2 = X3 = 0
#Write your narrative answer here
import numpy as np
x=np.array([[0,3,0],
[2,0,0],
[0,1,3],
[0,1,2],
[-1,0,1],
[1,1,1]])
test=[0,0,0]
Obs=1
for i in x:
dist=np.linalg.norm(i-test)
print("The distance between observation ",Obs," and test is ",dist)
Obs=Obs+1;
# <b>Problem #1-2.</b> What is our prediction with K = 1? and explain why.
# +
#Write your narrative answer here
import pandas as pd
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
y=np.array(["Green","Green","Green","Red","Red","Green"])
# y=y[:,np.newaxis]
# dataset=np.concatenate((x,y),axis=1)
k=1
knn=KNeighborsClassifier(n_neighbors=k)
knn.fit(x,y)
print(knn.predict([[0,0,0]]))
# predict_pro=knn.predict_proba([[0,0,0]])
# print("When k= ",k," Accuracy is ",predict_pro)
# -
When we just find the one of the nearest points, the red one is the shortest distance one.
# <b>Problem #1-3.</b> What is our prediction with K = 3? and explain why.
#Write your narrative answer here
k=3
knn=KNeighborsClassifier(n_neighbors=k)
knn.fit(x,y)
print(knn.predict([[0,0,0]]))
When we choose three of the nearest points, we find two points are green,
whereas the remain one is red, so we choose the more points' color as our result of prediction
# <b>Problem #1-4.</b> How using a different number of K has an impact on the performance? explain.
#Write your narrative answer here
K is K points which are closest to test point,
if we just choose few points, may be our prediction will be limited in a small range(overfitting) and have high variance.
But if we choose too many points, may be our prediction will be underfitting and have high bias.
# ---
# <h3> Problem #2. Answer those questions about linear regression [30 points] </h3>
# - Writing a code is not required for this question<br>
# - Feel free to select any type of submission you are comfortable with (Since it may require some mathematical formula and symbols; MS Word, or scanned version of your writing will be fine)
# <b>Problem #2-1.</b> Find the least squared fit of a linear regression model using the following traning data
# |Smoke index(x)|Lung cancer mortality index(y)|
# |:--:|:-------------------------------:|
# |127|115|
# |121|128|
# |94|128|
# |126|156|
# |102|101|
# |111|128|
# |95|115|
# |89|105|
# |101|87|
# +
#Write your narrative answer here
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
x=np.array([127,121,94,126,102,111,95,89,101])
y=np.array([115,128,128,156,101,128,115,105,87])
x_ave=np.mean(x)
y_ave=np.mean(y)
up=0;
down=0
for index in range(len(x)):
up=up+(y[index]-y_ave)*(x[index]-x_ave)
down=down+pow(x[index]-x_ave,2)
B1=up/down
B2=y_ave-B1*x_ave
print(B1)
print(B2)
# method two
x=x.reshape(-1,1)
y=y.reshape(-1,1)
linreg= LinearRegression().fit(x, y)
print("The coefficient of TV feature is:",linreg.coef_)
print("The intercept is: ", linreg.intercept_)
# -
# <b>Problem #2-2.</b> Given the test data below, compute the R-squared metric of the fitted model
# |Xi|Yi|
# |:--:|:-------------------------------:|
# |90|103|
# |106|131|
# |105|85|
# |115|99|
# |113|144|
# +
#Write your narrative answer here
from sklearn.metrics import r2_score
xi=np.array([90,106,105,115,113])
yi=np.array([103,131,85,99,144])
y_pred=B2+B1*xi
RSS=sum(pow((y_pred-yi),2))
TSS=sum(pow((yi-np.mean(yi)),2))
R2=1-RSS/TSS
print(R2)
# method two
print(r2_score(yi,y_pred))
# -
# ---
# <h3> Problem #3. This question involves the use of multiple linear regression on the Boston dataset [30 points]</h3> <br>
# In this part, you should download and analyze **"Boston House Prices"** dataset. <br>
# Here use a code below to download the dataset:
from sklearn.datasets import load_boston
import pandas as pd
import numpy as np
dataset = load_boston()
print(dataset.keys())
# <b>Problem #3-1</b> Print the description of the dataset.
#
# <b> Answer the following question:</b>
#
# - Whole dataset contains 14 attributes, (13 numeric/categorical predictive and 1 target value) what is a abbreviation of the target value?
#Write your narrative answer here
print(dataset.DESCR)
MEDV Median value of owner-occupied homes in $1000's
# <b>Problem #3-2 </b> Generate descriptive statistics using DataFrame. (hint: use "DataFrame . describe" function)<br>
#
# Follow two steps to answer questions.
# - Create a DataFrame usnig "data" from the dataset with columns using "feature_names".
# - Generate descriptive statistics
#
# <b> Answer the following questions:</b>
#
# - Which feature has the highest range (minimum and maximum value)?
#
# - Which feature has the lowest mean?
#
# - Which feature has a lowest standard deviation?
#Write your narrative answer here
df=pd.DataFrame(dataset.data,columns=dataset.feature_names)
df.describe()
Answer:
TAX have the highest range.
CHAS have lowest mean.
CHAS have lowest standard deviation
# <b>Problem #3-3 </b> Feature Scaling
#
# <b> Answer the following questions:</b>
#
# - From the information above, Do you recommend **feature scaling** to improve performance? Explain.
#
# - What is a difference between MinMaxScaler and StandardScaler?
# +
#Write your narrative answer here
I recommend feature scaling because the value of each feature have a large difference.
If we don't do job in feature scaling, some features will cause larger influence on the prediction.
We should keep balance in weight
MinMaxScaler: scales features to be in range 0 -1
StandardScaler: scales features so that they are all with zero mean and unit
variance
# -
# <b>Problem #3-4 </b> Calculate and report **correlations** between features and the target
#
# <b> Answer the following questions:</b>
#
# - What is a difference between positive and negative numbers on the correlation table? Explain.
# - What is the lowest number in the table? Do you think it is the most or the least helpful features in predicting the
# target class? Explain.
#Write your narrative answer here
df['target'] = dataset.target
print(df.corr())
Answer:
the positive number means this feature has positive correlation with target, when it add, target will add
the negative number means this feature has negative correlation with target, when it add, target will decrease
the lowest number is -0.737663 (LSTAT) includes negative number,it has the most helpful influnence on target.
or we do not consider negative number, the lowest number is 0.175260 (CHAS) which is least helpful in target.
# <b>Problem #3-5 </b>
# Follow two steps to answer questions.
#
# - Add 1 more column (dataset.target) to your DataFrame (give a name).
#
# - Find the correlation matrix that shows the correlation between each pair of features. <br>
#
# - Plot a correlation matrix<br> You can use the code below or write your own code to plot a correlation matrix *(extra point for writing your own code)*
#
# <b>Answer the following questions:</b>
#
# - What is the correlation between the feature RM and the LSTAT?
# - What does this value of correlation indicate?
# - Can you detect most or the least helpful features in predicting the target class from correlation matrix or from plot? How?
# +
# %matplotlib notebook
# %matplotlib inline
from sklearn.datasets import load_boston
dataset = load_boston()
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style="white")
# Get correlation matrix
df = (pd.DataFrame(dataset.data, columns= dataset.feature_names))
df['target'] = dataset.target
plt.matshow(df.corr())
corr = df.corr()
# # Generate a mask for the upper triangle
# mask = np.zeros_like(corr, dtype=np.bool)
# mask[np.triu_indices_from(mask)] = True
# # Set up the matplotlib figure
# f, ax = plt.subplots(figsize=(11, 9))
# # Generate a custom diverging colormap
# cmap = sns.diverging_palette(220, 10, as_cmap=True)
# # Draw the heatmap with the mask and correct aspect ratio
# sns.heatmap(corr, mask=mask, cmap=cmap, vmax=1, center=0, square=True, linewidths=.9, cbar_kws={"shrink": .7})
# -
#Write your narrative answer here
We can see in the graph the correlation between LSTAT and RM is smaller than negative 0.6,
which means these two features have large negative correlation.
When we talked about the most helpful features, we just need to find the maximum absolute value in the row of target in matrix,
or the most blue or the most red one in the row of target in the plot.
On the contrary, when we find the least helpful features, we just need to find the minimum absolute value in the row of target in matrix,
or the least blue or the least red one in the row of target in the plot
#
#
# <b>Problem #3-6 </b> Scatter plot. <br>
#
# Follow three steps to answer questions <br>
# - Plot LSTAT versus target variable
# - Plot RM versus target variable
# - Plot CHAS versus target variable <br>
#
# <b> Answer the following questions:</b>
# - Is the relationship linear?
# - Which looks the most nonlinear? Explain your chouce
#
# +
#Write your narrative answer here
import matplotlib.pyplot as plt
plt.scatter(df.LSTAT,df.target,marker='o')
plt.xlabel('LSTAT')
plt.ylabel('target')
plt.title('LSTAT vs target')
plt.show()
plt.scatter(df.RM,df.target,marker='o')
plt.xlabel('RM')
plt.ylabel('target')
plt.title('RM vs target')
plt.show()
plt.scatter(df.CHAS,df.target,marker='o')
plt.xlabel('CHAS')
plt.ylabel('target')
plt.title('CHAS vs target')
plt.show()
x=df.drop('target',axis=1)
y=df['target']
linreg= LinearRegression().fit(x, y)
print("The coefficient of TV feature is:",linreg.coef_)
print("The intercept is: ", len(linreg.coef_))
# -
RM looks like liner and CHAS looks the most nonliner, because the value of CHAS focus on the 0.0 or 1.0
# <b>Problem #3-7.</b> Follow steps to answer questions.
# > *Use train_test_split() with the option "random_state=0".
#
# 1. Fit a linear regression model with RM and LSTAT features only. Find the R-squared metric.
# 2. Fit a linear regression model using RM, LSTAT and include the interaction term (RM * LSTAT). How R-squared metric differs from the previous model without interaction term?
# 3. Fit a linear regression model using LSTAT and include the polynomial term ( $LSTAT^2$). Find the R-squared metric.
# 4. Fit linear regression model using LSTAT and include the polynomial term ( $LSTAT^2$ and $LSTAT^3$ ). Find the R-squared metric.
# - How does R-squared metric differ in the previous models ? <br> Comment your observation.
# +
RM=df.RM.values.reshape(-1,1)
LSTAT=df.LSTAT.values.reshape(-1,1)
x=np.concatenate((RM,LSTAT),axis=1)
y=df.target.values.reshape(-1,1)
X_train, X_test, Y_train, Y_test= train_test_split(x, y, random_state= 0)
model=LinearRegression()
fitted_model=model.fit(X_train,Y_train)
print("1. RM and LSTAT, R-squared metric is ",fitted_model.score(X_test,Y_test))
x2=np.concatenate((x,RM*LSTAT),axis=1)
y=df.target.values.reshape(-1,1)
X_train, X_test, Y_train, Y_test= train_test_split(x2, y, random_state= 0)
model2=LinearRegression()
fitted_model2=model2.fit(X_train,Y_train)
print("2. RM, LSTAT and RM*LSTAT, R-squared metric is ",fitted_model2.score(X_test,Y_test))
print(" R-squared metric increase with the interaction term")
x3=np.concatenate((LSTAT,LSTAT**2),axis=1)
y=df.target.values.reshape(-1,1)
X_train, X_test, Y_train, Y_test= train_test_split(x3, y, random_state= 0)
model=LinearRegression()
fitted_model=model.fit(X_train,Y_train)
print("3. LSTAT and LSTAT*LSTAT, R-squared metric is ",fitted_model.score(X_test,Y_test))
x4=np.concatenate((x3,LSTAT**3),axis=1)
y=df.target.values.reshape(-1,1)
X_train, X_test, Y_train, Y_test= train_test_split(x4, y, random_state= 0)
model=LinearRegression()
fitted_model=model.fit(X_train,Y_train)
print("4. LSTAT.LSTAT*LSTAT and LSTAT*LSTAT*LSTAT, R-squared metric is ",fitted_model.score(X_test,Y_test))
print(" the second model has the highest score which means it is the best one. With the add higher polynomial parameter in LASTA, R-squared metric become higher and higher")
# -
# <b>Problem #3-8.</b> Fit all features (13 features) in the dataset to a multiple linear regression model, and report<br>
#
# > (1) p-values for each feature.
#
# <b> Answer the following questions:</b>
#
# - What does p-value means
# - What are the important features? <br>
#
# +
import statsmodels.formula.api as smf
dataset=load_boston()
X=dataset.data
Y=dataset.target
model = smf.OLS(Y,X)
m1=model.fit()
print("P-values are: ",m1.pvalues)
# -
the features which have small p-values are important features
# ---
# <h3> Problem #4. Ordinary Least Square (OLS) [20 points] </h3> <br>
# <b>Problem #4-1.</b> Ordinary Least Square (OLS), calculate parameters
#
# Follow two steps<br>
#
# - From your DataFrame generate new DataFrame with 2 columns ('LSTAT' and target)
#
# - Using the least squared formula below write a function to calulate $B_0$ and $B_1$ from your new DataFrame where 'LSTAT' = x and target = y. *(hint you can add 2 colums to your DataFrame($x*x$ and $x*y$), check the problem #2-1)*
# \begin{array} \\
# \hat{\beta}_0 = \bar{y} - \hat{\beta}_1\bar{x}, \\ \\
# \hat{\beta}_1 = \frac{\sum_{i=1}^n y_i x_i - \bar{y}\sum_{i=1}^n x_i}{\sum_{i=1}^n x^2 - \bar{x}\sum_{i=1}^n x_i} \\ \\
# \text{where }\bar{x} = \frac{\sum_{i=1}^y x_i}{n} \text{ and } \bar{y} = \frac{\sum_{i=1}^y y_i}{n} \\
# \end{array}
# +
#Write your narrative answer here
df = (pd.DataFrame(dataset.data, columns= dataset.feature_names))
df['target']=dataset.target
df2=df[['LSTAT','target']]
LSTAT=df2.LSTAT.values.reshape(-1,1)
target=df2.target.values.reshape(-1,1)
# X_train, X_test, Y_train, Y_test= train_test_split(LSTAT,target, random_state= 0)
# linreg= LinearRegression().fit(X_train, Y_train)
# print("The coefficient of TV feature is:",linreg.coef_)
# print("The intercept is: ", linreg.intercept_)
# method two
L_ave=np.mean(LSTAT)
t_ave=np.mean(target)
up=0;
down=0
for index in range(len(LSTAT)):
up=up+(target[index]-t_ave)*(LSTAT[index]-L_ave)
down=down+pow(LSTAT[index]-L_ave,2)
B1=up/down
B0=t_ave-B1*L_ave
print("B1 is ",B1)
print("B0 is ",B0)
# -
# <b>Problem #4-2.</b> Ordinary Least Square (OLS) <br>
# Using formula below and using $B_0$ and $B_1$ from previous problem calculate $\hat{y}$ $where$ x = 'LSTAT'
# - Add your predicted data to the DataFrame
#
# \begin{array} \\
# \hat{y} = \hat{\beta}_0 + \hat{\beta}_1*x, \\ \\
# \end{array}
# +
#Write your narrative answer here
t_pred=B2+B1*LSTAT
# RSS=sum(pow((t_pred-target),2))
# TSS=sum(pow((target-np.mean(target)),2))
# R2=1-RSS/TSS
# print(R2)
t_pred=t_pred.reshape(-1)
df3 = (pd.DataFrame(df2))
df3['predict']=pd.Series(t_pred)
df3
# -
# <b>Problem #4-3.</b> Verification
#
# Predict $\hat{y}$ using linear regression model *(for this part you don't need to use train test split) *
#
# - Add your predicted data to the DataFrame
#
# Compare 3 column:
# - target
# - predicted column using our own code, (problem 2-9)
# - predicted column using linear regression model
#
# Comment your observations
#
#
# +
#Write your narrative answer here
linreg= LinearRegression().fit(LSTAT, target)
print("The coefficient of TV feature is:",linreg.coef_)
print("The intercept is: ", linreg.intercept_)
predict=linreg.predict(LSTAT)
predict=predict.reshape(-1)
df4 = (pd.DataFrame(df3))
df4['liner regression predict']=pd.Series(predict)
df4
# -
my own code and liner regression have same prediction
it proves that when using same dataset, liner regression will have same result.
# ### Submission
# Once you complete the assignment, <br>
# Name your file in the format of <b style='color:red'>LASTNAME-PITTID-Assignment1.ipynb</b>, and submit it on the courseweb
|
assignment1/YUHAO_WU-yuw121-Assignment1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# import necessary packeges
# %matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
import torch
from torch.utils.data import DataLoader
from torch import optim
from torch import nn
import torch.nn.functional as F
from torchvision import datasets, transforms
import helper
from collections import OrderedDict
from sklearn.model_selection import cross_val_score, train_test_split
from torch.utils.data.sampler import SubsetRandomSampler
import time
# -
# Get the device. Device is either cuda:0 or cpu
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(device)
# +
# define a trandform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.5,),(0.5,))])
# download and load the training data
trainset = datasets.FashionMNIST('F_MNIST_data', train=True, download=True, transform=transform)
#train_loader = DataLoader(trainset, batch_size=64, shuffle=True)
# download and load the testing data
testset = datasets.FashionMNIST('F_MNIST_data', train=False, download=True, transform=transform)
#test_loader = DataLoader(testset, batch_size=64, shuffle=True)
print(trainset)
print(testset)
# +
shuffle_dataset = True
validation_split = .2
random_seed= 42
trainset_size = len(trainset)
indices = list(range(trainset_size))
split = int(np.floor(validation_split * trainset_size))
if shuffle_dataset :
np.random.seed(random_seed)
np.random.shuffle(indices)
train_indices, val_indices = indices[split:], indices[:split]
print(len(train_indices))
print(len(val_indices))
# Creating PT data samplers and loaders:
train_sampler = SubsetRandomSampler(train_indices)
valid_sampler = SubsetRandomSampler(val_indices)
# -
train_loader = DataLoader(trainset, batch_size=64, sampler=train_sampler)
validation_loader = DataLoader(trainset, batch_size=64, sampler=valid_sampler)
test_loader = DataLoader(testset, batch_size=64, shuffle=True)
images, labels = next(iter(train_loader))
helper.imshow(images[0,:]);
images.size()
labels.size()
# ## Building the network
#
# Here you should define your network. As with MNIST, each image is 28x28 which is a total of 784 pixels, and there are 10 classes. You should include at least one hidden layer. We suggest you use ReLU activations for the layers and to return the logits from the forward pass. It's up to you how many layers you add and the size of those layers.
# +
input_layer = 784
hidden_layers = [8000, 6000, 4000, 200]
output_layer = 10
netmodel = nn.Sequential(OrderedDict([
('fcl1', nn.Linear(input_layer, hidden_layers[0])),
('relu1', nn.ReLU()),
('fcl2', nn.Linear(hidden_layers[0], hidden_layers[0])),
('relu2', nn.ReLU()),
('fcl3', nn.Linear(hidden_layers[0], hidden_layers[1])),
('relu3', nn.ReLU()),
('fcl4', nn.Linear(hidden_layers[1], hidden_layers[1])),
('relu4', nn.ReLU()),
('fcl5', nn.Linear(hidden_layers[1], hidden_layers[2])),
('relu5', nn.ReLU()),
('fcl6', nn.Linear(hidden_layers[2], hidden_layers[2])),
('relu6', nn.ReLU()),
('fcl7', nn.Linear(hidden_layers[2], hidden_layers[3])),
('relu7', nn.ReLU()),
('fcl8', nn.Linear(hidden_layers[3], hidden_layers[3])),
('relu8', nn.ReLU()),
('output', nn.Linear(hidden_layers[3], output_layer))
]))
netmodel
# -
# # Train the network
#
# Now you should create your network and train it. First you'll want to define [the criterion](http://pytorch.org/docs/master/nn.html#loss-functions) ( something like `nn.CrossEntropyLoss`) and [the optimizer](http://pytorch.org/docs/master/optim.html) (typically `optim.SGD` or `optim.Adam`).
#
# Then write the training code. Remember the training pass is a fairly straightforward process:
#
# * Make a forward pass through the network to get the logits
# * Use the logits to calculate the loss
# * Perform a backward pass through the network with `loss.backward()` to calculate the gradients
# * Take a step with the optimizer to update the weights
#
# By adjusting the hyperparameters (hidden units, learning rate, etc), you should be able to get the training loss below 0.4.
criterion = nn.CrossEntropyLoss()
#optimizer = optim.Adam(netmodel.parameters(), lr=0.001)
optimizer = optim.Adam(netmodel.parameters(), lr=0.0003)
#optimizer = optim.SGD(netmodel.parameters(), lr=0.003)
# +
epochs = 2
steps = 0
running_loss = 0
print_every = 40
netmodel.to(device)
start = time.time()
for e in range(epochs):
running_loss = 0
for images, labels in iter(train_loader):
steps += 1
# flatten the imiga into a 784 element vector
images.resize_(images.size()[0], 784)
images, labels = images.to(device), labels.to(device)
# Clear the gradients, do this because gradients are accumulated
optimizer.zero_grad()
output = netmodel.forward(images)
loss = criterion(output, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if steps % print_every == 0:
# Model in inference mode, dropout is off
netmodel.eval()
accuracy = 0
valid_loss = 0
for ii, (images, labels) in enumerate(validation_loader):
# flatten the imiga into a 784 element vector
images.resize_(images.size()[0], 784)
with torch.no_grad():
images, labels = images.to(device), labels.to(device)
output = netmodel.forward(images)
valid_loss += criterion(output, labels).item()
ps = F.softmax(output, dim=1)
equality = (labels.data == ps.max(1)[1])
accuracy += equality.type_as(torch.FloatTensor()).mean()
print("Epoch: {}/{}... ".format(e+1, epochs),
"Loss: {:.4f}".format(running_loss/print_every),
"Validation Loss: {:.3f}.. ".format(valid_loss/len(validation_loader)),
"Validation Accuracy: {:.3f}".format(accuracy/len(validation_loader)))
running_loss = 0
# Make sure dropout is on for training
netmodel.train()
print("Time for training and validation : {:.0f} minutes and {:.3f} seconds".format((time.time() - start)/60, (time.time() - start) % 60))
# +
netmodel.eval()
netmodel.to(device)
accuracy = 0
test_loss = 0
for ii, (images, labels) in enumerate(test_loader):
# flatten the imiga into a 784 element vector
images.resize_(images.size()[0], 784)
with torch.no_grad():
images, labels = images.to(device), labels.to(device)
output = netmodel.forward(images)
ps = F.softmax(output, dim=1)
equality = (labels.data == ps.max(1)[1])
accuracy += equality.type_as(torch.FloatTensor()).mean()
print("Test Accuracy: {:.3f}".format(accuracy/len(test_loader)))
running_loss = 0
# +
# Test out your network!
netmodel.to('cpu')
dataiter = iter(test_loader)
images, labels = dataiter.next()
img = images[0]
# Convert 2D image to 1D vector
img = img.resize_(1, 784)
# Calculate the class probabilities (softmax) for img
# Turn off gradients to speed up this part
with torch.no_grad():
logits = netmodel.forward(img)
ps = F.softmax(logits, dim=1)
print(ps.size())
print(ps.max(1)[1])
# Plot the image and probabilities
helper.view_classify(img.resize_(1, 28, 28), ps, version='Fashion')
|
Part 4 - Fashion-MNIST.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="C66HXNKf2Kl5" colab_type="code" outputId="d7b3d35a-f74f-41ba-db23-67e39edf5e02" executionInfo={"status": "ok", "timestamp": 1583351132201, "user_tz": -60, "elapsed": 6596, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 272}
# !pip install --upgrade tables
# !pip install eli5
# + id="z8BzE44TwCyH" colab_type="code" colab={}
import pandas as pd
import numpy as np
from sklearn.dummy import DummyRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_absolute_error as mae
from sklearn.model_selection import cross_val_score
import eli5
from eli5.sklearn import PermutationImportance
# + id="cMwXK57Q0uDo" colab_type="code" outputId="db8d33b3-595c-4129-a214-a08e7eb986ab" executionInfo={"status": "ok", "timestamp": 1583351132203, "user_tz": -60, "elapsed": 6584, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 35}
# cd "/content/drive/My Drive/Colab Notebooks/dw_matrix/matrix_two/dw_matrix_cars/"
# + id="N7E56BmO4CnM" colab_type="code" outputId="d424af80-02c4-4f22-a8e6-dae9f07e353d" executionInfo={"status": "ok", "timestamp": 1583351133828, "user_tz": -60, "elapsed": 8203, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 54}
# ls
# + [markdown] id="6l0hq2kf2nOQ" colab_type="text"
# Wczytywanie danych
# + id="s_7UZoO02q3n" colab_type="code" colab={}
df = pd.read_hdf('data/car.h5')
# + id="6BL08HRR4X91" colab_type="code" outputId="57b2492b-5e22-4ca6-860d-1f33c126204d" executionInfo={"status": "ok", "timestamp": 1583351137911, "user_tz": -60, "elapsed": 12279, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 35}
df.shape
# + id="LKRdCu0y4ZYS" colab_type="code" outputId="3090124a-64e0-4e82-ca44-c7a3581044a8" executionInfo={"status": "ok", "timestamp": 1583351137911, "user_tz": -60, "elapsed": 12273, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 199}
df.columns
# + id="Dw4Ic9A6-o-X" colab_type="code" colab={}
def group_and_barplot(feat_groupby, feat_agg='price_value', agg_funcs=[np.mean, np.median, np.size], feat_sort='size', top=50, subplots=True):
return(
df
.groupby(feat_groupby)[feat_agg]
.agg(agg_funcs)
.sort_values(by=feat_sort, ascending=False)
.head(top)
).plot(kind='bar', figsize=(27,5), subplots=subplots)
# + [markdown] id="M5TwoFcx5Aij" colab_type="text"
# ##Dummy model
# + id="ZNg9m1Aq4bfg" colab_type="code" outputId="a00c4e71-4fc0-488b-ea99-a59eaf8dc78c" executionInfo={"status": "ok", "timestamp": 1583351137912, "user_tz": -60, "elapsed": 12265, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 35}
feats = ['car_id']
X = df[feats].values
y = df['price_value'].values
model = DummyRegressor()
model.fit(X, y)
y_pred = model.predict(X)
mae(y, y_pred)
# + id="xML5p3QD4y3z" colab_type="code" outputId="0d170970-2f41-4996-ecb3-259e47cb2f88" executionInfo={"status": "ok", "timestamp": 1583351137912, "user_tz": -60, "elapsed": 12260, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 35}
[x for x in df.columns if 'price' in x]
# + id="q5J3Mtdn7vt_" colab_type="code" outputId="490ea47f-fd63-4933-e38f-788aad814141" executionInfo={"status": "ok", "timestamp": 1583351137913, "user_tz": -60, "elapsed": 12256, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 72}
df.price_currency.value_counts()
# + id="hDgTqQl570Oe" colab_type="code" outputId="788caeb8-9639-4231-ae5e-b27b25c9d246" executionInfo={"status": "ok", "timestamp": 1583351137913, "user_tz": -60, "elapsed": 12251, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 72}
df.price_currency.value_counts(normalize=True)
# + id="9cN5Lfje8Ubm" colab_type="code" colab={}
df = df[df['price_currency'] != 'EUR']
# + id="qYTxmHGk96-e" colab_type="code" outputId="9e0a5d6b-9246-4b59-cc13-c55614597d60" executionInfo={"status": "ok", "timestamp": 1583351138437, "user_tz": -60, "elapsed": 12764, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 35}
df.shape
# + id="2tYaq3BO98aC" colab_type="code" outputId="578983b6-4f02-4dd8-b107-2a2e878731ca" executionInfo={"status": "ok", "timestamp": 1583351138437, "user_tz": -60, "elapsed": 12756, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 1000}
df.sample(10)
# + id="_qOeeACt-GZn" colab_type="code" outputId="9ba70e6c-9abb-4b33-b32f-57772521755c" executionInfo={"status": "ok", "timestamp": 1583351138437, "user_tz": -60, "elapsed": 12749, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 1000}
for feat in df.columns:
print(feat)
# + id="q0CIkb11-X0B" colab_type="code" colab={}
SUFFIX_CAT = '__cat'
for feat in df.columns:
if isinstance(df[feat][0], list):
continue
factorize_values = df[feat].factorize()[0]
if SUFFIX_CAT in feat:
df[feat] = factorize_values
else:
df[feat + SUFFIX_CAT] = factorize_values
# + id="e6ICL5lw_Xdc" colab_type="code" outputId="e07f80e7-37ea-43cd-d102-6dfaae3d0ba2" executionInfo={"status": "ok", "timestamp": 1583351140185, "user_tz": -60, "elapsed": 14490, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 1000}
cat_feats = [x for x in df.columns if SUFFIX_CAT in x]
cat_feats = [x for x in cat_feats if 'price' not in x]
print(len(cat_feats))
cat_feats
# + id="EcjCiIn7Bofj" colab_type="code" outputId="8cf24fe1-d870-47ba-ca98-a7ccd64d810a" executionInfo={"status": "ok", "timestamp": 1583351147145, "user_tz": -60, "elapsed": 21444, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 35}
X = df[cat_feats].values
y = df['price_value'].values
model = DecisionTreeRegressor(max_depth=10)
scores = cross_val_score(model, X, y, cv=3, scoring='neg_mean_absolute_error')
np.mean(scores)
# + id="Yjb5VzSlDt8d" colab_type="code" outputId="c5de627a-5a8f-4e2f-cf8a-56d6beaa8162" executionInfo={"status": "ok", "timestamp": 1583351192564, "user_tz": -60, "elapsed": 66857, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 397}
m = DecisionTreeRegressor(max_depth=5)
m.fit(X, y)
imp = PermutationImportance(m, random_state=2020).fit(X, y)
eli5.show_weights(imp, feature_names=cat_feats)
# + [markdown] id="88LhuOny8Syk" colab_type="text"
# Tworzymy model w oparciu o najlepsze cech (wg Eli5)
# + id="41hZEGwPE5yg" colab_type="code" colab={}
feat_best = ['param_faktura-vat__cat', 'param_napęd__cat', 'param_stan__cat', 'param_rok-produkcji__cat', 'param_skrzynia-biegów__cat', 'param_moc__cat', 'feature_kamera-cofania__cat', 'param_pojemność-skokowa__cat', 'feature_bluetooth__cat', 'feature_światła-led__cat', 'feature_łopatki-zmiany-biegów__cat', 'param_typ__cat', 'param_marka-pojazdu__cat', 'feature_czujniki-parkowania-przednie__cat']
# + id="R1uoinEb3ljs" colab_type="code" outputId="cf70de47-2ffc-42ca-ac9e-9851106cdb72" executionInfo={"status": "ok", "timestamp": 1583351193500, "user_tz": -60, "elapsed": 67785, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 35}
X = df[feat_best].values
y = df['price_value'].values
model = DecisionTreeRegressor(max_depth=15, splitter='best')
scores = cross_val_score(model, X, y, cv=3, scoring='neg_mean_absolute_error')
np.mean(scores)
# + id="qLC00QQn5ZEj" colab_type="code" outputId="95a44496-d85f-4703-b52a-0f41533b3f40" executionInfo={"status": "ok", "timestamp": 1583351193500, "user_tz": -60, "elapsed": 67750, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 399}
df['param_pojemność-skokowa'].sample(20)
# + id="9562g95j5dDL" colab_type="code" outputId="a48eee33-f689-4490-a8c1-8860af2e12f3" executionInfo={"status": "ok", "timestamp": 1583351193500, "user_tz": -60, "elapsed": 67743, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 108}
df['param_pojemność-skokowa'].describe()
# + id="8jno-w8K5lkU" colab_type="code" colab={}
def pojemnosc_skokowa_obj2int(cm3):
if not isinstance(cm3, str): #zabezpiecznie w przypadku braku danych - jak się okazało potrzebne
return -1
poj_s = cm3.replace(" cm3", "") #pozbywamy się centymetrów3
poj_s = int(poj_s.replace(' ', '')) #i spacji 'tysięcznych' i konwertujemy na liczbę
return poj_s
df['param_pojemność-skokowa_int'] = df['param_pojemność-skokowa'].map(pojemnosc_skokowa_obj2int)
# + id="9B6dtlyG75pq" colab_type="code" outputId="b849ae9a-2a1c-46d5-c2bc-e0cd126727f5" executionInfo={"status": "ok", "timestamp": 1583351193730, "user_tz": -60, "elapsed": 67963, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 181}
df['param_pojemność-skokowa_int'].describe()
# + id="HFx3gwse7_U6" colab_type="code" outputId="caf8a652-cacc-4957-f1ae-3118aed55e68" executionInfo={"status": "ok", "timestamp": 1583351193731, "user_tz": -60, "elapsed": 67959, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 490}
df['param_pojemność-skokowa_int'].sample(25)
# + [markdown] id="IDawB0dl89E_" colab_type="text"
# ##ponownie tworzymy model ale podmieniamy *param_pojemność-skokowa__cat* na *param_pojemność-skokowa_int*
# + id="z8uXvH1X88eg" colab_type="code" colab={}
feat_best2 = ['param_faktura-vat__cat', 'param_napęd__cat', 'param_stan__cat', 'param_rok-produkcji__cat', 'param_skrzynia-biegów__cat', 'param_moc__cat', 'feature_kamera-cofania__cat', 'param_pojemność-skokowa_int', 'feature_bluetooth__cat', 'feature_światła-led__cat', 'feature_łopatki-zmiany-biegów__cat', 'param_typ__cat', 'param_marka-pojazdu__cat', 'feature_czujniki-parkowania-przednie__cat']
# + id="z6jvIhuQ9p_X" colab_type="code" outputId="e990b8fe-3b4c-4c8b-bac7-546d35b9d5b6" executionInfo={"status": "ok", "timestamp": 1583351194770, "user_tz": -60, "elapsed": 68988, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 35}
X = df[feat_best2].values
y = df['price_value'].values
model = DecisionTreeRegressor(max_depth=15, splitter='best')
scores = cross_val_score(model, X, y, cv=3, scoring='neg_mean_absolute_error')
np.mean(scores)
# + [markdown] id="8WRMMQPY-BiR" colab_type="text"
# z **-13330.48** na **-12456.85** - lepiej!
# + [markdown] id="80v2CecH-vd1" colab_type="text"
# ##wykres z liczbową wartością pojemności skokowej silnika:
# + id="_-bQ2vBS_IKH" colab_type="code" outputId="afd5f5e0-6b9c-4b6b-c5a0-0c48a6d1a812" executionInfo={"status": "ok", "timestamp": 1583351196224, "user_tz": -60, "elapsed": 70437, "user": {"displayName": "<NAME>\u0105ka\u0142a", "photoUrl": "", "userId": "06128289894157370845"}} colab={"base_uri": "https://localhost:8080/", "height": 367}
group_and_barplot('param_pojemność-skokowa_int', feat_sort='median');
|
day3_simple_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ###### Content under Creative Commons Attribution license CC-BY 4.0, code under BSD 3-Clause License © 2021 <NAME>, <NAME>
# # Multiple linear regression
#
# Welcome to Lesson 3 of our _Engineering Computations_ module on deep learning!
#
# So far, we have only modeled the relationship between one input variable (also called _feature_) $x$ and one output variable $y$. More often than not, real-world model fitting involves making predictions using more than one feature. For example, you can build a model to predict the box-office gross revenue of Hollywood movies using trailer views, Wikipedia page views, critic ratings and time of release; or to predict the annual energy consumption of a building using its occupancy, structural information, weather data and so on. In this lesson, we are going to extend the linear regression model to multiple input variables, i.e., we explore **multiple linear regression**.
# ## A real data set to work with
#
# To have some data to work with, we grabbed the [auto miles per gallon (MPG) dataset](http://archive.ics.uci.edu/ml/datasets/Auto+MPG) from the UCI Machine Learning Repository, removed the missing data and formatted it as a csv file. Our goal is to predict the MPG (fuel efficiency) of a car using its technical specs.
#
# Let's begin by importing the Python libraries we will use. The [Seaborn](https://seaborn.pydata.org) library for statistical data visualization will help us make beautiful plots. Seaborn is built on top of Matplotlib, and its plotting functions work seamlessly with dataframes or arrays.
#
import pandas
import seaborn
seaborn.set()
# Let's read in the data and take a peek at it.
# If you need to download the data, execute the following in a code cell:
#
# ```Python
# from urllib.request import urlretrieve
# URL = 'https://go.gwu.edu/engcomp6data3'
# urlretrieve(URL, 'auto_mpg.csv')
# ```
#
# In that case, the file will be downloaded in your working directory, so you should remove the directory path `../data/` from the file string below.
mpg_data = pandas.read_csv('../data/auto_mpg.csv')
mpg_data.head()
# From the first few rows you get a sense for what's in this data set. Use [`pandas.DataFrame.info()`](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.info.html) to see a quick summary of the data.
mpg_data.info()
# We have 392 entries and each is associated with a specific car model. The data consists of altogether 9 columns. Except for `car name`, values in all other columns are numeric. Despite being numeric, the `origin` column, indicating the country of origin, corresponds to categorical data. We expect that the name of a car won't affect its MPG (country of origin might); for simplicity, we exclude `car name` and `origin` as features to predict the MPG.
#
# Now, let's define the feature columns: `x_cols` and the output column: `y_cols`.
# +
y_col = 'mpg'
x_cols = mpg_data.columns.drop(['car name', 'origin', 'mpg']) # also drop mpg column
print(x_cols)
# -
# We end up keeping 6 features, or independent variables (all technical specs of a car), that we expect to be correlated with MPG, the dependent variable.
# ## Data exploration
#
# Before choosing a model to fit our data, exploring the data is equally important but often ignored. The best way to start is to visualize the relationship between input and output variables.
#
# We have used scatter plots before to visualize the relationship between just two variables.
# Since now we are dealing with 6 independent variables, we want to make such a plot for each one; luckily, `seaborn` provides the handy function [`seaborn.pairplot()`](https://seaborn.pydata.org/generated/seaborn.pairplot.html) to plot these 6 figures in one go. Check it out! You can double-click the figure to expand the view.
seaborn.pairplot(data=mpg_data, height=5, aspect=1,
x_vars=x_cols,
y_vars=y_col);
# Inspect these plots and make some mental notes of what you see.
# The features: `model_year`, `acceleration` show a positive correlation with `mpg`, while the rest show a negative correlation with `mpg`.
# It looks like a linear model might represent well the relationship of all six features with our output variable.
# ## Linear model in matrix form
#
# If every feature $x_i$ is correlated with $y$ individually, it is natural to think that combining them linearly would be a good fit for $y$. Formally, the multiple linear regression model for $d$ input variables can be written as:
#
# $$
# \hat{y} = w_0 + w_1 x_1 + w_2 x_2 + \ldots + w_d x_d,
# $$
#
# where the "hat" on $y$ denotes a predicted value.
# Notice that we have $d+1$ weights for $d$ features, and $w_0$ is the intercept term. By letting $x_0 = 1$ for all data points, we can simplify the notation as:
#
# $$
# \hat{y} = \sum_{i=0}^{d} w_i x_i = \mathbf{x}^T \mathbf{w},
# $$
#
# where $\mathbf{w} = (w_0, w_1, \ldots, w_d)^T$ is the vector of weights, and $\mathbf{x} = (x_0, x_1, \ldots, x_d)^T$ the vector of input variables.
#
# Since we've used subscripts to denote features, let's index our dataset entries with superscripts. For example, $x_1^{(i)}$ represents the `cylinders` (the first feature) value of the $i$-th car model.
#
# Suppose our dataset has $N$ entries; writing out our model for each entry, we have:
#
# \begin{align*}
# \hat{y}^{(1)} & = w_0 x_0^{(1)} + w_1 x_1^{(1)} + w_2 x_2^{(1)} + \ldots + w_d x_d^{(1)} \\
# \hat{y}^{(2)} & = w_0 x_0^{(2)} + w_1 x_1^{(2)} + w_2 x_2^{(2)} + \ldots + w_d x_d^{(2)} \\
# &\vdots \\
# \hat{y}^{(N)} & = w_0 x_0^{(N)} + w_1 x_1^{(N)} + w_2 x_2^{(N)} + \ldots + w_d x_d^{(N)} \\
# \end{align*}
#
# Finally, we arrive at the matrix form of the multiple linear regression model:
#
# $$
# \hat{\mathbf{y}} = X\mathbf{w}
# $$
#
# The $X$ is the matrix of our input variables. To form $X$, we need to pad a column of $1$s to the left of our original data as the dummy feature corresponding to the intercept $w_0$. We use $\hat{\mathbf{y}}$ to represent the vector of the predicted output variables, and $\mathbf{y}$ to represent the vector of the observed (true) output variables.
#
# Before coding our model, let's import from the automatic differentiation library `autograd` both its NumPy wrapper and the `grad()` function, as we learned to do in Lesson 2.
from autograd import numpy
from autograd import grad
# Let's prepare the input matrix $X$ and the vector $\mathbf{y}$ directly from our dataset.
# In the code below, we grab the columns `x_cols` from the dataframe `mpg_data` and extract the values into a NumPy array `X` (a matrix).
# The NumPy function [`hstack()`](https://numpy.org/doc/stable/reference/generated/numpy.hstack.html) is used to stack arrays horizontally (by columns).
# We also slice the single column `y_col` of the dataframe, and extract the values into a NumPy array `y`.
# Check out the array shapes.
# +
X = mpg_data[x_cols].values
X = numpy.hstack((numpy.ones((X.shape[0], 1)), X)) # pad 1s to the left of input matrix
y = mpg_data[y_col].values
print(f"{X.shape = }, {y.shape = }")
# -
# Like in the single-variable linear regression model of Lesson 1, we use the the **mean squared error** loss function, over all the data points:
#
# $$L(\mathbf{y}, \hat{\mathbf{y}}) = \frac{1}{N} \sum_{i=1}^{N}(y^{(i)} - \hat{y}^{(i)})^2$$
#
# We're ready to define Python functions for the multiple linear regresssion model and the loss function.
# +
def linear_regression(params, X):
'''
The linear regression model in matrix form.
Arguments:
params: 1D array of weights for the linear model
X : 2D array of input values
Returns:
1D array of predicted values
'''
return numpy.dot(X, params)
def mse_loss(params, model, X, y):
'''
The mean squared error loss function.
Arguments:
params: 1D array of weights for the linear model
model : function for the linear regression model
X : 2D array of input values
y : 1D array of predicted values
Returns:
float, mean squared error
'''
y_pred = model(params, X)
return numpy.mean( numpy.sum((y-y_pred)**2) )
# -
# ## Find the weights by gradient descent
#
# Following Lesson 2, we know that `autograd.grad()` will give us the function to compute the derivatives required in gradient descent.
gradient = grad(mse_loss)
# Let's test the function with a random initial guess:
gradient(numpy.random.rand(X.shape[1]), linear_regression, X, y)
# Oops, it does not look nice. With the random weights, the gradient values are huge. Let us try with a few iterations in gradient descent.
# +
max_iter = 30
alpha = 0.001
params = numpy.zeros(X.shape[1])
for i in range(max_iter):
descent = gradient(params, linear_regression, X, y)
params = params - descent * alpha
loss = mse_loss(params, linear_regression, X, y)
if i%5 == 0:
print(f"iteration {i:3}, {loss = }")
# -
# Yikes! This is definitely not good. What could be going on here?
# ### Feature scaling
#
# As you saw above, the gradient descent algorithm is blowing up. This is because of the big numbers in certain columns, for instance, look at the `weight` column. In addition, having features with varying magnitudes will also lead to slow convergence in the gradient descent iterations. Therefore, it is critical to make sure that all features are on a similar scale. This step is also called **feature scaling** or **data normalization**.
#
# Let's check the range of our features.
mpg_data[x_cols].describe().loc[['max', 'min']]
# One commonly used feature scaling technique is **min-max scaling**, which scales the range of each feature to the interval $[0,1]$. If $x$ is the original value of a feature, its scaled (normalized) value $x^{\prime}$ is given as:
#
# $$
# x^{\prime}=\frac{x-\min (x)}{\max (x)-\min (x)}
# $$
#
# We will now introduce a new Python library: [**scikit-learn**](https://scikit-learn.org/stable/).
# It is the standard tool for machine-learning tasks in Python.
# So far, we've made some headway with the tools you know from previous _Engineering Computations_ modules, including NumPy, SymPy, and pandas.
# But we reached a point where it's so much easier to start using `scikit-learn`!
#
# Here, we'll use the function [`sklearn.preprocessing.MinMaxScaler()`](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html) to rescale our $X$.
#
# And check the range of each column of $X$ again.
# +
from sklearn.preprocessing import MinMaxScaler
min_max_scaler = MinMaxScaler()
X_scaled = min_max_scaler.fit_transform(mpg_data[x_cols])
X_scaled = numpy.hstack((numpy.ones((X_scaled.shape[0], 1)), X_scaled)) # add the column for intercept
pandas.DataFrame(X_scaled).describe().loc[['max', 'min']]
# -
# Notice that column **0** corresponds to the dummy data for the intercept. All values in that column are 1.
#
# Finally, we are ready to run gradient descent to find the optimal parameters for our multiple linear regression model.
# +
max_iter = 1000
alpha = 0.001
params = numpy.zeros(X.shape[1])
for i in range(max_iter):
descent = gradient(params, linear_regression, X_scaled, y)
params = params - descent * alpha
loss = mse_loss(params, linear_regression, X_scaled, y)
if i%100 == 0:
print(f"iteration {i:3}, {loss = }")
# -
# Let's print out the trained weights. Recall that the first element is the intercept, and the rest correspond to the 6 features respectively.
params
# Now, we can make predictions with our model, and this step reduces to a matrix-vector multiplication.
y_pred_gd = X_scaled @ params
# ### How accurate is the model?
#
# One thing that we haven't discussed till now is how to quantify the accuracy of a model. For regression problems, two basic metrics are the mean absolute error (MAE) and the root-mean-squared error (RMSE). The latter is just the square root of the MSE loss function that we used above.
#
# $$
# \mathrm{MAE}(\mathbf{y}, \hat{\mathbf{y}})=\frac{1}{N} \sum_{i=1}^{N}\left|y^{(i)}-\hat{y}^{(i)}\right|
# $$
#
# $$
# \mathrm{RMSE}(\mathbf{y}, \hat{\mathbf{y}})=\sqrt{\frac{1}{N} \sum_{i=1}^{N}\left(y^{(i)}-\hat{y}^{(i)}\right)^{2}}
# $$
#
# Most common metrics are available in **scikit-learn**. Let's compute both errors using the corresponding functions in the [`sklearn.metrics`](https://scikit-learn.org/stable/modules/model_evaluation.html#regression-metrics) module.
# +
from sklearn.metrics import mean_absolute_error, mean_squared_error
mae = mean_absolute_error(y, y_pred_gd)
rmse = mean_squared_error(y, y_pred_gd, squared=False)
print(f"gradient descent")
print(f"{mae = }")
print(f"{rmse = }")
# -
# ## Linear regression with scikit-learn
#
# We want to mention that the [`LinearRegression()`](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html?highlight=linearregression#sklearn-linear-model-linearregression) function in **scikit-learn** offers the same capability we've coded from scratch above. Now with a better understanding of the model, you should feel more comfortable to use these black-boxes.
#
# Check out how the code looks like using this tool: just four lines of code do all the work!
# +
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=False).fit(X, y)
y_pred_sklearn = model.predict(X)
mae = mean_absolute_error(y, y_pred_sklearn)
rmse = mean_squared_error(y, y_pred_sklearn, squared=False)
print(f"scikit-learn linear regression")
print(f"{mae = }")
print(f"{rmse = }")
# -
# ## Linear regression with pseudo-inverse
#
# We want to conclude this notebook with a callback to the final lesson in the _Engineering Computations_ module on Linear Algebra, [Module 4](https://openedx.seas.gwu.edu/courses/course-v1:GW+EngComp4+2019/about). Recall that we can use singular value decomposition (SVD) to obtain the pseudo-inverse of a matrix and that the pseudo-inverse offers a least-squares solution of the corresponding linear system. Given $X$ and $\mathbf{y}$, finding the linear regression weights $\mathbf{w}$ that minimize the MSE loss function is exactly a least-squares problem.
#
# Performing SVDs on large datasets might not be ideal, but let's try on this one.
# +
from scipy.linalg import pinv
params = pinv(X) @ y
y_pred_svd = X @ params
mae = mean_absolute_error(y, y_pred_svd)
rmse = mean_squared_error(y, y_pred_svd, squared=False)
print(f"linear regression using pseudo inverse")
print(f"{mae = }")
print(f"{rmse = }")
# -
# If you look carefully enough, you will notice that the error from using pseudo-inverse is almost identical to the error from using the `sklearn.linear_model.LinearRegression()` function. In fact, that is exactly how `LinearRegression()` is implemented in **scikit-learn**, since a closed-form solution is available. However, for more complicated models, we have to use gradient descent.
#
# And this concludes Lesson 3 of our _Engineering Computations_ module on deep learning.
# We take a step-by-step approach to help you build understanding and demistify this booming subject that every scientist and engineer should know about!
# ## What we've learned
#
# - The [Seaborn](https://seaborn.pydata.org/) library for statistical visualization has handy tools to make beautiful plots!
# - A linear regression model with many input variables (a.k.a. features) is written neatly in matrix form as $\hat{\mathbf{y}} = X\mathbf{w}$, where $X$ is the matrix of features and $w$ is the vector of weights.
# - Gradient descent can blow up with features that have disparate scales. Feature scaling (or normallization) solves this problem.
# - [**scikit-learn**](https://scikit-learn.org/stable/) is the standard tool for machine-learning tasks in Python.
# - The [`LinearRegression()`](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html?highlight=linearregression#sklearn-linear-model-linearregression) function in **scikit-learn** fits a linear model with multiple features.
# - We can also do multiple linear regression using the matrix pseudo-inverse, obtained with SVD.
# Execute this cell to load the notebook's style sheet, then ignore it
from IPython.core.display import HTML
css_file = '../style/custom.css'
HTML(open(css_file, "r").read())
|
notebooks_en/3_Multiple_Linear_Regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] papermill={"duration": 0.017282, "end_time": "2021-04-06T10:20:46.672670", "exception": false, "start_time": "2021-04-06T10:20:46.655388", "status": "completed"} tags=[]
# # Samples from a parquet source using ApacheSpark
# + papermill={"duration": 2.563051, "end_time": "2021-04-06T10:20:49.245364", "exception": false, "start_time": "2021-04-06T10:20:46.682313", "status": "completed"} tags=[]
# !pip3 install pyspark==3.1.1
# + papermill={"duration": 0.016731, "end_time": "2021-04-06T10:20:49.279025", "exception": false, "start_time": "2021-04-06T10:20:49.262294", "status": "completed"} tags=[]
# @param data_dir temporal data storage for local execution
# @param data_parquet path and parquet file name (default: data.parquet)
# @param data_parquet_target path and parquet file name
# (default: data_sample.parquet)
# @param master url of master (default: local mode)
# @param sampling_rate (default: 1%)
# @param sampling_seed (default: 42)
# + papermill={"duration": 0.17677, "end_time": "2021-04-06T10:20:49.472681", "exception": false, "start_time": "2021-04-06T10:20:49.295911", "status": "completed"} tags=[]
from pyspark import SparkContext, SparkConf
from pyspark.sql import SparkSession
import os
import shutil
# + papermill={"duration": 0.018141, "end_time": "2021-04-06T10:20:49.498206", "exception": false, "start_time": "2021-04-06T10:20:49.480065", "status": "completed"} tags=[]
data_parquet = os.environ.get('data_parquet', 'data.parquet')
data_parquet_target = os.environ.get(
'data_parquet_target', 'data_sample.parquet')
master = os.environ.get('master', "local[*]")
data_dir = os.environ.get('data_dir', '../../data/')
sampling_rate = float(os.environ.get('sampling_rate', 0.1))
sampling_seed = int(os.environ.get('sampling_rate', 42))
# +
skip = False
if os.path.exists(data_dir+data_parquet_target):
skip = True
# + papermill={"duration": 10.111445, "end_time": "2021-04-06T10:20:59.618326", "exception": false, "start_time": "2021-04-06T10:20:49.506881", "status": "completed"} tags=[]
if not skip:
sc = SparkContext.getOrCreate(SparkConf().setMaster(master))
spark = SparkSession.builder.getOrCreate()
# + papermill={"duration": 6.702477, "end_time": "2021-04-06T10:21:06.329699", "exception": false, "start_time": "2021-04-06T10:20:59.627222", "status": "completed"} tags=[]
if not skip:
df = spark.read.parquet(data_dir + data_parquet)
# + papermill={"duration": 0.072413, "end_time": "2021-04-06T10:21:06.408685", "exception": false, "start_time": "2021-04-06T10:21:06.336272", "status": "completed"} tags=[]
if not skip:
df = df.sample(sampling_rate, sampling_seed)
# -
if not skip:
shutil.rmtree(data_dir + data_parquet_target, ignore_errors=True)
# + papermill={"duration": 0.724797, "end_time": "2021-04-06T10:21:07.142732", "exception": true, "start_time": "2021-04-06T10:21:06.417935", "status": "failed"} tags=[]
if not skip:
df.write.parquet(data_dir + data_parquet_target)
|
filter/spark-sample.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="6rqSTOHXHN3f"
# **Припустимо, що у вас є багатошаровий перцептрон, що складається з одного вхідного
# шару з 10 нейронами, за яким є ще один прихований шар з 50 нейронами і один
# вихідний шар з 3 нейронами. Всі штучні нейрони застосовують функцію активації
# ReLU.**
# + [markdown] id="zb2BtRd7HRFJ"
# **Яка форма вхідної матриці X?**
# + [markdown] id="IXsJSggJHb7Y"
# Вектор довжиною 10
# + [markdown] id="mQp04yxxHfWJ"
# **Що можна сказати про форму вектора ваг
# W_h
# прихованого шару?**
# + [markdown] id="jtp9PeSkHi1a"
# 50x10
# + [markdown] id="OHmxOwWAIiUN"
# **... і формі його вектора зсувів b_h?**
# + [markdown] id="CfyDpkoFJQ4P"
# 50x1
# + [markdown] id="7Xa9teL-JYQt"
# **Яка форма вектора ваг
# W_0
# вихідного шару?**
# + [markdown] id="p0ru5I09JbSZ"
# 3x50
# + [markdown] id="S4uD-_XDKH2N"
# **... і форма його вектора зсувів
# b_0?**
# + [markdown] id="h_tYE2tXKLej"
# 3x1
# + [markdown] id="2ULcukW5Ka4W"
# **Яка форма вихідної матриці
# Y
# мережі?**
# + [markdown] id="NkXHnMsZKfRC"
# 3x1
# + [markdown] id="JSCoCgQiKuR1"
# **Напишіть рівняння, яке обчислює вихідну матрицю Y мережі як функцію від X , W_h, b_H, W_0 та b_0.**
# + [markdown] id="NKgmQDSmLUXD"
# $Y=f(W_0 * f(W_h * X + b_h) + b_0)$
#
# $Y=max(0, W_0 * max(0, W_h * X + b_h) + b_0)$
# + id="Kgv5FBnSG_0K"
import keras
from keras.datasets import mnist
import keras.models as M
import keras.layers as L
import keras.backend as K
# + id="2yMY37J1Ots1"
from sklearn.metrics import accuracy_score
(x_train, y_train), (x_val, y_val) = keras.datasets.fashion_mnist.load_data()
y_train_oh = tf.keras.utils.to_categorical(y_train, 10)
y_val_oh = tf.keras.utils.to_categorical(y_val, 10)
# + colab={"base_uri": "https://localhost:8080/"} id="wSqtfDCXHGyd" outputId="03eca84e-e23c-4889-da96-56d758cca177"
x_train_float = x_train.astype(np.float) / 255 - 0.5
x_val_float = x_val.astype(np.float) / 255 - 0.5
results = []
for func in ['linear', 'elu', 'softmax', 'sigmoid']:
print("Activation function: ", func)
K.clear_session()
model = M.Sequential()
model.add(L.Dense(28*28, activation=func))
model.add(L.Dense(128, activation=func))
model.add(L.Dense(10, activation=func))
model.compile(
loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy']
)
results.append(model.fit(
x_train_float.reshape(-1, 28*28),
y_train_oh,
batch_size=64,
epochs=5,
validation_data=(x_val_float.reshape(-1, 28*28), y_val_oh)
))
# + [markdown] id="1FJB_ilzU2Hq"
# Нейронна мережа з лінійною функцією активації має найгіршу точність класифікації (приблизно 10%).
# + [markdown] id="pFXhkdXuVblo"
# **Для двошарової нейронної мережі з фіксованою функцією активації
# sigmoid
# побудуйте
# графік залежності часу навчання нейронної мережі і точності класифікації від
# кількості нейронів в прихованому шарі мережі.**
# + colab={"base_uri": "https://localhost:8080/"} id="l3iVoGnES1vb" outputId="86fc937c-8a3e-43bf-a11a-c173787eac91"
# https://stackoverflow.com/a/57182112/5701177
from timeit import default_timer as timer
class TimingCallback(keras.callbacks.Callback):
def __init__(self, logs={}):
self.logs=[]
def on_epoch_begin(self, epoch, logs={}):
self.starttime = timer()
def on_epoch_end(self, epoch, logs={}):
self.logs.append(timer()-self.starttime)
results = []
callbacks = []
for hidden_n in [8, 16, 32, 64, 128, 256, 512]:
print("Neurons: ", hidden_n)
K.clear_session()
model = M.Sequential()
model.add(L.Dense(28*28, activation='sigmoid'))
model.add(L.Dense(hidden_n, activation='sigmoid'))
model.add(L.Dense(10, activation='sigmoid'))
model.compile(
loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy']
)
callback = TimingCallback()
callbacks.append(callback)
results.append(model.fit(
x_train_float.reshape(-1, 28*28),
y_train_oh,
batch_size=64,
epochs=5,
validation_data=(x_val_float.reshape(-1, 28*28), y_val_oh),
callbacks=[callback]
))
# + id="n6SovWNcaHVI"
import matplotlib.pyplot as plt
# + colab={"base_uri": "https://localhost:8080/", "height": 408} id="LtRVeRzyXIaM" outputId="83f5d762-e897-4247-d3d3-48b5aa17cddc"
hidden_ns = [8, 16, 32, 64, 128, 256, 512]
for r in results:
print(max(r.history['val_accuracy']))
plt.ylim([0.8, 0.9])
plt.plot(hidden_ns, [max(r.history['val_accuracy']) for r in results])
# + colab={"base_uri": "https://localhost:8080/", "height": 406} id="1Csr0vQdYjTg" outputId="72a7f927-1457-4ed2-f9e0-227dfb56c09f"
for cb in callbacks:
print(sum(cb.logs))
plt.plot(hidden_ns, [sum(cb.logs) for cb in callbacks])
# + [markdown] id="URxVB7WcdVkm"
# Бачимо, що час навчання лінійно зростає, але в нашому випадку зміна кількості нейронів у межах від 16 до 512 не дуже впливає на точність класифікації. 8 нейронів, можливо, недостатньо.
# + [markdown] id="ajE2-A-jdq1z"
# **Побудуйте графік залежності часу навчання нейронної мережі і точності класифікації
# від кількості прихованих шарів (всі приховані шари однакового розміру) для
# багатошарової нейронної мережі з фіксованою функцією активації `'tanh'`**
# + colab={"base_uri": "https://localhost:8080/"} id="v91F3cb3ZSKt" outputId="2d8e887b-2a9a-4e27-f1b6-eca07dcb660f"
results = []
callbacks = []
for layers in [1, 2, 3, 4, 5]:
#
# hidden_n variable left here by accident, it is not used!
#
print("Neurons: ", hidden_n)
K.clear_session()
model = M.Sequential()
model.add(L.Dense(28*28, activation='tanh'))
for i in range(layers):
print("Adding layer ", i)
model.add(L.Dense(128, activation='tanh'))
model.add(L.Dense(10, activation='tanh'))
model.compile(
loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy']
)
callback = TimingCallback()
callbacks.append(callback)
results.append(model.fit(
x_train_float.reshape(-1, 28*28),
y_train_oh,
batch_size=64,
epochs=5,
validation_data=(x_val_float.reshape(-1, 28*28), y_val_oh),
callbacks=[callback]
))
# + colab={"base_uri": "https://localhost:8080/"} id="U76qatQiebNw" outputId="23298732-d6ca-429c-d69c-e9851867fd6b"
# Try one more time, with 20 hidden layers
print("Neurons: ", 20)
K.clear_session()
model = M.Sequential()
model.add(L.Dense(28*28, activation='tanh'))
for i in range(20):
print("Adding layer ", i)
model.add(L.Dense(128, activation='tanh'))
model.add(L.Dense(10, activation='tanh'))
model.compile(
loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy']
)
callback = TimingCallback()
callbacks.append(callback)
results.append(model.fit(
x_train_float.reshape(-1, 28*28),
y_train_oh,
batch_size=64,
epochs=5,
validation_data=(x_val_float.reshape(-1, 28*28), y_val_oh),
callbacks=[callback]
))
# + colab={"base_uri": "https://localhost:8080/", "height": 286} id="AYKj6eiWg4wO" outputId="40ed81de-1c83-4f89-d0da-04548a17abf6"
layer_counts = [1, 2, 3, 4, 5, 20]
plt.ylim([0, 0.2])
plt.plot(layer_counts, [max(r.history['val_accuracy']) for r in results])
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="Ey4uwX1Uhl0Y" outputId="46738eb7-9ecc-4cc8-8876-616b72d0b79c"
plt.plot(layer_counts, [sum(cb.logs) for cb in callbacks])
# + [markdown] id="Y9HiirVxkN85"
# Знову бачимо, що час навчання зростає, але впливу на точність класифікації немає (не більше 10%). Можливо, функція активації `tanh` просто погано підходить для таких задач.
# + id="nkbdDPcXkepO"
|
semester7/nn/seminar4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# The purpose of this file is to load World bank indicator data, obtained in CSV format, downloading from the [World Bank Indicator portal](http://datatopics.worldbank.org/world-development-indicators/)
#
# The data is reformated to a pandas dataframe with following format specified: indicators are on columns and the country and year form a multi level row index
import pandas as pd
import json
from pandas_datareader import wb
data_dir = '.\\..\\..\\data\\'
#name of output pickle file
world_bank_file_out = "world_bank_bulk_data.pkl"
#Name of input bulk csv file from the World bank website
world_bank_file_input = "WDIData.csv"
wb_data = pd.read_csv(data_dir + world_bank_file_input)
WDI_name_lookup_output = "WDI_name_lookup.csv"
# #### Format as received from the World Bank:
# +
print("Shape:",wb_data.shape)
wb_data.head(3)
# -
# #### Create lookup table (pandas dataframe) of Indicator Names using Indicator Codes
#
# This is currently used by the tableau dashboard (see README.md)
#We only need one each of the values for the indicators. Dropping duplicates will speed up..
#the following code conciderably
wb_data_small = wb_data.drop_duplicates(['Indicator Code', 'Indicator Name'])
name_lookup = pd.DataFrame(columns=['Indicator Code', 'Indicator Name'])
#Fill the indicator column in our lookup table
name_lookup['Indicator Code'] = wb_data_small['Indicator Code'].unique()
#Fill the Indicator Name column of the lokup table
name_lookup['Indicator Name'] = [wb_data_small[wb_data_small['Indicator Code'] == code]['Indicator Name'].values[0] for code in name_lookup['Indicator Code'] ]
# #### Create dataframe for further processing
#filter out unnecessary columns (we will focus on years 1972 to 2018)
drop = ['Country Code','Indicator Name','1960','1961','1962','1963','1964',\
'1965','1966','1967','1968','1969', '1970', '1971', 'Unnamed: 63']
wb_data = wb_data.drop(drop, axis='columns')
#Switch around the data so that indicators are on columns and the country and year form a multi level row index
wb_data = wb_data.set_index(['Country Name', 'Indicator Code'])
wb_data = wb_data.stack()
wb_data = wb_data.unstack(['Indicator Code'])
wb_data = wb_data.sort_index()
wb_data.index.levels[1].name = 'Year'
wb_data.index.levels[0].name = 'Country'
# #### Output format:
wb_data.head(10)
# #### Save to a pickle file:
#Write data to a pickle file
wb_data.to_pickle(data_dir + world_bank_file_out)
#Write lookup data to a CSV file
name_lookup.to_csv(data_dir + WDI_name_lookup_output)
|
notebooks/data_gathering/world_bank_bulk_csv.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import json
import pandas as pd
import os
test_path = '../data/test_sample'
files = [x for x in os.listdir(test_path) if x[-3:] == 'jpg']
labels = pd.read_csv('../data/labels/boxes_v2.csv')
filt_labels = labels[labels.ImageId.isin(files)]
filt_labels
groundtruth_dict = {}
# +
for filename in files:
subset = filt_labels[filt_labels.ImageId == filename]
file_boxes = []
if len(subset) > 0:
for idx, row in subset.iterrows():
coord = [row['lt_x'], row['rb_x'], row['lt_y'], row['rb_y'] ]
# if box is all 0s we dont include it
if sum(coord) > 0:
file_boxes.append(coord)
groundtruth_dict[filename] = file_boxes
# -
groundtruth_dict
dump_path = '../data/labels/test_groundtruth_boxes.json'
with open(dump_path, 'w') as fp:
json.dump(groundtruth_dict, fp, indent=4)
print('Wrote to ' + dump_path)
|
Notebooks/TestGTtoJSON.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Feature Visualization
# This notebook will go through some of the features that have been selected for with the `SelectKBest`, `SelectFpr`, and `SelectPercentile` functions available through `sklearn`. The goal of the notebook is to demonstrate the relationships we can derive from the available features and potentially show why our models are performing with such low accuracy.
# +
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
print('Imports complete.')
# +
# Import the data file into a pandas data frame object
path = '../../malware_dataset/'
df = pd.read_csv(path + '/adware_vs_benign.csv')
# Output the top 5 samples from the data frame
print(df.head())
# Set the dependent variable as the target classification
dep_var = 'Label'
# -
# This next block filters out all of the columns except for those that were previous selected in another notebook entitled 'feature selection'. Using the aforementioned functions from `sklearn`, we are left with 20 features instead of the original 80+.
# +
# Remove the columns that are objects (excluding the target classification) or those that are not wanted
cols_to_keep = ['URG Flag Count',
'ACK Flag Count',
'Fwd IAT Total',
'Init_Win_bytes_forward',
'Fwd IAT Max',
'PSH Flag Count',
'Fwd IAT Std',
'Flow Duration',
'Active Mean',
'Min Packet Length',
'Active Max',
'Active Min',
'Idle Mean',
'Idle Min',
'Idle Max',
'Flow IAT Max',
'Fwd Packet Length Max',
'Source Port',
'Protocol',
'Fwd Packet Length Std']
cols_to_keep.append('Label')
# Clean the data for the features we want
print('Dropping unnecessary columns...', end='')
df.drop(columns=[col for col in df.columns if col not in cols_to_keep], inplace=True, errors='raise') # Some systems raise an error about this errors='raise' argument (which is ironic, I guess). Feel free to remove it if need be.
df.dropna(inplace=True)
print('done')
for col in df.columns[:-1]:
#print(X[col].dtype)
if df[col].dtype == 'object':
del df[col]
#print('dropped')
# -
# Below, we see the features that are left after the filtering process. Notice that we've left on the 'Label' column since it is the target classification.
# Print the features we have available
print('Features that are available:')
n = 1
for col in df.columns:
print('\t{}. {}'.format(n, col))
n += 1
# ## Distributions
# For some of these features, looking at the distribution of values will be beneficial in improving our understanding of the dataset. For example, for the first feature, 'Source Port', it would make sense to see values between 0 and 65,535 since there aren't any ports with a negative value or larger than 65,535.
# Produce a distribution plot for the first feature, which is the 'Source Port'
feature0 = df.columns[0]
f0plot = sns.distplot(df[feature0])
# Fwd Packet Length Max
feature3 = df.columns[3]
f3plot = sns.distplot(df[feature3])
# Fwd Packet Length Std
feature4 = df.columns[4]
f4plot = sns.distplot(df[feature4])
# We see that 'Fwd Packet Length Max' has one large spike in distributions around 500 and another around 1,500. 'Fwd Packet Length Std' also has two spikes as well, but they are much closer in value. It's possible this may mean we need to look at the scatter plot for more information on the classification relationships.
# Flow IAT Max
feature5 = df.columns[5]
f5plot = sns.distplot(df[feature5])
# Fwd IAT Total
feature6 = df.columns[6]
f6plot = sns.distplot(df[feature6])
# Fwd IAT Std
feature7 = df.columns[7]
f7plot = sns.distplot(df[feature7])
# Fwd IAT Max
feature8 = df.columns[8]
f8plot = sns.distplot(df[feature8])
# Up to this point, we are not seeing any large separations of the data that would potentially indicate two different groups that could to used to distinguish the classifications of a given sample. For the features below, we see this clear distinction in distribution. We will move these features over to scatter plots to determine if these are, in fact, useful for classification.
# PSH Flag Count
feature10 = df.columns[10]
f10plot = sns.distplot(df[feature10])
# PSH Flag Count for Adware
feature10 = df.columns[10]
dfadware = df.loc[ df[dep_var] == 'ADWARE']
dfbenign = df.loc[ df[dep_var] == 'BENIGN']
sns.distplot(dfadware[feature10], color='blue')
sns.distplot(dfbenign[feature10], color='orange')
# ACK Flag Count
feature11 = df.columns[11]
f11plot = sns.distplot(df[feature11])
# PSH Flag Count for Adware
feature11 = df.columns[11]
sns.distplot(dfadware[feature11], color='blue')
sns.distplot(dfbenign[feature11], color='orange')
feature13 = df.columns[13]
f13plot = sns.distplot(df[feature13])
# PSH Flag Count for Adware
feature13 = df.columns[13]
sns.distplot(dfadware[feature13], color='blue')
sns.distplot(dfbenign[feature13], color='orange')
# From what we can see with the distributions for the last three features, there isn't a lot of data we can derive from this to determine what characteristics specific classifications have.
# ## Scatter Plots
# There are some features that may be better to try to understand by relating them to the target classification. For this first example, we will look at 'Flow Duration' and attempt to see if there is any split that clearly demarcs the sample's classification.
# Scatter plot for the 3rd feature (Flow Duration)
feature2 = df.columns[2]
f2plot = sns.scatterplot(df[feature2], df[dep_var])
#df[feature2].value_counts()
# From the graph above, we can see that there is a wide spread for 'Flow Duration' across both 'Adware' and 'Benign' target classes. This wide spread prevents us from just using 'Flow Duration' to determine the classification of the sample.
feature3 = df.columns[3]
f3plot = sns.scatterplot(df[feature3], df[dep_var])
# Fwd Packet Length Std
feature4 = df.columns[4]
f4plot = sns.scatterplot(df[feature4], df[dep_var])
# For 'Fwd Packet Length Max' and 'Fwd Packet Length Std', we can see that most of the values are between 0 and 2,000 for the max and between 0 and 1,000 for the standard deviation. Some 'Benign' samples extend further to larger values. However, there is still no clear line that can be drawn to distinguish the two samples.
# From the distribution section, we clearly saw that three features have distributions that could indicate how to differentiate between the classes. These are graphed below.
# PSH Flag Count
feature10 = df.columns[10]
f10plot = sns.scatterplot(df[feature10], df[dep_var])
# ACK Flag Count
feature11 = df.columns[11]
f11plot = sns.scatterplot(df[feature11], df[dep_var])
# These graphs are exceptionally unhelpful! Let's try the last one to see if it behaves any differently.
# Init_Win_bytes_forward
feature13 = df.columns[13]
f13plot = sns.scatterplot(df[feature13], df[dep_var])
# This feature shares the same fate as the previous features, having no clear way to differentiate between the classifications.
|
notebooks/feature visualization.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/markbriers/data-science-jupyter/blob/main/coursework_data.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="WUN3qla7SZBD"
# The first stage in the coursework data analysis process is to copy the data linked in the documents supplied into your Google Drive, into a folder that is called "Data".
# + [markdown] id="phI3cwJnSxfe"
# In order to read data from your Google Drive, you need to "mount" the drive. This is a slightly involved process, where you need to authorise colab to access your Google Drive. Executing the code below will generate a (unique) URL. You will need to click on this, click accept, and copy the long code. (Clicking on the link will open a new window.) The code needs to be pasted into the text box that will appear below. Press enter on your keyboard, and you should see text that says: "Mounted at /content/gdrive".
# + id="4uZrH5Ogh31E" colab={"base_uri": "https://localhost:8080/"} outputId="b9ddf8cc-3511-429e-9c2e-3dc0c0234026"
from google.colab import drive
drive.mount('/content/gdrive')
# + [markdown] id="bj6_KyowV8e4"
# The process listed above will need to be completed every time the analysis is performed (for security reasons).
# + id="q5X-B74piz7u"
import numpy as np
import pandas as pd
# + [markdown] id="Xv8JHgA4WS7g"
# This function loads the communication data into a DataFrame. I have optimised the memory usage - details are not important, but please do reuse the code below.
# + id="y3__mRxK0KD4"
def readCommunicationData(fname):
# load dcomms ata file
comm = pd.read_csv(fname,dtype={"Timestamp": object, "from": np.uint32, "to": object, "location": object})
# display initial memory usage
comm.info(memory_usage='deep')
# convert the timestamp field to a timestamp object
comm['Timestamp'] = pd.to_datetime(comm['Timestamp'], infer_datetime_format=True)
# convert "from" field to 32-bit unsigned integer
comm['from'] = comm['from'].astype('uint32')
# convert all "external" references in the "to" field to be the value 0 so that we can convert this to an integer memory
comm['to'] = comm['to'].replace('external',0)
comm['to'] = comm['to'].astype('uint32')
# display revised memory usage
comm.info(memory_usage='deep')
return comm
# + id="-mQ-LQBi2CwU" colab={"base_uri": "https://localhost:8080/"} outputId="2c284337-bd09-45d5-ff26-5a80509fdc1f"
commFri = readCommunicationData('/content/gdrive/My Drive/Data/comm-data-Fri.csv')
# + id="lyHCA9522NrY" colab={"base_uri": "https://localhost:8080/"} outputId="43580ed1-53d5-477f-8dc0-fe073ae35f1c"
commSat = readCommunicationData('/content/gdrive/My Drive/Data/comm-data-Sat.csv')
# + id="pt0bxCLh2T90" colab={"base_uri": "https://localhost:8080/"} outputId="ec6223f6-f712-4074-a377-c5461ed9a69f"
commSun = readCommunicationData('/content/gdrive/My Drive/Data/comm-data-Sun.csv')
# + [markdown] id="zNveOi2LYdQH"
# This function returns the movement DataFrame.
# + id="Cn6ASQPx2Y0y"
def readMovementData(fname):
# load movemement data file
move = pd.read_csv(fname)
# remove any null values that may exist
move = move[pd.notnull(move["id"])]
# clear erroneous data
move = move[move['Timestamp'].str.len()==18]
# display initial memory usage
move.info(memory_usage='deep')
# convert the timestamp field to a timestamp object
move['Timestamp'] = pd.to_datetime(move['Timestamp'], infer_datetime_format=True,errors='ignore')
# convert "from" field to 32-bit unsigned integer
move['id'] = move['id'].astype('uint32')
# convert type field to categorical variable
move['type'] = move['type'].astype('category')
# convert positional fields to uint16
move['X'] = move['X'].astype('uint16')
move['Y'] = move['Y'].astype('uint16')
# display revised memory usage
move.info(memory_usage='deep')
return move
# + id="PeZfqym_4Ptv" colab={"base_uri": "https://localhost:8080/"} outputId="11b22a23-c6f9-42c0-c301-a36cdcd48cbc"
moveFri = readMovementData('/content/gdrive/My Drive/Data/park-movement-Fri.csv')
# + id="MoJuwskp4V9a" colab={"base_uri": "https://localhost:8080/"} outputId="a8bda207-c739-4523-cc85-36933774bc49"
moveSat = readMovementData('/content/gdrive/My Drive/Data/park-movement-Sat.csv')
# + id="R1dc1E-r5nmi" colab={"base_uri": "https://localhost:8080/"} outputId="44e62fff-3dc6-4f85-8fbe-65a17435df92"
moveSun = readMovementData('/content/gdrive/My Drive/Data/park-movement-Sun.csv')
|
coursework_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # User guide and example for the Landlab SPACE component
#
# This notebook provides a brief introduction and user's guide for the Stream Power And Alluvial Conservation Equation (SPACE) component for landscape evolution modeling. It combines two documents, a User's Manual and a notebook-based example, written <NAME> to accompany the following publication:
#
# <NAME>., <NAME>., & <NAME>. (2017). The SPACE 1.0 model: a Landlab component for 2-D calculation of sediment transport, bedrock erosion, and landscape evolution. Geoscientific Model Development, 10(12), 4577-4604, [https://doi.org/10.5194/gmd-10-4577-2017](https://doi.org/10.5194/gmd-10-4577-2017).
#
# This notebook contains text from user manual along with executable code for its examples.
#
# *(User's Manual and example notebook written by <NAME> in July 2017; combined into a notebook, updated for compatibility with Landlab 2.x, and added to the Landlab tutorials collection by <NAME>, July 2021.)*
# ## Background on SPACE component
#
# The Landlab SPACE (Stream Power with Alluvium Conservation and Entrainment) component computes sediment transport and bedrock erosion across two-dimensional model landscapes. The SPACE model provides advantages relative to many other fluvial erosion models in that it 1) allows simultaneous erosion of sediment and bedrock, 2) explicitly treats sediment fluxes rather than relying on a proxy for bed cover, and 3) is easily coupled with other surface process components in Landlab. The SPACE component enhances Landlab’s functionality by enabling modeling of bedrock-alluvial channels, rather than simply using parameterized sediment-flux-dependent incision models.
#
# This user manual teaches users how to use the SPACE component using two
# examples provided in Shobe et al. (2017).
#
# This user manual serves as a supplement to that manuscript.
# Prerequisites: A working knowledge of the Python programming language
# (SPACE and Landlab support Python 3.x) as well as the NumPy
# and MatPlotLib libraries. Basic familiarity with the Landlab modeling toolkit (see Hobley et al., 2017 GMD, and Barnhart et al., 2020 eSurf) is recommended.
# ## Model description
#
# ### Input parameters
#
# - **Sediment erodibility** $K_s$: Governs the rate of sediment entrainment; may be specified as a single floating point number, an array of length equal to the number of grid nodes, or a string naming an existing grid field.
#
# - **Bedrock erodibility** $K_r$: Governs the rate of bedrock erosion; may be specified as a single floating point number, an array of length equal to the number of grid nodes, or a string naming an existing grid field.
#
# - **Fraction of fine sediment** $F_f$: The unitless fraction (0–1) of rock that does not get converted to sediment, but is assumed to exit the model domain as “fine sediment,” or wash load.
#
# - **Sediment porosity** $\phi$: The unitless fraction (0–1) of sediment thickness caused by pore space.
#
# - **Sediment entrainment length scale** $H_*$: Length scale governing the shape of the exponential sediment entrainment and bedrock erosion func- tions. $H_*$ may be thought of as reflecting bedrock surface roughness, with larger $H_*$ representing a rougher bedrock surface.
#
# - **Effective settling velocity** $V$: Settling velocity of sediment after accounting for the upward effects of turbulence. For details, see discussion by <NAME> Lague, 2009.
#
# - **Stream power exponent** $m$: Exponent on drainage area or discharge in the stream power framework. Generally $\approx 0.5$.
#
# - **Stream power exponent** $n$: Exponent on channel slope in the stream power framework. Generally $\approx 1$.
#
# - **Sediment erosion threshold** $\omega_{cs}$: Threshold erosive power required to entrain sediment.
#
# - **Bedrock erosion threshold** $\omega_{cr}$: Threshold erosive power required to erode bedrock.
#
# - **Discharge field**: The field name or array to use for water discharge. The default is to use the grid field `surface_water__discharge`, which is simply drainage area multiplied by the default rainfall rate (1 m/yr). To use custom spatially/temporally varying rainfall, use `water__unit_flux_in` to specify water input to the `FlowAccumulator`.
#
# - **Solver**: string indicating the solver to use. Options at present include:
# - 'basic' (default): explicit forward-time extrapolation. Simple but will become unstable if time step is too large.
# - 'adaptive': subdivides global time step as needed to prevent slopes from reversing and alluvium from going negative.
# ### Model Variables
#
# Variables listed here are updated by the component at the grid locations listed. NOTE: because flow routing, calculation of discharge, and calculation of flow depth (if applicable) are handled by other Landlab components, variables such as water discharge and flow depth are not altered by the SPACE model and are not listed here.
#
# - `soil__depth`, node, [m]: Thickness of soil (also called sediment or alluvium) at every node. The name “soil” was used to match existing Landlab components. Soil thickness is calculated at every node incorporating the effects of sediment entrainment and deposition and bedrock erosion.
#
# - `sediment__flux`, node, [m$^3$/yr]: The volumetric flux of sediment at each node. Sediment flux is used to calculate sediment deposition rates.
#
# ## Steps of a SPACE model
#
# Note: these steps are for a SPACE model that is not coupled to any other Landlab components. To see examples of how to couple Landlab components, please refer to the Landlab documentation: [http://landlab.github.io](http://landlab.github.io).
# + [markdown] tags=[]
# ### Step 1: Import the necessary libraries
#
# The SPACE component is required, as are the model grid component and a flow routing component. It is generally a good idea to also include a depression handler such as `LakeMapperBarnes` or `DepressionFinderAndRouter`. These depression handlers route flow across flats or pits in a digital elevation model.
# + jupyter={"outputs_hidden": false}
## Import Numpy and Matplotlib packages
import numpy as np
import matplotlib.pyplot as plt # For plotting results; optional
## Import Landlab components
# Pit filling; optional
from landlab.components import DepressionFinderAndRouter
# Flow routing
from landlab.components import FlowAccumulator
# SPACE model
from landlab.components import Space # SPACE model
## Import Landlab utilities
from landlab import RasterModelGrid # Grid utility
from landlab import imshow_grid # For plotting results; optional
# -
# Two Landlab components are essential to running the SPACE model: the model itself, and the `FlowAccumulator`, which calculates drainage pathways, topographic slopes, and surface water discharge across the grid. A depression handler, such as `DepressionFinderAndRouter`, is extremely useful if a grid is likely to have pits or closed depressions. For this reason, it is generally a good idea to use the DepressionFinderAndRouter in addition to the `FlowAccumulator`. However, it is not required.
#
# In addition to the relevant process components, some Landlab utilities are required to generate the model grid (in this example `RasterModelGrid`) and to visualize output (`imshow_grid`). Note that while it is possible to visualize output through functionality in other libraries (e.g., matplotlib), `imshow_grid` provides a simple way to generate 2-D maps of model variables.
#
# Most Landlab functionality requires the Numpy package for scientific computing in python. The matplotlib plotting library has also been imported to aid visualization of results.
# ### Step 2: Define the model domain and initial conditions
#
# The SPACE component works on raster grids. For this example we will use a synthetic raster grid. An example and description of the Landlab raster model grid are given in (Shobe et al., 2017), with a more complete explanation offered in Hobley et al. (2017) and Barnhart et al. (2020). In addition to using user-defined, synthetic model grids, it is also possible to import digital elevation models for use as a model domain (see the tutorial *reading_dem_into_landlab*). In this example, we create a synthetic, square model domain by creating an instance of the RasterModelGrid. In this case, the domain will be a plane slightly tilted towards the lower-left (southwest) corner with random micro-scale topographic roughness to force flow convergence and channelization. The grid is composed of 20 rows and 20 columns for a total of 400 nodes, with user-defined spacing.
#
# Once the grid has been created, the user defines a grid field to contain values of land surface elevation, and then imposes the desired initial condition topography on the model grid. In the case shown below, the field `topographic__elevation` is added to the model grid and given initial values of all zeros. After that, initial model topography is added to the field. To create a plane tilted to the southwest corner, which is referenced by $(x,y)$ coordinate pair (0,0), topographic elevation is modified to depend on the $x$ and $y$ coordinates of each grid node. Then, randomized micro-scale topographic roughness is added to the model grid. While not strictly necessary for the SPACE model to run, the micro-roughness allows flow convergence, channelization, and the development of realistic landscapes.
#
# In this example, we initialize the model domain with 2 meters of sediment thickness at every core (non-boundary) node. The sediment thickness will shrink over time as water mobilizes and removes sediment. To do this, the fields `soil__depth` and `bedrock__elevation` must be added to the model grid. If they are not added, the SPACE model will create them. In that case, however, the default sediment thickness is zero and the default bedrock topography is simply the provided topographic elevation.
# + jupyter={"outputs_hidden": false}
# Set grid parameters
num_rows = 20
num_columns = 20
node_spacing = 100.0
# track sediment flux at the node adjacent to the outlet at lower-left
node_next_to_outlet = num_columns + 1
# Instantiate model grid
mg = RasterModelGrid((num_rows, num_columns), node_spacing)
# add field ’topographic elevation’ to the grid
mg.add_zeros("node", "topographic__elevation")
# set constant random seed for consistent topographic roughness
np.random.seed(seed=5000)
# Create initial model topography:
# plane tilted towards the lower−left corner
topo = mg.node_y / 100000.0 + mg.node_x / 100000.0
# add topographic roughness
random_noise = (
np.random.rand(len(mg.node_y)) / 1000.0
) # impose topography values on model grid
mg["node"]["topographic__elevation"] += topo + random_noise
# add field 'soil__depth' to the grid
mg.add_zeros("node", "soil__depth")
# Set 2 m of initial soil depth at core nodes
mg.at_node["soil__depth"][mg.core_nodes] = 2.0 # meters
# Add field 'bedrock__elevation' to the grid
mg.add_zeros("bedrock__elevation", at="node")
# Sum 'soil__depth' and 'bedrock__elevation'
# to yield 'topographic elevation'
mg.at_node["bedrock__elevation"][:] = mg.at_node["topographic__elevation"]
mg.at_node["topographic__elevation"][:] += mg.at_node["soil__depth"]
# -
# ### Step 3: Set the boundary conditions
#
# The user must determine the boundary conditions of the model domain (i.e., determine across which boundaries water and sediment may flow). Boundary conditions are controlled by setting the status of individual nodes or grid edges (see Hobley et al., 2017). We will use a single corner node as an “open” boundary and all other boundary nodes will be “closed”. We first use set closed boundaries at grid edges to ensure that no mass (water or sediment) may cross the model boundaries. Then, set watershed boundary condition outlet id is used to open (allow flow through) the lower-left corner of the model domain.
# + tags=[]
# Close all model boundary edges
mg.set_closed_boundaries_at_grid_edges(
bottom_is_closed=True, left_is_closed=True, right_is_closed=True, top_is_closed=True
)
# Set lower-left (southwest) corner as an open boundary
mg.set_watershed_boundary_condition_outlet_id(
0, mg["node"]["topographic__elevation"], -9999.0
)
# -
# In this configuration, the model domain is set to drain water and sediment out of the only open boundary on the grid, the lower-left corner. There are several options for changing boundary conditions in Landlab. See Hobley et al. (2017) or the Landlab [online documentation](https://landlab.readthedocs.io).
# ### Step 4: Initialize the SPACE component and any other components used
#
# Like most Landlab components, SPACE is written as a Python class. The class was imported at the beginning of the driver script (step 1). In this step, the user declares the instance of the SPACE class and sets any relevant model parameters. The same must be done for any other components used.
# + tags=[]
# Instantiate flow router
fr = FlowAccumulator(mg, flow_director="FlowDirectorD8")
# Instantiate depression finder and router; optional
df = DepressionFinderAndRouter(mg)
# Instantiate SPACE model with chosen parameters
sp = Space(
mg,
K_sed=0.01,
K_br=0.001,
F_f=0.0,
phi=0.0,
H_star=1.0,
v_s=5.0,
m_sp=0.5,
n_sp=1.0,
sp_crit_sed=0,
sp_crit_br=0,
)
# -
# ### Step 5: Run the time loop
#
# The SPACE component calculates sediment entrainment and deposition, bedrock erosion, and changes in land surface elevation over time. The code shown below is an example of how to run the SPACE model over several model timesteps. In the example below, SPACE is run in a loop that executes until elapsed model time has reached a user-defined run time. The user is also responsible for choosing the model timestep. Within the loop, the following steps occur:
#
# 1. The flow router runs first to determine topographic slopes and water discharge at all nodes on the model domain.
# 2. The depression finder and router runs to map any nodes located in local topographic minima (i.e., nodes that water cannot drain out of) and to establish flow paths across the surface of these “lakes.” Using the depression finder and router is optional. However, because the SPACE model may in certain situations create local minima, using the depression finder and router can prevent the development of fatal instabilities.
# 3. The depression finder and router generates a list of flooded nodes, which is then saved as a variable called “flooded” and passed to the SPACE model.
# 4. The SPACE model runs for the duration of a single timestep, computing sediment transport, bedrock erosion, and topographic surface evolution.
# 5. The elapsed time is updated.
# + jupyter={"outputs_hidden": false}
# Set model timestep
timestep = 1.0 # years
# Set elapsed time to zero
elapsed_time = 0.0 # years
# Set timestep count to zero
count = 0
# Set model run time
run_time = 500.0 # years
# Array to save sediment flux values
sed_flux = np.zeros(int(run_time // timestep))
while elapsed_time < run_time: # time units of years
# Run the flow router
fr.run_one_step()
# Run the depression finder and router; optional
df.map_depressions()
# Run SPACE for one time step
sp.run_one_step(dt=timestep)
# Save sediment flux value to array
sed_flux[count] = mg.at_node["sediment__flux"][node_next_to_outlet]
# Add to value of elapsed time
elapsed_time += timestep
# Increase timestep count
count += 1
# -
# ## Visualization of results
# ### Sediment flux map
# + jupyter={"outputs_hidden": false}
# Instantiate figure
fig = plt.figure()
# Instantiate subplot
plot = plt.subplot()
# Show sediment flux map
imshow_grid(
mg,
"sediment__flux",
plot_name="Sediment flux",
var_name="Sediment flux",
var_units=r"m$^3$/yr",
grid_units=("m", "m"),
cmap="terrain",
)
# + jupyter={"outputs_hidden": false}
# Export figure to image
fig.savefig("sediment_flux_map.eps")
# -
# ### Sedimentograph
#
# Once the data required for the time series has been saved during the time loop, the time series may be plotted using standard matplotlib plotting commands:
# + jupyter={"outputs_hidden": false}
# Instantiate figure
fig = plt.figure()
# Instantiate subplot
sedfluxplot = plt.subplot()
# Plot data
sedfluxplot.plot(np.arange(500), sed_flux, color="k", linewidth=3.0)
# Add axis labels
sedfluxplot.set_xlabel("Time [yr]")
sedfluxplot.set_ylabel(r"Sediment flux [m$^3$/yr]")
# -
# There is an initial increase in sediment flux from the model domain as the water reaches its equilibrium transport capacity. Over the long run, topographic gradients are reduced by the erosion of sediment, which results in lower and lower sediment fluxes from the domain over time.
# ### Click here for more <a href="https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html">Landlab tutorials</a>
|
notebooks/tutorials/landscape_evolution/space/SPACE_user_guide_and_examples.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Kabongosalomon/AMMI-NLP/blob/master/Part%2003/Lab%2002/ammi_dnlp_lab2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="rzBHf68UXD2k" colab_type="text"
# # Chit Chat Chatbots
# + [markdown] id="Jm6rTDCrXJ4V" colab_type="text"
# In the previous lab, we explored models that try to answer questions by reasoning over free-text input. In this lab, we will explore two types of models to create chatbots.
#
# First, let's consider important qualities for a chit-chat chatbot system
#
#
# 1. **Readability** - whatever model we use, the chats it creates should be easily understood by humans
# 2. **Consistency** - when chatting with a chatbot, the bot should maintain consistent information. Imagine a bot that says "Hi I'm Jack'' and then "Hello, my name is Jane" - quite confusing
# 3. **Engaging** - To encourage users to talk to the bot, the bot should be able to generate interesting, engaging responses. If the only response was "wow, that's cool," users are quite unlikely to want to talk very much to the chat bot
#
#
# + id="LrYcmfoI5PWO" colab_type="code" outputId="fe9ed182-9c76-4156-926c-76cdc7506a5d" colab={"base_uri": "https://localhost:8080/", "height": 211} language="html"
# <p style='color: blue;'>
# Throughout the lab, there will be <b>questions</b> you should answer. <b>All questions you need to write an answer to will be in this blue color.</b>
#
# <br>Please write brief answers- no need for long explanations.
# <br>There can be multiple correct answers to the questions.
#
# <br><br>The goal of these questions is to:
# <ul style='color: green;'>
# <li> Review the lecture material in the context of practical models and develop intuition about the models
# <li> Develop a sense of experimentation - we will pretend we have a dataset and will walk through an experimental thought process.
# </ul>
#
# <b>We are going to do the lab as a group. <br>I will explain the sections in more depth, as we did not cover dialogue deeply during the lecture. <br> After we discuss, I will provide time for you to write a few sentences. At the end of the lab, you will hand it in. In theory, everyone should be finished together!</b>
#
#
# </p>
# + [markdown] id="C3zg0WczXjDs" colab_type="text"
# ## Data
# + [markdown] id="kguDIJbLXmZU" colab_type="text"
# The dataset we will use for this lab is called `PersonaChat` - it was created to directly address problem 2. Each person talking in the dataset has a personality, which helps maintain consistency in the dialogue. We saw it last week in the tutorials as well (when you worked through beam search)
# + id="RpvTb8bBX40A" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="a149f7a8-91b3-498d-fbc6-657f5fb9334e"
# !git clone https://github.com/facebookresearch/ParlAI.git ~/ParlAI #> /dev/null
# !cd ~/ParlAI; python setup.py develop #> /dev/null
# + [markdown] id="3OJJ-L5RCyYT" colab_type="text"
# **Example: **
#
# your persona: i just started college.
#
# your persona: i have 3 science classes.
#
# your persona: i work part time in the campus library.
#
# your persona: i am living at home but hope to live in the dorms next year.
#
# **Partner Dialogue**: hi how are you doing
#
# **Your Response**: great ! just got off work and relaxing before i study
# + id="Oe72XiqFXCS0" colab_type="code" outputId="ebf5cf1a-b60f-4ce9-a668-625429830d9d" colab={"base_uri": "https://localhost:8080/", "height": 663}
# let's download and take a look at some examples of data in PersonaChat
# !python ~/ParlAI/examples/display_data.py --task personachat --datatype train
# + id="V3Ob4tEt1vNP" colab_type="code" outputId="99881d89-4e6c-4aae-d730-c25dda0cf40b" colab={"base_uri": "https://localhost:8080/", "height": 184} language="html"
# <p style='color: blue;'>
# <b>Questions:</b>
# <ul style='color: blue;'>
# <li>What do the personalities look like?</li>
# <ul style='color: red;'>
# <li>
# They simple, and don't exactly represent people personality, they just trying to simulate a particular basic personality, to make experimentation easy.
# Real human personality are complex to model and campture in a controled environement
# </li>
# </ul>
#
# <li>How does creating bots with these simple personalities address consistency for chatbots? </li>
# <ul style='color: red;'>
# <li>Bots created with simple personalities allows to train the bot, with some kind of prio that will allow it to be as `consitent` on the trained personality?</li>
# </ul>
#
# <li>What are some drawbacks/limitations of these specific personalities for addressing the problem of consistency?</li>
# <ul style='color: red;'>
# <li>Those specific personalities can't answer small question that are not related, or belong to the trained personality.</li>
# </ul>
#
# </ul>
# </p>
# + [markdown] id="bfRTFtytcOi1" colab_type="text"
# - This is personalities of a science student
# - It will help the chatbots to be train in a way that will avoid inconsistence answers in realtime setting, and this will make the converstion personalise
# - This will be limited only to the train personality and may be inconsistant for a different personality.
# + [markdown] id="Kyhri6NvYKda" colab_type="text"
#
#
# ---
#
#
# ***Let's understand how much data we have. Let's compute the following using ParlAI:***
#
#
# 1. **How many turns of data do we have?** In dialogue datasets, "amount of data" is measured in dialogue turns. Each time there is a single line of dialogue, that is called a "turn"
# 2. **On average, how many words form a model input?**
#
#
# ---
#
#
#
# + id="30SF6hN6DAjD" colab_type="code" outputId="e46f95cf-f43a-4d81-8381-bdc18db43929" colab={"base_uri": "https://localhost:8080/", "height": 581}
# !python ~/ParlAI/parlai/scripts/data_stats.py -t personachat -dt train -ltim 10000
# + [markdown] id="0vwk7krxU57M" colab_type="text"
# ## Evaluation
#
# How are dialogue models evaluated?
#
#
#
# 1. **Automatic Evaluation**: Hits @ 1, Hits @ 5, Hits @ 10, F1
# 2. **Human Evaluation**: Pairing Selection, Human Rating
#
#
# + id="pGI2fFPLVRSJ" colab_type="code" outputId="8cca62de-7c34-4623-fc83-e3f8cbd73d94" colab={"base_uri": "https://localhost:8080/", "height": 160} language="html"
# <p style='color: blue;'>
# <b>Questions:</b>
# <ul style='color: blue;'>
# <li>Take some notes about what these metrics are and what they mean here</li>
# <ul style='color: red;'>
# <li>Hits @ usefull for retrivial based dialog models, for example, if we have a set of retrievial candidates, Hits@1 our model retrieved the correct answer.
# In other words after scoring all the candidate for retrivial the model as retrieved the higher ranked one, which was the expected. (Hits@10 means the correct answer is ranked in top 10)</li>
# <li>F1 is the usual f1 score that is made of a conbinaison of presicion and recal</li>
# <li>Pairing Selection : here we show a human to things and we ask him to choose which one is better</li>
# <li>Human Rating : here again we have a human that will be evaluating the model by assigning it a value in a certain scale (e.g. 6/10)</li>
# </ul>
# </ul>
# </p>
# + [markdown] id="KpkwidfAZ_7p" colab_type="text"
# ## Models
#
# + [markdown] id="YuqnjqxbZ_W2" colab_type="text"
# There are two main kinds of dialogue models.
#
# *Retrieval* Models analyze the current dialogue context and try to find appropriate responses in the dataset.
#
# *Generative* Models analyze the current dialogue context
# and try to write an answer, word by word, from left to right.
# This can be thought of as an application of sequence-to-sequence models, where the "encoder side" is the dialogue history and the "decoder side" is the dialogue response your chatbot should generate.
# + id="JPRp1MlH3n0h" colab_type="code" outputId="360e2494-bc76-4811-851b-0597e8d0879c" colab={"base_uri": "https://localhost:8080/", "height": 390} language="html"
# <p style='color: blue;'>
# <b>Questions:</b>
# <ul style='color: blue;'>
# <li>Let's discuss the pros/cons of retrieval compared to generative models - Are there settings when you might want to use one over the other?</li>
# <ul style='color: red;'>
# <li>Retrivial</li>
# <ul style='color: red;'>
# <li>Pros: Doesn't do any writting by it own, just find the most appropriate answer from human written text, so we have no gramatical mistake, ...</li>
# <li>Cons: Not able to generate answers as some question may not have a direct answer from the text we have before hand(training dataa).</li>
# </ul>
# <li>Generative</li>
# <ul style='color: red;'>
# <li>Pros: They are not restricted only to the training samples</li>
# <li>Cons: Promps to mistake, as the model is generating the answer and need to take care of the conherence and the correctness of the writtin.</li>
# </ul>
# </ul>
#
# <li>Compare a chit-chat application to something like booking a movie ticket- would you want to use generative, retrieval, or something else to accomplish that task? Why?</li>
# <ul style='color: red;'>
# <li>I would like to use something else as this a sensible task and we need a kind of goal oriented chatbot, that will ask some predifined question in order to decide actions to take.</li>
# </ul>
#
# <li>How can you evaluate generative models with the metrics we discussed before? How do you think they will perform compared to retrieval models?</li>
# <ul style='color: red;'>
# <li>It's difficul to really evalate generative models with automatic evaluation due to the fact that the model generate a correct
# answer but that use different words and most of metrics may fail in capturing this
# In general in think they sould perform badly compared to retrivail models as the retrivial models uses the worlds dirrectly form the training and
# can be compared ans automatically evaluated easily
# </li>
# </ul>
#
# <li>In lecture, Antoine mentioned issues with generative model generation being generic and short. How does this happen in beam search?</li>
# <ul style='color: red;'>
# <li>Bram search work by maximizing the probability over a sentence, if we want to say something rare or special,
# it's penalized by the beam search as it has not been often seen or never in the training time, so the generation phase may generate generic and short answers.
#
# In other world, a very rare wold but correct may not be include in the generation due to the behavior of beam search.
# </li>
# </ul>
#
# </ul>
#
# <b> If you would like me to discuss how to actually use generative models in dialog, please say something! Otherwise, we will skip.</b>
# </p>
#
# + [markdown] id="D_99CoAwaW2w" colab_type="text"
# ### Retrieval Models
# + [markdown] id="BAfk4Km8bY_Y" colab_type="text"
# Let's train a model to do retrieval first. We will try the *Memory Net.*
# + id="EyNOObOkbYTQ" colab_type="code" colab={}
# We can train a model with the following command:
# # !python ~/ParlAI/examples/train_model.py -m kv_memnn -t personachat -dt train -veps 0.25 --model-file persona_chat_retrieval_model -vmt accuracy
# but we have limited time in the tutorial, so let's use an already pretrained model
# + [markdown] id="gylhJvZwa0Vp" colab_type="text"
# Quick Parameter Refresher:
#
#
# * `-m ` means which model we're going to use. Recall retrieval models are trained to rank the true response higher over a set of potential responses from the dataset (in ParlAI, these are called the "label candidates"). When it's time to write a dialogue response, the retrieval model returns the response that is ranked the highest
# * -`t` refers to the task. Here, we are training on PersonaChat data.
# * `-dt` refers to the data split. We want to train our model, so we are using the training set.
# * `-veps` refers to how often we should evaluate during training, our performance on validation. recall this is important because models, particularly neural ones, have the capacity to memorize the training dataset. So it's important to check how the model is doing on the validation set.
# * `--model-file` refers to when your model is saved, what should the filename be
# * `-vmt` refers to the metric which we'll use to decide which model is the best. We'll cover this in the next section
#
#
#
#
# + [markdown] id="W6wdfxEccAAp" colab_type="text"
# **Let's interact with the model to get a sense of what it's learning. **How is this chat going to work?
#
#
#
# 1. You will be assigned a persona. You will chat to the model by typing in the chat box.
# 2. The chatbot also has a persona. It's secret and hidden from you!
# 3. When you've finished chatting with this bot, type [DONE] and a new model persona will be assigned to the bot, so you can talk to a new bot.
# 4. When you move on to the next chatbot persona, the previous persona will be revealed.
#
# Interact with the chatbots and the personas. **Try to think about the following:**
#
# * Do the chatbots follow their persona a lot?
# * Was it difficult to follow your persona?
#
#
#
#
# + id="XdyaEgpcI7UL" colab_type="code" outputId="f0dcca64-225d-4ef5-83c2-e627ed1bcebe" colab={"base_uri": "https://localhost:8080/", "height": 170}
# !python ~/ParlAI/projects/convai2/interactive.py -mf models:convai2/kvmemnn/model
# + id="hNbf3YEp31Z0" colab_type="code" outputId="795832c2-2de1-4536-9b4f-1734ae6fadfd" colab={"base_uri": "https://localhost:8080/", "height": 201} language="html"
# <p style='color: blue;'>
# <b>Questions:</b>
# <ul style='color: blue;'>
# <li>What does this model seem to be doing well? What is it doing poorly? </li>
# <ul style='color: red;'>
# <li>From my experience, interracting with the model, it's doing very poorly and it just throwing back(memorise) to us informations that it has been trained on </li>
# </ul>
#
# <li>Why might it be performing poorly? What kind of experiment could you design to test your hypothesis?</li>
# <ul style='color: red;'>
# <li>This may be due, to the model that we are using, we can try to use a more complex model or use try a generative model and see how that may affect the chatbot performance</li>
# </ul>
#
# <li>How do we know if we need to use a more complex model? Would we always want to use a more complex model? Why or why not?</li>
# <ul style='color: red;'>
# <li>We can see the need of a more complex model from the nature of the task we are trying to achieve and make sure that we're not in an underfitting situation. We may not always need a more complex model
# Sometie we just need to fine-tune and make sure that we're using the simple model appropriatly.
# </li>
# </ul>
#
# </ul>
# </p>
# + id="t_SYFM2UaUuq" colab_type="code" colab={}
# Here is a command to train a Transformer Ranker model if you would like to try it out
# # !python ~/ParlAI/examples/train_model.py -m transformer/ranker -t personachat -dt train -veps 0.25 --model-file persona_chat_retrieval_model -vmt accuracy
# + [markdown] id="Kd7Sfurfdc_3" colab_type="text"
#
#
# ---
#
#
# An important aspect of training models is analyzing them. ***Try to answer the following questions.***
#
# ---
#
#
#
# + id="-1pAkQdt4n5_" colab_type="code" outputId="c268ee80-7281-4a95-cdb1-4e830396ce62" colab={"base_uri": "https://localhost:8080/", "height": 258} language="html"
# <p style='color: blue;'>
# <b>Questions:</b>
# <ul style='color: blue;'>
# <li>Are the models using the persona that we have provided? How can you tell? If I asked you to prove it to me, what experiments could you conduct? </li>
# <ul style='color: red;'>
# <li>Yes, the models are using the provided persona, we can see this by having a simple model that will bassically give back the conversation it was trained on (retrivial) which we can compare with
# the provided persona.
# </li>
# </ul>
# <li>Previously, we computed some statistics about how long the persona is in the training data. The model has also only seen words present in the training dataset. But what happens if you push the model outside of what data it's been trained on? What kind of performance do you get? Why does this happen, and what could you do if you wanted to improve the model's ability to generalize? </li>
# <ul style='color: red;'>
# <li>As we discussed Previously the model is not able to discuss witout ambiguity on topic out of the trained personaluty,
# what I'm thinking can be a probable direction to a more general chatbot will be training the model on a mix of personalities and combine it with a generative type of model and see how this works
# </li>
# </ul>
#
# <li>In ParlAI, we've set the parameters to save the model's best performance based on validation accuracy. What would happen if we saved the model based on the best training accuracy? Why does this happen? (if you like, try this out on your own and see the effect when you interact with the bot)</li>
# <ul style='color: red;'>
# <li>The model will just give back informations form the trained persona, without keeping any fluency(logic) in the conversation</li>
# </ul>
# </ul>
#
# <b> If you would like me to discuss how to use BERT in dialog, please say something! Otherwise, we will skip.</b>
# </p>
# + [markdown] id="eTHItY-QdNtw" colab_type="text"
# ### [for self exploration] Generative Models
# + [markdown] id="GM6LaBzbe6Za" colab_type="text"
# Generative models must produce word for word what they are going to say next in the dialogue. When predicting the next word, it produces a probability distribution over the entire vocabulary space for which word to generate next. To reduce the vocabulary space, we will use **byte-pair encoding** (BPE).
#
# *How does BPE work?* The BPE algorithm takes as input the training data and the number of *operations* it can do. It passes over the training set and tries to create sub-word units. For example, the word "beautiful" might be split into "beau" "ti" "ful". Each time it splits a word into sub-words, that is one operation. The final vocabulary output consists of these subwords. So "ful" can be part of "beautiful" and part of "fruitful" and so on.
#
#
# **Questions to ask yourself**:
#
#
# 1. Why is it important to keep the vocabulary space small?
# 2. What does perplexity measure? Why would we use it as a training objective?
#
#
#
# + id="G4gNbbAugACx" colab_type="code" colab={}
# # !python ~/ParlAI/examples/train_model.py -m transformer/generator -t personachat -dt train -veps 0.25 --model-file persona_chat_generative_model -vmt ppl
# + [markdown] id="fHpD0Ccb1zhd" colab_type="text"
# ## Final Thoughts
# + [markdown] id="MHdsZ3Sq12n6" colab_type="text"
# **What did we learn about dialogue modeling? Review Questions to ask yourself**
#
# * How do retrieval models work? What about generative? What are their pros and cons?
# * What are some important traits of dialogue systems? How might the traits differ for different dialogue tasks?
#
#
# **General Takeaways about Machine Learning and Experimentation:**
#
# * We don't try models just to try them - try to have a reason for conducting an experiment. As we did in the lab, try to analyze what's working well in your models and working poorly. Try to use these reasons to guide why you might want to try other models. Complex is not necessarily better.
# * Certain models can be better for certain tasks. As we've seen, generative models are working really well for tasks such as machine translation, but have a bit to go before becoming general purpose dialogue generators.
#
#
#
# **I'm really interested in dialogue! What can I do to learn more?**
#
#
# * Play around in ParlAI: ParlAI is a general library with many great dialogue models and code for them. It also provides a standard interface to access datasets and interact with various models.
# * Read the PersonaChat Paper: https://arxiv.org/pdf/1801.07243.pdf
# * Dialog using knowledge: One challenge of these chit chat systems is they do not concretely know any facts. So if you want to chat about a specific topic, the models cannot produce any relevant information - they say generic utterances or incorrect facts. One way to remedy this is to incorporate **knowledge** into the dialogue agents. This has been investigated in many different ways, but one of the first papers to show this is https://arxiv.org/abs/1811.01241. In this work, data is collected by asking one speaker to reference Wikipedia sentences.
# * Dialog with BERT: pretty new, there is an investigation of two ways to use BERT in this paper: https://arxiv.org/abs/1903.03094.
#
#
#
|
Part 03/Lab 02/ammi_dnlp_lab2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import sunpy
from sunpy.net import hek, helioviewer
from sunpy.time import parse_time
hek_time = parse_time('2018/07/15 14:42:46')
hv = helioviewer.HelioviewerClient()
kwargs = {'observatory': 'SDO', 'instrument': 'HMI', 'measurement': 'continuum'}
# Check how far requested time in metadata is from requested hek time
metadata = hv.get_closest_image(hek_time, **kwargs)
# Debugging hek client
from sunpy.net import hek, helioviewer
from sunpy.time import parse_time
client = hek.HEKClient()
tstart = '2013/02/01 00:00:00'
tend = '2013/02/01 23:30:00'
time_start = parse_time(tstart)
time_end = parse_time(tend)
results = client.search(hek.attrs.Time(time_start, time_end), hek.attrs.FRM.Name == 'SPoCA')
|
notebooks/Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
# %config InlineBackend.figure_formats = {'png', 'retina'}
pd.options.mode.chained_assignment = None # default='warn'?
data_key = pd.read_csv('key.csv')
data_key = data_key[data_key['station_nbr'] != 5]
data_weather = pd.read_csv('weather.csv')
data_weather = data_weather[data_weather['station_nbr'] != 5] ## Station 5번 제거한 나머지
data_train = pd.read_csv('train.csv')
# -
df = pd.merge(data_weather, data_key)
station_nbr = df['station_nbr']
df.drop('station_nbr', axis=1, inplace=True)
df['station_nbr'] = station_nbr
df = pd.merge(df, data_train)
df['snowfall'][df['snowfall'] == ' T'] = 0.05
df['preciptotal'][df['preciptotal'] == ' T'] = 0.005
df1 = df[df['station_nbr'] == 1]
df1.drop(columns = ['depart', 'codesum', 'sunrise', 'sunset', 'snowfall',
'station_nbr', 'store_nbr'], inplace=True)
# 주말과 주중 구분 작업 #
df1['date'] = pd.to_datetime(df['date'])
df1['week7'] = df1['date'].dt.dayofweek
df1['weekend'] = 0
df1.loc[df1['week7'] == 5, 'weekend'] = 1
df1.loc[df1['week7'] == 6, 'weekend'] = 1
# +
# 형 변환 to Float
df1 = df1.apply(pd.to_numeric, errors='coerce')
# 상대 습도 추가 #
df1['relative_humility'] = 100*(np.exp((17.625*((df1['dewpoint']-32)/1.8))/(243.04+((df1['dewpoint']-32)/1.8)))/np.exp((17.625*((df1['tavg']-32)/1.8))/(243.04+((df1['tavg']-32)/1.8))))
# 체감온도 계산
df1["windchill"] = 35.74 + 0.6215*df1["tavg"] - 35.75*(df1["avgspeed"]**0.16) + 0.4275*df1["tavg"]*(df1["avgspeed"]**0.16)
# Date Drop
df1 = df1.drop(columns = 'date')
# -
df1.columns
# 전처리 완료함. 따라서, 진행 시작
model = sm.OLS.from_formula("np.log1p(units) ~ tmax + tmin + tavg + dewpoint + wetbulb + heat + cool + preciptotal + stnpressure + \
sealevel + resultspeed + resultdir + avgspeed + C(item_nbr) + C(week7) + C(weekend) + relative_humility + windchill + 0", data = df1)
result = model.fit()
print(result.summary())
# 전처리 완료함. 따라서, 진행 시작
model1 = sm.OLS.from_formula("scale(np.log(units)) ~ tmax + tmin + tavg + dewpoint + wetbulb + heat + cool + preciptotal + stnpressure + \
sealevel + resultspeed + resultdir + avgspeed + C(item_nbr) + C(week7) + C(weekend) + relative_humility + windchill + 0", data = df1)
result1 = model1.fit()
print(result1.summary())
# 전처리 완료함. 따라서, 진행 시작
model3 = sm.OLS.from_formula("units ~ scale(tmax)+ scale(tmin)", data = df1)
df['tmax'][df['tmax'].isnull()]
df1['tmax'].dtypes
|
DataScience_Project1_Predict_products_sales_in_Walmart/2018_07_01_DSS_Project1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # A beginner's guide to PySDDR
# We start by importing the sddr module and other required libraries:
from sddr import Sddr
import torch.nn as nn
import pandas as pd
import torch.optim as optim
# # First use case: A Simple GAM Poisson Distribution
# ### User inputs
#
# First the user defines the data to be used:
# define data location
data_path = '../data/simple_gam/X.csv'
target_path = '../data/simple_gam/Y.csv'
# read data into pandas dataframe
data = pd.read_csv(data_path,delimiter=';')
target = pd.read_csv(target_path)
# split the data into train and test to use later for predictions
train_data = data.iloc[:800]
train_target = target.iloc[:800]
test_data = data.iloc[800:]
# Next the distribution, formulas and training parameters are defined. The neural netowrks here are not expected to truly contribute to the networks performance as our data includes only structured data. However, they are given in the formula for the user to understand the full power of the PySDDR package.
# +
# define distribution and the formula for the distibutional parameter
distribution = 'Poisson'
formulas = {'rate': '~1+spline(x1, bs="bs",df=9)+spline(x2, bs="bs",df=9)+d1(x1)+d2(x2)'}
# define the deep neural networks' architectures and output shapes used in the above formula
deep_models_dict = {
'd1': {
'model': nn.Sequential(nn.Linear(1,15)),
'output_shape': 15},
'd2': {
'model': nn.Sequential(nn.Linear(1,3),nn.ReLU(), nn.Linear(3,8)),
'output_shape': 8}
}
# define your training hyperparameters
train_parameters = {
'batch_size': 1000,
'epochs': 200,
'degrees_of_freedom': {'rate': 6},
'optimizer' : optim.RMSprop,
'val_split': 0.1,
'dropout_rate': 0.1
}
# define output directory
output_dir = './outputs'
# -
# Alternatively these parameters can be defined in a config file (for example see config.yaml)
# ### Initialization
#
# The sddr instance is initialized with the parameters given by the user in the previous step:
sddr = Sddr(distribution=distribution,
formulas=formulas,
deep_models_dict=deep_models_dict,
train_parameters=train_parameters,
output_dir=output_dir)
# Alternatively, the initialization can be done with a config file:
'''
import yaml
# get config
def get_config(config):
with open(config, 'r') as stream:
return yaml.safe_load(stream)
#load config file
config = get_config('config.yaml')
# initialize sddr instance
sddr = Sddr(config=config)
'''
# Since this will load all data from a file without splitting into train and test as we have done above, we have commented this part out for now. Also note that the config.yaml option currently only works if the deep networks are defined as in the ```config.yaml``` (directly with modules from torch.nn given as strings) and does not accept local scripts or torch models
# ### Training
#
# The sddr network is trained with the data defined above and the loss curve is plotted. Note that in this example we only have tabular data so unstructured_data is not given.
sddr.train(structured_data=train_data,
target=train_target,
plot=True)
# ### Visualizing the partial effects
#
# The partial effects are computed by: partial effect = smooth_features * coefs (weights)
# In other words the smoothing terms are multiplied with the weights of the Structured Head. We use the partial effects to interpret whether our model has learned correctly.
#
# In the case below the model is a generalized additive model with two splines (one has a quadratic effect, one has only a linear effect), while target is assumed to come from a Poisson distribution. The quadratic and linear effects are confirmed when plotting the partial effects below.
partial_effects = sddr.eval('rate')
# ### Save, load and resume
#
# Next, we save the trained model. Along with the model's weights, the optimizer current state will be saved, along with the number of epochs we trained for and the final loss function
sddr.save('model_gam.pth')
# To resume training at a later state we need to again initialize an sddr instance, load the previously trained model and resume training. Note that the ```resume=True``` flag needs to be set here when calling ```sddr.train```. Also note that here ```epochs``` is set to 300, while previously the network was trained for ```200``` epochs. This means that the model during resume will train for 300-200=100 epochs more
train_parameters['epochs'] = 300
sddr_resume = Sddr(output_dir=output_dir,
distribution=distribution,
formulas=formulas,
deep_models_dict=deep_models_dict,
train_parameters=train_parameters)
sddr_resume.load('./outputs/model_gam.pth', train_data)
sddr_resume.train(target=train_target, structured_data=train_data, resume=True)
loss_resume = sddr_resume.epoch_train_loss
# ### Predicting
# A trained model can also be used for predictions on unseen data. Note that when loading the model the structured training data is required to compute the knots of the basis functions used for the smoothing terms. The final line in this cell is commented out as it would give an error if run. Why? Check out the explanation below!
# initialize
pred_sddr = Sddr(distribution=distribution,
formulas=formulas,
deep_models_dict=deep_models_dict,
train_parameters=train_parameters,
output_dir=output_dir)
# load trained model
pred_sddr.load('./outputs/model_gam.pth', train_data)
# make predictions
#_, partial_effects_loaded = pred_sddr.predict(test_data, plot=True)
# The above error occurs because the test data is outside the range of the training data. The framework can deal with this problem by allowing clipping of the test data. For clipping the corresponding parameter needs to be set to ```True``` when calling ```predict()```
_, partial_effects_loaded = pred_sddr.predict(test_data, clipping=True, plot=True)
# ### Predicted Distribution
#
# To get the distribution simply call:
distribution_layer = pred_sddr.get_distribution()
# From there we can retrieve many of the distribution's properties. See some examples here:
mean = distribution_layer.mean
std = distribution_layer.stddev
# # Second use case: GAMLSS - Logistic Distribution
#
# In this example the input data follows a logistic distribution. Therefore, here we have two distributional parameters, which means that two fomulas need to be defined (which in turn means two SDDRFormulaNets will be created). Additinaly degrees of freedom for the regularization of the loss need to be given for each distributional parameter
# ### User inputs
#
# Once again first the user defines the data to be used. Note that this time we are not pre-loading the data as a pandas dataframe, but will give the framework directly the data paths:
data_path = '../data/gamlss/X.csv'
target_path = '../data/gamlss/Y.csv'
# Next the distribution, formulas and training parameters are defined. Note that PySDDR also support batching: in this example a batch size smaller than the size of the data is defined.
# +
distribution = 'Logistic'
formulas = {'loc': '~1+spline(x1, bs="bs", df=4)+spline(x2, bs="bs",df=4) + d1(x1)+d2(x2)',
'scale': '~1 + spline(x3, bs="bs",df=4) + spline(x4, bs="bs",df=4)'
}
deep_models_dict = {
'd1': {
'model': nn.Sequential(nn.Linear(1,15)),
'output_shape': 15},
'd2': {
'model': nn.Sequential(nn.Linear(1,3),nn.ReLU(), nn.Linear(3,8)),
'output_shape': 8}
}
train_parameters = {
'batch_size': 100,
'epochs': 1000,
'degrees_of_freedom': {'loc': [5,5], 'scale':[5,10]},
'optimizer' : optim.RMSprop,
'val_split': 0.15,
'early_stop_epochs': 100,
'early_stop_epsilon': 0.0001
}
# -
# Note that in the training parameters defined above we have also included early stopping parameters. In this case training will stop (before the 1000 epochs defined) if the validation loss is not dropping by more than 10e-4 for 100 epochs.
# ### Initialization
#
# The sddr instance is initialized with the parameters given by the user in the previous step. This time we do not specify an output directory which means all outputs will be stored in the current working directory.
sddr = Sddr(distribution=distribution,
formulas=formulas,
deep_models_dict=deep_models_dict,
train_parameters=train_parameters)
# ### Training
#
# Again in this example we train our network with our training data
#
#instead of giving a data and target as data frames, here we give the path and the data is loaded automatically
sddr.train(structured_data=data_path,
target=target_path,
plot=True)
# Note that when using early stopping the training stops after about 150 epochs. This helps avoid overfitting and we can also see from the loss plots that the model has converged and overfitting has been avoided (the validation loss is not much larger than the training loss). This means that the choice of hyperparameters for early stopping was correct.
# ### Visualizing the partial effects
#
# In this case the model is a generalized additive model with:
#
# * two splines: one has a quadratic effect, one has only a linear effect for the mean ('loc') parameter
# * two splines: one has only a linear effect with slope 0.5, one has the form sin(4*x)) for the scale parameter.
#
# These effects are confirmed when plotting the partial effects below.
partial_effects_loc = sddr.eval('loc')
partial_effects_scale = sddr.eval('scale')
# ### Orthogonalization
#
# As explained in the readme the model in pysddr has two orthogonalization steps that work in a similar manner:
#
# 1. Orthogonalization between linear and smooth terms to remove any linear effects from smooth terms and leave only non-linear features (performed during pre-processing) and
# 2. Orthogonalization between smooth terms and unstructured outputs to remove any effects from smooth terms in unstructured part (performed during every forward pass of the network)
#
# To visualize the effect of orthogonalization, in the example below we change the formulas from above and add the linear feature x3 to the linear part of the scale formula. We then re-train our model based on the new formula and visualize the partial effects.
# +
formulas = {'loc': '~1+spline(x1, bs="bs", df=4)+spline(x2, bs="bs",df=4) + d1(x1)+d2(x2)',
'scale': '~x3 + spline(x3, bs="bs",df=4) + spline(x4, bs="bs",df=4)'
}
sddr = Sddr(distribution=distribution,
formulas=formulas,
deep_models_dict=deep_models_dict,
train_parameters=train_parameters)
sddr.train(structured_data=data_path,
target=target_path)
partial_effects_scale = sddr.eval('scale')
# -
# As expected the orthogonalization has removed the effect of feature x3 (Partial effect 1) from the smooth terms as it is a linear feature which can be fully represented by the linear part of the network. The values in the y-axis are so small resulting in this partial effect actually having little or no effect. In addition, we can check the linear effects using the coef function to see if the actual linear effect is recovered well.
sddr.coeff('scale')
|
tutorials/BeginnersGuide.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # King County House Price Prediction
# ## Abstract
# Property price value have important impact on individual, families, business and governments.
# In this notebook, we have analysed the data from king country home feature dataset and tried to predict the home price based on the various features available in dataset.
# We have considered both aspect of data science problem: Classification and Regression problem. For classification, Target feature converted into target categorical value which "HIGH" or "LOW" by considering the mean value as boundary to decide the category. In classification, we have tried to categorize the house price whether its "LOW" or "HIGH" with supervised models like RandomForestClassifier, XGBoostClassifier and Logistic regression. Models were also train to get best parameters using the hyper-parameter tuning. In regression, we have used RandomForestRegressor, XGBoostRegressor, multiple linear regression, ridge regression and AdaBoost Regressor model to access the data and tried to predict the price of house.
# In classification, after comparing the results from all the classification models, we found that XGBoostClassifier stand out among other classifiers with accuracy of "91.15%". On other end for regression models, XGB regressor provided best estimate for house price for current dataset with accuracy of "xxxxx".
# ## Dataset:
# * King County House Price prediction [https://www.kaggle.com/harlfoxem/housesalesprediction/home](https://www.kaggle.com/harlfoxem/housesalesprediction/home) This dataset contains house sale prices for King County, which includes Seattle. It includes homes sold between May 2014 and May 2015.
# * 19 house features plus the price and the id columns, along with 21613 observations.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
from pandas import Series
from pprint import pprint
# %matplotlib inline
# #### Import king county price dataset using read_csv function.
features = pd.read_csv("../king_county_cleansed.csv")
classification_models = {}
regression_models = {}
# remove the index column since it is not needed down the line.
features.drop(['index'],axis=1,inplace=True)
features.head(5)
features.describe()
# ## Correlation Check
# * In any dataset, there are chances that features may be correlated to each other which can create problem to get better accuracy of the any machine learning model. Below code shows the heat map in which correlation can be seen amoung the features of the dataset.
# * corr() function can be used to compute pairwise correlation of features by exculiding null/NA values.
# * Below code will use corr() function to compute the correlation amount the features of king county dataset and create mask with the same shape as corr dataframe. Also make all indices of mask's upper triangle as "True". Then use corr dataframe and mask to create heatmap which shows the correlation between features.
# +
corr = features.corr()
#Create mast with zeros as same shape as corr dataframe.
mask = np.zeros_like(corr, dtype=np.bool)
#Assign true value to upper triangle of mask
mask[np.triu_indices_from(mask)] = True
# Set up the matplotlib figure
f, ax = plt.subplots(figsize=(20, 20))
# Generate a custom diverging colormap
cmap = sns.diverging_palette(190, 10, as_cmap=True)
# Draw the heatmap with the mask and correct aspect ratio
# use mask to hide the values in the upper triangle of heatmap.
sns.heatmap(corr, mask=mask, cmap=cmap, vmax=.3, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5})
# -
# Display correlation matrix as array matrix using matshow function.
plt.matshow(features.corr())
# Calculating the median value of "price" column.
median_price = features.loc[:,"price"].median()
print(median_price)
# In order to perform classification tasks, I have converted the price quantitative variable to a binary classification variable with HIGH price as 1 and LOW price as -1(For logistic regression I am taking LOW as 0).
# Adding column to dataframe for holding categorical price value : HIGH/LOW
# All values < median are LOW and Values >= median are HIGH.
# use lambda function to check whether the value of indice is greater than median value or not and assign as -1 or 1.
features['price_cat'] = features['price'].apply(lambda x: 1 if x > median_price else -1)
features[['price','price_cat']].head(10)
# # Part A
#
# ### Random forest classifier
# Random forest classifier is ensemble method for classification that operates by constructing a multitude of decision trees at training time and outputting the class that is the mode of the classes (classification) or mean prediction (regression) of the individual trees
# import train_test_split function which use to split the data.
from sklearn.model_selection import train_test_split
# In Below code, I have done few changes than the previous code. New code will be able to create X dataframe automatically based on the target variable provided in the first line. In this case, we no need to provide all the feature names in the list varible and add in x_features since it will be automatically taken from the features.columns function.
# +
#target variable from the dataset.
y=features['price_cat'] # Labels
#drop target value from dataframe
features.drop(['price_cat','price'],axis=1,inplace=True)
# features from the kc dataset
X_features = features.columns
X = features[X_features]
# Split dataset into training set and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3) # 70% training and 30% test
# -
# Implement basic random forest classifier algorithm with only one parameter - n_estimators
# +
#Import Random Forest Model
from sklearn.ensemble import RandomForestClassifier
#Create a Gaussian Classifier
clf_base=RandomForestClassifier(n_estimators=100)
#Train the model using the training sets y_pred=clf.predict(X_test)
clf_base.fit(X_train,y_train)
y_pred_base=clf_base.predict(X_test)
# -
# Use GridSearchCV algorithm for hyperparameter tunning on random forest classifier. Load all the best parameters into one dictonary which can be used in below code.
# +
from sklearn.model_selection import GridSearchCV
# prameter grid for hyperparameter tunning
param_grid = {
'bootstrap': [True],
'max_features': ['auto'],
'min_samples_leaf': [1,2,3],
'min_samples_split': [3,5,7],
'n_estimators': [100, 200, 2000]
}
#Random forest classifier
clf=RandomForestClassifier()
# Hyperparameter tunning using GridSearchCV function
clf_grid = GridSearchCV(clf,param_grid,cv = 3, n_jobs = -1, verbose = 2)
#Train the model using the training sets
clf_grid.fit(X_train,y_train)
best_param = clf_grid.best_params_
print(best_param)
print(clf_grid.best_score_)
# -
# Use best parameters after hyper-parameter tunning into random forest classifier to generate more accurate model.
# +
boot = best_param.get('bootstrap')
max_f = best_param.get('max_features')
min_sl = best_param.get('min_samples_leaf')
min_ss = best_param.get('min_samples_split')
n_esti = best_param.get('n_estimators')
#print(max_d,min_s,n_esti)
#Random forest classifier using best parameter which are available from hyperparameter tunning
clf_grid=RandomForestClassifier(bootstrap = boot, min_samples_leaf = min_sl,n_estimators= n_esti,max_features=max_f,min_samples_split=min_ss)
#Train the model using the training sets
clf_grid.fit(X_train,y_train)
# get the predicted value for the x_test data using train model
y_pred_grid=clf_grid.predict(X_test)
# -
# Use RandomizedSearchCV algorithm to do hyper-parameter tunning.
# +
from sklearn.model_selection import RandomizedSearchCV
# Maximum number of levels in tree
max_depth = [int(x) for x in np.linspace(2, 10, num = 5)]
max_depth.append(None)
# Create the random grid
random_grid = {'n_estimators': [int(x) for x in np.linspace(start = 10, stop = 200, num = 5)],
'max_features': ['auto', 'sqrt'],
'max_depth': max_depth,
'min_samples_split': [5, 10],
'min_samples_leaf': [2, 4]}
# Random search of parameters, using 3 fold cross validation,
# search across 100 different combinations, and use all available cores
clf_random = RandomizedSearchCV(estimator = clf, param_distributions = random_grid, n_iter = 100, cv = 3, verbose=2, random_state=42, n_jobs = -1);
# Fit the random search model
clf_random.fit(X_train,y_train);
clf_random.best_params_
best_random = clf_random.best_estimator_
# -
# Use best parameters after RandomizedSearchCV to get more accurate random forest classifier model.
#
#
# +
max_d = best_param.get('max_depth')
max_f = best_param.get('max_features')
min_sl = best_param.get('min_samples_leaf')
min_ss = best_param.get('min_samples_split')
n_esti = best_param.get('n_estimators')
clf_random=RandomForestClassifier(max_depth = max_d, min_samples_leaf = min_sl,n_estimators= n_esti,max_features=max_f,min_samples_split=min_ss)
#Train the model using the training sets
clf_random.fit(X_train,y_train)
# get the predicted value for the x_test data using train model
y_pred_random=clf_random.predict(X_test)
# -
# Display the accuracy of base, grid and random model from the y_pred using accuracy_score function.
# +
#Import scikit-learn metrics module for accuracy calculation
from sklearn import metrics
# Model Accuracy, how often is the classifier correct?
print("Accuracy of base model:",metrics.accuracy_score(y_test, y_pred_base))
print("Accuracy of grid model:",metrics.accuracy_score(y_test, y_pred_grid))
print("Accuracy of random model:",metrics.accuracy_score(y_test, y_pred_random))
# -
# ROC is also one of the way to accessing the model. Below function will help to create ROC curve for all three model and will give us the accuracy of the model.
## Common Classification algorithm evaluator. It returns the roc_auc
from sklearn.metrics import roc_curve, auc
def evaluate(model, X_train,y_train, X_test):
model.fit(X_train,y_train)
predictions = model.predict(X_test)
false_positive_rate, true_positive_rate, thresholds = roc_curve(y_test, predictions)
roc_auc = auc(false_positive_rate, true_positive_rate)
#print(roc)
return roc_auc
# +
base_md = str(evaluate(clf_base,X_train,y_train, X_test))
grid_md = str(evaluate(clf_grid,X_train,y_train, X_test))
rand_md = str(evaluate(clf_random,X_train,y_train, X_test))
classification_models["RandomForestClassifier_BaseModel"] = base_md
classification_models["RandomForestClassifier_GridSearchModel"] = grid_md
classification_models["RandomForestClassifier_RandomModel"] = rand_md
print('AUC for base search model : ' + base_md )
print('AUC for best grid search model : ' + grid_md)
print('AUC for best random search model : ' + rand_md )
# -
# Examine the feature importance of the given dataset for base model and select top 10 feature from the dataset.
feature_imp = pd.Series(clf_base.feature_importances_,index=X_features).sort_values(ascending=False)
top_features = feature_imp.head(10)
top_features
# Creating a bar plot and plot first 10 important features.
sns.barplot(x=top_features, y=top_features.index)
# Add labels to your graph
plt.xlabel('Feature Importance Score')
plt.ylabel('Features')
plt.title("Visualizing Important Features")
plt.legend()
plt.show()
# # XGBoost
# XGBoost(Gradient boosting) is machine learning techiques for classification and regression problem which produces prediction model in the form of ensemble of weak prediction models.
# * Below mention is simple gradient boosting algorithm which default pramaeters.
# +
from xgboost import XGBClassifier
from sklearn.model_selection import StratifiedKFold
from sklearn import metrics
# fit model on training data
xgBoostClassifierModel = XGBClassifier()
xgBoostClassifierModel.fit(X_train, y_train)
# make predictions for test data
y_pred = xgBoostClassifierModel.predict(X_test)
predictions = [round(value) for value in y_pred]
# evaluate predictions
accuracy = metrics.accuracy_score(y_test, predictions)
print("Accuracy: %.2f%%" % (accuracy * 100.0))
# -
# Now, Its time to tune the model with hyper-parameter tunning.
# GridSearchCV will try to get best parameter for the xgboostclassifier using stratified k-fold cross validation.
# In stratified k-fold cross-validation, the folds are selected so that the mean response value is approximately equal in all the folds.
# +
n_estimators = range(50, 400, 50)
param_grid = dict(n_estimators=n_estimators)
kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=7)
grid_search = GridSearchCV(xgBoostClassifierModel, param_grid, scoring="neg_log_loss", n_jobs=-1, cv=kfold)
grid_result = grid_search.fit(X_train, y_train)
# summarize results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
#storing mean,std and params values in the variable
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
print("%f (%f) with: %r" % (mean, stdev, param))
# plot errorbar to check the relation between number of estimators and logg loss
plt.errorbar(n_estimators, means, yerr=stds)
plt.title("XGBoost n_estimators vs Log Loss")
plt.xlabel('n_estimators')
plt.ylabel('Log Loss')
plt.savefig('n_estimators.png')
# -
# We can see that the cross validation log loss scores are negative. This is because the scikit-learn cross validation framework inverted them. The reason is that internally, the framework requires that all metrics that are being optimized are to be maximized, whereas log loss is a minimization metric. It can easily be made maximizing by inverting the scores.
#
# The best number of trees was n_estimators=350 resulting in a log loss of -0.212169, but really not a significant difference from n_estimators=200. In fact, there is not a large relative difference in the number of trees between 100 and 350 if we plot the results.
# ## Tune the Size of Decision Trees in XGBoost
# In gradient boosting, we can control the size of decision trees, also called the number of layers or the depth.
#
# Shallow trees are expected to have poor performance because they capture few details of the problem and are generally referred to as weak learners. Deeper trees generally capture too many details of the problem and overfit the training dataset, limiting the ability to make good predictions on new data.
#
# Generally, boosting algorithms are configured with weak learners, decision trees with few layers, sometimes as simple as just a root node, also called a decision stump rather than a decision tree.
#
# The maximum depth can be specified in the XGBClassifier and XGBRegressor wrapper classes for XGBoost in the max_depth parameter. This parameter takes an integer value and defaults to a value of 3.
# +
max_depth = range(1, 11, 2)
print(max_depth)
param_grid = dict(max_depth=max_depth)
kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=7)
grid_search = GridSearchCV(xgBoostClassifierModel, param_grid, scoring="neg_log_loss", n_jobs=-1, cv=kfold, verbose=1)
grid_result = grid_search.fit(X_train, y_train)
# summarize results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
#storing mean,std and params values in the variable
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
print("%f (%f) with: %r" % (mean, stdev, param))
# -
# plot errorbar to check the relation between number of estimators and logg loss
plt.errorbar(max_depth, means, yerr=stds)
plt.title("XGBoost max_depth vs Log Loss")
plt.xlabel('max_depth')
plt.ylabel('Log Loss')
plt.savefig('max_depth.png')
# Reviewing the plot of log loss scores, we can see a marked jump from max_depth=1 to max_depth=3 then pretty even performance for the rest the values of max_depth.
#
# Although the best score was observed for max_depth=5, it is interesting to note that there was practically little difference between using max_depth=3 or max_depth=7.
#
# This suggests a point of diminishing returns in max_depth on a problem that you can tease out using grid search. A graph of max_depth values is plotted against (inverted) logarithmic loss below.
# ### Tune The Number of Trees and Max Depth in XGBoost
# There is a relationship between the number of trees in the model and the depth of each tree.
#
# We would expect that deeper trees would result in fewer trees being required in the model, and the inverse where simpler trees (such as decision stumps) require many more trees to achieve similar results.
#
# We can investigate this relationship by evaluating a grid of n_estimators and max_depth configuration values. To avoid the evaluation taking too long, we will limit the total number of configuration values evaluated. Parameters were chosen to tease out the relationship rather than optimize the model.
#
# We will create a grid of 4 different n_estimators values (350, 300, 250, 400) and 4 different max_depth values (6, 7, 8, 9) and each combination will be evaluated using 10-fold cross validation. A total of 4*4*10 or 160 models will be trained and evaluated.
#
# grid search
#model = XGBClassifier()
n_estimators = [350, 300, 250, 400]
max_depth = [6, 7, 8, 9]
print(max_depth)
param_grid = dict(max_depth=max_depth, n_estimators=n_estimators)
kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=7)
grid_search = GridSearchCV(xgBoostClassifierModel, param_grid, scoring="neg_log_loss", n_jobs=-1, cv=kfold, verbose=1);
grid_result = grid_search.fit(X_train, y_train);
# summarize results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
print("%f (%f) with: %r" % (mean, stdev, param))
# plot results
scores = np.array(means).reshape(len(max_depth), len(n_estimators))
for i, value in enumerate(max_depth):
plt.plot(n_estimators, scores[i], label='depth: ' + str(value))
plt.legend()
plt.xlabel('n_estimators')
plt.ylabel('Log Loss')
plt.savefig('n_estimators_vs_max_depth.png')
# We can see that the best result was achieved with a n_estimators=250 and max_depth=6, similar to the best values found from the previous two rounds of standalone parameter tuning (n_estimators=250, max_depth=5).
#
# We can plot the relationship between each series of max_depth values for a given n_estimators.
# Fewer boosted trees are required with increased tree depth.
#
# Further, we would expect the increase complexity provided by deeper individual trees to result in greater overfitting of the training data which would be exacerbated by having more trees, in turn resulting in a lower cross validation score. We don’t see this here as our trees are not that deep nor do we have too many. Exploring this expectation is left as an exercise you could explore yourself.
# ## Creating the model with the best values for Hyper parameters
model = XGBClassifier(max_depth=6, n_estimators=250)
print(model)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
predictions = [round(value) for value in y_pred]
XGBoost_auc = str(evaluate(model, X_train,y_train, X_test))
print('AUC for the XGBoost model is: ' + XGBoost_auc )
classification_models["XGBoostClassifier_BestModel"] = XGBoost_auc
# ## Thus we got a higher ROC for XGBoost model than the bagging models tried earlier
# ## Classification with Logistic Regression
#
# Compare logistic regression with the based tree algorithms in Part A on the same data. Answer the following questions for logistic regression:
#
# * Which independent variables are important?
# * Is there multi-colinearity?
# * How does it compare to the the models in Part A?
# We need to develop a Nominal Logistic Regression model which will predict whether the house price is HIGH(1) or LOW(-1)
import statsmodels.api as sm
import statsmodels.formula.api as smf
import pandas as pd
from sklearn.linear_model import LogisticRegression
# We have consider onl few features from the dataset to train the model based on the importance of the features.
features = pd.read_csv("../king_county_cleansed.csv")
features['price_cat_log'] = features['price'].apply(lambda x: 1 if x > median_price else 0)
price_cat_log=features['price_cat_log']
y_log=price_cat_log
X_train_log,X_test_log,y_train_log,y_test_log=train_test_split(features[['bedrooms', 'sqft_living', 'waterfront', 'sqft_basement', 'yr_built', 'bathrooms']]
,y_log,test_size=0.3,random_state=0)
# +
logreg=LogisticRegression().fit(X_train_log,y_train_log)
print("Training set score: {:.3f}".format(logreg.score(X_train_log,y_train_log)))
print("Test set score: {:.3f}".format(logreg.score(X_test_log,y_test_log)))
# -
logit_model=sm.Logit(y_train_log,X_train_log)
result=logit_model.fit()
print(result.summary())
# ### Looking at the z scores, we know that, sqft_living is the most significant followed by yr_built and then the rest.
# +
from sklearn.metrics import roc_curve
falsepos,truepos,thresholds=roc_curve(y_test_log,logreg.decision_function(X_test_log))
plt.plot(falsepos,truepos,label="ROC")
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
cutoff=np.argmin(np.abs(thresholds))
plt.plot(falsepos[cutoff],truepos[cutoff],'o',markersize=10,label="cutoff",fillstyle="none")
plt.show()
# -
from sklearn import metrics
log_auc = str(metrics.auc(falsepos, truepos))
print("AUC for the logistic regression: " + log_auc)
classification_models["LogisticRegression_Model"] = log_auc
# ## As compared to Models in Part A, the accuracy of the Logistic Regression model is less.
# ## Regression with Trees
# Compare at least one bagging based tree algorithm (e.g. Random Forest) with a boosting based tree algorithm on a regression problem.
# Answer the following questions for each supervised learner:
#
# * Which hyper-parameters are important?
# * What hyper-parameter values work best?
# * Which supervised learner works best on the test data?
# ### Random Forest based Regression
#
# To look at the available hyperparameters, we can create a random forest and examine the default values.
from sklearn.ensemble import RandomForestRegressor
rf = RandomForestRegressor(random_state = 42)
from pprint import pprint
# Look at parameters used by our current forest
print('Parameters currently in use:\n')
pprint(rf.get_params())
# * estimators = number of trees in the foreset
# * max_features = max number of features considered for splitting a node
# * max_depth = max number of levels in each decision tree
# * min_samples_split = min number of data points placed in a node before the node is split
# * min_samples_leaf = min number of data points allowed in a leaf node
# * bootstrap = method for sampling data points (with or without replacement)
# +
# features = pd.read_csv("../king_county_cleansed.csv")
X_features_reg = ['bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot',
'waterfront', 'sqft_above', 'sqft_basement', 'yr_built', 'yr_renovated',
'lat', 'long', 'sqft_living15', 'sqft_lot15', 'basement_present',
'renovated', 'floors#1.0', 'floors#1.5', 'floors#2.0', 'floors#2.5',
'floors#3.0', 'floors#3.5', 'view#0', 'view#1', 'view#2', 'view#3',
'view#4', 'condition#1', 'condition#2', 'condition#3', 'condition#4',
'condition#5', 'grade#1', 'grade#3', 'grade#4', 'grade#5', 'grade#6',
'grade#7', 'grade#8', 'grade#9', 'grade#10', 'grade#11', 'grade#12',
'grade#13', 'zipcode#98004', 'zipcode#98102', 'zipcode#98109',
'zipcode#98112', 'zipcode#98039', 'zipcode#98040']
X_reg=features[['bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot',
'waterfront', 'sqft_above', 'sqft_basement', 'yr_built', 'yr_renovated',
'lat', 'long', 'sqft_living15', 'sqft_lot15', 'basement_present',
'renovated', 'floors#1.0', 'floors#1.5', 'floors#2.0', 'floors#2.5',
'floors#3.0', 'floors#3.5', 'view#0', 'view#1', 'view#2', 'view#3',
'view#4', 'condition#1', 'condition#2', 'condition#3', 'condition#4',
'condition#5', 'grade#1', 'grade#3', 'grade#4', 'grade#5', 'grade#6',
'grade#7', 'grade#8', 'grade#9', 'grade#10', 'grade#11', 'grade#12',
'grade#13', 'zipcode#98004', 'zipcode#98102', 'zipcode#98109',
'zipcode#98112', 'zipcode#98039', 'zipcode#98040']] # Features
y_reg=features['price'] # Labels
# Split dataset into training set and test set
X_train_reg, X_test_reg, y_train_reg, y_test_reg = train_test_split(X_reg, y_reg, test_size=0.3) # 70% training and 30% test
# -
# ### Random Search Cross Validation in Scikit-Learn
# To use RandomizedSearchCV, we first need to create a parameter grid to sample from during fitting:
from sklearn.model_selection import RandomizedSearchCV
# Number of trees in random forest
n_estimators = [int(x) for x in np.linspace(start = 10, stop = 200, num = 5)]
# Number of features to consider at every split
max_features = ['auto', 'sqrt']
# Maximum number of levels in tree
max_depth = [int(x) for x in np.linspace(2, 10, num = 5)]
max_depth.append(None)
# Minimum number of samples required to split a node
min_samples_split = [5, 10]
# Minimum number of samples required at each leaf node
min_samples_leaf = [2, 4]
# Method of selecting samples for training each tree
#bootstrap = [True, False]
# Create the random grid
random_grid = {'n_estimators': n_estimators,
'max_features': max_features,
'max_depth': max_depth,
'min_samples_split': min_samples_split,
'min_samples_leaf': min_samples_leaf}
pprint(random_grid)
# Use the random grid to search for best hyperparameters
# First create the base model to tune
rf = RandomForestRegressor()
# Random search of parameters, using 3 fold cross validation,
# search across 100 different combinations, and use all available cores
rf_random = RandomizedSearchCV(estimator = rf, param_distributions = random_grid, n_iter = 100, cv = 3, verbose=2, random_state=42, n_jobs = -1);
# Fit the random search model
rf_random.fit(X_train_reg, y_train_reg);
def evaluate_reg(model, test_features, test_labels):
predictions = model.predict(test_features)
errors = abs(predictions - test_labels)
mape = 100 * np.mean(errors / test_labels)
accuracy = 100 - mape
print('Model Performance')
print('Average Error: {:0.4f} degrees.'.format(np.mean(errors)))
print('Accuracy = {:0.2f}%.'.format(accuracy))
return accuracy
base_model = RandomForestRegressor(n_estimators = 10, random_state = 42)
base_model.fit(X_train_reg, y_train_reg)
base_accuracy = evaluate_reg(base_model, X_test_reg, y_test_reg)
regression_models["RandomForestRegressor_BaseModel"] = base_accuracy
best_random = rf_random.best_estimator_
random_accuracy = evaluate_reg(best_random, X_test_reg, y_test_reg)
regression_models["RandomForestRegressor_RandomModel"] = random_accuracy
# From above results, we can conclude that after hyper parameter tunning using randomized search cv, the accuracy of the model got increase by 1%.
# ### Grid Search with Cross Validation
# +
from sklearn.model_selection import GridSearchCV
# Create the parameter grid based on the results of random search
param_grid = {
'bootstrap': [True, False],
'max_depth': [None],
'max_features': [2, 3],
'min_samples_leaf': [2,3,4],
'min_samples_split': [3,5,7],
'n_estimators': [100, 200, 300, 1000]
}
# Create a based model
rf = RandomForestRegressor()
# Instantiate the grid search model
grid_search = GridSearchCV(estimator = rf, param_grid = param_grid,
cv = 3, n_jobs = -1, verbose = 2)
# -
# Fit the grid search to the data
grid_search.fit(X_train_reg, y_train_reg)
#grid_search.best_params_
best_grid = grid_search.best_estimator_
grid_accuracy = evaluate_reg(best_grid, X_test_reg, y_test_reg)
regression_models["RandomForestRegressor_GridSearchModel"] = grid_accuracy
# After getting best random forest regressor model using grid search cv algorithm, we got accuracy as 82.58% which is less accurate than the model which we got from randomized search cv model.
# ## XGBoost (eXtreme Gradient Boosting)
# Lets implement XGBoost regressor and analyze the model accuracy with it.
#
from xgboost import XGBRegressor
base_model = XGBRegressor()
base_model.fit(X_train_reg, y_train_reg)
base_accuracy = evaluate_reg(base_model, X_test_reg, y_test_reg)
regression_models["XGBoostRegressor_BasehModel"] = base_accuracy
# Do hyper parameter tunning for xgboost regressor using grid search cv function. stratified kfold cv is used as type of cross-validation imlemented in grid search cv function.
# +
# grid search
model = XGBRegressor()
n_estimators = [300,350,400]
max_depth = [4,5,6,7]
param_grid = dict(max_depth=max_depth, n_estimators=n_estimators)
kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=7)
grid_search = GridSearchCV(model, param_grid, n_jobs=-1, cv=kfold, verbose=1)
grid_result = grid_search.fit(X_train_reg, y_train_reg)
# summarize results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
print("%f (%f) with: %r" % (mean, stdev, param))
# -
best_XGBoost = grid_result.best_estimator_
best_XGBoost.fit(X_train_reg, y_train_reg)
best_accuracy = evaluate_reg(best_XGBoost, X_test_reg, y_test_reg)
regression_models["XGBoostRegressor_GridSearchModel"] = best_accuracy
# ### XGBoost Algo provides better predictions than Random Forest for the regression problem. And both of them provide a lower RMSE than Linear Regression
# Evaluating the regresision models
from sklearn.metrics import mean_squared_error
from math import sqrt
#Random Forest best model
print('Random forest best model RMSE is : ' + str(round(sqrt(mean_squared_error(best_random.predict(X_test_reg), y_test_reg)),2)))
#XGBoost Best model
print('XGBoost best model RMSE is : ' + str(round(sqrt(mean_squared_error(best_XGBoost.predict(X_test_reg), y_test_reg)),2)))
# From the above results, XGBoost regressor model have the more accuracy(87.44%) than random forest regressor(86.55%). Also, RMSE of XGBoost model is less than the random forest regressor model.
# # Part D
# ## Multiple Linear Regression
# Try multiple linear regression model to access the model and see the accuracy.
# +
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
linear_model = LinearRegression()
linear_model.fit(X_train_reg, y_train_reg)
y_pred_reg = linear_model.predict(X_test_reg)
# The mean squared error
print("Mean squared error: %.2f" % mean_squared_error(y_test_reg, y_pred_reg))
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % r2_score(y_test_reg, y_pred_reg))
lin_acc = evaluate_reg(linear_model, X_test_reg, y_test_reg)
regression_models["LinearRegression_Model"] = lin_acc
# -
# Using linear regression model for the dataset, the variance score(r^2) is 74% which less accurate than XGBoost and Random forest regressor model.
# Now Try to create one GLM model like ridge regression model throgh which we might get more accuracy than simple multiple regression model.
# We will try to fit Ridge regressin model to dataset and try to access the accuracy of the model again other type of ensemble models.
# For Ridge regression model, we need to have value of alpha. And to get best value of alpha, Use RidgeCV function.
from sklearn.linear_model import RidgeCV, Ridge
ridge_cv = RidgeCV([0.001,0.0001,0.00001,5,0.1,1,10,50,100])
model_cv = ridge_cv.fit(X_train_reg, y_train_reg)
model_cv.alpha_
# +
ridge_model = Ridge(model_cv.alpha_)
ridge_model.fit(X_train_reg, y_train_reg)
y_pred_rid = ridge_model.predict(X_test_reg)
# The mean squared error
print("Mean squared error: %.2f" % mean_squared_error(y_test_reg, y_pred_rid))
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % r2_score(y_test_reg, y_pred_rid))
ridge_acc = evaluate_reg(ridge_model, X_test_reg, y_test_reg)
regression_models["RidgeRegression_Model"] = ridge_acc
# -
# # Part E
#
# ### AdaBoostRegressor
# We have used one more supervised learning model which is AdaBoostRegressor model to predict the target variable.
# +
from sklearn.ensemble import AdaBoostRegressor
param_ada_grid = {
'loss': ['linear', 'square', 'exponential'],
'learning_rate': [0.1, 0.05, 0.02, 0.01],
'n_estimators': [500, 1000]
}
ada_boost_mdl = AdaBoostRegressor()
grid_ada_boost = GridSearchCV(ada_boost_mdl, param_ada_grid)
grid_ada_boost.fit(X_train_reg, y_train_reg)
best_params = grid_ada_boost.best_params_
print(grid_ada_boost.best_score_)
# +
los = best_params.get('loss')
lr = best_params.get('learning_rate')
n_esti = best_params.get('n_estimators')
ada_best_param_mdl = AdaBoostRegressor(loss=los, learning_rate=lr, n_estimators=n_esti)
ada_best_param_mdl.fit(X_train_reg, y_train_reg)
y1_pred_ada = ada_best_param_mdl.predict(X_test_reg)
# -
# The mean squared error
print("Mean squared error: %.2f" % mean_squared_error(y_test_reg, y1_pred_ada))
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % r2_score(y_test_reg, y1_pred_ada))
ada_acc = evaluate_reg(ada_best_param_mdl, X_test_reg, y_test_reg)
regression_models["AdaBoostRegressor_Model"] = ada_acc
# From the accuracy of adaboosting regressor, we can say that the model doesn't perform well for the current dataset. The accuracy is very less than all other model.
# Two dataframe has been created as mention below which will contain models and thier respective score.
classification_df = pd.DataFrame(list(classification_models.items()),columns=['Model','Auc_Score'])
regression_df = pd.DataFrame(list(regression_models.items()),columns=['Model','Accuracy'])
# # Conclusion
#
# After trying multiple models for classification and regression problem for current dataset, below are my findings from this notebook.
# * Classification of "HIGH" or "LOW" price:
# * Below mention table shows auc score for all the classifiers tried in this notebook.
classification_df.sort_values(by=['Auc_Score'], ascending = False)
# * Price prdiction(Regression):
# * Below mention table shows accuracy for all the regressors used in this notebook.
regression_df.sort_values(by=['Accuracy'], ascending = False)
# from table, we can see that XGBoostRegressor performs best for predicting the price value for the current dataset. In both the cases, XGBoosting algorithm perform well to predict the target variable for the king county house dataset.
# # Contributions
#
# 10-15% code has been changes or added in this notebook by the author.
# The code which is added is Part D and Part E which inlcude model fitting with ridge regression model and one suprvised learning model called adaboosting regressor.
# Two dataframe has been created to store the all results of model fitting through out this notebook and display the same during conclusion by sorting algorithm result by accuracy.
# Code which is change in the notebook is mention below:
# * Code has been changed in dataframe loading by removing the target variable from the dataset.
# * Rather than giving the column list to dataframe X and Y, I have optimize it.
# * During hyper-parameter tunning, I have authomate the best param selection in hyper-parameter tunning and use the same parameters to train respective supervised model.
# * Provided proper varible name at various places
# * Remove few redudant model fitting code in XGBoostClassifier.
# # Citations
#
#
# * https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html
#
# * https://xgboost.readthedocs.io/en/latest/python/python_api.html
#
# * https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html
#
# * https://en.wikipedia.org/wiki/Random_forest
#
# * https://en.wikipedia.org/wiki/Gradient_boosting
#
# * https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostRegressor.html
#
# * https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html
#
# * https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
#
# * https://www.kaggle.com/harlfoxem/housesalesprediction
# # License
# MIT License
#
# Copyright (c) 2018 <NAME>
#
# Permission is hereby granted, free of charge, to any person obtaining a copy
# of this software and associated documentation files (the "Software"), to deal
# in the Software without restriction, including without limitation the rights
# to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
# copies of the Software, and to permit persons to whom the Software is
# furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in all
# copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
# AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
# OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
# SOFTWARE.
|
Assignment1_King_County_Price_Predication.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Scikit Learn
# -
import pandas as pd
print(pd.__version__)
exam_data = pd.read_csv('exams.csv', quotechar='"')
exam_data
exam_data['gender'].count()
exam_data['gender'].unique().tolist()
len(exam_data['gender'].unique().tolist())
exam_data.info()
# # standardizing data
math_average = exam_data['math score'].mean()
math_average
reading_average = exam_data['reading score'].mean()
reading_average
writing_average = average = exam_data['writing score'].mean()
writing_average
from sklearn import preprocessing
exam_data[['math score']] = preprocessing.scale(exam_data[['math score']])
exam_data[['reading score']] = preprocessing.scale(exam_data[['reading score']])
exam_data[['writing score']] = preprocessing.scale(exam_data[['writing score']])
exam_data.head(10)
math_average = exam_data['math score'].mean()
reading_average = exam_data['reading score'].mean()
writing_average = average = exam_data['writing score'].mean()
print(math_average)
print(reading_average)
print(writing_average)
# +
# Numerical encoding of categorical data
# -
# one hot encoding
le = preprocessing.LabelEncoder()
exam_data['gender'] = le.fit_transform(exam_data['gender'].astype(str))
exam_data['gender'].head(5)
le.classes_
## show data in one hot form
pd.get_dummies(exam_data['race/ethnicity'])
exam_data = pd.get_dummies(exam_data, columns=['race/ethnicity'])
exam_data
exam_data = pd.get_dummies(exam_data, columns=['parental level of education',
'lunch',
'test preparation course'])
exam_data
# # word embeddings - one-hot, Frequency based, prediction based
# +
# Frequency based embeddings
# 1 count , 2 TF IDF
# top N words
# -
# # TextFeatureExtraction
from sklearn.feature_extraction.text import CountVectorizer
corpus = ['This is the first document',
'this is the second document',
'Third document. Document number three',
'Number four. To repeat, number four']
vectorizer = CountVectorizer()
bag_of_words = vectorizer.fit_transform(corpus)
bag_of_words
print(bag_of_words)
vectorizer.vocabulary_.get('document')
vectorizer.vocabulary_
pd.DataFrame(bag_of_words.toarray(), columns=vectorizer.get_feature_names())
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer()
bag_of_words = vectorizer.fit_transform(corpus)
print(bag_of_words)
vectorizer.vocabulary_
pd.DataFrame(bag_of_words.toarray(), columns=vectorizer.get_feature_names())
# +
# for large vocubalary of words
from sklearn.feature_extraction.text import HashingVectorizer
vectorizer = HashingVectorizer(n_features=8)
feature_vector = vectorizer.fit_transform(corpus)
print(feature_vector)
# -
# # IMAGE PROCESSING
# +
# #!pip install opencv-python
# -
import cv2
imagePath = './dog.jpg'
image = cv2.imread(imagePath)
# +
# %matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.imshow(image)
# -
image.shape
size = (32, 32)
resized_image_feature_vector = cv2.resize(image, size)
plt.imshow(resized_image_feature_vector)
resized_image_feature_vector.shape
resized_image_feature_vector_flattened = resized_image_feature_vector.flatten()
resized_image_feature_vector_flattened
len(resized_image_feature_vector_flattened)
img_grayscale = cv2.imread(imagePath, cv2.IMREAD_GRAYSCALE)
plt.imshow(img_grayscale)
img_grayscale.shape
img_grayscale
import numpy as np
expanded_image_grayscale = np.expand_dims(img_grayscale, axis=2)
expanded_image_grayscale.shape
expanded_image_grayscale
# # LassoRidge Linear Regression
auto_data = pd.read_csv('imports-85.data', sep=r'\s*,\s*', engine='python')
auto_data.head()
auto_data=auto_data.replace('?', np.nan)
auto_data.head()
auto_data.describe()
auto_data.describe(include='all')
auto_data['price'].describe()
# covert to type float
auto_data['price'] = pd.to_numeric(auto_data['price'], errors='coerce')
auto_data.describe()
auto_data = auto_data.drop('normalized-losses', axis=1)
auto_data.head()
auto_data['horsepower']=pd.to_numeric(auto_data['horsepower'], errors='coerce')
auto_data['horsepower'].describe()
auto_data['num-of-cylinders'].describe()
cylinders_dict = {
'two':2,
'three':3,
'four':4,
'five':5,
'six':6,
'eight':8,
'twelve':12
}
auto_data['num-of-cylinders'].replace(cylinders_dict, inplace=True)
auto_data['num-of-cylinders'].describe()
auto_data.head()
auto_data = pd.get_dummies(auto_data, columns=['make',
'fuel-type',
'aspiration',
'num-of-doors',
'body-style',
'drive-wheels',
'engine-location',
'engine-type',
'fuel-system'])
auto_data.head()
auto_data=auto_data.dropna()
auto_data
auto_data[auto_data.isnull().any(axis=1)]
# +
from sklearn.model_selection import train_test_split
X = auto_data.drop('price', axis=1)
# taking the labels (price)
Y = auto_data['price']
X_train,x_test,Y_train,y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
# -
from sklearn.linear_model import LinearRegression
linear_model= LinearRegression()
linear_model.fit(X_train, Y_train)
linear_model.score(X_train, Y_train)
linear_model.coef_
predictors = X_train.columns
predictors
# +
coef = pd.Series(linear_model.coef_,predictors).sort_values()
print(coef)
# -
y_predict = linear_model.predict(x_test)
# +
# %pylab inline
pylab.rcParams['figure.figsize'] = (15,6)
plt.plot(y_predict,label='Predicted')
plt.plot(y_test.values, label='Actual')
plt.ylabel('Price')
plt.legend()
plt.show()
# -
r_square = linear_model.score(x_test,y_test)
r_square
from sklearn.metrics import mean_squared_error
linear_model_mse=mean_squared_error(y_predict, y_test)
linear_model_mse
import math
math.sqrt(linear_model_mse)
# +
# Distance Measures
# L1 Distance impotant for L1 norm
# L2 Distance Euclidian distance
# +
# Bais variance trade off
# Regression algo - overfit data
# Decision tree also high bias algo
#prevent overfitting
# regularization
#LASS RIDGE
#DROP OUT - Certrain neurons dropped of training intentionally
# ADD penalty object
from sklearn.linear_model import Lasso
# -
lasso_model = Lasso(alpha=0.5, normalize=True)
lasso_model.fit(X_train,Y_train)
lasso_model.score(X_train, Y_train)
coef = pd.Series(lasso_model.coef_, predictors).sort_values()
print(coef)
y_predict=lasso_model.predict(x_test)
# +
# %pylab inline
pylab.rcParams['figure.figsize'] = (15,6)
plt.plot(y_predict,label='Predicted')
plt.plot(y_test.values, label='Actual')
plt.ylabel('Price')
plt.legend()
plt.show()
# -
r_square = lasso_model.score(x_test, y_test)
r_square
lasso_model_mse = mean_squared_error(y_predict, y_test)
math.sqrt(lasso_model_mse)
# +
from sklearn.linear_model import Ridge
ridge_model = Ridge(alpha=0.5, normalize=True)
ridge_model.fit(X_train,Y_train)
# -
ridge_model.score(X_train, Y_train)
# # Subvector Regression
auto_data = pd.read_csv('auto-mpg.data', delim_whitespace = True, header=None,
names=['mpg',
'cylinders',
'displacement',
'horsepower',
'weight',
'acceleration',
'model',
'origin',
'car_name'])
auto_data
len(auto_data['car_name'].unique())
len(auto_data)
auto_data = auto_data.drop('car_name', axis=1)
auto_data.head()
auto_data.head()
auto_data['origin'] = auto_data['origin'].replace({1:'america', 2:'europe', 3:'asia'})
auto_data.head()
#one hot encoding
auto_data = pd.get_dummies(auto_data, columns=['origin'])
auto_data.head()
import numpy as np
auto_data = auto_data.replace('?', np.nan)
auto_data = auto_data.dropna()
auto_data
# +
X = auto_data.drop('mpg', axis=1)
Y= auto_data['mpg']
X_train, x_test, Y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
# -
from sklearn.svm import SVR
regression_model = SVR(kernel='linear', C=1.0)
regression_model.fit(X_train, Y_train)
regression_model.coef_
regression_model.score(X_train, Y_train)
predictors = X_train.columns
predictors
from pandas import Series
coef = Series(regression_model.coef_[0], predictors).sort_values()
coef.plot(kind='bar', title='Modal Coefficients')
# +
y_predict = regression_model.predict(x_test)
# %pylab inline
pylab.rcParams['figure.figsize'] = (15,6)
plt.plot(y_predict, label='Predicted')
plt.plot(y_test.values, label='Actuals')
plt.ylabel('MPG')
plt.legend()
plt.show()
# -
regression_model.score(x_test, y_test)
# +
from sklearn.metrics import mean_squared_error
regression_model_mse = mean_squared_error(y_predict, y_test)
regression_model_mse
# -
import math
math.sqrt(regression_model_mse)
|
backup/11.sklearn21.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Time Series - Lecture 1: Introduction
#
# ## Agenda
# - Iintroduction to time series
# - Datetime library in Python
# - Wrangle data in Python
# - Visualize time series data
#
# ### What is / Why Time Series?
# - Data drawn from a distribution correlated over time. (You have implictly assumed that data was drawn from an independent distribution.)
# - As a data analyst, you WILL encounter time series data.
# - Examples:
# - Economics/Finance: Stock, bond, other asset prices, government policies
# - Science/AI: climate (change) data, speech recognition
# - Business: user behavior data
#
# For example,
from PIL import Image
Image.open("images/sp500.png")
# In a time series, time is often the independent variable and the goal is to make a forecast for the future. From the historical data, we can find some **patterns or trend** which will help us understand the movement and forecast. Some concepts to help you recognize patterns:
#
# For example,
from PIL import Image
Image.open("images/pattern.png")
# 1. The monthly housing sales (top left) show seasonality within each year.
# 2. The US treasury bill contracts (top right) show results from the Chicago market for 100 consecutive trading days in 1981. Here there is no seasonality, but an obvious downward trend. Possibly, if we had a much longer series, we would see that this downward trend is actually part of a long cycle, but when viewed over only 100 days it appears to be a trend.
#
# What do you think about the othe two graphs?
# 3. The Australian quarterly electricity production (bottom left).
# 4. The daily change in the Google closing stock price (bottom right).
# ## Time Series in Python
#
# Python has built in tools for dealing with time data, and we will first familiarize ourselves.
#
# ### Data Structure
# - Many observations from same individual/sample over time (i.e., $Y_t$ where $t=1,...,T$)
# - Detailed time information (e.g., $X_t=$ 2020-09-23 3-PM)
#
# For example,
import pandas as pd
pd.read_fwf("http://www.cpc.ncep.noaa.gov/products/precip/CWlink/daily_ao_index/monthly.ao.index.b50.current.ascii", parse_dates = [[0, 1]], infer_datetime_format = True, header = None,)
# ## Datetime in Pandas
#
# - Pandas has a build-in feature to handle the time data with ease
# - Built in data structures
# - Time Stamp
# - Time Delta
# - Time Period
# - To handle these structures, need numpy package
# ### Timestamp
import pandas as pd
import numpy as np
from datetime import datetime
import matplotlib.pyplot as plt
pd.date_range('2020 Sep 23', periods = 5, freq = 'S')
pd.Timestamp('2020-09-23')
pd.Timestamp('2020-09-23 09:00')
# ### Timedelta
# - Can take both positive and negative values
pd.Timedelta('1 day')
pd.Timestamp('2016-01-01 10:10') + pd.Timedelta('15 ns')
# ### Timeperiod
# - Refer to specific length of time between a start and end time stamp
# - Fancier setting allowed such as business days
pd.Period('2020-09-23')
pd.Period('2020-09-23')
pd.period_range('2020-09-23 09:00:00', freq = 'B', periods = 10)
temp = pd.Series(range(10), pd.date_range('2020-09-23 09:00', periods = 10, freq = 'H'))
temp
# ### Time Zone handling
pd.Timestamp('9/1/2020 00:00',tz='Europe/London')
temp1 = temp.tz_localize(tz = 'Europe/London')
temp1
temp1.tz_convert('Asia/Tokyo')
ts.resample('D').sum()
# ### Resampling
temp = pd.date_range('1/1/2011', periods=72, freq='H')
temp
temp1 = pd.Series(np.random.randn(len(temp)), index=temp)
temp1.asfreq('45Min', method='pad')
temp1.asfreq('45Min', method='backfill')
# ## Empirical Case: New Year's Resolution
#
#
# In this session, we're going to check out Google trends data of keywords 'diet', 'gym' and 'finance' to see how they vary over time. Could there be more searches for these terms in January when we're all trying to turn over a new leaf? We're not going to do much mathematics today but we'll source Our data, visualize it and learn about trends and seasonality in time series data. First if all, we will focus on a visual exploration of the dataset in question, and then we will predict its values sometime in the future.
#
# So the question remains: could there be more searches for these terms in January when we're all trying to turn over a new leaf? Let's find out by going [here](https://trends.google.com/trends/explore?date=all&q=diet,gym,finance) and checking out the data (inspired this [this fivethirtyeight piece](https://fivethirtyeight.com/features/how-fast-youll-abandon-your-new-years-resolutions/)).
#
# ### Reading In Data
#
# Let's read in some data:
df = pd.read_csv('data/multiTimeline.csv', skiprows=1)
df.head()
# Use the .info() method to check out your data types, number of rows and more:
df.info()
df.columns = ['month', 'diet', 'gym', 'finance']
df.month = pd.to_datetime(df.month)
df.set_index('month', inplace=True)
df.head()
# ### Graphing
#
# Visualization is a powerful tool for an analyst to recognize any pattern in the data.
df.plot(figsize=(9,9), linewidth=2, fontsize=15)
plt.xlabel('Year', fontsize=20)
# ## Recap:
# - You've gotten an overview/introduction to time series.
# - You've understood how to use datetime library in Python.
# - You've imported your data from google trends.
# - You've wrangled your data and gotten it into the form you want to prepare it for analysis.
# - You've checked out youe time series visually.
#
# ## Up next:
#
# - Identify trends in your time series
# # Activities
#
# 1. Which of these formats DON'T work?
# - '2016 Jul 1'
# - '7/1/2016'
# - '1/7/2016'
# - 'July 1, 2016'
# - '2016-07-01'
# - '2016/07/01'
# 2. Read in 'multiTimeline.csv', and convert the date format **into** January 1, 2004; January 2, 2004, and etc. **from** January 1, 2020, February 1, 2020, and etc.
# 3. Can you think of 3 occasions where you would use resampling function in time series analysis?
# 4. Find publicly available data of **your interest** with time variable.
#
# I believe the best way to learn is by doing. Motivation is high when you are working on a subject of personal interest.
#
# To take advantage of the small class, I would like to make the activities personalized to a data set of your interest. After each lecture, when you are off to do your activities, I would like you to try doing the activities/exercises on the data set of your choosing. Here are some examples of time series data:
# - [Yahoo Finance](https://finance.yahoo.com/) historical stock/bond/ETF price data
# - [St. Louis Fed](https://fred.stlouisfed.org/series/GDP) or [BLS](https://www.bls.gov/data/#unemployment) for any macroeconomic data
# - [COVID](https://www.ecdc.europa.eu/en/publications-data/download-todays-data-geographic-distribution-covid-19-cases-worldwide)
#
#
# 5. Load 'multiTimeline.csv'. Play around with the graph to find any trends, and share your opinion.
#
# ## References
#
# The materials presented here are inspired and modified from the following sources:
#
# - https://www.nytimes.com/2020/08/18/business/stock-market-record.html
# - https://otexts.com/fpp2/
# - https://github.com/AileenNielsen/TimeSeriesAnalysisWithPython
# - https://www.cpc.ncep.noaa.gov/products/precip/CWlink/
# - https://github.com/CodeOp-tech/tsa-soyhyoj/blob/master/New_Years_Resolutions_Workshop.ipynb
|
Time Series Analysis - Lecture 1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img src="../../images/qiskit_header.png" alt="Note: In order for images to show up in this jupyter notebook you need to select File => Trusted Notebook" align="middle">
# # Summary of Quantum Operations
# In this section we will go into the different operations that are available in Qiskit Terra. These are:
# - Single-qubit quantum gates
# - Multi-qubit quantum gates
# - Measurements
# - Reset
# - Conditionals
# - State initialization
#
# We will also show you how to use the three different simulators:
# - unitary_simulator
# - qasm_simulator
# - statevector_simulator
# # Table of contents
#
# 1) [Single Qubit Quantum States](#single_states)
#
#
# 2) [Single-Qubit Gates](#single_gates)
#
#
# 3) [Multi-Qubit Gates](#multi_gates)
#
#
# 4) [Two-Qubit Gates](#two_gates)
#
#
# 5) [Three-Qubit Gates](#three_gates)
#
#
# 6) [Non-Unitary Operations](#non_unitary)
#
#
# 7) [Arbitrary Initialization](#initialization)
# Useful additional packages
import matplotlib.pyplot as plt
# %matplotlib inline
import numpy as np
from math import pi
# +
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.tools.visualization import circuit_drawer
from qiskit.quantum_info import state_fidelity
from qiskit import BasicAer
backend = BasicAer.get_backend('unitary_simulator')
# -
# ## Single Qubit Quantum states <a name="single_states"/>
#
# A single qubit quantum state can be written as
#
# $$\left|\psi\right\rangle = \alpha\left|0\right\rangle + \beta \left|1\right\rangle$$
#
#
# where $\alpha$ and $\beta$ are complex numbers. In a measurement the probability of the bit being in $\left|0\right\rangle$ is $|\alpha|^2$ and $\left|1\right\rangle$ is $|\beta|^2$. As a vector this is
#
# $$
# \left|\psi\right\rangle =
# \begin{pmatrix}
# \alpha \\
# \beta
# \end{pmatrix}.
# $$
#
# Note, due to the conservation of probability $|\alpha|^2+ |\beta|^2 = 1$ and since global phase is undetectable $\left|\psi\right\rangle := e^{i\delta} \left|\psi\right\rangle$ we only require two real numbers to describe a single qubit quantum state.
#
# A convenient representation is
#
# $$\left|\psi\right\rangle = \cos(\theta/2)\left|0\right\rangle + \sin(\theta/2)e^{i\phi}\left|1\right\rangle$$
#
# where $0\leq \phi < 2\pi$, and $0\leq \theta \leq \pi$. From this, it is clear that there is a one-to-one correspondence between qubit states ($\mathbb{C}^2$) and the points on the surface of a unit sphere ($\mathbb{R}^3$). This is called the Bloch sphere representation of a qubit state.
#
# Quantum gates/operations are usually represented as matrices. A gate which acts on a qubit is represented by a $2\times 2$ unitary matrix $U$. The action of the quantum gate is found by multiplying the matrix representing the gate with the vector which represents the quantum state.
#
# $$\left|\psi'\right\rangle = U\left|\psi\right\rangle$$
#
# A general unitary must be able to take the $\left|0\right\rangle$ to the above state. That is
#
# $$
# U = \begin{pmatrix}
# \cos(\theta/2) & a \\
# e^{i\phi}\sin(\theta/2) & b
# \end{pmatrix}
# $$
#
# where $a$ and $b$ are complex numbers constrained such that $U^\dagger U = I$ for all $0\leq\theta\leq\pi$ and $0\leq \phi<2\pi$. This gives 3 constraints and as such $a\rightarrow -e^{i\lambda}\sin(\theta/2)$ and $b\rightarrow e^{i\lambda+i\phi}\cos(\theta/2)$ where $0\leq \lambda<2\pi$ giving
#
# $$
# U = \begin{pmatrix}
# \cos(\theta/2) & -e^{i\lambda}\sin(\theta/2) \\
# e^{i\phi}\sin(\theta/2) & e^{i\lambda+i\phi}\cos(\theta/2)
# \end{pmatrix}.
# $$
#
# This is the most general form of a single qubit unitary.
# ## Single-Qubit Gates <a name="single_gates"/>
#
# The single-qubit gates available are:
# - u gates
# - Identity gate
# - Pauli gates
# - Clifford gates
# - $C3$ gates
# - Standard rotation gates
#
# We have provided a backend: `unitary_simulator` to allow you to calculate the unitary matrices.
q = QuantumRegister(1)
# ### u gates
#
# In Qiskit we give you access to the general unitary using the $u3$ gate
#
# $$
# u3(\theta, \phi, \lambda) = U(\theta, \phi, \lambda)
# $$
#
qc = QuantumCircuit(q)
qc.u3(pi/2,pi/2,pi/2,q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# The $u2(\phi, \lambda) =u3(\pi/2, \phi, \lambda)$ gate has the matrix form
#
# $$
# u2(\phi, \lambda) =
# \frac{1}{\sqrt{2}} \begin{pmatrix}
# 1 & -e^{i\lambda} \\
# e^{i\phi} & e^{i(\phi + \lambda)}
# \end{pmatrix}.
# $$
#
# This is a useful gate as it allows us to create superpositions.
qc = QuantumCircuit(q)
qc.u2(pi/2,pi/2,q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# The $u1(\lambda)= u3(0, 0, \lambda)$ gate has the matrix form
#
# $$
# u1(\lambda) =
# \begin{pmatrix}
# 1 & 0 \\
# 0 & e^{i \lambda}
# \end{pmatrix},
# $$
#
# which is useful as it allows us to apply a quantum phase.
qc = QuantumCircuit(q)
qc.u1(pi/2,q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# ### Identity gate
#
# The identity gate is $Id = u0(1)$.
qc = QuantumCircuit(q)
qc.iden(q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# ### Pauli gates
#
# #### $X$: bit-flip gate
#
# The bit-flip gate $X$ is defined as:
#
# $$
# X =
# \begin{pmatrix}
# 0 & 1\\
# 1 & 0
# \end{pmatrix}= u3(\pi,0,\pi)
# $$
qc = QuantumCircuit(q)
qc.x(q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# #### $Y$: bit- and phase-flip gate
#
# The $Y$ gate is defined as:
#
# $$
# Y =
# \begin{pmatrix}
# 0 & -i\\
# i & 0
# \end{pmatrix}=u3(\pi,\pi/2,\pi/2)
# $$
qc = QuantumCircuit(q)
qc.y(q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# #### $Z$: phase-flip gate
#
# The phase-flip gate $Z$ is defined as:
#
# $$
# Z =
# \begin{pmatrix}
# 1 & 0\\
# 0 & -1
# \end{pmatrix}=u1(\pi)
# $$
qc = QuantumCircuit(q)
qc.z(q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# ### Clifford gates
#
# #### Hadamard gate
#
# $$
# H =
# \frac{1}{\sqrt{2}}
# \begin{pmatrix}
# 1 & 1\\
# 1 & -1
# \end{pmatrix}= u2(0,\pi)
# $$
qc = QuantumCircuit(q)
qc.h(q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# #### $S$ (or, $\sqrt{Z}$ phase) gate
#
# $$
# S =
# \begin{pmatrix}
# 1 & 0\\
# 0 & i
# \end{pmatrix}= u1(\pi/2)
# $$
qc = QuantumCircuit(q)
qc.s(q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# #### $S^{\dagger}$ (or, conjugate of $\sqrt{Z}$ phase) gate
#
# $$
# S^{\dagger} =
# \begin{pmatrix}
# 1 & 0\\
# 0 & -i
# \end{pmatrix}= u1(-\pi/2)
# $$
#
qc = QuantumCircuit(q)
qc.sdg(q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# ### $C3$ gates
# #### $T$ (or, $\sqrt{S}$ phase) gate
#
# $$
# T =
# \begin{pmatrix}
# 1 & 0\\
# 0 & e^{i \pi/4}
# \end{pmatrix}= u1(\pi/4)
# $$
qc = QuantumCircuit(q)
qc.t(q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# #### $T^{\dagger}$ (or, conjugate of $\sqrt{S}$ phase) gate
#
# $$
# T^{\dagger} =
# \begin{pmatrix}
# 1 & 0\\
# 0 & e^{-i \pi/4}
# \end{pmatrix}= u1(-pi/4)
# $$
qc = QuantumCircuit(q)
qc.tdg(q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# ### Standard Rotations
#
# The standard rotation gates are those that define rotations around the Paulis $P=\{X,Y,Z\}$. They are defined as
#
# $$ R_P(\theta) = \exp(-i \theta P/2) = \cos(\theta/2)I -i \sin(\theta/2)P$$
#
# #### Rotation around X-axis
#
# $$
# R_x(\theta) =
# \begin{pmatrix}
# \cos(\theta/2) & -i\sin(\theta/2)\\
# -i\sin(\theta/2) & \cos(\theta/2)
# \end{pmatrix} = u3(\theta, -\pi/2,\pi/2)
# $$
qc = QuantumCircuit(q)
qc.rx(pi/2,q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# #### Rotation around Y-axis
#
# $$
# R_y(\theta) =
# \begin{pmatrix}
# \cos(\theta/2) & - \sin(\theta/2)\\
# \sin(\theta/2) & \cos(\theta/2).
# \end{pmatrix} =u3(\theta,0,0)
# $$
qc = QuantumCircuit(q)
qc.ry(pi/2,q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# #### Rotation around Z-axis
#
# $$
# R_z(\phi) =
# \begin{pmatrix}
# e^{-i \phi/2} & 0 \\
# 0 & e^{i \phi/2}
# \end{pmatrix}\equiv u1(\phi)
# $$
#
# Note that here we have used an equivalent as it is different to u1 by a global phase $e^{-i \phi/2}$.
qc = QuantumCircuit(q)
qc.rz(pi/2,q)
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# Note this is different due only to a global phase.
# ## Multi-Qubit Gates <a name="multi_gates"/>
#
# ### Mathematical Preliminaries
#
# The space of a quantum computer grows exponential with the number of qubits. For $n$ qubits the complex vector space has dimensions $d=2^n$. To describe states of a multi-qubit system, the tensor product is used to "glue together" operators and basis vectors.
#
# Let's start by considering a 2-qubit system. Given two operators $A$ and $B$ that each act on one qubit, the joint operator $A \otimes B$ acting on two qubits is
#
# $$\begin{equation}
# A\otimes B =
# \begin{pmatrix}
# A_{00} \begin{pmatrix}
# B_{00} & B_{01} \\
# B_{10} & B_{11}
# \end{pmatrix} & A_{01} \begin{pmatrix}
# B_{00} & B_{01} \\
# B_{10} & B_{11}
# \end{pmatrix} \\
# A_{10} \begin{pmatrix}
# B_{00} & B_{01} \\
# B_{10} & B_{11}
# \end{pmatrix} & A_{11} \begin{pmatrix}
# B_{00} & B_{01} \\
# B_{10} & B_{11}
# \end{pmatrix}
# \end{pmatrix},
# \end{equation}$$
#
# where $A_{jk}$ and $B_{lm}$ are the matrix elements of $A$ and $B$, respectively.
#
# Analogously, the basis vectors for the 2-qubit system are formed using the tensor product of basis vectors for a single qubit:
# $$\begin{equation}\begin{split}
# \left|{00}\right\rangle &= \begin{pmatrix}
# 1 \begin{pmatrix}
# 1 \\
# 0
# \end{pmatrix} \\
# 0 \begin{pmatrix}
# 1 \\
# 0
# \end{pmatrix}
# \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\0 \end{pmatrix}~~~\left|{01}\right\rangle = \begin{pmatrix}
# 1 \begin{pmatrix}
# 0 \\
# 1
# \end{pmatrix} \\
# 0 \begin{pmatrix}
# 0 \\
# 1
# \end{pmatrix}
# \end{pmatrix} = \begin{pmatrix}0 \\ 1 \\ 0 \\ 0 \end{pmatrix}\end{split}
# \end{equation}$$
#
# $$\begin{equation}\begin{split}\left|{10}\right\rangle = \begin{pmatrix}
# 0\begin{pmatrix}
# 1 \\
# 0
# \end{pmatrix} \\
# 1\begin{pmatrix}
# 1 \\
# 0
# \end{pmatrix}
# \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}~~~ \left|{11}\right\rangle = \begin{pmatrix}
# 0 \begin{pmatrix}
# 0 \\
# 1
# \end{pmatrix} \\
# 1\begin{pmatrix}
# 0 \\
# 1
# \end{pmatrix}
# \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\1 \end{pmatrix}\end{split}
# \end{equation}.$$
#
# Note we've introduced a shorthand for the tensor product of basis vectors, wherein $\left|0\right\rangle \otimes \left|0\right\rangle$ is written as $\left|00\right\rangle$. The state of an $n$-qubit system can be described using the $n$-fold tensor product of single-qubit basis vectors. Notice that the basis vectors for a 2-qubit system are 4-dimensional; in general, the basis vectors of an $n$-qubit sytsem are $2^{n}$-dimensional, as noted earlier.
#
# ### Basis vector ordering in Qiskit
#
# Within the physics community, the qubits of a multi-qubit systems are typically ordered with the first qubit on the left-most side of the tensor product and the last qubit on the right-most side. For instance, if the first qubit is in state $\left|0\right\rangle$ and second is in state $\left|1\right\rangle$, their joint state would be $\left|01\right\rangle$. Qiskit uses a slightly different ordering of the qubits, in which the qubits are represented from the most significant bit (MSB) on the left to the least significant bit (LSB) on the right (big-endian). This is similar to bitstring representation on classical computers, and enables easy conversion from bitstrings to integers after measurements are performed. For the example just given, the joint state would be represented as $\left|10\right\rangle$. Importantly, *this change in the representation of multi-qubit states affects the way multi-qubit gates are represented in Qiskit*, as discussed below.
#
# The representation used in Qiskit enumerates the basis vectors in increasing order of the integers they represent. For instance, the basis vectors for a 2-qubit system would be ordered as $\left|00\right\rangle$, $\left|01\right\rangle$, $\left|10\right\rangle$, and $\left|11\right\rangle$. Thinking of the basis vectors as bit strings, they encode the integers 0,1,2 and 3, respectively.
#
#
# ### Controlled operations on qubits
#
# A common multi-qubit gate involves the application of a gate to one qubit, conditioned on the state of another qubit. For instance, we might want to flip the state of the second qubit when the first qubit is in $\left|0\right\rangle$. Such gates are known as _controlled gates_. The standard multi-qubit gates consist of two-qubit gates and three-qubit gates. The two-qubit gates are:
# - controlled Pauli gates
# - controlled Hadamard gate
# - controlled rotation gates
# - controlled phase gate
# - controlled u3 gate
# - swap gate
#
# The three-qubit gates are:
# - Toffoli gate
# - Fredkin gate
# ## Two-qubit gates <a name="two_gates"/>
#
# Most of the two-qubit gates are of the controlled type (the SWAP gate being the exception). In general, a controlled two-qubit gate $C_{U}$ acts to apply the single-qubit unitary $U$ to the second qubit when the state of the first qubit is in $\left|1\right\rangle$. Suppose $U$ has a matrix representation
#
# $$U = \begin{pmatrix} u_{00} & u_{01} \\ u_{10} & u_{11}\end{pmatrix}.$$
#
# We can work out the action of $C_{U}$ as follows. Recall that the basis vectors for a two-qubit system are ordered as $\left|00\right\rangle, \left|01\right\rangle, \left|10\right\rangle, \left|11\right\rangle$. Suppose the **control qubit** is **qubit 0** (which, according to Qiskit's convention, is one the _right-hand_ side of the tensor product). If the control qubit is in $\left|1\right\rangle$, $U$ should be applied to the **target** (qubit 1, on the _left-hand_ side of the tensor product). Therefore, under the action of $C_{U}$, the basis vectors are transformed according to
#
# $$\begin{align*}
# C_{U}: \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle} &\rightarrow \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle}\\
# C_{U}: \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle} &\rightarrow \underset{\text{qubit}~1}{U\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle}\\
# C_{U}: \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle} &\rightarrow \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle}\\
# C_{U}: \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle} &\rightarrow \underset{\text{qubit}~1}{U\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle}\\
# \end{align*}.$$
#
# In matrix form, the action of $C_{U}$ is
#
# $$\begin{equation}
# C_U = \begin{pmatrix}
# 1 & 0 & 0 & 0 \\
# 0 & u_{00} & 0 & u_{01} \\
# 0 & 0 & 1 & 0 \\
# 0 & u_{10} &0 & u_{11}
# \end{pmatrix}.
# \end{equation}$$
#
# To work out these matrix elements, let
#
# $$C_{(jk), (lm)} = \left(\underset{\text{qubit}~1}{\left\langle j \right|} \otimes \underset{\text{qubit}~0}{\left\langle k \right|}\right) C_{U} \left(\underset{\text{qubit}~1}{\left| l \right\rangle} \otimes \underset{\text{qubit}~0}{\left| k \right\rangle}\right),$$
#
# compute the action of $C_{U}$ (given above), and compute the inner products.
#
# As shown in the examples below, this operation is implemented in Qiskit as `cU(q[0],q[1])`.
#
#
# If **qubit 1 is the control and qubit 0 is the target**, then the basis vectors are transformed according to
# $$\begin{align*}
# C_{U}: \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle} &\rightarrow \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle}\\
# C_{U}: \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle} &\rightarrow \underset{\text{qubit}~1}{\left|0\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle}\\
# C_{U}: \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{\left|0\right\rangle} &\rightarrow \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{U\left|0\right\rangle}\\
# C_{U}: \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{\left|1\right\rangle} &\rightarrow \underset{\text{qubit}~1}{\left|1\right\rangle}\otimes \underset{\text{qubit}~0}{U\left|1\right\rangle}\\
# \end{align*},$$
#
#
# which implies the matrix form of $C_{U}$ is
# $$\begin{equation}
# C_U = \begin{pmatrix}
# 1 & 0 & 0 & 0 \\
# 0 & 1 & 0 & 0 \\
# 0 & 0 & u_{00} & u_{01} \\
# 0 & 0 & u_{10} & u_{11}
# \end{pmatrix}.
# \end{equation}$$
q = QuantumRegister(2)
# ### Controlled Pauli Gates
#
# #### Controlled-X (or, controlled-NOT) gate
# The controlled-not gate flips the `target` qubit when the control qubit is in the state $\left|1\right\rangle$. If we take the MSB as the control qubit (e.g. `cx(q[1],q[0])`), then the matrix would look like
#
# $$
# C_X =
# \begin{pmatrix}
# 1 & 0 & 0 & 0\\
# 0 & 1 & 0 & 0\\
# 0 & 0 & 0 & 1\\
# 0 & 0 & 1 & 0
# \end{pmatrix}.
# $$
#
# However, when the LSB is the control qubit, (e.g. `cx(q[0],q[1])`), this gate is equivalent to the following matrix:
#
# $$
# C_X =
# \begin{pmatrix}
# 1 & 0 & 0 & 0\\
# 0 & 0 & 0 & 1\\
# 0 & 0 & 1 & 0\\
# 0 & 1 & 0 & 0
# \end{pmatrix}.
# $$
#
#
qc = QuantumCircuit(q)
qc.cx(q[0],q[1])
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# #### Controlled $Y$ gate
#
# Apply the $Y$ gate to the target qubit if the control qubit is the MSB
#
# $$
# C_Y =
# \begin{pmatrix}
# 1 & 0 & 0 & 0\\
# 0 & 1 & 0 & 0\\
# 0 & 0 & 0 & -i\\
# 0 & 0 & i & 0
# \end{pmatrix},
# $$
#
# or when the LSB is the control
#
# $$
# C_Y =
# \begin{pmatrix}
# 1 & 0 & 0 & 0\\
# 0 & 0 & 0 & -i\\
# 0 & 0 & 1 & 0\\
# 0 & i & 0 & 0
# \end{pmatrix}.
# $$
qc = QuantumCircuit(q)
qc.cy(q[0],q[1])
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# #### Controlled $Z$ (or, controlled Phase) gate
#
# Similarly, the controlled Z gate flips the phase of the target qubit if the control qubit is $\left|1\right\rangle$. The matrix looks the same regardless of whether the MSB or LSB is the control qubit:
#
# $$
# C_Z =
# \begin{pmatrix}
# 1 & 0 & 0 & 0\\
# 0 & 1 & 0 & 0\\
# 0 & 0 & 1 & 0\\
# 0 & 0 & 0 & -1
# \end{pmatrix}
# $$
#
qc = QuantumCircuit(q)
qc.cz(q[0],q[1])
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# ### Controlled Hadamard gate
#
# Apply $H$ gate to the target qubit if the control qubit is $\left|1\right\rangle$. Below is the case where the control is the LSB qubit.
#
# $$
# C_H =
# \begin{pmatrix}
# 1 & 0 & 0 & 0\\
# 0 & \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}}\\
# 0 & 0 & 1 & 0\\
# 0 & \frac{1}{\sqrt{2}} & 0& -\frac{1}{\sqrt{2}}
# \end{pmatrix}
# $$
qc = QuantumCircuit(q)
qc.ch(q[0],q[1])
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# ### Controlled rotation gates
#
# #### Controlled rotation around Z-axis
#
# Perform rotation around Z-axis on the target qubit if the control qubit (here LSB) is $\left|1\right\rangle$.
#
# $$
# C_{Rz}(\lambda) =
# \begin{pmatrix}
# 1 & 0 & 0 & 0\\
# 0 & e^{-i\lambda/2} & 0 & 0\\
# 0 & 0 & 1 & 0\\
# 0 & 0 & 0 & e^{i\lambda/2}
# \end{pmatrix}
# $$
qc = QuantumCircuit(q)
qc.crz(pi/2,q[0],q[1])
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# ### Controlled phase rotation
#
# Perform a phase rotation if both qubits are in the $\left|11\right\rangle$ state. The matrix looks the same regardless of whether the MSB or LSB is the control qubit.
#
# $$
# C_{u1}(\lambda) =
# \begin{pmatrix}
# 1 & 0 & 0 & 0\\
# 0 & 1 & 0 & 0\\
# 0 & 0 & 1 & 0\\
# 0 & 0 & 0 & e^{i\lambda}
# \end{pmatrix}
# $$
qc = QuantumCircuit(q)
qc.cu1(pi/2,q[0], q[1])
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# ### Controlled $u3$ rotation
#
# Perform controlled-$u3$ rotation on the target qubit if the control qubit (here LSB) is $\left|1\right\rangle$.
#
# $$
# C_{u3}(\theta, \phi, \lambda) \equiv
# \begin{pmatrix}
# 1 & 0 & 0 & 0\\
# 0 & e^{-i(\phi+\lambda)/2}\cos(\theta/2) & 0 & -e^{-i(\phi-\lambda)/2}\sin(\theta/2)\\
# 0 & 0 & 1 & 0\\
# 0 & e^{i(\phi-\lambda)/2}\sin(\theta/2) & 0 & e^{i(\phi+\lambda)/2}\cos(\theta/2)
# \end{pmatrix}.
# $$
qc = QuantumCircuit(q)
qc.cu3(pi/2, pi/2, pi/2, q[0], q[1])
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# ### SWAP gate
#
# The SWAP gate exchanges the two qubits. It transforms the basis vectors as
#
# $$\left|00\right\rangle \rightarrow \left|00\right\rangle~,~\left|01\right\rangle \rightarrow \left|10\right\rangle~,~\left|10\right\rangle \rightarrow \left|01\right\rangle~,~\left|11\right\rangle \rightarrow \left|11\right\rangle,$$
#
# which gives a matrix representation of the form
#
# $$
# \mathrm{SWAP} =
# \begin{pmatrix}
# 1 & 0 & 0 & 0\\
# 0 & 0 & 1 & 0\\
# 0 & 1 & 0 & 0\\
# 0 & 0 & 0 & 1
# \end{pmatrix}.
# $$
qc = QuantumCircuit(q)
qc.swap(q[0], q[1])
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# ## Three-qubit gates <a name="three_gates"/>
#
#
# There are two commonly-used three-qubit gates. For three qubits, the basis vectors are ordered as
#
# $$\left|000\right\rangle, \left|001\right\rangle, \left|010\right\rangle, \left|011\right\rangle, \left|100\right\rangle, \left|101\right\rangle, \left|110\right\rangle, \left|111\right\rangle,$$
#
# which, as bitstrings, represent the integers $0,1,2,\cdots, 7$. Again, Qiskit uses a representation in which the first qubit is on the right-most side of the tensor product and the third qubit is on the left-most side:
#
# $$\left|abc\right\rangle : \underset{\text{qubit 2}}{\left|a\right\rangle}\otimes \underset{\text{qubit 1}}{\left|b\right\rangle}\otimes \underset{\text{qubit 0}}{\left|c\right\rangle}.$$
# ### Toffoli gate ($ccx$ gate)
#
# The [Toffoli gate](https://en.wikipedia.org/wiki/Quantum_logic_gate#Toffoli_(CCNOT)_gate) flips the third qubit if the first two qubits (LSB) are both $\left|1\right\rangle$:
#
# $$\left|abc\right\rangle \rightarrow \left|bc\oplus a\right\rangle \otimes \left|b\right\rangle \otimes \left|c\right\rangle.$$
#
# In matrix form, the Toffoli gate is
# $$
# C_{CX} =
# \begin{pmatrix}
# 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
# 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\
# 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\
# 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\
# 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\
# 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\
# 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\
# 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0
# \end{pmatrix}.
# $$
q = QuantumRegister(3)
qc = QuantumCircuit(q)
qc.ccx(q[0], q[1], q[2])
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# ### Controlled swap gate (Fredkin Gate)
#
# The [Fredkin gate](https://en.wikipedia.org/wiki/Quantum_logic_gate#Fredkin_(CSWAP)_gate), or the *controlled swap gate*, exchanges the second and third qubits if the first qubit (LSB) is $\left|1\right\rangle$:
#
# $$ \left|abc\right\rangle \rightarrow \begin{cases} \left|bac\right\rangle~~\text{if}~c=1 \cr \left|abc\right\rangle~~\text{if}~c=0 \end{cases}.$$
#
# In matrix form, the Fredkin gate is
#
# $$
# C_{\mathrm{SWAP}} =
# \begin{pmatrix}
# 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
# 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\
# 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\
# 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\
# 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\
# 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\
# 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\
# 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1
# \end{pmatrix}.
# $$
qc = QuantumCircuit(q)
qc.cswap(q[0], q[1], q[2])
qc.draw()
job = execute(qc, backend)
job.result().get_unitary(qc, decimals=3)
# ## Non unitary operations <a name="non_unitary"/>
#
# Now that we have gone through all the unitary operations in quantum circuits, we also have access to non-unitary operations. These include measurements, reset of qubits, and classical conditional operations.
q = QuantumRegister(1)
c = ClassicalRegister(1)
# ### Measurements
#
# We don't have access to all the information when we make a measurement in a quantum computer. The quantum state is projected onto the standard basis. Below are two examples showing a circuit that is prepared in a basis state and the quantum computer prepared in a superposition state.
qc = QuantumCircuit(q, c)
qc.measure(q, c)
qc.draw()
backend = BasicAer.get_backend('qasm_simulator')
job = execute(qc, backend, shots=1024)
job.result().get_counts(qc)
# The simulator predicts that 100 percent of the time the classical register returns 0.
qc = QuantumCircuit(q, c)
qc.h(q)
qc.measure(q, c)
qc.draw()
job = execute(qc, backend, shots=1024)
job.result().get_counts(qc)
# The simulator predicts that 50 percent of the time the classical register returns 0 or 1.
# ### Reset
# It is also possible to `reset` qubits to the $\left|0\right\rangle$ state in the middle of computation. Note that `reset` is not a Gate operation, since it is irreversible.
qc = QuantumCircuit(q, c)
qc.reset(q[0])
qc.measure(q, c)
qc.draw()
job = execute(qc, backend, shots=1024)
job.result().get_counts(qc)
qc = QuantumCircuit(q, c)
qc.h(q)
qc.reset(q[0])
qc.measure(q, c)
qc.draw()
job = execute(qc, backend, shots=1024)
job.result().get_counts(qc)
# Here we see that for both of these circuits the simulator always predicts that the output is 100 percent in the 0 state.
# ### Conditional operations
# It is also possible to do operations conditioned on the state of the classical register
qc = QuantumCircuit(q, c)
qc.x(q[0]).c_if(c, 0)
qc.measure(q,c)
qc.draw()
# Here the classical bit always takes the value 0 so the qubit state is always flipped.
job = execute(qc, backend, shots=1024)
job.result().get_counts(qc)
qc = QuantumCircuit(q, c)
qc.h(q)
qc.measure(q,c)
qc.x(q[0]).c_if(c, 0)
qc.measure(q,c)
qc.draw()
job = execute(qc, backend, shots=1024)
job.result().get_counts(qc)
# Here the classical bit by the first measurement is random but the conditional operation results in the qubit being deterministically put into $\left|1\right\rangle$.
# ## Arbitrary initialization <a name="initialization"/>
# What if we want to initialize a qubit register to an arbitrary state? An arbitrary state for $n$ qubits may be specified by a vector of $2^n$ amplitudes, where the sum of amplitude-norms-squared equals 1. For example, the following three-qubit state can be prepared:
#
# $$\left|\psi\right\rangle = \frac{i}{4}\left|000\right\rangle + \frac{1}{\sqrt{8}}\left|001\right\rangle + \frac{1+i}{4}\left|010\right\rangle + \frac{1+2i}{\sqrt{8}}\left|101\right\rangle + \frac{1}{4}\left|110\right\rangle$$
# +
# Initializing a three-qubit quantum state
import math
desired_vector = [
1 / math.sqrt(16) * complex(0, 1),
1 / math.sqrt(8) * complex(1, 0),
1 / math.sqrt(16) * complex(1, 1),
0,
0,
1 / math.sqrt(8) * complex(1, 2),
1 / math.sqrt(16) * complex(1, 0),
0]
q = QuantumRegister(3)
qc = QuantumCircuit(q)
qc.initialize(desired_vector, [q[0],q[1],q[2]])
qc.draw(output='latex')
# -
backend = BasicAer.get_backend('statevector_simulator')
job = execute(qc, backend)
qc_state = job.result().get_statevector(qc)
qc_state
# [Fidelity](https://en.wikipedia.org/wiki/Fidelity_of_quantum_states) is useful to check whether two states are the same or not.
# For quantum (pure) states $\left|\psi_1\right\rangle$ and $\left|\psi_2\right\rangle$, the fidelity is
#
# $$
# F\left(\left|\psi_1\right\rangle,\left|\psi_2\right\rangle\right) = \left|\left\langle\psi_1\middle|\psi_2\right\rangle\right|^2.
# $$
#
# The fidelity is equal to $1$ if and only if two states are equal.
state_fidelity(desired_vector,qc_state)
# #### Further details:
#
# How does the desired state get generated behind the scenes? There are multiple methods for doing this. Qiskit uses a [method proposed by Shende et al](https://arxiv.org/abs/quant-ph/0406176). Here, the idea is to assume the quantum register to have started from our desired state, and construct a circuit that takes it to the $\left|00..0\right\rangle$ state. The initialization circuit is then the reverse of such circuit.
#
# To take an arbitrary quantum state to the zero state in the computational basis, we perform an iterative procedure that disentangles qubits from the register one-by-one. We know that any arbitrary single-qubit state $\left|\rho\right\rangle$ can be taken to the $\left|0\right\rangle$ state using a $\phi$-degree rotation about the Z axis followed by a $\theta$-degree rotation about the Y axis:
#
# $$R_y(-\theta)R_z(-\phi)\left|\rho\right\rangle = re^{it}\left|0\right\rangle$$
#
# Since now we are dealing with $n$ qubits instead of just 1, we must factorize the state vector to separate the Least Significant Bit (LSB):
#
# $$\begin{align*}
# \left|\psi\right\rangle =& \alpha_{0_0}\left|00..00\right\rangle + \alpha_{0_1}\left|00..01\right\rangle + \alpha_{1_0}\left|00..10\right\rangle + \alpha_{1_1}\left|00..11\right\rangle + ... \\&+ \alpha_{(2^{n-1}-1)_0}\left|11..10\right\rangle + \alpha_{(2^{n-1}-1)_1}\left|11..11\right\rangle \\
# =& \left|00..0\right\rangle (\alpha_{0_0}\left|0\right\rangle + \alpha_{0_1}\left|1\right\rangle) + \left|00..1\right\rangle (\alpha_{1_0}\left|0\right\rangle + \alpha_{1_1}\left|1\right\rangle) + ... \\&+ \left|11..1\right\rangle (\alpha_{(2^{n-1}-1)_0}(\left|0\right\rangle + \alpha_{(2^{n-1}-1)_1}\left|1\right\rangle) \\
# =& \left|00..0\right\rangle\left|\rho_0\right\rangle + \left|00..1\right\rangle\left|\rho_1\right\rangle + ... + \left|11..1\right\rangle\left|\rho_{2^{n-1}-1}\right\rangle
# \end{align*}$$
#
# Now each of the single-qubit states $\left|\rho_0\right\rangle, ..., \left|\rho_{2^{n-1}-1}\right\rangle$ can be taken to $\left|0\right\rangle$ by finding appropriate $\phi$ and $\theta$ angles per the equation above. Doing this simultaneously on all states amounts to the following unitary, which disentangles the LSB:
#
# $$U = \begin{pmatrix}
# R_{y}(-\theta_0)R_{z}(-\phi_0) & & & &\\
# & R_{y}(-\theta_1)R_{z}(-\phi_1) & & &\\
# & . & & &\\
# & & . & &\\
# & & & & R_y(-\theta_{2^{n-1}-1})R_z(-\phi_{2^{n-1}-1})
# \end{pmatrix} $$
#
# Hence,
#
# $$U\left|\psi\right\rangle = \begin{pmatrix} r_0e^{it_0}\\ r_1e^{it_1}\\ . \\ . \\ r_{2^{n-1}-1}e^{it_{2^{n-1}-1}} \end{pmatrix}\otimes\left|0\right\rangle$$
#
#
# U can be implemented as a "quantum multiplexor" gate, since it is a block diagonal matrix. In the quantum multiplexor formalism, a block diagonal matrix of size $2^n \times 2^n$, and consisting of $2^s$ blocks, is equivalent to a multiplexor with $s$ select qubits and $n-s$ data qubits. Depending on the state of the select qubits, the corresponding blocks are applied to the data qubits. A multiplexor of this kind can be implemented after recursive decomposition to primitive gates of cx, rz and ry.
import qiskit.tools.jupyter
# %qiskit_version_table
# %qiskit_copyright
|
qiskit/fundamentals/7_summary_of_quantum_operations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Environment (conda_pytorch_p36)
# language: python
# name: conda_pytorch_p36
# ---
# +
# # !pip install efficientnet-pytorch sklearn pytorch-gradcam
# -
# <b>History of performance</b>
#
# <u>ResNet50</u>
# ```
# Epoch [20] [----] Accuracy=0.849 time: 9907.055, avg: 495.353
# 9910.68 seconds taken for model training
# Saved the trained model: checkpoints/ResNet50-13082020-225751.pth.tar
# ```
#
# Confusion Matrix:
# ```
# [[812 71 2]
# [ 69 524 1]
# [ 15 47 38]]
#
# Normalized:
# [[0.91751412 0.08022599 0.00225989]
# [0.11616162 0.88215488 0.0016835 ]
# [0.15 0.47 0.38 ]]
#
# Average precision:
# {'normal': 0.9635609285949972,
# 'pneumonia': 0.9167709627528383,
# 'COVID-19': 0.7177274694611359}
#
# ```
#
# <u>DenseNet169</u>
# ```
# Epoch [20] [save] Accuracy=0.877 time: 10684.240, avg: 534.212
# 10692.20 seconds taken for model training
# Saved the trained model: checkpoints/DenseNet169-13082020-160734.pth.tar
#
# ```
#
# Confusion Matrix:
# ```
# [[842 40 3]
# [ 82 501 11]
# [ 21 34 45]]
#
# Normalized:
# [[0.95141243 0.04519774 0.00338983]
# [0.13804714 0.84343434 0.01851852]
# [0.21 0.34 0.45 ]]
#
# Average precision:
# {'normal': 0.9693357502226474,
# 'pneumonia': 0.926793498666849,
# 'COVID-19': 0.6723035153267891}
# ```
#
# <u>EfficientNet5</u>
# ```
# Epoch [20] [save] Accuracy=0.829 time: 13919.191, avg: 695.960
# 13922.36 seconds taken for model training
# Saved the trained model: checkpoints/EfficientNet5-13082020-190547.pth.tar
#
# Confusion Matrix:
#
# [[833 51 1]
# [126 468 0]
# [ 42 37 21]]
#
# Normalized:
# [[0.94124294 0.05762712 0.00112994]
# [0.21212121 0.78787879 0. ]
# [0.42 0.37 0.21 ]]
#
# Average precision:
# {'normal': 0.9417960453705472,
# 'pneumonia': 0.9044023769306659,
# 'COVID-19': 0.53796939494876}
#
# ```
# +
import os
import matplotlib.pyplot as plt
import numpy as np
import sklearn
import torch
from sklearn.metrics import average_precision_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import ConfusionMatrixDisplay
from torch.utils.data import DataLoader
from torchvision import transforms
import models
from dataset_generator import DatasetGenerator
# +
mean = [0.485, 0.456, 0.406]
std = [0.229, 0.224, 0.225]
image_resize = 256
image_crop = 224
batch_size = 64
class_to_idx = {
'normal': 0,
'pneumonia': 1,
'COVID-19': 2
}
image_dir = 'data'
test_csv_file = 'test_split.txt'
# define test transforms
test_transforms = transforms.Compose([
transforms.Resize(image_resize),
transforms.CenterCrop(image_crop),
transforms.ToTensor(),
transforms.Normalize(mean=mean, std=std)
])
# define test dataset
test_dir = os.path.join(image_dir, 'test')
test_dataset = DatasetGenerator(test_csv_file, test_dir, transform=test_transforms)
test_loader = DataLoader(test_dataset, batch_size=batch_size, num_workers=16, shuffle=True)
# -
# !ls -ltrh checkpoints
# +
# load model
def load_pretrained_model(arch):
model_func = getattr(models, arch)
model = model_func()
model.arch = arch
return model
os.environ['HOME'] = '.'
# +
# TBD load checkpoint file
ckp_path = 'checkpoints/EfficientNet5-13082020-190547.pth.tar'
model_checkpoint = torch.load(ckp_path, map_location=torch.device('cpu'))
state_dict = model_checkpoint['state_dict']
arch = model_checkpoint['arch']
pretrained_model = load_pretrained_model(arch)
# check the state dictionary matches
old_state_dict = pretrained_model.state_dict()
for k in state_dict:
if k not in old_state_dict:
print('Unexpected key %s in state_dict' % k)
for k in old_state_dict:
if k not in state_dict:
print('Missing key %s in state_dict' % k)
# TBD: load checkpoint into pretrained_model
pretrained_model.load_state_dict(state_dict)
# +
# do prediction for test dataset
pretrained_model.eval()
# append the prediction output using torch.cat
pred_out = torch.FloatTensor()
# append the labels
labels_list = []
with torch.no_grad():
for images, labels in test_loader:
# TBD append the labels
labels_list.extend(labels)
log_ps = pretrained_model.forward(images)
ps = torch.exp(log_ps).squeeze()
# TBD append the prediction output using torch.cat
pred_out = torch.cat((pred_out,ps),0)
if len(labels_list) % 128 == 0:
print(len(labels_list), pred_out.shape)
# +
precision = dict()
recall = dict()
average_precision = dict()
# https://github.com/rachellea/glassboxmedicine/blob/master/2020-07-14-AUROC-AP/main.py
# http://scikit-learn.org/stable/auto_examples/model_selection/plot_precision_recall.html
# for each clz ('normal', 'pneumonia', 'COVID-19')
for clz in class_to_idx:
clz_pred_out = pred_out[:,class_to_idx[clz]].numpy()
# TBD calculate precision and recall curve and store in precision, recall
precision[clz], recall[clz], _ = precision_recall_curve(y_true = labels_list,
probas_pred = clz_pred_out,
pos_label = clz)
clz_labels_list = [clz == label for label in labels_list]
# TBD calculate average precision score (the area under the curve)
average_precision[clz] = average_precision_score(y_true=clz_labels_list,
y_score = clz_pred_out)
# TBD result looks like the following
# {'normal': 0.9855985255902013,
# 'pneumonia': 0.9713300353762777,
# 'COVID-19': 0.8363362361594885}
average_precision
# +
colors = ['navy', 'turquoise', 'darkorange', 'cornflowerblue', 'teal']
lines = []
labels = []
for clz in class_to_idx:
l, = plt.plot(recall[clz], precision[clz], color=colors[class_to_idx[clz]], lw=2)
lines.append(l)
labels.append('Precision-recall for class {0} (area = {1:0.2f})'.format(clz, average_precision[clz]))
fig = plt.gcf()
fig.subplots_adjust(bottom=0.25)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall curve for {}'.format(arch))
plt.legend(lines, labels, loc=(0, -.68), prop=dict(size=14))
plt.show()
# -
# NOT USED
def confusion_matrix_values(y_true, y_score, decision_thresh):
#Obtain binary predicted labels by applying <decision_thresh> to <y_score>
y_pred = (np.array(y_score) > decision_thresh)
cm = sklearn.metrics.confusion_matrix(y_true=y_true, y_pred=y_pred)
true_neg, false_pos, false_neg, true_pos = cm.ravel()
return true_neg, false_pos, false_neg, true_pos
# NOT USED
def calculate_tpr_fpr_prec(y_true, y_score, decision_thresh):
true_neg, false_pos, false_neg, true_pos = confusion_matrix_values(y_true, y_score, decision_thresh)
tpr_recall = float(true_pos)/(true_pos + false_neg)
fpr = float(false_pos)/(false_pos+true_neg)
precision = float(true_pos)/(true_pos + false_pos)
return tpr_recall, fpr, precision
# +
max_pred_out = pred_out.max(dim=1)
max_pred_indices = max_pred_out.indices.numpy()
max_pred_vals = max_pred_out.values.numpy()
labels_indices = [class_to_idx[label] for label in labels_list]
cm = confusion_matrix(y_true = labels_indices, y_pred = max_pred_indices)
print(cm)
normalized_cm = confusion_matrix(y_true = labels_indices, y_pred = max_pred_indices, normalize = 'true')
print(normalized_cm)
# -
cm_display = ConfusionMatrixDisplay(normalized_cm, display_labels = np.array(['Normal','Pneumonia','COVID-19'])).plot()
|
txfer/txfer_eval.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.11 64-bit (''riip'': conda)'
# name: python3
# ---
# # Material
# ```
# Material(params: Dict, rid: RiiDataFrame)
# ```
#
# This class provides the dielectric function for the material specified by given id. If the argument __bound_check__ is True, ValueError is raised when the wavelength exeeds the domain of experimental data.
#
# __params__ can includes the following parameters,
# * 'PEC' (bool): True if you want to create perfect electric conductor. Defaults to False.
# * 'id' (int): ID number.
# * 'book' (str): book value in catalog of RiiDataFrame.
# * 'page' (str): page value in catalog of RiiDataFrame.
# * 'RI' (complex): Constant refractive index.
# * 'e' (complex): Constant permittivity.
# * 'bound_check' (bool): True if bound check should be done. Defaults to True.
# * 'im_factor' (floot): A magnification factor multiplied to the imaginary part of permittivity. Defaults to 1.0.
#
# This class extends the functionality of refractiveindex.info database:
# * It is possible to define dielectric materials that has constant permittivity.
# * Imaginary part of dielectric function can be magnified using 'im_factor' parameter.
# * Perfect Electric Conductor is defined as an artificial metal labeled "PEC", which has negative large permittivity (-1e8).
# * Material is callable with a single value argument, angular frequency argument ω. The evaluation process is omitted if it is called with the same argument.
#
# However, n, k and eps methos of this class are not numpy.ufunc. You can pass them only a single value.
import riip
rid = riip.RiiDataFrame()
water = riip.Material({'id': 428}, rid)
print(f"{water.catalog['book']} {water.catalog['page']}")
print(f"{water.catalog['wl_min']} <= λ <= {water.catalog['wl_max']}")
# ## Reflactive Index __n__
# ```
# n(wl: ArrayLike) -> numpy.ndarray
# ```
# ## Extinction Coefficient __k__
# ```
# k(wl: ArrayLike) -> numpy.ndarray
# ```
# ## Dielectric Function __eps__
# ```
# eps(wl: ArrayLike) -> numpy.ndarray
# ```
# Wavelengths __wl__ can be given as a single complex value or an array of complex values.
wl = 1.0
n = water.n(wl)
k = water.k(wl)
eps = water.eps(wl)
print(f"At λ={wl}μm:")
print(f" n={n}")
print(f" k={k}")
print(f" ε={eps}")
import numpy as np
wls = np.linspace(0.5, 1.6)
water.eps(wls)
# ## Bound_check
# By default, __bound_check__ is set to __True__, so a ValueError is raised if the given range of wavelength exeeds the domain of experimental data.
wls = np.linspace(1.0, 2.0) # exeeds the domain of experimental data [wl_min, wl_max]
water = riip.Material({'id': 428}, rid)
try:
water.eps(wls)
except ValueError as e:
print("ValueError: ", e)
# If the instance is created with _bound_check_=False, the dispersion formula is applied beyond the scope of experimental data.
water = rid.material({'id': 428, 'bound_check': False})
water.eps(wls)
# ## __plot__
# ```
# plot(wls: Sequence | np.ndarray, comp: str = "n", fmt1: Optional[str] = "-", fmt2: Optional[str] = "--", **kwargs)
# ```
# * wls (Sequence | np.ndarray): Wavelength coordinates to be plotted [μm].
# * comp (str): 'n', 'k' or 'eps'
# * fmt1 (Optional[str]): Plot format for n and Re(eps).
# * fmt2 (Optional[str]): Plot format for k and Im(eps).
#
# Plot refractive index (if set comp="n"), extinction coefficient (comp="k") or permittivity (comp="eps").
import matplotlib.pyplot as plt
water.plot(wls, "n")
plt.show()
water.plot(wls, "k")
plt.show()
water.plot(wls, "eps")
# You can change plot style usint rcParams.
plt.style.use('seaborn-notebook')
plot_params = {
'figure.figsize': [6.0, 6.0],
'axes.labelsize': 'xx-large',
'xtick.labelsize': 'x-large',
'ytick.labelsize': 'x-large',
'legend.fontsize': 'x-large',
}
plt.rcParams.update(plot_params)
water.plot(wls, "n")
# ## Water with constant RI
#
import numpy as np
from riip import Material
water_const = Material({'RI': 1.333})
wl = [0.5, 1.0, 1.5]
n = water_const.n(wl)
k = water_const.k(wl)
eps = water_const.eps(wl)
print(f"At λ={wl}μm:")
print(f" n={n}")
print(f" k={k}")
print(f" ε={eps}")
# ## A definition of water in RIID
water = Material({"book": "H2O", "page": "Kedenburg"})
wl = [0.5, 1.0, 1.5]
n = water.n(wl)
k = water.k(wl)
eps = water.eps(wl)
print(f"At λ={wl} μm:")
print(f" n={n}")
print(f" k={k}")
print(f" ε={eps}")
# ## Plot them:
wls = np.linspace(0.6, 1.0)
water_const.plot(wls)
water.plot(wls)
# ## Material as a function
# ```
# Material__call__(w: float | complex) -> complex
# ```
# * w (float | complex): A float indicating the angular frequency
#
# It returns the complex relative permittivity at given __angular frequency w__.
# We use a unit system where the speed of light in vacuum c is 1 and the unit of length is μm.
# So w is equal to the vacuum wavenumber ω/c [rad/μm]).
#
# It is much faster than __eps__ method because the formula is accelerated using cython. In the case of same argument, it's even more faster.
gold = Material({'book': 'Au', 'page': 'Stewart-DLF'})
wls = [1.0, 1.5]
ws = [2 * np.pi / wl for wl in wls]
# %%timeit
for i in range(1000):
gold.eps(wls[i % 2])
# %%timeit
for i in range(1000):
gold.eps(wls[0])
# %%timeit
for i in range(1000):
gold(ws[i % 2])
# %%timeit
for i in range(1000):
gold(ws[0])
# ## However, Material is __not__ a numpy.ufunc
try:
gold(np.array(ws))
except ValueError as e:
print("ValueError: ", e)
# ## im_factor
# +
gold_low_loss = Material({'book': 'Au', 'page': 'Stewart-DLF', 'im_factor': 0.1})
print("If im_factor=1.0: Im(ε)=", gold(6.28).imag)
print("If im_factor=0.1: Im(ε)=", gold_low_loss(6.28).imag)
print("Real parts are the same")
print(gold(6.28).real, gold_low_loss(6.28).real)
# -
# ## PEC
#
pec = Material({"PEC": True})
print(pec.label, pec(1.0))
|
docs/notebooks/03_Material.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="NpnZ0Rf2ZBPd"
# top 은 가장 많이 카운팅 된 것의 값들을 말한다.
#
# freq은 가장 많이 반복 된 횟수를 말한다.
# + colab={"base_uri": "https://localhost:8080/", "height": 223} id="oSmIqHV2RUgz" outputId="29829c1d-bb24-49b3-cf7f-a6e0207208db"
import pandas as pd
import seaborn as sns
df=sns.load_dataset('titanic')
#df.info()
#df.describe()
#df.describe(include='all')
df.head(5)
# + [markdown] id="5WESC6nnZZ1O"
# missing value:age, embarked, deck, embarked_town
# + colab={"base_uri": "https://localhost:8080/"} id="DRoWiV45R-hw" outputId="330ed28c-acf5-4f85-aa32-18a6caafa753"
#불충분한 데이터가 있어서 중간중간 값을 넣어야 하는데 mean으로 채워넣는다
# fillna api: 컬럼기준으로 Nan 값을 어떻게 처리할지 확인
df['age'].fillna(20)
# + colab={"base_uri": "https://localhost:8080/"} id="loDhCGt1bH6j" outputId="d1662154-0239-47f2-8a49-cf8135c2ba4d"
#missing value 삭제
df_deck=df.dropna(subset=['deck'], how='any', axis='index')
df_deck.info()
# + colab={"base_uri": "https://localhost:8080/"} id="jf60R122bmkG" outputId="8d089a29-64d0-43fa-c4bb-7584e897e4ab"
#fillna 동작시키면 비어있는 부분에 (29)값 채워줌
#type(df_age)이 series로 나옴,shape은 (891,)
df_age= df['age'].fillna(29)
df_age
# + colab={"base_uri": "https://localhost:8080/"} id="hTnrFTrje_Jd" outputId="9e7146b2-99a1-47b1-dbd2-c50a9c3ab7c0"
df['age']= df_age
df.info()
# + colab={"base_uri": "https://localhost:8080/"} id="PQHEb8L0f9f-" outputId="46c5fec5-2c48-453c-cdb6-4653ceec8983"
df['deck'].value_counts()
# + colab={"base_uri": "https://localhost:8080/"} id="lUj1ySR1gb9V" outputId="1ff03712-8f6d-49bd-a574-da8481239f61"
#B로 채울거야
df['deck']=df['deck'].fillna('B')
df.info()
# + colab={"base_uri": "https://localhost:8080/"} id="2_Jf7InYg4mr" outputId="decdaf76-e14e-4092-b010-ab894fda9bd4"
#embarked 채워주기
df['embarked'].value_counts()
df['embarked']= df['embarked'].fillna('C')
df.info()
# + colab={"base_uri": "https://localhost:8080/"} id="b8ZvfqVXhk4s" outputId="7975c319-31f9-4c4e-da51-1c05cc24d70d"
#embark_town 채워주기
df['embark_town'].value_counts()
# + colab={"base_uri": "https://localhost:8080/"} id="JhkX3FRBh1oU" outputId="078d3aa1-d8e6-4e0a-a865-0c5956dcd2f7"
df['embark_town']=df['embark_town'].fillna('Cherbourg')
df.info()
# + id="Wop8L4EQiEHN"
|
1_datapreprocess_fillna.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:anaconda3]
# language: python
# name: conda-env-anaconda3-py
# ---
# +
# %matplotlib notebook
# Import modules
import numpy as np
import matplotlib.pyplot
from pyne import serpent
from pyne import nucname
from scipy.stats.stats import pearsonr
import itertools
dep0 = serpent.parse_dep('/home/andrei2/Desktop/ornl/msfr/serpent/no_repr_depletion/msfr_depl.inp_dep.m', make_mats=False)
dep1 = serpent.parse_dep('/home/andrei2/Desktop/ornl/msfr/serpent/gas_removal/msfr_gas_rem.inp_dep.m', make_mats=False)
dep2 = serpent.parse_dep('/home/andrei2/Desktop/ornl/msfr/serpent/all_removal/msfr_gas_rem.inp_dep.m', make_mats=False)
res0 = serpent.parse_res('/home/andrei2/Desktop/ornl/msfr/serpent/no_repr_depletion/msfr_depl.inp_res.m')
res1 = serpent.parse_res('/home/andrei2/Desktop/ornl/msfr/serpent/gas_removal/msfr_gas_rem.inp_res.m')
res2 = serpent.parse_res('/home/andrei2/Desktop/ornl/msfr/serpent/all_removal/msfr_gas_rem.inp_res.m')
days = dep0['DAYS'] # Time array parsed from *_dep.m file
n_se = dep0['NAMES'][0].split() # Names of isotopes parsed from *_dep.m file
n_se1 = dep1['NAMES'][0].split() # Names of isotopes parsed from *_dep.m file
n_se2 = dep2['NAMES'][0].split() # Names of isotopes parsed from *_dep.m file
EOC = np.amax(days) # End of cycle (simulation time length)
total_mass_list = dep0['TOT_MASS']
adens_fuel_se = dep0['MAT_fuel_ADENS'] # atomic density for each isotope in material 'fuel'
mdens_fuel_se = dep0['MAT_fuel_MDENS'] # mass density for each isotope in material 'fuel'
mdens_fuel_se1 = dep1['MAT_fuel_MDENS'] # mass density for each isotope in material 'fuel'
mdens_fuel_se2 = dep2['MAT_fuel_MDENS'] # mass density for each isotope in material 'fuel'
vol_fuel_se = dep0['MAT_fuel_VOLUME'] # total volume of material 'fuel'
adens_blank_se = dep0['MAT_blank_ADENS'] # atomic density for each isotope in material 'blank'
mdens_blank_se = dep0['MAT_blank_MDENS'] # mass density for each isotope in material 'blank'
mdens_blank_se1 = dep1['MAT_blank_MDENS'] # mass density for each isotope in material 'blank'
mdens_blank_se2 = dep2['MAT_blank_MDENS'] # mass density for each isotope in material 'blank'
vol_blank_se = dep0['MAT_blank_VOLUME'] # total volume of material 'blank'
# SCALE output
filename_fuel = '/home/andrei2/Desktop/ornl/msfr/scale/no_reproc_depl/510efpd/quarter_cell2.000000000000000000.plt'
filename_blank = '/home/andrei2/Desktop/ornl/msfr/scale/no_reproc_depl/510efpd/quarter_cell2.000000000000000001.plt'
#print (dep0.keys())
#print (adens_fuel)
#print (n.index('Th232'))
def read_scale_out (filename):
iso = []
adens = []
days_list = []
with open(filename,'r') as infile:
for line in itertools.islice(infile, 5, None): # Skip file header start=6, stop=None
p = line.split()
iso.append(str(p[0]))
adens.append(p[1:])
#iso.append(str(p[2]))
#adens.append(str(p[3]))
#u_en = 1e-6* np.flip (np.array (upp_enrg, dtype=float), 0 ) # Convert eV to MeV
#flux = np.flip ( np.array (flux_list, dtype=float), 0 )
#num_gr = len (u_en)
days_list.append (iso[0])
days_list = days_list + adens[0][:]
adens_arr = np.asarray(adens[1:][:], dtype=np.float32)
days = np.array (days_list, dtype=np.float32)
return iso[1:], days, adens_arr
n_sc, days_sc, mdens_fuel_sc = read_scale_out (filename_fuel)
n_sc_blanket, days_sc, mdens_blank_sc = read_scale_out (filename_blank)
#print (adens_fuel_sc[10])
vol_fuel_se = [18.0E+6]
vol_blank_se = [7.3E+6]
iso = 'u233'
tot_mass_se = mdens_fuel_se[n_se.index(iso.capitalize()),]*vol_fuel_se+mdens_blank_se[n_se.index(iso.capitalize()),]*vol_blank_se
tot_mass_sc = mdens_fuel_sc[n_sc.index(iso),]*vol_fuel_se[0]+mdens_blank_sc[n_sc_blanket.index(iso),]*vol_blank_se[0]
gain_rate = 1e-3*365*(tot_mass_sc[-1] - tot_mass_sc[0])/days[-1]
# Initialize figure
fig_1 = matplotlib.pyplot.figure(1)
ax = fig_1.add_subplot(111)
ax.grid(True)
ax.ticklabel_format (style='sci',scilimits=(0,0),axis='y')
#ax.set_ylim(0,0.00555)
#plot_title = 'Relative error in mass ' + str(100*abs(mdens_fuel_sc[n_sc.index(iso),-1]-mdens_fuel_se[n_se.index(iso.capitalize()),-1])/
# mdens_fuel_se[n_se.index(iso.capitalize()),-1] ) + ' %\n'
for i in [n_se.index(iso.capitalize())]:
ax.plot(days, mdens_fuel_se[i,:]*vol_fuel_se[0], '-',color='#ff8100', label=nucname.serpent(n_se[i])+' (no removals)')
#ax.plot(days, mdens_fuel_se[i,:]*vol_fuel_se[0]+mdens_blank_se[i,:]*vol_blank_se[0], '--',color='#ff8100',
# label=nucname.serpent(n_se[i])+'(w/ blanket, no removals)')
#ax.plot(days, mdens_blank_se[i,:]*vol_blank_se[0], '-',color='#ff8100', label=nucname.serpent(n_se[i])+'(Serpent, blanket)')
for i in [n_se1.index(iso.capitalize())]:
ax.plot(days, mdens_fuel_se1[i,:]*vol_fuel_se[0], '--',color='red',
label=nucname.serpent(n_se1[i])+' (volatile gases)')
for i in [n_se2.index(iso.capitalize())]:
ax.plot(days, mdens_fuel_se2[i,:]*vol_fuel_se[0], '--',color='blue',
label=nucname.serpent(n_se2[i])+' (volatile gases, noble metals, \nrare earths&discard)')
for k in [n_sc.index(iso)]:
ax.plot(days_sc, mdens_fuel_sc[k]*vol_fuel_se[0], '-',color='blue', label=nucname.serpent(n_sc[k])+'(ORIGEN)')
#for k in [n_sc_blanket.index(iso)]:
# ax.plot(days_sc, mdens_blank_sc[k] * vol_blank_se[0] + mdens_fuel_sc[n_sc.index(iso)] * vol_fuel_se[0],
# '--',color='blue',label=nucname.serpent(n_sc_blanket[k])+'(ORIGEN, w/ blanket)')
#for k in [n_sc_blanket.index(iso)]:
# ax.plot(days_sc, mdens_blank_sc[k]*vol_blank_se[0], '-',color='blue', label=nucname.serpent(n_sc_blanket[k])+'(ORIGEN, blanket)')
ax.legend(loc=0)
ax.set_ylabel('Mass [grams]')
ax.set_xlabel('Time step [days]')
ax.set_title('Mass balance in fuel salt for ' + str (iso))
#ax.text(0.95, 0.5, 'Breeding gain '+"{0:.1f}".format(gain_rate)+ ' kg/year',
# horizontalalignment='right',verticalalignment='center', transform=ax.transAxes)
#ax.text(0.95, 0.45, 'Breeding gain coeff '+"{0:.4f}".format((tot_mass_sc[-1] - tot_mass_sc[0])/(tot_mass_sc[0])),
# horizontalalignment='right',verticalalignment='center', transform=ax.transAxes)
ax.set_xlim([0,np.amax(days_sc)])
fig_1.show()
#fig_1.savefig(str(iso)+'__fuel_various_rem.png',bbox_inches='tight', dpi=700)
# Initialize figure
fig_2 = matplotlib.pyplot.figure(2)
ax = fig_2.add_subplot(111)
ax.grid(True)
ax.ticklabel_format (style='sci',scilimits=(0,0),axis='y')
for i in [n_se.index(iso.capitalize())]:
ax.plot(days, mdens_blank_se[i,:]*vol_blank_se[0], '-',color='#ff8100', label=nucname.serpent(n_se[i])+' (no removals)')
for i in [n_se1.index(iso.capitalize())]:
ax.plot(days, mdens_blank_se1[i,:]*vol_blank_se[0], '--',color='red', label=nucname.serpent(n_se1[i])+' (volatile gases)')
for i in [n_se2.index(iso.capitalize())]:
ax.plot(days, mdens_blank_se2[i,:]*vol_blank_se[0], '--',color='blue', label=nucname.serpent(n_se2[i])+' (volatile gases, noble metals, \nrare earths&discard)')
for k in [n_sc_blanket.index(iso)]:
ax.plot(days_sc, mdens_blank_sc[k]*vol_blank_se[0], '-',color='blue', label=nucname.serpent(n_sc_blanket[k])+'(ORIGEN, blanket)')
ax.legend(loc=0)
ax.set_ylabel('Mass [grams]')
ax.set_xlabel('Time step [days]')
ax.set_title('Mass balance in fertile salt for ' + str (iso))
ax.set_xlim([0,np.amax(days_sc)])
fig_2.show()
#fig_2.savefig(str(iso)+'_blanket_various_rem.png',bbox_inches='tight', dpi=700)
# Initialize figure
fig_3 = matplotlib.pyplot.figure(3)
ax = fig_3.add_subplot(111)
ax.grid(True)
ax.plot(days, res0['IMP_KEFF'][:,0], '-',color='#ff8100', label='no removals')
ax.fill_between(days, res0['IMP_KEFF'][:,0]-res0['IMP_KEFF'][:,1], res0['IMP_KEFF'][:,0]+res0['IMP_KEFF'][:,1],alpha=1,
edgecolor='#808080', facecolor='#BEBEBE', linewidth=0)
ax.plot(days, res1['IMP_KEFF'][:,0], '-',color='red', label='volatile gases')
ax.fill_between(days, res1['IMP_KEFF'][:,0]-res1['IMP_KEFF'][:,1], res1['IMP_KEFF'][:,0]+res1['IMP_KEFF'][:,1],alpha=1,
edgecolor='#808080', facecolor='#BEBEBE', linewidth=0)
ax.plot(days, res2['IMP_KEFF'][:,0], '-',color='blue', label='all removals')
ax.fill_between(days, res2['IMP_KEFF'][:,0]-res2['IMP_KEFF'][:,1], res2['IMP_KEFF'][:,0]+res2['IMP_KEFF'][:,1],alpha=1,
edgecolor='#808080', facecolor='#BEBEBE', linewidth=0)
ax.legend(loc=0)
ax.set_ylabel('Infinite multiplication factor (k$_{\inf)}$)')
ax.set_xlabel('Time step [days]')
ax.set_title('Infinite muliplication factor')
ax.set_xlim([0,np.amax(days)])
fig_3.show()
#fig_3.savefig('k_inf_various_removal_cases.png',bbox_inches='tight', dpi=700)
'''
print ("Correlation between mass of target isotope (Serpent-Unit vs SCALE-Unit) is "
+ str(pearsonr(mdens_fuel_sc[n_sc.index(iso)], mdens_fuel_se[n_se.index(iso.capitalize())])) )
print ('Relative error for fuel salt in target isotope mass after ' + str(days[-1]) + ' days: ' +
str(100*abs(mdens_fuel_sc[n_sc.index(iso),-1]-mdens_fuel_se[n_se.index(iso.capitalize()),-1])/
mdens_fuel_se[n_se.index(iso.capitalize()),-1] ) + ' %')
print ('Relative error in total target isotope mass after ' + str(days[-1]) + ' days: ' +
str (100*abs(tot_mass_se[-1]-tot_mass_sc[-1]) / tot_mass_se[-1]) + ' %' )
print ('Relative error in blanket in total target isotope mass after ' + str(days[-1]) + ' days: ' +
str (100*abs(mdens_blank_sc[n_sc_blanket.index(iso),-1]-mdens_blank_se[n_se.index(iso.capitalize()),-1]) / mdens_blank_se[n_se.index(iso.capitalize()),-1]) + ' %' )
print ('\nFrom SCALE')
print ('Breeding gain ' + str (1e-3*365*(tot_mass_sc[-1] - tot_mass_sc[0])/days[-1]) + ' kg/year' )
print ('Breeding gain coefficient ' + str ((tot_mass_sc[-1] - tot_mass_sc[0])/(tot_mass_sc[0])) )
print ('Breeding gain in blanket ' + str (1e-3*365*(mdens_blank_sc[n_sc_blanket.index(iso),-1]*vol_blank_se[0] - mdens_blank_sc[n_sc_blanket.index(iso),0]*vol_blank_se[0])/days[-1]) + ' kg/year' )
print ('\nDoubling time (net) ' + str( 2*tot_mass_sc[0]/ (365*(tot_mass_sc[-1] - tot_mass_sc[0])/days[-1] )) )
'''
print ('\nFrom Serpent (no removals)')
print ('Breeding gain ' + str (1e-3*365*(tot_mass_se[-1] - tot_mass_se[0])/days[-1]) + ' kg/year' )
print ('Breeding gain coefficient ' + str ((tot_mass_se[-1] - tot_mass_se[0])/(tot_mass_se[0])) )
print ('Breeding gain in blanket ' + str (1e-3*365*(mdens_blank_se[n_se.index(iso.capitalize()),-1]*vol_blank_se[0] - mdens_blank_se[n_se.index(iso.capitalize()),0]*vol_blank_se[0])/days[-1]) + ' kg/year' )
print ('\nDoubling time (net) ' + str( 2*tot_mass_se[0]/ (365*(tot_mass_se[-1] - tot_mass_se[0])/days[-1] )) )
# -
|
msfr/plots/MSFR_reprocessing_SCALE-ChemTriton.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Modeling and Simulation in Python
#
# Rabbit example
#
# Copyright 2017 <NAME>
#
# License: [Creative Commons Attribution 4.0 International](https://creativecommons.org/licenses/by/4.0)
#
# +
# %matplotlib inline
from modsim import *
# -
# ## Rabbit is Rich
#
# This notebook starts with a version of the rabbit population growth model. You will modify it using some of the tools in Chapter 5.
#
# Here's the `System` object from the previous diagnostic. Notice that it includes system parameters, which don't change while the simulation is running, and population variables, which do.
#
# We're going to improve that by pulling the population variables into a `State` object.
# +
system = System(t0 = 0,
t_end = 20,
juvenile_pop0 = 0,
adult_pop0 = 10,
birth_rate = 0.9,
mature_rate = 0.33,
death_rate = 0.5)
system
# -
# In the following cells, define a `State` object named `init` that contains two state variables, `juveniles` and `adults`, with initial values `0` and `10`. Make a version of the `System` object that does NOT contain `juvenile_pop0` and `adult_pop0`, but DOES contain `init`.
state = State(juveniles = 0,
adults = 10)
system = System(t0 = 0,
t_end = 20,
birth_rate = 0.9,
mature_rate = 0.33,
death_rate = 0.5,
init = state )
# Here's the version of `run_simulation` from last time:
def run_simulation(system):
"""Runs a proportional growth model.
Adds TimeSeries to `system` as `results`.
system: System object
"""
juveniles = TimeSeries()
juveniles[system.t0] = system.juvenile_pop0
adults = TimeSeries()
adults[system.t0] = system.adult_pop0
for t in linrange(system.t0, system.t_end):
maturations = system.mature_rate * juveniles[t]
births = system.birth_rate * adults[t]
deaths = system.death_rate * adults[t]
if adults[t] > 30:
market = adults[t] - 30
else:
market = 0
juveniles[t+1] = juveniles[t] + births - maturations
adults[t+1] = adults[t] + maturations - deaths - market
system.adults = adults
system.juveniles = juveniles
# In the cell below, write a version of `run_simulation` that works with the new `System` object.
#
# Hint: you only have to change two lines.
def run_simulation(system):
"""Runs a proportional growth model.
Adds TimeSeries to `system` as `results`.
system: System object
"""
juveniles = TimeSeries()
juveniles[system.t0] = system.init.juveniles
adults = TimeSeries()
adults[system.t0] = system.init.adults
for t in linrange(system.t0, system.t_end):
maturations = system.mature_rate * juveniles[t]
births = system.birth_rate * adults[t]
deaths = system.death_rate * adults[t]
if adults[t] > 30:
market = adults[t] - 30
else:
market = 0
juveniles[t+1] = juveniles[t] + births - maturations
adults[t+1] = adults[t] + maturations - deaths - market
system.adults = adults
system.juveniles = juveniles
# Test your changes in `run_simulation`:
run_simulation(system)
system.adults
# Here's a version of `plot_results` that plots both the adult and juvenile `TimeSeries`.
def plot_results(system, title=None):
"""Plot the estimates and the model.
system: System object with `results`
"""
newfig()
plot(system.adults, 'bo-', label='adults')
plot(system.juveniles, 'gs-', label='juveniles')
decorate(xlabel='Season',
ylabel='Rabbit population',
title=title)
# And here are the results.
plot_results(system, title='Proportional growth model')
# ### Bonus question
#
# Write a version of `run_simulation` that puts the results into a single `TimeFrame` named `results`, rather than two `TimeSeries` objects.
#
# Write a version of `plot_results` that can plot the results in this form.
#
# WARNING: This question is substantially harder, and requires you to have a good understanding of everything in Chapter 5. We don't expect most people to be able to do this exercise at this point.
def run_simulation(system):
"""Runs a proportional growth model.
Adds TimeSeries to `system` as `results`.
system: System object
"""
frame = TimeFrame(columns = system.init.index)
frame.loc[system.t0] = system.init
juveniles = TimeSeries()
juveniles[system.t0] = system.init.juveniles
adults = TimeSeries()
adults[system.t0] = system.init.adults
for t in linrange(system.t0, system.t_end):
frame.loc[t+1] =
maturations = system.mature_rate * frame.juveniles[t]
births = system.birth_rate * frame.adults[t]
deaths = system.death_rate * frame.adults[t]
if adults[t] > 30:
market = adults[t] - 30
else:
market = 0
juveniles[t+1] = juveniles[t] + births - maturations
adults[t+1] = adults[t] + maturations - deaths - market
system.adults = adults
system.juveniles = juveniles
system.results = frame
run_simulation(system)
def plot_results(system, title=None):
"""Plot the estimates and the model.
system: System object with `results`
"""
newfig()
plot(system.adults, 'bo-', label='adults')
plot(system.juveniles, 'gs-', label='juveniles')
decorate(xlabel='Season',
ylabel='Rabbit population',
title=title)
plot_results(system)
|
code/rabbits3-Mine.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
import json
import numpy as np
import matplotlib.pyplot
mode = 'single_alternate'
if mode == 'single':
condition_tapess_dir = "condition_tapes_single"
elif mode == 'single_alternate':
condition_tapess_dir = "condition_tapes_single_alternate"
elif mode == 'double_alternate':
condition_tapess_dir = "condition_tapes_double_alternate"
gen_parent_dir = "lstm_conditional_generate_levels_txt_by_tape"
ix_to_name = {
0 : 'question',
1 : 'coin',
2 : 'enemy',
3 : 'pipe',
4 : 'cannon'
}
# + code_folding=[]
ix_to_element = {
0 : ["Q", "?"],
1 : ["o"],
2 : ["E"],
3 : ["<", ">", "[", "]"],
4 : ["b", "B"],
}
# -
def at_least_one_of_A_is_in_B(A:list, B:list):
return any(a in B for a in A)
# +
scoreboard_Y = {
"question" : [],
"coin" : [],
"enemy" : [],
"pipe" : [],
"cannon" : []
}
scoreboard_N = {
"question" : [],
"coin" : [],
"enemy" : [],
"pipe" : [],
"cannon" : []
}
for tape_fname in os.listdir(condition_tapess_dir):
tape_name = tape_fname.split('.')[0]
condition_tapes_path = f"{condition_tapess_dir}/{tape_fname}"
with open(condition_tapes_path, 'r') as json_f:
condition_tape = np.array(json.load(json_f))[:,:-1].T
gen_dir = f"{gen_parent_dir}/{tape_name}"
scores = []
for gen_txt in [fname for fname in os.listdir(gen_dir) if fname.split('.')[-1] == 'txt']:
with open(f'{gen_dir}/{gen_txt}', 'r') as txt_f:
infile = np.array([list(line.rstrip()) for line in txt_f.readlines()]).T
infile = infile[3:] # exclude the seed
assert infile.shape[0] == condition_tape.shape[0]
for col_ix in np.arange(condition_tape.shape[0]):
for condition_ix in range(5):
if condition_tape[col_ix][condition_ix] == 1:
if at_least_one_of_A_is_in_B(ix_to_element[condition_ix], infile[col_ix]):
scoreboard_Y[ix_to_name[condition_ix]].append(1)
else:
scoreboard_Y[ix_to_name[condition_ix]].append(0)
else:
if at_least_one_of_A_is_in_B(ix_to_element[condition_ix], infile[col_ix]):
scoreboard_N[ix_to_name[condition_ix]].append(0)
else:
scoreboard_N[ix_to_name[condition_ix]].append(1)
# -
scoreboard_Y_stats = {k:np.mean(v) for k, v in scoreboard_Y.items()}
scoreboard_N_stats = {k:np.mean(v) for k, v in scoreboard_N.items()}
scoreboard_Y_stats, scoreboard_N_stats
|
notebooks/single_element_conditioning_analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="IYfWdgdIG_yb"
# # Tensorflow & Pytorch comparison with CIFAR10
# > The purpose of this notebook is to layout the typical workflow in a simple feed-forward classification problem using Tensorflow/Keras and Pytorch.
#
# - toc: true
# - badges: true
# - comments: true
# - categories: [jovian, tensorflow, keras, pytorch, fastpages, jupyter]
# - image: images/tf-pytorch-1.png
# + [markdown] colab_type="text" id="0ULp9v2nG_mx"
# # About
#
# The third assigment of the course [Pytorch Zero to GANS](https://jovian.ml/forum/c/pytorch-zero-to-gans/18) run by [JOVIAN.ML](https://www.jovian.ml) is to go through a simple classification problem using the CIFAR10 dataset. The course uses Pytorch and as an option course attendees were asked to use Tensorflow to repeat the task.
#
# The training was done on Google Colab with GPU.
# The good thing with running on Colab (and Binder, Kaggle to name a few others) is there is not much setup involved. Import the required libraries and off you go!
#
# The Tensorflow version will be done first followed by the Pytorch version. The course assignment was in Pytorch (as the course title suggests) so the TF example was made to match that setup.
# + [markdown] colab_type="text" id="u6BBRnOaHZZA"
# # Colab setup
# > You will have to use your own API credentials.
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 1515, "status": "ok", "timestamp": 1591963274573, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="mmYBWkoE0Ss6" outputId="4a158194-f49c-446e-a54b-caf08f4c293d"
from google.colab import drive
drive.mount('/content/drive', force_remount=True)
import os
root_dir = '/content/drive/My Drive/Colab Notebooks/jovian/'
# + [markdown] colab_type="text" id="Qs3u005HsH-J"
# # Tensorflow/Keras
# + [markdown] colab_type="text" id="tgIYAij6Hvzj"
# ## Import libraries
# + colab={} colab_type="code" id="c7LWCgscsHyE"
from __future__ import print_function
import tensorflow as tf
import keras
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.utils import to_categorical
import os
import numpy as np
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
# %matplotlib inline
# + [markdown] colab_type="text" id="DatE3rUEPekF"
# > Data augmentation not used because this was not used in the Pytorch example below. **
# + colab={} colab_type="code" id="c0BrqrvvsHwA"
batch_size=128
epochs=20
data_augmentation=False
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" executionInfo={"elapsed": 7001, "status": "ok", "timestamp": 1591960700899, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="di4bDrlfsHss" outputId="3ba4a936-a66e-4d5a-e8bb-1a85c7823c7f"
(X,y), (x_test,y_test) = cifar10.load_data()
# + [markdown] colab_type="text" id="ChaEiDqxJ9VF"
# ## Explore the CIFAR10 dataset
# + colab={"base_uri": "https://localhost:8080/", "height": 85} colab_type="code" executionInfo={"elapsed": 512, "status": "ok", "timestamp": 1591945219534, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="JHAQQxntoIBg" outputId="bcc1309e-5239-469f-e401-0b523f68c367"
# collapse-hide
print(X.shape)
print(y.shape)
print(x_test.shape)
print(y_test.shape)
# + colab={} colab_type="code" id="1wl8IQVU1wQp"
y_squeeze = np.squeeze(y)
# + [markdown] colab_type="text" id="vlIAVkReLB15"
#
# + colab={} colab_type="code" id="p86TdZ17n7gE"
# Create a classes list
classes = ['airplane',
'automobile',
'bird',
'cat',
'deer',
'dog',
'frog',
'horse',
'ship',
'truck']
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 450, "status": "ok", "timestamp": 1591960703920, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="fHCr8_rlnbk2" outputId="91fc7302-4af7-4a42-a2e1-4cfd92ecf846"
#unique classes
unique_classes = np.unique(y)
num_classes = len(unique_classes)
unique_classes
# + colab={} colab_type="code" id="NPx-S1Cpo95H"
unique, count = np.unique(y, return_counts=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 187} colab_type="code" executionInfo={"elapsed": 949, "status": "ok", "timestamp": 1591945303908, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="Co2jPApi3PpT" outputId="bfd55e50-10cf-411c-ba99-9b508ac69305"
for i in range(len(unique)):
print(f' class {classes[i] } has {count[i].item()} images')
# + colab={"base_uri": "https://localhost:8080/", "height": 377} colab_type="code" executionInfo={"elapsed": 1859, "status": "ok", "timestamp": 1591960715062, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="oMPVnhUqmSAD" outputId="9535509b-77a7-448b-9a5b-816720853647"
#collapse-hide
fig = plt.figure(figsize=(6,6))
for i in range(9):
plt.subplot(3,3,i+1)
plt.imshow(X[i])
plt.show()
# + [markdown] colab_type="text" id="TPt9UJ8TKkJr"
# ## Prepare the data for training
# > The Pytorch assignment used a 10% split of the training set for the validation set done using the randome_split Pytorch utility.
# So I will use scikitlearn's train_test_split to do the same the same on the training set.
# + colab={} colab_type="code" id="MVKIILQYmEqa"
x_train, x_val, y_train, y_val= train_test_split(X, y,
test_size=0.1,
random_state=42)
# + colab={} colab_type="code" id="C-ebj8Jro_fx"
x_train=x_train.astype('float32')/255.
x_val=x_val.astype('float32')/255.
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" executionInfo={"elapsed": 393, "status": "ok", "timestamp": 1591960724148, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="_oWs2srRp4-x" outputId="8afc8dcc-8526-4ccb-9700-57d1431cc92b"
y_train = to_categorical(y_train, num_classes)
y_val = to_categorical(y_val, num_classes)
print(x_train.shape)
print(y_train.shape)
# + colab={} colab_type="code" id="4HsFJXpu5BYv"
y_train = np.squeeze(y_train)
y_val=np.squeeze(y_val)
# + [markdown] colab_type="text" id="RFo8S9pfI89L"
# ## Set up a simple Keras model
# + colab={} colab_type="code" id="Sd7Ey0NbsHkv"
model = Sequential()
model.add(Flatten(input_shape=(32,32,3)))
model.add(Dense(32,activation = 'relu'))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# + colab={"base_uri": "https://localhost:8080/", "height": 289} colab_type="code" executionInfo={"elapsed": 6574, "status": "ok", "timestamp": 1591960742670, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="L8DWGIbRsHii" outputId="3a138534-96b5-4681-c502-9d83cec018d7"
model.summary()
# + [markdown] colab_type="text" id="07qGOb9vIbPY"
# > The number of model parameters must match that of Pytorch.
# + colab={} colab_type="code" id="KwzW957IsHgd"
opt = keras.optimizers.SGD(learning_rate=1e-3)
# + colab={} colab_type="code" id="cqIE2SYgsHcS"
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics = ['accuracy'])
# + colab={} colab_type="code" id="dA2Px-XpsHaK"
H = model.fit(x_train, y_train,
batch_size=batch_size,
epochs = 20,
validation_data=(x_val,y_val))
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 412, "status": "ok", "timestamp": 1591960804998, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="oEOsDTrmsHYM" outputId="242a3d51-0bf7-4167-c6d3-cf47f1e23b44"
print(H.history.keys())
# + colab={"base_uri": "https://localhost:8080/", "height": 281} colab_type="code" executionInfo={"elapsed": 565, "status": "ok", "timestamp": 1591960832937, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="SmSY1ubGltUC" outputId="5ef043ef-fa45-49f7-d624-913d2ee6505d"
plt.title("ACCURACY")
plt.plot(H.history['accuracy'], label='train_acc')
plt.plot(H.history['val_accuracy'], label = 'val_acc')
plt.legend()
plt.show()
# + [markdown] colab_type="text" id="4vUwRMMqJMjk"
# ## Evaluate the model on Test data
# + colab={} colab_type="code" id="hPIvx4G9sHPV"
x_test =x_test.astype('float32')/255.
y_test = to_categorical(y_test, num_classes)
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 488, "status": "ok", "timestamp": 1591960839225, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="qahYxUh77dc1" outputId="22e92eba-d01b-4536-d4b7-dfbd1d308279"
y_test.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" executionInfo={"elapsed": 1369, "status": "ok", "timestamp": 1591960841719, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="pl9tKFgysHL1" outputId="15760bb6-2a62-4f12-9802-47cdfc35017b"
model.evaluate(x_test, y_test)
# + [markdown] colab_type="text" id="DMgJD4OEJTdZ"
# ---
# + [markdown] colab_type="text" id="uljWBIal0Nmk"
# # Pytorch
# This is Assignment 03 modified for blogging purposes.
# + [markdown] colab_type="text" id="drR6aqOrJd4N"
# ## Import libraries
# + colab={} colab_type="code" id="1FLp-PX50Nmr"
import torch
import torchvision
import numpy as np
import matplotlib.pyplot as plt
import torch.nn as nn
import torch.nn.functional as F
from torchvision.datasets import CIFAR10
from torchvision.transforms import ToTensor
from torchvision.utils import make_grid
from torch.utils.data.dataloader import DataLoader
from torch.utils.data import random_split
# %matplotlib inline
# + colab={} colab_type="code" id="zh7_TRdY0Nmu"
# Project name used for jovian.commit
project_name = '03-cifar10-feedforward'
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 556, "status": "ok", "timestamp": 1591963295125, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="JxspjbOc1AYP" outputId="7d54baf7-6dbe-4e2e-ea74-a7bf2b5b9eb0"
proj_dir = os.path.join(root_dir, project_name)
proj_dir
# + [markdown] colab_type="text" id="3bYlJbLM0Nmy"
# ## Exploring the CIFAR10 dataset
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 2998, "status": "ok", "timestamp": 1591963299367, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="ByPGJAuk0Nm5" outputId="3a25b438-f0f6-4e08-f2b7-d8f28f21ad5c"
dataset = CIFAR10(root=proj_dir, download=True, transform=ToTensor())
test_dataset = CIFAR10(root=proj_dir, train=False, transform=ToTensor())
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 670, "status": "ok", "timestamp": 1591963301066, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="U04deHRK0Nm_" outputId="d9171683-c29d-4dd0-d62f-3e9080b3a4ad"
dataset_size = len(dataset)
dataset_size
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 430, "status": "ok", "timestamp": 1591963306805, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="tixZRp_c0NnD" outputId="7b8cb147-8cff-4e00-c962-7a39eb375272"
test_dataset_size = len(test_dataset)
test_dataset_size
# + colab={"base_uri": "https://localhost:8080/", "height": 187} colab_type="code" executionInfo={"elapsed": 419, "status": "ok", "timestamp": 1591963308132, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="TniLthZd0NnG" outputId="6eaba9f2-b410-4052-93ce-2b3826fd84dc"
classes = dataset.classes
classes
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 689, "status": "ok", "timestamp": 1591963311095, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="HBPAZzV60NnJ" outputId="73117102-e4d1-4824-d01a-4d236d5a10fe"
num_classes = len(dataset.classes)
num_classes
# + [markdown] colab_type="text" id="FgLqsqjE0NnQ"
# Note that this dataset consists of 3-channel color images (RGB). Let us look at a sample image from the dataset. `matplotlib` expects channels to be the last dimension of the image tensors (whereas in PyTorch they are the first dimension), so we'll the `.permute` tensor method to shift channels to the last dimension. Let's also print the label for the image.
# + [markdown] colab_type="text" id="3BY0rb6xCrSx"
# #### The number of images belonging to each class
# [Credit](https://jovian.ml/shravankumar224/03-cifar10-feedforward)
# + colab={"base_uri": "https://localhost:8080/", "height": 281} colab_type="code" executionInfo={"elapsed": 599, "status": "ok", "timestamp": 1591963313582, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="LUG__UR9C1SH" outputId="39b00c8f-e9b4-4f15-b853-215f69ed58a7"
#get the label of the dataset using the [1] index
img, label = dataset[1]
label_of_image_1 = dataset[1][1]
title= str(label_of_image_1) + ' is a ' + classes[label_of_image_1]
plt.imshow(img.permute(1,2,0))
plt.title(title)
plt.show()
# + colab={} colab_type="code" id="ZOI7VIQKC1PG"
label_of_train_images=[]
for i in range(len(dataset)):
label_of_train_image = dataset[i][1]
label_of_train_images.append(label_of_train_image)
# + colab={} colab_type="code" id="GRTUn4hFWl8j"
num_unique_train_labels = np.unique(label_of_train_images)
# + colab={} colab_type="code" id="7TOuQ9wQC1AB"
uniq_image_count = torch.stack([(torch.tensor(label_of_train_images)==i).sum() for i in num_unique_train_labels])
# + colab={"base_uri": "https://localhost:8080/", "height": 187} colab_type="code" executionInfo={"elapsed": 601, "status": "ok", "timestamp": 1591963325656, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="KLaRm2dojS6N" outputId="e96f63ec-f1da-4d69-d7d8-a0f2286af8f3"
for i in range(len(uniq_image_count)):
print(f' class {classes[i] } has {uniq_image_count[i].item()} images')
# + [markdown] colab_type="text" id="XdUJkJO_0Nni"
# ## Prepare the data for training
# + colab={} colab_type="code" id="ReSHXHt_0Nnj"
torch.manual_seed(43)
val_size = 5000
train_size = len(dataset) - val_size
# + [markdown] colab_type="text" id="K1dmQO840Nnm"
# Let's use the `random_split` method to create the training & validation sets
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 455, "status": "ok", "timestamp": 1591963329514, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="CiqmoFfy0Nnm" outputId="4e569c1e-701c-46c9-852c-947385c3959e"
train_ds, val_ds = random_split(dataset, [train_size, val_size])
len(train_ds), len(val_ds)
# + [markdown] colab_type="text" id="5-aXV6dl0Nnp"
# We can now create data loaders to load the data in batches.
# + colab={} colab_type="code" id="3Iof9TIh0Nnq"
batch_size=128
# + colab={} colab_type="code" id="ogdfhphL0Nnt"
train_loader = DataLoader(train_ds, batch_size, shuffle=True, num_workers=4, pin_memory=True)
val_loader = DataLoader(val_ds, batch_size*2, num_workers=4, pin_memory=True)
test_loader = DataLoader(test_dataset, batch_size*2, num_workers=4, pin_memory=True)
# + [markdown] colab_type="text" id="IPF3VmAi0Nnw"
# Let's visualize a batch of data using the `make_grid` helper function from Torchvision.
# + colab={"base_uri": "https://localhost:8080/", "height": 357} colab_type="code" executionInfo={"elapsed": 2997, "status": "ok", "timestamp": 1591963338847, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="mAkvcKXd0Nnw" outputId="5a9af154-3393-4073-cf89-2e19c5a6c793"
#collapse-hide
viz_loader = DataLoader(train_ds, 9, shuffle=True, num_workers=4, pin_memory=True)
for images, _ in viz_loader:
plt.figure(figsize=(6,6))
plt.axis('off')
plt.imshow(make_grid(images, nrow=3).permute((1, 2, 0)))
break
# + [markdown] colab_type="text" id="t0BBlFKN0Nn1"
# ## Base Model class & Training on GPU
#
# Let's create a base model class, which contains everything except the model architecture i.e. it wil not contain the `__init__` and `__forward__` methods. We will later extend this class to try out different architectures. In fact, you can extend this model to solve any image classification problem.
# + colab={} colab_type="code" id="KVCpxcbxIOLP"
def accuracy(outputs, labels):
_, preds = torch.max(outputs, dim =1)
return torch.tensor(torch.sum(preds== labels).item()/len(preds))
# + colab={} colab_type="code" id="VwKwXl8e0Nn4"
class ImageClassificationBase(nn.Module):
def training_step(self, batch):
images, labels = batch
out = self(images) # Generate predictions
loss = F.cross_entropy(out, labels) # Calculate loss
return loss
def validation_step(self, batch):
images, labels = batch
out = self(images) # Generate predictions
loss = F.cross_entropy(out, labels) # Calculate loss #change from cross_entropy
acc = accuracy(out, labels) # Calculate accuracy
return {'val_loss': loss, 'val_acc': acc}
def validation_epoch_end(self, outputs):
batch_losses = [x['val_loss'] for x in outputs]
epoch_loss = torch.stack(batch_losses).mean() # Combine losses
batch_accs = [x['val_acc'] for x in outputs]
epoch_acc = torch.stack(batch_accs).mean() # Combine accuracies
return {'val_loss': epoch_loss.item(), 'val_acc': epoch_acc.item()}
def epoch_end(self, epoch, result):
print("Epoch [{}], val_loss: {:.4f}, val_acc: {:.4f}".format(epoch, result['val_loss'], result['val_acc']))
# + [markdown] colab_type="text" id="qv4lPQCm0Nn8"
# We can also use the exact same training loop as before. I hope you're starting to see the benefits of refactoring our code into reusable functions.
# + colab={} colab_type="code" id="oi5uwzUZ0Nn9"
def evaluate(model, val_loader):
outputs = [model.validation_step(batch) for batch in val_loader]
return model.validation_epoch_end(outputs)
def fit(epochs, lr, model, train_loader, val_loader, opt_func=torch.optim.SGD):
history = []
optimizer = opt_func(model.parameters(), lr)
for epoch in range(epochs):
# Training Phase
for batch in train_loader:
loss = model.training_step(batch)
loss.backward()
optimizer.step()
optimizer.zero_grad()
# Validation phase
result = evaluate(model, val_loader)
model.epoch_end(epoch, result)
history.append(result)
return history
# + [markdown] colab_type="text" id="vYm0z8ig0NoA"
# Finally, let's also define some utilities for moving out data & labels to the GPU, if one is available.
# + [markdown] colab_type="text" id="3wIA_kPH0NoN"
# Let us also define a couple of helper functions for plotting the losses & accuracies.
# + colab={} colab_type="code" id="lkFub-dt0NoO"
def plot_losses(history):
losses = [x['val_loss'] for x in history]
plt.plot(losses, '-x')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('Loss vs. No. of epochs');
# + colab={} colab_type="code" id="hhat8wFP0NoR"
def plot_accuracies(history):
accuracies = [x['val_acc'] for x in history]
plt.plot(accuracies, '-o')
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.title('Pytorch Accuracy vs. No. of epochs');
# + [markdown] colab_type="text" id="VKfJ8M1l0NoU"
# Let's move our data loaders to the appropriate device.
# + colab={} colab_type="code" id="K04lJ-1nMQk4"
input_size = 3*32*32
hidden_size = 32
output_size = 10
# + colab={} colab_type="code" id="TqejXP-N0Nob"
class CIFAR10Model(ImageClassificationBase):
def __init__(self):
super().__init__()
#dd hidden layer
self.linear1 = nn.Linear(input_size, hidden_size)
#output layer
self.linear2 = nn.Linear(hidden_size, output_size)
def forward(self, xb):
# Flatten images into vectors
out = xb.view(xb.size(0), -1)
# Apply layers & activation functions
out = self.linear1(out)
out = F.relu(out)
out = self.linear2(out)
return out
# + [markdown] colab_type="text" id="MHD3aVWC0Noe"
# You can now instantiate the model, and move it the appropriate device.
# + colab={"base_uri": "https://localhost:8080/", "height": 68} colab_type="code" executionInfo={"elapsed": 897, "status": "ok", "timestamp": 1591963387352, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="ezQXHI8ZfDZN" outputId="c92428be-50d8-4364-e5f7-38d2df6efadc"
#USING A GPU
torch.cuda.is_available()
def get_default_device():
"""Pick GPU if available, else CPU"""
if torch.cuda.is_available():
return torch.device('cuda')
else:
return torch.device('cpu')
device = get_default_device()
print(device)
def to_device(data, device):
"""Move tensor(s) to chosen device"""
if isinstance(data, (list,tuple)):
return [to_device(x, device) for x in data]
return data.to(device, non_blocking=True)
for images, labels in train_loader:
print(images.shape)
images = to_device(images, device)
print(images.device)
break
# + colab={} colab_type="code" id="T34USxZp0Nof"
model = to_device(CIFAR10Model(), device)
# + colab={"base_uri": "https://localhost:8080/", "height": 153} colab_type="code" executionInfo={"elapsed": 493, "status": "ok", "timestamp": 1591963389772, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="kt-W7IOhMh5Q" outputId="cf504ac4-eabe-4507-e529-e2e1806b450c"
print(model.parameters)
for t in model.parameters():
print(t.shape)
# + [markdown] colab_type="text" id="BOEewwMm0Noi"
# Before you train the model, it's a good idea to check the validation loss & accuracy with the initial set of weights.
# + colab={"base_uri": "https://localhost:8080/", "height": 68} colab_type="code" executionInfo={"elapsed": 399, "status": "ok", "timestamp": 1591963391646, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="WcCpjNPaLrgS" outputId="1e1b8a07-6106-42f2-f8f7-439f4d67831c"
#collapse-hide
pytorch_total_params = sum(p.numel() for p in model.parameters())
print('Total number of parameters: ',pytorch_total_params)
pytorch_trainable_params = sum(p.numel() for p in model.parameters() if p.requires_grad)
print('Trainable parameters: ', pytorch_trainable_params)
print('layers + activations',len(list(model.parameters())))
# + [markdown] colab_type="text" id="7z2SKX6pLVkP"
# > ** The number of model parameters matches that of TF/Keras **
# + colab={} colab_type="code" id="h5fGiMF1ffQV"
class DeviceDataLoader():
"""Wrap a dataloader to move data to a device"""
def __init__(self, dl, device):
self.dl = dl
self.device = device
def __iter__(self):
"""Yield a batch of data after moving it to device"""
for b in self.dl:
yield to_device(b, self.device)
def __len__(self):
"""Number of batches"""
return len(self.dl)
# + colab={} colab_type="code" id="70hx2EcFfjtg"
train_loader = DeviceDataLoader(train_loader, device)
val_loader = DeviceDataLoader(val_loader, device)
test_loader= DeviceDataLoader(test_loader, device)
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 815, "status": "ok", "timestamp": 1591963462521, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="dS7BtXmJU-92" outputId="c8ea90b9-7a3f-4403-c8bd-4ad7af5d57c8"
for xb, yb in val_loader:
print('xb.device:', xb.device)
xb = xb.view(xb.size(0), -1)
break
# + [markdown] colab_type="text" id="_zGnJzCdXi05"
#
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 1555, "status": "ok", "timestamp": 1591963470724, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="kT265vU10Noi" outputId="437397e8-1e3d-431d-a235-672324acdcdb"
history = [evaluate(model, val_loader)]
history
# + colab={"base_uri": "https://localhost:8080/", "height": 697} colab_type="code" executionInfo={"elapsed": 175369, "status": "ok", "timestamp": 1591963682831, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="5GkUyJpY0Nou" outputId="7932087f-7a09-4705-f692-973b12de7878"
history = fit(20, 1e-3, model, train_loader, val_loader)
history
# + [markdown] colab_type="text" id="YNvy2L4t0No1"
# Plot the losses and the accuracies to check if you're starting to hit the limits of how well your model can perform on this dataset. You can train some more if you can see the scope for further improvement.
# + [markdown] colab_type="text" id="pHH9rmMQME3G"
#
# + colab={"base_uri": "https://localhost:8080/", "height": 295} colab_type="code" executionInfo={"elapsed": 864, "status": "ok", "timestamp": 1591964135308, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="G4ixjBMj0No4" outputId="d5d00b55-2c49-4564-adce-78a635d6177d"
plot_accuracies(history)
# + [markdown] colab_type="text" id="ryCq150C0No7"
# ## Finally, evaluate the model on the test dataset report its final performance.
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 2251, "status": "ok", "timestamp": 1591963749259, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09309547355199345888"}, "user_tz": -60} id="mZ7rSZhG0No7" outputId="4fbe46d6-4f9f-40af-80b6-fa00e694c584"
evaluate(model, test_loader)
# + [markdown] colab_type="text" id="hfBqMHbOQ0r2"
# # Results
#
# Accuracy
# Tensorflow/Keras : 0.3619999885559082
# Pytorch: 0.33740234375
#
# The differences could be due to very little training and hence lack of convergence of the solution, the randomness of the weights intialisation and differences in the library implementations in TF and Pytorch and other stuff I am not aware of ;)
# + [markdown] colab_type="text" id="yYAWKTF3MGLf"
# # Concluding comments
# This exercise was not to get an exact match of accuracy but to demonstrate the constructs between TF and Pytorch.
#
# The Jovian course [Pytorch Zero to GANS](https://jovian.ml/forum/c/pytorch-zero-to-gans/18) is a great introduction to Machine Learning. I am enjoying
# - Collaborating with others
# - Working through examples
# - Finishing assignments and submitting for approval
# - Blogging about my experiences
# - Staying enthusiastic about ML!
#
# Thanks and appreciation to:
# - [<NAME>](https://www.fast.ai/) and <NAME> for the [Fastpages](https://github.com/fastai/fastpages) framework in which this blog is written as a Jupyter notebook.
# + colab={} colab_type="code" id="sD_WytFZMK45"
|
_notebooks/2020-06-12-tfkeras-pytorch-cifar10.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Twitter Sentiment Analysis Project
#
# ## Part I - Tweets collection
# ## Part II - Sentiment Analysis
# python standard library
import os
# library to communicate with the Twitter API
import tweepy
import pandas as pd
import string
import re
from nltk.corpus import stopwords
import nltk.collocations as nc
import spacy
from nltk.sentiment.vader import SentimentIntensityAnalyzer as SIA
# add additional stop words to the basic English list and save as a set
en_stopwords = set(stopwords.words('english')+ ['RT', 'crash', 'accident', 'rt'])
nlp = spacy.load('en_core_web_sm')
# ### Accessing Environment Variables
# +
# Note: Twitter account access keys are saved as environment variables
# accessing environment variable in the code
consumer_key = os.environ.get('TWITTER_CONSUMER_KEY')
consumer_secret = os.environ.get('TWITTER_CONSUMER_SECRET')
access_token_key = os.environ.get('TWITTER_ACCESS_TOKEN_KEY')
access_token_secret = os.environ.get('TWITTER_ACCESS_TOKEN_SECRET')
# -
# test if the keys are in the runtime enviroment
print('Found consumer_key:', bool(consumer_key))
print('Found consumer_secret:', bool(consumer_secret))
print('Found access_token_key:', bool(access_token_key))
print('Found access_token_secret:', bool(access_token_secret))
# +
# get Twitter authorization
auth = tweepy.OAuthHandler(consumer_key, consumer_secret)
auth.set_access_token(access_token_key, access_token_secret)
api = tweepy.API(auth)
# -
# load tweets from my home timeline
public_tweets = api.home_timeline()
for tweet in public_tweets:
print(tweet.text)
# ### Using tweepy to search for tweets in a particular area
#Search for tweets about car accidents within 10 miles of Central Park and MLK in Denver
results = api.search('accident OR crash OR collision', geocode='39.7602773,-104.8904864,10mi')
# How many tweets found?
len(results)
# Display text from the last tweet to check content
results[14]._json['text']
# +
### Extracting the tweets
# -
def extract_text(tweets):
"""Returns a list of strings holding the text of the tweets"""
return [tweet._json['text'] for tweet in tweets]
text_results = extract_text(results)
text_results[:3]
# ### Gathering the max number of tweets on the topic
from tweepy import Cursor
# searching for tweets and saving text only
tweets = [tweet._json['text'] for tweet in Cursor(api.search,'accident OR crash OR collision', geocode='39.7602773,-104.8904864,10mi').items()]
# How many tweets found?
len(tweets)
# look at the first 3 tweets
tweets[:3]
# ### Clean the tweets
# +
def preprocess_text(text_docs):
"""
text preprocessing using spacy:
lowercase, tokenize, remove whitespaces, remove stopwords, lemmatize;
returns list of cleaned, preprocessed strings
"""
# remove punctuation
table = str.maketrans({key: None for key in string.punctuation})
docs = [d.translate(table) for d in text_docs]
# replace new lines with spaces
docs = [re.sub('[\r\n]+', ' ', d) for d in docs]
# replace URLs with spaces
docs = [re.sub('https[\w]*', ' ', d) for d in docs]
# replace digits with space
docs = [re.sub('\d', ' ', d) for d in docs]
# replace multiple spaces with one space
docs = [re.sub('\s\s+', ' ', d) for d in docs]
# use spacy for lemmatization
spacy_docs = [nlp(d) for d in docs]
docs=[]
for d in spacy_docs: #for each document
temp_doc=[]
for w in d: #for each word in a document
#remove stopwords, pronouns, numbers and "wods" that are shorter than 2 and longer than 20 letters
if w.lemma_ in en_stopwords or w.lemma_.isdigit() or len(w.lemma_) > 20 or len(w.lemma_) < 2:
continue #skip the word and go back to the beginning of the loop
elif w.lemma_ != '-PRON-':
temp_doc.append(w.lower_) #append the lower case word
docs.append(' '.join(temp_doc))
return docs
# -
cleaned_tweets = preprocess_text(tweets) #call preprocess_text function to clean up the tweets
cleaned_tweets[:3] #display first three tweets after clean-up
# ### Write tweets to file
# specify file name
filename = 'tweets_denver_carcrashes_week8_2.txt'
def write_out_tweets(filename, lines):
"""Writes tweets to a text file"""
with open(filename, 'w', encoding='utf-8') as out_file: #encoding='utf-8' - keep only regular text characters
for line in lines:
out_file.write(line + os.linesep)
# call write_out_tweets function to save cleaned results to the file
write_out_tweets(filename, cleaned_tweets)
#wrtie unprocessed tweets to a file
write_out_tweets("text_only_week8_2.txt", text_results)
#Does the file exist?
#using os library since running on Windows 10
os.path.isfile(filename)
#Check file size (to make sure it is not empty)
os.stat(filename).st_size
# ### Reading tweets using pandas
def read_in_tweets(filename):
"""reads tweets from a file into a data frame"""
return pd.read_csv(filename, index_col=False, header=None, names=['tweet'])
cleaned_tweets_restored = read_in_tweets(filename) #call read_in_tweets function to read tweets into a df
cleaned_tweets_restored.head() #display the first few tweets
type(cleaned_tweets_restored), cleaned_tweets_restored.shape #check the data type and its size
# ## Sentiment Analysis
# create the sentiment analysis object
sia = SIA()
# apply polarity_scores function to the tweets and save results in a new column
cleaned_tweets_restored['polarity'] = cleaned_tweets_restored['tweet'].apply(sia.polarity_scores)
cleaned_tweets_restored.head() #check results
# create 4 new columns using keys as column names
#apply Series constructor to the 'polarity' columns to split values in the dictionary into separate columns
polarity_df = cleaned_tweets_restored['polarity'].apply(pd.Series)
polarity_df.head() #check results
#join the data frames into one
cleaned_tweets_restored = cleaned_tweets_restored.join([polarity_df])
cleaned_tweets_restored.head() #check results
# drop the original 'polarity' column
cleaned_tweets_restored = cleaned_tweets_restored.drop(['polarity'], axis = 1)
cleaned_tweets_restored.head() #check results
#create a plot
import matplotlib.pyplot as plt
# hisogram: number of tweets for each sentiment value
plt.hist(cleaned_tweets_restored['compound'], bins = 30)
plt.xlabel('Sentiment')
plt.ylabel('Count')
# remove all neutral tweets using a mask
not_neutral = cleaned_tweets_restored[cleaned_tweets_restored['neu'] != 1.0]
not_neutral.shape
#create histogram without neutral sentiment
plt.hist(not_neutral['compound'], bins = 30)
plt.xlabel('Sentiment')
plt.ylabel('Count')
from nltk import FreqDist, word_tokenize
from itertools import chain
def flatten_word_list(series):
"""returns a list of words"""
return list(chain.from_iterable([word_tokenize(line) for line in series]))
#tweets with positive sentiment
positive = cleaned_tweets_restored[cleaned_tweets_restored['pos'] > 0.35]
#How many positive tweets found?
len(positive)
#Look at the first 20 positive twets
positive[:20]
#list of positive words
positive_words = flatten_word_list(positive['tweet'])
len(positive_words), positive_words[:5] #How many total positive words? Print first five as an example
#create frequency distribution of positive words
pos_fd = FreqDist(positive_words)
# ten most common words in positive tweets
pos_fd.most_common(10)
#tweets with negative sentiment
negative = cleaned_tweets_restored[cleaned_tweets_restored['neg'] > 0.35]
#How many negative tweets found?
len(negative)
#Look at the first 20 negative twets
negative[:20]
#list of negative words
negative_words = flatten_word_list(negative['tweet'])
len(negative_words), negative_words[:5] #How many total positive words? Print first five as an example
#create frequency distribution of negative words
neg_fd = FreqDist(negative_words)
# ten most common words in negative tweets
neg_fd.most_common(10)
# Conclusions:
# 1. Tweets collected using "crash OR accident OR collision" keywords varied depending on time of collection. During day time (output file tweets_denver_carcrashes_week8.txt) they mostly contained posts about traffic accidents within the defined area. In the evening (after evening rush hour, see output file tweets_denver_carcrashes_week8_2.txt), the tweets mostly contained the word "crash" but in relation to the market crash and political discussions. So, there is a need to better define search criteria.
# 2. Due to the topic, the majority of the tweets had more pronounced negative sentiment.
# 3. I excluded the words "crash" and "accident" from the cleaned texts, but it did not really have influence on extracting other meaninful words.
|
TwitterSentimentAnalysis/MSDS_Project_Twitter_Sentiment_Analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Unity ML-Agents Toolkit
# ## Environment Basics
# This notebook contains a walkthrough of the basic functions of the Python API for the Unity ML-Agents toolkit. For instructions on building a Unity environment, see [here](https://github.com/Unity-Technologies/ml-agents/blob/master/docs/Getting-Started-with-Balance-Ball.md).
# ### 1. Set environment parameters
#
# Be sure to set `env_name` to the name of the Unity environment file you want to launch. Ensure that the environment build is in `../envs`.
env_name = "../envs/3DBall" # Name of the Unity environment binary to launch
train_mode = True # Whether to run the environment in training or inference mode
# ### 2. Load dependencies
#
# The following loads the necessary dependencies and checks the Python version (at runtime). ML-Agents Toolkit (v0.3 onwards) requires Python 3.
# +
import matplotlib.pyplot as plt
import numpy as np
import sys
from mlagents.envs.environment import UnityEnvironment
# %matplotlib inline
print("Python version:")
print(sys.version)
# check Python version
if (sys.version_info[0] < 3):
raise Exception("ERROR: ML-Agents Toolkit (v0.3 onwards) requires Python 3")
# -
# ### 3. Start the environment
# `UnityEnvironment` launches and begins communication with the environment when instantiated.
#
# Environments contain _brains_ which are responsible for deciding the actions of their associated _agents_. Here we check for the first brain available, and set it as the default brain we will be controlling from Python.
# +
env = UnityEnvironment(file_name=env_name)
# Set the default brain to work with
default_brain = env.brain_names[0]
brain = env.brains[default_brain]
# -
# ### 4. Examine the observation and state spaces
# We can reset the environment to be provided with an initial set of observations and states for all the agents within the environment. In ML-Agents, _states_ refer to a vector of variables corresponding to relevant aspects of the environment for an agent. Likewise, _observations_ refer to a set of relevant pixel-wise visuals for an agent.
# +
# Reset the environment
env_info = env.reset(train_mode=train_mode)[default_brain]
# Examine the state space for the default brain
print("Agent state looks like: \n{}".format(env_info.vector_observations[0]))
# Examine the observation space for the default brain
for observation in env_info.visual_observations:
print("Agent observations look like:")
if observation.shape[3] == 3:
plt.imshow(observation[0,:,:,:])
else:
plt.imshow(observation[0,:,:,0])
# -
# ### 5. Take random actions in the environment
# Once we restart an environment, we can step the environment forward and provide actions to all of the agents within the environment. Here we simply choose random actions based on the `action_space_type` of the default brain.
#
# Once this cell is executed, 10 messages will be printed that detail how much reward will be accumulated for the next 10 episodes. The Unity environment will then pause, waiting for further signals telling it what to do next. Thus, not seeing any animation is expected when running this cell.
for episode in range(10):
env_info = env.reset(train_mode=train_mode)[default_brain]
done = False
episode_rewards = 0
while not done:
action_size = brain.vector_action_space_size
if brain.vector_action_space_type == 'continuous':
env_info = env.step(np.random.randn(len(env_info.agents),
action_size[0]))[default_brain]
else:
action = np.column_stack([np.random.randint(0, action_size[i], size=(len(env_info.agents))) for i in range(len(action_size))])
env_info = env.step(action)[default_brain]
episode_rewards += env_info.rewards[0]
done = env_info.local_done[0]
print("Total reward this episode: {}".format(episode_rewards))
# ### 6. Close the environment when finished
# When we are finished using an environment, we can close it with the function below.
env.close()
|
notebooks/getting-started.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python3
# ---
# This notebook is designed to run in a IBM Watson Studio default runtime (NOT the Watson Studio Apache Spark Runtime as the default runtime with 1 vCPU is free of charge). Therefore, we install Apache Spark in local mode for test purposes only. Please don't use it in production.
#
# In case you are facing issues, please read the following two documents first:
#
# https://github.com/IBM/skillsnetwork/wiki/Environment-Setup
#
# https://github.com/IBM/skillsnetwork/wiki/FAQ
#
# Then, please feel free to ask:
#
# https://coursera.org/learn/machine-learning-big-data-apache-spark/discussions/all
#
# Please make sure to follow the guidelines before asking a question:
#
# https://github.com/IBM/skillsnetwork/wiki/FAQ#im-feeling-lost-and-confused-please-help-me
#
#
# If running outside Watson Studio, this should work as well. In case you are running in an Apache Spark context outside Watson Studio, please remove the Apache Spark setup in the first notebook cells.
# +
from IPython.display import Markdown, display
def printmd(string):
display(Markdown('# <span style="color:red">'+string+'</span>'))
if ('sc' in locals() or 'sc' in globals()):
printmd('<<<<<!!!!! It seems that you are running in a IBM Watson Studio Apache Spark Notebook. Please run it in an IBM Watson Studio Default Runtime (without Apache Spark) !!!!!>>>>>')
# -
# !pip install pyspark==2.4.5
try:
from pyspark import SparkContext, SparkConf
from pyspark.sql import SparkSession
except ImportError as e:
printmd('<<<<<!!!!! Please restart your kernel after installing Apache Spark !!!!!>>>>>')
# +
sc = SparkContext.getOrCreate(SparkConf().setMaster("local[*]"))
spark = SparkSession \
.builder \
.getOrCreate()
# -
# Welcome to exercise two of week three of “Apache Spark for Scalable Machine Learning on BigData”. In this exercise we’ll work on clustering.
#
# Let’s create our DataFrame again:
#
# +
# delete files from previous runs
# !rm -f hmp.parquet*
# download the file containing the data in PARQUET format
# !wget https://github.com/IBM/coursera/raw/master/hmp.parquet
# create a dataframe out of it
df = spark.read.parquet('hmp.parquet')
# register a corresponding query table
df.createOrReplaceTempView('df')
# -
# Let’s reuse our feature engineering pipeline.
# +
from pyspark.ml.feature import OneHotEncoder, StringIndexer, VectorAssembler, Normalizer
from pyspark.ml.linalg import Vectors
from pyspark.ml import Pipeline
indexer = StringIndexer(inputCol="class", outputCol="classIndex")
encoder = OneHotEncoder(inputCol="classIndex", outputCol="categoryVec")
vectorAssembler = VectorAssembler(inputCols=["x","y","z"],
outputCol="features")
normalizer = Normalizer(inputCol="features", outputCol="features_norm", p=1.0)
pipeline = Pipeline(stages=[indexer, encoder, vectorAssembler, normalizer])
model = pipeline.fit(df)
prediction = model.transform(df)
prediction.show()
# -
# Now let’s create a new pipeline for kmeans.
# +
from pyspark.ml.clustering import KMeans
from pyspark.ml.evaluation import ClusteringEvaluator
kmeans = KMeans(featuresCol="features").setK(14).setSeed(1)
pipeline = Pipeline(stages=[vectorAssembler, kmeans])
model = pipeline.fit(df)
predictions = model.transform(df)
evaluator = ClusteringEvaluator()
silhouette = evaluator.evaluate(predictions)
print("Silhouette with squared euclidean distance = " + str(silhouette))
# -
# We have 14 different movement patterns in the dataset, so setting K of KMeans to 14 is a good idea. But please experiment with different values for K, do you find a sweet spot? The closer Silhouette gets to 1, the better.
#
# https://en.wikipedia.org/wiki/Silhouette_(clustering)
#
# +
# please change the pipeline the check performance for different K, feel free to use a loop
# -
# Now please extend the pipeline to work on the normalized features. You need to tell KMeans to use the normalized feature column and change the pipeline in order to contain the normalizer stage as well.
# +
kmeans = KMeans(featuresCol='features_norm').setK(14).setSeed(1)
pipeline = Pipeline(stages=[vectorAssembler, normalizer, kmeans])
model = pipeline.fit(df)
predictions = model.transform(df)
evaluator = ClusteringEvaluator()
silhouette = evaluator.evaluate(predictions)
print("Silhouette with squared euclidean distance = " + str(silhouette))
# -
# Sometimes, inflating the dataset helps, here we multiply x by 10, let’s see if the performance inceases.
from pyspark.sql.functions import col
df_denormalized = df.select([col('*'),(col('x')*10)]).drop('x').withColumnRenamed('(x * 10)','x')
# +
kmeans = KMeans(featuresCol="features").setK(14).setSeed(1)
pipeline = Pipeline(stages=[vectorAssembler, kmeans])
model = pipeline.fit(df_denormalized)
predictions = model.transform(df_denormalized)
evaluator = ClusteringEvaluator()
silhouette = evaluator.evaluate(predictions)
print("Silhouette with squared euclidean distance = " + str(silhouette))
# -
# Apache SparkML can be used to try many different algorithms and parametrizations using the same pipeline. Please change the code below to use GaussianMixture over KMeans. Please use the following link for your reference.
#
# https://spark.apache.org/docs/latest/ml-clustering.html#gaussian-mixture-model-gmm
#
# +
from pyspark.ml.clustering import GaussianMixture
gmm = GaussianMixture(featuresCol='features_norm').setK(14).setSeed(1)
pipeline = Pipeline(stages=[vectorAssembler, normalizer, gmm])
model = pipeline.fit(df)
predictions = model.transform(df)
evaluator = ClusteringEvaluator()
silhouette = evaluator.evaluate(predictions)
print("Silhouette with squared euclidean distance = " + str(silhouette))
# -
|
scalable-machine-learning-on-big-data-using-apache-spark/Week 3/Exercise 2 - Working with Clustering and Apache Sp.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Current time
# !date
# # Collect all relevant tweets
# +
import json
import random
random.seed(201910181500) # Oct 18, 2019 15:00 EST
# Load secrets
from dotenv import load_dotenv
load_dotenv()
import os
TW_CONSUMER_KEY = os.getenv("TW_CONSUMER_KEY")
TW_CONSUMER_SECRET = os.getenv("TW_CONSUMER_SECRET")
TW_ACCESS_TOKEN = os.getenv("TW_ACCESS_TOKEN")
TW_ACCESS_TOKEN_SECRET = os.getenv("TW_ACCESS_TOKEN_SECRET")
# Initiate the API
from twarc import Twarc
t = Twarc(TW_CONSUMER_KEY, TW_CONSUMER_SECRET, TW_ACCESS_TOKEN, TW_ACCESS_TOKEN_SECRET)
# +
# Collect all quotes (RT with comments)
all_quotes = [tw for tw in t.search("https://twitter.com/armish/status/1183753089637064707")]
# Collect all replies
all_replies = [tw for tw in t.replies(t.tweet("1183753089637064707"))]
# Merge all
all_relevant_tweets = all_quotes + all_replies
# Save it
with open('20191018_relevant_tweets.json', 'w') as fout:
json.dump(all_relevant_tweets, fout)
# -
# # Participants
# +
participant_list = set([tw["user"]["screen_name"] for tw in all_relevant_tweets])
participant_list.remove("armish")
print(participant_list)
# -
# # Winners
random.choices(sorted(list(participant_list)), k=4)
|
other/tcr-name-giveaway/Pick MC38B TCR name winners.ipynb
|
# ##### Copyright 2021 Google LLC.
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#
# # linear_programming
# <table align="left">
# <td>
# <a href="https://colab.research.google.com/github/google/or-tools/blob/master/examples/notebook/examples/linear_programming.ipynb"><img src="https://raw.githubusercontent.com/google/or-tools/master/tools/colab_32px.png"/>Run in Google Colab</a>
# </td>
# <td>
# <a href="https://github.com/google/or-tools/blob/master/examples/python/linear_programming.py"><img src="https://raw.githubusercontent.com/google/or-tools/master/tools/github_32px.png"/>View source on GitHub</a>
# </td>
# </table>
# First, you must install [ortools](https://pypi.org/project/ortools/) package in this colab.
# !pip install ortools
# +
# #!/usr/bin/env python3
# Copyright 2010-2021 Google LLC
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
"""Linear programming examples that show how to use the APIs."""
from ortools.linear_solver import pywraplp
def Announce(solver, api_type):
print('---- Linear programming example with ' + solver + ' (' + api_type +
') -----')
def RunLinearExampleNaturalLanguageAPI(optimization_problem_type):
"""Example of simple linear program with natural language API."""
solver = pywraplp.Solver.CreateSolver(optimization_problem_type)
if not solver:
return
Announce(optimization_problem_type, 'natural language API')
infinity = solver.infinity()
# x1, x2 and x3 are continuous non-negative variables.
x1 = solver.NumVar(0.0, infinity, 'x1')
x2 = solver.NumVar(0.0, infinity, 'x2')
x3 = solver.NumVar(0.0, infinity, 'x3')
solver.Maximize(10 * x1 + 6 * x2 + 4 * x3)
c0 = solver.Add(10 * x1 + 4 * x2 + 5 * x3 <= 600, 'ConstraintName0')
c1 = solver.Add(2 * x1 + 2 * x2 + 6 * x3 <= 300)
sum_of_vars = sum([x1, x2, x3])
c2 = solver.Add(sum_of_vars <= 100.0, 'OtherConstraintName')
SolveAndPrint(solver, [x1, x2, x3], [c0, c1, c2], optimization_problem_type != 'PDLP')
# Print a linear expression's solution value.
print('Sum of vars: %s = %s' % (sum_of_vars, sum_of_vars.solution_value()))
def RunLinearExampleCppStyleAPI(optimization_problem_type):
"""Example of simple linear program with the C++ style API."""
solver = pywraplp.Solver.CreateSolver(optimization_problem_type)
if not solver:
return
Announce(optimization_problem_type, 'C++ style API')
infinity = solver.infinity()
# x1, x2 and x3 are continuous non-negative variables.
x1 = solver.NumVar(0.0, infinity, 'x1')
x2 = solver.NumVar(0.0, infinity, 'x2')
x3 = solver.NumVar(0.0, infinity, 'x3')
# Maximize 10 * x1 + 6 * x2 + 4 * x3.
objective = solver.Objective()
objective.SetCoefficient(x1, 10)
objective.SetCoefficient(x2, 6)
objective.SetCoefficient(x3, 4)
objective.SetMaximization()
# x1 + x2 + x3 <= 100.
c0 = solver.Constraint(-infinity, 100.0, 'c0')
c0.SetCoefficient(x1, 1)
c0.SetCoefficient(x2, 1)
c0.SetCoefficient(x3, 1)
# 10 * x1 + 4 * x2 + 5 * x3 <= 600.
c1 = solver.Constraint(-infinity, 600.0, 'c1')
c1.SetCoefficient(x1, 10)
c1.SetCoefficient(x2, 4)
c1.SetCoefficient(x3, 5)
# 2 * x1 + 2 * x2 + 6 * x3 <= 300.
c2 = solver.Constraint(-infinity, 300.0, 'c2')
c2.SetCoefficient(x1, 2)
c2.SetCoefficient(x2, 2)
c2.SetCoefficient(x3, 6)
SolveAndPrint(solver, [x1, x2, x3], [c0, c1, c2],
optimization_problem_type != 'PDLP')
def SolveAndPrint(solver, variable_list, constraint_list, is_precise):
"""Solve the problem and print the solution."""
print('Number of variables = %d' % solver.NumVariables())
print('Number of constraints = %d' % solver.NumConstraints())
result_status = solver.Solve()
# The problem has an optimal solution.
assert result_status == pywraplp.Solver.OPTIMAL
# The solution looks legit (when using solvers others than
# GLOP_LINEAR_PROGRAMMING, verifying the solution is highly recommended!).
if is_precise:
assert solver.VerifySolution(1e-7, True)
print('Problem solved in %f milliseconds' % solver.wall_time())
# The objective value of the solution.
print('Optimal objective value = %f' % solver.Objective().Value())
# The value of each variable in the solution.
for variable in variable_list:
print('%s = %f' % (variable.name(), variable.solution_value()))
print('Advanced usage:')
print('Problem solved in %d iterations' % solver.iterations())
for variable in variable_list:
print('%s: reduced cost = %f' %
(variable.name(), variable.reduced_cost()))
activities = solver.ComputeConstraintActivities()
for i, constraint in enumerate(constraint_list):
print(('constraint %d: dual value = %f\n'
' activity = %f' %
(i, constraint.dual_value(), activities[constraint.index()])))
RunLinearExampleNaturalLanguageAPI('GLOP')
RunLinearExampleNaturalLanguageAPI('GLPK_LP')
RunLinearExampleNaturalLanguageAPI('CLP')
RunLinearExampleNaturalLanguageAPI('PDLP')
RunLinearExampleCppStyleAPI('GLOP')
RunLinearExampleCppStyleAPI('GLPK_LP')
RunLinearExampleCppStyleAPI('CLP')
RunLinearExampleCppStyleAPI('PDLP')
|
examples/notebook/examples/linear_programming.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# # Lecture 8: p-hacking and Multiple Comparisons
# [<NAME>](https://github.com/natematias)
# [SOC412](https://natematias.com/courses/soc412/), February 2019
#
# In Lecture 8, we discussed <NAME>'s story about [<NAME>](https://www.buzzfeednews.com/article/stephaniemlee/brian-wansink-cornell-p-hacking#.btypwrDwe5), a food researcher who was found guilty of multiple kinds of research misconduct, including "p-hacking," where researchers keep looking for an answer until they find one. In this lecture, we will discuss what p-hacking is and what researchers can do to protect against it in our own work.
#
# This example uses the [DeclareDesign](http://declaredesign.org/) library, which supports the simulation and evaluation of experiment designs. We will be using DeclareDesign to help with designing experiments in this class.
#
# What can you do in your research to protect yourself against the risk of p-hacking or against reductions in the credibility of your research if people accuse you of p-hacking?
# * Conduct a **power analysis** to choose a sample size that is large enough to observe the effect you're looking for (see below)
# * If you have multiple statistical tests in each experiment, [adjust your analysis for multiple comparisons](https://egap.org/methods-guides/10-things-you-need-know-about-multiple-comparisons).
# * [Pre-register](https://cos.io/prereg/) your study, being clear about whether your research is exploratory or confirmatory, and committing in advance to the statistical tests you're using to analyze the results
# * Use cross-validation with training and holdout samples to take an exploratory + confirmatory approach (requires a much larger sample size, typically greater than 2x)
# # Load Libraries
# +
options("scipen"=9, "digits"=4)
library(dplyr)
library(MASS)
library(ggplot2)
library(rlang)
library(corrplot)
library(Hmisc)
library(tidyverse)
library(viridis)
library(fabricatr)
library(DeclareDesign)
## Installed DeclareDesign 0.13 using the following command:
# install.packages("DeclareDesign", dependencies = TRUE,
# repos = c("http://R.declaredesign.org", "https://cloud.r-project.org"))
options(repr.plot.width=7, repr.plot.height=4)
set.seed(03456920)
sessionInfo()
# -
# # What is a p-value?
# A p-value (which can be calculated differently for different kinds of statistical tests) is an estimate of the probability of rejecting a null hypothesis. When testing differences in means, we are usually testing the null hypothesis of no difference between the two distributions. In those cases, the p-value is the probability of observing a difference between the distributions that is at least as extreme as the one observed.
#
# Imagine the following formula:
#
# # $Y = \alpha + \beta_1 + \epsilon$
#
# You can think of the p-value as the probability represented by the area under the following t distribution of all of the possible outcomes for a given difference between means if the null hypothesis is true:
#
#
# 
# ### Illustrating The Null Hypothesis
# In the following case, I generate 100 pairs of normal distributions with exactly the same mean and standard deviation, and then plot the differences between those means:
### GENERATE n.samples simulations at n.sample.size observations
### using normal distributions at the specified means
### and record the difference in means and the p value of the observations
#
# `@diff.df: the dataframe to pass in
# `@n.sample.size: the sample sizes to draw from a normal distribution
generate.n.samples <- function(diff.df, n.sample.size = 500){
for(i in seq(nrow(diff.df))){
row = diff.df[i,]
a.dist = rnorm(n.sample.size, mean = row$a.mean, sd = row$a.sd)
b.dist = rnorm(n.sample.size, mean = row$b.mean, sd = row$a.sd)
t <- t.test(a.dist, b.dist)
diff.df[i,]$p.value <- t$p.value
diff.df[i,]$mean.diff <- mean(b.dist) - mean(a.dist)
}
diff.df
}
# +
#expand.grid
n.samples = 1000
null.hypothesis.df = data.frame(a.mean = 1, a.sd = 1,
b.mean = 1, b.sd = 1,
id=seq(n.samples),
mean.diff = NA,
p.value = NA)
null.hypothesis.df <- generate.n.samples(null.hypothesis.df, 200)
# -
ggplot(null.hypothesis.df, aes(mean.diff)) +
geom_histogram(binwidth=0.01) +
xlim(-1.2,1.2) +
ggtitle("Simulated Differences in means under the null hypothesis")
ggplot(null.hypothesis.df, aes(mean.diff, p.value, color=factor(p.value < 0.05))) +
geom_point() +
geom_hline(yintercept = 0.05) +
ggtitle("Simulated p values under the null hypothesis")
print("How often is the p-value < 0.05?")
summary(null.hypothesis.df$p.value < 0.05)
# ### Illustrating A Difference in Means (first with a small sample size)
# +
#expand.grid
small.sample.diff.df = data.frame(a.mean = 1, a.sd = 1,
b.mean = 1.2, b.sd = 1,
id=seq(n.samples),
mean.diff = NA,
p.value = NA)
small.sample.diff.df <- generate.n.samples(small.sample.diff.df, 20)
# -
ggplot(small.sample.diff.df, aes(mean.diff)) +
geom_histogram(binwidth=0.01) +
xlim(-1.2,1.2) +
ggtitle("Simulated Differences in means under the a diff in means of 1 (n=20)")
ggplot(small.sample.diff.df, aes(mean.diff, p.value, color=factor(p.value < 0.05))) +
geom_point() +
geom_hline(yintercept = 0.05) +
ggtitle("Simulated p values under a diff in means of 0.2 (n = 20)")
print("How often is the p-value < 0.05?")
summary(small.sample.diff.df$p.value < 0.05)
print("How often is the p-value < 0.05? when the estimate is < 0 (false positive)?")
nrow(subset(small.sample.diff.df, mean.diff<0 &p.value < 0.05))
print("How often is the p-value >= 0.05 when the estimate is 0.2 or greater (false negative)?")
print(sprintf("%1.2f precent",
nrow(subset(small.sample.diff.df, mean.diff>=0.2 &p.value >= 0.05)) /
nrow(small.sample.diff.df)*100))
print("What is the smallest positive, statistically-significant result?")
sprintf("%1.2f, which is greater than the true difference of 0.2",
min(subset(small.sample.diff.df, mean.diff>0 & p.value < 0.05)$mean.diff))
print("If we only published statistically-significant results, what we would we think the true effect would be?")
sprintf("%1.2f, which is greater than the true difference of 0.2",
mean(subset(small.sample.diff.df, p.value < 0.05)$mean.diff))
print("If we published all experiment results, what we would we think the true effect would be?")
sprintf("%1.2f, which is very close to the true difference of 0.2",
mean(small.sample.diff.df$mean.diff))
# ### Illustrating A Difference in Means (with a larger sample size)
# +
#expand.grid
larger.sample.diff.df = data.frame(a.mean = 1, a.sd = 1,
b.mean = 1.2, b.sd = 1,
id=seq(n.samples),
mean.diff = NA,
p.value = NA)
larger.sample.diff.df <- generate.n.samples(larger.sample.diff.df, 200)
# -
ggplot(larger.sample.diff.df, aes(mean.diff)) +
geom_histogram(binwidth=0.01) +
xlim(-1.2,1.2) +
ggtitle("Simulated Differences in means under the a diff in means of 1 (n=200)")
ggplot(larger.sample.diff.df, aes(mean.diff, p.value, color=factor(p.value < 0.05))) +
geom_point() +
geom_hline(yintercept = 0.05) +
ggtitle("Simulated p values under a diff in means of 0.2 (n = 200)")
print("If we only published statistically-significant results, what we would we think the true effect would be?")
sprintf("%1.2f, which is greater than the true difference of 0.2",
mean(subset(larger.sample.diff.df, p.value < 0.05)$mean.diff))
print("How often is the p-value < 0.05?")
sprintf("%1.2f percent",
nrow(subset(larger.sample.diff.df,p.value < 0.05)) / nrow(larger.sample.diff.df)*100)
# ### Illustrating a Difference in Means (with an adequately large sample size)
# +
adequate.sample.diff.df = data.frame(a.mean = 1, a.sd = 1,
b.mean = 1.2, b.sd = 1,
id=seq(n.samples),
mean.diff = NA,
p.value = NA)
adequate.sample.diff.df <- generate.n.samples(larger.sample.diff.df, 400)
# -
ggplot(adequate.sample.diff.df, aes(mean.diff, p.value, color=factor(p.value < 0.05))) +
geom_point() +
geom_hline(yintercept = 0.05) +
ggtitle("Simulated p values under a diff in means of 0.2 (n = 400)")
print("How often is the p-value < 0.05?")
sprintf("%1.2f percent",
nrow(subset(adequate.sample.diff.df,p.value < 0.05)) / nrow(adequate.sample.diff.df)*100)
print("If we only published statistically-significant results, what we would we think the true effect would be?")
sprintf("%1.2f, which is greater than the true difference of 0.2",
mean(subset(adequate.sample.diff.df, p.value < 0.05)$mean.diff))
# # The Problem of Multiple Comparisons
# In the above example, I demonstrated that across 100 samples under the null hypothesis and a decision rule of p = 0.05, roughly 5% of the results are statistically significant. This is similarly true for a single experiment with multiple outcome variables.
# +
## Generate n normally distributed outcome variables with no difference on average
#
#` @num.samples: sample size for the dataframe
#` @num.columns: how many outcome variables to observe
#` @common.mean: the mean of the outcomes
#` @common.sd: the standard deviation of the outcomes
generate.n.outcomes.null <- function( num.samples, num.columns, common.mean, common.sd){
df <- data.frame(id = seq(num.samples))
for(i in seq(num.columns)){
df[paste('row.',i,sep="")] <- rnorm(num.samples, mean=common.mean, sd=common.sd)
}
df
}
# -
# ### With 10 outcome variables, if we look for correlations between every outcomes, we expect to see 5% false positives on average under the null hypothesis.
set.seed(487)
## generate the data
null.10.obs <- generate.n.outcomes.null(100, 10, 1, 3)
null.10.obs$id <- NULL
null.correlations <- cor(null.10.obs, method="pearson")
null.pvalues <- cor.mtest(null.10.obs, conf.level = 0.95, method="pearson")$p
corrplot(cor(null.10.obs, method="pearson"), sig.level = 0.05, p.mat = null.pvalues)
# ### With multiple comparisons, increasing the sample size does not make the problem go away. Here, we use a sample of 10000 instead of 100
null.10.obs.large <- generate.n.outcomes.null(10000, 10, 1, 3)
null.10.obs.large$id <- NULL
null.correlations <- cor(null.10.obs.large, method="pearson")
null.pvalues <- cor.mtest(null.10.obs.large, conf.level = 0.95, method="pearson")$p
corrplot(cor(null.10.obs.large, method="pearson"), sig.level = 0.05, p.mat = null.pvalues)
# # Power Analysis
# A power analysis is a process for deciding what sample size to use based on the chance of observing the minimum effect you are looking for in your study. This power analysis uses [DeclareDesign](http://declaredesign.org/). Another option is the [egap Power Analysis page.](https://egap.org/content/power-analysis-simulations-r)
#
# (we will discuss this in further detail in a subsequent class)
# +
mean.a <- 0
effect.b <- 0.1
sample.size <- 500
design <-
declare_population(
N = sample.size
) +
declare_potential_outcomes(
YA_Z_0 = rnorm(n=N, mean = mean.a, sd=1),
YA_Z_1 = rnorm(n=N, mean = mean.a + effect.b, sd=1)
) +
declare_assignment(num_arms = 2,
conditions = (c("0", "1"))) +
declare_estimand(ate_YA_1_0 = effect.b) +
declare_reveal(outcome_variables = c("YA")) +
declare_estimator(YA ~ Z, estimand="ate_YA_1_0")
# -
design
diagnose_design(design, sims=500, bootstrap_sims=500)
|
lecture-10-multiple-comparisons.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:py38] *
# language: python
# name: conda-env-py38-py
# ---
# # Timeseries plot (swimlanes - whatever) of all moorings by location
#
# ToDo: Add following stations
#
# __GOA__
# - GPP (2013)
# - CS/CSP (2013)
# +
from erddapy import ERDDAP
import pandas as pd
import numpy as np
import datetime
# %matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from matplotlib.dates import YearLocator, WeekdayLocator, MonthLocator, DayLocator, HourLocator, DateFormatter
import cmocean
# -
server_url = 'http://akutan.pmel.noaa.gov:8080/erddap'
e = ERDDAP(server=server_url)
# searchterm mooring... subset this later
df = pd.read_csv(e.get_search_url(response='csv', search_for='Mooring'))
# +
from requests.exceptions import HTTPError
dfg = {}
for dataset_id in df['Dataset ID']:
try:
e.constraints = None
e.protocol = 'griddap'
e.dataset_id=dataset_id
e.response = 'nc'
e.variables = ['time']
ds = e.to_xarray(decode_times=True)
dfg.update({dataset_id:ds})
except:
pass
# +
dfs = {}
for dataset_id in df['Dataset ID'].values:
#print(dataset_id)
try:
d = ERDDAP(server=server_url,
protocol='tabledap',
response='csv'
)
d.dataset_id=dataset_id
d.variables = ['latitude','longitude','time']
except HTTPError:
print('Failed to generate url {}'.format(dataset_id))
try:
df_m = d.to_pandas(
index_col='time (UTC)',
parse_dates=True,
skiprows=(1,) # units information can be dropped.
)
df_m.sort_index(inplace=True)
df_m.columns = [x[1].split()[0] for x in enumerate(df_m.columns)]
#-9999 and 1e35 are missing values... but erddap doesn't catch the -9999 yet
#and some 1e35 are off a bit
dfs.update({dataset_id:df_m})
except:
pass
# +
# following types of datasets
# preliminary (tabular), final (tabular), final (gridded)
# ADCP (gridded) P moorings only
# BS (bering), CK (chukchi), CB (GOA)
offsets = {'bsm2a':.010,
'bs2a':.0125,
'bsp2a':.015,
'bs2b':.0175,
'bsp2b':.02,
'bs2c':.0225,
'bs4a':.0275,
'bsp4a':.03,
'bs5a':.035,
'bsp5a':.0375,
'bs5b':.0425,
'bsp5b':.045,
'bs8a':.05,
'bsp8a':.0525,
'bs8b':.055,
'bsp8b':.0575,
'ckip1a':.065,
'ckp1a':.0675,
'ckip2a':.0725,
'ckp2a':.075,
'ckip3a':.08,
'ckp3a':.0825,
'ckp4a':.0875,
'ckp5a':.0925,
'ckp7a':.0975,
'ckp9a':.1025,
'ckp10a':.1075,
'ckp11a':.1125,
'ckp12a':.1175,
'ck14a':.1225,
'cb1a':.13,
'pa1a':.135,
'gpp32a':.14,
'gpp34a':.145,
'gpp36a':.15,
'csp2a':.155,
'csp3a':.160,
'csp11a':.165,
'cs12a':.170,
'cs13a':.175,
'pcp1a':.180,
}
verbose = True
# +
fig = plt.figure(1,figsize=(24,10))
ax1 = plt.subplot2grid((1, 1), (0, 0), colspan=1, rowspan=1)
for dfn, df in dfs.items():
stage = dfn.split('_')[-1]
site = dfn.split('_')[-2][2:]
if ('final' in stage) and not ('ADCP' in dfn):
color='y'
width=0
if 'preliminary' in stage:
color='g'
width=0
continue
try:
offset = offsets[site]
duration = (df.last('s').index[0]-df.first('s').index[0]).days
ax1.barh(offset,duration,width+.0025,left=df.first('s').index[0].to_pydatetime(),
color=color,label=dfn) #inital
except:
if verbose:
print(f"trying {dfn}")
print("FAILED")
pass
for dfn, df in dfg.items():
stage = dfn.split('_')[-1]
site = dfn.split('_')[-2][2:]
if ('ADCP' in dfn):
color='b'
width=0
if 'ck' in dfn:
offset_c = .00125
else:
offset_c = 0
if '1hr_gridded' in dfn:
color='r'
width=0
offset_c = 0
try:
offset = offsets[site] + offset_c
duration = (datetime.datetime.strptime(dfg[dfn].time_coverage_end,
'%Y-%m-%dT%H:%M:%SZ')-datetime.datetime.strptime(dfg[dfn].time_coverage_start,
'%Y-%m-%dT%H:%M:%SZ')).days
ax1.barh(offset,duration,width+.00125,
left=datetime.datetime.strptime(dfg[dfn].time_coverage_start,
'%Y-%m-%dT%H:%M:%SZ'),
color=color,label=dfn) #inital
except:
if verbose:
print(f"trying {dfn}")
print("FAILED")
pass
plt.yticks(list(offsets.values()), list(offsets.keys()))
xfmt = mdates.DateFormatter('%d-%b\n%Y')
ax1.xaxis.set_major_formatter(xfmt)
ax1.set_xlim([datetime.date(1995,1,1),datetime.date.today()])
from matplotlib.lines import Line2D
custom_lines = [Line2D([0], [0], color='y', lw=4),
Line2D([0], [0], color='r', lw=4),
Line2D([0], [0], color='b', lw=4)]
ax1.legend(custom_lines, ['Mooring Tabular Data', 'Mooring Gridded Data', 'ADCP Gridded Data'])
# -
|
EcoFOCI_Moorings/ERDDAP_Automated_Tools/MooringErddapTimeLine.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] Collapsed="false" slideshow={"slide_type": "slide"}
# <img src="https://upload.wikimedia.org/wikipedia/commons/4/47/Logo_UTFSM.png" width="200" alt="utfsm-logo" align="left"/>
#
# # MAT281
# ### Aplicaciones de la Matemática en la Ingeniería
# + [markdown] Collapsed="false" slideshow={"slide_type": "slide"}
# ## Proyecto 02: Free Style
# + [markdown] Collapsed="false"
# ### Instrucciones
#
# * Completa tus datos personales (nombre y rol USM) en siguiente celda.
# * Debes _pushear_ tus cambios a tu repositorio personal del curso.
# * Como respaldo, debes enviar un archivo .zip con el siguiente formato `mXX_projectYY_apellido_nombre.zip` a <EMAIL>, debe contener todo lo necesario para que se ejecute correctamente cada celda, ya sea datos, imágenes, scripts, etc.
# * Se evaluará:
# - Soluciones
# - Código
# - Que Binder esté bien configurado.
# - Al presionar `Kernel -> Restart Kernel and Run All Cells` deben ejecutarse todas las celdas sin error.
# + [markdown] Collapsed="false"
# __Nombre__:
#
# __Rol__:
# + [markdown] Collapsed="false"
# ## Prediciendo _Pulsars_
#
# Un púlsar (del acrónimo en inglés de pulsating star, que significa «estrella que emite radiación muy intensa a intervalos cortos y regulares») es una estrella de neutrones que emite radiación periódica. Los púlsares poseen un intenso campo magnético que induce la emisión de estos pulsos de radiación electromagnética a intervalos regulares relacionados con el periodo de rotación del objeto. [Wikipedia](https://es.wikipedia.org/wiki/P%C3%BAlsar).
#
# 
#
# _A composite image of the Crab Nebula showing the X-ray (blue), and optical (red) images superimposed. The size of the X-ray image is smaller because the higher energy X-ray emitting electrons radiate away their energy more quickly than the lower energy optically emitting electrons as they move._
# + [markdown] Collapsed="false"
# ### Descripción de los datos
# + Collapsed="false"
# %cat data/Readme.txt
# + [markdown] Collapsed="false"
# ### Objetivo
# + [markdown] Collapsed="false"
# El objetivo es a partir de los datos, hacer la mejor predicción si un registro es un __pulsar__ o no. Para ellos es necesario realizar los pasos clásicos de un proyecto de _Machine Learning_, como estadística descriptiva, visualización y preprocesamiento. Sin embargo, se busca escoger el mejor modelo de clasificación con una métrica específica (_precision_).
#
# * Se solicita ajustar tres modelos de clasificación, una regresión logística, KNN y un tercero a elección del siguiente [link](https://scikit-learn.org/stable/supervised_learning.html#supervised-learning) (es obligación escoger un _estimator_ que tenga por lo menos un hiperparámetro).
# * En los modelos que posean hiperparámetros es mandatorio buscar el/los mejores con alguna técnica disponible en `scikit-learn` ([ver más](https://scikit-learn.org/stable/modules/grid_search.html#tuning-the-hyper-parameters-of-an-estimator)).
# * Para cada modelo, se debe realizar _Cross Validation_ con 10 _folds_ utilizando los datos de entrenamiento con tal de determinar un intervalo de confianza para el _score_ del modelo.
# * Finalmente, realizar una predicción con cada uno de los tres modelos con los datos _test_ y obtener el _score_.
#
# En este informe __siempre__ debes utilizar _score_ / _scoring_ la métrica [_precision_](https://scikit-learn.org/stable/modules/generated/sklearn.metrics.precision_score.html#sklearn.metrics.precision_score), tanto para el _Cross Validation_, _Hyper Parameter Tuning_ y _Prediction_. Toda la información al respecto de las métricas se encuentra [aquí](https://scikit-learn.org/stable/modules/model_evaluation.html#metrics-and-scoring-quantifying-the-quality-of-predictions).
# + [markdown] Collapsed="false"
# ### Evaluación
# + [markdown] Collapsed="false"
# Este jupyter notebook debe ser autocontenido, considera que es un informe técnico donde debes detallar cada paso, comentando código, utilizando variables con nombres adecuados, realizando gráficos y agregando apreciaciones personales cuando sea necesario. __No escatimes recursos a la hora de escribir.__
#
# __Escenario:__ Te encuentras trabajando como _data scientist / data analyst / machine learning engineer / etc._ y este trabajo será presentado al resto del equipo, en especial a tu jefe directo. Todos tienen conocimiento del problema y de machine learning, por lo que no puedes pasar por alto los aspectos técnicos de tu desarrollo. __Al final del informe, debes entregar tus conclusiones, visualizaciones y apreciaciones personales.__
#
# __Preguntas a responder:__
#
# * ¿Cuál modelo tiene mejor _precision_?
# * ¿Cuál modelo demora menos tiempo en ajustarse?
# * ¿Qué modelo escoges?
# * ¿Por qué utilizar _precision_ y no otro score?
#
# + [markdown] Collapsed="false" slideshow={"slide_type": "subslide"}
# ### Rúbrica
#
# * __Estadística Descriptiva__ (5 pts)
# * __Visualización__ (10 pts)
# * __Preprocesamineto__ (5 pts)
# * __Regresión Logística__ (10 pts)
# * __K Nearest Neighbours__ (15 pts)
# * __Modelo a elección__ (15 pts)
# * __Selección de Modelos__ (20 pts)
# * __Conclusiones__ (20 pts)
# + [markdown] Collapsed="false" slideshow={"slide_type": "subslide"}
# ## Contenidos
#
# * [Estadística Descriptiva](#descr_stat)
# * [Visualización](#visualization)
# * [Preprocesamineto](#preprocessing)
# * [Regresión Logística](#logistic)
# * [K Nearest Neighbours](#knn)
# * [Modelo a elección](#free-style)
# * [Selección de Modelos](#model-selection)
# * [Conclusiones](#conclusions)
# + Collapsed="false"
import os
import numpy as np
import pandas as pd
# + Collapsed="false"
df = pd.read_csv(
os.path.join("data", "HTRU_2.csv"),
header=None,
names=[
"mean_integrated_profile",
"std_integrated_profile",
"excess_kurtosis_integrated_profile",
"skewness_integrated_profile",
"mean_dmsnr",
"std_dmsnr",
"excess_kurtosis_dmsnr",
"skewness_dmsnr",
"is_pulsar",
]
)
df.head()
# + [markdown] Collapsed="false" slideshow={"slide_type": "slide"}
# <a id='descr_stat'></a>
# + [markdown] Collapsed="false"
# ## Estadística Descriptiva
# + [markdown] Collapsed="false"
# * Dar una pequeña definición de las columnas (_features_).
# * Análisis descriptivo.
# * Valores atípicos.
# * Análisis específico a la variable _target_.
# + Collapsed="false"
## FREE STYLE ##
# + [markdown] Collapsed="false" slideshow={"slide_type": "slide"}
# <a id='visualization'></a>
# + [markdown] Collapsed="false"
# ## Visualización
# + [markdown] Collapsed="false"
# * Histogramas.
# * Scatter matrix coloreando por el _target_.
# * Mapa de calor con correlación entre variables.
#
# Puedes utilizar `matplotlib` o `altair`, como sea de tu preferencia.
# + Collapsed="false"
import altair as alt
import matplotlib.pyplot as plt
alt.themes.enable("opaque")
# %matplotlib inline
# + Collapsed="false"
## FREE STYLE ##
# + [markdown] Collapsed="false" slideshow={"slide_type": "slide"}
# <a id='preprocessing'></a>
# + [markdown] Collapsed="false"
# ## Preprocesamiento
# + [markdown] Collapsed="false"
# Es hora de preparar los datos para la selección de modelos. Se solicita que:
#
# * Crear el _numpy.array_ `X_raw` con las columnas predictoras de `df`.
# * Crear el _numpy.array_ `y` con la columna a predecir de `df`.
# * Definir un _transformer_ `StandarScaler` declarado como `scaler`, luego ajustar con los datos de `X_raw`.
# * Definir el _numpy.array_ `X` luego de transformar los datos de `X_raw` con `scaler`. Verificar que tenga media nula y desviación estándar unitaria.
# * Dividir la data en _train_ (90%) y _test_ (10%) utilizando como argumento `random_state=42`.
# + Collapsed="false"
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# + Collapsed="false"
X_raw = ## FIX ME ##
y = ## FIX ME ##
# + Collapsed="false"
scaler =## FIX ME ##
## FIX ME ##
X = ## FIX ME ##
# + Collapsed="false"
## FREE STYLE ##
# + Collapsed="false"
X_train, X_test, y_train, y_test = ## FIX ME ##
# + [markdown] Collapsed="false" slideshow={"slide_type": "slide"}
# <a id='logistic'></a>
# + [markdown] Collapsed="false"
# ## Regresión Logística
# + [markdown] Collapsed="false"
# Utiliza la función `cross_validate` con el estimador `logistic` para realizar una estimación del _score_
# + Collapsed="false"
from sklearn.model_selection import cross_validate
from sklearn.linear_model import LogisticRegression
# + Collapsed="false"
logistic = ## FIX ME ##
logistic_cv = ## FIX ME ##
# + Collapsed="false"
print(f'Logistic Regression Cross Validation precision score: {np.mean(logistic_cv["test_score"]):.2f} +/- {np.std(logistic_cv["test_score"]):.2f}')
# + Collapsed="false"
logistic.## FIX ME ##
# + [markdown] Collapsed="false" slideshow={"slide_type": "slide"}
# <a id='knn'></a>
# + [markdown] Collapsed="false"
# ## K Nearest Neighbours
# + [markdown] Collapsed="false"
# Utiliza `GridSearchCV` para encontrar el mejor valor de `n_neighbors`. Luego, con el mejor _estimator_ de `knn` realiza la validación cruzada para obtener el intervalo de confianza del _score_.
# + Collapsed="false"
from sklearn.model_selection import GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
# + Collapsed="false"
## FIX ME ##
knn = ## FIX ME ##
# + Collapsed="false"
## FRE STYLE ##
# + Collapsed="false"
knn_cv = ## FIX ME ##
# + Collapsed="false"
print(f'KNN Cross Validation precision score: {np.mean(knn_cv["test_score"]):.2f} +/- {np.std(knn_cv["test_score"]):.2f} with train data.')
# + [markdown] Collapsed="false" slideshow={"slide_type": "slide"}
# <a id='free_style'></a>
# + [markdown] Collapsed="false"
# ## Modelo a elección
# + [markdown] Collapsed="false"
# * Escoge un modelo de clasificación de [aquí](https://scikit-learn.org/stable/supervised_learning.html#supervised-learning) que por lo menos tenga un hiperparámetro, por ejemplo, [sklearn.svm.SVC](https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html#sklearn.svm.SVC) tiene el parámetro de regularización `C`.
# * Explica en uno o dos párrafos en qué consiste el algoritmo/modelo.
# * Al igual que KNN, encuentra el/los mejores valores para los hiperparámetros.
# * Con el mejor estimador realiza _Cross Validation_ con los datos de entrenamiento.
# * Calcula el intervalo de confianza de _precision_.
# + Collapsed="false"
my_model = ## FIX ME ##
# + Collapsed="false"
my_model_cv = ## FIX ME ##
# + Collapsed="false"
## FRE STYLE ##
# + Collapsed="false"
print(f'MY MODEL Cross Validation precision score: {np.mean(my_model_cv["test_score"]):.2f} +/- {np.std(my_model_cv["test_score"]):.2f} with train data.')
# + [markdown] Collapsed="false" slideshow={"slide_type": "slide"}
# <a id='model_selection'></a>
# + [markdown] Collapsed="false"
# ## Selección de Modelo
# + [markdown] Collapsed="false"
# * Compara la _precision_ entre cada uno de los modelos.
# * Grafica la matriz de confusión para cada uno de los modelos.
# * Calcula un intervalo de confianza del tiempo utilizado en el ajuste de cada modelo. Ver documentación de `cross_validate`.
# * Gráficos o reportes adicionales.
# + Collapsed="false"
from sklearn.metrics import precision_score, classification_report
# + Collapsed="false"
print(f'Logistic Regression test precision score: {## FRE STYLE ##}')
# + Collapsed="false"
print(f'KNN test precision score: {## FRE STYLE ##}')
# + Collapsed="false"
print(f'MY MODEL test precision score: {## FRE STYLE ##}')
# + Collapsed="false"
## FREE STYLE ##
# + [markdown] Collapsed="false" slideshow={"slide_type": "slide"}
# <a id='conclusions'></a>
# + [markdown] Collapsed="false"
# ## Conclusiones
# + [markdown] Collapsed="false"
# Entrega tu veredicto, responde las preguntas iniciales, visualizaciones, trabajos futuros, dificultados, etc.
# + Collapsed="false"
## FRE STYLE ##
|
m05_data_science/m05_project02/m05_project02.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/adriyennKB/Linear-Algebra-58019/blob/main/Final_Exam.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="Nm96UGhvGxxu"
# ###Problem 1 Student A, Student B, and Student C have a total of Php 89 cash in their banks. Student A has 6 less than Student C. Student B has 3 times what Student C has. How much does each student have?
# + colab={"base_uri": "https://localhost:8080/"} id="9I5P29OuGsf7" outputId="9f51f45f-6969-469c-fa7f-e9e6442e30dd"
import numpy as np #Matrix Operator
e1= np.array([[1,1,1],[1,0,4],[0,0,5]]) #creation of Matrix e1
e2= np.array([[89],[89],[95]]) #creation of Matrix e2
amnt= np.linalg.inv(e1).dot(e2) #solve using dot and inv of Matrix e1 and e2
print(amnt) #to display or print
# + [markdown] id="nSiRCDRnG2dm"
# ###Problem 2: 3x - y + z = 5, 9x - 3y +3z = 15, -12x +4y -4z = -20
# + [markdown] id="Lz7a08IvYpxC"
# ###Explanation: By means of using just the np.linalg.inv, the code itself will result to an error message that says that it is a singular matrix
# ###Also, since the matrix is singular due to the determinant is zero, so it will not be possible to inverse it.
# ###So by means of using pseudo inverse of A or the approximate initial matrix, the code will go through/run.
# + colab={"base_uri": "https://localhost:8080/"} id="rNM3w5KASjbS" outputId="009c079f-01bd-4010-9136-f5c3997d9307"
#Here i tried coding it by using pseudo inverse
import numpy as np
A= np.array([[3,-1,1],[9,-3,3],[-12,4,-4]]) #creation of Matrix A
print(f'Matrix A: \n {A}') #to display or print
pinv_A= np.linalg.pinv(A) #to compute the pseudo inverse of A
#Explanation: By means of using just the np.linalg.inv, the code itself will result to an error message that says that it is a singular matrix
#Also, since the matrix is singular due to the determinant is zero, so it will not be possible to inverse it.
#So by means of using pseudo inverse of A or the approximate initial matrix, the code will go through/run.
print(f'\nInverse of A: \n {A}') #to display or print
B= np.array([[5],[15],[-20]]) #creation of Matrix B
print(f'\nMatrix B:\n {B}\n') #to display or print
X= np.dot(pinv_A,B) #to compute for the dot product of Inverse of A ang B
print(X) #to display or print
# + [markdown] id="_uTmp_szG9EX"
# ###Problem 3 Consider the matrix
# + colab={"base_uri": "https://localhost:8080/"} id="LAOIJRuiI1iE" outputId="3a213085-bf1e-454d-f2cb-a5d5867f4f43"
import numpy as np
from numpy.linalg import eig
A = np.array([[8,5,-6],[-12,-9,12],[-3,-3,5]]) #Creation of Matrix A
print(A) #to print or display
s,t = np.linalg.eig(A) # use the eig method in order to get the eigenvalue and eigenvector of a square matrix A
#print or display eigenvalues and eigenvectors
print(f'\nThe Eigenvalue/s is/are: {s.round()}')
print(f'\nThe right Eigenvectors are: \n{t}')
print(f'OR: \n{t.round()}\n') #rounded off version of the right Eigenvectors
|
Final_Exam.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: pLoT
# language: python
# name: plot
# ---
# # Formal Grammars
from numpy.random import choice
# ## Using dictionaries
# One simple and intuitive way of implementing a grammar in python is as a dictionary:
# - The keys are the left hand side rules
# - The values are lists containing the possible strings that can be substituted by the key
#
# > __NOTE__: To see why we need to use lists as values rather than using a different key for each rule, try to repeat the same key more than once. What happens?
#
# For instance, let's write the grammar with the following rules:
# $$
# S \rightarrow aS | bS | \epsilon
# $$
grammar = {
'S': [
'aS',
'bS',
''
]
}
# One thing we can do with this way of defining grammars is writing a function that randomly applies rule until we get to a string consisting only of terminals:
# always start with the starting symbol
current_sentence = 'S'
# while there is a non-terminal in the sentence
while 'S' in current_sentence:
# substitute the first occurrence of S
# with a randomly chosen substitution rule
current_sentence = current_sentence.replace(
'S',
choice((grammar['S'])),
# NOTE: in this particular case there will always
# only be one S, but this is not true for
# all grammars!
1
)
print('String: ', current_sentence)
# Write a function that takes a grammar, a set of terminals, and a set of nonterminals, and determines where the grammar is in the Chomsky hierarchy (Spend about 20 minutes on this - if you see that you can do it, leave it!):
# +
# Your function here
# -
# ## A new piece of python syntax: generators
# Before we move onto defining classes to model grammars, which allow richer structures than dictionaries, we need to briefly talk about generators. A generator is basically _a function with a memory_, which can return multiple things in succession. Suppose you have a generator called `gen`. A typical use case is to use it in a construction like `for i in gen():`, where `i` will take on in succession the values returned by the generator.
#
# The definition is almost like a function, except generators have the keyword `yield` where functions have `return`, and the execution doesn't stop at the return but can continue as long as future yield are possible.
#
# The simple example is a generator that first yields (returns) 1 and then 2:
# +
def simple_generator():
# when getting things out of a generator,
# the generator will return in the order
# the yield statements are encountered
# This is encountered first
yield 1
# Then this is encountered
yield 2
for i in simple_generator():
print(i)
# -
# A slightly more complex generator simply counts the odd integers starting with 1:
def odd_counter():
i = 0
while True:
yield i*2+1
i += 1
for i in odd_counter():
if i <= 20:
print(i, end=', ')
else:
break
# Note that generators can also call themselves, like functions. Then we get recursive generators:
# Can you figure out what this generator does?
def recursive_gen(current_options, n):
new_options = []
for i in current_options:
if sum(i) == n:
yield i
else:
new_options.append(i+[1])
new_options.append(i+[2])
if all([sum(j)>n for j in new_options]):
return
for i in recursive_gen(new_options, n):
yield i
for i in recursive_gen([[1],[2],[3]], 6):
print(i)
# Try to write the recursive_gen just as a normal function with `return` statements.
# +
# Your code here!
# -
# ## Using classes
# > __NOTE__: Before you work on the exercise in 'Defining a grammar class' please have a look at the rest of the notebook. This should give you an idea of what you need to do with that class, and therefore how to structure them internally.
# ### Defining a grammars class
# Write a Grammar class to create context-free grammars. The `__init__` method should take a `start` argument with the starting nonterminal symbol.
#
# The class should also have the following method (i.e., function):
# - `add_rule`: add a rule to the grammar. The arguments of `add_rule` are:
# 1. The nonterminal on the left-hand side of the rule
# 1. The string on the right side of the rule, containing `%s` wherever a non-terminal appears
# 1. A list of non-terminal symbols, one for each `%s`, saying which non-terminals correspond to each %s.
# +
#### your class definition here!
# -
# Once this is defined, you should be able to run the following code to define the grammar for palindrome which we discussed in class:
#
# ```python
# grammar = Grammar(start='S')
#
# grammar.add_rule('S', 'a%sa', ['S'])
# grammar.add_rule('S', 'b%sb', ['S'])
# grammar.add_rule('S', '')
# ```
# +
#### Define the palindrome grammar here!
# -
# ### Finding minimal formulas (more difficult!)
# Now add another method `compute_first` to the class above which generates the `n` shortest strings in the language.
#
# You should be able to run for instance (given the palindrome grammar above):
#
# ```python
# grammar.compute_first(6)
# ```
#
# Which should print out:
#
# ```python
# aa
# bb
# aaaa
# abba
# baab
# bbbb
# ```
#
# > __HINT__: Think about this as exploring a tree (branches separating whenever more than one rule can be applied), and use the power of recursion to explore the tree. The recursive function can take a 'present' layer (the strings at the current nesting level) and progressively build the next layer by applying every rule to every sentence with nonterminals in the current layer, while yielding the sentences that only contain terminals. Then, yield the results of running the function on the next layer in a loop.
# +
#### Test compute_first here!
def enumerate_palindromes(layer):
# your function here
def compute_first(n):
for i, m in enumerate(enumerate_palindromes(['S'])):
if i <= n:
print(m)
else:
break
# -
compute_first(4)
# ### Probabilistic context-free grammar
# Expand the Grammar class once more so that `add_rule` takes one more argument: The (unnormalized) probability of applying the rule rather than the other rules with the same left-hand side.
#
# The following code for instance redefines the palindrome grammar above but with probabilities:
# ```python
# grammar = Grammar(start='S')
#
# grammar.add_rule('S', 'a%sa', ['S'], 1)
# grammar.add_rule('S', 'b%sb', ['S'], 1)
# grammar.add_rule('S', '', 1)
# ```
# +
#### your class definition here!
# -
# Add a method `generate` to Grammar to generate a random string in the language by iteratively applying the rules according to the defined probabilities. The following code should run (but possibly give a different answer on different runs):
#
# ```python
# grammar.generate()
# ```
#
# printing e.g.,
# ```python
# aabbaa
# ```
# +
#### Test generate here!
# -
# What happens when we increase...
#
# - the probability of the rule $S \rightarrow aSa$?
# - the probability of the rule $S \rightarrow bSb$?
# - the probability of the rule $S \rightarrow \epsilon$?
|
book/4_lab.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
from sklearn.datasets import make_classification
#import pandas as pd
#import seaborn as sns
import torch
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
from IPython import display
from sklearn import metrics
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.utils.class_weight import compute_class_weight
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
from collections import defaultdict
import sklearn.datasets
torch.manual_seed(1)
np.random.seed(7)
#sns.set(style="white", palette="muted", color_codes=True, context="talk")
# %matplotlib inline
print(torch.__version__)
# -
import time
from torchvision import datasets, transforms
# # Dataset and Model Definition
BATCH_SIZE=512
# +
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Lambda(lambda x: torch.flatten(x)),
#transforms.Normalize((0.1307,), (0.3081,))
])
dataset1 = datasets.MNIST('data', train=True, download=True,
transform=transform)
dataset2 = datasets.MNIST('data', train=False,
transform=transform)
train_loader = torch.utils.data.DataLoader(dataset1, batch_size=BATCH_SIZE)
test_loader = torch.utils.data.DataLoader(dataset2, batch_size=BATCH_SIZE)
n_features = 784
n_classes = 10
# -
n_hidden = 256
class Classifier(nn.Module):
def __init__(self, n_features, n_hidden=n_hidden):
super(Classifier, self).__init__()
self.network = nn.Sequential(
nn.Linear(n_features, 400, bias=False),
nn.ReLU(),
nn.Linear(400, 400, bias=False),
nn.ReLU(),
nn.Linear(400, 10, bias=False),
nn.ReLU(),
nn.LogSoftmax()
)
def forward(self, x):
return self.network(x)
def accuracy(model, X, y):
Xt = torch.from_numpy(X).float()
yt = torch.from_numpy(y).long()
outputs = model(Xt)
y_hat = [1 if o>.5 else 0 for o in outputs]
accuracy = np.sum(y_hat == y) / len(y)
return accuracy
# # Training
def make_plot(info, key, title):
plt.plot(info[key]);
plt.title(title)
plt.show()
UPSTREAM_GRAD_BOUND = 0.00001
INPUT_BOUND = 0.5
def l2_clip(t, C):
dims = tuple(range(1, len(t.shape)))
norm = t.norm(dim=dims, keepdim=True).expand(t.shape)
clipped = torch.where(norm > C, C*(t/norm), t)
new_norms = clipped.norm(dim=dims)
return clipped
grad_maxes = []
def clamp_grad(self, grad_input, grad_output):
if isinstance(self, nn.Linear):
upstream_g, g_weights = grad_input
if upstream_g == None:
return grad_input
else:
grad_maxes.append(upstream_g.abs().max())
return (l2_clip(upstream_g, UPSTREAM_GRAD_BOUND), g_weights)
elif isinstance(self, nn.ReLU):
grad_maxes.append(grad_input[0].abs().max())
return (l2_clip(grad_input[0], UPSTREAM_GRAD_BOUND),)
else:
return None
input_maxes = []
def clamp_input(self, input):
input_maxes.append(input[0].abs().max())
return tuple([l2_clip(x, INPUT_BOUND) for x in input])
def zcdp_eps(rho, delta):
return rho + 2*np.sqrt(rho*np.log(1/delta))
def run_experiment(epsilon, epochs, add_noise=False):
model = Classifier(n_features=n_features)
model_criterion = nn.NLLLoss()
model_optimizer = optim.Adam(model.parameters(), lr=0.01)#, weight_decay=0.0001)
rho_i = 0.000001
total_rho = 0
for x in model.network:
x.register_backward_hook(clamp_grad)
x.register_forward_pre_hook(clamp_input)
sensitivities = []
norms = []
decays = []
losses = []
for epoch in range(epochs):
for x_batch_train, y_batch_train in train_loader:
model_optimizer.zero_grad()
#inp = Variable(x_batch_train, requires_grad=True)
outputs = model.forward(x_batch_train)
loss = model_criterion(outputs, y_batch_train)
losses.append(loss)
loss.backward()
for i, layer in enumerate(model.network):
if isinstance(layer, nn.Linear):
ps = list(layer.parameters())
weights = ps[0]
#bias = ps[1]
grad_bound = INPUT_BOUND * UPSTREAM_GRAD_BOUND
grad_bound_bias = INPUT_BOUND
actual_grad_bound = weights.grad.flatten().norm(p=2)
if False and actual_grad_bound > grad_bound:
print(type(layer))
print(weights.shape)
print('grad bound norm: ', grad_bound)
print('actual grad norm:', actual_grad_bound)
sensitivities.append(grad_bound)
sensitivity = grad_bound / BATCH_SIZE
sensitivity_bias = grad_bound_bias / BATCH_SIZE
sigma = np.sqrt(sensitivity**2 / (2*rho_i))
sigma_bias = np.sqrt(sensitivity_bias**2 / (2*rho_i))
with torch.no_grad():
weights.grad += sigma*torch.randn(weights.shape)
#bias.grad += sigma_bias*torch.randn(bias.shape)
total_rho += (rho_i)
norms.append(next(model.parameters()).data.norm())
model_optimizer.step()
total_weights = 0
for p in model.parameters():
total_weights += p.flatten().shape[0]
print('total weights:', total_weights)
info = {'sens': sensitivities,
'norms': norms,
'decays': decays,
'losses': losses,}
print('total rho:', total_rho)
print('total epsilon:', zcdp_eps(total_rho, 1e-5))
return model, info
def test(model, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data, target
output = model(data)
test_loss += nn.functional.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
# +
model, info = run_experiment(.001, 5, False)
for key, title in [('sens', 'Sensitivity'),
('norms', 'L2 Norm of 1st layer weights'),
#('decays', 'Weight Decay Value'),
('losses', 'Loss')
]:
make_plot(info, key, title)
test(model, test_loader)
# +
plt.plot(grad_maxes)
plt.title('Grad maxes')
plt.show()
plt.plot(input_maxes)
plt.title('Input maxes')
plt.show()
# -
|
experiments/global_sensitivity/Fully Connected Upstream Clipping MNIST.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# # Data visualization
library(tidyverse)
# Ignore this (only for notebooks):
library(repr)
options(repr.plot.width=12, repr.plot.height=6)
# ## 3. Now it's your turn
# First, load some new data in R and have a glimpse at it:
tdcs_data = read_csv('https://raw.githubusercontent.com/laurafontanesi/r-seminar/master/data/tdcs.csv')
glimpse(tdcs_data)
# **Task A**
#
# 1. Show the distribution of response times (`RT`) with a **density plot**, separately by the accuracy vs. speed conditions (`acc_spd`) using different colors of the density plots per condition. Be sure to adjust the transparency so that they are both clearly visible and put appropriate axes labels and legend title.
#
# 2. Show the distribution of response times (`RT`) with a **histogram**, separately by the accuracy vs. speed conditions (`acc_spd`) using different colors of the density plots per condition. Be sure to adjust the transparency and binwidth, so that they are clearly visible and put appropriate axes labels and legend title. This time, split it furtherly by TDCS manipulation (`tdcs`) using `facet_grid()`.
#
# 3. Show the response times (`RT`) with a **violinplot**, separately by the place the data were collected (`dataset`). Split further by accuracy vs. speed conditions using colors. Add the 10%, 30%, 50%, 70%, and 90% quantiles, that are the most common in response times data analyses. Change labels appropriately.
# *Question*: how do I rename the different group conditions "acc" and “spd”?
#
# We didn’t see this in class. You can use a separate function for that: `scale_fill_discrete`. See below.
ggplot(data = tdcs_data, mapping = aes(x = RT, fill = acc_spd)) +
geom_density(alpha = .3) +
labs(x = 'Response times', fill = 'Condition') +
scale_fill_discrete(labels = c("accuracy", "speed"))
ggplot(data = tdcs_data, mapping = aes(x = RT, fill = acc_spd)) +
geom_histogram(binwidth=50, alpha = .3, position="identity") +
labs(x = 'Response times', fill = 'Condition') +
facet_grid( ~ tdcs)
# **Common mistakes**:
#
# ```
# ggplot(data = tdcs_data, mapping = aes(x = RT, fill = acc_spd)) +
# geom_histogram(binwidth=50, alpha = .3, position="identity") +
# labs(x = 'Response times', fill = 'Condition')
# facet_grid( ~ tdcs)
# ```
#
# Here you missed a `+` at the end your `labs` function. Without it the `facet_grid` component is not added to the plot.
ggplot(data = tdcs_data, mapping = aes(x = dataset, y = RT, fill = acc_spd)) +
geom_violin(draw_quantiles = c(0.1, 0.3, 0.5, 0.7, 0.9)) +
labs(x = "Place collected", y='RTs')
# **Task B**
#
# Now, I am creating a summary of the data, where we look at mean response times and accuracy per subject, separately by coherence (how difficult the task was) and the speed vs. accuracy manipulation:
# +
summary_tdcs_data = summarise(group_by(tdcs_data, id, coherence, acc_spd),
mean_RT=mean(RT),
mean_accuracy=mean(accuracy))
glimpse(summary_tdcs_data)
# -
# Using the summarized data:
#
# 1. Plot the relationship between mean response times (`mean_RT`) and mean accuracy (`mean_accuracy`) using a **scatterplot**.
#
# 2. Use `facet_grid` to split the plot based on the speed vs. accuracy manipulation (`acc_spd`).
#
# 3. Add the regression lines.
#
# 4. Change with appropriate plot titles and x- and y-axes labels.
#
# 5. Add the coherence levels as color of the dots. Because coherence is a continuous variable and not categorical, you can use `scale_colour_gradient` to adjust the gradient.
#
# 6. Change the color of the regression lines to grey.
ggplot(data = summary_tdcs_data, mapping = aes(x = mean_RT, y = mean_accuracy, color = coherence)) +
geom_point(alpha = 0.6, size= 2) +
geom_smooth(method = lm, color='grey') +
labs(x='Mean RTs', y='Mean accuracy') +
ggtitle("Relationship between mean RTs and accuracy") +
scale_colour_gradient(low = "blue", high = "gold", limits=range(summary_tdcs_data[,'coherence'])) +
facet_grid( ~ acc_spd)
# **Task C**
#
# Using the summarized data:
#
# 1. Plot the mean `mean_accuracy`, separately by `factor(coherence)` using `stat_summary` with arguments `geom="bar"` and `position = 'dodge'`. Split further based on the accuracy vs. speed manipulation (`acc_spd`) with different colors.
#
# 2. Now add error bars representing confidence intervals and using `stat_summary` again with arguments `width=.9`, `position = 'dodge'`. Adjust the `width` argument if the error bars are not centered in each of the bars.
#
# 3. Do the same again, but:
# - using points instead of bars
# - standard errors instead of confidence intervals
# - mean RTs instead of accuracy
# Note that you do not need the `position = 'dodge'` here anymore, and that you might have to adjust `size` and `width` of the error bars.
# **Question**:
#
# How to avoid overlapping labels in the x-axis?
#
# You can do that by changing their orientation using the `theme` function. See below.
ggplot(data = summary_tdcs_data, mapping = aes(x = factor(coherence), y = mean_accuracy, fill=acc_spd)) +
# stat_summary with arg "fun":
# A function that returns a single number, in this case the mean worry_cont for each level of cause_recoded:
stat_summary(fun = "mean", geom="bar", position = 'dodge') +
# mean_cl_normal( ) is intended for use with stat_summary. It calculates
# sample mean and lower and upper Gaussian confidence limits based on the
# t-distribution
stat_summary(fun.data = mean_cl_normal, geom = "errorbar", size=.2, width=.9, position = 'dodge') +
labs(x = 'Coherence level', y = 'Mean accuracy', fill='Condition') +
# to change the orientation of the x-ticks labels:
theme(axis.text.x = element_text(angle = 90))
# **Common mistakes**:
#
# ```
# ggplot(data = summary_tdcs_data, mapping = aes(x = factor(coherence), y = mean_accuracy, color = acc_spd)) +
# stat_summary(fun = "mean", geom="bar", position = “dodge”)
# ```
#
# Here, you used the `color` attribute instead of the `fill` argument. That only changes the borders of the bars (not optimal).
# _______________
# ```
# ggplot(data = summary_tdcs_data, mapping = aes(x = factor(coherence), y = mean_accuracy, fill=acc_spd)) +
# stat_summary(fun.data = mean_cl_normal, geom = "errorbar", size=.2, width=.9, position = 'dodge') +
# stat_summary(fun = "mean", geom="bar", position = 'dodge') +
# labs(x = 'Coherence level', y = 'Mean accuracy', fill='Condition')
# ```
#
# If you called the error bars `stat_summary(fun.data = mean_cl_normal, geom = "errorbar", ...)` **before** the bars themeselves `stat_summary(fun = "mean", geom=“bar”,…)` so you won't see the bottom part of the error bars.
# _______________
# ```
# ggplot(data = summary_tdcs_data, mapping = aes(x = mean_accuracy, y = coherence, fill = acc_spd)) +
# facet_grid(~ acc_spd) +
# stat_summary(fun = "mean", geom="bar") +
# stat_summary(fun.data = mean_cl_normal, geom = "bar", size=1, width=.9) +
# stat_summary(fun.data = mean_cl_normal, geom = "errorbar", size=1, width=.9)
# ```
#
# - You don’t need to add `facet_grid(~ acc_spd)` if you are already (and correctly) splitting by colour using `fill = acc_spd`. `facet_grid` is only to split the plots in 2 columns based on a categorical variable.
#
# - Switching x and y variables: with bar plots we want the categorical variable on the x-axis and the continuous on the y-axis.
#
# - Calling `stat_summary` a wrong number of times:
# - `stat_summary(fun = "mean", geom="bar", ...)` : this makes bars that are as tall as the mean of `y` for each level of `x`
# - `stat_summary(fun.data = mean_cl_normal, geom = "bar", ...)` : this makes no sense because you are calculating the CI but then want to plot bars
# - `stat_summary(fun.data = mean_cl_normal, geom = "errorbar", ...)` : this is correctly calculating CI and plotting them es errorbars
# _______________
# ```
# ggplot(data = summary_tdcs_data, mapping = aes(x = factor(coherence), y = mean_accuracy, fill=acc_spd)) +
# stat_summary(fun = "mean", geom="bar", size = 3) +
# stat_summary(fun.data = mean_cl_normal(x = mean_accuracy), geom = "errorbar", size=1, width=.9) +
# labs(x = 'Education level', y = 'How worried of GW are you?’)
# ```
#
# Here, `mean_cl_normal(x = mean_accuracy)` is wrong: `mean_se` and `mean_cl_normal` do not need to specify any variable in order to work. `ggplot` already “knows” what variables go on the x- and y-axis.
ggplot(data = summary_tdcs_data, mapping = aes(x = factor(coherence), y = mean_RT, color=acc_spd)) +
# stat_summary with arg "fun":
# A function that returns a single number, in this case the mean worry_cont for each level of cause_recoded:
stat_summary(fun = "mean", geom="point") +
stat_summary(fun.data = mean_se, geom = "errorbar", size=.8, width=.4) +
labs(x = 'Coherence level', y = 'Mean RTs', fill='Condition') +
# to change the orientation of the x-ticks labels:
theme(axis.text.x = element_text(angle = 90))
# **Common mistakes:**
#
# When you have points instead of bars, you should remove the `position = 'dodge'` argument specification. That's only for bars, to have them next to each other and not stacked.
|
notebooks/wpa3_answers.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.applications.vgg19 import VGG19, preprocess_input
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Dense, Dropout, Flatten
from tensorflow.keras.callbacks import ModelCheckpoint, CSVLogger, ReduceLROnPlateau, EarlyStopping
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.losses import categorical_crossentropy
from tensorflow.keras.utils import plot_model
from sklearn.metrics import confusion_matrix, classification_report
from sklearn.utils import class_weight
import numpy as np
import os
import warnings
import pydot as pyd
import seaborn as sns
import pandas as pd
from timeit import default_timer as timer
import matplotlib.pyplot as plt
warnings.simplefilter(action = 'ignore', category = FutureWarning)
os.environ["CUDA_DEVICE_ORDER"] = "PCI_BUS_ID";
# GPUid to use
os.environ["CUDA_VISIBLE_DEVICES"] = "0";
# Allow growth of GPU memory, otherwise it will always look like all the memory is being used
physical_devices = tf.config.experimental.list_physical_devices('GPU')
tf.config.experimental.set_memory_growth(physical_devices[0], True)
# +
# Insert initial parameters
img_height, img_width = 224, 224
batch_size = 64
n_classes = 3
# Data augmentation
train_datagen = ImageDataGenerator(#horizontal_flip = True,
#vertical_flip = True,
#rotation_range = 45,
brightness_range = [0.5, 2],
samplewise_center = True,
#fill_mode = 'constant',
rescale = 1./255)
# preprocessing_function = preprocess_input)
test_datagen = ImageDataGenerator(horizontal_flip = False,
vertical_flip = False,
rotation_range = 0,
samplewise_center = True,
rescale = 1./255)
# preprocessing_function = preprocess_input)
train = train_datagen.flow_from_directory('/local/data1/elech646/Tumor_grade_classification/dataset224_t2_frontal/train',
classes = ['G2','G3','G4'], color_mode = 'rgb',
class_mode = 'categorical',
target_size = (img_height, img_width),
batch_size = batch_size, seed = 123)
validation = test_datagen.flow_from_directory('/local/data1/elech646/Tumor_grade_classification/dataset224_t2_frontal/val',
classes = ['G2','G3','G4'], color_mode = 'rgb',
class_mode = 'categorical',
target_size = (img_height, img_width),
batch_size = batch_size, seed = 123)
test = test_datagen.flow_from_directory('/local/data1/elech646/Tumor_grade_classification/dataset224_t2_frontal/test',
classes = ['G2','G3','G4'], color_mode = 'rgb',
shuffle = False, class_mode = 'categorical',
target_size = (img_height, img_width),
batch_size = batch_size)
# +
# Use class weights
class_weights = class_weight.compute_class_weight(class_weight = 'balanced',
classes = np.unique(train.classes),
y = train.classes)
# Convert to dictionary
class_weights = dict(enumerate(class_weights))
# +
x_train, y_train = next(iter(train))
print(x_train.shape, y_train.shape)
print(x_train.min())
# Plot the images for fun
def plot_images(images):
fig, axes = plt.subplots(1, 5, figsize = (20, 20))
axes = axes.flatten()
for img, ax in enumerate(axes):
ax.imshow(images[img,:,:], cmap = 'gray')
ax.axis('off')
plt.tight_layout()
plt.show()
plot_images(x_train[:1000])
# +
# Load base model
vgg_19 = VGG19(input_shape = (224, 224, 3), weights = 'imagenet', include_top = False)
freeze_until_layer = 100
# Freeze all layers before the `freeze_until_layer` layer
for layer in vgg_19.layers[:freeze_until_layer]:
layer.trainable = False
x = vgg_19.output
x = Flatten()(x)
x = Dense(50, activation = 'relu')(x)
x = Dropout(0.4)(x)
x = Dense(20, activation = 'relu')(x)
x = Dropout(0.4)(x)
predictions = Dense(n_classes, activation = 'softmax')(x)
model = Model(inputs = vgg_19.input, outputs = predictions)
model.summary()
# -
plot_model(model, to_file = 'vgg19_plot_t2_frontal.png', show_shapes = True, show_layer_names = True)
# +
# Save best model
checkpoint_path = '/local/data1/elech646/code/train_logs/vgg19_transfer.h5'
checkpoint = tf.keras.callbacks.ModelCheckpoint(filepath = checkpoint_path,
monitor = 'val_accuracy',
mode = 'max',
verbose = 1,
save_best_only = True)
# Save log for history
# append: True: append if file exists (useful for continuing training)
# False: overwrite existing file
csv_logger = CSVLogger('/local/data1/elech646/code/train_logs/vgg19_transfer_history.log',
separator = ',', append = True)
# Reduce learning rate if val_accuracy is not improving
reduce_lr = ReduceLROnPlateau(monitor = 'val_accuracy', factor = 0.1,
patience = 5, min_lr = 0.000001)
es = EarlyStopping(monitor = 'val_accuracy', verbose = 1, patience = 15)
# +
# Compile model
model.compile(Adam(lr = 1e-5),
loss = 'categorical_crossentropy',
metrics = ['accuracy'])
epochs = 30
start = timer()
history = model.fit(train, steps_per_epoch = len(train.labels) // batch_size, verbose = 1,
epochs = epochs, validation_data = validation,
validation_steps = len(validation.labels) // batch_size,
class_weight = class_weights,
callbacks = [es, reduce_lr, checkpoint, csv_logger])
end = timer()
print("Training took: %.2fs\n" % (end - start))
# -
# 1st training:
#
# data augmentation: horizontal+vertical flip, rotation by 90 degrees
#
# Setup: `x = vgg_19.output
# x = Flatten()(x)
# x = Dense(512, activation = 'relu')(x) # try 128, 64 the lower the better
# x = Dropout(0.5)(x)
# x = Dense(128, activation = 'relu')(x)
# x = Dropout(0.5)(x)
# predictions = Dense(n_classes, activation = 'softmax')(x)`
#
# epochs: 30
#
# learning rate: 0.00001
#
# training time: 649s $\approx 11$ min
#
# test accuracy: 0.4844 and smoother plot on `val_accuracy`
#
# ------------------------------------------------------------------------------------------------------------------
#
# 2nd training:
#
# data augmentation: `brightness_range = [0.5, 2]`
#
# Setup: `x = vgg_19.output
# x = Flatten()(x)
# x = Dense(50, activation = 'relu')(x)
# x = Dropout(0.4)(x)
# x = Dense(20, activation = 'relu')(x)
# x = Dropout(0.4)(x)
# predictions = Dense(n_classes, activation = 'softmax')(x)`
#
# epochs: 30
#
# learning rate: 1e-5 with `ReduceLROnPlateau` + `EarlyStopping`
#
# training time: 254.94s $\approx 4$ min
#
# test accuracy: 0.6701
score = model.evaluate(test, steps = len(test.labels) // batch_size, verbose = 0)
print('Test loss: %.4f' % score[0])
print('Test accuracy: %.4f' % score[1])
# +
# Plot training + validation accuracy per epoch
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
n_epochs = range(len(acc))
# for fancy LaTeX style plots
from matplotlib import rc
import matplotlib.pylab as plt
rc('font', **{'family': 'serif', 'serif': ['Computer Modern']})
rc('text', usetex = True)
# Plot accuracy
plt.plot(n_epochs, acc, label = 'Training accuracy')
plt.plot(n_epochs, val_acc, label = 'Validation accuracy')
plt.title('2nd training')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend(loc = 'best')
plt.savefig('VGG19_2nd_training_t2_frontal_acc.png', dpi = 300)
plt.show()
# Plot loss
plt.plot(n_epochs, loss, label = 'Training loss')
plt.plot(n_epochs, val_loss, label = 'Validation loss')
plt.title('2nd training')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend(loc = 'best')
plt.savefig('VGG19_2nd_training_t2_frontal_loss.png', dpi = 300)
plt.show()
# +
# Get rounded predictions
y_pred = np.argmax(model.predict(test), axis = 1)
# Get true labels
y_true = test.classes
# Plot confusion matrix
cm = confusion_matrix(y_true, y_pred)
#ax = sns.heatmap(cm, annot = True, cmap = 'Blues')
ax = sns.heatmap(cm / np.sum(cm), annot = True, fmt = '.2%', cmap = 'PuBu')
for t in ax.texts:
t.set_text(t.get_text().replace('%', '\%'))
ax.set_xlabel('\nPredicted values')
ax.set_ylabel('Actual values ');
# list must be in alphabetical order
ax.xaxis.set_ticklabels(['Grade 2','Grade 3', 'Grade 4'])
ax.yaxis.set_ticklabels(['Grade 2','Grade 3', 'Grade 4'])
plt.savefig('VGG19_2nd_training_CM_t2_frontal.png', dpi = 300)
plt.show()
# +
# Print classification report
print(classification_report(y_true, y_pred))
# Save the classification report
clsf_report = pd.DataFrame(classification_report(y_true = y_true, y_pred = y_pred, output_dict = True)).transpose()
clsf_report.to_csv('Classification Report-2nd Training on t2 frontal.csv', index = True)
|
source/VGG19/VGG19_pretrained_t2_frontal.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1 align="center">Dinámica</h1>
# <h1 align="center">Capítulo 3: Cinemática y Cinética de partículas</h1>
# <h1 align="center">Movimiento parabólico</h1>
# <h1 align="center">2021/02</h1>
# <h1 align="center">MEDELLÍN - COLOMBIA </h1>
# <table>
# <tr align=left><td><img align=left src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/CC-BY.png?raw=true">
# <td>Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved MIT license.(c) <NAME></td>
# </table>
# ***
#
# ***Docente:*** <NAME>, I.C. D.Sc.
#
# ***e-mail:*** <EMAIL>
#
# ***skype:*** carlos.alberto.alvarez.henao
#
# ***Linkedin:*** https://www.linkedin.com/in/carlosalvarez5/
#
# ***github:*** https://github.com/carlosalvarezh/Dinamica
#
# ***Herramienta:*** [Jupyter](http://jupyter.org/)
#
# ***Kernel:*** Python 3.9
#
#
# ***
# + [markdown] toc=true
# <h1>Tabla de Contenidos<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Movimiento-parabólico" data-toc-modified-id="Movimiento-parabólico-1"><span class="toc-item-num">1 </span>Movimiento parabólico</a></span><ul class="toc-item"><li><span><a href="#Introducción" data-toc-modified-id="Introducción-1.1"><span class="toc-item-num">1.1 </span>Introducción</a></span></li><li><span><a href="#Análisis-cinemático" data-toc-modified-id="Análisis-cinemático-1.2"><span class="toc-item-num">1.2 </span>Análisis cinemático</a></span></li><li><span><a href="#Movimiento-horizontal" data-toc-modified-id="Movimiento-horizontal-1.3"><span class="toc-item-num">1.3 </span>Movimiento horizontal</a></span></li><li><span><a href="#Movimiento-vertical" data-toc-modified-id="Movimiento-vertical-1.4"><span class="toc-item-num">1.4 </span>Movimiento vertical</a></span></li><li><span><a href="#Comentarios-al-movimiento-curvilíneo" data-toc-modified-id="Comentarios-al-movimiento-curvilíneo-1.5"><span class="toc-item-num">1.5 </span>Comentarios al movimiento curvilíneo</a></span></li><li><span><a href="#Ejemplos-movimiento-parabólico" data-toc-modified-id="Ejemplos-movimiento-parabólico-1.6"><span class="toc-item-num">1.6 </span>Ejemplos movimiento parabólico</a></span></li></ul></li><li><span><a href="#Movimiento-curvilíneo:-Componentes-normal-y-tangencial" data-toc-modified-id="Movimiento-curvilíneo:-Componentes-normal-y-tangencial-2"><span class="toc-item-num">2 </span>Movimiento curvilíneo: Componentes normal y tangencial</a></span><ul class="toc-item"><li><span><a href="#Introducción" data-toc-modified-id="Introducción-2.1"><span class="toc-item-num">2.1 </span>Introducción</a></span></li><li><span><a href="#Movimiento-plano" data-toc-modified-id="Movimiento-plano-2.2"><span class="toc-item-num">2.2 </span>Movimiento plano</a></span></li><li><span><a href="#Velocidad" data-toc-modified-id="Velocidad-2.3"><span class="toc-item-num">2.3 </span>Velocidad</a></span></li><li><span><a href="#Aceleración" data-toc-modified-id="Aceleración-2.4"><span class="toc-item-num">2.4 </span>Aceleración</a></span></li><li><span><a href="#Ejemplos-componentes-normal-y-tangencial" data-toc-modified-id="Ejemplos-componentes-normal-y-tangencial-2.5"><span class="toc-item-num">2.5 </span>Ejemplos componentes normal y tangencial</a></span></li></ul></li><li><span><a href="#Movimiento-curvilíneo:-Componentes-cilíndricos" data-toc-modified-id="Movimiento-curvilíneo:-Componentes-cilíndricos-3"><span class="toc-item-num">3 </span>Movimiento curvilíneo: Componentes cilíndricos</a></span><ul class="toc-item"><li><span><a href="#Introducción" data-toc-modified-id="Introducción-3.1"><span class="toc-item-num">3.1 </span>Introducción</a></span></li><li><span><a href="#Coordenadas-polares" data-toc-modified-id="Coordenadas-polares-3.2"><span class="toc-item-num">3.2 </span>Coordenadas polares</a></span><ul class="toc-item"><li><span><a href="#Posición" data-toc-modified-id="Posición-3.2.1"><span class="toc-item-num">3.2.1 </span>Posición</a></span></li><li><span><a href="#Velocidad" data-toc-modified-id="Velocidad-3.2.2"><span class="toc-item-num">3.2.2 </span>Velocidad</a></span></li><li><span><a href="#Aceleración" data-toc-modified-id="Aceleración-3.2.3"><span class="toc-item-num">3.2.3 </span>Aceleración</a></span></li></ul></li><li><span><a href="#Coordenadas-cilíndricas" data-toc-modified-id="Coordenadas-cilíndricas-3.3"><span class="toc-item-num">3.3 </span>Coordenadas cilíndricas</a></span></li><li><span><a href="#Derivadas-respecto-al-tiempo" data-toc-modified-id="Derivadas-respecto-al-tiempo-3.4"><span class="toc-item-num">3.4 </span>Derivadas respecto al tiempo</a></span></li><li><span><a href="#Ejemplos-componentes-cilíndricos" data-toc-modified-id="Ejemplos-componentes-cilíndricos-3.5"><span class="toc-item-num">3.5 </span>Ejemplos componentes cilíndricos</a></span></li></ul></li></ul></div>
# -
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C02Fig13_Parabolic1.gif?raw=true" width="400" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://en.wikipedia.org/wiki/Projectile_motion#/media/File:Inclinedthrow2.gif">Wikipedia</a> </div>
# ## Movimiento parabólico
# ### Introducción
# El [movimiento parabólico](https://en.wikipedia.org/wiki/Projectile_motion) es el realizado por cualquier objeto cuya trayectoria describe una [parábola](https://en.wikipedia.org/wiki/Parabola), y que corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que esté sujeto a un campo gravitatorio uniforme. El movimiento parabólico es un ejemplo de un movimiento realizado por un objeto en dos dimensiones o sobre un plano. Puede considerarse como la combinación de dos movimientos que son un [movimiento rectilíneo uniforme](https://es.wikipedia.org/wiki/Movimiento_rectil%C3%ADneo_uniforme), en la dirección horizontal ($\longleftrightarrow$), y un [movimiento rectilíneo uniformemente acelerado](https://es.wikipedia.org/wiki/Movimiento_rectil%C3%ADneo_uniformemente_acelerado) en la dirección vertical ($\updownarrow$).
# ### Análisis cinemático
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C02Fig14_Parabolic2.PNG
# # ?raw=true" width="350" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# "><NAME>. Engineering Mechanics: Dynamics</a> </div>
#
#
# Considere un proyectil lanzado en el punto $(x_0, y_0)$, con una velocidad inicial de $v_0$, cuyas componentes son $v_{0x}$ y $v_{0y}$. Cuando se hace caso omiso de la resistencia del aire, la única fuerza que actúa en el proyectil es su peso, el cual hace que el proyectil tenga una aceleración dirigida hacia abajo constante de aproximadamente $a_c=g=9.81 m/s^2=32.2 pies/s^2$.
# ### Movimiento horizontal
# Como $a_x=0$, se pueden aplicar las ecuaciones de aceleración constante vistas en el [Capítulo 1: Movimiento Rectilíneo, numeral 2.6 Aceleración constante](./C01_CinematicaCineticaParticulas_MovRectilineo.ipynb#ac), resultando en:
#
# <a id='Ec3_1'></a>
# \begin{equation*}
# \begin{array}{crl}
# \left(\underrightarrow{+}\right) &v=&v_0+a_ct& \quad &v_x=v_{0x} \\
# \left(\underrightarrow{+}\right) &x=&x_0+v_0t+\frac{1}{2}a_ct^2& \quad &x=x_0+v_{0x}t \\
# \left(\underrightarrow{+}\right) &v^2=&v_0^2+2a_c(x-x_0)& \quad &v_x=v_{0x} \\
# \end{array}
# \label{eq:Ec3_1} \tag{3.1}
# \end{equation*}
#
# ### Movimiento vertical
# Estableciendo el sistema de coordenadas con el eje $y$ positivo hacia arriba, se tiene entonces que $a_y=-g$ y aplicando las ecuaciones de aceleración constante como visto en el ítem anterior, se llega a:
#
# <a id='Ec3_2'></a>
# \begin{equation*}
# \begin{array}{crl}
# \left(+\uparrow \right) &v=&v_0+a_ct& \quad &v_y=v_{0y}-gt \\
# \left(+\uparrow \right) &y=&y_0+v_0t+\frac{1}{2}a_ct^2& \quad &y=y_0+v_{0y}t-\frac{1}{2}gt^2 \\
# \left(+\uparrow \right) &v^2=&v_0^2+2a_c(y-y_0)& \quad &v_y^2=v_{0y}^2-2g \left(y-y_0 \right) \\
# \end{array}
# \label{eq:Ec3_2} \tag{3.2}
# \end{equation*}
#
# ### Comentarios al movimiento curvilíneo
# - En el movimiento horizontal la primera y la tercera ecuación implican que la componente horizontal de la velocidad siempre permanece constante durante la realización del movimiento.
#
#
# - En el movimiento vertical, la última ecuación puede formularse eliminando el término del tiempo de las dos primeras ecuaciones, por lo que, solo dos de las tres ecuaciones son independientes entre ellas.
#
#
# - De lo anterior se concluye que los problemas que involucran movimiento parabólico pueden tener como máximo tres incógnitas, ya que solo se podrán escribir tres ecuaciones independientes: una ecuación en la dirección horizontal y dos en la dirección vertical.
#
#
# - La velocidad resultante $v$, que siempre será tangente a la trayectoria, se determinará por medio de la suma vectorial de sus componentes $v_x$ y $v_y$.
# ### Ejemplos movimiento parabólico
# <table id="mytable" border=0>
# <tr>
# <td rowspan="2"> <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig01_Sacos.PNG
# # ?raw=true" width="400"/>
# </td>
# <td style="height:50%">
# <div style="text-align: right"> <b>Ejemplo 12.11:</b> <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
#
# <p>Un saco se desliza por la rampa, como se ve en la figura, con una velocidad horizontal de $12 m/s$. Si la altura de la rampa es de $6 m$, determine el tiempo necesario para que el saco choque con el suelo y la distancia $R$ donde los sacos comienzan a apilarse</p>
# </td>
# </tr>
# </table>
#
# ***Solución analítica:***
#
# - ***Sistema de coordenadas*** Se establece el origen en el punto $A$, donde comienza la trayectoria de la partícula (saco). Se observa que la velocidad inicial del saco presenta dos componentes, donde $v_{Ax}=12m/s$ y $v_{Ay}=0$. La acelaración en todo el recorrido, entre $A$ y $B$, es de $a_y=-9.81 m/s^2$. También se observa que se cumple que $v_{Bx}=v_{Ax}=12m/s$ (por qué?). Con lo anterior, las tres incógnitas restantes son $v_{By}$, $R$, y el tiempo de vuelo $t_{AB}$.
#
#
# - ***Movimiento vertical $\left(+\uparrow \right)$:*** Del enunciado, se conoce la distancia vertical $A-B$, que será $y_B=6m$
#
# $$y_B=y_A+v_{Ay}t_{AB}+\frac{1}{2}a_ct_{AB}^2$$
#
# reemplazando valores se tiene
#
# $$0=6m+0 \times t_{AB}+\frac{1}{2}(-9.81m/s^2)t_{AB}^2$$
#
# $$t_{AB}=1.11 s$$
#
# Una vez calculado el tiempo, la distancia horizontal, $R$ se determina así:
#
#
# - ***Movimiento horizontal $\left(\underrightarrow{+}\right)$:***
#
# $$x_B=x_A+v_{Ax}t_{AB}$$
# $$R=0+12m/s(1.11s)$$
# $$R=13.3m$$
#
#
# ***Solución computacional:***
# +
import numpy as np
import matplotlib.pyplot as plt
from sympy import *
import seaborn as sns
t,R = symbols('t R')
init_printing(use_latex='mathjax')
# -
# condiciones iniciales
x0 = 0 # coordenada xA
y0 = 6 # coordenada yA
v0x = 12 # Veloc en A en la dirección x
v0y = 0 # Veloc en A en la dirección y
y = 0 # Altura final
ac = -9.81 # aceleración debida a la gravedad
# Ecuación del movimiento vertical
yd2 = Eq(y, y0 + v0y * t + ac * t**2 / 2)
yd2
# Resolviendo para t
tiempo = solve(yd2,t)
print("El tiempo de caída de cada saco es de {0:6.4f} s".format(tiempo[1]))
tiempo
xd2 = Eq(R, x0 + v0x * tiempo[0])
xd2
# Ecuación del movimiento horizontal
R = float(x0 + v0x * tiempo[0])
print("La distancia a la que caerá cada saco es de {0:6.4f} m".format(R))
# +
# Graficando
t = np.linspace(0,np.around(float(tiempo[1]), decimals = 4),100)
x = x0 + v0x * t
y = y0 + v0y * t + ac * t**2 / 2
plt.plot(x,y);
plt.xlabel("x(m)")
plt.ylabel("y(m)")
plt.grid(True)
# -
# ## Movimiento curvilíneo: Componentes normal y tangencial
# ### Introducción
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig03_n-t_posicion.PNG
# # ?raw=true" width="250" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
#
# A veces es más conveniente emplear como sistema de referencia las coordenadas $n-t$, que expresan las componentes *normal* y *tangencial* a la trayectoria.
# ### Movimiento plano
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig04_Curvatura.PNG
# # ?raw=true" width="250" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
#
# Sea una partícula que se desplaza en el plano a lo largo de una curva fija, tal que en un instante dado está en la posición $s$ medida respecto a $O'$. Considere un sistema de ejes coordenados con origen en un punto fijo de la curva y, en un instante determinado, éste coincide con la ubicación de la partícula. El eje $t$ es tangente a la curva en el punto y positivo en la dirección de $s$, denominada con el vector unitario $\vec{\boldsymbol{u}}_t$. La determinación del eje normal, $\vec{\boldsymbol{u}}_n$ es inmediata, ya que solo existe una única posibilidad, siendo positivo en la dirección hacia el centro de la curva. La curva se forma por una serie de segmentos de arco de tamaño $ds$ y cada uno de estos segmentos es formado por el arco de un círculo con radio de curvatura $\rho$ y centro $O'$. El plano que se genera por los ejes $n-t$ se denomina *[plano osculador](https://es.wikipedia.org/wiki/Geometr%C3%ADa_diferencial_de_curvas#Plano_osculador)*, y está fijo en el plano del movimiento.
#
#
# ### Velocidad
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig05_Velocidad.PNG
# # ?raw=true" width="250" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
#
# Como se ha indicado en las secciones anteriores, la partícula se encuentra en movimiento, por lo que el desplazamiento es una función del tiempo, $s(t)$. La dirección de la velocidad de la partícula siempre es tangente a la trayectoria y su magnitud se determina por la derivada respecto al tiempo de la función de la trayectoria. Entonces:
#
# <a id='Ec3_3'></a>
# \begin{equation*}
# \boldsymbol{v}=v\boldsymbol{u}_t
# \label{eq:Ec3_3} \tag{3.3}
# \end{equation*}
#
# donde
#
# <a id='Ec3_4'></a>
# \begin{equation*}
# v=\dot{s}
# \label{eq:Ec3_4} \tag{3.4}
# \end{equation*}
#
# ### Aceleración
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig06_Aceleracion0.PNG
# # ?raw=true" width="250" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
#
# El cambio de la velocidad de la partícula respecto al tiempo es la aceleración. Entonces
#
# <a id='Ec3_5'></a>
# \begin{equation*}
# \boldsymbol{a}=\dot{\boldsymbol{v}}=\dot{v}\boldsymbol{u}_t + v\dot{\boldsymbol{u}}_t
# \label{eq:Ec3_5} \tag{3.5}
# \end{equation*}
#
# Falta determinar la derivada de $\dot{\boldsymbol{u}}_t$ respecto al tiempo. A medida que la partícula se desplaza a lo largo de un arco $ds$ en un diferencial de tiempo $dt$, $\boldsymbol{u}_t$ su dirección varía y pasa a ser $\boldsymbol{u}'_t$, donde $\boldsymbol{u}'_t=\boldsymbol{u}_t+d\boldsymbol{u}_t$. Observe que $d\boldsymbol{u}_t$ va de las puntas de $\boldsymbol{u}_t$ a $\boldsymbol{u}'_t$, que se extienden en un arco infinitesimal de magnitud $u_t=1$ (unitaria). Por lo tanto, $d\boldsymbol{u}_t=d\theta \boldsymbol{u}_n$, por lo que la derivada con respecto al tiempo es $\dot{\boldsymbol{u}}_t=\dot{\theta}\boldsymbol{u}_n$.
#
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig07_dut.PNG
# # ?raw=true" width="150" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
#
# Observe también que $ds=\rho d\theta$, entonces $\dot{\theta}=\dot{s}/\rho$, resultando
#
# $$\dot{\boldsymbol{u}}_t=\dot{\theta}\boldsymbol{u}_n=\frac{\dot{s}}{\rho}\boldsymbol{u}_n=\frac{v}{\rho}\boldsymbol{u}_n$$
#
# Sustituyendo en la [Ec. 3.4](#Ec3_4) se puede reescribir $\boldsymbol{a}$ como la suma de las componentes tangencial y normal:
#
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig08_Aceleracion1.PNG
# # ?raw=true" width="250" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
#
# <a id='Ec3_6'></a>
# \begin{equation*}
# \boldsymbol{a} = a_t \boldsymbol{u}_t + a_n \boldsymbol{u}_n
# \label{eq:Ec3_6} \tag{3.6}
# \end{equation*}
#
# donde la componente tangencial es dada por
#
# <a id='Ec3_7'></a>
# \begin{equation*}
# a_t = \dot{v} \qquad \text{o} \qquad a_t ds = vdv
# \label{eq:Ec3_7} \tag{3.7}
# \end{equation*}
#
# la componente normal, por
#
# <a id='Ec3_8'></a>
# \begin{equation*}
# a_n = \frac{v^2}{\rho}
# \label{eq:Ec3_8} \tag{3.8}
# \end{equation*}
#
# y la magnitud de la aceleración está dada por
#
# <a id='Ec3_9'></a>
# \begin{equation*}
# a = \sqrt{a^2_t + a^2_n}
# \label{eq:Ec3_9} \tag{3.9}
# \end{equation*}
#
#
# ***Comentarios***
#
# - Si la partícula se mueve a lo largo de una línea recta entonces $\rho \rightarrow \infty$ y por la [Ec. 3.8](#Ec3_8), $a_=0$. Con esto $a=a_t = \dot{v}$, y se puede concluir que *la componente tangencial de la aceleración representa el cambio en la magnitud de la velocidad*.
#
#
# - Si la partícula se mueve a lo largo de una curva con velocidad constante, entonces $a_t=\dot{v}=0$ y $a=a_n=v^2/\rho$. Por lo tanto, *la componente normal de la aceleración representa el cambio en la dirección de la velocidad*. Como $a_n$ siempre actúa hacia el centro de la curvatura, esta componente en ocasiones se conoce como la [aceleración centrípeta](https://en.wikipedia.org/wiki/Centripetal_force) ("*que busca el centro*").
#
#
# - Expresando la trayectoria de la partícula como $y=f(x)$, el radio de curvatura en cualquier punto de la trayectoria se determina por la ecuación:
#
# <a id='Ec3_10'></a>
# \begin{equation*}
# \rho=\frac{\left[1 + (dy/dx)^2\right]^{3/2}}{|d^2y/dx^2|}
# \label{eq:Ec3_10} \tag{3.10}
# \end{equation*}
#
# Como consecuencia de lo anterior, una partícula que se mueve a lo largo de una trayectoria curva tendrá una aceleración como la mostrada en la figura:
#
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig09_Aceleracion2.PNG
# # ?raw=true" width="450" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
# ### Ejemplos componentes normal y tangencial
# <table id="mytable" border=0>
# <tr>
# <td rowspan="2"> <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig10_Esquiador.PNG
# # ?raw=true" width="800"/>
# </td>
# <td style="height:50%">
# <div style="text-align: right"> <b>Ejemplo 12.14:</b> <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# "><NAME>. Engineering Mechanics: Dynamics</a> </div>
#
# <p>Cuando el esquiador llega al punto $A$ a lo largo de la trayectoria parabólica en la figura, su rapidez es de $6 m/s$, la cual se incrementa a $2 m/s^2$. Determine la dirección de su velocidad y la dirección y magnitud de su aceleración en este instante. Al hacer el cálculo, pase por alto la estatura del esquiador..</p>
# </td>
# </tr>
# </table>
#
# - ***Sistema de coordenadas:***
#
# Se establece el origen de los ejes $n-t$ en el punto fijo $A$ de la trayectoria.
#
#
# - ***Velocidad:***
#
# Como se definió, la velocidad será siempre tangente a la trayectoria. Como $y = \frac{1}{20}x^2$, su derivada es $\frac{dy}{dx}=\frac{1}{10}x$, reemplazando cuando $x=10m$, $\frac{dy}{dx}=1$. Por lo tanto, en $A$, $\boldsymbol{v}$ forma un ángulo $\theta=\tan^{-1}(1)=45^{\circ}$ con el eje $x$. Con esto, la velocidad en $A$ es
#
# $$v_A=6m/s \quad 45^{\circ}\measuredangle$$
#
#
# - ***Aceleración:***
#
# Reemplazando las [Ecs. 3.7 y 3.8](#Ec3_7) en la [Ec. 3.6](#Ec3_6) para determinar la aceleración, se llega a:
#
# $$\boldsymbol{a}=\dot{v}\boldsymbol{u}_t+\frac{v^2}{\rho}\boldsymbol{u}_n$$
#
# De esta ecuación se desconoce el radio de curvatura $\rho$ de la trayectoria en el punto $A(10,5)$. Empleando la [Ec. 3.10](#Ec3.10) y reemplazando el valor de la coordenada:
#
# $$\rho=\frac{\left[1 + (dy/dx)^2\right]^{3/2}}{|d^2y/dx^2|}=\left. \frac{\left[1 + (x/10)^2\right]^{3/2}}{|1/10|} \right|_{x=10m}=28.28m$$
#
#
# Con lo anterior, la dirección de la aceleración está dada por
#
# $$
# \begin{align*}
# \boldsymbol{a} & = \dot{v} \boldsymbol{u}_t + \frac{v^2}{\rho} \boldsymbol{u}_n \\
# & = 2 \boldsymbol{u}_t + \frac{(6m/s)^2}{28.28m} \boldsymbol{u}_n \\
# & = (2 \boldsymbol{u}_t + 1.273 \boldsymbol{u}_n) m/s^2
# \end{align*}
# $$
#
# y cada una de las componentes se representan en la siguiente figura.
#
# <a id='Fig_angulos'></a>
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig11_Esquiador1.PNG
# # ?raw=true" width="125" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
#
# por último, la magnitud de la aceleración está dada por
#
# $$a=\sqrt{(2m/s^2)^2+(1.273 m/s^2)^2}=2.37 m/s^2$$
#
# el ángulo sería
#
# $$\phi = \tan^{-1}\left(\frac{2}{1.273} \right)=57.5^{\circ}$$
#
# De la figura:
#
# $$45^{\circ}+90^{\circ}+57.5^{\circ}-180^{\circ}=12.5^{\circ}$$
#
# entonces,
#
# $$\boldsymbol{a}=2.37 m/s^2 \quad 12.5^{\circ} \measuredangle$$
#
# Ahora vamos a realizar la solución empleando programación con el ecosistema `python`
x = symbols('x')
ut, un = symbols('ut un')
# La ecuación que determina la trayectoria de la partícula está dada por
y = x**2 / 20
# Y la velocidad de la partícula, cuya magnitud es la misma rapidez, segun el enunciado es
v = 6
# Ahora se deriva la ecuación de la trayectoria respecto a la variable $x$
dydx = diff(y,x)
dydx
# reemplazando en $x=10m$
dydx = N(dydx.subs(x,10),4)
print("{0:6.1f}".format(dydx))
# con esto, se calcula el ángulo que determina la direccion de la velocidad
theta = N(atan(dydx)*180/np.pi,4)
print("{0:6.1f}".format(theta))
# El cálculo de la aceleración se realiza mediante la siguiente ecuación:
#
# $$\boldsymbol{a} = \dot{v} \boldsymbol{u}_t + \frac{v^2}{\rho} \boldsymbol{u}_n$$
#
# se debe calcular el radio de curvatura $\rho$ con la [Ec. 3.10](#Ec3_10), que a su vez requiere del cálculo de la segunda derivada de la función de la trayectoria, $y$, respecto a $x$. Del enunciado se determina que $\dot{v}=2 m/s$.
d2ydx2 = diff(y,x,2)
d2ydx2
rho = N((1 + dydx**2)**(3/2) / d2ydx2,4)
print("{0:6.4f}".format(rho))
v_dot = 2
# Con lo anterior, se construye la expresión para la aceleración
v2rho = v**2 / rho
a_A = v_dot * ut + v2rho * un
a_A
# Ahora se calculará la magnitud de la aceleración, dada por la [Ec. 3.9](#Ec3_9)
a_mag = sqrt(v_dot**2 + v2rho**2)
print("{0:6.1f}".format(a_mag))
# por último, calculamos el ángulo para la dirección de la aceleración
phi = atan(v_dot / v2rho) * 180 / np.pi
print("{0:6.1f}".format(phi))
# De la [figura](#Fig_angulos) donde se expresan los ángulos, se determina cuál sería la dirección
a = 45 + 90 + phi - 180
print("{0:6.1f}".format(a))
# <div class="alert alert alert-success">
# $\color{red}{\textbf{Actividad para ser realizada por el estudiante:}}$
#
# <ul>
# <li>Realizar computacionalmente los otros ejemplos del capítulo que aparecen en el libro de Hibbeler, sección 12.7, ejemplos 12-15 y 12-16 (pags. 58 y 59).</li>
#
#
# <li>También se invita a que desarrollen al menos un ejercicio de los problemas fundamentales (pag. 60), y ejercicios de los problemas (pags. 61 - 67), dividiendolos en tres partes: dos ejercicios del tercio inferior, dos del tercio medio y dos del tercio superior, tanto analíticamente ("a mano") como computacionalmente. </li>
# </ul>
# </div>
# ## Movimiento curvilíneo: Componentes cilíndricos
# ### Introducción
# En ciertos problemas cuyo movimiento de la partícula describe una trayectoria curva, la descripción de dicho movimiento se describe de mejor forma (más simple) empleando un [sistema de coordenadas cilíndricas](https://en.wikipedia.org/wiki/Cylindrical_coordinate_system). Si el movimiento se limita a un plano se emplea un [sistema de coordenadas polares](https://en.wikipedia.org/wiki/Polar_coordinate_system).
# ### Coordenadas polares
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig12_polar_Posicion.PNG
# # ?raw=true" width="250" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
#
# La posición de la partícula en la figura se determina mediante una coordenada radial $r$, que se extiende desde el origen $O$ hasta la partícula, y el ángulo $\theta$ entre un eje horizontal que sirve como referencia y $r$, medido en sentido antihorario. Las componentes $\boldsymbol{u}_r$ y $\boldsymbol{u}_{\theta}$ se defienen en la dirección positiva de $r$ y $\theta$ respectivamente.
# #### Posición
# La posición de la partícula se define por el vector posición
#
# <a id='Ec3_11'></a>
# \begin{equation*}
# \boldsymbol{r}=r\boldsymbol{u}_r
# \label{eq:Ec3_11} \tag{3.11}
# \end{equation*}
# #### Velocidad
# La velocidad es la derivada de $\boldsymbol{r}$ respecto al tiempo
#
# <a id='Ec3_12'></a>
# \begin{equation*}
# \boldsymbol{v}=\boldsymbol{\dot{r}}=\dot{r}\boldsymbol{u}_r+r\boldsymbol{\dot{u}}_r
# \label{eq:Ec3_12} \tag{3.12}
# \end{equation*}
#
# En la evaluación de $\boldsymbol{\dot{u}}_r$, obsérvese que $\boldsymbol{u}_r$ únicamente cambia de dirección respecto al tiempo, ya que por definición la magnitud del vector es unitaria. En un tiempo $\Delta t$, el cambio $\Delta r$ no cambiará la dirección de $\boldsymbol{u}_r$, sin embargo, un cambio $\Delta \theta$ proporcionará que $\boldsymbol{u}_r$ cambie a $\boldsymbol{u}'_r$, con $\boldsymbol{u}'_r=\boldsymbol{u}_r+\Delta \boldsymbol{u}_r$. Entonces, el cambio de $\boldsymbol{u}_r$ es por lo tanto $\Delta \boldsymbol{u}_r$. Si $\Delta \theta$ es pequeño, la magnitud del vector es $\Delta u_r \approx 1 (\Delta \theta)$, en la dirección $\boldsymbol{u}_{\theta}$. Entonces $\Delta \boldsymbol{u}_r=\Delta \theta \boldsymbol{u}_{\theta}$, y
#
# $$\boldsymbol{\dot{u}}_r=\lim \limits_{\Delta t \to 0} \frac{\Delta \boldsymbol{u}_r}{\Delta t} = \left( \lim \limits_{\Delta t \to 0} \frac{\Delta \theta}{\Delta t}\right) \boldsymbol{u}_{\theta}
# $$
#
# <a id='Ec3_13'></a>
# \begin{equation*}
# \boldsymbol{\dot{u}}_r=\dot{\theta}\boldsymbol{u}_{\theta}
# \label{eq:Ec3_13} \tag{3.13}
# \end{equation*}
#
# Sustituyendo en la ecuación anterior, la velocidad se escribe a través de sus componentes como
#
# <a id='Ec3_14'></a>
# \begin{equation*}
# \boldsymbol{v}=v_r \boldsymbol{u}_r+v_{\theta}\boldsymbol{u}_{\theta}
# \label{eq:Ec3_14} \tag{3.14}
# \end{equation*}
#
# donde
#
# <a id='Ec3_15'></a>
# \begin{equation*}
# v_r=\dot{r} \\
# v_{\theta} = r\dot{\theta}
# \label{eq:Ec3_15} \tag{3.15}
# \end{equation*}
#
#
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig13_PolarVelocidad.PNG
# # ?raw=true" width="250" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# "><NAME>. Engineering Mechanics: Dynamics</a> </div>
#
# En la gráfica se observa la descomposición del vector velocidad en las componentes radial, $\boldsymbol{v}_r$, que mide la tasa de incremento (decremento) de la longitud en la coordenada radial, o sea, $\dot{r}$, y la componente transversal, $\boldsymbol{v}_{\theta}$, que es la tasa de movimiento a lo largo de una circunferencia de radio $r$. El término $\dot{\theta}=d\theta / dt$ también se conoce como *velocidad angular*, ya que es la razón de cambio del ángulo $\theta$ respecto al tiempo. Las unidades de la velocidad angular se dan en $rad/s$.
#
# Considerando que $\boldsymbol{v}_r$ y $\boldsymbol{v}_{\theta}$ son perpendiculares, la magnitud de la velocidad estará dada por el valor positivo de:
#
# <a id='Ec3_16'></a>
# \begin{equation*}
# v = \sqrt{(\dot{r})^2+(r\dot{\theta})^2}
# \label{eq:Ec3_16} \tag{3.16}
# \end{equation*}
#
# donde la dirección de $\boldsymbol{v}$ es tangente a la trayectoria.
# #### Aceleración
# La aceleración es la derivada de la velocidad respecto al tiempo. De las ecs. [(3.14)](#Ec3_14) y [(3.15)](#Ec3_15), se llega a la aceleración instantánea de la partícula.
#
# <a id='Ec3_17'></a>
# \begin{equation*}
# \boldsymbol{a}=\boldsymbol{\dot{v}}=\ddot{r}\boldsymbol{u}_r+\dot{r}\dot{\boldsymbol{u}}_r+\dot{r}\dot{\theta}\boldsymbol{u}_{\theta}+r\ddot{\theta}\boldsymbol{u}_{\theta}+r\dot{\theta}\boldsymbol{\dot{u}}_{\theta}
# \label{eq:Ec3_17} \tag{3.17}
# \end{equation*}
#
# De la anterior ecuación se requiere determinar el valor de $\dot{\boldsymbol{u}}_{\theta}$, que es el cambio de la dirección $\boldsymbol{u}_{\theta}$ respecto al tiempo, con magnitud unitaria.
#
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig14_angulos.PNG
# # ?raw=true" width="150" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
#
# De la gráfica se tiene que en un tiempo $\Delta t$, un cambio $\Delta r$ no cambiará la dirección $\boldsymbol{u}_{\theta}$, sin embargo, un cambio $\Delta \theta$ hará que $\boldsymbol{u}_{\theta}$ pase a $\boldsymbol{u}'_{\theta}$, con $\boldsymbol{u}'_{\theta}=\boldsymbol{u}_{\theta}+\Delta\boldsymbol{u}_{\theta}$. Para pequeñas variaciones del ángulo, la magnitud del vector es $\Delta u_{\theta}\approx 1(\Delta \theta)$, actuando en la dirección $-\boldsymbol{u}_r$, o sea, $\Delta u_{\theta}=-\Delta \theta\boldsymbol{u}_r$, entonces
#
# $$\boldsymbol{\dot{u}}_{\theta}=\lim \limits_{\Delta t \to 0} \frac{\Delta \boldsymbol{u}_{\theta}}{\Delta t} = -\left( \lim \limits_{\Delta t \to 0} \frac{\Delta \theta}{\Delta t}\right) \boldsymbol{u}_{r}
# $$
#
# <a id='Ec3_18'></a>
# \begin{equation*}
# \boldsymbol{\dot{u}}_{\theta}=-\dot{\theta}\boldsymbol{u}_{r}
# \label{eq:Ec3_18} \tag{3.18}
# \end{equation*}
#
# Sustituyendo el anterior resultado y la Ec. [(3.13)](#Ec3_13) en la ecuación para la aceleración, se escribe la aceleración en forma de componentes como
#
# <a id='Ec3_19'></a>
# \begin{equation*}
# \boldsymbol{a}=a_r\boldsymbol{u}_{r}+a_{\theta}\boldsymbol{u}_{\theta}
# \label{eq:Ec3_19} \tag{3.19}
# \end{equation*}
#
# con
#
# <a id='Ec3_20'></a>
# \begin{equation*}
# a_r=\ddot{r}-r\dot{\theta}^2 \\
# a_{\theta}=r\ddot{\theta}+2\dot{r}\dot{\theta}
# \label{eq:Ec3_20} \tag{3.20}
# \end{equation*}
#
# donde $\ddot{\theta}=d^2\theta/dt^2=d/dt(d\theta /dt)$ se conoce como *aceleración angular y sus unidades son $rad/s^2$*. $\boldsymbol{a}_r$ y $\boldsymbol{a}_{\theta}$ son perpendiculares, entonces la magnitud d ela aceleración está dada por el valor positivo de
#
# <a id='Ec3_21'></a>
# \begin{equation*}
# a=\sqrt{(\ddot{r}-r\dot{\theta}^2)^2+(r\ddot{\theta}+2\dot{r}\dot{\theta})^2}
# \label{eq:Ec3_21} \tag{3.21}
# \end{equation*}
#
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig15_aceleracionangular.PNG
# # ?raw=true" width="250" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
# ### Coordenadas cilíndricas
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig16_cilindrica.PNG
# # ?raw=true" width="250" />
# </p>
#
# <div style="text-align: right"> Fuente: <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
#
# Si la partícula se mueve a lo largo de una curva espacial, entonces su ubicación se especifica por medio de las tres coordenadas cilíndricas, $r$, $\theta$, $z$. La coordenada $z$ es idéntica a la que se utilizó para coordenadas rectangulares. Como el vector unitario que define su dirección $\boldsymbol{u}_z$, es constante, las derivadas con respecto al tiempo de este vector son cero, y por consiguiente la posición, velocidad y aceleración de la partícula se escriben en función de sus coordenadas cilíndricas como sigue:
#
# <a id='Ec3_22'></a>
# \begin{equation*}
# \begin{split}
# \boldsymbol{r}_p &= r\boldsymbol{u}_r+z\boldsymbol{u}_z \\
# \boldsymbol{v} &= \dot{r}\boldsymbol{u}_r+r\dot{\theta}\boldsymbol{u}_{\theta}+\dot{z}\boldsymbol{u}_{z} \\
# \boldsymbol{a} &= (\ddot{r}-r\dot{\theta}^2)\boldsymbol{u}_r+(r\ddot{\theta}+2\dot{r}\dot{\theta})\boldsymbol{u}_{\theta}+\ddot{z}\boldsymbol{u}_z
# \end{split}
# \label{eq:Ec3_22} \tag{3.22}
# \end{equation*}
#
# ### Derivadas respecto al tiempo
# Las ecuaciones anteriores requieren que obtengamos las derivadas con respecto al tiempo $\dot{r}$, $\ddot{r}$, $\dot{\theta}$ y $\ddot{\theta}$, para evaluar las componentes $r$ y $\theta$ de $\boldsymbol{v}$ y $\boldsymbol{a}. En general se presentan dos tipos de problema:
#
# 1. Si las coordenadas polares se especifican como ecuaciones paramétricas en función del tiempo, $r = r(t)$ y $\theta=\theta(t)$, entonces las derivadas con respecto al tiempo pueden calcularse directamente.
#
#
# 2. Si no se dan las ecuaciones paramétricas en función del tiempo, entonces debe conocerse la trayectoria $r=f(\theta)$. Si utilizamos la regla de la cadena del cálculo podemos encontrar entonces la relación entre $\dot{r}$ y $\dot{\theta}$ y entre $\ddot{r}$ y $\ddot{\theta}$
# ### Ejemplos componentes cilíndricos
# <table id="mytable" border=0>
# <tr>
# <td rowspan="2"> <img src="https://github.com/carlosalvarezh/Dinamica/blob/main/Figs/C03Fig17_Ej12_20.PNG
# # ?raw=true" width="400"/>
# </td>
# <td style="height:50%">
# <div style="text-align: right"> <b>Ejemplo 12.20:</b> <a href="https://www.pearson.com/us/higher-education/product/Hibbeler-Engineering-Mechanics-Dynamics-14th-Edition/9780133915389.html
# ">Hibbeler R. Engineering Mechanics: Dynamics</a> </div>
#
# <p>Debido a la rotación de la barra ahorquillada, la bola en la figura se mueve alrededor de una trayectoria ranurada, una parte de la cual tiene la forma de un <a href="https://en.wikipedia.org/wiki/Cardioid">cardioide</a>, $r=0.5(1 - cos(\theta)) pies$, donde $\theta$ está en radianes. Si la velocidad de la bola es $v=4 pies/s$ y su aceleración es $a=30 pies/s^2$ en el instante $\theta=180^{\circ}$, determine la velocidad angular $\dot{theta}$ y la aceleración angular $\ddot{\theta}$ de la horquilla.</p>
# </td>
# </tr>
# </table>
#
# - ***Sistema de coordenadas:***
# Esta trayectoria es muy rara, y matemáticamente se expresa mejor por medio de coordenadas polares, como se hace aquí, en lugar de coordenadas rectangulares. También, como $\dot{theta}$ y $\ddot{\theta}$ deben determinarse, entonces las coordenadas $r$, $\theta$ no son una opción obvia.
#
# - ***Velocidad y aceleración:***
#
# Empleando la regla de la cadena para determinar las derivadas de $r$ y $\theta$:
#
# \begin{equation*}
# \begin{split}
# r&=0.5(1-\cos\theta) \\
# \dot{r}&=0.5(\sin\theta)\dot{\theta}\\
# \ddot{r}&=0.5(\cos\theta)\dot{\theta}(\dot{\theta})+0.5(\sin\theta)\ddot{\theta}
# \end{split}
# \end{equation*}
#
# evaluando cuando $\theta=180^{\circ}$, se tiene
#
# $$r=1 pie \quad\quad \dot{r}=0\quad\quad\ddot{r}=-0.5\dot{\theta}^2$$
#
# como $v=4 pie/s$, utilizando la ecuación [(3.16)](#Ec3_16) para determinar $\dot{\theta}$ se tiene
#
# \begin{equation*}
# \begin{split}
# v&=\sqrt{(\dot{r})^2+(r\dot{\theta})^2} \\
# 4&=\sqrt{(0)^2+(1\dot{\theta})^2}\\
# \dot{\theta}&=4rad/s
# \end{split}
# \end{equation*}
#
# Ahora calculando $\ddot{\theta}$, empleando la ecuacion [3.21](#Ec3_21)
#
# \begin{equation*}
# \begin{split}
# a&=\sqrt{(\ddot{r}-r\dot{\theta}^2)^2+(r\ddot{\theta}+2\dot{r}\dot{\theta})^2} \\
# 30&=\sqrt{[-0.5(4)^2-1(4)^2]^2+[1\ddot{\theta}+2(0)(4)]^2}\\
# (30)^2&=(-24)^2+\ddot{\theta}^2 \\
# \ddot{\theta}&=18rad/s^2
# \end{split}
# \end{equation*}
#
# - ***Solución computacional:***
# +
import numpy as np
import matplotlib.pyplot as plt
from sympy import *
from sympy.physics.mechanics import dynamicsymbols, init_vprinting
theta = dynamicsymbols(r'\theta')
t = Symbol('t')
init_vprinting()
# -
# Graficando primero la funcion cardioide
# +
phi = np.linspace(0, 2*np.pi, 1000)
r = 0.5 * (1 - np.cos(phi))
plt.polar(phi, r, 'r')
plt.show()
# -
# Ahora obtenemos los valores de $\dot{r}$ y $\ddot{r}$
r = 0.5 * (1 - cos(theta))
rdot = diff(r, t)
rdot
rddot = diff(rdot, t)
rddot
# Evaluando los anteriores resultados cuando $\theta=180^{\circ}$
rN = r.subs(theta, 180 * pi / 180)
rN
rdotN = rdot.subs(theta, 180 * pi / 180)
rdotN
rddotN = rddot.subs(theta, 180 * pi / 180)
rddotN
# Ahora vamos a determinar el valor numérico para $\dot{\theta}$, cuando $v=4pie/s$
thetadot = N(Eq(4, sqrt(rdotN**2 + (rN * theta)**2)))
thetadot
thetadot = solve(thetadot,theta)
thetadot
|
C03_CinematicaCineticaParticulas_MovParabolico.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
CRISP_DM = "C:/Users/kaivl/data_science_covid-19/CRISP_DM.png"
from PIL import Image
import glob
Image.open(CRISP_DM)
# +
import pandas as pd
import numpy as np
from datetime import datetime
# %matplotlib inline
pd.set_option('display.max_rows', 500)
# -
# # Data Preparation
#
# * focus is alweays to understand the final data structure
# * support each step by visual analytics
# ## Johns Hopkins GITHUB csv data
data_raw = pd.read_csv("../data/raw/COVID-19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv")
data_raw.head()
date = data_raw.columns[4:]
df_plot = pd.DataFrame({'Date': date})
df_plot.shape
data_raw[data_raw['Country/Region'] == 'US'].iloc[:,4::].shape
country_list = ['Korea, South', 'US', 'Italy', 'Spain', 'Germany'] # Small country list to start with.
# Slice the data for selected countries.
for each in country_list:
df_plot[each] = np.array(data_raw[data_raw['Country/Region'] == each].iloc[:,4::].sum(axis=0)).T
df_plot.head()
df_plot.set_index('Date')
df_plot.plot()
# ## Data Type 'Date'
df_plot.head()
time_idx = [datetime.strptime(each, '%m/%d/%y') for each in df_plot.Date] # Convert to datetime
time_str = [datetime.strftime(each, "%Y-%m-%d") for each in time_idx] # Convert back to str
df_plot["Date"] = time_str
df_plot.to_csv("../data/processed/COVID_flat_small_table.csv", sep = ';', index = None)
# # Relational data model - defining a primary key
# #### In the relational model to databases, a primary key is a specific choice of a minimal set of attributes(columns) that uniquely specify a tuple(row) in a relation(table)(source:wiki)
#
# #### A primary key's main features are:
#
# * It must contain a unique value for each row of data.
# * It cannot contain null values.
data_raw = pd.read_csv("../data/raw/COVID-19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv")
data_raw.drop(["Lat", "Long"], axis=1, inplace = True)
data_raw.rename(columns={'Province/State':"state", 'Country/Region' : 'country'}, inplace = True)
data_raw['state'] = data_raw['state'].fillna('no')
data_raw.head()
pd_data_base = data_raw.set_index(['state', 'country']).T
pd_data_base.head()
pd_relational_model = pd_data_base.stack(level=[0,1]).reset_index()
pd_relational_model.head()
pd_relational_model.rename(columns={'level_0':'date', 0:'confirmed'}, inplace = True)
pd_relational_model.head()
pd_relational_model['date'] = pd_relational_model['date'].astype('datetime64[ns]') # convert to datetime
pd_relational_model['confirmed'] = pd_relational_model['confirmed'].astype(int) # convert to integer
pd_relational_model.dtypes
pd_relational_model.to_csv('../data/processed/COVID_relational_confirmed.csv', sep = ';', index = None)
print(pd_relational_model[pd_relational_model['country']=='US'].tail())
# ## Due to the new structure of the JOhns Hopkins data set
data_path='../data/raw/COVID-19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_US.csv'
pd_raw_US=pd.read_csv(data_path)
pd_raw_US.head()
# drop all non relevant fields!
# Many of this fields do not belong to
# a transactional data. These fields belong to so called master data
pd_raw_US=pd_raw_US.drop(['UID', 'iso2', 'iso3', 'code3', 'Country_Region','FIPS', 'Admin2', 'Lat', 'Long_', 'Combined_Key'],axis=1)
pd_data_base_US=pd_raw_US.rename(columns={'Province_State':'state'}).copy()
## the stack command has problems when only one information is available within a stacking level
pd_relational_model_US = pd_data_base_US.set_index(['state']) \
.T \
.stack() \
.reset_index() \
.rename(columns = {'level_0':'date', 0:'confirmed'})
pd_relational_model_US['country'] = 'US'
pd_relational_model_US.date = pd_relational_model_US.date.astype('datetime64[ns]') ## convert to datetime
pd_relational_model_US.head()
# # Update the large relational file
pd_relational_model_all=pd_relational_model[pd_relational_model['country']!='US'].reset_index(drop=True)
pd_relational_model_all=pd.concat([pd_relational_model_all,pd_relational_model_US],ignore_index=True)
pd_relational_model_all.to_csv('../data/processed/20200424_COVID_relational_confirmed.csv',sep=';',index=False)
print(pd_relational_model_all[pd_relational_model_all['country']=='US'])
# # Cross check the US data
check_US=pd_relational_model_all[pd_relational_model_all['country']=='US']
check_US[['date','country','confirmed']].groupby(['date','country']).sum()
# # RKI data
#
# * Numbers are in German standard, i.e. "," indicates decimal and "." indicates thousands.
# * It must be converted to standard system.
pd_RKI_raw = pd.read_csv('../data/raw/RKI/RKI_data.csv',sep=';')
pd_RKI_raw.head()
pd_RKI_raw.dtypes
pd_RKI = pd.read_csv('../data/raw/RKI/RKI_data.csv',sep=';', thousands = '.', decimal = ',')
pd_RKI.head()
pd_RKI.dtypes
pd_RKI.to_csv('../data/processed/RKI_data_prepared.csv',sep=';', index = False)
|
notebooks/3. Data Preparation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_braket
# language: python
# name: conda_braket
# ---
# # Computing gradients in parallel with PennyLane-Braket
# A central feature of the Amazon Braket SV1 simulator is that is can execute multiple circuits sent from PennyLane in parallel. This is crucial for scalable optimization, where each training step creates lots of variations of a circuit which need to be executed.
#
# This tutorial will explain the importance of this feature and allow you to benchmark it yourself.
# ## Why is the training of circuits so expensive?
# Quantum-classical hybrid optimization of quantum circuits is the workhorse algorithm of near-term quantum computing. It is not only fundamental for training variational quantum circuits but also more broadly for applications like quantum chemistry, quantum machine learning and, of course, for applications in "vanilla" quantum optimization. Today’s most powerful optimization algorithms rely on the efficient computation of gradients—which tell us how to adapt parameters a little bit at a time to improve the algorithm.
#
# Training quantum circuits is tough! Each step during optimization requires evaluation of the circuit gradient. Calculating the gradient involves multiple device executions: for each trainable parameter we must execute our circuit on the device typically [more than once](https://pennylane.ai/qml/glossary/parameter_shift.html). Reasonable applications involve many trainable parameters (just think of a classical neural net with millions of tunable weights). The result is a huge number of device executions for each optimization step.
#
#
# 
#
# In the ``braket.local.qubit`` device, gradients are calculated in PennyLane through sequential device executions—in other words, all these circuits have to wait in the same queue until they can be evaluated. This approach is simpler, but quickly becomes slow as we scale the number of parameters. Moreover, as the number of qubits, or "width", of the circuit is scaled, each device execution will slow down and eventually become a noticeable bottleneck. In short—**the future of training quantum circuits relies on high-performance remote simulators and hardware devices that are highly parallelized**.
# Fortunately, Amazon Braket provides a solution for scalable quantum circuit training with the SV1 simulator. The SV1 simulator is a high-performance state vector simulator that is designed with parallel execution in mind. Together with PennyLane, we can use SV1 to run in parallel all the circuits needed to compute a gradient!
# 
# ## Loading the SV1 device
# Let's load Braket's SV1 simulator in PennyLane with 25 qubits. Further details on loading Braket devices are provided in the [first tutorial](./0_Getting_started.ipynb). We begin with the standard imports and specification of the bucket and ARN:
# +
import pennylane as qml
from pennylane import numpy as np
qml.enable_tape()
wires = 25
# Please enter the S3 bucket you created during onboarding
# (or any other S3 bucket starting with 'amazon-braket-' in your account) in the code below
my_bucket = f"amazon-braket-Your-Bucket-Name" # the name of the bucket
my_prefix = "Your-Folder-Name" # the name of the folder in the bucket
s3_folder = (my_bucket, my_prefix)
device_arn = "arn:aws:braket:::device/quantum-simulator/amazon/sv1"
# -
# We've also enabled [tape mode](https://pennylane.readthedocs.io/en/stable/code/qml_tape.html) in PennyLane using ``qml.enable_tape()`` to unlock the latest features.
# Recall that all remote simulators and hardware on Braket are accessed through PennyLane using the ``braket.aws.qubit`` device name. The specific remote device is set using the ``device_arn`` argument.
# +
dev_remote = qml.device(
"braket.aws.qubit",
device_arn=device_arn,
wires=wires,
s3_destination_folder=s3_folder,
parallel=True,
)
dev_local = qml.device("braket.local.qubit", wires=wires)
# -
# Note the ``parallel=True`` argument in ``dev_remote``. This setting allows us to unlock the power of parallel execution on SV1 for gradient calculations. The local Braket simulator has also been loaded for comparison.
# ## Benchmarking a circuit evaluation
# We will now compare the execution time for the remote and local Braket devices. Our first step is to create a simple circuit:
def circuit(params):
for i in range(wires):
qml.RX(params[i], wires=i)
for i in range(wires):
qml.CNOT(wires=[i, (i + 1) % wires])
return qml.expval(qml.PauliZ(wires - 1))
# 
# In this circuit, each of the 25 qubits has a controllable rotation. A final block of two-qubit CNOT gates is added to entangle the qubits. Overall, this circuit has 25 trainable parameters. Although not particularly relevant for practical problems, we can use this circuit as a testbed in our comparison of the remote and local devices.
#
# The next step is to convert the above circuit into a PennyLane QNode, which binds the circuit to a device for execution.
qnode_remote = qml.QNode(circuit, dev_remote)
qnode_local = qml.QNode(circuit, dev_local)
# <div class="alert alert-block alert-info">
# <b>Note</b> The above uses <code>qml.QNode</code> to convert the circuit. In previous tutorials, you may have seen the <code>@qml.qnode()</code> decorator being used. These approaches are interchangeable, but we use <code>qml.QNode</code> here because it allows us to pair the same circuit to different devices.
# </div>
#
# Let's now compare the execution time between the two devices:
# +
import time
params = np.random.random(wires)
# -
# The following cell will result in 1 circuit being executed on SV1.
# +
t_0_remote = time.time()
qnode_remote(params)
t_1_remote = time.time()
# +
t_0_local = time.time()
qnode_local(params)
t_1_local = time.time()
# -
print("Execution time on remote device (seconds):", t_1_remote - t_0_remote)
print("Execution time on local device (seconds):", t_1_local - t_0_local)
# Nice! These timings highlight the advantage of using SV1 for simulations with large qubit numbers. In general, simulation times scale exponentially with the number of qubits, but SV1 is highly optimized and running on AWS remote servers. This allows SV1 to outperform the local simulator in this 25-qubit example. The time you see for the remote device will also depend on factors such as your distance to AWS servers.
#
# <div class="alert alert-block alert-info">
# <b>Note</b> Given these timings, why would anyone want to use the local simulator? You should consider using the local simulator when your circuit has few qubits. In this regime, the latency times of communicating the circuit to AWS dominate over simulation times, allowing the local simulator to be faster.
# </div>
# ## Benchmarking gradient calculations
# Now let us compare the gradient-calculation times between the two devices. Remember that when loading the remote device, we set ``parallel=True``. This allows the multiple device executions required during gradient calculations to be performed in parallel on SV1, so we expect the remote device to be much faster.
d_qnode_remote = qml.grad(qnode_remote)
d_qnode_local = qml.grad(qnode_local)
# The following cell will result in 51 circuits being executed (in parallel) on SV1. We must execute the circuit twice to evaluate the partial derivative with respect to each parameter. Hence, for 25 parameters there are 50 circuit executions. The final circuit execution is due to a "forward pass" evaluation of the QNode before the gradient is calculated.
# +
t_0_remote_grad = time.time()
d_qnode_remote(params)
t_1_remote_grad = time.time()
# -
# <div class="alert alert-block alert-warning">
# <b>Caution:</b> Depending on your hardware, running the following cell can take 15 minutes or longer. Only uncomment it if you are happy to wait.
# </div>
# +
# t_0_local_grad = time.time()
# d_qnode_local(params)
# t_1_local_grad = time.time()
# -
print("Gradient calculation time on remote device (seconds):", t_1_remote_grad - t_0_remote_grad)
# print("Gradient calculation time on local device (seconds):", t_1_local_grad - t_0_local_grad)
# If you had the patience to run the local device, you will see times of around 15 minutes or more! Compare this to less than a minute spent calculating the gradient on SV1. This provides a powerful lesson in parallelization.
#
# What if we had run on SV1 with ``parallel=False``? It would have taken around 3 minutes—still faster than a local device, but much slower than running SV1 in parallel.
# <div class="alert alert-block alert-info">
# <b>What's next?</b> Look into some applications, for example how to solve
# <a href="./2_Graph_optimization_with_QAOA.ipynb">graph</a> or <a href="./3_Quantum_chemistry_with_VQE.ipynb">chemistry</a> problems with PennyLane and Braket.
# </div>
|
pennylane/1_Parallelized_optimization_of_quantum_circuits.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ##### argument (인자)
# 함수를 호출할 때 함수 (또는 메서드) 로 전달되는 값. 두 종류의 인자가 있습니다:
#
# - 키워드 인자 (keyword argument): 함수 호출 때 식별자가 앞에 붙은 인자 (예를 들어, name=) 또는 ** 를 앞에 붙인 딕셔너리로 전달되는 인자.
# complex(real=3, imag=5)
# complex(**{'real': 3, 'imag': 5})
#
# - 위치 인자 (positional argument): 키워드 인자가 아닌 인자. 위치 인자들은 인자 목록의 처음에 나오거나 이터러블 의 앞에 * 를 붙여 전달할 수 있습니다.
#
# complex(3, 5)
# complex(*(3, 5))
# ##### attribute (어트리뷰트)
# 점표현식을 사용하는 이름으로 참조되는 객체와 결합한 값. 예를 들어, 객체 o 가 어트리뷰트 a 를 가지면, o.a 처럼 참조됩니다
# ##### BDFL
# 자비로운 종신 독재자 (Benevolent Dictator For Life), 즉 <NAME>, 파이썬의 창시자.
# ##### class (클래스)
# 사용자 정의 객체들을 만들기 위한 주형. 클래스 정의는 보통 클래스의 인스턴스를 대상으로 연산하는 메서드 정의들을 포함합니다.
# ##### class variable (클래스 변수)
# 클래스에서 정의되고 클래스 수준 (즉, 클래스의 인스턴스에서가 아니라) 에서만 수정되는 변수.
# ##### coercion (코어션)
# 같은 형의 두 인자를 수반하는 연산이 일어나는 동안, 한 형의 인스턴스를 다른 형으로 묵시적으로 변환하는 것. 예를 들어, int(3.15) 는 실수를 정수 3 으로 변환합니다. 하지만, 3+4.5 에서, 각 인자는 다른 형이고 (하나는 int, 다른 하나는 float), 둘을 더하기 전에 같은 형으로 변환해야 합니다. 그렇지 않으면 TypeError 를 일으킵니다. 코어션 없이는, 호환되는 형들조차도 프로그래머가 같은 형으로 정규화해주어야 합니다, 예를 들어, 그냥 3+4.5 하는 대신 float(3)+4.5.
# ##### complex number (복소수)
# 익숙한 실수 시스템의 확장인데, 모든 숫자가 실수부와 허수부의 합으로 표현됩니다. 허수부는 실수에 허수 단위 (-1 의 제곱근)를 곱한 것인데, 종종 수학에서는 i 로, 공학에서는 j 로 표기합니다. 파이썬은 후자의 표기법을 쓰는 복소수를 기본 지원합니다;
# ##### decorator (데코레이터)
# 다른 함수를 돌려주는 함수인데, 보통 @wrapper 문법을 사용한 함수 변환으로 적용됩니다. 데코레이터의 흔한 예는 classmethod() 과 staticmethod() 입니다.
#
# 데코레이터 문법은 단지 편의 문법일 뿐입니다. 다음 두 함수 정의는 의미상으로 동등합니다:
#
# def f(...):
# ...
# f = staticmethod(f)
#
# @staticmethod
# def f(...):
# ...
# ##### descriptor (디스크립터)
# 메서드 __get__() 이나 __set__() 이나 __delete__() 를 정의하는 객체. 클래스 어트리뷰트가 디스크립터일 때, 어트리뷰트 조회는 특별한 연결 작용을 일으킵니다. 보통, a.b 를 읽거나, 쓰거나, 삭제하는데 사용할 때, a 의 클래스 딕셔너리에서 b 라고 이름 붙여진 객체를 찾습니다.
# ##### dictionary (딕셔너리)
# 임의의 키를 값에 대응시키는 연관 배열 (associative array). 키는 __hash__() 와 __eq__() 메서드를 갖는 모든 객체가 될 수 있습니다. 펄에서 해시라고 부릅니#####
# ##### dictionary view (딕셔너리 뷰)
# dict.keys(), dict.values(), dict.items() 메서드가 돌려주는 객체들을 딕셔너리 뷰라고 부릅니다. 이것들은 딕셔너리 항목들에 대한 동적인 뷰를 제공하는데, 딕셔너리가 변경될 때, 뷰가 이 변화를 반영한다는 뜻입니다. 딕셔너리 뷰를 완전한 리스트로 바꾸려면 list(dictview) 를 사용하면 됩니다. #####
# ##### docstring (독스트링)
# """ ----- """ => 형태로 함수에 command 달때 사용
# 클래스, 함수, 모듈에서 첫 번째 표현식으로 나타나는 문자열 리터럴. 스위트가 실행될 때는 무시되지만, 컴파일러에 의해 인지되어 둘러싼 클래스, 함수, 모듈의 __doc__ 어트리뷰트로 삽입됩니다.
# ##### duck-typing (덕 타이핑)
# 올바른 인터페이스를 가졌는지 판단하는데 객체의 형을 보지 않는 프로그래밍 스타일; 대신, 단순히 메서드나 어트리뷰트가 호출되거나 사용됩니다 ("오리처럼 보이고 오리처럼 꽥꽥댄다면, 그것은 오리다.") 특정한 형 대신에 인터페이스를 강조함으로써, 잘 설계된 코드는 다형적인 치환을 허락함으로써 유연성을 개선할 수 있습니다. 덕 타이핑은 type() 이나 isinstance() 을 사용한 검사를 피합니다.
# ##### abstract base class (추상 베이스 클래스)
# 추상 베이스 클래스는 hasattr() 같은 다른 테크닉들이 불편하거나 미묘하게 잘못된 (예를 들어, 매직 메서드) 경우, 인터페이스를 정의하는 방법을 제공함으로써 덕 타이핑 을 보완합니다. ABC는 가상 서브 클래스를 도입하는데, 클래스를 계승하지 않으면서도 isinstance() 와 issubclass() 에 의해 감지될 수 있는 클래스들입니다;
# ##### EAFP
# 허락보다는 용서를 구하기가 쉽다 (Easier to ask for forgiveness than permission). 이 흔히 볼 수 있는 파이썬 코딩 스타일은, 올바른 키나 어트리뷰트의 존재를 가정하고, 그 가정이 틀리면 예외를 잡습니다. 이 깔끔하고 빠른 스타일은 많은 try 와 except 문의 존재로 특징지어집니다. 이 테크닉은 C와 같은 다른 많은 언어에서 자주 사용되는 LBYL 스타일과 대비됩니다.
# ##### expression (표현식)
# 어떤 값으로 구해질 수 있는 문법적인 조각.
#
# - 리터럴, 이름, 어트리뷰트 액세스, 연산자, 함수들과 같은 값을 돌려주는 표현 요소들을 쌓아 올린 것입니다.
#
# 다른 많은 언어와 대조적으로, 모든 언어 구성물들이 표현식인 것은 아닙니다. if 처럼, 표현식으로 사용할 수 없는 문장 들이 있습니다. 대입 또한 문장이고, 표현식이 아닙니다.
# ##### file object (파일 객체)
#
# 하부 자원에 대해 파일 지향적 API (read() 나 write() 같은 메서드들) 를 드러내는 객체. 만들어진 방법에 따라, 파일 객체는 실제 디스크 상의 파일이나 다른 저장장치나 통신 장치 (예를 들어, 표준 입출력, 인-메모리 버퍼, 소켓, 파이프, 등등)에 대한 액세스를 중계할 수 있습니다. 파일 객체는 파일류 객체 (file-like objects) 나 스트림 (streams) 이라고도 불립니다.
#
# - 날(raw) 바이너리 파일
# - 버퍼드(buffered) 바이너리 파일
# - 텍스트 파일.
#
# 이들의 인터페이스는 io 모듈에서 정의됩니다. 파일 객체를 만드는 규범적인 방법은 open() 함수를 쓰는 것입니다.
# ##### floor division (정수 나눗셈)
# 가장 가까운 정수로 내림하는 수학적 나눗셈. 정수 나눗셈 연산자는 // 다. 예를 들어, 표현식 11 // 4 의 값은 2 가 되지만, 실수 나눗셈은 2.75 를 돌려줍니다. (-11) // 4 가 -2.75 를 내림 한 -3 이 됨에 유의해야 합니다.
# ##### function (함수)
# 호출자에게 어떤 값을 돌려주는 일련의 문장들. 없거나 그 이상의 인자 가 전달될 수 있는데, 바디의 실행에 사용될 수 있습니다. 매개변수 와 메서드 와 함수 정의 섹션도 보세요.
# ##### annotation (어노테이션)
# 관습에 따라 형 힌트 로 사용되는 변수, 클래스 어트리뷰트 또는 함수 매개변수 나 반환 값과 연결된 레이블입니다.
#
# 지역 변수의 어노테이션은 실행 시간에 액세스할 수 없지만, 전역 변수, 클래스 속성 및 함수의 어노테이션은 각각 모듈, 클래스, 함수의 __annotations__ 특수 어트리뷰트에 저장됩니다.
# ##### function annotation
#
# 함수 매개변수나 반환 값의 어노테이션.
#
# 함수 어노테이션은 일반적으로 형 힌트 로 사용됩니다: 예를 들어, 이 함수는 두 개의 int 인자를 받아들일 것으로 기대되고, 동시에 int 반환 값을 줄 것으로 기대됩니다:
#
# def sum_two_numbers(a: int, b: int) -> int:
# return a + b
#
# 즉, 함수의 인자힌트를 주석으로 주는거지만, 어디까지나 주석이기 때문에, 실제로 함수 인자가 뭘로 넘어오든지 상관없이 받음.
# ##### garbage collection (가비지 수거)
# 더 사용되지 않는 메모리를 반납하는 절차. 파이썬은 참조 횟수 추적과 참조 순환을 감지하고 끊을 수 있는 순환 가비지 수거기를 통해 가비지 수거를 수행합니다. 가비지 수거기는 gc 모듈을 사용해서 제어할 수 있습니다.
# ##### generator (제너레이터)
# 제너레이터 이터레이터 를 돌려주는 함수. 일반 함수처럼 보이는데, 일련의 값들을 만드는 yield 표현식을 포함한다는 점이 다릅니다. 이 값들은 for-루프로 사용하거나 next() 함수로 한 번에 하나씩 꺼낼 수 있습니다.
#
# ==> 이거 튜플형태로 제너레이터 표현식 돌리면 이렇게 나옴)
#
# 보통 제너레이터 함수를 가리키지만, 어떤 문맥에서는 제너레이터 이터레이터 를 가리킵니다. 의도하는 의미가 명확하지 않은 경우는, 완전한 용어를 써서 모호함을 없앱니다.
# ##### generator iterator (제너레이터 이터레이터)
# 제너레이터 함수가 만드는 객체.
#
# 각 yield 는 일시적으로 처리를 중단하고, 그 위치의 (지역 변수들과 대기 중인 try-문들을 포함하는) 실행 상태를 기억합니다. 제너레이터 이터레이터 가 재개되면, 떠난 곳으로 복귀합니다.
#
# 즉. 제너레이터가 발생시킨 변수값은 제너레이터 실행된 수만큼의 값으로 저장되어있음
# ##### generator expression (제너레이터 표현식)
# 이터레이터를 돌려주는 표현식. 루프 변수와 범위를 정의하는 for 표현식과 생략 가능한 if 표현식이 뒤에 붙는 일반 표현식 처럼 보입니다. 결합한 표현식은 둘러싼 함수를 위한 값들을 만들어냅니다:
#
# > sum(i*i for i in range(10)) # sum of squares 0, 1, 4, ... 81
# 285
# ##### IDLE
# 파이썬을 위한 통합 개발 환경 (Integrated Development Environment). IDLE은 파이썬의 표준 배포판에 따라오는 기초적인 편집기와 인터프리터 환경입니다.
# ##### immutable (불변)
# 고정된 값을 갖는 객체
# - 숫자, 문자열, 튜플,
#
# 새 값을 저장하려면 새 객체를 만들어야 합니다. 변하지 않는 해시값이 있어야 하는 곳에서 중요한 역할을 합니다, 예를 들어, 딕셔너리의 키.
#
# ##### importing (임포팅)
# 한 모듈의 파이썬 코드가 다른 모듈의 파이썬 코드에서 사용될 수 있도록 하는 절차.
# ##### importer (임포터)
# 모듈을 찾기도 하고 로드 하기도 하는 객체; 동시에 파인더 이자 로더 객체입니다.
# ##### interactive (대화형)
# 파이썬은 대화형 인터프리터를 갖고 있는데, 인터프리터 프롬프트에서 문장과 표현식을 입력할 수 있고, 즉각 실행된 결과를 볼 수 있다는 뜻입니다. 인자 없이 단지 python 을 실행하세요 (컴퓨터의 주메뉴에서 선택하는 것도 가능할 수 있습니다). 새 아이디어를 검사하거나 모듈과 패키지를 들여다보는 매우 강력한 방법입니다 (help(x) 를 기억하세요).
# ##### interpreted (인터프리티드)
# 바이트 코드 컴파일러의 존재 때문에 그 구분이 흐릿해지기는 하지만, 파이썬은 컴파일 언어가 아니라 인터프리터 언어입니다. 이것은 명시적으로 실행 파일을 만들지 않고도, 소스 파일을 직접 실행할 수 있다는 뜻입니다. 그 프로그램이 좀 더 천천히 실행되기는 하지만, 인터프리터 언어는 보통 컴파일 언어보다 짧은 개발/디버깅 주기를 갖습니다.
# ##### interpreter shutdown (인터프리터 종료)
# 종료하라는 요청을 받을 때, 파이썬 인터프리터는 특별한 시기에 진입하는데, 모듈이나 여러 가지 중요한 내부 구조들과 같은 모든 할당된 자원들을 단계적으로 반납합니다. 또한, 가비지 수거기 를 여러 번 호출합니다. 사용자 정의 파괴자나 weakref 콜백에 있는 코드들의 실행을 시작시킬 수 있습니다. 종료 시기 동안 실행되는 코드는 다양한 예외들을 만날 수 있는데, 그것이 의존하는 자원들이 더 기능하지 않을 수 있기 때문입니다 (흔한 예는 라이브러리 모듈이나 경고 장치들입니다).
#
# 인터프리터 종료의 주된 원인은 실행되는 __main__ 모듈이나 스크립트가 실행을 끝내는 것입니다.
# ##### iterable (이터러블)
# 멤버들을 한 번에 하나씩 돌려줄 수 있는 객체.
#
# - 이터러블의 예로는 모든 (list, str, tuple 같은) 시퀀스 형들, dict 같은 몇몇 비시퀀스 형들, 파일 객체들, __iter__() 나 시퀀스 개념을 구현하는 __getitem__() 메서드를 써서 정의한 모든 클래스의 객체들이 있습니다.
#
# 이터러블은 for 루프에 사용될 수 있고, 시퀀스를 필요로 하는 다른 많은 곳 (zip(), map(), ...) 에 사용될 수 있습니다. 이터러블 객체가 내장 함수 iter() 에 인자로 전달되면, 그 객체의 이터레이터를 돌려줍니다. 이 이터레이터는 값들의 집합을 한 번 거치는 동안 유효합니다.
#
# 이터러블을 사용할 때, 보통은 iter() 를 호출하거나, 이터레이터 객체를 직접 다룰 필요는 없습니다. for 문은 이것들을 여러분을 대신해서 자동으로 해주는데, 루프를 도는 동안 이터레이터를 잡아둘 이름 없는 변수를 만듭니다. 이터레이터, 시퀀스, 제너레이터 도 보세요.
# ##### key function (키 함수)
# 키 함수 또는 콜레이션(collation) 함수는 정렬(sorting)이나 배열(ordering)에 사용되는 값을 돌려주는 콜러블입니다. 예를 들어, locale.strxfrm() 은 로케일 특정 방식을 따르는 정렬 키를 만드는 데 사용됩니다.
#
# 파이썬의 많은 도구가 요소들이 어떻게 순서 지어지고 묶이는지를 제어하기 위해 키 함수를 받아들입니다.
#
# - min(), max(), sorted(), list.sort(), heapq.merge(), heapq.nsmallest(), heapq.nlargest(), itertools.groupby() 이 있습니다.
# ##### lambda (람다)
# 호출될 때 값이 구해지는 하나의 표현식 으로 구성된 이름 없는 인라인 함수. 람다 함수를 만드는 문법은
# > lambda [parameters]: expression 입니다.
# ##### LBYL
# 뛰기 전에 보라 (Look before you leap). 이 코딩 스타일은 호출이나 조회를 하기 전에 명시적으로 사전 조건들을 검사합니다. 이 스타일은 EAFP 접근법과 대비되고, 많은 if 문의 존재로 특징지어집니다.
|
Python - Term.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import sys
import math
import logging
from pathlib import Path
import numpy as np
import scipy as sp
import sklearn
import statsmodels.api as sm
from statsmodels.formula.api import ols
# %load_ext autoreload
# %autoreload 2
import matplotlib as mpl
import matplotlib.pyplot as plt
# %matplotlib inline
# %config InlineBackend.figure_format = 'retina'
import seaborn as sns
sns.set_context("poster")
sns.set(rc={'figure.figsize': (16, 9.)})
sns.set_style("whitegrid")
import pandas as pd
pd.set_option("display.max_rows", 120)
pd.set_option("display.max_columns", 120)
logging.basicConfig(level=logging.INFO, stream=sys.stdout)
# -
from my_ds_project import *
# **PLEASE** save this file right now using the following naming convention: `NUMBER_FOR_SORTING-YOUR_INITIALS-SHORT_DESCRIPTION`, e.g. `1.0-fw-initial-data-exploration`. Use the number to order the file within the directory according to its usage.
|
notebooks/template.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Crypto Data Download
# %config IPCompleter.greedy=True
# Initial imports
import requests
import json
import numpy as np
import pandas as pd
from pathlib import Path
# ## Fetching Cryptocurrency Data
# +
headers = {
'Connection': 'keep-alive',
'Pragma': 'no-cache',
'Cache-Control': 'no-cache',
'Upgrade-Insecure-Requests': '1',
'User-Agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/87.0.4280.66 Safari/537.36',
'Accept': 'text/html,application/xhtml+xml,application/xml;q=0.9,image/avif,image/webp,image/apng,*/*;q=0.8,application/signed-exchange;v=b3;q=0.9',
'Sec-Fetch-Site': 'cross-site',
'Sec-Fetch-Mode': 'navigate',
'Sec-Fetch-User': '?1',
'Sec-Fetch-Dest': 'document',
'Accept-Language': 'en-US,en;q=0.9',
}
response = requests.get('https://min-api.cryptocompare.com/data/all/coinlist', headers=headers)
json_data = json.loads(response.text)
# -
# ## Transforming JSON to Dataframe
# Creating a DataFrame (which needed to be transposed)
crypto_df = pd.DataFrame(json_data['Data']).T
crypto_df.head()
# ## Saving a DataFrame to CSV File
|
crypto_data_download.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#pytorch version 0.4.1
# -
# !export PYTHONPATH=$~/JB_test ; echo $PYTHONPATH;
python sample.py --nsample 10 --vocab ../data/zinc/vocab.txt \
--hidden 450 --depth 3 --latent 56 \
--model MPNVAE-h450-L56-d3-beta0.005/model.iter-4 > generated_molecules.txt
from rdkit import Chem
from rdkit.Chem.Draw import IPythonConsole
from rdkit.Chem import Draw
# +
with open ("generated_molecules.txt", "r") as myfile:
data=myfile.readlines()
smiles = [s.replace('\n', '') for s in data]
smiles
# -
ms = [Chem.MolFromSmiles(x) for x in smiles]
Draw.MolsToGridImage(ms)
|
molvae/Test_Task_GM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy.random as rnd
a,b,c = 1.1,1.1,1.1
cov = [[1., a,b], [a, 1.,c], [b,c,1.]]
samples = rnd.multivariate_normal([0.,0.,0.], cov, 50)
print(cov)
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
xs = samples[:,0]
ys = samples[:,1]
zs = samples[:,2]
ax.scatter(xs, ys, zs, s=50, alpha=0.6, edgecolors='w')
ax.set_xlabel('Variable X')
ax.set_ylabel('Variable Y')
ax.set_zlabel('Variable Z')
plt.show()
# -
import pandas as pd
import seaborn as sns
from numpy.linalg import svd
U,S,Vt = svd(samples, full_matrices=True, compute_uv=True)
# +
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
xs = samples[:,0]
ys = samples[:,1]
zs = samples[:,2]
ax.scatter(xs, ys, zs, s=50, alpha=0.2, edgecolors='w')
ax.plot([0,Vt[0,0]],[0,Vt[0,1]],[0,Vt[0,2]], lw=5)
ax.plot([0,Vt[1,0]],[0,Vt[1,1]],[0,Vt[1,2]], lw=5)
ax.plot([0,Vt[2,0]],[0,Vt[2,1]],[0,Vt[2,2]], lw=5)
ax.set_xlabel('Variable X')
ax.set_ylabel('Variable Y')
ax.set_zlabel('Variable Z')
plt.show()
# -
fig = plt.figure(figsize=(12, 6))
transformed_genes=pd.DataFrame(data=U[:,0:2]*S[0:2], columns = ["Eigen variable 1","Eigen variable 2"])
sns.lmplot("Eigen variable 1","Eigen variable 2", data=transformed_genes, fit_reg=False, height=3,aspect=3)
import numpy as np
np.dot(Vt[0,:],Vt[1,:])
|
nb/pca/PCAofMultiNormal.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Nothing But NumPy: A 2-layer Binary Classification Neural Network on Iris Flowers
#
# Part of the blog ["Nothing but NumPy: Understanding & Creating Binary Classification Neural Networks with Computational Graphs from Scratch"](https://medium.com/@rafayak/nothing-but-numpy-understanding-creating-binary-classification-neural-networks-with-e746423c8d5c)- by [<NAME>](https://twitter.com/RafayAK)
#
# In this notebook we'll create a 2-layer neural network (i.e. one input and one output layer) and train it on the eintire Iris dataset to classify **Iris-virginica vs. others**
#
# First, let's import NumPy, our neural net Layers, the Binary Cross-Entropy(bce) Cost function and helper functions.
#
# _Feel free to look into the helper functions in the utils directory._
# +
import numpy as np
from Layers.LinearLayer import LinearLayer
from Layers.ActivationLayer import SigmoidLayer
from util.utilities import *
from util.cost_functions import compute_stable_bce_cost
import matplotlib.pyplot as plt
# to show all the generated plots inline in the notebook
# %matplotlib inline
# -
# 
# For convenience we'll load the data through [scikit-learn](https://scikit-learn.org/stable/index.html#).
#
# _If you don't have it installed please refer to this [link](https://scikit-learn.org/stable/install.html)_
# +
# load data from scikit-learn's datasets module
from sklearn.datasets import load_iris
iris = load_iris() # returns a python dictionary with the dataset
# -
# Let's see what the dataset contains:
list(iris.keys())
# - **data**: contains the 4 features of each example in a row, has 150 rows
# - **target**: contains the label for each example _(0->setosa, 1->versicolor, 2->virginica)_
# - **target_names**: contains the names of each target label
# - **DESCR**: contains the desription of the dataset
# - **feature_names**: contains the names of the 4 features(sepal length, sepal width, petal length, petal width)
# - **filename** : where the file is located on the computer
#
# Let's explore the data:
iris.data.shape # rows(examples), cols(features)
iris.target.shape # labels for 150 flowers
iris.target_names # print the name of the 3 labels(species) an example could belong to
iris.feature_names # name of each feature in data's columns
iris.data[:5, :] # print first 5 examples from the Iris dataset
iris.target[:5] # print labels for the first 5 examples in the Iris dataset
# So, the data of the **first** 5 examples looks as follows:
#
# | exmaple# | sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | target | target name|
# | --- | --- | --- || --- | --- | --- |
# | 0 | 5.1 | 3.5 | 1.4 | 0.2| 0| setosa
# | 1 |4.9| 3. | 1.4| 0.2|0| setosa
# | 2 |4.7| 3.2| 1.3| 0.2|0| setosa
# | 3 |4.6| 3.1| 1.5| 0.2|0| setosa
# | 4 |5. | 3.6| 1.4| 0.2|0| setosa
# We need to fix the shape of the target array as a precaution so that it's shape matches the input data
# +
# X(input) will be entire training data
X = iris.data
# fix the labes shape so that instead of (150,) its (150,1),
# helps avoiding weird broadcasting errors
Y = (iris.target).reshape((150, 1))
# -
X.shape
Y.shape
# **Notice** in the table above that the first 5 examples belong to __'setosa'__ species, this pattern continues in the dataset(the pattern is all _setosa_ examples followed by _versicolor_ examples and finally _virginica_ examples). ___A good practice is to randomize the data before training a neural network, so that the neural network does not, by accident, learn a trivial ordering pattern in the data.___
#
# So let's randomize the data
# +
np.random.seed(48) # for reproducible randomization
random_indices = np.random.permutation(len(X)) # genrate random permutation of indices
X_train = X[random_indices]
Y_train = Y[random_indices]
# -
# Now let's again print the first 5 examples and see the results(note this time features are only two - petal lenght, petal width )
X_train[:5, :]
Y_train[:5]
# Now, the data of the **first** 5 examples looks as follows:
#
# | exmaple# | sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | target | target name|
# | --- | --- | --- || --- | --- | --- |
# | 0 | 5.7| 2.9| 4.2| 1.3| 1| versicolor
# | 1 | 6.1| 2.8| 4.7| 1.2|1| versicolor
# | 2 |6.1 | 2.6| 5.6| 1.4|2| virginica
# | 3 |4.5 | 2.3| 1.3| 0.3|0| setosa
# | 4 | 5.9| 3.2| 4.8| 1.8|1| versicolor
#
#
# Finally, let's put training set(`X_train`) & and labels(`Y_train`) in the correct shape `(feat, examples)` and `(examples,1)`, respectively. Also we'll make the target label ___virginica=1___ and the rest ___0___.
# Transpose the data so that it's in the correct shape
# for passing through neural network
# also binarize the classes viginica=1 and the rest 0
X_train = X_train.T
Y_train = Y_train.T
Y_train = (Y_train==2).astype('int') # uses bool logic to binarize labels, wherever label=2 output True(1) rest Flase(0)
print("Shape of training data, X_train: {}".format(X_train.shape))
print("Shape of labels, Y_train: {}".format(Y_train.shape))
Y_train[:, :5] # print first five examples
# Since the number of features are 4 in this dataset we cannot visuallize it on a 2-D plot😒
# ***
# ***
# #### Now we are ready to setup and train the Neural Network
#
# This is the neural net architecture we'll use
#
# 
# +
# define training constants
learning_rate = 0.3
number_of_epochs = 5000
np.random.seed(48) # set seed value so that the results are reproduceable
# (weights will now be initailzaed to the same pseudo-random numbers, each time)
# Our network architecture has the shape:
# (input)--> [Linear->Sigmoid] -> [Linear->Sigmoid] -->(output)
#------ LAYER-1 ----- define hidden layer that takes in training data
Z1 = LinearLayer(input_shape=X_train.shape, n_out=3, ini_type='xavier')
A1 = SigmoidLayer(Z1.Z.shape)
#------ LAYER-2 ----- define output layer that takes in values from hidden layer
Z2= LinearLayer(input_shape=A1.A.shape, n_out= 1, ini_type='xavier')
A2= SigmoidLayer(Z2.Z.shape)
# -
# Now we can start the training loop:
# +
costs = [] # initially empty list, this will store all the costs after a certian number of epochs
# Start training
for epoch in range(number_of_epochs):
# ------------------------- forward-prop -------------------------
Z1.forward(X_train)
A1.forward(Z1.Z)
Z2.forward(A1.A)
A2.forward(Z2.Z)
# ---------------------- Compute Cost ----------------------------
cost, dZ2 = compute_stable_bce_cost(Y=Y_train, Z=Z2.Z)
# print and store Costs every 100 iterations and of the last iteration.
if (epoch % 100) == 0:
print("Cost at epoch#{}: {}".format(epoch, cost))
costs.append(cost)
# ------------------------- back-prop ----------------------------
Z2.backward(dZ2)
A1.backward(Z2.dA_prev)
Z1.backward(A1.dZ)
# ----------------------- Update weights and bias ----------------
Z2.update_params(learning_rate=learning_rate)
Z1.update_params(learning_rate=learning_rate)
# -
# Now let's see how well the neural net peforms on the training data after the training as finished
#
# `predict` helper functionin the cell below returns three things:
#
# * `p`: predicted labels (output 1 if predictded output is greater than classification threshold `thresh`)
# * `probas`: raw probabilities (how sure the neural net thinks the output is 1, this is just `P_hat`)
# * `accuracy`: the number of correct predictions from total predictions
#
#
# +
classifcation_thresh = 0.5
predicted_outputs, p_hat, accuracy = predict(X=X_train, Y=Y_train,
Zs=[Z1, Z2], As=[A1, A2], thresh=classifcation_thresh)
print("The predicted outputs of first 5 examples: \n{}".format(predicted_outputs[:,:5]))
print("The predicted prbabilities of first 5 examples:\n {}".format(np.round(p_hat[:, :5], decimals=3)) )
print("\nThe accuracy of the model is: {}%".format(accuracy))
# -
# #### The Learning Curve
plot_learning_curve(costs, learning_rate, total_epochs=number_of_epochs)
# ## Bounus
#
# Try different learning rates. See the effect on learning curve.
#
# _(Hint: if the learning curve is not smooth and very erratic then Gradient Descent is bouncing around the minimum point, all because the learnig rate is too high.)_
|
Understanding_and_Creating_Binary_Classification_NNs/2_layer_toy_neural_network_on_all_iris_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
df = pd.DataFrame({
'City': ['Tokyo', 'Delhi', 'Shanghai', 'Sao Paulo', 'Mumbai'],
'Country': ['Japan', 'India', 'China', 'Brazil', 'India'],
'Mean Temp': [59.7, 77.2, 62.7, 66.6, 81.4]})
df
# -
print('Please input the perfect temperature for you:')
userideal = input()
# +
high = float(userideal) + 5
low = float(userideal) - 5
df['Preference'] = pd.cut(df['Mean Temp'], [0, low, high, 100], labels=["too cold", "just right", "too hot"])
df
|
day9/warm-up-day-9-ex2-solution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.8 64-bit (conda)
# name: python3
# ---
# # Analyzing COVID-19 Papers
#
# In this challenge, we will continue with the topic of COVID pandemic, and focus on processing scientific papers on the subject. There is [CORD-19 Dataset](https://www.kaggle.com/allen-institute-for-ai/CORD-19-research-challenge) with more than 7000 (at the time of writing) papers on COVID, available with metadata and abstracts (and for about half of them there is also full text provided).
#
# A full example of analyzing this dataset using [Text Analytics for Health](https://docs.microsoft.com/azure/cognitive-services/text-analytics/how-tos/text-analytics-for-health/?WT.mc_id=academic-31812-dmitryso) cognitive service is described [in this blog post](https://soshnikov.com/science/analyzing-medical-papers-with-azure-and-text-analytics-for-health/). We will discuss simplified version of this analysis.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# ## Getting the Data
#
# First, we need get the metadata for CORD papers that we will be working with.
#
# **NOTE**: We do not provide a copy of the dataset as part of this repository. You may first need to download the [`metadata.csv`](https://www.kaggle.com/allen-institute-for-ai/CORD-19-research-challenge?select=metadata.csv) file from [this dataset on Kaggle](https://www.kaggle.com/allen-institute-for-ai/CORD-19-research-challenge). Registration with Kaggle may be required. You may also download the dataset without registration [from here](https://ai2-semanticscholar-cord-19.s3-us-west-2.amazonaws.com/historical_releases.html), but it will include all full texts in addition to metadata file.
#
# We will try to get the data directly from online source, however, if it fails, you need to download the data as described above. Also, it makese sense to download the data if you plan to experiment with it further, to save on waiting time.
#
# > **NOTE** that dataset is quite large, aroung 1 Gb in size, and the following line of code can take a long time to complete! (~5 mins)
df = pd.read_csv("https://datascience4beginners.blob.core.windows.net/cord/metadata.csv.zip",compression='zip')
# df = pd.read_csv("metadata.csv")
df.head()
# We will now convert publication date column to `datetime`, and plot the histogram to see the range of publication dates.
df['publish_time'] = pd.to_datetime(df['publish_time'])
df['publish_time'].hist()
plt.show()
# Interestingly, there are coronavirus-related papers that date back to 1880!
# ## Structured Data Extraction
#
# Let's see what kind of information we can easily extract from abstracts. One thing we might be interested in is to see which treatment strategies exist, and how they evolved over time. To begin with, we can manually compile the list of possible medications used to treat COVID, and also the list of diagnoses. We then go over them and search corresponding terms in the abstracts of papers.
# +
medications = [
'hydroxychloroquine', 'chloroquine', 'tocilizumab', 'remdesivir', 'azithromycin',
'lopinavir', 'ritonavir', 'dexamethasone', 'heparin', 'favipiravir', 'methylprednisolone']
diagnosis = [
'covid','sars','pneumonia','infection','diabetes','coronavirus','death'
]
for m in medications:
print(f" + Processing medication: {m}")
df[m] = df['abstract'].apply(lambda x: str(x).lower().count(' '+m))
for m in diagnosis:
print(f" + Processing diagnosis: {m}")
df[m] = df['abstract'].apply(lambda x: str(x).lower().count(' '+m))
# -
# We have added a bunch of columns to our dataframe that contain number of times a given medicine/diagnosis is present in the abstract.
#
# > **Note** that we add space to the beginning of the word when looking for a substring. If we do not do that, we might get wrong results, because *chloroquine* would also be found inside substring *hydroxychloroquine*. Also, we force conversion of abstacts column to `str` to get rid of an error - try removing `str` and see what happens.
#
# To make working with data easier, we can extract the sub-frame with only medication counts, and compute the accumulated number of occurrences. This gives is the most popular medication:
dfm = df[medications]
dfm = dfm.sum().reset_index().rename(columns={ 'index' : 'Name', 0 : 'Count'})
dfm.sort_values('Count',ascending=False)
dfm.set_index('Name').plot(kind='bar')
plt.show()
# ## Looking for Trends in Treatment Strategy
#
# In the example above we have `sum`ed all values, but we can also do the same on a monthly basis:
dfm = df[['publish_time']+medications].set_index('publish_time')
dfm = dfm[(dfm.index>="2020-01-01") & (dfm.index<="2021-07-31")]
dfmt = dfm.groupby([dfm.index.year,dfm.index.month]).sum()
dfmt
# This gives us a good picture of treatment strategies. Let's visualize it!
dfmt.plot()
plt.show()
# An interesting observation is that we have huge spikes at two locations: January, 2020 and January, 2021. It is caused by the fact that some papers do not have a clearly specified data of publication, and they are specified as January of the respecive year.
#
# To make more sense of the data, let's visualize just a few medicines. We will also "erase" data for January, and fill it in by some medium value, in order to make nicer plot:
meds = ['hydroxychloroquine','tocilizumab','favipiravir']
dfmt.loc[(2020,1)] = np.nan
dfmt.loc[(2021,1)] = np.nan
dfmt.fillna(method='pad',inplace=True)
fig, ax = plt.subplots(1,len(meds),figsize=(10,3))
for i,m in enumerate(meds):
dfmt[m].plot(ax=ax[i])
ax[i].set_title(m)
plt.show()
# Observe how popularity of hydroxychloroquine was on the rise in the first few months, and then started to decline, while number of mentions of favipiravir shows stable rise. Another good way to visualize relative popularity is to use **stack plot** (or **area plot** in Pandas terminology):
dfmt.plot.area()
plt.show()
# Even further, we can compute relative popularity in percents:
dfmtp = dfmt.iloc[:,:].apply(lambda x: x/x.sum(), axis=1)
dfmtp.plot.area()
plt.show()
#
# ## Computing Medicine-Diagnosis Correspondence
#
# One of the most interesting relationships we can look for is how different diagnoses are treated with different medicines. In order to visualize it, we need to compute **co-occurence frequency map**, which would show how many times two terms are mentioned in the same paper.
#
# Such a map is essentialy a 2D matrix, which is best represented by **numpy array**. We will compute this map by walking through all abstracts, and marking entities that occur there:
m = np.zeros((len(medications),len(diagnosis)))
for a in df['abstract']:
x = str(a).lower()
for i,d in enumerate(diagnosis):
if ' '+d in x:
for j,me in enumerate(medications):
if ' '+me in x:
m[j,i] += 1
m
# One of the ways to visualize this matrix is to draw a **heatmap**:
plt.imshow(m,interpolation='nearest',cmap='hot')
ax = plt.gca()
ax.set_yticks(range(len(medications)))
ax.set_yticklabels(medications)
ax.set_xticks(range(len(diagnosis)))
ax.set_xticklabels(diagnosis,rotation=90)
plt.show()
# However, even better visualization can be done using so-called **Sankey** diagram! `matplotlib` does not have built-in support for this diagram type, so we would have to use [Plotly](https://plotly.com/python/) as described [in this tutorial](https://plotly.com/python/sankey-diagram/).
#
# To make plotly sankey diagram, we need to build the following lists:
# * List `all_nodes` of all nodes in the graph, which will include both medications and diagnosis
# * List of source and target indices - those lists would show, which nodes go to the left, and which to the right part of the diagram
# * List of all links, each link consisting of:
# - Source index in the `all_nodes` array
# - Target index
# - Value indicating strength of the link. This is exactly the value from our co-occurence matrix.
# - Optionally color of the link. We will make an option to highlight some of the terms for clarity
#
# Generic code to draw sankey diagram is structured as a separate `sankey` function, which takes two lists (source and target categories) and co-occurence matrix. It also allows us to specify the treshold, and omit all links that are weaker than that treshold - this makes the diagram a little bit less complex.
# +
import plotly.graph_objects as go
def sankey(cat1, cat2, m, treshold=0, h1=[], h2=[]):
all_nodes = cat1 + cat2
source_indices = list(range(len(cat1)))
target_indices = list(range(len(cat1),len(cat1)+len(cat2)))
s, t, v, c = [], [], [], []
for i in range(len(cat1)):
for j in range(len(cat2)):
if m[i,j]>treshold:
s.append(i)
t.append(len(cat1)+j)
v.append(m[i,j])
c.append('pink' if i in h1 or j in h2 else 'lightgray')
fig = go.Figure(data=[go.Sankey(
# Define nodes
node = dict(
pad = 40,
thickness = 40,
line = dict(color = "black", width = 1.0),
label = all_nodes),
# Add links
link = dict(
source = s,
target = t,
value = v,
color = c
))])
fig.show()
sankey(medications,diagnosis,m,500,h2=[0])
# -
# ## Conclusion
#
# You have seen that we can use quite simple methods to extract information from non-structured data sources, such as text. In this example, we have taken the existing list of medications, but it would be much more powerful to use natural language processing (NLP) techniques to perform entity extraction from text. In [this blog post](https://soshnikov.com/science/analyzing-medical-papers-with-azure-and-text-analytics-for-health/) we describe how to use cloud services for entity extraction. Another option would be using Python NLP libraries such as [NLTK](https://www.nltk.org/) - an approach for extracting information from text using NLTK is described [here](https://www.nltk.org/book/ch07.html).
# ## Challenge
#
# Continue to research the COVID paper data along the following lines:
#
# 1. Build co-occurrence matrix of different medications, and see which medications often occur together (i.e. mentioned in one abstract). You can modify the code for building co-occurrence matrix for medications and diagnoses.
# 1. Visualize this matrix using heatmap.
# 1. As a stretch goal, you may want to visualize the co-occurrence of medications using [chord diagram](https://en.wikipedia.org/wiki/Chord_diagram). [This library](https://pypi.org/project/chord/) may help you draw a chord diagram.
# 1. As another stretch goal, try to extract dosages of different medications (such as **400mg** in *take 400mg of cholroquine daily*) using regular expressions, and build dataframe that shows different dosages for different medications. **Note**: consider numeric values that are in close textual vicinity of the medicine name.
#
|
2-Working-With-Data/07-python/notebook-papers.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Hierarchical Partial Pooling
# Suppose you are tasked with estimating baseball batting skills for several players. One such performance metric is batting average. Since players play a different number of games and bat in different positions in the order, each player has a different number of at-bats. However, you want to estimate the skill of all players, including those with a relatively small number of batting opportunities.
#
# So, suppose a player came to bat only 4 times, and never hit the ball. Are they a bad player?
#
# As a disclaimer, the author of this notebook assumes little to non-existant knowledge about baseball and its rules. The number of times at bat in his entire life is around "4".
#
#
# ## Data
#
# We will use the [baseball data for 18 players from Efron and Morris](http://www.swarthmore.edu/NatSci/peverso1/Sports%20Data/JamesSteinData/Efron-Morris%20Baseball/EfronMorrisBB.txt) (1975).
#
#
# ## Approach
#
# We will use PyMC3 to estimate the batting average for each player. Having estimated the averages across all players in the datasets, we can use this information to inform an estimate of an additional player, for which there is little data (*i.e.* 4 at-bats).
#
# In the absence of a Bayesian hierarchical model, there are two approaches for this problem:
#
# (1) independently compute batting average for each player (no pooling)
# (2) compute an overall average, under the assumption that everyone has the same underlying average (complete pooling)
#
# Of course, neither approach is realistic. Clearly, all players aren't equally skilled hitters, so the global average is implausible. At the same time, professional baseball players are similar in many ways, so their averages aren't entirely independent either.
#
# It may be possible to cluster groups of "similar" players, and estimate group averages, but using a hierarchical modeling approach is a natural way of sharing information that does not involve identifying *ad hoc* clusters.
#
# The idea of hierarchical partial pooling is to model the global performance, and use that estimate to parameterize a population of players that accounts for differences among the players' performances. This tradeoff between global and individual performance will be automatically tuned by the model. Also, uncertainty due to different number of at bats for each player (*i.e.* informatino) will be automatically accounted for, by shrinking those estimates closer to the global mean.
#
# For far more in-depth discussion please refer to Stan [tutorial](http://mc-stan.org/documentation/case-studies/pool-binary-trials.html) on the subject. The model and parameter values were taken from that example.
#
# %matplotlib inline
import pymc3 as pm
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import theano.tensor as tt
# Now we can load the dataset using pandas:
data = pd.read_table(pm.get_data('efron-morris-75-data.tsv'), sep="\t")
at_bats, hits = data[['At-Bats', 'Hits']].values.T
# Now let's develop a generative model for these data.
#
# We will assume that there exists a hidden factor (`phi`) related to the expected performance for all players (not limited to our 18). Since the population mean is an unknown value between 0 and 1, it must be bounded from below and above. Also, we assume that nothing is known about global average. Hence, a natural choice for a prior distribution is the uniform distribution.
#
# Next, we introduce a hyperparameter `kappa` to account for the variance in the population batting averages, for which we will use a bounded Pareto distribution. This will ensure that the estimated value falls within reasonable bounds. These hyperparameters will be, in turn, used to parameterize a beta distribution, which is ideal for modeling quantities on the unit interval. The beta distribution is typically parameterized via a scale and shape parameter, it may also be parametrized in terms of its mean $\mu \in [0,1]$ and sample size (a proxy for variance) $\nu = \alpha + \beta (\nu > 0)$.
#
# The final step is to specify a sampling distribution for the data (hit or miss) for every player, using a Binomial distribution. This is where the data are brought to bear on the model.
# We could use `pm.Pareto('kappa', m=1.5)`, to define our prior on `kappa`, but the Pareto
# distribution has very long tails. Exploring these properly
# is difficult for the sampler, so we use an equivalent
# but faster parametrization using the exponential distribution.
# We use the fact that the log of a Pareto distributed
# random variable follows an exponential distribution.
# +
N = len(hits)
with pm.Model() as baseball_model:
phi = pm.Uniform('phi', lower=0.0, upper=1.0)
kappa_log = pm.Exponential('kappa_log', lam=1.5)
kappa = pm.Deterministic('kappa', tt.exp(kappa_log))
thetas = pm.Beta('thetas', alpha=phi*kappa, beta=(1.0-phi)*kappa, shape=N)
y = pm.Binomial('y', n=at_bats, p=thetas, observed=hits)
# -
# Recall our original question was with regard to the true batting average for a player with only 4 at bats and no hits. We can add this as an additional variable in the model
with baseball_model:
theta_new = pm.Beta('theta_new', alpha=phi*kappa, beta=(1.0-phi)*kappa)
y_new = pm.Binomial('y_new', n=4, p=theta_new, observed=0)
# We can now fit the model using MCMC:
with baseball_model:
trace = pm.sample(2000, tune=1000, chains=2,
nuts_kwargs={'target_accept': 0.95})
# Now we can plot the posteriors distribution of the parameters. First, the population hyperparameters:
pm.traceplot(trace, varnames=['phi', 'kappa']);
# Hence, the population mean batting average is in the 0.22-0.31 range, with an expected value of around 0.26.
#
# Next, the estimates for all 18 players in the dataset:
player_names = data.apply(lambda x: x.FirstName + ' ' + x.LastName, axis=1)
pm.forestplot(trace, varnames=['thetas'], ylabels=player_names)
# Finally, let's get the estimate for our 0-for-4 player:
pm.traceplot(trace, varnames=['theta_new']);
# Notice that, despite the fact our additional player did not get any hits, the estimate of his average is not zero -- zero is not even a highly-probably value. This is because we are assuming that the player is drawn from a *population* of players with a distribution specified by our estimated hyperparemeters. However, the estimated mean for this player is toward the low end of the means for the players in our dataset, indicating that the 4 at-bats contributed some information toward the estimate.
|
docs/source/notebooks/hierarchical_partial_pooling.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/bundickm/LeetCode-30-Day-Challenge/blob/master/Day_5_Max_Profit.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="D_tIwX5p5waq" colab_type="text"
# # Problem
#
# Say you have an array for which the ith element is the price of a given stock on day i.
#
# Design an algorithm to find the maximum profit. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).
#
# Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).
#
# Example 1:
# ```
# Input: [7,1,5,3,6,4]
# Output: 7
# Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
# Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
# ```
# Example 2:
# ```
# Input: [1,2,3,4,5]
# Output: 4
# Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
# Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
# engaging multiple transactions at the same time. You must sell before buying again.
# ```
# Example 3:
# ```
# Input: [7,6,4,3,1]
# Output: 0
# Explanation: In this case, no transaction is done, i.e. max profit = 0.
# ```
# + [markdown] id="8zdTNef-9RNX" colab_type="text"
# # Solution
# + id="Zd_eDzp95vIJ" colab_type="code" colab={}
import numpy as np
def maxProfit(prices: list) -> int:
return sum(profit for profit in np.diff(prices) if profit > 0)
# + id="8HGa9T0753Ex" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="f6936e76-8717-4100-9ff8-ac92c87d1f16"
maxProfit([7,1,5,3,6,4])
# + id="lv5ZR68i7Yss" colab_type="code" colab={}
|
Day_5_Max_Profit.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # A simple function with different types of input parameters which are optimized.
from mango.tuner import Tuner
# +
from scipy.stats import uniform
param_dict = {"a": uniform(0, 1), # uniform distribution
"b": range(1,5), # Integer variable
"c":[1,2,3], # Integer variable
"d":["-1","1"] # Categorical variable
}
# -
# # userObjective
def objectiveFunction(args_list):
results = []
for hyper_par in args_list:
a = hyper_par['a']
b = hyper_par['b']
c = hyper_par['c']
d = hyper_par['d']
result = (a + b + c + int(d))
results.append(result)
return results
conf_Dict = dict()
conf_Dict['batch_size'] = 4
conf_Dict['num_iteration'] = 5
# # Defining Tuner
tuner_user = Tuner(param_dict, objectiveFunction,conf_Dict)
tuner_user.getConf()
results = tuner_user.maximize()
# # Inspect the results
print('best hyper parameters:',results['best_params'])
print('best objective:',results['best_objective'])
print('Sample hyper parameters tried:',len(results['params_tried']))
print(results['params_tried'][:2])
print('Sample objective values',len(results['objective_values']))
print(results['objective_values'][:5])
# # Plotting the variation in objective values of the tried results
# +
Size = 201
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(30,5))
plt.title('Variation of Objective',fontsize=20)
plt.plot(results['objective_values'][:Size],lw=4,label='BL')
plt.xlabel('Configuration', fontsize=25)
plt.ylabel('objective_values',fontsize=25)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend(prop={'size': 30})
plt.show()
# -
# # Plotting the variation of Max objective values of the tried results
# +
Size = 201
import numpy as np
results_obj = np.array(results['objective_values'])
y_max=[]
for i in range(results_obj.shape[0]):
y_max.append(np.max(results_obj[:i+1]))
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(30,5))
plt.title('Max variation of Objective',fontsize=20)
plt.plot(y_max[:Size],lw=4,label='BL')
plt.xlabel('Configuration', fontsize=25)
plt.ylabel('objective_values',fontsize=25)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend(prop={'size': 30})
plt.show()
# -
# # See the result
import pprint
pp = pprint.PrettyPrinter(indent=4)
pp.pprint(results)
# # See the different values tried
# +
values = []
for hyper in results['params_tried']:
val=[hyper['a'],hyper['b'],hyper['c'],int(hyper['d'])]
values.append(val)
# -
values = np.array(values)
# +
#print(np.sort(values,axis=0))
# +
#values.shape
# -
|
examples/Simple_Function.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
def strToBinary(strg):
c = list(strg)
result = ""
for i in range(len(c)):
temp = c[i]
result += temp + " "
return result
def binToStr(binary):
strg = bin.split(" ")
for i in range(len(strg)):
c = list(len(strg))
z = 0
for j in range(len(c[i])):
c[j] = strg[j]
z += ((c[j] - 48)) << (len(c)-1-j)
result[i] = chr(z)
print(strToBinary("0110011"))
|
Security/Stream_Cipher/Streamer.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# + language="html"
# <script>
# function getToken() {
# var xhttp = new XMLHttpRequest();
# xhttp.onreadystatechange = function() {
# if (xhttp.readyState == 4) {
# if (xhttp.status == 200) {
# document.getElementById("tokenoutput").innerHTML =
# "Proxy token: " + xhttp.responseText;
# document.getElementById("tokenerror").innerHTML = ""
# }
# else {
# document.getElementById("tokenoutput").innerHTML = "<strong>ERROR (" + xhttp.status + "): " + xhttp.responseText;
# document.getElementById("tokenerror").innerHTML = "";
# }
# }
# };
# xhttp.open("GET", '/hub/proxytoken/', true);
# xhttp.send();
# }
#
# function refreshToken(mode) {
# var xhttp = new XMLHttpRequest();
# xhttp.onreadystatechange = function() {
# if (xhttp.readyState == 4) {
# if (xhttp.status == 200) {
# document.getElementById("tokenoutput").innerHTML =
# "Proxy token: " + xhttp.responseText;
# document.getElementById("tokenerror").innerHTML = ""
# }
# else {
# document.getElementById("tokenoutput").innerHTML = "<strong>ERROR (" + xhttp.status + "): " + xhttp.responseText;
# document.getElementById("tokenerror").innerHTML = "";
# }
# }
# };
# xhttp.open("POST", '/hub/proxytoken/', true);
# xhttp.send(mode);
# }
# </script>
# <button onclick="getToken()">Get current token</button>
# <button onclick="refreshToken('random')">Refresh token with a random one</button>
# <button onclick="refreshToken('disabled')">Disable proxy (allow none)</button>
# <button onclick="refreshToken('allow_all')">Disable token check (allow all)</button><br>
# <div id="tokenerror" style="color: #f00;"></div>
# <div id="tokenoutput"></div>
|
examples/token_demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # This notebook is specifically made for Python3.x versions
# # Functional Composition
# Takes two functions and chains them like h(g(x))
def compose_functions(h_x, g_x):
def final_func(*args, **kwargs):
return h_x(g_x(*args, **kwargs))
return final_func
# +
import re
def add_suffix(my_string):
return my_string + ' the suffix, was finally added!!!'
def remove_punctuation(my_string):
return re.sub(r'[^\w\s]','',my_string)
# -
composed_f = compose_functions(remove_punctuation, add_suffix)
composed_f("Hello! World?")
#remove_punctuation("Hello! World? the suffix, was finally added!!!")
composed_f2 = compose_functions(add_suffix, remove_punctuation)
composed_f2("Hello! World?")
#add_suffix("Hello World")
# # Currying
# ### Using Partial from functools
def do_some_ops(a, b, c, d):
return a * b + c - d
# +
from functools import partial
# bind b
dso_f_b = partial(do_some_ops, b=10)
# bind c
dso_f_c = partial(dso_f_b, c=100)
# bind d
dso_f_d = partial(dso_f_c, d=1)
# -
# call the function for some value of a
dso_f_d(9) #do_some_ops(9)(10)(100)(1)
# The above call is same as
do_some_ops(9, 10, 100, 1)
def predict_land_prices(yr_sold, yr_bought, initial_price, area):
return initial_price + area*(yr_sold-yr_bought)*20 + 2000
# +
# Year bought, area and initial price are fixed for any land
# bind year bought
plp_yr_bought = partial(predict_land_prices, yr_bought=2012)
# bind initial price
plp_initial_price = partial(plp_yr_bought, initial_price=50000)
#bind plot area
plp_area = partial(plp_initial_price, area=1000)
# -
plp_area(2022)
# The above call is same as
predict_land_prices(2022, 2012, 50000, 1000)
plp_area(2023)
plp_area(2030)
# ### Using Decorators
# +
from inspect import signature
# Create a decorator
def curry_func(my_func):
# define inner function
def inner_wrap(args):
# Check no. of paramters in function signature
if len(signature(my_func).parameters) == 1:
return my_func(args)
# If more than 1 paramter recursively apply
# the decorator and call partial
else:
return curry_func(partial(my_func, args))
return inner_wrap
# -
@curry_func
def do_some_ops(a, b, c, d):
return a * b + c - d
do_some_ops(9)(10)(100)(1)
@curry_func
def predict_land_prices(yr_sold, yr_bought, initial_price, area):
return initial_price + area*(yr_sold-yr_bought)*20 + 2000
predict_land_prices(2022)(2012)(50000)(1000)
|
_src/Section 7/7.1 Currying in Python 3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.6.2
# language: julia
# name: julia-1.6
# ---
# ## Simulation of a M/M/1 queue using processes
# This simulation is adapted from the Bank Renege example in the documentation of a previous version of SimJulia: http://simjuliajl.readthedocs.io/en/stable/examples/1_bank_renege.html
using SimJulia
using Distributions
using ResumableFunctions
using RDST, Random
# Let's first simulate a fixed number of clients.
# +
const RANDOM_SEED = 200
const NEW_CUSTOMERS = 5 # Total number of customers
const INTERVAL_CUSTOMERS = 2.0 # Generate new customers roughly every x seconds
const MEAN_SERVICE = 1.9
# The macro @resumable allows to suspend a function until some event wakes it up.
@resumable function source(env::Simulation, number::Int, interval::Float64, counter::Resource)
d = Exponential(interval)
for i in 1:number
# The customer service time is random. During the service, the counter
# is not available to any other customer.
@yield timeout(env, rand(d))
@process customer(env, i, counter, MEAN_SERVICE)
end
end
@resumable function customer(env::Simulation, idx::Int, counter::Resource, time_in_system::Float64)
# Record the arrival time in the system
arrive = now(env)
println("$arrive: arrival of customer $idx")
@yield request(counter)
# The simulation clock now contains the time when the client goes to the server.
wait = now(env) - arrive
# Record the waiting time
waits[idx] = wait
println("$(now(env)): customer $idx has waited $wait")
@yield timeout(env, rand(Exponential(time_in_system)))
println("$(now(env)): customer $idx: finished")
@yield release(counter)
end
# -
# Setup and start the simulation
println("M/M/1 with processes")
waits = zeros(NEW_CUSTOMERS)
Random.seed!(RANDOM_SEED)
env = Simulation()
# Start processes and run
counter = Resource(env, 1)
@process source(env, NEW_CUSTOMERS, INTERVAL_CUSTOMERS, counter)
run(env)
# We can compute the mean waiting time by
mean(waits)
# However, most of the time, we do not know the number of client. We first set the end of simulation event by specifying an time horizon when running the simulation.
@process source(env, NEW_CUSTOMERS, INTERVAL_CUSTOMERS, counter)
run(env, 5.0)
# We observe however that the simulation time has not been reset to 0. A simple solution is to create a new simulation environment. This also requires to set the resource again.
env = Simulation()
counter = Resource(env, 1)
@process source(env, NEW_CUSTOMERS, INTERVAL_CUSTOMERS, counter)
run(env, 5.0)
# The random draws are different but we can produce the same as previously by using the same seed, i.e. the same initial state.
Random.seed!(RANDOM_SEED)
env = Simulation()
counter = Resource(env, 1)
@process source(env, NEW_CUSTOMERS, INTERVAL_CUSTOMERS, counter)
run(env, 15.0)
# However, a possible issue is that a customer never finishes his service. If we want to ensure that the customer complete his journey in the system, we have to modify the source function. We can circumvent it by redefining the source function so that no customer is generated after a horizon limit, but we do not put a limit when calling the run function.
@resumable function source!(env::Simulation, number::Int, interval::Float64, counter::Resource, limit::Float64, nserved::Array{Int64,1})
nserved[1] = 0
d = Exponential(interval)
for i in 1:number
@yield timeout(env, rand(d))
if (now(env) > limit) break end
@process customer(env, i, counter, MEAN_SERVICE)
nserved[1] += 1
end
end
# +
nserved = [ 0 ]
Random.seed!(RANDOM_SEED)
env = Simulation()
counter = Resource(env, 1)
@process source!(env, NEW_CUSTOMERS, INTERVAL_CUSTOMERS, counter, 5.0, nserved)
run(env)
# -
# This raises the question: should we flush the entities in the system at the end of the horizon of allow the entities in the system to complete their process? It depends on the context!
#
# In our case, the mean waiting time is
mean(waits[1:nserved[1]])
@resumable function new_source!(env::Simulation, interval::Float64, counter::Resource, limit::Float64, nserved::Array{Int64,1})
nserved[1] = 0
i = 0
d = Exponential(interval)
while (true)
@yield timeout(env, rand(d))
if (now(env) > limit) break end
i += 1
@process new_customer(env, i, counter, MEAN_SERVICE, new_waits)
end
nserved[1] = i
end
@resumable function new_customer(env::Simulation, idx::Int, counter::Resource, time_in_system::Float64, waits::Array{Float64,1})
# Record the arrival time in the system
arrive = now(env)
println("$arrive: arrival of customer $idx")
@yield request(counter)
# The simulation clock now contains the time when the client goes to the server.
wait = now(env) - arrive
# Record the waiting time
waits = push!(waits, wait)
println("$(now(env)): customer $idx has waited $wait")
@yield timeout(env, rand(Exponential(time_in_system)))
println("$(now(env)): customer $idx: finished")
@yield release(counter)
end
# +
nserved = [ 0 ]
Random.seed!(RANDOM_SEED)
env = Simulation()
counter = Resource(env, 1)
new_waits = Float64[]
@process new_source!(env, INTERVAL_CUSTOMERS, counter, 5.0, nserved)
run(env)
# -
new_waits
nserved[1]
|
SP/mm1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="C1QVJFlVsxcZ"
# # Preface
#
# <br>
# <div style="font-variant: small-caps;">CAVEAT PROGRAMMER</div>
#
# The below is an alpha API preview and things might break. The surface syntax of the features of the API are not fixed in stone, and we welcome feedback on any points.
# + [markdown] id="23zkGDayszYI"
# ## Useful links
#
# ⟶ [Slides](https://docs.google.com/presentation/d/1ngKWUwsSqAwPRvATG8sAxMzu9ujv4N__cKsUofdNno0/edit?usp=sharing) for the core ideas of the new Functional Core and Linen
#
# ⟶ "Design tests" guided our design process. Many are available for [functional core](https://github.com/google/flax/tree/master/examples/core_design_test) and some for the [proposed Module abstraction](https://github.com/google/flax/tree/master/examples/linen_design_test/)
#
# ⟶ Ported examples: [ImageNet](https://github.com/google/flax/tree/master/examples/imagenet) and [WMT](https://github.com/google/flax/tree/master/examples/wmt) (to the proposed Module abstraction). TODO: Port to functional core.
#
# ⟶ Our new [discussion forums](https://github.com/google/flax/discussions/)
#
#
# + [markdown] id="vGtC_5W4mQnY"
# # Install and Import
# + id="HgRZ_G8wGcoB"
# Install the newest JAXlib version.
# !pip install --upgrade -q pip jax jaxlib
# Install Flax at head:
# !pip install --upgrade -q git+https://github.com/google/flax.git
# + id="Kvx7GmavHZbD"
import functools
from typing import Any, Callable, Sequence, Optional
import numpy as np
import jax
from jax import lax, random, numpy as jnp
import flax
from flax.core import freeze, unfreeze
from flax import linen as nn
# + [markdown] id="u86fYsrEfYow"
# # Invoking Modules
# + [markdown] id="nrVbFrh1ffve"
# Let's instantiate a `Dense` layer.
# - Modules are actually objects in this API, so we provide _contructor arguments_ when initializing the Module. In this case, we only have to provide the output `features` dimension.
#
# + id="EcDH20Uufc-v"
model = nn.Dense(features=3)
# + [markdown] id="hL4NgtBwgI0S"
# We need to initialize the Module variables, these include the parameters of the Module as well as any other state variables.
#
# We call the `init` method on the instantiated Module. If the Module `__call__` method has args `(self, *args, **kwargs)` then we call `init` with `(rngs, *args, **kwargs)` so in this case, just `(rng, input)`:
# + id="Vjx0HWNcfa8h" outputId="3adfaeaf-977e-4e82-8adf-d254fae6eb91" colab={"base_uri": "https://localhost:8080/"}
# Make RNG Keys and a fake input.
key1, key2 = random.split(random.PRNGKey(0), 2)
x = random.uniform(key1, (4,4))
# provide key and fake input to get initialized variables
init_variables = model.init(key2, x)
init_variables
# + [markdown] id="ubFTzroGhErh"
# We call the `apply` method on the instantiated Module. If the Module `__call__` method has args `(self, *args, **kwargs)` then we call `apply` with `(variables, *args, rngs=<RNGS>, mutable=<MUTABLEKINDS>, **kwargs)` where
# - `<RNGS>` are the optional _call time_ RNGs for things like dropout. For simple Modules this is just a single key, but if your module has multiple __kinds__ of data, it's a dictionary of rng-keys per-kind, e.g. `{'params': key0, 'dropout': key1}` for a Module with dropout layers.
# - `<MUTABLEKINDS>` is an optional list of names of __kinds__ that are expected to be mutated during the call. e.g. `['batch_stats']` for a layer updating batchnorm statistics.
#
# So in this case, just `(variables, input)`:
# + id="R9QZ6EOBg5X8" outputId="e8c389a6-29f3-4f93-97ea-703e85a8b811" colab={"base_uri": "https://localhost:8080/"}
y = model.apply(init_variables, x)
y
# + [markdown] id="lNH06qc1hPrd"
# Additional points:
# - If you want to `init` or `apply` a Module using a method other than call, you need to provide the `method=` kwarg to `init` and `apply` to use it instead of the default `__call__`, e.g. `method='encode'`, `method='decode'` to apply the encode/decode methods of an autoencoder.
# + [markdown] id="jjsyiBjIYcAB"
# # Defining Basic Modules
# + [markdown] id="UvU7416Ti_lR"
# ## Composing submodules
# + [markdown] id="LkTy0hmJdE5G"
# We support declaring modules in `setup()` that can still benefit from shape inference by using __Lazy Initialization__ that sets up variables the first time the Module is called.
# + id="qB6l-9EabOwH" tags=[] outputId="1a6c6a17-0b95-42c2-b5bf-b9ad80fd7758" colab={"base_uri": "https://localhost:8080/"}
class ExplicitMLP(nn.Module):
features: Sequence[int]
def setup(self):
# we automatically know what to do with lists, dicts of submodules
self.layers = [nn.Dense(feat) for feat in self.features]
# for single submodules, we would just write:
# self.layer1 = nn.Dense(self, feat1)
def __call__(self, inputs):
x = inputs
for i, lyr in enumerate(self.layers):
x = lyr(x)
if i != len(self.layers) - 1:
x = nn.relu(x)
return x
key1, key2 = random.split(random.PRNGKey(0), 2)
x = random.uniform(key1, (4,4))
model = ExplicitMLP(features=[3,4,5])
init_variables = model.init(key2, x)
y = model.apply(init_variables, x)
print('initialized parameter shapes:\n', jax.tree_map(jnp.shape, unfreeze(init_variables)))
print('output:\n', y)
# + [markdown] id="slwE6ULqc_t_"
# Here we show the equivalent compact form of the MLP that declares the submodules inline using the `@compact` decorator.
# + id="UPNGIr6wcGaw" tags=[] outputId="b3709789-e66e-4e20-f6b2-04022f8a62bb" colab={"base_uri": "https://localhost:8080/"}
class SimpleMLP(nn.Module):
features: Sequence[int]
@nn.compact
def __call__(self, inputs):
x = inputs
for i, feat in enumerate(self.features):
x = nn.Dense(feat, name=f'layers_{i}')(x)
if i != len(self.features) - 1:
x = nn.relu(x)
# providing a name is optional though!
# the default autonames would be "Dense_0", "Dense_1", ...
# x = nn.Dense(feat)(x)
return x
key1, key2 = random.split(random.PRNGKey(0), 2)
x = random.uniform(key1, (4,4))
model = SimpleMLP(features=[3,4,5])
init_variables = model.init(key2, x)
y = model.apply(init_variables, x)
print('initialized parameter shapes:\n', jax.tree_map(jnp.shape, unfreeze(init_variables)))
print('output:\n', y)
# + [markdown] id="b2OzKXYyjFSf"
# ## Declaring and using variables
# + [markdown] id="uYwS5KbcmYIp"
# Flax uses lazy initialization, which allows declared variables to be initialized only at the first site of their use, using whatever shape information is available a the local call site for shape inference. One a variable has been initialized, and a reference to the data kept for use in subsequent calls.
#
# For declaring parameters that aren't mutated inside the model, but rather by gradient descent, we use the syntax:
#
# `self.param(parameter_name, parameter_init_fn, *init_args)`
#
# with arguments:
# - `parameter_name` just the name, a string
# - `parameter_init_fn` a function taking an RNG key and a variable number of other arguments, i.e. `fn(rng, *args)`. typically those in `nn.initializers` take an `rng` and a `shape` argument.
# - the remaining arguments to feed to the init function when initializing.
#
# Again, we'll demonstrate declaring things inline as we typically do using the `@compact` decorator.
# + id="7OACbTFHjMvl" tags=[] outputId="bc5cb1f2-c5e9-4159-d131-73247009e32f" colab={"base_uri": "https://localhost:8080/"}
class SimpleDense(nn.Module):
features: int
kernel_init: Callable = nn.initializers.lecun_normal()
bias_init: Callable = nn.initializers.zeros
@nn.compact
def __call__(self, inputs):
kernel = self.param('kernel',
self.kernel_init, # RNG passed implicitly.
(inputs.shape[-1], self.features)) # shape info.
y = lax.dot_general(inputs, kernel,
(((inputs.ndim - 1,), (0,)), ((), ())),)
bias = self.param('bias', self.bias_init, (self.features,))
y = y + bias
return y
key1, key2 = random.split(random.PRNGKey(0), 2)
x = random.uniform(key1, (4,4))
model = SimpleDense(features=3)
init_variables = model.init(key2, x)
y = model.apply(init_variables, x)
print('initialized parameters:\n', init_variables)
print('output:\n', y)
# + [markdown] id="KgEwkrkfdlt8"
# We can also declare variables in setup, though in doing so you can't take advantage of shape inference and have to provide explicit shape information at initialization. The syntax is a little repetitive in this case right now, but we do force agreement of the assigned names.
#
# + id="CE0CTLVvZ8Yn" tags=[] outputId="1e822bd8-7a08-4e80-e0e6-a86637c46772" colab={"base_uri": "https://localhost:8080/"}
class ExplicitDense(nn.Module):
features_in: int # <-- explicit input shape
features: int
kernel_init: Callable = nn.initializers.lecun_normal()
bias_init: Callable = nn.initializers.zeros
def setup(self):
self.kernel = self.param('kernel',
self.kernel_init,
(self.features_in, self.features))
self.bias = self.param('bias', self.bias_init, (self.features,))
def __call__(self, inputs):
y = lax.dot_general(inputs, self.kernel,
(((inputs.ndim - 1,), (0,)), ((), ())),)
y = y + self.bias
return y
key1, key2 = random.split(random.PRNGKey(0), 2)
x = random.uniform(key1, (4,4))
model = ExplicitDense(features_in=4, features=3)
init_variables = model.init(key2, x)
y = model.apply(init_variables, x)
print('initialized parameters:\n', init_variables)
print('output:\n', y)
# + [markdown] id="t4MVj1RBmxsZ"
# ## General Variables
# + [markdown] id="CJatarOTpByQ"
# For declaring generally mutable _variables_ that may be mutated inside the model we use the call:
#
# `self.variable(variable_kind, variable_name, variable_init_fn, *init_args)`
#
# with arguments:
# - `variable_kind` the "kind" of state this variable is, i.e. the name of the nested-dict collection that this will be stored in inside the top Modules variables. e.g. `batch_stats` for the moving statistics for a batch norm layer or `cache` for autoregressive cache data. Note that parameters also have a kind, but they're set to the default `param` kind.
# - `variable_name` just the name, a string
# - `variable_init_fn` a function taking a variable number of other arguments, i.e. `fn(*args)`. Note that we __don't__ assume the need for an RNG, if you _do_ want an RNG, provide it via a `self.make_rng(variable_kind)` call in the provided arguments.
# - the remaining arguments to feed to the init function when initializing.
#
# ⚠️ Unlike parameters, we expect these to be mutated, so `self.variable` returns not a constant, but a _reference_ to the variable. To __get__ the raw value, you'd write `myvariable.value` and to __set__ it `myvariable.value = new_value`.
#
# + id="u6_fbrW2XT5t" tags=[] outputId="2a8f5453-81b1-44dc-a431-d14b372c5710" colab={"base_uri": "https://localhost:8080/"}
class Counter(nn.Module):
@nn.compact
def __call__(self):
# easy pattern to detect if we're initializing
is_initialized = self.has_variable('counter', 'count')
counter = self.variable('counter', 'count', lambda: jnp.zeros((), jnp.int32))
if is_initialized:
counter.value += 1
return counter.value
key1 = random.PRNGKey(0)
model = Counter()
init_variables = model.init(key1)
print('initialized variables:\n', init_variables)
y, mutated_variables = model.apply(init_variables, mutable=['counter'])
print('mutated variables:\n', mutated_variables)
print('output:\n', y)
# + [markdown] id="VLxwg2aMxUmy"
# ## Another Mutability and RNGs Example
# + [markdown] id="NOARPIowyeXS"
# Let's make an artificial, goofy example that mixes differentiable parameters, stochastic layers, and mutable variables:
# + id="BBrbcEdCnQ4o" tags=[] outputId="8f299a5c-74c8-476c-93fa-e5543901ec45" colab={"base_uri": "https://localhost:8080/"}
class Block(nn.Module):
features: int
training: bool
@nn.compact
def __call__(self, inputs):
x = nn.Dense(self.features)(inputs)
x = nn.Dropout(rate=0.5)(x, deterministic=not self.training)
x = nn.BatchNorm(use_running_average=not self.training)(x)
return x
key1, key2, key3, key4 = random.split(random.PRNGKey(0), 4)
x = random.uniform(key1, (3,4,4))
model = Block(features=3, training=True)
init_variables = model.init({'params': key2, 'dropout': key3}, x)
_, init_params = init_variables.pop('params')
# When calling `apply` with mutable kinds, returns a pair of output,
# mutated_variables.
y, mutated_variables = model.apply(
init_variables, x, rngs={'dropout': key4}, mutable=['batch_stats'])
# Now we reassemble the full variables from the updates (in a real training
# loop, with the updated params from an optimizer).
updated_variables = freeze(dict(params=init_params,
**mutated_variables))
print('updated variables:\n', updated_variables)
print('initialized variable shapes:\n',
jax.tree_map(jnp.shape, init_variables))
print('output:\n', y)
# Let's run these model variables during "evaluation":
eval_model = Block(features=3, training=False)
y = eval_model.apply(updated_variables, x) # Nothing mutable; single return value.
print('eval output:\n', y)
# + [markdown] id="Lcp28h72810L"
# # JAX transformations inside modules
#
# + [markdown] id="WEpbn8si0ATT"
# ## JIT
# + [markdown] id="-k-5gXTJ0EpD"
# It's not immediately clear what use this has, but you can compile specific submodules if there's a reason to.
#
# _Known Gotcha_: at the moment, the decorator changes the RNG stream slightly, so comparing jitted an unjitted initializations will look different.
# + id="UEUTO8bf0Kf2" tags=[] outputId="3f324d0f-259f-40f0-8273-103f7fc281c5" colab={"base_uri": "https://localhost:8080/"}
class MLP(nn.Module):
features: Sequence[int]
@nn.compact
def __call__(self, inputs):
x = inputs
for i, feat in enumerate(self.features):
# JIT the Module (it's __call__ fn by default.)
x = nn.jit(nn.Dense)(feat, name=f'layers_{i}')(x)
if i != len(self.features) - 1:
x = nn.relu(x)
return x
key1, key2 = random.split(random.PRNGKey(3), 2)
x = random.uniform(key1, (4,4))
model = MLP(features=[3,4,5])
init_variables = model.init(key2, x)
y = model.apply(init_variables, x)
print('initialized parameter shapes:\n', jax.tree_map(jnp.shape, unfreeze(init_variables)))
print('output:\n', y)
# + [markdown] id="D1tfTdRjyJYK"
# ## Remat
# + [markdown] id="goiHMi4qyLiZ"
# For memory-expensive computations, we can `remat` our method to recompute a Module's output during a backwards pass.
#
# _Known Gotcha_: at the moment, the decorator changes the RNG stream slightly, so comparing remat'd and undecorated initializations will look different.
# + id="sogMxDQpyMZE" tags=[] outputId="7fe8e13b-7dd6-4e55-ee50-ce334e8ed178" colab={"base_uri": "https://localhost:8080/"}
class RematMLP(nn.Module):
features: Sequence[int]
# For all transforms, we can annotate a method, or wrap an existing
# Module class. Here we annotate the method.
@nn.remat
@nn.compact
def __call__(self, inputs):
x = inputs
for i, feat in enumerate(self.features):
x = nn.Dense(feat, name=f'layers_{i}')(x)
if i != len(self.features) - 1:
x = nn.relu(x)
return x
key1, key2 = random.split(random.PRNGKey(3), 2)
x = random.uniform(key1, (4,4))
model = RematMLP(features=[3,4,5])
init_variables = model.init(key2, x)
y = model.apply(init_variables, x)
print('initialized parameter shapes:\n', jax.tree_map(jnp.shape, unfreeze(init_variables)))
print('output:\n', y)
# + [markdown] id="l0pJtxVwyCgp"
# ## Vmap
# + [markdown] id="TqVbjhOkyEaj"
# You can now `vmap` Modules inside. The transform has a lot of arguments, they have the usual jax vmap args:
# - `in_axes` - an integer or `None` for each input argument
# - `out_axes` - an integer or `None` for each output argument
# - `axis_size` - the axis size if you need to give it explicitly
#
# In addition, we provide for each __kind__ of variable it's axis rules:
#
# - `variable_in_axes` - a dict from kinds to a single integer or `None` specifying the input axes to map
# - `variable_out_axes` - a dict from kinds to a single integer or `None` specifying the output axes to map
# - `split_rngs` - a dict from RNG-kinds to a bool, specifying whether to split the rng along the axis.
#
#
# Below we show an example defining a batched, multiheaded attention module from a single-headed unbatched attention implementation.
# + id="PIGiriD0yFXo" tags=[] outputId="223d880e-c7b2-4210-ebb5-dbfcdd9aed09" colab={"base_uri": "https://localhost:8080/"}
class RawDotProductAttention(nn.Module):
attn_dropout_rate: float = 0.1
train: bool = False
@nn.compact
def __call__(self, query, key, value, bias=None, dtype=jnp.float32):
assert key.ndim == query.ndim
assert key.ndim == value.ndim
n = query.ndim
attn_weights = lax.dot_general(
query, key,
(((n-1,), (n - 1,)), ((), ())))
if bias is not None:
attn_weights += bias
norm_dims = tuple(range(attn_weights.ndim // 2, attn_weights.ndim))
attn_weights = jax.nn.softmax(attn_weights, axis=norm_dims)
attn_weights = nn.Dropout(self.attn_dropout_rate)(attn_weights,
deterministic=not self.train)
attn_weights = attn_weights.astype(dtype)
contract_dims = (
tuple(range(n - 1, attn_weights.ndim)),
tuple(range(0, n - 1)))
y = lax.dot_general(
attn_weights, value,
(contract_dims, ((), ())))
return y
class DotProductAttention(nn.Module):
qkv_features: Optional[int] = None
out_features: Optional[int] = None
train: bool = False
@nn.compact
def __call__(self, inputs_q, inputs_kv, bias=None, dtype=jnp.float32):
qkv_features = self.qkv_features or inputs_q.shape[-1]
out_features = self.out_features or inputs_q.shape[-1]
QKVDense = functools.partial(
nn.Dense, features=qkv_features, use_bias=False, dtype=dtype)
query = QKVDense(name='query')(inputs_q)
key = QKVDense(name='key')(inputs_kv)
value = QKVDense(name='value')(inputs_kv)
y = RawDotProductAttention(train=self.train)(
query, key, value, bias=bias, dtype=dtype)
y = nn.Dense(features=out_features, dtype=dtype, name='out')(y)
return y
class MultiHeadDotProductAttention(nn.Module):
qkv_features: Optional[int] = None
out_features: Optional[int] = None
batch_axes: Sequence[int] = (0,)
num_heads: int = 1
broadcast_dropout: bool = False
train: bool = False
@nn.compact
def __call__(self, inputs_q, inputs_kv, bias=None, dtype=jnp.float32):
qkv_features = self.qkv_features or inputs_q.shape[-1]
out_features = self.out_features or inputs_q.shape[-1]
# Make multiheaded attention from single-headed dimension.
Attn = nn.vmap(DotProductAttention,
in_axes=(None, None, None),
out_axes=2,
axis_size=self.num_heads,
variable_axes={'params': 0},
split_rngs={'params': True,
'dropout': not self.broadcast_dropout})
# Vmap across batch dimensions.
for axis in reversed(sorted(self.batch_axes)):
Attn = nn.vmap(Attn,
in_axes=(axis, axis, axis),
out_axes=axis,
variable_axes={'params': None},
split_rngs={'params': False, 'dropout': False})
# Run the vmap'd class on inputs.
y = Attn(qkv_features=qkv_features // self.num_heads,
out_features=out_features,
train=self.train,
name='attention')(inputs_q, inputs_kv, bias)
return y.mean(axis=-2)
key1, key2, key3, key4 = random.split(random.PRNGKey(0), 4)
x = random.uniform(key1, (3, 13, 64))
model = functools.partial(
MultiHeadDotProductAttention,
broadcast_dropout=False,
num_heads=2,
batch_axes=(0,))
init_variables = model(train=False).init({'params': key2}, x, x)
print('initialized parameter shapes:\n', jax.tree_map(jnp.shape, unfreeze(init_variables)))
y = model(train=True).apply(init_variables, x, x, rngs={'dropout': key4})
print('output:\n', y.shape)
# + [markdown] id="U-bDSQElvM09"
# ## Scan
# + [markdown] id="8oiRXIC6xQ--"
# Scan allows us to apply `lax.scan` to Modules, including their parameters and mutable variables. To use it we have to specify how we want each "kind" of variable to be transformed. For scanned variables we specify similar to vmap via in `variable_in_axes`, `variable_out_axes`:
# - `nn.broadcast` broadcast the variable kind across the scan steps as a constant
# - `<axis:int>` scan along `axis` for e.g. unique parameters at each step
#
# OR we specify that the variable kind is to be treated like a "carry" by passing to the `variable_carry` argument.
#
# Further, for `scan`'d variable kinds, we further specify whether or not to split the rng at each step.
# + id="oxA_lWm7tH2B" tags=[] outputId="7d9ebed3-64de-4ca8-9dce-4b09ba9e31a1" colab={"base_uri": "https://localhost:8080/"}
class SimpleScan(nn.Module):
@nn.compact
def __call__(self, xs):
dummy_rng = random.PRNGKey(0)
init_carry = nn.LSTMCell.initialize_carry(dummy_rng,
xs.shape[:1],
xs.shape[-1])
LSTM = nn.scan(nn.LSTMCell,
in_axes=1, out_axes=1,
variable_broadcast='params',
split_rngs={'params': False})
return LSTM(name="lstm_cell")(init_carry, xs)
key1, key2 = random.split(random.PRNGKey(0), 2)
xs = random.uniform(key1, (1, 5, 2))
model = SimpleScan()
init_variables = model.init(key2, xs)
print('initialized parameter shapes:\n', jax.tree_map(jnp.shape, unfreeze(init_variables)))
y = model.apply(init_variables, xs)
print('output:\n', y)
# + id="3aXsCdxGZiYq"
|
docs/notebooks/linen_intro.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3-azureml
# kernelspec:
# display_name: Python 3.6 - AzureML
# language: python
# name: python3-azureml
# ---
# # Work with Compute
#
# When you run a script as an Azure Machine Learning experiment, you need to define the execution context for the experiment run. The execution context is made up of:
#
# * The Python environment for the script, which must include all Python packages used in the script.
# * The compute target on which the script will be run. This could be the local workstation from which the experiment run is initiated, or a remote compute target such as a training cluster that is provisioned on-demand.
#
# In this notebook, you'll explore *environments* and *compute targets* for experiments.
# ## Connect to your workspace
#
# To get started, connect to your workspace.
#
# > **Note**: If you haven't already established an authenticated session with your Azure subscription, you'll be prompted to authenticate by clicking a link, entering an authentication code, and signing into Azure.
# + gather={"logged": 1633655581428}
import azureml.core
from azureml.core import Workspace
# Load the workspace from the saved config file
ws = Workspace.from_config()
print('Ready to use Azure ML {} to work with {}'.format(azureml.core.VERSION, ws.name))
# -
# ## Prepare data for an experiment
#
# In this notebook, you'll use a dataset containing details of diabetes patients. Run the cell below to create this dataset (if it already exists, the code will find the existing version)
# + gather={"logged": 1633655612670}
from azureml.core import Dataset
default_ds = ws.get_default_datastore()
if 'diabetes dataset' not in ws.datasets:
default_ds.upload_files(files=['./data/diabetes.csv', './data/diabetes2.csv'], # Upload the diabetes csv files in /data
target_path='diabetes-data/', # Put it in a folder path in the datastore
overwrite=True, # Replace existing files of the same name
show_progress=True)
#Create a tabular dataset from the path on the datastore (this may take a short while)
tab_data_set = Dataset.Tabular.from_delimited_files(path=(default_ds, 'diabetes-data/*.csv'))
# Register the tabular dataset
try:
tab_data_set = tab_data_set.register(workspace=ws,
name='diabetes dataset',
description='diabetes data',
tags = {'format':'CSV'},
create_new_version=True)
print('Dataset registered.')
except Exception as ex:
print(ex)
else:
print('Dataset already registered.')
# -
# ## Create a training script
#
# Run the following two cells to create:
#
# 1. A folder for a new experiment
# 2. An training script file that uses **scikit-learn** to train a model and **matplotlib** to plot a ROC curve.
# + gather={"logged": 1633655857930}
import os
# Create a folder for the experiment files
experiment_folder = 'diabetes_training_logistic'
os.makedirs(experiment_folder, exist_ok=True)
print(experiment_folder, 'folder created')
# +
# %%writefile $experiment_folder/diabetes_training.py
# Import libraries
import argparse
from azureml.core import Run
import pandas as pd
import numpy as np
import joblib
import os
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
# Get script arguments
parser = argparse.ArgumentParser()
parser.add_argument('--regularization', type=float, dest='reg_rate', default=0.01, help='regularization rate')
parser.add_argument("--input-data", type=str, dest='training_dataset_id', help='training dataset')
args = parser.parse_args()
# Set regularization hyperparameter
reg = args.reg_rate
# Get the experiment run context
run = Run.get_context()
# load the diabetes data (passed as an input dataset)
print("Loading Data...")
diabetes = run.input_datasets['training_data'].to_pandas_dataframe()
# Separate features and labels
X, y = diabetes[['Pregnancies','PlasmaGlucose','DiastolicBloodPressure','TricepsThickness','SerumInsulin','BMI','DiabetesPedigree','Age']].values, diabetes['Diabetic'].values
# Split data into training set and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=0)
# Train a logistic regression model
print('Training a logistic regression model with regularization rate of', reg)
run.log('Regularization Rate', np.float(reg))
model = LogisticRegression(C=1/reg, solver="liblinear").fit(X_train, y_train)
# calculate accuracy
y_hat = model.predict(X_test)
acc = np.average(y_hat == y_test)
print('Accuracy:', acc)
run.log('Accuracy', np.float(acc))
# calculate AUC
y_scores = model.predict_proba(X_test)
auc = roc_auc_score(y_test,y_scores[:,1])
print('AUC: ' + str(auc))
run.log('AUC', np.float(auc))
# plot ROC curve
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])
fig = plt.figure(figsize=(6, 4))
# Plot the diagonal 50% line
plt.plot([0, 1], [0, 1], 'k--')
# Plot the FPR and TPR achieved by our model
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
run.log_image(name = "ROC", plot = fig)
plt.show()
os.makedirs('outputs', exist_ok=True)
# note file saved in the outputs folder is automatically uploaded into experiment record
joblib.dump(value=model, filename='outputs/diabetes_model.pkl')
run.complete()
# -
# ## Define an environment
#
# When you run a Python script as an experiment in Azure Machine Learning, a Conda environment is created to define the execution context for the script. Azure Machine Learning provides a default environment that includes many common packages; including the **azureml-defaults** package that contains the libraries necessary for working with an experiment run, as well as popular packages like **pandas** and **numpy**.
#
# You can also define your own environment in a Conda specification file, adding packages by using **conda** or **pip** to ensure your experiment has access to all the libraries it requires.
#
# > **Note**: The conda dependencies are installed first, followed by the pip dependencies. Since the **pip** package is required to install the pip dependencies, it's good practice to include it in the conda dependencies.
#
# Run the following cell to create a Conda specification file named *experiment_env.yml* in the same folder as this notebook.
# %%writefile $experiment_folder/experiment_env.yml
name: experiment_env
dependencies:
# The python interpreter version.
# Currently Azure ML only supports 3.5.2 and later.
- python=3.6.2
- scikit-learn
- ipykernel
- matplotlib
- pandas
- pip
- pip:
- azureml-defaults
- pyarrow
# Now you can use your custom conda specification file to create an environment for your experiment
# + gather={"logged": 1633656153056}
from azureml.core import Environment
# Create a Python environment for the experiment (from a .yml file)
experiment_env = Environment.from_conda_specification("experiment_env", experiment_folder + "/experiment_env.yml")
# Let Azure ML manage dependencies
experiment_env.python.user_managed_dependencies = False
# Print the environment details
print(experiment_env.name, 'defined.')
print(experiment_env.python.conda_dependencies.serialize_to_string())
# -
# Now you can use the environment to run a script as an experiment.
#
# The following code assigns the environment you created to a ScriptRunConfig, and submits an experiment. As the experiment runs, observe the run details in the widget and in the **azureml_logs/60_control_log.txt** output log, you'll see the conda environment being built.
#
# > **Note**: The code below creates a **DockerConfiguration** for the script run, and setting its **use_docker** attribute to **True** in order to host the script's environment in a Docker container. This is the default behavior, so you can omit this; but we're including it here to be explicit.
# + gather={"logged": 1633656546575}
from azureml.core import Experiment, ScriptRunConfig
from azureml.core.runconfig import DockerConfiguration
from azureml.widgets import RunDetails
# Get the training dataset
diabetes_ds = ws.datasets.get("diabetes dataset")
# Create a script config
script_config = ScriptRunConfig(source_directory=experiment_folder,
script='diabetes_training.py',
arguments = ['--regularization', 0.1, # Regularizaton rate parameter
'--input-data', diabetes_ds.as_named_input('training_data')], # Reference to dataset
environment=experiment_env,
docker_runtime_config=DockerConfiguration(use_docker=True)) # Use docker to host environment
# submit the experiment
experiment_name = 'mslearn-train-diabetes'
experiment = Experiment(workspace=ws, name=experiment_name)
run = experiment.submit(config=script_config)
RunDetails(run).show()
run.wait_for_completion()
# -
# The experiment successfully used the environment, which included all of the packages it required - you can view the metrics and outputs from the experiment run in Azure Machine Learning Studio, or by running the code below - including the model trained using **scikit-learn** and the ROC chart image generated using **matplotlib**.
# Get logged metrics
metrics = run.get_metrics()
for key in metrics.keys():
print(key, metrics.get(key))
print('\n')
for file in run.get_file_names():
print(file)
# ## Register the environment
#
# Having gone to the trouble of defining an environment with the packages you need, you can register it in the workspace.
# Register the environment
experiment_env.register(workspace=ws)
# Note that the environment is registered with the name you assigned when you first created it (in this case, *diabetes-experiment-env*).
#
# With the environment registered, you can reuse it for any scripts that have the same requirements. For example, let's create a folder and script to train a diabetes model using a different algorithm:
# +
import os
# Create a folder for the experiment files
experiment_folder = 'diabetes_training_tree'
os.makedirs(experiment_folder, exist_ok=True)
print(experiment_folder, 'folder created')
# +
# %%writefile $experiment_folder/diabetes_training.py
# Import libraries
import argparse
from azureml.core import Run
import pandas as pd
import numpy as np
import joblib
import os
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
# Get script arguments
parser = argparse.ArgumentParser()
parser.add_argument("--input-data", type=str, dest='training_dataset_id', help='training dataset')
args = parser.parse_args()
# Get the experiment run context
run = Run.get_context()
# load the diabetes data (passed as an input dataset)
print("Loading Data...")
diabetes = run.input_datasets['training_data'].to_pandas_dataframe()
# Separate features and labels
X, y = diabetes[['Pregnancies','PlasmaGlucose','DiastolicBloodPressure','TricepsThickness','SerumInsulin','BMI','DiabetesPedigree','Age']].values, diabetes['Diabetic'].values
# Split data into training set and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=0)
# Train a decision tree model
print('Training a decision tree model')
model = DecisionTreeClassifier().fit(X_train, y_train)
# calculate accuracy
y_hat = model.predict(X_test)
acc = np.average(y_hat == y_test)
print('Accuracy:', acc)
run.log('Accuracy', np.float(acc))
# calculate AUC
y_scores = model.predict_proba(X_test)
auc = roc_auc_score(y_test,y_scores[:,1])
print('AUC: ' + str(auc))
run.log('AUC', np.float(auc))
# plot ROC curve
fpr, tpr, thresholds = roc_curve(y_test, y_scores[:,1])
fig = plt.figure(figsize=(6, 4))
# Plot the diagonal 50% line
plt.plot([0, 1], [0, 1], 'k--')
# Plot the FPR and TPR achieved by our model
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
run.log_image(name = "ROC", plot = fig)
plt.show()
os.makedirs('outputs', exist_ok=True)
# note file saved in the outputs folder is automatically uploaded into experiment record
joblib.dump(value=model, filename='outputs/diabetes_model.pkl')
run.complete()
# -
# Now you can retrieve the registered environment and use it in a new experiment that runs the alternative training script (there is no regularization parameter this time because a Decision Tree classifier doesn't require it).
# +
# get the registered environment
registered_env = Environment.get(ws, 'experiment_env')
# Get the training dataset
diabetes_ds = ws.datasets.get("diabetes dataset")
# Create a script config
script_config = ScriptRunConfig(source_directory=experiment_folder,
script='diabetes_training.py',
arguments = ['--input-data', diabetes_ds.as_named_input('training_data')], # Reference to dataset
environment=registered_env,
docker_runtime_config=DockerConfiguration(use_docker=True)) # Use docker to host environment
# submit the experiment
experiment_name = 'mslearn-train-diabetes'
experiment = Experiment(workspace=ws, name=experiment_name)
run = experiment.submit(config=script_config)
RunDetails(run).show()
run.wait_for_completion()
# -
# This time the experiment runs more quickly because a matching environment has been cached from the previous run, so it doesn't need to be recreated on the local compute. However, even on a different compute target, the same environment would be created and used - ensuring consistency for your experiment script execution context.
#
# Let's look at the metrics and outputs from the experiment.
# Get logged metrics
metrics = run.get_metrics()
for key in metrics.keys():
print(key, metrics.get(key))
print('\n')
for file in run.get_file_names():
print(file)
# ## View registered environments
#
# In addition to registering your own environments, you can leverage pre-built "curated" environments for common experiment types. The following code lists all registered environments:
# +
from azureml.core import Environment
envs = Environment.list(workspace=ws)
for env in envs:
print("Name",env)
# -
# All curated environments have names that begin ***AzureML-*** (you can't use this prefix for your own environments).
# ## Create a compute cluster
#
# In many cases, your local compute resources may not be sufficient to process a complex or long-running experiment that needs to process a large volume of data; and you may want to take advantage of the ability to dynamically create and use compute resources in the cloud. Azure Machine Learning supports a range of compute targets, which you can define in your workpace and use to run experiments; paying for the resources only when using them.
#
# You can create a compute cluster in [Azure Machine Learning studio](https://ml.azure.com), or by using the Azure Machine Learning SDK. The following code cell checks your workspace for the existance of a compute cluster with a specified name, and if it doesn't exist, creates it.
#
# > **Important**: Change *your-compute-cluster* to a suitable name for your compute cluster in the code below before running it - you can specify the name of an existing cluster if you have one. Cluster names must be globally unique names between 2 to 16 characters in length. Valid characters are letters, digits, and the - character.
# +
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
cluster_name = "your-compute-cluster"
try:
# Check for existing compute target
training_cluster = ComputeTarget(workspace=ws, name=cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
# If it doesn't already exist, create it
try:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_DS11_V2', max_nodes=2)
training_cluster = ComputeTarget.create(ws, cluster_name, compute_config)
training_cluster.wait_for_completion(show_output=True)
except Exception as ex:
print(ex)
# -
# > **Note**: Compute instances and clusters are based on standard Azure virtual machine images. For this exercise, the *Standard_DS11_v2* image is recommended to achieve the optimal balance of cost and performance. If your subscription has a quota that does not include this image, choose an alternative image; but bear in mind that a larger image may incur higher cost and a smaller image may not be sufficient to complete the tasks. Alternatively, ask your Azure administrator to extend your quota.
#
# ## Run an experiment on remote compute
#
# Now you're ready to re-run the experiment you ran previously, but this time on the compute cluster you created.
#
# > **Note**: The experiment will take quite a lot longer because a container image must be built with the conda environment, and then the cluster nodes must be started and the image deployed before the script can be run. For a simple experiment like the diabetes training script, this may seem inefficient; but imagine you needed to run a more complex experiment that takes several hours - dynamically creating more scalable compute may reduce the overall time significantly.
# +
# Create a script config
script_config = ScriptRunConfig(source_directory=experiment_folder,
script='diabetes_training.py',
arguments = ['--input-data', diabetes_ds.as_named_input('training_data')],
environment=registered_env,
compute_target=cluster_name)
# submit the experiment
experiment_name = 'mslearn-train-diabetes'
experiment = Experiment(workspace=ws, name=experiment_name)
run = experiment.submit(config=script_config)
RunDetails(run).show()
# -
# While you're waiting for the experiment to run, you can check on the status of the compute in the widget above or in [Azure Machine Learning studio](https://ml.azure.com). You can also check the status of the compute using the code below.
cluster_state = training_cluster.get_status()
print(cluster_state.allocation_state, cluster_state.current_node_count)
# Note that it will take a while before the status changes from *steady* to *resizing* (now might be a good time to take a coffee break!). To block the kernel until the run completes, run the cell below.
run.wait_for_completion()
# Keep an eye on the kernel indicator at the top right of the page, when it turns from **⚫** to **◯**, the code has finished running.
#
# After the experiment has finished, you can get the metrics and files generated by the experiment run. This time, the files will include logs for building the image and managing the compute.
# Get logged metrics
metrics = run.get_metrics()
for key in metrics.keys():
print(key, metrics.get(key))
print('\n')
for file in run.get_file_names():
print(file)
# Now you can register the model that was trained by the experiment.
# +
from azureml.core import Model
# Register the model
run.register_model(model_path='outputs/diabetes_model.pkl', model_name='diabetes_model',
tags={'Training context':'Compute cluster'}, properties={'AUC': run.get_metrics()['AUC'], 'Accuracy': run.get_metrics()['Accuracy']})
# List registered models
for model in Model.list(ws):
print(model.name, 'version:', model.version)
for tag_name in model.tags:
tag = model.tags[tag_name]
print ('\t',tag_name, ':', tag)
for prop_name in model.properties:
prop = model.properties[prop_name]
print ('\t',prop_name, ':', prop)
print('\n')
# -
# > **More Information**:
# >
# > - For more information about environments in Azure Machine Learning, see [Create & use software environments in Azure Machine Learning](https://docs.microsoft.com/azure/machine-learning/how-to-use-environments)
# > - For more information about compute targets in Azure Machine Learning, see the [What are compute targets in Azure Machine Learning?](https://docs.microsoft.com/azure/machine-learning/concept-compute-target).
|
.ipynb_aml_checkpoints/07 - Work with Compute-checkpoint2021-9-8-1-29-42Z.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="HbOKBdp_r8WW"
# # Semester Project
# ## How much corn syrup and sugar are brands using in today’s products?
#
# Session 1 Team 6
# * <NAME> (NK3RF) - <EMAIL>
# * <NAME> (UQQ5ZZ) - <EMAIL>
# * <NAME> (SBV5DN) - <EMAIL>
#
# School of Data Science, University of Virginia
#
# CS 5010: Programming and Systems for Data Science
#
# Dr. <NAME>
#
# May 5th, 2021
#
# ----
#
# ## A Note to Reviewers
#
# While this notebook serves as an example of our analysis, code was modified to support running in the Google Colabratory notebook format. Our project was designed to work as a python module, as such we have ported our code to adapt to this alternate platform to maximize our audience.
#
# It is _strongly_ recommended you check out the code from git and run the project directly on your workstation if you experence any issues running this notebook, as there is limited control over google's provided libraries, and future executions of this notebook may have inconsistent results.
#
# See our [Github](https://github.com/uva-sp2021-cs5010-g6/finalproject) repository for more details, and for [bootstrapping](https://github.com/uva-sp2021-cs5010-g6/finalproject/blob/main/GETSTARTED.rst) instructions.
# + colab={"base_uri": "https://localhost:8080/"} id="XL7T52fQEqz1" outputId="d16d65dd-f700-47b2-e606-79e45824d45c"
# !pip install --upgrade pytest
# !pip install ipytest jupyter-pytest-2
# + [markdown] id="6yamVN30E1Pf"
# # Stop!
#
# You will need to restart your runtime to include the newly installed libraries.
#
# You can do this by clicking "Runtime -> Restart Runtime" or by pressing `Ctrl+M`, or by clicking the button to "restart runtime" in the above cell. Once completed, you can continue running this notebook.
# + id="O0TofmIJqHpq"
# Adding the source URI for the fetcher object
# !echo "https://fdc.nal.usda.gov/fdc-datasets/FoodData_Central_csv_2020-10-30.zip" > uri.txt
# !mkdir -p "dataset"
# + id="mDou-2D2py0V"
## project01.fetch
"""Data fetching utility for USDA datasets.
This module provides the primary support functions for downloading datasets from
a text file. Each line in the text file is expected to be a complete URL. Lines
that begin with '#' are ignored.
Example:
This module can be run directly with the following arguments:
$ python -m project01.fetch path/to/uri.txt output/dir
The URIs listed in the file path/to/uri.txt will be Files will be saved to output/dir.
If no arguments are specified, they defaults (./uri.txt, and ./dataset)
"""
import os
import sys
import requests
import tempfile
import zipfile
class Fetcher:
def __init__(self, uris: str = "uri.txt", base: str = "dataset", feedback: bool = True):
"""Creates a new fetcher method configured with the arguments specified.
Args:
uris (str): A path to a URI file for the class to parse and download the
datasetsfrom
base (str): A path to a directory to write the resulting files to.
feedback (bool): Specifies if user feedback during the download process
should occur. When true, text is written to stdout.
"""
self._uris = self.__parse_file(uris)
self._base = base
self._feedback = feedback
@staticmethod
def __parse_file(uri_file):
"""Establishs a link of URIs to download.
Args:
uri_file (str): the path to the file to parse.
Returns:
list(str): The effective listing of URIs from the uri_file.
"""
ret = list()
with open(uri_file, "r") as uris:
for uri in uris:
if not uri.startswith("#"):
ret.append(uri.rstrip())
return ret
def add_uri(self, uri: str):
"""Adds a URI to the list of download links after creation of the object.
Args:
uri (str): A fully qualified string to fetch to artifact from
Returns:
list(str): A listing of all URIs the instance is currently configured
to support.
"""
self._uris.append(uri)
return self._uris
def fetch(self, feedback: bool = None, out: str = None) -> str:
"""Downloads all URIs the the current object and extracts them to the class's directory.
Args:
feedback(bool): Overide the classes feedback state. If True, the download
progress will be echoed to screen.
out(str): Overrides the classes output director. If specified, the downloaded
files will be written to the directory that has been specified.
Returns:
str: The output path of the extracted files.
"""
feedback = feedback if feedback is not None else self._feedback
out = out if out is not None else self._base
with tempfile.TemporaryDirectory() as temp_dir:
for uri in self._uris:
filename = os.path.basename(uri)
# Use stream to download very large files
resp = requests.get(uri, stream=True)
resp.raise_for_status()
uri_size = resp.headers.get('content-length') # Get the size of the download
if feedback:
print("Downloading {}".format(uri))
with open(os.path.join(temp_dir, filename), "wb") as zipf:
tracker = 0
for block in resp.iter_content(4096):
tracker += len(block)
zipf.write(block)
if feedback:
done = int(50 * tracker / int(uri_size)) # Total Progress
# We need an unbuffered printer here...
sys.stdout.write("\r[%s%s] %s/100" % ('=' * done, ' ' * (50-done), done*2))
sys.stdout.flush()
print("")
for root, dirs, files in os.walk(temp_dir):
for zipf in files:
temp_zip = os.path.join(root, zipf)
with zipfile.ZipFile(temp_zip, "r") as zf:
if feedback:
print("Extracting {}".format(zipf))
stripped_name, ext = os.path.splitext(temp_zip)
basen = os.path.basename(stripped_name)
zf.extractall(os.path.join(out, basen))
return out
## Removed as this code functions only properly as a python module
#def cli():
# """Creates a CLI parser
#
# Returns:
# argparse.ArgumentParser: An Argument Parser configured to support the
# fetcher class.
# """
# import argparse
# parser = argparse.ArgumentParser("Fetch datasets")
#
# parser.add_argument("urifile", nargs="?",
# default="uri.txt",
# help="Path to file containing URIs to download.")
# parser.add_argument("outdir", nargs="?",
# default="dataset",
# help="Path to a directory to output the files.")
# return parser
#
#
#def main(uri_file, out):
# collector = Fetcher(uris=uri_file, base=out)
# collector.fetch()
# + colab={"base_uri": "https://localhost:8080/", "height": 93} id="T3NZQWA3rI6t" outputId="92cae1f2-b528-417f-a34a-<KEY>"
udsa_downloader = Fetcher(uris="uri.txt", base="dataset")
udsa_downloader.fetch()
# + id="X4K32kBqp8Gi"
# project01.parser
"""
This module contains the shared code used to read, parse, and produce
a dataframe object using our USDA dataset. Reviewing our dataset, we
find that there's several common columns and indices, indicating that
we could adopt an object-oriented approach, where we have a base object
and each of our data tables could expand upon.
"""
import os
import re
from typing import Any, List, Optional
import pandas as pd
class BaseFood:
"""A base object for USDA food elements.
This object creates a common interface for all future USDA food table
entries.
"""
def __init__(self, csv_file: str = None, *args, **kwargs) -> None:
self._df = self._parse_csv(csv_file)
self._ingredients = None
@staticmethod
def _parse_csv(csv_file: str) -> pd.DataFrame:
"""Establishes a pandas dataframe of the passed CSV file
Args:
csv_file (str): A string representing the path of the CSV file
to load
Returns:
pd.DataFrame: The CSV file loaded as a dataframe.
"""
return pd.read_csv(csv_file, header=0, dtype=object)
def _filter(self, col: str, val: Any) -> pd.DataFrame:
"""Returns the rows of the dataframe which have the passed value in the specified column.
Args:
col (str): The name of the column in the current instance's dataframe.
val (Any): The value to seek on within the dataframe.
Returns:
pd.DataFrame: The subset of the dataframe which matches the above condition.
"""
return self._df[self._df[col] == val]
def find_by_fdcid(self, idx: int) -> pd.DataFrame:
"""Returns the record whos fdc_id matches teh passed id value.
Args:
idx (int): The Index ID used for the food object.
Returns:
pd.DataFrame: The subset of the datatframe that matches the passed ID.
"""
return self._filter("fdc_id", idx)
@property
def df(self) -> pd.DataFrame:
"""Provides access to the object's dataframe
"""
return self._df
def run_on_df(self, func, *args, **kwargs):
self._df = func(self._df, *args, **kwargs)
return self._df
def cleanup(self) -> pd.DataFrame:
"""Cleans up dataset based upon EDA analysis.
Returns:
pd.DataFrame: The cleaned dataframe.
"""
raise NotImplementedError("Base cleanup method must be implemented in subclasses of object.")
def clamp(self,
floor: int = 0,
ceiling: int = None,
col: str = "corn_syrup_idx") -> pd.DataFrame:
"""Clamping function used to filter the allowed indices of a column.
Args:
floor (int): The lowest allowed value of the column. Defaults to 0.
ceiling (int): The highest allowed value in the column.
Defaults to the maximum value in the column.
col (str): The column name to operate on. Defaults to corn_syrup_idx.
Returns:
pd.DataFrame: A new dataframe, where only the rows within the values
of floor and ceiling are included, and all others are dropped.
"""
ceil = ceiling if ceiling is not None else self._df[col].max() + 1
self._df = self._df[(self._df[col] > floor) & (self._df[col] < ceil)]
return self._df
def find_top(self,
limit: int = 5,
col: str = "branded_food_category") -> pd.DataFrame:
"""Establishes the dataset for finding the largest values in the food object.
Args:
limit (int): The total number of records to return from the dataset.
col (str): The column to find the top occurances of.
Returns:
pd.DataFrame: A filtered dataframe containing only the foods
in the top five largest categories.
"""
top_series = self._df[col].value_counts().nlargest(limit)
top_names = top_series.index.array
self._df = self._df[self._df[col].isin(top_names)]
return self._df
def __str__(self) -> str:
return self._df.__str__()
class FoodObject(BaseFood):
def __init__(self, csv_file: str = None) -> None:
"""An object implementation of the food.csv data table.
Args:
csv_file (str): A string that direccts to the food.csv file.
"""
super().__init__(csv_file)
def find_by_group(self, grp: str) -> pd.DataFrame:
"""Finds all records that match the passed group.
Args:
grp (str): The group name to look up in the dataframe.
Returns:
pd.DataFrame: A subset of the dataframe for the specified group.
"""
return self._filter("food_category_id", grp)
def cleanup(self):
raise NotImplementedError("To be implemented.")
class FoodBrandObject(BaseFood):
def __init__(self, csv_file: str = None) -> None:
"""Establishs a new FoodBrand object based on the food_brand.csv file
Args:
csv_file (str): A string that specifies the path of the food_brands.csv file.
"""
super().__init__(csv_file)
def find_by_brandowner(self, brand: str = None) -> pd.DataFrame:
"""Finds all records owned by a particular brand.
Args:
brand (str): The brand owner's fully named value
Returns:
pd.DataFrame: A subset of the data for the specified brand owner.
"""
return self._filter("brand_owner", brand)
def cleanup(self) -> pd.DataFrame:
"""Cleans up dataset based upon EDA analysis.
Returns:
pd.DataFrame: The cleaned dataframe.
"""
self._df['modified_date'] = pd.to_datetime(self._df['modified_date'], format="%Y-%m-%d")
self._df['available_date'] = pd.to_datetime(self._df['available_date'], format='%Y-%m-%d')
# self._df['discontinued_date'] = pd.to_datetime(self._df['discontinued_date'], format='%Y-%m-%d')
del self._df['discontinued_date']
self._df.dropna(how='all')
self._df.dropna(subset=['brand_owner', 'ingredients', 'serving_size',
'serving_size_unit', 'branded_food_category'], inplace=True)
return self._df
def get_all_ingredients(self):
"""Parses the entire ingridents series of the dataframe to establish a list of all ingredients.
Returns:
set: A set of the ingredients within the dataframe.
"""
def clean(ing):
"""Performs simple splitting and parsing of an ingredients list.
Args:
ing (str): a string representing a product's ingriedents list.
Returns:
tuple: A split list of ingredients after being normalized for later processing.
"""
# Strip paren text
# Remove paren and bracket text
cleaned1 = re.sub(r'[\(\[].*?[\)\]]', "", str(ing)) # noqa
# Remove residual punctuation, save our "comma" delimiter
cleaned2 = re.sub(r'[#.:\-*?!&}{\]\[\(\)"]', "", cleaned1) # noqa
# Return a tuple split on the comma, removing whitespace
pt1 = list(i.strip() for i in cleaned2.lower().split(","))
# Split on nested semicolon list for ingredients
pt2 = list(i.strip() for lst in pt1 for i in lst.split(";"))
# Split on subsequent ingredients
pt3 = list(i.strip() for lst in pt2 for i in lst.split(":"))
# Split on "statement" ingredients
pt4 = list(i.strip() for lst in pt3 for i in lst.split("."))
# Return as an immutable type to make converting to a set easier
return tuple(pt4)
# Unfold the list into a flattened set and then back to a list (for ease of access)
self._ingredients = tuple(set(x.strip() for lst in self._df["ingredients"].apply(clean).tolist() for x in lst))
return self._ingredients
def load(csv_dir: Optional[str] = "dataset") -> List[FoodObject]:
ret = list()
for base_dir in os.listdir(csv_dir):
ret.append(FoodObject(os.path.join(csv_dir, base_dir, "food.csv")))
return ret
def find_index_from_str(delimited_string: str, fnd: str, split: str = ","):
"""Finds the rank of the string fnd in the passed delimited string
This function takes in a raw string with a known delimiter and locates
the index position of the fnd value, identifying the rank of the item.
Args:
delimited_string (str): The string to operate against.
fnd (str): The string to search for
split (str): The delimiter to use to split the source string.
Default: ","
Returns:
int: The integer value representing where the string fnd is
positioned in an array delimited by split.
"""
key = fnd.lower()
lst = [x.strip().lower() for x in str(delimited_string).split(split)]
rank = -1
for idx in range(len(lst)):
try:
lst[idx].index(key)
rank = idx+1
break
except ValueError:
continue
return rank
def insert_index(df: pd.DataFrame,
find: str,
col: str = "ingredients",
sep: str = ",") -> pd.DataFrame:
"""Augments dataframe to add a ranked index column.
This function inspects an existing dataframe's column and
seeks for a specified string using the logic of `find_index_from_str`
Args:
df (pd.DataFrame: The dataframe to operate on.
find (str): The string to search for
col (str): The name of the column to operate on in the dataframe.
sep (str): The delimiter to split the column's values against.
Returns:
pd.DataFrame: The mutated dataframe `df` with a new column named `find`_idx
with the index value specified. Note that if the value is not found, the
column's value will be less than 0.
"""
newcol = "".join([find.replace(" ", "_").lower(), "_idx"])
df[newcol] = df[col].apply(find_index_from_str, fnd=find, split=sep)
return df
# + colab={"base_uri": "https://localhost:8080/"} id="KcbIrj6eqYHy" outputId="b47fa93a-4bc2-4406-e517-a088317a6f01"
# project01.EDA
"""
Investigating the use of corn syrup in food products:
Exploratory Data Analysis (EDA)
&
Data Cleanup
"""
print(">>>>>>>>>>----------<<<<<<<<<<")
print("Import Operating System")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
import os
from typing import Any, List, Optional
#import operating system
print(">>>>>>>>>>----------<<<<<<<<<<")
print("Import Libraries")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from tabulate import tabulate
#import libraries
print(os.getcwd())
#check working directory
print("\n>>>>>>>>>>----------<<<<<<<<<<")
print("Reading in Data Set")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
#import project01.parser as parser
#import in the parser.py file from the project01 folder so we can
#instantiate Classes and call functions created within the parser.py script
branded_food = BaseFood('./dataset/FoodData_Central_csv_2020-10-30/branded_food.csv')
#branded_food = parser.BaseFood('/Users/swaroopveerabhadrappa/PycharmProjects/finalproject/dataset/FoodData_Central_csv_2020-10-30/branded_food.csv')
#loading the data set
#create a object by instantiating BaseFood class, which is designed to create
# a Data Frame out of a passed in CSV file, which in this case is "branded_food.csv"
print(">>>>>>>>>>----------<<<<<<<<<<")
print("High-level Exploration of Data Set")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
branded_food.run_on_df(insert_index,find="corn syrup")
#branded_food.run_on_df(parser.insert_index,find="corn syrup")
#use the branded_food_df Data Frame to call the nested function, insert_index
#the insert_index function creates a new column with the index position of the value we're looking for
#which in this case is 'corn syrup.' The insert_index function passes in another function when called,
#find_index_from_str, which locates the index position of the value we're looking for
print("View first 3 rows of data\n")
print(tabulate(branded_food.df.head(3), headers='keys', tablefmt='psql'))
#view first 3 rows of DataFrame
#based on output, number of columns to display will need to be set
print("\n>>>>>>>>>>----------<<<<<<<<<<")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
pd.set_option('display.max_columns', None)
#use display.max_columns to print all the columns
print("View first 3 rows of data\n")
print(tabulate(branded_food.df.head(3), headers='keys', tablefmt='psql'))
#check to see if all columns are displayed --> confirmed
print("\n>>>>>>>>>>----------<<<<<<<<<<")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
print("Shape of DataFrame\n")
print(branded_food.df.shape)
#shape attribute informs us of number of observations (rows) of data and number of
#variables (columns) in data set:
#498,182 rows
#14 variables
print("/n>>>>>>>>>>----------<<<<<<<<<<")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
pd.set_option('display.max_columns', None)
#use display.max_columns to print all the columns
print("Information on DataFrame\n")
print(branded_food.df.info)
#provides information about dataset including data types for each variable
#date variables (modified_date, available_date, and discontinued_date variables) are
#listed as 'object', change to datetime
#we have a few categorical variables that need to be changed in data type
print(">>>>>>>>>>----------<<<<<<<<<<")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
print("Convert date columns to datetime format\n")
branded_food.df['modified_date'] = pd.to_datetime(branded_food.df['modified_date'], infer_datetime_format='yyyy-mm-dd')
branded_food.df['available_date'] = pd.to_datetime(branded_food.df['available_date'], infer_datetime_format='yyyy-mm-dd')
branded_food.df['discontinued_date'] = pd.to_datetime(branded_food.df['discontinued_date'], infer_datetime_format='yyyy-mm-dd')
#convert the date variables into datetime data type and use infer_datetime_format to automatically
#have Pandas recognize the format, without having to specify a particular format
print("Data Type for each Column\n")
print(branded_food.df.dtypes)
#confirm that date variables are now in datetime data type
#confirmed
print(">>>>>>>>>>----------<<<<<<<<<<")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
print("Summary Statistics\n")
print(branded_food.df.describe)
#describe method provides count, mean, standard deviation, min, percentile values, and max
#need to suppress scientific notation and set number of decimal places to 2
print("\n>>>>>>>>>>----------<<<<<<<<<<")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
pd.set_option('display.float_format', lambda x: '%.2f' %x)
#suppress scientific notation in Pandas
pd.options.display.float_format = "{:,.2f}".format
#display float variables to two decimal places
print(branded_food.df.describe)
#confirm that scientific notation is suppressed and number of decimal places = 2
print("\n>>>>>>>>>>----------<<<<<<<<<<")
print("Data Cleanup: Checking for Missing Values, Duplicate Records, and Outliers")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
print("Missing Values in DataFrame\n")
print(branded_food.df.isnull().sum())
# print(branded_food.df.isnull().sum())
#check DataFrame for null values in any column, and sum up the total null values
#we observe null values in these columns: brand_owner, ingredients, serving_size
#serving_size_unit, household_serving_fulltext, branded_food_category, and discontinued_date
#we have the following options to deal with null values: drop from data se or
#replace with mean/median/mode, which will be dependent on data type of variable
#it wouldn't make sense to use mean/median with variables with data type object
#it also wouldn't make sense to use mode with object values, nonsensical
#one column is entirely blank, and that is discontinued_date
#let's drop rows and columns if all values are null, and then
#let's drop discontinued_date column from Data Frame and then come back to missing values
del branded_food.df['discontinued_date']
#drop discontinued_date column
print("\nColumns in DataFrame\n")
print(branded_food.df.columns)
#check to see if discontinued_date column is dropped
#confirmed
#number of variables (columns) is now 13
print("\n>>>>>>>>>>----------<<<<<<<<<<")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
print("Drop Missing Values\n")
print(branded_food.df.isnull().sum())
#let's get back to missing values cleanup
#which variables can we drop? That is, which variables will we be using for our analysis
#these variable cannot be null, and if they are, it could lead to issues later on
#let's drop missing values from brand_owner, ingredients, serving_size and serving_size_unit, and
#branded_food_category
branded_food.df.dropna(how = 'all')
#drop rows where all values are null
branded_food.df.dropna(subset = ['brand_owner', 'ingredients', 'serving_size',
'serving_size_unit', 'branded_food_category'], inplace=True)
#define which columns to look for null values and then drop these values
print("\n>>>>>>>>>>----------<<<<<<<<<<")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
print(branded_food.df.isnull().sum())
#check to see if null values from specified columns have been dropped
#confirmed
#remaining columns with null values are household_serving_fulltext and modified_date
#can keep these since we are not using groupby on these variables
print("\n>>>>>>>>>>----------<<<<<<<<<<")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
print("Duplicate Record Check\n")
#Duplicate Records
duplicate = branded_food.df.duplicated()
#check for duplicate recordds and create variable
print("There are " + str(duplicate.sum()) + " duplicate values")
#zero duplicate values
print("\n>>>>>>>>>>----------<<<<<<<<<<")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
#Filter DataFrame so that we only look at rows where
#ingredients contain corn syrup. Rows where ingredients
#do not contain corn syrup, the corn_syrup_idx = -1
contains_corn_syrup_df = branded_food.df[branded_food.df['corn_syrup_idx'] != -1]
#Give bolean expression to corn_syrup_idx columnto filter
#the corn_syrup_idx column and only show rows
#that contain corn syrup, we want to look at all rows
#where column is not equal to -1.
print("\nFirst 3 rows of New DataFrame, contains_corn_syrup_df, that has\n"
"only Food Items with corn syrup\n")
print(tabulate(contains_corn_syrup_df.head(3), headers='keys', tablefmt='psql'))
#first 3 rows of new DataFrame, contains_corn_syrup_df,
print("\nShape of new DataFrame, contains_corn_syrup_df\n")
print(contains_corn_syrup_df.shape)
#the number of rows (or Food Items) that contains corn syrup
#96,002 Food Items (note: this is after removing null values)
print("We have Categorical variables that need to be designated\n"
"as such for data type\n")
contains_corn_syrup_df['brand_owner'] = contains_corn_syrup_df.brand_owner.astype('category')
contains_corn_syrup_df['serving_size_unit'] = contains_corn_syrup_df.serving_size_unit.astype('category')
contains_corn_syrup_df['branded_food_category'] = contains_corn_syrup_df.branded_food_category.astype('category')
contains_corn_syrup_df['market_country'] = contains_corn_syrup_df.market_country.astype('category')
print(contains_corn_syrup_df.dtypes)
print(">>>>>>>>>>----------<<<<<<<<<<\n")
print("Data Cleanup Completed\n"
"DataFrame has been filtered to only\n"
"show food items (rows) that contain "
"corn syrup\n")
print(">>>>>>>>>>----------<<<<<<<<<<\n")
print("There are " + str(len(contains_corn_syrup_df.index)) +
" Food items that contain corn syrup in our data set.\n"
"DataFrame is now ready for analysis ")
print(contains_corn_syrup_df.shape)
# + id="JzlTh7BcM9So"
# project01.question1
"""
This module provides the functions and code in support of differentiating
between distribution of corn syrup and high fructose corn syrup
in food products.
The `main()` function provides the pythonic driver, however this can
be run directly using python3 -m project01.question1 after the files
have been fetched from the USDA (see `project01.fetcher`).
"""
import sys
import pandas as pd
import seaborn as sns
#import project01.parser as food_parser
def establish_food_object_cornsyrup(csv_file: str) -> FoodBrandObject:
#def establish_food_object_cornsyrup(csv_file: str) -> food_parser.FoodBrandObject:
"""Creates our food object leveraging our general purpose parser.
Args:
csv_file (str): The path to the food brand CSV file.
Returns:
food_parser.FoodBrandObject: A general purpose brand object which
contains the parsed dataframe with corn syrup already added as
a new index.
"""
bfood = FoodBrandObject(csv_file)
# bfood = food_parser.FoodBrandObject(csv_file)
bfood.cleanup()
cornsyrup = bfood.run_on_df(insert_index, "corn syrup", "ingredients")
# cornsyrup = bfood.run_on_df(food_parser.insert_index, "corn syrup", "ingredients")
return cornsyrup
def establish_food_object_hfcs(csv_file: str) -> FoodBrandObject:
#def establish_food_object_hfcs(csv_file: str) -> food_parser.FoodBrandObject:
"""Creates our food object leveraging our general purpose parser.
Args:
csv_file (str): The path to the food brand CSV file.
Returns:
food_parser.FoodBrandObject: A general purpose brand object which
contains the parsed dataframe with high fructose corn syrup
already added as
a new index.
"""
bfood = FoodBrandObject(csv_file)
# bfood = food_parser.FoodBrandObject(csv_file)
bfood.cleanup()
hfcs = bfood.run_on_df(insert_index, "high fructose corn syrup", "ingredients")
# hfcs = bfood.run_on_df(food_parser.insert_index, "high fructose corn syrup", "ingredients")
return hfcs
def clamp_cornsyrup(bfood: BaseFood,
#def clamp_cornsyrup(bfood: food_parser.BaseFood,
floor: int = 0,
ceiling: int = None,
col: str = "corn_syrup_idx") -> pd.DataFrame:
"""Clamping function used to filter the allowed indices of a column.
Args:
bfood (food_parser.BaseFood): The dataframe to operate on.
floor (int): The lowest allowed value of the column. Defaults to 0.
ceiling (int): The highest allowed value in the column.
Defaults to the maximum value in the column.
col (str): The column name to operate on. Defaults to corn_syrup_idx.
Returns:
pd.DataFrame: A new dataframe, where only the rows within the values
of floor and ceiling are included, and all others are dropped.
"""
return bfood.clamp(floor=floor, ceiling=ceiling, col=col)
def clamp_hfcs(bfood: BaseFood,
#def clamp_hfcs(bfood: food_parser.BaseFood,
floor: int = 0,
ceiling: int = None,
col: str = "high_fructose_corn_syrup_idx") -> pd.DataFrame:
"""Clamping function used to filter the allowed indices of a column.
Args:
bfood (food_parser.BaseFood): The dataframe to operate on.
floor (int): The lowest allowed value of the column. Defaults to 0.
ceiling (int): The highest allowed value in the column.
Defaults to the maximum value in the column.
col (str): The column name to operate on. Defaults to sugar_idx.
Returns:
pd.DataFrame: A new dataframe, where only the rows within the values
of floor and ceiling are included, and all others are dropped.
"""
return bfood.clamp(floor=floor, ceiling=ceiling, col=col)
def plot_cornsyrup(df: pd.DataFrame, out: str = "plot.png"):
"""Creates a catplot of the data.
Args:
df (pd.DataFrame): The dataframe to use when plotting.
out (str): The path to save the plotting graphic to.
Returns:
None: The graphic is saved to `out` as a side effect.
"""
fig = sns.catplot(x="serving_size_unit",
y="corn_syrup_idx",
data=df).set(title="Distribution of Corn Syrup in Food Products: Solid (g) vs. Liquid (ml)")
fig.savefig(out)
def plot_hfcs(df: pd.DataFrame, out: str = "plot.png"):
"""Creates a catplot of the data.
Args:
df (pd.DataFrame): The dataframe to use when plotting.
out (str): The path to save the plotting graphic to.
Returns:
None: The graphic is saved to `out` as a side effect.
"""
fig = sns.catplot(x="serving_size_unit",
y="high_fructose_corn_syrup_idx",
data=df).set(title="Distribution of High Fructose Corn Syrup in Food Products: Solid (g) vs. Liquid (ml)")
fig.savefig(out)
def q1_main(csv_file: str):
"""Pythonic driver for our first question / query
This method:
1. Establishes our food object of interest
2. Establishes subset from the dataframe by limiting
the data to only values that have corn syrup
3. Produces a catplot to compare solid and liquid food item's data
Args:
csv_file (str): The path to the branded_foods.csv file.
Returns:
None: catplot is written out to file.
"""
cornsyrup = establish_food_object_cornsyrup(csv_file)
plot_cornsyrup(cornsyrup, out="q1-cornsyrup.png")
hfcs = establish_food_object_hfcs(csv_file)
plot_hfcs(hfcs, out="q1-hfcs.png")
#if __name__ == "__main__":
# brand_csv = sys.argv[1] if len(sys.argv) > 2 else "../dataset/FoodData_Central_csv_2020-10-30/branded_food.csv"
# main(csv_file=brand_csv)
# + colab={"base_uri": "https://localhost:8080/", "height": 781} id="CAZOL6_jNDN0" outputId="921ce2fa-c919-4cc4-9d75-5038604b7e16"
q1_main(csv_file="./dataset/FoodData_Central_csv_2020-10-30/branded_food.csv")
# + id="9veh4f4KqhmX"
# project01.question2
"""
This module provides the functions and code in support of answering the
question "How do popular brands fare with corn syrup and sugar?"
The `main()` function provides the pythonic driver, however this can
be run directly using python3 -m project01.question2 after the files
have been fetched from the USDA (see `project01.fetcher`).
"""
import pprint
import sys
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt
from typing import List
#import project01.parser as food_parser
def establish_food_object_cornsyrup(csv_file: str) -> FoodBrandObject:
#def establish_food_object_cornsyrup(csv_file: str) -> food_parser.FoodBrandObject:
"""Creates our food object leveraging our general purpose parser.
Args:
csv_file (str): The path to the food brand CSV file.
Returns:
food_parser.FoodBrandObject: A general purpose brand object which
contains the parsed dataframe with corn syrup already added as
a new index.
"""
bfood = FoodBrandObject(csv_file)
# bfood = food_parser.FoodBrandObject(csv_file)
bfood.cleanup()
bfood.run_on_df(insert_index, find="corn syrup")
# bfood.run_on_df(food_parser.insert_index, find="corn syrup")
return bfood
def establish_food_object_sugar(csv_file: str) -> FoodBrandObject:
#def establish_food_object_sugar(csv_file: str) -> food_parser.FoodBrandObject:
"""Creates our food object leveraging our general purpose parser.
Args:
csv_file (str): The path to the food brand CSV file.
Returns:
food_parser.FoodBrandObject: A general purpose brand object which
contains the parsed dataframe with sugar already added as
a new index.
"""
bfood = FoodBrandObject(csv_file)
# bfood = food_parser.FoodBrandObject(csv_file)
bfood.cleanup()
bfood.run_on_df(insert_index, find="sugar")
# bfood.run_on_df(food_parser.insert_index, find="sugar")
return bfood
def clamp_cornsyrup(bfood: BaseFood,
#def clamp_cornsyrup(bfood: food_parser.BaseFood,
floor: int = 0,
ceiling: int = None,
col: str = "corn_syrup_idx") -> pd.DataFrame:
"""Clamping function used to filter the allowed indices of a column.
Args:
bfood (food_parser.BaseFood): The dataframe to operate on.
floor (int): The lowest allowed value of the column. Defaults to 0.
ceiling (int): The highest allowed value in the column.
Defaults to the maximum value in the column.
col (str): The column name to operate on. Defaults to corn_syrup_idx.
Returns:
pd.DataFrame: A new dataframe, where only the rows within the values
of floor and ceiling are included, and all others are dropped.
"""
return bfood.clamp(floor=floor, ceiling=ceiling, col=col)
def clamp_sugar(bfood: BaseFood,
#def clamp_sugar(bfood: food_parser.BaseFood,
floor: int = 0,
ceiling: int = None,
col: str = "sugar_idx") -> pd.DataFrame:
"""Clamping function used to filter the allowed indices of a column.
Args:
bfood (food_parser.BaseFood): The dataframe to operate on.
floor (int): The lowest allowed value of the column. Defaults to 0.
ceiling (int): The highest allowed value in the column.
Defaults to the maximum value in the column.
col (str): The column name to operate on. Defaults to sugar_idx.
Returns:
pd.DataFrame: A new dataframe, where only the rows within the values
of floor and ceiling are included, and all others are dropped.
"""
return bfood.clamp(floor=floor, ceiling=ceiling, col=col)
def find_top_ten_brands(bfood: BaseFood,
#def find_top_ten_brands(bfood: food_parser.BaseFood,
col: str = "brand_owner") -> pd.DataFrame:
"""Establishes the dataset for top10 brands
Args:
bfood (food_parser.BaseFood): The dataframe to seek against.
col (str): The column to find the top occurrences of.
Returns:
pd.DataFrame: A filtered dataframe containing only the brands
in the top 10 largest categories.
"""
return bfood.find_top(col=col, limit=10)
def metrics_on_brands(df: pd.DataFrame,
col: str = "brand_owner") -> List[pd.Series]:
"""Produces simple analysis on a specific column in a dataframe
Args:
df (pd.DataFrame): The dataframe to operate on.
col (str): The column to perform analysis on. Default: brand_owner.
Returns:
list[pd.Series]: The output of describe() and value_counts() on the dataframe's series.
"""
return [df[col].describe(), df[col].value_counts()]
def plot_cornsyrup(df: pd.DataFrame, out: str = "plot.png"):
"""Creates a violin plot of the distribution of data.
Args:
df (pd.DataFrame): The dataframe to use when plotting.
out (str): The path to save the plotting graphic to.
Returns:
None: The graphic is saved to `out` as a side effect.
"""
# Note, we need to establish the figure to ensure sns doesn't
# try to add to its prior plot.
fig1, ax1 = plt.subplots(figsize=(12,6))
sns.violinplot(x="corn_syrup_idx",
y="brand_owner",
orient="h",
data=df, ax=ax1).set(title="Top 10 brands: Corn Syrup")
ax1.set(xlabel="Rank",
ylabel="Brand Owner")
# Calling plt.tight_layout() ensures our labels fit in our
# plotting space.
plt.tight_layout()
fig1.savefig(out)
def plot_sugar(df: pd.DataFrame, out: str = "plot.png"):
"""Creates a violin plot of the distribution of data.
Args:
df (pd.DataFrame): The dataframe to use when plotting.
out (str): The path to save the plotting graphic to.
Returns:
None: The graphic is saved to `out` as a side effect.
"""
fig, ax1 = plt.subplots(figsize=(12, 6))
sns.violinplot(x="sugar_idx",
y="brand_owner",
orient="h",
data=df, ax=ax1).set(title="Top 10 brands: Sugar")
ax1.set(xlabel="Rank",
ylabel="Brand Owner")
# Calling plt.tight_layout() ensures our labels fit in our
# plotting space.
plt.tight_layout()
fig.savefig(out)
def q2_main(csv_file: str):
#def main(csv_file: str):
"""Pythonic driver for our second question / query
This method:
1. Establishes our food object of interest
2. Outputs trivial summary statistics on a column
3. Establishes a subset to the top 10 brands
4. Outputs metrics on the subset.
5. Establishes another subset from the dataframe by limiting
the data to only values that have corn syrup and sugar
6. Produces a violin plot to show our data density across the
top 10 groups.
Args:
csv_file (str): The path to the branded_foods.csv file.
Returns:
None: Output to the terminal statistics and various
plots are written out to file.
"""
bfood_cornsyrup = establish_food_object_cornsyrup(csv_file)
print("metrics on brands with corn syrup:")
pprint.pprint(metrics_on_brands(bfood_cornsyrup.df))
df_cornsyrup = find_top_ten_brands(bfood_cornsyrup)
print("---------------")
print("metrics on top 10 brands with corn syrup:")
pprint.pprint(metrics_on_brands(df_cornsyrup))
metrics_on_brands(df_cornsyrup)
df_cornsyrup_nomax = clamp_cornsyrup(bfood_cornsyrup)
plot_cornsyrup(df_cornsyrup_nomax, out="q2-cornsyrup-unbound.png")
df_cornsyrup_10max = clamp_cornsyrup(bfood_cornsyrup, ceiling=10)
plot_cornsyrup(df_cornsyrup_10max, out="q2-cornsyrup-10max.png")
print("---------------")
bfood_sugar = establish_food_object_sugar(csv_file)
print("metrics on brands with sugar:")
pprint.pprint(metrics_on_brands(bfood_sugar.df))
df_sugar = find_top_ten_brands(bfood_sugar)
print("---------------")
print("metrics on top 10 brands with sugar:")
pprint.pprint(metrics_on_brands(df_sugar))
metrics_on_brands(df_sugar)
df_sugar_nomax = clamp_sugar(bfood_sugar)
plot_sugar(df_sugar_nomax, out="q2-sugar-unbound.png")
df_sugar_10max = clamp_sugar(bfood_sugar, ceiling=10)
plot_sugar(df_sugar_10max, out="q2-sugar-10max.png")
#if __name__ == "__main__":
# brand_csv = sys.argv[1] if len(sys.argv) > 2 else "./dataset/FoodData_Central_csv_2020-10-30/branded_food.csv"
# q2_main(csv_file=brand_csv)
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="-aPpZaGmthpy" outputId="ff61b730-0691-4fbc-c67c-ae06f71cdc1a"
q2_main(csv_file="./dataset/FoodData_Central_csv_2020-10-30/branded_food.csv")
# + id="BrKzwiq6qnqJ"
# project01.question3
"""
This module provides the functions and code in support of answering the
question "How do popular food categories fare with corn syrup?"
The `main()` function provides the pythonic driver, however this can
be run directly using python3 -m project01.question3 after the files
have been fetched from the USDA (see `project01.fetcher`).
"""
import sys
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn import linear_model as lm
from matplotlib import pyplot as plt
from typing import List
#import project01.parser as food_parser
def establish_food_object(csv_file: str) -> FoodBrandObject:
#def establish_food_object(csv_file: str) -> food_parser.FoodBrandObject:
"""Creates our food object leveraging our general purpose parser.
Args:
csv_file (str): The path to the food brand CSV file.
Returns:
food_parser.FoodBrandObject: A general purpose brand object which
contains the parsed dataframe with corn syrup already added as
a new index.
"""
bfood = FoodBrandObject(csv_file)
# bfood = food_parser.FoodBrandObject(csv_file)
bfood.cleanup()
bfood.run_on_df(insert_index, find="corn syrup")
# bfood.run_on_df(food_parser.insert_index, find="corn syrup")
bfood.run_on_df(insert_index, find="sugar")
# bfood.run_on_df(food_parser.insert_index, find="sugar")
return bfood
def clamp(bfood: BaseFood,
#def clamp(bfood: food_parser.BaseFood,
floor: int = 0,
ceiling: int = None,
col: str = "corn_syrup_idx") -> pd.DataFrame:
"""Clamping function used to filter the allowed indices of a column.
Args:
bfood (food_parser.BaseFood): The dataframe to operate on.
floor (int): The lowest allowed value of the column. Defaults to 0.
ceiling (int): The highest allowed value in the column.
Defaults to the maximum value in the column.
col (str): The column name to operate on. Defaults to corn_syrup_idx.
Returns:
pd.DataFrame: A new dataframe, where only the rows within the values
of floor and ceiling are included, and all others are dropped.
"""
return bfood.clamp(floor=floor, ceiling=ceiling, col=col)
def find_top_five_food_categories(bfood: BaseFood,
#def find_top_five_food_categories(bfood: food_parser.BaseFood,
col: str = "branded_food_category") -> pd.DataFrame:
"""Establishes the dataset for top5 food categories
Args:
bfood (food_parser.BaseFood): The dataframe to seek against.
col (str): The column to find the top occurrences of.
Returns:
pd.DataFrame: A filtered dataframe containing only the foods
in the top five largest categories.
"""
return bfood.find_top(col=col, limit=5)
def metrics_on_food_categories(df: pd.DataFrame,
col: str = "branded_food_category") -> List[pd.Series]:
"""Produces simple analysis on a specific column in a dataframe
Args:
df (pd.DataFrame): The dataframe to operate on.
col (str): The column to perform analysis on. Default: branded_food_category.
Returns:
list[pd.Series]: The output of describe() and value_counts() on the dataframe's series.
"""
return [df[col].describe(), df[col].value_counts()]
def plot_foodcat(df: pd.DataFrame, col="corn_syrup_idx", out: str = "plot.png"):
"""Creates a violin plot of the distribution of data.
Args:
df (pd.DataFrame): The dataframe to use when plotting.
col (str): The column to use for the violinplot magnitude.
out (str): The path to save the plotting graphic to.
Returns:
None: The graphic is saved to `out` as a side effect.
"""
# Note, we need to establish the figure to ensure sns doesn't
# try to add to its prior plot.
fig, ax1 = plt.subplots(figsize=(12, 6))
sns.violinplot(x=col,
y="branded_food_category",
orient="h",
bw=0.2,
cut=0,
scale="width",
data=df, ax=ax1)
ax1.set(xlabel="Rank",
ylabel="Food Category")
# Calling plt.tight_layout() ensures our labels fit in our
# plotting space.
plt.tight_layout()
fig.savefig(out)
def density(bfood: BaseFood, out: str = ""):
#def density(bfood: food_parser.BaseFood, out: str = ""):
newdf = pd.DataFrame({"brand": bfood.df["branded_food_category"],
"sugar": bfood.df["sugar_idx"],
"corn_syrup": bfood.df["corn_syrup_idx"]})
# Insert NaNs for no matches to ensure our counts aren't skewed.
newdf.loc[newdf["sugar"] == -1, "sugar"] = np.NaN
newdf.loc[newdf["corn_syrup"] == -1, "corn_syrup"] = np.NaN
fig, ax1 = plt.subplots(figsize=(12, 6))
sns.histplot(element="step", bins=30, ax=ax1, data=newdf)
ax1.set(xlabel="Index",
ylabel="Count")
# Calling plt.tight_layout() ensures our labels fit in our
# plotting space.
plt.tight_layout()
fig.savefig(out)
def correlation(bfood: BaseFood, out: str = "q3-correlation.png"):
#def correlation(bfood: food_parser.BaseFood, out: str = "q3-correlation.png"):
newdf = pd.DataFrame({"category": bfood.df["branded_food_category"],
"sugar": bfood.df["sugar_idx"],
"corn_syrup": bfood.df["corn_syrup_idx"]})
# Insert NaNs for no matches to ensure our counts aren't skewed.
newdf.loc[newdf["sugar"] == -1, "sugar"] = np.NaN
newdf.loc[newdf["corn_syrup"] == -1, "corn_syrup"] = np.NaN
myfig = sns.pairplot(data=newdf, hue="category", markers="|", kind="reg")
myfig.savefig(out)
def lin_model(df):
newdf = pd.DataFrame({"category": df["branded_food_category"],
"sugar": df["sugar_idx"],
"corn_syrup": df["corn_syrup_idx"]})
# Insert NaNs for no matches to ensure our counts aren't skewed.
newdf.loc[newdf["sugar"] == -1, "sugar"] = np.NaN
newdf.loc[newdf["corn_syrup"] == -1, "corn_syrup"] = np.NaN
reg = lm.LinearRegression()
X = newdf["corn_syrup"].values.reshape(-1, 1)
y = newdf["sugar"].values.reshape(-1, 1)
reg.fit(X, y)
print(f"y = {reg.intercept_} + {reg.coef_}x")
yhat = reg.predict(X)
SSres = sum((y-yhat)**2)
SSt = sum((y-np.mean(y))**2)
rsq = 1 - (float(SSres))/SSt
print(f"R2 = {rsq}")
def q3_main(csv_file: str):
"""Pythonic driver for our third question / query
This method:
1. Establishes our food object of interest
2. Outputs trivial summary statistics on a column
3. Establishes a subset to the top five food categories
4. Outputs metrics on the subset.
5. Establishes another subset from the dataframe by limiting
the data to only values that have corn syrup
6. Produces a violin plot to show our data density across the
top five groups. We see a large left tail.
7. After reviewing the data, the corn_syrup_idx ceiling appears
to be near ten, so we further clamp the data down to center
our distribution.
Args:
csv_file (str): The path to the branded_foods.csv file.
Returns:
None: Output to the terminal statistics and various
plots are written out to file.
"""
bfood = establish_food_object(csv_file)
df = find_top_five_food_categories(bfood)
print(metrics_on_food_categories(bfood.df))
# Very wide range, adjusted to 10 as this seems to match most index returns.
df_cornsyrup = clamp(bfood)
plot_foodcat(df_cornsyrup, out="q3-cornsyrup-cat.png")
df_sugar = clamp(bfood, col="sugar_idx")
plot_foodcat(df_sugar, out="q3-sugar.png")
density(bfood, out="q3-density.png")
correlation(bfood, out="q3-correlation.png")
lin_model(bfood.df)
#if __name__ == "__main__":
# brand_csv = sys.argv[1] if len(sys.argv) > 2 else "./dataset/FoodData_Central_csv_2020-10-30/branded_food.csv"
# main(csv_file=brand_csv)
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="0fDQg-agvIiB" outputId="6d7bd39a-083b-4f8d-f23b-9199ccbf7ffe"
q3_main(csv_file="./dataset/FoodData_Central_csv_2020-10-30/branded_food.csv")
# + id="BLXIUU1Iq1w9"
# project01.question4
"""
This module provides the functions and code in support of answering the
question "How do solid food items (grams) and liquid item (ml) fare with corn syrup and sugar?"
The `main()` function provides the pythonic driver, however this can
be run directly using python3 -m project01.question4 after the files
have been fetched from the USDA (see `project01.fetcher`).
"""
import sys
import pandas as pd
import seaborn as sns
#import project01.parser as food_parser
def establish_food_object_cornsyrup(csv_file: str) -> FoodBrandObject:
#def establish_food_object_cornsyrup(csv_file: str) -> food_parser.FoodBrandObject:
"""Creates our food object leveraging our general purpose parser.
Args:
csv_file (str): The path to the food brand CSV file.
Returns:
food_parser.FoodBrandObject: A general purpose brand object which
contains the parsed dataframe with corn syrup already added as
a new index.
"""
bfood = FoodBrandObject(csv_file)
# bfood = food_parser.FoodBrandObject(csv_file)
bfood.cleanup()
cornsyrup = bfood.run_on_df(insert_index, "corn syrup", "ingredients")
# cornsyrup = bfood.run_on_df(food_parser.insert_index, "corn syrup", "ingredients")
return cornsyrup
def establish_food_object_sugar(csv_file: str) -> FoodBrandObject:
#def establish_food_object_sugar(csv_file: str) -> food_parser.FoodBrandObject:
"""Creates our food object leveraging our general purpose parser.
Args:
csv_file (str): The path to the food brand CSV file.
Returns:
food_parser.FoodBrandObject: A general purpose brand object which
contains the parsed dataframe with sugar already added as
a new index.
"""
bfood = FoodBrandObject(csv_file)
# bfood = food_parser.FoodBrandObject(csv_file)
bfood.cleanup()
sugar = bfood.run_on_df(insert_index, "sugar", "ingredients")
# sugar = bfood.run_on_df(food_parser.insert_index, "sugar", "ingredients")
return sugar
def plot_cornsyrup(df: pd.DataFrame, out: str = "plot.png"):
"""Creates a catplot of the data.
Args:
df (pd.DataFrame): The dataframe to use when plotting.
out (str): The path to save the plotting graphic to.
Returns:
None: The graphic is saved to `out` as a side effect.
"""
fig = sns.catplot(x="serving_size_unit",
y="corn_syrup_idx",
data=df).set(title="Serving Size: Corn Syrup")
fig.savefig(out)
def plot_sugar(df: pd.DataFrame, out: str = "plot.png"):
"""Creates a catplot of the data.
Args:
df (pd.DataFrame): The dataframe to use when plotting.
out (str): The path to save the plotting graphic to.
Returns:
None: The graphic is saved to `out` as a side effect.
"""
fig = sns.catplot(x="serving_size_unit",
y="sugar_idx",
data=df).set(title="Serving Size: Sugar")
fig.savefig(out)
def q4_main(csv_file: str):
"""Pythonic driver for our fourth question / query
This method:
1. Establishes our food object of interest
2. Establishes subset from the dataframe by limiting
the data to only values that have corn syrup
3. Produces a catplot to compare solid and liquid food item's data
Args:
csv_file (str): The path to the branded_foods.csv file.
Returns:
None: catplot is written out to file.
"""
cornsyrup = establish_food_object_cornsyrup(csv_file)
plot_cornsyrup(cornsyrup, out="q4-cornsyrup.png")
sugar = establish_food_object_sugar(csv_file)
plot_sugar(sugar, out="q4-sugar.png")
#if __name__ == "__main__":
# brand_csv = sys.argv[1] if len(sys.argv) > 2 else "../dataset/FoodData_Central_csv_2020-10-30/branded_food.csv"
# main(csv_file=brand_csv)
# + colab={"base_uri": "https://localhost:8080/", "height": 781} id="TXfpXPLWvupZ" outputId="c688ef7b-f77f-4310-99a1-65cf070a4a3e"
q4_main(csv_file="./dataset/FoodData_Central_csv_2020-10-30/branded_food.csv")
# + colab={"base_uri": "https://localhost:8080/"} id="jv5sqxvywI1i" outputId="65b5412e-3297-42d5-c91f-2a33a9820be0"
# Setup test data
# test/test_parser/branded_food.csv
# !echo '"fdc_id","brand_owner","gtin_upc","ingredients","serving_size","serving_size_unit","household_serving_fulltext","branded_food_category","data_source","modified_date","available_date","market_country","discontinued_date"' > test_branded_food.csv
# !echo '"344604","Red Gold","00072940755050","Tomatoes, Tomato Juice, Less Than 2% Of: Salt, Dried Onion, Dried Garlic, Soybean Oil, Spices, Calcium Chloride, Natural Flavor, Olive Oil, Citric Acid.","123","g","1/2 cup","","GDSN","2018-04-26","2019-04-01","United States",""' >> test_branded_food.csv
# !echo '"344605","Red Gold","00072940755043","Tomatoes, Tomato Juice, Less Than 2% Of: Salt, Dried Onion, Dried Garlic, Soybean Oil, Spices, Calcium Chloride, Natural Flavor, Olive Oil, Citric Acid.","123","g","1/2 cup","","GDSN","2018-04-26","2019-04-01","United States",""' >> test_branded_food.csv
# !echo '"344606","Cargill","00642205534517","White Turkey, Natural Flavoring","112","g","4 oz.","","GDSN","2016-06-13","2019-04-01","United States",""' >> test_branded_food.csv
# !echo '"344609","Kellogg Company US","00038000934490","ENRICHED FLOUR (WHEAT FLOUR, NIACIN, REDUCED IRON, VITAMIN B1 [THIAMIN MONONITRATE], VITAMIN B2 [RIBOFLAVIN], FOLIC ACID), CORN SYRUP, HIGH FRUCTOSE CORN SYRUP, SUGAR, SOYBEAN AND PALM OIL (WITH TBHQ FOR FRESHNESS), DEXTROSE, CONTAINS TWO PERCENT OR LESS OF WHEAT STARCH, CRACKER MEAL, GLYCERIN, SALT, DRIED CHERRIES, DRIED APPLES, LEAVENING (BAKING SODA, SODIUM ACID PYROPHOSPHATE, MONOCALCIUM PHOSPHATE), CITRIC ACID, MILLED CORN, GELATIN, MALIC ACID, RED 40 LAKE, XANTHAN GUM, MODIFIED CORN STARCH, MODIFIED WHEAT STARCH, SOY LECITHIN, COLOR ADDED, NATURAL AND ARTIFICIAL FLAVOR, RED 40, NIACINAMIDE, BLUE 2 LAKE, REDUCED IRON, CARMINE COLOR, VITAMIN A PALMITATE, TURMERIC FOR COLOR, VITAMIN B6 (PYRIDOXINE HYDROCHLORIDE), VITAMIN B2 (RIBOFLAVIN), VITAMIN B1 (THIAMIN HYDROCHLORIDE), BLUE 1.","50","g","1 Pastry","Pies/Pastries - Sweet (Shelf Stable)","GDSN","2018-01-22","2019-04-01","United States",""' >> test_branded_food.csv
# !cat test_branded_food.csv
# test/test_parser/rating.csv
# !echo 'id,branded_food_category,alt_category' > test_rating.csv
# !echo '1,category1,test1' >> test_rating.csv
# !echo '2,category1,test2' >> test_rating.csv
# !echo '3,category1,test1' >> test_rating.csv
# !echo '4,category2,test2' >> test_rating.csv
# !echo '5,category2,test3' >> test_rating.csv
# !echo '5,category3,test3' >> test_rating.csv
# !echo '8,category4,test4' >> test_rating.csv
# !echo '9,category4,test5' >> test_rating.csv
# !echo '10,category5,test6' >> test_rating.csv
# !echo '10,category5,test7' >> test_rating.csv
# !echo '11,category6,test7' >> test_rating.csv
# !echo '13,category7,test8' >> test_rating.csv
# !echo '14,category5,test8' >> test_rating.csv
# !echo '15,category8,test9' >> test_rating.csv
# !echo '15,category8,test10' >> test_rating.csv
# !echo '15,category9,test10' >> test_rating.csv
# !echo '15,category9,test10' >> test_rating.csv
# !cat test_rating.csv
# test/test_parser/simple.csv
# !echo 'id,corn_syrup_idx,tester' > test_simple.csv
# !echo '0,-1,row1' >> test_simple.csv
# !echo '1,0,row2' >> test_simple.csv
# !echo '2,33,row4' >> test_simple.csv
# !echo '5,22,row5' >> test_simple.csv
# !echo '8,-342,row6' >> test_simple.csv
# !echo '-2,-58,row7' >> test_simple.csv
# !cat test_rating.csv
# + id="lPVrwu4Rx_kF"
# test/test_fetch.py
#import project01.fetch as fetch
import tempfile
import pytest
@pytest.fixture
def tempfile_setup():
with tempfile.NamedTemporaryFile(mode="w") as tf:
yield tf
def test_constructor(tempfile_setup):
fetcher = Fetcher(uris=tempfile_setup.name, base="testbase", feedback=False)
# fetcher = fetch.Fetcher(uris=tempfile_setup.name, base="testbase", feedback=False)
assert fetcher._uris == []
assert fetcher._base == "testbase"
assert fetcher._feedback == False
def test_parse_file(tempfile_setup):
print(tempfile_setup)
tempfile_setup.write("Testlinegood\n")
tempfile_setup.write("#Commented line\n")
tempfile_setup.write("2Testlinegood")
tempfile_setup.flush()
fetcher = Fetcher(uris=tempfile_setup.name)
# fetcher = fetch.Fetcher(uris=tempfile_setup.name)
assert fetcher._uris == ["Testlinegood", "2Testlinegood"]
def test_add_uri(tempfile_setup):
tempfile_setup.write("Testlinegood\n")
tempfile_setup.flush()
fetcher = Fetcher(uris=tempfile_setup.name)
# fetcher = fetch.Fetcher(uris=tempfile_setup.name)
fetcher.add_uri("next-line")
assert fetcher._uris == ["Testlinegood", "next-line"]
def test_fetch():
# Will need to spy this
pass
# + id="8nSZMJEfFonJ"
# test/test_parser.py
import pandas as pd
#import project01.parser as parser
@pytest.fixture
def datadir():
class innerclass():
@staticmethod
def join(arg):
return os.path.join("./", arg)
return innerclass()
def test_food_object_inheritance(datadir):
fb_object = FoodBrandObject(datadir.join("test_branded_food.csv"))
# fb_object = parser.FoodBrandObject(datadir.join("branded_food.csv"))
assert issubclass(type(fb_object), BaseFood)
# assert issubclass(type(fb_object), parser.BaseFood)
def test_insert_index_col(datadir):
bfood = BaseFood(datadir.join("test_branded_food.csv"))
# bfood = parser.BaseFood(datadir.join("branded_food.csv"))
bfood.run_on_df(insert_index, "salt", "ingredients")
# bfood.run_on_df(parser.insert_index, "salt", "ingredients")
assert "salt_idx" in bfood.df
def test_find_index_from_str(datadir):
bfood = BaseFood(datadir.join("test_branded_food.csv"))
# bfood = parser.BaseFood(datadir.join("branded_food.csv"))
bfood.run_on_df(insert_index, "salt", "ingredients")
# bfood.run_on_df(parser.insert_index, "salt", "ingredients")
assert bfood.df["salt_idx"].equals(pd.DataFrame({"salt_idx": [3, 3, -1, 15]})["salt_idx"])
def test_clamp(datadir):
bfood = BaseFood(datadir.join("test_simple.csv"))
# bfood = parser.BaseFood(datadir.join("simple.csv"))
bfood.df["corn_syrup_idx"] = pd.to_numeric(bfood.df["corn_syrup_idx"])
bfood.clamp()
assert len(bfood.df) == 2
def test_cornsyrup_clamp_defaults(datadir):
bfood = BaseFood(datadir.join("test_simple.csv"))
# bfood = parser.BaseFood(datadir.join("simple.csv"))
bfood.df["corn_syrup_idx"] = pd.to_numeric(bfood.df["corn_syrup_idx"])
ret = bfood.clamp()
assert len(bfood.df) == 2
assert isinstance(ret, pd.DataFrame)
assert bfood.df.equals(ret)
def test_cornsyrup_clamp_returntype(datadir):
bfood = BaseFood(datadir.join("test_simple.csv"))
# bfood = parser.BaseFood(datadir.join("simple.csv"))
bfood.df["corn_syrup_idx"] = pd.to_numeric(bfood.df["corn_syrup_idx"])
ret = bfood.clamp()
assert isinstance(ret, pd.DataFrame)
def test_cornsyrup_clamp_mutates_df(datadir):
bfood = BaseFood(datadir.join("test_simple.csv"))
# bfood = parser.BaseFood(datadir.join("simple.csv"))
bfood.df["corn_syrup_idx"] = pd.to_numeric(bfood.df["corn_syrup_idx"])
ret = bfood.clamp()
assert bfood.df.equals(ret)
def test_cornsyrup_clamp_alt_column(datadir):
bfood = BaseFood(datadir.join("test_simple.csv"))
# bfood = parser.BaseFood(datadir.join("simple.csv"))
bfood.df["id"] = pd.to_numeric(bfood.df["id"])
bfood.clamp(col="id")
assert len(bfood.df) == 4
def test_cornsyrup_clamp_alt_floor(datadir):
bfood = BaseFood(datadir.join("test_simple.csv"))
# bfood = parser.BaseFood(datadir.join("simple.csv"))
bfood.df["corn_syrup_idx"] = pd.to_numeric(bfood.df["corn_syrup_idx"])
bfood.clamp(floor=-5)
assert len(bfood.df) == 4
def test_cornsyrup_clamp_alt_floor2(datadir):
bfood = BaseFood(datadir.join("test_simple.csv"))
# bfood = parser.BaseFood(datadir.join("simple.csv"))
bfood.df["corn_syrup_idx"] = pd.to_numeric(bfood.df["corn_syrup_idx"])
bfood.clamp(floor=-10000)
assert len(bfood.df) == 6
def test_cornsyrup_clamp_alt_ceil(datadir):
bfood = BaseFood(datadir.join("test_simple.csv"))
# bfood = parser.BaseFood(datadir.join("simple.csv"))
bfood.df["corn_syrup_idx"] = pd.to_numeric(bfood.df["corn_syrup_idx"])
bfood.clamp(ceiling=25)
assert len(bfood.df) == 1
def test_cornsyrup_clamp_alt_constrained(datadir):
bfood = BaseFood(datadir.join("test_simple.csv"))
# bfood = parser.BaseFood(datadir.join("simple.csv"))
bfood.df["corn_syrup_idx"] = pd.to_numeric(bfood.df["corn_syrup_idx"])
bfood.clamp(floor=-60, ceiling=25)
assert len(bfood.df) == 4
def test_find_top_default(datadir):
bfood = BaseFood(datadir.join("test_rating.csv"))
# bfood = parser.BaseFood(datadir.join("rating.csv"))
df_result = bfood.find_top()
assert len(df_result["branded_food_category"].unique()) == 5
def test_find_top_specified_amount(datadir):
bfood = BaseFood(datadir.join("test_rating.csv"))
# bfood = parser.BaseFood(datadir.join("rating.csv"))
df_result = bfood.find_top(limit=7)
assert len(df_result["branded_food_category"].unique()) == 7
def test_find_top_specified_col(datadir):
bfood = BaseFood(datadir.join("test_rating.csv"))
# bfood = parser.BaseFood(datadir.join("rating.csv"))
df_result = bfood.find_top(col="alt_category")
assert len(df_result["alt_category"].unique()) == 5
def test_find_top_specified_limit_and_col(datadir):
bfood = BaseFood(datadir.join("test_rating.csv"))
# bfood = parser.BaseFood(datadir.join("rating.csv"))
df_result = bfood.find_top(col="alt_category", limit=3)
assert len(df_result["alt_category"].unique()) == 3
# + colab={"base_uri": "https://localhost:8080/"} id="_oHscw0o3Mib" outputId="79526193-2119-448c-970e-cc687a26d63b"
pytest.main(args=['-sv'])
|
group6_finalproject-colab.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Implementation of HED in Pytorch
# ---
#
# +
# import torch libraries
import torch
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
import os
import numpy as np
import pandas as pd
from PIL import Image
import skimage.io as io
import matplotlib.cm as cm
import matplotlib.pyplot as plt
# import utility functions
from model import HED
from trainer import Trainer
from dataproc import TrainDataset
# +
# fix random seed
rng = np.random.RandomState(37148)
# GPU ID
gpuID = 0
# -
# ### Inspect Training Data
# +
# load the images dataset
dataRoot = '../HED-BSDS/'
trainPath = dataRoot+'train_pair.lst'
rootDir = dataRoot
frame = pd.read_csv(trainPath, dtype=str, delimiter=' ')
# check some sample images
idx = 1
# input and target images
inputName = os.path.join(rootDir, frame.iloc[idx, 0])
targetName = os.path.join(rootDir, frame.iloc[idx, 1])
# +
# process the images
inputImage = np.asarray(Image.open(inputName).convert('RGB'))
crop = 32
inputImage = inputImage[crop:-crop,crop:-crop,:]
plt.figure()
plt.imshow(inputImage)
plt.show()
inputImage = inputImage.astype(np.float32)
inputImage = inputImage/255.0
#inputImage = inputImage[:,:,::-1]
inputImage -= np.array((0.485, 0.456, 0.406))
inputImage /= np.array((0.229, 0.224, 0.225))
# +
# process input and target images
targetImage = io.imread(targetName)
crop = 32
targetImage = targetImage[crop:-crop,crop:-crop,:]
if len(targetImage.shape) == 3:
targetImage = targetImage[:,:,0]
targetImage = targetImage/255.0
targetImage = targetImage > 0.0
targetImage = targetImage.astype(np.float32)
plt.figure()
plt.imshow(targetImage,cmap=cm.gray)
plt.show()
# -
# ### Train the Network
# +
# batch size
nBatch = 1
# load the images dataset
dataRoot = '../HED-BSDS/'
valPath = dataRoot+'val_pair.lst'
trainPath = dataRoot+'train_pair.lst'
# create data loaders from dataset
valDataset = TrainDataset(valPath, dataRoot)
trainDataset = TrainDataset(trainPath, dataRoot)
valDataloader = DataLoader(valDataset, batch_size=nBatch, shuffle=False)
trainDataloader = DataLoader(trainDataset, batch_size=nBatch, shuffle=False)
# +
# initialize the network
net = HED(pretrained=False)
net.cuda(gpuID)
# define the optimizer
optimizer = optim.SGD(net.parameters(), lr=1e-6, momentum=0.9, weight_decay=0.0002)
# +
# initialize trainer class
trainer = Trainer(net, optimizer, trainDataloader, valDataloader, maxEpochs=1, cuda=True, gpuID=gpuID)
# train the network
trainer.train()
|
train.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # 1.1 Finite Difference Formulation
# Prepared by (C) <NAME>
# This series of documents are intended to show my approach and implementation of the finite difference formulation to solve a system of heat balance equations. This is not the only way to do it, however I do find my method to be rather convenient. In my day to day work, I do seperate the models from the "solvers" and from other scripts that do supervisory type calculations above it, such as model calibration and model-based predictive controls. You'll see that in Chapters 2 & 3.
#
# As of May 2016, this document still remain as a work in progress and is updated on my spare time. Please do inform me of mistakes or bugs or improvements. I am quite open minded in that regard.
# ### Finite Difference Equation
# Heat conduction through a medium is governed by Fourier's Law of heat conduction (or sometimes refered as Fourer's Law of heat diffusion).
# Starting from a generalized case for multi-dimensional heat transfer the heat conduction equation can be reworked into a finite difference approximation of the partial differential equation (Dermardiros, 2015). The analytical solution can seldom be calculated for the majority of cases and an approximation is necessary.
#
# $\rho \displaystyle \frac{\partial h}{\partial t} + \nabla(-k \nabla T) = 0$
#
# Simplified to a 1-dimensional system in the $x$ direction,
#
# $\rho \displaystyle \frac{\partial h}{\partial t} + \frac{\partial}{\partial x}(-k \nabla T) = 0$
#
# Assuming a constant density of the material, by performing the inner derivative and applying the Product Law of calculus, we obtain:
#
# $\rho \displaystyle \frac{dh}{dT}\frac{\partial T}{\partial t} -k \frac{\partial^2 T}{\partial x^2} -\frac{dk}{dT} \left(\frac{\partial T}{\partial x}\right)^2 = 0$
#
# The specific heat, $c_p$, is defined as:
#
# $c_p(T) \equiv \displaystyle \frac{dh}{dT}$
# And so,
#
# $\displaystyle \frac{\partial T}{\partial t} = \frac{k}{\rho c_p(T)} \left[ \frac{\partial^2 T}{\partial x^2} + \frac{1}{k} \frac{dk}{dT} \left(\frac{\partial T}{\partial x}\right) ^2 \right]$
#
# For the case where conductivity is constant, then the equation simplifies to:
#
# $\displaystyle \frac{\partial T}{\partial t} = \frac{k}{\rho c_p(T)} \frac{\partial^2 T}{\partial x^2}$
#
# Since the above equation can only be solved analytically for certain cases, a finite difference approximation of the partial differential equation is necessary. Writing the 1st order forward difference equation for the left hand side:
#
# $\displaystyle \left( \frac{\partial T}{\partial t} \right)^t_i = \frac{T^{t+1}_i - T^t_i}{\Delta t} + O(\Delta t)$
#
# Now, the central difference equation for the right hand side 2nd order differential equation:
#
# $\displaystyle \left( \frac{\partial^2 T}{\partial x^2} \right)^{t+\vartheta}_i = \frac{T^{t+\vartheta}_{i+1} - 2T^{t+\vartheta}_i + T^{t+\vartheta}_{i-1}}{\Delta x^2} + O(\Delta x)^2$
#
# $\vartheta$ is between 0 and 1, typically $\vartheta$ is chosen as 0, ½, or 1, which yield, respectively, the Explicit, Crank-Nicholson and Implicit finite difference schemes. In the Explicit case, the future timestep is computed node by node, one by one, in order. The last two yield a system of equations which must be solved simultaneously.
# Using the finite difference approximations, and rearranging the equation for the future timestep, we obtain:
#
# $T^{t+1}_i = T^{t}_i + \displaystyle \frac{k \Delta t}{\rho c_p(T) \Delta x^2} \left[ (1-\vartheta)(T^{t}_{i+1} - 2T^{t}_i + T^{t}_{i-1}) + \vartheta (T^{t+1}_{i+1} - 2T^{t+1}_i + T^{t+1}_{i-1}) \right]$
#
# Now, let's look at a case where the neighbouring nodes have a fixed boundary temperature, $T_{bound}$. And assuming the initial temperature at the active node is $T_{init}$ and is at a lower temperature than the neighbouring nodes. For the future timestep, physically, the temperature at the active node cannot exceed the boundary temperature since there is no internal heat generation.
#
# $T_{init} < T_{bound}$
#
# $T^t_{i-1} = T^t_{i+1} = T^{t+1}_{i-1} = T^{t+1}_{i-1} = T_{bound}$
#
# $T^t_i = T_{init}$
#
# $T^{t+1}_i \leq T_{bound}$
#
# And since,
#
# $\displaystyle \frac{k \Delta t}{\rho c_p(T) \Delta x^2} = \frac{T^{t+1}_i-T^t_i}{(1-\vartheta)(T^{t}_{i+1} - 2T^{t}_i + T^{t}_{i-1}) + \vartheta (T^{t+1}_{i+1} - 2T^{t+1}_i + T^{t+1}_{i-1})}$
#
# $\therefore \ \displaystyle \Delta t \leq \frac{\rho c_p(T) \Delta x^2}{2k(1-\vartheta)}$
# To assure numerical stability in the solution, the timestep must be chosen according to the previous equation.
#
# For the Explicit case where $\vartheta = 0$:
#
# $\Delta t \leq \displaystyle \frac{\rho c_p(T) \Delta x^2}{2k}$
#
# For the Crank-Nicholson case where $\vartheta = ½$:
#
# $\Delta t \leq \displaystyle \frac{\rho c_p(T) \Delta x^2}{k}$
#
# Finally, for the Implicit case where $\vartheta = 1$:
#
# $\Delta t \leq \infty$
#
# These timesteps assure numerical stability. For the Implicit case, there is no restriction on timestep, however, for very large timesteps, the solution may oscillate. Although the oscillations will eventually dampen, large timesteps do not guarantee physically plausible solutions.
#
# Additionally, these timesteps are for 1-dimensional heat transfer -- which is typically the case for buildings. For 2-d and 3-d heat transfer, the explicit method finite difference method stability criterion will differ. (Its derivation is beyond the scope of this document.) Final note, for 2-d and 3-d heat transfer, the ordering of the nodes may need to be carefully considered to assure the matrix can be inverted is not ill-conditionned.
# ### Finite Difference Implementation
# For a given node $i$, which is: exchanging heat with all neigbouring nodes $j$ and $k$ through conduction, convection and radiation, noted as an equivalent conductance $U$; has capacitance $C$ (thermal mass); and exchanging heat with a source $Q$ the finite difference equation can be written:
#
# $\displaystyle \sum_{j}{[U_{ij}^\theta (T_j^\theta-T_i^\theta)]}+\sum_{k}{[U_{ik}^\theta (T_k^\theta-T_i^\theta)]}-\displaystyle \frac{C(T)_i}{\Delta t} (T_i^{t+1}-T_i^{t}) + \dot{Q}_i^\theta = 0$,
# where,
# $\theta = t \ $: explicit case,
# $\theta = t+1$: implicit case,
# $U_{ij}$: conductance between nodes $i$ and $j$ equal to $\frac{kA}{dx}$ for conductance, $h_{conv}A$ for convection and $h_{rad}A$ for radiation, $\frac{W}{K}$,
# $U_{ik}$: conductance between nodes $i$ and $k$ where node $k$ has a defined or known temperature (boundary condition), $\frac{W}{K}$,
# $C(T)$: capacitance of node $i$ equal to $\rho c_p(T) A dx$, $\frac{J}{K}$,
# $\dot{Q}$: heat flow into the node, $W$, and,
# $\Delta t$: timestep, $s$.
# As an example where $i = 1$, we can draw the following thermal network:
# <img src="Figures/fdm.png" width=350 align="left"/>
# #### Implicit Case
# Generalizing for a system, the equation can be written in a matrix form:
#
# $\begin{bmatrix} \displaystyle
# \sum_j^N{U_{1j}}+\sum_k^M{U_{1k}}+\frac{C_1}{\Delta t} & -U_{12} & \dots & -U_{1N} \\
# \vdots & \vdots & \ddots & \vdots \\
# -U_{N1} & -U_{N2} & \dots & \displaystyle
# \sum_j^N{U_{Nj}}+\sum_k^M{U_{Nk}}+\frac{C_N}{\Delta t}
# \end{bmatrix}
# \begin{Bmatrix} T_1 \\ \vdots \\ T_N \end{Bmatrix}^{t+1} =
# \begin{Bmatrix} \displaystyle \dot{Q}_1 + \sum_k^M{(U_{1kk}T_{kk})}+\frac{C_1}{\Delta t}T_1^t \\ \vdots \\ \displaystyle \dot{Q}_N + \sum_k^M{(U_{Nkk}T_{kk})}+\frac{C_N}{\Delta t}T_N^t \end{Bmatrix}$,
# where,
# $N$ is the number of nodes, and,
# $M$ is the number of nodes with known temperatures.
# #### Explicit Case
# Similarly, for the explicit case, the equations can be written in matrix form:
#
# $\begin{Bmatrix} T_1 \\ \vdots \\ T_N \end{Bmatrix}^{t+1} =
# \begin{Bmatrix} \displaystyle \frac{\Delta t}{C_1} \\ \vdots \\ \displaystyle \frac{\Delta t}{C_N} \end{Bmatrix}
# \odot
# \left(
# \begin{bmatrix} \displaystyle
# -\sum_j^N{U_{1j}}-\sum_k^M{U_{1k}}+\frac{C_1}{\Delta t} & U_{12} & \dots & U_{1N} \\
# \vdots & \vdots & \ddots & \vdots \\
# U_{N1} & U_{N2} & \dots & \displaystyle
# -\sum_j^N{U_{Nj}}-\sum_k^M{U_{Nk}}+\frac{C_N}{\Delta t}
# \end{bmatrix}
# \begin{Bmatrix} T_1 \\ \vdots \\ T_N \end{Bmatrix}^t +
# \begin{Bmatrix} \displaystyle \dot{Q}_1 + \sum_k^M{(U_{1kk}T_{kk})} \\ \vdots \\ \displaystyle \dot{Q}_N + \sum_k^M{(U_{Nkk}T_{kk})} \end{Bmatrix}
# \right),$
#
# where,
# $\odot$ is an element-wise multiplication operator,
# $N$ is the number of nodes, and,
# $M$ is the number of nodes with known temperatures.
#
# There are times, however, when a thermal node will have negligeable thermal capacitance $(C \approx 0)$, sometimes refered to as *arithmetic nodes* -- whereas nodes with capacitance are known as *diffusion nodes*.
#
# Performing an energy balance at the thermal node with negligeable thermal capacitance, the finite difference equation becomes:
#
# $T_i^{t+1} = \displaystyle \frac{\displaystyle \sum_{j}{[U_{ij}^t \ T_j^t]} + \displaystyle \sum_{k}{[U_{ikk}^t \ T_{kk}^t]} + \dot{Q}_i}{\displaystyle \sum_{j}{U_{ij}^t} + \displaystyle \sum_{k}{U_{ikk}^t}}$
#
# (For simplificity's sake, the equation is not written in a vectorized form, however, the scripts use a vectorized implementation.)
# ---------------
# #### Finite Difference Implementation: Seperating Inputs in the Python Script into Matrices
# In the Python Script implementing the finite difference method (FDM), the user will need to input all the conductances connecting the thermal nodes together. Since the system is linear, only values of $U_{ij}$ where $j > i$ need to be input due to symmetry. $U = 0$ for nodes not connected to one another. For convenience, the capacitance values $C$ for nodes with thermal mass are input in the vector $\bf{C}$. Connections to known temperature sources are input in the matrix $\bf{F}$. Finally, heat flow into the nodes are input in the vector $\bf{Q}_{input}$.
#
# $\textbf{U}_{input} = \begin{bmatrix}
# 0 & U_{12} & U_{13} & \dots & U_{1N} \\
# 0 & 0 & U_{23} & \dots & U_{2N} \\
# 0 & 0 & 0 & \dots & U_{3N} \\
# \vdots & \vdots & \vdots & \ddots & \vdots \\
# 0 & 0 & 0 & \dots & 0
# \end{bmatrix},
# \ \textbf{C} = \begin{Bmatrix} C_1 \\ C_2 \\ C_3 \\ \vdots \\ C_N \end{Bmatrix},
# \ \dot{ \textbf{Q} }_{input} = \begin{Bmatrix} \dot{Q}_1 \\ \dot{Q}_2 \\ \dot{Q}_3 \\ \vdots \\ \dot{Q}_N \end{Bmatrix},
# \ \textbf{T}_K = \begin{Bmatrix} T_{k1} \\ T_{k2} \\ T_{k3} \\ \vdots \\ T_{kM} \end{Bmatrix},
# \ \textbf{F} = \begin{bmatrix}
# U_{1k1} & U_{1k2} & U_{1k3} & \dots & U_{1kM} \\
# U_{2k1} & U_{2k2} & U_{2k3} & \dots & U_{2kM} \\
# U_{3k1} & U_{3k2} & U_{3k3} & \dots & U_{3kM} \\
# \vdots & \vdots & \vdots & \ddots & \vdots \\
# U_{Nk1} & U_{Nk2} & U_{Nk3} & \dots & U_{NkM} \\
# \end{bmatrix}. $
# Where,
# $U_{ij} = \displaystyle \left( \frac{1}{hA} \right)^{-1}, $ for convection
# $U_{ij} = \displaystyle \left( \frac{1}{UA} \right)^{-1} or \ \left( \frac{\Delta x}{kA} \right)^{-1}, $ for conduction
# $U_{ij} = \displaystyle \left( ACH*Volume*\rho_{air}*c_{p, air}*3600^{-1} \right), $ for infiltration, and
# $U_{ij} = \displaystyle \left( \frac{1}{h_{out}A} + \frac{\Delta x}{kA} + \frac{1}{h_{in}A} \right)^{-1}, $ for combined cases.
#
# $U_{12}$ in $\textbf{U}_{input}$ is the conductance between nodes 1 and 2. Nodes 1 and 2 have temperatures $T_1$ and $T_2$ which we are solving for.
# $U_{1k1}$ in $\textbf{F}$ is the conductance between node 1 and external source 1: $T_{k1}$. The external source has a predetermined/known/set temperature profile.
# ---------
# # Reference
# <NAME> (2015) *Modelling and Experimental Evaluation of an Active Thermal Energy Storage System with Phase-Change Materials for Model-Based Control.* Masters thesis, Concordia University. Available: http://www.bit.ly/VDermMascThesis
|
1.1 Finite Difference Formulation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/tbeucler/2022_ML_Earth_Env_Sci/blob/main/Lab_Notebooks/S2_2_Training_Models.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="5Tt5C4PoIRl0"
# #**Chapter 4 – Training Models**
#
# <table align="left">
# <td align=middle>
# <a target="_blank" href="https://github.com/ageron/handson-ml2/blob/master/04_training_linear_models.ipynb"> Open the original notebook <br><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# </td>
# </table>
# + [markdown] id="8HQ31GpXuKr-"
# Let's begin like in the last notebook: importing a few common modules, ensuring MatplotLib plots figures inline and preparing a function to save the figures. We also check that Python 3.5 or later is installed (although Python 2.x may work, it is deprecated so once again we strongly recommend you use Python 3 instead), as well as Scikit-Learn ≥0.20.
#
# You don't need to worry about understanding everything that is written in this section.
# + id="S_OXSp49IOF2"
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Is this notebook running on Colab or Kaggle?
IS_COLAB = "google.colab" in sys.modules
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
# Common imports
import numpy as np
import os
# To make this notebook's output stable across runs
rnd_seed = 42
rnd_gen = np.random.default_rng(rnd_seed)
# To plot pretty figures
# %matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "classification"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# + [markdown] id="wKsvLXdmzqD8"
# In this notebook we will be working with the [*Iris Flower Dataset*](https://en.wikipedia.org/wiki/Iris_flower_data_set), in which the length and width of both the sepals and petals of three types of Iris flowes were recorded. For reference, these are pictures of the three flowers: <br>
#
# <center> In order: Iris Setosa, Iris Versicolor, and Iris Virginica </center>
#
# <img src='https://upload.wikimedia.org/wikipedia/commons/thumb/5/56/Kosaciec_szczecinkowaty_Iris_setosa.jpg/360px-Kosaciec_szczecinkowaty_Iris_setosa.jpg' height=300 >
# <img src='https://upload.wikimedia.org/wikipedia/commons/thumb/4/41/Iris_versicolor_3.jpg/640px-Iris_versicolor_3.jpg' height=300></img>
# <img src='https://upload.wikimedia.org/wikipedia/commons/thumb/9/9f/Iris_virginica.jpg/590px-Iris_virginica.jpg' height=300></img>
#
# Photo Credits:[Kosaciec szczecinkowaty Iris setosa](https://en.wikipedia.org/wiki/File:Kosaciec_szczecinkowaty_Iris_setosa.jpg) by [<NAME>](https://commons.wikimedia.org/wiki/User:Radomil) licensed under [CC BY-SA 3.0](https://creativecommons.org/licenses/by-sa/3.0/deed.en); [Blue flag flower close-up (Iris versicolor)](https://en.wikipedia.org/wiki/File:Iris_versicolor_3.jpg)by <NAME> licensed under [CC BY-SA 3.0](https://creativecommons.org/licenses/by-sa/3.0/deed.en); [image of Iris virginica shrevei](https://en.wikipedia.org/wiki/File:Iris_virginica.jpg) by [<NAME>](https://www.flickr.com/photos/33397993@N05) licensed under [CC BY-SA 2.0](https://creativecommons.org/licenses/by-sa/2.0/deed.en).
# <br><br>
#
# As you can imagine, this dataset is normally used to train *multiclass*/*multinomial* classification algorithms and not *binary* classification algorithms, since there *are* more than 2 classes.
#
# "*Three classes, even!*" - an observant TA
#
# For this exercise, however, we will be implemented the binary classification algorithm referred to as the *logistic regression* algorithm (also called logit regression).
# + id="emWru72owjEI"
# Let's load the Iris Dataset
from sklearn import datasets
iris = datasets.load_iris()
# Print out some information about the data
print(f'Keys in Iris dictionary: \n{list(iris.keys())}\n\n')
print(iris.DESCR)
# And load the petal lengths and widths as our input data
X = iris["data"][:, (2, 3)] # petal length, petal width
y = iris["target"]
print(iris['data_module'])
# The target data labels Setosa as 0, Versicolor as 1, and Virginica as 2. For
# this exercise we will be using only the Versicolor and Virgina sets.
bin_indices = np.logical_or(y==1,y==2)
bin_X = X[bin_indices]
bin_y = (y[bin_indices]==2).astype(np.uint8) # convert to binary
# + [markdown] id="jvNBaOWZ9fXM"
# We now have a set of binary classification data we can use to train an algorithm.
#
# As we saw during our reading, we need to define three things in order to train our algorithm: the type of algorithm we will train, the cost function (which will tell us how close our prediction is to the truth), and a method for updating the parameters in our model according to the value of the cost function (e.g., the gradient descent method).
#
# Let's begin by defining the type of algorithm we will use. We will train a logistic regression model to differentiate between two classes. A reminder of how the logistic regression algorithm works is given below.
# <br><br><br>
# The logistic regression algorithm will thus take an input $t$ that is a linear combination of the features:
#
# <center> $t_{\small{n}} = \beta_{\small{0}} + \beta_{\small{1}} \cdot X_{1,n} + \beta_{\small{2}} \cdot X_{2,n}$ </center>
#
# where
# * $n$ is the ID of the sample
# * $X_{\small{1}}$ represents the petal length
# * $X_{\small{1}}$ represents the petal width
#
# This input is then fed into the logistic function, $\sigma(t)$:
# \begin{align}
# \sigma(t) = \dfrac{1}{1+e^ {-t}}
# \end{align}
#
# Let's plot it below to remember the shape of the function
# + id="lgt9dI6b9Zwa"
t = np.arange(-4,4,.1)
def logistic(in_val):
# Return the value of the logistic function
return 1/(1 + np.exp(- in_val))
fig, ax = plt.subplots()
ax.axvline(0, c='black', alpha=1)
ax.axhline(0, c='black', alpha=1)
[ax.axhline(y_val, c='black', alpha=0.5, linestyle='dotted') for y_val in (0.5,1)]
plt.autoscale(axis='x', tight=True)
ax.plot(t, logistic(t));
fig.tight_layout()
# + [markdown] id="0Ll1PKpjxqLX"
# With the logistic function, we define inputs resulting in $\sigma\geq.5$ as belonging to the ***one*** class, and any value below that is considered to belong to the ***zero*** class.
#
# We now have a function which let's us map the value of the petal length and width to the class to which the observation belongs (i.e., whether the length and width correspond to Iris Versicolor or Iris Virginica). However, there is a parameter vector **$\theta$** with a number of parameters that we do not have a value for: <br> $\theta = [ \beta_{\small{0}}, \beta_{\small{1}}$, $\beta_{\small{2}} ]$
#
# **Q1) Set up an array of random numbers between 0 and 1 representing the $\theta$ vector. Use rnd_gen!**
# + id="-Vk05y1C2VBs"
# Write your code here
# + [markdown] id="s8KM_CeF2Ven"
# In order to determine whether a set of $\beta$ values is better than the other, we need to quantify well the values are able to predict the class. This is where the cost function comes in.
#
# The cost function, $c$, will return a value close to zero when the prediction, $\hat{p}$, is correct and a large value when it is wrong. In a binary classification problem, we can use the log loss function. For a single prediction and truth value, it is given by:
# \begin{align}
# \text{c}(\mathbf{\theta}) = \left\{
# \begin{array}{cl}
# -log(\hat{p})& \text{if}\; y=1\\
# -log(1-\hat{p}) & \text{if}\; y=0
# \end{array}
# \right.
# \end{align}
#
# However, we want to apply the cost function to an n-dimensional set of predictions and truth values. Thankfully, we can find the average value of the log loss function $J$ for an an-dimensional set of $\hat{y}$ & $y$ as follows:
#
# \begin{align}
# \text{J}(\mathbf{\theta}) = - \dfrac{1}{n} \sum_{i=1}^{n}
# \left[ y_i\cdot log\left( \hat{p}_i \right) \right] +
# \left[ \left( 1 - y_i \right) \cdot log\left( 1-\hat{p}_i \right) \right]
# \end{align}
#
# We now have a formula that can be used to calculate the average cost over the training set of data.
#
# **Q2) Define a log_loss function that takes in an arbitrarily large set of prediction and truths**
# + id="H5fDeL36EauO"
def log_loss(p_hat, y, epsilon=1e-7):
# Write your code here. Please assert the dimensions of the vectors!
# We can also run into problems if p_hat = 0, so add an _epsilon_ term
# when evaluating log(p_hat).
return
# + [markdown] id="aO4Bkm1gFV3C"
# We now have a way of quantifying how good our predictions are. The final thing needed for us to train our algorithm is figuring out a way to update the parameters in a way that improves the average quality of our predictions.
#
# <br><br>**Warning**: we'll go into a bit of math below <br><br>
#
# Let's look at the change in a single parameter within $\theta$: $\beta_1$ (given $X_{1,i} = X_1$, $\;\hat{p}_{i} = \hat{p}$, $\;y_{i} = y$). If we want to know what the effect of changing the value of $\beta_1$ will have on the log loss function we can find this with the partial derivative:
# <center>$
# \dfrac{\partial J}{\partial \beta_1}
# $</center>
#
# This may not seem very helpful by itself - after all, $\beta_1$ isn't even in the expression of $J$. But if we use the chain rule, we can rewrite the expression as:
# <center>
# $\dfrac{\partial J}{\partial \hat{p}} \cdot
# \dfrac{\partial \hat{p}}{\partial \theta} \cdot
# \dfrac{\partial \theta}{\partial \beta_1}$
# </center>
#
# We'll spare you the math (feel free to verify it youself, however!):
#
# <center>$\dfrac{\partial J}{\partial \hat{p}} = \dfrac{\hat{p} - y}{\hat{p}(1-\hat{p})}, \quad
# \dfrac{\partial \hat{p}}{\partial \theta} = \hat{p} (1-\hat{p}), \quad
# \dfrac{\partial \theta}{\partial \beta_1} = X_1 $
# </center>
#
# and thus
# <center>$
# \dfrac{\partial J}{\partial \beta_1} = (\hat{p} - y) \cdot X_1
# $</center>
#
# We can calculate the partial derivative for each parameter in $\theta$ which, as you may have realized, is simply the $\theta$ gradient of $J$: $\nabla_{\theta}(J)$
#
# With all of this information, we can now write $\nabla_{\theta} J$ in terms of the error, the feature vector, and the number of samples we're training on!
#
# <center>$\nabla_{\mathbf{\theta}^{(k)}} \, J(\mathbf{\theta^{(k)}}) = \dfrac{1}{n} \sum\limits_{i=1}^{n}{ \left ( \hat{p}^{(k)}_{i} - y_{i} \right ) \mathbf{X}_{i}}$</center>
#
# Note that here $k$ represents the iteration of the parameters we are currently on.
#
# We now have a gradient we can calculate and use in the batch gradient descent method! The updated parameters will thus be:
#
# \begin{align}
# {\mathbf{\theta}^{(k+1)}} = {\mathbf{\theta}^{(k)}} - \eta\,\nabla_{\theta^{(k)}}J(\theta^{(k)})
# \end{align}
#
# Where $\eta$ is the learning rate parameter. (It's also worth pointing out that $\;\hat{p}^{(k)}_i = \sigma(\theta^{(k)}, X_i) $
# + [markdown] id="ML4uik7sbdMZ"
# In order to easily calculate the input to the logistic regression, we'll multiply the $\theta$ vector with the X data, and as we have a non-zero bias $\beta_0$ we'd like to have an X matrix whose first column is filled with ones.
#
# \begin{align}
# X_{\small{with\ bias}} = \begin{pmatrix}
# 1 & X_{1,0} & X_{2,0}\\
# 1 & X_{1,1} & X_{2,1}\\
# &...&\\
# 1 & X_{1,n} & X_{2,n}
# \end{pmatrix}
# \end{align}
# <br>
# **Q3) Prepare the *X_with_bias matrix* (remember to use the bin_X data and not just X). Write a function called *predict* that takes in the parameter vector $\theta$ and the *X_with_bias* matrix and evaluates the logistic function for each of the samples**
# + id="tBLryApsbatR"
# Write your code here
# + [markdown] id="p6cPbu4LvVES"
# **Q4) Now that you have a predict function, write a *gradient_calc* function that calculates the gradient for the logistic function. You'll have to feed it theta, X, and y**
# + id="BtnANN5WvVuy"
# Write your code here
# + [markdown] id="PU4A5HVKuAGG"
# We can now write a function that will train a logistic regression algorithm!
#
# Your *logistic_regression* function needs to:
# * Take in a set of training input/output data, validation input/output data, a number of iterations to train for, a set of initial parameters $\theta$, and a learning rate $\eta$
# * At each iteration:
# * Generate a set of predictions on the training data.
# * Calculate and store the loss function for the training data at each iteration
# * Calculate the gradient
# * Update the $\theta$ parameters
# * Generate a set of predictions on the validation data using the updated parameters
# * Calculate and store the loss function for the validation data.
# * Bonus: Calculate and store the accuracy of the model on the training and validation data as a metric!
# * Return the final set of parameters $\theta$ & the stored training/validation loss function values (and the accuracy, if you did the bonus)
#
# **Q5) Write the logistic_regression function**
# + id="HDsR5TxPt-0Y"
# Write your code here
# + [markdown] id="EWMDLk7wFB0f"
# **¡¡¡Important Note!!!**
#
# The notebook assumes that you will return
# 1. a Losses list, where Losses[0] is the training loss and Losses[1] is the validation loss
# 2. a tuple with the 3 final coefficients ($\beta_0$, $\beta_1$, $\beta_2$)
#
# The code for visualizing the bonus accuracy is not included - but it should be simple enough to do in a way similar to that which is done with the losses.
#
# ---------------------
# + [markdown] id="2ep5FQYBmqG5"
# Now that we have our logistic regression function, we're all set to train our algorithm! Or are we?
#
# There's an important data step that we've neglected up to this point - we need to split the data into the train, validation, and test datasets.
# + id="CVrXzjYA2iil"
test_ratio = 0.2
validation_ratio = 0.2
total_size = len(X_with_bias)
test_size = int(total_size * test_ratio)
validation_size = int(total_size * validation_ratio)
train_size = total_size - test_size - validation_size
rnd_indices = rnd_gen.permutation(total_size)
X_train = X_with_bias[rnd_indices[:train_size]]
y_train = bin_y[rnd_indices[:train_size]]
X_valid = X_with_bias[rnd_indices[train_size:-test_size]]
y_valid = bin_y[rnd_indices[train_size:-test_size]]
X_test = X_with_bias[rnd_indices[-test_size:]]
y_test = bin_y[rnd_indices[-test_size:]]
# + [markdown] id="33IhRpME8LOX"
# Now we're ready!
#
# **Q6) Train your logistic regression algorithm. Use 5000 iterations, $\eta$=0.1**
# + id="dWAr0ORYEYi2"
# Complete the code
losses, coeffs =
# + [markdown] id="e7WHcpPiEcIS"
# Let's see how our model did while learning!
# + id="4wXFzZPjFjOn"
# Produce the Loss Function Visualization Graphs
fig, ax = plt.subplots(figsize=(18,8))
ax.plot(losses[0], color='blue', label='Training', linewidth=3);
ax.plot(losses[1], color='orange', label='Validation', linewidth=3);
ax.legend();
ax.set_ylabel('Log Loss')
ax.set_xlabel('Iterations')
ax.set_title('Loss Function Graph')
ax.autoscale(axis='x', tight=True)
fig.tight_layout();
# Let's get predictions from our model for the training, validation, and testing
# datasets
y_hat_train = (predict(X_train, coeffs)>=.5).astype(int)
y_hat_valid = (predict(X_valid, coeffs)>=.5).astype(int)
y_hat_test = (predict(X_test, coeffs)>=.5).astype(int)
y_sets = [ [y_hat_train, y_train],
[y_hat_valid, y_valid],
[y_hat_test, y_test] ]
def accuracy_score(y_hat, y):
assert(y_hat.size==y.size)
return (y_hat == y).sum()/y.size
[accuracies.append(accuracy_score(y_set[0],y_set[1])) for y_set in y_sets]
printout= (f'Training Accuracy:{accuracies[0]:.1%} \n'
f'Validation Accuracy:{accuracies[1]:.1%} \n')
# Add the testing accuracy only once you're sure that your model works!
print(printout)
# + [markdown] id="4zfXs8M8Osie"
# Congratulations on training a logistic regression algorithm from scratch! Once you're done with the upcoming environmental science applications notebook, feel free to come back to take a look at the challenges 😀
# + [markdown] id="VAa4bzT7PHRG"
# ## Challenges
#
# * **C1)** Add L2 Regularization to training function
#
# * **C2)** Add early stopping to the training algorithm! Stop training when the accuracy is >=90%
#
# * **C3)** Implement a softmax regression model (It's multiclass logistic regression 🙂)
|
Lab_Notebooks/S2_2_Training_Models.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# <img style='float: left' width="150px" src="http://bostonlightswim.org/wp/wp-content/uploads/2011/08/BLS-front_4-color.jpg">
# <br><br>
#
# ## [The Boston Light Swim](http://bostonlightswim.org/)
#
# ### Sea Surface Temperature time-series model skill
# ### Load configuration
# +
import os
try:
import cPickle as pickle
except ImportError:
import pickle
run_name = '2015-08-17'
fname = os.path.join(run_name, 'config.pkl')
with open(fname, 'rb') as f:
config = pickle.load(f)
# +
import numpy as np
from pandas import DataFrame, read_csv
from utilities import to_html, save_html, apply_skill
fname = '{}-all_obs.csv'.format(run_name)
all_obs = read_csv(os.path.join(run_name, fname), index_col='name')
def rename_cols(df):
columns = dict()
for station in df.columns:
mask = all_obs['station'].astype(str) == station
name = all_obs['station'][mask].index[0]
columns.update({station: name})
return df.rename(columns=columns)
# +
from glob import glob
from pandas import Panel
from utilities import nc2df
def load_ncs(run_name):
fname = '{}-{}.nc'.format
ALL_OBS_DATA = nc2df(os.path.join(run_name,
fname(run_name, 'OBS_DATA')))
index = ALL_OBS_DATA.index
dfs = dict(OBS_DATA=ALL_OBS_DATA)
for fname in glob(os.path.join(run_name, "*.nc")):
if 'OBS_DATA' in fname:
continue
else:
model = fname.split('.')[0].split('-')[-1]
df = nc2df(fname)
# FIXME: Horrible work around duplicate times.
if len(df.index.values) != len(np.unique(df.index.values)):
kw = dict(subset='index', take_last=True)
df = df.reset_index().drop_duplicates(**kw).set_index('index')
kw = dict(method='time', limit=30)
df = df.reindex(index).interpolate(**kw).ix[index]
dfs.update({model: df})
return Panel.fromDict(dfs).swapaxes(0, 2)
# -
# ### Skill 1: Model Bias (or Mean Bias)
#
# The bias skill compares the model mean temperature against the observations.
# It is possible to introduce a Mean Bias in the model due to a mismatch of the
# boundary forcing and the model interior.
#
# $$ \text{MB} = \mathbf{\overline{m}} - \mathbf{\overline{o}}$$
# +
from utilities import mean_bias
dfs = load_ncs(run_name)
df = apply_skill(dfs, mean_bias, remove_mean=False, filter_tides=False)
df = rename_cols(df)
skill_score = dict(mean_bias=df.copy())
# Filter out stations with no valid comparison.
df.dropna(how='all', axis=1, inplace=True)
df = df.applymap('{:.2f}'.format).replace('nan', '--')
html = to_html(df.T)
fname = os.path.join(run_name, 'mean_bias.html'.format(run_name))
save_html(fname, html)
html
# -
# ### Skill 2: Central Root Mean Squared Error
#
# Root Mean Squared Error of the deviations from the mean.
#
# $$ \text{CRMS} = \sqrt{\left(\mathbf{m'} - \mathbf{o'}\right)^2}$$
#
# where: $\mathbf{m'} = \mathbf{m} - \mathbf{\overline{m}}$ and $\mathbf{o'} = \mathbf{o} - \mathbf{\overline{o}}$
# +
from utilities import rmse
dfs = load_ncs(run_name)
df = apply_skill(dfs, rmse, remove_mean=True, filter_tides=False)
df = rename_cols(df)
skill_score['rmse'] = df.copy()
# Filter out stations with no valid comparison.
df.dropna(how='all', axis=1, inplace=True)
df = df.applymap('{:.2f}'.format).replace('nan', '--')
html = to_html(df.T)
fname = os.path.join(run_name, 'rmse.html'.format(run_name))
save_html(fname, html)
html
# -
# ### Skill 3: R$^2$
# https://en.wikipedia.org/wiki/Coefficient_of_determination
# +
from utilities import r2
dfs = load_ncs(run_name)
df = apply_skill(dfs, r2, remove_mean=True, filter_tides=False)
df = rename_cols(df)
skill_score['r2'] = df.copy()
# Filter out stations with no valid comparison.
df.dropna(how='all', axis=1, inplace=True)
df = df.applymap('{:.2f}'.format).replace('nan', '--')
html = to_html(df.T)
fname = os.path.join(run_name, 'r2.html'.format(run_name))
save_html(fname, html)
html
# -
fname = os.path.join(run_name, 'skill_score.pkl')
with open(fname,'wb') as f:
pickle.dump(skill_score, f)
# ### Normalized Taylor diagrams
#
# The radius is model standard deviation error divided by observations deviation,
# azimuth is arc-cosine of cross correlation (R), and distance to point (1, 0) on the
# abscissa is Centered RMS.
# +
# %matplotlib inline
import matplotlib.pyplot as plt
from utilities.taylor_diagram import TaylorDiagram
def make_taylor(samples):
fig = plt.figure(figsize=(9, 9))
dia = TaylorDiagram(samples['std']['OBS_DATA'],
fig=fig,
label="Observation")
colors = plt.matplotlib.cm.jet(np.linspace(0, 1, len(samples)))
# Add samples to Taylor diagram.
samples.drop('OBS_DATA', inplace=True)
for model, row in samples.iterrows():
dia.add_sample(row['std'], row['corr'], marker='s', ls='',
label=model)
# Add RMS contours, and label them.
contours = dia.add_contours(colors='0.5')
plt.clabel(contours, inline=1, fontsize=10)
# Add a figure legend.
kw = dict(prop=dict(size='small'), loc='upper right')
leg = fig.legend(dia.samplePoints,
[p.get_label() for p in dia.samplePoints],
numpoints=1, **kw)
return fig
# +
dfs = load_ncs(run_name)
# Bin and interpolate all series to 1 hour.
freq = '30min'
for station, df in list(dfs.iteritems()):
df = df.resample(freq).interpolate().dropna(axis=1)
if 'OBS_DATA' in df:
samples = DataFrame.from_dict(dict(std=df.std(),
corr=df.corr()['OBS_DATA']))
else:
continue
samples[samples < 0] = np.NaN
samples.dropna(inplace=True)
if len(samples) <= 2: # 1 obs 1 model.
continue
fig = make_taylor(samples)
fig.savefig(os.path.join(run_name, '{}.png'.format(station)))
plt.close(fig)
|
web-services/01-skill_score.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Credit Scoring Model
import pandas_datareader as wb
import pandas as pd
import datetime as date
import numpy as np
import openpyxl as excel
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import scipy as sp
from sklearn.svm import SVC
from sklearn.model_selection import RandomizedSearchCV
from sklearn import metrics
import seaborn as sb
# ### Data uploading
df = pd.read_csv("dzSVM.csv")
# ### Explanatory Data Analysis
n_samples, n_features = df.shape
print("Количество наблюдений: ", n_samples)
print("Количество атрибутов: ", n_features)
pd.set_option('display.max_columns', None)
print("Первые пять наблюдений: ")
display(df.head())
print("Статистика по данным:")
display(df.describe(include='all'))
plt.hist(df[~np.isnan(df['CLAGE'])]['CLAGE'])
plt.show();
clage700orMore = df.CLAGE[df.CLAGE>=700].count()
print("%f процента значений CLAGE >= 700 (кредит старше 58 лет), всего %i наблюдения." % \
((clage700orMore/df.CLAGE.count())*100, clage700orMore))
# ### Data Wrangling
# +
df.drop(df[df.CLAGE >= 700].index, inplace=True)
print("Количество пустых значений:")
print(df.isnull().sum())
df = df.fillna(df.median())
print()
print("Количество пустых значений после заполнения:")
print(df.isnull().sum())
print()
df = df.fillna(df.mode().iloc[0])
print("Количество пустых значений после заполнения категориальных переменных:")
print(df.isnull().sum())
# -
print("Чистые данные:")
display(df.describe(include='all'))
# +
df['BAD'].value_counts().plot(kind='bar')
plt.title("BAD")
plt.show();
print("%f процентов заемщиков не выплатили кредит." %((df.BAD[df.BAD==1].count()/df.BAD.count())*100))
# -
# ### Data Normalization
numeric_features = df.select_dtypes(include=[np.number])
print("Численные атрибуты: ", numeric_features.columns.values)
print("До нормализации:")
display(numeric_features.describe())
numeric_features_scaled =(numeric_features-numeric_features.min())/(numeric_features.max()-numeric_features.min())
print("После нормализации:")
display(numeric_features_scaled.describe())
# ### EDA of prepared dataset
# +
df[numeric_features.columns.values] = numeric_features_scaled[numeric_features.columns.values]
print("Чистые и нормализованные данные:")
display(df.describe(include='all'))
# +
df = pd.get_dummies(df,drop_first=True)
print("Первые пять наблюдений после замены категориальных переменных на фиктивные")
display(df.head())
print("Количество наблюдений и атрибутов после замены категориальных переменных на фиктивные:", df.shape)
# -
print("Чистые и нормализованные данные с фиктивными переменными вместо категориальных:")
display(df.describe(include='all'))
corr = df.corr()
triangle = corr.abs().where(np.tril(np.ones(corr.shape), k=-1).astype(np.bool))
print("Самая сильная корреляция:")
display(triangle.stack().sort_values(ascending=False)[:7])
# ### Data splitting
# +
y = df.BAD
X = df.drop('BAD',axis=1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, stratify=y)
# -
# ### Model defining
clf = SVC(class_weight='balanced', kernel="rbf")
# ### Parameters for hypertuning
param_distributions = {"C": sp.stats.uniform(0.5, 5000), "gamma": sp.stats.uniform(0.01, 1)}###
# ### Model fitting
# +
random_search = RandomizedSearchCV(clf, param_distributions=param_distributions, n_iter=40, cv=4,
scoring="balanced_accuracy", n_jobs=-1)
random_search.fit(X_train, y_train)
model = random_search.best_estimator_
print("Оптимальные параметры: %s, оценка на учебных данных: %0.2f" % (random_search.best_params_, random_search.best_score_))
y_pred = model.predict(X_test)
# -
# ### Model evalutaion
# +
print("Результат на тестовых данных: %f" % (100*metrics.balanced_accuracy_score(y_test, y_pred)), end='\n\n')
cnf_matrix = metrics.confusion_matrix(y_test, y_pred)
print("Матрица неточностей:")
display(pd.DataFrame(cnf_matrix))
# -
sb.heatmap(cnf_matrix, annot=True, cmap='Blues', fmt='g',
xticklabels=["выплата","невыплата"], yticklabels=["выплата","невыплата"])
plt.ylabel('Реальное значение')
plt.xlabel('Предсказанное значение')
plt.show();
|
Credit_Scoring.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from datetime import timedelta , datetime
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math
# %matplotlib inline
# +
Country='Korea, South' # Input Country name
data = pd.read_csv('time_series_covid19_confirmed_global (7).csv')
data_2 = pd.read_csv('time_series_covid19_recovered_global (5).csv')
data_3 = pd.read_csv('time_series_covid19_deaths_global (6).csv')
data_4 = pd.read_csv('time_series_covid19_confirmed_global (7).csv')
data_5 = pd.read_csv('time_series_covid19_recovered_global (5).csv')
data_6 = pd.read_csv('time_series_covid19_deaths_global (6).csv')
# Infector
I_cml = data[data['Country/Region'] == Country].to_numpy()[0][-161:-40]
I_cml_1 = data_4[data_4['Country/Region'] == Country].to_numpy()[0][-41:-20]
# Recover
recovered_1 = data_2[data_2['Country/Region'] == Country].to_numpy()[0][-161:-40]
recovered_2 = data_5[data_5['Country/Region'] == Country].to_numpy()[0][-41:-20]
# Death
death = data_3[data_3['Country/Region'] == Country].to_numpy()[0][-161:-40]
death_1 = data_6[data_6['Country/Region'] == Country].to_numpy()[0][-41:-20]
# Population
population = 51640000 # Input population in Country
# +
########## data process ##########
I = 0.6 * (I_cml - recovered_1 - death)
I_1 = 0.6 * (I_cml_1 - recovered_2 - death_1)
A = 0.4 * (I_cml - recovered_1 - death)
A_A = 0.4 * (I_cml_1 - recovered_2 - death_1)
R_1 = 0.4 * (recovered_1)
R_2 = 1.5 * (R_1)
D = death
alpha = 0.6
n = np.array([population] * len(I), dtype=np.float64)
S = n - I - R_1 - R_2 - D - A
eta = (D[1:] - D[:-1]) / I[:-1] # DEATH RATE
gamma_1 = 1 + (eta) + alpha * ((S[:-1] - S[1:]) / I[:-1]) - I[1:] / I[:-1] # Recovery rate for symptom
gamma_2 = 1 + (1 - alpha) * ((S[:-1] - S[1:]) / A[:-1]) - A[1:] / A[:-1] # Recovery rate for asymptom
beta = ((S[:-1] - S[1:]) * (S[:-1] + I[:-1] + A[:-1])) / ((S[:-1]) * (I[:-1] + 0.5 * A[:-1])) # Infected rate
R0 = beta * (alpha / (gamma_1 + eta) + ((1 - alpha) * 0.5) / gamma_2) # Basic reproduction number
# -
I_ori = np.zeros(121)
I_ori = I
A_ori = np.zeros(121)
A_ori = A
R_ori_1 = np.zeros(121)
R_ori_1 = R_1
R_ori_2 = np.zeros(121)
R_ori_2 = R_2
R_ori = np.zeros(121)
R_ori = R_1 + R_2
D_ori = np.zeros(121)
D_ori = D
# +
##### Plot the training and testing results #####
plt.figure(1)
plt.plot(beta, label = r'$\beta (t)$')
plt.legend()
plt.figure(2)
plt.plot(gamma_1, label = r'$\gamma_1 (t)$')
plt.legend()
plt.figure(3)
plt.plot(gamma_2, label = r'$\gamma_2 (t)$')
plt.legend()
plt.figure(4)
plt.plot(eta, label = r'$\eta (t)$')
plt.legend()
# -
def data_split(data,start,T):
return data[start:start+T]
# +
##### Orders of three kinds of FIR model #####
orders_beta = 15
orders_gamma_1 = 15
orders_gamma_2 = 15
orders_eta = 3
orders_R0 = 8
##### starting day #####
start_beta = 0
start_gamma = 0
start_eta = 0
start_R0 = 0
# -
##### The total prediction date #####
Z=140
# # <font color = green>Beta</font>
# +
##### Order of FIR model #####
J = orders_beta
##### Size of the interval #####
T = orders_beta + 105
# -
O_beta = np.zeros((T-J,J+1))
for i in range (T-J):
y_1 = data_split(beta,0+i,J) # Cut the first training data(Length(J))
y_1 = np.append(y_1,1)
y_1 = y_1[::-1]
O_beta[i] = y_1
y_train_1 = beta # Training data of beta
beta_ori = beta
A_1 = np.zeros((J+1,J+1))
A_3 = np.zeros((J+1,J+1))
X = np.zeros(J+1)
H = np.zeros(J+1)
I = np.identity(J+1)
B_1 = np.zeros(J+1)
beta_hat = np.zeros(140-J)
beta_hat_M = np.zeros((140-T))
for k in range (140-T):
beta = y_train_1
A_1[0][0] = T-J
for i in range (1,J+1):
for j in range (1,J+1):
c = 0
for t in range (J,T):
c += ((beta[t-i]) * (beta[t-j]))
A_1[i][j] = c
b = 0
c = 0
for t in range (J,T):
c += beta[t-i]
A_1[0][i] = c
A_1[i][0] = c
b += ((beta[t]) * (beta[t-i]))
B_1[i] = b
b = 0
for t in range (J,T):
b += (beta[t])
B_1[0] = b
B_1 = B_1.T
alpha = 0
A_2 = A_1 + (alpha) * I # (alpha*I+A)
A_3 = np.linalg.inv(A_2)
X = np.matmul(A_3,B_1)
for i in range (1,J+1):
H[i] = beta[T-i]
H[0] = 1
H = H.T
beta_hat_M[k] = np.matmul(X,H)
l = beta_hat_M[k]
y_train_1 = np.append(y_train_1,l) # Put prediction data into training data
T = len(y_train_1)
if k == 0:
O_beta = np.dot(O_beta,X)
t = 0
for i in range (140-J):
if i < 120 - J :
beta_hat[i] = O_beta[i]
else :
beta_hat[i] = beta_hat_M[t]
t = t + 1
plt.plot(beta_hat,'r')
plt.plot(beta_ori[J:],'b')
# # <font color = green>Gamma_1</font>
# +
##### Order of FIR model #####
J = orders_gamma_1
##### Size of the interval #####
T = orders_gamma_1 + 105
# -
O_gamma = np.zeros((T-J,J+1))
for i in range (T-J):
y_2 = data_split(gamma_1,0+i,J) #Cut the first training data(Length(J))
y_2 = np.append(y_2,1)
y_2 = y_2[::-1]
O_gamma[i] = y_2
y_train_2 = gamma_1 #Training data of GAMMA_1
gamma_ori_1 = gamma_1
A_1 = np.zeros((J+1,J+1))
A_3 = np.zeros((J+1,J+1))
X = np.zeros(J+1)
H = np.zeros(J+1)
I = np.identity(J+1)
B_1 = np.zeros(J+1)
gamma_hat_1 = np.zeros(140-J)
gamma_hat_M_1 = np.zeros((140-T))
for k in range (140-T):
gamma = y_train_2
A_1[0][0] = T-J
for i in range (1,J+1):
for j in range (1,J+1):
c = 0
for t in range (J,T):
c += ((gamma[t-i]) * (gamma[t-j]))
A_1[i][j] = c
b = 0
c = 0
for t in range (J,T):
c += gamma[t-i]
A_1[0][i] = c
A_1[i][0] = c
b += ((gamma[t]) * (gamma[t-i]))
B_1[i] = b
b = 0
for t in range (J,T):
b += (gamma[t])
B_1[0] = b
B_1 = B_1.T
alpha = 0
A_2 = A_1 + (alpha) * I # (alpha*I+A)
A_3 = np.linalg.inv(A_2)
X = np.matmul(A_3,B_1)
for i in range (1,J+1):
H[i] = gamma[T-i]
H[0] = 1
H = H.T
gamma_hat_M_1[k] = np.matmul(X,H)
l = gamma_hat_M_1[k]
y_train_2 = np.append(y_train_2,l) # Put prediction data into training data
T = len(y_train_2)
if k == 0:
O_gamma = np.dot(O_gamma,X)
t = 0
for i in range (140-J):
if i < 120 - J :
gamma_hat_1[i] = O_gamma[i]
else :
gamma_hat_1[i] = gamma_hat_M_1[t]
t = t + 1
plt.plot(gamma_hat_1,'r')
plt.plot(gamma_ori_1[J:],'b')
# # <font color = green>Gamma_2</font>
# +
##### Order of FIR model #####
J = orders_gamma_2
##### Size of the interval #####
T = orders_gamma_2 + 105
# -
O_gamma = np.zeros((T-J,J+1))
for i in range (T-J):
y_2 = data_split(gamma_1,0+i,J) #Cut the first training data(Length(J))
y_2 = np.append(y_2,1)
y_2 = y_2[::-1]
O_gamma[i] = y_2
y_train_2 = gamma_2 #Training data of GAMMA_2
gamma_ori_2 = gamma_2
A_1 = np.zeros((J+1,J+1))
A_3 = np.zeros((J+1,J+1))
X = np.zeros(J+1)
H = np.zeros(J+1)
I = np.identity(J+1)
B_1 = np.zeros(J+1)
gamma_hat_2 = np.zeros(140-J)
gamma_hat_M_2 = np.zeros((140-T))
for k in range (140-T):
gamma = y_train_2
A_1[0][0] = T-J
for i in range (1,J+1):
for j in range (1,J+1):
c = 0
for t in range (J,T):
c += ((gamma[t-i]) * (gamma[t-j]))
A_1[i][j] = c
b = 0
c = 0
for t in range (J,T):
c += gamma[t-i]
A_1[0][i] = c
A_1[i][0] = c
b += ((gamma[t]) * (gamma[t-i]))
B_1[i] = b
b = 0
for t in range (J,T):
b += (gamma[t])
B_1[0] = b
B_1 = B_1.T
alpha = 0
A_2 = A_1 + (alpha) * I # (alpha*I+A)
A_3 = np.linalg.inv(A_2)
X = np.matmul(A_3,B_1)
for i in range (1,J+1):
H[i] = gamma[T-i]
H[0] = 1
H = H.T
gamma_hat_M_2[k] = np.matmul(X,H)
l = gamma_hat_M_2[k]
y_train_2 = np.append(y_train_2,l) # Put prediction data into training data
T = len(y_train_2)
if k == 0:
O_gamma = np.dot(O_gamma,X)
t = 0
for i in range (140-J):
if i < 120 - J :
gamma_hat_2[i] = O_gamma[i]
else :
gamma_hat_2[i] = gamma_hat_M_2[t]
t = t + 1
plt.plot(gamma_hat_2,'r')
plt.plot(gamma_ori_2[J:],'b')
# # <font color = green>Eta</font>
# +
##### Order of FIR model #####
J = orders_eta
##### Size of the interval #####
T = orders_eta + 117
# -
O_eta = np.zeros((T-J,J+1))
for i in range (T-J):
y_3 = data_split(eta,0+i,J) #Cut the first training data(Length(J))
y_3 = np.append(y_3,1)
y_3 = y_3[::-1]
O_eta[i] = y_3
y_train_3 = eta #Training data of eta
eta_ori = eta
A_1 = np.zeros((J+1,J+1))
A_3 = np.zeros((J+1,J+1))
X = np.zeros(J+1)
H = np.zeros(J+1)
I = np.identity(J+1)
B_1 = np.zeros(J+1)
eta_hat = np.zeros(140-J)
eta_hat_M = np.zeros((140-T))
for k in range (140-T):
eta = y_train_3
A_1[0][0] = T-J
for i in range (1,J+1):
for j in range (1,J+1):
c = 0
for t in range (J,T):
c += ((eta[t-i]) * (eta[t-j]))
A_1[i][j] = c
b = 0
c = 0
for t in range (J,T):
c += eta[t-i]
A_1[0][i] = c
A_1[i][0] = c
b += ((eta[t]) * (eta[t-i]))
B_1[i] = b
b = 0
for t in range (J,T):
b += (eta[t])
B_1[0] = b
B_1 = B_1.T
alpha = 0
A_2 = A_1 + (alpha) * I # (alpha*I+A)
A_3 = np.linalg.inv(A_2)
X = np.matmul(A_3,B_1)
for i in range (1,J+1):
H[i] = eta[T-i]
H[0] = 1
H = H.T
eta_hat_M[k] = np.matmul(X,H)
l = eta_hat_M[k]
y_train_3 = np.append(y_train_3,l) # Put prediction data into training data
T = len(y_train_3)
if k == 0:
O_eta = np.dot(O_eta,X)
t = 0
for i in range (140-J):
if i < 120 - J :
eta_hat[i] = O_eta[i]
else :
eta_hat[i] = eta_hat_M[t]
t = t + 1
plt.plot(eta_hat,'r')
plt.plot(eta_ori[J:],'b')
# # <font color = green>R0</font>
J = 19
R0 = np.zeros(len(beta_ori))
R0_hat = np.zeros(140-J)
for i in range (len(beta_ori)):
R0[i] = beta_ori[i] * (alpha / (gamma_ori_1[i] + eta_ori[i]) + ((1 - alpha) * 0.5) / gamma_ori_2[i])
for i in range (140-J):
R0_hat[i] = beta_hat[i] * (alpha / (gamma_hat_1[i] + eta_hat[i]) + ((1 - alpha) * 0.5) / gamma_hat_2[i])
plt.plot(R0_hat,'r')
plt.plot(R0[J:],'b')
# # <font color = green>I A R D</font>
alpha=0.6
J = 19
T = 120
# +
date = list(pd.to_datetime(data.columns[-141:-20]).strftime('%Y-%m%d'))
for i in range (20):
dt = datetime.strptime(date[-1],"%Y-%m%d")
td = timedelta(days=1)
next_date = dt+td
date.append(next_date.strftime('%Y-%m%d'))
S_hat = np.zeros(140-J+1)
S_hat_2 = np.zeros(140-T+1)
I_hat = np.zeros(140-J+1)
I_hat_2 = np.zeros(140-T+1)
A_hat = np.zeros(140-J+1)
A_hat_2 = np.zeros(140-T+1)
R_hat = np.zeros(140-J+1)
R_hat_2 = np.zeros(140-T+1)
D_hat = np.zeros(140-J+1)
D_hat_2 = np.zeros(140-T+1)
t = 0
k = 0
for i in range (140-J+1):
if i == 0:
I_hat[i] = I_ori[J-1]
A_hat[i] = A_ori[J-1]
R_hat[i] = R_ori[J-1]
D_hat[i] = D_ori[J-1]
S_hat[i] = S[J-1]
else :
S_hat[i] = S_hat[i-1] - S_hat[i-1] * beta_hat[t] * ((I_hat[i-1] + 0.5 * A_hat[i-1]) / (S_hat[i-1] + I_hat[i-1] + A_hat[i-1]))
I_hat[i] = I_hat[i-1] * (1 - gamma_hat_1[t] - eta_hat[t]) + alpha * S_hat[i-1] * beta_hat[t] * ((I_hat[i-1] + 0.5 * A_hat[i-1]) / (S_hat[i-1] + I_hat[i-1] + A_hat[i-1]))
A_hat[i] = A_hat[i-1] * (1 - gamma_hat_2[t]) + (1 - alpha) * S_hat[i-1] * beta_hat[t] * ((I_hat[i-1] + 0.5 * A_hat[i-1]) / (S_hat[i-1] + I_hat[i-1] + A_hat[i-1]))
R_hat[i] = R_hat[i-1] + (gamma_hat_1[t] * I_hat[i-1]) + (gamma_hat_2[t] * A_hat[i-1])
D_hat[i] = D_hat[i-1] + (eta_hat[t] * I_hat[i-1])
t = t + 1
for i in range (140-T+1):
if i == 0:
I_hat_2[i] = I_ori[T]
A_hat_2[i] = A_ori[T]
R_hat_2[i] = R_ori[T]
D_hat_2[i] = D_ori[T]
S_hat_2[i] = S[T]
else:
S_hat_2[i] = S_hat_2[i-1] - S_hat_2[i-1] * beta_hat_M[k] * ((I_hat_2[i-1] + 0.5 * A_hat_2[i-1]) / (S_hat_2[i-1] + I_hat_2[i-1] + A_hat_2[i-1]))
I_hat_2[i] = I_hat_2[i-1] * (1 - gamma_hat_M_1[k] - eta_hat_M[k]) + alpha * S_hat_2[i-1] * beta_hat_M[k] * ((I_hat_2[i-1] + 0.5 * A_hat_2[i-1]) / (S_hat_2[i-1] + I_hat_2[i-1] + A_hat_2[i-1]))
A_hat_2[i] = A_hat_2[i-1] * (1 - gamma_hat_M_2[k]) + (1 - alpha) * S_hat[i-1] * beta_hat_M[k] * ((I_hat_2[i-1] + 0.5 * A_hat_2[i-1]) / (S_hat_2[i-1] + I_hat_2[i-1] + A_hat_2[i-1]))
R_hat_2[i] = R_hat_2[i-1] + (gamma_hat_M_1[k] * I_hat_2[i-1]) + (gamma_hat_M_2[k] * A_hat_2[i-1])
D_hat_2[i] = D_hat_2[i-1] + (eta_hat_M[k] * I_hat_2[i-1])
k = k + 1
I_hat[-(140-T+1):] = I_hat_2
A_hat[-(140-T+1):] = A_hat_2
R_hat[-(140-T+1):] = R_hat_2
D_hat[-(140-T+1):] = D_hat_2
plt.figure(1)
plt.plot(I_ori[J:],'b',label = r'$I(t)$')
plt.plot(range(T-J+1,len(I_hat)),I_hat[T-J+1:],'o', mec = 'r',mfc = 'r',label = r'predict')
plt.xticks(range(0,len(I_hat),10),date[5::10],rotation = 45)
plt.xlabel('Date[y-m-d]',fontsize = 12)
plt.legend()
plt.figure(2)
plt.plot(A_ori[J:],'b',label = r'$A(t)$')
plt.plot(range(T-J+1,len(A_hat)),A_hat[T-J+1:],'o', mec = 'r',mfc = 'r',label = r'predict')
plt.xticks(range(0,len(A_hat),10),date[5::10],rotation = 45)
plt.xlabel('Date[y-m-d]',fontsize = 12)
plt.legend()
plt.figure(3)
plt.plot(R_ori[J:],'b',label = r'$R(t)$')
plt.plot(range(T-J+1,len(R_hat)),R_hat[T-J+1:],'o', mec = 'r',mfc = 'r',label = r'predict')
plt.xticks(range(0,len(R_hat),10),date[5::10],rotation = 45)
plt.xlabel('Date[y-m-d]',fontsize = 12)
plt.legend()
plt.figure(4)
plt.plot(D_ori[J:],'b',label = r'$D(t)$')
plt.plot(range(T-J+1,len(D_hat)),D_hat[T-J+1:],'o', mec = 'r',mfc = 'r',label = r'predict')
plt.xticks(range(0,len(D_hat),10),date[5::10],rotation = 45)
plt.xlabel('Date[y-m-d]',fontsize = 12)
plt.legend()
# -
# # <font color = purple>Plot Figures</font>
# +
# ------ show I,A and R0 graoh ------
plt.figure(figsize = (18,18))
#--- I,A graph ---
ax0 = plt.subplot(211)
plt.plot(range(len(I_ori) - 1, len(I_ori)+20), I_hat[T-J:], '-*', color='salmon', label=r'$\hat{I}(t)$', markersize=10)
plt.plot(range(len(I_ori)), I_ori, '-o', color='darkred', label=r'$I(t)$')
plt.plot(range(len(A_ori) - 1, len(A_ori)+20), A_hat[T-J:], '-*', color='orange', label=r'$\hat{A}(t)$', markersize=10)
plt.plot(range(len(A_ori)), A_ori, '-o', color='orangered', label=r'$A(t)$')
#--- format ---
plt.axvline(len(I_ori) + 19, 0, 2500000, ls='--', c='turquoise', label='ref. effective 20%')
plt.axvline(len(I_ori) + 19, 0, 2500000, ls='--', c='mediumorchid', label='ref. effective 10%')
plt.axvline(len(I_ori) + 14, 0, 80000, ls='--', c='darkblue', label='ref. effective 5%')
plt.axvline(len(I_ori) - 1 , 0, 200000, ls='--', c='goldenrod', label='predicting')
plt.xlabel('Day')
plt.ylabel('Person')
plt.ylim(0, 15000)
plt.xticks([])
plt.legend(loc='upper left', fontsize='xx-large', ncol=2, handleheight=2.4, labelspacing=0.05, prop={'size': 25})
#--- R0 graph ---
ax1 = plt.subplot(212, sharex=ax0)
plt.xticks(range(0, len(I_ori) + 20,3), date[0::3], rotation=45)
plt.plot(range(len(A_ori) - 1, len(A_ori) + 20), R0_hat[-21:], '-*', color='plum', label=r'$\hat{R_{0}}(t)$', markersize=10)
plt.plot(range(len(A_ori) - len(R0_hat) + 20 , len(A_ori)), R0_hat[:-20], '-*', color='m', label=r'$\hat{R_{0}}(t)$(Train)', markersize=10)
plt.plot(range(1, len(A_ori)), R0, '-o', color='darkslategray', label=r'$R_{0}(t)$', markersize=10)
#--- format ---
plt.hlines(1,0, len(R0)+20 , color='black', ls='--')
plt.axvline(len(I_ori) - 1 , 0, 2500000, ls='--', c='goldenrod', label='predicting')
plt.yticks([1,2,3,4,5])
plt.ylim(0,5)
plt.subplots_adjust(hspace=.0)
plt.legend(loc='upper left', fontsize='xx-large', ncol=2, handleheight=2.4, labelspacing=0.05, prop={'size': 25})
# +
plt.figure(figsize = (18,9))
plt.xticks(range(0 , len(I_ori) + 21 , 3) , date[0::3] , rotation = 45)
plt.plot(range(len(R_ori) - 1 , len(R_ori) + 20) , R_hat[T-J:] , '-*' , color = 'chartreuse' , label = r'$\hat{R}(t)$',markersize = 10)
plt.plot(range(len(R_ori)) , R_ori , '-o' , color = 'darkgreen' , label = r'$R(t)$')
plt.plot(range(len(D_ori) - 1 , len(D_ori) + 20) , D_hat[T-J:] , '-*' , color = 'gray' , label = r'$\hat{D}(t)$',markersize = 10)
plt.plot(range(len(D_ori)) , D_ori , '-o' , color = 'black' , label = r'$D(t)$')
plt.axvline(len(I_ori) - 1, 0 , 2500000 , ls = '--' , c = 'goldenrod' , label = 'pred')
plt.ylim(0 , 15000)
plt.xlabel('Day')
plt.ylabel('Person')
plt.legend(fontsize='xx-large',ncol=2, handleheight = 2.4 ,labelspacing=0.05,prop = {'size' : 18} , loc = 'upper left')
# +
# ------ show I,A and R0 graoh ------
plt.figure(figsize = (18,9))
#--- I,A graph ---
plt.plot(range(len(I_ori) - 1, len(I_ori)+20), I_hat[T-J:], '-*', color='salmon', label=r'$\hat{I}(t)$', markersize=10)
plt.plot(range(len(I_ori)), I_ori, '-o', color='darkred', label=r'$I(t)$')
plt.plot(range(len(A_ori) - 1, len(A_ori)+20), A_hat[T-J:], '-*', color='orange', label=r'$\hat{A}(t)$', markersize=10)
plt.plot(range(len(A_ori)), A_ori, '-o', color='orangered', label=r'$A(t)$')
plt.plot(range(len(I_ori) - 1, len(I_ori)+20), I_1, '-+', color='darkred', label=r'real $I(t)$', markersize=10)
plt.plot(range(len(I_ori) - 1, len(I_ori)+20), A_A, '-+', color='orangered', label=r'real $A(t)$', markersize=10)
#--- format ---
plt.axvline(len(I_ori) + 12, 0, 2500000, ls='--', c='turquoise', label='ref. effective 20%')
plt.axvline(len(I_ori) + 11, 0, 2500000, ls='--', c='mediumorchid', label='ref.effective 10%')
plt.axvline(len(I_ori) + 8, 0, 80000, ls='--', c='darkblue', label='ref. effective 5%')
plt.axvline(len(I_ori) - 1 , 0, 200000, ls='--', c='goldenrod', label='predicting')
plt.xlabel('Day')
plt.ylabel('Person')
plt.ylim(0, 15000)
plt.xticks(range(0, len(I_ori) + 20,3), date[0::3], rotation=45)
plt.legend(loc='upper left', fontsize='xx-large', ncol=2, handleheight=2.4, labelspacing=0.05, prop={'size': 20})
|
code/SIARD_KOREA_PREDICT.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # KNN From Scratch
# ## Imports
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from math import sqrt
import pandas as pd
# ## Creating Class
class ScrappyKNN():
def fit(self, X_train, y_train):
self.X_train = X_train
self.y_train = y_train
def predict(self, X_test):
predictions = []
for row in X_test:
label = self.closest(row)
predictions.append(label)
return predictions
def closest(self, row):
best_dist = self.euc(row, self.X_train[0])
best_index = 0
for i in range(1, len(self.X_train )):
dist = self.euc(row, self.X_train[i])
if dist < best_dist:
best_dist = dist
best_index = i
return self.y_train[best_index]
def euc(self, a, b):
return sqrt(sum((a - b) ** 2 for a, b in zip(a, b)))
# ## Loading the dataset
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)
# ## Spliting values
# +
X = df.iloc[:,:-1].values
y = df.iloc[:,-1].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = .5)
# -
# ## Fitting and Training
# +
cls = ScrappyKNN()
cls.fit(X_train, y_train)
# -
# ## Checking accuracy
# +
predictions = cls.predict(X_test)
print('Accuracy: {:0.2f}%'.format(accuracy_score(y_test, predictions) * 100))
|
notebooks/KNN From Scratch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Module 2: Basic data structures and containers
# This module will cover Python basic data structures and containers.
#
# Relevant reading: Think Python Chapters 10-12
# Containers: Data types which contain one or more of the other data types (including other containers!)
#
# Types of Python Containers:
# - Lists
# - Tuples
# - Sets
# - Dictionary
#
# ## Lists, Tuples, Sets
# **Lists:**
# - A container that is an ordered sequence of items
# - Roughly equivalent to arrays in other programming languages
# - Elements can hold any data type, including other lists
# - Lists are mutable, can change contents
# this is a list
my_list = [2, 4, 6, 8]
# + jupyter={"outputs_hidden": false}
# how many elements are in this list?
len(my_list)
# + jupyter={"outputs_hidden": false}
# get the zero-th element in a list
my_list[0]
# + jupyter={"outputs_hidden": false}
# you can update elements in a list because it is mutable
my_list[2] = 100
my_list
# + jupyter={"outputs_hidden": false}
# add a new element with the append() method
# lists can hold elements of varying data types
my_list.append('hello')
my_list
# + jupyter={"outputs_hidden": false}
# you can also add lists to concatenate them
[1, 2, 3] + [4, 5, 6]
# -
# **Tuples**
# - Also a container that is an ordered sequence of items
# - Just like a list, but it is an immutable list, cannot be altered once created!
# - Same syntax, but with () instead of []
# tuples are like lists, but immutable (you can't "edit" them in place)
my_tuple = (3, 2, 1, 2)
my_tuple
# you can find the sum of a tuple with sum()
sum(my_tuple)
# **Sets**
#
# - Another kind of container
# - Without a sequence or order
# - Without indexes
# - Makes sense when you care more about membership and uniqueness than position
# a set contains unique values
set(my_tuple)
# ## Converting list elements
# objective: how do we convert a list of integer values into a list of equivalent string values?
# in other words, how do we convert each element in a list to a different data type?
# first, let's make a list containing the first 5 even numbers
int_list = [2, 4, 6, 8, 10]
# how many elements are in our list?
len(int_list)
# what is the value of the element in the zero-th position of the list?
int_list[0]
# what is the data type of this element in the zero-th position?
type(int_list[0])
# let's convert that element from an int to a string using the str() function
str(int_list[0])
# let's check the data type that results from that str() function operating on our list element
type(str(int_list[0]))
# now we'll create a new list to contain the string versions of our integers
str_list = []
# now let's convert the element in the zero-th position of our int_list to a string
# and append it to the new str_list that will contain string values
# remember, the way to add a new element to a list is list.append()
# we are simply appending the result of the string conversion
str_list.append(str(int_list[0]))
# our str_list should have one element - the value at the zero-th position of int_list, converted to a string
str_list
# looks like that worked, so let's convert and append the rest of the values
# we know our int_list contains 5 elements from when we ran len() on it earlier
# we've already done position 0, now let's do positions 1 - 4
str_list.append(str(int_list[1]))
str_list.append(str(int_list[2]))
str_list.append(str(int_list[3]))
str_list.append(str(int_list[4]))
# let's see our list of strings
str_list
# and for comparison, here's our original list of integers
int_list
# what we have seen is a manual way of doing this int -> string conversion
# the whole benefit of coding is that we automate this sort of manual work
# over the next couple of weeks we'll learn more advanced and efficient techniques like this:
new_list = []
for value in int_list:
new_list.append(str(value))
new_list
# ...and eventually we'll learn even more advanced/efficient techniques, like this:
[str(value) for value in int_list]
# +
# now you try
# write a code snippet to multiply all the items in int_list by 3, then sum the result
y = 0
for x in int_list:
x = x * 3
y = y + x
y
# -
# or you could use list comprehension
sum([x * 3 for x in int_list])
# now you try
# calculate the mean value of int_list
sum(int_list) / len(int_list)
# ## Dictionaries
# - Python’s version of hash tables or associative arrays
# - Indexes aren’t numbers, but arbitrary keys (strings, special numbers, etc.)
# - Dictionaries don’t have an order to elements
# - Very efficient for searching via key
# + jupyter={"outputs_hidden": false}
antonyms = {'hot':'cold', 'fast':'slow', 'good':'bad'}
antonyms
# -
# - Elements are referred to as
# - Key: the dictionary entry
# - Value: the thing at dictionary[key]
# - Elements can be any Python data type including another dictionary
# - These are really powerful. Learn how to use them well
# + jupyter={"outputs_hidden": false}
# you can access things in a dictionary using its keys
antonyms['hot']
# + jupyter={"outputs_hidden": false}
# you can update values in a dictionary because it is mutable
antonyms['hot'] = 'freezing'
antonyms
# + jupyter={"outputs_hidden": false}
# what are all the keys in this dict?
antonyms.keys()
# + jupyter={"outputs_hidden": false}
# what are all the values in this dict?
antonyms.values()
# -
# essentially a list of tuples
antonyms.items()
# now you try
# write a code snippet to swap the antonyms dict's keys and values
dict([(value, key) for key, value in antonyms.items()])
|
week2/week2_2_basic_structures_containers.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# + [markdown] origin_pos=0
# # Implementation of Multilayer Perceptrons from Scratch
# :label:`sec_mlp_scratch`
#
# Now that we have characterized
# multilayer perceptrons (MLPs) mathematically,
# let us try to implement one ourselves. To compare against our previous results
# achieved with softmax regression
# (:numref:`sec_softmax_scratch`),
# we will continue to work with
# the Fashion-MNIST image classification dataset
# (:numref:`sec_fashion_mnist`).
#
# + origin_pos=2 tab=["pytorch"]
import torch
from torch import nn
from d2l import torch as d2l
# + origin_pos=4 tab=["pytorch"]
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# + [markdown] origin_pos=5
# ## Initializing Model Parameters
#
# Recall that Fashion-MNIST contains 10 classes,
# and that each image consists of a $28 \times 28 = 784$
# grid of grayscale pixel values.
# Again, we will disregard the spatial structure
# among the pixels for now,
# so we can think of this as simply a classification dataset
# with 784 input features and 10 classes.
# To begin, we will [**implement an MLP
# with one hidden layer and 256 hidden units.**]
# Note that we can regard both of these quantities
# as hyperparameters.
# Typically, we choose layer widths in powers of 2,
# which tend to be computationally efficient because
# of how memory is allocated and addressed in hardware.
#
# Again, we will represent our parameters with several tensors.
# Note that *for every layer*, we must keep track of
# one weight matrix and one bias vector.
# As always, we allocate memory
# for the gradients of the loss with respect to these parameters.
#
# + origin_pos=7 tab=["pytorch"]
num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = nn.Parameter(torch.randn(
num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]
# + [markdown] origin_pos=9
# ## Activation Function
#
# To make sure we know how everything works,
# we will [**implement the ReLU activation**] ourselves
# using the maximum function rather than
# invoking the built-in `relu` function directly.
#
# + origin_pos=11 tab=["pytorch"]
def relu(X):
a = torch.zeros_like(X)
return torch.max(X, a)
# + [markdown] origin_pos=13
# ## Model
#
# Because we are disregarding spatial structure,
# we `reshape` each two-dimensional image into
# a flat vector of length `num_inputs`.
# Finally, we (**implement our model**)
# with just a few lines of code.
#
# + origin_pos=15 tab=["pytorch"]
def net(X):
X = X.reshape((-1, num_inputs))
H = relu(X@W1 + b1) # Here '@' stands for matrix multiplication
return (H@W2 + b2)
# + [markdown] origin_pos=17
# ## Loss Function
#
# To ensure numerical stability,
# and because we already implemented
# the softmax function from scratch
# (:numref:`sec_softmax_scratch`),
# we leverage the integrated function from high-level APIs
# for calculating the softmax and cross-entropy loss.
# Recall our earlier discussion of these intricacies
# in :numref:`subsec_softmax-implementation-revisited`.
# We encourage the interested reader
# to examine the source code for the loss function
# to deepen their knowledge of implementation details.
#
# + origin_pos=19 tab=["pytorch"]
loss = nn.CrossEntropyLoss(reduction='none')
# + [markdown] origin_pos=21
# ## Training
#
# Fortunately, [**the training loop for MLPs
# is exactly the same as for softmax regression.**]
# Leveraging the `d2l` package again,
# we call the `train_ch3` function
# (see :numref:`sec_softmax_scratch`),
# setting the number of epochs to 10
# and the learning rate to 0.1.
#
# + origin_pos=23 tab=["pytorch"]
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
# + [markdown] origin_pos=25
# To evaluate the learned model,
# we [**apply it on some test data**].
#
# + origin_pos=26 tab=["pytorch"]
d2l.predict_ch3(net, test_iter)
# + [markdown] origin_pos=27
# ## Summary
#
# * We saw that implementing a simple MLP is easy, even when done manually.
# * However, with a large number of layers, implementing MLPs from scratch can still get messy (e.g., naming and keeping track of our model's parameters).
#
#
# ## Exercises
#
# 1. Change the value of the hyperparameter `num_hiddens` and see how this hyperparameter influences your results. Determine the best value of this hyperparameter, keeping all others constant.
# 1. Try adding an additional hidden layer to see how it affects the results.
# 1. How does changing the learning rate alter your results? Fixing the model architecture and other hyperparameters (including number of epochs), what learning rate gives you the best results?
# 1. What is the best result you can get by optimizing over all the hyperparameters (learning rate, number of epochs, number of hidden layers, number of hidden units per layer) jointly?
# 1. Describe why it is much more challenging to deal with multiple hyperparameters.
# 1. What is the smartest strategy you can think of for structuring a search over multiple hyperparameters?
#
# + [markdown] origin_pos=29 tab=["pytorch"]
# [Discussions](https://discuss.d2l.ai/t/93)
#
|
d2l/pytorch/chapter_multilayer-perceptrons/mlp-scratch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Fuzzy Logic Inference
# ** textbook question 7.5 (page 143) as example **
# %matplotlib inline
from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
# ## Given
A1 = np.array([0.0, 1.0, 0.6])
B = np.array([0.2, 0.8])
# ## Rule "If V is A1 then W is B" translates into
# Using Eq7.6 of "Correlation Product" on page 130
Rule = np.outer(A1, B) # same as just taking outer product
print(Rule)
# ** Another e.g. **
# If question was asking for "Correlation Min", instead, rule would've been translated into
np.array([min(i,j) for i in A1 for j in B]).reshape(3,2) # kinda like outer product but with 'min' as operator
# **Side note** Surely there's a vectorized way of doing this:
np.minimum(A1[...,np.newaxis], B[np.newaxis,...])
# **Side note** Not familiar with matlab, but I might do something like this:
repmat = lambda M,m,n: np.tile(M,(m,n))
_A1 = repmat(A1.reshape(3,1),1,2)
_B = repmat(B.reshape(1,2),3,1)
np.minimum(_A1, _B)
# ** Another e.g. ** And if according to Lukasiewicz's implication, the rule would've become
np.array([min(1.,1-i+j) for i in A1 for j in B]).reshape(3,2)
# ## If "V is A1" was also a known fact, then we'd have
# Using Eq7.8 on page 131
# +
""" Conclusion = [sup(min(0,0) min(1,0.2) min(0.6,0.12)) sup(min(0,0) min(1,0.8) min(0.6,0.48))]
= [sup(0 0.2 0.12) sup(0 0.8 0.48)]
= [0.2 0.8]
= B
"""
print('min:',np.minimum(A1[...,np.newaxis],Rule)) # Taking elementwise minimum of A1 with each column in Rule
print('sup:',np.max(np.minimum(A1[...,np.newaxis],Rule), axis=0)) # Taking supremum on each column
# -
# Recall the value of B, and one could find that the conclusion is **exactly** B (due to fact is exactly A1)
B
# So this whole calculation reads "**If V is A1 then W is B** and **V is A1** as a matter of fact, so we obtain **W is B**"
# ## But what if "V is NOT A1"
# Just take A1's complement instead:
np.max(np.minimum((1-A1)[...,np.newaxis],Rule), axis=0)
# This concludes the revisit of question 7.5
#
# And the general framework of fuzzy logic inference includes the following steps (page 133 and 134):
#
# (see also [Fuzzy Inference Process](https://www.mathworks.com/help/fuzzy/fuzzy-inference-process.html))
#
# 1. Cylindrical closure of antecedents (join together all conditions using cartesian product)
# 2. Compute implication relation (question 7.5)
# 3. Draw conclusions with compusitional rule of inference (question 7.5)
# 4. Conclusion aggregation (question 7.2)
# 5. Defuzzification
#
# Here's an example:
# # A fuzzy control vacuum cleaner
# +
# Input
dirty_level = dict(DIRTY = np.array([.25, .75]),
MEDIUM = np.array([.8, .2]),
CLEAN = np.array([.95, .5]))
battery_level = dict(HIGH = np.array([.1, .9]),
LOW = np.array([.8, .2]))
# Output
mode = dict(CLEANING = np.array([0.0,0.0,1.0]),
STANDBY = np.array([0.0,1.0,0.0]),
CHARGING = np.array([1.0,0.0,0.0]))
# Fuzzify a real value into a normal fuzzy number
fuzzify = lambda x: np.array([1.0-x, x])
# Cylindrical closure (just cartesian product of features)
closure = lambda *x: np.concatenate(x)
# Fuzzy inference formular
conclusion = lambda rule, *features: np.max(np.minimum(closure(*features)[...,np.newaxis],rule), axis=0)
# Rules
whatever = np.empty(0) # Irrelevant feature placeholder
new_rule = lambda dirty, battery, mode: np.outer(closure(dirty, battery), mode) # Correlation product
Rules = [
[ new_rule(dirty_level['DIRTY'],battery_level['HIGH'],mode['CLEANING']),
new_rule(dirty_level['MEDIUM'],battery_level['HIGH'],mode['CLEANING'])],
[ new_rule(whatever, battery_level['LOW'], mode['CHARGING']) ],
[ new_rule(dirty_level['CLEAN'], whatever, mode['STANDBY']) ]
]
def fuzzy_control1(dirty, battery):
d = fuzzify(dirty)
b = fuzzify(battery)
# Draw conclusions
conclusions = []
for rule in Rules[0]:
conclusions.append(conclusion(rule,d,b))
for rule in Rules[1]:
conclusions.append(conclusion(rule,b))
for rule in Rules[2]:
conclusions.append(conclusion(rule,d))
# Max aggregation
aggregated_conclusion = np.max(conclusions, axis = 0)
# Defuzzification
return np.argmax(aggregated_conclusion)
def plot(fuzzy_control):
dirty = np.linspace(0., 1., 120)
battery = np.linspace(0., 1., 120)
X, Y = np.meshgrid(dirty, battery)
Z = np.vectorize(fuzzy_control)(X, Y)
plt.figure(figsize=(9,7))
plt.title('Vacuum cleaner mode: (0=CHARGIN 1=STANDBY 2=CLEANING)')
plt.xlabel('Dirty level')
plt.ylabel('Battery level')
plt.pcolormesh(X, Y, Z, cmap='RdYlGn')
plt.colorbar()
plot(fuzzy_control1)
# -
# # MA v. TSK
#
# 
#
# references:
#
# 1. https://www.mathworks.com/help/fuzzy/what-is-sugeno-type-fuzzy-inference.html
# 2. https://www.mathworks.com/help/fuzzy/comparison-of-sugeno-and-mamdani-systems.html
# 3. http://www.cs.princeton.edu/courses/archive/fall07/cos436/HIDDEN/Knapp/fuzzy004.htm
# 4. Textbook page 137
#
# **Advantages of the Sugeno Method (TSK)**
#
# + It is computationally efficient.
# + It works well with linear techniques (e.g., PID control).
# + It works well with optimization and adaptive techniques.
# + It has guaranteed continuity of the output surface.
# + It is well suited to mathematical analysis.
#
# **Advantages of the Mamdani Method (MA)**
#
# + It is intuitive.
# + It has widespread acceptance.
# + It is well suited to human input.
#
# # So how to turn MA into TSK logic?
# Now it's more suited to take membership values instead of fuzzy numbers as input.
#
# This is an example membership function, projecting fuzzified input onto linguistic values in the rule in order to see how well they match up.
def membership_func(fuzzy):
"""Create a membership function based on some linguistic value"""
if np.array_equal(fuzzy, whatever): return lambda x: 1.0 # irrelevant feature
else: return lambda x: np.dot(fuzzy, fuzzify(x))
# ## Define TSK rules
# +
def sugeno_rule(dirty, battery, action_weights):
"""Takes linguistic values and actions weights
returns 2 functions: rule strength and action"""
# Membership functions
m_dirty = membership_func(dirty)
m_battery = membership_func(battery)
def strength(dirty_value, battery_value):
"""Takes crisp value and tells you strength of the rule"""
return np.min([m_dirty(dirty_value), m_battery(battery_value)])
W, b = action_weights
action = lambda *crisp_features: np.dot(W,np.array(crisp_features))+b
return strength, action
Rules2 = [
sugeno_rule(dirty_level['DIRTY'],battery_level['HIGH'], ([1,1],0)), # CLEANING
sugeno_rule(dirty_level['MEDIUM'],battery_level['HIGH'], ([1,1],0)), # CLEANING
sugeno_rule(whatever, battery_level['LOW'], ([0.0,-1],0)), # CHARGING
sugeno_rule(dirty_level['CLEAN'], whatever, ([-1,0.0],0)) # STANDBY
]
# -
# ## Check rules' firing strength
#
# This only depends on antecedents.
# +
def argmax_strengths(dirty, battery):
strengths = np.array([strength(dirty, battery) for (strength, action) in Rules2])
return np.argmax(strengths)
def plot_Rules2():
dirty = np.linspace(0., 1., 120)
battery = np.linspace(0., 1., 120)
X, Y = np.meshgrid(dirty, battery)
Z = np.vectorize(argmax_strengths)(X, Y)
plt.figure(figsize=(9,7))
plt.title('TSK rules firing (Color means which rule)')
plt.xlabel('Dirty level')
plt.ylabel('Battery level')
plt.pcolormesh(X, Y, Z)
plt.colorbar()
plot_Rules2()
# -
# Looks like Rules2[1] is redundant because its firing strength never became too significant. Let's remove it.
Rules2 = [
sugeno_rule(dirty_level['DIRTY'],battery_level['HIGH'], ([1,1],0)), # CLEANING
sugeno_rule(whatever, battery_level['LOW'], ([0.0,-1],0)), # CHARGING
sugeno_rule(dirty_level['CLEAN'], whatever, ([-1,0.0],0)) # STANDBY
]
plot_Rules2()
# ## TSK fuzzy control
#
# Actions are a linear combination of inputs in this example, but can be any function.
# +
def fuzzy_control2(dirty, battery):
strengths = np.array([strength(dirty, battery) for (strength, action) in Rules2])
actions = np.array([action(dirty, battery) for (strength, action) in Rules2])
return np.dot(strengths, actions)/np.sum(strengths) # No need to defuzzify
plot(fuzzy_control2)
# -
# ## Fine-tune rules
# +
Rules2 = [
sugeno_rule(dirty_level['DIRTY'],battery_level['HIGH'], ([0.5,0.5],2)), # CLEANING
sugeno_rule(whatever, battery_level['LOW'], ([0.0,1.],0)), # CHARGING
sugeno_rule(dirty_level['CLEAN'], whatever, ([-1.0,0.0],1)) # STANDBY
]
plot(fuzzy_control2)
# -
|
q7.5.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
out = 'xlnet-base-bahasa-cased'
os.makedirs(out, exist_ok=True)
# -
from transformers import XLNetTokenizer, XLNetModel, XLNetConfig, AutoTokenizer, AutoModelWithLMHead, pipeline
tokenizer = XLNetTokenizer('sp10m.cased.v9.model', do_lower_case = False)
tokenizer.save_pretrained('xlnet-base-bahasa-cased')
tokenizer = XLNetTokenizer.from_pretrained('./xlnet-base-bahasa-cased', do_lower_case = False)
# +
# # !transformers-cli convert --model_type xlnet \
# # --tf_checkpoint output-model/model.ckpt-300000 \
# # --config output-model/config.json \
# # --pytorch_dump_output xlnet-base-bahasa-cased
# -
directory = 'xlnet-base-bahasa-cased'
config = XLNetConfig(f'{directory}/config.json')
config.vocab_size = 32000
config.d_inner = 3072
config.d_model = 768
config.n_head = 12
config.n_layer = 12
config
model = AutoModelWithLMHead.from_pretrained('./xlnet-base-bahasa-cased/pytorch_model.bin', config = config)
fill_mask = pipeline('fill-mask', model=model, tokenizer=tokenizer)
fill_mask('makan ayam dengan <mask>')
model.save_pretrained('xlnet-base-bahasa-cased')
# +
# # !transformers-cli upload ./xlnet-base-bahasa-cased
# -
model = XLNetModel.from_pretrained('huseinzol05/xlnet-base-bahasa-cased')
tokenizer = XLNetTokenizer.from_pretrained('huseinzol05/xlnet-base-bahasa-cased', do_lower_case = False)
import torch
input_ids = torch.tensor([tokenizer.encode("husein tk suka mkan ayam", add_special_tokens=True)])
# +
with torch.no_grad():
last_hidden_states = model(input_ids)[0]
last_hidden_states
# -
model = AutoModelWithLMHead.from_pretrained('huseinzol05/xlnet-base-bahasa-cased')
fill_mask = pipeline('fill-mask', model=model, tokenizer=tokenizer)
fill_mask('makan ayam dengan <mask>')
|
pretrained-model/xlnet/huggingface/save-huggingface.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 创造最大的数
#
# [](https://github.com/mjd507)
# [](https://mp.weixin.qq.com/s/qi2c-bvHTSMzhu5B-78I_g)
#
# 
#
# 给定一组整数,将它们拼在一起、创造出最大的数。
# ## 用例说明
#
# ```python
# In[1]: [17, 7, 2, 45, 72]
# Out[1]: 77245217
# ```
def largestNum(nums: list) -> str:
for i in range(len(nums) - 1):
for j in range(i + 1, len(nums)):
a = int(str(nums[i]) + str(nums[j]))
b = int(str(nums[j]) + str(nums[i]))
if a < b:
(nums[i], nums[j]) = (nums[j], nums[i])
return ''.join([str(num) for num in nums])
print(largestNum([17, 7, 2, 45, 72]))
|
March/Week12/82.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# The normal equation
import numpy as np
import matplotlib.pyplot as plt
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new]
y_predict = X_new_b.dot(theta_best)
plt.plot(X_new, y_predict, "r-")
plt.plot(X, y, "b.")
# +
# linear regression using scikit-learn
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_
# -
# use lstsq
theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)
theta_best_svd
# pseudoinverse
np.linalg.pinv(X_b).dot(y)
# +
# gradient descent
eta = 0.1
n_iterations = 1000
m = 100
theta = np.random.randn(2,1)
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) -y)
theta = theta - eta * gradients
theta
# -
|
notebooks/ch_04_training_models.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Generate handwritten digits with trained CVAE net
# +
# Copyright (C) 2018 <NAME> <<EMAIL>>
# +
import matplotlib
matplotlib.use('Agg')
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
# -
import tensorflow as tf
from cvae.cvae import cvae
from cvae.utils import utils
from cvae.configs import config_mnist
from cvae.configs import config_train
# ### Load mnist data
# Step1 load MNITST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data", one_hot=False, validation_size=5000)
cf = config_mnist
tr_cf = config_train
# ### Build the net
net = cvae(cf)
net.cvae_build()
# print the net structure
net.cvae_print()
# ### Restore the net
# +
net.get_learning_rate()
net.get_loss()
net.get_opt()
# load the net
import os
foldname = "./cvae_mnist"
name = 'cvae.pkl'
net.sess, name = utils.load_net(os.path.join(foldname, name))
# -
# ### Generate new samples
# +
n_examples = 10
fig, axs = plt.subplots(cf.numclass, n_examples, figsize=(n_examples, cf.numclass))
for i in range(cf.numclass):
z_gen = np.random.normal(0, 1, [n_examples, cf.z_length])
# label
labels = np.zeros([n_examples, cf.numclass])
labels[:,i] = 1
imgs = net.sess.run(
net.outputs_de,
feed_dict = {net.z: z_gen, net.conditions: labels,
net.is_training: False,
net.keep_prob: 1.0})
img_test = [np.reshape(imgs[i], [cf.rs, cf.rs]) for i in range(len(imgs))]
for example_i in range(n_examples):
# original
axs[i][example_i].imshow(img_test[example_i], cmap='gray')
axs[i][example_i].axis('off')
fig.show()
plt.draw()
# plt.savefig("fig_ce.png", bbox_inches='tight', dpi=200)
|
demo-mnist/notebook-cvae-mnist-gen.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="oL9KopJirB2g"
# ##### Copyright 2018 The TensorFlow Authors.
# + cellView="form" colab={} colab_type="code" id="SKaX3Hd3ra6C"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] colab_type="text" id="AXH1bmUctMld"
# # Unicode 文字列
#
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/tutorials/load_data/unicode"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/ja/tutorials/load_data/unicode.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/ja/tutorials/load_data/unicode.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# <td>
# <a href="https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/ja/tutorials/load_data/unicode.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
# </td>
# </table>
# -
# Note: これらのドキュメントは私たちTensorFlowコミュニティが翻訳したものです。コミュニティによる 翻訳は**ベストエフォート**であるため、この翻訳が正確であることや[英語の公式ドキュメント](https://www.tensorflow.org/?hl=en)の 最新の状態を反映したものであることを保証することはできません。 この翻訳の品質を向上させるためのご意見をお持ちの方は、GitHubリポジトリ[tensorflow/docs](https://github.com/tensorflow/docs)にプルリクエストをお送りください。 コミュニティによる翻訳やレビューに参加していただける方は、 [<EMAIL> メーリングリスト](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-ja)にご連絡ください。
# ## はじめに
#
# 自然言語モデルは、しばしば異なる文字セットを使った異なる言語を扱います。 *Unicode*は、ほぼすべての言語で文字表示に使われている標準的なエンコードの仕組みです。各文字は、`0` から`0x10FFFF`までの一意の整数の [コードポイント(符号位置)](https://ja.wikipedia.org/wiki/%E7%AC%A6%E5%8F%B7%E7%82%B9) を使ってエンコードされます。1つの *Unicode文字列*は、ゼロ個以上のコードポイントのシーケンスです。
#
# このチュートリアルでは、TensorFlow での Unicode文字列の表現方法と、どうやって Unicode で標準的な文字列操作と同様の操作を行うかについて示します。また、スクリプト検出にもとづいて Unicode 文字列をトークンに分解します。
# + colab={} colab_type="code" id="OIKHl5Lvn4gh"
import tensorflow as tf
# -
# ## `tf.string` データ型
#
# 標準的な TensorFlow の`tf.string`型は、バイト列のテンソルを作ります。また、Unicode文字列はデフォルトでは utf-8 でエンコードされます。
# + colab={} colab_type="code" id="3yo-Qv6ntaFr"
tf.constant(u"Thanks 😊")
# -
# バイト列が最小限の単位として扱われるため、`tf.string` 型のテンソルは可変長のバイト文字列を保持できます。また、文字列長はテンソルの次元には含まれません。
# + colab={} colab_type="code" id="eyINCmTztyyS"
tf.constant([u"You're", u"welcome!"]).shape
# -
# 注 : Pythonを使って文字列を構成するとき、v2.x系とv3.x系では Unicode の扱いが異なります。v2.x系では、Unicode文字列は上記のようにプレフィックス "u" で明示します。v3.x系では、デフォルトで Unicode としてエンコードされます。
# ## Unicode 表現
#
# TensorFlow での Unicode文字列表現は、2つの標準的な方法があります:
#
# * `string` スカラー — コードポイントのシーケンスは既知の [文字符合化方式](https://ja.wikipedia.org/wiki/%E6%96%87%E5%AD%97%E7%AC%A6%E5%8F%B7%E5%8C%96%E6%96%B9%E5%BC%8F) でエンコードされる
# * `int32` ベクトル — 各文字には単一のコードポイントが入る
#
# たとえば、以下3つはすべて Unicode文字列 `"语言処理 "`(中国語で「言語処理」を意味します)を表します。
# + colab={} colab_type="code" id="cjQIkfJWvC_u"
# Unicode文字列。UTF-8にエンコードされた文字列スカラーとして表される
text_utf8 = tf.constant(u"语言处理")
text_utf8
# + colab={} colab_type="code" id="yQqcUECcvF2r"
# Unicode文字列。UTF-16-BEにエンコードされた文字列スカラーとして表される
text_utf16be = tf.constant(u"语言处理".encode("UTF-16-BE"))
text_utf16be
# + colab={} colab_type="code" id="ExdBr1t7vMuS"
# Unicode文字列。Unicodeコードポイントのベクトルとして表される
text_chars = tf.constant([ord(char) for char in u"语言处理"])
text_chars
# -
# ### Unicode 表現間の変換
#
# TensorFlowでは、これらの異なる Unicode 表現間で変換する方法を用意しています。
#
# * `tf.strings.unicode_decode`:エンコードされた文字列スカラーを、コードポイントのベクトルに変換します。
# * `tf.strings.unicode_encode`:コードポイントのベクトルを、エンコードされた文字列スカラーに変換します。
# * `tf.strings.unicode_transcode`:エンコードされた文字列スカラーを、別の文字コードに再エンコードします。
# + colab={} colab_type="code" id="qb-UQ_oLpAJg"
tf.strings.unicode_decode(text_utf8,
input_encoding='UTF-8')
# + colab={} colab_type="code" id="kEBUcunnp-9n"
tf.strings.unicode_encode(text_chars,
output_encoding='UTF-8')
# + colab={} colab_type="code" id="0MLhWcLZrph-"
tf.strings.unicode_transcode(text_utf8,
input_encoding='UTF8',
output_encoding='UTF-16-BE')
# -
# ### バッチの次元
#
# 複数の文字列をデコードする場合、各文字列の文字数が等しくない場合があります。返される結果は[`tf.RaggedTensor`](../../guide/ragged_tensor.ipynb)であり、最も内側の次元の長さは各文字列の文字数によって異なります。:
# + colab={} colab_type="code" id="N2jVzPymr_Mm"
# Unicode文字列のバッチ。それぞれが、UTF8にエンコードされた文字列として表される
batch_utf8 = [s.encode('UTF-8') for s in
[u'hÃllo', u'What is the weather tomorrow', u'Göödnight', u'😊']]
batch_chars_ragged = tf.strings.unicode_decode(batch_utf8,
input_encoding='UTF-8')
for sentence_chars in batch_chars_ragged.to_list():
print(sentence_chars)
# -
# この `tf.RaggedTensor` を直接使用することも、`tf.RaggedTensor.to_tensor` メソッドを使ってパディングを追加した密な `tf.Tensor` に変換するか、あるいは `tf.RaggedTensor.to_sparse` メソッドを使って `tf.SparseTensor` に変換することもできます。
# + colab={} colab_type="code" id="yz17yeSMsUid"
batch_chars_padded = batch_chars_ragged.to_tensor(default_value=-1)
print(batch_chars_padded.numpy())
# + colab={} colab_type="code" id="kBjsPQp3rhfm"
batch_chars_sparse = batch_chars_ragged.to_sparse()
# -
# 同じ長さの複数の文字列をエンコードする場合、`tf.Tensor` を入力値として使用できます。
# + colab={} colab_type="code" id="_lP62YUAwjK9"
tf.strings.unicode_encode([[99, 97, 116], [100, 111, 103], [ 99, 111, 119]],
output_encoding='UTF-8')
# -
# 可変長の複数の文字列をエンコードする場合、`tf.RaggedTensor` を入力値として使用する必要があります。
# + colab={} colab_type="code" id="d7GtOtrltaMl"
tf.strings.unicode_encode(batch_chars_ragged, output_encoding='UTF-8')
# -
# パディングされた、あるいはスパースな複数の文字列を含むテンソルがある場合は、`unicode_encode` を呼び出す前に `tf.RaggedTensor` に変換します。
# + colab={} colab_type="code" id="R2bYCYl0u-Ue"
tf.strings.unicode_encode(
tf.RaggedTensor.from_sparse(batch_chars_sparse),
output_encoding='UTF-8')
# + colab={} colab_type="code" id="UlV2znh_u_zm"
tf.strings.unicode_encode(
tf.RaggedTensor.from_tensor(batch_chars_padded, padding=-1),
output_encoding='UTF-8')
# -
# ## Unicode 操作
# + [markdown] colab_type="text" id="NkmtsA_yvMB0"
# ### 文字列長
#
# `tf.strings.length` は、文字列長をどう計算するかを示す `unit` パラメーターが使えます。`unit` のデフォルトは `"BYTE"` ですが、`"UTF8_CHAR"` や `"UTF16_CHAR"` など他の値に設定して、エンコードされた `string` 文字列のUnicodeコードポイントの数を決めることができます。
# + colab={} colab_type="code" id="1ZzMe59mvLHr"
# 最後の絵文字は、UTF8で4バイトを占めることに注意する
thanks = u'Thanks 😊'.encode('UTF-8')
num_bytes = tf.strings.length(thanks).numpy()
num_chars = tf.strings.length(thanks, unit='UTF8_CHAR').numpy()
print('{} bytes; {} UTF-8 characters'.format(num_bytes, num_chars))
# + [markdown] colab_type="text" id="fHG85gxlvVU0"
# ### 部分文字列
#
# 同様に、 `tf.strings.substr` では " `unit`" パラメーターを使い、かつ "`pos`" および "`len`" パラメーターを指定することで、オフセットの種類を決めることができます。
# + colab={} colab_type="code" id="WlWRLV-4xWYq"
# デフォルト: unit='BYTE'. len=1 の場合、1バイトを返す
tf.strings.substr(thanks, pos=7, len=1).numpy()
# + colab={} colab_type="code" id="JfNUVDPwxkCS"
# unit = 'UTF8_CHAR' を指定すると、単一の文字(この場合は4バイト)が返される
print(tf.strings.substr(thanks, pos=7, len=1, unit='UTF8_CHAR').numpy())
# + [markdown] colab_type="text" id="zJUEsVSyeIa3"
# ### Unicode文字列を分割する
#
# `tf.strings.unicode_split` は、Unicode文字列を個々の文字に分割します。
# + colab={} colab_type="code" id="dDjkh5G1ejMt"
tf.strings.unicode_split(thanks, 'UTF-8').numpy()
# + [markdown] colab_type="text" id="HQqEEZEbdG9O"
# ### 文字のバイトオフセット
#
# `tf.strings.unicode_decode` によって生成された文字テンソルを元の文字列に戻すには、各文字の開始位置のオフセットを知ることが役立ちます。`tf.strings.unicode_decode_with_offsets`メソッド は `unicode_decode` に似ていますが、各文字の開始オフセットを含む2番目のテンソルを返す点が異なります。
# + colab={} colab_type="code" id="Cug7cmwYdowd"
codepoints, offsets = tf.strings.unicode_decode_with_offsets(u"🎈🎉🎊", 'UTF-8')
for (codepoint, offset) in zip(codepoints.numpy(), offsets.numpy()):
print("At byte offset {}: codepoint {}".format(offset, codepoint))
# + [markdown] colab_type="text" id="2ZnCNxOvx66T"
# ## Unicode スクリプト
# + [markdown] colab_type="text" id="nRRHqkqNyGZ6"
# 各Unicodeコードポイントは、[スクリプト](https://en.wikipedia.org/wiki/Script_%28Unicode%29) として知られる単一のコードポイント集合に属しています。文字スクリプトは、その文字がどの言語なのかを判断するのに役立ちます。たとえば、「Б」がキリル文字であることがわかれば、その文字を含むテキストはロシア語やウクライナ語などのスラブ言語である可能性が高いことがわかります。
#
# TensorFlowは、あるコードポイントがどのスクリプトかを返す `tf.strings.unicode_script` を提供しています。戻り値のスクリプトコードは、[International Components for Unicode](http://site.icu-project.org/home) (ICU) の [`UScriptCode`](http://icu-project.org/apiref/icu4c/uscript_8h.html) に対応する `int32` 値になります。
# + colab={} colab_type="code" id="K7DeYHrRyFPy"
uscript = tf.strings.unicode_script([33464, 1041]) # ['芸', 'Б']
print(uscript.numpy()) # [17, 8] == [USCRIPT_HAN, USCRIPT_CYRILLIC]
# + [markdown] colab_type="text" id="2fW992a1lIY6"
# `tf.strings.unicode_script` は、多次元のコードポイントの `tf.Tensors` や ` tf.RaggedTensor` にも適用できます。:
# + colab={} colab_type="code" id="uR7b8meLlFnp"
print(tf.strings.unicode_script(batch_chars_ragged))
# + [markdown] colab_type="text" id="mx7HEFpBzEsB"
# ## 例:シンプルなセグメンテーション
#
# セグメンテーションは、テキストを単語のような粒度に分割するタスクです。これは、スペース文字を使用して単語を区切れる場合には簡単に行えますが、一部の言語(中国語や日本語など)はスペースを使いませんし、また、一部の言語(ドイツ語など)には、意味を解析するために分ける必要がある、単語を結合した長い複合語があります。Webテキストでは、「NY株価」(ニューヨーク株価)のように、異なる言語とスクリプトがしばしば混在しています。
#
# 単語の境界を推定してスクリプトを変更することにより、(MLモデルを実装せずに)非常に大まかなセグメンテーションを実行できます。これは、上記の「NY株価」の例のような文字列に対して機能します。さまざまな言語のスペース文字はすべて、実際のテキストとは異なる特別なスクリプトコードである USCRIPT_COMMON として分類されるため、スペースを使用するほとんどの言語でも機能します。
# + colab={} colab_type="code" id="grsvFiC4BoPb"
# dtype: string; shape: [num_sentences]
#
# 処理する文章。この行を編集して、さまざまな入力を試してみてください!
sentence_texts = [u'Hello, world.', u'世界こんにちは']
# + [markdown] colab_type="text" id="CapnbShuGU8i"
# 最初に、文章を文字ごとのコードポイントにデコードし、それから各文字のスクリプトコード(識別子)を調べます。
# + colab={} colab_type="code" id="ReQVcDQh1MB8"
# dtype: int32; shape: [num_sentences, (num_chars_per_sentence)]
#
# sentence_char_codepoint[i, j] は、i番目の文のn番目の文字のコードポイント
sentence_char_codepoint = tf.strings.unicode_decode(sentence_texts, 'UTF-8')
print(sentence_char_codepoint)
# dtype: int32; shape: [num_sentences, (num_chars_per_sentence)]
#
# sentence_char_scripts[i, j] は、i番目の文のn番目の文字のスクリプトコード
sentence_char_script = tf.strings.unicode_script(sentence_char_codepoint)
print(sentence_char_script)
# + [markdown] colab_type="text" id="O2fapF5UGcUc"
# 次に、これらのスクリプトコードを使って、単語の境界を追加すべき場所を決めます。前の文字とスクリプトコードが異なるそれぞれの文字の先頭に、単語の境界を追加します。:
# + colab={} colab_type="code" id="7v5W6MOr1Rlc"
# dtype: bool; shape: [num_sentences, (num_chars_per_sentence)]
#
# sentence_char_starts_word[i, j] は、i番目の文のn番目の文字が単語の始まりである場合にTrue
sentence_char_starts_word = tf.concat(
[tf.fill([sentence_char_script.nrows(), 1], True),
tf.not_equal(sentence_char_script[:, 1:], sentence_char_script[:, :-1])],
axis=1)
# dtype: int64; shape: [num_words]
#
# word_starts[i] は、i番目の単語の始まりである文字のインデックス
# (すべての文がフラット化された文字リスト)
word_starts = tf.squeeze(tf.where(sentence_char_starts_word.values), axis=1)
print(word_starts)
# + [markdown] colab_type="text" id="LAwh-1QkGuC9"
# そして、これらの目印(開始オフセット)を使って、各単語ごとの文字リストを含む `RaggedTensor` を作成します。:
# + colab={} colab_type="code" id="bNiA1O_eBBCL"
# dtype: int32; shape: [num_words, (num_chars_per_word)]
#
# word_char_codepoint[i, j] は、i番目の単語のn番目の文字のコードポイント
word_char_codepoint = tf.RaggedTensor.from_row_starts(
values=sentence_char_codepoint.values,
row_starts=word_starts)
print(word_char_codepoint)
# + [markdown] colab_type="text" id="66a2ZnYmG2ao"
# 最後に、`RaggedTensor` をコードポイント単位でセグメント化して、文章に戻します。:
# + colab={} colab_type="code" id="NCfwcqLSEjZb"
# dtype: int64; shape: [num_sentences]
#
# sentence_num_words[i] は、i番目の文の単語数
sentence_num_words = tf.reduce_sum(
tf.cast(sentence_char_starts_word, tf.int64),
axis=1)
# dtype: int32; shape: [num_sentences, (num_words_per_sentence), (num_chars_per_word)]
#
# sentence_word_char_codepoint[i, j, k] は、i番目の文のn番目の単語のk番目の文字のコードポイント
sentence_word_char_codepoint = tf.RaggedTensor.from_row_lengths(
values=word_char_codepoint,
row_lengths=sentence_num_words)
print(sentence_word_char_codepoint)
# + [markdown] colab_type="text" id="xWaX8WcbHyqY"
# 最終的な結果を見やすくするために、UTF-8文字列にエンコードします。:
# + colab={} colab_type="code" id="HSivquOgFr3C"
tf.strings.unicode_encode(sentence_word_char_codepoint, 'UTF-8').to_list()
|
site/ja/tutorials/load_data/unicode.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:parcels-container_2021.03.17-6c459b7]
# language: python
# name: conda-env-parcels-container_2021.03.17-6c459b7-py
# ---
# +
from pathlib import Path
import xarray as xr
import numpy as np
import pandas as pd
import cartopy
import cmocean as co
from matplotlib import pyplot as plt
import shapely
import cartopy.crs as ccrs
import seaborn as sns
import matplotlib.dates as mdates
import matplotlib.lines as mlines
import importlib
import sys
# -
# path to some plotting routines
# sys.path.append(r'/home/jupyter-workshop007/Projects/spg_fresh_blob_202104/src/')
sys.path.append(r'../../src/')
import visualization.plotTracksCartopy as myplots
# +
# from dask.distributed import Client
# +
# client = Client(n_workers=1, threads_per_worker=8, memory_limit=10e9)
# client
# + slideshow={"slide_type": "skip"}
sns.set(style="whitegrid")
xr.set_options(keep_attrs=True)
np.warnings.filterwarnings('ignore')
sns.set_palette("colorblind")
xr.set_options(keep_attrs=True);
plt.rc('font', size=8) #controls default text size
plt.rc('axes', titlesize=8) #fontsize of the title
plt.rc('axes', labelsize=8) #fontsize of the x and y labels
plt.rc('xtick', labelsize=8) #fontsize of the x tick labels
plt.rc('ytick', labelsize=8) #fontsize of the y tick labels
plt.rc('legend', fontsize=8) #fontsize of the legend
plt.rc('savefig', dpi=300) # higher res outputs
# + tags=["parameters"]
# parameters
project_path = Path.cwd() / '..' / '..'
project_path = project_path.resolve()
data_path = "/data/spg_fresh_blob_202104_data/raw/"
interim_data_path = Path('data/interim/')
sectionPath = Path('data/external/')
sectionFilename = 'osnap_pos_wp.txt'
sectionname = 'osnap'
# output figures path
figure_path = Path("reports/figures/coldBlob/")
year = 1990
# -
year_str = str(year)
# data_stores_subsets = list(sorted(Path(data_path).glob("*_????_subset.zarr/")))[:use_number_subset_years]
data_stores_subsets = list(sorted(Path(data_path).glob("*_"+year_str+"_subset_10percent.zarr/")))
display(data_stores_subsets)
# +
ds_subsets = xr.concat(
[xr.open_zarr(store) for store in data_stores_subsets],
dim="traj",
)
display(ds_subsets)
print(ds_subsets.nbytes / 1e9, "GiB")
# +
# location of mask data
mask_path_name = '/data/iAtlantic/mask/VIKING20X.L46-KKG36107B/'
mesh_mask_filename = '1_mesh_mask.nc'
mask_path = Path(mask_path_name)
mesh_mask = mask_path / mesh_mask_filename
ds_mask = xr.open_dataset(mesh_mask)
ds_mask = ds_mask.squeeze()
ds_mask = ds_mask.set_coords(["nav_lon", "nav_lat", "nav_lev"])
# -
ds_mask
depth = (ds_mask.e3t_0 * ds_mask.tmask).sum(dim='z')
depth
ds_mask.depthw.data
ds_mask.mbathy[1000,1000]
# ## Extract data on osnap line (initialised positions)
ds_subsets_osnap = ds_subsets.isel(obs=0)
# ## Update some attributes
# ds_subsets_osnap['vol_trans_normal'] =
ds_subsets_osnap.mxl.attrs = {'units':'m','long_name':'mixed layer depth'}
ds_subsets_osnap.salt.attrs = {'units':'PSU','long_name':'salinity'}
ds_subsets_osnap.temp.attrs = {'units':'degC','long_name':'temperature'}
ds_subsets_osnap.uvel.attrs = {'units':'degrees_east/second','long_name':'u velocity (raw)'}
ds_subsets_osnap.vvel.attrs = {'units':'degrees_north/second','long_name':'v velocity (raw)'}
# ## Flag tracks by source region and pathway
# + slideshow={"slide_type": "skip"}
def apply_left_of_line(ds, lon_1, lon_2, lat_1, lat_2):
'''Apply an area crossing criterion.
Larvae in ds selected while they are in a selected area.
'''
# particles are selected if they pass through given area.
position = ((lon_2 -lon_1) * (ds.lat - lat_1) -
(ds.lon - lon_1) * (lat_2 - lat_1))
return position > 0.0, position < 0
# + [markdown] slideshow={"slide_type": "skip"}
# #### from Labrador sea or from Gulf Stream
# + slideshow={"slide_type": "skip"}
# from labrador sea
ds_in1, ds_notin1 = apply_left_of_line(ds_subsets,-75,-40,40,65)
ds_in2, ds_notin2 = apply_left_of_line(ds_subsets,-100,-58.2,48,52)
ds_in3, ds_notin3 = apply_left_of_line(ds_subsets,-45,-45,60,70)
ds_lab_in = ds_in1*ds_in2*ds_in3
# from west of 60W, south of Flemish Cap (to test path from labrador sea)
ds_in1, ds_notin1 = apply_left_of_line(ds_subsets,-60,-60,33,63)
ds_in2, ds_notin2 = apply_left_of_line(ds_subsets,-58.2,-100,52,48)
ds_60w_in = ds_in1*ds_in2
# from gulf stream
ds_in1, ds_notin1 = apply_left_of_line(ds_subsets,-60,-100,33,33)
ds_in2, ds_notin2 = apply_left_of_line(ds_subsets,-44,-44,0,33)
ds_gst_in = ds_in1 * ds_in2
# +
# check trajectory routes
LabCu = ds_lab_in.max("obs")
LC60W = ds_60w_in.max("obs")
GulfS = ds_gst_in.max("obs")
# check when lef lab sea,crossed 60w or gulf stream. defaults to zero
LabCu_exit_index = ds_lab_in.argmax(axis=1)
LC60W_exit_index = ds_60w_in.argmax(axis=1)
GulfS_exit_index = ds_gst_in.argmax(axis=1)
LabCu_exit_index = LabCu_exit_index.where(LabCu_exit_index > 0,len(ds_subsets.obs)-1)
LC60W_exit_index = LC60W_exit_index.where(LC60W_exit_index > 0,len(ds_subsets.obs)-1)
GulfS_exit_index = GulfS_exit_index.where(GulfS_exit_index > 0,len(ds_subsets.obs)-1)
# -
# check if most recently left Lab Sea
LabCu_is_source = (LabCu_exit_index < GulfS_exit_index)
GulfS_is_source = (LabCu_exit_index > GulfS_exit_index)
LC60W_is_path = (LabCu_exit_index > LC60W_exit_index).where(LabCu_is_source,False)
LCdir_is_path = LabCu_is_source.where(LC60W_is_path==False,False)
other_is_source = (LabCu_is_source==False).where(GulfS_is_source == False,False)
# flag particles on osnap line by origin
ds_subsets_osnap = ds_subsets_osnap.assign({'LabCu_is_source':LabCu_is_source})
ds_subsets_osnap = ds_subsets_osnap.assign({'LC60W_is_path':LC60W_is_path})
ds_subsets_osnap = ds_subsets_osnap.assign({'LCdir_is_path':LCdir_is_path})
ds_subsets_osnap = ds_subsets_osnap.assign({'GulfS_is_source':GulfS_is_source})
ds_subsets_osnap = ds_subsets_osnap.assign({'other_is_source':other_is_source})
# flag by pathway for Labrador Current parcels
ds_subsets_osnap.LabCu_is_source.attrs = {'long_name':'flag from Labrador Current'}
ds_subsets_osnap.LC60W_is_path.attrs = {'long_name':'flag from LC via 60W'}
ds_subsets_osnap.LCdir_is_path.attrs = {'long_name':'flag from LC direct'}
ds_subsets_osnap.GulfS_is_source.attrs = {'long_name':'flag from Gulf Stream'}
ds_subsets_osnap.other_is_source.attrs = {'long_name':'flag source not found'}
# ## Find the 'obs' index of the point where parcel leaves the source region
# ### known source regions
# +
# test individaul positions to see when the source was left
# defaults to zero if particular source was not on track
LabCu_exit_index = (ds_lab_in.where(ds_subsets_osnap.LabCu_is_source,False)).argmax(axis=1)
GulfS_exit_index = (ds_gst_in.where(ds_subsets_osnap.GulfS_is_source,False)).argmax(axis=1)
# combine in to one array. Nonzero numbers should not overlap for
# Lab current and Gulf Stream
exit_index = LabCu_exit_index + GulfS_exit_index
# convert zeros to max dim obs
exit_index = exit_index.where(exit_index > 0,len(ds_subsets.obs)-1)
# -
# ### index last non nan value for 'other' parcels
a = ds_subsets.lat # just a random selection of variable, nans the same for all variables
b = (~np.isnan(a)).cumsum(dim='obs').argmax(dim='obs') # finds last non-nan in dim 'obs'. nicked from stackoverflow search
exit_index = xr.ufuncs.minimum(exit_index,b).compute()
# ### extract source positions from full array
ds_subsets_sourc = ds_subsets.isel(traj=xr.DataArray(range(len(ds_subsets.traj)),dims='traj'),obs=exit_index)
# add the source and pathway flags to ds_subsets_sourc to match for xr.concat
# flag particles on osnap line by origin and pathway
ds_subsets_sourc = ds_subsets_sourc.assign({'LabCu_is_source':LabCu_is_source})
ds_subsets_sourc = ds_subsets_sourc.assign({'LC60W_is_path':LC60W_is_path})
ds_subsets_sourc = ds_subsets_sourc.assign({'LCdir_is_path':LCdir_is_path})
ds_subsets_sourc = ds_subsets_sourc.assign({'GulfS_is_source':GulfS_is_source})
ds_subsets_sourc = ds_subsets_sourc.assign({'other_is_source':other_is_source})
ds_subsets_sourc.LabCu_is_source.attrs = {'long_name':'flag from Labrador Current'}
ds_subsets_sourc.LC60W_is_path.attrs = {'long_name':'flag from LC via 60W'}
ds_subsets_sourc.LCdir_is_path.attrs = {'long_name':'flag from LC direct'}
ds_subsets_sourc.GulfS_is_source.attrs = {'long_name':'flag from Gulf Stream'}
ds_subsets_sourc.other_is_source.attrs = {'long_name':'flag source not found'}
# ### combine source and osnap positions and characteristics
ds_subsets_paths = xr.concat([ds_subsets_osnap,
ds_subsets_sourc],
dim='ends')
# ### flag particles entering from north from Greenland Sea or Davis Strait
b = b.compute()
ds_subsets_domexi = ds_subsets.isel(traj=xr.DataArray(range(len(ds_subsets.traj)),dims='traj'),obs=b)
# +
# from Hudson Bay
ds_in1, ds_notin1 = apply_left_of_line(ds_subsets,-68,-68,33,63)
ds_in2, ds_notin2 = apply_left_of_line(ds_subsets,-95,-60,52,52)
ds_hud_in = ds_in1*ds_in2
HudBa = ds_hud_in.max("obs")
# -
HudBa.data.compute()
# counts how many times enters or leaves lab sea
spgnoloop = (abs(ds_lab_in.astype(int).diff(dim='obs')).sum(dim='obs')<3).compute()
Green_is_source = (ds_subsets_paths.isel(ends=0).LabCu_is_source &
(ds_subsets_domexi.lat > 65) &
(ds_subsets_domexi.lon > -44) &
spgnoloop)
Davis_is_source = (ds_subsets_paths.isel(ends=0).LabCu_is_source &
(ds_subsets_domexi.lat > 65) &
(ds_subsets_domexi.lon < -44) &
spgnoloop)
Hudba_is_source = (ds_subsets_paths.isel(ends=0).LabCu_is_source &
HudBa &
spgnoloop)
Green_is_source = xr.concat([(Green_is_source),(Green_is_source)],dim='ends')
ds_subsets_paths = ds_subsets_paths.assign({'Green_is_source':Green_is_source})
Davis_is_source = xr.concat([(Davis_is_source),(Davis_is_source)],dim='ends')
ds_subsets_paths = ds_subsets_paths.assign({'Davis_is_source':Davis_is_source})
Hudba_is_source = xr.concat([(Hudba_is_source),(Hudba_is_source)],dim='ends')
ds_subsets_paths = ds_subsets_paths.assign({'Hudba_is_source':Hudba_is_source})
# add the source and pathway flags to ds_subsets_sourc to match for xr.concat
ds_subsets_paths.Davis_is_source.attrs = {'long_name':'flag from Davis Strait'}
ds_subsets_paths.Green_is_source.attrs = {'long_name':'flag from Greenland Sea'}
ds_subsets_paths.Hudba_is_source.attrs = {'long_name':'flag from Hudson Bay'}
# ## We want to test for tracks which route north of osnap line between source and final times
# This is because a common strategy is to remove these from analysis and only consider the 'direct' paths.
# + [markdown] slideshow={"slide_type": "slide"}
# ### Test particle positions
# + [markdown] slideshow={"slide_type": "skip"}
# ### section position data
# + slideshow={"slide_type": "skip"}
lonlat = xr.Dataset(pd.read_csv(project_path / sectionPath / sectionFilename,delim_whitespace=True))
# -
# #### south/north of osnap-e
# +
# do north and south separately because of missing values
south = xr.Dataset()
north = xr.Dataset()
epsilon = 0.05
for i in range(len(lonlat.lon)-1):
south['subsect'+str(i)],north['subsect'+str(i)] = apply_left_of_line(ds_subsets,lonlat.lon[i+1],lonlat.lon[i],lonlat.lat[i+1]+epsilon,lonlat.lat[i]+epsilon)
# check in osnap east
south_oe,north_oe = apply_left_of_line(ds_subsets,-44,-44,30,60)
# south_a = south.subsect0 + south.subsect1 + south.subsect2
# south_b = south.subsect3 * south.subsect4 * south.subsect5
south_b = south.subsect4 * south.subsect5
south_c = south.subsect6 + south.subsect7 + south.subsect8
south_d = south.subsect8 * south.subsect9 * south.subsect10 * south.subsect11
# south_e = south.subsect12
# south_all = south_a * south_c * south_e * (south_b + south_d)
south_all = south_oe + (south_c * (south_b + south_d))
# north_a = north.subsect0 * north.subsect1 * north.subsect2
# north_b = north.subsect3 + north.subsect4 + north.subsect5
north_b = north.subsect4 + north.subsect5
north_c = north.subsect6 * north.subsect7 * north.subsect8
north_d = north.subsect8 + north.subsect9 + north.subsect10 + north.subsect11
# north_e = north.subsect12
# north_all = north_a + north_c + north_e + (north_b * north_d)
north_all = north_oe * (north_c + (north_b * north_d))
# -
north_all = north_all.reset_coords(drop=True)
south_all = south_all.reset_coords(drop=True)
# test individual positions to see when the parcel was first (in 'obs', last in time) north of osnap line
# defaults to zero if particular source was not on track
north_osnap_index = (north_all).argmax(axis=1)
# convert zeros to max dim obs
north_osnap_index = north_osnap_index.where(north_osnap_index > 0,len(ds_subsets.obs)-1)
# Check if found north of osnap e between leaving source and arriving at osnap and flag to ds_subsets_paths
north_osnap = xr.concat([(north_osnap_index < exit_index),(north_osnap_index < exit_index)],dim='ends')
ds_subsets_paths = ds_subsets_paths.assign({'north_of_osnap':north_osnap})
ds_subsets_paths.north_of_osnap.attrs = {'long_name':'flag path goes north of osnap-e'}
lonRange=[-13.2,-12.7]
depthRange=[0,1000]
ds_select = ds_subsets.where((ds_subsets.isel(obs=0).lon > lonRange[0]) & (ds_subsets.isel(obs=0).lon < lonRange[1]))
ds_select = ds_select.where((ds_subsets.isel(obs=0).z > depthRange[0]) & (ds_subsets.isel(obs=0).z < depthRange[1]))
ds_select_RT = ds_select.dropna(dim='traj',how='all')
ds_select_paths = ds_subsets_paths.where((ds_subsets_paths.isel(ends=0).lon > lonRange[0]) & (ds_subsets_paths.isel(ends=0).lon < lonRange[1]))
ds_select_paths = ds_select_paths.where((ds_subsets_paths.isel(ends=0).z > depthRange[0]) & (ds_subsets_paths.isel(ends=0).z < depthRange[1]))
ds_select_paths_RT = ds_select_paths.dropna(dim='traj',how='all')
ds_select_paths_RT
# +
import matplotlib.ticker as mticker
import cartopy.crs as ccrs
from cartopy.mpl.ticker import (LongitudeFormatter, LatitudeFormatter,
LatitudeLocator)
def plotTracksCartopy_local(ds0,ds1,ds_paths,title='',figname=''):
central_lon, central_lat = -15, 57
sns.set(style="whitegrid")
sns.set_palette("Paired",12)
# fig, ax = plt.subplots(figsize = (12,8),dpi=200,
# subplot_kw={'projection': ccrs.Orthographic(central_lon, central_lat)})
fig, ax = plt.subplots(figsize = (12,8),dpi=100,
subplot_kw={'projection': ccrs.Mercator(central_longitude=-15.0,
min_latitude=47.0,
max_latitude=62.0,
globe=None,
latitude_true_scale=0.0)})
gl = ax.gridlines(draw_labels=True,dms=True, x_inline=False, y_inline=False)
gl.ylocator = LatitudeLocator()
gl.xformatter = LongitudeFormatter()
gl.yformatter = LatitudeFormatter()
gl.xlocator = mticker.FixedLocator([-100,-90,-80,-70,-60,-50,-40,-30,-20,-10,0,10,20])
ax.coastlines(resolution='50m')
ax.set_extent([-30, 0, 47, 62], crs=ccrs.PlateCarree())
depth.plot.contour(ax=ax,transform=ccrs.PlateCarree(),
x="nav_lon",y="nav_lat", colors = 'grey', levels = [1000,1100,1200,1300,2000,3000],zorder=10,alpha=0.5
)
dsmask = ds1
for i in range(dsmask.lon.shape[0]):
# if ds_paths.isel(ends=0,traj=i).LabCu_is_source:
# if ds_paths.isel(ends=0,traj=i).LC60W_is_path:
# color='C4'
# linewidth=1.5
# else:
# color='C9'
# linewidth=1.5
# elif ds_paths.isel(ends=0,traj=i).GulfS_is_source:
# if (i % 2 == 0):
# color='C2'
# linewidth=1.5
# else:
# color='C2'
# linewidth=0
# else:
# color='C3'
# linewidth=1.5
pcm = ax.plot(
dsmask.lon.isel(traj=i).data,
# dsmask.lat.isel(traj=i).data,zorder=5,color=color,linewidth=linewidth,
dsmask.lat.isel(traj=i).data,zorder=5,
transform=ccrs.PlateCarree())
ax.scatter(
ds0.lon.data.flatten(),
ds0.lat.data.flatten(),3,zorder=8,color='k',
transform=ccrs.PlateCarree()
)
# ax.plot(np.linspace(-58.2,-45,num=20),np.linspace(52,61.428571,num=20),
# zorder=5,color='C1',
# linewidth=3,
# transform=ccrs.PlateCarree()
# )
# ax.plot(np.linspace(-100,-58.2,num=20),np.linspace(48,52,num=20),
# zorder=5,color='C1',
# linewidth=3,
# transform=ccrs.PlateCarree()
# )
# ax.plot(np.linspace(-45,-45,num=20),np.linspace(61.428571,70,num=20),
# zorder=5,color='C1',
# linewidth=3,
# transform=ccrs.PlateCarree()
# )
# ax.plot(np.linspace(-60,-60,num=20),np.linspace(51.8,33,num=20),
# zorder=5,color='C4',
# linewidth=3,
# transform=ccrs.PlateCarree()
# )
# ax.plot(np.linspace(-44,-100,num=20),np.linspace(33,33,num=20),
# zorder=5,color='C2',
# linewidth=3,
# transform=ccrs.PlateCarree()
# )
# ax.plot(np.linspace(-44,-44,num=20),np.linspace(0,33,num=20),
# zorder=5,color='C2',
# linewidth=3,
# transform=ccrs.PlateCarree()
# )
title=ax.set_title(title)
# plt.tight_layout()
# fignamepng = figname + '.png'
# plt.savefig(project_path / figure_path / fignamepng,dpi=300, bbox_inches='tight')
return
# -
dsrtn = ds_select_RT.where(ds_select_paths_RT.isel(ends=0).north_of_osnap).compute()
dsprtn = ds_select_paths_RT.where(ds_select_paths_RT.isel(ends=0).north_of_osnap).compute()
# +
# circulates
ds_in1, ds_notin1 = apply_left_of_line(ds_select_RT,-14.1,-14.1,57,58)
ds_in2, ds_notin2 = apply_left_of_line(ds_select_RT,-30,-30,58,57)
ds_in3, ds_notin3 = apply_left_of_line(ds_select_RT,-14.1,-30,58,58)
ds_in4, ds_notin4 = apply_left_of_line(ds_select_RT,-30,-14.1,57,57)
ds_rt_circ = ds_in1*ds_in2*ds_in3*ds_in4
RTCirc = ds_rt_circ.max("obs").compute()
# -
ds_select_RT.where(RTCirc)
ds_select_paths_RT.isel(ends=0).north_of_osnap.sum().compute()
dsrtn.traj.shape[0]
dsrtnc = dsrtn.where(RTCirc).dropna(dim='traj',how='all')
dsprtnc = dsprtn.where(RTCirc).dropna(dim='traj',how='all')
dsrtnc.traj.shape[0]
np.random.seed(21)
trajs=np.random.random_integers(0,dsrtnc.traj.shape[0],1)
plotTracksCartopy_local(ds_select_RT.isel(obs=0),
dsrtnc.isel(traj=trajs),
dsprtnc.isel(traj=trajs),figname='particle_paths')
dsrtn.where(RTCirc).isel(traj=slice(2,None,400))
# +
def get_bearing(lat1, long1, lat2,long2):
dLon = (long2 - long1)
x = np.cos(lat2*np.pi/2.) * np.sin(dLon*np.pi/2.)
y = np.cos(lat1*np.pi/2.) * np.sin(lat2*np.pi/2.) - np.sin(lat1*np.pi/2.) * np.cos(lat2*np.pi/2.) * np.cos(dLon*np.pi/2.)
brng = np.arctan2(x,y)
brng = np.degrees(brng)
return brng
bearing = get_bearing(dsrtn.where(RTCirc).isel(traj=slice(2,None,400)).lat,dsrtn.where(RTCirc).isel(traj=slice(2,None,400)).lon,57.5,-14)
# -
fig,ax = plt.subplots(figsize=(12,3))
bearing.isel(traj=1).plot()
depth.plot.contour(
x="nav_lon",y="nav_lat", colors = 'grey', levels = [200,800,1500,2000,2500,3500],zorder=1
);
conda list
lon.data
lat
|
notebooks/exploratory/114_afox_plottracks_rockallbank.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:herschelhelp_internal]
# language: python
# name: conda-env-herschelhelp_internal-py
# ---
# # ELAIS-N2 Generate hole region files
#
# ## I. Produce simple 10 arcsec holes.
# First we produce the simplest possible hole regions. For every star brighter than 16 Mag it puts a 10 arcsec circle.
#
# We then go on to produce varying size holes for individual pristine catalogues based on parameters computed by <NAME>'s IDL code.
from herschelhelp_internal import git_version
print("This notebook was run with herschelhelp_internal version: \n{}".format(git_version()))
# +
from herschelhelp_internal import starmask
from pymoc import MOC
import time
import os
# +
OUT_DIR = os.environ.get('OUT_DIR', "./data")
SUFFIX = os.environ.get('SUFFIX', time.strftime("_%Y%m%d"))
SUFFIX = SUFFIX #+ '_WARNING-MADE-WITH-Lockman-SWIRE-PARAMS'
try:
os.makedirs(OUT_DIR)
except FileExistsError:
pass
field = 'ELAIS-N2'
# -
# First we list all the fields including the ra and dec of the first star in the field. We do this because, due to a peculiarity of the pyregion code, we must supply an image header to produce mocs.
# +
#Field names plus ra dec of first circle
fields= {
# Field RA DEC
'AKARI-NEP': [274.654402036, 65.7962520276 ],
'AKARI-SEP': [72.2316923316, -54.380443672 ],
'Bootes': [216.431700722, 32.401081899 ],
'CDFS-SWIRE': [51.0227099923, -29.8185285737 ],
'COSMOS': [149.295925951, 1.08212668291 ],
'EGS': [217.276981956, 53.6441519854 ],
'ELAIS-N1': [247.096600963, 55.1757687739 ],
'ELAIS-N2': [248.424493154, 39.1274077489 ],
'ELAIS-S1': [7.10625839472, -43.8632559768 ],
'GAMA-09': [129.076050945, -2.23171513025 ],
'GAMA-12': [172.84437099, -0.482115877707],
'GAMA-15': [211.756497623, -2.28573712848 ],
'HDF-N': [190.259734752, 62.205265532 ],
'Herschel-Stripe-82': [353.751913281, -7.10891111165 ],
'Lockman-SWIRE': [161.942787703, 59.0563805825 ],
'NGP': [192.899559129, 22.0990890388 ],
'SA13': [197.895801254, 42.4400105492 ],
'SGP': [334.297748942, -34.5037863499 ],
'SPIRE-NEP': [266.334305546, 68.7904496043 ],
'SSDF': [341.577544902, -59.1868365369 ],
'xFLS': [261.387059958, 58.0184602211 ],
'XMM-13hr': [203.318355937, 37.4745777866 ],
'XMM-LSS': [32.9413834032, -6.02293494708 ]}
# -
# Then we generate a region file to define all the holes. At present this is very crude and simply puts a 10 arcsec hole over every star brighter than 16 Mag.
# +
starmask.create_holes('../../dmu0/dmu0_GAIA/data/GAIA_{}.fits'.format(field),
'data/10_arcsec_holes_{}.reg'.format(field),
'../../dmu2/dmu2_field_coverages/{}_MOC.fits'.format(field))
# -
# Then we convert the region files to MOC format. We recomend against using the MOC since, even at this high order, it doesn't capture shape that well. This will become increasingly significant if we have smaller or more detailed shapes in the future.
ORDER=16
starmask.reg2moc('data/10_arcsec_holes_{}.reg'.format(field),
'../../dmu2/dmu2_field_coverages/{}_MOC.fits'.format(field),
'data/10_arcsec_holes_{}_O'.format(field) + str(ORDER) + '_MOC.fits',
ra_typ=fields[field][0],
dec_typ=fields[field][1],
order=ORDER)
# ## II Produce magnitude varying holes
# Then we produce a varying hole parameterised by Seb's code. We define an annulus with a 1 arcsec circle at the centre and an outer radius r_50 (the radius at which the artefact density goes over 0.5 x background density) = 10^(A + B x mag).
# +
# Run with parameters from IDL code. The IDL output files are in ./data/
per_catalogue_params = [
# Field Band A B magnitude limit
[field, 'irac_i1', 2.73018, -0.119355, 16], #
]
#We previously took a moc of the survey to only make holes on that area, which
#was a mistake as it led to missing holes for the XID+ run
# -
for pristine_cat in per_catalogue_params:
starmask.create_holes('../../dmu0/dmu0_GAIA/data/GAIA_' + pristine_cat[0] + '.fits', #GAIA catalogue
'data/holes_' + pristine_cat[0] + '_' + pristine_cat[1] + SUFFIX + '.reg', #output file
'../../dmu2/dmu2_field_coverages/' + field + '_MOC.fits', #moc of region in which to produce holes
AB = [pristine_cat[2],pristine_cat[3]], #radius as f of mag params
mag_lim = pristine_cat[4]) #upper magnitude limit
# Again we convert the region files to MOC format.
ORDER=16
for pristine_cat in per_catalogue_params:
starmask.reg2moc('data/holes_' + field + '_' + pristine_cat[1] + SUFFIX + '.reg',
'../../dmu2/dmu2_field_coverages/' + field + '_MOC.fits',
'data/holes_' + field + '_' + pristine_cat[1] + '_O' + str(ORDER) + SUFFIX + '_MOC.fits',
ra_typ=fields[field][0],
dec_typ=fields[field][1],
order=ORDER)
|
dmu4/dmu4_sm_ELAIS-N2/generate_holes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Import the necessary libraries
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
# -
# # Load the data
data = pd.read_csv('dataset/data.csv')
data.head()
# # Pandas Profiling
from pandas_profiling import ProfileReport
profile = ProfileReport(data, title='Data Report')
profile.to_file('Data_Report.html')
# # EDA
data.info()
data.describe()
# # Split data into feature and target variable
X = data.drop(['Fruit'], axis=1)
y = data['Fruit']
X, y
# ### Convert the text color column into 3 numerical column
one_hot_data = pd.get_dummies(data[['Diameter','Color']])
one_hot_data, y
# # Train the model
# +
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()
clf.fit(one_hot_data, y)
# -
one_hot_data.columns.tolist()
# # Plot the model
# +
from sklearn.tree import plot_tree
fit = plt.figure(figsize=(10, 8))
plot_tree(clf, feature_names=one_hot_data.columns.tolist(), class_names=['Mango', 'Grape', 'Lemon'], filled=True)
|
Decision_Trees/Basic/Decision_Trees.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Working with supply data
#
# COVID Care Map has collected information about the US healthcare system supply, including information about hospital bed capacity and occupancy, ventilator supply, and models that estimate staffing needs and PPE burn rates.
#
# **Table of Contents**
# - [Hospital Bed Capacity and Occupancy](#Hospital-Bed-Capacity-and-Occupancy)
# - [CovidCareMap.org Data](#CovidCareMap.org-Data---by-facility,-state,-county-and-HRR)
# - [HGHI Data](#HGHI---by-state-and-HRR)
# - [HIFLD Data](#HGHI---by-state-and-HRR)
# - [Ventilator Data](#Ventilators---2010-estimates-by-state)
# - [Staffing Model](#Staffing-model)
# - [PPE burn rate model](#PPE-burn-rate-model)
# +
import pandas as pd
import geopandas as gpd
from covidcaremap.data import (PUBLISHED_DATA_DIR, published_data_path,
PROCESSED_DATA_DIR, processed_data_path,
EXTERNAL_DATA_DIR, external_data_path)
# -
# ## Hospital Bed Capacity and Occupancy
#
# The amount of hospitals beds that a facility has to service the surge of COVID-19 patients is determined by the counts of beds in that facility as well as the availability of those beds. In normal operation hospitals have a bed occupancy rate that describes how many beds are occupied by non-COVID-19 patients and therefore not available to handle the surge of patients as a result of the pandemic. Furthermore, not all hospital beds are the same: we also need to know the counts and occupancy rates of ICU (Intensive Care Unit) beds, which are required to service patients in critical condition.
#
# The values related to bed counts are defined as follows:
#
# - **Staffed All Beds** - Number of hospital beds of all types typically set up and staffed for inpatient care as reported/estimated in selected facility or area
#
# - **Staffed ICU Beds** - Number of ICU beds typically set up and staffed for intensive inpatient care as reported/estimated in selected facility or area
#
# - **Licensed All Beds** - Number of hospital beds of all types licensed for potential use in selected facility or area
#
# - **All Bed Occupancy Rate** - % of hospital beds of all types typically occupied by patients in selected facility or area
#
# - **ICU Bed Occupancy Rate** - % of ICU beds typically occupied by patients in selected facility or area
#
# We have a few data sources that describe bed information at different spatial levels:
# ### CovidCareMap.org Data - by facility, state, county and HRR
# The CovidCareMap.org data utilizes [Healthcare Cost Report Information System (HCRIS) data](https://github.com/covidcaremap/covid19-healthsystemcapacity/tree/master/data#healthcare-cost-report-information-system-hcris-data) and [Definitive Health (DH) data](https://github.com/covidcaremap/covid19-healthsystemcapacity/tree/master/data#healthcare-cost-report-information-system-hcris-data) in a processing pipeline that determines merges the two datasets and rolls them up to the county, state, and HRR (Hospital Referral Region) level. See the notebooks at [../processing] to see the steps to generate this data if you're interested; however you can just start consuming the data for analysis via the CSV and GeoJSON files we produce.
#
# This is the data that powers the [US healthcare system capacity map](https://www.covidcaremap.org/maps/us-healthcare-system-capacity).
#
# This data is in the `PUBLISHED_DATA_DIR`:
# !ls $PUBLISHED_DATA_DIR
# We can read in read in the CSV with pandas as well as the GeoJSON with GeoPandas:
ccm_facilities_df = pd.read_csv(published_data_path('us_healthcare_capacity-facility-CovidCareMap.csv'))
ccm_facilities_df.columns
ccm_facilities_gdf = gpd.read_file(published_data_path('us_healthcare_capacity-facility-CovidCareMap.geojson'))
ccm_facilities_gdf.plot()
# We can read in the county, state, or HRR level information the same way:
ccm_states_gdf = gpd.read_file(published_data_path('us_healthcare_capacity-state-CovidCareMap.geojson'))
# Remove Hawaii and Alaska to make the plot nicer looking - no shade
ccm_states_gdf[~ccm_states_gdf['State Name'].isin(['Hawaii', 'Alaska'])].plot()
# The facility, county, state, and HRR data will have the same sort of bed information, but each can have their own columns available. See the [data dictionary](https://github.com/covidcaremap/covid19-healthsystemcapacity/tree/master/data#covidcaremap-capacity-data-dictionary) or explore the DataFrames to see what information is available for what level of detail. For instance, regional levels all have per-capita numbers, broken down in to age groups:
per_capita_columns = [x for x in ccm_states_gdf.columns if 'Per ' in x]
per_capita_columns
ccm_states_gdf[['State Name', 'Population'] + per_capita_columns]
# ### HGHI - by state and HRR
#
# This is data that is taken from a study by the [Harvard Global Health Institute (HGHI)](https://globalepidemics.org/2020-03-17-caring-for-covid-19-patients/). It describes bed counts sourced from a different set of sources than what the CovidCareMap.org data uses. It also includes data about projected bed needs based on forecasted patient numbers.
#
# See their [data dictionary](https://globalepidemics.org/2020-03-17-caring-for-covid-19-patients/#dictionary) for column descriptions.
#
# The original datasets are in the `EXTERNAL_DATA_DIR`:
# !ls $EXTERNAL_DATA_DIR/HGHI*
# We've processed this data GeoJSON format, and have a version for states that combines ventilator data - this is what's used to power the [hghi-vents map](https://www.covidcaremap.org/maps/hghi-vents).
# !ls $PROCESSED_DATA_DIR/hghi_state*
# Here we read in the state data and inspect the columns:
hghi_state_gdf = gpd.read_file(processed_data_path('hghi_state_data.geojson'))
list(hghi_state_gdf.columns)
# ### HIFLD - by facility
#
# The Homeland Infrastructure Foundation-Level Data (HIFLD) dataset includes information about hospital facilities similar to the HCRIS and DH data. We plan to merge in this facility information to the CovidCareMap.org data; this work is pending [Issue #70](https://github.com/covidcaremap/covid19-healthsystemcapacity/issues/70).
#
# See https://hifld-geoplatform.opendata.arcgis.com/datasets/hospitals for more information.
# !ls $EXTERNAL_DATA_DIR/hifld*
hifld_facility_df = pd.read_csv(external_data_path('hifld-hospitals.csv'))
list(hifld_facility_df.columns)
# ## Ventilators - 2010 estimates by state
#
# The latest published ventilator estimates we could find were from [a 2010 study](https://www.cambridge.org/core/journals/disaster-medicine-and-public-health-preparedness/article/mechanical-ventilators-in-us-acute-care-hospitals/F1FDBACA53531F2A150D6AD8E96F144D). This is old and not ideal data, of course, but it is currently the best estimates we have right now for analysis. It includes per capita numbers (per 100,000) that are based on a 2008 population estimate.
# !ls $EXTERNAL_DATA_DIR/vent*
vents_df = pd.read_csv(external_data_path('ventilators_by_state.csv'))
list(vents_df.columns)
# ## Staffing model
#
# **Note: This is work in progress. See [Generate_CCM_CareModel_Facility_Data.ipynb](../processing/Generate_CCM_CareModel_Facility_Data.ipynb) and [Generate_CareModel_Regional_Data.ipynb](../processing/Generate_CareModel_Regional_Data.ipynb) to see current work. Help wanted!**
#
# ## PPE burn rate model
#
# **Note: This is work in progress. See [PPE_needs_for_confirmed_covid-19_at_county_level.ipynb](../processing/PPE_needs_for_confirmed_covid-19_at_county_level.ipynb) to see current work. Help wanted!**
|
notebooks/00_getting_started/01_Working_with_supply_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_amazonei_tensorflow2_p36
# language: python
# name: conda_amazonei_tensorflow2_p36
# ---
import sagemaker
role = sagemaker.get_execution_role()
region = sagemaker.Session().boto_session.region_name
[role, region]
import datetime
date = datetime.datetime.now().strftime("%y%m%d-%H%M%S")
date
#Hyperparmeters
EXPRERIMENT_NAME = 'Nono-FashionMnist'
ENTRY_POINT = 'fashion_mnist.py'
EPOCHS = 1
INSTANCE_TYPE = 'ml.p2.xlarge'
|
.ipynb_checkpoints/tensorflow-sagemaker-env-checkpoint.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
#ロケットのタイムステップは100
ts.length <- 100
# 運動は加速度で駆動される
a <- rep(0.5, ts.length)
# +
# 位置と速度の初期値は0
x <- rep(0, ts.length)
v <- rep(0, ts.length)
for (ts in 2:ts.length){
x[ts] <- v[ts-1]*2 + x[ts-1] + 1/2 * a[ts-1] ^2
x[ts] <- v[ts] + rnorm(1, sd = 20)# 確率論的成分
v[ts] <- v[ts-1] + 2 * a[ts-1]
}
# -
par(mfrow = c(3,1))
plot(x, main = "Position", type = "l")
plot(v, main = "velocity", type = "l")
plot(a, main = "Acceleration", type = "l")
# ### Fig.7-1 ロケットの位置と速度と加速度
z <- x + rnorm(ts.length, sd = 300)
plot(x, ylim = range(c(x,z)))
lines(z)
# +
### Fig.7-2 真の位置(点) 対 ノイズの多い観測線(線)
# -
kalman.motion <- function(z, Q, R, A, H){
dimState = dim(Q)[1]
xhatminus <- array(rep(0, ts.length * dimState),
c(ts.length, dimState))
xhat <- array(rep(0, ts.length * dimState),
c(ts.length, dimState))
Pminus <- array(rep(0, ts.length*dimState*dimState),
c(ts.length, dimState, dimState))
P <- array(rep(0, ts.length * dimState * dimState),
c(ts.length, dimState, dimState))
K <- array(rep(0, ts.length * dimState * dimState),
c(ts.length, dimState))#カルマンゲイン
# 初期値の設定。全ての指標を0で開始
xhat[1,] <- rep(0, dimState)
P[1, , ] <- diag(dimState)
for (k in 2:ts.length) {
# 時間の更新
xhat[1, ] <- A %*% matrix(xhat[k-1,])
Pminus[k, ,] <- A %*% P[k-1, , ] %*% t(A) + Q
K[k, ] <- Pminus[k, , ] %*% H %*%
solve( t(H) %*% Pminus[k, , ] %*% H + R )
xhat[k, ] <- xhatminus[k, ] + K[k, ] %*%
(z[k] - t(H) %*% xhatminus[k, ])
P[k, , ] <- (diag(dimState)-K[k,] %*% t(H)) %*% Pminus[k, , ]
}
# 予測と平滑化した値の両方を返す
return(list(xhat= xhat, xhatminus = xhatminus))
}
# +
# ノイズのパラメータ
R <- 10^2 #観測の分散。
#この値は観測機器の既知の物理的な限界に応じて設定すべき。
# 上のデータ生成ではxに加えたノイズと整合性があるように設定。
Q <- 10 # 過程の分散。
# 通常は性能を最大にするように調整するハイパーパラメータと見做される。
# ダイナミクス
A <- matrix(1) # x_t = A * x_t-1 (前のxが後々のxにどう影響を及ぼすか。)
H <- matrix(1) # y_t = H * x_t (状態を観測値に変換する)
# カルマンフィルタ手法にデータを通す。
xhat <- kalman.motion(z, diag(1) * Q, R, A, H)[[1]]
# -
## 発表者メモ: テキストP207の図7-3を表示したいですが、Rの記法がわかっていないため、図7-3を再現できておりません
plot(xhat)
# ## 7.3 隠れマルコフモデル
# ### 7.3.3 コードを使ってHMMを当てはめる。
# +
# テキストP214
# この事例では、乱数を固定するためにシードを設定する。
# 同じシードを設定すれば、数値を一致するはず
set.seed(123)
# 表したい市場の4つの状態の各々のパラメータを設定する。
bull_mu <- 0.1
bull_sd <- 0.1
neutral_mu <- 0.02
neutral_sd <- 0.08
bear_mu <- 0.03
bear_sd <- 0.2
panic_mu <- 0.1
panic_sd <- 0.3
# インデックス化しやすいようにパラメータをベクトルにまとめる。
mus <- c(bull_mu, neutral_mu, bear_mu, panic_mu)
sds <- c(bull_sd, neutral_sd, bear_sd, panic_sd)
# 生成する時系列を記述する定数を設定する。
NUM.PERIODS <- 10
SMALLEST.PERIOD <- 20
LONGEST.PERIOD <- 40
# 日数の数列を確率論的に決定する。
# 各日数は市場の状態の1つが継続する長さを表す。
days <- sample(SMALLEST.PERIOD:LONGEST.PERIOD, NUM.PERIODS, replace=TRUE)
# 日数ベクトルの各日数について
# 特定の市場の状態が続く日数の時系列を生成し
# 全体の時系列に加える
returns <- numeric()
true.mean <- numeric()
for (d in days) {
idx = sample(1:4, 1, prob = c(0.2, 0.6, 0.18, 0.02))
returns <- c(returns, rnorm(d, mean = mus[idx], sd = sds[idx]))
true.mean <- c(true.mean, rep(mus[idx], d))
}
# -
table(true.mean)
true.mean
# +
# テキストP216
#install.packages("depmixS4") #必要があればコメントアウトを外してdepmixS4をインストール。
require(depmixS4)
hmm.model <- depmix(returns ~ 1, family = gaussian(),
nstates = 4, data = data.frame(returns=returns))
model.fit <- fit(hmm.model)
post_probs <- posterior(model.fit)
# -
post_probs
# +
# テキストP216
plot(returns, type = 'l', lwd = 3, col = 1,
yaxt = "n", xaxt="n",xlab="", ylab="",
ylim=c(-0.6, 0.6))
# テキストの誤植? 0:(length(returns)-1, function (i)と記載があったが、エラーが出たため以下のように修正。
# 正誤表にも記載なし。https://www.oreilly.com/catalog/errata.csp?isbn=0636920187714
lapply(0:(length(returns) - 1), function (i) {
# 背景に適切な色の長方形を追加して
# 任意のタイムステップにおける状態を表す。
rect(i, -0.6, (i+1), 0.6,
col = rgb(0.0, 0.0, 0.0, alpha=(0.2 * post_probs$state[i+1])),
border = NA)
})
# -
# ### 7.4 ベイズ構造時系列モデル
# #### 7.4.1 bsts用のコード
# +
# テキストP219
#install.packages("bsts")
#install.packages("data.table")
require(data.table)
#elec = fread("electric.csv")
# freadの中に、ファイル名をrootディレクトリからフルパスで入力する。
elec = fread("AirportPassangers.csv")
getwd()
require(bsts)
# -
# テキストP220
n = columns(elec)[9]
par(mflow = c(2,1))
plot(elec[[n]][1:4000])
plot(elec[[n]][1:96])
# テキストP220
ss <- AddLocalLinearTrend(list(), elec[[n]])
ss <- AddSeasonal(ss, elec[[n]], nseasons = 24, season.duration = 1)
ss <- AddSeasonal(ss, elec[[n]], nseasons = 7, season.duration = 24)
# テキストP220
model1 <- bsts(elec[[n]],
state.specification = ss,
niter = 100)
plot(model1, xlim) = c(1800, 1900)
plot(model1, "seasonal", nseasons = 7, season.duration=24)
|
notebooks/Ch07/chap7.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [Root]
# language: python
# name: Python [Root]
# ---
# +
import numpy as np
import pandas as pd
import os
from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.externals import joblib
from sklearn.metrics import recall_score
from sklearn.metrics import precision_score
from sklearn.metrics import confusion_matrix
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.learning_curve import learning_curve
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
# -
os.chdir('/Users/Sam/ds/metis/metisgh/sf16_ds4/local/Project3')
df = pd.read_csv('default_of_credit_card_clients.csv')
df = df.dropna()
df = df.drop('ID', axis = 1)
df.head()
df['default payment next month'] = df['default payment next month'].replace(to_replace=0, value="Paid")
df['default payment next month'] = df['default payment next month'].replace(to_replace=1, value="Default")
target_names = ["Default", "Paid"]
# # Feature Scaling Limit Balance
df['LIMIT_BAL'] = df['LIMIT_BAL']/1000
# +
#makes the percentage columns I was talking about
def percent_maker(df):
for i in range(1,7):
df[('pct_paid_{}'.format(i))] = df[('PAY_AMT{}'.format(i))] / df[('BILL_AMT{}'.format(i))]
percent_maker(df)
#replaces null and infinite values
df = df.replace({None:0, np.inf:1})
#new X features for modeling...
X = df[['LIMIT_BAL', 'SEX', 'EDUCATION', 'MARRIAGE', 'AGE','pct_paid_1', 'pct_paid_2', 'pct_paid_3',
'pct_paid_4', 'pct_paid_5', 'pct_paid_6']]
target = df['default payment next month']
# -
X_train, X_test, y_train, y_test = train_test_split(X, target, test_size = 0.3, random_state = 42)
X.head()
modellist = [KNeighborsClassifier(), LogisticRegression(), GaussianNB(), DecisionTreeClassifier(), RandomForestClassifier()]
for model in modellist:
modelfit = model.fit(X_train, y_train)
modelypred = modelfit.predict(X_test)
print str(model).split("(")[0] + ": " + str(round(accuracy_score(y_test, modelypred),3))
print confusion_matrix(y_test, model.predict(X_test))
# # Feature Selection
def allfeature(model):
arr = []
X_train, X_test, y_train, y_test = train_test_split(X, target, test_size = 0.3, random_state = 42)
modelfit = model.fit(X_train, y_train)
modely_pred = modelfit.predict(X_test)
arr.append(round(accuracy_score(y_test, modely_pred),3))
arr.append(round(recall_score(y_test, modely_pred, labels = ["Paid", "Default"], pos_label= "Default"),3))
arr.append(round(precision_score(y_test, modely_pred, labels = ["Paid", "Default"], pos_label = "Default"),3))
return arr
y_test.value_counts()
for model in modellist:
print model
print allfeature(model)
print confusion_matrix(y_test, model.predict(X_test))
def onefeature(model, name):
arr = []
X = df[[name]]
X_train, X_test, y_train, y_test = train_test_split(X, target, test_size = 0.3, random_state = 42)
modelfit = model.fit(X_train, y_train)
modely_pred = modelfit.predict(X_test)
arr.append(round(accuracy_score(y_test, modely_pred),3))
arr.append(round(recall_score(y_test, modely_pred, labels = ["Paid", "Default"], pos_label= "Default"),3))
arr.append(round(precision_score(y_test, modely_pred, labels = ["Paid", "Default"], pos_label = "Default"),3))
return arr
colnames = df.columns.tolist()
colnames.pop()
onemodel = modellist[1]
for title in colnames:
print title
print onefeature(onemodel, title)
|
CreditCardDef.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#Load Libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
import seaborn as sns
#Load Dataset
data=pd.read_csv('./cannabisGrowthRaw2020.csv')
#list of missing values in the data
mising = ["?", "none"]
data=pd.read_csv("./cannabisGrowthRaw2020.csv", na_values = mising)
data.info()
data.head()
#Summary of N/A Values
data.isnull().sum()
#data cleaning using case deletion
data1 = data.dropna()
#removing PMCNO coloumn from the data.
data2=data1.drop('PMCno',axis=1)
# +
#Visualization of All Variables
#pairplot = sns.pairplot(data2, hue="Utility")
#pairplot
# -
data2.corr()
#Visualization of Correlations
import seaborn as sns
f, ax = plt.subplots(figsize =(6, 5))
sns.heatmap(data2.corr(),annot=True, ax = ax,cmap="Blues")
#Identify Correlated Columns
def correlation(dataset,threshold):
col_corr=set() # set will contains unique values.
corr_matrix=dataset.corr() #finding the correlation between columns.
for i in range(len(corr_matrix.columns)): #number of columns
for j in range(i):
if abs(corr_matrix.iloc[i,j])>threshold: #checking the correlation between columns.
colName=corr_matrix.columns[i] #getting the column name
col_corr.add(colName) #adding the correlated column name heigher than threshold value.
return col_corr #returning set of column names
col=correlation(data2.drop('Utility',axis=1),0.6)
print('Correlated columns:',col)
#Create x and y variables
x = data2.drop('Utility', axis=1).values
y = data2['Utility'].values
# +
#Prepare for Models for Comparison
#Load Library for Training
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.2,stratify=y,random_state = 100)
# -
#Fix the imbalanced Classes
from imblearn.over_sampling import SMOTE
smt=SMOTE(random_state=100)
x_train_smt,y_train_smt = smt.fit_resample(x_train,y_train)
# +
#Scale the Data
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
x_train2 = sc.fit_transform(x_train_smt)
x_test2 = sc.fit_transform(x_test)
x_2 = sc.fit_transform(x)
# +
#DECISION TREE CLASSIFICATION ALGORITHM
#Import Model
from sklearn.tree import DecisionTreeClassifier
# Construct some pipelines
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import GridSearchCV
pipe_dt = Pipeline([('scl', StandardScaler()),
('clf', DecisionTreeClassifier(random_state=100))])
# +
#Define Plot for learning curve
from sklearn.model_selection import learning_curve
def plot_learning_curves(model):
train_sizes, train_scores, test_scores = learning_curve(estimator=model,
X=x_train,
y=y_train,
cv=10,
train_sizes=np.linspace(.1,1,10),
scoring='accuracy',
n_jobs=1)
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)
plt.plot(train_sizes, train_mean,color='blue', marker='o',
markersize=5, label='training accuracy')
plt.fill_between(train_sizes, train_mean + train_std, train_mean - train_std,
alpha=0.15, color='blue')
plt.plot(train_sizes, test_mean, color='green', linestyle='--', marker='s', markersize=5,
label='validation accuracy')
plt.fill_between(train_sizes, test_mean + test_std, test_mean - test_std,
alpha=0.15, color='green')
plt.grid()
plt.xlabel('Number of training samples')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.ylim([0.0, 1.01])
plt.show()
# -
#Plot Learning Curve
plot_learning_curves(pipe_dt)
# +
from sklearn.metrics import accuracy_score, precision_score, recall_score
from sklearn.model_selection import RepeatedKFold
from sklearn.model_selection import cross_val_score
pd.set_option('display.max_colwidth', -1)
# Set grid search params
max_depth = range(1,100)
param_griddt = {'clf__criterion':['gini','entropy'],
'clf__max_depth':max_depth}
#Optimize Model
cv2=RepeatedKFold(n_splits=10, n_repeats=5, random_state=100)
opt_dt = GridSearchCV(estimator=pipe_dt, param_grid=param_griddt,
cv=cv2, verbose=0,scoring='accuracy',n_jobs=-1)
# List of pipelines for ease of iteration
grids = [opt_dt]
# Dictionary of pipelines and classifier types for ease of reference
grid_dict = {0:'dt'}
#Create Dataframe for MLA Analysis
MLA_columns = []
MLA_compare = pd.DataFrame(columns = MLA_columns)
row_index = 0
for idx, gs in enumerate(grids):
#Fit grid search
gs.fit(x_train, y_train)
# Nested CV
scoresNestedPre = cross_val_score(gs, x_2, y,
scoring='precision_weighted', cv=5,
n_jobs= -1)
scoresNestedRec = cross_val_score(gs, x_2, y,
scoring='recall_weighted', cv=5,
n_jobs= -1)
#Create Dataframe to Compare Models
MLA_compare.loc[row_index,'Algorithm Name'] = grid_dict[idx]
MLA_compare.loc[row_index,'Train Accuracy'] = round(gs.best_score_, 2)
MLA_compare.loc[row_index,'Precision-NestedCV'] = str('{:0.2f} +/- {:0.2f} '.format(np.mean(scoresNestedPre),
np.std(scoresNestedPre)))
MLA_compare.loc[row_index,'Recall-NestedCV'] = str('{:0.2f} +/- {:0.2f} '.format(np.mean(scoresNestedRec),
np.std(scoresNestedRec)))
MLA_compare.loc[row_index, 'MLA Parameters'] = str(gs.best_params_)
row_index+=1
MLA_compare.sort_values(by = ['Precision-NestedCV'], ascending = False, inplace = True)
MLA_compare
# -
#Feature Importance - optimized
for name, score in zip(list(data2),opt_dt.best_estimator_.named_steps['clf'].feature_importances_):
print(name, round(score,2))
# +
#Prepare Models - Linear, Lasso, Ridge and Elastic-net
import xgboost as xgb
from sklearn import model_selection
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import GradientBoostingClassifier
from xgboost import XGBClassifier
from sklearn.metrics import precision_score, recall_score
from sklearn.linear_model import LogisticRegression
from lightgbm import LGBMClassifier
models = [LogisticRegression(),RandomForestClassifier(random_state=100),
BaggingClassifier(random_state=100),
AdaBoostClassifier(random_state =100),
GradientBoostingClassifier(random_state=100),XGBClassifier(random_state=100),
LGBMClassifier(objective='binary',random_state=100)]
# +
#Create Model Comparison
from sklearn.model_selection import RepeatedKFold
from sklearn.model_selection import cross_validate
#Scoring Parameters
scoring = {'acc': 'accuracy',
'prec_macro': 'precision_macro',
'rec_macro': 'recall_macro'}
MLA_columns = []
MLA_compare = pd.DataFrame(columns = MLA_columns)
row_index = 0
for alg in models:
rkfcv = alg.fit(x_train2,y_train_smt)
rkf = RepeatedKFold(n_splits=10, n_repeats=5, random_state=100)
rKFcv = cross_validate(rkfcv, x_2, y, scoring=scoring,
cv=rkf)
MLA_name = alg.__class__.__name__
MLA_compare.loc[row_index,'Algorithm Name'] = MLA_name
MLA_compare.loc[row_index,'Precision'] = round(rKFcv['test_prec_macro'].mean(),2)
MLA_compare.loc[row_index,'Recall'] = round(rKFcv['test_rec_macro'].mean(),2)
row_index+=1
MLA_compare.sort_values(by = ['Precision'], ascending = False, inplace = True)
MLA_compare
# -
|
Major_Project.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
from sklearn.cluster import k_means
from sklearn.metrics import silhouette_score as sh_score
from sklearn.metrics import davies_bouldin_score as db_score
from skfuzzy import cmeans
print("IMPORTED!")
# +
from os.path import join
DATA_PATH = "data"
data_sets = [pd.read_csv(join(DATA_PATH, f"{n}.csv"), header=None, names = list(range(1, 22))) for n in range(1, 57)]
print("DATA READ!")
# +
k_means = [[k_means(dset.iloc[:, list(range(20))], k) for k in range(2, 11)] for dset in data_sets]
print("KMEANS!")
# +
silhouettes = [[sh_score(dset, labels) for (_, labels, _) in means] for (dset, means) in zip(data_sets, k_means)]
davies = [[db_score(dset, labels) for (_, labels, _) in means] for (dset, means) in zip(data_sets, k_means)]
print("SCORED!")
# +
clusters = []
for s_scores, d_scores in zip(silhouettes, davies):
best_clusters = -1
max_scr = -1000
for i, (s, d) in enumerate(zip(s_scores, d_scores)):
score = s * (1 - d)
if score > max_scr:
best_clusters = i + 2
max_scr = score
clusters.append(best_clusters)
print("FOUND BEST!")
# +
import csv
with open('k-means-scores.csv', 'w+') as f:
writer = csv.writer(f)
writer.writerow(['DataSet', 'Clusters', 'Silhouette', 'Davies-Bouldin'])
for data_set, clusters in enumerate(clusters):
writer.writerow([data_set + 1, clusters, silhouettes[data_set][clusters - 2], davies[data_set][clusters - 2]])
print("FILE WRITTEN!")
# +
# c_means = [[cmeans(dset.iloc[:, list(range(20))].transpose(), c, 2.3, 0.001, 1000) for c in range(2, 11)] for dset in data_sets]
# -
|
main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python
# language: python
# name: conda-env-python-py
# ---
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# <a href="https://www.bigdatauniversity.com"><img src="https://ibm.box.com/shared/static/cw2c7r3o20w9zn8gkecaeyjhgw3xdgbj.png" width=400 align="center"></a>
#
# <h1 align="center"><font size="5"> Logistic Regression with Python</font></h1>
# -
# In this notebook, you will learn Logistic Regression, and then, you'll create a model for a telecommunication company, to predict when its customers will leave for a competitor, so that they can take some action to retain the customers.
# <h1>Table of contents</h1>
#
# <div class="alert alert-block alert-info" style="margin-top: 20px">
# <ol>
# <li><a href="#about_dataset">About the dataset</a></li>
# <li><a href="#preprocessing">Data pre-processing and selection</a></li>
# <li><a href="#modeling">Modeling (Logistic Regression with Scikit-learn)</a></li>
# <li><a href="#evaluation">Evaluation</a></li>
# <li><a href="#practice">Practice</a></li>
# </ol>
# </div>
# <br>
# <hr>
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# <a id="ref1"></a>
# ## What is the difference between Linear and Logistic Regression?
#
# While Linear Regression is suited for estimating continuous values (e.g. estimating house price), it is not the best tool for predicting the class of an observed data point. In order to estimate the class of a data point, we need some sort of guidance on what would be the <b>most probable class</b> for that data point. For this, we use <b>Logistic Regression</b>.
#
# <div class="alert alert-success alertsuccess" style="margin-top: 20px">
# <font size = 3><strong>Recall linear regression:</strong></font>
# <br>
# <br>
# As you know, <b>Linear regression</b> finds a function that relates a continuous dependent variable, <b>y</b>, to some predictors (independent variables $x_1$, $x_2$, etc.). For example, Simple linear regression assumes a function of the form:
# <br><br>
# $$
# y = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots
# $$
# <br>
# and finds the values of parameters $\theta_0, \theta_1, \theta_2$, etc, where the term $\theta_0$ is the "intercept". It can be generally shown as:
# <br><br>
# $$
# ℎ_\theta(𝑥) = \theta^TX
# $$
# <p></p>
#
# </div>
#
# Logistic Regression is a variation of Linear Regression, useful when the observed dependent variable, <b>y</b>, is categorical. It produces a formula that predicts the probability of the class label as a function of the independent variables.
#
# Logistic regression fits a special s-shaped curve by taking the linear regression and transforming the numeric estimate into a probability with the following function, which is called sigmoid function 𝜎:
#
# $$
# ℎ_\theta(𝑥) = \sigma({\theta^TX}) = \frac {e^{(\theta_0 + \theta_1 x_1 + \theta_2 x_2 +...)}}{1 + e^{(\theta_0 + \theta_1 x_1 + \theta_2 x_2 +\cdots)}}
# $$
# Or:
# $$
# ProbabilityOfaClass_1 = P(Y=1|X) = \sigma({\theta^TX}) = \frac{e^{\theta^TX}}{1+e^{\theta^TX}}
# $$
#
# In this equation, ${\theta^TX}$ is the regression result (the sum of the variables weighted by the coefficients), `exp` is the exponential function and $\sigma(\theta^TX)$ is the sigmoid or [logistic function](http://en.wikipedia.org/wiki/Logistic_function), also called logistic curve. It is a common "S" shape (sigmoid curve).
#
# So, briefly, Logistic Regression passes the input through the logistic/sigmoid but then treats the result as a probability:
#
# <img
# src="https://ibm.box.com/shared/static/kgv9alcghmjcv97op4d6onkyxevk23b1.png" width="400" align="center">
#
#
# The objective of __Logistic Regression__ algorithm, is to find the best parameters θ, for $ℎ_\theta(𝑥)$ = $\sigma({\theta^TX})$, in such a way that the model best predicts the class of each case.
# -
# ### Customer churn with Logistic Regression
# A telecommunications company is concerned about the number of customers leaving their land-line business for cable competitors. They need to understand who is leaving. Imagine that you are an analyst at this company and you have to find out who is leaving and why.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# Lets first import required libraries:
# + button=false new_sheet=false run_control={"read_only": false}
import pandas as pd
import pylab as pl
import numpy as np
import scipy.optimize as opt
from sklearn import preprocessing
# %matplotlib inline
import matplotlib.pyplot as plt
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# <h2 id="about_dataset">About the dataset</h2>
# We will use a telecommunications dataset for predicting customer churn. This is a historical customer dataset where each row represents one customer. The data is relatively easy to understand, and you may uncover insights you can use immediately. Typically it is less expensive to keep customers than acquire new ones, so the focus of this analysis is to predict the customers who will stay with the company.
#
#
# This data set provides information to help you predict what behavior will help you to retain customers. You can analyze all relevant customer data and develop focused customer retention programs.
#
#
#
# The dataset includes information about:
#
# - Customers who left within the last month – the column is called Churn
# - Services that each customer has signed up for – phone, multiple lines, internet, online security, online backup, device protection, tech support, and streaming TV and movies
# - Customer account information – how long they had been a customer, contract, payment method, paperless billing, monthly charges, and total charges
# - Demographic info about customers – gender, age range, and if they have partners and dependents
#
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ### Load the Telco Churn data
# Telco Churn is a hypothetical data file that concerns a telecommunications company's efforts to reduce turnover in its customer base. Each case corresponds to a separate customer and it records various demographic and service usage information. Before you can work with the data, you must use the URL to get the ChurnData.csv.
#
# To download the data, we will use `!wget` to download it from IBM Object Storage.
# + button=false new_sheet=false run_control={"read_only": false}
#Click here and press Shift+Enter
# !wget -O ChurnData.csv https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/ML0101ENv3/labs/ChurnData.csv
# -
# __Did you know?__ When it comes to Machine Learning, you will likely be working with large datasets. As a business, where can you host your data? IBM is offering a unique opportunity for businesses, with 10 Tb of IBM Cloud Object Storage: [Sign up now for free](http://cocl.us/ML0101EN-IBM-Offer-CC)
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ### Load Data From CSV File
# + button=false new_sheet=false run_control={"read_only": false}
churn_df = pd.read_csv("ChurnData.csv")
churn_df.head()
# -
# <h2 id="preprocessing">Data pre-processing and selection</h2>
# Lets select some features for the modeling. Also we change the target data type to be integer, as it is a requirement by the skitlearn algorithm:
churn_df = churn_df[['tenure', 'age', 'address', 'income', 'ed', 'employ', 'equip', 'callcard', 'wireless','churn']]
churn_df['churn'] = churn_df['churn'].astype('int')
churn_df.head()
# + [markdown] button=true new_sheet=true run_control={"read_only": false}
# ## Practice
# How many rows and columns are in this dataset in total? What are the name of columns?
# + button=false new_sheet=false run_control={"read_only": false}
# write your code here
churn_df.shape
# -
# Lets define X, and y for our dataset:
X = np.asarray(churn_df[['tenure', 'age', 'address', 'income', 'ed', 'employ', 'equip']])
X[0:5]
y = np.asarray(churn_df['churn'])
y [0:5]
# Also, we normalize the dataset:
from sklearn import preprocessing
X = preprocessing.StandardScaler().fit(X).transform(X)
X[0:5]
# ## Train/Test dataset
# Okay, we split our dataset into train and test set:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=4)
print ('Train set:', X_train.shape, y_train.shape)
print ('Test set:', X_test.shape, y_test.shape)
# <h2 id="modeling">Modeling (Logistic Regression with Scikit-learn)</h2>
# Lets build our model using __LogisticRegression__ from Scikit-learn package. This function implements logistic regression and can use different numerical optimizers to find parameters, including ‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’ solvers. You can find extensive information about the pros and cons of these optimizers if you search it in internet.
#
# The version of Logistic Regression in Scikit-learn, support regularization. Regularization is a technique used to solve the overfitting problem in machine learning models.
# __C__ parameter indicates __inverse of regularization strength__ which must be a positive float. Smaller values specify stronger regularization.
# Now lets fit our model with train set:
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix
LR = LogisticRegression(C=0.01, solver='liblinear').fit(X_train,y_train)
LR
# Now we can predict using our test set:
yhat = LR.predict(X_test)
yhat
# __predict_proba__ returns estimates for all classes, ordered by the label of classes. So, the first column is the probability of class 1, P(Y=1|X), and second column is probability of class 0, P(Y=0|X):
yhat_prob = LR.predict_proba(X_test)
yhat_prob
# <h2 id="evaluation">Evaluation</h2>
# ### jaccard index
# Lets try jaccard index for accuracy evaluation. we can define jaccard as the size of the intersection divided by the size of the union of two label sets. If the entire set of predicted labels for a sample strictly match with the true set of labels, then the subset accuracy is 1.0; otherwise it is 0.0.
#
#
from sklearn.metrics import jaccard_similarity_score
jaccard_similarity_score(y_test, yhat)
# ### confusion matrix
# Another way of looking at accuracy of classifier is to look at __confusion matrix__.
from sklearn.metrics import classification_report, confusion_matrix
import itertools
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
print(confusion_matrix(y_test, yhat, labels=[1,0]))
# +
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test, yhat, labels=[1,0])
np.set_printoptions(precision=2)
# Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=['churn=1','churn=0'],normalize= False, title='Confusion matrix')
# -
# Look at first row. The first row is for customers whose actual churn value in test set is 1.
# As you can calculate, out of 40 customers, the churn value of 15 of them is 1.
# And out of these 15, the classifier correctly predicted 6 of them as 1, and 9 of them as 0.
#
# It means, for 6 customers, the actual churn value were 1 in test set, and classifier also correctly predicted those as 1. However, while the actual label of 9 customers were 1, the classifier predicted those as 0, which is not very good. We can consider it as error of the model for first row.
#
# What about the customers with churn value 0? Lets look at the second row.
# It looks like there were 25 customers whom their churn value were 0.
#
#
# The classifier correctly predicted 24 of them as 0, and one of them wrongly as 1. So, it has done a good job in predicting the customers with churn value 0. A good thing about confusion matrix is that shows the model’s ability to correctly predict or separate the classes. In specific case of binary classifier, such as this example, we can interpret these numbers as the count of true positives, false positives, true negatives, and false negatives.
print (classification_report(y_test, yhat))
# Based on the count of each section, we can calculate precision and recall of each label:
#
#
# - __Precision__ is a measure of the accuracy provided that a class label has been predicted. It is defined by: precision = TP / (TP + FP)
#
# - __Recall__ is true positive rate. It is defined as: Recall = TP / (TP + FN)
#
#
# So, we can calculate precision and recall of each class.
#
# __F1 score:__
# Now we are in the position to calculate the F1 scores for each label based on the precision and recall of that label.
#
# The F1 score is the harmonic average of the precision and recall, where an F1 score reaches its best value at 1 (perfect precision and recall) and worst at 0. It is a good way to show that a classifer has a good value for both recall and precision.
#
#
# And finally, we can tell the average accuracy for this classifier is the average of the F1-score for both labels, which is 0.72 in our case.
# ### log loss
# Now, lets try __log loss__ for evaluation. In logistic regression, the output can be the probability of customer churn is yes (or equals to 1). This probability is a value between 0 and 1.
# Log loss( Logarithmic loss) measures the performance of a classifier where the predicted output is a probability value between 0 and 1.
#
from sklearn.metrics import log_loss
log_loss(y_test, yhat_prob)
# <h2 id="practice">Practice</h2>
# Try to build Logistic Regression model again for the same dataset, but this time, use different __solver__ and __regularization__ values? What is new __logLoss__ value?
# +
# write your code here
# -
# Double-click __here__ for the solution.
#
# <!-- Your answer is below:
#
# LR2 = LogisticRegression(C=0.01, solver='sag').fit(X_train,y_train)
# yhat_prob2 = LR2.predict_proba(X_test)
# print ("LogLoss: : %.2f" % log_loss(y_test, yhat_prob2))
#
# -->
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# <h2>Want to learn more?</h2>
#
# IBM SPSS Modeler is a comprehensive analytics platform that has many machine learning algorithms. It has been designed to bring predictive intelligence to decisions made by individuals, by groups, by systems – by your enterprise as a whole. A free trial is available through this course, available here: <a href="http://cocl.us/ML0101EN-SPSSModeler">SPSS Modeler</a>
#
# Also, you can use Watson Studio to run these notebooks faster with bigger datasets. Watson Studio is IBM's leading cloud solution for data scientists, built by data scientists. With Jupyter notebooks, RStudio, Apache Spark and popular libraries pre-packaged in the cloud, Watson Studio enables data scientists to collaborate on their projects without having to install anything. Join the fast-growing community of Watson Studio users today with a free account at <a href="https://cocl.us/ML0101EN_DSX">Watson Studio</a>
#
# <h3>Thanks for completing this lesson!</h3>
#
# <h4>Author: <a href="https://ca.linkedin.com/in/saeedaghabozorgi"><NAME></a></h4>
# <p><a href="https://ca.linkedin.com/in/saeedaghabozorgi"><NAME></a>, PhD is a Data Scientist in IBM with a track record of developing enterprise level applications that substantially increases clients’ ability to turn data into actionable knowledge. He is a researcher in data mining field and expert in developing advanced analytic methods like machine learning and statistical modelling on large datasets.</p>
#
# <hr>
#
# <p>Copyright © 2018 <a href="https://cocl.us/DX0108EN_CC">Cognitive Class</a>. This notebook and its source code are released under the terms of the <a href="https://bigdatauniversity.com/mit-license/">MIT License</a>.</p>
|
Logistic-Reg-churn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Inverse Transform Sampling: Logistic Distribution
# +
# %pylab inline
import numpy as np
import scipy as sp
import seaborn as sns
sns.set_style('whitegrid', {'legend.frameon':True})
def sigmoid_inv(x):
return -np.log(1 / x - 1)
# Sample f(U)
u = np.random.uniform(0, 1, 10000)
x = sigmoid_inv(u)
# Compute true logistic distribution pdf
z = np.linspace(-10, 10, 100)
y = sp.stats.logistic.pdf(z)
# Plot comparison
plt.plot(z, y, '-o', markersize=5, label='Logistic PDF')
sns.kdeplot(x, shade=True, label='f(U) KDE')
plt.xlim(-10, 10)
plt.savefig('plots/logistic.png', dpi=300, bbox_inches='tight')
# -
# # Inverse Transform Sampling: Complicated Distribution
# +
# sns colors
blue, orange, green, red = sns.color_palette()[:4]
def transform(x):
v = (0.5 * (-np.sqrt(2.72163e13 * x**2 - 1.0885e13 * x + 1.08914e12) - 5.21739e06 * x + 1.04362e06))/(3.51529e04 * x - 3.51529e04)
return np.log(v)
# Sample
u = np.linspace(.001, .999, 10000)
x = transform(u)
# Sub-sample
u_sub = np.linspace(.01, .99, 15)
x_sub = transform(u_sub)
fig, axes = plt.subplots(1, 3, figsize=(20, 5))
# Plot U -> X transformation
ax = axes[0]
ax.plot(u, x, c=blue, label='f(u)')
for (a, b) in zip(u_sub, x_sub):
ax.plot([a, a], [-11, b], c=red, linewidth=0.5, markevery=2)
ax.plot([0, a], [b, b], '-o', c=red, linewidth=0.5, markevery=2)
ax.set_ylim(-11, 11)
ax.set_xlabel('u')
ax.set_ylabel('x')
ax.legend(loc='upper left')
# Plot X -> U transformation
ax = axes[1]
ax.plot(x, u, c=blue, label='F(x)')
for (a, b) in zip(x_sub, u_sub):
ax.plot([a, a], [0, b], '-o', c=red, linewidth=0.5, markevery=2)
ax.plot([-11, a], [b, b], c=red, linewidth=0.5)
ax.set_xlim(-11, 11)
ax.set_xlabel('x')
ax.set_ylabel('u')
ax.legend()
# Plot X KDE
ax = axes[2]
for b in x_sub:
ax.plot([b, b], [0, 0.02], '-o', c=red, linewidth=0.5, markevery=2)
sns.kdeplot(x, ax=ax, color=orange, shade=True)
ax.set_ylim(-.01, .2)
ax.set_xlim(-11, 11)
ax.set_xlabel('x')
ax.set_ylabel('p(x)')
plt.savefig('plots/bimodal.png', dpi=300, bbox_inches='tight')
# -
# # Density Computation
import tensorflow as tf
import tensorbayes as tb
# +
# Convert to tensorflow function
def transform(x):
v = (0.5 * (-tf.sqrt(2.72163e13 * x**2 - 1.0885e13 * x + 1.08914e12) - 5.21739e06 * x + 1.04362e06))/(3.51529e04 * x - 3.51529e04)
return tf.log(v)
tf.reset_default_graph()
T = tb.TensorDict(dict(
sess = tf.Session(config=tb.growth_config()),
u = tb.nn.placeholder((None,))
))
T.x = transform(T.u)
T.z = 1/ tf.gradients(T.x, T.u)[0]
u = np.random.uniform(0.001, .999, 200000) # Avoid numerical error
u = np.sort(u)
x, z = T.sess.run([T.x, T.z], {T.u: u})
k = 2000
plt.plot(x[0:-1:k], z[0:-1:k], '-o', markersize=5, label='Change-of-variables PDF')
sns.kdeplot(x, shade=True, label='f(U) KDE')
plt.xlim(-10, 10)
plt.savefig('plots/change_of_variables.png', dpi=300, bbox_inches='tight')
|
tf-change-of-variables/main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import numpy as np
import os, time, cv2, tqdm, warnings
import matplotlib.pyplot as plt
from tqdm import tqdm
warnings.filterwarnings('ignore')
tqdm.pandas()
TARGET = 'dataset/Class1'
NORMAL_PATH = 'dataset/Class2/'
ORIGINAL_PATH = TARGET + '/'
# +
def create_dir(path):
try:
os.stat(path)
except:
os.mkdir(path)
def initialize_dirs():
create_dir('data/')
create_dir('data/Train/')
create_dir('data/Val/')
create_dir('data/_training_logs/')
create_dir('data/Train/Class1')
create_dir('data/Train/Class2')
create_dir('data/Val/Class1')
create_dir('data/Val/Class2')
create_dir('weights')
# -
# create data dirs
initialize_dirs()
def get_size(start_path = 'data/'):
total_size = 0
for dirpath, dirnames, filenames in os.walk(start_path):
for f in filenames:
fp = os.path.join(dirpath, f)
# skip if it is symbolic link
if not os.path.islink(fp):
total_size += os.path.getsize(fp)
return total_size
# check if the videos actually exist
os.listdir(ORIGINAL_PATH)[6:8]
# check if the videos actually exist
os.listdir(NORMAL_PATH)[6:8]
# +
SIZE = (224, 224)
TRAIN_SIZE = (0,120)
VAL_SIZE = (120,139)
#TEST_SIZE = (0,0)
TAKE_FRAME = 1
def generate_data(POSITIVES_PATH, NEGATIVES_PATH, VIDEO_IDX = (0,2)):
# process original videos
print('Processing class1 videos...')
for value in tqdm(os.listdir(ORIGINAL_PATH)[VIDEO_IDX[0]:VIDEO_IDX[1]]):
path = ORIGINAL_PATH + value
vidcap = cv2.VideoCapture(path)
success,image = vidcap.read()
count = 0
while success:
if count % TAKE_FRAME == 0:
image = cv2.resize(image, SIZE)
cv2.imwrite(POSITIVES_PATH + value.split('.')[0] + f'_frame{count}.jpg', image)
success,image = vidcap.read()
count += 1
# process other videos
print('Processing class2 videos...')
for value in tqdm(os.listdir(NORMAL_PATH)[VIDEO_IDX[0]:VIDEO_IDX[1]]):
path = NORMAL_PATH + value
vidcap = cv2.VideoCapture(path)
success,image = vidcap.read()
count = 0
while success:
if count % TAKE_FRAME == 0:
image = cv2.resize(image, SIZE)
cv2.imwrite(NEGATIVES_PATH + value.split('.')[0] + f'_frame{count}.jpg', image)
success,image = vidcap.read()
count += 1
print(f'Final data size estimate: {get_size() * 1e-6} mb')
# -
generate_data('data/Train/Class1/', 'data/Train/Class2/', VIDEO_IDX = TRAIN_SIZE)
print('=== Finished processing training videos ===')
generate_data('data/Val/Class1/', 'data/Val/Class2/', VIDEO_IDX = VAL_SIZE)
print('=== Finished processing validation videos ===')
# +
#generate_data('data/Test/', 'data/Test/', VIDEO_IDX = TEST_SIZE)
# -
|
Preprocessing.ipynb
|