problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
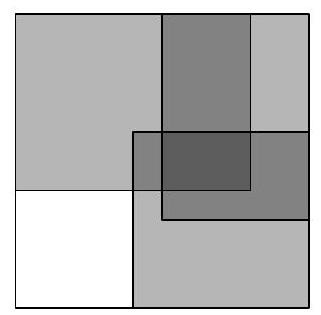
Problem 9.4. From left to right, intersecting squares with sides $12, 9, 7, 3$ are depicted respectively. By how much is the sum of the black areas greater than the sum of the gray areas?
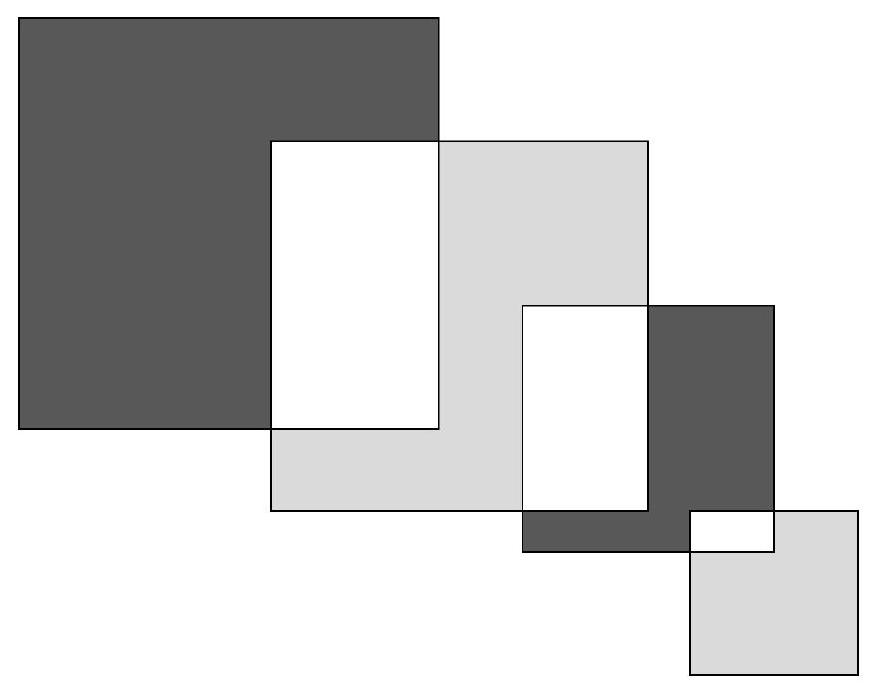
|
Answer: 103.
Solution. Let's denote the areas by $A, B, C, D, E, F, G$.
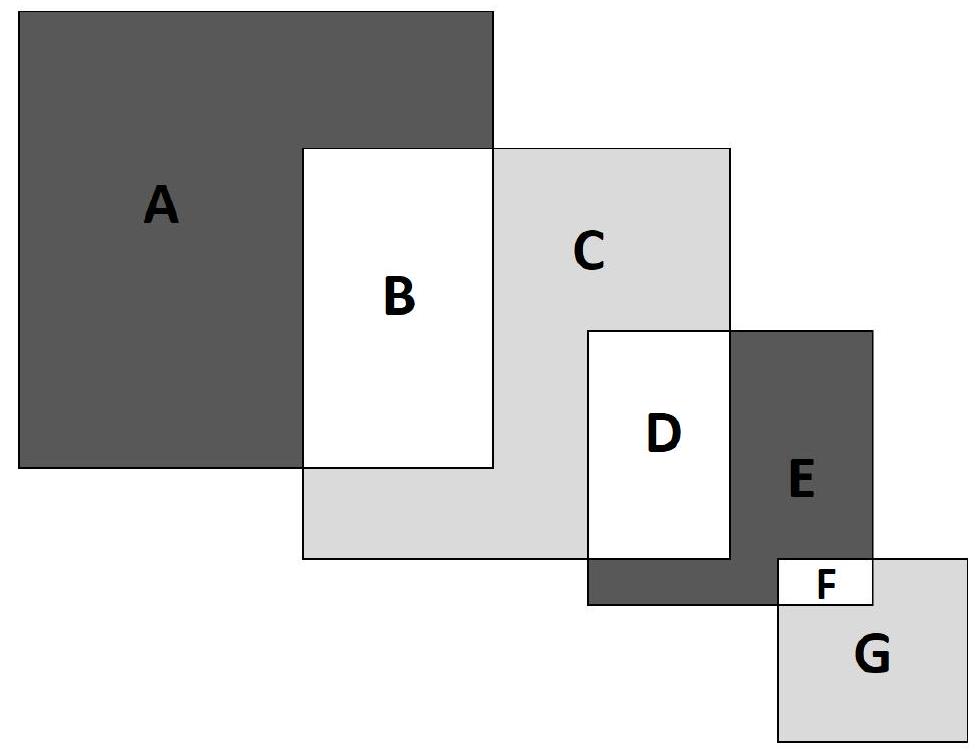
We will compute the desired difference in areas:
$$
\begin{aligned}
A+E-(C+G) & =A-C+E-G=A+B-B-C-D+D+E+F-F-G= \\
& =(A+B)-(B+C+D)+(D+E+F)-(F+G)= \\
& =12^{2}-9^{2}+7^{2}-3^{2}=103
\end{aligned}
$$
|
103
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.7. In triangle $ABC$, the bisector $AL$ is drawn. Points $E$ and $D$ are marked on segments $AB$ and $BL$ respectively such that $DL = LC$, $ED \parallel AC$. Find the length of segment $ED$, given that $AE = 15$, $AC = 12$.
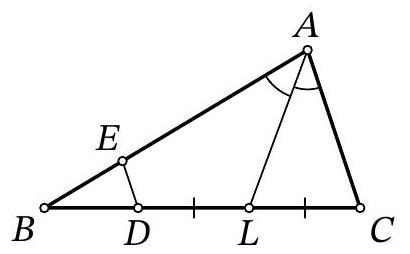
|
Answer: 3.
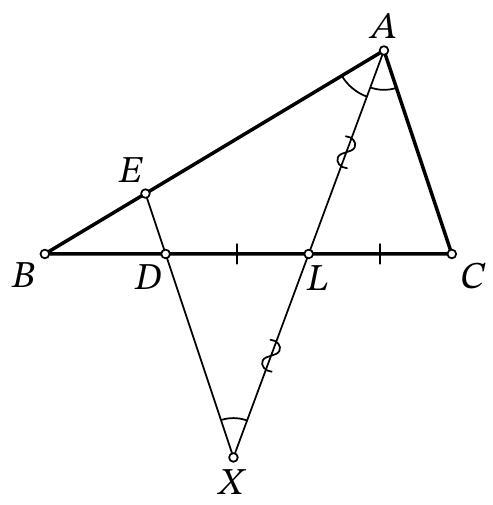
Fig. 5: to the solution of problem 9.7
Solution. On the ray $AL$ beyond point $L$, mark a point $X$ such that $XL = LA$ (Fig. 5). Since in the quadrilateral $ACXD$ the diagonals are bisected by their intersection point $L$, it is a parallelogram (in particular, $AC = DX$). Therefore, $DX \parallel AC$. Since $AC \parallel ED$ by the problem's condition, the points $X, D, E$ lie on the same line.
Since $AC \parallel EX$, then $\angle EAX = \angle CAX = \angle AXE$, i.e., triangle $AEX$ is isosceles, $EA = EX$. Then
$$
ED = EX - XD = EA - AC = 15 - 12 = 3
$$
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
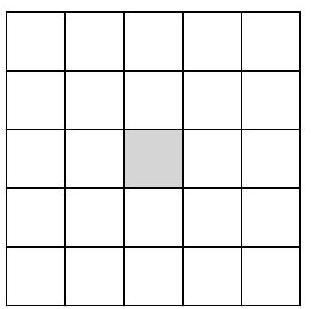
Problem 10.1. In each cell of a $5 \times 5$ table, a natural number is written in invisible ink. It is known that the sum of all the numbers is 200, and the sum of three numbers inside any $1 \times 3$ rectangle is 23. What is the central number in the table?
|
Answer: 16.
Solution. Divide the $5 \times 5$ square without the central cell into four $2 \times 3$ rectangles, and each of these into two $1 \times 3$ rectangles.
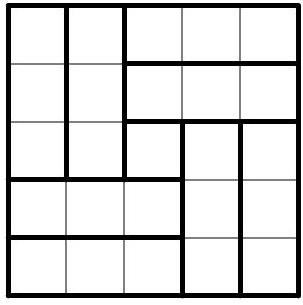
This results in 8 rectangles of $1 \times 3$, the sum of the numbers in each of which is 23. Since the sum of all the numbers is 200, we find the number in the central cell as $200 - 23 \cdot 8 = 16$.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
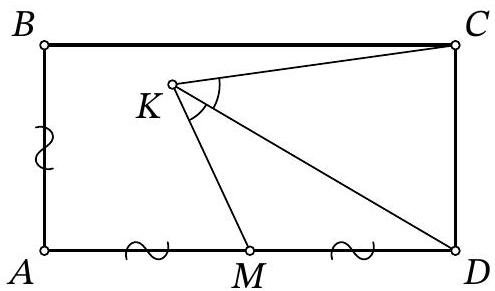
Problem 10.8. Rectangle $ABCD$ is such that $AD = 2AB$. Point $M$ is the midpoint of side $AD$. Inside the rectangle, there is a point $K$ such that $\angle AMK = 80^{\circ}$ and ray $KD$ is the bisector of angle $MKC$. How many degrees does angle $KDA$ measure?
|
Answer: 35.
Solution. Let's start with the assumption that the quadrilateral KMDС is inscribed (several proofs of this fact will be proposed below).
Using the fact that in the inscribed quadrilateral $K M D C$ the sum of opposite angles is $180^{\circ}$, we get $\angle M K D=\frac{\angle M K C}{2}=\frac{180^{\circ}-\angle M D C}{2}=45^{\circ}$. The angle $A M K$ as an external angle for triangle $K D M$ is equal to the sum of angles $M K D$ and $K D A$, so the required angle КDA is $80^{\circ}-45^{\circ}=35^{\circ}$.

Fig. 8: to the solution of problem 10.8
Let's provide the first possible proof of the inscribed nature of quadrilateral KMDC. Consider triangle $M K C$ and its circumscribed circle. Note that point $D$ lies on the bisector of angle $M K C$, and is equidistant from vertices $M$ and $C$ (Fig. 8). However, the bisector of an angle in a non-isosceles triangle and the perpendicular bisector of its opposite side, as is known, intersect at the midpoint of the "smaller" arc of the circumscribed circle of the triangle. In other words, $D$ is the midpoint of the arc $M C$ of the circumscribed circle of triangle $M K C$, not containing point $K$. It should also be noted that $M K \neq K C$ (otherwise, triangles $K M D$ and $K C D$ would be equal, but $\angle K M D>90^{\circ}>\angle K C D$ ).
Let's provide the second possible proof of the inscribed nature of quadrilateral KMDC. It will use the fourth criterion for the equality of triangles: if two sides and an angle not between them are equal in two triangles, then these triangles are either equal or the sum of the other two angles not between them is $180^{\circ}$. The fourth criterion is satisfied for triangles $M D K$ and $C D K (M D=D C, D K$ - common, $\angle M K D=\angle C K D)$. However, angles $K M D$ and $K C D$ are not equal (again, the first is obtuse, and the second is acute), so their sum is $180^{\circ}$, which are the opposite angles of quadrilateral KMDC. Therefore, it is inscribed.
## 11th grade
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
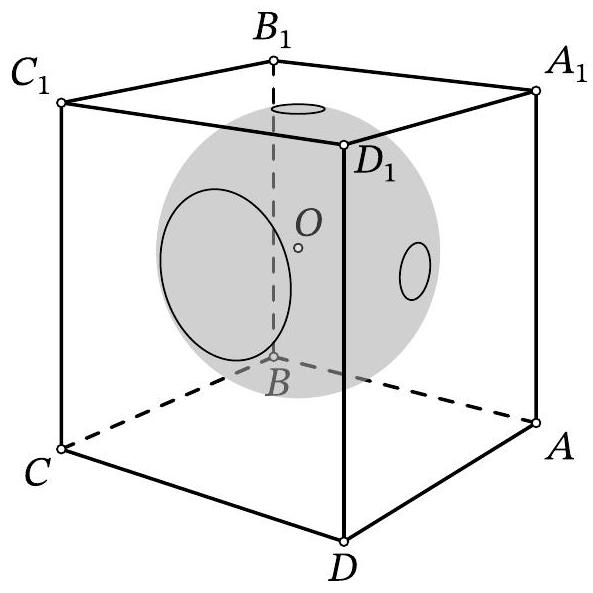
Problem 11.6. Inside the cube $A B C D A_{1} B_{1} C_{1} D_{1}$, there is the center $O$ of a sphere with radius 10. The sphere intersects the face $A A_{1} D_{1} D$ along a circle with radius 1, the face $A_{1} B_{1} C_{1} D_{1}$ along a circle with radius 1, and the face $C D D_{1} C_{1}$ along a circle with radius 3. Find the length of the segment $O D_{1}$.
|
Answer: 17.
Solution. Let $\omega$ be the circle that the sphere cuts out on the face $C D D_{1} C_{1}$. From point $O$
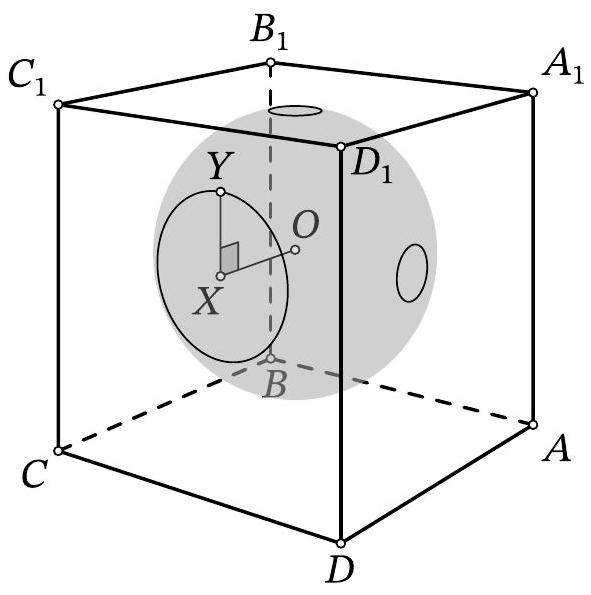
Fig. 10: to the solution of problem 11.6
drop a perpendicular $O X$ to this face, then point $X$ is the center of $\omega$ (point $O$ is equidistant from all points of $\omega$, so the projection of $O$ onto the plane of $\omega$ is also equidistant from them). Let $Y$ be an arbitrary point on $\omega$ (Fig. 10). Triangle $OXY$ is a right triangle; by the problem's condition, $X Y=3$ and $O Y=10$. By the Pythagorean theorem, we get $O X^{2}=10^{2}-3^{2}=91$.
Similarly, we find the squares of the distances from point $O$ to the planes $A_{1} B_{1} C_{1} D_{1}$ and $A D D_{1} A_{1}$, which are both equal to $10^{2}-1^{2}=99$.
By the spatial Pythagorean theorem, the square of the length of segment $O D_{1}$ is equal to the sum of the squares of the distances from point $O$ to the three faces containing point $D_{1}$. Therefore, $O D_{1}^{2}=$ $91+99+99=289$, from which $O D_{1}=17$.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. On the side $AC$ of triangle $ABC$, a point $M$ is taken. It turns out that $AM = BM + MC$ and $\angle BMA = \angle MBC + \angle BAC$. Find $\angle BMA$.
|
Answer: $60^{\circ}$. Solution. First, we show that triangle $A B C$ is isosceles. Indeed, this follows from the condition $\angle B M A=\angle M B C+\angle B A C$ and the property of the exterior angle: $\angle B M A=\angle M B C+\angle B C A$. From these two equalities, we have $\angle B C A=\angle B A C$, and thus, triangle $A B C$ is isosceles. Next, we take a point $K$ on side $A C$ that is symmetric to point $M$ with respect to point $O$ - the midpoint of $A C$. Then $A K=M C$ and therefore from the relation $A M=B M+M C$ it follows that point $M$ lies between $C$ and $O$ and, hence, this relation gives $K M=B M$. Since $\triangle A B C$ is isosceles, point $O$ coincides with the projection of point $B$ onto the base $A C$, and therefore $B M=B K$. Thus, in triangle $K B M$ all sides are equal, meaning it is equilateral and all its angles are $60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (7 points) The first term of the sequence is 934. Each subsequent term is equal to the sum of the digits of the previous term, multiplied by 13. Find the $2019-$th term of the sequence.
|
Solution. Let's find the first few terms of the sequence:
$a_{1}=934 ; a_{2}=16 \cdot 13=208 ; a_{3}=10 \cdot 13=130 ; a_{4}=4 \cdot 13=52 ;$
$a_{5}=7 \cdot 13=91 ; a_{6}=10 \cdot 13=130=a_{3}$.
Since each subsequent number is calculated using only the previous number, the terms of the sequence will repeat with a period of 3 from this point on. The number 2019 is a multiple of 3, so $a_{2019}=a_{3}=130$.
Answer. 130.
|
130
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) The function $f$ is such that for any $x>0, y>0$ the equality $f(x y)=f(x)+f(y)$ holds. Find $f(2019)$, if $f\left(\frac{1}{2019}\right)=1$.
|
Solution. When $y=1 \quad f(x)=f(x)+f(1), f(1)=0$.
When $x=2019 \quad y=\frac{1}{2019} f(1)=f(2019)+f\left(\frac{1}{2019}\right)$,
$f(2019)=f(1)-f\left(\frac{1}{2019}\right)$
$f(2019)=-f\left(\frac{1}{2019}\right)=-1$.
Answer. $f(2019)=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (7 points) On side $AB$ of triangle $ABC$, a point $K$ is marked, and on side $AC$ - a point $M$. Segments $BM$ and $CK$ intersect at point $P$. It turns out that angles $APB$, $BPC$, and $CPA$ are each $120^{\circ}$, and the area of quadrilateral $AKPM$ is equal to the area of triangle $BPC$. Find the angle $BAC$.
#
|
# Solution.
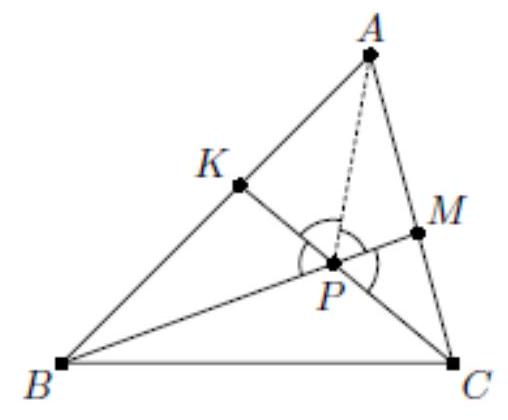
Add the area of triangle $B P K$ to both sides of the equality $S_{\text {AKPM }}=S_{\text {BPC }}$:
$$
\begin{aligned}
& S_{A K P M}+S_{B P K}=S_{B P C}+S_{B P K}, \\
& S_{A B M}=S_{B C K} .
\end{aligned}
$$
Therefore, $\frac{1}{2} A B \cdot A M \cdot \sin \angle A=\frac{1}{2} B K \cdot B C \cdot \sin \angle B$.
Then $\frac{B K}{A M}=\frac{A B \cdot \sin \angle A}{B C \cdot \sin \angle B}$.
By the Law of Sines: $\quad \frac{B C}{\sin \angle A}=\frac{A C}{\sin \angle B}$. Thus, $\quad \frac{\sin \angle A}{\sin \angle B}=\frac{B C}{A C}$, $\frac{B K}{A M}=\frac{A B \cdot B C}{B C \cdot A C} \Leftrightarrow \frac{B K}{A B}=\frac{A M}{A C}$.
Thus, points $K$ and $M$ divide segments $B A$ and $A C$ in the same ratio, counting from vertices $B$ and $A$ respectively, that is, $\frac{B K}{K A}=\frac{A M}{M C}$.
$\angle B P K=\angle K P A=\angle A P M=\angle M P C=60^{\circ}$ (angles adjacent to the given angles of $120^{\circ}$). Therefore, $P K$ and $P M$ are the angle bisectors of triangles $A P B$ and $A P C$ respectively. By the Angle Bisector Theorem, we get: $\frac{B K}{K A}=\frac{B P}{P A}$ and $\frac{A M}{M C}=\frac{A P}{P C}$. Considering equality (1), we get that $\frac{B P}{P A}=\frac{A P}{P C}$.
Moreover, $\angle B P A=\angle A P C=120^{\circ}$. Thus, triangles $B P A$ and $A P C$ are similar (by two sides and the angle between them). Therefore, $\angle P A C=\angle P B A$.
Thus, $\angle B A C=\angle B A P+\angle P A C=\angle B A P+\angle P B A=180^{\circ}-120^{\circ}=60^{\circ}$.
Answer. $60^{0}$.
Maximum points - 35.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1 Four princesses each thought of a two-digit number, and Ivan thought of a four-digit number. After they wrote down their numbers in a row in some order, the result was 132040530321. Find Ivan's number.
Answer: 5303
|
Solution: Let's go through the options. Option 1320 is not suitable because the remaining part of the long number is divided into segments of two adjacent digits: $40,53,03,21$, and the segment 03 is impossible as it is not a two-digit number. Option 3204 is impossible due to the invalid segment 05 (or the segment 1 from a single digit). Option 2040 results in the segment 03, which is not possible. Option 0405 is not an option - it is a three-digit number. Option 4053 results in the impossible segment 03. Option 0530 is not possible. Option 5303 is the only possible one, as option 3032 leads to a segment of one digit 1.
|
5303
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3 It is known that for some natural number $n$ each of the numbers $3 n-1$ and $n-10$ is divisible by a prime number p. Find the number p.
|
Answer: 29
Solution. The number $3 n-1-3(n-10)=29$ is divisible by p. Since $29$ is a prime number, then $\mathrm{p}=29$.
|
29
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4 In the class, there are more than 30 people but less than 40. Any boy is friends with three girls, and any girl is friends with five boys. How many people are in the class?
|
Answer: 32
Solution. Let $\mathrm{m}$ be the number of boys, $\mathrm{d}$ be the number of girls, and $\mathrm{r}$ be the number of friendly pairs "boy-girl". According to the problem, $\mathrm{r}=3 \mathrm{~m}$ and $\mathrm{r}=5 \mathrm{~d}$. Therefore, r is divisible by 3 and 5, and thus by 15: $\mathrm{r}=15 \mathrm{k}$. Then $\mathrm{m}=5 \mathrm{k}, \mathrm{d}=3 \mathrm{k}$, and the total number of students is $\mathrm{m}+\mathrm{d}=8 \mathrm{k}$, which means it is divisible by 8. The only number between 30 and 40 that is divisible by 8 is 32.
|
32
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. In the first grade, there are more than 10 but fewer than 15 children. On New Year's morning, Father Frost came to them with a bag of candies and distributed them equally to everyone, and found that he had 9 candies left. How many candies did each child receive if there were initially 207 candies in the bag?
|
Solution. 207-9=198 candies were given out by Father Frost. 198=18$\cdot$11 - factorization taking into account that one of the factors meets the condition of being between 10 and 15. Therefore, 11 children received 18 candies each.
Answer: 18 candies.
## Criteria:
7 points - complete solution;
6 points - factorization obtained, but not explained that other possible factorizations do not meet the condition "more than 10, but less than 15";
4 points - factorization obtained, but the conclusion is incorrect (for example, swapping the values of the number of children and the number of candies received by each child);
3 points - the answer is guessed, a check is performed, but it is not proven that there can be no other options;
1 point - factorization of the number of candies distributed is obtained, further progress is absent;
0 points - only the answer without justification.
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Find the GCD of all numbers obtained by all possible permutations of the digits of the number 202120222023
Solution. By the divisibility rule, all these numbers are divisible by 9 (the sum of the digits is 18). A sufficient condition to prove that there are no other numbers is that the difference between any two such numbers is also divisible by the GCD. For example, 222222100032 - 222222100023 = 9 is divisible by 9 and cannot be greater than 9.
|
Answer: 9.
## Criteria
7 points - complete solution;
3 points - GCD found, but not proven that there can be no other divisors.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. On December 31, 2011, Yevgeny Alexandrovich's age coincided with the sum of the digits of his birth year. How old was Yevgeny Alexandrovich on December 31, 2014? Prove the uniqueness of the answer.
Solution. The maximum sum of the digits of the birth year can be $1+9+9+9=28$, and the minimum - 2. Therefore, Y.A. was born no earlier than 1983 and no later than 2009. Note that if we change only the last digit of the birth year, the sum of the digits will increase, while the age will decrease (and vice versa) by the same amount. Therefore, in each decade, there can be no more than one suitable year. It remains to check the possible decades. If the birth year falls in the 2000s, we get the equation $2+0+0+x=11-x$. Thus, $2x=9$, which has no solution in integers. If the birth year falls in the 1980s, we get the equation $1+9+8+x=31-x$ or $2x=13$, which also has no solution in integers. Finally, for the 1990s, we get the equation $1+9+9+x=21-x$. Solving it, we get the only solution: $x=1$. Therefore, Y.A. was born in 1991. Thus, in 2014, he was 23 years old.
|
Answer: 23 years.
## Criteria:
7 points - complete solution;
4 points - equations are correctly set up;
3 points - the earliest and latest year of birth are estimated;
2 points - noted that in each decade there is no more than one suitable year.
|
23
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
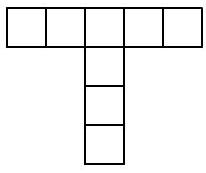
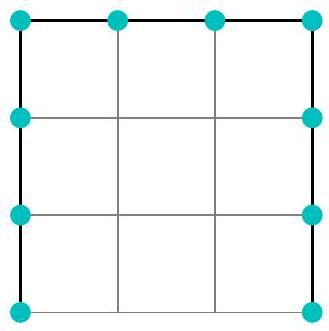
Problem 4.3. How many rectangles exist on this picture with sides running along the grid lines? (A square is also a rectangle.)
|
Answer: 24.
Solution. In a horizontal strip $1 \times 5$, there are 1 five-cell, 2 four-cell, 3 three-cell, 4 two-cell, and 5 one-cell rectangles. In total, $1+2+3+4+5=15$ rectangles.
In a vertical strip $1 \times 4$, there are 1 four-cell, 2 three-cell, 3 two-cell, and 4 one-cell rectangles. In total, $1+2+3+4=10$ rectangles. At the same time, one one-cell rectangle at the intersection of the strips is counted twice (and only it is). Therefore, the answer to the problem is the number $15+10-1=24$.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.3. A cuckoo clock is hanging on the wall. When a new hour begins, the cuckoo says "cuckoo" a number of times equal to the number the hour hand points to (for example, at 19:00, "cuckoo" sounds 7 times). One morning, Maxim approached the clock when it was 9:05. He started turning the minute hand until he advanced the clock by 7 hours. How many times did "cuckoo" sound during this time?

|
Answer: 43.
Solution. The cuckoo will say "cuckoo" from 9:05 to 16:05. At 10:00 it will say "cuckoo" 10 times, at 11:00 - 11 times, at 12:00 - 12 times. At 13:00 (when the hand points to the number 1) "cuckoo" will sound 1 time. Similarly, at 14:00 - 2 times, at 15:00 - 3 times, at 16:00 - 4 times. In total
$$
10+11+12+1+2+3+4=43
$$
|
43
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
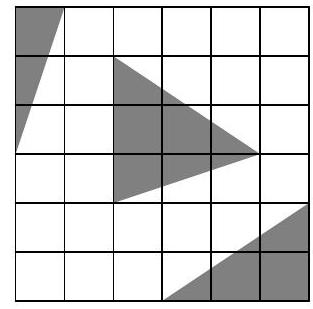
Problem 5.5. From a $6 \times 6$ square grid, gray triangles have been cut out. What is the area of the remaining figure? The side length of each cell is 1 cm. Give your answer in square centimeters.
|
Answer: 27.
Solution. The area of the entire square is $6 \cdot 6=36$ sq. cm.
Divide the triangle located in the middle of the square into two smaller triangles, as shown in the picture on the left. Then the dark gray triangles can be combined into a rectangle $1 \times 3$, and the light gray triangles into a rectangle $2 \times 3$. Therefore, the area of the figure that remains after cutting out all the triangles is 36-3-6 $=27$ sq. cm.
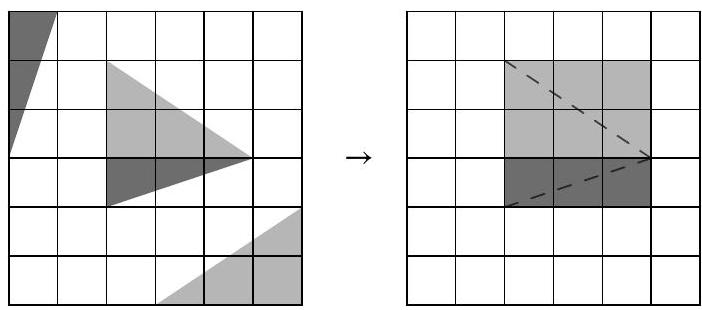
|
27
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.5. In the park, paths are laid out as shown in the figure. Two workers started to asphalt them, starting simultaneously from point $A$. They lay asphalt at constant speeds: the first on the section $A-B-C$, the second on the section $A-D-E-F-C$. In the end, they finished the work simultaneously, spending 9 hours on it. It is known that the second works 1.2 times faster than the first. How many minutes did the second spend laying asphalt on the section $D E$?
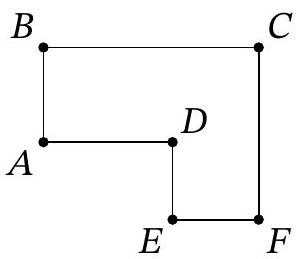
|
Answer: 45.
Solution. Let the line $A D$ intersect the line $C F$ at point $G$, as shown in the figure below. Since $A B C G$ and $D E F G$ are rectangles, we have $A B=C G, B C=A G, E F=D G$ and $D E=F G$.
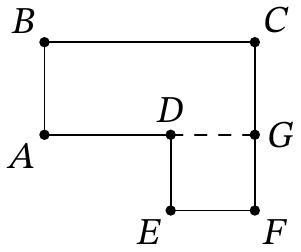
The second worker works 1.2 times faster than the first, and the working time was the same, so the second worker laid 1.2 times more asphalt than the first. Let the first worker lay $x=A B+B C$ asphalt on the section $A-B-C$, then the second worker on the section $A-D-E-F-C$ laid
$$
\begin{aligned}
1.2 x & =A D+D E+E F+F G+G C=(A D+E F+C G)+(D E+F G)= \\
& =(B C+A B)+(D E+D E)=x+2 D E
\end{aligned}
$$
From this, we find that $D E=0.1 x$, which is 12 times less than the total amount of asphalt on the second section. Therefore, the second worker spent 12 times less time on the section $D E$ than on his entire path. He worked a total of $9 \cdot 60=540$ minutes, so he spent $\frac{540}{12}=45$ minutes on $D E$.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.8. There are exactly 120 ways to color five cells in a $5 \times 5$ table so that each column and each row contains exactly one colored cell.
There are exactly 96 ways to color five cells in a $5 \times 5$ table without a corner cell so that each column and each row contains exactly one colored cell.
How many ways are there to color five cells in a $5 \times 5$ table without two corner cells so that each column and each row contains exactly one colored cell?

|
Answer: 78.
Solution. Consider the colorings of a $5 \times 5$ table described in the problem (i.e., such that in each column and each row exactly one cell is colored).
For convenience, let's introduce some notations. The top-left corner cell of the $5 \times 5$ table will be called $A$, and the bottom-right corner cell will be called $B$. Suppose that among the colorings of the first table, exactly $a$ have the cell $A$ colored, and exactly $b$ have the cell $B$ colored. Clearly, $a=b$ due to symmetry.
Notice that the number of colorings of the second table is equal to the number of colorings of the first table where the cell $A$ is not colored. The number of colorings of the third table is equal to the number of colorings of the first table where neither $A$ nor $B$ is colored. To find this, we subtract from 120 the number of colorings of the first table where $A$ or $B$ is colored. To count the number of such colorings, we add $a$ and $b$, and then subtract what has been counted twice - the ways where both $A$ and $B$ are colored.
All colorings of the first table can be divided into two types: those in which the cell $A$ is colored, and those in which it is not. This leads to the equation $120=a+96$, i.e., $a=24$. Then $b=24$ as well.
The number of colorings where both $A$ and $B$ are colored is the same as the number of ways to color the central $3 \times 3$ square. It is easy to see that there are exactly $3!=6$ such ways (to choose the colored cell in its top row, there are 3 ways, in the middle row - 2 ways, and in the bottom row - 1 way).
Thus, the answer to the problem is the number $120-(24+24-6)=78$.
## 7th grade
|
78
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.7. In three of the six circles of the diagram, the numbers 4, 14, and 6 are recorded. In how many ways can natural numbers be placed in the remaining three circles so that the products of the triples of numbers along each of the three sides of the triangular diagram are the same?
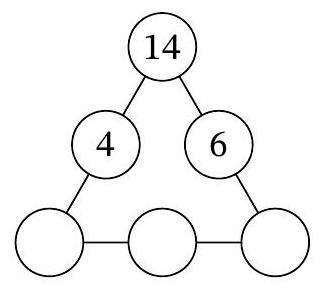
|
Answer: 6.
Solution. Let $a, b, c$ be the natural numbers in the three lower circles, from left to right. According to the condition, $14 \cdot 4 \cdot a = 14 \cdot 6 \cdot c$, i.e., $2a = 3c$. From this, it follows that $3c$ is even, and therefore $c$ is even. Thus, $c = 2k$ for some natural number $k$, and from the equation $2a = 3c$ it follows that $a = 3k$.
It must also hold that $14 \cdot 4 \cdot 3k = 3k \cdot b \cdot 2k$, which means $b \cdot k = 28$. Note that by choosing the number $k$, which is a natural divisor of 28, the natural numbers $a, b, c$ are uniquely determined. The number 28 has exactly 6 natural divisors: $1, 2, 4, 7, 14, 28$. Therefore, there are also 6 ways to place the numbers in the circles.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.8. Given an isosceles triangle $ABC (AB = BC)$. On the ray $BA$ beyond point $A$, point $E$ is marked, and on side $BC$, point $D$ is marked. It is known that
$$
\angle ADC = \angle AEC = 60^{\circ}, AD = CE = 13.
$$
Find the length of segment $AE$, if $DC = 9$.
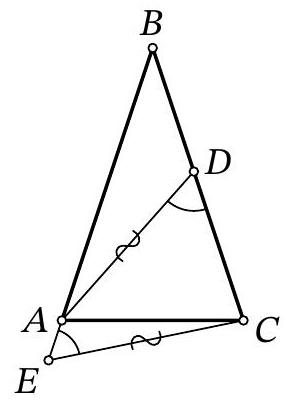
|
Answer: 4.
Solution. Mark point $K$ on ray $B C$ such that $B E=B K$. Then $A E=C K$ as well.
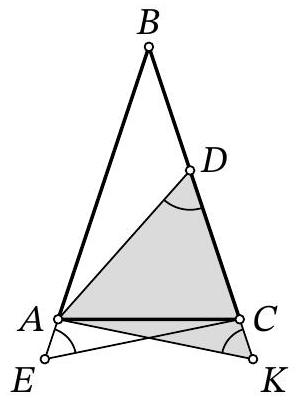
Notice that triangles $A C E$ and $C A K$ are congruent by two sides ($A E=C K, A C$ - common side) and the angle between them ($\angle C A E=\angle A C K$ - adjacent to the equal base angles of the isosceles triangle). Therefore, $A K=C E=13$ and $\angle A K C=\angle A E C=60^{\circ}$.
In triangle $A D K$, the angles at vertices $D$ and $K$ are $60^{\circ}$, so it is equilateral, and $D K=A K=A D=13$. Therefore, $A E=C K=D K-D C=13-9=4$.
## 8th grade
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. In a $5 \times 5$ square, some cells have been painted black as shown in the figure. Consider all possible squares whose sides lie along the grid lines. In how many of them is the number of black and white cells the same?

|
Answer: 16.
Solution. An equal number of black and white cells can only be in squares $2 \times 2$ or $4 \times 4$ (in all other squares, there is an odd number of cells in total, so there cannot be an equal number of black and white cells). There are only two non-fitting $2 \times 2$ squares (both of which contain the center of the table, but do not contain any cells above the center), so there are exactly $16-2=14$ fitting $2 \times 2$ squares. And among the $4 \times 4$ squares, only the two lower ones fit.
Thus, the total number of squares with an equal number of black and white cells is exactly $14+2=16$.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.3. In triangle $ABC$, the sides $AC=14$ and $AB=6$ are known. A circle with center $O$, constructed on side $AC$ as the diameter, intersects side $BC$ at point $K$. It turns out that $\angle BAK = \angle ACB$. Find the area of triangle $BOC$.
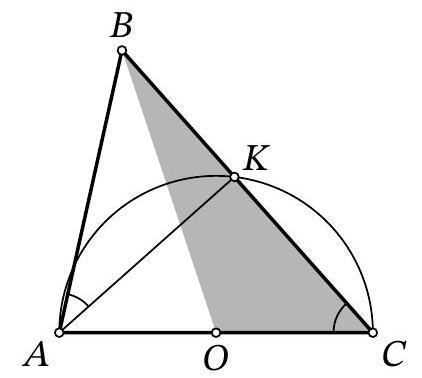
|
Answer: 21.
Solution. Since $AC$ is the diameter of the circle, point $O$ is the midpoint of $AC$, and $\angle AKC = 90^{\circ}$.
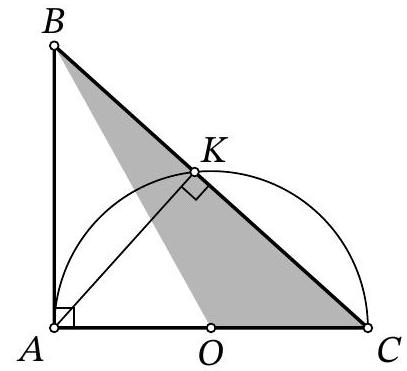
Then
$$
\angle BAC = \angle BAK + \angle CAK = \angle BCA + \angle CAK = \angle BKA = 90^{\circ}.
$$
The area of the right triangle $ABC$ can be found as $\frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot 6 \cdot 14 = 42$. Since the median $BO$ divides its area in half, the area of triangle $BOC$ is $\frac{42}{2} = 21$.
|
21
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. Given an isosceles triangle $A B C$, where $A B=A C$ and $\angle A B C=53^{\circ}$. Point $K$ is such that $C$ is the midpoint of segment $A K$. Point $M$ is chosen such that:
- $B$ and $M$ are on the same side of line $A C$;
- $K M=A B$
- angle $M A K$ is the maximum possible.
How many degrees does angle $B A M$ measure?
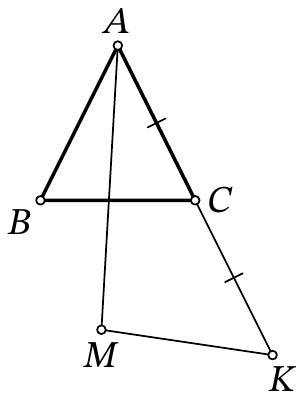
|
Answer: 44.
Solution. Let the length of segment $AB$ be $R$. Draw a circle with center $K$ and radius $R$ (on which point $M$ lies), as well as the tangent $AP$ to it such that the point of tangency $P$ lies on the same side of $AC$ as $B$. Since $M$ lies inside the angle $PAK$ or on its boundary, the angle $MAK$ does not exceed the angle $PAK$, and these angles are equal only if points $M$ and $P$ coincide. Therefore, $M$ is this point of tangency.
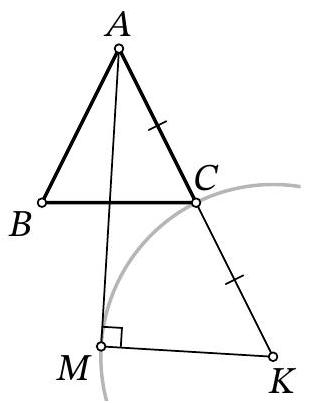
The radius $KM$ of the circle is perpendicular to the tangent $AM$. Also, in the right triangle $AMK$, the leg $MK$ is half the hypotenuse $AK$, so $\angle MAK=30^{\circ}$. Additionally, from the condition, we get that $\angle BAC=180^{\circ}-2 \cdot 53^{\circ}=74^{\circ}$. Therefore,
$$
\angle BAM=\angle BAC-\angle MAK=74^{\circ}-30^{\circ}=44^{\circ}
$$
|
44
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.1. An equilateral triangle with a side of 10 is divided into 100 small equilateral triangles with a side of 1. Find the number of rhombi consisting of 8 small triangles (such rhombi can be rotated).
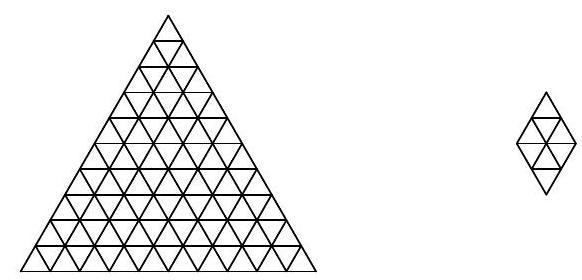
|
Answer: 84.
Solution. Rhombuses consisting of eight triangles can be of one of three types:

It is clear that the number of rhombuses of each orientation will be the same, so let's consider only the vertical ones. Each of them is uniquely determined by its top triangle. Now it is easy to count the number of such triangles.
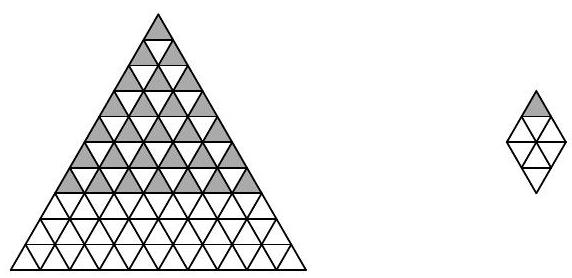
In the first row, there is 1 such triangle, in the second row - 2, in the third row - 3, ..., in the seventh row - 7. In total, \(1+2+3+\ldots+7=28\) vertical rhombuses, and therefore, the answer to the problem is \(28 \cdot 3 = 84\).
|
84
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.5. A circle $\omega$ is inscribed in trapezoid $A B C D$, and $L$ is the point of tangency of $\omega$ and side $C D$. It is known that $C L: L D=1: 4$. Find the area of trapezoid $A B C D$, if $B C=9$, $C D=30$.
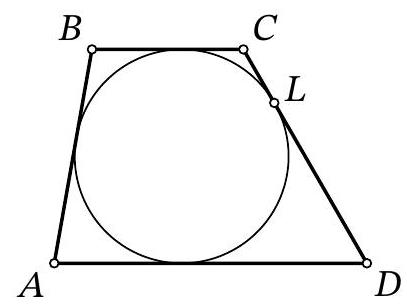
|
Answer: 972.
Solution. Let's mark the center of the circle $I$, as well as the points of tangency $P, Q, K$ with the sides $B C$, $A D, A B$ respectively. Note that $I P \perp B C, I Q \perp A D$, i.e., points $P, I, Q$ lie on the same line, and $P Q$ is the height of the given trapezoid, equal to the diameter of its inscribed circle. Also, the segments of tangents $A K=A Q, B K=B P, C P=C L, D L=D Q$ are equal.
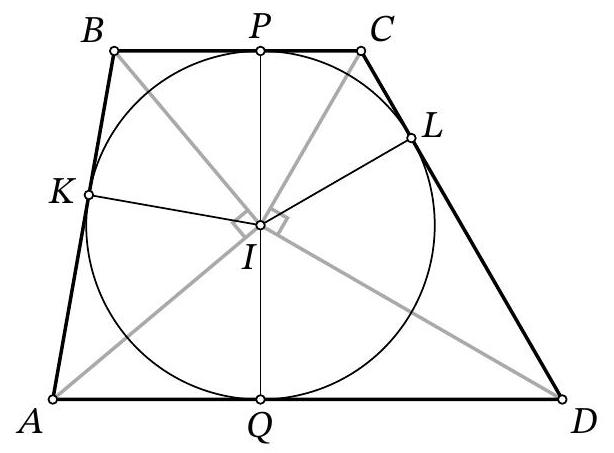
From the condition, it follows that $C P=C L=\frac{1}{5} \cdot 30=6, D Q=D L=\frac{4}{5} \cdot 30=24$. Then $B K=B P=$ $B C-C P=9-6=3$.
Since the lines $C I$ and $D I$ are the angle bisectors of angles $C$ and $D$ of the trapezoid, we have $\angle I C D+$ $\angle I D C=\frac{1}{2}(\angle C+\angle D)=\frac{180^{\circ}}{2}=90^{\circ}$, i.e., triangle $C I D$ is a right triangle with a right angle at vertex $I$. Since $I L$ is its height dropped to the hypotenuse, $I L=$ $\sqrt{C L \cdot D L}=12$. This is the radius of the circle.
Similarly, considering the height $I K$ in the right triangle $A I B$, we get $12=$ $I K=\sqrt{A K \cdot B K}$. Using $B K=3$, we extract $A K=A Q=48$.
Thus, the area of the trapezoid is
$$
S_{A B C D}=\frac{B C+A D}{2} \cdot C H=\frac{9+(48+24)}{2} \cdot 24=972
$$
|
972
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. A tangent $FK$ is drawn to the circumcircle $K$ of triangle $FDC$, and $\angle KFC=58^{\circ}$. Points $K$ and $D$ lie on opposite sides of line $FC$, as shown in the figure. Find the acute angle between the angle bisectors of $\angle CFD$ and $\angle FCD$. Express your answer in degrees.
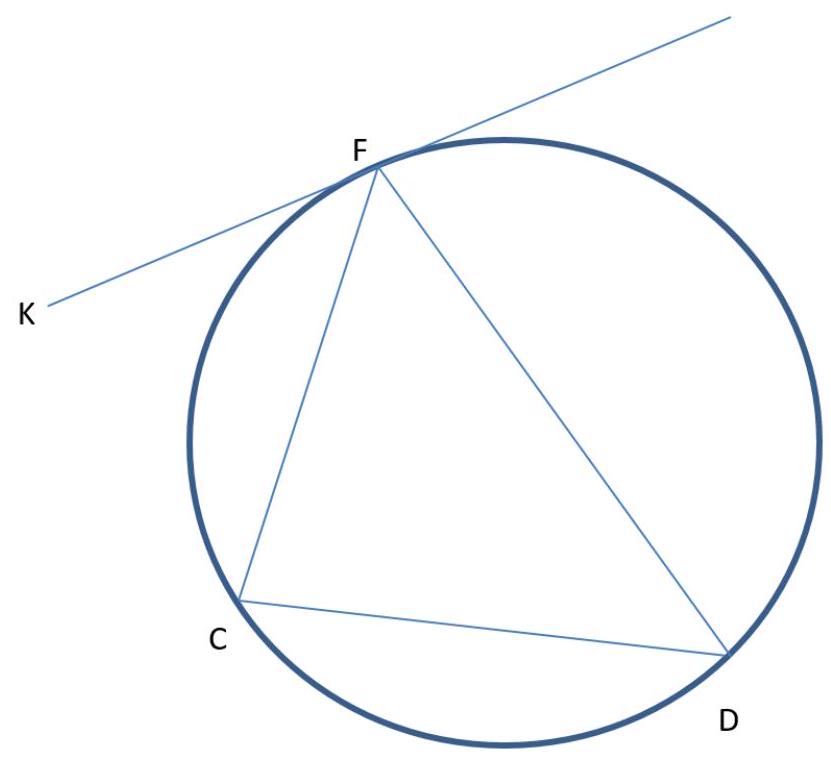
|
Answer: 61
Solution. Let's refer to the picture:
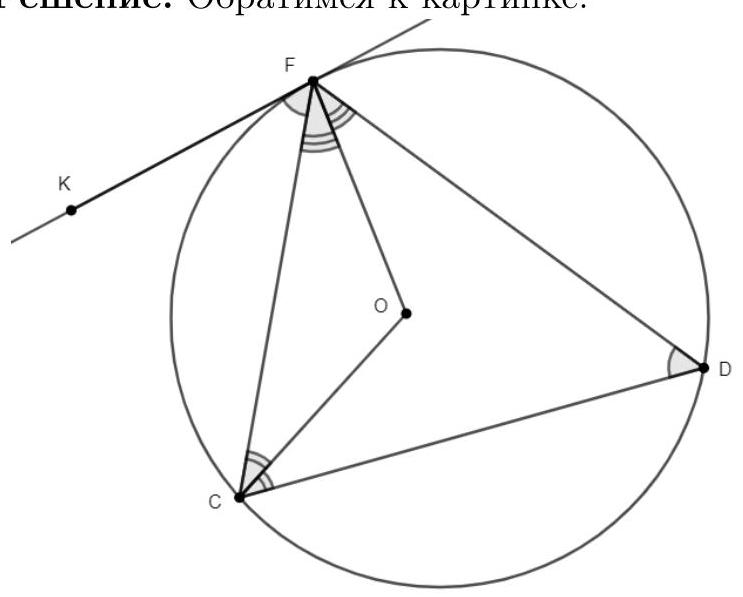
$\angle KFC$ is the angle between the chord and the tangent, which is equal to half the arc $FC$, just like the inscribed angle $\angle FDC$ that subtends it. Let $O$ be the point of intersection of the angle bisectors of $\triangle FCD$. Then $\angle FOC = 180^{\circ} - (\angle FCO + \angle CFO) = 180^{\circ} - \frac{1}{2} \cdot (\angle FCD + \angle CFD) = 180^{\circ} - \frac{1}{2} \cdot (180^{\circ} - \angle FDC) = 90^{\circ} + \frac{1}{2} \angle FDC = 90^{\circ} + 29^{\circ} = 119^{\circ}$. The required acute angle is $180^{\circ} - 119^{\circ} = 61^{\circ}$.
Remark. O is not the center of the circumscribed circle.
|
61
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. Among fifty consecutive natural numbers, exactly 8 are divisible by 7 without a remainder. What is the remainder when the eleventh number in the sequence is divided by 7?
#
|
# Answer: 3
Solution. The closest numbers that give the same remainder when divided by 7 differ by 7. Therefore, among fifty consecutive numbers, 6 groups of numbers with the same remainder are formed, each containing 7 numbers, and only one group containing 8 numbers, with the first and last numbers among them. Thus, the first number is exactly divisible by 7. Then the eleventh number gives the same remainder when divided by 7 as the fourth, and this remainder is 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. Four chess players - Ivanov, Petrov, Vasiliev, and Kuznetsov - played a round-robin tournament (each played one game against each other). A win earns 1 point, a draw earns 0.5 points each. It turned out that the player who took first place had 3 points, and the player who took last place had 0.5 points. How many variants of point distribution among the named chess players exist, if some of them could have scored the same number of points? (For example, the variants where Ivanov has 3 points and Petrov has 0.5, and where Petrov has 3 points and Ivanov has 0.5, are considered different!)
|
Answer: 36
Solution. First, let's determine what quantities of points the four participants can have under the given conditions. Since the one who took first place has 3 points, he won against everyone, and the one who took second place could not have scored more than 2, as he lost to the first. There were a total of 6 games in the tournament, which means 6 points were distributed (regardless of the outcome of the game, 1 point is always at stake), so the second and third places together have $6-3-0.5=2.5$ points. Therefore, they could have scored 2 and 0.5 or 1.5 and 1 point. In the first case, we need to find the number of ways to distribute the points $3 ; 2 ; 0.5$ and 0.5 among the four given chess players. This can be done in $4 \cdot 3=12$ ways, as any of the four can be in first place, and any of the remaining three can be in second place, with no further choice. In the second case, there will be $4 \cdot 3 \cdot 2=24$ ways, since here the points are different for all. In the end, we get $12+24=36$ ways to distribute the points.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. People stand in a circle - liars who always lie, and ryiars who always tell the truth. And each of them said that among the people standing next to them, there are as many liars as ryiars. How many people are there in total if there are 48 ryiars?
|
Answer: 72
Solution. Let's denote a knight as $\mathrm{P}$, and a liar as L. Notice that each knight stands between a knight and a liar, otherwise he would have told a lie. Therefore, knights stand in groups of two. Liars cannot stand in groups larger than one, as in such a case, the liar standing at the edge of the group would have told the truth. Thus, groups of two knights and one liar alternate: ... PPPLPPPLPPP... Since there are 48 knights, there are 24 liars. Therefore, there are 72 people in total.
|
72
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A merchant bought several bags of salt in Tver and sold them in Moscow with a profit of 100 rubles. With all the money earned, he again bought salt in Tver (at the Tver price) and sold it in Moscow (at the Moscow price). This time the profit was 120 rubles. How much money did he spend on the first purchase?
|
Solution. Let the merchant pay $x$ rubles for the salt during the first purchase in Tver. Then he sold it in Moscow for $x+100$ rubles. The second time, he spent $x+100$ rubles in Tver and received $x+100+120=x+220$ rubles in Moscow. Since the ratio of Moscow and Tver prices did not change, we can set up the proportion $\frac{x}{x+100}=\frac{x+100}{x+220}$, from which we get $x^{2}+220 x=x^{2}+200 x+10000, 20 x=10000, x=500$.
Answer: 500 rubles.
|
500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a triangle, two medians are perpendicular to each other, their lengths are 18 cm and 24 cm. Calculate the area of the triangle.
|
Solution. $S=\frac{1}{2} A C \cdot B M$ (see the figure). By the property of medians, we have $A O=\frac{2}{3} \cdot A E=16, O C=\frac{2}{3} \cdot C D=12$. From $\triangle A O C$, we find $A C=\sqrt{A E^{2}+O C^{2}}=20$. Let $D F \perp A C, O K \perp A C$,
moreover, $B M \perp A C$. Note that $S_{A O C}=\frac{1}{2} A O \cdot O C=\frac{1}{2} K O \cdot A C$, hence $K O=\frac{A O \cdot O C}{A C}=9.6$. Triangles $F D C$ and $K O C$ are similar, so $\frac{D F}{K O}=\frac{D C}{O C}$, from which we get $D F=\frac{D C \cdot K O}{O C}=14.4$, and $B M=2 D F=28.8$. Therefore, we have $S=\frac{1}{2} A C \cdot B M=288$.
Answer: 288.
|
288
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. We will build a sequence of numbers in the following way. We will place the number 7 in the first position, and after each number, we will place the sum of the digits of its square, increased by one. For example, the second position will hold the number 14, since $7^{2}=49$, and $4+9+1=14$. The third position will hold the number 17, since $14^{2}=196$, and $1+9+6+1=17$, and so on. What number stands in the 2016th position?
|
Solution Let's continue finding the first few terms of the sequence: $7 ; 14 ; 17 ; 20 ; 5 ; 8 ; 11 ; 5 ; \ldots$ - the number 5 is repeated. This means the sequence has a period of length 3: the numbers 5; 8; 11 will repeat subsequently. The number 8 is in the sixth position, so for any $\mathrm{k}>0$, the number 8 will also be in the $3 \mathrm{k}$-th position. Since $2016=3 \times 672$, the number 8 is in the 2016-th position.
Answer: 8.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Thirty students from five classes came up with 40 tasks, and students from one class came up with the same number of tasks, while students from different classes came up with a different number. How many students came up with one task?
|
Solution: We will choose 5 students, one from each class. Each of them came up with a different number of problems. Therefore, the total number of problems they came up with is no less than $1+2+3+4+5=$ 15. The remaining 25 students came up with no more than $40-15=25$ problems. It is clear that each of them came up with one problem.
Answer: 26 students.
|
26
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.3. Zhenya drew a square with a side of 3 cm, and then erased one of these sides. A figure in the shape of the letter "P" was obtained. The teacher asked Zhenya to place dots along this letter "P", starting from the edge, so that the next dot was 1 cm away from the previous one, as shown in the picture, and then count how many dots he got. He got 10 dots.
Then the teacher decided to complicate the task and asked to count the number of dots, but for the letter "P" obtained in the same way from a square with a side of 10 cm. How many dots will Zhenya have this time?
|
Answer: 31.
Solution. Along each of the three sides of the letter "П", there will be 11 points. At the same time, the "corner" points are located on two sides, so if 11 is multiplied by 3, the "corner" points will be counted twice. Therefore, the total number of points is $11 \cdot 3-2=31$.
|
31
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.5. Hooligan Dima made a construction in the shape of a $3 \times 5$ rectangle using 38 wooden toothpicks. Then he simultaneously set fire to two adjacent corners of this rectangle, marked in the figure.
It is known that one toothpick burns for 10 seconds. How many seconds will it take for the entire construction to burn?
(Fire spreads along the toothpicks at a constant speed. The fire continues to spread from each burned toothpick to all adjacent unburned toothpicks.)

|
Answer: 65.
Solution. In the picture below, for each "node", the point where the toothpicks connect, the time in seconds it takes for the fire to reach it is indicated. It will take the fire another 5 seconds to reach the middle of the middle toothpick in the top horizontal row (marked in the picture).
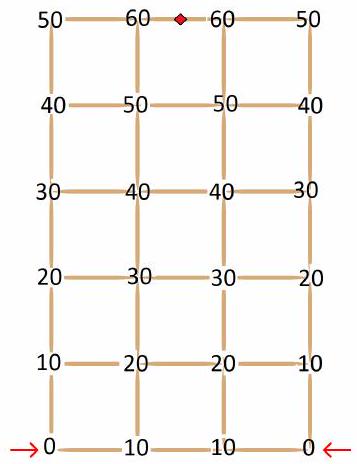
|
65
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. The school principal, the caretaker, and the parent committee, failing to agree with each other, each bought a carpet for the school auditorium, which is $10 \times 10$. After thinking about what to do, they decided to place all three carpets as shown in the picture: the first carpet $6 \times 8$ - in one corner, the second carpet $6 \times 6$ - in the opposite corner, and the third carpet $5 \times 7$ - in one of the remaining corners (all dimensions are in meters).
Find the area of the part of the hall covered by carpets in three layers (give the answer in square meters).
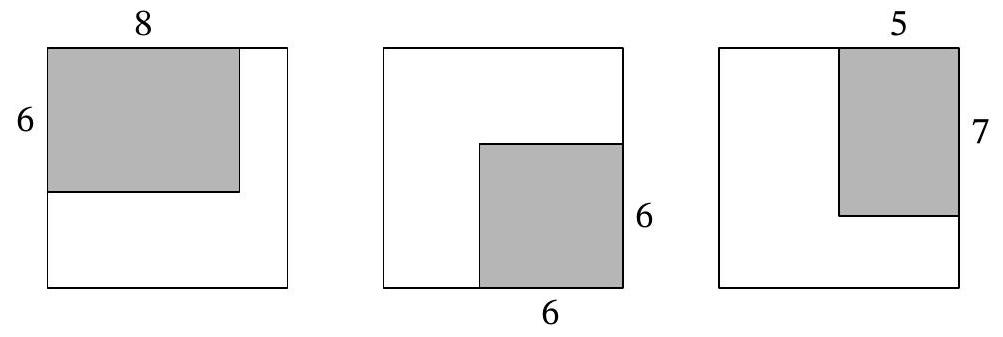
|
Answer: 6.
Solution. We will measure all dimensions in meters and the area in square meters.
Let's look at the overlap of the second and third carpets. This will be a rectangle $5 \times 3$ (5 along the horizontal, 3 along the vertical), adjacent to the right side of the square room, 4 units from the top side, and 3 units from the bottom side.
The first carpet intersects this rectangle horizontally between the 5th and 8th meters from the left side of the square room, and vertically between the 4th and 6th meters from the top side. In the end, we get a rectangle $2 \times 3$, the area of which is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.8. Inside a large triangle with a perimeter of 120, several segments were drawn, dividing it into nine smaller triangles, as shown in the figure. It turned out that the perimeters of all nine small triangles are equal to each other. What can they be equal to? List all possible options.
The perimeter of a figure is the sum of the lengths of all its sides.
|
Answer: 40.
Solution. Let's add the perimeters of the six small triangles marked in gray in the following figure:
From the obtained value, subtract the perimeters of the other three small white triangles. Since the perimeters of the small triangles are equal, on one side, we get three times the perimeter of a small triangle. On the other side, in this sum, there will only be segments that make up the perimeter of the large triangle, which is 120. Therefore, the perimeter of a small triangle is $120: 3=40$.
## 6th grade
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.7. Anya places pebbles on the sand. First, she placed one stone, then added pebbles to form a pentagon, then made a larger outer pentagon with pebbles, then another outer pentagon, and so on, as shown in the picture. The number of stones she had arranged on the first four pictures: 1, 5, 12, and 22. If she continues to create such pictures, how many stones will be on the 10th picture?
-
|
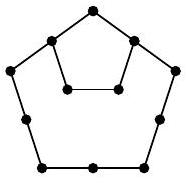
Answer: 145.
Solution. On the second picture, there are 5 stones. To get the third picture from it, you need to add three segments with three stones on each. The corner stones will be counted twice, so the total number of stones in the third picture will be $5+3 \cdot 3-2=12$.
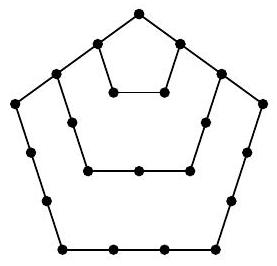
To get the fourth picture from the third, you need to add three segments with four stones on each. The corner stones will be counted twice, so the total number of stones will be $12+3 \cdot 4-2=22$.
Similarly, we will calculate the number of stones on each of the remaining pictures:
on the 5th: $22+3 \cdot 5-2=35$;
on the 6th: $\quad 35+3 \cdot 6-2=51$;
on the 7th: $51+3 \cdot 7-2=70$;
on the 8th: $\quad 70+3 \cdot 8-2=92$;
on the 9th: $92+3 \cdot 9-2=117$
on the 10th: ~ 117+3 \cdot 10-2=145$.
|
145
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. In the chat of students from one of the schools, a vote was held: "On which day to hold the disco: October 22 or October 29?"
The graph shows how the votes were distributed an hour after the start of the voting.
Then, 80 more people participated in the voting, voting only for October 22. After that, the voting ended. The final distribution of votes is also shown on the graph.
How many people participated in the voting?
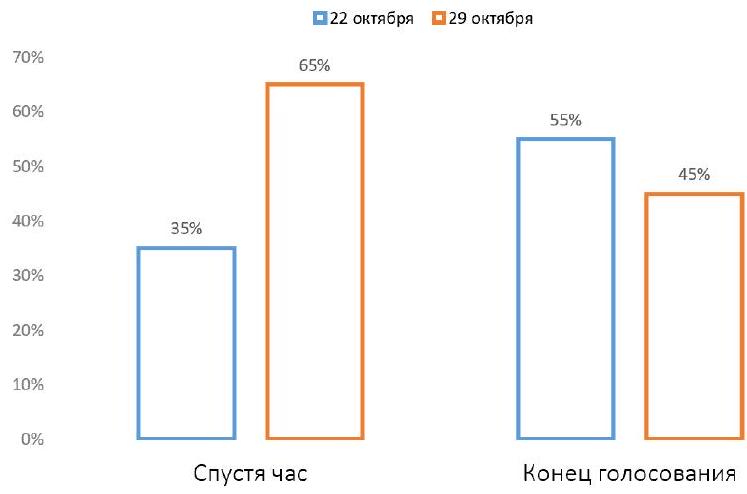
|
Answer: 260.
Solution. Let $x$ be the number of people who voted an hour after the start. From the left chart, it is clear that $0.35 x$ people voted for October 22, and $-0.65 x$ people voted for October 29.
In total, $x+80$ people voted, of which $45\%$ voted for October 29. Since there are still $0.65 x$ of them, we get the equation
$0.65 x=0.45(x+80)$, from which we find $x=180$. Therefore, a total of $180+80=260$ people participated in the voting.
|
260
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. The figure shows two equal triangles: $A B C$ and $E B D$. It turns out that $\angle D A E = \angle D E A = 37^{\circ}$. Find the angle $B A C$.
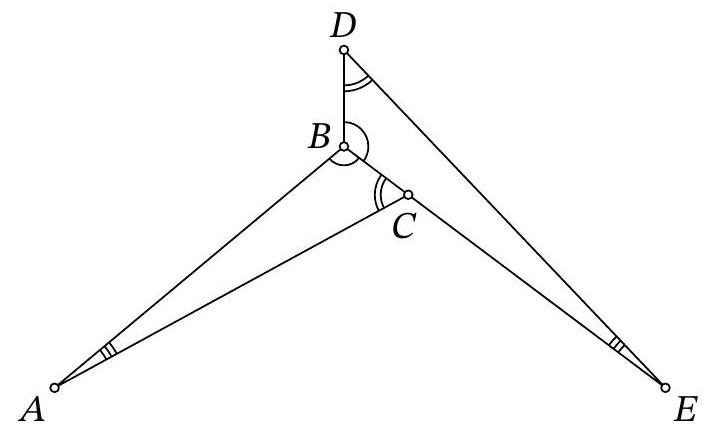
|
Answer: 7.
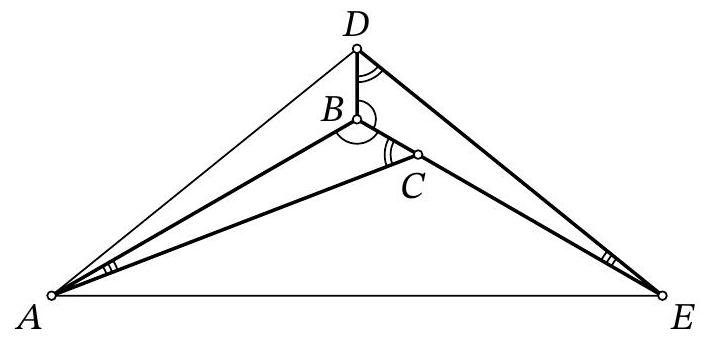
Fig. 4: to the solution of problem 8.7
Solution. Draw segments $A D$ and $A E$ (Fig. 4). Since $\angle D A E=\angle D E A=37^{\circ}$, triangle $A D E$ is isosceles, $A D=D E$.
Notice that triangle $A B D$ is equal to triangle $E B D$ by three sides: $B D$ is a common side, $A D=D E, A B=B E$ from the equality of triangles $A B C$ and $E B D$. Then $\angle D A B=$ $\angle B E D=\angle B A C$ and $\angle A B D=\angle D B E=\angle A B E=\frac{1}{3} \cdot 360^{\circ}=120^{\circ}$.
Since $A B=B E$, triangle $A B E$ is isosceles with an angle of $120^{\circ}$, so $\angle B A E=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$. Therefore,
$$
\angle B A C=\angle D A B=\angle D A E-\angle B A E=37^{\circ}-30^{\circ}=7^{\circ}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. A line $\ell$ is drawn through vertex $A$ of rectangle $ABCD$, as shown in the figure. Perpendiculars $BX$ and $DY$ are dropped from points $B$ and $D$ to line $\ell$. Find the length of segment $XY$, given that $BX=4$, $DY=10$, and $BC=2AB$.
|
Answer: 13.
Fig. 5: to the solution of problem 9.4
Solution. Note that since $\angle Y A D=90^{\circ}-\angle X A B$ (Fig. 5), right triangles $X A B$ and $Y D A$ are similar by the acute angle $\angle Y A D=\angle X B A$. The similarity ratio is the ratio $A B: A D$, which is $\frac{1}{2}$. From this, we get $X A=\frac{1}{2} D Y=5$ and $A Y=2 B X=8$, which in total gives $X Y=13$.
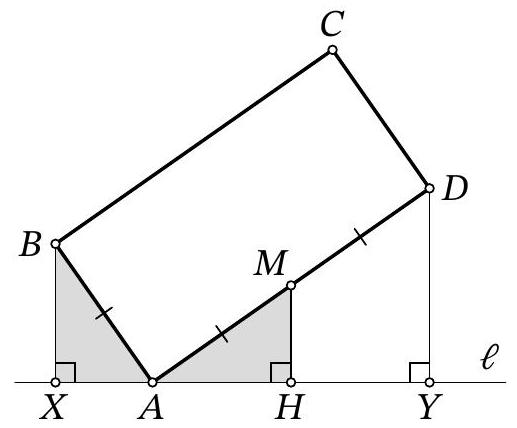
Fig. 6: to the solution of problem 9.4
Another solution. Let $M$ be the midpoint of segment $A D$, then $A M=M D=\frac{A D}{2}=\frac{B C}{2}=A B$ (Fig. 6). Drop a perpendicular from $M$ to $M H$ on line $\ell$. Since in triangle $A D Y$ the segment $M H$ passes through the midpoint of side $A D$ and is parallel to side $D Y$, it is the midline, $A H=H Y$ and $M H=\frac{D Y}{2}=\frac{10}{2}=5$.
Note that $\angle A B X=90^{\circ}-\angle B A X=90^{\circ}-\left(180-90^{\circ}-\angle M A H\right)=\angle M A H$. Then right triangles $A B X$ and $M A H$ are equal by hypotenuse $A B=A M$ and acute angle $\angle A B X=\angle M A H$. From this, it follows that $A X=M H=5$ and $A H=B X=4$.
Thus, $X Y=A X+A H+H Y=5+4+4=13$.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.6. In triangle $A B C$, the angles $\angle B=30^{\circ}$ and $\angle A=90^{\circ}$ are known. On side $A C$, point $K$ is marked, and on side $B C$, points $L$ and $M$ are marked such that $K L=K M$ (point $L$ lies on segment $B M$).
Find the length of segment $L M$, if it is known that $A K=4, B L=31, M C=3$.
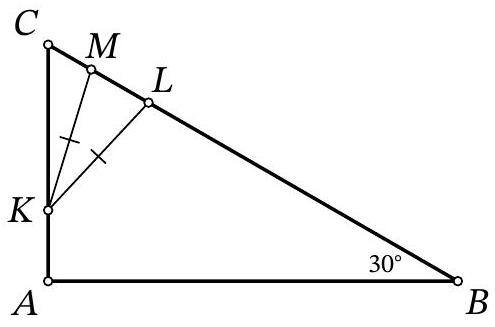
|
Answer: 14.
Solution. In the solution, we will use several times the fact that in a right-angled triangle with an angle of $30^{\circ}$, the leg opposite this angle is half the hypotenuse. Drop the height $K H$ from the isosceles triangle $K M L$ to the base (Fig. 7). Since this height is also a median, then $M H=H L=x$. In the right-angled triangle $C K H$ we have $\angle C K H=90^{\circ}-\angle C=\angle A=30^{\circ}$, so $K C=2 \cdot C H=2 \cdot(C M+M H)=$ $2 \cdot(3+x)=6+2 x$. In the right-angled triangle $A B C$ we have $\angle A=30^{\circ}$, so $B C=2 \cdot A C$. Setting up and solving the corresponding equation $31+2 x+3=2 \cdot(4+6+2 x)$, we find $x=7$. Then $L M=2 x=2 \cdot 7=14$.
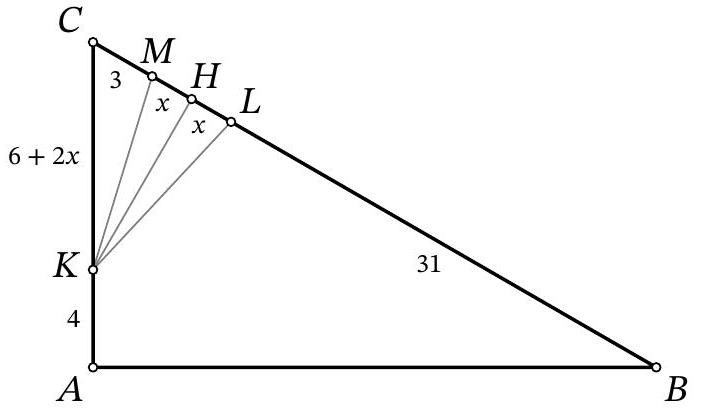
Figure 7: to the solution of problem 9.6
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.2. Points $A, B, C, D, E, F, G$ are located clockwise on a circle, as shown in the figure. It is known that $A E$ is the diameter of the circle. Also, it is known that $\angle A B F=81^{\circ}, \angle E D G=76^{\circ}$. How many degrees does the angle $F C G$ measure?
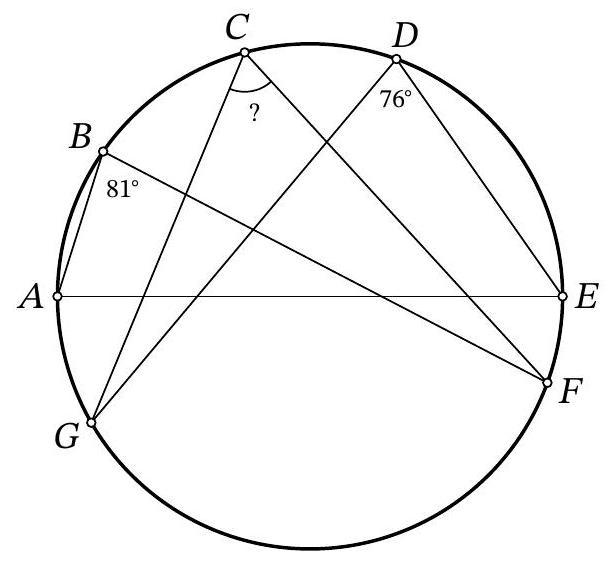
|
Answer: 67.
Solution. Since inscribed angles subtended by the same arc are equal, then $\angle A C F=$ $\angle A B F=81^{\circ}$ and $\angle E C G=\angle E D G=76^{\circ}$. Since a right angle is subtended by the diameter,
$$
\angle F C G=\angle A C F+\angle E C G-\angle A C E=81^{\circ}+76^{\circ}-90^{\circ}=67^{\circ}
$$
|
67
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
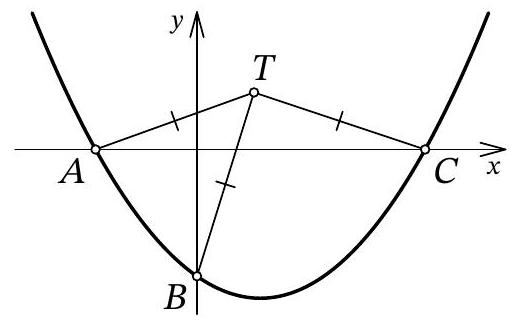
Problem 10.7. The graph of the function $f(x)=\frac{1}{12} x^{2}+a x+b$ intersects the $O x$ axis at points $A$ and $C$, and the $O y$ axis at point $B$, as shown in the figure. It turned out that for the point $T$ with coordinates $(3 ; 3)$, the condition $T A=T B=T C$ is satisfied. Find $b$.
|
Answer: -6.
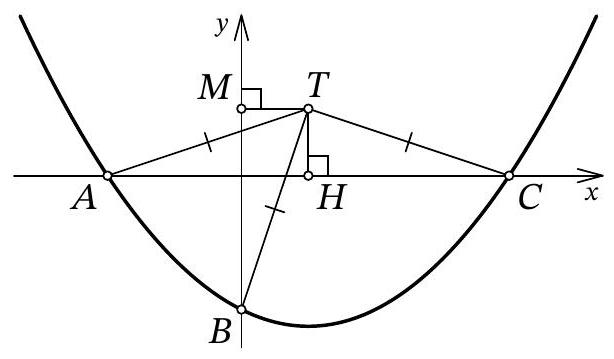
Fig. 11: to the solution of problem 10.7
Solution. Let point $A$ have coordinates $\left(x_{1} ; 0\right)$, and point $C$ have coordinates $\left(x_{2} ; 0\right)$. From the condition, it is clear that $x_{1} < 0$ and $x_{2} > 0$. Since $x_{1}$ and $x_{2}$ are the roots of the quadratic trinomial $f(x)$, by Vieta's theorem, we have $x_{1} \cdot x_{2} = 12b$, from which we get $b = \frac{x_{1} \cdot x_{2}}{12} < 0$.
Let $H$ be the point with coordinates $(3 ; 0)$ (Fig. 11). Clearly, in the isosceles triangle $A T C$, the segment $T H$ is the height, and therefore it is also the median. Thus, $3 - x_{1} = A H = H C = x_{2} - 3$, from which we get $x_{1} = 6 - x_{2}$.
Let $M$ be the point with coordinates $(0, 3)$. Since $T H = T M = 3$ and $T A = T B$, the right triangles $A T H$ and $B T M$ are equal by the leg and hypotenuse. Therefore, $3 - x_{1} = H A = M B = 3 - b$, that is, $x_{1} = b = \frac{x_{1} \cdot x_{2}}{12}$ (by Vieta's theorem), from which we find $x_{2} = 12$. Finally, $x_{1} = 6 - x_{2} = 6 - 12 = -6$ and $b = x_{1} = -6$.
Another solution. As in the previous solution, let the abscissas of points $A$ and $C$ be $x_{1}$ and $x_{2}$, respectively; we will also use the fact that point $B$ has coordinates $(0 ; b)$. Immediately, we understand that $O A = |x_{1}| = -x_{1}$, $O C = |x_{2}| = x_{2}$, and $O B = |b| = -b$.
Let's find the second intersection of the circle with the y-axis, let this be point $D$ with coordinates $(0 ; d)$ (Fig. 12). The chords $A C$ and $B D$ of the circle intersect at the origin $O$; from the properties of the circle, we know that $O A \cdot O C = O B \cdot O D$. We get $-x_{1} \cdot x_{2} = -b \cdot d$, from which, replacing $x_{1} \cdot x_{2}$ with $12b$ by Vieta's theorem, we get $d = 12$.
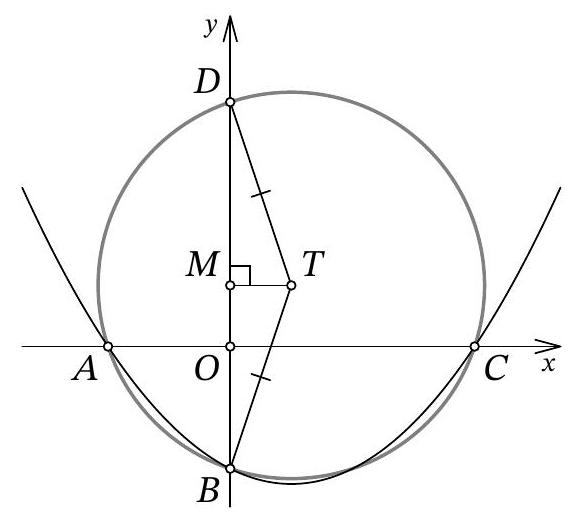
Fig. 12: to the solution of problem 10.7
It remains to note that triangle $BTD$ is isosceles, and the midpoint of its base, point $M$, has coordinates $(0 ; 3)$. Reflecting point $D(0 ; 12)$ relative to it, we get $B(0 ; -6)$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.2. A square was cut into five rectangles of equal area, as shown in the figure. The width of one of the rectangles is 5. Find the area of the square.

|
Answer: 400.
Solution. The central rectangle and the rectangle below it have a common horizontal side, and their areas are equal. Therefore, the vertical sides of these rectangles are equal, let's denote them by $x$ (Fig. 13). The vertical side of the lower left rectangle is $2x$, and we will denote its horizontal side by $y$. Since its area $2xy$ is the same as the area of the central rectangle, the horizontal side of the central rectangle is $2y$. Then the horizontal side of the upper left rectangle is $3y$, and its area $3y \cdot 5 = 15y$ should be equal to $2xy$, from which we find $x=7.5$. Then the side of the entire square is $5+2x=5+2 \cdot 7.5=20$, and its area is $20^2=400$.
|
400
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. In a football tournament, 15 teams participated, each playing against each other exactly once. For a win, 3 points were awarded, for a draw - 1 point, and for a loss - 0 points.
After the tournament ended, it turned out that some 6 teams scored at least $N$ points each. What is the greatest integer value that $N$ can take?
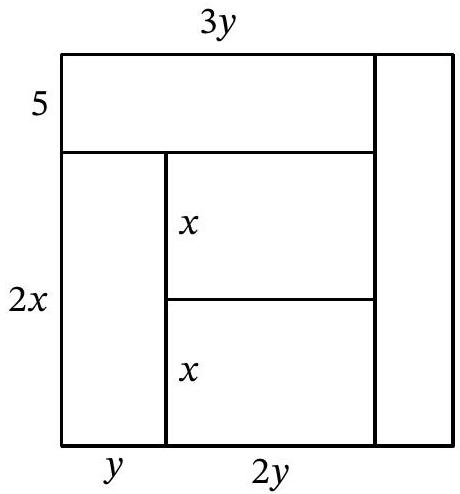
Fig. 13: to the solution of problem 11.2
#
|
# Answer: 34.
Solution. Let's call these 6 teams successful, and the remaining 9 teams unsuccessful. We will call a game between two successful teams an internal game, and a game between a successful and an unsuccessful team an external game.
First, note that for each game, the participating teams collectively earn no more than 3 points. Clearly, there were exactly $\frac{6 \cdot 5}{2}=15$ internal games, and only from these games did all successful teams collectively earn no more than $15 \cdot 3=45$ points. There were exactly $6 \cdot 9=54$ external games, and in each such game, a successful team earned no more than 3 points. Therefore, collectively, all successful teams earned no more than $54 \cdot 3=162$ points from external games. According to the problem, the successful teams collectively earned at least $6 \mathrm{~N}$ points, so we get the inequality $6 N \leqslant 45+162$. From this, it follows that $N \leqslant \frac{207}{6}<35$ and $N \leqslant 34$. Now let's provide an example for $N=34$. Number the teams from 1 to 15. We will show how teams from 1 to 6 can earn at least 34 points.
- Suppose each team from 1 to 6 won against each team from 7 to 15, then each team from 1 to 6 earned $9 \cdot 3=27$ points just from these games.
- Suppose teams from 1 to 6 played among themselves as indicated in the following table (in each cell, the number of points is shown that the team from the corresponding row received in the game with the team from the corresponding column):
| | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $\mathbf{1}$ | | 3 | 3 | 1 | 0 | 0 |
| $\mathbf{2}$ | 0 | | 3 | 3 | 1 | 0 |
| $\mathbf{3}$ | 0 | 0 | | 3 | 3 | 1 |
| $\mathbf{4}$ | 1 | 0 | 0 | | 3 | 3 |
| $\mathbf{5}$ | 3 | 1 | 0 | 0 | | 3 |
| $\mathbf{6}$ | 3 | 3 | 1 | 0 | 0 | |
- Suppose in each game between teams from 7 to 15, the team with the higher number won (the outcome of these games does not matter).
In total, teams from 1 to 6 earned at least $27+7=34$ points.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.8. Given a parallelepiped $A B C D A_{1} B_{1} C_{1} D_{1}$. A point $X$ is chosen on the edge $A_{1} D_{1}$, and a point $Y$ is chosen on the edge $B C$. It is known that $A_{1} X=5, B Y=3, B_{1} C_{1}=14$. The plane $C_{1} X Y$ intersects the ray $D A$ at point $Z$. Find $D Z$.
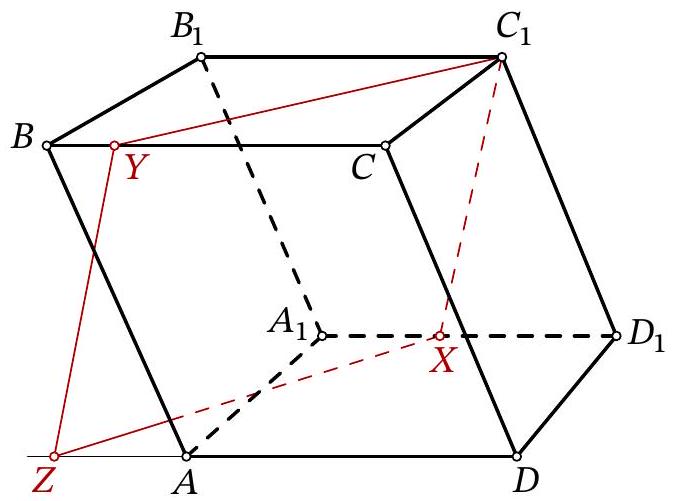
|
Answer: 20.
Solution. Lines $C_{1} Y$ and $Z X$ lie in parallel planes $B B_{1} C_{1} C$ and $A A_{1} D_{1} D$, so they do not intersect. Since these two lines also lie in the same plane $C_{1} X Z Y$, they are parallel. Similarly, lines $Y Z$ and $C_{1} X$ are parallel. Therefore, quadrilateral $C_{1} X Z Y$ is a parallelogram.
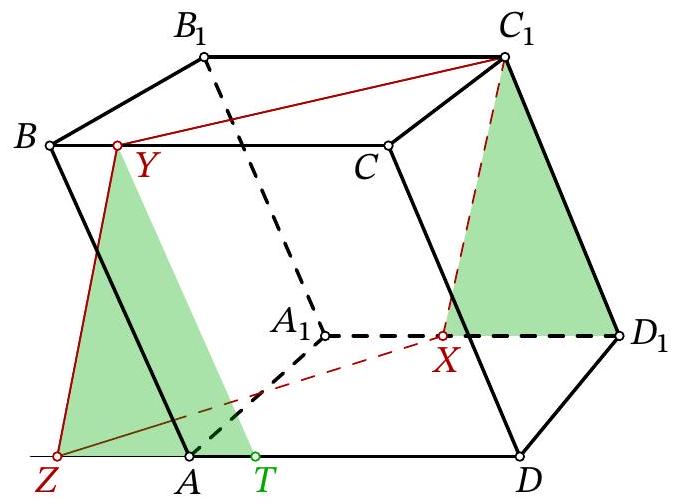
Fig. 15: to the solution of problem 11.8
Let us lay off segment $A T$ on $A D$, equal to $B Y$ (Fig. 15). Quadrilateral $B Y T A$ is a parallelogram, meaning segments $Y T, B A$, and $C_{1} D_{1}$ are parallel and equal. Additionally, segments $Y Z$ and $C_{1} X$ are parallel and equal; from the parallelism follows the equality of angles $Z Y T$ and $X C_{1} D_{1}$, which gives the equality of triangles $Z Y T$ and $X C_{1} D_{1}$.
Then
$$
\begin{aligned}
D Z & =Z T+A D-A T=X D_{1}+B_{1} C_{1}-B Y= \\
& =\left(A_{1} D_{1}-A_{1} X\right)+B_{1} C_{1}-B Y=(14-5)+14-3=20
\end{aligned}
$$
Another solution. As in the previous solution, we will use the fact that $C_{1} X Z Y$ is a parallelogram.
Consider the chain of vector equalities:
$$
\overrightarrow{D Z}=\overrightarrow{D C}+\overrightarrow{C Y}+\overrightarrow{Y Z}=\overrightarrow{D_{1} C_{1}}+\overrightarrow{C Y}+\overrightarrow{C_{1} X}=\overrightarrow{C Y}+\overrightarrow{D_{1} X}
$$
In the last part, all vectors are oriented the same as $\overrightarrow{D Z}$, so we can transition to the equality of segments and continue:
$$
D Z=C Y+D_{1} X=(C B-B Y)+\left(D_{1} A_{1}-A_{1} X\right)=2 B_{1} C_{1}-B Y-A_{1} X
$$
Substituting the lengths given in the condition, we get $D Z=2 \cdot 14-3-5=20$.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2 Points A, B, C, D are consecutive vertices of a regular n-gon. What is n if $\angle \mathrm{ACD}=120^{\circ}$?
|
Solution. We consider the given n-gon as inscribed.
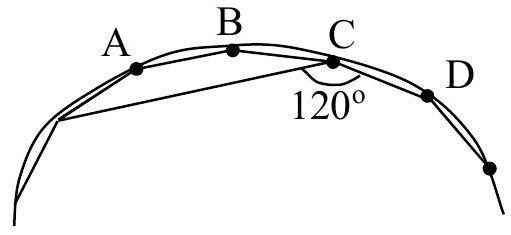
Each small arc between adjacent vertices is $\frac{1}{\mathrm{n}} \cdot 360^{\circ}$. The angle $\mathrm{ACD}$ is an inscribed angle and subtends an arc consisting of $\mathrm{n}-3$ small arcs, i.e., an arc of $(\mathrm{n}-3) \cdot \frac{1}{\mathrm{n}} \cdot 360^{\circ}$. Therefore, $\angle \mathrm{ACD}=\frac{1}{2} \cdot \frac{\mathrm{n}-3}{\mathrm{n}} \cdot 360^{\circ}=\frac{\mathrm{n}-3}{\mathrm{n}} \cdot 180^{\circ}$. According to the problem, $\frac{\mathrm{n}-3}{\mathrm{n}} \cdot 180^{\circ}=240^{\circ}$. Solving for $\mathrm{n}$, we get $\mathrm{n}=9$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3 Let a, b, c be non-negative integers such that $28a + 30b + 31c = 365$. Prove that $a + b + c = 12$.
|
Solution. If it were $\mathrm{a}+\mathrm{b}+\mathrm{c} \leq 11$, then we would have $28 \mathrm{a}+30 \mathrm{~b}+31 \mathrm{c} \leq 31(\mathrm{a}+\mathrm{b}+\mathrm{c}) \leq 31 \cdot 11 < 365$. Therefore, $\mathrm{a}+\mathrm{b}+\mathrm{c} \geq 12$. We will show that the inequality $\mathrm{a}+\mathrm{b}+\mathrm{c} \geq 13$ is also excluded. For this, note that due to the equality $28 \mathrm{a}+30 \mathrm{~b}+31 \mathrm{c}=365$, the number $\mathrm{c}$ is odd (otherwise, the left side of the equality would represent an even number, while 365 is an odd number). Therefore, $c \geq 1$. Further, if $\mathrm{a}+\mathrm{b}+\mathrm{c} \geq 13$, then we get
$28 \mathrm{a}+30 \mathrm{~b}+31 \mathrm{c}=28(\mathrm{a}+\mathrm{b}+\mathrm{c})+2 \mathrm{~b}+3 \mathrm{c} \geq 28 \cdot 13+2 \cdot 0+3 \cdot 1=267-$ too much! Therefore, $\mathrm{a}+\mathrm{b}+\mathrm{c} \leq 12$. Finally, $\mathrm{a}+\mathrm{b}+\mathrm{c}=12$.
|
12
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.1. In class 7 "B", there are more than 3 but less than 15 children. On New Year's, Santa Claus came to them with a bag containing 195 candies. After distributing the candies equally among all the children in the class, Santa Claus found that there were 8 candies left in the bag. How many candies did each child receive?
|
Answer: 17.
Solution. The children received $195-8=187=11 \cdot 17$ candies. This number must be divisible by the number of children in the class, which is more than 3 and less than 15. Therefore, there are 11 children in the class, and each of them received $187: 11=17$ candies.
|
17
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.3. In the example with fractions, some two-digit natural numbers have been replaced by the letters $A$ and $B$.
$$
\frac{A-5}{A}+\frac{4}{B}=1
$$
(a) (2 points) What is the smallest value that $A$ can take?
(b) (2 points) What is the largest value that $B$ can take?
|
# Answer:
(a) (2 points) 15.
(b) (2 points) 76.
Solution. According to the condition,
\[
1=\frac{A-5}{A}+\frac{4}{B}=1-\frac{5}{A}+\frac{4}{B}
\]
from which we obtain \(\frac{A}{5}=\frac{B}{4}\) and \(4A=5B\). It follows that for some integer \(k\), the equalities \(A=5k\) and \(B=4k\) hold.
Since \(B=4k \geqslant 10\), we get \(k \geqslant 3\) and \(A=5k \geqslant 5 \cdot 3=15\). The value \(A=15\) is possible if \(B=12\).
Since \(A=5k \leqslant 99\), we get \(k \leqslant 19\) and \(B=4k \leqslant 4 \cdot 19=76\). The value \(B=76\) is possible if \(A=95\).
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
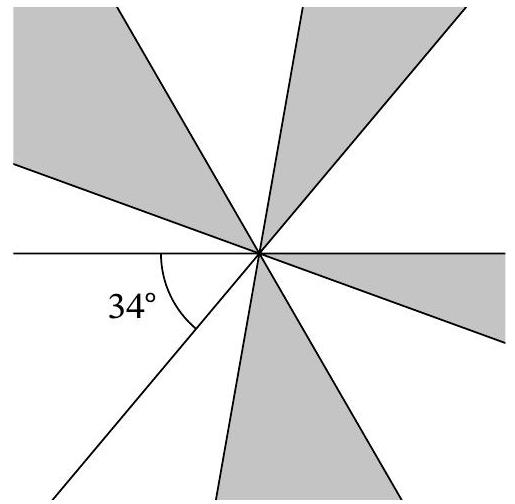
Problem 7.4. The figure shows 5 lines intersecting at one point. One of the resulting angles is $34^{\circ}$. How many degrees is the sum of the four angles shaded in gray?
|
Answer: $146^{\circ}$.
Solution. Replace the two "upper" gray angles with their equal vertical angles, as shown in the picture:
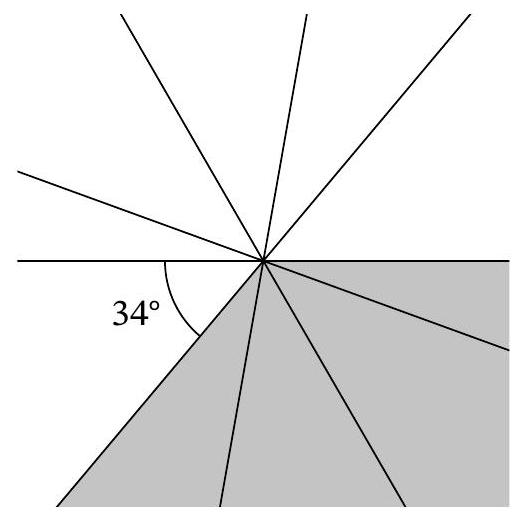
Now it is clear that the gray angles, together with the $34^{\circ}$ angle, sum up to $180^{\circ}$. Therefore, the sum of the gray angles is $146^{\circ}$.
|
146
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.5. On an island, there live knights who always tell the truth, and liars who always lie. One day, 35 inhabitants of the island sat down at 7 tables, with 5 people at each table. Each of these 35 inhabitants was asked: "Are there more than three tables where at least 3 knights are sitting?"
(a) (1 point) What is the maximum number of inhabitants who could have answered "Yes"?
(b) (3 points) What is the maximum number of inhabitants who could have answered "No"?
|
Answer:
(a) (1 point) 35.
(b) (3 points) 23.
Solution. (a) It is clear that all 35 people could have answered "Yes" if they were knights. More than 35 could not be.
(b) Consider two cases.
First case. The statement "There are more than three tables where at least 3 knights are sitting" is true.
Then there are at least 4 tables where at least 3 knights are sitting, meaning there are at least 12 knights in total. Therefore, there are no more than $35-12=23$ liars, so there were no more than 23 "no" answers.
It is not difficult to construct an example in this case:
- At the first four tables, there are 3 knights and 2 liars each;
- At the remaining three tables, there are 5 liars each.
Second case. The statement "There are more than three tables where at least 3 knights are sitting" is false.
Then there are no more than 3 tables where at least 3 knights are sitting. Thus, there are at least 4 tables where no more than 2 knights are sitting. Therefore, there are at least 4 tables where at least 3 liars are sitting, meaning there are at least 12 liars.
Therefore, there were no more than $35-12=23$ knights, so there were no more than 23 "no" answers.
It is not difficult to construct an example in this case:
- At the first three tables, there are 5 knights each;
- At the remaining four tables, there are 2 knights and 3 liars each.
|
23
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.8. In a chess tournament, 30 chess players participated, each playing against each other exactly once. A win was awarded 1 point, a draw - $1 / 2$, and a loss - 0. What is the maximum number of chess players who could have ended up with exactly 5 points by the end of the tournament?
|
Answer: 11.
Solution. Let $N-$ be the number of chess players with 5 points.
Assume $N \geqslant 12$. In each game between two playing chess players, 1 point is played, so the sum of points of all chess players who scored 5 points at the end of the tournament is no less than $\frac{N \cdot(N-1)}{2}$. Then, by the pigeonhole principle, there will be one among them with points no less than $\frac{\stackrel{2}{N-1}}{2} \geqslant 5.5$, a contradiction. Therefore, $N \leqslant 11$.
We will show that the value $N=11$ is possible. Divide the 30 chess players into two groups: the first with 11 people, and the second with 19. Let each person in each group play to a draw with each other, and also let each person in the first group lose to each person in the second group. It is easy to see that exactly 5 points were scored by all chess players in the first group, and there are 11 of them.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.3. In each of the three chests, Ali-Baba found gold and silver coins; in total, there were 40 gold and 40 silver coins. In the first chest, there were 7 more gold coins than silver coins, in the second chest, there were 15 fewer silver coins than gold coins. Which type of coin is more in the third chest and by how many? Explain your answer.
|
Answer: There are 22 more silver coins.
Solution. In the first two chests, the total number of gold coins is $7+15=22$ more than the total number of silver coins. Since initially there were an equal number of gold and silver coins, there are 22 fewer gold coins than silver coins in the third chest.
## Evaluation criteria:
+ complete and justified solution
$\pm$ correct line of reasoning, but an arithmetic error was made in addition
$\pm$ the correct answer and the operation $7+15=22$ are provided
干 the correct answer is obtained based on the specific values of the number of coins in the chests
干 only the correct answer is provided
- the task is not solved or is solved incorrectly
|
22
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.4. The frame for three square photographs has the same width everywhere (see figure). The perimeter of one opening is 60 cm, the perimeter of the entire frame is 180 cm. What is the width of the frame?
|
Answer: 5 cm.
Solution. From the condition of the problem, it follows that the length of one hole's side is 15 cm. Let $d$ cm be the width of the frame, then the perimeter of the rectangle is $8 \cdot 15 + 12 d = 120 + 12 d$ (cm). According to the condition, $120 + 12 d = 180$, which means $d = 5$.
Similar reasoning can be conducted without setting up an equation.
## Evaluation Criteria:
+ fully justified solution
$\pm$ the equation is correctly set up (correct line of reasoning), but an arithmetic error is made in solving the equation (in performing a certain operation)
干 the correct answer is guessed and verified that it satisfies the condition
- only the answer is provided
- the problem is not solved or is solved incorrectly
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.5. The arithmetic mean of four numbers is 10. If one of these numbers is erased, the arithmetic mean of the remaining three increases by 1; if instead another number is erased, the arithmetic mean of the remaining numbers increases by 2; and if only the third number is erased, the arithmetic mean of the remaining increases by 3. By how much will the arithmetic mean of the remaining three numbers change if the fourth number is erased?
|
Answer: will decrease by 6.
Solution. From the fact that the arithmetic mean of four numbers is 10, it follows that the sum of these numbers is 40. Similarly, the sum of three numbers (excluding the first) is 33, the sum of three numbers (excluding the second) is 36, and the sum of three numbers (excluding the third) is 39. From these conditions, we get: the first number is 7, the second is 4, the third is 1. Thus, the arithmetic mean of the first three numbers is 4, which is 6 less than 10.
Similar reasoning can be conducted algebraically. Denoting the four numbers by $a, b, c$, and $d$ respectively, we get four equations: $(a+b+c+d): 4=10, (b+c+d): 3=11, (a+c+d): 3=12$, $(a+b+d): 3=13$. The solution to this system is the set of numbers: $(7,4,1,28)$.
## Evaluation Criteria:
+ fully justified solution
$\pm$ correct line of reasoning (the system of equations is correctly set up), but an arithmetic error is made
the answer is not obtained, but it is proven that the arithmetic mean of the first three numbers is less than 10
$\mp$ the correct answer is obtained by selecting a set of four numbers and verifying that it satisfies the condition (but it is not proven that the found set of four numbers is the only possible one)
- a set of four numbers is given, but it is not even verified
- an error is made in the definition of the arithmetic mean
- the problem is not solved or is solved incorrectly
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.6. What is the smallest natural number $a$ for which there exist integers $b$ and $c$ such that the quadratic trinomial $a x^{2}+b x+c$ has two distinct positive roots, each not exceeding $\frac{1}{1000} ?$
(A. Khryabrov)
|
Answer. $a=1001000$.
First solution. We will prove that $a \geqslant 1001000$. Notice that if $y$ is a root of the quadratic polynomial $a x^{2}+b x+c$, then $1 / y$ is a root of the quadratic polynomial $c x^{2}+b x+a$. Therefore, in the problem, we need to find the smallest natural $a$ for which the roots $x_{1}$ and $x_{2}$ of some quadratic polynomial $c x^{2}+b x+a$ (with integer $b$ and $c$) are greater than 1000. Since $x_{1}$ and $x_{2}$ are positive and $x_{1} x_{2}=a / c$ (by Vieta's theorem), we have $c>0$.
If $c=1$, then $\left|x_{1}-x_{2}\right|=\sqrt{b^{2}-4 a} \geqslant 1$. Since the smaller root is at least 1000, the larger root is at least 1001, and thus $a=x_{1} x_{2} \geqslant 1001 \cdot 1000$. If $c \geqslant 2$, then $a=c x_{1} x_{2} \geqslant 2 x_{1} x_{2}>2000000$. In both cases, the required estimate is proven.
It remains to note that the quadratic polynomial $x^{2}-(1000+1001) x+1001 \cdot 1000$ has roots 1000 and 1001, so $a=1001000$ works.
Second solution. Let for brevity $n=1000$. Let $x_{1}$ and $x_{2}$ be two distinct roots of the quadratic polynomial $f(x)=a x^{2}+b x+c$, where $0-\frac{n b}{2}$.
Since the roots are distinct, the discriminant $D=b^{2}-4 a c$ is positive. Therefore, $b^{2}>4 a c>-2 n b c$ and, thus, $-b>2 n c$. Therefore, $a>(-b) \cdot \frac{n}{2}>2 n c \cdot \frac{n}{2}=n^{2} c$. Let $a=n^{2} c+d$, where $d$ is a natural number.
Suppose that $a<n^{2}+n$. Then $c=1$ and $d<n$. Therefore, $0 \leqslant f\left(\frac{1}{n}\right)=\frac{a}{n^{2}}+\frac{b}{n}+c=\frac{d}{n^{2}}+\frac{b}{n}+2<\frac{1}{n}+\frac{b}{n}+2$ and, thus, $-b<2 n+1$. Consequently, $-b \leqslant 2 n$ and $D=b^{2}-4 a c \leqslant 4 n^{2}-4\left(n^{2}+d\right)=-4 d<0$. This contradiction shows that $d \geqslant n$.
If $a=n^{2}+n$, then for $b=-2 n-1$ and $c=1$, the quadratic polynomial has roots $x_{1}=\frac{1}{n+1}$ and $x_{2}=\frac{1}{n}$.
|
1001000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (7 points) 45 candies cost as many rubles as can be bought for 20 rubles. How many candies can be bought for 50 rubles?
Answer: 75 candies.
|
Solution. Let $x$ be the cost of one candy in rubles. Then $45 x=\frac{20}{x}$, from which $x=\frac{2}{3}$. Then with 50 rubles, one can buy $\frac{50}{x}=75$ candies.
Criteria. Any correct solution: 7 points.
The equation $45 x=\frac{20}{x}$ is correctly set up, but an arithmetic error is made in solving it or in subsequent steps: 5 points.
In the solution, it is claimed that the price of one candy is $\frac{2}{3}$, it is verified that this price fits the condition of the problem, and the correct answer is obtained: 4 points.
Only the correct answer is provided: 1 point.
|
75
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. When composing the options for the district mathematics olympiad for grades $7, 8, 9, 10, 11$, the jury aims to ensure that in the option for each grade, there are exactly 7 problems, of which exactly 4 do not appear in any other option. What is the maximum number of problems that can be included in the olympiad?
|
Answer: 27.
Solution. The number of non-repeating tasks will be 20, the number of repeating tasks does not exceed $3 \cdot 5 / 2<8$. We will provide an example of variants with exactly 7 repeating tasks: 7th grade: $1,2,3$; 8th grade: $1,2,3$; 9th grade: $4,5,6$; 10th grade: $4,5,7$; 11th grade: $4,6,7$.
|
27
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. One hundred integers are written in a circle. Each number is greater than the sum of the two numbers following it in a clockwise direction. What is the maximum number of positive numbers that can be among the written ones
(S. Berlov)
|
Answer: 49.
Solution: Suppose that two non-negative numbers stand next to each other. Then the number preceding them is greater than their sum, meaning it is positive. Similarly, the number before it is also positive, and so on. In the end, we get that all numbers are non-negative; but then the smallest of them cannot be greater than the sum of the next two - a contradiction.
Thus, among any two consecutive numbers, there is at least one negative number. This means there are no more than 50 positive numbers. Suppose there are exactly 50, then they alternate with negative numbers. Now consider three consecutive numbers $-a, b, -c$ (here $a, b, c > 0$). Then $-a > b - c > -c$, meaning any negative number is strictly greater than the next negative number. Since the numbers are arranged in a circle, this is impossible. Therefore, there are no more than 49 positive numbers.
It remains to provide an example where there are exactly 49 positive numbers. For instance, the following arrangement works:
$-200, 1, -202, 1, -204, 1, -206, 1, \ldots, -296, 1, -298, -99$.
|
49
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.6. The field is a square grid of $41 \times 41$ cells, one of which conceals a tank. The fighter aircraft shoots at one cell per shot. If a hit occurs, the tank moves to an adjacent cell along a side; if not, it remains in place. After each shot, the pilot does not know whether a hit occurred. To destroy the tank, it must be hit twice. What is the minimum number of shots required to guarantee that the tank is destroyed?
(S. Berlov, A. Magazinov)
|
Answer. $\frac{3 \cdot 41^{2}-1}{2}=2521$ shots.
Solution. Color the cells in a checkerboard pattern so that the corners of the field are black. Suppose the pilot first shoots at all the white cells, then at all the black cells, and then again at all the white cells. If the tank was on a white cell, the pilot will destroy it in the first and second series; if it was on a black cell, then in the second and third series. In this case, the pilot will make $41^{2}+\frac{41^{2}-1}{2}=\frac{3 \cdot 41^{2}-1}{2}$ shots.
It remains to show that fewer shots will not suffice. Suppose the pilot has a sequence of shots after which the tank will be guaranteed to be destroyed. Clearly, he must shoot at least once at any cell (otherwise, the tank in that cell will not be destroyed).
Assume there are two adjacent cells $A$ and $B$, at which he shot exactly once, and the shot at $B$ occurred later. Then, if the tank was initially in $B$, it could have moved to $A$ after the shot at $B$, and the second hit would not have occurred. This is impossible; hence, such pairs of cells do not exist.
Now, divide the entire board into $\frac{41^{2}-1}{2}$ rectangles of $1 \times 2$ and one cell. By the proven fact, the fighter must make at least three shots in each rectangle, and at least one shot in the remaining cell. In total, he made no fewer than $3 \cdot \frac{41^{2}-1}{2}+1=\frac{3 \cdot 41^{2}-1}{2}$ shots.
|
2521
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.8. On the board, there are $N \geqslant 9$ different non-negative numbers, each less than one. It turns out that for any eight different numbers on the board, there is a ninth, different from them, such that the sum of these nine numbers is an integer. For which $N$ is this possible?
(F. Nilov)
|
Answer. Only for $N=9$.
Solution. It is clear that for $N=9$ the required is possible - it is sufficient to write 9 different positive numbers on the board with a unit sum. We will show that for $N>9$ the required is impossible. Suppose the opposite; let $S$ be the sum of all numbers on the board.
Choose arbitrary numbers $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{7}$ with sum $T$; let $A$ be the set of all other numbers on the board. By the condition, for any number $\beta \in A$ there exists a number $\gamma \in A$ different from it such that the number $T+\beta+\gamma$ is an integer. We say that the number $\gamma$ corresponds to the number $\beta$. Note that such a number $\gamma$ is unique. Indeed, if there were another number $\gamma^{\prime} \in A$ for which the sum $T+\beta+\gamma^{\prime}$ is an integer, then the number $\gamma-\gamma^{\prime}=(T+\beta+\gamma)-\left(T+\beta+\gamma^{\prime}\right)$ would also be an integer; this is impossible, since $0<|\gamma-\gamma^{\prime}|<1$, as $N=7+2 \ell>9$.
Now consider the sum
$$
\Sigma=\left(T+\beta_{1}+\gamma_{1}\right)+\left(T+\beta_{2}+\gamma_{2}\right)+\ldots+\left(T+\beta_{\ell}+\gamma_{\ell}\right)
$$
Then $\Sigma$ is an integer. On the other hand, each number from $A$ appears in $\Sigma$ exactly once; hence, $\Sigma=\ell T+(S-T)=S+(\ell-1) T$, from which $T=\frac{\Sigma-S}{\ell-1}$.
Now, choosing the numbers $\alpha_{2}, \alpha_{3}, \alpha_{4}, \ldots, \alpha_{8}$ on the board and denoting their sum by $T^{\prime}$, we similarly obtain that $T^{\prime}=\frac{\Sigma^{\prime}-S}{\ell-1}$ for an integer $\Sigma^{\prime}$. Therefore,
$$
\alpha_{1}-\alpha_{8}=\frac{\Sigma-S}{\ell-1}-\frac{\Sigma^{\prime}-S}{\ell-1}=\frac{\Sigma-\Sigma^{\prime}}{\ell-1}
$$
Since $\alpha_{1}$ and $\alpha_{8}$ could be any two numbers on the board, we get that the difference of any two numbers on the board has the form $\frac{k}{\ell-1}$ for an integer $k$.
Let $\mu$ be the smallest number on the board. Then the board can only contain the numbers $\mu, \mu+\frac{1}{\ell-1}, \ldots, \mu+\frac{\ell-2}{\ell-1}$ (all larger numbers will already be at least 1) - a total of $\ell$ numbers. However, the total number of numbers on the board is $N=7+2 \ell>\ell$; hence, they cannot all be different. Contradiction.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 1. CONDITION
How many integers between 100 and 10000 are there such that their representation contains exactly 3 identical digits?
|
Solution. If the digit that repeats three times is zero, then by adding one of the other 9 digits in front, we get 9 numbers. If the digit $a \neq 0$ repeats in the number, then the number of numbers with different $b, b \neq a$, will be $9 \cdot 4 \cdot 9$. Therefore, in total, there are 333 numbers.
Answer: 333.
|
333
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. The price for a ride on the "Voskhod" carousel in February 2020 was 300 rubles per person. In March, the price was reduced, and the number of visitors increased by $50 \%$, while the revenue increased by $25 \%$. By how many rubles was the price reduced?
|
Answer: 50.
Solution. The entry fee for two people in February 2020 was 600 rubles. In March, instead of every two people, the stadium is visited by three people, as the number of visitors increased by $50 \%$. Since the total collection increased by $25 \%$, they will pay $600+0.25 \cdot 600=750$ (rub.), and thus one ticket will cost $750: 3=250$ (rub.), which is 50 rubles less than in February.
Comment. Answer without justification - 1 point.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. The external angles of a triangle are proportional to the numbers $5: 7: 8$. Find the angle between the altitudes of this triangle drawn from the vertices of its smaller angles.
|
Answer: $90^{0}$.
Solution. The sum of the exterior angles of a triangle is
$$
180^{\circ} \cdot 3-180^{\circ}=360^{\circ}
$$
From this, we get that one of the exterior angles of the triangle is $\frac{360^{\circ}}{5+7+8} \cdot 5=90^{0}$, and therefore the adjacent interior angle of the triangle is $90^{0}$. Consequently, the other two angles are the smaller angles of the triangle, and the heights drawn from them coincide with the legs of the triangle, the angle between which is $90^{\circ}$.
Comment. An answer without justification - 0 points.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the island, there are 217 residents, 17 of whom are knights, and the remaining 200 are tricksters. One day, a private detective arrived on the island and decided to find out who is who. For this, he asked each resident to write a list of 200 people they consider to be tricksters. The detective does not know who wrote which list, but he knows that the knights honestly wrote down 200 real tricksters, while the tricksters could have written down any residents of the island (including themselves). Can the detective always identify at least 13 residents who are definitely tricksters based on the received lists? All residents of the island have different names, so a name written in the list always uniquely corresponds to one resident of the island.
|
Answer: Yes, it can always.
Solution. We will combine identical lists into groups. Let's call a group important if it contains at least 17 lists. Note that the number of important groups is no more than 12 (otherwise, the number of residents is at least $13 * 17 = 221$, which is more than 217).
Since all the knights should have ended up with the same list (all wrote down the same tricksters), the lists of all the knights ended up in one group.
Since there are 17 knights, this group contains at least 17 lists, meaning it is important. Thus, in one of the important groups, all the tricksters are listed.
We will prove that there are at least 13 residents who are listed in all important groups. We will mark the people who are not listed in the important groups. In each group, only 17 residents of the island are not listed. Therefore, since there are no more than 12 important groups, a total of no more than 17 * 12 = 204 residents will be marked. At least 13 residents will not be marked, meaning they are listed in all important groups. Regardless of which important group contains the lists of the knights, these 13 residents are definitely tricksters.
Thus, to detect the tricksters, the private detective should combine identical lists into groups and find 13 names that appear in all important (containing at least 17 lists) groups.
Criteria. Only the answer - 0 points. Considering only individual special cases (for example, that all residents wrote down the real tricksters) - 0 points. The solution contains the idea of combining identical lists into groups and highlighting groups with a size of 17 or more lists (but no further progress) - 1 point.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Does there exist a ten-digit number, divisible by 11, in which all digits from 0 to 9 appear?
|
Answer. Yes, for example, 9576843210.
Solution. Let's consider a possible way to find the required number. Note that a number is divisible by 11 if the difference between the sum of the digits in the odd positions and the sum of the digits in the even positions is divisible by 11. If we write all ten digits in descending order, that is, 9876543210, then this difference will be 5. If we swap 5 and 8, the first sum will increase by 3, and the second sum will decrease by 3, so their difference will become 11. Therefore, the number 9576843210 is divisible by 11.
Comment. Any correct number provided - 7 points.
|
9576843210
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. There is a balance scale without weights and 11 visually identical coins, among which one may be counterfeit, and it is unknown whether it is lighter or heavier than the genuine coins (genuine coins have the same weight). How can you find at least 8 genuine coins in two weighings?
|
Solution. Let's divide the coins into three piles of three coins each. Compare pile 1 and pile 2, and then compare pile 2 and pile 3. If all three piles weigh the same, then all the coins in them are genuine, and we have found 9 genuine coins. Otherwise, one of the piles differs in weight from the others, and the counterfeit coin can only be in it. Then the genuine coins are in the other two piles plus the two remaining coins that we did not weigh.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. Find all numbers of the form $22 \ldots 2$ that can be represented as the sum of two perfect squares.
|
Answer: 2.
Solution. Let $22 \ldots 2=a^{2}+b^{2}$ for some integers $a$ and $b$.
If the numbers $a$ and $b$ are even, then the sum of their squares is divisible by 4, but the number $22 \ldots 2$ is not.
Thus, the numbers $a$ and $b$ can only be odd:
$$
a=2 k+1, b=2 l+1(k, l \in Z)
$$
Therefore, the sum
$$
a^{2}+b^{2}=(2 k+1)^{2}+(2 l+1)^{2}=4 k(k+1)+4 l(l+1)+2
$$
when divided by 8 leaves a remainder of 2.
On the other hand, among the numbers of the form 222... 2, only the number 2 leaves a remainder of 2 when divided by 8, since if the number of twos in this number is greater than 1, then
$22 \ldots 2=22 \ldots 2200+22$, in which the first term of the obtained sum is divisible by 8, and the second term leaves a remainder of 6 when divided by 8.
Comments on evaluation. It is shown that the numbers $a$ and $b$ can only be odd - 2 points.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 10.1. Find any natural $x$ such that the value of the expression $2^{x}+2^{8}+2^{11}$ is a square of a natural number.
|
Answer: 12.
Solution. Note that $x=12$ works: $2^{12}+2^{8}+2^{11}=\left(2^{6}\right)^{2}+\left(2^{4}\right)^{2}+2 \cdot 2^{6} \cdot 2^{4}=\left(2^{6}+2^{4}\right)^{2}$. Remark. The number $x=12$ is the only one that fits the condition of the problem.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.2. There are 36 balls lying in a circle, each of which is either red or blue (balls of each of these colors are present). It is known that:
- for any red ball, there is exactly one red ball such that there is exactly one ball between them;
- for any red ball, there is exactly one red ball such that there are exactly three balls between them.
(a) (2 points) Suppose there are no two adjacent red balls. How many red balls can lie in a circle? Indicate all possible options.
(b) (2 points) Suppose there are two adjacent red balls. How many red balls can lie in a circle? Indicate all possible options.
|
Answer:
(a) (2 points) 12.
(b) (2 points) 24.
Solution. By the condition, there will be two red balls, between which lies exactly one ball. Number the balls clockwise with numbers \(1, 2, \ldots, 36\) such that the 1st and 3rd balls are red. From the condition, it follows that the 35th ball is blue (otherwise, the first condition is false for the 1st ball), the 5th ball is blue (otherwise, the first condition is false for the 3rd ball), the 7th ball is red (otherwise, the second condition is false for the 3rd ball), and the 9th ball is red (otherwise, the first condition is false for the 7th ball). Thus, assuming that the 1st and 3rd balls are red, we have that the 5th ball is blue, and the 7th and 9th balls are red. Continuing this reasoning, we get that the 11th ball is blue, the 13th and 15th balls are red, and so on.
Two-thirds of the balls are red, and one-third are blue.
(a) Suppose there are no two adjacent red balls. It is easy to see that then there are no red balls among the balls with even numbers. Therefore, the total number of red balls is \(\frac{36}{2} \cdot \frac{2}{3} = 12\). An example with 12 red balls is shown below.
(b) Suppose there are two adjacent red balls. It is easy to see that then among the balls with even numbers, red balls also constitute two-thirds. Therefore, the total number of red balls is \(36 \cdot \frac{2}{3} = 24\). An example with 24 red balls is shown below.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.3. Quadrilateral $ABCD$ is such that $\angle ABD = \angle ACD = 90^\circ$, $\angle CAD = 42^\circ$. Rays $CB$ and $DA$ intersect at point $K$. It is known that $BK = 3$, $AD = 6$.
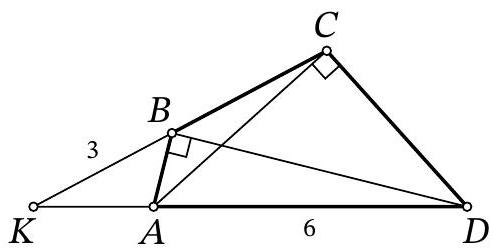
(a) (2 points) How many degrees does the angle $BKA$ measure?
(b) (2 points) How many degrees does the angle $BAC$ measure?
|
# Answer:
(a) (2 points) $28^{\circ}$.
(b) (2 points) $34^{\circ}$.
Solution. From the condition, it follows that points $A, B, C, D$ lie on a circle with diameter $A D$. Connect point $B$ to the midpoint $O$ of segment $A D$, which is the center of this circle (Fig. 6). Clearly, $A O=O D=O B=B K=3$.
Triangles $K B O$ and $B O D$ are isosceles. Let $\alpha=\angle B K A=\angle B O K$. The angle $B O K$, equal to $\alpha$, is an exterior angle for triangle $B O D$ and is equal to the sum of the two interior angles at vertices $B$ and $D$, so $\angle O B D=\angle O D B=\frac{\alpha}{2}$.
Since quadrilateral $A B C D$ is inscribed, $\angle C B D=\angle C A D=42^{\circ}$. The angle $C B D$, equal to $42^{\circ}$, is an exterior angle for triangle $K B D$ and is equal to the sum of the two interior angles at vertices $K$ and $D$, so $42^{\circ}=\alpha+\frac{\alpha}{2}$, from which we find $\angle B K A=\alpha=$ $\frac{2}{3} \cdot 42^{\circ}=28^{\circ}$.
Fig. 6: to the solution of problem 10.3
In the right triangle $A B D$, the sum of the angles at vertices $A$ and $D$ is $90^{\circ}$, so $90^{\circ}=\angle B A C+\angle C A D+\angle A D B=\angle B A C+42^{\circ}+\frac{1}{2} \cdot 28^{\circ}$, from which we find $\angle B A C=34^{\circ}$.
|
34
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.4. Given a rectangular grid of cells. It is known that:
- there are exactly 940 ways to cut out a $1 \times 2$ rectangle from it along the grid lines;
- there are exactly 894 ways to cut out a $1 \times 3$ rectangle from it along the grid lines.
How many ways are there to cut out a $1 \times 5$ rectangle from it along the grid lines?
When counting the number of ways to cut out a rectangle, both vertical and horizontal orientations are considered.
|
Answer: 802.
Solution. Let the table have $a$ rows and $b$ columns. Without loss of generality, $a \leqslant b$. It is clear that at least one of the numbers $a$ and $b$ is not less than 2.
- Suppose $a=1$. Then from the table $1 \times b$, a rectangle $1 \times 2$ can be cut in $b-1=940$ ways, and a rectangle $1 \times 3$ can be cut in $b-2=894$ ways. Clearly, such values of $b$ do not exist.
- Suppose $b \geqslant a \geqslant 2$. Then from the table $a \times b$, a rectangle $1 \times 2$ can be cut in $a(b-1)+b(a-1)$ ways, and a rectangle $1 \times 3$ can be cut in $a(b-2)+b(a-2)$ ways. Therefore, $a(b-1)+b(a-1)=940$ and $a(b-2)+b(a-2)=894$. Subtracting the second equation from the first, we get $a+b=46$. From this, it follows that $ab=493$. By the converse of Vieta's theorem, the numbers $a$ and $b$ are the roots of the polynomial $x^{2}-46x+493=(x-17)(x-29)$, so $a=17$ and $b=29$. A rectangle $1 \times 5$ can be cut from the table $17 \times 29$ in exactly $17 \cdot 25+13 \cdot 29=802$ ways.
|
802
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.5. Several sweet-tooths participated in a candy eating contest. Each participant ate an integer number of candies, and any two participants ate a different number of candies. Summarizing the contest, the jury ranked all the people in descending order of the number of candies eaten (for example, the winner ate the most candies, and the person who came in last place ate the fewest candies).
It is known that:
- the winner ate 14 times fewer candies than all the other participants combined;
- the participant who came in third place ate 20 times fewer candies than all the other participants combined;
- the participant who came in last place ate 21 times fewer candies than all the other participants combined.
How many sweet-tooths participated in the contest?
|
Answer: 21.
Solution. Let there be $n$ sweet-tooth participants in total, and they ate $S$ candies in total. From the condition, it follows that the winner ate $\frac{S}{15}$ candies, the person in third place $-\frac{S}{21}$ candies, and the person in last place $-\frac{S}{22}$ candies.
All participants, except the last one, ate more than $\frac{S}{22}$ candies. Therefore, $S > n \cdot \frac{S}{22}$, from which we get $n < 22$. On the other hand, since the person in third place ate $-\frac{S}{21}$ candies, and the person in last place ate $-\frac{S}{22}$ candies, we have $-\frac{S}{21} > -\frac{S}{22}$, which means $n \geqslant 21$.
Additionally, for $n=21$, we can provide an example. Suppose the 1st sweet-tooth participant ate 924 candies, the 2nd - 783 candies, the 3rd - 660 candies, and from the 4th to the 21st - from 647 to 630 candies respectively (a total of 13860 candies eaten). It is not difficult to verify that all conditions of the problem are satisfied.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.6. Given trapezoid $ABCD$. Segments $AB$ and $CD$ - its lateral sides - are equal to 24 and 10, respectively. Points $X$ and $Y$ are marked on side $AB$ such that $AX=6, XY=8, YB=10$. It is known that the distances from points $X$ and $Y$ to line $CD$ are 23 and 27, respectively.
(a) (1 point) Find the area of triangle $ACD$.
(b) (3 points) Find the area of trapezoid $ABCD$.
|
# Answer:
(a) (1 point) 100.
(b) (3 points) 260.
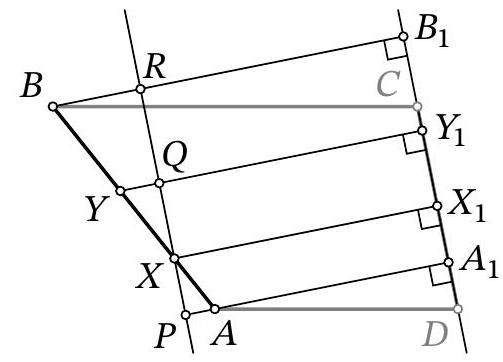
Fig. 7: to the solution of problem 10.6
Solution. We will prove that the distances from points $A$ and $B$ to the line $C D$ are 20 and 32, respectively. Let $A_{1}, X_{1}, Y_{1}, B_{1}$ be the projections of points $A, X, Y, B$ onto the line $C D$ respectively (Fig. 7). Draw a line through $X$ parallel to $C D$, and let it intersect the lines $A A_{1}$, $Y Y_{1}$, $B B_{1}$ at points $P, Q, R$ respectively. In the similar right triangles $A P X$, $Y Q X$, $B R X$, the hypotenuses are in the ratio $A X: X Y: Y B=6: 8: 18=3: 4: 9$, so $A P: Y Q: B R=3: 4: 9$. Considering that $Y Q=Y Y_{1}-Q Y_{1}=Y Y_{1}-X X_{1}=27-23=4$, we get that $A P=3$ and $B R=9$. Then $A A_{1}=X X_{1}-A P=23-3=20$ and $B B_{1}=X X_{1}+B R=23+9=32$. Therefore, $S_{A C D}=\frac{1}{2} \cdot A A_{1} \cdot C D=\frac{1}{2} \cdot 20 \cdot 10=100$ and $S_{B C D}=\frac{1}{2} \cdot B B_{1} \cdot C D=\frac{1}{2} \cdot 32 \cdot 10=160$.
In the trapezoid $A B C D$, the areas of triangles $A B C$ and $B C D$ are equal, since side $B C$ is common to both, and the heights dropped from points $A$ and $D$ to $B C$ are equal. Therefore,
$$
S_{A B C D}=S_{A C D}+S_{A B C}=S_{A C D}+S_{B C D}=100+160=260
$$
|
260
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. On an island, there are 23 knights and 200 liars; all residents have different names. A tourist who knows this asked each of the 223 residents to write down 200 names of liars on a piece of paper. Each knight correctly wrote down 200 names of liars, while each liar wrote down an arbitrary list of 200 names, which definitely does not include their own name. What is the maximum number of liars the tourist can definitely identify from these data?
|
Answer: 16.
Solution. First, let's outline a strategy for the liars that allows identifying no more than 16 of them. Let's call the knights $R_{1}, R_{2}, \ldots, R_{23}$, and the liars $-L_{1}, L_{2}, \ldots, L_{200}$. All knights will list $L_{1}, L_{2}, \ldots, L_{200}$ in their lists. For each integer $0 \leqslant i \leqslant 7$, the group of liars $L_{23 i+1}, L_{23 i+2}, \ldots, L_{23 i+23}$ will list $R_{1}, R_{2}, \ldots, R_{23}$, as well as all liars except for themselves. The 16 liars $L_{185}, L_{186}, \ldots, L_{200}$ will list $R_{1}, R_{2}, \ldots, R_{23}, L_{1}, L_{2}, \ldots, L_{177}$ in their lists. The tourist, upon seeing the received lists, will not be able to reliably identify any liar among $L_{1}, L_{2}, \ldots, L_{184}$ (which means he will identify no more than 16 liars). Indeed, if the tourist were to claim that $L_{k}$ is a liar, he could be wrong: the group of 23 people, which included $L_{k}$, could consist entirely of knights who, in their lists, uniformly indicated all other people who could turn out to be liars.
Now, let's understand why the tourist will always be able to identify at least 16 liars. The fact that a person lists 200 names of supposed liars is equivalent to them calling the remaining 23 people (including themselves) knights. All 23 knights will definitely call each other knights. Note that if a person $A$ calls a group of 23 people knights, and not all of them call the same group of people knights, then $A$ is definitely a liar (if he were a knight, then all the people he named would also be knights, and they would call the same group of people knights). There are no more than 9 groups of 23 people who call each other knights (since $10 \cdot 23 > 223$), and these groups do not overlap. Therefore, the tourist can definitely guarantee that the remaining people, who do not belong to such groups, are liars. And there are at least $223 - 9 \cdot 23 = 16$ such people.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.3. Zhenya drew a square with a side of 3 cm, and then erased one of these sides. A figure in the shape of the letter "P" was obtained. The teacher asked Zhenya to place dots along this letter "P", starting from the edge, so that the next dot was 1 cm away from the previous one, as shown in the picture, and then count how many dots he got. He got 10 dots.
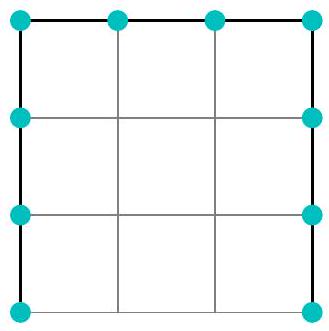
Then the teacher decided to complicate the task and asked to count the number of dots, but for the letter "P" obtained in the same way from a square with a side of 10 cm. How many dots will Zhenya have this time?
|
Answer: 31.
Solution. Along each of the three sides of the letter "П", there will be 11 points. At the same time, the "corner" points are located on two sides, so if 11 is multiplied by 3, the "corner" points will be counted twice. Therefore, the total number of points is $11 \cdot 3-2=31$.
|
31
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.5. Hooligan Dima made a construction in the shape of a $3 \times 5$ rectangle using 38 wooden toothpicks. Then he simultaneously set fire to two adjacent corners of this rectangle, marked in the figure.
It is known that one toothpick burns for 10 seconds. How many seconds will it take for the entire construction to burn?
(Fire spreads along the toothpicks at a constant speed. The fire continues to spread from each burned toothpick to all adjacent unburned toothpicks.)

|
Answer: 65.
Solution. In the picture below, for each "node", the point where the toothpicks connect, the time in seconds it takes for the fire to reach it is indicated. It will take the fire another 5 seconds to reach the middle of the middle toothpick in the top horizontal row (marked in the picture).
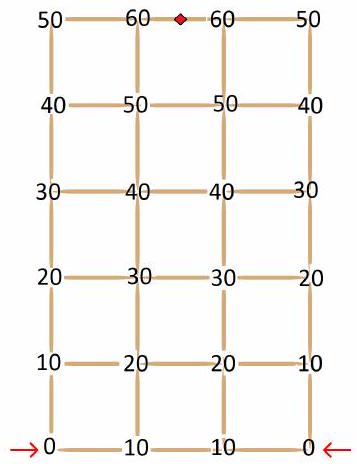
|
65
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. The school principal, the caretaker, and the parent committee, failing to agree with each other, each bought a carpet for the school auditorium, which is $10 \times 10$. After thinking about what to do, they decided to place all three carpets as shown in the picture: the first carpet $6 \times 8$ - in one corner, the second carpet $6 \times 6$ - in the opposite corner, and the third carpet $5 \times 7$ - in one of the remaining corners (all dimensions are in meters).
Find the area of the part of the hall covered by carpets in three layers (give the answer in square meters).
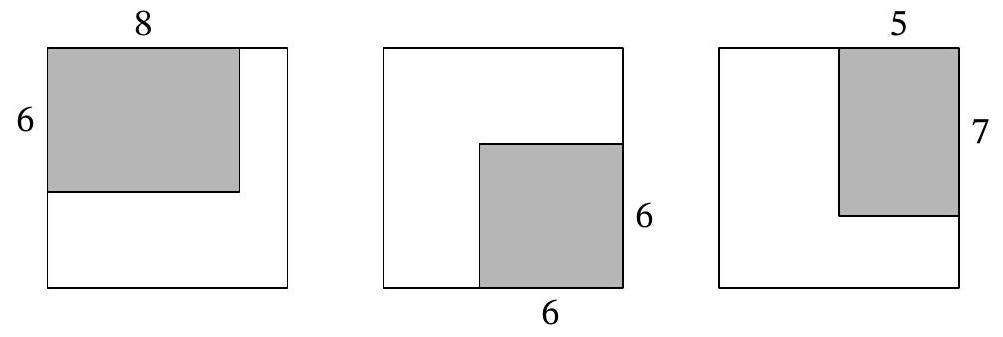
|
Answer: 6.
Solution. We will measure all dimensions in meters and the area in square meters.
Let's look at the overlap of the second and third carpets. This will be a rectangle $5 \times 3$ (5 along the horizontal, 3 along the vertical), adjacent to the right side of the square room, 4 units from the top side, and 3 units from the bottom side.
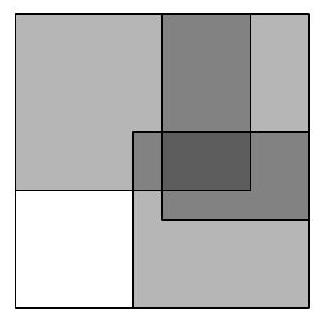
The first carpet intersects this rectangle horizontally between the 5th and 8th meters from the left side of the square room, and vertically between the 4th and 6th meters from the top side. In the end, we get a rectangle $2 \times 3$, the area of which is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.8. Inside a large triangle with a perimeter of 120, several segments were drawn, dividing it into nine smaller triangles, as shown in the figure. It turned out that the perimeters of all nine small triangles are equal to each other. What can they be equal to? List all possible options.
The perimeter of a figure is the sum of the lengths of all its sides.
|
Answer: 40.
Solution. Let's add the perimeters of the six small triangles marked in gray in the following figure:
From the obtained value, subtract the perimeters of the other three small white triangles. Since the perimeters of the small triangles are equal, on one side, we get three times the perimeter of a small triangle. On the other side, in this sum, there will only be segments that make up the perimeter of the large triangle, which is 120. Therefore, the perimeter of a small triangle is $120: 3=40$.
## 6th grade
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.7. Anya places pebbles on the sand. First, she placed one stone, then added pebbles to form a pentagon, then made a larger outer pentagon with pebbles, then another outer pentagon, and so on, as shown in the picture. The number of stones she had arranged on the first four pictures: 1, 5, 12, and 22. If she continues to create such pictures, how many stones will be on the 10th picture?
-
|
Answer: 145.
Solution. On the second picture, there are 5 stones. To get the third picture from it, you need to add three segments with three stones on each. The corner stones will be counted twice, so the total number of stones in the third picture will be $5+3 \cdot 3-2=12$.
To get the fourth picture from the third, you need to add three segments with four stones on each. The corner stones will be counted twice, so the total number of stones will be $12+3 \cdot 4-2=22$.
Similarly, we will calculate the number of stones on each of the remaining pictures:
on the 5th: $22+3 \cdot 5-2=35$;
on the 6th: $\quad 35+3 \cdot 6-2=51$;
on the 7th: $51+3 \cdot 7-2=70$;
on the 8th: $\quad 70+3 \cdot 8-2=92$;
on the 9th: $92+3 \cdot 9-2=117$
on the 10th: ~ 117+3 \cdot 10-2=145$.
|
145
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. In the chat of students from one of the schools, a vote was held: "On which day to hold the disco: October 22 or October 29?"
The graph shows how the votes were distributed an hour after the start of the voting.
Then, 80 more people participated in the voting, voting only for October 22. After that, the voting ended. The final distribution of votes is also shown on the graph.
How many people participated in the voting?
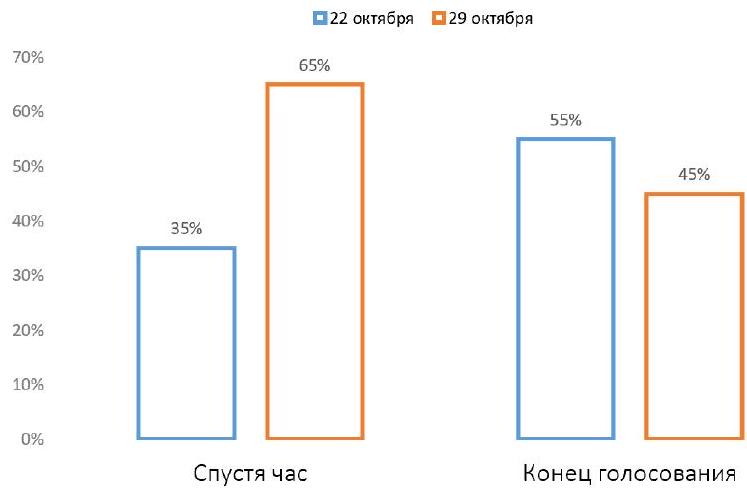
|
Answer: 260.
Solution. Let $x$ be the number of people who voted an hour after the start. From the left chart, it is clear that $0.35 x$ people voted for October 22, and $-0.65 x$ people voted for October 29.
In total, $x+80$ people voted, of which $45\%$ voted for October 29. Since there are still $0.65 x$ of them, we get the equation
$0.65 x=0.45(x+80)$, from which we find $x=180$. Therefore, a total of $180+80=260$ people participated in the voting.
|
260
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. The figure shows two equal triangles: $A B C$ and $E B D$. It turns out that $\angle D A E = \angle D E A = 37^{\circ}$. Find the angle $B A C$.
|
Answer: 7.
Fig. 4: to the solution of problem 8.7
Solution. Draw segments $A D$ and $A E$ (Fig. 4). Since $\angle D A E=\angle D E A=37^{\circ}$, triangle $A D E$ is isosceles, $A D=D E$.
Notice that triangle $A B D$ is equal to triangle $E B D$ by three sides: $B D$ is a common side, $A D=D E, A B=B E$ from the equality of triangles $A B C$ and $E B D$. Then $\angle D A B=$ $\angle B E D=\angle B A C$ and $\angle A B D=\angle D B E=\angle A B E=\frac{1}{3} \cdot 360^{\circ}=120^{\circ}$.
Since $A B=B E$, triangle $A B E$ is isosceles with an angle of $120^{\circ}$, so $\angle B A E=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$. Therefore,
$$
\angle B A C=\angle D A B=\angle D A E-\angle B A E=37^{\circ}-30^{\circ}=7^{\circ}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. A line $\ell$ is drawn through vertex $A$ of rectangle $ABCD$, as shown in the figure. Perpendiculars $BX$ and $DY$ are dropped from points $B$ and $D$ to line $\ell$. Find the length of segment $XY$, given that $BX=4$, $DY=10$, and $BC=2AB$.
|
Answer: 13.
Fig. 5: to the solution of problem 9.4
Solution. Note that since $\angle Y A D=90^{\circ}-\angle X A B$ (Fig. 5), the right triangles $X A B$ and $Y D A$ are similar by the acute angle $\angle Y A D=\angle X B A$. The similarity ratio is the ratio $A B: A D$, which is $\frac{1}{2}$. From this, we get $X A=\frac{1}{2} D Y=5$ and $A Y=2 B X=8$, which in total gives $X Y=13$.
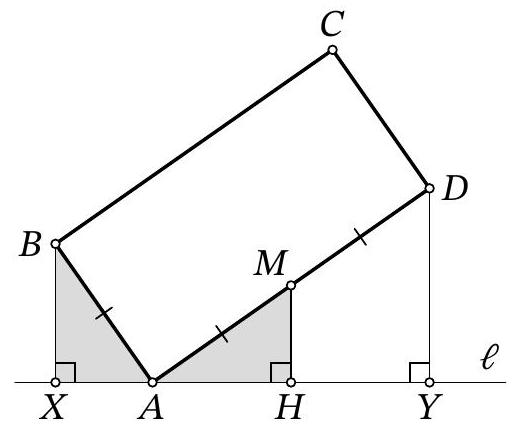
Fig. 6: to the solution of problem 9.4
Another solution. Let $M$ be the midpoint of segment $A D$, then $A M=M D=\frac{A D}{2}=\frac{B C}{2}=A B$ (Fig. 6). Drop a perpendicular from $M$ to $M H$ on line $\ell$. Since in triangle $A D Y$ the segment $M H$ passes through the midpoint of side $A D$ and is parallel to side $D Y$, it is the midline, $A H=H Y$ and $M H=\frac{D Y}{2}=\frac{10}{2}=5$.
Note that $\angle A B X=90^{\circ}-\angle B A X=90^{\circ}-\left(180-90^{\circ}-\angle M A H\right)=\angle M A H$. Then the right triangles $A B X$ and $M A H$ are equal by hypotenuse $A B=A M$ and acute angle $\angle A B X=\angle M A H$. From this, it follows that $A X=M H=5$ and $A H=B X=4$.
Thus, $X Y=A X+A H+H Y=5+4+4=13$.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.6. In triangle $A B C$, the angles $\angle B=30^{\circ}$ and $\angle A=90^{\circ}$ are known. On side $A C$, point $K$ is marked, and on side $B C$, points $L$ and $M$ are marked such that $K L=K M$ (point $L$ lies on segment $B M$).
Find the length of segment $L M$, if it is known that $A K=4, B L=31, M C=3$.
|
Answer: 14.
Solution. In the solution, we will use several times the fact that in a right-angled triangle with an angle of $30^{\circ}$, the leg opposite this angle is half the hypotenuse. Drop the height $K H$ from the isosceles triangle $K M L$ to the base (Fig. 7). Since this height is also a median, then $M H=H L=x$. In the right-angled triangle $C K H$ we have $\angle C K H=90^{\circ}-\angle C=\angle A=30^{\circ}$, so $K C=2 \cdot C H=2 \cdot(C M+M H)=$ $2 \cdot(3+x)=6+2 x$. In the right-angled triangle $A B C$ we have $\angle A=30^{\circ}$, so $B C=2 \cdot A C$. Setting up and solving the corresponding equation $31+2 x+3=2 \cdot(4+6+2 x)$, we find $x=7$. Then $L M=2 x=2 \cdot 7=14$.
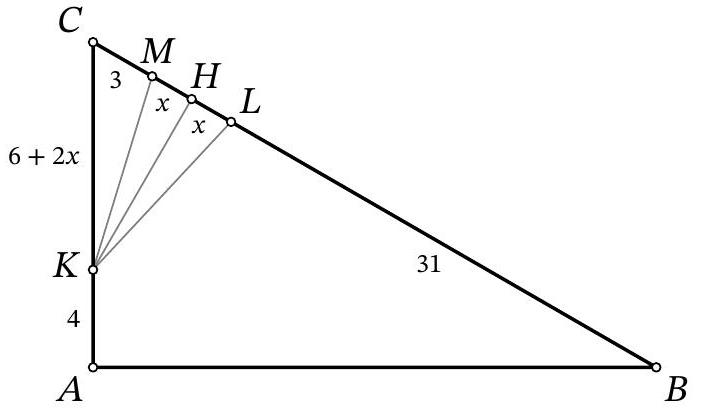
Figure 7: to the solution of problem 9.6
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.2. Points $A, B, C, D, E, F, G$ are located clockwise on a circle, as shown in the figure. It is known that $A E$ is the diameter of the circle. Also, it is known that $\angle A B F=81^{\circ}, \angle E D G=76^{\circ}$. How many degrees does the angle $F C G$ measure?
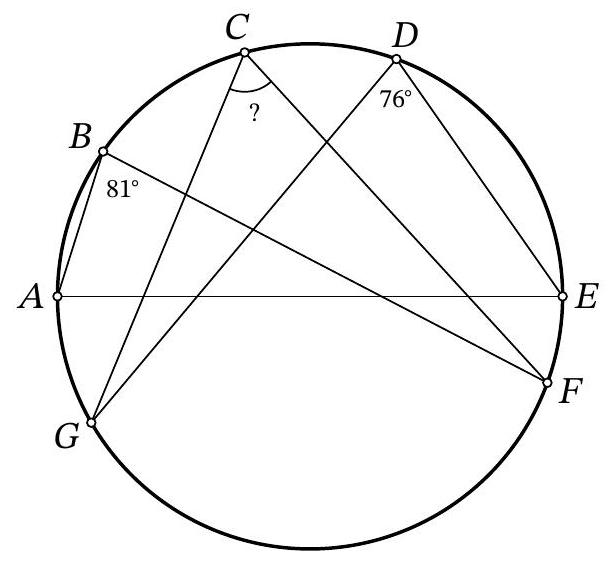
|
Answer: 67.
Solution. Since inscribed angles subtended by the same arc are equal, then $\angle A C F=$ $\angle A B F=81^{\circ}$ and $\angle E C G=\angle E D G=76^{\circ}$. Since a right angle is subtended by the diameter,
$$
\angle F C G=\angle A C F+\angle E C G-\angle A C E=81^{\circ}+76^{\circ}-90^{\circ}=67^{\circ}
$$
|
67
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. The graph of the function $f(x)=\frac{1}{12} x^{2}+a x+b$ intersects the $O x$ axis at points $A$ and $C$, and the $O y$ axis at point $B$, as shown in the figure. It turned out that for the point $T$ with coordinates $(3 ; 3)$, the condition $T A=T B=T C$ is satisfied. Find $b$.

|
Answer: -6.
Fig. 11: to the solution of problem 10.7
Solution. Let point $A$ have coordinates $\left(x_{1} ; 0\right)$, and point $C$ have coordinates $\left(x_{2} ; 0\right)$. From the condition, it is clear that $x_{1} < 0$ and $x_{2} > 0$. Since $x_{1}$ and $x_{2}$ are the roots of the quadratic trinomial $f(x)$, by Vieta's theorem, we have $x_{1} \cdot x_{2} = 12b$, from which we get $b = \frac{x_{1} \cdot x_{2}}{12} < 0$.
Let $H$ be the point with coordinates $(3 ; 0)$ (Fig. 11). Clearly, in the isosceles triangle $A T C$, the segment $T H$ is the height, and therefore it is also the median. Thus, $3 - x_{1} = A H = H C = x_{2} - 3$, from which we get $x_{1} = 6 - x_{2}$.
Let $M$ be the point with coordinates $(0, 3)$. Since $T H = T M = 3$ and $T A = T B$, the right triangles $A T H$ and $B T M$ are equal by the leg and hypotenuse. Therefore, $3 - x_{1} = H A = M B = 3 - b$, that is, $x_{1} = b = \frac{x_{1} \cdot x_{2}}{12}$ (by Vieta's theorem), from which we find $x_{2} = 12$. Finally, $x_{1} = 6 - x_{2} = 6 - 12 = -6$ and $b = x_{1} = -6$.
Another solution. As in the previous solution, let the abscissas of points $A$ and $C$ be $x_{1}$ and $x_{2}$, respectively; we will also use the fact that point $B$ has coordinates $(0 ; b)$. Immediately, we understand that $O A = |x_{1}| = -x_{1}$, $O C = |x_{2}| = x_{2}$, and $O B = |b| = -b$.
Let's find the second intersection of the circle with the y-axis, let this be point $D$ with coordinates $(0 ; d)$ (Fig. 12). The chords $A C$ and $B D$ of the circle intersect at the origin $O$; from the properties of the circle, we know that $O A \cdot O C = O B \cdot O D$. We get $-x_{1} \cdot x_{2} = -b \cdot d$, from which, replacing $x_{1} \cdot x_{2}$ with $12b$ by Vieta's theorem, we get $d = 12$.
Fig. 12: to the solution of problem 10.7
It remains to note that triangle $BTD$ is isosceles, and the midpoint of its base, point $M$, has coordinates $(0 ; 3)$. Reflecting point $D(0 ; 12)$ relative to it, we get $B(0 ; -6)$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.2. A square was cut into five rectangles of equal area, as shown in the figure. The width of one of the rectangles is 5. Find the area of the square.
|
Answer: 400.
Solution. The central rectangle and the rectangle below it have a common horizontal side, and their areas are equal. Therefore, the vertical sides of these rectangles are equal, let's denote them as $x$ (Fig. 13). The vertical side of the lower left rectangle is $2x$, and we will denote its horizontal side as $y$. Since its area $2xy$ is the same as the area of the central rectangle, the horizontal side of the central rectangle is $2y$. Then the horizontal side of the upper left rectangle is $3y$, and its area $3y \cdot 5 = 15y$ should be equal to $2xy$, from which we find $x=7.5$. Then the side of the entire square is $5+2x=5+2 \cdot 7.5=20$, and its area is $20^2=400$.
|
400
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. In a football tournament, 15 teams participated, each playing against each other exactly once. For a win, 3 points were awarded, for a draw - 1 point, and for a loss - 0 points.
After the tournament ended, it turned out that some 6 teams scored at least $N$ points each. What is the greatest integer value that $N$ can take?
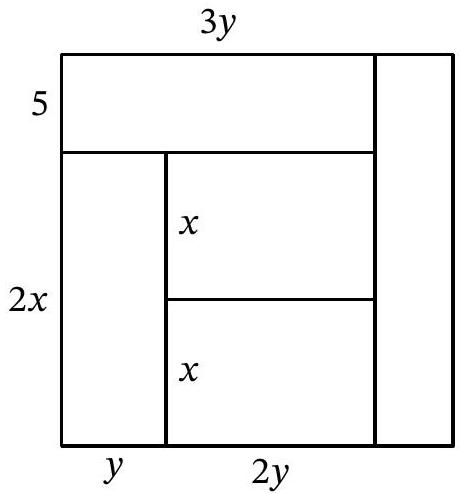
Fig. 13: to the solution of problem 11.2
#
|
# Answer: 34.
Solution. Let's call these 6 teams successful, and the remaining 9 teams unsuccessful. We will call a game between two successful teams an internal game, and a game between a successful and an unsuccessful team an external game.
First, note that for each game, the participating teams collectively earn no more than 3 points. Clearly, there were exactly $\frac{6 \cdot 5}{2}=15$ internal games, and only from these games did all successful teams collectively earn no more than $15 \cdot 3=45$ points. There were exactly $6 \cdot 9=54$ external games, and in each such game, a successful team earned no more than 3 points. Therefore, collectively, all successful teams earned no more than $54 \cdot 3=162$ points from external games. According to the problem, the successful teams collectively earned at least $6 \mathrm{~N}$ points, so we get the inequality $6 N \leqslant 45+162$. From this, it follows that $N \leqslant \frac{207}{6}<35$ and $N \leqslant 34$. Now let's provide an example for $N=34$. Number the teams from 1 to 15. We will show how teams from 1 to 6 can earn at least 34 points.
- Suppose each team from 1 to 6 won against each team from 7 to 15, then each team from 1 to 6 earned $9 \cdot 3=27$ points just from these games.
- Suppose teams from 1 to 6 played among themselves as indicated in the following table (in each cell, the number of points is shown that the team from the corresponding row received in the game with the team from the corresponding column):
| | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $\mathbf{1}$ | | 3 | 3 | 1 | 0 | 0 |
| $\mathbf{2}$ | 0 | | 3 | 3 | 1 | 0 |
| $\mathbf{3}$ | 0 | 0 | | 3 | 3 | 1 |
| $\mathbf{4}$ | 1 | 0 | 0 | | 3 | 3 |
| $\mathbf{5}$ | 3 | 1 | 0 | 0 | | 3 |
| $\mathbf{6}$ | 3 | 3 | 1 | 0 | 0 | |
- Suppose in each game between teams from 7 to 15, the team with the higher number won (the outcome of these games does not matter).
In total, teams from 1 to 6 earned at least $27+7=34$ points.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.8. Given a parallelepiped $A B C D A_{1} B_{1} C_{1} D_{1}$. A point $X$ is chosen on the edge $A_{1} D_{1}$, and a point $Y$ is chosen on the edge $B C$. It is known that $A_{1} X=5, B Y=3, B_{1} C_{1}=14$. The plane $C_{1} X Y$ intersects the ray $D A$ at point $Z$. Find $D Z$.
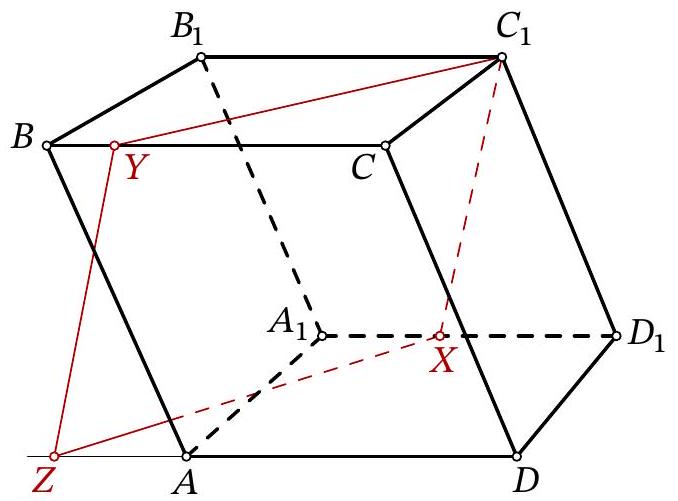
|
Answer: 20.
Solution. Lines $C_{1} Y$ and $Z X$ lie in parallel planes $B B_{1} C_{1} C$ and $A A_{1} D_{1} D$, so they do not intersect. Since these two lines also lie in the same plane $C_{1} X Z Y$, they are parallel. Similarly, lines $Y Z$ and $C_{1} X$ are parallel. Therefore, quadrilateral $C_{1} X Z Y$ is a parallelogram.
Fig. 15: to the solution of problem 11.8
Let us lay off segment $A T$ on $A D$, equal to $B Y$ (Fig. 15). Quadrilateral $B Y T A$ is a parallelogram, meaning segments $Y T, B A$, and $C_{1} D_{1}$ are parallel and equal. Additionally, segments $Y Z$ and $C_{1} X$ are parallel and equal; from the parallelism follows the equality of angles $Z Y T$ and $X C_{1} D_{1}$, which gives the equality of triangles $Z Y T$ and $X C_{1} D_{1}$.
Then
$$
\begin{aligned}
D Z & =Z T+A D-A T=X D_{1}+B_{1} C_{1}-B Y= \\
& =\left(A_{1} D_{1}-A_{1} X\right)+B_{1} C_{1}-B Y=(14-5)+14-3=20
\end{aligned}
$$
Another solution. As in the previous solution, we will use the fact that $C_{1} X Z Y$ is a parallelogram.
Consider the chain of vector equalities:
$$
\overrightarrow{D Z}=\overrightarrow{D C}+\overrightarrow{C Y}+\overrightarrow{Y Z}=\overrightarrow{D_{1} C_{1}}+\overrightarrow{C Y}+\overrightarrow{C_{1} X}=\overrightarrow{C Y}+\overrightarrow{D_{1} X}
$$
In the last part, all vectors are oriented the same as $\overrightarrow{D Z}$, so we can transition to the equality of segments and continue:
$$
D Z=C Y+D_{1} X=(C B-B Y)+\left(D_{1} A_{1}-A_{1} X\right)=2 B_{1} C_{1}-B Y-A_{1} X
$$
Substituting the lengths given in the condition, we get $D Z=2 \cdot 14-3-5=20$.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Petya runs twice as fast as Kolya and three times as fast as Masha. On the running track of the stadium, Petya, Kolya, and Masha started at the same time. Petya reached the finish line 12 seconds earlier than Kolya. By how many seconds did Petya finish earlier than Masha?
|
Answer: By 24 seconds.
Solution: Since Kolya runs twice as slow as Petya, he spends twice as much time covering the distance. Therefore, Kolya ran the distance in 24 seconds, and Petya in 12 seconds. Then Masha ran the distance in $12 \cdot 3=36$ seconds and fell behind Petya by $36-12=24$ seconds.
Comment: Just the answer without explanation - 3 points.
Any text showing that the answer is not just guessed can be considered as an explanation.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the line AB, point O is marked and from it rays OC, OD, OE, OF are drawn in the specified order into one half-plane of line AB (ray OC lies between rays OA and OD). Find the sum of all angles with vertex O, whose sides are rays OA, OC, OD, OE, OF, OB, if $\angle \mathrm{COF}=97^{\circ}, \angle \mathrm{DOE}=35^{\circ}$.
|
Answer: $1226^{\circ}$.
Instructions. There are four pairs of adjacent angles and a straight angle, which sum up to $180^{\circ}$ or are equal to $180^{\circ}$. There are two pairs of angles whose sum equals $\angle \mathrm{COF}$, and the angle itself. And there is still $\angle \mathrm{DOE}$. Therefore, the sum of the measures of all the required angles is
$5 \cdot 180^{\circ}+3 \cdot 97^{\circ}+1 \cdot 35^{\circ}=900^{\circ}+291^{\circ}+35^{\circ}=1226^{\circ}$.
Criteria. Correct answer without justification: 2 points.
For a computational error with correct reasoning, 3 points are deducted.
|
1226
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a room, 15 chairs are arranged in a circle. Three jewelers, when no one is watching, sit on three adjacent chairs, and the one sitting in the middle chair hides a diamond in the chair he is sitting on. The inspector has several detectors that show whether someone has sat on a chair or not. What is the minimum number of detectors he should place on the chairs before the jewelers arrive, so that he can determine from their readings where the diamond is?
|
Answer: 9 detectors.
Instructions. Evaluation. Consider five chairs such that between any two nearest ones there are two other chairs. If there is no detector in two nearest ones, then by adding to the two chairs between them any of them, we get two possible seating arrangements of jewelers, in which the detector readings are the same. To have a detector in any two nearest ones, it is necessary to place at least three detectors in them. Such different quintets can be formed three times. This means that at least $3 \cdot 3=9$ detectors are needed. Example. They need to be placed in groups of three on adjacent chairs in intervals, between which there are two chairs without detectors. The number of activated detectors easily determines which three chairs were occupied.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.5. A large rectangle consists of three identical squares and three identical small rectangles. The perimeter of the square is 24, and the perimeter of the small rectangle is 16. What is the perimeter of the large rectangle?
The perimeter of a figure is the sum of the lengths of all its sides.
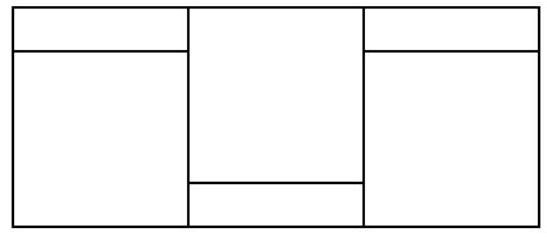
|
Answer: 52.
Solution. All sides of a square are equal, and its perimeter is 24, so each side is $24: 4=6$. The perimeter of the rectangle is 16, and its two largest sides are each 6, so the two smallest sides are each $(16-6 \cdot 2): 2=2$. Then the entire large rectangle has dimensions $8 \times 18$, and its perimeter is $2 \cdot(8+18)=$ 52.
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.1. The set includes 8 weights: 5 identical round, 2 identical triangular, and one rectangular weight weighing 90 grams.
It is known that 1 round and 1 triangular weight balance 3 round weights. Additionally, 4 round weights and 1 triangular weight balance 1 triangular, 1 round, and 1 rectangular weight.
How much does the triangular weight weigh?
|
Answer: 60.
Solution. From the first weighing, it follows that 1 triangular weight balances 2 round weights.
From the second weighing, it follows that 3 round weights balance 1 rectangular weight, which weighs 90 grams. Therefore, a round weight weighs $90: 3=30$ grams, and a triangular weight weighs $30 \cdot 2=60$ grams.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. A jeweler has six boxes: two contain diamonds, two contain emeralds, and two contain rubies. On each box, it is written how many precious stones are inside.
It is known that the total number of rubies is 15 more than the total number of diamonds. What is the total number of emeralds in the boxes?

#
|
# Answer: 12.
Solution. The total number of rubies is no more than $13+8=21$, and the number of diamonds is no less than $2+4=6$. According to the condition, their quantities differ by 15. This is only possible if the rubies are in the boxes with 13 and 8 stones, and the diamonds are in the boxes with 2 and 4 stones. Then the emeralds are in the two remaining boxes, and there are a total of $5+7=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.4. Seven boxes are arranged in a circle, each containing several coins. The diagram shows how many coins are in each box.
In one move, it is allowed to move one coin to a neighboring box. What is the minimum number of moves required to equalize the number of coins in all the boxes?
|
Answer: 22.
Solution. Note that there are a total of 91 coins, so after all moves, each box should have exactly 13 coins. At least 7 coins need to be moved from the box with 20 coins. Now consider the boxes adjacent to the box with 20 coins. Initially, they have a total of 25 coins, and at least 7 more coins will be transferred from the box with 20 coins. In the end, these two boxes should have a total of 26 coins, so at least \(25 + 7 - 26 = 6\) coins need to be moved from these boxes. Next, consider the boxes with 17 and 18 coins, from which at least 4 and 5 coins need to be moved, respectively. In total, there should be at least \(7 + 6 + 4 + 5 = 22\) moves.
Let's provide an example of how to equalize all the boxes in exactly 22 moves. From the box with 20 coins, we move 3 coins to the box with 10 (it becomes 13), and 4 coins to the box with 15 (it becomes 19). From the box that now has 19 coins, we move 6 coins to the box with 5 coins (it becomes 11). From the box with 17 coins, we move 2 coins to the box with 11, and 2 coins to the box with 6 (it becomes 8). Finally, we move 5 coins from the box with 18 coins to the box with 8 coins. In the end, each box has exactly 13 coins. It is easy to verify that exactly 22 moves were made.
|
22
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.