problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3. In triangle $\mathrm{ABC}$, angle $\mathrm{C}$ is twice as small as angle $\mathrm{B}$. $\mathrm{BB}_{1}$ is the bisector of angle $\mathrm{B}, \mathrm{D}$ is the point of intersection of the circumcircle of triangle $\mathrm{ABB}_{1}$ and side $\mathrm{AB} . \mathrm{BD}=14$, $\mathrm{CD}=18$. Find the length of $\mathrm{AC}$.
If there are multiple correct answers, list them in any order separated by a semicolon.
|
Answer: 30.
## Examples of answer notation:
45
#
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Three consecutive terms of a geometric progression with a common ratio $q$ were used as coefficients of a quadratic trinomial, with the middle term being the leading coefficient. For what largest integer $q$ will the resulting trinomial have two distinct roots regardless of how the other two coefficients are arranged?
|
Answer: -1
## Examples of answer notation:
2
5;9
#
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. $A B C D E$ - a pentagon inscribed in circle $S$. Lines $D E$ and $A B$ are parallel, $B C=C D$, $A D=D E=20, \cos C B D=5 / 8$. Find the radius of circle $S$.
|
Answer: 16.
## Examples of how to write answers:
## $1 / 4$
0.25
1
#
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) On the Island of Misfortune, there live knights, who always tell the truth, and liars, who always lie. One day, $n$ islanders gathered in a room. $\quad 30$
The first one said: "Exactly every first person present in this room is a liar."
The second one said: "Exactly every second person present in this room is a liar." and so on
The person with number $n$ said: "Exactly every $n$-th person present in this room is a liar." How many people could have been in the room?
|
# Answer: 2
## Solution:
Let's note that among these people, there is definitely one knight, otherwise it would mean that the first islander is a liar telling the truth, which is impossible. Moreover, the first person is definitely a liar.
Furthermore, there is exactly one knight, since all the speakers contradict each other. This means there are no more than half knights. On the other hand, all the islanders claim that there are no fewer than half knights. Therefore, there are exactly half, i.e., there are two people in the room.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (3 points) Anya, Vanya, Danya, Sanya, and Tanya were collecting apples. It turned out that each of them collected a whole percentage of the total number of apples collected, and all these numbers are different and greater than zero. What is the minimum number of apples that could have been collected?
Answer: 20
|
Solution:
Example: there are many different examples, for instance $1+2+3+4+10$ or $2+3+4+5+6=20$
Estimate (proof that there are no fewer than 20 apples):
Let Anna have collected the fewest apples, and this number is at least 2. Then we get that the total collected is no less than $2+3+4+5+6=20$ apples.
If Anna has 1 apple and there are a total of $n$ apples, then $\frac{1}{n}$ is an integer percentage, i.e., $n$ is a divisor of 100, and at least $1+2+3+4+5=15$. The smallest suitable number is 20.
|
20
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (4 points) In an $8 \times 8$ table, integers from 0 to 10 are arranged (naturally, numbers can repeat, not all specified numbers necessarily appear). It is known that in each rectangle $3 \times 2$ or $2 \times 3$, the sum of the numbers is 10. Find the smallest possible value of the sum of the numbers in the entire table.
#
|
# Answer: 105
## Solution:
Let's look at the left part of the figure below. Consider the rectangles $3 \times 2$ and $2 \times 3$, which contain the left upper $2 \times 2$ square. The remaining parts of these two rectangles are the leftmost upper rectangles $1 \times 2$ and $2 \times 1$, shaded in gray. Since the sum of the numbers in both rectangles $3 \times 2$ and $2 \times 3$ is 10, the sum of the numbers in these two gray rectangles is equal.
Similarly, it can be proven that the sums of the numbers in all gray rectangles in the picture, as well as in all white $2 \times 2$ squares, are equal. Let the sum of the numbers in each white square be $x$, then the sum of the numbers in each gray rectangle is $10-x$. Therefore, the total sum of the numbers in the table is at least $9x + 12(10-x) = 120 - 3x$. If $x > 5$, the result is a number greater than 105.
Thus, the sum of all numbers in the table is at least 105.
An example is provided in the right part of the figure, cells filled with zeros are left blank for convenience.
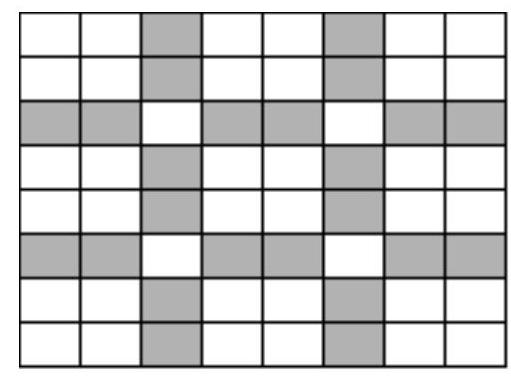
| | | 5 | | | 5 | | |
| ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: |
| | 5 | | | 5 | | | 5 |
| 5 | | | 5 | | | 5 | |
| | | 5 | | | 5 | | |
| | 5 | | | 5 | | | 5 |
| 5 | | | 5 | | | 5 | |
| | | 5 | | | 5 | | |
| | 5 | | | 5 | | | 5 |
|
105
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) On the Island of Misfortune, there live knights who always tell the truth, and liars who always lie. One day, $n$ islanders gathered in a room.
The first one said: "Exactly every second person in this room is a liar."
The second one said: "Exactly every third person in this room is a liar."
and so on
The person with number $n$ said: "Exactly every ( $n_{33} 1$ )-th person in this room is a liar."
How many people could have been in the room, given that not all of them are liars?
|
# Answer: 2
Solution:
According to the condition, there is at least one knight among these people. Therefore, there must be at least two people, otherwise the first person would be a knight who is lying.
Moreover, there is exactly one knight, as all the speakers contradict each other. Thus, there cannot be more than half knights. On the other hand, all the islanders, including the knight who tells the truth, claim that there are at least half knights. Therefore, there must be exactly half, i.e., there are two people in the room.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (3 points) Anya, Vanya, Danya, Manya, Sanya, and Tanya were collecting apples. It turned out that each of them collected a whole percentage of the total number of apples collected, and all these numbers are different and greater than zero. What is the minimum number of apples that could have been collected?
Answer: 25
|
Solution:
Example: there are many different examples, for instance $1+2+3+4+5+10$.
Evaluation (proof that there are no fewer than 25 apples):
Let Anya have collected the fewest apples, and this number is at least 2. Then we get that the total collected is no less than $2+3+4+5+6+7=27$ apples.
If Anya has 1 apple and there are a total of $n$ apples, then $\frac{1}{n}$ is an integer percentage, i.e., $n$ is a divisor of 100, and at least $1+2+3+4+5+6=21$. The smallest suitable number is 25.
|
25
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
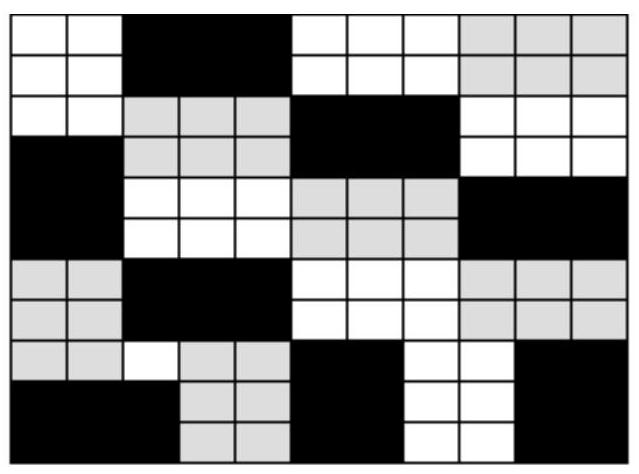
8. (4 points) In an $11 \times 11$ table, integers from 0 to 10 are arranged (naturally, numbers can repeat, not all specified numbers necessarily appear). It is known that in each $3 \times 2$ or $2 \times 3$ rectangle, the sum of the numbers is 10. Find the smallest possible value of the sum of the numbers in the entire table.
Answer: 200
#
|
# Solution:
The right part of the figure below shows the table divided into 20 rectangles and one cell. This means that the sum of the numbers in the entire table is no less than the sum of the numbers in these 20 rectangles, which is 200.
An example is provided in the left part of the figure, cells filled with zeros are left blank for convenience.
| | | 5 | | | 5 | | | 5 | | |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | 5 | | | 5 | | | 5 | | | 5 |
| 5 | | | 5 | | | 5 | | | 5 | |
| | | 5 | | | 5 | | | 5 | | |
| | 5 | | | 5 | | | 5 | | | 5 |
| 5 | | | 5 | | | 5 | | | 5 | |
| | | 5 | | | 5 | | | 5 | | |
| | 5 | | | 5 | | | 5 | | | 5 |
| 5 | | | 5 | | | 5 | | | 5 | |
| | | 5 | | | 5 | | | 5 | | |
| | 5 | | | 5 | | | 5 | | | 5 |
|
200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (4 points) At a knight's tournament, each knight gave each of his acquainted ladies as many flowers as she had acquainted knights, except for him. After this, every two knights arranged as many duels as they had common acquainted ladies. What was more: the given flowers or the arranged duels, and by how many times?
Answer: Flowers were more by two times.
|
Solution: For each trio consisting of a lady and two of her acquainted knights, one duel will take place. Regarding the flowers, the first knight will give the lady one flower for introducing him to the second, and the second will give one for being introduced to the first, making a total of two flowers.
## Grade 9 2nd variant
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (2 points) Anya was making pancakes, planning for each of the three members of her family to get an equal number of pancakes. But something went wrong: every third pancake Anya couldn't flip; $40 \%$ of the pancakes that Anya managed to flip burned; and $\frac{1}{5}$ of the edible pancakes Anya dropped on the floor. What percentage of the intended number of pancakes was Anya able to offer her family?
Answer: $32 \%$.
|
Solution:
In total, Anya managed to save $\frac{2}{3} \cdot 0.6 \cdot 0.8=0.32$ of the number of pancakes.
|
32
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (4 points) With the number written on the board, one of the following operations is allowed:
1) If there is a digit in the original number that is not 9 and has two neighboring digits greater than 0, you can increase this digit by 1, and decrease the neighboring digits by 1.
2) Subtract 1 from any non-zero digit except the last one, and add 3 to the next digit.
3) Decrease any sufficiently large digit by 7.
If, as a result of any of these operations, there are zeros in the leading positions of the number, they are automatically discarded.
Initially, the number on the board was a hundred eights. In the end, a single-digit number remained. Which one exactly?
|
Answer: 3
Solution:
The first operation corresponds to subtracting a number of the form $910 \cdot 0$, the second and third - subtracting $70 \cdot 0$. Both these operations do not change the remainder of the original number when divided by 7, since 91 is divisible by 7.
$1001=c d o t 91$, and $888888=888 \cdot 1001$. Therefore, to find the remainder of the original number when divided by 7, the number of eights that are multiples of 6 can be discarded. The remaining number is $8888=8008+875+5=8 \cdot 1001+7 \cdot 125+5$ which gives a remainder of 5.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (5 points) From a $12 \times 12$ grid, a $4 \times 4$ square was cut out, lying at the intersection of the third to sixth horizontal lines and the same vertical lines. What is the maximum number of non-attacking rooks that can be placed on this field, if the rooks do not attack through the cut-out cells?
## Answer: 14
#
|
# Solution:
The available part of the board is divided into the following four areas, in each of which no more than the specified number of rooks can be placed (see the left figure), as in each rectangle, no more rooks can be placed than the length of its shorter side. Therefore, the total number of rooks does not exceed 14.
An example for 14 rooks is shown in the right figure.
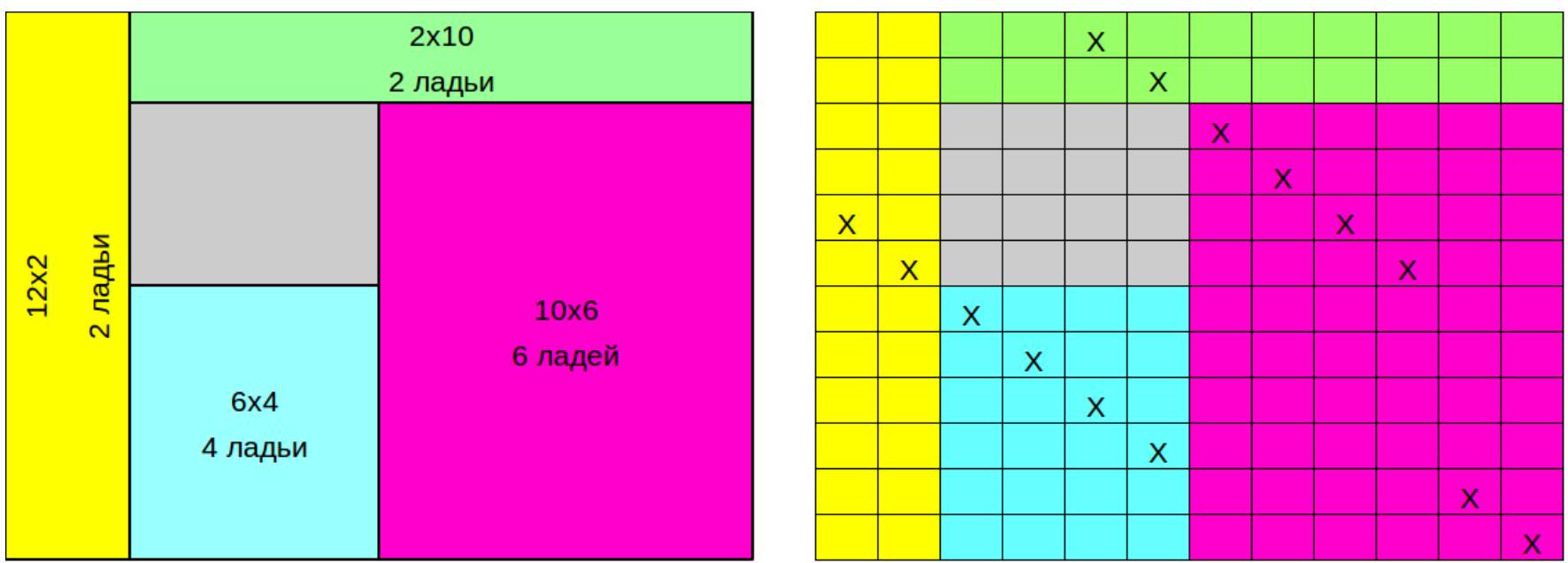
## Open Mathematical Olympiad for Schoolchildren
March 11, 2018
## 7th Grade 2nd Variant Solutions
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (2 points) Anya was making pancakes, planning for each of the five members of her family to get an equal number of pancakes. But something went wrong: every fifth pancake Anya couldn't flip; $49\%$ of the pancakes that Anya managed to flip burned; and $\frac{1}{6}$ of the edible pancakes Anya dropped on the floor. What percentage of the intended number of pancakes was Anya able to offer her family?
Answer: $34\%$.
|
# Solution:
In total, Anya managed to save $0.8 \cdot 0.51 \cdot \frac{5}{6}=0.34$ of the pancakes.
|
34
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (4 points) With the number written on the board, one of the following operations is allowed:
1) If there is a digit in the original number that is not equal to 9 and has two neighboring digits greater than 0, you can increase this digit by 1, and decrease the neighboring digits by 1.
2) Subtract 1 from any non-zero digit except the last one, and add 3 to the next digit.
3) Decrease any sufficiently large digit by 7.
If, as a result of any of these operations, there are zeros in the number on one or more of the leading positions, they are automatically discarded.
Initially, the number consisting of one hundred nines was written on the board. In the end, a single-digit number remained. Which one exactly?
|
# Answer: 3
Solution:
The first operation corresponds to subtracting a number of the form $910 \cdot 0$, the second and third - subtracting $70 \cdot 0$. Both these operations do not change the remainder of the original number when divided by 7, since 91 is divisible by 7.
$1001 = 91 \cdot 11$, and $999999 = 999 \cdot 1001$. Therefore, to find the remainder of the original number when divided by 7, the number of nines that are multiples of 6 can be discarded. The remaining number is $9999 = 9009 + 987 + 3 = 9 \cdot 1001 + 7 \cdot 141 + 3$, which gives a remainder of 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (5 points) From a $12 \times 12$ grid, a $4 \times 4$ square was cut out, lying at the intersection of the fourth to seventh horizontal and vertical lines. What is the maximum number of non-attacking rooks that can be placed on this field, if the rooks do not attack through the cut-out cells?
## Answer: 15
#
|
# Solution:
The available part of the board is divided into the following four areas, in each of which no more than the specified number of rooks can stand (see the left figure), as in each rectangle, no more rooks can stand than the length of its shorter side. Therefore, the total number of rooks does not exceed 15.
An example with 15 rooks is shown in the right figure.
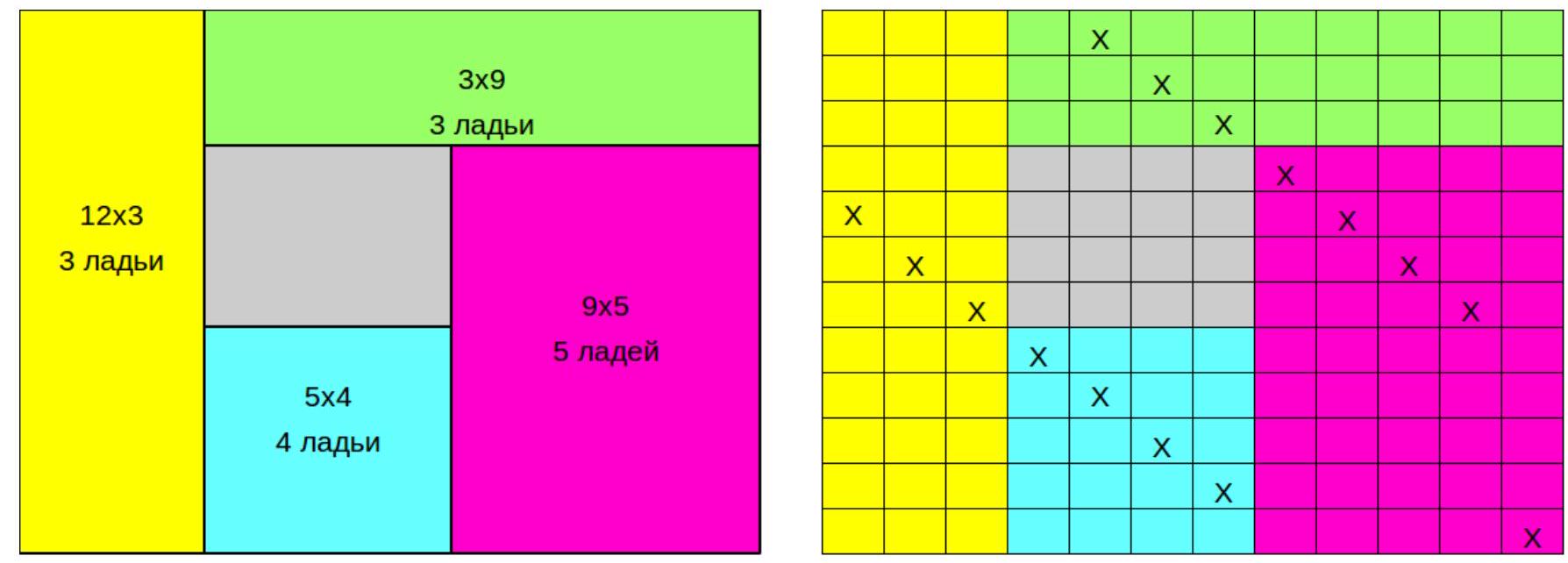
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (4 points) Find what $x+y$ can be equal to, given that $x^{3}-6 x^{2}+15 x=12$ and $y^{3}-6 y^{2}+15 y=16$.
|
Answer: 4.
Solution:
Let $u=x-2$ and $v=y-2$. Then the original equations transform into $u^{3}+3 u=-2$ and $v^{3}+3 v=2$. Adding these equations, we get $(u+v)\left(u^{2}-u v+v^{2}+3\right)=0$. The second bracket is always positive, so the first one must be zero, from which we have $x+y=u+v+4=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (4 points) Find what $x+y$ can be equal to, given that $x^{3}+6 x^{2}+16 x=-15$ and $y^{3}+6 y^{2}+16 y=-17$.
|
Answer: -4
Solution: Let $u=x+2$ and $v=y+2$. Then the original equations transform into $u^{3}+4 u=1$ and $v^{3}+4 v=-1$. Adding these equations, we get $(u+v)\left(u^{2}-u v+v^{2}+4\right)=0$. The second bracket is always positive, so the first one must be zero, from which we have $x+y=u+v-4=-4$.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Point $O$ is the center of a certain circle, $A$ is a point outside the circle, $B$ is a point on the circle such that $AB$ is a tangent. $AO=6$. Find the greatest possible value of the area of triangle $AOB$.
|
Answer: 9.
## Examples of answer notations:
17
$1 / 7$
1.7
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A five-digit number ABCDE, consisting of different digits, is divisible by both the three-digit number CDE and the two-digit number AB. Find the smallest possible value of ABCDE.
|
Answer: 12480
## Examples of answer recording:
12345
#
|
12480
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On Misfortune Island, a table tennis tournament was held in a round-robin format (i.e., everyone played against everyone else once). After each match, both participants approached the Chief Referee separately and reported the result. Among the participants, there were only three types of people: knights, who always tell the truth, liars, who always lie, and politicians, who always say what is advantageous to them - each politician claimed after each match that they had won.
After the tournament, it turned out that the Chief Referee, incognito, had attended several matches, as a result of which he was lucky enough to not only be able to determine the results of all matches but also to find out that there were exactly six politicians. What is the minimum number of matches he could have attended?
(There are no draws in table tennis. The Chief Referee did not know in advance which players belonged to which type, and did not receive information in any other way except as described in the condition)
|
Answer: 16
## Examples of answer recording:
17
#
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A circle with radius 12 and center at point $O$ and a circle with radius 3 touch internally at point $H$. The line $X H$ is their common tangent, and the line $O X$ is tangent to the smaller circle. Find the square of the length of the segment $O X$.
|
Answer: 162
2.. A circle with radius 12 and center at point $O$ and a circle with radius 4 touch internally at point $H$. Line $X H$ is their common tangent, and line $O X$ is tangent to the smaller circle. Find the square of the length of segment $O X$.
Answer: 192
|
162
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A circle of radius 20 with center at point $O$ and a circle of radius 8 touch internally at point $H$. The line $X H$ is their common tangent, and the line $O X$ is tangent to the smaller circle. Find the square of the length of the segment $O X$.
|
Answer: 720
## Examples of how to write answers:
17
$1 / 7$
1.7
|
720
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. There are 12 students in the class. Each of them was asked how many friends they have in the class. Each number \( n \) was either mentioned exactly \( n \) times or not at all. What is the maximum value that the sum of all the numbers mentioned can take?
|
Answer: 90
Only digits are allowed as input.
## Problem 5. (3 points)
|
90
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Each vertex of a tetrahedron with a volume of 216 was symmetrically reflected relative to the point of intersection of the medians of the opposite face. The four resulting points formed a new tetrahedron. Find its volume.
|
Answer: 1000
Allowed for input are digits, a dot or comma, and a division sign
#
|
1000
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Circle $S_{1}$ intersects circle $S_{2}$ at points $A$ and $B$ and is tangent to circle $S_{3}$ at point $Z$. The common tangent of circles $S_{1}$ and $S_{3}$ intersects line $A B$ at point $C$. Also, through $C$ passes line $X Y$, which is tangent to circle $S_{2}$ at point $X$ and to circle $S_{3}$ at point $Y$.
It is known that $A B=7, B C=5, X Z=4 \sqrt{6}$. Find $Y Z$.
It is assumed that points denoted by different letters do not coincide. If there are multiple possible answers, write them in any order separated by a semicolon.
|
Answer: 12
Allowed for input are digits, a period or comma, a division sign, a semicolon
#
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a rectangle $\mathrm{ABCD}$. The length of side $\mathrm{BC}$ is one and a half times less than the length of side $\mathrm{AB}$. Point $\mathrm{K}$ is the midpoint of side AD. Point $\mathrm{L}$ on side $\mathrm{CD}$ is such that $\mathrm{CL}=\mathrm{AK}$. Point $\mathrm{M}$ is the intersection of line BL and the perpendicular bisector of segment DL. It is known that $\mathrm{KL}=4$. Find the length of segment BM.
(A rectangle is a figure such that its opposite sides are equal, and the angles are each $90^{\circ}$. )
|
Answer: 8
## Examples of answer recording:
#
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A $10 x 10$ grid is filled with non-negative numbers. It is known that in each (vertical or horizontal) strip of 1 x 3, the sum of the numbers is 9. What is the maximum value that the sum of all numbers in the grid can take?
|
Answer: 306
Examples of writing answers:
14
|
306
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The function $f(x)$ is such that $f(x+1)+f(x-1)=5.2 f(x)$. It is known that $f(0)=-98$, and $\mathrm{f}(3)=249.2$. Find $f(1)$.
|
Answer: -10
## Examples of how to write answers:
17
$-1.7$
$1 / 7$
#
|
-10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
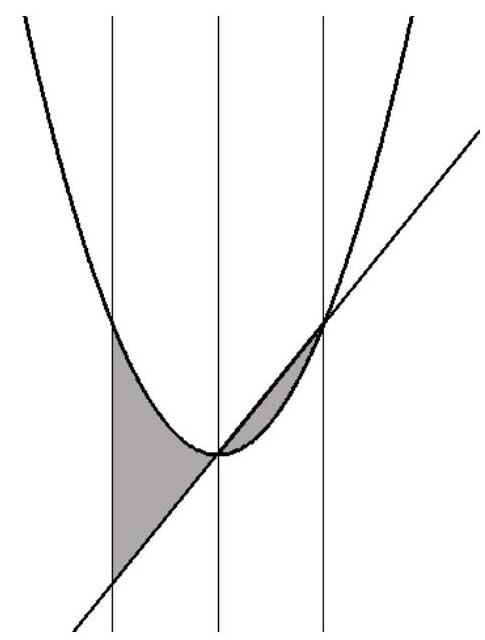
1. The graphs of a quadratic trinomial with a positive leading coefficient 2 and its derivative intersect at the vertex of the parabola with abscissa $x_{0}$ and at another point with abscissa $x_{1}$. Find the total area of both regions bounded by the graphs of the trinomial, its derivative, and the line symmetric to the line $x=x_{1}$ with respect to the line $x=x_{0}$ (see figure).
|
Answer: 16
## Examples of answer notations:
17
$-1.7$
$1 / 7$
#
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Around a circle, 129 (not necessarily integer) numbers from 5 to 25 inclusive were written. From each number, the logarithm to the base of the next number in the clockwise direction was taken, after which all the obtained logarithms were added. What is the maximum value that the sum of these logarithms can take?
|
Answer: 161
## Examples of answer notations:
17
$-1.7$
$1 / 7$
## 10th grade
#
|
161
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) In a certain country, there are 100 cities. The Ministry of Aviation requires that every two cities be connected by a two-way flight operated by exactly one airline, and that it should be possible to travel from any city to any other city using the flights of each airline (possibly with layovers). What is the maximum number of airlines for which this is possible?
Answer: 50
|
Solution: Evaluation: in order to connect all cities, the airline must have at least 99 flights. In total, there are $100 \cdot 99 / 2$ pairs of cities, which means there are no more than 50 airlines.
Example: let's denote the cities as $a_{1}, a_{2}, \ldots a_{50}, b_{1}, b_{2}, \ldots, b_{50}$ in some way. Then the airline with number $k$ will connect
1) cities $a_{k}$ and $b_{k}$;
2) $a_{k}$ and each city $a_{i}$, where $i < k$
3) $a_{k}$ and each city $b_{i}$, where $i > k$
4) $b_{k}$ and each city $a_{i}$, where $i > k$
5) $b_{k}$ and each city $b_{i}$, where $i < k$.
Thus, cities $a_{i}$ and $a_{j}$ are connected by a flight of the airline with number $\max \left(a_{i}, a_{j}\right)$, cities $b_{i}$ and $b_{j}$ by the airline with number $\max \left(b_{i}, b_{j}\right)$, and cities $a_{i}$ and $b_{j}$ by the airline with number $\min \left(b_{i}, b_{j}\right)$.
|
50
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) Prove that for $n=6002$ the sum of binomial coefficients with a step of 6, i.e., $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$, gives a remainder of 1 when divided by 3.
$C_{n}^{k}-$ the number of ways to choose $k$ items from $n$, which is $\frac{n!}{k!(n-k)!}$ if $0 \leqslant k \leqslant n$ and 0 in all other cases.
|
# Solution:
It is easy to verify that $C_{n}^{k}=C_{n-3}^{k-3}+3 C_{n-3}^{k-2}+3 C_{n-3}^{k-1}+C_{n-3}^{k}$, therefore, $C_{n}^{k}$ gives the same remainder when divided by 3 as $C_{n-3}^{k-3}+C_{n-3}^{k}$.
Thus, $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$ gives the same remainder when divided by 3 as $C_{n-3}^{1}+C_{n-3}^{4}+\ldots+$ $C_{n-3}^{n-7}+C_{n-3}^{n-4}$ (here the two extreme terms, equal to 0, are discarded).
Let's denote this sum as $S_{n-3}$.
Similarly, we transition to $2 C_{n-6}^{1}+2 C_{n-3}^{4}+\ldots+2 C_{n-3}^{n-7}+2 C_{n-3}^{n-4}=2 S_{n-6}$.
Applying this procedure 1998 more times, we get that the formula from the condition gives the same remainder when divided by 3 as $2^{1999} S_{2}=4^{999} \cdot 2 C_{2}^{1}=4^{1000}$, which gives a remainder of 1 when divided by 3.
|
1
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) In a certain country, there are 50 cities. The Ministry of Aviation requires that every two cities be connected by a two-way flight operated by exactly one airline, and that it should be possible to travel from any city to any other using the flights of each airline (possibly with layovers). What is the maximum number of airlines for which this is possible?
## Answer: 25
|
Solution: Evaluation: in order to connect all cities, the airline must have at least 49 flights. In total, there are $50 \cdot 49 / 2$ pairs of cities, so there are no more than 25 airlines.
Example: let the cities be denoted as $a_{1}, a_{2}, \ldots a_{25}, b_{1}, b_{2}, \ldots, b_{25}$ in some way. Then the airline with number $k$ will connect
1) cities $a_{k}$ and $b_{k}$
2) $a_{k}$ and each city $a_{i}$, where $i < k$
3) $a_{k}$ and each city $b_{i}$, where $i > k$
4) $b_{k}$ and each city $a_{i}$, where $i > k$
5) $b_{k}$ and each city $b_{i}$, where $i < k$.
Thus, cities $a_{i}$ and $a_{j}$ are connected by a flight of the airline with number $\max \left(a_{i}, a_{j}\right)$, cities $b_{i}$ and $b_{j}$ - by the airline with number $\max \left(b_{i}, b_{j}\right)$, and cities $a_{i}$ and $b_{j}$ - by the airline with number $\min \left(b_{i}, b_{j}\right)$.
4. (3 points) Prove that for $n=3002$, the sum of binomial coefficients with a step of 6, i.e., $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$, gives a remainder of 1 when divided by 3.
$C_{n}^{k}$ - the number of ways to choose $k$ items from $n$, which is $\frac{n!}{k!(n-k)!}$ if $0 \leqslant k \leqslant n$ and 0 in other cases.
Solution:
It is easy to verify that $C_{n}^{k}=C_{n-3}^{k-3}+3 C_{n-3}^{k-2}+3 C_{n-3}^{k-1}+C_{n-3}^{k}$, therefore, $C_{n}^{k}$ gives the same remainder when divided by 3 as $C_{n-3}^{k-3}+C_{n-3}^{k}$.
Thus, $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$ gives the same remainder when divided by 3 as $C_{n-3}^{1}+C_{n-3}^{4}+\ldots+$ $C_{n-3}^{n-7}+C_{n-3}^{n-4}$ (here the two extreme terms, equal to 0, are omitted).
Denote this sum by $S_{n-3}$.
Similarly, we transition to $2 C_{n-6}^{1}+2 C_{n-3}^{4}+\ldots+2 C_{n-3}^{n-7}+2 C_{n-3}^{n-4}=2 S_{n-6}$.
Applying this procedure 998 more times, we get that the formula from the condition gives the same remainder when divided by 3 as $2^{999} S_{2}=4^{499} \cdot 2 C_{2}^{1}=4^{500}$, which gives a remainder of 1 when divided by 3.
|
25
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) In a certain country, there are 200 cities. The Ministry of Aviation requires that every two cities be connected by a two-way flight operated by exactly one airline, and that it should be possible to travel from any city to any other using the flights of each airline (possibly with layovers). What is the maximum number of airlines for which this is possible?
#
|
# Answer: 100
Solution: Evaluation: for the airline to connect all cities, it must have at least 199 flights. The total number of city pairs is $200 \cdot 199 / 2$, so there are no more than 100 airlines.
Example: let's denote the cities as $a_{1}, a_{2}, \ldots a_{100}, b_{1}, b_{2}, \ldots, b_{100}$ in some way. Then the airline with number $k$ will connect
1) cities $a_{k}$ and $b_{k}$
2) $a_{k}$ and each city $a_{i}$, where $i < k$
3) $a_{k}$ and each city $b_{i}$, where $i > k$
4) $b_{k}$ and each city $a_{i}$, where $i > k$
5) $b_{k}$ and each city $b_{i}$, where $i < k$.
Thus, cities $a_{i}$ and $a_{j}$ are connected by a flight of the airline with number $\max \left(a_{i}, a_{j}\right)$, cities $b_{i}$ and $b_{j}$ by the airline with number $\max \left(b_{i}, b_{j}\right)$, and cities $a_{i}$ and $b_{j}$ by the airline with number $\min \left(b_{i}, b_{j}\right)$.
|
100
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) Prove that for $n=9002$ the sum of binomial coefficients with a step of 6, i.e., $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$, gives a remainder of 1 when divided by 3.
$C_{n}^{k}-$ the number of ways to choose $k$ items from $n$, which is $\frac{n!}{k!(n-k)!}$ if $0 \leqslant k \leqslant n$ and 0 in all other cases.
|
Solution:
It is easy to verify that $C_{n}^{k}=C_{n-3}^{k-3}+3 C_{n-3}^{k-2}+3 C_{n-3}^{k-1}+C_{n-3}^{k}$, therefore, $C_{n}^{k}$ gives the same remainder when divided by 3 as $C_{n-3}^{k-3}+C_{n-3}^{k}$.
Thus, $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$ gives the same remainder when divided by 3 as $C_{n-3}^{1}+C_{n-3}^{4}+\ldots+$ $C_{n-3}^{n-7}+C_{n-3}^{n-4}$ (here the two extreme terms, equal to 0, are discarded).
Let's denote this sum as $S_{n-3}$.
Similarly, we transition to $2 C_{n-6}^{1}+2 C_{n-3}^{4}+\ldots+2 C_{n-3}^{n-7}+2 C_{n-3}^{n-4}=2 S_{n-6}$.
Applying this procedure 2998 more times, we get that the formula from the condition gives the same remainder when divided by 3 as $2^{2999} S_{2}=4^{1499} \cdot 2 C_{2}^{1}=4^{1500}$, which gives a remainder of 1 when divided by 3.
|
1
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) In a certain country, there are 120 cities. The Ministry of Aviation requires that every two cities be connected by a two-way flight operated by exactly one airline, and that it should be possible to travel from any city to any other using the flights of each airline (possibly with layovers). What is the maximum number of airlines for which this is possible?
## Answer: 60
|
Solution: Evaluation: in order to connect all cities, the airline must have at least 119 flights. The total number of city pairs is $120 \cdot 119 / 2$, so there are no more than 60 airlines.
Example: let's denote the cities as $a_{1}, a_{2}, \ldots a_{60}, b_{1}, b_{2}, \ldots, b_{60}$ in some way. Then the airline with number $k$ will connect
1) cities $a_{k}$ and $b_{k}$
2) $a_{k}$ and each city $a_{i}$, where $i < k$
3) $a_{k}$ and each city $b_{i}$, where $i > k$
4) $b_{k}$ and each city $a_{i}$, where $i > k$
5) $b_{k}$ and each city $b_{i}$, where $i < k$.
Thus, cities $a_{i}$ and $a_{j}$ are connected by a flight of the airline with number $\max \left(a_{i}, a_{j}\right)$, cities $b_{i}$ and $b_{j}$ by the airline with number $\max \left(b_{i}, b_{j}\right)$, and cities $a_{i}$ and $b_{j}$ by the airline with number $\min \left(b_{i}, b_{j}\right)$.
|
60
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) Prove that for $n=12002$ the sum of binomial coefficients with a step of 6, i.e., $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$, gives a remainder of 1 when divided by 3.
$C_{n}^{k}-$ the number of ways to choose $k$ items from $n$, which is $\frac{n!}{k!(n-k)!}$ if $0 \leqslant k \leqslant n$ and 0 in all other cases.
|
# Solution:
It is easy to verify that $C_{n}^{k}=C_{n-3}^{k-3}+3 C_{n-3}^{k-2}+3 C_{n-3}^{k-1}+C_{n-3}^{k}$, therefore, $C_{n}^{k}$ gives the same remainder when divided by 3 as $C_{n-3}^{k-3}+C_{n-3}^{k}$.
Thus, $C_{n}^{1}+C_{n}^{7}+\ldots+C_{n}^{n-1}$ gives the same remainder when divided by 3 as $C_{n-3}^{1}+C_{n-3}^{4}+\ldots+$ $C_{n-3}^{n-7}+C_{n-3}^{n-4}$ (here the two extreme terms, equal to 0, are discarded).
Let's denote this sum as $S_{n-3}$.
Similarly, we transition to $2 C_{n-6}^{1}+2 C_{n-3}^{4}+\ldots+2 C_{n-3}^{n-7}+2 C_{n-3}^{n-4}=2 S_{n-6}$.
Applying this procedure 3998 more times, we get that the formula from the condition gives the same remainder when divided by 3 as $2^{3999} S_{2}=4^{1999} \cdot 2 C_{2}^{1}=4^{2000}$, which gives a remainder of 1 when divided by 3.
|
1
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. (2 points) A chess piece called a quadraliner attacks two verticals and two horizontals adjacent to the square it occupies. What is the maximum number of non-attacking quadraliners that can be placed on a $10 \times 10$ board?
|
Answer: 25
## Solution:
Example: place the four-line rulers at the intersections of even columns and even rows.
Evaluation: In each pair of rows, the four-line rulers can only stand on one row. At the same time, they cannot stand on two adjacent cells.
|
25
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (4 points) Prove that if a convex 102-gon can be divided into triangles by non-intersecting diagonals such that from each vertex either exactly three diagonals or none emanate, then the number of resulting triangles, all three sides of which are diagonals of the original polygon, will be exactly 34.
#
|
# Solution:
A 102-gon is divided into 100 triangles by 99 diagonals. Each diagonal has two ends, so the sum of the number of diagonals emanating from the vertices of the polygon is 198. Therefore, the number of vertices from which three diagonals emanate is 66, and the number of remaining vertices from which no diagonals emanate is 36.
There are three types of triangles. The first type - triangles with two sides being sides of the polygon. Between these two sides is a vertex from which no diagonals emanate, and conversely, each such vertex corresponds to one triangle of the first type. Therefore, there are also 36 such triangles.
The triangles of the first type contain 72 sides of the polygon. The remaining 30 sides are included in triangles of the second type, each containing one side of the polygon. Therefore, there are also 30 triangles of the second type.
The remaining triangles are of the third type, the number of which is \(100-36-30=34\), as required.
|
34
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. A grid rectangle $4 \times 11$ is divided into $2 \times 2$ squares and strips of three cells. What is the maximum number of strips that can participate in this division?
|
Answer: 12
## Examples of answer notation:
100
90
#
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Point $O$ is the center of a certain circle, $A$ is a point outside the circle, $B$ is a point on the circle such that $AB$ is a tangent. $AO=6$. Find the greatest possible value of the area of triangle $AOB$.
|
Answer: 9.
## Examples of answer notations:
17
$1 / 7$
1.7
#
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In country Gamma, there are 101 cities. It is known that at least 2 roads lead out of each city. It is also known that if there is a road from city A to city B and from city B to city C, then there is also a road from city A to city C. What is the minimum number of roads that can be in the country?
|
Answer: 205
## Examples of answer notation:
17
#
|
205
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. It is known that the number $\sqrt{3}+\sqrt{5}$ is a root of a polynomial of the fourth degree with integer coefficients, the leading coefficient of which is 1. What is the sum of the coefficients of this polynomial?
|
Answer: -11
2. It is known that the number $\sqrt{3}+\sqrt{7}$ is a root of a polynomial of the fourth degree with integer coefficients, the leading coefficient of which is 1. What is the sum of the coefficients of this polynomial?
Answer: -3
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. It is known that the number $\sqrt{5}+\sqrt{7}$ is a root of a polynomial of the fourth degree with integer coefficients, the leading coefficient of which is 1. What is the sum of the coefficients of this polynomial?
|
Answer: -19
## Examples of how to write answers:
17
$1 / 7$
1.7
## Problem 8
|
-19
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. It is known that the function $f(x)$ satisfies the equality for any $x$:
$3 \sin x+f(x)=f(x+2)$
Find the value of $\mathrm{f}(2017) \sin 1$, given that $f(1)=\frac{3 \cos ^{2} 1008}{\sin 1}$.
|
Answer: 3
## Examples of answer notations:
17
$1 / 7$
1.7
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (3 points) On the Island of Misfortune, there live knights who always tell the truth, and liars who always lie. One day, $n$ islanders gathered in a room.
The first one said: "Exactly 1 percent of those present in this room are liars."
The second one said: "Exactly 2 percent of those present in this room are liars."
and so on
The person with number $n$ said: "Exactly $n$ percent of those present in this room are liars."
How many people could have been in the room, given that it is known for sure that at least one of them is a knight?
|
Answer: 100
## Solution:
There must be exactly one knight, as all other islanders in the room contradict each other. This means that the knights are $\frac{1}{n}$ of the total number of people. Let them be $k$ percent of the total number of people present, which means the person with the number $100-k$ is telling the truth.
We get that $\frac{1}{n}=\frac{k}{100}$, where $100-k \leqslant n$.
This can be rewritten as $n k=100$ and $k+n \geqslant 100$, from which $n k-k-n \leqslant 0$.
Therefore, $n-k-n+1 \leqslant 1$, that is, $(n-1)(k-1) \leqslant 1$. Since $n$ and $k$ are both natural numbers, we get that either one of them is 1, or both are 2. The latter case does not satisfy the equation $n k=100$.
If $n=1$, we get that the only person is a liar, which contradicts the condition.
If $k=1$, then $n=100$ and the first person is telling the truth. This is the answer.
|
100
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) Anya, Vanya, Danya, and Tanya were collecting apples. It turned out that each of them collected a whole percentage of the total number of apples collected, and all these numbers were different and greater than zero. Then Tanya, who collected the most apples, ate her apples. After this, it turned out that each of the children still had a whole percentage, but now of the remaining number of apples. What is the minimum number of apples that could have been collected?
Answer: 20 : for example $2+3+5+10$
|
# Solution:
Let Anya have collected the fewest apples, which is $k$, and the total number of apples is $n$. Then we get that the total number of apples collected is no less than $4k + 6$. For $k \geq 5$, we already get more than 20 apples. For $k < 5$, we need to consider the cases where $k$ is 1, 2, 3, or 4.
If $k = 4$, then the total number of apples is at least $4 \times 4 + 6 = 22$, which is more than 20.
If $k = 3$, then the total number of apples is at least $4 \times 3 + 6 = 18$, which is less than 20. However, since $\frac{n}{k}$ must be an integer and a divisor of 100, we get that at least $10k$ apples were collected, which is 30, more than 20.
If $k = 2$, then the total number of apples is at least $4 \times 2 + 6 = 14$, which is less than 20. However, since $\frac{n}{k}$ must be an integer and a divisor of 100, we get that at least $10k$ apples were collected, which is 20.
If $k = 1$, we get that Anya, Vanya, and Sanya collected at least 6 apples, and thus, by similar reasoning, there are at least 10 of them. Therefore, the four of them together had at least 20 apples (the next divisor of 100).
|
20
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (3 points) Given a convex pentagon $A B C D E$. Point $P$ is the intersection of $B E$ and $A C$, point $Q$ is the intersection of $C E$ and $A D$, point $O$ is the intersection of $A D$ and $B E$. It turns out that triangles $A B P$ and $D E Q$ are isosceles triangles with the angle at the vertex (exactly at the vertex, not at the base) equal to 80 degrees. Find the value of angle $A C E$, given that triangles $A P O$ and $E Q O$ are also isosceles.
|
Answer: $60^{\circ}$ or $105^{\circ}$
Solution: Consider triangle $A B P$. The angle $\angle A P B$ in it can be $80^{\circ}$ or $50^{\circ}$. Then the adjacent $\angle A P O$ is $100^{\circ}$ or $130^{\circ}$. Therefore, in triangle $A P O$, this is the angle at the vertex and $\angle A O P$ is $40^{\circ}$ or $25^{\circ}$.
We can make similar considerations for triangles $B Q E$ and $E Q O$, obtaining that $\angle Q O E$ is also $40^{\circ}$ or $25^{\circ}$ depending on $\angle D Q E$. But $\angle Q O E=\angle A O P$ as vertical angles, so $\angle A P B=\angle D Q E$.
$\angle A C E=360^{\circ}-\angle C P O-\angle C Q O-\angle P O Q=360^{\circ}-540^{\circ}+\angle A P O+\angle E Q O+\angle A O P$, which is $60^{\circ}$ or $105^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (4 points) On the board, all three-digit natural numbers are written, the first digits of which are odd and greater than 1. What is the maximum number of quadratic equations of the form $a x^{2}+b x+c=0$ that can be formed using these numbers as $a, b$ and $c$, each no more than once, such that all these equations have roots.
#
|
# Answer: 100
## Solution:
In each equation, there must be a coefficient less than five hundred. Otherwise, the discriminant $b^{2}-4 a c$ 2 variant
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) Anya, Vanya, Danya, Sanya, and Tanya were collecting apples. It turned out that each of them collected a whole percentage of the total number of collected apples, and all these numbers were different and greater than zero. Then Tanya, who collected the most apples, ate her apples. After that, it turned out that each of the children still had a whole percentage, but now of the remaining number of apples. What is the minimum number of apples that could have been collected?
|
Answer: 20, for example $1+2+3+4+10$
## Solution:
Let Anna have collected the fewest apples, and this number is $k$, and the total number of apples is $n$. Then we get that the total number of apples collected is no less than $4 k+10$. For $k \geq 3$, we already get more than 20 apples. For $k=2$, we get $n \geq 18=9 k$. Since $\frac{n}{k}$ must be an integer and a divisor of a hundred, it turns out that no fewer than $10 k$ apples were collected, that is, at least 20 again. For $k=1$, we get that the children collected at least 15 apples, and this number, as in the previous considerations, must be a divisor of a hundred, that is, at least 20 apples again.
|
20
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (3 points) Given a rectangle $A B C D, A B=5, B C=6$. Point $K$ lies on side $C D$, point $L$ lies on side $A B$, point $M$ lies on side $B C$, point $N$ lies on side $C D$. Prove that the length of the closed broken line $A K L M N A$ is not greater than 26.
|
Solution:
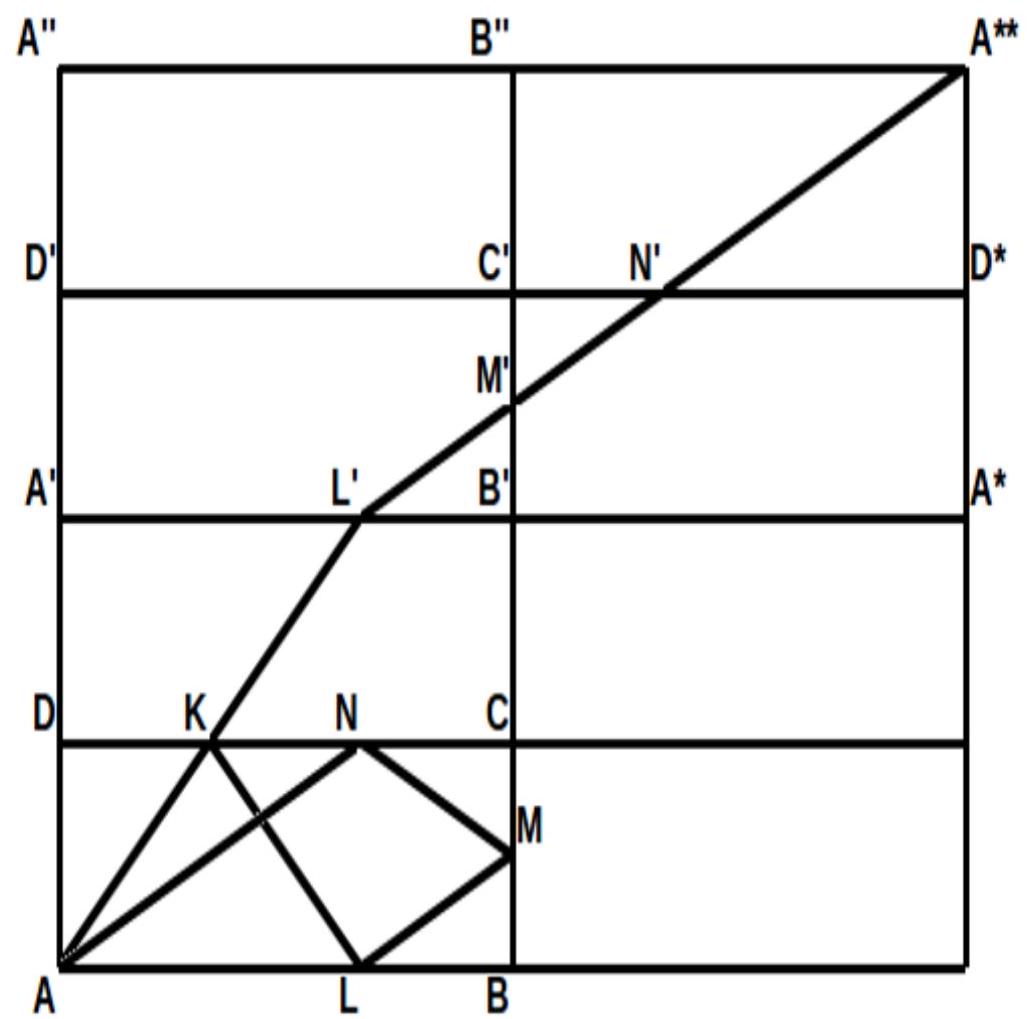
Let's add several more rectangles equal to the given one, as shown in the figure. Take point $L^{\prime}$ such that $A L=A L^{\prime}$, point $M$ such that $B^{\prime} M^{\prime}=B M$, and point $N^{\prime}$ such that $C^{\prime} N^{\prime}=C N$.
From the construction, it is clear that the length of the broken line $A K L M N A$ is equal to the length of the broken line $A K L^{\prime} M^{\prime} N^{\prime} A * *$, which is longer than $A B^{\prime \prime}$. The length of this segment can be calculated using the Pythagorean theorem and is equal to 26.
|
26
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
7. (3 points) Given a convex pentagon $A B C D E$. Point $P$ is the intersection of $B E$ and $A C$, point $Q$ is the intersection of $C E$ and $A D$, point $O$ is the intersection of $A D$ and $B E$. It turns out that triangles $A B P$ and $D E Q$ are isosceles triangles with the angle at the vertex (exactly at the vertex, not at the base) equal to 40 degrees. Find the value of angle $A C E$, given that triangles $A P O$ and $E Q O$ are also isosceles.
|
Answer: $120^{\circ}$ or $75^{\circ}$
Solution: Consider triangle $A B P$. The angle $\angle A P B$ in it can be $40^{\circ}$ or $70^{\circ}$. Then the adjacent $\angle A P O$ is $140^{\circ}$ or $110^{\circ}$. Therefore, in triangle $A P O$, this is the angle at the vertex and $\angle A O P$ is $20^{\circ}$ or $35^{\circ}$.
We can make similar considerations for triangles $B Q E$ and $E Q O$, obtaining that $\angle Q O E$ is also $20^{\circ}$ or $35^{\circ}$ depending on $\angle D Q E$. But $\angle Q O E=\angle A O P$ as vertical angles, so $\angle A P B=\angle D Q E$.
$\angle A C E=360^{\circ}-\angle C P O-\angle C Q O-\angle P O Q=360^{\circ}-540^{\circ}+\angle A P O+\angle E Q O+\angle A O P$, which is $120^{\circ}$ or $75^{\circ}$.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (4 points) On the board, all three-digit natural numbers are written, the first digits of which are odd and greater than 1. What is the maximum number of quadratic equations of the form $a x^{2}+b x+c=0$ that can be formed using these numbers as $a, b$, and $c$, each no more than once, such that all these equations have roots.
|
Answer: 100.
Solution:
In each equation, there must be a coefficient less than five hundred. Otherwise, the discriminant $b^{2}-4 a c<1000^{2}-4 \cdot 500^{2}=0$ and the equation has no roots. Thus, we get no more than 100 equations.
Now for an example: Take $b$ as numbers starting with 9, and for each equation, take $a$ and $c$ as $500-k$ and $399+k$ respectively, where $k$ takes natural values from 0 to 99. Then $a c=(500-k)(399+k)<(500-k)(400+k)=200000+100 k-k^{2}=202500-(k-50)^{2} \leqslant 202500$. Therefore, $4 a c<810000$, on the other hand, $b^{2} \geq 900^{2}=810000$, hence $b \geqslant a c$.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) In space, there is a cube $1000 \times 1000 \times 1000$ with a vertex at the origin and faces parallel to the coordinate planes. Vectors are drawn from the origin to all integer points inside and on the boundary of this cube. Find the remainder when the sum of the squares of the lengths of these vectors is divided by 13.
#
|
# Answer: 0
Solution:
The sum of the squares of the lengths of these vectors is the sum of the squares of all their coordinates, that is, $3 \cdot 1001^{2} \cdot\left(0^{2}+1^{2}+\right.$ $2^{2}+\ldots+1000^{2}$ ), which is divisible by 13, since 1001 is divisible by 13.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) In space, there is a cube $1000 \times 1000 \times 1000$ with a vertex at the origin and faces parallel to the coordinate planes. Vectors are drawn from the origin to all integer points inside and on the boundary of this cube. Find the remainder when the sum of the squares of the lengths of these vectors is divided by 11.
#
|
# Answer: 0
## Solution:
The sum of the squares of the lengths of these vectors is the sum of the squares of all their coordinates, that is, $3 \cdot 1001^{2} \cdot\left(0^{2}+1^{2}+\right.$ $\left.2^{2}+\ldots+1000^{2}\right)$, which is divisible by 11, since 1001 is divisible by 11.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The train was supposed to travel 300 km. Having traveled 212 km at a certain speed, it then reduced its speed by 50 km/h. As a result, the train arrived 40 minutes later than the scheduled time. Find the initial speed of the train. Answer in km/h.
|
Answer: 110
3rd option. The train was supposed to travel 300 km. After traveling 50 km at a certain speed, it then reduced its speed by 40 km/h. As a result, the train arrived 1 hour and 40 minutes later than the scheduled time. Find the initial speed of the train. Record your answer in km/h.
Answer: 100
#
|
110
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Four different numbers $a, b, c, d$, greater than one and not divisible by 5, are such that $\gcd(a, b) = \gcd(c, d)$ and $\operatorname{lcm}(a, b) = \operatorname{lcm}(c, d)$. What is the smallest possible value of $a + b + c + d$?
|
Answer: 24
## Examples of how to write the answer:
17
#
|
24
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. At a round table, raccoons, hedgehogs, and hamsters were sitting, a total of 134 animals. When asked: "Are there any animals of the same kind as you among your neighbors?", everyone answered "No." What is the maximum number of hedgehogs that could have been sitting at the table, given that hamsters and hedgehogs always tell the truth, raccoons almost always lie (except when a raccoon is sitting between two raccoons, in which case he tells the truth), and hamsters heard the question differently: "Are your neighbors animals of the same kind?"
|
Answer: 44
## Examples of how to write the answer:
17
#
|
44
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8. (5 points)
A figure called a "half-bishop" moves one square diagonally. What is the maximum number of non-attacking half-bishops that can be placed on a $7 \times 7$ chessboard?
Answer: 28
|
Solution:
Consider all diagonals of one direction. On each diagonal of even length, no more than half of the cells can be occupied by semi-bishops, as it can be divided into pairs of cells that cannot be simultaneously occupied.
On each diagonal of odd length $2n+1$, no more than $n+1$ semi-bishops can be placed for the same reasons.
There are a total of 7 odd diagonals, so the maximum possible number of semi-bishops is $\frac{49-7}{2}+7=28$.
An example can be constructed by placing semi-bishops in all cells of rows with odd numbers.
## 2nd Option
#
|
28
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8. (5 points)
A figure called a "half-bishop" moves one square diagonally. What is the maximum number of non-attacking half-bishops that can be placed on a $9 \times 9$ chessboard?
|
Answer: 45
Solution:
Consider all diagonals of one direction. On each diagonal of even length, no more than half of the cells can be occupied by pseudo-bishops, as it can be divided into pairs of cells that cannot be simultaneously occupied.
On each diagonal of odd length $2n+1$, no more than $n+1$ pseudo-bishops can be placed for the same reasons.
There are a total of 9 odd diagonals, so the maximum possible number of pseudo-bishops is $\frac{81-9}{2}+9=45$.
An example can be constructed by placing pseudo-bishops in all cells of the rows with odd numbers.
## 7th grade
#
|
45
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) In trapezoid $A B C D$ with bases $A D=16$ and $B C=10$, the circles constructed on sides $A B, B C$ and $C D$ as diameters intersect at one point. The length of diagonal $A C$ is 10. Find the length of $B D$.
|
Answer: 24
## Solution:
Let the intersection point of the three circles be $O$. Then, since the circles are constructed on the sides of the trapezoid $AB, BC$, and $CD$ as diameters, the angles $\angle AOB, \angle BOC$, and $\angle COD$ are right angles. Therefore, points $A, O, C$ lie on the same line and points $B, O, D$ lie on the same line, meaning that $O$ is the intersection point of the diagonals of the trapezoid.
Let the midpoints of sides $AB, BC$, and $CD$ be $K, L$, and $M$ respectively. Since $KL$ and $LM$ are the midlines in triangles $ABC$ and $BCD$, $KL \parallel AC$ and $LM \parallel BD$. Thus, $KL \perp LM$, meaning that triangle $KLM$ is a right triangle. Moreover, $KL = \frac{AC}{2} = 5$, and $KM = \frac{AD + BC}{2} = 13$, so by the Pythagorean theorem, $LM = 12$. Therefore, $BD = 2LM = 24$.
Instead of reasoning with midlines, we can consider triangles $BOC$ and $AOD$, which are similar with a ratio of $10:16 = 5:8$. Since $AC = 10$, then $OC = \frac{5}{13}AC = \frac{50}{13}$. By the Pythagorean theorem in triangle $BOC$, we find $OB = \sqrt{10^2 - \frac{2500}{169}} = \frac{120}{13}$. Therefore, $BD = \frac{13}{5}OB = \frac{13}{5} \cdot \frac{120}{13} = 24$.
|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) Let $x, y, z$ and $t$ be non-negative numbers such that $x+y+z+t=5$. Prove the inequality
$$
\sqrt{x^{2}+y^{2}}+\sqrt{x^{2}+1}+\sqrt{z^{2}+y^{2}}+\sqrt{z^{2}+t^{2}}+\sqrt{t^{2}+9} \geqslant 10
$$
|
# Solution:
Consider the following points on the plane: $A(0,0) ; B(x, 1) ; C(x+y, 1+x) ; D(x+y+z, 1+$ $x+y) ; E(x+y+z+t, 1+x+y+z) ; F(x+y+z+t+3,1+x+y+z+t)$. Then the length of the broken line $A B C D E F$ coincides with the expression that needs to be evaluated. By the triangle inequality, the length of the broken line $A B C D E F$ is not less than the length of the segment $A F$. Given that $x+y+z+t=5$, the coordinates of point $F$ are $(8,6)$ and the length of segment $A F=10$.
|
10
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) In trapezoid $A B C D$ with bases $A D=12$ and $B C=8$, the circles constructed on sides $A B, B C$, and $C D$ as diameters intersect at one point. The length of diagonal $A C$ is 12. Find the length of $B D$.
|
Answer: 16
## Solution:
Let the intersection point of the three circles be $O$. Then, since the circles are constructed on the sides of the trapezoid $AB, BC$, and $CD$ as diameters, the angles $\angle AOB, \angle BOC$, and $\angle COD$ are right angles. Therefore, points $A, O, C$ lie on the same line and points $B, O, D$ lie on the same line, meaning that $O$ is the intersection point of the diagonals of the trapezoid.
Let the midpoints of sides $AB, BC$, and $CD$ be $K, L$, and $M$ respectively. Since $KL$ and $LM$ are the midlines in triangles $ABC$ and $BCD$, $KL \parallel AC$ and $LM \parallel BD$. Thus, $KL \perp LM$, meaning that triangle $KLM$ is a right triangle. Moreover, $KL = \frac{AC}{2} = 6$, and $KM = \frac{AD + BC}{2} = 10$, so by the Pythagorean theorem, $LM = 8$. Therefore, $BD = 2LM = 16$.
Instead of reasoning with midlines, we can consider triangles $BOC$ and $AOD$, which are similar with a ratio of $8:12 = 2:3$. Since $AC = 12$, then $OC = \frac{2}{5}AC = \frac{24}{5}$. By the Pythagorean theorem in triangle $BOC$, we find $OB = \sqrt{8^2 - \frac{24^2}{5^2}} = \frac{32}{5}$. Therefore, $BD = \frac{5}{2}OB = \frac{5}{2} \cdot \frac{32}{5} = 16$.
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) Let $x, y, z$ and $t$ be non-negative numbers such that $x+y+z+t=4$. Prove the inequality
$$
\sqrt{x^{2}+t^{2}}+\sqrt{z^{2}+1}+\sqrt{z^{2}+t^{2}}+\sqrt{y^{2}+x^{2}}+\sqrt{y^{2}+64} \geqslant 13
$$
|
# Solution:
Consider the following points on the plane: $A(0,0) ; B(x, t) ; C(x+z, t+1) ; D(x+z+t, t+1+z)$; $E(x+z+t+y, t+1+z+x) ; F(x+z+t+y+8, t+1+z+x+y)$. Then the length of the broken line $A B C D E F$ coincides with the expression that needs to be evaluated. By the triangle inequality, the length of the broken line $A B C D E F$ is not less than the length of the segment $A F$. Given that $x+y+z+t=4$, the coordinates of point $F$ are $(12,5)$ and the length of segment $A F=13$.
|
13
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) In trapezoid $A B C D$ with bases $A D=20$ and $B C=14$, the circles constructed on sides $A B, B C$ and $C D$ as diameters intersect at one point. The length of diagonal $A C$ is 16. Find the length of $B D$.
|
Answer: 30
## Solution:
Let the intersection point of the three circles be $O$. Then, since the circles are constructed on the sides $AB$, $BC$, and $CD$ of the trapezoid as diameters, the angles $\angle AOB$, $\angle BOC$, and $\angle COD$ are right angles. Therefore, points $A$, $O$, and $C$ lie on the same line, and points $B$, $O$, and $D$ lie on the same line, meaning that $O$ is the intersection point of the diagonals of the trapezoid.
Let the midpoints of sides $AB$, $BC$, and $CD$ be $K$, $L$, and $M$ respectively. Since $KL$ and $LM$ are the midlines in triangles $ABC$ and $BCD$, $KL \parallel AC$ and $LM \parallel BD$. Thus, $KL \perp LM$, meaning that triangle $KLM$ is a right triangle. Moreover, $KL = \frac{AC}{2} = 8$, and $KM = \frac{AD + BC}{2} = 17$, so by the Pythagorean theorem, $LM = 15$. Therefore, $BD = 2LM = 30$.
Instead of reasoning with midlines, we can consider triangles $BOC$ and $AOD$, which are similar with a ratio of $14:20 = 7:10$. Since $AC = 16$, then $OC = \frac{7}{17} AC = \frac{112}{17}$. By the Pythagorean theorem in triangle $BOC$, we find $OB = \sqrt{14^2 - \frac{112^2}{17^2}} = \frac{210}{17}$. Therefore, $BD = \frac{17}{7} OB = \frac{17}{7} \cdot \frac{210}{17} = 30$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) Let $x, y, z$ and $t$ be non-negative numbers such that $x+y+z+t=7$. Prove the inequality
$$
\sqrt{x^{2}+y^{2}}+\sqrt{x^{2}+1}+\sqrt{z^{2}+y^{2}}+\sqrt{t^{2}+64}+\sqrt{z^{2}+t^{2}} \geqslant 17
$$
|
Solution:
Consider the following points on the plane: $A(0,0) ; B(x, y) ; C(x+1, y+x) ; D(x+1+y, y+x+z) ; E(x+1+y+t, y+x+z+8) ; F(x+1+y+t+z, y+x+z+8+t)$. Then the length of the broken line $A B C D E F$ coincides with the expression that needs to be evaluated. By the triangle inequality, the length of the broken line $A B C D E F$ is not less than the length of the segment $A F$. Given that $x+y+z+t=7$, the coordinates of point $F$ are $(8,15)$ and the length of segment $A F=17$.
|
17
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) In trapezoid $A B C D$ with bases $A D=20$ and $B C=10$, circles constructed on sides $A B, B C$, and $C D$ as diameters intersect at one point. The length of diagonal $A C$ is 18. Find the length of $B D$.
|
Answer: 24
## Solution:
Let the intersection point of the three circles be $O$. Then, since the circles are constructed on the sides of the trapezoid $AB, BC$, and $CD$ as diameters, the angles $\angle AOB, \angle BOC$, and $\angle COD$ are right angles. Therefore, points $A, O, C$ lie on the same line and points $B, O, D$ lie on the same line, meaning that $O$ is the intersection point of the diagonals of the trapezoid.
Let the midpoints of sides $AB, BC$, and $CD$ be $K, L$, and $M$ respectively. Since $KL$ and $LM$ are the midlines in triangles $ABC$ and $BCD$, $KL \parallel AC$ and $LM \parallel BD$. Thus, $KL \perp LM$, meaning that triangle $KLM$ is a right triangle. Moreover, $KL = \frac{AC}{2} = 9$, and $KM = \frac{AD + BC}{2} = 15$, so by the Pythagorean theorem, $LM = 12$. Therefore, $BD = 2LM = 24$.
Instead of reasoning with midlines, we can consider triangles $BOC$ and $AOD$, which are similar with a ratio of $10:20 = 1:2$. Since $AC = 18$, then $OC = \frac{1}{3}AC = 6$. By the Pythagorean theorem in triangle $BOC$, we find $OB = \sqrt{10^2 - 6^2} = 8$. Therefore, $BD = \frac{3}{1}OB = 3 \cdot 8 = 24$.
|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) Let $x, y, z$ and $t$ be non-negative numbers such that $x+y+z+t=2$. Prove the inequality
$$
\sqrt{x^{2}+z^{2}}+\sqrt{x^{2}+1}+\sqrt{z^{2}+y^{2}}+\sqrt{y^{2}+t^{2}}+\sqrt{t^{2}+4} \geqslant 5
$$
|
Solution:
Consider the following points on the plane: $A(0,0) ; B(x, z) ; C(x+1, z+x) ; D(x+1+z, z+x+y) ; E(x+1+z+y, z+x+y+t) ; F(x+1+z+y+t, z+x+y+t+2)$. Then the length of the broken line $A B C D E F$ coincides with the expression that needs to be evaluated. By the triangle inequality, the length of the broken line $A B C D E F$ is not less than the length of the segment $A F$. Given that $x+y+z+t=2$, the coordinates of point $F$ are $(3,4)$ and the length of segment $A F=5$.
|
5
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. A four-digit number ABCD, consisting of different digits, is divisible by both the two-digit number CD and the two-digit number AB. Find the smallest possible value of ABCD.
|
Answer: 1248
## Examples of answer recording:
1234
#
|
1248
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In country Gamma, there are 83 cities. It is known that at least 2 roads lead out of each city. It is also known that if there is a road from city A to city B and from city B to city C, then there is also a road from city A to city C. What is the minimum number of roads that can be in the country?
|
Answer: 87
## Examples of answer notation:
17
#
|
87
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
In trapezoid $A B C D$, the lateral side $A B$ is equal to the diagonal $A C$. On the smaller arc $A D$ of the circumscribed circle of triangle $A B D$, a point $E$ is chosen such that $A B=A E$. Find the angle $\angle C E D$.
|
Answer: $90^{\circ}$.
Solution:
From the isosceles property of triangle $ABC$ and the parallelism of $BC$ and $AD$, we get $\angle ABC = \angle ACB = \angle CAD = \alpha$.
Let the line $BC$ intersect the circumcircle of triangle $ABD$ at point $F$. Then $ABFD$ is an inscribed, i.e., isosceles, trapezoid, from which the arcs $AB, AE$, and $DF$ are equal. Hence, $\angle ABE = \angle DBF = \beta$.
$\angle EAD = \angle EBD = \gamma$, since these angles subtend the same arc.
$\angle ABD = \angle ABE + \angle EBD = \beta + \gamma$.
$\angle EAC = \angle EAD + \angle CAD = \gamma + \alpha$. Therefore, in the isosceles triangle $EAC$, the equality $\angle ACE = \angle AEC = \frac{180^{\circ} - \alpha - \gamma}{2}$ holds.
Moreover, $\alpha = \angle ABC = \angle ABF = \angle ABD + \angle DBF = 2\beta + \gamma$.
$\angle CED = \angle AED - \angle AEC = (180^{\circ} - \angle ABD) - \frac{180^{\circ} - \alpha - \gamma}{2} = 180^{\circ} - \beta - \gamma - 90^{\circ} + \frac{2\beta + 2\gamma}{2} = 90^{\circ}$
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8. (5 points)
Girl Katya doesn't like the number 239. She listed several different numbers, none of which contain the sequence of digits 239 (in a row and exactly in that order). Prove that the sum of the reciprocals of these numbers is no more than 30000.
#
|
# Solution:
The number of suitable $3 n+1$-digit numbers is no more than $9 \cdot 999^{n}: 9$ options for the first digit and no more than 999 options for each subsequent triplet of digits. Each of them is no less than $10^{3 n}$.
The number of suitable $3 n+2$-digit numbers is no more than $90 \cdot 999^{n}$. Each of them is no less than $10^{3 n+1}$.
The number of suitable $3 n+3$-digit numbers is no more than $899 \cdot 999^{n}$. Each of them is no less than $10^{3 n+2}$.
Let the number of digits in the largest written number not exceed $3 N+3$. Then the total sum of the numbers is no more than
$$
\sum_{n=0}^{N}\left(\frac{9 \cdot 999^{n}}{1000^{n}}+\frac{90 \cdot 999^{n}}{10 \cdot 1000^{n}}+\frac{899 \cdot 999^{n}}{100 \cdot 1000^{n}}\right)=(9+9+8.99) \sum_{n=0}^{N}\left(\frac{999^{n}}{1000^{n}}\right) \leqslant 30 \cdot \frac{1}{1-0.999}=
$$
30000.
## 2nd Option
#
|
30000
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
In trapezoid $A B C D$, the lateral side $B C$ is equal to the diagonal $B D$. On the smaller arc $A B$ of the circumscribed circle of triangle $A B C$, a point $E$ is chosen such that $B C=B E$. Find the angle $\angle A E D$.
|
Answer: $90^{\circ}$.
## Solution:
From the isosceles triangle $B C D$ and the parallelism of $A B$ and $C D$, we get $\angle B C D = \angle B D C = \angle D B A = \alpha$.
Let the line $C D$ intersect the circumcircle of triangle $A B C$ at point $F$. Then $B C F A$ is an inscribed, i.e., isosceles, trapezoid, from which the arcs $B C, B E$, and $A F$ are equal. Hence, $\angle B C E = \angle A C F = \beta$.
$\angle E B A = \angle E C A = \gamma$, since these angles subtend the same arc.
$\angle B C A = \angle B C E + \angle E C A = \beta + \gamma$.
$\angle E B D = \angle E B A + \angle D B A = \gamma + \alpha$. Therefore, in the isosceles triangle $E B D$, the equality $\angle B D E = \angle B E D = \frac{180^{\circ} - \alpha - \gamma}{2}$ holds.
Moreover, $\alpha = \angle B C D = \angle B C F = \angle B C A + \angle A C F = 2 \beta + \gamma$.
$\angle A E D = \angle B E A - \angle B E D = (180^{\circ} - \angle B C A) - \frac{180^{\circ} - \alpha - \gamma}{2} = 180^{\circ} - \beta - \gamma - 90^{\circ} + \frac{2 \beta + 2 \gamma}{2} = 90^{\circ}$
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8. (5 points)
Boy Kolya doesn't like the number 1234. He listed several different numbers, none of which contain the sequence of digits 1234 (in a row and exactly in that order). Prove that the sum of the reciprocals of these numbers is no more than 400000.
|
Solution:
The number of suitable $4 n+1$-digit numbers is no more than $9 \cdot 9999^{n}: 9$ options for the first digit and no more than 9999 options for each subsequent quartet of digits. Each of them is no less than $10^{4 n}$.
The number of suitable $4 n+2$-digit numbers is no more than $90 \cdot 9999^{n}$. Each of them is no less than $10^{4 n+1}$.
The number of suitable $4 n+3$-digit numbers is no more than $900 \cdot 9999^{n}$. Each of them is no less than $10^{4 n+2}$.
The number of suitable $4 n+4$-digit numbers is no more than $8999 \cdot 9999^{n}$. Each of them is no less than $10^{4 n+3}$.
Let the number of digits in the largest written number not exceed $4 N+4$.
Then the total sum of the numbers is no more than $\sum_{n=0}^{N}\left(\frac{9 \cdot 9999^{n}}{10000^{n}}+\frac{90 \cdot 9999^{n}}{10 \cdot 10000^{n}}+\frac{900 \cdot 9999^{n}}{100 \cdot 10000^{n}}+\frac{8999 \cdot 9999^{n}}{1000 \cdot 10000^{n}}\right)$ $=(9+9+9+8.999) \sum_{n=0}^{N}\left(\frac{9999^{n}}{10000^{n}}\right) \leqslant 40 \cdot \frac{1}{1-0.9999}=400000$.
## 3rd variant
#
|
400000
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
In trapezoid $A B C D$, the lateral side $C D$ is equal to the diagonal $A C$. On the smaller arc $B C$ of the circumscribed circle of triangle $B C D$, a point $E$ is chosen such that $C D=C E$. Find the angle $\angle A E B$.
|
Answer: $90^{\circ}$.
Solution:
From the isosceles triangle $A C D$ and the parallelism of $B C$ and $A D$, we get $\angle A D C = \angle C A D = \angle A C B = \alpha$.
Let the line $A D$ intersect the circumcircle of triangle $B C D$ at point $F$. Then $C D F B$ is an inscribed, i.e., isosceles, trapezoid, from which the arcs $C D, C E$, and $B F$ are equal. Hence, $\angle C D E = \angle B D F = \beta$.
$\angle E C B = \angle E D B = \gamma$, since these angles subtend the same arc.
$\angle C D B = \angle C D E + \angle E D B = \beta + \gamma$.
$\angle E C A = \angle E C B + \angle A C B = \alpha + \gamma$. Therefore, in the isosceles triangle $E C A$, the equality $\angle C A E = \angle A E C = \frac{180^{\circ} - \alpha - \gamma}{2}$ holds.
Moreover, $\alpha = \angle A D C = \angle C D F = \angle C D B + \angle B D F = 2 \beta + \gamma$.
$\angle A E B = \angle C E B - \angle A E C = (180^{\circ} - \angle C D B) - \frac{180^{\circ} - \alpha - \gamma}{2} = 180^{\circ} - \beta - \gamma - 90^{\circ} + \frac{2 \beta + 2 \gamma}{2} = 90^{\circ}$
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8. (5 points)
Girl Masha doesn't like the number 729. She listed several different numbers, none of which contain the sequence of digits 729 (in a row and exactly in that order). Prove that the sum of the reciprocals of these numbers is no more than 30000.
#
|
# Solution:
The number of suitable $3 n+1$-digit numbers is no more than $9 \cdot 999^{n}: 9$ options for the first digit and no more than 999 options for each subsequent triplet of digits. Each of them is no less than $10^{3 n}$.
The number of suitable $3 n+2$-digit numbers is no more than $90 \cdot 999^{n}$. Each of them is no less than $10^{3 n+1}$.
The number of suitable $3 n+3$-digit numbers is no more than $899 \cdot 999^{n}$. Each of them is no less than $10^{3 n+2}$.
Let the number of digits in the largest written number not exceed $3 N+3$. Then the total sum of the numbers is no more than
$$
\sum_{n=0}^{N}\left(\frac{9 \cdot 999^{n}}{1000^{n}}+\frac{90 \cdot 999^{n}}{10 \cdot 1000^{n}}+\frac{899 \cdot 999^{n}}{100 \cdot 1000^{n}}\right)=(9+9+8.99) \sum_{n=0}^{N}\left(\frac{999^{n}}{1000^{n}}\right) \leqslant 30 \cdot \frac{1}{1-0.999}=
$$
30000.
## 4th variant
#
|
30000
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
In trapezoid $A B C D$, the lateral side $A D$ is equal to the diagonal $B D$. On the smaller arc $C D$ of the circumscribed circle of triangle $A C D$, a point $E$ is chosen such that $A D=D E$. Find the angle $\angle B E C$.
|
Answer: $90^{\circ}$.
## Solution:
From the isosceles triangle $B A D$ and the parallelism of $A B$ and $C D$, we get $\angle B A D = \angle D B A = \angle B D C = \alpha$.
Let the line $A B$ intersect the circumcircle of triangle $A C D$ at point $F$. Then $D A F C$ is an inscribed, i.e., isosceles, trapezoid, from which the arcs $D A, D E$, and $C F$ are equal. Hence, $\angle D A E = \angle C A F = \beta$.
$\angle E D C = \angle E A C = \gamma$, since these angles subtend the same arc.
$\angle D A C = \angle D A E + \angle E A C = \beta + \gamma$.
$\angle E D B = \angle E D C + \angle B D C = \gamma + \alpha$. Therefore, in the isosceles triangle $E B D$, the equality $\angle D B E = \angle B E D = \frac{180^{\circ} - \alpha - \gamma}{2}$ holds.
Moreover, $\alpha = \angle B A D = \angle D A F = \angle D A C + \angle C A F = 2 \beta + \gamma$.
$\angle B E C = \angle D E C - \angle D E B = (180^{\circ} - \angle D A C) - \frac{180^{\circ} - \alpha - \gamma}{2} = 180^{\circ} - \beta - \gamma - 90^{\circ} + \frac{2 \beta + 2 \gamma}{2} = 90^{\circ}$
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8. (5 points)
Boy Anton does not like the number 2048. He listed several different numbers, none of which contain the sequence of digits 2048 (in a row and exactly in this order). Prove that the sum of the reciprocals of these numbers is no more than 400000.
#
|
# Solution:
The number of suitable $4 n+1$-digit numbers is no more than $9 \cdot 9999^{n}: 9$ options for the first digit and no more than 9999 options for each subsequent quartet of digits. Each of them is no less than $10^{4 n}$.
The number of suitable $4 n+2$-digit numbers is no more than $90 \cdot 9999^{n}$. Each of them is no less than $10^{4 n+1}$.
The number of suitable $4 n+3$-digit numbers is no more than $900 \cdot 9999^{n}$. Each of them is no less than $10^{4 n+2}$.
The number of suitable $4 n+4$-digit numbers is no more than $8999 \cdot 9999^{n}$. Each of them is no less than $10^{4 n+3}$.
Let the number of digits in the largest written number not exceed $4 N+4$.
Then the total sum of the numbers is no more than $\sum_{n=0}^{N}\left(\frac{9 \cdot 9999^{n}}{10000^{n}}+\frac{90 \cdot 9999^{n}}{10 \cdot 10000^{n}}+\frac{900 \cdot 9999^{n}}{100 \cdot 10000^{n}}+\frac{8999 \cdot 9999^{n}}{1000 \cdot 10000^{n}}\right)$ $=(9+9+9+8.999) \sum_{n=0}^{N}\left(\frac{9999^{n}}{10000^{n}}\right) \leqslant 40 \cdot \frac{1}{1-0.9999}=400000$.
|
400000
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. $\mathrm{ABCD}$ is an isosceles trapezoid, $\mathrm{AB}=\mathrm{CD}=25, \mathrm{BC}=40, \mathrm{AD}=60$. $\mathrm{BCDE}$ is also an isosceles trapezoid. Find AE. (Points A and E do not coincide) If there are multiple possible values, list them in any order separated by a semicolon.
|
Answer: 44
## Examples of answer recording:
45
$45 ; 56$
Problem 10 (4 points).
|
44
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) Does there exist a four-digit natural number with the sum of its digits being 21, which is divisible by $14 ?$
|
Answer: Yes, for example 6384.
|
6384
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (2 points) Boys were collecting apples. Each collected either 10 apples or $10\%$ of the total number of apples collected, and there were both types. What is the smallest number of boys there could have been?
|
# Answer: 6
Solution: Example: one boy collected 10 apples, the rest collected 2 each, totaling 20.
Evaluation: Let's prove that there could not have been fewer boys. We know that $10\%$ of the total number of apples is an integer, let's denote it as $k$. Suppose $n$ people collected ten apples each, and $m$ people collected $10\%$ each, then $10n = (10-m)k$, which means $10n$ is divisible by $10-m$. When $m=1$ or $m=3$, we get that $10n$ is divisible by 9 or 7, respectively, meaning $n$ is divisible by 9 or 7, which is too large. When $m=2$ or $m=4$, we get that $10n$ is divisible by 8 or 6, respectively, meaning $n$ is divisible by 4 or 3, and $m+n \geqslant 6$. When $m \geqslant 5$, the total number of boys is at least 1 more, meaning, again, at least 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) Solve the system of equations: $\left\{\begin{array}{l}x y=6(x+y) \\ x z=4(x+z) \\ y z=2(y+z)\end{array}\right.$
|
Answer: $x=y=z=0$ or $x=-24, y=\frac{24}{5}, y=\frac{24}{7}$
Solution: It is easy to verify that if one of the variables is 0, then the others are also 0. Otherwise, the system can be transformed into
$\left\{\begin{array}{l}\frac{1}{6}=\frac{1}{x}+\frac{1}{y} \\ \frac{1}{4}=\frac{1}{x}+\frac{1}{z} \\ \frac{1}{2}=\frac{1}{z}+\frac{1}{y}\end{array}\right.$
By adding the first two equations and subtracting the last one, we get $\frac{1}{6}+\frac{1}{4}-\frac{1}{2}=\frac{2}{x}$, from which $-\frac{1}{12}=\frac{2}{x}$, that is, $x=-24$. Similarly, we find the other unknowns.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (3 points) Given the rebus: MIMIMI + NYANYANYA = OLALAOY. Identical letters represent identical digits, different letters represent different digits. Find MI + NY.
#
|
# Answer: 119
Solution: The rebus can be rewritten as OLAOLOY = (MI + NYA) $\cdot$10101. First, this means that the last digit of MI + NYA is Y. Second, if MI + NYA $<100$, the result will be a four-digit number. Let MI + NYA $=1 Z$ Y, where $Z$ is some digit.
Then OLAOLOY $=1 Z$ Y $0000+1 Z$ Y $00+1 Z$ Y. If Y $<9$, then the sixth and fourth digits of this number should match, but they do not match. Therefore, Y $=9$. Consequently, I + A $=9$. The digit $Z$ is actually $O$, which is 1. Therefore, MI + NYA $=119$.
An example exists: $848484+353535=1202019$.
|
119
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) A quadrilateral is divided into 1000 triangles. What is the maximum number of different points at which the vertices of these triangles can be located?
|
Answer: 1002
Solution: The sum of the angles of a quadrilateral is $360^{\circ}$, and for thousands of triangles, it is $180000^{\circ}$. Where did the extra $1796400^{\circ}$ come from? Each internal vertex, where only the angles of triangles meet, adds $360^{\circ}$. Each vertex on the side of the original triangle or on the side of one of the triangles in the partition adds $180^{\circ}$. To achieve the maximum, it is necessary to have only points of the second type, and there should be $179640: 180=998$ of them. The example is constructed by sequentially adding new points to the boundaries of the original quadrilateral and the previously constructed triangles.
Adding the three vertices of the original quadrilateral, we get the answer 1002
|
1002
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) Does there exist a four-digit natural number with the sum of its digits being 14, which is divisible by $14 ?$
|
Answer: Yes, for example 6314.
|
6314
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (3 points) Given the puzzle: ЛЯЛЯЛЯ + ФУФУФУ = ГГЫГЫЫР. Identical letters represent identical digits, different letters represent different digits. Find ЛЯ + ФУ.
|
Answer: 109
Solution: The rebus can be rewritten as GGUGUUU $=(\text{LYA} + \text{FU}) 10101$. First, this means that the last digit of $\text{LYA} + \text{FU}$ is R. Second, if $\text{LYA} + \text{FU} < 100$, the result will be a four-digit number. Let $\text{LYA} + \text{FU} = 1ZP$, where $Z$ is some digit.
Then OLAOAOY $=1ZP0000 + 1ZP00 + 1ZP$. If $P < 9$, the sixth and fourth digits of this number should match, but they do not. Therefore, $P = 9$ and the fourth digit (G) is one more than the sixth (U) due to the carry from the fifth to the fourth place.
Thus, Y + U = 9. The digit $Z$ is actually U, so $\Gamma - 1 = 0$. This means $\text{LYA} + \text{FU} = 109$.
An example exists, indeed $757575 + 343434 = 1101009$.
6. (3 points) A quadrilateral is divided into 1000 triangles. What is the smallest number of different points where the vertices of these triangles can be located?
## Answer: 503
Solution: The sum of the angles of a quadrilateral is $360^{\circ}$, and the sum of the angles of a thousand triangles is $180000^{\circ}$. Where did the extra $1796400^{\circ}$ come from? Each internal vertex, where only the angles of the triangles meet, adds $360^{\circ}$. Each vertex on the side of the original quadrilateral or on the side of one of the triangles in the division adds $180^{\circ}$. To achieve the minimum, there should only be points of the first type, and there should be $179640: 360 = 499$ of them. An example can be constructed by sequentially adding new points inside (not on the boundary) of the existing triangles.
Adding the four vertices of the original quadrilateral, we get the answer 503.
|
109
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Boy Zhenya lives in a building with a total of 100 floors. The elevator takes 1 second to travel between adjacent floors. Unfortunately, only two buttons in the elevator work: “+13 floors” and “-7 floors”. The buttons are pressed instantly.
How many seconds will it take Zhenya to get home from the 1st floor to the 24th floor? (The elevator can only travel to existing floors)
|
Answer: 107
Examples of writing answers:
45
|
107
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Two quadratic trinomials have a common root -3, and for one of them, it is the larger root, while for the other, it is the smaller root. The length of the segment cut off by the graphs of these trinomials on the y-axis is 12. Find the length of the segment cut off by the graphs of the trinomials on the x-axis.
|
Answer: 4
Allowed for input are digits, the division sign, and a period or comma as a decimal separator
#
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A 103-gon is inscribed in a circle with diameter $\mathrm{XY}=4$ and has an axis of symmetry perpendicular to this diameter. Find the sum of the squares of the distances from the vertices of the 103-gon to the point $X$.
|
Answer: 824
## Examples of how to write the answer:
1,7
$1 / 7$
17
#
|
824
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given 50 quadratic trinomials. The graphs of these trinomials have their vertices on the $x$-axis. No three graphs intersect at the same point. What is the minimum number of intersection points they can form?
|
Answer: 600
## Examples of how to write the answer:
## 17
#
|
600
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. From the digits $1,2,3,4,5,6,7$, all possible seven-digit numbers with all different digits were formed. The obtained numbers were written in ascending order. Find which number will be in the 1972nd place.
|
Answer: 3641572
## Examples of how to write the answer:
1234567
#
|
3641572
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On Misfortune Island, a table tennis tournament was held in a round-robin format (i.e., everyone played against everyone else once). After each match, both participants separately approached the Chief Referee and reported the result. Among the participants, there were only three types of people: knights, who always tell the truth, liars, who always lie, and politicians, who always say what is advantageous to them—each politician claimed after each match that they had won.
After the tournament, it turned out that the Chief Referee, incognito, had attended several matches, as a result of which he was lucky enough to not only be able to determine the results of all the matches but also to find out that there were exactly six politicians. What is the minimum number of matches he could have attended?
(There are no draws in table tennis. The Chief Referee did not know in advance which players belonged to which type, and did not receive information in any other way except as described in the condition)
|
Answer: 16
## Examples of answer recording:
17
#
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Two racers with speeds of $100 \mathrm{~m} / \mathrm{c}$ and $70 \mathrm{~m} / \mathrm{c}$ started simultaneously in the same direction from the same place on a circular track of length $800 \mathrm{m}$. How many times did the racers meet after the start if both drove for 320 seconds?
|
Answer: 12
## Examples of writing answers:
45
## Problem 4 (2 points).
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Mitya wrote on the board the sum of the digits of each of the numbers from 1 to 800 inclusive. What is the sum of the numbers on the board
|
Answer: 10008
## Examples of answer notation:
12345
#
|
10008
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Boy Zhenya lives in a building with a total of 100 floors. The elevator takes 1 second to travel between adjacent floors. Unfortunately, only two buttons in the elevator work: “+13 floors” and “-7 floors”. The buttons are pressed instantly.
How many seconds will it take Zhenya to get home from the 1st floor to the 24th floor? (The elevator can only go to existing floors)
|
Answer: 107
Examples of writing answers:
45
|
107
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Seven dwarfs lined up by height, starting with the tallest. The first (i.e., the tallest) said: "My height is 60 cm." The second said: "My height is 61 cm." In order next: "My height is 62 cm," "My height is 63 cm," "My height is 64 cm," "My height is 65 cm," and finally the shortest said: "My height is 66 cm." What is the maximum number of dwarfs who could have told the truth?
|
1. Answer: 1.
No two dwarfs could tell the truth, because in this case the taller one would name the shorter height. However, one dwarf (any one) could tell the truth.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. A lot of snow fell, and the children decided to build snowmen. For this, they rolled 99 snowballs with masses of 1 kg, 2 kg, 3 kg, ..., 99 kg. A snowman consists of three snowballs stacked on top of each other, and one snowball can be placed on another if and only if the mass of the first is at least twice as small as the mass of the second. What is the maximum number of snowmen the children can build?
|
11. Answer: 24.
Two snowballs with masses from 50 to 99 kg cannot end up in the same snowman, so in each snowman, there will be at least two snowballs with masses from 1 to 49 kg. Therefore, there cannot be more than 24 snowmen.
An example can be constructed greedily: first, take three snowballs with masses, for example, 96, 48, and 24 kg. Now, if the mass of each is reduced by 1, the snowman can still be formed. Indeed, if the larger snowball decreases by 1, then to maintain the inequality, the smaller one must decrease by at least 0.5, but it also decreases by 1.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. Find the largest natural number that cannot be represented as the sum of two composite numbers. (Recall that a natural number is called composite if it is divisible by some natural number other than itself and one.)
|
17. Answer: 11.
All large numbers can be represented in the required way: odd numbers as "9 + an even number greater than two", and even numbers as "8 + an even number greater than two".
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. Among 65 residents of the village, two are tricksters, and the rest are knights. A knight always tells the truth, while a trickster can either tell the truth or lie. You can show any resident a list of a group of residents (including a group of one person) and ask if they are all knights. How can you find both tricksters by asking no more than 30 questions?
|
18. In fact, 16 questions are enough (and this is not the minimum).
In the first four questions, we will find a knight. We will do this as follows: ask the first and second residents about the third. If both answered that he is a knight, then he is a knight (otherwise, all three are liars, which is impossible).
If not, then ask the fourth and fifth residents about the sixth. If someone here said that he is a liar, then among $1,2,3$ there is a liar and among $4,5,6$ there is a liar, so the remaining 59 residents are knights, and the remaining questions will definitely be enough. Otherwise, the sixth is a knight.
The remaining questions will be asked to the found knight about the other 64 residents. Using dichotomy, we will find one liar in 6 questions, and in the next 6 questions - another one.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.