problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
19. Grandfather Frost has many identical dials in the form of regular 12-sided polygons, on which numbers from 1 to 12 are printed. He places these dials in a stack on top of each other (one by one, face up). In doing so, the vertices of the dials coincide, but the numbers in the coinciding vertices do not necessarily match. The Christmas tree will light up as soon as the sums of the numbers in all 12 columns have the same remainder when divided by 12. How many dials can be in the stack at this moment?
|
19. Answer: 12.
Let there be $k$ clock faces in the stack. Consider any two adjacent columns. The sum of the numbers in them differs by either $k$ or $k-12s$ (where $s$ is the number of clock faces for which one column has 12 and the next has 1). For $k=1,2, \ldots, 11$, all these differences are not divisible by 12, but for $k=12$ they become divisible by 12.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21. Baron Münchhausen told a story. "A whole crowd gathered. We reached a crossroads. Then half of our group turned left, a third - right, and a fifth - straight ahead." "But excuse me," the duke noticed, - the sum of a half, a third, and a fifth is not equal to one, so you are lying!" The baron objected: "I am not lying, I am rounding. For example, 17 people are walking. I say that a third turned. According to you, should one of the people split? No, with rounding, it turns out that six turned. After all, the closest whole number to the fraction $17 / 3$ is 6. And if I say that half of 17 people turned - that means 8 or 9 people." It is known that Baron Münchhausen never lies. What is the largest number of people that could have been in the crowd?
## 7th grade
|
21. Answer: 37 (18 to the left, 12 to the right, 7 straight).
Evaluation: $\frac{1}{2}+\frac{1}{3}+\frac{1}{5}=\frac{31}{30}$. If there were a total of people, then $\frac{1}{30} \cdot$ is the error. Let's calculate the maximum error (in fractions of a person): $\frac{1}{2}+\frac{1}{3}+\frac{2}{5}=\frac{37}{30}$. Therefore, $\frac{37}{30} \geqslant \frac{1}{30}$, from which $x \leqslant 37$.
## 7th grade
|
37
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32. In the country, there are 1000000 people, each of whom is acquainted with at least one resident. After surveys, a paradoxical situation has emerged: exactly $90 \%$ of the population admitted that they believe in Santa Claus, however, each resident can claim that among their acquaintances, exactly $10 \%$ believe in Santa Claus. Prove that someone among the residents is acquainted with at least 810 people.
|
32. Each person knows at least 10 people. In total, we have 900,000 people who believe in Santa Claus, and they have at least 8,100,000 acquaintances with those who do not believe in him. In total, 100,000 people do not believe in Santa Claus, so among them, there will be someone who has at least 81 acquaintances who believe in him, therefore, he has at least 810 acquaintances.
|
810
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
35. There is a pile of 660 stones on the table. In one move, you can split any of the existing piles into two smaller ones. At the same time, the sizes of any two piles on the table at the same time must differ by less than a factor of two. What is the maximum number of piles that can result?
## 9th Grade
## Plot 1
Let $I$ be the center of the inscribed circle $\alpha$ of triangle $ABC$. The circumcircle of triangle $AIC$ intersects $\alpha$ at points $P$ and $Q$ such that $P$ and $A$ lie on the same side of line $BI$, and $Q$ and $C$ lie on the opposite side. Let $M$ be the midpoint of the smaller arc $AB$ of the circumcircle of triangle $ABC$, and $N$ be the midpoint of the smaller arc $BC$.
|
35. Answer: 30
Example: Let's go in reverse - we will combine two piles into one without violating the conditions of the problem. Let's say we initially had piles (two of each kind): $15,15,16,16, \ldots, 29,29$. It is easy to see that the condition is not violated, and the sum is 660. We will combine the two smallest piles (both 15), then again the two smallest (both 16), and so on until the piles of
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
40.
$$
\frac{x^{2}}{x^{2}+2 y z}+\frac{y^{2}}{y^{2}+2 z x}+\frac{z^{2}}{z^{2}+2 x y} \geqslant 1
$$
|
40. Since $2 x y \leqslant x^{2}+y^{2}$, we get
$$
\begin{aligned}
\frac{x^{2}}{x^{2}+2 y z}+\frac{y^{2}}{y^{2}+2 z x} & +\frac{z^{2}}{z^{2}+2 x y} \geqslant \\
& \geqslant \frac{x^{2}}{x^{2}+y^{2}+z^{2}}+\frac{y^{2}}{x^{2}+y^{2}+z^{2}}+\frac{z^{2}}{x^{2}+y^{2}+z^{2}}=1
\end{aligned}
$$
|
1
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
41.
$$
\frac{x^{2}+2 y^{2}+2 z^{2}}{x^{2}+y z}+\frac{y^{2}+2 z^{2}+2 x^{2}}{y^{2}+z x}+\frac{z^{2}+2 x^{2}+2 y^{2}}{z^{2}+x y}>6
$$
|
41. Transform the left side using $2 x y \leqslant x^{2}+y^{2}$, multiplying the numerator and denominator by 2:
$$
\begin{aligned}
& \frac{x^{2}+2 y^{2}+2 z^{2}}{x^{2}+y z}+\frac{y^{2}+2 z^{2}+2 x^{2}}{y^{2}+z x}+\frac{z^{2}+2 x^{2}+2 y^{2}}{z^{2}+x y} \geqslant \\
& \geqslant 2\left(\frac{x^{2}+2 y^{2}+2 z^{2}}{2 x^{2}+y^{2}+z^{2}}+\frac{y^{2}+2 z^{2}+2 x^{2}}{2 y^{2}+z^{2}+x^{2}}+\frac{z^{2}+2 x^{2}+2 y^{2}}{2 z^{2}+x^{2}+y^{2}}\right) \geqslant \\
& \quad \geqslant 2\left(\frac{x^{2}+y^{2}+2 z^{2}}{2 x^{2}+y^{2}+z^{2}}+\frac{y^{2}+z^{2}+2 x^{2}}{2 y^{2}+z^{2}+x^{2}}+\frac{z^{2}+x^{2}+2 y^{2}}{2 z^{2}+x^{2}+y^{2}}\right)
\end{aligned}
$$
Now apply the transinequality (for the numerators and the reciprocals of the denominators) to the expression in parentheses:
$$
\begin{aligned}
& 2\left(\frac{x^{2}+y^{2}+2 z^{2}}{2 x^{2}+y^{2}+z^{2}}+\frac{y^{2}+z^{2}+2 x^{2}}{2 y^{2}+z^{2}+x^{2}}+\frac{z^{2}+x^{2}+2 y^{2}}{2 z^{2}+x^{2}+y^{2}}\right) \geqslant \\
& \quad \geqslant 2\left(\frac{y^{2}+z^{2}+2 x^{2}}{2 x^{2}+y^{2}+z^{2}}+\frac{z^{2}+x^{2}+2 y^{2}}{2 y^{2}+z^{2}+x^{2}}+\frac{x^{2}+y^{2}+2 z^{2}}{2 z^{2}+x^{2}+y^{2}}\right)=6
\end{aligned}
$$
|
6
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
65. What is the smallest degree that a polynomial $P$ can have if it is known that there exists an integer $b$ such that $A_{P}$ contains elements both greater and less than $b$, but does not contain $b$?
|
65. Answer: 4.
For example, consider the polynomial $P(x)=(x-3)(x-1)(x+1)(x+3)$. It is even. Therefore, if $c \neq P(0)$, then $l_{P}(c)$ is even. Therefore, in $A$ there can only be one odd number, namely, $l_{P}(P(0))$. Thus, $b=1$ or $b=3$ is the desired number, since $0,4 \in A_{P}$. Why can't the degree be less? Consider, for example, a cubic polynomial $P$. Since its derivative is a quadratic polynomial, it has no more than two roots, and thus $P$ has no more than three intervals of monotonicity, specifically 1 or 3. Let's consider the most complex case immediately - when $P$ has three intervals of monotonicity. Suppose it has a local minimum $m$ and a local maximum $M$. Then for $x \in(-\infty, m) \cup(M,+\infty)$, $l_{P}(x)=1$, $l_{P}(m)=l_{P}(M)=2$, and for $x \in(m, M)$, $l_{P}(x)=3$. The other cases are even simpler to analyze.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
65. What is the smallest degree that a polynomial $P$ can have if it is known that there exists an integer $b$ such that $A_{P}$ contains elements both greater and smaller than $b$, but does not contain $b$?
|
65. Answer: 4.
For example, consider the polynomial $P(x)=(x-3)(x-1)(x+1)(x+3)$. It is even. Therefore, if $c \neq P(0)$, then $l_{P}(c)$ is even. Therefore, in $A$ there can only be one odd number, namely, $l_{P}(P(0))$. Thus, $b=1$ or $b=3$ is the desired number, since $0,4 \in A_{P}$. Why can't the degree be less? Consider, for example, a cubic polynomial $P$. Since its derivative is a quadratic polynomial, it has no more than two roots, and thus $P$ has no more than three intervals of monotonicity, specifically 1 or 3. Let's consider the most complex case immediately - when $P$ has three intervals of monotonicity. Suppose it has a local minimum $m$ and a local maximum $M$. Then for $x \in(-\infty, m) \cup(M,+\infty)$, $l_{P}(x)=1$, $l_{P}(m)=l_{P}(M)=2$, and for $x \in(m, M)$, $l_{P}(x)=3$. The other cases are even simpler to analyze.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The number 2015 was divided into 12 addends, after which all numbers that can be obtained by adding some of these addends (from one to nine) were written down. What is the minimum number of numbers that could have been written down?
|
5.
Answer: 10
Example: Let's break down 2015 into 11 numbers of 155 and one number of 310. In this case, the sum of the addends can range from $155 \times 1$ to $155 \times 10$.
We will prove that it is impossible to get fewer than 10 different numbers: first, note that 2015 is not divisible by 12, so we will have at least 2 different numbers. Arrange all the numbers in ascending order. First, select only the first number, then the first and second, and so on—finally, select the first 9 numbers—this gives us 9 different sums. Now, take the last 9 numbers—the new sum exceeds all previous sums, so there are at least 10 different numbers on the board.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. There are 1000 crows sitting on a wire. At the end of each minute, every third (third, sixth, ninth, and so on) crow flies away.
a) Which crows, by their initial count, will remain on the wire in the end?
b) How many minutes will pass before the crows stop flying away?
|
Solution. a) It is clear that at the end there will be no more than two ravens left, and the first and second never fly away. Therefore, it will be precisely these two. Answer: 1 and 2.
b) It is easy to see that the number of ravens flying away in the next minute is one-third of their number, rounded down. Thus, it only remains to carefully count:
| minute | $\sqrt{1}$ | | 2 | 3 | $\overline{4}$ | 5 | 6 | 7 | 8 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| ravens at the start | 1000 | | 57 | 445 | 297 | 198 | 132 | 88 | 59 |
| will fly away at the end | 333 | | 22 | 128 | 99 | 66 | 44 | 29 | 19 |
| minute | 9 | 10 | 11 | $\overline{12}$ | 13 | 14 | 15 | 16 | 17 |
| ravens at the start | 40 | 27 | 18 | 12 | 8 | 6 | 4 | 3 | 2 |
| will fly away at the end | 13 | 9 | 6 | 4 | 2 | 2 | 1 | 1 | 0 |
We see that the ravens stopped flying away on the 17th minute, thus we get the answer: 16 minutes.
|
16
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Seven natives from several tribes are sitting in a circle by the fire. Each one says to the neighbor on their left: “Among the other five, there are no members of my tribe.” It is known that the natives lie to foreigners and tell the truth to their own. How many tribes are represented around the fire?
|
Solution. If there are at least 4 natives from one tribe, then two of them sit next to each other, and one of them will lie to the other, although they should tell the truth. If there is only one native from a certain tribe, then he tells the truth to his left neighbor, although he should lie. Therefore, each tribe has two or three representatives.
Then, with two tribes, there are no more than $3+3=6$, so there are exactly three tribes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On a 5 by 5 board, a certain number of bishops and knights were placed. Then, they counted how many times each bishop is attacked, and all the obtained numbers were added together. What is the maximum sum that could have been obtained?
#
|
# Solution:
Answer: 80.
The example is constructed through a chessboard coloring - bishops on one color, rooks on the other.
Evaluation: First, place bishops everywhere. The total sum will be 64. Now, in each cell, write the number of points that can be gained by replacing a bishop with a knight. We will get the following table:
| 1 | 1 | 2 | 1 | 1 |
| :--- | :--- | :--- | :--- | :--- |
| 1 | 0 | 2 | 0 | 1 |
| 2 | 2 | 4 | 2 | 2 |
| 1 | 0 | 2 | 0 | 1 |
| 1 | 1 | 2 | 1 | 1 |
Divide this table into 4 smaller tables:
| 1 | 1 | 1 |
| :--- | :--- | :--- |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
In each of these smaller tables, we can definitely get no more than 4 points, as the cells with 1 can be paired by a knight's move. Therefore, we can gain no more than 16 additional points by replacing bishops with knights.
Criteria for determining winners and prize winners of the final stage of the Youth Mathematical School Olympiad, 2015-16.
Each problem is worth 1 point.
For 4th grade:
A winner is a participant who solves 6 problems.
A prize winner is a participant who solves at least 4 problems.
For 5th grade:
A winner is a participant who solves at least 6 problems.
A prize winner is a participant who solves at least 4 problems.
For 6th grade:
A winner is a participant who solves 7 problems.
A prize winner is a participant who solves at least 5 problems.
For 7th grade:
A winner is a participant who solves 7 problems.
A prize winner is a participant who solves at least 5 problems.
For 8th grade:
A winner is a participant who solves 6 problems.
A prize winner is a participant who solves at least 4 problems.
For 9th grade:
A winner is a participant who solves 8 problems.
A prize winner is a participant who solves at least 6 problems.
For 10th grade:
A winner is a participant who solves 9 problems.
A prize winner is a participant who solves at least 5 problems.
For 11th grade:
A winner is a participant who solves 7 problems.
A prize winner is a participant who solves at least 5 problems.
|
80
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.3. Let $N=15$ and only the second operation is allowed. Prove that from any arrangement, less than $10^{4}$ others can be obtained.
|
Solution. We will paint the positions in three colors; the parity of the number of blacks on all positions changes simultaneously. With a fixed set of parities, there are exactly $2^{12}$ arrangements, and with a fixed set up to inversion $-2^{13}<10000$.
|
10000
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. Timur thought of a three-digit number and told it to Anton, who then wrote down three numbers that result from replacing one of the digits of the original number with 1 (for example, if the number 215 was thought of, Anton would write down 115, 215, 211). The sum of all the numbers written down by Anton turned out to be 1243. What number could Timur have thought of? Provide all possible options, and prove that there are no others.
|
Solution: Notice that from the number abc, we get the sum $1 b c + a 1 c + a b 1 = 111 + 2^{\star} a b c$. From the equation $1243 = 111 + 2 * a b c$, it follows that $a b c = 566$.
|
566
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In each cell of a $10 \times 10$ board, there sits a rabbit. Between rabbits in adjacent cells, there are partitions that can be removed. What is the minimum number of partitions that need to be removed so that any rabbit can visit any other rabbit, traveling through no more than 17 cells (not counting the starting and ending cells)?
|
Solution. An example for 100 partitions is given in the figure. The correctness of the example follows from the fact that, as can be easily seen, any rabbit can reach the central 4-cell square by moving no more than 8 cells. From the central square to any cell, it can also be reached in no more than 8 moves. No more than 2 moves are required for movement within the central square. In total, $8+2+8=18$ cells, counting the final one.
We will show that fewer than 100 partitions cannot be removed. Consider
a graph where the vertices are cells and the edges are the missing partitions. Since the graph is connected, it has at least 99 edges, and we only need to show that exactly 99 cannot be. Suppose this is the case. Then the graph is a tree. Let's mentally divide the board into two halves: the upper and the lower. Then there must be a path from A1 to K1 (i.e., from the lower left to the lower right corner) that lies in the lower half - if it rises to the upper half, it will be longer than the required 18 edges. Similarly, the path from A10 to K10 must lie only in the upper half, the path from A1 to A10 only in the left half, and the path from K1 to K10 only in the right half. By combining these paths and shortening the edges traversed in both directions, we will obtain a non-trivial cycle (we go from the lower left quarter to the upper left, then from there to the upper right, then to the lower right, and back), which cannot exist in a tree.
Criteria for determining winners and prizewinners of the final stage of the Youth Mathematical School Olympiad, 2015-16.
Each problem is worth 1 point.
For 4th grade:
A winner is a participant who solves 6 problems.
A prizewinner is a participant who solves at least 4 problems.
For 5th grade:
A winner is a participant who solves at least 6 problems.
A prizewinner is a participant who solves at least 4 problems.
For 6th grade:
A winner is a participant who solves 7 problems.
A prizewinner is a participant who solves at least 5 problems.
For 7th grade:
A winner is a participant who solves 7 problems.
A prizewinner is a participant who solves at least 5 problems.
For 8th grade:
A winner is a participant who solves 6 problems.
A prizewinner is a participant who solves at least 4 problems.
For 9th grade:
A winner is a participant who solves 8 problems.
A prizewinner is a participant who solves at least 6 problems.
For 10th grade:
A winner is a participant who solves 9 problems.
A prizewinner is a participant who solves at least 5 problems.
For 11th grade:
A winner is a participant who solves 7 problems.
A prizewinner is a participant who solves at least 5 problems.
|
100
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In the company, several employees have a total monthly salary of 10000 dollars. A kind manager proposes to triple the salary for everyone earning up to 500 dollars, and increase the salary by 1000 dollars for the rest, so the total salary will become 24000 dollars. A mean manager proposes to reduce the salary to 500 dollars for everyone earning more than 500 dollars, and leave the rest as is. What will the total salary be in this case?
|
Solution. Note that the increase proposed by the kind manager is twice as large as the salary proposed by the evil manager (this is true for both poor and rich employees). The increase according to the kind manager's proposal is 14000, so the salary according to the evil manager's proposal is 7000.
|
7000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. There are 30 people in the bar. The bartender knows that among them, there are 10 knights (who always tell the truth), 10 liars (who always lie), and 10 troublemakers. The bartender can ask person $X$ about person $Y$: "Is it true that $Y$ is a troublemaker?" If $X$ is not a troublemaker, they will answer the question, but if $X$ is a troublemaker, they will throw $Y$ out of the bar in response. The bartender can kick out anyone they want, but their goal is to get rid of the troublemakers and leave as many peaceful customers in the bar as possible. How should he proceed? Don't forget to prove that he cannot leave more peaceful customers.
## SOLUTION:
## TRANSLATION:
6. There are 30 people in the bar. The bartender knows that among them, there are 10 knights (who always tell the truth), 10 liars (who always lie), and 10 troublemakers. The bartender can ask person $X$ about person $Y$: "Is it true that $Y$ is a troublemaker?" If $X$ is not a troublemaker, they will answer the question, but if $X$ is a troublemaker, they will throw $Y$ out of the bar in response. The bartender can kick out anyone they want, but their goal is to get rid of the troublemakers and leave as many peaceful customers in the bar as possible. How should he proceed? Don't forget to prove that he cannot leave more peaceful customers.
## SOLUTION:
|
Answer: 19. Indeed, with the first question, a peaceful client may be identified, so the bartender cannot guarantee to keep all peaceful clients.
Let's show how the bartender can leave 19 peaceful clients.
Solution 1. First, he asks everyone about client $A$ until someone throws him out of the bar. Let's say $B$ threw him out (thus, $B$ is a troublemaker). Now we start asking about $B$ until $B$ is thrown out, and so on. In the end, we will have a situation where a troublemaker $X$ is not thrown out by anyone. This means there are no more troublemakers (except for $X$). The bartender then throws out $X$, and everyone becomes calm. Note that all those thrown out, except the first one, were definitely troublemakers.
Solution 2. First, we ask client $B$ about $A$, then we ask $C$ about $B$. With the first question, we get information on whether $B$ is a troublemaker, and with the second question, we learn whether $C$ is a knight, a liar, or a troublemaker. If $C$ is not a troublemaker, we will ask $C$ about all the clients and find out who the troublemakers are (if $C$ is a liar, then his answers should be interpreted in reverse). These are the ones to be thrown out.
If $C$ is a troublemaker, we ask $D$ about $C$. Either $D$ will answer, or $D$ is also a troublemaker (then we will ask about $D$, and so on). When we get any answer, we act as in the previous case.
|
19
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In a $100 \times 100$ square, 10000 cuts were made along the grid lines (each cut one cell long), and it split into 2500 four-cell figures. How many of them are $2 \times 2$ squares?
|
Solution:
Answer: 2300.
Solution. Note that the perimeter of a $2 \times 2$ square is 8, while for the other four-cell figures (rectangle $1 \times 4$, T-shape, L-shape, or S-shape) it is 10. Let the number of squares be $x$, and the number of other figures be $2500-x$. Then their total perimeter is $8 x + 10 \cdot (2500 - x) = 25000 - 2 x$. On the other hand, this is the perimeter of the square plus twice the length of the cut, i.e., 20400 cells. Therefore, $2 x = 25000 - 20400 = 4600$, and as a result, $x = 2300$.
|
2300
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Milla was writing the letters M and L in uppercase. At the end, she counted that the letter matched the previous one 59 times, and did not match 40 times. Determine the maximum number of letters M that Milla could have written, and prove that it is indeed the maximum.
|
Solution. Answer: 80 letters.
For each letter except the first, it is known whether it matches the previous letter or not. Therefore, Milla wrote $1+59+40=100$ letters.
Divide all the written letters into groups of consecutive identical letters. Then, groups of M (M-groups) will alternate with groups of L (L-groups). At the beginning of each group, except the first group, there is a letter that does not match the previous letter. All other letters in the groups match the previous letter. Therefore, there are a total of $1+40=41$ groups.
If the first letter is $M$, then there will be 21 M-groups and 20 L-groups. If the first letter is L, then
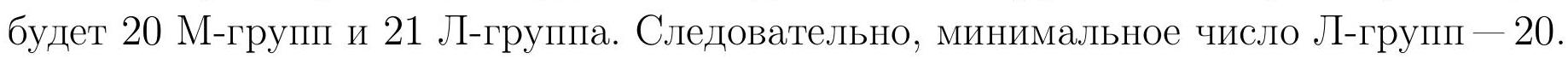
The minimum number of letters in one group is one. Therefore, Milla wrote at least $20 \times 1=20$ letters L. Thus, the number of letters M cannot be more than $100-20=80$.
It remains to show that Milla could indeed write 80 letters M. This is not difficult: first, write 60 letters M, and then 20 pairs LM.
|
80
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There are 20 chocolate candies on the table. Masha and Bear are playing a game according to the following rules. Players take turns. In one move, a player can take one or several candies from the table and eat them. Masha goes first, but on this move, she cannot take all the candies. In all other moves, players cannot take more candies than anyone has already taken in one move. The player who takes the last candy wins. For this, he will get a whole cake! Who among the players can ensure their victory?
|
Solution. Masha will win if she eats 4 candies on her first move.
Let's arrange the candies in a row, number them, and assume that the players take candies in a row from left to right.
Suppose Masha eats one candy on her first move. In this case, she will lose, as until the end of the game, the players will take one candy each, and all even-numbered candies, including the last 20th candy, will go to the Bear.
Suppose Masha eats two candies on her first move. Then the Bear will take two candies until Masha takes one candy. If Masha never takes one candy, the Bear will take candies 3, 4, 7, 8, 11, 12, 15, 16, 19, 20 and win. If Masha takes one candy, its number will be odd. Then the players will take one candy each in turn, and the Bear will get candies with even numbers. Masha will lose again.
Suppose Masha eats three candies on her first move. Then the Bear will take one candy on his first move, and with the remaining moves, he will again eat all the remaining even-numbered candies, and Masha will lose.
Suppose Masha eats 4 candies on her first move. Then Masha will act as follows: if the Bear eats 4 candies, Masha will also eat 4; if the Bear eats 3 candies, Masha will eat one; if the Bear eats 2 candies, Masha will also eat 2; if the Bear eats one candy, Masha will also eat one. If the Bear always takes 4 candies, Masha will eat candies 1, 2, 3, 4, 9, 10, 11, 12, 17, 18, 19, 20 and win. After the Bear eats three or one candy, an odd number of candies will remain on the table, and all the remaining candies with even numbers will go to Masha. Masha will win again. After the Bear eats two candies, 20 - 4 - 2 = 14 or 20 - 4 - 4 - 4 - 2 = 6 candies will remain on the table. Then the players will eat two candies each (the case with one candy we have already discussed), and Masha will get the 19th and 20th candies. Therefore, in this game, Masha will win if she eats 4 candies on her first move.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Petya thought of a 9-digit number obtained by rearranging the digits of the number 123456789. Vitya is trying to guess it. For this, he chooses any 9-digit number (possibly with repeated digits and zeros) and tells it to Petya, who then responds with how many digits of this number match the ones in his thought number. Can Vitya find out the first digit of Petya's number in no more than 4 moves? (A match is a digit standing in the same place.)
|
Solution. Vitya's first move is to name the number 122222 222. Then Petya can only respond with 0, 1, or 2.
If Petya answers 0, then neither the one nor the two hit their places. This means the two must be in the first position. There's no need to ask further.
If Petya answers 2, then both the one and the two hit their places. This means the one is in the first position. There's no need to ask further.
If Petya answers 1, then neither the one nor the two can be in the first position. In this case, Vitya will name the next number 344444444. After Petya's response, Vitya will either learn the first digit of Petya's number or understand that it is neither a three nor a four. Next, Vitya will name the numbers 566666666 and 788888888 until he learns the first digit. If Petya also answers 1 to the number 788888888, then the first digit of his number will be the only remaining unchecked digit - 9.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.4. Prove that Shakti will always be able to find a strange sociable set of no more than 82 troglodytes.
#
|
# Solution.
Consider a communicative set $A$ of the smallest size. Note that we can choose $A$ such that for each troglodyte $a$ in $A$, there exists a troglodyte $v_{a}$ whose only friend in the set $A$ is the troglodyte $a$. Indeed, otherwise, if $a$ is friends with someone in $A$, it can simply be removed, and if it is not friends with anyone in $A$, it can be replaced with any of its friends.
By the Pigeonhole Principle, some troglodyte $u \in A$ is acquainted with at least $(100-|A|) /|A|$ troglodytes not in $A$.
Let $B$ be the set of maximum size containing $u$ such that no one in it is friends. Note that $B$ is a strange communicative set, let's estimate its size. Note that $B$ does not contain friends of $u$, and also no more than one troglodyte from each pair $a, v_{a}$, where $a \in A \backslash\{u\}$.
Since the friends of $u$ not in $A$, by construction, do not belong to the pairs $\left(a, v_{a}\right)$ and there are at least $(100-|A|) /|A|$, we get
$$
|B| \leqslant 100-\frac{100-|A|}{|A|}-(|A|-1)=102-\frac{100}{|A|}-|A| \leqslant 82
$$
which is what we needed.
## Plot 2.
There is a square with side 2. Vasya colored a finite number of polygons in it such that there were no colored points at a distance of 1 (the boundary is considered uncolored). Let $A-$ be the colored set, $S(A)$ - its area.
|
82
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
4. The number 100 is represented as the sum of several two-digit numbers, and in each addend, the digits are swapped. What is the largest number that could result from the new sum?
|
Solution. If the digits in the two-digit number $\overline{b a}$ are swapped, the number increases by $9(a-b)$. Therefore, the new sum is $S=100+9 U-9 D$, where $D$ is the sum of the tens digits, and $U$ is the sum of the units digits in the original addends. Since $10 D+U=100$, then $S=1000-99 D$. Thus, we need to minimize $D$ - the sum of the tens digits. It can be 6, for example, $100=19 \cdot 4+24$, but not less. Suppose $D<6$, then there are no more than 5 numbers. Thus, $U$ is no more than $5 \cdot 9=45$, and the sum of the numbers before swapping the digits does not exceed $10 \cdot 5+45=95<100$. Contradiction. Therefore, the minimum possible $D$ is 6, and the maximum sum is $1000-99 \cdot 6=406$.
|
406
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Given a string of 2021 letters A and B. Consider the longest palindromic substring. What is its minimum possible length? A palindrome is a string that reads the same from right to left and from left to right.
|
Solution. The minimum possible length of the maximum palindrome is 4.
We will prove that it cannot be less than 4. Consider the 5 letters in the center of the string. If these are alternating letters, then it is a palindrome of length 5. Suppose among these five letters there are two identical letters standing next to each other. Take the maximal contiguous block of identical letters. It is at least 2 in length, and adding one opposite letter on each side, we get 4 (if there are no other letters on the sides, then we have reached the end of the string and there are many identical letters in a row, since we started from the center of the string).
Let's provide an example of a string where the maximum palindrome has a length of 4. This is a string where the sequence ABABAB repeats periodically: ABABABABABABABABABAB.... By checking all possible positions of the centers of palindromes, one can verify that there are no palindromes longer than 4 in this string. Due to the periodicity of the string, only a small number of cases need to be checked.
Comments. The specified example is unique up to shift and reflection.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the bus route, there are only four stops - "Initial", "First", "Final", and "Last". At the first two stops, passengers only got on, and at the remaining stops, they only got off. It turned out that 30 passengers got on at the "Initial" stop, and 14 passengers got off at the "Last" stop. At the "First" stop, three times fewer passengers got on than got off at the "Final" stop. Which passengers are more - those traveling from "Initial" to "Last", or those traveling from "First" to "Final", and by how many?
Solution:
|
Answer: Those traveling from "First" to "Final" are six more.
Let $x$ be the number of people who got on at "First". Then, $3x$ people got off at "Final". Since the number of people getting on equals the number of people getting off, we have $30 + x = 3x + 14$, from which $x = 8$. Let $y$ be the number of people traveling from "Initial" to "Final". Then, the number of people traveling from "Initial" to "Final" is $8 - y$. Together with those traveling from "First" to "Final", they make up 14 people. Therefore, the number of people traveling from "First" to "Final" is $14 - 8 + y = 6 + y$. That is, six more people are traveling from "First" to "Final" than from "Initial" to "Final".
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Baron Munchausen placed a horse in some cells of an $N \times N$ board. He claims that no one will find two different $4 \times 4$ squares on this board (with sides along the grid lines) with the same number of horses. For what largest $N$ can his words be true?
#
|
# Solution:
Answer: $N=7$.
The number of knights in a $4 \times 4$ square can range from 0 to 16, i.e., there are 17 possible variants. The number of $4 \times 4$ squares on an $N \times N$ board is $(N-3)^{2}$ (since the top-left cell of the square can occupy positions from the far left to the fourth from the right horizontally, and the same vertically). To avoid repetitions, the number of squares must be no more than 17, i.e., $(N-3)^{2} \leqslant 17$. Therefore, $N$ cannot be greater than seven, since then $(N-3)^{2} \geqslant(8-3)^{2}=25>17$.
For $N=7$, an example can be constructed as shown on the right (knights are placed in the shaded cells, and the number of knights in each square is indicated in the top-left cell of each $4 \times 4$ square).
| 16 | 15 | 14 | 13 | | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 12 | 11 | 10 | 9 | | | |
| 8 | 7 | 6 | 5 | | | |
| 4 | 3 | 2 | 1 | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Pompous Vova has an iPhone XXX, and on that iPhone there is a voice-command calculator: "Multiply my number by two and subtract two from the result," "Be so kind as to multiply my number by three and then add four," and finally, "Add seven to my number!" The iPhone knows that Vova initially had the number 1. How many four-digit numbers could the iPhone XXX theoretically obtain by obediently following Vova's commands?
## Solution:
|
Answer: 9000 (or 18000, if negative numbers are considered).
We will prove that we can obtain all four-digit numbers. Note that the command +7 allows us to obtain from the current number all larger numbers with the same remainder when divided by seven. Therefore, it is sufficient to use the first two buttons to obtain a representative of each of the seven remainders $(0,1, \ldots, 6)$.
Initially, we have 1. From 1, we can obtain the number $7 (3 \cdot 1 + 4 = 7)$ - a representative of the remainder 0. From the number 7, we can obtain representatives of the remainder $5 (2 \cdot 7 - 2 = 12)$ and the remainder $4 (3 \cdot 7 + 4 = 25)$. From the number 25, we can obtain a representative of the remainder $6 (2 \cdot 25 - 2 = 48)$ and the remainder $2 (3 \cdot 25 + 4 = 79)$. From the number 79, we can obtain a representative of the remainder $3 (3 \cdot 79 + 4 = 241)$. Thus, we have obtained representatives of all remainders, from which we can obtain all four-digit numbers using the +7 button. And there are 9000 four-digit numbers in total.
Remark. In the problem, natural four-digit numbers were implied. However, a similar solution works for negative numbers, except that we need to obtain a multi-digit negative number with a remainder of 1 when divided by 7 using repeated application of the operation $2 \cdot x - 2$ (the remainders alternate $1-0-5-1$).
|
9000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Winnie-the-Pooh decided to give Eeyore a pot of honey. On the way to Eeyore, he tried the honey from the pot several times. When he tried the honey for the first time, the pot became half as heavy. And after the second time, the pot became half as heavy again. And after the third! And after the fourth! Indeed, after the fourth time, there was no honey left. How much honey did Winnie-the-Pooh eat if the pot without honey weighs 200 grams?
|
Solution. $\quad$ Answer: 3000 g. Indeed, $3000=(((200 \cdot 2) \cdot 2) \cdot 2) \cdot 2)-200$.
|
3000
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Petya has several 5-ruble coins and several 2-ruble coins. Vanya has as many 5-ruble coins as Petya has 2-ruble coins, and as many 2-ruble coins as Petya has 5-ruble coins. Petya has 60 rubles more than Vanya. Which coins does Petya have more of - 5-ruble or 2-ruble? By how many?
|
Solution. Answer: Petya has 20 more 5-ruble coins.
Suppose Petya has more 2-ruble coins than 5-ruble coins. Let Petya remove one 2-ruble coin, and Vanya remove one 5-ruble coin. Then the difference in the sums of Petya's and Vanya's coins will increase by 3. If they repeat this operation until Petya has an equal number of 5-ruble and 2-ruble coins, the sums of Petya's and Vanya's coins should become equal (since the composition of the coins will be the same), but their difference will be no less than 60. This is a contradiction. Therefore, Petya has more 5-ruble coins.
Let Petya then remove one 5-ruble coin, and Vanya remove one 2-ruble coin. Then the difference in the sums of Petya's and Vanya's coins will decrease by 3. If they repeat this operation until Petya has an equal number of 5-ruble and 2-ruble coins, the sums of Petya's and Vanya's coins will become equal (since the composition of the coins will be the same). This means they performed this operation $60: 3=20$ times. Therefore, initially, Petya had 20 more 5-ruble coins than 2-ruble coins.
If briefly,
$$
60=5 n+2 k-(5 k+2 n)=3(n-k)
$$
Therefore, $n-k=60: 3=20$.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The Elector George has 100 coins, some of which are counterfeit (possibly all or none). George can show the expert from 10 to 20 coins, and the expert will tell him how many of them are counterfeit. The problem is that the only expert in the entire region is Baron Münchhausen, and he exaggerates: the result given by the baron is always greater than the true number by some fixed (and unknown to George) natural number. The baron is not bothered by the fact that he might say "thirteen," for example, if he was given only twelve coins. Can George reliably determine which coins are counterfeit by consulting the expert fewer than 120 times?
|
Solution. It will work. We will submit $X$ random coins for expertise, and then the same $X$ plus 1 more. If the baron says the same number both times, the added coin is genuine; otherwise, it is counterfeit. This way, we can divide the coins into groups of 10, and check each group for counterfeits in 11 queries: first, submit 10 other coins, and then add one coin from the group being checked. The total number of queries will be $11 \cdot 10 = 110 < 120$.
## Criteria.
Full solution - 7 points.
Solutions where only one coin is submitted for each query - 0 points.
Identifying the number by which the baron lies - 0 points.
|
110
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. There are several cards. On each of them, on each of the two sides, a circle is drawn: red, blue, or yellow. Among any 30 cards, there is a card with a red circle, among any 40 cards, there is a yellow circle, and among any 50, there is a blue one. In total, there are 20 cards with circles of different colors. Prove that there are no more than 48 monochromatic cards.
#
|
# Solution:
There are no more than 29 cards without red circles, no more than 39 cards without yellow, and no more than 49 cards without blue. Adding all these numbers, we get no more than 117. In this process, single-colored cards have been counted twice, and two-colored cards have been counted once. Therefore, the doubled number of single-colored cards is no more than 97, i.e., the number of single-colored cards is no more than 48.
|
48
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
7. Kopyatych took some natural number, raised it to the 1st, 2nd, 3rd, 4th, and 5th powers. Then he encrypted the numbers by replacing the same digits with the same letters and different digits with different letters. He wrote each encrypted number on a separate piece of paper. But Nyusha left only a fragment of each piece of paper, preserving only the last two letters, and even those were mixed up. The result was: OK, SY, YZ, SH, LI. Find the value of the expression
$$
\text { Yo } \cdot Z \cdot I \cdot \mathrm{K}-L \cdot O \cdot \mathrm{C} \cdot \text { Y. Sh. }
$$
|
# Solution:
It is clear that the letters К, Ё, Ж, И are of the same parity, and among them there are no 0 or 5.
If К, Ё, Ж, И are even, then all powers except the first one must be divisible by 4, and then О, Ш are also even digits, which is not good.
The last digit of the number in the first and fifth power is the same, so ШИ are the last two digits of the first and fifth power of the number. But then the fourth power of this number ends in 01.
Then, up to the permutation of the factors,
$$
\text { Ё } \cdot \text { K } \cdot \text { И } \cdot \mathrm{K}-Л \cdot \mathrm{O} \cdot \mathrm{C} \cdot \text { Я } \cdot \amalg=1 \cdot 3 \cdot 7 \cdot 9-0 \cdot 2 \cdot 4 \cdot 6 \cdot 8=189 .
$$
Remark. There are examples in this problem, and not just one. There are $07,49,43,01,07$ and $43,49,07,01$, 43. It is important that we cannot determine which letter is Ш and which is О.
|
189
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. We remind you that the sum of the angles in a triangle equals 180 degrees. In triangle $A B C$, angle $A$ is a right angle. Let $B M$ be the median of the triangle, and $D$ be the midpoint of $B M$. It turns out that $\angle A B D = \angle A C D$. What are these angles?
|
# Solution.
Draw $A D$. Since triangle $A B M$ is a right triangle, its median $A D$ equals half the hypotenuse $B M$. Therefore, $\angle A B D = \angle B A D = \alpha$, and $\angle A D M$ equals $2 \alpha$, as the exterior angle of triangle $A B D$. However, since $D M = A D$, $\angle D A M = \angle D M A = 90^{\circ} - \alpha$. This means triangle $A D C$ is a right triangle, because $\angle A C D + \angle D A C = 90^{\circ}$. Since $D M$ is the median of the right triangle $A D C$, it equals half the hypotenuse. We previously established that it also equals one of the legs of this triangle $(A D)$. Therefore, $\angle A C D$, which lies opposite this leg, equals 30 degrees.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the Magic and Wizardry club, all first and second-year students wear red robes, third-year students wear blue, and fourth-year students wear black.
Last year, at the general assembly of students, there were 15 red, 7 blue, and several black robes, while this year - blue and black robes are equal in number, and red robes are twice as many as blue ones.
(a) How many black robes will there be at the general assembly next year? (1 point)
(b) How many first-year students are there this year? (3 points)
(c) In what minimum number of years will the number of blue and black robes be equal again? (6 points)
(d) Suppose it is additionally known that each year the number of first-year students is 1 less than the number of fourth-year students. In how many years will the number of red robes first be three times the number of blue ones? (10 points)
|
# Solution.
(a) 7 mantles. Since 7 blue mantles from last year will turn black this year and there are an equal number of blue and black mantles this year, there will also be 7 blue mantles this year, which will turn black next year.
(b) 6 students. This year, there are 7 blue, 7 black, and $14=2 \times 7$ red mantles. Therefore, last year there were $8=15-7$ first-year students who will become second-year students this year. Thus, this year there are $14-8=6$ first-year students.
(c) In three years. Last year, 8 new students joined the club, and this year 6 did. If 6 new students join next year, then in three years there will be 6 blue and 6 black mantles:
$$
(6,8,7,7) \rightarrow(6,6,8,7) \rightarrow(?, 6,6,8) \rightarrow(?, ?, 6,6)
$$
If a different number of new students join next year, the number of blue and black mantles will differ for the next three years. Therefore, the smallest number of years after which the number of blue and black mantles can be equal is three.
(d) In 17 years. The composition of students for the next year is uniquely determined by the composition of students for the current year: $(a, b, c, d) \rightarrow(c-1, a, b, c)$. If we sequentially list the composition of students for each year:
$$
(6,8,7,7) \rightarrow(6,6,8,7) \rightarrow(7,6,6,8) \rightarrow(5,7,6,6) \rightarrow \ldots
$$
then in 17 years, we will first obtain a composition of students that satisfies the condition. This will be the composition $(2,1,1,3)$, in which $2+1=3$ red mantles and one blue mantle.
|
17
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Each of five friends multiplied several consecutive numbers starting from 1. It turned out that one of the products is equal to the sum of the other four. Find all possible values of this product and show that there are no other values.
|
Solution. The product of all consecutive numbers from 1 to $x$ is called the factorial of the number $x$ and is denoted by $x!$. Thus, we need to solve the equation $x!=a!+b!+c!+d!$. Let the numbers $a, b, c, d$ be ordered in ascending order. Then $x>d$, i.e., $x! \geqslant x \cdot d!$. But we know that $x! \leqslant 4 d!$, because $a! \leqslant d!, b! \leqslant d!$, and $c! \leqslant d!$. Therefore, $x \leqslant 4$.
If $x=4$, then the values $a=b=c=d=3$ fit (and this is the only solution).
If $x=3$, then the only option is $3!=1!+1!+2!+2!$. This option does not fit because each multiplied several (i.e., more than one) numbers.
Clearly, $x \leqslant 2$ cannot be.
Thus, the only answer is 24.
Criteria. Full solution - 5 points.
2 points - proof of the estimate $x \leqslant 4$;
1 point - consideration of the case $x=4$;
1 point - consideration of the case $x=3$;
1 point - consideration of the case $x=1,2$;
The above points are cumulative.
1 point - Correct answer without any solution.
|
24
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
6. In a $4 \times 4$ square, cells are colored in several colors such that in any $1 \times 3$ rectangle, there are two cells of the same color. What is the maximum number of colors that can be used?
|
Solution. Maximum 9 colors. See example in the picture. We will prove that more is not possible. Any row (row or column) gives a maximum of three colors, so the first row + first column will give a maximum of $3+3-1=5$ colors.
We will prove that the remaining $3 \times 3$ square will give a maximum of 4 colors. Indeed, suppose we used 5 colors in it. Since in one row there are no more than two different colors, there will be two rows in which 4 different colors are used, 2 colors in each row. Then in the remaining row, there will be at least one cell of the fifth color. In the column containing this cell, all cells will be of different colors. Contradiction.
Thus, on the entire board, there are no more than $4+5=9$ different colors.
Criteria. Full solution (there is an estimate and there is an example) - 7 points.
Of these:
There is an example for 9 colors - 2 points.
Full proof of the estimate - 5 points, of which: 2 points for one row + one column and 3 points for the proof that the $3 \times 3$ square will give a maximum of 4 colors.

|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Captain Billy the pirate plundered 1010 gold doubloons and set sail on his ship to a deserted island to bury them as treasure. Every evening of the voyage, he paid each of his pirates one doubloon. On the eighth day of the voyage, the pirates plundered a Spanish caravel, and Billy's treasure doubled, while the number of pirates was halved. On the 48th day of the voyage, the pirates arrived at the deserted island, and Billy buried all his treasure in a spot marked with a cross - exactly 1000 doubloons. How many pirates set out with Billy to the deserted island?
|
Solution. Answer: 30
Before the pirates looted the caravel, Billy managed to pay the pirates their daily wages 7 times. After this, his fortune doubled. This is equivalent to Billy having 2020 doubloons before the voyage, and he paid the wages 14 times. After this, Billy paid the wages 40 times to half of the remaining pirates. This is equivalent to him paying the wages 20 times to all the pirates. In total, Billy paid the full wages 34 times during the voyage. Therefore, initially, there were $(2020-1000) / 34 = 30$ pirates.
If briefly, $1000 = (1010 - 7n) \cdot 2 - 40 \cdot \frac{n}{2}$.
|
30
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The length of the escalator is 200 steps. When Petya walks down the escalator, he manages to count 50 steps. How many steps will he count if he runs twice as fast?
|
Solution. 80 steps. Let's call the step of the escalator from which Petya begins his descent the first step. When Petya walks down, he passes 50 steps. During this time, the first step manages to descend $200-50=150$ steps. Therefore, the escalator moves three times faster than Petya walks. When Petya runs, the speed ratio will be $3:2$ in favor of the escalator. Thus, Petya will count $200 \cdot 2:(3+2)=80$ steps.
|
80
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In the company, there are elves, fairies, and gnomes. Each elf is friends with all fairies except for three, and each fairy is friends with twice as many elves. Each elf is friends with exactly three gnomes, and each fairy is friends with all gnomes. Each gnome is friends with exactly half of the elves and fairies combined. How many gnomes are there in the company?
|
Solution. Answer: 12.
Let $n$ be the number of elves, $m$ be the number of fairies, and $k$ be the number of gnomes. Then the number of friendly pairs "elf-fairy" is $n(m-3)$, and "fairy-elf" is $-m \cdot 2(m-3)$. But these are the same pairs, therefore,
$$
n(m-3)=2 m(m-3)
$$
From which, $n=2 m$. Counting the friendly pairs with gnomes, we arrive at the equation
$$
k \cdot \frac{n+m}{2}=3 n+m k
$$
Substituting $n=2 m$, we get
$$
k \cdot \frac{3}{2} m=6 m+m k
$$
Dividing by $m$, we get $k=12$.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A number is written on the board. In one move, you can either increase or decrease any of its digits by three (if it results in a digit), or swap two adjacent digits. Show how to transform the number 123456 into 654321 in 11 moves.
|
Solution. In the first 5 moves, we move 6 to the beginning: 612345. Then we swap 1 and 2, 4 and 5, getting 621354. Now we increase 2 and 1 by three, and decrease 5 and 4 by three - resulting in 654321.
|
654321
|
Logic and Puzzles
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. A group of toddlers in a kindergarten has 90 teeth in total. Any two toddlers together do not have more than 9 teeth. What is the minimum number of toddlers that can be in the group?
|
Solution. If all children have fewer than 5 teeth, then there are no fewer than $90 / 4$, i.e., no fewer than 23 children.
If one child has exactly 5 teeth, then the others have no more than 4, and there are no fewer than $1+85 / 4$, i.e., also no fewer than 23 children.
If any of the children have between 6 and 9 teeth, then the others have no more than three, and there are more than $81 / 3=27$ children.
Thus, in any case, there are no fewer than 23 children.
Examples with 23 exist (for example, 5+1+21$\cdot$4 or 2+22$\cdot$4).
|
23
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. A chessboard $(8 \times 8)$ was cut into several equal parts in such a way that all white cells remained uncut, while each black cell was cut. How many parts could have been obtained?
|
Solution. Note that there are 32 white cells, and each part contains an integer number of white cells, so the answer must be a divisor of 32.
Obviously, it cannot be 1. The answers $2, 4, 8, 16$, and 32 are possible. To achieve them,
we need to cut the board into rectangles $8 \times 8, 8 \times 4, 8 \times 2, 4 \times 2, 2 \times 2$, and then divide each of them into two equal parts. Constructions for two rectangles are shown in the figure; the others are similar.
Criteria for determining winners and prizewinners of the final stage of the Youth Mathematical School Olympiad, 2015-16.
Each problem is worth 1 point.
For 4th grade:
A winner is a participant who solved 6 problems.
A prizewinner is a participant who solved at least 4 problems.
For 5th grade:
A winner is a participant who solved at least 6 problems.
A prizewinner is a participant who solved at least 4 problems.
For 6th grade:
A winner is a participant who solved 7 problems.
A prizewinner is a participant who solved at least 5 problems.
For 7th grade:
A winner is a participant who solved 7 problems.
A prizewinner is a participant who solved at least 5 problems.
For 8th grade:
A winner is a participant who solved 6 problems.
A prizewinner is a participant who solved at least 4 problems.
For 9th grade:
A winner is a participant who solved 8 problems.
A prizewinner is a participant who solved at least 6 problems.
For 10th grade:
A winner is a participant who solved 9 problems.
A prizewinner is a participant who solved at least 5 problems.
For 11th grade:
A winner is a participant who solved 7 problems.
A prizewinner is a participant who solved at least 5 problems.
|
32
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. 99 people - knights and liars (knights always tell the truth, while liars always lie) - are standing in a row. Each of them said one of two phrases: "To the left of me, there are twice as many knights as liars" or "To the left of me, there are as many knights as liars." In reality, there were more knights than liars, and more than 50 people said the first phrase. How many liars said the first phrase?
|
Answer: 49.
Solution:
There are more knights than half, so:
1) Either they alternate like this: KRK...LK, but this option does not work: the phrase "there are twice as many knights as liars" cannot be said by any knight, but there are more than 50 such phrases.
2) Or some two knights stand next to each other. Two knights standing next to each other cannot both say the same phrases, and they can say different phrases only in one case: the third says that there are as many knights as liars before him, and the fourth says that there are twice as many knights as liars before him (this can be derived from simple equations). There are no other places where knights stand next to each other, so to have at least 50 knights, the picture can only be like this: KLRKRL...LK. All knights, except the first and the fourth from the left, definitely say that there are as many knights as liars to their left, as they cannot say anything else. There are 48 of them. To have more than 50 opposite phrases, all the remaining ones must say exactly these. Therefore, all liars, who are a total of 49, say the first phrase.
|
49
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Today's date is written as: 22.11.2015. How many other days in this year can be written with the same set of digits?
|
Solution. The month number cannot start with a two, so it is either 11 or 12. In the first case, it is 22.11, in the second case 12.12 and 21.12. Answer: two.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A group of toddlers in a kindergarten has 90 teeth in total. Any two toddlers together do not have more than 9 teeth. What is the minimum number of toddlers that can be in the group
|
Solution. If all children have fewer than 5 teeth, then there are no fewer than $90 / 4$, i.e., no fewer than 23 children.
If one child has exactly 5 teeth, then the others have no more than 4, and there are no fewer than $1 + 85 / 4$, i.e., also no fewer than 23 children.
If any of the children have between 6 and 9 teeth, then the others have no more than three, and there are more than $81 / 3 = 27$ children.
Thus, in any case, there are no fewer than 23 children.
Examples with 23 children exist (for example, $5 + 1 + 21 \cdot 4$ or $2 + 22 \cdot 4$).
## Grade 4. Target Audience
## Solutions
|
23
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.4. Let initially each island is inhabited by one colony, and let one of the islands have $d$ neighboring islands. What can the maximum possible number of colonies that can settle on this island be equal to?
|
Solution. Answer: $d+1$.
Example. We will prove that in a vertex of degree $d$, $d+1$ colonies can gather. Suspend the tree from this vertex as the root and prove that in each vertex from which $e$ edges go down, $e+1$ colonies can gather, conducting only migrations within its subtree. We will prove this by "induction from the lower vertices to the upper ones." For leaves, the statement is obvious (they already have one colony), and for any other vertex, it is sufficient to gather the required number of colonies in its immediate children, after which perform one migration for each of them.
Estimate. We will show that any available distribution of numbers on the tree can be obtained by organizing migrations so that each colony does not move further than to a neighboring island. From this, it will follow that the answer is no more than $d+1$.
We prove this by induction on the number of migrations. Base case - zero migrations, is obvious.
Inductive step. Suppose a migration is about to occur from island $v$. By the inductive hypothesis, all colonies on it are from it and neighboring islands. Since a migration is possible, by the inductive hypothesis, there are colonies on the island from at least $\operatorname{deg} v-1$ neighboring islands; we will send them back to their islands. If there is a colony from the remaining neighboring island, we will also send it back, and if there is a colony from the island itself, we will send it to any of the neighboring islands.
## Plot 2.
Two circles inscribed in an angle with vertex $R$ intersect at points $A$ and $B$. A line through $A$ intersects the smaller circle at point $C$ and the larger circle at point $D$. It turns out that $A B=A C=A D$.
|
+1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. From head to tail of the zebra Hippotigris - 360 stripes of the same width. Flea Masha and flea Dasha started crawling from the head of the zebra to its tail. At the same time, flea Sasha started crawling from the tail to the head. Flea Dasha crawls twice as fast as flea Masha. Before meeting flea Sasha, Masha overcame exactly 180 stripes. How many stripes will flea Dasha overcome before she meets flea Sasha?
|
Solution: 240 stripes.
Mashka crawled half of the zebra. Let her speed be $v$, then the closing speed of Mashka and Sashka is $2v$, and the closing speed of Dashka and Sashka is $3v$. Therefore, Sashka will crawl $3/2$ times fewer stripes before meeting Dashka than before meeting Mashka, i.e., 120 stripes. The remaining 240 stripes will be crawled by Dashka.
|
240
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a row, 100 knights and 100 liars are standing (in some order). The first person was asked: "Are you a knight?", and the rest were asked in turn: "Is it true that the previous person answered 'Yes'?" What is the maximum number of people who could have said "Yes"? Knights always tell the truth, liars always lie.
|
Solution. 150, for example, if there are 100 knights followed by 100 liars. We will now prove that this is the maximum.
Consider any liar, except possibly the first one. Either they said "no," or the previous person said "no." Thus, to each of the 99 liars, we can associate at least one "no" response (either theirs or the previous person's), and each "no" response is associated with no more than two liars. Therefore, there are at least 50 "no" responses.
|
150
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The gnomes went to work, and Snow White is feeling lonely. She laid out a pile of 36 stones on the table. Every minute, Snow White splits one of the existing piles into two, and then adds a new stone to one of them. After some time, she had seven piles, each with an equal number of stones. How many stones ended up in each pile?
|
Solution. There will be seven piles after six moves. After six moves, there will be $36+6=42$ stones - meaning, 6 stones in each pile.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a certain city, the fare scheme for traveling by metro with a card is as follows: the first trip costs 50 rubles, and each subsequent trip costs either the same as the previous one or one ruble less. Petya spent 345 rubles on several trips, and then on several subsequent trips - another 365 rubles. How many trips did he make?
|
Solution. A total of 710 rubles was spent. The total number of trips could not have been 14 or less (for 14 trips, a maximum of 700 rubles could be spent), but it also could not have been 17 or more $(50+49+48+\cdots+35+$ $34=714$, and this is the minimum that could be spent). Therefore, the choice is between two options - 15 or 16 trips.
Notice that 345 rubles could have been spent only over 7 trips (for 8 trips, a minimum of $50+49+48+47+46+45+$ $44+43=372>345$ could be spent, while for 6 trips - a maximum of $6 \cdot 50=300365$.
Answer: 15 times.
|
15
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Seven people stood in a circle, each of whom is either a knight, who always tells the truth, or a liar, who always lies, or a traveler, who alternates between truth and lies.
The first and second said in unison: "Among us there is exactly 1 liar," the second and third: "Among us there are exactly 2 knights," the third and fourth: "Among us there are exactly 3 liars," $\vdots$
the sixth and seventh: "Among us there are exactly 6 knights," the seventh and first: "Among us there are exactly 7 liars."
Who is who among them?
|
Solution. If all 7 statements are lies, then everyone lied, meaning everyone is a liar, and then 7 and 1 told the truth. This means that at least one statement is true. On the other hand, there are no more than 2 true statements (one about the liars, the other about the knights). That is, there are either 0 or 1 knights, but the latter is impossible, since everyone said there are more than 1 knight. Therefore, there are no knights, but someone told the truth. This means the statement about the liars was true, and it was told by two visitors. Hence, 5 and 6 are visitors, and all others are liars.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. When the child was born, their parents were not yet 40 years old, but they were already adults. When the child turned 2 years old, the age of exactly one of the parents was divisible by 2; when the child turned 3 years old, the age of exactly one of the parents was divisible by 3, and so on. How long could such a pattern have continued?
|
Solution. The condition means that at the moment of the child's birth, the age of exactly one of the parents was divisible by 2, the age of exactly one of the parents - by 3, and so on (as long as this pattern continued).
Let one of the parents be 24 years old, and the other 35 years old. Then this pattern could continue until the child turned 8. Beyond that, the pattern must break. Indeed, suppose the child turned 9, and the pattern continues. Then at the moment of the child's birth, exactly one of the parents had an even number of years, exactly one - a multiple of 3, exactly one - a multiple of 6, exactly one - a multiple of 8, and exactly one - a multiple of 9. So it is the same parent, and they must be at least 72 years old, i.e., they are too old.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In a company, several employees have a total monthly salary of 10000 dollars. A kind manager proposes to triple the salary for those earning up to 500 dollars, and increase the salary by 1000 dollars for the rest, so the total salary will become 24000 dollars. A mean manager proposes to reduce the salary to 500 dollars for those earning more than 500 dollars, and leave the rest as is. What will the total salary be in this case?
|
Solution. Note that the increase proposed by the kind manager is twice as large as the salary proposed by the evil manager (this is true for both poor and rich employees). The increase according to the kind manager's proposal is 14000, so the salary according to the evil manager's proposal is 7000.
|
7000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. 31 cars started simultaneously from one point on a circular track: the first car at a speed of 61 km/h, the second at 62 km/h, and so on (the 31st at 91 km/h). The track is narrow, and if one car overtakes another by a full lap, they crash into each other, both fly off the track, and are eliminated from the race. In the end, only one car remained. At what speed is it traveling?
|
Solution. First, the fastest car collides with the slowest, then the second fastest collides with the second slowest, and so on. In the end, the car with the median speed remains, i.e., the 16th. It travels at a speed of $76 \mathrm{Km} /$ h.
Criteria. Full solution - 3 points.
1 point if only the answer 76 is written.
1 point is deducted for correct reasoning but an answer of 75 or 77.
|
76
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Five brothers were dividing their father's inheritance equally. The inheritance included three houses. Since the houses couldn't be divided, the three older brothers took them, and the younger brothers were given money: each of the three older brothers paid $2000. How much did one house cost?
## Solution:
|
Answer: $5000.
Since each of the brothers who received money got $3000, the total inheritance was estimated at $15000. Therefore, each house was worth a third of this amount.
|
5000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the Parliament of the Emerald City, 5 parties are represented, which together developed 100 laws over the year (each law was developed by exactly one of the parties). It is known that any three parties together developed no fewer than 50 laws. What is the maximum number of laws that the Green Lenses party could have developed?
|
Solution:
Answer: 33.
Evaluation. Let this quantity be $x$. Since any three parties together have developed no less than 50, any party together with the Green Lenses party has developed no more than 50. Therefore, each of the four other parties has developed no more than $50-x$, and all of them together have developed no more than $200-4x$. Thus, the total number of laws is no more than $200-3x$. Since the total number of laws is 100, we have $3x \leqslant 100$, from which $x \leqslant 33$.
Example. $33,17,17,17,16$.
|
33
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Andrey placed chips of a hundred different colors in the cells of a $10 \times 10$ board. Each minute, one of the chips changes color, and only a chip that was unique (i.e., differed in color from all others) in its row or column before this operation can change color. After $N$ minutes, it turned out that no chip could change color anymore. What is the smallest value $N$ could have been?
|
Solution. Let's look at the moment when there are no moves left. Suppose we have $k$ colors left, then we have repainted at least $100-k$ cells. Note that if nothing can be repainted, then there are at least 4 cells of each color. In total, there are at least 25 colors left after this process. Therefore, we will repaint at least 75 cells. Thus, $N \geqslant 75$. The example is constructed simply by $2 \times 2$ squares. That is, we divide the board into $2 \times 2$ squares and repaint each square to the color of its lower left corner.
|
75
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In triangle $A B C$, angle $A$ is equal to $50^{\circ}, B H$ is the altitude. Point $M$ on $B C$ is such that $B M=B H$. The perpendicular bisector of segment $M C$ intersects $A C$ at point $K$. It turns out that $A C=2 \cdot H K$. Find the angles of triangle $A B C$.
|
Solution. Draw a perpendicular to $BC$ from point $M$. Let $K^{\prime}$ be the point of its intersection with $AC$. Then the segment $MK$ is the midline in $\triangle K^{\prime}MC$, that is, $K^{\prime}K = KC$. From the fact that $HK = KC + AH$, we get $AH = HK^{\prime}$. Right triangles $BHA$ and $BHK^{\prime}$ are equal by two legs, $BHK^{\prime}$ and $BMK^{\prime}$ are equal by a leg and hypotenuse. Then
$$
\angle B = 3 \angle AHB = 3 \cdot (90^{\circ} - 50^{\circ}) = 120^{\circ} \text{.}
$$
The remaining angle $C$ is
$$
180^{\circ} - 50^{\circ} - 120^{\circ} = 10^{\circ}
$$
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Masha bought 2021 weights of pairwise distinct masses. Now Masha places one weight on each pan of a two-pan balance (weights placed on the balance previously are not removed). Each time the balance is in equilibrium, Masha rejoices. What is the maximum number of times she can find a reason to be happy
|
Solution. Answer: 673 times.
Example. Let Masha have bought 673 triples of the form $x, y, x+y$ (we will choose the weights of the new triples so that they do not duplicate the old ones). The last two weights are any. Masha puts $x$ on the left pan, then $y$ on the same left pan, and finally $x+y$ on the right pan and rejoices.
Estimate. Suppose the scales are in balance. By placing the next two weights on the scales, Masha will be sad (the first weight will tip the scales out of balance, and the second, being different from the first, will not be able to return them to balance). Thus, the first two weighings Masha will not be able to rejoice, and thereafter in each triple she will find no more than one reason for joy.
|
673
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Seven fishermen stand in a circle. The fishermen have a professional habit of exaggerating numbers. Each fisherman has a measure of lying (each has their own, an integer) - how many times the number mentioned by the fisherman is greater than the true value. For example, if a fisherman with a lying measure of 3 catches two fish, he will say he caught six fish. In response to the question: "How many fish did your left neighbor catch?", the answers (not necessarily in the order in which the fishermen stand) were $12,12,20,24,32,42$ and 56. In response to the question: "How many fish did your right neighbor catch?", six fishermen answered $12,14,18$, $32,48,70$. What did the seventh one answer?
|
Solution. Note that the product of all the numbers named by the fishermen in each of the surveys is the product of the number of fish caught, multiplied by the product of all the measures of lying of these fishermen. Therefore, the seventh answered $\frac{12 \cdot 12 \cdot 20 \cdot 24 \cdot 32 \cdot 42 \cdot 56}{12 \cdot 14 \cdot 18 \cdot 32 \cdot 48 \cdot 70}=16$.
Note that such a situation could indeed arise if the fishermen caught $2,7,3,8,4,2,2$ fish, and their measure of lying was $10,6,6,8,7,8,6$, respectively.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The gnomes have gone to work, and Snow White is feeling lonely. She laid out a pile of fifteen stones on the table. Every minute, Snow White splits one pile into two non-empty piles and adds a stone to one of them. How can Snow White use these actions to get seven identical piles?
|
Solution. First, let's understand how many stones are in the piles. With each action, the number of piles increases by one, as does the number of stones. Therefore, 7 piles will arise after 6 actions, with the total number of stones being $15+6=21$. This means each pile should have three stones. From these considerations, it is easy to construct an example - each time, the largest pile should be split into $3+X$, and a stone should be added to $X$:
$15-313-3311-3339-333337-3333335-3333333$
Note: Other sequences of actions are possible, but if an even number arises at any point, the example will not converge, as splitting an even pile always results in piles of different parity (and, thus, unequal size)
|
3333333
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the company, several employees have a total monthly salary of 10000 dollars. A kind manager proposes to double the salary for everyone earning up to 500 dollars, and increase the salary by 500 dollars for the rest, so the total salary will become 17000 dollars. A mean manager proposes to reduce the salary to 500 dollars for everyone earning more than 500 dollars, and leave the rest as is. What will the total salary be in this case?
|
Solution. Answer: 7000
Let's look at the difference between the total salary from the kind manager and the current one, and we will understand that this is the total salary from the evil manager:
up to 500 - from the doubled we subtract the current, we get the current
over 500 - from the increased by 500 we subtract the current, we get 500
|
7000
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Konstantin pronounced the names of all natural numbers from 180 to 220 inclusive, while Mikhail - from 191 to 231 inclusive. Who pronounced more words and by how many?
|
Solution. Let's remove the numbers that both have: 191-220. Then each will have 11 numbers left: Konstantin has 180-190, and Mikhail has 221-231. Note that in the names of the numbers 181-189, 221-229, and 231, there are three words each, while in 180, 190, and 230, there are two words each. This means that Mikhail said one more word.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. At the festival "Hobbits - for cultural diversity!", more than 20 participants arrived. A correspondent found out that among any 15 participants of the festival, there are at least 4 humans and at least 5 elves. How many hobbits participated in the festival? Provide all possible answers and prove that there are no others.
|
Solution. Suppose there is at least one hobbit. If there are 10 people among the participants, then in their company with the hobbit and 4 other participants, there will not be 5 elves, which contradicts the condition. Therefore, there are no more than 9 people. Since the total number of participants is more than 20, there will be 12 participants who are not people. But then, by adding 3 participants to them, we will get a company that contradicts the condition. This means that there were no hobbits at all.
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Cheburashka bought as many mirrors from Galina in the store as Gen bought from Shapoklyak. If Gen had bought from Galina, he would have 27 mirrors, and if Cheburashka had bought from Shapoklyak, he would have 3 mirrors. How many mirrors would Gen and Cheburashka buy together if Galina and Shapoklyak agreed and set the price of mirrors to the average of their current prices? (The average of two numbers is half of their sum, for example, for the numbers 22 and 28, the average is 25.)
|
Solution. Let Gena have $x$ times more money than Cheburashka. If we swap Gena's and Cheburashka's money, then with the second method of purchase, the number of mirrors should be equal. Therefore, $3 x=\frac{27}{x}$, from which $3 x^{2}=27$, and $x=3$. So, Gena initially had three times more money than Cheburashka, and the price at Shapoklyak is three times higher than at Galya. Thus, they had four times more money in total than Cheburashka, and the average price is twice as high as at Galya. Initially, Cheburashka could buy $3 \cdot 3=9$ mirrors, then together with Gena at the average price, they would buy $\frac{4 \cdot 9}{2}=18$ mirrors.
|
18
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let $N=400$. What is the maximum number of balls that the magician can guarantee are not in their correct vessels?
#
|
# Solution:
Answer: 533.
Let's imagine that inside the vessels, the balls are divided into cells, and each cell contains one ball. Then we can imagine that (regardless of whether they are in the same vessel or different ones) balls $i$ and $j$ simply swap cells upon the command ( $i j$ ). Thus, any sequence of commands simply performs a fixed permutation of the balls in the cells. (Note that transpositions allow us to perform any permutation). We will make a permutation of the type "a pile of cycles of 3 and one of 5", then in each cycle of 3, at least two will change ownership, and in the cycle of length 5, at least three. In total, 533. We cannot guarantee more than this— in a cycle of length $k$, we can guarantee a maximum of $(k+1) / 2 \leqslant \frac{2}{3} k$ changes in ownership (the cycle can consist of pairs of neighboring balls (standing next to each other on the cycle) + possibly one unpaired ball), and two-thirds of 800 is less than 534.
|
533
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. 31 cars started simultaneously from one point on a circular track: the first car at a speed of 61 km/h, the second at 62 km/h, and so on (the 31st at 91 km/h). The track is narrow, and if one car overtakes another by a full lap, they crash into each other, both fly off the track, and are eliminated from the race. In the end, only one car remained. At what speed is it traveling?
|
Solution. First, the fastest car collides with the slowest, then the second fastest collides with the second slowest, and so on. In the end, the car with the median speed remains, i.e., the 16th. It travels at a speed of $76 \mathrm{Km} /$ h.
Criteria. Full solution - 7 points.
Solution that correctly describes the overall sequence of collisions but with an incorrect answer in the count - 6 points.
Correct answer + cars that have been eliminated are written out and crossed out, but the principle (order of elimination) is not explained - 4 points.
|
76
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Each cell of a $10 \times 10$ board is painted black or white. A cell is said to be out of place if it has at least seven neighbors of a different color than itself. (Neighbors are cells that share a common side or corner.) What is the maximum number of cells on the board that can be out of place at the same time?
|
# Solution.
Answer 26. The example consists of 13 dominoes, which do not share any cells and do not touch the border of the board (see right).
Estimation. Let's call a cell that is not in its place an NVCT-cell. Obviously, NVCT-cells cannot be adjacent to the border. Let's examine what form a connected component of NVCT-cells can have, considering cells to be neighbors if they share a side or a corner. The simplest case is an isolated cell
(case $a$ in the figure).
Now, let's consider two neighboring NVCT-cells of the same color (say, the first). Then their neighbors - cells of the second color, each of which has at least two neighbors of the second color, are of the second color and each, by definition, borders cells of the second color, each of which has at least two neighbors of the second color, meaning they are not NVCT. We get cases $b$ and $c$.
Consider two neighboring NVCT-cells of different colors. They can only be adjacent by a corner, and such a picture is uniquely defined up to reflection. Further, among the neighboring cells, only those marked with "?" can be NVCT-cells, and so on, resulting in a "snake" (with two or more NVCT-cells - $g$).
$a$
$b$
Now, for each cell, let's draw its 0.5-neighborhood - a square with a side of 2 (its sides do not follow the grid lines), in which our cell is in the center. The components into which the NVCT-cells are divided - single cells, dominoes, and "snakes" of $n$ cells (including 2 cells of the same color) - have neighborhoods of size 4, 6, and $3n+1$ cells, respectively. These neighborhoods do not overlap and lie within the central $9 \times 9$ square.

The area of the neighborhood of a component is at least three times the area of the component itself, and equality is only achieved for a domino. If there are 27 NVCT-cells, then the minimum area of the neighborhoods is exactly equal to the area of the $9 \times 9$ square ($27 \cdot 3 = 81$), but the ratio is exactly 3 only if everything is divided into dominoes, and 27 is odd - a contradiction.
|
26
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Each cell of a $10 \times 10$ board is painted black or white. A cell is said to be out of place if it has at least seven neighbors of a different color than itself. (Neighbors are cells that share a common side or corner.) What is the maximum number of white cells on the board that can be out of place at the same time?
|
Solution. Answer: 26
Example: 13 dominoes, not touching each other or the edge of the board.

Estimate. Let's call a cell that is not in its own place an OOP cell. For each OOP cell, we draw its neighborhood: a square with side 2, centered on it (its sides are not aligned with the grid lines!). White OOP cells are divided into components - single cells, dominoes, and diagonal dominoes. They have neighborhoods of size 4, 6, and 7 cells, respectively. These neighborhoods do not overlap and lie within the central $9 \times 9$ square. Also, it can be noted that the area of the neighborhoods is at least three times the area of the cells themselves. If there are 27 OOP cells, then $27 \cdot 3 = 81$ (exactly three times!), but the ratio can be exactly 3 only if everything is divided into dominoes, and 27 is odd.
|
26
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Masha bought 2021 weights of pairwise distinct masses. Now Masha places one weight on each pan of a two-pan balance (weights placed on the balance previously are not removed). Each time the balance is in equilibrium, Masha rejoices. What is the maximum number of times she can find a reason to be happy
|
Solution. Answer: 673 times.
Example. Let Masha have bought 673 triples of the form $x, y, x+y$ (we will choose the weights of the new triples so that they do not duplicate the old ones). The last two weights are any. Masha puts $x$ on the left pan, then $-y$ on the same left pan, and finally $x+y$ on the right pan and rejoices.
Estimate. Suppose the scales are in balance. By placing the next two weights on the scales, Masha will be sad (the first weight will tip the scales out of balance, and the second, being different from the first, will not be able to return them to balance). Thus, the first two weighings Masha will not be able to rejoice, and in each subsequent triple, she will find no more than one reason for joy, since between two joyful weighings there will be at least two unjoyful ones.
|
673
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Seven fishermen stand in a circle. The fishermen have a professional habit of exaggerating numbers. Each fisherman has a measure of lying (each has their own, an integer) - how many times the number mentioned by the fisherman is greater than the true value. For example, if a fisherman with a lying measure of 3 catches two fish, he will say he caught six fish. In response to the question: "How many fish did your left neighbor catch?", the answers (not necessarily in the order in which the fishermen stand) were $12,12,20,24,32,42$ and 56. In response to the question: "How many fish did your right neighbor catch?", six fishermen answered $12,14,18,32$, 48,70. What did the seventh fisherman answer?
|
Solution. Note that the product of all the numbers named by the fishermen in each of the surveys is the product of the number of fish caught, multiplied by the product of all the measures of lying of these fishermen. Therefore, the seventh answered $\frac{12 \cdot 12 \cdot 20 \cdot 24 \cdot 32 \cdot 42 \cdot 56}{12 \cdot 14 \cdot 18 \cdot 32 \cdot -48 \cdot 70}=16$.
Note that such a situation could indeed arise if the fishermen caught $2,7,3,8,4,2,2$ fish, and their measure of lying was $10,6,6,8,7,8,6$, respectively.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. The lye trader Matti wrote several three-digit palindromic numbers on the board. It turned out that no two of them add up to a palindrome. Could he have written more than half of all three-digit palindromes? Recall that a palindrome is a number that remains the same when its digits are reversed.
|
Solution. No. There are $9 \cdot 10$ three-digit palindromes in total (9 options for the first digit, 10 for the second, and the third is uniquely determined by the first). We will prove that at least 45 palindromes are missing from the board.
If $a, b, c, d$ are such digits that $a+c=b+d=11$, then
$$
\overline{a b a}+\overline{c d c}=1221
$$
which means all palindromes consisting of digits from 2 to 9 can be paired, and from each pair, no more than one can be written. There are 64 such palindromes in total (8 options for the first digit and 8 for the second), so at least 32 of them are missing.
Now consider the following group of 13 palindromes:
$$
\begin{gathered}
\text { 101, 111, 121, 131, 141, 151 } \\
202,303,404,505 \\
212,313,414
\end{gathered}
$$
No more than one of them can be written, as adding any two of them does not result in a carry, so the sum will be a palindrome. Therefore, at least 12 of them are missing.
Finally, there are also pairs $(161,616),(171,717)$, and $(181,818)$, and from each pair, at least one palindrome is missing. So, at least 3 in total.
In the end, Vasya will be missing at least $32+12+3=47$ palindromes, which is more than 45.
Moreover, this estimate seems quite rough, so there may be many unpleasant solutions that need to be listened to with extreme caution, requiring the presenter to formulate strict statements and clearly explain which cases they are considering, etc. And generally, it is not advisable to hesitate to seek help if it is unclear whether it is a fake or not.
|
47
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Andrey named all natural numbers from 180 to 220 inclusive ("one hundred eighty", "one hundred eighty one", etc.). How many words did he say?
|
Solution. A total of 41 numbers are named. In each, the hundreds place is named (a total of 41 words). In addition to the hundreds place, the numbers 180, 190, 201-220 each contain one more word (this is 22 words). The number 200 does not contribute any more words, while the remaining 18 numbers each contain two more words. In total, $41+22+2 \cdot 18=99$ words.
|
99
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Yesterday at the market, with one hundred tugriks you could buy 9 gingerbreads and 7 pastries (and even get some change), but today this amount is no longer enough. However, with the same one hundred tugriks today, you can buy two gingerbreads and 11 pastries (also with some change), but yesterday this amount would not have been enough. A gingerbread and a pastry cost a whole number of tugriks, and the price of each sweet changed by no more than one tugrik overnight. $A$ How much does one gingerbread cost today?
|
Solution. Note that something has become more expensive (otherwise, the situation where we could buy a set yesterday but not today could not have arisen), and another sweet has become cheaper for similar reasons. Nine cookies and seven cakes together have become more expensive, so the cookie has become more expensive, and the cake has become cheaper. This set has become 2 tugriks more expensive overnight, i.e., it cost 99 tugriks yesterday and 101 tugriks today. Thus, today 9 cookies = 101 tugriks - 7 cakes, i.e., by subtracting a multiple of 7 from 101, we should get a number that is a multiple of 9. This is only possible in one case: 101 - 56 = 45. Then a cookie today costs 5 tugriks, and a cake costs 8 tugriks.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. The set contained weights of 43, 70, and 57 grams, with an equal number of each type. Maly lost several weights (less than half), weighed the remaining on the scales, and got 20172 grams. How many and which weights were lost?
|
Solution (1). If the weights had not been lost, the total weight would end in 0. Therefore, the weight of the lost weights ends in 8. This can only be the case if 4 weights of 57 g are lost (losing 70 g or the pair $43+57$ does not affect the last digit of the total weight).
Solution (2). Let's divide the initial set of weights into triples $43+70+57$. In each triple, the total weight is 170 g. Note that no more than $4 \cdot 70=280$ g has been lost. Therefore, we need to find all numbers from 20172 to 20452 that are multiples of 170. There are only two such numbers: 20230 and 20400 g.
In the first case, 58 g have been lost, which is impossible. In the second case, 228 g have been lost. This is only possible if 4 weights of 57 g have been lost. Indeed, the number of lost 70-gram weights must be even (otherwise, the lost weight would be odd). If no 70-gram weights have been lost, the maximum possible lost weight is $4 \cdot 57=228$ g. If two 70-gram weights have been lost, 88 g remain for the two remaining weights, which is clearly impossible to achieve.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Each boy is friends with 5 girls, while all girls are friends with a different number of boys. What is the minimum number of children that can be in this group?
|
Solution. If there is a girl who does not have any friends, we can exclude her (the number of children will decrease, but the condition of the problem will remain).
Let us have $m$ boys and $d$ girls. Draw a segment between a boy and a girl if they are friends. Then $5m$ segments are drawn from the boys, and at least $\frac{d(d+1)}{2}$ segments are drawn from the girls. Indeed, let's order the girls by the number of acquaintances in ascending order; then the first girl is friends with at least one boy, the second with at least two, and so on. We also note that from this it follows that $m \geqslant d$ (the last girl is friends with at least $d$ boys, so there must be at least $d$ boys).
Then
$$
\frac{d(d+1)}{2} \geqslant 5 m \geqslant 5 d
$$
from which $d \geqslant 9$ and $m \geqslant 9$. An example with 9 boys and 9 girls is easy to construct: let the ninth girl know all the boys, the eighth - all except the first, the first - only the first boy, the seventh - except the second and third, the second - only the second and third, and so on.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a volleyball tournament, $n$ teams from city $A$ and $2 n$ teams from city $B$ participated. Each team played exactly one game against each other team. The ratio of the number of wins by teams from city $B$ to the number of wins by teams from city $A$ is $3: 4$. Find $n$, given that there were no draws in the tournament.
|
(12 points) Solution. The number of games in which only teams from city $A$ participated is $\frac{(n-1) n}{2}$. In these games, teams from city $A$ won $\frac{(n-1) n}{2}$ games. The number of games in which only teams from city $B$ participated is $\frac{(2 n-1) 2 n}{2}$. In these games, teams from city $B$ won $(2 n-1) n$ games. The number of matches between teams from city $A$ and teams from city $B$ is $2 n^{2}$. Let $m$ be the number of wins in these matches by teams from city $A$, then teams from city $B$ won $2 n^{2}-m$ games in these matches. In total, teams from city $A$ won $\frac{(n-1) n}{2}+m$ games, and teams from city $B$ won $(2 n-1) n+2 n^{2}-m$ games. According to the condition, we have $\frac{\frac{(n-1) n}{2}+m}{(2 n-1) n+2 n^{2}-m}=\frac{4}{3}$, $3 n^{2}-3 n+6 m=32 n^{2}-8 n-8 m, 14 m=29 n^{2}-5 n, m=\frac{29 n^{2}-5 n}{14}, \frac{29 n^{2}-5 n}{14} \leq 2 n^{2}, n^{2}-5 n \leq 0$. The number $n$ can be $1,2,3,4,5$. By substituting into the equation $m=\frac{29 n^{2}-5 n}{14}$, we get that $m$ is an integer only when $n=5$.
Answer: 5.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. What is the smallest area that a figure on the plane $Oxy$ can have, located between the lines $x=-26$ and $x=2$, bounded below by the $x$-axis, and above by the tangent to the graph of the function $y=5+\sqrt{4-x}$ at the point of tangency with abscissa $x_{0}$, where $x_{0}$ lies in the interval $-26 \leq x_{0} \leq 2$?
(12 points)
|
Solution. Solution. We will write the equation of the tangent line to the graph of the function $y=5+\sqrt{4-x}$ at the point with abscissa $x_{0}$
$$
y_{\text {tan }}=-\frac{1}{2 \sqrt{4-x_{0}}}\left(x-x_{0}\right)+5+\sqrt{4-x_{0}}
$$
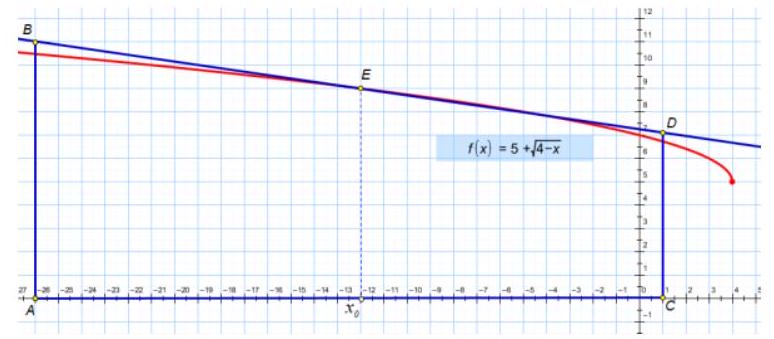
The figure is a trapezoid with bases equal to $y_{\text {tan }}(-26)$ and $y_{\text {tan }}(2)$. The height of the trapezoid is 28. We have
$y_{\text {tan }}(-26)=\frac{1}{2 \sqrt{4-x_{0}}}\left(26+x_{0}\right)+5+\sqrt{4-x_{0}}, \quad y_{\text {tan }}(2)=\frac{1}{2 \sqrt{4-x_{0}}}\left(x_{0}-2\right)+5+\sqrt{4-x_{0}}$,
$S=14\left(y_{\text {tan }}(-26)+y_{\text {tan }}(2)\right)=14\left(\frac{x_{0}+12}{\sqrt{4-x_{0}}}+10+2 \sqrt{4-x_{0}}\right)=14\left(\frac{20-x_{0}}{\sqrt{4-x_{0}}}+10\right)$. We find the derivative $S^{\prime}=14\left(\frac{20-x_{0}}{\sqrt{4-x_{0}}}\right)^{\prime}=\frac{-7\left(x_{0}+12\right)}{\sqrt{\left(4-x_{0}\right)^{3}}}$. The function $S\left(x_{0}\right)$ takes its minimum value at $x_{0}=-12$, $S_{\text {min }}=S(-12)=504$.
Answer: 504.
|
504
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find all natural numbers $n \geq 2$, for which the equality $4 x_{n}+2 y_{n}=20 n^{2}+13 n-33$ holds, where $x_{n}=1 \cdot 2+2 \cdot 3+\cdots+(n-1) \cdot n, y_{n}=1^{2}+2^{2}+3^{2}+\cdots+(n-1)^{2}$.
(20 points)
|
Solution: Let $z_{n}=1+2+\cdots+n=\frac{(n+1) n}{2}=\frac{n^{2}+n}{2}$. We have
$$
\begin{aligned}
& x_{n}=1 \cdot 2+2 \cdot 3+\cdots+(n-1) \cdot n=(2+3+\cdots n)+(3+4+\cdots n)+\cdots((n-1)+n)+n= \\
& =\left(z_{n}-z_{1}\right)+\left(z_{n}-z_{2}\right)+\cdots+\left(z_{n}-z_{n-1}\right)=(n-1) z_{n}-\left(z_{1}+z_{2}+\cdots+z_{n-1}\right)= \\
& =\frac{1}{2}\left((n-1) n(n+1)-\left(1^{2}+1+2^{2}+2+\cdots+(n-1)^{2}+(n-1)\right)=\right. \\
& =\frac{1}{2}\left((n-1) n(n+1)-\left(y_{n}+z_{n-1}\right)\right)
\end{aligned}
$$
Substitute the obtained expression into the equation $4 x_{n}+2 y_{n}=20 n^{2}+13 n-33$. We get
$$
\begin{aligned}
& 2\left((n-1) n(n+1)-\left(y_{n}+z_{n-1}\right)\right)+2 y_{n}=20 n^{2}+13 n-33,2(n-1) n(n+1)-n(n-1)=20 n^{2}+13 n-33, \\
& (n-1)(2 n(n+1)-n)=(n-1)(20 n+33), 2 n^{2}-19 n-33=0, n=11 .
\end{aligned}
$$
Answer: $n=11$.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Compute the coefficient of $x^{80}$ in the polynomial $\left(1+x+x^{2}+\cdots+x^{80}\right)^{3}$ after combining like terms.
|
Solution: $\left(1+x+x^{2}+\cdots+x^{80}\right)^{3}=\left(1+x+x^{2}+\cdots+x^{80}\right)\left(1+x+x^{2}+\cdots+x^{80}\right)\left(1+x+x^{2}+\cdots+x^{80}\right)$
Let after expanding the brackets, the term $x^{p} \cdot x^{q} \cdot x^{r}$ is obtained if the factor $x^{p}$ is chosen from the first bracket, $x^{q}$ - from the second bracket, $x^{r}$ - from the third bracket. Then $x^{p} \cdot x^{q} \cdot x^{r}=x^{80}, p+q+r=80$, $0 \leq p, q, r \leq 80, p, q, r \in N$. We need to calculate the number of such terms after expanding the brackets. Let $p=0$, the number of different sums $q+r=80$ is 81. Let $p=1$, the number of different sums $q+r=79$ is 80. And so on. Let $p=80$, the number of different sums $q+r=0$ is 1. Calculate the total number of such terms: $1+2+3+\cdots+81=\frac{82 \cdot 81}{2}=3321$.
Answer: 3321.
|
3321
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Shooting at a target, with each shot the athlete scored only eight, nine, or ten points (all these points were scored at least once). Making more than 11 shots, in total he scored 100 points. How many 8-point shots did the athlete make?
|
Solution. $8 x+9 y+10 z=100, x, y, z \in \mathbb{N} \Rightarrow 8(x+y+z)<100$
$$
\begin{gathered}
\Rightarrow 11<x+y+z<\frac{100}{8}=12.5 \Rightarrow x+y+z=12 \\
\Rightarrow\left\{\begin{array} { c }
{ x + y + z = 1 2 } \\
{ 8 x + 9 y + 1 0 z = 1 0 0 }
\end{array} \Rightarrow \left\{\begin{array} { c }
{ x + y + z = 1 2 } \\
{ 9 6 + y + 2 z = 1 0 0 }
\end{array} \Rightarrow \left\{\begin{array}{c}
x+y+z=12 \\
y+2 z=4
\end{array} \Rightarrow y=2, z=1, x=9\right.\right.\right.
\end{gathered}
$$
Answer: 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The Fibonacci sequence is defined recursively: $a_{1}=a_{2}=1$, $a_{n+2}=a_{n+1}+a_{n}$ for all natural $n$. What is the last digit of $a_{2020}$?
|
Solution. By induction, it is proved that
1) the parity of the numbers alternates as: OOEEOOEEO...
2) the number with an index divisible by 5 is divisible by 5.
Since 2020 is divisible by 5 and leaves a remainder of 1 when divided by 3, the number $a_{2020}$ is odd and divisible by 5.
Answer: 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. What is the smallest area that a right triangle can have, with its hypotenuse containing the point \( M(1 ; 0) \), and its legs lying on the lines \( y = -2 \) and \( x = 0 \)?
(12 points)
|
Solution. $A B: \quad y=k x+b, \quad M \in A B \Rightarrow b=-k$
$$
\begin{aligned}
& A(a ;-2) \in A B \Rightarrow-2=k a+b \Rightarrow a=1-\frac{2}{k} \\
& S_{A B C}=\frac{1}{2} B C \cdot C A=\frac{1}{2}(b+2) a=\frac{1}{2}(2-k)(1-2 / k) \\
& S^{\prime}=\frac{(2-k)(2+k)}{2 k^{2}}=0, k_{\min }=-2, \quad S_{\min }=4
\end{aligned}
$$
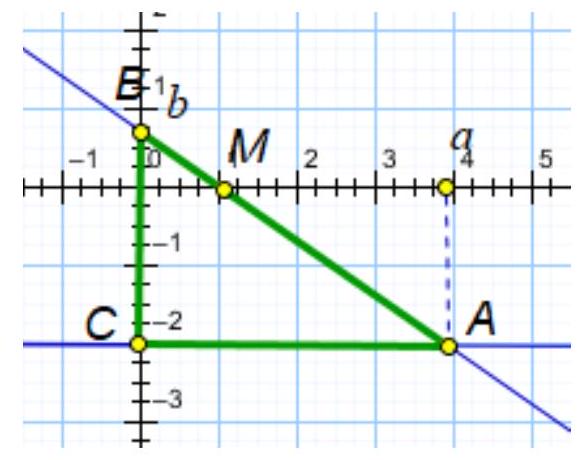
## Answer: 4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Specify the greatest value of the parameter $a$ for which there is a unique solution to the system
$$
\left\{\begin{array}{l}
y=1-\sqrt{x} \\
a-2(a-y)^{2}=\sqrt{x}
\end{array}\right.
$$
|
# Solution:
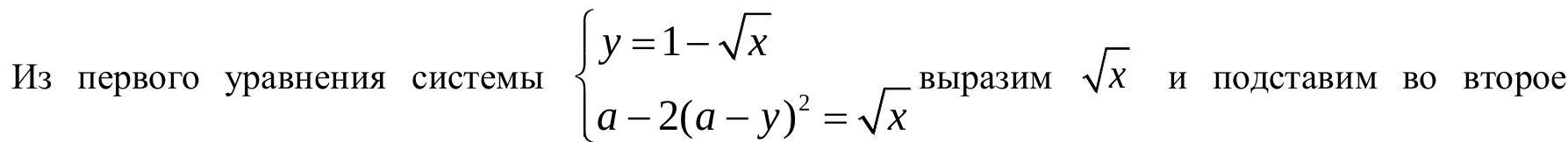
Equation: $\left\{\begin{array}{l}\sqrt{x}=1-y \\ a-2(a-y)^{2}=1-y\end{array}\right.$, considering that $1-y \geq 0$, we solve the resulting quadratic equation:
$$
\begin{aligned}
& a-2(a-y)^{2}=1-y \quad \Rightarrow \quad 2 y^{2}-y(4 a+1)+2 a^{2}-a+1=0 \\
& y_{1,2}=\frac{(4 a+1) \pm \sqrt{(4 a+1)^{2}-8\left(2 a^{2}-a+1\right)}}{4}=\frac{4 a+1 \pm \sqrt{16 a-7}}{4}
\end{aligned}
$$
For the equation to have a unique solution, and thus for the original system to have a unique solution, either the discriminant must be zero and the root must be no greater than one, or one of the two roots satisfies the condition while the other does not.
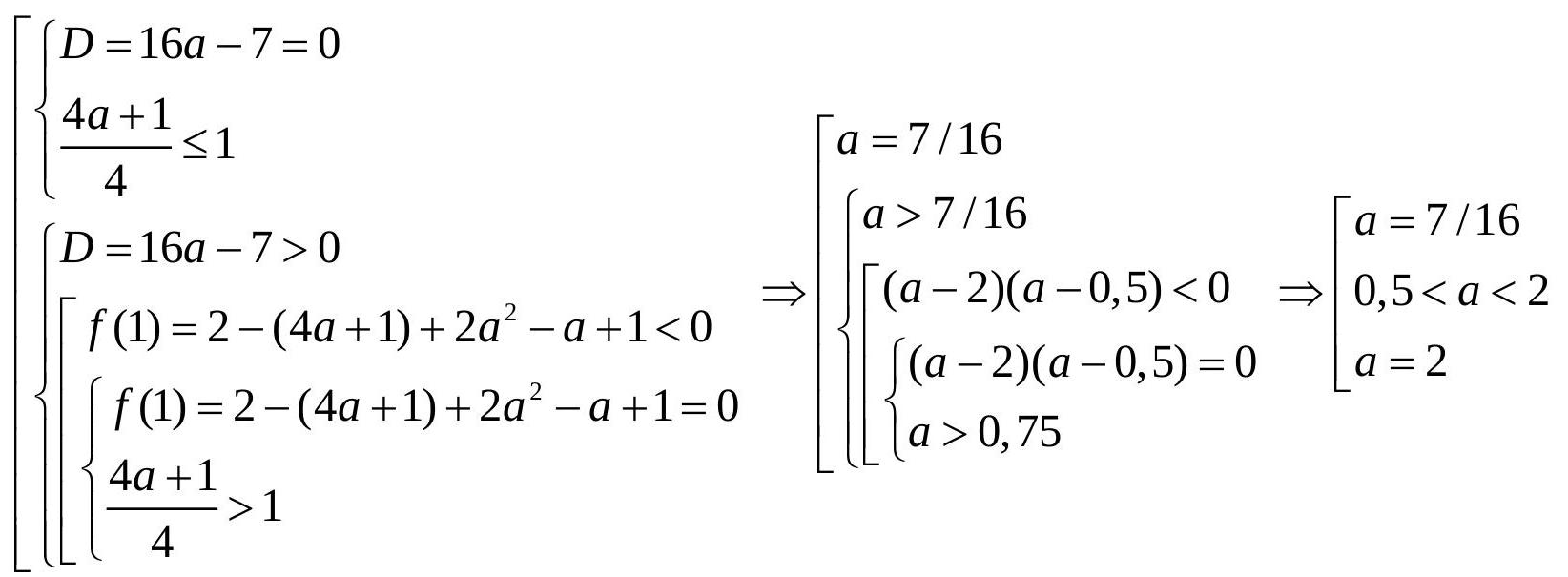
Therefore, the maximum value of the parameter for which the system has a unique solution is $a=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The resistance to bending of a beam with a rectangular cross-section is proportional to the product of the width of this section and the square of its height. What should be the width of the cross-section of a beam cut from a round log with a diameter of $15 \sqrt{3}$ so that its resistance to bending is maximized?
(5 points)
|
# Solution.
$F(a)=k a b^{2}, a-$ width of the beam, $b$ - height of the beam. Since $b^{2}=225 \cdot 3-a^{2}$, then
$F(a)=k a\left(225 \cdot 3-a^{2}\right)=k\left(225 \cdot 3 a-a^{3}\right), F^{\prime}(a)=k\left(225 \cdot 3-3 a^{2}\right)=3 k\left(225-a^{2}\right)$.
The derivative equals zero and changes sign from positive to negative at $a=15$, at which point the resistance to bending will be the greatest.
Answer: 15.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find all pairs of integers $(x, y)$ that satisfy the equation $x y=20-3 x+y$. For each found pair $(x, y)$, calculate the product $x y$. In the answer, write the sum of these products.
|
Solution. $\quad x y=20-3 x+y, \quad x y=17+3(1-x)+y, \quad(x-1) y+3(x-1)=17$, $(x-1)(y+3)=17$. Since x and y are integers, we have four cases:
1) $\left\{\begin{array}{c}y+3=17, \\ x-1=1,\end{array} \Leftrightarrow\left\{\begin{array}{c}y=14 \\ x=2\end{array}\right.\right.$
2) $\left\{\begin{array}{c}y+3=-17, \\ x-1=-1,\end{array} \Leftrightarrow\left\{\begin{array}{c}y=-20 \\ x=0\end{array}\right.\right.$
3) $\left\{\begin{array}{c}y+3=1, \\ x-1=17,\end{array} \Leftrightarrow\left\{\begin{array}{l}y=-2 \\ x=18\end{array}\right.\right.$
4) $\left\{\begin{array}{c}y+3=-1, \\ x-1=-17,\end{array} \Leftrightarrow\left\{\begin{array}{c}y=-4 \\ x=16\end{array}\right.\right.$
Answer: 56.
|
56
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find all natural solutions to the inequality
$$
\frac{4}{5}+\frac{4}{45}+\frac{4}{117}+\cdots+\frac{4}{16 n^{2}-8 n-3}>n-5
$$
In your answer, write the sum of all found solutions.
|
Solution. We have $16 n^{2}-8 n-3=(4 n-3)(4 n+1), \quad \frac{1}{4 n-3}-\frac{1}{4 n+1}=\frac{4}{16 n^{2}-8 n-3}$,
$\frac{4}{1 \cdot 5}+\frac{4}{5 \cdot 9}+\frac{4}{9 \cdot 13}+\cdots+\frac{4}{(4 n-3)(4 n+1)}>n-5$,
$1-\frac{1}{5}+\frac{1}{5}-\frac{1}{9}+\cdots+\frac{1}{4 n-3}-\frac{1}{4 n+1}>n-5,1-\frac{1}{4 n+1}>n-5,4 n^{2}-23 n-5<0$,
$n \in\left(\frac{23-\sqrt{609}}{8} ; \frac{23-\sqrt{609}}{8}\right) \cap \mathbb{N}, 1+2+3+4+5=15$.
Answer: 15.
|
15
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. There is an unlimited supply of square glasses in 10 colors. In how many ways can 4 glasses be inserted into a $2 \times 2$ window frame so that some color appears in both the upper and lower halves of the window.
|
Solution. If the upper half of the glass is of one color (one of 10), then the colors of the lower glasses can be chosen in $10^{2}-9^{2}=19$ ways. If the upper glasses are different $\left(10 * 9=90\right.$ ways to choose), then the colors of the lower ones can be chosen in $10^{2}-8^{2}=36$ ways.
In total $10 * 19+90 * 36=190+3240=3430$ ways.
Answer: 3430.
|
3430
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let $x, y, z$ be the roots of the equation $t^{3}-5 t-3=0$. Find $x^{3} y^{3}+x^{3} z^{3}+y^{3} z^{3}$.
|
Solution. The polynomial has 3 different real roots, since $\mathrm{P}(-100)0, \mathrm{P}(0)0$. By Vieta's theorem, $\mathrm{x}+\mathrm{y}+\mathrm{z}=0, \mathrm{xy}+\mathrm{xz}+\mathrm{yz}=-5, \mathrm{xyz}=3$.
$$
\begin{gathered}
x^{3} y^{3}+x^{3} z^{3}+y^{3} z^{3}=(5 x+3)(5 y+3)+(5 x+3)(5 z+3)+(5 y+3)(5 z+3) \\
=25(x y+x z+y z)+30(x+y+z)+27=-98
\end{gathered}
$$
Answer: -98.
|
-98
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. What is the smallest area that a right triangle can have, with its hypotenuse containing the point \( M(1; 3) \), and its legs lying on the lines \( y = x \) and \( y = -x \)?
(12 points)
|
Solution.
$A B: \quad y=k x+d, \quad M \in A B \Rightarrow d=3-k$
$A(a ;-a) \in A B \Rightarrow-a=k a+3-k \Rightarrow a=\frac{3-k}{k+1}$,
$B(b ; b) \in A B \Rightarrow b=k b+3-k \Rightarrow b=\frac{k-3}{k-1}$,
$S_{A B O}=\frac{1}{2} d \cdot(b-a)=\frac{3-k}{2}\left(\frac{k-3}{k-1}-\frac{k-3}{k+1}\right)=\frac{(k-3)^{2}}{1-k^{2}}$,
$S'=\frac{2(k-3)(1-3 k)}{\left(k^{2}-1\right)^{2}}=0, k_{\min }=\frac{1}{3}, \quad S_{\text {min }}=8$.
Answer: 8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Find all integer values of the parameter $a$ for which the system $\left\{\begin{array}{l}x-2 y=y^{2}+2, \\ a x-2 y=y^{2}+x^{2}+0.25 a^{2}\end{array}\right.$. has at least one solution. In your answer, specify the sum of the found values of the parameter $a$.
|
Solution: Transform the system
$$
\left\{\begin{array} { l }
{ x - 1 = ( y + 1 ) ^ { 2 } } \\
{ ( y + 1 ) ^ { 2 } + ( x - 0.5 a ) ^ { 2 } = 1 }
\end{array} \Rightarrow \left\{\begin{array}{l}
x-1=(y+1)^{2} \\
x-2+(x-0.5 a)^{2}=0
\end{array}\right.\right.
$$
Consider the second equation of the system
$x^{2}+x(1-a)+\left(a^{2}-8\right) / 4=0, \quad D=(a-1)^{2}-\left(a^{2}-8\right)=9-2 a$
A solution exists when $a \leq 9 / 2, x=\frac{a-1 \pm \sqrt{9-2 a}}{2}$, and $x \geq 1$. For the solution to exist, the following conditions must be met:
$$
\left\{\begin{array} { l }
{ D = 9 - 2 a \geq 0 } \\
{ \left[ \begin{array} { l }
{ f ( 1 ) = ( a ^ { 2 } - 4 a ) / 4 > 0 } \\
{ \frac { a - 1 } { 2 } > 1 }
\end{array} \right. } \\
{ f ( 1 ) = ( a ^ { 2 } - 4 a ) / 4 \leq 0 }
\end{array} \Rightarrow \left\{\begin{array}{l}
a \leq 9 / 2 \\
{\left[\begin{array}{l}
a(a-4)>0 \\
a-1>2 \\
a(a-4) \leq 0
\end{array}\right.}
\end{array} \Rightarrow a \in[0,9 / 2]\right.\right.
$$
Summing the integer values of the parameter, we get $0+1+2+3+4=10$.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. There are 5 pieces of transparent glass of the same square shape and size. Each piece of glass is conditionally divided into 4 equal parts (right triangles) by its diagonals, and one of these triangles is painted with an opaque paint of its individual color, different from the colors of the painted parts of the other glasses. Then all these glasses are stacked on top of each other (with precise alignment of edges and vertices) with the painted parts facing up. How many different ways are there to stack the glasses so that the entire stack ends up completely opaque in the vertical direction. (12 points)
|
Solution. First, consider some fixed vertical order of laying the glasses (from bottom to top). It is clear that by rotating the entire layout by some angle, we will not change the layout (we will not get a new layout). Therefore, we can assume that the bottom glass in the layout is always fixed (does not rotate). Then the layouts (with a fixed vertical order of glasses) will differ from each other by the rotation of each of the subsequent 4 upper glasses by $0^{\circ}, 90^{\circ}, 180^{\circ}$, and $270^{\circ}$ relative to the fixed bottom glass. Therefore, we will get a total of $4^{4}=256$ layout options with a fixed vertical order of glasses. Adding now all possible vertical permutations of the five glasses (5! = 120 options), we get the total number of possible glass layouts in a stack: $5!4^{4}=120 \cdot 256=30720$ pieces. But not all these layouts meet the condition of the problem. The layouts that meet the condition of the problem are only those in which the entire stack turns out to be vertically opaque. Consider columns of triangles located above each of the four fixed triangles of the bottom glass. The condition of the problem will be met when each of these four columns is opaque. In this case, one of these columns is already opaque by default (the one that stands on the bottom shaded triangle). Consider the ordered set (vector) of possible angles of rotation (for definiteness, clockwise) of the shaded triangles on each of the 4 upper glasses relative to the bottom shaded triangle: $\left(\alpha_{1}, \alpha_{2}, \alpha_{3}, \alpha_{4}\right)$, where $\alpha_{k} \in\left\{0^{\circ}, 90^{\circ}, 180^{\circ}, 270^{\circ}\right\}, k=1,2,3,4$.
All "columns" of glass triangles will be opaque if in this set of rotation angles there is at least one angle $90^{\circ}$, at least one angle $180^{\circ}$, and at least one angle $270^{\circ}$ (while the angle $0^{\circ}$ does not have to appear, although it will not hurt if it does appear). To count the total number of such sets (and thus the number of layouts with a fixed vertical order of glasses), we will divide them into four groups:
- sets in which all rotation angles are different, i.e., all $\alpha_{k}$ are pairwise different, such sets (due to permutations) are a total of $4!=24$ pieces;
- sets in which the rotation angles $180^{\circ}$ and $270^{\circ}$ appear once each, and the rotation angle $90^{\circ}$ appears twice, such sets (due to permutations) are a total of $6 \cdot 2=12$ pieces (here 6 is the number of places in the vector for two angles of $90^{\circ}$, and 2 is the two permutations of the angles $180^{\circ}$ and $270^{\circ}$ in the remaining two places);
- sets in which the rotation angles $90^{\circ}$ and $270^{\circ}$ appear once each, and the rotation angle $180^{\circ}$ appears twice; similarly, such sets (due to permutations) are also a total of $6 \cdot 2=12$ pieces;
- sets in which the rotation angles $90^{\circ}$ and $180^{\circ}$ appear once each, and the rotation angle $270^{\circ}$ appears twice; similarly, such sets (due to permutations) are a total of $6 \cdot 2=12$ pieces.
In the end, we get a total of $24+12+12+12=60$ ordered sets of rotation angles that meet the required condition. This is the total number of layouts with a fixed vertical order of glasses, in which the final stack turns out to be opaque. Finally, by permuting the glasses $5!=120$ ways, we get the total number of $120 \cdot 60=7200$ layouts, in which the final stack turns out to be opaque.
Answer: 7200 ways.
|
7200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A student wrote a program to recolor a pixel into one of 128 different colors. These colors he numbered with natural numbers from 1 to 128, and the primary colors received the following numbers: white color - number 1, red - 5, orange - 13, yellow - 19, green - 23, blue - 53, blue - 55, purple - 83, black - 128. If the initial color of the pixel has a number \( n \leq 17 \), then the student's program recolors it to the color with the number \( 3n - 2 \), and if the initial color of the pixel has a number \( n \geq 18 \), then the pixel is recolored to the color with the number \( |129 - 2n| \). Initially, the pixel was red. The student applied his program 2019 times sequentially. What color did the pixel end up with?
|
Solution. The final pixel color number is equal to $f^{[2019]}(5)$, where $f^{[k]}(n)=\underbrace{f(f(f(\ldots(f}_{k \text { times }}(n) \ldots)-k$ is the $k$-fold composition of the function $f(n)$, which is equal to $3 n-2$ for $n \leq 17$, and equal to $|129-2 n|$ for $n \geq 18$. Let's compute and write down the first few values: $f(5)=13, \quad f^{[2]}(5)=37, f^{[3]}(5)=55, \quad f^{[4]}(5)=19, f^{[5]}(5)=91, \quad f^{[6]}(5)=53, \quad f^{[7]}(5)=23$, $f^{[8]}(5)=83, f^{[9]}(5)=37=f^{[2]}(5)$. We have obtained a cycle of length 7 operations. Therefore, for any natural value of $k$ and any $r=0,1, \ldots, 6$, we have $f^{[2+7 k+r]}(5)=f^{[r]}(37)$. Since $2019=2+288 \cdot 7+1$, then $r=1$, and $f^{[2019]}(5)=f^{[1]}(37)=55$. The pixel will be blue.
Answer: blue.
|
55
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The wolf saw a roe deer several meters away from him and chased after her along a straight forest path. The wolf's jump is $22\%$ shorter than the roe deer's jump. Both animals jump at a constant speed. All the roe deer's jumps are of the same length, and the wolf's jumps are also equal to each other. There is a period of time during which both the wolf and the roe deer make a certain whole number of jumps. Each time, it turns out that the wolf has made $t\%$ more jumps than the roe deer. Find the greatest integer value of $\mathrm{t}$, for which the wolf will not be able to catch the roe deer.
|
Solution: Let x be the length of the roe deer's jump, then $0.78x$ is the length of the wolf's jump; y - the number of jumps the roe deer makes in a unit of time specified in the condition, $y\left(1+\frac{t}{100}\right)$ - the number of jumps the wolf makes in the same unit of time. The wolf will not be able to catch up with the roe deer if the distance covered by the roe deer in a unit of time - xy - is always greater than the distance covered by the wolf in the same unit of time $0.78xy\left(1+\frac{t}{100}\right)$. We will form the inequality: $0.78xy\left(1+\frac{t}{100}\right)<xy ; 1+\frac{t}{100}<\frac{50}{39} ; t<\frac{1100}{39}$. The maximum value of $t$ that satisfies this inequality, $t=28\%$.
Answer: 28.
|
28
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the arithmetic progression $\left(a_{n}\right) a_{1000}=75, d=0.25$.
Calculate: $99 \cdot 100 \cdot\left(\frac{1}{a_{1580} \cdot a_{1581}}+\frac{1}{a_{1581} \cdot a_{1582}}+\ldots+\frac{1}{a_{2019} \cdot a_{2020}}\right)$.
|
Solution: The expression in parentheses consists of several terms of the form $\frac{1}{x \cdot(x+d)}$, which can be decomposed into the sum of simpler fractions: $\frac{1}{x \cdot(x+d)}=\frac{1}{d}\left(\frac{1}{x}-\frac{1}{x+d}\right)$. Transform the original expression: $99 \cdot 100 \cdot\left(\frac{1}{a_{1580} \cdot a_{1581}}+\frac{1}{a_{1581} \cdot a_{1582}}+\ldots+\frac{1}{a_{2019} \cdot a_{2020}}\right)=$ $=99 \cdot 100 \cdot \frac{1}{d}\left(\frac{1}{a_{1580}}-\frac{1}{a_{1581}}+\frac{1}{a_{1581}}-\frac{1}{a_{1582}}+\ldots+\frac{1}{a_{2019}}-\frac{1}{a_{2020}}\right)=$ $=99 \cdot 100 \cdot \frac{1}{d}\left(\frac{1}{a_{1580}}-\frac{1}{a_{2020}}\right)=99 \cdot 100 \cdot \frac{1}{d}\left(\frac{a_{2020}-a_{1580}}{a_{2020} \cdot a_{1580}}\right)=99 \cdot 100 \cdot \frac{1}{d}\left(\frac{(2019-1579) d}{a_{2020} \cdot a_{1580}}\right)=$
$=99 \cdot 100 \cdot \frac{1}{d}\left(\frac{(2019-1579) d}{a_{2020} \cdot a_{1580}}\right)=99 \cdot 100 \cdot \frac{1}{d} \cdot \frac{440 d}{330 \cdot 220}=60$,
since $a_{2020}=a_{1000}+1020 d=75+1020 \cdot 0.25=330$, and
$$
a_{1580}=a_{1000}+580 d=75+580 \cdot 0.25=220
$$
Answer: 60.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In $\triangle A B C$ with $\angle B=120^{0}$, the angle bisectors $A A_{1}, B B_{1}, C C_{1}$ are drawn.
Segment $A_{1} B_{1}$ intersects the bisector $C C_{1}$ at point M. Find the angle $\Delta B_{1} C_{1} M$.
#
|
# Solution.
Extend side $A B$ beyond point $B$, then $B C$ is the bisector of angle $\angle B B_{1} B K$, which means point $A_{1}$ is equidistant from sides $B_{1} B$ and $B K$.
Considering that point $A_{1}$ lies on the bisector of $\angle B A C$, and thus is equidistant from its sides, we get that $A_{1}$ is equidistant from sides $B_{1} B$ and $B_{1} C$, and therefore lies on the bisector of $\angle B B_{1} C$. Similarly, we prove that $B_{1} C_{1}$ is the bisector of $\angle A B_{1} B$.
Therefore, $\angle C_{1} B_{1} A_{1}=90^{\circ}$, as the angle between the bisectors of adjacent angles.
In $\triangle B B_{1} C M$, the intersection point of the bisectors $B_{1} A_{1}$ and $C C_{1}$, and thus $B M$ is also the bisector of $\angle B_{1} B C$, so $\angle B_{1} B M=\angle M B C=30^{\circ}$.
$\angle A B M=\angle C_{1} B B_{1}+\angle B_{1} B M=60^{\circ}+30^{\circ}=90^{\circ}$, and therefore a circle can be circumscribed around quadrilateral $B M B_{1} C_{1}$. Thus, $\angle B_{1} M C_{1}=\angle B_{1} B C_{1}=60^{\circ}$, as they subtend the same arc.
Answer: 60.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. What is the minimum value that the function $F(x ; y)=6 y+8 x-9$ can take, given that $x^{2}+y^{2}+25=10(x+y)$.
#
|
# Solution:
$x^{2}+y^{2}+25=10(x+y) \Leftrightarrow (x-5)^{2}+(y-5)^{2}=5^{2}$ - this is a circle with center $(5 ; 5)$ and radius 5. Let $F(x ; y)=\mathrm{M}$, then $\mathrm{M}=6 y+8 x-9$ - this is a straight line.
The condition for the minimum of the function is equivalent to the condition for the minimum of $\mathrm{M}$, under which the given line will be tangent to the circle. That is, the distance from the center of the circle to the line is equal to its radius.
$$
\frac{|30+40-9-M|}{\sqrt{36+64}}=5 \Rightarrow |61-M|=50 \Rightarrow M=11 \text{ or } M=111.
$$
## Answer: 11.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. What is the minimum number of cells that need to be painted in a square with a side of 65 cells (65x65 - there are a total of 4225 cells in the square), so that among any four of its cells forming a corner (an "L" shape), there is at least one painted cell.
#
|
# Solution.
Shading should be done diagonally every 3rd (see fig.). Thus, $\left[\frac{N^{2}}{3}\right]$ cells will be shaded. This is the minimum possible number, as within any $3 \times 3$ square, at least three cells need to be shaded. $\left[\frac{65^{2}}{3}\right]=1408$.
Answer: 1408.
|
1408
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Find the sum of all integer values of c for which the equation $10|p-3|+|2 p-| p+c \mid|=6$ has at least one root with respect to p
#
|
# Solution:
Consider the function $\mathrm{f}(\mathrm{r})=10|\mathrm{p}-3|+|2 \mathrm{p}-| \mathrm{p}+\mathrm{c}||-6 \mathrm{p}$. The coefficient of the first modulus in absolute value is greater than the sum of the other coefficients of $\mathrm{p}$. $10>2+1+6$. Therefore, on all intervals up to $\mathrm{p}=3$, the coefficient of the linear increment is negative, and after $\mathrm{p}=3$ it is positive. $\mathrm{p}=3$ is a point of minimum. For the equation $\mathrm{f}(\mathrm{p})=0$ to have at least one root, it is necessary and sufficient that the inequality:
$\mathrm{f}(3) \leq 0$
$\Rightarrow$ Let $|c+3|=\mathrm{t} ;|6-\mathrm{t}|-18 \leq 0$
$(6-\mathrm{t})^{2}-18^{2} \geq 0$
$(24-t)(t+12) \geq 0$
$\mathrm{t} \in[-12 ; 24]$
$|c+3| \leq 24$
Answer: -147.
|
-147
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Ivan Ivanovich approached a source with two empty cans; one held 10 liters, and the other held 8 liters. Water from the source flowed in two streams - one stronger, the other weaker. Ivan Ivanovich simultaneously placed the cans under the streams and, when half of the smaller can was filled, he switched the cans. To Ivan Ivanovich's surprise, the cans filled up simultaneously. How many times more water does the stronger stream provide compared to the weaker one?
|
Solution: Let x liters of water fill the larger can while 4 liters fill the smaller can. After the switch, (10-x) liters fill the larger can while 4 liters again fill the smaller can. Since the flow rates are constant, the ratio of the volumes of water filled in the same time is also constant. We can set up the equation: $\frac{4}{x}=\frac{10-x}{4} ; x^{2}-10 x+16=0$, which has two roots $x_{1}=2, x_{2}=8$. The two roots of the equation correspond to two possibilities: placing the smaller can under the stronger or the weaker stream first. However, in both cases, the answer is the same: one stream provides twice as much water as the other.
Answer: 2.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.