problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3. In the arithmetic progression $\left(a_{n}\right) a_{1}=1, d=4$.
$$
\text { Calculate } A=\frac{1}{\sqrt{a_{1}}+\sqrt{a_{2}}}+\frac{1}{\sqrt{a_{2}}+\sqrt{a_{3}}}+\ldots+\frac{1}{\sqrt{a_{1579}}+\sqrt{a_{1580}}}
$$
In the answer, write the smallest integer greater than $A$.
|
Solution: We transform the expression by multiplying the numerator and denominator of each fraction by the expression conjugate to the denominator:
$$
\begin{aligned}
& A=\frac{1}{\sqrt{a_{1}}+\sqrt{a_{2}}}+\frac{1}{\sqrt{a_{2}}+\sqrt{a_{3}}}+\ldots+\frac{1}{\sqrt{a_{1579}}+\sqrt{a_{1580}}}= \\
& =\frac{\sqrt{a_{2}}-\sqrt{a_{1}}}{a_{2}-a_{1}}+\frac{\sqrt{a_{3}}-\sqrt{a_{2}}}{a_{3}-a_{2}}+\ldots+\frac{\sqrt{a_{1580}}-\sqrt{a_{1579}}}{a_{1580}-a_{1579}}=
\end{aligned}
$$
$=\frac{\sqrt{a_{2}}-\sqrt{a_{1}}}{d}+\frac{\sqrt{a_{3}}-\sqrt{a_{2}}}{d}+\ldots+\frac{\sqrt{a_{1580}}-\sqrt{a_{1579}}}{d}=$
$=\frac{\sqrt{a_{1580}}-\sqrt{a_{1}}}{d}=\frac{\sqrt{a_{1}+1579 d}-\sqrt{a_{1}}}{d}=\frac{\sqrt{1+1579 \cdot 4}-\sqrt{1}}{4}=\frac{\sqrt{6317}-1}{4}$
We estimate the value of $A: \quad 19<\frac{\sqrt{6317}-1}{4}<20$, and write the smallest integer greater than $A$ in the answer.
Answer: 20.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
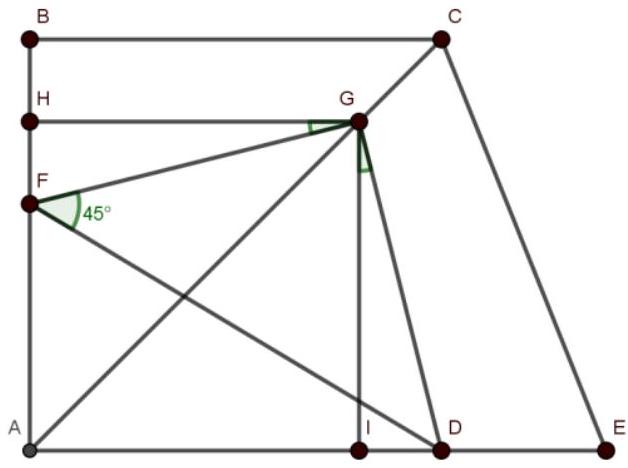
4. Right triangles $\triangle M D C$ and $\triangle A D K$ have a common right angle $\angle D$. Point $K$ lies on $C D$ and divides it in the ratio $2: 3$ from point $C$. Point $M$ is the midpoint of side $A D$. Find the sum of $\angle A K D$ and $\angle M C D$, if $A D: C D=2: 5$.
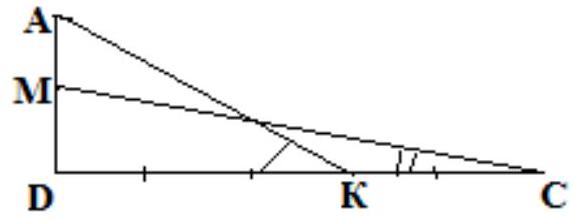
|
# Solution
Complete $\triangle A D C$ to a square $L J C D$. Choose point $H$ on side $L J$ such that $L H: H J=2: 3$, point $N$ on side $C J$ such that $C N: N J=3: 2$, and point $B$ on side $C J$ such that $C B: B J=2: 3$. Then $\triangle A H N$ is a right isosceles triangle with $\angle A=45^{0}$, $\angle L A H=\angle A K D$, $\angle N A B=\angle M C D$. $\angle L A B=\angle L A H+\angle H A N+\angle N A B=90^{\circ}$.
From this, $\angle L A H+\angle N A B=\angle A K D+\angle M C D=45^{\circ}$.
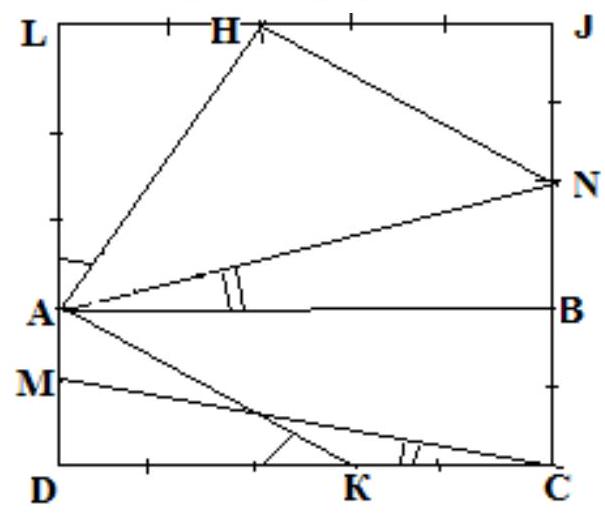
Answer: 45.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the first alloy of copper and lead, the mass ratio is $1: 3$; in the second alloy, it is $1: 2$. How many grams of the first alloy should be taken to obtain 10 g of a new alloy with a mass ratio of copper to lead of $3: 7$?
|
Solution. Let there be x g of copper and 3x g of lead in the first alloy. In the second alloy, there are y g of copper and 2y g of lead. Then $k \cdot 4x + n \cdot 3y = 10 ; \frac{kx + n \cdot y}{k \cdot 3x + n \cdot 2y} = \frac{3}{7}$; we need to find $k \cdot 4x$ and 3ny. Let $ny = b ; kx = a$
$\cdot \frac{a + b}{3a + 2b} = \frac{3}{7} \cdot 7a + 7b = 9a + 6b ; b = 2a$ Using
$4a + 6a = 10 ; a = 1 ; b = 2$ Therefore, $k \cdot 4x = 4 ; 3$ n $= 6$
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. For all non-negative values of the real variable $x$, the function $f(x)$ satisfies the condition $f(x+1)+1=f(x)+\frac{20}{(x+1)(x+2)}$. Calculate $\frac{2019}{f(2019)}$, if $\quad f(0)=2019$.
|
# Solution.
Notice that
$f(x+2019)-f(x)=(f(x+2019)-f(x+2018))+(f(x+2018)-f(x+2017))+\cdots+(f(x+$ 1) $-f(x))=\frac{20}{(x+2019)(x+2020)}-1+\frac{20}{(x+2018)(x+2019)}-1+\cdots+\frac{20}{(x+1)(x+2)}-1$. Therefore, $f(2019)-f(0)=20\left(\frac{1}{2019}-\frac{1}{2020}+\ldots+1-\frac{1}{2}\right)-2019=20\left(1-\frac{1}{2020}\right)-2019$. Thus, $\frac{2019}{f(2019)}=\frac{2020}{20}=101$
Answer: 101.
|
101
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. What is the minimum number of cells that need to be painted in a square with a side of 65 cells (a total of $65 \times 65$ cells, which is 4225 cells in the square), so that from any unpainted cell it is impossible to move to another unpainted cell with a knight's move in chess?
|
# Solution
Cells should be colored in a checkerboard pattern. Thus, $\left[\frac{N^{2}}{2}\right]$ cells will be colored. Since any "knight's move" lands on a cell of a different color, there is no move to a cell of the same color. A "knight's move" can traverse any square table larger than 4x4 such that the knight visits each cell exactly once (see, for example, a 5x5 table). If these moves are numbered, it is clear that fewer than $\left[\frac{N^{2}}{2}\right]$ cells cannot be colored because then there would necessarily be two consecutive uncolored cells in this sequence, i.e., a move from one to the other would be possible. The $35 \times 35$ table needs to be divided into 169 $5 \times 5$ tables, and they should be numbered sequentially, starting with the first $5 \times 5$ table. $\left[\frac{65^{2}}{2}\right]=2112$.
| 21 | 16 | 5 | 10 | 23 | |
| :--- | :--- | :--- | :--- | :--- | :--- |
| 6 | 11 | 22 | 17 | 4 | |
| 1 | 20 | 15 | 24 | 9 | 26 |
| 12 | 7 | 18 | 3 | 14 | |
| 19 | 2 | 13 | 8 | 25 | |
| | | | | | |
Answer: 2112.
|
2112
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Find the sum of all integer values of $\mathrm{h}$ for which the equation ||$r+h|-r|-4 r=9|r-3|$ in terms of $r$ has no more than one solution.
#
|
# Solution
Consider the function $\mathrm{f}(\mathrm{r})=9|\mathrm{r}-3|-|| \mathrm{r}+\mathrm{h}|-\mathrm{r}|+4 \mathrm{r}$. The coefficient of the first modulus in absolute value is greater than the sum of the other coefficients of $\mathrm{r}$. $9>1+1+4$. Therefore, on all intervals up to $r=3$, the coefficient of the linear increment is negative, and after $\mathrm{r}=3$ it is positive. $\mathrm{r}=3$ is a point of minimum. For the equation $\mathrm{f}(\mathrm{r})=0$ to have no more than one root, it is necessary and sufficient that the inequality:
$$
\mathrm{f}(3) \geq 0
$$
$\Rightarrow$ Let $|\mathrm{h}+3|=\mathrm{t} ; 12-|t-3| \geq 0$
$(\mathrm{t}-3)^{2}-12^{2} \leq 0$
$(\mathrm{t}-15)(\mathrm{t}+9) \leq 0$
$\mathrm{t} \in[-9 ; 15]$
$|\mathrm{h}+3| \leq 15$
Answer: -93.
|
-93
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. A table consisting of 1861 rows and 1861 columns is filled with natural numbers from 1 to 1861 such that each row contains all numbers from 1 to 1861. Find the sum of the numbers on the diagonal that connects the top left and bottom right corners of the table, if the table is filled symmetrically with respect to this diagonal.
#
|
# Solution:
We will show that all numbers from 1 to 1861 are present on the diagonal. Suppose the number $a \in\{1,2,3 \ldots, 1861\}$ is not on the diagonal. Then, due to the symmetry of the table, the number $a$ appears an even number of times. On the other hand, since the number $a$ appears once in each row, the total number of $a$ in the table is odd (1861). This is a contradiction.
There are 1861 cells on the diagonal, so each number from the set $\{1,2, \ldots 1861\}$ will appear exactly once on the diagonal. By calculating the sum of the arithmetic progression, we find the answer.
Answer: 1732591.
|
1732591
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Ilya takes a triplet of numbers and transforms it according to the rule: at each step, each number changes to the sum of the other two. What is the difference between the largest and the smallest numbers in the triplet after 1989 applications of this rule, if the initial triplet of numbers was $\{70 ; 61 ; 20\}$? If the question of the problem allows for multiple answers, then specify all of them in the form of a set.
|
# Solution:
Let's denote the 3 numbers as $\{x ; x+a ; x+b\}$, where $0<a<b$. Then the difference between the largest and the smallest number at any step, starting from the zeroth step, will be an invariant, that is, unchanged and equal to $b . \quad b=70-20=50$.
Answer: 50.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Two points are moving along a circle. When moving in the same direction, the faster point catches up with the slower point every 16 seconds. If they move in opposite directions at the same speeds, they meet every 4 seconds. It is known that when moving towards each other along the circle, the distance between the approaching points decreases by 64 cm every 2 seconds (until the moment of meeting). Find the speed of the faster point (in cm/sec).
|
# Solution:
Let $v-$ be the speed of the faster point, and $u-$ be the speed of the slower point. According to the problem, we set up the system of equations: $\left\{\begin{array}{l}(u+v) \cdot 4=(v-u) \cdot 16 \\ (u+v) \cdot 2=64\end{array} ;\left\{\begin{array}{l}3 v=5 u \\ u+v=32\end{array} ;\left\{\begin{array}{l}u=12 \\ v=20\end{array}\right.\right.\right.$. The speed of the faster point is 20 cm/sec.
Answer: 20.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In triangle $A B C$, side $B C$ is 18 cm. The perpendicular $D F$, drawn from the midpoint of side $A B$ - point $D$, intersects side $B C$ at point $F$. Find the perimeter of triangle $A F C$, if side $A C$ is $9 \, \text{cm}$.
|
# Solution:
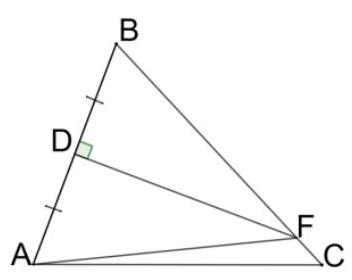
Triangle $ABF (BF = AF)$ is isosceles, since $DF \perp AB$, and $D$ is the midpoint of $AB$. $P_{AFC} = AF + FC + AC = BF + FC + AC = BC + AC = 27 \text{ cm}$.
Answer: 27 cm.
|
27
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. There are two types of containers: 27 kg and 65 kg. How many containers of the first and second type were there in total, if the cargo in the first type of containers exceeds the cargo in the second type of containers by 34 kg, and the number of 65 kg containers does not exceed 44 units?
#
|
# Solution:
Let $x$ be the number of containers weighing 27 kg, and $y$ be the number of containers weighing 65 kg. We get the equation $27 x - 65 y = 34$.
$27(x - 2y) - 11y = 34$, let $x - 2y = k$
$27k - 11y = 34$
$11(2k - y) + 5k = 34$, let $2k - y = t(2)$
$11t + 5k = 34$
$5(2t + k) + t = 34$, let $2t + k = n(3)$
$5n + t = 34, t = 34 - 5n$
Substitute into (3), $k = 11n - 68$
Substitute into (2), $y = 27n - 170$
Substitute into (1), $x = 65n - 408$
Since $x > 0, 0 \leq y \leq 44$, then $n = 7$. Therefore, $x = 47, y = 19$.
This results in 47 and 19 containers, a total of 66 containers.
Answer: 66.
|
66
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. A farmer presented 6 types of sour cream in barrels of $9,13,17,19,20,38$ liters at the market. On the first day, he sold sour cream from three barrels completely, and on the second day, from two more barrels completely. The volume of sour cream sold on the first day was twice the volume of sour cream sold on the second day. Which barrels were emptied on the first day? In your answer, indicate the largest possible sum of the volumes of sour cream sold on the first day.
#
|
# Solution:
A total of 116 liters were delivered; $116=3 \cdot 38+2$; therefore, the unsold barrel, when divided by 3, gives a remainder of 2.
1) If it is 17 liters, then $116-17=99$, then on the second day, one third of 99 liters were sold, which is $33=13+20$, then on the first day, barrels with capacities of $9, 19, 38$ liters were sold, their total volume is 66 liters.
2) If it is 20 liters, then $116-20=96$; one third of 96 is $32=13+19$, then on the first day, barrels with capacities of $9, 17, 38$ liters were sold, their total volume is 2 liters less than the previous one;
3) If the 38-liter barrel is unsold, then $116-38=78$, two thirds of 78 is 52, 52 is less than 66.
Answer: 66.
|
66
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. In triangle $A B C$ with $\angle B=120^{\circ}$, the angle bisectors $A A_{1}, B B_{1}, C C_{1}$ are drawn. Segment $A_{1} B_{1}$ intersects the angle bisector $C C_{1}$ at point M. Find $\angle C B M$.
#
|
# Solution:
Extend side $A B$ beyond point $B$, then $B C$ is the bisector of angle $\angle B_{1} B K$, which means point $A_{1}$ is equidistant from sides $B_{1} B$ and $B K$.
Considering that point $A_{1}$ lies on the bisector of $\angle B A C$, and therefore is equidistant from its sides.
We obtain that $A_{1}$ is equidistant from sides $B_{1} B$ and $B_{1} C$, which means it lies on the bisector of $\angle B B_{1} C$. In triangle $B B_{1} C M$ - point $A_{1}$ is the intersection of the bisectors $B_{1} A_{1}$ and $C C_{1}$, and therefore $B M$ is also the bisector of $\angle B_{1} B C$, hence $\angle B_{1} B M=\angle M B C=30^{\circ}$
Answer: $\angle C B M=30^{\circ}$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. For what values of the parameter $\boldsymbol{a}$ does the equation $|f(x)-5|=p(x)$, where $f(x)=\left|\frac{x^{2}-10 x+25}{x-5}-\frac{x^{2}-3 x}{3-x}\right|$, $p(x)=a \quad$ have three solutions? If there is more than one value of the parameter, indicate their product in the answer.
|
# Solution:
Simplify $f(x)=\left|\frac{x^{2}-10 x+25}{x-5}-\frac{x^{2}-3 x}{3-x}\right|$, we get $f(x)=$ $|2 x-5|$, where $x \neq 5, x \neq 3$.
Solve the equation || $2 x-5|-5|=a$, where $x \neq 5, x \neq 3$ graphically in the system $x O a$.
The equation has three solutions when $a=4, a=5$.
The product is 20.
Answer: 20.
## Solution for Variant #2
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. If a two-digit number is decreased by 54, the result is a number written with the same digits but in reverse order. In the answer, specify the arithmetic mean of the resulting numbers.
#
|
# Solution:
$\overline{x y}=10 x+y-$ the original two-digit number, then $\overline{y x}=10 y+x$ - the number written with the same digits but in reverse order. We get the equation $10 x+y=10 y+x+54$.
From the equation, it is clear that the two-digit number is greater than 54. Let's start the investigation with the tens digit equal to 6.
| $\boldsymbol{x}$ | equation | $\boldsymbol{y}$ | number |
| :---: | :---: | :---: | :---: |
| 6 | $60+y=10 y+6+54$ | $y=0$ | 60 does not fit the condition |
| 7 | $70+y=10 y+7+54$ | $y=1$ | 71 |
| 8 | $80+y=10 y+8+54$ | $y=2$ | 82 |
| 9 | $90+y=10 y+9+54$ | $y=3$ | 93 |
These could be the numbers 71, 82, 93. The arithmetic mean of the numbers is 82.
Answer: 82.
|
82
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. During the shooting practice, each soldier fired 10 times. One of them successfully completed the task and scored 90 points. How many times did he score 9 points, if there were 4 tens, and the results of the other hits were sevens, eights, and nines. There were no misses at all.
|
# Solution:
Since the soldier scored 90 points and 40 of them were scored in 4 shots, he scored 50 points with the remaining 6 shots. As the soldier only hit the 7, 8, and 9, let's assume he scored 24 points with three shots (one each in 7, 8, and 9). Then, for the remaining three shots, he scored 26 points, which is only possible with the unique combination of numbers $7, 8, 9$: $8+9+9=26$. Therefore, the shooter hit the 7 once, the 8 twice, and the 9 three times.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Players divide the chips. The first player takes $m$ chips and a sixth of the remainder; the second $-2 m$ chips and a sixth of the new remainder; the third $-3 m$ chips and a sixth of the new remainder, and so on. It turned out that the chips were divided equally in this way. How many players were there?
|
# Solution:
Let $x$ be the number of players, and $y$ be the number of chips each has. The last player took $y=m x$ chips, with no remainder, otherwise the condition of equal distribution would not be met. The second-to-last player took $y=(x-$ 1)m plus one-sixth of the remainder, and $\frac{5}{6}$ of the remainder equals $xm$; thus, one-sixth of the remainder equals $\frac{x m}{5} ; x m=(x-1) m+\frac{x m}{5} ; 5 m=x m ; x=5$.
## Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In rectangle $A B C D$, point $E$ is located on diagonal $A C$ such that $B C=E C$, point $M$ is on side $B C$ such that $E M=M C$. Find the length of segment $M C$, if $B M=6, A E=3$. If the answer is not an integer, round the result to tenths according to rounding rules.
|
# Solution:

Draw $A F$ parallel to $B E$ (point $F$ lies on line $B C$), then $\angle C B E=\angle C F A, \angle C E B=$ $\angle C A F$. Considering that $B C=C E$, we get that triangle $F C A$ is isosceles, hence $F C$ $=A C$ and $F B=A E$. Triangles $F B A$ and $A E F$ are congruent, as $F B=A E, \angle A F B=\angle F A E, A F$ is common. We obtain that $\angle F B A=\angle A E F=90^{\circ}$, from which $\angle F E C=90^{\circ}$. Triangle $F C E$ is right-angled and $M C=M E$, so $F M=M C$ and $F M=F B+B M=A E+B M=M C=9$.
Answer: 9 cm.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Given triangle $A B C . \angle A=\alpha, \angle B=\beta$. Lines $O_{1} O_{2}, O_{2} O_{3}, O_{1} O_{3}$ are the bisectors of the external angles of triangle $A B C$, as shown in the figure. Point O is the center of the inscribed circle of triangle $A B C$. Find the angle between the lines $\mathrm{CO}_{1}$ and $\mathrm{O}_{2} \mathrm{O}_{3}$.
|
# Solution:
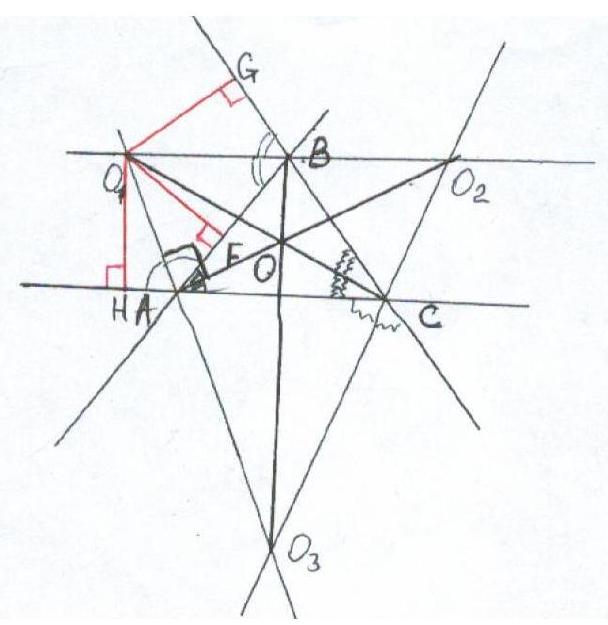
We will prove that the bisectors of two external angles and one internal angle intersect at one point. Let \( O_{1} G, O_{1} H, O_{1} F \) be the perpendiculars to \( B C, A C \) and \( A B \) respectively. Then triangles \( A H O_{1} \) and \( B F O_{1} \), \( B F O_{1} \) and \( B G O_{1} \) are right triangles and are equal by the hypotenuse and acute angle. From the equality of the triangles, it follows that \( H O_{1} = G O_{1} \). Therefore, \( O_{1} \) is equidistant from the sides of angle \( C \), which means \( C O_{1} \) is the bisector of angle \( C \). Similarly, it can be proven that \( A O_{2} \) and \( B O_{3} \) are the bisectors of angles \( A \) and \( B \). The point \( O \) is the point of intersection of the bisectors of triangle \( \mathrm{ABC} \). The angle \( O_{1} A O_{2} \) is a right angle, as it is formed by the bisectors of adjacent angles. Similarly, the angles \( O_{1} B O_{3} \) and \( O_{1} C O_{2} \) are right angles, and therefore, \( O \) is the point of intersection of the altitudes of triangle \( O_{1} O_{2} O_{3} \). Thus, \( \mathrm{CO}_{1} \) is perpendicular to \( \mathrm{O}_{2} \mathrm{O}_{3} \).
Answer: \( 90^{\circ} \).
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. For what values of the parameter a does the equation $f(x)=p(x)$ have one solution, if $f(x)=$ $\left|\frac{2 x^{3}-5 x^{2}-2 x+5}{(1.5 x-3)^{2}-(0.5 x-2)^{2}}\right|, \quad p(x)=|2 x+5|+a$. If there are more than one value of the parameter, then in the answer, specify their sum.
#
|
# Solution:
Simplify $f(x)=\left|\frac{2 x^{3}-5 x^{2}-2 x+5}{(1.5 x-3)^{2}-(0.5 x-2)^{2}}\right|$, we get
$$
f(x)=|x+1|, \text { where } x \neq 1, x \neq 2.5 \text {. }
$$
Solve the equation $|x+1|=|5+2 x|+a$, where $x \neq 1, x \neq 2.5$ graphically in the system $x O a$.
1) $\left\{\begin{array}{c}x<-2.5 \\ -x-1=-2 x-5+a\end{array} \quad\left\{\begin{array}{l}x<-2.5 \\ a=x+4\end{array}\right.\right.$
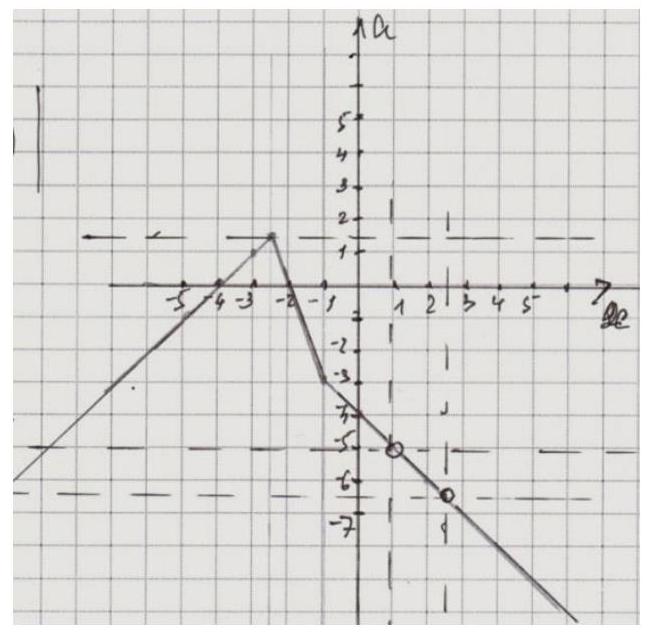
2) $\left\{\begin{array}{c}-2.5 \leq x<-1 \\ -x-1=2 x+5+a\end{array} \quad\left\{\begin{array}{c}-2.5 \leq x<-1 \\ a=-3 x-6\end{array}\right.\right.$
3) $\left\{\begin{array}{c}x \geq-1 \\ x+1=2 x+5+a\end{array} \quad\left\{\begin{array}{c}x \geq-1 \\ a=-x-4\end{array}\right.\right.$
The equation has one solution when $a=-6.5, a=-5, a=1.5$. The sum is -10.
Answer: -10.
|
-10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
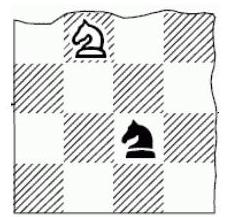
1. In how many ways can two knights - a white one and a black one - be placed on a chessboard consisting of $16 \times 16$ cells so that they threaten each other? (A knight moves in an "L" shape, i.e., it can move to one of
the fields closest to the one it is on, but not on the same row, column, or diagonal.) (12 points)
|
Solution: Let's connect an $n \times n (n>2)$ rectangular coordinate system to the board. Denote the coordinates of the two knights as $\left(x_{1} ; y_{1}\right)$ and $\left(x_{2} ; y_{2}\right)$, where $x_{k}, y_{k} \in\{1,2, \ldots, n\}, k=1,2$. The knights threaten each other if 1) $\left|x_{1}-x_{2}\right|=1, \quad\left|y_{1}-y_{2}\right|=2$ or 2) $\left|x_{1}-x_{2}\right|=2, \quad\left|y_{1}-y_{2}\right|=1$. In the first case, there are four such possibilities:
$1 \leq x_{1} \leq n-1, x_{2}=x_{1}+1, \quad 1 \leq y_{1} \leq n-2, y_{2}=y_{1}+2 ;$
$1 \leq x_{1} \leq n-1, x_{2}=x_{1}+1, \quad 1 \leq y_{2} \leq n-2, y_{1}=y_{2}+2$
$1 \leq x_{2} \leq n-1, x_{1}=x_{2}+1, \quad 1 \leq y_{1} \leq n-2, y_{2}=y_{1}+2$
$1 \leq x_{2} \leq n-1, x_{1}=x_{2}+1, \quad 1 \leq y_{2} \leq n-2, y_{1}=y_{2}+2$.
Each of these sub-cases corresponds to $(n-1)(n-2)$ positions. The second case differs from the first by a $90^{\circ}$ rotation. For $n=16$, we have $8(n-1)(n-2)=8 \cdot 15 \cdot 14=1680$.
Answer: 1680.
|
1680
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the smallest natural number that has exactly 70 natural divisors (including 1 and the number itself).
$(16$ points $)$
|
Solution: Let $n$ be the required natural number, $n=p_{1}^{k_{1}} \cdot p_{2}^{k_{2}} \cdot \ldots \cdot p_{m}^{k_{m}}$ - the prime factorization of the number $n$. Any natural divisor of this number has the form $d=p_{1}^{h_{1}} \cdot p_{2}^{l_{2}} \cdot \ldots \cdot p_{m}^{l_{m}}$, where $l_{i} \in\left\{0,1, \ldots, k_{i}\right\}, i=1, \ldots, m$. The number of divisors of the number $n$ is $\left(k_{1}+1\right)\left(k_{2}+1\right) \cdots\left(k_{m}+1\right)=70$. We factorize the number 70 into non-unit factors in all possible ways and choose the smallest number $n$. Since $70=2 \cdot 5 \cdot 7$, we have five cases:
1) $70=70$, the smallest number $n=2^{69}>40000$;
2) $70=35 \cdot 2$, the smallest number $n=2^{34} \cdot 3^{1}>40000$;
3) $70=14 \cdot 5$, the smallest number $n=2^{13} \cdot 3^{4}>40000$;
4) $70=10 \cdot 7$, the smallest number $n=2^{9} \cdot 3^{6}=512 \cdot 81>40000$;
5) $70=7 \cdot 5 \cdot 2$, the smallest number $n=2^{6} \cdot 3^{4} \cdot 5^{1}=25920$.
Answer: 25920.
|
25920
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find all values of $n, n \in N$, for which the sum of the first terms of the sequence $a_{k}=3 k^{2}-3 k+1, \quad k \in N$, is equal to the sum of the first $n$ terms of the sequence $b_{k}=2 k+89, k \in N . \quad(12$ points)
|
Solution. Note that $a_{k}=3 k^{2}-3 k+1=k^{3}-(k-1)^{3}$, and the sum is $S_{n}=n^{3}$. For the second sequence, $b_{k}=2 k+89=(k+45)^{2}-(k+44)^{2}$, the sum is $S_{n}=(n+45)^{2}-45^{2}=n(n+90)$.
We get the equation $n^{3}=n(n+90) \Rightarrow n^{2}-n-90=0 \Rightarrow n=10$.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A student wrote a program for recoloring a pixel into one of 128 different colors. These colors he numbered with natural numbers from 1 to 128, and the primary colors received the following numbers: white color - number 1, red - 5, orange - 13, yellow - 21, green - 45, blue - 75, indigo - 87, violet - 91, black - 128. If the initial color of the pixel has a number \( n \leq 19 \), then the student's program recolors it to the color with the number \( n+4 \), and if the initial color of the pixel has a number \( n \geq 20 \), then the pixel is recolored to the color with the number \( |129-2n| \). Initially, the pixel was red. The student applied his program 2019 times sequentially. What color did the pixel end up as a result?
|
Solution. The final pixel color number is equal to $f^{[2019]}(5)$ where $f^{[k]}(n)=\underbrace{f(f(f(\ldots(f}_{k \text { times }}(n) \ldots)-k$-fold composition of the function $f(n)$, which is equal to $n+4$ when $n \leq 19$, and equal to $|129-2 n|$ when $n \geq 20$. Let's compute and write down the first few values: $f(5)=9, \quad f^{[2]}(5)=13, f^{[3]}(5)=17, \quad f^{[4]}(5)=21, f^{[5]}(5)=87, \quad f^{[6]}(5)=45, \quad f^{[7]}(5)=39$, $f^{[8]}(5)=51, \quad f^{[9]}(5)=27, \quad f^{[10]}(5)=75, f^{[11]}(5)=21=f^{[4]}(5) . \quad$ We have obtained a cycle of length 7 operations. Therefore, for any natural value of $k$ and any $r=0,1, \ldots, 6$, we have $f^{[4+7 k+r]}(5)=f^{[r]}(21)$. Since $2019=4+287 \cdot 7+6$, then $r=6$, and $f^{[2019]}(5)=f^{[6]}(21)=75$. The pixel will be blue. Answer: blue.
|
75
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (10 points) On a tourist base, the number of two-room cottages is twice the number of one-room cottages. The number of three-room cottages is a multiple of the number of one-room cottages. If the number of three-room cottages is tripled, it will be 25 more than the number of two-room cottages. How many cottages are there in total on the tourist base, given that there are no fewer than 70?
|
Solution. Let the number of one-bedroom houses be $x$, two-bedroom houses $2 \mathrm{x}$, and three-bedroom houses nx.
$3 n x-25=2 x ; x(3 n-2)=25 ; \Rightarrow 25:(3 n-2) \Rightarrow 3 n-2=1 ; 5 ; 25$. If
$3 n-2=1 ; n=1 ; x=25 ; 25+50+25=100$ total houses.
If $3 n-2=5 ; 3 n=7$, which is impossible. If $3 n-2=25 ; 3 n=27 ; n=9 ; x=1 ; 1+2+9 is an insufficiently justified solution |
| 0 points | Incorrect reasoning or only the answer is written. |
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (15 points) For what values of the parameter $a$ is the sum of the squares of the roots of the equation $x^{2}+a x+2 a=0$ equal to $21?$
|
Solution: By Vieta's theorem: $x_{1}+x_{2}=-a, x_{1} \cdot x_{2}=2 a, \quad$ therefore, $x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=a^{2}-4 a$. From the condition, we get that $a^{2}-4 a=21$ or $a \in\{-3 ; 7\}$.
The discriminant of the equation is $D=a^{2}-8 a$, when $a=7$ it is negative, meaning the equation has no solutions, when $a=-3$ the equation has two roots. Therefore, the answer is $a=-3$.
Answer: $a=-3$.
## Criteria:
| Points | Conditions for awarding |
| :---: | :--- |
| 15 | The correct answer is obtained with justification |
| 10 | The number of solutions of the equation depending on the value of the parameter is not investigated or an incorrect answer is obtained due to an arithmetic error |
| 0 | The solution does not meet any of the above conditions |
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (20 points) Dasha added 158 numbers and got 1580. Then Seryozha tripled the largest of these numbers and decreased another number by 20. The resulting sum did not change. Find the smallest of the original numbers.
#
|
# Solution:
Let x be the largest of the original numbers, and y be the number that Seryozha decreased. Then: $x+y=3 x+y-20$, i.e., $x=10$.
Since the arithmetic mean of the original numbers is 10, and the largest of these numbers is also 10, each of the given numbers is 10.
Answer: 10.
## Criteria:
| 20 points | Any complete and correct solution. |
| :--- | :--- |
| 15 points | A generally correct solution with minor flaws. |
| 5 points | The largest number is found. |
| 0 points. | The solution does not meet any of the criteria listed above or only the answer is provided. |
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. $x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}$, but according to Vieta's theorem $\left\{\begin{array}{l}D \geq 0 \\ x_{1}+x_{2}=-(m+1) . \text { Then, } \mathrm{c} \\ x_{1} x_{2}=2 m-2\end{array}\right.$ considering that $D=(m+3)^{2} \geq 0$, we have $x_{1}^{2}+x_{2}^{2}=$
$(-(m+1))^{2}-2(2 m-2)=m^{2}+2 m+1-4(m-1)=m^{2}-2 m+5=(m-1)^{2}+4$
From which $y=(m-1)^{2}+4$ and $y_{\text {min }}=4$ when $m=1$.
|
Answer: For the equation $x^{2}+(m+1) x+2 m-2=0$, the smallest sum of the squares of its roots is 4 when $m=1$.
## Grading Criteria.
| 15 points | Correct and justified solution. |
| :--- | :--- |
| 10 points | Using Vieta's theorem, the expression for the sum of the squares of the roots is correctly written, but there is an error in the transformation of the expression. |
| 5 points | Vieta's theorem (considering D) is correctly written. |
| 0 points | Other solutions that do not meet the above criteria. |
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. According to the theorem inverse to Vieta's theorem, we form a quadratic equation. We get $x^{2}-\sqrt{2019} x+248.75=0$.
Next, solving it, we find the roots $a$ and $b$: $a=\frac{\sqrt{2019}}{2}+\frac{32}{2}$ and $b=\frac{\sqrt{2019}}{2}-\frac{32}{2}$, and consequently, the distance between the points $a$ and $b$: $a-b=32$.
|
Answer: 32
| 15 points | The correct answer is obtained justifiably |
| :---: | :---: |
| 10 points | The quadratic equation is solved, but an arithmetic error is made or the distance between the points is not found |
| 5 points | The quadratic equation is correctly formulated according to the problem statement. |
| 0 points | The solution does not meet any of the criteria listed above |
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Initially, the farmer placed his produce in boxes with a capacity of 8 kg each, but one box was not fully loaded. Then the farmer repackaged all the produce into boxes with a capacity of 6 kg each, which required 8 more boxes, but in this case, one box was also not fully loaded. When the produce was finally placed in boxes with a capacity of 5 kg each, all boxes were fully loaded, but it required an additional 5 boxes. How many kilograms did the farmer's produce weigh? Provide the answer as a number without specifying the unit.
points)
|
Solution. Let $x$ kg be the weight of the farmer's produce. Then $\quad 8(n-1)<x<8 n$, $6(n+7)<x<6(n+8), \quad 5(n+13)=x, \Rightarrow 8(n-1)<5(n+13)<8 n, \quad 6(n+7)<5(n+13)<6(n+8)$, $\Rightarrow 21 \frac{2}{3}<n<23, \quad n=22, \quad x=35 \cdot 5=175$.
Answer: 175.
|
175
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Solve the equation $8 \sin ^{4}(\pi x)-\sin ^{2} x=\cos ^{2} x-\cos (4 \pi x)$. In your answer, specify the sum of the roots that belong to the interval $[-1 ; 2]$.
points)
|
Solution. Considering the basic trigonometric identity, we get
$8 \sin ^{4}(\pi x)-1+\cos (4 \pi x)=0 \quad \Rightarrow \quad 8 \sin ^{4}(\pi x)-2 \sin ^{2}(2 \pi x)=0 \quad \Rightarrow$
$\left(2 \sin ^{2}(\pi x)-2 \sin (\pi x) \cos (\pi x)\right)\left(2 \sin ^{2}(\pi x)+2 \sin (\pi x) \cos (\pi x)\right)=0 \Rightarrow$ $\sin ^{2}(\pi x)\left(\sin ^{2}(\pi x)-\cos ^{2}(\pi x)\right)=0 \Rightarrow \sin ^{2}(\pi x)(\cos (2 \pi x))=0$.
Therefore, $\left[\begin{array}{l}\sin (\pi x)=0, \\ \cos (2 \pi x)=0,\end{array} \Rightarrow\left[\begin{array}{l}\pi x=\pi k, k \in Z, \\ 2 \pi x=\frac{\pi}{2}+\pi n, n \in Z,\end{array} \Rightarrow\left[\begin{array}{l}x=k, k \in Z, \\ x=\frac{1}{4}+\frac{n}{2}, n \in Z,\end{array}\right.\right.\right.$ then the roots of the equation belonging to the interval $[-1 ; 2]$, will be $-1,1,2,-0.75,-0.25,0.25,0.75,1.25,1.75$. Their sum is 5.
## Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the country of Landia, which breeds an elite breed of horses, an annual festival is held to test their speed, in which only one-year-old, two-year-old, three-year-old, and four-year-old horses can participate. For each horse that meets the speed standard, the festival organizers pay a fixed amount of money to the stud farm where the horse was raised: 1 landric for a one-year-old, 2 landrics for a two-year-old, 3 landrics for a three-year-old, and 4 landrics for a four-year-old. Each stud farm participating in the festival annually enters four new horses (of any age combination as they wish) for testing, which have not previously participated in the tests, as well as personally all horses (not older than four years) that previously participated in the tests at a younger age and met the standard. What is the maximum amount of money a stud farm can earn in the first six years of its participation in the festival $\quad(12$ points)
|
Solution. A four-year-old horse can earn a maximum of 4 landricks over its entire participation in festivals. If the horse starts participating in festivals at 1 year old, it can participate for another 3 years after that. In the case of annual victories, it will earn $1+2+3+4=10$ landricks over 4 years. If the horse starts participating in festivals at 2 years old, it can earn a maximum of $2+3+4=9$ landricks over its 3 possible years of participation. If the horse starts participating in festivals at 3 years old, it can earn a maximum of $3+4=7$ landricks. Therefore, the most optimal strategy is as follows. In the first year, the stable enters 4 one-year-old horses. The maximum winnings are 4 landricks. In the second year, the stable enters 4 new one-year-old horses and 4 two-year-olds that participated and won in the first year. The maximum winnings are $4+4 \cdot 2=12$ landricks. In the third year, the stable enters 4 new one-year-old horses, 4 two-year-olds that participated in the second year, and 4 three-year-olds that participated in the previous 2 years. The maximum bonus is $4+4 \cdot 2+4 \cdot 3=24$ landricks. In the fourth year, there is no point in entering one-year-old horses, as they will only be able to participate for 2 more years. Therefore, it makes sense to enter 4 new two-year-old horses. The winnings will be $4 \cdot 2+4 \cdot 2+4 \cdot 3+4 \cdot 4=44$ landricks. Horses that start participating in the 5th year will only participate once after that, so it makes sense to enter new three-year-olds. The winnings will be $4 \cdot 3+4 \cdot 3+4 \cdot 3+4 \cdot 4=52$ landricks. In the sixth year,
landricks. In total, over 6 years of participation in festivals, the stable can earn a maximum of $4+12+24+44+52+64=200$ landricks.
Answer: 200.
|
200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The number $N$ is written as the product of consecutive natural numbers from 2019 to 4036: $N=2019 \cdot 2020 \cdot 2021 \cdot \ldots \cdot 4034 \cdot 4035 \cdot 4036$. Determine the power of two in the prime factorization of the number $N$.
(points)
|
Solution. The number $N$ can be represented as
$$
\begin{aligned}
& N=\frac{(2 \cdot 2018)!}{2018!}=\frac{1 \cdot 2 \cdot 3 \cdot 4 \cdot \ldots \cdot 4034 \cdot 4035 \cdot 4036}{2018!}=\frac{(1 \cdot 3 \cdot \ldots \cdot 4035) \cdot(2 \cdot 4 \cdot \ldots \cdot 4034 \cdot 4036)}{2018!}= \\
& =\frac{(1 \cdot 3 \cdot \ldots \cdot 4035) \cdot 2 \cdot 2 \cdot \ldots \cdot 2 \cdot(1 \cdot 2 \cdot \ldots \cdot 2017 \cdot 2018)}{2018!}=(1 \cdot 3 \cdot \ldots \cdot 4035) \cdot 2^{2018}
\end{aligned}
$$
We obtained the product of odd numbers and a power of two.
Answer: 2018.
|
2018
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. What is the smallest area that a right triangle can have, if its hypotenuse lies on the tangent to the graph of the function $y=\sqrt{x-3}$, one of its legs lies on the $y$-axis, and one of its vertices coincides with the point of tangency
points)
|
Solution. $\quad f(x)=\sqrt{x-3}, \quad f^{\prime}\left(x_{0}\right)=\frac{1}{2 \sqrt{x-3}}$
$S_{A B C}=\frac{1}{2} A B \cdot B C, x_{0}-$ abscissa of the point of tangency $A$,
$A\left(x_{0}, f\left(x_{0}\right)\right), \quad B\left(0, f\left(x_{0}\right)\right), \quad C \quad$ - the point of intersection of the tangent with the $y$-axis. Let $C(0, c)$. The equation
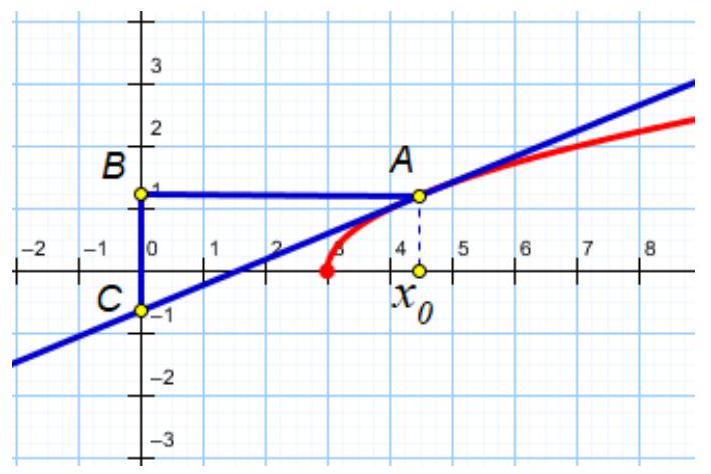
of the tangent to the graph of the function $f(x)=\sqrt{x-3}$ is $y=f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+f\left(x_{0}\right)$. Point $C$ belongs to the tangent, we substitute its coordinates into the equation of the tangent: $c=-f^{\prime}\left(x_{0}\right) x_{0}+f\left(x_{0}\right)$.
Then $\quad A B=x_{0}, \quad B C=f\left(x_{0}\right)-c=f^{\prime}\left(x_{0}\right) x_{0}, \quad S_{A B C}=\frac{1}{2} A B \cdot B C=\frac{1}{2} f^{\prime}\left(x_{0}\right)\left(x_{0}\right)^{2}=\frac{x_{0}^{2}}{2 \sqrt{x_{0}-3}} . \quad$ To find the extrema of the function $S_{A B C}=S\left(x_{0}\right)=\frac{x_{0}{ }^{2}}{4 \sqrt{x_{0}-3}}$ we find the zeros of the derivative of this function $S^{\prime}\left(x_{0}\right)=\frac{3\left(x_{0}{ }^{2}-4 x_{0}\right)}{8 \sqrt{\left(x_{0}-3\right)^{3}}} . \quad$ Since $x_{0} \geq 3$, the only extremum point, and specifically, the point of minimum for this function is the point $\quad x_{0}=4, \quad S_{\min }=S(4)=\frac{4^{2}}{4 \sqrt{4-3}}=4$.
Answer: 4.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In triangle $A B C$, altitudes $A D, B E, C F$ are drawn. The length of side $A C$ is $1+\sqrt{3}$. The distances from the center of the inscribed circle in triangle $D E F$ to points $A$ and $C$ are $\sqrt{2}$ and 2, respectively. Find the length of side $A B$.
points)
|
Solution. $\quad A D, B E, C F$ are the altitudes of triangle $A B C, D A, E B, F C$ are the angle bisectors of angles $D, E, F$ of triangle $D E F, O$ is the point of intersection of the altitudes of triangle $A B C$, which is also the center of the inscribed circle of triangle $D E F$. Thus, $A O=\sqrt{2}, C O=2$. Let $O E=x, A E=y$. Then we arrive at the system $\left\{\begin{array}{c}x^{2}+y^{2}=2, \\ (1+\sqrt{3}-y)^{2}+x^{2}=4\end{array}\right.$. Solving the system, we get $\quad y=1, x=1 . \quad$ Then $\quad \angle D A C=\angle B C A=45^{\circ}$,
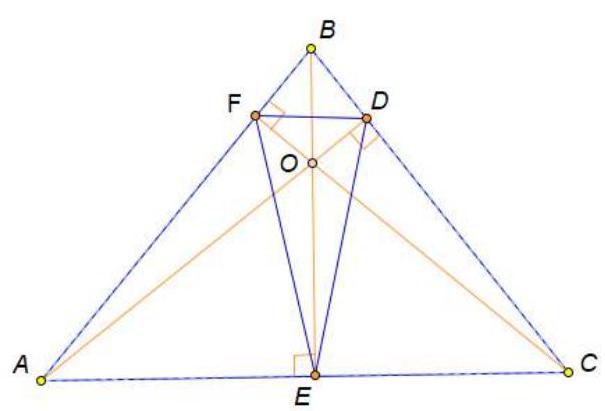
$B C=\sqrt{6}, \angle F C A=\operatorname{arctg} \frac{1}{\sqrt{3}}=30^{\circ}$,
$\angle A B E=30^{\circ}, \quad A B=2$.
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A vessel with a capacity of 10 liters is filled with air containing $24\%$ oxygen. A certain volume of air was pumped out of the vessel and an equal volume of argon was added. Then, the same volume of the mixture as the first time was pumped out and again topped up with the same volume of argon. In the new mixture, $11.76\%$ oxygen was found. How many liters of the mixture were released each time from the vessel? Give your answer as a number without specifying the unit.
points)
|
Solution. Let $x$ be the volume of the mixture released each time from the vessel. Then, the first time, the amount of oxygen left in the vessel is $2.4 - 0.24x$. The percentage of oxygen in the mixture after adding argon is $(2.4 - 0.24x) \times 10$. The second time, the amount of oxygen left in the vessel is $2.4 - 0.24x - (2.4 - 0.24x) \times 0.1x$. The percentage of oxygen in the mixture after adding argon in this case is $10(2.4 - 0.24x - (2.4 - 0.24x) \times 0.1x)$. According to the condition, $10(2.4 - 0.24x - (2.4 - 0.24x) \times 0.1x) = 11.76$. Solving the equation, we arrive at the quadratic equation $x^2 - 20x + 51 = 0, x_1 = 3, x_2 = 17$. The second root does not fit the condition.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Determine the smallest natural number $N$, among the divisors of which are all numbers of the form $x+y$, where $x$ and $y$ are natural solutions to the equation $6 x y-y^{2}-5 x^{2}=7$. points)
|
Solution. Transform the equation by factoring the right-hand side
$6 x y-y^{2}-5 x^{2}-x^{2}+x^{2}=7 \Rightarrow 6 x(y-x)-(y+x)(y-x)=7 \Rightarrow(y-x)(6 x-y-x)=7 \Rightarrow$ $(y-x)(5 x-y)=7$.
Considering that the variables are natural numbers, and 7 is a prime number, we get
$$
\left\{\begin{array} { l }
{ y - x = 7 , } \\
{ 5 x - y = 1 , \text { or } }
\end{array} \quad \left\{\begin{array} { l }
{ y - x = - 7 , } \\
{ 5 x - y = - 1 , \text { or } }
\end{array} \quad \left\{\begin{array} { l }
{ y - x = 1 , } \\
{ 5 x - y = 7 , \text { or } }
\end{array} \quad \left\{\begin{array}{l}
y-x=-1 \\
5 x-y=-7
\end{array}\right.\right.\right.\right.
$$
the second and fourth systems do not have natural solutions. The solution to the first system is the pair $(2 ; 9)$, and the third system is $(2 ; 3)$. Therefore, $x+y=11$ or $x+y=5$. The smallest natural number that has 5 and 11 as divisors is 55.
Answer: 55.
|
55
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. From point $A$ of a circular track, a car and a motorcycle started simultaneously and in the same direction. The car drove two laps without stopping in one direction. At the moment when the car caught up with the motorcyclist, the motorcyclist turned around and increased his speed by 16 km/h, and after $3 / 8$ hours from the turn, he arrived at point $A$ simultaneously with the car. Find the entire distance (in km) traveled by the motorcyclist, if this distance is 5.25 km shorter than the entire track. Provide the answer as a number without specifying the unit.
|
Solution. Let $x$ (km/h) be the speed of the motorcyclist, $x$ (km/h) be the speed of the car, $S$ (km) be the distance the motorcyclist travels before turning around, then the total length of the track is $2 S+5.25$. We have $\frac{S}{x}=\frac{3 S+5.25}{y}, \frac{3 x}{8}+6=S, \frac{3 y}{8}=S+5.25$. This leads to the quadratic equation $4 S^{2}-36 S-63=0$, its positive solution is $S=10.5$, the entire distance traveled by the motorcyclist is $2 S=21$.
Answer: 21.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given 2019 indistinguishable coins. All coins have the same weight, except for one, which is lighter. What is the minimum number of weighings required to guarantee finding the lighter coin using a balance scale without weights? (12 points)
|
Solution. We will prove the following statement by induction on $k$: if there are $N$ visually identical coins, with $3^{k-1}<N \leq 3^{k}$, and one of them is lighter, then it can be found in $k$ weighings. Base case: $k=0, N=1$, no weighing is needed for a single coin. Inductive step: suppose the statement is true for $0,1,2$, $\ldots, k$. Now let $3^{k}<N \leq 3^{k+1}$. Place no less than $N / 3$ coins, but no more than $3^{k}$ coins, on the left pan, and the same number on the right pan. If the left pan is lighter, then the lighter coin is on it; if the right pan is lighter, then the lighter coin is on it; if the scales are balanced, then the lighter coin is among the remaining coins, the number of which is less than or equal to $N / 3 \leq 3^{k}$. As a result, we need to find the lighter coin among no more than $3^{k}$ coins, and it will take no more than $k$ additional weighings. Since $3^{6}<2019 \leq 3^{7}$, the number of weighings $k$ is 7.
Answer: 7.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the sum of all numbers of the form $x+y$, where $x$ and $y$ are natural number solutions to the equation $5 x+17 y=307$.
points)
|
Solution. We solve the auxiliary equation $5 x+17 y=1$. For example, its solutions can be 7 and 2. Multiplying them by 307 and considering linear combinations for integer $t$, we get values in natural numbers
$\left\{\begin{array}{l}x=7 \cdot 307-17 t, \\ y=-2 \cdot 307+5 t,\end{array} t \in Z, x>0, y>0 \Rightarrow t \in\{123,124,125,126\} \Rightarrow\right.$
(58,1), (41,6), $(24,11),(7,16)$
$59+47+35+23=164$
Answer: 164.
|
164
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In 100 containers of three types with capacities of $1 \pi$, 10 liters, and 50 liters, 500 liters of oil have been distributed. How many containers of each type were used, if the amount of oil in each container corresponds to its capacity?
(12 points)
|
Solution. Let $n, m, k$ be the number of containers with capacities of 1 liter, 10 liters, and 50 liters, respectively. Then $\left\{\begin{array}{c}n+10 m+50 k=500, \\ n+m+k=100 .\end{array}\right.$ Since $n=500-10 m-50 k=10(50-m-5 k)$, $n$ is divisible by 10, i.e., $n=10 l, l \in N, n \leq 100, l \leq 10 .\left\{\begin{array}{c}l+m+5 k=50, \\ 10 l+m+k=100,\end{array} \quad\left\{\begin{array}{c}l+m+5 k=50, \\ 9 l-4 k=50,\end{array} \Rightarrow l=5+(5+4 k) / 9\right.\right.$ , $(5+4 k) / 9 \leq 5,(5+4 k) / 9 \in N$. From this, we have $k \leq 10,(5+4 k) / 9 \in N, \Rightarrow$ $k=1, k=10 . \quad$ Then 1) $k=1, l=6, n=60, m=39 ; 2) \quad k=10, l=10, n=100, m<0, \quad$ there are no non-negative integer solutions.
Answer: 60 of 1 liter, 39 of 10 liters, 1 of 50 liters.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find all natural numbers $n \geq 2$, for which the equality $4 x_{n}+2 y_{n}=55 n^{2}+61 n-116$ holds, where $x_{n}=1 \cdot 2+2 \cdot 3+\cdots+(n-1) \cdot n, y_{n}=1^{2}+2^{2}+3^{2}+\cdots+(n-1)^{2}$.
(20 points)
|
Solution: Let $z_{n}=1+2+\cdots+n=\frac{(n+1) n}{2}=\frac{n^{2}+n}{2}$. We have
$$
\begin{aligned}
& x_{n}=1 \cdot 2+2 \cdot 3+\cdots+(n-1) \cdot n=(2+3+\cdots n)+(3+4+\cdots n)+\cdots((n-1)+n)+n= \\
& =\left(z_{n}-z_{1}\right)+\left(z_{n}-z_{2}\right)+\cdots+\left(z_{n}-z_{n-1}\right)=(n-1) z_{n}-\left(z_{1}+z_{2}+\cdots+z_{n-1}\right)= \\
& =\frac{1}{2}\left((n-1) n(n+1)-\left(1^{2}+1+2^{2}+2+\cdots+(n-1)^{2}+(n-1)\right)=\right. \\
& =\frac{1}{2}\left((n-1) n(n+1)-\left(y_{n}+z_{n-1}\right)\right)
\end{aligned}
$$
Substitute the obtained expression into the equation $4 x_{n}+2 y_{n}=55 n^{2}+61 n-116$. We get
$$
\begin{aligned}
& 2\left((n-1) n(n+1)-\left(y_{n}+z_{n-1}\right)\right)+2 y_{n}=55 n^{2}+61 n-116,2(n-1) n(n+1)-n(n-1)=55 n^{2}+61 n-116 \\
& (n-1)(2 n(n+1)-n)=(n-1)(55 n+116), 2 n^{2}-54 n-116=0, n^{2}-27 n-58=0, n=29
\end{aligned}
$$
Answer: $n=29$.
|
29
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In triangle $ABC$, lines parallel to the sides of the triangle are drawn through an arbitrary point $O$. As a result, triangle $ABC$ is divided into three parallelograms and three triangles. The areas of the resulting triangles are $6 \text{ cm}^2$, $24 \text{ cm}^2$, and $54 \text{ cm}^2$. Find the area of triangle $ABC$.
$$
\text { (20 points) }
$$
|
# Solution:
The triangles are similar. Let the first and third be similar with a similarity coefficient $k_{1}$, and the second and third with a similarity coefficient $k_{2}$. Then for the areas of these triangles, we have the ratios $\frac{S_{1}}{S_{3}}=k_{1}^{2}, \frac{S_{2}}{S_{3}}=k_{2}^{2}$.
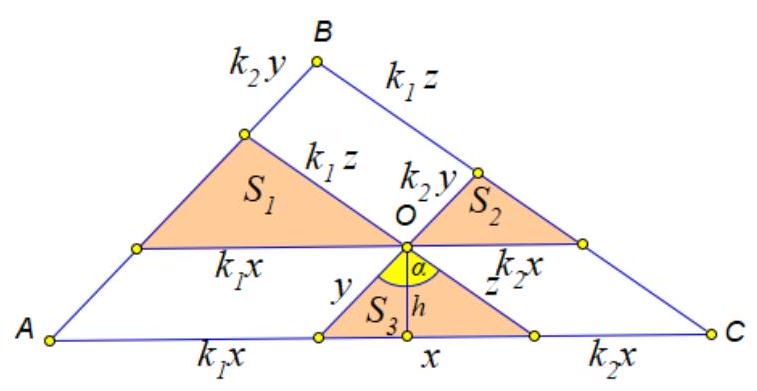
The areas of the parallelograms are expressed as follows: $S_{1 p}=k_{1} x h=2 k_{1} S_{3}, S_{2 p}=k_{2} x h=2 k_{2} S_{3}, S_{3 p}=k_{1} k_{2} y z \sin \alpha=2 k_{1} k_{2} S_{3}$. $S_{A B C}=S_{1}+S_{2}+S_{3}+2\left(k_{1}+k_{2}+k_{1} k_{2}\right) S_{3}=S_{1}+S_{2}+S_{3}+2\left(\sqrt{\frac{S_{1}}{S_{3}}}+\sqrt{\frac{S_{2}}{S_{3}}}+\frac{\sqrt{S_{1} S_{2}}}{S_{3}}\right) S_{3}=$ $=S_{1}+S_{2}+S_{3}+2 \sqrt{S_{1} S_{3}}+2 \sqrt{S_{2} S_{3}}+2 \sqrt{S_{1} S_{2}}=6+24+54+2 \sqrt{6 \cdot 54}+2 \sqrt{24 \cdot 54}+2 \sqrt{6 \cdot 24}=216$.
Answer: 216.
## Solution for Variant #2
|
216
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Schoolchildren were given 7 sheets of paper and asked to cut some of them into 7 pieces. The resulting pieces of paper were mixed and they were asked again to cut some of them into 7 pieces. This was repeated several times. How many pieces of paper need to be cut so that in the end there are 331 pieces.
|
Solution. After $k$ cuts, there remain $6 k+7$ pieces. Therefore, to determine the number of cuts made, we solve the equation $6 k+7=331 \Rightarrow k=54$.
Answer: 54.
|
54
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the equation $10 x-6+x^{2}=\sqrt{2 x^{2}-2 x+1} \cdot \sqrt{36+(x+4)^{2}}$
|
Solution. Transform the equation $10 x-6+x^{2}=\sqrt{2 x^{2}-2 x+1} \cdot \sqrt{36+(x+4)^{2}}$
$10 x-6+x^{2}=\sqrt{x^{2}+x^{2}-2 x+1} \cdot \sqrt{36+(x+4)^{2}} \Rightarrow 6 x-6+x^{2}+4 x=\sqrt{x^{2}+(x-1)^{2}} \cdot \sqrt{6^{2}+(x+4)^{2}}$,
This equation can be interpreted as the scalar product of vectors $\vec{a}=(x-1, x), \quad \vec{b}=(6, x+4)$, written in two ways - the sum of the products of corresponding coordinates and the product of the lengths of the vectors times the cosine of the angle between them, which in this case is 1. The cosine is equal to one if the vectors are collinear, i.e., their coordinates are proportional
$$
\frac{x-1}{6}=\frac{x}{x+4} \Rightarrow x^{2}+3 x-4=6 x \Rightarrow x^{2}-3 x-4=0 \Rightarrow x=\left[\begin{array}{l}
-1 \\
4
\end{array}, \text { but } x=-1\right. \text { is an extraneous root. }
$$
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (15 points) Two medians of a triangle, equal to 18 and 24, are perpendicular to each other. Find the length of the third median of this triangle.
|
Solution. Let $\mathrm{AP}=18$ and $\mathrm{BH}=24$. We will find the length of the median $\mathrm{CM}$. By the property of medians in $\triangle A B C$ we have:
$A O: O P=B O: O H=2: 1 \Rightarrow A O=$
$=\frac{2}{3} A P=\frac{2}{3} \cdot 18=12 ; B O=\frac{2}{3} B H=\frac{2}{3} \cdot 24=16$.
Then, by the Pythagorean theorem in the right-angled
$\triangle A O B: A B=\sqrt{A O^{2}+B O^{2}}==\sqrt{12^{2}+16^{2}}=20$. Since $O M$ is the median of this triangle, drawn from the vertex of the right angle,
$O M=\frac{1}{2} A B=\frac{1}{2} \cdot 20=10$. Considering that $C O: O M=2: 1$,
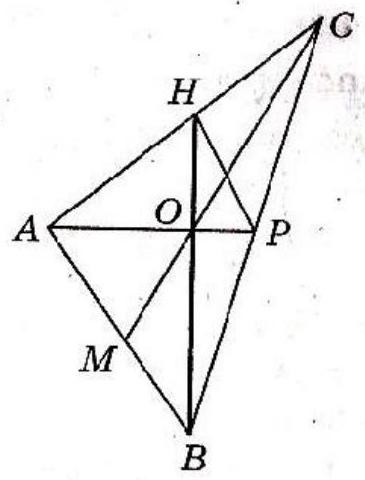
we get: $C M=3 O M=3 \cdot 10=30$.
Answer: 30.
| Criterion | Points |
| :--- | :---: |
| The correct answer is obtained with justification. | 15 |
| The solution contains a computational error, possibly leading to an incorrect answer, but the solution has a correct sequence of all steps. | 10 |
| In the solution of the problem, one or two formulas are correctly written, which could be the beginning of a possible solution. | 5 |
| The solution does not meet any of the criteria described above. | 0 |
| Maximum score | 15 |
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (20 points) Calculate the value of the expression:
$$
1 \cdot 2 \cdot(1+2)-2 \cdot 3 \cdot(2+3)+3 \cdot 4 \cdot(3+4)-\cdots+2019 \cdot 2020 \cdot(2019+2020)
$$
|
Solution. We will prove by mathematical induction for natural n that:
$$
\begin{gathered}
-0 \cdot 1 \cdot(0+1)+1 \cdot 2 \cdot(1+2)-2 \cdot 3 \cdot(2+3)+3 \cdot 4 \cdot(3+4)-\cdots- \\
-(2 n-2) \cdot(2 n-1) \cdot(4 n-3)+(2 n-1) \cdot 2 n \cdot(4 n-1)= \\
=(2 n-1) \cdot 2 n \cdot(2 n+1) .
\end{gathered}
$$
Base: \( n=1 \Rightarrow -0 \cdot 1 \cdot(0+1)+1 \cdot 2 \cdot(1+2)=1 \cdot 2 \cdot 3 \) - true.
Assume it is true for \( n=k \), then for \( n=k+1 \):
$$
\begin{gathered}
-0 \cdot 1 \cdot(0+1)+1 \cdot 2 \cdot(1+2)-2 \cdot 3 \cdot(2+3)+3 \cdot 4 \cdot(3+4)-\cdots \\
\ldots+(2 k-1) \cdot 2 k \cdot(4 k-1)- \\
=(2 k-1) \cdot 2 k \cdot(2 k+1)+(2 k+1) \cdot((2 k+2 k) \cdot(4 k+3)-2 k \cdot(4 k+1))= \\
=(2 k+1) \cdot\left(4 k^{2}-2 k+8 k^{2}+14 k+6-8 k^{2}-2 k\right)=(2 k+1) \cdot\left(4 k^{2}+10 k+6\right) \\
=\quad=(2 k+1) \cdot(2 k+2) \cdot(2 k+3), \text { the statement is proved. }
\end{gathered}
$$
Therefore,
\( 1 \cdot 2 \cdot(1+2)-2 \cdot 3 \cdot(2+3)+3 \cdot 4 \cdot(3+4)-\cdots+2019 \cdot 2020 \cdot(2019+2020)=2019 \cdot 2020 \cdot \) \( 2021=2020^{3}-2020=8000 \cdot 101^{3}-2020=8000 \cdot 1030301-2020=8242408000-2020= \) 8242405980.
Answer: 8242405980.
| Criterion Content | Points |
| :--- | :---: |
| The correct answer is obtained with justification. | 20 |
| There is an arithmetic error or the solution is insufficiently justified in an otherwise correct and justified solution. | 14 |
| The beginning of a possible solution is provided, some intermediate results are obtained (but the formula for \( (2 n-1) \cdot 2 n \cdot(2 n+1) \) is not proved), further solution is incorrect or missing. | 6 |
| The solution does not meet any of the criteria listed above. | 0 |
| Maximum score | 20 |
## Solution for Variant 7
|
8242405980
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (15 points) The area of an isosceles trapezoid is 100, and its diagonals are perpendicular to each other. Find the height of this trapezoid.
|
Solution. Let $ABCD$ be an isosceles trapezoid, the diagonals $AC$ and $BD$ of which are perpendicular to each other. Denote $O = AC \cap BD$, point $M$ is the midpoint of $BC$, and point $H$ is the midpoint of $AD$. Draw the segment $MH: O \in MH, MH \perp AD$. Since $MH$ is the axis of symmetry of the given trapezoid, then $OB = OC, OA = OD$. Therefore, the right triangles $BOC$ and $AOD$ are isosceles, meaning $\angle OBM = \angle OAH = 45^\circ$. Then the right triangles $MOB$ and $AOH$ are also isosceles: $OM = BM, OH = AH$.
We have:
$OM = BM = 0.5 BC, OH = AH = 0.5 AD \Rightarrow MH = OM + OH = 0.5 BC + 0.5 AD = 0.5(BC + AD)$, which means the height $MH$ of the trapezoid is equal to its midline. This means that for the area of the given trapezoid we get: $S_{ABCD} = 0.5(BC + AD) MH = MH \cdot MH = MH^2$. Then $MH = \sqrt{S_{ABCD}} = \sqrt{100} = 10$.
Answer: 10.
| Criterion Content | Points |
| ---: | :---: |
| The correct answer is obtained with justification. | 15 |
| The solution contains a computational error, possibly leading to an incorrect answer, but the solution has a correct sequence of all steps. | 10 |
| In the solution of the problem, one or two formulas are correctly written, which are the beginning of a possible solution. | 5 |
| The solution does not meet any of the criteria described above. | 0 |
| Maximum score | 15 |
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find all values of the parameter $a$ for which the equation
$$
\left(\left|\frac{a x^{2}-a x-12 a+x^{2}+x+12}{a x+3 a-x-3}\right|-a\right) \cdot|4 a-3 x-19|=0
$$
has one solution. In your answer, write the largest value of the parameter $a$
|
Solution:
Simplify $\frac{a x^{2}-a x-12 a+x^{2}+x+12}{a x+3 a-x-3}=\frac{a x^{2}-x^{2}+(-a x+x)+(-12 a+12)}{a(x+3)-(x+3)}=$
$=\frac{x^{2}(a-1)-x(a-1)-12(a-1)}{(x+3)(a-1)}=\frac{(a-1)\left(x^{2}-x-12\right)}{(x+3)(a-1)}=$
$=\frac{x^{2}+3 x-4 x-12}{x+3}=\frac{(x+3)(x-4)}{x+3}=x-4$
We get $\left\{\begin{array}{c}(|x-4|-a) \cdot|4 a+3 x-19|=0 \\ a \neq 1 \\ x \neq-3\end{array} ;\left\{\begin{array}{c}{\left[\begin{array}{c}|x-4|-a=0 \\ 4 a+3 x-19=0 \\ a \neq 1 \\ x \neq-3\end{array} ;\right.} \\ \text {; }\end{array}\right.\right.$
$$
\left\{\begin{array}{c}
a=|x-4| \\
a=-0.75 x+4.75 \\
\quad a \neq 1 \\
x \neq-3
\end{array}\right.
$$
Construct the graph in the coordinate system $\chi O a$ $a=-0.75 x+4.75-$ line
| $x$ | -3 | 5 |
| :--- | :--- | :--- |
| $y$ | 7 | 1 |
$a=|x-4|$ the graph is obtained from $a=|x|$ by shifting 4 units to the right
Since $x \neq-3$, then $a \neq 7$
$a \neq 1$, then $x \neq 3 ; x \neq 5$
Points $(-3 ; 7) ;(3 ; 1) ;(5 ; 1)$ - are excluded
For $a \in(-\infty ; 0) \cup\{7\}$ - one solution
For $a \in(0 ; 1) \cup(1 ; 7) \cup(7 ;+\infty)$ - three solutions
For $a=0$ two solutions
For $a=1$ no solutions
Answer: 7
## №3: Triangles.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. When adding two natural numbers, Alyosha accidentally added an extra digit, so instead of the number 23456, he got the number 55555.
Determine which digit Alyosha accidentally added.
## solution.
Let Alyosha be adding numbers $x$ and $y$. When he appended an extra digit $a$ to one of them (let's say to $x$), the number became $10x + a$. We get the system of equations: $\left\{\begin{array}{c}x + y = 23456; \\ (10x + a) + y = 55555\end{array}9x + a = 320999x = 32099 - a \\ a = 5 \\ 9x = 32094$
$x = 3566 \quad y = 19890$. Answer: 5;
## №5: Percentages.
A flask is filled with a 96% hydrochloric acid solution. From it, 12 liters of acid were poured out and the flask was topped up with water. Then, 18 liters were poured out again and the flask was topped up with water, after which the concentration of acid in the flask was 32%. Find the volume of the flask.
|
Answer: 36 liters
## №6: Plane Geometry.
№2. From points B and C of the acute angle BAC, perpendiculars CM and BK are drawn, intersecting at point E, such that point M lies on AB, and K lies on AC. A circle is drawn through points A, M, and C, intersecting BK at point O, and $BE=17, OK=72$. AK: $KC=1:4$. Find the tangent of angle BAC. (the ratio of BK to AK).
## Solution.
1) Let $\mathrm{OE}=x=\succ \mathrm{BO}=\mathrm{BE}-\mathrm{OE}=17=x$ and $\mathrm{BK}=\mathrm{BO}+\mathrm{OK}=17-x+72=89-x$.
2) $\mathrm{BK} \perp \mathrm{AC}=\succ \mathrm{KO}=\mathrm{KH}=72=\succ \mathrm{BH}=\mathrm{BO}+\mathrm{OH}=17-x+144=161-x$.
3) $\triangle \mathrm{ABK} \sim \triangle \mathrm{EMB} \Rightarrow \succ \mathrm{BM} / \mathrm{BK}=\mathrm{BE} / \mathrm{AB}=\succ \mathrm{BM} \cdot \mathrm{AB}=\mathrm{BK} \cdot \mathrm{BE}$.
4) $\mathrm{BA}$ and $\mathrm{BE}-$ secants $=\succ \mathrm{BM} \cdot \mathrm{AB}=\mathrm{BO} \cdot \mathrm{BH}$.
5) From (3 and 4) $\Rightarrow \succ \mathrm{BO} \cdot \mathrm{BH}=\mathrm{BK} \cdot \mathrm{BE}=\succ \quad(17-x)(161-x)=(89-x) 17=\succ x^{2}-$ $161 x+1224=0=\succ x=8$ or $x=153=\succ \mathrm{OE}=8 ; \mathrm{BO}=9 ; \mathrm{BK}=81$.
6) $\mathrm{AK} \cdot \mathrm{KC}=K \mathrm{KO} \cdot \mathrm{H}=\succ 4 \mathrm{AK}^{2}=72^{2} \Rightarrow \succ \mathrm{AK}=36=\succ \mathrm{BK} / \mathrm{AK}=81 / 36=2.25$.
Answer: 2.25.
## №7: Number Theory.
Find the smallest natural $\mathrm{n}$, for which $1999!$ does not divide $34^{\mathrm{n}}$. (n!=1$\cdot$2$\cdot$3$\cdot$... $\mathrm{n}$)
## Solution:
$34=2 \cdot 17$. Determine the power to which the number 17 will enter the factorization of 1999! (2 will obviously enter this factorization in a higher power). $117<\frac{1999}{17}<118 ; 6<\frac{1999}{17^{2}}<7$ from this, 17 enters $1999!$ 123 times, and to not divide, we add one more.
Answer: 124
## №8: Parameter.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Determine for which $a$ the system $x+y-144=0, xy-5184-0.1a^2=0$ has one solution. Answer: 0.
Solution. $\left\{\begin{array}{c}x+y=144 \\ xy=5184+0.1a^2\end{array}\right.$
This means that $x$ and $y$ are equal to the roots of the quadratic equation
$p^2 - 144p + (5184 + 0.1a^2) = 0$. Therefore, $D = 72^2 - (5184 + 0.1a^2) = -0.1a^2$.
Thus, the equation can have a solution only when $a = 0$. $p = 72$, so $x = y = 72$. Answer: 0.
## №9: Divisibility.
Find the smallest number among the natural numbers exceeding 2022 that divides the number $2021!! + 2022!!$. (The symbol $n!!$ denotes the product of all natural numbers not exceeding $n$ and having the same parity: $n!! = n \cdot (n-2) \cdot (n-4) \ldots$)
|
Answer. 2023.
## Solution.
We will prove that $2021!! + 2022!!$ is divisible by the number 2023. Indeed,
$$
2022!! = (2023-1)(2023-3)(2023-5) \ldots (2023-2021)
$$
the remainder of this number when divided by 2023 is the same as the remainder of the product
$$
(-1)(-3)(-5) \ldots (-2021) = (-1)^{\frac{2022}{2}} \cdot 2021!! = -2021!!
$$
when divided by 2023. Therefore, $2021!! + 2022!!$ is divisible by the number 2023. Since 2023 is the smallest number among natural numbers greater than 2022, we get the answer.
Answer. 2023.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Variant №1
№1. The number of male students in the university is $35 \%$ more than the number of female students. All students are distributed between two buildings, with $\frac{2}{5}$ of all male students in the first building and $\frac{4}{7}$ of all female students in the second building. How many students are there in total in the university, if it is known that fewer than 2500 students are in the first building, and more than 2500 students are in the second building?
|
# Solution:
Let $n$ be the number of girls studying at the university, then the number of boys is $1.35 n = \frac{27}{20} n$, from which we can conclude that $n$ is a multiple of 20, i.e., $n = 20 m$.
Thus, the number of girls is $20 m$, and the number of boys is $27 m$.
In the first building, $\frac{2}{5}$ of all boys study, i.e., $\frac{2}{5} \cdot 27 m = \frac{54}{5} m$ students, and in the second building, $\frac{4}{7}$ of all girls study, i.e., $\frac{4}{7} \cdot 20 m = \frac{80}{7} m$ students. For the condition of integrality to be satisfied, the number $m$ must be a multiple of 35, i.e., $m = 35 k$.
Then in the first building, $\frac{2}{5} \cdot 27 m = \frac{54}{5} m = \frac{54}{5} \cdot 35 k = 378 k$ students, $\frac{3}{7} \cdot 20 m = \frac{60}{7} m = \frac{60}{7} \cdot 35 k = 300 k$ students, and a total of $678 k$ people, and in the second building, $\frac{3}{5} \cdot 27 m = \frac{81}{5} m = \frac{81}{5} \cdot 35 k = 567 k$ students, $\frac{4}{7} \cdot 20 m = \frac{80}{7} m = \frac{80}{7} \cdot 35 k = 400 k$ students, and a total of $967 k$ people.
By the condition of the problem $\left\{\begin{array}{l}678 k < 2500 \\ 967 k > 2500\end{array} \Leftrightarrow\left\{\begin{array}{l}k < \frac{2500}{678} \\ k > \frac{2500}{967}\end{array}\right.\right.$, hence, $k = 3$, and
the total number of students is $678 k + 967 k = 1645 k = 4935$.
Answer: 4935.
## Criteria
| Points | Criteria for awarding points |
| :---: | :---: |
| 10 | Complete solution. The correct answer is justified. |
| 5 | The problem model is correctly formulated and there are some advances in the solution. |
| 0 | The solution does not meet any of the above criteria. |
#2. In triangle $\mathrm{ABC}$, angle C is a right angle. Line MK is perpendicular to the median CM and intersects AC at point K. It is known that CK: KA = 5: 3. Point O is the center of the circle circumscribed around triangle MAK. Find the area of triangle OBC if $\mathrm{BC}=4$.
## Solution.
By the property of the median of a right triangle, $\mathrm{CM}=\mathrm{BM}=\mathrm{AM}=x$. Let $CK=k$, KA $=n$. Triangles $\mathrm{ABC}$ and CKM are right and similar by the acute angle $\angle M A C = \angle M C A$ (MCA is isosceles). Therefore, $x: k = (k+n): 2x$ or $x = \sqrt{\frac{k(k+n)}{2}}$.
By the Law of Sines for triangle MAK, we get: $2 R = \frac{M K}{\sin \angle M A C} = \frac{M K}{\sin \angle M C A} = C K$, i.e., the radii of the circles circumscribed around triangles MAK and CMK with centers at points O and N, respectively, are equal. Since MK is a common chord of equal circles, $N O$ is the perpendicular bisector of it and $N O = \sqrt{4 R^{2} - M K^{2}} = \sqrt{k^{2} - C K^{2} + C M^{2}} = C M$.
By the condition of the problem, $\mathrm{CM} \perp \mathrm{MK} \Rightarrow \mathrm{CM} \| \mathrm{ON} \Rightarrow C M O N$ is a parallelogram, i.e., $\mathrm{OM} = \mathrm{CN} = k / 2, \mathrm{C} N \| \mathrm{OM} \Rightarrow \mathrm{OM} \perp B C$. Therefore, OH is the height of triangle OBC and
$\mathrm{OH} = \mathrm{OM} + \mathrm{MH} = \mathrm{OM} + \frac{A C}{2} = R + \frac{k+n}{2} = \frac{k}{2} + \frac{k+n}{2} = k + \frac{n}{2}$.
By the condition $k: n = 5: 3 \Rightarrow 0 \mathrm{H} = 1.3 k$. From the original triangle, by the Pythagorean Theorem $(\mathrm{BC}=4, \mathrm{AC}=1.6 k, A B=2 x=4 k \sqrt{0.2}): 16 + 2.26 k^{2} = 3.2 k^{2} \Rightarrow k^{2} = 25 \Rightarrow k = 5$.
$$
S_{B O C} = \frac{1}{2} \cdot 4 \cdot 1.3 \cdot 5 = 13
$$
Answer: 13.
## Criteria
| Points | Criteria for awarding points |
| :---: | :---: |
| 10 | Complete solution. The correct answer is justified. |
| 5 | It is proved that CMON is a parallelogram. |
| 0 | The solution does not meet any of the above criteria. |
#3. For what values of the parameter $a$ does there
|
4935
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given the vertices of a regular 100-gon $A_{1}, A_{2}, A_{3}, \ldots, A_{100}$. In how many ways can three vertices be chosen from them to form an obtuse triangle? (10 points)
|
Solution. Let the vertices be numbered clockwise.
Denote the selected vertices clockwise as $K, L, M$, where angle $K L M$ is obtuse. If $K=A_{k}, L=A_{l}, M=A_{m}$, then $\alpha=\angle K L M=\frac{180^{\circ}}{100}(100-(m-k))>90^{\circ}, 0<m-k<50$.
The difference $m-k$ is taken modulo 100
(for example, $15-\left.70\right|_{\bmod 100}=45$ ).
Let's count the number of ways to choose vertices $K, L, M$. First, choose vertex $K$ in one of 100 ways. Then choose any two of the vertices $A_{k+1}, A_{k+2}, \ldots, A_{k+49}$ (vertex numbers are taken modulo 100). The closer of these vertices to $K$ will be $L$, and the farther one will be $M$. Thus, we have $100 \cdot \mathrm{C}_{49}^{2}=100 \cdot 49 \cdot 24=117600$.
Answer: 117600.
|
117600
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given the vertices of a regular 120-gon $A_{1}, A_{2}, A_{3}, \ldots, A_{120}$. In how many ways can three vertices be chosen from them to form an obtuse triangle? (10 points)
|
Solution. Let the vertices be numbered clockwise.
Denote the selected vertices clockwise as $K, L, M$, where angle $K L M$ is obtuse. If $K=A_{k}, L=A_{l}, M=A_{m}$, then $\alpha=\angle K L M=\frac{180^{\circ}}{120}(120-(m-k))>90^{\circ}, 0<m-k<60$.
The difference $m-k$ is taken modulo 120
(for example, $15-\left.90\right|_{\text {mod } 120}=45$ ).
Let's count the number of ways to choose vertices $K, L, M$.
First, choose vertex $K$ in one of 120 ways. Then choose any two of the vertices $A_{k+1}, A_{k+2}, \ldots, A_{k+59}$ (vertex numbers are taken modulo 120). The closer of these vertices to $K$ will be $L$, and the farther one will be $M$. Thus, we have $120 \cdot$ C $_{59}^{2}=120 \cdot 59 \cdot 29=205320$.
## Answer: 205320.
|
205320
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The sequence of real numbers $a_{1}, a_{2}, a_{3}, \ldots, a_{100}$ satisfies the inequalities $a_{n}-2022 a_{n+1}+2021 a_{n+2} \geq 0 \quad$ for $\quad n=1,2,3, \ldots, 98$, and $\quad a_{99}-2022 a_{100}+2021 a_{1} \geq 0$, $a_{100}-2022 a_{1}+2021 a_{2} \geq 0$. Find $a_{22}$, if $a_{10}=10$. (10 points)
|
# Solution.
Let $b=a_{1}+a_{2}+a_{3}+\cdots+a_{100}, b_{n}=a_{n}-2022 a_{n+1}+2021 a_{n+2}, n=1,2,3, \ldots, 98$, $b_{99}=a_{99}-2022 a_{100}+2021 a_{1}, b_{100}=a_{100}-2022 a_{1}+2021 a_{2}$. By the condition $b_{n} \geq 0$, for $n=$ $1,2,3, \ldots, 100$. We have $b_{1}+b_{2}+b_{3}+\cdots+b_{100}=b-2022 b+2021 b=0 . \quad$ Therefore, $b_{n}=0$, for $n=1,2,3, \ldots, 100$. From this, we get $\left(a_{n}-a_{n+1}\right)+2021\left(a_{n+2}-a_{n+1}\right)=0, n=$ $1,2,3, \ldots, 98, a_{99}-a_{100}+2021\left(a_{1}-a_{100}\right)=0,\left(a_{100}-a_{1}\right)+2021\left(a_{2}-a_{1}\right)=0$.
We have $a_{2}-a_{3}=\frac{a_{1}-a_{2}}{2021}, \quad a_{3}-a_{4}=\frac{a_{1}-a_{2}}{2021^{2^{2}}}, \ldots, a_{99}-a_{100}=\frac{a_{1}-a_{2}}{2021^{1^{8}}}, a_{100}-a_{1}=\frac{a_{1}-a_{2}}{2021^{1^{9}}}$. Considering the equality $a_{100}-a_{1}=2021\left(a_{1}-a_{2}\right)$, we have $\frac{a_{1}-a_{2}}{2021^{99}}=2021\left(a_{1}-a_{2}\right)$. From this, we get $a_{n}=a_{1}$ for all $n=1,2,3, \ldots, 100$. Therefore, $a_{22}=a_{10}=10$.
## Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. There are two types of containers: 27 kg and 65 kg. How many containers of the first and second type were there in total, if the cargo in the first type of containers exceeds the cargo in the second type of containers by 34 kg, and the number of 65 kg containers does not exceed 44 units?
|
Solution. Let $x$ be the number of containers weighing 27 kg, and $y$ be the number of containers weighing 65 kg. We obtain the equation $27 x - 65 y = 34$.
$27(x - 2y) - 11y = 34$, let $x - 2y = k$.
$27k - 11y = 34$,
$11(2k - y) + 5k = 34$, let $2k - y = t$.
$11t + 5k = 34$,
$5(2t + k) + t = 34$, let $2t + k = n$.
$5n + t = 34, t = 34 - 5n$.
Substitute into (3), $k = 11n - 68$.
Substitute into (2), $y = 27n - 170$.
Substitute into (1), $x = 65n - 408$.
Since $x > 0, 0 < y \leq 44$, then $n = 7$. Therefore, $x = 47, y = 19$ or 47 and 19 containers, a total of 66 containers.
Answer: 66.
|
66
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In triangle $A B C$ with angle $\angle B=120^{\circ}$, the angle bisectors $A A_{1}, B B_{1}, C C_{1}$ are drawn. Find the degree measure of angle $C_{1} B_{1} A_{1}$.
|
# Solution.
Extend side $A B$ beyond point $B$, then $B C$ is the bisector of angle $\angle B B_{1} B K$, which means point $A_{1}$ is equidistant from sides $B_{1} B$ and $B K$. Considering that point $A_{1}$ lies on the bisector of $\angle B A C$, and is therefore equidistant from its sides, we get that $A_{1}$ is equidistant from sides $B_{1} B$ and $B_{1} C$, and thus lies on the bisector of $\angle B B_{1} C$. Therefore, $B_{1} A_{1}$ is the bisector of $\angle B B_{1} C$.
Similarly, we prove that $B_{1} C_{1}$ is the bisector of $\angle A B_{1} B$. Therefore, $\angle C_{1} B_{1} A_{1}=90^{0}$, as the angle between the bisectors of adjacent angles.
Answer: 90.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Given a rectangular trapezoid $\mathrm{ABCE}$, the bases of which $\mathrm{BC}$ and $\mathrm{AE}$ are equal to 5 and 7, respectively. The smaller lateral side $\mathrm{AB}$ is equal to $\mathrm{BC}$. On $\mathrm{AB}$, a point $\mathrm{F}$ is marked such that $\mathrm{BF}: \mathrm{FA}=2: 3$, on $\mathrm{AC}$, a point $\mathrm{G}$ is marked such that $\mathrm{AG}: \mathrm{GC}=4: 1$; on $\mathrm{AE}$, a point $\mathrm{D}$ is marked such that $\mathrm{AD}: \mathrm{DE}=5: 2$. Determine the degree measure of angle DFG.
|
Solution. Construct perpendiculars GI and GH.
1) $\Delta G I D = \Delta G F H$ - by two legs, since $G I = G H = 4; F H = I D = 1$, therefore $F G = G D$, $\angle F G H = \angle D G I = \alpha$.
2) $G I A H$ is a square, so $\angle I G H = 90^{\circ}, \angle I G H = \angle F G H + \angle I G F = \alpha + \angle I G F$.
3) $\angle D G F = \angle D G I + \angle I G F = \alpha + \angle I G F = 90^{\circ}$.
4) $\triangle D F G$ is a right isosceles triangle, since $F G = G D$, and thus $\angle D F G = 45^{\circ}$.
Answer: 45.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. A chemistry student conducted an experiment: from a tank filled with syrup solution, he poured out several liters of liquid, refilled the tank with water, then poured out twice as much liquid and refilled the tank with water again. As a result, the amount of syrup in the tank decreased by $\frac{8}{3}$ times. Determine how many liters of liquid the student poured out the first time, if the tank's volume is 1000 liters.
#
|
# Solution.
1) Let the syrup content in the original solution be $p \%$ and let $\mathcal{X}$ liters of the solution be poured out the first time.
2) Then after pouring out the liquid, there are $(1000-x)$ liters of solution left, and in it $(1000-x) \cdot \frac{p}{100}$ liters of syrup and $(1000-x) \cdot \frac{100-p}{100}$ water.
3) After adding $X$ liters of water, there are 1000 liters of solution in the tank, and in it $(1000-x) \cdot \frac{p}{100}$ liters of syrup and $(1000-x) \cdot \frac{100-p}{100}+x$ liters of water.
4) At the end of all the pouring, there are 1000 liters of solution in the tank with a syrup content of $\frac{3 p}{8} \%$, which is $1000 \cdot \frac{\frac{3 p}{8}}{100}=\frac{30 p}{8}$ liters of syrup and $1000-\frac{30 p}{8}$ liters of water.
5) Then before the last addition of $2 x$ liters of water, there were $(1000-2 x)$ liters of solution in the tank, and in it $\frac{30 p}{8}$ liters of syrup and $1000-\frac{30 p}{8}-2 x$ water. This is the same liquid as in point 3) of the solution, so the ratio of syrup to liquid in it is the same.
We can set up the equation:
$$
\frac{(1000-x) \cdot \frac{p}{100}}{1000}=\frac{\frac{30 p}{8}}{1000-2 x} \Leftrightarrow 2 x^{2}-3000 x+\frac{5}{8} \cdot 1000^{2}=0 \Leftrightarrow
$$
$\Leftrightarrow x \in\{1250 ; 250\}, 1250$ liters does not satisfy the condition of the problem.
Answer: 250.
## Solution variant № 2
1. If a two-digit natural number is decreased by 27, the result is a two-digit number with the same digits but in reverse order. In the answer, indicate the median of the numerical sequence formed from all such numbers.
## Solution.
Let $\overline{x y}=10 x+y$ be the original two-digit number, and $\overline{y x}=10 y+x$ be the number with the digits in reverse order. We get the equation $10 x+y=10 y+x+27$. From the equation, it is clear that the two-digit number is greater than 27. Let's start the investigation with the tens digit equal to 3.
| $\boldsymbol{x}$ | equation | $\boldsymbol{y}$ | number |
| :--- | :--- | :---: | :--- |
| 3 | $30+y=10 y+3+27$ | $y=0$ | 30 does not fit the condition |
| 4 | $40+y=10 y+4+27$ | $y=1$ | 41 |
| 5 | $50+y=10 y+5+27$ | $y=2$ | 52 |
| 6 | $60+y=10 y+6+27$ | $y=3$ | 63 |
| 7 | $70+y=10 y+7+27$ | $y=4$ | 74 |
| 8 | $80+y=10 y+8+27$ | $y=5$ | 85 |
| 9 | $90+y=10 y+9+27$ | $y=6$ | 96 |
These can be the numbers $41,52,63,74,85,96$. The median of the sequence is 68.5.
Answer: 68.5.
|
250
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. During the shooting practice, each soldier fired 10 times. One of them completed the task successfully and scored 90 points. How many times did he score 8 points, if there were 4 tens, and the results of the hits were sevens, eights, and nines. There were no misses at all.
|
Solution. Since the soldier scored 90 points and 40 of them were scored in 4 attempts, he scored 50 points with the remaining 6 shots. Since the soldier only hit the seven, eight, and nine, let's assume that for three shots (once in the seven, once in the eight, and once in the nine), he scored 24 points. Then, for the remaining three shots, he scored 26 points, which is only possible with the unique combination of the numbers $7, 8, 9: 8+9+9=26$. Therefore, the shooter hit the seven once, the eight twice, and the nine three times.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The grandmother and granddaughter were picking strawberries. The granddaughter was using a children's bucket with a capacity of 2.5 liters, while the grandmother was using a two-liter jar. The grandmother had poor eyesight and found it hard to bend down, so the granddaughter was always picking berries faster than her. When the grandmother had filled half of her jar, they switched their containers and, after some time, filled them simultaneously. How many liters of berries did the granddaughter collect in total, assuming that the work efficiency of both the grandmother and the granddaughter remained constant throughout?
|
Solution. Let the granddaughter collect $X$ liters of berries in the time it takes the grandmother to collect 1 liter, $x>1$ according to the problem. After swapping containers, the granddaughter collected 1 liter of berries, while the grandmother collected $(2.5-x)$ liters. Since their work efficiency does not change, the ratio of the amount of berries collected remains constant.
We can set up the equation: $\frac{1}{x}=\frac{2.5-x}{1} ; 2 x^{2}-5 x+2=0$, which has two roots $x_{1}=2, x_{2}=0.5$. The second root does not fit the problem's conditions. In total, the granddaughter collected $2+1=3$ liters of berries.
Answer: 3.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Elvira takes a triplet of numbers and transforms it according to the rule: at each step, each number is replaced by the sum of the other two. What is the difference between the largest and the smallest numbers in the triplet after 2019 applications of this rule, if the initial triplet was $\{100 ; 89 ; 60\}$? If the question allows multiple answers, write them without spaces in ascending order.
|
Solution. Let's denote the 3 numbers as $\{x ; x+a ; x+b\}$, where $0<a<b$. Then the difference between the largest and the smallest number at any step, starting from the zeroth step, will be an invariant, that is, unchanged and equal to $b$.
$b=100-60=40$.
Answer: 40.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On the sides $\mathrm{AB}$ and $\mathrm{AC}$ of the right triangle $\mathrm{ABC}\left(\angle B A C=90^{\circ}\right)$, right triangles АВТ and АСК are constructed externally such that $\angle A T B=\angle A K C=90^{\circ}$, $\angle A B T=\angle A C K=30^{\circ}$. On the side $\mathrm{BC}$, a point М is chosen such that $\mathrm{BM}=\mathrm{MC}$. Determine the degree measure of angle КМТ.
|
Solution. Mark points P and O at the midpoints of sides AB and AC, respectively. Connect point P with points M and T, and point O with points K and M.
Then: 1) $\triangle T P M = \Delta K O M$, by two sides and the angle between them, since
$$
\begin{gathered}
A O = \frac{1}{2} A C = K O = P M \\
A P = \frac{1}{2} A B = T P = O M \\
\angle T P M = \angle T P A + \angle A P M = \angle A O K + \angle A O M = \angle K O M
\end{gathered}
$$
Thus, TM = MK, $\angle P M T = \angle M K O$, and $\angle P T M = \angle K M O$.
2) Find the sum of angles $\angle P M T$ and $\angle K M O$:
$$
\angle P M T + \angle K M O = \angle M K O + \angle K M O = 180^{\circ} - \angle M O K.
$$
In turn, $\angle M O K = 360^{\circ} - \angle K O C - \angle M O C = 360^{\circ} - 120^{\circ} - \angle B A C = 240^{\circ} - \angle B A C$. 3) $\angle K M T = \angle P M O - (\angle P M T + \angle K M O) = \angle B A C - (180^{\circ} - \angle M O K) = \angle K M T = \angle B A C - 180^{\circ} + 240^{\circ} - \angle B A C = 60^{\circ}$.
Answer: 60.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. A chemistry student conducted an experiment: from a bottle filled with syrup solution, he poured out one liter of liquid, refilled the bottle with water, then poured out one liter of liquid again and refilled the bottle with water. As a result, the percentage of syrup decreased from 9 to 4 percent. Determine the volume of the bottle in liters.
|
# Solution.
1) Let $X$ be the volume of the bottle in liters.
2) Then after pouring out one liter of liquid, there are $(x-1)$ liters of solution left, and in it $(x-1) \cdot \frac{9}{100}$ liters of syrup and $(x-1) \cdot \frac{91}{100}$ liters of water.
3) After adding one liter of water to the bottle, there are $X$ liters of solution, and in it $(x-1) \cdot \frac{9}{100}$ liters of syrup and $(x-1) \cdot \frac{91}{100}+1$ liters of water.
4) At the end of all the pouring, there are $X$ liters of solution in the bottle, and in it $x \cdot \frac{4}{100}$ liters of syrup and $x \cdot \frac{96}{100}$ liters of water.
5) Then before the last addition of one liter of water, there were $(x-1)$ liters of solution in the bottle, and in it $x \cdot \frac{4}{100}$ liters of syrup and $x \cdot \frac{96}{100}-1$ liters of water. This is the same liquid as in point 3) of the solution, so the ratio of syrup to water in it is the same.
We can set up the equation:
$$
\begin{aligned}
& \frac{(x-1) \cdot \frac{9}{100}}{x \cdot \frac{4}{100}}=\frac{(x-1) \cdot \frac{91}{100}+1}{x \cdot \frac{96}{100}-1} \Leftrightarrow \frac{(x-1) \cdot 9}{x \cdot 4}=\frac{(x-1) \cdot 91+100}{x \cdot 96-100} \Leftrightarrow \\
& \frac{9 x-9}{4 x}=\frac{91 x+9}{96 x-100} \Leftrightarrow(9 x-9)(96 x-100)=4 x(91 x+9) \Leftrightarrow \\
& 5 x^{2}-18 x+9=0 \Leftrightarrow x \in\{3 ; 0.6\}
\end{aligned}
$$
0.6 liters does not satisfy the condition of the problem.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In triangle $\mathrm{ABC}$, angle $\mathrm{C}$ is a right angle, and $\mathrm{CD}$ is the altitude. Find the length of the radius of the circle inscribed in triangle $\mathrm{ABC}$, if the lengths of the radii of the circles inscribed in triangles $\mathrm{ACD}$ and $\mathrm{BCD}$ are 6 and 8, respectively.
|
Answer: 10
## №4: Progression.
The numbers $5 \mathrm{x}-\mathrm{y} ; 2 \mathrm{x}+3 \mathrm{y} ; \mathrm{x}+2 \mathrm{y}$ are consecutive terms of an arithmetic progression. The numbers $(\mathrm{y}+1)^{2} ; \mathrm{xy}+1 ;(\mathrm{x}-1)^{2}$ are consecutive terms of a geometric progression. Find the numbers x and y. If there are multiple values, write the negative sum $x+y$ rounded to the nearest integer in the answer.
## Answer: -1
## №5: Percentages.
A flask is completely filled with a 96% hydrochloric acid solution (by volume). From it, 12 liters of the solution were poured out, the flask was topped up to the brim with water and mixed. Then, 18 liters of the resulting solution were poured out again, the flask was topped up to the brim with water and mixed. After this, the concentration of acid in the flask was 32%. Find the volume of the flask (in liters)?
Answer: 36
## №6: Set
Solve the equation $\frac{\sqrt{x+3.3}+\sqrt{x+11.3}+\sqrt{x+27.3}}{\sqrt{x+2.3}+\sqrt{x+6.3}+\sqrt{x+18.3}}=\frac{3}{2}$. In the answer, specify the root or the sum of the roots if there are several.
## Solution:
$$
\begin{aligned}
& \text { Rewrite } \quad \text { the equation } \\
& 2(\sqrt{x+3.3}+\sqrt{x+11.3}+\sqrt{x+27.3})=3(\sqrt{x+2.3}+\sqrt{x+6.3}+\sqrt{x+18.3}) \text {, and then in } \\
& \text { the form } \\
& 2(\sqrt{x+3.3}-\sqrt{x+2.3}+\sqrt{x+11.3}-\sqrt{x+6.3}+\sqrt{x+27.3}-\sqrt{x+18.3})=\sqrt{x+2.3}+\sqrt{x+6.3}+\sqrt{x+18.3}
\end{aligned}
$$
Let the left side of the equation be $f(x)$, and the right side be $g(x)$. $g(x)$ is monotonically increasing on the interval $[-2.3 ;+\infty)$ as the sum of three increasing functions. Transform the left side - $f(x)$. $f(x)=2\left(\frac{1}{\sqrt{x+3.3}+\sqrt{x+2.3}}+\frac{5}{\sqrt{x+11.3}+\sqrt{x+6.3}}+\frac{9}{\sqrt{x+27.3}+\sqrt{x+18.3}}\right)$.
$f(x)$ is monotonically decreasing on $[-2.3 ;+\infty)$ as the sum of monotonically decreasing functions. Therefore, the equation $f(x)=g(x)$ has no more than one root. Notice that $f(-2.3)=g(-2.3)$, so $x=-2.3$ is the only root of the equation.
Answer: $-2.3$
## №7: Circles.
In triangle $A B C$, the height $B H$ is drawn. A circle with its center lying on the height $B H$ passes through the vertices of the triangle $B, C$ and intersects the side $A B$ at point $E$. Find the length of the segment $A E$, if $A B=8, B C=6$.
## Solution:
Let the line $B H$ and the circle intersect at point $D$. Right triangles $B H A$ and $B E D$ are similar ( $\angle B$ is common), $\angle B C E=\angle B D E$ (as inscribed angles subtending the same arc), therefore, $\angle B A C=\angle B D E=\angle B C E$. Next, triangles $C B E$ and $A B C$ are similar (by two angles: $\angle B$ is common, $\angle B A C=\angle B C E)$.
From the equality of the ratios of corresponding sides, we find:
$$
\frac{B E}{B C}=\frac{B C}{A B^{\prime}}, B E=\frac{B C^{2}}{A B}=\frac{36}{8}=4.5
$$
Therefore, $A E=8-4.5=3.5$.
Answer: 3.5
## №8: Parameter.
Find all values of the parameter $a$ for which the equation $a^{2}+13|x-1|+3 \sqrt{4 x^{2}-8 x+13}=3 a+3|4 x-3 a-4|$ has at least one root. In the answer, specify the sum of all integer values of the parameter that satisfy the condition of the problem.
## Solution:
Rewrite the equation as $a^{2}-3 a+3 \sqrt{(2 x-2)^{2}+9}=3|4 x-3 a-4|-13|x-1|$ and consider the functions $f(x)=a^{2}-3 a+3 \sqrt{(2 x-2)^{2}+9}$ and $g(x)=3|4 x-3 a-4|-13|x-1|$, defined and continuous on the set of real numbers. The graph of the function $y=g(x)$ represents a piecewise-linear function consisting of segments of lines and rays. For $x \geq 1$ each segment of the graph is part of a line of the form $y=k x+b$, where $k<0$ (since for any expansion of the first modulus, the coefficient of $x$ will be negative). Therefore, on the interval $[1 ;+\infty)$ the function $y=g(x)$ decreases from $g(0)$ to $-\infty$. Similarly, it can be shown that on the interval $(-\infty ; 1]$ the function $g(x)$ increases from $-\infty$ to $g(0)$. Therefore, at the point $x=1$ this function reaches its maximum value. $g_{\text {max. }}=g(1)=3|3 a|=9|a|$.
Based on the properties of monotonic functions, the function $f(x)$ takes its minimum value at $x=1 . f_{\text {min. }}=f(1)=a^{2}-3 a+9$. On $[1 ;+\infty) f(x)$ increases from $f(0)$ to $+\infty$, and on the interval $(-\infty ; 0]$ it decreases from $+\infty$ to $f(0)$.
Therefore, the equation $f(x)=g(x)$ has at least one root only when $f_{\text {min. }} \leq g_{\text {max., }}$, that is, when the inequality $a^{2}-3 a+9 \leq 9|a|$ is satisfied. For $a \geq 0 \quad$ we get $a^{2}-3 a+9 \leq 9 a ; a^{2}-12 a+9 \leq 0 ; \frac{D}{4}=36-9=27$; $a_{1,2}=6 \pm 3 \sqrt{3} ; \quad a \in[6-3 \sqrt{3} ; 6+3 \sqrt{3}] . \quad$ For $\quad a<0 \quad$ we have $a^{2}+6 a+9 \leq 0 ;(a+3)^{2} \leq 0 ; a=-3$. Thus, the equation has at least one root for $a \in\{-3\} \cup[6-3 \sqrt{3} ; 6+3 \sqrt{3}]$. Estimate between which integers the boundaries of the interval lie: $0<6-3 \sqrt{3}<1 ; 11<6+3 \sqrt{3}<12$. Therefore, the integers on the considered interval are from 1 to 11 inclusive. Sum all the integers that satisfy the condition of the problem: $1+2+3+4+5+6+7+8+9+10+11-3=63$.
Answer: 63
## №9: Divisibility.
Find the smallest number among natural numbers exceeding 2022 that divides the number 2021!! + 2022!!. (The symbol n!! denotes the product of all natural numbers not exceeding $n$ and having the same parity: $n!!=n \cdot(n-2) \cdot(n-4) \ldots)$
## Solution.
We will prove that 2021!! + 2022!! is divisible by the number 2023. Indeed,
$$
2022!!=(2023-1)(2023-3)(2023-5) \ldots(2023-2021)
$$
the remainder of the division of this number by 2023 is equal to the remainder of the division of the product
$$
(-1)(-3)(-5) \ldots(-2021)=(-1)^{\frac{2022}{2}} \cdot 2021!!=-2021!!
$$
by 2023. Therefore, 2021!! + 2022!! is divisible by the number 2023. Since 2023 is the smallest number among natural numbers exceeding 2022, we get the answer.
Answer. 2023.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the value of the expression $\left(\left(\frac{3}{a-b}+\frac{3 a}{a^{3}-b^{3}} \cdot \frac{a^{2}+a b+b^{2}}{a+b}\right)\right.$ ? $\left.\frac{2 a+b}{a^{2}+2 a b+b^{2}}\right) \cdot \frac{3}{a+b}$ when $a=2023, b=2020$
|
Solution:
$$
\begin{aligned}
& \left(\left(\frac{3}{a-b}+\frac{3 a}{(a-b)(a+b)}\right) \text { back } \frac{2 a+b}{(a+b)^{2}}\right) \cdot \frac{3}{a+b}=\left(\left(\frac{3(a+b)+3 a}{(a-b)(a+b)}\right) \cdot \frac{(a+b)^{2}}{2 a+b}\right) \cdot \frac{3}{a+b}=\left(\frac{3(2 a+b)}{(a-b)} \cdot\right. \\
& \left.\frac{(a+b)}{2 a+b}\right) \cdot \frac{3}{a+b}=\frac{3(a+b)}{a-b} \cdot \frac{3}{a+b}=\frac{9}{a-b} \\
& \text { We get the answer: } \frac{9}{a-b}=\frac{9}{2023-2020}=\frac{9}{3}=3
\end{aligned}
$$
Answer: 3
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Inside the square $A B C D$ with a side length of 5, there is a point $X$. The areas of triangles $A X B, B X C$, and $C X D$ are in the ratio $1: 5: 9$. Find the sum of the squares of the distances from point $X$ to the sides of the square.
|
Solution:
Let the side of the square be $a=5$, and the distances from point $X$ to sides $AB$, $BC$, $CD$, and $DA$ be $h_{1}$, $h_{2}$, $h_{3}$, and $h_{4}$, respectively. Since the area of a triangle is $S=\frac{1}{2} a h$, we conclude that $h_{1}: h_{2}: h_{3}=1: 5: 9$ or $h_{1}=x$, $h_{2}=5 x, h_{3}=9 x$. However, the sums of the distances from a point inside the square to the sides are equal to the side of the square, $h_{1}+h_{3}=h_{2}+h_{4}=a$, then $h_{1}=\frac{1}{10} a, h_{2}=\frac{5}{10} a=\frac{1}{2} a$, $h_{3}=\frac{9}{10} a, h_{4}=\frac{5}{10} a=\frac{1}{2} a$. We get that $h_{1}^{2}+h_{2}^{2}+h_{3}^{2}+h_{4}^{2}=a^{2}\left(\frac{1}{100}+\frac{1}{4}+\frac{81}{100}+\frac{1}{4}\right)=25 \cdot \frac{132}{100}=33$.
Answer: 33.
|
33
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The boat traveled 165 km upstream against the current and then returned. On the return trip, it took 4 hours less than the trip there. Find the boat's own speed if the river's current speed is 2 km/h.
|
# Solution:
$$
\begin{aligned}
& v_{\text {down}}=v_{\mathrm{c}}+v_{\text {current}} \\
& v_{\text {up}}=v_{\mathrm{c}}-v_{\text {current}}
\end{aligned}=>v_{\text {down}}-v_{\text {up}}=2 v_{\text {current}}=2 \cdot 2=4
$$
Then $\quad v_{\text {up}}=x$ km/h, $v_{\text {down}}=x+4$ km/h
Preliminary (online) stage of the "Step into the Future" School Students' Olympiad in the subject of Mathematics
Let the time for the boats $t_{\text {up}}=y$ h, $t_{\text {down}}=y-4$ h
We get $x y=165$ and $(x+4)(y-4)=165=>x y=(x+4)(y-4)=>$ $=>4 y-4 x=16=>y-x=4 \Rightarrow y=x+4$
Then $x(x+4)=165$
$$
\begin{aligned}
& x^{2}+4 x+4-4-165=0 \\
& (x+2)^{2}-169=0 \\
& {\left[\begin{array}{l}
x+2-13=0 \\
x+2+13=0
\end{array} ; \begin{array}{c}
x=11 \\
x=-15
\end{array}\right.}
\end{aligned}
$$
-15 is an extraneous root
$$
v_{\mathrm{c}}=v_{\text {up}}+v_{\mathrm{current}}=11+2=13(\mathrm{km} / \mathrm{h})
$$
Answer: 13 km/h.
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. . Find all values of the parameter $a$ for which the equation
$$
\left(\left|\frac{a x^{2}-a x-12 a+x^{2}+x+12}{a x+3 a-x-3}\right|-a\right) \cdot|4 a-3 x-19|=0
$$
has one solution. In your answer, write the largest value of the parameter $a$
|
Solution:
Simplify $\frac{a x^{2}-a x-12 a+x^{2}+x+12}{a x+3 a-x-3}=\frac{a x^{2}-x^{2}+(-a x+x)+(-12 a+12)}{a(x+3)-(x+3)}=$
$=\frac{x^{2}(a-1)-x(a-1)-12(a-1)}{(x+3)(a-1)}=\frac{(a-1)\left(x^{2}-x-12\right)}{(x+3)(a-1)}=$
Preliminary (correspondence) online stage of the "Step into the Future" School Students' Olympiad in the subject of Mathematics
$$
=\frac{x^{2}+3 x-4 x-12}{x+3}=\frac{(x+3)(x-4)}{x+3}=x-4
$$
$$
\text { We get }\left\{\begin{array}{c}
(|x-4|-a) \cdot|4 a+3 x-19|=0 \\
a \neq 1 \\
x \neq-3
\end{array} ; \quad\left\{\begin{array}{c}
|x-4|-a=0 \\
4 a+3 x-19=0 \\
a \neq 1 \\
x \neq-3
\end{array}\right.\right.
$$
$$
\left\{\begin{array}{c}
a=|x-4| \\
a=-0.75 x+4.75 \\
\quad a \neq 1 \\
\quad x \neq-3
\end{array}\right.
$$
We will plot the graph in the coordinate system $x O a$
| $a=-0.75 x+4.75$ | | |
| :--- | :--- | :--- |
| $x$ | -3 | 5 |
| $y$ | 7 | 1 |
$a=|x-4|$ the graph will be obtained from $a=|x|$ by shifting 4 units to the right
Since $x \neq-3$, then $a \neq 7$
$$
a \neq 1 \text {, then } x \neq 3 ; x \neq 5
$$
The points $(-3 ; 7) ;(3 ; 1) ;(5 ; 1)$ are punctured
For $a \in(-\infty ; 0) \cup\{7\}-$ one solution
For $a \in(0 ; 1) \cup(1 ; 7) \cup(7 ;+\infty)-$ three
solutions
For $a=0$ two solutions
For $a=1$ no solutions
Answer: 7
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In the right-angled triangle $ABC$ with the right angle at vertex $B$, on the longer leg $BC$, a segment $BD$ equal to the shorter leg is laid off from point $B$. Points $K$ and $N$ are the feet of the perpendiculars dropped from points $B$ and $D$ to the hypotenuse, respectively. Find the length of segment $BK$, if $AK=ND=2$.
|
Solution:
Drop a perpendicular from point $D$ to segment $B K$, let the foot of this perpendicular be point $M$. Then the right triangles $A K B$ and $B M D$ are equal by hypotenuse and acute angle, therefore, $B M=A K=2$. Quadrilateral $M K N D$ is a rectangle and $M K=N D=2$, then $B K=B M+M K=2+2=4$.
Answer: 4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. The production of x thousand units of a product costs $q=0.5 x^{2}-2 x-10$ million rubles per year. At a price of p thousand rubles per unit, the annual profit from selling this
Preliminary (online) stage of the "Step into the Future" School Students' Olympiad in the subject of Mathematics
product (in million rubles) is $p x - q$. The factory produces the product in such a quantity that the profit is maximized. For what minimum value of p will the total profit over three years be at least 126 million rubles.
|
# Solution:
Let the annual profit $f(x)=p x-q=p x-0.5 x^{2}+2 x+10=$
$-0.5 x^{2}+x(p+2)+10=-0.5\left(x^{2}-2 x(p+2)-20\right)=$
$=-0.5\left(x^{2}-2 x(p+2)+(p+2)^{2}-(p+2)^{2}-20\right)=$
$=-0.5(x-(p+2))^{2}+(p+2)^{2} / 2+10$
The quadratic trinomial $\mathrm{f}(\mathrm{x})$ reaches its maximum value at $\mathrm{x}=\mathrm{p}+2$ and is equal to $(p+2)^{2} / 2+10$
In three years, the total profit should be at least 126 million rubles, so we get
$(p+2)^{2} / 2+10 \geq 126 / 3$
$(p+2)^{2} \geq 42 \cdot 2-20$
but $\mathrm{p}>0=>p \geq 6$.
Answer: $\mathrm{p}=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. In triangle $A B C$, sides $A B, A C, B C$ are equal to 5, 6, and 7 respectively. On the median $A M$, segment $A K$ equal to 2 is laid off. Find the ratio of the areas of triangles $A B K$ and $A C K$. Write the answer as $\frac{S_{A B K}}{S_{A C K}}$.
|
# Solution:
The median of a triangle divides the triangle into two equal-area (equal in area) triangles. In triangle $ABC$, the areas of triangles $ABM$ and $ACM$ are equal because $AM$ is its median. In triangle $KBC$, the segment $KM$ is the median, so the areas of triangles $KBM$ and $KCM$ are equal. $S_{ABK} = S_{ABM} - S_{\text{KBM}} = S_{ACM} - S_{\text{KCM}} = S_{ACK}$, thus we get $S_{ABK} : S_{ACK} = 1$.
Answer: 1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. How many solutions in integers $x, y$ does the inequality $|y-x|+|3 x-2 y| \leq a$ have a) for $a=2$; b) for $a=20$?
|
Answer: a) 13; b) 841. Solution. Let $m=y-x, n=3 x-2 y$, then (expressing $x$, y from these equations) we get $x=2 m+n$ and $y=3 m+n$ and thus, for any integers m, n there correspond integers $x, y$ (and vice versa), i.e., there is a one-to-one correspondence between ordered pairs (m.n) and ( $x, y$ ). Therefore, we need to determine how many pairs (m.n) of integers satisfy the inequality $|m|+|n| \leq a$.
a) For $a=2$ such pairs can be easily listed: these are four pairs $( \pm 1, \pm 1)$ plus four pairs $( \pm 1,0)$, $( \pm 2,0)$ plus four pairs $(0, \pm 1),(0, \pm 2)$ and one more zero pair $(0,0)$. In total, there are 13 pairs (m.n), corresponding to 13 solutions of the original inequality. b) First, let's find the number of pairs of natural numbers ( $m . n$ ), for which $m+n=c$ for a given natural $c$. It is easy to see that the number of such pairs is $c-1$ (solutions are the pairs $(1, c-1),(2, c-2), \ldots,(c-1,1))$. Therefore, the number of pairs of natural numbers satisfying the inequality $m+n \leq 20$ is $1+2+\ldots .+19=190$. Then the total number of pairs of non-zero integers satisfying the inequality $|m|+|n| \leq a$ will be four times greater, i.e., 760. The number of solutions of the form $(m, 0)$ is 41 (these are the pairs $(-20,0),(-19,0) \ldots,(20,0))$ and, similarly, there are 41 solutions of the form $(0, n)$, but in this case, we counted the zero pair twice. Thus, the total number of solutions is $760+41+40=841$.
|
13
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. In 7a grade, there are 33 students. At the beginning of the school year, two clubs were organized in the class. According to school rules, a club can be organized if at least $70 \%$ of all students in the class sign up for it. What is the smallest number of students who could have signed up for both clubs simultaneously?
|
Answer: 15 students. Solution. In each club, there should be no less than $33 \cdot 0.7=23.1$ people, which means no less than 24 people. Let $n_{1}, n_{2}$ be the number of students who signed up for the first and second club, respectively, and $n$ be the number of students who signed up for at least one club. Obviously, $n \leq 33$ (note that it is not necessarily $n=33$, as the problem does not state that every student signed up for a club). Then the number of students who signed up for both clubs is $n_{1}+n_{2}-n$, since in the sum $n_{1}+n_{2}$, those who signed up for both clubs are counted twice. Therefore, $n_{1}+n_{2}-n \geq 24+24-33=15$, and this number is achieved when 9 people signed up for only one club and 15 people signed up for both clubs.
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. In a three-digit number, the first digit was crossed out to obtain a two-digit number. If the original number is divided by the obtained number, the quotient is 8 and the remainder is 6. Find the original number.
|
Answer: 342. Solution. Let $a$ be the first digit of the original number, and $b$ be the two-digit number formed by the last two digits. According to the condition, $100 a+b=8 b+6 \Leftrightarrow 7 b=2(50 a-3)=2 \cdot 49 a+2(a-3)$. Thus, the number $a-3$ must be divisible by 7. Considering that $0<a \leq 9$, we get that $a=3$. Then $b=42$.
|
342
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. There are 200 matches. How many ways are there to form, using all the matches, a square and (separately) an equilateral triangle? (Different ways differ in the sizes of the square and the triangle).
|
Answer: 16. Solution. Let $x$ (matches) be the side length of the square, and $y$ (matches) be the side length of the triangle. Then $4 x+3 y=200 \Leftrightarrow 3 y=4(50-x)$. Thus, for divisibility by 3, we need to consider all natural numbers up to 50 as $x$ that give a remainder of 2 when divided by 3 (i.e., the same remainder as the number 50). We have 16 such numbers, namely numbers of the form $2+3 k, k=0,1, \ldots, 15$, from 2 to 47 (the number 50 itself should not be considered, as otherwise only a square would be formed, without a triangle). Then the corresponding value of $y$ is $4 \cdot(16-k)$.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. How many points on the hyperbola $y=\frac{2013}{x}$ have integer coordinates $(x ; y)$?
|
Answer: 16. Solution. Integer points in the first quadrant correspond to the natural divisors of the number $2013=3 \cdot 11 \cdot 61$. The number of such divisors is 8 (they can be listed directly or the formula $\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right) \ldots\left(\alpha_{k}+1\right)$ for the number of natural divisors of the number $N=p_{1}{ }^{\alpha_{1}} \cdot p_{2}{ }^{\alpha_{2}} \cdot \ldots \cdot p_{k}{ }^{\alpha_{k}}$ can be used.). Taking into account the symmetric points in the third quadrant, we get the answer.
|
16
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. a) Given the quadratic equation $x^{2}-9 x-10=0$. Let $a$ be its smallest root. Find $a^{4}-909 a$. b) For the quadratic equation $x^{2}-9 x+10=0$, where $b$ is the smallest root, find $b^{4}-549 b$.
|
Answer: a) 910; b) -710. Solution. a) Let's solve the problem in general. Let $x^{2}-c x+d=0-$ be a quadratic equation, and $a-$ be its root. Then $a^{4}=(c a-d)^{2}=c^{2} a^{2}-2 a c d+d^{2}=$ $c^{2}(c a-d)-2 a c d+d^{2}=a\left(c^{3}-2 c d\right)+d^{2}-c^{2} d$. Therefore, $a^{4}-\left(c^{3}-2 c d\right) a=d^{2}-c^{2} d$. When $c=9, d=-10$, we get $a^{4}-909 a=910$, and when $c=9, d=10$, we have $b^{4}-549 b=-710$. (In part a), the result can be easily and directly obtained).
|
910
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. There are 12 matches, each 2 cm long. Can a polygon with an area of 16 cm $^{2}$ be formed from them? (The matches cannot be broken, and all matches must be used.)
|
Answer: It is possible. Solution. The result follows from the Pythagorean theorem (since $10^{2}=6^{2}+8^{2}$) and construction (see figure). The area of the polygon is $\frac{6 \cdot 8}{2}-8=16$.
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. A truck and a car are moving in the same direction on adjacent lanes at speeds of 65 km/h and 85 km/h, respectively. At what distance from each other will they be 3 minutes after they are side by side?
|
Answer: 1 km. Solution. The difference in the speeds of the cars is 20 km/h, so in 3 minutes they will be separated by a distance equal to 20 (km/h) $\cdot \frac{1}{20}$ (hour) $=1$ km.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. On a line, several points were marked, after which two points were placed between each pair of adjacent points, and then the same procedure (with the entire set of points) was repeated again. Could there be 82 points on the line as a result?
|
Answer: Yes. Solution. Let there be x points marked on the line initially. Then after the first procedure, $2(x-1)$ points are added to them, and there are a total of $3x-2$ points. After the second procedure, $2(3x-3)$ points are added to these points. Thus, there are a total of $3x-2+2(3x-3)=9x-8$ points on the line. Therefore, we need to solve the equation in integers $9x-8=82$. From this, $x=10$. This means that if there were 10 points initially, then after two procedures, there will be 82 points.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. In triangle $A B C$, the angles $A$ and $C$ at the base are $20^{\circ}$ and $40^{\circ}$ respectively. It is known that $A C - A B = 5$ (cm). Find the length of the angle bisector of angle $B$.
|
Answer: 5 cm. Solution. Let $B M$ be the bisector of angle $B$. Mark a point $N$ on the base $A C$ such that $A N=A B$. Then triangle $A B N$ is isosceles and $\angle A B N=\angle A N B=80^{\circ}$. Since $\angle A B M=\frac{180^{\circ}-20^{\circ}-40^{\circ}}{2}=60^{\circ}$, then $\angle B M N=\angle A+\angle A B M=20^{\circ}+60^{\circ}=80^{\circ}$. Thus, the angles at the base of $\triangle M B N$ are equal, which means $\triangle M B N$ is isosceles: $M B=B N$. In $\triangle B N C$, the angles $\angle N C B$ and $\angle C N B$ are equal to $40^{\circ}$ (since $\angle B N C=180^{\circ}-80^{\circ}=100^{\circ}$ and $\angle N B C=180^{\circ}-40^{\circ}-100^{\circ}=40^{\circ}$). Therefore, $\triangle B N C$ is isosceles: $B N=N C$. As a result, we have $B M=B N=N C=5$ cm (since $N C=A C-A N=A C-A B)$.
## 8th grade
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. In triangle $ABC$, side $BC$ is equal to segment $AM$, where $M$ is the point of intersection of the medians. Find the angle $\angle BMC$.
|
Answer: $90^{\circ}$. Solution. Let $A N-$ be the median. By the property of the intersection point of medians, $M N=\frac{1}{2} A M=\frac{1}{2} B C$. Thus, in triangle $B M C$, the median $M N$ is equal to half of side $B C$. Therefore, $\triangle B M N$ is a right triangle with a right angle at $B M N$ (this is a known fact, which can be easily proven by considering isosceles triangles $B M N$ and $C M N$: the doubled sum of the angles at their base equals $180^{\circ}$ ).
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. What is the smallest number of digits that need to be appended to the right of the number 2014 so that the resulting number is divisible by all natural numbers less than $10?$
|
Answer: 4 digits. Solution. If three digits are appended to 2014, the resulting number will be $\leq 2014$ 999. Dividing 2014999 by $2520=$ LCM $(1,2, \ldots, 9)$, we get a quotient of 799 and a remainder of 1519. Since $1519>1000$, there is no integer multiple of 2520 between the numbers 2014000 and 2014999. Therefore, it is impossible to append three digits to 2014. From this, it follows that it is also impossible to append one or two digits (otherwise, it would be possible to append zeros to make up three digits). Four digits will be sufficient, since $10000>2520$, and therefore there is an integer multiple of 2520 between 20140000 and 20149999 (the smallest of such numbers is $20142360=2520 \cdot 7993$).
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Solve the equation $\sin ^{2} x+1=\cos (\sqrt{2} x)$.
|
The answer is $x=0$. Solution. The left side of the equation $\geq 1$, and the right side $\leq 1$. Therefore, the equation is equivalent to the system: $\sin x=0, \cos \sqrt{2} x=1$. We have $x=\pi n, \sqrt{2} x=2 \pi k$ ( $n, k$ - integers). From this, $n=k \cdot \sqrt{2}$. Since $\sqrt{2}$ is an irrational number, the last equality is possible only when $n=k=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Is the number
$$
\sqrt[3]{2016^{2}+2016 \cdot 2017+2017^{2}+2016^{3}}
$$
- rational or irrational?
|
Answer: the whole rational number 2017. Solution. Let $a=2017, b=2016$. Then $b^{2}+a b+a^{2}+b^{3}=\frac{a^{3}-b^{3}}{a-b}+b^{3}=a^{3}-b^{3}+b^{3}=a^{3}$ (since $a-b=1$ ). Thus, we get $\sqrt[3]{a^{3}}=a=2017$
|
2017
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. How many five-digit natural numbers exist, each of which has adjacent digits with different parity
|
Answer: 5625. Solution. If the first digit is even, then it can be chosen in four ways $(2,4,6,8)$. And all subsequent ones can be chosen in five ways $(1,3,5,7,9$ - for the second and fourth digits and $0,2,4,6,8$ - for the third and fifth). In the end (by the rule of product), we have a total of $4 \cdot 5^{4}=2500$ numbers. Similarly, in the case of an odd first digit, we get $5^{5}=3125$ numbers. Thus, the total number of numbers is 5625. Remark. The same result can be obtained if we immediately use the rule of product. The first (most significant) digit can be chosen in nine ways (taking any digit except 0), after which the second digit can be chosen in five ways (taking any digit with a different parity from the first digit), and so on: the following digits can be chosen in five ways (and the number of ways does not depend on the previous digits). Therefore, by the rule of product, we get the result: $9 \cdot 5^{4}$.
|
5625
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. Andrey and Seva are going to visit Borya. Andrey is at point $A$, and Borya is at point $B$, 30 km away from point $A$ along a straight highway. Seva is at point $C$, exactly halfway between $A$ and $B$. The friends decided to leave simultaneously: Andrey on a bicycle, and Seva on foot, but Andrey will leave the bicycle at an agreed location so that Seva can use it (Andrey will finish the journey on foot). The boys move at a speed of 20 km/hour on the bicycle and 5 km/hour on foot. Where should the bicycle be left so that the friends can arrive at Borya's place together as soon as possible?
|
Answer: 5 km before point $B$. Solution. Let $a=15$ (km), $u=5$ (km/h), $v=20$ (km/h). Let $x$ (km) be the distance from point $B$ to the place where the bicycle is left. Then Andrei's travel time is $t_{A}=\frac{2 a-x}{v}+\frac{x}{u}$, and Seva's travel time is $t_{C}=\frac{a-x}{u}+\frac{x}{v}$. We need to find such a value of $x$ for which the maximum of the two times $t_{A}$ and $t_{C}$ is as small as possible (if, for example, $t_{A}t_{C}$ and in each of these cases it is easy to show how to improve the time by leaving the bicycle a little closer or, respectively, a little further from the given place). Without proving this fact, the solution is rated less than half of the maximum score.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Find the value of the expression $\frac{\left(a^{2}+b^{2}\right)^{2}-c^{2}-4 a^{2} b^{2}}{a^{2}+c-b^{2}}$ for $a=2017, b=2016, c=2015$. Justify your result.
|
Answer: 2018. Solution. The numerator equals $a^{4}+2 a^{2} b^{2}+b^{4}-4 a^{2} b^{2}-c^{2}=\left(a^{2}-b^{2}\right)^{2}-c^{2}=$ $\left(a^{2}-b^{2}+c\right)\left(a^{2}-b^{2}-c\right)$, and after dividing by the denominator we get $a^{2}-b^{2}-c=$ $(a-b)(a+b)-c=2017+2016-2015=2018$.
|
2018
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. Find the natural number $x$ that satisfies the equation
$$
x^{3}=2011^{2}+2011 \cdot 2012+2012^{2}+2011^{3}
$$
|
Answer: 2012. Solution: Let $a=2011, \quad b=2012$. Then $a^{2}+a b+b^{2}=\frac{b^{3}-a^{3}}{b-a}=b^{3}-a^{3}$ (since $b-a=1$). Therefore, $x^{3}=b^{3}-a^{3}+a^{3}=b^{3}$. Hence, $x=b=2012$.
|
2012
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. In a five-digit number, one of the digits was crossed out, and this four-digit number was subtracted from the original number. As a result, the number 54321 was obtained. Find the original number.
|
Answer: 60356. Solution. Let $x$ be the four-digit number obtained after crossing out a digit. Note that the crossed-out digit was the last digit of the five-digit number, because otherwise the last digit after subtraction would be zero. Let this digit be $y$. We have the equation $10 x+y-x=54321 \Leftrightarrow 9 x+y=54321=9 \cdot 6035+6$. Therefore, $x=6035$ and $y=6$ (the quotient and remainder when 54321 is divided by 9).
|
60356
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. From a rectangular table of $m \times n$ cells, several squares of different sizes need to be cut out along the grid lines. What is the maximum number of squares that can be cut out if: a) $m=8$, $n=11$; b) $m=8, n=12 ?$
|
Answer: a) 5; b) 5. Solution. a) Note that the area of six different squares is no less than $1+4+9+16+25+36=91>88$. Therefore, it is impossible to cut out more than five different squares. A possible example for five squares (even in a rectangle $8 \times 9$) is shown in the figure. b) Suppose, for the sake of contradiction, that it is possible to cut out 6 squares of different sizes. Then these must be squares of sizes $1 \times 1, 2 \times 2, 3 \times 3, 4 \times 4, 5 \times 5$, and $6 \times 6$. After cutting out the $6 \times 6$ square from one side, a strip of width no more than 2 will remain on one side, and a strip of width no more than 6 on the other side. Therefore, the squares $4 \times 4$ and $5 \times 5$ must be located in the strip (no more than) $6 \times 8$. But after cutting out the $5 \times 5$ square from this strip, the remaining part will have strips of width no more than 3, and thus it will be impossible to place the $4 \times 4$ square.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Is it possible to place the 12 numbers $1,2, \ldots, 12$ on the edges of a cube such that the product of the four numbers on the top face equals the product of the four numbers on the bottom face?
|
Answer: It is possible. Solution. An example of such an arrangement can be as follows: on the top face, place the numbers $2,4,9,10$; on the bottom face, place the numbers $3,5,6,8$; the remaining numbers $1,7,11,12$ are placed on the side edges. The products on the top and bottom faces are the same and equal to 720. (To arrive at such an example, one needs to select the prime numbers 7 and 11 for the side edges and distribute the powers of two and three on the top and bottom faces, which significantly reduces the number of combinations to check.)
|
720
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. There are ten coins of different weights and a balance scale without weights. It is required to select the heaviest and the lightest coin. Can this be achieved in 13 weighings?
|
Answer: It is possible. Solution. First, divide all the coins into 5 pairs and in 5 weighings compare the weight of each pair. By selecting the heavier coin in each pair, we form a "heavy" group of 5 coins. The remaining 5 coins will form the "light" group. Now, in the heavy group, over 4 sequential weighings, select the heaviest coin. Similarly, in the light group, over 4 weighings, select the lightest coin. In total, $5+4+4=13$ weighings have been conducted.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. In a five-digit number, one digit was crossed out, and the resulting four-digit number was added to the original. The sum turned out to be 54321. Find the original number.
|
Answer: 49383. Solution. Note that the crossed-out digit must be the last digit of the number $N$, because otherwise the sum of the two numbers would have an even digit in the last place. Let's denote this crossed-out digit by $x$ and let $y$ be the four-digit number obtained after the crossing out. Then the condition can be written as: $10 y + x + y = 54321 \Leftrightarrow 11 y + x = 54321$. Dividing 54321 by 11 with a remainder, we get $54321 = 11 \cdot 4938 + 3$ and considering that $x < 11$, we will have the unique solution (due to the uniqueness of division with a remainder) $x = 3, y = 4938$.
|
49383
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. How many roots does the equation $\sqrt{14-x^{2}}(\sin x-\cos 2 x)=0$ have?
|
Answer: 6 roots. Solution. The domain of the equation: $14-x^{2} \geq 0 \Leftrightarrow|x| \leq \sqrt{14}$. On this domain, we solve the trigonometric equation $\sin x-\cos 2 x=0 \Leftrightarrow \sin x+2 \sin ^{2} x-1=0$; $\sin x=\frac{-1 \pm 3}{4}$, i.e., $\sin x=-1$ or $\sin x=\frac{1}{2}$. From this, we get three series of solutions: 1) $\left.\left.x=-\frac{\pi}{2}+2 \pi k ; 2\right) x=\frac{\pi}{6}+2 \pi n ; 3\right) x=\frac{5 \pi}{6}+2 \pi m(k, n, m \in Z)$. Solutions of the first series lie in the domain of definition only when $k=0$ (since for $k \neq 0,|x| \geq 2 \pi-\frac{\pi}{2}=\frac{3 \pi}{2}>\frac{9}{2}>\sqrt{14}$ ). Solutions of the second series also lie in the domain of definition only when $n=0$ (since $\left|\frac{\pi}{6}-2 \pi\right|=\frac{11 \pi}{6}>\frac{11}{2}>\sqrt{14}$ ). Solutions of the third series lie in the domain of definition for $m=0$ and $m=-1$. Indeed, $\frac{5}{6} \pi2 \pi>\sqrt{14}$ ). Adding the roots of the first factor $\sqrt{14-x^{2}}$ of the original equation, namely $\pm \sqrt{14}$, we get a total of 6 roots.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. The number $a$ is a root of the quadratic equation $x^{2}-x-50=0$. Find the value of $a^{4}-101 a$.
|
Answer: 2550. Solution. We have $a^{2}=a+50$, therefore $a^{4}=(a+50)^{2}=a^{2}+100 a+2500=$ $a+50+100 a+2500=101 a+2550$. Hence $a^{4}-101 a=2550$.
|
2550
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. In triangle $A B C$, side $B C$ is equal to segment $A M$, where $M$ is the point of intersection of the medians. Find the angle $\angle B M C$.
|
Answer: $90^{\circ}$. Solution. Let $A N-$ be the median. By the property of the intersection point of medians, $M N=\frac{1}{2} A M=\frac{1}{2} B C$. Thus, in triangle $B M C$, the median $M N$ is equal to half of side $B C$. Therefore, $\triangle B M N$ is a right triangle with a right angle at $B M N$ (this is a known fact, which can be easily proven by considering isosceles triangles $B M N$ and $C M N$: the doubled sum of the angles at their base equals $180^{\circ}$ ).
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. How many a) rectangles; b) right-angled triangles with integer sides exist, for which the area is numerically equal to the perimeter? (Congruent figures are counted as one).
|
Answer: a) two; b) two. Solution. a) Let the sides of the rectangle be integers $a$ and $b$ ( $a \leq b$ ). Then $a b=2(a+b)$, which is equivalent to the equation $(a-2)(b-2)=4$. The number 4 can be factored into the product of two integers in four ways: $(1 ; 4),(2,2),(-4 ;-1),(-2,-2)$, of which the first two give rectangles $(3,6)$ and $(4,4)$. b) Let the legs of the right triangle be $a$ and $b(a \leq b)$. We have the equation $a+b+\sqrt{a^{2}+b^{2}}=\frac{a b}{2}$. Let $u=a+b, v=a b$ Then the equation can be written as $2 u+2 \sqrt{u^{2}-2 v}=v$. After isolating the square root on the left side, squaring both sides, and dividing the equation by $v$, we get: $v-4 u+8=0$, i.e., $a b-4 a-4 b+8$, or $(a-4)(b-4)=8$. The number 8 can be factored into the product of two integers in four ways: ( $1 ; 8),(2,4),(-8 ;-1),(-4,-2)$, of which the first two give right triangles $(5,12,13)$ and $(6,8,10)$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Solve the equation $\cos ^{2}(\sqrt{2} x)-\sin ^{2} x=1$.
|
Answer: $x=0$. Solution. The left side of the equation does not exceed one, and it can equal one only if the following two conditions are simultaneously satisfied: $\cos ^{2}(\sqrt{2} x)=1$ and $\sin x=0$. Hence, $\sqrt{2} x=\pi n$ and $x=\pi k, k, n \in \mathbf{Z}$. Then $\frac{\pi n}{\sqrt{2}}=\pi k$, i.e., $n=\sqrt{2} k$ for some integers $n, k$. Since $\sqrt{2}$ is an irrational number, it follows from the last equation that $k$ must be zero. Therefore, $k=n=0$, and $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.