problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
11.4. $n$ vectors in space are such that any pair of them forms an obtuse angle. What is the largest value that $n$ can take?
|
Answer: 4. Solution. Let $\vec{a}_{1}, \vec{a}_{2}, \ldots, \vec{a}_{n}$ be the given vectors. Direct the $z$-axis of the coordinate space along $\vec{a}_{n}$. Then the $z$-coordinate of the other vectors must be negative (this follows from the formula for the cosine of the angle between vectors through the scalar product of vectors). Let $\vec{a}_{1}=\left(x_{1}, y_{1}, z_{1}\right), \ldots, \vec{a}_{n-1}=\left(x_{n-1}, y_{n-1}, z_{n-1}\right)$ be the coordinates of the vectors, and let the two-dimensional vectors $\vec{b}_{1}=\left(x_{1}, y_{1}\right), \ldots, \vec{b}_{n-1}=\left(x_{n-1}, y_{n-1}\right)$ be the projections of these vectors onto the $x O y$ plane. Then the angle between any pair of vectors $\vec{b}_{i}$ and $\vec{b}_{j}$ is obtuse: indeed, $\cos \left(\vec{b}_{i} \wedge \vec{b}_{j}\right)=\frac{x_{i} x_{j}+y_{i} y_{j}}{\left|\vec{b}_{i}\right| \cdot\left|\vec{b}_{j}\right|}<0$, since $x_{i} x_{j}+y_{i} y_{j}<x_{i} x_{j}+y_{i} y_{j}+z_{i} z_{j}<0$ (in the first of these inequalities, it is used that $z_{i}$ and $z_{j}$ are negative, and in the second, that the angle between $\vec{a}_{i}$ and $\vec{a}_{j}$ is obtuse). Thus, on the $x O y$ plane, the vectors $\vec{b}_{1}, \ldots, \vec{b}_{n-1}$ have the same property, namely: the angle between any pair of them is obtuse. Therefore, $n-1 \leq 3$ (this is easy to show if, by placing the vectors from one point, we sum the adjacent angles around the circle, since they sum up to $360^{\circ}$). Thus, we obtain the estimate $n \leq 4$. An example for four vectors can be given as follows: $\vec{a}_{1}=(1,0,-\varepsilon), \vec{a}_{2}=\left(\cos \frac{2 \pi}{3}, \sin \frac{2 \pi}{3},-\varepsilon\right), \vec{a}_{3}=\left(\cos \frac{4 \pi}{3}, \sin \frac{4 \pi}{3},-\varepsilon\right), \vec{a}_{4}=(0,0,1)$, where $\varepsilon$ is a sufficiently small positive number, which can be taken as $\varepsilon=0.1$.
## 11th Grade
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Find all values of the parameter $a$ for which the equation $a x^{2}+\sin ^{2} x=a^{2}-a$ has a unique solution.
|
Answer: $a=1$. Solution. Note that only $x=0$ can be the unique root of the equation, since due to the evenness of the functions involved, for any solution $x_{0} \neq 0$, $(-x_{0})$ will also be a solution. Therefore, we necessarily get $a^{2}-a=0 \Leftrightarrow a=0$ or $a=1$. Let's check these values. When $a=0$, we have the equation $\sin ^{2} x=0$, which has an infinite set of solutions $x=k \pi(k \in Z)$. If $a=1$, then the equation $x^{2}+\sin ^{2} x=0$ has a unique solution $x=0$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. In 7a class, $52\%$ are girls. All students in the class can line up in such a way that boys and girls alternate. How many students are in the class?
|
Answer: 25 students. Solution: Considering that there are more girls than boys in the class, from the condition of alternation, we get that there are exactly one more girl than boys. Therefore, one person constitutes $52-48=4 \%$ of the class size. Thus, the number of students in the class (i.e., $100 \%$) is $100 / 4=25$ people.
|
25
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. Given a rectangular grid of $7 \times 14$ (cells). What is the maximum number of three-cell corners that can be cut out from this rectangle?
|
Answer: 32 corners. Solution: It is obvious that no more than 32 corners can be cut out, as otherwise, the rectangle must contain no fewer than $33 \cdot 3=99>98$ cells. The image below shows an example of cutting one

7x7 square into 16 corners. The adjacent 7x7 square is cut in the same way.
|
32
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. a) Prove that there exists a pair of two-digit numbers such that if 15 is added to the first number and 20 is subtracted from the second, the resulting numbers will remain two-digit, and their product will be equal to the product of the original numbers. b) How many such pairs are there?
|
Answer: b) 16 pairs. Solution. The sought numbers $x$ and $y$ must satisfy the condition $(x+15)(y-20)=xy$. Expanding the brackets and transforming, we get the equation $3y-4x=60$. From this equation, it follows that the number $x$ must be divisible by 3, and $y$ by 4, i.e., $x=3x_{1}, y=4y_{1}$ for some natural $x_{1}, y_{1}$. Then the equation will take the form $y_{1}=5+x_{1}$. We need to find integer solutions satisfying the inequalities $10 \leq x<85$ and $30 \leq y<100$, which correspond to the inequalities $4 \leq x_{1} \leq 28$ and $9 \leq y_{1} \leq 24$. Considering the equation $y_{1}=5+x_{1}$, we get that $x_{1}$ can be any natural number from 4 to 19 (=24-5), in total $x_{1}$ takes 16 values. For each such $x_{1}$, the pair $\left(3x_{1}, 4(5+x_{1})\right)$ is the sought one. For example, when $x_{1}=10$ the pair $(30,60)$ satisfies the conditions (any similar example answers the question in part a).
|
16
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
11.4. On the coordinate plane, the parabola $y=x^{2}$ is drawn. On the positive $O y$-axis, a point $A$ is taken, and through it, two lines with positive slopes are drawn. Let $M_{1}, N_{1}$ and $M_{2}, N_{2}$ be the points of intersection with the parabola of the first and second line, respectively. Find the ordinate of point $A$, given that $\angle M_{1} O N_{1}=\angle M_{2} O N_{2}$, where $O$ is the origin.
|
Answer. 1. Solution. Let $a$ be the ordinate of point A. The line passing through point $A$ has the equation $\mathrm{y}=k \cdot x+a$, and the abscissas $x_{1}, x_{2}$ of points M and $N$ of intersection of the line with the parabola are the roots of the equation $x^{2}=k \cdot x+a$. From Vieta's theorem, we have $x_{1} \cdot x_{2}=-a$ and $x_{1}+x_{2}=k$. We calculate $\cos (\angle M O N)=$ $\frac{(\overrightarrow{M O}, \overrightarrow{N O})}{|M \hat{O}||\overrightarrow{O O}|}=\frac{x 1 \cdot x 2 \cdot(1+x 1 \cdot x 2)}{|x 1 \cdot x 2| \sqrt{\left(1+x 1^{2}\right)\left(1+x 2^{2}\right)}}=\frac{-a(1-a)}{a \sqrt{1+a^{2}-2 a+k^{2}}}=\frac{a-1}{\sqrt{1+a^{2}-2 a+k^{2}}}$. When $a=1$, we have $\cos (\angle M O N)=0$ and, therefore, $\angle M O N$ does not depend on $k$. If $a \neq 1$ and for two angular coefficients $k_{1}, k_{2}>0$ the corresponding angles are equal, then from the equality $\frac{a-1}{\sqrt{1+a^{2}-2 a+k 1^{2}}}=\frac{a-1}{\sqrt{1+a^{2}-2 a+k 2^{2}}}$ it follows that $k_{1}^{2}=k_{2}^{2}$, i.e., $k_{1}=$ $k_{2}$ (due to the positivity of $k_{1}, k_{2}$). Thus, we obtain the answer $a=1$. (The equality $k_{1}=k_{2}$ can also be obtained without using the dot product: instead, the tangent of the angle $M O N$ can be calculated using the tangent addition formula for angles MOA and NOA.)
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. Solve the equation $(\sqrt{2023}+\sqrt{2022})^{x}-(\sqrt{2023}-\sqrt{2022})^{x}=\sqrt{8088}$.
|
Answer: $x=1$.
Solution. Notice that $\sqrt{8088}=2 \sqrt{2022}$. This observation suggests that $x=1$ is a root of the equation. We will show that there are no other roots. Indeed, the left side represents the difference of two exponential functions: the base of the first is greater than one, and the base of the second is less than one (it can be noted that the product of these bases equals one). Therefore, the left side is the difference of an increasing and a decreasing function over the entire real line, i.e., it is a strictly increasing function, and thus it takes the value equal to the number on the right side at the unique point $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. In triangle $A B C$, the bisector $A M$ and the median $B N$ intersect at point $O$. It turns out that the areas of triangles $A B M$ and $M N C$ are equal. Find $\angle M O N$.
|
Answer: $90^{\circ}$. Solution. Since $S_{A M N}=S_{M N C}$ (because $A N=N C$), from the condition of the problem we have $S_{A B M}=S_{A N M}$. Therefore, in triangles $A B M$ and $A M N$, the heights drawn from vertices $B$ and $N$ are equal. Let $B_{1}$ and $N_{1}$ be the bases of these heights. Then the right triangles $A B B_{1}$ and $A N N_{1}$ are equal, since $B B_{1}=N N_{1}$ and $\angle B A B_{1}=\angle N A N_{1}$. Therefore, $A B=A N$ and thus points $B_{1}$ and $N_{1}$ coincide with each other and coincide with point $O$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. 10 girls and 10 boys stood in a row such that girls and boys alternate, specifically from left to right: girl-boy-girl-boy and so on. Every minute, in one (any) pair of neighbors "girl-boy," the children can swap places, provided that the girl is to the left of the boy. Can such an "exchange process" continue for more than an hour?
|
Answer: It cannot. Solution. Consider the numbers in order (from left to right) of all ten boys. Initially, these were all even numbers $2,4,6, \ldots, 20$. Every minute, the number of one of the boys decreases by one, and the process will continue until the numbers of the boys become $1,2,3, \ldots, 10$ (i.e., until all the boys are to the left of all the girls). The sum of the boys' numbers was initially $(2+4+\ldots+20)=2(1+2+\ldots+10)=2 \cdot 55$, and at the end, it is $(1+2+\ldots+10)=55$. Therefore, it will decrease by 55. Since this sum decreases by 1 each minute, the entire process will take 55 minutes.
|
55
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. The number $a$ is a root of the quadratic equation $x^{2}-x-50=0$. Find the value of $a^{3}-51 a$.
|
Answer: 50. Solution. We have $a^{2}=a+50$, therefore $a^{3}=a^{2}+50 a=a+50+50 a=51 a+50$. Hence $a^{3}-51 a=50$.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. How many solutions in natural numbers $x, y$ does the system of equations have
$$
\left\{\begin{array}{l}
\text { GCD }(x, y)=20! \\
\text { LCM }(x, y)=30!
\end{array} \quad(\text { where } n!=1 \cdot 2 \cdot 3 \cdot \ldots \cdot n) ?\right.
$$
|
Answer: $2^{8}$. Solution. If for the given two numbers $x, y$ the set of their prime divisors is denoted as $p_{1}, p_{2}, \cdots, p_{k}$ and we write $x=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \cdots p_{k}^{\alpha_{k}}, y=p_{1}^{\beta_{1}} p_{2}^{\beta_{2}} \cdots p_{k}^{\beta_{k}}$ (where $\alpha_{i}, \beta_{i}$ are non-negative integers), then
$$
\begin{aligned}
& \operatorname{GCD}(x, y)=p_{1}^{\min \left(\alpha_{1}, \beta_{1}\right)} \cdot p_{2}^{\min \left(\alpha_{2}, \beta_{2}\right)} \cdots \cdots p_{k}^{\min \left(\alpha_{k}, \beta_{k}\right)} \\
& \operatorname{LCM}(x, y)=p_{1}^{\max \left(\alpha_{1}, \beta_{1}\right)} \cdot p_{2}^{\max \left(\alpha_{2}, \beta_{2}\right)} \cdots \cdots p_{k}^{\max \left(\alpha_{k}, \beta_{k}\right)}
\end{aligned}
$$
The problem is to find $x, y$ for given $A, B$ from the equations GCD $(x, y)=A$, LCM $(x, y)=B$. If the factorizations of $A$ and $B$ are $A=p_{1}^{n_{1}} p_{2}^{n_{2}} \cdots p_{k}^{n_{k}}, B=p_{1}^{m_{1}} p_{2}^{m_{2}} \cdots p_{k}^{m_{k}}$ and $n_{1}=m_{1}$, then $\alpha_{1}=\beta_{1}$. If $n_{1}n_{i}$, specifically 2,3, 5,7,11,13,23,29 (all prime numbers less than 30 except 17 and 19). Therefore, the number of different ways to choose ordered sets $\alpha_{i}, \beta_{i}$ is $2^{8}=256$.
|
256
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. In triangle $A B C$, angle $A$ is the largest. Points $M$ and $N$ are symmetric to vertex $A$ with respect to the angle bisectors of angles $B$ and $C$ respectively. Find $\angle A$, if $\angle M A N=50^{\circ}$.
|
Answer: $80^{\circ}$. Solution. See problem 8.2
|
80
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3 How many right-angled triangles with integer sides exist, where one of the legs is equal to 2021.
|
Answer: 4. Solution. Let the hypotenuse of a right triangle be $x$, one of the legs be $-y$, and the other be 2021. Then, by the Pythagorean theorem, $x^{2}-y^{2}=2021^{2}$, i.e., $(x-y) \cdot(x+y)=2021^{2}$. Considering that $x>y$, we have: $x+y>x-y>0$. Since the prime factorization of 2021 is $2021=43 \cdot 47$, the prime factorization of $2021^{2}$ is $2021^{2}=43^{2} \cdot 47^{2}$, and therefore $2021^{2}$ can be represented as the product of two natural numbers in five ways:
$2021^{2}=1 \cdot\left(43^{2} \cdot 47^{2}\right)=43 \cdot\left(43 \cdot 47^{2}\right)=47 \cdot\left(43^{2} \cdot 47\right)=43^{2} \cdot 47^{2}=(43 \cdot 47) \cdot(43 \cdot 47)$.
Since in the product $(x-y) \cdot(x+y)$ the factors are different and the second factor is greater than the first, we have four systems of two equations:
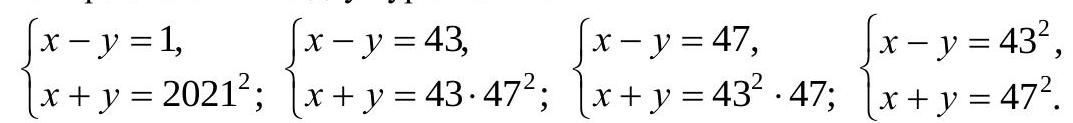
Solving each of these systems, we obviously get natural $x, y$ (which follows from the oddness of the right-hand sides). Therefore, there exist four right triangles with integer sides, one of which has a leg equal to 2021.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. In a class of 30 people, for New Year's, each person sent greeting cards to no fewer than 16 classmates. Prove that there were no fewer than 45 pairs of mutual greetings.
|
Solution. A total of no less than $30 \cdot 16=480$ letters were sent, while the number of pairs of classmates is $(30 \cdot 29) / 2=435$. For each pair of classmates, there can be one of three situations: a) neither of them wrote to the other; b) only one wrote to the other; c) they exchanged letters. Let the number of such pairs be denoted by $A, B$, and $C$, respectively. Then $B+2 C \geq 480$ and $A+B+C=435$. From this, $C-A \geq 480-435=45$. Therefore, $C \geq 45+A \geq 45$.
## 11th Grade
|
45
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
11.5. On the coordinate plane, the graph of $y=\frac{2020}{x}$ is constructed. How many points on the graph have a tangent that intersects both coordinate axes at points with integer coordinates?
|
Answer: 40 points. Solution. The equation of the tangent at the point $\left(x_{0}, y_{0}\right)$ to the hyperbola $y=k / x$ is $y-y_{0}=-\left(k / x_{0}^{2}\right)\left(x-x_{0}\right)$, where $y_{0}=k / x_{0}$. From this equation, the coordinates $x_{1}$ and $y_{1}$ of the points of intersection with the axes O $x$ and O $y$ are obtained, specifically, $x_{1}=2 x_{0}$ and $y_{1}=2 y_{0}$. Therefore, $2 x_{0}$ is an integer. Let $n=2 x_{0}$. Then $y_{1}=2 y_{0}=2 k / x_{0}=4 k / n$. Thus, $n$ can take the value of any divisor of the number $4 k$. For $k=2020$, we need to find the number of integer divisors of the number $4 \cdot 2020=8080=2^{4} \cdot 5 \cdot 101$. The number of natural divisors of this number is $20=(4+1)(1+1)(1+1)$ (here we calculated the number of natural divisors using the powers of prime numbers in the prime factorization of the number 8080). Taking into account the negative divisors (corresponding to points of tangency in the third quadrant), we get double the number, i.e., a total of 40 points.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. For what values of the parameter $a$ do the equations $a x+a=7$ and $3 x-a=17$ have a common integer root?
|
Answer: $a=1$.
Solution. Solving these two equations as a system with unknowns $x$ and $a$, express $a$ from the second equation and substitute it into the first. We get the quadratic equation $3 x^{2}-14 x-24=0$. It has two roots: 6 and (-4/3). For the integer root $x=6$, the corresponding value of $a=3 x-17=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Given two coprime natural numbers $p$ and $q$, differing by more than one. a) Prove that there exists a natural number $n$ such that the numbers $p+n$ and $q+n$ will not be coprime. b) Find the smallest such $n$ for $p=2, q=2023$.
|
Answer: b) 41.
Solution. See the solution to problem 8.2 (including the notation and comments). If both numbers $p+n$ and $q+n$ are divisible by some $k>1$, then $m=q-p$ is also divisible by $k$, and therefore $k$ is not less than the smallest prime divisor of the number $m$. For $p=2, q=2023$, we have $m=2021=43 \cdot 47$—the factorization into prime factors. Therefore, to the numbers 2 and 2023 for divisibility by 43, one needs to add $43-2=41$.
|
41
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Append a digit to the left and right of the eight-digit number 20222023 so that the resulting 10-digit number is divisible by 72. (List all possible solutions.)
|
Answer: 3202220232.
Solution. Since $72=8 \cdot 9$, it is required to append digits so that the resulting number is divisible by both 8 and 9. Divisibility by 8 is determined by the last three digits: thus, to the two-digit number 23, we need to append a digit on the right to form a three-digit number that is a multiple of 8. There is only one digit, namely 2, for which this is possible ( $232: 8=29$ ). After this, the first digit of the desired number is determined by the divisibility rule for 9 (the sum of the digits must be divisible by 9, so we need to add 3 to the existing sum of digits, which is 15).
|
3202220232
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. The number $a$ is a root of the quadratic equation $x^{2}-x-100=0$. Find the value of $a^{4}-201 a$
|
Answer: 10100.
Solution. Squaring the expression $a^{2}=a+100$, we get $a^{4}=a^{2}+200a+10000=a+100+200a+10000=201a+10100$. From this, we obtain the answer.
|
10100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. How many points are there on the hyperbola $y=\frac{2013}{x}$ such that the tangent at these points intersects both coordinate axes at points with integer coordinates
|
Answer: 48 points. Solution. Let $k=2013$. The equation of the tangent to the hyperbola $y=\frac{k}{x}$ at the point $\left(x_{0}, y_{0}\right)$ is $y-y_{0}=-\frac{k}{x_{0}^{2}}\left(x-x_{0}\right)$, where $y_{0}=\frac{k}{x_{0}}$. From this, we find the coordinates of the points of intersection of the tangent with the axes $O x$ and $O y$, specifically $x_{1}=2 x_{0}, y_{1}=\frac{2 k}{x_{0}}=2 y_{0}$. Thus, $2 x_{0}$ is an integer; let us denote it by $n$. Then $y_{1}=\frac{2 k}{x_{0}}=\frac{4 k}{n}=\frac{4 \cdot 2013}{n}$. Therefore, $n$ can take any value of a divisor of the number $N=4 \cdot 2013=2^{2} \cdot 3^{1} \cdot 11^{1} \cdot 61^{1}$. The number of natural divisors of the number $N$ is $(2+1)(1+1)(1+1)(1+1)=24$ (since any divisor has the form $2^{\alpha_{1}} \cdot 3^{\alpha_{2}} \cdot 11^{\alpha_{3}} \cdot 61^{\alpha_{4}}$, where $0 \leq \alpha_{1} \leq 2$, $0 \leq \alpha_{2,3,4} \leq 1$). Taking into account the negative divisors (corresponding to tangents in the third quadrant), we get a total of 48 points.
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. How many solutions in integers $x, y$ does the equation $|3 x+2 y|+|2 x+y|=100$ have?
|
Answer: 400. Solution. Note that for any integers $a, b$ the system of equations $\left\lvert\,\left\{\begin{array}{l}3 x+2 y=a \\ 2 x+y=b\end{array}\right.$ has an integer solution $\left\lvert\,\left\{\begin{array}{l}x=2 b-a \\ y=2 a-3 b\end{array}\right.$, and different ordered pairs $(a, b)$ correspond to different solutions ( $x, y$ ). Therefore, for any natural number $n$ from 1 to 99, taking $a, b$ as numbers of the form $a= \pm n, b= \pm(100-n)$, we get $99 \cdot 4=396$ solutions. In addition, there will be two solutions corresponding to the numbers $a= \pm 100, b=0$ and, similarly, there will be two more solutions corresponding to the numbers $a=0, b= \pm 100$. In total, 400 solutions.
|
400
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. How many solutions in natural numbers $x, y$ does the equation $x+y+2 x y=2023$ have?
|
Answer: 6.
Solution. Multiply the equation by 2, add one to both sides, and factor the left side, while expressing the right side as a product of prime factors:
$$
2 x+4 x y+2 y+1=4047 \Leftrightarrow(2 x+1)(2 y+1)=4047 \Leftrightarrow(2 x+1)(2 y+1)=3 \cdot 19 \cdot 71
$$
Since \(x\) and \(y\) are natural numbers, each factor on the left side is at least three, so the number one cannot appear in the factorization options, and the possible options are:
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. Solve the equation $2 \cos (\pi x)=x+\frac{1}{x}$.
|
Answer: $x=-1$.
Solution. The left side of the equation is no more than two in absolute value, while the right side is no less than two in absolute value: for the right side, this follows from elementary inequalities, for example (for $x>0$), - from the inequality between the arithmetic mean and the geometric mean, and for $x<0$ it is true for the absolute value due to the oddness of the function $y=x+1 / x$; the same conclusion can also be reached by studying the range of values of this function using the derivative. The value of 2 (in absolute value) is only achieved at $x=1$ or $x=-1$. Checking these numbers, we find that only $x=-1$ works.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. How many three-digit natural numbers $n$ exist for which the number $n^{3}-n^{2}$ is a perfect square
|
Answer: 22. Solution. Let $n^{3}-n^{2}=m^{2}$ for some natural number $m$. Then $n^{2}(n-1)=m^{2}$, and therefore $n-1$ must also be a perfect square: $n-1=a^{2}$. Thus, $n=a^{2}+1$ and $m=\left(a^{2}+1\right) a$. Therefore, we need to find all three-digit numbers $n$ that are one more than perfect squares. Such numbers are $101=10^{2}+1, 122=11^{2}+1, \ldots, 962=31^{2}+1$ (the next square $32^{2}=1024-$ is already too large).
## 9th grade
|
22
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Given a right triangle, the height dropped to the hypotenuse is 4 times smaller than the hypotenuse. Find the acute angles of this triangle.
|
Answer: $15^{\circ}$ and $75^{\circ}$. Solution. See problem 8.4.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. In triangle $A B C$, angle $A$ is the largest. Points $M$ and $N$ are symmetric to vertex $A$ with respect to the angle bisectors of angles $B$ and $C$ respectively. Find $\angle A$, if $\angle M A N=50^{\circ}$.
|
Answer: $80^{\circ}$. Solution. Let $\angle A=\alpha, \angle B=\beta, \angle C=\gamma$. Then $\angle A M B=90^{\circ}-\frac{\beta}{2}, \angle A N C=90^{\circ}-\frac{\gamma}{2}$ (since triangles $A M B$ and $\quad$ are isosceles). Therefore, $\angle M A N=180^{\circ}-\left(90^{\circ}-\frac{\beta}{2}\right)-\left(90^{\circ}-\frac{\gamma}{2}\right)=\frac{\beta+\gamma}{2}=90^{\circ}-\frac{\alpha}{2}$. From the problem statement, $90^{\circ}-\frac{\alpha}{2}=50^{\circ}$, hence, $\alpha=80^{\circ}$.
|
80
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. The bisector of angle $ABC$ forms an angle with its sides that is three times smaller than the adjacent angle to $ABC$. Find the measure of angle $ABC$.
|
Answer. $\quad 72^{\circ}$. Solution. Let $x$ be the degree measure of angle $ABC$. From the condition of the problem, we get the equation $\frac{x}{2}=\frac{180-x}{3} \Leftrightarrow 5 x=360 \Leftrightarrow x=72$ (degrees).
|
72
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. A natural number is called curious if, after subtracting the sum of its digits from it, the result is a number consisting of identical digits. How many three-digit curious numbers exist?
|
Answer: 30 numbers. Solution: Let $\overline{x y z}$ be a curious three-digit number. Then the number
$$
A=\overline{x y z}-(x+y+z)=100 x+10 y+z-(x+y+z)=9(11 x+y)
$$
is divisible by 9 and consists of identical digits, and $100-27 \leq A \leq 999-1$. Thus, $A$ can be either 99, 333, or 666.
In the case of $A=99$, we have $11 x+y=11$, then $x=1, y=0, z$ - any digit, i.e., in this case, there are 10 curious numbers: $100,101, \ldots, 109$.
In the case of $A=333$, we get $11 x+y=37$, then we sequentially determine the digits: $x=3, y=4$, $z$ - any digit, i.e., in this case, there are also 10 curious numbers.
In the case of $A=666$, we have $11 x+y=74$, and then $x=6, y=8, z$ - any digit, again we have 10 curious numbers.
|
30
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Given the sequence $a_{n}=(-1)^{1+2+\ldots+n}$. Find $a_{1}+a_{2}+\ldots+a_{2017}$.
|
Answer: -1. Solution. We have $a_{n}=(-1)^{\text {sn }}$, where $S_{n}=\frac{n(n+1)}{2}$. It is easy to notice and prove that the parity of the number $S_{n}$ repeats with a period of 4: indeed, $S_{n+4}-S_{n}=\frac{(n+4)(n+5)-n(n+1)}{2}=\frac{8 n+20}{2}=4 n+10$, i.e., an even number. Therefore, $a_{1}+a_{2}+\ldots+a_{2017}=(-1-1+1+1)+(-1-1+1+1)+\ldots+(-1-1+1+1)+(-1)=0+0+\ldots+0+(-$ $1)=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.7 Find all values of the parameter \(a\), for each of which the system of equations
\[
\left\{
\begin{array}{l}
x^{2}+y^{2}=2 a, \\
x+\log _{2}\left(y^{2}+1\right)=a
\end{array}
\right.
\]
has a unique solution.
|
Answer: $a=0$.

Solution. Note that if $(x, y)$ is a solution to the system, then $(x, -y)$ is also a solution to this system. Therefore, if for a parameter $a$ the system has a unique solution, the value of $y$ must be zero. Then from the second equation, we have $x=a$, and substituting $x=a$, $y=0$ into the first equation, we get $a^2 = 2a$. Thus, $a=0$ or $a=2$. Now we need to check these values of $a$ (note that they are derived as a consequence of the uniqueness of the solution to the system, but do not yet guarantee uniqueness).
For $a=0$, the first equation is equivalent to the equalities $x=y=0$, and for these zero values of the unknowns, the second equation is satisfied, i.e., the value $a=0$ works.
For $a=2$, the system has the solution $x=2, y=0$, but for the system, this solution is not unique. Indeed, the curve $x=2-\log_2(y^2+1)$ intersects the circle $x^2+y^2=4$ not only at the point $(2; 0)$ but also at two symmetric points in the second and third quadrants. (see figure). This follows from the fact that the points $(1; 1)$ and $(1; -1)$ lie on the given curve and are inside the circle $x^2+y^2=4$ (or one can verify that the points $(0; \pm \sqrt{3})$ on the y-axis will also be such points), and for $|y|>2$, the corresponding points on the curve are outside the circle.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. In the 7th grade, there are 25 people, and each attends a dance club or a drama club (some attend both clubs). Everyone took a math test, and the teacher calculated the percentage of students who received a failing grade (2) separately among the "dancers" and among the "actors." It turned out that the percentage is the same and equals $30 \%$. Can the percentage of failing grades in the entire class be more than $35 \%$?
|
Answer. It can. Solution. Consider the following example. Suppose there are 10 "dancers" and 20 "actors" in the class, then the number of "dancing actors" will be $10+20-25=5$ people, and the number of "pure dancers" will be $10-5=5$ and the number of "pure actors" will be $20-5=15$. Suppose that three "dancers" and six "actors" received twos, and the "dancing actors" did not receive any twos. Then the percentage of twos among "dancers" and among "actors" is $\frac{3}{10}=\frac{6}{20}=30 \%$, while the percentage of twos in the entire class is $\frac{9}{25}=36 \%$. Comment. A complete solution to the problem is considered any example that meets the conditions. In the given example, the "round" numbers of dancers and actors (10 and 20) are "suggested" by the round percentage ( $=30 \%$ ).
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. Find a six-digit number that, when multiplied by 9, is written with the same digits as the original number but in reverse order? How many such six-digit numbers are there?
|
Answer. 109989 is the only number. Solution See problem 7.3.
|
109989
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. Given a triangle $A B C$. On the side $A C$, the largest in the triangle, points $M$ and $N$ are marked such that $A M=A B$ and $C N=C B$. It turns out that angle $N B M$ is three times smaller than angle $A B C$. Find $\angle A B C$.
|
Answer: $108^{\circ}$.
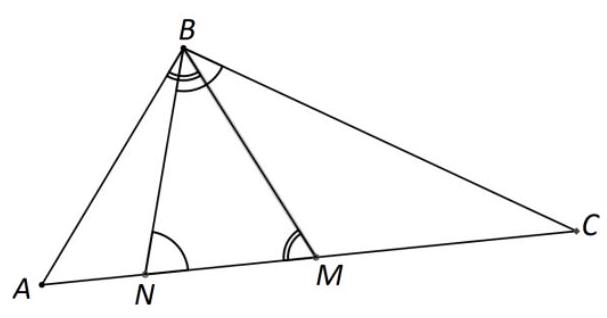
Solution. Point $N$ lies between $A$ and $M$, since $A M+C V=A B+B C > AC$. Let $\angle N B M = x$, then $\angle A B M + \angle N B C = \angle A B C + \angle N B M = 3x + x = 4x$. According to the problem, triangles $A B M$ and $N B C$ are isosceles, and therefore $\angle A B M + \angle N B C = \angle B M N + \angle B N M = 180^{\circ} - \angle N B M = 180^{\circ} - x$. Thus, we have the equation $4x = 180^{\circ} - x$, from which $x = 36^{\circ}$ and $\angle A B C = 3x = 108^{\circ}$.
|
108
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Find the smallest natural number divisible by 5, with the sum of its digits being 100. Justify your answer.
|
Answer: 599999999995 (between two fives there are 10 nines). Solution. Due to divisibility by 5, the last digit of the number $N$ can be either 5 or 0. If the last digit is 0, without changing the sum of the digits, we can replace 0 with 5 and subtract one from each of the five non-zero digits in other positions. Then we get a smaller number that satisfies the conditions of the problem. Next, if any digit of $N$ between the first and the last is not a nine, then by increasing it by one and decreasing the digit in the higher position by one, we again get a smaller number. Thus, all digits of $N$, except the first and the last, are nines (say, $n$ of them), and the last one is five. The first digit $x$ is found from the condition for the sum of the digits: $x+9n+5=100$, i.e., $9n=95-x$. Obviously, the digit $x$ for the divisibility of the right side by 9 is uniquely determined: $x=5$. Hence the answer.
|
599999999995
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. On the edges of a cube, numbers $1,2, \ldots, 12$ were placed in some order, and for each face, the sum of the four numbers on its edges was calculated. Prove that there is a face for which this sum is greater than 25.
|
Solution. Let's calculate the corresponding sum on each face and then add these sums for all six faces. We will get $(1+2+\ldots+12) \cdot 2$ as a result, since in this calculation any edge will be counted twice. Thus, the total sum is 156, and then the sum for at least one face is not less than $\frac{156}{6}=26$. (Indeed, otherwise we would get a total sum not exceeding $25 \cdot 6=150<156$).
|
26
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
8.4. Given a right triangle, the height dropped to the hypotenuse is 4 times smaller than the hypotenuse. Find the acute angles of this triangle.
|
Answer: $15^{\circ}$ and $75^{\circ}$. Solution. Let $A B C$ be the given triangle, $C M$ the height from vertex $C$ of the right angle, and $C O$ the median. Consider the right triangle $C M O$. By the property of the median from the vertex of the right angle, $C O=\frac{A B}{2}$, and therefore (by the condition) $C O$ is twice as long as $C M$. Therefore (by the property of a right triangle with a leg equal to half the hypotenuse) $\angle C O M=30^{\circ}$. Then, considering the isosceles $\triangle C O B$ with the external angle $C O M$, we get $\angle O C B=\angle O B C=15^{\circ}$, $\angle C A B=90^{\circ}-15^{\circ}=75^{\circ}$.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Petya says to Kolya: «I placed some numbers at the vertices of a cube, and then on each face I wrote the sum of the four numbers at its vertices. Then I added all six numbers on the faces and got 2019. Can you figure out what the sum of the eight numbers at the vertices of the cube is?» How would you answer this question if you were Kolya?
|
Answer: 673. Solution. Each vertex of the cube belongs to three faces (which meet at this vertex) and therefore the number placed at this vertex participates three times in the calculation of the sums on the faces. Thus, the sum of the numbers at the vertices is $2019: 3=673$. Comment: another way to solve (direct) is as follows: by denoting the 8 unknown numbers at the vertices of the cube and expressing through them the sum of the numbers on the faces, after factoring out the threes, in parentheses we will get the sum of all the numbers at the vertices.
|
673
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
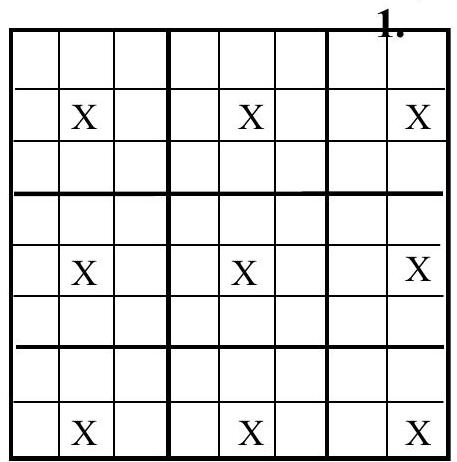
7.4. What is the minimum number of kings that need to be placed on a chessboard so that they attack all unoccupied squares? (A king attacks the squares that are adjacent to its square by side or corner).
|
Answer: 9 kings. Solution. The required arrangement of nine kings is shown in the figure. Let's prove that it is impossible to manage with a smaller number. Indeed, consider the 9 rectangular zones outlined on the figure with bold lines. If we assume the opposite, then at least one of these zones does not contain a king. However, in this case, the cell in this zone marked with a cross will not be attacked by any king located in another zone, since this cell does not border with other zones.
## 11th grade
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2 In a company of $n$ people, 100000 ruble coins need to be distributed equally. How many different values of $n$ exist for which such a distribution is possible?
|
Answer: 36. Solution: Let's calculate the number of natural divisors of the number $100000=2^{5} \cdot 5^{5}$. Any such divisor has the form $2^{i} \cdot 5^{j}$, where the integers $i, j$ can take six values: from 0 to 5. Then the number of different ordered pairs ( $i ; j$ ) will be $6 \cdot 6=36$.
|
36
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. How many Pythagorean triangles exist with one of the legs equal to 2013? (A Pythagorean triangle is a right triangle with integer sides. Equal triangles are counted as one.).
|
Answer: 13. Solution. From the Pythagorean theorem, we obtain the equation in integers $2013^{2}+x^{2}=y^{2} \Leftrightarrow(y-x)(y+x)=2013^{2}=3^{2} \cdot 11^{2} \cdot 61^{2}$. This equation is equivalent to the system $\left\{\begin{array}{l}y-x=d_{1} \\ y+x=d_{2}\end{array}\right.$, where $d_{1}, d_{2}=\frac{2013^{2}}{d_{1}}-$ are natural divisors of the number 2013 2. The solution of the system $x=\frac{d_{2}-d_{1}}{2}, y=\frac{d_{2}+d_{1}}{2}$ will be integer, since $d_{1}$ and $d_{2}-$ are odd numbers. For the number $x$ to be natural, the divisor $d_{2}$ must be greater than $d_{1}$, i.e. $d_{2}>2013, d_{1}<2013$ (we discard the "central" divisor $d=2013$, and the remaining divisors are divided into pairs $\left(d_{1}, d_{2}\right)$, where $d_{1} \cdot d_{2}=2013$, and from each pair we choose $\left.d_{2}>d_{1}\right)$.
|
13
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1 The length of a rectangle is $25 \%$ greater than its width. By a straight cut, parallel to the shorter side, this rectangle is cut into a square and a rectangular strip. By what percentage is the perimeter of the square greater than the perimeter of the strip?
|
Answer: By $60 \%$. Solution: Let $a$ be the width of the rectangle, then its length is $1.25 a$. The perimeter of the resulting square is $4 a$, and the perimeter of the strip is $2 a+0.5 a=2.5 a$. The ratio of the perimeters is $4 a: 2.5 a=1.6$. Therefore, the perimeter of the square is greater than the perimeter of the strip by $0.6 \cdot 100 \% = 60 \%$
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2 Can 8 numbers be chosen from the first hundred natural numbers so that their sum is divisible by each of them
|
Answer. Yes. Solution. An example of the required numbers can be $1 ; 2 ; 3 ; 6 ; 12 ; 24 ; 48 ; 96.3$ here the sum 192 is divisible by each of the numbers. This example is not unique; others can be provided, such as $1 ; 2 ; 3 ; 4 ; 5 ; 15 ; 30 ; 60$ with a sum of 120.
|
120
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2 In the glass, there was a solution in which water made up $99 \%$. The glass with the solution was weighed, and the weight turned out to be 500 gr. After that, part of the water evaporated, so that in the end, the proportion of water was $98 \%$. What will be the weight of the glass with the resulting solution, if the weight of the empty glass is 300 gr.?
|
Answer: 400 g. Indication. Initially, the weight of the solution was $500-300=200$ (g)., and the amount of water was $0.99 \cdot 200=198$ (g.), and thus, the substance was $200-198=2$ (g.). After the evaporation of water, 2 g of the substance make up $100 \% -98 \% =2 \%$ of the weight of the solution, so the entire solution weighs 100 g, and together with the glass 400 g.
|
400
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Given a triangle $A B C$, point $O$ is the center of the inscribed circle. Find the angle $A$ if it is known that the radii of the circumscribed circles of triangles $A B C$ and $B O C$ are the same.
|
Answer. $\quad 60^{\circ}$.
Solution. Let $\angle A=\alpha$. Note that $\angle B O C=90^{\circ}+\frac{\alpha}{2}$; indeed, $\angle B O C=180^{\circ}-(\angle O B C+\angle B C O)=180^{\circ}-\frac{1}{2}(\angle B+\angle C)=180^{\circ}-\frac{1}{2}\left(180^{\circ}-\alpha\right)=90^{\circ}+\frac{\alpha}{2}$. Then $B C=2 R_{A B C} \sin \alpha=2 R_{B O C} \sin \left(90^{\circ}+\frac{\alpha}{2}\right)=2 R_{B O C} \cos \frac{\alpha}{2} \Leftrightarrow \quad \sin \alpha=\cos \frac{\alpha}{2} \Leftrightarrow$ $\sin \frac{\alpha}{2}=\frac{1}{2} \Leftrightarrow \frac{\alpha}{2}=30^{\circ}$
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. A natural number $n$ was multiplied by the sum of the digits of the number $3 n$, and the resulting number was then multiplied by 2. As a result, 2022 was obtained. Find $n$.
|
Answer: 337. Solution. Let $s(N)$ denote the sum of the digits of the number $N$. Then the condition of the problem can be written as $2 n \cdot s(3 n)=2 \cdot 3 \cdot 337$, i.e., $n \cdot s(3 n)=3 \cdot 337=1011$. Therefore, $n \leq 1011$, so $3 n$ is at most a four-digit number, and $s(3 n)<4 \cdot 9=36$. Thus, $s(3 n)$ cannot equal 337, but must equal either 3 or 1. However, it is clear that the equality $s(3 n)=1$ leads to a contradiction (in this case, $3 n$ would be a power of ten). Therefore, $s(3 n)=3, n=337$. Verification confirms this solution, since $3 n=1011$.
|
337
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Let $a$ be the number of six-digit numbers divisible by 13 but not divisible by 17, and $b$ be the number of six-digit numbers divisible by 17 but not divisible by 13.
Find $a-b$.
|
Answer: 16290. Solution. Let $c$ be the number of six-digit numbers divisible by both 13 and 17. Then $a+c$ is the number of all six-digit numbers divisible by 13, and therefore $a+c=\left[\frac{999999}{13}\right]-\left[\frac{99999}{13}\right]=76923-7692=69231$.
denotes the integer part of the number $x$ ). Similarly,
$b+c=\left[\frac{999999}{17}\right]-\left[\frac{99999}{17}\right]=58823-5882=52941$. Thus, $a-b=(a+c)-(b+c)=$ $=16290$.
|
16290
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Find the largest natural number, all digits of which are different, and the product of these digits is a cube of some natural number.
|
Answer: 984321. Solution. Obviously, among the digits of the desired number $x$, there is no zero. The product of all digits from 1 to 9 is $2^{7} \cdot 3^{4} \cdot 5^{1} \cdot 7^{1}$. Therefore, $x$ cannot contain the digit 5 or the digit 7 (otherwise, the product of the digits of the number $x$ would have to be divisible by $5^{3}$ or $7^{3}$). This means that $x$ contains no more than seven of the remaining digits, and $2^{7} \cdot 3^{4}$ is divisible by the product of the digits of the number $x$. Since $2^{7} \cdot 3^{4}$ is not a cube of a natural number, $x$ cannot contain all seven of these digits. If we remove the digit 6, the remaining six digits will give a product of $2^{6} \cdot 3^{3}=12^{3}$. Removing any other digit instead of 6 clearly does not yield a product equal to the cube of a natural number. Removing several digits results in a number consisting of five or fewer digits. Therefore, $x$ consists of the digits 1, 2, 3, 4, 8, 9, and the requirement for maximality leads to the result: $x=984321$.
|
984321
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. Find the largest natural number, all digits of which are different, and the product of these digits is a cube of some natural number.
|
Answer: 984321. Solution. See problem 7.4
|
984321
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. In an $n \times n$ grid, each cell is colored either white or black. For what smallest $n$ is it always true (i.e., for any coloring) that there exists a rectangle whose vertices coincide with the centers of four cells of the same color?
|
Answer: $n=5$. Proof. We will prove that for $n=5$ (and thus for $\mathrm{n}>5$) such a rectangle will exist. Consider the bottom row of the table. In it, there are at least 3 cells of the same color. Let's assume for definiteness that these are white cells. Then consider the three columns with these cells at the base, i.e., we consider a smaller table of size $5 \times 3$, the bottom row of which consists of three white cells. If in any of the four remaining rows of this smaller table there are two white cells, then the desired "white" rectangle is formed by their centers and the centers of the corresponding cells in the bottom row.

Now, suppose in each of these four rows there are at least two black cells. Then among these four rows, there will be at least two rows with the same arrangement of black cells, since there are only 3 different arrangements of two black (denoted by b) cells, namely: (bb?), (b?b), and (?bb)), and thus their centers form a "black" rectangle. An example of coloring a $4 \times 4$ square for which there is no such rectangle is shown in the figure (it is easy to verify that for this example, there are no "monochromatic" rectangles even with sides not parallel to the grid lines).
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. Girls stood in a circle, some of them wearing scarves. A circle is called correct if each girl without a scarf has a neighbor wearing a scarf. a) What is the minimum number of scarves in a correct circle of 25 girls? b) Prove that if in this correct circle of 25 girls there are more than 12 scarves, then some girls can take off their scarves, and the circle will still be correct.
|
Answer: a) 9. Solution. a) Note that among three consecutive girls, there is at least one handkerchief: otherwise, the girl in the middle would not have a neighbor with a handkerchief. Fix one girl with a handkerchief in the circle, say Tanya, and consider three girls in sequence clockwise after Tanya. There are a total of 8 such triplets, and in each of them, there is at least one handkerchief. Thus, the total number of handkerchiefs is no less than $1+8=9$, and the estimate is obtained. Now let's construct an example of a correct circle with 9 handkerchiefs: for this, we can put a handkerchief on Tanya, and in each of the specified triplets, on the girl standing in the middle. b) Suppose there are more than 12 handkerchiefs in the circle. Fix a girl without a handkerchief, say Olya (if all 25 girls have handkerchiefs, the situation is obvious: any of them can take off their handkerchief). The remaining 24 girls can be divided into six quartets, counting clockwise after Olya. Then in one of these quartets, there will be at least three handkerchiefs (by the pigeonhole principle or reasoning by contradiction: otherwise, there would be no more than $2 \cdot 6=12$ handkerchiefs in total). Therefore, among the three girls with handkerchiefs in this quartet, the middle girl can obviously take off her handkerchief and the circle will remain correct.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. The inscribed circle of triangle $A B C$ with center $O$ touches the sides $A B, B C$ and $A C$ at points $M, N$ and $K$ respectively. It turns out that angle $A O C$ is four times the angle $M K N$. Find angle $B$.
|
Answer: $108^{\circ}$. Solution. Let $\angle A=\alpha, \angle B=\beta, \angle C=\gamma$. Then, in the isosceles triangle $A K M$, the angle at the base is $\angle A K M=\left(180^{\circ}-\alpha\right) / 2$. Similarly, in triangle $C K N$, we find $\angle C K N=\left(180^{\circ}-\gamma\right) / 2$. Therefore, $\angle M K N=180^{\circ}-\angle C K N-\angle A K M=(\alpha+\gamma) / 2=\left(180^{\circ}-\beta\right) / 2=$ $=90^{\circ}-\frac{\beta}{2}$. Next, $\angle A O C=180^{\circ}-\frac{\alpha}{2}-\frac{\gamma}{2}=180^{\circ}-\left(180^{\circ}-\beta\right) / 2=90^{\circ}+\frac{\beta}{2}$. Thus, from the condition of the problem, we have $90^{\circ}+\frac{\beta}{2}=4\left(90^{\circ}-\frac{\beta}{2}\right) \Leftrightarrow \beta=\frac{540^{\circ}}{5}=108^{\circ}$.
|
108
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Append a digit to the left and right of the eight-digit number 20222023 so that the resulting 10-digit number is divisible by 72. (List all possible solutions.)
|
Answer: 3202220232.
Solution. Since $72=8 \cdot 9$, it is required to append digits so that the resulting number is divisible by both 8 and 9. Divisibility by 8 is determined by the last three digits: thus, to the two-digit number 23, we need to append a digit on the right to form a three-digit number that is a multiple of 8. There is only one digit, namely 2, for which this is possible ( $232: 8=29$ ). After this, the first digit of the desired number is determined by the divisibility rule for 9 (the sum of the digits must be divisible by 9, so we need to add 3 to the existing sum of digits, which is 15).
|
3202220232
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. Given an isosceles triangle $A B C$ with base $A C$. Points $K$ and $N$ are marked on the side $B C$ ( $K$ lies between $B$ and $N$ ). It turns out that $K N=A N$ and $\angle B A K=\angle N A C$. Find $\angle B A N$.
|
Answer: $60^{\circ}$. Solution. Let $\angle B A K=\angle N A C=x, \angle K A N=y$. In the isosceles triangle $A K N$, the angle $A K N$ (at the base) is also equal to $y$. The angles at the base of triangle $A B C$ are equal to $2 x+y$, and the angle at the vertex $B$ is therefore equal to $180^{\circ}-2(2 x+y)$. The exterior angle $\angle A K N=y$ in triangle $A K B$ is equal to $x+180^{\circ}-2(2 x+y)=180^{\circ}-3 x-2 y$. Then from the equation $y=180^{\circ}-3 x-2 y$ we get $x+y=60^{\circ}$, i.e., $\angle B A N=60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. $\quad$ A cyclist planned to travel from point $A$ to point $B$ in 5 hours, moving at a constant speed. He traveled at the planned speed until the midpoint of the journey, then increased his speed by $25 \%$. He completed the journey to point $B$ at the new speed. How long did the entire trip take?
|
Answer: 4 hours 30 minutes. Solution. See problem 7.1.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Find the sum of all three-digit natural numbers that do not contain the digits 0 or 9 in their representation.
|
Answer: 255 744. Solution. We will add the numbers in a column. Each last digit (for example, two) appears in the units place as many times as there are three-digit numbers of the specified form with this last digit (in our case -- these are numbers of the form $\overline{x y 2}$, where $x, y$ are any digits from 1 to 8 inclusive.). This means that the digit two, like any other digit from 1 to 8, will appear in the units place $8 \cdot 8 = 64$ times. Thus, the sum of the digits in the units place is $64 \cdot (1+2+\ldots+8)=2304$. Similarly, in the tens and hundreds places, we get the same sum of 2304. In the end, the sum of all the numbers is
$$
2304 \cdot 100 + 2304 \cdot 10 + 2304 = 2304 \cdot 111 = 255744
$$
|
255744
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Find the sum of all four-digit natural numbers composed of the digits 3, 6, and 9.
|
Answer: 539946. Solution. We will add the numbers in a column. Each last digit (for example, six) appears in the units place as many times as there are three-digit numbers of the specified type with this last digit (in our case -- these are numbers of the form $\overline{x y z 6}$, where $x, y, z$ are arbitrary sets of digits 3, 6, and 9. Thus, the digit six, like three and nine, will appear in the units place $3 \cdot 3 \cdot 3=27$ times. Therefore, the sum of the digits in the units place is $27 \cdot(3+6+9)=486$. Similarly, in the tens, hundreds, and thousands places, we get the same sum of 486. In the end, the sum of all the numbers is
$$
486 \cdot 1000+486 \cdot 100+486 \cdot 10+486=486 \cdot 1111=539946
$$
|
539946
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. The sequence $a_{n}$ is defined as follows: $a_{1}=2^{20}, a_{n+1}=s\left(a_{n}\right)$ for all $n$, where $s(a)$ denotes the sum of the digits of the natural number $a$. Find $a_{100}$.
|
Answer: 5. Solution. The main fact used is that the sum of the digits of any number has the same remainder when divided by 9 as the number itself. This fact is proven in the same way as the well-known divisibility rule for 9. We will show that the sequence $a_{n}$ decreases rapidly until it becomes less than 10, and after that, it obviously becomes constant. Indeed, if the number $n$ is $k$-digit, then $n>10^{k-1}$, and $s(n) \leq 9 k < 10^{k / 2} = \sqrt{10}^{k}$ for $k \geq 4$ (the last inequality is easily proven by induction). The initial number $a_{1}=2^{20}$ is less than $10^{1024}$, since $2^{2015} < (2^{3})^{672} < 10^{1024}$. Therefore, $a_{2}<10^{528}, a_{3}<10^{256}, \ldots, a_{9}<10^{4}$, i.e., $a_{9}$ has no more than three digits. Hence, $a_{10} \leq 3 \cdot 9 = 27$ and, obviously, $a_{12}<10$. It remains to find the remainder of $2^{2015}$ when divided by 9. Since $2^{3}$ has the form $9 p - 1$ (i.e., it has a remainder of 8 when divided by 9), then $2^{2013} = (2^{3})^{671}$ also has such a form (as the product of an odd number of factors of the form $9 p - 1$), and $2^{2015} = 2^{2013} \cdot 4 = (9 p - 1) \cdot 4 = 9 q + 5$ (where $q = 4 p - 1$).
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Find the smallest natural number divisible by 5, with the sum of its digits being 100. Justify your answer.
|
Answer: 599999999995 (between two fives there are 10 nines).
Solution. Due to divisibility by 5, the last digit of the number $N$ can be either 5 or 0. If the last digit is 0, without changing the sum of the digits, we can replace 0 with 5 and subtract one from each of the five non-zero digits in other positions. Then we get a smaller number that satisfies the conditions of the problem. Next, if any digit of $N$ between the first and last is not a nine, then by increasing it by one and decreasing the digit in the higher position by one, we again get a smaller number. Thus, all digits of $N$ except the first and last are nines (say, $n$ of them), and the last one is a five. The first digit $x$ is found from the condition for the sum of the digits: $x+9n+5=100$, i.e., $9n=95-x$. Obviously, the digit $x$ for the divisibility of the right side by 9 is uniquely determined: $x=5$. Hence the answer.
|
599999999995
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. In triangle $A B C$, the angles $A$ and $C$ at the base are $20^{\circ}$ and $40^{\circ}$, respectively. It is known that $A C - A B = 5$ (cm). Find the length of the angle bisector of angle $B$.
|
Answer: 5 cm. Solution. Let $B M$ be the bisector of angle $B$. Mark a point $N$ on the base $A C$ such that $A N=A B$. Then triangle $A B N$ is isosceles and $\angle A B N=\angle A N B=80^{\circ}$. Since $\angle A B M=\frac{180^{\circ}-20^{\circ}-40^{\circ}}{2}=60^{\circ}$, then $\angle B M N=\angle A+\angle A B M=20^{\circ}+60^{\circ}=80^{\circ}$. Thus, the angles at the base of $\triangle M B N$ are equal, which means $\triangle M B N$ is isosceles: $M B=B N$. In $\triangle B N C$, the angles $\angle N C B$ and $\angle C N B$ are equal to $40^{\circ}$ (since $\angle B N C=180^{\circ}-80^{\circ}=100^{\circ}$ and $\angle N B C=180^{\circ}-40^{\circ}-100^{\circ}=40^{\circ}$). Therefore, $\triangle B N C$ is isosceles: $B N=N C$. As a result, we have $B M=B N=N C=5$ cm (since $N C=A C-A N=A C-A B)$.
## 8th grade
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. What is the smallest number of digits that can be appended to the right of the number 2013 so that the resulting number is divisible by all natural numbers less than 10?
|
Answer: three digits. Solution. The least common multiple of the numbers $(1,2, \ldots, 9)$ is 2520. If two digits are appended to 2013, the resulting number will not exceed 201399. Dividing 201399 by 2520 with a remainder, we get a remainder of 2319. Since 2319 > 99, there is no integer multiple of 2520 between the numbers 201300 and 201399. Therefore, it is impossible to append two digits to 2013. Clearly, it is also impossible to append one digit (otherwise, it would be possible to add another zero at the end). Three digits will suffice; indeed, when dividing 2013999 by 2520, the remainder is 519, and since $519<999$, we find the required number $2013999-519=$ 2013480, which is a multiple of 2520.
|
2013480
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Find the sum of all three-digit natural numbers that do not contain the digit 0 or the digit 5.
|
Answer: 284160. Solution. We will add the numbers in a column. Each last digit appears in the units place as many times as there are three-digit numbers ending with this digit. Therefore, it will appear $8 \cdot 8=64$ times (since a total of 8 digits are used for the hundreds and tens places). Thus, the sum of the digits in the last place is $64 \cdot(1+2+3+4+6+7+8+9)=2560$. Similarly, in the tens and hundreds places, we get the same sum. In the end, we get $2560 \cdot 100+2560 \cdot 10+2560=2560 \cdot 111=284160$.
|
284160
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1 The average age of the teaching staff of a school, consisting of 20 teachers, was 49 years. When another teacher joined the school, the average age became 48 years. How old is the new teacher?
|
Answer: 28 years old. Solution: Before the new teacher arrived, the total age of the teachers was 49*20=980. Then the total age became 48*21=1008. Therefore, the new teacher is $1008-$ $980=28$ years old.
|
28
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4 On a grid sheet of paper sized $60 \times 70$ cells (horizontally and vertically respectively), Lena drew a coordinate system (the origin is at the center of the sheet, the $x$-axis is horizontal, the $y$-axis is vertical, and the axes are drawn to the edges of the sheet) and plotted the graph $y=0.83 x$. Then Lena shaded all the cells that the graph passes through, i.e., cells that contain points of the graph. How many shaded cells are there in total?
|
Answer: 108. Solution: The graph passes through the first and third quadrants. Let's count the number of shaded cells in the first quadrant (in the third quadrant, there will be the same number, since the graph is a straight line passing through the origin, and therefore centrally symmetric). The graph intersects 29 vertical grid lines: $x=1, x=2, \ldots, x=29$ (inside the quadrant) and 24 horizontal grid lines: $y=1, y=2, \ldots$, $y=24$ (since at $x=30$ the value of $y=24.9$). We also note that the points of intersection with these lines are not grid nodes, since $0.83 x$ is not an integer for $x=1,2, \ldots, 29$, because 83 is a prime number. Thus, there are a total of $29+24=53$ points of intersection with the grid lines inside the quadrant, and the number of segments in the first quadrant into which the graph is divided by these points is 54. Each such segment corresponds to a shaded cell (to which it belongs). Therefore, in both quadrants, there will be 108 shaded cells.
## 1st round. 11.11 .2018
## 8th grade
|
108
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2 Let $s(n)$ denote the sum of the digits of a natural number $n$. Solve the equation $n+s(n)=2018$.
|
Answer: $n=2008$. Solution. Since $n2018-29=1989$, i.e., $n$ is written in the form $\overline{199 x}$ or $\overline{200 x}$ or $\overline{201 x}$ where $x$ is some digit. In the first case, we have the equation $1990+x+19+x=2018$, which gives a non-integer value of $x$. Similarly, in the third case, the equation $2010+2 x+3=2018$ gives a non-integer $x$. In the second case, the equation $2000+2 x+2=2018$ gives $x=8$, i.e., $n=2008$.
|
2008
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. Find all values of the parameter $a$ for which the equation $|x+a|=\frac{1}{x}$ has exactly two roots.
|
Answer: $a=-2$. Solution. The intersection of the graphs of the right and left parts can only be in the first
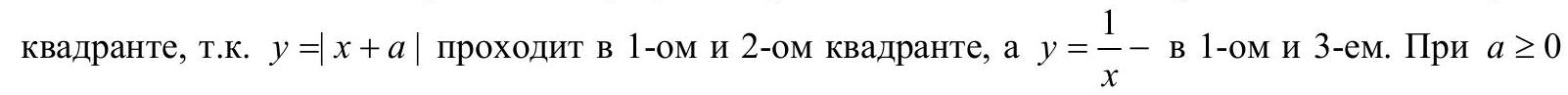
the graph $y=|x+a|$ in the first quadrant represents the line $y=x+a$, which intersects with the hyperbola $y=\frac{1}{x}$ at exactly one point (since $y=\frac{1}{x}$ is a decreasing function). Now consider the values $a<0$. For $x \geq -a$, we have (reasoning similarly) one point of intersection of the graphs. Therefore, we need to find $a$ such that there is exactly one more point of intersection for $x \in (0, -a)$. We have $-x-a=\frac{1}{x} \Leftrightarrow x^{2}+a x+1=0 \Leftrightarrow x=\left(-a \pm \sqrt{a^{2}-4}\right) / 2$, hence $a=-2$ (for $-2<a<0$ the quadratic equation has no roots, and for $a<-2$ it has two positive roots, both less than $|a|$).
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. Given a convex quadrilateral $A B C D$, where $A B=A D=1, \angle A=80^{\circ}$, $\angle C=140^{\circ}$. Find the length of the diagonal $A C$.
|
Answer: 1. Solution. We will prove that $A C=1$ by contradiction. If $A C>1$, then in triangle $A B C$ the larger side $A C$ is opposite the larger angle: $\angle B>\angle B C A$. Similarly, for triangle $A D C$ we have $\angle D>\angle D C A$. Adding these inequalities, we get $\angle B+\angle D>\angle C=140^{\circ}$. Thus, the sum of all angles of the quadrilateral $(\angle A+\angle C)+(\angle B+\angle D)>\left(80^{\circ}+140^{\circ}\right)+140^{\circ}=360^{\circ}$ - a contradiction. Similarly, if we assume that $A C<1$, then $\angle B+\angle D<\angle C$, and as a result, we get the sum of the angles of the quadrilateral less than $360^{\circ}$ - again, a contradiction. Comment. Another solution method uses the properties of inscribed angles: if we assume that point $C$ lies inside the unit circle centered at point $A$, then angle $C$ will be greater than $\frac{1}{2}\left(360^{\circ}-\angle A\right)=140^{\circ}$, and if $C$ lies outside the circle, then angle $C$ will be less than $140^{\circ}$. Therefore, $C$ lies on the circle.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. From a three-digit number, the sum of its digits was subtracted and the result was 261. Find the second digit of the original number.
|
Answer: 7. Solution. Let $\overline{x y z}=100 x+10 y+z$ be the original number. According to the condition, $99 x+9 y=261$, i.e., $11 x+y=29$. Since $y \leq 9$, for $29-y$ to be divisible by 11, we get $y=7$ (and then $x=2$).
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Kolya and Petya exchanged stamps. Before the exchange, Kolya had 5 more stamps than Petya. After Kolya exchanged $24\%$ of his stamps for $20\%$ of Petya's stamps, Kolya had one stamp less than Petya. How many stamps did the boys have before the exchange?
|
Answer. Petya had 45 stamps, Kolya had 50 stamps. Solution. Let Petya have $x$ stamps before the exchange, then Kolya had $(x+5)$ stamps. After the exchange, Petya had $x-\frac{x}{5}+(x+5) \cdot \frac{6}{25}$, and Kolya had $x+5-(x+5) \cdot \frac{6}{25}+\frac{x}{5}$. Solving the equation $x-\frac{x}{5}+(x+5) \cdot \frac{6}{25}-x-5+(x+5) \cdot \frac{6}{25}-\frac{x}{5}=1$, we find $x=45$.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. For a 92-digit natural number n, the first 90 digits are known: from the 1st to the 10th - ones, from the 11th to the 20th - twos, and so on, from the 81st to the 90th - nines. Find the last two digits of the number n, given that n is divisible by 72.
|
Answer: 36. Solution: Let the last digits be $x$ and $y$. The number $n$ must be divisible by 9 and 8. The number consisting of the first 90 digits is divisible by 9, since the sum of its digits is divisible by 9. Therefore, the number $\overline{x y}$ is also divisible by 9. In addition, by the divisibility rule for 4, the number $\overline{x y}$ is divisible by 4. Therefore, $\overline{x y}$ is either 00, 36, or 72. Since $n$ is divisible by 8, the number $\overline{9 x y}$ (consisting of the last three digits) is divisible by 8. Among the numbers 900, 936, and 972, only 936 has this property.
|
36
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. $\quad$ In the 7a class, $60 \%$ of the students are girls. When two boys and one girl were absent due to illness, the percentage of girls present was $62.5 \%$. How many girls and boys are there in the class according to the list?
|
Answer: 21 girls and 14 boys. Solution. Let there be $d$ girls and $m$ boys in the class. From the conditions of the problem, we have two equations: $\frac{d}{d+m}=0.6$ and $\frac{d-1}{d+m-3}=0.625$. From the first equation, $2 d=3 m$. Substituting $m=\frac{2}{3} d$ into the second equation and solving it, we get $d=21$, and then $m=14$.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. There are 11 kg of cereal. How can you measure out 1 kg of cereal using two weighings on a balance scale, if you have one 3 kg weight?
|
Solution. First weighing: place a weight (3 kg) on one scale pan, and on the other, initially 11 kg of grain, and keep pouring grain onto the first pan until equilibrium is achieved. We get 3 kg (weight) + 4 kg (grain) $=7$ kg (grain) (since $3+x=11-x=>x=4$). Second weighing: from the obtained 4 kg of grain, pour out 3 kg of grain to balance the 3 kg weight. The weight of the remaining grain is 1 kg.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. Find a six-digit number that, when multiplied by 9, is written with the same digits as the original number but in reverse order? How many such six-digit numbers are there?
|
Answer: 109989 is the only number. Solution. Let $\overline{a b c d e f}$ be the desired number, i.e., $\overline{a b c d e f} \cdot 9=\overline{f e d c b a}$. Then it is obvious that $a=1, b=0$ (otherwise, multiplying by 9 would result in a seven-digit number). Therefore, $f=9$, and the second-to-last digit $e=8$ (which follows from multiplying in columns). Then the third digit $c$ can be 8 or 9. But if $c=8$, then $d=1$, since the sum of the digits is divisible by 9, but the number 108189 does not fit upon checking. If, however, $c=9$, then $d=9$ and the number 109989 is the only one that satisfies the condition, and it fits upon checking.
|
109989
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Find the natural number $x$ that satisfies the equation
$$
x^{3}=2011^{2}+2011 \cdot 2012+2012^{2}+2011^{3} .
$$
|
Answer. $\quad 2012$.
Solution. See problem 8.4.
|
2012
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. On the side $AC$ of triangle $ABC$, a point $M$ is taken. It turns out that $AM = BM + MC$ and $\angle BMA = \angle MBC + \angle BAC$. Find $\angle BMA$.
|
Answer. $\quad 60^{\circ}$. Solution. First, we will show that triangle $A B C$ is isosceles. Indeed, this follows from the condition $\angle B M A=\angle M B C+\angle B A C$ and the property of the exterior angle: $\angle B M A=\angle M B C+\angle B C A$. From these two equalities, we have $\angle B C A=\angle B A C$. Next, we take a point $K$ on side $A C$ that is symmetric to point $M$ with respect to the midpoint of $A C$. Then $A K=M C$ and therefore from the relation $A M=B M+M C$ it follows that point $M$ lies between $C$ and the midpoint of $A C$, and thus this relation can be written as $K M=B M$. Since $\triangle A B C$ is isosceles, the midpoint of $A C$ coincides with the projection of point $B$, and therefore $B M=B K$. Thus, in triangle $K B M$ all sides are equal, and all angles are $60^{\circ}$.
## SOLUTION 2 variant
## 9th grade
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. A father had three sons, and he left them 9 ares of land as an inheritance - a rectangle measuring 25 m $\times 36$ m. The brothers decided to divide the land into three rectangular plots - three ares for each brother. How many options are there for the division (in terms of the length and width of the plots), and in which of the options will the total length of the fences between the plots be the smallest?
|
Answer: 4 options; the smallest length is 49 m in the option of dividing into a plot of $25 \times 12$ and two plots of $12.5 \times 24$. Solution. Let $ABCD$ be the original rectangle; $AB=25, BC=36$. Since it has 4 vertices and 3 plots, two vertices must belong to one plot. First, consider the case where the vertices of the shorter side (say, $AB$) belong to such a plot $ABNM$ (see figure). In this case, the remaining part - rectangle $MNCD$ - needs to be divided into two equal rectangles, which can be done in two ways (see figure).
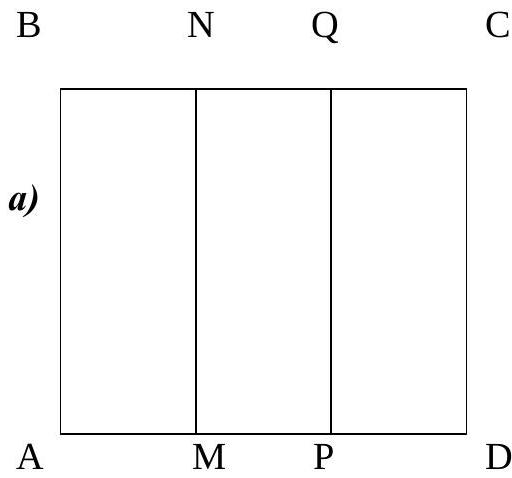
C $\quad$ B $\quad \mathrm{N}$
C
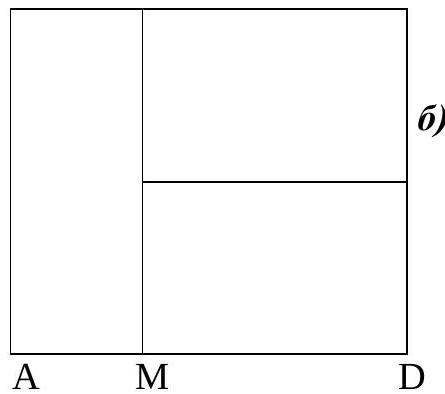
Similarly, in the second case (when $B, C$ belong to one plot), there can be two division options (see figure). From the condition of equal areas, we get the plot sizes: in the first case - a) three plots $25 \times 12$ or b) one plot $25 \times 12$ and two plots $12.5 \times 24$; in the second case - a) three plots $\frac{25}{3} \times 36$ or b) one plot $\frac{25}{3} \times 36$ and two plots $\frac{50}{3} \times 18$.
B
a)
C
B
b)
C
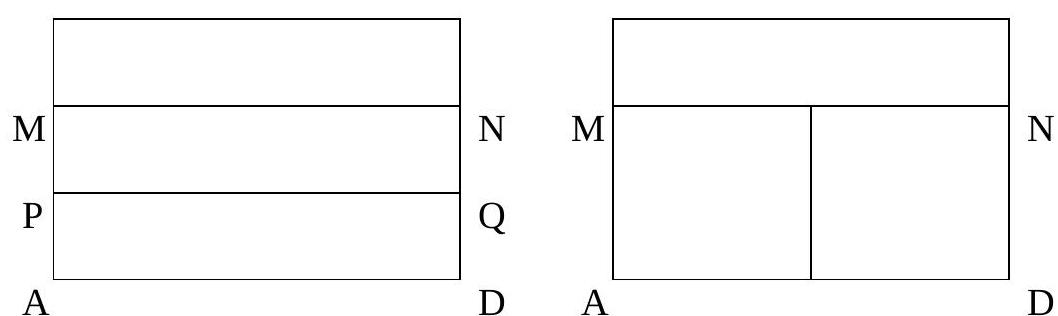
The total length of the fences in these four options will be 50 or 49 (in the first case) and 72 or $\frac{158}{3}$ (in the second case). Therefore, 49 is the smallest length.
|
49
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. The numbers $a, b$, and $c$ satisfy the relation $\frac{a+b}{c}=\frac{b+c}{a}=\frac{a+c}{b}$. Find $a+b+c$, given that $b \neq c$.
|
Answer: 0. Solution. From the equality $\frac{a+b}{c}=\frac{a+c}{b}$, we get $a(b-c)=(c-b)(c+b)$. Dividing this equality by $b-c \neq 0$, we obtain $b+c=-a$. Therefore, $a+b+c=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. How many zeros does the product $s(1) \cdot s(2) \cdot \ldots \cdot s(100)$ end with, where $s(n)$ denotes the sum of the digits of the natural number $n$?
|
Answer: .19 zeros. Solution. Consider the numbers from the first hundred for which the sum of the digits is divisible by 5. Such numbers have a digit sum of either 5, 10, or 15. There are 6 numbers with a digit sum of 5: these are $5, 14, 23, 32, 41, 50$. There are 9 numbers with a digit sum of 10: these are $19, 28, \ldots, 91$. There are 4 numbers with a digit sum of 15: these are $69, 78, 87, 96$. Thus, in the product $P=s(1) \cdot s(2) \cdot \ldots \cdot s(100)$, the factor 5 appears 19 times. The factor 2 in $P$ appears in a (much) higher degree (it is sufficient to consider, for example, numbers with a digit sum of 8; there are 9 such numbers, and each contributes a factor of $2^{3}$ to $P$, so the factor 2 appears in $P$ in a degree $\left.\geq 3 \cdot 9 = 27\right)$. Therefore, $P$ ends with 19 zeros.
|
19
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. A father had three sons, and he left them 9 ares of land as an inheritance - a rectangle measuring 25 m $\times 36$ m. The brothers decided to divide the land into three rectangular plots - three ares for each brother. How many options are there for the division (in terms of the length and width of the plots), and in which of the options will the total length of the fences between the plots be the smallest?
|
Answer: 4 options; the shortest length is 49 m in the option of dividing into a plot of $25 \times 12$ and two plots of $12.5 \times 24$. Solution. See problem 7.2
|
49
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Let $s(n)$ denote the sum of the digits (in decimal notation) of a natural number $n$. Find all natural $n$ for which $n+s(n)=2011$.
|
Answer: 1991. Hint. Since $n<2011$, then $s(n) \leq 2+9+9+9=29$. Therefore, $n=2011-$ $s(n) \geq 1982$. Since the numbers $n=2011$ and $n=2010$ obviously do not fit, the first three digits of the number $n$ can be one of three possibilities: 198, or 199, or 200. Let the last (fourth) digit of the number $n$ be $x$. Then in each of the cases mentioned, we get the equation: either 1) $1980+x+18+x=2011$, or 2) $1990+x+19+x=2011$, or 3) $2000+x+2+x=2011$. Only in the second case does the equation have an integer solution, namely, $x=1$.
|
1991
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The unit square in the first quadrant of the coordinate plane ( $0 \leq x, y \leq 1$ ) is divided into squares with side length $2 \cdot 10^{-4}$. How many nodes of this partition (inside the unit square) lie on the parabola $y=x^{2}$?
|
Answer: 49. Note. The nodes of the partition have coordinates of the form ( $i / 5000, j / 5000$ ), where $i$, $j=1,2, \ldots, 4999$. The condition that a given node lies on the parabola is $\frac{j}{5000}=\left(\frac{i}{5000}\right)^{2}$, i.e., $i^{2}=j \cdot 5^{4} \cdot 2^{3}$. Therefore, the number $i$ must have the form $i=5^{2} \cdot 2^{2} \cdot k=100 k$, where $k-$ is any natural number less than $\frac{5000}{100}=50$.
## "Future Researchers - Future of Science" Mathematics Olympiad (Final Round) Variant 2
## 9th Grade
|
49
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. The bisectors of the external angles $B$ and $C$ of triangle $ABC$ intersect at point $M$. a) Can angle $BMC$ be obtuse? b) Find angle $BAC$ if it is known that $\angle BMC = \frac{\angle BAM}{2}$.
|
Answer: a) cannot; b) $120^{\circ}$. Hint. Let $\angle A=\alpha, \angle B=\beta, \angle C=\gamma$. Then $\angle B M C=180^{\circ}-\left(\frac{180^{\circ}-\beta}{2}+\frac{180^{\circ}-\gamma}{2}\right)=\frac{\beta+\gamma}{2}=90^{\circ}-\frac{\alpha}{2}$. a) Therefore, angle $B M C$ cannot be obtuse. b) from the equation $\frac{\alpha}{2}=90^{\circ}-\frac{\alpha}{4}$ we get the value $\alpha=120^{\circ}$ (here we used the fact that point $M$ must lie on the bisector of angle $A$ ).
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. Let $s(n)$ denote the sum of the digits of a natural number $n$. How many zeros does the number equal to the product $s(1) \cdot s(2) \cdot \ldots \cdot s(100)$ end with?
|
Answer: 19 zeros. Hint. Consider the numbers from the first hundred for which the sum of the digits is divisible by 5. Such numbers have a sum of digits of either 5, 10, or 15. There are 6 numbers with a sum of 5: these are $5,14,23,32,41,50$. There are 9 numbers with a sum of digits 10: these are $19,28, \ldots, 91$. There are 4 numbers with a sum of digits 15: these are $69,78,87,96$. Thus, in the product $P=s(1) \cdot s(2) \cdot \ldots \cdot s(100)$, the factor 5 appears 19 times. And the factor 2 in $P$ appears in a (much) higher degree (it is enough to consider, for example, numbers with a sum of digits 8; there are 9 such numbers, and each contributes a factor of $2^{3}$ to $P$, so the factor 2 appears in $P$ in a degree $\geq 3 \cdot 9=27$). Therefore, $P$ ends with 19 zeros.
|
19
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. A rectangular grid with a cell side of 1 cm and an area of $2021 \mathrm{~cm}^{2}$ is cut into four rectangular pieces by two perpendicular cuts along the grid lines. Prove that at least one of the pieces has an area of at least $528 \mathrm{~cm}^{2}$.
|
Solution. The prime divisors of the number 2021 are 43 and 47, and $2021=43 \cdot 47$. Therefore, the integer sides $a$ and $b$ of the original rectangle can be either 1) $a=2021, b=1$, or 2) $a=47, b=43$. However, it is obvious that case 1) $a=2021, b=1$ is impossible, since such a rectangle cannot be cut into square cells. In the second case, the largest of the four parts will have an area of at least $24 \cdot 22=528$.
|
528
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
10.3. The sum $1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{45}$ is represented as a fraction with the denominator $45!=1 \cdot 2 \cdots 45$. How many zeros (in decimal notation) does the numerator of this fraction end with?
|
Answer: 8 zeros. Solution. The numerator of the fraction is the sum of numbers of the form $1 \cdot 2 \cdot \ldots \cdot(k-1)(k+1) \cdot \ldots .45$ (the product lacks one of the natural numbers from 1 to 45). Let's denote such a term as $c_{k}$. Note that $45!=5^{10} \cdot 2^{n} \cdot \boldsymbol{p}$, where $\boldsymbol{p}$ is coprime with 10, and $n>$ 15 (in fact, $\boldsymbol{n}=\left[\frac{45}{2}\right]+\left[\frac{45}{2^{2}}\right]+\ldots+\left[\frac{45}{2^{5}}\right]=22+11+5+2+1=41$), i.e., 45! ends with 10 zeros. In the numerator, in the given sum, the terms $c_{k}$ for $k$ not divisible by five will be divisible by $5^{10} \cdot 2^{10}$, i.e., such terms end with 10 zeros. The terms $c_{k}$ for $k$ divisible by five but not equal to 25 will be divisible by $5^{9} \cdot 2^{9}$ and, therefore, will end with 9 zeros. There is only one term, namely, $c_{25}$, in which 5 enters to the 8th power, and only this term ends with 8 zeros. Therefore, the numerator ends with 8 zeros.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. From points $A$ and $B$, two cyclists set off towards each other at the same time. They traveled at constant speeds. After meeting, the first cyclist took 40 minutes to reach point $B$, and the second cyclist took one and a half hours to reach point $A$. Find the time from the start of the journey until they met and the ratio of the cyclists' speeds.
|
Answer. Time until the meeting - 1 hour. The speed of the first cyclist is 1.5 times greater than the speed of the second. Solution. Let $v_{1}, v_{2}$ be the speeds of the cyclists, $t$ - the time until the meeting. Then the first cyclist traveled the distance $\mathrm{v}_{1} t$ before the meeting, and the second - the distance $\mathrm{v}_{2} t$. From the conditions of the problem, we then have $\frac{\mathrm{v}_{2} t}{\mathrm{v}_{1}}=40$ (min.) and $\frac{\mathrm{v}_{1} t}{\mathrm{v}_{2}}=90$ (min.). From these equations, by eliminating $t$, we get that $\left(\frac{\mathrm{v}_{1}}{\mathrm{v}_{2}}\right)^{2}=\frac{9}{4}$, i.e., $\frac{\mathrm{v}_{1}}{\mathrm{v}_{2}}=\frac{3}{2}$. Then the value of $t=60$ (min).
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. There are 19 kg of cereal. Can 1 kg be measured with three weighings on a balance scale if there is one 3 kg weight?
|
Answer: It is possible. Solution. The first weighing can yield 8 kg of cereal. If a weight is placed on one (left) pan of the scales and, by pouring cereal from the right pan to the left, the scales are balanced. Indeed, from the equation $3+x=19-x$ we get $x=8$, i.e., there will be 8 kg of cereal on the pan with the weight. Leave 8 kg of cereal on the scales and, with the second weighing, divide this weight in half by pouring and balancing the pans of the scales. The last weighing will yield 1 kg if the weight is placed on one pan, and 4 kg of cereal on the other, and then 1 kg is poured (into a bag) to achieve balance.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. On a chessboard, the centers of some cells are marked in such a way that no triangle with marked vertices is a right triangle. What is the maximum number of points that could have been marked?
|
Answer: 14 points. Solution. Let's call a marked point vertical if there are no other marked points on its vertical line. Similarly, we define a horizontal point. Note that any marked point is either vertical or horizontal (or both at the same time). Indeed, if the marked point $A$ had another point $B$ on its vertical line and a point $C$ on its horizontal line, then the triangle $BAC$ would be a right triangle. It is not difficult to provide an example of 14 points satisfying the condition: mark the central points in the cells a2, a3,...,a8 and in the cells $\mathrm{b} 1, \mathrm{c} 1, \ldots, \mathrm{h} 1$ (i.e., in all cells of the first vertical and the first horizontal except the bottom-left cell). Obviously, all triangles with vertices at these marked points are obtuse. We will now show that there cannot be more than 14 points. If there are 8 vertical points, then they lie in eight different vertical lines, and therefore there are no other marked points. Similarly, if there are 8 horizontal points, then there cannot be a ninth marked point. Therefore, in the optimal example, there are no more than 7 horizontal and no more than 7 vertical marked points, and the total number of marked points is no more than 14.
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 2. (10 points)
In a right triangle $A B C$ (angle $C$ is right), medians $A M$ and $B N$ are drawn, the lengths of which are 19 and 22, respectively. Find the length of the hypotenuse of this triangle.
|
# Solution.
Let $AC = 2x$ and $BC = 2y$. By the Pythagorean theorem, we have
$$
\left\{\begin{array}{c}
(2 x)^{2}+y^{2}=19^{2} \\
x^{2}+(2 y)^{2}=22^{2}
\end{array} \Rightarrow 5 x^{2}+5 y^{2}=19^{2}+22^{2}=845 \Rightarrow\right.
$$
Answer: 26.
|
26
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 4. (12 points)
Solve the equation $x^{2}+y^{2}+1=x y+x+y$.
#
|
# Solution
$$
\begin{gathered}
x^{2}+y^{2}+1=x y+x+y \Leftrightarrow(x-y)^{2}+(x-1)^{2}+(y-1)^{2}=0 \Leftrightarrow \\
x=y=1 .
\end{gathered}
$$
Answer: $x=y=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 8. (16 points)
Let all companies in the country have a certain rank, which is a natural number. When two companies of ranks $m$ and $n$ merge, a new company of rank $(m+n)$ is formed. The profit of the resulting company will be $m \cdot n$ more than the sum of the profits of the companies forming it. The profit of a company of the first rank is 1 d.e. Is there a rank at which the profit of the company will be 2016 d.e.?
|
# Solution.
Let $p_{n}$ be the profit of the company of rank $n$. Then, according to the problem statement,
$$
p_{m+n}=p_{m}+p_{n}+m n
$$
Notice that for any $n$,
$$
p_{n}=p_{n-1}+p_{1}+(n-1) \cdot 1=p_{n-1}+1+n-1=p_{n-1}+n
$$
We will prove that $p_{n}=1+2+\ldots+n$.
We use mathematical induction.
1) Base case: $p_{1}=1$.
2) Assume $p_{k}=1+2+\ldots+k$. We need to prove that $p_{k+1}=1+2+\ldots+k+(k+1)$.
Indeed, $p_{k+1}=p_{k}+(k+1)=(1+2+\ldots+k)+(k+1)$.
Therefore, $p_{n}=1+2+\ldots+n=\frac{n(n+1)}{2}$.
For a company to have a profit of 2016 units, its rank must satisfy the equation
$$
\frac{n(n+1)}{2}=2016
$$
The last equation has a natural solution $n=63$.
Answer: yes, the rank is 63.
|
63
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. (10 points)
Find the denominator of the fraction $\frac{100!}{28^{20}}$ after it has been reduced to its simplest form.
(The expression 100! is equal to the product of the first 100 natural numbers: $100!=1 \cdot 2 \cdot 3 \cdot 4 \cdot \ldots \cdot 100$.$) .$
|
# Solution.
It can be noticed that among the numbers from 1 to 100, exactly 14 numbers are divisible by 7, and exactly two are divisible by 49. Therefore, in the prime factorization of $1 \cdot 2 \cdot 3 \cdot 4 \cdot \ldots \cdot 100$, the number 7 will appear in the power of 16. Among the numbers from 1 to 100, exactly 50 are even, so in the prime factorization of $1 \cdot 2 \cdot 3 \cdot 4 \cdot \ldots \cdot 100$, the number 2 will appear in a power no less than 50. Therefore, in the fraction $\frac{100!}{28^{20}}=\frac{100!}{7^{20} \cdot 2^{40}}$, after simplification, only $7^{4}=2401$ will remain in the denominator.
Answer: 2401.
| Criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 10 |
| A minor computational error was made. | $\pm$ | 7 |
| The main idea of the solution was found. The solution is incomplete. The answer is correct. | $+/ 2$ | 5 |
| The main idea of the solution was found. The solution is incomplete. The answer is incorrect. | $\mp$ | 2 |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | | 10 |
|
2401
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 4. (12 points)
A shooting tournament involves several series of 10 shots each. In one series, Ivan scored 82 points, as a result of which the average number of points he scored per series increased from 75 to 76 points. How many points does Ivan need to score in the next series of shots to make the average number of points scored per series equal to 77?
|
# Solution.
Let $N$ be the points scored in the $n$ considered series, in the last of which Ivan scored 82 points. Then $N=76n$ and $N-82=75(n-1)$. Solving the obtained system, we find $n=7$ and $N=532$.
Let $x$ be the points Ivan needs to score to meet the condition of the problem. In this case, we get $77 \cdot 8 = 532 + x \Rightarrow x = 84$.
Answer: 84.
| Criterion Content | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 12 |
| All main logical steps of the solution are provided. There is no strict justification for some conclusions. The answer is correct. | $\pm$ | 9 |
| All main logical steps of the solution are justified. The answer is incorrect due to a computational error or typo. | | |
| All main logical steps of the solution are provided. The system of equations is correctly set up. The solution of the system contains errors or is not completed. | $+/ 2$ | 6 |
| The main idea of the solution is found. The answer is missing or incorrect. | 干 | 2 |
| The answer is correct, but the solution is missing or does not contain substantial progress. | | |
All-Russian School Olympiad "Mission Possible. Your Calling - Financier!"
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| :---: | :---: | :---: |
| Maximum score | | 12 |
|
84
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 6. (14 points)
According to the regulations of the chess tournament, each participant must play one game with every other participant. After exactly 99 games were played, it turned out that the set of participants could be divided into two unequal groups such that all opponents belonging to the same group had already played their games with each other. At the same time, no more than four games were played between opponents belonging to different groups. What is the maximum possible number of participants in this chess tournament?
|
# Solution.
Let the number of participants in the tournament be $n$, and the number of those who fell into the 1st group be $k$. Then the number of matches played is:
$\frac{k(k-1)}{2}+\frac{(n-k)((n-k)-1)}{2}+m=99$, where $m$ is small, $\Rightarrow$
$k^{2}-k+(n-k)^{2}-(n-k)+2 m-198=0$
$k^{2}-k+k^{2}-2 k n+n^{2}-n+k+2 m-198=0$
$2 k^{2}-2 k n+\left(n^{2}-n+2 m-198\right)=0$
$\frac{D}{4}=n^{2}-2\left(n^{2}-n+2 m-198\right)=-n^{2}+2 n-4 m+396 \geq 0$
$n^{2}-2 n+(4 m-396) \leq 0 \quad(n-1)^{2}-(397-4 m) \leq 0$
$n_{\max }=1+\sqrt{397-4 m} \leq 20$.
If $n=20$, then
$2 k^{2}-40 k+(400-20+2 m-198)=0$
$k^{2}-20 k+91+m=0$
$k=10, n-k=10, m=9$ - contradiction;
$k=11, n-k=9, m=8$ - contradiction;
$k=12, n-k=8, m=5$ - contradiction;
$k=13, n-k=7, m=0$ - contradiction;
for $k>13 m13 m$ of the maximum number of participants in the tournament. There is no strict justification for the estimates provided or the answer. | $\pm$ | 11 |
|  | $+/ 2$ | 7 |
| The answer is correct. Correct but unexplained estimates for the maximum number of participants in the tournament are provided. A strict justification for the answer based on the given estimates is provided. | | |
| The answer is incorrect or missing. Justified estimates for the maximum number of participants in the tournament or correct relationships from which they are derived are provided in the solution. | $\mp$ | 3 |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | | 14 |
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 7. (14 points)
In a company, there are 168 employees. Among any four people, at least one can be chosen who is acquainted with the other three. What is the minimum possible number of people who are acquainted with everyone? #
|
# Solution.
If there are no strangers, then the number of people who know everyone is 168. Let $A$ and $B$ not know each other, then all other people know each other (if $C$ does not know $D$, then in the group $A, B, C, D$ no one knows the other three). If $A$ and $B$ know all the others, then 166 people know everyone. If $A$ also does not know $C$, where $C \neq D$, then $A$, $B$, and $C$ know all the other 165 people (since in any group $A, B, C, D$ only $D$ can be known by the other three), who also know each other. Thus, the minimum number of people who know everyone is 165.
Answer. 165
| Criterion Content Full solution. | Evaluation | Points |
| :---: | :---: | :---: |
| The answer is correct. All main logical steps of the solution are provided. Some rigorous justifications of individual conclusions are missing. | $\pm$ | 11 |
| The answer is correct. The solution is missing or incorrect. | $\mp$ | 14 |
| The main idea of the solution is found. The answer is missing or | | 3 |
All-Russian School Olympiad "Mission Possible. Your Calling - Financier!"
| incorrect. | | |
| :---: | :---: | :---: |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | | 14 |
|
165
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 8. (16 points)
Vova was playing with old domino tiles, on which all the dots had worn off, making them indistinguishable. Each tile is a $2 \times 1$ rectangle, and their total number is 24. Vova decided to arrange the tiles in a new pattern each day to form a $2 \times 12$ path, ensuring that the pattern of the arrangement never repeats. How many days can Vova continue arranging the tiles in this way, making one arrangement per day, until all possible arrangements are exhausted?
|
# Solution.
We will assume that the paths are arranged horizontally, with the longer side along the x-axis. The dominoes in such paths can be of two types: vertical (placed across the path) and horizontal, placed along the path.
Each vertical domino "cuts" the path and divides it into two parts, to the right and left of itself.
Each horizontal domino must have a paired horizontal domino, together forming a $2 \times 2$ square.
Indeed, if there were a pair of horizontal dominoes that did not form a square (i.e., were arranged as shown in the figure), then both parts of the path to the right and left of this pair of dominoes would contain an odd number of dominoes and could not be covered by dominoes.
Let $F(n)$ be the number of possible tilings of a path of size $2 \times n$ with dominoes of size $2 \times 1$. Then, obviously, $F(1)=1, F(2)=2, F(3)=3$.
Each tiling of a path $2 \times n$ has at its right end either a vertical domino (removing which can yield a tiling of a path $2 \times(n-1)$) or a pair of horizontal dominoes (removing which can yield a tiling of a path $2 \times(n-2))$. This fact justifies the formula: $F(n)=F(n-1)+F(n-2)$, i.e., the sequence $F(n)$ is the Fibonacci sequence. Answer: $F(12)=233$.
| Full solution. | + | 16 |
| :---: | :---: | :---: |
| The answer is correct. All main logical steps of the solution are provided. Some individual conclusions lack rigorous justification. | $\pm$ | 12 |
| All main logical steps of the solution are provided. Some individual conclusions lack rigorous justification. A computational error or typo may result in an incorrect answer. | $+/ 2$ | 8 |
| The solution is generally incorrect or incomplete, but contains some progress in the right direction. The answer is missing. | $\mp$ | 3 |
| The solution does not meet any of the criteria described | | |
| above. | | |
|
233
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Assignment 1. (10 points)
Each of the 2017 middle school students studies English or German. English is studied by $70 \%$ to $85 \%$ of the total number of students, and both languages are studied by $5 \%$ to $8 \%$. What is the maximum number of students who can study German.
|
# Solution.
Let $A$ be the number of people who study English, $N$ be the number of people who study German, and $AN$ be the number of people who study both languages.
Then $N=2017-A+AN$.
It is known that $A \geq 2017 \cdot 0.7=1411.9$ and $AN \leq 0.08 \cdot 2017=161.36$.
Therefore, $N \leq 2017-1412+161=766$.
Note that $N=766$, if $A=1412, AN=161$.
Answer: 766.
| Criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 10 |
| A minor computational error was made. Main estimates are provided. Lack of necessary rigor in obtaining the answer. The answer is correct. | .+ | 8 |
| Main estimates are provided. Lack of necessary rigor in obtaining the answer. The answer is incorrect. | $+/ 2$ | 7 |
| Not all estimates are provided. The answer is not obtained or is incorrect. | $\mp$ | 2 |
| The answer is correct, but the solution is missing. | + | $-/ 0$ |
| The solution does not meet any of the criteria described above. | 0 | |
| Maximum score | | 10 |
|
766
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 4. (12 points)
Find the smallest positive integer in which the product of the digits is 5120.
|
# Solution.
Since $5120=2^{10} \cdot 5$, the main question is how many digits are in this number. Clearly, there are no 0s and there is a 5. From the ten factors of 2, we can form a minimum of 4 digits. This can be done in two ways: $2,8,8,8$ or $4,4,8,8$. Then, from the two sets of digits $5,2,8,8,8$ and $5,4,4,8,8$, we need to form the smallest number. The first digit should be the smallest, i.e., 2.
Answer: 25888.
| Criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 12 |
| The idea of factoring the number into prime factors is presented. Not all factorization options are presented. The answer is correct. | $\pm$ | 9 |
| The main idea of the solution is found. All factorization options are presented. An incorrect answer is obtained. | $+/ 2$ | 6 |
| | | |
| The idea of factoring the number into prime factors is presented. Not all factorization options are presented. The answer is incorrect. | $\mp$ | 2 |
| :---: | :---: | :---: |
| The answer is correct, but the solution is missing. | | |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | | 10 |
|
25888
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 7. (14 points)
In a certain company, no two employees have jobs of the same difficulty, and no two employees receive the same salary. On April 1, each employee made two statements:
(a) There will not be 12 employees with more difficult jobs.
(b) At least 30 employees have a higher salary. How many employees are in the company if some employees told the truth twice, and the rest lied twice.
#
|
# Solution.
If on April 1st all employees of the company told the truth, then the second statement about the highest salary is false, which cannot be. If, however, all of them lied, then the first statement for the employee with the highest salary would be true, again leading to a contradiction.
Thus, there is at least one liar and at least one truth-teller.
Let's take the employee who told the truth with the highest salary among all truthful employees. Since from his second statement it follows that at least 30 "liars" have a higher salary than he does. The second statement of the lying employee with the lowest salary among all "liars" is false, thus, no more than 29 "liars" have a higher salary, and no more than 30 "liars" in total. That is, there are 30 liars in total.
The first statement for the "liar" with the most difficult job among all "liars" is false, so there are at least 12 truthful employees with more difficult jobs.
The first statement for the truthful employee with the least difficult job among all truthful employees is true, so there are no more than 12 truthful employees in total. That is, there are exactly 12 truthful employees.
Ultimately, we get that the company employs 42 employees. Answer: 42
| Content of the criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 14 |
| The answer is correct. There is no strict proof that there are 30 liars or that there are 12 truthful employees. | $\pm$ | 11 |
| The answer is correct. It is claimed that there are 30 liars and 12 truthful employees, but neither of these facts is proven. | $+/ 2$ | 7 |
| The correct answer is provided. The solution does not specify that there are 30 liars and 12 truthful employees. | $\mp$ | 3 |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | 14 | |
|
42
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 1. (10 points)
How many natural numbers $n$ exist such that the equation $n x-12=3 n$ has an integer solution
#
|
# Solution.
Since $n x-12=3 n \Rightarrow x=3+\frac{12}{n}$, the condition of the problem is satisfied if 12 is divisible by $n$. Therefore, $n$ can take the values $1,2,3,4,6,12$.
Answer. 6
| Criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 10 |
| All main logical steps of the solution are provided. Integer values of $\boldsymbol{n}$ are calculated. | | |
| All main logical steps of the solution are provided. The answer is incorrect. | $+/ 2$ | 5 |
| The answer is correct. The solution is missing or incorrect. | $\mp$ | 2 |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | 10 | |
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. (12 points)
The arithmetic mean of ten different natural numbers is 20, and the arithmetic mean of any nine of these numbers is not less than 17. Find the maximum possible value of the largest of these numbers.
#
|
# Solution.
We will order the 10 given numbers in ascending order.
According to the problem, the sum of the first 9 numbers cannot be less than $9 \cdot 17=153$.
Therefore, the 10th largest number cannot be greater than $20 \cdot 10-153=47$.
At the same time, the set 17, 17, $, 17, 47$ satisfies the condition of the problem.
Answer. 47
| Content of the criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 12 |
| The answer is correct. It is shown that the maximum possible value cannot be greater than 47. The set containing 47 is not specified. | $+/ 2$ | 6 |
| All main logical steps of the solution are provided. Due to a computational error or typo, an incorrect answer is obtained. | | |
| The answer is correct. It is not shown that 47 is the maximum possible value. | $\mp$ | 2 |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
|
47
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.