problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
# Task 4. (12 points)
A numerical sequence is such that $x_{n}=\frac{n+2}{n x_{n-1}}$ for all $n \geq 2$. Find the product $x_{1} x_{2} x_{3} \ldots x_{2016} x_{2017}$, if $x_{1}=1$.
#
|
# Solution.
Notice that $x_{n} x_{n-1}=\frac{n+2}{n}$, therefore,
$$
x_{1} x_{2} x_{3} \ldots x_{2016} x_{2017}=x_{1}\left(x_{2} x_{3}\right)\left(x_{4} x_{5}\right) \ldots\left(x_{2016} x_{2017}\right)=1 \frac{5}{3} \frac{7}{5} \ldots \frac{2017}{2015} \frac{2019}{2017}=673
$$
Answer. 673
| Criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete | + | 12 |
| Due to a computational error or typo, an incorrect answer is obtained. | $\pm$ | 9 |
| It is shown in general that $x_{n} x_{n-1}=\frac{n+2}{n}$. The answer is incorrect or missing. | $+/ 2$ | 6 |
| :---: | :---: | :---: |
| It is shown for some $n$ that $x_{n} x_{n-1}=\frac{n+2}{n}$. The answer is incorrect or missing. | $\mp$ | 2 |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | 12 | |
|
673
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6. (14 points)
The function $f(x)$ is such that $f(f(x))=x$ and $f(f(x+2)+2)=x$ for any $x$.
Find $f(2017)$, given that $f(0)=1$.
#
|
# Solution.
From the equality $f(x)=f(f(f(x+2)+2))=f(x+2)+2$, we obtain the formula $f(x+2)=f(x)-2$.
Moreover, $f(1)=f(f(0))=0$.
We will prove by induction that $f(x)=1-x$ for any integer $x$.
First, we will prove that the given equality holds for even $x$.
1) $f(0)=1$ - true.
2) Let $f(2n)=1-2n$.
3) We will prove that $f(2(n+1))=1-2(n+1)$
Indeed, $f(2(n+1))=f(2n)-2=1-2n-2=1-2(n+1)$.
Now we will prove that the given equality holds for odd $x$.
1) $f(1)=0$ - true.
2) Let $f(2n+1)=1-(2n+1)$ for some $n$.
3) We will prove that $f(2(n+1)+1)=1-(2(n+1)+1)$
Indeed, $f(2(n+1)+1+2)=f(2n+1)-2=1-(2n+1)-2=1-(2(n+1)+1)$.
Therefore, $f(2017)=1-2017=-2016$.
Answer. -2016.
| Content of the criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 14 |
| All main logical steps of the solution are presented. It is proven that $f(x+2)=f(x)-2$. The solution lacks some justifications. The answer is correct. | $\pm$ | 11 |
| Several initial values of the sequence $f(n)$ are written out. It is assumed that $f(x)=1-x$, but the proof of this fact is not provided. The answer is correct. | $+/ 2$ | 7 |
| It is noted that $f(x)=1-x$. Justifications, as well as partial confirmations of this fact, are not provided. The answer is correct. | $\mp$ | 3 |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | 14 | |
|
-2016
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 1. (10 points)
Six consecutive natural numbers from 10 to 15 are written in circles on the sides of a triangle in such a way that the sums of the three numbers on each side are equal.
What is the maximum value that this sum can take?
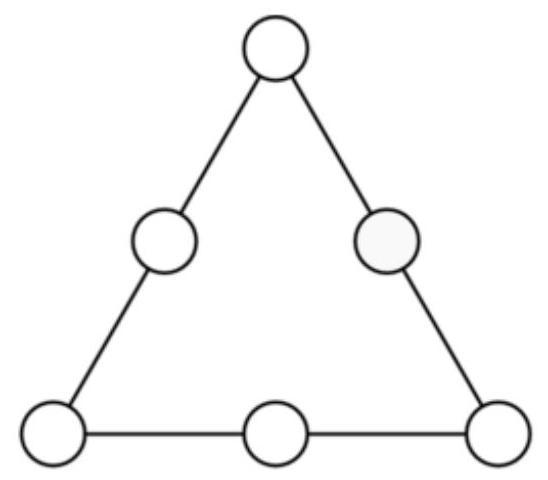
|
# Solution.
Let $a, b, c, d, e, f$ be the given numbers, written in the order of their arrangement in the circles when traversed clockwise, and the numbers $a$, $c$, $e$ are located at the vertices of the triangle. If $S$ is the considered sum, then we have
$$
\left\{\begin{array}{l}
a+b+c=S \\
c+d+e=S \\
e+f+a=S
\end{array}\right.
$$
Adding all the equations of this system, we get,
$$
\begin{gathered}
(a+b+c+d+e+f)+a+c+e=3 S \Rightarrow \\
(10+11+12+13+14+15)+a+c+e=75+a+c+e=3 S \Rightarrow \\
S=25+\frac{a+c+e}{3}
\end{gathered}
$$
Therefore, the number $S$ cannot be greater than the number $25+\frac{15+14+13}{3}=39$.
The figure below shows that the number $S$ can be equal to 39.
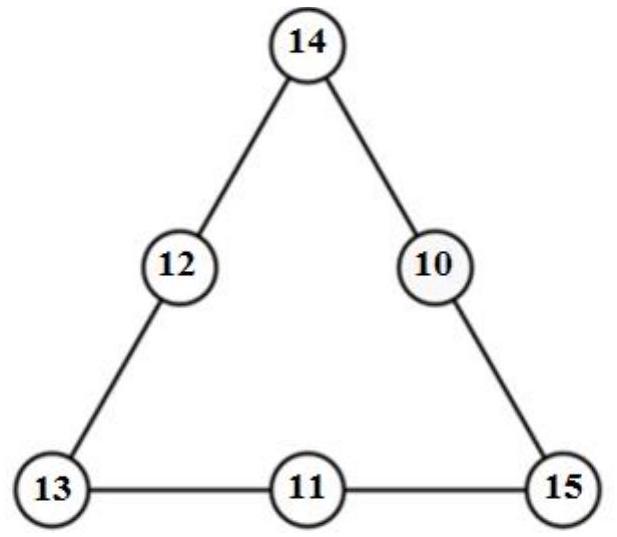
Answer: 39.
|
39
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 3. (12 points)
Egorov decided to open a savings account to buy a car worth 900000 rubles. The initial deposit amount is 300000 rubles. After one month and subsequently every month, Egorov plans to top up his account by 15000 rubles. The bank accrues interest monthly at an annual rate of $12 \%$. Interest accrued for the month is credited to the account, and in the following month, interest is also accrued on this interest. What is the minimum number of months required for the account to have a sufficient amount to buy the car?
|
# Solution
Let $S_{n}$ be the sum of the deposit after $n$ months, after interest accrual and after making additional contributions $D (15000$ rubles).
Since the bank accrues $1 \%$ per month, then
$$
\begin{gathered}
S_{1}=300000(1+0.01)+D \\
S_{2}=S_{1}(1+0.01)+D=\left(S_{0}(1+0.01)+D\right)(1+0.01)+D=S_{0}(1+0.01)^{2}+D(1+(1+0.01)) \\
S_{3}=S_{2}(1+0.01)=\left(S_{0}(1+0.01)^{2}+D(1+0.01)+D\right)(1+0.01)+D= \\
=S_{0}(1+0.01)^{3}+D\left((1+0.01)^{2}+(1+0.01)+1\right) \\
\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\
S_{n}=S_{0}(1+0.01)^{n}+D\left((1+0.01)^{n-1}+(1+0.01)^{n-2}+\ldots+(1+0.01)+1\right)
\end{gathered}
$$
By the formula for the sum of $n$ terms of a geometric progression, we get
$$
(1+0.01)^{n-1}+(1+0.01)^{n-2}+\ldots+(1+0.01)+1=\frac{1.01^{n}-1}{1.01-1}=\frac{1.01^{n}-1}{0.01} .
$$
Therefore, $S_{n}=S_{0}(1+0.01)^{n}+D \frac{1.01^{n}-1}{0.01}$.
The required number of months satisfies the inequality
$$
\begin{gathered}
300000 \cdot 1.01^{n}+15000 \frac{1.01^{n}-1}{0.01} \geq 900000 \Leftrightarrow \\
\Leftrightarrow 3 \cdot 1.01^{n}+15\left(1.01^{n}-1\right) \geq 9 \Leftrightarrow \\
\Leftrightarrow 18 \cdot 1.01^{n} \geq 24 \Leftrightarrow 1.01^{n} \geq \frac{24}{18} \Leftrightarrow n \geq 28.91
\end{gathered}
$$
Thus, the sufficient amount for buying the car will be in the deposit after 29 months.
## Answer: 29.
|
29
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6. (14 points)
A finite sequence of numbers $x_{1}, x_{2}, \ldots, x_{N}$ has the following property:
$$
x_{n+2}=x_{n}-\frac{1}{x_{n+1}} \text { for all } 1 \leq n \leq N-2 \text {. }
$$
Find the maximum possible number of terms in this sequence if $x_{1}=20 ; x_{2}=16$.
|
# Solution
The sequence will have the maximum number of terms if its last term is equal to zero. Otherwise, this sequence can be continued.
For all $1 \leq n \leq N-2$ we have
$$
x_{n+2}=x_{n}-\frac{1}{x_{n+1}} \Leftrightarrow x_{n+2} \cdot x_{n+1}=x_{n+1} \cdot x_{n}-1 \Leftrightarrow x_{n+1} \cdot x_{n}=x_{n+2} \cdot x_{n+1}+1
$$
Let $x_{N}=0$, then
$$
\begin{gathered}
x_{N-1} \cdot x_{N-2}=x_{N} \cdot x_{N-1}+1=1 \\
x_{N-2} \cdot x_{N-3}=x_{N-1} \cdot x_{N-2}+1=1+1=2 \\
\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\
x_{3} \cdot x_{2}=(N-4)+1=N-3 \\
x_{2} \cdot x_{1}=(N-3)+1=N-2=20 \cdot 16 \Rightarrow N=20 \cdot 16+2=322
\end{gathered}
$$
Answer: 322.
|
322
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 7. (14 points)
Several businessmen decided to open a company and divide all the profits into equal parts. One of the businessmen was appointed as the director. One day, this director of the company transferred part of the profit from the company's account to his own personal account. This amount of money was three times more than the share each of the others would have received if they had divided the remaining profit equally among themselves. After this, the director left the company. The next director of the company, one of the remaining businessmen, immediately did the same as the previous one, and so on. In the end, the penultimate director of the company transferred part of the profit to his own account, which was also three times more than what was left for the last businessman. As a result of these profit distributions, the last businessman received 190 times less money than the first director of the company. How many businessmen opened this company?
|
# Solution.
Let $n$ be the number of businessmen and $d_{i}$ be the profit of the $i$-th director, $i=1, \ldots, n$.
By the condition $d_{i}=3 \frac{d_{i+1}+d_{i+2}+\ldots+d_{n}}{n-i}$. Then
$$
\begin{gathered}
d_{i-1}=3 \frac{d_{i}+d_{i+1}+\ldots+d_{n}}{n-i+1}=3 \frac{3 \frac{d_{i+1}+d_{i+2}+\ldots+d_{n}}{n-i}+d_{i+1}+\ldots+d_{n}}{n-i+1}= \\
=3 \frac{(n-i+3)\left(d_{i+1}+d_{i+2}+\ldots+d_{n}\right)}{(n-i)(n-i+1)}
\end{gathered}
$$
Thus, $\frac{d_{i-1}}{d_{i}}=\frac{n-i+3}{n-i+1}, \quad i=2, \ldots, n$.
Multiplying these equalities, we get
$$
\frac{d_{1}}{d_{n}}=\frac{d_{1}}{d_{2}} \cdot \frac{d_{2}}{d_{3}} \cdot \ldots \cdot \frac{d_{n-1}}{d_{n}}=\frac{n+1}{n-1} \cdot \frac{n}{n-2} \cdot \ldots \cdot \frac{4}{2} \cdot \frac{3}{1}=\frac{(n+1) n}{2}
$$
By the condition $\frac{d_{1}}{d_{n}}=190$, that is, $(n+1) n=380$, from which $n=19$.
Answer: 19.
|
19
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 2. (10 points)
It is known that the graph of the function $f(x)=x^{2}-2016 x+2015$ passes through two different points with coordinates ( $a, c$ ) and ( $b, c$ ). Find the sum $a+b$.
#
|
# Solution
According to the problem,
$$
\begin{gathered}
f(a)=a^{2}-2016 a+2015=f(b)=b^{2}-2016 b+2015 \Leftrightarrow \\
\Leftrightarrow a^{2}-b^{2}=2016 a-2016 b \Leftrightarrow(a-b)(a+b)=2016(a-b) \Leftrightarrow a+b=2016
\end{gathered}
$$
Answer: 2016.
|
2016
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 3. (12 points)
In a school, there are 1200 students, each of whom has five lessons every day. Any teacher in this school gives 4 lessons per day. How many teachers work in the school if there are exactly 30 students in each class?
|
# Solution
Since each student has 5 lessons per day, if there was only one student in the class, the total number of lessons per day would be $5 \times 1200=6000$. Since there are 30 students in the class, the number of lessons conducted in the school each day is $\frac{6000}{30}=200$. Therefore, the number of teachers in the school is $\frac{200}{4}=50$.
Answer: 50.
|
50
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 4. (12 points)
Consider the sequence of numbers $x_{1}, x_{2}, \ldots, x_{2015}$. In this case,
$$
x_{n}= \begin{cases}7, & \text { if } n \text { is divisible by } 9 \text { and } 32 ; \\ 9, & \text { if } n \text { is divisible by } 7 \text { and } 32 ; \\ 32, & \text { if } n \text { is divisible by } 7 \text { and } 9 ; \\ 0, & \text { in all other cases. }\end{cases}
$$
Find the sum of all terms of this sequence.
|
# Solution
Since $7 \cdot 9 \cdot 32=2016$, then
$$
x_{n}= \begin{cases}7, & \text { if } n=9 \cdot 32 \cdot k, \text { where } k=1, \ldots, 6 \\ 9, & \text { if } n=7 \cdot 32 \cdot k, \text { where } k=1, \ldots, 8 \\ 32, & \text { if } n=7 \cdot 9 \cdot k, \text { where } k=1, \ldots, 31 \\ & 0, \quad \text { in all other cases. }\end{cases}
$$
The desired sum is
$$
7 \cdot 6+9 \cdot 8+32 \cdot 31=1106
$$
Answer: 1106.
|
1106
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 5. (12 points)
On a plane, there are four different circles. We will call an intersection point a point where at least two circles intersect. Find the maximum possible number of intersection points of four circles.
#
|
# Solution
Any two circles can intersect at no more than two points. From four circles, we can choose 6 different pairs of circles. Therefore, the number of intersection points cannot exceed 12.
The figure below shows a case where there are exactly 12 intersection points.
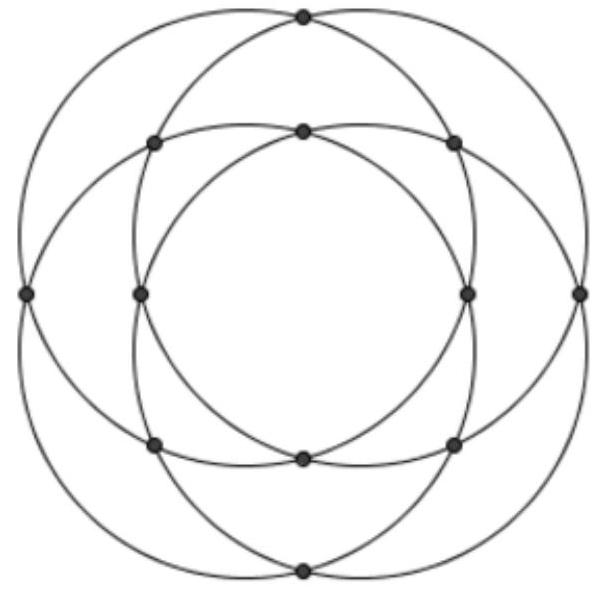
Answer: 12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 7. (14 points)
In the analysis of bank accounts, it was found that the remaining balance on each of them is more than 10 rubles. It also turned out that there is a group of clients, each of whom has the same amount of money on their account. This amount is a number consisting of only ones. If you add up all the money on the accounts of this group of clients, the resulting sum will also be represented by a number consisting of only ones. Find the smallest number of clients in the group for which this is possible, if the group has more than one person.
|
# Solution
This problem is equivalent to the following.
Find the smallest natural number $m$, for which there exist natural numbers $n$ and $k$, such that $n>k>1$ and $\underbrace{11 \ldots 1}_{n}=\underbrace{11 \ldots 1}_{k} \cdot m$.
Obviously, $m>9$. If $m=\overline{a b}$, where $a \geq 1$, then the equality $\underbrace{11 \ldots 1}_{n}=\underbrace{11 \ldots 1}_{k} \cdot \overline{a b}$ means that $b=1$. However, in this case, regardless of $a$, the second digit from the right in the number $\underbrace{11 \ldots 1}_{k} \cdot \overline{a b}$ is $a+1$, and this cannot be 1. Therefore, $m \geq 100$. Clearly, $n=100$ does not satisfy the condition because $\underbrace{11 \ldots 1 \cdot 100}_{k}=\underbrace{11 \ldots 100}_{k}$.
On the other hand, $n=101$ works, since 101$\cdot$11=1111.
Answer: 101.
|
101
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 1. (10 points)
How many natural numbers $n$ not exceeding 2017 exist such that the quadratic trinomial $x^{2}+x-n$ can be factored into linear factors with integer coefficients
#
|
# Solution.
According to the problem, \(x^{2}+x-n=(x-a)(x-b)\). Therefore, \(ab = -n\), which means the numbers \(a\) and \(b\) have different signs and are not zero. Without loss of generality, we assume that \(a \geq 0\). Since \(a + b = -1 \Rightarrow b = -1 - a\), we have
\[
ab = -n = a(-1 - a) \Rightarrow a^{2} + a = n \leq 2017 \Rightarrow a \leq 44
\]
Thus, we obtain 44 pairs of numbers \(a\) and \(b\) that satisfy the given conditions.
Answer. 44.
| Content of the criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 10 |
| All logical steps of the solution are provided, including the estimate for one of the roots and the relationship between the roots of the quadratic trinomial. The answer is incorrect. | \(\pm\) | 7 |
| The estimate for one of the roots of the quadratic trinomial is correct. The answer is incorrect or missing. | \(+/ 2\) | 5 |
| The relationship between \(n\) and the roots of the quadratic trinomial is shown. Incorrect estimates for one of the roots and/or the number of numbers \(n\) satisfying the problem's condition are provided. | \(\mp\) | 2 |
| The solution does not meet any of the criteria described above. | \(-/ 0\) | 0 |
| Maximum score | | 10 |
|
44
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 6. (14 points)
Natural numbers $a, b, c, d$, and $e$ are consecutive terms of an arithmetic progression. Find the smallest possible value of the number $c$, if the sum $b+c+d$ is a perfect square, and the sum $a+b+c+d+e$ is a perfect cube.
|
# Solution.
Since $b+d=2c$, then $3c=n^2$ for some natural number $n$.
Therefore, $n$ is divisible by 3 and $c=3l^2$ for some natural number $l$.
Since $a+b+d+e=4c$, then $5c=m^3$ for some natural number $m$.
Therefore, $m$ is divisible by 5 and $c=5^2 l^3$ for some natural number $l$.
The smallest number that satisfies these conditions is $5^2 3^3=675$.
Answer: 675.
| Content of the criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 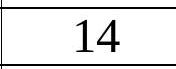 |
| Main logical steps of the solution are presented. Some justifications are missing in the solution. The answer is correct. | $\pm$ | 11 |
| Main logical steps of the solution are presented. The answer is incorrect. | $+/ 2$ | 7 |
| The solution contains a certain advancement in the right direction. The answer is correct. | | |
| The solution is generally incorrect or incomplete, but contains a certain advancement in the right direction. The answer is incorrect or missing. | 干 | 3 |
| The answer is correct. The solution is missing or incorrect. | | |
| The solution does not meet any of the above criteria. | -10 | 0 |
|
675
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 11.1. (10 points)
Given a sequence of numbers $x_{1}, x_{2}, \ldots$, such that $x_{1}=79$ and $x_{n}=\frac{n}{x_{n-1}}$ for all $n>1$. How many zeros does the number equal to the product $x_{1} x_{2} \ldots x_{2018}$ end with?
|
# Solution.
From the condition of the problem, it follows that $x_{n} x_{n-1}=n$. Therefore,
$$
x_{1} x_{2} \ldots x_{2018}=\left(x_{1} x_{2}\right)\left(x_{3} x_{4}\right) \ldots\left(x_{2017} x_{2018}\right)=2 \cdot 4 \cdot 6 \cdot \mathrm{K} \cdot 2018=2^{1009} \cdot 1009!
$$
In the obtained product, 201 numbers are divisible by 5, 40 numbers are divisible by 25, 8 numbers are divisible by 125, and 1 number is divisible by 625.
Thus, in the obtained product, the number 5 is included in the power of $201+40+8+1=250$. At the same time, 2 is included in the given product in a power greater than 250.
The remaining numbers do not end in 0 or 5 and are even, so their product also does not end in 0.
Therefore, the given product ends with 250 zeros.
Answer. 250.
| Content of the criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 10 |
| All main logical steps of the solution are justified. Due to a computational error or typo, an incorrect answer is obtained. | .+ | 8 |
| All main logical steps of the solution are provided. There is no strict justification for some conclusions. The answer is correct. | $\pm$ | 7 |
| All main logical steps of the solution are justified, including showing that divisibility by a power of 5 needs to be considered. Due to an incorrect consideration of a separate case of divisibility by a power of 5, an incorrect answer is obtained. | | |
| There is no strict justification for some conclusions. | $+/ 2$ | 5 |
All-Russian School Olympiad "Mission Possible. Your Calling - Financier!"
| As a result of a computational error or typo, an incorrect answer may be obtained. | | |
| :---: | :---: | :---: |
| There is no strict justification for some conclusions. It is shown that divisibility by a power of 5 needs to be considered, but due to an error, an incorrect answer is obtained. | | |
| The answer is correct. The solution is missing or incorrect. | $\mp$ | 2 |
| The main idea of the solution is found. Numbers divisible by 25, 125, and 625 are not considered. | | |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | | 10 |
|
250
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 11.3. (12 points)
How many distinct roots does the equation $f(f(f(x)))=1$ have, if $f(x)=x-\frac{2}{x}$.
|
# Solution.
Let $f(x)=k=x-\frac{2}{x}, f(f(x))=f(k)=k-\frac{2}{k}, f(f(f(x)))=f(f(k))=f(k)-\frac{2}{f(k)}$. The equation $f(f(f(x)))=f(k)-\frac{2}{f(k)}=1 \Leftrightarrow f^{2}(k)-f(k)-2=0$ has two solutions $f_{1}(k)=-1$ and $f_{2}(k)=2$.
We obtain $\left[\begin{array}{l}f(k)=k-\frac{2}{k}=-1 \\ f(k)=k-\frac{2}{k}=2\end{array} \Leftrightarrow\left[\begin{array}{l}k^{2}+k-2=0 \\ k^{2}-2 k-2=0\end{array}\right.\right.$.
The system has four distinct roots $k_{1}, k_{2}, k_{3}, k_{4}$.
Notice that the equations $x-\frac{2}{x}=k \Leftrightarrow x^{2}-k_{i} x-2=0$ have two distinct roots and these equations with different $k_{i}$ do not have common roots.
(Schoolchildren should strictly prove this or find the roots $x$ explicitly).
Thus, the original equation has 8 distinct roots.
Answer. 8.
| Content of the criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 12 |
| The answer is correct. All main logical steps of the solution are provided. There are arithmetic errors or typos that did not affect the overall course of the solution. | +. | 10 |
| The answer is correct. All main logical steps of the solution are provided. There is no strict justification for some conclusions. | $\pm$ | 9 |
| All main logical steps of the solution are provided. The incorrect reasoning led to an incorrect answer. | $+/ 2$ | 6 |
| The answer is correct. The main logical steps of the solution are provided. There is no proof that the equations $x^{2}-k_{i} x-2=0$ for different $k_{i}$ do not have common roots. | | |
| The answer is correct. The solution is missing or incorrect. | $\mp$ | 2 |
| :---: | :---: | :---: |
| Some steps reflecting the general idea of the solution are provided. The answer is missing or incorrect. | | |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | 12 | |
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 11.4. (12 points)
Employees of the company are divided into hard workers and slackers. In 2016, the average salary of hard workers was twice the average salary of slackers. After improving their qualifications, hard workers in 2017 began to earn $50 \%$ more, while the salary of slackers remained unchanged. At the end of 2016, some slackers were laid off. The average salary of all employees in 2017 became $20 \%$ higher than it was in 2016. Find what percentage of the total number of employees were hard workers in 2017, if in 2016 they were $10 \%$.
|
# Solution.
Let the number of hard workers in the company in 2016 be $x$, then the number of slackers was $9x$, and the total number of people in the company was $10x$. Let the average salary of a slacker be $s$, then the average hard worker received $2s$, and the average salary across the entire company was $\frac{2sx + 9xs}{x + 9x} = \frac{11s}{10}$.
Let the number of slackers remaining in 2017 be $y$, then the average salary across the entire company (considering the 50% salary increase for hard workers) became: $\frac{3sx + ys}{x + y}$.
Thus, we get the equation:
$\frac{3sx + ys}{x + y} = \frac{11s}{10} \cdot \frac{12}{10}$
$100(3sx + ys) = 132(x + y)$
$50(3sx + ys) = 66(x + y)$
$150x + 50y = 66x + 66y$
$84x = 16y$
$y = \frac{21}{4}x$
In the end: $\frac{x \cdot 100\%}{x + y} = \frac{x \cdot 100\%}{x + \frac{21}{4}x} = \frac{4 \cdot 100\%}{4 + 21} = \frac{4 \cdot 100\%}{25} = 16\%$.
Answer. $16\%$.
All-Russian School Olympiad "Mission Possible. Your Calling - Financier!"
| Content of the criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 12 |
| Correct answer. All main logical steps of the solution are provided. The solution contains arithmetic errors or typos that did not affect the overall course of the solution. | .+ | 10 |
| Correct answer. All main logical steps of the solution are provided. The solution lacks a strict justification for some conclusions. | $\pm$ | 9 |
| The idea of the solution is found, but it is not completed or contains errors. | | |
| At the same time, a significant part of the solution is completed, in particular, the system of equations is correctly set up. | $+/ 2$ | 6 |
| The solution is generally incorrect or incomplete, but contains a certain advancement in the right direction. The corresponding system of equations is set up incorrectly. | $\mp$ | 2 |
| The idea of the solution is found, but it is not completed or contains errors. A significant part of the solution is completed. | $+/ 2$ | 6 |
| The solution is generally incorrect or incomplete, but contains a certain advancement in the right direction. | $\mp$ | 2 |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | | 12 |
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 11.6. (14 points)
Real numbers $a$ and $b$ are such that $\left(a+\sqrt{1+a^{2}}\right)\left(b+\sqrt{1+b^{2}}\right)=1$. Find the sum $a+b$.
#
|
# Solution.
$$
\begin{aligned}
& b+\sqrt{1+b^{2}}=\frac{1}{a+\sqrt{1+a^{2}}}=-a+\sqrt{1+a^{2}} \\
& a+\sqrt{1+a^{2}}=\frac{1}{b+\sqrt{1+b^{2}}}=-b+\sqrt{1+b^{2}}
\end{aligned}
$$
By adding the obtained equations, we get
$$
a+b+\sqrt{1+a^{2}}+\sqrt{1+b^{2}}=-a-b+\sqrt{1+a^{2}}+\sqrt{1+b^{2}} \Rightarrow a+b=0
$$
## Answer. 0.
| Criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 14 |
| All main logical steps of the solution are presented. Some justifications are missing in the solution. The answer is correct. | $\pm$ | 11 |
| The idea of the solution is found. The main logical steps of the solution are presented. The answer is incorrect or missing. | $+/ 2$ | 7 |
| The answer is correct. The solution is missing or incorrect. | $\mp$ | 3 |
| The solution does not meet any of the criteria described | | |
| above. | | |
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 2. (10 points)
Given 2018 numbers $x_{1}, x_{2}, \ldots, x_{2018}$, each of which is either $2-\sqrt{3}$ or $2+\sqrt{3}$. Find the greatest possible value of the sum $x_{1} x_{2}+x_{3} x_{4}+x_{5} x_{6}+\ldots+x_{2017} x_{2018}$, given that it is an integer.
|
# Solution.
Note that the product $x_{2 k-1} x_{2 k}$ can take one of three values:
$$
\begin{aligned}
& (2-\sqrt{3})(2-\sqrt{3})=7-2 \sqrt{3} \\
& (2+\sqrt{3})(2+\sqrt{3})=7+2 \sqrt{3}
\end{aligned}
$$
or
$$
(2-\sqrt{3})(2+\sqrt{3})=1
$$
Let $a$ be the number of times the number $2-\sqrt{3}$ appears in the considered sum, and $b$ be the number of times the number $2+\sqrt{3}$ appears. Then the number of terms equal to 1 in this sum will be $1009-a-b$. In this case, the sum is
$$
a(7-2 \sqrt{3})+b(7+2 \sqrt{3})+1009-a-b=1009+6 a+6 b+7(b-a) \sqrt{3}
$$
Since the sum is an integer, then $a=b$, and the sum is $1009+12 a$.
Since $a$ can take values from 0 to 504
$(2 a=a+b \leq 1009 \Rightarrow a \leq 504.5)$, the maximum value of the considered sum is $1009+12 \cdot 504=7057$.
Answer. 7057.
| Criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 10 |
| All main logical steps of the solution are provided. The answer is incorrect due to a computational error or typo. | $\pm$ | 7 |
| Main logical steps of the solution are provided. | $+/ 2$ | 5 |
| Main idea of the solution is found. The answer is missing or incorrect. | $\mp$ | 2 |
| The answer is correct. The solution is missing or incorrect. | $\mp$ | 0 |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | 10 | |
All-Russia School Olympiad "Mission Possible. Your Calling - Financier!"
| The solution lacks a rigorous justification of individual conclusions. In particular, it may not be proven that the given answer corresponds to the maximum value. The answer is correct. | | |
| :---: | :---: | :---: |
| The main idea of the solution is found. The answer is missing or incorrect. | $\mp$ | 2 |
| The answer is correct. The solution is missing or incorrect. | $\mp$ | 0 |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | 10 | |
|
7057
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 4. (12 points)
The angle bisectors of angles $A, B$, and $C$ of triangle $A B C$ intersect the circumcircle of this triangle at points $A_{1}, B_{1}$, and $C_{1}$, respectively. Find the distances between point $A_{1}$ and the center of the inscribed circle of triangle $A B C$, given that $\angle A_{1} B_{1} C_{1}=50^{\circ}, \angle A_{1} C_{1} B_{1}=70^{\circ}, B_{1} C_{1}=\sqrt{3}$.
|
# Solution.
In the figure, identical numbers mark equal angles (this follows from the fact that $A A_{1}, B B_{1}, C C_{1}$ are the angle bisectors of triangle $ABC$, the angle marked "1+2" near point $O$ (which is the center of the inscribed circle) is equal to $\angle O A B + \angle O B A = \angle 1 + \angle 2$ by the exterior angle theorem of a triangle. Therefore, triangle $O B A_{1}$ is isosceles and $A_{1} B = A_{1} O$ is the desired segment.
$\angle A B_{1} C_{1} = 50^{\circ}, \angle A C_{1} B_{1} = 70^{\circ}$, hence $\angle B_{1} A_{1} C_{1} = 60^{\circ}$. By the Law of Sines,
$\frac{B_{1} C_{1}}{\sin \angle B_{1} A_{1} C_{1}} = 2 R, \frac{\sqrt{3}}{\sin 60^{\circ}} = 2 R, R = 1$. Next,
$\angle A = \angle A_{1} B_{1} C_{1} + \angle A_{1} C_{1} B_{1} - \angle B_{1} A_{1} C_{1} = 60^{\circ}$,
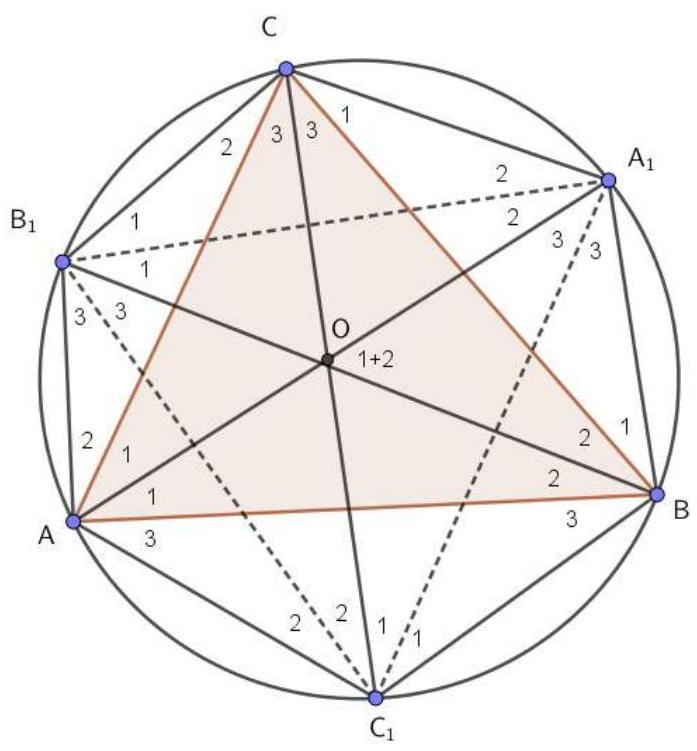
from which $\angle 1 = 30^{\circ}$. Then
$A_{1} O = A_{1} B = 2 \cdot R \cdot \sin \angle 1 = 1$.
Answer: 1.
| Criterion for Evaluation Full solution. | Rating + | Points |
| :---: | :---: | :---: |
| The main logical steps of the solution are presented. The solution lacks some justifications or has a computational error or typo. | $\pm$ | 9 |
| The idea of the solution is found, but it is not completed. However, a significant part of the task is performed. | $+/ 2$ | 6 |
| The solution is generally incorrect or incomplete, but contains some progress in the right direction. | $\mp$ | 2 |
| The solution does not meet any of the criteria described | | |
| above. | | |
All-Russian School Olympiad "Mission Possible. Your Calling - Financier!"
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 8. (16 points)
How many solutions in integers does the equation $x_{1}^{4}+x_{2}^{4}+\cdots+x_{14}^{4}=2031$ have.
|
# Solution.
Note that if the number $n$ is even, then $n^{4}$ is divisible by 16.
If $n$ is odd, then the number
$$
n^{4}-1=(n-1)(n+1)\left(n^{2}+1\right)
$$
is divisible by 16.
Therefore, the remainder of the left-hand side of the equation $x_{1}^{4}+x_{2}^{4}+\cdots+x_{14}^{4}$ when divided by 16 is equal to the number of odd numbers in the set $x_{1}, x_{2}, \ldots, x_{14}$, i.e., it does not exceed 14. On the other hand, 2031 has a remainder of 15 when divided by 16, which means the equality of the left and right sides is impossible.
Answer: 0 (no solutions).
All-Russian School Olympiad "Mission Possible. Your Calling - Financier!"
| Content of the criterion | Evaluation | Points |
| :---: | :---: | :---: |
| Complete solution. | + | 16 |
| Main logical steps of the solution are presented. Some justifications are missing in the solution. | $\pm$ | 12 |
| The idea of the solution is found, but it is not completed. A significant part of the task is completed. | $+/ 2$ | 8 |
| The solution is generally incorrect or incomplete, but contains some progress in the right direction. In particular, estimates for $x_{1}, x_{2}, \ldots, x_{14}$ and the correct answer may be provided. | $\mp$ | 4 |
| The solution does not meet any of the criteria described above. | $-/ 0$ | 0 |
| Maximum score | 16 | |
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. On a sausage, thin rings are drawn across. If you cut along the red rings, you get 5 pieces; if along the yellow ones, you get 7 pieces; and if along the green ones, you get 11 pieces. How many pieces of sausage will you get if you cut along the rings of all three colors?
$[3$ points] (A. V. Shipovalov)
|
Answer: 21 pieces.
Solution: Note that the number of pieces is always one more than the number of cuts. Therefore, there are 4 red rings, 6 yellow ones, and 10 green ones. Thus, the total number of cuts is $4+6+10=20$, and the number of pieces is 21.
|
21
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. At the exchange office, there are two types of operations: 1) give 2 euros - get 3 dollars and a candy as a gift; 2) give 5 dollars - get 3 euros and a candy as a gift.
When the wealthy Pinocchio came to the exchange office, he only had dollars. When he left, he had fewer dollars, no euros appeared, but he received 50 candies. How much did such a "gift" cost Pinocchio in dollars?
[6 points] (I.V. Raskina)
|
Answer: $10.
Solution: Since Buratino received 50 candies, he performed exactly 50 operations. At the same time, he exchanged all the euros he received back into dollars. Therefore, for every 3 operations of the first type, there were 2 operations of the second type. That is, Buratino received $3 30 times and gave away $5 20 times. Thus, he spent $20 \cdot 5 - 30 \cdot 3 = 10$ dollars.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Yura has a calculator that allows multiplying a number by 3, adding 3 to a number, or (if the number is divisible by 3) dividing the number by 3. How can one use this calculator to get from the number 1 to the number 11? $\quad[3$ points] (T. I. Golenishcheva-Kutuzova)
|
Answer. For example, $((1 \cdot 3 \cdot 3 \cdot 3)+3+3): 3=11$ or $(1 \cdot 3+3): 3+$ $3+3+3=11$.
Comment. Note that on Yura's calculator, any number can be increased by $1:(x \cdot 3+3): 3=x+1$. Therefore, in principle, any natural number can be obtained from one on it.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Little kids were eating candies. Each one ate 7 candies less than all the others together, but still more than one candy. How many candies were eaten in total?
[5 points] (A. V. Shapovalov)
|
Answer: 21 candies.
Solution. Let's choose one of the children, for example, Petya. If we take away 7 candies from all the others, there will be as many left as Petya has. This means that twice the number of candies Petya has equals the total number of candies minus seven. The same can be said about any of the children, which means that all the children have the same number of candies - let's say, in piles.
It is clear that each one ate one whole pile less than the others together. Therefore, 7 is divisible by the size of the pile. Since each one ate more than 1 candy according to the condition, there are 7 candies in each pile, i.e., each one ate one pile less than the others together. Petya ate one pile, so the others ate two. Therefore, there are three piles in total, and 21 candies.
This solution can also be written algebraically.
Let $S$ be the total number of candies eaten by the children. If one of the children ate $a$ candies, then according to the condition, all the others ate $a+7$ candies, and together they ate $S=a+(a+7)=$ $=2a+7$ candies. This reasoning is valid for each child, so all the children ate the same number of candies: $a=(S-7)/2$ each.
Now let $N$ be the number of children. Then the condition can be written as $a=a(N-1)-7$, from which $7=a(N-2)$. The number 7 is prime, so one of the factors is 1, and the other is 7. But according to the condition $a>1$, so $a=7, N-2=1$. Thus, $N=3$, and a total of $S=aN=21$ candies were eaten.
|
21
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. In a singing competition, a Rooster, a Crow, and a Cuckoo participated. Each member of the jury voted for one of the three performers. The Woodpecker calculated that there were 59 judges in total, and that the Rooster and the Crow received a total of 15 votes, the Crow and the Cuckoo received 18 votes, and the Cuckoo and the Rooster received 20 votes. The Woodpecker is a poor counter, but each of the four numbers he mentioned differs from the correct one by no more than 13. How many judges voted for the Crow? [6 points] (I.V.Raschina)
|
Answer: 13 judges.
Solution. The number of votes for the Rooster and the Raven cannot be more than $15+13=28$. Similarly, the number of votes for the Raven and the Cuckoo cannot exceed $18+13=31$, and the number of votes for the Cuckoo and the Rooster cannot exceed $20+13=33$. Adding these three quantities of votes, we get twice the total number of votes (each vote is counted in two of the three sums). Thus, the total number of jury members is no more than $(28+31+33) / 2=46$. On the other hand, from the first announcement of the Woodpecker, it is no less than $59-13=46$. Therefore, there are exactly 46 jury members, and all the inequalities are actually equalities.
Finally, the number of votes for the Raven can be found as the difference between the total number of jury members and the sum of those who voted for the Cuckoo and the Rooster: $46-33=13$ votes.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Three sides of a quadrilateral are equal, and the angles of the quadrilateral formed by these sides are $90^{\circ}$ and $150^{\circ}$. Find the other two angles of this quadrilateral.
|
Answer: $45^{\circ}$ and $75^{\circ}$.
Solution. Let's denote the vertices of the quadrilateral as shown in the diagram.
Extend $A B C$ to form a square $A B C X$. In triangle $X C D$, the angle $\angle X C D$ is equal to $\angle B C D - \angle B C X = 150^{\circ} - 90^{\circ} = 60^{\circ}$, and the sides $C X$ and $C D$ are equal. Therefore, triangle $X C D$ is isosceles with an angle of $60^{\circ}$, meaning it is equilateral (in particular, segment $X D$ is also equal to the side of the square).
Now that we understand that
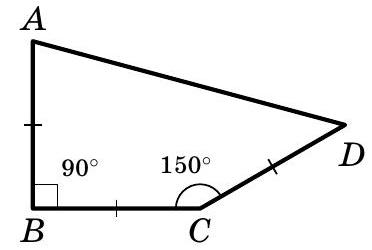
our quadrilateral is formed by
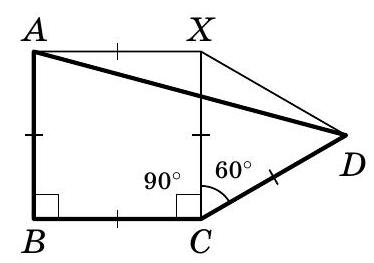
a square and an equilateral triangle, we can calculate its angles. Triangle $A X D$ is isosceles with an angle of $90^{\circ} + 60^{\circ} = 150^{\circ}$ at the vertex.
Therefore,
$$
\angle X A D = \angle X D A = \frac{180^{\circ} - 150^{\circ}}{2} = 15^{\circ}
$$
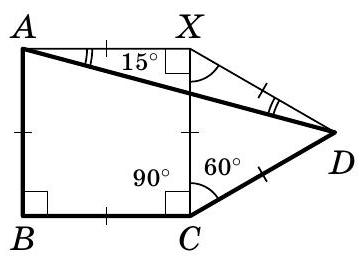
Thus,
$$
\begin{aligned}
& \angle B A D = \angle B A X - \angle X A D = 90^{\circ} - 15^{\circ} = 75^{\circ} \\
& \angle A D C = \angle X D C - \angle X D A = 60^{\circ} - 15^{\circ} = 45^{\circ}
\end{aligned}
$$
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In a small town, there is only one tram line. It is circular, and trams run along it in both directions. There are stops on the loop: Circus, Park, and Zoo. The journey from Park to Zoo via Circus is three times longer than not via Circus. The journey from Circus to Zoo via Park is twice as short as not via Park. Which route from Park to Circus is shorter - via Zoo or not via Zoo - and by how many times?
(A.V. Shapovalov)
|
Answer: The path not through the Zoo is 11 times shorter.
Solution. Let's board the tram at the Zoo stop and travel through the Circus to the Park, and then, without leaving the tram, return to the Zoo. The second part of the journey is three times shorter than the first, meaning the first part takes up three quarters of the full circle, and the second part takes up one quarter. Let's mark the Zoo and the Park on the map, and somewhere on the longer arc between them, mark the Circus (see the diagram). Now, on the same tram, let's travel from the Circus to the Zoo (passing the Park, as shown on the map).
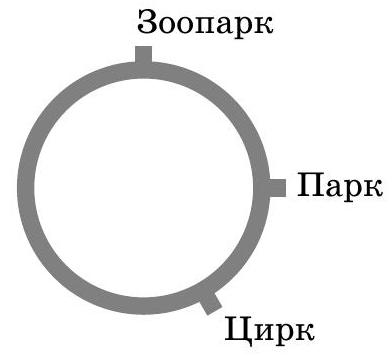
Having arrived at the Zoo, we will return to the Circus on the same tram, completing a full circle. The first part of the journey is twice as short as the second, meaning it takes up one third of the circle. This means that the path (still on the same tram) from the Circus to the Park will not pass through the Zoo and will constitute $\frac{1}{3}-\frac{1}{4}=\frac{1}{12}$ of the full circle. The path through the Zoo is $1-\frac{1}{12}=\frac{11}{12}$ of the circle, which is 11 times longer.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. An equilateral triangle with a side length of 8 was divided into smaller equilateral triangles with a side length of 1 (see figure). What is the minimum number of small triangles that need to be shaded so that all intersection points of the lines (including those on the edges) are vertices of at least one shaded triangle? Provide an example and prove that it is impossible to shade fewer triangles.
[6 points] (
|
Answer: 15 small triangles. See the example in the figure.
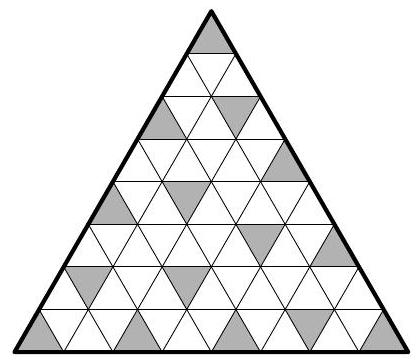
Solution: The total number of intersection points of the lines is $1+2+3+\ldots+9=45$. Since a triangle has three vertices, at least $45:3=15$ triangles will need to be shaded.
Comment: It can be shown that there is only one (up to axial symmetry) way to shade 15 triangles.
In the coloring we found, no vertex is shaded twice. The side length of 8 of the large triangle is the minimum for which such an "economical" coloring is possible. It is definitely impossible if the side length is a multiple of three. A more complex version of this problem (for a triangle with side length 2015) was published in the "Problems" section of the journal "Mathematics in School" (Issue 1, 2016).
|
15
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. The robot invented a cipher for writing words: he replaced some letters of the alphabet with single or double-digit numbers, using only the digits 1, 2, and 3 (different letters he replaced with different numbers). First, he wrote himself in code: РОБОТ $=3112131233$. After encrypting the words КРОКОДИЛ and БЕГЕМОТ, he was surprised to notice that the numbers turned out to be exactly the same! Then the robot wrote the word МАТЕМАТИКА. Write down the number he got. Justify your answer.
[7 points]
(A. V. Khachatryan)
|
Answer: 2232331122323323132.
Solution. Consider the word ROBOT $=3112131233$. It contains 5 letters and 10 digits, so all codes are two-digit and can be determined without difficulty. Let's write down all twelve possible codes and the letters we definitely know:
$$
\begin{array}{llll}
1= & 11= & 21= & 31=P \\
2= & 12=O & 22= & 32= \\
3= & 13=B & 23= & 33=T
\end{array}
$$
Now let's think about how the word КРОКОДИЛ $=$ БЕГЕМОТ would be written. It starts with $Б=13$, so $К=1$. Now we can write the beginning of the word: КРОКО... $=13112112 \ldots$ We start reading it as the word БЕГЕМОТ: $\mathrm{Б}=13, \mathrm{E} \neq 1$, so $\mathrm{E}=11$, and then $\Gamma=2$, otherwise the second $\mathrm{E}$ would not work. And M starts with 2, so $\mathrm{M}=2 *$. Now let's look at the end of the word, ...ОТ, which is ...1233. This means that $Л=3$ and $И=23$, and Д ends with 1, so $Д=* 1$. The asterisk is the only remaining undeciphered digit. It is not difficult to decipher: $31=\mathrm{P}, 11=\mathrm{E}$, so $Д=* 1=21$.
Then $\mathrm{M}=22$, and we have almost fully deciphered the code:
$$
\begin{array}{llll}
1=\mathrm{K} & 11=\mathrm{E} & 21=\mathrm{D} & 31=\mathrm{P} \\
2=\Gamma & 12=\mathrm{O} & 22=\mathrm{M} & 32= \\
3=\mathrm{J} & 13=\mathrm{E} & 23=\mathrm{U} & 33=\mathrm{T}
\end{array}
$$
Now we know everything we need to write the word МАТЕМАТИКА in code, except one thing - how the letter А is encoded. But since Robot was able to write this word, there must be a code for А. And this code is 32, because all the others have been used.
|
2232331122323323132
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. Forty children were playing in a ring. Of them, 22 were holding hands with a boy and 30 were holding hands with a girl. How many girls were in the ring? [8 points] (E.V. Bakayev)
|
Answer: 24 girls.
Solution: $22+30=52$, so $52-40=12$ children held hands with both a boy and a girl. Therefore, $30-12=18$ children held hands only with girls. These 18 children held $18 \cdot 2=36$ girls' hands, and the other 12 held one girl's hand each, so the girls had a total of $36+12=48$ hands. Thus, there were $48: 2=24$ girls.
Comment: An arrangement of children in a circle that meets the conditions of the problem exists, for example, as shown in the figure. Other arrangements are possible.
Knowing the answer (24 girls and, therefore, 16 boys), we can observe that the number of girls is greater than the number of boys by exactly the same amount by which the number of children holding a girl's hand is greater than those holding a boy's hand: $24-16=30-22=8$. This is not a coincidence. Knowing this fact, the problem can be easily solved. However, proving this fact is not very simple. We will provide one possible proof.
Let $Д$ and $M$ be the number of girls and boys in the circle, and let $X$ and $Y$ be the number of children holding a girl's hand and a boy's hand, respectively.
Consider several (more than one) girls standing in a row. Ask them to leave the circle one by one—first those in the "middle" (i.e., standing between two girls), and then, when only two girls remain, one of the remaining. We will track how $Д, M$, and $Д-M$, as well as $X$, $Y$, and $X-Y$, change. We will create a table (using the small letter "д" to denote the girl leaving the circle):
| | Д | $\bar{M}$ | $\bar{Д}-M$ | $\bar{X}$ | $\bar{Y}$ | $\overline{X-Y}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| ...ДдД... | -1 | no change | -1 | -1 | no change | -1 |
| ...МдДМ... | -1 | no change | -1 | -2 | -1 | -1 |
We see that the differences $Д-M$ and $X-Y$ change in the same way (decrease by 1) with the departure of each girl. We will do the same with rows of boys—similarly, we can show that both differences will increase by 1 with the departure of each boy from the circle.
After all this, we will have a circle where boys and girls alternate, meaning there are an equal number of each, and $Д-M=0$. But $X-Y=0$ as well, because in this case $X=M$, and $Y=Д$.
Thus, $Д-M$ and $X-Y$ changed in the same way with each child leaving the circle, and in the end, $Д-M=X-Y$. This means that in the original circle, $Д-M=X-Y$, which is what we needed to prove.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. On the surface of a planet shaped like a donut, two snails crawled, leaving trails behind: one along the outer equator, and the other along a spiral line (see figure). Into how many parts did the snails' trails divide the surface of the planet? (It is sufficient to write the answer.)
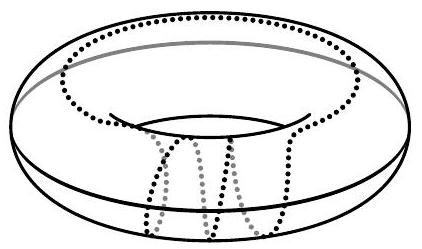
## [4 points] (S.K. Smirnov, I.V. Yashchenko)
|
Answer: 3.
Comment. Let's imagine the surface of a donut made of paper. Cut it along the path of the first snail and unfold it. We will get the lateral surface of a cylinder. The path of the second snail will be cut in three places. That is, on the resulting surface, the trail of the second snail represents three lines connecting the bottom base of the cylinder with the top. It is not difficult to realize that they divide the lateral surface of the cylinder into 3 parts.
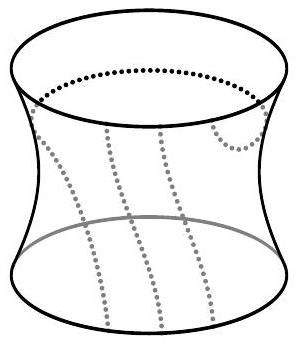
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. Three frogs on a swamp jumped in turn. Each landed exactly in the middle of the segment between the other two. The length of the second frog's jump is 60 cm. Find the length of the third frog's jump.
$[4$ points]
(A. V. Shapovalov)
|
Answer: 30 cm.
Solution. Regardless of how the frogs were sitting initially, after the first jump, they will be on one straight line, with the first (A) in the middle.
B $\qquad$ A B
Now the second frog (B) jumps. It flies a distance to A and then half of this distance, which, according to the condition, is 60 cm. Therefore, the distance between it and A (as well as between A and B) was 40 cm.

Thus, now the distance between A and B is 40 cm, and B is exactly in the middle between them, and it's V's turn to jump. She will fly 20 cm and then half of this distance, which is a total of 30 cm.
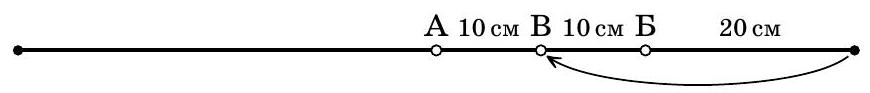
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. The maze for mice (see the figure) is a $5 \times 5$ meter square, and the mice can only run along the paths. Two pieces of cheese (marked with crosses) are placed at two intersections. At another intersection, a mouse (marked with a circle) is sitting. She can smell the cheese, but she needs to run the same distance to both pieces, so she doesn't know which one to choose and sits thoughtfully in place.
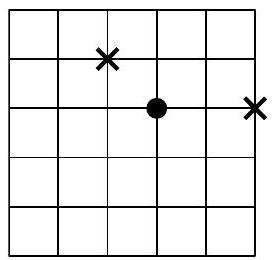
a) Mark five more intersections where the mouse could sit thoughtfully (from where she would need to run the same distance to both pieces of cheese).
[2 points]
b) Come up with two intersections where you can place a piece of cheese so that there are as many suitable intersections for a thoughtful mouse as possible.
[up to 5 points]
|
Answer. a)
b) The maximum number of places for thoughtful mice is 26:
Comments. 1. In any example for part b), one end of each of the following 10 segments must be free (if both ends are marked, then the pieces of cheese must be placed on a line perpendicular to this segment, which means there will be exactly 6 suitable places.
From this, we can also conclude that there cannot be more than 26 thoughtful mice: if one end is free, then we have at least 10 unmarked intersections.
|
26
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. A row of new recruits stood facing the sergeant. On the command "left," some turned left, while the rest turned right. It turned out that six times more soldiers were looking at the back of their neighbor than in the face. Then, on the command "about face," everyone turned in the opposite direction. Now, seven times more soldiers were looking at the back of their neighbor than in the face. How many soldiers are in the row?
$[8$ points] (A. V. Shipovalov)
|
Answer: 98.
Solution. Let's assume that the sergeant lined up the soldiers between two posts. After the first command, each recruit either looks at the back of the neck of the neighbor or at the face, except for the two soldiers at the ends, who can look at the posts.
If a soldier is looking at the back of the neck of a neighbor, then after the turn, this neighbor will be looking at the back of the neck of the first soldier. Therefore, the number of those looking at the back of the neck will not change.
The soldier at the end, who was looking at the post, will not be doing so after the turn; conversely, if he was not looking at the post, he will be after the turn. Thus, the number of those looking at the post will either remain the same (was 1 and will remain 1), or increase by 2 (was 0, will become 2), or decrease by 2 (was 2, will become 0).
Since the total number of soldiers is constant, the number of those looking at the face will also either remain the same, or increase or decrease by 2.
According to the problem, the number of soldiers looking at the face was initially one-sixth of the number looking at the back of the neck, and then one-seventh. This means that their number decreased (and, therefore, decreased by 2). On the other hand, it changed by $1/6 - 1/7 = 1/42$ of the constant number of those looking at the back of the neck. That is, there were $2 \cdot 42 = 84$ people looking at the back of the neck, and 14 people looking at each other before the turn, which is $84: 6 = 14$. There were no soldiers looking at the posts. Thus, the total number of recruits is $84 + 14 = 98$.
|
98
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. The she-rabbit bought seven drums of different sizes and seven pairs of sticks of different lengths for her seven bunnies. If a bunny sees that both its drum is larger and its sticks are longer than those of one of its brothers, it starts to drum loudly. What is the maximum number of bunnies that can start drumming? [3 points] (D.V. Baranov)
|
Answer: 6 baby rabbits.
Solution: Not all baby rabbits can play the drum, as the baby rabbit that gets the smallest drum will not play it. On the other hand, if the same baby rabbit is also given the shortest drumsticks, then all the other baby rabbits will play the drum.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. There were several whole cheese heads on the warehouse. At night, rats came and ate 10 heads, and everyone ate equally. Several rats got stomachaches from overeating. The remaining 7 rats the next night finished off the remaining cheese, but each rat could eat only half as much cheese as the night before. How much cheese was originally on the warehouse? [5 points] (A.D. Blyunkov, I. V. Raskina)
|
Answer: 11 cheese heads
Solution: Let the total number of rats be $k$ ( $k>7$ ), then each rat ate $10 / k$ cheese heads on the first night. On the second night, each rat ate half as much, that is, $5 / k$ cheese heads. Thus, the 7 rats ate a total of $35 / k$ cheese heads. This is an integer. The only divisor of the number 35 that exceeds $7$ is the number 35 itself. Therefore, $35 / k=1$, and the total number of cheese heads on the warehouse before the rat invasion was $10+1=11$ cheese heads.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. A number was multiplied by the sum of its digits and the result was 2008. Find this number.
$[4$ points] (I. V. Yashchenko)
|
Answer: 251.
Solution: The desired number is a divisor of the number 2008. Let's factorize the number 2008 into prime factors: $2008=2 \cdot 2 \cdot 2 \cdot 251$. List all divisors of the number $2008: 1,2,4,8,251,502,1004,2008$. By finding the sum of the digits of each of them, we notice that the condition of the problem is only satisfied by the number $251(2008=251 \cdot(2+5+1))$.
|
251
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Dima lives in a nine-story building. He descends from his floor to the first floor by elevator in 1 minute. Due to his small stature, Dima cannot reach the button for his floor. Therefore, when going up, he presses the button he can reach, and then walks the rest of the way. The entire journey upwards takes 1 minute 10 seconds. The elevator moves up and down at the same speed, and Dima climbs at half the speed of the elevator. On which floor does Dima live?
[6 points] (D.E. Shnol)
|
Answer. Dima lives on the seventh floor.
First solution. Consider the part of the journey that Dima travels down by elevator and up on foot. On the one hand, the walk takes twice as long, and on the other, it is 10 seconds longer. Therefore, he traveled this part by elevator in 10 seconds and walked it in 20 seconds. Since the entire elevator ride takes 60 seconds, he walked $1 / 6$ of the way.
Notice that he walked a whole number of intervals between floors. Since the building is nine-story, he walked 1 interval and rode 5. Therefore, Dima lives on the 7th floor.
Second solution. Let the elevator move at a speed of $v$ floors per second, Dima lives on the $n$-th floor, and usually gets off on the $m$-th floor. Then
$$
\left\{\begin{array}{l}
\frac{n-1}{v}=60 \\
\frac{m-1}{v}+\frac{n-m}{v} \cdot 2=70
\end{array}\right.
$$
from which $m-1+2 n-2 m=70 v$. Substitute $v=\frac{n-1}{60}$ from the first equation:
$$
\begin{gathered}
2 n-m-1=\frac{n-1}{6} \cdot 7 \\
12 n-6 m-6=7 n-7 \\
5 n+1=6 m
\end{gathered}
$$
Since $m<9$, it is not difficult to find that $n=7$, and $m=6$.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Bus stop $B$ is located on a straight highway between stops $A$ and $C$. After some time following departure from $A$, the bus found itself at a point on the highway such that the distance from this point to one of the three stops is equal to the sum of the distances to the other two. After the same amount of time, the bus was again at a point with this property, and after another 25 minutes, it arrived at $B$. How much time does the bus need for the entire journey from $A$ to $C$, if its speed is constant and it stops at $B$ for 5 minutes?
$[6$ points] (A.V.Khachaturyan)
|
Answer: 3 hours.
Solution. At both moments in time mentioned in the problem, the sum of distances will obviously be the distance from the bus to the farthest stop from it. This cannot be $B$, as it is closer than $C$. Therefore, these were $C$ (before the bus had traveled halfway from $A$ to $C$) and $A$ (after this moment).
In the first case, the bus was at point $X$ and the distance from it to $C$ was equal to the sum of the distances to $A$ and to $B$. But this distance is also equal to the sum of the distance to $B$ and the distance $B C$. Therefore, the bus had traveled exactly the distance $B C$. On the diagram, we marked equal distances with arcs.
By the second moment, the bus had traveled another distance $B C$ and was at point $Y$. The sum of the distances from it to $B$ and to $C$ is equal to $B C$ and $Y B$, counted twice. According to the problem, this is the distance to $A$, so $Y B$ is half the length of $B C$.
Since $Y B$ was traveled in 25 minutes, $B C$ will be traveled in 50 minutes, and the entire journey will take $3 \cdot 50 + 25 + 5 = 180$ minutes, which is three hours.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. In quadrilateral $A B C D$, it is known that $A B=$ $=B C=C D, \angle A=70^{\circ}$ and $\angle B=100^{\circ}$. What can the angles $C$ and $D$ be equal to? $\quad[8$ points] (M.A.Volchkevich)
|
Answer: $60^{\circ}$ and $130^{\circ}$ or $140^{\circ}$ and $50^{\circ}$.
First Solution. Draw segment $B E$ such that point $E$ lies on $A D$, and angle $A B E$ is $40^{\circ}$. Then $\angle A E B = 180^{\circ} - 70^{\circ} - 40^{\circ} = 70^{\circ}$, hence triangle $A B E$ is isosceles, $A B = B E$. Consider triangle $B C E$: $\angle C B E = 100^{\circ} - 40^{\circ} = 60^{\circ}$ and $B E = A B = B C$, thus triangle $B C E$ is equilateral, and $C E = B C = A B$. This means that quadrilateral $A B C E$ satisfies the condition, and one possible answer is that angle $C$ of such a quadrilateral is $60^{\circ}$, and the remaining angle is $\angle A E B + \angle B E C = 70^{\circ} + 60^{\circ} = 130^{\circ}$.
Notice that for any point $D^{\prime}$ on segment $A E$, $C D^{\prime} > C E = B C$ (since $C D^{\prime}$ is the largest side in the obtuse triangle $C E D^{\prime}$). Let point $D$ lie on ray $A E$ beyond point $E$, and $C D = B C = C E$. Then $\angle C E D = 180^{\circ} - \angle A E B - \angle B E C = 180^{\circ} - 70^{\circ} - 60^{\circ} = 50^{\circ}$, and since $C E = C D$, $\angle C D E = \angle C E D = 50^{\circ}$, thus $\angle E C D = 180^{\circ} - 2 \cdot 50^{\circ} = 80^{\circ}$ and $\angle B C D = 60^{\circ} + 80^{\circ} = 140^{\circ}$.
Second Solution. In the isosceles triangle $A B C$, angle $A B C$ is $100^{\circ}$, so $\angle B A C = \angle A C B = 40^{\circ}$, and then $\angle C A D = 70^{\circ} - 40^{\circ} = 30^{\circ}$. Mark the midpoint $M$ of segment $A C$ and the foot $P$ of the perpendicular dropped from point $C$ to line $A D$. Then, in the right triangle $A C P$, the side opposite the $30^{\circ}$ angle is $C P$, so $C P = \frac{1}{2} A C = C M$. Therefore, right triangles $B C M$ and $D C P$ are congruent by the hypotenuse and one leg, so $\angle C D P = \angle M B C = 50^{\circ}$, i.e., depending on whether point $P$ lies inside segment $A D$ or outside, either angle $A D C$ or its adjacent angle is $50^{\circ}$. Accordingly, in the first case, $\angle A D C = 50^{\circ}$ and $\angle B C D = 140^{\circ}$, and in the second case, $\angle A D^{\prime} C = 130^{\circ}$ and $\angle B C D^{\prime} = 60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. The year 2009 has the following property: by swapping the digits of the number 2009, it is impossible to obtain a smaller four-digit number (numbers do not start with zero). In which year will this property reoccur for the first time?
|
Answer. In 2022.
Solution. In the years $2010, 2011, \ldots, 2019$ and in 2021, the year number contains a one, and if it is moved to the first position, the number will definitely decrease. The number 2020 can be reduced to 2002. However, the number 2022 cannot be decreased by rearranging the digits.
|
2022
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. In the park, there were lindens and maples. Maples among them were $60 \%$. In spring, lindens were planted in the park, after which maples became $20 \%$. In autumn, maples were planted, and maples became $60 \%$ again. By what factor did the number of trees in the park increase over the year?
[6 points] (D.E. Shnol)
|
Answer: 6 times.
First solution. Before the planting, lindens constituted $2 / 5$, and maples $-3 / 5$ of all the trees in the park. By summer, the number of maples did not change, but they began to constitute $1 / 5$ of all the trees. Therefore, the total number of trees in the park increased threefold. At the same time, lindens constituted $4 / 5$ of all the trees.
By winter, the number of lindens did not change, but they began to constitute $2 / 5$ of all the trees. Therefore, the total number of trees increased by another factor of two. Thus, over the year, the number of trees increased by a factor of 6.
Second solution. At first, there were 1.5 times fewer lindens than maples, and then there were 4 times more. While the number of maples did not change. Therefore, the number of lindens increased by $1.5 \cdot 4 = 6$ times. Note that by the end of the year, the ratio of the number of maples to the number of lindens became the same as it was at the beginning.
Since the number of lindens did not change in the fall, the number of maples also increased by six times. That is, the number of trees in the park increased by six times.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 5. A curious tourist wants to stroll through the streets of the Old Town from the station (point $A$ on the map) to their hotel (point $B$). The tourist wants their route to be as long as possible, but it is not interesting for them to visit the same intersection twice, and they do not do so. Draw the longest possible route on the map and prove that there is no longer one.
$[7$ points] (I. V. Yashchenko)
|
Solution. One of the possible routes of the tourist is shown in the figure. By following this path, the tourist will walk 34 streets (a street is defined as a segment between two adjacent intersections). We-
claim that a longer route is impossible.
There are a total of 36 intersections in the Old Town. Every time the tourist walks another street, he arrives at a new intersection. Therefore, the tourist cannot walk more than 35 streets (the initial intersection $A$ is not counted). We will show that the curious tourist cannot visit 35 intersections (and, consequently, walk 35 streets). To do this, we will color the intersections in black and white in a checkerboard pattern (see the figure). Every time the tourist walks a street, he arrives at an intersection of the opposite color. Both the hotel and the station are located on white intersections. Therefore, any route contains an even number of streets, and the number 35 is odd.
|
34
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Two sums are written on the board:
$$
\begin{array}{r}
1+22+333+4444+55555+666666+7777777+ \\
+88888888+999999999
\end{array}
$$
$9+98+987+9876+98765+987654+9876543+$
$+98765432+987654321$
Determine which of them is greater (or if they are equal).
$[4$ points] (G. Galperin)
|
Answer: The sums are equal.
Solution. Let's write both sums in a column, and for better clarity, the second one in reverse order. In both sums, the digits from 1 to 9 will be added in the units place, the digits from 2 to 9 in the tens place, the digits from 3 to 9 in the hundreds place, and so on. The digit obtained in each place and the carry to the higher place will be the same in both cases. Therefore, the result of the addition will be the same.
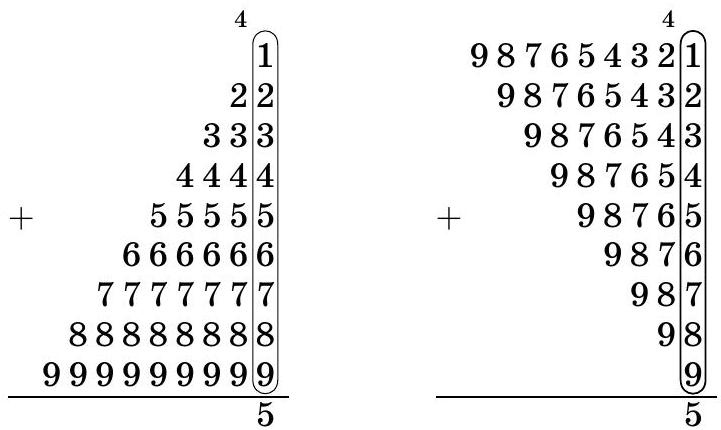
Of course, both sums can be calculated directly, and the result is 1097393685. But this is a rather laborious and uninteresting way.
Comment. One can imagine the digits in the second example "falling down," and the second example turning into the first.
|
1097393685
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. The figure "violinist" attacks the cell to the left on the side (with the elbow) and the cell to the upper right diagonally (with the bow), if he is right-handed, and, conversely, the right cell on the side and the upper left cell diagonally, if he is left-handed (all violinists are facing us). Place as many "violinists" as possible in an "orchestra" of $8 \times 8$ cells, so that they do not attack each other. (You can use any combination of right-handed and left-handed violinists.)
this is how a right-handed violinist attacks
and this is how a left-handed violinist attacks
(M. Khachaturian)
|
Solution. Placing 32 violinists is not difficult: for example, you can fill four columns every other one (it doesn't matter whether they are right-handed or left-handed). However, it is possible to place more. An example with 34 violinists is shown in the figure.
| $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | $\Lambda$ | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | | $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | 1 |
| $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | $\Lambda$ | | |
| | | $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | $\Lambda$ |
| $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | $\Lambda$ | | |
| | | $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | $\Lambda$ |
| $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | $\wedge$ | | $\mathrm{p}$ |
| $\Lambda$ | | $\mathrm{p}$ | $\wedge$ | | $\mathrm{p}$ | | $\Lambda$ |
Comment. It can be proven that it is impossible to place more than 34 violinists. Indeed, consider a vertical strip two cells wide. Any violinist standing in this strip and not in the top row will hit one cell in the same strip. We can associate this empty cell with the given violinist. If it turns out that two violinists hit the same empty cell (there are two similar cases of this, one of which is shown in the figure), then the cell below the twice-hit one must also be empty, so it can be associated with one of the two violinists, say the lower one. If this cell is hit by a bow from a violinist standing even lower, we can associate this violinist with the adjacent cell horizontally (which is necessarily empty), and so on.
Thus, in the strip, there can be a maximum of 9 violinists - two in the top cells and seven more in the remaining 14 cells, because each violinist there corresponds to an empty cell, meaning that the occupied cells do not exceed half.
However, two strips with nine violinists cannot be adjacent, otherwise four violinists would sit in a row in the top row. Therefore, there can be no more than two such strips, and in the remaining two strips, there can be a maximum of 8 violinists each, so there are no more than $9+9+8+8=34$ musicians in the orchestra.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Anya calls a date beautiful if all 6 digits of its notation are different. For example, 19.04.23 is a beautiful date, while 19.02.23 and 01.06.23 are not. How many beautiful dates are there in 2023? 3 $[4$ points] (M. Evdokimov)
|
Answer: 30.
Solution: The digits 2 and 3 are already used in the year number, so we need to consider only the months 01, 04, 05, 06, 07, 08, 09, and 10. Each of these month numbers contains a 0, so in a beautiful date, there will be no day number starting with 0, 2, or 3, and there will also be no days 10, 11, 12, and 13—only the 6 days from 14 to 19 remain. However, in each of these months, a beautiful date starts with 1, and only 6 months, from 04 to 09, are suitable. It remains to note that for each suitable month, exactly one day ending in the same digit will not be beautiful—thus, in each of the 6 months, there are 5 beautiful dates, and in total, in 2023, there are 30.
|
30
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Children went to the forest to pick mushrooms. If Anya gives half of her mushrooms to Vitya, all the children will have the same number of mushrooms, and if instead Anya gives all her mushrooms to Sasha, Sasha will have as many mushrooms as all the others combined. How many children went mushroom picking?
|
Answer: 6 children.
Solution: Let Anya give half of her mushrooms to Vitya. Now all the children have the same number of mushrooms (this means that Vitya did not have any mushrooms of his own). For Sanya to now get all of Anya's mushrooms, he needs to take the mushrooms from Vitya and Anya. Then he will have the mushrooms of three children - Vitya's, Anya's, and his own. The others will have just as many, so with Vitya, Anya, and Sanya, there were three more children in the forest.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. In the morning, a dandelion blooms, it flowers yellow for two days, on the third day in the morning it turns white, and by evening it sheds its seeds. Yesterday afternoon, there were 20 yellow and 14 white dandelions on the meadow, and today there are 15 yellow and 11 white.
a) How many yellow dandelions were there on the meadow the day before yesterday
b) How many white dandelions will there be on the meadow tomorrow? [6 points] (
|
Answer. a) 25 yellow dandelions; b) 9 white dandelions.
Solution. a) All dandelions that were yellow the day before yesterday have turned white yesterday or today. Therefore, there were $14+11=25$.
b) Out of the yellow dandelions from yesterday, 11 turned white today, and the remaining $20-11=9$ will turn white tomorrow.
|
25
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Mom baked pies - three with rice, three with cabbage, and one with cherries - and laid them out in a circle on a plate (see fig.). Then she put the plate in the microwave to warm them up. On the outside, all the pies look the same.
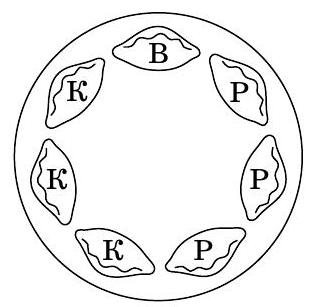
Masha knows how they were arranged, but she doesn't know how the plate was rotated. She wants to eat the cherry pie, considering the others to be unappetizing. How can Masha definitely achieve this, biting into as few unappetizing pies as possible
[7 points] (A. V. Khachaturyan)

|
Solution. It is clear that Masha cannot solve the task with one bite. If Masha, for example, tried a cabbage pie, she cannot determine which of the three she got, and therefore cannot confidently find the pie with the cherry.
Let's show how Masha can solve the task in two bites.
Suppose Masha bit into a pie, and it turned out to be not with cherry, but with cabbage. Then she can try the pie that lies one position clockwise from it. If this is the pie with cherry, Masha has achieved her goal; if it is with rice, then the desired pie is between the bitten ones; and if it is again with cabbage, then she should take the next one clockwise, and this will definitely be the pie with cherry.
If the first pie is with rice, Masha can act similarly, but move counterclockwise.
Comment. Masha can act similarly with a larger number of "unpalatable" pies. Suppose there are $N$ cold pies with cabbage on the plate, then a pie with cherry, and again $N$ pies with rice. Masha can notice the middle pie with cabbage (and if $N$ is even, then any of the two middle ones) and remember how many pies she needs to count clockwise to take the pie with cherry. When the pies warm up, Masha tries one pie. Suppose she is unlucky, and it turns out to be with cabbage. Masha can then imagine that she tried the very middle pie and count from it as needed. If she guessed correctly, she will get the cherry, and if not, she will understand whether she is closer to the desired pie than the chosen middle one or farther from it. In any case, the uncertainty is reduced by half: after one attempt, Masha has "under suspicion" no more than half of the pies with cabbage.
A lot of interesting information about problems on the amount of information can be found in the book by K.A. Knop "Weighings and Algorithms: From Puzzles to Problems" (Moscow, MCCME, 2011).
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. In the morning, a dandelion blooms, it flowers yellow for three days, on the fourth day in the morning it turns white, and by the evening of the fifth day, it withers. On Monday afternoon, there were 20 yellow and 14 white dandelions on the meadow, and on Wednesday there were 15 yellow and 11 white. How many white dandelions will there be on the meadow on Saturday?
[6 points] (D.E. Shnol)
|
Answer: 6 white dandelions.
Solution: A blooming dandelion is white on the fourth and fifth day. Therefore, on Saturday, the dandelions that bloomed on Tuesday or Wednesday will be white. Let's determine how many there are.
14 dandelions that were white on Monday had all their seeds dispersed by Wednesday, while 20 yellow ones definitely survived until Wednesday (possibly turning white).
On Wednesday, there were $15+11=26$ dandelions on the meadow. We know that 20 of them were on the meadow since Monday, and the remaining $26-20=6$ bloomed on Tuesday and Wednesday.
Comment: It is not hard to notice that the number of white dandelions on Monday does not affect the answer.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Children visited the dolphinarium. Katya remembered that there were exactly 7 either otters or seals; Yura that there were exactly 6 either sea lions or seals; Igor - that there were exactly 5 either otters or sea lions; Seryozha - that there were the fewest either seals or otters. No one was wrong. How many otters, seals, and sea lions were there in the dolphinarium?
[4 points] (T. Kazitsyna)
|
Answer: 5 otters, 7 seals, 6 sea lions.
Solution: Since none of the children made a mistake, one of the otters, sea lions, and seals was exactly 5, one was exactly 6, and one was exactly 7. Sergey remembered that the fewest (meaning 5) were either seals or otters, and Igor remembered that 5 were either otters or sea lions. Therefore, 5 were exactly otters. Then 7 were not otters, but seals. Therefore, 6 were sea lions.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. An isosceles triangle $ABC (AB = BC)$ and a square $AKLM$ are positioned as shown in the figure. Point $S$ on $AB$ is such that $AS = SL$. Find the measure of angle $SLB$.
[8 points] (L. Ponov)
|
Answer: $90^{\circ}$.
Solution. Consider triangles $A K S$ and $L K S$. They are equal by three sides.
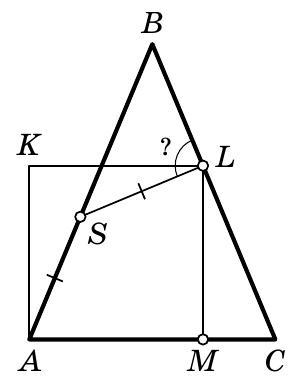
Therefore, angles $K A S$ and $K L S$ are equal.
In the isosceles triangle $A B C$, angles $B A C$ and $A C B$ are equal. Lines $K L$ and $A C$ are parallel, so angles $A C B$ and $K L B$ are equal as corresponding angles. Then $\angle S L B=\angle S L K + \angle K L B=\angle K A S + \angle A C B=\angle K A S + \angle B A C=\angle K A M=90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. A monkey becomes happy when it eats three different fruits. What is the maximum number of monkeys that can be made happy with 20 pears, 30 bananas, 40 peaches, and 50 tangerines? Justify your answer. $[8$ points] (A.V. Shapovalov)
|
Answer: 45.
Solution. Let's set the tangerines aside for now. There are $20+30+40=90$ fruits left. Since we feed the monkeys no more than one tangerine each, each monkey will eat at least two of these 90 fruits. Therefore, there can be no more than $90: 2=45$ monkeys. Let's show how 45 monkeys can be made happy:
5 monkeys eat: a pear, a banana, a tangerine;
15 monkeys eat: a pear, a peach, a tangerine;
25 monkeys eat: a peach, a banana, a tangerine.
In total, 45 happy monkeys - and there are still five unused tangerines left!
|
45
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In an aquarium, there are three types of fish: gold, silver, and red. If the cat eats all the gold fish, the number of fish will be 1 less than $2 / 3$ of the original number. If the cat eats all the red fish, the number of fish will be 4 more than $2 / 3$ of the original number. Which fish - gold or silver - are there more of, and by how many?
[4 points] (I.R. Vysotsky, I.V. Raskina)
|
Answer: There are 2 more silver fish.
Solution: From the first condition, there is 1 more goldfish than a third. From the second condition, there are 4 fewer red fish than a third. Therefore, there are 3 more silver fish than a third.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. There is a set of two cards: 1 and 2. In one operation, it is allowed to form an expression using the numbers on the cards, arithmetic operations, and parentheses. If its value is a non-negative integer, it is issued on a new card. (For example, having cards 3, 5, and 7, you can form the expression 7 [ 5/3 and get a card with the number 25, or form the expression 3 哒 and get a card with the number 35.)
How to get a card with the number 2015 a) in 4 operations; b) in 3 operations $[8$ points] (I.V. Yashchenko)
|
Answer. a) For example
$[1+2=3 ; \quad 3+2=5 ; \quad 3-2-11=0 ; \quad 201[5=2015$
or
$[1+2=3 ; \quad[1]=[13 ; \quad 3[1=31 ; \quad([2+3) \cdot 13 \cdot 31=2015$.
b) $[1+2=3 ; \quad 3 \cdot 2-1=63 ; \quad(63+2) \cdot 31=2015$.
Comments. 1. To solve the problem, it is useful to first factorize 2015 into prime factors: $2015=5 \cdot 13 \cdot 31$.
|
2015
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. A $3 \times 3$ square is filled with digits as shown in the figure on the left. It is allowed to move along the cells of this square, transitioning from one cell to an adjacent one (by side), but it is not allowed to visit any cell more than once.
| 1 | 8 | 4 |
| :--- | :--- | :--- |
| 6 | 3 | 9 |
| 5 | 7 | 2 |
Petya walked as shown in the figure on the right and wrote down all the digits he encountered in order - resulting in the number 84937561. Draw another path so that the resulting number is larger (the larger, the better).
|
Answer. The largest number that can be obtained is -573618492 (see fig.).
Comments. 1. Let's explain how the problem could be solved (this was not required of the participants).
Notice that a number larger than the one given
| 1 | 8 | 4 |
| :---: | :---: | :---: |
| 6 | 3 | 9 |
| 5 | 7 | 2 |
in the problem can be obtained by starting the traversal from the number 9 (for example, it is not difficult to get the number 94836572). However, if all the cells of the board are traversed, a 9-digit number will result, which, of course, will be greater than any 8-digit number.
And a 9-digit number is also the larger the greater its first digit. One can notice that it is impossible to construct a 9-digit number starting with 9. In general, for none of the black cells (see fig. below) does there exist a path starting from it and passing through all the cells of the board (see the next comment).
Therefore, the largest number will be obtained by starting from the largest white cell, i.e., the digit 5. Next, one should move to its largest neighbor, the digit 7, then to its largest neighbor, the digit 3. But if one then goes to the largest neighbor of the digit 3, the digit 9, it will not be possible to traverse all the cells of the square. Similarly, it is not advisable to go to the digit 8. Therefore, from 3, one should move to 6. The path is then unique.
|
573618492
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. Having defeated Koschei, Ivan demanded gold to ransom Vasilisa from the bandits. Koschei led him to a cave and said:
"In the chest lie gold ingots. But you cannot simply take them: they are enchanted. Put one or several into your bag. Then I will put one or several from the bag back into the chest, but it must be a different number. We will take turns moving them: you into the bag, I into the chest, each time a new number. When a new move becomes impossible, you can take your bag with the ingots."
What is the maximum number of ingots Ivan can take, no matter how Koschei acts, if the chest initially contains a) 13; b) 14 gold ingots? How can he do it?
[8 points for both parts, 5 points for one] (A. V. Shapovalov)
|
Answer. a) 13; b) 13.
Solution. Ivan will act in such a way that each time Kashchey's move will be the only one possible: all other numbers have either already appeared in previous moves or are too large - Ivan does not have that many ingots at that moment. We will record the moves of the game as follows: the number of ingots moved (the number of ingots Ivan has after the move).
a) +2 (2), -1 (1), +3 (4), -4 (0), +6 (6), -5 (1), +7 (8), -8 (0), +10 (10), -9 (1), +11 (12), -12 (0), +13 (13).
At the end, all possible moves have been made, Ivan has all 13 ingots, so he can take them.
b) We will act the same way as in the previous part. After the move “+13 (13)”, only the move 14 is not made, but it is impossible, so Ivan can take 13 ingots.
We will prove that Ivan cannot take 14 ingots. Suppose at some point there were 14 ingots in the bag. This means there are no ingots in the chest, so the last move was made by Ivan. Then the total number of moves made is odd, and therefore some number from 1 to 14 has not appeared. Kashchey can make a move with this number, so the ingots cannot be taken yet.
Comment. One can notice that for 17, 21, and generally $4k+1$ ingots, the problem is solved similarly to part a), and for 14, 18, and generally $4k+2$ ingots - similarly to part b). One can think about solving the problem in the remaining cases (when there are $4k$ or $4k+3$ ingots).

The first issue of the new magazine for students in grades 5-8 - "Kvantik" - has been published. The magazine is dedicated to interesting questions and problems in mathematics, linguistics, physics, and other natural sciences. You will learn a lot about the world around you.
On the pages of this issue, you will read about a remarkable scientist, learn about a president who proved theorems, conduct fascinating experiments with a Möbius strip, puzzle over seemingly simple problems, learn how to construct certain regular polygons. You will meet with amazing numbers, amusing picture problems, linguistic quirks, and other often quite unexpected things.
In each issue of the magazine
look for the problems of our contest - anyone can try their hand, and the winners will receive prizes.
"Kvantik" is published
monthly. You can subscribe at any post office of Russia Post, subscription index 84252.
All issues are always
available for purchase at the MCCME store at the address: Moscow, Bol. Vlasyevsky per., 11. Store phone: (499) 241-72-85.
Our email: kvantik@mccme.ru, website: www.kvantik.com, phone: (499) 241-74-83.
## Information on enrollment in grades 5-8 with advanced mathematics in 2012
| School | Phone | Address, URL | Grades | Periods |
| :---: | :---: | :---: | :---: | :---: |
| 2 | $(499) 137-17-69$ $(499) 137-69-31$ | Fotieva St., 18 (m. "Oktyabrskaya") www.sch2.ru | 7,8 | from March 23 to May 25 |
| 54 | $(499) 245-99-72$ $(499) 245-54-25$ | Dovatora St., 5/9 (m. "Sportivnaya") moscowschool54.ru | 8 | from February to May |
| 57 | $(495) 691-85-72$ $(495) 691-54-58$ | Mal. Znamensky per., 7/10, bld. 5 (m. "Borovitskaya") sch57.msk.ru | 8 | from March 21 on Wednesdays at $16^{00}$ |
| 179 | (495) 692-48-51 | Bol. Dmitrovka St., 5/6, bld. 7 (m. "Okhotny Ryad") www.179.ru | 8 | from March 16 on Fridays at $16^{00}$ |
| 192 | $(499) 137-33-55$ $(499) 137-72-85$ | Leninsky Prospekt 34-A (m. "Leninsky Prospekt") www.sch192.ru | 5,7; additional in 8 | from April 6 on Fridays at $16^{00}$ |
| 218 | $(495) 976-63-45$ $(495) 976-19-85$ | Dmitrovskoye Shosse, 5a (m. "Dmitrovskaya") school218.ru | 8 (IUP), 5-7 (diff. edu.) | April-May |
| 1543 | $(495) 433-16-44$ $(495) 434-26-44$ | 26 Baku Commissars St., 3, bld. 5 (m. "Yugo-Zapadnaya") www.1543.ru | 8 | April |
| Intel- lectual | (495) 445-52-10 | Kremenchugskaya St., 13 (m. "Slavyanskiy Bulvar") int-sch.ru | 5; additional in 7 | registration on the site from January, interviews from March |
Information provided by the schools to MCCME. Published free of charge.
Detailed information on enrollment in these and other classes on the website www.mccme.ru
## The Oral City Mathematical Olympiad for grades 6-7 will take place on March 9, 2012.
Students who have received a diploma of prizewinner or a certificate at least in one of the following mathematical competitions (of the current or previous academic year) are invited to the olympiad:
- Mathematical Festival (13.02.11 or 19.02.12),
- IX City Oral Olympiad (13.03.11),
- Winter Archimedes Tournament (23.01.11 or 22.01.12),
- Spring Archimedes Tournament for 5th grade (in the individual event, 3.04.11).
To participate in the olympiad, you need to register in advance by February 27, 2012. Details on the website olympiads.mccme.ru/ustn/
Operational information about olympiads - on the website www.olimpiada.ru
The page of the Mathematical Festival (problems, solutions, lists of winners) www.mccme.ru/matprazdnik/
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. "This is for you to see a bit too early,"- said Baba Yaga to her 33 students and commanded: "Close your eyes!" The right eye was closed by all the boys and a third of the girls. The left eye was closed by all the girls and a third of the boys. How many students still saw what they were not supposed to see yet? [3 points] (A. V. Shapovalov)
|
Answer: 22 students.
Solution: What is seen is still too early, two-thirds of the girls saw with their right eye, and two-thirds of the boys saw with their left eye. In total, then, one eye was not closed by two-thirds of all students - 22 people.
|
22
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. A wooden block was cut into eight smaller blocks with three cuts. On Fig. 5, the surface area of seven blocks is indicated. What is the surface area of the invisible block?
$[8$ points] (A. V. Shapovalov)
|
Answer: 22.
Solution: For each small block, the surface of the cuts constitutes half of its entire surface. We will only consider this. We will color the small blocks in black and white as shown in Fig. 6 (the invisible block is black). Then, every two identical rectangles touching on the cut are of different colors. Therefore, the sum of the areas of the black cuts is equal to the sum of the areas of the white ones.
Fig. 5
Fig. 6
Thus, the sum of the areas of the surfaces of the white blocks is equal to the sum of the areas of the surfaces of the black ones. Therefore, the area of the surface of the invisible black block is
$$
(148+46+72+28)-(88+126+58)=22
$$
|
22
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. The magician taught Kashtanka to bark as many times as he showed her secretly. When Kashtanka correctly answered how much two times two is in this way, he hid a delicious cake in a suitcase with a combination lock and said:
- The eight-digit code for the suitcase is the solution to the puzzle УЧУЙ $=\kappa \mathrm{E} \times$ КС. You need to replace the same letters with the same digits, and different letters with different digits, so that the equation is correct. Bark the necessary number of times for each of the eight letters, and you will get a treat.
But then a mishap occurred. Kashtanka, from excitement, barked one more time for each letter than she should have. Of course, the suitcase did not open. Suddenly, a child's voice exclaimed: "Unfair! The dog solved the puzzle correctly!" And indeed, if each digit of the solution the magician had in mind is increased by 1, another solution to the puzzle is obtained!
Can we restore: a) what exact solution the magician had in mind; b) what the number УЧУЙ was in this solution?
[7 points] (A. K. Kulikov, T. A. Korchemkina, I. V. Raskina)
|
Answer. a) No. b) Yes, УЧУЙ $=2021$.
Solution. a) Note that КЕ and КС represent different numbers, but swapping them does not change the product УЧУЙ. Therefore, for each solution to the puzzle, there is a paired solution where the digits corresponding to $\mathrm{E}$ and $\mathrm{C}$ are swapped. Thus, it is impossible to uniquely determine the solution the magician intended.
b) After increasing all digits by 1, we again get a solution to the puzzle, so,
$$
\begin{aligned}
& \text { УЧУЙ }+1111=(К \mathrm{~K}+11)(К \mathrm{~K}+11)= \\
& \quad=\mathrm{КE} \cdot К \mathrm{C}+11 \cdot \mathrm{KE}+11 \cdot \text { КС }+11 \cdot 11 .
\end{aligned}
$$
Since УЧУЙ $=$ КЕ $\cdot$ КС, we get that
$$
\begin{gathered}
1111=11 \cdot \kappa \mathrm{E}+11 \cdot \kappa \mathrm{C}+11 \cdot 11 \\
101=\kappa \mathrm{E}+\kappa \mathrm{C}+11 \\
\kappa \mathrm{E}+\kappa \mathrm{C}=90
\end{gathered}
$$
which means
$$
\begin{gathered}
10 \cdot \mathrm{K}+\mathrm{E}+10 \cdot \mathrm{K}+\mathrm{C}=90 \\
20 \cdot \mathrm{K}+\mathrm{E}+\mathrm{C}=90
\end{gathered}
$$
Note that $\mathrm{E}+\mathrm{C}$ is a number from 1 to 17, so $20 \cdot \mathrm{K}$ is a number from 73 to 89 that is divisible by 20. Therefore, $20 \cdot К=80$ and $К=4$, and $\mathrm{E}+\mathrm{C}=10$.
The digits $\mathrm{E}$ and $\mathrm{C}$ are different, neither is 4, and neither is 9 (otherwise, adding 1 to each digit would cause a carry-over, which would change exactly one of the digits in the positions of У or К, and the result would not be a solution to the puzzle). Therefore, for the equation $\mathrm{E}+\mathrm{C}=10$, only two options remain: $2+8$ and $3+7$.
Then, $К Е \cdot К С=42 \cdot 48=2016$ or $К \mathrm{E} \cdot К \mathrm{C}=43 \cdot 47=2021$. But in the word УЧУЙ, the first and third letters are the same, so only the variant УЧУЙ $=2021$ fits.
|
2021
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Given an equilateral triangle $ABC$. On side $AB$, point $K$ is marked, and on side $BC$ - points $L$ and $M$ ( $L$ lies on segment $BM$ ) such that $KL=KM, BL=2, AK=3$. Find $CM$.
[7 points]
(E. V. Bakayev)
|
Answer: 5.
Solution. Mark a point $T$ on the extension of segment $L M$ beyond point $M$ such that $M T=2$. Angles $B L K$ and $T M K$ are equal because they are adjacent to the equal angles of the isosceles triangle $K L M$. Therefore, triangles $B L K$ and $T M K$ are congruent by two sides and the included angle. Then their corresponding angles are equal: $\angle K T M=\angle K B L=60^{\circ}$.
In triangle $K B T$, two angles are $60^{\circ}$, so it is equilateral, and $B K=B T$. Since triangle $A B C$ is also equilateral and $B A=B C$, then $C T=B C-B T=B A-B K=A K=3$ (and point $T$ lies on side $B C$, not on its extension). Then $C M=C T+M T=3+2=5$.
Second solution. Draw the height $K H$ of the isosceles triangle $K L M$. It is also its median, so $L H=H M$. Let $L H=H M=x$. Triangle $K B H$ is a right triangle with angle $B$ equal to $60^{\circ}$, so its hypotenuse $K B$ is twice its leg $B H$. Since $B H=2+x$, then $K B=2 B H=4+2 x$, and thus $B A=B K+K A=4+2 x+3=7+2 x$. Triangle $A B C$ is equilateral, so $B C=B A=7+2 x$. Therefore, $M C=B C-B M=(7+2 x)-(2+2 x)=5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Inside a rectangular grid with a perimeter of 50 cells, a rectangular hole with a perimeter of 32 cells is cut out along the cell boundaries (the hole does not contain any boundary cells). If the figure is cut along all horizontal grid lines, 20 strips 1 cell wide will be obtained. How many strips will be obtained if, instead, it is cut along all vertical grid lines? (A $1 \times 1$ square is also a strip!)
[6 points]
(A. V. Shapovalov)
|
Answer: 21.
First solution. Let the rectangle occupy $a$ cells vertically and $b$ horizontally, $a+b=50: 2=25$. Similarly, let the dimensions of the hole be $x$ cells vertically and $y$ horizontally, $x+y=32: 2=16$.
If there were no hole, there would be $a$ horizontal strips. The hole cuts $x$ of them into two parts, so the total number of horizontal strips is $a+x$, which is 20 according to the problem. Similarly, the number of vertical strips will be $b+y$. But $a+b+x+y=25+16=41$ and $a+x=20$. Therefore, $b+y=41-20=21$.
Second solution. For each horizontal strip, mark its left and right sides, and for each vertical strip, mark its top and bottom. Clearly, we have marked all the boundaries of the cells on the contour of the rectangle and the contour of the hole, i.e., $50+32=82$ boundaries. Each strip gave us two boundaries, so the total number of strips is $82: 2=41$. There are 20 horizontal strips, so there are 21 vertical strips.
Comment. The second solution is more general - it works even in the case where the figure and the hole have a complex polygonal shape (see figure).
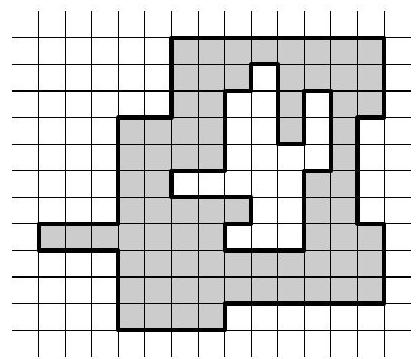
|
21
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. In the showcase of a jewelry store, there are 15 diamonds. Next to them are signs indicating their weights, which are $1, 2, \ldots, 15$ carats. The seller has a balance scale and four weights with masses of $1, 2, 4,$ and 8 carats. The customer is allowed only one type of weighing: place one of the diamonds on one pan of the scale, and the weights on the other pan to verify that the weight indicated on the corresponding sign is correct. However, for each weight taken, the customer must pay the seller 100 coins. If a weight is removed from the scale and does not participate in the next weighing, the seller keeps it. What is the smallest amount that will have to be paid to check the weights of all the diamonds?
$[8$ points]
(A. V. Gribalko)
|
Answer: 800 coins.
Solution. Example.
| Which weights we buy | What we weigh | How many coins we paid |
| :---: | :--- | :---: |
| 1 | $\mathbf{1 = 1}$ | 100 |
| 2 | $1+2=\mathbf{3}, 2=\mathbf{2}$ | 200 |
| 4 | $2+4=\mathbf{6}$ | 300 |
| 1 | $1+2+\mathbf{4}=\mathbf{7}, 1+\mathbf{4}=\mathbf{5}, \mathbf{4}=\mathbf{4}$ | 400 |
| 8 | $\mathbf{4}+8=\mathbf{12}$ | 500 |
| 1 | $1+\mathbf{4}+8=\mathbf{13}$ | 600 |
| 2 | $1+2+\mathbf{4}+8=\mathbf{15}, 2+\mathbf{4}+8=\mathbf{14}, 2+8=\mathbf{10}$ | 700 |
| 1 | $1+2+8=\mathbf{11}, \mathbf{1}+8=\mathbf{9}, 8=\mathbf{8}$ | 800 |
Estimate. At each weighing, we either buy one or several weights or return them to the seller. Therefore, we have bought and returned a total of $N \geqslant 15$ weights. After the last weighing, we still have at least one weight in our possession, so we bought more than we returned. This means we bought more than half of $N$, i.e., at least 8 weights, and thus paid the greedy seller no less than 800 coins.
Estimate (alternative method). Imagine that the payment for each weight is divided into two parts: 50 coins are paid by the buyer when they take the weight, and another 50 when they return it. If we assume that all weights are returned to the seller at the end, the total payment remains the same under this method of calculation.
Consider 16 moments: the beginning, when the buyer takes the first weights, 14 intervals between weighings, and the end, when the buyer returns the remaining weights. At each of these moments, the buyer performs some action (taking or returning something), so they must pay at least 50 coins, and in total, they will have to pay no less than $50 \cdot 16 = 800$ coins.
Comment. From the solution, it is clear that the optimal order of weighing involves going through all possible sets of weights, with adjacent sets differing by the addition or removal of exactly one weight. Such a sequence of sets is called a Gray code.
Why were Gray codes invented? Imagine that we want to know the position of a rotating disk. If we only need a rough idea, we can paint one half of the disk black and the other half white and place a photodetector. Now we always know which half of the disk is facing the detector.
But suppose we want more precision. We can place several photodetectors and paint several rings on the disk, with each sector labeled with its number in black and white stripes as a binary code (see the left image).
But then, at the boundary between sectors, the detectors might not trigger simultaneously, and between 001 and 010, we might "see" 011 or 000. For such a situation, Gray codes were invented: if only one ring changes color at the boundary of two sectors, we can only get the code of one of these sectors.
Any optimal solution to the problem turns out to be a Gray code for 4 rings and 16 sectors (the Gray code from the solution is used in the right image).
|
800
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Sasha wrote down the numbers from one to one hundred, and Misha erased some of them. Among the remaining numbers, 20 numbers have a one in their notation, 19 numbers have a two in their notation, and 30 numbers have neither a one nor a two. How many numbers did Misha erase?
$[4$ points] (A. V. Shapovalov)
|
Answer: 33.
Solution: Among the numbers from 1 to 100, the digit 1 appears exactly twenty times: the number 1 itself, ten numbers from 10 to 19, the numbers $21, 31, \ldots, 91$ (eight of them), and the number 100. Therefore, none of these numbers were erased. Similarly, the digit 2 appears exactly nineteen times: the number 2 itself, ten numbers in the third decade, and $12, 32, 42, \ldots, 92$ (eight such numbers). Thus, none of these were erased by Misha either. In total, there are $19+20-2=37$ such numbers (we subtract 2 because the numbers 12 and 21 were counted twice). In total, $37+30=67$ numbers remained, and Misha erased $100-67=33$ numbers.
|
33
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Senya cannot write some letters and always makes mistakes in them. In the word TETRAHEDRON he would make five mistakes, in the word DODECAHEDRON - six, and in the word ICOSAHEDRON - seven. How many mistakes would he make in the word OCTAHEDRON?
|
# Answer. 5.
Solution. If Senya mistakenly writes D, then out of the letters O, E, K, A, E, R, which are also in DODEKAEDR, he makes three mistakes and writes three correctly. But all these letters, except E, are also in IKOSAEDR, which means he will write at least two letters correctly and cannot make 7 mistakes. Therefore, Senya writes the letter D correctly. Then he inevitably makes mistakes in writing all the other letters in the words DODEKAEDR and IKOSAEDR, and in the word TETRAEDR, he writes the letter D correctly and also writes the letter T correctly, but makes mistakes in all the others. Now it is clear that in the word OKTAEDR, Senya will make five mistakes.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Seven cities are connected in a circle by seven one-way flights (see figure). Assign (draw with arrows) several more one-way flights so that from any city to any other, one could get there with no more than two transfers. Try to make the number of additional flights as small as possible.
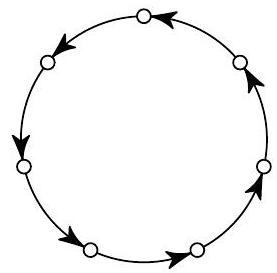
(up to 6 points) (V.A. Klepinin)
|
Solution. An example with five additional flights is shown in the figure. It can be proven that it is impossible to add a smaller number of flights.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. Each face of a cube $6 \times 6 \times 6$ is divided into $1 \times 1$ cells. The cube is covered with $2 \times 2$ squares such that each square covers exactly four cells, no squares overlap, and each cell is covered by the same number of squares. What is the maximum value that this identical number can take? (Squares can be bent over the edges.) [8 points] (A.V. Shyakov)
|
Answer: 3.
Solution: Estimation. A cell in the corner of a face can be covered in three ways (entirely within the face, with a fold over one edge of the corner, with a fold over the other edge of the corner). Therefore, each cell is covered by no more than three squares.
Example. Consider the usual covering of a cube with squares, where each face is covered by nine squares. From the usual covering, we can obtain a rotated one: leave two opposite faces untouched, and on the other four faces, shift all squares in a ring by one cell. Since a pair of opposite faces can be chosen in three ways, there will be exactly three rotated coverings. We will show that no two squares on coverings rotated differently coincide.
Indeed, consider one face. On the diagram, the centers of the squares covering it are marked: with crosses if this face was not shifted, with black and white dots if it was shifted in one or the other direction. It is clear that no centers, and therefore no squares, coincide.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. A group of tourists is dividing cookies. If they evenly distribute two identical packs, one extra cookie will remain. But if they evenly distribute three such packs, 13 extra cookies will remain. How many tourists are in the group? [7 points] (I.V. Raskina)
|
Answer: 23.
First solution. Distribute three times two packs, 3 * 1 = 3 cookies will remain. But the same six packs of cookies can be distributed differently - three and another three, and then 2 * 13 = 26 cookies will remain. Therefore, 26 - 3 = 23 cookies can be divided equally among the tourists. Since the number 23 is prime, this is only possible if there are 23 tourists.
Second solution. First, divide two packs of cookies. One extra cookie remains. Divide the third pack. It contains 13 - 1 = 12 extra cookies. But then there should have been 12 * 2 = 24 extra cookies in the two packs. Why is there actually only one? Because 24 - 1 = 23 cookies the tourists were able to divide equally. Since the number 23 is prime, this is only possible if there are 23 tourists.
Comment. The number of cookies in a pack cannot be determined from the problem statement. There could have been 12, 35, 58, etc.
|
23
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Given a square $ABCD$. On the extension of the diagonal $AC$ beyond point $C$, a point $K$ is marked such that $BK=AC$. Find the angle $BKC$. $[6$ points] (
|
Answer: $30^{\circ}$.
Solution: Since the picture is symmetric with respect to the line $A C$, we have $D K=B K$. By the condition, $B K=A C$.
And since the diagonals in a square are equal, $A C=B D$. Thus, in triangle $B K D$ all sides are equal, i.e., it is equilateral, and $\angle B K D=60^{\circ}$. Again, due to symmetry with respect to the line $A C$, we have $\angle B K C=\angle D K C$, and together these angles sum to $60^{\circ}$, i.e., each of them is $30^{\circ}$.
Comment: The equalities $D K=B K$ and $\angle B K C=\angle D K C$ can also be proven without using the concept of symmetry.
Indeed, in triangles $B C K$ and $D C K$, side $C K$ is common, $B C=C D$ as sides of the square, $\angle B C K=\angle C K D$, since each is adjacent to a $45^{\circ}$ angle. Therefore, triangles $B C K$ and $D C K$ are congruent by two sides and the included angle. Consequently, $D K=B K$ and $\angle B K C=\angle D K C$ as corresponding elements of congruent triangles.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Find a six-digit number where the first digit is 6 times less than the sum of all digits to the right of it and the second digit is 6 times less than the sum of all digits to the right of it.
$[4$ points] (A. V. Shapovalov)
|
Answer: 769999.
First solution. The sum of the last five digits of the number, by condition, is divisible by 6 (the quotient is equal to the first digit). The sum of the last four digits of the number is also divisible by 6 (the quotient is equal to the second digit). Therefore, the second digit, as the difference of two numbers divisible by 6, is also divisible by 6. This means the second digit is 0 or 6. If it is 0, then the sum of the last four digits is also 0, and thus the first digit is 0, but a six-digit number cannot start with 0. Therefore, this option does not work, and the second digit is 6. Then the sum of the last four digits is $6 \cdot 6 = 36$, so all of them are 9. Finally, the sum of the last five digits is 42, and thus the first digit is $42 : 6 = 7$. Therefore, the required number is 769999.
Second solution. The sum of the last 4 digits is 6 times the second digit, so the sum of the last 5 digits is 7 times the second digit and 6 times the first digit. Therefore, 7 times the second digit equals 6 times the first digit, which means the first digit is 7, and the second digit is 6; then the sum of the last four is 36, and this is only possible if all 4 last digits are nines.
Comment. The problem can be solved by trying all possible values (from 0 to 9) of the second digit of the number. For example, if this digit is 9, then the sum of the digits to the right of it is 6 times greater, i.e., $9 \cdot 6 = 54$, but then the sum of all digits to the right of the first is $9 + 54 = 63$. Since the number 63 is not divisible by 6, the option that the second digit is 9 does not work, and so on.
|
769999
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Petya observes two ants crawling along a straight path at constant speeds. After 3 minutes of observation, the distance between the ants was 9 meters, after 5 minutes - 5 meters, after 9 minutes - 3 meters. What was the distance between the ants after 8 minutes of observation?
$[5$ points]
| 1a | 1b | 2a | 2b | 2c | 2d | 3a | 3b | 3c | 4 | $\Sigma$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | | | | | | | | | | |
| | | | | | | | | | | |
|
4. The faster ant is ahead of the slower one and is moving away from it.
It is clear that situation 1 can over time turn into situation 2, and situation 3 can turn into situation 4. But if the ants at some point find themselves in situation 2 or 4, then from that moment on, they will always be moving away from each other.
We know the distance between the ants at three moments in time. Note that between the first and second moment, 2 minutes have passed, and the distance between the ants has decreased by 4 meters. Between the second and third moment, 4 minutes have passed, and the distance has decreased by 2 meters. Since the distance decreased both times, we can be sure that 3 minutes and 5 minutes after the start of the observation, the ants were not in a "moving away" state, meaning they could only be in states 1 or 3.
If the meeting between them had not occurred in the next 4 minutes (from the 5th to the 9th minute), they would have remained in the same state (1 or 3) and continued to approach each other at a rate of 4 meters in 2 minutes, meaning they should have closed the distance by 8 meters in 4 minutes. However, the distance between them decreased by only 2 meters, so at some point between the 2nd and 3rd moments, a meeting must have occurred.
After the meeting, the ants move away from each other at the same speed they approached (in situations 1 and 2, the speeds of approaching and moving away are equal to the sum of the ants' speeds, while in situations 3 and 4, they are equal to the difference in their speeds). Therefore, in 4 minutes, the distance between the ants decreased from 5 meters to zero and then increased from zero to 3 meters. In total, 8 meters in 4 minutes, which matches the previously found rate of approaching. One minute earlier, the distance was 2 meters less. Therefore, 8 minutes after the start of the movement, the distance between the ants was 1 meter.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 2.
Here is a fairly simple rebus: EKH is four times greater than OI. AI is four times greater than OH. Find the sum of all four.
[4 points
|
Answer: 150.
Solution: The digits Й and Х are even because ЭХ and АЙ are divisible by 4. The numbers ОЙ and ОХ are less than 25, otherwise, when multiplied by 4, they would no longer be two-digit numbers. Therefore, $\mathrm{O}=2$ or $\mathrm{O}=1$. Let's consider the first case. The number 20 as $\mathrm{OX}$ or ОЙ is not suitable because 80 ends with the same digit. 22 is also not suitable due to identical digits. The only option left is 24, but the numbers ОЙ and ОХ must be different.
Thus, $\mathrm{O}=1$. The number 10 is not suitable for the same reason as 20. Taking $O X=16$, we get $А И ̆=64$, but then $A=X$, which is not allowed. For the same reason, ОЙ $=16$ is also impossible. Taking $\mathrm{OX}=14$, we find АЙ $=56$, then ОЙ $=16$, which, as we have seen, is impossible. Therefore, ОХ and ОЙ can only be 12 and 18 (in any order), and ЭХ and АЙ are then 48 and 72, respectively. We find the sum: $12+48+18+72=150$.
Comment: The answer can be obtained without finding the actual numbers. As we know, $\mathrm{O}=1$, and the digits Й and $\mathrm{X}$ are even. On the other hand, if you add a number that is four times larger to any even number, you get a number divisible by 10. Therefore, Й $+\mathrm{X}=10$. Then ОЙ $+\mathrm{OX}=10+$ $+10+10=30$, and the sum of all four numbers is five times greater, i.e., 150.
|
150
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. A dog and a cat simultaneously grabbed a sausage loaf with their teeth from different sides. If the dog bites off its piece and runs away, the cat will get 300 g more than the dog. If the cat bites off its piece and runs away, the dog will get 500 g more than the cat. How much sausage will be left if both bite off their pieces and run away?
$[2$ points] (A. V. Shapovalov)
|
Answer: 400 g.
Solution: If two identical dogs grab the sausage from both sides, there will be a piece of 300 g between them. If two identical cats grab the sausage from both sides, there will be a piece of 500 g between them (see the figure).

It is clear that a dog bites off ( $500-300$ ) $: 2=100$ g more than a cat. Therefore, when the dog and the cat bite off their pieces and run away, 300 + 100 = 400 g of sausage will remain.
Alternatively, we can reason as follows. The dog intends to bite off 300 g less from the sausage than leave. If he bit off 150 g more, leaving 150 g less, he would get exactly half of the entire sausage. Similarly, the cat would get half of the entire sausage if he bit off 250 g more than he intended. In this case, the entire sausage would be eaten, so the remaining weight is 150 + 250 = 400 g.
Comment: The problem can also be solved algebraically (see solutions for seventh-grade problems).
|
400
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. 13 children sat at a round table and agreed that boys would lie to girls, but tell the truth to each other, and girls, on the contrary, would lie to boys, but tell the truth to each other. One of the children said to their right neighbor: "The majority of us are boys." The latter said to their right neighbor: "The majority of us are girls," and he to his right neighbor: "The majority of us are boys," and so on, until the last child said to the first: "The majority of us are boys." How many boys were at the table?
[6 points] (A. V. Khachatryan)
|
# Answer: 7.
Solution. It is clear that there were both boys and girls at the table. Let's see how the children were seated. After a group of boys sitting next to each other comes a group of girls, then boys again, then girls, and so on (a group can consist of just one person). Groups of boys and girls alternate, so their number is even. The incorrect statements were made at the transitions from one group to another, so their number is also even. Since seven statements of "most of us are boys" were made, six of the statements "most of us are girls" must be incorrect, and there were also six groups.
The alternation of correct and incorrect statements means that there were two children in each group. Only the first and last child sitting next to each other said the same thing, so there were three people in their group. These are boys, as they are in the majority. In total, there were $2+2+2=6$ girls and $2+2+3=7$ boys sitting at the table.
The diagram shows exactly how the children were seated at the table. The first speaker is outlined in a frame.
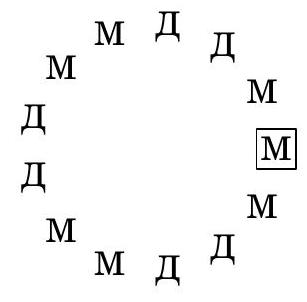
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Small Island and Big Island have a rectangular shape and are divided into rectangular counties. In each county, a road is laid along one of the diagonals. On each island, these roads form a closed path that does not pass through any point more than once. Here is how Small Island is organized, with a total of 6 counties (see Fig. 1). Draw how Big Island might be organized if it has an odd number of counties. How many counties did you get?
[7 points] (A. V. Shapovalov)
Fig. 1
Fig. 2
|
Answer. Figure 2 provides an example for 9 counties.
Comment. We will show that examples do not exist for 7 counties (or fewer), while at the same time pointing out a property characteristic of all such examples.
All roads can be divided into two types: some roads connect the top-left corner of a county with the bottom-right, while others connect the bottom-left with the top-right. If the roads of different types always alternated when traversing a closed path, their total number would be even (just like the groups of boys and girls in the previous problem). On the Large Island, where the number of counties is odd, there must, therefore, be two roads of the same type in a row.
For example, suppose two roads $A B$ and $B C$ of the same type are in a row (see the figure). In addition to the counties in which they are constructed, two more counties, shaded in gray, adjoin vertex $B$. By the condition, the roads in these counties do not pass through point $B$. Let's draw them.
Now there are four roads on the figure. To have a total of seven, three segments are needed to connect them into a single chain. To do this, it would be necessary to connect some two ends of the roads in the "gray counties" with a segment, which is impossible.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. Thirty-three bogatyrs (Russian knights) were hired to guard Lake Luka for 240 coins. The cunning Chernomor can divide the bogatyrs into squads of any size (or record all in one squad), and then distribute the entire salary among the squads. Each squad divides its coins equally, and the remainder goes to Chernomor. What is the maximum number of coins Chernomor can get if:
a) Chernomor distributes the salary among the squads as he pleases
b) Chernomor distributes the salary among the squads equally? [8 points] (I.V.Raskina, A.V.Khachaturyan)
|
Answer. a) 31 coins; b) 30 coins.
Solution. From each detachment of $N$ bogatyrs, Chernomor will receive at most $N-1$ coins in the best case, since the remainder is less than the divisor. Therefore, he will receive no more than $33-K$ coins in total, where $K$ is the number of detachments. Can Chernomor get 32 coins if there is only one detachment? No, because $240: 33=7$ (remainder 9), so Chernomor will receive only 9 coins. He can try to get 31 coins by dividing the bogatyrs into two detachments.
If (part a) the money does not necessarily have to be divided equally, this is quite possible. For example, let the first detachment have 32 bogatyrs, and the second only one. Then the first detachment can be given 63 coins (from which Chernomor will receive 31), and the remaining 177 coins can be given to the single bogatyr in the second detachment. There are many other ways to divide the money.
However, if (part b) the money must be divided equally, this cannot be done. To show this, one could enumerate all the ways to divide the bogatyrs into two detachments, but there is a simpler way. If, by giving a detachment of $N$ people 120 coins, Chernomor expects to receive $N-1$ coins, then the number 121 must be divisible by $N$. However, 121 is only divisible by 1, 11, and 121, and it is impossible to add up to 33 from two such numbers.
However, it is possible to get 30 coins in part b) by dividing the bogatyrs into three detachments and giving each detachment $240: 3 = 80$ coins. The number of people in each detachment must be a divisor of the number $80+1=81$. From three divisors of 81, it is possible to add up to 33: $33=27+3+3$. Let's check: from detachments of three people, Chernomor will receive 2 coins each, and from the detachment of 27 people, he will receive 26 coins, totaling $26+2+2=30$.
## 7th grade
|
31
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In the square, some cells are shaded as shown in the figure. It is allowed to fold the square along any grid line and then unfold it back. Cells that coincide with shaded cells when folded are also shaded. Can the entire square be shaded:
a) in 5 or fewer;
b) in 4 or fewer;

c) in 3 or fewer such foldings?
(If yes, write the number of the fold after which each cell will be shaded for the first time, draw the fold line and mark it with the same number. If no, prove it.) [4 points] (T. I. Goleneva-Kutuzova, M. A. Raskin, I. V. Yashchenko)
|
Answer. It is possible (even with 3 bends).
Solution. For example, it is possible to paint the entire lower half of the board with two vertical bends, after which the upper half can be painted with one horizontal bend - see the figure. (There are other solutions as well.)
Comment. It is impossible to paint all cells in 2 bends. Indeed, with each bend, the number of cells increases by no more than 2 times. Initially, there are 6 painted cells; therefore, after two bends, no more than $6 \cdot 2 \cdot 2=24$ cells out of 36 will be painted.
| 3 | 3 | 3 | 3 | 3 | 3 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 3 | 3 | 3 | 3 | 3 | 3 |
| 3 | 3 | 3 | 3 | 3 | 3 |
| | 1 | | 1 | 2 | 2 |
| 2 | | 1 | 2 | 2 | |
| 1 | 2 | 2 | | | 2 |
| | | 1 | 2 | | |
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. A bag of sunflower seeds was passed around a table. The first person took 1 seed, the second took 2, the third took 3, and so on: each subsequent person took one more seed than the previous one. It is known that in the second round, the total number of seeds taken was 100 more than in the first round. How many people were sitting at the table?
$[4$ points
(A. V. Shapovalov)
|
Answer: 10 people.
Solution: Let there be $n$ people sitting at the table. Then on the second round, the first person took the $n+1$-th sunflower seed, the second person took the $n+2$-th - and generally, each person took $n$ more seeds than on the first round. Altogether, on the second round, they took $n \cdot n=n^{2}$ more seeds than on the first. Since $n^{2}=100$, then $n=10$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Three square paths with a common center are 1 m apart from each other (see figure). Three ants start simultaneously from the lower left corners of the paths and run at the same speed: Mu and Ra counterclockwise, and Wei clockwise. When Mu reaches the lower right corner of the largest path, the other two, who have not yet completed a full circle, are on the right sides of their paths, and all three are on the same straight line. Find the sides of the squares.
[6 points] (A. V. Shapovalov)
|
Answer: 4 m, 6 m, 8 m.
Solution: The lengths of the sides of two adjacent paths differ by 2 m (Fig. 3). Therefore, at the moment when Mu reached the corner, Ra had run 2 m along the right side of the path and was at a distance of $2+1=3$ m from the "lower" side of the outer path. Since $\mathrm{Pa}$ is halfway between Mu and Vee, Vee is at twice the distance from this side, 6 m (since the two highlighted right triangles in Fig. 4 are equal in hypotenuse and angles). That is, Vee still has to run $6-1-1=4$ m along the side.
Fig. 3
Fig. 4
But if Vee had run counterclockwise, he would have run the entire lower side and another 4 m along the right side (since this side is 4 m shorter than the side of the outer square), i.e., he would have ended up at the same point. Since Vee ends up at the same point whether he runs clockwise or counterclockwise, this point is the upper right corner of the square. Therefore, the side of this square is 4 m. Accordingly, the sides of the other two squares are $4+2=6$ m and $6+2=8$ m.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. Fox Alice and Cat Basil have grown 20 fake banknotes on a tree and are now filling in seven-digit numbers on them. Each banknote has 7 empty cells for digits. Basil calls out one digit at a time, either "1" or "2" (he doesn't know any others), and Alice writes the called digit in any free cell of any banknote and shows the result to Basil.
When all cells are filled, Basil takes as many banknotes with different numbers as possible (if there are several with the same number, he takes only one), and the rest go to Alice. What is the maximum number of banknotes Basil can get, no matter how Alice acts? [8 points] (A. V. Shapovalov)
|
Answer: 2.
Solution: Basil can always get two banknotes: he knows the place where the last digit should be written and names it so that it differs from the digit in the same place on some other banknote. Then the numbers on these two banknotes will be different, and the cat can take them.
We will show how Alice can ensure that there are no more than two different numbers. She arranges the banknotes one above the other so that the cells for the digits form a table.
When the cat names a one, Alice writes it in the leftmost column where there is a free cell (in any of the cells), and when the cat names a two - in the rightmost column.
If both ones and twos start to appear in some column, then all other columns are already filled: ones on the left, twos on the right. This means there will be at most one column where both ones and twos appear. Therefore, if the numbers do differ, they will differ only by the digit in this column. Since there are only two digits, there will be no more than two different numbers.
$\begin{array}{lllllllllllll}1 & 1 & 1 & 1 & 2 & 2 & 2\end{array}$


$\begin{array}{lllllll}1 & 1 & 1 & 2 & 2 & 2 & 2\end{array}$
$\begin{array}{lllllll}1 & 1 & 1 & 2 & 2 & 2 & 2\end{array}$
The 11th Oral City Mathematical Olympiad for 6-7 grades will take place on March 17, 2013.
Students who have received a diploma or certificate as a prize winner or honorable mention in at least one of the following mathematical competitions are invited to participate:
- Mathematical Festival (19.02.12 or 17.02.13),
- 10th City Oral Olympiad (09.03.12),
- Winter Archimedes Tournament (22.01.12 or 20.01.13),
- Spring Archimedes Tournament for 5th grade (individual competition, 01.04.12).
To participate in the Olympiad, you need to register in advance by March 5, 2013. Details on the website olympiads.mccme.ru/ustn/
## Information on Enrollment in 5-8 Grades with Advanced Mathematics in 2013
| School | Phone, URL | Address | Grades | Periods |
| :---: | :---: | :---: | :---: | :---: |
| 2 | (499) $137-17-69$ (499) $137-69-31$ www.sch2.ru | Fotieva St., 18 (m. "Oktyabrskaya") | 7,8 | March-May |
| 25 | sch25.ru nabor@mathbaby.ru | University Ave., 7 (m. "University") | $7 ;$ additional in 8 | from February |
| 54 | (499) 245-99-72 (499) 245-54-25 moscowschool54.ru | Dovator St., 5/9 (m. "Sportivnaya") | 8 | February-May |
| 57 | (495) $691-85-72$ (495) $691-54-58$ sch57.msk.ru | Mal. Znamensky Lane, 7/10, bld. 5 (m. "Borovitskaya") | 8 | from March 13 Wednesdays |
| 179 | (495) $692-48-51$ www.179.ru | Bol. Dmitrovka St., 5/6, bld. 7 (m. "Okhotny Ryad") | 7,8 | from March 22 |
| 192 | (499) $137-33-55$ (499) $137-72-85$ www.sch192.ru | Leninsky Prospekt 34-A (m. "Leninsky Prospekt") | 5,$7 ;$ additional in 8 | April-May Fridays at $16^{00}$ |
| 218 | (499) 976-19-85 school218.ru | Dmitrovskoye Shosse, 5a (m. "Dmitrovskaya") | 8 (IUP) | from March 25 to May 18 |
| 444 | (495) 465-23-52 $(495) 465-60-52$ schv444.mskobar.ru | Nizh. Pervomayskaya St., 14 (m. "Pervomayskaya") | 8 | March-May |
| 1329 | co1329.mskzapad.ru nabor@mathbaby.ru | Nikulin St., 10 (m. "Yugo-Zapadnaya") | 5,8 | from February |
| 1543 | (495) $433-16-44$ $(495) 434-26-44$ www. $1543 . r u$ | 26 Baku Commissars St., 3, bld. 5 (m. "Yugo-Zapadnaya") | 8 | April |
| 2007 | (495) 716-29-35 fmsh2007.ru | Gorchakova St., 9, bld. 1 (m. "Gorchakova St.") | $5-7 ;$ additional in 8 | April |
| Intel- lectual | (499) 445-52-10 sch-int.ru | Kremenchugskaya St., 13 (m. "Slavyanskiy Bulvar") | $5 ;$ additional in 6,7 | March-June |
The information is provided by the schools to the MCCME. It is published free of charge.
Detailed information on enrollment in these and other classes is available on the website www.mccme.ru
Current information on olympiads is available on the website www.olimpiada.ru
The page of the Mathematical Festival (problems, solutions, lists of winners) www.mccme.ru/matprazdnik /
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. In a singing competition, a Rooster, a Crow, and a Cuckoo participated. Each member of the jury voted for one of the three performers. The Woodpecker calculated that there were 59 judges in total, and that the Rooster and the Crow received a total of 15 votes, the Crow and the Cuckoo received 18 votes, and the Cuckoo and the Rooster received 20 votes. The Woodpecker is a poor counter, but each of the four numbers he mentioned differs from the correct one by no more than 13. How many judges voted for the Crow? [6 points] (I.V. Raskina)
|
Answer: 13 judges.
Solution. The number of votes for the Rooster and the Raven cannot be more than $15+13=28$. Similarly, the number of votes for the Raven and the Cuckoo cannot exceed $18+13=31$, and the number of votes for the Cuckoo and the Rooster cannot exceed $20+13=33$. Adding these three quantities of votes, we get twice the total number of votes (each vote is counted in two of the three sums). Thus, the total number of jury members is no more than $(28+31+33) / 2=46$. On the other hand, from the first announcement of the Woodpecker, it is no less than $59-13=46$. Therefore, there are exactly 46 jury members, and all the inequalities are actually equalities.
Finally, the number of votes for the Raven can be found as the difference between the total number of jury members and the sum of those who voted for the Cuckoo and the Rooster: $46-33=13$ votes.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. An equilateral triangle with a side length of 8 was divided into smaller equilateral triangles with a side length of 1 (see figure). What is the minimum number of small triangles that need to be shaded so that all intersection points of the lines (including those on the edges) are vertices of at least one shaded triangle? Provide an example and prove that it is impossible to shade fewer triangles.
[6 points] (
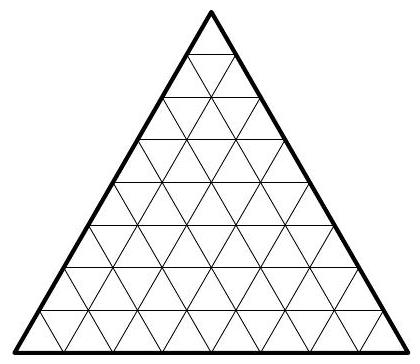
|
Answer: 15 small triangles. See the example in the figure.
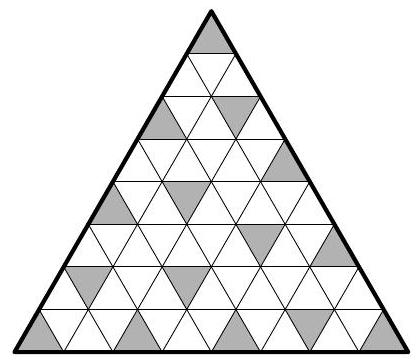
Solution: The total number of intersection points of the lines is $1+2+3+\ldots+9=45$. Since a triangle has three vertices, at least $45: 3=15$ triangles will need to be shaded.
Comment: It can be shown that there is only one (up to axial symmetry) way to shade 15 triangles.
In the coloring we found, no vertex is shaded twice. The side length of 8 of the large triangle is the minimum for which such an "economical" coloring is possible. It is definitely impossible if the side length is a multiple of three. A more complex version of this problem (for a triangle with side length 2015) was published in the "Problems" section of the journal "Mathematics in School" (Issue 1, 2016).
|
15
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. On the surface of a planet shaped like a donut, two snails crawled, leaving trails behind: one along the outer equator, and the other along a spiral line (see figure). Into how many parts did the snails' trails divide the surface of the planet? (It is sufficient to write the answer.)
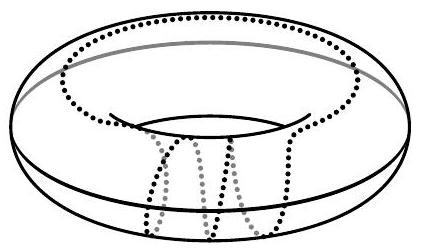
## [4 points] (S.K. Smirnov, I.V. Yashchenko)
|
Answer: 3.
Comment. Let's imagine the surface of a donut made of paper. Cut it along the path of the first snail and unfold it. We will get the lateral surface of a cylinder. The path of the second snail will be cut in three places. That is, on the resulting surface, the trail of the second snail represents three lines connecting the bottom base of the cylinder with the top. It is not difficult to realize that they divide the lateral surface of the cylinder into 3 parts.
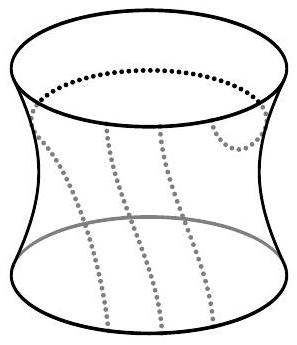
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In Fedia the gardener's garden, there is a wonder-tree with seven branches. On each branch, either 6 apples, 5 pears, or 3 oranges can grow. Fedia noticed that there are fruits of all types on the tree, and the most pears have grown, while the fewest apples have grown.
How many fruits have grown on the wonder-tree?
$[3$ points $]$
Space for answers

|
# Problem 1.
Answer: 30.
Since the tree ended up with fruits of all kinds, there must be at least one branch with apples, meaning there are no fewer than 6 apples. Since apples are the fewest, oranges must have grown on at least three branches, meaning there are at least 9.
There are three branches left. Suppose that on one of them, pears did not grow. Then pears grew on no more than two branches, which means there are no more than 10 pears. In this case, on another branch, either apples grew, which would make 12 apples, or oranges, which would also make 12 oranges. In both cases, pears would not be the most, so our assumption is impossible. Therefore, on one branch, 6 apples grew, on three other branches, 3 oranges each, and on the remaining three branches, 5 pears each. In total, $6+9+15=30$ fruits.
|
30
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the side $AB$ of an equilateral triangle $ABC$, a point $K$ is chosen, and on the side $BC$, points $L$ and $M$ are chosen such that $KL = KM$, with point $L$ being closer to $B$ than $M$.
a) Find the angle $MKA$ if it is known that $\angle BKL = 10^{\circ}$.
b) Find $MC$ if $BL = 2$ and $KA = 3$.
Justify your answers for each part.

| 5 | 6a | 6b | $\Sigma$ |
| :--- | :--- | :--- | :--- |
| | | | |
|
# Problem 6.
Answer: a) $130^{\circ} ;$ b) 5 .
First solution. Mark a point $N$ on the segment $MC$ such that $NM = BL$. Since triangle $LKM$ is isosceles, the angles $KLM$ and $KML$ at its base are equal. Therefore, the adjacent angles $KLB$ and $KMN$ are also equal. This implies the equality of triangles $BKL$ and $NKM$ by the second criterion of triangle congruence. Thus, $\angle KNB = \angle KBL = 60^{\circ}$, meaning triangle $BKN$ is also equilateral.
To solve part a), note that from the congruence of the triangles, it follows that $\angle MKN = \angle BKL = 10^{\circ}$. Then $\angle AKM = \angle AKN + \angle NKM = 180^{\circ} - \angle BKN + \angle NKM = 180^{\circ} - 60^{\circ} + 10^{\circ} = 130^{\circ}$. To solve part b)
it remains to note that $BK = BN$ and $BA = BC$, so $NC = KA$. Then $MC = MN + NC = BL + KA = 2 + 3 = 5$.
Second solution. Draw the altitude $KF$ in triangle $LKM$. Since this triangle is isosceles, this altitude is also the bisector and median. Then, by the sum of the angles in triangle $BKF$, we find that $\angle BKF = 180^{\circ} - \angle KBF - \angle KFB = 30^{\circ}$. Then $\angle LKF = \angle BKF - \angle BKL = 30^{\circ} - 10^{\circ} = 20^{\circ}$. Since $KF$ is the bisector of angle $LKM$, we get that $\angle FKM = \angle FKL = 20^{\circ}$. Then $\angle AKM = 180^{\circ} - \angle BKL - \angle LKF - \angle FKM = 180^{\circ} - 10^{\circ} - 20^{\circ} - 20^{\circ} = 130^{\circ}$.
To solve part b), let the segment $LF$ be denoted by $x$. Then, since $BF$ is the median of triangle $LKM$, $FM = FL = x$. On the other hand, it is known that in a triangle with angles $30^{\circ}, 60^{\circ}, 90^{\circ}$, the side opposite the $30^{\circ}$ angle is half the hypotenuse. Using this fact for triangle $BKF$, we get that $BK = 2 \cdot (x + 2) = 2x + 4$. Using the equality of sides $AB$ and $BC$, we can set up the equation: $3 + 2x + 4 = 2 + 2x + MC$, from which $MC = 5$.
|
130
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. A phone charges fully in 1 hour 20 minutes on fast charging, and in 4 hours on regular charging. Fedya first plugged in a completely discharged phone to regular charging, and then, when he found the necessary adapter, switched it to fast charging until it was fully charged. Find the total charging time of the phone, given that it was on fast charging for one third of the total charging time. Assume that the phone charges at a constant rate both on fast and regular charging. [6 points] (based on problem 7.3 of the Math Festival 2007)
|
Answer: 144 minutes = 2 hours 24 minutes.
Solution. Since the fast charging lasts 1 hour 20 minutes, which is 80 minutes, the phone charges by $1 / 80$ of the full charge per minute. For the regular charging, which lasts 4 hours, or 240 minutes, the phone charges by $1 / 240$ of the full charge per minute.
Let's denote the total charging time of the phone in minutes by $t$. Then $t / 3$ is the time for fast charging, and $2 t / 3$ is the time for regular charging. During the fast charging, the phone charges to $\frac{t}{3} \cdot \frac{1}{80}=\frac{t}{240}$ of the full charge. During the regular charging, it charges to $\frac{2 t}{3} \cdot \frac{1}{240}=\frac{t}{360}$ of the full charge. Since the phone is fully charged at the end of the charging process, we can set up the equation $\frac{t}{240}+\frac{t}{360}=1$, solving which we find
$$
t=\frac{1}{\frac{1}{240}+\frac{1}{360}}=\frac{1}{\frac{3}{720}+\frac{2}{720}}=\frac{720}{5}=144
$$
|
144
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. On the sides \(AB\) and \(BC\) of square \(ABCD\) with side length 10, points \(K\) and \(L\) are marked such that \(AK = CL = 3\). On segment \(KL\), a point \(P\) is chosen, and on the extension of segment \(AB\) beyond point \(B\), a point \(Q\) is chosen such that \(AP = PQ = QL\) (see figure).
a) Prove that \(\angle PAB = \angle BLQ\).
b) Find the length of segment \(BQ\).
[4 points]
[4 points] * In solving part b), you can use the statement from part a).
(F. A. Ivlev, A. A. Mardanov)
a) Solution. Note that \(KB = AB - AK = 10 - 3 = BC - CL = BL\). Therefore, triangle \(KBL\) is isosceles and right-angled, so \(\angle KLB = 45^\circ\).
Let \(\angle BLQ = \alpha\). Since triangle \(PQL\) is isosceles, we have \(\angle LPQ = \angle PLQ = 45^\circ + \alpha\). From the sum of the angles in triangle \(PQL\), we find \(\angle PQL = 180^\circ - 2 \cdot (45^\circ + \alpha) = 90^\circ - 2\alpha\).
From the sum of the angles in triangle \(BLQ\), we find that \(\angle LQB = 90^\circ - \alpha\). Now we find \(\angle PQA = \angle LQA - \angle LQP = 90^\circ - \alpha - (90^\circ - 2\alpha) = \alpha\). Finally, since triangle \(APQ\) is isosceles, \(\angle PQA = \angle PAQ = \alpha = \angle BLQ\), which is what we needed to prove.
b) Answer. \(BQ = 4\).
|
Solution. Drop a perpendicular $PH$ from point $P$ to side $AB$. Since triangle $KBL$ is isosceles and right-angled, $\angle PKH = 45^\circ$. Therefore, triangle $KPH$ is also isosceles and $KH = HP$.
Notice that right triangles $APH$ and $LQB$ are equal by hypotenuse ($AP = LQ$) and acute angle ($\angle PAH = \angle BLQ$). Therefore, $KH = PH = BQ$.
Since $PH$ is the height in the isosceles triangle $APQ$ drawn to its base, it is also the median. Then $AH = HQ$ and we can write the following relationship:
\[
\begin{gathered}
AB + BQ = AQ = 2AH = 2(AK + KH) = 2(AK + BQ) \\
10 + BQ = 2(3 + BQ) = 6 + 2BQ
\end{gathered}
\]
from which $BQ = 4$.
|
4
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 2.
Here is a rather simple rebus: EKH is four times greater than OY. AY is four times greater than OH. Find the sum of all four.
$[4 points]
|
Answer: 150.
Solution: The digits Y and X are even because EH and AI are divisible by 4. The numbers OY and OX are less than 25, otherwise, when multiplied by 4, they will no longer be two-digit numbers. Therefore, O = 2 or O = 1. Let's consider the first case. The number 20 as OX or OY is not suitable because 80 ends with the same digit. 22 is also not suitable due to identical digits. Only 24 remains, but the numbers OY and OX must be different.
Thus, O = 1. The number 10 is not suitable for the same reason as 20. Taking OX = 16, we get AI = 64, but then A = X, which should not be the case. For the same reason, OY = 16 is also impossible. Taking OX = 14, we find AI = 56, then OY = 16, which, as we have seen, is impossible. Therefore, OX and OY can only be 12 and 18 (in any order), and EH and AI are then 48 and 72, respectively. We find the sum: 12 + 48 + 18 + 72 = 150.
Comment: The answer can be obtained without finding the actual numbers. As we know, O = 1, and the digits Y and X are even. On the other hand, if you add a number that is four times larger to any even number, you get a number divisible by 10. Therefore, Y + X = 10. Then OY + OX = 10 + 10 + 10 = 30, and the sum of all four numbers is five times greater, i.e., 150.
|
150
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Small Island and Big Island have a rectangular shape and are divided into rectangular counties. In each county, a road is laid along one of the diagonals. On each island, these roads form a closed path that does not pass through any point more than once. Here is how Small Island is organized, with a total of 6 counties (see Fig. 1). Draw how Big Island might be organized if it has an odd number of counties. How many counties did you get?
[7 points] (A. V. Shapovalov)

Fig. 1

Fig. 2
|
Answer. Figure 2 provides an example for 9 counties.
Comment. We will show that examples do not exist for 7 counties (or fewer), while at the same time pointing out a property characteristic of all such examples.
All roads can be divided into two types: some roads connect the top-left corner of a county with the bottom-right, while others connect the bottom-left with the top-right. If the roads of different types always alternated when traversing a closed path, their total number would be even (just like the groups of boys and girls in the previous problem). On the Large Island, where the number of counties is odd, there must, therefore, be two roads of the same type in a row.
For example, suppose two roads $A B$ and $B C$ of the same type are in a row (see the figure). In addition to the counties in which they are constructed, two more counties, shaded in gray, adjoin vertex $B$. By the condition, the roads in these counties do not pass through point $B$. Let's draw them.
Now there are four roads on the figure. To have a total of seven, three segments are needed to connect them into a single chain. To do this, it would be necessary to connect some two ends of the roads in the "gray counties" with a segment, which is impossible.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In the square, some cells are shaded as shown in the figure. It is allowed to fold the square along any grid line and then unfold it back. Cells that coincide with shaded cells when folded are also shaded. Can the entire square be shaded:
a) in 5 or fewer;
b) in 4 or fewer;

c) in 3 or fewer such foldings?
(If yes, write the number of the fold after which each cell will be shaded for the first time, draw the fold line and mark it with the same number. If no, prove it.) [4 points] (T. I. Golenishcheva-Kutuzova, M. A. Raskin, I. V. Yashchenko)
|
Answer. It is possible (even with 3 bends).
Solution. For example, it is possible to paint the entire lower half of the board with two vertical bends, after which the upper half can be painted with one horizontal bend - see the figure. (There are other solutions as well.)
Comment. It is impossible to paint all cells in 2 bends. Indeed, with each bend, the number of cells increases by no more than 2 times. Initially, there are 6 painted cells; therefore, after two bends, no more than $6 \cdot 2 \cdot 2=24$ cells out of 36 will be painted.
| 3 | 3 | 3 | 3 | 3 | 3 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 3 | 3 | 3 | 3 | 3 | 3 |
| 3 | 3 | 3 | 3 | 3 | 3 |
| | 1 | | 1 | 2 | 2 |
| 2 | | 1 | 2 | 2 | |
| 1 | 2 | 2 | | | 2 |
| | | 1 | 2 | | |
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. The numbers $2,3,4, \ldots, 29,30$ are written on the board. For one ruble, you can mark any number. If a number is already marked, you can freely mark its divisors and numbers that are multiples of it. What is the minimum number of rubles needed to mark all the numbers on the board? [6 points]
(I.V. Yashchenko)
|
Answer. For 5 rubles.
Solution. Let's mark the numbers $17, 19, 23$, and 29, spending four rubles. Then mark the number 2, spending another ruble. After this, we can freely mark all even numbers (since they are divisible by 2), and then all odd numbers not exceeding 15 - for any of them (let's say for the number $n$), the even number $2n$ is marked, and we can mark $n$ as its divisor. It remains to mark 21, 25, and 27, and this is also done for free: 25 is divisible by the marked number 5, and 21 and 27 are divisible by the marked number 3. In any way of solving the problem, the prime numbers 17, 19, 23, and 29, which exceed 15, will have to be marked for money, as they are not divisors or multiples of any numbers on the board. So, 4 rubles will be spent only on them. To mark anything else, we will have to spend a fifth ruble. Therefore, it is impossible to fulfill the conditions of the problem for less than five rubles.
Comment. In fact, after marking the "large" prime numbers, we could have marked any of the remaining numbers on the board instead of two. Indeed, then we will freely mark its smallest prime divisor $p$. If $p=2$, we act according to the algorithm described above. If not, we mark $2p$ (this is possible since $p<15$), then mark two, and then everything else in the known way.
A similar solution is applicable for an arbitrarily long set $2, 3, 4, \ldots, N$ - we are forced to mark all "large" prime numbers (exceeding $N / 2$) for money, and then mark any of the remaining numbers for a ruble. Then we freely mark two in the way described above, then all even numbers, then all "small" prime numbers (not exceeding $N / 2$), because any "small" $p$ will be a divisor of $2p$. Now we can mark all other unmarked numbers: each of them will be divisible by its minimal prime divisor - a "small" prime number.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. In the forest, there live 40 animals - foxes, wolves, hares, and badgers. Every year they organize a masquerade ball: each one wears a mask of another animal type, and they do not wear the same mask for two consecutive years. Two years ago, at the ball, there were 12 "foxes" and 28 "wolves", last year there were 15 "hares", 10 "foxes", and 15 "badgers", and this year there are 15 "hares" and 25 "foxes". Which animals are the most numerous in the forest?
|
Answer. The most numerous are the badgers.
Solution. Let's record the data from the problem in a table.
| | "Wolves" | "Foxes" | "Rabbits" | "Badgers" |
| :--- | :---: | :---: | :---: | :---: |
| Two years ago | 28 | 12 | | |
| Last year | | 10 | 15 | 15 |
| This year | | 25 | 15 | |
Let's look at the "rabbits." Over the last two years, there were 30 animals in rabbit masks. All these are different animals, as no one will wear a rabbit mask for two consecutive years. And these are not real rabbits. This means there are at least 30 non-rabbits in the forest, so the number of rabbits is no more than $40-30=10$. The same reasoning about the animals that were "foxes" for the last two years shows that the number of real foxes is no more than $40-10-25=5$. Two years ago, there were 28 "wolves" at the masquerade, and all of them were not real wolves. The number of real wolves is no more than $40-28=12$. Thus, the total number of wolves, foxes, and rabbits is no more than $12+5+10=27$. This means that the number of badgers is at least $40-27=13$, and this is the most numerous species in the forest.
Note that it is possible to choose the number of animals of each species and distribute the masks in such a way that all the conditions of the problem are satisfied. The participants in the olympiad were not required to provide such an example, but we hope that an inquisitive reader will be able to come up with it if they wish.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. Vanya is coming up with a number consisting of non-repeating digits without zeros - a password for his phone. The password works as follows: if, without lifting his finger from the screen, he sequentially connects the points corresponding to the digits of the password with line segments, the phone will unlock. However, the phone does not allow connecting two points with a segment if there is a third point between them: if Vanya connects, for example, 1 and 3, the phone will "think" that Vanya is entering 1-2-3.
Vanya wants the line traced by his finger when entering the password not to intersect itself. Additionally, he wants that by rearranging the digits of the password, no other such line can be obtained, except in reverse order. For example, the password 1263 is not to Vanya's liking because the line $6-3-2-1$ is different but also does not have self-intersections.
Vanya came up with the password 723 (see the figure). These three digits - 2, 3, and 7 - indeed cannot be connected in any other way. It's a pity, though, that the password is so short.
Help Vanya come up with a longer password. In your answer, write the password itself and draw the only line that can be formed from these digits.
[8 points]
(I.V. Yashchenko)
|
Answer. For example, 12769. See the figure.
This password meets Vanya's requirements. Let's see how we can connect its digits without any intersections. The digit 7 must be connected to some digit, which can be either 2 or 6. Suppose, for example, we draw the segment $7-6$. Now 9 can only be connected to 6. Next, it is inevitable to draw the segments $7-2$ and $2-1$, and we get the line shown in the figure. If we had drawn $7-2$ instead of $7-6$ first, the line would have been the same. Thus, this line is unique.
Comment. Interestingly, it is impossible to come up with a four-digit password that meets Vanya's requirements. There is also no password with six or more digits. There are eight possible five-digit passwords: $12769,96721,14389,98341,32947,74923,78163,36187$. However, the lines for all eight passwords are of the same form, differing only in rotation, symmetry, or the direction of drawing.
|
12769
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. In a multicolored family, there were an equal number of white, blue, and striped octopus children. When some blue octopus children became striped, the father decided to count the children. There were 10 blue and white children in total, while white and striped children together amounted to 18. How many children are there in the multicolored family?
|
Answer: 21.
First solution. Note that the white octopuses were one third of the total number, and they did not change color. If we add 10 and 18, we get the total number of all children, plus the number of white ones, which is $4 / 3$ of the total number of all children. Thus, $4 / 3$ of the number of children in the family is 28, which means there are 21 children in total.
Second solution. After recoloring, the number of striped octopuses became $18-10=8$ more than the blue ones. This means that $8: 2=4$ blue octopuses turned striped. There were $18-4=14$ white and "old striped" octopuses, which means there were $14: 2=7$ of each color. Therefore, there are $3 \cdot 7=21$ children in the colorful family.
|
21
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. The figure "violinist" attacks the cell to the left on the side (with the elbow) and the cell to the upper right diagonally (with the bow), if he is right-handed, and, conversely, the right cell on the side and the upper left cell diagonally, if he is left-handed (all violinists are facing us). Place as many "violinists" as possible in an "orchestra" of $8 \times 8$ cells, so that they do not attack each other. (You can use any combination of right-handed and left-handed violinists.)
This is how a right-handed violinist attacks
and this is how a left-handed violinist attacks
(M. Khachaturian)
|
Solution. Placing 32 violinists is not difficult: for example, you can fill four columns every other one (it doesn't matter whether they are right-handed or left-handed). However, it is possible to place more. An example with 34 violinists is shown in the figure.
| $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | $\Lambda$ | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | | $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | 1 |
| $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | $\Lambda$ | | |
| | | $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | $\Lambda$ |
| $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | $\Lambda$ | | |
| | | $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | $\Lambda$ |
| $\mathrm{p}$ | $\Lambda$ | | | $\mathrm{p}$ | $\wedge$ | | $\mathrm{p}$ |
| $\Lambda$ | | $\mathrm{p}$ | $\wedge$ | | $\mathrm{p}$ | | $\Lambda$ |
Comment. It can be proven that it is impossible to place more than 34 violinists. Indeed, consider a vertical strip two cells wide. Any violinist standing in this strip and not in the top row will hit one cell in the same strip. We can associate this empty cell with the given violinist. If it turns out that two violinists hit the same empty cell (there are two similar cases of this, one of which is shown in the figure), then the cell below the twice-hit one must also be empty, so it can be associated with one of the two violinists, say the lower one. If this cell is hit by a bow from a violinist standing even lower, we can associate this violinist with the adjacent cell horizontally (which is necessarily empty), and so on.
Thus, in the strip, there can be a maximum of 9 violinists - two in the top cells and seven more in the remaining 14 cells, because each violinist there corresponds to an empty cell, meaning that the occupied cells do not exceed half.
However, two strips with nine violinists cannot be adjacent, otherwise four violinists would sit in a row in the top row. Therefore, there can be no more than two such strips, and in the remaining two strips, there can be a maximum of 8 violinists each, so there are no more than $9+9+8+8=34$ musicians in the orchestra.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. Along the path between the houses of Nезнайка (Nезнayka) and Синеглазка (Sineglazka), there were 15 peonies and 15 tulips growing in a row, mixed together.
Setting out from home to visit Nезнайка, Синеглазка watered all the flowers in a row. After the 10th tulip, the water ran out, and 10 flowers remained unwatered.
The next day, setting out from home to visit Синеглазка, Незнайка picked flowers for her one by one. After picking the 6th tulip, he decided that it was enough for the bouquet. How many flowers remained growing along the path?
|
Answer: 19 flowers.
Solution: 10 flowers were left unwatered, which means $30-10=20$ flowers were watered. Consider the last flower watered by Blue-Eyes, which is a tulip. Since there are 15 tulips in total, there are $15-10=5$ tulips after this tulip.
Therefore, Nезнайка will pick these 5 tulips and finish picking flowers right at the last tulip watered by Blue-Eyes. This means that all the other watered flowers survived. That is, $20-1=19$ flowers survived.
|
19
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. A rectangular sheet of paper was folded, aligning a vertex with the midpoint of the opposite shorter side (Fig. 12). It turned out that triangles I and II are equal. Find the longer side of the rectangle if the shorter side is 8.
[6 points] (A. V. Khachatryan)
|
Answer: 12.
Fig. 12
Solution. Let's mark the equal segments (Fig. 13 - here we used the fact that in congruent triangles, sides opposite equal angles are equal). We see that the length of the larger side is $a+b+4$, and the length of the smaller side is $a+b$. Therefore, $a+b=8$ and the larger side has a length of $a+b+4=8+4=12$.
Fig. 13
Comment. By applying the Pythagorean theorem, we can find the lengths of the sides of triangles I and II. It turns out that these are Egyptian triangles - triangles with sides 3, 4, and 5.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Pete liked the puzzle, he decided to glue it together and hang it on the wall. In one minute, he glued together two pieces (initial or previously glued). As a result, the entire puzzle was joined into one complete picture in 2 hours. How long would it have taken to assemble the picture if Pete had glued together three pieces per minute instead of two?
[5 points] (A. V. Shapovalov)
|
Answer: In one hour.
Solution 1. Each gluing reduces the number of pieces on the table by 1. Since after 120 gluings one piece (the complete puzzle) was obtained, there were 121 pieces at the beginning. Now, if three pieces are glued together per minute (i.e., the number of pieces is reduced by 2), one piece will remain after 60 minutes.
Solution 2. In one minute, Petya made one gluing and spent 2 hours assembling the puzzle. If he glued three pieces together, he would make two gluings per minute, i.e., work twice as fast and thus spend 1 hour.
Comment. The time spent gluing the entire puzzle does not depend on the order in which Petya took the pieces. For example, he could add one piece at a time to the already glued part. Or he could glue the pieces in pairs or triplets and then glue them together. In the first case, it would take him 2 hours, and in the second case, 1 hour. In the first solution, this fact is proven by counting the total number of pieces. In the second solution, it is taken as obvious. Therefore, strictly speaking, the second solution is incomplete: it provides the correct answer, but does not prove its uniqueness.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. The inhabitants of the Island of Misfortune, like us, divide the day into several hours, an hour into several minutes, and a minute into several seconds. But they have 77 minutes in a day and 91 seconds in a minute. How many seconds are there in a day on the Island of Misfortune?
[5 points] (I. V. Raskina)
|
Answer: 1001.
Solution: If you divide 77 by the number of minutes in an hour, you get the number of hours in a day. If you divide 91 by the number of minutes in an hour, you get the number of seconds in a minute. Therefore, both 77 and 91 are divisible by the number of minutes in an hour. Since there are obviously more than one minute in an hour, the number of minutes in an hour is 7—no other number greater than one divides both 77 and 91. Then, the number of hours in a day is $77: 7=11$ and $11 \cdot 91=1001$ seconds.
Comment: The same solution can be expressed algebraically. Specifically, let there be $a>1$ hours in a day, $b>1$ minutes in an hour, and $c>1$ seconds in a minute. Then $77=a b, 91=b c$. On the other hand, $77=7 \cdot 11$ and $91=7 \cdot 13$, and the numbers $7,11,13$ are prime, i.e., they cannot be factored further. Therefore, $b=7$, from which $a=11, c=13$. The total number of seconds in a day is $a b c=1001$.
|
1001
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. The cake is packed in a box with a square base. The height of the box is half the side of this square. A ribbon of length 156 cm can be used to tie the box and make a bow on top (as shown in the left image). To tie it with the same bow on the side (as shown in the right image), a ribbon of length 178 cm is needed. Find the dimensions of the box.
(I. V. Raskina)

|
Answer: 22 cm $\times$ 22 cm $\times$ 11 cm.
Solution: In the first method of tying, the ribbon encircles the box twice along the length, twice along the width, and four times along the height, meaning its length is equal to six sides of the base plus the bow. In the second method of tying, the ribbon encircles the box twice along the length, four times along the width, and twice along the height, meaning its length is equal to seven sides of the base plus the bow. Now it is clear that the difference in the lengths of the ribbons, $178-156=22$ cm, is exactly equal to the side of the base of the box. Therefore, the dimensions of the box are 22 cm $\times$ 22 cm $\times$ 11 cm. Let's check: in the first case, 132 cm is used for wrapping the box ($22 \times 6=132$ cm), and 24 cm is used for the bow. In the second case, 154 cm is used for wrapping the box ($22 \times 7=154$ cm), and the same 24 cm is used for the bow.
|
22
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.