problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Task 5. Replace in the equation
$$
\text { PIE = SLICE + SLICE + SLICE + ... + SLICE }
$$
identical letters with identical digits, and different letters with different digits, so that the equation is true, and the number of "slices of pie" is the largest possible.
|
Answer. The maximum number of "pieces" is seven, for example: ПИРОГ $=95207$, КУСОК $=13601$.
Solution. An example for seven "pieces" is given above. We will show that there cannot be more than seven "pieces". For this, it is convenient to rewrite the condition as a multiplication example: ПИРОГ $=$ КУСОК $\cdot n$, where $n$ is the number of "pieces".
It is clear that if there are 10 or more "pieces", the right side will exceed 100000, so there will be no solutions.
A solution is also impossible for nine "pieces". For ПИРОГ $=$ КУСОК $\cdot 9$ to be a five-digit number, $К$ must be 1. But then ПИРОГ starts and ends with a nine, which should not be the case.
Now we will prove that there cannot be eight "pieces". Let КУСОК $\cdot 8=$ ПИРОГ. Since all the digits in ПИРОГ are different, ПИРОГ $\leqslant 98765$, and then КУСОК $\leqslant 98765 / 8=12345.675$, so КУСОК $\leqslant 12345$. Then it is clear that $К=1$ and $\Gamma=8$. The letter О represents a digit, the product of which by 8 ends in the same digit. It is easy to see that this can only be zero. Since the digits 0 and 1 are already used, and $\mathrm{V} \leqslant 2$ and $\mathrm{C} \leqslant 3$, then $\mathrm{V}=2$ and $\mathrm{C}=3$. Thus, there is only one possibility: КУСОК $=12301$. But this number does not work, as $12301 \cdot 8=98408$, and in 98408 the digits are repeated, which should not be the case.
The example given for seven "pieces" is not the only one; there are three more: $14051 \cdot 7=98357, 12351 \cdot 7=86457, 12051 \cdot 7=84357$. Of course, it was sufficient to provide one example.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. First-year students admitted to the university were distributed into study groups so that each group had the same number of students. Due to a reduction in the number of specialties, the number of groups decreased by 9, and all first-year students were redistributed into groups; as a result, the groups were again equal in number, and each had fewer than 30 students. It is known that there were 2376 first-year students in total. How many groups are there now?
Answer: 99.
|
Let the new number of groups be $n$, then initially there were ( $n+9$ ) groups. In each group, there was an equal number of students, so $2376: n$ and $2376:(n+9)$. We factorize 2376 into prime factors ( $2376=2^{3} \cdot 3^{3} \cdot 11$ ) and list all divisors: $1,2,4,8,3,6,12,24,9,18,36,72,27,54$, $108,216,11,22,44,88,33,66,132,264,99,198,396,792,297,594,1188,2376$. According to the condition, the groups now contain fewer than 30 students, hence $\frac{2376}{n}<30$. This means we need to find among the divisors of 2376 two such that they differ by 9 and are greater than 79. These are 99 and 108. Therefore, $n=99$.
|
99
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the sum of the first thirty-three terms of an arithmetic progression, given that the sum of the seventh, eleventh, twentieth, and thirtieth terms of this progression is 28.
|
Answer. $S_{33}=231$.
Solution Let $a_{k}$ be the $k$-th term of the arithmetic progression, and $d$ be its common difference. Then, according to the condition, $a_{7}+a_{11}+a_{20}+a_{30}=28$, from which we have $a_{7}+\left(a_{7}+4 d\right)+\left(a_{7}+13 d\right)+\left(a_{7}+23 d\right)=28 \Leftrightarrow a_{7}+10 d=7$, i.e., $a_{17}=7$. The sum of the first thirty-three terms is
$$
S_{33}=\frac{a_{1}+a_{33}}{2} \cdot 33=\frac{\left(a_{17}-16 d\right)+\left(a_{17}+16 d\right)}{2} \cdot 33=33 a_{17}=231
$$
|
231
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. An infinite geometric progression consists of natural numbers. It turned out that the product of the first four terms equals param1. Find the number of such progressions.
The infinite geometric progression consists of positive integers. It turned out that the product of the first four terms equals param1. Find the number of such progressions.
| param1 | Answer |
| :---: | :---: |
| $2^{200} 3^{300}$ | 442 |
| $2^{200} 5^{400}$ | 578 |
| $3^{200} 5^{600}$ | 867 |
| $2^{300} 7^{600}$ | 1326 |
| $3^{300} 7^{500}$ | 1092 |
## Condition
An infinite geometric progression consists of natural numbers. It turned out that the product of the first four terms equals $2^{200} 3^{300}$. Find the number of such progressions.
## Answer.
442
|
Solution
If $b_{1}$ is the first term of the progression and $q$ is its common ratio, then the product of the first four terms of the progression is $b_{1}^{4} q^{6}$. Therefore, $b_{1}^{2} q^{3}=2^{100} \cdot 3^{150}$. Hence, $b_{1}=2^{a} 3^{b}, q=2^{c} 3^{d}$, and we obtain the system: $2 a+3 c=100, 2 b+3 d=150$. The first equation has 17 solutions in non-negative integers ( $c$ is an even number, i.e., $c=2 n$, from which $a+3 n=50$, and we get $0 \leq n \leq 16$ ), the second has 26 solutions ( $b=3 m, 2 m+d=50$, i.e., $0 \leq m \leq 25$ ).
Each solution to the first equation can correspond to any solution of the second. The total number of progressions is $17 \cdot 26=442$.
|
442
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a function $f: \sqcup \rightarrow \sqcup$ such that $f(1)=1$, and for any $x \in \sqcup, y \in \sqcup$ the equality $f(x)+f(y)+x y+1=f(x+y)$ holds. Find all integers $n$ for which the equality $f(n)=$ param 1 holds. In the answer, write down the sum of cubes of all such values of $n$.
Function $f: \sqcup \rightarrow \sqcup$ such that $f(1)=1$ satisfies the equality $f(x)+f(y)+x y+1=f(x+y)$ for any real $x, y$. Find all integers $n$ for which $f(n)=$ param1. In the answer write down the sum of cubes of all such values of $n$.
| param1 | Answer |
| :---: | :---: |
| $2 n^{2}-10$ | 19 |
| $3 n^{2}-6 n-11$ | 63 |
| $2 n^{2}-9 n+14$ | 133 |
| $3 n^{2}+19 n+29$ | -91 |
## Condition
Given a function $f: \sqcup \rightarrow \sqcup$ such that $f(1)=1$, and for any $x \in \sqcup, y \in \sqcup$ the equality $f(x)+f(y)+x y+1=f(x+y)$ holds. Find all integers $n$ for which the equality $f(n)=2 n^{2}-10$ holds. In the answer, write down the sum of cubes of all such values of $n$.
## Answer.
19
|
# Solution
Substituting $y=1$ into the given functional equation, we get: $f(x)+f(1)+x+1=f(x+1)$, which means $f(k)-f(k-1)=k+1$. Therefore, $f(n)-f(1)=(f(n)-f(n-1))+(f(n-1)-f(n-2))+\ldots$ $+f(2)-f(1)=n+1+n+\ldots+2$. Hence, $f(n)=\frac{n^{2}+3 n-2}{2}$. Reasoning similarly,
we get $f(n)=\frac{n^{2}+3 n-2}{2}$ for $n \leq 0$. Therefore, we need to solve the equation $n^{2}+3 n$ $-2=2\left(2 n^{2}-10\right)$. This gives us the equation $3 n^{2}-3 n-18=0$. The roots of this equation are 3 and -2. The sum of the cubes of these numbers is 19.
|
19
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In a convex pentagon $A B C D E$, a point $M$ is taken on side $A E$, and a point $N$ is taken on side $D E$. Segments $C M$ and $B N$ intersect at point $P$. What is the smallest possible area of the pentagon $A B C D E$, given that the quadrilaterals $A B P M$ and $D C P N$ are parallelograms with areas param1 and param2, respectively?
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| 8 | 9 | 29 |
| 10 | 45 | 85 |
| 9 | 50 | 89 |
| 6 | 75 | 111 |
| 8 | 49 | 85 |
## Condition
In a convex pentagon $A B C D E$, a point $M$ is taken on side $A E$ and a point $N$ is taken on side $D E$. Segments $C M$ and $B N$ intersect at point $P$. What is the smallest possible area of the pentagon $A B C D E$, given that the quadrilaterals $A B P M$ and $D C P N$ are parallelograms with areas 8 and 9, respectively?
## Answer.
#
|
# Solution
Let the areas of parallelograms ABPM and DCPN, triangle BCP, and quadrilateral MPNE be $S_{1}, S_{2}, S_{3}$, and $S_{4}$, respectively. According to the problem, $A M \sqcup B \mathcal{B}$ and $P N \sqcup C \mathcal{D}$. Therefore, $\mathrm{AE} \sqcup \mathcal{B} N \cup C D$. Similarly, $D E \sqcup C M \sqcup A B$. Then, M PNE is also a parallelogram, and thus $S_{4}: S_{1}=N P: P B$ (parallelograms ABPM and M PNE have equal heights). Similarly, triangle $BCP$ and parallelogram $DCPN$ have equal heights, so $S_{3}: S_{2}=\frac{1}{2} B P: P N$. Multiplying the written equalities, we get: $\frac{S_{4}}{S_{1}} \cdot \frac{S_{3}}{S_{2}}=\frac{1}{2} \cdot$ Therefore, $S=S_{1}+S_{2}+$ $S_{3}+S_{4}=$
$=S_{1}+S_{2}+S_{3}+\frac{S_{1} S_{2}}{2 S_{3}} \geq S_{1}+S_{2}+2 \sqrt{S_{3} \cdot \frac{S_{1} S_{2}}{2 S_{3}}}=S_{1}+S_{2}+\sqrt{2 S_{1} S_{2}}=29$. The obtained minimum is achieved when $S_{3}=S_{4}$.
|
29
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Let param1. What is the largest possible value of param2?
It is given that param1. Find the largest possible value of param2.
| param 1 | param 2 | Answer |
| :---: | :---: | :---: |
| $\frac{9 \cos ^{2} x-7+12 \sin x}{16-9 \sin ^{2} x+6 \sqrt{5} \cos x}=3$ | $6 \sin x$ | 4 |
| $\frac{25 \sin ^{2} x-37+40 \cos x}{35-25 \cos ^{2} x-30 \sin x}=4$ | $10 \cos x$ | 8 |
| $\frac{33-16 \cos ^{2} x-24 \sin x}{16 \sin ^{2} x-19-8 \sqrt{7} \cos x}=2$ | $12 \sin x$ | 9 |
| :---: | :---: | :---: |
| $\frac{15-9 \cos ^{2} x+6 \sin x}{9 \sin ^{2} x-7+12 \sqrt{2} \cos x}=\frac{1}{2}$ | | |
## Condition
Let $\frac{9 \cos ^{2} x-7+12 \sin x}{16-9 \sin ^{2} x+6 \sqrt{5} \cos x}=3$. What is the largest possible value of $6 \sin x$?
Answer.
4
#
|
# Solution
Notice that $\frac{9 \cos ^{2} x-7+12 \sin x}{16-9 \sin ^{2} x+6 \sqrt{5} \cos x}=\frac{6-(3 \sin x-2)^{2}}{2+(3 \cos x+\sqrt{5})^{2}}$. The obtained expression can equal 3 only if $3 \sin x-2=0$ and $3 \cos x+\sqrt{5}=0$. Therefore, the expression $6 \sin x$ can only take the value 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The clock hand points to 12. Jack writes a sequence consisting of param 1 symbols, each symbol being plus or minus. After that he gives this sequence to a robot. The robot reads it from right to left. If he sees a plus he turns the clock hand $120^{\circ}$ clockwise and if he sees a minus he turns it $120^{\circ}$ counterclockwise. Find the number of sequences such that after the robot finishes the program the clock hand still points to 12.
| param1 | Answer |
| :---: | :---: |
| 11 | 682 |
| 12 | 1366 |
| 13 | 2730 |
| 14 | 5462 |
| 15 | 10922 |
Condition
The clock hand points to 12. Jack writes a sequence consisting of 11 symbols, each symbol being plus or minus. After that he gives this sequence to a robot. The robot reads it from right to left. If he sees a plus he turns the clock hand $120^{\circ}$ clockwise and if he sees a minus he turns it $120^{\circ}$ counterclockwise. Find the number of sequences such that after the robot finishes the program the clock hand still points to 12.
## Answer.
|
# Solution
Let $a_{n}$ be the number of sequences of length $n$ that result in the arrow pointing at 12 o'clock, and $b_{n}$ be the number of sequences of length $n$ that result in the arrow pointing at 4 or 8 o'clock. It is not difficult to understand that $a_{n+1}=2 b_{n}, b_{n+1}=a_{n}+b_{n}$. From this, we get that $b_{n+2}=b_{n+1}+2 b_{n}, a_{n+2}=a_{n+1}+2 a_{n}$. Since $a_{0}=1, a_{1}=0$, we can write the formula $a_{n}=\frac{2^{n}+2 \cdot(-1)^{n}}{3} \cdot$ In our case, we get the answer $a_{11}=682$.
|
682
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. Let $S(k)$ denote the sum of all the digits in the decimal representation of a positive integer $k$. Let $n$ be the smallest positive integer satisfying the condition $S(n)+S(n+1)=$ param1. As the answer to the problem, write down a five-digit number such that its first two digits coincide with the first two digits of $n$ and its last three digits coincide with the last three digits of $n$. For example, if $\mathrm{n}=1234567890$, then the answer must be 12890.
| param1 | Answer |
| :---: | :---: |
| 2016 | 59989 |
| 664 | 49989 |
| 1580 | 39989 |
| 4000 | 79989 |
## Condition
Let $S(k)$ denote the sum of all the digits of the number $k$. Let $n$ be the smallest natural number such that $S(n)+S(n+1)=2016$. As the answer to the problem, write down a five-digit number such that its first two digits coincide with the first two digits of $n$, and its last three digits coincide with the last three digits of $n$. For example, if $\mathrm{n}=1234567890$, then the answer should be 12890.
## Answer.
59989
## Solution
If the number $n$ does not end in 9, then $S(n+1)=S(n)+1$, and the sum $S(n)+S(n+1)$ is odd, which means it cannot equal 2016. Therefore, the number $n$ must end in 9. If it ends in one 9, then $S(n+1)=S(n)-8$, and thus $S(n)=1012$. The smallest number with such a sum of digits is 599...989 (the total number of 9s is 111). If the number of 9s at the end of $n$ is not less than two, then by similar reasoning, the sum $S(n)$ will be larger, and the number $n$ will also be larger. Therefore, the answer is 59989.
12. Let $A C$ be the largest side of triangle $A B C$. Points $K$ and $M$ are chosen on side $A C$ such that $A M=A B$ and $C K=C B$. It is given that the radius of the circumcircle of triangle $K B M$ is param1, and the radius of the incircle of triangle $A B C$ is param2, and this incircle touches side $B C$ at point $T$. Find the square of the length of segment $B T$.
Let $A C$ be the largest side of triangle $A B C$. Points $K$ and $M$ are chosen on side $A C$ so that $A M=$ $A B$ and $C K=C B$. It is given that the radius of the circumcircle of the triangle $K B M$ equals param1, and the radius of the incircle of the triangle $A B C$ equals param2. Find the length of $B T$ squared if $T$ is the point where the incircle of $A B C$ touches its side $B C$.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| 7 | 5 | 24 |
| 8 | 5 | 39 |
| 9 | 7 | 32 |
| 11 | 8 | 57 |
| 13 | 9 | 88 |
## Condition
Let $A C$ be the largest side of triangle $A B C$. Points $K$ and $M$ are chosen on side $A C$ such that $A M=A B$ and $C K=C B$. It is given that the radius of the circumcircle of triangle $K B M$ is 7, and the radius of the incircle of triangle $A B C$ is 5, and this incircle touches side $B C$ at point $T$. Find the square of the length of segment $B T$.
## Answer.
24
|
# Solution
Let $R$ be the radius of the circumcircle of triangle KBM and $r$ be the radius of the incircle of triangle ABC. First, we will prove that the centers of the circles mentioned in the problem statement coincide. Indeed, the center $I$ of the incircle of triangle $ABC$ lies on the bisector of angle $BAC$, which is also the bisector of the isosceles triangle $BAM$. This means that point $I$ lies on the perpendicular bisector of segment $BM$. Similarly, it lies on the perpendicular bisector of segment $BK$. Therefore, it is the center of the circumcircle of triangle $KBM$. It is known that $B T=\frac{B C+B A-A C}{2}=\frac{C K+A M-A C}{2}=\frac{K M}{2}$. Triangle $K I M$ is isosceles: $І \mathrm{~K}=\mathrm{I} M$ as radii of the circumcircle of triangle $\mathrm{K} B \mathrm{~L}$. Let the incircle touch side $AC$ at point $S$. Then $K M=2 \mathrm{KS}=$ $=2 \sqrt{I K^{2}-\mid S^{2}}=2 \sqrt{R^{2}-r^{2}}$, so $B T^{2}=R^{2}-r^{2}=24$.
|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. In a convex pentagon $A B C D E$, a point $M$ is taken on side $A E$, and a point $N$ is taken on side $D E$. Segments $C M$ and $B N$ intersect at point $P$. Find the area of pentagon $A B C D E$ if it is known that quadrilaterals $A B P M$ and $D C P N$ are parallelograms with areas param1 and param2, respectively, and the area of triangle $B C P$ is param3.
| param1 | param2 | param3 | Answer |
| :---: | :---: | :---: | :---: |
| 5 | 8 | 10 | 25 |
| 6 | 10 | 3 | 29 |
| 7 | 9 | 7 | 27.5 |
| 8 | 11 | 20 | 41.2 |
| 9 | 12 | 4 | 38.5 |
## Condition
In a convex pentagon $A B C D E$, a point $M$ is taken on side $A E$, and a point $N$ is taken on side $D E$. Segments $C M$ and $B N$ intersect at point $P$. Find the area of pentagon $A B C D E$ if it is known that quadrilaterals $A B P M$ and $D C P N$ are parallelograms with areas 5 and 8, respectively, and the area of triangle $B C P$ is 10.
## Answer.
25
|
# Solution
Let the areas of parallelograms ABP M and DCPN, triangle BCP, and quadrilateral

$A E \sqcup B N N C D$. Similarly, $D E \sqcup C M \sqcup\{B$. Then M PNE is also a parallelogram, and thus $S_{4}: S_{1}=N P: P B$ (parallelograms ABPM and M PNE have equal heights). Similarly, triangle $B C P$ and parallelogram $D C P N$ have equal heights, so $S_{3}: S_{2}=$ $\frac{1}{2} B P: P N$. Multiplying the written equalities, we get: $\frac{S_{4}}{S_{1}} \cdot \frac{S_{3}}{S_{2}}=\frac{1}{2} \cdot$ Therefore, $S=S_{1}+S_{2}+$ $S_{3}+S_{4}=S_{1}+S_{2}+S_{3}+\frac{S_{1} S_{2}}{2 S_{3}}=25$
|
25
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. The difference of the squares of two different real numbers is param 1 times greater than the difference of these numbers, and the difference of the cubes of these numbers is param 2 times greater than the difference of these numbers. By how many times is the difference of the fourth powers of these numbers greater than the difference of the squares of these numbers?
The difference between the squares of two different real numbers is param 1 times greater than the difference between these numbers. The difference between the cubes of these numbers is param2 times greater than the difference between these numbers. Find the ratio of difference between the fourth powers of these numbers to the difference between squares of these numbers.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| 37 | 1069 | 769 |
| 40 | 1209 | 818 |
| 37 | 1039 | 709 |
| 40 | 1201 | 802 |
| 31 | 741 | 521 |
## Condition
The difference of the squares of two different real numbers is 37 times greater than the difference of these numbers, and the difference of the cubes of these numbers is 1069 times greater than the difference of these numbers. By how many times is the difference of the fourth powers of these numbers greater than the difference of the squares of these numbers?
## Answer.
#
|
# Solution
From the equalities $a^{2}-b^{2}=k(a-b)$ and $a^{3}-b^{3}=m(a-b)$ (in the problem $k=37, m=1069$), it follows that $a+b=k$ and $a^{2}+a b+b^{2}=m$. Squaring the first equality and subtracting the second from it, we get: $a b=k^{2}-m$. Then the ratio $\left(a^{4}-b^{4}\right):\left(a^{2}-b^{2}\right)=a^{2}+b^{2}=m-a b=2 m-k^{2}=769$.
|
769
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Out of two hundred ninth-grade students, 80% received excellent grades on the first exam, 70% on the second exam, and 59% on the third exam. What is the smallest number of participants who could have received excellent grades on all three exams?
Answer: 18.
|
Let $M_{i}$ be the number of students who received excellent grades only on the $i$-th exam; $M_{ij}$ be the number of students who received excellent grades only on exams $i$ and $j$; $M_{123}$ be the number of students who received excellent grades on all three exams. Then, according to the problem,
$$
\left\{\begin{array}{l}
M_{1}+M_{12}+M_{13}+M_{123}=160 \\
M_{2}+M_{12}+M_{23}+M_{123}=140 \\
M_{3}+M_{23}+M_{13}+M_{123}=118
\end{array}\right.
$$
Adding all three equations:
$$
M_{1}+M_{2}+M_{3}+2\left(M_{12}+M_{13}+M_{23}\right)+3 M_{123}=418
$$
Notice that
$$
M_{1}+M_{2}+M_{3}+M_{12}+M_{13}+M_{23}+M_{123} \leq 200
$$
(on the left side of this inequality, the number of students who received at least one excellent grade is recorded, and on the right side - the total number of students). Subtracting (2) from (1), we get
$$
M_{12}+M_{13}+M_{23}+2 M_{123} \geq 218 \Leftrightarrow\left(M_{12}+M_{13}+M_{23}\right) \geq 218-2 M_{123}
$$
Since $M_{23} \leq 200-160=40, M_{13} \leq 200-140=60, M_{12} \leq 200-118=82$, then $M_{12}+M_{13}+M_{23} \leq 182$. Considering (3), we get that $182 \geq 218-2 M_{123}$, from which $M_{123} \geq 18$.
It is not difficult to verify that the value $M_{123}=18$ can be achieved. For this, take $M_{12}=82$, $M_{13}=60, M_{23}=40, M_{1}=M_{2}=M_{3}=0$.
|
18
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Piglet ran down a moving escalator and counted 66 steps. Then he ran up the same escalator at the same speed relative to the escalator and counted 198 steps. How many steps would he have counted if he had gone down a stationary escalator?
Answer. 99.
|
Let \( u \) be the speed of Piglet, \( v \) be the speed of the escalator (both measured in steps per unit time), and \( L \) be the length of the escalator (in steps). Then, the time Piglet spent descending the moving escalator is \( \frac{L}{u+v} \), and during this time, he counted \( \frac{L}{u+v} \cdot u \) steps. For the ascent against the movement, the time spent was \( \frac{L}{u-v} \), i.e., he counted \( \frac{L}{u-v} \cdot u \) steps. We obtain the equations \( L u = 66 u + 66 v \) and \( L u = 198 u - 198 v \), from which \( 66 u + 66 v = 198 u - 198 v \), hence \( u = 2 v \). Then, \( L u = 66 u + 33 u \), so \( L = 99 \).
|
99
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The remainder of dividing a certain natural number $n$ by 22 is 7, and the remainder of dividing $n$ by 33 is 18. Find the remainder of dividing $n$ by 66.
|
Answer: 51.
Solution: According to the condition $n=22l+7, \quad l \in Z$ and $n=33m+18, m \in Z$. By equating these two expressions, we get $22l+7=33m+18, 2l=3m+1$. Since the left side of the equation is even, the right side must also be divisible by 2, so $m$ is an odd number, i.e., $m=2q+1, q \in Z$. Then $n=33(2q+1)+18=66q+51$, and the remainder of dividing $n$ by 70 is 51.
|
51
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Out of three hundred eleventh-grade students, excellent and good grades were received by $77 \%$ on the first exam, $71 \%$ on the second exam, and $61 \%$ on the third exam. What is the smallest number of participants who could have received excellent and good grades on all three exams?
Answer: 27.
|
Let $M_{i}$ be the number of students who received excellent grades only on the $i$-th exam; $M_{ij}$ be the number of students who received excellent grades only on exams $i$ and $j$; $M_{123}$ be the number of students who received excellent grades on all three exams. Then, according to the conditions,
\[
\left\{\begin{array}{l}
M_{1}+M_{12}+M_{13}+M_{123}=231 \\
M_{2}+M_{12}+M_{23}+M_{123}=213 \\
M_{3}+M_{23}+M_{13}+M_{123}=183
\end{array}\right.
\]
Adding all three equations:
\[
M_{1}+M_{2}+M_{3}+2\left(M_{12}+M_{13}+M_{23}\right)+3 M_{123}=627 .
\]
Notice that
\[
M_{1}+M_{2}+M_{3}+M_{12}+M_{13}+M_{23}+M_{123} \leq 300
\]
(on the left side of this inequality, the number of students who received at least one excellent grade is recorded, and on the right side - the total number of students). Subtracting (2) from (1), we get
\[
M_{12}+M_{13}+M_{23}+2 M_{123} \geq 327 \Leftrightarrow\left(M_{12}+M_{13}+M_{23}\right) \geq 327-2 M_{123}
\]
Since $M_{23} \leq 300-231=69, M_{13} \leq 300-213=87, M_{12} \leq 300-183=117$, then $M_{12}+M_{13}+M_{23} \leq 273$. Taking (3) into account, we get that $273 \geq 327-2 M_{123}$, from which $M_{123} \geq 27$.
It is not difficult to verify that the value $M_{123}=27$ can be achieved. For this, take $M_{12}=117$, $M_{13}=87, M_{23}=69, M_{1}=M_{2}=M_{3}=0$.
|
27
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Winnie the Pooh ran down a moving escalator and counted 55 steps. Then he ran up the same escalator at the same speed relative to the escalator and counted 1155 steps. How many steps would he have counted if he had gone down a stationary escalator?
Answer: 105.
|
Let \( u \) be the speed of Winnie the Pooh, \( v \) be the speed of the escalator (both measured in steps per unit time), and \( L \) be the length of the escalator (in steps). Then, the time Winnie the Pooh spent descending the moving escalator is \( \frac{L}{u+v} \), and during this time, he counted \( \frac{L}{u+v} \cdot u \) steps. For the ascent against the movement, the time spent was \( \frac{L}{u-v} \), i.e., he counted \( \frac{L}{u-v} \cdot u \) steps. We obtain the equations \( L u = 55 u + 55 v \), \( L u = 1155 u - 1155 v \), from which \( 55 u + 55 v = 1155 u - 1155 v \), \( 10 u = 11 v \). Then \( L u = 55 u + 50 u \), \( L = 105 \).
|
105
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. Let $S(k)$ denote the sum of all the digits in the decimal representation of a positive integer $k$. Let $n$ be the smallest positive integer satisfying the condition $S(n)+S(n+1)=$ param1. As the answer to the problem, write down a five-digit number such that its first two digits coincide with the first two digits of $n$ and its last three digits coincide with the last three digits of $n$. For example, if $\mathrm{n}=1234567890$, then the answer must be 12890.
| param1 | Answer |
| :---: | :---: |
| 2016 | 59989 |
| 664 | 49989 |
| 1580 | 39989 |
| 4000 | 79989 |
## Condition
Let $S(k)$ denote the sum of all the digits in the decimal representation of a positive integer $k$. Let $n$ be the smallest positive integer such that $S(n)+S(n+1)=2016$. As the answer to the problem, write down a five-digit number such that its first two digits coincide with the first two digits of $n$ and its last three digits coincide with the last three digits of $n$. For example, if $\mathrm{n}=1234567890$, then the answer must be 12890.
## Answer.
59989
## Solution
If the number $n$ does not end in 9, then $S(n+1)=S(n)+1$, and the sum $S(n)+S(n+1)$ is odd, which means it cannot equal 2016. Therefore, the number $n$ must end in 9. If it ends in one 9, then $S(n+1)=S(n)-8$, and thus $S(n)=1012$. The smallest number with such a sum of digits is 599...989 (the total number of 9s is 111). If the number of 9s at the end of $n$ is not less than two, then by similar reasoning, the sum $S(n)$ will be larger, and the number $n$ will also be larger. Therefore, the answer is 59989.
12. Let $A C$ be the largest side of triangle $A B C$. Points $K$ and $M$ are chosen on side $A C$ such that $A M=A B$ and $C K=C B$. It is given that the radius of the circumcircle of triangle $K B M$ equals param1, and the radius of the incircle of triangle $A B C$ equals param2. Find the length of $B T$ squared if $T$ is the point where the incircle of $A B C$ touches its side $B C$.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| 7 | 5 | 24 |
| 8 | 5 | 39 |
| 9 | 7 | 32 |
| 11 | 8 | 57 |
| 13 | 9 | 88 |
## Condition
Let $A C$ be the largest side of triangle $A B C$. Points $K$ and $M$ are chosen on side $A C$ such that $A M=A B$ and $C K=C B$. It is given that the radius of the circumcircle of triangle $K B M$ equals 7, and the radius of the incircle of triangle $A B C$ equals 5. Find the length of $B T$ squared if $T$ is the point where the incircle of $A B C$ touches its side $B C$.
## Answer.
24
|
# Solution
Let $R$ be the radius of the circumcircle of triangle KBM and $r$ be the radius of the incircle of triangle ABC. First, we will prove that the centers of the circles mentioned in the problem statement coincide. Indeed, the center $I$ of the incircle of triangle $ABC$ lies on the bisector of angle $BAC$, which is also the bisector of the isosceles triangle $BAM$. This means that point $I$ lies on the perpendicular bisector of segment $BM$. Similarly, it lies on the perpendicular bisector of segment $BK$. Therefore, it is the center of the circumcircle of triangle $KBM$. It is known that $B T=\frac{B C+B A-A C}{2}=\frac{C K+A M-A C}{2}=\frac{K M}{2}$. Triangle $K I M$ is isosceles: $І \mathrm{~K}=\mathrm{I} M$ as radii of the circumcircle of triangle $\mathrm{K} B \mathrm{~L}$. Let the incircle touch side $AC$ at point $S$. Then $K M=2 \mathrm{KS}=$ $=2 \sqrt{I K^{2}-\mid S^{2}}=2 \sqrt{R^{2}-r^{2}}$, so $B T^{2}=R^{2}-r^{2}=24$.
|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given a strictly increasing function $f: \mathbb{N}_{0} \rightarrow \mathbb{N}_{0}$ (where $\mathbb{N}_{0}$ is the set of non-negative integers), which satisfies the relation $f(n+f(m))=f(n)+m+1$ for any $m, n \in \mathbb{N}_{0}$. Find all possible values that $f(2023)$ can take.
(T.A. Garmanova)
|
Solution. 1) Substituting $m=0, n=0$, we get $f(f(0))=f(0)+1$.
If $f(0)=0$, then we get $f(0)=f(0)+1$, which is impossible.
2) Let $f(0)=a$, then $a \in \mathbb{N}$. From the first point, we get that $f(a)=a+1$. If we substitute $m=0, n=a$, then we get that $f(2a)=f(a)+1=a+2$. Therefore, the values of the function at the ends of the segment $[a ; 2a]$ are two consecutive natural numbers. According to the condition, the function $f: \mathbb{N}_{0} \rightarrow \mathbb{N}_{0}$ is strictly increasing, which means there should be no other integer points on the segment $[a ; 2a]$ except $a$ and $2a$, because otherwise, the values at these points would coincide with $a+1$ or $a+2$, which would contradict the strict increase. $2a-a=1$, i.e., $a=1$.
Substituting $m=0$ into the original relation and considering the equality $f(0)=1$, we get $f(n+1)=$ $f(n)+1$. Thus, $f(n)=n+1$, therefore, $f(2023)=2024$.
|
2024
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. What is the smallest number of different integers that need to be taken so that among them one can choose both a geometric and an arithmetic progression of length $5$?
(M.A. Evdokimov)
|
Solution. Let's provide an example of six integers that satisfy the condition: $-8, -2, 1, 4, 10, 16$. The numbers $1, -2, 4, -8, 16$ form a geometric progression, while the numbers $-8, -2, 4, 10, 16$ form an arithmetic progression.
We will show that no five distinct integers satisfy the condition of the problem. Suppose the contrary: let there be five integers that simultaneously form a geometric progression and, possibly in a different order, an arithmetic progression. Then they have the form $b$, $b q, b q^{2}, b q^{3}, b q^{4}$ where $b \in \mathbb{Z}$. Note that $b \neq 0$ and $q \neq 0$ by the definition of a geometric progression. The numbers $b, b q^{2}, b q^{4}$ are always of the same sign and in an arithmetic progression, they either appear consecutively for $q > 0$ or $q < 0$. In any case, the equality $2 b q^{2} = b + b q^{4}$ must hold, i.e., $b\left(q^{2}-1\right)^{2}=0$, from which $q = \pm 1$, but then there are equal numbers among them. Contradiction. Therefore, five numbers are insufficient.
Answer: 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the smallest natural number $N>9$, which is not divisible by 7, but if any of its digits is replaced by 7, the resulting number is divisible by 7.
|
(M. A. Evdokimov) Solution. Let the smallest such number be of the form $\overline{a_{1} a_{2} \ldots a_{n}}$. From the condition, it follows that among its digits there are no 0 and 7. If the number contains digits 8 or 9, then they can be replaced by 1 or 2, respectively, to obtain a smaller number with the same property. Thus, the desired number consists of digits from 1 to 6.
Consider $a_{k}$ and $a_{k+1}$. By the condition, the numbers $\overline{a_{1} a_{2} \ldots 7 a_{k+1} \ldots a_{n}}$ and $\overline{a_{1} a_{2} \ldots a_{k} 7 \ldots a_{n}}$ are divisible by 7, hence their difference is also divisible by 7, i.e., $10 a_{k} \equiv a_{k+1}(\bmod 7)$ for any $k$. Therefore, the number can only be structured as follows: 1 is followed by 3, 3 is followed by 2 (since the digit 9 is not in the number), and so on (see Fig. 11-2-3).
By the condition, the original number, with 7 instead of the last digit, is divisible by 7. Therefore, the original number without the last digit $\overline{a_{1} a_{2} a_{3} \ldots a_{n-1}}$ is divisible by 7. Using the congruence $10 a_{k} \equiv a_{k+1}(\bmod 7)$ several times, we get:
$$
\begin{gathered}
\overline{a_{1} a_{2} \ldots a_{n-1}}=a_{1} 10^{n-2}+a_{2} 10^{n-3}+a_{3} 10^{n-4}+\ldots+a_{n-1} \equiv 10 a_{1} \cdot 10^{n-3}+a_{2} 10^{n-3}+a_{3} 10^{n-4}+\ldots+a_{n-1} \equiv \\
\equiv 2 a_{2} 10^{n-3}+a_{3} 10^{n-4} \ldots+a_{n-1} \equiv \ldots \equiv(n-1) a_{n-1} \quad(\bmod 7)
\end{gathered}
$$
Since $a_{n-1}$ is not divisible by 7, we conclude that $n-1$ is divisible by 7, so the smallest possible $n$ is 8. Thus, the smallest possible number consists of at least eight digits. It remains to note that the number 13264513 satisfies the condition of the problem, and since it starts with 1, this number is the smallest.
|
13264513
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In the relay race Moscow - Petushki, two teams of 20 people each participated. Each team divided the distance into 20 not necessarily equal segments and distributed them among the participants so that each ran exactly one segment (the speed of each participant is constant, but the speeds of different participants may vary). The first participants of both teams started simultaneously, and the baton handover happens instantaneously. What is the maximum number of overtakes that could occur in such a race? Overtaking at the segment boundaries is not counted as an overtake.
(2023-96, E. Neustroeva)
|
Answer: 38 overtakes.
Solution. First, let's prove that no more than 38 overtakes occurred. Note that between the start and the first overtake, and between two consecutive overtakes, at least one of the teams must have changed the runner. There were 19 changes of runners in each team, meaning a total of 38 changes, so there could not have been more than 38 overtakes.
Let's prove that 38 overtakes were possible. We will illustrate the movement trajectories of the teams on a graph with the horizontal axis representing time and the vertical axis representing the segments, directed upwards and to the right. The lower-left end of each broken line coincides with the origin, and the upper-right ends of the broken lines have the same vertical coordinate. In this situation, an overtake is a point of intersection of the broken lines that is not a vertex.
So, let's provide an example. First, draw a broken line consisting of 40 consecutive sides of a regular 160-gon, such that the last side is horizontal. In other words, the first segment of the broken line starts from the point with coordinates \((0,0)\) and is rotated at an angle of \(9/4^{\circ}\), and each subsequent segment is rotated by \(9/4^{\circ}\) clockwise compared to the previous one. Thus, the last segment will be horizontal, i.e., rotated by \(40 \cdot 9/4^{\circ} = 90^{\circ}\) relative to the vertical axis. Connect the vertices of the auxiliary broken line with numbers \(1, 2, 4, 6, \ldots, 50\) sequentially with line segments; this will be the trajectory of the first team. The trajectory of the second team will be a broken line connecting the vertices with numbers \(1, 3, 5, \ldots, 51\). The segments \((i, i+2)\) and \((i+1, i+3)\) for \(i=1, 2, \ldots, 38\) will intersect, and their points of intersection will be the 38 overtakes we are looking for.
Let's illustrate the example for the case of teams consisting of two participants.
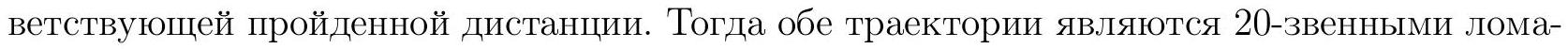
Fig. 1: to the solution of problem 2
|
38
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On an island, there live chameleons of five colors. When one chameleon bites another, the color of the bitten chameleon changes according to some rule, and the new color depends only on the color of the biter and the color of the bitten. It is known that 2023 red chameleons can agree on a sequence of bites, after which all of them will turn blue. For what smallest $k$ can it be guaranteed that $k$ red chameleons can agree to turn blue?
For example, the rules might be: if a red chameleon bites a green one, the bitten one changes color to blue; if a green chameleon bites a red one, the bitten one remains red, i.e., "changes color to red"; if a red chameleon bites a red one, the bitten one changes color to yellow, and so on. (The specific rules for color changes may be different.)
(2022-60, M. Raskin)
|
# Answer. For $k=5$. Solution.
First, let's provide an example of rules under which the described recoloring would require at least 5 red chameleons. Let's number the colors so that red is the first color and blue is the last. Then, let the rules be as follows: if a chameleon of color $k1$ can reduce the number of its color by means of a bite from a chameleon of color $l<k$. In other words, chameleons of colors $1, \ldots, k$ can become colors $1, \ldots, k-1$. By applying this reasoning several times, we will get that our chameleons can all change their color to blue.
Comment. It is not hard to notice that for $n$ colors, $n$ chameleons will be needed. In fact, this problem is one of many questions around (in general) Petri nets. With slight modifications to the problem, the minimum size of the initial population can increase significantly.
For example, suppose that upon biting, both chameleons can change their color differently, and the goal is to reach a state with one green chameleon and many blue ones. In this case, the minimum number can grow faster than any polynomial in $n$, and even faster than
known as the Ackermann function.
Fortunately, if all chameleons must be of the same color both at the beginning and at the end, the situation simplifies significantly. The requirement that only one of the chameleons changes color upon biting even further simplifies the situation. It corresponds to "immediate observation" or "one-way communication" in Petri nets (immediate observation, one-way communication).
In this variant, for example, it is shown—using combinatorial methods accessible to school students—that if two sets of chameleon colors, and after adding the same number of blue chameleons to the first, it becomes possible to obtain the second, then it is sufficient to add $n^{3}$ chameleons.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (B. Novikov) On each cell of an $8 \times 8$ board, a guard is placed. Each guard can look in one of four directions (along the lines of the board) and watch all the guards on the line of his sight. For what largest $k$ can the guards' gazes be directed so that each guard is watched by at least $k$ other guards?
|
Solution: Answer: 5. We will prove that $k \leq 5$. For this, assume that $k \geqslant 6$. Consider the guards standing at the corners of the board. Each of them is watched by at least 6 guards, and these guards must stand at the edge of the board. Moreover, if a guard sees one of the corner guards, they do not see the other corner guards. Thus, at least 24 guards standing at the edge of the board are looking along the sides of the board. Then, inside the board, not at the corner guards, there are no more than four guards standing at the boundaries.
Now consider the guards standing in the central $6 \times 6$ square. Let's count the maximum possible number of "incoming gazes" for them. (We will not count gazes directed at guards on the boundary of the board). This number does not exceed $184=24+100+48+12$. (24 - from four guards on the boundary, 100 - 5 gazes from each of the 20 guards on the boundary of the $6 \times 6$ square, 48 - 4 gazes from each of the 12 guards on the boundary of the $4 \times 4$ square, 12 - 3 gazes from each of the 4 guards in the central $2 \times 2$ square.) Thus, for 36 guards, there are $184=36 \cdot 5+4<36 \cdot 6$ gazes. Therefore, among the guards, there are those who received fewer than 6 gazes.
Examples for $k=5$ can be arranged differently. One of the variants is shown in the figure (long arrows mean that several guards in a row are looking in the same direction, guards in the center can look in any direction).
## Criteria.
Arithmetic errors (or errors in counting the number of certain cells) do not affect the evaluation if they did not affect the solution process. “+” - a correct and justified solution is provided;
“土” - a correct example and evaluation with minor (easily fixable) flaws that do not simplify the evaluation;
“干” - a correct example or a correct evaluation is provided;
“-.“ - an evaluation with minor flaws is provided;
“-” - all other cases, including if an evaluation with any significant flaws is provided, the evaluation is greater than 5, or the example is less than 5.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the largest natural number $n$ with the following property: for any odd prime $p$ less than $n$, the difference $n-p$ is also a prime number.
(I. Akulich)
|
Answer: 10
Solution: Suppose that $n>10$. Notice that the numbers $n-3, n-5, n-7$ are all greater than three, and one of them is divisible by three, and consequently composite. Contradiction.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Among any five nodes of a regular grid paper, there will definitely be two nodes, the midpoint of the segment between which is also a node of the grid paper. What is the minimum number of nodes of a grid made of regular hexagons that need to be taken so that among them, there will definitely be two nodes, the midpoint of the segment between which is also a node of this grid?
(A. Kulygin)
#
|
# Answer. 9
Lemma. Among any five nodes of a grid of equilateral triangles, there will be two such that the midpoint of the segment between them is also a grid node.
Proof. Introduce the origin at one of the grid nodes and denote by $\vec{a}$ and $\vec{b}$ the radius vectors to the two nearest nodes (see picture). Then the nodes of the grid are points of the form $m \vec{a}+n \vec{b}$ for integers $m$ and $n$. By the pigeonhole principle, among five points, there will be two points $m_{1} \vec{a}+n_{1} \vec{b}$ and $m_{2} \vec{a}+n_{2} \vec{b}$, for which the parity of $m_{1}$ and $m_{2}$ and the parity of $n_{1}$ and $n_{2}$ coincide simultaneously. The midpoint of the segment connecting these two points is the point $\frac{m_{1}+m_{2}}{2} \vec{a}+\frac{n_{1}+n_{2}}{2} \vec{b}$. It is a grid node due to the identical parity of $m_{1}$ and $m_{2}, n_{1}$ and $n_{2}$.
Solution. In the first picture, you can see an example of the placement of 8 grid nodes, among which there are no two such that the midpoint of the segment between them is a grid node. We will prove that nine nodes are sufficient. Note that the hexagonal grid is divided into the union of two triangular grids (see the second picture). By the pigeonhole principle, among any nine nodes, at least five will be in one of these two triangular grids. By the lemma, among these five nodes, there will be two of the required ones.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given a polynomial of degree 2022 with integer coefficients and leading coefficient 1. What is the maximum number of roots it can have on the interval $(0,1)$?
(A. Kanel-Belov)
|
Answer: 2021
Solution. If the interval $(0,1)$ contains all 2022 roots of the polynomial, then by Vieta's theorem, the constant term of the polynomial must be equal to their product, and thus will also lie in the interval $(0,1)$ and will not be an integer. We will prove that the polynomial $P(x)=x^{2022}+(1-$ $4042 x)(3-4042 x) \ldots(4041-4042 x)$ can serve as an example. Notice that for all $k=0,1, \ldots, 2021$, the number $P\left(\frac{2 k}{4042}\right)=\left(\frac{2 k}{4042}\right)^{n}+(-1)^{k}(2 k-1)!!(4041-2 k)!!$ is positive for even $k$ and negative for odd $k$. Thus, on the interval $(0,1)$, the polynomial $P(x)$ changes sign at least 2021 times, and therefore has at least 2021 roots.
|
2021
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. M. Evdokimov
}
A natural number is written on the board. If the last digit (in the units place) is erased, the remaining non-zero number will be divisible by 20, and if the first digit is erased, the remaining number will be divisible by 21. What is the smallest number that can be written on the board if its second digit is not equal to 0?
|
Answer: 1609.
Solution.
The second to last digit of the number is 0, since the number without the last digit is divisible by 20. Therefore, the number is at least four digits. Note that the number remaining after erasing the last digit cannot be 100 according to the condition. Also, this number cannot be 120 or 140, as numbers of the form $\overline{20 a}$ and $\overline{40 a}$ are not divisible by 21. For 160, there is only one example: 1609.
|
1609
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. proposed by A. Shen
There is an infinite one-way strip of cells, numbered with natural numbers, and a bag with ten stones. Initially, there are no stones in the cells of the strip. The following actions are allowed:
- moving a stone from the bag to the first cell of the strip or back;
- if there is a stone in the cell with number $i$, then a stone can be moved from the bag to the cell with number $i+1$ or back.
Is it possible, acting according to these rules, to place a stone in the cell with number $1000 ?$
|
Answer: $\partial a$.
Solution. Note that for each action there is an inverse to it. Therefore, if we get from situation $A$ to situation $B$ by following the rules, we can also get from situation $B$ to situation $A$ by following the rules.
We will show by induction that if there is a reserve of $n$ stones, then, acting according to the above rules, we can place a stone in any cell from 1 to $2^{n}-1$.
Base of induction: $n=1$. This is obvious.
Inductive step. Suppose we have proven that with a reserve of $n$ stones, we can place a stone in all cells up to the $\left(2^{n}-1\right)$-th. Now let's assume we have $n$ black stones and one red stone. We will act as follows:
(1) Without removing the red stone from the bag, place a black stone in the $\left(2^{n}-1\right)$-th cell. This can be done by the inductive hypothesis.
(2) Place the red stone in the $2^{n}$-th cell.
(3) Perform the operations as in step (1), but in reverse and in the opposite order. It is clear that the red stone will not hinder this. In the end, all black stones will be back in the bag, and on the strip, there will be exactly one stone - the red stone in cell $2^{n}$. Let's agree that we will not remove the red stone from now on.
(4) The cells with numbers from $2^{n}+1$ to $2^{n+1}-1$ form a strip of length $2^{n}-1$. The inductive hypothesis for $n$ stones applies to this strip, as the red stone allows operations with the leftmost cell of this strip. Therefore, we can place a stone in the last cell.
Thus, with a reserve of 10 stones, we can place a stone in all cells numbered from 1 to $1023=2^{10}-1$.
Comment: In fact, a strip of length 1000 is sufficient. Indeed, note that among the cells numbered from 1000 to 1023, the first stone will be placed in cell 1000. That is, to place a stone in the 1000th cell, cells numbered from 1001 to 1023 are not necessary, which means that with a reserve of 10 stones, we can place a stone in the last cell of a strip of length 1000.
|
1000
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A polyhedron with vertices at the midpoints of the edges of a certain cube is called a cuboctahedron. When the cuboctahedron is intersected by a plane, a regular polygon is obtained. What is the maximum number of sides this polygon can have?
(M. A. Evdokimov)
|
Solution.
Let the edge of the original cube, from which the cuboctahedron is obtained, be 1. Consider the sections of the cuboctahedron by a plane parallel to the base of the cube at a distance of $08$. Then the vertices of this $n$-gon must lie on the edges of the cuboctahedron, and no more than two vertices of the $n$-gon can belong to one edge. Consider the section of the original cube, which is a regular hexagon (see fig.), as well as sections that are obtained from this by rotating by $90^{\circ}, 180^{\circ}$, and $270^{\circ}$ about the vertical axis of the cube. Note that the union of the sides of these four regular hexagons is the union of all the edges of the cuboctahedron. We will show that on the sides of one of the four chosen regular hexagons, there lie at least 3 vertices of the $n$-gon. Indeed, if on the sides of each such hexagon there are no more than two vertices, then the total number of vertices will not exceed eight. Therefore, the plane of the section of the $n$-gon coincides with the plane of this hexagon, and a hexagon is obtained in the section of the cuboctahedron. This leads to a contradiction.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (I. Akulich) Find the largest natural $n$ with the following property: for any odd prime $p$ less than $n$, the difference $n-p$ is also a prime number.
|
Solution: Answer: 10. Indeed, $10=3+7=5+5$. We will prove that numbers greater than 10 do not work. Let $n$ be a number greater than 10. Note that the numbers $3, 5, 7$ give different remainders when divided by 3. Then the numbers $n-3, n-5, n-7$ give different remainders when divided by 3, meaning one of them is divisible by 3. It remains to note that this number is greater than 3, so it is composite. Contradiction.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. Sasha writes down the numbers 1, 2, 3, 4, 5 in some order, places the arithmetic operation signs "++", "-", "×" and parentheses, and looks at the result of the obtained expression. For example, he can get the number 8 using the expression $(4-3) \times (2+5)+1$. Can he get the number 123?
Forming numbers from several others is not allowed (for example, from the numbers 1 and 2, the number 12 cannot be formed).
(A. Gолованов, A. Sokolov)
|
Answer: 2 yes
Solution. For example, $3 \times(2 \times 4 \times 5+1)=123$.
|
123
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In Alik's collection, there are two types of items: badges and bracelets. There are more badges than bracelets. Alik noticed that if he increases the number of bracelets by a certain (not necessarily integer) factor, without changing the number of badges, then his collection will have 100 items. And if, conversely, he increases the initial number of badges by the same factor, leaving the number of bracelets unchanged, then he will have 101 items. How many badges and how many bracelets could Alik have in his collection?
|
Solution. Let Alik have $x$ badges and $y$ bracelets, and the increase occurs by a factor of $n$. Then we get the system
$$
x+n y=100, \quad n x+y=101
$$
By adding and subtracting the equations and eliminating $n$, we obtain
$$
\frac{201}{x+y}-\frac{1}{x-y}=2
$$
We transform this equation to the form
$$
(201-2 u)(2 v+1)=201=3 \cdot 67
$$
where $u=x+y, v=x-y$ are natural numbers.
There are two cases:
1) $2 v+1=3,201-2 u=67$, then $x=34, y=33, n=2$.
2) $2 v+1=67,201-2 u=3$, then $x=66, y=33, n=\frac{34}{33}$.
Answer. 34 badges and 33 bracelets, or 66 badges and 33 bracelets.
|
34
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. The Sultan gathered 300 court wise men and proposed a test. There are 25 different colors of hats, known in advance to the wise men. The Sultan informed them that one of these hats would be placed on each of the wise men, and if the number of hats of each color is written down, all the numbers will be different. Each wise man will see the hats of the others, but not his own. Then all the wise men will simultaneously announce the supposed color of their own hat. Can the wise men agree in advance to act in such a way that at least 150 of them will definitely name the correct color?
|
(A. V. Grialko) Solution. Since $0+1+2+\ldots+24=300$, the quantities of caps of different colors take all values from 0 to 24.
Next, each sage counts the number of caps of each color. For two colors, the quantities of caps coincide, and the sage understands that he is wearing a cap of one of these two colors. It only remains to choose which of these two colors to name.
There are various ways to agree (in advance!) on how each sage should make this choice. For example, a regular bipartite graph can be constructed and Hall's lemma for Arab countries can be used. The strategy presented below is based on the concept of the parity of a permutation.
Let the sages pre-number the colors with numbers from 0 to 24. Then the true distribution of caps corresponds to the permutation
$$
\begin{gathered}
\text { color number } \\
\text { number of caps }
\end{gathered}\left(\begin{array}{ccccccccc}
0 & 1 & 2 & \ldots & i & \ldots & j & \ldots & 24 \\
a_{0} & a_{1} & a_{2} & \ldots & a_{i} & \ldots & a_{j} & \ldots & a_{24}
\end{array}\right)
$$
If a sage sees an equal number of caps of color $i$ and color $j$ (with $k$ caps of each of these two colors), then he needs to decide which of these two colors to attribute his cap to, that is, to choose between two permutations
$$
\left(\begin{array}{ccccccccc}
0 & 1 & 2 & \ldots & i & \ldots & j & \ldots & 24 \\
a_{0} & a_{1} & a_{2} & \ldots & k & \ldots & k+1 & \ldots & a_{24}
\end{array}\right) \quad\left(\begin{array}{ccccccccc}
0 & 1 & 2 & \ldots & i & \ldots & j & \ldots & 24 \\
a_{0} & a_{1} & a_{2} & \ldots & k+1 & \ldots & k & \ldots & a_{24}
\end{array}\right) .
$$
One of these permutations corresponds to the true distribution of colors, and the specified permutations differ in the placement of exactly two elements, so they have different parities.
The sages can agree in advance that exactly 150 of them will make their choice in favor of the even permutation, and the other 150 will choose the odd permutation.
Then exactly half of the sages will correctly name the color of their cap.
Remark. The strategy according to which the sages agree in advance that 150 of them choose the color with the higher number (of the two between which they need to choose), and the other 150 choose the color with the lower number, does not guarantee 150 correct answers.
Indeed, let the true distribution of caps correspond to the permutation
$$
\begin{gathered}
\text { color number } \\
\text { number of caps }
\end{gathered}\left(\begin{array}{llllllllllllll}
0 & 1 & 2 & \ldots & 15 & 16 & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24 \\
0 & 1 & 2 & \ldots & 15 & 16 & 17 & 24 & 23 & 22 & 21 & 20 & 19 & 18
\end{array}\right)
$$
and let the sages who received caps of colors 3-17 (exactly 150 people) choose the color with the lower number, while the other 150 sages choose the color with the higher number. Then all the sages, except for the sages with caps of colors 1, 2, and 24, will name the color incorrectly.
|
150
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. Provide an example of a nine-digit natural number that is divisible by 2 if the second (from the left) digit is erased, by 3 if the third digit is erased in the original number, ..., and by 9 if the ninth digit is erased in the original number.
|
1. Answer. For example, 900900000.
Note. In fact, there are 28573 numbers that satisfy the conditions of the problem, the smallest of which is 100006020, and the largest is 999993240.
|
900900000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Tanya was sequentially writing down numbers of the form $n^{7}-1$ for natural numbers $n=2,3, \ldots$ and noticed that for $n=8$ the resulting number is divisible by 337. For what smallest $n>1$ will she get a number divisible by $2022?$
|
(T. A. Garmanova) Solution. Let the natural number $n$ be such that $n^{7}-1$ is divisible by $2022=2 \cdot 3 \cdot 337$. Then $n^{7}-1$ is divisible by 2 and 3, so $n$ is an odd number, having a remainder of 1 when divided by 3. In addition, $n^{7}-1$ is divisible by 337. Note that if two numbers are congruent modulo 337 (i.e., they give the same remainder when divided by 337), then their seventh powers are also congruent modulo 337. This means that to find the desired number, it is sufficient to consider all integers $n$ in the interval $[0 ; 336]$, satisfying the congruence $n^{7} \equiv 1(\bmod 337)$.
Now let's prove that any congruence of the form $P_{k}(n) \equiv 0(\bmod 337)$ has no more than $k$ solutions on the interval $[0 ; 336]$, where $P_{k}(n)$ is a polynomial of degree $k$ with integer coefficients. We will prove this by induction on $k$. For $k=1$, we get a congruence of the form $a n+b \equiv 0(\bmod 337)$, which has no more than one solution, since any integer $n \in(0 ; 336]$ is coprime with 337. Suppose the statement is true for all polynomials of degree $\leqslant k-1$. Consider the polynomial $P_{k}(n)$. If it has no roots, then the statement is satisfied. If it has a root, then the polynomial can be represented as $P_{k}(n)=(n-a) Q_{k-1}(n)$, and by the induction hypothesis, the polynomial $Q_{k-1}(n)$ has no more than $k-1$ roots. The statement is proved.
Now let's find all solutions to the congruence $n^{7} \equiv 1(\bmod 337)$ on the interval $[0 ; 336]$. We know two solutions: $n_{1}=1, n_{2}=8$. Note that if $n$ is a solution to the congruence $n^{7} \equiv 1(\bmod 337)$, then for any natural number $s$, the numbers $n^{s}$ are also solutions. Therefore, the solutions to this congruence are the numbers
$$
\begin{gathered}
8^{2}=64 \equiv 64 \quad(\bmod 337) \\
8^{3}=512 \equiv 175 \quad(\bmod 337) \\
8^{4} \equiv 8 \cdot 175 \equiv 52 \quad(\bmod 337) \\
8^{5} \equiv 8 \cdot 52 \equiv 79 \quad(\bmod 337) \\
8^{6} \equiv 8 \cdot 79 \equiv 295 \quad(\bmod 337)
\end{gathered}
$$
Thus, we have found seven solutions on the interval $[0 ; 336]: n_{1}=1, n_{2}=8, n_{3}=52, n_{4}=64, n_{5}=79$, $n_{6}=175, n_{7}=295$. According to the proof above, there are no other solutions on this interval. Among them, the odd numbers that have a remainder of 1 when divided by 3 are $n_{1}=1, n_{5}=79, n_{6}=175$ and $n_{7}=295$. The smallest one greater than 1 is $n_{5}=79$.
Answer: 79.
|
79
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. (A. Zaslavsky) In a certain state, there are 32 cities, each of which is connected by a road with one-way traffic. The Minister of Communications, a secret villain, decided to organize traffic in such a way that after leaving any city, it would be impossible to return to it. To achieve this, he can change the direction of traffic on one of the roads every day, starting from June 1, 2021. Prove that he can achieve his goal by 2022 (that is, he has 214 days).
|
Solution. We will prove the general formula. Let there be $2^{n}$ cities in the state. Then the prime minister can achieve the desired result in no more than $2^{n-2}\left(2^{n}-n-1\right)$ days.
Lemma. Suppose there are $2k$ cities in the state, each two of which are connected by a one-way road. Choose half of them with the largest number of outgoing roads. Then the total number of roads outgoing from the selected cities is not less than $k^{2}$.
Proof. Suppose from $k$ selected cities, the total number of outgoing roads is less than $k^{2}$. Then, by the pigeonhole principle, there is a city from which no more than $k-1$ roads go out. Since the cities with the largest number of outgoing roads are chosen, from each of the remaining $k$ cities, no more than $k-1$ roads also go out. In total, there are fewer than $k^{2}+k(k-1)=2k^{2}-k$ outgoing roads, while the total number of roads is exactly $\frac{2k(2k-1)}{2}=2k^{2}-k$. Contradiction, the lemma is proved.
Now let's proceed to the proof of the main formula. We will prove it by induction. Base case $n=1$: between two cities, there is only one road, and it is already in one direction. No changes are needed.
Step. Suppose the statement is true for $2^{n}$ cities. We will prove it for $2^{n+1}$. Divide the cities into two groups of $2^{n}$ cities each. In the first group, place the cities with the largest number of outgoing roads. According to the lemma, from all cities in this group, the total number of outgoing roads is not less than $2^{2n}$.
Of these roads, $\frac{2^{n}(2^{n}-1)}{2}$ are roads within the group, so from the first group to the second, there are not fewer than $2^{n-1}(2^{n}+1)$ roads. Then, out of $2^{2n}$ roads between the first and second groups, no more than $2^{n-1}(2^{n}-1)$ are directed into the first group. The prime minister can redirect all these roads to the second group in no more than $2^{n-1}(2^{n}-1)$ days. And in no more than $2 \cdot 2^{n-2}(2^{n}-n-1)$ days, he will ensure that in each group, it is impossible to leave a city and return to it. Therefore, in total, it will take no more than $2^{n-1}(2^{n+1}-n-2)$ days.
Since $32=2^{5}$, the minister will need no more than $2^{3}(2^{5}-5-1)=208$ days, which is less than the 214 days remaining until 2022.
Comment. If there are $n$ cities in the country, then an estimate for the number of $f(n)$ changes can be obtained from the relations $f(2n) \leq \frac{n(n-1)}{2} + 2f(n)$ (essentially proven in the problem) and $f(2n+1) \leq n + f(2n)$ (obvious). The jury does not know whether this estimate is exact.
|
208
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
4. First solution. Let $a_{1}, a_{2}, \ldots, a_{15}$ be the days of the month that were sunny. Then Andrey Stepanovich will not drink a single drop from the 1st to the $a_{1}$-th day, he will drink one drop per day from the $a_{1}$-th day to the $a_{2}$-th day (including the $a_{1}$-th day but not the $a_{2}$-th day), and so on. In total, he will drink
$$
\begin{aligned}
& 1 \cdot\left(a_{2}-a_{1}\right)+2 \cdot\left(a_{3}-a_{2}\right)+\ldots \\
& \quad \ldots+14 \cdot\left(a_{15}-a_{14}\right)+15 \cdot\left(30-a_{15}+1\right)= \\
& \quad=15 \cdot 31-\left(a_{1}+a_{2}+\ldots+a_{15}\right)
\end{aligned}
$$
Ivan Petrovich, on the other hand, will drink a number of drops equal to the sum of the numbers of all days except $a_{i}$:
$$
\begin{aligned}
(1+2+\ldots+30)-\left(a_{1}+a_{2}+\ldots\right. & \left.+a_{15}\right) \\
& =15 \cdot 31-\left(a_{1}+a_{2}+\ldots+a_{15}\right)
\end{aligned}
$$
|
The second solution. First, let's consider the situation where the first fifteen days of April were cloudy, and the last fifteen were sunny. It is easy to check that both characters in the problem will drink $1+2+3+\ldots+15=120$ drops of valerian - indeed, equally.
Let's swap some sunny day $s$ with some cloudy day $p$ and see how the monthly doses of valerian change for both. Suppose that $s > p$. Note that Andrei Stepanovich, starting from day $p$ (not inclusive) to day $s$ (inclusive), will drink one drop of valerian more each day than before the swap, and in all other days, he will drink the same amount. Thus, he will drink $s-p$ drops more in total than before the swap. As for Ivan Petrovich, after the swap, he will also drink $s-p$ drops more than before, as he stopped drinking valerian on day $p$ and started on day $s$. Similarly, it can be proven that if $s < p$, the amount of valerian each character drinks will decrease by $p-s$.
Thus, the operation of swapping a cloudy and a sunny day changes the dose of valerian taken by both by the same number of drops. It remains to note that by swapping days, we can transform the initial month (with 15 cloudy days at the beginning) into any other.
The third solution. Consider a checkered "staircase": a figure consisting of 30 columns corresponding to the days in April, with as many cells in each column as the number of that day in the month (see figure). In each column, we will gray out as many cells as the number of drops of valerian Andrei Stepanovich drank on the corresponding day, and each column corresponding to a cloudy day will be filled with crosses.
Thus, Andrei Stepanovich drank as many drops of valerian as there are grayed-out cells, and Ivan Petrovich drank as many as there are crosses in the table. It is sufficient to prove that the number of crosses in the unshaded cells is the same as the number of shaded cells without crosses.
The shaded cells without crosses are in the "sunny" columns. On each sunny day, Andrei Stepanovich drank one drop of valerian more than on the previous sunny day (on the first sunny day, he drank 1 drop). Therefore, the number of shaded cells without crosses is $1+2+3+\ldots+15$.
Now let's count the number of crosses in the unshaded cells. Suppose the $n$-th day was cloudy and there were $k$ sunny days before it. Then in the corresponding column, there will be $n-k$ "unshaded" crosses (and $k$ "shaded" ones). Note that this is the $(n-k)$-th cloudy day, so in the first cloudy day, there will be one unshaded cross, in the second - two, and so on. Thus, the number of unshaded crosses is $1+2+3+\ldots+15$.
|
120
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. At the vertices of the quadrilateral $A_{1} A_{2} A_{3} A_{4}$ (Fig. 62), the following masses are placed: $2, 6, 2, 3$. Calculate the moment of inertia of the resulting system of material points relative to the point $S$. (The side of each square on Fig. 62 is 1 unit.) (O. 117, P. 177.)
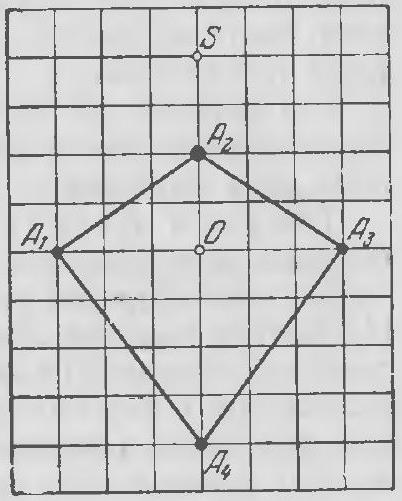
Fig. 62.
|
1. The sought moment of inertia is
$$
\begin{aligned}
J_{S}=2 \cdot S A_{1}^{2} & +6 \cdot S A_{2}^{2}+2 \cdot S A_{3}^{2}+3 \cdot S A_{4}^{2}= \\
& =2\left(3^{2}+4^{2}\right)+6 \cdot 2^{2}+2\left(3^{2}+4^{2}\right)+3 \cdot 8^{2}=316
\end{aligned}
$$
|
316
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. There are two solutions of wine spirit in water ${ }^{1}$ ): The first solution weighs 4002 and contains $30 \%$ spirit, the second solution weighs 6002 and contains $80 \%$ spirit.
From these two solutions, one solution is made. What percentage of spirit will it contain? (O. 117, U. 126, P. 215.$)$
|
2. a) Let's represent the solutions using material points. For this, we will take a segment $AB$ of one unit length (Fig. 172). Let point $A$ represent pure water

[Boda] (cimupm.)
Fig. 172.
$(100\%$ water), and $B$—pure alcohol ( $100\%$ alcohol). The first solution will then be represented by the material point $K_{1} \equiv\left(K_{1}, 400\right)$, where $A K_{1}=0.3$ (the mark "30" next to point $K_{1}$ indicates that $A K_{1}$ contains 30 parts out of 100). The second solution will be represented by the material point $K_{2} \equiv\left(K_{2}, 600\right)$. The combination of these two solutions will be the solution $K \equiv(K, 1000)$, where $K \equiv Z\left[K_{1}, K_{2}\right]$. According to the lever rule,
$$
\frac{K_{1} K}{K K_{2}}=\frac{600}{400}=\frac{3}{2}
$$
Let $A K=x$. Then we get: $\frac{x-0.3}{0.8-x}=\frac{3}{2}$, from which $x=0.6$. Therefore, the concentration of alcohol in the solution $(1000)$ is $60\%$. The same result could have been obtained from the relation
$$
\operatorname{Mom}_{A} K \equiv \operatorname{Mom}_{A} K_{1}+\text{Mom}_{A} \boldsymbol{K}_{2},
$$
i.e., $1000 \cdot x=400 \cdot 0.3+600 \cdot 0.8$. The problem can also be solved purely graphically.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. What is the smallest number of triangular pyramids (tetrahedrons) into which a cube can be divided?
|
14. It is easy to see that the cube $A B C D A_{1} B_{1} C_{1} D_{1}$ can be divided into five tetrahedra: if we cut off the tetrahedra $B A C B_{1}$ and $D A C D_{1}$, as well as the tetrahedra $A_{1} B_{1} D_{1} A$ and $C_{1} B_{1} D_{1} C$, we will have one more (fifth) tetrahedron $A C B_{1} D_{1}$ left (Fig. 51; the tetrahedron $A C B_{1} D_{1}$ is even a regular one). It is more difficult to establish that the cube cannot be divided into fewer than five tetrahedra.
Indeed, suppose that the cube $A B C D A_{1} B_{1} C_{1} D_{1}$ is divided into some number of tetrahedra. In this case, the face $A B C D$ of the cube is divided into parts that are faces of at least two tetrahedra (the square $A B C D$ can be divided into two or more triangles), and the sum of the areas
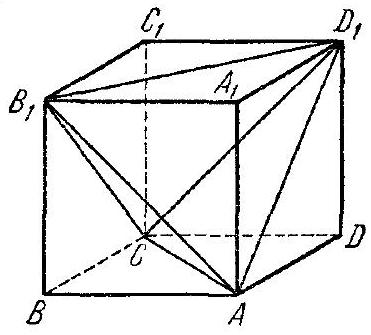
Fig. 51. of the bases of these tetrahedra is equal to $a^{2}$, and the height of each of them does not exceed $a$; therefore, the sum of the volumes of the tetrahedra adjacent to the face $A B C D$ of the division does not exceed $\frac{1}{3} a^{2} \cdot a = \frac{a^{3}}{3}$. Similarly, the face $A_{1} B_{1} C_{1} D_{1}$ of the cube is adjacent to at least two tetrahedra, and the total volume of these tetrahedra also does not exceed $\frac{a^{3}}{3}$. Since no tetrahedron can simultaneously have faces that are part of the square $A B C D$ and part of the square $A_{1} B_{1} C_{1} D_{1}$ (since no tetrahedron has parallel faces!), we already have at least four tetrahedra, and the total number of tetrahedra in the division is not yet exhausted, since the total volume of the specified tetrahedra does not exceed $\frac{a^{3}}{3} + \frac{a^{3}}{3} = \frac{2}{3} a^{3}$, which is less than the volume $a^{3}$ of the cube. Hence, the number of tetrahedra in the division cannot be less than five.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. On the plane, there are a (generally non-convex) quadrilateral and a pentagon, and no vertex of one lies on the side of the other. What is the maximum possible number of intersection points of their sides?
|
15. Note that no line can intersect the sides of a polygon in an odd number of points, since otherwise, moving along this line in a certain direction - after entering the polygon for the last time, we would not be able to leave its boundaries. Therefore, each side of the quadrilateral can have no more than four intersection points with the contour of the pentagon. Hence, the total number of intersection points between the sides of the quadrilateral and the pentagon cannot exceed $4 \times 4=16$. The fact that this number can equal 16 follows from Fig. 52.
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. Every two adjacent sides of a flat (self-intersecting!) 14-sided polygon are mutually perpendicular; no two sides of it lie on the same line. What is the maximum possible number of self-intersection points of the sides of such a polygon?
|
16. Let's agree to consider that all sides of the 14-sided polygon are either "horizontal" or "vertical." Clearly, in this case, exactly 7 sides are horizontal (and 7 are vertical): after all, from each vertex, one horizontal (and one vertical) side extends. Summing over all 14 vertices, we count 14 horizontal sides; but in doing so, each side is counted twice (corresponding to its two vertices).
Fig. 52.
(further, the highest and the lowest of the horizontal sides of the 14-sided polygon cannot contain any intersection points with other sides (since there are no vertices of the polygon above, respectively below, these sides); the second from the top and the second from the bottom sides can contain only two intersection points (since there are only 2 vertices above, respectively below, these sides); the third from the top and the third from the bottom of the horizontal sides can contain up to 4 intersection points (since there are 4 vertices of the 14-sided polygon above and below these sides). Finally, the middle horizontal side by height can contain no more than 6 intersection points, since there are 6 vertices of the 14-sided polygon above and below it; however, the number 6 is actually impossible here, because otherwise each vertex above this middle side would be connected to one of the lower vertices and vice versa, and thus the vertices belonging to the "middle" side itself would not be connected to any other vertices.
Thus, the maximum possible number of intersection points of our 14-sided polygon is
$$
2+4+5+4+2=17
$$
the fact that such a number of intersection points is possible is shown by the example (Fig. 53).
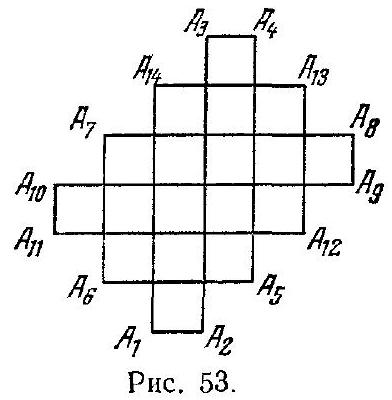
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. a) Into how many parts can a plane be divided by two closed curves, one of which is a circle and the other is the boundary of a square?
b) $* *$ Into how many parts can space be divided by two closed surfaces, one of which is a sphere and the other is the surface of a cube?
|
18. a) The boundary of a square and a circle can divide the plane into parts of the following types:
1) the part located outside the square and outside the circle; such a part is always one;
2) the part located inside the square and inside the circle; if the square does not intersect the circle, then there are no such parts; otherwise, there is one such part;
3) the part located outside the circle but inside the square; such a part always contains at least one corner of the square, and for brevity, we will call it a "corner"; the number of "corners" does not exceed the number of corners of the square, i.e., four;
4) the part located outside the square but inside the circle; if the circle and the square intersect, then the boundary of such a part (a "segment") includes a segment of at least one of the four sides of the square; therefore, the total number of "segments" cannot exceed the number of sides of the square, i.e., four.
Thus, the maximum number of parts into which a square and a circle can divide the plane is
$$
1+1+4+4=10
$$
(Fig. 56, a). The minimum number of parts into which a square and a circle can divide the plane is, obviously, three: each line already divides the plane into 2 parts, and since they are different, the second line increases the number of parts by at least 1 (Fig. 56, b, c). It is easy to see that the number of parts into which a square and a circle divide the plane can be any number \( N \), where \( 3 \leqslant N \leqslant 10 \) (Fig. 56, a-u; the number of "corners" \( U \) and the number of "segments" \( C \) are indicated in parentheses).
b) A sphere and the surface of a cube can divide space into parts of four types:
1) outside the sphere and the cube (there is always 1 such part);
2) inside the sphere and the cube (there can be 0 or 1 such part);
3) outside the sphere but inside the cube (such a part must include at least one three-dimensional corner of the cube; for brevity, we will call such a part a "corner"; the number of them does not exceed the number of vertices of the cube, i.e., 8;
4) outside the cube but inside the sphere (if the sphere and the cube intersect, then the boundary of such a part must include at least one flat face; we will call such a part a "cap"; the number of them does not exceed the number of faces of the cube, i.e., 6).
Thus, the total number of parts cannot exceed
$$
1+1+8+6=16
$$
In Fig. 57, a case of the mutual position of the sphere and the cube is shown, where the number of parts into which both surfaces divide the space is maximal, i.e., 16 (the sphere touches all the edges of the cube).
The minimum number of parts into which a sphere and a cube can divide space is, obviously, 3 (compare the solution of part a)). Therefore, the total number of parts lies between 3 and 16.

Fig. 56.
Fig. 57.
space, is maximal, i.e., 16 (the sphere touches all the edges of the cube).
In Fig. 57a, examples are given where the number of parts is 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 (in parentheses—the number of "corners" \( U \) and the number of "caps" \( Ш \)). We will now prove that the sphere and the surface of the cube cannot divide space into 13, 14, or 15 parts.
The division of space into 13, 14, or 15 parts can only be achieved with the following values of \( (U, Ш): (8,3), (8,4), (8,5), (7,4), (7,5), (7,6), (6,5), (6,6) \), and \( (5,6) \); we will prove that none of these values can be taken by the pair \( (U, Ш) \). Leaving aside the "extreme" values \( (8,3) \) and \( (5,6) \), note that in all other cases \( Ш \geqslant 4 \) and \( U \geqslant 6 \). But if an edge \( AB \) of the cube lies entirely inside the sphere, then the planes of the four faces of the cube converging at vertices \( A \) and \( B \) cut off four spherical segments from the sphere, which together form one part of space inside the sphere and outside the cube; therefore, the number of \( Ш \) "caps," which can be at most 6, cannot exceed 3 in this case. Therefore, when \( Ш \geqslant 4 \), all 12 edges of the cube must intersect the sphere, touch it, or lie outside it, i.e., the mutual position of the sphere and the cube must be covered by the following table:
| Number of edges | Number of "caps" | 5 | 5 | |
| :--- | :---: | :---: | :---: | :---: | :---: | :---: |
| intersecting the sphere | 0 | 1 | 2 | 3 |
| touching the sphere or lying outside it | 12 | 11 | 10 | 9 |
(The number of "caps," which can be at most 6, can decrease only due to the presence of edges of the cube that intersect the sphere or lie inside it.)
The number of edges touching the sphere cannot exceed 6. Indeed, if there were 7 or more, then at least 3 of them would belong to one face of the cube: since if among the four edges bounding each face of the cube, the sphere touched no more than two, the total number of edges of the cube touching the sphere could not exceed \( \frac{1}{2}(2 \cdot 6) = 6 \). (The product \( 2 \cdot 6 \) is divided by 2 because when counting edges "by faces," each edge is counted twice.) But if the sphere touches three edges belonging to one face \( \alpha \) of the cube, then the sphere intersects the plane \( \alpha \) along an inscribed circle in the face \( \alpha \), and the center of the sphere lies on the axis of symmetry of the cube perpendicular to the face \( \alpha \). Moving the center of the sphere along the line \( a \), we see that in this case the pair \( (U, Ш) \) can take the following values: \( (1,1), (1,5), (1,6) \), and \( (8,6) \) (the value \( (8,6) \), corresponding to the maximum number of 16 parts of space, is achieved when the sphere intersects two faces \( \alpha \) and \( \beta \) along inscribed circles in these faces); but none of these values \( (U, Ш) \) coincide with the ones we are interested in. Thus, the values \( (8,4), (8,5), (7,4), (7,5), (7,6), (6,5) \), and \( (6,6) \) of the pair \( (U, Ш) \) are impossible.
The value \( (5,6) \) of the pair \( (U, Ш) \) is impossible because when \( Ш = 6 \), all 12 edges of the cube touch the sphere or lie outside it (see the table above); but in this case, at least 6 edges of the cube lie outside the sphere, and therefore the number \( U \) of "corners" cannot equal 5 (it cannot exceed 2).
Finally, consider the value \( (8,3) \) of the pair \( (U, Ш) \). From \( U = 8 \), it follows that all 12 edges of the cube intersect the sphere or touch it; but since we have established that the number of edges touching the sphere cannot exceed 6, at least 6 edges intersect the sphere. But (we have already used this fact above) the presence of an edge \( AB \) of the cube intersecting the sphere leads to a decrease by one in the total number of \( Ш \) "caps," because in this case, the planes of the adjacent faces \( \alpha \) and \( \beta \) of the cube cut off segments from the sphere, which together form one part of space inside the sphere and outside the cube; therefore, when \( U = 8 \), \( Ш \) must be 2, which proves the impossibility of the case \( (U, Ш) = (8,3) \).
[Note that in part a), in the case of the maximum possible number \( N = 10 \) of parts of the plane, we can, by specifying a square, place the circle in different ways so that \( N \) equals 10. The nature of the case of the maximum possible number
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
49. Let $h_{a}=\beta_{b}=m_{c}$, where $h_{a}=A P, \beta_{b}=B L$ and $m_{c}=C F-$ are the altitude, bisector, and median drawn from three different vertices of some triangle $A B C$. What value can the ratio of the greatest side of triangle $A B C$ to its smallest side have?
|
49. First of all, note that if for triangle \(ABC\) the inequality \(m_{a}b = CA\) holds. This immediately follows from the known formula \(^{2}\) \(m_{a} = \frac{1}{2} \sqrt{2 b^{2} + 2 c^{2} - a^{2}}\), but it can also be proven without calculations. Translate triangle \(ABC\) parallel to vector \(\overline{ED}\) to position \(A' B' C'\) (Fig. 128). Since \(B' D = B E\), by the condition \(B' D = B E > A D\); therefore,
Fig. 128. thus \(B' P > A P\), where \(P\) is the projection of point \(D\) on \(AB\). Since \(A A' = B B'\), then \(B P > A' P\), and consequently,
\[
\frac{a}{2} = B D > A' D = \frac{b}{2}, \quad \text{or} \quad a > b.
\]
Now suppose triangle \(ABC\) is such that \(h_{a} = \beta_{b} = m_{c}\). Since, by the result of problem 48, \(h_{u} = \beta_{b} \geqslant h_{b}\) and \(h_{a} = m_{c} \geqslant h_{c}\), the height \(h_{a}\)
1) This also follows from the fact that in any other arrangement of points \(P, K\), and \(D\), the problem of constructing triangle \(ABC\) from three segments \(h_{a}, \beta_{a}\), and \(m_{n}\) would be unsolvable, as mentioned later (compare with problem 112 from book [17]).
\(^{2}\) See, for example, Adamar [13], p. 124.
is the largest; therefore, from the equality \(h_{a} = m_{c}\) it follows that \(\angle C < 60^{\circ}\) (see problem 50 below). On the other hand, the median \(m_{c}\) is the smallest in triangle \(ABC\), because \(m_{c} = h_{\alpha} \leqslant m_{\alpha}\) and \(m_{c} = \beta_{b} \leqslant m_{b}\) (see problem 48); therefore, by what has just been proven, \(c\) is the largest side of triangle \(ABC\), and \(C\) is its largest angle. Since the sum of the three angles of a triangle is \(180^{\circ} = 3 \cdot 60^{\circ}\), and since \(\angle C \leqslant 60^{\circ}\), all angles of the triangle are \(60^{\circ}\), triangle \(ABC\) is equilateral, and the ratio of its largest side to its smallest side is 1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In space, there are 4 points not lying in the same plane. How many planes can be drawn equidistant from these points?
|
1. Since the four points do not lie in the same plane, the plane equidistant from these points cannot be located on the same side of all of them. Therefore, there are only two possible cases: 1) three points lie on one side of the considered plane, and the fourth point lies on the other side, and 2) two points lie on each side of the plane.
Fig. 27.
Consider the first case. Let points \(A, B\), and \(C\) lie on one side of the plane \(\Pi\), equidistant from points \(A, B, C\), and \(D\), while point \(D\) lies on the other side (Fig. 27). Points \(A, B\), and \(C\) cannot lie on the same line—otherwise, all four points would lie in the same plane. Since the plane \(\Pi\) is equidistant from points \(A, B\), and \(C\), which are located on the same side of it, this plane must be parallel to the plane \(ABC\). For the distance from point \(D\) to this plane to be equal to the distance from it to the three points \(A, B\), and \(C\), the plane \(\Pi\) must pass through the midpoint of the perpendicular \(DP\) dropped from point \(D\) to the plane \(ABC\) (see Fig. 27). Thus, the plane \(\Pi\), equidistant from points \(A, B, C\), and \(D\), with points \(A, B\), and \(C\) on one side and point \(D\) on the other, is uniquely determined.
Similarly, the plane equidistant from the given four points, with only point \(C\) (or point \(B\), or point \(A\)) on one side and the other three points on the other side, can be found. In total, there are four planes equidistant from the given four points such that only one point is on one side of them, and the other three are on the other side.
Consider the second case. Let points \(A\) and \(B\) lie on one side of the plane \(\Pi\), equidistant from points \(A, B, C\), and \(D\), while points \(C\) and \(D\) lie on the other side (Fig. 28). Since the plane \(\Pi\) is equidistant from points \(A\) and \(B\), which lie on the same side of \(\Pi\), it must be parallel to the line \(AB\). Similarly, it can be proven that this plane must be parallel to the line \(CD\). Since points \(A, B, C\), and \(D\) do not lie in the same plane, the lines \(AB\) and \(CD\) must be skew. Draw two parallel planes through the skew lines \(AB\) and \(CD\); it is clear that the plane \(\Pi\) must be parallel to these planes and equidistant from them, i.e., it must pass exactly midway between these planes (see Fig. 28). Thus, there is a unique plane equidistant from points \(A, B, C\), and \(D\) such that points \(A\) and \(B\) lie on one side of it, and points \(C\) and \(D\) lie on the other.
Similarly, there is a unique plane equidistant from our four points such that the point \(A\) and only the point \(C\) (or point \(D\)) lie on the same side, while the other two points (\(B\) and \(D\) or \(B\) and \(C\)) lie on the other side. Therefore, there are three planes equidistant from the given four points such that two of the four points lie on one side of each of them, and the other two lie on the other side.
Thus, the total number of planes equidistant from the given four points in space is \(4 + 3 = 7\). If we consider a triangular pyramid (tetrahedron) with vertices \(A, B, C\), and \(D\),
a)
b)
Fig. 29.
then four of these seven planes will pass parallel to the faces of the pyramid through the midpoints of the corresponding heights (Fig. 29, a), and the remaining three will pass parallel to pairs of opposite edges at equal distances from them (Fig. 29, b).
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How many spheres exist that touch all the faces of the given triangular pyramid $T$?
|
3. The task is to determine how many points (centers of the sought spheres) are equidistant from the four faces of the pyramid.
The geometric locus of points equidistant from the faces of a given dihedral angle is a plane passing through the edge of the dihedral angle and bisecting this angle — the bisector plane of the dihedral angle.
Since two intersecting planes form two pairs of vertical dihedral angles, the geometric locus of points equidistant from two intersecting planes consists of two planes passing through the line of intersection of the first two planes.
The geometric locus of points equidistant from the faces of a trihedral angle is the line of intersection of the bisector planes of the three dihedral angles of the trihedral angle — the bisector line of the trihedral angle.
Since three intersecting planes form four pairs of vertical trihedral angles, the geometric locus of points equidistant from three intersecting planes consists of four lines passing through the point of intersection of the three planes.
Let $\mathrm{II}_{1}, \mathrm{II}_{2}, \mathrm{II}_{3}$, and $\mathrm{II}_{4}$ be the planes of the faces of the pyramid. Consider the trihedral angle of the pyramid formed by the planes $\mathrm{II}_{1}, \mathrm{II}_{2}$, and $\mathrm{II}_{3}$. The geometric locus of points equidistant from the three faces of this angle consists of four lines $\beta_{1}, \beta_{2}, \beta_{3}$, and $\beta_{4}$. Further, the geometric locus of points equidistant from the planes $\mathrm{II}_{1}$ and $\mathrm{II}_{4}$ consists of two planes $B_{1}$ and $B_{2}$. It is clear that each of the points of intersection of one of the lines $\beta_{1}, \beta_{2}, \beta_{3}$, and $\beta_{4}$ with one of the planes $B_{1}$ and $B_{2}$ (and only these points) will be equidistant from the planes $\mathrm{II}_{1}, \mathrm{II}_{2}, \mathrm{II}_{3}$, and $\mathrm{II}_{4}$. Thus, in general, we obtain eight points equidistant from the planes of the faces of the pyramid, and consequently, eight spheres tangent to these faces. It is not difficult to see that out of these eight spheres, one is enclosed inside the pyramid (the inscribed sphere; Fig. 35, a), four are located outside the pyramid, one inside each of its trihedral angles (the "exscribed" spheres; Fig. 35, b), and three are located inside the dihedral angles of the pyramid and inside the angles vertical to the opposite dihedral angles (Fig. 35, c).
a)
b)
c:
Fig. 35.
Note that in special cases, a tetrahedral pyramid may have fewer than eight spheres tangent to the planes of all its faces. For example, a regular tetrahedron has only five such spheres (spheres of only the types shown in Fig. 35, a and b). This is because in some cases, some of the lines $\beta_{1}, \beta_{2}, \beta_{3}$, and $\beta_{4}$ may be parallel to some of the planes $B_{1}$ and $B_{2}$.
Remark. It can be shown that if the sum of the areas of two faces of a triangular pyramid is equal to the sum of the areas of the other two faces, then there are only 7 spheres tangent to the planes of all the faces; if the areas of the faces are pairwise equal, then there are 6 such spheres; finally, if all the faces of the pyramid are equal in area (and therefore equal; see, for example, problem 29 in the book by D. O. Shklyarsky, N. N. Chentsov, and I. M. Yaglom, Selected Problems and Theorems of Elementary Mathematics, part 3, "Mathematical Circle Library," issue 3), then there are only 5 such spheres. See "Elementary Geometry" by J. Hadamard, part 2 (Moscow, Uchpedgiz, 1951), solution to problem 701.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In how many different ways can the faces of a cube be painted using six given colors (each face must be painted entirely with one color), if only those colorings are considered different that cannot be made to coincide by rotating the cube?
|
4. Suppose the faces of a cube are painted green, blue, red, yellow, white, and black. Let's place the cube so that the green face is at the bottom. In this case, the top face can be painted one of the five remaining colors. It is clear that no two colorings, in which the top (i.e., opposite the green) face is painted different colors, can be aligned with each other by rotation. Now let's determine the number of colorings in which the top face is painted a certain color (say, blue); the total number of colorings is five times this number (since the top face can be painted any of the 5 remaining colors).
Choose one of the four colors remaining after removing green and blue (say, red) and place our cube so that the red face is the back face; this can always be achieved by rotating the cube around the vertical axis. We have 3 colors left - yellow, white, and black, with which we need to paint the 3 faces (the front and two side faces). Clearly, none of the resulting colorings can be aligned with each other by rotation - with any rotation, either the bottom face will no longer be green, or the back face will no longer be red. The three faces can be painted with the three colors in six different ways (the front face can be painted any of the three colors, and for each of these colorings, we can choose the color of the left face in two ways).
Therefore, the total number of colorings that cannot be aligned by rotating the cube is $5 \cdot 6=30$.
|
30
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In how many different ways can 30 workers be divided into 3 teams of 10 people each?
|
5. 10 workers, forming the first brigade, can be chosen from thirty in $C_{30}^{10}=\frac{30 \cdot 29 \cdot \ldots \cdot 21}{10!}$ ways. After this, from the remaining 20 workers, 10 workers for the second brigade can be chosen in $C_{20}^{10}=\frac{20 \cdot 19 \cdots 11}{10!}$ ways. By combining each way of forming the first brigade with each way of forming the second brigade, we get a total of $\frac{30 \cdot 29 \cdot \ldots \cdot 11}{(10!)^{2}}=\frac{30!}{(10!)^{3}}$ ways to distribute the workers into three brigades. However, here the distributions that differ only by the numbering of the brigades are counted as different; therefore, the obtained number must be divided by $3!$ — the number of ways to assign three numbers to three brigades. Thus, the desired number of ways is
$$
\frac{30!}{3!(10!)^{3}}=2775498395670
$$
Note. Similarly, it can be concluded that from $n k$ workers, $k$ brigades of $n$ workers each can be formed in $\frac{(n k)!}{(n!)^{k} k!}$ ways.
|
2775498395670
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. The commission consists of 11 people. The materials that the commission works on are stored in a safe. How many locks should the safe have, and how many keys should each member of the commission be provided with, so that access to the safe is possible when a majority of the commission members gather, but not possible if fewer than half of the members gather?
|
7. According to the problem statement, for any five members of the committee, there should be a lock for which the key is absent from all these committee members (but is present with each of the six absent members, since the presence of any of the nine absent members already makes the meeting of the committee possible). Thus, the smallest possible number of locks is equal to the number of ways to choose five members from the 11 members of the committee, i.e., the number of combinations of 11 elements taken 5 at a time:
$$
C_{11}^{5}=\frac{11 \cdot 10 \cdot 9 \cdot 8 \cdot 7}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5}=462
$$
Since each lock should have six keys, the total number of keys will be
$$
462 \cdot 6=2772
$$
Each member of the committee will have
$$
2772: 11=252
$$
keys.
For the conditions stated in the problem to be met, the keys must be distributed in a specific way. Specifically, the six keys to each of the $C_{11}^{5}$ locks should be held by a specific group of six committee members, and for each group of six members, there should be a lock for which the key is held by this group of six members and only by them. Then, a meeting of the committee will be impossible if six (or more) members of the committee are absent.
If the number of committee members were $n$ and it were required that the safe could be opened with the presence of $m$ members, then the number of locks on the safe should be
$$
C_{n}^{m-1}=\frac{n(n-1) \ldots(n-m-2)}{1 \cdot 2 \cdot 3 \ldots(m-1)}
$$
and the number of keys each committee member should have is
$$
\frac{m}{n} C_{n}^{m-1}=\frac{m(n-1) \ldots(n-m-2)}{1.2 \cdot 3 \ldots(m-1)}
$$
The obtained answer indicates that such a method of storing documents is practically unfeasible (even with a relatively small committee, opening the safe would take an entire day).
|
252
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. The numbers from 1 to 1000 are written in a circle. Starting from the first, every 15th number is crossed out (i.e., the numbers $1, 16, 31$, etc.), and during subsequent rounds, already crossed-out numbers are also taken into account. The crossing out continues until it turns out that all the numbers to be crossed out have already been crossed out previously. How many numbers will remain uncrossed out?
|
8. After the first cycle, all numbers that give a remainder of 1 when divided by 15 will be crossed out; the last such number will be 991. The first number to be crossed out during the second cycle will be $991+15-1000=6$; subsequently, during the second cycle, all numbers that give a remainder of 6 when divided by 15 will be crossed out (the last such number is 996). The first number to be crossed out during the third cycle will be $996+15-1000=11$; subsequently, during the third cycle, all numbers that give a remainder of 11 when divided by 15 will be crossed out (the last such number is 986). The first number to be crossed out during the fourth cycle will be $986+15-1000=1$. Since this number has already been crossed out earlier, further counting intervals of 15 numbers will always land on already crossed out numbers, so no new numbers will be crossed out.
Thus, ultimately, all numbers that give a remainder of 1, 6, or 11 when divided by 15, and only these numbers, will be crossed out. However, numbers that give a remainder of 1, 6, or 11 when divided by 15 coincide with all numbers that give a remainder of 1 when divided by 5. There are $\frac{1000}{5}=200$ such numbers among the first 1000 (numbers $1,6,11,16, \ldots, 996=5 \cdot 199+1$). Therefore, $1000-200=$ $=800$ numbers will remain uncrossed.
|
800
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. All numbers from 1 to 10000000000 are written in a row. Which numbers will be more - those in which the digit 1 appears, or those in which 1 does not appear?
|
9. First solution. Let's calculate the number of numbers in our sequence that do not contain the digit 1. Add the number 0 (zero) at the very beginning of this sequence and omit the last number 10000000000; we will get a sequence of $10^{10}$ numbers, containing one more number, in the notation of which the digit 1 does not appear, than the original sequence. Let's agree to prepend as many zeros to all numbers in the obtained sequence that are less than ten digits, so that they become ten-digit. The new sequence will consist of $10^{10}$ ten-digit numbers, starting from 0000000000 and ending with 9999999999. If a number in this sequence does not contain the digit 1, then this means that the first digit in this number is one of the nine digits 0, $2,3,4,5,6,7,8,9$. The second digit of the number must also be one of the same nine digits; combining 9 possible values of the first digit with 9 values of the second, we get a total of $9^{2}$ different possibilities for the first pair of digits. Similarly, for the first three digits of our number, we get $9^{3}$ different possibilities, for the first four digits $9^{4}$ different possibilities, and so on; finally, for the first ten digits, we get $9^{10}$ different possibilities. This means that in the sequence of numbers from 0000000000 to 9999999999, there are $9^{10}$ different numbers that do not contain the digit 1. Therefore, in the sequence of numbers from 1 to 10000000000, such numbers will be
$$
9^{10}-1=3486784401-1=3486784400
$$
and the numbers that contain the digit 1 will be
$$
10000000000-3486784400=6513215600 .
$$
Thus, the numbers that contain the digit 1 will be more.
Second solution. Let's calculate the number of numbers in our sequence that contain the digit 1. Let's agree that a decade means ten consecutive positive integers, starting from a number ending in zero and ending with a number ending in 9; a hundred means a hundred consecutive integers, starting from a number ending in two zeros and ending with a number ending in two nines; a thousand means a thousand consecutive integers, starting from a number ending in three zeros and ending with a number ending in three nines, and so on. To make the first decade, the first hundred, the first thousand, and so on, complete, we will prepend the number 0 to the beginning of our sequence of numbers.
In the first decade, there is a single number that contains the digit 1--this is the number 1. The same number of numbers containing the digit 1 will be included in any other decade of the first hundred, except the second--the second decade (numbers from 10 to 19) consists entirely of numbers containing 1.
Therefore, the first hundred contains
$$
9 \cdot 1+10
$$
numbers that contain the digit 1.
Exactly the same number of numbers that contain the digit 1 are contained in any other hundred of the first thousand, except the second--the second hundred consists entirely of numbers containing 1. Therefore, the first thousand contains
$$
9(9 \cdot 1+10)+100=9^{2}+9 \cdot 10+10^{2}
$$
numbers that contain the digit 1.
In each thousand of the first ten thousand, except the second, there will be the same number of numbers that contain the digit 1, and the second thousand will consist entirely of such numbers. Thus, among the first 10000 numbers, there will be
$$
9\left(9^{2}+9 \cdot 10+10^{2}\right)+1000=9^{3}+9^{2} \cdot 10+9 \cdot 10^{2}+10^{3}
$$
numbers that contain the digit 1.
Continuing to reason in the same way, we can easily show that among the first 10000000000 numbers from 0 to 9999999999, there are
$$
9^{9}+9^{8} \cdot 10+9^{7} \cdot 10^{2}+\ldots+9 \cdot 10^{8}+10^{9}
$$
numbers that contain the digit 1. This sum is easily calculated using the formula for the sum of the terms of a geometric progression:
$$
\begin{aligned}
& 9^{9}+9^{8} \cdot 10+9^{7} \cdot 10^{2}+\ldots+9 \cdot 10^{8}+10^{9}= \\
&= \frac{10^{9} \cdot \frac{10}{9}-9^{9}}{\frac{10}{9}-1}=\frac{\frac{10^{10}}{9}-9^{9}}{\frac{1}{9}}=10^{10}-9^{10}
\end{aligned}
$$
In the sequence from 1 to 10000000000, the numbers containing 1 will be one more, i.e.,
$$
10^{10}-9^{10}+1=6513215600
$$
This result, naturally, coincides with the one obtained in the first solution. It shows that in this sequence, the numbers containing the digit 1 will be more than the numbers that do not contain 1.
|
6513215600
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. All integers from 1 to 222222222 are written in sequence. How many times does the digit 0 appear in the recording of these numbers?
## 2. Factorization of numbers into products and their decomposition into sums
In solving some of the subsequent problems, the following notations prove useful.
The symbol $[x]$ (read as "the integer part of $x$") denotes the greatest integer not exceeding $x$. For example,
$\left[\frac{3}{2}\right]=1, \quad[10.85]=10, \quad[5]=5, \quad[-8.2]=-9$, etc.
(however, we will only need the symbol $[x]$ for positive numbers $x$).
The symbol $(x)$ (read as "the nearest integer to $x$") denotes the integer closest to the number $x$. For example,
$$
(5.4)=5, \quad(8.73)=9, \quad(6)=6, \quad(-2.8)=-3
$$
and so on.
Clearly, $(x)$ will be equal to $[x]$ or $[x]+1$ depending on whether the difference $x - [x]$ is less than or greater than half. In the case where $x - [x] = \frac{1}{2}$, $(x)$ can be taken as either $[x]$ or $[x]+1$; in this case, it is agreed to consider $(x) = [x]$ (however, we will use the symbol $(x)$ only in cases where $x - [x] \neq \frac{1}{2}$, so there will be no ambiguity as to whether to consider $(x)$ equal to $[x]$ or $[x]+1$).
In all subsequent problems where the number $n$ is mentioned in the condition, this number is considered to be a positive integer.
|
10. Obviously, among the first 222222222 integers, there will be 22222222 numbers ending in zero (numbers 10, $20,30, \ldots, 222222220$). Further, among them, there will be 2222222 numbers ending in the digits 00 (numbers $100,200,300, \ldots, 222222200$); 2222222 numbers ending in the digits 01 (numbers 101, 201, 301, ..., 222222201); 2222222 numbers ending in the digits 02; 2222222 numbers ending in the digits 03, and so on, finally, 2222222 numbers ending in the digits 09. Thus, in the sequence of all numbers from 1 to 222222222, the digit 0 will stand in the second-to-last place $2222222+2222222+\ldots+2222222=$ $=10 \cdot 2222222=22222220$ times.
Similarly, among the first 222222222 numbers, there will be 222222 numbers ending in the digits 000; 222222 numbers ending in the digits 001, and so on, finally, 222222 numbers ending in the digits 099. Thus, the digit 0 will stand in the third-to-last place $100 \cdot 222222=22222200$ times. Further, it is shown that the digit 0 will stand in the fourth-to-last place $1000 \cdot 22222=22222000$ times; in the fifth-to-last place $10000 \cdot 2222=22220000$ times; in the sixth-to-last place $100000 \cdot 222=22200000$ times; in the seventh-to-last place $1000000 \cdot 22=22000000$ times; finally, in the eighth-to-last place $10000000 \cdot 2=20000000$ times.
Thus, the digit 0 appears a total of
$22222222+22222220+22222200+22222000+$
$+22220000+22200000+22000000+20000000=$
$=175308642$
times.
|
175308642
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. a) How many integers less than 1000 are not divisible by 5 or 7?
b) How many of these numbers are not divisible by 3, 5, or 7?
|
11. a) There are a total of 999 numbers less than 1000 (numbers $1,2,3, \ldots, 999$). Now, let's strike out those that are divisible by 5; there are $\left[\frac{999}{5}\right]=199$ such numbers (numbers $5,10,15,20, \ldots, 995=199.5$). Next, let's strike out all numbers divisible by 7; there are $\left[\frac{999}{7}\right]=142$ such numbers (numbers 7, $14,21,28, \ldots, 994=142 \cdot 7$). But among the numbers divisible by 7, there are $\left[\frac{993}{35}\right]=28$ numbers that are also divisible by 5 (i.e., divisible by $5.7=35$); these numbers are $35,70,105, \ldots, 980=28.35$. These 28 numbers will be struck out twice (both when striking out numbers divisible by 5 and when striking out numbers divisible by 7). Therefore, a total of $199+142-28=313$ numbers will be struck out. Thus, among the numbers less than 1000, $999-313=686$ numbers will remain unstruck; these are the numbers that are not divisible by 5 or 7.
b) Let's strike out all numbers divisible by 5 and all numbers divisible by 7 again; in this case, we will strike out 313 numbers (problem 11a)). Now, let's strike out all numbers divisible by 3; there are $\left[\frac{999}{3}\right]=333$ such numbers. But among these numbers, all numbers that are also divisible by 5 or 7, i.e., all numbers divisible by 15 or 21, have already been struck out earlier. Among the numbers less than 1000, $\left[\frac{999}{15}\right]=66$ numbers are divisible by 15, and $\left[\frac{999}{21}\right]=47$ numbers are divisible by 21. But $\left[\frac{999}{105}\right]=9$ of these numbers are divisible by both 15 and 21 (105 is the least common multiple of 15 and 21) and, therefore, among the 66 numbers divisible by 15 and the 47 numbers divisible by 21, there are 9 common numbers. Therefore, among the 333 numbers divisible by 3, 104 numbers were already struck out earlier, i.e., in the last strike-out, we will strike out another $333-104=229$ numbers. Thus, the total number of unstruck numbers (i.e., not divisible by 3, 5, or 7) is $686-229=457$.
Note. Reasoning similarly to the solution of problem 11, it is not difficult to show that the number of numbers less than some $N$ and not divisible by any of the pairwise coprime numbers $p_{1}, p_{2}, p_{3}, \ldots, \ldots, p_{n-1}, p_{n}$ is
$$
\begin{aligned}
N-\left[\frac{N}{p_{1}}\right]- & {\left[\frac{N}{p_{2}}\right]-\ldots-\left[\frac{N}{p_{n}}\right]+} \\
& +\left[\frac{N}{p_{1} p_{2}}\right]+\left[\frac{N}{p_{1} p_{3}}\right]+\ldots+\left[\frac{N}{p_{n-1} p_{n}}\right]- \\
& -\left[\frac{N}{p_{1} p_{2} p_{3}}\right]-\ldots+\left[\frac{N}{p_{n-2} p_{n-1} p_{n}}\right]+ \\
& \left.\ldots \ldots \ldots \ldots \ldots \cdots \cdots \cdots \cdots+\frac{N}{p_{1} p_{2} \ldots p_{n}}\right]
\end{aligned}
$$
(see the first solution of problem 78a).
|
457
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12*. How many integers are there that are less than the number 56700000 and coprime with it?
|
12. The problem is very close to the previous one. The factorization of the number 56700000 is $56700000=2^{5} \cdot 3^{4} \cdot 5^{5} \cdot 7$; thus, the problem reduces to determining how many numbers less than 56700000 are not divisible by 2, 3, 5, or 7.
Let's list all numbers from 1 to 56700000. We will strike out all numbers divisible by 2 (their number is $\frac{1}{2} \cdot 56700000=28350000$); all numbers divisible by 3 (their number is $\left.\frac{1}{3} \cdot 56700000=18900000\right)$; all numbers divisible by 5 (their number is $\frac{1}{5} \cdot 56700000=11340000$); all numbers divisible by 7 (their number is $\frac{1}{7} \cdot 56700000=8100000$). The total number of all these numbers is $28350000+18900000+11340000+8100000=$
$=66690000$.
But among these 66690000 numbers, there are: $\frac{1}{2 \cdot 3} \cdot 56700000=9450000$ numbers divisible by 2 and 3; $\frac{1}{2 \cdot 5} \cdot 56700000=5670000$ numbers divisible by 2 and 5; $\frac{1}{2 \cdot 7} \cdot 56700000=4050000$ numbers divisible by 2 and 7; $\frac{1}{3 \cdot 5} \cdot 56700000=3780000$ numbers divisible by 3 and 5; $\frac{1}{3 \cdot 7} \cdot 56700000=2700000$ numbers divisible by 3 and 7; $\frac{1}{5 \cdot 7} \cdot 56700000=1620000$ numbers divisible by 5 and 7.
All these numbers are counted twice in the sum of all numbers divisible by 2, or 3, or 5, or 7. Therefore, the total number of these numbers, equal to
$$
\begin{gathered}
9450000+5670000+4050000+3780000+ \\
+2700000+1620000=27270000
\end{gathered}
$$
must be subtracted from the sum obtained above:
$$
66690000-27270000=39420000
$$
In the difference $66690000-27270000$, obviously, all numbers divisible by only one of the factors 2, 3, 5, and 7, and all numbers divisible by two of these factors (the first are counted once in the minuend; the second are counted twice in the minuend and once in the subtrahend) are included once. Now let's determine how any number divisible by three of these factors, for example, by 2, 3, and 5, is counted in this difference. This number is counted three times in the minuend (among the numbers divisible by 2, among the numbers divisible by 3, and among the numbers divisible by 5) and three times in the subtrahend (among the numbers divisible by 2 and 3, among the numbers divisible by 2 and 5, and among the numbers divisible by 3 and 5). Therefore, all numbers divisible by any three of the four factors 2, 3, 5, and 7 are not counted at all in our difference, and we must add to the difference the total number of all such numbers. The total number of these numbers (not exceeding 56700000) is obviously
$$
\begin{aligned}
& \frac{1}{2 \cdot 3 \cdot 5} \cdot 56700000+\frac{1}{2 \cdot 3 \cdot 7} \cdot 56700000+\frac{1}{2 \cdot 5 \cdot 7} \cdot 56700000+ \\
&+\frac{1}{3 \cdot 5 \cdot 7} \cdot 56700000= \\
&=1890000+1350000+810000+540000=4590000
\end{aligned}
$$
Thus, we get:
$$
66690000-27270000+4590000=44010000
$$
In the expression $66690000-27270000+4590000$, all numbers divisible by one of the factors 2, 3, 5, and 7; by two of these factors; and by three of these factors are counted once. Now let's determine how numbers divisible by 2, 3, 5, and 7 are counted in this expression. They are obviously counted four times in the first term 66690000 (as divisible by 2, 3, 5, and 7); six times in the second term 27270000 (as divisible by 2 and 3; 2 and 5; 2 and 7; 3 and 5; 3 and 7; 5 and 7); and four times in the last term (as divisible by 2, 3, and 5; 2, 3, and 7; 2, 5, and 7; 3, 5, and 7). Therefore, these numbers are counted in our expression $4-6+4=2$ times, and their number, equal to $\frac{1}{2 \cdot 3 \cdot 5 \cdot 7} \cdot 56700000=270000$, must be subtracted:
$66690000-27270000+4590000-270000=43740000$.
Thus, from 1 to 56700000, there are 43740000 numbers divisible by at least one of the factors 2, 3, 5, or 7. Therefore, the number of numbers not divisible by any of these factors (coprime with the number 56700000) is
$$
56700000-43740000=12960000
$$
Note. It can be shown in the same way that if the factorization of the number $N$ into prime factors is
$$
N=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} p_{3}^{\alpha_{3}} \ldots p_{k}^{\alpha_{k}}
$$
then the number $\varphi(N)$ of numbers less than $N$ and coprime with it is
$$
\begin{aligned}
\varphi(N)= & N-\frac{N}{p_{1}}-\frac{N}{p_{2}}-\ldots-\frac{N}{p_{k}}+\frac{N}{p_{1} p_{2}}+\frac{N}{p_{2} p_{3}}+\ldots+\frac{N}{p_{k-1} p_{k}}- \\
& -\frac{N}{p_{1} p_{2} p_{3}}-\ldots-\frac{N}{p_{k-2} p_{k-1} p_{k}}+\ldots+(-1)^{k} \frac{N}{p_{1} p_{2} \ldots p_{k}}= \\
= & N\left(1-\frac{1}{p_{1}}\right)\left(1-\frac{1}{p_{2}}\right)\left(1-\frac{1}{p_{3}}\right) \ldots\left(1-\frac{1}{p_{k}}\right)
\end{aligned}
$$
(see the note to the solution of problem 11b).
|
12960000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. How many positive integers $x$, less than 10000, are there for which the difference $2^{x}-x^{2}$ is not divisible by 7?
|
13. $2^{0}=1$ gives a remainder of $1$ when divided by 7, $2^{1}=2$ gives a remainder of $2$, $2^{2}=4$ gives a remainder of $4$, $2^{3}$ gives a remainder of $1$ again, $2^{4}$ gives a remainder of $2$ again, $2^{5}$ gives a remainder of $4$ again, $2^{6}$ gives a remainder of $1$ for the third time, and so on. Thus, when dividing $2^{x}$ by 7, the remainders can only be the numbers 1, 2, and 4, and these remainders periodically repeat in the following order: 1, 2, 4; 1, 2, 4; 1, 2, 4; ...
Now, let's represent $x$ as $x=7t+s$, where $s<7$. Then the remainders from dividing $x^{2}$ by 7 are the same as the remainders from dividing $s^{2}$ by 7. If $s$ takes the values $0, 1, 2, 3, 4, 5$, and 6, then the remainders from dividing $s^{2}$ by 7 will be the numbers $0, 1, 4, 2, 2, 4$, and 1, respectively. Therefore, the remainders from dividing $x^{2}$ by 7 can only be the numbers $0, 1, 4$, and 2, and these remainders periodically repeat in the following order: $0, 1, 4, 2, 2, 4, 1$. Since the remainders from dividing $2^{x}$ by 7 periodically repeat every 3 values of $x$, and the remainders from dividing $x^{2}$ by 7 periodically repeat every 7 values of $x$, the remainders from dividing $2^{x}-x^{2}$ by 7 will periodically repeat every 21 values of $x$. Let's write out the first 21 remainders from dividing $2^{x}$ and $x^{2}$ by 7 one under the other:
$$
\begin{array}{rrrrrrrrrrrrrrrrrrrrr}
-1 & 2 & 4 & 1 & 2 & 4 & 1 & 2 & 4 & 1 & 2 & 4 & 1 & 2 & 4 & 1 & 2 & 4 & 1 & 2 & 4 \\
0 & 1 & 4 & 2 & 2 & 4 & 1 & 0 & 1 & 4 & 2 & 2 & 4 & 1 & 0 & 1 & 4 & 2 & 2 & 4 & 1 .
\end{array}
$$
From this, we see that the remainders from dividing $2^{x}$ and $x^{2}$ by 7 coincide 6 times (for $x=2, 4, 5, 6, 10, 15$). Therefore, among the numbers $2^{x}-x^{2}$, where $x=0, 1, 2, \ldots, 20$, exactly 6 numbers are divisible by 7 without a remainder.
Since $10000=21 \cdot 476+4$, there are 476 complete intervals of 21 numbers among the numbers less than 10000. Therefore, for $x$ not exceeding $9996=21 \cdot 476$, the number $2^{x}-x^{2}$ is divisible by 7 exactly $476 \cdot 6=2856$ times. The remaining three numbers less than 10000 give remainders of 1, 2, and 3 when divided by 21; therefore, one of these numbers (specifically 9998) gives the 2857th value of $x$ for which $2^{x}-x^{2}$ is divisible by 7 without a remainder. Thus, there are a total of $2856+1=2857$ numbers $x$ less than 10000 for which $2^{x}-x^{2}$ is divisible by 7. For the remaining $9999-2857=7142$ numbers $x$ less than 10000, the expression $2^{x}-x^{2}$ is not divisible by 7.
|
7142
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. How many different pairs of integers $x, y$, lying between 1 and 1000, are there such that $x^{2}+y^{2}$ is divisible by 49?
|
14. If $x^{2}+y^{2}$ is divisible by 49, then $x^{2}+y^{2}$ is also divisible by 7. But $x^{2}$, when divided by 7, can only give remainders of $0, 1, 4$, or 2 (see the solution to problem 13). The remainder from dividing $x^{2}+y^{2}$ by 7 is equal to the sum of the remainders from dividing the numbers $x^{2}$ and $y^{2}$ by 7. But it is easy to check that out of all the sums of any two (the same or different) of the numbers $0, 1, 4$, and 2, only the sum $0+0=0$ is divisible by 7. Therefore, $x^{2}+y^{2}$ is divisible by 7 only when both $x^{2}$ and $y^{2}$ are divisible by 7, i.e., when both $x$ and $y$ are divisible by 7. On the other hand, if $x$ and $y$ are two numbers divisible by 7, then the sum $x^{2}+y^{2}$ is divisible by 49. Thus, the required number is the number of different pairs of positive integers $x$ and $y$ less than 1000 that are divisible by 7.
But $1000=7 \cdot 142+6$, so there are 142 numbers less than 1000 that are multiples of 7. Combining each of the 142 numbers $x$ with each of the 142 numbers $y$, we get a total of $142^{2}$ pairs of $x, y$. 142 of these pairs consist of the same numbers; all the other pairs we counted twice: once as the pair $x, y$ and
the second time as the pair $y, x$. Therefore, the number of different pairs $x, y$ is
$$
\frac{142^{2}-142}{2}+142=\frac{142 \cdot 143}{2}=10153
$$
|
10153
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. In how many ways can a million be factored into three factors? Factorizations that differ only in the order of the factors are considered the same.
|
15. Since a million is equal to $2^{6} \cdot 5^{6}$, any of its divisors has the form $2^{\alpha} \cdot 5^{\beta}$, and the factorization of a million into 3 factors has the form
$$
1000000=\left(2^{\alpha_{1}} \cdot 5^{\beta_{2}}\right)\left(2^{\alpha_{2}} \cdot 5^{\beta_{2}}\right)\left(2^{\alpha_{3}} \cdot 5^{\beta_{3}}\right) ;
$$
here $\alpha_{1}, \alpha_{2}, \alpha_{3} ; \beta_{1}, \beta_{2}, \beta_{3}-$ are non-negative integers satisfying the equations
$$
\alpha_{1}+\alpha_{2}+\alpha_{3}=6, \quad \beta_{1}+\beta_{2}+\beta_{3}=6
$$
Let's count how many such systems of numbers $\alpha_{1}, \alpha_{2}, \alpha_{3}$; $\beta_{1}, \beta_{2}, \beta_{3}$ can be.
If $\alpha_{1}=6$, then $\alpha_{2}$ and $\alpha_{3}$ must be equal to 0; thus, in this case, we have a unique system of numbers $\alpha_{1}, \alpha_{2}, \alpha_{3}$.
If $\alpha_{1}=5$, then there are two systems:
$$
\alpha_{1}=5, \alpha_{2}=1, \alpha_{3}=0 \text { and } \alpha_{1}=5, \alpha_{2}=0, \alpha_{3}=1
$$
If $\alpha_{1}=4$, then there are three systems:
$$
\begin{gathered}
\alpha_{1}=4, \alpha_{2}=2, \alpha_{3}=0 ; \alpha_{1}=4, \alpha_{2}=1, \alpha_{3}=1 \\
\alpha_{1}=4, \alpha_{2}=0, \alpha_{3}=2
\end{gathered}
$$
Similarly, it can be shown that if $\alpha_{1}=3$, there are four systems; if $\alpha_{1}=2$, there are five systems; if $\alpha_{1}=1$, there are six systems, and if $\alpha_{1}=0$, there are seven systems. Therefore, the total number of systems of numbers $\alpha_{1}, \alpha_{2}, \alpha_{3}$ satisfying the equation $\alpha_{1}+\alpha_{2}+\alpha_{3}=6$ is
$$
1+2+3+4+5+6+7=28
$$
Similarly, there are 28 different systems of numbers $\beta_{1}, \beta_{2}$, $\beta_{3}$ satisfying the equation $\beta_{1}+\beta_{2}+\beta_{3}=6$. Since in the factorization of the number 1000000 into three factors, we can combine any triplet of numbers $\alpha_{1}, \alpha_{2}, \alpha_{3}$ with any triplet of numbers $\beta_{1}, \beta_{2}, \beta_{8}$, the total number of factorizations is
$$
28 \cdot 28=784
$$
However, in this count, factorizations that differ only by the order of the factors are considered different, i.e., many factorizations are counted multiple times.
Let's determine how many times each factorization is counted. 1) Only one factorization, namely
$$
10^{8}=\left(2^{2} \cdot 5^{2}\right) \cdot\left(2^{2} \cdot 5^{2}\right) \cdot\left(2^{2} \cdot 5^{2}\right)
$$
is counted once.
2) If in the factorization of $10^{6}$ into three factors, two of them are equal (and the third is different), then such a factorization is counted three times: the factor that is different from the others can stand in the product in the first, second, or third position.
Let's count the number of such factorizations. Suppose the factor that appears twice in the factorization has the form $2^{\alpha} \cdot 5^{\beta}$ (i.e., the factorization has the form $10^{6}=\left(2^{\chi} \cdot 5^{\beta}\right) \cdot\left(2^{\alpha} \cdot 5^{\beta}\right)\left(2^{6-2 \alpha} \cdot 5^{6-2 \beta}\right)$; then $\alpha$ can be $0,1,2$ or $3, \beta$ can also be $0,1,2$ or 3. Since any $\alpha$ can be combined with any $\beta$, the total number of possibilities is $4 \cdot 4=16$. We need to exclude one possibility $\alpha=2, \beta=2$, since in this case we get the factorization
$$
10^{6}=\left(2^{2} \cdot 5^{2}\right) \cdot\left(2^{2} \cdot 5^{2}\right) \cdot\left(2^{2} \cdot 5^{2}\right)
$$
highlighted earlier. Thus, 15 factorizations are counted three times.
3) The remaining factorizations are counted six times. Indeed, if all three factors are different from each other, then the following six factorizations differ only by the order of the factors:
$$
\begin{aligned}
& \left(2^{\alpha_{1}} \cdot 5^{\beta_{1}}\right) \cdot\left(2^{\alpha_{3}} \cdot 5^{\beta_{3}}\right) \cdot\left(2^{\gamma_{3}} \cdot 5^{\beta_{3}}\right) ; \quad\left(2^{\alpha_{1}} \cdot 5^{\beta_{1}}\right) \cdot\left(2^{\pi_{3}} \cdot 5^{\beta_{3}}\right) \cdot\left(2^{\alpha_{3}} \cdot 5^{\beta_{3}}\right) ; \\
& \left(2^{\alpha_{2}} \cdot 5^{\beta_{2}}\right) \cdot\left(2^{\alpha_{1}} \cdot 5^{\beta_{1}}\right) \cdot\left(2^{\alpha_{3}} \cdot 5^{\beta_{3}}\right) ; \quad\left(2^{\alpha_{1}} \cdot 5^{\beta_{3}}\right) \cdot\left(2^{\alpha_{3}} \cdot 5^{\beta_{3}}\right) \cdot\left(2^{\alpha_{1}} \cdot 5^{\beta_{1}}\right) ; \\
& \left(2^{\gamma_{3}} \cdot 5^{\beta_{3}}\right) \cdot\left(2^{\alpha_{1}} \cdot 5^{\beta_{2}}\right) \cdot\left(2^{\alpha_{1}} \cdot 5^{\beta_{2}}\right) ; \quad\left(2^{\alpha_{3}} \cdot 5^{\beta_{3}}\right) \cdot\left(2^{\alpha_{2}} \cdot 5^{\beta_{2}}\right) \cdot\left(2^{z_{1}} \cdot 5^{\beta_{1}}\right) .
\end{aligned}
$$
Therefore, the total number of different factorizations of a million into three factors is:
$$
\begin{aligned}
1+15+\frac{784-15 \cdot 3-1 \cdot 1}{6} & =1+15+\frac{738}{6}= \\
& =1+15+123=139
\end{aligned}
$$
|
139
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. How many different pairs of integers $A, B$ exist for which the least common multiple is 59400000?
|
17. The prime factorization of the number 59400000 is
$$
59400000=2^{6} \cdot 3^{3} \cdot 5^{5} \cdot 11
$$
Therefore, if the least common multiple of two numbers $A$ and $B$ is 59400000, then it must be
$$
A=2^{x_{1}} \cdot 3^{\beta_{1}} \cdot 5 \gamma_{1} \cdot 11^{\delta_{1}}, \quad B=2^{\alpha_{2}} \cdot 3^{\beta_{2}} \cdot 5 \tau_{2} \cdot 11^{\delta_{3}}
$$
In this case, it must be:
$\alpha_{1} \leqslant 6, \alpha_{2} \leqslant 6, \max \left(\alpha_{1}, \alpha_{2}\right)=6 ; \beta_{1} \leqslant 3, \beta_{2} \leqslant 3, \max \left(\beta_{1}, \beta_{2}\right)=3 ;$ $\gamma_{1} \leqslant 5, \gamma_{2} \leqslant 5, \max \left(\gamma_{1}, \gamma_{2}\right)=5 ; \hat{c}_{1} \leqslant 1, \hat{c}_{2} \leqslant 1, \max \left(\hat{c}_{1}, \delta_{2}\right)=1$, where $\max (a, b)$ denotes the maximum of two numbers $a$ and $b$.
These conditions are satisfied by 13 possible pairs of values $\alpha_{1}, \alpha_{2}\left(\alpha_{1}=6, \alpha_{2}=0,1,2,3,4,5 ; \alpha_{1}=0,1,2,3,4,5\right.$, $\left.\alpha_{2}=6 ; \alpha_{1}=\alpha_{2}=6\right) ; 7$ possible pairs of values $\beta_{1}, \beta_{2}\left(\beta_{1}=3\right.$, $\left.\beta_{2}=0,1,2 ; \beta_{1}=0,1,2, \beta_{2}=3 ; \beta_{1}=\beta_{2}=3\right) ; 11$ possible
1) Another example of a multiplicative function of a number $N$ is the Euler function $\varphi(N)$ - the number of numbers less than $N$ and coprime with $N$ (see note to the solution of problem 12).
pairs of values $\gamma_{1}, \gamma_{2}\left(\gamma_{1}=5, \gamma_{2}=0,1,2,3,4 ; \gamma_{1}=0\right.$, $1,2,3,4, \gamma_{2}=5 ; \gamma_{1}=\gamma_{2}=5$ ) and 3 possible pairs of values $\delta_{1}, \delta_{2}\left(\hat{\delta}_{1}=1, \delta_{2}=0 ; \delta_{1}=0, \delta_{2}=1 ; \delta_{1}=\delta_{9}=1\right)$. By combining all these values, we get a total of
$$
13 \cdot 7 \cdot 11 \cdot 3=3003
$$
pairs of numbers $A, B$.
However, in our count, two pairs of numbers that differ only in order are considered different. Therefore, each pair of numbers, having the same least common multiple 59400000, except for the pair $A=B=59400000$, is counted twice. Therefore, the number of essentially different pairs of numbers $A, B$ will be
$$
\frac{3003-1}{2}+1=1502
$$
Note. In the same way, it can be shown that if the prime factorization of a number $N$ is
$$
N=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \ldots p_{k}^{\alpha_{k}}
$$
then the number $m$ of all possible pairs of integers, the least common multiple of which is $N$, can be calculated by the formula
$$
m=\frac{\left(2 x_{1}+1\right)\left(2 x_{2}+1\right) \ldots\left(2 x_{k}+1\right)-1}{2}+1
$$
|
1502
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. Find the coefficients of $x^{17}$ and $x^{18}$ after expanding the brackets and combining like terms in the expression
$$
\left(1+x^{5}+x^{7}\right)^{20}
$$
|
18. Let's repeat 20 times the trinomial $1+x^{3}+x^{7}$ and multiply it according to the usual rules. Each term of the resulting sum will represent a product of 20 factors, each equal to either 1, or $x^{5}$, or $x^{7}$. It is essential that in these products of twenty factors, any of the three expressions can stand in each of the 20 positions: the sum will contain terms that are products of all possible combinations of the specified factors (i.e., the product of 20 ones, the product of 19 ones and one factor $x^{5}$, the product of 19 ones and one factor $x^{7}$, the product of 18 ones, one factor $x^{5}$, and one factor $x^{7}$, and so on), taken in all possible orders (for example, we will have 20 different terms that are the product of 19 ones and $x^{5}$, because the factor $x^{5}$ can stand in such a product in the first, second, third, ..., twentieth position, and all these will be different terms of our sum).
All such products will represent $x$ raised to some power, which is the sum of a certain number of fives and a certain number of sevens. But it is easy to check that the number 18 cannot be represented as the sum of addends taking the values 5 and 7; hence, the term $x^{18}$ will not be present in our sum (the desired coefficient of $x^{18}$ is zero).
The number 17 can be uniquely represented as the sum of fives and sevens: $17=5+5+7$. Therefore, $x^{17}$ will be equal to those terms of our sum that are the product of two factors $x^{5}$, one factor $x^{7}$, and 17 factors 1. We need to determine the number of such products in our sum. The factor $x^{7}$ can stand in any of the 20 positions. Let's assume for definiteness that it stands in the first position. After this, there are still 19 free positions, two of which must be occupied by factors $x^{5}$, and the remaining 17 by ones. If one of the factors $x^{5}$ stands in a certain position, then the second can stand in any of the remaining 18 positions. Thus, we get 18 terms in which the first unoccupied position by $x^{7}$ (i.e., the second) is occupied by $x^{5}$, 18 terms in which the second of these free positions is occupied by $x^{5}$, 18 terms in which the third such position is occupied by $x^{5}$, and so on, finally, 18 terms in which the last (nineteenth) free position is occupied by $x^{5}$. At first glance, it seems that there are 19.18 terms of the required form in which the factor $x^{7}$ stands in the first position. However, in reality, there are half as many. Indeed, in each of these terms, the factors $x^{5}$ stand in two positions (for example, in the $i$-th and $k$-th positions), so in our count, each of these terms is counted twice (in our example, the considered term is counted among the 18 products in which the $i$-th position is occupied by $x^{5}$, and among the 18 products in which the $k$-th position is occupied by $x^{5}$). Therefore, the actual number of terms of the required form in which the factor $x^{7}$ stands in the first position is $\frac{19 \cdot 18}{2}=171$. There will be as many such terms in which $x^{7}$ stands in the second, third, ..., twentieth position. Thus, the total number of such terms, equal to the coefficient of $x^{17}$ in $\left(1+x^{\overline{5}}+x^{7}\right)^{20}$, is $20 \cdot 171=3420$.
|
3420
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. In how many ways can 20 kopecks be exchanged for coins worth 5 kopecks, 2 kopecks, and 1 kopeck?
|
19. Let's list all the ways to change 20 kopecks. In such a change, we can use either four 5-kopeck coins, or three such coins, or two, or one, or none.
There is only one way to change 20 kopecks using four 5-kopeck coins (since four 5-kopeck coins already make 20 kopecks).
If we use three 5-kopeck coins, we need to make up another 5 kopecks with coins of other denominations. This can be done in three ways: take two 2-kopeck coins and one 1-kopeck coin, or one 2-kopeck coin and three 1-kopeck coins, or, finally, no 2-kopeck coins and five 1-kopeck coins.
Thus, we have indicated three more ways to change 20 kopecks.
If we use two 5-kopeck coins, we need to make up another 10 kopecks with 2-kopeck and 1-kopeck coins. This can be done in six ways. We can take:
1) 5 coins of 2 kopecks, 0 coins of 1 kopeck.
2) 4 » 2 » 2 » » 1 »
3) 3 » " 2 » 4 » » 1 »
4) 2 » » 2 » 6 » » 1 »
5) 1 » " 2 » 8 » » 1 »
6) 0 » " 2 » 10 » " 1 » 20 kopecks.
Thus, we have indicated six more ways to change 20 kopecks.
If we use one 5-kopeck coin, we need to make up another 15 kopecks with coins of other denominations. This can be done in the following ways:
1) 7 coins of 2 kopecks, 1 coin of 1 kopeck.
2) 6 " " 2 » 3 » » 1 »

Thus, we have indicated eight more ways to change 20 kopecks.
Finally, if 5-kopeck coins are not used at all in the change, the following ways are possible:
| 1) 10 | coins | of | 2 kopecks, | | coins | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | » | » | 2 " | 2 | " | » | 1 |
| 3) | » | » | 2 » | 4 | " | » | 1 |
| 7 | " | » | 2 » | 6 | » | » | 1 |
| 6 | » | » | 2 » | 8 | » | » | 1 |
| 5 | » | » | 2 » | 10 | » | » | 1 |
| 4 | » | » | 2 " | 12 | » | » | 1 |
| 3 | » | » | 2 " | 14 | » | » | 1 |
| 2 | » | » | 2 " | 16 | » | " | 1 |
| 1 | " | » | 2 " | 18 | » | " | 1 |
| n | » | ” | 2 " | 20 | » | " | 1 |
i.e., 11 more ways.
All the indicated ways of changing are different, and there are no other ways. Therefore, the total number of ways to change 20 kopecks is
$$
1+3+6+8+11=29
$$
|
29
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
22**. In how many ways can you make up a ruble using coins of 1, 2, 5, 10, 20, and 50 kopecks?
|
22. Since from coins of 10, 20, and 50 kopecks, only a whole number of tens of kopecks can be formed, then from 1, 2, and 5 kopeck coins, a whole number of tens of kopecks must also be formed. Therefore, the following cases are possible:
1) The ruble is composed of coins worth 10, 20, and 50 kopecks,
2) Coins worth 10, 20, and 50 kopecks form 90 kopecks.
Let's consider each of these possibilities separately.
1) One ruble can be composed of coins worth 10, 20, and 50 kopecks in the same number of ways as 10 kopecks can be composed of coins worth 1, 2, and 5 kopecks. According to problem 21b), this number is
$$
\left(\frac{(10+4)^{2}}{20}\right)=\left(\frac{196}{20}\right)=(9.8)=10
$$
2) 90 kopecks can be composed of coins worth 10, 20, and 50 kopecks in the same number of ways as 9 kopecks can be composed of coins worth 1, 2, and 5 kopecks, i.e., $\left(\frac{(9+4)^{2}}{20}\right)$ ways. This number is
$$
\left(\frac{169}{20}\right)=(8.45)=8
$$
In this case, we need to form 10 kopecks with coins worth 1, 2, and 5 kopecks. The number of different ways to do this is
$$
\left(\frac{(10+4)^{2}}{20}\right)=\left(\frac{196}{20}\right)=10
$$
Therefore, the total number of different ways to form 90 kopecks with coins worth 10, 20, and 50 kopecks, and 10 kopecks with coins worth 1, 2, and 5 kopecks, is
$8 \cdot 10=80$.
3) By similar reasoning, the total number of different ways is
$$
\begin{aligned}
\left(\frac{(8+4)^{2}}{20}\right) \cdot\left(\frac{(20+4)^{2}}{20}\right) & =\left(\frac{144}{20}\right) \cdot\left(\frac{576}{20}\right)= \\
& =(7.2) \cdot(28.8)=7 \cdot 29=203
\end{aligned}
$$
4) The total number of different ways is
$$
\begin{aligned}
\left(\frac{(7+4)^{2}}{20}\right) \cdot\left(\frac{(30+4)^{2}}{20}\right) & =\left(\frac{121}{20}\right) \cdot\left(\frac{1156}{20}\right)= \\
& =(6.05) \cdot(57.8)=6 \cdot 58=348
\end{aligned}
$$
5) The total number of different ways is
$$
\begin{aligned}
\left(\frac{(6+4)^{2}}{20}\right)\left(\frac{(40+4)^{2}}{20}\right) & =\left(\frac{100}{20}\right) \cdot\left(\frac{1936}{20}\right)= \\
& =(5)(96.8)=5 \cdot 97=485
\end{aligned}
$$
6) The total number of different ways is
$$
\begin{aligned}
\left(\frac{(5+4)^{2}}{20}\right)\left(\frac{(50+4)^{2}}{20}\right) & =\left(\frac{81}{20}\right)\left(\frac{2916}{20}\right)= \\
& =(4.05)(145.8)=4 \cdot 146=584
\end{aligned}
$$
7) The total number of different ways is
$$
\begin{aligned}
\left(\frac{(4+4)^{2}}{20}\right)\left(\frac{(60+4)^{2}}{20}\right) & =\left(\frac{64}{20}\right)\left(\frac{4096}{20}\right)= \\
& =(3.2)(204.8)=3 \cdot 205=615
\end{aligned}
$$
23-24] PROBLEMS IN COMBINATORICS AND PROBABILITY 123
8) The total number of different ways is
$$
\begin{aligned}
\left(\frac{(3+4)^{2}}{20}\right)\left(\frac{(70+4)^{2}}{20}\right) & =\left(\frac{49}{20}\right)\left(\frac{5476}{20}\right)= \\
& =(2.45) \cdot(273.8)=2 \cdot 274=548
\end{aligned}
$$
9) The total number of different ways is
$$
\begin{aligned}
\left(\frac{(2+4)^{2}}{20}\right) \cdot\left(\frac{(80+4)^{2}}{20}\right) & =\left(\frac{36}{20}\right) \cdot\left(\frac{7056}{20}\right)= \\
& =(1.8) \cdot(352.8)=2 \cdot 353=706
\end{aligned}
$$
10) The total number of different ways is
$$
\begin{aligned}
\left(\frac{(1+4)^{2}}{20}\right)\left(\frac{(90+4)^{2}}{20}\right) & =\left(\frac{25}{20}\right)\left(\frac{8836}{20}\right)= \\
& =(1.25)(441.8)=1.442=442
\end{aligned}
$$
11) The total number of all different ways is
$$
\begin{aligned}
\left(\frac{(0+4)^{2}}{20}\right)\left(\frac{(100+4)^{2}}{20}\right) & =\left(\frac{16}{20}\right)\left(\frac{10816}{20}\right)= \\
& =(0.8)(540.8)=1 \cdot 541=541
\end{aligned}
$$
Thus, the final total number of ways to form a ruble with coins worth 1, 2, 5, 10, 20, and 50 kopecks is:
$$
\begin{gathered}
10+80+203+348+485+584+615+ \\
+548+706+442+541=4562
\end{gathered}
$$
|
4562
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
24. How many integer solutions does the inequality
$$
|x|+|y|<100 ?
$$
have? Here, for $x \neq y$, the solutions $x, y$ and $y, x$ should be considered different.
|
24. We need to find the number of pairs of integers \(x, y\) such that \(|x| + |y|\) is 0, 1, 2, 3, ..., or 99. Let's count the number of pairs \(x, y\) for which \(|x| + |y| = k\). Here, \(|x|\) can take \(k + 1\) different values, namely \(0, 1, 2, \ldots, k-1, k\); in this case, \(|y|\) will be \(k, k-1, k-2, \ldots, 1, 0\). If \(|x| = l\) and \(|y| = k - l\), where neither \(l\) nor \(k - l\) is 0, then \(x\) and \(y\) can each take two values differing in sign; thus, we get four different solutions to the equation \(|x| + |y| = k\), namely: \((l, k-l)\),
\((-l, k-l)\), \((l, -k+l)\) and \((-l, k-l)\). If \(l = k\) or \(l = 0\), then we get only two solutions to the equation \(|x| + |y| = k\), namely: \((0, k)\) and \((0, -k)\) or \((k, 0)\) and \((-k, 0)\). Therefore, for \(k \neq 0\), the equation \(|x| + |y| = k\) has \(2 + 4(k-1) + 2 = 4k\) different solutions. If \(k = 0\), then the equation \(|x| + |y| = k\) (i.e., the equation \(|x| + |y| = 0\)) has one unique solution: \(x = 0, y = 0\). Therefore, the number of different integer solutions to the inequality \(|x| + |y| < 100\) is \(1 + 4(1 + 2 + 3 + \ldots + 99) = 1 + 4 \cdot \frac{99 \cdot 100}{2} =\)
\[
= 1 + 19800 = 19801
\]
|
19801
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32. a) What is the maximum number of rooks that can be placed on a chessboard of $n^{2}$ squares so that no two rooks threaten each other? In how many different ways can this be done?
b) What is the minimum number of rooks that can be placed on a chessboard of $n^{2}$ squares so that these rooks threaten all the squares of the board? In how many different ways can this be done?
|
32. a) A chessboard consisting of $n^{2}$ squares (see Fig. 39, where the case $n=8$ is shown) contains $n$ rows and $n$ columns. To ensure that no two rooks placed on this board threaten each other, it is necessary that no two rooks stand on the same row or the same column. It is clear, therefore, that the total number of rooks cannot exceed $n$, and $n$ rooks can be placed so that no two of them threaten each other: for example, by placing these rooks along one of the main diagonals of the chessboard.
Fig. 39.
Now let's determine how many different arrangements of $n$ rooks satisfy our conditions. We will call the first rook the one standing on the first column, the second the one standing on the second column, and so on, up to the $n$-th rook standing on the $n$-th column. The first rook can be placed on any of the $n$ rows, after which the second can be placed on any of the $n-1$ remaining rows (the row occupied by the first rook is excluded, as no two rooks should threaten each other), the third rook on any of the $n-2$ remaining unoccupied rows, and so on, up to the $(n-1)$-th rook, for which two unoccupied rows remain, and the last rook, for which only one unoccupied row remains. By combining $n$ different placements of the first rook with $n-1$ different placements of the second rook, we get $n(n-1)$ possible placements of the first two rooks; similarly, we get $n(n-1)(n-2)$ possible placements of the first three rooks, $n(n-1)(n-2)(n-3)$ placements of the first four rooks, ..., $n(n-1)(n-2) \ldots 2 \cdot 1$ different placements of all $n$ rooks. Therefore, the number of different arrangements is
$$
1 \cdot 2 \cdot 3 \ldots(n-1) n=n!
$$
In particular, for a standard chessboard, where $n=8$, we get:
$$
8!=8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=40320
$$
different arrangements.
b) All the squares of a chessboard consisting of $n^{2}$ squares cannot be under threat if there are fewer than $n$ rooks on the board. Indeed, in this case, there is at least one column without any rook; the $n$ squares of this column cannot all be under threat from the placed rooks, as the number of rooks is less than $n$ and none of them can threaten two squares of the considered column simultaneously; $n$ rooks, satisfying the conditions of the problem, can obviously be placed (see, for example, Fig. 39).
If $n$ rooks, placed on a chessboard consisting of $n^{2}$ squares, threaten all the squares of the board, then either there is one rook on each column of the board or one rook on each row. Indeed, if there were both a column and a row free from rooks, then the square at the intersection of these column and row would not be under threat. The number of ways to place rooks, one on each of the $n$ columns, is $n^{n}$ (the first rook can be placed in $n$ ways on one of the squares of the first column; the second, independently of the first, in $n$ ways on one of the squares of the second column, and so on). The number of ways to place $n$ rooks, one on each of the $n$ rows, is obviously also $n^{n}$. At first glance, it might seem that the total number of arrangements of $n$ rooks, under which they threaten all the squares of the board, is $n^{n}+n^{n}=2 n^{n}$. However, in this count, each arrangement where there is one rook on each column and simultaneously one rook on each row is counted twice. Since the total number of these latter arrangements is $n!$ (see the solution to part a)), the correct answer to the question is $2 n^{n}-n!$.
In particular, for a standard chessboard ($n=8$), we get:
$$
2 \cdot 8^{8}-8!=33514312
$$
different arrangements.
|
33514312
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
47. a) How many different squares, in terms of size or position, consisting of whole cells, can be drawn on a chessboard of 64 cells?
b) The same question for a chessboard of $n^{2}$ cells.
|
47. a) This problem is close to the previous one. The number of all possible squares consisting of $k^{2}$ cells that can be chosen on a chessboard of 64 cells is $(9-k)^{2}$ (see the solution to problem 46 a)). From this, it follows that the number of all squares is $8^{2}+7^{2}+6^{2}+\ldots+1^{2}=$
$$
=64+49+36+25+16+9+4+1=204
$$
b) Similarly to the solution of part a), we conclude that the desired number is
$$
1^{2}+2^{2}+3^{2}+\cdots+n^{2}=\frac{n(n+1)(2 n+1)}{6}
$$
(see, for example, the formula derived in the footnote on page 179; this formula differs from the one we need only by replacing $n$ with $n-1$).
Note. Since by a well-known formula (this formula is not difficult to derive using mathematical induction or prove similarly to the footnote on page $179^{11}$ ))
$$
1^{3}+2^{3}+3^{3}+\ldots+n^{3}=\left(\frac{n(n+1)}{2}\right)^{2}
$$
the results of parts a) and b) can be given the following symmetric form:
The number of different squares consisting of an integer number of cells that can be drawn on an $n^{2}$-cell board is
$$
1^{2}+2^{2}+3^{2}+\ldots+n^{2}
$$
the number of different rectangles consisting of an integer number of cells that can be drawn on an $n^{2}$-cell board is
$$
1^{3}+2^{3}+3^{3}+\ldots+n^{3}
$$
|
204
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
69. What is more likely: to win 3 games out of 4 or 5 games out of 8 against an equally matched opponent?
|
69. The total number of possible outcomes of a sequence of four matches we get by combining a win or loss in the first match with a win or loss in the second, third, and fourth matches. This number is equal to $2^{4}=16$. All these outcomes are equally probable, as the opponents are of equal strength, and for each separate match, the probability of winning is the same for each of the two opponents. Favorable outcomes here are those in which the first of the opponents wins in three out of four cases; the number of such outcomes is obviously 4 (these four cases correspond to losing the first, second, third, or fourth match and winning the rest). Thus, the desired probability is $\frac{4}{16}=\frac{1}{4}$. Similarly, in the case of eight matches, the total number of outcomes is $2^{8}=256$. The number of favorable outcomes here is the number of ways in which five matches can be won out of eight, i.e., it is equal to $C_{8}^{5}=$ $=\frac{8 \cdot 7 \cdot 6}{1 \cdot 2 \cdot 3}=56$. Therefore, the probability of winning five matches out of eight is $\frac{56}{256}=\frac{7}{32}<\frac{1}{4}$.
Answer: winning three matches out of four against an equally strong opponent is more likely than winning five matches out of eight ${ }^{1}$).
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
103*. The bus network of the city, consisting of several (more than two) routes, is organized in such a way that:
$1^{\circ}$ each route has at least three stops,
$2^{\circ}$ from any stop to any other stop, one can travel without transferring, and
$3^{\circ}$ for each pair of routes, there is one (and only one) stop where one can transfer from one of these routes to the other.
a) Prove that each bus route has the same number of stops and that each stop is served by the same number of routes (equal to the number of stops on each route).
b) Find the number of stops on each bus route if the total number of routes in the city is 57.
|
103. a) Let \( n \) be the number of stops on one of the bus routes in the city. We need to prove that in this case, each route will have exactly \( n \) stops and that exactly 2 routes will pass through each stop.
Let's denote the route with \( n \) stops by \( a \), and the stops on this route by \( A_{1}, A_{2}, \ldots, A_{n} \). Consider an arbitrary bus stop \( B \) located outside the route \( a \) (Fig. 92). According to condition \( 2^{\circ} \), from stop \( B \) one can reach each of the \( n \) stops \( A_{1}, A_{2}, \ldots, A_{n} \) by one of the routes. By condition \( 3^{\circ} \), each of the routes passing through \( B \) must pass through one of the stops \( A_{1}, A_{2}, \ldots, A_{n} \) (otherwise, it would be impossible to transfer to route \( a \) from this route), and only through one of them (otherwise, it would be possible to transfer to route \( a \) from this route at two stops), and no two routes passing through \( B \) pass through the same stop on route \( a \) (otherwise, it would be possible to transfer from one of these routes to another at two stops: at stop \( B \) and at the stop where they meet route \( a \)). Therefore, the number of routes passing through stop \( B \) is the same as the number of stops on route \( a \), i.e., exactly \( n \) routes.
Now consider an arbitrary route \( c \) different from \( a \) (Fig. 93). According to condition \( 1^{\circ} \), route \( c \) has at least three stops, and by condition \( 3^{\circ} \), one of these stops is also a stop on route \( a \). Outside route \( c \), there are obviously \( n-1 \) stops of route \( a \); let's show that there is at least one more stop outside \( c \) that does not lie on \( a \). Indeed, let \( A_{1} \) be one of the \( n-1 \) stops of route \( a \) located outside \( c \), and let \( C_{1} \) be one of the stops of route \( c \) located outside \( a \) (there are at least 2 such stops). By condition \( 2^{\circ} \), there is a bus route \( b \) passing through stops \( A_{1} \) and \( C_{1} \), and by condition \( 3^{\circ} \), this route has at least one more stop \( B \) outside \( c \) and outside \( a \).
We know that exactly \( n \) routes pass through each bus stop located outside \( a \); this applies, in particular, to stop \( B \). Each of the \( n \) routes passing through \( B \) intersects route \( c \) at exactly one stop by condition \( 3^{\circ} \); furthermore, by condition \( 2^{\circ} \), at least one route passing through \( B \) also passes through each stop of route \( c \). Therefore, the number of stops on route \( c \) is equal to the number of routes passing through \( B \), i.e., \( n \). Thus, we have proved that each bus route in the city has the same number \( n \) of stops.
It remains to prove that exactly \( n \) routes pass through each of the stops \( A_{1}, A_{2}, \ldots, A_{n} \) on route \( a \). To do this, it is sufficient to show that for any of these stops, there is a route that does not pass through this stop: indeed, this route, like any other, will have \( n \) stops, and we already know that exactly \( n \) routes pass through any stop located outside a route with \( n \) stops (see the proof at the beginning of the solution that \( n \) routes pass through \( B \)). Since the total number of routes is at least two, there is another route \( b \) besides \( a \) that, by condition \( 3^{\circ} \), intersects route \( a \) at exactly one stop. Let this stop be \( A_{1} \); then the stops \( A_{2}, A_{3}, \ldots, A_{n} \) will be located outside \( b \) and, therefore, exactly \( n \) routes will pass through them. Furthermore, on \( b \) there are other stops besides \( A_{1} \) (at least two); let \( B \) be one of these stops. In this case, the route passing through \( B \) and \( A_{2} \) (such a route exists by \( 2^{\circ} \)) will not pass through \( A_{1} \); therefore, there is at least one route outside \( A_{1} \) and exactly \( n \) routes pass through \( A_{1} \). Thus, the problem is solved.
b) By the result of part a), in this case, each route has the same number \( n \) of stops, and exactly \( n \) routes pass through each stop. Let \( a \) be one of the routes; through each of the \( n \) stops of this route, besides \( a \), \( n-1 \) other routes pass. From condition \( 3^{\circ} \), it easily follows that no two of the \( n(n-1) \) routes obtained in this way coincide with each other and that each of the routes different from \( a \) is among these \( n(n-1) \) routes (see the solution of part a)). Thus, the total number of bus routes in the city (including \( a \)) is \( n(n-1)+1 \). From this, we obtain the quadratic equation for determining \( n \):
\[
\begin{aligned}
n(n-1)+1 & =57 \\
n^{2}-n-56 & =0 ; \\
n & =8
\end{aligned}
\]
(the second root of the equation \( n=-7 \) is, of course, not suitable).
|
8
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1.2. Given a cube with an edge of 1. Find the angle and distance between the skew diagonals of two of its adjacent faces.
|
1.2. Consider the diagonals $A B_{1}$ and $B D$ of the cube $A B C D A_{1} B_{1} C_{1} D_{1}$. Since $B_{1} D_{1} \| B D$, the angle between the diagonals $A B_{1}$ and $B D$ is equal to the angle $A B_{1} D_{1}$. But the triangle $A B_{1} D_{1}$ is equilateral, so $\angle A B_{1} D_{1}=60^{\circ}$.
It is easy to check that the line $B D$ is perpendicular to the plane $A C A_{1} C_{1}$; therefore, when projected onto this plane, it passes through the midpoint $M$ of the segment $A C$. Similarly, the point $B_{1}$ is projected onto the midpoint $N$ of the segment $A_{1} C_{1}$. Thus, the distance between the lines $A B_{1}$ and $B D$ is equal to the distance from the point $A M$ to the line $A N$. If the legs of a right triangle are $a$ and $b$, and its hypotenuse is $c$, then the distance from the vertex of the right angle to the hypotenuse is $a b / c$. In the right triangle $A M N$, the legs are 1 and $1 / \sqrt{2}$, so its hypotenuse is $\sqrt{3 / 2}$, and the desired distance is $1 / \sqrt{ } \sqrt{3}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.10. At the base of a regular triangular prism lies a triangle $ABC$ with side $a$. Points $A_{1}, B_{1}$, and $C_{1}$ are taken on the lateral edges, the distances from which to the plane of the base are $a / 2$, $a$, and $3 a / 2$. Find the angle between the planes $ABC$ and $A_{1} B_{1} C_{1}$.
## § 3. Lines forming equal angles with lines and planes
|
1.10. Let $O$ be the point of intersection of the lines $A B$ and $A_{1} B_{1}$, $M$ be the point of intersection of the lines $A C$ and $A_{1} C_{1}$. First, we will prove that $M O \perp O A$. For this, we will take points $B_{2}$ and $C_{2}$ on the segments $B B_{1}$ and $C C_{1}$ such that $B B_{3}=C C_{2}=A A_{1}$. It is clear that $M A: A A_{1}=$ $=A C: C_{1} C_{2}=1$ and $O A: A A_{1}=A B: B_{1} B_{2}=2$. Therefore, $M A: O A=1: 2$. Moreover, $\angle M A O=60^{\circ}$, which means $\angle O M A=90^{\circ}$. Therefore, the plane $A M A_{i}$ is perpendicular to the line $M O$, along which the planes $A B C$ and $A_{1} B_{1} C_{1}$ intersect. Hence, the angle between these planes is equal to the angle $A M A_{1}$, which is $45^{\circ}$.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.28. Through the vertex $A$ of a right circular cone, a section of maximum area is drawn. Its area is twice the area of the section passing through the axis of the cone. Find the angle at the vertex of the axial section of the cone.
|
2.28. Consider an arbitrary section passing through the vertex $A$. This section is a triangle $A B C$, and its sides $A B$ and $A C$ are the generators of the cone, i.e., they have a constant length. Therefore, the area of the section is proportional to the sine of the angle $B A C$. The angle $B A C$ varies from $0^{\circ}$ to $\varphi$,
where $\varphi$ is the angle at the vertex of the axial section of the cone. If $\varphi \leqslant 90^{\circ}$, then the axial section has the maximum area, and if $\varphi > 90^{\circ}$, then the section with a right angle at the vertex $A$ has the maximum area. Thus, from the problem statement, it follows that $\boldsymbol{\operatorname { s i n }} \varphi=0.5$ and $\varphi > 90^{\circ}$, i.e., $\varphi=120^{\circ}$.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.11. The centers of three spheres, with radii of 3, 4, and 6, are located at the vertices of an equilateral triangle with a side length of 11. How many planes exist that are tangent to all three spheres simultaneously?
## § 3. Two intersecting circles lie on the same sphere
|
4.11. Consider a plane tangent to all three given spheres, and draw a plane through the center of the sphere of radius 3 parallel to it. The resulting plane is tangent to the spheres of radii $4 \pm 3$ and $6 \pm 3$, concentric with the spheres of radii 4 and 6. When the signs of the number 3 are the same, the tangency is external, and when they are different, the tangency is internal. It is also clear that for each plane tangent to all spheres, the plane symmetric to it with respect to the plane passing through the centers of the spheres is also tangent to all spheres.
To determine whether there exists a plane passing through a given point and tangent to two given spheres, we can use the result of problem 12.11. In all cases except for the internal tangency with spheres of radii 1 and 9, the tangent planes exist (see Fig. 36). We will prove that there is no plane tangent internally to the spheres of radii 1 and 9 with centers $B$ and $C$ and passing through the point $A$. Let $\alpha$ be the angle between the line $A B$ and the tangent from $A$ to the sphere with center $B$, and $\beta$ be the angle between the line $A C$ and the tangent from $A$ to the sphere with center $C$. It is sufficient to check that $\alpha + \beta > 60^{\circ}$, i.e., $\cos (\alpha + \beta) < 1 / 2$. Since $\sin \alpha = 1 / 11$ and $\sin \beta = 9 / 11$, we have $\cos \alpha = \sqrt{120} / 11$, $\cos \beta = \sqrt{40} / 11$. Then $\cos (\alpha + \beta) = (40 \sqrt{3} - 9) / 121$. Thus, the inequality $\cos (\alpha + \beta) < 1 / 2$ is equivalent to the inequality $80 \sqrt{3} < 139$; the latter inequality is verified by squaring.
In the end, we find that there are 3 pairs of tangent planes.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.19. Chord $A B$ of a sphere with radius 1 has a length of 1 and is positioned at an angle of $60^{\circ}$ to the diameter $C D$ of this sphere. It is known that $A C=\sqrt{2}$ and $A C<B C$. Find the length of the segment $B D$.
|
4.19. Let $O$ be the center of the sphere. Take a point $E$ such that $\overrightarrow{C E}=\overrightarrow{A B}$. Since $\angle O C E=60^{\circ}$ and $C E=1=O C$, then $O E=1$. Point $O$ is equidistant from all vertices of the parallelogram $A B E C$, so $A B E C$ is a rectangle and the projection $O_{1}$ of point $O$ onto the plane of this rectangle coincides with its center, i.e., with the midpoint of segment $B C$. Segment $O O_{1}$ is the midline of triangle $C B D$, therefore $B D=20 O_{1}=2 \sqrt{O C^{2}-B C^{2} / 4} \Rightarrow$ $=2 \sqrt{1-\left(A B^{2}+A C^{2}\right) / 4}=1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.21. In the tetrahedron \(ABCD\), the plane angles at vertex \(A\) are right angles, and \(AB = AC + AD\). Prove that the sum of the plane angles at vertex \(B\) is \(90^\circ\).
|
6.21. Let's take points $P$ and $R$ on rays $A C$ and $A D$ such that $A P = A R = A B$, and consider the square $A P Q R$. It is clear that $\triangle A B C = \triangle R Q D$ and $\triangle A B D = \triangle P Q C$, and therefore, $\triangle B C D = \triangle Q D C$. Thus, the sum of the planar angles at vertex $B$ is $\angle P Q C + \angle C Q D + \angle D Q R = \angle P Q R = 90^{\circ}$.
|
90
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
6.35. a) Prove that the sum of the cosines of the dihedral angles of a regular tetrahedron is 2.
b) The sum of the plane angles of a trihedral angle is \(180^{\circ}\). Find the sum of the cosines of its dihedral angles.
## § 5. Orthocentric Tetrahedron
Definition. A tetrahedron is called orthocentric if all its altitudes (or their extensions) intersect at one point.
|
6.35. a) Let $\mathbf{e}_{1}, \mathbf{e}_{2}, \mathbf{e}_{3}$ and $\mathbf{e}_{4}$ be unit vectors, non-perpendicular to the faces and directed outward. Since the areas of all faces are equal, then $\mathbf{e}_{1}+\mathbf{e}_{2}+\mathbf{e}_{3}+\mathbf{e}_{4}=0$ (see problem 7.19). Therefore, $0=\left|e_{1}+\mathbf{e}_{2}+\mathbf{e}_{3}+\mathbf{e}_{4}\right|^{2}=$ $=4+2 \sum\left(\mathrm{e}_{i}, \mathbf{e}_{j}\right)$. It remains to note that the scalar product $\left(\mathrm{e}_{i}, \mathrm{e}_{j}\right)$ is equal to $-\cos \varphi_{i j}$, where $\varphi_{i j}$ is the dihedral angle between the faces numbered $i$ and $j$.
b) Take an arbitrary point $A$ on one edge of the given trihedral angle with vertex $S$ and draw segments $A B$ and $A C$ to intersect the other edges such that $\angle S A B=$ $=\angle A S C$ and $\angle S A C=\angle A S B$. Then $\triangle S C A=\triangle A B S$. Since the sum of the angles of triangle $A C S$ is equal to the sum of the planar angles at vertex $S$, then $\angle S C A=\angle C S B$. Therefore, $\triangle S C A=$ $=\triangle C S B$, which means the tetrahedron $A B C S$ is equifacial. According to problem a), the sum of the cosines of the dihedral angles at the edges of this tetrahedron is 2, and this sum is twice the sum of the cosines of the dihedral angles of the given trihedral angle.
|
2
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
7.37. What is the maximum number of planes of symmetry that a spatial figure consisting of three pairwise non-parallel lines can have?
Symmetry with respect to a line $l$ is a transformation of space that maps a point $X$ to a point $X^{\prime}$ such that the line $l$ passes through the midpoint of the segment $X X^{\prime}$ and is perpendicular to it. This transformation is also called axial symmetry, and $l$ is called the axis of symmetry:
|
7.37. Let $P$ be a plane of symmetry of a figure consisting of three pairwise non-parallel lines. There are only two possible cases: 1) each given line is symmetric relative to $P$; 2) one line is symmetric relative to $P$, and the other two lines are symmetric to each other.
In the first case, either one line is perpendicular to $P$, and the other two belong to $P$, or all three lines belong to $P$. Thus, the plane $P$ is defined by some pair of the given lines. Therefore, the number of planes of symmetry of this type is no more than 3.
In the second case, the plane $P$ passes through the bisector of the angle between two given lines and is perpendicular to the plane containing these lines. For each pair of lines, there are exactly 2 such planes, so the number of planes of symmetry of this type is no more than 6.
Thus, the total number of planes of symmetry is no more than 9. Moreover, a figure consisting of three pairwise perpendicular lines passing through one point has exactly 9 planes of symmetry.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.26. a) How many pairwise non-equal spatial quadrilaterals exist with one and the same set of side vectors?
b) Prove that the volumes of all tetrahedra defined by these spatial quadrilaterals are equal.
|
8.26. a) We fix one of the vectors of the sides. It can be followed by any of the three remaining vectors, and then by any of the two remaining ones. Therefore, there are exactly 6 different quadrilaterals.
b) Let $\mathbf{a}, \mathbf{b}, \mathbf{c}$, and $\mathbf{d}$ be the given vectors of the sides. Consider the parallelepiped defined by the vectors $\mathbf{a}$, $\mathbf{b}$, and $\mathbf{c}$ (Fig. 61); its diagonal is the vector $\mathbf{d}$. A simple enumeration shows that all 6 different quadrilaterals are among the quadrilaterals whose sides are the edges of this parallelepiped and its diagonal $\mathbf{d}$ (it is convenient to fix the vector $\mathbf{d}$ during enumeration). The volume of each corresponding tetrahedron is $1/6$ of the volume of the parallelepiped.
|
6
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
9.9. a) Prove that it is possible to choose 8 vertices of a dodecahedron such that they are the vertices of a cube. How many ways can this be done?
b) Prove that it is possible to choose 4 vertices of a dodecahedron such that they are the vertices of a regular tetrahedron.
|
9.9. a) From the solution to problem 9.2, it is clear that there exists a cube whose vertices are located at the vertices of the dodecahedron. Moreover, one edge of the cube is located on each face of the dodecahedron. It is also clear that choosing any of the five diagonals of a certain face of the dodecahedron as an edge of the cube uniquely determines the entire cube. Therefore, there are 5 different cubes with vertices at the vertices of the dodecahedron.
b) By placing the cube such that its vertices are located at the vertices of the dodecahedron, it is then possible to place a regular tetrahedron such that its vertices are located at the vertices of that cube.
|
5
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
11.18. The height of a regular quadrilateral prism $A B C D A_{1} B_{1} C_{1} D_{1}$ is half the length of the side of the base. Find the maximum value of the angle $A_{1} M C_{1}$, where $M$ is a point on the edge $A B$.
|
11.18. Let $A A_{1}=1, A M=x$. Introduce a coordinate system, the axes of which are parallel to the edges of the prism. The vectors $\overrightarrow{M A}_{\text {}}$ and $\overrightarrow{M C}_{1}$ have coordinates $(0,1,-x)$ and ( $2,1,2-x$ ); their scalar product is equal to $1-2 x+x^{2}=(1-x)^{2} \geqslant 0$. Therefore, $\angle A_{1} M C_{1} \leqslant 90^{\circ}$; when $x=1$ this angle is $90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15.22. What is the smallest number of tetrahedra into which a cube can be cut?
|
15.22. If a tetrahedron \(A^{\prime} B C^{\prime} D\) is cut out from the cube \(A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}\), the remaining part of the cube splits into 4 tetrahedra, i.e., the cube can be cut into 5 tetrahedra.
We will prove that the cube cannot be cut into fewer than 5 tetrahedra. The face \(A B C D\) cannot be a face of the tetrahedra into which the cube is divided, so at least two tetrahedra adjoin it. Consider all tetrahedra adjacent to the face \(A B C D\). Their heights dropped onto this face do not exceed \(a\), where \(a\) is the edge of the cube, and the sum of the areas of their faces lying on \(A B C D\) is equal to \(a^{2}\). Therefore, the sum of their volumes does not exceed \(a^{3} / 3\). Since the faces of one tetrahedron cannot lie on opposite faces of the cube, at least 4 tetrahedra adjoin the faces \(A B C D\) and \(A^{\prime} B^{\prime} C^{\prime} D^{\prime}\), and the sum of their volumes does not exceed \(2 a^{3} / 3 < a^{3}\). Therefore, there is still one more tetrahedron in the partition.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15.26. Into how many parts do the planes of the faces divide the space a) of a cube; b) of a tetrahedron?
|
15.26. The planes of the faces of both polyhedra intersect only along the lines containing their edges. Therefore, the space divided into parts, into which the space is split, has a common point with the polyhedron. Moreover, to each vertex, each edge, and each face, one can correspond exactly one adjacent part to it, and these will exhaust all parts, except for the interior of the polyhedron. Thus, the required number is $1+\mathrm{B}+$ $+\Gamma+P$. For a cube, it is $1+8+6+12=27$, and for a tetrahedron, it is $1+4+4+6=15$.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15.32. A plane intersects the lower base of a cylinder along its diameter and has only one common point with the upper base. Prove that the area of the cut-off part of the lateral surface of the cylinder is equal to the area of its axial section.
|
15.32. Let 0 be the center of the lower base of the cylinder; $AB$ - the diameter along which the plane intersects the base; $\alpha$ - the angle between the base and the intersecting plane; $r$ - the radius of the cylinder. Consider an arbitrary generatrix $XY$ of the cylinder, having a common point $Z$ with the intersecting plane (point $X$ lies on the lower base). If $\angle AOX = \varphi$, then the distance from point $X$ to the line $AB$ is $r \sin \varphi$. Therefore, $XZ = r \sin \varphi \operatorname{tg} \alpha$. It is also clear that $r \operatorname{tg} \alpha = h$, where $h$ is the height of the cylinder.
268
Unfold the surface of the cylinder onto a plane tangent to it at point $A$. Introduce a coordinate system on this plane, choosing point $A$ as the origin, and directing the $Oy$ axis upwards, parallel to the axis of the cylinder. Point $X$ transitions to point $(r \varphi, 0)$ upon unfolding, and point $Z$ transitions to point $(r \varphi, h \sin \varphi)$. Thus, the unfolded surface of the section is bounded by the $Ox$ axis and the graph of the function $y = h \sin (x / r)$ (Fig. 112). Its area is
$$
\int_{0}^{\pi r} h \sin (x / r) d x = \left.(-h r \cos (x / r))\right|_{0} ^{\pi r} = 2 h r
$$
It remains to note that the area of the axial section of the cylinder is also equal to $2 h r$.
|
2
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
15.34. In space, 4 points are given, not lying in the same plane. How many different parallelepipeds exist for which these points serve as vertices?
|
15.34. Consider a parallelepiped for which the given points are vertices, and mark its edges connecting these points. Let \( n \) be the maximum number of marked edges of this parallelepiped emanating from one vertex; the number \( n \) can vary from 0 to 3. A simple enumeration shows that only the variants depicted in Fig. 113 are possible. First, any of the four points can be the first, the second can be any of the remaining three, and so on, i.e., the 4 points can be numbered in 24 different ways. After numbering the given points, the parallelepiped in each case is uniquely restored, so we need to determine which numberings lead to the same parallelepiped.
a) \( n=0 \)
\( \delta \quad n=2 \)
b) \( n=2 \)
\( 2 n=3 \)
Fig. 113
a) The parallelepiped in case a) does not depend on the numbering.
b) Numberings \( 1,2,3,4 \) and \( 4,3,2,1 \) lead to the same parallelepiped, i.e., there are 12 different parallelepipeds in total.
c) Numberings \( 1,2,3,4 \) and \( 1,4,3,2 \) lead to the same parallelepiped, i.e., there are 12 different parallelepipeds in total.
d) The parallelepiped depends only on the choice of the first point, i.e., there are 4 different parallelepipeds in total.
In the end, we get that there are \( 1 + 12 + 12 + 4 = 29 \) different parallelepipeds.
Let a sphere \( S \) with center \( O \) and radius \( R \) be given in space. Inversion with respect to the sphere \( S \) is a transformation that maps any point \( A \), different from \( O \), to a point \( A^{*} \) lying on the ray \( O A \) at a distance \( O A^{*} = R^{2} / O A \) from the point \( O \). Inversion with respect to \( S \) will also be called inversion with center \( O \) and power \( R^{2} \).
Throughout this chapter, the image of a point \( A \) under inversion is denoted by \( A^{*} \).
|
29
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16.16. Given three pairwise tangent spheres $\Sigma_{1}$, $\Sigma_{2}$, $\Sigma_{3}$ and a set of spheres $S_{1}, S_{2}, \ldots, S_{n}$, such that each sphere $S_{i}$ is tangent to all three spheres $\Sigma_{1}$, $\Sigma_{2}$, $\Sigma_{3}$, as well as to the spheres $S_{i-1}$ and $S_{i+1}$ (it is meant that $S_{0}=S_{n}$ and $S_{n+1}=$ $=S_{1}$). Prove that if all points of tangency of the spheres are pairwise distinct and $n>2$, then $n=6$.
|
16.16. Consider the inversion with the center at the point of tangency of spheres $\Sigma_{1}$ and $\Sigma_{2}$. In this case, they transform into a pair of parallel planes, and the images of all other spheres touch these planes, and therefore their radii are equal. Thus, in a section by a plane equidistant from these parallel planes, we obtain what is shown in Fig. 117.
|
6
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
61. Determine the remainder of the division by 7 of the number
$$
3^{100}
$$
The 10-arithmetic and 7-arithmetic we have discussed are special cases of residue arithmetic modulo $m$, or $m$-arithmetic. Let $m$ be any positive integer. The elements of $m$-arithmetic are the numbers $0,1,2, \ldots, m-1$. Addition and multiplication in $m$-arithmetic are defined as follows: to add (or multiply) two numbers, one must take the remainder of the division by $m$ of their ordinary sum (respectively product).
|
61. Let's compute $3^{100}$ in 7-arithmetic:
$$
3^{2}=2,3^{8}=6,3^{4}=4,3^{5}=5,3^{6}=1
$$
Therefore,
$$
3^{100}=3^{6 \cdot 16+4}=\left(3^{6}\right)^{16} \cdot 3^{4}=3^{4} \Rightarrow 4
$$
$14^{*}$
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
112. Make sure that the last digits of the numbers in the Fibonacci sequence $^{\circ}$ repeat periodically. What is the length of the period?
Ensure that the last digits of the numbers in the Fibonacci sequence $^{\circ}$ repeat periodically. What is the length of the period?
|
112. The last digits of the Fibonacci sequence $\varnothing^{0}$ themselves form a Fibonacci sequence in the sense of 10-arithmetic (sequence $\Phi_{10}^{0}$).
Let's write out the terms of this sequence:
$0,1,1,2,3,5,8,3,1,4,5,9,4,3,7$, $0,7,7,4,1,5,6,1,7,8,5,3,8,1,9$, $0,9,9,8,7,5,2,7,9,6,5,1,6,7,3$, $0,3,3,6,9,5,4,9,3,2,5,7,2,9,1$, $0,1,1,2,3,5, \ldots$
We notice that $c_{60}=0, c_{61}=1$. Therefore, if we discard the first 60 terms $\left(c_{0}, c_{1}, c_{2}, \ldots, c_{60}\right)$ of the sequence, we are left with a Fibonacci sequence starting with the numbers 0,1, i.e., the sequence $\Phi_{10}^{0}$ again. This means that $c_{62}=c_{2}, c_{63}=c_{3}, \ldots, c_{60+k}=$ $=c_{k}, \ldots$, i.e., the sequence $\Phi_{10}^{0}$ is periodic with a period length of 60.
|
60
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
117. Let three elements $x, y, z$ of the circular sequence $\breve{\Phi}_{m}$ be arranged such that the distance between $x$ and $y$ is equal to the distance between $y$ and $z$ (Fig. 54). Prove that if $x=y=0$, then $z=0$.
|
117. The number $y=0$ is at an equal distance from $x$ and $z$. Therefore, based on problem 116, either $x+z=0$ or $x-z=0$. Since $x=0$, in both cases $z=0$,
|
0
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
120. Prove that if a circular sequence without repetitions $\Phi_{m}$ contains zero and consists of an odd number of elements, then the number of its elements is three.
|
120. If the circular sequence $\breve{\Phi}_{m}$ contains zero and consists of an odd number of terms, then there will be a pair of adjacent elements $x, y$ located at the same distance from zero (Fig. 143). According to problem 116, either
Fig. 143.
Fig. 144.
$x+y=0$, or $x-y=0$ and, therefore, one of the elements of the sequence adjacent to the pair $x, y$ is equal to zero. By problem 117, the second element adjacent to this pair is also equal to zero. From this, it follows that $x=y$, and since the sequence in question is a sequence without repetitions, it has the form shown in Fig. 144.
|
3
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
191. The following experiment is conducted. Two urns that look identical are placed in a room. The left one contains $a$ balls, and the right one contains $b$ balls. People enter the room one by one, and each person moves a ball from the left urn to the right or from the right urn to the left. It is assumed that the probability of a ball being moved from the left urn to the right is the same as the probability of a ball being moved from the right urn to the left, which is $\frac{1}{2}$. The experiment continues until one of the urns is empty. What is the probability that the left urn will be empty? What is the probability that the right urn will be empty? What is the probability that the experiment will never end?
Fig. 63.
|
191. We will represent the number of balls in the left urn using a chip placed on a number line. At the initial
1) A. P. Kiselev, Algebra, Part 2, 23rd edition, Uchpedgiz, M., 1946, p. 78.
18 Law. Zzya. E. Dynkin and V. Uspenskii
moment, the chip is located at point $a$ (Fig. 156). After each unit of time, it moves to the right with a probability of $\frac{1}{2}$ (a ball is moved from the right urn to the left, increasing the number of balls in the left urn by one) and to the left with a probability of $\frac{1}{2}$ (a ball is moved from the left urn to the right, decreasing the number of balls in the left urn by one), until it first reaches one of the points 0 or $a+b$. The arrival of the chip at point 0 means that the left urn is empty, and its arrival at point $a+b$ means that the right urn is empty. Let the probability of the chip reaching 0, given that it started from point $k$, be denoted by $p_{k}$ (we need to find $p_{a}$). Clearly, $p_{0}=1, p_{a+b}=0$.
Suppose the chip is at point $k$.
Consider two events:
$A$: "the chip moves to $k+1$ in one step,"

Fig. 156.
By the condition, $\mathbf{P}(A)=\mathbb{P}(B)=1 / 2$. If event $A$ occurs, the probability of the chip reaching 0 is $p_{k+1}$, and if event $B$ occurs, the probability of the chip reaching 0 is $p_{k-1}$. By the formula for total probability, we have
$$
p_{k}=\frac{1}{2} p_{k+1}+\frac{1}{2} p_{k-1}
$$
or after transformation
$$
2 p_{k}=p_{k+1}+p_{k-1}, \quad p_{k+1}-p_{k}=p_{k}-p_{k-1}
$$
Denoting the constant difference $p_{k+1}-p_{k}$ by $d$, we write
$$
\begin{array}{r}
p_{k}-p_{k-1}=d_{2} \\
p_{k-1}-p_{k-2}=d \\
\cdots \cdot \cdot \cdot \\
p_{2}-p_{1}=d \\
p_{1}-p_{0}=d
\end{array}
$$
Adding these equations, we get
$$
\begin{aligned}
& p_{k}-p_{0}=k d, \\
& p_{k}-1=k d, \\
& p_{k}=1+k d
\end{aligned}
$$
or, setting $k=a+b$,
$$
\begin{gathered}
0=p_{a+b}=1+(a+b) d, \quad d=-\frac{1}{a+b} \\
p_{k}=1-\frac{k}{a+b}=\frac{a+b-k}{a+b}
\end{gathered}
$$
The probability we are interested in is
$$
p_{a}=\frac{b}{a+b}
$$
it is clear,
The probability that the right urn will be empty is
$$
p_{b}=\frac{a}{a+b}
$$
The probability that the experiment will end, i.e., that one of the urns will be empty, is, by property 2
$$
\frac{b}{a+b}+\frac{a}{a+b}=1
$$
The probability that the experiment will never end is $1-1=0$ (property 3).
Remark. This problem is known in the history of mathematics as the "ruin problem." The classical formulation of this problem is as follows:
Two players are playing. The probability of winning each game for each of them is $\frac{1}{2}$. The first player has $a$ rubles, and the second player has $b$ rubles. The game continues until one of the players is left with no money. What is the probability of ruin for each player?
In problem 191, the players are replaced by urns, and the money by balls.
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In triangle $ABC$, the median $AD$ is drawn. $\widehat{D A C} + \widehat{A B C} = 90^{\circ}$. Find $\widehat{B A C}$, given that $|A B| = |A C|$.
|
1. Take a point $A_{1}$ on the line $B A$ such that $\left|A_{1} B\right|=\left|A_{1} C\right|$. The points $A_{1}, A, D$ and $C$ lie on the same circle $\left(\widehat{D A_{1} C}=90^{\circ}-\widehat{A B C}=\widehat{D A C}\right)$. Therefore, $\widehat{A_{1} A C}=\widehat{A_{1} D C}=90^{\circ}$, which means $\widehat{B A C}=90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Three circles with radii 1, 2, and 3 touch each other externally. Find the radius of the circle passing through the points of tangency of these circles.
|
2. Note that the circle passing through the points of tangency is inscribed in a triangle with vertices at the centers of the circles. By equating the expressions for the area of the triangle obtained using Heron's formula and as the product of the semiperimeter and the radius of the inscribed circle, we find \( r=1 \).
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In a trapezoid, the diagonals are equal to 3 and 5, and the segment connecting the midpoints of the bases is equal to 2. Find the area of the trapezoid.
|
7. Let (Fig. 2) $ABCD$ be the given trapezoid ($BCAD$). Draw a line through $C$ parallel to $BD$, and denote by $K$ the point of intersection of this line with the line $AD$. The area of $\triangle ACK$ is equal to the area of the trapezoid, the sides $AC$ and $CK$ are equal to the diagonals of the trapezoid, and the median $CL$ is equal to the distance between the midpoints of $AD$ and $BC$. Extend $CL$ and take a point $M$ on the extension such that $|LLM| = |CL|$. We obtain $\triangle CKM$, which is equal in area to trapezoid $ABCD$, with sides equal to its diagonals and twice the distance between the midpoints of the bases. In our case, the sides of $\triangle CKM$ are 3.5 and 4.
Answer: $S=6$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. A circle of radius 1 is inscribed in triangle $A B C$, where $\cos \widehat{A B C}=0.8$. This circle touches the midline of triangle $A B C$, parallel to side $A C$. Find the length of side $A C$.
|
9. It follows from the condition that the height to side $AC$ is equal to two diameters of the inscribed circle, i.e., 4. If $M, N$ and $K$ are the points of tangency with $AB, BC$ and $CA$, then
$$
|BM|=|BN|=r \operatorname{ctg} \frac{\widehat{ABC}}{2}=1 \cdot \sqrt{\frac{1+0.8}{1-0.8}}=\sqrt{9}=3
$$
If $|MA|=|AK|=x,|KC|=|NC|=y$, then, expressing the area through the semiperimeter and the radius of the inscribed circle and through the base and height, we get
$$
(3+x+y)=(x+y) 2, \quad x+y=3
$$
Answer: $|AC|=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
58. Determine the measure of angle $\hat{A}$ of triangle $ABC$, if it is known that the bisector of this angle is perpendicular to the line passing through the point of intersection of the altitudes and the center of the circumscribed circle of this triangle.
|
58. Let $O$ be the center of the circumscribed circle, $H$ the intersection point of the altitudes of $\triangle ABC$. Since the line $OH$ is perpendicular to the bisector of angle $A$, it intersects sides $AB$ and $AC$ at points $K$ and $M$ such that $|AK|=|AM|$. Thus, $|AO|=|OB|$ and $\widehat{AOB}=2 \hat{C}$ (assuming angle $C$ is acute), $\widehat{OAK}=90^{\circ}-\hat{C}=\widehat{HAM}$. Therefore, $\triangle OAK=\triangle HAM$ and $|OA|=|HA|=R$ (where $R$ is the radius of the circumscribed circle). If $D$ is the foot of the perpendicular dropped from $O$ to $BC$, then $|OD|=\frac{1}{2}|AH|=\frac{R}{2}$. Consequently, $\cos \hat{A} = \cos \widehat{DOC} = \frac{1}{2}$ and $A=60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
61. In trapezoid $A B C D$, the lateral side $A B$ is perpendicular to $A D$ and $B C$, and $|A B|=\sqrt{|A D| \cdot|B C|}$. Let $E$ be the point of intersection of the non-parallel sides of the trapezoid, $O$ be the point of intersection of the diagonals, and $M$ be the midpoint of $A B$. Find $\widehat{E O M}$.
|
61. Let $|A D|=a,|B C|=b$. Drop a perpendicular $O K$ from $O$ to $A B$. Now we can find $|B K|=\sqrt{\overline{a b}} \frac{b}{b+a},|B E|=\sqrt{\overline{a b}} \frac{b}{a-b}$, $|M K|=\frac{\sqrt{a b}}{2}-\sqrt{\overline{a b}} \frac{b}{b+a}=\sqrt{\overline{a b}} \frac{a-b}{2(a+b)},|E K|=|B E|+|B K|=$ $=\sqrt{a \bar{b}} \frac{2 a b}{(a-b)(a+b)},|0 K|=\frac{a b}{a+b}$. It is easy to verify that $|O K|^{2}=$ $=|E K| \cdot|M K|$.
Answer: $\widehat{E O M}=90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
63. Two circles touch each other internally at point $A$. From the center of the larger circle, a radius $O B$ is drawn, touching the smaller circle at point $C$. Find $\widehat{B A C}$.
|
63. If $O_{1}$ is the center of the smaller circle, and $\widehat{B O A}=\varphi$, then $\widehat{B A O}=90^{\circ}-\frac{\varphi}{2}$, $\widehat{C O_{1} A}=90^{\circ}+\varphi$, $\widehat{C A O_{1}}=45^{\circ}-\frac{\varphi}{2}$. Therefore,
$$
\begin{gathered}
\widehat{B A C}=\widehat{B A O}-\widehat{C A O_{1}}=45^{\circ} . \\
\text { Answer: } 45^{\circ} .
\end{gathered}
$$
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
64. Inside the square $A B C D$, a point $M$ is taken such that $\widehat{M A B}=60^{\circ}, \widehat{M C D}=15^{\circ}$. Find $\widehat{M B C}$.
|
64. Construct an equilateral triangle $A B K$ on $A B$ inside the square. Then $\widehat{K A B}=60^{\circ}, \widehat{K C D}=15^{\circ}$, i.e., $K$ coincides with $M$. Answer: $30^{\circ}$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
65. In triangle $ABC$ with angle $\widehat{ABC}=60^{\circ}$, the bisector of angle $A$ intersects $BC$ at point $M$. On side $AC$, a point $K$ is taken such that $\widehat{AM} K=30^{\circ}$. Find $\widehat{OKC}$, where $O$ is the center of the circumcircle of triangle $AMC$.
|
65. If $\widehat{B A C}=2 \alpha$, it is easy to find that $\widehat{K M C}=\widehat{M K C}=$ $=30^{\circ}+\alpha$, i.e., $|M C|=|K C|$. Extend $M K$ until it intersects the circle at point $N$; $\triangle K M C$ is similar to $\triangle K A N$, so $|A N|=|K N|=R$ - the radius of the circle (since $\widehat{A M N}=30^{\circ}$).
Points $A, K$ and $O$ lie on a circle with center at $N$, $\widehat{A N O}=60^{\circ}$; therefore, $\widehat{A K O}=30^{\circ}$ or $150^{\circ}$, depending on whether angle $A M C$ is obtuse or acute.
Answer: $30^{\circ}$ or $150^{\circ}$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
66. Given a triangle $A B C$, where $|A B|=|A C|$, $\widehat{B A C}=80^{\circ}$. Inside the triangle, a point $M$ is taken such that $\widehat{M} \overrightarrow{B C}=30^{\circ}, \widehat{M C B}=10^{\circ}$. Find $\widehat{A M C}$.
|
66. Let's draw (Fig. 12) the angle bisector of $\angle A$ and extend $B M$ until it intersects with the bisector at point N. Since $|B N|=|N C|$, then $\widehat{B N C}=120^{\circ} ;$ therefore, the angles $\widehat{B N A}, \widehat{C N A}$ are also $120^{\circ}$ each, $\widehat{N C A}=\widehat{N C M}=20^{\circ}, \quad$ i.e., $\triangle N M C=\triangle N C A,|M C|=$ $=|A C|, \quad \triangle A M C$ is isosceles.
Answer: $70^{\circ}$.
|
70
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
67. In triangle $ABC$, given are $\widehat{ABC}=100^{\circ}, \widehat{ACB}=$ $=65^{\circ}$. On $AB$, a point $M$ is taken such that $\widehat{MCB}=55^{\circ}$, and on $AC$ - a point $N$ such that $\widehat{NBC}=80^{\circ}$. Find $\widehat{NMC}$.
|
67. Describe a circle around $\triangle M C B$ (Fig. 13) and extend $B N$ until it intersects with the circle
Fig. 12. at point $M_{1} ;\left|C M_{1}\right|=|C M|$, since the angles subtended by them $\left(80^{\circ}\right.$ and $\left.100^{\circ}\right)$ sum up to $180^{\circ}$; $\widehat{M_{1} C M}=\widehat{M_{1} B M}=20^{\circ}$, i.e., $N C$ is the bisector of angle $M_{1} C M$, and $\triangle M_{1} C N=\triangle N C M, \widehat{N M C}=\widehat{N M_{1} C}=\widehat{C M B}=25^{\circ}$.
Answer: $25^{\circ}$.
Fig. 13.
Fig. 14.
|
25
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
68. In triangle $ABC$, it is given that $|AB|=|BC|, \widehat{ABC}=$ $=20^{\circ}$; on $AB$ a point $M$ is taken such that $\widehat{MCA}=60^{\circ}$; on side $CB$ - a point $N$ such that $\widehat{NAC}=50^{\circ}$. Find $\widehat{NMA}$.
|
68. Let's take a point $K$ on $BC$ (Fig. 14) such that $\widehat{K A C}=60^{\circ}$, $M K \| A C$. Let $L$ be the intersection point of $A K$ and $M C$; $\triangle A L C$ is equilateral, $\triangle A N C$ is isosceles (calculate the angles), so $\triangle L N C$ is also isosceles, $\widehat{L C N}=20^{\circ}$. Now let's find the angles $N L M$ and $M K N$ - they are both $100^{\circ}$; since $\triangle M K L$ is equilateral, the angles $\widehat{K L N}$ and $\widehat{N K L}$ are both $40^{\circ}$, i.e., $|K N|=|L N|$ and $\triangle M K N = \triangle M L N, \widehat{N M L}=\widehat{K M N}=30^{\circ}$.
Answer: $30^{\circ}$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
69. In triangle $ABC$, given are $\widehat{ABC}=70^{\circ}, \widehat{ACB}=$ $=50^{\circ}$. On $AB$, a point $M$ is taken such that $\widehat{MCB}=40^{\circ}$, and on $AC$-point $N$ such that $\widehat{NBC}=50^{\circ}$. Find $\widehat{NMC}$.
|
69. Let's take point $K$ (Fig. 15) such that $\widehat{K B C}=\widehat{K C B}=30^{\circ}$, and denote by $L$ the intersection point of the lines $M C$ and $B K$.
Fig. 15. Since $\triangle B N C$ is isosceles $\left(\widehat{N B C}=\widehat{N C B}=50^{\circ}\right)$, then $\widehat{K N C}=$ $=40^{\circ}$. Point $L$ is the intersection of the angle bisectors of triangle $N K C$ ( $L K$ and $L C$ are angle bisectors). Therefore, $N L$ is also the angle bisector of $\angle K N C$ and $\widehat{L N B}=60^{\circ} ; B N$, in turn, is the angle bisector of $\angle M B L$; moreover, $B N \perp M L$; thus, $B N$ bisects $M L$ and $\widehat{M N B}=\widehat{B N L}=60^{\circ}$, and $\widehat{N M C}=$ $=30^{\circ}$.
Answer: $30^{\circ}$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.