problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
75. In quadrilateral $A B C D$, it is given that $\widehat{D A B}=150^{\circ}$, $\widehat{D A C}+\widehat{A B D}=120^{\circ}, \widehat{D B C}-\widehat{A B \bar{D}}=60^{\circ}$. Find $\widehat{B D C}$.
|
75. Let $\widehat{A B D}=\alpha, \widehat{B D C}=\varphi$. By the condition, $\widehat{D A C}=$ $=120^{\circ}-\alpha, \widehat{B A C}=30^{\circ}+\alpha, \widehat{A D B}=30^{\circ}-\alpha, \widehat{D B C}=60^{\circ}+\alpha$. Using the Law of Sines for triangles $A B C, B C D, A C D$, we get
$$
\begin{aligned}
& \frac{|B C|}{|A C|}=\frac{\sin \left(30^{\circ}+\alpha\right)}{\sin \left(60^{\circ}+2 \alpha\right)}=\frac{1}{2 \cos \left(30^{\circ}+\alpha\right)}, \\
& \frac{|D C|}{|B C|}=\frac{\sin \left(60^{\circ}+\alpha\right)}{\sin \varphi}, \\
& \frac{|A C|}{|D C|}=\frac{\sin \left(30^{\circ}-\alpha+\varphi\right)}{\sin \left(120^{\circ}-\alpha\right)} .
\end{aligned}
$$
Multiplying these equations, we have
$\sin \left(30^{\circ}-\alpha+\varphi\right)=\sin \left(30^{\circ}+\alpha+\varphi\right)-\sin \left(30^{\circ}+\alpha-\varphi\right) \Rightarrow$
$\Rightarrow \sin \left(30^{\circ}-\alpha+\varphi\right)+\sin \left(30^{\circ}+\alpha-\varphi\right)=\sin \left(30^{\circ}+\alpha+\varphi\right) \Rightarrow$
$\Rightarrow \cos (\varphi-\alpha)=\sin \left(30^{\circ}+\alpha+\varphi\right) \Rightarrow$
$\Rightarrow \sin \left(90^{\circ}-\varphi+\alpha\right)-\sin \left(30^{\circ}+\alpha+\varphi\right)=$
$$
=2 \cos \left(60^{\circ}+\alpha\right) \sin \left(30^{\circ}-\varphi\right)=0 ;
$$
thus, $\varphi=30^{\circ}$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35*. What is the greatest number of rays in space that form pairwise obtuse angles?
|
35. It is easy to see that it is possible to draw four rays, each pair of which forms obtuse angles: for example, it is sufficient to connect the center $O$ of a regular tetrahedron $ABCD$ with all its vertices (it is clear, for example, that $\angle AOB > \angle AO_1B = 90^\circ$, where $O_1$ is the center of the face $BCD$ of the tetrahedron). Now let's prove that it is impossible to specify more than four rays in space, each pair of which forms obtuse angles.
Let $l_1, l_2, l_3$, and $l_4$ be four rays emanating from a point $O$ and forming obtuse angles with each other, and let $\pi_1, \pi_2, \pi_3$, and $\pi_4$ be planes passing through the point $O$ and perpendicular to the rays $l_1, l_2, l_3$, and $l_4$, respectively. All rays forming obtuse angles with the ray $l_1$ must lie on the other side of the plane $\pi_1$ from the ray $l_1$. All rays forming obtuse angles with both rays $l_1$ and $l_2$ must lie within the dihedral angle formed by the half-planes $\pi_1$ and $\pi_2$; this dihedral angle (Fig. 83a) is acute, since the angle between the rays perpendicular to its faces is obtuse. All rays forming obtuse angles with each of the three rays $l_1, l_2, l_3$ must lie within the intersection of the dihedral angles $\pi_1\pi_2$ and $\pi_1\pi_3$. This intersection is a trihedral angle $\pi_1\pi_2\pi_3$, or $OABC$ (Fig. 83b), which, as proven above, has all dihedral angles acute. The ray $l_4$ must lie within it; we will show that it forms acute angles with all other rays lying inside this angle.
Let the plane passing through $OA$ and the ray $l_4$ intersect the face $BOC$ along the ray $OA'$. One of the dihedral angles with edge $OA'$ is acute; let this be the angle $AOA'C$. Then all dihedral angles of the trihedral angle $OAA'C$ are acute; hence, all plane angles of this trihedral angle are also acute (see, for example, the solution to problem 28 in the book by D. O. Sharygin et al., cited in the footnote on page 151). But $\angle AOL_4$ is only a part of the angle $AOA'$; therefore, the angle between the rays $OA$ and $l_4$ is acute. Similarly, the ray $l_4$ forms acute angles with $OB$ and $OC$. Therefore, all
1) Consider how this reasoning changes if we are talking about points in space (although the case where all points lie in the same plane does not contradict the condition of problem b).
three rays $OA, OB, OC$ lie on the same side of the plane $\pi_4$ as the ray $l_4$, and thus all internal points of the trihedral angle $OABC$ lie on the same side of $\pi_4$ as the ray $l_4$. Therefore, any ray $l_5$ located inside the trihedral angle $\pi_1\pi_2\pi_3$,
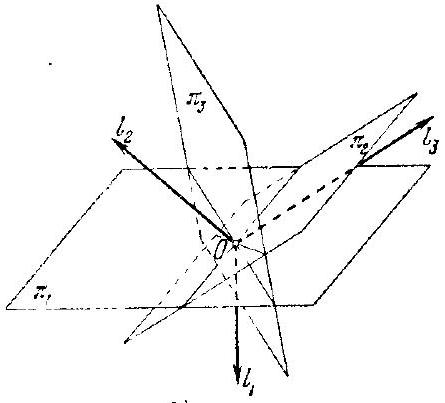
a)
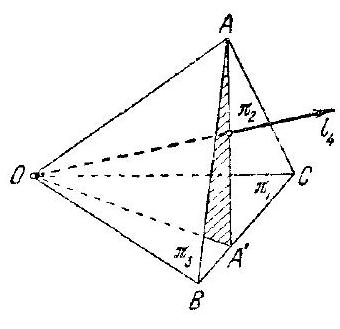
b)
Fig. 83.
lies on the same side of the plane $\pi_4$, and thus no such ray $l_5$ can form an obtuse angle with $l_4$. This proves the required statement.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
52. Given a triangle $T$.
a) Place a centrally symmetric polygon $m$ of the largest possible area inside $T$.
What is the area of $m$ if the area of $T$ is 1?
b) Enclose $T$ in a convex centrally symmetric polygon $M$ of the smallest possible area.
What is the area of $M$ if the area of $T$ is 1?
|
52. a) If $O$ is the center of the sought centrally symmetric polygon $m$, then by symmetrically reflecting the given $\triangle ABC \equiv T$ together with $m$ (which will transform into itself), we can see that $m$ is also inscribed in $\triangle A_{1} B_{1} C_{1} \equiv T_{1}$, which is symmetric to $\triangle ABC$ with respect to $O$. Since the intersection ${ }^{1}$ ) $n=T \cap T_{1}$ of triangles $T$ and $T_{1}$ is clearly a centrally symmetric polygon with center $O$, the smallest centrally symmetric polygon inscribed in $T$ with center $O$ has an area of $\frac{1}{2} S_{ABC}$, because if the height $OP$ of triangle $AOB$ were less than half the height $CH$ of triangle $ABC$, then point $C'$ would lie outside $\triangle ABC$ (beyond side $AB$) and the intersection of $\triangle ABC$ and $\triangle A'B'C'$ would not be a parallelogram.
In the second case, the convex hull of the considered points is a centrally symmetric hexagon $A C' B A' C B'$ (Fig. $109, \sigma$), the area of which is exactly twice the area of $\triangle ABC$. Indeed,
\[
\begin{aligned}
& S_{A C' B A' C B'} = S_{O A B'} + S_{O A' B} + S_{O C A'} + S_{O C' A} + S_{O B C'} + S_{O B' C} = \\
&= 2 S_{O A B'} + 2 S_{O C A'} + 2 S_{O B C'}
\end{aligned}
\]
but
\[
S_{O A B'} = S_{O A B}
\]
since $AO$ is the median of triangle $AB'B$, and similarly
\[
S_{O C A'} = S_{O C A}, \quad S_{O B C'} = S_{O B C}
\]
thus,
\[
S_{A C' B A' C B'} = 2 S_{O A B} + 2 S_{O C A} + 2 S_{O B C} = 2 S_{ABC}
\]
The simplest example of a centrally symmetric polygon (of the smallest possible area) with an area of $2 S_{ABC}$ (i.e., an area of 2 if $S_{ABC} = 1$), containing $\triangle ABC$ inside, is the parallelogram $A B A' C$ (Fig. $109, b$).
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
90. On a plane, there are 4 points $A_{1}, A_{2}, A_{3}, A_{4}$, the distance between any two of which is not less than 1. What is the maximum possible number of line segments $A_{i} A_{j}$ of length 1 connecting these points pairwise?
|
90. The number $v_{2}(4)<6$, otherwise the number of diameters of a system of four points on a plane could equal the "complete" number of six segments connecting our points, and by the result of problem 87 a) this is not the case. However, the number of segments equal to 1, connecting the points of our system of four points on a plane, can equal 5:
$$
v_{2}(4)=5
$$
(Fig. 159).
Note. It is also obvious that $v_{2}(3)=3$ and generally
$v_{k}(n)=C_{n}^{2}\left(=\frac{n(n-1)}{2}\right) \quad$ for $\quad n \leqslant k+1$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. a) Points $A$ and $B$ move uniformly and with equal angular velocities along circles centered at $O_{1}$ and $O_{2}$, respectively (clockwise). Prove that vertex $C$ of the equilateral triangle $A B C$ also moves uniformly along some circle.
b) The distances from a fixed point $P$ on the plane to two vertices $A, B$ of an equilateral triangle $A B C$ are $A P=2$ and $B P=3$. Determine the maximum value that the distance $C P$ can have.
|
6. a) Let $\overrightarrow{\mathrm{O}_{1} \mathrm{O}_{3}}$ be the vector obtained by rotating $\overrightarrow{O_{1} O_{2}}$ by $60^{\circ}$ (in the same direction as the rotation that transforms $\overrightarrow{A B}$ into $\overrightarrow{A C}$). Points $A^{\prime}$ and $B^{\prime}$ are the images of $A$ and $B$ under the same rotation around $O_{1}$. When vectors $\overrightarrow{O_{1} A}$ and $\overrightarrow{O_{2} B}$ rotate uniformly with the same angular velocity, $\triangle O_{1} A^{\prime} A$ will rotate around $O_{1}$, vectors $\overrightarrow{O_{3} B^{\prime}}$ and $\overrightarrow{B^{\prime} C}=\overrightarrow{A^{\prime} A}$, and thus their sum $\overrightarrow{O_{3} C}$ will rotate around $O_{8}$ (Fig. 23).
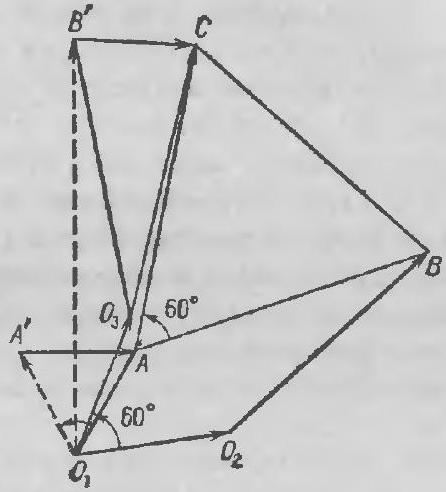
Fig. 23
Fig. 24
b) Answer: 5. Fix point $B$ at a distance of 3 from $P$ (Fig. 24). As point $A$ moves along a circle of radius 2 centered at $P$, vertex $C$ will move along a circle of radius 2, with its center $O$ located at a distance $O P=3$ from $P$ ( $\triangle O P B$ is equilateral). The farthest point on this circle from $P$ is at a distance $C O + O P = 5$.
$\nabla$ In the inequality to be proven, $P C \leqslant A P + B P$ (for any equilateral triangle $A B C$ and any point $P$), equality is achieved for all points $P$ on the arc $A B$ of the circumscribed circle of $\triangle A B C$, not containing point $C$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Kolya and Petya are dividing $2 n+1$ nuts, $n \geqslant 2$, with each wanting to get as many as possible. There are three ways of dividing (each goes through three stages).
1st stage: Petya divides all the nuts into two parts, each containing no fewer than two nuts.
2nd stage: Kolya divides each part again into two, each containing no fewer than one nut.
(1st and 2nd stages are common for all three ways.)
3rd stage: in the first way, Kolya takes the larger and the smaller parts; in the second way, Kolya takes both middle parts; in the third way, Kolya takes either the larger and the smaller parts or both middle parts, but in exchange for the right to choose, he gives Petya one nut.
Determine which way is the most advantageous for Kolya and which is the least advantageous for him.
|
10. Answer: the most profitable way for Kolya is the first one; with the second and third, he will get one nut less with correct play. (In general, as we will see, the dispute in this division is over one nut.)
No matter what piles (of $a$ and $b$ nuts, $a<b$) form after Petya's first move, Kolya can split the larger one into two parts of 1 and $b-1$ nuts, which will be the largest and the smallest, i.e., with the first division method, he can take $b \geqslant n+1$ nuts. (By taking $a=n, b=n+1$, Petya can prevent him from achieving more.) With the second division method, after the first move, $a=2, b=2n+1$, and with the best response $2=1+1$, $2n-1=n-1+n$, Kolya will get only $n$ nuts. (But with any other first move, he can get no less than $n+1$.) With the third method, Petya's move $a=n, b=n+1$ does not allow Kolya to achieve more than taking $n+1$ nuts (the sums of the two middle piles and the two outer ones will always be $n$ and $n+1$), so the extra nut that needs to be given away becomes decisive.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21. Let's take any 1962-digit number divisible by 9. The sum of its digits will be denoted by $a$, the sum of the digits of $a$ by $b$, and the sum of the digits of $b$ by $c$. What is $c$?[^0]
|
21. Answer. $c=9$. The sum of the digits of any number gives the same remainder when divided by 9 as the number itself (PZ). On the other
Fig. 30 hand, $a \leqslant 1962.9<19999$, so $b \leqslant 1+4 \cdot 9=37$ and $c \leqslant 9$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
23. What is the maximum area that a triangle with sides \(a, b, c\) can have, given the following constraints:
\[
0 \leqslant a \leqslant 1 \leqslant b \leqslant 2 \leqslant c \leqslant 3 \text { ? }
\]
|
23. Answer: 1. Among triangles with two sides $a, b$ that satisfy the conditions $0<a \leqslant 1,1 \leqslant b \leqslant 2$, the one with the largest area is the right triangle with legs $a=1, b=2$ (indeed, $s \leqslant a b / 2 \leqslant 1$, since the height dropped to side $b$ is no more than $a$). The third side of this triangle $c=\sqrt{5}$ satisfies the condition $2 \leqslant c \leqslant 3$, therefore, among all the considered triangles, it has the largest area.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
43. For each of the numbers from 1 to 1000000000, the sum of its digits is calculated, and for each of the resulting billion numbers, the sum of its digits is calculated again, and so on, until a billion single-digit numbers are obtained. Which number will there be more of: 1 or 2?
|
43. Answer: the number of ones will be one more than the number of twos.
Any number gives the same remainder when divided by 9 as the sum of its digits (DS). Therefore, in our problem, ones come from numbers that give a remainder of 1 when divided by 9, i.e., from the numbers 1, 10, 19, 28, ..., 999999991, 1000000000, and twos come from numbers that give a remainder of 2, i.e., from the numbers $2,11,20,29, \ldots$ ... 999999992.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
46. Solve the equation in integers
$$
\sqrt{\sqrt{x+\sqrt{x+\sqrt{x+\ldots+\sqrt{x}}}}}=y
$$
|
46. Answer: the only solution is $x=y=0$.
Let $\boldsymbol{x}$ and $\boldsymbol{y}$ be integers satisfying the condition. After a series of squaring, we are convinced that $\sqrt{x+\sqrt{x}}=\boldsymbol{m}$ and $\sqrt{x}=k$ are integers, and
$$
m^{2}=k(k+1)
$$
If $k>0$, then it must be that $k^{2}<m^{2}<(k+1)^{2}$, so $k<m<k+1$ and therefore $m$ is not an integer. Thus, $k=0$, i.e., $x=0$.
$\nabla$ Note that the contradiction of equation (*) also follows from problem 42.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
53. What is the smallest number of non-overlapping tetrahedra into which a cube can be divided?
|
53. It is easy to see that a cube can be divided into 5 tetrahedra. In Fig. 40, these are the tetrahedra $A A^{\prime} B^{\prime} D^{\prime}, A B^{\prime} B C, A C D D^{\prime}, B^{\prime} C^{\prime} D^{\prime} C$, and $A C D^{\prime} B^{\prime}$.
Let us now prove that it is impossible to divide the cube into fewer tetrahedra. Suppose the cube is divided into several tetrahedra. There are at least two of them whose bases lie on the face $A B C D$ of the cube. Similarly, there are at least 2 tetrahedra with bases on the face $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$.
These tetrahedra are certainly different from the first two, since a tetrahedron cannot have two parallel faces. Thus, we already have 4 tetrahedra. Their total volume is no more than $2 a^{3} / 3$, i.e., less than the volume of the cube. Therefore, it is impossible to divide the cube into 4 tetrahedra.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
64*. Can 1965 points be placed in a square with a side of 1 so that any rectangle of area $1 / 200$ with sides parallel to the sides of the square contains at least one of these points?
|
64. Answer: it is possible.
In the square $0 \leqslant x \leqslant 1, 0 \leqslant y \leqslant 1$ and on the line $y=1 / 2$, uniformly place $c_{0}=200$ points: ( $\left.k / 201 ; 1 / 2\right), k=1,2, \ldots$ $\ldots, 200$. Then on each of the lines $y=1 / 4$ and $y=3 / 4$, place $c_{1}=100$ points ( $\left.k / 101 ; 1 / 4\right),(k / 101 ; 3 / 4), k=1,2, \ldots$ $\ldots, 100$. Repeating this process, for $m=2,3, \ldots, 7$ and on each line $y=(2 l-1) 2^{-m-1}, 1 \leqslant l \leqslant 2^{m}$, place $c_{m}$ points $\left(\frac{k}{c_{m}+1} ; \frac{2 l-1}{2^{m j+1}}\right)$, where $c_{m}=\left[200 \cdot 2^{-m}\right]$ (when $m=7$, 128 corresponding lines will have one point each). In total, the number of points placed is
$$
\begin{aligned}
& \sum_{m=0}^{7} 2^{m} c_{m}=200+2 \cdot 100+4 \\
& \cdot 50+8 \cdot 25+16 \cdot 12+32 \cdot 6+ \\
& \quad+64 \cdot 3+128=1704 \text { points. }
\end{aligned}
$$
This construction is illustrated in Fig. 45.
It is clear that no rectangle of area $1 / 200$ can fit between the placed points. If it intersects the line $y=1 / 2$, then its base is not
Fig. 45 greater than $1 / 201$; if not, then it is located entirely above or below this line. In this case, if it intersects the line $y=3 / 4$ or $y=1 / 4$, its height is not more than $1 / 2$, and its base is not more than $1 / 101$, and so on. If the rectangle is entirely located between lines of the form $y=$ $=n / 256$ ( $n=1,2, \ldots, 255$ ), then its height is not more than $1 / 256$.
|
1704
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
90. In a sequence of integers (positive), each term, starting from the third, is equal to the absolute difference of the two preceding ones.
What is the maximum number of terms such a sequence can have if each of its terms does not exceed 1967?
|
90. Answer: 2952. We will prove that the length (number of terms) of a sequence satisfying the condition of the problem, where the largest term is the second and equals $n$, does not exceed $d_{n} = [3(n+1) / 2]$, and for the sequence $n-1, n, 1, \ldots, \ldots, 1,1$ the length is exactly $d_{n}$.
We will reason by induction. For $n \leqslant 4$, the statement is easily verified by enumeration ($d_{1}=2, d_{2}=3, d_{3}=6, d_{4}=7$). Let's estimate the maximum length of a sequence starting with $a$, $n, n-a, a, \ldots (a<n)$, assuming that the statement is proven for smaller $n$. For $1 \leqslant a < n / 2$, its length does not exceed $d_{n-a}+1$, since by removing the first term $a$, we can replace its beginning with: $n-2a, n-a, \ldots$; for $n / 2 \leqslant a < n-1$, it does not exceed $d_{a}+2$ - it is sufficient to remove the first two terms. Thus, it remains to verify that for such $a$, the inequalities $d_{n-a}+1 \leqslant d_{n}$ and $d_{a}+2 \leqslant d_{n}$ are satisfied. For $a=1$ or $a=n-1$ - for the sequence $n-1, n, 1, n-1, n-2,1, 1-3, \ldots, 1,1$ - it is sufficient to remove the first three terms and rearrange the next two, to leave only the verification of the equality $d_{n-8}+3=d_{n}$.
From the general statement for $n=1967$, we get the answer $d_{1967}=[3 \cdot 1968 / 2]=2952$.
|
2952
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
92. Three consecutive vertices of a rhombus lie on the sides $A B, B C, C D$ of a given square with side 1. Find the area of the figure filled by the fourth vertices of such rhombi.
|
92. Answer: $S=1$.
Let $K, L, N$ be the vertices of the rhombus on the sides $A B, B C$, and $A D$ of the square (Fig. $52, a$). Note that the length $K B$ is equal to the distance from point $M$ to the line $A D$. Therefore, if we fix point $K$, the possible positions of point $M$ fill a certain segment $M_{1} M_{2}$ parallel to side $A D$.
The lower position $M_{1}$ of point $M$ corresponds to the case $N_{1}=A$, and the upper position $M_{2}$ corresponds to the case $L_{2}=C$.
To determine the positions of points $M_{1}$ and $M_{2}$ depending on the location of point $K$, we introduce a coordinate system as shown in Fig. 52.
Simple calculations show that if the abscissa of point $K$ is $x>0$, then $M_{1}=(-x, \sqrt{2 x})$, and $M_{2}=(-x, \sqrt{1-2 x}+1)$. Using the symmetry of the set of points $M$ with respect to the $O y$ axis, we find that this set forms a figure marked with hatching. There is no need to take integrals to calculate the area: in Fig. 51, the figures marked with the numbers 1 and 2 are equal.

Fig. 52

6
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
99. In a regular $n$-gon ( $n>5$ ), the difference between the largest and smallest diagonals is equal to the side. Find $n$.
|
99. Answer: $n=9$.
Let $a_{n}$ be the side length, and $D_{n}$ and $d_{n}$ be the lengths of the largest and smallest diagonals of a regular $n$-gon. For $n=4$ and $n=5$, all diagonals are equal. For $n=6$ and $n=7$, $D_{n}-a_{n}=2 A K=D_{8}-d_{8}$. For $n=9$ (Fig. 55,6), similarly, we get $\angle A B K=30^{\circ}$, so $A B=a_{9}=2 A K=D_{9}-d_{9}$.
We will further consider the $n$-gon inscribed in a circle of radius 1. For $n>9$, obviously, $D_{n} \geqslant D_{9}, d_{n}D_{9}-d_{9}=a_{9}>a_{n}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
123. In a certain state, the airline system is arranged in such a way that any city is connected by air routes to no more than three other cities, and from any city to any other, one can travel with no more than one layover.
What is the maximum number of cities that can be in this state?
|
123. Answer: 10 cities.
From any city $A$, one can reach no more than three cities, and from each of them no more than two (excluding $A$). Thus, the total number of cities is no more than $1+3+3 \cdot 2=$ $=10$.
The example in Fig. 60 shows that the required system of air routes in a state with ten cities exists.
$\nabla$ The graph in Fig. 60 is often used as an example and even has a special name, the "Petersen graph".
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
126*. In the country's football championship, 20 teams are participating. What is the minimum number of games that must be played so that among any three teams, there are two that have already played against each other?
|
126. Answer: 90 games.
Let among any three teams, there be two that have already played against each other. Choose a team $A$ that has played the least number of games $-k$. Each of the $k$ teams that have already played with $A$, as well as team $A$ itself, has played no fewer than $k$ games. From the $(19-k)$ teams that have not played with $A$, each has played with all the other $(18-k)$ of them - otherwise, there would be a trio of teams, none of which have played against each other. Thus, the doubled number of all games - which can be obtained by summing the number of games played by all teams - is no less than,
$$
\begin{aligned}
k^{2}+k+(19-k)(18-k)=2 k^{2}-36 k+ & 18 \cdot 19= \\
= & 2(k-9)^{2}+180 \geqslant 180
\end{aligned}
$$
An example of a situation where 90 games have been played and the conditions of the problem are satisfied is given by two groups of 10 teams each, where all teams within each group have played against each other, but none have played against a team from the other group.
$\nabla$ If the teams are represented by points, and the teams that have not played against each other are connected by a segment, then the resulting graph, when the conditions of the problem are met, will be a triangle-free graph. It can be proven that in such a graph with $n$ vertices, the maximum number of edges is $\left[n^{2} / 4\right]$.
The reasoning conducted in the solution is similar to the proof of the "cross lemma" in solution 156 and the estimates in 246v).
|
90
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
131. How many sides in a convex polygon can be equal in length to the longest diagonal?
|
131. Answer: no more than two. An example of a polygon with two sides equal to the largest diagonal is shown in Fig. 61.
Suppose there are more than two such sides. We select two of them, $A B$ and $C D$, which do not share any vertices (this is possible, [^3] since a polygon with diagonals is not a triangle). Then at least one of the diagonals $A C$ or $B D$ is longer than side $A B$: if these diagonals intersect at some point $K$, then
$$
\begin{aligned}
& A C+B D=A K+K C+B K+ \\
& \quad+K D>A B+C D=2 A B
\end{aligned}
$$
Fig. 61
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
161. Find the greatest integer $x$ such that the number
$$
4^{27}+4^{1000}+4^{x}
$$
is a perfect square.
|
161. Answer: $x=1972$. Since $4^{27}+4^{1000}+4^{x}=$ $=2^{54}\left(1+2 \cdot 2^{1945}+2^{2 x-54}\right)$, the expression in parentheses will be a perfect square when $2 x-54=2 \cdot 1945$, i.e., when $x=1972$. If $x>1972$, then $2^{2(x-27)}<1+2 \cdot 2^{1945}+2^{2(x-27)}<\left(2^{x-27}+1\right)^{2}$, i.e., the given number is between the squares of two consecutive natural numbers.
|
1972
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
179. The Tennis Federation has assigned qualification numbers to all its tennis players: the strongest player gets the first number, the next strongest gets the second number, and so on. It is known that in matches where the qualification numbers differ by more than 2, the player with the lower number always wins. A tournament involving the 1024 strongest tennis players is held according to the Olympic system: participants in each round are randomly paired, and the winner of each pair advances to the next round, so the number of participants is halved after each round. Thus, after the tenth round, the winner will be determined. What is the highest number he can have?
|
179. Answer! The highest possible number of the winner is 20.
Since a tennis player with number $k$ can lose (not counting stronger ones) only to the $(k+1)$-th and $(k+2)$-th tennis players, the number of the strongest winner after each round cannot increase by more than 2. Thus, the number of the winner of the entire tournament cannot be more than 21. However, we will show that the 21st tennis player cannot become the winner. For this, after the first round, the 1st and 2nd players must be eliminated, losing to the 3rd and 4th (otherwise, the number of the winner would be less than 21), in the second round, the 3rd and 4th must be eliminated, and the 5th and 6th must win against them, and so on up to the 9th round, where the 19th and 20th must win against the 17th and 18th. Thus, the 21st tennis player does not make it to the final, where two players meet.
It remains to provide an example of a tournament where the 20th player wins. For this, we will divide all the players into two groups of 512 people each. The first group will include the 19th, 20th, and 510 weaker players. We will organize the tournament in this group so that the 20th wins (which is obviously possible). The second group will include the 1st, 2nd, ..., 18th, and the remaining weaker players, and we will organize the tournament so that the 18th wins. This can be done by organizing the tournament as described above: in the first round, the 3rd and 4th win against the 1st and 2nd, in the second round, the 5th and 6th win against the 3rd and 4th, and so on until the eighth round, when the 17th and 18th win against the 15th and 16th, after which, in the ninth round, the 18th wins against the 17th. In the final, the 20th and 18th meet, and thus the 20th can win.
$\nabla$ It can be proven by induction that in the case of $2^n$ players, the highest number of the winner is $2n$.
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
190. Among the numbers of the form $36^{k}-5^{l}$, where $k$ and $l$ are natural numbers, find the smallest in absolute value. Prove that the found number is indeed the smallest.
|
190. Answer: $11=36-5^{2}$.
The last digit of the number $36^{h}=6^{2 k}$ is 6, the last digit of the number $5^{t}$ is 5. Therefore, the number $\left|6^{2 k}-5^{t}\right|$ ends in either 1 (if $6^{2 k}>5^{t}$) or 9 (if $6^{2 k}<5^{t}$).
The equation $6^{2 k}-5^{t}=1$ is impossible, because then it would be $5^{l}=\left(6^{k}-1\right)\left(6^{k}+1\right)$, and the number $6^{k}+1$ is not divisible by 5. For $k=1$ and $l=2$, we get $36^{k}-5^{t}=11$.
The equation $5^{t}-6^{2 k}=9$ is also impossible, because $5^{t}$ for a natural $l$ is not divisible by 3.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
226. In a regular 1976-gon, the midpoints of all sides and the midpoints of all diagonals are marked. What is the greatest number of marked points that can lie on one circle?
|
226. Answer: 1976. All marked points, except for the center $O$ of the 1976-gon, lie 1976 each on 987 circles with center $O$. Any other circle $\gamma$ intersects each of these 987 circles at two points; besides these intersection points, there can be only one more marked point on $\gamma$: $O$. Therefore, there are no more than $987 \cdot 2 + 1 = 1975$ marked points on such a circle $\gamma$.
|
1976
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
238. Several black and white chips are arranged in a circle. Two players take turns performing the following operation: the first player removes all black chips that have a white neighbor (at least on one side), and the second player then removes all white chips that have a black neighbor. They continue doing this until only chips of one color remain.
a) Suppose there were 40 chips initially. Is it possible that after each player makes two moves, only one chip remains on the circle?
b)* Initially, there were 1000 chips on the circle. What is the minimum number of moves after which only one chip can remain on the circle?
|
238. Answers: a) yes, b) 8 moves (each player - per move).
Fig. 102 shows an example of arranging 41 chips; next to each chip is its rank-number, indicating how many moves before the end it will be removed. The construction of such an arrangement is convenient "from the end"; to the remaining last black chip of rank 0, add two white chips of rank 1, next to each of them add two black chips of rank 2 (on both sides), next to each black chip add two white chips of rank 3, and so on. It is clear that this method gives the maximum possible number of chips of the corresponding rank at each step. Thus, for each $t$, an arrangement is obtained with the maximum possible number $a_{t}=b_{t}+w_{t}$ of chips - $b_{t}$ black and $w_{t}$ white, which can be transformed into one black chip in $t$ moves ($b_{0}=1$, $w_{0}=0$); the rule for sequential calculation of ($b_{t}, w_{t}$) is very simple: when transitioning from $\boldsymbol{t}$ to $\boldsymbol{t}+1$, the larger of the numbers $\boldsymbol{b}_{t}$, $w_{t}$ does not change, and to the smaller, the doubled larger is added.
| $\boldsymbol{t}$ | 0 | 1 | 2 | 3 | 4 | 5 | | 7 | |
| :---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: |
| $b_{t}$ | 1 | 1 | 5 | 5 | 29 | 29 | 169 | 169 | 985 |
| $w_{t}$ | 0 | 2 | 2 | 12 | 12 | 70 | 70 | 408 | 408 |
| $a_{t}$ | 1 | 3 | 7 | 17 | 41 | 99 | 239 | 577 | 1393 |
To solve problem a), it is sufficient to remove one chip of rank 4 from the 41 points in Fig. 102, which does not affect the situation after the first move (i.e., standing next to another chip "4"), for example, to maintain symmetry, the one marked with a star.
The transition from 1000 chips to one cannot occur in fewer than 8 moves, as can be seen from the table, $a_{7}=577<1000$. An example with exactly 1000 chips can be obtained from the maximum arrangement for 8 moves with $a_{8}=1393$ chips, by removing 393 chips of rank 8, which do not affect the situation after the first move - this can be done since $2 \cdot 408=816$ chips of rank 8, placed among 577 chips of rank no more than 7, form no fewer than $816-577=239$ pairs of adjacent chips.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
252. Let $a_{n}$ denote the integer closest to $\sqrt{n}$. Find the sum
$$
\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{1980}}
$$
|
252. Answer: 88.
Each number $k=1,2,3, \ldots$ appears in the sequence $(a_{n})$ $2 k$ times, since the condition $a_{n}=k$ is equivalent to
$$
k-\frac{1}{2}<\sqrt{n}<k+\frac{1}{2}, \quad \text { or } \quad k^{2}-k<n \leqslant k^{2}+k
$$
Therefore, in the sum
$$
\begin{aligned}
&\left(\frac{1}{a_{1}}+\frac{1}{a_{2}}\right)+\left(\frac{1}{a_{3}}+\frac{1}{a_{4}}+\frac{1}{a_{5}}\right.\left.+\frac{1}{a_{6}}\right)+\ldots \\
& \ldots+\left(\frac{1}{a_{44 \cdot 43+1}}+\ldots+\frac{1}{a_{44 \cdot 45}}\right)
\end{aligned}
$$
each of the 44 round brackets equals $2 k \cdot 1 / k=2$.
|
88
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
270. A kangaroo jumps in the corner $x \geqslant 0, y \geqslant 0$ of the coordinate plane $O x y$ as follows: from the point ( $x ; y$ ) the kangaroo can jump to the point ( $x-5$; $y+7)$ or to the point $(x+1 ; y-1)$, and jumping to points with a negative coordinate is not allowed. From which initial points $(x ; y)$ can the kangaroo not reach a point that is more than 1000 units away from the origin? Draw the set of all such points ( $x ; y$ ) and find its area.
|
270. Answer: the set of points from which one cannot escape *to infinity* has an area of 15; this is the stepped figure $T$, shown in Fig. 112.
From any point outside $T$, one can reach the region $x \geq 5$ in several steps $(1; -1)$, and then make steps $(-5; 7) + 5(1; -1) = (0; 2)$
$\nabla$ Even more interesting shapes of figures are formed in this problem if the number of allowed jumps is 3 or more.
Fig. 111
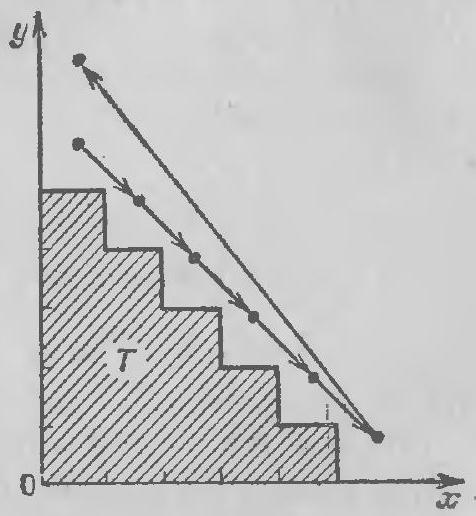
Fig. 112
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
281*. The final sequence $a_{1}, a_{2}, \ldots, a_{n}$ of numbers 0 and 1 must satisfy the following condition: for any integer $k$ from 0 to $n-1$, the sum
$$
a_{1} a_{k+1}+a_{2} a_{k+2}+\ldots+a_{n-k} a_{n}
$$
is an odd number.
a) Come up with such a sequence for $n=25$.
b) Prove that such a sequence exists for some $n>1000$.
|
281. The value specified in the problem condition
$$
p_{k}=a_{1} a_{k+1}+a_{2} a_{k+2}+\ldots+a_{n-k} a_{n}
$$
is conveniently calculated as follows: the sequence $A_{n}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ is signed under itself with a shift of $k$ digits; in this case, $p_{k}=p_{k}\left(A_{n}\right)$ is the number of digits where ones are present in both rows.
A sequence $A_{n}$ of length $n$ satisfies the problem condition if all $p_{k}\left(A_{n}\right)$ for $0 \leqslant k \leqslant n-1$ are odd.
The following construction allows constructing $A_{l}=A_{n} \sqcup A_{m}$ of length $l=1$ 238
$=(2 m-1) n-(m-1)=2 m n-m-n+1$. Replace each 1 in $A_{n}$ with the block $A_{m} \underbrace{0 \ldots 0}_{m-1}$ of $2 m-1$ digits, each 0 in $A_{n}$ with a block of $2 m-1$ zeros, and discard the last $m-1$ zeros. When calculating $p_{k}$ for $A_{l}$ using the method described above for any shift $k$, each block $A_{m}$ in the upper row touches only one block $A_{m}$ in the lower row; if $k=(2 m-1) q+r$ or $k=(2 m-1) q-r$, where $0 \leqslant r \leqslant m-1$, $0 \leqslant q \leqslant n-1$, then $p_{k}\left(A_{l}\right)=p_{q}\left(A_{n}\right) \cdot p_{r}\left(A_{m}\right)$, since exactly $p_{q}\left(A_{n}\right)$ pairs of blocks $A_{m}$ touch each other and they are shifted by $r$ digits. From this, it is clear that the constructed sequence $A_{l}=A_{n} \sqcup A_{m}$ satisfies the problem condition along with $A_{n}$ and $A_{m}$.
This construction allows creating the answer $A_{25}=A_{4} \sqcup A_{4}$ for part (a) from $A_{4}=1101$:
$$
A_{25}=110100011010000000000 \text{. } 1101 .
$$
Further, $A_{25} \sqcup A_{25}$ already has $2 \cdot 25^{2}-50+1=1201-$ more than 1000 digits, as required in part (b),
$\nabla$ There are other series of sequences that satisfy the problem condition. One of them was devised by the olympiad participant A. A. Razborov. It is interesting to obtain their complete description. A similar problem can be considered on a circle.
|
1201
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
306. We will say that a number has the property $\mathrm{P}(k)$ if it can be factored into the product of $k$ consecutive natural numbers, all greater than 1.
a) Find $k$ such that some number $N$ simultaneously has the properties $\mathrm{P}(k)$ and $\mathrm{P}(k+2)$.
b) Prove that there are no numbers that simultaneously have the properties $P(2)$ and $\mathbf{P}(4)$.
|
306. a) $k=3 ; 720=2 \cdot 3 \cdot 4 \cdot 5 \cdot 6=8 \cdot 9 \cdot 10$.
b) If $m(m+1)=n(n+1)(n+2)(n+3)$, then $m^{2}+m+1=\left(n^{2}+3 n+1\right)^{2}$, which is impossible.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
322. Find at least one natural number $n$ such that each of the numbers $n, n+1, n+2, \ldots, n+20$ has a common divisor with the number $30030=2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13$ that is greater than one.
|
322. Answer: for example, 9440. Let $m=2 \cdot 3 \cdot 5 \cdot 7 \cdot k$. By choosing $k$ such that $m-1$ is divisible by 11, and $m+1$ is divisible by 13, we get that the number $n=m-10$ satisfies the condition of the problem (P2).
|
9440
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
325. a) Find the smallest possible value of the polynomial
$$
P(x, y)=4+x^{2} y^{4}+x^{4} y^{2}-3 x^{2} y^{2}
$$
b) ${ }^{*}$ Prove that this polynomial cannot be represented as a sum of squares of polynomials in the variables $x, y$.
|
325. a) Answer: 3 at $x=y=1$.
From the inequality of the arithmetic mean, it follows that $1+x^{2} y^{4}+x^{4} y^{2} \geqslant 3 x^{2} y^{2}$.
b) Let $P(x, y)=g_{1}^{2}(x, y)+g_{2}^{2}(x, y)+\ldots+g_{n}^{2}(x, y)$, where $g_{i}(x, y), i=1,2, \ldots, n-$ are polynomials. Since $P(x, 0)=$ $=P(0, y)=4$, the polynomials $g_{i}$ cannot contain monomials of the form $a x^{k}$ and $b y^{2}$. Therefore, the coefficient of $x^{2} y^{2}$ must be positive.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
337. Natural numbers from 1 to 1982 are arranged in some order. A computer scans pairs of adjacent numbers (the first and second, the second and third, etc.) from left to right up to the last pair and swaps the numbers in the scanned pair if the larger number is to the left. Then it scans all pairs from right to left from the last pair to the first, swapping the numbers in pairs by the same rule. At the end of this scan, the operator working with the computer received information that the number in the hundredth position did not move from its place during both scans. Find this number.
|
337. Answer: 100. Consider the number $a$-the largest of the first 99 numbers, and the number $b$-the smallest of the last 1882 numbers and ensure that $a<100<b$.
|
100
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
389. The sequence $x_{n}$ is defined recursively: $\quad x_{1}=1 ; x_{2}=1 ; x_{n+2}=x_{n+1}^{2}-\frac{1}{2} x_{n}, \quad$ if $n \geqslant 1$. Prove that the sequence $x_{n}$ has a limit, and find it.
390 *. In the white cells of a chessboard of size $1983 \times 1984$, numbers 1 or -1 are written such that for any black cell, the product of the numbers in the adjacent white cells is 1. Prove that this is possible only if all the written numbers are 1.
|
389. Answer: $\lim _{n \rightarrow \infty} x_{n}=0\left(\left|x_{n+7}\right| \leqslant \frac{1}{4}\left(\frac{5}{6}\right)^{n}\right.$ for $\left.n \geqslant 1\right)$.
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
432. Milk is poured into 30 glasses. A boy is trying to make the amount of milk equal in all glasses. For this, he takes any two glasses and pours milk from one to the other until the amount of milk in them is equal. Is it possible to pour milk into the glasses in such a way that the boy cannot achieve his goal, no matter how long he spends pouring?
|
432. Answer: it is possible. You need to pour 100 g of milk into all the glasses except one, and into the remaining one - 200 g
256
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
456. Every evening, Uncle Chernomor appoints 9 or 10 out of 33 bogatyrs for duty, at his discretion. What is the smallest number of days after which it can happen that each of the bogatyrs has been on duty the same number of times?
|
456. Answer: 7 days. Let $k$ be the number of days when 9 bogatyrs were on duty, and $l$ be the number of days when 10 bogatyrs were on duty, with each of them being on duty $m$ times. Then $9 k + 10 l = 33 m$. For $m=1$ there are no solutions, but for $m=2$ we have $k=4$ and $l=3$.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.3. Replace the ellipsis with such a natural number $p$ so that the answer to the following question is unique: how many lines are drawn on the plane, if it is known that they intersect at ... different points?
|
1.3. Answer. $p=2$.
We will prove that if there are two intersection points, there can only be three lines. Suppose there are only two intersection points $A$ and $B$, and let $l_{1}$ and $l_{2}$ be the lines intersecting at point $A$, and $l_{3}$ be a line not passing through $A$ (such a line exists, otherwise all lines would intersect at $A$). Line $l_{3}$ intersects only one of the lines $l_{1}, l_{2}$, say $l_{1}$, at point $B$, and is parallel to the other line $l_{2}$ (figure a). Verify that no more lines can be drawn without increasing the number of intersection points.
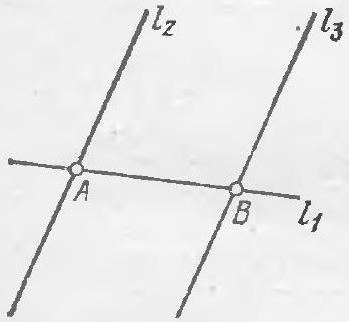
a)
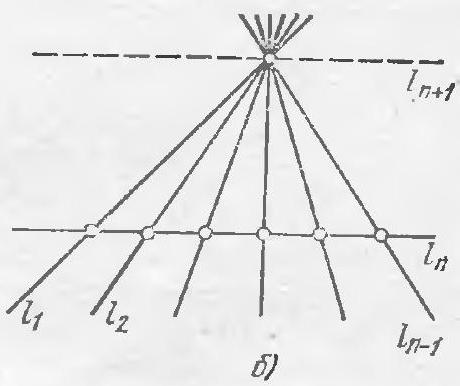
Fig. 1.3.
Note that the proof uses Euclid's "fifth postulate" - the axiom stating that through a point, no more than one line can be drawn parallel to a given line.
We will prove that the number of intersection points cannot be different from 2. If there is only one intersection point, the number of lines can be any number starting from 2, provided that all lines pass through this point. If the number of intersection points $n>2$, the number of lines is not uniquely determined. This is illustrated by the example of the arrangement of lines shown in figure b: a line $l_{n+1}$ can be drawn parallel to $l_{n}$, or it can be not drawn, without affecting the number of intersection points.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.9. What is the maximum number of strings connecting adjacent nodes in a volleyball net with square cells that can be cut so that the net does not fall apart into separate pieces? The size of the net is $10 \times 100$ cells.
## PARALLEL SEGMENTS
|
1.9. Answer. 1000.
Suppose that so many strings have been torn that the net has not yet split into pieces, but no more strings can be torn. This means that there are no closed loops of strings left in the net. Prove that in this case, the number of unbroken strings is one less than the total number of nodes (including nodes located on the edges and at the corners of the net).
This can be verified, for example, as follows. Fix some node $A$. From it, you can travel along the unbroken strings to any other node $B$. Correspond to each node $B$ of the net the last string on the path leading from $A$ to $B$. This path is uniquely determined because there are no closed paths of strings. Therefore, the correspondence between the remaining strings and nodes $B$ (different from $A$) is one-to-one. Thus, the number of strings left is one less than the total number of nodes in the net, which, as is easy to calculate, is 1111. The total number of strings in the new unbroken net is 2110. Therefore, to leave 1110 strings, 1000 must be torn.
An example where 1000 strings are torn and the net has not yet split into pieces is easy to provide. For instance, you can tear all the horizontal strings in all rows except the top one. Then the net will turn into a "fringe." In essence, we have proved above that you can sequentially tear any 1000 strings, ensuring only that each time a string loop is cut, and on the 1001st time, this will not be possible.
|
1000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. The altitudes of triangle $ABC$ intersect at point $O$. It is known that $OC = AB$. Find the angle at vertex $C$.
|
## 5.1. Answer. $45^{\circ}$.
Let $D$ be the foot of the perpendicular dropped from point $A$. Prove that triangles $C O D$ and $A B D$ are congruent. Then show that $\angle O B D=45^{\circ}$, and from this, deduce that the required angle is also $45^{\circ}$.
Another solution can be obtained by almost verbatim repeating the reasoning presented in the second solution of problem 5.3.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.3. Find the angle $C$ of triangle $ABC$, if the distance from vertex $C$ to the orthocenter of the triangle is equal to the radius of the circumscribed circle.
|
5.3. Answer. $60^{\circ}$.
1st solution. Let $O$ be the center of the circumcircle of triangle $ABC$, $M$ be the orthocenter, and $CC'$ be the diameter of the circumcircle (see figure a). Inscribed angles $ABC$ and $AC'C$ are equal, so the acute angles $MCB$ and $ACO$, which complement them to $90^{\circ}$, are also equal.
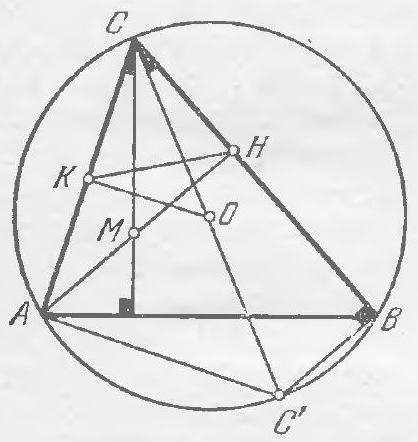
a)
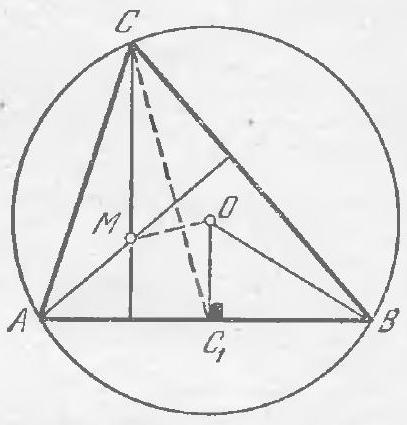
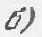
Fig. 5.3.
Let $K$ be the midpoint of $AC$, and $H$ be the foot of the altitude dropped from $A$ to $BC$. The median $KH$ of the right triangle $ACH$ is equal to $AC / 2 = KC$ (it is the radius of the circumcircle of $ACH$).
Both of these facts are true for any triangle $ABC$. Additionally, in this triangle, $KC = CH$. This follows from the equality of the right triangles $KCO$ and $CHM$ ($CM = CO$ by the condition and $\angle KCO = \angle HCM$ as proven). Therefore, triangle $KCH$ is equilateral, and the desired angle $C$ is $60^{\circ}$.
2nd solution. This solution is based on the following observation: in any triangle, the distance from the orthocenter to a vertex is twice the distance from the center of the circumcircle to the opposite side (in figure b, $CM = 2OC_1$). This fact is incidentally obtained during the proof of Euler's theorem (see the solution to problem 4.8). Now, from the condition of the problem, it immediately follows that in the right triangle $BOC_1$, the leg $OC_1$ is equal to $BO / 2$, and thus $\angle BOC_1 = 60^{\circ}$. But $\angle BCA = \angle BOC_1$, since both the inscribed angle $BCA$ and the central angle $BOC_1$ measure half the arc $BA$. Therefore, $\angle BCA = 60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.5. In triangle $A B C$ with an angle of $120^{\circ}$ at vertex $A$, the angle bisectors $A A_{1}, B B_{1}$ and $C C_{1}$ are drawn. Find the angle $C_{1} A_{1} B_{1}$.
|
5.5. Answer. $90^{\circ}$.
Let the length of side $AB$ be denoted by $c$, $AC$ by $b$, and $BC$ by $a$. First, we will prove that $AA_1 = \frac{bc}{b+c}$.
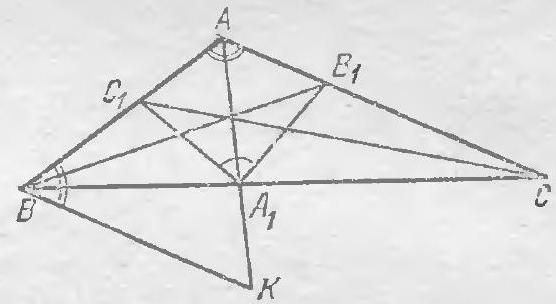
Fig. 5.5.
Extend $AA_1$ and draw a line $BK$ parallel to $AC$ (see the figure). In triangle $ABK$, angles $A$ and $K$ are both $60^{\circ}$, so it is equilateral and thus $AK = BK = c$. Now, from the similarity of triangles $BA_1K$ and $AA_1C$, we get $\frac{c - AA_1}{AA_1} = \frac{c}{b}$, from which it follows that $AA_1 = \frac{bc}{b+c}$.
Since the bisector of an internal angle of a triangle divides the opposite side into segments proportional to the adjacent sides, we have $\frac{BA_1}{a - BA_1} = \frac{c}{b}$, from which $BA_1 = \frac{ac}{b+c}$. Therefore, $AA_1 : BA_1 = b : a$. The base $C_1$ of the bisector $CC_1$ divides side $BA$ in the same ratio. Hence, $A_1C_1$ is the bisector of angle $A_1$ in triangle $BA_1A$. Similarly, it can be shown that $A_1B_1$ is the bisector of angle $AA_1C$. Therefore, $\angle C_1A_1B_1 = \left(\angle BA_1A + \angle AA_1C\right) / 2 = 90^{\circ}$. 5.6. Answer. $36^{\circ}, 36^{\circ}, 108^{\circ}$.
It is clear that this triangle $ABC$ is isosceles. Let $AB$ be its base, and $O$ be the center of the circumscribed circle. Prove that $\angle ACO = \angle CAO = \frac{3}{2} \angle CAB$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.7. In an isosceles triangle \(ABC\) with lateral sides \(AB = BC\), the angle \(ABC\) is \(80^\circ\). Inside the triangle, a point \(O\) is taken such that the angle \(OAC\) is \(10^\circ\) and the angle \(OCA\) is \(30^\circ\). Find the angle \(AOB\).
|
5.7. Answer. $70^{\circ}$.
Let $K$ be the point of intersection of the altitude dropped from vertex $B$ and the bisector of angle $OAB$ (see figure). First, show that point $K$ lies on the extension of $OC$. Then prove that triangles
Fig. 5.7.
$ABK$ and $AOK$ are congruent (by side and two adjacent angles) and from the isosceles triangle $OAB$, find the required angle.
|
70
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.3. Six pennies lie on the table, forming a closed chain (i.e., the first penny touches the second, the second touches the third, and so on, the sixth touches the first). A seventh penny, also lying on the table, rolls without slipping along the outer side of the chain, touching each of the six pennies in the chain in turn. How many revolutions will this penny make before returning to its original position?
## QUADRILATERAL AND FOUR CIRCLES
|
6.3. Answer. 4 turns.
From figure $a$, it can be seen that during the time the moving coin, depicted with a dashed line, rolls along the arc $\alpha$ of the stationary coin with center $O$, it rotates by an angle of $2 \alpha$: in this figure, $M^{\prime} A^{\prime}$ is the new position of the radius $M A$, the radii $M A$ and $M^{\prime} A^{\prime \prime}$ are parallel, $\angle A^{\prime \prime} M^{\prime} B = \angle A O B = \alpha$, and since the arcs $A^{\prime} B$ and $A B$ are equal, $\angle B M^{\prime} A^{\prime} = \alpha$, therefore, the entire angle $\angle A^{\prime \prime} M^{\prime} A^{\prime}$, by which the moving coin rotates, is $2 \alpha$.
a)
b)
Fig. 6.3.
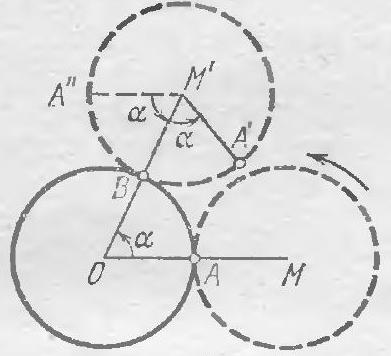
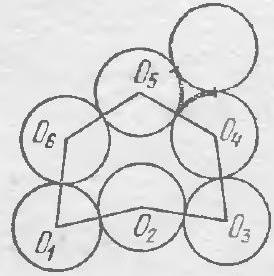
Now let's find the sum of the arcs (in degrees) consisting of points of the stationary coins that the moving coin touched while rolling along the chain. Let $O_{1}, O_{2}, \ldots, O_{6}$ be the centers of the stationary coins (see figure b). The sum of the arcs lying inside the hexagon $O_{1} O_{2} \ldots O_{6}$ is equal to the sum of its interior angles, i.e., $180^{\circ} \cdot 6 - 360^{\circ} = 720^{\circ}$. Indeed, the sum of the interior angles of any $n$-sided polygon, not necessarily convex, is $180^{\circ} n - 360^{\circ}$ (prove this yourself or read the proof, for example, in the book by D. O. Shklyarsky et al., "Selected Problems and Theorems in Planimetry," "Nauka," 1967, problem 108). The sum of the arcs lying outside this hexagon is $360^{\circ} \cdot 6 - 720^{\circ} = 1440^{\circ}$. From this, we need to subtract the sum of the arcs lying in the indentations between two adjacent coins, where the moving coin will not reach; in each of the six indentations, the sum of the two such arcs is $120^{\circ}$ (on figure 6, these arcs are shown with a bold line). Thus, the total sum of the arcs along which the coin will roll is $1440^{\circ} - 120^{\circ} \cdot 6 = 720^{\circ}$, and the desired number of turns is obtained by multiplying this value by 2 and dividing by $360^{\circ}$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. In a city, there are 10 streets parallel to each other and 10 others intersect them at right angles. What is the minimum number of turns a closed route can have, passing through all intersections?
|
8.5. Answer. 20.
It is easy to provide an example with 20 turns. We will prove that fewer than 20 turns are not possible. Consider 10 streets of a certain direction. If the route passes through each of them, then there are already at least two turns of the route on each of them, and the proof is complete. If there is a street that the route does not pass through at all, then it must pass through all ten perpendicular streets. We can apply the same reasoning to them.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Let $S(x)$ denote the sum of the digits of a natural number $x$. Solve the equations:
a) $x+S(x)+S(S(x))=1993$
b)* $x+S(x)+S(S(x))+S(S(S(x)))=1993$.
2*. It is known that the number $n$ is the sum of the squares of three natural numbers. Show that the number $n^{2}$ is also the sum of the squares of three natural numbers.
|
1. a) According to the divisibility rule for 3 (see fact 6), the numbers $x$ and $S(x)$ give the same remainder when divided by 3. The same remainder will also be given by the number $S(S(x))$. Therefore, the sum
$$
x + S(x) + S(S(x))
$$
is divisible by 3 (since it is the sum of three numbers with the same remainder when divided by 3). However, 1993 is not divisible by 3, so there are no solutions.
b) It is clear that $x < 1993$. It is not difficult to see that among the numbers less than 1993, the largest sum of digits, 27, is achieved by the numbers 1989 and 999. Therefore, $S(x) \leq 27$. Further, $S(S(x)) \leq S(19) = 10$. Finally, $S(S(S(x))) \leq 9$. From the equation, it follows that
$$
\begin{aligned}
& x = 1993 - S(x) - S(S(x)) - S(S(S(x))) \geq \\
& \quad \geq 1993 - 27 - 10 - 9 = 1947
\end{aligned}
$$
Similarly to part "a", all numbers $x, S(x), S(S(x))$, and $S(S(S(x)))$ give the same remainder when divided by 9, while 1993 gives a remainder of 4, so the number $x$ must give a remainder of 1 (see the comment). Among the numbers from 1947 to 1993, the numbers that give a remainder of 1 when divided by 9 are 1954, 1963, 1972, 1981, and 1990. Checking these numbers, we find that only 1963 fits.
Comment. We used the following statement: if the sum of four numbers with the same remainder when divided by 9 gives a remainder of 4 when divided by 9, then each of these numbers gives a remainder of 1. This can be strictly proven either by enumeration or as follows: let the desired remainder be $x$. Then $4x$ gives a remainder of 4 when divided by 9. That is, $4(x-1) = 4x - 4$ is divisible by 9, and thus $x-1$ is divisible by 9. Therefore, $x = 1$, see fact 7.
|
1963
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Petya has a total of 28 classmates. Any two of the 28 have a different number of friends in this class. How many friends does Petya have?
|
4. Petya's classmates can have $0,1,2, \ldots, 28$ friends - a total of 29 options. However, if someone is friends with everyone, then everyone has at least one friend. Therefore, either there is someone who is friends with everyone, or there is someone who is not friends with anyone. In both cases, there are 28 options left: $1,2, \ldots, 28$ or $0,1, \ldots, 27$.
Let's denote the person with the most friends as $A$, and the person with the fewest friends as $B$. In the first case, $A$ is friends with everyone, and $B$ is only friends with one person, i.e., only with $A$. In the second case, $B$ is not friends with anyone, and $A$ is friends with everyone except one, i.e., with everyone except $B$.
Thus, in each case, $A$ is friends with Petya, and $B$ is not. We will transfer $A$ and $B$ to another class. As we have already seen, $A$ is friends with everyone left, and $B$ is not friends with anyone left. Therefore, after the transfer, each of the remaining classmates has one fewer friend (among classmates). This means that the remaining classmates of Petya will again have a different number of friends among classmates.
Now, we will again transfer the most "friendly" and the most "unsociable" to another class, and so on.
By repeating these arguments 14 times, we will transfer 14 pairs of students to another class, in each of which exactly one is Petya's friend. Thus, Petya has 14 friends.
Commentary. $1^{\circ}$. Several ideas are at work in the solution: the symmetry of friendship, the principle of the extreme, and inductive descent.
$2^{\circ}$. There is a very short but incorrect solution: let Petya have $x$ friends. Let's make all friends quarrel, and those who were not friends become friends, then Petya's classmates will again have a different number of friends, and thus Petya will again have $x$ friends. We get the equation $x=28-x$. Where is the mistake? If it were proven that the answer in the problem is unique, then the reasoning would be correct. Nevertheless, this reasoning allows us to guess the answer.
$3^{\circ}$. Solve the problem if Petya has 27 classmates.
$4^{\circ}$. This problem is a continuation of another well-known problem: prove that in any company, there will be two people who have the same number of friends in this company (possibly none).
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Each pair of numbers $x$ and $y$ is assigned a number $x * y$. Find $1993 * 1935$, given that for any three numbers $x, y$ and $z$ the identities $x * x=0$ and $x *(y * z)=(x * y)+z$ are satisfied.
|
5. Let's take $y=z$ in the second identity. Then we get
$$
(x * y)+y=x *(y * y)=x * 0
$$
Thus, $x * y=x * 0 - y$. It remains to compute $x * 0$. For this, take $x=y=z$ in the second identity:
$$
x * 0=x *(x * x)=x * x + x=0 + x=x.
$$
Thus, $x * y=x * 0 - y=x - y$. Therefore, $1993 * 1935=1993 - 1935=58$.
Comment. Check that if you take $x * y=x - y$, then both identities are indeed satisfied.
|
58
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A cooperative receives apple and grape juice in identical barrels and produces an apple-grape drink in identical cans. One barrel of apple juice is enough for exactly 6 cans of the drink, and one barrel of grape juice is enough for exactly 10 cans. When the recipe for the drink was changed, one barrel of apple juice became enough for exactly 5 cans of the drink. How many cans of the drink will one barrel of grape juice now be enough for? (The drink is not diluted with water.)
|
1. The first method. For one can of the drink, $\frac{1}{6}$ of a barrel of apple juice and $\frac{1}{10}$ of a barrel of grape juice are used, so the volume of the can is
$$
\frac{1}{6}+\frac{1}{10}=\frac{4}{15}
$$
of the barrel's volume.
After changing the recipe, for one can of the drink, $\frac{1}{5}$ of a barrel of apple juice and $\frac{1}{x}$ of a barrel of grape juice are used, so the volume of the can is
$$
\frac{1}{5}+\frac{1}{x}
$$
of the barrel's volume. Thus, we get the equation:
$$
\frac{1}{5}+\frac{1}{x}=\frac{4}{15}
$$
From this, we find
$$
\frac{1}{x}=\frac{4}{15}-\frac{1}{5}=\frac{1}{15}
$$
Therefore, $x=15$.
The second method. For 30 cans, 5 barrels of apple juice and 3 barrels of grape juice were used. In total, 8 barrels. According to the new recipe, 6 barrels of apple juice will be used for 30 cans. Therefore, 2 barrels of grape juice will be used. Thus, one barrel of grape juice is enough for 15 cans.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A student did not notice the multiplication sign between two three-digit numbers and wrote a single six-digit number, which turned out to be seven times greater than their product. Find these numbers.
|
2. First method. Let $x, y$ be the desired three-digit numbers. If we append three zeros to the number $x$, we get the number $1000 x$, and if we append $y$, we get $1000 x + y$ (see fact 11).
Thus, the student wrote the number $1000 x + y$. According to the problem, this number is seven times greater than $x \cdot y$. This gives us the equation
$$
7 x \cdot y = 1000 x + y
$$
Divide both sides of equation (1) by $x$:
$$
7 y = 1000 + \frac{y}{x}
$$
The number $\frac{y}{x}$ is positive and less than 10, since $y \leqslant 999$ and $x \geqslant 100$. Therefore,
$$
1000 < 7 y < 1010
$$
Dividing this inequality by 7, we get
$$
142 \frac{6}{7} < y < 144 \frac{2}{7}
$$
Since $y$ is an integer, $y$ is either 143 or 144. Let $y = 143$. Substituting this value of $y$ into equation (1), we get:
$$
7 x \cdot 143 = 1000 x + 143
$$
Solving this equation, we find $x = 143$. If $y = 144$, then the analogous equation gives $x = 18$, which is not valid because $x$ is a three-digit number.
In the second method. Rewrite equation (1) as $1000 x = (7 x - 1) y$. It is easy to see that $x$ and $7 x - 1$ have no common divisors other than 1 and -1. Indeed, if $d$ is a common divisor of the numbers $x$ and $7 x - 1$, then $d$ is a divisor of the number $7 x$, and therefore a divisor of the number $1 = 7 x - (7 x - 1)$ (see fact 5). But 1 is divisible only by 1 and -1.
Thus, the number $7 x - 1$ is a divisor of the product $1000 \cdot x$ and is coprime with the second factor. Then, by a known theorem (see fact 9), the number $7 x - 1$ is a divisor of the number 1000. But
$$
7 x - 1 \geqslant 7 \cdot 100 - 1 = 699
$$
so $7 x - 1 = 1000$ (the only divisor of the number 1000 that is greater than or equal to 699 is the number 1000 itself), from which $x = 143$. Substituting $x = 143$ into the original equation, we find $y = 143$.
Comment. Compare with problem 1 for 10th grade.
Fig. 41
|
143
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5*. Find the largest natural number, not ending in zero, which, when one (not the first) digit is erased, decreases by an integer factor.
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
5. Let $x$ be the deleted digit, $a$ be the part of the number to the left of $x$, and $c$ be the part of the number to the right of $x$. Then the number has the form $\overline{a x c}$, see fact 11. Suppose the digit $x$ is in the $(n+1)$-th place (counting from the right). Then
$$
\overline{a x c}=a \cdot 10^{n+1}+x \cdot 10^{n}+c .
$$
After deleting the digit $x$, the resulting number is $\overline{a c}=a \cdot 10^{n}+c$. Consider the ratio of the original number to the resulting number
$$
r=\frac{a \cdot 10^{n+1}+x \cdot 10^{n}+c}{a \cdot 10^{n}+c}, \quad \text { where } c0$. Therefore,
$$
-8 \leqslant l \leqslant 9
$$
It is also clear that $l \neq 0$ (otherwise, the decimal representation of the number $c$ ends in zero).

Proof. Consider two cases: $l>0$ and $l0$. From equation (3), it follows that $x-l a>0$, so,
$$
a18$ ). Therefore, $n \leqslant 4$. Let $n=4$, then $l+9=16$, and equation (3) can be rewritten as
$$
(x-7 a) \cdot 5^{4}=c
$$
Since $x$ is a digit, $a=1, x=8$ or $x=9$. For $x=9$, the number $c$ ends in zero, and thus is not suitable. For $x=8$, we get $c=625$ and the answer
$$
\overline{a x c}=180625
$$
$2^{\circ}$. Suppose the number $c$ does not contain fives. The number $l+9$ is divisible by a power of five no higher than the first, so $n \leqslant 1$, and the number is definitely not the maximum.
|
180625
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A rectangle of size $1 \times k$ for any natural number $k$ will be called a strip. For which natural numbers $n$ can a rectangle of size $1995 \times n$ be cut into pairwise distinct strips?
|
3. Idea of the solution: take the maximum strip (equal to the maximum side of the rectangle). The remaining strips will be combined in pairs, giving the sum of the maximum strip. If we have filled the rectangle, the problem is solved; otherwise, reasoning with areas shows that the rectangle cannot be cut into different strips.
Consider two cases: $n \leqslant 1995$ and $n>1995$.
For the case $n \leqslant 1995$. If $n \leqslant 998$, we will cut the rectangle into $n$ strips of length 1995. We keep the first one, cut the second one into two strips of length 1 and 1994, the third one into two strips of length 2 and 1993, and so on. The last strip $1 \times 1995$ will be cut into parts $1 \times(n-1)$ and $1 \times(1996-n)$. We will get strips with lengths:
$$
1,2, \ldots, n-1,1996-n,(1996-n)+1, \ldots, 1994,1995
$$
It is clear that the first $n-1$ strips are different, and the remaining strips are also different. However, to ensure that among the first $n-1$ strips there are no strips equal to one of the remaining strips, it is necessary (and sufficient) that $n-1 \leqslant 997$. This condition is satisfied for $n \leqslant 998$.
For the case $n \geqslant 1995$. The case $n \geqslant 1995$ is analogous. We cut the rectangle into 1995 strips of length $n$. We keep the first one, cut the second one into two strips of length 1 and $n-1$, and so on. We will get strips with lengths:
$$
1,2, \ldots, 1994, n-1994,(n-1994)+1, \ldots, n
$$
They will be different if $1994 < n-1994$, i.e., $n \geqslant 3989$. To prove the necessity of this condition, we again compare the areas. Since the total area of the strips does not exceed $\frac{n(n+1)}{2}$, we get the inequality
$$
1995 n \leqslant \frac{n(n+1)}{2},
$$
From this, $n \geqslant 2 \cdot 1995-1=3989$.
Comments. $1^{\circ}$. A rectangle $n \times m$ with $n \geqslant m$ can be cut into strips of different lengths if and only if $n \geqslant 2 m-1$.
$2^{\circ}$. We used the formula $1+2+\ldots+n=\frac{n(n+1)}{2}$. This formula can be proven by induction. Moreover, it is a special case of the formula for the sum of an arithmetic progression. Nevertheless, we will provide an elegant proof of this formula. Let $1+2+\ldots+n=X$ and calculate the sum of all numbers in the table:
$$
\begin{array}{ccccccc}
1 & 2 & 3 & \ldots & n-2 & n-1 & n \\
n & n-1 & n-2 & \ldots & 3 & 2 & 1
\end{array}
$$
Since the sum in each column is $n+1$, and there are $n$ columns, the sum of all numbers in the table is $n(n+1)$. On the other hand, the sum in each row is $X$, so the sum of all numbers in the table is $2 X$. Therefore, $2 X=n(n+1)$, from which our statement follows.
|
3989
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Is it enough to make a closed rectangular box from all sides, enclosing no less than 1995 unit cubes, a) 962; b) 960; c) 958 square units of material?
|
4. It is sufficient to take a box of size $11 \times 13 \times 14$. Its volume is 2002, which is sufficient; and the total area of its walls is $2 \cdot(11 \cdot 13+11 \cdot 14+13 \cdot 14)=958$.
Comments. $1^{\circ}$. How can one guess such a solution? It is known that among all parallelepipeds with a given volume, the cube has the minimum surface area - this follows from the inequality between the arithmetic mean and the geometric mean, see fact 26. However, a cube with a volume of 1995 would have irrational side lengths. Therefore, one needs to try to find a box that is close in shape to a cube but with integer side lengths. The "nearest" cubes are $12 \times 12 \times 12$ and $13 \times 13 \times 13$ (their volumes are 1728 and 2197, respectively). It might seem that the most "economical" option is $12 \times 13 \times 13$. Unfortunately, this parallelepiped only provides a solution for part "a". Continuing to search for parallelepipeds close to a cube, one can find the solution to the problem.
$2^{\circ}$. 957 units of material are not enough to make the box.
|
958
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
6. A line cuts off triangle $A K N$ from a regular hexagon $A B C D E F$ such that $A K+A N=A B$. Find the sum of the angles under which segment $K N$ is seen from the vertices of the hexagon ( $\angle K A N+\angle K B N+\angle K C N+\angle K D N+\angle K E N+$ $+\angle K F N$).
## 9 t h g r a d e
|
6. Let's assume that $N$ lies on $A B$, and $K$ lies on $A F$ (Fig. 60). Note that $F K = A N$. We choose point $P$ on $B C$, point $R$ on $C D$, point $S$ on $D E$, and point $T$ on $E F$ such that the equalities $F K = A N = B P = C R = D S = E T$ hold. Then $\angle K B N = \angle T A K$, $\angle K C N = \angle S A T$, $\angle K D N = \angle R A S$, $\angle K E N = \angle P A R$, $\angle K F N = \angle N A P$, from which
$$
\begin{gathered}
\angle K A N + \angle K B N + \angle K C N + \angle K D N + \\
+ \angle K E N + \angle K F N = \\
= \angle K A N + \angle T A K + \angle S A T + \angle R A S + \\
+ \angle P A R + \angle N A P = \\
= \angle K A N + \angle K A N = 120^{\circ} + 120^{\circ} = 240^{\circ}.
\end{gathered}
$$
Fig. 60
9th grade
|
240
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In a $10 \times 10$ grid, the centers of all unit squares are marked (a total of 100 points). What is the minimum number of lines, not parallel to the sides of the square, needed to cross out all the marked points?
|
2. Let's draw all lines parallel to one of the diagonals of the square and containing more than one of the marked points - there are 17 such lines. The un-
Fig. 77 erased will be the two corner points. They can be erased by drawing one more line - the other diagonal (Fig. 77).
We will prove that it is impossible to manage with a smaller number of lines. Indeed, consider the centers of the unit squares located along the perimeter of the large square. It is clear that a line not parallel to the side of the square can erase no more than two such points, but there are 36 such points in total (see also fact 1).
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given an equilateral triangle $A B C$. Side $B C$ is divided into three equal parts by points $K$ and $L$, and point $M$ divides side $A C$ in the ratio $1: 2$, starting from vertex $A$. Prove that the sum of angles $A K M$ and $A L M$ is $30^{\circ}$.
|
4. Without loss of generality, we can assume that point $K$ is closer to point $B$ than point $L$ (Fig. 72). Then triangle $M K C$ is equilateral (since $M C = K C, \angle M C K = 60^{\circ}$). Therefore, $A B \| M K$ (since $\left.\angle M K C = \angle A B C = 60^{\circ}\right)$. This means that angles $A K M$ and $B A K$ are equal as alternate interior angles.
Notice that angles $B A K$ and $C A L$ are equal due to symmetry (or because $\triangle B A K = \triangle C A L$ by the first criterion). Therefore, $\angle A K M = \angle C A L$. Hence,
$$
\begin{aligned}
\angle A K M + & \angle A L M = \\
& = \angle C A L + \angle A L M = \angle L M C
\end{aligned}
$$
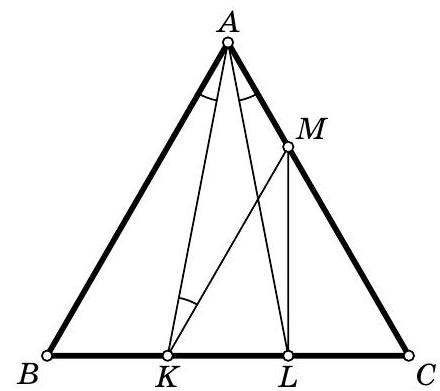
Fig. 72
The last equality follows from the fact that $\angle L M C$, being an exterior angle in triangle $A M L$, is equal to the sum of the two interior angles.
Thus, it remains to prove that $\angle L M C = 30^{\circ}$. But segment $M L$ is the median of the equilateral triangle $M K C$, and therefore $M L$ is also the angle bisector of this triangle.
Comment. Compare with problem 3 for 10th grade.
|
30
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
6. Ali-Baba and the bandit are dividing a treasure consisting of 100 gold coins, arranged in 10 piles of 10 coins each. Ali-Baba chooses 4 piles, places a cup next to each, and sets aside several coins from each pile (at least one, but not the entire pile). The bandit must then rearrange the cups, changing their initial positions, after which the coins are poured from the cups into the piles next to which the cups are placed. Ali-Baba then again chooses 4 piles out of 10, places cups next to them, and so on. At any point, Ali-Baba can leave, taking with him any three piles of his choice. The remaining coins go to the bandit. What is the maximum number of coins Ali-Baba can take if the bandit also tries to get as many coins as possible?
## 10th grade
|
6. We will show that Ali-Baba can achieve no more than 4 coins in 7 piles, while the robber can ensure that there are no piles with fewer than 4 coins. Therefore, Ali-Baba will take $100 - 7 \cdot 4 = 72$ coins.
First, we will prove that the robber can act in such a way that there are no piles with fewer than 4 coins. Indeed, this is true for the initial situation. Suppose that at some step this is true and part of the coins have already been placed in cups. Then, if two cups contain the same number of coins, the robber can swap these cups, and the situation does not change. If the number of coins in all cups is different, then in the two largest of them there are at least 3 and 4 coins, respectively, and the robber can swap these cups. As a result, in all new piles there will again be no fewer than 4 coins.
Now we will show that Ali-Baba can achieve no more than 4 coins in 7 piles.
Suppose there are 4 piles, each containing more than 4 coins, and $x_{1}^{(0)} \geqslant x_{2}^{(0)} \geqslant x_{3}^{(0)} \geqslant x_{4}^{(0)} \geqslant 5$ are the numbers of coins in these piles. We will show that Ali-Baba can achieve that in one of these piles there will be fewer than 4 coins, while the number of coins in each of the remaining six piles does not change. Let's distribute these piles as follows:
$$
x_{1}^{(0)}=y_{1}+1, \quad x_{2}^{(0)}=y_{2}+2, \quad x_{3}^{(0)}=y_{3}+3, \quad x_{4}^{(0)}=y_{4}+4
$$
by placing 1, 2, 3, and 4 coins in the cups, respectively. After swapping the cups, we get new piles consisting of
$$
x_{1}^{(1)}=y_{1}+z_{1}, \quad x_{2}^{(1)}=y_{2}+z_{2}, \quad x_{3}^{(1)}=y_{3}+z_{3}, \quad x_{4}^{(1)}=y_{4}+z_{4}
$$
coins, where $z_{1}, z_{2}, z_{3}$, and $z_{4}$ are some permutation of the numbers 1, 2, 3, and 4. The process is then repeated by replacing the numbers $x_{1}^{(0)}, \ldots, x_{4}^{(0)}$ with the numbers $x_{1}^{(1)}, \ldots, x_{4}^{(1)}$ arranged in non-increasing order.
We will prove that at some step the process will terminate, i.e., in one of these piles there will be fewer than 5 coins. One of the following three possibilities will occur:
1) $x_{1}^{(1)}>x_{1}^{(0)}$ (if the first cup is swapped);
2) $x_{1}^{(1)}=x_{1}^{(0)}, x_{2}^{(1)}>x_{2}^{(0)}$ (if the first cup is left in place and the second cup is swapped);
3) $x_{1}^{(1)}=x_{1}^{(0)}, x_{2}^{(1)}=x_{2}^{(0)}, x_{3}^{(1)}>x_{3}^{(0)}$ (if the first two cups remain in place).
On each step, the number of coins in the first pile does not decrease. Therefore, the number of steps where the first possibility is realized is finite. The total number of coins in the first and second piles also does not decrease, so the number of steps where the second possibility is realized is also finite. Similarly, it can be verified that the number of steps realizing the third possibility is also finite. Therefore, at some step the process will terminate, which corresponds to the fact that in some pile there will be no more than 4 coins. In this case, the number of piles with no more than 4 coins will increase. By repeating this process, eventually we will reach a point where there are no more than three piles containing more than 4 coins.
10 c l a s s
|
72
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. From the volcano station to the summit of Stromboli volcano, it takes 4 hours to walk along the road, and then 4 hours along the path. At the summit, there are two craters. The first crater erupts for 1 hour, then remains silent for 17 hours, then erupts again for 1 hour, and so on. The second crater erupts for 1 hour, remains silent for 9 hours, then erupts again for 1 hour, and so on. During the eruption of the first crater, it is dangerous to walk both on the path and the road, while during the eruption of the second crater, only the path is dangerous. Vanya saw that at exactly 12 o'clock, both craters started erupting simultaneously. Will he ever be able to climb to the summit of the volcano and return, without risking his life?
|
2. The path along the road and the trail (there and back) takes 16 hours. Therefore, if you start immediately after the eruption of the first crater, it will not be dangerous.
Movement along the trail (there and back) takes 8 hours. Therefore, if you start moving along the trail immediately after the eruption of the second crater, it will not be dangerous.
For Vanya to climb safely, it is sufficient for the first crater to stop erupting by the start of the movement along the road, and for the second crater to stop erupting 4 hours later, by the start of the movement along the trail.
Let's find such a moment in time. The first crater erupts on the 1st, 19th, 37th hours. The second crater erupts on the 1st, 11th, 21st, 31st, 41st hours. Therefore, if you start at the beginning of the 38th hour, Vanya will reach the start of the trail just as the second crater finishes erupting, which is what we need.
Comment. We solved the problem by enumeration. In fact, we could have set up a Diophantine equation. The first crater erupts in hours numbered $18x + 1$, where $x$ is an integer; the second crater - in hours numbered $10y + 1$. We need them to erupt with a 4-hour shift, leading to the equation
$$
10y - 18x = 4 \text{.}
$$
The smallest solution in natural numbers is $y = 4, x = 2$.
|
38
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5*. In rhombus $A B C D$ the measure of angle $B$ is $40^{\circ}, E-$ is the midpoint of $B C, F$ - is the foot of the perpendicular dropped from $A$ to $D E$. Find the measure of angle $D F C$.
|
5. Let lines $D E$ and $A B$ intersect at point $G$ (Fig. 83). Then triangles $D E C$ and $B E G$ are congruent by the second criterion. Therefore, $B G=C D=B A$. Hence, points $A, G$, and $C$ lie on a circle with center at point $B$, and $A G$ is the diameter. Since $\angle A F G=90^{\circ}$, point $F$ lies on the same circle by the theorem about angles subtended by a diameter (see fact 14).
Fig. 83
By the inscribed angle theorem, we have $\angle G F C=\frac{1}{2} \angle G B C=\frac{1}{2}\left(180^{\circ}-40^{\circ}\right)=70^{\circ}$. Therefore, $\angle D F C=180^{\circ}-$ $-\angle G F C=110^{\circ}$.
Alternative solution. We can solve the problem without using circles. It is known that the median of a right triangle drawn to the hypotenuse is equal to half the hypotenuse (see fact 14). Applying this statement to triangle $A F G$, we get $B F=B A=B G$.
Triangles $C B F$ and $F B A$ are isosceles, so the sum of angles $B C F$ and $B A F$ equals angle $C F A$.
The sum of the angles in quadrilateral $A B C F$ is $360^{\circ}$. Therefore,
$$
\angle C F A+\angle C F A+40^{\circ}=360^{\circ},
$$
from which $\angle C F A=160^{\circ}$. Hence, $\angle C F D=360^{\circ}-\angle A F C-$ $-\angle A F D=360^{\circ}-160^{\circ}-90^{\circ}=110^{\circ}$.
|
110
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A road 1 km long is fully illuminated by street lamps, each of which illuminates a section of the road 1 m long. What is the maximum number of street lamps that can be on the road, given that after turning off any street lamp, the road will no longer be fully illuminated?
|
3. Let's number the street lamps with natural numbers in the order of their placement along the road. If the segments illuminated by the $n$-th and $(n+2)$-th street lamps intersect (at least at one point), then the $(n+1)$-th street lamp can be turned off. Therefore, segments with different odd numbers do not intersect. On a segment of length 1000 m, it is impossible to place more than 999 non-intersecting segments of length 1 m. If there were at least 1999 street lamps, then there would be at least 1000 street lamps with odd numbers. Thus, there are no more than 1998 street lamps.
Let's place 1998 street lamps such that the centers of the illuminated segments form an arithmetic progression, the first term of which is $\frac{1}{2}$ m, and the 1998-th term is $999 \frac{1}{2}$ m. (The common difference of this progression is $\frac{999}{1997}$.) The distance between the $n$-th and $(n+2)$-th street lamps is $\frac{1998}{1997}$. Therefore, there is a gap of $\frac{1}{1997}$ m between the segments illuminated by these street lamps. This gap is illuminated only by the $(n+1)$-th street lamp. Therefore, no street lamp can be turned off.
Comment. Compare with problem 6 for 8th grade.
|
1998
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On the board in the laboratory, two numbers are written. Every day, senior researcher Petya erases both numbers from the board and writes down their arithmetic mean and harmonic mean instead. On the morning of the first day, the numbers 1 and 2 were written on the board. Find the product of the numbers written on the board in the evening of the 1999th day. (The arithmetic mean of two numbers $a$ and $b$ is the number $\frac{a+b}{2}$, and the harmonic mean is the number $\frac{2}{1 / a+1 / b}$.)
|
1. The product of the numbers on the board does not change. Indeed,
$$
\frac{a+b}{2} \cdot \frac{2}{1 / a+1 / b}=\frac{a+b}{2} \cdot \frac{2 a b}{a+b}=a b
$$
Therefore, on the 1999th day, the product will be the same as it was on the first day. See also fact 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 *. Find all pairs of natural numbers $x, y$ such that $x^{3}+y$ and $y^{3}+x$ are divisible by $x^{2}+y^{2}$.
|
3. Let's first prove that $x$ and $y$ are coprime. Assume the opposite. Then $x$ and $y$ are divisible by some prime number $p$. Let $p$ enter the prime factorizations of $x$ and $y$ with powers $a \geqslant 1$ and $b \geqslant 1$ respectively (see fact 10). Without loss of generality, we can assume that $a \geqslant b$. Then the maximum power of $p$ that divides $x^{3}+y$ is $b$ (since $x^{3}$ is divisible by $p^{3 a}$ and therefore by $p^{b+1}$, but $y$ is divisible by $p^{b}$ and not by $p^{b+1}$). On the other hand, $x^{2}+y^{2}$ is divisible by $p^{2 b}$, so $x^{3}+y$ cannot be divisible by $x^{2}+y^{2}$. This contradiction shows that $x$ and $y$ are coprime (see fact 5).
Next, by the condition, $x\left(x^{2}+y^{2}\right)-\left(x^{3}+y\right)=y(x y-1)$ must be divisible by $x^{2}+y^{2}$. Note that $y$ and $x^{2}+y^{2}$ cannot have a common divisor greater than 1 (since $x$ and $y$ are coprime), so $x y-1$ must be divisible by $x^{2}+y^{2}$ (see fact 9). But if we assume that $x y-1>0$, this is impossible, since $x^{2}+y^{2} \geqslant 2 x y>x y-1$. Therefore, $x y=1$, which means $x=y=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Pete's bank account contains 500 dollars. The bank allows only two types of transactions: withdrawing 300 or adding 198 dollars. What is the maximum amount Pete can withdraw from his account if he has no other money?
|
4. Since 300 and 198 are divisible by 6, Petya will only be able to withdraw an amount that is a multiple of 6 dollars (see fact 5). The maximum number that is a multiple of 6 and does not exceed 500 is 498.
Let's show how to withdraw 498 dollars. We will perform the following operations: $500-300=200, 200+198=398, 398-300=98, 98+198=296, 296+198=494$. The amount in the bank has decreased by 6 dollars.
By repeating this procedure 16 times, Petya will withdraw 96 dollars. Then he can withdraw 300, deposit 198, and withdraw 300 again. As a result, he will have 498 dollars.
|
498
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4*. Find all such positive integers $k$ for which the number
$$
\underbrace{1 \ldots 1 \overbrace{2 \ldots 2}^{k}}_{2000}-\underbrace{2 \ldots 2}_{1001}
$$
is a perfect square.
|
4. Let $n=1000$. Consider two cases.
$1^{\circ} . k>n$. Then
$$
\underbrace{1 \ldots 12 \ldots 2}_{2 n}-\underbrace{2 \ldots 2}_{n+1}=\underbrace{1 \ldots 1}_{2 n-k} \overbrace{2 \ldots 2}^{k-(n+1)} \underbrace{0 \ldots 0}_{n+1} .
$$
This number ends with $n+1=1001$ zeros. But if a number is a square of a natural number, it must end with an even number of zeros! Therefore, this number cannot be a square of a natural number.
$2^{\circ} . k \leqslant n$. Then
$$
\begin{aligned}
\underbrace{1 \ldots 1 \overbrace{2 \ldots 2}^{k}}_{2 n}-\underbrace{2 \ldots 2}_{n+1}=\underbrace{1 \ldots 10 \ldots 0}_{2 n-k}-\underbrace{2 \ldots 20 \ldots 0}_{k} & = \\
& =10^{k}(\underbrace{1 \ldots 1}_{2 n-k}-\underbrace{2 \ldots 2}_{n+1-k})
\end{aligned}
$$
This number ends with $k$ zeros. As explained above, for it to be a square of a natural number (henceforth, we will call squares of natural numbers perfect squares), $k$ must be even. Let $l=\frac{k}{2}$.
It is clear that the number (1) is a perfect square if and only if the number
$$
A=\underbrace{1 \ldots 1}_{2 n-2 l}-\underbrace{2 \ldots 2}_{n+1-2 l}
$$
is a perfect square.
Notice that
$$
A=\frac{1}{9} \cdot \underbrace{9 \ldots 9}_{2 n-2 l}-\frac{2}{9} \cdot \underbrace{9 \ldots 9}_{n+1-2 l}=\frac{1}{9}\left(10^{2 n-2 l}-1-2\left(10^{n+1-2 l}-1\right)\right)
$$
(see fact 11). Let $B=9 A$. The number $A$ is a perfect square if and only if $B=9 A$ is a perfect square. Write the expression for $B$ in the following form:
$$
B=10^{2 n-2 l}-2 \cdot 10^{n+1-2 l}+1=\left(10^{n-l}\right)^{2}-2 \cdot 10^{n-l} \cdot 10^{1-l}+1
$$
For $l=1$, the right-hand side of (2) becomes the formula for the square of a difference:
$$
B=\left(10^{n-1}\right)^{2}-2 \cdot 10^{n-1}+1=\left(10^{n-1}-1\right)^{2}
$$
Let $l>1$.
Now notice that if $X=Y^{2}$ is a square of a natural number, then the nearest perfect square (less than $X$) is $(Y-1)^{2}=Y^{2}-2 Y+1$. That is, if a number $Z$ is such that
$$
Y^{2}-2 Y+1\left(10^{n-l}\right)^{2}-2 \cdot 10^{n-l}+1
$$
Then, by the previous observation, this number cannot be a perfect square, so only $l=1$ (and, therefore, only $k=2$) satisfies the condition.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In the elections to the 100-seat parliament, 12 parties participated. Parties that received strictly more than $5 \%$ of the voters' votes enter the parliament. Among the parties that entered the parliament, seats are distributed proportionally to the number of votes they received (i.e., if one party received $x$ times more votes than another, it will also receive $x$ times more seats in the parliament). After the elections, it turned out that each voter voted for exactly one party (there were no invalid ballots, votes "against all," etc.) and each party received an integer number of seats. Moreover, the Party of Mathematics Enthusiasts received $25 \%$ of the votes. What is the maximum number of seats in the parliament that the Party of Mathematics Enthusiasts could have received? (Explain your answer.)
|
2. Idea of the solution: The Party of Mathematics Enthusiasts (PME) will receive the maximum number of seats in parliament if the total number of votes cast for non-qualifying (i.e., receiving no more than $5 \%$ of the votes) parties is maximized.
If 10 parties receive exactly $5 \%$ of the votes each, and two, including the Party of Mathematics Enthusiasts (PME), receive $25 \%$ each, then only two parties will enter parliament. Each of them will receive exactly 50 seats in parliament.
We will prove that PME cannot receive more seats. If 11 parties did not qualify for parliament, then together they would have received no more than $55 \%$ of the votes, but $55 \% + 25 \% < 100 \%$. Therefore, a maximum of 10 parties did not qualify for parliament, and they collectively received no more than $50 \%$ of the votes.
Thus, the parties that qualified for parliament received at least $50 \%$ of the votes. Since PME received $25 \%$ of the votes, it received no more than half of the seats in parliament, i.e., no more than 50 seats.
|
50
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. What is the maximum number of knights that can be placed on a $5 \times 5$ board such that each one attacks exactly two others? (Provide an example and explain why it is not possible to place more knights.)
## 9 t h g r a d e
|
6. Fig. 116 shows the arrangement of 16 knights that satisfies the problem's condition. We will show that it is impossible to place more knights. Let's color the cells of the board in black and white, as shown in Fig. 116. Note that the number of knights on black cells is equal to the number of knights on white cells. Indeed, if we connect the knights that attack each other with segments, then each segment will connect a white cell with a black one. On the other hand, from each cell, two segments emerge. Therefore, the number of segments is equal to twice the number of knights on white cells and twice the number of knights on black cells. Hence, the number of knights on white cells is equal to the number of knights on black cells.
There are 12 white cells and 13 black cells in total. If the number of empty white cells is $n$, then the number of empty black cells
Fig. 116
Fig. 117 is $n+1$, and it is sufficient to prove that $n \geqslant 4$ (then at least $4+(4+1)=9$ cells are empty).
In any optimal arrangement of knights, the central cell is empty. Otherwise, out of the eight cells that the knight on the central cell attacks, exactly six are empty white cells. Hence, $n \geqslant 6$, and the number of knights does not exceed $25-6-(6+1)=12$.
Consider the cell marked with the number 1 in Fig. 117. If a knight stands on this cell, then 4 out of the 6 black cells it attacks are empty. By the proven fact, the central cell is also empty. Therefore, at least 5 black cells are empty, and the proof is complete. Therefore, we can assume that this cell is empty. Similarly, we can assume that cells 2, 3, and 4 are empty. But then $n \geqslant 4$, which is what we needed to prove.
9 c l a s s
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Six words are given: ZANOZA, ZIPUNY, KAZINO, KEFAL', OTMEL', SHELEST. In one step, you can replace any letter in any of these words with any other letter (for example, in one step, you can get the word ZKNOZA from ZANOZA). How many steps are needed to make all the words the same (nonsense words are allowed)? Provide an example and prove that it is impossible to do so with fewer steps.
|
3. Let's write the words in a column:
|  | | | |
| :---: | :---: | :---: | :---: |
After all the letter replacements in each column, the letters should become the same. The number of replacements will be the smallest if, in each column, the most frequent letter (any of them if there are several) is retained. For example, in the first column, we can keep the letters 3 or К. In both cases, to make the first letters the same, four replacements will be required. In the second column, four replacements will also be needed. However, in the third column, all the letters are different, so five replacements will be required. In the last three columns, four replacements will be needed each. The minimum number of replacements in all columns is \(4+4+5+4+4+4=25\).
Comment. Among the words that can result, there are meaningful ones, such as ЗЕЛЕНЬ (GREEN), КАПЕЛЬ (DROPLETS), or КАФЕЛЬ (TILE).
|
25
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a convex quadrilateral $A B C D$, points $E$ and $F$ are the midpoints of sides $B C$ and $C D$ respectively. Segments $A E, A F$, and $E F$ divide the quadrilateral into 4 triangles, the areas of which are consecutive natural numbers. What is the maximum possible value of the area of triangle $A B D$?
|
3. Let the areas of the triangles be $n, n+1, n+2$, $n+3$. Then the area of the quadrilateral $A B C D$ is $4 n+6$. It is easy to see that the area of triangle $B C D$ is four times the area of triangle $E C F$, so this area is at least $4 n$. Therefore,
$$
S_{A B D}=S_{A B C D}-S_{B C D} \leqslant(4 n+6)-4 n=6 .
$$
Equality is achieved if triangle $E C F$ has the smallest area
Fig. 151 of the four triangles mentioned.
It remains to prove that the value 6 is possible. An example is an isosceles trapezoid with bases $A D=6, B C=4$ and height 2 (the numbers in Fig. 151 denote the areas of the triangles).
Comment. It is easy to see that the area of triangle $A B D$ is always either 2 or 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the city of Udoyev, mayoral elections proceed as follows. If in a given round of voting no candidate receives more than half of the votes, then a subsequent round is held with the participation of all candidates except the one who received the fewest votes. (No two candidates ever receive the same number of votes; if a candidate receives more than half of the votes, they become the mayor and the election ends.) Each voter votes for one candidate in each round. If this candidate advances to the next round, the voter votes for them again. If the candidate is eliminated, all their voters vote for the same remaining candidate.
In the upcoming election, 2002 candidates ran. Ostap Bender became the mayor, finishing in $k$-th place in the first round by the number of votes. Determine the maximum possible value of $k$ if Ostap was elected a) in the 1002nd round; b)* in the 1001st round.
|
5. a) Ostap could not take the last, 2002nd place in the first round, as otherwise he would have been immediately eliminated from the list of candidates. Therefore, $k \leqslant 2001$.
Suppose all candidates in the first round received almost the same number of votes, Ostap took the second-to-last place, and in each subsequent round, he received all the votes of the eliminated candidate. Then Ostap will win at the moment when the number of eliminated candidates reaches half. This will happen precisely in the 1002nd round.
Let's perform an exact calculation in the case where the candidates in the first round received $10^{6}, 10^{6}+1, \ldots, 10^{6}+2001$ votes. Then in the 1001st round, Ostap still has less than half of the votes, specifically: the votes of all candidates who took the last 1001 places in the first round. However, in the 1002nd round, he already has more than half of all the votes. Indeed, in the 1002nd round, Ostap has
\[
\begin{array}{r}
10^{6}+\left(10^{6}+1\right)+\ldots+\left(10^{6}+1001\right)=1002 \cdot 10^{6}+\frac{1001 \cdot 1002}{2}= \\
=1002 \cdot 10^{6}+1001 \cdot 501=1002501501
\end{array}
\]
votes, and the total number of voters is
\[
\begin{aligned}
10^{6}+\left(10^{6}+1\right)+\ldots+ & \left(10^{6}+2001\right)=2002 \cdot 10^{6}+\frac{2001 \cdot 2002}{2}= \\
& =2002 \cdot 10^{6}+2001 \cdot 1001=2004003001
\end{aligned}
\]
It is easy to verify that this is less than twice the number of votes Ostap has.
b) Suppose $k>1$. Those who were eliminated in the first thousand rounds will be called underdogs, and all other candidates except Ostap will be called leaders. The candidate who took first place in the first round will be called the favorite. Since the number of underdogs is 1000 and the number of leaders is 1001, one of the leaders did not receive votes from the underdogs. In the first round (and later), he had more votes than any underdog (since in the end, the underdog was eliminated, not this leader). Therefore, the favorite also had more votes in the first round than any underdog. Hence, the favorite is a leader.
The maximum number of votes Ostap could have collected by the 1001st round is all the votes of the underdogs at the moment of their elimination and the votes of Ostap's initial voters. Any leader in any of the first thousand rounds (and especially in the 1001st) has more votes than the underdog of that round. The favorite definitely has more votes than Ostap had in the first round. Therefore, the leaders and the favorite together have more votes in the 1001st round than Ostap, and he cannot become the winner.
Comments. $1^{\circ}$. Additional question: Would the answer change in the problem if the votes of the eliminated candidate were arbitrarily divided among the remaining candidates?
$2^{\circ}$. Note that in part "a" we get a very large city (with more than two billion voters). It is interesting to understand how the answer depends on the number of voters. Note that from the condition, it follows that the city has at least
\[
0+1+\ldots+2001=2003001
\]
voters - otherwise, the number of votes for all candidates could not have been different.
|
2001
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. There are 4 people in the family. If Masha's scholarship is doubled, the total income of the entire family will increase by $5 \%$, if instead, Mom's salary is doubled - then by $15 \%$, if Dad's salary is doubled - then by $25 \%$. By what percentage will the family's total income increase if Grandpa's pension is doubled?
|
1. The first method. If Masha's scholarship is doubled, the family income will increase by the amount of this scholarship. Therefore, Masha's scholarship constitutes $5 \%$ of the total income. Similarly, Mom's salary is $15 \%$, and Dad's is $25 \%$. The remaining share $100 \% - 5 \% - 15 \% - 25 \% = 55 \%$ is attributed to Grandpa's pension. Thus, if his pension is doubled, the family's total income will increase by $55 \%$.
The second method. If all family members suddenly started getting paid twice as much, the total income would increase by $100 \%$. Out of this increase, $5 \%$ is attributed to Masha, $15 \%$ to Mom, $25 \%$ to Dad, and the remaining $55 \%$ to Grandpa.
|
55
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In the country, there are 15 cities, some of which are connected by air routes belonging to three airlines. It is known that even if any one of the airlines ceases operations, it will still be possible to travel from any city to any other (possibly with layovers), using the flights of the remaining two airlines. What is the minimum number of air routes that can exist in the country?
|
5. We will prove that fewer than 21 airlines are not sufficient. First, note that if 15 cities are connected by airlines in such a way that one can travel from any city to any other, then there are no fewer than 14 airlines. Indeed, starting from an arbitrary city, we will try to visit all the others, and visiting each subsequent city will require at least one new airline (see fact 3).
Let the number of lines of the airlines be denoted by $a$, $b$, and $c$. By the proven fact, any two companies together have no fewer than 14 lines, i.e., $a+b \geqslant 14, b+c \geqslant 14, c+a \geqslant 14$. Adding these inequalities, we get: $2(a+b+c) \geqslant 42$, i.e., the three companies together have no fewer than 21 airlines.
It remains to provide an example with 21 airlines. Two such examples are shown in Fig. 157.
Fig. 157
|
21
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. For a convex polyhedron, the internal dihedral angle at each edge is acute. How many faces can the polyhedron have?
|
5. For each of the faces, consider the vector of the external normal, i.e., a vector perpendicular to this face and directed outward from the polyhedron.
$1^{\circ}$. Let's prove that the angle between any two external normals is obtuse or straight. Suppose this is not the case, and there exist two faces $\Gamma_{1}$ and $\Gamma_{2}$, the external normals of which form an angle not greater than $\pi / 2$. Then the faces $\Gamma_{1}$ and $\Gamma_{2}$ belong to half-planes $\Pi_{1}$ and $\Pi_{2}$, which form a dihedral angle of at least $\pi / 2$.
Take a point $P$ on the face $\Gamma_{2}$. Let $P^{\prime}$ be the projection of the point $P$ onto the plane of the face $\Gamma_{1}$. Since the angle between
Fig. 167 the external normals to the faces $\Gamma_{1}$ and $\Gamma_{2}$ is not greater than $\pi / 2$, and our polyhedron is convex, the point $P^{\prime}$ lies outside the polygon $\Gamma_{1}$. Therefore, there exists a line containing some edge $r$ of the face $\Gamma_{1}$ and separating $P^{\prime}$ from $\Gamma_{1}$. The polyhedron lies inside the acute dihedral angle corresponding to the edge $r$, but $P$ lies outside this dihedral angle (Fig. 167). Contradiction.
$2^{\circ}$. It remains to show that in space, there do not exist more than four vectors, the pairwise angles between which are obtuse or straight.
Suppose this is not the case, and $\vec{u}_{0}, \vec{u}_{1}, \vec{u}_{2}, \vec{u}_{3}, \vec{u}_{4}$ are five vectors, the pairwise angles between which are obtuse or straight. Introduce a rectangular coordinate system such that the $O z$ axis is directed along $\vec{u}_{0}$.
Denote by $\vec{v}_{i}$ the projection of the vector $\vec{u}_{i}$ onto the plane $O x y$. Let $\vec{u}_{i}=\left(x_{i}, y_{i}, z_{i}\right)$, then $x_{0}=y_{0}=0, z_{0}>0$ and $v_{0}=0$.
The condition that all angles are obtuse or straight is equivalent to all scalar products being negative. In particular,
$$
z_{0} z_{i}=\left(\vec{u}_{0}, \vec{u}_{i}\right) < 0 \quad \text{for} \quad 1 \leqslant i \leqslant 4.
$$
Since $z_{0} > 0$, it follows that $z_{i} < 0$ for $1 \leqslant i \leqslant 4$. Now consider the scalar products between the projections:
$$
\left(\vec{v}_{i}, \vec{v}_{j}\right)=\left(\vec{u}_{i}, \vec{u}_{j}\right)-z_{i} z_{j} < 0 \quad \text{for} \quad 1 \leqslant i, j \leqslant 4.
$$
Thus, $\vec{v}_{1}, \vec{v}_{2}, \vec{v}_{3}, \vec{v}_{4}$ are four vectors on the plane, the angles between which are obtuse or straight. But this is impossible.
Therefore, a polyhedron has four faces. Note that a polyhedron with four faces can only be a tetrahedron.
Idea of another solution. First, prove that at each vertex of the polyhedron, three faces meet. For this, it is sufficient to prove that the sum of the dihedral angles of any $n$-hedral angle is greater than $\pi(n-2)$. Since an $n$-hedral angle can be cut into $n-2$ trihedral angles, it is sufficient to prove this statement for a trihedral angle. Now, it can be shown that all planar angles at each vertex are acute. From this, it is not difficult to deduce that all faces are triangles. Now, it is not difficult to verify that the polyhedron is a tetrahedron.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the shore of a round island called Somewhere, there are 20 villages, each inhabited by 20 wrestlers. A tournament was held where each wrestler faced all wrestlers from all other villages. Village A is considered stronger than Village B if at least $k$ matches between wrestlers from these villages end with a victory for a wrestler from Village A. It turned out that each village is stronger than the next one in the clockwise direction. What is the maximum value that $k$ can have? (All wrestlers have different strengths, and the stronger wrestler always wins in a match.)
|
6. Let's provide an example showing that the described situation is possible when $k \leqslant 290$. We will order all the wrestlers by strength and renumber them in ascending order of strength (the first being the weakest). We will call the 210 weakest wrestlers novices, and the 190 strongest - masters. In particular, any novice will be weaker than any master. We will number the villages counterclockwise. We will place in the first village one of the weakest novices and 19 of the weakest masters; in the second village - two of the weakest remaining novices and 18 of the weakest remaining masters; in the third village - three of the weakest remaining novices and 17 of the weakest remaining masters, and so on; in the last village, we will place the 20 strongest novices. This placement in the villages is shown in the table (in the "Wrestlers" column, numbers in regular font indicate the strengths of masters, and numbers in italics indicate the strengths of novices).
| Villages | Wrestlers | Villages | Wrestlers |
| :---: | :--- | :---: | :--- |
| 1 | $1,211-229$ | 11 | $56-66,356-364$ |
| 2 | $2-3,230-247$ | 12 | $67-78,365-372$ |
| 3 | $4-6,248-264$ | 13 | $79-91,373-379$ |
| 4 | $7-10,265-280$ | 14 | $92-105,380-385$ |
| 5 | $11-15,281-295$ | 15 | $106-120,386-390$ |
| 6 | $16-21,296-309$ | 16 | $121-136,391-394$ |
| 7 | $22-28,310-322$ | 17 | $137-153,395-397$ |
| 8 | $29-36,323-334$ | 18 | $154-171,398-399$ |
| 9 | $37-45,335-345$ | 19 | $172-190,400$ |
| 10 | $46-55,346-355$ | 20 | $191-210$ |
We will show that the $i$-th village is stronger than the $(i-1)$-th village for $i>1$. Indeed, in the $i$-th village, there are $i$ novices and $20-i$ masters. In this case, the masters of the $i$-th village will defeat all in the $(i-1)$-th village, and the novices will defeat the novices, and the total number of victories will be $20(20-i)+i(i-1)=i^{2}-21 i+400$. The vertex of this parabola is at the point $i=10.5$, and the branches are directed upwards, so the minimum value at an integer point is achieved exactly at two values $i=10$ and $i=11$ - and is equal to $10^{2}-21 \cdot 10+400=290$. That is, the $i$-th village is stronger than the $(i-1)$-th village for $k \leqslant 290$. Moreover, the masters of the first village will defeat the novices of the 20th village, and the total number of victories will be $20 \cdot 19=380>290$, i.e., all conditions are met.
We will show that such a situation is impossible when $k>290$. We will order the wrestlers in each village by decreasing strength and select the tenth strongest wrestler in each village. We will show that the village in which the weakest of the selected wrestlers lives cannot be stronger than the next village. Let's denote the selected wrestlers in our and the next village as $A$ and $B$ respectively. Then in our village, there are 11 wrestlers who are not stronger than $A$, and in the next village, there are 10 wrestlers who are at least as strong as $B$. All matches between these wrestlers will end in favor of the next village, and there are 110 such matches, i.e., the number of matches won by a wrestler from our village is no more than $20 \cdot 20-110=290$.
|
290
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. An extrasensory perception (ESP) practitioner has a deck of 36 cards face down in front of him (four suits, nine cards of each suit). He names the suit of the top card, after which the card is revealed to him. Then he names the suit of the next card, and so on. The task of the ESP practitioner is to guess the suit as many times as possible.
The backs of the cards are not symmetrical, and the ESP practitioner can see which of the two positions the top card is in. The ESP practitioner's assistant knows the order of the cards in the deck, cannot change it, but can position the back of each card in one of two ways.
Could the ESP practitioner have agreed with the assistant, before the assistant knew the order of the cards, to ensure guessing the suit of at least a) 19 cards; b) 23 cards?
If you have come up with a way to guess a different number of cards, more than 19, please also write it down.
10 k l a s s
|
6. a) Note that guessing 18 cards is not difficult. Indeed, the first two backs can "encode" the suit of the second card (by associating each suit with one of the four possible arrangements of the two backs), the next two backs can encode the suit of the fourth card, and so on.
When only two cards remain in the deck, the clairvoyant knows what they are (since he saw which 34 cards came out), and therefore the assistant only needs to encode the order in which they lie; this is easily done using the back of the 35th card. Indeed, the clairvoyant and the assistant can agree on which suit is "older," after which the assistant can indicate with the position of the 35th card which of the cards is older - the 35th or the 36th. Thus, the clairvoyant will guess the suits of 19 cards.
b) We will call the 1st, 3rd, 5th, ..., 35th cards odd. Consider the following 17 cards: all odd cards except the first and the second-to-last, and the second card. By the pigeonhole principle (see fact 1), among these seventeen cards, there must be five cards of the same suit. We will call this suit the main suit. The position of the first two cards in the deck can encode the main suit. The position of the $(2k-1)$-th and $2k$-th cards (for $2 \leqslant k \leqslant 17$) can encode the suit of the $2k$-th card. The position of the back of the second-to-last card can encode the suits of the last two cards (see the solution to part "a").
The clairvoyant should name the main suit for each of the selected seventeen cards. Then he will guess the suits of at least five of the selected seventeen cards. In addition, the clairvoyant will guess the suits of all even cards except the second and the last, as well as the suits of the last two cards. In total, he will guess the suits of at least 23 cards.
Comment. We will show how the clairvoyant could guess the suits of 24 cards. For this, it is sufficient to guess the suits of at least 22 out of the first 34 cards (see the end of the solution to part "a"). Divide these 34 cards, except the first, into 11 consecutive triplets. The position of the first card (not included in any triplet) will indicate whether there are more black or red suits in the first triplet. Without loss of generality, assume there are more black suits.
Consider the cards of the first triplet. Call the first two black cards natural. The remaining card is called unnatural (it can be either black or red). By rotating the back of each of the two natural cards, the assistant will show which of the two black suits the clairvoyant should name. Using this information, the clairvoyant will guess the suits of both natural cards. By rotating the back of the unnatural card, the assistant encodes the color that is more frequent in the next triplet. (Note that if the red card in the first triplet is not the last, the clairvoyant will be able to recognize its unnaturalness only after it is revealed.)
Now the same can be done with the second triplet - in this case, the clairvoyant will guess two suits out of three and learn the dominant color of the next triplet, and so on. Thus, he will guess the suits of all cards except, perhaps, the first card and one card in each triplet, i.e., at least 24 cards in total.
A (much more complex) algorithm is known that ensures the guessing of the suits of 26 cards (see [89], [90]).
10 c l a s s
|
26
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A square sheet of checkered paper $8 \times 8$ was folded several times along the grid lines so that a $1 \times 1$ square was obtained. It was then cut along a segment connecting the midpoints of two opposite sides of the square. Into how many pieces could the square have split as a result?
|
2. Let the cut be vertical (the case of a horizontal cut is analogous). Draw vertical segments in all $1 \times 1$ squares, connecting the midpoints of opposite sides. Notice that when folding along the grid lines, these
Fig. 180 segments overlap each other. Therefore, when cutting, only these segments are cut. By counting the number of resulting parts, we see that the square has split into 9 parts.
Comment. It was important to solve the problem for any folding, not just a specific example. In particular, the problem does not specify that each fold was made in half.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. To some natural number, two two-digit numbers were appended sequentially to the right. The resulting number turned out to be equal to the cube of the sum of the three original numbers. Find all possible triples of the original numbers.
|
5. Let $a$ denote the first natural number, and $b$ and $c$ the two-digit numbers written after it. Let $x=a+b+c$. According to the condition, the numbers $a, b, c$ and $x$ satisfy the equation $10^{4} a+100 b+c=x^{3}$ (see fact 11). Therefore,
$$
x^{3}=10^{4} a+100 b+c44$;
2) $x=45(x-1=44), 45^{3}=91125, a=9, b=11, c=25$;
3) $x=54(x+1=55), 54^{3}=157464,15+74+64>54$;
4) $x=55(x-1=54), 55^{3}=166375,16+63+75>55$;
5) $x=89(x-1=88, x+1=90), 89^{3}=704969,70+49+$ $+69>89$
6) $x=98(x+1=99), 98^{3}=941192,94+11+92>98$;
7) $x=99,99^{3}=970299,97+2+99>99,2-$ is not a two-digit number.
|
91125
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35. Given a line $l$, two points $A$ and $B$ on the same side of it, and a segment $a$. Find a segment $X Y$ on the line $l$ of length $a$ such that the length of the broken line $A X Y B$ is the smallest (Fig. 42).
|
35. Since the length of the segment $X Y$ is equal to $a$, it is necessary that the sum $A X + B Y$ be minimal. Suppose that the segment $X Y$ is laid out. The sliding symmetry with the axis $l$ "of the parallel translation magnitude $a$ translates point $B$ to $B'$, and point $Y$ to $X$ (Fig. 144); therefore, $B Y = B' X$ and, consequently, $A X + B Y = A X + B' X$. Thus, it is required that the length of the broken line $A X B'$ be the smallest. From this, it follows that $X$ is the point of intersection of the line $l$ with the segment $A B'$.
Fig. 144.
Fig. 145.
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
42. Given three lines $l_{1}, l_{2}$ and $l_{3}$ and three points $A, B$ and $C$-one point on each of the lines. Draw a line $m$ intersecting lines $l_{1}, l_{2}$ and $l_{3}$ at points $X, Y$ and $Z$ such that $A X=B Y=C Z$.
|
42. Let the lines $l_{1}, l_{2}$ and $l_{3}$ not all be parallel to each other, for example, $l_{3}$ is not parallel to either $l_{1}$ or $l_{2}$. Suppose the problem is solved (Fig. 155). By Theorem 1, there exists
Fig. 155.
a rotation that maps $A X$ to $C Z$, and a rotation that maps $B Y$ to $C Z$; the angles of rotation $\alpha_{1}$ and $\alpha_{2}$ are equal to the angles between $l_{1}$ and $l_{3}$, and $l_{2}$ and $l_{3}$, respectively, and the centers of rotation $O_{1}$ and $O_{2}$ are located as in the first solution of problem 41 a) - r). From the isosceles triangles $O_{1} X Z$ and $O_{2} Y Z$ with angles at the vertices $O_{1}$ and $O_{2}$, respectively, equal to $\alpha_{1}$ and $\alpha_{2}$, we find $\angle O_{1} Z X = 90^{\circ} - \frac{\alpha_{1}}{2}$, $\angle O_{2} Z Y = 90^{\circ} - \frac{\alpha_{2}}{2}$. Therefore, $\angle O_{1} Z O_{2} = \frac{\alpha_{1} \pm \alpha_{2}}{2}$, and thus, the point $Z$ can be found as the intersection of the line $l_{3}$ with the arc of the circle subtended by the segment $O_{1} O_{2}$, containing the known angle $\frac{\alpha_{1} + \alpha_{2}}{2}$ or $\frac{\alpha_{1} - \alpha_{2}}{2}$.
I. M. Yaglom
Each of the angles of rotation $\alpha_{1}$ and $\alpha_{2}$, and the corresponding centers of rotation $O_{1}$ and $O_{2}$, can be determined in two different ways (compare with the solution of the previous problems). Therefore, the maximum possible number of solutions to the problem is 16.
If $l_{1} \| l_{2} \| l_{3}$, then the problem has three solutions in the case where the points $A, B$, and $C$ do not lie on the same line (the solutions are given by the medians of the triangle $ABC$), and infinitely many solutions when $A B C$ is a straight line.
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-ча 1. How many real solutions does the system of two equations with three unknowns have:
$$
\left\{\begin{aligned}
x+y & =2 \\
x y-z^{2} & =1 ?
\end{aligned}\right.
$$
|
Sol 1. From the second equation, it follows that $x y \geqslant 1$. The numbers $x$ and $y$ cannot both be negative, since their sum is 2. Therefore, the numbers $x$ and $y$ are positive and $x+y \geqslant 2 \sqrt{x y} \geqslant 2$, and the equality $x+y=2$ is possible only when $x=y=1$. In this case, $z=0$.
Part 2. Solve the system of equations:
$$
\left\{\begin{aligned}
x^{3}-y^{3} & =26 \\
x^{2} y-x y^{2} & =6
\end{aligned}\right.
$$
Sol 2. Let $y=k x$. Immediately note that $k \neq 1$. From the equations
$$
\begin{aligned}
x^{3}-k^{3} x^{3} & =26 \\
k x^{3} y-k^{2} x^{3} & =6
\end{aligned}
$$
we get $x^{3}=\frac{26}{1-k^{3}}$ and $x^{3}=\frac{6}{k-k^{2}}$. Therefore,
$$
\frac{26}{1-k^{3}}=\frac{6}{k-k^{2}}
$$
This equation can be multiplied by $1-k$. As a result, we get
$$
\frac{26}{1+k+k^{2}}=\frac{6}{k}
$$
from which $k=3$ or $\frac{1}{3}$. Therefore, $x^{3}=-1$ or $x^{3}=27$. In the end, we get the following solutions: $(-1,-3)$, $\left(\frac{1 \pm i \sqrt{3}}{2}, \frac{3}{2}(1 \pm i \sqrt{3})\right),(3,1),\left(\frac{-3 \pm 3 i \sqrt{3}}{2}, \frac{1}{2}(-1 \pm i \sqrt{3})\right)$.
Part 3. Find the sum
$$
1^{3}+3^{3}+5^{3}+\cdots+(2 n-1)^{3}
$$
Sol 3. By induction on $m$, it is easy to prove that $1^{3}+2^{3}+3^{3}+\cdots+m^{3}=\left(\frac{m(m+1)}{2}\right)^{2}$. Indeed, the base of induction is obvious, so we only need to check the equality
$$
\frac{m^{2}(m+1)^{2}}{2}+(m+1)^{3}=\frac{(m+1)^{2}(m+2)^{2}}{.}
$$
After canceling by $m+1$ and multiplying by 4, we get the obvious equality $m^{2}+4(m+1)=(m+2)^{2 *}$
Thus, $1^{3}+2^{3}+3^{3}+\cdots+(2 n-1)^{3}+(2 n)^{3}=\left(\frac{2 n(2 n+1)}{2}\right)$, i.e., $1^{3}+3^{3}+5^{3}+\cdots+(2 n-1)^{3}+2^{3}\left(1^{3}+2^{3}+\cdots+n^{3}\right)=\left(\frac{2 n(2 n+1)}{2}\right)^{2}$. Transform the last equality, using the fact that $1^{3}+2^{3}+\cdots+n^{3}=\left(\frac{n(n+1)}{2}\right)^{2}$. As a result, we get $1^{3}+3^{3}+5^{3}+\cdots+(2 n-1)^{3}=n^{2}\left(2 n^{2}-1\right)$.
## Series C
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-ча 1. Six different colors are chosen; it is required to paint 6 faces of a cube, each in a special color from the chosen ones. In how many geometrically distinct ways can this be done? Geometrically distinct are two such colorings that cannot be made to coincide with each other by rotating the cube around its center.
Solve the same problem for the case of coloring the faces of a regular dodecahedron in twelve different colors.
(This problem was not solved by any of the participants in the olympiad.)
|
Solution 1. A cube can be rotated so that the face painted the first color takes the specified position. There are 5 different options for painting the opposite face; different colorings of the opposite face give geometrically different colorings of the cube.
Among the remaining four faces, one can choose the face painted a given color and translate it to a given position (without changing the position of the first two faces). Different colorings of the three remaining faces give geometrically different colorings of the cube. One of these faces can be painted in 3 ways, and one of the remaining in 2 ways. In total, we get $5 \cdot 3 \cdot 2=30$ geometrically different colorings.
Now let's solve the problem for a 12-faced polyhedron (dodecahedron). The total number of possible colorings of the dodecahedron is $12!=1 \cdot 2 \cdots \cdots 12$. To find the number of geometrically different colorings, we need to divide 12! by the number of self-coincidences of the dodecahedron. Any of the 12 faces can be translated to any other. In addition, there are 5 rotations (including the identity) that preserve a given face. In total, there are 60 self-coincidences. Therefore, the number of geometrically different colorings of the dodecahedron is $12!/ 60=7983360$.
|
30
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-4. In how many different ways can 1000000 be represented as a product of three natural ${ }^{1}$ numbers? Products that differ only in the order of the factors are considered identical.
(This problem was not solved by any of the olympiad participants.)
|
Solution 4. Let the factors have the form $2^{a_{1}} 5^{b_{1}}, 2^{a_{2}} 5^{b_{2}}$ and $2^{a_{3}} 5^{b_{3}}$. Then $a_{1}+a_{2}+a_{3}=6$ and $b_{1}+b_{2}+b_{3}=6$. Here, the numbers $a_{i}$ and $b_{i}$ can be zero. If $a_{1}=k$, then for the decomposition $a_{2}+a_{3}=6-k$ we get $7-k$ options. Therefore, for the decomposition $a_{1}+a_{2}+a_{3}=6$ we get $7+6+5+4+3+2+1=28$ options. In total, we get $(28)^{2}=784$ ways.
However, we have not yet taken into account the identity of decompositions that differ only in the order of the factors. There is exactly one decomposition, independent of the order of the factors, in which all factors are equal to 100. The decompositions in which there are two equal factors, we have counted three times. In each of the equal factors, 2 can enter in degrees $0,1,2$ or 3, i.e., in four different ways; 5 can also enter in four different ways. In total, we get 16 decompositions of this kind, but one of them is the decomposition considered above with three equal factors. There remain 15 decompositions, each of which we have counted three times. The number of decompositions with pairwise distinct factors is $784-1-45=738$. Each of them we have counted 6 times, so among them there will be $738 / 6=123$ different decompositions. In total, we get $1+15+123=139$ decompositions.
|
139
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-4. How many natural ${ }^{2}$ numbers less than a thousand are there that are not divisible by 5 or 7?
|
Solution 4. Answer: 686 numbers. First, let's strike out from the set of numbers $1,2, \ldots, 999$ the numbers that are multiples of 5; their quantity is $\left[\frac{999}{5}\right]=199$. Then, from the same set of numbers $1,2, \ldots, 999$, let's strike out the numbers that are multiples of 7; their quantity is $\left[\frac{999}{7}\right]=142$. In this process, numbers that are multiples of 35 will be struck out twice. Their quantity is $\left[\frac{999}{35}\right]=28$. Therefore, we have struck out a total of $199+142-28=313$ numbers, and $999-313=686$ numbers remain. [^1]
## V Olympiad $(1939)$
## First Round
|
686
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-5. The factorial of a number $n$ is defined as the product of all integers from 1 to $n$ inclusive. Find all three-digit numbers that are equal to the sum of the factorials of their digits.
|
Solve 5. Answer: 145. Let $N=100x+10y+z$ be the desired number, for which $N=x!+y!+z!$. The number $7!=5040$ is four-digit, so no digit of the number $N$ exceeds 6. Therefore, the number $N$ is less than 700. But then no digit of the number $N$ exceeds 5, since $6!=720$. The inequality $3 \cdot 4!=72<100$ shows that at least one digit of the number $N$ is 5. At the same time, $x \neq 5$, since $3 \cdot 5!=360<500$. This inequality also shows that $x \leqslant 3$. Moreover, $x \leqslant 2$, since $3!+2 \cdot 5!=246<300$. The number 255 does not satisfy the condition of the problem, and if only one digit of the desired number is 5, then $x \leqslant 1$, since $2!+5!+4!=146<200$. Since $1!+5!+4!=145<150$, we get $y \leqslant 4$. Therefore, $z=5$. Considering that $x=1$ and $0 \leqslant y \leqslant 4$, we find the unique solution $N=145$.
## Second Round
## 7 - 8 grades
|
145
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-ча 1. Find a four-digit number that is a perfect square, and such that the first two digits are the same as each other and the last two digits are also the same.
|
Solution 1. Let $a$ be the first and second digits, $b$ be the third and fourth. Then the given number is equal to $11(b+100a)$, so $b+100a=11x^2$ for some natural number $x$. Moreover, $100 \leqslant b+100a \leqslant 908$, which means $3 \leqslant x \leqslant 9$. By calculating the squares of the numbers $33, 44, \ldots, 99$, we find that exactly one of them has the required form: $88^2=7744$.
Part 2. Points $A, B, C$ are the vertices of an equilateral triangle inscribed in a circle. Point $D$ lies on the smaller arc $AB$. $\quad DC=AD+BD$. Prove.
Solution 2. First, note that $\angle ADC=\angle ABC=60^\circ$, since these angles subtend the same arc. Similarly, $\angle BDC=60^\circ$. Mark points $K$ and $L$ on segment $CD$ such that triangles $BDK$ and $ADL$ are equilateral. Triangles $ADB$ and $ALC$ are equal by two sides and the angle between them. Therefore, $CL=DB$, which means $DC=DL+LC=AD+BD$.
|
7744
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-4. How many pairs of integers $x, y$, lying between 1 and 1000, are there such that $x^{2}+y^{2}$ is divisible by 7.
|
Solve 4. Answer: $142^{2}=20164$. The number $x^{2}+y^{2}$ is divisible by 7 if and only if both numbers $x$ and $y$ are divisible by 7. Indeed, the square of an integer when divided by 7 gives remainders of 0, 2, and 4. The number of integers between 1 and 1000 that are divisible by 7 is 142. Therefore, the desired number is $142^{2}=20164$.
## 9 - 10 grades
|
20164
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-5. How many positive integers $x$, less than 10000, are there for which $2^{x}-x^{2}$ is divisible by 7?
|
Solve 5. Answer: 2857. The remainders of the division by 7 of the numbers $2^{x}$ and $x^{2}$ repeat with periods of 3 and 7, respectively, so the remainders of the division by 7 of the numbers $2^{x} - x^{2}$ repeat with a period of 21. Among the numbers $x$ from 1 to 21, the numbers that give equal remainders from the division by 7 of the numbers $2^{x}$ and $x^{2}$ are exactly 6 numbers. Therefore, among the numbers from 1 to $9996 = 7 \cdot 476$, there are $476 \cdot 6 = 2856$ required numbers. Direct verification using the obtained sequence of remainders shows that among the remaining numbers 9997, 9998, and 9999, only the number 9998 has the required property.
## VII Olympiad (1941)
## First Round
## 7 - 8 grades
|
2857
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-4. Construct triangle $ABC$ given points $M$ and $N$ - the feet of the altitudes $AM$ and $BN$ - and the line on which side $AB$ lies.
|
Sol 4. Points $M$ and $N$ lie on a circle with diameter $AB$. The center $O$ of this circle is the intersection of line $AB$ and the perpendicular bisector of segment $NM$, so we can construct it. Points $A$ and $B$ are the points of intersection of line $AB$ and the circle centered at $O$ passing through point $M$. Therefore, points $A$ and $B$ can be constructed. Point $C$ is then constructed as the intersection of lines $AN$ and $BM$.
3 - part 5. Solve the equation:
$$
|x+1|-|x|+3|x-1|-2|x-2|=x+2
$$
Sol 5. Answer: $x=-2$ or $x \geqslant 2$.
If $x \geqslant 2$, we get an identity.
If $1 \leqslant x<2$, we get the equation $4x=8$, which has no solutions in this interval.
If $0 \leqslant x<1$, we get the equation $-2x=2$, which has no solutions in this interval.
If $-1 \leqslant x<0$, we get $0=2$, which is impossible.
If $x<-1$, we get the root $x=-2$.
3 - part 6. How many roots does the equation
$$
\sin x=\frac{x}{100} ?
$$
Sol 6. Answer: 63.
First, note that the number of positive roots is equal to the number of negative roots, and there is also the root 0. Therefore, it is sufficient to verify that the number of positive roots is 31. If $\sin x=\frac{x}{100}$, then $|x|=100|\sin x| \leqslant 100$. Consider the graphs of the functions $y=x / 100$ and $y=\sin x$. The segment of the $Ox$ axis from 0 to 100 contains 15 segments of length $2\pi$ and one segment of length less than $2\pi$. By examining the specified graphs, it is easy to see that on the first segment of length $2\pi$ there is one root of the given equation, and on each of the other 14 segments of length $2\pi$ there are two roots. Calculations show that the length of the last segment is greater than $\pi$, so there are also two roots on it. In total, we get 31 positive roots.
## Second Round
## 7 - 8 grades
|
63
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-2. Find a three-digit number, every integer power of which ends in the same three digits as the original number (in the same order).
|
Let $N$ be the desired number. Then $N^{2}-N=N(N-1)$ is divisible by 1000. The numbers $N$ and $N-1$ are coprime, so one of them is divisible by 8, and the other by 125. Let's first assume $N=125 k$. Then $k \leqslant 8$. Among the numbers $125 k-1, k=1, \ldots, 8$, only the number 624 is divisible by 8. Now let $N-1=125 k$. Then $N=125 k+1$, so $k \leqslant 7$. Among the numbers $125 k+1, k=1, \ldots, 7$, only the number 376 is divisible by 8.
If $N^{2}-N=N(N-1)$ is divisible by 1000, then $N^{k}-N=N\left(N^{k-1}-1\right)$ is also divisible by 1000, since $N^{k-1}-1$ is divisible by $N-1$.
|
376
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-ча 1. Given 6 digits: $0,1,2,3,4,5$. Find the sum of all four-digit even numbers that can be written using these digits (the same digit can be repeated in a number).
|
Solution 1. Answer: 1769580.
We will separately calculate the sum of thousands, hundreds, tens, and units for the considered numbers. The first digit can be any of the five digits $1,2,3,4,5$. The number of all numbers with a fixed first digit is $6 \cdot 6 \cdot 3=108$, since the second and third places can be any of the six digits, and the fourth place can be any of the three digits $0,2,4$ (we are considering only even numbers). Therefore, the sum of thousands is $(1+2+3+4+5) \cdot 108 \cdot 1000=1620000$. The number of numbers with a fixed second digit is $5 \cdot 6 \cdot 3=90$ (the first place can be any of the five digits). Therefore, the sum of hundreds is $(1+2+3+4+5) \cdot 90 \cdot 100=135000$. Similarly, the sum of tens is $(1+2+3+4+5) \cdot 90 \cdot 10=13500$, and the sum of units is $(2+4) \cdot 5 \cdot 6 \cdot 6=1080$.
|
1769580
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-2. Two identical polygons were cut out of cardboard, aligned, and pierced with a pin at some point. When one of the polygons is rotated around this "axis" by $25^{\circ} 30^{\prime}$, it aligns again with the second polygon. What is the smallest possible number of sides of such polygons?
|
Solution 2. Answer: 240. First, note that $\frac{1}{360} \cdot 25 \frac{1}{2}=\frac{17}{240}$, and the numbers 17 and 240 are coprime. Consider a ray emanating from the "axis" to the vertex of the first polygon. Rotations of this ray around the "axis" by angles $k \cdot 25^{\circ} 30^{\prime}$, where $k=1,2, \ldots, 240$, are distinct. Indeed, if the rotations of the ray by angles $k_{1} \cdot 25^{\circ} 30^{\prime}$ and $k_{2} \cdot 25^{\circ} 30^{\prime}$ coincide, then the number $\frac{\left(k_{1}-k_{2}\right) 17}{240}$ is an integer, which means that $k_{1}-k_{2}$ is divisible by 240. On each of these 240 rays, there is a vertex of the polygon, so the number of sides of the polygon is at least 240. On the other hand, when a regular 240-gon is rotated by an angle of $25^{\circ} 30^{\prime}$ around its center, it coincides with itself.
|
240
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-3. A circle with a radius equal to the height of a certain equilateral triangle rolls along the side of this triangle. Prove that the arc intercepted by the sides of the triangle on the circle is always $60^{\circ}$.
|
Solution 3. Let the angular measure of the arc cut off by the sides of the given equilateral triangle $ABC$ be denoted by $\alpha$. We will assume that the circle is tangent to the side $BC$. Consider the arc cut off by the extensions of the sides of the triangle $ABC$ on the circle, and denote its angular measure by $\alpha^{\prime}$. Then $\left(\alpha+\alpha^{\prime}\right) / 2=\angle B A C=60^{\circ}$. But $\alpha=\alpha^{\prime}$, since these arcs are symmetric with respect to the line passing through the center of the circle parallel to the side $BC$. Therefore, $\alpha=\alpha^{\prime}=60^{\circ}$.
## IX Olympiad (1946)
## First Round
## 7 - 8 grades
|
60
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3-ча 3. Find a four-digit number that, when divided by 131, gives a remainder of 112, and when divided by 132, gives a remainder of 98.
|
Solve 3. Answer: 1946. Let $N$ be the desired number. By the condition, $N=131 k+112=132 l+98$, where $k$ and $l$ are natural numbers. Moreover, $N<10000$, so $l=\frac{N-98}{132}<\frac{10000-98}{132} \leqslant 75$. Further, $131 k+112=$ $132 l+98$, so $131(k-l)=l-14$. Therefore, if $k \neq l$, then $|l-14| \geqslant 131$. But $l \leqslant 75$, so $k=l$ and $l-14=0$. Thus, $N=131 \cdot 14+112=132 \cdot 14+98=1946$.
Solve 4. Answer: $x_{1}=-x_{8}=1, x_{2}=-x_{2}=2, x_{3}=-x_{6}=3, x_{4}=-x_{5}=4$.
Adding all the equations, we get $3\left(x_{1}+x_{2}+\cdots+x_{8}\right)=0$. Then add the first, fourth, and seventh equations. The result is $2 x_{1}+x_{2}+x_{3}+\cdots+x_{8}=1$, so $x_{1}=1$. The other unknowns are found similarly.
|
1946
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-5. The city's bus network is organized as follows: 1) from any stop to any other stop, you can get without transferring;
2) for any pair of routes, there is, and only one, stop where you can transfer from one of these routes to the other;
3) on each route, there are exactly three stops.
How many bus routes are there in the city?
|
Solve 5. Answer: 7. We will prove that if the given conditions are satisfied, then the number of stops $n$ and the number of routes $N$ are related by the formula $N=n(n-1)+1$. Let $a$ be one of the routes, and $B$ be a stop that route $a$ does not pass through. Each route passing through $B$ intersects route $a$. Therefore, exactly $n$ routes pass through $B$. Similarly, it can be proven that through each stop of route $a$, $n-1$ routes different from $a$ pass. In total, we get $n(n-1)$ different routes and the route $a$ itself.
## 9 - 10 grades
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-ча 1. In a chess tournament, students from grades IX and X participated. There were 10 times more students from grade X than from grade IX, and they scored 4.5 times more points in total than all the students from grade IX. How many points did the students from grade IX score? Find all solutions.
|
Solution 1. Let $x$ be the number of ninth graders in the tournament. Then there were a total of $11x$ participants, and they scored $\frac{11x(11x-1)}{2}$ points. According to the problem, the ratio of the number of points scored by the ninth graders to the number of points scored by the tenth graders is $1:4.5$. Therefore, the ninth graders scored $x(11x-1)$ points, which means each ninth grader won all $11x-1$ games they played. However, if there were two ninth graders among the participants, they would have had to both win their game against each other, which is impossible. Therefore, only one ninth grader participated in the tournament; he scored 10 points.
Part 2. Given the sequence of numbers: $0,1,1,2,3,5,8,13,21,34,55,89, \ldots$, where each number, starting from the third, is the sum of the two preceding numbers. Will there be a number among the first hundred million ($10^8 + 1$) terms of this sequence that ends with four zeros?
Solution 2. Answer: Yes, there will be. Replace each of the given numbers with its remainder when divided by 1000. Let $a_{1}=0, a_{2}, \ldots$ be the resulting numbers. If we know the numbers $a_{k}$ and $a_{k+1}$, then we also know $a_{k-1}$, since in the original sequence the $(k-1)$-th term is the difference between the $(k+1)$-th and $k$-th terms. Therefore, if for some $k$ and $n$ the equalities $a_{k}=a_{k+n}$ and $a_{k+1}=a_{k+n+1}$ hold, then $a_{k-1}=a_{k+n-1}, a_{k-2}=a_{k+n-2}, \ldots, a_{1}=a_{n+1}$. But $a_{1}=0$, so $a_{n+1}=0$, i.e., in the original sequence, the number at the $(n+1)$-th position ends with four zeros.
It remains to prove that among the pairs $\left(a_{1}, a_{2}\right),\left(a_{2}, a_{3}\right), \ldots,\left(a_{10^{8}}, a_{10^{8}+1}\right),\left(a_{10^{8}+1}, a_{10^{8}+2}\right)$, there will be two identical pairs. But from the numbers $0,1,2, \ldots, 9999$, it is impossible to form more than $10^8$ different pairs, while we are considering $10^8 + 1$ pairs.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-4. In the city, there are 57 bus routes. It is known that:
1) from any stop to any other stop, one can travel without transferring;
2) for any pair of routes, there is one, and only one, stop where one can transfer from one of these routes to the other;
3) each route has no fewer than three stops.
How many stops does each of the 57 routes have?
|
Solution 4. Answer: 8. We will prove that if the given conditions are satisfied, then the number of stops $n$ and the number of routes $N$ are related by the formula $N=n(n-1)+1$. First, we will show that if a route has $n$ stops, then any other route also has $n$ stops, and furthermore, each stop is served by $n$ routes. Let's take a stop $B$ that is not on the considered route $a$. From $B$, there is a route to each of the $n$ stops on route $a$, and such a route is unique, since two different routes cannot have two common stops. Each route passing through $B$ intersects route $a$. Therefore, exactly $n$ routes pass through $B$. Now it is clear that a route $b$ that does not pass through stop $B$ also has exactly $n$ stops. Indeed, exactly $n$ routes pass through $B$, each intersecting $b$ at one point, two routes cannot intersect $b$ at the same point, and each stop on route $b$ is served by one of these routes. Now it is clear that each stop is served by $n$ routes. In particular, each stop on route $a$ is served by $n-1$ routes other than $a$ itself. In total, we get $n(n-1)$ different routes and the route $a$ itself.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-ча 1. Determine the coefficients that will stand by $x^{17}$ and $x^{18}$ after expanding the brackets and combining like terms in the expression
$$
\left(1+x^{5}+x^{7}\right)^{20}
$$
|
Solution 1. The number 18 cannot be represented as the sum of the numbers 5 and 7, so the coefficient of $x^{18}$ will be zero.
The number 17 can be represented as the sum of the numbers 5 and 7 as follows: $17=7+5+5$; this representation is unique up to the order of the terms. In one of the 20 expressions $1+x^{5}+x^{7}$, we must choose $x^{7}$, and in two of the 19 remaining such expressions, we must choose $x^{5}$. Therefore, the coefficient of $x^{17}$ is $20 \cdot \frac{19 \cdot 18}{2}=3420$.
|
3420
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-rd 5. From point \(A\) to other points, one can get there in two ways:
1. Exit immediately and walk.
2. Call a car and, after waiting for a certain amount of time, ride in it.
In each case, the mode of transportation that requires the least time is used. It turns out that
\begin{tabular}{|c|c|}
\hline if the final point is & then the travel time will be \\
\hline \(1 \mathrm{km}\) & 10 min \\
\(2 \mathrm{km}\) & 15 min \\
\(3 \mathrm{km}\) & \(17 \frac{1}{2}\) min \\
\hline
\end{tabular}
The speeds of the pedestrian and the car, as well as the waiting time for the car, are assumed to be constant. How much time will be required to reach a point that is 6 km away from \(A\)?
|
Solution 5. Answer: 25 min.
Let \(v\) be the pedestrian's speed, \(V\) be the car's speed, and \(T\) be the waiting time for the car. (We will measure speed in km/h and time in hours.) If walking, the time required for 1.2 km and 3 km would be \(1 / v\), \(2 / v\), and \(3 / v\) hours, respectively, and if traveling by car, it would be \(T+\frac{1}{V}\), \(T+\frac{2}{V}\), and \(T+\frac{3}{V}\) hours. Suppose that walking 2 km is no slower than traveling by car, i.e., \(T+\frac{2}{V} \geqslant \frac{2}{v}\). Then \(T+\frac{1}{V} \geqslant \frac{T}{2}+\frac{1}{V} \geqslant \frac{1}{v}\), meaning that 1 km can also be walked. However, if 1 km and 2 km can be walked, then the time spent on 2 km would be exactly twice that of 1 km, which is not the case according to the problem. Therefore, \(T+\frac{2}{V} \leqslant \frac{2}{v}\), and thus \(T+\frac{3}{V} \leqslant \frac{3}{2}\left(T+\frac{2}{V}\right) \leqslant \frac{3}{v}\). Consequently, \(1 / v=1 / 6\), \(T+2 / V=1 / 4\), and \(T+3 / V=7 / 24\). Solving this system of equations, we find: \(v=6\), \(T=1 / 6\), and \(V=24\). If walking 6 km, it would take 1 hour, and if traveling by car, it would take \(\frac{1}{6}+\frac{6}{24}=\frac{5}{12}\), i.e., 25 min.
\section*{9th - 10th Grades}
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-ча 1. In a convex 13-sided polygon, all diagonals are drawn. They divide it into polygons. Let's take among them a polygon with the largest number of sides. What is the maximum number of sides it can have
|
Solve 1. Answer: 13. From each vertex of the original 13-gon, no more than two diagonals emerge that are sides of the considered polygon. Each diagonal corresponds to two vertices, so the number of sides of the considered polygon does not exceed 13. An example of a regular 13-gon shows that the number of sides of the polygon obtained by cutting can be equal to 13.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-4. On a circle, there are 20 points. These 20 points are connected by 10 (non-intersecting - ed. note) chords. In how many ways can this be done?
|
Solution 4. Answer: 16796. Let \(a_{n}\) be the number of ways to connect \(2 n\) points on a circle with \(n\) non-intersecting chords. It is clear that \(a_{1}=1\) and \(a_{2}=2\). We will show that
\[
a_{n}=a_{n-1}+a_{n-2} a_{1}+a_{n-3} a_{2}+\cdots+a_{1} a_{n-2}+a_{n-1}.
\]
Fix one of the \(2 n\) points. The chord emanating from it divides the circle into two arcs, with an even number of given points on each arc: from 0 to \(2 n-2\). If there are \(2 k\) points on one arc, then there are \(2(n-k-1)\) points on the other arc; these points can be connected by non-intersecting chords (not intersecting the chord emanating from the fixed point) in \(a_{n-k-1} a_{k}\) ways.
Thus, \(a_{3}=a_{2}+a_{1}^{2}+a_{2}=5, a_{4}=14, a_{5}=42, a_{6}=132, a_{7}=429, a_{8}=1430, a_{9}=4862\) and \(a_{10}=16796\).
Remark. It can be proven that \(a_{n}=\frac{(2 n)!}{n!(n+1)!}=\frac{1}{2 n+1}\binom{2 n+1}{n}\).
\section*{9th - 10th Grades}
|
16796
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-ча 1. In a convex 1950-gon, all diagonals are drawn. They divide it into polygons. Among them, we take the polygon with the largest number of sides. What is the maximum number of sides it can have?
|
Solution 1. Answer: 1949. The same reasoning as in the solution to problem 1 for grades 7-8 shows that the resulting polygon has no more than 1950 sides, and if the number of its sides is 1950, then exactly two diagonals emanate from each vertex of the original polygon, bounding the resulting polygon. Suppose two diagonals \(A_{1} A_{p}\) and \(A_{1} A_{q}\) emanate from vertex \(A_{1}\), bounding the resulting polygon. Then \(A_{p}\) and \(A_{q}\) are adjacent vertices, since otherwise there would be a diagonal inside the angle \(A_{p} A_{1} A_{q}\) that cuts the resulting polygon. Indeed, a vertex lying between \(A_{p}\) and \(A_{q}\) would have to be connected to a vertex lying between \(A_{1}\) and \(A_{p}\) or between \(A_{1}\) and \(A_{q}\). By changing the direction of vertex numbering if necessary, we can assume that \(q=p+1\) and \(p \leqslant 1950 / 2=975\). If we exclude the diagonal \(A_{1} A_{p+1}\), then any other diagonal bounding the resulting polygon connects one of the vertices numbered from 2 to \(p\) with some vertex. Therefore, the resulting polygon can have no more than \(1+974 \cdot 2=1949\) sides. To obtain an example of a 1950-gon, the cutting of which results in a 1949-gon, one can take a regular 1949-gon and cut off a small triangle, i.e., instead of vertex \(A_{1}\), take two vertices \(A_{1}^{\prime}\) and \(A_{1950}\), located on the sides \(A_{1} A_{2}\) and \(A_{1} A_{1949}\) near vertex \(A_{1}\).
|
1949
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-5. There is a piece of chain consisting of 60 links, each weighing 1 g. What is the smallest number of links that need to be unbuckled so that from the resulting parts, all weights of 1 g, 2 g, 3 g, \(\ldots, 60\) g can be formed (an unbuckled link also weighs 1 g)
|
Solution 5. Answer: 3 links. Let's determine the greatest \(n\) for which it is sufficient to break \(k\) links of an \(n\)-link chain so that all weights from 1 to \(n\) can be formed from the resulting parts. If \(k\) links are broken, then any number of links from 1 to \(k\) can be formed from them. But \(k+1\) links cannot be formed if there is no part with \(k+1\) or fewer links (we do not consider the broken links here). The most advantageous situation is to have a part with exactly \(k+1\) links. Then we can get any number of links from 1 to \(2k+1\). (Otherwise, we can only get a number of links from 1 to \(l_1 + k\), where \(l_1 \leq k\).) Next, the most advantageous situation is to have a part with \(2(k+1)\) links, then with \(4(k+1)\) links, and so on. Thus, if we break \(k\) links, the most advantageous situation is when the \(k+1\) parts obtained consist of \(k+1, 2(k+1), 4(k+1), 8(k+1)\), \(\ldots, 2^k(k+1)\) links (we do not consider the broken links here). In this case, any number of links from 1 to \(n = 2^{k+1}(k+1) - 1\) can be formed. Therefore, if \(2^k k \leq n \leq 2^{k+1}(k+1) - 1\), then \(k\) breaks are sufficient and \(k-1\) breaks are insufficient. In particular, if \(24 \leq n \leq 63\), then the minimum number of broken links is 3. The four parts of the chain obtained by breaking should consist of \(4, 8, 16, 29\) links.
\footnotetext{
\({ }^{6}\) It is allowed for the vertices of the quadrilateral to lie not only on the sides of the trapezoid but also on their extensions. (Editor's note)
}
\section*{9 - 10 grades}
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-4. There is a piece of chain consisting of 150 links, each weighing 1 g. What is the smallest number of links that need to be unbuckled so that from the resulting parts, all weights of 1 g, 2 g, 3 g, \(\ldots, 150\) g can be formed (an unbuckled link also weighs 1 g)?
|
Solution 4. Answer: 4 links. According to the solution of problem 5 for grades \(7-8\) for a chain consisting of \(n\) links, where \(64 \leqslant n \leqslant 159\), it is sufficient to unfasten 4 links.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-rd 5. When dividing the polynomial \(x^{1951}-1\) by \(x^{4}+x^{3}+2 x^{2}+x+1\), a quotient and a remainder are obtained. Find the coefficient of \(x^{14}\) in the quotient.
|
Solve 5. Answer: -1. The equalities \(x^{4}+x^{3}+2 x^{2}+x+1=\left(x^{2}+1\right)\left(x^{2}+x+1\right)\) and \(x^{12}-1=(x-1)\left(x^{2}+x+\right.\)
1) \(\left(x^{3}+1\right)\left(x^{2}+1\right)\left(x^{4}-x^{2}+1\right)\) show that
\[
\begin{aligned}
x^{4}+x^{3}+2 x^{2}+x+1 & =\frac{x^{12}-1}{(x-1)\left(x^{3}+1\right)\left(x^{4}-x^{2}+1\right)}= \\
& =\frac{x^{12}-1}{x^{8}-x^{7}-x^{6}+2 x^{5}-2 x^{3}+x^{2}+x-1}
\end{aligned}
\]
Therefore, dividing the polynomial \(x^{1951}-1\) by \(x^{4}+x^{3}+2 x^{2}+x+1\) is the same as first dividing it by \(x^{12}-1\) and then multiplying by \(x^{8}-x^{7}-x^{6}+2 x^{5}-2 x^{3}+x^{2}+x-1\). But
\[
\frac{x^{1951}-1}{x^{12}-1}=x^{1939}+x^{1927}+x^{1915}+\cdots+x^{19}+x^{7}+\frac{x^{7}-1}{x^{12}-1}
\]
so the desired coefficient is the coefficient of \(x^{14}\) in the product
\[
\left(x^{1939}+\cdots+x^{19}+x^{7}+\frac{x^{7}-1}{x^{12}-1}\right)\left(x^{8}-x^{7}-x^{6}+2 x^{5}-2 x^{3}+x^{2}+x-1\right)
\]
\section*{9th - 10th Grades}
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-5. Determine the maximum value of the ratio of a three-digit number to the number equal to the sum of the digits of this number.
|
Solve 5. Answer: 100. The sum of the digits of a three-digit number \(100a + 10b + c\) is \(a + b + c\). It is clear that \(\frac{100a + 10b + c}{a + b + c} \leqslant 100\). Moreover, for the number 100, the given ratio is 100.
\section*{8th Grade}
|
100
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.