problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3-5. Five people play several games of dominoes (two on two) so that each player has each other as a partner once and as an opponent twice. Find the number of games played and all possible ways of distributing the players.
|
Solution 5. Answer: 5 games; the distribution of players is unique (up to their numbering). First, let's see who the 1st player played with. We can assume that the 1st and 2nd played against the 3rd and 4th, and the 1st and 5th played against the 2nd and 3rd (this can be achieved by swapping the 3rd and 4th). The 3rd player has already been an opponent of the 1st twice, so the 2nd and 5th play against the 1st and 4th. After this, the 2nd cannot play against the 1st, so the 4th and 5th play against the 1st and 3rd. The last game remains: the 2nd and 4th play against the 3rd and 5th.
\section*{10th Grade}
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-4. Find all numbers by which the fraction \(\frac{5 l+6}{8 l+7}\) can be reduced when \(l\) is an integer.
|
Solution 4. We will compute \(\text{GCD}(5l+6, 8l+7)\), using the fact that \(\text{GCD}(a, b) = \text{GCD}(a-b, b)\). As a result, we get \(\text{GCD}(5l+6, 8l+7) = \text{GCD}(5l+6, 3l+1) = \text{GCD}(2l+5, 3l+1) = \text{GCD}(2l+5, l-4) = \text{GCD}(l+9, l-4) = \text{GCD}(13, l-4)\). The number 13 is prime, so the fraction can only be reducible by 13. When \(l=4\), we get the fraction \(\frac{26}{39}\), which is indeed reducible by 13.
|
13
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-5. What is the smallest number of points that can be chosen on a circle of length 1956 so that for each of these points there is exactly one chosen point at a distance of 1 and exactly one at a distance of 2 (distances are measured along the circumference)?
|
Solve 5. Answer: 1304.
Let \(A\) be one of the selected points, \(B\) and \(C\) be the selected points, located at distances 1 and 2 from it, respectively. The arrangement \(A B C\) is impossible, since in this case, for point \(B\), there are two selected points at a distance of 1. Therefore, the points are arranged in the following order: \(C \quad A B\) (or \(B A \quad C\)). Let \(D\) be the point located at a distance of 1 from \(C\). The arrangement \(C D A B\) is clearly impossible. Therefore, the arrangement is as follows: \(D C \quad A B\). Let \(E\) be the point located at a distance of 1 from \(B\). It is arranged as follows: \(D C \quad A B \quad E\). Continuing these considerations, we will see that the circle of length 1956 will be divided into \(1956 / 3 = 652\) arcs of length 3 (the endpoints of these arcs are the points \(A, C, E, \ldots\)). Each arc contains one point. In total, we get \(2 \cdot 652 = 1304\) points. All these points must be present.
\section*{8th Grade}
|
1304
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-2. Points \(A_{1}, A_{2}, A_{3}, A_{4}, A_{5}, A_{6}\) divide a circle of radius 1 into six equal parts. From \(A_{1}\), a ray \(l_{1}\) is drawn in the direction of \(A_{2}\), from \(A_{2}\) - a ray \(l_{2}\) in the direction of \(A_{3}, \ldots\), from \(A_{6}\) - a ray \(l_{6}\) in the direction of \(A_{1}\). From point \(B_{1}\), taken on ray \(l_{1}\), a perpendicular is dropped onto ray \(l_{6}\), from the foot of this perpendicular a perpendicular is dropped onto \(l_{5}\), and so on. The foot of the sixth perpendicular coincides with \(B_{1}\). Find the segment \(B_{1} A_{1}\).
|
Solve 2. Answer: \(B_{1} A_{1}=2\).
Let \(B_{2}, B_{3}, \ldots, B_{7}\) be the feet of the perpendiculars dropped from \(l_{6}, l_{5}, \ldots, l_{1} ; x_{1}=A_{2} B_{1}, x_{2}=\) \(A_{1} B_{2}, x_{3}=A_{6} B_{3}, \ldots, x_{7}=A_{2} B_{7}\). Then \(x_{k+1}=\frac{1}{2}\left(1+x_{k}\right)\). By the condition \(x_{1}=x_{7}\). But
\[
x_{7}=\frac{1}{2}\left(1+x_{6}\right)=\frac{1}{2}\left(1+\frac{1}{2}\left(1+x_{5}\right)\right)=\frac{1}{2}\left(1+\frac{1}{2}\left(1+\frac{1}{2}\left(1+x_{5}\right)\right)\right)=\ldots
\]
therefore
\[
x_{7}=\frac{1}{2}+\frac{x_{6}}{2}=\frac{3}{4}+\frac{x_{5}}{4}=\frac{7}{8}+\frac{x_{4}}{8}=\cdots=\frac{63}{64}+\frac{x_{1}}{64}
\]
Thus, we get the equation \(\frac{63}{64}+\frac{x_{1}}{64}=x_{1}\), from which \(x_{1}=1\). It is also clear that \(B_{1} A_{1}=1+x\).
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-3. We took three numbers \(x, y, z\). We calculated the absolute values of the pairwise differences \(x_{1}=|x-y|\), \(y_{1}=|y-z|, z_{1}=|z-x|\). In the same way, from the numbers \(x_{1}, y_{1}, z_{1}\) we constructed the numbers \(x_{2}, y_{2}, z_{2}\) and so on. It turned out that for some \(n\), \(x_{n}=x\), \(y_{n}=y\), \(z_{n}=z\). Knowing that \(x=1\), find \(y\) and \(z\).
|
Solve 3. Answer: \(y=z=0\).
The numbers \(x_{n}, y_{n}, z_{n}\) are non-negative, so the numbers \(x, y, z\) are also non-negative. If all the numbers \(x\), \(y, z\) were positive, then the largest of the numbers \(x_{1}, y_{1}, z_{1}\) would be strictly less than the largest of the numbers \(x, y, z\), and then the largest of the numbers \(x_{n}, y_{n}, z_{n}\) would be strictly less than the largest of the numbers \(x, y, z\). Therefore, among the numbers \(x, y, z\) there is a 0. Similarly, it is proved that among the numbers \(x_{1}, y_{1}, z_{1}\) there is a 0 (for \(n=1\) there is nothing to prove, because then \(x_{1}=x, y_{1}=y, z_{1}=z\)). This means that two of the numbers \(x, y, z\) are equal. In the end, we get that the unordered set of numbers \(x, y, z\) can be either 0,0, 1, or \(0,1,1\). Obviously, the second set does not have the required property.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-4. In a rectangular table composed of positive numbers, the product of the sum of the numbers in any column and the sum of the numbers in any row equals the number at their intersection. Prove that the sum of all numbers in the table is one.
|
Solution 4. First solution. Let \(x_{1}, \ldots, x_{n}\) be the sums of the numbers in the rows, and \(y_{1}, \ldots, y_{m}\) be the sums of the numbers in the columns. At the intersection of the \(i\)-th row and the \(j\)-th column, the number \(x_{i} y_{j}\) is placed. Therefore, the sum of the numbers in the \(i\)-th row is \(x_{i} y_{1} + x_{i} y_{2} + \cdots + x_{i} y_{m}\). On the other hand, this sum is equal to \(x_{i}\). Thus, \(x_{i} = x_{i} (y_{1} + y_{2} + \cdots + y_{m})\). The number \(x_{i}\) is positive; in particular, it is not zero, so \(y_{1} + y_{2} + \cdots + y_{m} = 1\). But the sum \(y_{1} + y_{2} + \cdots + y_{m}\) is precisely the sum of all the numbers in the table.
\(s s l\) Let \(a_{j i}\) be the number at the intersection of the \(i\)-th column and the \(j\)-th row. By the condition, \(a_{j i} = \left(\sum_{p=1}^{m} a_{p i}\right) \left(\sum_{q=1}^{n} a_{j q}\right)\).
Therefore, \(\sum_{i, j} a_{j i} = \sum_{i, j} \left(\sum_{p=1}^{m} a_{p i}\right) \left(\sum_{q=1}^{n} a_{j q}\right) = \left(\sum_{i, j} a_{j i}\right)^{2}\). For the number \(S = \sum_{i, j} a_{j i}\), we have obtained the equation \(S^{2} = S\). But \(S > 0\), so \(S = 1\).
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3-5. The distance from \(A\) to \(B\) is 999 km. Along the road, there are kilometer markers indicating the distances to \(A\) and to \(B: 0\) ।999, 1 ।998, \(\ldots, 999\) ।0. How many of these markers have only two different digits?
|
Solve 5. Answer: 40.
Assume that on the kilometer post, the number \(\overline{a b d a_{1} b_{1} c_{1}}\) is written. Then \(\overline{a b c} + \overline{a_{1} b_{1} c_{1}} = 999\), so \(a_{1} = 9 - a\), \(b_{1} = 9 - b\), and \(c_{1} = 9 - c\). If \(a = b = c\), then the required condition is satisfied. There will be exactly 10 such posts. Now, let's assume that among the digits \(a, b, c\) there are exactly two different digits. Among the digits \(a_{1}, b_{1}, c_{1}\) there will be exactly the same two digits if and only if these two digits sum to 9. There are exactly 5 such pairs of digits: \((0,9), (1,8), (2,7), (3,6)\), and \((4,5)\). There are exactly six three-digit numbers that can be written using two given digits: three of them are written with two digits \(a\) and one digit \(b\) (which stands in one of three positions), and the other three are written with one digit \(a\) and two digits \(b\). This gives us another \(5 \cdot 6 = 30\) posts, making a total of \(10 + 30 = 40\) posts.
\section*{8th Grade}
|
40
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-ча 1. In a chess tournament, 12 people participated. After the tournament, each participant made 12 lists. The first list includes only himself, the second list includes him and those he defeated, the third list includes all people from the second list and those they defeated, and so on. The 12th list includes all people from the 11th list and those they defeated. It is known that for any participant in the tournament, the 12th list includes a person who was not in the 11th list. How many draws were played in the tournament?
|
Solution 1. Answer: 54. If the \((k+1)\)-th list is the same as the \(k\)-th, then the lists numbered \(k+2, \ldots, 11, 12\) will also be exactly the same. However, according to the condition, the 11th list and the 12th list are different. Therefore, each participant's \(k\)-th list contains exactly \(k\) people. In particular, the 2nd list contains exactly two people. This means that each participant won exactly one game. Therefore, the number of draws is \(\frac{12 \cdot 11}{2} - 12 = 54\).
Part 2. Given the numbers: \(4, 14, 24, \ldots, 94, 104\). Prove that it is impossible to first cross out one number, then two more from the remaining, then three more, and finally four more numbers such that after each crossing out, the sum of the remaining numbers is divisible by eleven.
Solution 2. There are 11 numbers in total, and 10 numbers need to be crossed out. Therefore, in the end, one number that is divisible by 11 should remain, i.e., the number 44. On the other hand, the number 44 must be crossed out first. Indeed, the sum of all the given numbers is \(\frac{11 \cdot 108}{2}\), so it is divisible by 11. Consequently, if the sum of the remaining numbers is divisible by 11 after crossing out one number, then the crossed-out number must also be divisible by 11.
|
54
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-6. All values of the quadratic trinomial \(a x^{2}+b x+c\) on the interval \([0,1]\) do not exceed 1 in absolute value. What is the maximum value that the quantity \(|a|+|b|+|c|\) can have in this case?
|
Solve 6.
\section*{9th Grade}
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.40. The leg $BC$ of the right triangle $ABC$ with a right angle at $C$ is divided by points $D$ and $E$ into three equal parts. Prove that if $BC = 3AC$, then the sum of the angles $AEC$, $ADC$, and $ABC$ is $90^{\circ}$.
|
1.40. First solution. Consider the square $B C M N$ and divide its side $M N$ into three equal parts by points $P$ and $Q$ (Fig. 1.9). Then $\triangle A B C = \triangle P D Q$ and $\triangle A C D = \triangle P M A$. Therefore, triangle $P A D$ is an isosceles right triangle and $\angle A B C + \angle A D C = \angle P D Q + \angle A D C = 45^{\circ}$.
Fig. 1.9
Second solution. Since $D E = 1, E A = \sqrt{2}, E B = 2, A D = \sqrt{5}$, and $B A = \sqrt{10}$, we have $D E: A E = E A: E B = A D: B A$ and $\triangle D E A \sim \triangle A E B$. Therefore, $\angle A B C = \angle E A D$. Additionally, $\angle A E C = \angle C A E = 45^{\circ}$. Therefore, $\angle A B C + \angle A D C + \angle A E C = (\angle E A D + \angle C A E) + \angle A D C = \angle C A D + \angle A D C = 90^{\circ}$.
|
90
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
2.15. A circle with a radius equal to the height of an equilateral triangle rolls along one of its sides. Prove that the angular measure of the arc cut off on the circle by the sides of the triangle is always $60^{\circ}$.
|
2.15. Let the angular measure of the arc cut off by the sides of triangle $ABC$ on the circle be denoted by $\alpha$. Consider the arc cut off by the extensions of the sides of the triangle on the circle, and denote its angular measure by $\alpha^{\prime}$. Then $\left(\alpha+\alpha^{\prime}\right) / 2=\angle B A C=60^{\circ}$. But $\alpha=\alpha^{\prime}$, since these arcs are symmetric with respect to the line passing through the center of the circle parallel to side $BC$. Therefore, $\alpha=\alpha^{\prime}=60^{\circ}$.
|
60
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3.45*. On the diameter $A B$ of the circle $S$, a point $K$ is taken, and a perpendicular is erected from it, intersecting $S$ at point $L$. Circles $S_{A}$ and $S_{B}$ are tangent to the circle $S$, the segment $L K$, and the diameter $A B$, with $S_{A}$ touching the segment $A K$ at point $A_{1}$, and $S_{B}$ touching the segment $B K$ at point $B_{1}$. Prove that $\angle A_{1} L B_{1}=45^{\circ}$.
|
3.45. Let $\angle L A B=\alpha$ and $\angle L B A=\beta\left(\alpha+\beta=90^{\circ}\right)$. According to problem 3.42, b) $A B_{1}=A L$, so $\angle A B_{1} L=90^{\circ}-\alpha / 2$. Similarly, $\angle B A_{1} L=90^{\circ}-\beta / 2$. Therefore, $\angle A_{1} L B_{1}=(\alpha+\beta) / 2=45^{\circ}$.
|
45
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
5.33. In triangle $A B C$ with angle $A$ equal to $120^{\circ}$, the angle bisectors $A A_{1}, B B_{1}$ and $C C_{1}$ intersect at point $O$. Prove that $\angle A_{1} C_{1} O=30^{\circ}$.
|
5.33. According to the solution of the previous problem, ray $A_{1} C_{1}$ is the bisector of angle $A A_{1} B$. Let $K$ be the point of intersection of the angle bisectors of triangle $A_{1} A B$. Then $\angle C_{1} K O=\angle A_{1} K B=90^{\circ}+\angle A / 2=120^{\circ}$. Therefore, $\angle C_{1} K O+\angle C_{1} A O=180^{\circ}$, i.e., quadrilateral $A O K C_{1}$ is cyclic. Hence, $\angle A_{1} C_{1} O=\angle K C_{1} O=$ $=\angle K A O=30^{\circ}$.
|
30
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
6.90. What is the maximum number of acute angles a convex polygon can have
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
6.90. Let a convex $n$-gon have $k$ acute angles. Then the sum of its angles is less than $k \cdot 90^{\circ} + (n-k) \cdot 180^{\circ}$. On the other hand, the sum of the angles of an $n$-gon is $(n-2) \cdot 180^{\circ}$. Therefore, $(n-2) \cdot 180^{\circ} < k \cdot 90^{\circ} + (n-k) \cdot 180^{\circ}$, i.e., $k < 4$. Since $k$ is an integer, $k \leqslant 3$.
For any $n \geqslant 3$, there exists a convex $n$-gon with three acute angles (Fig. 6.17).
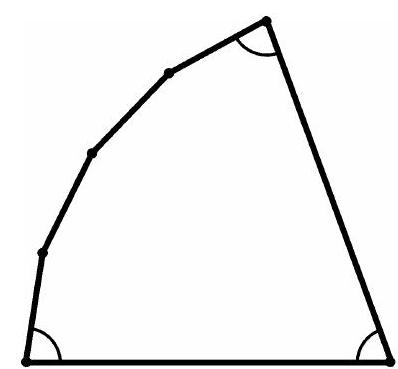
Fig. 6.17
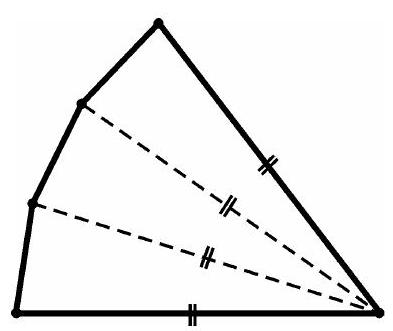
Fig. 6.18
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.68. Using a compass and a ruler, divide an angle of $19^{\circ}$ into 19 equal parts.
|
8.68. If there is an angle of magnitude $\alpha$, then angles of magnitude $2 \alpha, 3 \alpha$, etc., can be constructed. Since $19 \cdot 19^{\circ}=361$, an angle of $361^{\circ}$, which coincides with an angle of $1^{\circ}$, can be constructed.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.18*. How many sides can a convex polygon have if all its diagonals have the same length?
|
9.18. We will prove that the number of sides of such a polygon does not exceed 5. Suppose that all diagonals of the polygon $A_{1} \ldots A_{n}$ have the same length and $n \geqslant 6$. Then the segments $A_{1} A_{4}, A_{1} A_{5}, A_{2} A_{4}$, and $A_{2} A_{5}$ have the same length, as they are diagonals of this polygon. However, in the convex quadrilateral $A_{1} A_{2} A_{4} A_{5}$, the segments $A_{1} A_{5}$ and $A_{2} A_{4}$ are opposite sides, while $A_{1} A_{4}$ and $A_{2} A_{5}$ are diagonals. Therefore, $A_{1} A_{5} + A_{2} A_{4} < A_{1} A_{4} + A_{2} A_{5}$. This leads to a contradiction.
It is also clear that a regular pentagon and a square satisfy the required condition.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.22. In a triangle, the lengths of two sides are 3.14 and 0.67. Find the length of the third side, given that it is an integer.
|
9.22. Let the length of the third side be $n$. By the triangle inequality, $3.14-0.67<n<3.14+$ $+0.67$. Since $n$ is an integer, then $n=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.32. The perimeter of a convex quadrilateral is 4. Prove that its area does not exceed 1.
|
9.32. According to problem $9.31 S_{A B C D} \leqslant(A B+C D)(B C+A D) / 4$. Since $a b \leqslant(a+$ $+b)^{2} / 4$, then $S_{A B C D} \leqslant(A B+C D+A D+B C)^{2} / 16=1$.
|
1
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
11.30. The diagonals of a convex quadrilateral $ABCD$ intersect at point $O$. What is the smallest area that this quadrilateral can have if the area of triangle $AOB$ is 4 and the area of triangle $COD$ is 9?
|
11.30. Since $S_{A O B}: S_{B O C}=A O: O C=S_{A O D}: S_{D O C}$, then $S_{B O C} \cdot S_{A O D}=$ $=S_{A O B} \cdot S_{D O C}=36$. Therefore, $S_{B O C}+S_{A O D} \geqslant 2 \sqrt{S_{B O C} \cdot S_{A O D}}=12$, and equality is achieved if $S_{B O C}=S_{A O D}$, i.e., $S_{A B C}=S_{A B D}$, from which $A B \| C D$. In this case, the area of the quadrilateral is $4+9+12=25$.
|
25
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.42. If five points are given on a plane, then by considering all possible triples of these points, one can form 30 angles. Let the smallest of these angles be $\alpha$. Find the maximum value of $\alpha$.
If five points are given on a plane, then by considering all possible triples of these points, one can form 30 angles. Let the smallest of these angles be $\alpha$. Find the maximum value of $\alpha$.
|
11.42. First, assume that the points are the vertices of a convex pentagon. The sum of the angles of a pentagon is $540^{\circ}$, so one of its angles does not exceed $540^{\circ} / 5=108^{\circ}$. The diagonals divide this angle into three angles, so one of them does not exceed $108^{\circ} / 3=36^{\circ}$. In this case, $\alpha \leqslant 36^{\circ}$.
If the points are not the vertices of a convex pentagon, then one of them lies inside the triangle formed by the other three. One of the angles of this triangle does not exceed $60^{\circ}$. The segment connecting the corresponding vertex to the internal point divides this angle into two angles, so one of them does not exceed $30^{\circ}$. In this case, $\alpha \leqslant 30^{\circ}$. In all cases, $\alpha \leqslant 36^{\circ}$. It is clear that for a regular pentagon, $\alpha=36^{\circ}$.
|
36
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.43*. In a city, there are 10 streets parallel to each other, and 10 streets intersecting them at right angles. What is the minimum number of turns a closed bus route can have, passing through all intersections?
|
11.43. A closed route passing through all intersections can have 20 turns (Fig. 11.8). It remains to prove that such a route cannot have fewer than 20 turns. After each turn, there is a transition from a horizontal street to a vertical one or vice versa. Therefore, the number of horizontal segments in a closed route is equal to the number of vertical segments and is half the number of turns. Suppose a closed route has fewer than 20 turns. Then there will be streets of both directions that the route does not pass through. Therefore, the route does not pass through the intersection of these streets.

Fig. 11.8

Fig. 11.9
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.44*. What is the maximum number of cells on an $8 \times 8$ chessboard that can be cut by a single straight line?
|
11.44. A line can intersect 15 cells (Fig. 11.9). We will now prove that a line cannot intersect more than 15 cells. The number of cells intersected by a line is one less than the number of points of intersection with the segments that form the sides of the cells. Inside the square, there are 14 such segments. Therefore, inside the square, there are no more than 14 points of intersection of the line with the sides of the cells. No line can intersect the boundary of the board in more than two points, so the number of points of intersection with the segments does not exceed 16. Therefore, the maximum number of cells on an $8 \times 8$ chessboard that can be intersected by a single line is 15.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.45*. What is the maximum number of points that can be placed on a segment of length 1 so that on any segment of length $d$ contained in this segment, there are no more than $1+1000 d^{2}$ points?
See also problems $15.1,17.20$.
## §7. Extremal Properties of Regular Polygons
|
11.45. First, let's prove that it is impossible to place 33 points in such a way. Indeed, if 33 points are on a segment of length 1, then the distance between some two of them does not exceed \(1 / 32\). The segment with endpoints at these points contains two points, but it should contain no more than \(1 + 1000 / 32^2\) points, i.e., fewer than two points.
Now, let's prove that 32 points can be placed. Take 32 points that divide the segment into equal parts (the endpoints of the given segment are included in these 32 points). Then a segment of length \(d\) contains either \([31d]\) or \([31d] + 1\) points. We need to prove that \([31d] \leq 1000d^2\). If \(31d < 1\), then \([31d] = 0 < 1000d^2\). If \(31d \geq 1\), then \([31d] \leq 31d \leq (31d)^2 = 961d^2 < 1000d^2\).
Note. \([x]\) is the integer part of the number \(x\), i.e., the greatest integer not exceeding \(x\).
Fig. 11.10
|
32
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.52. In triangle $A B C$, the height $A H$ is equal to the median $B M$. Find the angle $M B C$.
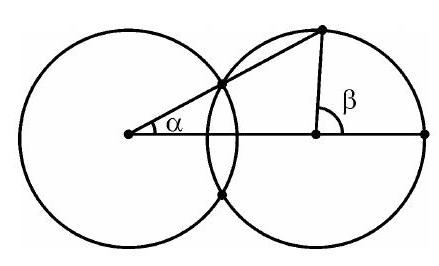
Fig. 12.2
|
12.52. Drop a perpendicular $M D$ from point $M$ to line $B C$. Then $M D = A H / 2 = B M / 2$. In the right triangle $B D M$, the leg $M D$ is equal to half of the hypotenuse $B M$. Therefore, $\angle M B C = \angle M B D = 30^{\circ}$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.53. In triangle $ABC$, the angle bisectors $AD$ and $BE$ are drawn. Find the measure of angle $C$, given that $AD \cdot BC = BE \cdot AC$ and $AC \neq BC$.
|
12.53. The quantities $A D \cdot B C \sin A D B$ and $B E \cdot A C \sin A E B$ are equal, as they are equal to twice the area of triangle $A B C$. Therefore, $\sin A D B = \sin A E B$. There are two possible cases.
1. $\angle A D B = \angle A E B$; in this case, points $A, E, D, B$ lie on the same circle, so $\angle E A D = \angle E B D$, i.e., $\angle A = \angle B$, which cannot be true according to the condition.
2. $\angle A D B + \angle A E B = 180^{\circ}$; in this case, $\angle E C D + \angle E O D = 180^{\circ}$, where $O$ is the point of intersection of the angle bisectors. Since $\angle E O D = 90^{\circ} + \angle C / 2$ (Problem 5.3), then $\angle C = 60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.54. Find the angle $B$ of triangle $A B C$, if the length of the height $C H$ is half the length of side $A B$, and $\angle B A C=75^{\circ}$.
|
12.54. Let $B'$ be the point of intersection of the perpendicular bisector of segment $AC$ with line $AB$. Then $AB' = CB'$ and $\angle AB'C = 180^\circ - 2 \cdot 75^\circ = 30^\circ$. Therefore, $AB' = CB' = 2CH = AB$, i.e., $B' = B$ and $\angle B = 30^\circ$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.55*. In a right triangle $ABC$ with a right angle at $A$, a circle is constructed on the altitude $AD$ as a diameter, intersecting side $AB$ at point $K$ and side $AC$ at point $M$. Segments $AD$ and $KM$ intersect at point $L$. Find the acute angles of triangle $ABC$, given that $AK: AL = AL: AM$.
|
12.55. It is clear that $A K D M$ is a rectangle and $L$ is the point of intersection of its diagonals. Since $A D \perp B C$ and $A M \perp B A$, then $\angle D A M = \angle A B C$. Similarly, $\angle K A D = \angle A C B$. Drop a perpendicular $A P$ from point $A$ to the line $K M$. Let's assume for definiteness that $\angle B < \angle C$. Then the point $P$ lies on the segment $K L$. From the similarity of triangles $A K P$ and $M K A$, we get $A K : A P = M K : M A$. Therefore, $A K \cdot A M = A P \cdot M K = A P \cdot A D = 2 A P \cdot A L$. By the condition $A L^2 = A K \cdot A M$, hence $A L = 2 A P$, i.e., $\angle A L P = 30^{\circ}$. It is clear that $\angle K M A = \angle A L P / 2 = 15^{\circ}$. Therefore, the acute angles of triangle $A B C$ are 15 and $75^{\circ}$.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18.5. On the sides $C B$ and $C D$ of the square $A B C D$, points $M$ and $K$ are taken such that the perimeter of triangle $C M K$ is equal to twice the side of the square. Find the measure of angle $M A K$.
|
18.5. Rotate the given square around point $A$ by $90^{\circ}$ so that vertex $B$ moves to $D$. Let $M^{\prime}$ be the image of point $M$ under this rotation. Since by the condition $M K+M C+C K=(B M+M C)+(K D+C K)$, then $M K=B M+K D=D M^{\prime}+K D=K M^{\prime}$. Moreover, $A M=A M^{\prime}$, therefore $\triangle A M K=\triangle A M^{\prime} K$, which means $\angle M A K=\angle M^{\prime} A K=\angle M A M^{\prime} / 2=45^{\circ}$.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18.34*. In the circus arena, which is a circle with a radius of 10 m, a lion is running. Moving along a broken line, he ran $30 \mathrm{km}$. Prove that the sum of all his turning angles is not less than 2998 radians.
## §4. Compositions of Rotations
|
18.34. Suppose the lion ran along the broken line $A_{1} A_{2} \ldots A_{n}$. Let's straighten the lion's trajectory as follows. Rotate the circus arena and the subsequent trajectory around point $A_{2}$ so that point $A_{3}$ falls on the ray $A_{1} A_{2}$. Then rotate the circus arena and the subsequent trajectory around point $A_{3}$ so that point $A_{4}$ falls on the ray $A_{1} A_{2}$, and so on. The center $O$ of the circus arena successively moves to points $O_{1}=O, O_{2}, \ldots, O_{n-1}$; points $A_{1}, \ldots, A_{n}$ move to points $A_{1}^{\prime}, \ldots, A_{n}^{\prime}$, lying on the same straight line (Fig. 18.5).
Let $\alpha_{i-1}$ be the angle of the lion's turn at point $A_{i}^{\prime}$. Then $\angle O_{i-1} A_{i}^{\prime} O_{i}=\alpha_{i-1}$ and $A_{i}^{\prime} O_{i-1}=A_{i}^{\prime} O_{i} \leqslant 10$, so $O_{i} O_{i-1} \leqslant 10 \alpha_{i-1}$. Therefore, $30000=$ $=A_{1}^{\prime} A_{n}^{\prime} \leqslant A_{1}^{\prime} O_{1}+O_{1} O_{2}+\ldots+O_{n-2} O_{n-1}+O_{n-1} A_{n}^{\prime} \leqslant 10+10\left(\alpha_{1}+\ldots+\alpha_{n-2}\right)+10$, i.e., $\alpha_{1}+\ldots+\alpha_{n-2} \geqslant 2998$.
|
2998
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
21.7*. Each of the two disks is divided into 1985 equal sectors, and 200 sectors on each are painted in an arbitrary color (one color). The disks are placed on top of each other, and one is rotated by angles that are multiples of $360^{\circ} / 1985$. Prove that there are at least 80 positions in which no more than 20 colored sectors coincide.
|
21.7. Let's take 1985 disks colored the same as the second of our disks and place them on the first disk so that they occupy all possible positions. Then above each colored sector of the first disk, there are 200 colored sectors, i.e., there are a total of $200^{2}$ pairs of coinciding colored sectors. Let there be $n$ positions of the second disk where at least 21 pairs of colored sectors coincide. Then the number of coinciding colored sectors is not less than $21 n$. Therefore, $21 n \leqslant 200^{2}$, i.e., $n \leqslant 1904.8$. Since $n$ is an integer, $n \leqslant 1904$. Consequently, for at least $1985-1904=81$ positions, no more than 20 pairs of colored sectors coincide.
|
81
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
21.9*. In the park, there are 10000 trees planted in a square grid pattern (100 rows of 100 trees each). What is the maximum number of trees that can be cut down so that the following condition is met: if you stand on any stump, you will not see any other stump? (The trees can be considered thin enough.)
|
21.9. Let's divide the trees into 2500 quartets, as shown in Fig. 21.3. In each such quartet, no more than one tree can be cut down. On the other hand, all the trees growing in the upper left corners of the squares formed by our quartets of trees can be cut down. Therefore, the maximum number of trees that can be cut down is 2500.
|
2500
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
22.4. Among all such numbers $n$ that any convex 100-gon can be represented as the intersection (i.e., common part) of $n$ triangles,
find the smallest.
|
22.4. First, note that 50 triangles are sufficient. Indeed, let $\Delta_{k}$ be the triangle whose sides lie on the rays $A_{k} A_{k-1}$ and $A_{k} A_{k+1}$ and which contains the convex polygon $A_{1} \ldots A_{100}$. Then this polygon is the intersection of the triangles $\Delta_{2}, \Delta_{4}, \ldots, \Delta_{100}$. On the other hand, the 100-gon shown in Fig. 22.2 cannot be represented as the intersection of fewer than 50 triangles. Indeed, if three of its sides lie on the sides of one triangle, then one of these sides is the side $A_{1} A_{2}$. All sides of this polygon lie on the sides of $n$ triangles, so $2 n + 1 \geqslant 100$, i.e., $n \geqslant 50$.
Fig. 22.2
|
50
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25.25*. A regular octagon with side 1 is cut into parallelograms. Prove that among them there are at least two rectangles, and the sum of the areas of all rectangles is 2.
## §5. Plane, cut by lines
Let $n$ pairwise non-parallel lines be drawn on the plane, with no three intersecting at the same point. Problems 25.26-25.30 consider the properties of the figures into which these lines divide the plane. A figure is called $n$-linked if it is bounded by $n$ links (i.e., segments or rays).
|
25.25. Let us consider two mutually perpendicular pairs of opposite sides in a regular octagon and, as in problem 25.1, chains of parallelograms connecting opposite sides. At the intersections of these chains, there are rectangles. By considering two other pairs of opposite sides, we will obtain at least one more rectangle.
The parallelograms in each chain can be further cut so that the chain splits into several "paths," where in each path, adjacent parallelograms touch each other with entire sides, not parts of sides. The union of the rectangles in the new partition coincides with the union of the rectangles in the original partition, so the proof is sufficient to conduct for the new partition. Each path has a constant width; therefore, the length of one side of each rectangle in the path is equal to the width of the path, and the sum of the lengths of all other sides is equal to the sum of the widths of the paths corresponding to the second pair of sides. Consequently, the area of all rectangles in one path is equal to the product of the width of the path by the length of the side of the polygon, i.e., numerically equal to the width of the path. Therefore, the area of all rectangles corresponding to two perpendicular pairs of opposite sides is 1, and the area of all rectangles in general is 2.
|
2
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
27.7. Ten points are marked on a circle. How many non-closed, non-self-intersecting nine-segment broken lines with vertices at these points exist?
|
27.7. The first point can be chosen in ten ways. Each of the following eight points can be chosen in two ways, as it must be adjacent to one of the previously chosen points (otherwise, a self-intersecting broken line would result). Since the beginning and end are not distinguished in this calculation, the result must be divided by 2. Therefore, there are $10 \cdot 2^{8} / 2=1280$ broken lines.
|
1280
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
43. It is obvious that any figure with a diameter of 1 can be enclosed within a square with a side of 2: for this, it is sufficient for the center of the square to coincide with any point of the figure. What is the side of the smallest square that can enclose any figure with a diameter of 1?
Note. One can also pose a problem analogous to problems 42 and 43, replacing the square (problem 43) or circle (problem 42) with any other figure. For example, it can be shown that the smallest equilateral triangle that can enclose any figure with a diameter of 1 is a triangle with a side of \(\sqrt{3}\), and the smallest regular hexagon with the same property is a hexagon with a side of \(\frac{\sqrt{3}}{3}\) (see problem 31 in the book by I. M. Yaglom and V. G. Boltyansky, cited on page 10).
|
43. It is obvious that a circle with a diameter of 1 cannot be enclosed in any square whose side is less than 1. On the other hand, it is almost equally clear that any figure with a diameter of 1 can be enclosed in a square with a side of 1. Indeed, any square that encloses some figure $\Phi$ can always be reduced so that at least one pair of opposite sides of the square "touch" the figure (Fig. 123). But if $A$ and $B$ are points of the figure $\Phi$ with a diameter of 1, lying on opposite sides of the square containing $\Phi$ inside itself, then the distance between these sides of the square (or, equivalently, the side of the square) does not exceed $AB$, and $AB \leqslant 1$.
Thus, the smallest square in which any figure with a diameter of 1 can be enclosed has a side equal to 1.

Fig. 123.
Fig. 124.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
49. How many circles of radius 1 can be applied ${ }^{1}$ ) to a given unit circle $\mathcal{S}$ so that no two of these circles intersect? So that no one of these circles contains the center of another circle inside itself?
|
49. Since a unit circle tangent to $S$ is seen from the center $O$ of circle $S$ at an angle of $60^{\circ}$ (Fig. $132, a$), no more than $6\left(=\frac{360}{60^{\circ}}\right)$ non-overlapping unit circles can be applied to $S$. Six circles can obviously be applied (Fig. 132, b).
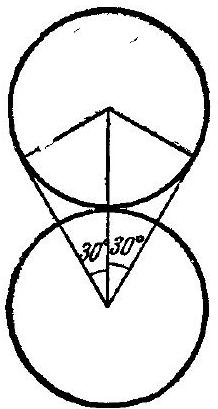
Further, if $O_{1}$ and $O_{2}$ are the centers of two unit circles $C_{1}$ and $C_{2}$ applied to $S$ such that $O_{1}$ does not lie inside $C_{2}$ and $O_{2}$ does not lie inside $C_{1}$ (Fig. $133, a$), then $O_{1} O_{2} \geqslant 1, O O_{1}=$ $=O O_{2}=2$ and $\angle O_{1} O O_{2} \geqslant 2 \arcsin \frac{1}{4} \approx 29.0^{\circ}$. It follows that no more than 12 (12 is the integer part of the fraction $\frac{360^{\circ}}{29.0^{\circ}}$) unit circles can be applied to $S$ such that no circle contains the center of another circle; 12 circles can obviously be applied (Fig. 133, b).
a)
Fig. 132.
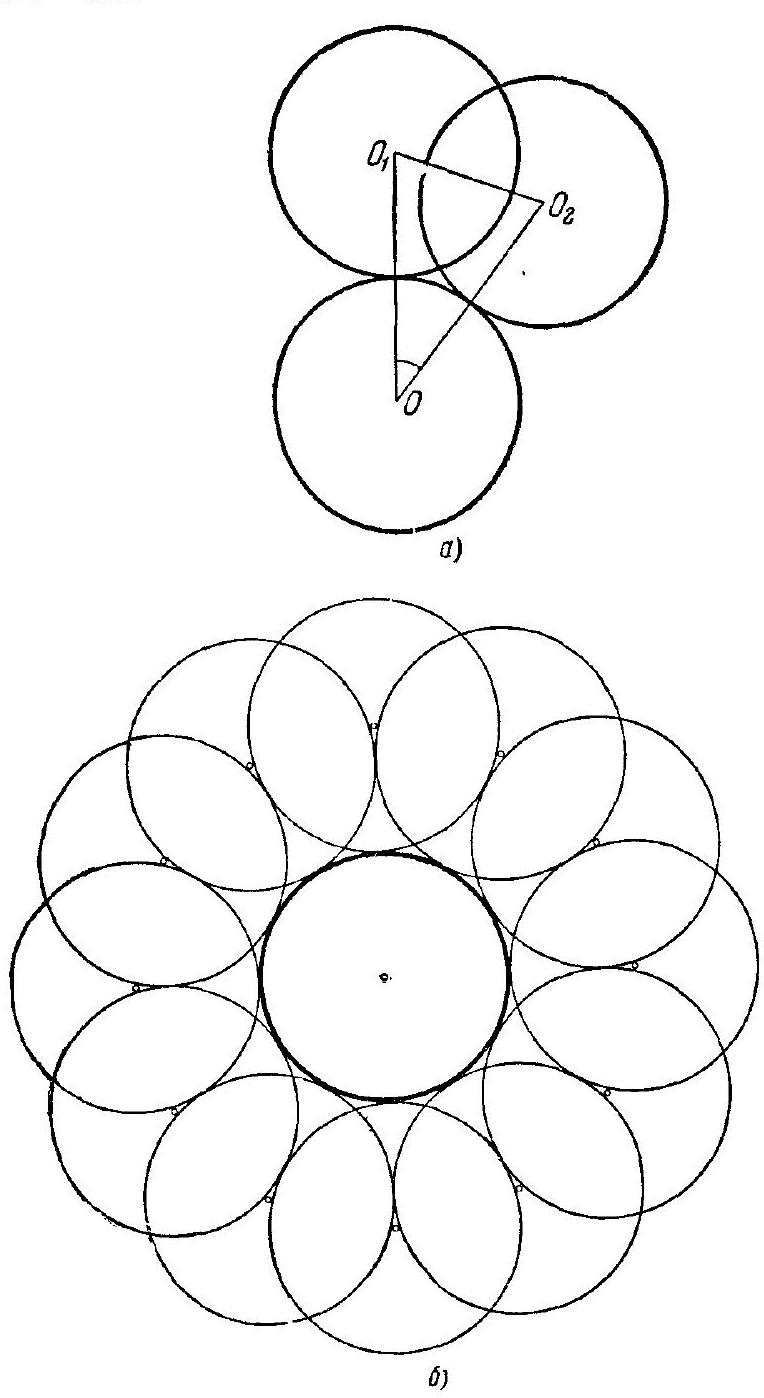
Fig. 133.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
50*. What is the greatest number of circles of radius 1 that can be placed on a plane so that they all intersect a certain fixed unit circle $S$ and no one of them contains the center of $S$ or the center of another circle inside it?
|
50. Fig. 134 shows that 18 circles satisfying the condition of the problem can be placed (six circles in Fig. 134 have centers at the vertices of a regular hexagon inscribed in $S$, the other 12 - at the vertices of squares constructed on the sides of the inscribed hexagon outside it; compare with Fig. 130). The fact that more than 18 circles cannot be placed follows from the result of problem 48: otherwise, the centers of all circles (including the center $O$ of circle $S$) would form a system of 20 or more points enclosed within a circle of radius 2 centered at one of these points $O$ and such that the distance between any two of these points is not less than 1, while according to the theorem of problem 48, such a system of points cannot exist.
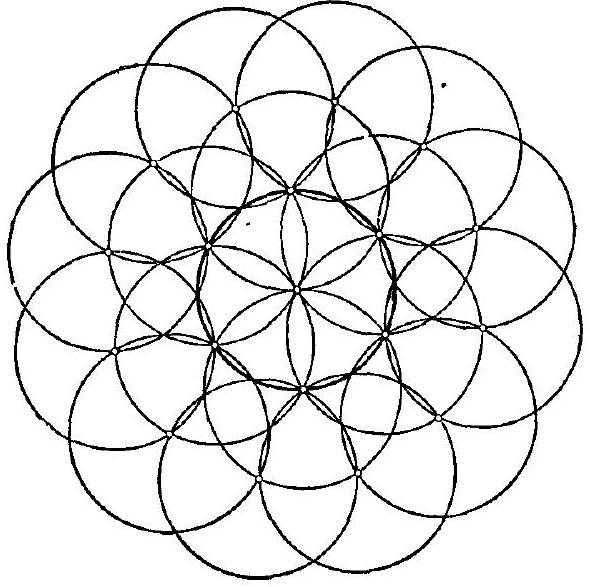
Fig. 134.
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
51. What is the greatest number of squares with side 1 that can be placed ${ }^{1}$ ) next to a given unit square $K$ so that no two of them intersect?
$^{1}$) The superscript "1" is kept as is, since it might refer to a footnote or additional information in the original text.
|
51. First solution. Let $O$ be the center of the main square $K$, and $O_{1}$ and $O_{2}$ be the centers of the non-overlapping squares $K_{1}$ and $K_{2}$ attached to it (Fig. $135, a$). Since the smallest distance from the center of a unit square to its boundary is $\frac{1}{2}$, the segments $O O_{1}$, $O O_{2}$, and $O_{1} O_{2}$ are not less than 1. Furthermore, since the squares $K$ and $K_{1}$ touch at some point $A$, we have $O O_{1} \leqslant O A + O_{1} A \leqslant \sqrt{2}$ (since the greatest distance from the center of a unit square to its boundary is $\frac{\sqrt{2}}{2}$). Therefore, the points $O_{1}$ and $O_{2}$ lie within the annulus centered at $O$ and bounded by circles of radii 1 and $\sqrt{2}$; and since $O_{1} O_{2} \geqslant 1$, the angle $O_{1} O O_{2}$, by the result of problem 46, is not less than $2 \arcsin \frac{1}{2 \sqrt{2}} \approx 41.4^{\circ}$. From this,
a)

b)
Fig. 135.
it follows that more than eight non-overlapping unit squares cannot be attached to the square $K$, since $9 \times 41.4^{\circ} > 360^{\circ}$. That eight squares can be attached is evident from Fig. 135, b.
Note. This problem can also be solved without using trigonometric tables. $2 \arcsin \frac{1}{2 \sqrt{2}}$ is the angle at the vertex of an isosceles triangle with legs $\sqrt{2}$ and base 1. If we attach nine such triangles to each other as shown in Fig. 136, the sum of the lengths of the bases of all these triangles will exceed the length of the circumference of radius $\sqrt{2}$; indeed, $2 \pi \sqrt{2} < 360^{\circ}$, which is what we needed to show.
Second solution. Let $A B C D$ be the original square $K$; we will take the length of its side as the unit. Consider the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ with side 2, having the same center as the square $K$ and the same orientation of sides (Fig. $137, a$); the perimeter of the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is obviously 8. We will show that the length $l$ of the part of the perimeter of the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ cut by the side of one attached square cannot be less than 1; from this it will follow that no more than eight non-overlapping squares can be attached to $K$. Consider all possible positions of the attached square.
a)
b)
Fig. 137.
$1^{\circ}$ Suppose no vertex of the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ falls inside the attached square (cases of squares $E F G H$ and $E_{1} F_{1} G_{1} H_{1}$ in Fig. 137, a). If in this case only one vertex of the attached square falls inside the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ (as in the case of square $E F G H$), then, denoting the angle between the sides $B C$ and $E F$ by $\alpha$, we have
$$
\begin{aligned}
& l = M K + K N = E K \operatorname{tg} \alpha + E K \operatorname{ctg} \alpha = \frac{1}{2} \left( \operatorname{tg} \alpha + \frac{1}{\operatorname{tg} \alpha} \right) = \\
& = 1 + \frac{1}{2} \left( \sqrt{\operatorname{tg} \alpha} - \frac{1}{\sqrt{\operatorname{tg} \alpha}} \right)^2 \geqslant 1
\end{aligned}
$$
If two vertices of the attached square fall inside the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ (as in the case of square $E_{1} F_{1} G_{1} H_{1}$), then obviously $l = M_{1} N_{1} \geqslant N_{1} L_{1} = 1$.
$2^{\circ}$ Suppose one vertex of the square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ falls inside the attached square (squares $A F_{2} C_{2} H_{2}$, $E_{3} F_{3} C_{3} H_{3}$, and $E_{4} F_{4} G_{4} H_{4}$ in Fig. 137, b). If the attached square touches the square $A B C D$ at a point on the boundary other than a vertex (case of square $E_{3} F_{3} G_{3} H_{3}$), then
$$
\begin{aligned}
l = M B^{\prime} + B^{\prime} N & = \left( P B^{\prime} + B^{\prime} Q \right) + (Q N - P M) = \\
& = 1 + (Q N - P M).
\end{aligned}
$$
But (Fig. $137, \sigma$)
$P M = E_{3} P \operatorname{tg} \alpha, \quad Q N = R Q \operatorname{tg} \alpha, \quad R Q - E_{3} P = R B - E_{3} B \geqslant 0$, since $\alpha \leqslant 45^{\circ}$. Therefore, $Q N > P M$ and $l > 1$. These same arguments apply in the case where the attached square touches the square $A B C D$ at a vertex (case of square $A F_{2} G_{2} H_{2}$); in this case only $P^{\prime} M^{\prime} = Q^{\prime} N^{\prime}$ and, therefore, $l = M^{\prime} A^{\prime} + A^{\prime} N^{\prime} = 1$. Finally, if the attached square touches the vertex of the square $A B C D$ with a side (case of square $E_{4} F_{4} G_{4} H_{4}$), then
$$
l = M_{1} D^{\prime} + D^{\prime} N_{1} > M_{1} N_{1} \geqslant G_{4} F_{4} = 1
$$
Thus, in all cases, the length of the part $M N$ of the perimeter of $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ indeed cannot be less than 1.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
54. What is the smallest number of circles with which a circle of twice the radius can be completely covered?
|
54. Since the diameter of the smaller circles is equal to the radius $R$ of the larger circle, each such circle intersects the circumference of the larger circle at points no more than $R$ apart, and thus covers an arc of this circumference no greater than $60^{\circ}$. It follows that at least six smaller circles are required to cover the entire circumference of the larger circle; in this case, six circles are sufficient only when these circles have diameters equal to the six sides of a regular hexagon inscribed in the larger circle, and in all other cases, at least seven circles are required. However, if the circumference of the larger circle is covered by six circles, then at least one more small circle is required to cover the remaining part of the larger circle (since the first six circles do not cover, for example, the center of the larger circle). In this case, one circle is sufficient to cover the remaining part of the larger circle (Fig. 143; from the fact that $O_{1} M=\frac{1}{2} R$, it follows that $O_{1} M$ is the median of the right triangle $O O_{1} A$ with an angle of $30^{\circ}$ and, therefore, $\left.O M=\frac{1}{2} R\right)$. Thus, we see that the smallest number of circles with radius $\frac{1}{2} R$ required to cover a circle with radius $R$ is 7.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
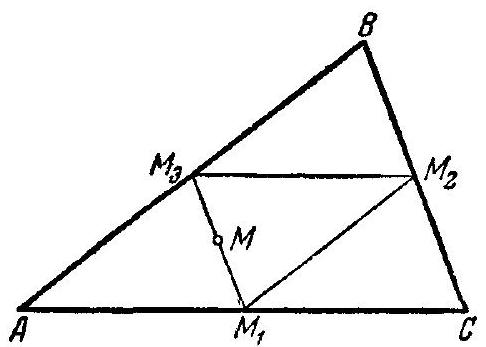
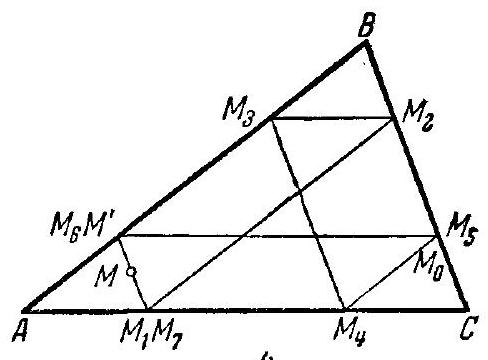
102. Given a triangle $ABC$. A point $M$, located inside the triangle, moves parallel to side $BC$ until it intersects side $CA$, then moves parallel to $AB$ until it intersects side $BC$, then - parallel to $AC$ until it intersects $AB$, and so on. Prove that after a certain number of such steps, the point will return to its initial position, and find this number of steps.
Fig. 25.
|
102. If point $M$ lies on any of the medians of triangle $ABC$, for example, on $M_{3} M_{1}$, then it is obvious that after four steps it will return to its initial position (Fig. $227, a$). Now suppose that $M$ does not lie on any of the three medians of triangle $ABC$.
Let $M_{1}, M_{2}, M_{3}, M_{4}, M_{5}, M_{6}, M_{7}$ be the points on the sides of triangle $ABC$ that point $M$ sequentially reaches during its movement (Fig. 227, b). We need to prove that $M_{7}$ coincides with $M_{1}$. Let $M^{\prime}$ be the point of intersection of $M M_{1}$ with $AB$. It is sufficient to show that $M_{6}$ coincides with $M^{\prime}$. Draw a line through point $M^{\prime}$ parallel to $AC$. Let $M_{0}$ be the point of intersection of this line with $BC$.
a)
b)
Fig. 227.
Triangle $M^{\prime} B M_{0}$ is equal to triangle $M_{1} M_{2} C$, triangle $M_{1} M_{2} C$ is equal to triangle $A M_{3} M_{4}$, and triangle $A M_{3} M_{4}$ is equal to triangle $B M_{5} M_{6}$. Therefore, triangle $M^{\prime} B M_{0}$ is equal to triangle $B M_{5} M_{6}$, and thus $M_{6} M_{5} = M^{\prime} M_{0}$. From this, it follows that $M_{6}$ coincides with $M^{\prime}$, and $M_{5}$ with $M$; hence, $M_{7}$ coincides with $M_{1}$. This will happen in seven steps.
|
7
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
31. a) The third term of an arithmetic progression is equal to 0. Find the sum of the first 5 terms.
b) The third term of a geometric progression is equal to 4. Find the product of the first 5 terms.
|
31. a) We know that for an arithmetic progression $u_{1}=u_{3}-2 d ; u_{2}=u_{3}-d$; $u_{4}=u_{3}+d ; \quad u_{5}=u_{3}+2 d$. Therefore, the sum of the first five terms is
$$
\begin{aligned}
& \delta_{5}=u_{1}+u_{2}+u_{3}+u_{4}+u_{5}=\left(u_{3}-2 d\right)+ \\
& +\left(u_{3}-d\right)+u_{3}+\left(u_{3}+d\right)+ \\
& +\left(u_{3}+2 d\right)=5 u_{3}=0
\end{aligned}
$$
b) We need to find
$$
P_{5}=u_{1} \cdot u_{2} \cdot u_{3} \cdot u_{4} \cdot u_{5}
$$
We know that for a geometric progression
$\boldsymbol{u}_{1}=\frac{u_{3}}{q^{2}} ; \quad u_{2}=\frac{u_{3}}{q} ; \quad u_{4}=u_{3} q ; \quad u_{5}=u_{3} q^{2}$.
Therefore,
$$
P_{5}=\frac{u_{3}}{q^{2}} \cdot \frac{u_{3}}{q} \cdot u_{3} \cdot u_{3} q \cdot u_{3} q^{2}=u_{3}^{5}=4^{5}=1024
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
33. Someone arrives in the city with very interesting news and after 10 minutes reports it to two people. Each of the newly informed people, after 10 minutes, reports it to two more (who have not yet heard it) and so on. *). How long will it take for the entire city to know this news, if the city has three million residents?
|
33. It is easy to see that the number of people who were told the news at the end of the 1st ten-minute period is 2, the number of people who were told the news after the 2nd ten-minute period is 4, and generally, the number of people who were told the news at the end of the $k$-th ten-minute period is $2^{k}$.
The number of all people who will know the news after $10 k$ minutes is equal to the number of people who learned this news after 0 minutes (i.e., 1 person), plus the number of people who learned the news after 10 minutes (2 people), plus the number of people who learned the news after 20 minutes (4 people), and so on up to the people who learned the news after $k \cdot 10$ minutes ($2^{k}$ people),
Therefore, this number of people is
$$
S_{k}=1+2+4+\ldots+2^{k}
$$
We see that $S_{k}$ is the sum of the first $k+1$ terms of a geometric progression with the first term 1 and common ratio 2. Therefore,
$$
S_{k}=\frac{1 \cdot 2^{k+1}-1}{2-1}=2^{k+1}-1 .
$$
Now, to solve the problem, we need to find the smallest $k$ for which $S_{k}$, i.e., the number of all people who know the news after $k \cdot 10$ minutes, will be greater than 3000000 (the total population of the city). It is easy to see that the smallest $k=21$, since
$$
2^{22}-1=4194303
$$
Thus, all residents of the city will know the news after 210 minutes $=$ $=3$ hours 30 minutes.
|
210
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35. Find the sum of all positive odd numbers not exceeding a thousand.
|
35. We need to find the sum $1+3+$ $+5+\ldots+997+999$. It is clear that this is the sum of the first 500 terms of an arithmetic progression with the first term 1 and common difference 2. Therefore, our sum is
$1 \cdot 500+\frac{500 \cdot 499}{2} \cdot 2=500+500 \cdot 499=$
$$
=500 \cdot 500=250000
$$
|
250000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
36. Find the sum of all positive three-digit numbers that are not divisible by 2 or 3.
|
36. Subtract from the sum of all positive three-digit numbers $S^{(1)}$ the sum of positive three-digit numbers divisible by 2 ($S^{(2)}$), and the sum of positive three-digit numbers divisible by 3 ($S^{(3)}$). In this process, numbers divisible by both 2 and 3, i.e., divisible by 6, are subtracted twice.
Therefore, to get the answer, we need to add the sum of all positive three-digit numbers divisible by 6 ($S^{(6)}$) to the obtained difference, i.e., take the value
$$
S=S^{(1)}-S^{(2)}-S^{(3)}+S^{(6)}
$$
Each of the four sums written on the right is the sum of a certain number of terms of the corresponding arithmetic progression. The number of terms and the common difference of the progression are given in the table.
| | $u_{1}$ | $n$ | $d$ |
| :---: | :---: | :---: | :---: |
| I | 100 | 900 | 1 |
| II | 100 | 450 | 2 |
| III | 102 | 300 | 3 |
| IV | 102 | 150 | 6 |
Therefore, $S^{(1)}=100 \cdot 900+\frac{900 \cdot 899}{2} \cdot 1=$ $=90000+404550=494550$,
$S^{(2)}=100 \cdot 450+\frac{450 \cdot 449}{2} \cdot 2=247050$,
$$
\begin{aligned}
S^{(3)} & =102 \cdot 300+\frac{300 \cdot 299}{2} \cdot 3= \\
& =30600+134550=165150 \\
S^{(6)} & =102 \cdot 150+\frac{150 \cdot 149}{2} \cdot 6=82350 \\
S & =S^{(1)}-S^{(2)}-S^{(3)}+S^{(6)}=164700
\end{aligned}
$$
|
164700
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
44. In the kitchen, there are five light bulbs. How many lighting options exist?
Do you understand what lighting options mean? Each lamp can be on or off. Two options are considered different if they differ in the state of at least one lamp (see Fig. 7 and 8).
|
44. First solution. The number of ways to illuminate with one lamp out of five is equal to the number of ways to illuminate with four lamps out of five (Fig. 32).
$$
\begin{aligned}
& 000 \sim 0000 \\
& 10000000 \\
& 0000 \text { } \\
& 1000 \\
& 0000 \sim 0000
\end{aligned}
$$
## Fig. 32
Similarly, the number of ways to illuminate with two lamps out of five is equal to the number of ways in which two lamps out of five do not light up (i.e., three lamps out of five light up). These methods are shown in Fig. 33 (10 ways in which two lamps light up and 10 ways in which three lamps light up).
## $00 \bullet \bullet \sim \bullet 000$ $0 \bullet 0 \cdot \sim \sim 000$ $0 \bullet 0 \cdot \sim 00 \bullet 0$ $0 \cdot \bullet \cdot 0 \sim 000$ $-00 \cdot \sim 0 \cdot 000$ $-0 \cdot 0 \sim 0 \cdot 00$ $-0 \cdot 0 \sim 000$ $\cdot 00 \cdot \sim 00 \cdot 0$ $\bullet 0.0 \sim 00 \cdot 0$ $\bullet \bullet 00 \sim 000 \bullet$
## Beo naunes ropar:
00000
All lamps in the roper: $-00$
Fig. 3 s
2 lamps, and 10 ways in which 3 lamps light up). There are also two more ways (Fig. 34) (all lamps light up, all lamps do not light up). We have considered all ways of illumination and it is now easy to count them. Second solution. 1) Suppose there is one lamp in the kitchen. It can be in two states: not lit or lit 0, i.e., there are 2 ways of illumination.
2) 2 lamps. The first lamp can be in two states: and $\bigcirc$.
Each of these can be combined with any of the two states of the second lamp: if the second lamp is not lit, we get 2 ways of illumination.
If the second lamp is lit, we get 2 more ways
In total, there are 4 ways of illumination:

3) 3 lamps. The first two lamps can be in four states. Each of these four states can be combined with any of the two states of the third lamp.

In total, there are 8 ways of illumination:

4) 4 lamps. The first three lamps can be in eight states. Each of these can be combined with any of the two states of the fourth lamp. There are $8 \cdot 2=16$ ways of illumination.
5) 5 lamps. There are $16 \cdot 2=32$ ways of illumination. The method of solution considered allows for minor modifications: the transition from two lamps to three
can be illustrated not only by the above scheme but also by the following schemes:

Both of them also show that adding one lamp (which can be in two states) doubles the number of ways of illumination.
|
32
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
55. What is the maximum number of bishops that can be placed on a chessboard so that they do not threaten each other? Prove that the number of ways to arrange the bishops in such a way is the square of some number.
To understand the condition, of course, you need to know how a bishop moves. A bishop moves diagonally. For example, from the square $d 3$, a bishop can move in one move to any of the squares marked in Fig. 11 ( $b 1, c 2$, etc.). Thus, 2 bishops threaten each other if they stand on the same diagonal.
|
55. The instruction to the problem shows a specific example of placing 14 bishops. Therefore, it is possible to place 14 bishops. If we prove that it is impossible to place more than 14 bishops, the first part of the problem will be solved. Let's first consider the black-square bishops. How many can be placed on a chessboard so that they do not threaten each other? 7 can be placed; let's prove that it is impossible to place more. We choose 7 black diagonals, parallel to each other (Fig. 35). On one diagonal, a maximum of one bishop can stand. Therefore, the answer is: 7. If we take the "black" diagonals perpendicular to the specified ones, there will be 8 (with the outermost ones containing one cell each). Considering these diagonals, we could also convince ourselves that it is impossible to place more than seven bishops (indeed, if eight bishops are placed, not threatening each other, then two of them must be on the outermost diagonals, but since each of these diagonals consists of one cell, these two bishops must be in opposite corners of the board, i.e., threatening each other). However, this reasoning is unnecessary, as we obtain the same result more simply by choosing the diagonals as shown in Fig. 35.
The maximum number of white-square bishops that do not threaten each other is also 7. White-square and black-square bishops cannot threaten each other. Therefore, a total of 14 bishops can be placed on the board without threatening each other.
Let \( B \) be the number of ways to place 7 white-square bishops that do not threaten each other; \( C \) be the number of ways to place 7 black-square bishops that do not threaten each other; and finally, \( C \) be the number of ways to place 14 bishops that do not threaten each other. Clearly, \( B = C \), \( C = B \cdot C = (C)^2 \), i.e., \( C \) is the square of some number.
Remark. Solve a more general problem. Suppose the board has dimensions \( n \times n \), where \( n \) is even. Prove that the maximum number of bishops that do not threaten each other is \( 2n - 2 \). Prove that the number of ways to place \( 2n - 2 \) bishops that do not threaten each other is \( 2^n \).
|
14
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
56. Mom has two apples and three pears. Every day for five consecutive days, she gives out one fruit. In how many ways can this be done?
|
56. Here is one way to distribute apples and pears: 000 'on the 1st and 3rd day - apples, on the 2nd, 4th, and 5th days - pears),
## 000
(on the first three days - pears, on the last two days - apples). Thus, we need to count all the tables with two light and three dark circles; but we have already done this when solving problem 44. The answer is $C_{5}^{2}=10$
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
81. Determine the sum of the coefficients of the polynomial that results from expanding and combining like terms in the expression $\left(1+x-3 x^{2}\right)^{1965}$.
|
81. If we expand the expression $\left(1+x-3 x^{2}\right)^{1965}$ and combine like terms, we get a polynomial $a_{0}+a_{1} \cdot x+$ $+a_{2} \cdot x^{2}+a_{3} \cdot x^{3}+\ldots$. Note that the sum of its coefficients is equal to the value of the polynomial at $x=1$
$$
\begin{aligned}
& a_{0}+a_{1} \cdot 1+a_{2} \cdot 1^{2}+a_{3} \cdot 1^{3}+\ldots= \\
&=a_{0}+a_{1}+a_{2}+a_{3}+\ldots
\end{aligned}
$$
Of course, there is no need to actually expand the brackets and combine like terms. It is sufficient to substitute $x=1$ into the original expression
$$
\left(1+1-3 \cdot 1^{2}\right)^{1965}=(-1)^{1965}=-1
$$
Thus, $a_{0}+a_{1}+a_{2}+a_{3}+\ldots=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
93. How many phone numbers contain the combination 12? (The number consists of six digits.)
|
93. Let's consider the following five sets of phone numbers:

B

-

E

(for example, set \( B \) consists of numbers where the second and third digits are 12, and the other digits can be anything). Each of these sets contains \( 10^4 \) numbers. Sets \( A \) and \( B \) do not have any common numbers. Sets \( A \) and \( C \) have \( 10^2 \) common numbers, which are numbers of the form

It is easy to calculate that there are \( 6 \cdot 10^2 \) numbers that belong to any two sets simultaneously. Finally, only one number (1212 12) belongs to three sets. Now, using either the method from problem 91 or the method from problem 92, it is easy to show that the desired number is \( 5 \cdot 10^4 - 6 \cdot 10^2 + 1 = 49401 \).
## Chapter 3
|
49401
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
105. Is it true that there exists a number $C$ such that for all integers $k$ the inequality
$$
\left|\frac{k^{8}-2 k+1}{k^{4}-3}\right|<C ?
$$
|
105. Let's see how the expression $\left|\frac{k^{3}-2 k+1}{k^{4}-3}\right|$ behaves for large (in absolute value) values of $k$. Clearly, in the numerator, the term $k^{3}$ plays the main role, and in the denominator, $k^{4}$. Therefore, we can expect that for large values of $k$, our expression is approximately equal to $\left|\frac{k^{3}}{k^{4}}\right|=\frac{1}{|k|}$. Now let's investigate how much the exact value of our expression differs from the found approximate value. For this, we will perform the following transformation:
$$
\begin{aligned}
&\left|\frac{k^{3}-2 k+1}{k^{4}-3}\right|=\left|\frac{k^{3}\left(1-\frac{2}{k^{2}}+\frac{1}{k^{3}}\right)}{k^{4}\left(1-\frac{3}{k^{4}}\right)}\right|= \\
&=\frac{1}{|k|} \frac{\left|1-\frac{2}{k^{2}}+\frac{1}{k^{3}}\right|}{\left|1-\frac{3}{k^{4}}\right|}
\end{aligned}
$$
Let $|k| \geqslant 2$; then
$$
\begin{gathered}
\left|1-\frac{2}{k^{2}}+\frac{1}{k^{3}}\right| \leqslant 1+\frac{2}{k^{2}}+\frac{1}{|k|^{3}} \leqslant \\
\leqslant 1+\frac{1}{2}+\frac{1}{8}\frac{1}{2}
\end{gathered}
$$
Therefore, for $|k| \geqslant 2$, the inequality
$$
\frac{1}{|k|} \frac{\left|1-\frac{2}{k^{2}}+\frac{1}{k^{3}}\right|}{\left|1-\frac{3}{k^{4}}\right|}<\frac{1}{2} \cdot \frac{2}{\frac{1}{2}}=2
$$
holds. Thus, for $|k| \geqslant 2$, our expression does not exceed 2. It remains to see what values it takes for $k=$ $=-1,0,1$. These values are respectively $1,1 / 3,0$.
Answer: the number $C$ exists, for example, we can take
$$
C=2
$$
Remark. In the same way, we can obtain more accurate estimates for our expression and verify that the maximum value, equal to 1, it takes at $k=-1$. Do this independently.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
148. To compute the square root of a positive number $a$, one can use the following method of successive approximations. Take any number $x_{0}$ and construct a sequence according to the following rule:
$$
x_{n+1}=\frac{1}{2}\left(x_{n}+\frac{a}{x_{n}}\right)
$$
Prove that if $x_{0}>0$, then $\lim _{n \rightarrow \infty} x_{n}=\sqrt{a}$, and if $x_{0}<0$, then $\lim _{n \rightarrow \infty} x_{n}=-\sqrt{a}$. (By $\sqrt{a}$ we denote the arithmetic square root of $a$.)
How many successive approximations (i.e., how many terms of the sequence $\left\{x_{n}\right\}$ need to be computed) are required to find the value of $\sqrt{10}$ with an accuracy of 0.00001, if the initial value is taken as $x_{0}=3$?
|
148. First, let's prove that if the limit of $\{x_{n}\}$ exists, then it equals $\pm \sqrt{a}$. Indeed, let $\lim _{n \rightarrow \infty} x_{n}=b$. Then $\lim _{n \rightarrow \infty} \frac{1}{2}\left(x_{n}+\frac{a}{x_{n}}\right)=\frac{1}{2}\left(b+\frac{a}{b}\right)$. We obtain the equation $b=\frac{1}{2}\left(b+\frac{a}{b}\right)$, from which $b^{2}=a, b= \pm \sqrt{a}$.
It remains to note that if $x_{0}>0$, then all terms of the sequence are positive; if $x_{0}>0$ (Fig. 47). Let us denote by $y_{n}$ the difference between $x_{n}$ and $\sqrt{a}$, divided by $\sqrt{a}$. Substituting the expression $x_{n}=\sqrt{a}\left(1+y_{n}\right)$ into the equality $x_{n+1}=\frac{1}{2}\left(x_{n}+\frac{a}{x_{n}}\right)$, we get
$$
\begin{aligned}
& \sqrt{a}\left(1+y_{n+1}\right)= \\
& \quad=\frac{1}{2}\left(\sqrt{a}\left(1+y_{n}\right)+\frac{a}{\sqrt{a}\left(1+y_{n}\right)}\right)
\end{aligned}
$$
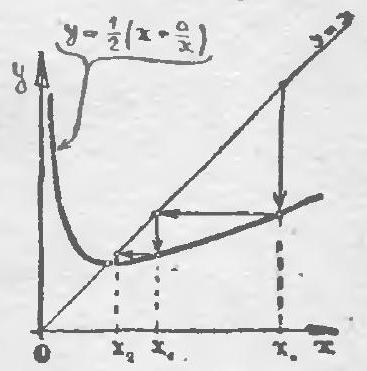
Fig. 47
from which
$$
y_{n+1}=\frac{y_{n}^{2}}{2\left(1+y_{n}\right)}
$$
We need to prove that the sequence $\{y_{n}\}$ tends to zero. Note first that since
$$
1+y_{0}=1+\frac{x_{0}-\sqrt{a}}{\sqrt{a}}=\frac{x_{0}}{\sqrt{a}}>0
$$
all numbers $y_{n}$ for $n \geqslant 1$ are positive. Therefore,
$$
\left|y_{n+1}\right|=y_{n+1}=\frac{y_{n}^{2}}{2\left(1+y_{n}\right)}<\frac{y_{n}^{2}}{2}
$$
If $x_{0}=3$ and $a=10$, then $\sqrt{10}<3.2$.
Therefore, $\left|y_{0}\right|=\left|\frac{3-\sqrt{10}}{\sqrt{10}}\right|<\frac{0.2}{3}=\frac{1}{15}$ and, hence,
$$
\left|y_{1}\right|=\frac{y_{0}^{2}}{2\left(1+y_{0}\right)}<\frac{\left(\frac{1}{15}\right)^{2}}{2\left(1-\frac{1}{15}\right)}<\frac{1}{400}
$$
Further,
$$
\left|y_{2}\right|=\frac{y_{1}^{2}}{2\left(1+y_{1}\right)}<\frac{\left(\frac{1}{400}\right)^{2}}{2}<\frac{1}{320000}
$$
Therefore, $\left|x_{2}-\sqrt{10}\right|=y_{2} \sqrt{10}<\frac{\sqrt{10}}{320000}<$ $<0.00001$. Thus, to find $\sqrt{10}$ with an accuracy of 0.00001, it is sufficient to find the term $x_{2}$. We have
$$
\begin{aligned}
x_{1}=\frac{1}{2}\left(x_{0}+\frac{10}{x_{0}}\right)= & \frac{1}{2}\left(3+\frac{10}{3}\right)= \\
= & 3 \frac{1}{6}=3.166666 \ldots \\
x_{2}=\frac{1}{2}\left(x_{1}+\frac{10}{x_{1}}\right)= & \frac{1}{2}\left(3 \frac{1}{6}+\frac{10}{3 \frac{1}{6}}\right)= \\
& =3 \frac{37}{228}=3.162280 \ldots
\end{aligned}
$$
In fact, $\sqrt{10}=3.16227765 \ldots$
As you can see, the value we found indeed differs from the true value by less than 0.00001.
|
2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
228. Given an angle MAN and a point $O$ not lying on the side of the angle. Draw a line through $O$ intersecting the sides of the angle at points $X$ and $Y$, such that the product $O X \cdot O Y$ has a given value $k$.
|
228. Suppose the problem is solved. From OX. $O Y=k$, it follows that $X$ is obtained from point $Y$ by the inversion with center $O$ and power $k$; therefore, $X$ lies on the circle $S$, which is obtained from the line $A N$ by the inversion with center $O$ and power $k$ (i.e., $k$), i.e., $X$ is the intersection point of the line $A M$ and the circle $S$ (which can be constructed). The problem can have up to four solutions.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
298. The set of all cycles in Lobachevsky's non-Euclidean geometry that are perpendicular to two given cycles \( S_{1} \) and \( S_{2} \) is called a bundle of cycles. List all possible types of bundles of cycles in Lobachevsky's non-Euclidean geometry. Prove that for each bundle II, there are infinitely many cycles that are not perpendicular to all cycles in this bundle; these cycles form a new bundle \(\overline{\mathrm{I}}\), which it is natural to call perpendicular to the bundle II.
|
298. Obviously, the pencil of cycles of Lobachevsky's hyperbolic geometry does not differ from the pencil of circles of ordinary (Euclidean) geometry (see § 3 of this chapter); only in accordance with the definition of points in hyperbolic geometry, here one should consider not the entire circles but only arcs of them, contained within the circle K (see, however, the note to the solution of problem 300). Accordingly, the last statement of the problem follows directly from the results of § 3 (see pp. $219-221$ ).
An elliptic pencil of circles is defined by the given two points $P$ and $Q$, through which all the circles of the pencil pass. Therefore, in Lobachevsky's non-Euclidean geometry, there are six different "elliptic pencils of cycles," corresponding to the six possible arrangements of points $P$ and $Q$:
$1^{\circ}$ points $P$ and $Q$ are located inside $K$;
$2^{\circ}$ point $P$ is located inside $K$, and $Q$ is on the circumference $\Sigma$;
$3^{\circ}$ point $P$ is located inside $K$, and $Q$ is outside $K$;
$4^{\circ}$ points $P$ and $Q$ are located on the circumference $\Sigma$ (see Fig. 254, b on p. 334);
$5^{\circ}$ point $P$ is located on the circumference $\Sigma$, and $Q$ is outside $K$;
$6^{\circ}$ points $P$ and $Q$ are located outside $K$.
A hyperbolic pencil of circles can be defined as a pencil perpendicular to an elliptic pencil. Therefore, the six types of "elliptic pencils of cycles" in Lobachevsky's non-Euclidean geometry correspond to six types of perpendicular "hyperbolic pencils of cycles." However, it is advisable to single out one more special case - when the circumference $\Sigma$ itself belongs to the considered pencil (see Fig. 254, a on p. 333); the perpendicular elliptic pencil of type $3^{\circ}$ is characterized by the fact that points $P$ and $Q$ are symmetric with respect to the circumference $\Sigma$ - from a certain point of view, this type of "elliptic pencils of cycles" should also be considered special. Thus, we will have seven types of "hyperbolic pencils of cycles" in total.
Finally, a parabolic pencil of circles is characterized by the given point $A$ and a line $l$ passing through this point - all the circles of the pencil touch the line $l$ at point $A$. Accordingly, it is natural to distinguish the following six types of "parabolic pencils of cycles" in Lobachevsky's non-Euclidean geometry:
$1^{\circ}$ point $A$ lies inside the circle $K$;
$2^{\circ}$ point $A$ lies on the circumference $\Sigma$, and the line $l$ intersects $\Sigma$;
$3^{\circ}$ point $A$ lies on the circumference $\Sigma$, and the line $l$ is tangent to $\Sigma$ (see Fig. 254, c on p. 335);
$4^{\circ}$ point $A$ lies outside the circle $K$, and the line $l$ intersects $\Sigma$;
$5^{\circ}$ point $A$ lies outside $K$, and the line $l$ is tangent to $\Sigma$;
$6^{\circ}$ point $A$ lies outside $K$, and the line $l$ has no common points with $\Sigma$.
Thus, there are $6+7+6=19$ different types of pencils of cycles. We recommend that the reader make the corresponding drawings and figure out what kind of cycles are included in the pencil of each of the listed types.
|
19
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
2.12. (GDR, 77). How many pairs of values $p, q \in \mathbf{N}$, not exceeding 100, exist for which the equation
$$
x^{5}+p x+q=0
$$
has solutions in rational numbers?
|
2.12. Let for some values
$$
p, q \in\{1 ; 2 ; \ldots ; 100\}
$$
the number $x \in \mathbf{Q}$ satisfies the equation
$$
x^{5}+p x+q=0
$$
Since all coefficients of the polynomial on the left side of the equation are integers, and the coefficient of the leading term is 1, by Theorem 60, any rational root of this polynomial, including the number $x$, is an integer. We will prove that $-30 < x < 3$.
If $x \geq 3$, then
$$
x^{5}+p x+q \geq 3^{5} + 3p + q > 0
$$
If $x \leq -3$, then
$$
x^{5}+p x+q \leq -3^{5} - 3p + q < 0
$$
Thus, the only possible integer values for $x$ are $-2, -1, 0, 1, 2$. For each of these values, we can find pairs $(p, q)$ such that the equation holds. If $x > 0$, then $q = -x^5 - px$, and since $p$ and $q$ are positive integers, $p$ must be less than or equal to 99. If $x < 0$, then $q = -x^5 - px$, and since $p$ and $q$ are positive integers, $p$ must be less than or equal to 34. If all the pairs obtained are distinct, the number of such pairs is $99 + 34 = 133$.
|
133
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.2. (Belgium, 79). Find the sum of all $7!$ numbers that can be obtained by all possible permutations of the digits in the number 1234567.
|
4.2. For any values of $i, i \in\{1 ; \ldots ; 7\}$, the number of numbers in which the $i$-th place is occupied by the digit $j$ is 61. Therefore, the sum of all numbers is
$$
\begin{aligned}
& (61 \cdot 1+\ldots+61 \cdot 7)+(61 \cdot 1+\ldots+61 \cdot 7) 10+ \\
& \quad+(61 \cdot 1+\ldots+61 \cdot 7) 10^{2}+\ldots+(61 \cdot 1+\ldots+61 \cdot 7) 10^{6}= \\
& =61(1+2+\ldots+7)\left(1+10+\ldots+10^{6}\right)=720 \cdot 28 \cdot 1111111=22399997760 .
\end{aligned}
$$
|
22399997760
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.17*. (NRP, 83). Find all values of $n \in \mathbf{N}$ for each of which there exists a permutation
$$
\left(a_{1} ; a_{2} ; \ldots ; a_{n}\right)
$$
of the numbers $0,1, \ldots, n-1$, such that all numbers
$$
a_{1}, a_{1} a_{2}, a_{1} a_{2} a_{3}, \ldots, a_{1} a_{2} \ldots a_{n}
$$
give different remainders when divided by $n$.
|
4.17. For $n=1$ the permutation $\left(a_{1}\right)=(0)$ satisfies the condition of the problem. For $n=4$, the permutation
$$
\left(a_{1} ; a_{2} ; a_{8} ; a_{4}\right)=(1 ; 3 ; 2 ; 0)
$$
possesses the required property. Let $n$ be a prime number. According to the Chinese "remainder theorem" (Theorem 23), for each value of $k=2, \ldots, n$ there exists a number $b_{k}$ satisfying the conditions
$$
b_{k} \equiv 0(\bmod k-1), b_{k} \equiv k(\bmod n)
$$
Let $a_{k}$ be the remainder of the division of $c_{k}=b_{k} /(k-1)$ by $n$, then
$$
b_{k}=c_{k}(k-1)=a_{k}(k-1)(\bmod n)
$$
Let $a_{i}=1$ and prove that all numbers $a_{1}, a_{2}, \ldots, a_{n}$ are distinct. Indeed, we have $a_{n}=0$ and $a_{k} \neq a_{n}$ for $k=1, \ldots, n-1$ (since $a_{n}(n-1) \equiv 0(\bmod n), a_{1}=1, a_{k}(k-1) \equiv k(\bmod n)$ for $\left.k=2, \ldots, n-1\right)$. Further, if the equality $a_{l}=a_{k}=a$ holds, where $14$ does not satisfy the condition of the problem. If $n=p^{2}$, then let $q=2 p<n$, otherwise the number $n$ can be represented as a product $p q$, where $1<p<q<n$. In both cases
$$
p q=0(\bmod n) .
$$
Suppose there exists a permutation ( $a_{1} ; a_{2} ; \ldots ; a_{n}$ ) satisfying the condition of the problem. Then
$$
a_{k} \neq 0 \text { for } k=1, \ldots, n-1 \text {, }
$$
since otherwise
$$
a_{1} \ldots a_{k} \equiv 0(\bmod n)
$$
and
$$
a_{i} \ldots a_{k} a_{k+1}=0(\bmod n)
$$
Take such values of $k, l<n$ for which $a_{k}=p, a_{l}=q$. Denote
$$
m=\max (k, l)
$$
then
$$
a_{1} a_{2} \ldots a_{m} \vdots a_{k} a_{l}
$$
therefore
$$
a_{1} a_{2} \ldots a_{m}=0(\bmod n)
$$
and
$$
a_{1} a_{2} \ldots a_{m} a_{m+1} \equiv 0(\bmod n)
$$
which contradicts the assumption. Thus, the numbers 1, 4, and all prime numbers satisfy the condition of the problem.
|
14
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.6. (Yugoslavia, 83). Find all values of $n \in \mathbf{N}$ that have the following property: if the numbers $n^{3}$ and $n^{4}$ are written next to each other (in the decimal system), then in the resulting record each of the 10 digits $0,1, \ldots, 9$ will appear exactly once.
|
5.6. Let $f(m)$ denote the number of digits in the decimal representation of the number $m \in N$, then for the desired number $n$ we have
$$
f\left(n^{3}\right)+f\left(n^{4}\right)=10
$$
Moreover, $f\left(n^{9}\right) \geqslant 4$, because otherwise the inequalities $n^{3}4$, then $n>10, n^{4}>10 n^{3}$, from which
$$
f\left(n^{3}\right) \geqslant 5, \quad f\left(n^{4}\right) \geqslant f\left(n^{3}\right)+1
$$
and
$$
f\left(n^{3}\right)+f\left(n^{4}\right) \geqslant 5+6>10
$$
Thus, $f\left(n^{9}\right)=4$ and $f\left(n^{4}\right)=6$. Further, from the inequality $n^{3}10000$. Similarly, from the inequality $n^{4} \geqslant 100000$ we have the estimate $n>17$, since $17^{4}<100000$. Therefore, $18 \leqslant n \leqslant 21$. Since any natural number is congruent modulo 9 to the sum of its digits, then
$$
n^{3}+n^{4} \equiv(0+1+\ldots+9)(\bmod 9)
$$
from which
$$
n^{3}(n+1)=0(\bmod 9) .
$$
The last condition is not satisfied by the values $n=19$ and $n=20$, and the value $n=21$ does not have the required property in the problem, since both numbers $21^{3}$ and $21^{4}$ end in the digit 1. Finally, checking shows that the only possible value $n=18$ satisfies the condition of the problem ( $18^{3}=5832,18^{4}=104976$ ).
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. (GDR, 74). What is greater: $\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}-\sqrt{2}$ or 0?
|
7.1. Using Theorem 4, we get
$$
\begin{aligned}
& \sqrt{4+\sqrt{7}}=\sqrt{4-\sqrt{7}}-\sqrt{\overline{2}}= \\
& =\left(\sqrt{\frac{4+\sqrt{16-7}}{2}}+\sqrt{\frac{4-\sqrt{16-7}}{2}}\right)- \\
& -\left(\sqrt{\frac{4+\sqrt{16-7}}{2}}-\sqrt{\frac{4-\sqrt{16-7}}{2}}\right)-\sqrt{2}= \\
& =\sqrt{\frac{7}{2}}+\sqrt{\frac{1}{2}}-\sqrt{\frac{7}{2}}+\sqrt{\frac{1}{2}}-V^{\overline{2}}=0
\end{aligned}
$$
i.e., the given numbers are equal to each other.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. (England, 75). Solve the equation
$$
[\sqrt[3]{1}]+[\sqrt[3]{2}]+\ldots+\left[\sqrt[3]{x^{3}-1}\right]=400
$$
in natural numbers.
|
8.2. Note that the relation $[\sqrt[3]{m}]=k$, where $m, k \in \mathrm{N}$, is equivalent to the inequality $k^{3} \leqslant m \leqslant(k+1)^{3}-1$. The number of natural numbers $m$ satisfying this condition (for a fixed $k$) is $(k+1)^{3}-k^{3}=3 k^{2}+3 k+1$. Therefore, the left side of the equation is $\sum_{k=1}^{x-1} S_{k}$, where
$$
S_{k}=k\left(3 k^{2}+3 k+1\right)
$$
Since $S_{k}>0$ for $k \in \mathrm{N}$, $S_{1}=1 \cdot 7 = 7$, $S_{2}=2 \cdot 19 = 38$, $S_{3}=3 \cdot 37 = 111$, $S_{4}=4 \cdot 61 = 244$, and $S_{1}+S_{2}+S_{3}+S_{4}=400$, the original equation has a unique solution in natural numbers: $x=5$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. (Sweden, 82). Find all values of $n \in \mathbf{N}$ for each of which there exists a number $m \in \mathbf{N}$, a triangle $A B C$ with sides $A B=33, A C=21, B C=n$ and points $D$, $E$ on sides $A B, A C$ respectively, satisfying the conditions $A D=D E=E C=m$.
|
9.3. Let the numbers $m, n \in \mathbf{N}$ satisfy the condition of the problem. Then $m = CE < AC = 21$ and from triangle $ADE$ (Fig. 3) we have $21 - m = AE < AD + DE = 2m$, hence
$$
7 < m < 21
$$
Furthermore, since $AD = DE$, for the angle $\alpha = \angle BAC$ we find
$$
\cos \alpha = AE / (2 \cdot AD) = (21 - m) / 2m
$$
Fig. 3
Finally, by the cosine rule for triangle $ABC$ we obtain
$$
\begin{aligned}
& n^{2} = BC^{2} = AB^{2} + AC^{2} - \\
& - 2 AB \cdot AC \cdot \cos \alpha = \\
& = 33^{2} + 21^{2} - 2 \cdot 33 \cdot 21 \cdot \frac{21 - m}{2m} = \\
& = 2223 - \frac{27 \cdot 49 \cdot 11}{m}
\end{aligned}
$$
from which it follows that the number $m$ is a divisor of the number $27 \cdot 49 \cdot 11$. Of the two possible values $m = 9$ and $m = 11$, the first does not work (since $n^{2} \neq 606$), while the second gives the equation $n^{2} = 900$, i.e., $n = 30$. Verification shows that all conditions of the problem are satisfied for the found value of $n$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.20. (SFRY, 83). Inside triangle $A B C$, a point $M$ is taken, for which $\angle M B A=30^{\circ}, \angle M A B=10^{\circ}$. Find $\angle A M C$, if $\angle A C B=80^{\circ}$ and $A C=B C$.
|
9.20. Let the height $CH$ of triangle $ABC$ intersect the line
Fig. 16
$BM$ at point $E$ (Fig. 16). Then $AE = BE$ and
\[
\begin{aligned}
& \angle EAM = \angle EAB - \angle MAB = 30^\circ - 10^\circ = 20^\circ, \\
& \angle ACE = (1/2) \angle ACB = 40^\circ, \\
& \angle EAC = \angle CAH - \angle EAB = (90^\circ - 40^\circ) - 30^\circ = 20^\circ, \\
& \angle AME = \angle MAB + \angle MBA = 10^\circ + 30^\circ = 40^\circ
\end{aligned}
\]
which means that triangles $AME$ and $ACE$ are equal by the common side and two angles. Therefore,
\[
AM = AC, \angle AMC = \angle ACM = (1/2)(180^\circ - \angle CAM) = 70^\circ
\]
|
70
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.21. (England, 70). On the sides $B C$ and $A C$ of triangle $A B C$, points $D$ and $E$ are chosen respectively such that $\angle B A D=50^{\circ}, \angle A B E=30^{\circ}$. Find $\angle B E D$, if
$\angle A B C=\angle A C B=50^{\circ}$
|
9.21. Let $O$ be the point of intersection of lines $A D$ and $B E$ (Fig. 17), then $\angle A O B=180^{\circ}-30^{\circ}-50^{\circ}=100^{\circ}$, $\angle B D A=180^{\circ}-50^{\circ}-50^{\circ}=80^{\circ}$, $\angle C B E=50^{\circ}-30^{\circ}=20^{\circ}$, $\angle A E B=\angle C B E+\angle E C B=70^{\circ}$, $\angle C A D=180^{\circ}-\angle A C B$ -
$-\angle A B C-\angle B A D=30^{\circ}$
By the Law of Sines, we have
$$
\begin{gathered}
\frac{O D}{O B}=\frac{\sin 20^{\circ}}{\sin 80^{\circ}}, \quad \frac{O B}{O A}=\frac{\sin 50^{\circ}}{\sin 30^{\circ}}, \\
\frac{O A}{O E}=\frac{\sin 70^{\circ}}{\sin 30^{\circ}}
\end{gathered}
$$
from which we obtain
Fig. 17
$$
\begin{aligned}
& \frac{O D}{O E}=\frac{O D}{O B} \cdot \frac{O B}{O A} \cdot \frac{O A}{O E}=\frac{\sin 20^{\circ} \sin 50^{\circ} \sin 70^{\circ}}{\sin 80^{\circ} \sin ^{2} 30^{\circ}}= \\
& \quad=\frac{4 \sin 20^{\circ} \cos 40^{\circ} \cos 20^{\circ}}{\sin 80^{\circ}}=\frac{2 \sin 40^{\circ} \cos 40^{\circ}}{\sin 80^{\circ}}=\frac{\sin 80^{\circ}}{\sin 80^{\circ}}=1
\end{aligned}
$$
i.e., $O D=O E$ and
$$
\angle B E D=\angle O D E=\frac{1}{2}\left(180^{\circ}-\angle E O D\right)=\frac{1}{2}\left(180^{\circ}-100^{\circ}\right)=40^{\circ}
$$
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.22. (GDR, 64). On the side $BC$ of triangle $ABC$, a point $P$ is taken such that $PC = 2BP$. Find $\angle ACB$ if $\angle ABC = 45^\circ$ and $\angle APC = 60^\circ$.
|
9.22. If point $C_{1}$ is symmetric to point $C$ with respect to line $A P$ (Fig. 18), then $C_{1} P = C P = 2 B P$ and $\angle C_{1} P B = 180^{\circ} - \angle A P C - \angle A P C_{1} = 180^{\circ} - 60^{\circ} - 60^{\circ} = 60^{\circ}$. Therefore, $\angle C_{1} B P = 90^{\circ}$ (since triangle $C_{1} P B$ is similar to a right triangle with hypotenuse 2 and leg 1), which means that $B A$ is the bisector of angle $C_{1} B P$. Thus, point $A$, which is equidistant from the lines $C_{1} P$, $P C$, and $C_{1} B$, lies on the bisector of angle $P C_{1} D$ (where point $D$ lies on the extension of segment $B C_{1}$ beyond point $C_{1}$). Therefore,
$$
\angle A C B = \angle A C_{1} P = \frac{1}{2} \left(180^{\circ} - \angle B C_{1} P \right) = \frac{1}{2} \left(180^{\circ} - 30^{\circ} \right) = 75^{\circ}
$$
|
75
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.16. (England, 66). Find the number of sides of a regular polygon if for four of its consecutive vertices \( A, B, C, D \) the equality
\[
\frac{1}{A B}=\frac{1}{A C}+\frac{1}{A D}
\]
is satisfied.
|
11.16. Let a circle with center 0 and radius $R$ be circumscribed around a polygon (Fig. 58). Denote $\alpha=\angle A O B$, then $0<\alpha<$ $<120^{\circ}$ and
$A B=2 R \sin (\alpha / 2), A C=2 R \sin \alpha$,
$$
A D=2 R \sin (3 \alpha / 2)
$$
from which we have
$$
\frac{1}{\sin (\alpha / 2)}=\frac{1}{\sin \alpha}+\frac{1}{\sin (3 \alpha / 2)}
$$
Therefore, we obtain
$$
\begin{array}{r}
0=\sin \alpha \sin \frac{3 \alpha}{2}-\left(\sin \alpha+\sin \frac{3 \alpha}{2}\right) \times \\
\times \sin \frac{\alpha}{2}=\frac{1}{2}\left(\cos \frac{\alpha}{2}-\cos \frac{5 \alpha}{2}\right)-\frac{1}{2}\left(\cos \frac{\alpha}{2}-\cos \frac{3 \alpha}{2}\right)- \\
-\frac{1}{2}(\cos \alpha-\cos 2 \alpha)=\frac{1}{2}\left(\left(\cos \frac{3 \alpha}{2}+\cos 2 \alpha\right)-\left(\cos \alpha+\cos \frac{5 \alpha}{2}\right)\right)= \\
=\cos \frac{7 \alpha}{4}\left(\cos \frac{\alpha}{4}-\cos \frac{3 \alpha}{4}\right)=2 \cos \frac{7 \alpha}{4} \sin \frac{\alpha}{4} \sin \frac{\alpha}{2}
\end{array}
$$
from which
$$
7 \alpha / 4=90^{\circ} \text { and } \alpha=360^{\circ} / 7
$$
i.e., the original polygon has seven sides.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.10. (SFRY, 76). Find all values of $n \in \mathbf{N}$, greater than 2, for which it is possible to select $n$ points on a plane such that any two of them are vertices of an equilateral triangle, the third vertex of which is also one of the selected points.
|
12.10. We will prove that the condition of the problem is satisfied only by the value $n=3$ (in which case the points can be placed at the vertices of an equilateral triangle). Indeed, suppose that it is possible to arrange $n \geqslant 4$ points in the manner specified in the problem. We select two points $A$ and $B$, the distance between which is maximal, and a third point $C$, such that the triangle $A B C$ is equilateral. Then all the other points lie within the figure $M$, which is the intersection of three circles of radius $A B$ centered at points $A, B$, and $C$ (Fig. 68). If point $O$ is the center of the triangle $A B C$, then the segments $A O, B O$, and $C O$ divide the set $M$ into three equal parts, none of which can contain any of the $n$ points, except those already mentioned. Indeed, suppose, for example, that part $M_{B C}$, consisting of the triangle $B O C$ and the segment of the circle centered at $A$ with the arc $B C$, contains another point $D$. Then there exists a point $D^{\prime}$ such that the triangle $A D D^{\prime}$ is equilateral. Consequently, when rotating (in a certain direction) around point $A$ by an angle of $60^{\circ}$, point $D$ transitions to point $D^{\prime}$, which thus lies simultaneously in the image $M_{B C}^{\prime}$ of part $M_{B C}$ under this rotation and in the set $M$. But since $\angle B A C=60^{\circ}$, either $C^{\prime}=B$ or $B^{\prime}=C$. For definiteness, assume that $B^{\prime}=C$. Then the sets $M_{B C}^{\prime}$ and $M$ lie in different half-planes relative to the line $B^{\prime} O^{\prime}$, because
$$
\angle B B^{\prime} O^{\prime}=\angle B C A+\angle A B^{\prime} O^{\prime}=60^{\circ}+30^{\circ}=90^{\circ},
$$
i.e., the line $B^{\prime} O^{\prime}$ is tangent to the arc $A C$. Therefore, $M_{B C}^{\prime}$ and $M$ have only one common point $B^{\prime}$, from which it follows that $D^{\prime}=B^{\prime}$ and $D=B$, which contradicts the choice of point $D$. The statement is proved.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.11. (CSSR, 80). The set $M$ is obtained from the plane by removing three distinct points $A, B$, and $C$. Find the smallest number of convex sets whose union is the set $M$.
|
12.11. Let points $A, B$, and $C$ initially lie on the same line. Then these points divide the line into 4 intervals, and no points from different intervals can lie in the same convex set. Therefore, the number of required sets cannot be less than 4. The number 4 is achieved if the set $M$ is divided into parts as shown in Fig. 69.

Fig. 69
Now, let points $A, B$, and $C$ not lie on the same line. Then points $B$ and $C$ divide the line $BC$ into 3 intervals, and points from different intervals must lie in different convex sets. Therefore, the number of required sets cannot be less than 3, and 3 sets can be chosen as shown in Fig. 70.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.12. (Jury, SRP, 79). Prove that for any value of $n \in \mathbf{N}$, greater than some number $n_{0}$, the entire plane can be divided into $n$ parts by drawing several lines, among which there must be intersecting ones. Find the smallest such value of $n_{0}$.
|
12.12. Among the lines drawn according to the condition, there are necessarily intersecting lines that already divide the plane into 4 parts. If another line is drawn, then, as a simple case analysis shows, the number of parts will increase by at least 2. Therefore, it is impossible to get exactly 5 parts, from which it follows that \( n_{0} \geqslant 5 \). On the other hand, any number \( n > 5 \) of parts can be obtained in the required way: if \( n = 2k \) ( \( k \in \mathbf{N} \) ), then the division of the plane can be constructed as shown in Fig. 71; if \( n = 4k + 3 \), see Fig. 72; and if \( n = 4k + 5 \), see Fig. 73. Thus, the smallest value of \( n_{0} \) is 5.
Fig. 70

Fig. 71
Fig. 72
Fig. 73
|
5
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
12.17*. (CSSR, 73). In a square with side 50, a broken line is located. Prove that if the distance from any point of the square to at least one point of the broken line is no more than 1, then the length of the broken line is greater than 1248.
|
12.17. Let $U(M)$ denote the union of all circles of radius 1, the centers of which belong to a set $M$ on the plane. We will prove by induction on $n \in \mathbb{N}$ that for any broken line $A_{0} A_{1} \ldots A_{n}$, the inequality
$$
S_{U\left(A_{0} \ldots A_{n}\right)} \leqslant 2 \sum_{i=1}^{n} A_{i-1} A_{i} + \pi
$$
holds. For $n=1$, the set $U\left(A_{0} A_{1}\right)$ is divided into two semicircles of radius 1 and a rectangle with sides $A_{0} A_{1}$ and 2, so
$$
S_{U\left(A_{0} A_{1}\right)} = 2 \cdot A_{0} A_{1} + \pi
$$
i.e., the statement is true. Suppose it is already proven for some value $n-1 \in \mathbb{N}$. Let
$$
X = U\left(A_{0} \ldots A_{n-1}\right), \quad Y = U\left(A_{n-1} A_{n}\right), \quad Z = X \cap Y
$$
then $S_{Z} \geqslant \pi$ (since $Z \supset U\left(A_{n-1}\right)$) and, using the induction hypothesis, we have
$$
\begin{aligned}
& S_{U\left(A_{0} \cdots A_{n-1} A_{n}\right)} = S_{X \cup Y} = S_{X \backslash Z} + S_{Y \backslash Z} + S_{Z} = \\
& \quad = \left(S_{X \backslash Z} + S_{Z}\right) + \left(S_{Y \backslash Z} + S_{Z}\right) - S_{Z} = S_{X} + S_{Y} - S_{Z} \leqslant \\
& \quad \leqslant \left(2 \sum_{i=1}^{n-1} A_{i-1} A_{i} + \pi\right) + \left(2 A_{n-1} A_{n} + \pi\right) - \pi = 2 \sum_{i=1}^{n} A_{i-1} A_{i} + \pi
\end{aligned}
$$
which completes the proof of the inequality. For the broken line given in the problem, the set $U\left(A_{0} \ldots A_{n}\right)$ contains the entire square with side 50, so its length is at least
$$
\left(S_{U\left(A_{0} \cdots A_{n}\right)} - \pi\right) / 2 > \left(50^{2} - 4\right) / 2 = 1248
$$
which is what we needed to prove.
|
1248
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
15.7. (NBR, 68). Inside the tetrahedron $A B C D$ is a point $O$ such that the lines $A O, B O, C O, D O$ intersect the faces $B C D, A C D, A B D, A B C$ of the tetrahedron at points $A_{1}, B_{1}$, $C_{1}, D_{1}$ respectively, and the ratios
$$
\frac{A O}{A_{1} O}, \frac{B O}{B_{1} O}, \frac{C O}{C_{1} O}, \frac{D O}{D_{1} O}
$$
are all equal to the same number. Find all possible values that this number can take.
|
15.7. Let \( V \) be the volume of the tetrahedron \( ABCD \), and \( k \) be the desired number. Then we have
\[
\frac{V}{V_{OBCD}} = \frac{AA_1}{OA_1} = \frac{AO}{A_1O} + \frac{OA_1}{OA_1} = k + 1
\]
\[
\frac{V}{V_{OACD}} = \frac{V}{V_{OABD}} = \frac{V}{V_{OABC}} = k + 1,
\]
from which
\[
k + 1 = \frac{4V}{V_{OBCD} + V_{OACD} + V_{OABD} + V_{OABC}} = \frac{4V}{V} = 4, \text{ i.e., } k = 3
\]
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16.15. (England, 68). Find the maximum number of points that can be placed on a sphere of radius 1 so that the distance between any two of them is: a) not less than $\sqrt{2} ;$ b) greater than $\sqrt{2}$.
|
16.15. a) Let's prove that if points $A_{1}, A_{2}, \ldots, A_{n}$ are located on a sphere with center $O$ and radius 1 such that the distance between any points $A_{i}, A_{j} (i \neq j)$ is at least $\sqrt{2}$, then $n \leqslant 6$. Indeed, let $n>6$. By the cosine theorem, we have
$$
A_{i} A_{j}^{2}=2-2 \cos \angle A_{i} O A_{j} \geq 2
$$
from which $\angle A_{i} O A_{j} \geqslant 90^{\circ}$ and $\overrightarrow{O A_{i}} \cdot \overrightarrow{O A_{j}} \leq 0$. Let's choose a rectangular coordinate system in space with the origin at point $O$ as follows. First, note that among the vectors $\overrightarrow{O A}_{i}$, there must be three non-coplanar vectors (otherwise, all $n>4$ vectors would lie in the same plane, and the angle between some two of them would be acute). Without loss of generality, we can assume that the vectors $\overrightarrow{O A}_{1}, \overrightarrow{O A}_{2}, \overrightarrow{O A}_{3}$ are non-coplanar. The axis $O X$ is directed along the line $O A_{i}$ so that the abscissa of point $A_{1}$ is 1. Next, the axis $O Y$ is directed so that point $A_{2}$ lies in the plane $X O Y$ and has a positive ordinate. Finally, the axis $O Z$ is directed so that the applicate of point $A_{3}$ is positive. Let $x_{i}, y_{i}, z_{i}$ be the coordinates of point $A_{i}$. Then
$$
\overrightarrow{O A}_{1}=(1 ; 0 ; 0), \overrightarrow{O A}_{2}=\left(x_{2} ; y_{2} ; 0\right), \overrightarrow{O A}_{3}=\left(x_{8} ; y_{8} ; z_{3}\right),
$$
where $y_{2}>0, z_{3}>0$, so for all values of $i>1$ we have
$$
\overrightarrow{O A}_{i} \cdot \overrightarrow{O A}_{1}=x_{i} \leqslant 0
$$
further, for all values of $i>2$ we have
$$
\overrightarrow{O A}_{i} \cdot \overrightarrow{O A_{2}}=x_{i} x_{2}+y_{i} y_{2} \leqslant 0
$$
from which $y_{i} \leqslant 0$ (since $x_{2} \leqslant 0, x_{i} \leqslant 0, y_{2}>0$); finally, for all values of $i>3$ we have
$$
\overrightarrow{O A}_{i} \cdot \overrightarrow{O A_{3}}=x_{i} x_{3}+y_{i} y_{3}+z_{i} z_{3} \leqslant 0
$$
from which $z_{i} \leqslant 0$ (since $x_{3} \leqslant 0, x_{i} \leqslant 0, y_{3} \leqslant 0, y_{i} \leqslant 0, z_{3}>0$). Among the four vectors $\overrightarrow{O A}_{4}, \overrightarrow{O A}_{5}, \overrightarrow{O A}_{8}, \overrightarrow{O A}_{7}$, at least two have the same negative coordinate, and therefore their scalar product is positive. The obtained contradiction proves that $n \leqslant 6$. Since 6 points with coordinates
$$
( \pm 1 ; 0 ; 0),(0 ; \pm 1 ; 0),(0 ; 0 ; \pm 1)
$$
satisfy the condition of part a), the maximum number of points is 6. 276
b) Let's prove that if points $A_{1}, A_{2}, \ldots, A_{n}$ are located on the same sphere such that the distance between any points $A_{i}, A_{j} (i \neq j)$ is greater than $\sqrt{2}$, then $n \leq 4$. Then $\overrightarrow{O A}_{i} \cdot \overrightarrow{O A}_{j} < 0$ for all $i \neq j$. For $n \geq 3$ we will have $x_{i} < 1 / 2$ and $n < 6$
(the last inequality also follows from the fact that the dihedral angle $\angle A_{1} H A_{2} = 360^{\circ} / n$ at the lateral edge $O A_{0}$ is greater than the plane angle $\angle A_{1} A_{0} A_{2} = 60^{\circ}$ of the pyramid's base), and for the other values of $n=2,3,4,5$ we have
$$
r_{n}=\sqrt{1-\frac{1}{4 \sin ^{2}\left(180^{\circ} / n\right)}}
$$
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16.21. (England, 70). Find the smallest number of planes that divide a cube into at least 300 parts.
16.22\%. (SRP, 78). On planes $\alpha$ and $\alpha^{\prime}$, intersecting along a line $l$, three points each are chosen: $A, B, C$ and $A^{\prime}, B^{\prime}, C^{\prime}$ respectively. The plane $\alpha^{\prime}$ rotates around the line $l$. Prove that if the lines $A A^{\prime}, B B^{\prime}, C C^{\prime}$ intersect at a single point for some position of the plane $\alpha^{\prime}$, then for any other position of the plane $\alpha^{\prime}$, different from the plane $\alpha$, they also intersect at a single point. Find the geometric locus of these points of intersection.
|
16.21. We will prove by induction on $n$ that $n$ lines divide the plane into no more than
$$
p(n)=\frac{n(n+1)}{2}+1
$$
parts, and exactly $p(n)$ parts are obtained if no two lines are parallel and no three lines pass through the same point. Indeed, $p(0)=1$, and for any value of $n \in \mathbb{N}$, we have the inequality
$$
p(n) \leqslant p(n-1)+n=\frac{(n-1) n}{2}+1+n=\frac{n(n+1)}{2}+1,
$$
with equality being achieved (the $n$-th line, intersecting with each of the other lines, itself is divided into no more than $n$ parts, each of which defines a new part of the plane). Similarly, we will prove that $n$ planes divide space into no more than
$$
q(n)=\frac{n^{3}+5 n+6}{6}
$$
parts, and exactly $q(n)$ parts are obtained if no two planes are parallel, no three planes pass through the same line, and no four planes pass through the same point. Indeed, $q(0)=1$ and for any value of $n \in \mathbf{N}$, we have the inequality
$$
\begin{aligned}
q(n) \leqslant q(n-1) & +p(n-1)= \\
& =\frac{(n-1)^{3}+5(n-1)+6}{6}+\frac{(n-1) n}{2}+1=\frac{n^{3}+5 n+6}{6}
\end{aligned}
$$
with equality being achieved (the $n$-th plane, intersecting with the other planes, itself is divided into no more than $p(n-1)$ parts, each of which defines a new part of space). The required number of planes is 13, since
$$
q(12)=299<300<378=q(13)
$$
Indeed, 12 planes are insufficient, while 13 planes can divide the entire space into $q(13)$ parts, then we can choose one point inside each of them and take a cube containing all $q(13)$ points, after which it remains to subject the entire construction to a similarity transformation with the appropriate coefficient.
|
13
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
17.3. (New York, 74). Let
$$
a_{n}=\frac{1 \cdot 3 \cdot 5 \ldots(2 n-1)}{2 \cdot 4 \cdot 6 \ldots 2 n}, n \in \mathrm{N}
$$
Find $\lim a_{n}$.
$$
n \rightarrow \infty
$$
|
17.3. Since
$$
\begin{aligned}
a_{n}^{2}=\frac{1^{2} \cdot 3^{2} \cdot \ldots \cdot(2 n-1)^{2}}{2^{2} \cdot 4^{2} \cdot \ldots \cdot(2 n)^{2}} & = \\
& =\frac{1 \cdot 3}{2^{2}} \cdot \frac{3 \cdot 5}{4^{2}} \cdots \frac{(2 n-1)(2 n+1)}{(2 n)^{2}} \cdot \frac{1}{2 n+1}<\frac{1}{2 n+1}
\end{aligned}
$$
for any $n \in \mathbf{N}$, then
$$
0<a_{n}<1 / \sqrt{2 n+1} \quad \text { and } \quad \lim _{n \rightarrow \infty} a_{n}=0
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21.5. (Austria, 83). Find all values of $a$ for which the roots $x_{1}, x_{2}, x_{3}$ of the polynomial $x^{3}-6 x^{2}+a x+a$ satisfy the equation
$$
\left(x_{1}-3\right)^{3}+\left(x_{2}-3\right)^{3}+\left(x_{3}-3\right)^{3}=0
$$
|
21.5. Let's make the substitution $y=x-3$, then the numbers $y_{1}=x_{1}-3, y_{2}=$ $=x_{2}-3$ and $y_{3}=x_{3}-3$ are the roots of the polynomial
$$
(y+3)^{3}-6(y+3)^{2}+a(y+3)+a=y^{3}+3 y^{2}+(a-9) y+4 a-27
$$
By Vieta's theorem, we have the equalities
$$
\begin{aligned}
& y_{1}+y_{2}+y_{3}=-3 \\
& y_{1} y_{2}+y_{1} y_{3}+y_{2} y_{3}=a-9 \\
& y_{1} y_{2} y_{3}=27-4 a
\end{aligned}
$$
and in addition, the relation $y_{1}^{3}+y_{2}^{3}+y_{3}^{3}=0$ must hold. By direct verification, we confirm the validity of the identity $y_{1}^{3}+y_{2}^{3}+y_{3}^{3}=$
$$
\equiv\left(y_{1}+y_{2}+y_{3}\right)^{3}-3\left(y_{1} y_{2}+y_{1} y_{3}+y_{2} y_{3}\right)\left(y_{1}+y_{2}+y_{3}\right)+3 y_{1} y_{2} y_{3}
$$
from which we obtain the necessary and sufficient condition for $a$ :
$$
0=(-3)^{3}-3(a-9) \cdot(-3)+3(27-4 a)=-27-3 a
$$
i.e. $a=-9$.
|
-9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
23.13*. (CSSR, 74). Let $M$ be the set of all polynomials of the form
$$
P(x)=a x^{3}+b x^{2}+c x+d \quad(a, b, c, d \in \mathbf{R})
$$
satisfying the inequality $|P(x)| \leqslant 1$ for $x \in[-1 ; 1]$. Prove that some number $k$ provides the estimate $|a| \leqslant k$ for all polynomials $P(x) \in M$. Find the smallest value of $k$.
|
23.13. The polynomial $P_{0}(x)=4 x^{3}-3 x$ belongs to the set $M$, since $P_{0}(-1)=-1, P_{0}(1)=1$, and at its extremum points we have $P_{0}(-1 / 2)=1, P_{0}(1 / 2)=-1$. Let's prove that for any polynomial $P(x) \in M$ the estimate $|a| \leqslant 4$ holds. Suppose, on the contrary, that there exists a polynomial $P(x)=a x^{3}+b x^{2}+c x+d$, satisfying the inequalities $|a|>4$ and $|P(x)| \leq 1$ for $|x| \leq 1$. Then consider the non-zero polynomial
$$
Q(x)=P_{0}(x)-\frac{4}{a} P(x)
$$
the degree of which does not exceed two. Since $\left|\frac{4}{a} P(x)\right|0, Q(1 / 2)0$, and thus the polynomial $Q(x)$ has at least three roots. The obtained contradiction proves that the desired number $k$ is 4.
|
4
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
25.2. (USA, 82). In a society consisting of 1982 people, among any four people, at least one can be chosen who is acquainted with the other three. What is the minimum possible number of people who are acquainted with everyone?
|
25.2. If there are no strangers, then the number of people who know everyone is 1982. Let $A$ and $B$ not know each other. Then all other people know each other (if $C$ does not know $D$, then in the group $A, B, C, D$ no one knows the other three). If $A$ and $B$ know all the others, then 1980 people know everyone. If $A$ does not know $C$ as well, where $C \neq B$, then $A$, $B$, and $C$ are not familiar with all the other 1979 people (since in any group $A, B, C, D$ only $D$ can be familiar with the other three), who are also familiar with each other. Thus, the minimum number of people who know everyone is 1979.
|
1979
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25.6. (USSR, 81; USA, 81). In a certain country, any two cities are directly connected by one of the following means of transportation: bus, train, or airplane. It is known that there is no city provided with all three types of transportation, and at the same time, there do not exist three cities such that any two of them are connected by the same means of transportation. Find the largest possible number of cities in this country.
|
25.6. Suppose there are five cities connected in the manner indicated in the problem. First, let's prove that no city has three lines of the same type of transport leading out of it. Let city \( A \) be connected to cities \( B, C \), and \( D \), for example, by airplane. Then, according to the condition, no pair of cities \( B, C \), and \( D \) can be connected by airplane. Suppose \( B \) and \( C \) are connected, for example, by train. Cities \( C \) and \( D \) cannot be connected by bus, as otherwise city \( C \) would have all three types of transport. Therefore, \( C \) and \( D \) are connected by train. For the same reasons, cities \( B \) and \( D \) are also connected by train. We have obtained that \( B, C \), and \( D \) are pairwise connected by train. Contradiction. Thus, from each city, two transport lines of one type and two transport lines of another type lead out. Then each city is served by exactly two types of transport. Therefore, at least one type of transport serves no more than three cities (otherwise, there would be at least \( 4 \cdot 3 / 2 = 6 \) cities in total). If it serves exactly two cities, then from each of these cities, only one transport line of this type leads out, which is impossible. If it serves exactly three cities, then they must be pairwise connected by this type of transport, which is also impossible. Thus, we have proved that the condition of the problem is unfulfillable for five cities. It is even more unfulfillable for a larger number of cities. If, however, we consider four cities \( A, B \), \( C \), and \( D \), which are connected as follows: \( A \) with \( B \) by train, \( C \) with \( D \) by bus, and all other pairs by airplane, then all conditions of the problem will be met. Therefore, the maximum number of cities is 4.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
27.5. (Jury, Brazil, 82; Australia, 83). An urn contains $n$ white and $m$ black balls, and next to the urn is a box with a sufficiently large number of black balls. The following operation is performed: a pair of balls is randomly drawn from the urn; if they are of the same color, a black ball from the box is moved to the urn; if they are of different colors, the white ball is returned to the urn. The operation is repeated until only one ball remains in the urn. What is the probability that it will be white?
|
27.5. Since the parity of the number of white balls contained in the urn does not change after each operation, the last ball will be white if and only if the number $n$ is odd. Therefore, the desired probability is either 1 (if $n$ is odd), or 0 (if $n$ is even).
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
27.11. (Belgium, 77). Three shooters $A, B, C$ decided to duel simultaneously. They positioned themselves at the vertices of an equilateral triangle and agreed on the following: the first shot is taken by $A$, the second by $B$, the third by $C$, and so on in a circle; if one of the shooters is eliminated, the duel continues between the two remaining. It is known that shooter $A$ hits the target with a probability of 0.3, shooter $C$ with a probability of 0.5, and shooter $B$ never misses. Each shooter aims at one of the two others or at the air in such a way as to maximize their probability of winning the duel. Where should shooter $A$ direct his first shot: 1) at shooter $C$; 2) at shooter $B$; 3) at the air?
|
27.11. Let's consider three events that may occur after the first shot of shooter $A$.
1) $C$ is hit. Then with probability 1, shooter $A$ will be hit by the first shot of $B$.
2) $B$ is hit. Then: either with probability 0.5, shooter $C$ will hit $A$ with his first shot, or with probability $0.5 \cdot 0.3$, shooter $A$ will hit $C$ with his second shot, or with probability $0.5 \cdot 0.7 \cdot 0.5$, shooter $C$ will hit $A$ with his second shot, or with probability $0.5 \cdot 0.7 \cdot 0.5 \cdot 0.3$, shooter $A$ will hit $C$ with his third shot, and so on. Therefore, the probability for $A$ to win the duel in this case is
$$
\begin{aligned}
& 0.5 \cdot 0.3 + 0.5 \cdot 0.7 \cdot 0.5 \cdot 0.3 + 0.5 \cdot 0.7 \cdot 0.5 \cdot 0.7 \cdot 0.5 \cdot 0.3 + \ldots = \\
& \quad = 0.15 \left(1 + 0.35 + 0.35^2 + \ldots \right) = 0.15 \frac{1}{1 - 0.35} = \frac{15}{100} \cdot \frac{100}{65} = \frac{3}{13}
\end{aligned}
$$
3) No one is hit. After this, $B$ will shoot at $C$ (as the more accurate of his opponents) and hit him. Then $A$ with probability 0.3 will hit $B$, winning the duel.
Thus, the most advantageous situation for shooter $A$ is when no one is hit after his shot. Therefore, he should shoot into the air the first time.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. In the city of "Diversity," 10,000 residents live, and any two of them are either enemies or friends. Each day, no more than one resident can "start a new life," which means breaking up with all their friends and befriending all their enemies; meanwhile, any three residents can become friends with each other. Prove that all residents can become friends with each other. What is the smallest number of days that is definitely sufficient for this?
|
10. Let $A, B$ and $C$ be three residents of the city. It is clear that it is possible for all of them to be friends with each other; it is also possible that one of them (say, $A$) is not friends with either $B$ or $C$, while $B$ and $C$ are friends with each other: in this case, for $A, B$, and $C$ to all become friends, it is sufficient for $A$ to "start a new life." It is not difficult
1) For more on this, see, for example, [64], pp. 122-123.
to see that the two other cases: when all three residents $A, B$, and $C$ are enemies with each other, and when one resident, for example, the same $A$, is friends with both $B$ and $C$, while they are enemies with each other, are not possible: in these cases, among the three pairs $A, B; A, C$ and $B, C$ of residents of the city, there is an odd (3 or 1) number of pairs of enemies and an even (0 or 2) number of pairs of friends; with any changes in the relationships within this trio (in all cases where $A, B$ or $C$ "start a new life"), the parity of the numbers of enemies and friends does not change (an odd number of enemies can only be replaced by another odd number of enemies, and an even number of friends by another even number of friends), which is why all three residents $A, B$ and $C$ will never be able to become friends with each other (the number of enemies cannot become 0).
The described structure of the "friendship relationship" between any three individuals $A, B$, and $C$ proves that within the entire city, this relationship can be described quite simply: in the city, there are two groups of residents (two parties $\mathscr{M}$ and $\mathfrak{N}$), such that all residents belong to either one or the other party (but never to both at the same time), and every two members of the same party are friends with each other, while residents belonging to different parties are necessarily enemies. Indeed, let us add another resident $D$ to our three residents $A, B$, and $C$ of the city; in this case, if $A$ and $B$ are friends with each other and $D$ is friends with at least one of them, then he is also friends with the other - and, therefore, belongs to the party that includes both $A$ and $B$; if, however, $A$ and $B$ are enemies with each other, then $D$ is friends with only one of them (but he is necessarily friends with one!). This reasoning ensures the possibility of dividing the quartet of residents $A, B$, $C$, and $D$ into two parties $\mathscr{K}$ and $\mathcal{N}$ (although one of these parties may be "empty": this will be the case if all residents $A, B, C$, and $D$ are friends with each other). Proceeding in the same way and further, i.e., sequentially adding one person to the already considered residents of the city, we will prove the possibility of dividing all 10000 residents of the city into two parties.
Now, the proof of the statement of the problem presents no difficulty. If all residents of the city are friends with each other, then there is nothing to prove; if, however, neither of the parties $\mathscr{M}$ and $\mathscr{N}$ is "empty," then we will suggest that each day one of the members of party $\mathscr{M}$ "start a new life," i.e., simply switch to party $\mathscr{P}$. If party $\mathscr{M}$ has $k$ people, then all residents of the city will be able to become friends in $k$ days; from this, it is clear that 5000 days (≈ 14 years) will certainly be sufficient for all residents of the city to become friends (since at least one of the parties $\mathscr{M}$ and $\mathcal{N}$ contains no more than 5000 members).
|
5000
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
14. Some of the 20 metal cubes, identical in size and appearance, are aluminum, the rest are duralumin (heavier). How can you determine the number of duralumin cubes using no more than 11 weighings on a balance scale without weights?
Note. The problem assumes that all cubes can be aluminum, but they cannot all be duralumin (since if all the cubes were of the same weight, we would have no way to determine whether they are aluminum or duralumin without this condition).
|
14. Let's place one cube on each pan of the scales (first weighing). In this case, two different scenarios may occur.
$1^{\circ}$. During the first weighing, one pan of the scales tips. In this case, one of the two weighed cubes is definitely aluminum, and the other is duralumin. Next, we place these two cubes on one pan of the scales, and on the other pan, we sequentially place pairs of the remaining cubes (we randomly divide the 18 remaining cubes into 9 pairs). If any pair of cubes tips the scales, it means that both cubes in the second pair are duralumin; if the first pair tips the scales, it means that both cubes in the second pair are aluminum; if both pairs have the same weight, it means that the second pair also contains one aluminum and one duralumin cube. Thus, in case $1^{\circ}$, we can determine the number of duralumin cubes using 10 weighings (one weighing and 9 more).
$2^{\circ}$. During the first weighing, the scales remain in balance. In this case, the cubes of the first pair are either both aluminum or both duralumin. Next, we place these two cubes on one pan of the scales, and on the other pan, we sequentially place pairs of cubes from the remaining 18. Suppose the first $k$ of these pairs have the same weight as the initial pair, while the $(k+1)$-th pair has a different weight. (If $k=9$, all the cubes have the same weight, and thus there are no duralumin cubes at all; the case $k=0$ is no different from the general case). For definiteness, let's assume that the $(k+1)$-th pair is heavier than the initial pair (the reasoning would be similar if the $(k+1)$-th pair were lighter). In this case, the first two cubes, and therefore the cubes of the $k$ pairs that have the same weight as them, are definitely aluminum. Thus, we have performed $1+(k+1)=k+2$ weighings and identified $k+1$ pairs of aluminum cubes. Now, we place one cube from the last weighed pair on each pan of the scales (the $(k+3)$-th weighing). If both cubes have the same weight, they must both be duralumin; otherwise, one is aluminum and the other is duralumin. In both cases, after $k+3$ weighings, we can identify a pair of two cubes, one of which is aluminum and the other is duralumin. Using this pair, we can determine the number of duralumin cubes among the remaining $20-2(k+2)=16-2k$ cubes with $8-k$ weighings, similar to how we proceeded in case $1^{\circ}$. The total number of weighings in case $2^{\circ}$ will be $k+3+(8-k)=11$.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. a) One day, a guest came to the hotel owner, K, without money but with a silver chain consisting of seven links. The owner agreed to keep the guest for a week on the condition that the guest would give him one of the chain links as payment each day. What is the minimum number of links that need to be cut so that the chain owner can pay the hotel owner daily for seven days (possibly taking back previously given links and giving other ones in exchange)?
b) The chain consists of 2000 links. What is the minimum number of links that need to be cut so that any number of links from 1 to 2000 can be collected by taking some number of the resulting parts?
|
16. a) It is sufficient to saw off one third link; in this case, the chain will break into two parts, containing 2 and 4 links respectively, and one separate (sawed) link. On the first day, the guest will give this link; on the second day, he will take it back and give in exchange the part of the chain consisting of two links; on the third day, he will add the sawed link again; on the fourth day, he will take back everything he gave earlier and hand over the part of the chain consisting of four links; on the fifth day, he will add the sawed link again; on the sixth day, he will take back this link and give in exchange the part of the chain consisting of two links; on the seventh day, he will give the last link.
b) It is convenient to first solve the following problem: for what maximum $n$ is it sufficient to saw $k$ links of an $n$-link chain so that any number of links from 1 to $n$ can be obtained by taking some of the resulting parts? To solve this problem, let's consider the most advantageous arrangement of $k$ sawed links. Since after sawing $k$ links, we will have $k$ separate (sawed) links, we can already collect any number of links from 1 to $k$ from them. But we cannot get $k+1$ links if we do not have a part consisting of $k+1$ or fewer links. It is clear that it is most advantageous to have a part exactly of $k+1$ links; then from this part and $k$ separate links, we can collect any number from 1 to $2k+1$. To be able to get $2k+2=2(k+1)$ links, we need to have a part containing $2(k+1)$ or fewer links; the most advantageous for us will be if this part contains exactly $2(k+1)$ links. Now we can already form all numbers from 1 to $2k+1+2(k+1)=4k+3$; the next largest part we need is a part containing $4(k+1)$ links. Continuing to reason in the same way, we will see that the most advantageous will be if the $k+1$ parts, obtained after we saw $k$ links (the $k$ separate links obtained in this process are not counted here as parts), will have the following numbers of links:
$$
k+1, 2(k+1), 4(k+1), 8(k+1), \ldots, 2^k(k+1)
$$
In this case, any number of links from 1 to
$$
\begin{aligned}
n=k+\{k+1+2(k+1)+ & \left.4(k+1)+\ldots+2^k(k+1)\right\}= \\
& =k+\left(2^{k+1}-1\right)(k+1)=2^{k+1}(k+1)-1
\end{aligned}
$$
can be formed from the parts of the chain.
Thus, if $2^k k \leqslant n \leqslant 2^{k+1}(k+1)-1$, then $k$ cuts of the chain are sufficient, but $k-1$ cuts are not sufficient. In particular,
| for $-2 \leqslant n \leqslant 7$ | $k=1$, | for $160 \leqslant n \leqslant 383$ | $k=5$, |
| :--- | :--- | :--- | :--- |
| for $8 \leqslant n \leqslant 23$ | $k=2$, | for $384 \leqslant n \leqslant 895$ | $k=6$, |
| for $24 \leqslant n \leqslant 63$ | $k=3$, | for $896 \leqslant n \leqslant 2047$ | $k=7$. |
| for $64 \leqslant n \leqslant 159$ | $k=4$, | | |
Thus, we see that for $n=2000$, the minimum number of sawed links is 7. The conditions of the problem will be met if these links are chosen so that the 8 resulting parts of the chain (7 separate links are not counted here) have 8, 16, 32, 64, 128, 256, 512, and 977 links respectively.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
27. Five friends, one of whom had a monkey, once bought a bag of nuts, which they intended to divide among themselves the next morning. However, one of the friends woke up at night and wanted nuts; he divided all the nuts in the bag into five equal parts, with one extra nut left over, which he gave to the monkey, and took one fifth for himself. Soon after, another of the nut owners woke up; not knowing that someone had already taken nuts, he divided all the remaining contents of the bag again into five parts, with one extra nut left over, which he gave to the monkey, and took one fifth for himself. Then the remaining three friends successively performed the same operation; each of them, not knowing about the actions of the others, divided all the nuts into five parts, took one fifth for himself, and each time one extra nut remained, which was given to the monkey. Finally, in the morning, all five of them together took out the bag, divided the remaining nuts into five parts, and one nut, which turned out to be extra, was again given to the monkey. It is required to determine the smallest number of nuts in the bag for which such a division is possible.
|
27. First solution. Let $n$ be the number of nuts each friend received in the morning; in this case, $5n + 1$ is the number of nuts that were in the bag in the morning. The last of those who woke up at night, obviously, took $\frac{5n + 1}{4}$ for himself, and before that, there were $5 \frac{5n + 1}{4} + 1 = \frac{25n + 9}{4}$ nuts in the bag. The second to last who woke up took $\frac{1}{4} \cdot \frac{25n + 9}{4}$ for himself, and before that, there were $5 \cdot \frac{1}{4} \cdot \frac{25n + 9}{4} + 1 = \frac{125n + 61}{16}$ nuts in the bag; the third took $\frac{1}{4} \cdot \frac{125n + 61}{16}$ for himself, and before that, there were $5 \cdot \frac{1}{4} \cdot \frac{125n + 61}{16} + 1 = \frac{625n + 369}{64}$ nuts in the bag; the second took $\frac{1}{4} \cdot \frac{625n + 369}{64}$ for himself, and before that, there were $5 \cdot \frac{1}{4} \cdot \frac{625n + 369}{64} + 1 = \frac{3125n + 2101}{256}$ nuts in the bag; finally, the first took $\frac{1}{4} \cdot \frac{3125n + 2101}{256}$ for himself, and initially, there were
$N = 5 \cdot \frac{1}{4} \cdot \frac{3125n + 2101}{256} + 1 = \frac{15625n + 11529}{1024} \Rightarrow$
$$
= 15n + 11 + \frac{265n + 265}{1024}
$$
nuts. Since this number must be an integer, $265(n + 1)$ must be divisible by 1024. The smallest value of $n$ that satisfies this condition is, obviously, 1023, and in this case,
$$
N = 15 \cdot 1023 + 11 + 265 = 15621
$$
Second solution. This problem can be solved much faster and almost without any calculations if we carefully consider the conditions that the content of the problem imposes on the total number $N$ of nuts. The first condition of the problem is that during the first division into five parts, one nut remains. This condition means that $N$ when divided by 5 gives a remainder of 1, i.e., $N = 5l + 1$; numbers that satisfy this condition occur in the natural sequence of numbers with an interval of five numbers, and knowing one such number, we can find an unlimited number of others by adding (or subtracting) multiples of 5. The second condition of the problem states that $k = \frac{4}{5}(N - 1) = 4l$ gives a remainder of 1 when divided by 5, i.e., $k = 5l_1 + 1$. This requirement is equivalent to $l$ giving a remainder of 4 when divided by 5 or that $N = 5l + 1$ gives a remainder of 21 when divided by 25; numbers that satisfy this condition occur in the number sequence with an interval of 25 numbers, and knowing one such number, we can obtain as many as we want by adding (or subtracting) multiples of 25. Similarly, the third condition of the problem states that $k_1 = \frac{4}{5}(k - 1) = 4l_1$ gives a remainder of 1 when divided by 5; this condition determines the remainder from the division of the number $l_1$ by 5 or the remainders from the division of the numbers $k$ and $l$ by 25, or the remainder from the division of $N$ by 125. All conditions of the problem determine the remainder from the division of the number $N$ by $5^6 = 15625$; numbers that satisfy these conditions occur in the natural sequence of numbers with an interval of 15625.
We could calculate the remainder that the number $N$ gives when divided by 58, but there is no need for this. The fact is that one number that satisfies all the conditions of the problem is obvious. This number is -4. Indeed, when -4 is divided by 5, it gives a quotient of -1 and a remainder of +1; therefore, if we subtract 1 from -4 and take $\frac{4}{5}$ of the resulting difference, which is already divisible by 5, we will get the same number -4. Similarly, in all subsequent divisions by 5, we will have the same remainder +1. True, the number -4 cannot serve as an answer to our problem, as, by condition, the number $N$ must be positive; but knowing one number that satisfies the conditions of the problem, we can obtain as many as we want by adding multiples of $5^6$. The smallest positive number that satisfies the conditions is, obviously, $-4 + 5^6 = 15625 - 4 = 15621$.
|
15621
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28. Two brothers sold a flock of sheep that belonged to both of them, taking as many rubles for each sheep as there were sheep in the flock. The money received was divided as follows: first, the elder brother took ten rubles from the total amount, then the younger brother took ten rubles, after that the elder brother took another ten rubles, and so on. In the end, the younger brother did not have enough ten rubles; therefore, he took all the small change left after the division, and in addition, to make the division fair, the elder brother gave the younger brother his pocket knife. What was the pocket knife valued at?
|
28. Let the number of sheep in the flock be denoted by $n$; in this case, the brothers received $n$ rubles for each sheep, and thus the total amount they received is $N=n \cdot n=n^{2}$ rubles. Let $d$ be the number of whole tens in the number $n$, and $e$ be the number of units; then $n=10 d+e$ and
$$
N=(10 d+e)^{2}=100 d^{2}+20 d e+e^{2}
$$
From the conditions of the division, it follows that the elder brother received one ten more than the younger brother, i.e., that the total sum $N$ contains an odd number of tens (and some remainder). But $100 d^{2}+20 d e=20 d(5 d+e)$ is divisible by 20 (contains an even number of tens); therefore, the number $e^{2}$ must contain an odd number of tens. Since $e$ is less than 10 ( $e$ is the remainder of the division of the number $n$ by 10 ), then $e^{2}$ can only have one of the following values:
$$
1,4,9,16,25,36,49,64,81
$$
But of these numbers, only 16 and 36 contain an odd number of tens; therefore, $e^{2}$ is equal to 16 or 36. Both these numbers end in 6; hence, the remainder that the younger brother received in place of the 10 rubles he was short is 6 rubles, and the elder received 4 rubles more than the younger. Therefore, for the division to be fair, the elder should still pay the younger 2 rubles. Thus, the pocketknife was valued at 2 rubles.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
34. a) Find the smallest integer starting with the digit 1 such that if this digit is moved to the end, the number triples. Find all such numbers.
b) What digits can non-zero integers start with if they triple when the first digit is moved to the end? Find all such numbers.
|
34. a) First solution. Let's denote the (m-digit) number obtained by removing the first digit 1 from the desired number as \(X\). In this case, according to the problem, we have:
\[
\left(1 \cdot 10^{m} + X\right) \cdot 3 = 10 X + 1
\]
from which
\[
X = \frac{3 \cdot 10^{m} - 1}{7}
\]
From the last equation, it is not difficult to determine the number \(X\). For this, we need to divide the number \(3 \cdot 10^{m} = 30000\) ... by 7 until the remainder is 1. As a result, we have:
Thus, the smallest possible value of the number \(X\) is 42857, and the smallest value of the desired number is 142857.
In the division process, we could have continued beyond the first 1 and continued dividing until the next 1, and so on; in this case, we would have obtained numbers

that also satisfy the condition of the problem.
Second solution. Let's denote the second digit of the desired number by \(x\), the third by \(y\), and so on, i.e., assume that the desired number has the form \(1 x y \ldots z t\) (the bar above indicates that here we have not the product \(1 \cdot x \cdot y \ldots z \cdot t\), but a number composed of the digits \(1, x, y, \ldots, z, t\)). In this case, according to the problem, we have:
\[
\overline{1 x y \ldots z t} \cdot 3 = x \overline{x y \ldots z t 1}
\]
From this, it follows that \(t = 7\) (in no other case would the product on the left end in 1). Therefore, the tens digit of the number on the right is 7. This is only possible if the product \(z \cdot 3\) ends in \(7 - 2 = 5\) (two tens on the right are obtained from the product of the last digit of the desired number 7 by 3), i.e., \(z = 5\). Now we know the hundreds digit of the number on the right: 5; therefore, the hundreds digit of the desired number must give a number ending in \(5 - 1 = 4\) (1 is the tens digit of the product 5.3). The calculations will end when we reach the first digit 1. It is convenient to arrange them as follows:
\[
\begin{array}{ccccc}
1 & 4 & 2 & 8 & 57 \\
4-1=3, & 2-\dot{0}=2, & 8-\dot{2}=6, & 5-1=4, & 7-\dot{2}=\dot{5}
\end{array} \times 3 = \cdots \cdots 142857
\]
(calculations are performed from right to left). Thus, the smallest number satisfying the conditions of the problem is 142857.
If we do not stop at the first obtained 1 in our calculations and continue further, we will obtain other numbers,
b) Since the number of digits does not increase when such a number is tripled, the first digit of the number can only be 1, 2, or 3.
As we saw in the solution to part a), it can be 1. Let's now show that it cannot be 3.
Indeed, if the first digit of the desired number is 3, then the second digit, equal to the first digit of the tripled given number, is 9. But the result of multiplying a number starting with the digits 39 by 3 has more digits than the original number; therefore, it cannot be obtained from the original number by moving the first digit to the end.
We leave it to the readers to prove independently that the desired numbers can start with the digit 2. The smallest such number is 285714; all such numbers starting with the digit 2 have the form
(the proof is analogous to the solution of part a)).
|
142857
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35. Find the smallest natural number ending in the digit 6 that quadruples when its last digit is moved to the beginning of the number.
|
35. First solution. Let the number $X$ satisfy the conditions of the problem:
$$
X=\widehat{a_{1} a_{2} \ldots a_{n-1} 6} \quad \text { and } \quad 4 X=\widehat{6 a_{1} a_{2} \ldots a_{n-1}},
$$
where $a_{1}, a_{2}, \ldots, a_{n-1}, 6$ are the digits of the number $X$. Since the last digit of $X$ is 6, the last digit of $a_{n-1}$ of the number $4 X$ is 4; thus, $X=\overline{a_{1} a_{2} \ldots a_{n-2} 46}$, which allows us to find the second-to-last digit $a_{n-2}=8$ of the number $4 X$. Writing $X$ now as $\ldots 846$, we can find that $a_{n-3}=3$, and so on. We will continue this process until we get the digit 6 in the number $4 X$, which can be considered as carried from the end of the number $X$. Thus, we find that the smallest possible number satisfying the condition of the problem is $X=153846$; in this case, $4 X=615384$.
Second solution. Since the desired number $X$ ends with the digit 6, it can be written in the form $X=10 x+6$, where $x$ is the number obtained from $X$ by erasing the last digit 6. If the number $x$ is $n$-digit, then from the condition of the problem it follows that
$$
4 \cdot(10 x+6)=6 \cdot 10^{n}+x
$$
i.e.,
$$
39 x=6 \cdot\left(10^{n}-4\right), \text { or } \quad x=\frac{2\left(10^{n}-4\right)}{13}
$$
The number $10^{n}-4$ is obviously 6, or 96, or 996, or $9996, \ldots$ The smallest of such numbers that is a multiple of 13 is the number $99996=13.7692$; it corresponds to the value $n=5$. But in this case, the equality (*) gives $x=15384$, and thus, $X=153846$.
|
153846
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
39. Find the smallest integer starting with the digit 7 that decreases threefold when this digit is moved to the end. Find all such numbers.
|
39. First solution. Let the unknown digits of the desired number be denoted by $x, y, \ldots, z, t$. In this case, using the notation from the second solution of problem 34 a), we have:
$$
\text { - } \overline{7 x y \ldots z t} \cdot \frac{1}{3}=\overline{x y \ldots z t 7}
$$
or
$$
\overline{x y \ldots z t 7} \cdot 3=\overline{7 x y \ldots z t}
$$
It is immediately clear that $t=1$; after this, we can determine the digit $z$ (17.3 ends in 51; hence, $z=5$) and thus sequentially find new digits of the desired number. The calculation should be stopped when we reach the digit 7. It is convenient to arrange it as follows:
241379310344827586206896551
7241379310344827586206896551
(calculations are performed from right to left). Thus, the smallest number satisfying the conditions of the problem is 7241379310344827586206896551.
If we do not stop our calculations at the first 7 and continue further, we will obtain other numbers that satisfy the condition of the problem. All such numbers will have the form
Second solution. Let $\overline{7 x y z \ldots t}$ be the desired number. Then, when dividing it by 3, we get the number $\overline{x^{\prime} z \ldots t 7}$. Let's write this as
From this, it is clear that $x=2$. If we write this value in the dividend and the quotient, we can find the second digit of the quotient; using it, we can find the third digit of the dividend; from this, we can find the third digit of the quotient, and so on. The process will end when the last obtained digit of the quotient is 7, and the written dividend is divisible by 3 without a remainder.
It is easy to see that this number is the desired one, since if we move the 7 from the beginning to the end in it, we get the number we wrote as the quotient, i.e., one-third of it.
Since up to this point we were necessarily obtaining the next digit from the already written ones, the indicated number will be the smallest with the required property. The calculations can be arranged as follows: in the top line, we will write the digits of the dividend, in the second line - the number, dividing which by 3 gives the next digit of the quotient, and in the third line - this digit; $\begin{array}{llllllllllllllllllll}7 & 2 & 4 & 1 & 3 & 7 & 9 & 3 & 1 & 0 & 3 & 4 & 4 & 8 & 2 & 7 & 5 & 8 & 6 & 2\end{array}$ 71241123279311013142482217251862 $\begin{array}{llllllllllllllllllll}2 & 4 & 3 & 3 & 9 & 3 & 1 & 0 & 3 & 4 & 4 & 8 & 2 & 7 & 5 & 8 & 6 & 2 & 0\end{array}$
$$
\begin{array}{rrrrrrrrr}
0 & 6 & 8 & 9 & 6 & 5 & 5 & 1 \\
20 & 26 & 28 & 19 & 16 & 15 & 5 & 21 \\
6 & 8 & 9 & 6 & 5 & 5 & 1 & 7
\end{array}
$$
Thus, the smallest number with the required property is: 7241379310344827586206896551.
Third solution. Analogously to the first solution of problem 34 a), using similar notation, we will have:
$$
\left(7 \cdot 10^{m}+X\right) \cdot \frac{1}{3}=10 X+7
$$
from which
$$
X=\frac{7 \cdot 10^{m}-21}{29}
$$
Thus, the problem reduces to determining a number of the form $70000 \ldots$ which, when divided by 29, gives a remainder of 21. We leave it to the reader to verify that in this case, we arrive at the same result as in the first two solutions.
Note. Similarly, we can solve the following problem:
Find the smallest number starting with a known digit that decreases by 3 times when the first digit is moved to the end. To be able to search for solutions starting with the digits 1 and 2, we will assume that 0 can stand at the beginning of the number.
If the number starts with the digit 0, it is easy to verify that the only number with the required property is 0. Let's write down the other numbers with this property:
| 1 | 034 | 482 | 758 | 620 | 689 | 655 | 172 | 413 | 793 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 2 | 068 | 965 | 517 | 241 | 379 | 310 | 344 | 827 | 586 |
| 3 | 103 | 448 | 275 | 862 | 068 | 965 | 517 | 241 | 379 |
| 4 | 137 | 931 | 034 | 482 | 758 | 620 | 689 | 655 | 172 |
| 5 | 172 | 413 | 793 | 103 | 448 | 275 | 862 | 068 | 965 |
| 6 | 206 | 896 | 551 | 724 | 137 | 931 | 034 | 482 | 758 |
| 8 | 275 | 862 | 068 | 965 | 517 | 241 | 379 | 310 | 344 |
| 9 | 310 | 344 | 827 | 586 | 206 | 896 | 551 | 724 | 137 |
In the same way, we can solve the problem:
Find the smallest integer starting with a given digit $a$ and decreasing by moving this digit to the end by a factor of 3. Find all such numbers.
|
7241379310344827586206896551
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
41. a) Find a six-digit number that increases by 6 times when the last three digits of the number, without changing their order, are moved to the beginning of the number.
b) Prove that there does not exist an eight-digit number that increases by 6 times when the last four digits are moved to the first four positions while maintaining their order.
|
41. a) Let the number formed by the first three digits of the desired number $N$ be denoted by $p$, and the number formed by the last three digits of $N$ be denoted by $q$. In this case, the condition of the problem gives
$$
1000 q + p = 6(1000 p + q) \quad(=6 N)
$$
from which we get
$$
(1000 q + p) - (1000 p + q) = 999(q - p) = 5 N
$$
i.e., $N$ is divisible by 999.
Further, $p + q = (1000 p + q) - 999 p = N - 999 p$, from which it follows that $p + q$ is also divisible by 999. But $p$ and $q$ are three-digit numbers, which obviously cannot both equal 999; therefore,
$$
p + q = 999
$$
Now we easily find:
$$
(1000 q + p) + (1000 p + q) = 1001(p + q) = 7 N
$$
and, thus,
$$
7 N = 999999, \quad N = 142857
$$
b) Analogously to the solution of part a), denoting by $p$ the number formed by the first four digits of the desired number $N$, and by $q$ the number formed by the last four digits, we find:
$$
7 N = 10001(p + q) = 99999999
$$
which is impossible for an integer $N$ (since 99999999 is not divisible by 7).
|
142857
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
42. Find a six-digit number, the products of which when multiplied by 2, 3, 4, 5, and 6 are written with the same digits as the number itself, but in a different order.
|
42. Let $x$ be the number satisfying this condition. Since $6x$, like $x$, is a six-digit number, the first digit of the decimal representation of the number $x$ is 1. Therefore:
1) the first digits of the decimal representation of the numbers $x, 2x, 3x, 4x, 5x$, and $6x$ are all different, so they form a complete set of digits participating in the decimal representation of the number $x$;
2) all digits in the decimal representation of the number $x$ are different from each other.
Among these digits, there is no 0, so the last digit of the number $x$ is odd (otherwise $5x$ would end in zero) and different from 5 (otherwise $2x$ would end in zero). Therefore, the last digits of the decimal representation of the numbers $x, 2x, 3x, 4x, 5x$, and $6x$ are all different, and thus also form a complete set of digits participating in the decimal representation of the number $x$. Therefore, among them there is a 1. The number $3x$ can end in 1, as $2x, 4x$, and $6x$ end in even digits, $5x$ ends in 5, and the decimal representation of $x$ already has a 1 (the first digit). Therefore, $x$ ends in the digit 7, $2x$ in the digit 4, $3x$ in the digit 1, $4x$ in the digit 8, $5x$ in the digit 5, and $6x$ in the digit 2. Since the first digits of these numbers are the digits of the same set, arranged in ascending order, we can write:
$$
\begin{aligned}
& x \cdot 1=1 * * * * 7 \\
& x \cdot 2=2 * * * * 4 \\
& x \cdot 3=4^{* * * * 1} \\
& x \cdot 4=5 * * * * 8 \\
& x \cdot 5=7 * * * * 5 \\
& x \cdot 6=8^{* * * * 2}
\end{aligned}
$$
(stars stand in place of the unknown digits).
Note now that in the written table, not only in each row do the six different digits $1,2,4,5$, 7, and 8 appear in some order, but also in each column, the same six different digits appear in some order. Indeed, suppose, for example, that in the numbers $x \cdot 2$ and $x \cdot 5$ the same digit $a$ (which can have one of two values not occupied by the first and last digits of the two numbers being considered) stands in the third place. In this case, the difference $x \cdot 5 - x \cdot 2 = x \cdot 3$ will represent a six-digit number, in the decimal representation of which the third place will be the digit 0 or the digit 9 (this follows from the rule of subtracting multi-digit numbers "in a column"). But this is impossible, since we know that the number $x \cdot 3$ is written with the digits $1,2,4,5,7$, and 8.
Now let's add the numbers
$$
\begin{aligned}
& x \cdot 1=1 * * * * 7 \\
& x \cdot 2=2 * * * * 4 \\
& x \cdot 3=4^{* * * * 1} \\
& x \cdot 4=5 * * * * 8 \\
& x \cdot 5=7 * * * * 5 \\
& x \cdot 6=8 * * * * 2
\end{aligned}
$$
"column-wise," considering that the sum of the digits in each column is $1 + 2 + 4 + 5 + 7 + 8 = 27$. We get:
$$
x \cdot 21=2999997
$$
or $x=142857$. This is the desired number; indeed,
$$
\begin{aligned}
x & =142857, \\
2x & =285714 \\
3x & =428571, \\
4x & =571428, \\
5x & =714285 \\
6x & =857142
\end{aligned}
$$
|
142857
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
51. What remainders can the hundredth power of an integer give when divided by 125?
|
51. Any integer either is divisible by 5 or can be represented in one of the following four forms: $5k+1, 5k+2, 5k-2$, or $5k-1$. If a number is divisible by 5, then its hundredth power is clearly divisible by $5^3 = 125$. Further, using the binomial theorem, we get:
$$
(5k \pm 1)^{100} = (5k)^{100} \pm \ldots + \frac{100 \cdot 99}{1 \cdot 2}(5k)^2 \pm 100 \cdot 5k + 1
$$
where all the omitted terms contain a factor of $5k$ raised to a power of at least 3, and thus are divisible by 125. Similarly,
$$
(5k \pm 2)^{100} = (5k)^{100} \pm \ldots + \frac{100 \cdot 99}{1 \cdot 2}(5k)^2 \cdot 2^{98} \pm 100 \cdot 5k \cdot 2^{99} + 2^{100}
$$
But $\frac{100 \cdot 99}{1 \cdot 2}(5k)^2 = 125 \cdot 990k^2$ and $100 \cdot 5k = 125 \cdot 4k$ are divisible by 125. As for the number $2^{100}$, it can be represented as
$$
(5-1)^{50} = 5^{50} - \ldots + \frac{50 \cdot 49}{1 \cdot 2} \cdot 5 - 50 \cdot 5 + 1
$$
from which it is clear that it gives a remainder of 1 when divided by 125.
Thus, the hundredth power of a number divisible by 5 is divisible by 125; the hundredth power of a number not divisible by 5 gives a remainder of 1 when divided by 125.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
54*. Let $N$ be an even number not divisible by 10. What will be the tens digit of the number $N^{20}$? What will be the hundreds digit of the number $N^{200}$?
|
54. Let's find the last two digits of the number \(N^{20}\). The number \(N^{20}\) is divisible by 4 (since \(N\) is even). Further, the number \(N\) is not divisible by 5 (otherwise it would be divisible by 10) and, therefore, can be represented in the form \(5k \pm 1\) or in the form \(5k \pm 2\) (see the solution to problem 51). But the number
\[
(5k \pm 1)^{20} = (5k)^{20} \pm 20(5k)^{19} + \ldots + \frac{20 \cdot 19}{1 \cdot 2}(5k)^{2} \pm 20 \cdot 5k + 1
\]
gives a remainder of 1 when divided by 25, and the number
\[
\begin{aligned}
&(5k \pm 2)^{20} = (5k)^{20} \pm 20(5k)^{19} \cdot 2 + \ldots \\
& \ldots + \frac{20 \cdot 19}{1 \cdot 2}(5k)^{2} \cdot 2^{18} \pm 20 \cdot 5k \cdot 2^{19} + 2^{20}
\end{aligned}
\]
gives the same remainder when divided by 25 as the number \(2^{20} = (2^{10})^2 = (1024)^2 = (1025-1)^2\), i.e., also a remainder of 1. From the fact that the number \(N^{20}\) gives a remainder of 1 when divided by 25, it follows that the last two digits of this number can only be 01, 26, 51, or 76. Considering that \(N^{20}\) must be divisible by 4, we get that the last two digits of this number can only be 76. Therefore, the tens digit of the number \(N^{20}\) is 7.
Now let's find the last three digits of the number \(N^{200}\). The number \(N^{200}\) is divisible by 8. Further, since \(N\) is coprime with 5, \(N^{100}\) gives a remainder of 1 when divided by 125 (see the solution to problem 51): \(N^{100} = 125k + 1\). But then \(N^{200} = (125k + 1)^2 = 125^2 k^2 + 250k + 1\) also gives a remainder of 1 when divided by 125. Therefore, \(N^{200}\) can end in the digits 126, 251, 376, 501, 626, 751, or 876; but since \(N^{200}\) is divisible by 8, it must end in the digits 376. Therefore, the hundreds digit of the number \(N^{200}\) is 3.
Note. It is easy to see that the number \(N^{100}\) must already end in the three digits 376.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
57. The number $123456789(10)(11)(12)(13)(14)$ is written in the base-15 numeral system, i.e., this number is equal to
(14) $+(13) \cdot 15+(12) \cdot 15^{2}+(11) \cdot 15^{3}+\ldots+2 \cdot 15^{12}+15^{13}$. What remainder does it give when divided by 7?
|
57. The number 15 gives a remainder of 1 when divided by 7. Therefore, it follows that
$$
15^{2}=(7 \cdot 2+1) \cdot(7 \cdot 2+1)=7 n_{1}+1
$$
gives a remainder of 1 when divided by 7,
$$
15^{3}=15^{2} \cdot 15=\left(7 n_{1}+1\right) \cdot(7 \cdot 2+1)=7 n_{2}+1
$$
gives a remainder of 1 when divided by 7, and generally, any power of the number 15 gives a remainder of 1 when divided by 7. If we now subtract from the given number the sum \(1+2+3+4+\ldots+14=105\), then, by grouping the terms appropriately, we get:
$$
\begin{aligned}
& 13(15-1)+12\left(15^{2}-1\right)+ \\
& \quad+11\left(15^{3}-1\right)+\ldots+2\left(15^{12}-1\right)+1\left(15^{13}-1\right)
\end{aligned}
$$
i.e., a number that is divisible by 7. But from the fact that the difference between the given number and the number \(105=7 \cdot 15\) is divisible by 7, it follows that the original number is also divisible by 7.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
65. Find the remainder when the number
$$
10^{10}+10^{\left(10^{0}\right)}+\ldots+10^{\left(10^{10}\right)}
$$
is divided by 7.
|
65. First of all, note that \(10^{6}-1=999999\) is divisible by 7 (since \(999999=7 \cdot 142857\)). From this, it easily follows that \(10^{\mathrm{N}}\), where \(N\) is any integer, gives the same remainder when divided by 7 as \(10^{r}\), where \(r\) is the remainder from dividing \(N\) by 6. Indeed, if \(N=6k+r\), then
\[
\begin{aligned}
& 10^{k}-10^{r}=10^{6k+r}-10^{r}=10^{r}\left(10^{6k}-1\right)= \\
& =10^{r} \cdot \left(10^{6}-1\right)\left(10^{6k-6}+10^{6k-12} \ldots+10^{6}+1\right)
\end{aligned}
\]
is divisible by 7.
But any integer power of 10 gives a remainder of 4 when divided by 6; indeed, \(10^{n}-4=\underset{(n-1) \text{ times }}{999 \ldots 9}\) is always divisible by \(2 \cdot 3=6\) (due to the divisibility rules for 2 and 3). Thus, all the complex exponents of the terms in our sum give a remainder of 4 when divided by 6. Consequently, each of these 10 terms gives the same remainder when divided by 7 as the number \(10^{4}\), and the entire sum gives the same remainder as the number
\[
\begin{aligned}
10^{4}+10^{4}+10^{4}+10^{4}+10^{4}+10^{4}+10^{4} & +10^{4}+10^{4}+10^{4}= \\
& =10^{5}=100000=7 \cdot 14285+5
\end{aligned}
\]
Thus, the desired remainder is 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
68. a) What is the last digit of the number
$$
\left(\ldots\left(\left(\left(7^{7}\right)^{7}\right)^{7}\right)^{\ldots 7}\right)
$$
(raising to the power of 7 is repeated 1000 times)? What are the last two digits of this number?
b) What is the last digit of the number
$$
7\left(7^{\left(.7^{\left(7^{7}\right)}\right)} \ldots\right)
$$
written using 1001 sevens, similar to the number in problem a), but with a different order of exponentiation? What are the last two digits of this number?
|
68. a) If you multiply two numbers, one of which ends in the digit $a$, and the second in the digit $b$, then their product will end in the same digit as the product $a b$. This observation allows us to easily solve the given problem. We will sequentially raise to powers, keeping track only of the last digit of the number: $7^{2}$ ends in the digit $9, 7^{3} = 7^{2} \cdot 7$ ends in the digit $3, 7^{4} = 7^{3} \cdot 7$ ends in the digit 1, and $7^{7} = 7^{4} \cdot 7^{3}$ ends in the digit 3.
Next, in the same way, we find that $\left(7^{7}\right)^{7}$ ends again in the digit 7 (indeed, $\left(7^{7}\right)^{2}$ ends in the digit $9, \left(7^{7}\right)^{3}$ ends in the digit $7, \left(7^{7}\right)^{4}$ ends in the digit 1, and $\left(\left(7^{7}\right)^{7}\right)$ ends in the digit 7). From this, it follows that the number $\left(\left(7^{\prime}\right)^{1}\right)^{\top}$ ends in the same digit as the number $7^{7}$, i.e., the digit 3, the number $\left.\left(\left(7^{7}\right)^{7}\right)^{7}\right)^{7}$ ends again in the digit 7, and so on. Continuing in the same way, after an odd number of exponentiations by 7, we will always arrive at a number ending in the digit 3, and after an even number of exponentiations by 7, a number ending in the digit 7. Since 1000 is an even number, the number of interest to us ends in the digit 7.
If one number ends in a two-digit number $A$, and the second in a two-digit number $B$, then their product ends in the same two digits as the product $A \cdot B$. This allows us to find the last two digits of the number of interest to us. As before, we check that $7^{7}$ ends in the two digits 43, and $\left(7^{7}\right)^{7}$ ends in the same digits as $43^{7}$, namely the digits 07. From this, it follows that, raising the numbers 7, 77, $\left(7^{7}\right)^{7}, \ldots$ sequentially to the power of 7, we will after an odd number of exponentiations end up with a number ending in the digits 43, and after an even number of exponentiations, a number ending in the digits 07. Therefore, the number of interest to us ends in the digits 07.
b) In the solution to part a), we saw that $7^{4}$ ends in the digit 1. From this, it follows that $7^{4 k} = \left(7^{4}\right)^{k}$ also ends in the digit 1 and $7^{4 k + l}$, where $l$ is one of the numbers $0, 1, 2$ or 3, ends in the same digit as $7^{l} \left(7^{4 k + l} = 7^{4 k} \cdot 7^{l}\right)$. Thus, the problem reduces to determining the remainder when the exponent, to which 7 is raised to obtain the number in the problem, is divided by 4.
The exponent to which 7 is raised in the problem itself is 7 raised to a very large power; we need to determine the remainder when this power of 7 is divided by 4. But $7 = 8 - 1$; from this, it follows that $7^{2} = (8 - 1) \cdot (8 - 1)$ gives a remainder of 1 when divided by 4, $7^{3} = 7^{2} \cdot (9 - 1)$ gives a remainder of -1 (or, equivalently, a remainder of 3) when divided by 4, and generally, every even power of 7 gives a remainder of 1 when divided by 4, and every odd power gives a remainder of -1 (i.e., +3). But the power of 7 of interest to us in this case is necessarily an odd number (since it itself is a power of 7), and therefore, the number in the problem has the form $7^{4 k + 3}$ and, consequently, ends in the same digit as $7^{3}$, i.e., the digit 3.
Since $7^{4}$ ends in the digits 01, $7^{4 k + l}$ ends in the same two digits as $7^{l}$. Therefore, the number of interest to us ends in the same two digits as the number $7^{3}$, i.e., the digits 43.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
69*. Determine the five last digits of the number
$$
\left.N=9^{\left(9^{(} \cdot 9^{\left(9^{9}\right)}\right)} \ldots\right),
$$
written using 1001 nines in a similar manner to the number in problem 68).
|
69. Let's consider the sequence of numbers:
$$
\begin{aligned}
& 1^{\circ} \cdot Z_{1}=9 \\
& \begin{aligned}
2^{\circ} \cdot Z_{2} & =9^{Z_{1}}=(10-1)^{Z_{1}}= \\
& =10^{Z_{1}}-C_{Z_{1}}^{1} \cdot 10^{Z_{1}-1}+\ldots+C_{Z_{1}}^{1} \cdot 10-1
\end{aligned}
\end{aligned}
$$
where the omitted terms in the expansion are all divisible by 100. But \( C_{Z_{1}}^{1}=9 \); therefore, the last two digits of the number \( Z_{2} \) will be the same as the last two digits of the number \( 9 \cdot 10-1=89 \).
$$
\text { 3. } \begin{aligned}
Z_{3}=9^{Z_{2}} & =(10-1)^{Z_{2}}= \\
& =10^{Z_{2}}-C_{Z_{2}}^{1} \cdot 10^{Z_{1}-1}+\ldots-C_{Z_{3}}^{2} \cdot 10^{2}+C_{Z_{2}}^{1} \cdot 10-1 .
\end{aligned}
$$
But \( Z_{2} \) ends in 89; therefore, \( C_{Z_{2}}^{1}=Z_{2} \) ends in 89, and \( C_{Z_{2}}^{2}=\frac{Z_{2}\left(Z_{2}-1\right)}{1 \cdot 2}=\frac{\ldots 89 \cdot \ldots 88}{1 \cdot 2} \) (dots represent unknown digits) ends in 6. Therefore, the last three digits of the number \( Z_{3} \) will be the same as the last three digits of the number \( -600+890-1=289 \).
$$
\begin{aligned}
4^{7} & : Z_{4}=9^{Z_{3}}=(10-1)^{Z_{3}}= \\
& =10^{Z_{3}}-C_{Z_{3}}^{1} \cdot 10^{Z_{3}-1}+\ldots \div C_{Z_{1}}^{3} \cdot 10^{3}-C_{Z_{3}}^{2} \cdot 10^{2}+C_{Z_{3}}^{1} \cdot 10-1
\end{aligned}
$$
$$
C_{Z_{3}}^{2}=\frac{Z_{3}\left(Z_{3}-1\right)}{1 \cdot 2}=\frac{\ldots 289 \cdot \ldots 288}{1 \cdot 2}
$$
ends in 16;
$$
C_{Z_{3}}^{3}=\frac{Z_{3}\left(Z_{3}-1\right)\left(Z_{3}-2\right)}{1 \cdot 2 \cdot 3}=\frac{\ldots 289 \ldots 288 \ldots 287}{1 \cdot 2 \cdot 3}
$$
ends in 4. Therefore, the last four digits of the number \( Z_{4} \) will be the same as the last four digits of the number \( 4000-1600+2890-1=5289 \).
$$
\begin{aligned}
5^{0} \cdot Z_{5}=9^{Z_{k}}= & (10-1)^{Z_{k}}=10^{Z_{4}}-C_{Z_{1}}^{1} \cdot 10^{Z_{4}-1}+\ldots \\
& \ldots-C_{Z_{4}}^{1} \cdot 10^{1}+C_{Z_{4}}^{3} \cdot 10^{3}-C_{Z_{4}}^{2} \cdot 10^{2}+C_{Z_{k}}^{1} \cdot 10-1
\end{aligned}
$$
Since \( Z_{4} \) ends in 5289, \( C_{Z_{4}}^{1}=Z_{4} \) ends in 5289;
$$
\cdot C_{Z_{4}}^{\prime 2}=\frac{Z_{4}\left(Z_{1}-1\right)}{1 \cdot 2}=\frac{\ldots 5289 \cdot \ldots 5288}{1 \cdot 2}
$$
ends in 116;
$$
C_{Z_{4}}^{3}=\frac{Z_{4}\left(Z_{4}-1\right)\left(Z_{4}-2\right)}{1 \cdot 2 \cdot 3}=\frac{\ldots 5289 \cdot \ldots .5288 \cdot \ldots 5287}{1 \cdot 2 \cdot 3}
$$
ends in 64; finally,
$$
C_{Z_{4}}^{4}=\frac{Z_{4}\left(Z_{4}-1\right)\left(Z_{4}-2\right)\left(Z_{4}-3\right)}{1 \cdot 2 \cdot 3 \cdot 4}=\frac{\ldots 5289 \ldots 5288 \cdot \ldots 5287 \ldots 5286}{1 \cdot 2 \cdot 3 \cdot 4}
$$
ends in 6. Therefore, \( Z_{5} \) ends in the same last five digits as the number
$$
-60000+64000-11600+52890-1=45289
$$
From the fact that the last four digits of the number \( Z_{5} \) coincide with the last four digits of the number \( Z_{4} \), it follows that the last five digits of the number \( Z_{6}=9^{Z_{6}}=(10-1)^{Z_{\overline{5}}} \) coincide with the last five digits of the number \( Z_{5} \) ( \( \left.=9^{Z_{4}}\right) \). Similarly, it can be shown that all numbers in the sequence
$$
Z_{3}, \quad Z_{6}=9^{Z_{5}}, Z_{7}=9^{Z_{5}}, \ldots, Z_{1000}=9^{Z_{289}}, Z_{1001}=9^{Z_{1000}}
$$
end in the same five digits, namely 45289. But \( Z_{1001} \) is the number \( N \) in the problem condition.
|
45289
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
70. For which natural numbers $n$ is the sum $5^{n}+n^{5}$ divisible by 13? What is the smallest $n$ that satisfies this condition?
|
70. First, let's find the remainders of the division by 13 of the numbers \(5^n\) and \(n^5\) for the first few values of \(n = 0, 1, 2, \ldots\). It is more convenient to start with the numbers \(5^n\):
\(n\)
| 0 | 1 | 2 | 3 | 4 | . | . | . |
| ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: |
| 1 | 5 | 25 | 125 | 625 | . | . | . |
| 1 | 5 | -1 | -5 | 1 | . | . | . |
[Here we write the remainder -1 instead of "remainder 12" and "remainder -3" instead of "remainder 8", which allows us to easily find all subsequent remainders: if \(5^n\) gives a remainder of -1 when divided by 13, i.e., \(5^n = 13k - 1\), where \(k\) is an integer, then \(5^{n+1} = 5^n \cdot 5 = (13k - 1) \cdot 5 = 13(5k) - 5\) gives a remainder of -5 when divided by 13; similarly, if \(5^m\) gives a remainder of -5 when divided by 13, i.e., \(5^m = 13l - 5\), then \(5^{m+1} = 5^m \cdot 5 = (13l - 5) \cdot 5 = 13(5l) - 25 = 13(5l - 2) + 1\) gives a remainder of 1 when divided by 13.] There is no need to continue the table further: since \(5^4 = 13q + 1\), then \(5^5 = 5^4 \cdot 5 = (13q + 1) \cdot 5\) gives the same remainder as the number 5 (remainder 5) when divided by 13; the number \(5^6 = 5^4 \cdot 5^2 = (13q + 1) \cdot 5^2\) gives the same remainder as the number \(5^2\) (remainder -1) when divided by 13, and so on; thus, in our "sequence of remainders," the numbers \(1, 5, -1, -5\) alternate sequentially.
Similarly, we can create a table of remainders from the division by 13 of the numbers \(n^5\), where \(n = 0, 1, 2, \ldots\), and so on. But the number \((13p + r)^5 = \frac{(13p + r)(13p + r) \ldots (13p + r)}{5 \text{ factors}}\) gives the same remainder as the number \(r^5\) when divided by 13; therefore, it is sufficient to limit ourselves to the values \(n = 0, 1, 2, 3, \ldots, 12\). Further, if the number \(n\) is equal to (or gives a remainder of) \(s\) when divided by 13, and the number \(n^2\) gives a remainder of \(t\) when divided by 13, then the number \(n^5 = n^2 \cdot n^2 \cdot n\) gives the same remainder as the product \(t \cdot t \cdot s\) when divided by 13—this fact can simplify the creation of the required table for the values \(n = 4, 5, 6\). Finally, note that if the number \(n^5\) gives a remainder of \(u\) when divided by 13, then the number \((13 - n)^5 = \underbrace{(13 - n)(13 - n) \ldots (13 - n)}\) gives the same remainder as the number \((-n)^5\), i.e., the remainder -u, or \(13 - u\).
Now we can create our table:
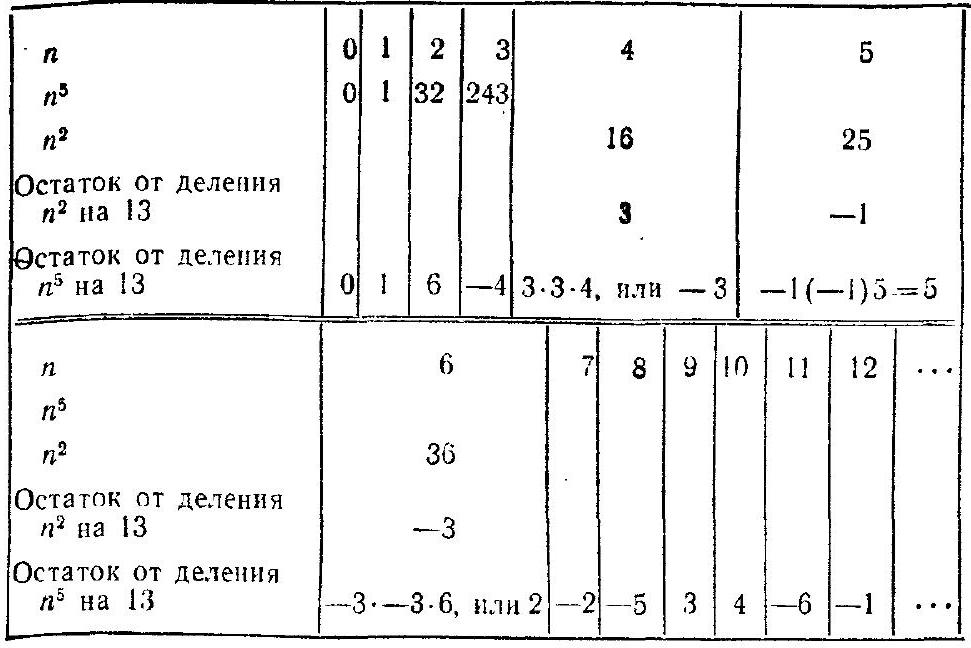
(The remainders corresponding to the values \(n = 7, 8, \ldots, 12\) are written based on the fact that the numbers \(n^5\) and \((13 - n)^5\) give "complementary" remainders \(u\) and \(-u\).) After the value \(n = 12\) in our table, the same remainders \(0, 1, 6, -4, -3, 5, 2, -2, -5, 3, 4, -6, -1\) will "periodically" repeat.
Since the first table has a "period" of 4, and the second has a "period" of 13, the value \(4 \cdot 13 = 52\) is the "period" of the combination of both tables: increasing \(n\) by 52 (or any multiple of 52) does not change the remainders of the division by 13 of both numbers \(5^n\) and \(n^5\). Further, we are only interested in those columns of the second table that correspond to remainders \(\pm 1\) and \(\pm 5\) (since in the first table, only the remainders \(1, 5, -1, -5\) alternate). But within the range from \(n = 0\) to \(n = 51\), the remainder 1 in the second table corresponds to the values \(n = 1, 1 + 13 = 14\), \(1 + 2 \cdot 13 = 27\), and \(1 + 3 \cdot 13 = 40\); of these four numbers, only 14 has the form \(4x + 2\), which in the first table corresponds to the remainder -1; thus, the number \(n = 14\) satisfies the required condition \((5^{14} + 14^5\) is divisible by 13\). Similarly, the remainder -1 in the second table within the same range corresponds to the values \(n = 12, 12 + 13 = 25\), \(12 + 2 \cdot 13 = 38\), and \(12 + 3 \cdot 13 = 51\); of these numbers, only 12 has the form \(4y\), which in the first table leads to the remainder 1. Similarly, the remainder 5 in the second table corresponds to the values \(n = 5, 5 + 13 = 18\), \(5 + 2 \cdot 13 = 31\), and \(5 + 3 \cdot 13 = 44\), and the remainder -5 to the values \(n = 8, 8 + 13 = 21\), \(8 + 2 \cdot 13 = 34\), and \(8 + 3 \cdot 13 = 47\); but of the first four numbers, only 31 has the form \(4z + 3\), ensuring a remainder of -5 from the division of \(5^{31}\) by 13, and of the last four numbers, only 21 has the form \(4\tau + 1\), ensuring a remainder of 5 from the division of \(5^{21}\) by 13. Thus, within the range \(0 \leq n \leq 52\), the required condition is satisfied by the following four natural numbers: \(n = 12, 14\), 21, and 31; the entire set of natural numbers satisfying the condition of the problem consists of the following four "series" of numbers:
\[
\begin{gathered}
n = 52m + 12, \quad n = 52m + 14 \text{ (i.e., } n = 26(2m) + 12 \quad n \\
= 26(2m + 1) - 12)
\end{gathered}
\]
\[
n = 52m + 21 \quad \text{and} \quad n = 52m + 31 \text{ (i.e., } n = 52m \pm 21 \text{);}
\]
here \(m = 0, 1, 2, \ldots\) (and in the formula \(n = 52m - 21\) we must have \(m > 0\)).
Clearly, the smallest \(n\) that satisfies the conditions of the problem is \(n = 12\).
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
71. What are the last two digits of the number
$$
n^{a}+(n+1)^{a}+(n+2)^{a}+\ldots+(n+99)^{a}
$$
a) $a=4$
b) $a=8$ ?
|
71. It is clear that the last two digits of the numbers $n, n^{2}, n^{3}, \ldots$, where $n$ is a non-negative integer, depend only on the last two digits of the number $n$ - this follows from the rule of multiplying multi-digit numbers "in a column". On the other hand, the last digits of 100 consecutive non-negative integers necessarily run through the values $00,01,02, \ldots, 99 \cdot$ (although, generally speaking, not in this order); therefore, our problem reduces to finding the last two digits of the sum (for $a=4$ and $a=8$)
$$
N_{a}=0^{a}+1^{a}+2^{a}+\ldots+99^{a}
$$
a) If $n=10 x+y$ is a two-digit number, then
$$
n^{4}=(10 x+y)^{4}=10^{4} x^{4}+4 \cdot 10^{3} x^{3} y+6 \cdot 10^{2} x^{2} y^{2}+4 \cdot 10 x y^{3}+y^{4}
$$
where only the last two terms affect the last two digits of the number $n^{4}$, since all other terms end with two zeros. Therefore, we need to find only the last two digits of the sums
$$
\sum_{x} \sum_{y} 4 \cdot 10 x y^{3} \quad \text { and } \sum_{x} \sum_{y} x^{0} y^{4} \quad\left(=10 \sum_{y} y^{4}\right)
$$
where $x$ and $y$ independently take values from 0 to 9 and it is assumed that $0^{0}=1$ (so $\left.\sum_{x} x^{0}=0^{0}+1^{0}+\ldots+9^{0}=10\right)$.
Notice now that for a fixed $y$
$\sum_{x} 4 \cdot 10 x y^{3}=4 \cdot 10(0+1+2+3+4+5+6+7+8+9) \cdot y^{3}=1800 y^{3}$
ends with two zeros; therefore, $\sum_{x} \sum_{y} 4 \cdot 10 x y^{3}$ also ends with two zeros - and does not contribute to the last two digits of the number $N_{4}$. Thus, we are left to find only the last two digits of the number
$10 \sum_{y} y^{4}=10\left(0^{4}+1^{4}+2^{4}+3^{4}+4^{4}+5^{4}+6^{4}+7^{4}+8^{4}+9^{4}\right)=10 S_{4}$, or the last digit of the sum $S_{4}$.
But this task is easy to solve: in the following table, the last digits of the numbers $y, y^{2}$ and $y^{4}$ are sequentially listed:
$$
\begin{array}{c|cccccccccc}
y & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\
y^{2} & 0 & 1 & 4 & 9 & 6 & 5 & 6 & 9 & 4 & 1 \\
\boldsymbol{v}^{4} & 0 & 1 & 6 & 1 & 6 & 5 & 6 & 1 & 6 & 1
\end{array}
$$
Therefore, the last digit of the sum $S_{4}$ coincides with the last digit of the sum
$$
0+1+6+1+\ldots+1=4(1+6)+5=33
$$
which means that the last two digits of the sum $N_{4}$ (and the number in the problem statement) are 30.
6) In exactly the same way as in part a), we find that for $a=8$ the last two digits of the sum $N_{8}$ (and thus the number of interest to us) coincide with the last two digits of the number $10 S_{8}$, where $S_{8}=0^{8}+1^{8}+\ldots+9^{8}$. But from the written table of the last digits of the numbers $y^{4}$, and the equality $y^{4 k}=\left(y^{4}\right)^{k}$, it follows that the number $y^{4 k}$ (where $y$ is a digit) ends with the same digit as $y^{4}$. Therefore, for $a=8$ the last two digits of the number in question will be the same as for $a=4$, i.e., they will be the digits 30.
Note. It is not difficult to see that we will get the same result for all multiples of 4 values of $a$, i.e., for $a=4,8,12,16, \ldots$
|
30
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
74. How many zeros does the product of all integers from 1 to 100 inclusive end with?
In the future, we will use the following notation:
$$
1 \cdot 2 \cdot 3 \cdot 4 \ldots(n-1) \cdot n=n!
$$
(read as: $n$ factorial). Thus, the previous problem can be more succinctly stated as: how many zeros does the number 100! end with?
|
74. The number of bullets at the end of a number indicates how many times 10 is a factor in that number. The number 10 is equal to the product of $2 \cdot 5$; in the product of all integers from 1 to 100, the factor 2 appears in a higher power than the factor 5. Therefore, the product $1 \cdot 2 \cdot 3 \ldots 100$ is divisible by such a power of 10 (i.e., ends with such a number of zeros) as this product contains factors of 5. But up to 100, there are 20 numbers that are multiples of five, and four of them (25, 50, 75, and 100) are also multiples of 25, i.e., contain two factors of 5 each. Therefore, in the product $1 \cdot 2 \cdot 3 \ldots 100$, the number 5 appears as a factor 24 times; hence, there will be 24 zeros at the end of this product.
|
24
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
81. The square of an integer ends with four identical digits. Which ones?
|
81. A perfect square can only end in the digits 0, 1, 4, 9, 6, and 5. Furthermore, the square of any even number is clearly divisible by 4, while the square of any odd number gives a remainder of 1 when divided by 4 \(\left((2 k)^{2}=4 k^{2},(2 k+1)^{2}=4\left(k^{2}+k\right)+1\right)\); therefore, the square of no number can end in the digits 11, 99, 66, or 55 (numbers ending in two digits 11, 99, 66, or 55 give remainders of 3, 3, 2, and 3, respectively, when divided by 4). Finally, let's consider what remainders the square of an integer can give when divided by 16. Any integer can be represented in one of the following forms:
$$
8 k, 8 k \pm 1,8 k \pm 2,8 k \pm 3 \text { or } 8 k+4 \text {; }
$$
the squares of these numbers are of the form
$$
\begin{gathered}
16 \cdot\left(4 k^{2}\right), \quad 16\left(4 k^{2} \pm k\right)+1, \quad 16\left(4 k^{2} \pm 2 k\right)+4 \\
16\left(4 k^{2} \pm 3 k\right)+9 \quad \text { or } \quad 16\left(4 k^{2}+4 k+1\right) .
\end{gathered}
$$
Thus, we see that the square of an integer is either divisible by 16 or gives a remainder of 1, 4, or 9 when divided by 16. A number ending in the digits 4444 gives a remainder of 12 when divided by 16 and, therefore, cannot be a perfect square.
Therefore, if a perfect square ends in four identical digits, these digits must be four zeros (for example, \(100^{2}=10000\)).
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
86. a) Prove that the fraction $\frac{a^{3}+2 a}{a^{4}+3 a^{2}+1}$ is irreducible for any integer value of $a$.
b) Indicate all (natural) numbers by which the fraction $\frac{5 n+6}{8 n+7}$ can be reducible for integer $n$.
|
86. The fraction $\frac{a^{3}+2 a}{a^{4}+3 a^{2}+1}$ is reducible or irreducible simultaneously with the fraction $\frac{a^{4}+3 a^{2}+1}{a^{3}+2 a} \Rightarrow a+\frac{a^{2}+1}{a^{3}+2 a}$, or - simultaneously with the fraction $\frac{a^{2}+1}{a^{3}+2 a}$. The fraction $\frac{a^{2}+1}{a^{3}+2 a}$ is reducible or irreducible simultaneously with the fraction $\frac{a^{3}+2 a}{a^{2}+1}=a+\frac{a}{a^{2}+1}$, and - simultaneously with the fraction $\frac{a}{a^{2}+1} \cdot$ The fraction $\frac{a}{a^{2}+1}$ is reducible or irreducible simultaneously with the fraction $\frac{a^{2}+1}{a}=a+\frac{1}{a}$, and - simultaneously with the fraction $\frac{1}{a}$, which, for integer $a$, is clearly irreducible.
b) If the number $4=5 n+6$, as well as the number $3=8 n+7$, are divisible by the integer $d$, then $d$ also divides their difference $p=3-4=$ $=3 n+1$ and the difference $p_{1}=4-p=2 n+5$, as well as the differences $p_{2}=$ $=p-p_{1}=n-4 ; p_{3}=p_{1}-p_{2}=n+9 ; p_{4}=p_{3}-p_{2}=13$. Thus, $d$ must necessarily divide (the prime!) number 13, from which it is clear that $d$ can have only one value, 13. The fact that the value $d=13$ is possible is easily shown by example; for instance, if $n=4$, then the fraction $\frac{5 n+6}{8 n+7}=\frac{26}{39}$ is reducible by 13.
|
13
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
99. Find the smallest square that starts with six twos.
|
99. Since the number 222222 is not a perfect square, the decimal representation of the unknown number has the form $222222 a_{7} a_{8} \ldots a_{n}$, where $a_{7}, a_{8}, \ldots, a_{n}$ are some unknown digits.
First, assume that the number of digits $n$ of the unknown number is even: $n=2 k$. We will now extract the square root of this number according to the usual rules:
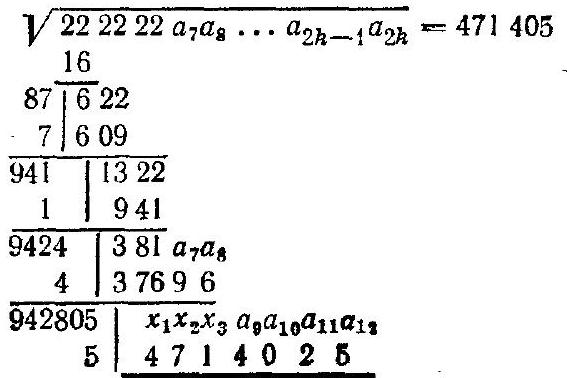
'The fifth digit of the result is 0, since $x_{1}$ can only be 4 or 5 and, therefore, less than 9; for the same reason, the sixth digit, if it is the last, is 5).
The remainder is zero if $a_{9}=4, a_{10}=0, a_{11}=2, a_{12}=5$; $x_{1}=4, x_{2}=7, x_{3}=1$, from which we easily deduce $a_{8}=6+1=7, a_{7}=(7+9)-10=6$. Thus, the smallest number with an even number of digits that satisfies the condition of the problem is $222222674025=471405^{2}$.
Similarly, consider the case when $n=2 k+1$ is odd:
$$
\begin{aligned}
& \sqrt{222222 a_{7} a_{5} a_{9} \ldots a_{2 k} a_{2 k+1}}=149071 \ldots \\
& 24 \left\lvert\, \frac{1}{122}\right. \\
& \frac{4 \mid 96}{289 \mid 2622} \\
& \frac{9 \mid 2601}{29807 \mid 21} 2 a_{7} a_{8} a_{8}
\end{aligned}
$$

Since the number formed by the digits $x_{1}, x_{2}$ is less than $33=$ ( $=119-86$ ) and not more than $43(=129-86)$, the sixth digit of the root is 1, and the process of extracting the root does not stop here but continues further. Therefore, the smallest number with an odd number of digits that satisfies the condition of the problem is at least thirteen digits, i.e., exceeds the number 222222674025. Thus, the number we are looking for is 222222674025.
|
222222674025
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.