problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
102. Find a four-digit number that, when divided by 131, gives a remainder of 112, and when divided by 132, gives a remainder of 98.
|
102. Let $N$ be the desired number. According to the problem, we have:
$$
N=131 k+112=132 l+98
$$
where $k$ and $l$ are positive integers. Since $N$ is a four-digit number, it is clear that:
$$
l=\frac{N-98}{132}<\frac{10000-98}{132} \leqslant 75
$$
Further, we have:
$$
131 k+112=132 l+98 ; \quad 131(k-l)=l-14
$$
From this, it is evident that if $k-l$ is not zero, then $l-14$ in absolute value exceeds 130, which is impossible if $l \leqslant 75$. Therefore, it must be that $k-l=0, k=l$, from which we immediately obtain:
$$
\begin{gathered}
l-14=0, k=l=14 \\
N=131 \cdot 14+112=(132 \cdot 14+98)=1946
\end{gathered}
$$
|
1946
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
103. a) Prove that the sum of all n-digit numbers $(n>2)$ is $494 \underbrace{99 \ldots 9}_{(n-3) \text { times }} 5 \underbrace{00 \ldots 0}_{(n-2) \text { times }}$ (thus, the sum of all three-digit numbers is 494550, and the sum of all six-digit numbers is 494999550000).
b) Find the sum of all four-digit even numbers that can be written using the digits $0,1,2,3,4,5$ (the same digit can be repeated in a number).
|
103. a) The $2n$-digit number given in the condition of the problem can be expressed as follows:
$$
\begin{gathered}
4 \cdot 10^{2n-1} + 9 \cdot 10^{2n-2} + 4 \cdot 10^{2n-3} + 9(10^{2n-4} + 10^{2n-5} + \cdots \\
\ldots + 10^n) + 5 \cdot 10^{n-1} + 5 \cdot 10^{n-2} = 4 \cdot 10^{2n-1} + 9 \cdot 10^{2n-2} + \\
+ 4 \cdot 10^{2n-3} + 9 \cdot 10^n \frac{10^{n-3} - 1}{9} + 5 \cdot 10^{n-1} + 5 \cdot 10^{n-2} = \\
-4 \cdot 10^{-2n-1} + 9 \cdot 10^{2n-2} + 5 \cdot 10^{2n-3} - 10^n + 5 \cdot 10^{n-1} \div \\
+ 5 \cdot 10^{n-2} = \frac{1}{2} \left(8 \cdot 10^{2n-1} + 18 \cdot 10^{2n-2} + 10 \cdot 10^{2n-3} - \right. \\
\left. - 2 \cdot 10^n + 10^n + 10^{n-1} \right) = \frac{1}{2} \left(9 \cdot 10^{2n-1} + 9 \cdot 10^{2n-2} - 9 \cdot 10^{n-1} \right) = \\
= \frac{\left( (10^n - 1) + 10^{n-1} \right) \cdot 9 \cdot 10^{n-1}}{2}
\end{gathered}
$$
But this is also equal to the sum of an arithmetic progression with a common difference of 1, the first term being $10^{n-1}$ and the last term being $10^n - 1$ (the number of terms in the progression is $10^n - 10^{n-1} = 8 \cdot 10^{n-1}$), which is the sum of all $n$-digit numbers.
b) The number of the considered numbers that start with a given digit $a$ (where $a$ can be 1, 2, 3, 4, or 5) is $6 \cdot 6 \cdot 3 = 108$ (because on the second and third places, any of the six digits $0, 1, 2, 3, 4, 5$ can stand, and on the third place, any of the three digits $0, 2, 4$, since only even numbers are considered). Therefore, the total sum of all thousands contained in all our numbers is $(1+2+3+4+5) \cdot 108 \cdot 1000 = 1620000$.
Similarly, the number of numbers in which a given digit stands on the second place is $5 \cdot 6 \cdot 3 = 90$, because on the first place, one of the five digits $1, 2, 3, 4,$ or $5$ can stand. Therefore, the total sum of all hundreds (after subtracting all thousands) contained in all our numbers is $(1+2+3+4+5) \cdot 90 \cdot 100 = 135000$.
In the same way, we find that the total sum of all tens is $(1+2+3+4+5) \cdot 90 \cdot 10 = 13500$ and, finally, the sum of units is $(2+4) \cdot 5 \cdot 6 \cdot 6 \cdot 1 = 1080$.
The desired sum is
$$
1620000 + 135000 + 13500 + 1080 = 1769580
$$
|
1769580
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
104. How many and which digits will be needed to write down all integers from 1 to 100000000 inclusive?
|
104. Let's first consider all integers from 0 to 99999999; for those numbers that have fewer than eight digits, we will pad them with leading zeros to make them eight-digit numbers. We will thus have 100000000 eight-digit numbers, which will require, obviously, 800000000 digits for their representation. In this case, each of the 10 digits will be used an equal number of times, since they are all equally valid (zero can stand in the first place just as any other digit). Therefore, each digit will be used 80000000 times.
Now let's count how many extra zeros (i.e., zeros added at the front of numbers with fewer than eight digits) there will be. There are nine single-digit numbers (excluding zero), 99 - 9 = 90 two-digit numbers, 999 - 99 = 900 three-digit numbers, and so on. Since we added seven zeros to the left of a single-digit number, six zeros to a two-digit number, and so on, the total number of extra zeros (excluding the first number 00000000, which was written as 00000000) will be
$7 \cdot 9 + 6 \cdot 90 + 5 \cdot 900 + 4 \cdot 9000 + 3 \cdot 90000 + 2 \cdot 900000 +$
$$
+1 \cdot 9000000 = 11111103,
$$
Now, if we add 1 to the left of the first number 00000000, we will get all integers from 1 to 100000000. We see that for writing these numbers, 80000000 twos, threes, and so on up to nines are required, 80000001 ones (one extra one was added to the left of the number 00000000), and $80000000 - 11111103 = 68888897$ zeros.
|
68888897
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
105. All integers are written in a row, starting from one. Determine which digit stands at the $206788-\mathrm{th}$ place.
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
105. There are nine single-digit numbers, $99-9=90$ two-digit numbers, $999-99=900$ three-digit numbers, and generally $9 \cdot 10^{n-1}$ $n$-digit numbers.
Single-digit numbers will occupy nine places in the sequence we have written, two-digit numbers $90 \cdot 2=180$ places, three-digit numbers $900 \cdot 3=2700$ places, four-digit numbers $9000 \cdot 4=36000$ places, and five-digit numbers $90000 \cdot 5=$ $\Leftarrow 450000$ places. From this, it is clear that the digit we are interested in will belong to a five-digit number.
Digits belonging to numbers with no more than four digits will have numbers from 1 to $9+180+2700+36000=38889$. To find out how many five-digit numbers will fit in the interval from the 38889th place to the 206788th, we need to divide the difference $206788-38889=167899$ by 5 (division with remainder):
$$
206788-38889=5 \cdot 33579+4
$$
Thus, the digit we are looking for will belong to the 33579th five-digit number, i.e., the number 43579 (since the first five-digit number is 10000). In this number, the digit we are interested in is in the 4th place. Therefore, the digit we are looking for is 7.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
107. Each of the integers from one to a billion inclusive is replaced by the sum of the digits of the number; single-digit numbers, of course, do not change, while the others decrease. Then each of the newly obtained numbers is again replaced by the sum of its digits, and so on until a billion single-digit numbers are obtained. Which numbers will be more among the resulting numbers - ones or twos?
|
107. It is a good fact to know that every positive integer $N$ gives the same remainder when divided by 9 as the sum of its digits. (This follows from the fact that the digit $a_{k}$ in the $(k+1)$-th position from the end in the decimal representation of $N$ represents the term $a_{k} \cdot 10^{k}$ in the expansion of $N$ in powers of ten; but $a_{k} \cdot 10^{k} = a_{k} \cdot (99 \ldots 9 + 1) = 99 \ldots 9 a_{h} + a_{h}$ gives the same remainder when divided by 9 as $a_{h}$.) From this, it follows that if the number $N$ gives a remainder $r \neq 0$ when divided by 9, then by repeatedly replacing the number with the sum of its digits, we will eventually arrive at a single-digit number $r$, and if $N$ is divisible by 9, we will arrive at the number 9. Thus, among our billion single-digit numbers, the ones will correspond to the numbers $1, 10, 19, 28, \ldots, 1000000000$, which give a remainder of 1 when divided by 9, and the twos will correspond to the numbers $2, 11, 20, 29, \ldots, 999999992$, which give a remainder of 2 when divided by 9. But the first set of numbers is obviously one more than the second set; therefore, we will get one more one than two.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
110. Find all ten-digit numbers such that the 1st digit of the number equals the number of zeros in its decimal representation, the 2nd digit - the number of ones, and so on up to the 10th digit, which equals the number of nines in the number's representation.
|
110. Let the desired number $X=\overline{a_{0} a_{1} a_{2} \ldots a_{9}}$ (where $a_{0}, a_{1}, \ldots, a_{9}$ are the digits of the number); in this case, $a_{0}$ is the number of zeros among the digits of $X$, $a_{1}$ is the number of ones, $a_{2}$ is the number of twos, and so on. Therefore, the sum of all the digits of $X$ is
$$
a_{0}+a_{1}+a_{2}+\ldots+a_{9}=a_{0} \cdot 0+a_{1} \cdot 1+a_{2} \cdot 2+\ldots+a_{9} \cdot 9
$$
from which we obtain
$$
a_{0}=a_{2}+2 a_{3}+3 a_{4}+4 a_{5}+5 a_{6}+6 a_{7}+7 a_{3}+8 a_{9}
$$
The equality $a_{0}=0$ is excluded by the conditions of the problem (otherwise the number $X$ would not be 10-digit; however, the condition $a_{0} \neq 0$ immediately follows from (*)); the equality $a_{0}=1$ leads to impossible values $a_{0}=a_{2}=1, a_{1}=8$ (since we should have 10 digits in total), all other digits are zeros; the equality $a_{0}=2$ is compatible only with (also impossible!) values $a_{0}=a_{2}=2, a_{1}=6$, all other digits are zeros, or $a_{0}=2, a_{3}=1, a_{1}=7$, all other digits are zeros. Let now $a_{0}=i>2$; we rewrite equality (*) as follows:
$$
a_{0}=i=a_{2}+2 a_{3}+\ldots+(i-1) a_{i}+\ldots+8 a_{9}
$$
(if $i=3$, then the terms $2 a_{3}$ and $(i-1) a_{i}$ coincide; if $i=9$, then $(i-1) a_{i}$ and $8 a_{9}$ coincide). In this case, $a_{i}$, the number of digits equal to $i$ in the number $X$, is non-zero (since $a_{0}=i$); on the other hand, (**) is impossible for $a_{i}>1$, so $a_{i}=1$. Therefore, (**) can be rewritten as:
$$
1=a_{2}+2 a_{3}+\ldots+(i-2) a_{i-1}+i a_{i+1}+\ldots+8 a_{9}, \quad(* * *)
$$
from which it immediately follows that $a_{2}=1$, and all digits of the number $X$ different from $a_{0}, a_{1}, a_{2}$ and $a_{i}$ are zero. But if $a_{2}=1$, then among the digits of the number $X$ there is a two, which, obviously, can only be the digit $a_{1}$. Thus, in the decimal representation of $X$, only the digits $a_{0}(=i), a_{1}=2, a_{2}=1$ and $a_{i}=1$ are non-zero, i.e., among the digits of $X$ there are $i$ zeros, 2 ones, 1 two, and 1 digit $i$, from which (since $X$ is 10-digit) $i=10-2-1-1=6$.
Thus, $X=6210001000$ (it is easy to check that this number indeed satisfies all the conditions of the problem).
|
6210001000
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
116. The distance from point $A$ to point $B$ is 899 km. Along the road connecting $A$ and $B$, there are kilometer markers indicating the distances to $A$ and to $B$ - the inscriptions on them look like this:
$$
0|999,1| 998,2|997, \ldots, 999| 0
$$
How many of these markers have only two different digits?
|
116. It is clear that if the numbers on the pole are $\overline{\lambda y z} \mid \overline{x_{1} y_{1} z_{i}}$ (where $x$, $\boldsymbol{y}, \ldots$ are digits), then $\overline{x_{1} y_{1} z_{1}}=999-x y z$ and, therefore, $z_{1}=9-z, y_{1}=$ $=9-y, x_{1}=9-x$. (If $x=9$ or $x=y=9$, then the digits $x_{1}=$ $=0$, or $x_{1}=y_{1}=0$ are not indicated on the pole.) From this, it immediately follows that if $x=y=z$ (and, therefore, $x_{1}=y_{1}=z_{1}=9-x$), then our conditions will be satisfied; this gives 10 poles satisfying the condition of the problem (corresponding to distances $0=000$, 11, $222, \ldots, 999$ km from point $A$). If the number $\overline{x y z}$ is written with two different digits, then these digits must be such that each of them complements the other to the number 9—in this case, the number $\overline{x_{1} y_{1} z_{1}}=9-x, 9-y \cdot 9-z$ will also be written with the same digits. Clearly, there are five such pairs of digits: $(0,9),(1,8),(2,7)$, $(3,6)$, and $(1,5)$; and there are six three-digit numbers written with two given digits $a$ and $b$: three of them are written with two digits $a$ and one digit $b$ (which can occupy any of the 3 available positions) and, similarly, three numbers are written with one digit $a$ and two digits $b$. Thus, we get another $5 \cdot 6=30$ distances satisfying the condition of the problem for the pole from point $A$; therefore, the total number of poles satisfying the formulated requirements is: $10+30=40$.
|
40
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
119. What is the greatest possible value of the ratio of a three-digit number to the sum of its digits?
|
119. Let \( N = \overline{a b} c \), where \( a, b, c \) are the digits of the number; it is clear that for "round" numbers \( N = 100, 200, \ldots, 900 \) we have \( \frac{N}{a+b+c} = 100 \). Furthermore, if the number \( N \) is not "round," then \( b+c > 0 \) and \( a+b+c \geqslant a+1 \), and since the leading digit of \( N \) is \( a \), we have \( N < (a+1) \cdot 100 \) and
\[
\frac{N}{a+b+c} < \frac{(a+1) \cdot 100}{a+1} = 100.
\]
Thus, the maximum value of the considered ratio is 100; this value is achieved only for "round" numbers.
Note. In the same way, it can be proven that the maximum value of the ratio of a \( k \)-digit number \( N = \overline{a_{k} a_{k-1} \ldots a_{1}} \) to the sum \( a_{k} + a_{k-1} + \ldots + a_{1} \) of its digits is \( 10^{k-1} \); this value is achieved only for "round" numbers, where the last \( k-1 \) digits are zeros.
|
100
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
150. a) Find a four-digit number that is a perfect square and such that its first two digits are equal to each other and the last two digits are also equal to each other.
b) A two-digit number, when added to the number formed by the same digits in reverse order, results in a perfect square. Find all such numbers.
|
150. a) Let $a$ be the first and $b$ the last digit of the number $N$ we are looking for. Then this number is equal to $1000 a + 100 a + 10 b + b = 1100 a + 11 b = 11(100 a + b)$. Since the number $N$ is a perfect square, it follows from its divisibility by 11 that it is also divisible by 121, i.e., $\frac{N}{11} = 100 a + b$ is divisible by 11. But
$$
100 a + b = 99 a + (a + b) = 11 \cdot 9 a + (a + b)
$$
Therefore, $a + b$ is divisible by 11. Since both $a$ and $b$ are no greater than 9 and $a$ is not equal to 0, we have $1 \leqslant a + b \leqslant 18$, and thus $a + b = 11$.
From this,
$$
\begin{aligned}
100 a + b & = 11 \cdot 9 a + 11 = 11(9 a + 1) \\
\frac{N}{121} & = \frac{100 a + b}{11} = 9 a + 1
\end{aligned}
$$
Since $N$ is a perfect square, $\frac{N}{121}$ is also a perfect square. But among the numbers of the form $9 a + 1$, where $a$ ranges from 1 to 9, only $9 \cdot 7 + 1 = 64$ is a perfect square. Therefore, $N = 121 \cdot 64 = 7744 = 88^2$.
b) Let $a$ be the tens digit of this number, and $b$ the units digit. Then the number is $10 a + b$, and the number written with the same digits in reverse order is $10 b + a$. According to the problem's condition, $10 a + b + 10 b + a = 11(a + b) = k^2$.
From this, it follows that $k^2$ is divisible by 11, so $a + b$ is also divisible by 11. Since $a + b \leqslant 18$, this is only possible if $a + b = 11, k^2 = 121$. Thus, the numbers we are looking for are
$$
29, 38, 47, 56, 65, 74, 83, 92 \text{. }
$$
|
7744
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
153. a) Find all three-digit numbers that are equal to the sum of the factorials of their digits.
b) Find all integers that are equal to the sum of the squares of their digits.
|
153. a) Let the hundreds, tens, and units digits of the desired number \( N \) be denoted by \( x, y \), and \( z \), respectively, so that \( N = 100x + 10y + z \). In this case, the condition of the problem gives
\[
100x + 10y + z = x! + y! + z!
\]
Note that \( 7! = 5040 \) is a four-digit number; therefore, no digit of the number \( N \) can exceed 6. Consequently, the number \( N \) itself does not exceed 700, from which it follows that no digit of \( N \) can exceed 5 (since \( 6! = 720 > 700 \)). At least one digit of the number \( N \) is 5, because even \( 3 \cdot 4! = 72 < 100 \), and \( N \) is a three-digit number. The digit \( x \) cannot be 5, since even \( 3 \cdot 5! = 360 < 500 \). It follows from this that \( x \) does not exceed 3. Furthermore, we can assert that \( x \) does not exceed 2, since even \( 3! + 2 \cdot 5! = 246 < 300 \). But the number 255 does not satisfy the condition of the problem, and if only one digit of the desired number is 5, then \( x \) cannot be greater than 1, because even \( 2! + 5! + 4! = 146 < 200 \). Moreover, since \( 1! + 5! + 4! = 145 < 150 \), we conclude that \( y \) cannot exceed 4; therefore, \( z = 5 \), since at least one digit of the number \( N \) must be 5. Thus, we have \( x = 1 \), \( 4 \geqslant y \geqslant 0 \), and \( z = 5 \); this allows us to easily find the only solution to the problem: \( N = 145 \).
b) The desired number \( N \) cannot have more than three digits, since even \( 4 \cdot 9^2 = 324 \) is a three-digit number. Therefore, we can write \( N = 100x + 10y + z \), where \( x, y, z \) are the digits of the number; here, \( x \) or even \( x \) and \( y \) simultaneously can be zero.
From the condition of the problem, we have \( 100x + 10y + z = x^2 + y^2 + z^2 \), from which
\[
(100 - x)x + (10 - y)y = z(z - 1)
\]
From the last equation, it follows first of all that \( x = 0 \), otherwise the number on the left side of the equation is not less than \( 90 \) (since \( x \geqslant 1 \), \( 100 - x \geqslant 90 \), \( (10 - y)y \geqslant 0 \)), and the number on the right side is not more than \( 9 \cdot 8 = 72 \) (since \( z \leqslant 9 \)). Therefore, the equation (") has the form \( (10 - y)y = z(z - 1) \). It is easy to check that this last equation is not satisfied for any positive integers \( x \) and \( y \) not exceeding 9, unless \( y \neq 0 \). If \( y = 0 \), then we have the only obvious solution \( z = 1 \).
Thus, the condition of the problem is satisfied by the only number \( N = 1 \).
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
169. In a chess tournament, two 7th-grade students and a certain number of 8th-grade students participated. Each participant played one game with every other participant. The two 7th-graders together scored 8 points, and all the 8th-graders scored the same number of points (in the tournament, each participant earns 1 point for a win and $1 / 2$ point for a draw). How many 8th-graders participated in the tournament?
|
169. Let $n$ be the number of eighth-graders, and $m$ be the number of points earned by each of them. In this case, the number of points scored by all participants in the tournament is $m n + 8$. This number is equal to the number of games played. Since the number of participants in the tournament is $n + 2$ and each played once with each of the $n + 1$ others, they played a total of $\frac{(n+2)(n+1)}{2}$ games (in the product $(n+2)(n+1)$, each game is counted twice). Thus, we have:
$$
m n + 8 = \frac{(n+2)(n+1)}{2}
$$
or, after some transformations,
$$
n(n + 3 - 2m) = 14
$$
Here, $n$ is an integer; the number in parentheses is also an integer (since $m$ is either an integer or a fraction with a denominator of 2).
Since $n$ is a divisor of 14, $n$ can be one of the numbers $1, 2, 7, 14$. The values $n = 1$ and $n = 2$ should be discarded, as in these cases, the total number of participants does not exceed 4, and two seventh-graders could not have scored a total of 8 points.
This leaves $n = 7$ and $n = 14$.
If $n = 7$, then $7(7 + 3 - 2m) = 14; m = 4$.
If $n = 14$, then $14(14 + 3 - 2m) = 14; m = 8$.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
188. Among the first 100000001 Fibonacci numbers (see problem 185), is there a number that ends with four zeros?
|
188. Let's leave in each member of the Fibonacci series, written with five or more digits, only the last four digits. We will get a sequence of numbers, each of which is less than $10^{4}$. Let's denote by $a_{k}$ the member of this sequence standing at the $k$-th place. Note that if we know $a_{k+1}$ and $a_{k}$, then we can calculate $a_{k-1}$, because the $(k-1)$-th member of the Fibonacci series is equal to the difference between the $(k+1)$-th and $k$-th members, and the last four digits of the difference can be determined by the last four digits of the minuend and subtrahend. From this it follows that if for some numbers $k$ and $n$ it turns out that $a_{k}=a_{n+k}, a_{k+1}=a_{n+k+1}$, then $a_{k-1}=a_{n+k-1}, a_{k-2}=a_{n+k-2}, \ldots, a_{1}=a_{n+1}$. But since $a_{1}=0$, this will mean that $a_{n+1}=0$, i.e., that in the Fibonacci series, the $(n+1)$-th place is occupied by a number ending in four zeros.
It remains to show that among $10^{8}+1$ pairs
| $a_{1}$, | | $a_{2}$, |
| :---: | :---: | :---: |
| $a_{2}$, | | $a_{3}$, |
| $\cdots . . . .$. | | |
| $a_{10^{8}}$ | | $a_{10^{8}+1}$, |
| $a_{10^{8}+1}$, | | $a_{10^{8}+2}$ |
there will be at least two identical ones. But this will certainly be the case, because all numbers $a_{1}, a_{2}, a_{3}, \ldots, a_{10^{8}+2}$ do not exceed $10^{4}$, and from $10^{4}$ numbers $0,1,2,3,4, \ldots, 9999$ only $10^{4} \cdot 10^{4}=10^{8}$ different pairs can be formed (because the first number can take $10^{4}$ different values and the second number can take $10^{4}$ different values).
Note. It is even possible to precisely indicate the first number in the Fibonacci series ending in four zeros; the number of this number is 7501 (see problem 174 of the book [5] and the corollaries from it).
|
7501
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
195. Let's consider the following sequence of sets of (natural) numbers. The first set $I_{0}$ consists of
two ones 1,1. Then we insert their sum $1+1=2$ between these numbers; we get the set $I_{1}: 1,2,1$. Next, between every two numbers in the set $I_{1}$, we insert the sum of these numbers; we get the set $I_{2}: 1,3,2,3,1 ;$ then, proceeding in the same way with the set $I_{2}$, we arrive at the set $I_{3}: 1,4,3,5,2,5,3,4,1$, and so on. How many times will the number 1973 appear in the millionth set $I_{1000000}$?
|
195. First of all, note that each of the sets $I_{0}, I_{1}$, $I_{2}, \ldots$ is obtained from the preceding one by adding a certain number of new numbers; at the same time, all the numbers that were previously present are retained in the new set. It is easy to see, furthermore, that all the new numbers appearing in the set $I_{n}$ will be greater than $n$; therefore, the number 1973 does not appear in sets with numbers greater than 1973, and all such sets contain the same number of 1973s. Let us now prove that a fixed pair of numbers $a, b$ (where $a$ stands, say, to the left of $b$; thus, $a, b$ and $b, a$ are considered different pairs!) will appear in the sequence $I_{0}, I_{1}$, $I_{2}, \ldots, I_{n}, \ldots$ of sets exactly once if the numbers $a$ and $b$ are coprime, and will not appear at all otherwise. This statement is obvious for pairs of numbers $a, b$, the largest of which does not exceed 2 (there are only two such pairs: 1,2 and 2,1 - and each of these pairs appears only once, namely, in the sequence $I_{1}: 1,2,1$); let us prove it by mathematical induction. Suppose that our statement has already been proven for all such pairs of numbers $a, b$ for which $\max [a, b] \leq 1$. "But from this it immediately follows that the pair of numbers $a, b$ appears in our sets once if $a$ and $b$ are coprime, and does not appear at all otherwise: for the numbers $a$ and $b$ are coprime if and only if the numbers $a$ and $b-\alpha$ are coprime.
Now it is clear that, since the number 1973 is prime (check this!), each of the pairs of numbers 1,1972; 2,1971; 3,1970; ...; 1971,2; 1972,1 will appear in our sets exactly once - since all these are pairs of coprime numbers. And from this it follows that the number 1973 appears in the sets $I_{n}$ with numbers $n>1973$ (in particular, in the set $I_{1}$ 000 000) exactly 1972 times (this number is equal to the number of pairs 1,1972; 2,1971; ...; 1972,1).
Note. From the solution of the problem, it also follows that any natural number $N$ appears in the sets $I_{n}$ (where $n > N$) exactly $\varphi(N)$ times, where $\varphi(N)$ is the number of numbers less than $N$ and coprime with $N$; regarding the calculation (from the number $N$) of the value $\varphi(N)$, see the Note to problem 341 (pp. 71-72).
|
1972
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
200. Let $t$ be an arbitrary positive number; the number of irreducible fractions $\frac{p}{q}$, where the numerator $p$ and the denominator $q$ do not exceed $t$, is denoted by $d(t)$,
## What is the sum
$-S=d\left(\frac{100}{1}\right)+d\left(\frac{100}{2}\right)+d\left(\frac{100}{3}\right)+\ldots+d\left(\frac{100}{99}\right)+d\left(\frac{100}{100}\right) ?$
|
200. To each irreducible fraction $\frac{p}{q}$, where
$$
0<p \leqslant 100, \quad 0<q \leqslant 100
$$
we associate a point $M$ with coordinates $p$, $q$; the inequalities ( ${ }^{*}$ ) indicate that the point $M$ is located inside the shaded square $\mathscr{K}=O A C B$ bounded by the coordinate axes and the lines $x=100$ and $y=100$ (or, in the extreme case, $M$ belongs to the side $A C$ or the side $B C$ of the square $\mathscr{K}$ ), and the irreducibility of the fraction $\frac{p}{q}$ means that there are no other "integer" points (points with integer coordinates) on the segment $O M$ (indeed, the equalities $p=k p_{1}, q_{1}=k q_{1}$, indicating that the fraction $\frac{p}{q}$ can be reduced by $k$, mean that the segment $O M$ also contains the integer point $M_{1}\left(p_{1} q_{1}\right)$). In this case, if the segment $O P$ cut out by the square $\mathscr{K}$ on a line $l$ passing through $O$ contains $n$ integer points ( $p_{0}, q_{0}$ ), $\left(2 p_{0}, 2 q_{0}\right),\left(3 p_{0}, 3 q_{0}\right), \ldots,\left(n p_{0}, n q_{0}\right)$ (where $M_{0}\left(p_{0}, q_{0}\right)$ is the closest to $O$ of these points), then (since $n p_{0} \leqslant 100, n q_{0} \leqslant 100$ ) we have $p_{0} \leqslant \frac{100}{n}$ $\left(<\frac{100}{n-1}<\frac{100}{n-2}<\ldots<\frac{100}{1}\right)$ and $q_{0} \leqslant \frac{100}{n}\left(<\frac{100}{n-1}<\frac{100}{n-2}<\ldots<\frac{100}{1}\right)$ and, thus, the irreducible fraction $\frac{p_{0}}{q_{0}}$ is counted in the terms $d\left(\frac{100}{1}\right)$,
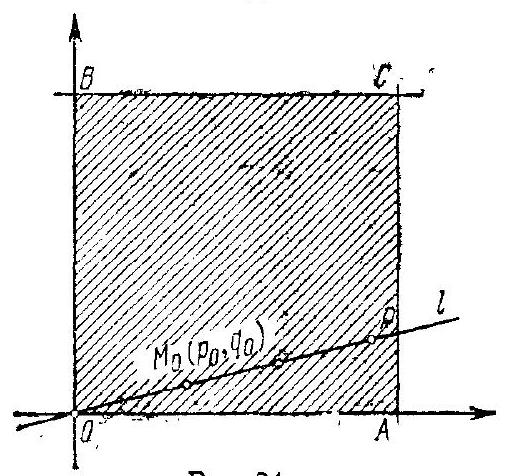
Fig. 24.
$d\left(\frac{100}{2}\right), \ldots, d\left(\frac{100}{n}\right)$ of the sum $S$, i.e., it is counted $n$ times in this sum (while the reducible fractions $\frac{2 p_{0}}{2 q_{0}}, \frac{3 p_{0}}{3 q_{0}}, \ldots, \frac{n p_{0}}{n q_{0}}$ are, of course, not counted in the sum $S$ at all). Thus, the contribution of the fraction $\frac{p_{0}}{q_{0}}$ to the sum $S$ is $n$, i.e., it is equal to the number of integer points on the segment $O P$.
From what has been proven, it follows that the total number of fractions counted in the sum $S$ - i.e., the numerical value of the sum $S$ - is equal to the total number of integer points in the square $\mathscr{K}$, i.e., $S=100 \cdot 100=10000$.
|
10000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
211. How many digits does the number $2^{100}$ have?
|
211. It is easy to check that $2^{10}=1024$; thus, $2^{100}=$ $=1024^{10}$. Since $1000^{10}=10^{30}$ represents a number consisting of a one followed by 30 zeros, and $1024^{10}>1000^{10}$, the number $2^{100}=$ $=1024^{10}$ cannot have fewer than 31 digits. On the other hand,
$$
\begin{aligned}
\frac{1024^{10}}{1000^{10}}<\left(\frac{1025}{1000}\right)^{10} & =\left(\frac{41}{40}\right)^{10}= \\
& =\frac{41}{40} \cdot \frac{41}{40} \cdot \frac{41}{40} \cdot \frac{41}{40} \cdot \frac{41}{40} \cdot \frac{41}{40} \cdot \frac{41}{40} \cdot \frac{41}{40} \cdot \frac{41}{40} \cdot \frac{41}{40}< \\
& <\frac{41}{40} \cdot \frac{40}{39} \cdot \frac{39}{38} \cdot \frac{38}{37} \cdot \frac{37}{36} \cdot \frac{36}{35} \cdot \frac{35}{34} \cdot \frac{34}{33} \cdot \frac{33}{32} \cdot \frac{32}{31}=\frac{41}{31}<10
\end{aligned}
$$
since
$$
\begin{gathered}
\frac{41}{40}<\frac{40}{39}<\frac{39}{38} \ldots, \text { and so on. } \\
\left(\text { because } \frac{41}{40}=1+\frac{1}{40} ; \frac{40}{39}=1+\frac{1}{39}, \text { and so on. }\right) .
\end{gathered}
$$
Thus,
$$
2^{100}=1024^{10}<10 \cdot 1000^{10}
$$
from which it follows that $2^{100}$ contains fewer than 32 digits. Therefore, the number $2^{100}$ consists of 31 digits.
Note. This problem is very easy to solve using logarithms: since $\log 2=0.30103$, then $\log 2^{100}=$ $=100 \log 2=30.103$ and, consequently, the number $2^{100}$ has 31 digits. The point of the problem is to obtain this result without using logarithms.
|
31
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
229*. Find the integer part of the number
$$
\frac{1}{\sqrt[3]{4}}+\frac{1}{\sqrt[3]{5}}+\frac{1}{\sqrt[3]{6}}+\ldots+\frac{1}{\sqrt[3]{1000000}}
$$
|
229. First, note that from the comparison of two expressions
$$
\left(1+\frac{1}{n}\right)^{2}=1+2 \frac{1}{n}+\frac{1}{n^{2}}
$$
and
$$
\left(1+\frac{2}{3} \frac{1}{n}\right)^{3}=1+2 \frac{1}{n}+\frac{4}{3} \frac{1}{n^{2}}+\frac{8}{27} \frac{1}{n^{3}}
$$
it follows that for each positive integer $n$
$$
\left(1+\frac{2}{3} \frac{1}{n}\right)^{3}>\left(1+\frac{1}{n}\right)^{2}
$$
From this, we have: $1+\frac{2}{3} \frac{1}{n}>\left(1+\frac{1}{n}\right)^{\frac{2}{3}}$. Multiplying the last inequality by $n^{\frac{2}{3}}$, we get: $n^{\frac{2}{3}}+\frac{2}{3} n^{-\frac{1}{3}}>(n+1)^{\frac{2}{3}}$ and finally
$$
\frac{1}{\sqrt[3]{n}}>\frac{3}{2}\left[\sqrt[3]{(n+1)^{2}}-\sqrt[3]{n^{2}}\right]
$$
Similarly,
$$
\begin{array}{r}
\left(1-\frac{2}{3} \frac{1}{n}\right)^{3}=1-2 \frac{1}{n}+\frac{4}{3} \frac{1}{n^{2}}-\frac{8}{27} \frac{1}{n^{3}}>1-2 \frac{1}{n}+\frac{1}{n^{2}}= \\
=\left(1-\frac{1}{n}\right)^{2}
\end{array}
$$
(because $\frac{1}{3} \frac{1}{n^{2}}-\frac{8}{27} \frac{1}{n^{3}}>\frac{1}{3} \frac{1}{n^{2}}-\frac{1}{3} \frac{1}{n^{3}} \geqslant 0$), from which it follows
$$
\begin{aligned}
1-\frac{2}{3} \frac{1}{n}> & \left(1-\frac{1}{n}\right)^{\frac{2}{3}}, \quad n^{\frac{2}{3}}-\frac{2}{3} n^{-\frac{1}{3}}>(n-1)^{\frac{2}{3}} \\
& \frac{1}{\sqrt[3]{n}} \\
& >\frac{3}{2}\left[\left(\sqrt[3]{5^{2}}-\sqrt[3]{4^{2}}\right)+\left(\sqrt[3]{6^{2}}-\sqrt[3]{5^{2}}\right)+\ldots\right. \\
& \left.\quad \cdots+\left(\sqrt[3]{1000001^{2}}-\sqrt[3]{1000000^{2}}\right)\right]= \\
& =\frac{3}{2}(\sqrt[3]{1000002000001}-\sqrt[3]{16})>\frac{3}{2} \cdot 10000-\sqrt[3]{54}>
\end{aligned}
$$
$$
>15000-4=14996 .
$$
On the other hand,
$$
\begin{aligned}
& \frac{1}{\sqrt[3]{4}}+\frac{1}{\sqrt[3]{5}}+\ldots+\frac{1}{\sqrt[3]{1000000}}< \\
& <\frac{3}{2}\left[\left(\sqrt[3]{4^{2}}-\sqrt[3]{3^{2}}\right)+\left(\sqrt[3]{5^{2}}-\sqrt[3]{4^{2}}\right)+\ldots\right. \\
& \left.\quad \cdots+\left(\sqrt[3]{1000000^{2}}-\sqrt[3]{999999^{2}}\right)\right]= \\
& \quad=\frac{3}{2}(\sqrt[3]{1000000000000}-\sqrt[3]{9}) .<\frac{3}{2}(10000-2)=14997
\end{aligned}
$$
Thus, the integer part of the sum $\frac{1}{\sqrt[3]{4}}+\frac{1}{\sqrt[3]{5}}+\ldots+\frac{1}{\sqrt[3]{1000000}}$ is 14996.
|
14996
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
232. Prove that if in the sum
$$
1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\ldots+\frac{1}{n}
$$
all terms where the denominator contains the digit 9 are removed, then the sum of the remaining terms for any $n$ will be less than 80.
|
232. Let $n_{k}$ denote the number of unstruck terms between $\frac{1}{10^{k}}$ and $\frac{1}{10^{k+1}}$, including $\frac{1}{10^{k}}$ but not $\frac{1}{10^{k+1}}$. If the term $-\frac{1}{q}$, located between $\frac{1}{10^{h-1}}$ and $\frac{1}{10^{h}}$, is not struck out, then among the terms $\frac{1}{10 q}, \frac{1}{10 q+1}, \frac{1}{10 q+2}, \ldots, \frac{1}{10 q+8}, \frac{1}{10 q+9}$, located between $\frac{1}{10^{k}}$ and $\frac{1}{10^{k+1}}$, only the last one will be struck out; if the term $\frac{1}{q}$ was struck out, then all terms $\frac{1}{10 q}, \frac{1}{10 q+1}, \ldots, \frac{1}{10 q+8}$, $\frac{1}{10 q+9}$ will also be struck out. From this, it follows that
$$
n_{k}=9 n_{k-1}
$$
Since $n_{0}=8$ (from the terms $1, \frac{1}{2}, \frac{1}{3}, \ldots, \frac{1}{8}, \frac{1}{9}$, only $\frac{1}{9}$ is struck out), then
$$
n_{1}=8 \cdot 9=72, \quad n_{2}=8 \cdot 9^{2}, \ldots, n_{k}=8 \cdot 9^{k}
$$
Now, let in the sum $1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{n}$ the number $n < 10^{m+1}$. Extend it to the sum $1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{10^{m+1}-1}$, strike out the terms whose denominators contain the digit 9, and group the remaining terms:
$$
\begin{aligned}
& \left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{8}\right)+ \\
& \quad+\left(\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+\ldots+\frac{1}{18}+\frac{1}{20}+\ldots+\frac{1}{88}\right)+ \\
& +\left(\frac{1}{100}+\frac{1}{101}+\ldots+\frac{1}{888}\right)+\ldots+\left(\frac{1}{10^{m}}+\ldots+\underbrace{\frac{1}{88 \ldots 8}}_{(m+1) \text{ digits}}\right)< \\
& \quad<1 \cdot n_{0}+\frac{1}{10} \cdot n_{1}+\frac{1}{100} \cdot n_{2}+\ldots+\frac{1}{10^{m-1}} \cdot n_{m-1}+\frac{1}{10^{m}} \cdot n_{m}
\end{aligned}
$$
since in each group, the product of the largest term in the group and the number of terms in the group is used. Continue this estimation further:
$$
\begin{gathered}
1 \cdot n_{0}+\frac{1}{10} \cdot n_{1}+\frac{1}{100} \cdot n_{2}+\ldots+\frac{1}{10^{m-1}} \cdot n_{m-1}+\frac{1}{10^{m}} \cdot n_{m}= \\
=8\left(1+\frac{9}{10}+\frac{9^{2}}{10^{2}}+\ldots+\frac{9^{m-1}}{10^{m-1}}+\frac{9^{m}}{10^{m}}\right)= \\
=8 \cdot \frac{1-\frac{9^{m+1}}{10^{m+1}}}{1-\frac{9}{10}}<8 \cdot \frac{1}{1-\frac{9}{10}}=8 \cdot 10=80
\end{gathered}
$$
Thus, the statement of the problem is proved.
|
80
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
256. Let all numbers $a_{1}, a_{2}, \ldots, a_{n}$ (where $n \geqslant 2$) be positive; how many real solutions does the system of equations have:
$$
x_{1} x_{2}=a_{1}, x_{2} x_{2}=a_{2}, \ldots, x_{n-1} x_{n}=a_{n-1}, x_{n} x_{1}=a_{n} ?
$$
|
256. Let's consider two cases separately.
$1^{\circ} . n$ is even. By multiplying the "odd" (i.e., $1$-st, $3$-rd, ..., $(n-1)$-th) and "even" equations of our system, we get:
$$
x_{1} x_{2} x_{3} \ldots x_{n}=a_{1} a_{3} a_{5} \ldots a_{n-1} \text { and } x_{1} x_{2} x_{3} \ldots x_{n}=a_{2} a_{4} a_{6} \ldots a_{n}
$$
from which it is clear that if $a_{1} a_{3} a_{5} \ldots a_{n-1} \neq a_{2} a_{4} a_{6} \ldots a_{n}$, the system has no solutions. If, however, $a_{1} a_{3} a_{5} \ldots a_{n-1}=a_{2} a_{4} a_{6} \ldots a_{n}$, then by taking any value for $x_{1}$ (certainly different from 0), we can subsequently find from the 1-st, 2-nd, ..., $(n-1)$-th equations of the system:
$$
x_{2}=\frac{a_{1}}{x_{1}}, \quad x_{3}=\frac{a_{2}}{x_{2}}, \ldots, \quad x_{n}=\frac{a_{n-1}}{x_{n-1}}
$$
Substituting all these values into the last equation shows that it is also satisfied.
$2^{\circ} . n$ is odd. Dividing the product of the "odd" (1-st, 3-rd, ..., $n$-th) equations by the product of the "even" equations, we get:
$$
x_{1}^{2}=\frac{a_{1} a_{3} a_{5} \ldots a_{n}}{a_{2} a_{4} \ldots a_{n-1}}, \quad \text { hence } x_{1}= \pm \sqrt{\frac{a_{1} a_{3} a_{5} \ldots a_{n}}{a_{2} a_{4} a_{6} \ldots a_{n-1}}}
$$
(we recall that all $a_{i}$ are positive). Then from the 1-st, 2-nd, ..., $(n-1)$-th equations, we sequentially find:
$$
x_{2}=\frac{a_{1}}{x_{1}}, \quad x_{3}=\frac{a_{2}}{x_{2}}, \ldots, \quad x_{n}=\frac{a_{n-1}}{x_{n-1}}
$$
Verification shows that, due to (*), the last equation of the system is also satisfied.
Answer: 0, if $n$ is even and $a_{1} a_{3} \ldots a_{n-1} \neq a_{2} a_{4} \ldots a_{n}$; infinitely many, if $n$ is even and $a_{1} a_{3} \ldots a_{n-1}=a_{2} a_{4} \ldots a_{n}$; 2, if $n$ is odd.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
257. a) How many roots does the equation
$$
\sin x=\frac{x}{100} ?
$$
b) How many roots does the equation
$$
\sin x=\lg x ?
$$
|
257. a) First of all, note that if $x_{0}$ is a root of the equation, then $-x_{0}$ is also a root. Therefore, the number of negative roots is the same as the number of positive roots. Furthermore, the number 0 is a root of the equation. Thus, it is sufficient to find the number of positive roots. Now, let's note that if $\frac{x}{100}=\sin x$, then
$$
|x|=100|\sin x| \leqslant 100 \cdot 1=100
$$
We obtain that the root of the equation cannot have an absolute value greater than 100.
Divide the segment of the $O x$ axis from $x=0$ to $x=100$ into segments of length $2 \pi$ (the last segment may be shorter) and count the number of roots of our equation on each of these segments. Refer to Fig. 29.
On the first segment (from 0 to $2 \pi$), there is one positive root (and one root zero), on each subsequent segment, except the last one, there are two roots. To determine the number of roots on the last segment, let's estimate its size: $\frac{100}{2 \pi}$ is obviously between 15 and $16\left(\frac{100}{15}=6.66 \ldots>2 \pi ; \quad \frac{100}{16}=6.255>\pi \right)$; therefore, on this segment, a complete positive half-wave of the sine wave fits and, thus, there are also two roots on it.
Thus, we have $1+14 \cdot 2+2=31$ positive roots of our equation. There are as many negative roots, and one root is zero.
Finally, the total number of roots is $31 \cdot 2+1=63$.

Fig. 29.
b) The solution to this problem is analogous to the solution of part a). First of all, it is obvious that if $\sin x=\lg x$, then $x \leqslant 10$ (otherwise, the left side of our equality is no more than 1, while the right side is greater). Since $2 \cdot 2 \pi>10$, on the segment of the $O x$ axis from $x=0$ to $x=10$, one complete wave of the sine curve $y=\sin x$ and part of the next wave fit (Fig. 30). The graph of $y=\lg x$,
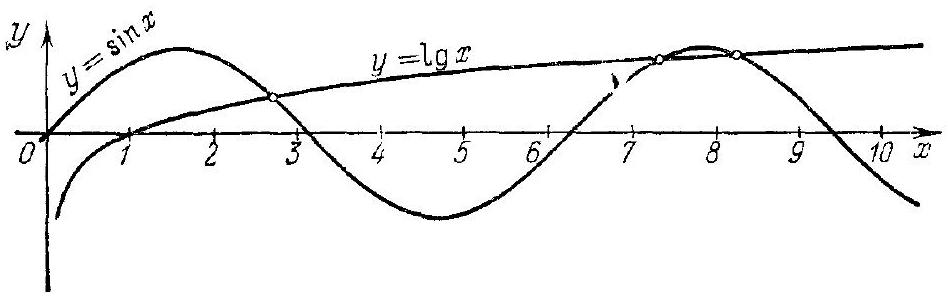
Fig. 30.
obviously intersects the first wave of the sine curve at one point. Further, since $2 \pi+\frac{\pi}{2} \lg x$ and, thus, the graph of $y=\lg x$ intersects the first half of the second positive half-wave; since $\lg x=1>\sin x$ at the point $x=10$, it must intersect the second half of this half-wave as well. Thus, we conclude that the equation $\sin x=\lg x$ has a total of three roots.
|
63
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
299. When dividing the polynomial $x^{1051}-1$ by $x^{4}+x^{3}+2 x^{2}+x+1$, a quotient and a remainder are obtained. Find the coefficient of $x^{14}$ in the quotient.
|
299. The polynomial $x^{4}+x^{8}+2 x^{2}+x+1$ can be factored; it equals $\left(x^{2}+1\right)\left(x^{2}+x+1\right)$. From this, it is easy to see that this polynomial is a divisor of the polynomial
$$
x^{12}-1=\left(x^{6}-1\right)\left(x^{6}+1\right)=\left(x^{3}-1\right)\left(x^{3}+1\right)\left(x^{2}+1\right)\left(x^{4}-x^{2}+1\right)
$$
specifically:
$$
\begin{aligned}
x^{4}+x^{3}+2 x^{2}+x+1= & \frac{x^{12}-1}{(x-1)\left(x^{3}+1\right)\left(x^{4}-x^{2}+1\right)}= \\
& =\frac{x^{12}-1}{x^{3}-x^{7}-x^{6}+2 x^{5}-2 x^{3}+x^{2}+x-1}
\end{aligned}
$$
Dividing $x^{1951}-1$ by $x^{4}+x^{3}+2 x^{2}+x+1$ is the same as dividing $x^{1951}-1$ by $x^{12}-1$, and then multiplying the result by $x^{8}-x^{7}-x^{6}+2 x^{5}-2 x^{3}+x^{2}+x-1$. But it is easy to see that
$$
\frac{x^{1951}-1}{x^{12}-1}=x^{1939}+x^{1927}+x^{1915}+x^{1903}+\ldots+x^{19}+x^{7}+\frac{x^{7}-1}{x^{12}-1}
$$
(it is easy to verify this by performing polynomial division or by noting that $x^{1951}-1=x^{7}\left[\left(x^{12}\right)^{162}-1\right]+x^{7}-1$ and using the known formula for dividing the difference of even powers of two monomials by the difference of their bases). From this, it follows that the desired coefficient coincides with the coefficient of $x^{14}$ in the product
$$
\begin{aligned}
\left(x^{1939}+x^{1927}+\ldots+x^{31}+\right. & \left.x^{19}+x^{7}+\frac{x^{7}-1}{x^{12}-1}\right) \times \\
& \times\left(x^{8}-x^{7}-x^{6}+2 x^{5}-2 x^{3}+x^{2}+x-1\right)
\end{aligned}
$$
which is equal to -1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
53. Prove that for any convex polyhedron with a sufficiently large number of faces, at least one face has no fewer than six neighbors. Find the minimum number $N$ such that for any convex polyhedron with a number of faces not less than $N$, this statement is true.
|
53. Let a certain convex polyhedron $W$ have the number of neighbors of each face less than six, i.e., not exceeding five.
It is easy to see that in each vertex of such a polyhedron, no more than five edges (and thus faces) can meet. To show this, consider any face of the polyhedral angle. This face has at least three sides. Two of these sides, adjacent to the vertex of the considered angle, are adjacent to the faces of this angle, and the others are adjacent to other faces. If six or more edges met at the vertex of the polyhedral angle, then with our face, there would be five or more faces of the angle and at least one more face, i.e.,
the number of its neighbors would be at least six, which contradicts the made assumption. We will show that if in some vertices of the polyhedron $W$ more than three edges meet, then $W$ can be replaced by a polyhedron $W_{1}$, in which exactly three edges meet at each vertex and the number of neighbors of each face is also no more than five. For this, we will cut off all vertices where four or more edges meet with planes, so that the cutting planes intersect only the faces of the corresponding angle (Fig. 108). In this process, new faces will appear, which, according to the above remark, will have four or five sides. Since all newly formed polyhedral angles will be trihedral, the new faces will have no more than five neighbors. The number of neighbors of each face can only decrease. Indeed, if in one of the vertices of a face of the polyhedron $W$ four or five faces met, then only two of them could share a common edge with this face, consequently, at least one face from the number of faces meeting at this vertex was adjacent to the first face only at the vertex. After cutting, this face (or several such faces) ceased to be a neighbor, while one (and only one) new face became adjacent. Thus, the number of neighbors of the old faces did not increase.
Thus, we have transitioned from the polyhedron $W$ to the polyhedron $W_{1}$, where the number of neighbors of each face did not increase, the number of faces only increased, and in each vertex of $W_{1}$, three edges meet.
Let $\mathscr{B}$, $\mathscr{P}$, and $\mathscr{F}$ be the number of vertices, edges, and faces of the polyhedron $W_{1}$. Since three edges meet at each vertex and each edge has ends in two vertices, we have
$$
\mathscr{P} = \frac{3}{2} \mathscr{B}
$$
By assumption, each face of the polyhedron $W$ had no more than five neighbors, so each face of $W_{1}$ also has no more than five neighbors and, consequently, no more than five vertices. Therefore, the sum of the number of vertices of all faces does not exceed $5 \mathscr{F}$. Since each vertex of the polyhedron is counted three times, we have the inequality
$$
\mathscr{B} \leqslant \frac{5}{3} \mathscr{F}
$$
Now, let's use Euler's theorem, which states that $\mathscr{B} - \mathscr{P} + \mathscr{F} = 2$. Considering the relations (*) and (**), we get sequentially $\mathscr{B} - \frac{3}{2} \mathscr{B} + \mathscr{F} = 2$ or $\mathscr{F} = \frac{\mathscr{B}}{2} + 2$ and, further, $\mathscr{F} \leqslant \frac{5}{6} \mathscr{B} + 2$, from which
$$
\mathscr{F} \leqslant 12 \text{. }
$$
Thus, the number of faces of the polyhedron $W_{1}$, and therefore of $W$, does not exceed 12, i.e., any polyhedron, each face of which has no more than five neighbors, contains no more than 12 faces. At the same time, a dodecahedron has exactly 12 faces, and each of them has five neighbors. Therefore, the desired number $N$ is 12.
|
12
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
85. The diagonals of a convex 17-gon, drawn from one vertex, divide it into 15 triangles. Can a convex 17-gon be cut into 14 triangles?
What about a non-convex 17-gon? What is the smallest number of triangles into which a 17-gon can be cut?
|
85. Each of the angles of a convex polygon is less than $2 d$, so the vertices cannot lie on the sides of the triangles of the partition. When a convex polygon is divided into triangles (not necessarily by diagonals), all the angles of the polygon will be divided into parts, which will
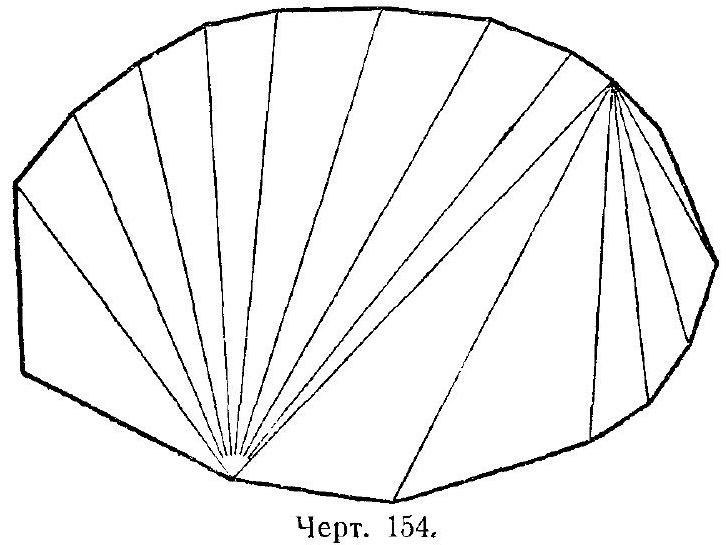
serve as angles of the triangles of the partition (Fig. 154). It follows that the sum of the angles of all the triangles of the partition must be no less than the sum of the angles of the polygon. But the sum of the angles of 14 triangles is $28 d$, while the sum of the angles of a 17-sided polygon is $30 d$. Therefore, a convex 17-sided polygon cannot be divided into 14 triangles.
It is easy to construct a non-convex 17-sided polygon that can be divided into six triangles (see, for example, Fig. 155, a, σ).
We will now show that no 17-sided polygon (convex or non-convex) can be cut into five triangles (if the 17-sided polygon does not have angles of $180^{\circ}$ ).
Fig. 155.
Indeed, each vertex of the 17-sided polygon either coincides with the vertices of several (possibly one) triangles of the partition, or lies on the side of a triangle of the partition; in the latter case, the corresponding angle of the 17-sided polygon is obviously greater than $180^{\circ}$. Therefore, the remaining part of this angle must be filled by at least one more triangle of the partition; hence, in this case, the vertex also coincides with the vertex of at least one triangle. It follows that the total number of vertices of all the triangles of the partition is no less than the number of vertices of the 17-sided polygon, i.e., 17.
Therefore, if $T$ is the number of triangles in the partition, then
$$
3 T \geqslant 17
$$
from which
$$
T \geqslant 5 \frac{2}{3}
$$
Since $T$ is an integer, $T$ cannot be less than six.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
92. Cut a rectangular parallelepiped with side ratios $8: 8: 27$ into four parts, from which a cube can be assembled.
|
92. The given parallelepiped is cut into two equal stepped parts, as shown in Fig. 165, $a$ (the height of the step is 9, and the width is 4). From these parts, we form a new
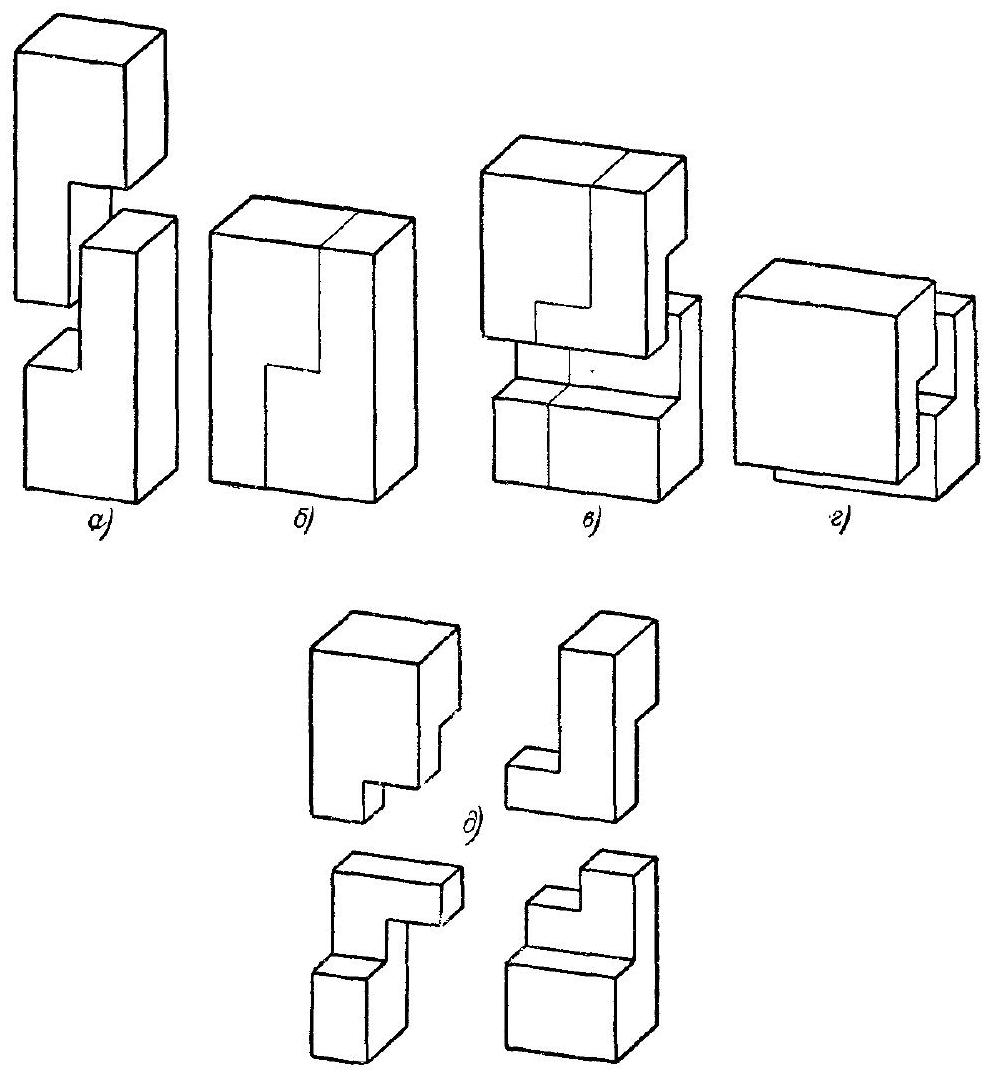
Fig. 165.
parallelepiped with the ratio of sides 12:8:18 (Fig. 165, b). This parallelepiped is then cut into stepped bodies, as shown in Fig. 165, c (the height of the step is 6, and the width is 4). From such parts, we form a cube with a side of 12 (Fig. 165, d). In Fig. 165, $\partial$ the four parts into which the original parallelepiped splits during such cutting are shown separately.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
71. A segment $AB$ of unit length, which is a chord of a sphere with radius 1, is positioned at an angle of $\pi / 3$ to the diameter $CD$ of this sphere. The distance from the end $C$ of the diameter to the nearest end $A$ of the chord $AB$ is $\sqrt{2}$. Determine the length of the segment $BD$.
|
71. Draw a line through $C$ parallel to $A B$, and take a point $E$ on it such that $|C E|=|A B|$, making $A B E C$ a parallelogram. If $O$ is the center of the sphere, then since $\widehat{O C E}=\pi / 3$ and $|C E|=1$ (as follows from the condition), $\triangle O C E$ is equilateral. Therefore, point $O$ is equidistant from all vertices of the parallelogram $A B E C$. This implies that $A B E C$ is a rectangle, the projection of $O$ onto the plane $A B E C$ is the point $K$ - the center of $A B E C$, and $|B D|=2|O K|=$ $=2 \sqrt{|O C|^{2}-\frac{1}{4}|B C|^{2}}=1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
104. The centers of three spheres, with radii of 3, 4, and 6, are located at the vertices of an equilateral triangle with a side length of 11. How many planes exist that are tangent to all three spheres simultaneously?
|
104. Any tangent plane divides space into two parts, and either all three spheres are located on one side, or two are on one side and one on the other. It is obvious that if a certain plane is tangent to the spheres, then the plane symmetric to it relative to the plane passing through the centers of the spheres is also tangent. We will show that there is no plane tangent to the given spheres such that the spheres of radii 3 and 4 are on one side of it, and the sphere of radius 6 is on the other.
Let the centers of the spheres of radii 3, 4, and 6 be at points $A, B$, and $C$. A plane tangent to the given spheres in the manner described above will divide the sides $A C$ and $B C$ in the ratios $1: 2$ and $2: 3$, i.e., it will pass through points $K$ and $L$ on $A C$ and $B C$ such that $|C K|=22 / 3$, $|C L|=33 / 5$. It is not difficult to find the distance from $C$ to $K L$. It is equal to $33 \sqrt{3 / 91}<6$. Therefore, it follows that a plane tangent to the sphere of radius 6 with center at $C$ cannot be drawn through $K L$. It can be shown that all other tangent planes exist, and there will be 6 of them in total.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
108. The volume of the tetrahedron \(ABCD\) is 5. A plane is drawn through the midpoints of the edges \(AD\) and \(BC\), intersecting the edge \(CD\) at point \(M\). The ratio of the length of segment \(DM\) to the length of segment \(CM\) is \(2/3\). Calculate the area of the section of the tetrahedron by the specified plane, given that the distance from this plane to vertex \(A\) is 1.
|
108. Let $K$ and $L$ be the midpoints of edges $AD$ and $BC$, and let $N$ and $P$ be the points of intersection of the plane with lines $AB$ and $AC$ (Fig. 16). We need to find the ratios $\frac{|PA|}{|PC|}$ and $\frac{|PK|}{|PM|}$. Draw $KQ$ and $AR$ parallel to $DC$, with $Q$ being the midpoint of $AC$.
$$
|AR|=|DM|, \quad \frac{|PA|}{|PC|}=\frac{|AR|}{|MC|}=\frac{|DM|}{|MC|}=\frac{2}{3}
$$
$$
\frac{|PK|}{|PM|}=\frac{|KQ|}{|MC|}=\frac{|DC|}{2|MC|}=\frac{5}{6}
$$
Next, we find
$$
\begin{gathered}
\frac{|AN|}{|NB|}=\frac{2}{3}, \quad \frac{|PN|}{|PL|}=\frac{4}{5} \\
\frac{V_{PAKN}}{V_{ABCD}}=\frac{|PA| \cdot|AK| \cdot|AN|}{|AC| \cdot|AD| \cdot|AB|}=\frac{2}{5}
\end{gathered}
$$
i.e., $V_{PAKN}=2$. Since the height dropped from $A$ to $PNK$ is $1$, and $S_{PNK}=6$,
$$
\frac{S_{PML}}{S_{PNK}}=\frac{|PK| \cdot|PN|}{|PM| \cdot|PL|}=\frac{3}{2}, \quad S_{PML}=9
$$
Thus, the area of the section will be $S_{PML}-S_{PNK}=3$.
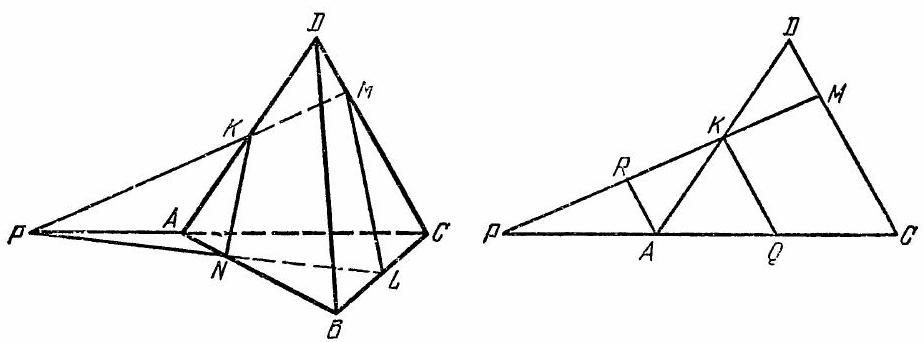
Fig. 16.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
156. Given a cube $A B C D A_{1} B_{1} C_{1} D_{1}$. Points $M$ and $N$ are taken on segments $A A_{1}$ and $B C_{1}$ such that the line $M N$ intersects the line $B_{1} D$. Find
$$
\frac{\left|B C_{1}\right|}{|B N|}-\frac{|A M|}{\left|A A_{1}\right|}
$$
|
156. Projecting a cube onto a plane perpendicular to $B_{i} D_{\text {, }}$ we obtain a regular hexagon $A B C C_{1} D_{1} A_{1}$ (Fig. 35) with side
Fig. $35_{s}$ equal to $\sqrt{\frac{2}{3}} a=b$, where $a$ is the edge of the cube (the equilateral triangle $B C_{\overline{\mathbf{1}}} A_{\mathbf{1}}$ projects into an equal triangle, as the plane $B C_{1} A_{\mathbf{i}}$ is perpendicular to $B_{1} D$). Consider $\triangle K A C_{i}$, in it $|K A|=\left|A C_{\mathbf{i}}\right|=2 b$, the line $N M$ passes through the midpoint of $A C_{\mathbf{i}}$. Let
$$
\frac{|A M|}{\left|A A_{1}\right|}=x
$$
Draw $C_{\overline{1}} L$ parallel to $M N_{9}$, we will have:
$$
\frac{|K N|}{\left|K C_{1}\right|}=\frac{|M L|=|A M|}{|K L|}=\frac{\mid K+x}{2+2 x}
$$
then
$$
\begin{aligned}
\frac{|B N|}{\left|B C_{1}\right|}=\frac{2\left(|K N|-\left|B C_{1}\right|\right)}{\left|K C_{1}\right|} & = \\
& =2 \frac{|K N|}{\left|K C_{1}\right|}-1=\frac{2+x}{1+x}-1=\frac{1}{1+x}
\end{aligned}
$$
Thus,
$$
\frac{\left|B C_{1}\right|}{|B N|}-\frac{|A M|}{\left|A A_{1}\right|}=1+x-x=1
$$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
195. Given a tetrahedron $A B C D$. In the planes defining its faces, points $A_{i}, B_{i}, C_{i}, D_{i}$ are taken such that the lines $A A_{i}, B B_{i}, C C_{i}, D D_{i}$ are parallel to each other. Find the ratio of the volumes of the tetrahedrons $A B C D$ and $A_{1} B_{1} C_{1} D_{\mathrm{i}}$.
|
195. Let $M$ be the point of intersection of the lines $C B_{1}$ and $C_{1} B$. The vertex $A$ lies on $D M$. We draw a plane through the points $D, D_{1}$, and $A$. Denote by $K$ and $L$ its points of intersection with $C_{1} B_{i}$ and $C B$, and by $A_{2}$ the point of intersection of the line $A A_{\hat{1}}$ with $D_{\mathrm{i}} K$ (Fig. 43). From the fact that ${ }^{A_{2}} C_{1} B_{1} B$ is a trapezoid and $K L$ passes through the intersection of its diagonals, it follows that $|K M|=|M L|$. Further, considering the trapezoid $D_{\mathrm{i}} K L D$, we will prove that $\left|A A_{1}\right|=\frac{1}{2}\left|A A_{2}\right|$. Therefore,
$$
v_{A B C D}=\frac{1}{3} v_{A_{2} B C D}
$$
But from the previous problem, it follows that $V_{A_{2} B C D}=V_{A_{1} B_{1} C_{1} D_{1}}$. Thus, the ratio of the volumes of the pyramids $A_{1} B_{1} C_{1} D_{i}$ and $A B C D$ is 3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
212. Given a parallelepiped $A B C D A_{1} B_{1} C_{1} D_{i}$, the diagonal $A C_{1}$ of which is equal to $d$, and the volume $V$. Prove that from the segments equal to the distances from the vertices $A_{i}, B$ and $D$ to the diagonal $A C_{1}$, a triangle can be constructed and that if $s$ is the area of this triangle, then $V=2 d s$.
|
212. Let $M$ be the point of intersection of the diagonal $A C_{i}$ with the plane $A_{1} B D$. Then $M$ is the point of intersection of the medians of triangle $A_{1} B D$, and, moreover, $M$ divides the diagonal $A C_{1}$ in the ratio $1: 2$, i.e., $|A M|=\frac{1}{3}d$.
Consider the pyramid $A B A_{1} D$ (Fig. 45). Take a point $K$ on the line $B M$ such that $|M K|=|B M|$, and construct the prism $M K D A N P$. It is not difficult to note that the distances between the lateral edges of this prism are equal to the corresponding distances from the points $A_{\mathrm{i}}, B$ and $D$ to $A M$. Therefore, the sides of the section perpendicular to the lateral edges of the prism $M K D A N P$ are equal to these distances. Furthermore, the volume of the pyramid $A B A_{1} D$ is equal to the volume of the constructed prism and is $\frac{1}{6}$ of the volume of the parallelepiped, i.e., $\frac{1}{6} V=\frac{1}{3} d S, V=2 d S$.
Fig. 45.
|
2
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
306. The sum of the planar angles of a trihedral angle is $180^{\circ}$. Find the sum of the cosines of the dihedral angles of this trihedral angle.
|
306. Consider a tetrahedron, all faces of which are equal triangles, the angles of which are respectively equal to the plane angles of a given trihedral angle. (Prove that such a tetrahedron exists.) All trihedral angles of this tetrahedron are equal to the given trihedral angle. The sum of the cosines of the dihedral angles of such a tetrahedron (see problem 304) is 2. Therefore, the sum of the cosines of the dihedral angles of the given trihedral angle is 1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
335. What is the greatest number of balls of radius 7 that can simultaneously touch, without intersecting, a ball of radius 3?
Transition to space.
|
335. We will prove that there cannot be more than six such spheres. Suppose there are seven. We connect the centers of all seven spheres with the center of the given sphere and denote by $O_{1}, O_{2}, \ldots, O_{7}$ the points of intersection of these segments with the surface of the given sphere. For each point $O_{i}$, we consider the set of points on the sphere for which the distance (along the surface of the sphere) to the point $O_{i}$ is no greater than the distance to any other point $O_{k}, k \neq i$. The sphere will be divided into seven spherical polygons. Each polygon is the intersection of six hemispheres containing the point $O_{i}$, the boundaries of which are great circles, along which the plane passing through the midpoint of the segment $O_{i} O_{k}$ and perpendicular to it intersects the sphere.
Each of the resulting polygons contains a circle inside it, the spherical radius of which is seen from the center of the original sphere at an angle $\alpha, \sin \alpha=0.7$.
Let $K$ and $N$ be the number of sides and vertices of the resulting partition, respectively. (Each side is a common side of two adjacent polygons and is counted once. The same applies to vertices.) It is easy to see that for such a partition, Euler's formula holds (see problem 324). In our case, this gives $K=N+5$. On the other hand, $K \geqslant \frac{3}{2} N$, since at least three sides emanate from each vertex, and each side is counted twice.
It is not difficult to obtain that $K \leqslant 15, N \leqslant 10$. In problem 325, we proved that among all spherical $n$-gons containing a given circle, the smallest area is that of a regular $n$-gon. Moreover, it can be shown that the sum of the areas of regular $n$- and $(n+2)$-gons is greater than twice the area of a regular $n$-gon. (We consider polygons circumscribed around the same circle.) It is also obvious that the area of a regular circumscribed $n$-gon decreases with increasing $n$. From this, it follows that the sum of the areas of the resulting seven polygons cannot be less than the sum of the areas of five regular quadrilaterals and two regular pentagons circumscribed around circles with a spherical radius corresponding to the central angle $\alpha=\arcsin 0.7$. The area of the corresponding regular pentagon will be
$$
s_{5}=9\left[10 \arccos \left(\cos \alpha \sin \frac{\pi}{5}\right)-3 \pi\right]
$$
and the area of the regular quadrilateral
$$
s_{1}=9\left[8 \arccos \left(\frac{\sqrt{2}}{2} \cos \alpha\right)-2 \pi\right]
$$
It is not difficult to prove that $2 s_{5}+5 s_{4}>36 \pi$. Thus, seven spheres of radius 7 cannot simultaneously, without intersecting, touch a sphere of radius 3. At the same time, it is easy to show that six spheres can be arranged in such a way.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In a bus without a conductor, there were 20 people. Although they only had coins worth 10, 15, and 20 kopecks, each of them paid for the fare and received the change they were due. How could this have happened? Prove that they had no fewer than 25 coins. (One ticket costs 5 kopecks.)
|
7. Let's first prove that the passengers had no less than 25 coins. Indeed, each passenger should receive change, i.e., no fewer than twenty coins should remain in the hands of the passengers. One ruble was dropped into the cash box, so there must be no fewer than five coins (since the largest coin available is 20 kopecks).
Now let's show that the situation described in the problem could have happened. Indeed, there could have been five groups of four people in the bus, and in each group, one person had two ten-kopeck coins, two people had one fifteen-kopeck coin each, and one person had a twenty-kopeck coin. The first person gave 10 kopecks to the second and third persons and took 15 kopecks from the second person. The third person gave his 15 kopecks to the fourth person, and the fourth person dropped his 20 kopecks into the cash box.
|
25
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. The bus network in the city of Lisse is arranged in such a way that: a) each route has three stops; b) any two routes either have no common stops at all or have only one common stop. What is the maximum number of routes that can exist in this city, given that there are only nine different stops?
|
10. Let's consider some stop $A$. Define how many routes can pass through it. Besides $A$, there are eight other stops in the city. On each route passing through $A_{\text {r }}$, there are two more stops. Since no two of these routes can have common stops other than $A$, a total of no more than $8: 2=4$ routes can pass through $A$.
Let's number all the stops and denote by $a_{i}$ the number of routes passing through the $i$-th stop. Since each route has three stops, we have
$$
a_{1}+a_{2}+\ldots+a_{9}=3 n
$$
where $\eta$ is the total number of routes. By the proven fact, all terms do not exceed four. Therefore,
$$
3 n \leqslant 4 \cdot 9 = 36 \text { and } n \leqslant 12
$$
In Fig. 14, a scheme is shown that satisfies the conditions of the problem and contains 12 routes (eight straight and four curved).
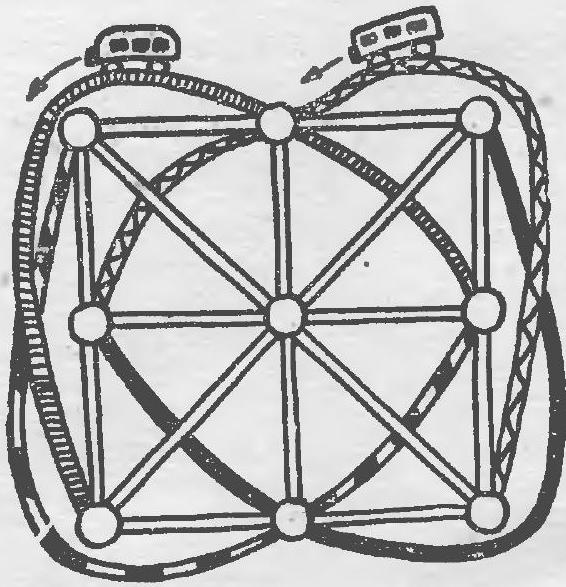
Fig. 14.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14**. Let the game be played until three signs in a row are achieved. What is the minimum number of cells the board should contain so that the first player can win, regardless of how his opponent plays? [Draw a board (of arbitrary shape) with the minimum number of cells and prove that on any board with fewer cells, the second player can avoid losing.]
|
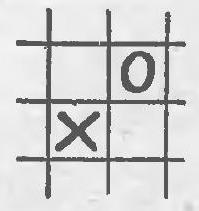
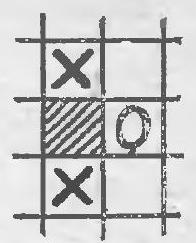
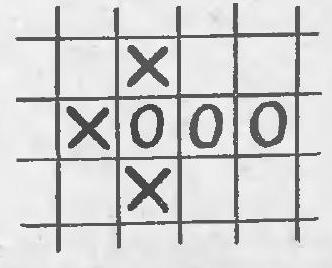
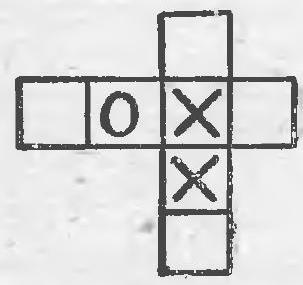
14. On a board of seven cells, shown in Fig. $16, a$, the first player can win regardless of how the opponent plays: first, he places a cross at the intersection of rows, and then on one of the middle cells in the row that does not have a zero.
No matter what move the opponent makes, the first player can win on the third move. If the board consists of no more than six cells, the second player can always prevent the first player from winning. Let's prove this.
We will call a triplet three adjacent cells. In Fig. 16,6 there are four triplets: $(1,2,3)$; $(2,3,4)$; $(3,4,5)$ and $(4,5,6)$, while in Fig. $16, \partial$ there are three triplets: $(1,2,3)$; $(3,5,6)$ and $(1,4,6)$
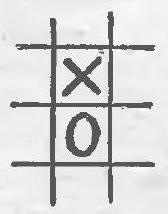
a)
b)
c)

d)

e)
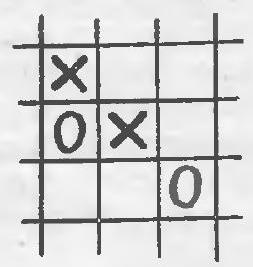
f)
g)
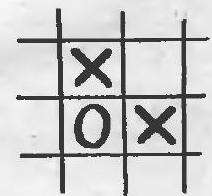
h)
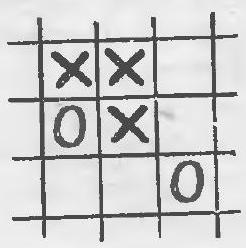
i)
Fig. 15.
To prevent the first player from winning, the second player only needs to place one zero on each triplet. If there are no more than two triplets, the second player can cover them with two moves.
Suppose there are more than two triplets. If five or six cells are adjacent, all triplets are in this row (Fig. 16, b and c). By placing a zero in the third or
a)

b)

c)

d)
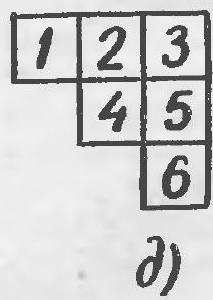
e)
Fig. 16.
fourth cell from the edge, the second player leaves only one uncovered triplet. With the second move, he can cover this triplet as well. If there are four adjacent cells, there is at most one triplet not in this row (Fig. 16, g). By occupying one of the two middle cells of the row of length 4, the second player covers both triplets in this row.
It remains to consider the case where no four cells are in a row (it is easy to see that in this case, six cells can contain no more than three triplets). If there are three triplets, then any two of them must have a common cell (Fig. $16, \partial$) and there are three such cells where two triplets intersect. By placing a zero on one of these cells, the second player can cover two of the three triplets with the first move; the third he will cover with the second move.
|
7
|
Logic and Puzzles
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
18. Prince Gvidon had three sons. Among his descendants, 93 each had two sons and no daughters, while all the others died childless. How many descendants did Prince Gvidon have in total?
|
18. Each of the descendants who have children adds two more descendants to the three descendants of the first generation. Since 93 descendants had children, this added $2 \cdot 93 = 186$ descendants, making a total of $3 + 186 = 189$. This problem ad-
a)
mits a beautiful geometric interpretation. Let's draw the family tree of Prince Gvidon (Fig. 18). From each vertex of this tree, either two segments or none emerge. The vertices of the first type are circled in black. The total number of descendants is equal to the number of segments in the tree. But each segment (except the three upper ones) emerges from a circled
b)
Fig. 17.
black vertex (of which there are 93). Therefore, the total number of segments is $2 \cdot 93 + 3 = 189$
3 E. B. Dynkin et al.
|
189
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25. A chocolate bar consists of $5 \times 8$ square pieces. The bar is broken along straight lines, separating the pieces, until 40 individual pieces are obtained. How many times will the bar need to be broken? (Find all solutions.)
|
25. Each time we break one piece, we get two smaller pieces, i.e., the total number of pieces increases by one. Initially, there was one piece. Therefore, we will have to break the chocolate bar 39 times.
Fig. 25.
Fig. 26.
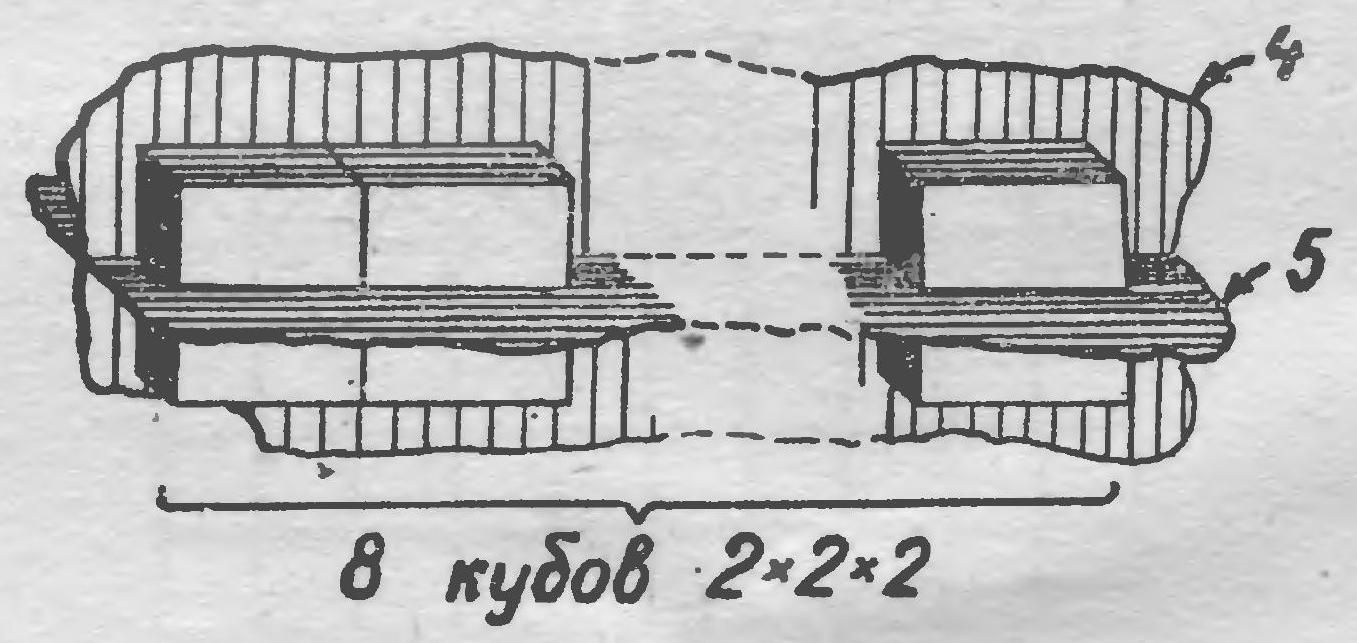
Fig. 27.
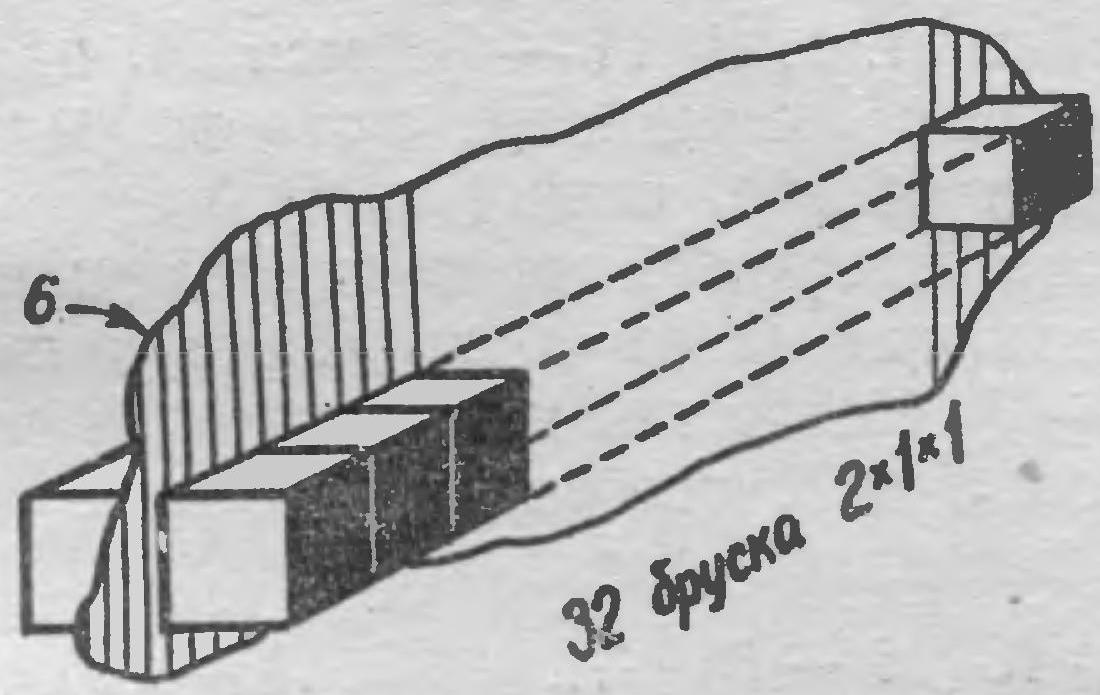
Fig. 28.
|
39
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
27**. In how many different ways can 25 identical coins be distributed among four schoolchildren? (Two ways are considered different if at least one of the schoolchildren receives a different amount of money in each way.)
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
27. Let's put three matches on the table and arrange the coins in a row so that the coins of the first schoolboy lie before the first match, between the first and second - the coins of the second, between the second and third - the coins of the third, and finally, after the third match - the coins of the fourth schoolboy. It is possible that some schoolboy will not receive any coins, then the corresponding matches will be placed next to each other. The coins and matches occupy 28 positions, and the number of ways to distribute them is equal to the number of ways to arrange three matches in 28 positions, or, equivalently, the number of ways to choose 3 numbers from the numbers 1 to 28. According to the corollary of the main lemma, this number is
$$
C_{28}^{3}=\frac{28 \cdot 27 \cdot 26}{1 \cdot 2 \cdot 3}=3276
$$
|
3276
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
30. There are 111 lamps, and each lamp has its own switch. It is allowed to simultaneously switch 13 of them. At the initial moment, some lamps are on, and some are off.
a) Is it possible to turn off all the lamps?
b) How many switches will be required for this if all the lamps were initially on?
|
30. Let's show that we can always turn off all the lamps. We can assume that initially more than 13 lamps were on (otherwise, we would have turned on 13 lamps from the extinguished ones). Moreover, for the same reason, we can assume that the number of extinguished lamps is more than 6. We will select 13 lamps such that 7 are on and 6 are off. We will perform the switch. As a result, the number of burning lamps will decrease by one. By repeating this procedure several times, we will achieve that exactly 13 lamps are burning and we will turn them off with one switch.
Of course, this method is not the most economical. Let's ensure that in task b) 9 switches are sufficient. (8 switches are not enough. Why?) We can act as follows: first, turn off 13 lamps, then turn off another 7 (for which we will switch 10 burning and 3 extinguished lamps). After two stages, 91 burning lamps will remain, which can be turned off with seven switches.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32. On a $10 \times 10$ board for playing "Battleship," a four-cell "ship" $\square \square$ ( $\square$ is located. What is the minimum number of "shots" needed to hit the ship? (Indicate the method of delivering this number of shots and prove that with fewer shots, the ship can always be placed in such a way that it will not be detected.)
|
32. Let's color the fields of the board as shown in Fig. 31 (instead of colors, we will write letters: k - red, s - blue, 3 - green, y - yellow). A direct count shows that the board has 24 yellow, 26 blue, 25 green, and 25 red fields. - It is clear that each four-cell ship occupies exactly one cell of each color. Therefore, by sequentially "shooting" at the yellow fields, we will hit a ship in no more than 24 "shots." Note that on a $10 \times 10$ board, 24 four-cell ships can be placed (we leave this task to the reader). From this, it follows that a number of shots less than 24 may not be sufficient.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
58. The numbers $1,2,3, \ldots, 1000000000$ are written down. Then each number is replaced by the sum of its digits, and so on, until only single-digit numbers remain in the sequence. Which digit appears more frequently in this sequence: ones or fives?
|
58. From the divisibility rule for 9, which we have used several times, it follows that the numbers in the last row give the same remainders when divided by 9 as the numbers in the first row above them. From this, it easily follows that in the first 999999999 positions of the last row, the digits $1,2,3,4,5,6$, $7,8,9$ repeat sequentially, and in the last position stands 1, i.e., there is one more 1 than 5 in the last row.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
71. Kolya, Lena, and Misha pooled their money and bought a football. The amount of money each of them contributed does not exceed half of the total amount contributed by the other two. How much money did Misha contribute if the ball cost 6 rubles?
|
71. According to the condition, the doubled amount of money invested by each boy does not exceed the sum invested by the other two. If one of the boys had given more than two rubles, then the other two would have given less than four, i.e., less than the doubled amount of money of the first. Therefore, each gave no more than two rubles. Since the ball cost 6 rubles, each gave 2 rubles.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
74. 30 students from five courses came up with 40 problems for the olympiad, with students from the same course coming up with the same number of problems, and students from different courses coming up with a different number of problems. How many students came up with exactly one problem?
|
74. Let's choose 5 students, one from each year. Each of them came up with a different number of problems. Therefore, the total number of problems proposed by them is no less than $1+2+3+4+5=15$. The remaining 25 students came up with no more than $40-15=25$ problems. It is clear that each of them came up with one problem, and thus, a total of 26 people came up with one problem each.
|
26
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
85. Bacteria have the following development rule: each one lives for 1 hour and every half hour it produces one new one (a total of two during its life). What will be the offspring of one bacterium 6 hours after its birth?
|
85. Let's call bacteria "young" if their age does not exceed half an hour, and "old" if they have lived for more than half an hour. Let's take half an hour as the unit of time. Denote the number of bacteria at moment $n$ by $u_{n}$. At moment $n-1$, $u_{n-1}$ bacteria are born, so by moment $n$ there are $u_{n-1}$ young bacteria, each of which produces one new bacterium, and $u_{n}-u_{n-1}$ old bacteria, each of which also reproduces. Therefore, by moment $n+1$, the number of bacteria is $u_{n-1}+u_{n-1}+u_{n}-u_{n-1}$, i.e.,
$$
u_{n+1}=u_{n}+u_{n-1}
$$
Given that $u_{1}=1, u_{2}=2$. The required number of bacteria is (*) shows that $u_{13}=377$.
The sequence $u_{n}$ coincides with the Fibonacci sequence (see N. N. Vorobiev, Fibonacci Numbers, 3rd ed., "Nauka", 1969$)$
|
377
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
86. At some point on a straight line, there is a particle. In the first second, it splits in half, and the halves move in opposite directions to a distance I from the previous position. In the next second, the resulting particles again split in half, and the halves move in opposite directions to a distance 1 from their previous positions. Upon colliding, any two particles are destroyed, so, for example, after two seconds, only two particles remain. How many particles will remain after 129 seconds?
|
86. The number and position of particles at moments $t=0$, $1,2,3$ and 4 sec are shown in Fig. 44. We will prove that after
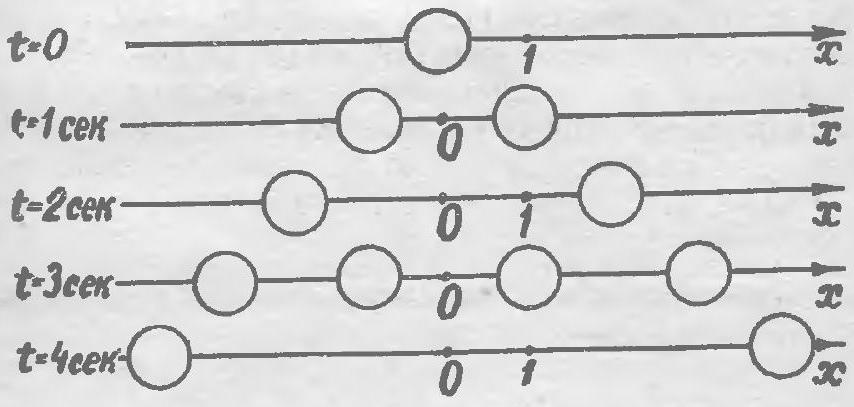
Fig. 44.
$2^{n}-1$ sec there will be $2^{n}$ particles, arranged in a row at a distance of 2 from each other, with the outermost particles being at a distance of $2^{n}-1$ from the initial position, and after $2^{n}$ sec, only two particles will remain at a distance of $2^{n}$ from the initial position. The validity of this statement for $n=1$ and $n=2$ is clear from Fig. 44. Let this statement be already proven for $n=k$. We will prove it for $n=k+1$.
According to the induction hypothesis, at the moment $t=2^{k}$, only two particles will remain at a distance of $2^{k}$ from the initial position. Then, during the time $2^{k}-1$ sec, the "offspring" of the first particle will not interact with the "offspring" of the second, and therefore, as follows from the induction hypothesis, at the moment $t=2^{k}+2^{k}-1=2^{k+1}-1$ sec, $2 \cdot 2^{k}=2^{k+1}$ particles will form, arranged in a row at a distance of 2 from each other. It is clear that at the moment $t+1=2^{k+1}$, only two particles will remain at a distance of $2^{k+1}$ from the initial position.
For $k=7$, we get from this that after 128 sec, there will be two particles at a distance of 128 from the initial position, and the number of particles after 129 sec is 4.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
99. There is a certain number of cards. Each card has a natural number written on it. For each $n \leqslant 1968$, there are exactly $n$ cards on which the numbers are divisors of $n$. Prove that the number $2^{10}=$ $=1024$ is written on at least one card.
|
99. We will prove by induction the following statement: the number $2^{n}$ (where $n \leqslant 10)$ is written on exactly $2^{n-1}$ cards. For $n=1$, the statement is trivial. Consider the number $2^{n}$. Its divisors are written on $2^{n}$ cards. But the divisors of the number $2^{n}$ are it itself and the divisors of the number $2^{n-1}$. The divisors of the number $2^{n-1}$ are, by the problem's condition, written on $2^{n-1}$ cards. Therefore, the number $2^{n}$ is written on $2^{n}-2^{n-1}=2^{n-1}$ cards. The statement is proved. In particular, for $n=10$ the number 1024 is written on 512 cards.
|
1024
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Example 1 (to item $1^{\circ}$). Given the matrix
$$
A=\left(\begin{array}{rrrrr}
1 & 2 & 3 & 5 & 8 \\
0 & 1 & 4 & 6 & 9 \\
0 & 0 & 1 & 7 & 10
\end{array}\right)
$$
Determine its rank.
|
Solution. We have
$$
M_{1}=|1| \neq 0, \quad M_{2}=\left|\begin{array}{ll}
1 & 2 \\
0 & 1
\end{array}\right| \neq 0, \quad M_{3}=\left|\begin{array}{lll}
1 & 2 & 3 \\
0 & 1 & 4 \\
0 & 0 & 1
\end{array}\right| \neq 0
$$
Minors of higher orders cannot be formed.
Answer: $\operatorname{rank} A=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2 (to item $2^{\circ}$). Find the rank of the matrix
$$
A=\left(\begin{array}{rrrrr}
3 & -1 & 1 & 2 & -8 \\
7 & -1 & 2 & 1 & -12 \\
11 & -1 & 3 & 0 & -16 \\
10 & -2 & 3 & 3 & -20
\end{array}\right)
$$
|
Solution. After subtracting the first row from all the others (from the last one with a factor of 2), we obtain the equivalent matrix
$$
A \sim\left(\begin{array}{rrrrr}
3 & -1 & 1 & 2 & -8 \\
4 & 0 & 1 & -1 & -4 \\
8 & 0 & 2 & -2 & -8 \\
4 & 0 & 1 & -1 & -4
\end{array}\right) \sim\left(\begin{array}{rrrrr}
3 & -1 & 1 & 2 & -8 \\
4 & 0 & 1 & -1 & -4
\end{array}\right)
$$
Since three rows of the intermediate matrix were proportional, we can obtain two zero rows from them, which we have discarded.
It is clear that $\operatorname{rank} A=2$, because $M_{2}=\left|\begin{array}{rr}3 & -1 \\ 4 & 0\end{array}\right|=4$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find the volume of the parallelepiped constructed on the vectors $\vec{a}\{1,2,3\}, \vec{b}\{0,1,1\}, \vec{c}\{2,1,-1\}$.
|
Solution. The desired volume $V=|\vec{a} \cdot \vec{b} \cdot \vec{c}|$. Since
$$
\left|\begin{array}{rrr}
1 & 2 & 3 \\
0 & 1 & 1 \\
2 & 1 & -1
\end{array}\right|=-4
$$
then $V=4$
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Determine that the planes with equations $2 x+3 y-$ $-4 z+1=0$ and $5 x-2 y+z+6=0$ are perpendicular.
|
Solution. Let's write down the normal vectors of the given planes: $\vec{N}_{1}=\{2,3,-4\}$ and $\vec{N}_{2}=\{5,-2,1\}$. The planes are perpendicular if and only if the scalar product $\vec{N}_{1} \vec{N}_{2}=0$. We have $2 \cdot 5+3 \cdot(-2)+(-4) \cdot 1=0$ (see point $\left.8^{\circ}\right)$
|
0
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Given the vertices of the tetrahedron \( A(2,3,1), B(4,1,-2) \), \( C(6,3,7), D(-5,-4,8) \). Find:
Fig. 4.11
1) the length of the edge \( A B \)
2) the angle between the edges \( A B \) and \( A D \);
3) the angle between the edge \( A D \) and the plane \( A B C \)
4) the volume of the tetrahedron \( A B C D \)
5) the equation of the edge \( A B \)
6) the equation of the plane \( A B C \);
7) the equation of the height dropped from \( D \) to \( A B C \)
8) the projection \( O \) of point \( D \) onto the base \( A B C \)
9) the height \( D O \).
|
Solution. The condition of the problem is satisfied by the constructed drawing (Fig. 4.11).
1) $AB$ is calculated by the formula
$$
\begin{aligned}
d & =\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}} \\
AB & =\sqrt{(4-2)^{2}+(1-3)^{2}+(-2-1)^{2}}=\sqrt{17}
\end{aligned}
$$
2) The angle $\varphi=(\widehat{\overrightarrow{AB}, \overrightarrow{AD}})$ is calculated by the formula (Ch. III, § 2)
$$
\cos \varphi=\frac{\overrightarrow{AB} \cdot \overrightarrow{AD}}{|\overrightarrow{AB}| \cdot|\overrightarrow{AD}|}
$$
a) $\overrightarrow{AB}=\{2,-2,-3\}, AB=\sqrt{17}, \overrightarrow{AD}=\{-7,-7,7\}, AD=7 \sqrt{3}$;
b) $\overrightarrow{AB} \cdot \overrightarrow{AD}=-14+14-21=-21$
c) $\cos \varphi=-\frac{21}{\sqrt{17} \cdot 7 \sqrt{3}} \approx-0.42, \quad \varphi \approx 180^{\circ}-65^{\circ}=115^{\circ}$.
3) The sine of the angle $\theta$ between the edge $AD$
Fig. 4.12 and the plane $ABC$ is equal to the cosine of the angle between the edge $AD$ and the normal vector $N$ of the plane $ABC$ (Fig. 4.12). The vector $\vec{N}$ is collinear with the vector product $\overrightarrow{AB} \times \overrightarrow{AC}$ (Ch. III, § 3)
a) $\overrightarrow{AB}=\{2,-2,-3\}, \overrightarrow{AC}=2\{2,0,3\}$
$$
\overrightarrow{AB} \times \overrightarrow{AC}=2 \cdot\left|\begin{array}{ccc}
\vec{i} & \vec{j} & \vec{k} \\
2 & -2 & -3 \\
2 & 0 & 3
\end{array}\right|=4 \cdot\{-3,-6,2\}
$$
We take $\vec{N}=\{-3,-6,2\}$.
b) $\overrightarrow{AD}=7\{-1,-1,1\}, \quad \sin \theta=\frac{3+6+2}{\sqrt{3} \cdot 7} \approx 0.92 ; \quad \theta \approx 67^{\circ}$.
4) The volume of the tetrahedron $ABCD$ is equal to $1 / 6$ of the modulus of the mixed product of the vectors $(\overrightarrow{AB} \times \overrightarrow{AC}) \cdot \overrightarrow{AD}$ (Ch. III, § 4).
We have: $\overrightarrow{AB}=\{2,-2,-3\}, \quad \overrightarrow{AC}=2\{2,0,3\}, \quad \overrightarrow{AD}=-7\{1,1,-1\};$
$$
\left|\begin{array}{ccc}
2 & -2 & -3 \\
2 & 0 & 3 \\
1 & 1 & -1
\end{array}\right|=2 \cdot\left|\begin{array}{cc}
0 & 3 \\
1 & -1
\end{array}\right|+2 \cdot\left|\begin{array}{cc}
2 & 3 \\
1 & -1
\end{array}\right|-3\left|\begin{array}{cc}
2 & 0 \\
1 & 1
\end{array}\right|=-22
$$
The desired volume is: $V=\frac{2 \cdot 7 \cdot 22}{6}=\frac{154}{3}$.
5) The equations of the line passing through two points have the form (§ 2) $\frac{x-x_{0}}{m}=\frac{y-y_{0}}{n}=\frac{z-z_{0}}{p} ;\{m, n, p\}$ - the direction vector $\vec{l}$ of the line. We take $\vec{l}=\overrightarrow{AB}=\{2,-2,-3\}$. Then
$$
(AB): \quad \frac{x-2}{2}=\frac{y-3}{-2}=\frac{z-1}{-3}
$$
6) The equation of the plane passing through three given points (§ 1):
$$
\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1}
\end{array}\right|=0
$$
We have
$$
(ABC):\left|\begin{array}{ccc}
x-2 & y-3 & z-1 \\
2 & -2 & -3 \\
2 & 0 & 3
\end{array}\right|=0
$$
or, after expanding the determinant: $3 x+6 y-2 z-22=0$.
7) As the direction vector $\vec{l}$ of the line $DO$, we can take the vector $\vec{l}=\vec{N}=\vec{N}(ABC)=\{3,6,-2\}(\S 2)$,
$$
(DO): \frac{x+5}{3}=\frac{y+4}{6}=\frac{z-8}{-2}
$$
or
$$
x=-5+3 t, y=-4+6 t, z=8-2 t
$$
8) The projection of $D$ on $ABC$ is the point $O$ (the intersection point of $DO$ with $ABC$). We substitute the values of $x, y$ and $z$, expressed in terms of the parameter $t$, into the equation of $ABC$. We find the value of $t$ and substitute it back into the expressions for $x, y$ and $z(\oint 3)$.
We get $3(3 t-5)+6(6 t-4)-2(8-2 t)-22=0,49 t=77, t=\frac{11}{7}$.
Then $x=-5+\frac{33}{7}=-\frac{2}{7}, y=\frac{38}{7}, z=\frac{34}{7}, O\left(-\frac{2}{7}, \frac{38}{7}, \frac{34}{7}\right)$
9) The height $DO$ can be calculated as the distance between $D$ and $O$, or as the distance from $D$ to the plane, or using the formula for the volume of the tetrahedron (§ 1).
In any case, we get $H=OD=\sqrt{\frac{33^{2}}{49}+\frac{66^{2}}{49}+\frac{22^{2}}{49}}=11$.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Find the differential of the function $y=e^{x}\left(x^{2}+3\right)$. Calculate the value of the differential at the point $x=0$.
|
Solution. We have:
$$
\begin{gathered}
d y=y^{\prime} d x=\left(e^{x}\left(x^{2}+3\right)+2 x e^{x}\right) d x=\left(x^{2}+2 x+3\right) e^{x} d x \\
d y(0)=\left.\left(x^{2}+2 x+3\right) e^{x}\right|_{x=0} d x=3 d x
\end{gathered}
$$
## Exercises
Find the differentials of the functions.
1. $y=\ln \left(\frac{1+x}{1-x}\right)^{1 / 4}-\frac{1}{2} \operatorname{arctg} x$.
2. $y=\frac{3 x^{2}-1}{3 x^{3}}+\ln \sqrt{1+x^{2}}+\operatorname{arctg} x$.
3. $y=\operatorname{arctg} \frac{a}{x}+\ln \sqrt{\frac{x-a}{x+a}}$. 4. $y=\frac{1}{3} \ln \frac{\sqrt{x^{2}+1}-x}{\sqrt{x^{2}+1}+x}$.
Calculate the increments and differentials of the functions
5. $y=2 x^{2}-x$ at $x=1, \Delta x=0.01$.
6. $y=x^{3}+2 x, x=-1, \Delta x=0.02$.
Calculate the approximate values.
7. $\sin 60^{\circ} 18^{\prime}$.
8. $\sqrt[6]{735}$
9. $\operatorname{tg} 46^{\circ}$.
10. $\ln 1.07$
## Answers
1. $d y=\frac{x^{2} d x}{1-x^{4}}$. 2. $d y=\frac{x^{5}+1}{x^{6}+x^{4}} d x$. 3. $d y=\frac{2 a^{3}}{x^{4}-a^{4}} d x$. 4. $d y=-\frac{2 d x}{3 \sqrt{x^{2}+1}}$. 5. $\Delta y=0.0302, d y=0.03$. 6. $\Delta y=0.0988, d y=0.1$. 7. 0.86863 . 8. 3.0041 . 9. 1.03553 . 10. 0.0676586 .
## § 6. Derivatives and Differentials of Higher Orders
$1^{\circ}$. Suppose the derivative $y^{\prime}=f^{\prime}(x)$ of the function $y \doteq f(x)$ is a differentiable function. Then its derivative $\left(y^{\prime}\right)^{\prime}$ is called the second derivative of the function $f(x)$ and is denoted by $y^{\prime \prime}=f^{\prime \prime}(x)$. Higher-order derivatives are defined successively: $y^{\prime \prime \prime}=\left(y^{\prime \prime}\right)^{\prime}, y^{I V}=\left(y^{\prime \prime \prime}\right)^{\prime}$, and so on. Notations can also be: $y^{(1)}, y^{(2)}, y^{(3)}, \ldots, y^{(n)}$
For example, if $y=x^{2}+5 x-6$, then $y^{\prime}=2 x+5, y^{\prime \prime}=2, y^{\prime \prime \prime}=0$.
If $y=\cos x$, then the derivative of any order of this function is found as follows:
$$
\begin{aligned}
& y^{\prime}=(\cos x)^{\prime}=-\sin x=\cos \left(x+\frac{\pi}{2}\right) \\
& y^{\prime \prime}=-\cos x=\cos \left(x+2 \frac{\pi}{2}\right) \\
& y^{\prime \prime \prime}=\sin x=\cos \left(x+3 \frac{\pi}{2}\right) \\
& y^{I V}=\cos x=\cos \left(x+4 \frac{\pi}{2}\right) \\
& \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\
& y^{(n)}=\cos \left(x+n \frac{\pi}{2}\right) ; \quad n=1,2,3, \ldots
\end{aligned}
$$
$2^{\circ}$. Higher-order differentials are defined as follows: $d^{n} y=f^{(n)}(x) d x^{n}$. Hence $f^{(n)}(x)=\frac{d^{n} y}{d x^{n}}=\frac{d}{d x}\left(\frac{d^{n-1} y}{d x^{n-1}}\right)$.
For example, $d^{n}(\cos x)=\cos \left(x+\frac{n \pi}{2}\right) d x^{n}$.
## Exercises
Find the derivatives and differentials of order $n \in \mathbb{N}$.
1. $y=\frac{1}{a x-b}$
2. $e^{3 x}$.
3. $\frac{x^{2}+2 x+3}{x}$
4. $\sqrt{x}$.
5. $x^{\alpha}$.
6. $\ln \sqrt[33]{x+1}$
7. $\sin \alpha x$. 8. $\cos \beta x$.
## Answers
1. $y^{(n)}=(-1)^{n} \frac{a^{n} n!}{(a x-b)^{n+1}}$.
2. $y^{(n)}=3^{n} e^{3 x}$. 3. $y^{\prime}=1-\frac{3}{x^{2}}$, $y^{\prime \prime}=\frac{6}{x^{3}}, \quad y^{(n)}=(-1)^{n} 3 \frac{n!}{x^{n+1}}$
3. $y^{(n)}=(-1)^{n-1} \frac{1 \cdot 3 \cdot 5 \cdots(2 n-3)}{2^{n} \cdot \sqrt{x^{2 n-1}}}$
4. $y^{(n)}=\alpha(\alpha-1) \cdots(\alpha-n+1) x^{\alpha-n}$. 6. $y^{(n)}=\frac{1}{33}(-1)^{n+1} \frac{(n-1)!}{x^{n}}$.
5. $y^{(n)}=\alpha^{n} \sin \left(\alpha x+\frac{\pi}{2} n\right) \cdot 8 \cdot y^{(n)}=\beta^{n} \cos \left(\alpha x+n \frac{\pi}{2}\right)$.
## § 7. Differentiation of Inverse Functions. Differentiation of Functions Given Implicitly and Parametrically
$1^{\circ}$. Let $y=f(x)$ be a function defined and continuous on the interval $[a ; b]$ and $f(a)=A, f
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Check if Rolle's theorem is valid for the function $f(x)=x^{2}+2 x+7$ on the interval $[-6 ; 4]$, and if so, find the corresponding value of c.
|
Solution. $f(x)=x^{2}+2 x+7$ is continuous and differentiable on any interval, in particular, on $[-6 ; 4]$, and $f(6)=f(4)=31$. Therefore, $f^{\prime}(x)=2 x+2=0$ for some $x \in(-6 ; 4)$. We have $x=c=-1$.
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Calculate the limits:
a) $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{\tan\left(x^{2}+y^{2}\right)}{x^{2}+y^{2}}$, b) $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x^{2}-y^{2}}{x^{2}+y^{2}}$, c) $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x y}{\sqrt{4-x y}-2}$.
|
Solution. Note that the functions $\frac{\operatorname{tg}\left(x^{2}+y^{2}\right)}{x^{2}+y^{2}}$ and $\frac{x^{2}-y^{2}}{x^{2}+y^{2}}$ are undefined only at the point $(0,0)$, while $\frac{x y}{\sqrt{4-x y}-2}$ is undefined on the coordinate axes $x=0$ and $y=0$.
a) Transition to polar coordinates $x=r \cos \varphi, y=r \sin \varphi$, $\varphi \in[0,2 \pi)$. Then $x^{2}+y^{2}=r^{2}$ and $(x, y) \rightarrow(0,0)$ implies $r \rightarrow 0$. Using the corollary of the first remarkable limit, we get
$$
\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{\operatorname{tg}\left(x^{2}+y^{2}\right)}{x^{2}+y^{2}}=\left(\frac{0}{0}\right)=\lim _{r \rightarrow 0} \frac{\operatorname{tg} r^{2}}{r^{2}}=1
$$
b) If $(x, y) \rightarrow(0,0)$ along different rays $y=k x, k \in \mathbb{R}$, then
$$
\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x^{2}-y^{2}}{x^{2}+y^{2}}=\left(\frac{0}{0}\right)=\lim _{x \rightarrow 0} \frac{x^{2}-k^{2} x^{2}}{x^{2}+k^{2} x^{2}}=\frac{1-k^{2}}{1+k^{2}}
$$
The right-hand side of this equation depends on $k$, and therefore the limit of the given function as $(x, y) \rightarrow(0,0)$ does not exist (the limit must be unique).
c) Multiply the numerator and denominator by the conjugate of the denominator. We get
$$
\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x y(\sqrt{4-x y}+2)}{-x y}=-\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}}(\sqrt{4-x y}+2)=-4
$$
Note. From the definition of continuity, it follows that the functions
$$
f(x, y)=\left\{\begin{array}{l}
\frac{\operatorname{tg}\left(x^{2}+y^{2}\right)}{x^{2}+y^{2}} \quad \text { for }(x, y) \neq(0, y) \text { and }(x, y) \neq(x, 0) \\
1 \quad \text { for }(x, y)=(0, y) \text { or }(x, y)=(x, 0)
\end{array}\right.
$$
and
$$
g(x, y)=\left\{\begin{array}{l}
\frac{x y}{\sqrt{4-x y}-2} \quad \text { for }(x, y) \neq(0,0) \\
-4 \text { for }(x, y)=(0,0)
\end{array}\right.
$$
are continuous on the entire plane $O x y$, while the function $\varphi(x, y)=\frac{x^{2}-y^{2}}{x^{2}+y^{2}}$ cannot be extended at the point $(0,0)$ in such a way that it is continuous at this point.
## Exercises
Calculate the limits.
1. $\lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} \frac{\operatorname{tg} x y}{y}$. 2. $\lim _{\substack{x \rightarrow 3 \\ y \rightarrow 7}} \lg (x+y)$.
2. $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{\sin x y}{x}$.
3. $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x+y}{x}$
4. $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}}(x+y) \sin \frac{1}{x} \cdot \cos \frac{1}{y}$.
5. $\lim _{\substack{x \rightarrow 1 \\ y \rightarrow 2}} \frac{2(x-1)(y-2)}{(x-1)^{2}+(y-2)^{2}}$
6. $\lim _{\substack{x \rightarrow \infty \\ y \rightarrow \infty}} \frac{x^{2}+y^{2}}{x^{4}+y^{4}}$
7. $\lim _{\substack{x \rightarrow \infty \\ y \rightarrow \infty}} \frac{x+y}{x^{2}-x y+y^{2}}$.
8. $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x^{2} y}{x^{2}+y^{2}}$
9. $\lim _{\substack{x \rightarrow 1 \\ y \rightarrow 0}} \frac{\ln \left(1+e^{y}\right)}{\sqrt{x^{2}+y^{2}}}$
10. $\lim _{\substack{x \rightarrow 2 \\ y \rightarrow-2}} \frac{2 x+y}{(x-2)^{2}+(y+2)^{2}}$
11. $\lim _{\substack{x \rightarrow-1 \\ y \rightarrow 2}} \frac{x^{2}+2 x+y^{2}-4 y+5}{x+2 y}$.
## Answers
1. 2. 2. 3. 3. 0. 4. Does not exist. 5. 0. 6. Does not exist. 7. 0. 8.0. 9. 0. 10. $\ln 2.11 .+\infty$. 12.0 .
## § 3. Partial Derivatives and Differential of a Function of Two Variables
$1^{\circ}$. The partial increments of the function $z=f(x, y)$ with respect to the independent variables $x$ and $y$ are the differences
$$
\Delta_{x} z=f(x+\Delta x, y)-f(x, y), \quad \Delta_{y} z=f(x, y+\Delta y)-f(x, y)
$$
where $\Delta x$ and $\Delta y$ are the increments of the independent variables $x$ and $y$.
The total increment of the function $z=f(x, y)$ is the difference
$$
\Delta z=f(x+\Delta x, y+\Delta y)-f(x, y)
$$
In general, the total increment does not equal the sum of the partial increments:
$$
\Delta z \neq \Delta_{x} z+\Delta_{y} z
$$
$2^{\circ}$. The partial derivative of the function $z=f(x, y)$ with respect to the variable $x$ or $y$ is the limit of the ratio of the corresponding partial increment $\Delta_{x} z$ or $\Delta_{y} z$ to the increment of the given variable, provided that the increment of the variable tends to zero.
The notations for partial derivatives are
$$
\begin{aligned}
& z_{x}^{\prime}=\frac{\partial z}{\partial x}=\frac{\partial f(x, y)}{\partial x}=f_{x}^{\prime}(x, y)=\lim _{\Delta x \rightarrow 0} \frac{\Delta_{x} z}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f(x+\Delta x, y)-f(x, y)}{\Delta x} \\
& z_{y}^{\prime}=\frac{\partial z}{\partial y}=\frac{\partial f(x, y)}{\partial y}=f_{y}^{\prime}(x, y)=\lim _{\Delta y \rightarrow 0} \frac{\Delta_{y} z}{\Delta y}=\lim _{\Delta y \rightarrow 0} \frac{f(x, y+\Delta y)-f(x, y)}{\Delta y}
\end{aligned}
$$
$3^{\circ}$. When finding a partial derivative (differentiation) with respect to a certain variable, one uses the formulas and rules of differentiation of a function of one variable, treating the other variable as fixed, constant.
$4^{\circ}$. The partial derivative $z_{x}^{\prime}$ $\left(z_{y}^{\prime}\right)$ at a given point $\left(x_{0}, y_{0}\right)$ is equal to the tangent of the angle of inclination of the tangent to the curve obtained by the intersection of the surface
Figure 8.2 $z=f(x, y)$ with the plane $y=y_{0}$ $\left(x=x_{0}\right), z_{x}^{\prime}\left(x_{0}, y_{0}\right)=\operatorname{tg} \alpha\left(z_{y}^{\prime}\left(x_{0}, y_{0}\right)=\operatorname{tg} \beta\right)$ (Figure 8.2).
$5^{\circ}$. The partial differentials of the function $z=f(x, y)$ are the quantities
$$
d_{x} z=z_{x}^{\prime} d x, \quad d_{y} z=z_{y}^{\prime} d y, \quad d x=\Delta x, \quad d y=\Delta y
$$
$6^{\circ}$. The total differential of the function $z=f(x, y)$ is the expression
$$
d z=d_{x} z+d_{y} z=z_{x}^{\prime} d x+z_{y}^{\prime} d y=\frac{\partial z}{\partial x} d x+\frac{\partial z}{\partial y} d y
$$
The total differential $d z$ represents the principal linear (with respect to $\Delta x$ and $\Delta y$) part of the total increment of the function $z=f(x, y)$.
## Examples with Solutions
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find the derivative of the function $z=x^{2}+y^{2}$ at the point $M(3,1)$ in the direction of the point $M_{1}(0,5)$.
|
Solution. We have: $\overrightarrow{M M}_{1}=\{0-3,5-1\}=\{-3,4\},\left|\overrightarrow{M M}_{\mathrm{I}}\right|=$ $=\sqrt{(-3)^{2}+4^{2}}=5, \cos \alpha=-\frac{3}{5}, \sin \alpha=\frac{4}{5}$.
Let $\vec{l}=\left\{-\frac{3}{5}, \frac{4}{5}\right\}$ and find $\frac{\partial z}{\partial l}$.
We have: $z_{x}^{\prime}=2 x, z_{y}^{\prime}=2 y, z_{x}^{\prime}(3,1)=6, z_{y}^{\prime}(3,1)=2$.
Finally, $\frac{\partial z}{\partial l}=6\left(-\frac{3}{5}\right)+2 \cdot \frac{4}{5}=-2$. The negative sign of the derivative value $\frac{\partial z(3,1)}{\partial l}$ indicates that the function is decreasing in the direction of $\vec{l}$.
|
-2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Find the direction of the maximum increase of the function $z=3 x^{2}-2 y^{2}$ at the point $M(1,2)$. Also, find the greatest value of the derivatives in different directions at the point $M$.
|
Solution. Let's find the gradient of the function $z$ at the given point $(1,2)$. We have $z_{x}^{\prime}=6 x, z_{x}^{\prime}(1,2)=6, z_{y}^{\prime}=-4 y, z_{y}^{\prime}(1,2)=-8$. The gradient of the field at point $M(1,2)$ is $\overrightarrow{\operatorname{grad}} z=\{6,-8\}$. This vector indicates the direction of the maximum increase of $z$. The maximum value of the derivative at $(1,2)$ is $\sqrt{6^{2}+(-8)^{2}}=10$.
|
10
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1.1. Calculate
$$
\left|\begin{array}{rrr}
2 & -1 & 1 \\
3 & 2 & 2 \\
1 & -2 & 1
\end{array}\right|
$$
|
Solution:
$$
\begin{gathered}
\left|\begin{array}{rrr}
2 & -1 & 1 \\
3 & 2 & 2 \\
1 & -2 & 1
\end{array}\right|=2 \cdot\left|\begin{array}{rr}
2 & 2 \\
-2 & 1
\end{array}\right|-(-1) \cdot\left|\begin{array}{ll}
3 & 2 \\
1 & 1
\end{array}\right|+1 \cdot\left|\begin{array}{rr}
3 & 2 \\
1 & -2
\end{array}\right|= \\
=2 \cdot(2+4)+1 \cdot(3-2)+1 \cdot(-6-2)=12+1-8=5
\end{gathered}
$$
Let's consider the concept of the inverse matrix.
Definition. Let a matrix $A$ of order $n$ be given. If its product with some matrix $B$ of order $n$ equals the identity matrix $E$, i.e., $A \cdot B=E$ or $B \cdot A=E$, then the matrix $B$ is called the inverse of matrix $A$ and is denoted by $A^{-1}$.
It can be proven that if $A \cdot A^{-1}=E$, then $A^{-1} \cdot A=E$, i.e., mutually inverse matrices are commutative.
Theorem 1. Every square matrix $A$, whose determinant $\Delta \neq 0$, has a unique inverse matrix $A^{-1}=B$, the elements of which $b_{i j}$ are found by the formula
$$
b_{i j}=\frac{A_{j i}}{\Delta}
$$
From the theorem, the following rule follows: to find the inverse matrix of matrix (1.2), where $m=n$, the following transformations must be performed:
1. Calculate the determinant $\Delta$ of matrix $A$ ($\Delta \neq 0$).
2. Replace each element of matrix $A$ with its algebraic complement, i.e., form the matrix ($A_{i j}$).
3. Transpose the matrix ($A_{i j}$), i.e., write the matrix ($A_{j i}$).
4. Multiply the matrix ($A_{j i}$) by $\frac{1}{\Delta}$.
As a result, we obtain the matrix $A^{-1}$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1.17. Form the equation of the line $l$ passing through the point $A(2; -4)$ and being at a distance of 2 units from the origin.
|
Solution. Let the equation of the desired line have the form:
$$
y-y_{A}=k\left(x-x_{A}\right),
$$
or
$$
y+4=k(x-2)
$$
or
$$
k x-y-(4+2 k)=0 .
$$
To determine the slope $k$ of this line, we will use the fact that it is 2 units away from the origin. We will find this distance directly. The equation of the perpendicular dropped from the origin to the line $k x-y-(2+4 k)=0$ is $y=-\frac{1}{k} x$, or $x+k y=0$. Solving the equations of these two lines simultaneously
$$
\begin{aligned}
& k x-y-(2+4 k)=0 \\
& x+k y=0
\end{aligned}
$$
we obtain the coordinates of the point $C$ of their intersection:
$$
x_{C}=\frac{2 k(k+2)}{1+k^{2}} ; y_{C}=-\frac{2(k+2)}{1+k^{2}}
$$
From this, we find the distance from the origin to the line $l$ :
$$
\begin{gathered}
O C=\sqrt{x_{C}^{2}+y_{C}^{2}}=\frac{2}{1+k^{2}} \sqrt{k^{2}(k+2)^{2}+(k+2)^{2}}= \\
=\frac{2(k+2)}{1+k^{2}} \sqrt{k^{2}+1}=\frac{2(k+2)}{\sqrt{k^{2}+1}}
\end{gathered}
$$
On the other hand, by the condition $O C=2$. Thus, we obtain an equation for finding the slope $k$ of the desired line $l$ :
$$
\frac{2(k+2)}{\sqrt{k^{2}+1}}=2 \text { or } k+2=\sqrt{k^{2}+1},
$$
from which $k=-\frac{3}{4}$. Thus, substituting the found value $k=-\frac{3}{4}$ into the equation (*), we get the equation of the line:
$$
-\frac{3}{4} x-y-4-2 \cdot \frac{3}{4}=0
$$
or finally,
$$
3 x+4 y+10=0
$$
In conclusion, by seeking the equation of the line $l$ in the form $y-y_{A}=k\left(x-x_{A}\right)$, we assumed that this line is not parallel to the y-axis. However, it is clear that the line $x=2$ (parallel to the y-axis) also satisfies the condition of the problem, as it passes through the point $A(2 ;-4)$ and is 2 units away from the origin (Fig. 17).
Fig. 17
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5.2. Using the definition directly, show that the series converges, and find its sum.
\[
\sum_{n=1}^{\infty} \frac{1}{n(n+1)}=\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\frac{1}{3 \cdot 4}+\ldots+\frac{1}{n(n+1)}+\ldots
\]
|
Solution. By the definition of the partial sum of a series, we have:
$$
\begin{aligned}
& S_{1}=a_{1}=\frac{1}{2} \\
& S_{2}=a_{1}+a_{2}=\frac{1}{2}+\frac{1}{6}=\frac{2}{3} \\
& S_{3}=a_{1}+a_{2}+a_{3}=\frac{2}{3}+\frac{1}{12}=\frac{3}{4} \\
& S_{4}=a_{1}+a_{2}+a_{3}+a_{4}=\frac{3}{4}+\frac{1}{20}=\frac{4}{5}
\end{aligned}
$$
Thus, we obtain the following sequence of partial sums:
$$
\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \ldots
$$
the general term of which is: $\frac{n}{n+1}$. It is clear that this sequence converges and its limit is one:
$$
\lim _{n \rightarrow \infty} S_{n}=\lim _{n \rightarrow \infty} \frac{n}{n+1}=1
$$
This means that the given series converges and its sum is one.
## 5.2. Necessary Condition for Convergence of a Series. Sufficient Conditions for Convergence of Series with Positive Terms
A series can converge only if its general term $a_{n}$ tends to zero as the index $n$ increases without bound: $\lim _{n \rightarrow \infty} a_{n}=0$ - this is the necessary condition for the convergence of a series.
If $\lim _{n \rightarrow \infty} a_{n} \neq 0$, then the series diverges - this is the sufficient condition for the divergence of a series.
For series with positive terms, the following sufficient conditions can be used to determine their convergence or divergence.
1. Comparison Test. If the terms of a positive series
$$
a_{1}+a_{2}+\ldots+a_{n}+\ldots
$$
starting from some index, do not exceed the corresponding terms of the series
$$
b_{1}+b_{2}+\ldots+b_{n}+\ldots
$$
then the convergence of series (2) implies the convergence of series (1), and the divergence of series (1) implies the divergence of series (2).
When investigating series for convergence and divergence using this test, a geometric progression is often used:
$$
a+a q+a q^{2}+\ldots+a q^{n}+\ldots(a>0)
$$
which converges for $|q|<1$ and diverges for $|q|>1$ (the question of convergence remains unresolved for $l=1$).
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Example 5.9. Based on the D'Alembert's criterion, investigate the convergence of the series
$$
3+\frac{3^{2}}{2^{2}}+\frac{3^{3}}{3^{3}}+\frac{3^{4}}{4^{4}}+\ldots+\frac{3^{n}}{n^{n}}+\ldots
$$
|
Solution. Knowing the $n$-th term of the series $a_{n}=\frac{3^{n}}{n^{n}}$, we write the $(n+1)$-th term: $a_{n+1}=\frac{3^{n+1}}{(n+1)^{n+1}} \cdot$ From this,
\[
\begin{gathered}
\lim _{n \rightarrow \infty} \frac{a_{n+1}}{a_{n}}=\lim _{n \rightarrow \infty} \frac{3^{n+1}}{(n+1)^{n+1}}: \frac{3^{n}}{n^{n}}=\lim _{n \rightarrow \infty} \frac{3^{n+1} \cdot n^{n}}{3^{n}(n+1)^{n+1}}=\lim _{n \rightarrow \infty} \frac{3}{n+1} \cdot \frac{n}{n+1}{ }^{n}= \\
=3 \lim _{n \rightarrow \infty} 1-\frac{n}{n+1}{ }^{n} \cdot \frac{1}{n+1}=3 \cdot e^{-1} \cdot 0=0
\end{gathered}
\]
Since $l=0<1$, the series converges.
## 5.3. Leibniz's Convergence Test
An alternating series is a series of the form
\[
a_{1}-a_{2}+a_{3}-\ldots+(-1)^{n-1} a_{n}+\ldots
\]
where $a_{1}, a_{2}, a_{3}, \ldots, a_{n}$ are positive numbers.
For alternating series, the following convergence test applies.
Leibniz's Test. The series (1) converges if its terms decrease monotonically in absolute value and the general term tends to zero as $n \rightarrow \infty$.
The application of convergent series to approximate calculations is based on replacing the sum of the series with the sum of its first few terms. The error introduced by this is easily estimated for an alternating series that satisfies Leibniz's test - the error is less than the absolute value of the first of the discarded terms of the series.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5.18. Find the region of convergence of the power series
$$
x+2!x^{2}+3!x^{3}+\ldots+n!x^{n}+\ldots
$$
|
Solution. Here $u_{n}=n!|x|^{n}, u_{n+1}=(n+1)!|x|^{n+1}$.
From this,
$$
l=\lim _{n \rightarrow \infty} \frac{u_{n+1}}{u_{n}}=\lim _{n \rightarrow \infty} \frac{(n+1)!|x|^{n+1}}{n!|x|^{n}}=|x| \lim _{n \rightarrow \infty}(n+1)
$$
Thus,
$$
l=\begin{array}{ccc}
\infty & \text { when } & x \neq 0, \\
0 & \text { when } & x=0 .
\end{array}
$$
Therefore, according to the D'Alembert's ratio test, the series converges only at the point $x=0$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.2.1. Find the integral $\iiint_{V} x d x d y d z$, if the body $V$ is bounded by the planes: $x=0, y=0, x+4 y-2 z=0$ and $x+y+z-6=0$.
|
Solution. The body V is bounded by the coordinate planes $x \mathrm{Oz}$ and $y \mathrm{Oz}$, and from below and above by the planes: $z=\frac{1}{2}(x+4 y)$ and $z=6-x-y$. Let's find the line of intersection of these planes:
$$
\begin{aligned}
& z=\frac{1}{2}(x+4 y) \\
& z=6-x-y
\end{aligned}
$$
or
$$
\frac{1}{2}(x+4 y)=6-x-y
$$
or
$$
x+2 y-4=0 .
$$
We have $y=\frac{1}{2}(4-x)$. Let's construct the region $D$ on the plane $x \mathrm{Oy}$ (Fig. 62). We compute:
$$
\begin{gathered}
\iiint_{V} x d x d y d z=\int_{0}^{4} x d x \int_{0}^{\frac{1}{2}(4-x)} d y \int_{\frac{1}{2}(x+4 y)}^{6-x-y} d z=\left.\int_{0}^{4} x d x \int_{0}^{\frac{1}{2}(4-x)} d y z\right|_{\frac{1}{2}(x+4 y)} ^{6-x-y}= \\
=\int_{0}^{4} x d x \int_{0}^{\frac{1}{2}(4-x)} d y(6-x-y)-\frac{1}{2}(x+4 y)= \\
=\int_{0}^{4} x d x \int_{0}^{\frac{1}{2}(4-x)} 6-\frac{3}{2} x-3 y d y=3 \int_{0}^{4} x d x 2 y-\frac{1}{2} x y-\left.\frac{1}{2} y^{2}\right|_{0} ^{\frac{1}{2}(4-x)}= \\
=3 \int_{0}^{4} x d x 2 \cdot \frac{1}{2}(4-x)-\frac{1}{2} x \cdot \frac{1}{2}(4-x)-\frac{1}{2} \frac{1}{2}(4-x)^{2}= \\
=3 \int_{0}^{4} x 2-x+\frac{1}{8} x^{2} d x=3 \int_{0}^{4} 2 x-x^{2}+\frac{1}{8} x^{3} d x= \\
=32 \cdot \frac{x^{2}}{2}-\frac{1}{3} x^{3}+\left.\frac{1}{8} \frac{1}{4} x^{4}\right|_{0} ^{4}=316-\frac{64}{3}+8=8
\end{gathered}
$$
Fig. 62
|
8
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6.21. On average, $85 \%$ of the items coming off the conveyor are of the first grade. How many items need to be taken so that with a probability of 0.997, the deviation of the frequency of first-grade items from 0.85 in absolute value does not exceed 0.01?
|
Solution. Here $p=0.85, q=1-0.85=0.15, \varepsilon=0.01, P=0.997$, $n-$? Since in the equation $P\left|\frac{m}{n}-p\right|<\varepsilon \approx \Phi \varepsilon \sqrt{\frac{n}{p q}}$ the probability $P$ on the left is known, we first solve the equation $\Phi(t)=P$. Let $t_{P}$ be the root of this equation. Then $\varepsilon \sqrt{\frac{n}{p q}} \approx t_{P}, \varepsilon^{2} \frac{n}{p q} \approx t_{P}^{2}$ and, consequently, $n \approx \frac{p q t_{P}^{2}}{\varepsilon^{2}}$. For our case $t_{0.997}=3$, therefore
$$
n \approx \frac{0.85 \cdot 0.15 \cdot 3^{2}}{(0.01)^{2}}=\frac{1.1475}{0.0001}=11475
$$
## 6.3. Random Variables
A random variable (RV) is a variable that takes on a specific numerical value in each specific trial, which can vary from trial to trial.
Examples: the number of customers visiting a hair salon in a day; the monthly profit of a tailor shop; the development time of a photographic film.
Random variables represent the results of measurements in random experiments (trials). There are two types of random variables: discrete and continuous.
Discrete random variables are variables that take only distinct numerical values (which can be listed in advance).
Examples: grades in a grade book $(3,4,5)$; the number of students taking an exam
Continuous random variables can take any values from a closed or open interval. For example, the dimensions of the same part, determined by different people or using different tools, vary.
Combined (discrete-continuous) random variables are possible, which are continuous on some intervals and discrete on others.
|
11475
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
### 7.1.1. Optimal Production Task
For the production of two types of products I and II, three types of raw materials are used.
To produce one unit of product I, it is required to spend 13 kg of the first type of raw material, 32 kg of the second type of raw material, and 58 kg of the third type of raw material.
To produce one unit of product II, it is required to spend 24 kg of the first type of raw material, 32 kg of the second type of raw material, and 29 kg of the third type of raw material.
The production is supplied with 312 kg of the first type of raw material, 480 kg of the second type of raw material, and 696 kg of the third type of raw material.
The profit from the sale of one unit of finished product I is 4 conditional units, and for product II - 3 conditional units.
It is required to develop a production plan for products I and II that ensures maximum profit from their sale, if it is planned in advance to produce at least 10 units of products I and II.
|
Solution. Let's consider the mathematical model of the problem. If we take $x_{1}$ as the number of items I planned for production and $x_{2}$ as the number of items II, we obtain a linear programming problem.
Subject to the constraints
$$
\begin{gathered}
13 x_{1}+24 x_{2} \leq 312 \\
32 x_{1}+32 x_{2} \leq 480 \\
58 x_{1}+29 x_{2} \leq 696 \\
x_{1}+x_{2} \geq 10 \\
x_{1} \geq 0, x_{2} \geq 0
\end{gathered}
$$
find the maximum of the linear function
$$
Z=4 x_{1}+3 x_{2}
$$
## Geometric Solution of the Problem
Since the problem is two-dimensional, it can be solved graphically.
The system of constraints (7.1) gives a polygon of feasible solutions. To construct it, we draw the lines that are the boundaries of the polygon and use a test point, for example $(0 ; 0)$, to determine the half-planes defined by these lines (Fig. 86):
$$
\begin{aligned}
& l_{1}: 13 x_{1}+24 x_{2}=312, \\
& l_{2}: 32 x_{1}+32 x_{2}=480, \\
& l_{3}: 58 x_{1}+29 x_{2}=696, \\
& l_{4}: x_{1}+x_{2}=10 .
\end{aligned}
$$
In the intersection of the corresponding half-planes, we obtain the hexagon $A B C D E F$.
Fig. 86
To find $\max z$, we construct a vector $\bar{n}=(4 ; 3)$ from the origin and a line perpendicular to it, which is the level line $z=0$, i.e., the line $4 x_{1}+3 x_{2}=0$.
Next, we move the level line $z=$ const in the direction of increasing $z$, i.e., parallel to itself in the direction of the vector $\bar{n}$. In the last intersected vertex $D$, we obtain the maximum value of $z$. Vertex $D$ is the intersection point of lines $l_{2}$ and $l_{3}$.
To find the coordinates of point $D$, we solve the system:
$$
\begin{array}{rlrl}
32 x_{1}+32 x_{2} & =480, \quad x_{1}+x_{2}=15, \\
58 x_{1}+29 x_{2} & =696, \quad 2 x_{1}+x_{2} & =24 .
\end{array}
$$
Solving the system, we find that $x_{1}=9, x_{2}=6$, i.e., $D(9 ; 6)$ and at this point $z=4 \cdot 9+3 \cdot 6=54$ (conditional units).
To solve the problem using the simplex method, we convert the system of constraints (7.1) to the form of equalities by introducing non-negative slack variables $y_{i}(i=1,2,3,4)$:
$$
\begin{gathered}
13 x_{1}+24 x_{2}+y_{1}=312 \\
x_{1}+x_{2}+y_{2}=15 \\
2 x_{1}+x_{2}+y_{3}=24 \\
-x_{1}-x_{2}+y_{4}=-10 \\
-4 x_{1}-3 x_{2}+Z=0
\end{gathered}
$$
with $x_{j} \geq 0(j=1,2) ; y_{i} \geq 0(i=1,2,3,4)$.
We write the system using abbreviated tables (Table 7.1).
Table 7.1
| | $x_{1}$ | $x_{2}$ | 1 |
| :---: | :---: | :---: | :---: |
| $y_{1}$ | 13 | 24 | $=312$ |
| $y_{2}$ | 1 | 1 | $=15$ |
| $y_{3}$ | 2 | 1 | $=24$ |
| $y_{4}$ | -1 | -1 | $=-10$ |
| $Z$ | -4 | -3 | $=0$ |
Since there is a negative element in the I-column, we need to make it positive. We choose the $y_{4}$-row with the negative free term “-10”.
In this row, there are negative elements, and we choose one of them, for example, “-1” in the $x_{1}$-column. We take the $x_{1}$-column as the pivot column.
We divide the free terms by the corresponding elements of the pivot column, obtaining $\{24,15,12,10\}$, and the smallest positive ratio will correspond to the pivot row, so the $y_{4}$-row is the pivot row, and the element -1 is the pivot element. We perform a step of the modified Jordan elimination (MJSE) with the pivot element -1 according to the rule:
1) the pivot element is replaced by its reciprocal;
2) the elements of the pivot row are divided by the pivot element;
3) the elements of the pivot column are divided by the pivot element and the sign is changed;
4) the other elements of the new table are found by the rectangle formula [17, p. 52]
$$
\begin{aligned}
& \text { corresponding element } \\
& \underset{\text { new elements }}{\text { corresponding element }}=\underset{\text { old elements }}{\text { corresponding element }}-\frac{\text { pivot row elements pivot column elements }}{\text { pivot element }} .
\end{aligned}
$$
We obtain Table 7.2, in which the variables $x_{1}$ and $y_{4}$ swap places. From the table, it is clear that the free coefficients in the I-column are non-negative, so we have obtained a basic solution: $x_{1}=10, x_{2}=0, y_{1}=182, y_{2}=5, y_{3}=4, y_{4}=0, Z=40$. Geometrically, this means that we are at vertex $F(10 ; 0)$ of the polygon of feasible solutions $A B C D E F$.
Table 7.2
| | $y_{4}$ | $x_{2}$ | 1 |
| :---: | :---: | :---: | :---: |
| $y_{1}$ | 13 | 11 | $=182$ |
| $y_{2}$ | 1 | 0 | $=5$ |
| $y_{3}$ | 2 | -1 | $=4$ |
| $x_{1}$ | -1 | 1 | $=10$ |
| $Z$ | -4 | 1 | $=40$ |
This solution is not optimal, as there is a negative coefficient in the $Z$-row, so we improve the plan.
We choose the pivot element according to the rule: we choose the column with the smallest negative element in the $z$-row as the pivot column, divide the free terms in the I-column by the corresponding coefficients, and the smallest positive ratio corresponds to the pivot row. The pivot element is 2. Performing MJSE with the pivot element 2 according to the above rule, we obtain Table 7.3.
Table 7.3
| | $y_{3}$ | $x_{2}$ | 1 |
| :---: | :---: | :---: | :---: |
| $y_{1}$ | $-\frac{13}{2}$ | $\frac{35}{2}$ | $=156$ |
| $y_{2}$ | $-\frac{1}{2}$ | $\boxed{-\frac{1}{2}}$ | $=3$ |
| $y_{4}$ | $\frac{1}{2}$ | $-\frac{1}{2}$ | $=2$ |
| $x_{1}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $=12$ |
| $Z$ | 2 | -1 | $=48$ |
The solution obtained from Table 7.3 is also not optimal, as there is a negative coefficient in the $Z$-row. Determining the pivot element $\frac{1}{2}$ from Table 7.3 and
Table 7.4
| | $y_{3}$ | $y_{2}$ | 1 |
| :---: | :---: | :---: | :---: |
| $y_{1}$ | 11 | -35 | $=51$ |
| $x_{2}$ | -1 | 2 | $=6$ |
| $y_{4}$ | 0 | 1 | $=5$ |
| $x_{1}$ | 1 | -1 | $=9$ |
| $Z$ | 1 | 2 | $=54$ |
performing MJSE, we arrive at Table 7.4, in which all coefficients in the $Z$-row are non-negative, and thus $\max Z$ has been reached, corresponding to the solution $x_{1}=9, x_{2}=6$, with $Z_{\max }=54$ (conditional units).
Answer: The maximum profit $Z=54$ (conditional units) is achieved by producing 9 units of item I and 6 units of item II.
|
54
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the distance $d$ between points $A$ and $B$ in each of the following cases:
1) $A(2), B(3) ; 2) A(-4), B(-8)$.
|
Solution. Applying formula (2), we get:
1) $d=|3-2|=1 ; 2) d=|-8-(-4)|=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
75. Write the equation of a line parallel to the $O x$ axis and cutting off a segment equal to -2 from the $O y$ axis. Check if the points $A(2; -2)$ and $B(3; 2)$ lie on this line.
|
Solution. According to the problem, the slope $k=0$, the initial ordinate $b=-2$, therefore, the equation of the line we are looking for is $y=-2$. It is easy to see that the coordinates of any point $M(x; -2)$ satisfy this equation.
Point $A$ lies on the line we are looking for, since its coordinates satisfy the equation of the line $y=-2$. Point $B$ does not lie on the line, since its coordinates do not satisfy the equation of the line $y=-2$ (Fig. 14).
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
312. Find the scalar square of the vector $\bar{a}=2 \bar{i}-\bar{j}-2 \bar{k}$ and its length.
|
Solution. We will use formulas (10), (13), and (14):
$$
(\bar{a})^{2}=a^{2}=2^{2}+(-1)^{2}+(-2)^{2}=9
$$
from which $a=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
313. Find the scalar product of the vectors
$$
\bar{p}=\bar{i}-3 \bar{j}+\bar{k}, \bar{q}=\bar{i}+\bar{j}-4 \bar{k}
$$
|
Solution. The scalar product of the vectors will be found using formula (12):
$$
\bar{p} \bar{q}=1 \cdot 1+(-3) \cdot 1+1 \cdot (-4)=-6
$$
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
314. Find the angle $\varphi$ between two vectors
$$
\bar{a}=\bar{i}+\bar{j}-4 \bar{k} \text { and } \bar{b}=\bar{i}-2 \bar{j}+2 \bar{k} .
$$
|
Solution. We will use formula (16):
$$
\cos \varphi=\frac{\bar{a} \bar{b}}{a b}=\frac{1-2-8}{\sqrt{1+1+16} \sqrt{1+4+4}}=-\frac{\sqrt{2}}{2},
$$
therefore, $\varphi=135^{\circ}$.
|
135
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
626. Find $f^{\prime}(0)$, if $f(x)=e^{x} \arcsin x+\operatorname{arctg} x$.
|
Solution. $\quad f^{\prime}(x)=\left(e^{x} \arcsin x\right)^{\prime}+(\operatorname{arctg} x)^{\prime}=\left(e^{x}\right)^{\prime} \arcsin x+$ $+e^{x}(\arcsin x)^{\prime}+(\operatorname{arctg} x)^{\prime}=e^{x} \arcsin x+\frac{e^{x}}{\sqrt{1-\lambda^{2}}}+$ $+\frac{1}{x^{2}+1}=e^{x} \frac{1+\sqrt{1-x^{2}} \arcsin x}{\sqrt{1-x^{2}}}+\frac{1}{1+x^{2}}$.
Substituting the value $x=0$, we get $f^{\prime}(0)=1+1=2$.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
976. Find the following limits:
1) $\lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} \frac{\tan x y}{y}$
2) $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x+y}{x}$.
|
Solution. 1) $\lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} \frac{\operatorname{tg} x y}{y}=\lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} x \frac{\operatorname{tg} x y}{x y}=2 \cdot 1=2$,
since
$$
\lim _{\alpha \rightarrow 0} \frac{\operatorname{tg} \alpha}{\alpha}=1
$$
2) Let's use the definition of the limit of a function at a point. Take the sequences $x=\frac{1}{n} \rightarrow 0, y=\frac{1}{n} \rightarrow 0(n \rightarrow \infty)$,
then
$$
\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x+y}{x}=\lim _{n \rightarrow \infty} \frac{\frac{1}{n}+\frac{1}{n}}{\frac{1}{n}}=2
$$
Now take $x=\frac{1}{n} \rightarrow 0, y=\frac{2}{n} \rightarrow 0(n \rightarrow \infty), \quad$ then
$$
\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x+y}{x}=\lim _{n \rightarrow \infty} \frac{\frac{1}{n}+\frac{2}{n}}{\frac{1}{n}}=3
$$
Thus, for different sequences of points converging to the point $(0 ; 0)$, we get different limits. This means that the limit of the function at this point does not exist (see point 1).
Note that the given function is not defined at the point $(0 ; 0)$. Find the following limits:
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1020. Investigate the function for extremum
$$
f(x, y)=x^{2}+y^{2}-4 y+4
$$
|
Solution. Let's find the partial derivatives:
$$
f_{x}^{\prime}(x, y)=2 x ; f_{y}^{\prime}(x, y)=2 y-4
$$
Set them equal to zero, we get a system of two equations with two unknowns:
$$
\left\{\begin{array}{l}
2 x=0 \\
2 y-4=0
\end{array}\right.
$$
from which $x=0, y=2$.
The function at the critical point $M_{0}(0 ; 2)$ has a minimum $f(0 ; 2)=4-8+4=0$, since near this point for any points $M(x ; y)$, different from $M_{0}(0 ; 2)$, the values of the function are greater than zero. For example, let $x=0, y=1$, then $f(0 ; 1)=1-4+4=1>0$; let $x=-1, y=3$, then $f(-1 ; 3)=1+9-12+4=2>0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1287. Calculate the area of the figure bounded by the parabola $y=-x^{2}+$ $+6 x-5$ and the coordinate axes.
|
Solution. If the figure is located on opposite sides of the $O x$ axis (Fig. $82, a$), then the area $S$ should be calculated using the formula
$$
S=\int_{a}^{c} f(x) d x+\left|\int_{c}^{b} f(x) d x\right|
$$
Fig. 81
Fig. 82
From Fig. 82, b, it is clear that the area of the given figure will be equal to
$$
\begin{aligned}
& S=\left|\int_{0}^{1}\left(-x^{2}+6 x-5\right) d x\right|+\int_{1}^{5}\left(-x^{2}+6 x-5\right) d x= \\
& =\left|\left(-\frac{x^{3}}{3}+3 x^{2}-5 x\right)\right|_{0}^{1}+\left.\left(-\frac{x^{3}}{3}+3 x^{2}-5 x\right)\right|_{1} ^{5}=13
\end{aligned}
$$
|
13
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1348. Calculate the integral $\int_{0}^{6}\left(x^{2}+3\right) d \bar{x}$ using the Newton-Leibniz formula and approximate formulas of rectangles and trapezoids, dividing the interval of integration into 6 equal parts $(n=6)$. Find the absolute and relative errors of the results obtained by the approximate formulas.
|
Solution. By the Newton-Leibniz formula
$$
I=\int_{0}^{6}\left(x^{2}+3\right) d x=\left.\left(\frac{x^{3}}{3}+3 x\right)\right|_{0} ^{6}=90
$$
The interval $[0,6]$ is divided into 6 equal parts, and we construct a table of values of the integrand function $y=x^{2}+3$ :
$$
\begin{array}{lllr}
x_{0}=0 & y_{0}=3 & x_{4}=4 & y_{4}=19 \\
x_{1}=1 & y_{1}=4 & x_{5}=5 & y_{5}=28 \\
x_{2}=2 & y_{2}=7 & x_{6}=6 & y_{6}=39 \\
x_{3}=3 & y_{3}=12 & h=\frac{b-a}{n}=\frac{6-0}{6}=
\end{array}
$$
By the rectangle formula (2)
$$
I \approx \sum_{i=0}^{5} y_{i}=y_{0}+y_{1}+y_{2}+y_{3}+y_{4}+y_{5}=73
$$
Absolute error $\Delta=90-73=17$. Relative error $\delta=\frac{17}{90} \approx 0.189=18.9 \%$.
By the rectangle formula ( $2^{\prime}$ )
$$
I \approx \sum_{i=1}^{6} y_{i}=y_{1}+y_{2}+y_{3}+y_{4}+y_{5}+y_{6}=109
$$
Absolute error $\Delta=109-90=19$. Relative error $\delta=\frac{19}{90} \approx 0.211=21.1 \%$.
By the trapezoidal formula
$$
\begin{gathered}
I \approx \frac{y_{0}+y_{b}}{2}+\sum_{i=1}^{5} y_{i}=\frac{3+39}{2}+70=91 \\
\Delta=91-90=1 ; \quad \delta=\frac{1}{90}=0.011=1.1 \%
\end{gathered}
$$
|
90
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1429. Check that the series $\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{\sqrt{n}}$ converges. How many terms of this series need to be taken to compute its sum with an accuracy of 0.01?
|
Solution. For this series, all conditions of the Leibniz criterion are satisfied, so the series converges. We can write the sum of the series in the form: $S=S_{n}+r_{n},\left|r_{n}\right|<\left|a_{n+1}\right|$. We need to find such an $n$ that $\left|a_{n+1}\right|=\frac{1}{\sqrt{n+1}} \leqslant 0.01$. Solving the equation $\frac{1}{\sqrt{n+1}}=0.01$, we get $n=9999$, hence $\left|r_{9999}\right|<0.01$. Considering the conditions of the problem and this result, we find $0<r_{9999}<0.01$. Therefore, $S=S_{9999}+r_{9999}$, from which $S \approx S_{9999}$ with an accuracy of 0.01 (with a deficit). Note that this series converges very slowly, as do all other conditionally convergent series.
|
9999
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1586. The share of premium quality items in this enterprise is $31 \%$. What is the most probable number of premium quality items in a randomly selected batch of 75 items?
|
Solution. It is known that $p=0.31, n=75$, and $q=1-p=$ $=0.69$. We form the double inequality (1):
$$
\begin{gathered}
75 \cdot 0.31 - 0.69 \leqslant m_{0} \leqslant 75 \cdot 0.31 + 0.31 ; \\
22.56 \leqslant m_{0} \leqslant 23.56 .
\end{gathered}
$$
From this, it follows that $m_{0}=23$.
|
23
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1615. On average, $85 \%$ of the items coming off the conveyor are of the first grade. How many items need to be taken so that with a probability of 0.997, the deviation of the frequency of first-grade items from 0.85 in absolute value does not exceed 0.01?
|
Solution. Here $p=0.85, q=1-0.85=0.15, \varepsilon=0.01$, $P=0.997, n$-? Since in the equality $P\left(\left|\frac{m}{n}-p\right|<\varepsilon\right) \approx$ $\approx \Phi\left(\varepsilon \sqrt{\frac{n}{p q}}\right)$ the probability $P$ on the left is known, we first solve the equation $\Phi(t)=P$. Let $t_{P}$ be the root of this equation. Then $\varepsilon \sqrt{\frac{n}{p q}} \approx t_{p}, \varepsilon^{2} \frac{n}{p q} \approx t_{P}^{2}$ and, consequently, $n \approx$
$\approx \frac{p q t_{P}^{2}}{\varepsilon^{2}}$. For our case $t_{0.997}=3$, therefore
$$
n \approx \frac{0.85 \cdot 0.15 \cdot 3^{2}}{(0.01)^{2}}=\frac{1.1475}{0.0001}=11475
$$
|
11475
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1702. How many times does one need to measure a given quantity, the true value of which is equal to $a$, to be able to state with a probability of at least 0.95 that the arithmetic mean of these measurements differs from $a$ in absolute value by less than 2, if the root mean square deviation of each measurement is less than 10?
|
Solution. Let $X_{i}$ be the result of the $i$-th measurement. From the condition of the problem, it follows that $E X_{i}=a, D X_{i}<10^{2}=100$. Therefore,
$$
\frac{E X_{1}+E X_{2}+\ldots+E X_{n}}{n}=\frac{a+a+\ldots+a}{n}=a
$$
We need to find $n$ such that
$$
P\left(\left|\frac{X_{1}+X_{2}+\ldots+X_{n}}{n}-a\right|<2\right) \geqslant 0.95
$$
Since
$$
P\left(\left|\frac{X_{1}+X_{2}+\ldots+X_{n}}{n}-a\right|<\varepsilon\right) \geqslant 1-\frac{C}{n \varepsilon^{2}}
$$
where $C=100, \varepsilon=2$, the previous inequality will certainly be satisfied if
$$
1-\frac{C}{n \varepsilon^{2}} \geqslant 0.95
$$
From this,
$$
1-\frac{100}{n \cdot 2^{2}} \geqslant 0.95 ; 0.05 \geqslant \frac{100}{n \cdot 4} ; \quad n \geqslant \frac{100}{4 \cdot 0.05}=500
$$
|
500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1737. Let the dairy farm of a collective farm have data on the milk yield of cows for the lactation period:
| Milk yield, kg | Number of cows | Milk yield, kg | Number of cows |
| :---: | :---: | :---: | :---: |
| $400-600$ | 1 | $1600-1800$ | 14 |
| $600-800$ | 3 | $1800-2000$ | 12 |
| $800-1000$ | 6 | $2000-2200$ | 10 |
| $1000-1200$ | 11 | $2200-2400$ | 6 |
| $1200-1400$ | 15 | 2400 and above | 2 |
| $1400-1600$ | 20 | | |
Find the arithmetic mean of the milk yield of cows on this farm.
|
Solution. The arithmetic mean will be found using the simplified formula
$$
\bar{X}=k \bar{U}+x_{0} \quad\left(U=\frac{X-x_{0}}{k}\right)
$$
by setting $x_{0}=1500$ and $k=200$. All necessary calculations are presented in the following table:
| Interval $X_{i}^{\prime}-X_{i}^{\prime \prime}$ | Frequency $m_{i}$ | Midpoint of interval $x_{i}$ | $u_{i}=\frac{x_{i}-x_{0}}{k}$ | $m_{i} u_{i}$ |
| :---: | :---: | :---: | :---: | :---: |
| $400-600$ | 1 | 500 | -5 | -5 |
| $600-800$ | 3 | 700 | -4 | -12 |
| $800-1000$ | 6 | 900 | -3 | -18 |
| $1000-1200$ | 11 | 1100 | -2 | -22 |
| $1200-100$ | 15 | 1300 | 0 | -15 |
| $1400-1600$ | 20 | 1500 | 0 | 14 |
| $1600-1800$ | 14 | 1700 | 2 | 24 |
| $1800-2000$ | 12 | 1900 | 4 | 30 |
| $2000-200$ | 10 | 2100 | 5 | 24 |
| $2200-2400$ | 6 | 2300 | 5 | 10 |
| 2400 and above | 2 | 2500 | 5 | 30 |
| Sum | 100 | | | |
$$
\bar{U}=\frac{30}{100}=0.3, \quad \bar{X}=k \bar{U}+x_{0}=200 \cdot 0.3+1500=1560
$$
|
1560
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1776. What should be the sample size to ensure that when determining the percentage of non-standard items, the maximum error $\varepsilon=5\%$ is achieved with a confidence probability $P=0.99896$.
|
Solution. Given the confidence probability $P=$ $=0.99896$, we find the argument $t$ of the Laplace function $\Phi(t)$, for which $\Phi(t)=0.99896 ; t=3.28$. Therefore, the sample size, at which with a probability of 0.99896 it can be stated that the sample proportion differs from the population proportion in absolute value by less than $5 \%$, is determined by the formula
$$
n \approx \frac{t^{2} p(1-p)}{\varepsilon^{2}}=\frac{(3.28)^{2} p(1-p)}{(0.05)^{2}}
$$
If the proportion of the characteristic $p$ were known at least approximately, then the approximate value of $n$ would follow directly from this formula. Since there is no information about $p$ in the problem statement, let's consider $n$ as a function of $p$ and find its maximum value. The derivative of $n$ with respect to $p n^{\prime}=$ $=\frac{(3.28)^{2}}{(0.05)^{2}}[p(1-p)]^{\prime}=\frac{(3.28)^{2}}{(0.05)^{2}}(1-2 p)$ is zero at $p=0.5$, and changes sign from positive to negative as $p$ passes through this value. Thus, $n$ attains its maximum value at $p=0.5$:
$$
n_{\max }=\frac{(3.28)^{2}}{(0.05)^{2}} \cdot \frac{1}{4} \approx 1076
$$
|
1076
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1777. It is planned to conduct a selective survey of 5000 light bulbs to determine the average duration of their burning. What should be the volume of the non-repeated sample to ensure with a probability of 0.9802 that the general average differs from the sample average by less than 15 hours in absolute value, if the general variance is less than 10000?
|
Solution. According to the table (Appendix 2), we find that the argument $t=2.33$ corresponds to the given confidence probability of 0.9802. For sampling without replacement, the sample size is determined by the formula
$$
n \approx \frac{N t^{2} \sigma_{0}^{2}}{N \varepsilon^{2}+t^{2} \sigma_{0}^{2}}
$$
In our case $\sigma_{0}^{2}<10000$, therefore
$$
\begin{gathered}
n \approx \frac{5000 \cdot(2.33)^{2} \sigma_{0}^{2}}{5000 \cdot(15)^{2}+(2.33)^{2} \sigma_{0}^{2}}<\frac{5000 \cdot 5.4289 \cdot 10000}{5000 \cdot 225+5.4289 \cdot 10000}= \\
=230.2 ; n_{\max }=230
\end{gathered}
$$
|
230
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.7. Convert to polar coordinates and evaluate the double integrals.
a) $\iint_{\Omega} x y^{2} d x d y$, where the region $\Omega$ is bounded by the circles $x^{2}+(y-1)^{2}=1$ and $x^{2}+y^{2}=4 y$
b) $\iint_{\Omega} e^{-x^{2}-y^{2}} d x d y$, where $\Omega-$ is the circle $x^{2}+y^{2} \leqslant R^{2}$.
|
Solution.
a) First, let's depict the region $\Omega$ in the Cartesian coordinate system (Fig. 1.32).
The equations of the boundary circles in polar coordinates are obtained after the substitution $x=\rho \cos \varphi, y=\rho \sin \varphi$:
$$
\begin{aligned}
x^{2}+(y-1)^{2}=1 \Rightarrow x^{2}+y^{2} & =2 y \Rightarrow \rho=2 \sin \varphi, 0 \leqslant \varphi \leqslant \pi \\
x^{2}+y^{2} & =4 y \Rightarrow \rho=4 \sin \varphi, 0 \leqslant \varphi \leqslant \pi
\end{aligned}
$$
The region $\Omega$ in coordinates $x, y$ is transformed into the region $D$ in coordinates $\varphi, \rho: D=\{(\varphi, \rho): 0 \leqslant \varphi \leqslant \pi ; 2 \sin \varphi \leqslant \rho \leqslant 4 \sin \varphi\}$. We will perform the transformation to coordinates $\varphi, \rho$ and compute the original double integral:
$$
\begin{gathered}
\iint_{\Omega} x y^{2} d x d y=\iint_{D} \rho^{3} \cos \varphi \sin ^{2} \varphi \rho d \rho d \varphi= \\
=\int_{0}^{\pi} \sin ^{2} \varphi \cos \varphi d \varphi \int_{2 \sin \varphi}^{4 \sin \varphi} \rho^{4} d \rho=\int_{0}^{\pi} \sin ^{2} \varphi \cos \varphi\left(\left.\frac{\rho^{5}}{5}\right|_{2 \sin \varphi} ^{4 \sin \varphi}\right) d \varphi= \\
=\frac{992}{5} \int_{0}^{\pi} \sin ^{7} \varphi \cos \varphi d \varphi=\frac{992}{5} \int_{0}^{\pi} \sin ^{7} \varphi d(\sin \varphi)= \\
=\left.\frac{992}{5} \frac{\sin ^{8} \varphi}{8}\right|_{0} ^{\pi}=0
\end{gathered}
$$
b) Transform the integral to polar coordinates $x=\rho \cos \varphi, y=\rho \sin \varphi:$
$$
\begin{gathered}
\iint_{\Omega} e^{-x^{2}-y^{2}} d x d y=\iint_{D} e^{-\rho^{2}} \rho d \rho d \varphi= \\
=\int_{0}^{2 \pi} d \varphi \int_{0}^{R} e^{-\rho^{2}} \rho d \rho=\left.\int_{0}^{2 \pi}\left(-\frac{e^{-\rho^{2}}}{2}\right)\right|_{0} ^{R} d \varphi=\pi\left(1-e^{-R^{2}}\right)
\end{gathered}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.5. Compute the specified line integrals of the second kind:
a) $\int_{L} 2 y \sin 2 x d x - \cos 2 x d y$, where $L$ is any piecewise-smooth curve connecting the points $A\left(\frac{\pi}{2}, 2\right)$ and $B\left(\frac{\pi}{6}, 1\right)$.
b) $\int_{L} y x e^{x} d x - (x-1) e^{x} d y$, where $L$ is any piecewise-smooth curve connecting the points $A(0,2)$ and $B(1,2)$.
|
Solution.
a) It is not difficult to understand that the integrand is a complete differential of the function $u=-y \cos 2 x$, i.e.
$$
\begin{gathered}
\int_{L} 2 y \sin 2 x d x-\cos 2 x d y=\int_{L} d u=u(B)-u(A)= \\
=-\cos \frac{\pi}{3}+2 \cos \pi=-2-\frac{1}{2}=-\frac{5}{2}
\end{gathered}
$$
b) In this problem, the function $u$ can be taken as the function $u=y(x-1) e^{x}: d u=y x e^{x} d x-(x-1) e^{x} d y$. Therefore,
$$
\int_{L} y x e^{x} d x-(x-1) e^{x} d y=\int_{L} d u=u(B)-u(A)=0 .
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.21. Calculate the circulation of the vector field:
a) $\vec{A}=x^{2} y^{2} \vec{i}+\vec{j}+z \vec{k}$ along the circle $x^{2}+y^{2}=a^{2}, z=0$;
b) $\dot{A}=(x-2 z) \dot{i}+(x+3 y+z) \dot{j}+(5 x+y) \vec{k}$ along the perimeter of the triangle $A B C$ with vertices $A(1,0,0), B(0,1,0), C(0,0,1)$.
|
Solution.
a) For $z=0$ we obtain the planar field $\vec{A}=x^{2} y^{2} \dot{i}+\ddot{j}$, where $P=x^{2} y^{2}, Q=1$. To compute the circulation of this field along the circle $x^{2}+y^{2}=a^{2}$, we can use Green's formula (2.62):
$$
\begin{gathered}
\oint_{x^{2}+y^{2}=a^{2}} \vec{A} \cdot d \vec{l}=\iint_{x^{2}+y^{2} \leqslant a^{2}}\left(Q_{x}-P_{y}\right) d x d y=-2 \iint_{x^{2}+y^{2} \leqslant a^{2}} x^{2} y d x d y= \\
\quad=-2 \int_{-a}^{+a} x^{2} d x \int_{-\sqrt{a^{2}-x^{2}}}^{+\sqrt{a^{2}-x^{2}}} y d y=-\left.2 \int_{-a}^{+a} x^{2} d x y^{2}\right|_{-\sqrt{a^{2}-x^{2}}} ^{\sqrt{a^{2}-x^{2}}}=0 .
\end{gathered}
$$
b) By Stokes' formula, the circulation of the vector field along the triangle $A B C$ is equal to the flux of $\operatorname{rot} \ddot{A}$ through the plane of the triangle $A B C$ with the outward normal (the normal forms an acute angle with the $O Z$ axis), i.e.,
$$
\oint_{A B C} \dot{A} \cdot d \dot{l}=\iint_{S_{A B C}}(\operatorname{rot} \dot{A} \cdot \dot{n}) d S
$$
We will calculate the necessary quantities entering the right-hand side of Stokes' formula:
$$
\begin{aligned}
& \operatorname{rot} \dot{A}=\left|\begin{array}{ccc}
i & j & \dot{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
x-2 z & x+3 y+z & 5 x+y
\end{array}\right|=-\dot{j} \cdot 7+\dot{k} ; \\
& S_{A B C}: x+y+z=1 ; \\
& \vec{n}=\frac{1}{\sqrt{3}}(1,1,1) ; \\
& d S=\sqrt{1+z_{x}^{2}+z_{y}^{2}} d x d y=\sqrt{3} d x d y .
\end{aligned}
$$
Thus, the sought circulation is:
$$
\oint_{A B C} \dot{A} \cdot \vec{l}=-6 \int_{\substack{x+y \leqslant 1 \\ x \geqslant 0 \\ y \geqslant 0}} d x d y=-6 \int_{0}^{1} d x \int_{0}^{1-x} d y=-3
$$
General problems related to scalar and vector fields.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.179. $\frac{d x}{d t}=y, \frac{d y}{d t}=-4 x-2 y$.
|
Solution. We form the characteristic equation
$$
\left|\begin{array}{cc}
(0-\lambda) & 1 \\
-4 & (-2-\lambda)
\end{array}\right|=2 \lambda^{2}+2 \lambda+4=0
$$
The roots of the characteristic equation are complex conjugates, the real part is negative, and the imaginary part is non-zero:
$$
\left.\lambda_{1,2}=-\frac{1}{2} \pm \frac{\sqrt{3}}{2}, \alpha=-\frac{1}{2}<0, \beta=\frac{\sqrt{3}}{2} \neq 0 \text { (case } 2 a\right) .
$$
The equilibrium point is a stable focus.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.180. $\frac{d x}{d t}=x-y, \frac{d y}{d t}=x+y$.
|
Solution. We form the characteristic equation
$$
\left|\begin{array}{cc}
(1-\lambda) & -1 \\
1 & (1-\lambda)
\end{array}\right|=\lambda^{2}-2 \lambda+2=0
$$
The roots of the characteristic equation are complex conjugates, with a positive real part and a non-zero imaginary part:
$$
\lambda_{1,2}=1 \pm i (\text{case } 2 \mathrm{~b}: \alpha=1>0, \beta=1 \neq 0).
$$
The equilibrium point is an unstable focus.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.1. $I=\int_{0}^{2} x^{3} d x$
|
Solution. $I=\int_{0}^{2} x^{3} d x=\left.\frac{x^{4}}{4}\right|_{0} ^{2}=\frac{2^{4}}{4}-\frac{0^{4}}{4}=4$.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.2. $I=\int_{0}^{2}(x-1)^{3} d x$.
|
Solution.
$$
\begin{aligned}
I= & \int_{0}^{2}(x-1)^{3} d x=\int_{0}^{2}\left(x^{3}-3 x^{2}+3 x-1\right) d x= \\
& =\int_{0}^{2} x^{3} d x-3 \int_{0}^{2} x^{2} d x+3 \int_{0}^{2} x d x-\int_{0}^{2} d x= \\
& =\left.\frac{x^{4}}{4}\right|_{0} ^{2}-\left.3 \frac{x^{3}}{3}\right|_{0} ^{2}+\left.3 \frac{x^{2}}{2}\right|_{0} ^{2}-\left.x\right|_{0} ^{2}=0
\end{aligned}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.5. $I=\int_{-1}^{1} x|x| d x$.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
However, since the text provided is already in a form that is commonly used in English for mathematical expressions, the translation is essentially the same:
Example 2.5. $I=\int_{-1}^{1} x|x| d x$.
|
Solution. Since the integrand is an odd function and the limits of integration are symmetric about zero, then
$$
\int_{-1}^{1} x|x| d x=0
$$
In the following two examples, it will be demonstrated that the formal application of the Newton-Leibniz formula (without considering the integrand functions) can lead to an incorrect result.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.13. $\int_{-1}^{1}|x| e^{|x|} d x$.
|
Solution. Here the integrand is an even function, which needs to be utilized, and then apply the integration by parts formula (2.3):
$$
\begin{gathered}
\int_{-1}^{1}|x| e^{|x|} d x=2 \int_{0}^{1} x e^{x} d x=\left|\begin{array}{l}
u=x, d u=d x \\
d v=e^{x} d x, v=\int e^{x} d x=e^{x}
\end{array}\right|= \\
=2\left(\left.x e^{x}\right|_{0} ^{1}-\int_{0}^{1} e^{x} d x\right)=2\left(\left.x e^{x}\right|_{0} ^{1}-\left.e^{x}\right|_{0} ^{1}\right)= \\
=\left.2 e^{x}(x-1)\right|_{0} ^{1}=-2 e^{0}(0-1)=2
\end{gathered}
$$
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.14. $\int_{0}^{(\pi / 2)^{2}} \sin \sqrt{x} d x$.
|
Solution. First, let's show an incorrect solution leading to a non-integrable function. Transform the integrand as follows:
$$
\begin{gathered}
\int_{0}^{(\pi / 2)^{2}} \frac{\sin \sqrt{x} \cdot \sqrt{x} d x}{\sqrt{x}}=\left|\begin{array}{l}
u=\sqrt{x}, d u=\frac{d x}{2 \sqrt{x}} \\
d v=\frac{\sin \sqrt{x} d x}{\sqrt{x}}, v=-2 \cos \sqrt{x}
\end{array}\right|= \\
\quad=\left.\sqrt{x}(-2 \cos \sqrt{x})\right|_{0}^{(\pi / 2)^{2}}-\int_{0}^{(\pi / 2)^{2}} \frac{\cos \sqrt{x} d x}{\sqrt{x}}
\end{gathered}
$$
Since $\cos x=1$, and $\frac{1}{\sqrt{x}}$ does not exist at $x=0$, the integrand $\frac{\cos \sqrt{x}}{\sqrt{x}}$ on the interval $\left[0,\left(\frac{\pi}{2}\right)^{2}\right]$ is not integrable in the sense of the definitions provided at the beginning of this section.
To correctly compute the given definite integral, we will use the method of substitution and set $x=z^{2}, d x=2 z d z$, the value $x_{0}=0$ will correspond to $z_{0}=0$, and the value $x_{1}=\left(\frac{\pi}{2}\right)^{2}-z_{1}=\frac{\pi}{2}$. After the specified substitution, the original integral will take the form:
$$
\begin{gathered}
I=\int_{0}^{\pi / 2} \sin z(2 z d z)=\left\lvert\, \begin{array}{l}
u=z, d u=d z \\
d v=\sin z d z, v=-\cos z
\end{array}\right. \\
\quad=2\left(-\left.z \cos z\right|_{0}^{\pi / 2}-\int_{0}^{\pi / 2}(-\cos z) d z\right) \\
=-\left.2(-z \cos z+\sin z)\right|_{0}^{\pi / 2}=2
\end{gathered}
$$
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.21. Find the limit $\lim _{x \rightarrow 0}\left(\left(\int_{0}^{x^{2}} \cos x d x\right) / x\right)$.
|
Solution. We will use L'Hôpital's rule, as there is an indeterminate form of type «0/0».
$$
\lim _{x \rightarrow 0} \frac{\int_{0}^{x^{2}} \cos x d x}{x}=\lim _{x \rightarrow 0} \frac{\left(\int_{0}^{x^{2}} \cos x d x\right)^{\prime}}{x^{\prime}}=\lim _{x \rightarrow 0} \frac{\cos \left(x^{2}\right) \cdot 2 x}{1}=0
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.22. Find the limit
$$
\lim _{x \rightarrow 0}\left(\int_{0}^{\operatorname{arctg} x} e^{\sin x} d x / \int_{0}^{x} \cos \left(x^{2}\right) d x\right)
$$
|
Solution. According to L'Hôpital's rule and the rules for differentiating definite integrals, we transform the limit as follows:
$$
\lim _{x \rightarrow 0}\left(\int_{0}^{\operatorname{arctg} x} e^{\sin x} d x\right)^{\prime} /\left(\int_{0}^{x} \cos \left(x^{2}\right) d x\right)^{\prime}=\lim _{x \rightarrow 0} \frac{e^{\sin (\operatorname{arctg} x)}}{\left(1+x^{2}\right) \cos x^{2}}=1
$$
## 2.3 . IMPROPER INTEGRALS
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.25. $\int_{-\infty}^{0} e^{x} d x$.
Translate the text above into English, keeping the original text's line breaks and format, and output the translation result directly.
Example 2.25. $\int_{-\infty}^{0} e^{x} d x$.
|
Solution. According to formula (2.6), we get
$$
\int_{-\infty}^{0} e^{x} d x=\lim _{a \rightarrow-\infty} \int_{a}^{0} e^{x} d x=\left.\lim _{a \rightarrow -\infty} e^{x}\right|_{a} ^{0}=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.36. $I=\mathrm{V}$.p. $\int_{-\infty}^{\infty} \operatorname{arctg} x d x$.
Translating the above text into English, while preserving the original text's line breaks and format, yields:
Example 2.36. $I=\mathrm{V}$.p. $\int_{-\infty}^{\infty} \arctan x d x$.
|
Solution.
$$
\begin{gathered}
I=\lim _{a \rightarrow \infty} \int_{-a}^{a} \operatorname{arctg} x d x=\left|\begin{array}{l}
\left.u=\operatorname{arctg} x . d u=\frac{d x}{1+x^{2}} \right\rvert\,= \\
d v=x, v=x
\end{array}\right|= \\
=\lim _{a \rightarrow \infty}\left(\left.x \operatorname{arctg} x\right|_{-a} ^{a}-\int_{-a}^{a} \frac{x d x}{1+x^{2}}\right)= \\
=\lim _{a \rightarrow \infty}(a \operatorname{arctg} a-(-a) \operatorname{arctg}(-a)- \\
\left.-0.5 \ln \left(1+a^{2}\right)+0.5 \ln \left(1+(-a)^{2}\right)\right)=0
\end{gathered}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.41. $I=\int_{0}^{1} \ln x d x$.
|
Solution.
$$
\begin{gathered}
I=\left|\begin{array}{l}
u=\ln x, d u=\frac{d x}{x} \\
d v=d x, v=x
\end{array}\right|=\lim _{a \rightarrow+0}\left(\left.x \ln x\right|_{a} ^{1}-\int_{a}^{1} x \frac{d x}{x}\right)= \\
=-\lim _{a \rightarrow+0} \frac{\ln a}{1 / a}-1=[\text{ apply L'Hôpital's rule] }= \\
=\lim _{a \rightarrow+0} \frac{1 / a}{1 / \dot{a}^{2}}-1=-1 .
\end{gathered}
$$
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.45. $I=\mathrm{V} . \mathrm{p} . \int_{1 / e}^{e} \frac{d x}{x \ln x}$. Calculate the improper integral of the second kind in the sense of the principal value.
|
Solution. According to formula (2.18)
$$
\begin{gathered}
I=\lim _{a \rightarrow+0}\left(\int_{1 / e}^{1-a} \frac{d(\ln x)}{\ln x}+\int_{1+a}^{e} \frac{d(\ln x)}{\ln x}\right)= \\
=\lim _{a \rightarrow+0}\left(\ln \left|\ln x\left\|_{1 / e}^{1-a}+\ln \mid \ln x\right\|_{1+a}^{e}\right)=\right. \\
=\lim _{a \rightarrow+0}(\ln |\ln (1-a)|-\ln |\ln 1-\ln e|+\ln |\ln e|-\ln |\ln (1+a)|)= \\
=\lim _{a \rightarrow+0} \ln \left|\frac{\ln (1-a)}{\ln (1+a)}\right|=\ln \left|\lim _{a \rightarrow+0} \frac{(\ln (1-a))^{\prime}}{(\ln (1+a))^{\prime}}\right|= \\
=\ln \left|\lim _{a \rightarrow+0}\left(-\frac{1+a}{1-a}\right)\right|=\ln 1=0 .
\end{gathered}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.46. Find the average value of the function $u(x)=$ $=1 / \sqrt{x}$ on the half-interval $x \in(0,1]$.
|
Solution.
$$
M(x)=\lim _{a \rightarrow+0}\left(\int_{a}^{1} \frac{d x / \sqrt{x}}{1-0}\right)=\lim _{a \rightarrow+0} \frac{2 \sqrt{1}-2 \sqrt{a}}{1}=2
$$
## 2.4. GEOMETRIC APPLICATIONS OF DEFINITE INTEGRALS
## Area of a Plane Curve
The area of a plane figure bounded by curves given by their equations in Cartesian coordinates: above - $y=y_{1}(x)$, below - $y=y_{2}(x)$, and on the left and right by segments of the lines $x=a$ and $x=b$, is calculated by the formula
$$
S=\left|\int_{a}^{b}\left(y_{1}(x)-y_{2}(x)\right) d x\right|
$$
The area of a plane figure bounded by curves given by their equations in Cartesian coordinates: to the right - $x=x_{1}(y)$, to the left - $x=x_{2}(y)$, and below and above by segments of the lines $y=c$ and $y=d$, is calculated by the formula
$$
S=\left|\int_{c}^{d}\left(x_{1}(y)-x_{2}(y)\right) d y\right|
$$
The area of a closed plane figure bounded by a curve given by parametric equations: $x=x(t)$, $y=y(t), 0 \leqslant t \leqslant T$ can be calculated using one of three formulas (assuming that as $t$ increases from 0 to $T$, the curve is traversed counterclockwise).
$$
S=\int_{0}^{T} y(t) x^{\prime}(t) d t=\int_{0}^{T} x(t) y^{\prime}(t) d t=0.5 \int_{0}^{T}\left(x(t) y^{\prime}(t)+y(t) x^{\prime}(t)\right) d t
$$
The area of a figure bounded by a curve given by an equation in polar coordinates $\rho=\rho(\varphi)$ and segments of two rays $\varphi=\alpha$ and $\varphi=\beta$, is calculated by the formula
$$
S=0.5\left|\int_{\alpha}^{\beta}(\rho(\varphi))^{2} d \varphi\right|
$$
## Arc Length
The length of an arc of a smooth curve given by the equation in Cartesian coordinates $y=y(x)(a \leqslant x \leqslant b)$, is calculated by the formula
$$
L=\left|\int_{a}^{b} \sqrt{1+\left(y^{\prime}(x)\right)^{2}} d x\right|
$$
The length of an arc of a smooth curve given by the equation in Cartesian coordinates $x=x(y)(c \leqslant y \leqslant d)$, is calculated by the formula
$$
L=\left|\int_{c}^{d} \sqrt{1+\left(x^{\prime}(y)\right)^{2}} d y\right|
$$
The length of an arc of a smooth curve given by parametric equations $x=x(t)$ and $y=y(t)\left(t_{1} \leqslant t \leqslant t_{2}\right)$ is calculated by the formula
$$
L=\left|\int_{t_{1}}^{t_{2}} \sqrt{\left(x^{\prime}(t)\right)^{2}+\left(y^{\prime}(t)\right)^{2}} d t\right|
$$
The length of an arc of a smooth curve given by parametric equations in three-dimensional space $x=x(t), y=y(t)$, $z=z(t)\left(t_{1} \leqslant t \leqslant t_{2}\right)$ is calculated by the formula
$$
L=\left|\int_{t_{1}}^{t_{2}} \sqrt{\left(x^{\prime}(t)\right)^{2}+\left(y^{\prime}(t)\right)^{2}+\left(z^{\prime}(t)\right)^{2}} d t\right|
$$
The length of an arc of a smooth curve given by a polar equation, $\rho=\rho(\varphi), \alpha \leqslant \varphi \leqslant \beta$ is calculated by the formula
$$
L=\left|\int_{a}^{\beta} \sqrt{\left.\left.(\rho(\varphi))^{2}\right)+\left(\rho^{\prime}(\varphi)\right)^{2}\right)} d \varphi\right|
$$
## Surface Area of Revolution
If a segment of a smooth curve is rotated around an arbitrary axis, the area of the surface formed is calculated by the formula
$$
S=2 \pi\left|\int_{r_{1}}^{r_{2}} G(l(r)) d l(r)\right|
$$
where $d l$ is the differential of the arc $l, G(l(r))$ is the distance from a point on the curve to the axis of rotation, $r_{1}$ and $r_{2}$ are the values of the arc variable $r$ corresponding to the ends of the arc.
If a segment of a smooth curve given by the equation in Cartesian coordinates $y=f(x)(a \leqslant x \leqslant b)$ is rotated around the $O X$ axis, the area of the surface formed is calculated by the formula
$$
S_{x}=2 \pi\left|\int_{a}^{b} f(x) \sqrt{1+\left(f^{\prime}(x)\right)^{2}} d x\right|
$$
If a segment of a smooth curve given by the equation in Cartesian coordinates $x=g(y)(c \leqslant x \leqslant d)$ is rotated around the $O Y$ axis, the area of the surface formed is calculated by the formula
$$
S_{y}=2 \pi\left|\int_{a}^{b} g(y) \sqrt{1+\left(g^{\prime}(y)\right)^{2}} d y\right|
$$
If a segment of a smooth curve given by parametric equations $x=x(t)$ and $y=y(t)\left(t_{1} \leqslant t \leqslant t_{2}\right)$ is rotated around the $O X$ axis, the area of the surface formed is calculated by the formula
$$
S_{x}=2 \pi\left|\int_{t_{1}}^{t_{2}} y(t) \sqrt{\left(x^{\prime}(t)\right)^{2}+\left(y^{\prime}(t)\right)^{2}} d t\right|
$$
If a segment of a smooth curve given by parametric equations $x=x(t)$ and $y=y(t)\left(t_{1} \leqslant t \leqslant t_{2}\right)$ is rotated around the $O Y$ axis, the area of the surface formed is calculated by the formula
$$
S_{y}=2 \pi\left|\int_{t_{1}}^{t_{2}} x(t) \sqrt{\left(x^{\prime}(t)\right)^{2}+\left(y^{\prime}(t)\right)^{2}} d t\right|
$$
If a segment of an arc given by the equation in polar coordinates $\rho=\rho(\varphi)(\alpha \leqslant \varphi \leqslant \beta)$ is rotated around the polar axis, the area of the surface of revolution is calculated by the formula
$$
S_{x}=2 \pi\left|\int_{\alpha}^{\beta} \rho(\varphi) \sin \varphi \sqrt{(\rho(\varphi))^{2}+\left(\rho^{\prime}(\varphi)\right)^{2}} d \varphi\right|
$$
Volume of a Solid
Let $S(x)$ be a continuous function on the interval $[a, b]$ which is equal to the area of a cross-section perpendicular to the $O X$ axis of some solid, then the volume of this solid is calculated by the formula
$$
V=\left|\int_{a}^{b} S(x) d x\right|
$$
Let $Q(y)$ be a continuous function on the interval $[c, d]$ which is equal to the area of a cross-section perpendicular to the $O Y$ axis of some solid, then the volume of this solid is calculated by the formula
$$
V=\left|\int_{a}^{b} Q(y) d y\right|
$$
If the curvilinear trapezoid $y=y(x) \geqslant 0, a \leqslant x \leqslant b$ is rotated around the $O X$ axis, the volume of the resulting solid of revolution is found by the formula
$$
V=\pi \int_{a}^{b}(f(x))^{2} d x
$$
If the curve is given parametrically $x=x(t) \geqslant 0, y=$ $=y(t) \geqslant 0, t_{1} \leqslant t \leqslant t_{2}$, and on this segment $x^{\prime}(t) \geqslant 0$, then the volume of the solid of revolution around the $O X$ axis is
$$
V=\left|\pi \
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.48. Calculate the area of the figure bounded by the parabola $y=-x^{2}+3 x-2$ and the coordinate axes.
|
Solution. Since the figure $y=-x^{2}+3 x-2$ is located in the regions with $y \geqslant 0$ and $y<0$ (Fig. 2.3), the area $S$ should be calculated separately for the part $y \geqslant 0$ and the part $y<0$, and then the absolute values of the obtained integrals should be added:
$$
\begin{gathered}
S=\left|\int_{0}^{1}\left(-x^{2}+3 x-2\right) d x\right|+\left|\int_{1}^{2}\left(-x^{2}+3 x-2\right) d x\right|= \\
\left.=\left.\left|\left(-\frac{x^{3}}{3}+\frac{3 x^{2}}{2}-2 x\right)\right|_{0}^{1}|+|\left(-\frac{x^{3}}{3}+\frac{3 x^{2}}{2}-2 x\right)\right|_{1} ^{2} \right\rvert\,= \\
=\left|-\frac{5}{6}\right|+\left|\frac{1}{6}\right|=1
\end{gathered}
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.58. Compute the length of the arc of the astroid $x=\cos ^{3} t$, $y=\sin ^{3} t, 0 \leqslant t \leqslant 2 \pi$.
|
Solution. From Fig. 2.9, it is clear that due to symmetry, it is sufficient to compute only a quarter of the astroid for
Fig. 2.9.
$0 \leqslant t \leqslant \pi / 2$. We will use formula (2.26):
$$
\begin{gathered}
L=\int_{0}^{\pi / 2} \sqrt{9 \sin ^{2} t \cos ^{4} t+9 \sin ^{4} t \cos ^{2} t} d t= \\
=\int_{0}^{\pi / 2} \sqrt{9 \sin ^{2} t \cos ^{2} t\left(\sin ^{2} t+\cos ^{2} t\right)} d t= \\
=12 \int_{0}^{\pi / 2}|\sin t \cos t| d t=6 \int_{0}^{\pi / 2}|\sin 2 t| d t=\left.6(-\cos (2 t))\right|_{0} ^{\pi / 2}=12
\end{gathered}
$$
Under the integral, it is necessary to write the arithmetic value of the root. If this is not done, an incorrect result can be obtained. In the example considered here, if instead of $3 \int_{0}^{\pi / 2}|\sin t \cos t| d t$ the integral $3 \int_{0}^{\pi / 2} \sin t \cos t d t$ were written, the result would be $\left.\frac{3}{2} \sin ^{2} t\right|_{0} ^{2 \pi}=0-$ a zero arc length.
|
12
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2.59. Calculate the length of the arc of the cardioid $\rho=$ $=2(1+\cos \varphi), 0 \leqslant \varphi \leqslant 2 \pi$ (see Fig. 2.7).
|
Solution. We will use formula (2.28):
$$
\begin{aligned}
L & =\int_{0}^{2 \pi} \sqrt{(2(1+\cos \varphi))^{2}+(-2 \sin \varphi)^{2}} d \varphi=\int_{0}^{2 \pi} \sqrt{16 \cos ^{2}(\varphi / 2)} d \varphi= \\
& =4 \int_{0}^{2 \pi}|\cos (\varphi / 2)| d \varphi=4 \cdot 2 \int_{0}^{\pi} \cos (\varphi / 2) d \varphi=\left.16 \sin (\varphi / 2)\right|_{0} ^{\pi}=16
\end{aligned}
$$
(due to the properties of the function $\cos (\varphi / 2)$ ).
|
16
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.