problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Example 2.79. Determine the amount of heat $Q$ generated by the current $I=5+4 t$ in a conductor with resistance $R=40$ over time $t=10$, given that the amount of heat generated per unit time by a constant current flowing through a conductor with constant resistance is equal to the product of the square of the current and the resistance.
|
Solution.
$$
\begin{aligned}
& Q=\int_{t_{1}}^{t_{2}} I^{2}(t) R d t=R \int_{i_{1}}^{t_{2}} I^{2}(t) d t=40 \int_{0}^{10}(5+4 t)^{2} d t= \\
& =40 \int_{0}^{10}(5+4 t)^{2} \frac{1}{4} d(5+4 t)=\left.40 \frac{(5+4 t)^{3}}{3}\right|_{0} ^{10}=303750
\end{aligned}
$$
|
303750
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3.3. Find the level surfaces of the function $y=$ $=\sqrt{36-x_{1}^{2}-x_{2}^{2}-x_{3}^{2}}$ and the value of the function at the point $P(1,1,3)$.
|
Solution. According to the definition of level surfaces, we have: $\sqrt{36-x_{1}^{2}-x_{2}^{2}-x_{3}^{2}}=C$, where $C \geqslant 0$. From this, it follows that $36-x_{1}^{2}-x_{2}^{2}-x_{3}^{2}=C^{2}$, that is, $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=$ $=36-C^{2}$ (obviously, $0 \leqslant C \leqslant 6$). The obtained equation represents the equation of a sphere in the rectangular Cartesian coordinate system $O x_{1} x_{2} x_{3}$ with its center at the origin and radius $\sqrt{36-C^{2}}$. When $\overparen{C}=6$, the level surface degenerates into the point 0.
Now let's find the value of the function at the point $P(1,1,3)$. For this, we substitute $x_{1}=1, x_{2}=1, x_{3}=3$ into the analytical expression defining the function. We get $y=\sqrt{36-1^{2}-1^{2}-3^{2}}=$ $=\sqrt{25}=5$
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3.9. Find the limit of the function $f(x, y)=\left(x^{2}+\right.$ $\left.+y^{2}\right)^{2} x^{2} y^{2}$ as $x \rightarrow 0$ and $y \rightarrow 0$.
|
Solution. For the calculation of the specified limit, it is more convenient to switch to polar coordinates $x=r \cos \varphi, y=r \sin \varphi$. We obtain
$$
\begin{gathered}
\lim _{\substack{x \rightarrow 0 \\
y \rightarrow 0}}\left(x^{2}+y^{2}\right)^{2 x^{2} y^{2}}=\lim _{r \rightarrow 0}\left(r^{2}\right)^{2 r^{4} \cos ^{2} \varphi \sin ^{2} \varphi}= \\
=\lim _{r \rightarrow 0}\left(r^{2}\right)^{r^{4} \sin ^{2} 2 \varphi / 2}=e^{\lim _{r \rightarrow 0} r^{4} \sin ^{2} 2 \varphi \ln r}= \\
=e^{\sin ^{2} 2 \varphi \lim _{r \rightarrow 0} r^{4} \ln r}=e^{0}=1
\end{gathered}
$$
Note that the equality to zero of the exponent of the exponential in the considered example follows from the following considerations. The exponent of the exponential represents the product of a bounded function $\sin 2 \varphi$ by an infinitesimal quantity, since calculating the limit $\lim _{r \rightarrow 0} r^{4} \ln r$ by L'Hôpital's rule,
$$
\lim _{r \rightarrow 0} r^{4} \ln r=\lim _{r \rightarrow 0} \frac{(\ln r)^{\prime}}{\left(r^{-4}\right)^{\prime}}=\lim _{r \rightarrow 0}\left(-\frac{r^{4}}{4}\right)=0
$$
Therefore, the value of the exponent of the exponential as $r \rightarrow 0$ is zero.
A function $f(P)$ is called continuous at a point $P_{0} \in$ $D(f) \subset E^{n}$ if: 1) it is defined both at the point $P_{0}$ and in some neighborhood of it; 2) if for any $\varepsilon>0$ there exists $\delta(\varepsilon)>0$ such that for all points $P$ in the domain of definition of the function $D(f)$, for which $\rho\left(P, P_{0}\right)$ $>0\left(f\left(P_{0}\right)0(f(P)0$ there exists such $\delta(\varepsilon)>0$ that for any points $P_{1}, P_{2} \in X$, for which $\rho\left(P_{1}, P_{2}\right)<\delta$ the inequality $\left|f\left(P_{1}\right)-f\left(P_{2}\right)\right|<\varepsilon$ holds.
If a function $f(P)$ is continuous on a bounded closed set $X$, then it is uniformly continuous on $X$.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4.37. How many times can the trigonometric series $\sum_{k=1}^{\infty} \frac{\cos k x}{k^{4}}$ be differentiated term by term?
|
Solution. In this example, $a_{k}=\frac{1}{k^{4}}$ and the series with the general term $k^{s} a_{k}$ will converge for $s=1$ and $s=2$ (for $s=3$ we get the harmonic series, and for $s>3$ the general term of the series will be an infinitely large quantity). Therefore, by Theorem 4.28, this series can be term-by-term differentiated twice.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. Expand the function
$$
f(z)=\frac{z}{z^{2}-2 z-3}
$$
into a Taylor series in the neighborhood of the point $z_{0}=0$ using expansion (12), and find the radius of convergence of the series.
|
Solution. Let's decompose the given function into partial fractions:
$$
\frac{z}{z^{2}-2 z-3}=\frac{1}{4} \frac{1}{z+1}-\frac{3}{4} \frac{1}{z-3}
$$
Transform the right-hand side as follows:
$$
f(z)=\frac{1}{4} \frac{1}{1+z}-\frac{1}{4} \frac{1}{1-\frac{2}{3}}
$$
Using the expansion (12) of the function $\frac{1}{1+z}$, we get
$$
\begin{aligned}
f(z) & =\frac{1}{4}\left(1-z+z^{2}-z^{3}+\ldots\right)-\frac{1}{4}\left(1+\frac{z}{3}+\frac{z^{2}}{9}+\ldots\right)= \\
& =\frac{1}{4}\left(-\frac{4}{3} z+\frac{8}{9} z^{2}-\frac{28}{27} z^{3}+\ldots\right)=-\frac{z}{3}+\frac{2}{3^{2}} z^{2}-\frac{7}{3^{3}} z^{3}+\ldots
\end{aligned}
$$
The nearest singular point to the point $z_{0}=0$ of the given function is the point $z=-1$. Therefore, the radius of convergence of the obtained series is $R=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. Investigate the convergence of the infinite product
$$
\prod_{k=1}^{\infty}\left(1-\frac{1}{k+1}\right)=\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right) \ldots\left(1-\frac{1}{k+1}\right) \ldots
$$
|
Solution. Here all $u_{k}=-\frac{1}{k+1}$ are negative and the series (14)
$$
\sum_{k=1}^{\infty} u_{k}=-\sum_{k=1}^{\infty} \frac{1}{k+1}=-\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\ldots\right)
$$
obviously diverges.
Then, by Theorem 4, the infinite product (15) diverges.
Remark. Calculating the $n$-th partial product in (15), we get
$$
p_{n}=\frac{1}{2} \cdot \frac{2}{3} \cdot \frac{3}{4} \cdot \ldots \cdot \frac{n-1}{n} \cdot \frac{n}{n+1}=\frac{1}{n+1}
$$
Since $p=\lim _{n \rightarrow \infty} p_{n}=\lim _{n \rightarrow \infty} \frac{1}{n+1}=0$, the infinite product (15) diverges.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Find the order of the zero $z_{0}=0$ for the function
$$
f(z)=\frac{z^{8}}{z-\sin z}
$$
|
Solution. Using the Taylor series expansion of the function $\sin z$ in the neighborhood of the point $z_{0}=0$, we obtain
$$
\begin{aligned}
f(z) & =\frac{z^{8}}{z-\sin z}=\frac{z^{8}}{z-\left(z-\frac{z^{3}}{3!}+\frac{z^{5}}{5!}-\ldots\right)}= \\
& =\frac{z^{8}}{\frac{z^{3}}{3!}-\frac{z^{5}}{5!}+\ldots}=\frac{z^{5}}{\frac{1}{3!}-\frac{z^{2}}{5!}+\ldots}=z^{5} \frac{1}{\frac{1}{3!}-\frac{z^{2}}{5!}+\ldots}
\end{aligned}
$$
Let
$$
\varphi(z)=\frac{1}{\frac{1}{3!}-\frac{z^{2}}{5!}+\ldots}
$$
Then $f(z)=z^{5} \varphi(z)$, where $\varphi(z)$ is a function analytic at the point $z_{0}=0$, and $\varphi(0)=6 \neq 0$. Therefore, the point $z_{0}=0$ is a zero of the fifth order for the given function.
|
5
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 10. Determine the nature of the singular point $z=1$ of the function
$$
f(z)=\frac{\sin \pi z}{2 e^{z-1}-z^{2}-1}
$$
|
Solution. Consider the function
$$
\varphi(z)=\frac{1}{f(z)}=\frac{2 e^{z-1}-z^{2}-1}{\sin \pi z}
$$
The point $z=1$ is a zero of the third order for the numerator
$$
\psi(z)=2 e^{z-1}-z^{2}-1
$$
since
$$
\begin{gathered}
\psi(1)=0 ; \quad \psi^{\prime}(1)=\left.\left(2 e^{z-1}-2 z\right)\right|_{z=1}=0 ; \\
\psi^{\prime \prime}(1)=\left.\left(2 e^{z-1}-2\right)\right|_{z=1}=0 ; \quad \psi^{\prime \prime \prime}(1)=\left.2 e^{z-1}\right|_{z=1}=2 \neq 0
\end{gathered}
$$
The point $z=1$ is a zero of the first order for the denominator $\sin \pi z$ of the function $\varphi(z)$.
Therefore, the point $z=1$ will be a zero of order $3-1=2$ for the function $\varphi(z)$, and thus a pole of the second order for the given function.
## Problems for Independent Solution
Determine the nature of the singular point $z_{0}=0$ for the following functions:
300. a) $\frac{1}{z-\sin z}$
b) $\frac{1}{\cos z-1+\frac{1}{2} z^{2}}$
c) $\frac{1}{e^{-z}+z-1}$
301. a) $\frac{\sin z}{e^{-z}+z-1}$; b) $\frac{\operatorname{sh} z}{z-\operatorname{sh} z}$.
Find the singular points and determine their nature for the following functions:
302. a) $\frac{1}{1-\sin z}$;
b) $\frac{1-\cos z}{z^{2}}$
303. a) $e^{1 /(x+2)}$;
b) $\cos \frac{1}{z}$
304. a) $\frac{z}{z^{5}+2 z^{4}+z^{3}}$
b) $\frac{1}{e^{-z}-1}+\frac{1}{z^{2}}$.
305. a) $e^{-1 / z^{2}}$
b) $\sin \frac{\pi}{z+1}$
c) $\operatorname{ch} \frac{1}{z}$
306. a) $\frac{z^{2}}{\cos z-1}$
b) $\frac{1-\sin z}{\cos z}$
c) $\frac{z-\pi}{\sin ^{2} z}$
The following statements are true.
1. For a point $z_{0}$ to be a removable singular point of the function $f(z)$, it is necessary and sufficient that the Laurent series expansion of $f(z)$ in a neighborhood of the point $z_{0}$ does not contain the principal part.
2. For a point $z_{0}$ to be a pole of the function $f(z)$, it is necessary and sufficient that the principal part of the Laurent series expansion of $f(z)$ in a neighborhood of $z_{0}$ contains only a finite number of terms
$$
f(z)=\frac{c_{-k}}{\left(z-z_{0}\right)^{k}}+\ldots+\frac{c_{-1}}{z-z_{0}}+\sum_{n=0}^{\infty} c_{n}\left(z-z_{0}\right)^{n} \quad\left(c_{-k} \neq 0\right)
$$
The largest of the exponents of the powers of the differences $z-z_{0}$ contained in the denominators of the terms of the principal part of the Laurent series coincides with the order of the pole.
3. A point $z_{0}$ is a singular essential point for the function $f(z)$ if and only if the principal part of its Laurent series expansion in a neighborhood of the point $z_{0}$ contains infinitely many terms.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Find the residue of the function
$$
f(z)=z^{3} \cdot \sin \frac{1}{z^{2}}
$$
at its singular point.
|
Solution. A singular point of the function $f(z)$ is the point $z=0$. It is an essential singular point of the function $f(z)$. Indeed, the Laurent series expansion of the function in the neighborhood of the point $z=0$ is
$$
f(z)=z^{3}\left(\frac{1}{z^{2}}-\frac{1}{3!z^{6}}+\frac{1}{5!z^{10}}-\cdots\right)=z-\frac{1}{3!z^{3}}+\frac{1}{5!z^{7}}-\cdots
$$
i.e., it contains an infinite number of terms in the principal part. The residue of the function at the point $z=0$ is zero, since the coefficient $c_{-1}$ in the Laurent series expansion of $f(z)$ is zero.
If the function $f(z)$ is of the form $f(z)=\frac{\varphi(z)}{\psi(z)}$, where the analytic functions $\varphi(z)$ and $\psi(z)$ have zeros of higher than the first order at the point $z_{0}$, then in this case it is convenient to replace the functions $\varphi(z)$ and $\psi(z)$ with their Taylor series expansions in the neighborhood of the point $z_{0}^{\prime}$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. Find the residue at the point $z=0$ of the function
$$
f(z)=\frac{\sin 3z - 3 \sin z}{(\sin z - z) \sin z}
$$
|
Solution. The point $z=0$ is a zero of both the numerator $\varphi(z)=\sin 3 z-3 \sin z$ and the denominator $\psi(z)=(\sin z-z) \sin z$. Let's determine the orders of these zeros using the Taylor series expansion of $\sin z$ around the point $z=0$:
$$
\sin z=z-\frac{z^{3}}{3!}+\frac{z^{5}}{5!}-\ldots
$$
We have
$$
\begin{aligned}
\varphi(z) & =\sin 3 z-3 \sin z=3 z-\frac{3^{3} z^{3}}{3!}+\frac{3^{5} z^{5}}{5!}-\cdots-3\left(z-\frac{z^{3}}{3!}+\frac{z^{5}}{5!}-\ldots\right)= \\
& =-\frac{3^{3}-3}{3!} z^{3}+\frac{3^{5}-3}{5!} z^{5}-\ldots=z^{3} \varphi_{1}(z)
\end{aligned}
$$
where
$$
\begin{aligned}
& \varphi_{1}(z)=-\frac{3^{3}-3}{3!}+\frac{3^{5}-3}{5!} z^{2}-\ldots, \varphi_{1}(0)=-4 \neq 0 \\
& \psi(z)=(\sin z-z) \sin z=\left(-\frac{z^{3}}{3!}+\frac{z^{5}}{5!}-\cdots\right)\left(z-\frac{z^{3}}{3!}+\ldots\right)= \\
& =z^{4}\left(-\frac{1}{3!}+\frac{z^{2}}{5!}-\cdots\right)\left(1-\frac{z^{2}}{3!}+\ldots\right)=z^{4} \psi_{1}(z)
\end{aligned}
$$
where
$$
\psi_{1}(z)=\left(-\frac{1}{3!}+\frac{z^{2}}{5!}-\ldots\right)\left(1-\frac{z^{2}}{3!}+\ldots\right), \quad \psi_{1}(0)=-\frac{1}{6} \neq 0
$$
Therefore,
$$
f(z)=\frac{\sin 3 z-3 \sin z}{(\sin z-z) \sin z}=\frac{z^{3} \varphi_{1}(z)}{z^{4} \psi_{1}(z)}=\frac{\varphi_{1}(z)}{z \psi_{1}(z)}
$$
and since $\varphi_{1}(0) \neq 0, \psi_{1}(0) \neq 0$, the point $z=0$ is a simple pole of the function, so its residue at this point is found using the formula (5)
$$
\operatorname{res}_{z=0} \frac{\sin 3 z-3 \sin z}{(\sin z-z) \sin z}=\lim _{z \rightarrow 0} \frac{\varphi_{1}(z)}{z \psi_{1}(z)} z \stackrel{\psi_{-}}{=} \frac{\varphi_{1}(0)}{\psi_{1}(0)}=\frac{-4}{-\frac{1}{6}}=24
$$
## Problems for Independent Solution
Calculate the following residues:
318. $\underset{i=0}{\operatorname{res}} \frac{z^{n-1}}{\sin ^{n} z} \quad(n=1,2, \ldots)$.
319. $\operatorname{res}_{z=0} \frac{\sin 2 z-2 z}{(1-\cos z)^{2}}$.
320. $\operatorname{res}_{z=0} \frac{e^{z}-1-z}{(1-\cos 2 z) \sin z}$.
321. $\operatorname{res}_{z=0} \frac{(1-\operatorname{ch} z) \operatorname{sh} z}{(1-\cos z) \sin ^{2} z}$.
322. $\underset{x=0}{\operatorname{res}} \frac{\boldsymbol{z}^{n-2}}{\operatorname{sh}^{n} z} \quad(\boldsymbol{n}=2,3, \ldots)$.
|
24
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 9. Find the residue of the function
$$
f(z)=e^{1 / z^{2}} \cos z
$$
at the point $z=0$.
|
Solution. Since the residue at the point $z=0$ is equal to the coefficient of $z^{-1}$, we immediately obtain that in this case the residue is zero, since the function $f(z)$ is even and its expansion in the neighborhood of the point $z=0$ cannot contain odd powers of $z$.
## Problems for Independent Solution
Find the residues at the singular points of the following functions:
324. $f(z)=\frac{\tan z}{z^{2}-\frac{\pi}{4} z}$.
325. $f(z)=z^{3} e^{1 / x}$.
326. $f(z)=\frac{\cosh z}{\left(z^{2}+1\right)(z-3)}$.
327. $f(z)=\frac{e^{z}}{\frac{1}{4}-\sin ^{2} z}$.
328. $f(z)=\frac{e^{z}}{z^{3}(z-1)}$.
329. $f(z)=\frac{z}{(z+1)^{3}(z-2)^{2}}$.
330. $f(z)=\frac{e^{-1 / z^{2}}}{1+z^{4}}$.
331. $f(z)=z^{2} \sin \frac{1}{z}$.
332. $f(z)=\cos \frac{1}{z}+z^{3}$.
333. $f(z)=\frac{\sin 2 z}{(z+i)\left(z-\frac{i}{2}\right)^{2}}$.
334. $f(z)=\frac{1-\cos z}{z^{3}(z-3)}$.
335. $f(z)=e^{z^{2}+1 / z^{2}}$.
336. $f(z)=\frac{e^{i z}}{\left(z^{2}-1\right)(z+3)}$.
337. $f(z)=\frac{\cos z}{z^{3}-\frac{\pi}{2} z^{2}}$.
338. $f(z)=\frac{e^{\pi z}}{z-i}$.
339. $f(z)=\frac{z^{2 n}}{(z-1)^{n}} \quad(n>0-$ integer).
340. $f(z)=\cot ^{2} z$.
341. $f(z)=\sin z \cos \frac{1}{z}$.
342. $f(z)=e^{z /(z-1)}$.
343. $f(z)=\frac{\sin \frac{1}{z}}{1-z}$.
344. $f(z)=\frac{e^{1 / z}}{1+z}$.
345. $f(z)=e^{\left(z^{2}+1\right) / z}$ 346. $f(z)=e^{z} \sin \frac{1}{z}$.
## § 11. The Residue Theorem of Cauchy. Application of Residues to the Evaluation of Definite Integrals. Summation of Some Series Using Residues
## $1^{\circ}$. The Residue Theorem of Cauchy.
Theorem. If the function $f(z)$ is analytic on the boundary $C$ of the region $D$ and everywhere inside the region, except for a finite number of singular points $z_{1}, z_{2}, \ldots, z_{n}$, then
$$
\int_{C} f(z) d z=2 \pi i \sum_{k=1}^{n} \operatorname{res} f\left(z_{k}\right)
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Compute the integral
$$
\int_{|x|=2} \frac{1}{z-1} \sin \frac{1}{z} d z
$$
|
Solution. In the circle $|z| \leqslant 2$, the integrand has two singular points $z=1$ and $z=0$. It is easy to establish that $z=1$ is a simple pole, therefore
$$
\operatorname{res}\left(\frac{1}{z-1} \sin \frac{1}{z}\right)=\left.\frac{\sin \frac{1}{z}}{(z-1)^{\prime}}\right|_{z=1}=\sin 1
$$
To determine the nature of the singular point $z=0$, we write the Laurent series for the function $\frac{1}{z-1} \sin \frac{1}{z}$ in the neighborhood of this point. We have
$$
\begin{aligned}
\frac{1}{z-1} \sin \frac{1}{z}= & -\frac{1}{1-z} \sin \frac{1}{z}=-\left(1+z+z^{2}+\ldots\right)\left(\frac{1}{z}-\frac{1}{3!z^{3}}+\frac{1}{5!z^{5}}-\ldots\right)= \\
= & -\left(1-\frac{1}{31^{\prime}}+\frac{1}{5!}-\ldots\right) \frac{1}{z}+\frac{c_{-2}}{z^{2}}+\frac{c_{-3}}{z^{3}}+\ldots+\text { regular part } \\
& c_{-k} \neq 0, \quad k=2,3, \ldots
\end{aligned}
$$
Since the Laurent series contains an infinite number of terms with negative powers of $z$, the point $z=0$ is an essential singularity. The residue of the integrand at this point is
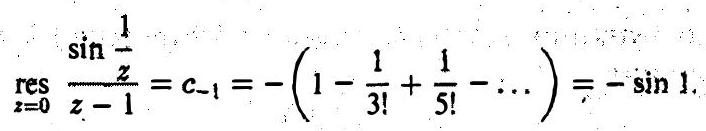
Therefore,
$$
\int_{|z| \neq 2} \frac{1}{z-1} \sin \frac{1}{z} d z=2 \pi i(\sin 1-\sin 1)=0
$$
## Problems for Independent Solution
Calculate the integrals:
347. $\int_{|z|=1} z \operatorname{tg} \pi z d z . \quad$ 348. $\int_{C} \frac{z d z}{(z-1)^{2}(z+2)}$, where $C: x^{2 / 3}+y^{2 / 3}=3^{2 / 3}$,
348. $\int_{\mid z==2} \frac{e^{z} d z}{z^{3}(z+1)}$
349. $\int_{|z-i|=3} \frac{e^{z^{2}}-1}{z^{3}-i z^{2}} d z . \quad 351 . \quad \int_{|z|=1 / 2} z^{2} \sin \frac{1}{z} d z$.
350. $\int_{|z|=\sqrt{3}} \frac{\sin \pi z}{z^{2}-z} d z$
351. $\int_{|z+1|=4} \frac{z d z}{e^{z}+3}$
352. $\int_{|z|=1} \frac{z^{2} d z}{\sin ^{3} z \cos z}$
353. $\int_{|z-i|=1} \frac{e^{z} d z}{z^{4}+2 z^{2}+1} \cdot 356 . \int_{|x|=-4} \frac{e^{i z} d z}{(z-n)^{3}}$.

359. $\int_{C} \frac{\sin \pi z}{\left(z^{2}-1\right)^{2}} d z, C: \frac{x^{2}}{4}+y^{2}=1 . \quad 360 . \int_{C} \frac{z+1}{z^{2}+2 z-3} d z, \quad C: x^{2}+y^{2}=16$.
361. $\int_{C} \frac{z \sin z}{(z-1)^{5}} d z, \quad C: \frac{x^{2}}{3}+\frac{y^{2}}{9}=1$. 362. $\int_{C} \frac{d z}{z^{4}+1} d z, \quad C: x^{2}+y^{2}=2 x$.
362. $\int_{|z|=1} z^{3} \sin \frac{1}{z} d z . \quad$ 364. $\int_{|z|=1 / 3}(z+1) e^{1 / z} d z$.
363. $\int_{|z|=2 / 3}\left(\sin \frac{1}{z^{2}}+e^{z^{2}} \cos z\right) d z$.
Residue of a function at the point at infinity
It is said that the function $f(z)$ is analytic at the point at infinity $z=\infty$, if the function
$$
\varphi(\zeta)=f\left(\frac{1}{\zeta}\right)
$$
is analytic at the point $\zeta=0$.
For example, the function $f(z)=\sin \frac{1}{z}$ is analytic at the point $z=\infty$, since the function
$$
\varphi(\zeta)=f\left(\frac{1}{\zeta}\right)=\sin \zeta
$$
is analytic at the point $\zeta=0$.
Let the function $f(z)$ be analytic in some neighborhood of the point at infinity (except the point $z=\infty$ itself).
The point $z=\infty$ is called an isolated singular point of the function $f(z)$ if there are no other singular points of the function $f(z)$ in some neighborhood of this point.
The function $f(z)=\frac{1}{\sin z}$ has a non-isolated singularity at infinity: the poles $z_{k}=k \pi$ of this function accumulate at infinity as $k \rightarrow \infty$.
It is said that $z=\infty$ is a removable singularity, a pole, or an essential singularity of the function $f(z)$ depending on whether $\lim _{z \rightarrow \infty} f(z)$ is finite, infinite, or does not exist.
The criteria for the type of singularity at infinity, related to the Laurent series expansion, differ from the criteria for finite singular points.
Theorem 1. If $z=\infty$ is a removable singularity of the function $f(z)$, then the Laurent series expansion of $f(z)$ in the neighborhood of this point does not contain positive powers of $z$; if $z=\infty$ is a pole, then this expansion contains a finite number of positive powers of $z$; in the case of an essential singularity - an infinite number of positive powers of $z$.
The Laurent series expansion of the function $f(z)$ in the neighborhood of the point at infinity is called the Laurent series expansion of $f(z)$ that converges everywhere outside a circle of sufficiently large radius $R$ centered at the point $z=0$ (except, perhaps, the point $z=\infty$ itself).
Let the function $f(z)$ be analytic in some neighborhood of the point $z=\infty$ (except, perhaps, the point $z=\infty$ itself).
The residue of the function $f(z)$ at infinity is defined as
$$
\operatorname{res} f(\infty)=\frac{1}{2 \pi i} \int_{\gamma^{-}} f(z) d z
$$
where $\gamma^{-}$ is a sufficiently large circle $|z|=\rho$, traversed clockwise (so that the neighborhood of the point $z=\infty$ remains on the left, as in the case of a finite point $z=a$).
From this definition, it follows that the residue of the function at infinity is equal to the coefficient of $z^{-1}$ in the Laurent series expansion of $f(z)$ in the neighborhood of $z=\infty$, taken with the opposite sign:
$$
\operatorname{res} f(\infty)=-c_{-1}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Compute the integral
$$
I=\int_{|z|=2} \frac{d z}{1+z^{4}}
$$
|
The poles (finite) of the integrand
$$
f(z)=\frac{1}{1+z^{4}}
$$
are the roots $z_{1}, z_{2}, z_{3}, z_{4}$ of the equation $z^{4}=-1$, which all lie inside the circle $|z|=2$. The function $f(z)=\frac{1}{1+z^{4}}$ has an expansion in the neighborhood of the infinitely distant point
$$
f(z)=\frac{1}{1+z^{4}}=\frac{1}{z^{4}} \frac{1}{1+\frac{1}{z^{4}}}=\frac{1}{z^{4}}-\frac{1}{z^{8}}+\frac{1}{z^{12}}-\cdots
$$
from which it is clear that res $f(\infty)=-c_{-1}=0$. By the equality (3)
$$
I=2 \pi i \sum_{k=1}^{4} \operatorname{res} f\left(z_{k}\right)=-2 \pi i \text { res } f(\infty)=0
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Find the logarithmic residue of the function
$$
f(z)=\frac{\operatorname{ch} z}{e^{i z}-1}
$$
with respect to the contour $C:|z|=8$.
|
Solution. We find the zeros $z_{k}$ of the function $f(z)$. For this, we solve the equation $\cosh z=0$ or $e^{z}+e^{-z}=0$. Writing the last equation as $e^{2 z}=-1$, we find
$2 z=\operatorname{Ln}(-1)=(2 k+1) \pi i$, so $z_{k}=\frac{2 k+1}{2} \pi i(k=0, \pm 1, \pm 2, \ldots)$ (all zeros are simple). To find the poles of the function $f(z)$, we solve the equation $e^{i z}-1=0$ or $e^{i z}=1$. We have $i z=\operatorname{Ln} 1=2 m \pi i, z_{m}=2 m \pi(m=0, \pm 1, \pm 2, \ldots)$. In the circle $|z|<8$ there are zeros
$$
z_{k}=\frac{2 k+1}{2} \pi i \quad(k=0, \pm 1, \pm 2,-3)
$$
and simple poles
$$
z_{m}=2 m \pi \quad(m=0, \pm 1)
$$
of the function $f(z)$. The number of zeros $N=6$, the number of poles $P=3$. Therefore,
$$
\frac{1}{2 \pi i} \int_{|z|=8} \frac{f^{\prime}(z)}{f(z)} d z=6-3=3
$$
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Find the logarithmic residue of the function
$$
f(z)=\frac{1+z^{2}}{1-\cos 2 \pi z}
$$
with respect to the circle $|z|=\pi$.
|
Solution. Setting $1+z^{2}=0$, we find two simple zeros of the function $f(z): a_{1}=-i, a_{2}=i$. Setting $1-\cos 2 \pi z=0$, we find the poles of the function $f(z): z_{n}=n, n=0, \pm 1, \pm 2, \ldots$. The multiplicity of the poles is $k=2$.
In the circle $|z|<\pi$, the function has two simple zeros $a_{1}=-i, a_{2}=i$ and seven double poles
$$
z_{1}=-3, \quad z_{2}=-2, \quad z_{3}=-1, \quad z_{4}=0, \quad z_{5}=1, \quad z_{6}=2, \quad z_{7}=3
$$
Thus, $N=2$ and $P=7$. By the logarithmic residue theorem, the logarithmic residue of the function $f(z)$ with respect to the circle $|z|=\pi$ is
$$
\frac{1}{2 \pi i} \int_{|z|=\pi} \frac{f^{\prime}(z)}{f(z)} d z=2-7 \cdot 2=-12
$$
## Problems for Independent Solution
Find the logarithmic residues of the given functions with respect to the specified contours:
429. $f(z)=\frac{z}{1+z^{3}}$,
$C:|z|=2$.
430. $f(z)=\cos z+\sin z$,
$C:|z|=4$.
431. $f(z)=\left(e^{z}-2\right)^{2}$,
$C:|z|=8$.
432. $f(z)=\operatorname{th} z$,
$C:|z|=8$.
433. $f(z)=\operatorname{tg}^{3} z$,
$C:|z|=6$.
434. $f(z)=1-\operatorname{th}^{2} z$,
$C:|z|=2$.
Principle of the Argument. The logarithmic residue of the function $f(z)$ with respect to a closed contour $C$ is equal to the increment $\Delta_{C} \operatorname{Arg} f(z)$ of the argument of $f(z)$ when the contour $C$ is traversed, divided by $2 \pi$:
$$
\frac{1}{2 \pi i} \int_{C} \frac{f^{\prime}(z)}{f(z)} d z=\frac{1}{2 \pi} \Delta_{C} \operatorname{Arg} f(z)
$$
Therefore, the difference between the number of zeros and poles of the function $f(z)$ enclosed in the domain $D$ is
$$
N-P=\frac{1}{2 \pi} \Delta_{C} \operatorname{Arg} f(z)
$$
In other words, the difference $N-P$ is equal to the number of turns made by the vector in the $w$-plane from the point $w=0$ to the point $w=f(z)$ as the point $z$ traces the contour $C$ (the number of turns is positive if the vector rotates counterclockwise and negative otherwise).
In the special case where the function $w=f(z)$ is analytic in the domain $D$ and on its boundary $C$, where it does not vanish, the logarithmic residue of $f(z)$ with respect to $C$ gives the number of zeros of $f(z)$ in $D$, which is equal to the change in $\operatorname{Arg} f(z)$ when the contour $C$ is traversed, divided by $2 \pi$:
$$
\frac{1}{2 \pi i} \int_{C} \frac{f^{\prime}(z)}{f(z)} d z=\frac{1}{2 \pi} \Delta_{C} \operatorname{Arg} f(z)=N
$$
This is the case, for example, for a polynomial $Q_{n}(z)=\sum_{k=0}^{n} a_{k} z^{k}$.
|
-12
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Find the number of roots in the right half-plane $\operatorname{Re} z>0$ of the equation
$$
Q_{5}(z) \equiv z^{5}+z^{4}+2 z^{3}-8 z-1=0
$$
|
Solution. By the argument principle, the number of zeros inside the contour $C$ is
$$
N=\frac{1}{2 \pi} \Delta_{C} \operatorname{Arg} Q_{5}(z)
$$
where the contour $C$ consists of the semicircle $C_{R}:|z|=R, \operatorname{Re} z>0$, and its diameter on the imaginary axis; the radius $R$ is taken to be so large that all the zeros of the polynomial $Q_{5}(z)$, located in the right half-plane, fall inside the semicircle $|z|>0$. We have
$$
Q_{5}(z)=z^{5}\left(1+\frac{1}{z}+\frac{2}{z^{2}}-\frac{8}{z^{4}}-\frac{1}{z^{5}}\right)
$$
Hence,
$$
\operatorname{Arg} Q_{5}(z)=\operatorname{Arg}\left[z^{3}\left(1+\frac{1}{z}+\frac{2}{z^{2}}-\frac{8}{z^{4}}-\frac{1}{z^{5}}\right)\right]=
$$
$$
\begin{aligned}
& =\operatorname{Arg} z^{5}+\operatorname{Arg}\left(1+\frac{1}{z}+\frac{2}{z^{2}}-\frac{8}{z^{4}}-\frac{1}{z^{5}}\right)= \\
& =5 \operatorname{Arg} z+\operatorname{Arg}\left(1+\frac{1}{z}+\frac{2}{z^{2}}-\frac{8}{z^{4}}-\frac{1}{z^{5}}\right)
\end{aligned}
$$
The increment of the argument of $Q_{5}(z)$ when traversing the semicircle $C_{R}$ in the positive direction will be
$$
\Delta_{C_{R}} \operatorname{Arg} Q_{5}(z)=5 \Delta_{C_{R}} \operatorname{Arg} z+\Delta_{C_{R}} \operatorname{Arg}\left(1+\frac{1}{z}+\frac{2}{z^{2}}-\frac{8}{z^{4}}-\frac{1}{z^{5}}\right)
$$
In this equality, we take the limit as $R \rightarrow \infty$:
$$
\lim _{R \rightarrow \infty} \Delta_{C_{R}} \operatorname{Arg} Q_{5}(z)=5 \lim _{R \rightarrow \infty} \Delta_{C_{R}} \operatorname{Arg} z+\lim _{R \rightarrow \infty} \Delta_{C_{R}} \operatorname{Arg}\left(1+\frac{1}{z}+\frac{2}{z^{2}}-\frac{8}{z^{4}}-\frac{1}{z^{5}}\right)
$$
Both limits on the right-hand side exist and are equal to
$$
\lim _{R \rightarrow \infty} \Delta_{C_{R}} \operatorname{Arg} z=\pi, \quad \lim _{R \rightarrow \infty} \Delta_{C_{R}} \operatorname{Arg}\left(1+\frac{1}{z}+\frac{2}{z^{2}}-\frac{8}{z^{4}}-\frac{1}{z^{5}}\right)=0
$$
Thus,
$$
\lim _{R \rightarrow \infty} \Delta_{C_{R}} \operatorname{Arg} Q_{5}(z)=5 \pi
$$
Now let the point $z$ move along the imaginary axis from $z=i R$ to $z=-i R$. Let $z=i t, -R \leqslant t \leqslant R$. Then
$$
\dot{Q}_{5}(i t)=u(t)+i v(t)=t^{4}-1+i\left(t^{5}-2 t^{3}-8 t\right)
$$
from which
$$
\left\{\begin{array}{l}
u=t^{4}-1 \\
v=t^{5}-2 t^{3}-8 t
\end{array}\right.
$$
These are the parametric equations of the curve described by the point $w=Q_{5}(z)$ in the $(\boldsymbol{u}, \boldsymbol{v})$ plane as the point $z$ traverses the imaginary axis from top to bottom. To construct this curve, we find the points of its intersection with the coordinate axes $O u$ and $O v$. Setting $u$ and $v$ to zero, we get respectively
$$
\begin{aligned}
& t^{4}-1=0, \quad \text { or } t= \pm 1 \\
& t^{5}-2 t^{3}-8 t=0, \text { or } t= \pm 2, \quad t=0
\end{aligned}
$$
Note that equations (2) and (3) do not have common real roots, so the polynomial $Q_{5}(z)$ has no zeros on the imaginary axis. Therefore, the application of the argument principle to the contour is valid. The roots of equations (2) and (3) are arranged in descending order, i.e., in the order of traversal of the contour, and we find the corresponding values of $\boldsymbol{u}$ and $v$:
| № | $t$ | $u$ | $v$ |
| :---: | ---: | ---: | ---: |
| 1 | 2 | 15 | 0 |
| 2 | 1 | 0 | -9 |
| 3 | 0 | -1 | 0 |
| 4 | -1 | 0 | 9 |
| 5 | -2 | 15 | 0 |
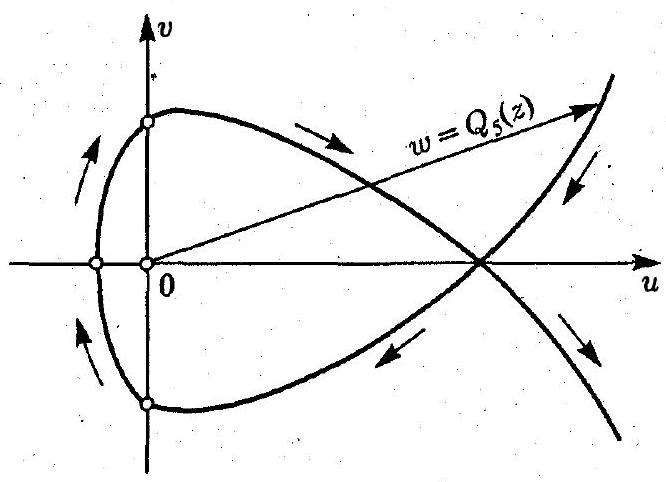
Figure 12
Further,
$$
\begin{aligned}
& \lim _{t \rightarrow \pm \infty} u=+\infty \\
& \lim _{t \rightarrow \pm \infty} v= \pm \infty
\end{aligned}
$$
These data allow us to construct the curve of interest (Figure 12).
From Figure 12, it is clear that the vector $w=Q_{5}(z)$ will rotate by an angle $\varphi=3 \pi$ in the negative direction. Therefore,
$\Delta_{C} \operatorname{Arg}_{5}(z)=5 \pi-3 \pi=2 \pi$,
from which the number of zeros in the right half-plane will be
$$
N=\frac{2 \pi}{2 \pi}=1
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. Find the number of roots of the equation
$$
Q_{7}(z) \equiv z^{7}-2 z-5=0
$$
in the right half-plane.
|
Solution. We choose the contour $C$ as indicated in Example 4. Then $\Delta_{C_{R}} \operatorname{Arg} Q_{7}(z)=\Delta_{C_{R}} \operatorname{Arg}\left(z^{7}-2 z-5\right)=$
$$
\begin{aligned}
& =\Delta_{C_{R}} \operatorname{Arg}\left[z^{7}\left(1-\frac{2}{z^{6}}-\frac{5}{z^{7}}\right)\right]=7 \Delta_{C_{R}} \operatorname{Arg} z+\Delta_{C_{R}} \operatorname{Arg}\left(1-\frac{2}{z^{6}}-\frac{5}{z^{7}}\right)= \\
& =7 \pi+\Delta_{C_{R}} \operatorname{Arg}\left(1-\frac{2}{z^{6}}-\frac{5}{z^{7}}\right) \rightarrow 7 \pi \quad \text { as } \quad R \rightarrow \infty
\end{aligned}
$$
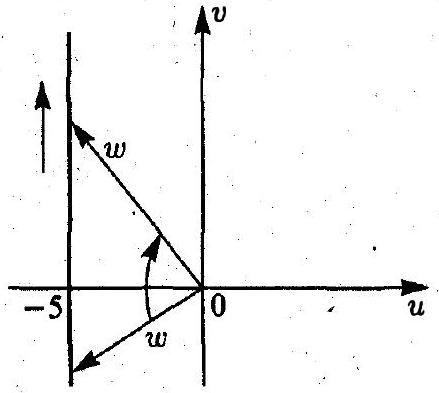
Fig. 13
Let $z=$ it $(-R \leqslant t \leqslant R)$. Then
$$
Q_{7}(i t)=u(t)+i v(t)=-5+i\left(-t^{7}-2 t\right)
$$
from which
$$
\left\{\begin{array}{l}
u=-5 \\
v=-t\left(t^{6}+2\right)
\end{array}\right.
$$
Since $u \neq 0$, the application of the argument principle is valid ( $Q_{7}(z)$ has no zeros on the imaginary axis). This line is a straight line (Fig. 13). The vector $w=Q_{7}(z)$ makes a turn in the negative direction by $\pi$ radians. Therefore,
$$
\Delta_{\dot{c}_{R}} \operatorname{Arg} Q_{1}(z) \xrightarrow[R \rightarrow \infty]{\longrightarrow} 7 \pi-\pi=6 \pi
$$
and
$$
N=\frac{6 \pi}{2 \pi}=3
$$
## Problems for Independent Solution
Determine the number of roots in the right half-plane for the following equations:
435. $z^{4}+2 z^{3}+3 z^{2}+z+2=0$. 436. $z^{3}-2 z-5=0$.
436. $z^{3}-4 z^{2}+5=0$.
437. $2 z^{3}-z^{2}-7 z+5=0$.
438. $z^{5}+5 z^{4}-5=0$.
440: $z^{12}-z+1=0$.
Rouche's Theorem. Suppose functions $f(z)$ and $\varphi(z)$, analytic in the closed domain $\bar{D}$, bounded by the contour $C$, satisfy the inequality $|f(z)|>|\varphi(z)|$ at all points of this contour. Then their sum $F(z)=f(z)+\varphi(z)$ and the function $f(z)$ have the same number of zeros (counting multiplicities) in the domain $D$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Find the number of zeros of the function
$$
F(z)=z^{8}-4 z^{5}+z^{2}-1
$$
inside the unit circle $|z|<1$.
|
Solution. Let us represent the function $F(z)$ as the sum of two functions $f(z)$ and $\varphi(z)$, which we choose, for example, as follows:
$$
f(z)=-4 z^{5}, \quad \varphi(z)=z^{8}+z^{2}-1
$$
Then on the circle $|z|=1$ we will have
$$
\begin{aligned}
& |f(z)|=\left|-4 z^{5}\right|=4 \\
& |\varphi(z)|=\left|z^{8}+z^{2}-1\right| \leqslant\left|z^{8}\right|+\left|z^{2}\right|+1=3
\end{aligned}
$$
Thus, on the boundary $|z|=1$ of the circle, the inequality $|f(z)|>|\varphi(z)|$ holds. The function $f(z)=-4 z^{5}$ has a fivefold zero at the origin. By Rouché's theorem, the function
$$
F(z)=f(z)+\varphi(z)=z^{8}-4 z^{5}+z^{2}-1
$$
has five zeros in the circle $|z|<1$. Note that a different choice of functions $f(z)$ and $\varphi(z)$ is also possible, for example, such as:
$$
f(z)=z^{8}-4 z^{5}, \quad \varphi(z)=z^{2}-1
$$
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 7. Determine the number of roots of the equation
$$
z^{6}-6 z+10=0
$$
inside the circle $|z|<1$.
|
Solution. Let, for example, $f(z)=10$ and $\varphi(z)=z^{6}-6 z$. On the circle $|z|=1$ we have
$$
|f(z)|=10, \quad|\varphi(z)|=\left|z^{6}-6 z\right| \leqslant\left|z^{6}\right|+6|z|=7
$$
Thus, in all points of the circle $|z|=1$, the inequality $|f(z)|>|\varphi(z)|$ holds. The function $f(z)=10$ has no zeros inside the circle $|z|<1$, and therefore, by Rouché's theorem, the function $z^{6}-6 z+10$ also has no zeros.
## Problems for Independent Solution
Using Rouché's theorem, find the number of roots of the given equations in the specified domains:
441. $z^{4}-3 z^{3}-1=0, \quad|z|<2$.
442. $z^{3}+z+1=0, \quad|z|<\frac{1}{2}$.
443. $z^{5}+z^{2}+1=0, \quad|z|<2$.
444. $z^{8}+6 z+10=0,|z|<1$.
445. $27 z^{11}-18 z+10=0,|z|<1$.
446. $z^{8}-6 z^{6}-z^{3}+2=0,|z|<1$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 8. How many roots of the equation
$$
z^{4}-5 z+1=0
$$
lie in the annulus $1<|z|<2 ?$
|
Solution. Let $N$ be the number of roots of equation (4) in the ring $1<|\varphi(z)|$, since $|f(z)|=|-5 z|=5,|\varphi(z)|=\left|z^{4}+1\right| \leqslant$ $\left|z^{4}\right|+1=2$. The function $f(z)=-5 z$ has one root in the circle $|z|<1$, and thus $N_{1}=1$.
In the circle $|z|<2$, $|f(z)|>\left|\varphi(z)\right|$, since $|f(z)|=\left|z^{4}\right|=2^{4}=16,|\varphi(z)|=|1-5 z| \leqslant 1+5|z|=11$. The function $f(z)=z^{4}$ has four roots in the circle $|z|<2$, and therefore $N_{2}=4$.
The number of roots of equation (4) in the ring $1<|z|<2$ will be $N=4-1=3$.
## Problems for Independent Solution
Determine the number of roots of the given equations in the specified rings:
447. $4 z^{4}-29 z^{2}+25=0, \quad 2<|z|<3$.
448. $z^{7}-5 z^{4}+z^{2}-2=0,1<|z|<2$.
449. $z^{6}-8 z+10=0, \quad 1<|z|<3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 9. Find the number of roots of the equation
$$
z^{2}-a e^{z}=0, \quad \text { where } \quad 0<a<e^{-1}
$$
in the unit circle $|z|<1$.
|
Solution. Let $f(z)=z^{2}$ and $\varphi(z)=-a e^{z}$. On the circle $|z|=1$ we have
$$
\begin{aligned}
& |f(z)|=\left|z^{2}\right|=1 \\
& |\varphi(z)|=\left|-a e^{z}\right|=a\left|e^{z}\right|=a\left|e^{x+i y}\right|=a e^{x} \leqslant a e|\varphi(z)|$, if $|z|=1$. The function $f(z)=z^{2}$ in the circle $|z|0, \quad \text { since } \quad 00, \quad \text { since } \quad a1), \quad|z|\frac{e^{R}}{R^{n}}, \quad|z|<R$.
452. $z^{2}-\cos z=0, \quad|z|<2$.
453. $z^{4}-\sin z=0, \quad|z|<\pi$.
454. $z^{2}+\operatorname{ch} i z=0, \quad|z|<0.5$.
455. $\operatorname{ch} z=z^{2}-4 z,|z|<1$.
456. $2^{z}=4 z, \quad|z|<1$.
Note: There are some parts in the original text that seem to be incomplete or contain errors, such as the conditions and inequalities. Please review the original text for clarity.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 10. Find the number of roots of the equation
$$
\lambda-\boldsymbol{z}-e^{-z}=0, \quad \lambda>1
$$
in the right half-plane $\operatorname{Re} z>0$.
|
Solution. Consider the contour composed of the segment $[-i R, i R]$ and the right semicircle $|z|=R$. Let $f(z)=z-\lambda$ and $\varphi(z)=e^{-z}$. On the segment $[-i R, i R]$, where $z=i y$, we have
$$
\begin{aligned}
& |f(z)|=|i y-\lambda|=\sqrt{\lambda^{2}+y^{2}} \geqslant \sqrt{\lambda^{2}}=\lambda>1 \\
& |\varphi(z)|=\left|e^{-z}\right|=\left|e^{-i y}\right|=1
\end{aligned}
$$
and, consequently, $|f(z)|>|\varphi(z)|$.
On the semicircle $|z|=R$, where $\operatorname{Re} z=x>0$ for sufficiently large $R$ $(R>\lambda+1)$, we have $|f(z)|>|\varphi(z)|$, since
$$
\begin{aligned}
& |f(z)|=|z-\lambda| \geqslant|z|-\lambda=R-\lambda>1 \\
& |\varphi(z)|=\left|e^{-z}\right|=\left|e^{-x-i y}\right|=\left|e^{-x} e^{-i y}\right|=e^{-x}\left|e^{-i y}\right|=e^{-x} \leqslant 1 \quad(x>0)
\end{aligned}
$$
By Rouché's theorem, inside the specified contour for any sufficiently large $R$, the given equation has as many roots as the equation $f(z)=z-\lambda=0$, i.e., one root. Therefore, in the entire right half-plane, the given equation has a unique root.
## Problems for Independent Solution
457. Show that the equation $z e^{\lambda-z}=1$, where $\lambda>1$, has a unique real and positive root in the unit disk $|z| \leqslant 1$.
458. Show that the equation $1+z+\alpha z^{n}=0$, where $n$ is a natural number greater than one, has at least one root in the disk $|z| \leqslant 2$ for any $\alpha$.
459. Let $f(z)$ and $\varphi(z)$ be functions that are analytic in some neighborhood of the point $a$, and $C$ be a circle centered at the point $a$ such that along the circumference of this circle we have
$$
|\alpha f(z)|+|\beta \varphi(z)|<r .
$$
Show that the equation $F(z)=z-a-\alpha f(z)-\beta f(z)=0$ has one and only one root inside the circle $C$.
## CHAPTER
## Conformal Mappings
## § 13. Conformal Mappings
## $1^{\circ}$. Concept of Conformal Mapping.
Definition. A mapping of a neighborhood of a point $z_{0}$ onto a neighborhood of a point $w_{0}$, realized by the function $w=f(z)$, is called conformal if at the point $z_{0}$ it has the property of preserving angles between curves and the constancy of dilations (Fig. 14).
This means that:
1) if under the mapping $w=f(z)$ the curves $\gamma_{1}$ and $\gamma_{2}$ are transformed into the curves $\Gamma_{1}$ and $\Gamma_{2}$, respectively, then the angle $\varphi$ between the tangents $k_{1}$ and $k_{2}$ to the curves $\gamma_{1}$ and $\gamma_{2}$ at the point $z_{0}$ will be equal to the angle $\Phi$ between the corresponding tangents $K_{1}$ and $K_{2}$ to the curves $\Gamma_{1}$ and $\Gamma_{2}$ at the point $w_{0}$, i.e., $\Phi=\varphi$.
2) if in the complex plane $z$ we take an infinitesimally small circle centered at the point $z_{0}$, then in the plane $w$ it will correspond to an infinitesimally small circle centered at the point $w_{0}$.
Therefore, it is said that a conformal mapping has the property of angle conservation and similarity in the small.
If under the mapping $w=f(z)$ the angles between corresponding directions are equal not only in magnitude but also in the direction of measurement, then such a mapping is called a conformal mapping of the first kind.
A conformal mapping in which angles are preserved only in absolute magnitude but the direction of their measurement is reversed is called a conformal mapping of the second kind.
A simple example of a conformal mapping of the first kind is the mapping $w=z$, and of the second kind is the mapping $w=\bar{z}$.
In the following, we will consider only conformal mappings of the first kind.
A mapping $w=f(z)$ is called conformal in a domain $D$ if it is conformal at every point of this domain.
Criterion for Conformality. For the mapping $w=f(z)$ to be conformal in a domain $D$, it is necessary and sufficient that in this domain the function $w=f(z)$ is univalent and analytic, and $f^{\prime}(z) \neq 0$ for all $z \in D$.
If we do not assume the univalence of $f(z)$, then the mapping realized by this function will not be one-to-one, and thus will not be conformal. For example, the function $w=z^{4}$, defined in the half-ring $1 \leqslant|z| \leqslant 2,0 \leqslant \arg z \leqslant \pi$, is analytic in it, and, moreover, the condition $w^{\prime}=4 z^{3} \neq 0$ is satisfied everywhere in the half-ring. However, the function $w=z^{4}$ maps the given half-ring onto the region $1 \leqslant|w| \leqslant 16,0 \leqslant \arg w \leqslant 4 \pi$, i.e., a region that twice covers the corresponding ring on the $w$-plane, which violates the one-to-one correspondence.
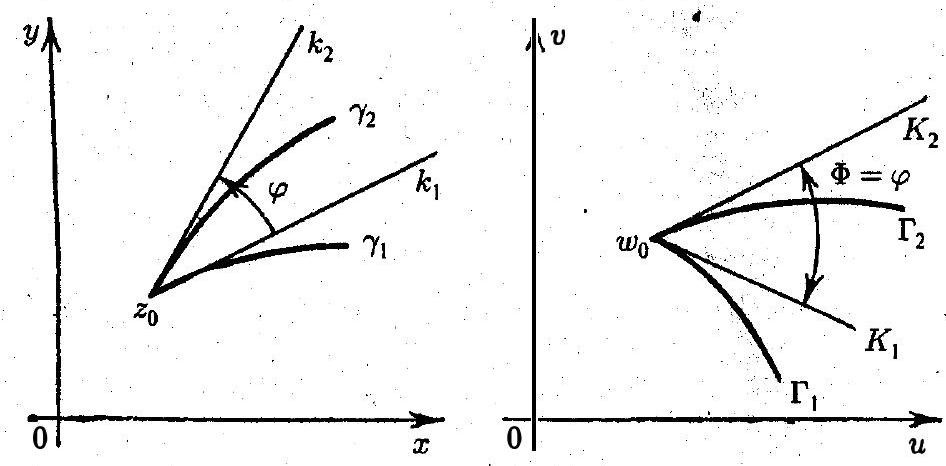
Fig. 14
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find the approximate value of the smallest characteristic number of the kernel by the Ritz method
$$
K(x, t)=x t ; \quad a=0, b=1
$$
|
Solution. As the coordinate system of functions $\psi_{n}(x)$, we choose the system of Legendre polynomials: $\psi_{n}(x)=P_{n}(2 x-1)$. In formula (1), we limit ourselves to two terms, so that
$$
\varphi_{2}(x)=a_{1} \cdot P_{0}(2 x-1)+a_{2} \cdot P_{1}(2 x-1) .
$$
Noting that
$$
\psi_{1} \equiv P_{0}(2 x-1)=1 ; \quad \psi_{2} \equiv P_{1}(2 x-1)=2 x-1,
$$
we find
$$
\begin{gathered}
\left(\psi_{1}, \psi_{1}\right)=\int_{0}^{1} d x=1, \quad\left(\psi_{1}, \psi_{2}\right)=\left(\psi_{2}, \psi_{1}\right)=\int_{0}^{1}(2 x-1) d x=0 \\
\left(\psi_{2}, \psi_{2}\right)=\int_{0}^{1}(2 x-1)^{2} d x=\frac{1}{3}
\end{gathered}
$$
Further,
$$
\begin{aligned}
& \left(K \psi_{1}, \psi_{1}\right)=\int_{0}^{1}\left(\int_{0}^{1} K(x, t) \psi_{1}(t) d t\right) \psi_{1}(x) d x=\int_{0}^{1} \int_{0}^{1} x t d x d t=\frac{1}{4} \\
& \left(K \psi_{1}, \psi_{2}\right)=\int_{0}^{1} \int_{0}^{1} x t(2 x-1) d x d t=\frac{1}{12} \\
& \left(K \psi_{2}, \psi_{2}\right)=\int_{0}^{1} \int_{0}^{1} x t(2 t-1)(2 x-1) d x d t=\frac{1}{36}
\end{aligned}
$$
In this case, system (3) takes the form
$$
\left|\begin{array}{cc}
\frac{1}{4}-\sigma & \frac{1}{12} \\
\frac{1}{12} & \frac{1}{36}-\frac{1}{3} \sigma
\end{array}\right|=0
$$
or
$$
\sigma^{2}-\sigma\left(\frac{1}{12}+\frac{1}{4}\right)=0
$$
From this, $\sigma_{1}=0, \sigma_{2}=\frac{1}{3}$. The largest eigenvalue $\sigma_{2}=\frac{1}{3}$, so the smallest characteristic number $\lambda=\frac{1}{\sigma_{2}}=3$.
## Problems for Independent Solution
Using the Ritz method, find the smallest characteristic numbers of the kernels ( $a=0$, $b=1):$
340. $K(x, t)=x^{2} t^{2} . \quad$ 341. $K(x, t)= \begin{cases}t, & x \geqslant t, \\ x, & x \leqslant t .\end{cases}$
341. $K(x, t)= \begin{cases}\frac{1}{2} x(2-t), & x \leqslant t, \\ \frac{1}{2} t(2-x), & x \geqslant t .\end{cases}$
$2^{\circ}$. Method of Traces. We call the $m$-th trace of the kernel $K(x, t)$ the number
$$
A_{m}=\int_{a}^{b} K_{m}(t, t) d t
$$
where $K_{m}(x, t)$ denotes the $m$-th iterated kernel.
For the smallest characteristic number $\lambda_{1}$, for sufficiently large $m$, the following approximate formula holds:
$$
\left|\lambda_{1}\right| \approx \sqrt{\frac{A_{2 m}}{A_{2 m+2}}}
$$
Formula (4) gives the value of $\left|\lambda_{1}\right|$ with a surplus.
Traces of even order for a symmetric kernel are computed by the formula
$$
A_{2 m}=\int_{a}^{b} \int_{a}^{b} K_{m}^{2}(x, t) d x d t=2 \int_{a}^{b} \int_{a}^{x} K_{m}^{2}(x, t) d t d x
$$
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Using the Kellogg method, calculate the smallest characteristic number of the kernel $K(x, t)=x^{2} t^{2}, 0 \leqslant x, t \leqslant 1$.
|
Solution. Let $\omega(x)=x$. Then
$$
\begin{aligned}
& \omega_{1}(x)=\int_{0}^{1} x^{2} t^{2} t d t=\frac{x^{2}}{4} \\
& \omega_{2}(x)=\int_{0}^{1} x^{2} t^{4} \frac{1}{4} d t=\frac{1}{4} x^{2} \cdot \frac{1}{5} \\
& \omega_{3}(x)=\int_{0}^{1} \frac{1}{4 \cdot 5} x^{2} t^{4} d t=\frac{1}{4 \cdot 5^{2}} x^{2} \\
& \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\
& \omega_{n}(x)=\frac{1}{4 \cdot 5^{n-1}} x^{2}
\end{aligned}
$$
Next,
$$
\left\|\omega_{n}(x)\right\|=\frac{1}{4 \cdot 5^{n-1}} \sqrt{\int_{0}^{1} x^{4} d x}=\frac{1}{4 \cdot 5^{n-1}} \cdot \frac{1}{\sqrt{5}}
$$
Thus, according to (7),
$$
\lambda_{1} \approx \frac{\frac{1}{4} \cdot \frac{1}{5^{n-2}} \cdot \frac{1}{\sqrt{5}}}{\frac{1}{4} \cdot \frac{1}{5^{n-1}} \cdot \frac{1}{\sqrt{5}}}=5
$$
## Problems for Independent Solution
Using the Kellogg method, find the smallest characteristic numbers of the following kernels:
347. $K(x, t)=x t$;
$0 \leqslant x, t \leqslant 1$.
348. $K(x, t)=\sin x \sin t$;
$-\pi \leqslant x, t \leqslant \pi$.
349. $K(x, t)=\left\{\begin{array}{ll}t, & x \geqslant t ; \\ x, & x \leqslant t ;\end{array} \quad 0 \leqslant x, t \leqslant 1\right.$.
350. $K(x, t)=\left\{\begin{array}{l}\frac{1}{2} x(2-t), \quad x \leqslant t, \\ \frac{1}{2} t(2-x), \quad x \geqslant t,\end{array} \quad 0 \leqslant x, t \leqslant 1\right.$.
Stability of a Compressed Rod (Longitudinal Bending of a Rod)
The equation of the deflected elastic line of the rod is
$$
\frac{d}{d x}\left(E I \frac{d y}{d x}\right)=M
$$
where $\boldsymbol{M}$ is the bending moment, $I$ is the moment of inertia of the cross-section of the rod with abscissa $x$, and $E$ is the Young's modulus.
Consider the case when the rod is compressed by forces applied to its ends. The magnitude of each of these forces is denoted by $P$. Then $M=-\boldsymbol{P} \cdot \boldsymbol{y}$ and equation (9) becomes
$$
\frac{d}{d x}\left(E I \frac{d y}{d x}\right)+P \cdot y=0
$$
The ends of the rod do not move in the direction perpendicular to the rod, so
$$
y(0)=y(l)=0,
$$
where $l$ is the length of the rod. Dividing both sides of equation (10) by $E$ and setting $\frac{\boldsymbol{P}}{\boldsymbol{E}}=\lambda$, we get
$$
\frac{d}{d x}\left(r \frac{d y}{d x}\right)+\lambda y=0
$$
Let $G(x, t)$ be the Green's function of the differential equation (12) with boundary conditions (11). Then the problem (12)-(11) is equivalent to the problem of solving the homogeneous Fredholm integral equation of the second kind
$$
y(x)=\lambda \int_{0}^{l} G(x, t) y(t) d t
$$
The kernel $G(x, t)$ of equation (13) is symmetric as the Green's function of a self-adjoint boundary value problem. Thus, the deflection $y(x)$ of the compressed rod satisfies the integral equation (13). For an arbitrarily chosen force $P$, the number $\lambda=\frac{P}{E}$ will not be a characteristic number, and the solution of equation (13) will be the function $y(x) \equiv 0$. In other words, an arbitrarily chosen compressive force will leave the rod straight. In the case when
$P=\lambda_{n} E$, where $\lambda_{n}$ is a characteristic number of the kernel $G(x, t)$, equation (13) will have a non-zero solution, which corresponds to the bending of the rod, i.e., the loss of its stability.
The smallest force $P$ at which the rod loses stability is called the critical force. It is obviously equal to $P_{\text {cr }}=\lambda_{1} E$, where $\lambda_{1}$ is the smallest characteristic number of equation (13). For practical purposes, a sufficiently good approximate formula is
$$
\lambda_{1} \approx \frac{1}{\sqrt{\int_{0}^{1} \int_{0}^{1} G^{2}(x, t) d x d t}}
$$
which gives $\lambda_{1}$ with a deficiency.
|
5
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Find the length of the arc of the curve $y=\arcsin \sqrt{x}-\sqrt{x-x^{2}}$ from $x_{1}=0$ to $x_{2}=1$.
|
Solution. We have $y^{\prime}=\frac{1}{2 \sqrt{x} \sqrt{1-x}}-\frac{1-2 x}{2 \sqrt{x-x^{2}}}=\frac{x}{\sqrt{x-x^{2}}}=$ $=\sqrt{\frac{x}{1-x}}$ $L=\int_{0}^{1} \sqrt{1+y^{\prime 2}} d x=\int_{0}^{1} \sqrt{1+\frac{x}{1-x}} d x=\int_{0}^{1} \frac{1}{\sqrt{1-x}} d x=-\left.2 \sqrt{1-x}\right|_{0} ^{1}=2$.
Answer. $L=2$.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Calculate the areas of figures bounded by the curves:
a) $\left\{\begin{array}{l}y=x \sqrt{9-x^{2}} \\ y=0(0 \leqslant x \leqslant 3)\end{array}\right.$
b) $\left\{\begin{array}{l}y=2 x-x^{2}+3 \\ y=x^{2}-4 x+3\end{array}\right.$
|
Solution. We will construct the corresponding regions (Fig. 3.8) and determine the appropriate limits of integration from them, omitting the systems of inequalities. Thus:
a) $S=\int_{D} \int d x d y=\int_{0}^{3} d x \int_{0}^{x \sqrt{9-x^{2}}} d y=$
$=\left.\int_{0}^{3} d x \cdot y\right|_{0} ^{x \sqrt{9-x^{2}}}=\int_{0}^{3} x \sqrt{9-x^{2}} d x=$
$=-\int_{0}^{3} \frac{1}{2}\left(9-x^{2}\right)^{1 / 2} d\left(9-x^{2}\right)=$
$=-\left.\frac{1}{3}\left(9-x^{2}\right)^{3 / 2}\right|_{0} ^{3}=9 ;$
b) $S=\iint_{D} d x d y=$
$$
=\int_{0}^{3}\left(2 x-x^{2}+3-x^{2}+4 x-3\right) d x=
$$
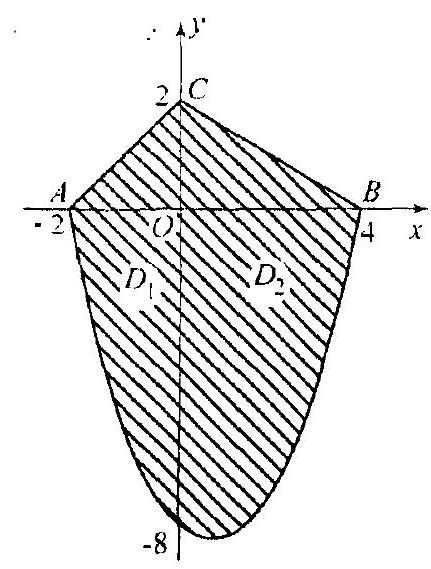
Fig. 3.9
$$
=\left.\left(-\frac{2 x^{3}}{3}+3 x^{2}\right)\right|_{0} ^{3}=9
$$
Answer. a) $S=9 ;$ b) $S=9$.
|
9
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 7. Calculate the area of the figure bounded above by the lines $x-y+2=0, y=2-\frac{1}{2} x$, and below by the parabola $y=x^{2}-2 x-$ $-8$.
|
Solution. Referring to Fig. 3.9. The equation of $AC$ is $y=x+2$, and $CB$ is described by the equation $y=2-\frac{1}{2} x$. Then,
$$
S=\int_{-2}^{0} d x \int_{x^{2}-2 x-8}^{x+2} d y+\int_{0}^{2} d x \int_{x^{2}-2 x-8}^{2-x / 2} d y=42
$$
Answer. $S=42$.
|
42
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Calculate the mass of the surface $z=x y$, located inside the cylinder $x^{2}+\frac{y^{2}}{4}=1$, if the density is $\rho=\frac{|z|}{\sqrt{1+x^{2}+y^{2}}}$.
|
Solution. Given the symmetries of the integration region $\sigma$: $x^{2}+\frac{y^{2}}{4} \leqslant 1$, the equation of the surface, and the density function, it is sufficient to compute the integral over one quarter of the region and multiply the result by 4: $m=4 \int_{D} \rho(x, y, z) d \sigma$, where $D$ is the quarter of the region $\sigma$ lying in the first quadrant of the $O x y$ plane. Further, we have:
$$
\begin{gathered}
z=x y, z_{x}^{\prime}=y, z_{y}^{\prime}=x, \sqrt{1+{z_{x}^{\prime}}^{2}+z_{y}^{\prime 2}}=\sqrt{1+x^{2}+y^{2}} \\
\rho d \sigma=\frac{|z| \sqrt{1+x^{2}+y^{2}}}{\sqrt{1+x^{2}+y^{2}}} d x d y=x y d x d y
\end{gathered}
$$
$$
\begin{array}{ll}
m=4 \cdot \int_{\substack{x^{2}+y^{2} / 4 \leqslant 1 \\
x \geqslant 0, y \geqslant 0}} x y d x d y=4 \int_{0}^{1} x d x \int_{0}^{2 \sqrt{1-x^{2}}} y d y= & \left.2 \int_{0}^{1} x d x \cdot y^{2}\right|_{0} ^{2 \sqrt{1-x^{2}}}= \\
& =8 \int_{0}^{1}\left(1-x^{2}\right) x d x=2 .
\end{array}
$$
Answer. $m=2$.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Calculate the mass of the tetrahedron bounded by the planes $x=0, y=0, z=0$ and $x / 10+y / 8+z / 3=1$, if the density distribution of mass at each point is given by the function $\rho=(1+x / 10+y / 8+z / 3)^{-6}$.
|
Solution. We have $m=\iint_{W} \int \rho d V$. The triple integral is reduced to a double and a definite one (see point $4^{\circ}$):
$$
m=\iint_{D} d x d y \int_{0}^{z} \frac{d z}{\left(1+\frac{x}{10}+\frac{y}{8}+\frac{z}{3}\right)^{6}}
$$
The upper limit, or the exit point from the region, is the ordinate of the point on the plane $\frac{x}{10}+\frac{y}{8}+\frac{z}{3}=1$ (Fig. 3.16), i.e., $z=3\left(1-\frac{x}{10}-\frac{y}{8}\right)$. The double integral is extended over the triangle, which is the base of the tetrahedron formed by
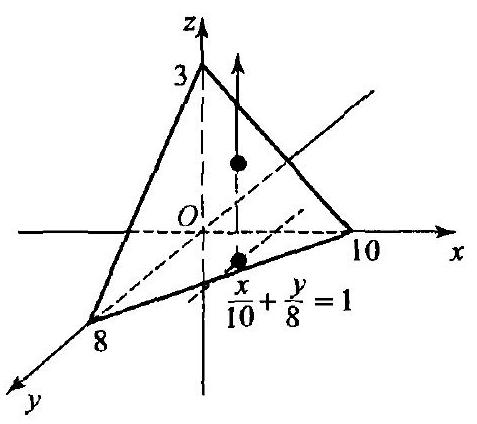
Fig. 3.16 the lines $x=0, y=0, \frac{x}{10}+\frac{y}{8}=1$; therefore (some steps are omitted):
$$
\begin{gathered}
m=\left.\iint_{D} d x d y\left[-\frac{3}{5}\left(1+\frac{x}{10}+\frac{y}{8}+\frac{z}{3}\right)^{-5}\right]\right|_{0} ^{3(1-x / 10-y / 8)}= \\
=\frac{3}{5} \int_{0}^{10} d x \int_{0}^{8(1-x / 10)}\left[2^{-5}-\frac{1}{\left(1+\frac{x}{10}+\frac{y}{8}\right)^{5}}\right] d y= \\
=-\left.\frac{3}{5} \int_{0}^{10} d x\left(\frac{y}{32}+\frac{8}{4}\left(1+\frac{x}{10}+\frac{y}{8}\right)^{-4}\right)\right|_{0} ^{8(1-x / 10)}= \\
=\frac{3}{5} \int_{0}^{10}\left(\frac{3}{8}-\frac{x}{40}-2\left(1+\frac{x}{10}\right)^{-4}\right) d x= \\
=-\left.\frac{3}{5}\left(\frac{3}{8} x-\frac{x^{2}}{80}+\frac{20}{3}\left(1+\frac{x}{10}\right)^{-3}\right)\right|_{0} ^{10}=2
\end{gathered}
$$
Answer. $m=2$.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 8. Check the conditions of Green's theorem for the line integral $\int_{L} 2 x y d x + x^{2} d y$ and compute this integral along the parabola $y=\frac{x^{2}}{4}$ from the origin to the point $A(2,1)$.
|
Solution. We have $P(x, y)=2 x y, Q(x, y)=x^{2}$. These functions are defined, continuous, and differentiable at any point $(x, y)$ in the plane. We have $\frac{\partial P}{\partial y}=2 x, \frac{\partial Q}{\partial x}=2 x$. The conditions of Green's theorem are satisfied. Therefore, the given integral is independent of the path of integration. Moreover, the expression $2 x y d x+x^{2} d y$ represents the total differential of some function $U(x, y)$. It is not difficult to guess that $U(x, y)=x^{2} y$. Therefore,
$$
\int_{O A} 2 x y d x+x^{2} d y=\left.x^{2} y\right|_{(0,0)} ^{(2, \mathrm{I})}=4
$$
Direct calculation gives $\left(y=\frac{x^{2}}{4}, d y=\frac{x}{2} d x\right)$ :
$$
\int_{O A} 2 x y d x+x^{2} d y=\int_{0}^{2}\left(\frac{x^{3}}{2}+\frac{x^{3}}{2}\right) d x=\left.\frac{x^{4}}{4}\right|_{0} ^{2}=4
$$
The answers match.
Answer. 4.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 10. Calculate the integral $I=\oint_{L}\left(x^{2}-y^{2}\right) d x+2 x y d y$, where $L-$ is the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$.
|
Solution. We apply Green's formula and compute the double integral, transitioning to "generalized" polar coordinates. We have: $P=x^{2}-y^{2}, Q=2 x y, \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=2 y+2 y=4 y$. Therefore,
$$
\begin{aligned}
& \int\left(x^{2}-y^{2}\right) d x+2 x y d y=4 \iint_{D} y d x d y= \\
& =\left\{\begin{aligned}
x & =a r \cos \varphi \\
y & =b r \cos \varphi, 0 \leqslant \varphi \leqslant 2 \pi, 0 \leqslant r \leqslant 1 \\
d x d y & =a b r d r d \varphi
\end{aligned}\right\}= \\
& =4 \iint_{D} a b^{2} r^{2} \sin \varphi d r d \varphi=4 a b^{2} \int_{0}^{2 \pi} \sin \varphi d \varphi \int_{0}^{1} r^{2} d r= \\
& =\left.\left.4 a b^{2} \cos \varphi\right|_{0} ^{2 \pi} \cdot \frac{r^{3}}{3}\right|_{0} ^{1}=0
\end{aligned}
$$
Answer. $I=0$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Investigate the convergence of the series $\sum_{n=2}^{\infty} \frac{18}{n^{2}+n-2}$ and, if possible, find its sum.
|
Solution. We have $\frac{18}{n^{2}+n-2}=\frac{6}{n-1}-\frac{6}{n+2}$. Let's form the partial sum and find its limit. Notice which terms cancel each other out (!). We have:
$$
\begin{aligned}
& S_{n}=u_{2}+u_{3}+\ldots+u_{n}= \\
& =6\left[\left(\frac{1}{1}-\frac{1}{A}\right)+\left(\frac{1}{2}-\frac{1}{b}\right)+\left(\frac{1}{3}-\frac{1}{6}\right)+\left(\frac{1}{A}-\frac{1}{7}\right)+\ldots\right. \\
& +\left(\frac{1}{n-4}-\frac{1 /}{n+1}\right)+\left(\frac{1 /}{n+3}-\frac{1}{n}\right)+ \\
& \left.+\left(\frac{1 /}{n-2}-\frac{1}{n+1}\right)+\left(\frac{1}{n-1}+\frac{1}{n+2}\right)\right]= \\
& =6\left(1+\frac{1}{2}+\frac{1}{3}-\frac{1}{n}-\frac{1}{n+1}-\frac{1}{n+2}\right)
\end{aligned}
$$
ll
$$
\lim _{n \rightarrow \infty} S_{n}=6 \lim _{n \rightarrow \infty}\left(\frac{11}{6}-\frac{1}{n}-\frac{1}{n+1}-\frac{1}{n+2}\right)=11
$$
Answer. The given series converges, and its sum is $S=11$.
|
11
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1 (scheduling problem). In how many ways can a daily school schedule be made, consisting of 6 subjects out of 10?
|
Solution. If we take, for example, BAGRIF (biology, algebra, geometry, Russian, history, physical education) as one of the possible schedules, then any other schedule must differ from it either in the order of subjects or in the subjects themselves, i.e., we are talking about permutations of six different subjects out of ten. Their number is equal to $A_{10}^{6}=10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5=151200$.
Answer. 151200.
Problem 2 (the number problem). How many different five-digit numbers can be formed from the digits $2,3,5,7$ and 9?
Solution. One of such numbers is 23579. Each new number is obtained from this by permuting its digits. Their number is equal to $P_{5}=5!=$ 120.
Answer. 120.
Problem 3 (the bouquet problem). In how many ways can a bouquet consisting of 5 flowers be composed, given 10 flowers?
Solution. Two bouquets should be considered different if they consist of different flowers, the order does not matter. This means that we are talking about combinations of five flowers out of ten. To determine the number of such bouquets, we reason as follows. Imagine that we have composed all possible bouquets of five flowers, and let the number of these bouquets be $N$. Take one of them and perform all possible permutations in it, the number of which is $P_{5}$. If we perform similar permutations in all bouquets, we get the number of arrangements of 10 out of 5. Thus, $A_{10}^{5}=N P_{5}$. From this, $N=A_{10}^{5}: P_{5}=252$. This number is $C_{10}^{5}$ (see above).
Answer. 252.
The problems are named to associate other problems with these.
|
151200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5 (Partition problem) In how many ways can 11 items be divided into two groups such that each group has no fewer than three items (selecting one group uniquely determines the other)?
|
Solution. All possibilities to divide 11 items into two groups are represented by the following decompositions: $11=3+8, 11=4+7$, $11=5+6$ (the possibilities $11=6+5, 11=7+4$ and $11=8+3$ coincide with the previous ones). It remains to understand in how many ways one can choose 3, 4, or 5 items out of 11. Since the order of selection does not matter, we are dealing with combinations: the corresponding number of ways are $C_{11}^{3}$, $C_{11}^{4}$, and $C_{11}^{5}$. Under these conditions, the addition rule applies to three objects. Therefore, dividing 11 items into two groups so that each group has at least three items is possible in $C_{11}^{3}+C_{11}^{4}+C_{11}^{5}=957$ ways.
Answer. 957
|
957
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Find the most probable number of hits in the ring in five throws, if the probability of hitting the ring with the ball in one throw is $p=0.6$.
|
Solution. We have $n=5 ; p=0.6 ; q=0.4$. For the number $k_{0}$, we obtain the estimate: $5 \cdot 0.6-0.4 \leqslant k_{0} \leqslant 5 \cdot 0.6+0.6$, i.e., $2.6 \leqslant k_{0} \leqslant 3.6$. Since $k_{0}$ is an integer, then $k_{0}=3$.
Direct calculations of $p_{5}(k)$ lead to the values: $p_{5}(0)=$ $=0.01024 ; p_{5}(1)=0.0768 ; \quad p_{5}(2)=0.2304 ; p_{5}(3)=0.3456 ; p_{5}(4)=$ $=0.2592 ; p_{5}(5)=0.07776$. The largest of the numbers $p_{5}(k)-$ is $p_{5}(3)=$ $=0.3456$; it corresponds to the value $k_{0}=3$.
Answer. 3 .
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 7. Among some products, the share of top-grade products is $31 \%$. What is the most probable number of top-grade products in a randomly selected batch of 75 products?
|
Solution. It is known that $p=0.31; q=1-p=0.69; n=75$. By formula (22) we have: $75 \cdot 0.31-0.69 \leqslant k_{0} \leqslant 75 \cdot 0.31+0.31 ; 22.56 \leqslant$ $\leqslant k_{0} \leqslant 23.56 ;$ since $k_{0}$ must be an integer, it follows that $k_{0}=23$.
Answer. 23.
## Exercises
1. Two equally skilled chess players play chess (draws are not considered). Find the probabilities of winning: 3 games out of 6; no more than 3 games out of 6; more than 3 games out of 6.
2. The probability of event $A$ in any of 4 independent trials is 0.8. Find the most probable number of occurrences of event $A$ and indicate the probability of this number.
3. The probability that a part is standard is 0.75. A batch of 10 parts is inspected. Find the most probable number of parts that will be considered standard.
4. How many trials need to be conducted so that the most probable number of occurrences of event $A$ in these trials is 30, if $p=p(A)=0.3$?
## Answers
1. $p_{6}(3)=0.3125 ; p_{6}(k \leqslant 3)=0.65625 ; p_{6}(k>3)=0.34375$. 2. $k_{0}=3$ or $k_{0}=4, p_{4}(3)=p_{4}(4)=0.4096$. 3. 8 4. From 99 to 102. Hint. Apply formula (22).
## § 8. Poisson's Formula. Event Flow
$1^{\circ}$. If the number of trials $n$ is large, and the probability of the occurrence of event $A$ in each trial is small ( $p<0.01$ ), then the numerical implementation of the Bernoulli formula becomes complex, although the formula is valid for any $n$ and $p$. In such cases, Poisson's theorem can be used.
Theorem 8 (Poisson). If $0<p<1$, then
$$
p_{n}(k)=\frac{\lambda^{k} \cdot e^{-\lambda}}{k!} \quad(\lambda=n p ; k=0,1, \ldots, n)
$$
This formula belongs to Poisson and is derived from the Bernoulli formula by taking the limit as $n \rightarrow+\infty$.
$2^{\circ}$. Poisson's formula is applicable for calculating the probabilities of events that form an event flow - a sequence of events that occur at random moments in time.
The intensity of the flow $\lambda$ is the average number of events that occur per unit of time.
A simple, or Poisson, flow of events is one for which the probability of the occurrence of $k$ events in the flow with intensity $\lambda$ is calculated using Poisson's formula
$$
\begin{aligned}
p_{t}(k)= & \frac{(\lambda t)^{k} \cdot e^{-\lambda t}}{k!}, \quad k=0,1,2, \ldots, n . \\
& \text { Problems with solutions }
\end{aligned}
$$
|
23
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. Given a statistical series - the number of days missed due to illness by employees of a laboratory.
| Number of days | 0 | 2 | 3 | 4 | 5 | 7 | 10 | Total |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| Number of employees | 7 | 3 | 5 | 2 | 5 | 6 | 2 | 30 |
Determine the average number of days missed due to illness per person and the dispersion of this number around the average.
|
Solution. Let's determine the sample mean of size $n=30(k=7)$ using formula (1):
$$
\bar{x}_{3}=\frac{1}{30}(7 \cdot 0+3 \cdot 2+5 \cdot 3+2 \cdot 4+5 \cdot 5+6 \cdot 7+2 \cdot 10)=\frac{116}{30}=3.87
$$
We will calculate the variance and standard deviation using formula (2):
$$
\begin{aligned}
\overline{x_{\mathrm{B}}^{2}}=\frac{1}{30}\left(7 \cdot 0^{2}+3 \cdot 2^{2}+5 \cdot 3^{2}+2 \cdot 4^{2}+5 \cdot 5^{2}+6 \cdot 7^{2}+2 \cdot\right. & \left.10^{2}\right)= \\
= & \frac{692}{30}=23.1
\end{aligned}
$$
We have $D_{\mathrm{B}}=\overline{x_{\mathrm{B}}^{2}}-\left(\bar{x}_{\mathrm{B}}\right)^{2}=23.1-3.87^{2}=8.3 ; \sigma=\sqrt{D}=2.8$. Rounding to the nearest whole number, we get that the average number (expected value) of absences in a year per person is 4 days, with a spread of 3 days.
Problem 2. The sample provided in the following table corresponds to the service time (in minutes) for a customer in a store:
| Time Interval | $34 \div 38$ | $38 \div 42$ | $42 \div 46$ | $46 \div 50$ | $50 \div 54$ | $54 \div 58$ | $\Sigma$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| Number of Customers | 2 | 3 | 15 | 18 | 10 | 2 | 50 |
Provide a forecast of the service time by the store and the standard deviation of this time. Find the mode of the variation series.
Solution. We transition from the interval table to the variation series by replacing the time interval with the center of this interval:
$$
\begin{array}{|c|c|c|c|c|c|c|c|}
\hline x_{i} & 36 & 40 & 44 & 48 & 52 & 56 & \Sigma \\
\hline n_{i} & 2 & 3 & 15 & 18 & 10 & 2 & 50 \\
\hline
\end{array}
$$
The mode is the variant with the maximum frequency; $M o=48$.
The numbers in the variation series are not convenient for calculations because they are large, so we transition to conditional variants with a new center $c=48$ and step (difference) $h=4$. Let $u_{i}=\frac{x_{i}-c}{h}=\frac{x_{i}-48}{4}$. We will calculate the sample mean and variance for the new variant. For convenience, we provide a table with intermediate calculations.
| $i$ | $x_{2}$ | $n_{2}$ | $u_{i}$ | $u_{2} n_{2}$ | $n_{i} u_{2}^{2}$ |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | 36 | 2 | -3 | -6 | 18 |
| 2 | 40 | 3 | -2 | -6 | 12 |
| 3 | 44 | 15 | -1 | -15 | 15 |
| 4 | 48 | 18 | 0 | 0 | 0 |
| 5 | 52 | 10 | 1 | 10 | 10 |
| 6 | 56 | 2 | 2 | 4 | 8 |
| $\Sigma$ | - | 50 | -3 | -13 | 63 |
Using the sums in the last row of the table, we calculate: $\bar{u}_{\mathrm{B}}=-\frac{13}{50}=-0.26, \overline{u_{\mathrm{B}}^{2}}=\frac{63}{50}=1.26, \quad D_{\mathrm{B}}=1.26-0.0676=1.1924$, $\sigma(x)=1.1$.
The reverse transition to the variants $x$ is carried out using formulas that follow from the formulas in point $8^{\circ}$:
$$
\bar{x}_{\mathrm{B}}=c+\bar{u}_{\mathrm{B}} \cdot h, \quad D_{\mathrm{B}}(x)=D_{\mathrm{B}}(u) h^{2}, \quad \sigma(x)=\sigma(u) h
$$
We get: $\bar{x}_{\mathrm{B}}=48-4 \cdot 0.26=46.96 ; D_{\mathrm{B}}(x)=19.08 ; \sigma(x)=4.4$.
Forecast of service time: $\approx 47$ min, spread $\approx 4.4$ min.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example. Compute the limit
$$
\lim _{n \rightarrow \infty} \frac{(2 n+1)^{2}-(n+1)^{2}}{n^{2}+n+1}
$$
|
Solution. Here $(2 n+1)^{2}-(n+1)^{2}=3 n^{2}+2 n-$ is a polynomial of the second degree (an infinitely large sequence of order $n^{2}$) and $n^{2}+n+1$ is a polynomial of the second degree (an infinitely large sequence of order $n^{2}$).
1. Factor out $n^{2}$ in the numerator, we get
$$
(2 n+1)^{2}-(n+1)^{2}=n^{2}\left(3+\frac{2}{n}\right)
$$
2. Factor out $n^{2}$ in the denominator, we get
$$
n^{2}+n+1=n^{2}\left(1+\frac{1}{n}+\frac{1}{n^{2}}\right)
$$
3. We have
$$
\lim _{n \rightarrow \infty} \frac{(2 n+1)^{2}-(n+1)^{2}}{n^{2}+n+1}=\lim _{n \rightarrow \infty} \frac{n^{2}(3+2 / n)}{n^{2}\left(1+1 / n+1 / n^{2}\right)}
$$
4. Canceling $n^{2}$ and using the theorem on the limit of a quotient, we get
$$
\lim _{n \rightarrow \infty} \frac{(2 n+1)^{2}-(n+1)^{2}}{n^{2}+n+1}=\frac{\lim _{n \rightarrow \infty}(3+2 / n)}{\lim _{n \rightarrow \infty}\left(1+1 / n+1 / n^{2}\right)}=3
$$
Answer. $\lim _{n \rightarrow \infty} \frac{(2 n+1)^{2}-(n+1)^{2}}{n^{2}+n+1}=3$.
Conditions of the Problems. Calculate the limit.
1. $\lim _{n \rightarrow \infty} \frac{(5-n)^{2}+(5+n)^{2}}{(5-n)^{2}-(5+n)^{2}}$. 2. $\quad \lim _{n \rightarrow \infty} \frac{(4-n)^{3}-(2-n)^{3}}{(1-n)^{2}-(2+n)^{4}}$.
2. $\lim _{n \rightarrow \infty} \frac{(3-n)^{3}-(2-n)^{3}}{(1-n)^{3}-(1+n)^{3}}$.
3. $\lim _{n \rightarrow \infty} \frac{(2-n)^{2}-(1+n)^{2}}{(1+n)^{2}-(2-n)^{2}}$.
4. $\lim _{n \rightarrow \infty} \frac{(3+n)^{2}-(2+n)^{2}}{(2+n)^{2}-(1-n)^{2}}$.
5. $\lim _{n \rightarrow \infty} \frac{(n+2)^{3}-(n+2)^{2}}{(n-2)^{3}-(n+2)^{3}}$.
6. $\lim _{n \rightarrow \infty} \frac{(1+3 n)^{3}-27 n^{3}}{(1+4 n)^{2}+2 n^{2}}$.
7. $\lim _{n \rightarrow \infty} \frac{(3-2 n)^{2}}{(n-3)^{3}-(n+3)^{3}}$.
8. $\lim _{n \rightarrow \infty} \frac{(2+n)^{3}}{(n+2)^{2}-(n+1)^{3}}$.
9. $\lim _{n \rightarrow \infty} \frac{(n+2)^{2}-(n+5)^{3}}{(3-n)^{3}}$.
Answers. 1. $-\infty$. 2.0.3.0. 4. $-1.5 .1 / 3.6 .-\infty .7 .9 .8 .-2 / 9$. 9. -1.10 .1 .
## 3.3. Calculation of $\lim _{n \rightarrow \infty}[f(n) / g(n)]$
Problem Statement. Calculate the limit
$$
\lim _{n \rightarrow \infty} \frac{f(n)}{g(n)}
$$
where $f(n)$ is an infinitely large sequence of order $n^{\alpha}$ and $g(n)$ is an infinitely large sequence of order $n^{\beta}$ $(\alpha, \beta \in \mathbb{R})$.
Plan of Solution.
1. Factor out $n^{\alpha}$ in the numerator, we get $f(n)=n^{\alpha} \varphi(n)$, where $\lim _{n \rightarrow \infty} \varphi(n)=a, a \neq 0$.
2. Factor out $n^{\beta}$ in the denominator, we get $g(n)=n^{\beta} \psi(n)$, where $\lim _{n \rightarrow \infty} \psi(n)=b, b \neq 0$.
3. We have
$$
\lim _{n \rightarrow \infty} \frac{f(n)}{g(n)}=\lim _{n \rightarrow \infty} \frac{n^{\alpha} \varphi(n)}{n^{\beta} \psi(n)}
$$
4. We get:
if $\alpha>\beta$, then $\lim _{n \rightarrow \infty} \frac{f(n)}{g(n)}=\infty$;
if $\alpha<\beta$, then $\lim _{n \rightarrow \infty} \frac{f(n)}{g(n)}=0$;
if $\alpha=\beta$, then by the theorem on the limit of a quotient
$$
\lim _{n \rightarrow \infty} \frac{f(n)}{g(n)}=\frac{\lim _{n \rightarrow \infty} \varphi(n)}{\lim _{n \rightarrow \infty} \psi(n)}=\frac{a}{b}
$$
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example. Compute the limit
$$
\lim _{n \rightarrow \infty} \frac{n \sqrt[6]{n}+\sqrt[5]{32 n^{10}+1}}{(n+\sqrt[4]{n}) \sqrt[3]{n^{3}-1}}
$$
|
Solution. The numerator $n \sqrt[6]{n}+\sqrt[5]{32 n^{10}+1}$ is an infinitely large sequence of order $n^{2}$, and the denominator $(n+\sqrt[4]{n}) \sqrt[3]{n^{3}-1}$ is an infinitely large sequence of order $n^{2}$.
1. Factor out $n^{2}$ in the numerator, we get
$$
n \sqrt[6]{n}+\sqrt[5]{32 n^{10}+1}=n^{2}\left(\frac{1}{n^{5 / 6}}+2 \sqrt[5]{1+\frac{1}{n^{10}}}\right)
$$
2. Factor out $n^{2}$ in the denominator, we get
$$
(n+\sqrt[4]{n}) \sqrt[3]{n^{3}-1}=n^{2}\left(1+\frac{1}{n^{3 / 4}}\right) \sqrt[3]{1-\frac{1}{n^{3}}}
$$
3. We have
$$
\lim _{n \rightarrow \infty} \frac{n \sqrt[6]{n}+\sqrt[5]{32 n^{10}+1}}{(n+\sqrt[4]{n}) \sqrt[3]{n^{3}-1}}=\lim _{n \rightarrow \infty} \frac{n^{2}\left(1 / n^{5 / 6}+2 \sqrt[5]{1+1 / n^{10}}\right)}{n^{2}\left(1+1 / n^{3 / 4}\right) \sqrt[3]{1-1 / n^{3}}}
$$
4. Canceling $n^{2}$ and using theorems about limits, we finally get
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{n \sqrt[6]{n}+\sqrt[5]{32 n^{10}+1}}{(n+\sqrt[4]{n}) \sqrt[3]{n^{3}-1}}=\lim _{n \rightarrow \infty} \frac{1 / n^{5 / 6}+2 \sqrt[5]{1+1 / n^{10}}}{\left(1+1 / n^{3 / 4}\right) \sqrt[3]{1-1 / n^{3}}}= \\
&=\frac{\lim _{n \rightarrow \infty}\left(1 / n^{5 / 6}+2 \sqrt[5]{1+1 / n^{10}}\right)}{\lim _{n \rightarrow \infty}\left(1+1 / n^{3 / 4}\right) \sqrt[3]{1-1 / n^{3}}}=2
\end{aligned}
$$
NOTE. In this case, the property of the root was used, according to which $\lim _{n \rightarrow \infty} \sqrt[5]{1+1 / n^{10}}=1$ and $\lim _{n \rightarrow \infty} \sqrt[3]{1-1 / n^{3}}=1$.
$$
\text { Answer. } \lim _{n \rightarrow \infty} \frac{n \sqrt[6]{n}+\sqrt[5]{32 n^{10}+1}}{(n+\sqrt[4]{n}) \sqrt[3]{n^{3}-1}}=2
$$
Conditions of the Problems. Calculate the limit.
1. $\lim _{n \rightarrow \infty} \frac{n \sqrt[3]{3 n^{2}}+\sqrt[4]{4 n^{8}+1}}{(n+\sqrt{n}) \sqrt{7-n+n^{2}}}$.
2. $\lim _{n \rightarrow \infty} \frac{\sqrt{n-1}-\sqrt{2 n^{2}+3}}{\sqrt[3]{n^{3}+3}+\sqrt[4]{n^{5}+2}}$.
3. $\lim _{n \rightarrow \infty} \frac{\sqrt{2 n^{3}+3}-\sqrt{n+5}}{\sqrt[3]{n^{3}+2}-\sqrt{n-1}}$.
4. $\lim _{n \rightarrow \infty} \frac{\sqrt[3]{n^{2}+3}+3 n^{3}}{\sqrt[4]{n^{12}+2 n+1}-n^{2}}$.
5. $\lim _{n \rightarrow \infty} \frac{\sqrt{3 n+2}-\sqrt[3]{125 n^{3}+n}}{\sqrt[5]{n}+n^{2}}$.
6. $\lim _{n \rightarrow \infty} \frac{n \sqrt{n}-\sqrt[3]{27 n^{6}+n^{4}}}{(n+\sqrt[4]{n}) \sqrt{4+n^{2}}}$.
7. $\lim _{n \rightarrow \infty} \frac{\sqrt{n+2}-\sqrt{n^{2}+2}}{\sqrt[4]{n^{4}+1}-\sqrt[3]{n^{2}-1}}$.
8. $\lim _{n \rightarrow \infty} \frac{\sqrt{n^{5}+3}+\sqrt{n-2}}{\sqrt[4]{n^{4}+2}-\sqrt{n-2}}$.
9. $\lim _{n \rightarrow \infty} \frac{10 n^{3}-\sqrt{n^{3}+2}}{\sqrt{4 n^{6}+3}-n}$.
10. $\lim _{n \rightarrow \infty} \frac{\sqrt{n+2}-\sqrt[3]{8 n^{3}+3}}{\sqrt[4]{n+5}+n}$.
Answers. 1. $\sqrt{2}$. 2.0.3. $+\infty .4$. 3. 5.5. 6. -3. 7. -1 . 8. $+\infty$. 9.5. 10. -2 .
## 3.4. Calculation of $\lim _{n \rightarrow \infty}\left[u(n)^{v(n)}\right]$
Problem Statement. Calculate the limit of the sequence
$$
\lim _{n \rightarrow \infty}\left[u(n)^{v(n)}\right]
$$
where $\lim _{n \rightarrow \infty} u(n)=1$ and $\lim _{n \rightarrow \infty} v(n)=\infty$.
## Plan of Solution.
1. Transform the expression under the limit so that we can use the second remarkable limit, i.e., factor out the one:
$$
\lim _{n \rightarrow \infty}\left[u(n)^{v(n)}\right]=\lim _{n \rightarrow \infty}\left((1+\alpha(n))^{1 / \alpha(n)}\right)^{\alpha(n) v(n)}
$$
where $\alpha(n)=u(n)-1$ is an infinitesimal sequence as $n \rightarrow \infty$. Since $\alpha(n) \rightarrow 0$ as $n \rightarrow \infty$, we have
$$
\lim _{n \rightarrow \infty}(1+\alpha(n))^{1 / \alpha(n)}=e
$$
2. If $\lim _{n \rightarrow \infty} a_{n}=a\left(a_{n}>0, a>0\right)$ and $\lim _{n \rightarrow \infty} b_{n}=b$, then
$$
\lim _{n \rightarrow \infty} a_{n}^{b_{n}}=a^{b}
$$
Therefore, if the limit
$$
\lim _{n \rightarrow \infty} \alpha(n) v(n)=\lim _{n \rightarrow \infty}(u(n)-1) v(n)
$$
exists, then we finally have
$$
\lim _{n \rightarrow \infty}\left[u(n)^{v(n)}\right]=e^{\lim _{n \rightarrow \infty}(u(n)-1) v(n)}
$$
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Example. Compute the limit
$$
\lim _{x \rightarrow 0} \frac{2 x \sin x}{1-\cos x}
$$
|
Solution. The expression under the limit sign is the ratio of two infinitesimals at the point $x=0$, since
$$
\lim _{x \rightarrow 0}(2 x \sin x)=0, \quad \lim _{x \rightarrow 0}(1-\cos x)=0
$$
The infinitesimals in the numerator and denominator are replaced by equivalent ones:
$$
\begin{array}{ll}
2 x \sin x \sim 2 x \cdot x, & x \rightarrow 0 \\
1-\cos x \sim \frac{x^{2}}{2}, & x \rightarrow 0
\end{array}
$$
Thus,
$$
\lim _{x \rightarrow 0} \frac{2 x \sin x}{1-\cos x}=\lim _{x \rightarrow 0} \frac{2 x \cdot x}{x^{2} / 2}=4
$$
Answer. $\lim _{x \rightarrow 0} \frac{2 x \sin x}{1-\cos x}=4$.
Conditions of the Problems. Calculate the limit.
1. $\lim _{x \rightarrow 0} \frac{\ln (1+\sin 2 x)}{\sin 3 x}$.
2. $\lim _{x \rightarrow 0} \frac{3 x^{2}+6 x}{\sin 3 x}$.
3. $\lim _{x \rightarrow 0} \frac{5^{x}-1}{\ln (1+x)}$.
4. $\lim _{x \rightarrow 0} \frac{1-\cos 2 x}{\cos 5 x-\cos 3 x}$.
5. $\lim _{x \rightarrow 0} \frac{1-\cos 2 x}{e^{2 x^{2}}-1}$.
6. $\lim _{x \rightarrow 0} \frac{\sqrt{9+x}-3}{3 \operatorname{arctg} 2 x}$.
7. $\lim _{x \rightarrow 0} \frac{\operatorname{tg} 2 x}{e^{2 x}-1}$.
8. $\lim _{x \rightarrow 0} \frac{1-\sqrt{\cos x}}{\sin ^{2} x}$.
9. $\lim _{x \rightarrow 0} \frac{\sin 2 x}{\ln (1-2 x)}$.
10. $\lim _{x \rightarrow 0} \frac{\arcsin 2 x}{\ln (e-2 x)-1}$.
Answers. 1. 2/3. 2. 2. 3. $\ln 5$.
4. $-1 / 4$.
5. 1 .
6. $1 / 12$. 7. 1. 8. $1 / 4$. 9. -1. 10. $-e$.
3.9. Calculation of $\lim _{x \rightarrow a}[f(x) / g(x)]$
PROBLEM STATEMENT. Calculate the limit
$$
\lim _{x \rightarrow a} \frac{f(x)}{g(x)}
$$
where $f(x)$ and $g(x)$ are infinitesimal functions at the point $x=a$.
SOLUTION PLAN.
1. We need to replace $f(x)$ and $g(x)$ with equivalent infinitesimal functions. However, the table of equivalent infinitesimal functions is compiled for the point $x=0$. Therefore, we first make a variable substitution $x-a=t$ and will find the limit as $t \rightarrow 0$.
2. Transform the expression under the limit sign using algebraic and trigonometric formulas, and replace the infinitesimal functions in the product and quotient with equivalent ones.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example. Calculate the limit
$$
\lim _{x \rightarrow \pi} \frac{\cos 3 x-\cos x}{\tan^{2} 2 x}
$$
|
Solution.
1. Since
$$
\lim _{x \rightarrow \pi}[\cos 3 x-\cos x]=0, \quad \lim _{x \rightarrow \pi} \operatorname{tg}^{2} 2 x=0
$$
the expression under the limit sign is a ratio of two infinitesimal functions as $x \rightarrow \pi$. We need to replace these infinitesimal functions with equivalent ones. For this, we first make the substitution $x-\pi=t$:
$$
\lim _{x \rightarrow \pi} \frac{\cos 3 x-\cos x}{\operatorname{tg}^{2} 2 x}=\lim _{t \rightarrow 0} \frac{\cos 3(\pi+t)-\cos (\pi+t)}{\operatorname{tg}^{2} 2(\pi+t)}
$$
2. Using trigonometric formulas and replacing the product and quotient of infinitesimal functions with equivalent ones, we get
$$
\begin{aligned}
& \lim _{t \rightarrow 0} \frac{\cos 3(\pi+t)-\cos (\pi+t)}{\operatorname{tg}^{2} 2(\pi+t)}= \\
& \quad=\lim _{t \rightarrow 0} \frac{\cos t-\cos 3 t}{\operatorname{tg}^{2} 2 t}=\lim _{t \rightarrow 0} \frac{-2 \sin 2 t \sin (-t)}{\operatorname{tg}^{2} 2 t}=\lim _{t \rightarrow 0} \frac{2 \cdot 2 t \cdot t}{4 t^{2}}=1
\end{aligned}
$$
Answer. $\lim _{x \rightarrow \pi} \frac{\cos 3 x-\cos x}{\operatorname{tg}^{2} 2 x}=1$.
Conditions of the Problems. Calculate the limits.
1. $\lim _{x \rightarrow 1} \frac{x^{3}-1}{\ln x}$.
2. $\lim _{x \rightarrow \pi} \frac{1+\cos 5 x}{\sin ^{2} 3 x}$.
3. $\lim _{x \rightarrow 1 / 2} \frac{1+\cos 2 \pi x}{\operatorname{tg}^{2} 2 \pi x}$.
4. $\lim _{x \rightarrow 2} \frac{\sin 3 \pi x}{\sin 8 \pi x}$.
5. $\lim _{x \rightarrow 2} \frac{\sqrt{x^{2}-x-1}-1}{\ln (x-1)}$.
6. $\lim _{x \rightarrow \pi / 2} \frac{\operatorname{tg} 5 x}{\operatorname{tg} 3 x}$.
7. $\lim _{x \rightarrow 1} \frac{1-x^{3}}{\sin \pi x}$.
8. $\lim _{x \rightarrow 1} \frac{2-\sqrt{5-x}}{\sin \pi x}$.
9. $\lim _{x \rightarrow \pi} \frac{\operatorname{tg} 5 x}{\sin 3 x}$.
10. $\lim _{x \rightarrow 2} \frac{2^{x}-4}{\sin \pi x}$.
Answers. 1. 3. 2. 5/18. 3. $1 / 2$. 4. 3/8. 5. 3/2. 6. 3/5. 7. $3 / \pi$. 8. $-1 /(4 \pi)$. 9. $-5 / 3$. 10. $(4 \ln 2) / \pi$.
### 3.10. Calculation of $\lim _{x \rightarrow 0}\left[u(x)^{v(x)}\right]$
Problem Statement. Calculate the limit
$$
\lim _{x \rightarrow 0}\left[u(x)^{v(x)}\right]
$$
where $\lim _{x \rightarrow 0} u(x)=1$ and $\lim _{x \rightarrow 0} v(x)=\infty$.
## PLAN OF SOLUTION.
1. Transform the expression under the limit sign:
$$
u(x)^{v(x)}=e^{v(x) \ln u(x)}
$$
2. Since the exponential function $e^{x}$ is continuous, we can take the limit under the sign of this function. We have
$$
\lim _{x \rightarrow 0}\left[u(x)^{v(x)}\right]=\lim _{x \rightarrow 0} e^{v(x) \ln u(x)}=e^{\lim _{x \rightarrow 0}[v(x) \ln u(x)]}
$$
3. Calculate the limit of the exponent
$$
\lim _{x \rightarrow 0}[v(x) \ln u(x)]
$$
replacing infinitesimal functions with equivalent ones.
4. Write the final answer.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example. Compute the limit
$$
\lim _{x \rightarrow 0} \sqrt[3]{x\left(2+\sin \frac{1}{x}\right)+8 \cos x}
$$
|
Solution.
1. Since the function $y=\sqrt[3]{x}$ is continuous for all $x$, by passing to the limit under the sign of a continuous function, we get
$$
\lim _{x \rightarrow 0} \sqrt[3]{x\left(2+\sin \frac{1}{x}\right)+8 \cos x}=\sqrt[3]{\lim _{x \rightarrow 0}\left[x\left(2+\sin \frac{1}{x}\right)+8 \cos x\right]}
$$
2. Since $x$ is an infinitesimal function at the point $x=0$, and $2+\sin (1 / x)$ is a bounded function in the neighborhood of the point $x=0$, then $x(2+\sin (1 / x))$ is an infinitesimal function at the point $x=0$, i.e.,
$$
\lim _{x \rightarrow 0} x\left(2+\sin \frac{1}{x}\right)=0
$$
3. Since $\cos x$ is continuous at the point $x=0$, then
$$
\lim _{x \rightarrow 0} \cos x=1
$$
and, using the properties of the limit of a function at a point, we get
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \sqrt[3]{x\left(2+\sin \frac{1}{x}\right)+8 \cos x}=\sqrt[3]{\lim _{x \rightarrow 0} x\left(2+\sin \frac{1}{x}\right)+8 \lim _{x \rightarrow 0} \cos x}=2 \\
& \text { Answer. } \lim _{x \rightarrow 0} \sqrt[3]{x\left(2+\sin \left(\frac{1}{x}\right)\right)+8 \cos x}=2
\end{aligned}
$$
Conditions of the Problems. Calculate the limit.
1. $\lim _{x \rightarrow 0} \sqrt{9 \cos 2 x+2 x \operatorname{arctg} \frac{1}{x}}$.
2. $\lim _{x \rightarrow \pi / 2} \sqrt{4 \sin x+(2 x-\pi) \sin \frac{x^{2}}{2 x-\pi}}$.
3. $\lim _{x \rightarrow 0} \sqrt{\cos x+\operatorname{arctg} x \cos ^{2} \frac{1}{x^{2}}}$.
4. $\lim _{x \rightarrow 0} \sqrt{4 \cos x+\ln (1+2 x) \sin \frac{1}{x}}$.
5. $\lim _{x \rightarrow 0} \sqrt{4 \cos ^{2} x+\left(e^{2 x}-1\right) \operatorname{arctg} \frac{1}{x^{2}}}$.
6. $\lim _{x \rightarrow 0} \ln \left[\left(e^{x^{3}}-\cos x\right) \cos \frac{2}{x}+\operatorname{tg}\left(x+\frac{\pi}{4}\right)\right]$.
7. $\lim _{x \rightarrow 0} \sqrt{4 \sin x+\left(e^{\sin ^{2} x}-1\right) \cos \frac{1}{x}}$.
8. $\lim _{x \rightarrow 2} \sqrt{\ln (x+2)+\sin \left(4-x^{2}\right) \cos \frac{x+2}{x-2}}$.
9. $\lim _{x \rightarrow 1} \operatorname{tg}\left(\arccos x+\sin \frac{x-1}{x+1} \cos \frac{x+1}{x-1}\right)$.
10. $\lim _{x \rightarrow 0} \ln \left(3+\operatorname{arctg} x \sin \frac{1}{x}\right)$.
Answers. 1. 3.
11. 2 .
12. 1 .
13. 2 .
14. 2 .
15. $0 . \quad 7.2$.
16. $\ln 2$.
17. $0 . \quad 10 . \ln 3$.
Chapter 4
## DIFFERENTIATION
In the study of the topic DIFFERENTIATION, you will become familiar with the concepts of the derivative and differential of a function of one variable through examples, learn to compute derivatives using the rules of differentiation for sums, products, quotients, and composite functions, learn to differentiate functions given parametrically, compute higher-order derivatives, and apply derivatives and differentials in approximate calculations and in solving geometric problems.
Using the package SOLVER.CA, you can compute limits, perform numerical calculations, and compute derivatives of any order to verify the correctness of the results you obtain.
## 4.1. The Concept of a Derivative
Problem Statement. Find the derivative of the function $f(x)$ at the point $x=0$ based on the definition.
Plan of Solution.
1. By definition,
$$
f^{\prime}(0)=\lim _{x \rightarrow 0} \frac{f(x)-f(0)}{x}
$$
(Recall that when computing the limit $x \rightarrow 0$, but $x \neq 0$.)
2. Compute the limit
$$
\lim _{x \rightarrow 0} \frac{f(x)-f(0)}{x}
$$
3. If the limit exists and equals $A$, then $f^{\prime}(0)=A$; if the limit does not exist, then $f^{\prime}(0)$ does not exist.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example. According to the definition, find the derivative of the function
$$
f(x)=\left[\begin{array}{ll}
1-\cos \left(x \sin \frac{1}{x}\right), & x \neq 0 \\
0, & x=0
\end{array}\right.
$$
at the point $x=0$.
|
Solution.
1. By definition
$$
f^{\prime}(0)=\lim _{x \rightarrow 0} \frac{f(x)-f(0)}{x}=\lim _{x \rightarrow 0} \frac{1-\cos (x \sin (1 / x))-0}{x}
$$
2. Since $\sin (1 / x)$ is a bounded function and $x$ is an infinitesimal function as $x \rightarrow 0$, by the theorem on the product of an infinitesimal function and a bounded function, $x \sin (1 / x) \rightarrow 0$ as $x \rightarrow 0$. Replacing the infinitesimal function in the numerator with an equivalent one and again using the mentioned theorem, we get
$$
\lim _{x \rightarrow 0} \frac{1-\cos (x \sin (1 / x))-0}{x} \lim _{x \rightarrow 0} \frac{x^{2} \sin ^{2}(1 / x)}{2 x}=0
$$
3. Thus, the limit exists and is equal to zero. Therefore, $f^{\prime}(0)=0$.
Answer. $f^{\prime}(0)=0$.
1. $f(x)=\left[\begin{array}{l}\sin \left(x^{3}+x^{2} \sin \frac{2}{x}\right), x \neq 0, \\ 0, x=0 .\end{array}\right.$
2. $f(x)=\left[\begin{array}{l}\operatorname{tg}\left(x^{2} \cos \frac{1}{9 x}\right)+2 x, x \neq 0, \\ 0, x=0 .\end{array}\right.$
3. $f(x)=\left[\begin{array}{l}\arcsin \left(x \cos \frac{1}{5 x}\right) \\ 0, x=0 .\end{array}\right.$
4. $f(x)=\left[\begin{array}{l}\ln \left(1-\operatorname{tg}\left(x^{2} \sin \frac{1}{x}\right)\right), x \neq 0, \\ 0, x=0 .\end{array}\right.$
5. $f(x)=\left[\begin{array}{l}\operatorname{tg}\left(x \sin \frac{3}{x}\right), x \neq 0, \\ 0, x=0 .\end{array}\right.$
6. $f(x)=\left[\begin{array}{l}\sqrt{1+\ln \left(1+x^{2} \sin \frac{1}{x}\right)}-1, x \neq 0, \\ 0, x=0 .\end{array}\right.$
7. $f(x)=\left[\begin{array}{l}\sin \left(e^{x^{2} \sin (5 / x)}-1\right), x \neq 0, \\ 0, \quad x=0 .\end{array}\right.$
8. $f(x)=\left[\begin{array}{l}x^{3} \cos \frac{4}{3 x}+3 x, \quad x \neq 0, \\ 0, \quad x=0 .\end{array}\right.$
9. $f(x)=\left[\begin{array}{l}\operatorname{arctg}\left(x-x^{2} \sin \frac{1}{3 x}\right), x \neq 0, \\ 0, x=0 .\end{array}\right.$
10. $f(x)=\left[\begin{array}{l}\sin ^{2} x \cos \frac{5}{x}+2 x, x \neq 0, \\ 0, x=0 .\end{array}\right.$
Answers. 1. 0. 2. 2. 3. Does not exist. 4. 0. 5. Does not exist. 6. 0. 7. 0. 8. 3. 9. 1. 10. 2.
## 4.2. Calculation of Derivatives
Problem Statement. Find the derivative of the function $y=f(x)$.
Solution Plan. The problem is solved in several stages. At each stage, it is necessary to recognize the type of function and apply the corresponding differentiation rule.
The following types of functions are possible.
- The function has the form $C_{1} u_{1}+C_{2} u_{2}+\ldots+C_{n} u_{n}$, where $u_{1}(x)$, $u_{2}(x), \ldots, u_{n}(x)$ are some functions and $C_{1}, C_{2}, \ldots, C_{n}$ are some constants. Use the formula for the derivative of a linear combination
$$
\left(C_{1} u_{1}+C_{2} u_{2}+\ldots+C_{n} u_{n}\right)^{\prime}=C_{1} u_{1}^{\prime}+C_{2} u_{2}^{\prime}+\ldots+C_{n} u_{n}^{\prime}
$$
- The function has the form $u \cdot v$. Use the formula for the derivative of a product
$$
(u \cdot v)^{\prime}=u^{\prime} \cdot v+u \cdot v^{\prime}
$$
- The function has the form $\frac{u}{v}$. Use the formula for the derivative of a quotient:
$$
\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} \cdot v-u \cdot v^{\prime}}{v^{2}}
$$
- The function has the form $u(v(x))$. Use the formula for the derivative of a composite function
$$
u(v(x))^{\prime}=u^{\prime}(v) \cdot v^{\prime}(x)
$$
- The function has the form $u(x)^{v(x)}$. The derivative of such a function is calculated using the formula
$$
u(x)^{v(x)}=e^{v \ln u}
$$
The transition from one stage to the next is made until each sign of the derivative contains a tabular function.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example. Find the area of the region bounded by the graphs of the functions
$$
y=x^{2}-4 x+3, \quad y=-x^{2}+2 x+3
$$
|
## Solution.
1. Find the abscissas $a$ and $b$ of the points of intersection of the graphs. For this, solve the equation
$$
x^{2}-4 x+3=-x^{2}+2 x+3
$$
We get $a=0, \quad b=3$.
2. Investigate the sign of the function $\varphi=x^{2}-4 x+3-\left(-x^{2}+2 x+3\right)$ on the interval $[a, b]=[0,3]$. For this, assign $x$ any value from $(0,3)$, for example $x=1$. We get that $\varphi(1)=-4$. Therefore, $\varphi<0$ when $x \in(0,3)$. Hence, $x^{2}-4 x+3 \leq-x^{2}+2 x+3$ when $x \in[0,3]$ and the region $D$ is defined by the system of inequalities
$$
\left\{\begin{aligned}
0 & \leq x \leq 3 \\
x^{2}-4 x+3 & \leq y \leq-x^{2}+2 x+3
\end{aligned}\right.
$$
3. Apply the formula (1) with $v(x)=-x^{2}+2 x+3, \quad u(x)=x^{2}-4 x+3, a=0$ and $b=3$:
$$
S_{D}=\int_{0}^{3}\left(-x^{2}+2 x+3-x^{2}+4 x-3\right) d x=\int_{0}^{3}\left(-2 x^{2}+6 x\right) d x=9
$$
Answer. $S=9(\text{units of length})^{2}$.
Conditions of the Problems. Calculate the areas of regions bounded by the graphs of the given functions.
1. $y=32-x^{2}, \quad y=-4 x$.
2. $y=3 \sqrt{x}, \quad y=3 / x, \quad x=4$.
3. $x=5-y^{2}, \quad x=-4 y$.
4. $y=\sqrt{e^{x}-1}, \quad y=0, \quad x=\ln 4$.
5. $y=\sin x, \quad y=\cos x, \quad x=0(x \geq 0)$.
6. $y=\sqrt{x}, \quad y=1 / x, \quad x=16$.
7. $x=27-y^{2}, \quad x=-6 y$.
8. $y=\sin x, \quad y=\cos x, \quad x=0(x \leq 0)$.
9. $y=\sqrt{9-x^{2}}, \quad y=0, \quad x=0, \quad x=3 / 2$.
10. $y=2 / x, \quad y=5 e^{x}, \quad y=2, \quad y=5$.
Answers. 1. 288. $2.14-3 \ln 4$. 3. 36. 4. $(6 \sqrt{3}-2 \pi) / 3$. 5. $\sqrt{2}-1$.
6. $42-\ln 16$.
7. 288.
8. $1+\sqrt{2}$.
9. $(3 \pi+\sqrt{3}) / 4$. 10. 3.
8.8. Calculation of arc lengths $y=f(x)$
PROBLEM STATEMENT. Calculate the length of the curve given by the equation
$$
y=f(x)
$$
and bounded by points with abscissas $x=a$ and $x=b$.
SOLUTION PLAN. The length $l$ of a piecewise smooth curve $y=f(x)$, bounded by points with abscissas $x=a$ and $x=b$, is equal to
$$
l=\int_{a}^{b} \sqrt{1+\left(y^{\prime}\right)^{2}} d x
$$
1. Find $y^{\prime}=f^{\prime}(x)$.
2. Compute the differential of the arc length
$$
d l=\sqrt{1+\left(y^{\prime}\right)^{2}} d x
$$
3. Find the arc length by evaluating the definite integral (1). Write the answer, not forgetting the dimension.
|
9
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example. Find the sum of the series
$$
\sum_{n=1}^{\infty} \frac{72}{n^{2}+5 n+4}
$$
|
Solution.
1. The roots of the denominator $n=-1$ and $n=-4$ differ by an integer, i.e., $n^{2}+5 n+4=(n+1)(n+1+3)$. Therefore, the terms of the sequence of partial sums of the series $\sum_{n=1}^{\infty} a_{n}$ are easily found, as many terms in the expression $S_{n}=a_{1}+a_{2}+\ldots+a_{n}$ cancel each other out.
2. We decompose the general term of the series into elementary fractions
$$
a_{n}=\frac{72}{n^{2}+5 n+4}=\frac{24}{n+1}-\frac{24}{n+4}
$$
and list several terms of the series:
$$
a_{1}=\frac{24}{2}-\frac{24}{5}, \quad a_{2}=\frac{24}{3}-\frac{24}{6}, \quad a_{3}=\frac{24}{4}-\frac{24}{7}
$$
$$
\begin{aligned}
& a_{4}=\frac{24}{5}-\frac{24}{8}, \quad a_{5}=\frac{24}{6}-\frac{24}{9}, \quad a_{6}=\frac{24}{7}-\frac{24}{10} \\
& \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\
& a_{n-5}=\frac{24}{n-4}-\frac{24}{n-1}, \quad a_{n-4}=\frac{24}{n-3}-\frac{24}{n} \\
& a_{n-3}=\frac{24}{n-2}-\frac{24}{n+1}, \quad a_{n-2}=\frac{24}{n-1}-\frac{24}{n+2} \\
& a_{n-1}=\frac{24}{n}-\frac{24}{n+3}, \quad a_{n}=\frac{24}{n+1}-\frac{24}{n+4}
\end{aligned}
$$
3. By canceling all possible terms, we find the $n$-th partial sum of the series:
$S_{n}=a_{1}+a_{2}+\ldots+a_{n}=$
$=\frac{24}{2}+\frac{24}{3}+\frac{24}{4}-\frac{24}{n+2}-\frac{24}{n+3}-\frac{24}{n+4}=26-\frac{24}{n+2}-\frac{24}{n+3}-\frac{24}{n+4}$.
4. We compute the sum of the series using formula (1):
$$
S=\lim _{n \rightarrow \infty} S_{n}=\lim _{n \rightarrow \infty}\left(26-\frac{24}{n+2}-\frac{24}{n+3}-\frac{24}{n+4}\right)=26
$$
Answer. $S=26$.
Problem Statements. Find the sums of the series.
1. $\sum_{n=1}^{\infty} \frac{6}{n^{2}+5 n+6}$.
2. $\quad \sum_{n=6}^{\infty} \frac{3}{n^{2}-5 n+6}$
3. $\quad \sum_{n=1}^{\infty} \frac{30}{25 n^{2}+5 n-6}$.
4. $\quad \sum_{n=1}^{\infty} \frac{4}{4 n^{2}-1}$.
5. $\quad \sum_{n=1}^{\infty} \frac{18}{n^{2}+3 n}$.
6. $\quad \sum_{n=1}^{\infty} \frac{90}{4 n^{2}+8 n-5}$.
7. $\quad \sum_{n=1}^{\infty} \frac{3}{9 n^{2}-3 n-2}$.
8. $\sum_{n=1}^{\infty} \frac{16}{16 n^{2}-8 n-3}$.
9. $\sum_{n=1}^{\infty} \frac{8}{n(n+1)(n+2)}$.
10. $\sum_{n=1}^{\infty} \frac{60}{(2 n+1)(2 n+3)(2 n+5)}$.
Answers. 1. $S=2$. 2. $S=1$. 3. $S=2$. 4. $S=2$. 5. $S=11$. 6. $S=23$. 7. $S=1$. 8. $S=4$. 9. $S=2$. 10. $S=1$.
## 10.2. First Comparison Theorem
Problem Statement. Investigate the convergence of the series with non-negative terms
$$
\sum_{n=1}^{\infty} a_{n}
$$
where $a_{n}=f\left(n, u_{1}(n), u_{2}(n), \ldots\right)$ and $u_{1}(n), u_{2}(n), \ldots-$ are functions with known minimum and maximum values (e.g., sine, cosine, etc.), and the function $f$ monotonically depends on $u_{1}, u_{2}, \ldots$
## Plan of Solution.
1. Check that $\lim _{n \rightarrow \infty} a_{n}=0$ (if $\lim _{n \rightarrow \infty} a_{n} \neq 0$, then the series diverges, as the necessary condition for the convergence of the series is not satisfied).
2. Since $a_{n} \geq 0$, apply the first comparison theorem.
Let there be two series with non-negative terms $\sum_{n=1}^{\infty} a_{n} \quad u$ $\sum_{n=1}^{\infty} b_{n}$
If $a_{n} \leq b_{n}$, then the convergence of the series $\sum_{n=1}^{\infty} b_{n}$ implies the convergence of the series $\sum_{n=1}^{\infty} a_{n}$.
If $a_{n} \geq b_{n}$, then the divergence of the series $\sum_{n=1}^{\infty} b_{n}$ implies the divergence of the series $\sum_{n=1}^{\infty} a_{n}$.
3. To draw a conclusion about the convergence (divergence) of the given series, we must establish the validity of one of the two hypotheses (we check them in any order).
I. The given series $\sum_{n=1}^{\infty} a_{n}$ converges.
II. The given series $\sum_{n=1}^{\infty} a_{n}$ diverges.
I. We check the first hypothesis. To establish that the given series $\sum_{n=1}^{\infty} a_{n}$ converges, we need to find a convergent series $\sum_{n=1}^{\infty} b_{n}$ such that
$$
a_{n} \leq b_{n}
$$
As the reference series $\sum_{n=1}^{\infty} b_{n}$, we use one of the following series:
a) convergent harmonic series $\sum_{n=1}^{\infty} \frac{c}{n^{p}}$ for $p>1$;
b) convergent geometric series $\sum_{n=1}^{\infty} c q^{n}$ for $0<q<1$;
c) convergent series $\sum_{n=1}^{\infty} \frac{c}{n(n+1)}$ (converges to $c$);
d) convergent series $\sum_{n=1}^{\infty} \frac{c}{n(n+1)(n+2)}$ (converges to $\frac{c}{2}$).
II. We check the second hypothesis. To establish that the given series $\sum_{n=1}^{\infty} a_{n}$ diverges, we need to find a divergent series $\sum_{n=1}^{\infty} b_{n}$ such that
$$
a_{n} \geq b_{n}
$$
As the reference series $\sum_{n=1}^{\infty} b_{n}$, we use one of the following series:
a) divergent harmonic series $\sum_{n=1}^{\infty} \frac{c}{n}$;
b) divergent series $\sum_{n=1}^{\infty} \frac{c}{n(n+1)}$ (diverges to $\infty$);
c) divergent series $\sum_{n=1}^{\infty} \frac{c}{n(n+1)(n+2)}$ (diverges to $\infty$).
4. To find the reference series, we use the known minimum and maximum values of the functions $u_{1}(n), u_{2}(n), \ldots$:
$$
\begin{aligned}
& 0 \leq \sin n \leq 1, \quad 0 \leq \cos n \leq 1, \quad 0 \leq \sin ^{2} n \leq 1, \quad 0 \leq \cos ^{2} n \leq 1, \\
& 0 \leq \sin ^{2} n+\cos ^{2} n=1, \quad 0 \leq \sin ^{2} n-\cos ^{2} n \leq 1, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \\
& 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \\
& 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \\
& 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \\
& 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \\
& 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \\
& 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \\
& 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \quad 0 \leq \sin ^{2} n \cos ^{2} n \leq \frac{1}{4}, \\
& 0 \leq \sin
|
26
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example. Evaluate the double integral
$$
\iint_{D}\left(54 x^{2} y^{2}+150 x^{4} y^{4}\right) d x d y
$$
where the region $D$ is bounded by the lines $x=1, y=x^{3}$ and $y=-\sqrt{x}$.
|
Solution.
1. Let's define the region $D$ by inequalities. It is obvious that $-\sqrt{x} \leq x^{3}$. Therefore, $-\sqrt{x} \leq y \leq x^{3}$. Since $x$ appears under the square root, $x \geq 0$. For $x$, the possible inequalities are $0 \leq x \leq 1$ or $1 \leq x$. In the second case, the region is unbounded, which is unacceptable.
Thus,
$$
D=\left\{\begin{array}{cc}
(x, y): & 0 \leq x \leq 1 \\
-\sqrt{x} \leq y \leq x^{3}
\end{array}\right\}
$$
2. We transition from the double integral to the iterated integral:
$$
\iint_{D}\left(54 x^{2} y^{2}+150 x^{4} y^{4}\right) d x d y=\int_{0}^{1} d x \int_{-\sqrt{x}}^{x^{3}}\left(54 x^{2} y^{2}+150 x^{4} y^{4}\right) d y
$$
3. Using the properties of the definite integral, we sequentially integrate first with respect to $y$ (considering $x$ as a constant), and then with respect to $x$:
$$
\begin{aligned}
& \int_{0}^{1} d x \int_{-\sqrt{x}}^{x^{3}}\left(54 x^{2} y^{2}+150 x^{4} y^{4}\right) d y= \\
& =\int_{0}^{1}\left[54 x^{2} \int_{-\sqrt{x}}^{x^{3}} y^{2} d y+150 x^{4} \int_{-\sqrt{x}}^{x^{3}} y^{4} d y\right] d x= \\
& =\int_{0}^{1}\left[\left.54 x^{2} \frac{y^{3}}{3}\right|_{-\sqrt{x}} ^{x^{3}}+\left.150 x^{4} \frac{y^{5}}{5}\right|_{-\sqrt{x}} ^{x^{3}}\right] d x= \\
& =\int_{0}^{1}\left[18 x^{11}+18 x^{7 / 2}+30 x^{19}+30 x^{13 / 2}\right] d x=11
\end{aligned}
$$
Answer. $\iint_{D}\left(54 x^{2} y^{2}+150 x^{4} y^{4}\right) d x d y=11$.
Conditions of the Problems. Calculate the double integrals over the regions $D$ bounded by the given lines.
1. $\iint_{D}(2 x-y) d x d y, \quad y=x^{2}, y=\sqrt{x}$.
2. $\iint_{D}(x-y) d x d y, \quad y=2-x^{2}, y=2 x-1$.
3. $\quad \iint_{D}(y \ln x) d x d y, \quad y=\frac{1}{x}, y=\sqrt{x}, x=2$.
4. $\quad \iint_{D}(\cos 2 x+\sin y) d x d y, \quad y=\frac{\pi}{4}-x, y=0, x=0$.
5. $\quad \iint_{D} \sin (x+y) d x d y, \quad y=x, y=\frac{\pi}{2}, x=0$.
6. $\iint_{D} \frac{x^{2}}{y^{2}} d x d y, \quad y=\frac{1}{x}, y=x, x=2$.
7. $\iint_{D}\left(x^{2}+y\right) d x d y, \quad y=x^{2}, y=\sqrt{x}$.
8. $\quad \iint_{D}(2 x-y) d x d y, \quad y=x^{2}, y=x, x=1, x=2$.
9. $\quad \int_{D} \sqrt{1-x^{2}-y^{2}} d x d y, \quad y=\sqrt{1-x^{2}}, \quad y=0, x=0$.
10. $\iint_{D} x^{2} y^{2} \sqrt{1-x^{3}-y^{3}} d x d y, \quad y=\sqrt[3]{1-x^{3}}, \quad y=0, \quad x=0$.
Answers. 1. $I=1 / 10 . \quad 2 . \quad I=64 / 15 . \quad$ 3. $I=5(2 \ln 2-1) / 8$.
4. $I=(\pi+1-2 \sqrt{2}) / 4 . \quad$ 5. $I=1 . \quad 6 . \quad I=9 / 4 . \quad$ 7. $I=33 / 140$.
5. $I=9 / 10$. $\quad 9 . \quad I=\pi / 6$. $\quad 10 . \quad I=4 / 135$.
## 12.3. Double Integral
## in Polar Coordinates
Problem Statement. Calculate the double integral
$$
\iint_{D} f(x, y) d x d y
$$
where the region $D$ is bounded by two circles
$$
y^{2}+a_{1} y+b_{1} x+x^{2}=0, \quad y^{2}+a_{2} y+b_{2} x+x^{2}=0
$$
$$
\left(a_{1}=0, a_{2}=0, \quad b_{1} b_{2}>0 \quad \text { or } \quad b_{1}=0, b_{2}=0, \quad a_{1} a_{2}>0\right)
$$
and two lines
$$
m_{1} y+k_{1} x=0, \quad\left(m_{1}^{2}+k_{1}^{2} \neq 0\right), \quad m_{2} y+k_{2} x=0, \quad\left(m_{2}^{2}+k_{2}^{2} \neq 0\right)
$$
## Plan of Solution.
1. Define the region $D$ by inequalities in the Cartesian coordinate system.
Notice that the circles $y^{2}+a_{1} y+b_{1} x+x^{2}=0$ and $y^{2}+a_{2} y+b_{2} x+x^{2}=0$ pass through the origin and their centers are located on the $O X$ axis (when $a_{1}=0, a_{2}=0$) or on the $O Y$ axis (when $b_{1}=0, b_{2}=0$) on the same side of the origin (since $b_{1} b_{2}>0$ or $a_{1} a_{2}>0$). Therefore, the circle with the smaller radius is located inside the other. Suppose, for example, this is the circle $y^{2}+a_{1} y+b_{1} x+x^{2}=0$. The region $D$ is between the circles, so the coordinates of the points in the region $D$ satisfy the inequalities
$$
y^{2}+a_{1} y+b_{1} x+x^{2} \geq 0, \quad y^{2}+a_{2} y+b_{2} x+x^{2} \leq 0
$$
The lines $m_{1} y+k_{1} x=0$ and $m_{2} y+k_{2} x=0$ pass through the origin. The region $D$ is located between them. Considering in which half-plane the circles and, consequently, the region $D$ are located, we determine which of the following pairs of inequalities the coordinates of the points in the region $D$ satisfy:
$$
\begin{array}{ll}
m_{1} y+k_{1} x \geq 0, & m_{2} y+k_{2} x \geq 0 \\
m_{1} y+k_{1} x \leq 0, & m_{2} y+k_{2} x \geq 0 \\
m_{1} y+k_{1} x \geq 0, & m_{2} y+k_{2} x \leq 0 \\
m_{1} y+k_{1} x \leq 0, & m_{2} y+k_{2} x \leq 0
\end{array}
$$
2. Since the region $D$ is bounded by circles and lines passing through the origin, it is easier to solve the given problem in polar coordinates
$$
\left\{\begin{array}{l}
x=\varrho \cos \varphi \\
y=\varrho \sin \varphi
\end{array}\right.
$$
In this case, $(\varrho, \varphi) \in D^{\prime}$, and the desired integral is defined by the formula
$$
\iint_{D} f(x, y) d x d y=\iint_{D^{\prime}} f(\varrho \cos \varphi, \varrho \sin \varphi) \varrho d \varrho d \varphi
$$
3. To find the region $D^{\prime}$, we replace $x$ with $\varrho \cos \varphi$ and $y$ with $\varrho \sin \varphi$ in the inequalities defining the region $D$. Then we solve the obtained inequalities for $\varrho$ and $\varphi$. Thus, we get
$$
D^{\prime}=\left\{\begin{array}{rlrl}
& =\varphi_{1} & \leq \varphi \leq \varphi_{2} \\
\varrho_{1}(\varphi) & \leq \varrho \leq \varrho_{2}(\varphi)
\end{array}\right\}
$$
4. We transition from the double integral to the iterated integral:
$$
S=\int_{\varphi_{1}}^{\varphi_{2}} d \varphi \int_{\varrho_{1}(\varphi)}^{\varrho_{2}(\varphi)} f(\varrho \cos \varphi, \varrho \
|
11
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example. Evaluate the double integral
$$
\iint_{D} \frac{x}{y^{5}} d x d y
$$
where the region $D$ is defined by the inequalities
$$
1 \leq \frac{x^{2}}{16}+y^{2} \leq 3, \quad y \geq \frac{x}{4}, \quad x \geq 0
$$
|
SOLUTION.
1. The region $D$ is defined by inequalities in the Cartesian coordinate system:
$$
D=\left\{(x, y): \begin{array}{c}
1 \leq \frac{x^{2}}{16}+y^{2} \leq 3 \\
\\
y \geq \frac{x}{4}, \quad x \geq 0
\end{array}\right\}
$$
2. Since the region $D$ is bounded by ellipses and lines passing through the origin, it is easier to solve the problem using generalized polar coordinates
$$
\left\{\begin{array}{l}
x=4 \varrho \cos \varphi \\
y=\varrho \sin \varphi
\end{array}\right.
$$
In this case, $(\varrho, \varphi) \in D^{\prime}$, and the desired integral is given by the formula
$$
\iint_{D} \frac{x}{y^{5}} d x d y=\iint_{D^{\prime}} \frac{4 \varrho \cos \varphi}{\varrho^{5} \sin ^{5} \varphi} 4 \varrho d \varrho d \varphi
$$
3. To find the region $D^{\prime}$, we replace $x$ with $a \varrho \cos \varphi$ and $y$ with $b \varrho \sin \varphi$ in the inequalities defining the region $D$:
$$
\left\{\begin{array}{l}
1 \leq \frac{16 \varrho^{2} \cos ^{2} \varphi}{16}+\varrho^{2} \sin ^{2} \varphi \leq 3 \\
\varrho \sin \varphi \geq \frac{4 \varrho \cos \varphi}{4}, \varrho \cos \varphi \geq 0
\end{array}\right.
$$
Solving these inequalities with respect to $\varrho$ and $\varphi$, we get
4. Transitioning from the double integral to the repeated integral and integrating sequentially, we obtain
$$
\iint_{D} \frac{x}{y^{5}} d x d y=\iint_{D^{\prime}} \frac{4 \varrho \cos \varphi}{\varrho^{5} \sin ^{5} \varphi} 4 \varrho d \varrho d \varphi=\int_{\pi / 4}^{\pi / 2} d \varphi \int_{1}^{\sqrt{3}} 16 \varrho^{-3} \cdot \frac{\cos \varphi}{\sin ^{5} \varphi} d \varrho=
$$
$$
=16 \int_{\pi / 4}^{\pi / 2} \frac{d \sin \varphi}{\sin ^{5} \varphi} \int_{1}^{\sqrt{3}} \varrho^{-3} d \varrho=\left.\left.16\left(-\frac{1}{4 \sin ^{4} \varphi}\right)\right|_{\pi / 4} ^{\pi / 2}\left(-\frac{1}{2 \varrho^{2}}\right)\right|_{1} ^{\sqrt{3}}=4
$$
Answer. $\iint_{D} \frac{x}{y^{5}} d x d y=4$.
PROBLEM CONDITIONS. Compute the double integrals.
1. $\iint_{D} \frac{y}{x} d x d y$
$$
D=\left\{1 \leq \frac{x^{2}}{9}+\frac{y^{2}}{4} \leq 2, y \geq 0, y \leq \frac{2 x}{3}\right\}
$$
2. $\int_{D}^{D} \int^{x} \frac{x}{y} d x d y$ $D=\left\{1 \leq \frac{x^{2}}{4}+\frac{y^{2}}{9} \leq 4, x \geq 0, y \geq \frac{3 x}{2}\right\}$.
3. $\iint_{D} \frac{x}{y} d x d y$ $D=\left\{1 \leq \frac{x^{2}}{16}+\frac{y^{2}}{4} \leq 4, x \geq 0, y \geq \frac{x}{2}\right\}$.
4. $\int_{D}^{D} \int^{3} y d x d y$ $D=\left\{1 \leq \frac{x^{2}}{4}+\frac{y^{2}}{9} \leq 1, x \geq 0, y \geq 0\right\}$.
5. $\iint_{D} \frac{x}{y} d x d y$
$D=\left\{1 \leq \frac{x^{2}}{4}+\frac{y^{2}}{16} \leq 5, x \geq 0, y \geq 2 x\right\}$.
6. $\iint_{D} \frac{x}{y} d x d y$
$D=\left\{1 \leq \frac{x^{2}}{9}+\frac{y^{2}}{4} \leq 5, x \geq 0, y \geq \frac{2 x}{3}\right\}$.
7. $\iint_{D} \frac{x}{y^{3}} d x d y$
$D=\left\{1 \leq \frac{x^{2}}{4}+y^{2} \leq 25, x \geq 0, y \geq \frac{x}{2}\right\}$.
8. $\int_{D}^{D} \int^{y} \frac{y}{x^{3}} d x d y$
$D=\left\{1 \leq x^{2}+\frac{y^{2}}{16} \leq 9, y \geq 0, y \leq 4 x\right\}$.
9. $\iint_{D} \frac{8 y}{x^{3}} d x d y$
$D=\left\{1 \leq \frac{x^{2}}{4}+y^{2} \leq 4, y \geq 0, y \leq \frac{x}{2}\right\}$.
10. $\iint_{D} \frac{9 x}{y^{3}} d x d y$
$D=\left\{1 \leq \frac{x^{2}}{4}+\frac{y^{2}}{9} \leq 36, x \geq 0, y \geq \frac{3 x}{2}\right\}$.
Answers. 1. $I=\ln 2$.
2. $I=3 \ln 2$.
3. $I=12 \ln 2$.
4. $I=6$.
5. $I=4 \ln 2$.
6. $I=9 \ln 2$.
7. $I=2 \ln 5$.
8. $I=8 \ln 3$.
9. $I=\ln 2$.
10. $I=2 \ln 6$.
## 12.5. Calculation of Volumes Using Double Integrals
PROBLEM STATEMENT. Find the volume of the body bounded by the surfaces
$g_{i}(x, y)=0(i=1,2, \ldots), \quad z=f_{1}(x, y), z=f_{2}(x, y)\left(f_{2}(x, y) \geq f_{1}(x, y)\right)$.
## PLAN OF SOLUTION.
1. The volume of the cylindrical prism bounded by the given surfaces is determined by the formula
$$
V=\iint_{D}\left[f_{2}(x, y)-f_{1}(x, y)\right] d x d y
$$
where $D$ is the projection of the body onto the $X O Y$ plane.
2. To find $D$, we define the body using inequalities and eliminate $z$.
For example, suppose the coordinates of the points of the body satisfy the inequalities $0 \leq z \leq f(x, y), g_{1}(x, y) \geq 0$ and $g_{2}(x, y) \leq 0$. Then the body is defined by the system of inequalities
$$
\left\{\begin{array}{l}
g_{1}(x, y) \geq 0 \\
g_{2}(x, y) \leq 0 \\
0 \leq z \leq f(x, y)
\end{array}\right.
$$
Eliminating $z$, we get
$$
D=\left\{\begin{array}{ll}
& g_{1}(x, y) \geq 0 \\
(x, y): & g_{2}(x, y) \leq 0 \\
0 \leq f(x, y)
\end{array}\right\}
$$
3. We compute the double integral using the formula (1) with $f_{2}=f(x, y)$ and $f_{1}=0$.
We write the answer, not forgetting the dimension.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find the volume of the body bounded by the surfaces
$$
x=17 \sqrt{2 y}, \quad x=2 \sqrt{2 y}, \quad z=1 / 2-y, \quad z=0
$$
|
## Solution.
1. By formula (1) with $f_{2}=1 / 2-y$ and $f_{1}=0$, the desired volume is
$$
V=\iint_{D}\left(\frac{1}{2}-y\right) d x d y
$$
where $D$ is the projection of the body onto the $X O Y$ plane.
2. To find $D$, we define the body using inequalities and eliminate $z$ from them. In this case, the body is defined by the system of inequalities
$$
\left\{\begin{array}{l}
x \leq 17 \sqrt{2 y} \\
x \geq 2 \sqrt{2 y} \\
0 \leq z \leq 1 / 2-y
\end{array}\right.
$$
Therefore,
$$
D=\left\{\begin{array}{ll}
(x, y): \begin{array}{l}
2 \sqrt{2 y} \leq x \leq 17 \sqrt{2 y} \\
0 \leq 1 / 2-y, \quad y \geq 0
\end{array}
\end{array}\right\}
$$
The inequality $y \geq 0$ is necessary because $y$ is under the square root.
3. We compute the double integral:
$$
\begin{aligned}
& V=\iint_{D}\left(\frac{1}{2}-y\right) d x d y=\int_{0}^{1 / 2} d y \int_{2 \sqrt{2 y}}^{17 \sqrt{2 y}}\left(\frac{1}{2}-y\right) d x= \\
&= 15 \sqrt{2} \int_{0}^{1 / 2}\left(\frac{1}{2}-y\right) \sqrt{y} d y=1
\end{aligned}
$$
Answer. $V=1$ unit of volume.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find the mass of the plate $D$ with surface density $\mu=16 x+9 y^{2} / 2$, bounded by the curves
$$
x=\frac{1}{4}, \quad y=0, \quad y^{2}=16 x \quad(y \geq 0)
$$
|
Solution.
1. The mass of the plate $D$ with surface density $\mu=16 x+9 y^{2} / 2$ is determined by the formula
$$
m=\iint_{D}\left(16 x+\frac{9 y^{2}}{2}\right) d x d y
$$
2. We compute the obtained double integral in Cartesian coordinates:
a) define the region $D$ by a system of inequalities:
$$
\left\{\begin{array}{l}
0 \leq x \leq 1 / 4 \\
0 \leq y \leq 4 \sqrt{x}
\end{array}\right.
$$
The inequality $0 \leq x$ follows from $y^{2}=16 x$, i.e., $x$ is non-negative
b) convert the double integral to an iterated integral:
$$
m=\iint_{D}\left(16 x+\frac{9 y^{2}}{2}\right) d x d y=\int_{0}^{1 / 4} d x \int_{0}^{4 \sqrt{x}}\left(16 x+\frac{9 y^{2}}{2}\right) d y
$$
c) integrate sequentially, using the properties of the definite integral:
$$
\begin{aligned}
m=\int_{0}^{1 / 4} d x \int_{0}^{4 \sqrt{x}}(16 x & \left.+\frac{9 y^{2}}{2}\right) d y= \\
& =\left.\int_{0}^{1 / 4}\left(16 x y+\frac{3 y^{3}}{2}\right)\right|_{0} ^{4 \sqrt{x}} d x=160 \int_{0}^{1 / 4} x^{3 / 2} d x=2
\end{aligned}
$$
Answer. $m=2$ units of mass.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Find the mass of the plate $D$ with surface density $\mu=x / y^{5}$, bounded by the curves
$$
\frac{x^{2}}{16}+y^{2}=1, \quad \frac{x^{2}}{16}+y^{2}=3, \quad y=\frac{x}{4}, \quad x=0 \quad\left(y \geq \frac{x}{4}, x \geq 0\right)
$$
|
Solution.
1. The mass of the plate $D$ with surface density $\mu=x / y^{5}$ is determined by the formula
$$
m=\iint_{D} \frac{x}{y^{5}} d x d y
$$
2. We calculate the obtained double integral:
a) define the region $D$ by inequalities in Cartesian coordinates
$$
D=\left\{(x, y): \begin{array}{c}
1 \leq \frac{x^{2}}{16}+y^{2} \leq 3 \\
\\
y \geq x / 4, \quad x \geq 0
\end{array}\right\}
$$
Since the region $D$ is bounded by ellipses and lines passing through the origin, it is easier to solve the problem in generalized polar coordinates
$$
\left\{\begin{array}{l}
x=4 \varrho \cos \varphi \\
y=\varrho \sin \varphi
\end{array}\right.
$$
In this case, $(\varrho, \varphi) \in D^{\prime}$, and the sought mass is determined by the formula
$$
m=\iint_{D} \frac{x}{y^{5}} d x d y=\iint_{D^{\prime}} \frac{4 \varrho \cos \varphi}{\varrho^{5} \sin ^{5} \varphi} 4 \varrho d \varrho d \varphi
$$
To find the region $D^{\prime}$, we replace $x$ with $4 \varrho \cos \varphi$ and $y$ with $\varrho \sin \varphi$ in the inequalities defining the region $D$:
$$
\left\{\begin{array}{l}
1 \leq \frac{16 \varrho^{2} \cos ^{2} \varphi}{16}+\varrho^{2} \sin ^{2} \varphi \leq 3 \\
\varrho \sin \varphi \geq 4 \varrho \cos \varphi / 4, \quad \varrho \cos \varphi \geq 0
\end{array}\right.
$$
Solving these inequalities with respect to $\varrho$ and $\varphi$, we get
$$
D^{\prime}=\left\{\begin{array}{lc}
& (\varrho, \varphi): \begin{array}{c}
1 \leq \varrho \leq \sqrt{3} \\
\frac{\pi}{4} \leq \varphi \leq \frac{\pi}{2}
\end{array}
\end{array}\right\}
$$
b) we transition from the double integral to the repeated integral:
$$
m=\iint_{D^{\prime}} \frac{4 \varrho \cos \varphi}{\varrho^{5} \sin ^{5} \varphi} 4 \varrho d \varrho d \varphi=\int_{\pi / 4}^{\pi / 2} d \varphi \int_{1}^{\sqrt{3}} 16 \varrho^{-3} \cdot \frac{\cos \varphi}{\sin ^{5} \varphi} d \varrho
$$
c) integrating sequentially, we get
$$
m=16 \int_{\pi / 4}^{\pi / 2} \frac{d \sin \varphi}{\sin ^{5} \varphi} \int_{1}^{\sqrt{3}} \varrho^{-3} d \varrho=\left.\left.16\left(-\frac{1}{4 \sin ^{4} \varphi}\right)\right|_{\pi / 4} ^{\pi / 2}\left(-\frac{1}{2 \varrho^{2}}\right)\right|_{1} ^{\sqrt{3}}=4
$$
Answer. $m=4$ units of mass.
Conditions of the Problem. Find the mass of the plate $D$ with surface density $\mu$, where $D$ is bounded by the given lines.
1. $\mu=2 x+y^{2}, \quad x=4, y=0, y=\sqrt{x}$.
2. $\mu=x^{2}+y, \quad x=1, y=0, y=2 \sqrt{x}$.
3. $\mu=x^{2}+2 y, \quad x=0, y=4, y=x^{2}(x \geq 0)$.
4. $\mu=x+y^{2}, \quad x=0, y=1, y=x^{2} / 4(x \geq 0)$.
5. $\quad \mu=\frac{x-y}{x^{2}+y^{2}}, \quad x=0, \quad y=0, \quad x^{2}+y^{2}=4, \quad x^{2}+y^{2}=9$
$$
(x \geq 0, y \leq 0)
$$
6. $\quad \mu=\frac{2 y-x}{x^{2}+y^{2}}$
$x=0, \quad y=0, \quad x^{2}+y^{2}=3, \quad x^{2}+y^{2}=5$ $(x \leq 0, y \geq 0)$.
7. $\quad \mu=\frac{y-x}{x^{2}+y^{2}}, \quad x=0, \quad y=0, \quad x^{2}+y^{2}=4, \quad x^{2}+y^{2}=16$
$$
(x \leq 0, \quad y \geq 0)
$$
8. $\quad \mu(x, y)=y, \quad y=0, \quad y=x \sqrt{3}, \quad x^{2}+\frac{y^{2}}{4}=1, \quad x^{2}+\frac{y^{2}}{4}=9$
$$
(y \geq 0, \quad y \leq x \sqrt{3})
$$
9. $\quad \mu(x, y)=\frac{y}{x^{2}}, \quad y=0, \quad y=x, \quad \frac{x^{2}}{4}+y^{2}=1, \quad \frac{x^{2}}{4}+y^{2}=4$ $(y \geq 0, \quad y \leq x)$.
10. $\mu(x, y)=\frac{x}{y^{2}}, \quad x=0, \quad y=x, \quad \frac{x^{2}}{9}+\frac{y^{2}}{4}=1, \quad \frac{x^{2}}{9}+\frac{y^{2}}{4}=25$
$(x \geq 0, y \geq x)$.
Answers. 1. $m=448 / 15$. 2. $m=11 / 7$. 3. $m=448 / 15$. 4. $m=11 / 7$. 5. $m=2$. 6. $m=3(\sqrt{5}-\sqrt{3})$. 7. $m=4$. 8. $m=52 / 3$. 9. $m=(\sqrt{2}-1) / 2$. 10. $m=18(\sqrt{2}-1)$.
## 12.9. Triple Integral
in Cartesian coordinates
Problem Statement. Calculate the triple integral
$$
\iiint_{\Omega} f(x, y, z) d x d y d z
$$
where the region $\Omega$ is bounded by certain surfaces.
Plan of Solution.
1. Define the region $\Omega$ by a system of inequalities, for example,
$$
\left\{\begin{aligned}
a & \leq x \leq b \\
y_{1}(x) & \leq y \leq y_{2}(x) \\
z_{1}(x, y) & \leq z \leq z_{2}(x, y)
\end{aligned}\right.
$$
2. Transition from the triple integral to the repeated integral:
$$
\iiint_{\Omega} f(x, y, z) d x d y d z=\int_{a}^{b} d x \int_{y_{1}(x)}^{y_{2}(x)} d y \int_{z_{1}(x, y)}^{z_{2}(x, y)} f(x, y, z) d z
$$
3. Using the properties of the definite integral, integrate sequentially first with respect to $z$ (considering $x$ and $y$ as constants), then with respect to $y$ (considering $x$ as a constant), and finally with respect to $x$.
Write the answer.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find the volume of the body $\Omega$, bounded by the surfaces
$$
x=17 \sqrt{2 y}, \quad x=2 \sqrt{2 y}, \quad z=\frac{1}{2}-y, \quad z=0
$$
|
Solution.
1. Define the region $\Omega$ by inequalities. Since $17 \sqrt{2 y} \geq 2 \sqrt{2 y}$, for $x$ we have the inequalities $2 \sqrt{2 y} \leq x \leq 17 \sqrt{2 y}$. Since $y$ appears under the square root, $y \geq 0$. For $z$, the possible inequalities are $0 \leq z \leq 1 / 2-y$ or $1 / 2-y \leq z \leq 0$. In the first case, $0 \leq y \leq 1 / 2$. In the second case, $y \geq 1 / 2$, i.e., the region is unbounded, which is unacceptable.
Thus,
$$
\Omega=\left\{\begin{array}{cc}
& 2 \sqrt{2 y} \leq x \leq 17 \sqrt{2 y} \\
(x, y, z): & 0 \leq y \leq 1 / 2 \\
& 0 \leq z \leq 1 / 2-y
\end{array}\right\}
$$
2. We compute the volume using formula (1), reducing the triple integral to an iterated integral:
$$
V=\iiint_{\Omega} 1 \cdot d x d y d z=\int_{0}^{1 / 2} d y \int_{2 \sqrt{2 y}}^{17 \sqrt{2 y}} d x \int_{0}^{1 / 2-y} d z=1
$$
Answer. $V=1$ unit of volume.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find the mass of the body $\Omega$ with density $\mu=2 x$, bounded by the surfaces
$$
x=2 \sqrt{2 y}, \quad x=\sqrt{2 y}, \quad z=1-y, \quad z=0
$$
|
Solution.
1. The mass of the body $\Omega$ with density $\mu=2 x$ is determined by the formula
$$
m=\iiint_{\Omega} 2 x d x d y d z
$$
2. Let's define the region $\Omega$ using inequalities. Since $2 \sqrt{2 y} \geq \sqrt{2 y}$, for $x$ we have the inequalities $\sqrt{2 y} \leq x \leq 2 \sqrt{2 y}$. Since $y$ appears under the square root, $y \geq 0$. For $z$, the possible inequalities are $0 \leq z \leq 1-y$ or $1-y \leq z \leq 0$. In the first case, $0 \leq y \leq 1$. In the second case, $y \geq 1$, i.e., the region is unbounded, which is unacceptable.
Thus,
$$
\Omega=\left\{\begin{array}{cc}
& \sqrt{2 y} \leq x \leq 2 \sqrt{2 y} \\
(x, y, z): & 0 \leq y \leq 1 \\
& 0 \leq z \leq 1-y
\end{array}\right\}
$$
3. We compute $m$ by reducing the triple integral to a repeated integral:
$$
m=\iiint_{\Omega} 2 x d x d y d z=\int_{0}^{1} d y \int_{\sqrt{2 y}}^{2 \sqrt{2 y}} 2 x d x \int_{0}^{1-y} d z=1
$$
Answer. $m=1$ unit of mass.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Find the derivative of the scalar field $u=x z^{2}+2 y z$ at the point $M_{0}(1,0,2)$ along the circle
$$
\left\{\begin{array}{l}
x=1+\cos t \\
y=\sin t-1 \\
z=2
\end{array}\right.
$$
|
Solution. The vector equation of the circle has the form
$$
\mathbf{r}(t)=(1+\cos t) \mathbf{i}+(\sin t-1) \mathbf{j}+2 \mathbf{k} .
$$
We find the vector $T$, tangent to it at any point $M$. We have
$$
\left.T=\frac{d r}{d t}=-\sin t \mathbf{i}+\cos t \mathbf{j}\right]
$$
The given point $M_{0}(1,0,2)$ lies in the $\boldsymbol{O} \boldsymbol{z}$ plane in the first octant, and corresponds to the parameter value $t=\frac{\pi}{2}$. At this point we will have
$$
\left.\tau\right|_{M_{0}}=-\sin \frac{\pi}{2} \mathbf{i}+\cos \frac{\pi}{2} \mathbf{j}=-\mathbf{i} .
$$
From this we obtain that the direction cosines of the tangent to the circle are $\cos \alpha=-1, \cos \beta=0, \cos \gamma=0$. The values of the partial derivatives of the given scalar field at the point $M_{0}(1,0,2)$ are
$$
\left.\frac{\partial u}{\partial x}\right|_{M_{0}}=\left.z^{2}\right|_{M_{0}}=4,\left.\quad \frac{\partial u}{\partial y}\right|_{M_{0}}=\left.2 z\right|_{M_{0}}=4,\left.\quad \frac{\partial u}{\partial z}\right|_{M_{0}}=\left.(2 x z+2 y)\right|_{M_{0}}=4
$$
Therefore, the sought derivative is
$$
\left.\frac{\partial u}{\partial l}\right|_{M_{0}}=\left.\frac{\partial u}{\partial r}\right|_{M_{0}}=4 \cdot(-1)+4 \cdot 0+4 \cdot 0=-4
$$
## Problems for Independent Solution
In the following problems, find the derivative of the given functions at the point $M_{0}\left(x_{0}, y_{0}, z_{0}\right)$ in the direction of the point $M_{1}\left(x_{1}, y_{1}, z_{1}\right)$.
58. $u=\sqrt{x^{2}+y^{2}+z^{2}}, \quad M_{0}(1,1,1), M_{1}(3,2,1)$
59. $u=x^{2} y+x z^{2}-2, \quad M_{0}(1,1,-1), M_{1}(2,-1,3)$.
60. $u=x e^{y}+y e^{x}-z^{2}, \quad M_{0}(3,0,2), M_{1}(4,1,3)$
61. $u=\frac{x}{y}-\frac{y}{x}, \quad M_{0}(1,1), M_{1}(4,5)$.
62. Find the derivative of the scalar field $u=\ln \left(x^{2}+y^{2}\right)$ at the point $M_{0}(1,2)$ of the parabola $y^{2}=4 x$ in the direction of this curve.
63. Find the derivative of the scalar field $u=\operatorname{arctg} \frac{y}{x}$ at the point $M_{0}(2,-2)$ of the circle $x^{2}+y^{2}-4 x=0$ along the arc of this circle.
64. Find the derivative of the scalar field $u=x^{2}+y^{2}$ at the point $M_{0}\left(x_{0}, y_{0}\right)$ of the circle $x^{2}+y^{2}=\boldsymbol{R}^{2}$ in the direction of this circle.
65. Find the derivative of the scalar field $u=2 x y+y^{2}$ at the point $(\sqrt{2}, 1)$ of the ellipse $\frac{x^{2}}{4}+\frac{y^{2}}{2}=1$ in the direction of the external normal to the ellipse at this point.
66. Find the derivative of the scalar field $u=x^{2}-y^{2}$ at the point $(5,4)$ of the hyperbola $x^{2}-y^{2}=9$ in the direction of this curve.
67. Find the derivative of the scalar field $u=\ln (x y+y z+x z)$ at the point $M_{0}(0,1,1)$ in the direction of the circle $x=\cos t, y=\sin t, z=1$.
68. Find the derivative of the scalar field $u=x^{2}+y^{2}+z^{2}$ at the point $M_{0}$ corresponding to the value of the parameter $t=\frac{\pi}{2}$ in the direction of the helical line $x=R \cos t$, $y=R \sin t, z=a t$.
## §9. Gradient of a Scalar Field
Let us have a scalar field defined by the scalar function
$$
u=f(x, y, z)
$$
the function $f$ is assumed to be differentiable.
Definition. The gradient of a scalar field at a given point $M$ is a vector denoted by the symbol grad $u$ and defined by the formula
$$
\operatorname{grad} u=\frac{\partial u}{\partial x} \mathbf{i}+\frac{\partial u}{\partial y} \mathbf{j}+\frac{\partial u}{\partial z} \mathbf{k}
$$
We have
Using the formula (1) from §8 for the directional derivative,
$$
\frac{\partial u}{\partial l}=\left(\operatorname{grad} u, \mathbf{l}^{0}\right)
$$
where $\mathbf{l}^{0}$ is the unit vector in the direction of $\mathbf{l}$, i.e.
$$
\mathbf{l}^{0}=\frac{\mathbf{l}}{|\mathbf{l}|}=\mathbf{i} \cos \alpha+\mathbf{j} \cos \beta+\mathbf{k} \cos \gamma
$$
## Properties of the Gradient
1. The gradient is directed along the normal to the level surface (or level line, if the field is planar).
2. The gradient is directed in the direction of the increase of the field function.
3. The magnitude of the gradient is equal to the maximum directional derivative at the given point of the field:
$$
\left.\max \frac{\partial u}{\partial l}=|\operatorname{grad} u|=\sqrt{\left(\frac{\partial u}{\partial x}\right)^{2}+\left(\frac{\partial u}{\partial y}\right)^{2}+\left(\frac{\partial u}{\partial z}\right)^{2}}\right)
$$
These properties provide an invariant characteristic of the gradient. They indicate that the vector grad $u$ points in the direction and magnitude of the greatest change in the scalar field at the given point.
|
-4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Using the invariant definition, calculate the divergence of the vector $a=x \mathbf{i}$ at the point $O(0,0,0)$, choosing as the surface $\sigma$ surrounding the point $O$, a sphere $\sigma_{\varepsilon}$ of radius $\varepsilon$ centered at this point.
|
Solution. By the definition of divergence at the given point, we have
$$
\operatorname{div} a(0)=\lim _{\left(\sigma_{k}\right) \rightarrow 0} \frac{\int\left(a, n^{0}\right) d \sigma}{v_{\varepsilon}}
$$
where $v_{\varepsilon}$ is the volume of the ball bounded by the sphere $\sigma_{\varepsilon}$, or
$$
\operatorname{div} a(0)=\lim _{k \rightarrow 0} \frac{\prod_{0}\left(a, n^{0}\right) d \theta}{v_{\varepsilon}}
$$
But since the volume of the ball is $v_{\varepsilon}=\frac{4}{3} \pi \varepsilon^{3}$, then
$$
\operatorname{div} a(0)=\lim _{\varepsilon \rightarrow 0} \frac{\sigma_{\varepsilon}\left(a, n^{0}\right) d \sigma}{(4 / 3) \pi \varepsilon^{3}}
$$
We will compute the flux $\oiint_{\sigma_{\varepsilon}}\left(a, n^{\dagger}\right) d \sigma$ of the given vector through the sphere $\sigma_{\varepsilon}$. The normal vector $n^{\dagger}$ to the sphere $\sigma_{\varepsilon}$ is directed along the radius of the sphere, so we can set
$$
\mathbf{n}^{\mathbf{n}}=\mathbf{r}^{\mathbf{0}}=\frac{\mathbf{r}}{|\mathbf{r}|}=\frac{\mathbf{r}}{\varepsilon}
$$
where $\mathbf{r}^{\mathbf{0}}$ is the unit vector of the radius vector $\mathbf{r}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k}$, or
$$
\mathbf{n}^{0}=\frac{x \mathbf{i}+y \mathbf{j}+z \mathbf{k}}{\varepsilon}
$$
The desired flux will be equal to
$$
\oiint_{\sigma_{\varepsilon}}\left(a, n^{0}\right) d \sigma=\oiint_{\sigma_{\varepsilon}} \frac{x^{2}}{\varepsilon} d \sigma
$$
Switching to coordinates on the sphere $\sigma_{\varepsilon}$
$$
x=\varepsilon \cos \varphi \sin \theta, \quad y=\varepsilon \sin \varphi \sin \theta, \quad z=\varepsilon \cos \theta .
$$
we get
$$
\begin{aligned}
\oiint_{\sigma_{\varepsilon}}\left(a, n^{0}\right) d \sigma=\iint_{\sigma_{\varepsilon}} \frac{\varepsilon^{2} \cos ^{2} \varphi \sin ^{2} \theta \varepsilon^{2} \sin \theta d \varphi d \theta}{\varepsilon}= \\
=\varepsilon^{3} \int_{0}^{2 \pi} \cos ^{2} \varphi d \varphi \int_{0}^{\pi} \sin ^{3} \theta d \theta=\frac{4}{3} \pi \varepsilon^{3} .
\end{aligned}
$$
Therefore,
$$
\operatorname{div} a(0)=\lim _{\varepsilon \rightarrow 0} \frac{(4 / 3) \pi \varepsilon^{3}}{(4 / 3) \pi \varepsilon^{3}}=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. Show that the vector field $a=\frac{2 \cos \theta}{r^{3}} \mathbf{e}_{r}+\frac{\sin \theta}{r^{3}} \mathbf{e}_{\theta}$
is solenoidal.
|
Solution. Using formula (5), we will have
$$
\begin{aligned}
& \operatorname{div}=\frac{1}{r^{2}} \frac{\theta}{\partial r}\left(r^{2} \frac{2 \cos \theta}{r^{3}}\right)+\frac{1}{r \sin \theta} \frac{\theta}{\partial \theta}\left(\sin \theta \frac{\sin \theta}{r^{3}}\right)+0= \\
&=\frac{1}{r^{2}}\left(-\frac{2 \cos \theta}{r^{2}}\right)+\frac{1}{r^{4} \sin \theta} 2 \sin \theta \cos \theta=0
\end{aligned}
$$
everywhere where $\boldsymbol{r} \neq 0$. This means that the vector field is solenoidal everywhere except at the point $\boldsymbol{r}=0$.
## Problems for Independent Solution
267. Find the equation of the vector lines of the following fields
a) $\mathbf{a}=e_{p}+\rho e_{4}+e_{z} ; 6$ 6) $=\rho e_{p}+\varphi e_{p}+z e_{z} ;$ c) $a=\frac{2 \alpha \cos \theta}{r^{3}} c+\frac{\alpha \sin \theta}{r^{3}} e_{\theta}, \alpha=$ const. Find the gradients of scalar fields:
a) In cylindrical coordinates
268. $u=\rho^{2}+2 \rho \cos \varphi-e^{8} \sin \varphi$.
269. $u=\rho \cos \varphi+2 \sin ^{2} \varphi-3^{\mu}$.
b) In spherical coordinates
270. $u=r^{2} \cos \theta$. 271. $u=3 r^{2} \sin \theta+e^{r} \cos \varphi-r$. 272. $u=\frac{\mu \cos \theta}{r^{2}}, \mu=$ const.
Calculate the divergence of the vector fields:
a) In cylindrical coordinates
273. $a=\rho e_{n}+x \sin \varphi e_{\varphi}+e^{\psi} \cos x \mathrm{e}_{2} . \quad 274.2=\varphi \operatorname{arctg} \rho e_{\rho}+2 e_{p}-x^{2} e^{2} e_{z}$.
b) In spherical coordinates
275. $a=r^{2} e_{s}-2 \cos ^{2} \varphi e_{\theta}+\frac{\varphi}{r^{2}+1} e_{\varphi}$.
Calculate the rotor of the following vector fields:
276. $a=(2 r+\alpha \cos \varphi) \mathrm{e}_{r}-\alpha \sin \theta \mathrm{e}_{\theta}+r \cos \theta \mathrm{e}_{\varphi}, \alpha=$ const.
277. $a=r^{2} \mathrm{e}_{r}+2 \cos \theta \mathrm{e}_{\theta}-\varphi \mathrm{e}_{\text {, }}$.
278. $\mathrm{a}=\cos \varphi \mathrm{e}_{5}-\frac{\sin \varphi}{\rho} \mathrm{e}_{5}+\rho^{2} \mathrm{e}_{2}$.
279. Show that the vector field $\mathrm{a}=\frac{2 \cos \theta}{\boldsymbol{r}^{3}} \mathbf{r}_{r}+\frac{\sin \theta}{\boldsymbol{r}^{3}} \mathbf{e}_{\text {, }}$ is potential.
280. Show that the vector field a $=f(r) e_{\text {, }}$, where $f(r)-$ any differentiable function, is potential.
$5^{\circ}$. Calculation of flux in curvilinear coordinates. Let $S$ be a part of the coordinate surface $q_{1}=C$, where $C=$ const, bounded by coordinate lines
$$
\begin{aligned}
& Q_{2}=\alpha_{1}, \quad Q_{2}=\alpha_{2} \quad\left(\alpha_{1}<\alpha_{2}\right) \\
& q_{3}=\beta_{1}, \quad q_{3}=\beta_{2} \quad\left(\beta_{1}<\beta_{2}\right)
\end{aligned}
$$
Then the flux of the vector field
$$
a=a_{1}\left(q_{1}, q_{2}, q_{3}\right) \mathbf{e}_{1}+a_{2}\left(q_{1}, q_{2}, q_{3}\right) e_{2}+a_{3}\left(q_{1}, q_{2}, q_{3}\right) e_{3}
$$
through the surface $S$ in the direction of the vector $\mathbf{e}_{1}$ is calculated by the formula
$$
\Pi=\int_{a_{1}}^{a_{1}} \int_{\beta_{1}}^{\beta_{2}} a_{1}\left(C, q_{2}, q_{3}\right) H_{2}\left(C, q_{2}, q_{3}\right) H_{3}\left(C, q_{2}, q_{3}\right) d q_{3} d q_{2}
$$
Similarly, the flux through a part of the surface $q_{2}=C$ or through a part of the surface $\varphi_{3}=C$, where $C=$ const, is calculated.
Example v. Calculate the flux of the vector field given in cylindrical coordinates: $a=\rho \mathrm{e}_{p}+\boldsymbol{z e} \mathbf{e}_{p}$ through the outer part of the lateral surface of the cylinder $\rho=1$, bounded by the planes $z=0, z=1$.
Solution. The cylinder is a coordinate surface $\rho=C=$ const, so the sought flux is
$$
\Pi=\int_{0}^{2 z} \int_{0}^{1} C^{2} d z d \varphi=2 \pi C^{2}
$$
From this, for the surface $\rho=1$, we get
$$
\Pi=2 \pi
$$
|
0
|
Calculus
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Example 12. Calculate the circulation of the vector field given in cylindrical coordinates: $2=\rho \sin \varphi \mathrm{e}_{\rho}+\rho z \mathrm{e}_{\varphi}+\rho^{3} \mathrm{e}_{z}$, along the curve L: $\{\rho=\sin \varphi, z=0,0 \leqslant \varphi \leqslant \pi\}$ directly and using Stokes' theorem.
|
Solution. Coordinates of the given vector
$$
a_{p}=\rho \sin \varphi, \quad a_{v}=\rho z, \quad a_{n}=\rho^{3}
$$
The contour $L$ represents a closed curve located in the plane $z=0$ (Fig. 41).
1) Direct calculation of circulation.
Substituting the coordinates of the vector into formula (13), we get
$$
\boldsymbol{\mu}=\oint_{\mathbf{L}} \rho \sin \varphi d \rho+\rho^{2} z d \varphi+\rho^{3} d z
$$
On the curve $L$ we have:
$$
z=0, d z=0 ; \quad \rho=\sin \varphi, d \rho=\cos \varphi d \varphi ; \quad 0 \leqslant \varphi \leqslant \pi
$$
Therefore, the sought circulation will be equal to
$$
\boldsymbol{\mu}=\oint_{L} \rho \sin \varphi d \rho=\int_{0}^{\pi} \sin ^{2} \varphi \cos \varphi d \varphi=0
$$
2) Calculation of circulation using Stokes' theorem. According to Stokes' theorem, the sought circulation is equal to
$$
\mu=\oint_{\mathbf{L}}(\mathrm{a}, d r)=\iint_{s}\left(\mathrm{rot} \mathrm{a}, \mathrm{n}^{0}\right) d S
$$
where $S$ is the surface stretched over the contour $L$.
We find the rotor of the given field
$$
\operatorname{rot} \alpha=\frac{1}{\rho}\left|\begin{array}{ccc}
e_{\phi} & \rho e_{\phi} & e_{z} \\
\frac{\theta}{\partial \rho} & \frac{\theta}{\partial \varphi} & \frac{\theta}{\partial z} \\
\rho \sin ^{2} \varphi & \rho^{2} z & \rho^{3}
\end{array}\right|=-\rho e_{\rho}-3 \rho^{2} e_{\varphi}+(2 z-\cos \varphi) e_{z} .
$$
At points where $\rho=0$, the value of the rotor is determined by continuity, assuming
$$
\text { rot } a(0, \varphi, z)=(2 z-\cos \varphi) e_{z} \text {. }
$$
Thus, the rotor is defined throughout the entire three-dimensional space. Since the curve $L$ lies in the plane $z=0$, we can take as the surface $S$ stretched over this curve, the part of the plane $z=0$ bounded by the curve $L$. Then, for the normal vector $\mathbf{n}^{\prime \prime}$ to the surface $S$, we can take the unit vector $\mathbf{e}_{z}$, i.e., $\mathbf{n}^{\prime \prime}=\mathbf{e}_{z}$. We find the scalar product:
$\left(\operatorname{rot} \mathrm{A}, \mathrm{n}^{0}\right)=\left(-\rho e_{\rho}-3 \rho^{2} \mathrm{e}_{\varphi}+(2 z-\cos \varphi) e_{z}, \mathrm{e}_{z}\right)=2 z-\cos \varphi_{.}$.
Since, due to the orthonormality of the basis vectors $e_{\rho}, \mathbf{e}_{\varphi}, \mathbf{e}_{z}$, we have
$$
\left(e_{\rho}, e_{z}\right)=\left(e_{\varphi}, e_{z}\right)=0, \quad\left(e_{z}, e_{z}\right)=1
$$
The sought circulation is equal to
$$
\zeta=\iint_{S}(2 z-\cos \varphi) d S
$$
Considering that $z=0$ on $S$ and the element of area $d S$ of the coordinate surface $z=0$ is equal to
$$
d S=\rho d \rho d \varphi
$$
we finally get
$$
\begin{aligned}
& \zeta=-\iint_{S} \cos \varphi d S=-\iint_{S} \cos \varphi \cdot \rho d \rho d \varphi= \\
& =-\int_{0}^{\pi} \cos \varphi d \varphi \int_{0}^{\sin \varphi} \rho d \rho=-\frac{1}{2} \int_{0}^{\pi} \sin ^{2} \varphi \cos \varphi d \varphi=0
\end{aligned}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
45. How many numbers need to be selected from a table of random numbers to be confident with a probability of at least 0.9 that among them there is at least one even number?
|
Solution. Let $n$ be the required number of random numbers. Consider the events:
$A_{k}$ - one randomly selected number is even $(k=1,2, \ldots, n)$;
$\overline{A_{k}}$ - one randomly selected number is odd;
$B$ - among $n$ random numbers there will be at least one even;
$\bar{B}$ - among $n$ random numbers there will be no even numbers.
The probabilities of all events $\overline{A_{k}}$ are equal. Let $P\left(A_{k}\right)=p$, $P\left(\bar{A}_{k}\right)=1-p=q$. Events $A_{k}$ and $\overline{A_{k}}$ are equally probable, so $p=q=0.5$. The probability of event $B$ is
$$
P(B)=1-P(\bar{B})
$$
Event $\bar{B}$ consists in all $n$ random numbers being odd. This means that $\bar{B}$ is the product of $\boldsymbol{n}$ independent events $\overline{A_{k}}: \bar{B}=\overline{A_{1}} \cdot \overline{A_{2}} \cdot \ldots \cdot \overline{A_{n}}$.
Applying the multiplication theorem of probabilities of independent events and equality $(*)$, we find $P(B)=1-q^{n}=1-0.5^{n}$.
By the condition $P(B) \geq 0.9$, we get: $1-0.5^{n} \geq 0.9$.
Solving this inequality, we sequentially find:
$$
\begin{gathered}
-0.5^{n} \geq-0.1 \\
0.5^{n} \leq 0.1 \\
n \cdot \lg 0.5 \leq \lg 0.1
\end{gathered}
$$
Since $\lg 0.5(\lg 0.1 / \lg 0.5) \approx 3.32$. Since $n$ is an integer, then $\boldsymbol{n} \geq 4$.
## 2.2. The Formula of Total Probability
The probability of an event $A$, which can occur given the occurrence of one of $n$ mutually exclusive events (hypotheses) $B_{i}(i=1,2, \ldots, n)$, forming a complete group, is found using the formula of total probability:
$$
P(A)=\sum_{i=1}^{n} P\left(B_{i}\right) P_{B_{i}}(A)
$$
In this formula, $P(A)$ is the probability of event $A$; $P\left(B_{i}\right)$ is the probability of event $B_{i}$, $P_{B_{i}}(A)$ is the conditional probability of event $A$, calculated given that event $B_{i}$ has occurred; $\sum_{i=1}^{n} P\left(B_{i}\right) P_{B_{i}}(A)$ is the sum of the products of the probabilities $P\left(B_{i}\right)$ of each of the events $B_{i}$ and the corresponding conditional probability $P_{B_{l}}(A)$.
The sum of the probabilities of the hypotheses $\sum_{i=1}^{n} P\left(B_{i}\right)=1$.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
63. A large batch of car tires contains $1.5\%$ defects. What should be the volume of a random sample so that the probability of finding at least one defective car tire in it would be more than $0.92?$
|
S o l u t i o n. Let the volume of the random sample be denoted by $n$. The experiment consists of checking car tires. Event $A$, which may or may not occur in each trial, is that the checked car tire turns out to be defective. The probability $p=0.015$; the probability $q=0.985$. Consider the events:
C - the sample of checked car tires contains at least one defective tire;
$\bar{C}$ - the sample of checked car tires contains no defective tires.
Using formulas (11) and (18), we get:
$$
P(C)=1-P(\bar{C})=1-P_{n}(0)=1-q^{n}=1-(0.985)^{n}
$$
By the condition $P(C)>0.92$. Thus, to find $n$, we need to solve the inequality:
$$
1-(0.985)^{n}>0.92
$$
Sequentially, we find
$$
(0.985)^{n}<0.08
$$
$$
n>\frac{\ln 0.08}{\ln 0.985} \approx 167.1608
$$
Thus, the random sample should contain no fewer than 168 car tires.
|
168
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
64. The probability of failure of each device during testing is 0.2. How many such devices need to be tested to assert with a probability of at least 0.9 that at least two devices will fail?
|
S o l u t i o n. Let the required number of devices be denoted by $n$. The event $A$, which may or may not occur in each trial, consists of a device failing. The probability $p=0.2$; the probability $q=0.8$.
Consider the events:
$B$ - at least two devices fail;
$\bar{B}$ - fewer than two devices fail.
The event $\bar{B}$ consists of either no device failing or one device failing. The probability of event $\bar{B}$ can be found using the Bernoulli formula and the theorem of addition of probabilities of mutually exclusive events:
$$
P(\bar{B})=P_{n}(0)+P_{n}(1)=p^{0} q^{n}+C_{n}^{1} p q^{n-1}=0.8^{n}+n \cdot 0.2 \cdot 0.8^{n-1}=0.8^{n}\left(1+\frac{n}{4}\right)
$$
According to formula (11)
$$
P(B)=1-P(\bar{B})=1-\frac{0.8^{n}(n+4)}{4}
$$
By the condition $P(B) \geq 0.9$. Therefore, to determine $n$, we need to solve the inequality:
$$
1-\frac{0.8^{n}(n+4)}{4} \geq 0.9
$$
We sequentially find
$$
\begin{aligned}
& \frac{0.8^{n}(n+4)}{4} \leq 0.1 \\
& 0.8^{n}(n+4)=0.4 \\
& n \cdot \lg 0.8+\lg (n+4) \leq \lg 0.4 \\
& 0.0969 n \geq \lg (n+4)+0.3979
\end{aligned}
$$
This inequality is satisfied for $n \geq 18$.
Thus, at least 18 devices need to be tested.
## 3.2. The Most Probable Number of Occurrences of an Event in Independent Trials
The most probable number $m_{0}$ (or the most probable frequency) of the occurrence of event $A$ in $n$ independent trials, in each of which it can occur with probability $p$ (and not occur with probability $q=1-p$), is found from the double inequality
$$
n p-q \leq m_{0} \leq n p+p
$$
|
18
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
76. When crossing two varieties of peas (with yellow and green seeds), G. Mendel found that in the second generation, the probability of green seeds appearing is 0.25. How many pea seeds need to be taken to expect with a probability of 0.9770 that the relative frequency of green seeds will deviate (in absolute value) from their probability of occurrence by no more than 0.02?
|
Solution. According to the condition $p=0.25 ; \varepsilon=0.02 ;$ we find $q=0.75$. It is known that $P\left(\left|\frac{m}{n}-0.25\right| \leq 0.02\right)=0.997$. We need to find the number of seeds $n$.
In accordance with formula (23) we have
$$
P\left(\left|\frac{m}{n}-p\right| \leq \varepsilon\right) \approx 2 \Phi\left(\varepsilon \sqrt{\frac{n}{p q}}\right)=0.997
$$
From this equality, we find $\Phi(x)=0.4985$, where $x=\varepsilon \sqrt{\frac{n}{p q}}$.
Using the table of values of the Laplace function (see table 3 in the appendix), we find $x=2.96$. Since
$$
\varepsilon \sqrt{\frac{n}{p q}}=0.02 \cdot \sqrt{\frac{n}{0.25 \cdot 0.75}}
$$
we obtain the following equality:
$$
0.02 \sqrt{\frac{n}{0.25 \cdot 0.75}}=2.96
$$
From the last equality, we determine $n=4107$. Therefore, we need to take 4107 seeds.
Chapter 4
## RANDOM VARIABLES
## AND THEIR DISTRIBUTION LAWS
I asked the cuckoo, how many years I will live... The tops of the pines trembled, a yellow ray sank into the grass, but there was no sound in the fresh air... I go home, and the cool wind caresses my hot forehead.
Anna Akhmatova
## ***
You don't often appear to me in dreams, my native
Golden my, bittersweet era. HOME,
But everything that will happen to me later, -
It all starts from here!
Alexander Galich
## 4.1. Series, frequency polygon, and distribution function of a discrete random variable
The distribution law of a discrete random variable can be represented by a series of distribution, a frequency polygon, and a distribution function.
A discrete random variable $X$, having a finite set of possible values $x_{i}$ with corresponding probabilities $p_{i}=P\left(X=x_{i}\right)(i=1,2, \ldots, n)$, can be defined by a series of distribution of the following form (Table 1):
Table 1
| $x_{i}$ | $x_{1}$ | $x_{2}$ | $\cdots$ | $x_{n}$ |
| :---: | :---: | :---: | :---: | :---: |
| $p_{i}$ | $p_{1}$ | $p_{2}$ | $\cdots$ | $p_{n}$ |
For the probabilities $p_{i}$ given in Table 1, the condition must be satisfied:
$$
\sum_{i=1}^{n} p_{i}=1
$$
A discrete random variable $X$, having an infinite (countable) set of possible values $x_{i}$ with corresponding probabilities $p_{i}=P\left(X=x_{i}\right)(i=1,2, \ldots, n, \ldots)$, can be defined by a series of distribution of the following form (Table 2):
Table 2
| $x_{i}$ | $x_{1}$ | $x_{2}$ | $\cdots$ | $x_{n}$ | $\cdots$ |
| :--- | :--- | :--- | :--- | :--- | :--- |
| $p_{i}$ | $p_{1}$ | $p_{2}$ | $\cdots$ | $p_{n}$ | $\cdots$ |
For the probabilities $p_{i}$ given in Table 2, the conditions must be satisfied: the series
$$
p_{1}+p_{2}+\ldots+p_{n}+\ldots
$$
converges and
$$
\sum_{i=1}^{\infty} p_{i}=1
$$
Graphically, the distribution of a discrete random variable $X$ can be represented by a frequency polygon. To construct a frequency polygon, points $\left(x_{i}, p_{i}\right)$ are plotted on a plane in the coordinate system $x O y$ and connected by a broken line. Figure 12 shows the frequency polygon of a random variable with $n=6$ possible values.
A discrete random variable $X$ can be defined by the distribution function $F(x)$, also called the integral distribution function:
For a discrete random variable defined by a series of distribution (Tables 1 and 2), the values of the distribution function are found using the formula
$$
F(x)=\sum_{x_{i}<x} p_{i}
$$
where the summation of probabilities $p_{i}$ is performed over all values of $i$ for which $x_{i}<x$.
$$
F(x)=P(X<x)
$$
Fig. 12
The probability that a random variable $X$ will take a value $\check{x} \in[\alpha, \beta)$ is expressed through the distribution function by the formula
$$
P(\alpha \leq X<\beta)=F(\beta)-F(\alpha)
$$
|
4107
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
90. Find the mathematical expectation of the random variable $Z=2 X+4 Y+5$, if the mathematical expectations of $X$ and $Y$ are known: $M(X)=3, M(Y)=5$.
|
Solution. Using the properties of mathematical expectation (formulas (31) - (33)), we get:
$$
\begin{aligned}
& M(Z)=M(2 X+4 Y+5)=2 M(X)+4 M(Y)+5= \\
& =2 \cdot 3+4 \cdot 5+5=31
\end{aligned}
$$
|
31
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
94. Random variables $X$ and $Y$ are independent. The variances of these variables are known: $D(X)=5 ; D(Y)=9$. Find the variance of the random variable $Z=2X-Y+5$.
|
S o l u t i o n. Using the properties of variance reflected in formulas (40), (41), and (42), we get
$$
D(Z)=D(2 X-Y+5)=2^{2} \cdot D(X)+(-1)^{2} \cdot D(Y)=4 \cdot 5+9=29
$$
|
29
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
118. The random variable $X$ is given by the distribution function:
$$
F(x)=\left\{\begin{array}{ccc}
0 & \text { if } & x \leq -c \\
\frac{1}{2}+\frac{1}{\pi} \arcsin \frac{x}{c} & \text { if } & -c < x \leq c \\
1 & \text { if } & x > c
\end{array}\right.
$$
( arcsine law ).
Find the mathematical expectation of this variable.
|
Solution. Let's find the probability density function of the random variable $X: f(x)=F^{\prime}(x)$. For $x \leq -c$ and for $x > c$, the function $f(x)=0$. For $-c < x \leq c$, we have
$$
f(x)=\left(\frac{1}{2}+\frac{1}{\pi} \arcsin \frac{x}{c}\right)^{\prime}=\frac{1}{\pi \sqrt{c^{2}-x^{2}}}
$$
The expected value of the random variable $X$ will be found using formula (54) with $a=-c$ and $b=c$:
$$
M(X)=\int_{-c}^{c} \frac{x d x}{\pi \sqrt{c^{2}-x^{2}}}
$$
Considering that the integrand is an odd function and the limits of integration are symmetric with respect to the origin, we conclude that the integral is zero; therefore, $M(X)=0$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
56. a) $29 \cdot 31$; b) $86^{2}-14^{2}$.
|
Solution. a) $29 \cdot 31=(30-1)(30+1)=30^{2}-1^{2}=900-1=899$;
b) $86^{2}-14^{2}=(86+14)(86-14)=100 \cdot 72=7200$.
|
899
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
120. Calculate $\left(\frac{9}{16}\right)^{-1 / 10}:\left(\frac{25}{36}\right)^{-3 / 2}-\left[\left(\frac{4}{3}\right)^{-1 / 2}\right]^{-2 / 5}\left(\frac{6}{5}\right)^{-3}$.
|
Solution. We will perform the actions sequentially:
1) $\left(\frac{9}{16}\right)^{-1 / 10}=\left[\left(\frac{3}{4}\right)^{2}\right]^{-1 / 10}=\left(\frac{3}{4}\right)^{-1 / 5}=\left(\frac{4}{3}\right)^{1 / 5}$;
2) $\left(\frac{25}{36}\right)^{-3 / 2}=\left[\left(\frac{5}{6}\right)^{2}\right]^{-3 / 2}=\left(\frac{5}{6}\right)^{-3}=\left(\frac{6}{5}\right)^{3}=\frac{216}{125}$;
3) $\left[\left(\frac{4}{3}\right)^{-1 / 2}\right]^{-2 / 5}=\left(\frac{4}{3}\right)^{1 / 5} ; \quad$ 4) $\left(\frac{6}{5}\right)^{-3}=\left(\frac{5}{6}\right)^{3}=\frac{125}{216}$.
Using the obtained results, we find
$$
\left(\frac{4}{3}\right)^{1 / 5} \cdot \frac{125}{216}-\left(\frac{4}{3}\right)^{1 / 5} \cdot \frac{125}{216}=0
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
137. $5^{x}=625$
|
Solution. Writing 625 as $5^{4}$, we get $5^{x}=5^{4}$, hence $x=4$. 138. $8^{x}=32$.
Solution. We have $32=2^{5} ; 8^{x}=\left(2^{3}\right)^{x}=2^{3 x}$. Therefore, $2^{3 x}=2^{5}$, hence $3 x=5$, i.e., $x=5 / 3$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
154. $(0,25)^{2-x}=\frac{256}{2^{x+3}}$.
154. $(0.25)^{2-x}=\frac{256}{2^{x+3}}$.
|
Solution. Let's convert all powers to base $2: 0.25=1/4=2^{-2}$; $256=2^{8}$. Therefore, $\left(2^{-2}\right)^{2-x}=\frac{2^{8}}{2^{x+3}}$. Applying the rule of dividing powers, we have
$$
\begin{gathered}
2^{-4+2 x}=2^{8-x-3} ; 2^{-4+2 x}=2^{5-x} ;-4+2 x=5-x ; 2 x+x=5+4 \\
3 x=9 ; x=3
\end{gathered}
$$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
161. $2^{x}+2^{x-1}-2^{x-3}=44$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
161. $2^{x}+2^{x-1}-2^{x-3}=44$.
|
Solution. Since the smallest exponent is $x-3$, we factor out $2^{x-3}$:
$$
2^{x-3} \cdot\left(2^{3}+2^{2}-1\right)=44 ; 2^{x-3}(8+4-1)=44 ; 2^{x-3} \cdot 11=44
$$
Dividing both sides of the equation by 11, we get
$$
2^{x-3}=4 ; 2^{x-3}=2^{2} ; x-3=2 ; x=5
$$
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
162. $7^{x}-3 \cdot 7^{x-1}+7^{x+1}=371$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
162. $7^{x}-3 \cdot 7^{x-1}+7^{x+1}=371$.
|
Solution. The least exponent is $x-1$; therefore, we factor out $7^{x-1}$:
$$
\begin{gathered}
7^{x-1} \cdot\left(7^{1}-3 \cdot 1+7^{12}\right)=371 ; 7^{x-1}(7-3+49)=371 \\
7^{x-1} \cdot 53=371 ; 7^{x-1}=7 ; x-1=1 ; x=2
\end{gathered}
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
171. $7^{2 x}-48 \cdot 7^{x}=49$
171. $7^{2 x}-48 \cdot 7^{x}=49$
|
Solution. Let $7^{x}=y$, we get the quadratic equation $y^{2}-$ $-48 y-49=0$. Let's solve it. Here $a=1, b=-48, c=-49 ; \quad D=b^{2}-$ $-4 a c=(-48)^{2}-4 \cdot 1(-49)=2304+196=2500 ; \sqrt{D}=50$. Using the formula $y_{1,2}=\frac{-b \pm \sqrt{D}}{2 a}$, we find
$$
y_{1}=\frac{48-50}{2}=\frac{-2}{2}=-1 ; \quad y_{2}=\frac{48+50}{2}=\frac{98}{2}=49
$$
Since $7^{x}=y$, then $7^{x}=-1$ (this equality is impossible, as the exponential function can only take positive values); $7^{x}=49 ; 7^{x}=7^{2}$, i.e., $x=2$. Thus, we get the answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
179. $5^{2}=25$.
|
Solution. Since the base of the power is 5, the exponent (logarithm) is 2, and the power is 25, then $\log _{5} 25=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
231. $\log _{4}(x+3)-\log _{4}(x-1)=2-3 \log _{4} 2$.
|
solution. Representing the number 2 as the logarithm of 16 to the base 4, we rewrite the given equation as
$$
\log _{4}(x+3)-\log _{4}(x-1)=\log _{4} 16-3 \log _{4} 2
$$
From this, we obtain
$$
\log _{4} \frac{x+3}{x-1}=\log _{4} \frac{16}{8}, \text { or } \frac{x+3}{x-1}=2
$$
We solve this equation:
$$
x+3=2(x-1) ; \quad x+3=2 x-2 ; \quad x=5
$$
To verify, substitute the value $x=5$ into the given equation:
$\log _{4}(5+3)-\log _{4}(5-1)=2-3 \log _{4} 2$
$\log _{4} 8-\log _{4} 4=\log _{4} 16-\log _{4} 8 ; \log _{4} \frac{8}{4}=\log \frac{16}{8} ; \log _{4} 2=\log _{4} 2$.
Thus, $x=5$.
Let's consider another type of logarithmic equations.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
319. $\sqrt{5-x}+2=7$.
319. $\sqrt{5-x}+2=7$.
The equation is already in English, so no translation was needed for the mathematical expression. However, if you meant to have the problem solved, here is the solution:
To solve the equation $\sqrt{5-x}+2=7$, we first isolate the square root term:
1. Subtract 2 from both sides:
\[
\sqrt{5-x} = 5
\]
2. Square both sides to eliminate the square root:
\[
5-x = 25
\]
3. Solve for \( x \):
\[
-x = 25 - 5
\]
\[
-x = 20
\]
\[
x = -20
\]
So, the solution is \( x = -20 \).
|
Solution. Isolate the radical and square both sides of the equation:
$$
\sqrt{5-x}=7-2 ;(\sqrt{5-x})^{2}=5^{2} ; 5-x=25 ;-x=20 ; x=-20
$$
Perform the check: $\sqrt{5-(-20)}+2=7 ; \sqrt{2} 5+2=7 ; 5+2=7$. Therefore, $x=-20$ is the solution to the equation.
|
-20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
320. $\sqrt{x-1} \cdot \sqrt{2 x+6}=x+3$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
320. $\sqrt{x-1} \cdot \sqrt{2 x+6}=x+3$.
|
Solution. First, we perform the multiplication of the roots:
$\sqrt{(x-1)(2 x+6)}=x+3 ; \sqrt{2 x^{2}-2 x+6 x-6}=x+3 ; \sqrt{2 x^{2}+4 x-6}=x+3$.
Now, we square both sides of the equation:
$\left(\sqrt{2 x^{2}+4 x-6}\right)^{2}=(x+3)^{2} ; 2 x^{2}+4 x-6=x^{2}+6 x+9 ; x^{2}-2 x-15=0$.
We solve the quadratic equation. Here $a=1, b=-2, c=-15, D=$ $=b^{2}-4 a c=4-4 \cdot 1 \cdot(-15)=64, \sqrt{D}=8$; therefore,
$$
x_{1,2}=\frac{-b \pm \sqrt{D}}{2 a} ; x_{1}=\frac{2-8}{2}=-3 ; x_{2}=\frac{2+8}{2}=5 ; x_{1}=-3, x_{2}=5
$$
Let's check both roots.
For $x=-3$ we have $\sqrt{(-3)-1} \cdot \sqrt{2(-3)+6}=-3+3$. We see that the first radical has no meaning in the set of real numbers; therefore, $x=-3$ is an extraneous root.
For $x=5$ we have $\sqrt{5-1} \cdot \sqrt{5 \cdot 2+6}=5+3 ; \sqrt{4} \cdot \sqrt{16}=8 ; 2 \cdot 4=8$. Thus, the root of the given equation is $x=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
321. $\sqrt{2 x+5}+\sqrt{x-1}=8$.
Translate the text above into English, keeping the original text's line breaks and format, and output the translation result directly.
321. $\sqrt{2 x+5}+\sqrt{x-1}=8$.
|
Solution. Isolate one of the radicals and square both sides of the equation:
$$
(\sqrt{2 x+5})^{2}=(8-\sqrt{x-1})^{2} ; 2 x+5=64-16 \sqrt{x-1}+(x-1)
$$
Move $16 \sqrt{x-1}$ to the left side, and all other terms to the right side:
$$
16 \sqrt{x-1}=64+x-1-2 x-5 ; 16 \sqrt{x-1}=58-x
$$
Square both sides of the equation again:
$(16 \sqrt{x-1})^{2}=(58-x)^{2} ; 256 x-256=3364-116 x+x^{2} ; x^{2}-372 x+3620=0$.
Solve the resulting quadratic equation. Since $a=1, b=-372$, $c=3620, \quad D=b^{2}-4 a c=(-372)^{2}-4 \cdot 1 \cdot 3620=138384-14480=123904$; $\sqrt{D}=352$, then
$$
x_{1}=\frac{-b-\sqrt{D}}{2 a}=\frac{372-352}{2}=10 ; \quad x_{2}=\frac{-b+\sqrt{D}}{2 a}=\frac{372+352}{2}=362
$$
Check both values $x_{1}=10 ; x_{2}=362$.
If $x=10$, then $\sqrt{2 \cdot 10+5}+\sqrt{10-1}=8 ; \sqrt{25}+\sqrt{9}=8 ; 5+3=8$; $8=8$
If $x=362$, then $\sqrt{2 \cdot 362+5}+\sqrt{362-1}=8 ; \sqrt{729}+\sqrt{361}=8 ; 27+$ $+19 \neq 8$; therefore, $x=362$ is an extraneous root.
The root of the given equation is $x=10$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
385. $(\tan \alpha+\cot \alpha)^{2}-(\tan \alpha-\cot \alpha)^{2}$.
|
Solution. We will use the formulas for the square of the sum and difference of two numbers:
$$
\begin{gathered}
(\operatorname{tg} \alpha+\operatorname{ctg} \alpha)^{2}-(\operatorname{tg} \alpha-\operatorname{ctg} \alpha)^{2}=\operatorname{tg}^{2} \alpha+2 \operatorname{tg} \alpha \operatorname{ctg} \alpha+\operatorname{ctg}^{2} \alpha-\operatorname{tg}^{2} \alpha+ \\
+2 \operatorname{tg} \alpha \operatorname{ctg} \alpha-\operatorname{ctg}^{2} \alpha=4 \operatorname{tg} \alpha \operatorname{ctg} \alpha=4
\end{gathered}
$$
(after combining like terms, we applied identity IV).
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
26. Compute the second-order determinants:
a) $\left|\begin{array}{rr}2 & 5 \\ -3 & -4\end{array}\right|$;
b) $\left|\begin{array}{ll}a^{2} & a b \\ a b & b^{2}\end{array}\right|$.
|
Solution. a) $\left|\begin{array}{rr}2 & 5 \\ -3 & -4\end{array}\right|=2(-4)-5(-3)=-8+15=7$;
b) $\left|\begin{array}{ll}a^{2} & a b \\ a b & b^{2}\end{array}\right|=a^{2} \cdot b^{2}-a b \cdot a b=a^{2} b^{2}-a^{2} b^{2}=0$.
27-32. Calculate the determinants:
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
33. Calculate the determinants of the third order:
a) $\left|\begin{array}{lll}3 & 2 & 1 \\ 2 & 5 & 3 \\ 3 & 4 & 3\end{array}\right|$
b) $\left|\begin{array}{lll}a & b & c \\ b & c & a \\ c & a & b\end{array}\right|$
|
Solution.
a) $\left|\begin{array}{lll}3 & 2 & 1 \\ 2 & 5 & 3 \\ 3 & 4 & 3\end{array}\right|=3 \cdot 5 \cdot 3+2 \cdot 3 \cdot 3+2 \cdot 4 \cdot 1-1 \cdot 5 \cdot 3-2 \cdot 2 \cdot 3-$ $-3 \cdot 3 \cdot 4=45+18+8-15-12-36=71-63=8$;
b) $\left|\begin{array}{lll}a & b & c \\ b & c & a \\ c & a & b\end{array}\right|=a c b+b a c+c b a-c \cdot c \cdot c-b \cdot b \cdot b-a \cdot a \cdot a=$ $=3 a b c-a^{3}-b^{3}-c^{3}$.
34-39. Calculate the determinants:
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
44. Determinant
$$
D=\left|\begin{array}{rrr}
3 & 1 & 2 \\
-1 & 2 & 5 \\
0 & -4 & 2
\end{array}\right|
$$
expand: a) by the elements of the 1st row; b) by the elements of the 2nd column.
|
Solution.
a) $D=3\left|\begin{array}{rr}2 & 5 \\ -4 & 2\end{array}\right|-1 \cdot\left|\begin{array}{rr}-1 & 5 \\ 0 & 2\end{array}\right|+2\left|\begin{array}{rr}-1 & 2 \\ 0 & -4\end{array}\right|=3(4+20)-$ $-1(-2-0)+2(4-0)=72+2+8=82$
b) $D=-1 \cdot\left|\begin{array}{rr}-1 & 5 \\ 0 & 2\end{array}\right|+2\left|\begin{array}{ll}3 & 2 \\ 0 & 2\end{array}\right|-(-4)\left|\begin{array}{rr}3 & 2 \\ -1 & 5\end{array}\right|=$ $=(-1)(-2)+2 \cdot 6-(-4) 17=2+12+68=82$.
If the determinant has a fourth or higher order, it can also be expanded along the elements of a row or column, and then reduce the order of the algebraic complements.
|
82
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
45. Calculate the determinant
$$
D=\left|\begin{array}{rrrr}
3 & 0 & 2 & 0 \\
2 & 3 & -1 & 4 \\
0 & 4 & -2 & 3 \\
5 & 2 & 0 & 1
\end{array}\right|
$$
|
Solution. We will expand the determinant along the elements of the 1st row (since it contains two zero elements):
$$
\begin{gathered}
D=\left|\begin{array}{rrrr}
3 & 0 & 2 & 0 \\
2 & 3 & -1 & 4 \\
0 & 4 & -2 & 3 \\
5 & 2 & 0 & 1
\end{array}\right|=3\left|\begin{array}{rrr}
3 & -1 & 4 \\
4 & -2 & 3 \\
2 & 0 & 1
\end{array}\right|-0 \cdot\left|\begin{array}{rrr}
2 & -1 & 4 \\
0 & -2 & 3 \\
5 & 0 & 1
\end{array}\right|+ \\
\\
+2\left|\begin{array}{lll}
2 & 3 & 4 \\
0 & 4 & 3 \\
5 & 2 & 1
\end{array}\right|-0 \cdot\left|\begin{array}{ccc}
2 & 3 & -1 \\
0 & 4 & -2 \\
5 & 2 & 0
\end{array}\right| .
\end{gathered}
$$
Since the second and fourth terms of the expansion are zero, we have
$$
\begin{aligned}
& D=3\left[3\left|\begin{array}{rr}
-2 & 3 \\
0 & 1
\end{array}\right|-(-1)\left|\begin{array}{ll}
4 & 3 \\
2 & 1
\end{array}\right|+4\left|\begin{array}{rr}
4 & -2 \\
2 & 0
\end{array}\right|\right]+2\left[2\left|\begin{array}{ll}
4 & 3 \\
2 & 1
\end{array}\right|-\right. \\
& \left.-3\left|\begin{array}{ll}
0 & 3 \\
5 & 1
\end{array}\right|+4\left|\begin{array}{ll}
0 & 4 \\
5 & 2
\end{array}\right|\right]=3[3(-2)-(-1)(4-6)+4 \cdot 4]+ \\
& +2[2(4-6)-3(-15)+4(-20)]=3(-6-2+16)+ \\
& +2(-4+45-80)=24-78=-54
\end{aligned}
$$
46-48. Calculate the third-order determinants:
|
-54
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
142. Calculate $3.27^{3}$.
|
Solution. We find $3.27 \cdot 3.27 \cdot 3.27 = 34.965 \approx 35.0$. The result is rounded to three significant figures, as the base of the power contains that many significant figures.
|
35
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
265. Find $z^{6}$, if $z=-\sqrt{3}+i$.
|
Solution. Let's write the number $z$ in trigonometric form, considering that $a=-\sqrt{3}, b=1$. We find $r=\sqrt{a^{2}+b^{2}} ; r=\sqrt{3+1}=2$. The point $z$ is located in the second quadrant. We form the ratios
$$
\cos \varphi=a / r=\sqrt{3} / 2, \sin \varphi=b / r=1 / 2
$$
Considering that the point $z$ is located in the second quadrant, we find $\arg z=$ $=\varphi=\pi-\frac{\pi}{6}=\frac{5 \pi}{6}$. Therefore, $z=2\left(\cos \frac{5 \pi}{6}+i \sin \frac{5 \pi}{6}\right)$.
According to the formula for raising to a power, we have $\left|z^{6}\right|=2^{6}$, $\arg \left(z^{6}\right)=$ $=\frac{5 \pi}{6} \cdot 6$ and, thus,
$$
\begin{gathered}
z^{6}=2^{6}\left(\cos \frac{5 \pi}{6} \cdot 6+i \sin \frac{5 \pi}{6} \cdot 6\right)=64(\cos 5 \pi+i \sin 5 \pi)= \\
=64(\cos \pi+i \sin \pi)=64(-1+i 0)=-64
\end{gathered}
$$
|
-64
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25. Find the length of the vector: a) $\vec{a}=(5 ; 12) ;$ b) $\vec{b}=(7 ;-1)$.
|
Solution. According to formula (1), we have:
a) $|\vec{a}|=\sqrt{x^{2}+y^{2}}=\sqrt{25+144}=\sqrt{169}=13$;
b) $|\vec{b}|=\sqrt{x^{2}+y^{2}}=\sqrt{49+1}=\sqrt{50}=5 \sqrt{2}$.
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
40. In an equilateral triangle $ABC$ with a side length of 6 (Fig. 42), find the scalar product of the vectors: a) $\overrightarrow{A B}$ and $\overrightarrow{A C} ;$ b) $\overrightarrow{A B}$ and $\overrightarrow{B C}$.
|
Solution. a) Since the angle $\varphi$ between the vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$ (and their directions) is $60^{\circ}$, for the scalar product of these vectors we get
$$
\overrightarrow{A B} \cdot \overrightarrow{A C}=|\overrightarrow{A B}| \cdot|\overrightarrow{A C}| \cdot \cos B \widehat{A C}=6 \cdot 6 \cdot \cos 60^{\circ}=36 \cdot 0.5=18
$$
Fig. 41
Fig. 42
b) The angle between the vectors $\overrightarrow{A B}$ and $\overrightarrow{B C}$ (i.e., the angle between their directions) is the angle $\varphi_{1}=120^{\circ}$, therefore
$\overrightarrow{A B}: \overrightarrow{B C}=|\overrightarrow{A B}| \cdot|\overrightarrow{B C}| \cdot \cos N \widehat{B C}=6 \cdot 6 \cdot \cos 120^{\circ}=6 \cdot 6 \cdot(-0.5)=-18$, since $\cos 120^{\circ}=\cos \left(180^{\circ}-60^{\circ}\right)=-\cos 60^{\circ}=-0.5$.
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
45. Find the scalar product of vectors $\vec{a}=(3 ; 5)$ and $\vec{b}=(-2 ; 7)$.
|
Solution. Here $x_{a}=3, x_{b}=-2, y_{a}=5, y_{b}=7$. Using formula (3), we get
$$
\vec{a} \vec{b}=3 \cdot(-2)+5 \cdot 7=-6+35=29
$$
46-51. Find the scalar product of the vectors:
|
29
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Determine the value of the function $f(x)=2 x^{2}-1$ at $x=3$.
|
Solution. Find $f(3)=y_{x=3}=2 \cdot 3^{2}-1=17$.
|
17
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
92. Show that as $t \rightarrow \infty$ the limit of the variable
$x=\frac{6 t^{3}-9 t+1}{2 t^{3}-3 t}$ is 3.
|
Solution. We find the difference between the variable $x$ and the number 3:
$$
\begin{gathered}
x-3=\frac{6 t^{3}+9 t+1}{2 t^{3}+3 t}-3=\frac{6 t^{3}+9 t+1-3\left(2 t^{3}+3 t\right)}{2 t^{3}+3 t}=\frac{6 t^{3}+9 t+1-6 t^{3}-9 t}{2 t^{3}+3 t}= \\
=\frac{1}{2 t^{3}+3 t}
\end{gathered}
$$
If $t \rightarrow \infty$, then $\frac{1}{2 t^{3}+3 t} \rightarrow 0$. Therefore, the condition $|x-3|<\varepsilon$ is satisfied, and consequently, $\lim _{t \rightarrow \infty} x=3$.
|
3
|
Calculus
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
94. Find $\lim _{x \rightarrow 2}\left(3 x^{2}-2 x\right)$.
|
Solution. Using properties 1, 3, and 5 of limits sequentially, we get
$$
\begin{gathered}
\lim _{x \rightarrow 2}\left(3 x^{2}-2 x\right)=\lim _{x \rightarrow 2}\left(3 x^{2}\right)-\lim _{x \rightarrow 2}(2 x)=3 \lim _{x \rightarrow 2} x^{2}-2 \lim _{x \rightarrow 2} x= \\
=3\left(\lim _{x \rightarrow 2} x\right)^{2}-2 \lim _{x \rightarrow 2} x=3 \cdot 2^{2}-2 \cdot 2=8 .
\end{gathered}
$$
|
8
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
95. Find $\lim _{x \rightarrow 4} \frac{x^{2}-2 x}{x-3}$.
|
Solution. To apply the property of the limit of a quotient, we need to check whether the limit of the denominator is not zero when $x=4$. Since $\lim _{x \rightarrow 4}(x-3)=$[^3]$=\lim _{x \rightarrow 4} x-\lim 3=4-3=1 \neq 0$, in this case, we can use property 4:
$$
\lim _{x \rightarrow 4} \frac{x^{2}-2 x}{x-3}=\frac{\lim _{x \rightarrow 1}\left(x^{2}-2 x\right)}{\lim _{x \rightarrow 4}(x-3)}
$$
But $\lim _{x \rightarrow 4}\left(x^{2}-2 x\right)=\left(\lim _{x \rightarrow 4} x\right)^{2}-2 \lim _{x \rightarrow 4} x$ and, therefore,
$$
\lim _{x \rightarrow 4} \frac{x^{2}-2 x}{x-3}=\frac{\left(\lim _{x \rightarrow 4} x\right)^{2}-2 \lim _{x \rightarrow 4} x}{\lim _{x \rightarrow 4} x-\lim 3}=\frac{4^{2}-2 \cdot 4}{4-3}=8
$$
96-98. Find the limits:
|
8
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
115. Find $\lim _{x \rightarrow 3} \frac{x^{2}-9}{3-x}$.
|
Solution. A direct transition to the limit is impossible here, since the limit of the denominator is zero: $\lim _{x \rightarrow 3}(3-x)=3-3=0$. The limit of the dividend is also zero: $\lim _{x \rightarrow 3}\left(x^{2}-9\right)=9-9=0$. Thus, we have an indeterminate form of $0 / 0$. However, this does not mean that the given function does not have a limit; to find it, we need to preliminarily transform the function by dividing the numerator and the denominator by the expression $x-3$:
$$
\frac{x^{2}-9}{3-x}=\frac{(x-3)(x+3)}{3-x}=-\frac{(x-3)(x+3)}{x-3}=-(x+3)
$$
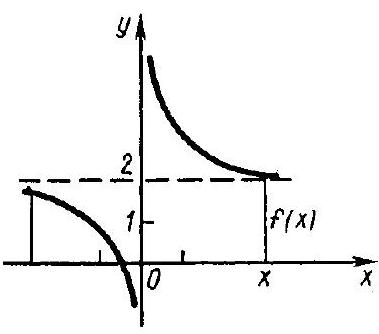
Fig. 95
$$
\begin{aligned}
& \text { For the expression }-(x+3) \text {, the limit as } \\
& x \rightarrow 3 \text { is easily found: } \lim _{x \rightarrow 3}(-(x+3))= \\
&=-\lim _{x \rightarrow 3}(x+3)=-6 .
\end{aligned}
$$
Remark. By canceling the fraction by $x-3$, we assume that $x \rightarrow 3$, but $x \neq 3$.
|
-6
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
116. Find $\lim _{x \rightarrow \infty} \frac{3}{x+5}$.
|
Solution. When $x \rightarrow \infty$, the denominator $x+5$ also tends to infinity, and its reciprocal $\frac{1}{x+5} \rightarrow 0$. Therefore, the product $\frac{1}{x+5} \cdot 3=\frac{3}{x+5}$ tends to zero if $x \rightarrow \infty$. Thus, $\lim _{x \rightarrow \infty} \frac{3}{x+5}=0$.
Identical transformations under the limit sign are applicable not only when the argument tends to a finite limit, but also when $x \rightarrow \infty$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
117. Find $\lim _{x \rightarrow \infty} \frac{2 x^{3}+x}{x^{3}-1}$.
|
Solution. Here, the numerator and denominator do not have a limit, as both increase indefinitely. In this case, it is said that there is an indeterminate form of $\infty / \infty$. We will divide the numerator and denominator term by term by $x^{3}$ (the highest power of $x$ in this fraction):
$$
\lim _{x \rightarrow \infty} \frac{2 x^{3}+x}{x^{3}-1}=\lim _{x \rightarrow \infty} \frac{2+\frac{1}{x^{2}}}{1-\frac{1}{x^{3}}}=\frac{\lim _{x \rightarrow \infty}\left(2+\frac{1}{x^{2}}\right)}{\lim _{x \rightarrow \infty}\left(1-\frac{1}{x^{3}}\right)}=2
$$
since $1 / x^{2}$ and $1 / x^{3}$ tend to zero as $x \rightarrow \infty$.
Remark. The method of dividing the numerator and denominator of a fraction by the highest power of the variable $x$, used to resolve indeterminate forms of $\infty / \infty$, cannot be used to find the limits of functions that do not lead to the indeterminate form of the specified type.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
118. Find $\lim _{\alpha \rightarrow 0} \frac{\sin 2 \alpha}{\alpha}$.
|
Solution. We will transform this limit into the form (1). For this, we multiply the numerator and the denominator of the fraction by 2, and take the constant factor 2 outside the limit sign. We have
$$
\lim _{\alpha \rightarrow 0} \frac{\sin 2 \alpha}{\alpha}=\lim _{\alpha \rightarrow 0} \frac{2 \sin 2 \alpha}{2 \alpha}=2 \lim _{\alpha \rightarrow 0} \frac{\sin 2 \alpha}{2 \alpha}
$$
Considering that if $\alpha \rightarrow 0$, then $2 \alpha \rightarrow 0$, we get
$$
\lim _{\alpha \rightarrow 0} \frac{\sin 2 \alpha}{\alpha}=2 \lim _{2 \alpha \rightarrow 0} \frac{\sin 2 \alpha}{2 \alpha}=2 \lim _{x \rightarrow 0} \frac{\sin x}{x}=2 \cdot 1=2
$$
If $x \rightarrow \infty$, then the following relation holds
$$
\lim _{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^{x}=e \approx 2.7182 \ldots
$$
which is known as the second remarkable limit. The proof of its validity is provided in detailed courses of mathematical analysis.
The number $e$ is of great importance in mathematics. Logarithms with base $e$ are called natural, and for them, the notation $\ln$ is used. Thus, $\ln x=\log _{e} x$. For example, $\ln 2 \approx 0.6931$.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
120. Find $\lim _{x \rightarrow 3}\left(x^{2}-7 x+4\right)$.
|
Solution. To find the limit of the given function, we will replace the argument $x$ with its limiting value:
$$
\lim _{x \rightarrow 3}\left(x^{2}-7 x+4\right)=3^{2}-7 \cdot 3+4=-8
$$
|
-8
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
135. Find $\lim _{x \rightarrow \infty} \frac{\sqrt{x^{2}+4}}{x}$.
|
Solution. As the argument $x$ tends to infinity, we have an indeterminate form of $\infty / \infty$. To resolve it, we divide the numerator and the denominator of the fraction by $x$. Then we get
$$
\lim _{x \rightarrow \infty} \frac{\sqrt{x^{2}+4}}{x}=\lim _{x \rightarrow \infty} \frac{\sqrt{\frac{x^{2}+4}{x^{2}}}}{1}=\lim _{x \rightarrow \infty} \sqrt{1+\frac{4}{x^{2}}}=1
$$
since $4 / x^{2} \rightarrow 0$ as $x \rightarrow \infty$.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
136. Find $\lim _{x \rightarrow \infty} \frac{3 x}{\sqrt{x^{2}-2 x+3}}$.
|
Solution. The limit transition as $x \rightarrow \infty$ can always be replaced by the limit transition as $\alpha \rightarrow 0$, if we set $\alpha=1 / x$ (the method of variable substitution).
Thus, setting $x=1 / \alpha$ in this case, we find that $\alpha \rightarrow 0$ as $x \rightarrow \infty$. Therefore,
$$
\begin{aligned}
\lim _{x \rightarrow \infty} \frac{3 x}{\sqrt{x^{2}-2 x+3}}= & \lim _{\alpha \rightarrow 0} \frac{3 \cdot \frac{1}{\alpha}}{\sqrt{\frac{1}{\alpha^{2}}-2 \cdot \frac{1}{\alpha}+3}}=\lim _{\alpha \rightarrow 0} \frac{3 \cdot \frac{1}{\alpha}}{\sqrt{\frac{1-2 \alpha+3 \alpha^{2}}{\alpha^{2}}}}= \\
& =\lim _{\alpha \rightarrow 0} \frac{3}{\sqrt{1-2 \alpha+3 \alpha^{2}}}=\frac{3}{1}=3
\end{aligned}
$$
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
137. Find $\lim _{x \rightarrow \infty} \frac{3 x^{2}+5 x+1}{x^{2}-2}$.
|
Solution. Method I. Dividing the numerator and the denominator by $x^{2}$, we find
$$
\lim _{x \rightarrow \infty} \frac{3 x^{2}+5 x+1}{x^{2}-2}=\lim _{x \rightarrow \infty} \frac{3+\frac{5}{x}+\frac{1}{x^{2}}}{1-\frac{2}{x^{2}}}=\frac{3}{1}=3
$$
Method II. Let $x=1 / a$; then $a \rightarrow 0$ as $x \rightarrow \infty$. Therefore,
$$
\lim _{x \rightarrow \infty} \frac{3 x^{2}+5 x+1}{x^{2}-2}=\lim _{a \rightarrow 0} \frac{3 \cdot \frac{1}{a^{2}}+5 \cdot \frac{1}{a}+1}{\frac{1}{a^{2}}-2}=\lim _{a \rightarrow 0} \frac{3+5 a+a^{2}}{1-2 a^{2}}=3
$$
138-141. Find the limits:
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
142. Find $\lim _{x \rightarrow \infty}(\sqrt{x+1}-\sqrt{x})$.
|
Solution. Here, it is required to find the limit of the difference of two quantities tending to infinity (indeterminate form of $\infty-\infty$). By multiplying and dividing the given expression by its conjugate, we get
$$
\sqrt{x+1}-\sqrt{x}=\frac{(\sqrt{x+1}-\sqrt{x})(\sqrt{x+1}+\sqrt{x})}{\sqrt{x+1}+\sqrt{x}}=\frac{1}{\sqrt{x+1}+\sqrt{x}}
$$
Therefore,
$$
\lim _{x \rightarrow \infty}(\sqrt{x+1}-\sqrt{x})=\lim _{x \rightarrow \infty} \frac{1}{\sqrt{x+1}+\sqrt{x}}=0
$$
Let's consider examples where remarkable limits are used.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
145. Find $\lim _{x \rightarrow 0} \frac{1-\cos 8 x}{2 x^{2}}$.
|
Solution. Transform the numerator to the form $1-\cos 8 x=2 \sin ^{2} 4 x$. Next, we find
$$
\begin{gathered}
\lim _{x \rightarrow 0} \frac{1-\cos 8 x}{2 x^{2}}=\lim _{x \rightarrow 0} \frac{2 \sin ^{2} 4 x}{2 x^{2}}=\lim _{x \rightarrow 0}\left(\frac{\sin 4 x}{x} \cdot \frac{\sin 4 x}{x}\right)= \\
=\lim _{x \rightarrow 0} \frac{\sin 4 x}{x} \cdot \lim _{x \rightarrow 0} \frac{\sin 4 x}{x}=4 \cdot 4=16
\end{gathered}
$$
|
16
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
168. Find the derivative of the function $y=5x$.
|
Solution. $1^{0} . y_{\mathrm{H}}=5(x+\Delta x)=5 x+5 \Delta x$.
$2^{0} . \Delta y=y_{\mathrm{k}}-y=(5 x+5 \Delta x)-5 x=5 \Delta x$.
$3^{0} . \frac{\Delta y}{\Delta x}=\frac{5 \Delta x}{\Delta x}=5$.
|
5
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.