problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
6.173. $2 \sqrt{5 \sqrt[4]{x+1}+4}-\sqrt{2 \sqrt[4]{x+1}-1}=\sqrt{20 \sqrt[4]{x+1}+5}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x+1 \geq 0, \\ 2 \sqrt[4]{x+1}-1 \geq 0\end{array} \Leftrightarrow\left\{\begin{array}{l}x \geq-1, \\ 2 \sqrt[4]{x+1} \geq 1,\end{array} \Leftrightarrow x \geq-\frac{15}{16}\right.\right.$.
Let $\sqrt[4]{x+1}=y$, where $y \geq 0$. The equation in terms of $y$ becomes $2 \sqrt{5 y+4}-\sqrt{2 y-1}=\sqrt{20 y+5}$. Squaring both sides of the equation, we get
$$
\begin{aligned}
& 20 y+16-4 \sqrt{(5 y+4)(2 y-1)}+2 y-1=20 y+5 \Leftrightarrow \\
& \Leftrightarrow y+5=2 \sqrt{(5 y+4)(2 y-1)} \Leftrightarrow y^{2}+10 y+25=4\left(10 y^{2}+3 y-4\right) \Leftrightarrow \\
& \Leftrightarrow 39 y^{2}+2 y-41=0, \text { from which } y_{1}=-\frac{41}{39}, y_{2}=1 ; y_{1}=-\frac{41}{39}<0 \text { is not suitable. }
\end{aligned}
$$
Hence, $\sqrt[4]{x+1}=1 \Leftrightarrow x+1=1, x=0$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.176. $(\sqrt{x+1}+\sqrt{x})^{3}+(\sqrt{x+1}+\sqrt{x})^{2}=2$.
6.176. $(\sqrt{x+1}+\sqrt{x})^{3}+(\sqrt{x+1}+\sqrt{x})^{2}=2$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x+1 \geq 0, \\ x \geq 0\end{array} \Leftrightarrow x \geq 0\right.$.
Let $\sqrt{x+1}+\sqrt{x}=y$, where $y \geq 0$. The equation in terms of $y$ becomes
$$
\begin{aligned}
& y^{3}+y^{2}-2=0 \Leftrightarrow y^{3}-1+y^{2}-1=0 \Leftrightarrow \\
& \Leftrightarrow(y-1)\left(y^{2}+y+1\right)+(y+1)(y-1)=0 \Leftrightarrow \\
& \Leftrightarrow(y-1)\left(y^{2}+y+1+y+1\right)=0,(y-1)\left(y^{2}+2 y+2\right)=0
\end{aligned}
$$
The obtained equation is equivalent to two equations: $y-1=0$ and $y^{2}+2 y+2=0$, solving which, we find $y_{1}=1$; the second equation has no solutions, since $D<0$.
Then $\sqrt{x+1}+\sqrt{x}=1 \Leftrightarrow x+1+2 \sqrt{(x+1) x}+x=1, \sqrt{(x+1) x}=-x$, where $x \leq 0$. From the domain of definition, we get $\left\{\begin{array}{l}x \geq 0 \\ x \leq 0\end{array} \Leftrightarrow x=0\right.$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.177. $\sqrt[3]{x+7}-\sqrt{x+3}=0$.
6.177. $\sqrt[3]{x+7}-\sqrt{x+3}=0$.
|
## Solution.
Domain of definition: $x+3 \geq 0, x \geq-3$.
From the condition $\sqrt[3]{x+7}=\sqrt{x+3}$ and raising both sides to the sixth power, we get $(x+7)^{2}=(x+3)^{3} \Leftrightarrow x^{2}+14 x+49=x^{3}+9 x^{2}+27 x+27 \Leftrightarrow$
$\Leftrightarrow x^{3}+8 x^{2}+13 x-22=0$. By checking, we find that $x_{1}=1$, since $1+8+13-22=0$. We divide the left side of the equation by $x-1$:
$\frac{x^{3}+8 x^{2}+13 x-22}{x-1}=x^{2}+9 x+22$.
Then $(x-1)\left(x^{2}+9 x+22\right)=0$.
From this, $x-1=0, x_{1}=1$, or $x^{2}+9 x+22=0$, no solutions exist since $D<0$. Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.250. For what values of $a$ do the equations $x^{2}+a x+1=0$ and $x^{2}+x+a=0$ have a common root?
|
Solution.
If for some $a$ and $x$ the left parts of the equations are equal to 0, then they are equal to each other:
$$
\left\{\begin{array}{l}
x^{2}+a x+1=0 \\
x^{2}+x+a=0
\end{array}\right.
$$
Subtracting the second equation of the system from the first, we get
$a x-x+1-a=0,(a-1) x-(a-1)=0,(a-1)(x-1)=0$, from which:
1) if $a-1=0$, then $a=1$ and each equation will take the form $a^{2}+a+1=0$, i.e., it has no roots;
2) if $a-1 \neq 0$, then $x=1$, from which $1+a+1=0$, i.e., $a=-2$.
Answer: $a=-2$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.160. Simplify the expression $\log _{a+b} m+\log _{a-b} m-2 \log _{a+b} m \cdot \log _{a-b} m$, given that $m^{2}=a^{2}-b^{2}$.
|
Solution.
$\log _{a+b} m+\log _{a-b} m-2 \log _{a+b} m \cdot \log _{a-b} m=\log _{a+b} m+\frac{\log _{a+b} m}{\log _{a+b}(a-b)}-$
$-2 \frac{\log _{a+b} m \cdot \log _{a+b} m}{\log _{a+b}(a-b)}=\log _{a+b} m \cdot\left(1+\frac{1}{\log _{a+b}(a-b)}-\frac{2 \log _{a+b} m}{\log _{a+b}(a-b)}\right)=$
$=\frac{\log _{a+b} m\left(\log _{a+b}(a-b)+1-2 \log _{a+b} m\right)}{\log _{a+b}(a-b)}$.
Since $m=\sqrt{a^{2}-b^{2}}$, we have
$$
\begin{aligned}
& \frac{\log _{a+b} \sqrt{a^{2}-b^{2}}\left(\log _{a+b}(a-b)+1-2 \log _{a+b} \sqrt{a^{2}-b^{2}}\right)}{\log _{a+b}(a-b)}= \\
& =\frac{\log _{a+b} \sqrt{a^{2}-b^{2}}\left(\log _{a+b}(a-b)+1-\log _{a+b}(a-b)-1\right)}{\log _{a+b}(a-b)}= \\
& =\frac{\log _{a+b} \sqrt{a^{2}-b^{2}} \cdot 0}{\log _{a+b}(a-b)}=0
\end{aligned}
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.166. $\sqrt{\log _{0.04} x+1}+\sqrt{\log _{0.2} x+3}=1$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}\frac{1}{2} \log _{0.2} x+1 \geq 0, \\ \log _{0.2}+3 \geq 0, \quad \Leftrightarrow 00\end{array} \quad\right.$
Switch to base 0.2. We have
$$
\begin{aligned}
& \sqrt{\frac{1}{2} \log _{0.2} x+1}+\sqrt{\log _{0.2} x+3}=1 \Leftrightarrow \\
& \Leftrightarrow \sqrt{\log _{0.2} x+2}+\sqrt{2 \log _{0.2} x+6}=\sqrt{2}
\end{aligned}
$$
Squaring both sides of the equation, we get
$$
\begin{aligned}
& \log _{0.2} x+2+2 \sqrt{\left(\log _{0.2} x+2\right)\left(2 \log _{0.2} x+6\right)}+2 \log _{0.2} x+6=2 \Leftrightarrow \\
& \Leftrightarrow 2 \sqrt{\left(\log _{0.2} x+2\right)\left(2 \log _{0.2} x+6\right)}=-3 \log _{0.2} x-6 \Rightarrow \\
& \Rightarrow 4\left(\log _{0.2} x+2\right)\left(2 \log _{0.2} x+6\right)=9\left(\log _{0.2} x+2\right)^{2} \text { when }-3 \log _{0.2} x-6 \geq 0 \Leftrightarrow \\
& \Leftrightarrow \log _{0.2} x+2 \leq 0
\end{aligned}
$$
Considering the domain of definition, we have $\log _{0.2} x+2=0$, from which $x=25$.
Answer: 25.
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.176. $2^{\log _{5} x^{2}}-2^{1+\log _{5} x}+2^{\log _{5} x-1}-1=0$.
7.176. $2^{\log _{5} x^{2}}-2^{1+\log _{5} x}+2^{\log _{5} x-1}-1=0$.
|
Solution.
Domain of definition: $x>0$.
Rewrite the equation as $2^{2 \log _{5} x}-2 \cdot 2^{\log _{5} x}+\frac{2^{\log _{5} x}}{2}-1=0 \Leftrightarrow$ $\Leftrightarrow 2 \cdot 2^{2 \log _{5} x}-3 \cdot 2^{\log _{5} x}-2=0$. Solving this equation as a quadratic equation in terms of $2^{\log _{5} x}$, we find $2^{\log _{5} x}=-\frac{1}{2}$ (not suitable) or $2^{\log _{5} x}=2$, from which $\log _{5} x=1, x=5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.177. $\frac{\log _{2}\left(9-2^{x}\right)}{3-x}=1$.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
7.177. $\frac{\log _{2}\left(9-2^{x}\right)}{3-x}=1$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}9-2^{x}>0, \\ 3-x \neq 0,\end{array} \Leftrightarrow 3 \neq x<\log _{2} 9\right.$.
## From the condition
$$
\log _{2}\left(9-2^{x}\right)=3-x \Leftrightarrow 9-2^{x}=2^{3-x} \Leftrightarrow 2^{2 x}-9 \cdot 2^{x}+8=0
$$
Solving it as a quadratic equation in terms of $2^{x}$, we find $\left(2^{x}\right)=1$, hence $x_{1}=0$ or $\left(2^{x}\right)_{2}=8$, hence $x_{2}=3 ; x_{2}=3$ does not satisfy the domain of definition.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.179. $\log _{a^{2}} x^{2}+\log _{a}(x-1)=\log _{a} \log _{\sqrt{5}} 5$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x>1, \\ 0<a \neq 1 .\end{array}\right.$
From the condition we have
$$
\log _{a} x+\log _{a}(x-1)=\log _{a} 2 \Rightarrow \log _{a} x(x-1)=\log _{a} 2
$$
from which $x^{2}-x-2=0 \Rightarrow x_{1}=2, x_{2}=-1 ; x_{2}=-1$ does not satisfy the domain of definition.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.186. $\log _{12}\left(4^{3 x}+3 x-9\right)=3 x-x \log _{12} 27$.
|
## Solution.
Domain of definition: $4^{3 x}+3 x-9>0$.
Rewrite the equation as
$$
\log _{12}\left(4^{3 x}+3 x-9\right)+\log _{12} 27^{x}=3 x \Rightarrow \log _{12} 27^{x}\left(4^{3 x}+3 x-9\right)=3 x
$$
from which $27^{x}\left(4^{3 x}+3 x-9\right)=12^{3 x} \Leftrightarrow 4^{3 x}+3 x-9=4^{3 x}, 3 x-9=0, x=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.187. $x^{2} \cdot \log _{x} 27 \cdot \log _{9} x=x+4$.
|
## Solution.
Domain of definition: $0<x \neq 1$.
Switch to base 3, then
$$
\frac{3 x^{2}}{\log _{3} x} \cdot \frac{\log _{3} x}{2}=x+4 \Leftrightarrow 3 x^{2}-2 x-8=0
$$
from which $x_{1}=2, x_{2}=-\frac{4}{3} ; x_{2}=-\frac{4}{3}$ does not satisfy the domain of definition.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.197. $5^{\frac{x}{\sqrt{x}+2}} \cdot 0.2^{\frac{4}{\sqrt{x}+2}}=125^{x-4} \cdot 0.04^{x-2}$.
|
## Solution.
Domain of definition: $x \geq 0$.
From the condition we have
$$
\begin{aligned}
& 5^{\frac{x}{\sqrt{x}+2}} \cdot 5^{-\frac{4}{\sqrt{x}+2}}=5^{3 x-12} \cdot 5^{-2 x+4} \Leftrightarrow 5^{\frac{x}{\sqrt{x}+2}-\frac{4}{\sqrt{x}+2}}=5^{3 x-12-2 x+4} \Leftrightarrow \\
& \Leftrightarrow \frac{x-4}{\sqrt{x}+2}=x-8 \Leftrightarrow x \sqrt{x}+x-8 \sqrt{x}-12=0
\end{aligned}
$$
Let $\sqrt{x}=y \geq 0$. The equation in terms of $y$ becomes $y^{3}+y^{2}-8 y-12=0,(y-3)(y+2)^{2}=0$, from which $y_{1}=3, y_{2,3}=-2 ; y_{2,3}=-2$ does not fit. Then $\sqrt{x}=3, x=9$.
Answer: 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.198. $\left(3 \cdot\left(3^{\sqrt{x}+3}\right)^{\frac{1}{2 \sqrt{x}}}\right)^{\frac{2}{\sqrt{x}-1}}=\frac{3}{\sqrt[10]{3}}$.
|
## Solution.
Domain of definition: $0<x \neq 1$.
From the condition
$$
3^{\frac{3(\sqrt{x}+1)}{2 \sqrt{x}} \cdot \frac{2}{\sqrt{x}-1}}=3^{\frac{9}{10}} \Leftrightarrow \frac{3(\sqrt{x}+1)}{2 \sqrt{x}} \cdot \frac{2}{\sqrt{x}-1}=\frac{9}{10} \Leftrightarrow 3 x-13 \sqrt{x}-10=0
$$
Solving this equation as a quadratic equation in terms of $\sqrt{x}$, we get $(\sqrt{x})_{1}=-\frac{2}{3}$ (not suitable), or $(\sqrt{x})_{2}=5$. Therefore, $x=25$.
Answer: 25.
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.200. $\frac{1+2 \log _{9} 2}{\log _{9} x}-1=2 \log _{x} 3 \cdot \log _{9}(12-x)$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}0<x<12, \\ x \neq 1 .\end{array}\right.$
Switch to base 3. Then we get
$$
\begin{aligned}
& \frac{1+\frac{2 \log _{3} 2}{\log _{3} 9}}{\frac{\log _{3} x}{\log _{3} 9}}-1=\frac{2}{\log _{3} x} \cdot \frac{\log _{3}(12-x)}{\log _{3} 9} \Leftrightarrow \frac{2+2 \log _{3} 2}{\log _{3} x}-1=\frac{\log _{3}(12-x)}{\log _{3} x} \Leftrightarrow \\
& \Leftrightarrow \frac{2+2 \log _{3} 2-\log _{3} x}{\log _{3} x}=\frac{\log _{3}(12-x)}{\log _{3} x} \Leftrightarrow 2+2 \log _{3} 2-\log _{3} x=\log _{3}(12-x) \Leftrightarrow \\
& \Leftrightarrow 2+2 \log _{3} 2=\log _{3} x+\log _{3}(12-x) \Leftrightarrow \\
& \Leftrightarrow \log _{3} 9+\log _{3} 4=\log _{3} x+\log _{3}(12-x), \log _{3} 36=\log _{3} x(12-x)
\end{aligned}
$$
$$
\text { hence } 36=x(12-x) \text { or } x^{2}-12 x+36=0,(x-6)^{2}=0, x=6 \text {. }
$$
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.201. $3 \lg 2+\lg \left(2^{\sqrt{x-1}-1}-1\right)=\lg \left(0.4 \sqrt{2^{\sqrt{x-1}}}+4\right)+1$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}2^{\sqrt{x-1}-1}-1>0, \\ x-1 \geq 0\end{array} \Leftrightarrow x>2\right.$.
Rewrite the equation in the form
$$
\begin{aligned}
& \lg 8+\lg \left(2^{\sqrt{x-1}-1}-1\right)=\lg \left(0.4 \sqrt{2^{\sqrt{x-1}}}+4\right)+\lg 10 \Leftrightarrow \\
& \Leftrightarrow \lg \left(8 \cdot\left(2^{\sqrt{x-1}-1}-1\right)\right)=\lg \left(4 \sqrt{2^{\sqrt{x-1}}}+40\right) \Leftrightarrow \\
& \Leftrightarrow 8\left(2^{\sqrt{x-1}-1}-1\right)=4\left(\sqrt{2^{\sqrt{x-1}}}+10\right) \Leftrightarrow\left(2^{\frac{\sqrt{x-1}}{2}}\right)^{2}-2^{\frac{\sqrt{x-1}}{2}}-12=0
\end{aligned}
$$
Solving this equation as a quadratic equation in terms of $2^{\frac{\sqrt{x-1}}{2}}$, we get $2^{\frac{\sqrt{x-1}}{2}}=-3$ (no solutions), or $2^{\frac{\sqrt{x-1}}{2}}=2^{2}$, from which $\frac{\sqrt{x-1}}{2}=2, \sqrt{x-1}=4$, $x-1=16, x=17$.
Answer: 17.
|
17
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.208. $2^{x-1}+2^{x-4}+2^{x-2}=6.5+3.25+1.625+\ldots$ (the expression on the right side is an infinite geometric progression).
|
Solution.
On the right side, we have the sum of the terms of an infinitely decreasing geometric progression $S$, where $b_{1}=6.5 ; q=\frac{3.25}{6.5}=0.5 \Rightarrow S=\frac{b_{1}}{1-q}=\frac{6.5}{1-0.5}=13$.
Rewrite the equation as $\frac{2^{x}}{2}+\frac{2^{x}}{16}+\frac{2^{x}}{4}=13 \Leftrightarrow \frac{13}{16} \cdot 2^{x}=13$, $2^{x}=16$, from which $x=4$.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.209. $49^{1+\sqrt{x-2}}-344 \cdot 7^{\sqrt{x-2}}=-7$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
7.209. $49^{1+\sqrt{x-2}}-344 \cdot 7^{\sqrt{x-2}}=-7$.
|
Solution.
Domain of definition: $x \geq 2$.
Rewrite the equation as $49 \cdot 7^{2 \sqrt{x-2}}-344 \cdot 7^{\sqrt{x-2}}+7=0$. Solving it as a quadratic equation in terms of $7^{\sqrt{x-2}}$, we get $\left(7^{\sqrt{x-2}}\right)=7^{-2}$ or $\left(7^{\sqrt{x-2}}\right)_{2}=7$, from which $(\sqrt{x-2})_{1}=-2$ (no solutions), or $(\sqrt{x-2})_{2}=1, x_{2}=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.212. $\frac{\log _{4 \sqrt{x}} 2}{\log _{2 x} 2}+\log _{2 x} 2 \cdot \log _{1 / 2} 2 x=0$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x>0, \\ x \neq \frac{1}{16}, \\ x \neq \frac{1}{2}, \\ x \neq 1 .\end{array}\right.$
Transition to base 2. We have
$\frac{\frac{\log _{2} 2}{\log _{2} 4 \sqrt{x}}}{\frac{\log _{2} 2}{\log _{2} 2 x}}+\frac{\log _{2} 2}{\log _{2} 2 x} \cdot \frac{\log _{2} 2 x}{\log _{2} \frac{1}{2}}=0 \Leftrightarrow \frac{1+\log _{2} x}{2+\frac{1}{2} \log _{2} x}-1=0$,
from which $\log _{2} x=2$ and $x=4$.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.214. $9^{x}+6^{x}=2^{2 x+1}$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
7.214. $9^{x}+6^{x}=2^{2 x+1}$.
|
Solution.
Rewrite the equation as $3^{2 x}+2^{x} \cdot 3^{x}-2 \cdot 2^{2 x}=0$ and divide it by $2^{2 x} \neq 0$. Then $\left(\frac{3}{2}\right)^{2 x}+\left(\frac{3}{2}\right)^{x}-2=0 \Rightarrow\left(\left(\frac{3}{2}\right)^{x}\right)=-2$ (no solutions) or $\left(\left(\frac{3}{2}\right)^{x}\right)_{2}=1 \Rightarrow x=0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.218. $\left(\frac{3}{5}\right)^{2 \log _{9}(x+1)} \cdot\left(\frac{125}{27}\right)^{\log _{27}(x-1)}=\frac{\log _{5} 27}{\log _{5} 243}$.
|
Solution.
Domain of definition: $x>1$.
From the condition we have
$\left(\frac{3}{5}\right)^{\log _{3}(x+1)} \cdot\left(\frac{3}{5}\right)^{\log _{3}(x-1)}=\frac{3}{5} \Leftrightarrow\left(\frac{3}{5}\right)^{\log _{3}(x+1)+\log _{3}(x-1)}=\frac{3}{5} \Rightarrow$
$\Rightarrow \log _{3}(x+1)+\log _{3}(x-1)=1 \Rightarrow \log _{3}\left(x^{2}-1\right)=1, x^{2}-1=3, x^{2}=4$.
From this, $x_{1}=-2, x_{2}=2 ; x_{1}=-2$ does not satisfy the domain of definition.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.219. $5^{1+x^{3}}-5^{1-x^{3}}=24$.
7.219. $5^{1+x^{3}}-5^{1-x^{3}}=24$.
|
Solution.
We have $5 \cdot 5^{x^{3}}-\frac{5}{5^{x^{3}}}-24=0 \Leftrightarrow 5 \cdot\left(5^{x^{3}}\right)^{2}-24 \cdot 5^{x^{3}}-5=0$. Solving this equation as a quadratic in terms of $5^{x^{3}}$, we get $5^{x^{3}}=-\frac{1}{5}$ (no solutions), or $5^{x^{3}}=5 \Rightarrow x^{3}=1, x=1$.
Answer: 1 .
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.220. $3^{2 x+4}+45 \cdot 6^{x}-9 \cdot 2^{2 x+2}=0$.
7.220. $3^{2 x+4}+45 \cdot 6^{x}-9 \cdot 2^{2 x+2}=0$.
(No change needed as the text is already in English and contains only a mathematical equation.)
|
Solution.
Rewrite the equation as $81 \cdot 3^{2 x}+45 \cdot 3^{x} \cdot 2^{x}-36 \cdot 2^{x}=0$. Dividing it by $9 \cdot 2^{2 x}$, we get $9 \cdot\left(\frac{3}{2}\right)^{2 x}+5 \cdot\left(\frac{3}{2}\right)^{x}-4=0 \Rightarrow\left(\frac{3}{2}\right)^{x}=-1$ (no solutions), or $\left(\frac{3}{2}\right)^{x}=\left(\frac{3}{2}\right)^{-2}$, from which $x=-2$.
Answer: -2 .
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.225. $\log _{3 x+7}(5 x+3)+\log _{5 x+3}(3 x+7)=2$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}0-\frac{3}{5}, x \neq-\frac{2}{5}\right.$.
Multiplying the equation by $\log _{3 x+7}(5 x+3) \neq 0$, we get
$$
\begin{aligned}
& \log _{3 x+7}^{2}(5 x+3)-2 \log _{3 x+7}(5 x+3)+1=0 \Leftrightarrow\left(\log _{3 x+7}(5 x+3)-1\right)^{2}=0 \Leftrightarrow \\
& \Leftrightarrow \log _{3 x+7}(5 x+3)=1 \Leftrightarrow 5 x+3=3 x+7, x=2 \\
& \text { Answer: } 2 .
\end{aligned}
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.227. $(\lg (x+20)-\lg x) \log _{x} 0.1=-1$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x+20>0, \\ 0<x \neq 1\end{array}\right.$ or $0<x \neq 1$.
Switch to base 10. We have $(\lg (x+20)-\lg x)\left(-\frac{1}{\lg x}\right)=-1 \Leftrightarrow$ $\Leftrightarrow \lg (x+20)-\lg x=\lg x \Leftrightarrow \lg (x+20)=2 \lg x \Leftrightarrow \lg (x+20)=\lg x^{2}$. Then $x+20=x^{2}, x^{2}-x-20=0$, from which $x_{1}=-4, x_{2}=5 ; x_{1}=-4$ does not satisfy the domain of definition.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.228. $5^{\lg x}=50-x^{\lg 5}$.
|
## Solution.
Domain of definition: $0<x \neq 1$.
Rewrite the equation as $5^{\lg x}=50-5^{\lg x}, 2 \cdot 5^{\lg x}=50, 5^{\lg x}=25$, from which $\lg x=2, x=10^{2}=100$.
Answer: 100.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.229. $27 \cdot 2^{-3 x}+9 \cdot 2^{x}-2^{3 x}-27 \cdot 2^{-x}=8$.
|
Solution.
Transform the equation:
$$
\begin{aligned}
& 27+9 \cdot 2^{4 x}-2^{6 x}-27 \cdot 2^{2 x}=8 \cdot 2^{3 x} \Leftrightarrow \\
& \Leftrightarrow 2^{6 x}-9 \cdot 2^{4 x}+8 \cdot 2^{3 x}+27 \cdot 2^{2 x}-27=0 \Leftrightarrow \\
& \Leftrightarrow 2^{6 x}-2^{4 x}-8 \cdot 2^{4 x}+8 \cdot 2^{3 x}+27 \cdot 2^{x}-27=0 \Leftrightarrow
\end{aligned}
$$
$$
\begin{aligned}
& \Leftrightarrow 2^{4 x}\left(2^{2 x}-1\right)-8 \cdot 2^{3 x}\left(2^{x}-1\right)+27\left(2^{x}-1\right)=0 \Leftrightarrow \\
& \Leftrightarrow 2^{4 x}\left(2^{x}-1\right)\left(2^{x}+1\right)-8 \cdot 2^{3 x}\left(2^{x}-1\right)+27\left(2^{x}-1\right)=0 \Leftrightarrow \\
& \Leftrightarrow\left(2^{x}-1\right)\left(2^{5 x}+2^{4 x}-8 \cdot 2^{3 x}+27\right)=0
\end{aligned}
$$
from which $2^{x}=1, x_{1}=0$. The equation $2^{5 x}+2^{4 x}-8 \cdot 2^{3 x}+27=0$ has no solutions.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.230. $\log _{x+1}(x-0.5)=\log _{x-0.5}(x+1)$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}0<x+1 \neq 1, \\ 0<x-0.5 \neq 1\end{array}\right.$ or $0.5<x \neq 1.5$.
Multiplying both sides of the equation by $\log _{x+1}(x-0.5) \neq 0$, we get
$$
\begin{aligned}
& \log _{x+1}^{2}(x-0.5)=1 \Rightarrow \log _{x+1}(x-0.5)=-1 \Rightarrow \\
& \Rightarrow x-0.5=\frac{1}{x+1}, 2 x^{2}+x-3=0, x_{1}=-\frac{3}{2} \text { (does not satisfy the domain of definition), }
\end{aligned}
$$
$x_{2}=1 ;$ or $\log _{x+1}(x-0.5)=1, x-0.5=x+1$, no solutions.
Answer: 1 .
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.231. $\log _{4} \log _{2} x+\log _{2} \log _{4} x=2$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}\log _{2} x>0, \\ \log _{4} x>0,\end{array} \Leftrightarrow x>1\right.$.
Switch to base 2. We have
$$
\begin{aligned}
& \frac{1}{2} \log _{2} \log _{2} x+\log _{2}\left(\frac{1}{2} \log _{2} x\right)=2 \Leftrightarrow \\
& \Leftrightarrow \log _{2} \log _{2} x+2 \log _{2}\left(\frac{1}{2} \log _{2} x\right)=4 \Leftrightarrow \\
& \Leftrightarrow \log _{2} \log _{2} x+\log _{2}\left(\frac{1}{4} \log _{2}^{2} x\right)=4 \Leftrightarrow \log _{2}\left(\log _{2} x \cdot \frac{1}{4} \log _{2}^{2} x\right)=4 \Leftrightarrow \\
& \Leftrightarrow \frac{1}{4} \log _{2}^{3} x=16, \log _{2}^{3} x=64
\end{aligned}
$$
Then $\log _{2} x=4, x=2^{4}=16$.
Answer: 16.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.235. $x \log _{x+1} 5 \cdot \log _{\sqrt[3]{1 / 5}}(x+1)=\frac{x-4}{x}$.
|
## Solution.
$$
\text { Domain: }\left\{\begin{array}{l}
0<x+1 \neq 1, \\
x \neq 0
\end{array} \Leftrightarrow-1<x \neq 0\right.
$$
Switch to base 5. We have $\frac{x}{\log _{5}(x+1)} \cdot(-3) \log _{5}(x+1)=\frac{x-4}{x}$,
$-3 x=\frac{x-4}{x}$ when $\log _{5}(x+1) \neq 0$. From here, $3 x^{2}+x-4=0, x_{1}=-\frac{4}{3}, x_{2}=1$; $x_{1}=-\frac{4}{3}$ does not satisfy the domain.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.241. $\frac{\log _{2}\left(x^{3}+3 x^{2}+2 x-1\right)}{\log _{2}\left(x^{3}+2 x^{2}-3 x+5\right)}=\log _{2 x} x+\log _{2 x} 2$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}x^{3}+3 x^{2}+2 x-1>0, \\ 0<x^{3}+2 x^{2}-3 x+5 \neq 1, \\ 0<x \neq \frac{1}{2} .\end{array}\right.$
By the formula for changing the base we have
$$
\begin{aligned}
& \log _{x^{3}+2 x^{2}-3 x+5}\left(x^{3}+3 x^{2}+2 x-1\right)=\log _{2 x} 2 x \Leftrightarrow \\
& \Leftrightarrow \log _{x^{3}+2 x^{2}-3 x+5}\left(x^{3}+3 x^{2}+2 x-1\right)=1 \Leftrightarrow
\end{aligned}
$$
$\Leftrightarrow x^{3}+3 x^{2}+2 x-1=x^{3}+2 x^{2}-3 x+5 \Leftrightarrow x^{2}+5 x-6=0 \Rightarrow x_{1}=1$, $x_{2}=-6 ; x_{2}=-6$ does not satisfy the domain of definition.
Answer: 1 .
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.242. $\left(16 \cdot 5^{2 x-1}-2 \cdot 5^{x-1}-0.048\right) \lg \left(x^{3}+2 x+1\right)=0$.
|
Solution.
Domain: $x^{3}+2 x+1>0$.
From the condition $16 \cdot 5^{2 x-1}-2^{x-1}-0.048=0$ or $\lg \left(x^{3}+2 x+1\right)=0$. Rewrite the first equation as
$\frac{16}{5} \cdot 5^{2 x}-\frac{2}{5} \cdot 5^{x}-0.048=0 \Leftrightarrow 16 \cdot 5^{2 x}-2 \cdot 5^{x}-0.24=0$.
Solving this equation as a quadratic in terms of $5^{x}$, we get $5^{x}=-\frac{3}{40}$ (no solutions), or $5^{x}=5^{-1} \Leftrightarrow x_{1}=-1$ (does not satisfy the domain). From the second equation, we have
$x^{3}+2 x+1=1 \Leftrightarrow x^{3}+2 x=0 \Leftrightarrow x\left(x^{2}+2\right)=0, x_{3}=0, x^{2}+2 \neq 0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.243. $5^{x} \cdot \sqrt[x]{8^{x-1}}=500$.
|
Solution.
Rewrite the equation as $5^{x} \cdot 8^{\frac{x-1}{x}}=500 \Leftrightarrow \frac{5^{x} \cdot 8}{8^{1 / x}}=500 \Leftrightarrow$ $\Leftrightarrow \frac{5^{x} \cdot 2}{8^{1 / x}}=125 \Leftrightarrow 5^{x-3}=2^{3 / x-1} \Rightarrow\left\{\begin{array}{l}x-3=0, \\ \frac{3}{x}-1=0,\end{array}\right.$ from which $x=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.245. $\log _{1+x}\left(2 x^{3}+2 x^{2}-3 x+1\right)=3$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}2 x^{3}+2 x^{2}-3 x+1>0, \\ -1<x \neq 0 .\end{array}\right.$
We have
$$
\begin{aligned}
& 2 x^{3}+2 x^{2}-3 x+1=(1+x)^{3} \Leftrightarrow 2 x^{3}+2 x^{2}-3 x+1=1+3 x+3 x^{2}+x^{3} \Leftrightarrow \\
& \Leftrightarrow x^{3}-x^{2}-6 x=0 \Leftrightarrow x\left(x^{2}-x-6\right)=0
\end{aligned}
$$
from which $x_{1}=0, x_{2}=-2, x_{3}=3 ; x_{1}=0, x_{2}=-2$ do not satisfy the domain of definition.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.246. $\log _{2} \sqrt[3]{x}+\sqrt[3]{\log _{2} x}=\frac{4}{3}$.
|
## Solution.
Domain of definition: $x>0$.
## From the condition we have
$$
\frac{1}{3} \log _{2} x+\sqrt[3]{\log _{2} x}=\frac{4}{3} \Leftrightarrow \log _{2} x+3 \sqrt[3]{\log _{2} x}-4=0
$$
Let $\sqrt[3]{\log _{2} x}=y$. The equation in terms of $y$ becomes
$$
\begin{aligned}
& y^{3}+3 y-4=0 \Leftrightarrow\left(y^{3}-1\right)+(3 y-3)=0 \Leftrightarrow \\
& \Leftrightarrow(y-1)\left(y^{2}+y+1\right)+3(y-1)=0 \Leftrightarrow(y-1)\left(y^{2}+y+4\right)=0
\end{aligned}
$$
from which $y-1=0$, since $y^{2}+y+4>0$. Therefore, $y=1, \sqrt[3]{\log _{2} x}=1$, $\log _{2} x=1, x=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.247. $\sqrt{\log _{5} x}+\sqrt[3]{\log _{5} x}=2$.
|
Solution.
Domain of definition: $\log _{5} x \geq 0$ or $x \geq 1$.
Rewrite the equation as $\sqrt[6]{\left(\log _{5} x\right)^{3}}+\sqrt[6]{\left(\log _{5} x\right)^{2}}-2=0$. Let $\sqrt[6]{\log _{5} x}=y$. The equation in terms of $y$ becomes
$$
y^{3}+y^{2}-2=0 \Leftrightarrow\left(y^{3}-1\right)+\left(y^{2}-1\right)=0 \Leftrightarrow
$$
$\Leftrightarrow(y-1)\left(y^{2}+y+1\right)+(y-1)(y+1)=0 \Leftrightarrow(y-1)\left(y^{2}+2 y+2\right)=0$, from which $y-1=0$, since $y^{2}+2 y+2>0$. We get $\sqrt[6]{\log _{5} x}=1, \log _{5} x=1$, $x=5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.252. $\frac{2}{15}\left(16^{\log _{9} x+1}-16^{\log _{3} \sqrt{x}}\right)+16^{\log _{3} x}-\log _{\sqrt{5}} 5 \sqrt{5}=0$.
|
## Solution.
Domain of definition: $x>0$.
Rewrite the equation as
$$
\begin{aligned}
& \frac{2}{15}\left(16 \cdot 16^{\frac{1}{2} \log _{3} x}-16^{\frac{1}{2} \log _{3} x}\right)+16^{\log _{3} x}-3=0 \Leftrightarrow \\
& \Leftrightarrow 16^{\log _{3} x}+2 \cdot 16^{\frac{\log _{3} x}{2}}-3=0
\end{aligned}
$$
Solving this equation as a quadratic in terms of $16^{\frac{\log _{3} x}{2}}$, we get $16^{\frac{\log _{3} x}{2}}=-3$ (no solutions), or $16^{\frac{\log _{3} x}{2}}=16^{0}$, from which $\frac{\log _{3} x_{2}}{2}=0$, $x=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.254. $\log _{2} \sqrt[3]{4}+\log _{8}\left(9^{x+1}-1\right)=1+\log _{8}\left(3^{x+1}+1\right)$.
|
## Solution.
Domain of definition: $9^{x+1}-1>0 \Leftrightarrow x>-1$.
Since $\log _{2} \sqrt[3]{4}=\frac{2}{3}$, we have
$$
\begin{aligned}
& \log _{8}\left(9 \cdot 3^{2 x}-1\right)-\log _{8}\left(3 \cdot 3^{x}+1\right)=\frac{1}{3} \Leftrightarrow \log _{8} \frac{9 \cdot 3^{2 x}-1}{3 \cdot 3^{x}+1}=\frac{1}{3} \Leftrightarrow \\
& \Leftrightarrow \frac{9 \cdot 3^{2 x}-1}{3 \cdot 3^{x}+1}=8^{\frac{1}{3}}=2 \Leftrightarrow 9 \cdot 3^{2 x}-6 \cdot 3^{x}-3=0
\end{aligned}
$$
Solving this equation as a quadratic in terms of $3^{x}$, we get $3^{x}=-\frac{1}{3}$ (no solutions), or $3^{x}=3^{0} \Rightarrow x=0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.255. $25^{\log _{4} x}-5^{\log _{16} x^{2}+1}=\log _{\sqrt{3}} 9 \sqrt{3}-25^{\log _{16} x}$.
|
## Solution.
Domain of definition: $x>0$.
Rewrite the equation as
$5^{\log _{2} x}-5 \cdot 5^{\frac{1}{2} \log _{2} x}=5-5^{\frac{1}{2} \log _{2} x} \Leftrightarrow 5^{\log _{2} x}-4 \cdot 5^{\frac{1}{2} \log _{2} x}-5=0$.
Solving this equation as a quadratic equation in terms of $5^{\frac{1}{\log _{2} x}}$, we get
$5^{\frac{1}{2} \log _{2} x}=-1$ (no solutions), or $5^{\frac{1}{2} \log _{2} x}=5 \Rightarrow \frac{1}{2} \log _{2} x=1, \log _{2} x=2$, $x=2^{2}=4$.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.257. $\log _{2} 3 \cdot \log _{3} 4 \cdot \log _{4} 5 \cdot \ldots \cdot \log _{n}(n+1)=10(n \in N)$.
|
Solution.
Let's switch to base 2.
$\log _{2} 3 \cdot \frac{\log _{2} 4}{\log _{2} 3} \cdot \frac{\log _{2} 5}{\log _{2} 4} \cdot \ldots \cdot \frac{\log _{2}(n+1)}{\log _{2} n}=10 \Leftrightarrow \log _{2}(n+1)=10 \Leftrightarrow$
$\Leftrightarrow n+1=2^{10} \Leftrightarrow n=1024-1=1023$.
Answer: 1023.
|
1023
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.111. Find the non-negative integer values of $x$ that satisfy the inequality $\frac{x+3}{x^{2}-4}-\frac{1}{x+2}<\frac{2 x}{2 x-x^{2}}$.
|
Solution.
Rewrite the inequality as $\frac{x+3}{x^{2}-4}-\frac{1}{x+2}+\frac{2 x}{x(x-2)}<0 \Leftrightarrow$
$$
\begin{aligned}
& \Leftrightarrow \frac{x+3}{(x-2)(x+2)}-\frac{1}{x+2}+\frac{2}{x-2}<0 \text { for } x \neq 0: \Leftrightarrow\left\{\begin{array}{l}
\frac{2 x+9}{(x-2)(x+2)}<0, \\
x \neq 0
\end{array} \Leftrightarrow\right. \\
& \Leftrightarrow\left\{\begin{array}{l}
(2 x+9)(x-2)(x+2)<0, \\
x \neq 0 .
\end{array}\right.
\end{aligned}
$$
Using the number line, we get $x=1$.
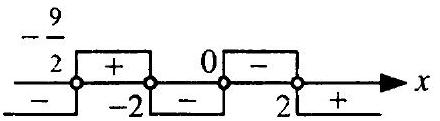
Answer: $x=1$.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.193. Inside a right angle, there is a point $M$, the distances from which to the sides of the angle are 4 and $8 \mathrm{~cm}$. A line passing through point $M$ cuts off a triangle from the right angle with an area of $100 \mathrm{~cm}^{2}$. Find the legs of the triangle.
|
Solution.
Given $\angle C=90^{\circ}, M P=4 \mathrm{~cm}, M Q=8 \mathrm{~cm}, S_{\triangle A B C}=100 \mathrm{~cm}^{2}$ (Fig. 10.3); we need to find $B C$ and $A C$. Let $B C=x, A C=y$; then $0.5 x y=100$, i.e., $x y=200$. Since $\triangle B P M \sim \triangle M Q A$, we have $\frac{M P}{A Q}=\frac{B P}{M Q}$ or $\frac{4}{y-4}=\frac{x-8}{8}$.
We have the system of equations
$$
\left\{\begin{array}{l}
\frac{4}{y-4}=\frac{x-8}{8}, \\
x y=200
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x+2 y=50, \\
x y=200
\end{array} \Rightarrow y^{2}-25 y+100=0, y_{1}=5 \right.\right. \text { cm }
$$
$y_{2}=20 \mathrm{~cm}$. We obtain two solutions: $x_{1}=40 \mathrm{~cm}, y_{1}=5 \mathrm{~cm} ; x_{2}=10 \mathrm{~cm}$, $y_{2}=20 \mathrm{~cm}$.
Answer: 40 and 5 cm or 10 and 20 cm.
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.195. The circle touches two adjacent sides of the square and divides each of the other two sides into segments equal to 2 and 23 cm. Find the radius of the circle.
|
## Solution.
Let $M$ and $K$ be the points of tangency of the circle with the sides $AB$ and $AD$ of the square $ABCD$ (Fig. 10.5), $M$ and $K$ being the points of intersection of the circle with the specified sides of the square, and $P$ and $E$ being the points of intersection with the sides $BC$ and $CD$. By the problem statement
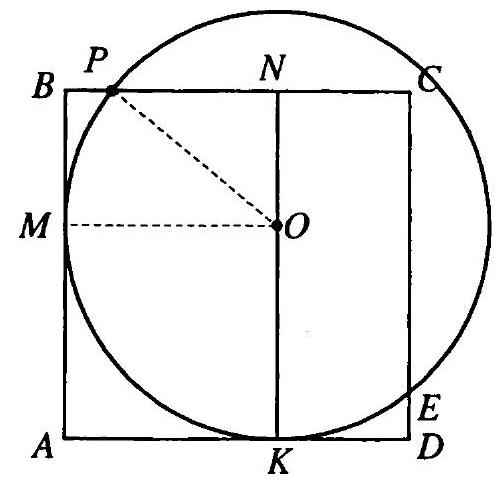
Fig. 10.5
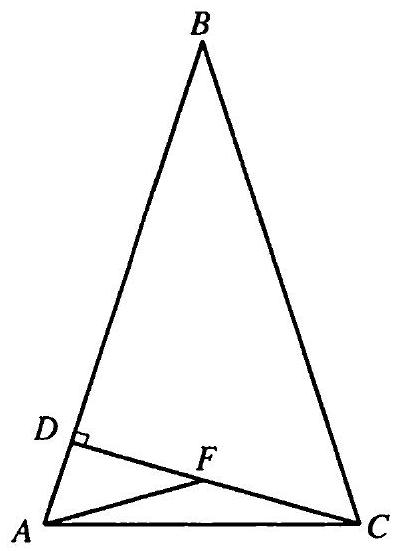
Fig. 10.6
$BP = DE = 2$ cm, $CP = CE = 23$ cm. Draw $ON \perp BC$. $OM = OP = NB = OK = R$, where $R$ is the radius of the given circle. $AB = NK = BC = CP + PB = 25$ cm, $ON = NK - KO = (25 - R)$ cm, $PN = BN - BP = (R - 2)$ cm. From the right triangle $PNO$: $OP^2 = ON^2 + NP^2$ or $R^2 = (R - 2)^2 + (25 - R)^2$, from which $\left[\begin{array}{l}R=17 \\ R=37\end{array}\right.$. The condition is satisfied by $R = 17$.
Answer: 17 cm.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.196. Given a triangle $A B C$, in which $2 h_{c}=A B$ and $\angle A=75^{\circ}$. Find the measure of angle $C$.
|
## Solution.
Let the height $CD$ be denoted by $h$, and the segment $AD$ by $x$ (Fig. 10.6). We have $\angle ACD = 90^{\circ} - 75^{\circ} = 15^{\circ}$. Draw $AF$ such that $\angle CAF = \angle ACD = 15^{\circ}$. Then $\angle AFD = 30^{\circ}$, and from $\triangle ADF$ we get $AF = FC = 2x$, $DF = x \sqrt{3}$. But $DF = h - FC = h - 2x \Rightarrow x = \frac{h}{2 + \sqrt{3}} = h(2 - \sqrt{3})$. Since $AB = 2h$, we have $BD = AB - AD = 2h - x = h \sqrt{3}$. From $\triangle BDC$ we have $BC = \sqrt{BD^2 + CD^2} = 2h \Rightarrow \angle B = 30^{\circ}$ and $\angle C = 180^{\circ} - 75^{\circ} - 30^{\circ} = 75^{\circ}$.
Answer: $75^{\circ}$.
|
75
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.199. The bases of the trapezoid are 4 and 16 cm. Find the radii of the inscribed and circumscribed circles of the trapezoid, given that these circles exist.
|
Solution.
In trapezoid $ABCD$ (Fig. 10.9) $BC \| AD, BC=4$ cm, $AD=16$ cm. Since a circle is circumscribed around the given trapezoid, then $AB=CD$. Since a circle can be inscribed in the given trapezoid, then $AD+BC=AB+CD=2AB; AB=\frac{AD+BC}{2}=10$ cm. $BK$ is the height of the trapezoid. Then $AK=\frac{AD-BC}{2}=6$ cm. From $\triangle AKB \quad (\angle AKB=90^{\circ})$: $BK=\sqrt{AB^{2}-AK^{2}}=8$ cm. The radius of the inscribed circle $r=\frac{1}{2} BK=4$ cm.
The radius $R$ of the circumscribed circle will be found as the radius of the circle circumscribed around $\triangle ABD: R=\frac{AB \cdot BD \cdot AD}{4 S_{\triangle ABD}}, KD=AD-AK=10$ cm. From $\triangle BKD$ $\left(\angle BKD=90^{\circ}\right): BD=\sqrt{BK^{2}+KD^{2}}=2 \sqrt{41}$ cm. $S_{\triangle ABD}=\frac{1}{2} AD \cdot BK=64$ cm$^2$. Then $R=\frac{10 \cdot 2 \sqrt{41} \cdot 16}{4 \cdot 64}=\frac{5 \sqrt{41}}{4}$ (cm).
Answer: $4$ cm; $\frac{5 \sqrt{41}}{4}$ cm.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.205. A circle with a radius of 5 cm is inscribed in some angle. The length of the chord connecting the points of tangency is 8 cm. Two tangents, parallel to the chord, are drawn to the circle. Find the sides of the resulting trapezoid.
|
Solution.
The circle with center $O$ (Fig. 10.15) touches the sides of angle $E$ at points $K$ and $L, K L=8 \text{ cm}, O K=5 \text{ cm}, A B\|C D\| K L$. Draw the diameter of the circle $M N \| K L, P$ is the intersection point of $E O$ and $K L, \angle K P O=90^{\circ}, \triangle K P O \sim$ $\sim \triangle O K M-$ by two angles ( $\left.\angle P K O=\angle K O M, \angle K P O=\angle O K M=90^{\circ}\right)$. Then $\frac{K P}{K O}=\frac{K O}{M O}, M O=\frac{K O^{2}}{K P}=\frac{25}{4}$ cm. $M N=2 M O=\frac{25}{2}$ cm. $M N-$ is the midline of trapezoid $A B C D$ and, since a circle is inscribed in this trapezoid, then $B C=A D=M N=\frac{25}{2}$ cm. $B B_{1}$ is the height of trapezoid $A B C D$, $B B_{1}=2 O K=10 \text{ cm}$. From $\triangle B B_{1} C\left(\angle B B_{1} C=90^{\circ}\right): B_{1} C=\sqrt{B C^{2}-B B_{1}^{2}}=7.5 \text{ cm}$. $C D-A B=2 B_{1} C=15$ cm, $C D+A B=2 B C=25$ cm. Then $C D=20$ cm, $A B=5$ cm.
Answer: 20 cm; 5 cm; 12.5 cm; 12.5 cm.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.206. What integers represent the sides of an isosceles triangle if the radius of the inscribed circle is $3 / 2 \mathrm{~cm}$, and the radius of the circumscribed circle is $25 / 8$ cm
|
Solution.
In $\triangle ABC$, $AB = BC$, $BD$ is the altitude, $O_1$ is the center of the inscribed circle, and $O_2$ is the center of the circumscribed circle (see Fig. 10.16). The radii of these circles are $r = \frac{3}{2}$ cm and $R = \frac{25}{8}$ cm, respectively. $E$ is the point of intersection of the ray $BD$ and the circumscribed circle. $AO_1$ is the bisector of $\angle BAC$. Let $\angle BAO_1 = \angle O_1AD = \alpha$. Then $\angle AO_1D = 90^\circ - \alpha$. Since $BE$ is the diameter of the circumscribed circle, $\angle BAE = 90^\circ$, $\angle O_1AE = 90^\circ - \alpha$, and $BE = 2R = \frac{25}{4}$ cm. Therefore, $AE = O_1E$. Let $DE = x$ cm. Then $AE = O_1E = O_1D + DE = r + x = \frac{3}{2} + x$. From $\triangle BAE$ ($\angle BAE = 90^\circ$, $AD$ is the altitude): $AE^2 = DE \cdot BE$; $\left(\frac{3}{2} + x\right)^2 = x \cdot \frac{25}{4}$; $x = \frac{9}{4}$ or $x = 1$. From $\triangle ADE$ ($\angle ADE = 90^\circ$): $AD = \sqrt{AE^2 - DE^2}$. When $x = \frac{9}{4}$: $AE = \frac{15}{4}$ cm, $AD = 3$ cm, $AC = 6$ cm. When $x = 1$: $AE = \frac{5}{2}$ cm, $AD = \frac{\sqrt{21}}{2}$ cm, and $AC$ is expressed as an irrational number. Therefore, $AC = 6$ cm, $AB = BC = \sqrt{BE^2 - AE^2} = 5$ cm.
Answer: 5 cm, 5 cm, 6 cm.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.208. Perpendiculars are drawn from the vertex of the acute angle of a rhombus to the lines containing the sides of the rhombus to which this vertex does not belong. The length of each perpendicular is 3 cm, and the distance between their bases is $3 \sqrt{3}$ cm. Calculate the lengths of the diagonals of the rhombus.
|
Solution.
Since $\triangle A E F$ is isosceles (Fig. 10.18), the bisector $A M$ is perpendicular to $E F$ and lies on the diagonal of the rhombus. We find $A M^{2}=A F^{2}-M F^{2}=9-\frac{27}{4}=\frac{9}{4}$, i.e., $A M=\frac{3}{2}$ (cm). In $\triangle A C F$, we have $\angle F=90^{\circ}$ and $F M \perp A C \Rightarrow A F^{2}=A C \cdot A M, 9=A C \cdot \frac{3}{2}, A C=6$ (cm).
Next, $\triangle A C D \sim \triangle A E F$ (the base angles are equal as angles with mutually perpendicular sides), so $\frac{A M}{O D}=\frac{E F}{A C} \Leftrightarrow \frac{3 / 2}{O D}=\frac{3 \sqrt{3}}{6}$, $O D=\sqrt{3}$ cm. We get $B D=2 \sqrt{3}$ cm, $A C=6$ cm.
Answer: 6 and $2 \sqrt{3}$ cm.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.211. On the larger leg of a right triangle, a circle is constructed with this leg as its diameter. Determine the radius of this circle if the smaller leg of the triangle is 7.5 cm, and the length of the chord connecting the vertex of the right angle with the point of intersection of the hypotenuse and the circle is 6 cm.
|
Solution.
In $\triangle ABC$ (Fig. 10.21) $\angle ACB=90^{\circ}, BC>AC, AC=7.5$ cm, $N$ is the intersection point of the circle mentioned in the condition and the hypotenuse $AB, CN=6$ cm. $\angle CNB$ is an inscribed angle and subtends the diameter. Therefore, $\angle CNB=90^{\circ}$. From $\triangle ANC \quad (\angle ANC=90^{\circ}): AN=\sqrt{AC^{2}-CN^{2}}=4.5$ cm. Since $CN$ is the altitude of the right $\triangle ACB$, $\triangle ANC \sim \triangle CNB$. Therefore, $\frac{AN}{AC}=\frac{CN}{BC}, BC=\frac{AC \cdot CN}{AN}=10$ cm. The desired radius $R=\frac{1}{2} BC=5$ cm.
Answer: 5 cm.
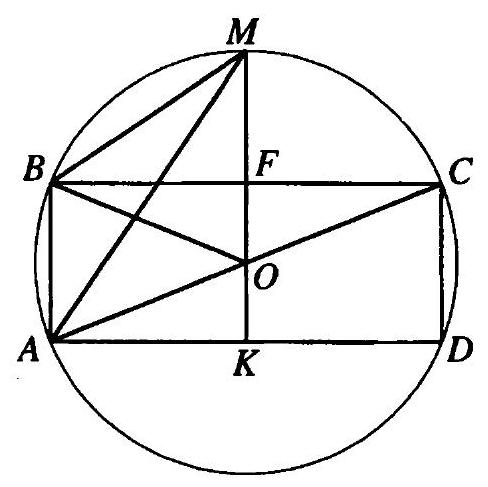
Fig. 10.22
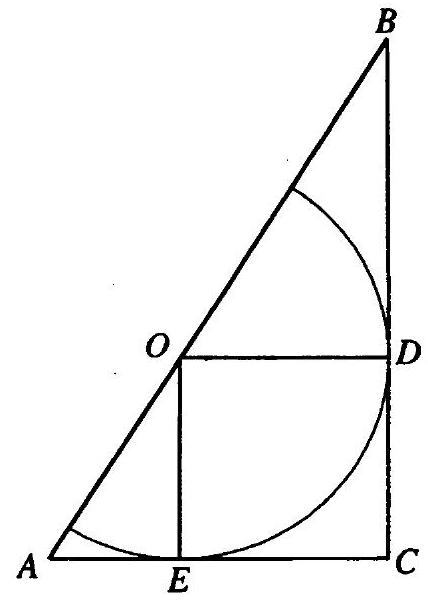
Fig. 10.23
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.212. The vertices of a rectangle inscribed in a circle divide it into four arcs. Find the distances from the midpoint of one of the larger arcs to the vertices of the rectangle, if its sides are 24 and 7 cm.
|
## Solution.
Since $AC$ is the diameter of the circle (Fig. 10.22), then $R=0.5 \sqrt{24^{2}+7^{2}}=12.5$ cm. In $\triangle B O F$, we have $O F=\sqrt{O B^{2}-B F^{2}}=\sqrt{12.5^{2}-12^{2}}=3.5$ cm; hence, $M F=12.5-3.5=9$ cm, $M K=12.5+3.5=16$ cm. From $\triangle M B F$ and $\triangle M A K$, we find the required distances: $M B=\sqrt{M F^{2}+B F^{2}}=\sqrt{9^{2}+12^{2}}=15 \text{ cm}$, $M A=\sqrt{M K^{2}+K A^{2}}=\sqrt{16^{2}+12^{2}}=20 \text{ cm}$.
Answer: 15 and $20 \text{ cm}$.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.215. In a right-angled triangle, the medians of the legs are $\sqrt{52}$ and $\sqrt{73}$. Find the hypotenuse of the triangle.
|
## Solution.
In $\triangle A B C$ (Fig. 10.25) $\angle A C B=90^{\circ}, B P$ and $A E$ are medians, $B P=\sqrt{52}$, $A E=\sqrt{73}$. Let $B C=x, A C=y$. Then $A B=\sqrt{x^{2}+y^{2}}$.
From $\triangle A C E\left(\angle A C E=90^{\circ}\right):$
$$
A C^{2}+C E^{2}=A E^{2} ; y^{2}+\frac{x^{2}}{4}=73
$$
From $\triangle B C P\left(\angle B C P=90^{\circ}\right)$ :
$$
B C^{2}+C P^{2}=B P^{2} ; x^{2}+\frac{y^{2}}{4}=52
$$
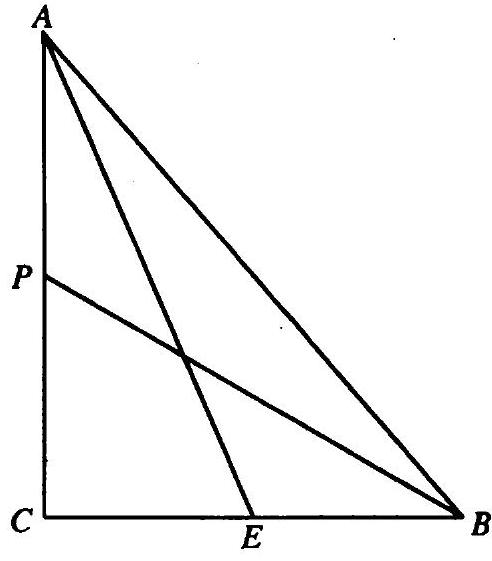
Fig. 10.25
We have $\left\{\begin{array}{l}4 y^{2}+x^{2}=292, \\ 4 x^{2}+y^{2}=208 ;\end{array} 5 x^{2}+5 y^{2}=500 ; x^{2}+y^{2}=100\right.$. Therefore, $A B=\sqrt{x^{2}+y^{2}}=10$.
Answer: 10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.216. Two circles, with radii of 4 and 8, intersect at a right angle. Determine the length of their common tangent.
|
Solution.
Let $A$ be the point of intersection of the circles with centers $O$ and $O_{1}$ (Fig. 10.26), $O A=8 \text{ cm}, O_{1} A=4 \text{ cm}$, $M N$ - their common tangent. According to the problem, the circles intersect at a right angle, so the tangents to them at point $A$ are perpendicular to each other. Therefore, the radii drawn to the point of tangency are also perpendicular. From $\triangle O A O_{1}: O O_{1}^{2}=O A^{2}+O_{1} A^{2}=80$. Draw $O_{1} D \| M N$. Then $O_{1} D \perp O M, M N=O_{1} D, M D=N O_{1}=4, O D=$ $=O M-M D=4$. From $\triangle O D O_{1}: O_{1} D=\sqrt{O O_{1}^{2}-O D^{2}}=8$.
Answer: 8.
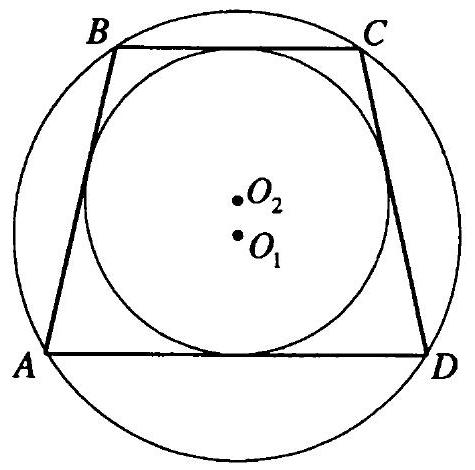
Fig. 10.27
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.218. A line parallel to the bases of a trapezoid passes through the point of intersection of its diagonals. Find the length of the segment of this line, enclosed between the lateral sides of the trapezoid, if the bases of the trapezoid are 4 and 12 cm.
|
## Solution.
In trapezoid $ABCD$ (Fig. 10.28) $BC \| AD, BC=4$ cm, $AD=12$ cm, $O$ is
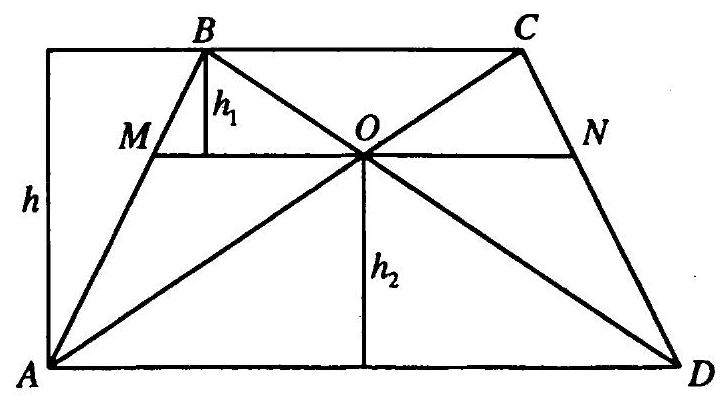
Fig. 10.28
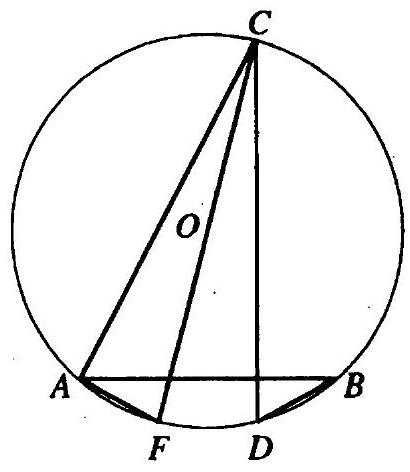
Fig. 10.29
the point of intersection of the diagonals, $MN$ is the segment of the desired length. Let $h_{1}$ be the distance between the lines $BC$ and $MN$, $h_{2}$ be the distance between $MN$ and $AD$, $h$ be the distance between $BC$ and $AD$, $h=h_{1}+h_{2}$. $\triangle MBO \sim \triangle ABD$. Then $\frac{MO}{AD}=\frac{h_{1}}{h}$ (1). $\triangle OCN \sim \triangle ACD$. Then $\frac{ON}{AD}=\frac{h_{1}}{h}$. Therefore, $MO=ON=\frac{1}{2} MN$. Let $MO=x$ cm. Then from (1) we have: $\frac{x}{12}=\frac{h_{1}}{h} \cdot \triangle MAO \sim \triangle BAC$. Then $\frac{MO}{BC}=\frac{h_{2}}{h} ; \frac{x}{4}=\frac{h_{2}}{h}$. Therefore, $\frac{x}{12}+\frac{x}{4}=\frac{h_{1}}{h}+\frac{h_{2}}{h} ; \frac{x}{3}=\frac{h_{1}+h_{2}}{h} ; x=3$. Thus, $MN=6$ cm.
Answer: 6 cm.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.224. Given an isosceles triangle with a base of 12 cm and a lateral side of $18 \mathrm{~cm}$. What segments need to be laid off from the vertex of the triangle on its lateral sides, so that by connecting their ends, a trapezoid with a perimeter of 40 cm is obtained?
|
## Solution.
By the condition in $\triangle A B C$ (Fig. 10.33) we have: $A B=B C=18, A C=12$. Let $B D=B E=x$. Then $A D=E C=18-x$. The perimeter of trapezoid $A D E C$ is: $P=A C+D E+2 A D=40$, from which $D E=40-(2 A D+A C)=2 x-8$. $\triangle A B C \sim$ $\sim \triangle D B E$, therefore, $\frac{B D}{D E}=\frac{A B}{A C}$ or $\frac{x}{2 x-8}=\frac{18}{12}, x=6$.
Answer: 6 cm.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.225. Two circles of different radii touch each other externally. Find the angle determined by the chords connecting the point of contact of the circles with the points of contact of their common external tangent.
|
Solution.
Let $AB$ be the common external tangent of the given circles, $C$ be the point of tangency, and $D$ be the intersection point of $AB$ and the common tangent of the circles at point $C$ (Fig. 10.34). Then $DB = DC$, $DA = DC$, hence $\angle DCB = \angle DBC$, $\angle DAC = \angle DCA$. From $\triangle ACB: \angle DAC + \angle DBC + \angle ACB = 180^{\circ}$, therefore, $\angle DAC + \angle DBC = \angle ACB$ and $2 \angle ACB = 180^{\circ}$, from which $\angle ACB = 90^{\circ}$.
Answer: $90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.229. A parallelogram with sides of 3 cm and 5 cm and a diagonal of 6 cm is inscribed in a triangle. Find the sides of the triangle, given that the diagonals of the parallelogram are parallel to the lateral sides of the triangle, and the smaller of its sides lies on the base of the triangle.
|
Solution.
Let in $\triangle A B C D K=E F=3 \text{cm}, D E=5 \text{cm}, D F=6$ cm, $D K \| E F$, $O$ - the point of intersection of the diagonals $D F$ and $E K$ of the parallelogram $D E F K$ (Fig. 10.38). Let $E O=x$ cm. Then $D F^{2}+E K^{2}=2\left(D E^{2}+E F^{2}\right)$; $36+4 x^{2}=2(25+9) ; x=2 \sqrt{2}$. OEBF is a parallelogram. Then $B E=F O=3 \text{cm}, B F=E O=2 \sqrt{2} \text{cm}$. K E F C is a parallelogram. Then $F C=E K=4 \sqrt{2}$ cm, $K C=E F=3 \text{cm}$. A E F D is a parallelogram. Then $A E=D F=6$ cm, $A D=E F=3$ cm. Therefore, $A B=A E+E B=9$ cm, $B C=B F+F C=6 \sqrt{2} \text{cm}, A C=A D+D K+K C=9 \text{cm}$.
Answer: 9 cm; 9 cm; $6 \sqrt{2}$ cm.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.230. The height, base, and sum of the lateral sides of the triangle are 24, 28, and 56 cm, respectively. Find the lateral sides.
|
Solution.
The area of the triangle $S=\frac{24 \cdot 28}{2}=336 \mathrm{~cm}^{2}$. Let one of the lateral sides be $x$ cm, then the second one is $(56-x)$ cm. The semi-perimeter of the triangle
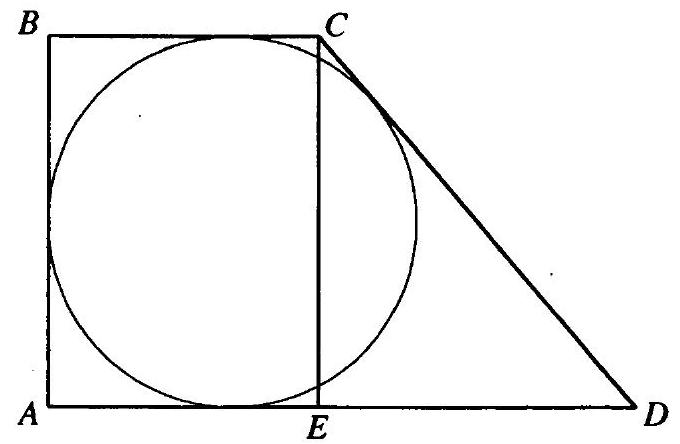
Fig. 10.39
$p=\frac{28+56}{2}=42$ (cm). Then, by Heron's formula, the area of the triangle $S=\sqrt{42 \cdot 14(42-x)(42-56+x)}$. Therefore, $\sqrt{3 \cdot 14^{2} \cdot(42-x)(x-14)}=336$; $\sqrt{3(42-x)(x-14)}=24 ;\left[\begin{array}{l}x=26, \\ x=30 .\end{array}\right.$ Thus, the lateral sides of the given triangle are 26 cm and 30 cm.
Answer: 26 cm; 30 cm.
|
26
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.234. A circle with a radius of 13 cm touches two adjacent sides of a square with a side length of $18 \mathrm{~cm}$. Into which two segments does the circle divide each of the other two sides of the square?
|
## Solution.
Draw the radius $O K$ (Fig. 10.42); then $K L=\sqrt{K O^{2}-L O^{2}}$. $L O=B E=18-13=5(\mathrm{~cm}) \Rightarrow K L=\sqrt{13^{2}-5^{2}}=12$ (cm), $B K=13-12=1$ (cm). We have found that the side of the square is divided into segments of 1 and 17 cm.
Answer: 1 and 17 cm.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.244. A circle with a radius of 3 cm is inscribed in a triangle. Calculate the lengths of the sides of the triangle if one of them is divided by the point of tangency into segments of 4 and $3 \mathrm{~cm}$.
|
Solution.
Let $O$ be the center of the circle with radius 3 inscribed in $\triangle ABC$ (Fig. 10.51). $M, N, K$ are the points of tangency of this circle with the sides $AB, BC, AC$ respectively. $BN=3 \text{ cm}, NC=4 \text{ cm}$. Then $ON \perp BC, OM \perp AB$, $ON=OM=3 \text{ cm}$. $BM=BN=3 \text{ cm}$. Therefore, $BMON$ is a rhombus, and since it has two right angles, $BMON$ is a square. Consequently, $\triangle ABC$ is a right triangle. Let $AM=x \text{ cm}$. Then $AK=AM=x \text{ cm}$. $CK=CN=4 \text{ cm}$. Therefore, $AB=(x+3) \text{ cm}$, $BC=7 \text{ cm}$, $AC=(x+4) \text{ cm}$, and $AC^2=AB^2+BC^2$. Then $(x+4)^2=49+(3+x)^2; x=21$. Thus, $AC=25 \text{ cm}$, $AB=24 \text{ cm}$.
Answer: 24 cm; 25 cm; 7 cm.
|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.251. Five circles are inscribed in an angle of $60^{\circ}$ such that each subsequent circle (starting from the second) touches the previous one. By what factor is the sum of the areas of all five corresponding circles greater than the area of the smallest circle?
|
## Solution.
Let $A$ be the vertex of the angle. $O_{i}$ and $r_{i}$ be the center and radius of the $i$-th circle $(i=1, \ldots, 5)$. Since $\frac{1}{2} \angle A=30^{\circ}$, then $A O_{i}=2 r_{i}, A O_{i-1}=2 r_{i-1}$, from which $A O_{i}=A O_{i-1}+r_{i-1}+r_{i}$ or $2 r_{i}=2 r_{i-1}+r_{i-1}+r_{i}$, i.e., $r_{i}=3 r_{i-1}$. Therefore, the radii of the circles form a geometric progression with a common ratio of 3, and the sum of the areas of the five circles will be $S=\pi r_{1}^{2}\left(1+9+9^{2}+9^{3}+9^{4}\right)=\frac{\pi r_{1}^{2}\left(9^{5}-1\right)}{9-1}=7381 \pi r_{1}^{2}$. Thus, $S: \pi r_{1}^{2}=7381$.
Answer: 7381 times.
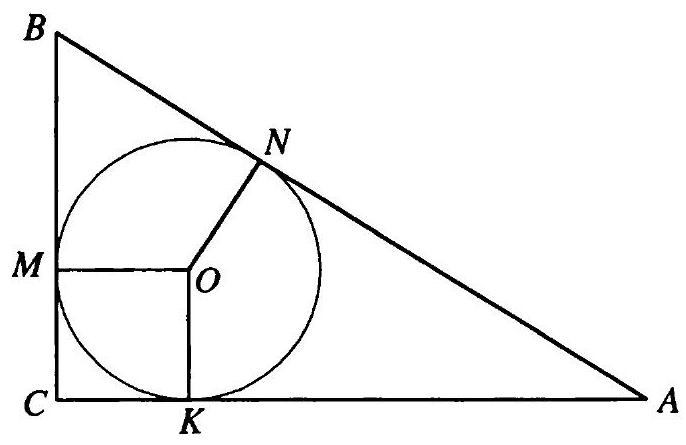
Fig. 10.58
|
7381
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.255. Through point $A$ of a circle with a radius of 10 cm, two mutually perpendicular chords $A B$ and $A C$ are drawn. Calculate the radius of the circle that is tangent to the given circle and the constructed chords, if $A B=16$ cm.
|
Solution.
$O$ is the center of a circle with a radius of 10 cm (Fig. 10.60), $O_{1}$ is the center of a circle that touches the chords $A B$ and $A C$ and the given circle at points $M, D$, and $K$ respectively. Then $O_{1} D \perp A C, O_{1} M \perp A B$. $\angle B A C$ is an inscribed and right angle. Therefore, $B C$ is the diameter of the given circle, $B C=20 \text{ cm}$, $A C=\sqrt{B C^{2}-A B^{2}}=\sqrt{20^{2}-16^{2}}=12$ (cm). Drop perpendiculars $O L$ and $O N$ to $A C$ and $A B$ respectively. Then $A L=L C=\frac{1}{2} A C=6$ cm, $A N=N B=\frac{1}{2} A B=8$ cm. Let the desired radius $O_{1} K=O_{1} D=O_{1} M=$ $=x$ cm. $E$ is the point of intersection of $O L$ and $O_{1} M$. Then $\angle O E O_{1}=90^{\circ}$, $O E=O L-E L=A N-O_{1} D=(8-x) \text{ cm}, Q_{1} E=O_{1} M-M E=O_{1} M-A L=(x-6) \text{ cm}$.
$O Q_{1}=O K-Q_{1} K=(10-x)$ cm. From $\triangle O E Q\left(\angle O E Q=90^{\circ}\right): O E^{2}+E O_{1}^{2}=O O_{1}^{2} ;$ $(8-x)^{2}+(x-6)^{2}=(10-x)^{2} ; x=8$.
Answer: 8 cm.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.256. The lengths of two sides of an acute triangle are $\sqrt{13}$ and $\sqrt{10} \mathrm{~cm}$. Find the length of the third side, knowing that this side is equal to the height drawn to it.
|
Solution.
Let in $\triangle A B C$ (Fig. 10.61) $A B=\sqrt{10}$ cm, $B C=\sqrt{13}$ cm, height $B D=A C$. Since $\triangle A B C$ is an acute-angled triangle, point $D$ lies on the segment $A C$. Let $B D=A C=x$ cm. From $\triangle A D B\left(\angle A D B=90^{\circ}\right)$: $A D=\sqrt{A B^{2}-B D^{2}}=\sqrt{10-x^{2}} \cdot$ And from $\triangle C D B\left(\angle C D B=90^{\circ}\right): C D=\sqrt{B C^{2}-B D^{2}}=$ $=\sqrt{13-x^{2}} \cdot$ Therefore, $A D+D C=A C ; \sqrt{10-x^{2}}+\sqrt{13-x^{2}}=x$; $\sqrt{13-x^{2}}=x-\sqrt{10-x^{2}} ; 13-x^{2}=x^{2}-2 x \cdot \sqrt{10-x^{2}}+10-x^{2} ; 2 x \sqrt{10-x^{2}}=x^{2}-3$; $\left\{\begin{array}{l}4 x^{2}\left(10-x^{2}\right)=x^{2}-6 x^{2}+9 \\ x^{2} \geq 3 ;\end{array}\left\{\begin{array}{l}5 x^{4}-46 x^{2}+9=0, \\ x^{2} \geq 3 ;\end{array}\left\{\begin{array}{l}{\left[\begin{array}{l}x^{2}=9, \\ x^{2}=\frac{1}{5},\end{array} x^{2}=9\right.} \\ x^{2} \geq 3 ;\end{array}\right.\right.\right.$
From this, $A C=3 \text{ cm}$.
Answer: 3 cm.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.259. On the segment $A C$ of length 12 cm, a point $B$ is constructed such that $A B=4 \text{ cm}$. On the segments $A B$ and $A C$ as diameters, semicircles are constructed in the same half-plane with boundary $A C$. Calculate the radius of the circle that is tangent to the constructed semicircles and $A C$.
|
## Solution.
Points $O_{1}$ and $O_{2}$ are the centers of semicircles with diameters $A B$ and $A C$ and radii $R_{1}=2$ cm and $R_{2}=6$ cm, respectively (Fig. 10.64). $O_{3}$ is the center of the circle with the unknown radius $x$ cm, $x>0$. Then $O_{1} O_{3}=(x+2)$ cm,
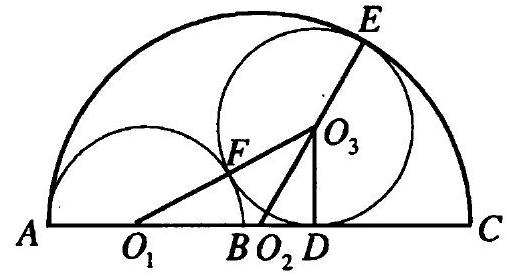
Fig. 10.64

Fig. 10.65
$O_{1} O_{2}=R_{2}-R_{1}=4 \text{ cm}, O_{2} O_{3}=(6-x) \text{ cm}$. $D$ is the point of tangency of the circle with center $O_{3}$ and $A C$. Then $O_{3} D \perp A C, O_{3} D=x$ cm. In $\Delta O_{1} O_{2} O_{3}$, the semiperimeter $p=\frac{O_{1} O_{3}+O_{2} O_{3}+O_{1} O_{2}}{2}=6$ cm. Then its area $S=\sqrt{p\left(p-O_{1} O_{3}\right)\left(p-O_{1} O_{2}\right)\left(p-O_{2} O_{3}\right)}=\sqrt{6(6-x-2)(6-4)(6-6+x)}=$ $=\sqrt{12 x(4-x)}$.
On the other hand, $S=\frac{1}{2} O_{1} O_{2} \cdot O_{3} D=2 x$. Then $\sqrt{12 x(4-x)}=2 x$; $3 x(4-x)=x^{2} ; x=3$.
Answer: 3 cm.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.281. A quadrilateral with angles of $120, 90, 60$, and $90^{\circ}$ is inscribed in a circle. The area of the quadrilateral is $9 \sqrt{3}$ cm $^{2}$. Find the radius of the circle, given that the diagonals of the quadrilateral are perpendicular to each other.
|
Solution.
Let $ABCD$ be the quadrilateral mentioned in the problem (Fig. 10.76), $\angle ABC = \angle ADC = 90^\circ$, $\angle BAD = 120^\circ$, $\angle BCD = 60^\circ$. $P$ is the intersection point of $AC$ and $BD$, and $AC \perp BD$. Since $\angle ABC = 90^\circ$, $AC$ is the diameter of the given circle. $BP$ is the height of the right triangle $\triangle ABC$. Therefore, $\angle ABD = \angle ACB$. $\angle ABD$ and $\angle ACD$ are inscribed angles subtending the chord $AD$. Thus, $\angle ABD = \angle ACD$. Consequently, $\angle ACB = \angle ACD = \frac{1}{2} \angle BCD = 30^\circ$. Therefore, $\triangle ABC = \triangle ADC$ (by hypotenuse and acute angle), $S_{\triangle ABC} = \frac{1}{2} S_{ABCD} = \frac{9\sqrt{3}}{2} \text{ cm}^2$. Let $AB = a$. Then $BC = AB \cot \angle ACB = a \sqrt{3}$ and $S_{\triangle ABC} = \frac{1}{2} AB \cdot BC = \frac{a^2 \sqrt{3}}{2}$. Therefore, $\frac{a^2 \sqrt{3}}{2} = \frac{9\sqrt{3}}{2}$, $a = 3$. The desired radius $R = \frac{1}{2} AC = AB = 3$ cm. Answer: 3 cm.
Fig. 10.77
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.283. The area of a right-angled triangle is $24 \mathrm{~cm}^{2}$, and the hypotenuse is 10 cm. Find the radius of the inscribed circle.
|
Solution.
Let $a$ and $b$ be the legs of the triangle. We have the system $\left\{\begin{array}{l}a b=48, \\ a^{2}+b^{2}=100,\end{array} \Rightarrow\right.$ $\Rightarrow a^{2}+2 a b+b^{2}=196, a^{2}-2 a b+b^{2}=4, \Rightarrow a+b=14, a-b=2$ and, consequently, $a=8$ (cm), $b=6$ (cm). Since $S=p r$, then $24=12 r, r=2$ (cm).
Answer: $2 \mathrm{~cm}$.
Fig. 10.78
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.309. The area of an isosceles trapezoid circumscribed about a circle is $32 \mathrm{~cm}^{2}$; the acute angle of the trapezoid is $30^{\circ}$. Determine the sides of the trapezoid.
|
## Solution.
Let the height $B H$ of the trapezoid be $h$ (Fig. 10.98). Then $A B=2 h$ (since $\angle A=30^{\circ}$), $B C+A D=4 h$ (since $B C+A D=A B+C D=2 A B$). The area of the trapezoid $S=\frac{(B C+A D) h}{2}=2 h^{2}=32\left(\mathrm{~cm}^{2}\right)$, from which $h=4$ cm. Therefore, $A B=C D=8 \mathrm{~cm}, B C+A D=16 \mathrm{~cm}$. But $B C+A D=2 B C+2 A H=$ $=2 B C+8 \sqrt{3}$. Thus, $A B=C D=8 \mathrm{~cm}, B C=8-4 \sqrt{3} \mathrm{~cm}, A D=8+4 \sqrt{3} \mathrm{~cm}$.
Answer: 8 cm; $8-4 \sqrt{3}$ cm; $8+4 \sqrt{3}$ cm.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.321. The medians of a triangle are 3, 4, and 5 cm. Find the area of the triangle.
|
## Solution.
Let $A N, B M, C P$ be the medians of $\triangle A B C$ (Fig. 10.110), $O$-the point of their intersection, $A N=3 \text{ cm}, B M=4 \text{ cm}, C P=5 \text{ cm}$. On the extension of segment $B M$ beyond point $M$, lay off segment $D M=O M$. Then $D O=B O=$ $=\frac{2}{3} B M=\frac{8}{3}$ cm. Drop a perpendicular $A K$ to $B M . S_{\triangle A D O}=$ $=\frac{1}{2} D O \cdot A K=\frac{1}{2} B O \cdot A K=S_{\triangle A B O}=\frac{1}{3} S_{\triangle A B C}$. Since $A O C D$ is a parallelogram, then $A D=O C=\frac{10}{3} \text{ cm} . A O=\frac{2}{3} A N=2 \text{ cm}$. Using Heron's formula, we find $S_{\triangle A D O}=\frac{8}{3} \text{ cm}^{2}$. Then $S_{\triangle A B C}=3 S_{\triangle 1 D O}=8 \text{ cm}^{2}$.
Answer: $8 \text{ cm}^{2}$.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.323. The diagonal of an isosceles trapezoid is $10 \mathrm{~cm}$, and the area is $48 \mathrm{~cm}^{2}$. Find the height of the trapezoid.
|
Solution.
In trapezoid $ABCD$ (Fig. 10.112) $AB=CD, AC=10$ cm, $CE$ is the height. Let $AE=x$ cm, $CE=y$ cm. Since $AE=\frac{AD+BC}{2}$, then by the condition $xy=48$ cm. From $\triangle AEC\left(\angle AEC=90^{\circ}\right): AE^{2}+CE^{2}=AC^{2} ; x^{2}+y^{2}=100$. We solve the system of equations: $\left\{\begin{array}{l}x^{2}+y^{2}=100 ; \\ xy=48 ;\end{array} ;\left\{\begin{array}{l}(x+y)^{2}-2xy=100 \\ xy=48 ;\end{array}\right.\right.$ $\left\{\begin{array}{l}(x+y)^{2}=196 ; \\ xy=48 .\end{array}\right.$ Since $x>0, y>0$, then $x+y=14$. Then $\left\{\begin{array}{l}x=8, \\ y=6,\end{array}\right.$ or $\left\{\begin{array}{l}x=6, \\ y=8 .\end{array}\right.$ Therefore, the height of the trapezoid is 6 cm or 8 cm.
Answer: 6 cm, 8 cm.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.333. Parallelogram $A B C D$, where $A B=153 \mathrm{~cm}, A D=180$ cm, $B E=135$ cm ( $B E$ - height), is divided into three equal-area figures by lines perpendicular to $A D$. At what distance from point $A$ are the points of intersection of these perpendiculars with $A D$?
|
## Solution.
Let $K M$ and $L H$ be the lines dividing the parallelogram $A B C D$ (Fig. 10.119) into three equal-area figures, and $D F$ be the height of the parallelogram. Then $B K=E M=H D=L F$. Let $B K=x$ cm. From $\triangle A E B\left(\angle A E B=90^{\circ}\right)$: $A E=\sqrt{A B^{2}-B E^{2}}=72$ cm. Then $A M=(x+72) \mathrm{cm}$ and $S_{A B K M}=$ $=\frac{A M+B K}{2} \cdot B E=135(x+36) \mathrm{cm}^{2} . S_{A B C D}=A D \cdot B E=180 \cdot 135 \mathrm{~cm}^{2}$. Since $S_{A B K M}=\frac{1}{3} S_{A B C D}$, then $135(x+36)=60 \cdot 135 ; x=24$. Therefore, $A M=96 \mathrm{cm}$, $A H=A D-H D=156 \mathrm{~cm}$.
Answer: 96 cm; 156 cm.
|
96
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.335. The perimeter of a sector is 28 cm, and its area is $49 \mathrm{~cm}^{2}$. Determine the length of the arc of the sector.
|
## Solution.
The perimeter of the sector $p=2 r+l$, where $r$ is the radius of the sector, $l$ is the length of the arc of the sector. The area of the sector $S=\frac{r l}{2}$.
Then $\left\{\begin{array}{l}2 r+l=28, \\ r l=98,\end{array}\left\{\begin{array}{l}r=\frac{28-l}{2} \\ r l=98\end{array}, l(28-l)=196 ; l^{2}-28 l+196=0 ; l=14\right.\right.$.
Answer: 14 cm.
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.346. A circle with center $O_{1}$ is divided by the diameter $A B$ into two semicircles. In one of them, two new semicircles are constructed, based on $O_{1} A$ and $O_{1} B$ as diameters. A circle is inscribed in the curvilinear figure bounded by the contours of these three semicircles. How many times smaller is its area compared to the area of the given circle?
|
## Solution.
Let $O_{2}$ be the midpoint of $A O_{1}$ - the center of one semicircle, $O_{3}$ be the midpoint of $B O_{1}$ - the center of the second semicircle, $O_{4}$ - the center of the circle inscribed in the curvilinear figure mentioned in the problem (Fig. 10.129).
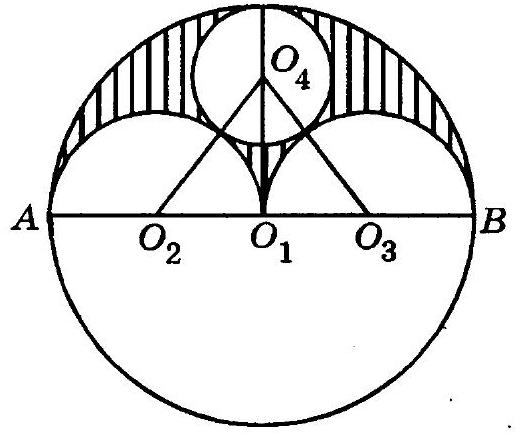
Fig. 10.129
Let $R$ be the radius of the circle with center $O_{1}$, and $S_{1}$ be its area, $r$ be the radius of the circle with center $O_{4}$, and $S_{2}$ be its area. We have: $O_{1} O_{2}=O_{1} O_{3}=\frac{R}{2}$, $O_{2} O_{4}=O_{3} O_{4}=\frac{R}{2}+r, O_{1} O_{4}=R-r$. In triangle $O_{2} O_{4} O_{3}: O_{2} O_{4}=O_{3} O_{4}$, point $O_{1}$ is the midpoint of $O_{2} O_{3}$. Therefore, $O_{1} O_{4} \perp O_{2} O_{3}$, then
Fig. 10.130
Fig. 10.131
$O_{2} O_{4}^{2}=O_{1} O_{2}^{2}+O_{1} O_{4}^{2}$, i.e., $\left(\frac{R}{2}+r\right)^{2}=\left(\frac{R}{2}\right)^{2}+(R-r)^{2} . R^{2}=3 R r, R=3 r$.
Therefore, $\frac{S_{1}}{S_{2}}=\frac{R^{2}}{r^{2}}=9$.
Answer: 9 times.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.357. In trapezoid $ABCD$, the lengths of the bases $AD=24$ cm and $BC=8$ cm, and the diagonals $AC=13$ cm, $BD=5\sqrt{17}$ cm are known. Calculate the area of the trapezoid.
|
## Solution.
Draw $B H \perp A D$ and $C F \perp A D$ (Fig. 10.137). Let $A H=x$; then $A F=8+x, D H=24-x$. Considering that $B H=C F$, in $\triangle A F C$ and $\triangle B H D$ we have $A C^{2}-A F^{2}=B D^{2}-D H^{2} . \Rightarrow 64 x=256, x=4$ cm.
Then $C F=\sqrt{A C^{2}-A F^{2}}=\sqrt{13^{2}-12^{2}}=5 \text{ cm}$.
Thus, $S=\frac{1}{2}(24+8) \cdot 5=80 \text{ cm}^{2}$.
Answer: $\quad 80 \text{ cm}^{2}$.
|
80
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.114. In a truncated triangular pyramid, the height is 10 m, the sides of one base are 27, 29, and 25 m, and the perimeter of the other base is 72 m (Fig. 11.12). Determine the volume of the truncated pyramid.
|
Solution.
Let $S_{1}$ and $S_{2}$ be the areas of the bases of the given truncated pyramid, and $P_{1}$ and $P_{2}$ be the perimeters of the bases, with $P_{2}=72 \text{ m}$. Then $P_{1}=27+29+52=108 \text{ (m)}$, from which, using Heron's formula, $S_{1}=270 \text{ m}^{2}$.

Fig. 11.12

Fig. 11.13
Since the bases of the truncated pyramid are similar, $\frac{S_{2}}{S_{1}}=\frac{P_{2}^{2}}{P_{1}^{2}}$; $S_{2}=S_{1} \cdot\left(\frac{P_{2}}{P_{1}}\right)^{2}=120 \text{ m}^{2}$
The volume of the truncated pyramid $V=\frac{1}{3} H\left(S_{1}+\sqrt{S_{1} S_{2}}+S_{2}\right)=1900 \text{ m}^{3}$.
Answer: $1900 \text{ m}^{3}$.
|
1900
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.117. The base of a right prism is an isosceles trapezoid $A B C D ; A B=C D=13$ cm, $B C=11$ cm, $A D=21$ cm. The area of its diagonal section is $180 \mathrm{~cm}^{2}$. Calculate the total surface area of the prism.
|
Solution.
$C K$ is the height of the base of the right prism $A B C D A_{1} B_{1} C_{1} D_{1}$ (Fig. 11.14). Given $A B=C D$, then $K D=\frac{A D-B C}{2}=5 \text{ cm}, A K=\frac{A D+B C}{2}=16 \text{ cm}$.
From $\triangle C K D\left(\angle C K D=90^{\circ}\right): C K=\sqrt{C D^{2}-K D^{2}}=12 \text{ cm}$.
From $\triangle A K C\left(A K C=90^{\circ}\right): A C=\sqrt{A K^{2}+C K^{2}}=20 \text{ cm}$. The diagonal section of the prism $A A_{1} C_{1} C$ is a rectangle with an area of $S_{1}=180 \text{ cm}^{2}$,
thus the height of the prism $H=C C_{1}=\frac{S_{1}}{A C}=9$ cm. The perimeter of the base of the prism $P=58$ cm, the area of the base $S_{\text {base }}=\frac{A D+B C}{2} \cdot C K=192 \text{ cm}^{2}$, the lateral surface area $S_{6}=P H=522 \text{ cm}^{2}$. The total surface area of the prism $S=S_{6}+2 S_{\text {base }}=906 \text{ cm}^{2}$.
Answer: $906 \text{ cm}^{2}$.
|
906
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.149. The base of a right parallelepiped is a parallelogram, one of the angles of which is $30^{\circ}$. The area of the base is 4 dm $^{2}$. The areas of the lateral faces of the parallelepiped are 6 and 12 dm ${ }^{2}$. Find the volume of the parallelepiped.
|
Solution.
The volume of the parallelepiped $V=S_{\text {base }} h$, where $h$ is the height of the parallelepiped. Since the parallelepiped is a right one, the heights of the lateral faces are also equal to $h$ (Fig. 11.44). According to the problem, $\angle B A D=30^{\circ}, A B \cdot h=6$ dm $^{2}, A D \cdot h=12$ dm $^{2}$, i.e., $A D=2 A B$. Let $B K \perp A D$; then $B K=\frac{1}{2} A B$.
Since $A D \cdot B K=4$ dm ${ }^{2}$, we have $2 A B \cdot \frac{1}{2} A B=4, A B=2$ (dm); therefore, $h=3$ dm. Finally, $V=4 \cdot 3=12$ dm $^{3}$.
Answer: 12 dm $^{3}$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.193. The base of the triangle is 4, and its median is $\sqrt{6}-\sqrt{2}$. One of the angles at the base is $15^{\circ}$. Show that the acute angle between the base of the triangle and its median is $45^{\circ}$.
|
Solution.
Let $BD$ be the median of $\triangle ABC, BD=\sqrt{6}-\sqrt{2}, AC=4, \angle A=15^{\circ}$ (Fig. 12.60), $\angle ADB=x$.
Then $\angle ABD=180^{\circ}-\left(x+15^{\circ}\right)$.
By the Law of Sines
from $\triangle ABD:$
$\frac{AD}{\sin \angle ABD}=\frac{BD}{\sin \angle A} \Rightarrow \frac{2}{\sin \left(x+15^{\circ}\right)}=\frac{\sqrt{6}-\sqrt{2}}{\sin 15^{\circ}} \Leftrightarrow \sin \left(x+15^{\circ}\right)=\frac{2 \sin 15^{\circ}}{\sqrt{6}-\sqrt{2}}$.
$$
\sin 15^{\circ}=\sin \left(45^{\circ}-30^{\circ}\right)=\sin 45^{\circ} \cos 30^{\circ}-\cos 45^{\circ} \sin 30^{\circ}=\frac{\sqrt{6}-\sqrt{2}}{4}
$$

Fig. 12.60

Fig. $12.60, \mathrm{a}$
From here $\sin \left(x+15^{\circ}\right)=\frac{2 \cdot \frac{\sqrt{6}-\sqrt{2}}{4}}{\sqrt{6}-\sqrt{2}}=\frac{1}{2} \Rightarrow x+15^{\circ}=30^{\circ}$ or $x+15^{\circ}=$ $=150^{\circ} ; x=15^{\circ}$ or $x=135^{\circ}$.
Thus, there are two triangles that satisfy the given conditions. In the first one, the smaller angle between the median and the base of the triangle - angle $ADB$ is equal to $15^{\circ}$ (Fig. 12.60), and in the second one, $-\angle BDC=180^{\circ}-\angle ADB=45^{\circ}$ (Fig. 12.60, a).
|
45
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
12.194. In a trapezoid, the smaller base is equal to 2, the adjacent angles are $135^{\circ}$ each. The angle between the diagonals, facing the base, is $150^{\circ}$. Find the area of the trapezoid.
Fig. 12.61
|
## Solution.
Let in trapezoid $A B C D$, $B C=2, \angle A B C=\angle D C B=135^{\circ}, O$ - the point of intersection of the diagonals, $\angle B O C=150^{\circ}$ (Fig. 12.61).
In $\triangle B O C: \angle A C B=\angle D B C=15^{\circ}$, then $\angle B A C=180^{\circ}-(\angle A B C+$ $+\angle A C B)=30^{\circ}$.
By the Law of Sines in $\triangle A B C$ :
$$
\begin{gathered}
\frac{A C}{\sin \angle A B C}=\frac{B C}{\sin \angle B A C} \Rightarrow A C=\frac{B C \sin \angle A B C}{\sin \angle A B C}=\frac{2 \sin 135^{\circ}}{\sin 30^{\circ}}=2 \sqrt{2} \\
S_{\triangle A B C D}=\frac{1}{2} A C \cdot B D \sin \angle B O C=\frac{1}{2} A C^{2} \sin \angle B O C=\frac{1}{2}(2 \sqrt{2})^{2} \sin 150^{\circ}=2
\end{gathered}
$$
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.195. Prove that if the bisector of one of the angles of a triangle is equal to the product of the sides enclosing it, divided by their sum, then this angle is $120^{\circ}$.

Fig. 12.62

Fig. 12.63
|
## Solution.
Let $B D$ be the bisector of $\triangle A B C$ (Fig.12.62), $B C=a, A B=b, B D=l$, $\angle A B C=\alpha$.
$S_{\triangle A B C}=S_{\triangle A B D}+S_{\triangle C B D} \Rightarrow \frac{a b}{2} \sin \alpha=\frac{a l}{2} \sin \frac{\alpha}{2}+\frac{b l}{2} \sin \frac{\alpha}{2} \Leftrightarrow$
$\Leftrightarrow 2 a b \sin \frac{\alpha}{2} \cos \frac{\alpha}{2}=l(a+b) \sin \frac{\alpha}{2} \Leftrightarrow \cos \frac{\alpha}{2}=\frac{l(a+b)}{2 a b}$.
By the condition $l=\frac{a b}{a+b}$ and $0^{\circ}<\frac{\alpha}{2}<90^{\circ}$, therefore $\cos \frac{\alpha}{2}=\frac{1}{2}$, $\frac{\alpha}{2}=60^{\circ}, \alpha=120^{\circ}$, which is what we needed to prove.
|
120
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
13.211. The digits of a certain three-digit number form a geometric progression. If in this number the digits of the hundreds and units are swapped, the new three-digit number will be 594 less than the desired one. If, however, in the desired number the digit of the hundreds is erased and the digits of the resulting two-digit number are rearranged, the new two-digit number will be 18 less than the number expressed by the last two digits of the desired number. Find this number.
|
## Solution.
Let the desired number have the form $100 x+10 y+z$, where $x, y, z$ form a geometric progression, which means $x z=y^{2}$. From the condition, we get:
$$
\begin{aligned}
& 100 z+10 y+x=100 x+10 y+z-594 \Rightarrow \\
& \Rightarrow x-z=6 ; 10 y+z=10 z+y+18 \Rightarrow y-z=2
\end{aligned}
$$
We have the system of equations
$$
\left\{\begin{array}{l}
x z=y^{2} \\
x-z=6, \\
y-z=2
\end{array}\right.
$$
Answer: 842.
|
842
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.213. Usually, two mechanisms are involved in performing a certain task simultaneously. The productivity of these mechanisms is not the same, and when working together, they complete the task in 30 hours. However, this time the joint operation of the two mechanisms lasted only 6 hours, after which the first mechanism was stopped and the second mechanism completed the remaining part of the task in 40 hours. How long would it take for each mechanism to complete the same task, working separately at its inherent productivity?
|
## Solution.
Let the entire volume of work be equal to one unit, the first mechanism completes the task in $x$ hours, and the second in $y$ hours. Then the productivity of the first mechanism is $\frac{1}{x}$, and the second is $-\frac{1}{y}$, the combined productivity when working together is $\frac{1}{x}+\frac{1}{y}$. Thus, we obtain the system of equations
$$
\left\{\begin{array}{l}
\frac{1}{x}+\frac{1}{y}=\frac{1}{30} \\
1-6\left(\frac{1}{x}+\frac{1}{y}\right)=\frac{40}{y}
\end{array} \Rightarrow x=75 \text { hours, } y=50\right. \text { hours }
$$
Answer: 75 and 50 hours.
|
75
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.215. A motorcyclist is moving away from point $A$ along a highway at a constant speed of $a$ km/h. After 30 minutes, a second motorcyclist starts from the same point at a constant speed of $1.25 a$ km/h. How many minutes after the start of the first motorcyclist was a third motorcyclist dispatched from the same point, if it is known that he developed a speed of $1.5 a$ km/h and caught up with the first motorcyclist at the same time as the second motorcyclist?
|
Solution.
Let $t$ be the time the third racer drove before catching up with the first. This means he drove $(1.5 a \cdot t)$ km. The first racer drove for $t_{1}$ hours.
So $t_{1} \cdot a=t \cdot 1.5 a$.
The second racer drove $\left(t_{1}-\frac{1}{2}\right)$ hours and covered $1.25 a\left(t_{1}-\frac{1}{2}\right)$ km.
Solving the system $\left\{\begin{array}{l}a \cdot t_{1}=1.5 a t, \\ 1.25 a\left(t_{1}-\frac{1}{2}\right)=1.5 a t,\end{array}\right.$ we find $t=\frac{5}{3} \text{ hours}; t_{1}=2.5 \text{ hours}$.
Therefore, the third racer started after the first racer's start by $t_{1}-t=\frac{5}{6} \text{ hours}=50$ minutes.
Answer: after 50 minutes.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.216. Two motorcyclists set off simultaneously towards each other from points $A$ and $B$, the distance between which is 600 km. While the first covers 250 km, the second covers 200 km. Find the speeds of the motorcyclists, assuming their movements are uniform, if the first motorcyclist arrives at $B$ 3 hours earlier than the second at $A$.
|
Solution.
Let $x$ km/h be the speed of the first motorcyclist; $y$ km/h be the speed of the second. The first covers 250 km in $\frac{250}{x}$ h; the second covers 200 km in $\frac{200}{y}$ h. According to the condition, $\frac{250}{x}=\frac{200}{y}$.
The first arrives at $B$ in $\frac{600}{x}$ h; the second arrives at $A$ in $\frac{600}{y}$ h.
According to the condition, $\frac{600}{x}+3=\frac{600}{y}$.
Solving the system $\left\{\begin{array}{l}\frac{250}{x}=\frac{200}{y}, \\ \frac{600}{x}+3=\frac{600}{y},\end{array}\right.$ we find $x=50$ km/h, $y=40$ km/h.
Answer: 40 and 50 km/h.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.219. The population of the city increases annually by $1 / 50$ of the current number of residents. In how many years will the population triple?
|
Solution.
Using the compound interest formula $x\left(\frac{1}{50}+1\right)^{n}=3 x$, we find $n=\log _{3} 1.02 \approx 55$.
Answer: $\approx 55$ years.
|
55
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.221. Two riders set out simultaneously from points $A$ and $C$ to point $B$, and despite the fact that $C$ was 20 km farther from $B$ than $A$ was from $B$, they arrived at $B$ simultaneously. Find the distance from $C$ to $B$, if the rider who set out from $C$ traveled each kilometer 1 minute 15 seconds faster than the rider who set out from $A$, and the rider who set out from $A$ arrived at $B$ after 5 hours.
|
Solution.
Let $AB = x$ km, $BC = x + 20$ km.
The speed of the rider from $A - \frac{x}{5}$ km/h, the speed of the rider from $C - \frac{x + 20}{5}$ km/h.
According to the condition $\frac{5}{x} - \frac{5}{x + 20} = \frac{1}{48}$, from which $x = 60$ km.
Then $CB = x + 20 = 80$ km.
Answer: 80 km.
|
80
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.222. The distance between stations $A$ and $B$ is 103 km. A train left $A$ for $B$ and, after traveling a certain distance, was delayed, and therefore the remaining distance to $B$ was traveled at a speed 4 km/h greater than the initial speed. Find the original speed of the train, given that the remaining distance to $B$ was 23 km longer than the distance traveled before the delay, and that the time taken to travel the remaining distance after the delay was 15 minutes more than the time taken to travel the distance before the delay.
|
## Solution.
Let $x$ km/h be the original speed of the train, $t$ h be the time until its stop.
Then $\left\{\begin{array}{l}x \cdot t=40, \\ (x+4)\left(t+\frac{1}{4}\right)=63,\end{array}\right.$ from which $x=80$ km/h.
Answer: $80 \mathrm{km} /$ h.
|
80
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.223. Point $C$ is located 12 km downstream from point $B$. A fisherman set out from point $A$, located upstream from point $B$, to point $C$. After 4 hours, he arrived at $C$, and the return trip took 6 hours. On another occasion, the fisherman used a motorboat, thereby tripling his own speed relative to the water, and reached from $A$ to $B$ in 45 minutes. It is required to determine the speed of the current, assuming it is constant.
|
Solution.
Let $v_{T}$ km/h be the speed of the current; $v_{,}$ km/h be the speed of the boat; $a$ km/h be the distance between $A$ and $B$. Then, according to the problem,
$$
\left\{\begin{array}{l}
\left(v_{T}+v_{T}\right) \cdot 4=12+a, \\
\left(v_{L}-v_{T}\right) \cdot 6=12+a, \\
a=\left(3 v_{T}+v_{T}\right) \cdot 0.75
\end{array}\right.
$$
Answer: 1 km/h.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.225. A certain order takes 3.6 hours longer to complete in workshop No.1 compared to workshop No.2, and 10 hours longer compared to workshop No.3. If under the same conditions, workshops No.1 and No.2 combine to complete the order, the completion time will be the same as in workshop No.3 alone. By how many hours more or less than one seven-hour workday does the completion of the specified order in workshop No.3 take?
|
## Solution.
Let $x$ hours be the time to complete the order in Workshop No.3. Then in the 1st workshop, this time is $x+10$ hours, and in the 2nd workshop, it is $-x+6.4$ hours.
$$
\text { According to the condition } \frac{1}{x+10}+\frac{1}{x+6.4}=\frac{1}{x} \text {, from which } x=8 \text { hours. }
$$
This means that the completion of the order in Workshop No.3 takes 1 hour longer than the 7-hour workday.
Answer: longer by 1 hour.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.226. A manuscript of 80 pages was given to two typists. If the first typist starts typing the manuscript 3 hours after the second, then each of them will type half of the manuscript. If both typists start working simultaneously, then after 5 hours, 15 pages will remain untyped. How long will it take for each typist to type the manuscript individually?
|
Solution.
Let the first typist can retype the manuscript in $x$ hours; the second - in $y$ hours. The first typist prints one page in $\frac{x}{80}$ hours, the second - in $\frac{y}{80}$ hours. The work rate of the first: $\frac{80}{x}$ pages/hour, the second: $\frac{80}{y}$ pages/hour.
According to the condition: $\left\{\begin{array}{l}\frac{40 y}{80}-\frac{40 x}{80}=3, \\ \frac{80}{x} \cdot 5+\frac{80}{y} \cdot 5=80-15,\end{array}\right.$ from which $x=10$ hours, $y=16$ hours.
Answer: 16 and 10 hours.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.227. Two workers were assigned a task. The second one started working an hour later than the first. After 3 hours from the time the first one started, they had 9/20 of the entire work left to complete. By the end of the work, it turned out that each had completed half of the entire work. How many hours would each, working separately, need to complete the entire task?
|
Solution.
Let the 1st worker can complete the entire job in $x$ hours, the second in $y$ hours. The productivity of the 1st: $\frac{1}{x} ; 2$nd: $\frac{1}{y}$.
$$
\text { According to the condition }\left\{\begin{array}{l}
\frac{1}{x} \cdot 3+\frac{1}{y} \cdot 2=1-\frac{9}{20}, \\
\frac{x}{2}-\frac{y}{2}=1
\end{array} \text { from which } x=10 \text { hours, } y=8\right. \text { hours. }
$$
Answer: 10 and 8 hours.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.228. Two workers were assigned to manufacture a batch of identical parts. After the first worked for 2 hours and the second for 5 hours, it turned out that they had completed half of the entire work. Working together for another 3 hours, they found that they had 0.05 of the entire work left to complete. In what time interval can each of them, working separately, complete the entire work?
|
## Solution.
Let the 1st worker can complete the entire job in $x$ hours, the second - in $y$ hours.
Productivity of the 1st: $\frac{1}{x}$, the second $-\frac{1}{y}$.
According to the condition $\left\{\begin{array}{l}\frac{1}{x} \cdot 2+\frac{1}{y} \cdot 5=\frac{1}{2}, \\ \frac{1}{2}+\left(\frac{1}{x}+\frac{1}{y}\right) \cdot 3=1-0.05,\end{array}\right.$ from which $x=12$ hours; $y=15$ hours.
Answer: 12 and 15 hours.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.232. From the railway station to the beach is 4.5 km. A boy and a scheduled bus left the station for the beach simultaneously. After 15 minutes, the boy met the bus returning from the beach, and he managed to walk another $9 / 28$ km from the place of the first meeting with the bus, when he was caught up by the same bus, which had reached the station and set off to the beach again. Find the speeds of the boy and the bus, assuming they are constant and neither the boy nor the bus stopped en route, but the bus made stops of 4 minutes each at the beach and at the station.
|
## Solution.
Let $v_{\text {m }}, v_{\text{a}}$ be the speeds of the boy and the bus, respectively.
According to the problem, we have the system
$\left\{\begin{array}{l}\frac{15}{60} v_{M}+\frac{15-4}{60} v_{\text{a}}=2 \cdot 4.5, \\ \frac{9}{28 v_{M}}=\frac{4}{60}+\frac{2 \frac{15}{60} v_{M}+\frac{9}{28}}{v_{\text{a}}},\end{array}\right.$
from which $v_{\text{M}}=3 \text{ km/h}, v_{\text{a}}=45 \text{ km/h}$.
Answer: 3 and 45 km/h.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.233. A tourist was returning from vacation on a bicycle. On the first leg of the journey, which was 246 km, he traveled on average 15 km less per day than he did on the last leg of the journey, which was 276 km. He arrived home right on time at the end of his last vacation day. It is also known that it took him one day more than half the number of days remaining until the end of his vacation to complete the first leg of the journey. How many days before the end of his vacation did the tourist set out for home?
|
## Solution.
Let the tourist travel 267 km in $x$ days, and 246 km in $\frac{x}{2}+1$. On the first segment of 246 km, his speed was $v$ km/day, and on the second segment of 276 km, it was $(v+15)$ km/day.
Then $\left\{\begin{array}{l}\left(\frac{x}{2}+1\right) v=246, \\ x(v+15)=276,\end{array}\right.$
from which $x=2$.
Therefore, the tourist set off for home $x+\frac{x}{2}+1=4$ days before the end of the vacation.
Answer: 4 days.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.236. The master is giving a simultaneous chess exhibition on several boards. By the end of the first two hours, he won $10 \%$ of the total number of games played, while 8 opponents drew their games with the master. Over the next two hours, the master won $10 \%$ of the games with the remaining opponents, lost two games, and drew the remaining 7 games. On how many boards was the game being played?
|
## Solution.
Let the game be played on $x$ boards. When in the first 2 hours $(0.1 x+8)$ games were played, in the next 2 hours: $0.1(x-0.1 x-8)+7+2$.
Then
$0.1 x+8+0.1(x-0.1 x-8)+7+2=x$,
from which $x=20$.
Answer: on 20 boards.
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.239. To the digital record of a certain two-digit number, the same number was appended to the right, and from the resulting number, the square of the intended number was subtracted. The difference was divided by $4 \%$ of the square of the intended number; in the quotient, half of the intended number was obtained, and in the remainder - the intended number. What number is intended?
To the digital record of a certain two-digit number, the same number was appended to the right, and from the resulting number, the square of the intended number was subtracted. The difference was divided by $4 \%$ of the square of the intended number; in the quotient, half of the intended number was obtained, and in the remainder - the intended number. What number is intended?
|
Solution.
Let $a$ be the number thought of. Then the new number is $100a + a = 101a$.
According to the condition, $101a - a^2 = 0.04a^2 \cdot \frac{1}{2}a + a$, from which $a = 50$.
Answer: 50.
Fig. 13.3
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.242. Two identical pools started filling with water simultaneously. In the first pool, 30 m$^3$ more water flows in per hour than in the second pool. At some point, the total amount of water in both pools was equal to the volume of each of them. After this, the first pool was filled after 2 hours and 40 minutes, and the second pool was filled after another 3 hours and 20 minutes. How much water flowed into each pool per hour?
|
Solution.
Let $x+30 \mathrm{~m}^{3} / \mathrm{h}$ be the filling rate of the first pool, $x \mathrm{~m}^{3} / \mathrm{h}$ the second; $V \mathrm{~m}^{3}$ the volume of the pools; $t$ the time when the pools contained $V \mathrm{~m}^{3}$.
According to the problem, $\left\{\begin{array}{l}(x+30) t+x t=V, \\ \left(t+2 \frac{2}{3}\right)(x+30)=V, \\ (t+6) x=V,\end{array}\right.$
from which $x=60$.
Answer: 60 and 90 $\mathrm{m}^{3}$.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.247. From milk with a fat content of $5 \%$, cottage cheese with a fat content of $15.5 \%$ is produced, leaving whey with a fat content of $0.5 \%$. How much cottage cheese can be obtained from 1 ton of milk?
|
Solution.
Let $x$ tons of cottage cheese with a fat content of $15.5\%$ be obtained, then $(1-x)$ tons of whey with a fat content of $0.5\%$ will remain. Therefore, in 1 ton of milk, there is
$$
\frac{15.5 x}{100}+\frac{0.5(1-x)}{100}=\frac{15 x+0.5}{100} \text { tons of fat. }
$$
According to the condition $\frac{15 x+0.5}{100}=\frac{5}{100}$, from which $x=0.3=300$ kg.
Answer: 300 kg.
|
300
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.249. It was planned to divide the bonus equally among the most distinguished employees of the enterprise. However, it turned out that there were three more employees deserving the bonus than was initially expected. In this case, each would receive 400 rubles less. The union and administration found a way to increase the total bonus amount by 9000 rubles, as a result of which each awarded employee received 2500 rubles. How many people received the bonus?
|
Solution.
Let the number of people who were supposed to receive the award be $x$ and $y$ be the original total amount of the award.
According to the problem,
$$
\left\{\begin{array}{l}
(x+3)\left(\frac{y}{x}-400\right)=y \\
y+9000=2500(x+3)
\end{array}\right.
$$
from which $x=15$ people.
Therefore, the number of people who received the award is $x+3=15+3=18$ people.
Answer: 18.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.251. The hour and minute hands coincide at midnight, and a new day begins. At what hour of this new day will the hour and minute hands coincide again for the first time, assuming that the clock hands move without jumps?
|
## Solution.
Let's assume the speed of the minute hand is 1, then the speed of the hour hand is $-\frac{1}{12} \cdot$ The hands will coincide when $\frac{1}{12} \cdot t + 60 = t$, where $t$ is the time of movement of the hands.
Solving the equation, we find $t = \frac{720}{11}$ (min).
Answer: 1 hr $5 \frac{5}{11}$ min.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.252. The duty maintenance worker descended on a downward-moving metro escalator. His entire journey from the upper platform to the lower one lasted $24 \mathrm{s}$. Then he climbed up and at the same pace descended again, but this time on a stationary escalator. It is known that the descent lasted 42 s. How many seconds would it take for a person to descend on a moving downward escalator while standing on a step?
|
## Solution.
Let $l$ be the path along the stationary escalator, $v_{\text {esc. }}$ be the speed of the escalator, and $v_{\text {tech. }}$ be the speed of the technician along the stationary escalator.
Then $\frac{l}{v_{\text {tech. }}}=42, \frac{l}{v_{\text {tech. }}+v_{\text {esc. }}}=24$. We need to find $\frac{l}{v_{\text {esc. }}}$. We get
$$
\frac{v_{\text {tech. }}}{l}=\frac{1}{42}, \frac{v_{\text {tech. }}}{l}+\frac{v_{\text {esc. }}}{l}=\frac{1}{24} ; \frac{v_{\text {esc. }}}{l}=\frac{1}{24}-\frac{1}{42}=\frac{1}{56} \Rightarrow \frac{l}{v_{\text {esc. }}}=56 \mathrm{~s} .
$$
Answer: in 56 s.
|
56
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.253. For hydrodynamic studies, a small model of a channel has been made. Several pipes of the same cross-section, supplying water, and several pipes of another, but also the same cross-section, intended for removing water, are connected to this model. If four inlet and three outlet pipes are opened simultaneously, then after 5 hours, the volume of water in the model will increase by 1000 m ${}^{3}$. If two inlet and two outlet pipes are opened simultaneously for 2 hours, the increase in the volume of water will be $180 \mathrm{~m}^{3}$. How much water does one inlet pipe and one outlet pipe pass in one hour?
|
## Solution.
Let $x$ m $^{3} /$ h be the flow rate of the inlet pipe, and $y$ m $^{3} /$ h be the flow rate of the outlet pipe. According to the problem,
$\left\{\begin{array}{l}5(4 x-3 y)=1000, \\ 2(2 x-2 y)=180,\end{array}\right.$
from which $x=65 \mathrm{~m}^{3}, y=20 \mathrm{~m}^{3}$.
Answer: 65 and $20 \mathrm{~m}^{3}$.
|
65
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.257. A courier on a moped left city $A$ for city $B$, which are 120 km apart. One hour after this, a second courier on a motorcycle left $A$ and, catching up with the first, immediately handed him an errand and then turned back, returning to $A$ at the moment the first courier reached $B$. What is the speed of the first courier if the speed of the second is 50 km/h?
|
Solution.
Let $v$ km/h be the speed of the first courier; he traveled for $t$ hours to the meeting point. According to the problem, $v t=50(t-1)$. The first courier arrived in $B$ after $\frac{120}{v}$ hours, and the second courier returned to $A$ after $\left(\frac{2 v t}{50}+1\right)$ hours.
$$
\text { According to the problem } \frac{2 v t+1}{50}+1=\frac{120}{v} \text {. }
$$
Solving the system $\left\{\begin{array}{l}v t=50(t-1), \\ \frac{2 v t}{50}+1=\frac{120}{v}\end{array}\right.$,
we find $v=30$ km/h.
Answer: 30 km/h.
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.