problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
13.259. A steamship, 2 hours after departure from pier $A$, stops for 1 hour and then continues its journey at a speed equal to 0.8 of its initial speed, as a result of which it is late to pier $B$ by 3.5 hours. If the stop had occurred 180 km further, then under the same conditions, the steamship would have been late to $B$ by 1.5 hours. Find the distance $A B$.
|
Solution.
Let $AB = x$ km, $v$ km/h be the speed of the steamboat.
According to the problem, $\left\{\begin{array}{l}\frac{x}{v} + 3.5 = 2 + 1 + \frac{x - 2v}{0.8v}, \\ \frac{x}{v} + 1.5 = \frac{2v + 180}{v} + 1 + \frac{x - 2v - 180}{0.8v},\end{array}\right.$ from which $x = 270$ km.
Answer: 270 km.
|
270
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.260. Two material particles, being 295 m apart from each other, started moving towards each other simultaneously. The first particle moves uniformly at a speed of $15 \mathrm{~m} / \mathrm{c}$, while the second particle moved 1 m in the first second and 3 m more in each subsequent second than in the previous one. Through what angle will the second hand of a clock move during the time that has passed from the start of the particles' movement until their meeting?
|
## Solution.
Let $t$ seconds have passed before the particles meet. In this time, the first particle has traveled $15 t \text{m}$, and the second particle has traveled $\frac{2+3(t-1)}{2} \cdot t$ (the formula for the sum of the first $n$ terms of an arithmetic progression was used).
According to the condition, $\frac{2+3(t-1)}{2} \cdot t + 15 t = 295$, from which $t = 10 \text{s}$.
The angle of the pointer's deflection $\alpha = \frac{360^{\circ}}{\frac{60}{10}} = 60^{\circ}$.
Answer: $60^{\circ}$.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.262. It is known that a freely falling body travels 4.9 m in the first second, and in each subsequent second, it travels 9.8 m more than in the previous one. If two bodies start falling from the same height, one 5 seconds after the other, then after what time will they be 220.5 m apart?
|
## Solution.
Let $t \mathrm{c}$ be the required time. In this time, the first body will travel $4.9 t^{2} \mathrm{M}$, and the second body will travel $4.9(t-5)^{2}$ m.
According to the condition, $4.9 t^{2}-4.9(t-5)^{2}=220.5$, from which $t=7 \mathrm{c}$.
Answer: 7 seconds after the first body starts falling.
Fig. 13.7
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.263. The path from $A$ to $B$ is traveled by a passenger train 3 hours and 12 minutes faster than by a freight train. In the time it takes the freight train to travel from $A$ to $B$, the passenger train travels 288 km more. If the speed of each train is increased by $10 \mathrm{~km} / \mathrm{h}$, the passenger train will travel from $A$ to $B$ 2 hours and 24 minutes faster than the freight train. Determine the distance from $A$ to $B$.
|
Solution.
In Fig. 13.7, the graphs of train movements before the speed changes are considered.
We have $\operatorname{tg} \angle M C N=v_{\text {pas. }}^{(0)}=288: 3.2=90$ km/h. If $v_{\text {tov. }}^{(0)}=x$ km/h, then $A B=N L=x t \mathrm{km}, C D=90(t-3.2)=x t \Rightarrow t=\frac{288}{90-x}$. After the speed changes, we get $v_{\text {pas. }}^{(1)}=100 \mathrm{km} / \mathrm{h}, v_{\text {tov. }}^{(1)}=x+10$ km/h. According to the condition $\frac{x t}{x+10}-\frac{x t}{100}=2.4$. Substituting $t=\frac{288}{90-x}$ here and solving the resulting equation, we find $x=50 \mathrm{km} / \mathrm{h}, t=7.2$ h. Therefore, $A B=x t=50 \cdot 7.2=360 \mathrm{km}$.
Answer: 360 km.
|
360
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.264. To rise in an ordinary elevator to the top floor of an eight-story building (height 33 m) with two 6-second intermediate stops, it takes as much time as it would to rise in an elevator of a high-rise building with one 7-second intermediate stop at the 20th floor (height 81 m). Determine the lifting speed of the elevator in the high-rise building, knowing that it exceeds the speed of the ordinary elevator by $1.5 \mathrm{~m} / \mathrm{c}$, but does not reach $5 \mathrm{~m} / \mathrm{c}$.
|
## Solution.
Let $v_{1}$ m/s be the speed of a regular elevator ($v_{1} \leq 3.5 \text{ m/s}$), and $v_{2}$ m/s be the speed of the elevator in a high-rise building, $v_{2}=v_{1}+1.5 \text{ m/s}$.
According to the condition,
$$
\frac{33}{v_{1}}+2 \cdot 6=\frac{81}{v_{1}+1.5}+7 \text{, from which } v_{1}=1.5 \text{ m/s}, v_{2}=v_{1}+1.5=3 \text{ m/s}
$$
Answer: $3 \text{ m/s}$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.267. Two motorcyclists started racing in the same direction from the same starting point simultaneously: one at a speed of 80 km/h, the other at a speed of 60 km/h. Half an hour later, a third racer started from the same starting point in the same direction. Find his speed, given that he caught up with the first racer 1 hour and 15 minutes later than the second.
|
Solution.
Let $x$ km/h be the speed of the third racer. He caught up with the first racer after $t_{1}$ hours, and the second racer after $t_{2}$ hours. According to the problem,
$$
\begin{aligned}
& \left\{\begin{array}{l}
80 t_{1}=x\left(t_{1}-0.5\right), \\
60 t_{2}=x\left(t_{2}-0.5\right) \\
t_{1}-t_{2}=1.25,
\end{array}\right. \\
& \text { from which } x=100 \text { km/h. }
\end{aligned}
$$
Answer: 100 km/h.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.269. At the pier, two passengers disembarked from a steamship and headed to the same village. One of them walked the first half of the way at a speed of 5 km/h and the second half at a speed of 4 km/h. The other walked the first half of the time at a speed of 5 km/h and the second half at a speed of 4 km/h, arriving at the village 1 minute earlier than the first. How long did each of them take to cover the entire distance, and what is the distance between the pier and the village?
|
Solution.
Let $x$ km be the distance between the pier and the village, $t$ h be the time it took the second passenger to walk to the village.
According to the problem, $\left\{\begin{array}{l}\frac{x}{2 \cdot 5}+\frac{x}{2 \cdot 4}=t+\frac{1}{60}, \\ 5 \cdot \frac{t}{2}+4 \cdot \frac{t}{2}=x,\end{array}\right.$
from which $x=6$ km; $t=\frac{4}{3} \text{ h}=1 \text{ h } 20$ min.
Answer: 1 h 21 min; 1 h 20 min; 6 km.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.271. The race track for the bicycle competition is a contour of a right-angled triangle with a difference in the lengths of the legs of 2 km. The hypotenuse runs along a dirt road, while both legs are on the highway. One of the participants covered the segment along the dirt road at a speed of $30 \mathrm{km} / \mathrm{h}$, and both segments along the highway in the same time at a speed of $42 \mathrm{km} / \mathrm{h}$. Determine the length of the track
|
## Solution.
Length of the route
$S=AB+BC+AC=a+a+2+\sqrt{a^{2}+(a+2)^{2}}$ (see Fig. 13.12).
By the condition $\frac{\sqrt{a^{2}+(a+2)^{2}}}{30}=\frac{a+a+2}{42}$, from which $a=8 \text{ km}$.
$S=8+8+2+\sqrt{8^{2}+10^{2}}=24$ km.
Answer: 24 km.
|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.272. From post office $A$, a car departed in the direction of post office $B$. After 20 minutes, a motorcyclist set off after it at a speed of 60 km/h. Catching up with the car, the motorcyclist handed a package to the driver and immediately turned back. The car arrived at $B$ at the moment when the motorcyclist was halfway between the meeting point and $A$. Determine the speed of the car, if the distance from $A$ to $B$ is 82.5 km.
|
Solution.
Let $t$ be the time it takes for the motorcyclist to catch up with the car, and $v$ be the speed of the car. According to the problem, we have the system
$\left\{\begin{array}{l}v\left(t+\frac{20}{60}\right)=60 \cdot t, \\ \frac{82.5-60 \cdot t}{v}=\frac{t}{2},\end{array}\right.$
from which $v=45(\mathrm{km} / \mathrm{h})$.
Answer: 45 km $/$ h.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.273. The ball is rolling perpendicular to the sideline of a football field. Suppose, moving uniformly decelerated, the ball rolled 4 m in the first second, and 0.75 m less in the next second. A football player, initially 10 m away from the ball, started running in the direction of the ball's movement to catch it. Moving uniformly accelerated, the player ran 3.5 m in the first second, and 0.5 m more in the next second. How long will it take for the player to catch the ball, and will he be able to catch it before the ball goes out of bounds, if the player needs to run 23 m to reach the sideline?
|
Solution.
Let $t$ be the desired time. In this time, the ball will roll $\frac{2 \cdot 4-0.75(t-1)}{2} \cdot t \mathrm{M}$, and the footballer will run $\frac{2 \cdot 3.5+0.5(t-1)}{2} \cdot t \mathrm{M}$. (The formula for the sum of $n$ terms of an arithmetic progression was used).
According to the condition,
$$
\frac{2 \cdot 3.5+0.5(t-1)}{2} \cdot t - \frac{2 \cdot 4-0.75(t-1)}{2} \cdot t = 10, \text{ from which } t = 5 \mathrm{s}
$$
The footballer will catch up with the ball, having run $\frac{2 \cdot 3.5+0.5 \cdot 4}{2} \cdot 5 = 22.5$ m, 0.5 m before the sideline.
Answer: in 5 s; 0.5 m before the line of the field.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.274. According to the schedule, the train covers a 120 km section at a constant speed. Yesterday, the train covered half of the section at this speed and was forced to stop for 5 minutes. To arrive on time at the final point of the section, the driver had to increase the train's speed by 10 km/h on the second half of the section. Today, the train was again stopped at the midpoint of the same section, but the delay lasted 9 minutes. At what speed did the driver operate the train today on the second half of the section, if the train again arrived at the final point of the section on schedule?
|
## Solution.
Let $x$ km/h be the original speed of the train. Considering the stop, it will take $\frac{1}{12}+\frac{60}{x+10}$ to travel the second half of the section, from which $x=80$ km/h.
Let $v$ km/h be the speed of the train today. Then $\frac{60}{80}=0.15+\frac{60}{v}$, from which $v=100$ km/h.
Answer: 100 km/h.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.283. Two pedestrians set out towards each other simultaneously from two points, the distance between which is 28 km. If the first pedestrian had not stopped for 1 hour at a distance of 9 km from the starting point, the meeting of the pedestrians would have taken place halfway. After the stop, the first pedestrian increased their speed by $1 \mathrm{~km} / \mathrm{h}$, and the meeting occurred 4 km from the place where the first pedestrian had stopped. Find the speeds of the pedestrians.
|
Solution.
Since pedestrians could meet halfway, their speeds are equal. Let $V$ be the initial speed of one of the pedestrians.
According to the condition $\frac{9}{V}+\frac{4}{V+1}+1=\frac{28-(9+4)}{V}$, from which $V=3$ (km/h).
Answer: initially, both were walking at the same speed of 3 km/h.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.285. On a 10 km stretch of highway, devoid of intersections, the bus stops only for passengers to get on and off. It makes a total of 6 intermediate stops, spending 1 minute at each, and always moves at the same speed. If the bus were to travel without stopping, it would cover the same distance at a speed exceeding the average speed of its movement with stops by 5 km/h. How many minutes is the bus in motion on this stretch of highway?
|
Solution.
Let $t$ min be the time the bus is in motion on the segment. Then its average speed without stops is $-\frac{10}{t}$, and with stops, it is $-\frac{10}{t+\frac{1}{60} \cdot 6}$.
According to the condition, $\frac{10}{t+0.1}+5=\frac{10}{t}$, from which $t=24$ (min).
Answer: 24 min.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.288. A master and his apprentice were tasked with manufacturing a batch of identical parts. After the master worked for 7 hours and the apprentice for 4 hours, it turned out that they had completed $5 / 9$ of the entire work. After working together for another 4 hours, they found that $1 / 18$ of the entire work remained to be done. How long would it take the apprentice to complete the entire work on his own?
|
Solution.
Let's take the entire volume of work as 1. Let $x, y$ be the labor productivity of the master and the apprentice per hour, respectively. According to the conditions, we have the system
$$
\left\{\begin{array}{l}
7 x+4 y=\frac{5}{9} \\
7 x+4 y+4(x+y)=1-\frac{1}{18}
\end{array}\right.
$$
The time required for the apprentice to complete the entire work is $-\frac{1}{y}=24$ (hours).
Answer: 24 hours.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.289. There are two alloys consisting of zinc, copper, and tin. It is known that the first alloy contains $40 \%$ tin, and the second - $26 \%$ copper. The percentage of zinc in the first and second alloys is the same. By melting 150 kg of the first alloy and 250 kg of the second, a new alloy was obtained, in which there turned out to be $30 \%$ zinc. How much tin is contained in the newly obtained alloy?
|
## Solution.
Let $x$ be the percentage of zinc in the first alloy. According to the condition, $\frac{x}{100} \cdot 150+\frac{x}{100} \cdot 250=\frac{30}{100}(150+250)$, from which $x=30 \%$. Then in the second alloy, there is $100 \%-(26 \%+30 \%)=44 \%$ of tin, and the new
$$
\text { alloy contains } \frac{40}{100} \cdot 150+\frac{44}{100} \cdot 250=170 \text { (kg) of tin. }
$$
Answer: 170 kg.
|
170
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.290. If both pipes are opened simultaneously, the pool will be filled in 2 hours and 24 minutes. In reality, however, only the first pipe was opened initially for $1 / 4$ of the time it takes the second pipe to fill the pool on its own. Then, the second pipe was opened for $1 / 4$ of the time it takes the first pipe to fill the pool on its own, after which it turned out that $11/24$ of the pool's full capacity remained to be filled. How much time is required for each pipe to fill the pool individually?
|
Solution.
Let's take the entire volume of the pool as 1. Let $x, y$ (liters) per hour leak through the first and second pipe, respectively. According to the conditions, we have the system
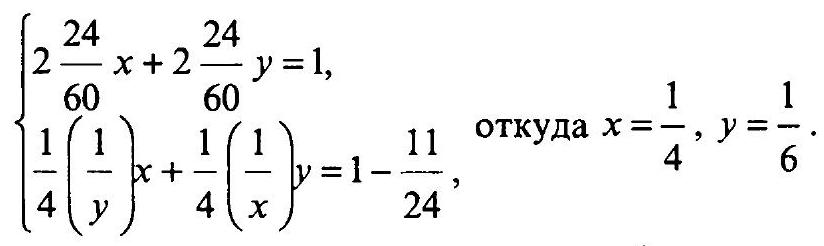
Then for the first pipe, it takes $\frac{1}{x}=4$ (hours) to fill the pool, and $\mathrm{a} \frac{1}{-}=6$ (hours) for the second.
Answer: 4 and $6$ hours.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.292. Two "mechanical moles" of different power, working simultaneously from different ends of the tunnel, could dig it in 5 days. In reality, however, both "moles" were used sequentially from one side of the tunnel, with the first digging $1 / 3$, and the second - the remaining $2 / 3$ of its length. The entire job took 10 days in this case. How many days would each "mole," working alone, need to dig the tunnel?
|
## Solution.
Let the length of the tunnel be 1. Let $x, y$ be the powers of the first and second "moles" respectively.
According to the problem, we have the system $\left\{\begin{array}{l}5(x+y)=1, \\ \frac{1}{3 x}+\frac{2}{3 y}=10\end{array}\right.$, from which $x=\frac{1}{15}, y=\frac{2}{15}$.
Then the first "mole" will dig the tunnel alone in $3 \times \frac{1}{x}=15$ (days), and the second $-3 \times \frac{1}{y}=7.5$ (days).
Answer: 15 and 7.5 days.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.293. Two pipes of different cross-sections are connected to a swimming pool. One is a uniform water supply pipe, and the other is a uniform water discharge pipe, with the first pipe filling the pool 2 hours longer than the second pipe empties it. When the pool was filled to $1 / 3$ of its capacity, both pipes were opened, and the pool was found to be empty after 8 hours. How many hours, acting separately, does the first pipe take to fill, and the second pipe to empty the pool?
|
## Solution.
Let's write down the values of the sought and given quantities in the form of a table:
| Pipe | Time, h | Capacity | Productivity |
| :---: | :---: | :---: | :---: |
| Supply | $x+2$ | 1 | $\frac{1}{x+2}$ |
| Discharge | $x$ | 1 | $\frac{1}{x}$ |
| Both together | 8 | $\frac{1}{3}$ | $\frac{1}{24}$ |
According to the condition $\frac{1}{x}-\frac{1}{x+2}=\frac{1}{24}$, from which $x=6$.
Answer: in 8 and 6 hours.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.294. Two workers were assigned to manufacture a batch of identical parts; after the first worked for $a$ hours, and the second for $0.6 a$ hours, it turned out that they had completed $5 / n$ of the entire work. After working together for another $0.6 a$ hours, they found that they still had to manufacture $1 / n$ of the entire batch of parts. How many hours will each of them, working separately, need to complete the entire work? The number $n$ is a natural number; find it.
|
## Solution.
Let the entire volume of work be 1. Let $x, y$ be the labor productivity (the number of parts produced per hour) of the first and second workers, respectively. According to the conditions, we have the system
$$
\left\{\begin{array}{l}
a x+0.6 a y=\frac{5}{n} \\
a x+0.6 a y+0.6 a(x+y)=1-\frac{1}{n}
\end{array} \text {, from which } x=\frac{11-n}{0.4 a n}, y=\frac{n-9}{0.24 a n} .\right.
$$
Then the first worker will manufacture all the parts in $\frac{1}{x}=\frac{0.4 a n}{11-n}$ (hours), and the second worker will do so in $\frac{1}{y}=\frac{0.24 a n}{n-9}$ (hours). The value of $n$ must satisfy the system of inequalities
$$
\left\{\begin{array}{l}
11-n>0, \\
n-9>0,
\end{array} \text { i.e., } n=10\right.
$$
Answer: $\frac{0.4 a n}{11-n} ; \frac{0.24 a n}{n-9} ; n=10$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.296. Two excavator operators must complete a certain job. After the first one worked for 15 hours, the second one starts and finishes the job in 10 hours. If, working separately, the first one completed $1 / 6$ of the job, and the second one completed $1 / 4$ of the job, it would take an additional 7 hours of their combined work to finish the job. How many hours would it take each excavator operator to complete the job individually?
|
Solution.
Let's take the entire volume of work as 1. Let $x, y$ be the work efficiency of the first and second excavator operators, respectively. According to the conditions, we have the system $\left\{\begin{array}{l}15 x+10 y=1, \\ 7(x+y)=1-\left(\frac{1}{6}+\frac{1}{4}\right),\end{array}\right.$ from which $x=\frac{1}{30}, y=\frac{1}{20}$.
Then the first excavator operator will complete the entire work in $\frac{1}{x}=30$ (hours), and $x$
the second $-3 \mathrm{a} \frac{1}{=}=20$ (hours).
$y$
Answer: in 20 and 30 hours.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.299. Two points rotate uniformly along two concentric circles. One of them completes a full revolution 5 seconds faster than the other, and therefore manages to make two more revolutions per minute. Let the rays directed from the center of the circle to these points coincide at the beginning of the motion. Calculate the magnitude of the angle between the rays after $1 \mathrm{s}$.
|
Solution.
Let $V_{1}, V_{2}$ be the rotational speeds of the points, $l$ be the length of the circumference, and $x$ be the length of the arc between the points after 1 second of rotation. Then the angle between the rays will be $\alpha=\frac{x \cdot 360^{\circ}}{l}$ (1). According to the problem, we have the system $\left\{\begin{array}{l}\frac{l}{V_{2}}-\frac{l}{V_{1}}=5, \\ 60\left(V_{1}-V_{2}\right)=2 l,\end{array}\right.$ from which $V_{1}=\frac{l}{10}, V_{2}=\frac{l}{15}$.
If the points rotate in the same direction, then $x=V_{1}-V_{2}=\frac{l}{30}$ and $\alpha=12^{\circ}$; if in opposite directions, then $x=V_{1}+V_{2}=\frac{l}{6}$ and $\alpha=60^{\circ}$.
Answer: 12 or $60^{\circ}$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.300. The smaller arc between points $A$ and $B$, located on a circle, is 150 m. If the points start moving towards each other along the smaller arc, they will meet after $10 \mathrm{c}$, and if they move along the larger arc, the meeting will occur after $14 \mathrm{c}$. Determine the speeds of the points and the length of the circumference, given that point $A$ can run the entire circumference in the time it takes for $B$ to travel only $90 \mathrm{M}$.
|
## Solution.
Let $V_{a}$ and $V_{b}$ be the speeds of points $A$ and $B$, and $l$ be the length of the circumference. According to the conditions, we have the system $\left\{\begin{array}{l}10\left(V_{a}+V_{b}\right)=150, \\ 14\left(V_{a}+V_{b}\right)=l-150, \\ \frac{l}{V_{a}}=\frac{90}{V_{b}},\end{array}\right.$
from which $V_{a}=12(\mathrm{m} / \mathrm{s}), V_{b}=3(\mathrm{m} / \mathrm{s}), l=360(\mathrm{m})$.
Answer: 12 m $/$ s and 3 m $/ s ; 360$ m.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.302. Two points move uniformly in the same direction along a circle 60 m in circumference. One of them completes a full revolution 5 seconds faster than the other. At the same time, the points coincide every 1 minute. Determine the speeds of the points.
|
Solution.
Let $V_{1}, V_{2}$ be the speeds of the points. According to the problem, we have the system
$$
\left\{\begin{array}{l}
\frac{60}{V_{2}}-\frac{60}{V_{1}}=5, \\
60\left(V_{1}-V_{2}\right)=60,
\end{array} \text { from which } V_{1}=4(\mathrm{M} / \mathrm{c}), V_{2}=3(\mathrm{M} / \mathrm{c})\right.
$$
Answer: 3 and $4 \mathrm{~m} / \mathrm{c}$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.306. Two hours after departure, the train stopped for 30 minutes. On the remaining part of the route to the station, repair work was being carried out, and the train was allowed a speed that was $1 / 3$ of its initial speed, as a result of which the train arrived at the station 1 hour and 10 minutes late. The next day, the train stopped 14 km closer to the final station, and under the same conditions, the delay was reduced to 50 minutes. Determine the distance between the stations and the speed of the train.
|
Solution.
Let $x$ be the distance between the stations, $V$ be the speed of the train. According to the problem, we have the system
$$
\left\{\begin{array}{l}
2+\frac{30}{60}+\frac{x-2 V}{\frac{1}{3} V}=\frac{x}{V}+1+\frac{10}{60} \\
\frac{2 V+14}{V}+\frac{30}{60}+\frac{x-(2 V+14)}{\frac{1}{4} V}=\frac{x}{V}+\frac{50}{60}
\end{array}\right.
$$
from which $x=196$ (km), $V=84$ (km/h).
Answer: 196 km; 84 km/h.
|
196
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.307. Find a three-digit number whose digits form a geometric progression, given that after reducing it by 495, the resulting number is written with the same digits as the desired number but in reverse order; if the digits of the number obtained after subtraction are decreased (from left to right) by 1, 1, and 2, respectively, then an arithmetic progression is formed.
|
Solution.
Let $100 x+10 y+z$ be the desired number. According to the condition, we have the system
$$
\left\{\begin{array}{l}
x z=y^{2}, \\
100 x+10 y+z-495=100 z+10 y+x, \text { from which } x=9, y=6, z=4 \\
(z-1)+(x-2)=2(y-1)
\end{array}\right.
$$
Answer: 964.
|
964
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.309. There are two gold and silver alloys. In one alloy, the quantities of these metals are in the ratio $1: 2$, in the other - $2: 3$.
How many grams should be taken from each alloy to obtain 19 g of an alloy in which gold and silver are in the ratio 7:12?
|
Solution.
Let $x$ (g) be the amount of the first alloy taken, which contains $\frac{1}{3} x$ gold and $\frac{2}{3} x$ silver. According to the problem, we have the system
$$
\left\{\begin{array}{l}
x+y=19 \\
\frac{1}{3} x+\frac{2}{5} y=\frac{7}{12}\left(\frac{2}{3} x+\frac{3}{5} y\right), \text{ from which } x=9(\mathrm{g}), y=10(\mathrm{g})
\end{array}\right.
$$
Answer: 9 and 10 g.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.310. There is scrap steel of two grades with nickel content of 5 and $40 \%$. How much of each of these grades of metal is needed to obtain 140 tons of steel with a $30 \%$ nickel content?
|
Solution.
Let $x, y$ be the mass of each type of metal taken. According to the condition
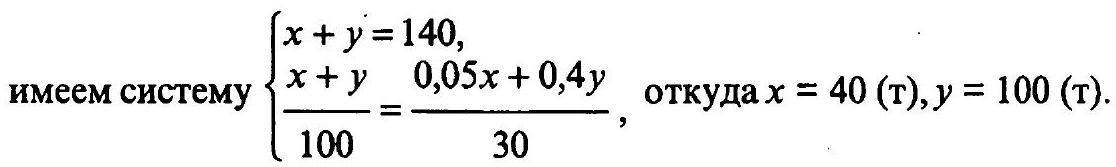
Answer: 40 and 100 tons.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.311. Two trains, a passenger train and an express train, set off towards each other simultaneously from two points that are 2400 km apart. Each train travels at a constant speed, and at some point in time, they meet. If both trains had traveled at the speed of the express train, they would have met 3 hours earlier than the actual meeting time. If both trains had traveled at the speed of the passenger train, they would have met 5 hours later than the actual meeting time. Find the speeds of the trains.
|
Solution.
Let $V_{1}, V_{2}$ be the speeds of the passenger and express trains, respectively, and $t$ be the time of travel until the trains meet. According to the problem, we have the system $\left\{\begin{array}{l}t\left(V_{1}+V_{2}\right)=2400, \\ 2 V_{2}(t-3)=2400, \text { from which } V_{1}=60(\text { km } / \text{h}), V_{2}=100(\text { km/h). } \\ 2 V_{1}(t+5)=2400,\end{array}\right.$
Answer: 60 and 100 km/h.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.315. The initial cost price of a unit of product was 50 rubles. During the first year of production, it increased by a certain percentage, and during the second year, it decreased (relative to the increased cost price) by the same percentage, as a result of which it became 48 rubles. Determine the percentages of the increase and decrease in the cost price of a unit of product.
|
## Solution.
Let the cost of a unit of production increase by x percent.
After the increase, the cost became $50+\frac{x}{100} \cdot 50=50+\frac{x}{2}$, and after the decrease - $\left(50+\frac{x}{2}\right)-\frac{x}{100} \cdot\left(50+\frac{x}{2}\right)=\left(50+\frac{x}{2}\right)\left(1-\frac{1}{100}\right) \cdot$ According to the condition, we have $\left(50+\frac{x}{2}\right)\left(1-\frac{x}{100}\right)=48$, from which $x=20 \%$.
Answer: $20 \%$.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.317. One tourist set out at 6 a.m., and the second - towards him at 7 a.m. They met at 8 a.m. and, without stopping, continued their journey. How much time did each of them spend on the entire journey, if the first arrived at the place where the second started 28 minutes later than the second arrived at the place where the first started? It is assumed that each walked without stopping at a constant speed.
|
## Solution.
Let $V_{1}, V_{2}$ be the speeds of the first and second tourists, respectively, and $x$ be the time it takes for the second tourist to cover the distance that the first tourist covers in 2 hours. According to the problem, we have the system $\left\{\begin{array}{l}x V_{2}=120 V_{1}, \\ V_{2} x+60 V_{2}=120 V_{1}+V_{1}(x+28) .\end{array}\right.$ From the first equation, we express $\frac{V_{1}}{V_{2}}$ and substitute it into the second equation. From the resulting equation, we find $x=72$ (min). Then the first tourist spent a total of $120+72+28=220$ (min) on the entire journey, and the second tourist spent $-60+72=132$ (min).
Answer: 3 hours 40 minutes and 2 hours 12 minutes.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.319. A vessel with a capacity of 8 liters is filled with a mixture of oxygen and nitrogen, with oxygen accounting for $16 \%$ of the vessel's capacity. From this vessel, a certain amount of the mixture is released and an equal amount of nitrogen is added, after which the same amount of the mixture is released again and the same amount of nitrogen is added once more. In the new mixture, the oxygen content is $9 \%$. What amount of the mixture was released each time?
|
Solution.
Initially, the vessel contained $16 \cdot \frac{8}{100}=\frac{32}{25}$ liters of oxygen. The released $x$ liters of the mixture contain $\frac{16 x}{100}=\frac{4 x}{25}$ liters of oxygen. Now, for every 8 liters of the mixture in the vessel, there are $\frac{32-4 x}{25}$ liters of oxygen, which constitutes $(16-2 x) \%$. The second release of $x$ liters of the mixture contains $(16-2 x) \frac{x}{100}=(8-x) \frac{x}{50}$ liters of oxygen. According to the problem, $\frac{32-4 x}{25}-\frac{(8-x) x}{50}=9 \cdot \frac{8}{100}$, from which $x_{1}=2, x_{2}=14$.
Answer: 2 liters.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.320. Impurities constitute $20 \%$ of the total volume of the solution. What is the smallest number of filters through which the solution must be passed so that the final impurity content does not exceed $0.01 \%$, if each filter absorbs $80 \%$ of the impurities? (It is known that $\lg 2 \approx 0.30$.)
|
Solution.
Impurities constitute $\frac{1}{5}$ of the solution. After the first filtration, $\left(\frac{1}{5}\right)^{2}$ of the impurities will remain, and after the $k$-th filtration, $-\left(\frac{1}{5}\right)^{k+1}$. According to the condition, $\left(\frac{1}{5}\right)^{k+1} \leq 10^{-4} ;-(k+1) \lg 5 \leq-4$, from which $k \geq 4.7$.
Answer: 5 filters.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.323. For the production of wheat bread, as many kilograms of flour were taken as the percentage that the leaven constitutes for this flour. For the production of rye bread, 10 kg more flour was taken, i.e., as many kilograms as the percentage that the leaven constitutes for rye flour. How many kilograms of each type of flour were taken if a total of 112.5 kg of bread was baked?
|
Solution.
Let $x$ be the mass of flour for wheat bread, and $(x+10)$ be for rye bread.
According to the condition, $x+x \cdot \frac{x}{100}+(x+10)+\frac{x+10}{100}(x+10)=112.5$ from which $x=35$.
Answer: 35 and 45 kg.
|
35
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.324. In the first week of his vacation, the engineer spent a few rubles less than $3 / 5$ of the amount of money he had taken with him; in the second week, $1 / 4$ of the remainder plus 30 rubles; in the third week, $2 / 5$ of the new remainder plus 12 rubles; after which $6 / 35$ of the amount of money taken remained. It is also known that the amount of money left unspent at the end of the first, second, and third weeks decreased in an arithmetic progression. How much money was spent over the three weeks of the vacation?
|
Solution.
Let $S$ be the total amount of money taken. We fill in the table:
| Period | Spent, rubles | Balance, rubles |
| :---: | :---: | :---: |
| first week | $x$ | $S-x$ |
| second week | $\frac{S-x}{4}+30$ | $\frac{3(S-x)}{4}-30$ |
| third week | $\frac{2}{5}\left(\frac{3(S-x)}{4}-30\right)+12$ | $\frac{6}{35} S$ |
By the condition $\left\{\begin{array}{l}x<\frac{3}{5} S, \\ \frac{S-x+\frac{6}{35} \cdot S}{2}=\frac{3(S-x)}{4}-30, \\ \frac{3(S-x)}{4}-30-\frac{2}{5}\left(\frac{3(S-x)}{4}-30\right)-12=\frac{6}{35} S,\end{array}\right.$
from which $S=1400$ rubles.
Then spent $S-\frac{6}{35} S=1160$ (rubles).
Answer: 1160 rubles.
|
1160
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.325. 9000 parts can be manufactured on several new machines of the same design and one machine of the old design, which works twice as slowly as each of the new machines. The old machine can also be replaced by a new machine of the same design as the others. In this second option, each machine would produce 200 fewer parts than one new machine in the first option. How many machines were there in total?
|
Solution.
Let $x$ parts be manufactured on one new machine, $\frac{x}{2}$ - on the old one, $n$ - the number of machines. According to the condition, we have the system
$$
\left\{\begin{array}{l}
(n-1) x+\frac{x}{2}=9000, \\
\frac{9000}{n}=x-200, \quad \text { from which } n=5
\end{array}\right.
$$
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.326. Three cars are dispatched from $A$ to $B$ at equal time intervals. They arrive in $B$ simultaneously, then proceed to point $C$, which is 120 km away from $B$. The first car arrives there one hour after the second. The third car, upon arriving at $C$, immediately turns back and meets the first car 40 km from $C$. Determine the speed of the first car, assuming that the speed of each car was constant throughout the route.
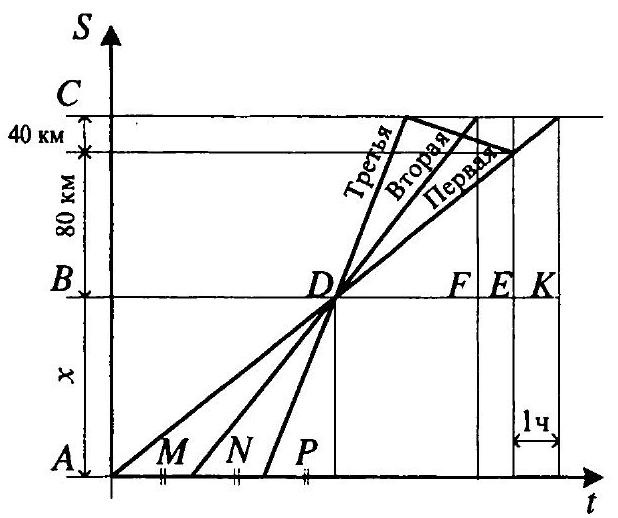
Fig. 13.16
|
Solution.
Let $V_{1}, V_{2}, V_{3}$ be the speeds of the cars. Compare the time intervals (see Fig. 13.16), expressing them as the ratio of distance to speed:
$A P=\frac{x}{V_{1}}, M P=\frac{x}{V_{2}}, N P=\frac{x}{V_{3}}$.
By the condition:
$$
\frac{x}{V_{1}}-\frac{x}{V_{2}}=\frac{x}{V_{2}}-\frac{x}{V_{3}}, \text { hence }
$$
$\frac{1}{V_{1}}+\frac{1}{V_{3}}=\frac{1}{V_{2}}$ (1). Further, $D E=\frac{80}{V_{1}}$ and $D E=\frac{80+40}{V_{3}}$, from which $\frac{80}{V_{1}}=\frac{120}{V_{3}}$ (2); $D K=\frac{120}{V_{1}} ; D F=\frac{120}{V_{2}}$, from which $\frac{120}{V_{1}}-\frac{120}{V_{2}}=1$ (3). Solving the system of equations (1), (2), (3), we find $V_{1}=30 \mathrm{km} / \mathrm{h}$.
Answer: 30 km/h.
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.328. A fishing brigade planned to catch 1800 tons of fish within a certain period. For $1 / 3$ of this period, there was a storm, as a result of which the planned daily target was underachieved by 20 tons. However, in the remaining days, the brigade managed to catch 20 tons more than the daily norm, and the planned target was completed one day ahead of schedule. How many tons of fish were planned to be caught daily?
|
## Solution.
Let $x$ be the planned period, and $y$ be the number of centners per day according to the plan. According to the conditions, we have the system $\left\{\begin{array}{l}x y=1800, \\ \frac{x}{3}(y-20)+\left(\frac{2 x}{3}-1\right)(y+20)=1800,\end{array}\right.$ from which $y=100$.
Answer: 100 centners.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.330. Two trucks were supposed to transport a certain cargo in 6 hours. The second truck was delayed in the garage, and when it arrived at the loading site, the first truck had already transported $3 / 5$ of the total cargo; the remaining part of the cargo was transported by the second truck, and the entire cargo was transported in this way in 12 hours. How much time would each truck need separately to transport the cargo?
|
Solution.
Let's take the entire volume of work as 1. Let $x, y$ be the weight of cargo transported by each machine in one trip. According to the conditions, we have the system
$$
\left\{\begin{array}{l}
\frac{1}{x+y}=6, \\
\frac{3}{5 x}+\frac{2}{5 y}=12,
\end{array} \text { from which } x=\frac{1}{10}, y=\frac{1}{15} \text { or } x=y=\frac{1}{12} .\right. \text { Then the first ma- }
$$
chine will transport the entire cargo in 10 hours, and the second in 15 hours, or each in 12 hours.
Answer: 10 and 15 hours or 12 hours each.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.331. Several balls of equal mass for bearings and several piston rings, also of equal mass, were made from a certain grade of metal. If the number expressing the mass of each ball in grams were 2 less than the number of rings made, and the number expressing the mass of each ring in grams were 2 more than the number of balls made, then the number expressing their total mass would exceed twice the difference between the number of rings and balls by 800, and if the number expressing the mass of each item in grams were equal to the number of items of the same kind made, then their total mass would be 881 g. How many balls and rings were made?
|
Solution.
Let $x$ be the number of balls, $m_{x}$ be the mass of one ball, $y$ be the number of rings, $m_{y}$ be the mass of one ring. According to the conditions, we have the system
$$
\left\{\begin{array}{l}
m_{x}+2=y \\
m_{y}=x+2 \\
x \cdot m_{x}+y \cdot m_{y}-800=2(y-x), \text{ from which } x=25, y=16 \text{ or } x=16, y=25 . \\
x^{2}+y^{2}=881
\end{array}\right.
$$
Answer: 25 balls and 16 rings or 16 balls and 25 rings.
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.333. A ball falls from a height of 2 m 43 cm and, upon hitting the ground, bounces back up, each time reaching $2 / 3$ of the height from which it falls again. After how many bounces will the ball rise to a height of 32 cm?
|
Solution.
The numbers expressing the height to which the ball rises form a geometric progression with $b_{1}=243 q$ and $q=\frac{2}{3}$. According to the condition $q_{n}=32=b_{1} q^{n-1}$, from which $n=5$.
Answer: after 5 bounces.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.335. If a two-digit number is divided by the product of its digits, the quotient is 3 and the remainder is 8. If the number, formed by the same digits but in reverse order, is divided by the product of the digits, the quotient is 2 and the remainder is 5. Find this number.
|
## Solution.
Let $10 x+y$ be the desired number. According to the condition, we have the system
$$
\left\{\begin{array}{l}
10 x+y=3 x y+8 \\
10 y+x=2 x y+5
\end{array}\right.
$$
Answer: 53.
|
53
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.338. The recording of a six-digit number starts with the digit 2. If this digit is moved from the first position to the last, keeping the order of the other five digits, the newly obtained number will be three times the original number. Find the original number.
|
Solution.
The original six-digit number has the form $2 \cdot 10^{5}+x$. After moving the digit 2 to the last place, we get the number $10 x+2$. According to the condition, $10 x+2=3\left(2 \cdot 10^{5}+x\right)$, from which $x=85714$.
Answer: 285714.
|
285714
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.340. It is known that the difference between the variable quantities $z$ and $y$ is proportional to the quantity $x$, and the difference between the quantities $x$ and $z$ is proportional to the quantity $y$. The coefficient of proportionality is the same and is a positive integer $k$. A certain value of the quantity $z$ is $5 / 3$ times the difference of the corresponding values of $x$ and $y$. Find the numerical value of the coefficient $k$.
|
Solution.
From the condition, we have the system $\left\{\begin{array}{l}z-y=k x, \\ x-z=k y, \\ x-y=\frac{3}{5} z\end{array}\right.$
From the first two equations, we express $\frac{x}{z}$ and $\frac{y}{z}$ in terms of $k$, then substitute the obtained expressions for $\frac{x}{z}$ and $\frac{y}{z}$ into the third equation and find $k=3$.
## Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.346. The volume of substance A is half the sum of the volumes of substances B and C, and the volume of substance B is 1/5 of the sum of the volumes of substances A and C. Find the ratio of the volume of substance C to the sum of the volumes of substances A and B.
|
Solution.
Given that $2 V_{A}=V_{B}+V_{C}$ and $5 V_{B}=V_{A}+V_{C}$. Let $V_{A}=x V_{C}$ and $V_{B}=y V_{C}$. Then we get the system $\left\{\begin{array}{l}2 x-y=1, \\ -x+5 y=1,\end{array}\right.$ from which $x=\frac{2}{3}, y=\frac{1}{3}$. Therefore, $\frac{V_{C}}{V_{A}+V_{B}}=\frac{1}{x+y}=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.349. From post office $A$ to village $B$, one needs to walk 9 km. The postman walks the entire path there and back, without stopping in the village, in 3 hours and 41 minutes. The road from $A$ to $B$ goes uphill first, then on flat ground, and finally downhill. Over what distance does the road run on flat ground, if the postman walks uphill at a speed of 4 km/h, on flat ground at 5 km/h, and downhill at 6 km/h?
|
## Solution.
Let $x, y, z$ be the lengths of the road uphill, on flat ground, and downhill, respectively. According to the problem, we have the system
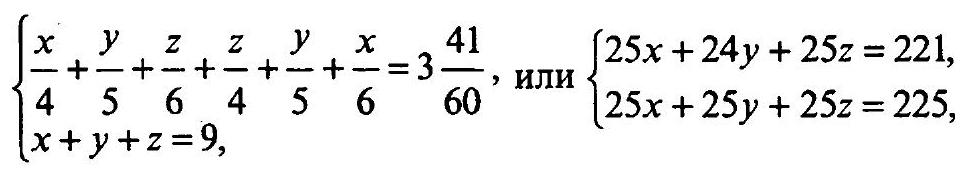
from which $y=4$ (km).
Answer: 4 km.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.352. A girl, an acquaintance of a young man sitting by the window of a tram, was walking towards the moving tram. 8 seconds after she passed by the window, the young man got off the tram and followed her. How much time passed from that moment until he caught up with the girl? The young man's speed is twice the girl's speed and five times less than the tram's speed.
|
Solution.
Let $x, 2x, 10x$ be the speeds of the girl, the boy, and the tram, respectively. According to the problem, $8 \cdot x + 8 \cdot 10x + t \cdot x = t \cdot 2x$, where $t$ is the desired time. Solving the equation, we find $t=88$ (s).
Answer: 88 s.
|
88
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.355. A car, having traveled a distance from $A$ to $B$, equal to 300 km, turned back and after 1 hour 12 minutes from leaving $B$, increased its speed by 16 km/h. As a result, it spent 48 minutes less on the return trip than on the trip from $A$ to $B$. Find the original speed of the car.
|
Solution.
Let $V$ be the original speed of the car. According to the condition, we have
$$
\frac{300}{V}-\left(1 \frac{12}{60}+\frac{300-1 \frac{12}{60} V}{V+16}\right)=\frac{48}{60}, \quad \text { from which } V=60 \text { (km/h) }
$$
Answer: 60 km/h.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.356. The distance between points $A$ and $B$ is 308 m. A point moves from point $A$ towards $B$, covering 15 m in the first second and 1 m less in each subsequent second. Another point moves from point $B$ in the opposite direction, covering 20 m in the first second and 3 m more in each subsequent second. At what distance from point $A$ will the meeting occur if the point that started from point $B$ began moving 3 seconds after the point that started from point $A$?
|
Solution.
Let's find the laws of motion of the points.
For the point from $A:\left\{\begin{array}{l}15=1 \cdot V_{1}-\frac{a_{1} \cdot 1^{2}}{2}, \\ 15+14=2 V_{1}-\frac{a_{1} \cdot 2^{2}}{2},\end{array}\right.$ from which $V_{1}=15.5(\mathrm{~m} / \mathrm{c})$, $a_{1}=1\left(\mathrm{m} / \mathrm{c}^{2}\right)$, and the law of its motion is $-S_{A}=15.5 t-\frac{t^{2}}{2}$.
For the point from $B$ :
$$
\left\{\begin{array}{l}
20=1 \cdot V_{2}+\frac{a_{1} \cdot 1^{2}}{2} \\
20+23=2 V_{2}+\frac{a_{1} \cdot 2^{2}}{2},
\end{array} \text { from which } V_{2}=18.5(\mathrm{m} / \mathrm{c})\right.
$$
$a_{2}=3\left(\mathrm{m} / \mathrm{c}^{2}\right)$, and the law of its motion is $-S_{B}=18.5 t+\frac{3 t^{2}}{2}$.
The point from $A$ will travel $15.5 \cdot 3-\frac{3^{2}}{2}=42$ (m) in 3 s, and its speed will become $V=V_{1}-3 a_{1}=12.5$ (m/s). According to the condition, $42+12.5 t-\frac{t^{2}}{2}+18.5 t+\frac{3 t^{2}}{2}=308$, from which $t=7(\mathrm{c})$.
Then the points will meet at a distance of $42+12.5 \cdot 7-\frac{7^{2}}{2}=105$ (m) from point $A$.
Answer: 105 m.
|
105
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.357. A cyclist traveled 96 km 2 hours faster than he had planned. During this time, for each hour, he traveled 1 km more than he had planned to travel in 1 hour and 15 minutes. At what speed did he travel?
|
Solution.
Let $V$ be the speed at which the cyclist was traveling, $\frac{1 \cdot V-1}{1 \frac{15}{60}}$ - the speed at which the cyclist intended to travel. According to the condition $\frac{96}{V}+2=\frac{96}{\frac{V-1}{1 \frac{1}{4}}}$, from which $V=16$ (km/h).
Answer: 16 km/h.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.358. Find a six-digit number starting with the digit 1 such that if this digit is moved to the end, the resulting number is three times the original number.
|
Solution.
The original six-digit number has the form $1 \cdot 10^{5}+x$. After moving the digit 1 to the last place, we get the number $10 x+1$. According to the condition, $10 x+1=3\left(1 \cdot 10^{5}+x\right)$, from which $x=42857$.
Answer: 142857.
|
142857
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.361. A red pencil costs 27 kopecks, a blue one - 23 kopecks. No more than 9 rubles 40 kopecks can be spent on purchasing pencils. It is necessary to purchase the maximum possible total number of red and blue pencils. At the same time, the number of red pencils should be as few as possible, but the number of blue pencils should not differ from the number of red pencils by more than 10. How many red and how many blue pencils should be purchased under the given conditions?
|
## Solution.
Let $x$ red and $y$ blue pencils be bought. According to the condition, $27 x + 23 y \leq 940$ and $y - x \leq 10$. Let's construct the lines $27 x + 23 y = 940$ (1) and $y - x = 10$ (2). From Fig. 13.18, it is clear that these lines intersect at point $A$, the coordinates of which satisfy equations (1) and (2), and at this point, the maximum possible sum $x + y$ is achieved. Solving the system (1), (2) and considering that the numbers $x$ and $y$ are natural, we get $x = 14, y = 24$.
Answer: 14 red and 24 blue.
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.362. A certain alloy consists of two metals in the ratio $1: 2$, while another contains the same metals in the ratio $2: 3$. How many parts of each alloy should be taken to obtain a third alloy containing the same metals in the ratio $17: 27?$
|
Solution.
Let $x$ parts of the first metal and $y$ parts of the second be taken. Then
$$
\frac{1}{3} x+\frac{2}{5} y=\frac{17}{44}(x+y), \text { hence } \frac{y}{x}=\frac{35}{9}
$$
Answer: 9 and 35 parts.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.367. Several students decided to buy a tape recorder priced between 170 and 195 dollars. However, at the last moment, two of them refused to participate in the purchase, so each of the remaining had to contribute 1 dollar more. What was the price of the tape recorder?
|
Solution.
Let $x$ be the amount each student was originally supposed to contribute; $y$ be the number of students. According to the problem,
\[
\left\{
\begin{array}{l}
2 x = y - 2, \\
x y \geq 170, \\
x y \leq 195,
\end{array}
\right.
\left\{
\begin{array}{l}
x = \frac{y}{2} - 1, \\
y\left(\frac{y}{2} - 1\right) \geq 170, \\
y\left(\frac{y}{2} - 1\right) \leq 195 .
\end{array}
\right.
\]
Solving the inequalities, we find $y = 20$, then $x = \frac{20}{2} - 1 = 9$ (dollars), and the cost of the tape recorder is $x y = 180$ dollars.
Answer: 180 dollars.
|
180
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.369. Around the house, lindens and birches are planted, and their total number is more than 14. If the number of lindens is doubled and the number of birches is increased by 18, then the number of birches will be greater than the number of lindens. If, however, the number of birches is doubled without changing the number of lindens, then the number of lindens will now be greater than the number of birches. How many lindens and how many birches were planted?
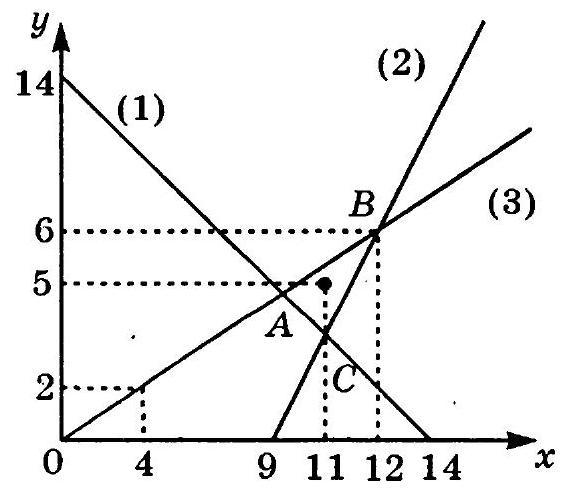
Fig. 13.20
|
Solution.
Let $x, y$ be the number of lindens and birches, respectively. According to the condition, we have the system of inequalities $\left\{\begin{array}{l}x+y>14, \\ y+18>2 x, \\ x>2 y .\end{array}\right.$
Construct the lines $x+y=14$ (1), $y+18=2 x$ (2), $x=2 y$ (3). From Fig. 13.20, it is clear that the point ( $11 ; 5$ ) is the only point with natural coordinates that lies inside the triangle $A B C$, i.e., satisfies our system of inequalities.
Answer: 11 lindens and 5 birches.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$1.4 \frac{3 a^{2}+2 a x-x^{2}}{(3 x+a)(a+x)}-2+10 \frac{a x-3 x^{2}}{a^{2}+9 x^{2}}$.
$1.5\left(\left(\frac{x}{y-x}\right)^{-2}-\frac{(x+y)^{2}-4 x y}{x^{2}-x y}\right)^{2} \frac{x^{4}}{x^{2} y^{2}-y^{4}}$.
|
1.4 According to formula (1.8), we have $a^{2}-9 x^{2}=(a-3 x)(a+3 x)$. Simplify the fraction $\frac{a x-3 x^{2}}{(a-3 x)(a+3 x)}$ by canceling $a-3 x$, assuming $a \neq 3 x$; we get $\frac{x}{a+3 x}$. Next, using formula (1.15), factor the numerator of the first fraction:
$$
\begin{aligned}
& 3 a^{2}+2 a x-x^{2}=-\left(x^{2}-2 a x-3 a^{2}\right)=-(x-3 a)(x+a)= \\
& =(3 a-x)(x+a)
\end{aligned}
$$
Now, cancel the first fraction by $a+x$, where $a \neq -x$, and we find
$$
\frac{3 a-x}{3 x+a}-2+\frac{10 x}{a+3 x}=\frac{3 a-x-2(3 x+a)+10 x}{a+3 x}=\frac{a+3 x}{a+3 x}=1
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$1.6 \frac{\left(\frac{1}{a}+\frac{1}{b}-\frac{2 c}{a b}\right)(a+b+2 c)}{\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{2}{a b}-\frac{4 c^{2}}{a^{2} b^{2}}} ; a=7,4, b=\frac{5}{37}$.
|
1.6 Perform the following transformations in the numerator and denominator:
$$
\begin{aligned}
& \frac{1}{a}+\frac{1}{b}-\frac{2 c}{a b}=\frac{b+a-2 c}{a b} \\
& \frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{2}{a b}-\frac{4 c^{2}}{a^{2} b^{2}}=\frac{b^{2}+a^{2}+2 a b-4 c^{2}}{a^{2} b^{2}}= \\
& =\frac{(b+a)^{2}-(2 c)^{2}}{a^{2} b^{2}}=\frac{(b+a-2 c)(b+a+2 c)}{a^{2} b^{2}}
\end{aligned}
$$
Thus,
$$
\frac{(b+a-2 c)(b+a+2 c)}{a b} : \frac{(b+a-2 c)(b+a+2 c)}{a^{2} b^{2}}=a b
$$
When $a=7.4=\frac{37}{5}, b=\frac{5}{37}$, we get $a b=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$1.24 \frac{\sqrt{\frac{a b c+4}{a}+4 \sqrt{\frac{b c}{a}}}}{\sqrt{a b c}+2} ; a=0.04$.
|
1.24 Assuming $a b c \neq 0$, we have:
$$
\begin{aligned}
& \frac{a b c+4}{a}+4 \sqrt{\frac{b c}{a}}=b c+\frac{4}{a}+4 \sqrt{\frac{b c}{a}}= \\
& =(\sqrt{b c})^{2}+4 \sqrt{\frac{b c}{a}}+\left(\frac{2}{\sqrt{a}}\right)^{2}=\left(\sqrt{b c}+\frac{2}{\sqrt{a}}\right)^{2} \\
& \frac{\sqrt{\left(\sqrt{b c}+\frac{2}{\sqrt{a}}\right)^{2}}}{\sqrt{a b c}+2}=\frac{\sqrt{a b c}+2}{\sqrt{a}(\sqrt{a b c}+2)}=\frac{1}{\sqrt{a}}
\end{aligned}
$$
For $a=0.04$, we find $\frac{1}{\sqrt{0.04}}=5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.26 Given the expression
$$
\begin{aligned}
& \frac{x^{3}-a^{-\frac{2}{3}} \cdot b^{-1}\left(a^{2}+b^{2}\right) x+b^{\frac{1}{2}}}{b^{\frac{3}{2}} x^{2}} \\
& \text { Substitute } x=a^{\frac{2}{3} b}-\frac{1}{2} \text { and simplify the result }
\end{aligned}
$$
Eliminate the irrationality in the denominator of the fraction (1.27-1.28):
|
1.26 After performing the specified substitution, we find
$$
\begin{aligned}
& \frac{\left(a^{\frac{2}{3}} b^{-\frac{1}{2}}\right)^{3}-a^{-\frac{2}{3}+\frac{2}{3}} b^{-1-\frac{1}{2}}\left(a^{2}+b^{2}\right)+b^{\frac{1}{2}}}{b^{\frac{3}{2}}\left(a^{\frac{2}{3}} b^{\left.-\frac{1}{2}\right)^{2}}\right.}= \\
& =\frac{a^{2} b^{-\frac{3}{2}}-b^{-\frac{3}{2}} a^{2}-b^{\frac{1}{2}}+b^{\frac{1}{2}}}{a^{\frac{4}{3}} b^{\frac{1}{2}}}=0
\end{aligned}
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.29 Calculate the sum of the cubes of two numbers if their sum and product are 11 and 21, respectively.
|
1.29 Let $a$ and $b$ be the required numbers; then $a+b=11$ and $ab=21$. According to formula (1.11), we have $(a+b)^{3}=a^{3}+b^{3}+3ab(a+b)$. Therefore, $a^{3}+b^{3}=(a+b)^{3}-3ab(a+b)$, i.e., $a^{3}+b^{3}=$ $=11^{3}-3 \cdot 21 \cdot 11=638$.
Answer: 638.
|
638
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$1.53 \frac{\sqrt{7+4 \sqrt{3}} \cdot \sqrt{19-8 \sqrt{3}}}{4-\sqrt{3}}-\sqrt{3}=2$.
|
1.53 Consider the equality
$$
\frac{\sqrt{7+4 \sqrt{3}} \cdot \sqrt{19-8 \sqrt{3}}}{4-\sqrt{3}}=2+\sqrt{3}
$$
Obviously, if this equality is true, then the given equality is also true. Let
$$
a=\frac{\sqrt{7+4 \sqrt{3}} \cdot \sqrt{19-8 \sqrt{3}}}{4-\sqrt{3}}, b=2+\sqrt{3}
$$
It is easy to establish that $a>0$ and $b>0$. If in this case the equality $a^{2}=b^{2}$ holds, then $a=b$. We find
$$
\begin{aligned}
& a^{2}=\frac{(7+4 \sqrt{3})(19-8 \sqrt{3})}{(4-\sqrt{3})^{2}}= \\
& =\frac{(7+4 \sqrt{3})(19-8 \sqrt{3})}{19-8 \sqrt{3}}=7+4 \sqrt{3} \\
& b^{2}=(2+\sqrt{3})^{2}=7+4 \sqrt{3}
\end{aligned}
$$
Since $a^{2}=b^{2}$, then $a=b$, i.e., the given equality is valid.
This example can be solved faster if one guesses that both expressions under the square roots in the condition are squares of positive numbers, specifically:
$7+4 \sqrt{3}=(2+\sqrt{3})^{2}$ and $19-8 \sqrt{3}=(4-\sqrt{3})^{2}$.
Then the left side of the given equality is
$$
\frac{(2+\sqrt{3})(4-\sqrt{3})}{(4-\sqrt{3})}-\sqrt{3}=2+\sqrt{3}-\sqrt{3}=2 \text { and } 2=2
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$1.54 \sqrt[3]{38+\sqrt{1445}}+\sqrt[3]{38-\sqrt{1445}}=4$.
|
### 1.54 Let
$\sqrt[3]{38+\sqrt{1445}}+\sqrt[3]{38-\sqrt{1445}}=x$.
Cubing both sides of this equation, and using formula (1.11), we get
$38+\sqrt{1445}+38-\sqrt{1445}+3 \sqrt[3]{(38+\sqrt{1445})(38-\sqrt{1445})} x=x^{3}$,
or $x^{3}+3 x-76=0$. By substitution, we verify that $x=4$ is one of the roots of the resulting cubic equation: $64+12-76=0$.
Transform this cubic equation:
$$
\begin{aligned}
& x^{3}-64=3(4-x) ;(x-4)\left(x^{2}+4 x+16\right)+3(x-4)=0 \\
& (x-4)\left(x^{2}+4 x+19\right)=0
\end{aligned}
$$
But the factor $x^{2}+4 x+19$ has no real roots. Therefore, 4 is the only possible real value for $x$, which proves the required equality (since it is obvious that $\sqrt[3]{38+\sqrt{1445}}+\sqrt[3]{38-\sqrt{1445}}$ is a real number).
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.1 \quad \frac{2}{3-x}+\frac{1}{2}=\frac{6}{x(3-x)}$.
|
2.1 Let's move all terms of the equation to the left side and transform the obtained equation to the form
$$
\frac{x^{2}-7 x+12}{2 x(3-x)}=0
$$
From the equation $x^{2}-7 x+12=0$, we find $x_{1}=3, x_{2}=4$. When $x=3$, the denominator becomes zero; therefore, 3 is not a root. Thus, $x=4$.
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.13 \sqrt{x-2}=x-4$.
Translate the text above into English, keeping the original text's line breaks and format, and output the translation result directly.
$2.13 \sqrt{x-2}=x-4$.
|
2.13 Let's square both sides of the equation:
$$
\begin{aligned}
& (\sqrt{x-2})^{2}=(x-4)^{2} ; x-2=x^{2}-8 x+16 \\
& x^{2}-9 x+18=0 ; x_{1}=3 ; x_{2}=6
\end{aligned}
$$
Let's check the found roots by substituting them into the original equation. If $x=3$, we get $1=-1$ - an incorrect equality; if $x=6$, we get $2=2$ - a correct equality. Therefore, the given equation has a single root $x=6$.
Note that we could have first found the domain of the given equation. For this, we solve the system of inequalities
$\left\{\begin{array}{l}x-2 \geqslant 0, \\ x-4 \geqslant 0,\end{array}\right.$
from which $x \geqslant 4$. Then it is immediately clear that $x_{1}=3$ is an extraneous root of the original equation. By checking, we confirm that $x=6$ satisfies the given equation.
Answer: $x=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.14 \sqrt{15-x}+\sqrt{3-x}=6$.
|
2.14 We have $\sqrt{15-x}=6-\sqrt{3-x}$. Squaring both sides of the equation, we get $15-x=36-12 \sqrt{3-x}+3-x$; $\sqrt{3-x}=2 ; 3-x=4 ; x=-1$. Checking shows that this value is a root of the equation.
Omвem: $x=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.18 \frac{\sqrt[3]{x^{4}}-1}{\sqrt[3]{x^{2}}-1}-\frac{\sqrt[3]{x^{2}}-1}{\sqrt[3]{x}+1}=4$.
|
2.18 Reducing the fractions in the left part of the equation, we get
$\sqrt[3]{x^{2}}+1-\sqrt[3]{x}+1=4$, or $\sqrt[3]{x^{2}}-\sqrt[3]{x}-2=0$.
From this, $\sqrt[3]{x}=-1$ or $\sqrt[3]{x}=2$. Since $\sqrt[3]{x}$ cannot be equal to -1 (as this would make the denominators of the original fractions zero), then $x=8$.
Omeem: $x=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.19 \frac{\sqrt{x}+\sqrt[3]{x}}{\sqrt{x}-\sqrt[3]{x}}=3$.
|
2.19 To solve the equation, we will use the following statement: if the equality $\frac{a}{b}=\frac{c}{d}$ is true, then the equality (check it!) $\frac{a+b}{a-b}=\frac{c+d}{c-d}$ is also valid. We have
$$
\begin{aligned}
& \frac{(\sqrt{x}+\sqrt[3]{x})+(\sqrt{x}-\sqrt[3]{x})}{(\sqrt{x}+\sqrt[3]{x})-(\sqrt{x}-\sqrt[3]{x})}=\frac{3+1}{3-1} ; \frac{2 \sqrt{x}}{2 \sqrt[3]{x}}=2 \\
& \sqrt{x}=2 \sqrt[3]{x} ; x^{3}=64 x^{2}
\end{aligned}
$$
Since $x \neq 0$, then $x=64$.
Answer: $x=64$.
|
64
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.20 \sqrt[7]{\frac{5-x}{x+3}}+\sqrt[7]{\frac{x+3}{5-x}}=2$.
|
2.20 Instruction. Use the substitution $\sqrt[7]{\frac{5-x}{x+3}}=z$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.49 \frac{x^{2}+1}{x+1}+\frac{x^{2}+2}{x-2}=-2$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
$2.49 \frac{x^{2}+1}{x+1}+\frac{x^{2}+2}{x-2}=-2$.
|
2.49 We have
$$
\left(x^{2}+1\right)(x-2)+\left(x^{2}+2\right)(x+1)=-2(x+1)(x-2)
$$
Performing the transformations, we get $2 x^{3}+x^{2}+x-4=0$. Since the sum of all coefficients is zero, then $x=1$. Let's write the last equation in the form
$2 x^{3}-2 x^{2}+3 x^{2}-3 x+4 x-4=0$,
or $(x-1)\left(2 x^{2}+3 x+4\right)=0$.
From this, $2 x^{2}+3 x+4=0$. Since the discriminant of this equation is negative, it has no roots.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.55 \sqrt{x+1}+\sqrt{4 x+13}=\sqrt{3 x+12}$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
$2.55 \sqrt{x+1}+\sqrt{4 x+13}=\sqrt{3 x+12}$.
|
2.55 By squaring both sides of the equation, we get
$$
\begin{aligned}
& x+1+4 x+13+2 \sqrt{(x+1)(4 x+13)}=3 x+12 \\
& \sqrt{(x+1)(4 x+13)}=-(x+1)
\end{aligned}
$$
Another squaring would eliminate the irrationality, but there is no need for this transformation here. We notice that the derived equation can have a solution only under the condition $x+1 \leqslant 0$. At the same time, one of the conditions for the existence of a solution to the original equation is the requirement $x+1 \geqslant 0$. Both these conditions are consistent in the unique case where $x+1=0$, from which $x=-1$. This value of $x$, as is easily verified, satisfies the original equation. Since the derived equation has no other roots, the original equation also has no other roots. Thus, $x=-1$.
Answer: $x=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.58 \sqrt{x}+\frac{2 x+1}{x+2}=2$.
Translate the text above into English, keeping the original text's line breaks and format, and output the translation result directly.
$2.58 \sqrt{x}+\frac{2 x+1}{x+2}=2$.
|
### 2.58 We have
$\sqrt{x}=2-\frac{2 x+1}{x+2}$, or $\sqrt{x}=\frac{3}{x+2}$.
After squaring and performing transformations, the equation will take the form $x^{3}+4 x^{2}+4 x-9=0$. Notice that the sum of the coefficients of the last equation is zero, which means it has a root $x=1$. Therefore,
$$
x^{3}-x^{2}+5 x^{2}-5 x+9 x-9=0
$$
or $(x-1)\left(x^{2}+5 x+9\right)=0$.
Since the equation $x^{2}+5 x+9=0$ has no roots, $x=1$ is the only root of the original equation.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.59 \sqrt{x+2}-\sqrt[3]{3 x+2}=0$.
Translate the text above into English, keeping the original text's line breaks and format, and output the translation result directly.
$2.59 \sqrt{x+2}-\sqrt[3]{3 x+2}=0$.
|
2.59 We have $\sqrt{x+2}=\sqrt[3]{3 x+2}$. After raising the equation to the sixth power, we get $(x+2)^{3}=(3 x+2)^{2}$, or $x^{3}-3 x^{2}+4=0$, or $(x+1)\left(x^{2}-4 x+4\right)=0$.
From this, $x_{1}=-1$ (extraneous root), $x_{2}=2$.
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.78 For what values of a do the equations $x^{2}+a x+1=0$ and $x^{2}+x+a=0$ have a common root?
|
2.78 Subtracting the second equation from the first, we get
$$
a x - x + 1 - a = 0, \text{ or } (a-1)(x-1) = 0
$$
$$
x^{2} + x + 1 = 0
$$
such an equation has no real roots. If $a \neq 1$, then $x = 1$ and, therefore, $1 + a + 1 = 2$, i.e., $a = -2$.
Answer: when $a = -2$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1 The tractor driver plowed three plots of land. The area of the first is $\frac{2}{5}$ of the total area of all three plots, and the area of the second is to the area of the third as $\frac{3}{2}: \frac{4}{3}$. How many hectares were there in all three plots if the third plot was 16 hectares smaller than the first?
|
3.1 The areas of the plots are equal to $x, y, x-16$ (ha). According to the condition, $x=\frac{2}{5}(x+y+x-16)$ and $y:(x-16)=\frac{3}{2}: \frac{4}{3}$, from which $y=\frac{9}{8}(x-16)$. Further, we have $x=\frac{2}{5}\left(2 x-16+\frac{9}{8} x-18\right)$, or $x=\frac{2}{5}\left(\frac{25 x}{8}-34\right)$, from which $x=\frac{272}{5}$. Now we find $y=\frac{9}{8}\left(\frac{272}{5}-16\right)=\frac{216}{5}$. The total area is $\frac{544}{5}+\frac{216}{5}-16=136$ (ha).
Omeem: 136 ha.
|
136
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.2 Two workers together produced 72 parts per shift. After the first worker increased their labor productivity by $15 \%$, and the second by $25 \%$, together they started producing 86 parts per shift. How many parts does each worker produce per shift after the increase in labor productivity?
|
3.2 Initially, workers produced $x$ and $72-x$ parts per shift, and then $1.15 x$ and $1.25(72-x)$ parts. According to the condition, $1.15 x + 90 - 1.25 x = 86 ; 0.1 x = 4 ; x = 40 ; 1.15 \cdot 40 = 46$.
Answer: 46 and 40 parts.
|
46
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.3 The areas of three plots of land are in the ratio $2 \frac{3}{4}: 1 \frac{5}{6}: 1 \frac{3}{8}$. It is known that 72 centners of grain more were harvested from the first plot compared to the second. Find the area of all three plots, if the average yield is 18 centners per hectare.
|
3.3 Let $x, y, z$ be the areas of the plots. Then $\frac{x}{y}=\frac{6}{4}, \frac{y}{z}=\frac{4}{3}$, from which $x=6 k, y=4 k, z=3 k$. According to the condition, $(6 k-4 k) \cdot 18=72$, from which $k=2$. Therefore, the total area of all plots is $x+y+z=2(6+4+3)=26$ (ha).
Omeem: 26 ha.
|
26
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.4 The working day has been reduced from 8 to 7 hours. By what percentage does labor productivity need to increase to ensure that, with the same rates, the wage increases by $5 \%$?
|
3.4 Let a master produce $a$ parts and earn $b$ rubles for 8 hours of work. Then the rate is $\frac{b}{a}$ rubles per part, and the labor productivity is $\frac{a}{8}$ parts per hour. After increasing productivity by $x \%$, the master started producing $\frac{a}{8}+\frac{x a}{8 \cdot 100}$ parts per hour. Therefore, in 7 hours, he produced $\frac{7 a}{8}\left(1+\frac{x}{100}\right)$ parts and earned $\frac{7 a}{8}\left(1+\frac{x}{100}\right) \frac{b}{a}=\frac{7 b}{8}\left(1+\frac{x}{100}\right)$ rubles.
According to the condition, $\frac{7 b}{8}\left(1+\frac{x}{100}\right)=1.05 b$, from which $x=20 \%$.
Answer: by $20 \%$.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.5 On the first day of the sports competition, $\frac{1}{6}$ of the boys' team and $\frac{1}{7}$ of the girls' team did not meet the qualifying standards and were eliminated from further competition. Over the remaining period of the competition, an equal number of athletes from both teams were eliminated due to non-compliance with the standards. In total, by the end of the trials, 48 people from the boys' team and 50 people from the girls' team did not meet the qualifying standards, but among the total number of athletes who met the qualifying standards, there were twice as many girls as boys. What was the initial number of athletes in each team?
## Relationships "more - less"
|
3.5 Let $x$ be the number of boys who met the credit standards and $2x$ be the number of girls. Thus, the initial number of team members consists of $x+48$ boys and $2x+50$ girls. By the end of the first day of the competition, $\frac{1}{6}(x+48)$ boys and $\frac{1}{7}(2x+50)$ girls dropped out. Later, an equal number of athletes dropped out from both teams, so
$48-\frac{1}{6}(x+48)=50-\frac{1}{7}(2x+50)$,
from which $x=24$. Therefore, the initial number of team members is 72 boys and 98 girls.
Answer: 72 boys and 98 girls.
|
72
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.7 Two parks with a total area of 110 hectares are divided into an equal number of plots. The plots of each park are equal in area to each other, but differ from those of the other park. If the first park were divided into plots of the same area as the second, it would have 75 plots, and if the second park were divided into plots of the same area as the first, it would contain 108 plots. Determine the area of each park.
## Geometric and Physical Problems
|
3.7 Let $S$ be the area of the park, $n$ be the number of equal-sized plots, and $Q$ be the area of a plot. Then $\frac{S}{n}=Q$. We will fill in the table with the given and required values in the sequence indicated by the numbers (2) and (12).
| Park | Initially | | | With new arrangement | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | $\underline{s}$ | $n$ | $Q$ | $S$ | $\bar{n}$ | $\ell$ |
| First | $7^{x}$ | (11) $\frac{108 x}{110-x}$ | $\frac{110-x}{9108}$ | (1) ${ }^{x}$ | $33^{75}$ | (5) $\frac{x}{75}$ |
| Second | 811 | $\frac{75(110-x)}{12)}$ | (10) $\frac{x}{75}$ | $\left(2^{10-x}\right.$ | (4) | $\frac{110-x}{6)}$ |
According to the condition,
$\frac{108 x}{110-x}=\frac{75(110-x)}{x}$,
from which $x=50$.
Answer: 50 and 60 hectares.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.8 The front wheel of a moving model makes 6 more revolutions than the rear wheel over a distance of 120 m. If the circumference of the front wheel is increased by $\frac{1}{4}$ of its length, and the circumference of the rear wheel is increased by $\frac{1}{5}$ of its length, then over the same distance, the front wheel will make 4 more revolutions than the rear wheel. Find the lengths of the circumferences of the front and rear wheels.
|
3.8 The circumference of a wheel $C$, the number of revolutions $n$, and the distance $s$ are related by the formula $C n=s$. We will fill in the table of values of these quantities in the order indicated by the numbers (1), (2), .., (12).
| Wheel | Before change | | | After change | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | $\bar{C}$ | $\boldsymbol{s}$ | $\bar{n}$ | $C$ | $s$ | $\boldsymbol{n}$ |
| Front | (1) ${ }^{x}$ | $(3)^{120}$ | (5) $\frac{120}{x}$ | (7) $\frac{5 x}{4}$ | $9^{120}$ | (11) $\frac{120 \cdot 4}{5 x}$ |
| Rear | (2) ${ }^{y}$ | (4) $^{120}$ | (6) $\frac{120}{y}$ | (8) $\frac{6 y}{5}$ | (10) $^{120}$ | (12) $\frac{120 \cdot 5}{6 y}$ |
According to the condition, we obtain the system
$$
\left\{\begin{array}{l}
\frac{120}{x}-\frac{120}{y}=6 \\
\frac{96}{x}-\frac{100}{y}=4
\end{array}\right.
$$
from which we find $x=4(m), y=5(m)$.
Answer: 4 and 5 m.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.10 Two skins with a total cost of 2250 rubles were sold at an auction with a profit of $40 \%$. What is the cost of each skin if a profit of $25 \%$ was made on the first one, and a loss of $-50 \%$ on the second one?
|
3.10 Let $x$ (rubles) be the cost of the first pelt, then $2250-x$ (rubles) is the cost of the second pelt. After selling, the first pelt was sold for $1.25 x$ (rubles), and the second for $1.5(2250-x)$ (rubles). According to the condition, we set up the equation
$1.25 x + 1.5(2250 - x) = 1.4 \cdot 2250$,
from which $x = 900$ (rubles); hence, $2250 - x = 1350$ (rubles).
Answer: 900 and 1350 rubles.
|
900
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.11 Apples of the first grade for a total of 228 rubles and apples of the second grade for a total of 180 rubles were delivered to the store. During unloading, the delivered apples were accidentally mixed. It was found that if all the apples are now sold at one price - 90 kopecks lower than the price per kilogram of first-grade apples, the planned amount will be received. How many kilograms of apples were delivered, if it is known that there were 5 kg more of second-grade apples than first-grade apples?
## Ratios between natural numbers
|
3.11 Let's construct the following table:
| Apple Variety | Cost, rub | Quantity, tons | Price, rub/kg |
| :---: | :---: | :---: | :---: |
| First | 228 | $x$ | $\frac{228}{x}$ |
| Second | 180 | $x+5$ | $\frac{180}{x+5}$ |
According to the problem, we have the equation
$\left(\frac{228}{x}-0.9\right)(2 x+5)=408$,
from which, after transformations, we arrive at the quadratic equation
$$
6 x^{2}-145 x-3800=0
$$
We find its roots:
$x_{1}=\frac{145+335}{12}=40, x_{2}=\frac{145-335}{12}<0$ (not suitable).
Thus, 40 tons of the first variety of apples and 45 tons of the second variety of apples were delivered, i.e., a total of 85 tons.
Answer: 85 tons.
|
85
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.12. The sum of the digits of a two-digit number is 12. If 36 is added to this number, the result is a number written with the same digits but in reverse order. Find the original number.
|
3.12 Let the desired number be of the form $10 x+y$. Then, by the condition,
$x+y=12$
and $10 x+y+36=10 y+x$, i.e.,
$x-y+4=0$.
Adding (1) and (2), we get $2 x=8$, hence $x=4$, and $y=8$.
Answer: 48.
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.13 A three-digit number ends with the digit 2. If it is moved to the beginning of the number, the resulting number will be 18 more than the original. Find the original number.
|
3.13 Let the desired three-digit number be of the form $100x + 10y + 2$; then after moving the digit 2, it will take the form
$200 + 10x + y$.
By the condition,
$200 + 10x + y - (100x + 10y + 2) = 18$
from which $10x + y = 20$. Substituting this expression into (1), we get $200 + 20 = 220$. Thus, the original three-digit number is 202.
Answer: 202.
|
202
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.14 A positive integer is thought of. To its representation, the digit 7 is appended on the right, and from the resulting new number, the square of the thought number is subtracted. The remainder is then reduced by $75\%$ of this remainder, and the thought number is subtracted again. In the final result, zero is obtained. What number was thought of?
## Motion: distance, speed, time
|
3.14 Let a number $x$ be thought of. Then, following the text of the condition, we get the numbers
$10 x+7, 10 x+7-x^{2}$ and the remainder $\frac{25}{100}\left(10 x+7-x^{2}\right)$.
Then $\frac{1}{4}\left(10 x+7-x^{2}\right)-x=0$, or $x^{2}-6 x-7=0$. Only the value $x=7$ works.
Answer: 7.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.16 A material particle entered the hole of a pipe, and 6.8 minutes later, a second particle entered the same hole. Upon entering the pipe, each particle immediately began linear motion along the pipe: the first particle moved uniformly at a speed of 5 m/min, while the second particle covered 3 m in the first minute and 0.5 m more in each subsequent minute than in the previous one. How many minutes did it take for the second particle to catch up with the first?
|
3.16 Let $t$ be the time (in minutes) it takes for the second particle to catch up with the first. The distance traveled by the second particle is equal to the sum of $t$ terms of an arithmetic progression, where $a_{1}=3, d=0.5$; therefore,
$s=\frac{2 a_{1}+d(t-1)}{2} t=\frac{6+0.5(t-1)}{2} t$.
The same distance traveled by the first particle is $5(6.8+t)=34+5 t$. Thus, $\frac{6+0.5(t-1)}{2} t=34+5 t$, from which $t=17$ (min).
|
17
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.18 The distance between points $A$ and $B$ is 270 m. A body moves uniformly from $A$ to $B$; upon reaching $B$, it immediately returns with the same speed. A second body, which leaves $B$ for $A$ 11 s after the first body leaves $A$, moves uniformly but more slowly. On its way from $\boldsymbol{B}$ to $\boldsymbol{A}$, it meets the first body twice: 10 and 40 s after its departure from $B$. Find the speed of each body.
|
3.18 A convenient model of the problem is a graph of uniform motion in the coordinate system "path" ($s$ - in meters), "time" ($t$ in seconds). Let $AC$ (Fig. 3.3) be the graph of the motion from $A$ to $B$ of the first body with speed $v_{1}=\operatorname{tg} \alpha$ (time axis $At$); $CD$ be the graph of the motion from $B$ to $A$ of the same body with the same speed $v_{1}=\operatorname{tg} \alpha$ (time axis $Bt$); $\boldsymbol{EF}$ be the graph of the motion of the second body from $B$ to $\boldsymbol{A}$ with speed $v_{2}=\operatorname{tg} \beta, \beta<\alpha$ (time axis $Bt$).
The time interval $BE=11$, the time interval to the first meeting $EH=10$, between the first and second meetings $HK=30$; then $NM=21 v_{1}, HM=10 v_{2}$, $KF=40 v_{2}, NM+HM=AB=270$, i.e.,
$21 v_{1}+10 v_{2}=270$
Fig. 3.3
The time interval $HC=\frac{HM}{v_{1}}=\frac{10 v_{2}}{v_{1}}$; the time interval $CK=\frac{KF}{v_{1}}=\frac{40 v_{2}}{v_{1}}$. Since $HC+CK=30$, then
$\frac{10 v_{2}}{v_{1}}+\frac{40 v_{2}}{v_{1}}=30$, hence
$5 v_{2}=3 v_{1}$.
Solving equations (1) and (2) simultaneously, we find $v_{1}=10 \mathrm{m} / \mathrm{s}$, $v_{2}=6 \mathrm{m} / \mathrm{s}$.
Answer: 10 and $6 \mathrm{~m} / \mathrm{s}$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.19 The first tourist, after riding a bicycle for 1.5 hours at a speed of $16 \mathrm{km} / \mathrm{h}$, makes a stop for 1.5 hours, and then continues the journey at the initial speed. After 4 hours from the departure of the first tourist, the second tourist sets off in pursuit on a motorcycle at a speed of 56 km/h. What distance will they have traveled before the second tourist catches up with the first?
|
3.19 An approximate graph of the movement is shown in Fig. 3.4.
Fig. 3.4
Let $t$ be the time (in hours) it takes for the second tourist to catch up with the first. Since
$$
\begin{aligned}
& v_{\text {bike }}=16 \mathrm{km} / \mathrm{h} \\
& v_{\text {motor }}=56 \mathrm{km} / \mathrm{h}, \text { then } \\
& s_{\text {bike }}=(2.5+t) \cdot 16
\end{aligned}
$$
$$
s_{\text {motor }}=56 t \text {. }
$$
From this, $56 t=16 t+40$, i.e., $t=1$ (hour). Therefore, $s=56$ km.
|
56
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.21 A motorcyclist set off from point $A$ to point $B$, which is 120 km away from $A$. On the way back, he set off at the same speed, but had to stop for 10 minutes one hour after departure. After this stop, he continued his journey to $A$, increasing his speed by 6 km/h. What was the initial speed of the motorcyclist, given that he spent as much time on the return trip as he did on the trip from $A$ to $B$?
|
3.21 According to the condition, $A C=C D$ (Fig. 3.6).
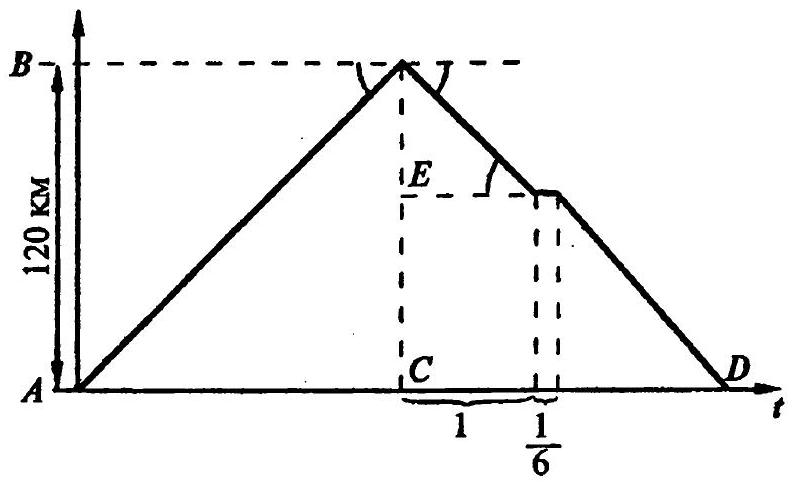
Fig. 3.6
We have $A C=\frac{120}{x}$, where $x$ is the initial speed;
$C D=1+\frac{1}{6}+\frac{120-x}{x+6}$. Therefore,
$$
\frac{120}{x}=\frac{7}{6}+\frac{120-x}{x+6}, \text { from which } x=48 \text { (km/h). }
$$
Answer: $48 \mathrm{~km} / \mathrm{h}$.
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.22 A pedestrian and a cyclist set off simultaneously towards each other from cities $A$ and $B$, the distance between which is $40 \mathrm{km}$, and meet 2 hours after departure. Then they continue their journey, with the cyclist arriving in $A$ 7 hours and 30 minutes earlier than the pedestrian in $B$. Find the speeds of the pedestrian and the cyclist, assuming that they remained constant throughout.
## Paboma
|
3.22 Fill in the table of speed, distance, and time values in the order indicated by the numbers (1), (2), .., (12):
| Tourist | Before Meeting | | | After Meeting | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | speed, km/h | time, h | distance, km | speed, km/h | time, h | distance, km |
| Pedestrian | (1) | $(3)^{2}$ | $5^{2 x}$ | $b^{x}$ | $\frac{40-2 x}{(1)}$ | $9^{40-2 x}$ |
| Cyclist | $\sqrt{20-x}$ | 4 | $40-2 x$ | $\sqrt[8]{20-x}$ | $\frac{2 x}{20-x}$ | $2 x$ |
By condition,
$$
\begin{aligned}
& \frac{40-2 x}{x}-\frac{2 x}{20-x}=\frac{15}{2} \\
& \text { from which } x=4(\text { km/h })
\end{aligned}
$$
Answer: 4 and 16 km/h.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.23 A team of workers completed a certain task. If the team is reduced by 20 people, then the same task will be completed 5 days later than with the original composition, and if the team is increased by 15 people, then the task will be completed 2 days earlier. How many workers were originally in the team and how many days did they take to complete the task?
|
3.23 Let $x$ workers completed the task in $y$ days; then according to the condition $x y=(x-20)(y+5)$ and $x y=(x+15)(y-2)$. We can write both equations as proportions:
$\frac{x-20}{x}=\frac{y}{y+5}$ and $\quad \frac{x+15}{x}=\frac{y}{y-2}$.
Each proportion of the form $\frac{a}{b}=\frac{c}{d}$ can be replaced by an equivalent proportion of the form $\frac{a-b}{b}=\frac{c-d}{d}$. Then we get
$\frac{-20}{x}=\frac{-5}{y+5}$ and $\frac{15}{x}=\frac{2}{y-2}$.
Now it is easy to find that $x=60$ and $y=10$. Thus, there were 60 people in the team, who completed the task in 10 days.
Answer: 60 workers; 10 days.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.24 One of the two machines processes a batch of parts for 3 days longer than the other. How long would the processing of this batch of parts take on each machine separately, if it is known that when working together, these machines processed a batch of parts three times larger in 20 days?
|
3.24 Time ( $t$ ), the amount of work done per unit of time, i.e., productivity ( $W$ ), and the total volume of work ( $V$ ) are related by the equation $V=W t$. Let $V=1$ and fill in the following table:
| Machine | Time, days | Volume of work | Productivity |
| :---: | :---: | :---: | :---: |
| First | $x$ | 1 | $\frac{1}{x}$ |
| Second | $x-3$ | 1 | $\frac{1}{x-3}$ |
| Both together | 20 | 3 | $\frac{3}{20}$ |
Since the productivities of the machines add up when they work together, $\frac{1}{x}+\frac{1}{x-3}=\frac{3}{20}$, from which $x=15$.
Answer: 15 and 12 days.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.25 Two snow-clearing machines are working on snow removal. The first can clear a street in 1 hour, while the second can do it in $75\%$ of this time. Starting the cleaning simultaneously, both machines worked together for 20 minutes, after which the first machine stopped. How much more time is needed for the second machine to finish the work?
|
3.25 Let's accept the entire volume of work as a unit. The productivity of the first machine is 1 (per hour), and the second is $1: \frac{3}{4}=\frac{4}{3}$ (per hour). Working together for $\frac{1}{3}$ hour, they will complete $\frac{1}{3} \cdot 1 + \frac{1}{3} \cdot \frac{4}{3} = \frac{7}{9}$ of the entire work. Then, the remaining work for the second machine will be $\frac{2}{9}$, which will require $\frac{2}{9} : \frac{4}{3} = \frac{1}{6}(h)$.
Answer: 10 min.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.29 The volume of substance $A$ is half the sum of the volumes of substances $B$ and $C$, and the volume of substance $B$ is $\frac{1}{5}$ of the sum of the volumes of substances $A$ and $C$. Find the ratio of the volume of substance $C$ to the sum of the volumes of substances $A$ and $B$.
|
3.29 According to the condition, $2 V_{A}=V_{B}+V_{C}$ and $5 V_{B}=V_{A}+V_{C}$. Let $V_{A}=x V_{C}$ and $V_{B}=y V_{C}$. Then we get the system
$\left\{\begin{array}{l}2 x-y=1 \\ -x+5 y=1\end{array}\right.$
from which $x=\frac{2}{3}, y=\frac{1}{3}$. Therefore,
$\frac{V_{C}}{V_{A}+V_{B}}=\frac{1}{x+y}=1$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.30 It is known that the difference between the variable quantities $z$ and $y$ is proportional to the quantity $x$, and the difference between the quantities $x$ and $z$ is proportional to the quantity $y$. The coefficient of proportionality is the same and is equal to a positive integer $k$. A certain value of the quantity $z$ is $\frac{5}{3}$ times the difference of the corresponding values of $x$ and $y$. Find the numerical value of the coefficient $k$.
|
3.30 I n s t r u c t i o n. Write the condition as a system of three equations. From the first two equations, express $\frac{x}{y}$ and $\frac{y}{z}$ in terms of $k$, and then substitute the obtained expressions for $\frac{x}{y}$ and $\frac{y}{z}$ into the third equation and calculate the desired value of $k$.
A n s w e r: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.33 From milk with a fat content of $5 \%$, cottage cheese with a fat content of $15.5 \%$ is produced, leaving behind whey with a fat content of $0.5 \%$. How much cottage cheese is obtained from 1 ton of milk?
## Geometric and Physical Problems
|
3.33 Let $x$ tons of cottage cheese with a fat content of $15.5\%$ be obtained; then $1-x$ tons of whey with a fat content of $0.5\%$ will remain. Therefore, in 1 ton of milk, there is
$\frac{15.5 x}{100}+\frac{0.5(1-x)}{100}=\frac{15.5 x+0.5}{100}$ tons of fat.
According to the condition, $\frac{15.5 x+0.5}{100}=\frac{5}{100}$, from which $x=0.3$ (tons).
Answer: $\quad 300 \text{kg}$.
|
300
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.38 It is known that a freely falling body travels 4.9 m in the first second, and in each subsequent second, it travels 9.8 m more than in the previous one. If two bodies start falling from the same height, one 5 s after the other, then after what time will they be 220.5 m apart from each other?
|
3.38 Instruction. Use the well-known physics formula $s=4.9 t^{2}$.
Answer: 7 seconds after the start of the fall of the first body.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.40 A red pencil costs 27 kopecks, a blue one - 23 kopecks. No more than 9 rubles 40 kopecks can be spent on purchasing pencils. It is necessary to purchase the maximum possible total number of red and blue pencils. At the same time, the number of red pencils should be as few as possible, but the number of blue pencils should not differ from the number of red pencils by more than 10. How many red and how many blue pencils should be purchased under the given conditions
|
3.40 Let $x$ red and $y$ blue pencils be bought. According to the conditions, $27 x+23 y \leqslant 940$ and $y-x \leqslant 10$. Let's construct the lines
\[
\begin{aligned}
& 27 x+23 y=940 \\
& y-x=10
\end{aligned}
\]
From Fig. 3.8, it is clear that these lines intersect at point $A$, the coordinates of which satisfy equations (1) and (2), and at this point, the maximum possible sum $x+y$ is achieved. Solving the system (1), (2) and considering that the numbers $x$ and $y$ are natural, we get $x=14, y=24$.
Answer: 14 red and 24 blue pencils.
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.41 Several students decided to buy an imported tape recorder priced between 170 and 195 dollars. However, at the last moment, two of them refused to participate in the purchase, so each of the remaining had to contribute 1 dollar more. What was the price of the tape recorder?
## Ratios between natural numbers
|
3.41 Let $x$ be the original number of students, and $p$ be the cost of the tape recorder. Then $\frac{p}{x}$ is the amount each student was originally supposed to contribute, and $\frac{p}{x-2}$ is the amount each of the tape recorder buyers contributed. Using one of the conditions of the problem, we get the equation
$$
\frac{p}{x-2}-\frac{p}{x}=1
$$
$$
p\left(\frac{1}{x-2}-\frac{1}{x}\right)=1 ; p \cdot \frac{2}{x(x-2)}=1 ; p=\frac{x(x-2)}{2}
$$
Now let's use the other condition:
$170<\frac{x(x-2)}{2}<195 ; 340<x^{2}-2 x<390 ;$
$341<(x-1)^{2}<391 ; 18.5<x-1<19.8$.
Since the number $x-1$ must be an integer, then $x-1=19$,
i.e., $x=20$. Therefore, the tape recorder cost $\frac{20 \cdot 18}{2}=180$ dollars.
Answer: 180 dollars.
|
180
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.42 The digits of a certain three-digit number form a geometric progression. If in this number the digits of the hundreds and units are swapped, the new three-digit number will be 594 less than the desired one. If, however, in the desired number the digit of the hundreds is erased and the digits of the resulting two-digit number are rearranged, the new two-digit number will be 18 less than the number expressed by the last two digits of the desired number. Find the original number.
|
3.42 The desired number has the form $100 x+10 y+z$, where $x, y, z$ form a geometric progression, i.e.
$x z=y^{2}$.
According to the condition, we have:
$100 z+10 y+x=100 x+10 y+z-594$, from which
$x-z=6$
$10 y+z=10 z+y+18$, from which
$y-z=2$.
The system of equations (1), (2), (3) is satisfied by $x=8$, $\boldsymbol{y}=4, z=2$. The desired number is 842.
Answer: 842.
|
842
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.45 The recording of a six-digit number starts with the digit 2. If this digit is moved from the first position to the last, keeping the order of the other five digits, the newly obtained number will be three times the original number. Find the original number.
## Distance: path, speed, time
|
3.45 The original six-digit number has the form $2 \cdot 10^{5}+x$. After moving the digit 2 to the last place, we get the number $10 x+2$. According to the condition, $10 x+2=3\left(2 \cdot 10^{5}+x\right)$, from which $x=85714$. Therefore, the original number is 285714.
Answer: 285714.
|
285714
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.