problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
11. Write down all the letter combinations that can be obtained by rearranging the letters in the word MAMA.
|
11. We will get the following 6 letter combinations: MAMA, MMAA, MAAM, AMAM, AAMM, AMMA.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. There are 5 different books: three on mathematics and two on physics. In how many ways can two books be selected: one on mathematics and one on physics?
|
14. Let's denote the mathematics books as $M_{1}, M_{2}, M_{3}$, and the physics books as $\Phi_{1}$, and $\Phi_{2}$. We obtain the following 6 ways: $M_{1} \Phi_{1}, M_{2} \Phi_{1}, M_{3} \Phi_{1}, M_{1} \Phi_{2}, M_{2} \Phi_{2}, M_{3} \Phi_{2}$. We can also reason as follows: the selection of a mathematics book can be done in three ways, and for each of these ways, there are 2 ways to choose a physics book. In total, we will have $3 \cdot 2=6$ ways.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. In how many ways can two letters be chosen from the word УЧЕБНИК so that one of the letters is a consonant and the other is a vowel?
|
15. The number of ways can be visually represented using the graph shown in Figure 94. In total, we get \(4 \cdot 3 = 12\) ways.
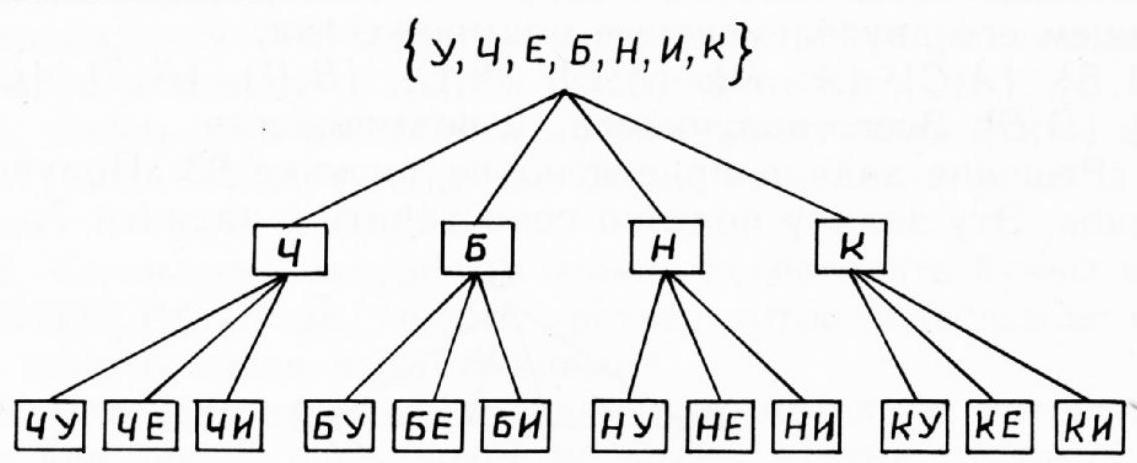
Fig. 94
After solving problems 14 and 15, it is appropriate to formulate the multiplication rule for two selections.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. From city $A$ to city $B$, one can travel by one of three types of transport, and from city $B$ to city $C$ - by one of four types of transport. In how many ways can one travel from city $A$ to city $C$, visiting city $B$ along the way?
|
16. From city $A$ to city $B$, there are three ways to travel, after which from city $B$ to city $C$, there are four ways. By the rule of product, from city $A$ to city $C$, there are $3 \cdot 4=12$ ways to travel.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
90. Several students went to take a math exam. One student calculated that even if none of them "fail," there could still be 59049 different exam outcomes. How many students were there?
|
90. Let there be $n$ students. For each of them, there are three possible outcomes of the exam: "satisfactory", "good", and "excellent". Therefore, for $n$ students, we get $3^{n}$ outcomes. We have the equation: $3^{n}=59049$, from which $n=10$.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. Cut a plate weighing 11 g into three pieces so that, using these pieces as weights, it is possible to weigh on balance scales any whole number of grams from 1 g to 11 g.
$(4-5$ grade.)
|
4.1. The plate needs to be cut into parts weighing 1 g, 3 g, and 7 g. To weigh 2 g, you need to place 3 g on one pan of the scales, and on the other pan - a 1 g counterweight and the substance to be weighed. For the other cases, we get: $4=3+1,5=7+1-3,6=7-1,8=7+1$, $9=7+3-1,10=7+3,11=7+3+1$.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. If Petya performs a certain task in such a way that each subsequent day he does twice as much as in all the previous days combined, then the entire task will take him 12 days. How many days will it take for Petya and Kolya to complete this task if Kolya works in the same way as Petya?
$$
\text { (4-8 grades) }
$$
|
9.1. It is clear that in 11 days, Petya will complete exactly half of the entire work, since on the twelfth day, he must complete as much work as he did in the previous 11 days combined, after which the entire work will be completed. If Kolya works together with Petya, then Kolya will also complete half of the entire work in 11 days. Thus, both boys together will complete the entire work in 11 days.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16.1. Calculate: $2^{15}-2^{14}-2^{13}-\ldots-2^{1}-1$.
$$
\text { (6-7 grades) }
$$
|
16.1. Noticing that $2^{15}-2^{14}=2 \cdot 2^{14}-2^{14}=2^{14}$, we will reduce the given expression to the following:
$$
2^{14}-2^{13}-2^{12}-\ldots-2-1
$$
Continuing to proceed in this manner further and further, we will find that the desired sum is 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20.1. A boy wrote a certain number. In the second place, he wrote the number 7, in the third place - the difference between the second and the first number, in the fourth place - the difference between the third and the second number, and so on. What number will be in the $200-\mathrm{m}$ place?
$$
\text { (6-8 grades) }
$$
4
|
20.1. Let the first number be denoted by $x$. Then, following the condition of the problem, we get the following sequence of numbers: $x, 7, 7-x, -x, -7, x-7, x, 7, \ldots$ 18
As we can see, the seventh and eighth numbers repeat the first and second, i.e., we have a periodic repetition of numbers with a period of 6. Since 200 divided by 6 leaves a remainder of 2, we will have the same number on the two hundredth place as on the second place, i.e., 7.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
22.1. Calculate the expression $2 x^{4}+3 x^{2} y^{2}+y^{4}+y^{2}$, given that $x^{2}+y^{2}=1$.
$$
\text { (7-8 grades) }
$$
|
22.1. Taking into account that $x^{2}+y^{2}=1$, we get:
$$
\begin{gathered}
2 x^{4}+3 x^{2} y^{2}+y^{4}+y^{2}=2 x^{4}+2 x^{2} y^{2}+x^{2} y^{2}+y^{4}+y^{2}= \\
=2 x^{2}\left(x^{2}+y^{2}\right)+y^{2}\left(x^{2}+y^{2}\right)+y^{2}=2 x^{2}+y^{2}+y^{2}= \\
=2\left(x^{2}+y^{2}\right)=2
\end{gathered}
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32.1. Find all such prime numbers that can be represented both as the sum of two prime numbers and as their difference. $(7-10$ grades $)$
|
32.1. It is obvious that neither of the prime numbers 2 and 3 can be represented as the sum of two prime numbers. Now, let's take a prime number \( p > 3 \). It can be represented as the sum of two prime numbers only if \( p-2 \) is a prime number, since in the sum of two prime numbers, one of the addends must be equal to 2. Similarly, if a prime number \( p > 3 \) can be represented as the difference of two prime numbers, then the number \( p+2 \) must be prime, since in the difference of two prime numbers, the subtrahend must be equal to 2. Therefore, if a prime number \( p \) can be represented both as the sum and as the difference of two prime numbers, then the numbers \( p-2 \) and \( p+2 \) must be prime simultaneously. It is clear that the number 5 satisfies the condition of the problem, since \( 5 = 3 + 2 = 7 - 2 \), where all four numbers \( 2, 3, 5, 7 \) are prime. We will prove that the problem has no other solutions. For this, it is sufficient to prove that for a prime \( p > 5 \), the numbers \( p-2 \) and \( p+2 \) cannot be prime simultaneously. Indeed, a prime number \( p > 5 \) when divided by 3 gives a remainder of 1 or 2, i.e., it has one of two forms: \( p = 3k + 1 \) or \( p = 3k + 2 \), where \( k > 1 \). In the first case, the number \( p + 2 = 3k + 1 + 2 = 3(k + 1) \) will be composite, and in the second case, the number \( p - 2 = 3k + 2 - 2 = 3k \) will be composite.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.2. One sixth of the fourth-grade students received fives on their math test, one third received threes, and half received fours. How many students in this class received unsatisfactory grades?
$$
\text { (4-5 grade) }
$$
|
4.2. From Figure 12, we see that
$$
\frac{1}{6}+\frac{1}{3}+\frac{1}{2}=\frac{1}{6}+\frac{2}{6}+\frac{3}{6}=1
$$
Fig. 12
i.e., the students who received grades of five, three, and four make up the entire class. Therefore, no student received an unsatisfactory grade.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.2. The sum of half and a third of a number is 7 units greater than its quarter. What is this number?
$$
(6-7 \text { grade })
$$
|
12.2. Let the desired number be denoted by $x$. Then
$$
\frac{1}{2} x+\frac{1}{3} x=\frac{1}{4} x+7, \text { from which } x=12
$$
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.2. A third of the sixth-grade students received threes for their math test. How many students received fives if only one student received a two, and fives were received by $\frac{5}{13}$ of the sixth-graders?
$$
(6-7 \text { grade) }
$$
|
13.2. Students who received threes and fours constitute
$$
\frac{1}{3}+\frac{5}{13}=\frac{28}{39} \text { of the entire class. }
$$
Therefore, the number of students in this class is divisible by 39. Since the class size does not exceed 50 students, there are 39 students in total in the class, with 28 of them receiving threes and fours on the test. Therefore, fives were received by $39-28-1=10$ students.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16.2. Every third student in the sixth grade is a member of the math club, every fourth is a member of the history club, every sixth is a member of the chemistry club, and all the others are members of the literature club. How many people are in the chemistry club if there are three more people in the math club than in the literature club?
$$
(6-7 \text { grade) }
$$
|
16.2. Students attending the literary club constitute $1-\frac{1}{3}-\frac{1}{4}-\frac{1}{6}=\frac{1}{4}$ of the class. If $x$ is the total number of students in the sixth grade, then according to the problem, $\frac{1}{3} x-\frac{1}{4} x=3$, from which $x=36$. Therefore, the number of students attending the chemistry club is $36: 6=6$.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19.2. What is the last digit of the sum
$$
3^{13}+3^{15}+3^{17}+\ldots+3^{43} ?
$$
|
19.2. There are 16 addends in total in this sum. By sequentially dividing them into 8 pairs, we get:
$$
\begin{gathered}
3^{13}(1+9)+3^{17}(1+9)+\ldots+3^{41}(1+9)= \\
=\left(3^{13}+3^{17}+\ldots+3^{41}\right) \cdot 10
\end{gathered}
$$
Thus, the considered sum ends in 0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28.2. Among all triangles for which the sum of the medians is 3, find the triangle with the greatest sum of altitudes.
$$
(7-9 \text { grades })
$$
|
28.2. In any triangle, the height dropped to any side is not greater than the median drawn to the same side. Therefore, the sum of the heights of the triangle is not greater than the sum of its medians. In the conditions of this problem, the greatest sum of heights is 3, which will be the case for an equilateral triangle.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15.3. Boys are dividing nuts. The first one took 3 nuts and a fifth of the remainder; the second took twice 3 nuts and a fifth of the new remainder; the third took thrice 3 nuts and a fifth of the next remainder, and so on. How many boys were there if it turned out that as a result of such division, each received an equal number of nuts?
$$
\text { (6-8 grades) }
$$
|
15.3. Let the number of all boys be denoted by $n$. Then the last boy received $3 n$ nuts with nothing left over. The second-to-last boy received $3(n-1)$ nuts and one fifth of the remainder. Since the second-to-last boy received as many nuts as the last one, i.e., $3 n$ nuts, the one fifth of the remainder amounts to $3 n-3(n-1)=3$ nuts, and the entire remainder before the second-to-last boy took his one fifth consisted of 15 nuts. Therefore, the last boy received $15-3=12$ nuts. Then $3 n=12$, from which $n=4$. Answer: There were 4 boys in total.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19.3. Can the number of diagonals of a polygon be exactly twice the number of its sides?
$(6-8$ grades $)$
|
19.3. From one vertex of an $n$-sided polygon, $n-3$ diagonals emanate. Then the product $n(n-3)$ expresses twice the number of all diagonals, since in this counting each diagonal was counted twice. It remains to check whether the equation $0.5 n(n-3)=2 n$ has a solution in natural numbers. It is easy to see that such a solution is $n=7$. Thus, the number of diagonals of a convex heptagon is twice the number of its sides.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
114*. What is the maximum number of natural numbers that can be written in a row so that the sum of any three consecutive numbers is even, and the sum of any four consecutive numbers is odd?
|
Let's denote the consecutive natural numbers of the row as $a_{1}, a_{2}, a_{3}$, and so on.
By the condition, the sums
$$
a_{1}+a_{2}+a_{3}, \quad a_{2}+a_{3}+a_{4}, \quad a_{3}+a_{4}+a_{5}, \quad a_{4}+a_{5}+a_{6}
$$
and others are even. By subtracting each sum, starting from the second, from the previous one, we get that the differences
$$
a_{4}-a_{1}, \quad a_{5}-a_{2}, \quad a_{6}-a_{3}, \ldots
$$
are even, and therefore, the pairs of numbers $a_{1}$ and $a_{4}, a_{2}$ and $a_{5}, a_{3}$ and $a_{6}$, etc., have the same parity.
Let's write down the odd sums consisting of four consecutive numbers:
$$
\begin{gathered}
a_{1}+a_{2}+a_{3}+a_{4}=\left(a_{1}+a_{2}+a_{3}\right)+a_{4} \\
a_{2}+a_{3}+a_{4}+a_{5}=\left(a_{2}+a_{3}+a_{4}\right)+a_{5} \\
a_{3}+a_{4}+a_{5}+a_{6}=\left(a_{3}+a_{4}+a_{5}\right)+a_{6}, \ldots
\end{gathered}
$$
From this, it follows that the numbers $a_{4}, a_{5}, a_{6}$, etc., are odd. But then the sum $a_{4}+a_{5}+a_{6}$ is odd, which contradicts the condition.
This contradiction arises every time the number of numbers is not less than 6. Let's try to take 5 numbers.
Reasoning similarly, we establish that the numbers $a_{4}$ and $a_{5}$ are odd, and therefore, by the previous, the numbers $a_{1}$ and $a_{2}$ are also odd. Then, since the sum $a_{1}+a_{2}+a_{3}$ is even, the number $a_{3}$ is even.
Let's do one more check and verify that if we take five numbers
$$
a_{1}, a_{2}, a_{3}, a_{4}, a_{5}
$$
where the number $a_{3}$ is even, and the others are odd, then each of the sums
$$
a_{1}+a_{2}+a_{3}, \quad a_{2}+a_{3}+a_{4}, \quad a_{3}+a_{4}+a_{5}
$$
is even, and each of the sums
$$
a_{1}+a_{2}+a_{3}+a_{4}, \quad a_{2}+a_{3}+a_{4}+a_{5}
$$
is odd.
Answer: 5
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
121. Find all values of the digit $a$, if the number $\overline{875 a}$ is divisible by 6.
|
$\triangle$ Since this number is divisible by 6, it is divisible by 2 and 3, and vice versa.
Let's apply the divisibility rule for 3. For this, we will find the sum of the digits of the number:
$$
8+7+5+a=20+a
$$
From the divisibility of $(20+a): 3$ it follows that the digit $a$ is 1, 4, or 7. But according to the divisibility rule for 2, this digit must be even, so only $a=4$ fits.
Answer: 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
141. Find all values of the digit $a$, if the number $\overline{a 719}$ is divisible by 11.
|
$\triangle$ Divisibility of this number by 11 is equivalent to the divisibility by 11 of the sum $a-7+1-9=$ $=a-15$. The difference $a-15$ is divisible by 11 only when $a=4$.
Answer: 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
146. From a natural number, the sum of its digits was subtracted, and then one digit was erased from the resulting difference. The sum of the remaining digits of the difference is 131. Which digit was erased?
|
$\triangle$ The difference between a natural number and the sum of its digits is divisible by 9 (see problem 130). Let the erased digit be denoted by $x$. Then the sum $131+x$ is divisible by 9, from which $x=4$.
Answer: 4
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
381. The numbers $p$ and $p+15$ are prime. Find all such $p$.
|
$\triangle$ When $p=2$, we get that the number $p+15=17$ is prime.
Let $p>2$. Then $p$ is odd. Consequently, the number $p+15$ is even. Hence, this number is composite. Therefore, no prime $p>2$ works.
Answer: 2.
$382^{\circ}$. Prove that the numbers $p, p+2$, and $p+4$ are all prime only in the case when they form the triplet $3,5,7$.
$\triangle$ Consider several cases depending on $p$.
When $p=2$, the number $p+2=4$ is composite, so the value $p=2$ is ruled out.
When $p=3$, we get the triplet $3,5,7$, mentioned in the problem statement.
When $p=5$, the number $p+2=7$ is prime, but the number $p+4=9$ is composite, so $p=5$ must be discarded.
When $p=7$, the number $p+2=9$ is composite.
When $p=11$, the number $p+4=15$ is also composite.
It seems that only $p=3$ works. Let's prove it.
It is not hard to notice that the values $p=5, p=7$, and $p=11$ did not work because either $p+2$ or $p+4$ is divisible by 3. Let's confirm that this will always be the case for a prime $p>3$.
A prime number greater than 3 does not divide by 3 and, therefore, when divided by 3, can only leave a remainder of 1 or 2. Let's consider both cases.
1) Suppose $p$ when divided by 3 leaves a remainder of $1: p=3k+1(k \in \mathbb{N})$. Then the number
$$
p+2=(3k+1)+2=3k+3
$$
is divisible by 3, and the quotient of this division is greater than 1. Thus, the number $p+2$ is composite.
2) Suppose $p=3k+2(k \in \mathbb{N})$. Then the number
$$
p+4=(3k+2)+4=3k+6
$$
is composite.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
427. If the numbers 826 and 4373 are divided by the same natural number, the remainders will be 7 and 8, respectively. Find all values of the divisor.
|
$\triangle$ Let's write the corresponding equalities:
$$
826=b q_{1}+7, \quad 4373=b q_{2}+8
$$
where $b-$ is the unknown divisor, $q_{1}$ and $q_{2}$ are the incomplete quotients. Then
$$
b q_{1}=819, \quad b q_{2}=4365
$$
Let's factorize the numbers 819 and 4365 into prime factors:
$$
819=3^{2} \cdot 7 \cdot 13, \quad 4365=3^{2} \cdot 5 \cdot 97
$$
Therefore, the common divisors of the numbers 819 and 4365 are the numbers 1, 3, and 9. But common divisors equal to 1 and 3 are impossible, as the remainder must be less than the divisor. The only remaining number is 9.
Answer: 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
431. When dividing a natural number $a$ by 2, the remainder is 1, and when dividing by 3, the remainder is 2. What remainder will be obtained when dividing $a$ by 6?
|
$\triangle$ Let
$$
a=6 q+r
$$
where the remainder $r$ satisfies the inequality $0 \leqslant r \leqslant 5$. We will consider all possible values of $r$.
The case $r=0$ is impossible, otherwise the number $a$ would be divisible by 2 and 3.
The case $r=1$ is also impossible, because then $a$ when divided by 3 would leave a remainder of 1, not 2.
For similar reasons, the cases $r=2, r=3$, and $r=4$ are also ruled out.
The case $r=5$ is possible, for example, when $a=5$ or $a=11$.
Answer: 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
438*. What remainder does $46^{925}$ give when divided by $21?$
|
$\triangle$ The solution method we applied in the last problems is too cumbersome here due to the large base of the exponent and the large divisor. Let's try to modify it.
Divide 46 by 21 with a remainder and transform the exponent:
$$
46^{925}=(21 \cdot 2+4)(21 \cdot 2+4) \ldots(21 \cdot 2+4)
$$
If we multiply 925 identical sums together, then all the terms in the resulting sum are divisible by 21, except for the term $4^{925}$. Therefore, the remainder of the division of the power $46^{925}$ by 21 coincides with the remainder of the division of the power $4^{925}$ by 21.
Let's use the fact that
$$
4^{3}=64=21 \cdot 3+1
$$
We get:
$4^{925}=4 \cdot 4^{924}=4 \cdot\left(4^{3}\right)^{308}=4 \cdot 64^{308}=4 \cdot(21 \cdot 3+1)^{308}=4 \cdot(21 k+1)=4 \cdot 21 k+4$.
Therefore, the desired remainder is 4.
Answer: 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
449. Find the greatest common divisor of all nine-digit numbers, in the representation of which each of the digits $1,2,3, \ldots, 9$ appears exactly once.
|
$\triangle$ Let's denote this greatest common divisor by $d$.
From all nine-digit numbers of the specified form, we will take only two - 123456798 and 123456789.
Since these numbers are divisible by $d$, their difference, which is 9, is also divisible by $d$: $9: d$. Therefore, $d=1, d=3$ or $d=9$.
Which of these cases gives the answer? To determine the truth, we will use the divisibility rules for 3 and 9 to check if each of the nine-digit numbers is divisible by 3 or 9. For this purpose, we will find the sum of the digits of any of them:
$$
1+2+3+\ldots+9=45
$$
Since 45 is divisible by 9, each of the nine-digit numbers is divisible by 9. From the previous, it follows that 9 is their greatest divisor.
Answer: 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
459. Find all values of the greatest common divisor of the numbers $8 a+3$ and $5 a+2$, where $a$ is a natural number.
|
$\triangle$ Let's denote the greatest common divisor of these numbers by $d$. Then
$$
(8 a+3): d, \quad(5 a+2): d
$$
Multiply the sum $8 a+3$ by 5, and the sum $5 a+2$ by 8. We get:
$$
(40 a+15): d, \quad(40 a+16): d
$$
But two consecutive natural numbers $40 a+15$ and $40 a+16$ are coprime (see the statement of problem 454), therefore, $d=1$.
Answer: 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
485. A father and son were walking one behind the other on a snow-covered road. The father's step length is $-80 \mathrm{~cm}$, the son's $-60 \mathrm{~cm}$. Their steps coincided 601 times, including at the beginning and the end of the journey. What distance did they cover?
|
$\triangle$ Let's find the distance that the father and son walked from one coincidence of steps to the next. It is equal to the least common multiple of the numbers 80 and 60, i.e., $240 \mathrm{~cm}=2.4$ m. Therefore, the entire distance they walked is
$$
600 \cdot 2.4 \mathrm{M}=1440 \mathrm{~m}=1 \mathrm{Km} 440 \mathrm{M}
$$
Answer: 1 km 440 m.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
582. The number $n^{2}+2 n(n \in N)$ ends with the digit 4. Find all possible values of its second-to-last digit.
|
$\triangle$ Add 1 to both sides of the equality
$$
n^{2}+2 n=10 a+4
$$
where $a-$ is the number of tens in the number $n^{2}+2 n$, to get:
$$
n^{2}+2 n+1=10 a+5, \quad(n+1)^{2}=10 a+5
$$
From this, it is clear that the number $n+1$ ends in 5, and therefore, its square ends in 25 (see the statement of problem 563). Then the number $a$ ends in 2, i.e., the second-to-last digit of the original number $n^{2}+2 n$ is 2.
Answer: 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
585. Find the last non-zero digit of the product of all natural numbers from 1 to 40.
|
$\triangle$ First, let's find the last non-zero digit of the product $1 \cdot 2 \cdot 3 \cdot \ldots \cdot 10$. For this, we will remove the factors 10, 2, and 5 from the number. The remaining product is
$$
3 \cdot 4 \cdot 6 \cdot 7 \cdot 8 \cdot 9
$$
which, as is not difficult to calculate, ends with the digit 8.
For the same reason, each of the products
$$
11 \cdot 12 \cdot 13 \cdot \ldots \cdot 20, \quad 21 \cdot 22 \cdot 23 \cdot \ldots \cdot 30, \quad 31 \cdot 32 \cdot 33 \cdot \ldots \cdot 40
$$
has the last digit, different from zero, equal to 8. Then the last non-zero digit of the entire given product coincides with the last digit of the number
$$
8 \cdot 8 \cdot 8 \cdot 8=8^{4}=2^{12}=4096
$$
i.e., it is equal to 6.
Answer: 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
635. What exact square is equal to the product of four consecutive odd numbers?
|
Let's denote the smallest of the odd numbers by $n$. Then
$$
n(n+2)(n+4)(n+6)=a^{2}
$$
where $a$ is an integer, and also odd. We transform the left side of this equation by multiplying the first factor by the fourth, and the second by the third:
$$
\left(n^{2}+6 n\right)\left(n^{2}+6 n+8\right)=a^{2}, \quad\left(n^{2}+6 n\right)^{2}+8\left(n^{2}+6 n\right)=a^{2}
$$
We complete the left side of the last equation to a perfect square. For this, we add 16 to both sides of the equation:
$$
\begin{gathered}
\left(n^{2}+6 n\right)^{2}+8\left(n^{2}+6 n\right)+16=a^{2}+16, \quad(n+6 n+4)^{2}=a^{2}+16 \\
\left(n^{2}+6 n+4\right)^{2}-a^{2}=16
\end{gathered}
$$
When do two perfect squares differ by 16? To answer this question, we list the sequence of perfect squares, starting from 0, until the difference between even consecutive squares becomes greater than 16:
$$
0 ; 1 ; 4 ; 9 ; 16 ; 25 ; 36 ; 49 ; 64 ; 81
$$
From this, we see that the difference between two perfect squares equals 16 in only two cases:
$$
16=16-0=25-9
$$
But since $a$ is odd, only the second option fits:
$$
\left(n^{2}+6 n+4\right)^{2}=25, \quad a^{2}=9
$$
We get two equations with $n$:
$$
n^{2}+6 n+4=5, \quad n^{2}+6 n+4=-5
$$
The first of these has non-integer roots, while from the second we find that $n=-3$.
Answer: $9=(-3) \cdot(-1) \cdot 1 \cdot 3$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
650. Find all natural $k$ for which the number
$$
2^{k}+8 k+5
$$
is a perfect square.
|
$\triangle$ Checking shows that the value $k=1$ does not work, the value $k=2$ works, and the values $k=3,4,5,6$ do not work. It seems that no $k>2$ satisfies the condition of the problem. Let's prove our assumption.
Assume that there exists such a $k>2$ that the number $2^{k}+8 k+5$ is a perfect square. Since this number is odd, we have
$$
2^{k}+8 k+5=(2 a-1)^{2},
$$
where $a$ is an integer. We get:
$$
2^{k}+8 k+5=4 a^{2}-4 a+1, \quad 2^{k}+8 k+4=4 a(a-1) .
$$
In the last equation, the right-hand side is divisible not only by 4 but also by 8. However, the left-hand side is not divisible by 8, so such an equation is impossible. We have reached a contradiction. Therefore, no $k>2$ has the required property.
Answer: 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
663. Find all natural $n$ for which the number $n^{2}+3 n$ is a perfect square.
|
$\triangle$ For a natural $n$, the inequality holds:
$$
(n+1)^{2} \leqslant n^{2}+3 n<(n+2)^{2}
$$
(check it!). But since the numbers $(n+1)^{2}$ and $(n+2)^{2}$ are the two closest perfect squares to each other, the number $n^{2}+3 n$ will be a perfect square only when the left inequality turns into an equality:
$$
n^{2}+3 n=(n+1)^{2}, \quad n^{2}+3 n=n^{2}+2 n+1, \quad n=1
$$
Answer: 1.
The method of solution we used in problem 663 is called the "pinching" method.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
678. The number 43 is written in the septenary (base-7) numeral system. In which system is it written with the same digits but in reverse order?
|
$\triangle$ First, let's convert the number 43 to the decimal system:
$$
43_{7}=4 \cdot 7+3=28+3=31
$$
139
Now, let's determine the base $d$ of the system in which the equality $31=34_{d}$ holds. We will have:
$$
31=3 d+4, \quad 3 d=27, \quad d=9
$$
Answer: in base 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
700*. In what number system is the number $11111_{d}$ a perfect square?
|
$\triangle$ Let's represent this number as a sum, decomposing it by powers of $d$:
$$
11111_{d}=d^{4}+d^{3}+d^{2}+d+1
$$
We need to find a natural number $d>1$ such that the resulting sum is a square of a quadratic trinomial with argument $d$ and integer coefficients.
We will bound this sum between two squares:
$$
\left(d^{2}+\frac{d}{2}\right)^{2}<d^{4}+d^{3}+d^{2}+d+1<\left(d^{2}+\frac{d}{2}+1\right)^{2}
$$
(verify the inequality!). Multiply the last inequality by 4 to avoid fractions:
$$
\left(2 d^{2}+d\right)^{2}<4 d^{4}+4 d^{3}+4 d^{2}+4 d+4<\left(2 d^{2}+d+2\right)^{2}
$$
Since the left and right parts of this double inequality are squares of natural numbers differing by 2, and the middle part must also be a square of a natural number, the base of the latter square can only be $2 d^{2}+d+1$. Solve the corresponding equation:
$$
\begin{gathered}
\left(2 d^{2}+d+1\right)^{2}=4 d^{4}+4 d^{3}+4 d^{2}+4 d+4 \\
4 d^{4}+d^{2}+1+4 d^{3}+4 d^{2}+2 d=4 d^{4}+4 d^{3}+4 d^{2}+4 d+4 \\
d^{2}-2 d-3=0, \quad d=3
\end{gathered}
$$
Answer: in the ternary system.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
719. Find all numbers of the form $222 \ldots 2$ that can be represented as the sum of two perfect squares.
|
$\triangle$ Let
$$
222 \ldots 2=a^{2}+b^{2}
$$
where $a$ and $b$ are integers. Then the numbers $a$ and $b$ can only be odd:
$$
a=2 k+1, b=2 l+1 \quad(k \in Z, l \in Z)
$$
Therefore, the sum $a^{2}+b^{2}$ when divided by 8 gives a remainder of 2:
$$
a^{2}+b^{2}=(2 k+1)^{2}+(2 l+1)^{2}=4 k(k+1)+4 l(l+1)+2
$$
On the other hand, of the numbers of the form $222 \ldots 2$, only the number 2 gives a remainder of 2 when divided by 8, since if the number of twos in this number is greater than 1, then
$$
22 \ldots 2=22 \ldots 2 \cdot 100+22
$$
where the first term of the obtained sum is divisible by 8, and the second term gives a remainder of 6 when divided by 8.
Answer: 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
746. There are containers of two types: 130 kg and 160 kg. How many containers of the first type and how many of the second type are there if together they weigh 3 tons? List all solutions.
|
Let's denote the number of containers of the first type by $x$, and the second type by $y$. We get the equation
$$
130 x + 160 y = 3000, \quad 13 x + 16 y = 300
$$
Let's try to use divisibility by 13. For this, we represent $16 y$ as $13 y + 3 y$, and divide 300 by 13 with a remainder:
$$
13 x + 13 y + 3 y = 13 \cdot 23 + 1, \quad 3 y - 1 = 13 \cdot 23 - 13 x - 13 y .
$$
The right side of the last equation is divisible by 13, so the left side must also be divisible by 13. To find the values of $y$ for which the difference $3 y - 1$ is divisible by 13, we will use trial and error. Instead of assigning $y$ consecutive values $1, 2, 3$, etc., it is easier to set $3 y - 1$ to numbers divisible by 13: $13, 26, 39, 52, 65$, etc., and determine each time whether the root of the corresponding equation is an integer or a fraction. Integer roots are obtained in the following cases:
$$
3 y - 1 = 26, \quad y = 9 ; \quad 3 y - 1 = 65, \quad y = 22
$$
and so on. But the value $y = 22$ is already too large, since in this case
$$
16 y = 16 \cdot 22 = 352 > 300 .
$$
For $y = 9$, we can find $x$ from the equation:
$$
13 x + 16 \cdot 9 = 300, \quad 13 x = 156, \quad x = 12
$$
Answer: 12 containers of 130 kg each and 9 of 160 kg each.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
925. What is the smallest number of members in a math club if the number of girls in it is more than $40 \%$, but less than $50 \%$?
|
Let in the club there be $a$ girls, and the total number of club members is $b$. Then the ratio of the number of girls to the total number of club members is $\frac{a}{b}$.
Since $40 \%$ is $\frac{2}{5}$, and $50 \% - \frac{1}{2}$ of the club members, then by the condition
$$
\frac{2}{5}<\frac{a}{b}<\frac{1}{2}
$$
We need to find the smallest natural number $b$, for which there exists such a natural number $a$, for which the written inequality is true.
This is a problem of the same type as problem 922. Therefore, the further solution is carried out in the same way. Complete it independently.
Answer: 7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1007. From a natural number, the sum of its digits was subtracted, and from the resulting difference, the sum of its digits was subtracted again. If this process continues, with what number will the calculations end?
|
$\triangle$ The difference between a natural number and the sum of its digits is divisible by 9 (see supporting problem 120 from § 5), and this property is preserved at each step of the computation. But such a difference is non-negative and decreases with further continuation of the computations, so its last value is zero.
Answer: 0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1061. There are candies in three boxes. In the first box, there are 8 candies less than in the other two together, and in the second box, there are 12 less than in the first and third together. How many candies are in the third box?
|
$\triangle$ Let the number of candies in the first, second, and third boxes be denoted by $a, b$, and $c$ respectively. We obtain the system of equations:
$$
\left\{\begin{array}{l}
a=b+c-8 \\
b=a+c-12
\end{array}\right.
$$
Adding these equations term by term:
$$
a+b=(a+b)+2 c-20
$$
Then
$$
2 c-20=0, \quad c=10
$$
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## PROBLEM 40. PERFECT NUMBERS
The ancient Greeks discovered that some natural numbers $n$ have a remarkable property: the sum of the divisors of the number $n$ equals the number $n$ itself (the number itself is not considered a divisor). For example, $n=28$ gives
$$
1+2+4+7+14=28
$$
Such numbers were called "perfect." Using the arithmetic function $\sigma(n)$, which denotes the sum of all positive divisors of the number $n$ (including the number $n$ itself), we can say that a number $n$ is perfect if $\sigma(n)=2 n$. Perfect numbers are very rare. The first five of them are $6,28,496,8128$, 33550336. In 1976, only 24 perfect numbers were known, with the largest being $2^{19936} \cdot\left(2^{19937}-1\right)$, containing about 6000 digits *).
In the eighteenth century, Euler proved that every even perfect number $m$ can be represented in the form $m=2^{n-1}\left(2^{n}-1\right)$, where $2^{n}-1$ is a prime number.
Prove the following two not-so-difficult statements independently, which we will need later:
1) $\sigma(n)$ is a multiplicative function, i.e., $\sigma(a \cdot b)=\sigma(a) \cdot \sigma(b)$ provided that $a$ and $b$ are coprime numbers.
2) If $2^{n}-1$ is a prime number, then the number $n$ is also a prime number.
*) By 1989, 52 had been found, the largest being $2^{56687} \cdot\left(2^{56667}-1\right) .-\Pi_{p}$ note by the translator.
74
In light of these premises, the task in this problem is to find all perfect numbers $n$ for which $\sigma[\sigma(n)]$ is also a perfect number.
|
Solution. First, let us assume that $n$ is an odd perfect number. Then $\sigma(n)=2n$, where 2 and $n$ are coprime, and we get
$$
\sigma[\sigma(n)]=\sigma(2n)=\sigma(2)\sigma(n)=3\sigma(n)=3 \cdot 2n=6n
$$
Clearly, $6n$ is even, and if it is also perfect, then for some prime number $p$ we must have
$$
6n=2^{p-1}(2^{p}-1)
$$
($p$ must be prime since $2^{p}-1$ is prime). However, since $n$ is odd, the number $6n$ contains the factor 2 only once (in the number 6). This means that
$$
2^{p-1}=2^{1}, \quad \text{so } p=2.
$$
Accordingly,
$$
6n=2(2^{2}-1)=6, \quad \text{so } n=1
$$
But 1 is not an odd perfect number, and we have reached a contradiction. Therefore, there are no odd perfect numbers $n$ for which $\sigma[\sigma(n)]$ is also a perfect number.
Now, let us assume that $n$ is an even perfect number. As stated, for some prime number $p$ we can write
$$
n=2^{p-1}(2^{p}-1)
$$
where $2^{p}-1$ is a prime number. In this case, 2 and $2^{p}-1$ are coprime, and we have
$$
\begin{aligned}
\sigma[\sigma(n)]=\sigma(2n)= & \sigma\left[2^{p}(2^{p}-1)\right]=\sigma\left(2^{p}\right) \cdot \sigma\left(2^{p}-1\right)= \\
& =\left(2^{p+1}-1\right)\left[(2^{p}-1)+1\right]=2^{p}(2^{p+1}-1),
\end{aligned}
$$
since $2^{p}-1$ is prime.
Clearly, this number is even, and if it is also perfect, then it is already represented in the Eulerian form for such numbers. This implies that the exponent $p+1$ must be a prime number. Thus, the numbers $p$ and $p+1$ must both be prime numbers and, since they are consecutive, they can only be 2 and 3. Therefore,
$$
n=2^{p-1}(2^{p}-1)=2 \cdot (2^{2}-1)=6
$$
and
$$
\sigma[\sigma(n)]=\sigma[\sigma(6)]=\sigma(12)=28
$$
Therefore, $n=6$ is the only solution.
|
6
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
## PROBLEM 44. COWS AND SHEEP
Two men jointly owned $x$ cows, which they sold for $x$ dollars a head. With the money they received, they bought sheep at 12 dollars a head. Since the proceeds from the sale of the cows did not divide by 12, they used the remaining money to buy a lamb. Then they divided the flock so that each of them had the same number of animals. The man with the lamb was therefore somewhat shortchanged. To make up for it, the second man gave him his harmonica. How much is the harmonica worth?
|
Solution. The revenue from sales equals $x^{2}$ dollars. If $x$ were divisible by 6, then $x^{2}$ would be divisible by 36, and consequently, by 12. Since this is not the case, $x$ is not divisible by 6. In this case, $x=12 k+r$, where $|r|=1,2,3,4$ or 5. Accordingly,
$$
\frac{x^{2}}{12}=\frac{(12 k+r)^{2}}{12}=\frac{144 k^{2}+24 k r+r^{2}}{12}=12 k^{2}+2 k r+\frac{r^{2}}{12}
$$
Now, since both people have the same number of animals, the total number of animals is even, which means there is an odd number of sheep and one lamb. Therefore, the quotient of dividing the number $x^{2}$ by 12, which equals the number of sheep bought for $x^{2}$ dollars, must be an odd number. But $12 k^{2}+2 k r$ is an even number. Therefore, the number $r^{2} / 12$ must contribute an odd value to the quotient. This implies that $r^{2}$ must exceed 12, leading to $|r|=4$ or 5. For $|r|=5$ we have
$$
\frac{r^{2}}{12}=\frac{25}{12}=2+\frac{1}{12}
$$
80
giving an even number as the contribution to the quotient. Therefore, $|r|$ must be 4 and $r^{2}=16$. Thus,
$$
\frac{r^{2}}{12}=\frac{16}{12}=1+\frac{4}{12}
$$
and the remainder is 4 (not -4). Therefore, the lamb costs 4 dollars. Consequently, one person had a 4-dollar lamb, and the other had a 12-dollar sheep, and the transfer of a 4-dollar harmonica would bring each of them to a level of 8 dollars.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{n^{3}-(n-1)^{3}}{(n+1)^{4}-n^{4}}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{n^{3}-(n-1)^{3}}{(n+1)^{4}-n^{4}}=\lim _{n \rightarrow \infty} \frac{n^{3}-n^{3}+3 n^{2}-3 n+1}{\left((n+1)^{2}-n^{2}\right) \cdot\left((n+1)^{2}+n^{2}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{3 n^{2}-3 n+1}{\left(n^{2}+2 n+1-n^{2}\right)\left(n^{2}+2 n+1+n^{2}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{\frac{1}{n^{3}}\left(3 n^{2}-3 n+1\right)}{\frac{1}{n^{3}}(2 n+1)\left(2 n^{2}+2 n+1\right)}=\lim _{n \rightarrow \infty} \frac{\frac{3}{n}-\frac{3}{n^{2}}+\frac{1}{n^{3}}}{\left(2+\frac{1}{n}\right)\left(2+\frac{2}{n}+\frac{1}{n^{2}}\right)}= \\
& =\frac{0-0+0}{(2+0) \cdot(2+0+0)}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 3-22
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{\sqrt[3]{n^{2}}-\sqrt{n^{2}+5}}{\sqrt[5]{n^{7}}-\sqrt{n+1}}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{\sqrt[3]{n^{2}}-\sqrt{n^{2}+5}}{\sqrt[5]{n^{7}}-\sqrt{n+1}}=\lim _{n \rightarrow \infty} \frac{n^{-\frac{7}{5}}\left(\sqrt[3]{n^{2}}-\sqrt{n^{2}+5}\right)}{n^{-\frac{7}{5}}\left(\sqrt[5]{n^{7}}-\sqrt{n+1}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{\sqrt[3]{n^{2} \cdot n^{-\frac{21}{5}}}-\sqrt{n^{2} \cdot n^{-\frac{14}{5}}+5 n^{-\frac{14}{5}}}}{\sqrt[5]{n^{7} \cdot n^{-7}}-\sqrt{n \cdot n^{-\frac{14}{5}}}+n^{-\frac{14}{5}}}= \\
& =\lim _{n \rightarrow \infty} \frac{\sqrt[3]{n^{-\frac{11}{5}}}-\sqrt{n^{-\frac{4}{5}}+5 n^{-\frac{14}{5}}}}{\sqrt[5]{1}-\sqrt{n^{-\frac{9}{5}}+n^{-\frac{14}{5}}}}= \\
& =\frac{\sqrt[3]{0}-\sqrt{0+5 \cdot 0}}{1-\sqrt{0+0}}=\frac{0}{1}=0
\end{aligned}
$$
Problem Kuznetsov Limits 4-22
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty}\left(\frac{n+3}{n+1}\right)^{-n^{2}}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty}\left(\frac{n+3}{n+1}\right)^{-n^{2}}=\lim _{n \rightarrow \infty}\left(\frac{n+1+2}{n+1}\right)^{-n^{2}}= \\
& =\lim _{n \rightarrow \infty}\left(1+\frac{2}{n+1}\right)^{-n^{2}}=\lim _{n \rightarrow \infty}\left(1+\frac{1}{\left(\frac{n+1}{2}\right)}\right)^{-n^{2}}= \\
& =\lim _{n \rightarrow \infty}\left(1+\frac{1}{\left(\frac{n+1}{2}\right)}\right)^{\left(\frac{n+1}{2}\right)\left(\frac{2}{n+1}\right)\left(-n^{2}\right)}= \\
& =\left(\lim _{n \rightarrow \infty}\left(1+\frac{1}{\left(\frac{n+1}{2}\right)}\right)^{\left(\frac{n+1}{2}\right)}\right)^{\lim _{n \rightarrow \infty}\left(\frac{2}{n+1}\right)\left(-n^{2}\right)} \\
& =\{\text { Using the second remarkable limit }\}= \\
& =e^{\lim _{n \rightarrow \infty} \frac{-2 n^{2}}{n+1}}=e^{\lim _{n \rightarrow \infty} \frac{\frac{1}{n}\left(-2 n^{2}\right)}{\frac{1}{n}(n+1)}}=e^{\lim _{n \rightarrow \infty} \frac{-2 n}{1+\frac{1}{n}}}= \\
& =\left\{e^{\frac{-\infty}{1+0}}=e^{-\infty}=\left(\frac{1}{e}\right)^{\infty}\right\}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 7-22
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt[7]{x}}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt[7]{x}}=\lim _{x \rightarrow 0} \frac{(\sqrt{1+x}-\sqrt{1-x})(\sqrt{1+x}+\sqrt{1-x})}{\sqrt[7]{x}(\sqrt{1+x}+\sqrt{1-x})}= \\
& =\lim _{x \rightarrow 0} \frac{1+x-(1-x)}{\sqrt[7]{x}(\sqrt{1+x}+\sqrt{1-x})}=\lim _{x \rightarrow 0} \frac{2 x}{x^{\frac{1}{7}}(\sqrt{1+x}+\sqrt{1-x})}= \\
& =\lim _{x \rightarrow 0} \frac{2 x^{\frac{6}{7}}}{\sqrt{1+x}+\sqrt{1-x}}=\frac{2 \cdot 0^{\frac{6}{7}}}{\sqrt{1+0}+\sqrt{1-0}}=\frac{0}{1+1}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 11-22
This problem may have a different condition (possibly due to different editions or errors). See below for more details.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0} \frac{e^{3 x}-e^{2 x}}{\sin 3 x-\tan 2 x}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{e^{3 x}-e^{2 x}}{\sin 3 x-\tan 2 x}=\lim _{x \rightarrow 0} \frac{\left(e^{3 x}-1\right)-\left(e^{2 x}-1\right)}{\sin 3 x-\tan 2 x}= \\
& =\lim _{x \rightarrow 0} \frac{\frac{1}{x}\left(\left(e^{3 x}-1\right)-\left(e^{2 x}-1\right)\right)}{\frac{1}{x}(\sin 3 x-\tan 2 x)}= \\
& =\frac{\lim _{x \rightarrow 0} \frac{1}{x}\left(\left(e^{3 x}-1\right)-\left(e^{2 x}-1\right)\right)}{\lim _{x \rightarrow 0} \frac{1}{x}(\sin 3 x-\tan 2 x)}= \\
& =\left(\lim _{x \rightarrow 0} \frac{e^{3 x}-1}{x}-\lim _{x \rightarrow 0} \frac{e^{2 x}-1}{x}\right) /\left(\lim _{x \rightarrow 0} \frac{\sin 3 x}{x}-\lim _{x \rightarrow 0} \frac{\tan 2 x}{x}\right)=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$e^{3 x}-1 \sim 3 x$, as $x \rightarrow 0(3 x \rightarrow 0)$
$e^{2 x}-1 \sim 2 x$, as $x \rightarrow 0(2 x \rightarrow 0)$
$\sin 3 x \sim 3 x$, as $x \rightarrow 0(3 x \rightarrow 0)$
$\tan 2 x \sim 2 x$, as $x \rightarrow 0(2 x \rightarrow 0)$
We get:
$$
=\frac{\lim _{x \rightarrow 0} \frac{3 x}{x}-\lim _{x \rightarrow 0} \frac{2 x}{x}}{\lim _{x \rightarrow 0} \frac{3 x}{x}-\lim _{x \rightarrow 0} \frac{2 x}{x}}=\frac{\lim _{x \rightarrow 0} 3-\lim _{x \rightarrow 0} 2}{\lim _{x \rightarrow 0} 3-\lim _{x \rightarrow 0} 2}=\frac{3-2}{3-2}=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0} \frac{1-\sqrt{\cos x}}{1-\cos \sqrt{x}}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{1-\sqrt{\cos x}}{1-\cos \sqrt{x}}=\lim _{x \rightarrow 0} \frac{(1-\sqrt{\cos x})(1+\sqrt{\cos x})}{(1-\cos \sqrt{x})(1+\sqrt{\cos x})}= \\
& =\lim _{x \rightarrow 0} \frac{1-\cos x}{(1-\cos \sqrt{x})(1+\sqrt{\cos x})}=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$$
\begin{aligned}
& 1-\cos x \sim \frac{x^{2}}{2}, \text { as } x \rightarrow 0 \\
& 1-\cos \sqrt{x} \sim \frac{(\sqrt{x})^{2}}{2}, \text { as } x \rightarrow 0
\end{aligned}
$$
We get:
$$
\begin{aligned}
& =\lim _{x \rightarrow 0} \frac{\frac{x^{2}}{2}}{\frac{(\sqrt{x})^{2}}{2}(1+\sqrt{\cos x})}= \\
& =\lim _{x \rightarrow 0} \frac{x^{2}}{x(1+\sqrt{\cos x})}=\lim _{x \rightarrow 0} \frac{x}{1+\sqrt{\cos x}}= \\
& =\frac{0}{1+\sqrt{\cos 0}}=\frac{0}{1+\sqrt{1}}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 16-22
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0}\left(\cos \left(\frac{x}{\pi}\right)\right)^{1+x}$
|
## Solution
$\lim _{x \rightarrow 0}\left(\cos \left(\frac{x}{\pi}\right)\right)^{1+x}=\left(\cos \left(\frac{0}{\pi}\right)\right)^{1+0}=1^{1}=1$
## Problem Kuznetsov Limits 18-22
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the cosine of the angle between vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$.
$A(-1 ; 2 ;-3), B(3 ; 4 ;-6), C(1 ; 1 ;-1)$
|
## Solution
Let's find $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\overrightarrow{A B}=(3-(-1) ; 4-2 ;-6-(-3))=(4 ; 2 ;-3)$
$\overrightarrow{A C}=(1-(-1) ; 1-2 ;-1-(-3))=(2 ;-1 ; 2)$
We find the cosine of the angle $\phi_{\text {between vectors }} \overrightarrow{A B}$ and $\overrightarrow{A C}$:
$$
\begin{aligned}
& \cos (\overrightarrow{A B, A \overrightarrow{A C}})=\frac{(\overrightarrow{A B}, \overrightarrow{A C})}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}= \\
& =\frac{4 \cdot 2+2 \cdot(-1)+(-3) \cdot 2}{\sqrt{4^{2}+2^{2}+(-3)^{2}} \cdot \sqrt{2^{2}+(-1)^{2}+2^{2}}}= \\
& =\frac{8-2-6}{\sqrt{16+4+9} \cdot \sqrt{4+1+4}}=\frac{0}{\sqrt{29} \cdot \sqrt{9}}=0
\end{aligned}
$$
Thus, the cosine of the angle:
$\cos (\overrightarrow{A B, A C})=0$
and consequently the angle
$\overrightarrow{A B, A C}=\frac{\pi}{2}$
## Problem Kuznetsov Analytic Geometry 4-4
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the cosine of the angle between vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$.
$A(2 ; 1 ;-1), B(6 ;-1 ;-4), C(4 ; 2 ; 1)$
|
## Solution
Let's find $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\overrightarrow{A B}=(6-2 ;-1-1 ;-4-(-1))=(4 ;-2 ;-3)$
$\overrightarrow{A C}=(4-2 ; 2-1 ; 1-(-1))=(2 ; 1 ; 2)$
We find the cosine of the angle $\phi_{\text{between vectors }} \overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\cos (\overrightarrow{A B,} \overrightarrow{A C})=\frac{(\overrightarrow{A B}, \overrightarrow{A C})}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}=$
$=\frac{4 \cdot 2+(-2) \cdot 1+(-3) \cdot 2}{\sqrt{4^{2}+(-2)^{2}+(-3)^{2}} \cdot \sqrt{2^{2}+1^{2}+2^{2}}}=$
$=\frac{8-2-6}{\sqrt{16+4+9} \cdot \sqrt{4+1+4}}=\frac{0}{\sqrt{29} \cdot \sqrt{9}}=0$
Thus, the cosine of the angle:
$\cos (\overrightarrow{A B,} \overrightarrow{A C})=0$
and consequently the angle
$\widehat{A B,} \overrightarrow{A C}=\frac{\pi}{2}$
## Problem Kuznetsov Analytic Geometry 4-11
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## problem statement
Let $k$ be the coefficient of similarity transformation with the center at the origin. Is it true that point $A$ belongs to the image of plane $a$?
$A(-2 ; 3 ;-3)$
$a: 3 x+2 y-z-2=0$
$k=\frac{3}{2}$
|
## Solution
When transforming similarity with the center at the origin of the plane
$a: A x+B y+C z+D=0_{\text{and coefficient }} k$ transitions to the plane
$a^{\prime}: A x+B y+C z+k \cdot D=0$. We find the image of the plane $a$:
$a^{\prime}: 3 x+2 y-z-3=0$
Substitute the coordinates of point $A$ into the equation $a^{\prime}$:
$3 \cdot(-2)+2 \cdot 3-(-3)-3=0$
$-6+6+3-3=0$
$0=0$
Since $0=0$, point $A$ belongs to the image of the plane $a$.
## Problem Kuznetsov Analytical Geometry 12-11
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$$
\lim _{n \rightarrow \infty} \frac{(2 n+1)!+(2 n+2)!}{(2 n+3)!}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{(2 n+1)!+(2 n+2)!}{(2 n+3)!}=\lim _{n \rightarrow \infty}\left(\frac{(2 n+1)!}{(2 n+3)!}+\frac{(2 n+2)!}{(2 n+3)!}\right)= \\
& =\lim _{n \rightarrow \infty}\left(\frac{1}{(2 n+2)(2 n+3)}+\frac{1}{2 n+3}\right)=0+0=0
\end{aligned}
$$
## Problem Kuznetsov Limits 6-2
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$$
\lim _{x \rightarrow-1} \frac{x^{3}-3 x-2}{x+x^{2}}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow-1} \frac{x^{3}-3 x-2}{x+x^{2}}=\left\{\frac{0}{0}\right\}=\lim _{x \rightarrow-1} \frac{\left(x^{2}-x-2\right)(x+1)}{x(x+1)}= \\
& =\lim _{x \rightarrow-1} \frac{x^{2}-x-2}{x}=\frac{(-1)^{2}-(-1)-2}{-1}=\frac{1+1-2}{-1}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 10-2
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0} \frac{e^{3 x}-e^{-2 x}}{2 \arcsin x-\sin x}$
|
## Solution
$\lim _{x \rightarrow 0} \frac{e^{3 x}-e^{-2 x}}{2 \arcsin x-\sin x}=\lim _{x \rightarrow 0} \frac{\left(e^{3 x}-1\right)-\left(e^{-2 x}-1\right)}{2 \arcsin x-\sin x}=$
$=\lim _{x \rightarrow 0} \frac{\frac{1}{x}\left(\left(e^{3 x}-1\right)-\left(e^{-2 x}-1\right)\right)}{\frac{1}{x}(2 \arcsin x-\sin x)}=$
$$
\begin{aligned}
& =\frac{\lim _{x \rightarrow 0} \frac{1}{x}\left(\left(e^{3 x}-1\right)-\left(e^{-2 x}-1\right)\right)}{\lim _{x \rightarrow 0} \frac{1}{x}(2 \arcsin x-\sin x)}= \\
& =\left(\lim _{x \rightarrow 0} \frac{e^{3 x}-1}{x}-\lim _{x \rightarrow 0} \frac{e^{-2 x}-1}{x}\right) /\left(\lim _{x \rightarrow 0} \frac{2 \arcsin x}{x}-\lim _{x \rightarrow 0} \frac{x}{x}\right)=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$e^{3 x}-1 \sim 3 x$, as $x \rightarrow 0(3 x \rightarrow 0)$
$e^{-2 x}-1 \sim-2 x$, as $x \rightarrow 0(-2 x \rightarrow 0)$
$\arcsin x \sim x$, as $x \rightarrow 0$
$\sin x \sim x$, as $x \rightarrow 0$
We get:
$=\frac{\lim _{x \rightarrow 0} \frac{3 x}{x}-\lim _{x \rightarrow 0} \frac{-2 x}{x}}{\lim _{x \rightarrow 0} \frac{2 x}{x}-\lim _{x \rightarrow 0} \frac{x}{x}}=\frac{\lim _{x \rightarrow 0} 3-\lim _{x \rightarrow 0}-2}{\lim _{x \rightarrow 0} 2-\lim _{x \rightarrow 0} 1}=\frac{3+2}{2-1}=5$
## Problem Kuznetsov Limits 15-2
|
5
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$$
\lim _{x \rightarrow 0} \frac{1+x \sin x-\cos 2 x}{\sin ^{2} x}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{1+x \sin x-\cos 2 x}{\sin ^{2} x}=\lim _{x \rightarrow 0} \frac{1+x \sin x-\left(1-2 \sin ^{2} x\right)}{\sin ^{2} x}= \\
& =\lim _{x \rightarrow 0} \frac{x \sin x+2 \sin ^{2} x}{\sin ^{2} x}=\lim _{x \rightarrow 0} \frac{x \sin x}{\sin ^{2} x}+\lim _{x \rightarrow 0} \frac{2 \sin ^{2} x}{\sin ^{2} x}= \\
& =\lim _{x \rightarrow 0} \frac{x}{\sin x}+\lim _{x \rightarrow 0} 2=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$\sin x \sim x$, as $x \rightarrow 0$
We get:
$$
=\lim _{x \rightarrow 0} \frac{x}{x}+2=\lim _{x \rightarrow 0} 1+2=3
$$
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0}\left(\frac{2+x}{3-x}\right)^{x}$
|
## Solution
$\lim _{x \rightarrow 0}\left(\frac{2+x}{3-x}\right)^{x}=\left(\frac{2+0}{3-0}\right)^{0}=\left(\frac{2}{3}\right)^{0}=1$
## Problem Kuznetsov Limits 18-2
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Condition of the problem
Calculate the limit of the function:
$\lim _{x \rightarrow \frac{\pi}{4}}(\operatorname{tg} x)^{\operatorname{ctg} x}$
|
Solution
$\lim _{x \rightarrow \frac{\pi}{4}}(\tan x)^{\cot x}=(\tan \frac{\pi}{4})^{\cot \frac{\pi}{4}}=1^{1}=1$
## Problem Kuznetsov Limits 20-2
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the cosine of the angle between vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$.
$A(-4 ; 0 ; 4), B(-1 ; 6 ; 7), C(1 ; 10 ; 9)$
|
## Solution
Let's find $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\overrightarrow{A B}=(-1-(-4) ; 6-0 ; 7-4)=(3 ; 6 ; 3)$
$\overrightarrow{A C}=(1-(-4) ; 10-0 ; 9-4)=(5 ; 10 ; 5)$
We find the cosine of the angle $\phi$ between the vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\cos (\overrightarrow{A B}, \overrightarrow{A C})=\frac{(\overrightarrow{A B}, \overrightarrow{A C})}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}=$
$=\frac{3 \cdot 5+6 \cdot 10+3 \cdot 5}{\sqrt{3^{2}+6^{2}+3^{2}} \cdot \sqrt{5^{2}+10^{2}+5^{2}}}=$
$=\frac{15+60+15}{\sqrt{9+36+9} \cdot \sqrt{25+100+25}}=\frac{90}{\sqrt{54} \cdot \sqrt{150}}=1$
Thus, the cosine of the angle:
$\cos (\overrightarrow{A B,} \overrightarrow{A C})=1$
and consequently the angle
$\overrightarrow{A B}, \overrightarrow{A C}=0$
Problem Kuznetsov Analytic Geometry 4-30
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{\sqrt[3]{n^{3}-7}+\sqrt[3]{n^{2}+4}}{\sqrt[4]{n^{5}+5}+\sqrt{n}}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{\sqrt[3]{n^{3}-7}+\sqrt[3]{n^{2}+4}}{\sqrt[4]{n^{5}+5}+\sqrt{n}}=\lim _{n \rightarrow \infty} \frac{\frac{1}{n}\left(\sqrt[3]{n^{3}-7}+\sqrt[3]{n^{2}+4}\right)}{\frac{1}{n}\left(\sqrt[4]{n^{5}+5}+\sqrt{n}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{\sqrt[3]{1-\frac{7}{n^{3}}}+\sqrt[3]{\frac{1}{n}+\frac{4}{n^{3}}}}{\sqrt[4]{n+\frac{5}{n^{4}}}+\sqrt{\frac{1}{n}}}=\left\{\frac{\sqrt[3]{1-0}+\sqrt[3]{0+0}}{\sqrt[4]{\infty+0}+\sqrt{0}}=\frac{1}{\infty}\right\}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 4-17
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 2} \frac{x^{3}-6 x^{2}+12 x-8}{x^{3}-3 x^{2}+4}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 2} \frac{x^{3}-6 x^{2}+12 x-8}{x^{3}-3 x^{2}+4}=\left\{\frac{0}{0}\right\}=\lim _{x \rightarrow 2} \frac{(x-2)\left(x^{2}-4 x+4\right)}{(x-2)\left(x^{2}-x-2\right)}= \\
& =\lim _{x \rightarrow 2} \frac{x^{2}-4 x+4}{x^{2}-x-2}=\left\{\frac{0}{0}\right\}=\lim _{x \rightarrow 2} \frac{(x-2)^{2}}{(x-2)(x+1)}= \\
& =\lim _{x \rightarrow 2} \frac{x-2}{x+1}=\frac{2-2}{2+1}=0
\end{aligned}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0} \frac{e^{\sin 2 x}-e^{\sin x}}{\tan x}$
|
## Solution
$\lim _{x \rightarrow 0} \frac{e^{\sin 2 x}-e^{\sin x}}{\tan x}=\lim _{x \rightarrow 0} \frac{\left(e^{\sin 2 x}-1\right)-\left(e^{\sin x}-1\right)}{\tan x}=$
$=\lim _{x \rightarrow 0} \frac{e^{\sin 2 x}-1}{\tan x}-\lim _{x \rightarrow 0} \frac{e^{\sin x}-1}{\tan x}=$
Using the substitution of equivalent infinitesimals:
$e^{\sin 2 x}-1 \sim \sin 2 x$, as $x \rightarrow 0(\sin 2 x \rightarrow 0)$
$e^{\sin x}-1 \sim \sin x$, as $x \rightarrow 0(\sin x \rightarrow 0)$
$\tan x \sim x$, as $x \rightarrow 0$
We get:
$=\lim _{x \rightarrow 0} \frac{\sin 2 x}{x}-\lim _{x \rightarrow 0} \frac{\sin x}{x}=$
Using the substitution of equivalent infinitesimals:
$\sin x \sim x$, as $x \rightarrow 0$
$\sin 2 x \sim 2 x$, as $x \rightarrow 0(2 x \rightarrow 0)$
We get:
$=\lim _{x \rightarrow 0} \frac{2 x}{x}-\lim _{x \rightarrow 0} \frac{x}{x}=\lim _{x \rightarrow 0} 2-\lim _{x \rightarrow 0} 1=2-1=1$
## Problem Kuznetsov Limits 16-17
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the cosine of the angle between vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$.
$A(-1 ; 2 ;-3), B(0 ; 1 ;-2), C(-3 ; 4 ;-5)$
|
## Solution
Let's find $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\overrightarrow{A B}=(0-(-1) ; 1-2 ;-2-(-3))=(1 ;-1 ; 1)$
$\overrightarrow{A C}=(-3-(-1) ; 4-2 ;-5-(-3))=(-2 ; 2 ;-2)$
We find the cosine of the angle $\phi_{\text {between vectors }} \overrightarrow{A B}$ and $\overrightarrow{A C}$:
$$
\begin{aligned}
& \cos (\overrightarrow{A B, \overrightarrow{A C}})=\frac{(\overrightarrow{A B}, \overrightarrow{A C})}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}= \\
& =\frac{1 \cdot(-2)+(-1) \cdot 2+1 \cdot(-2)}{\sqrt{1^{2}+(-1)^{2}+1^{2}} \cdot \sqrt{(-2)^{2}+2^{2}+(-2)^{2}}}= \\
& =\frac{-2-2-2}{\sqrt{1+1+1} \cdot \sqrt{4+4+4}}=\frac{-6}{\sqrt{3} \cdot \sqrt{12}}=-1
\end{aligned}
$$
Thus, the cosine of the angle:
$\cos (\overrightarrow{A B, A C})=-1$
and consequently the angle
$\widehat{A B,} \overrightarrow{A C}=\pi$
## Problem Kuznetsov Analytic Geometry 4-24
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the equation of the tangent line to the given curve at the point with abscissa $x_{0}$.
$y=\frac{2 x}{x^{2}+1}, x_{0}=1$
|
## Solution
Let's find $y^{\prime}:$
$$
\begin{aligned}
& y^{\prime}=\left(\frac{2 x}{x^{2}+1}\right)^{\prime}=\frac{2 x^{\prime}\left(x^{2}+1\right)-2 x\left(x^{2}+1\right)^{\prime}}{\left(x^{2}+1\right)^{2}}= \\
& =\frac{2 x^{2}+2-2 x \cdot 2 x}{\left(-2 x^{2}+2\right)^{2}}=\frac{2-2 x^{2}}{\left(x^{2}+1\right)^{2}}
\end{aligned}
$$
Then:
$$
y_{0}^{\prime}=y^{\prime}\left(x_{0}\right)=\frac{2-2 \cdot 1^{2}}{\left(1^{2}+1\right)^{2}}=\frac{0}{2^{2}}=0
$$
Since the function $y^{\prime}{ }_{\text {at point }} x_{0}$ has a finite derivative, the equation of the tangent line is:
$$
\begin{aligned}
& y-y_{0}=y_{0}^{\prime}\left(x-x_{0}\right), \text { where } \\
& y_{0}^{\prime}=0 \\
& y_{0}=y\left(x_{0}\right)=\frac{2 \cdot 1}{1^{2}+1}=\frac{2}{2}=1
\end{aligned}
$$
We get:
$y-1=0 \cdot(x-(-2))$
$y=1$
That is, the equation of the tangent line is:
$y=1$
## Problem Kuznetsov Differentiation 3-23
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## problem statement
Let $k$ be the coefficient of similarity transformation with the center at the origin. Is it true that point $A$ belongs to the image of plane $a$?
$A(2; -5; 4)$
$a: 5x + 2y - z + 3 = 0$
$k = \frac{4}{3}$
|
## Solution
When transforming similarity with the center at the origin of the plane
$a: A x+B y+C z+D=0_{\text{and coefficient }} k$ transitions to the plane
$a^{\prime}: A x+B y+C z+k \cdot D=0$. We find the image of the plane $a$:
$a^{\prime}: 5 x+2 y-z+4=0$
Substitute the coordinates of point $A$ into the equation of $a^{\prime}$:
$5 \cdot 2+2 \cdot(-5)-4+4=0$
$10-10-4+4=0$
$0=0$
Since $0=0$, point $A$ belongs to the image of the plane $a$.
## Problem Kuznetsov Analytical Geometry 12-9
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Based on the definition of the derivative, find $f^{\prime}(0)$:
$$
f(x)=\left\{\begin{array}{c}
2 x^{2}+x^{2} \cos \frac{1}{x}, x \neq 0 \\
0, x=0
\end{array}\right.
$$
|
## Solution
By definition, the derivative at the point $x=0$:
$f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}$
Based on the definition, we find:
$$
\begin{aligned}
& f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{2 \Delta x^{2}+\Delta x^{2} \cos \frac{1}{\Delta x}-0}{\Delta x}= \\
& =\lim _{\Delta x \rightarrow 0} \frac{2 \Delta x^{2}+\Delta x^{2} \cos \frac{1}{\Delta x}}{\Delta x}=\lim _{\Delta x \rightarrow 0}\left(2 \Delta x+\Delta x \cos \frac{1}{\Delta x}\right)=
\end{aligned}
$$
Since $\cos \frac{1}{\Delta x}$ is bounded, then
$\Delta x \cdot \cos \frac{1}{9 \Delta x} \rightarrow 0$, as $\Delta x \rightarrow 0$
Then:
$=2 \cdot 0+0=0$
Therefore, $f^{\prime}(0)=0$
## Problem Kuznetsov Differentiation 2-16
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the distance from point $M_{0}$ to the plane passing through three points $M_{1}, M_{2}, M_{3}$.
$M_{1}(2 ; 3 ; 1)$
$M_{2}(4 ; 1 ;-2)$
$M_{3}(6 ; 3 ; 7)$
$M_{0}(-5 ;-4 ; 8)$
|
## Solution
Find the equation of the plane passing through three points $M_{1}, M_{2}, M_{3}$:
$\left|\begin{array}{ccc}x-2 & y-3 & z-1 \\ 4-2 & 1-3 & -2-1 \\ 6-2 & 3-3 & 7-1\end{array}\right|=0$
Perform transformations:
$$
\begin{aligned}
& \left|\begin{array}{ccc}
x-2 & y-3 & z-1 \\
2 & -2 & -3 \\
4 & 0 & 6
\end{array}\right|=0 \\
& (x-2) \cdot\left|\begin{array}{cc}
-2 & -3 \\
0 & 6
\end{array}\right|-(y-3) \cdot\left|\begin{array}{cc}
2 & -3 \\
4 & 6
\end{array}\right|+(z-1) \cdot\left|\begin{array}{cc}
2 & -2 \\
4 & 0
\end{array}\right|=0 \\
& (x-2) \cdot(-12)-(y-3) \cdot 24+(z-1) \cdot 8=0 \\
& -12 x+24+(-24) y+72+8 z+(-8)=0 \\
& -12 x-24 y+8 z+88=0 \\
& -3 x-6 y+2 z+22=0
\end{aligned}
$$
The distance $d$ from a point $M_{0}\left(x_{0} ; y_{0} ; z_{0}\right)$ to the plane $A x+B y+C z+D=0$:
$d=\frac{\left|A x_{0}+B y_{0}+C z_{0}+D\right|}{\sqrt{A^{2}+B^{2}+C^{2}}}$
Find:
$$
d=\frac{|-3 \cdot(-5)-6 \cdot(-4)+2 \cdot 8+22|}{\sqrt{(-3)^{2}+(-6)^{2}+2^{2}}}=\frac{|15+24+16+22|}{\sqrt{9+36+4}}=\frac{77}{\sqrt{49}}=11
$$
## Problem Kuznetsov Analytic Geometry $8-29$
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Based on the definition of the derivative, find $f^{\prime}(0)$:
$f(x)=\left\{\begin{array}{c}x^{2} \cos \left(\frac{4}{3 x}\right)+\frac{x^{2}}{2}, x \neq 0 \\ 0, x=0\end{array}\right.$
|
## Solution
By definition, the derivative at the point $x=0$:
$f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}$
Based on the definition, we find:
$$
\begin{aligned}
& f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{x^{2} \cos \left(\frac{4}{3 x}\right)+\frac{x^{2}}{2}-0}{\Delta x}= \\
& =\lim _{\Delta x \rightarrow 0} \frac{x^{2} \cos \left(\frac{4}{3 x}\right)+\frac{x^{2}}{2}}{\Delta x}=\lim _{\Delta x \rightarrow 0}\left(x \cos \left(\frac{4}{3 x}\right)+\frac{x}{2}\right)=
\end{aligned}
$$
Since $\cos \left(\frac{4}{3 x}\right)$ is bounded, then
$\Delta x \cdot \cos \left(\frac{4}{3 x}\right) \rightarrow 0 \quad$, as $\Delta x \rightarrow 0$
Then:
$=0+\frac{0}{2}=0$
Therefore, $f^{\prime}(0)=0$
## Problem Kuznetsov Differentiation $2-8$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$$
\lim _{n \rightarrow \infty} \frac{2^{n+1}+3^{n+1}}{2^{n}+3^{n}}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{2^{n+1}+3^{n+1}}{2^{n}+3^{n}}=\lim _{n \rightarrow \infty} \frac{2 \cdot 2^{n}+3 \cdot 3^{n}}{2^{n}+3^{n}}= \\
& =\lim _{n \rightarrow \infty} \frac{2 \cdot 2^{n}+2 \cdot 3^{n}+3^{n}}{2^{n}+3^{n}}=\lim _{n \rightarrow \infty} \frac{2\left(2^{n}+3^{n}\right)+3^{n}}{2^{n}+3^{n}}= \\
& =\lim _{n \rightarrow \infty}\left(2+\frac{3^{n}}{2^{n}+3^{n}}\right)=2+\lim _{n \rightarrow \infty} \frac{\frac{1}{3^{n}} 3^{n}}{\frac{1}{3^{n}}\left(2^{n}+3^{n}\right)}= \\
& =2+\lim _{n \rightarrow \infty} \frac{1}{\left(\frac{2}{3}\right)^{n}+1}=2+\frac{1}{0+1}=2+1=3
\end{aligned}
$$
## Problem Kuznetsov Limits 6-4
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$$
\lim _{x \rightarrow 1} \frac{\left(2 x^{2}-x-1\right)^{2}}{x^{3}+2 x^{2}-x-2}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 1} \frac{\left(2 x^{2}-x-1\right)^{2}}{x^{3}+2 x^{2}-x-2}=\left\{\frac{0}{0}\right\}=\lim _{x \rightarrow 1} \frac{(2 x+1)^{2}(x-1)^{2}}{\left(x^{2}+3 x+2\right)(x-1)}= \\
& =\lim _{x \rightarrow 1} \frac{(2 x+1)^{2}(x-1)}{x^{2}+3 x+2}=\frac{(2 \cdot 1+1)^{2}(1-1)}{1^{2}+3 \cdot 1+2}=\frac{3^{2} \cdot 0}{6}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 10-4
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0} \frac{e^{5 x}-e^{3 x}}{\sin 2 x-\sin x}$
|
## Solution
$\lim _{x \rightarrow 0} \frac{e^{5 x}-e^{3 x}}{\sin 2 x-\sin x}=\lim _{x \rightarrow 0} \frac{\left(e^{5 x}-1\right)-\left(e^{3 x}-1\right)}{\sin 2 x-\sin x}=$
$=\lim _{x \rightarrow 0} \frac{\frac{1}{x}\left(\left(e^{5 x}-1\right)-\left(e^{3 x}-1\right)\right)}{\frac{1}{x}(\sin 2 x-\sin x)}=$
$=\frac{\lim _{x \rightarrow 0} \frac{1}{x}\left(\left(e^{5 x}-1\right)-\left(e^{3 x}-1\right)\right)}{\lim _{x \rightarrow 0} \frac{1}{x}(\sin 2 x-\sin x)}=$
$=\left(\lim _{x \rightarrow 0} \frac{e^{5 x}-1}{x}-\lim _{x \rightarrow 0} \frac{e^{3 x}-1}{x}\right) /\left(\lim _{x \rightarrow 0} \frac{\sin 2 x}{x}-\lim _{x \rightarrow 0} \frac{\sin x}{x}\right)=$
Using the substitution of equivalent infinitesimals:
$e^{5 x}-1 \sim 5 x$, as $x \rightarrow 0(5 x \rightarrow 0)$
$e^{3 x}-1 \sim 3 x$, as $x \rightarrow 0(3 x \rightarrow 0)$
$\sin 2 x \sim 2 x$, as $x \rightarrow 0(2 x \rightarrow 0)$
$\sin x \sim x$, as $x \rightarrow 0$
We get:
$=\frac{\lim _{x \rightarrow 0} \frac{5 x}{x}-\lim _{x \rightarrow 0} \frac{3 x}{x}}{\lim _{x \rightarrow 0} \frac{2 x}{x}-\lim _{x \rightarrow 0} \frac{x}{x}}=\frac{\lim _{x \rightarrow 0} 5-\lim _{x \rightarrow 0} 3}{\lim _{x \rightarrow 0} 2-\lim _{x \rightarrow 0} 1}=\frac{5-3}{2-1}=2$
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the cosine of the angle between vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$.
$A(2 ; 3 ; 2), B(-1 ;-3 ;-1), C(-3 ;-7 ;-3)$
|
## Solution
Let's find $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\overrightarrow{A B}=(-1-2 ;-3-3 ;-1-2)=(-3 ;-6 ;-3)$
$\overrightarrow{A C}=(-3-2 ;-7-3 ;-3-2)=(-5 ;-10 ;-5)$
We find the cosine of the angle $\phi$ between the vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\cos (\overrightarrow{A B}, \overrightarrow{A C})=\frac{(\overrightarrow{A B}, \overrightarrow{A C})}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}=$
$=\frac{(-3) \cdot(-5)+(-6) \cdot(-10)+(-3) \cdot(-5)}{\sqrt{(-3)^{2}+(-6)^{2}+(-3)^{2}} \cdot \sqrt{(-5)^{2}+(-10)^{2}+(-5)^{2}}}=$
$=\frac{15+60+15}{\sqrt{9+36+9} \cdot \sqrt{25+100+25}}=\frac{90}{\sqrt{54} \cdot \sqrt{150}}=1$
Thus, the cosine of the angle:
$\cos (\overrightarrow{A B,} \overrightarrow{A C})=1$
and consequently the angle
$\overrightarrow{A B}, \overrightarrow{A C}=0$
## Problem Kuznetsov Analytic Geometry 4-22
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Let $k$ be the coefficient of similarity transformation with the center at the origin. Is it true that point $A$ belongs to the image of plane $a$?
$A(3 ; 5 ; 2)$
$a: 5x - 3y + z - 4 = 0$
$k = \frac{1}{2}$
|
## Solution
When transforming similarity with the center at the origin of the plane
$a: A x+B y+C z+D=0_{\text{and coefficient }} k$ transitions to the plane
$a^{\prime}: A x+B y+C z+k \cdot D=0$. We find the image of the plane $a$:
$a^{\prime}: 5 x-3 y+z-2=0$
Substitute the coordinates of point $A$ into the equation $a^{\prime}$:
$5 \cdot 3-3 \cdot 5+2-2=0$
$15-15+2-2=0$
$0=0$
Since $0=0$, point $A$ belongs to the image of the plane $a$.
## Problem Kuznetsov Analytical Geometry 12-22
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Based on the definition of the derivative, find $f^{\prime}(0)$:
$$
f(x)=\left\{\begin{array}{c}
x^{2} e^{|x|} \sin \frac{1}{x^{2}}, x \neq 0 \\
0, x=0
\end{array}\right.
$$
|
## Solution
By definition, the derivative at the point $x=0$:
$f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}$
Based on the definition, we find:
$$
\begin{aligned}
& f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{\Delta x^{2} e^{|\Delta x|} \sin \frac{1}{\Delta x^{2}}-0}{\Delta x}= \\
& =\lim _{\Delta x \rightarrow 0} e^{|\Delta x|} \cdot \Delta x \cdot \sin \frac{1}{\Delta x^{2}}= \\
& \quad \sin \frac{1}{\Delta x^{2}} \text { - is bounded, so }
\end{aligned}
$$
$\Delta x \sin \frac{1}{\Delta x^{2}} \rightarrow 0$, as $\Delta x \rightarrow 0$
Then:
$=e^{|0|} \cdot 0=1 \cdot 0=0$
Thus, $f^{\prime}(0)=0$
## Problem Kuznetsov Differentiation $2-28$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{(n+1)^{4}-(n-1)^{4}}{(n+1)^{3}+(n-1)^{3}}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{(n+1)^{4}-(n-1)^{4}}{(n+1)^{3}+(n-1)^{3}}=\lim _{n \rightarrow \infty} \frac{\left((n+1)^{2}-(n-1)^{2}\right) \cdot\left((n+1)^{2}+(n-1)^{2}\right)}{(n+1)^{3}+(n-1)^{3}}= \\
& =\lim _{n \rightarrow \infty} \frac{\left(n^{2}+2 n+1-n^{2}+2 n-1\right) \cdot\left(n^{2}+2 n+1+n^{2}-2 n+1\right)}{(n+1)^{3}+(n-1)^{3}}= \\
& =\lim _{n \rightarrow \infty} \frac{4 n\left(2 n^{2}+2\right)}{(n+1)^{3}+(n-1)^{3}}=\lim _{n \rightarrow \infty} \frac{\frac{1}{n^{3}} 8 n\left(n^{2}+1\right)}{n^{3}\left((n+1)^{3}+(n-1)^{3}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{8\left(1+\frac{1}{n^{2}}\right)}{\left(1+\frac{1}{n}\right)^{3}+\left(1-\frac{1}{n}\right)^{3}}=\frac{8 \cdot 1}{1^{3}+1^{3}}=4
\end{aligned}
$$
## Problem Kuznetsov Limits 3-24
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{\sqrt[3]{n^{2}+2}-5 n^{2}}{n-\sqrt{n^{4}-n+1}}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{\sqrt[3]{n^{2}+2}-5 n^{2}}{n-\sqrt{n^{4}-n+1}}=\lim _{n \rightarrow \infty} \frac{\frac{1}{n^{2}}\left(\sqrt[3]{n^{2}+2}-5 n^{2}\right)}{\frac{1}{n^{2}}\left(n-\sqrt{n^{4}-n+1}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{\sqrt[3]{\frac{1}{n^{4}}+\frac{2}{n^{6}}}-5}{\frac{1}{n}-\sqrt{1-\frac{1}{n^{3}}+\frac{1}{n^{4}}}}=\frac{\sqrt[3]{0+0}-5}{0-\sqrt{1-0+0}}=\frac{-5}{-1}=5
\end{aligned}
$$
## Problem Kuznetsov Limits 4-24
|
5
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{2+4+6+\ldots+2 n}{1+3+5+\ldots+(2 n-1)}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{2+4+6+\ldots+2 n}{1+3+5+\ldots+(2 n-1)}=\lim _{n \rightarrow \infty} \frac{\left(\frac{(2+2 n) n}{2}\right)}{\left(\frac{(1+(2 n-1)) n}{2}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{(2+2 n) n}{(1+(2 n-1)) n}=\lim _{n \rightarrow \infty} \frac{2 n+2 n^{2}}{2 n^{2}}= \\
& =\lim _{n \rightarrow \infty}\left(\frac{1}{n}+1\right)=0+1=1
\end{aligned}
$$
## Problem Kuznetsov Limits 6-24
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$$
\lim _{x \rightarrow 0} \frac{\sqrt[3]{8+3 x-x^{2}}-2}{\sqrt[3]{x^{2}+x^{3}}}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{\sqrt[3]{8+3 x-x^{2}}-2}{\sqrt[3]{x^{2}+x^{3}}}= \\
& =\lim _{x \rightarrow 0} \frac{\left(\sqrt[3]{8+3 x-x^{2}}-2\right)\left(\sqrt[3]{\left(8+3 x-x^{2}\right)^{2}}+2 \sqrt[3]{8+3 x-x^{2}}+4\right)}{\left(\sqrt[3]{x^{2}+x^{3}}\right)\left(\sqrt[3]{\left(8+3 x-x^{2}\right)^{2}}+2 \sqrt[3]{8+3 x-x^{2}}+4\right)}= \\
& =\lim _{x \rightarrow 0} \frac{8+3 x-x^{2}-8}{\sqrt[3]{x^{2}} \sqrt[3]{1+x}\left(\sqrt[3]{\left(8+3 x-x^{2}\right)^{2}}+2 \sqrt[3]{8+3 x-x^{2}}+4\right)}= \\
& =\lim _{x \rightarrow 0} \frac{x(3-x)}{\sqrt[3]{x^{2}} \sqrt[3]{1+x}\left(\sqrt[3]{\left(8+3 x-x^{2}\right)^{2}}+2 \sqrt[3]{8+3 x-x^{2}}+4\right)}= \\
& =\lim _{x \rightarrow 0} \frac{\sqrt[3]{x}(3-x)}{\sqrt[3]{1+x}\left(\sqrt[3]{\left(8+3 x-x^{2}\right)^{2}}+2 \sqrt[3]{8+3 x-x^{2}}+4\right)}= \\
& =\frac{\sqrt[3]{0}(3-0)}{\sqrt[3]{1+0}\left(\sqrt[3]{\left(8+3 \cdot 0-0^{2}\right)^{2}}+2 \sqrt[3]{8+3 \cdot 0-0^{2}}+4\right)}= \\
& =\frac{0}{1 \cdot\left(\sqrt[3]{8^{2}}+2 \sqrt[3]{8}+4\right)}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 11-24
This problem may have a different condition (possibly due to different editions or errors). See below for more details.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow \pi} \frac{1-\sin \left(\frac{x}{2}\right)}{\pi-x}$
|
## Solution
Substitution:
$$
\begin{aligned}
& x=y+\pi \Rightarrow y=x-\pi \\
& x \rightarrow \pi \Rightarrow y \rightarrow 0
\end{aligned}
$$
We get:
$$
\begin{aligned}
& \lim _{x \rightarrow \pi} \frac{1-\sin \left(\frac{x}{2}\right)}{\pi-x}=\lim _{y \rightarrow 0} \frac{1-\sin \left(\frac{y+\pi}{2}\right)}{\pi-(y+\pi)}= \\
& =\lim _{y \rightarrow 0} \frac{1-\sin \left(\frac{y}{2}+\frac{\pi}{2}\right)}{-y}=\lim _{y \rightarrow 0} \frac{1-\cos \left(\frac{y}{2}\right)}{-y}=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$1-\cos y \sim \frac{y^{2}}{2}$, as $y \rightarrow 0$
We get:
$=\lim _{y \rightarrow 0} \frac{\frac{y^{2}}{2}}{-y}=\lim _{y \rightarrow 0}-\frac{y}{2}=-\frac{0}{2}=0$
## Problem Kuznetsov Limits 13-24
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$$
\lim _{x \rightarrow 0} \frac{e^{x}-e^{3 x}}{\sin 3 x-\tan 2 x}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{e^{x}-e^{3 x}}{\sin 3 x-\tan 2 x}=\lim _{x \rightarrow 0} \frac{\left(e^{x}-1\right)-\left(e^{3 x}-1\right)}{\sin 3 x-\tan 2 x}= \\
& =\lim _{x \rightarrow 0} \frac{\frac{1}{x}\left(\left(e^{x}-1\right)-\left(e^{3 x}-1\right)\right)}{\frac{1}{x}(\sin 3 x-\tan 2 x)}= \\
& =\frac{\lim _{x \rightarrow 0} \frac{1}{x}\left(\left(e^{x}-1\right)-\left(e^{3 x}-1\right)\right)}{\lim _{x \rightarrow 0} \frac{1}{x}(\sin 3 x-\tan 2 x)}= \\
& =\left(\lim _{x \rightarrow 0} \frac{e^{x}-1}{x}-\lim _{x \rightarrow 0} \frac{e^{3 x}-1}{x}\right) /\left(\lim _{x \rightarrow 0} \frac{\sin 3 x}{x}-\lim _{x \rightarrow 0} \frac{\tan 2 x}{x}\right)=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$e^{x}-1 \sim x$, as $x \rightarrow 0$
$e^{3 x}-1 \sim 3 x$, as $x \rightarrow 0(3 x \rightarrow 0)$
$\sin 3 x \sim 3 x$, as $3 x \rightarrow 0(3 x \rightarrow 0)$
$\tan 2 x \sim 2 x$, as $x \rightarrow 0(2 x \rightarrow 0)$
We get:
$=\frac{\lim _{x \rightarrow 0} \frac{x}{x}-\lim _{x \rightarrow 0} \frac{3 x}{x}}{\lim _{x \rightarrow 0} \frac{3 x}{x}-\lim _{x \rightarrow 0} \frac{2 x}{x}}=\frac{\lim _{x \rightarrow 0} 1-\lim _{x \rightarrow 0} 3}{\lim _{x \rightarrow 0} 3-\lim _{x \rightarrow 0} 2}=\frac{1-3}{3-2}=-2$
## Problem Kuznetsov Limits 15-24
|
-2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow \frac{\pi}{6}} \frac{2 \sin ^{2} x+\sin x-1}{2 \sin ^{2} x-3 \sin x+1}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow \frac{\pi}{6}} \frac{2 \sin ^{2} x+\sin x-1}{2 \sin ^{2} x-3 \sin x+1}= \\
& =\lim _{x \rightarrow \frac{\pi}{6}} \frac{2\left(\sin ^{2} x+\frac{1}{2} \cdot \sin x+\frac{1}{16}\right)-\frac{9}{8}}{2\left(\sin ^{2} x-\frac{3}{2} \sin x+\frac{9}{16}\right)-\frac{1}{8}}= \\
& =\lim _{x \rightarrow \frac{\pi}{6}} \frac{2\left(\sin x+\frac{1}{4}\right)^{2}-\frac{9}{8}}{2\left(\sin x-\frac{3}{4}\right)^{2}-\frac{1}{8}}=\lim _{x \rightarrow \frac{\pi}{6}} \frac{2\left(\left(\sin x+\frac{1}{4}\right)^{2}-\frac{9}{16}\right)}{2\left(\left(\sin x-\frac{3}{4}\right)^{2}-\frac{1}{16}\right)}= \\
& =\lim _{x \rightarrow \frac{\pi}{6}} \frac{\left(\sin x+\frac{1}{4}-\frac{3}{4}\right)\left(\sin x+\frac{1}{4}+\frac{3}{4}\right)}{\left(\sin x-\frac{3}{4}-\frac{1}{4}\right)\left(\sin x-\frac{3}{4}+\frac{1}{4}\right)}= \\
& =\lim _{x \rightarrow \frac{\pi}{6}} \frac{\left(\sin x-\frac{1}{2}\right)(\sin x+1)}{(\sin x-1)\left(\sin x-\frac{1}{2}\right)}=\lim _{x \rightarrow \frac{\pi}{6}} \frac{\sin x+1}{\sin x-1}= \\
& =\frac{\sin \frac{\pi}{6}+1}{\sin \frac{\pi}{6}-1}=\frac{\frac{1}{2}+1}{\frac{1}{2}-1}=\frac{\frac{3}{2}}{-\frac{1}{2}}=-3
\end{aligned}
$$
## Problem Kuznetsov Limits 16-24
|
-3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$$
\lim _{x \rightarrow 0}\left(\frac{\operatorname{arctg} 3 x}{x}\right)^{x+2}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 0}\left(\frac{\operatorname{arctg} 3 x}{x}\right)^{x+2}=\left(\lim _{x \rightarrow 0} \frac{\operatorname{arctg} 3 x}{x}\right)^{\lim _{x \rightarrow 0} x+2}= \\
& =\left(\lim _{x \rightarrow 0} \frac{\operatorname{arctg} 3 x}{x}\right)^{0+2}=\left(\lim _{x \rightarrow 0} \frac{\operatorname{arctg} 3 x}{x}\right)^{2}=
\end{aligned}
$$
$\operatorname{arctg} 3 x \sim 3 x$, as $x \rightarrow 0(3 x \rightarrow 0)$
We get:
$=\left(\lim _{x \rightarrow 0} \frac{3 x}{x}\right)^{2}=\left(\lim _{x \rightarrow 0} 3\right)^{2}=3^{2}=9$
## Problem Kuznetsov Limits 18-24
|
9
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Condition of the problem
Calculate the limit of the function:
$\lim _{x \rightarrow 0} \sqrt{\left(e^{\sin x}-1\right) \cos \left(\frac{1}{x}\right)+4 \cos x}$
|
## Solution
Since $\cos \left(\frac{1}{x}\right)_{\text {- is bounded, and }}$
$\lim _{x \rightarrow 0} e^{\sin x}-1=e^{\sin 0}-1=e^{0}-1=1-1=0$, then
$$
\left(e^{\sin x}-1\right) \cos \left(\frac{1}{x}\right) \rightarrow 0 \quad, \text { as } x \rightarrow 0
$$
Therefore:
$\lim _{x \rightarrow 0} \sqrt{\left(e^{\sin x}-1\right) \cos \left(\frac{1}{x}\right)+4 \cos x}=\sqrt{0+4 \cos 0}=\sqrt{4}=2$
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the definite integral:
$$
\int_{1 / 8}^{1} \frac{15 \sqrt{x+3}}{(x+3)^{2} \sqrt{x}} d x
$$
|
## Solution
$$
\int_{1 / 8}^{1} \frac{15 \sqrt{x+3}}{(x+3)^{2} \sqrt{x}} d x=\int_{1 / 8}^{1} \frac{15}{(x+3) \sqrt{(x+3) x}} d x=
$$
Substitution:
$$
\begin{aligned}
& t=\sqrt{\frac{x+3}{x}} \\
& d t=\frac{1}{2} \sqrt{\frac{x}{x+3}} \cdot \frac{1 \cdot x-(x+3) \cdot 1}{x^{2}} d x=\frac{1}{2} \sqrt{\frac{x}{x+3}} \cdot \frac{-3}{x^{2}} d x= \\
& =-\frac{3}{2 x \sqrt{(x+3) x}} d x \Rightarrow \frac{d x}{x \sqrt{(x+3) x}}=-\frac{2 d t}{3} \\
& x=\frac{1}{8} \Rightarrow t=\sqrt{\frac{\frac{1}{8}+3}{\frac{1}{8}}}=\sqrt{1+24}=5 \\
& x=1 \Rightarrow t=\sqrt{\frac{1+3}{1}}=\sqrt{4}=2
\end{aligned}
$$
We get:
$$
\begin{aligned}
& =\int_{1 / 8}^{1} \frac{15}{\frac{x+3}{x} \cdot x \sqrt{(x+3) x}} d x=\int_{5}^{2} \frac{15}{t^{2}} \cdot\left(-\frac{2 d t}{3}\right)=\int_{5}^{2} \frac{-10 d t}{t^{2}}= \\
& =\left.\frac{10}{t}\right|_{5} ^{2}=\frac{10}{2}-\frac{10}{5}=5-2=3
\end{aligned}
$$
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\�_ $\% \mathrm{D} 0 \% 9 \mathrm{~A} \% \mathrm{D} 1 \% 83 \% \mathrm{D} 0 \% \mathrm{~B} 7 \% \mathrm{D} 0 \% \mathrm{BD} \% \mathrm{D} 0 \% \mathrm{~B} 5 \% \mathrm{D} 1 \% 86 \% \mathrm{D} 0 \% \mathrm{BE} \% \mathrm{D} 0 \% \mathrm{~B} 2 \mathrm{\%} 0 \mathrm{D} 0 \% 98 \% \mathrm{D} 0 \% \mathrm{BD}$ $\% \mathrm{D} 1 \% 82 \% \mathrm{D} 0 \% \mathrm{~B} 5 \% \mathrm{D} 0 \% \mathrm{~B} 3 \% \mathrm{D} 1 \% 80 \% \mathrm{D} 0 \% \mathrm{~B} 0 \% \mathrm{D} 0 \% \mathrm{BB} \% \mathrm{D} 1 \% 8 \mathrm{~B}+11-15$ »
Categories: Kuznetsov's Problem Book Integrals Problem 11 | Integrals
- Last modified: 21:56, 18 June 2009.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals 11-16
## Material from PlusPi
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the definite integral:
$$
\int_{1 / 24}^{1 / 3} \frac{5 \sqrt{x+1}}{(x+1)^{2} \sqrt{x}} d x
$$
|
## Solution
$$
\int_{1 / 24}^{1 / 3} \frac{5 \sqrt{x+1}}{(x+1)^{2} \sqrt{x}} d x=\int_{1 / 24}^{1 / 3} \frac{5}{(x+1) \sqrt{(x+1) x}} d x=
$$
Substitution:
$$
\begin{aligned}
& t=\sqrt{\frac{x+1}{x}} \\
& d t=\frac{1}{2} \sqrt{\frac{x}{x+1}} \cdot \frac{1 \cdot x-(x+1) \cdot 1}{x^{2}} d x=\frac{1}{2} \sqrt{\frac{x}{x+1}} \cdot \frac{-1}{x^{2}} d x= \\
& =-\frac{1}{2 x \sqrt{(x+1) x}} d x \Rightarrow \frac{d x}{x \sqrt{(x+1) x}}=-2 d t \\
& x=\frac{1}{24} \Rightarrow t=\sqrt{\frac{\frac{1}{24}+1}{\frac{1}{24}}}=\sqrt{1+24}=5 \\
& x=\frac{1}{3} \Rightarrow t=\sqrt{\frac{\frac{1}{3}+1}{\frac{1}{3}}}=\sqrt{1+3}=2
\end{aligned}
$$
We get:
$$
\begin{aligned}
& =\int_{1 / 24}^{1 / 3} \frac{5}{\frac{x+1}{x} \cdot x \sqrt{(x+1) x}} d x=\int_{5}^{2} \frac{5}{t^{2}} \cdot(-2 d t)=\int_{5}^{2} \frac{-10 d t}{t^{2}}= \\
& =\left.\frac{10}{t}\right|_{5} ^{2}=\frac{10}{2}-\frac{10}{5}=5-2=3
\end{aligned}
$$
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\� \%D0\%9A\%D1\%83\%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD $\% \mathrm{D} 1 \% 82 \% \mathrm{D} 0 \% \mathrm{~B} 5 \% \mathrm{D} 0 \% \mathrm{~B} 3 \% \mathrm{D} 1 \% 80 \% \mathrm{D} 0 \% \mathrm{~B} 0 \% \mathrm{D} 0 \% \mathrm{BB} \% \mathrm{D} 1 \% 8 \mathrm{~B}+11-22 »
Categories: Kuznetsov's Problem Book Integrals Problem 11 | Integrals
- Last modified: 15:27, 26 June 2009.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals 11-23
## Material from PlusPi
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the definite integral:
$$
\int_{16 / 15}^{4 / 3} \frac{4 \sqrt{x}}{x^{2} \sqrt{x-1}} d x
$$
|
## Solution
## Problem 11.
## Calculate the definite integral:
$$
I=\int_{16 / 15}^{4 / 3} \frac{4 \sqrt{x}}{x^{2} \sqrt{x-1}} d x
$$
## Perform a variable substitution:
$$
\begin{aligned}
& t=\sqrt{\frac{x}{x-1}}, \text { hence } t^{2}=\frac{x}{x-1}, \text { that is } x=1+\frac{1}{t^{2}-1}, \text { and } \\
& d x=\frac{-2 t}{\left(t^{2}-1\right)^{2}} d t=-\frac{2 t d t}{\left(t^{2}-1\right)^{2}} . \\
& x=\frac{1}{t^{2}-1}+1=\frac{t^{2}}{t^{2}-1}
\end{aligned}
$$
Recalculate the limits of integration
$$
\begin{aligned}
& t_{1}=\sqrt{\frac{4 / 3}{4 / 3-1}}=2 \\
& t_{2}=\sqrt{\frac{16 / 15}{16 / 15-1}}=4
\end{aligned}
$$
## Take the resulting integral:
$$
I=\int_{4}^{2} \frac{4 t}{\frac{t^{4}}{\left(t^{2}-1\right)^{2}}} \cdot\left(-\frac{2 t}{\left(t^{2}-1\right)^{2}} d t\right)=8 \int_{2}^{4} \frac{1}{t^{2}} d t=-\left.\frac{8}{t}\right|_{2} ^{4}=-2+4=2
$$
Answer: $\int_{16 / 15}^{4 / 3} \frac{4 \sqrt{x}}{x^{2} \sqrt{x-1}} d x=2$
\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD\%D1\%82\%D0\%B5\%D0\%B3\%D1\%80\%D0\%B0\%D0\%BB $\%$ D1\%8B_11-26»
Categories: In scan form | Kuznetsov's Integral Problems 11 | Integrals
Ukrainian Banner Network
- Last modified on this page: 11:23, June 8, 2009.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals 11-27
## Material from Plusi
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$$
\lim _{n \rightarrow \infty} \frac{(n+2)^{2}-(n-2)^{2}}{(n+3)^{2}}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{(n+2)^{2}-(n-2)^{2}}{(n+3)^{2}}=\lim _{n \rightarrow \infty} \frac{n^{2}+4 n+4-n^{2}+4 n-4}{n^{2}+6 n+9}= \\
& =\lim _{n \rightarrow \infty} \frac{\frac{1}{n} 8 n}{\frac{1}{n}\left(n^{2}+6 n+9\right)}=\lim _{n \rightarrow \infty} \frac{8}{n+6+\frac{9}{n}}=\left\{\frac{8}{\infty}\right\}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 3-30
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{\sqrt{n+1}-\sqrt[3]{n^{3}+1}}{\sqrt[4]{n+1}-\sqrt[5]{n^{5}+1}}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{\sqrt{n+1}-\sqrt[3]{n^{3}+1}}{\sqrt[4]{n+1}-\sqrt[5]{n^{5}+1}}=\lim _{n \rightarrow \infty} \frac{\frac{1}{n}\left(\sqrt{n+1}-\sqrt[3]{n^{3}+1}\right)}{\frac{1}{n}\left(\sqrt[4]{n+1}-\sqrt[5]{n^{5}+1}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{\sqrt{\frac{1}{n}+\frac{1}{n^{2}}}-\sqrt[3]{1+\frac{1}{n^{3}}}}{\sqrt[4]{\frac{1}{n^{3}}+\frac{1}{n^{4}}}-\sqrt[5]{1+\frac{1}{n^{5}}}}=\frac{\sqrt{0+0}-\sqrt[3]{1+0}}{\sqrt[4]{0+0}-\sqrt[5]{1+0}}=\frac{-1}{-1}=1
\end{aligned}
$$
## Problem Kuznetsov Limits 4-30
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow-3} \frac{x^{3}+7 x^{2}+15 x+9}{x^{3}+8 x^{2}+21 x+18}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow-3} \frac{x^{3}+7 x^{2}+15 x+9}{x^{3}+8 x^{2}+21 x+18}=\left\{\frac{0}{0}\right\}=\lim _{x \rightarrow-3} \frac{(x+3)\left(x^{2}+4 x+3\right)}{(x+3)\left(x^{2}+5 x+6\right)}= \\
& =\lim _{x \rightarrow-3} \frac{x^{2}+4 x+3}{x^{2}+5 x+6}=\left\{\frac{0}{0}\right\}=\lim _{x \rightarrow-3} \frac{(x+3)(x+1)}{(x+3)(x+2)}= \\
& =\lim _{x \rightarrow-3} \frac{x+1}{x+2}=\frac{-3+1}{-3+2}=\frac{-2}{-1}=2
\end{aligned}
$$
## Problem Kuznetsov Limits 10-30
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$$
\lim _{x \rightarrow-8} \frac{10-x-6 \sqrt{1-x}}{2+\sqrt[3]{x}}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow-8} \frac{10-x-6 \sqrt{1-x}}{2+\sqrt[3]{x}}=\lim _{x \rightarrow-8} \frac{(10-x-6 \sqrt{1-x})(10-x+6 \sqrt{1-x})}{(2+\sqrt[3]{x})}= \\
& =\lim _{x \rightarrow-8} \frac{(10-x+6 \sqrt{1-x})}{(2+\sqrt[3]{x})(10-x+6 \sqrt{1-x})}=\lim _{x \rightarrow-8} \frac{100-20 x+x^{2}-36+36 x}{(2+\sqrt[3]{x})(10-x+6 \sqrt{1-x})}= \\
& =\lim _{x \rightarrow-8} \frac{64+16 x+x^{2}}{(2+\sqrt[3]{x})(10-x+6 \sqrt{1-x})}=\lim _{x \rightarrow-8} \frac{(8+x)^{2}}{(2+\sqrt[3]{x})(10-x+6 \sqrt{1-x})}=
\end{aligned}
$$
$$
\begin{aligned}
& =\lim _{x \rightarrow-8} \frac{\left((2+\sqrt[3]{x})\left(4-2 \sqrt[3]{x}+\sqrt[3]{x^{2}}\right)\right)^{2}}{(2+\sqrt[3]{x})(10-x+6 \sqrt{1-x})}=\lim _{x \rightarrow-8} \frac{(2+\sqrt[3]{x})\left(4-2 \sqrt[3]{x}+\sqrt[3]{x^{2}}\right)^{2}}{10-x+6 \sqrt{1-x}}= \\
& =\frac{(2+\sqrt[3]{-8})\left(4-2 \sqrt[3]{-8}+\sqrt[3]{(-8)^{2}}\right)^{2}}{10-(-8)+6 \sqrt{1-(-8)}}=\frac{(2-2)\left(4-2 \cdot(-2)+(-2)^{2}\right)^{2}}{10+8+6 \sqrt{9}}= \\
& =\frac{0(4+4+4)^{2}}{10+8+6 \sqrt{9}}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 11-30
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the distance from point $M_{0}$ to the plane passing through three points $M_{1}, M_{2}, M_{3}$.
$M_{1}(-4 ; 2 ; 6)$
$M_{2}(2 ;-3 ; 0)$
$M_{3}(-10 ; 5 ; 8)$
$M_{0}(-12 ; 1 ; 8)$
|
## Solution
Find the equation of the plane passing through three points $M_{1}, M_{2}, M_{3}$:
$$
\left|\begin{array}{ccc}
x-(-4) & y-2 & z-6 \\
2-(-4) & -3-2 & 0-6 \\
-10-(-4) & 5-2 & 8-6
\end{array}\right|=0
$$
Perform transformations:
$$
\begin{aligned}
& \left|\begin{array}{ccc}
x+4 & y-2 & z-6 \\
6 & -5 & -6 \\
-6 & 3 & 2
\end{array}\right|=0 \\
& (x+4) \cdot\left|\begin{array}{cc}
-5 & -6 \\
3 & 2
\end{array}\right|-(y-2) \cdot\left|\begin{array}{cc}
6 & -6 \\
-6 & 2
\end{array}\right|+(z-6) \cdot\left|\begin{array}{cc}
6 & -5 \\
-6 & 3
\end{array}\right|=0 \\
& (x+4) \cdot 8-(y-2) \cdot(-24)+(z-6) \cdot(-12)=0 \\
& 8 x+32+24 y-48-12 z+72=0 \\
& 8 x+24 y-12 z+56=0 \\
& 2 x+6 y-3 z+14=0
\end{aligned}
$$
The distance $d$ from a point $M_{0}\left(x_{0} ; y_{0} ; z_{0}\right)$ to the plane $A x+B y+C z+D=0$:
$$
d=\frac{\left|A x_{0}+B y_{0}+C z_{0}+D\right|}{\sqrt{A^{2}+B^{2}+C^{2}}}
$$
Find:
$$
d=\frac{|2 \cdot(-12)+6 \cdot 1-3 \cdot 8+14|}{\sqrt{2^{2}+6^{2}+(-3)^{2}}}=\frac{|-24+6-24+14|}{\sqrt{4+36+9}}=\frac{28}{\sqrt{49}}=4
$$
## Problem Kuznetsov Analytic Geometry $8-17$
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Let $k$ be the coefficient of similarity transformation with the center at the origin. Is it true that point $A$ belongs to the image of plane $a?$
$A(2 ; 1 ; 2)$
$a: x-2 y+z+1=0$
$k=-2$
|
## Solution
When transforming similarity with the center at the origin of the plane
$a: A x+B y+C z+D=0_{\text{and coefficient }} k$ transitions to the plane
$a^{\prime}: A x+B y+C z+k \cdot D=0$. We find the image of the plane $a$:
$a^{\prime}: x-2 y+z-2=0$
Substitute the coordinates of point $A$ into the equation $a^{\prime}:$
$2-2 \cdot 1+2-2=0$
$2-2+2-2=0$
$0=0$
Since $0=0$, point $A$ belongs to the image of the plane $a$.
## Problem Kuznetsov Analytical Geometry 12-2
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow-1} \frac{x^{3}-3 x-2}{x^{2}-x-2}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow-1} \frac{x^{3}-3 x-2}{x^{2}-x-2}=\left\{\frac{0}{0}\right\}=\lim _{x \rightarrow-1} \frac{\left(x^{2}-x-2\right)(x+1)}{x^{2}-x-2}= \\
& =\lim _{x \rightarrow-1}(x+1)=-1+1=0
\end{aligned}
$$
## Problem Kuznetsov Limits 10-9
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow \pi} \frac{\cos 5 x-\cos 3 x}{\sin ^{2} x}$
|
## Solution
$\lim _{x \rightarrow \pi} \frac{\cos 5 x-\cos 3 x}{\sin ^{2} x}=\lim _{x \rightarrow \pi} \frac{-2 \sin \frac{5 x+3 x}{2} \sin \frac{5 x-3 x}{2}}{\sin ^{2} x}=$
$=\lim _{x \rightarrow \pi} \frac{-2 \sin 4 x \sin x}{\sin ^{2} x}=\lim _{x \rightarrow \pi} \frac{-2 \sin 4 x}{\sin x}=$
Substitution:
$x=y+\pi \Rightarrow y=x-\pi$
$x \rightarrow \pi \Rightarrow y \rightarrow 0$
We get:
$=\lim _{y \rightarrow 0} \frac{-2 \sin 4(y+\pi)}{\sin (y+\pi)}=\lim _{y \rightarrow 0} \frac{-2 \sin (4 y+4 \pi)}{-\sin y}=$
$=\lim _{y \rightarrow 0} \frac{2 \sin 4 y}{\sin y}=$
Using the substitution of equivalent infinitesimals:
$\sin 4 y \sim 4 y_{\text {, as }} y \rightarrow 0(4 y \rightarrow 0)$
$\sin y \sim y$, as $y \rightarrow 0$
$=\lim _{y \rightarrow 0} \frac{2 \cdot 4 y}{y}=\lim _{y \rightarrow 0} \frac{8}{1}=8$
## Problem Kuznetsov Limits 13-9
|
8
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{(n+1)^{3}+(n-1)^{3}}{n^{3}+1}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{(n+1)^{3}+(n-1)^{3}}{n^{3}+1}=\lim _{n \rightarrow \infty} \frac{\frac{1}{n^{3}}\left((n+1)^{3}+(n-1)^{3}\right)}{\frac{1}{n^{3}}\left(n^{3}+1\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{\left(1+\frac{1}{n}\right)^{3}+\left(1-\frac{1}{n}\right)^{3}}{1+\frac{1}{n^{3}}}=\frac{1+1}{1}=2
\end{aligned}
$$
## Problem Kuznetsov Limits 3-29
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{n^{2}-\sqrt{n^{3}+1}}{\sqrt[3]{n^{6}+2}-n}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{n^{2}-\sqrt{n^{3}+1}}{\sqrt[3]{n^{6}+2}-n}=\lim _{n \rightarrow \infty} \frac{\frac{1}{n^{2}}\left(n^{2}-\sqrt{n^{3}+1}\right)}{\frac{1}{n^{2}}\left(\sqrt[3]{n^{6}+2}-n\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{1-\sqrt{\frac{1}{n}+\frac{1}{n^{4}}}}{\sqrt[3]{1+\frac{2}{n^{6}}}-\frac{1}{n}}=\frac{1-\sqrt{0+0}}{\sqrt[3]{1+0}-0}=\frac{1}{1}=1
\end{aligned}
$$
## Problem Kuznetsov Limits 4-29
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$$
\lim _{n \rightarrow \infty} n\left(\sqrt{n^{4}+3}-\sqrt{n^{4}-2}\right)
$$
|
## Solution
$\lim _{n \rightarrow \infty} n\left(\sqrt{n^{4}+3}-\sqrt{n^{4}-2}\right)=$
$$
\begin{aligned}
& =\lim _{n \rightarrow \infty} \frac{n\left(\sqrt{n^{4}+3}-\sqrt{n^{4}-2}\right)\left(\sqrt{n^{4}+3}+\sqrt{n^{4}-2}\right)}{\sqrt{n^{4}+3}+\sqrt{n^{4}-2}}= \\
& =\lim _{n \rightarrow \infty} \frac{n\left(n^{4}+3-\left(n^{4}-2\right)\right)}{\sqrt{n^{4}+3}+\sqrt{n^{4}-2}}=\lim _{n \rightarrow \infty} \frac{5 n}{\sqrt{n^{4}+3}+\sqrt{n^{4}-2}}= \\
& =\lim _{n \rightarrow \infty} \frac{\frac{1}{n^{2}} 5 n}{\frac{1}{n^{2}}\left(\sqrt{n^{4}+3}+\sqrt{n^{4}-2}\right)}=\lim _{n \rightarrow \infty} \frac{\frac{5}{n}}{\sqrt{1+\frac{3}{n^{4}}}+\sqrt{1-\frac{2}{n^{4}}}}= \\
& =\frac{0}{\sqrt{1+0}+\sqrt{1-0}}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 5-29
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 4} \frac{\sqrt{x}-2}{\sqrt[3]{x^{2}-16}}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 4} \frac{\sqrt{x}-2}{\sqrt[3]{x^{2}-16}}=\lim _{x \rightarrow 4} \frac{\sqrt{x}-2}{\sqrt[3]{(x-4)(x+4)}}= \\
& =\lim _{x \rightarrow 4} \frac{\sqrt{x}-2}{\sqrt[3]{(\sqrt{x}-2)(\sqrt{x}+2)(x+4)}}= \\
& =\lim _{x \rightarrow 4} \frac{\sqrt{x}-2}{\sqrt[3]{(\sqrt{x}-2)} \sqrt[3]{(\sqrt{x}+2)(x+4)}}= \\
& =\lim _{x \rightarrow 4} \frac{\sqrt[3]{(\sqrt{x}-2)^{2}}}{\sqrt[3]{(\sqrt{x}+2)(x+4)}}=\frac{\sqrt[3]{(\sqrt{4}-2)^{2}}}{\sqrt[3]{(\sqrt{4}+2)(4+4)}}=
\end{aligned}
$$
$=\frac{\sqrt[3]{0^{2}}}{\sqrt[3]{(2+2) 8}}=0$
## Problem Kuznetsov Limits 11-29
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.