problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{(2 n+1)^{3}-(2 n+3)^{3}}{(2 n+1)^{2}+(2 n+3)^{2}}$
|
## Solution
$\lim _{n \rightarrow \infty} \frac{(2 n+1)^{3}-(2 n+3)^{3}}{(2 n+1)^{2}+(2 n+3)^{2}}=\lim _{n \rightarrow \infty} \frac{8 n^{3}+3 \cdot 4 n^{2}+3 \cdot 2 n+1-8 n^{3}-3 \cdot 3 \cdot 4 n^{2}-3 \cdot 3^{2} \cdot 2 n-3^{3}}{(2 n+1)^{2}+(2 n+3)^{2}}=$
$=\lim _{n \rightarrow \infty} \frac{\frac{1}{n^{2}}\left(3 \cdot 4 n^{2}(1-3)+3 \cdot 2 n\left(1-3^{2}\right)+\left(1-3^{3}\right)\right)}{\frac{1}{n^{2}}\left((2 n+1)^{2}+(2 n+3)^{2}\right)}=\lim _{n \rightarrow \infty} \frac{-24-\frac{48}{n}-\frac{26}{n^{2}}}{\left(2+\frac{1}{n}\right)^{2}+\left(2+\frac{3}{n}\right)^{2}}=$
$=\frac{-24-0-0}{2^{2}+2^{2}}=-\frac{24}{8}=-3$
## Problem Kuznetsov Limits 3-21
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{n \sqrt[4]{11 n}+\sqrt{25 n^{4}-81}}{(n-7 \sqrt{n}) \sqrt{n^{2}-n+1}}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{n \sqrt[4]{11 n}+\sqrt{25 n^{4}-81}}{(n-7 \sqrt{n}) \sqrt{n^{2}-n+1}}=\lim _{n \rightarrow \infty} \frac{\frac{1}{n^{2}}\left(n \sqrt[4]{11 n}+\sqrt{25 n^{4}-81}\right)}{\frac{1}{n^{2}}(n-7 \sqrt{n}) \sqrt{n^{2}-n+1}}= \\
& =\lim _{n \rightarrow \infty} \frac{\sqrt[4]{\frac{11}{n^{3}}}+\sqrt{25-\frac{81}{n^{4}}}}{\left(\frac{1}{n}(n-7 \sqrt{n})\right)\left(\frac{1}{n} \sqrt{n^{2}-n+1}\right)}=\lim _{n \rightarrow \infty} \frac{\sqrt[4]{\frac{11}{n^{3}}}+\sqrt{25-\frac{81}{n^{4}}}}{\left(1-7 \sqrt{\frac{1}{n}}\right) \sqrt{1-\frac{1}{n}+\frac{1}{n^{2}}}}= \\
& =\frac{\sqrt[4]{0}+\sqrt{25-0}}{(1-7 \sqrt{0}) \sqrt{1-0+0}}=\frac{5}{1}=5
\end{aligned}
$$
## Problem Kuznetsov Limits 4-21
|
5
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$$
\lim _{n \rightarrow \infty}\left(\sqrt{\left(n^{2}+1\right)\left(n^{2}+2\right)}-\sqrt{\left(n^{2}-1\right)\left(n^{2}-2\right)}\right)
$$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty}\left(\sqrt{\left(n^{2}+1\right)\left(n^{2}+2\right)}-\sqrt{\left(n^{2}-1\right)\left(n^{2}-2\right)}\right)= \\
& =\lim _{n \rightarrow \infty} \frac{\left(\sqrt{\left(n^{2}+1\right)\left(n^{2}+2\right)}-\sqrt{\left(n^{2}-1\right)\left(n^{2}-2\right)}\right)\left(\sqrt{\left(n^{2}+1\right)\left(n^{2}+2\right)}+\sqrt{\left(n^{2}-1\right)\left(n^{2}-2\right)}\right)}{\sqrt{\left(n^{2}+1\right)\left(n^{2}+2\right)}+\sqrt{\left(n^{2}-1\right)\left(n^{2}-2\right)}}= \\
& =\lim _{n \rightarrow \infty} \frac{\left(n^{2}+1\right)\left(n^{2}+2\right)-\left(n^{2}-1\right)\left(n^{2}-2\right)}{\sqrt{\left(n^{2}+1\right)\left(n^{2}+2\right)}+\sqrt{\left(n^{2}-1\right)\left(n^{2}-2\right)}}= \\
& =\lim _{n \rightarrow \infty} \frac{n^{4}+n^{2}+2 n^{2}+2-n^{4}+n^{2}+2 n^{2}-2}{\sqrt{\left(n^{2}+1\right)\left(n^{2}+2\right)}+\sqrt{\left(n^{2}-1\right)\left(n^{2}-2\right)}}= \\
& =\lim _{n \rightarrow \infty} \frac{6 n^{2}}{\sqrt{\left(n^{2}+1\right)\left(n^{2}+2\right)}+\sqrt{\left(n^{2}-1\right)\left(n^{2}-2\right)}}= \\
& =\lim _{n \rightarrow \infty} \frac{\frac{1}{n^{2}} 6 n^{2}}{\frac{1}{n^{2}}\left(\sqrt{\left(n^{2}+1\right)\left(n^{2}+2\right)}+\sqrt{\left(n^{2}-1\right)\left(n^{2}-2\right)}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{6}{\sqrt{\left(1+\frac{1}{n^{2}}\right)\left(1+\frac{2}{n^{2}}\right)}+\sqrt{\left(1-\frac{1}{n^{2}}\right)\left(1-\frac{2}{n^{2}}\right)}}= \\
& =\frac{6}{\sqrt{(1+0)(1+0)}+\sqrt{(1-0)(1-0)}}=\frac{6}{2}=3
\end{aligned}
$$
## Problem Kuznetsov Limits 5-21
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty}\left(\frac{3 n^{2}-5 n}{3 n^{2}-5 n+7}\right)^{n+1}$
|
## Solution
$\lim _{n \rightarrow \infty}\left(\frac{3 n^{2}-5 n}{3 n^{2}-5 n+7}\right)^{n+1}=\lim _{n \rightarrow \infty}\left(\frac{3 n^{2}-5 n+7}{3 n^{2}-5 n}\right)^{-n-1}=$
$=\lim _{n \rightarrow \infty}\left(1+\frac{7}{3 n^{2}-5 n}\right)^{-n-1}=\lim _{n \rightarrow \infty}\left(1+\frac{1}{\left(\frac{3 n^{2}-5 n}{7}\right)}\right)^{-n-1}=$
$=\lim _{n \rightarrow \infty}\left(1+\frac{1}{\left(\frac{3 n^{2}-5 n}{7}\right)}\right)^{\left(\frac{3 n^{2}-5 n}{7}\right)\left(\frac{7}{3 n^{2}-5 n}\right)(-n-1)}=$
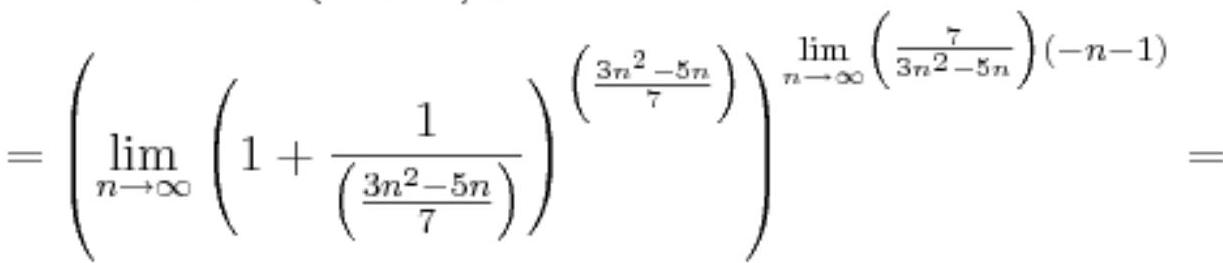
$=\{$ Using the second remarkable limit $\}=$
$=e^{\lim _{n \rightarrow \infty}\left(\frac{7}{3 n^{2}-5 n}\right)(-n-1)}=e^{\lim _{n \rightarrow \infty} \frac{7(-n-1)}{3 n^{2}-5 n}}=$
$=e^{\lim _{n \rightarrow \infty} \frac{\frac{1}{n^{2}} 7(-n-1)}{n^{2}\left(3 n^{2}-5 n\right)}}=e^{\lim _{n \rightarrow \infty} \frac{7\left(-\frac{1}{n}-\frac{1}{n^{2}}\right)}{3-\frac{5}{n^{2}}}}=e^{\frac{7(-0-0)}{3-0}}=e^{0}=1$
## Problem Kuznetsov Limits 7-21
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Condition of the problem
Calculate the limit of the function:
$$
\lim _{x \rightarrow-1} \frac{x^{3}-3 x-2}{x^{2}+2 x+1}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow-1} \frac{x^{3}-3 x-2}{x^{2}+2 x+1}=\left\{\frac{0}{0}\right\}=\lim _{x \rightarrow-1} \frac{(x+1)\left(x^{2}-x-2\right)}{(x+1)^{2}}= \\
& =\lim _{x \rightarrow-1} \frac{x^{2}-x-2}{x+1}=\left\{\frac{0}{0}\right\}=\lim _{x \rightarrow-1} \frac{(x+1)(x-2)}{x+1}= \\
& =\lim _{x \rightarrow-1}(x-2)=-1-2=-3
\end{aligned}
$$
## Problem Kuznetsov Limits 10-21
|
-3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{h \rightarrow 0} \frac{a^{x+h}+a^{x-h}-2 a^{x}}{h}$
|
Solution
$\lim _{h \rightarrow 0} \frac{a^{x+h}+a^{x-h}-2 a^{x}}{h}=\lim _{h \rightarrow 0} \frac{a^{x+h}-a^{x}+a^{x-h}-a^{x}}{h}=$
$=\lim _{h \rightarrow 0} \frac{a^{x+h}-a^{x}}{h}+\lim _{h \rightarrow 0} \frac{a^{x-h}-a^{x}}{h}=$
$=\lim _{h \rightarrow 0} \frac{a^{x}\left(a^{h}-1\right)}{h}+\lim _{h \rightarrow 0} \frac{a^{x}\left(a^{-h}-1\right)}{h}=$
$=\lim _{h \rightarrow 0} \frac{a^{x}\left(\left(e^{\ln a}\right)^{h}-1\right)}{h}+\lim _{h \rightarrow 0} \frac{a^{x}\left(\left(e^{\ln a}\right)^{-h}-1\right)}{h}=$
$=\lim _{h \rightarrow 0} \frac{a^{x}\left(e^{h \ln a}-1\right)}{h}+\lim _{h \rightarrow 0} \frac{a^{x}\left(e^{-h \ln a}-1\right)}{h}=$
Using the substitution of equivalent infinitesimals:
$e^{h \ln a}-1 \sim h \ln a$, as $h \rightarrow 0(h \ln a \rightarrow 0)$
$e^{-h \ln a}-1 \sim -h \ln a$, as $h \rightarrow 0(-h \ln a \rightarrow 0)$
We get:
$=\lim _{h \rightarrow 0} \frac{a^{x} \cdot h \ln a}{h}+\lim _{h \rightarrow 0} \frac{a^{x} \cdot(-h) \ln a}{h}=$
$=\lim _{h \rightarrow 0} a^{x} \ln a+\lim _{h \rightarrow 0}-a^{x} \ln a=a^{x} \ln a-a^{x} \ln a=0$
## Problem Kuznetsov Limits 16-21
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0}\left(\frac{\ln \left(1+x^{2}\right)}{x^{2}}\right)^{\frac{3}{x+8}}$
|
## Solution
$\lim _{x \rightarrow 0}\left(\frac{\ln \left(1+x^{2}\right)}{x^{2}}\right)^{\frac{3}{x+8}}=\left(\lim _{x \rightarrow 0} \frac{\ln \left(1+x^{2}\right)}{x^{2}}\right)^{\lim _{x \rightarrow 0} \frac{3}{x+8}}=$
$=\left(\lim _{x \rightarrow 0} \frac{\ln \left(1+x^{2}\right)}{x^{2}}\right)^{\frac{3}{0+8}}=\left(\lim _{x \rightarrow 0} \frac{\ln \left(1+x^{2}\right)}{x^{2}}\right)^{\frac{3}{8}}=$
Using the substitution of equivalent infinitesimals:
$\ln \left(1+x^{2}\right) \sim x^{2}$, as $x \rightarrow 0\left(x^{2} \rightarrow 0\right)$
We get:
$=\left(\lim _{x \rightarrow 0} \frac{x^{2}}{x^{2}}\right)^{\frac{3}{8}}=\left(\lim _{x \rightarrow 0} 1\right)^{\frac{3}{8}}=1^{\frac{3}{8}}=1$
## Problem Kuznetsov Limits 18-21
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$$
\lim _{x \rightarrow 1}\left(\ln ^{2} e x\right)^{\frac{1}{x^{2}+1}}
$$
|
## Solution
$$
\lim _{x \rightarrow 1}\left(\ln ^{2} e x\right)^{\frac{1}{x^{2}+1}}=\left(\ln ^{2}(e \cdot 1)\right)^{\frac{1}{1^{2}+1}}=\left(1^{2}\right)^{\frac{1}{2}}=1
$$
## Problem Kuznetsov Limits 20-21
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## problem statement
Based on the definition of the derivative, find $f^{\prime}(0)$ :
$$
f(x)=\left\{\begin{array}{c}
\sqrt[3]{1-2 x^{3} \sin \frac{5}{x}}-1+x, x \neq 0 \\
0, x=0
\end{array}\right.
$$
|
## Solution
By definition, the derivative at the point $x=0$:
$$
f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}
$$
Based on the definition, we find:
$$
\begin{aligned}
& f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{\sqrt[3]{1-2 \Delta x^{3} \sin \frac{5}{\Delta x}}-1+\Delta x-0}{\Delta x}= \\
& =\lim _{\Delta x \rightarrow 0} \frac{\sqrt[3]{1-2 \Delta x^{3} \sin \frac{5}{\Delta x}}-1}{\Delta x}+\lim _{\Delta x \rightarrow 0} \frac{\Delta x}{\Delta x}= \\
& =\lim _{\Delta x \rightarrow 0} \frac{\left(\sqrt[3]{1-2 \Delta x^{3} \sin \frac{5}{\Delta x}}-1\right)\left(\sqrt[3]{\left(1-2 \Delta x^{3} \sin \frac{5}{\Delta x}\right)^{2}}+\sqrt[3]{1-2 \Delta x^{3} \sin \frac{5}{\Delta x}}+1\right)}{\Delta x\left(\sqrt[3]{\left(1-2 \Delta x^{3} \sin \frac{5}{\Delta x}\right)^{2}}+\sqrt[3]{1-2 \Delta x^{3} \sin \frac{5}{\Delta x}}+1\right)}+\lim _{\Delta x \rightarrow 0} 1= \\
& =\lim _{\Delta x \rightarrow 0} \frac{1-2 \Delta x^{3} \sin \frac{5}{\Delta x}-1}{\Delta x\left(\sqrt[3]{\left(1-2 \Delta x^{3} \sin \frac{5}{\Delta x}\right)^{2}}+\sqrt[3]{1-2 \Delta x^{3} \sin \frac{5}{\Delta x}}+1\right)}+1= \\
& =\lim _{\Delta x \rightarrow 0} \frac{-2 \Delta x^{3} \sin \frac{5}{\Delta x}}{\Delta x\left(\sqrt[3]{\left(1-2 \Delta x^{3} \sin \frac{5}{\Delta x}\right)^{2}}+\sqrt[3]{1-2 \Delta x^{3} \sin \frac{5}{\Delta x}}+1\right)}+1= \\
& =\lim _{\Delta x \rightarrow 0} \frac{-2 \Delta x^{2} \sin \frac{5}{\Delta x}}{\sqrt[3]{\left(1-2 \Delta x^{3} \sin \frac{5}{\Delta x}\right)^{2}}+\sqrt[3]{1-2 \Delta x^{3} \sin \frac{5}{\Delta x}}+1}+1= \\
& \text { Since } \sin \frac{5}{\Delta x} \text { is bounded, then }
\end{aligned}
$$
$\Delta x \cdot \sin \frac{5}{\Delta x} \rightarrow 0$, as $\Delta x \rightarrow 0$
Then:
$=\frac{-2 \cdot 0}{\sqrt[3]{(1-2 \cdot 0)^{2}}+\sqrt[3]{1-2 \cdot 0}+1}+1=\frac{0}{\sqrt[3]{1}+\sqrt[3]{1}+1}+1=1$
Therefore, $f^{\prime}(0)=1$
## Problem Kuznetsov Differentiation $2-27$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the distance from point $M_{0}$ to the plane passing through three points $M_{1}, M_{2}, M_{3}$.
$M_{1}(7 ; 2 ; 4)$
$M_{2}(7 ;-1 ;-2)$
$M_{3}(-5 ;-2 ;-1)$
$M_{0}(10 ; 1 ; 8)$
|
## Solution
Find the equation of the plane passing through three points $M_{1}, M_{2}, M_{3}$:
$$
\left|\begin{array}{ccc}
x-7 & y-2 & z-4 \\
7-7 & -1-2 & -2-4 \\
-5-7 & -2-2 & -1-4
\end{array}\right|=0
$$
Perform transformations:
$$
\begin{aligned}
& \left|\begin{array}{ccc}
x-7 & y-2 & z-4 \\
0 & -3 & -6 \\
-12 & -4 & -5
\end{array}\right|=0 \\
& (x-7) \cdot\left|\begin{array}{ll}
-3 & -6 \\
-4 & -5
\end{array}\right|-(y-2) \cdot\left|\begin{array}{cc}
0 & -6 \\
-12 & -5
\end{array}\right|+(z-4) \cdot\left|\begin{array}{cc}
0 & -3 \\
-12 & -4
\end{array}\right|=0 \\
& (x-7) \cdot(-9)-(y-2) \cdot(-72)+(z-4) \cdot(-36)=0 \\
& -9 x+63+72 y-144-36 z+144=0 \\
& -9 x+72 y-36 z+63=0 \\
& -x+8 y-4 z+7=0
\end{aligned}
$$
The distance $d$ from a point $M_{0}\left(x_{0} ; y_{0} ; z_{0}\right)$ to the plane $A x+B y+C z+D=0$:
$d=\frac{\left|A x_{0}+B y_{0}+C z_{0}+D\right|}{\sqrt{A^{2}+B^{2}+C^{2}}}$
Find:
$$
d=\frac{|-10+8 \cdot 1-4 \cdot 8+7|}{\sqrt{(-1)^{2}+8^{2}+(-4)^{2}}}=\frac{|-10+8-32+7|}{\sqrt{1+64+16}}=\frac{27}{\sqrt{81}}=3
$$
## Problem Kuznetsov Analytic Geometry 8-18
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Let $k$ be the coefficient of similarity transformation with the center at the origin. Is it true that point $A$ belongs to the image of plane $a$?
$A\left(\frac{1}{3} ; 1 ; 1\right)$
$a: 3 x-y+5 z-6=0$
$k=\frac{5}{6}$
|
## Solution
When transforming similarity with the center at the origin of the plane
$a: A x+B y+C z+D=0_{\text{and coefficient }} k$ transitions to the plane
$a^{\prime}: A x+B y+C z+k \cdot D=0$. We find the image of the plane $a$:
$a^{\prime}: 3 x-y+5 z-5=0$
Substitute the coordinates of point $A$ into the equation $a^{\prime}$:
$3 \cdot \frac{1}{3}-1+5 \cdot 1-5=0$
$1-1+5-5=0$
$0=0$
Since $0=0$, point $A$ belongs to the image of the plane $a$.
Problem Kuznetsov Analytical Geometry 12-18
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Based on the definition of the derivative, find $f^{\prime}(x)$:
$f(x)=\left\{\begin{array}{c}\sin \left(e^{x^{2} \sin \frac{5}{x}}-1\right)+x, x \neq 0 \\ 0, x=0\end{array}\right.$
|
## Solution
By definition, the derivative at the point $x=0$:
$$
f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}
$$
Based on the definition, we find:
$$
\begin{aligned}
& f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim _{\Delta x \rightarrow 0}\left(\sin \left(e^{\Delta x^{2} \sin \frac{s}{\Delta x}}-1\right)+\Delta x-0\right) / \Delta x= \\
& =\lim _{\Delta x \rightarrow 0}\left(\sin \left(e^{\Delta x^{2} \sin \frac{5}{\Delta x}}-1\right)\right) / \Delta x+\lim _{\Delta x \rightarrow 0} \frac{\Delta x}{\Delta x}=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$$
e^{\Delta x^{2} \sin \frac{5}{\Delta x}}-1 \sim \Delta x^{2} \sin \frac{5}{\Delta x}, \text { as } \Delta x \rightarrow 0\left(\Delta x^{2} \sin \frac{5}{\Delta x} \rightarrow 0\right)
$$
We get:
$$
=\lim _{\Delta x \rightarrow 0}\left(\sin \left(\Delta x^{2} \sin \frac{5}{\Delta x}\right)\right) / \Delta x+\lim _{\Delta x \rightarrow 0} 1=
$$
Using the substitution of equivalent infinitesimals:
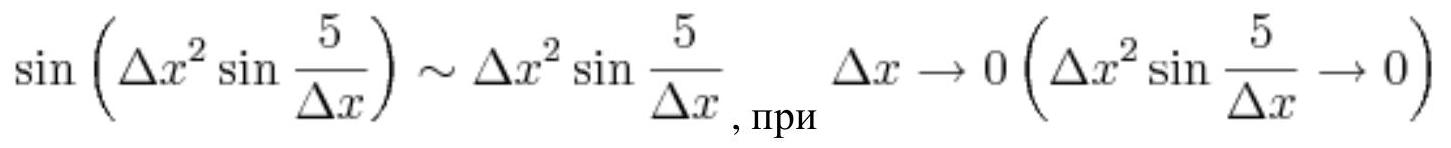
We get:
$=\lim _{\Delta x \rightarrow 0} \frac{\Delta x^{2} \sin \frac{5}{\Delta x}}{\Delta x}+1=\lim _{\Delta x \rightarrow 0} \Delta x \sin \frac{5}{\Delta x}+1=$
Since $\sin \left(\frac{5}{\Delta x}\right)$ is bounded,
$\Delta x \cdot \sin \left(\frac{5}{\Delta x}\right) \rightarrow 0 \quad$, as $\Delta x \rightarrow 0$
Then:
$=0+1=1$
Thus, $f^{\prime}(0)=1$
## Problem Kuznetsov Differentiation $2-7$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the volumes of the bodies bounded by the surfaces.
$$
\frac{x^{2}}{9}+y^{2}=1, z=y, z=0(y \geq 0)
$$
|
## Solution
The base of the considered area is a semi-ellipse, in which
$$
\begin{aligned}
& x=0 \text { when } y=1 \\
& y=0 \text { when } x=3
\end{aligned}
$$
That is, $x \in[-3,3], y \in[0,1]$
Consider the surface $z=y:$
$$
V_{z}=\int_{0}^{1} z d y=\int_{0}^{1} y d y=\left.\frac{y^{2}}{2}\right|_{0} ^{1}=\frac{1}{2}
$$
Now consider the area of the base and find the volume of the given body:
$$
\begin{aligned}
& \frac{x^{2}}{9}+y^{2}=1 \\
& y^{2}=1-\frac{x^{2}}{9} \\
& V=\frac{1}{2} \int_{-3}^{3}\left(1-\frac{x^{2}}{9}\right) d x=\left.\frac{1}{2}\left(x-\frac{x^{3}}{9 \cdot 3}\right)\right|_{-3} ^{3} d x=\frac{1}{2}\left(3-\frac{3^{3}}{27}\right)-\frac{1}{2}\left(-3-\frac{-3^{3}}{27}\right) \\
& =\frac{1}{2}(3-1)-\frac{1}{2}(-3+1)=1+1=2
\end{aligned}
$$
Answer: $V=2$
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\� \%D0\%9A\%D1\%83\%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD $\% \mathrm{D} 1 \% 82 \% \mathrm{D} 0 \% \mathrm{~B} 5 \% \mathrm{D} 0 \% \mathrm{~B} 3 \% \mathrm{D} 1 \% 80 \% \mathrm{D} 0 \% \mathrm{~B} 0 \% \mathrm{D} 0 \% \mathrm{BB} \% \mathrm{D} 1 \% 8 \mathrm{~B} \_20-1$ »
Categories: Kuznetsov's Problem Book Integrals Problem 20 | Integrals | Problems for Checking
Ukrainian Banner Network
- Last modified on this page: 08:06, 24 June 2010.
- Content is available under CC-BY-SA 3.0.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the volumes of the bodies bounded by the surfaces.
$$
\frac{x^{2}}{27}+y^{2}=1, z=\frac{y}{\sqrt{3}}, z=0(y \geq 0)
$$
|
## Solution
The base of the considered area is a semi-ellipse, in which
$$
\begin{aligned}
& x=0 \text { when } y=1 \\
& y=0 \text { when } x=3 \sqrt{3}
\end{aligned}
$$
That is,
$x \in[-3 \sqrt{3}, 3 \sqrt{3}], y \in[0,1]$
Therefore, the volume will be
$$
V=\int_{-3 \sqrt{3}}^{3 \sqrt{3}} d x \int_{0}^{\sqrt{1-x^{2} / 27}} d y \int_{0}^{y / \sqrt{3}} d z
$$
Consider the surface $z=\frac{y}{\sqrt{3}}:$
$$
V_{z}=\int_{0}^{\sqrt{1-x^{2} / 27}} z d y=\int_{0}^{\sqrt{1-x^{2} / 27}} \frac{y}{\sqrt{3}} d y=\left.\frac{y^{2}}{2 \sqrt{3}}\right|_{0} ^{\sqrt{1-x^{2} / 27}}=\frac{1}{2 \sqrt{3}} \cdot\left(1-\frac{x^{2}}{27}\right)
$$
Now the volume of the given body:
$$
\begin{aligned}
& V=\frac{1}{2 \sqrt{3}} \int_{-3 \sqrt{3}}^{3 \sqrt{3}}\left(1-\frac{x^{2}}{27}\right) d x=\left.\frac{1}{2 \sqrt{3}}\left(x-\frac{x^{3}}{27 \cdot 3}\right)\right|_{-3 \sqrt{3}} ^{3 \sqrt{3}} d x= \\
& =\frac{1}{2 \sqrt{3}}\left(3 \sqrt{3}-\frac{(3 \sqrt{3})^{3}}{81}\right)-\frac{1}{2 \sqrt{3}}\left(-3 \sqrt{3}-\frac{(-3 \sqrt{3})^{3}}{81}\right)= \\
& =\frac{\sqrt{3}}{2 \sqrt{3}}\left(3-\frac{27 \cdot 3}{81}\right)+\frac{\sqrt{3}}{2 \sqrt{3}}\left(3-\frac{27 \cdot 3}{81}\right)= \\
& =\frac{1}{2}(3-1)+\frac{1}{2}(3-1)=1+1=2
\end{aligned}
$$
Answer: $V=2$
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\� \%D0\%9A\%D1\%83\%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD $\% \mathrm{D} 1 \% 82 \% \mathrm{D} 0 \% \mathrm{~B} 5 \% \mathrm{D} 0 \% \mathrm{~B} 3 \% \mathrm{D} 1 \% 80 \% \mathrm{D} 0 \% \mathrm{~B} 0 \% \mathrm{D} 0 \% \mathrm{BB} \% \mathrm{D} 1 \% 8 \mathrm{~B}+20-26$ »
Categories: Kuznetsov's Problem Book Integrals Problem $20 \mid$ Integrals
Ukrainian Banner Network
- Last modified: 10:57, June 24, 2010.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals 20-27
## Material from Plusi
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Based on the definition of the derivative, find $f^{\prime}(0)$:
$f(x)=\left\{\begin{array}{c}\tan\left(2^{x^{2} \cos (1 /(8 x))}-1+x\right), x \neq 0 ; \\ 0, x=0\end{array}\right.$
|
## Solution
By definition, the derivative at the point $x=0$:
$f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}$
Based on the definition, we find:
$$
\begin{aligned}
& f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{\tan\left(2^{\Delta x^{2} \cos (1 /(8 \Delta x))}-1+\Delta x\right)-0}{\Delta x}= \\
& =\lim _{\Delta x \rightarrow 0} \frac{\tan\left(2^{\Delta x^{2} \cos (1 /(8 \Delta x))}-1+\Delta x\right)}{\Delta x}=
\end{aligned}
$$
We use the substitution of equivalent infinitesimals:
$\tan\left(2^{\Delta x^{2} \cos (1 /(8 \Delta x))}-1+\Delta x\right) \sim 2^{\Delta x^{2} \cos (1 /(8 \Delta x))}-1+\Delta x$, as
$\Delta x \rightarrow 0\left(2^{\Delta x^{2} \cos (1 /(8 \Delta x))}-1+\Delta x \rightarrow 0\right)$
We get:
$$
\begin{aligned}
& =\lim _{\Delta x \rightarrow 0} \frac{2^{\Delta x^{2} \cos (1 /(8 \Delta x))}-1+\Delta x}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{2^{\Delta x^{2} \cos (1 /(8 \Delta x))}-1}{\Delta x}+\lim _{\Delta x \rightarrow 0} \frac{\Delta x}{\Delta x}= \\
& =\lim _{\Delta x \rightarrow 0} \frac{\left(e^{\ln 2}\right)^{\Delta x^{2} \cos (1 /(8 \Delta x))}-1}{\Delta x}+\lim _{\Delta x \rightarrow 0} 1=1+\lim _{\Delta x \rightarrow 0} \frac{e^{\ln 2 \cdot \Delta x^{2} \cos (1 /(8 \Delta x))}-1}{\Delta x}=
\end{aligned}
$$
We use the substitution of equivalent infinitesimals:
$e^{\ln 2 \cdot \Delta x^{2} \cos (1 /(8 \Delta x))}-1 \sim \ln 2 \cdot \Delta x^{2} \cos (1 /(8 \Delta x))$, as
$\Delta x \rightarrow 0\left(\ln 2 \cdot \Delta x^{2} \cos (1 /(8 \Delta x)) \rightarrow 0\right)$
We get:
$$
=1+\lim _{\Delta x \rightarrow 0} \frac{\ln 2 \cdot \Delta x^{2} \cos (1 /(8 \Delta x))}{\Delta x}=1+\lim _{\Delta x \rightarrow 0} \ln 2 \cdot \Delta x \cos (1 /(8 \Delta x))=
$$
Since $\cos (1 /(8 \Delta x))$ is bounded, then
$\Delta x \cos (1 /(8 \Delta x)) \rightarrow 0$, as $\Delta x \rightarrow 0$
Then:
$=1+\ln 2 \cdot 0=1$
Therefore, $f^{\prime}(0)=1$
## Problem Kuznetsov Differentiation 2-12
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the lengths of the arcs of the curves given by the equations in polar coordinates.
$$
\rho=1-\sin \varphi, -\frac{\pi}{2} \leq \varphi \leq -\frac{\pi}{6}
$$
|
## Solution
The length of the arc of a curve given by an equation in polar coordinates is determined by the formula
$$
L=\int_{\phi_{1}}^{\phi_{2}} \sqrt{\rho^{2}+\left(\frac{d \rho}{d \phi}\right)^{2}} d \phi
$$
Let's find $\frac{d \rho}{d \phi}$:
$$
\frac{d \rho}{d \phi}=(-\cos \phi)
$$
We get:
$$
\begin{aligned}
L & =\int_{-\pi / 2}^{-\pi / 6} \sqrt{(1-\sin \phi)^{2}+(-\cos \phi)^{2}} d \phi= \\
& =\int_{-\pi / 2}^{-\pi / 6} \sqrt{1-2 \sin \phi+\sin ^{2} \phi+\cos ^{2} \phi} d \phi= \\
& =\int_{-\pi / 2}^{-\pi / 6} \sqrt{2-2 \sin \phi} d \phi= \\
& =\int_{-\pi / 2}^{-\pi / 6} \sqrt{2-2 \cos \left(\frac{\pi}{2}-\phi\right)} d \phi= \\
& =\int_{-\pi / 2}^{-\pi / 6} \sqrt{4 \sin ^{2}\left(\frac{\pi}{4}-\frac{\phi}{2}\right)} d \phi= \\
& =\int_{-\pi / 2}^{-\pi / 6} 2 \sin \left(\frac{\pi}{4}-\frac{\phi}{2}\right) d \phi=\left.4 \cdot \cos \left(\frac{\pi}{4}-\frac{\phi}{2}\right)\right|_{-\pi / 2} ^{-\pi / 6}= \\
& =4\left(\cos \left(\frac{\pi}{4}-\frac{1}{2} \cdot \frac{-\pi}{6}\right)-\cos \left(\frac{\pi}{4}-\frac{1}{2} \cdot \frac{-\pi}{2}\right)\right)=4\left(\cos \left(\frac{\pi}{3}\right)-\cos \left(\frac{\pi}{2}\right)\right)=4\left(\frac{1}{2}-0\right)=2
\end{aligned}
$$
Categories: Kuznetsov Problem Book Integrals Problem 19 | Integrals
Ukrainian Banner Network
- Last modified: 13:05, 27 May 2010.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals 19-12
## Material from PlusPi
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## problem statement
Find the cosine of the angle between vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$.
$A(-2 ; 1 ; 1), B(2 ; 3 ;-2), C(0 ; 0 ; 3)$
|
## Solution
Let's find $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$$
\begin{aligned}
& \overrightarrow{A B}=(2-(-2) ; 3-1 ;-2-1)=(4 ; 2 ;-3) \\
& \overrightarrow{A C}=(0-(-2) ; 0-1 ; 3-1)=(2 ;-1 ; 2)
\end{aligned}
$$
We find the cosine of the angle $\phi_{\text {between vectors }} \overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\cos (\widehat{A B,} \overrightarrow{A C})=\frac{(\overrightarrow{A B}, \overrightarrow{A C})}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}=$
$=\frac{4 \cdot 2+2 \cdot(-1)+(-3) \cdot 2}{\sqrt{4^{2}+2^{2}+(-3)^{2}} \cdot \sqrt{2^{2}+(-1)^{2}+2^{2}}}=$
$=\frac{8-2-6}{\sqrt{16+4+9} \cdot \sqrt{4+1+4}}=\frac{0}{\sqrt{29} \cdot \sqrt{9}}=0$
Thus, the cosine of the angle:
$\cos (\overrightarrow{A B,} \overrightarrow{A C})=0$
and consequently the angle
$\widehat{A B,} \overrightarrow{A C}=\frac{\pi}{2}$
Problem Kuznetsov Analytic Geometry 4-27
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task Condition
Are the vectors $a, b$ and $c$ coplanar?
$a=\{6 ; 3 ; 4\}$
$b=\{-1 ;-2 ;-1\}$
$c=\{2 ; 1 ; 2\}$
|
## Solution
For three vectors to be coplanar (lie in the same plane or parallel planes), it is necessary and sufficient that their scalar triple product $(a, b, c)$ be equal to zero.
$(a, b, c)=\left|\begin{array}{ccc}6 & 3 & 4 \\ -1 & -2 & -1 \\ 2 & 1 & 2\end{array}\right|=$
$=6 \cdot\left|\begin{array}{cc}-2 & -1 \\ 1 & 2\end{array}\right|-3 \cdot\left|\begin{array}{cc}-1 & -1 \\ 2 & 2\end{array}\right|+4 \cdot\left|\begin{array}{cc}-1 & -2 \\ 2 & 1\end{array}\right|=$
$=6 \cdot(-3)-3 \cdot 0+4 \cdot 3=-18-0+12=-6$
Since $(a, b, c)=-6 \neq 0$, the vectors $a, b$ and $c$ are not coplanar.
## Problem Kuznetsov Analytic Geometry 6-27
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## problem statement
Find the angle between the planes:
$2 x-6 y+14 z-1=0$
$5 x-15 y+35 z-3=0$
|
## Solution
The dihedral angle between planes is equal to the angle between their normal vectors. The normal vectors of the given planes:
$\overrightarrow{n_{1}}=\{2 ;-6 ; 14\}$
$\overrightarrow{n_{2}}=\{5 ;-15 ; 35\}$
The angle $\phi_{\text{between the planes is determined by the formula: }}$
$$
\begin{aligned}
& \cos \phi=\frac{\left(\overrightarrow{n_{1}}, \overrightarrow{n_{2}}\right)}{\left|\overrightarrow{n_{1}}\right| \cdot\left|\overrightarrow{n_{2}}\right|}=\frac{2 \cdot 5+(-6) \cdot(-15)+14 \cdot 35}{\sqrt{2^{2}+(-6)^{2}+14^{2}} \cdot \sqrt{5^{2}+(-15)^{2}+35^{2}}}= \\
& =\frac{10+90+490}{\sqrt{4+36+196} \cdot \sqrt{25+225+1225}}=\frac{590}{\sqrt{236} \cdot \sqrt{1475}}=\frac{590}{590}=1 \\
& \phi=\arccos 1=0
\end{aligned}
$$
## Problem Kuznetsov Analytic Geometry 10-27
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## problem statement
Calculate the limit of the function:
$\lim _{x \rightarrow-1} \frac{\left(x^{3}-2 x-1\right)(x+1)}{x^{4}+4 x^{2}-5}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow-1} \frac{\left(x^{3}-2 x-1\right)(x+1)}{x^{4}+4 x^{2}-5}=\left\{\frac{0}{0}\right\}=\lim _{x \rightarrow-1} \frac{\left(x^{3}-2 x-1\right)(x+1)}{\left(x^{3}-x^{2}+5 x-5\right)(x+1)}= \\
& =\lim _{x \rightarrow-1} \frac{x^{3}-2 x-1}{x^{3}-x^{2}+5 x-5}=\frac{(-1)^{3}-2(-1)-1}{(-1)^{3}-(-1)^{2}+5(-1)-5}= \\
& =\frac{-1+2-1}{-1-1-5-5}=\frac{0}{-12}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 10-1
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 1} \frac{x^{2}-1}{\ln x}$
|
## Solution
Substitution:
$x=y+1 \Rightarrow y=x-1$
$x \rightarrow 1 \Rightarrow y \rightarrow 0$
We get:
$\lim _{x \rightarrow 1} \frac{x^{2}-1}{\ln x}=\lim _{y \rightarrow 0} \frac{(y+1)^{2}-1}{\ln (y+1)}=$
Using the substitution of equivalent infinitesimals:
$\ln (1+y) \sim y$, as $y \rightarrow 0$
We get:
$=\lim _{y \rightarrow 0} \frac{y^{2}+2 y+1-1}{y}=\lim _{y \rightarrow 0} \frac{y^{2}+2 y}{y}=\lim _{y \rightarrow 0}(y+2)=0+2=2$
Problem Kuznetsov Limits 13-1
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0} \frac{e^{x}+e^{-x}-2}{\sin ^{2} x}$
|
## Solution
$\lim _{x \rightarrow 0} \frac{e^{x}+e^{-x}-2}{\sin ^{2} x}=\lim _{x \rightarrow 0} \frac{e^{-x}\left(e^{2 x}-2 e^{x}+1\right)}{\sin ^{2} x}=$
$=\lim _{x \rightarrow 0} \frac{e^{-x}\left(e^{x}-1\right)^{2}}{\sin ^{2} x}=$
Using the substitution of equivalent infinitesimals:
$e^{x}-1 \sim x$, as $x \rightarrow 0$
$\sin x \sim x$, as $x \rightarrow 0$
We get:
$$
=\lim _{x \rightarrow 0} \frac{e^{-x} \cdot x^{2}}{x^{2}}=\lim _{x \rightarrow 0} e^{-x}=e^{0}=1
$$
## Problem Kuznetsov Limits 16-1
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0}\left(\frac{\sin 2 x}{x}\right)^{1+x}$
|
## Solution
$\lim _{x \rightarrow 0}\left(\frac{\sin 2 x}{x}\right)^{1+x}=\left(\lim _{x \rightarrow 0}\left(\frac{\sin 2 x}{x}\right)\right)^{\lim _{x \rightarrow 0} 1+x}=$
$=\left(\lim _{x \rightarrow 0}\left(\frac{\sin 2 x}{x}\right)\right)^{1}=\lim _{x \rightarrow 0} \frac{\sin 2 x}{x}=$
Using the substitution of equivalent infinitesimals:
$\sin 2 x \sim 2 x$, as $x \rightarrow 0(2 x \rightarrow 0)$
We get:
$$
=\lim _{x \rightarrow 0} \frac{2 x}{x}=\lim _{x \rightarrow 0} \frac{2}{1}=2
$$
## Problem Kuznetsov Limits 18-1
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Condition of the problem
Calculate the limit of the function:
$$
\lim _{x \rightarrow 0} \sqrt{4 \cos 3 x+x \cdot \operatorname{arctg}\left(\frac{1}{x}\right)}
$$
|
## Solution
Since $\operatorname{arctg}\left(\frac{1}{x}\right)_{\text { is bounded, then }}$
$$
x \cdot \operatorname{arctg}\left(\frac{1}{x}\right) \rightarrow 0 \underset{\text { as } x \rightarrow 0}{ }
$$
Then:
$\lim _{x \rightarrow 0} \sqrt{4 \cos 3 x+x \cdot \operatorname{arctg}\left(\frac{1}{x}\right)}=\sqrt{4 \cos (3 \cdot 0)+0}=\sqrt{4}=2$
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the cosine of the angle between vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$.
$$
A(-3 ; -7 ; -5), B(0 ; -1 ; -2), C(2 ; 3 ; 0)
$$
|
## Solution
Let's find $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$$
\begin{aligned}
& \overrightarrow{A B}=(0-(-3) ;-1-(-7) ;-2-(-5))=(3 ; 6 ; 3) \\
& \overrightarrow{A C}=(2-(-3) ; 3-(-7) ; 0-(-5))=(5 ; 10 ; 5)
\end{aligned}
$$
We find the cosine of the angle $\phi$ between the vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$$
\begin{aligned}
& \cos (\overrightarrow{A B,} \overrightarrow{A C})=\frac{(\overrightarrow{A B}, \overrightarrow{A C})}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}= \\
& =\frac{3 \cdot 5+6 \cdot 10+3 \cdot 5}{\sqrt{3^{2}+6^{2}+3^{2}} \cdot \sqrt{5^{2}+10^{2}+5^{2}}}= \\
& =\frac{15+60+15}{\sqrt{9+36+9} \cdot \sqrt{25+100+25}}=\frac{90}{\sqrt{54} \cdot \sqrt{150}}=\frac{90}{\sqrt{8100}}=1
\end{aligned}
$$
Thus, the cosine of the angle:
$\cos (\overrightarrow{A B, A C})=1$
and consequently the angle
$\widehat{A B,} \overrightarrow{A C}=0$
## Problem Kuznetsov Analytic Geometry 4-7
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## problem statement
Let $k$ be the coefficient of similarity transformation with the center at the origin. Is it true that point $A$ belongs to the image of plane $a$?
$A\left(\frac{1}{4} ; \frac{1}{3} ; 1\right)$
a: $4 x-3 y+5 z-10=0$
$k=\frac{1}{2}$
|
## Solution
When transforming similarity with the center at the origin of the coordinate plane, the plane $a: A x + B y + C z + D = 0$ and the coefficient $k$ transitions to the plane $a^{\prime}: A x + B y + C z + k \cdot D = 0$. We find the image of the plane $a$:
$a^{\prime}: 4 x - 3 y + 5 z - 5 = 0$
Substitute the coordinates of point $A$ into the equation of $a^{\prime}$:
$4 \cdot \frac{1}{4} - 3 \cdot \frac{1}{3} + 5 \cdot 1 - 5 = 0$
$1 - 1 + 5 - 5 = 0$
$0 = 0$
Since $0 = 0$, point $A$ belongs to the image of the plane $a$.
## Problem Kuznetsov Analytical Geometry 12-12
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task Condition
Based on the definition of the derivative, find $f^{\prime}(0)$ :
$$
f(x)=\left\{\begin{array}{c}
x^{2} \cos ^{2} \frac{11}{x}, x \neq 0 \\
0, x=0
\end{array}\right.
$$
|
## Solution
By definition, the derivative at the point $x=0$:
$f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}$
Based on the definition, we find:
$$
\begin{aligned}
& f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{\Delta x^{2} \cos ^{2} \frac{11}{\Delta x}-0}{\Delta x}= \\
& =\lim _{\Delta x \rightarrow 0} \frac{\Delta x^{2} \cos ^{2} \frac{11}{\Delta x}}{\Delta x}=\lim _{\Delta x \rightarrow 0} \Delta x \cdot \cos ^{2} \frac{11}{\Delta x}=
\end{aligned}
$$
Since $\cos ^{2} \frac{11}{\Delta x}$ is bounded, then
$\Delta x \cdot \cos ^{2} \frac{11}{\Delta x} \rightarrow 0$, as $\Delta x \rightarrow 0$
Thus:
$=0$
Therefore, $f^{\prime}(0)=0$
## Problem Kuznetsov Differentiation $2-15$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{(2 n+1)^{3}+(3 n+2)^{3}}{(2 n+3)^{3}-(n-7)^{3}}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{(2 n+1)^{3}+(3 n+2)^{3}}{(2 n+3)^{3}-(n-7)^{3}}=\lim _{n \rightarrow \infty} \frac{\frac{1}{n^{3}}\left((2 n+1)^{3}+(3 n+2)^{3}\right)}{\frac{1}{n^{3}}\left((2 n+3)^{3}-(n-7)^{3}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{\left(2+\frac{1}{n}\right)^{3}+\left(3+\frac{2}{n}\right)^{3}}{\left(2+\frac{3}{n}\right)^{3}-\left(1-\frac{7}{n}\right)^{3}}=\frac{2^{3}+3^{3}}{2^{3}-1^{3}}=\frac{35}{7}=5
\end{aligned}
$$
## Problem Kuznetsov Limits 3-19
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{4 n^{2}-\sqrt[4]{n^{3}}}{\sqrt[3]{n^{6}+n^{3}+1}-5 n}$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{4 n^{2}-\sqrt[4]{n^{3}}}{\sqrt[3]{n^{6}+n^{3}+1}-5 n}=\lim _{n \rightarrow \infty} \frac{\frac{1}{n^{2}}\left(4 n^{2}-\sqrt[4]{n^{3}}\right)}{\frac{1}{n^{2}}\left(\sqrt[3]{n^{6}+n^{3}+1}-5 n\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{4-\sqrt[4]{\frac{1}{n^{5}}}}{\sqrt[3]{1+\frac{1}{n^{3}}+\frac{1}{n^{6}}}-\frac{5}{n}}=\frac{4-\sqrt[4]{0}}{\sqrt[3]{1+0+0}-0}=\frac{4}{1}=4
\end{aligned}
$$
## Problem Kuznetsov Limits 4-19
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the numerical sequence:
$\lim _{n \rightarrow \infty} \frac{2-5+4-7+\ldots+2 n-(2 n+3)}{n+3}$
|
## Solution
$\lim _{n \rightarrow \infty} \frac{2-5+4-7+\ldots+2 n-(2 n+3)}{n+3}=$
$=\{2-5=4-7=\ldots=2 n-(2 n+3)=-3\}=$
$=\lim _{n \rightarrow \infty} \frac{-3 \cdot n}{n+3}=\lim _{n \rightarrow \infty} \frac{\frac{1}{n} \cdot(-3) \cdot n}{\frac{1}{n}(n+3)}=$
$=\lim _{n \rightarrow \infty} \frac{-3}{1+\frac{3}{n}}=\frac{-3}{1}=-3$
## Problem Kuznetsov Limits 6-19
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0}\left(2-3^{\sin ^{2} x}\right)^{\frac{1}{\ln (\cos x)}}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 0}\left(2-3^{\sin ^{2} x}\right)^{\frac{1}{\ln (\cos x)}}= \\
& =\lim _{x \rightarrow 0}\left(e^{\ln \left(2-3^{\sin ^{2} x}\right)}\right)^{\frac{1}{\ln (\cos x)}}= \\
& =\lim _{x \rightarrow 0} e^{\ln \left(2-3^{\sin ^{2} x}\right) / \ln (\cos x)}= \\
& =\lim _{x \rightarrow 0} e^{\ln \left(1+\left(1-3^{\sin ^{2} x}\right)\right) / \ln \left(1-2 \sin ^{2} \frac{x}{2}\right)}= \\
& =\exp \left\{\lim _{x \rightarrow 0} \frac{\ln \left(1+\left(1-3^{\sin ^{2} x}\right)\right)}{\ln \left(1-2 \sin ^{2} \frac{x}{2}\right)}\right\}=
\end{aligned}
$$
$\ln \left(1+\left(1-3^{\sin ^{2} x}\right)\right) \sim\left(1-3^{\sin ^{2} x}\right)$, as $x \rightarrow 0\left(\left(1-3^{\sin ^{2} x}\right) \rightarrow 0\right)$ $\ln \left(1-2 \sin ^{2} \frac{x}{2}\right) \sim-2 \sin ^{2} \frac{x}{2}$, as $x \rightarrow 0\left(-2 \sin ^{2} \frac{x}{2} \rightarrow 0\right)$
We get:
$$
\begin{aligned}
& =\exp \left\{\lim _{x \rightarrow 0} \frac{1-3^{\sin ^{2} x}}{-2 \sin ^{2} \frac{x}{2}}\right\}=\exp \left\{\lim _{x \rightarrow 0} \frac{1-\left(e^{\ln 3}\right)^{\sin ^{2} x}}{-2 \sin ^{2} \frac{x}{2}}\right\}= \\
& =\exp \left\{\lim _{x \rightarrow 0} \frac{e^{\ln 3 \cdot \sin ^{2} x}-1}{2 \sin ^{2} \frac{x}{2}}\right\}=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$e^{\ln 3 \cdot \sin ^{2} x}-1 \sim \ln 3 \cdot \sin ^{2} x$, as $x \rightarrow 0\left(\ln 3 \cdot \sin ^{2} x \rightarrow 0\right)$
$\sin \frac{x}{2} \sim \frac{x}{2}$, as $x \rightarrow 0\left(\frac{x}{2} \rightarrow 0\right)$
We get:
$=\exp \left\{\lim _{x \rightarrow 0} \frac{\ln 3 \cdot \sin ^{2} x}{2\left(\frac{x}{2}\right)^{2}}\right\}=\exp \left\{\lim _{x \rightarrow 0} \frac{2 \ln 3 \cdot \sin ^{2} x}{x^{2}}\right\}=$
Using the substitution of equivalent infinitesimals:
$\sin x \sim x$, as $x \rightarrow 0$
We get:
$=\exp \left\{\lim _{x \rightarrow 0} \frac{2 \ln 3 \cdot x^{2}}{x^{2}}\right\}=\exp \left\{\lim _{x \rightarrow 0} 2 \ln 3\right\}=$
$=e^{2 \ln 3}=\left(e^{\ln 3}\right)^{2}=3^{2}=9$
## Problem Kuznetsov Limits 17-19
|
9
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## problem statement
Calculate the limit of the function:
$\lim _{x \rightarrow 0}\left(\frac{11 x+8}{12 x+1}\right)^{\cos ^{2} x}$
|
## Solution
$\lim _{x \rightarrow 0}\left(\frac{11 x+8}{12 x+1}\right)^{\cos ^{2} x}=\left(\frac{11 \cdot 0+8}{12 \cdot 0+1}\right)^{\cos ^{2} 0}=$
$=(8)^{\left(1^{2}\right)}=8^{1}=8$
## Problem Kuznetsov Limits 18-19
|
8
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 1}(\arcsin x)^{\tan \pi x}$
|
## Solution
$\lim _{x \rightarrow 1}(\arcsin x)^{\operatorname{tg} \pi x}=(\arcsin 1)^{\operatorname{tg} \pi}=\left(\frac{\pi}{2}\right)^{0}=1$
## Problem Kuznetsov Limits 20-19
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task Condition
Calculate the area of the figure bounded by the graphs of the functions:
$$
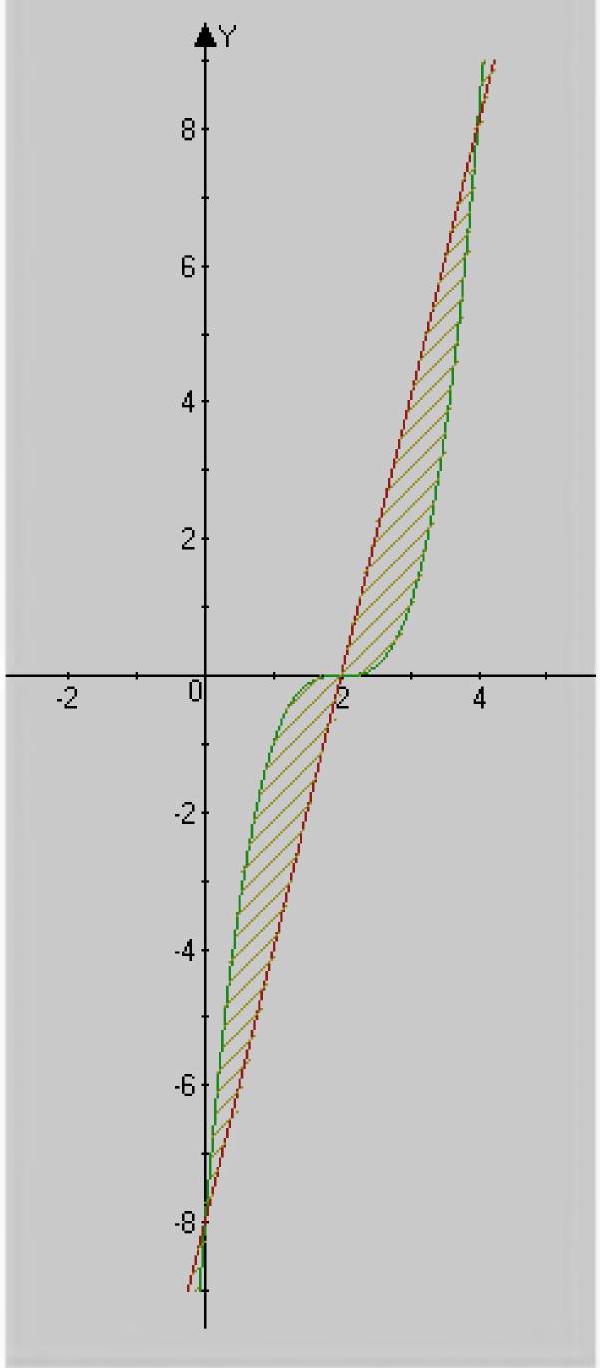
y=(x-2)^{3}, y=4 x-8
$$
|
## Solution
From the graph, it can be seen that the area between the curves consists of two identical parts:
$$
S_{(0,4)}=2 S_{(2,4)}
$$
We will find the area of the part where \( x \in (2,4) \) as the difference of two integrals:
$$
\begin{aligned}
& S=\int_{2}^{4}(4 x-8) d x-\int_{2}^{4}(x-2)^{3} d x= \\
& =\left.\left(4 \frac{x^{2}}{2}-8 x\right)\right|_{2} ^{4}-\int_{2}^{4}\left(x^{3}-6 x^{2}+12 x-8\right) d x= \\
& =\left.\left(2 x^{2}-8 x\right)\right|_{2} ^{4}-\left.\left(\frac{x^{4}}{4}-6 \frac{x^{3}}{3}+12 \frac{x^{2}}{2}-8 x\right)\right|_{2} ^{4}=
\end{aligned}
$$
Integrals \(14-1\)
$$
\begin{aligned}
& =(32-32)-(8-16)-\left(\frac{4^{4}}{4}-2 \cdot 4^{3}+6 \cdot 4^{2}-8 \cdot 4\right)+\left(\frac{2^{4}}{4}-2 \cdot 2^{3}+6 \cdot 2^{2}-8 \cdot 2\right)= \\
& =0+8-(64-128+96-32)+(4-16+24-16)=8-0+(-4)=4 \\
& S_{(0,4)}=2 \cdot S_{(2,4)}=2 \cdot 4=8
\end{aligned}
$$
%egraly_14-1»
Categories: Kuznetsov Integral Problems Problem 14 | Integrals
Ukrainian Banner Network
- Last edited on this page: 04:54, June 9, 2010.
- Content is available under CC-BY-SA 3.0.
Created by Geeteatoo
## Problem Kuznetsov Integrals 14-2
## Material from Plusi
|
8
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the area of the figure bounded by the graphs of the functions:
$$
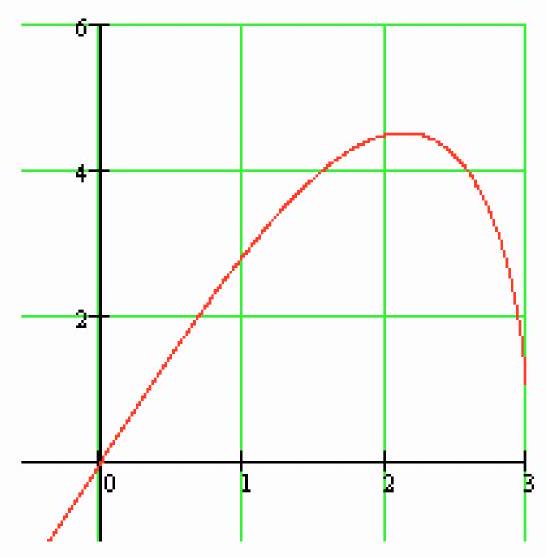
y=x \sqrt{9-x^{2}}, y=0, (0 \leq x \leq 3)
$$
|
## Solution
$$
\begin{aligned}
& S=\int_{0}^{3}\left(x \sqrt{9-x^{2}}\right) d x= \\
& =-\frac{1}{2} \int_{0}^{3}\left(9-x^{2}\right)^{\frac{1}{2}} d\left(9-x^{2}\right)= \\
& =-\left.\frac{1}{2} \cdot \frac{2}{3}\left(9-x^{2}\right)^{\frac{3}{2}}\right|_{0} ^{3}= \\
& =-\frac{1}{3} \cdot(0-27)=9
\end{aligned}
$$
--kasper 11:41, 23 May 2010 (UTC)
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\� \%D0\%9A\%D1\%83\%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD $\% \mathrm{D} 1 \% 82 \% \mathrm{D} 0 \% \mathrm{~B} 5 \% \mathrm{D} 0 \% \mathrm{~B} 3 \% \mathrm{D} 1 \% 80 \% \mathrm{D} 0 \% \mathrm{~B} 0 \% \mathrm{D} 0 \% \mathrm{BB} \% \mathrm{D} 1 \% 8 \mathrm{~B}+14-2$ »
Categories: Kuznetsov Problem Book Integrals Problem 14 | Integrals
- Last edited: 05:33, 9 June 2010.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals 14-3
## Material from PlusPi
|
9
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task Condition
Calculate the area of the figure bounded by the graphs of the functions:
$$
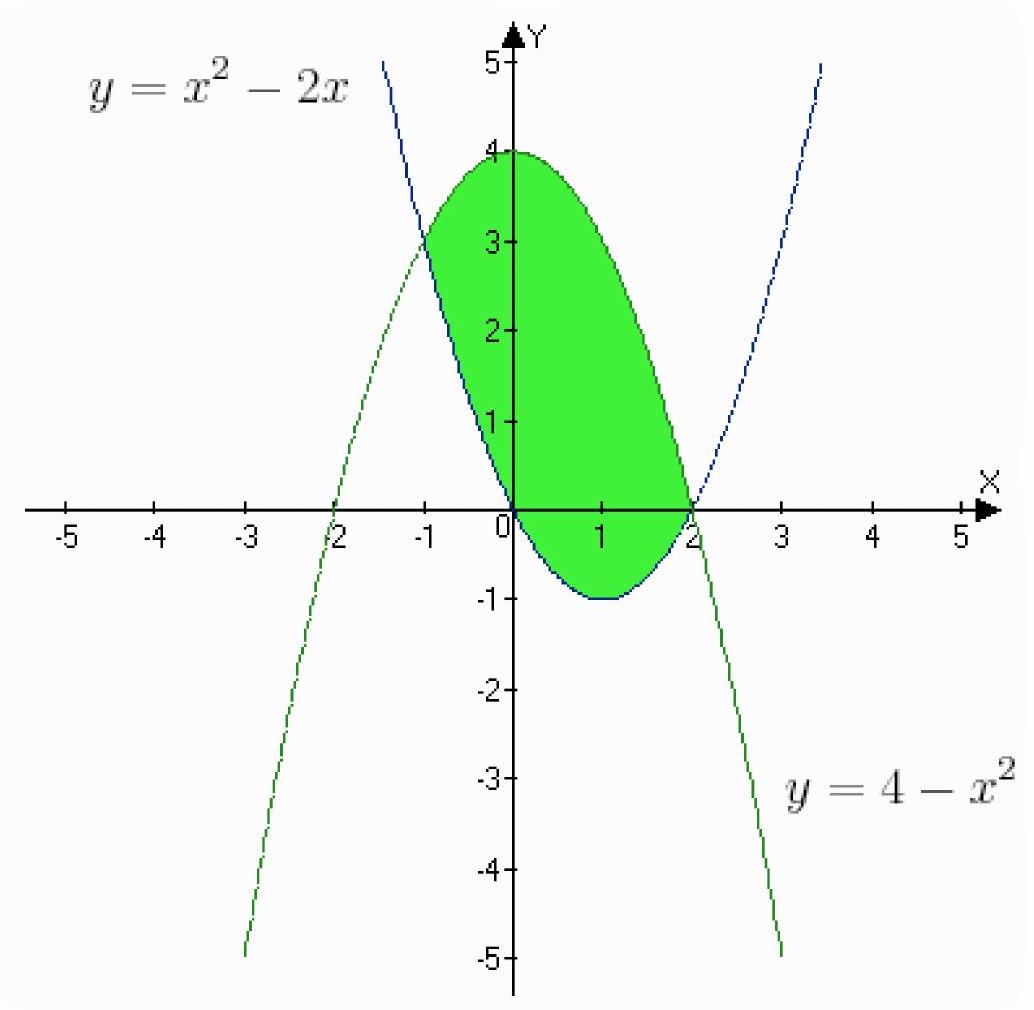
y=4-x^{2}, y=x^{2}-2 x
$$
|
## Solution
Find the abscissas of the points of intersection of the graphs of the functions:
$$
\begin{aligned}
& 4-x^{2}=x^{2}-2 x \\
& 2 x^{2}-2 x-4=0 \\
& x^{2}-x-2=0
\end{aligned}
$$
$$
\begin{aligned}
& D=(-1)^{2}-4 \cdot 1 \cdot(-2)=9 \\
& x_{1}=\frac{1-\sqrt{9}}{2 \cdot 1}=-1 \\
& x_{2}=\frac{1+\sqrt{9}}{2 \cdot 1}=2
\end{aligned}
$$
Calculate the area:
$$
\begin{aligned}
& S=\int_{-1}^{2}\left(\left(4-x^{2}\right)-\left(x^{2}-2 x\right)\right) d x=\int_{-1}^{2}\left(-2 x^{2}+2 x+4\right) d x= \\
& =\left.\left(-\frac{2 x^{3}}{3}+x^{2}+4 x\right)\right|_{-1} ^{2}=\left(-\frac{2 \cdot 2^{3}}{3}+2^{2}+4 \cdot 2\right)-
\end{aligned}
$$
$$
\begin{aligned}
& -\left(-\frac{2 \cdot(-1)^{3}}{3}+(-1)^{2}+4 \cdot(-1)\right)=-\frac{16}{3}+4+8-\frac{2}{3}-1+4= \\
& =-\frac{18}{3}+15=-6+15=9
\end{aligned}
$$
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\� \%D0\%9A\%D1\%83\%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD $\% \mathrm{D} 1 \% 84 \% \mathrm{D} 0 \% \mathrm{~B} 5 \% \mathrm{D} 0 \% \mathrm{~B} 3 \% \mathrm{D} 1 \% 80 \% \mathrm{D} 0 \% \mathrm{~B} 0 \% \mathrm{D} 0 \% \mathrm{BB} \% \mathrm{D} 1 \% 8 \mathrm{~B}+14-4$ » Categories: Kuznetsov's Problem Book Integrals Problem 14 | Integrals
Ukrainian Banner Network
- Last edited on this page: 16:15, 29 May 2010.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals 14-4
## Material from PlusPi
|
9
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the area of the figure bounded by the graphs of the functions:
$$
y=\frac{1}{x \sqrt{1+\ln x}}, y=0, x=1, x=e^{3}
$$
|
## Solution
Answer: 2
We construct the graphs:
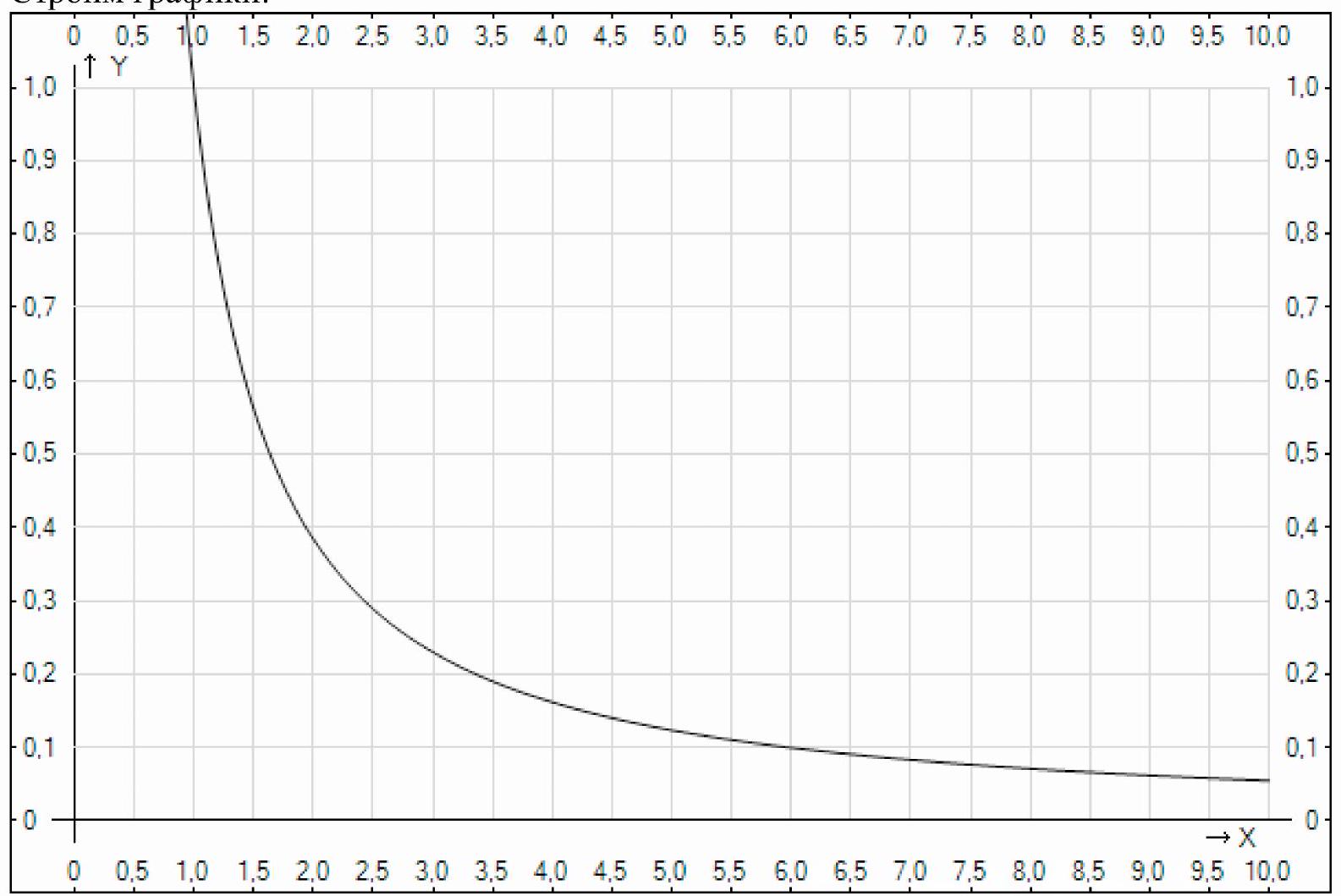
We obtain a figure bounded above by the curve $\frac{1}{x \cdot \sqrt{1+\ln x}}$, on the left by the line $x=1$, on the right by the line $x=e^{3}$, and below by $y=0$.
Thus, the area of the desired figure will be equal to the integral from 1 to $e^{3}$ of the function $\frac{1}{x \cdot \sqrt{1+\ln x}}$. We take the integral:
$$
\begin{aligned}
& \int_{1}^{e^{3}} \frac{1}{x \cdot \sqrt{1+\ln x}} d x=\int_{1}^{e^{3}} \frac{1}{\sqrt{1+\ln x}} d(\ln x)= \\
& =\int_{0}^{3} \frac{1}{\sqrt{1+x}} d x=\left.2 \cdot \sqrt{1+x}\right|_{0} ^{3}=2 \cdot(\sqrt{1+3}-\sqrt{1+0})= \\
& =2 \cdot(2-1)=2
\end{aligned}
$$
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\� \%D0\%9A\%D1\%83\%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD $\% \mathrm{D} 1 \% 84 \% \mathrm{D} 0 \% \mathrm{~B} 5 \% \mathrm{D} 0 \% \mathrm{~B} 3 \% \mathrm{D} 1 \% 80 \% \mathrm{D} 0 \% \mathrm{~B} 0 \% \mathrm{D} 0 \% \mathrm{BB} \% \mathrm{D} 1 \% 8 \mathrm{~B}+14-9$ »
Categories: Kuznetsov's Problem Book Integrals Problem 14 | Integrals
Ukrainian Banner Network
- Last edited on this page: 11:45, 24 May 2010.
- Content is available under CC-BY-SA 3.0.
Created by Gee Teatoo
## Problem Kuznetsov Integrals 14-10
## Material from PlusPi
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task Condition
Calculate the area of the figure bounded by the graphs of the functions:
$$
y=\arccos x, y=0, x=0
$$
|
## Solution
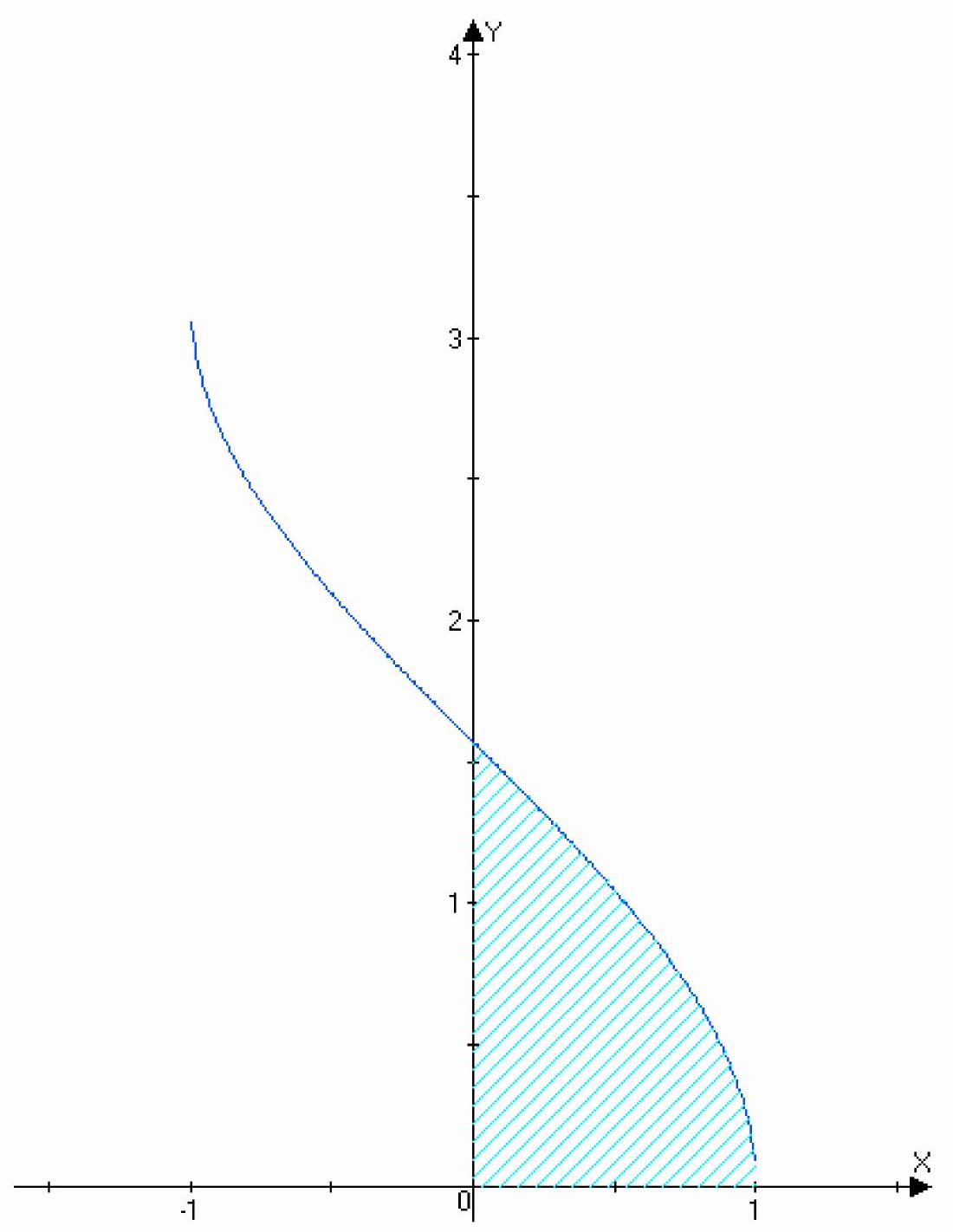
$S=\int_{0}^{1} \arccos x d x$
We will use the integration by parts formula:
$$
\begin{aligned}
& \int_{a}^{b} u d v=\left.u \cdot v\right|_{a} ^{b}-\int_{a}^{b} v d u \\
& \text{where} \\
& u=\arccos x ; v=x ; d u=-\frac{d x}{\sqrt{1-x^{2}}} ; d v=d x
\end{aligned}
$$
Then we get
$$
\begin{aligned}
& S=\int_{0}^{1} \arccos x d x= \\
& =\left.x \cdot \arccos x\right|_{0} ^{1}-\left(\int_{0}^{1} x \frac{-d x}{\sqrt{1-x^{2}}}\right)= \\
& =\left.x \cdot \arccos x\right|_{0} ^{1}+\int_{0}^{1} \frac{x d x}{\sqrt{1-x^{2}}}= \\
& =\left.x \cdot \arccos x\right|_{0} ^{1}-\frac{1}{2} \cdot \int_{0}^{1} \frac{d\left(1-x^{2}\right)}{\sqrt{1-x^{2}}}= \\
& =\left.x \cdot \arccos x\right|_{0} ^{1}-\left.\sqrt{1-x^{2}}\right|_{0} ^{1}= \\
& =\left(1 \cdot 0-0 \cdot \frac{\pi}{2}\right)-(\sqrt{0}-\sqrt{1})=1
\end{aligned}
$$
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\� \%D0\%9A\%D1\%83\%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD $\% \mathrm{D} 1 \% 82 \% \mathrm{D} 0 \% \mathrm{~B} 5 \% \mathrm{D} 0 \% \mathrm{~B} 3 \% \mathrm{D} 1 \% 80 \% \mathrm{D} 0 \% \mathrm{~B} 0 \% \mathrm{D} 0 \% \mathrm{BB} \% \mathrm{D} 1 \% 8 \mathrm{~B}+14-10$ » Categories: Kuznetsov's Problem Book Integrals Problem 14 | Integrals
Ukrainian Banner Network
- Last edited on this page: 10:42, June 9, 2010.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals 14-11
## Material from PlusPi
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task Condition
Calculate the area of the figure bounded by the graphs of the functions:
$$
y=2 x-x^{2}+3, y=x^{2}-4 x+3
$$
|
## Solution
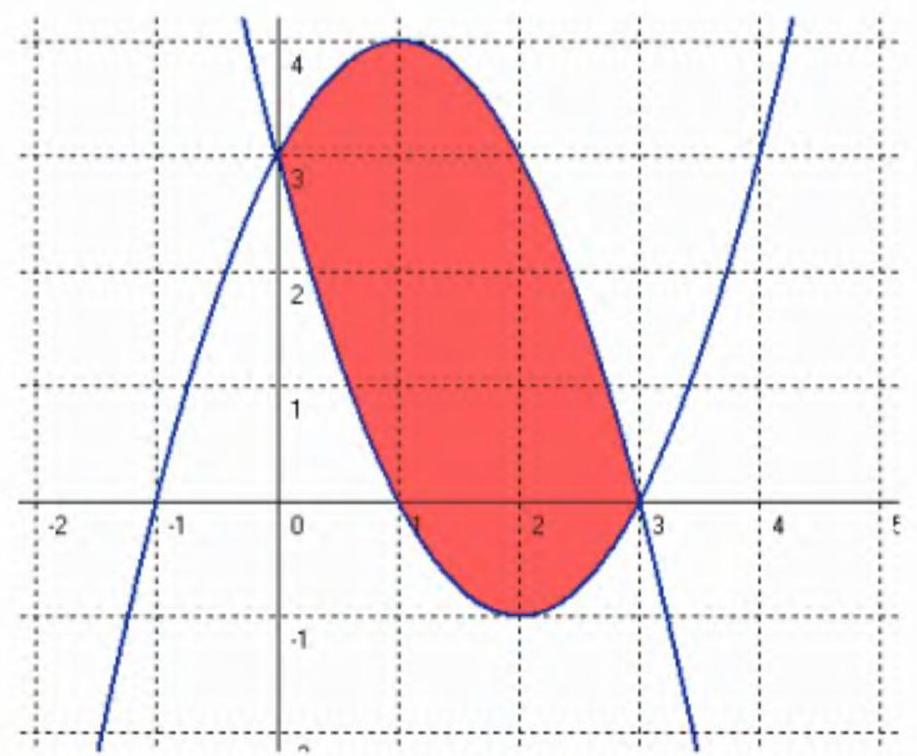
Let's find the points of intersection of the graphs of the functions:
$$
2 x - x^{2} + 3 = x^{2} - 4 x + 3 \Rightarrow \left[\begin{array}{l}
x = 0 \\
x = 3
\end{array}\right]
$$
Now let's find the area of the resulting figure:
$$
S = \int_{0}^{3} \left( \left( -x^{2} + 2 x + 3 \right) - \left( x^{2} - 4 x + 3 \right) \right) d x = \int_{0}^{3} \left( -2 x^{2} + 6 x \right) d x = -\left. \frac{2}{3} x^{3} \right|_{0}^{3} + \left. 3 x^{2} \right|_{0}^{3} = -18 + 27 = 9
$$
Source — "http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\�_\�\�\�\� \%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%B8\%D0\%B2\%D0\%B5\%D0\%B9\%D0\%B8\%D0\%BD\%D0\%B8\%D0\%B5\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8\%D0\%B8
|
9
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the area of the figure bounded by the graphs of the functions:
$$
y=\frac{1}{1+\cos x}, y=0, x=\frac{\pi}{2}, x=-\frac{\pi}{2}
$$
|
## Solution
$$
\begin{aligned}
S= & \int_{-\pi / 2}^{\pi / 2} \frac{1}{1+\cos x} d x= \\
& =\int_{-\pi / 2}^{\pi / 2} \frac{1}{2 \cos ^{2} \frac{x}{2}} d x= \\
& =\int_{-\pi / 2}^{\pi / 2} \frac{1}{\cos ^{2} \frac{x}{2}} d\left(\frac{x}{2}\right)= \\
& =\left.\operatorname{tg}_{\frac{1}{2}}\right|_{-\pi / 2} ^{\pi / 2}=1-(-1)=2
\end{aligned}
$$
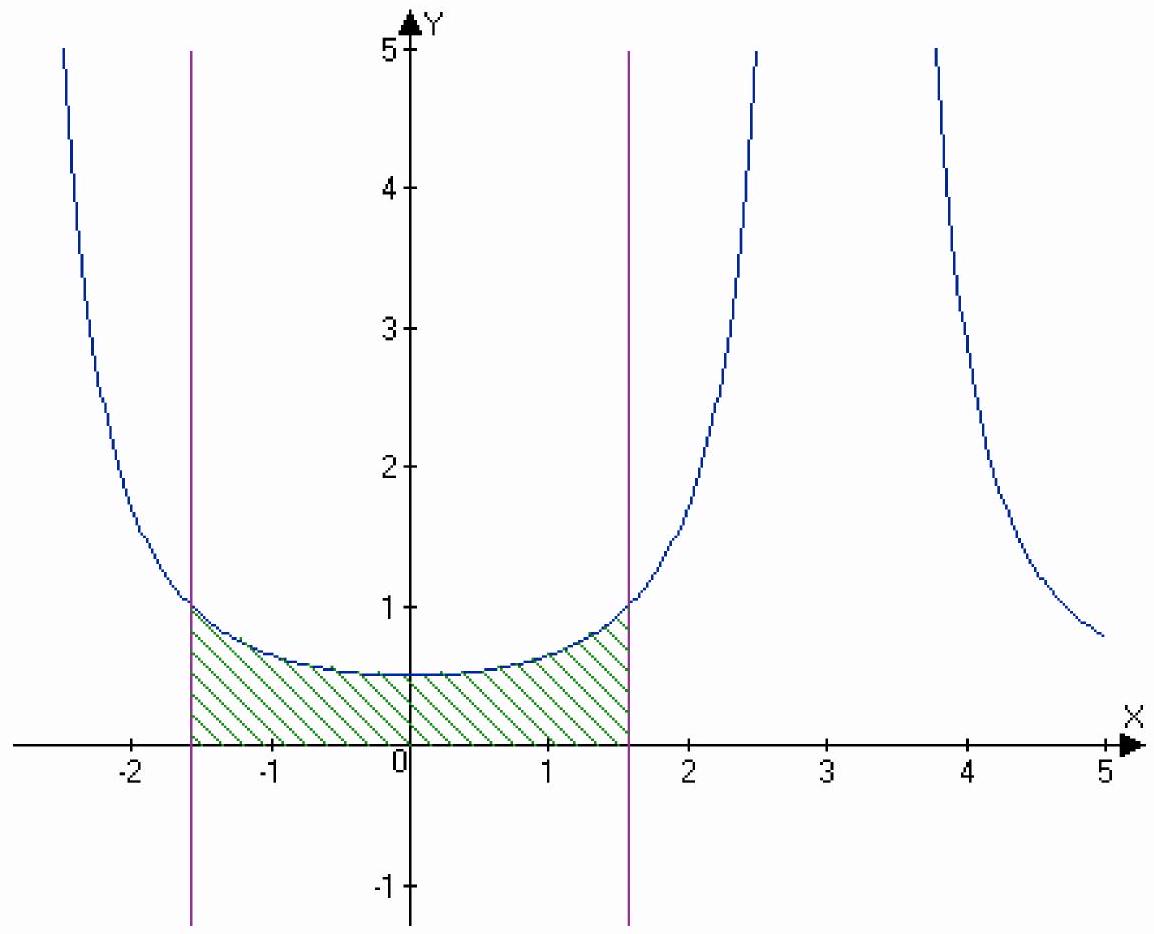
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\� \%D0\%9A\%D1\%83\%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD $\% \mathrm{D} 1 \% 82 \% \mathrm{D} 0 \% \mathrm{~B} 5 \% \mathrm{D} 0 \% \mathrm{~B} 3 \% \mathrm{D} 1 \% 80 \% \mathrm{D} 0 \% \mathrm{~B} 0 \% \mathrm{D} 0 \% \mathrm{BB} \% \mathrm{D} 1 \% 8 \mathrm{~B}+14-20$ » Categories: Kuznetsov Problem Book Integrals Problem 14 | Integrals
- Last edited: 08:08, June 11, 2010.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals 14-21
## Material from PlusPi
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task Condition
Calculate the area of the figure bounded by the graphs of the functions:
$$
x=(y-2)^{3}, x=4 y-8
$$
|
## Solution
$$
\begin{aligned}
& (y-2)^{3}=4(y-2) \\
& (y-2)\left[4-(y-2)^{2}\right]=0 \\
& \begin{array}{l}
4-y^{2}+4 y-4=0 \\
y(y-4)=0
\end{array} \\
& \frac{S}{2}=\int_{2}^{4}(4 y-8) d y-\int_{2}^{4}(y-3)^{3} d y= \\
& =\left.2 y^{2}\right|_{4} ^{2}-\left.8 y\right|_{4} ^{2}-\int_{2}^{4}\left(y^{3}-6 y^{2}+12 y-8\right) d y= \\
& =32-8-32+16-\left(\left.\frac{y^{4}}{4}\right|_{4} ^{2}-\left.6 \frac{y^{3}}{3}\right|_{4} ^{2}+\left.6 y^{2}\right|_{4} ^{2}-\left.8 y\right|_{4} ^{2}\right)= \\
& =8-\left(\frac{256}{4}-4-128+16+96-24-32+16\right)=4 \\
& S=2 \cdot \frac{S}{2}=8
\end{aligned}
$$
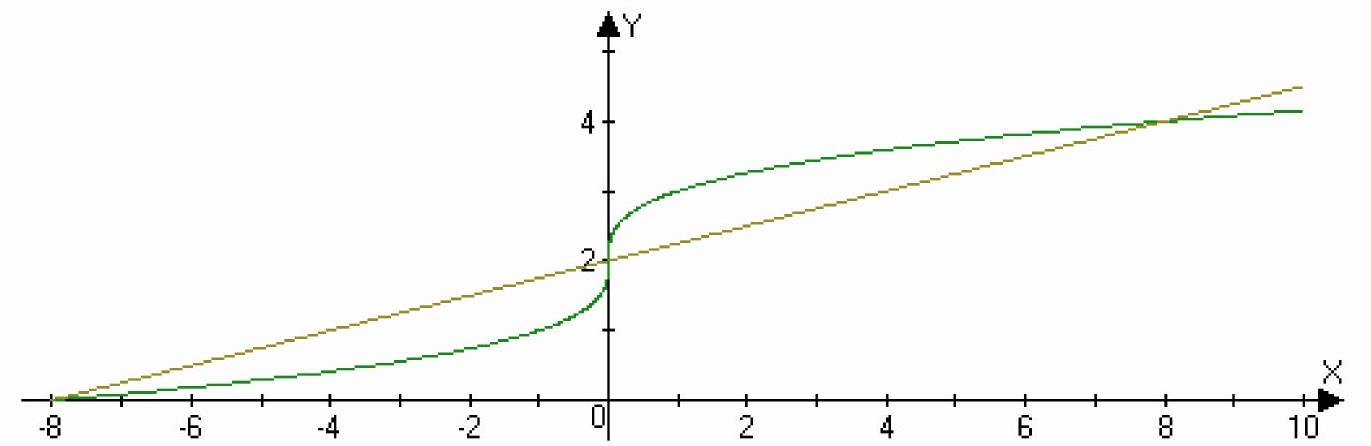
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\� \%D0\%9A\%D1\%83\%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD $\% \mathrm{D} 1 \% 82 \% \mathrm{D} 0 \% \mathrm{~B} \% \mathrm{D} 0 \% \mathrm{~B} 3 \% \mathrm{D} 1 \% 80 \% \mathrm{D} 0 \% \mathrm{~B} 0 \% \mathrm{D} 0 \% \mathrm{BB} \% \mathrm{D} 1 \% 8 \mathrm{~B}+14-21$ »
Categories: Kuznetsov's Problem Book Integrals Problem 14 | Integrals
Ukrainian Banner Network
- Last edited on this page: 08:22, 11 June 2010.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals 14-22
## Material from Plusi
|
8
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task Condition
Calculate the area of the figure bounded by the graphs of the functions:
$$
x=4-y^{2}, x=y^{2}-2 y
$$
|
## Solution
Let's find the limits of integration:
$$
\begin{aligned}
& \left(y^{2}-2 y\right)-\left(4-y^{2}\right)=0 \\
& 2 y^{2}-2 y-4=0 \\
& y^{2}-y-2=0
\end{aligned}
$$
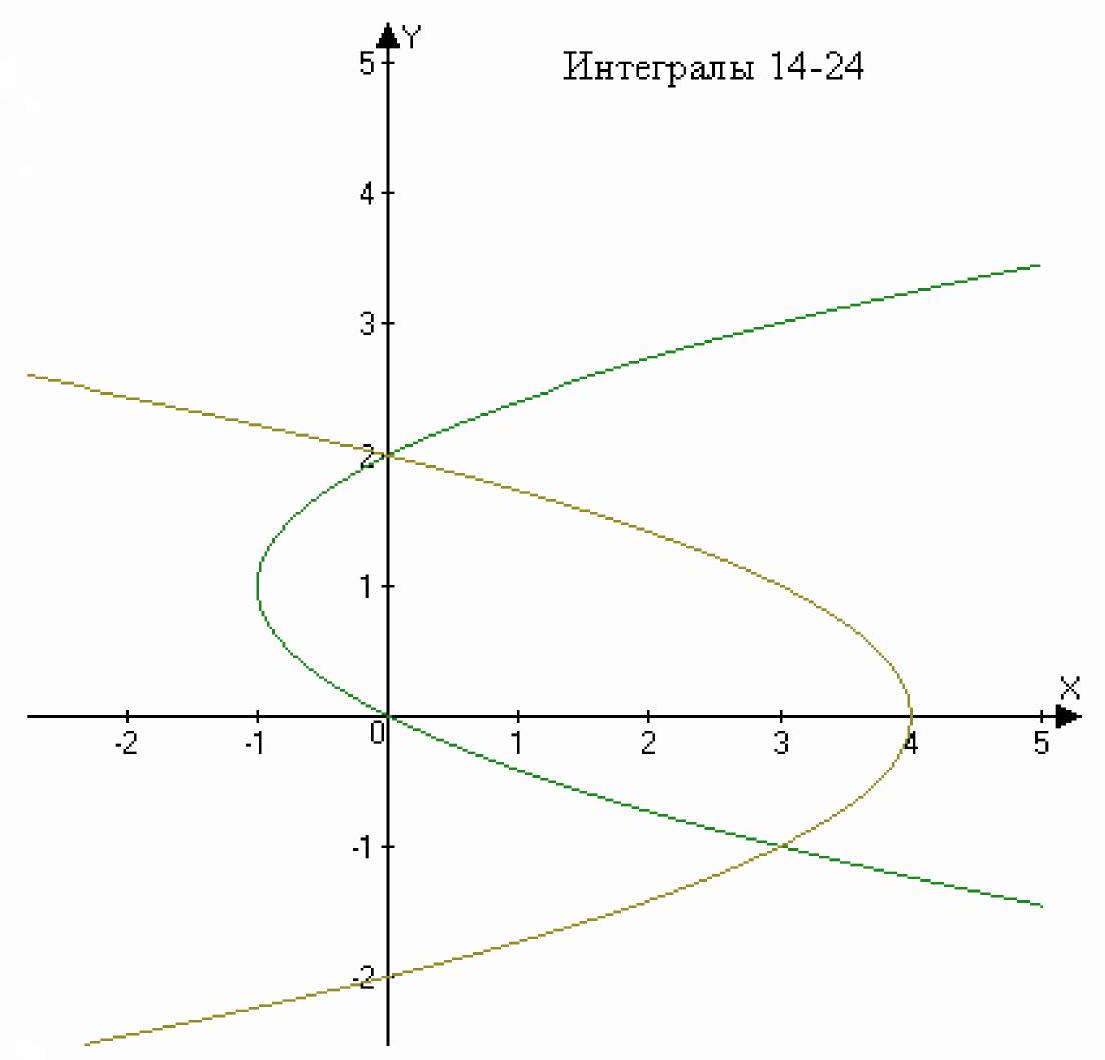
Then the area of the figure will be:
$$
\begin{aligned}
& S=\int_{-1}^{2}\left(4-y^{2}\right)-\left(y^{2}-2 y\right) d y= \\
& =\int_{-1}^{2}\left(-2 y^{2}+2 y+4\right) d y=
\end{aligned}
$$
$$
\begin{aligned}
& =\left.\left(-2 \frac{y^{3}}{3}+2 \frac{y^{2}}{2}+4 y\right)\right|_{-1} ^{2}= \\
& =\left(-2 \frac{8}{3}+4+8\right)-\left(2 \frac{1}{3}+1-4\right)=-\frac{16}{3}+4+8-\frac{2}{3}-1+4=9
\end{aligned}
$$
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\� \%D0\%9A\%D1\%83\%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD $\% \mathrm{D} 1 \% 84 \% \mathrm{D} 0 \% \mathrm{~B} 5 \% \mathrm{D} 0 \% \mathrm{~B} 3 \% \mathrm{D} 1 \% 80 \% \mathrm{D} 0 \% \mathrm{~B} 0 \% \mathrm{D} 0 \% \mathrm{BB} \% \mathrm{D} 1 \% 8 \mathrm{~B}+14-24$ » Categories: Kuznetsov's Problem Book Integrals Problem 14 | Integrals
- Last edited on this page: 10:09, 11 June 2010.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals $14-25$
## Material from PlusPi
|
9
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the area of the figure bounded by the graphs of the functions:
$$
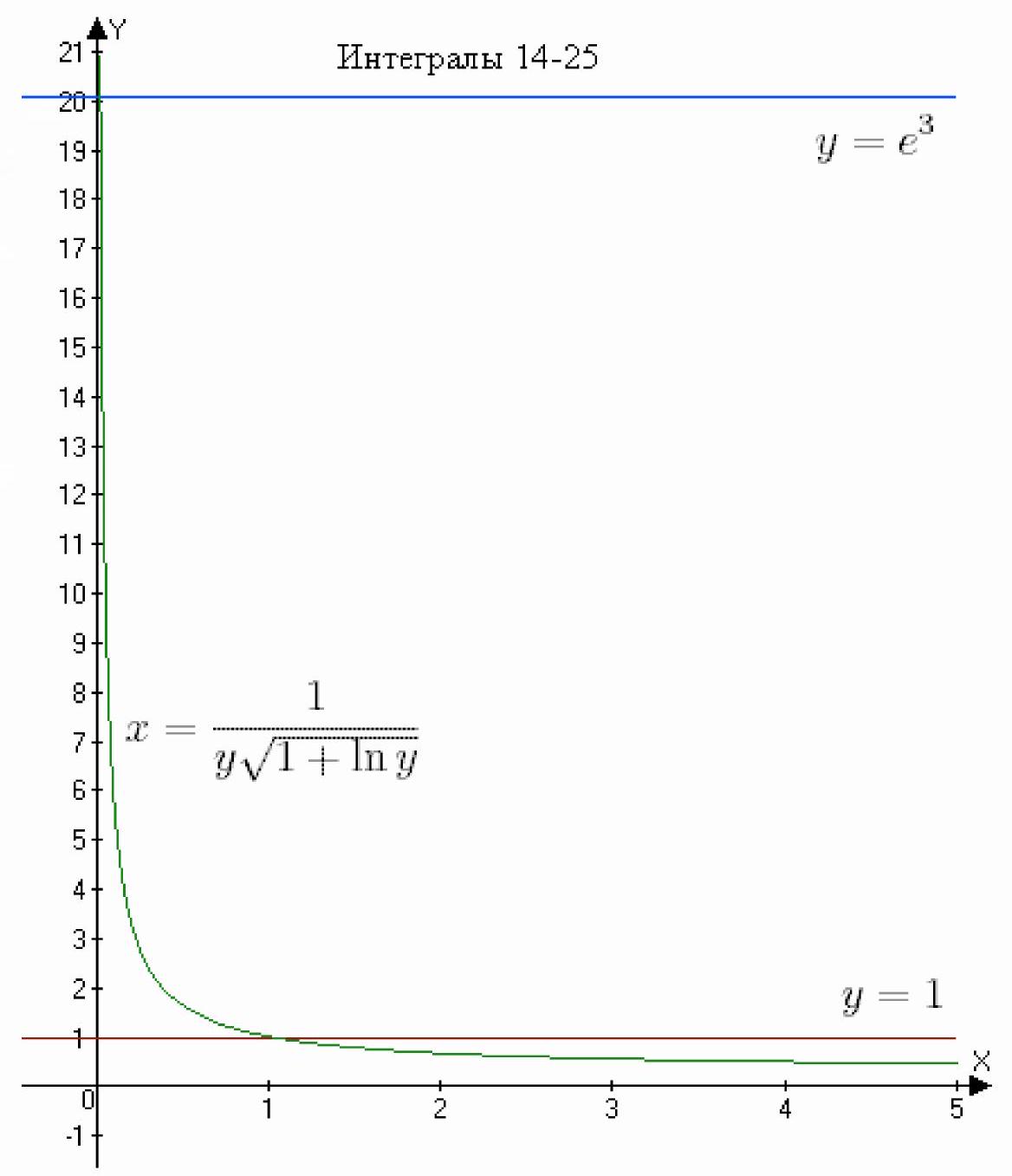
x=\frac{1}{y \sqrt{1+\ln y}}, x=0, y=1, y=e^{3}
$$
|
## Solution
The desired area $S$ is:
$S=\int_{1}^{e^{3}} \frac{1}{y \sqrt{\ln y+1}} d y$
We make a substitution of variables:
$t=\ln y$, hence
$d t=\frac{d y}{y}$
When $t=\ln 1 \Rightarrow t=0$ and when
$t=\ln e^{3} \Rightarrow t=3$
Then we get
$$
\begin{aligned}
& S=\int_{1}^{e^{3}} \frac{1}{y \sqrt{\ln y+1}} d y= \\
& =\int_{0}^{3} \frac{1}{\sqrt{t+1}} d t=\left.2 \sqrt{1+t}\right|_{0} ^{3}=2 \sqrt{4}-2 \sqrt{1}=2
\end{aligned}
$$
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\� \%D0\%9A\%D1\%83\%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD $\% \mathrm{D} 1 \% 82 \% \mathrm{D} 0 \% \mathrm{~B} \% \mathrm{D} 0 \% \mathrm{~B} 3 \% \mathrm{D} 1 \% 80 \% \mathrm{D} 0 \% \mathrm{~B} 0 \% \mathrm{D} 0 \% \mathrm{BB} \% \mathrm{D} 1 \% 8 \mathrm{~B}+14-25$ »
Categories: Kuznetsov's Problem Book Integrals Problem 14 | Integrals
Ukrainian Banner Network
- Last edited on this page: 10:36, 11 June 2010.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals 14-26
## Material from PlusPi
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task Condition
Calculate the area of the figure bounded by the graphs of the functions:
$$
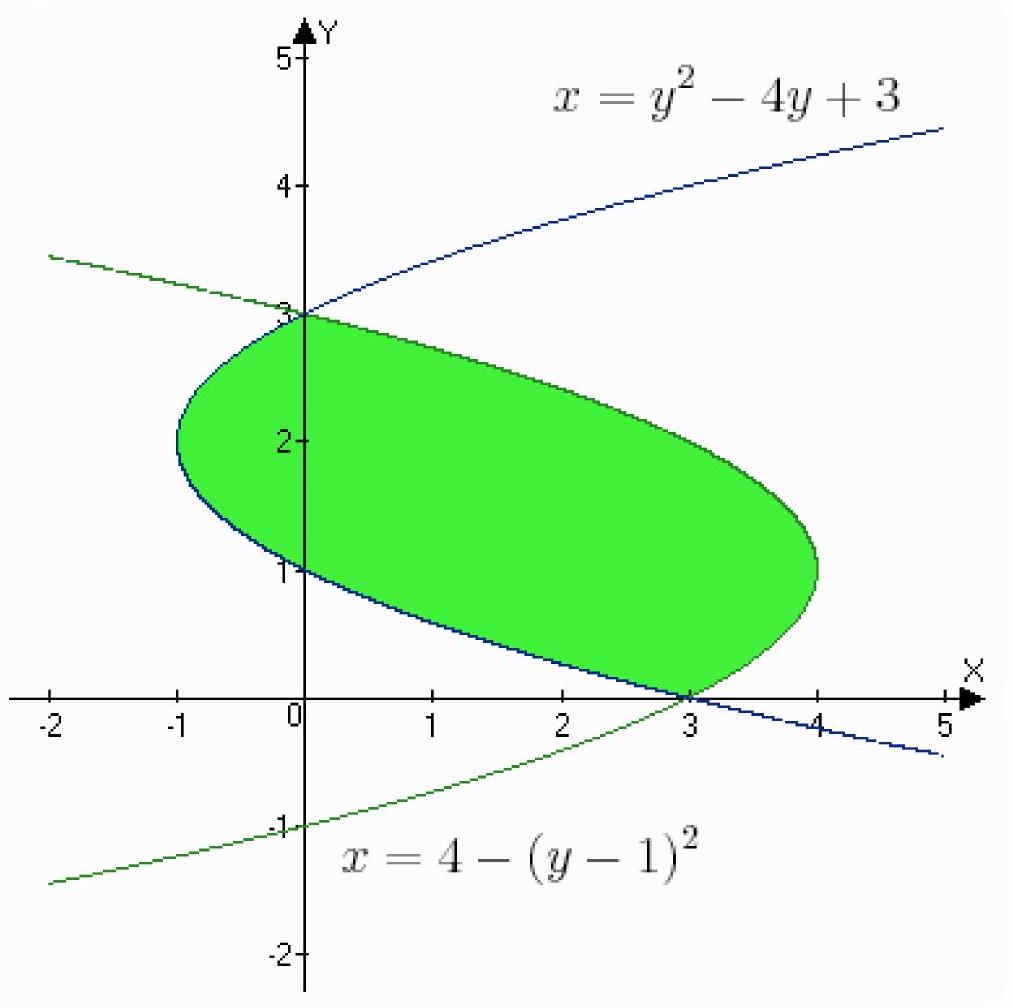
x=4-(y-1)^{2}, x=y^{2}-4 y+3
$$
|
## Solution
Find the ordinates of the points of intersection of the graphs of the functions $x=4-(y-1)^{2}$
, $x=y^{2}-4 y+3:$
$$
4-(y-1)^{2}=y^{2}-4 y+3
$$
$$
\begin{aligned}
& 4-y^{2}+2 y-1=y^{2}-4 y+3 \\
& 2 y^{2}-6 y=0 \\
& 2 y(y-3)=0 \\
& y=0, y=3
\end{aligned}
$$
Calculate the area:
$$
\begin{aligned}
& S=\int_{0}^{3}\left(\left(4-(y-1)^{2}\right)-\left(y^{2}-4 y+3\right)\right) d y= \\
& =\int_{0}^{3}\left(4-y^{2}+2 y-1-y^{2}+4 y-3\right) d y=
\end{aligned}
$$
$$
\begin{aligned}
& =\int_{0}^{3}\left(-2 y^{2}+6 y\right) d y=\frac{-2 y^{3}}{3}+\left.3 y^{2}\right|_{0} ^{3}= \\
& =\left(\frac{-2 \cdot 3^{3}}{3}+3 \cdot 3^{2}\right)-\left(\frac{-2 \cdot 0^{3}}{3}+3 \cdot 0^{2}\right)= \\
& =(-18+27)-(0+0)=9
\end{aligned}
$$
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\� \%D0\%9A\%D1\%83\%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD $\% \mathrm{D} 1 \% 84 \% \mathrm{D} 0 \% \mathrm{~B} 5 \% \mathrm{D} 0 \% \mathrm{~B} 3 \% \mathrm{D} 1 \% 80 \% \mathrm{D} 0 \% \mathrm{~B} 0 \% \mathrm{D} 0 \% \mathrm{BB} \% \mathrm{D} 1 \% 8 \mathrm{~B}+14-31$ » Categories: Kuznetsov's Problem Book Integrals Problem 14 | Integrals
Ukrainian Banner Network
- Last edited on this page: 08:28, 10 June 2010.
- Content is available under CC-BY-SA 3.0.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the lengths of the arcs of the curves given by the parametric equations.
$$
\begin{aligned}
& \left\{\begin{array}{l}
x=3(t-\sin t) \\
y=3(1-\cos t)
\end{array}\right. \\
& \pi \leq t \leq 2 \pi
\end{aligned}
$$
|
## Solution
The length of the arc of a curve defined by parametric equations is determined by the formula
$$
L=\int_{t_{1}}^{t_{2}} \sqrt{\left(x_{t}^{\prime}\right)^{2}+\left(y_{t}^{\prime}\right)^{2}} d t
$$
Let's find the derivatives with respect to $t$ for the given curve:
$$
\begin{aligned}
& x=3(t-\sin t) ; x_{t}^{\prime}=3(1-\cos t) \\
& y=3(1-\cos t) ; y_{t}^{\prime}=3 \sin t
\end{aligned}
$$
We get:
$$
\begin{aligned}
L & =\int_{\pi}^{2 \pi} \sqrt{9(1-\cos t)^{2}+9 \sin ^{2} t} d t= \\
& =3 \int_{\pi}^{2 \pi} \sqrt{(1-\cos t)^{2}+\sin ^{2} t} d t= \\
& =3 \int_{\pi}^{2 \pi} \sqrt{1-2 \cos t+\cos ^{2} t+\sin ^{2} t} d t= \\
& =3 \int_{\pi}^{2 \pi} \sqrt{2(1-\cos t)} d t=\left|\begin{array}{c}
\pi \leq t \leq 2 \pi ; \pi / 2 \leq t / 2 \leq \pi ; \sin (t / 2) \geq 0 \\
\sqrt{2(1-\cos t)}=\sqrt{4 \sin ^{2}(t / 2)}=2 \sin (t / 2)
\end{array}\right|= \\
& =3 \int_{\pi}^{2 \pi} 2 \sin (t / 2) d t=6 \int_{\pi}^{2 \pi} \sin (t / 2) d t=-\left.12 \cos (t / 2)\right|_{\pi} ^{2 \pi}=-12 \cdot(-1-0)=12
\end{aligned}
$$
Source — «http://pluspi.org/wiki/index.php/\�\�\�\�\�\�\�\�\�\�\�\� \%D0\%9A\%D1\%83\%D0\%B7\%D0\%BD\%D0\%B5\%D1\%86\%D0\%BE\%D0\%B2_\%D0\%98\%D0\%BD\%D1\%82
\%D0\%B5\%D0\%B3\%D1\%80\%D0\%B0\%D0\%BB\%D1\%8B_18-7»
Categories: Kuznetsov's Problem Book Integrals Problem 18 | Integrals
Ukrainian Banner Network
- Last modified on this page: 05:19, 21 May 2010.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals 18-8
## Material from PlusPi
|
12
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the lengths of the arcs of the curves given by the parametric equations.
$$
\begin{aligned}
& \left\{\begin{array}{l}
x=8 \cos ^{3} t \\
y=8 \sin ^{3} t
\end{array}\right. \\
& 0 \leq t \leq \frac{\pi}{6}
\end{aligned}
$$
|
## Solution
The length of the arc of a curve defined by parametric equations is determined by the formula
$$
L=\int_{t_{1}}^{t_{2}} \sqrt{\left(x_{t}^{\prime}\right)^{2}+\left(y_{t}^{\prime}\right)^{2}} d t
$$
From the equations of the curve, we find:
$$
\begin{aligned}
& x=8 \cos ^{3} t ; x_{t}^{\prime}=8 \cdot 3 \cos ^{2} t(\cos t)^{\prime}=-24 \cos ^{2} t \sin t \\
& y=8 \sin ^{3} t ; y_{t}^{\prime}=8 \cdot 3 \sin ^{2} t(\sin t)^{\prime}=24 \sin ^{2} t \cos t
\end{aligned}
$$
We obtain:
$$
\begin{aligned}
L & =\int_{0}^{\pi / 6} \sqrt{\left(-24 \cos ^{2} t \sin t\right)^{2}+\left(24 \sin ^{2} t \cos t\right)^{2}} d t= \\
& =24 \int_{0}^{\pi / 6} \sqrt{\cos ^{4} t \sin ^{2} t+\sin ^{4} t \cos ^{2} t} d t= \\
& =24 \int_{0}^{\pi / 6} \sqrt{\cos ^{2} t \sin ^{2} t} \cdot \sqrt{\sin ^{2} t+\cos ^{2} t} d t= \\
& =24 \int_{0}^{\pi / 6} \sqrt{\cos ^{2} t \sin ^{2} t} \cdot \sqrt{1} d t=\left|\begin{array}{c}
0 \leq t \leq \pi / 6 \\
\sin (t) \geq 0 \\
\cos (t) \geq 0
\end{array}\right|= \\
& =24 \int_{0}^{\pi / 6} \cos t \sin t \, dt=\frac{24}{4} \int_{0}^{\pi / 6} \sin (2 t) d(2 t)= \\
& =-\left.6 \cdot \cos (2 t)\right|_{0} ^{\pi / 6}=-6 \cdot\left(\cos \frac{\pi}{3}-\cos 0\right)=-6 \cdot\left(\frac{1}{2}-1\right)=3
\end{aligned}
$$
Source — «http://pluspi.org/wiki/index.php/%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%BD%D0%B8%D0%BA_%D0%9A%D1%83%D0%B7%D0%BD%D0%B5%D1%86%D0%BE%D0%B2_%D0%98%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B0%D0%BB%D1%8B_%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%B0_18-17»
Categories: Kuznetsov Problem Book Integrals Problem 18 | Integrals
- Last modified: 20:36, 29 May 2010.
- Content is available under CC-BY-SA 3.0.
Created by GeeTeatoo
## Problem Kuznetsov Integrals 18-18
## Material from PlusPi
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Based on the definition of the derivative, find $f^{\prime}(0)$:
$$
f(x)=\left\{\begin{array}{c}
e^{x \sin 5 x}-1, x \neq 0 \\
0, x=0
\end{array}\right.
$$
|
## Solution
By definition, the derivative at the point $x=0$:
$f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}$
Based on the definition, we find:
$$
\begin{aligned}
& f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{e^{\Delta x \sin 5 \Delta x}-1-0}{\Delta x}= \\
& =\lim _{\Delta x \rightarrow 0} \frac{e^{\Delta x \sin 5 \Delta x}-1}{\Delta x}=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$e^{\Delta x \sin 5 \Delta x}-1 \sim \Delta x \sin 5 \Delta x$, as $\Delta x \rightarrow 0(\Delta x \sin 5 \Delta x \rightarrow 0)$
We get:
$=\lim _{\Delta x \rightarrow 0} \frac{\Delta x \sin 5 \Delta x}{\Delta x}=\lim _{\Delta x \rightarrow 0} \sin 5 \Delta x=\sin 0=0$
Thus, $f^{\prime}(0)=0$
## Problem Kuznetsov Differentiation 2-20
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the cosine of the angle between vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$.
$A(0 ; 0 ; 4), B(-3 ;-6 ; 1), C(-5 ;-10 ;-1)$
|
## Solution
Let's find $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\overrightarrow{A B}=(-3-0 ;-6-0 ; 1-4)=(-3 ;-6 ;-3)$
$\overrightarrow{A C}=(-5-0 ;-10-0 ;-1-4)=(-5 ;-10 ;-5)$
We find the cosine of the angle $\phi_{\text {between vectors }} \overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\cos (\overrightarrow{A B, \overrightarrow{A C}})=\frac{(\overrightarrow{A B}, \overrightarrow{A C})}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}=$
$=\frac{(-3) \cdot(-5)+(-6) \cdot(-10)+(-3) \cdot(-5)}{\sqrt{(-3)^{2}+(-6)^{2}+(-3)^{2}} \cdot \sqrt{(-5)^{2}+(-10)^{2}+(-5)^{2}}}=$
$=\frac{15+60+15}{\sqrt{9+36+9} \cdot \sqrt{25+100+25}}=\frac{90}{\sqrt{54} \cdot \sqrt{150}}=1$
Thus, the cosine of the angle:
$\cos (\overrightarrow{A B, A C})=1$
and consequently the angle
$\widehat{A B, \overrightarrow{A C}}=0$
## Problem Kuznetsov Analytic Geometry 4-14
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the volume of the tetrahedron with vertices at points \( A_{1}, A_{2}, A_{3}, A_{4} \) and its height dropped from vertex \( A_{4} \) to the face \( A_{1} A_{2} A_{3} \).
\( A_{1}(2 ; 3 ; 1) \)
\( A_{2}(4 ; 1 ;-2) \)
\( A_{3}(6 ; 3 ; 7) \)
\( A_{4}(7 ; 5 ;-3) \)
|
## Solution
From vertex $A_{1}$, we draw vectors:
$$
\begin{aligned}
& \overrightarrow{A_{1} A_{2}}=\{4-2 ; 1-3 ;-2-1\}=\{2 ;-2 ;-3\} \\
& \vec{A}_{1} A_{3}=\{6-2 ; 3-3 ; 7-1\}=\{4 ; 0 ; 6\} \\
& \overrightarrow{A_{1} A_{4}}=\{7-2 ; 5-3 ;-3-1\}=\{5 ; 2 ;-4\}
\end{aligned}
$$
According to the geometric meaning of the mixed product, we have:
$$
V_{A_{1} A_{2} A_{3} A_{4}}=\frac{1}{6} \cdot\left|\left(\overrightarrow{A_{1} A_{2}}, \overrightarrow{A_{1} A_{3}}, \overrightarrow{A_{1} A_{4}}\right)\right|
$$
We compute the mixed product:
$$
\begin{aligned}
& \left(\overrightarrow{A_{1} A_{2}}, \overrightarrow{A_{1} A_{3}}, \overrightarrow{A_{1} A_{4}}\right)=\left|\begin{array}{ccc}
2 & -2 & -3 \\
4 & 0 & 6 \\
5 & 2 & -4
\end{array}\right|= \\
& =2 \cdot\left|\begin{array}{cc}
0 & 6 \\
2 & -4
\end{array}\right|-(-2) \cdot\left|\begin{array}{cc}
4 & 6 \\
5 & -4
\end{array}\right|+(-3) \cdot\left|\begin{array}{cc}
4 & 0 \\
5 & 2
\end{array}\right|= \\
& =2 \cdot(-12)+2 \cdot(-46)-3 \cdot 8=-24-92-24=-140
\end{aligned}
$$
We obtain:
$$
V_{A_{1} A_{2} A_{3} A_{4}}=\frac{1}{6} \cdot|-140|=\frac{70}{3}=23 \frac{1}{3}
$$
Since
$$
V_{A_{1} A_{2} A_{3} A_{4}}=\frac{1}{3} \cdot S_{A_{1} A_{2} A_{3}} \cdot h \Rightarrow h=\frac{3 V_{A_{1} A_{2} A_{3} A_{4}}}{S_{A_{1} A_{2} A_{3}}}
$$
According to the geometric meaning of the vector product:
$$
S_{A_{1} A_{2} A_{3}}=\frac{1}{2} \cdot\left|\overrightarrow{A_{1} A_{2}} \times \overrightarrow{A_{1} A_{3}}\right|
$$
We compute the vector product:
$A_{1} A_{2} \times A_{1} A_{3}=\left|\begin{array}{ccc}i & j & k \\ 2 & -2 & -3 \\ 4 & 0 & 6\end{array}\right|=i \cdot\left|\begin{array}{cc}-2 & -3 \\ 0 & 6\end{array}\right|-j\left|\begin{array}{cc}2 & -3 \\ 4 & 6\end{array}\right|+k \cdot\left|\begin{array}{cc}2 & -2 \\ 4 & 0\end{array}\right|=$
$=i \cdot(-12)-j \cdot 24+k \cdot 8=\{-12 ;-24 ; 8\}$
We obtain:
$S_{A_{1} A_{2} A_{3}}=\frac{1}{2} \cdot \sqrt{(-12)^{2}+(-24)^{2}+8^{2}}=\frac{1}{2} \cdot \sqrt{784}=\frac{28}{2}=14$
Then
$h=\frac{3 V_{A_{1} A_{2} A_{3} A_{4}}}{S_{A_{1} A_{2} A_{3}}}=\frac{3 \cdot \frac{70}{3}}{14}=5$
Volume of the tetrahedron: $23 \frac{1}{3}$
Height: 5
## Problem Kuznetsov Analytic Geometry 7-14
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Let $k$ be the coefficient of similarity transformation with the center at the origin. Is it true that point $A$ belongs to the image of plane $a$?
$A(2 ; 3 ;-2)$
$a: 3 x-2 y+4 z-6=0$
$k=-\frac{4}{3}$
|
## Solution
When transforming similarity with the center at the origin of the plane
$a: A x+B y+C z+D=0_{\text{and coefficient }} k$ transitions to the plane
$a^{\prime}: A x+B y+C z+k \cdot D=0$. We find the image of the plane $a$:
$a^{\prime}: 3 x-2 y+4 z+8=0$
Substitute the coordinates of point $A$ into the equation $a^{\prime}$:
$3 \cdot 2-2 \cdot 3+4 \cdot(-2)+8=0$
$6-6-8+8=0$
$0=0$
Since $0=0$, point $A$ belongs to the image of the plane $a$.
## Problem Kuznetsov Analytical Geometry 12-14
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the cosine of the angle between vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$.
$A(1, -2, 3), B(0, -1, 2), C(3, -4, 5)$
|
## Solution
Let's find $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\overrightarrow{A B}=(0-1 ;-1-(-2) ; 2-3)=(-1 ; 1 ;-1)$
$\overrightarrow{A C}=(3-1 ;-4-(-2) ; 5-3)=(2 ;-2 ; 2)$
We find the cosine of the angle $\phi_{\text {between vectors }} \overrightarrow{A B}$ and $\overrightarrow{A C}$:
$$
\begin{aligned}
& \cos (\overrightarrow{A B,} \overrightarrow{A C})=\frac{(\overrightarrow{A B}, \overrightarrow{A C})}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}= \\
& =\frac{(-1) \cdot 2+1 \cdot(-2)+(-1) \cdot 2}{\sqrt{(-1)^{2}+1^{2}+(-1)^{2}} \cdot \sqrt{2^{2}+(-2)^{2}+2^{2}}}= \\
& =\frac{-2-2-2}{\sqrt{1+1+1} \cdot \sqrt{4+4+4}}=\frac{-6}{\sqrt{3} \cdot \sqrt{12}}=\frac{-6}{\sqrt{36}}=-1
\end{aligned}
$$
Thus, the cosine of the angle:
$\cos (\overrightarrow{A B, A C})=-1$
and consequently the angle
$\widehat{A B,} \overrightarrow{A C}=\pi$
## Problem Kuznetsov Analytic Geometry 4-1
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task Condition
Calculate the area of the parallelogram constructed on vectors $a$ and $b$.
\[
\begin{aligned}
& a=p+2 q \\
& b=3 p-q \\
& |p|=1 \\
& |q|=2 \\
& (\widehat{p, q})=\frac{\pi}{6}
\end{aligned}
\]
|
## Solution
The area of the parallelogram constructed on vectors $a$ and $b$ is numerically equal to the modulus of their vector product:
$$
S=|a \times b|
$$
We compute \(a \times b\) using the properties of the vector product:
$$
\begin{aligned}
& a \times b=(p+2 q) \times(3 p-q)=3 \cdot p \times p-p \times q+2 \cdot 3 \cdot q \times p+2 \cdot(-1) q \times q= \\
& =-1 \cdot p \times q+6 \cdot q \times p=-1 \cdot p \times q-6 \cdot p \times q=(-1-6) \cdot p \times q=-7 \cdot p \times q
\end{aligned}
$$
$$
\begin{aligned}
& S=|a \times b|=|-7 \cdot p \times q|=7 \cdot|p \times q|=7 \cdot|p| \cdot|q| \cdot \sin (\widehat{p, q})= \\
& =7 \cdot 1 \cdot 2 \cdot \sin \frac{\pi}{6}=14 \cdot \sin \frac{\pi}{6}=14 \cdot \frac{1}{2}=7
\end{aligned}
$$
Thus, the area of the parallelogram constructed on vectors $a$ and $b$ is 7.
## Problem Kuznetsov Analytic Geometry 5-1
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Let $k$ be the coefficient of similarity transformation with the center at the origin. Is it true that point $A$ belongs to the image of plane $a$?
$A(4 ; 3 ; 1)$
$a: 3x - 4y + 5z - 6 = 0$
$k = \frac{5}{6}$
|
## Solution
When transforming similarity with the center at the origin of the plane
$a: A x+B y+C z+D=0$ and the coefficient $k$, the plane transitions to
$a^{\prime}: A x+B y+C z+k \cdot D=0$. We find the image of the plane $a$:
$a^{\prime}: 3 x-4 y+5 z-5=0$
Substitute the coordinates of point $A$ into the equation of $a^{\prime}$:
$3 \cdot 4-4 \cdot 3+5 \cdot 1-5=0$
$12-12+5-5=0$
$0=0$
Since $0=0$, point $A$ belongs to the image of the plane $a$.
## Problem Kuznetsov Analytical Geometry $12-21$
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
$$
\lim _{n \rightarrow \infty} \frac{\sqrt{n+2}-\sqrt{n^{2}+2}}{\sqrt[4]{4 n^{4}+1}-\sqrt[3]{n^{4}-1}}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{n \rightarrow \infty} \frac{\sqrt{n+2}-\sqrt{n^{2}+2}}{\sqrt[4]{4 n^{4}+1}-\sqrt[3]{n^{1}-1}}=\lim _{n \rightarrow \infty} \frac{\frac{1}{n}\left(\sqrt{n+2}-\sqrt{n^{2}+2}\right)}{\frac{1}{n}\left(\sqrt[4]{4 n^{\frac{1}{4}+1}}-\sqrt[3]{n^{4}-1}\right)}= \\
& =\lim _{n \rightarrow \infty} \frac{\sqrt{\frac{1}{n}+\frac{2}{n^{2}}}-\sqrt{1+\frac{2}{n^{2}}}}{\sqrt{4+\frac{1}{n^{4}}}-\sqrt[3]{n-\frac{1}{n^{3}}}}=\left\{\frac{\sqrt{0+0}-\sqrt{1+0}}{\sqrt[4]{4+0}-\sqrt[3]{\infty-0}}=\frac{-1}{-\infty}\right\}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 4-7
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$$
\lim _{x \rightarrow 0} \frac{(1+x)^{3}-(1+3 x)}{x+x^{5}}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{(1+x)^{3}-(1+3 x)}{x+x^{5}}=\left\{\frac{0}{0}\right\}=\lim _{x \rightarrow 0} \frac{1^{: 5}+3 \cdot 1^{2} \cdot x^{2}+3 \cdot 1 \cdot x^{2}+x^{3}-1-3 x}{x\left(1+x^{4}\right)}= \\
& =\lim _{x \rightarrow 0} \frac{1+3 x+3 x^{2}+x^{3}-1-3 x}{x\left(1+x^{4}\right)}=\lim _{x \rightarrow 0} \frac{3 x^{2}+x^{3}}{x\left(1+x^{4}\right)}= \\
& =\lim _{x \rightarrow 0} \frac{x^{2}(3+x)}{x\left(1+x^{4}\right)}=\lim _{x \rightarrow 0} \frac{x\left(3+x^{3}\right)}{1+x^{4}}=\frac{0(3+0)}{1+0^{4}}=\frac{0}{1}=0
\end{aligned}
$$
## Problem Kuznetsov Limits 10-7
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow \pi} \frac{\sin ^{2} x-\tan ^{2} x}{(x-\pi)^{4}}$
|
## Solution
$\lim _{x \rightarrow \pi} \frac{\sin ^{2} x-\tan ^{2} x}{(x-\pi)^{4}}=\lim _{x \rightarrow \pi} \frac{\frac{\sin ^{2} x \cdot \cos ^{2} x}{\cos ^{2} x}-\tan ^{2} x}{(x-\pi)^{4}}=$
$=\lim _{x \rightarrow \pi} \frac{\tan ^{2} x \cdot \cos ^{2} x-\tan ^{2} x}{(x-\pi)^{4}}=\lim _{x \rightarrow \pi} \frac{\tan ^{2} x\left(\cos ^{2} x-1\right)}{(x-\pi)^{4}}=$
$=\lim _{x \rightarrow \pi} \frac{\tan ^{2} x\left(-\sin ^{2} x\right)}{(x-\pi)^{4}}=$
Substitution:
$x=y+\pi \Rightarrow y=x-\pi$
$x \rightarrow \pi \Rightarrow y \rightarrow 0$
We get:
$=\lim _{y \rightarrow 0} \frac{\tan ^{2}(y+\pi)\left(-\sin ^{2}(y+\pi)\right)}{((y+\pi)-\pi)^{4}}=\lim _{y \rightarrow 0} \frac{\tan ^{2} y\left(-(-\sin y)^{2}\right)}{y^{4}}=$
$=\lim _{y \rightarrow 0} \frac{\tan ^{2} y\left(-\sin ^{2} y\right)}{y^{4}}=$
Using the substitution of equivalent infinitesimals:
$\sin y \sim y$, as $y \rightarrow 0$
$\tan y \sim y$, as $y \rightarrow 0$
We get:
$$
=\lim _{y \rightarrow 0} \frac{y^{2}\left(-y^{2}\right)}{y^{4}}=\lim _{y \rightarrow 0} \frac{-1}{1}=-1
$$
## Problem Kuznetsov Limits 13-7
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 3} \frac{\sin \left(\sqrt{2 x^{2}-3 x-5}-\sqrt{1+x}\right)}{\ln (x-1)-\ln (x+1)+\ln 2}$
|
## Solution
Substitution:
$x=y+3 \Rightarrow y=x-3$
$x \rightarrow 3 \Rightarrow y \rightarrow 0$
We get:
$$
\begin{aligned}
& \lim _{x \rightarrow 3} \frac{\sin \left(\sqrt{2 x^{2}-3 x-5}-\sqrt{1+x}\right)}{\ln (x-1)-\ln (x+1)+\ln 2}= \\
& =\lim _{y \rightarrow 0} \frac{\sin \left(\sqrt{2(y+3)^{2}-3(y+3)-5}-\sqrt{1+(y+3))}\right.}{\ln ((y+3)-1)-\ln ((y+3)+1)+\ln 2}= \\
& =\lim _{y \rightarrow 0} \frac{\sin \left(\sqrt{2 y^{2}+12 y+18-3 y-9-5}-\sqrt{y+4}\right)}{\ln (y+2)-\ln (y+4)+\ln 2}= \\
& =\lim _{y \rightarrow 0} \frac{\sin \left(\sqrt{2 y^{2}+9 y+4}-\sqrt{y+4}\right)}{\ln \frac{2(y+2)}{y+4}}= \\
& =\lim _{y \rightarrow 0} \frac{\sin \frac{\left(\sqrt{2 y^{2}+9 y+4}-\sqrt{y+4}\right)\left(\sqrt{2 y^{2}+9 y+4}+\sqrt{y+4}\right)}{\sqrt{2 y^{2}+9 y+4}+\sqrt{y+4}}}{\ln \left(1+\frac{y}{y+4}\right)}= \\
& =\lim _{y \rightarrow 0} \frac{\sin \frac{2 y^{2}+9 y+4-(y+4)}{\sqrt{2 y^{2}+9 y+4}+\sqrt{y+4}}}{\ln \left(1+\frac{y}{y+4}\right)}= \\
& =\lim _{y \rightarrow 0} \frac{\sin \frac{2 y^{2}+8 y}{\sqrt{2 y^{2}+9 y+4}+\sqrt{y+4}}}{\ln \left(1+\frac{y}{y+4}\right)}=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$$
\begin{aligned}
& \sin \frac{2 y^{2}+8 y}{\sqrt{2 y^{2}+9 y+4}+\sqrt{y+4}} \sim \frac{2 y^{2}+8 y}{\sqrt{2 y^{2}+9 y+4}+\sqrt{y+4}} \\
& \text {, as } \\
& y \rightarrow 0\left(\frac{2 y^{2}+8 y}{\sqrt{2 y^{2}+9 y+4}+\sqrt{y+4}} \rightarrow 0\right) \\
& \ln \left(1+\frac{y}{y+4}\right) \sim \frac{y}{y+4}{ }_{\text {, as }} y \rightarrow 0\left(\frac{y}{y+4} \rightarrow 0\right)
\end{aligned}
$$
We get:
$$
\begin{aligned}
& =\lim _{y \rightarrow 0} \frac{\frac{2 y^{2}+8 y}{\sqrt{2 y^{2}+9 y+4}+\sqrt{y+4}}}{\frac{y}{y+4}}= \\
& =\lim _{y \rightarrow 0} \frac{(2 y+8)(y+4)}{\sqrt{2 y^{2}+9 y+4}+\sqrt{y+4}}= \\
& =\frac{(2 \cdot 0+8)(0+4)}{\sqrt{2 \cdot 0^{2}+9 \cdot 0+4}+\sqrt{0+4}}=\frac{8 \cdot 4}{\sqrt{4}+\sqrt{4}}=\frac{8 \cdot 4}{2+2}=8
\end{aligned}
$$
## Problem Kuznetsov Limits 14-7
|
8
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$$
\lim _{x \rightarrow 0}\left(\frac{\ln (1+x)}{6 x}\right)^{\frac{x}{x+2}}
$$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 0}\left(\frac{\ln (1+x)}{6 x}\right)^{\frac{x}{x+2}}=\left(\lim _{x \rightarrow 0} \frac{\ln (1+x)}{6 x}\right)^{\lim _{x \rightarrow 0} \frac{x}{x+2}}= \\
& =\left(\lim _{x \rightarrow 0} \frac{\ln (1+x)}{6 x}\right)^{\frac{0}{0+2}}=\left(\lim _{x \rightarrow 0} \frac{\ln (1+x)}{6 x}\right)^{0}=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$\ln (1+x) \sim x$, as $x \rightarrow 0$
We get:
$$
=\left(\lim _{x \rightarrow 0} \frac{x}{6 x}\right)^{0}=\left(\lim _{x \rightarrow 0} \frac{1}{6}\right)^{0}=\left(\frac{1}{6}\right)^{0}=1
$$
## Problem Kuznetsov Limits 18-7
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Calculate the limit of the function:
$\lim _{x \rightarrow 3}\left(2-\frac{x}{3}\right)^{\sin (\pi x)}$
|
## Solution
$$
\begin{aligned}
& \lim _{x \rightarrow 3}\left(2-\frac{x}{3}\right)^{\sin (\pi x)}=\lim _{x \rightarrow 3}\left(e^{\ln \left(2-\frac{x}{3}\right)}\right)^{\sin (\pi x)}= \\
& =\lim _{x \rightarrow 3} e^{\sin (\pi x) \cdot \ln \left(2-\frac{x}{3}\right)}=\exp \left\{\lim _{x \rightarrow 3} \sin (\pi x) \cdot \ln \left(2-\frac{x}{3}\right)\right\}= \\
& =\exp \left\{\lim _{x \rightarrow 3} \sin (\pi x) \cdot \ln \left(1+\left(1-\frac{x}{3}\right)\right)\right\}=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$$
\ln \left(1+\left(1-\frac{x}{3}\right)\right) \sim 1-\frac{x}{3}, \text { as } \quad x \rightarrow 3\left(1-\frac{x}{3} \rightarrow 0\right)
$$
We get:
$$
\begin{aligned}
& =\exp \left\{\lim _{x \rightarrow 3} \sin (\pi x) \cdot\left(1-\frac{x}{3}\right)\right\}=\exp \left\{\sin (\pi \cdot 3) \cdot\left(1-\frac{3}{3}\right)\right\}= \\
& =\exp \{0\}=e^{0}=1
\end{aligned}
$$
## Problem Kuznetsov Limits 20-7
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## problem statement
Find the cosine of the angle between vectors $\overrightarrow{A B}$ and $\overrightarrow{A C}$.
$A(-4 ; 3 ; 0), B(0 ; 1 ; 3), C(-2 ; 4 ;-2)$
|
## Solution
Let's find $\overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\overrightarrow{A B}=(0-(-4) ; 1-3 ; 3-0)=(4 ;-2 ; 3)$
$\overrightarrow{A C}=(-2-(-4) ; 4-3 ;-2-0)=(2 ; 1 ;-2)$
We find the cosine of the angle $\phi_{\text {between vectors }} \overrightarrow{A B}$ and $\overrightarrow{A C}$:
$\cos (\overrightarrow{A B, A \overrightarrow{A C}})=\frac{(\overrightarrow{A B}, \overrightarrow{A C})}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}=$
$=\frac{4 \cdot 2+(-2) \cdot 1+3 \cdot(-2)}{\sqrt{4^{2}+(-2)^{2}+3^{2}} \cdot \sqrt{2^{2}+1^{2}+(-2)^{2}}}=$
$=\frac{8-2-6}{\sqrt{16+4+9} \cdot \sqrt{4+1+4}}=\frac{0}{\sqrt{29} \cdot \sqrt{9}}=0$
Thus, the cosine of the angle:
$\cos (\overrightarrow{A B,} \overrightarrow{A C})=0$
and consequently the angle
$\widehat{A B, A C}=\frac{\pi}{2}$
Problem Kuznetsov Analytic Geometry 4-19
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Find the distance from point $M_{0}$ to the plane passing through three points $M_{1}, M_{2}, M_{3}$.
$M_{1}(2 ; 1 ; 4)$
$M_{2}(3 ; 5 ;-2)$
$M_{3}(-7 ;-3 ; 2)$
$M_{0}(-3 ; 1 ; 8)$
|
## Solution
Find the equation of the plane passing through three points $M_{1}, M_{2}, M_{3}$:
$$
\left|\begin{array}{ccc}
x-2 & y-1 & z-4 \\
3-2 & 5-1 & -2-4 \\
-7-2 & -3-1 & 2-4
\end{array}\right|=0
$$
Perform transformations:
$$
\begin{aligned}
& \left|\begin{array}{ccc}
x-2 & y-1 & z-4 \\
1 & 4 & -6 \\
-9 & -4 & -2
\end{array}\right|=0 \\
& (x-2) \cdot\left|\begin{array}{cc}
4 & -6 \\
-4 & -2
\end{array}\right|-(y-1) \cdot\left|\begin{array}{cc}
1 & -6 \\
-9 & -2
\end{array}\right|+(z-4) \cdot\left|\begin{array}{cc}
1 & 4 \\
-9 & -4
\end{array}\right|=0 \\
& (x-2) \cdot(-32)-(y-1) \cdot(-56)+(z-4) \cdot 32=0 \\
& -32 x+64+56 y-56+32 z-128=0 \\
& -32 x+56 y+32 z-120=0 \\
& -4 x+7 y+4 z-15=0
\end{aligned}
$$
The distance $d_{\text {from point }} M_{0}\left(x_{0} ; y_{0} ; z_{0}\right)_{\text {to the plane }} A x+B y+C z+D=0$:
$$
d=\frac{\left|A x_{0}+B y_{0}+C z_{0}+D\right|}{\sqrt{A^{2}+B^{2}+C^{2}}}
$$
## Find:
$$
d=\frac{|-4 \cdot(-3)+7 \cdot 1+4 \cdot 8-15|}{\sqrt{(-4)^{2}+7^{2}+4^{2}}}=\frac{|12+7+32-15|}{\sqrt{16+49+16}}=\frac{36}{\sqrt{81}}=4
$$
## Problem Kuznetsov Analytic Geometry 8-19
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Based on the definition of the derivative, find $f^{\prime}(0)$:
$$
f(x)=\left\{\begin{array}{c}
e^{\sin \left(x^{\frac{3}{2}} \sin \frac{2}{x}\right)}-1+x^{2}, x \neq 0 \\
0, x=0
\end{array}\right.
$$
|
## Solution
By definition, the derivative at the point $x=0$:
$f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}$
Based on the definition, we find:
$$
\begin{aligned}
& f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim _{\Delta x \rightarrow 0}\left(e^{\sin \left(\Delta x^{\frac{3}{2}} \sin \frac{2}{\Delta x}\right)}-1+\Delta x^{2}-0\right) / \Delta x= \\
& =\lim _{\Delta x \rightarrow 0}\left(e^{\sin \left(\Delta x^{\frac{3}{2}} \sin \frac{2}{\Delta x}\right)}-1+\Delta x^{2}\right) / \Delta x= \\
& =\lim _{\Delta x \rightarrow 0}\left(e^{\sin \left(\Delta x^{\frac{3}{2}} \sin \frac{2}{\Delta x}\right)}-1\right) / \Delta x+\lim _{\Delta x \rightarrow 0} \frac{\Delta x^{2}}{\Delta x}=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$$
e^{\sin \left(\Delta x^{\frac{3}{2}} \sin \frac{2}{\Delta x}\right)}-1 \sim \sin \left(\Delta x^{\frac{3}{2}} \sin \frac{2}{\Delta x}\right) \text{, as } \Delta x \rightarrow 0\left(\sin \left(\Delta x^{\frac{3}{2}} \sin \frac{2}{\Delta x}\right) \rightarrow 0\right)
$$
We get:
$$
=\lim _{\Delta x \rightarrow 0} \frac{\sin \left(\Delta x^{\frac{3}{2}} \sin \frac{2}{\Delta x}\right)}{\Delta x}+\lim _{\Delta x \rightarrow 0} \Delta x=
$$
Using the substitution of equivalent infinitesimals:
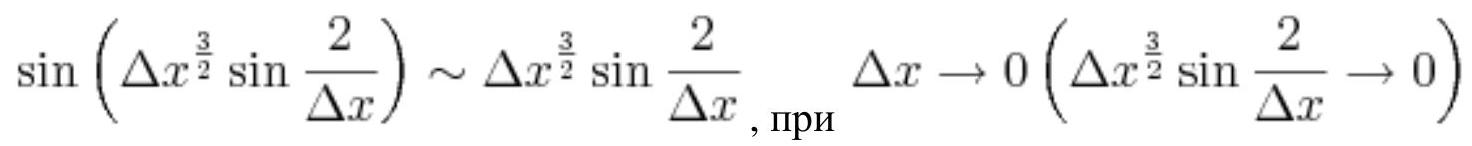
We get:
$=\lim _{\Delta x \rightarrow 0} \frac{\Delta x^{\frac{3}{2}} \sin \frac{2}{\Delta x}}{\Delta x}+0=\lim _{\Delta x \rightarrow 0} \Delta x^{\frac{1}{2}} \sin \frac{2}{\Delta x}=$
Since $\sin \frac{2}{\Delta x}$ is bounded, then
$\Delta x^{\frac{1}{2}} \cdot \sin \frac{2}{\Delta x} \rightarrow 0 \text{, as } \Delta x \rightarrow 0\left(\Delta x^{\frac{1}{2}} \rightarrow 0\right)$
Thus,
$=0$
Therefore, $f^{\prime}(0)=0$
Problem Kuznetsov Differentiation $2-26$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem Statement
Based on the definition of the derivative, find $f^{\prime}(0)$:
$f(x)=\left\{\begin{array}{c}\sqrt{1+\ln \left(1+x^{2} \sin \frac{1}{x}\right)}-1, x \neq 0 ; \\ 0, x=0\end{array}\right.$
|
## Solution
By definition, the derivative at the point $x=0$:
$$
f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}
$$
Based on the definition, we find:
$$
\begin{aligned}
& f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{\sqrt{1+\ln \left(1+x^{2} \sin \frac{1}{x}\right)}-1-0}{\Delta x}= \\
& =\lim _{\Delta x \rightarrow 0} \frac{\left(\sqrt{1+\ln \left(1+\Delta x^{2} \sin \frac{1}{\Delta x}\right)}-1\right) \cdot\left(\sqrt{1+\ln \left(1+\Delta x^{2} \sin \frac{1}{\Delta x}\right)}+1\right)}{\Delta x\left(\sqrt{1+\ln \left(1+\Delta x^{2} \sin \frac{1}{\Delta x}\right)}+1\right)}= \\
& =\lim _{\Delta x \rightarrow 0} \frac{1+\ln \left(1+\Delta x^{2} \sin \frac{1}{\Delta x}\right)-1}{\Delta x\left(\sqrt{1+\ln \left(1+\Delta x^{2} \sin \frac{1}{\Delta x}\right)}+1\right)}= \\
& =\lim _{\Delta x \rightarrow 0} \frac{\ln \left(1+\Delta x^{2} \sin \frac{1}{\Delta x}\right)}{\Delta x\left(\sqrt{1+\ln \left(1+\Delta x^{2} \sin \frac{1}{\Delta x}\right)}+1\right)}=
\end{aligned}
$$
Using the substitution of equivalent infinitesimals:
$\ln \left(1+\Delta x^{2} \sin \frac{1}{\Delta x}\right) \sim \Delta x^{2} \sin \frac{1}{\Delta x}_{\text {, as }} \Delta x \rightarrow 0\left(\Delta x^{2} \sin \frac{1}{\Delta x} \rightarrow 0\right)$
We get:
$$
=\lim _{\Delta x \rightarrow 0} \frac{\Delta x^{2} \sin \frac{1}{\Delta x}}{\Delta x\left(\sqrt{1+\ln \left(1+\Delta x^{2} \sin \frac{1}{\Delta x}\right)}+1\right)}=\lim _{\Delta x \rightarrow 0} \frac{\Delta x \sin \frac{1}{\Delta x}}{\sqrt{1+\ln \left(1+\Delta x^{2} \sin \frac{1}{\Delta x}\right)}+1}=
$$
Since $\sin \left(\frac{1}{\Delta x}\right)_{\text { is bounded, then }}$
$\Delta x \cdot \sin \left(\frac{1}{\Delta x}\right) \rightarrow 0 \quad$, as $\Delta x \rightarrow 0$
Then:
$=\frac{0}{\sqrt{1+\ln (1+0)}+1}=\frac{0}{\sqrt{1}+1}=0$
Thus, $f^{\prime}(0)=0$
## Problem Kuznetsov Differentiation 2-6
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.160. $\frac{\left(a^{2} b \sqrt{b}-6 a^{5 / 3} b^{5 / 4}+12 a b \sqrt[3]{a}-8 a b^{3 / 4}\right)^{2 / 3}}{a b \sqrt[3]{a}-4 a b^{3 / 4}+4 a^{2 / 3} \sqrt{b}}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}a^{1 / 3} b^{1 / 4} \neq 2, \\ a \neq 0, \\ b \neq 0 .\end{array}\right.$
$$
\begin{aligned}
& \frac{\left(a^{2} b \sqrt{b}-6 a^{5 / 3} b^{5 / 4}+12 a b \sqrt[3]{a}-8 a b^{3 / 4}\right)^{2 / 3}}{a b \sqrt[3]{a}-4 a b^{3 / 4}+4 a^{2 / 3} \sqrt{b}}= \\
& =\frac{\left(a^{2} b^{3 / 2}-6 a^{5 / 3} b^{5 / 4}+12 a^{4 / 3} b-8 a b^{3 / 4}\right)^{2 / 3}}{a^{4 / 3} b-4 a b^{3 / 4}+4 a^{2 / 3} b^{1 / 2}}= \\
& =\frac{\left(a b^{3 / 4}\left(a b^{3 / 4}-6 a^{2 / 3} b^{1 / 2}+12 a^{1 / 3} b^{1 / 4}-8\right)\right)^{2 / 3}}{a^{2 / 3} b^{1 / 2}\left(a^{2 / 3} b^{1 / 2}-4 a^{1 / 3} b^{1 / 4}+4\right)}= \\
& =\frac{a^{2 / 3} b^{1 / 2}\left(\left(a b^{3 / 4}-8\right)-6 a^{1 / 3} b^{1 / 4}\left(a^{1 / 3} b^{1 / 4}-2\right)\right)^{2 / 3}}{a^{2 / 3} b^{1 / 2}\left(a^{1 / 3} b^{1 / 4}-2\right)^{2}}= \\
& =\frac{\left(\left(\left(a^{1 / 3} b^{1 / 4}\right)^{3}-2^{3}\right)-6 a^{1 / 3} b^{1 / 4}\left(a^{1 / 3} b^{1 / 4}-2\right)\right)^{2 / 3}}{\left(a^{1 / 3} b^{1 / 4}-2\right)^{2}}= \\
& =\frac{\left(\left(a^{1 / 3} b^{1 / 4}-2\right)\left(a^{2 / 3} b^{1 / 2}+2 a^{1 / 3} b^{1 / 4}+4\right)-6 a^{1 / 3} b^{1 / 4}\left(a^{1 / 3} b^{1 / 4}-2\right)\right)^{2 / 3}}{\left(a^{1 / 3} b^{1 / 4}-2\right)^{2}}= \\
& =\frac{\left(\left(a^{1 / 3} b^{1 / 4}-2\right)\left(a^{2 / 3} b^{1 / 2}+2 a^{1 / 3} b^{1 / 4}+4-6 a^{1 / 3} b^{1 / 4}\right)\right)^{2 / 3}}{\left(a^{1 / 3} b^{1 / 4}-2\right)^{2}}= \\
& =\frac{\left(\left(a^{1 / 3} b^{1 / 4}-2\right)\left(a^{2 / 3} b^{1 / 2}-4 a^{1 / 3} b^{1 / 4}+4\right)\right)^{2 / 3}}{\left(a^{1 / 3} b^{1 / 4}-2\right)^{2}}= \\
& =\frac{\left(\left(a^{1 / 3} b^{1 / 4}-2\right)\left(a^{1 / 3} b^{1 / 4}-2\right)^{2}\right)^{2 / 3}}{\left(a^{1 / 3} b^{1 / 4}-2\right)^{2}}=\frac{\left(\left(a^{1 / 3} b^{1 / 4}-2\right)^{3}\right)^{2 / 3}}{\left(a^{1 / 3} b^{1 / 4}-2\right)^{2}}=\frac{\left(a^{1 / 3} b^{1 / 4}-2\right)^{2}}{\left(a^{1 / 3} b^{1 / 4}-2\right)^{2}}=1 .
\end{aligned}
$$
Answer: 1
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.196. $\frac{\left|x^{2}-1\right|+x^{2}}{2 x^{2}-1}-\frac{|x-1|}{x-1}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x \neq \pm \frac{\sqrt{2}}{2}, \\ x \neq 1 .\end{array}\right.$
Expanding the absolute values with consideration of the domain of definition, we consider three cases:
1) $\left\{\begin{array}{l}x \in(-\infty ;-1), \\ \frac{x^{2}-1+x^{2}}{2 x^{2}-1}+\frac{x-1}{x-1}=\frac{2 x^{2}-1}{2 x^{2}-1}+1=1+1=2 ;\end{array}\right.$
2) $\left\{\begin{array}{l}x \in\left[-1 ;-\frac{\sqrt{2}}{2}\right) \cup\left(-\frac{\sqrt{2}}{2} ; \frac{\sqrt{2}}{2}\right) \cup\left(\frac{\sqrt{2}}{2} ; 1\right), \\ \frac{-\left(x^{2}-1\right)+x^{2}}{2 x^{2}-1}+\frac{x-1}{x-1}=\frac{1}{2 x^{2}-1}+1=\frac{1+2 x^{2}}{2 x^{2}-1}=\frac{2 x^{2}}{2 x^{2}-1}\end{array}\right.$
3) $\left\{\begin{array}{l}x \in(1 ; \infty), \\ \frac{x^{2}-1+x^{2}}{2 x^{2}-1}-\frac{x-1}{x-1}=\frac{2 x^{2}-1}{2 x^{2}-1}-1=1-1=0 \text {. }\end{array}\right.$
Answer: 2, if $x \in(-\infty ;-1) ; \frac{2 x^{2}}{2 x^{2}-1}$, if $x \in\left[-1 ;-\frac{\sqrt{2}}{2}\right) \cup\left(-\frac{\sqrt{2}}{2} ; \frac{\sqrt{2}}{2}\right) \cup\left(\frac{\sqrt{2}}{2} ; 1\right) ; 0$, if $x \in(1 ; \infty)$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.204. $\sqrt{2+\sqrt{3}} \cdot \sqrt{2+\sqrt{2+\sqrt{3}}} \cdot \sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}} \cdot \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}$.
|
Solution.
$$
\begin{aligned}
& \sqrt{2+\sqrt{3}} \cdot \sqrt{2+\sqrt{2+\sqrt{3}}} \cdot \sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}} \cdot \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}= \\
& =\sqrt{2+\sqrt{3}} \cdot \sqrt{2+\sqrt{2+\sqrt{3}}} \cdot \sqrt{(2+\sqrt{2+\sqrt{2+\sqrt{3}}})(2-\sqrt{2+\sqrt{2+\sqrt{3}}})}= \\
& =\sqrt{2+\sqrt{3}} \cdot \sqrt{2+\sqrt{2+\sqrt{3}}} \cdot \sqrt{2^{2}-(\sqrt{2+\sqrt{2+\sqrt{3}}})^{2}}= \\
& =\sqrt{2+\sqrt{3}} \cdot \sqrt{2+\sqrt{2+\sqrt{3}}} \cdot \sqrt{4-2-\sqrt{2+\sqrt{3}}}= \\
& =\sqrt{2+\sqrt{3}} \cdot \sqrt{2+\sqrt{2+\sqrt{3}}} \cdot \sqrt{2-\sqrt{2+\sqrt{3}}}= \\
& =\sqrt{2+\sqrt{3}} \cdot \sqrt{(2+\sqrt{2+\sqrt{3}})(2-\sqrt{2+\sqrt{3}})}=\sqrt{2+\sqrt{3}} \cdot \sqrt{4-2-\sqrt{3}}= \\
& =\sqrt{2+\sqrt{3}} \cdot \sqrt{2-\sqrt{3}}=\sqrt{(2+\sqrt{3})(2-\sqrt{3})}=\sqrt{2^{2}-(\sqrt{3})^{2}}=\sqrt{4-3}= \\
& =\sqrt{1}=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.208. $\frac{\left((\sqrt[4]{m}+\sqrt[4]{n})^{2}-(\sqrt[4]{m}-\sqrt[4]{n})^{2}\right)^{2}-(16 m+4 n)}{4 m-n}+\frac{10 \sqrt{m}-3 \sqrt{n}}{\sqrt{n}+2 \sqrt{m}}$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}n \neq 4 m, \\ m>0, \\ n>0 .\end{array}\right.$
$$
\frac{\left((\sqrt[4]{m}+\sqrt[4]{n})^{2}-(\sqrt[4]{m}-\sqrt[4]{n})^{2}\right)^{2}-(16 m+4 n)}{4 m-n}+\frac{10 \sqrt{m}-3 \sqrt{n}}{\sqrt{n}+2 \sqrt{m}}=
$$
$=\frac{(\sqrt{m}+2 \sqrt[4]{m n}+\sqrt{n}-\sqrt{m}+2 \sqrt[4]{m n}-\sqrt{n})^{2}-(16 m+4 n)}{4 m-n}+\frac{10 \sqrt{m}-3 \sqrt{n}}{\sqrt{n}+2 \sqrt{m}}=$
$=\frac{(4 \sqrt[4]{m n})^{2}-(16 m+4 n)}{4 m-n}+\frac{10 \sqrt{m}-3 \sqrt{n}}{\sqrt{n}+2 \sqrt{m}}=\frac{16 \sqrt{m n}-(16 m+4 n)}{4 m-n}+$
$+\frac{10 \sqrt{m}-3 \sqrt{n}}{\sqrt{n}+2 \sqrt{m}}=\frac{-4(4 m-4 \sqrt{m n}+n)}{4 m-n}+\frac{10 \sqrt{m}-3 \sqrt{n}}{2 \sqrt{m}+\sqrt{n}}=$
$=\frac{-4\left((2 \sqrt{m})^{2}-2 \cdot 2 \sqrt{m n}+(\sqrt{n})^{2}\right)}{(2 \sqrt{m})^{2}-(\sqrt{n})^{2}}+\frac{10 \sqrt{m}-3 \sqrt{n}}{2 \sqrt{m}+\sqrt{n}}=$
$=\frac{-4(2 \sqrt{m}-\sqrt{n})^{2}}{(2 \sqrt{m}-\sqrt{n})(2 \sqrt{m}+\sqrt{n})}+\frac{10 \sqrt{m}-3 \sqrt{n}}{2 \sqrt{m}+\sqrt{n}}=\frac{-4(2 \sqrt{m}-\sqrt{n})}{2 \sqrt{m}+\sqrt{n}}+$
$+\frac{10 \sqrt{m}-3 \sqrt{n}}{2 \sqrt{m}+\sqrt{n}}=\frac{-8 \sqrt{m}+4 \sqrt{n}+10 \sqrt{m}-3 \sqrt{n}}{2 \sqrt{m}+\sqrt{n}}=\frac{2 \sqrt{m}+\sqrt{n}}{2 \sqrt{m}+\sqrt{n}}=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.219. $\left(\frac{9}{a+8}-\frac{a^{1 / 3}+2}{a^{2 / 3}-2 a^{1 / 3}+4}\right) \cdot \frac{a^{4 / 3}+8 a^{1 / 3}}{1-a^{2 / 3}}+\frac{5-a^{2 / 3}}{1+a^{1 / 3}}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}a \neq-8, \\ a \neq \pm 1 .\end{array}\right.$
$$
\begin{aligned}
& \left(\frac{9}{a+8}-\frac{a^{1 / 3}+2}{a^{2 / 3}-2 a^{1 / 3}+4}\right) \cdot \frac{a^{4 / 3}+8 a^{1 / 3}}{1-a^{2 / 3}}+\frac{5-a^{2 / 3}}{1+a^{1 / 3}}= \\
& =\left(\frac{9}{\left(a^{1 / 3}+2\right)\left(a^{2 / 3}-2 a^{1 / 3}+4\right)}-\frac{a^{1 / 3}+2}{a^{2 / 3}-2 a^{1 / 3}+4}\right) \cdot \frac{a^{1 / 3}(a+8)}{\left(1-a^{1 / 3}\right)\left(1+a^{1 / 3}\right)}+ \\
& +\frac{5-a^{2 / 3}}{1+a^{1 / 3}}=\frac{3^{2}-\left(a^{1 / 3}+2\right)^{2}}{\left(a^{1 / 3}+2\right)\left(a^{2 / 3}-2 a^{1 / 3}+4\right)} \cdot \frac{a^{1 / 3}(a+8)}{\left(1-a^{1 / 3}\right)\left(1+a^{1 / 3}\right)}+\frac{5-a^{2 / 3}}{1+a^{1 / 3}}= \\
& =\frac{\left(3-a^{1 / 3}-2\right)\left(3+a^{1 / 3}+2\right)}{a+8} \cdot \frac{a^{1 / 3}(a+8)}{\left(1-a^{1 / 3}\right)\left(1+a^{1 / 3}\right)}+\frac{5-a^{2 / 3}}{1+a^{1 / 3}}= \\
& =\frac{\left(5+a^{1 / 3}\right) a^{1 / 3}}{1+a^{1 / 3}}+\frac{5-a^{2 / 3}}{1+a^{1 / 3}}=\frac{5 a^{1 / 3}+a^{2 / 3}+5-a^{2 / 3}}{1+a^{1 / 3}}=\frac{5 a^{1 / 3}+5}{1+a^{1 / 3}}= \\
& =\frac{5\left(a^{1 / 3}+1\right)}{1+a^{1 / 3}}=5 .
\end{aligned}
$$
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.230. $\frac{\sqrt{x-2 \sqrt{2}}}{\sqrt{x^{2}-4 x \sqrt{2}+8}}-\frac{\sqrt{x+2 \sqrt{2}}}{\sqrt{x^{2}+4 x \sqrt{2}+8}} ; x=3$.
|
## Solution.
$$
\begin{aligned}
& \frac{\sqrt{x-2 \sqrt{2}}}{\sqrt{x^{2}-4 x \sqrt{2}+8}}-\frac{\sqrt{x+2 \sqrt{2}}}{\sqrt{x^{2}+4 x \sqrt{2}+8}}=\frac{\sqrt{x-2 \sqrt{2}}}{\sqrt{(x-2 \sqrt{2})^{2}}}-\frac{\sqrt{x+2 \sqrt{2}}}{\sqrt{(x+2 \sqrt{2})^{2}}}= \\
& =\frac{1}{\sqrt{x-2 \sqrt{2}}}-\frac{1}{\sqrt{x+2 \sqrt{2}}}=\frac{\sqrt{x+2 \sqrt{2}}-\sqrt{x-2 \sqrt{2}}}{\sqrt{(x-2 \sqrt{2})(x+2 \sqrt{2})}}= \\
& =\frac{\sqrt{x+2 \sqrt{2}}-\sqrt{x-2 \sqrt{2}}}{\sqrt{x^{2}-8}}=\frac{\sqrt{3+2 \sqrt{2}}-\sqrt{3-2 \sqrt{2}}}{\sqrt{9-8}}=\sqrt{3+2 \sqrt{2}}-\sqrt{3-2 \sqrt{2}}= \\
& =\sqrt{(\sqrt{3+2 \sqrt{2}}-\sqrt{3-2 \sqrt{2}})^{2}}= \\
& =\sqrt{3+2 \sqrt{2}-2 \sqrt{(3+2 \sqrt{2})(3-2 \sqrt{2})}+3-2 \sqrt{2}}=\sqrt{6-2 \sqrt{9-8}}= \\
& =\sqrt{6-2}=\sqrt{4}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.240. $\frac{\sqrt{\left(\frac{9-2 \sqrt{3}}{\sqrt{3}-\sqrt[3]{2}}+3 \sqrt[3]{2}\right) \cdot \sqrt{3}}}{3+\sqrt[6]{108}}$.
|
Solution.
$\frac{\sqrt{\left(\frac{9-2 \sqrt{3}}{\sqrt{3}-\sqrt[3]{2}}+3 \sqrt[3]{2}\right) \cdot \sqrt{3}}}{3+\sqrt[6]{108}}=\frac{\sqrt{\left(\frac{3^{2}-\sqrt{2^{2} \cdot 3}}{\sqrt{3}-\sqrt[3]{2}}+\sqrt[3]{3^{3} \cdot 2}\right) \cdot \sqrt{3}}}{3+\sqrt[6]{27 \cdot 4}}=$
$=\frac{\sqrt{\left(\frac{\sqrt[6]{3^{12}}-\sqrt[6]{2^{6} \cdot 3^{3}}}{\sqrt[6]{3^{3}}-\sqrt[6]{2^{2}}}+\sqrt[6]{3^{6} \cdot 2^{2}}\right) \cdot \sqrt[6]{3^{3}}}}{\sqrt[6]{3^{6}}+\sqrt[6]{3^{3} \cdot 2^{2}}}=$
$=\frac{\sqrt{\frac{\sqrt[6]{3^{12}}-\sqrt[6]{2^{6} \cdot 3^{3}}+\sqrt[6]{3^{9} \cdot 2^{2}}-\sqrt[6]{3^{6} \cdot 2^{4}}}{\sqrt[6]{3^{3}}-\sqrt[6]{2^{2}}} \cdot \sqrt[6]{3^{3}}}}{\sqrt[6]{3^{6}}+\sqrt[6]{3^{3} \cdot 2^{2}}}=$
$=\frac{\sqrt{\frac{\left(\sqrt[6]{3^{9}}-\sqrt[6]{2^{6}}+\sqrt[6]{3^{6} \cdot 2^{2}}-\sqrt[6]{3^{3} \cdot 2^{4}}\right) \cdot \sqrt[6]{3^{3}}}{\sqrt[6]{3^{3}}-\sqrt[6]{2^{2}}} \cdot \sqrt[6]{3^{3}}}}{\sqrt[6]{3^{3}}\left(\sqrt[6]{3^{3}}+\sqrt[6]{2^{2}}\right)}=$
$=\frac{\sqrt{\frac{\left(\sqrt[6]{3^{9}}-\sqrt[6]{3^{3} \cdot 2^{4}}\right)+\left(\sqrt[6]{3^{6} \cdot 2^{2}}-\sqrt[6]{2^{6}}\right)}{\sqrt[6]{3^{3}}-\sqrt[6]{2^{2}}} \cdot \sqrt[6]{3^{6}}}}{\sqrt[6]{3^{3}}\left(\sqrt[6]{3^{3}}+\sqrt[6]{2^{2}}\right)}=$
$=\frac{\sqrt{\frac{\sqrt[6]{3^{3}}\left(\sqrt[6]{3^{6}}-\sqrt[6]{2^{4}}\right)+\sqrt[6]{2^{2}}\left(\sqrt[6]{3^{3}}-\sqrt[6]{2^{4}}\right)}{\sqrt[6]{3^{6}}-\sqrt[6]{2^{2}}} \cdot \sqrt[6]{3^{6}}}}{\sqrt[6]{3^{3}}\left(\sqrt[6]{3^{3}}+\sqrt[6]{2^{2}}\right)}=$
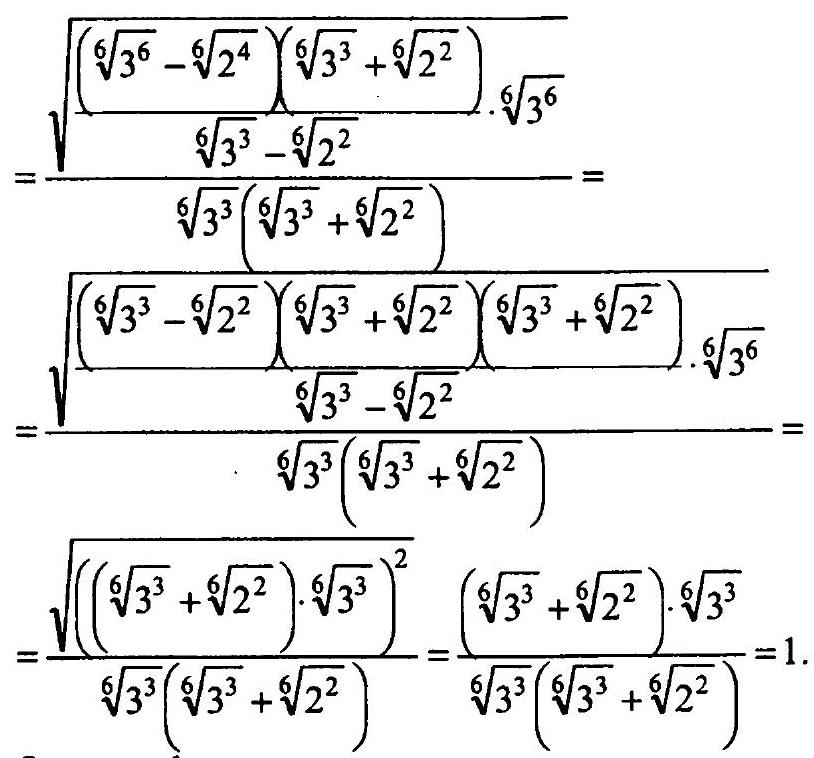
Answer: 1 .
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.254. $\left(\frac{x+2 y}{8 y^{3}\left(x^{2}+2 x y+2 y^{2}\right)}-\frac{(x-2 y): 8 y^{2}}{x^{2}-2 x y+2 y^{2}}\right)+\left(\frac{y^{-2}}{4 x^{2}-8 y^{2}}-\frac{1}{4 x^{2} y^{2}+8 y^{4}}\right)$ $x=\sqrt[4]{6}, \quad y=\sqrt[8]{2}$.
|
Solution.
$$
\begin{aligned}
& \left(\frac{x+2 y}{8 y^{3}\left(x^{2}+2 x y+2 y^{2}\right)}-\frac{(x-2 y): 8 y^{2}}{x^{2}-2 x y+2 y^{2}}\right)+\left(\frac{y^{-2}}{4 x^{2}-8 y^{2}}-\frac{1}{4 x^{2} y^{2}+8 y^{4}}\right)= \\
& =\left(\frac{x+2 y}{8 y^{3}\left(x^{2}+2 x y+2 y^{2}\right)}-\frac{x-2 y}{8 y^{3}\left(x^{2}-2 x y+2 y^{2}\right)}\right)+ \\
& +\left(\frac{1}{4 y^{2}\left(x^{2}-2 y^{2}\right)}-\frac{1}{4 y^{2}\left(x^{2}+2 y^{2}\right)}\right)= \\
& =\frac{(x+2 y)\left(x^{2}+2 y^{2}-2 x y\right)-(x-2 y)\left(x^{2}+2 y^{2}+2 x y\right)}{8 y^{3}\left(x^{2}+2 y^{2}+2 x y\right)\left(x^{2}+2 y^{2}-2 x y\right)}+ \\
& +\frac{x^{2}+2 y^{2}-x^{2}+2 y^{2}}{4 y^{2}\left(x^{2}-2 y^{2}\right)\left(x^{2}+2 y^{2}\right)}=\frac{8 y^{3}}{8 y^{3}\left(\left(x^{2}+2 y^{2}\right)^{2}-(2 x y)^{2}\right)}+
\end{aligned}
$$
$$
\begin{aligned}
& +\frac{4 y^{2}}{4 y^{2}\left(\left(x^{2}\right)^{2}-\left(2 y^{2}\right)^{2}\right)}=\frac{1}{x^{4}+4 y^{4}}+\frac{1}{x^{4}-4 y^{4}}= \\
& =\frac{x^{4}-4 y^{4}+x^{4}+4 y^{4}}{\left(x^{4}+4 y^{4}\right)\left(x^{4}-4 y^{4}\right)}=\frac{2 x^{4}}{x^{8}-16 y^{8}}=\frac{2(\sqrt[4]{6})^{4}}{(\sqrt[4]{6})^{8}-16(\sqrt[8]{2})^{8}}= \\
& =\frac{2 \cdot 6}{36-16 \cdot 2}=\frac{12}{36-32}=\frac{12}{4}=3
\end{aligned}
$$
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.259. $\left(\sqrt[3]{\frac{8 z^{3}+24 z^{2}+18 z}{2 z-3}}-\sqrt[3]{\frac{8 z^{2}-24 z^{2}+18 z}{2 z+3}}\right)-\left(\frac{1}{2} \sqrt[3]{\frac{2 z}{27}-\frac{1}{6 z}}\right)^{-1}$.
|
Solution.
Domain of definition: $z \neq \pm \frac{3}{2}, z \neq 0$.
$$
\begin{aligned}
& \left(\sqrt[3]{\frac{8 z^{3}+24 z^{2}+18 z}{2 z-3}}-\sqrt[3]{\frac{8 z^{2}-24 z^{2}+18 z}{2 z+3}}\right)-\left(\frac{1}{2} \sqrt[3]{\frac{2 z}{27}-\frac{1}{6 z}}\right)^{-1}= \\
& =\sqrt[3]{\frac{2 z\left(4 z^{2}+12 z+9\right)}{2 z-3}}-\sqrt[3]{\frac{2 z\left(4 z^{2}-12 z+9\right)}{2 z+3}}-\left(\frac{1}{2} \sqrt[3]{\frac{4 z^{2}-9}{54 z}}\right)^{-1}= \\
& =\sqrt[3]{\frac{2 z(2 z+3)^{2}}{2 z-3}}-\sqrt[3]{\frac{2 z(2 z-3)^{2}}{2 z+3}}-2 \sqrt[3]{\frac{54 z}{4 z^{2}-9}}= \\
& =\frac{\sqrt[3]{2 z(2 z+3)^{2}}}{\sqrt[3]{2 z-3}}-\frac{\sqrt[3]{2 z(2 z-3)^{2}}}{\sqrt[3]{2 z+3}}-\frac{2 \sqrt[3]{54 z}}{\sqrt[3]{(2 z-3)(2 z+3)}}=
\end{aligned}
$$
$$
\begin{aligned}
& =\frac{\sqrt[3]{2 z(2 z+3)^{3}}-\sqrt[3]{2 z(2 z-3)^{3}}-2 \sqrt[3]{54 z}}{\sqrt[3]{(2 z-3)(2 z+3)}}= \\
& =\frac{\sqrt[3]{2 z}(2 z+3-2 z+3-6)}{\sqrt[3]{4 z^{2}-9}}=\frac{\sqrt[3]{2 z} \cdot 0}{\sqrt[3]{4 z^{2}-9}}=0
\end{aligned}
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.274. $\frac{8-m}{\sqrt[3]{m}+2}:\left(2+\frac{\sqrt[3]{m^{2}}}{\sqrt[3]{m}+2}\right)+\left(\sqrt[3]{m}+\frac{2 \sqrt[3]{m}}{\sqrt[3]{m}-2}\right) \cdot \frac{\sqrt[3]{m^{2}}-4}{\sqrt[3]{m^{2}}+2 \sqrt[3]{m}}$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}m \neq 0, \\ m \neq \pm 8 .\end{array}\right.$
$\frac{8-m}{\sqrt[3]{m}+2}:\left(2+\frac{\sqrt[3]{m^{2}}}{\sqrt[3]{m}+2}\right)+\left(\sqrt[3]{m}+\frac{2 \sqrt[3]{m}}{\sqrt[3]{m}-2}\right) \cdot \frac{\sqrt[3]{m^{2}}-4}{\sqrt[3]{m^{2}}+2 \sqrt[3]{m}}=$
$=\frac{(2-\sqrt[3]{m})\left(4+2 \sqrt[3]{m}+\sqrt[3]{m^{2}}\right)}{\sqrt[3]{m}+2}: \frac{4+2 \sqrt[3]{m}+\sqrt[3]{m^{2}}}{\sqrt[3]{m}+2}+\frac{\sqrt[3]{m^{2}}-2 \sqrt[3]{m}+2 \sqrt[3]{m}}{\sqrt[3]{m}-2} \times$
$\times \frac{(\sqrt[3]{m}-2)(\sqrt[3]{m}+2)}{\sqrt[3]{m}(\sqrt[3]{m}+2)}=\frac{(2-\sqrt[3]{m})\left(4+2 \sqrt[3]{m}+\sqrt[3]{m^{2}}\right)}{\sqrt[3]{m}+2} \cdot \frac{\sqrt[3]{m}+2}{4+2 \sqrt[3]{m}+\sqrt[3]{m^{2}}}+\sqrt[3]{m}=$
$=2-\sqrt[3]{m}+\sqrt[3]{m}=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.282. $\left(\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}+\frac{1-x}{\sqrt{1-x^{2}}-1+x}\right) \cdot\left(\sqrt{\frac{1}{x^{2}}-1}-\frac{1}{x}\right)=0<x<1$.
|
## Solution.
$$
\begin{aligned}
& \left(\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}+\frac{1-x}{\sqrt{1-x^{2}}-1+x}\right) \cdot\left(\sqrt{\frac{1}{x^{2}}-1}-\frac{1}{x}\right)= \\
& =\left(\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}+\frac{\sqrt{(1-x)^{2}}}{\sqrt{(1-x)(1+x)}-\sqrt{(1-x)^{2}}}\right) \cdot\left(\sqrt{\frac{1-x^{2}}{x^{2}}}-\frac{1}{x}\right)= \\
& =\left(\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}+\frac{\sqrt{(1-x)^{2}}}{\sqrt{1-x}(\sqrt{1+x}-\sqrt{1-x})}\right) \cdot\left(\frac{\sqrt{1-x^{2}}}{x}-\frac{1}{x}\right)= \\
& =\left(\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}+\frac{\sqrt{1-x}}{\sqrt{1+x}-\sqrt{1-x}}\right) \cdot\left(\frac{\sqrt{1-x^{2}}-1}{x}\right)= \\
& =\frac{\sqrt{1+x}+\sqrt{1-x}}{\sqrt{1+x}-\sqrt{1-x}} \cdot \frac{\sqrt{1-x^{2}}-1}{x}= \\
& =\frac{(\sqrt{1+x}+\sqrt{1-x})(\sqrt{1+x}+\sqrt{1-x})}{(\sqrt{1+x}-\sqrt{1-x})(\sqrt{1+x}+\sqrt{1-x})} \cdot \frac{\sqrt{1-x^{2}}-1}{x}=
\end{aligned}
$$
$$
\begin{aligned}
& =\frac{(\sqrt{1+x}+\sqrt{1-x})^{2}}{(\sqrt{1+x})^{2}-(\sqrt{1-x})^{2}} \cdot \frac{\sqrt{1-x^{2}}-1}{x}=\frac{1+x+2 \sqrt{1-x^{2}}+1-x}{1+x-1+x} \cdot \frac{\sqrt{1-x^{2}}-1}{x}= \\
& =\frac{2+2 \sqrt{1-x^{2}}}{2 x} \cdot \frac{\sqrt{1-x^{2}}-1}{x}=\frac{\left(\sqrt{1-x^{2}}+1\right)\left(\sqrt{1-x^{2}}-1\right)}{x^{2}}=\frac{\left(\sqrt{1-x^{2}}\right)^{2}-1}{x^{2}}= \\
& =\frac{1-x^{2}-1}{x^{2}}=-\frac{x^{2}}{x^{2}}=-1
\end{aligned}
$$
Answer: -1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.283. $\frac{\left(p q^{-1}+1\right)^{2}}{p q^{-1}-p^{-1} q} \cdot \frac{p^{3} q^{-3}-1}{p^{2} q^{-2}+p q^{-1}+1}: \frac{p^{3} q^{-3}+1}{p q^{-1}+p^{-1} q-1}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}p \neq 0, \\ q \neq 0, \\ p \neq \pm q .\end{array}\right.$
$$
\begin{aligned}
& \frac{\left(p q^{-1}+1\right)^{2}}{p q^{-1}-p^{-1} q} \cdot \frac{p^{3} q^{-3}-1}{p^{2} q^{-2}+p q^{-1}+1}: \frac{p^{3} q^{-3}+1}{p q^{-1}+p^{-1} q-1}= \\
& =\frac{\left(\frac{p}{q}+1\right)^{2}}{\frac{p}{q}-\frac{q}{p}} \cdot \frac{\frac{p^{3}}{q^{3}}-1}{\frac{p^{2}}{q^{2}}+\frac{p}{q}+1}: \frac{\frac{p^{3}}{q^{3}}+1}{\frac{p}{q}+\frac{q}{p}-1}= \\
& =\frac{\left(\frac{p+q}{q}\right)^{2}}{\frac{p^{2}-q^{2}}{p q}} \cdot \frac{\frac{p^{3}-q^{3}}{q^{3}}}{\frac{p^{2}+p q+q^{2}}{q^{2}}}: \frac{\frac{p^{3}+q^{3}}{q^{3}}}{\frac{p^{2}-p q+q^{2}}{p q}}=
\end{aligned}
$$
$$
\begin{aligned}
& =\frac{(p+q)^{2}}{q^{2}} \cdot \frac{p q}{p^{2}-q^{2}} \cdot \frac{p^{3}-q^{3}}{q^{3}} \cdot \frac{q^{2}}{p^{2}+p q+q^{2}}:\left(\frac{p^{3}+q^{3}}{q^{3}} \cdot \frac{p q}{p^{2}-p q+q^{2}}\right)= \\
& =\frac{(p+q)^{2} p}{q(p+q)(p-q)} \cdot \frac{(p-q)\left(p^{2}+p q+q^{2}\right)}{q\left(p^{2}+p q+q^{2}\right)}:\left(\frac{(p+q)\left(p^{2}-p q+q^{2}\right) p}{q^{2}\left(p^{2}-p q+q^{2}\right)}\right)= \\
& =\frac{p(p+q)}{q^{2}}: \frac{p(p+q)}{q^{2}}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.288. Check that the number $x=\sqrt[3]{4+\sqrt{80}}-\sqrt[3]{\sqrt{80}-4}$ is a root of the equation $x^{3}+12 x-8=0$.
|
## Solution.
Let $x=\sqrt[3]{4+\sqrt{80}}-\sqrt[3]{\sqrt{80}-4}=\sqrt[3]{4+\sqrt{80}}+\sqrt[3]{4-\sqrt{80}}$.
Substituting this value of $x$ into the equation, we get
$$
(\sqrt[3]{4+\sqrt{80}}+\sqrt[3]{4-\sqrt{80}})^{3}+12(\sqrt[3]{4+\sqrt{80}}+\sqrt[3]{4-\sqrt{80}})-8=0
$$
$$
\begin{aligned}
& (\sqrt[3]{4+\sqrt{80}})^{3}+3(\sqrt[3]{4+\sqrt{80}})^{2} \cdot \sqrt[3]{4-\sqrt{80}}+3 \sqrt[3]{4+\sqrt{80}} \times \\
& \times(\sqrt[3]{4-\sqrt{80}})^{2}+(\sqrt[3]{4-\sqrt{80}})^{3}+12(\sqrt[3]{4+\sqrt{80}}+\sqrt[3]{4-\sqrt{80}})-8=0 \\
& 4+\sqrt{80}+3 \sqrt[3]{(4+\sqrt{80})(4-\sqrt{80})} \cdot(\sqrt[3]{4+\sqrt{80}}+\sqrt[3]{4-\sqrt{80}})+4-\sqrt{80}+ \\
& +12(\sqrt[3]{4+\sqrt{80}}+\sqrt[3]{4-\sqrt{80}})-8=0 \\
& 4+\sqrt{80}+3 \sqrt[3]{16-80} \cdot(\sqrt[3]{4+\sqrt{80}}+\sqrt[3]{4-\sqrt{80}})+4-\sqrt{80}+ \\
& +12(\sqrt[3]{4+\sqrt{80}}+\sqrt[3]{4-\sqrt{80}})-8=0 \\
& 4+\sqrt{80}-12(\sqrt[3]{4+\sqrt{80}}+\sqrt[3]{4-\sqrt{80}})+4-\sqrt{80}+ \\
& +12(\sqrt[3]{4+\sqrt{80}}+\sqrt[3]{4-\sqrt{80}})-8=0 \\
& 0=0 .
\end{aligned}
$$
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
2.297. $\sqrt[3]{26+15 \sqrt{3}} \cdot(2-\sqrt{3})=1$.
|
Solution.
$\sqrt[3]{26+15 \sqrt{3}} \cdot(2-\sqrt{3})=\sqrt[3]{26+15 \sqrt{3}} \cdot \sqrt[3]{(2-\sqrt{3})^{3}}=$ $=\sqrt[3]{26+15 \sqrt{3}} \cdot \sqrt[3]{8-12 \sqrt{3}+18-3 \sqrt{3}}=\sqrt[3]{26+15 \sqrt{3}} \cdot \sqrt[3]{26-15 \sqrt{3}}=$ $=\sqrt[3]{(26+15 \sqrt{3})(26-15 \sqrt{3})}=\sqrt[3]{26^{2}-(15 \sqrt{3})^{2}}=\sqrt[3]{676-675}=$ $=\sqrt[3]{1}=1$.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
2.301. $\frac{\sqrt{5-2 \sqrt{6}} \cdot(5+2 \sqrt{6})(49-20 \sqrt{6})}{\sqrt{27}-3 \sqrt{18}+3 \sqrt{12}-\sqrt{8}}=1$.
|
Solution.
$$
\begin{aligned}
& \frac{\sqrt{5-2 \sqrt{6}} \cdot(5+2 \sqrt{6})(49-20 \sqrt{6})}{\sqrt{27}-3 \sqrt{18}+3 \sqrt{12}-\sqrt{8}}= \\
& =\frac{\sqrt{3-2 \sqrt{3 \cdot 2}+2} \cdot(3+2 \sqrt{3 \cdot 2}+2)(49-20 \sqrt{6})}{\sqrt{9 \cdot 3}-3 \sqrt{9 \cdot 2}+3 \sqrt{4 \cdot 3}-\sqrt{4 \cdot 2}}=
\end{aligned}
$$
$$
\begin{aligned}
& =\frac{\sqrt{(\sqrt{3}-\sqrt{2})^{2}} \cdot(\sqrt{3}+\sqrt{2})^{2}(49-20 \sqrt{6})}{3 \sqrt{3}-9 \sqrt{2}+6 \sqrt{3}-2 \sqrt{2}}=\frac{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})^{2}(49-20 \sqrt{6})}{9 \sqrt{3}-11 \sqrt{2}}= \\
& =\frac{((\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})) \cdot(\sqrt{3}+\sqrt{2})(49-20 \sqrt{6})}{9 \sqrt{3}-11 \sqrt{2}}= \\
& =\frac{\left((\sqrt{3})^{2}-(\sqrt{2})^{2}\right) \cdot(49 \sqrt{3}-20 \sqrt{18}+49 \sqrt{2}-20 \sqrt{12})}{9 \sqrt{3}-11 \sqrt{2}}= \\
& =\frac{(3-2)(49 \sqrt{3}-20 \sqrt{9 \cdot 2}+49 \sqrt{2}-20 \sqrt{4 \cdot 3})}{9 \sqrt{3}-11 \sqrt{2}}= \\
& =\frac{49 \sqrt{3}-60 \sqrt{2}+49 \sqrt{2}-40 \sqrt{3}}{9 \sqrt{3}-11 \sqrt{2}}=\frac{9 \sqrt{3}-11 \sqrt{2}}{9 \sqrt{3}-11 \sqrt{2}}=1 .
\end{aligned}
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.235. $\frac{1-2 \cos ^{2} \alpha}{2 \operatorname{tg}\left(2 \alpha-\frac{\pi}{4}\right) \sin ^{2}\left(\frac{\pi}{4}+2 \alpha\right)}=1$.
|
## Solution.
$$
\begin{aligned}
& \frac{1-2 \cos ^{2} 2 \alpha}{2 \operatorname{tg}\left(2 \alpha-\frac{\pi}{4}\right) \sin ^{2}\left(\frac{\pi}{4}+2 \alpha\right)}=\frac{1-1-\cos 4 \alpha}{\frac{\sin \left(4 \alpha-\frac{\pi}{2}\right)}{1+\cos \left(4 \alpha-\frac{\pi}{2}\right)} \cdot\left(1-\cos \left(\frac{\pi}{4}+2 \alpha\right)\right)}= \\
& =\frac{-\cos 4 \alpha\left(1+\cos \left(4 \alpha-\frac{\pi}{2}\right)\right)}{\sin \left(4 \alpha-\frac{\pi}{2}\right)\left(1-\cos \left(\frac{\pi}{2}+4 \alpha\right)\right)}=\frac{-\cos 4 \alpha\left(1+\cos \left(\frac{\pi}{2}-4 \alpha\right)\right)}{-\sin \left(\frac{\pi}{2}-4 \alpha\right)\left(1-\cos \left(\frac{\pi}{2}+4 \alpha\right)\right)}=
\end{aligned}
$$
$=\frac{\cos 4 \alpha(1+\sin 4 \alpha)}{\cos 4 \alpha(1+\sin 4 \alpha)}=1$.
The identity is proven.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3.243. $(\cos 8 \alpha \tan 4 \alpha-\sin 8 \alpha)(\cos 8 \alpha \cot 4 \alpha+\sin 8 \alpha)$.
|
## Solution.
$$
\begin{aligned}
& (\cos 8 \alpha \tan 4 \alpha - \sin 8 \alpha)(\cos 8 \alpha \cot 4 \alpha + \sin 8 \alpha)= \\
& =\left(\frac{\cos 8 \alpha \sin 4 \alpha}{\cos 4 \alpha} - \sin 8 \alpha\right)\left(\frac{\cos 8 \alpha \cos 4 \alpha}{\sin 4 \alpha} + \sin 8 \alpha\right)= \\
& =\frac{\sin 4 \alpha \cos 8 \alpha - \cos 4 \alpha \sin 8 \alpha}{\cos 4 \alpha} \cdot \frac{\cos 8 \alpha \cos 4 \alpha + \sin 8 \alpha \sin 4 \alpha}{\sin 4 \alpha}= \\
& =\frac{\sin (-4 \alpha)}{\cos 4 \alpha} \cdot \frac{\cos 4 \alpha}{\sin 4 \alpha}=\frac{-\sin 4 \alpha \cos 4 \alpha}{\sin 4 \alpha \cos 4 \alpha}=-1 .
\end{aligned}
$$
Answer: -1 .
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.244. $\sin ^{2} 2 \alpha+\sin ^{2} \beta+\cos (2 \alpha+\beta) \cos (2 \alpha-\beta)$.
|
## Solution.
$$
\begin{aligned}
& \sin ^{2} 2 \alpha+\sin ^{2} \beta+\cos (2 \alpha+\beta) \cos (2 \alpha-\beta)= \\
& =\frac{1-\cos 4 \alpha}{2}+\frac{1-\cos 2 \beta}{2}+\cos (2 \alpha+\beta) \cos (2 \alpha-\beta)= \\
& =\frac{1}{2}(1-\cos 4 \alpha+1-\cos 2 \beta)+\cos (2 \alpha+\beta) \cos (2 \alpha-\beta)= \\
& =-\left(\frac{\cos 4 \alpha}{2}+\frac{\cos 2 \beta}{2}-1\right)+\cos (2 \alpha+\beta) \cos (2 \alpha-\beta)= \\
& =\left[\cos x \cos y=\frac{1}{2}(\cos (x-y)+\cos (x+y))\right]= \\
& =-\frac{\cos 4 \alpha}{2}-\frac{\cos 2 \beta}{2}+1+\frac{\cos 4 \alpha}{2}+\frac{\cos 2 \beta}{2}=1
\end{aligned}
$$
Answer: 1 .
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.247. $\left(1-\operatorname{ctg}^{2}\left(\frac{3}{2} \pi-2 \alpha\right)\right) \sin ^{2}\left(\frac{\pi}{2}+2 \alpha\right) \operatorname{tg}\left(\frac{5}{4} \pi-2 \alpha\right)+\cos \left(4 \alpha-\frac{\pi}{2}\right)$.
|
## Solution.
$$
\begin{aligned}
& \left(1-\operatorname{ctg}^{2}\left(\frac{3}{2} \pi-2 \alpha\right)\right) \sin ^{2}\left(\frac{\pi}{2}+2 \alpha\right) \operatorname{tg}\left(\frac{5}{4} \pi-2 \alpha\right)+\cos \left(4 \alpha-\frac{\pi}{2}\right)= \\
& =\left(1-\left(\operatorname{ctg}\left(\frac{3}{2} \pi-2 \alpha\right)\right)^{2}\right)\left(\sin \left(\frac{\pi}{2}+2 \alpha\right)\right)^{2} \times \\
& \times \operatorname{tg}\left(\pi+\left(\frac{\pi}{4}-2 \alpha\right)\right)+\cos \left(\frac{\pi}{2}-4 \alpha\right)= \\
& =\left(1-\operatorname{tg}^{2} 2 \alpha\right) \cos ^{2} 2 \alpha \operatorname{tg}\left(\frac{\pi}{4}-2 \alpha\right)+\sin 4 \alpha= \\
& =\left(1-\frac{\sin ^{2} 2 \alpha}{\cos ^{2} 2 \alpha}\right) \cos ^{2} 2 \alpha \operatorname{tg}\left(\frac{\pi}{4}-2 \alpha\right)+\sin 4 \alpha=
\end{aligned}
$$
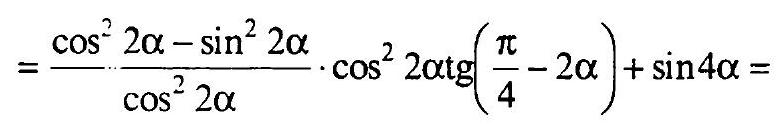
$=\cos 4 \alpha \operatorname{tg}\left(\frac{\pi}{4}-2 \alpha\right)+\sin 4 \alpha=\frac{\cos 4 \alpha\left(1-\cos \left(\frac{\pi}{2}-4 \alpha\right)\right)}{\sin \left(\frac{\pi}{2}-4 \alpha\right)}+\sin 4 \alpha=$
$=\frac{\cos 4 \alpha(1-\sin 4 \alpha)}{\cos 4 \alpha}+\sin 4 \alpha=1-\sin 4 \alpha+\sin 4 \alpha=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.282. $\frac{\sin 8 \alpha+\sin 9 \alpha+\sin 10 \alpha+\sin 11 \alpha}{\cos 8 \alpha+\cos 9 \alpha+\cos 10 \alpha+\cos 11 \alpha} \times$
$\times \frac{\cos 8 \alpha-\cos 9 \alpha-\cos 10 \alpha+\cos 11 \alpha}{\sin 8 \alpha-\sin 9 \alpha-\sin 10 \alpha+\sin 11 \alpha}$.
|
Solution.
$$
\begin{aligned}
& \frac{\sin 8 \alpha + \sin 9 \alpha + \sin 10 \alpha + \sin 11 \alpha}{\cos 8 \alpha + \cos 9 \alpha + \cos 10 \alpha + \cos 11 \alpha} \cdot \frac{\cos 8 \alpha - \cos 9 \alpha - \cos 10 \alpha + \cos 11 \alpha}{\sin 8 \alpha - \sin 9 \alpha - \sin 10 \alpha + \sin 11 \alpha} = \\
& = \frac{(\sin 11 \alpha + \sin 8 \alpha) + (\sin 10 \alpha + \sin 9 \alpha)}{(\cos 11 \alpha + \cos 8 \alpha) + (\cos 10 \alpha + \cos 9 \alpha)} \times \\
& \times \frac{(\cos 11 \alpha + \cos 8 \alpha) - (\cos 10 \alpha + \cos 9 \alpha)}{(\sin 11 \alpha + \sin 8 \alpha) - (\sin 10 \alpha + \sin 9 \alpha)} = \\
& = \left[\cos x + \cos y = 2 \cos \frac{x + y}{2} \cos \frac{x - y}{2}\right. \\
& \left.\sin x + \sin y = 2 \sin \frac{x + y}{2} \cos \frac{x - y}{2}\right] =
\end{aligned}
$$
$$
\begin{aligned}
& = \frac{2 \sin \frac{19 \alpha}{2} \cos \frac{3 \alpha}{2} + 2 \sin \frac{19 \alpha}{2} \cos \frac{\alpha}{2}}{2 \cos \frac{19 \alpha}{2} \cos \frac{3 \alpha}{2} + 2 \cos \frac{19 \alpha}{2} \cos \frac{\alpha}{2}} \times \\
& \times \frac{2 \cos \frac{19 \alpha}{2} \cos \frac{3 \alpha}{2} - 2 \cos \frac{19 \alpha}{2} \cos \frac{\alpha}{2}}{2 \sin \frac{19 \alpha}{2} \cos \frac{3 \alpha}{2} - 2 \sin \frac{19 \alpha}{2} \cos \frac{\alpha}{2}} = \\
& = \frac{2 \sin \frac{19 \alpha}{2} \left( \cos \frac{3 \alpha}{2} + \cos \frac{\alpha}{2} \right)}{2 \cos \frac{19 \alpha}{2} \left( \cos \frac{3 \alpha}{2} + \cos \frac{\alpha}{2} \right)} \cdot \frac{2 \cos \frac{19 \alpha}{2} \left( \cos \frac{3 \alpha}{2} - \cos \frac{\alpha}{2} \right)}{2 \sin \frac{19 \alpha}{2} \left( \cos \frac{3 \alpha}{2} - \cos \frac{\alpha}{2} \right)} = \\
& = \frac{\sin \frac{19 \alpha}{2}}{\cos \frac{19 \alpha}{2}} \cdot \frac{\cos \frac{19 \alpha}{2}}{\sin \frac{19 \alpha}{2}} = 1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.332. $\frac{\sin 24^{\circ} \cos 6^{\circ}-\sin 6^{\circ} \sin 66^{\circ}}{\sin 21^{\circ} \cos 39^{\circ}-\sin 39^{\circ} \cos 21^{\circ}}=-1$.
|
Solution.
$$
\begin{aligned}
& \frac{\sin 24^{\circ} \cos 6^{\circ}-\sin 6^{\circ} \sin 66^{\circ}}{\sin 21^{\circ} \cos 39^{\circ}-\sin 39^{\circ} \cos 21^{\circ}}=\frac{\sin 24^{\circ} \cos 6^{\circ}-\sin 6^{\circ} \sin \left(90^{\circ}-24^{\circ}\right)}{\sin 21^{\circ} \cos 39^{\circ}-\sin 39^{\circ} \cos 21^{\circ}}= \\
& =[\sin x \cos y-\cos x \sin y=\sin (x-y)]=\frac{\sin 24^{\circ} \cos 6^{\circ}-\cos 24^{\circ} \sin 6^{\circ}}{\sin 21^{\circ} \cos 39^{\circ}-\cos 21^{\circ} \sin 39^{\circ}}= \\
& =\frac{\sin 18^{\circ}}{\sin \left(-18^{\circ}\right)}=\frac{\sin 18^{\circ}}{-\sin 18^{\circ}}=-1
\end{aligned}
$$
The equality is valid.
|
-1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3.333. $\frac{\sin 20^{\circ} \cos 10^{\circ}+\cos 160^{\circ} \cos 100^{\circ}}{\sin 21^{\circ} \cos 9^{\circ}+\cos 159^{\circ} \cos 99^{\circ}}=1$.
|
## Solution.
$\frac{\sin 20^{\circ} \cos 10^{\circ}+\cos 160^{\circ} \cos 100^{\circ}}{\sin 21^{\circ} \cos 9^{\circ}+\cos 159^{\circ} \cos 99^{\circ}}=$
$$
\begin{aligned}
& =\frac{\sin 20^{\circ} \cos 10^{\circ}+\cos \left(180^{\circ}-20^{\circ}\right) \cos \left(90^{\circ}+10^{\circ}\right)}{\sin 21^{\circ} \cos 9^{\circ}+\cos \left(180^{\circ}-21^{\circ}\right) \cos \left(90^{\circ}+9^{\circ}\right)}= \\
& =\frac{\sin 20^{\circ} \cos 10^{\circ}+\cos 20^{\circ} \sin 10^{\circ}}{\sin 21^{\circ} \cos 9^{\circ}+\cos 21^{\circ} \sin 9^{\circ}}=\frac{\sin 30^{\circ}}{\sin 30^{\circ}}=1
\end{aligned}
$$
The equality holds.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3.335.
$$
\frac{\cos 64^{\circ} \cos 4^{\circ}-\cos 86^{\circ} \cos 26^{\circ}}{\cos 71^{\circ} \cos 41^{\circ}-\cos 49^{\circ} \cos 19^{\circ}}=-1
$$
|
Solution.
$$
\begin{aligned}
& \frac{\cos 64^{\circ} \cos 4^{\circ}-\cos 86^{\circ} \cos 26^{\circ}}{\cos 71^{\circ} \cos 41^{\circ}-\cos 49^{\circ} \cos 19^{\circ}}= \\
& =\frac{\cos \left(90^{\circ}-26^{\circ}\right) \cos 4^{\circ}-\cos \left(90^{\circ}-4^{\circ}\right) \cos 26^{\circ}}{\cos \left(90^{\circ}-19^{\circ}\right) \cos 41^{\circ}-\cos 19^{\circ} \cos \left(90^{\circ}-41^{\circ}\right)}= \\
& =[\sin x \cos y-\cos x \sin y=\sin (x-y)]= \\
& =\frac{\sin 26^{\circ} \cos 4^{\circ}-\sin 4^{\circ} \cos 26^{\circ}}{\sin 19^{\circ} \cos 41^{\circ}-\cos 19^{\circ} \sin 41^{\circ}}=\frac{\sin 22^{\circ}}{-\sin 22^{\circ}}=-1
\end{aligned}
$$
The equality is valid.
|
-1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3.336. $\frac{\cos 66^{\circ} \cos 6^{\circ}+\cos 84^{\circ} \cos 24^{\circ}}{\cos 65^{\circ} \cos 5^{\circ}+\cos 85^{\circ} \cos 25^{\circ}}=1$.
|
Solution.
$$
\begin{aligned}
& \frac{\cos 66^{\circ} \cos 6^{\circ}+\cos 84^{\circ} \cos 24^{\circ}}{\cos 65^{\circ} \cos 5^{\circ}+\cos 85^{\circ} \cos 25^{\circ}}= \\
& =\frac{\cos 66^{\circ} \cos 6^{\circ}+\cos \left(90^{\circ}-6^{\circ}\right) \cos \left(90^{\circ}-66^{\circ}\right)}{\cos 65^{\circ} \cos 5^{\circ}+\cos \left(90^{\circ}-5^{\circ}\right) \cos \left(90^{\circ}-65^{\circ}\right)}= \\
& =[\cos x \cos y+\sin x \sin y=\cos (x-y)]=\frac{\cos 66^{\circ} \cos 6^{\circ}+\sin 66^{\circ} \sin 6^{\circ}}{\cos 65^{\circ} \cos 5^{\circ}+\sin 65^{\circ} \sin 5^{\circ}}= \\
& =\frac{\cos 60^{\circ}}{\cos 60^{\circ}}=1
\end{aligned}
$$
The equality holds.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3.341. $\frac{\sin 20^{\circ} \sin 40^{\circ} \sin 60^{\circ} \sin 80^{\circ}}{\sin 10^{\circ} \sin 30^{\circ} \sin 50^{\circ} \sin 70^{\circ}}=3$.
|
Solution.
$$
\begin{aligned}
& \frac{\left(\sin 20^{\circ} \sin 40^{\circ}\right)\left(\sin 60^{\circ} \sin 80^{\circ}\right)}{\left(\sin 10^{\circ} \sin 30^{\circ}\right)\left(\sin 50^{\circ} \sin 70^{\circ}\right)}=\left[\sin x \sin y=\frac{1}{2}(\cos (x-y)-\cos (x+y))\right]= \\
& =\frac{\left(\cos 20^{\circ}-\cos 60^{\circ}\right)\left(\cos 20^{\circ}-\cos 140^{\circ}\right)}{\left(\cos 20^{\circ}-\cos 40^{\circ}\right)\left(\cos 20^{\circ}-\cos 120^{\circ}\right)}= \\
& =\frac{\left(\cos 20^{\circ}-\frac{1}{2}\right)\left(\cos 20^{\circ}-\cos \left(180^{\circ}-40^{\circ}\right)\right)}{\left(\cos 20^{\circ}-\cos 40^{\circ}\right)\left(\cos 20^{\circ}+\frac{1}{2}\right)}= \\
& =\frac{\left(2 \cos 20^{\circ}-1\right)\left(\cos 20^{\circ}+\cos 40^{\circ}\right)}{\left(\cos 20^{\circ}-\cos 40^{\circ}\right)\left(2 \cos 20^{\circ}+1\right)}= \\
& =\frac{2 \cos ^{2} 20^{\circ}+2 \cos 20^{\circ} \cos 40^{\circ}-\cos 20^{\circ}-\cos 40^{\circ}}{2 \cos ^{2} 20^{\circ}+\cos 20^{\circ}-2 \cos 40^{\circ} \cos 20^{\circ}-\cos 40^{\circ}}= \\
& =\left[\cos x \cos y=\frac{1}{2}(\cos (x-y)+\cos (x+y))\right]= \\
& =\frac{2 \cos ^{2} 20^{\circ}+\cos 20^{\circ}+\cos 60^{\circ}-\cos 20^{\circ}-\cos 40^{\circ}}{2 \cos ^{2} 20^{\circ}+\cos 20^{\circ}-\cos 60^{\circ}-\cos 20^{\circ}-\cos 40^{\circ}}= \\
& =\frac{2 \cos ^{2} 20^{\circ}+\frac{1}{2}-\cos 2\left(20^{\circ}\right)}{2 \cos ^{2} 20^{\circ}-\frac{1}{2}-\cos 2\left(20^{\circ}\right)}=\frac{2 \cos ^{2} 20^{\circ}+\frac{1}{2}-2 \cos ^{2} 20^{\circ}+1}{2 \cos ^{2} 20^{\circ}-\frac{1}{2}-2 \cos ^{2} 20^{\circ}}=\frac{\frac{3}{2}}{\frac{1}{2}}=3 .
\end{aligned}
$$
## The equality is valid.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.347. $8 \cos \frac{4 \pi}{9} \cos \frac{2 \pi}{9} \cos \frac{\pi}{9}=1$.
|
## Solution.
$$
8 \cos \frac{4 \pi}{9} \cos \frac{2 \pi}{9} \cos \frac{\pi}{9}=8 \cos 80^{\circ} \cos 40^{\circ} \cos 20^{\circ}=
$$
$=\frac{8 \cos 80^{\circ} \cos 40^{\circ} \cos 20^{\circ} \sin 20^{\circ}}{\sin 20^{\circ}}=\frac{4 \cos 80^{\circ} \cos 40^{\circ}\left(2 \cos 20^{\circ} \sin 20^{\circ}\right)}{\sin 20^{\circ}}=$
$=\frac{4 \cos 80^{\circ} \cos 40^{\circ} \sin 40^{\circ}}{\sin 20^{\circ}}=\frac{2 \cos 80^{\circ}\left(2 \cos 40^{\circ} \sin 40^{\circ}\right)}{\sin 20^{\circ}}=\frac{2 \cos 80^{\circ} \sin 80^{\circ}}{\sin 20^{\circ}}=$
$=\frac{\sin 160^{\circ}}{\sin 20^{\circ}}=\frac{\sin \left(180^{\circ}-20^{\circ}\right)}{\sin 20^{\circ}}=\frac{\sin 20^{\circ}}{\sin 20^{\circ}}=1$.
The equality holds.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3.348. $\operatorname{tg} 9^{\circ}+\operatorname{tg} 15^{\circ}-\operatorname{tg} 27^{\circ}-\operatorname{ctg} 27^{\circ}+\operatorname{ctg} 9^{\circ}+\operatorname{ctg} 15^{\circ}=8$.
|
## Solution.
$$
\begin{aligned}
& \operatorname{tg} 9^{\circ}+\operatorname{tg} 15^{\circ}-\operatorname{tg} 27^{\circ}-\operatorname{ctg} 27^{\circ}+\operatorname{ctg} 9^{\circ}+\operatorname{ctg} 15^{\circ}= \\
& =\left(\operatorname{tg} 9^{\circ}+\operatorname{ctg} 9^{\circ}\right)+\left(\operatorname{tg} 15^{\circ}+\operatorname{ctg} 15^{\circ}\right)-\left(\operatorname{tg} 27^{\circ}+\operatorname{ctg} 27^{\circ}\right)= \\
& =\left(\frac{\sin 9^{\circ}}{\cos 9^{\circ}}+\frac{\cos 9^{\circ}}{\sin 9^{\circ}}\right)+\left(\frac{\sin 15^{\circ}}{\cos 15^{\circ}}+\frac{\cos 15^{\circ}}{\sin 15^{\circ}}\right)-\left(\frac{\sin 27^{\circ}}{\cos 27^{\circ}}+\frac{\cos 27^{\circ}}{\sin 27^{\circ}}\right)= \\
& =\frac{\sin ^{2} 9^{\circ}+\cos ^{2} 9^{\circ}}{\sin 9^{\circ} \cos 9^{\circ}}+\frac{\sin ^{2} 15^{\circ}+\cos ^{2} 15^{\circ}}{\sin 15^{\circ} \cos 15^{\circ}}-\frac{\sin ^{2} 27^{\circ}+\cos ^{2} 27^{\circ}}{\sin 27^{\circ} \cos 27^{\circ}}= \\
& =\frac{1}{\sin 9^{\circ} \cos 9^{\circ}}+\frac{1}{\sin 15^{\circ} \cos 15^{\circ}}-\frac{1}{\sin 27^{\circ} \cos 27^{\circ}}= \\
& =\frac{2}{2 \sin 9^{\circ} \cos 9^{\circ}}+\frac{2}{2 \sin 15^{\circ} \cos 15^{\circ}}-\frac{2}{2 \sin 27^{\circ} \cos 27^{\circ}}= \\
& =\frac{2}{\sin 18^{\circ}}+\frac{2}{\sin 30^{\circ}}-\frac{2}{\sin 54^{\circ}}=\frac{2}{\sin 18^{\circ}}+\frac{2}{\frac{1}{2}}-\frac{2}{\sin 3\left(18^{\circ}\right)}= \\
& =\frac{2}{\sin 18^{\circ}}+4-\frac{2}{\sin 3\left(18^{\circ}\right)}=[\sin 3 x=3 \sin x-4 \sin x]= \\
& =\frac{2}{\sin 18^{\circ}}+4-\frac{2}{3 \sin 18^{\circ}-4 \sin ^{3} 18^{\circ}}=\frac{1}{\sin 18^{\circ}}+4-\frac{2}{3 \sin 18^{\circ}-4\left(\sin 18^{\circ}\right)^{3}}= \\
& =\left[\sin 18^{\circ}=\frac{\sqrt{5}-1}{4}\left(\mathrm{~cm} . N_{0} 3.339 \text { b) }\right)\right]=
\end{aligned}
$$
$$
\begin{aligned}
& =\frac{2}{\frac{\sqrt{5}-1}{4}}+4-\frac{2}{\frac{3(\sqrt{5}-1)}{4}-\frac{4(\sqrt{5}-1)^{3}}{64}}= \\
& =\frac{8}{\sqrt{5}-1}+4-\frac{128}{48(\sqrt{5}-1)-4(8 \sqrt{5}-16)}=\frac{8}{\sqrt{5}-1}+4-\frac{128}{16 \sqrt{5}+16}= \\
& =\frac{8}{\sqrt{5}-1}+4-\frac{8}{\sqrt{5}+1}=\frac{8(\sqrt{5}+1)-8(\sqrt{5}-1)}{5-1}+4=8
\end{aligned}
$$
The equality is valid.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.349. $\frac{\sin \left(\alpha-\frac{3}{2} \pi\right) \tan\left(\frac{\pi}{4}+\frac{\alpha}{2}\right)}{1+\cos \left(\alpha-\frac{5}{2} \pi\right)}=1$.
|
Solution.
$$
\begin{aligned}
& \frac{\sin \left(\alpha-\frac{3}{2} \pi\right) \tan\left(\frac{\pi}{4}+\frac{\alpha}{2}\right)}{1+\cos \left(\alpha-\frac{5}{2} \pi\right)}=\frac{-\sin \left(\frac{3}{2} \pi-\alpha\right) \tan\left(\frac{\pi}{4}+\frac{\alpha}{2}\right)}{1+\cos \left(\frac{5}{2} \pi-\alpha\right)}= \\
& =\left[\tan \frac{x}{2}=\frac{1-\cos x}{\sin x}, x \neq \pi+2 \pi n, n \in Z\right]=\frac{\cos \alpha \cdot \frac{1-\cos \left(\frac{\pi}{2}+\alpha\right)}{\sin \left(\frac{\pi}{2}+\alpha\right)}}{1+\sin \alpha}= \\
& =\frac{\cos \alpha \cdot \frac{1+\sin \alpha}{\cos \alpha}}{1+\sin \alpha}=1
\end{aligned}
$$
The equality is valid.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3.353. $\frac{1}{\sin 10^{\circ}}-\frac{\sqrt{3}}{\cos 10^{\circ}}=4$.
|
Solution.
$$
\begin{aligned}
& \frac{1}{\sin 10^{\circ}}-\frac{\sqrt{3}}{\cos 10^{\circ}}=\frac{\cos 10^{\circ}-\sqrt{3} \sin 10^{\circ}}{\sin 10^{\circ} \cos 10^{\circ}}=\frac{2\left(\frac{1}{2} \cos 10^{\circ}-\frac{\sqrt{3}}{2} \sin 10^{\circ}\right)}{\sin 10^{\circ} \cos 10^{\circ}}= \\
& =\frac{2 \cdot 2\left(\sin 30^{\circ} \cos 10^{\circ}-\cos 30^{\circ} \sin 10^{\circ}\right)}{2 \sin 10^{\circ} \cos 10^{\circ}}=
\end{aligned}
$$
$=[\sin x \cos y-\cos x \sin y=\sin (x-y) ; 2 \sin x \cos y=\sin 2 x]=$ $=\frac{4 \sin 20^{\circ}}{\sin 20^{\circ}}=4$.
The equality holds.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.358. $\frac{\cos 68^{\circ} \cos 8^{\circ}-\cos 82^{\circ} \cos 22^{\circ}}{\cos 53^{\circ} \cos 23^{\circ}-\cos 67^{\circ} \cos 37^{\circ}}$.
|
## Solution.
$$
\begin{aligned}
& \frac{\cos 68^{\circ} \cos 8^{\circ}-\cos 82^{\circ} \cos 22^{\circ}}{\cos 53^{\circ} \cos 23^{\circ}-\cos 67^{\circ} \cos 37^{\circ}}= \\
& =\frac{\cos 68^{\circ} \cos 8^{\circ}-\cos \left(90^{\circ}-8^{\circ}\right) \cos \left(90^{\circ}-68^{\circ}\right)}{\cos 53^{\circ} \cos 23^{\circ}-\cos \left(90^{\circ}-23^{\circ}\right) \cos \left(90^{\circ}-53^{\circ}\right)}= \\
& =\frac{\cos 68^{\circ} \cos 8^{\circ}-\sin 68^{\circ} \sin 8^{\circ}}{\cos 53^{\circ} \cos 23^{\circ}-\sin 53^{\circ} \sin 23^{\circ}}=[\cos x \cos y-\sin x \sin y=\cos (x+y)]=
\end{aligned}
$$
$$
=\frac{\cos 76^{\circ}}{\cos 76^{\circ}}=1
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.359. $\frac{\cos 70^{\circ} \cos 10^{\circ}+\cos 80^{\circ} \cos 20^{\circ}}{\cos 69^{\circ} \cos 9^{\circ}+\cos 81^{\circ} \cos 21^{\circ}}$.
|
## Solution.
$$
\frac{\cos 70^{\circ} \cos 10^{\circ}+\cos 80^{\circ} \cos 20^{\circ}}{\cos 69^{\circ} \cos 9^{\circ}+\cos 81^{\circ} \cos 21^{\circ}}=
$$
$$
\begin{aligned}
& =\frac{\cos \left(90^{\circ}-20^{\circ}\right) \cos 10^{\circ}+\cos \left(90^{\circ}-10^{\circ}\right) \cos 20^{\circ}}{\cos \left(90^{\circ}-21^{\circ}\right) \cos 9^{\circ}+\cos \left(90^{\circ}-9^{\circ}\right) \cos 21^{\circ}}= \\
& =\frac{\sin 20^{\circ} \cos 10^{\circ}+\cos 20^{\circ} \sin 10^{\circ}}{\sin 21^{\circ} \cos 9^{\circ}+\cos 21^{\circ} \sin 9^{\circ}}=[\sin x \cos y+\cos x \sin y=\sin (x+y)]= \\
& =\frac{\sin 30^{\circ}}{\sin 30^{\circ}}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.360. $\frac{\cos 67^{\circ} \cos 7^{\circ}-\cos 83^{\circ} \cos 23^{\circ}}{\cos 128^{\circ} \cos 68^{\circ}-\cos 38^{\circ} \cos 22^{\circ}}-\operatorname{tg} 164^{\circ}$.
|
## Решение.
$$
\frac{\cos 67^{\circ} \cos 7^{\circ}-\cos 83^{\circ} \cos 23^{\circ}}{\cos 128^{\circ} \cos 68^{\circ}-\cos 38^{\circ} \cos 22^{\circ}}-\operatorname{tg} 164^{\circ}=
$$
$$
=\frac{\cos 67^{\circ} \cos \left(90^{\circ}-83^{\circ}\right)-\cos 83^{\circ} \cos \left(90^{\circ}-67^{\circ}\right)}{\cos \left(90^{\circ}+38^{\circ}\right) \cos \left(90^{\circ}-22^{\circ}\right)-\cos 38^{\circ} \cos 22^{\circ}}-\operatorname{tg}\left(180^{\circ}-16^{\circ}\right)=
$$
$$
\begin{aligned}
& =\frac{\sin 83^{\circ} \cos 67^{\circ}-\cos 83^{\circ} \sin 67^{\circ}}{-\sin 38^{\circ} \sin 22^{\circ}-\cos 38^{\circ} \cos 22^{\circ}}+\operatorname{tg} 16^{\circ}= \\
& =\frac{\sin 83^{\circ} \cos 67^{\circ}-\cos 83^{\circ} \sin 67^{\circ}}{-\left(\cos 38^{\circ} \cos 22^{\circ}+\sin 38^{\circ} \sin 22^{\circ}\right)}+\operatorname{tg} 16^{\circ}= \\
& =[\sin x \cos y-\cos x \sin y=\sin (x-y) ; \\
& \cos x \cos y+\sin x \sin y=\cos (x-y)]= \\
& =\frac{\sin 16^{\circ}}{-\cos 16^{\circ}}+\operatorname{tg} 16^{\circ}=-\operatorname{tg} 16^{\circ}+\operatorname{tg} 16^{\circ}=0
\end{aligned}
$$
Oтвет: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.361. $\frac{\sin 22^{\circ} \cos 8^{\circ}+\cos 158^{\circ} \cos 98^{\circ}}{\sin 23^{\circ} \cos 7^{\circ}+\cos 157^{\circ} \cos 97^{\circ}}$.
|
Solution.
$$
\begin{aligned}
& \frac{\sin 22^{\circ} \cos 8^{\circ}+\cos 158^{\circ} \cos 98^{\circ}}{\sin 23^{\circ} \cos 7^{\circ}+\cos 157^{\circ} \cos 97^{\circ}}= \\
& =\frac{\sin 22^{\circ} \cos 8^{\circ}+\cos \left(180^{\circ}-22^{\circ}\right) \cos \left(90^{\circ}+8^{\circ}\right)}{\sin 23^{\circ} \cos 7^{\circ}+\cos \left(180^{\circ}-23^{\circ}\right) \cos \left(90^{\circ}+7^{\circ}\right)}= \\
& =\frac{\sin 22^{\circ} \cos 8^{\circ}+\cos 22^{\circ} \sin 8^{\circ}}{\sin 23^{\circ} \cos 7^{\circ}+\cos 23^{\circ} \sin 7^{\circ}}= \\
& =[\sin x \cos y+\cos x \sin y=\sin (x+y)]=\frac{\sin 30^{\circ}}{\sin 30^{\circ}}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.374. $\operatorname{tg} \frac{A}{2} \operatorname{tg} \frac{B}{2}+\operatorname{tg} \frac{B}{2} \operatorname{tg} \frac{C}{2}+\operatorname{tg} \frac{C}{2} \operatorname{tg} \frac{A}{2}=1$.
3.374. $\tan \frac{A}{2} \tan \frac{B}{2}+\tan \frac{B}{2} \tan \frac{C}{2}+\tan \frac{C}{2} \tan \frac{A}{2}=1$.
|
Solution.
$$
\begin{aligned}
& \tan \frac{A}{2} \tan \frac{B}{2} + \tan \frac{B}{2} \tan \frac{C}{2} + \tan \frac{C}{2} \tan \frac{A}{2} = \tan \frac{A}{2} \tan \frac{B}{2} + \left( \tan \frac{B}{2} + \tan \frac{A}{2} \right) \tan \frac{C}{2} = \\
& = \tan \frac{A}{2} \tan \frac{B}{2} + \left( \tan \frac{B}{2} + \tan \frac{A}{2} \right) \tan \frac{180^\circ - (A + B)}{2} =
\end{aligned}
$$
$$
\begin{aligned}
& = \tan \frac{A}{2} \tan \frac{B}{2} + \left( \tan \frac{B}{2} + \tan \frac{A}{2} \right) \tan \left( 90^\circ - \frac{A + B}{2} \right) = \\
& = \tan \frac{A}{2} \tan \frac{B}{2} + \left( \tan \frac{B}{2} + \tan \frac{A}{2} \right) \cot \frac{A + B}{2} = \left[ \tan x + \tan y = \frac{\sin (x + y)}{\cos x \cos y} \right] = \\
& = \tan \frac{A}{2} \tan \frac{B}{2} + \frac{\sin \frac{A + B}{2}}{\cos \frac{A}{2} \cos \frac{B}{2}} \cdot \frac{\cos \frac{A + B}{2}}{\sin \frac{A + B}{2}} = \tan \frac{A}{2} \tan \frac{B}{2} + \frac{\cos \left( \frac{A}{2} + \frac{B}{2} \right)}{\cos \frac{A}{2} \cos \frac{B}{2}} = \\
& = \left[ \cos (x + y) = \cos x \cos y - \sin x \sin y \right] = \\
& = \tan \frac{A}{2} \tan \frac{B}{2} + \frac{\cos \frac{A}{2} \cos \frac{B}{2} - \sin \frac{A}{2} \sin \frac{B}{2}}{\cos \frac{A}{2} \cos \frac{B}{2}} = \\
& = \tan \frac{A}{2} \tan \frac{B}{2} + \frac{\cos \frac{A}{2} \cos \frac{B}{2}}{\cos \frac{A}{2} \cos \frac{B}{2}} - \frac{\sin \frac{A}{2} \sin \frac{B}{2}}{\cos \frac{A}{2} \cos \frac{B}{2}} = \tan \frac{A}{2} \tan \frac{B}{2} + 1 - \tan \frac{A}{2} \tan \frac{B}{2} = 1.
\end{aligned}
$$
## The equality is valid.
|
1
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3.384. Prove that the expression $\frac{1-2 \sin ^{2}\left(\alpha-\frac{3}{2} \pi\right)+\sqrt{3} \cos \left(2 \alpha+\frac{3}{2} \pi\right)}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}$
does not depend on $\alpha$, where $\alpha \neq \frac{\pi n}{2}+\frac{\pi}{12}$.
|
## Solution.
$$
\begin{aligned}
& \frac{1-2 \sin ^{2}\left(\alpha-\frac{3}{2} \pi\right)+\sqrt{3} \cos \left(2 \alpha+\frac{3}{2} \pi\right)}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}= \\
& =\frac{1-2\left(-\sin \left(\frac{3}{2} \pi-\alpha\right)\right)^{2}+\sqrt{3} \cos \left(\frac{3}{2} \pi+2 \alpha\right)}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}= \\
& =\frac{1-2 \cos ^{2} \alpha+\sqrt{3} \sin 2 \alpha}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}=
\end{aligned}
$$
$$
\begin{aligned}
& =\frac{-\left(2 \cos ^{2} \alpha-1\right)+\sqrt{3} \sin 2 \alpha}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}=\frac{-\cos 2 \alpha+\sqrt{3} \sin 2 \alpha}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}= \\
& =\frac{-2\left(\frac{1}{2} \cos 2 \alpha-\frac{\sqrt{3}}{2} \sin 2 \alpha\right)}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}=\frac{-2\left(\sin \frac{\pi}{6} \cos 2 \alpha-\cos \frac{\pi}{6} \sin 2 \alpha\right)}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}= \\
& =\frac{-2 \sin \left(\frac{\pi}{6}-2 \alpha\right)}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}=-2
\end{aligned}
$$
Answer: -2.
|
-2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3.389. Prove that the expression $\cos ^{2} \alpha+\cos ^{2} \varphi+\cos ^{2}(\alpha+\varphi)-$ $2 \cos \alpha \cos \varphi \cos (\alpha+\varphi)$ does not depend on either $\alpha$ or $\varphi$.
|
## Solution.
$\cos ^{2} \alpha+\cos ^{2} \varphi+\cos ^{2}(\alpha+\varphi)-2 \cos \alpha \cos \varphi \cos (\alpha+\varphi)=$ $=\cos ^{2} \alpha+\cos ^{2} \varphi+(\cos (\alpha+\varphi))^{2}-2 \cos \alpha \cos \varphi \times$
$x(\cos \alpha \cos \varphi-\sin \alpha \sin \varphi)=\cos ^{2} \alpha+\cos ^{2} \varphi+\cos ^{2} \alpha \cos ^{2} \varphi-$ $-2 \sin \alpha \cos \alpha \sin \varphi \cos \varphi+\sin ^{2} \alpha \sin ^{2} \varphi-2 \cos ^{2} \alpha \cos ^{2} \varphi+2 \sin \alpha \cos \alpha \times$ $\times \sin \varphi \cos \varphi=\cos ^{2} \alpha+\cos ^{2} \varphi+\sin ^{2} \alpha \sin ^{2} \varphi-\cos ^{2} \alpha \cos ^{2} \varphi=$ $=\left(\cos ^{2} \alpha-\cos ^{2} \alpha \cos ^{2} \varphi\right)+\cos ^{2} \varphi+\sin ^{2} \alpha \sin ^{2} \varphi=$ $=\cos ^{2} \alpha\left(1-\cos ^{2} \varphi\right)+\cos ^{2} \varphi+\sin ^{2} \alpha \sin ^{2} \varphi=$ $=\left(\cos ^{2} \alpha \sin ^{2} \varphi+\sin ^{2} \alpha \sin ^{2} \varphi\right)+\cos ^{2} \varphi=$ $=\sin ^{2} \varphi\left(\cos ^{2} \alpha+\sin ^{2} \alpha\right)+\cos ^{2} \varphi=\sin ^{2} \varphi+\cos ^{2} \varphi=1$.
The number 1 does not depend on either $\alpha$ or $\varphi$, which is what we needed to prove. Answer: 1.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
4.041. Find the positive integer $n$ from the equation
$$
(3+6+9+\ldots+3(n-1))+\left(4+5.5+7+\ldots+\frac{8+3 n}{2}\right)=137
$$
|
## Solution.
In the first parentheses, there is the sum of the terms of an arithmetic progression $S_{k}$ where $a_{1}=3, d=3, a_{k}=3(n-1), k=\frac{a_{k}-a_{1}}{d}+1=\frac{3 n-3-3}{3}+1=n-1$; in the second parentheses, there is the sum of the terms of an arithmetic progression where $b_{1}=4, d=1.5, a_{m}=\frac{8+3 n}{2}, m=\frac{a_{m}-a_{1}}{d}+1=\frac{\frac{8+3 n}{2}-4}{1.5}+1=n+1$.
Then the original equation takes the form
$$
\frac{3+3(n-1)}{2} \cdot(n-1)+\frac{4+\frac{8+3 n}{2}}{2} \cdot(n+1)=137 \Leftrightarrow 9 n^{2}+13 n-532=0
$$
From this, $n_{1}=-\frac{76}{9}, n_{2}=7 ; n_{1}=-\frac{76}{9}$ is not suitable, as $n$ is an integer.
Answer: 7.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.