problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
4.056. Find the fifth term of an increasing geometric progression, given that its first term is equal to $7-3 \sqrt{5}$ and that each of its terms, starting from the second, is equal to the difference of the two adjacent terms.
|
Solution.
We have:
$$
\left\{\begin{array}{l}
b_{1}=7-3 \sqrt{5} \\
b_{2}=b_{3}-b_{1}, \\
|q|>1
\end{array}\right.
$$
$q_{1}=\frac{1-\sqrt{5}}{2}$ does not fit, as $\left|q_{1}\right|<1 ; q_{2}=\frac{1+\sqrt{5}}{2}$.
From this,
$$
b_{5}=b_{1} q^{4}=\frac{(7-3 \sqrt{5})(1+\sqrt{5})^{4}}{16}=\frac{(17-3 \sqrt{5}) 8(7+3 \sqrt{5})}{16}=\frac{49-45}{2}=2
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.061. Solve the equation
$$
\frac{x-1}{x}+\frac{x-2}{x}+\frac{x-3}{x}+\ldots+\frac{1}{x}=3
$$
where $x$ is a positive integer.
|
## Solution.
Multiplying both sides of the equation by $x$, we have
$$
(x-1)+(x-2)+(x-3)+\ldots+1=3 x
$$
The left side of this equation is the sum of the terms of an arithmetic progression, where $a_{1}=x-1, d=-1, a_{n}=1$,
$$
n=\frac{a_{n}-a_{1}}{d}+1=\frac{1-x+1}{-1}+1=x-1 . \text { Since } S_{n}=\frac{a_{1}+a_{n}}{2} \cdot n
$$
then $\frac{x-1+1}{2} \cdot(x-1)=3 x, x^{2}=7 x, x=7(x \neq 0)$.
Answer: $x=7$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.063. Given two geometric progressions consisting of the same number of terms. The first term and the common ratio of the first progression are 20 and $3 / 4$, respectively, while the first term and the common ratio of the second progression are 4 and $2 / 3$, respectively. If the terms of these progressions with the same indices are multiplied, the sum of all such products is 158.75. Find the number of terms in this progression.
|
## Solution.
Let $a_{1}, a_{2}, a_{3}, \ldots$ and $b_{1}, b_{2}, b_{3}, \ldots$ be the terms of two geometric progressions, where $a_{1}=20, q_{1}=\frac{3}{4}; b_{1}=4, q_{2}=\frac{2}{3}$ and $a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}+\ldots=$ $=158.75$. We find $a_{2}=a_{1} q_{1}=20 \cdot \frac{3}{4}=15, a_{3}=a_{1} q_{1}^{2}=20 \cdot \frac{9}{16}=\frac{45}{4}, b_{2}=b_{1} q_{2}=$ $=4 \cdot \frac{2}{3}=\frac{8}{3}, b_{3}=b_{1} q_{2}^{2}=4 \cdot \frac{4}{9}=\frac{16}{9}$. Then $20 \cdot 4+15 \cdot \frac{8}{3}+\frac{45}{4} \cdot \frac{16}{9}+\ldots=158.75$ or $80+40+20+\ldots=\frac{635}{4}$. The left side of this equation is the sum of the terms of a geometric progression, where the first term is 80 and the common ratio is $\frac{1}{2}$.
From this, we have
$$
\begin{aligned}
& \frac{80\left(1-\left(\frac{1}{2}\right)^{n}\right)}{1-\frac{1}{2}}=\frac{635}{4}, \frac{160\left(2^{n}-1\right)}{2^{n}}=\frac{635}{4}, \frac{32\left(2^{n}-1\right)}{2^{n}}=\frac{127}{4} \\
& 128\left(2^{n}-1\right)=127 \cdot 2^{n}, 2^{n}=2^{7}, n=7
\end{aligned}
$$
Answer: 7.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.136. $\frac{x^{2}+1}{x+1}+\frac{x^{2}+2}{x-2}=-2$.
6.136. $\frac{x^{2}+1}{x+1}+\frac{x^{2}+2}{x-2}=-2$.
(Note: The equation is the same in both languages, so the translation is identical to the original text.)
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}x \neq-1, \\ x \neq 2 .\end{array}\right.$
After bringing all terms of the equation to a common denominator, we have
$$
\begin{aligned}
& \frac{\left(x^{2}+1\right)(x-2)+\left(x^{2}+2\right)(x+1)+2(x+1)(x-2)}{(x+1)(x-2)}=0 \Leftrightarrow \\
& \Leftrightarrow \frac{2 x^{3}+x^{2}+x-4}{(x+1)(x-2)}=0 \Leftrightarrow 2 x^{3}+x^{2}+x-4=0 \text { for } x \neq-1 \text { and } x \neq 2
\end{aligned}
$$
Rewrite this equation as $\left(2 x^{3}-2\right)+\left(x^{2}-1\right)+(x-1)=0$, $2(x-1)\left(x^{2}+x+1\right)+(x-1)(x+1)+x-1=0 \Leftrightarrow(x-1)\left(2 x^{2}+3 x+4\right)=0$, from which $x-1=0$, or $2 x^{2}+3 x+4=0 ; x_{1}=1$, for the quadratic equation $D<0$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.145. $(x+1)^{2}(x+2)+(x-1)^{2}(x-2)=12$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
6.145. $(x+1)^{2}(x+2)+(x-1)^{2}(x-2)=12$.
|
## Solution.
We have:
$$
\begin{aligned}
& \left(x^{2}+2 x+1\right)(x+2)+\left(x^{2}-2 x+1\right)(x-2)-12=0 \Leftrightarrow \\
& \Leftrightarrow x^{3}+2 x^{2}+2 x^{2}+4 x+x+2+x^{3}-2 x^{2}-2 x^{2}+4 x+x-2-12=0 \\
& 2 x^{3}+10 x-12=0, x^{3}+5 x-6=0
\end{aligned}
$$
The last equation can be rewritten as:
$x^{3}+5 x-5-1=0,\left(x^{3}-1\right)+5(x-1)=0,(x-1)\left(x^{2}+x+1\right)+5(x-1)=0$, $(x-1)\left(x^{2}+x+6\right)=0$, from which $x-1=0, x_{1}=1$, or $x^{2}+x+6=0, D<0$ and there are no roots.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.146. $\frac{(x-1)(x-2)(x-3)(x-4)}{(x+1)(x+2)(x+3)(x+4)}=1$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x \neq-1, \\ x \neq-2, \\ x \neq-3, \\ x \neq-4 .\end{array}\right.$
$$
\begin{aligned}
& \text { From the condition } \frac{(x-1)(x-2)(x-3)(x-4)}{(x+1)(x+2)(x+3)(x+4)}-1=0 \Leftrightarrow \\
& \Leftrightarrow \frac{(x-1)(x-4)(x-2)(x-3)-(x+1)(x+4)(x+2)(x+3)}{(x+1)(x+4)(x+2)(x+3)}=0
\end{aligned}
$$
We have $(x-1)(x-4)(x-2)(x-3)-(x+1)(x+4)(x+2)(x+3)=0$ for $x \neq-1$, $x \neq-2, x \neq-3, x \neq-4 ;\left(x^{2}-5 x+4\right)\left(x^{2}-5 x+6\right)-\left(x^{2}+5 x+4\right)\left(x^{2}+5 x+6\right)=0$, $\left(x^{2}-5 x\right)^{2}+10\left(x^{2}-5 x\right)+24-\left(x^{2}+5 x\right)^{2}-10\left(x^{2}+5 x\right)-24=0 \Leftrightarrow$ $\Leftrightarrow-20 x\left(x^{2}+5\right)=0$, from which $x_{1}=0, x^{2}+5 \neq 0$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.158. $\sqrt[3]{9-\sqrt{x+1}}+\sqrt[3]{7+\sqrt{x+1}}=4$.
|
## Solution.
Domain of definition: $x+1 \geq 0$ or $x \geq-1$.
Let $\sqrt{x+1}=y \geq 0$. The equation in terms of $y$ becomes $\sqrt[3]{9-y}+\sqrt[3]{7+y}=4$. Raising both sides of the equation to the third power, we get
$$
\begin{aligned}
& 9-y+\sqrt[3]{(9-y)^{2}(7+y)}+3 \sqrt[3]{(9-y)(7+y)^{2}}+7+y=64 \Leftrightarrow \\
& \Leftrightarrow 3 \sqrt[3]{(9-y)^{2}(7+y)}+3 \sqrt[3]{(9-y)(7+y)^{2}}=48 \Leftrightarrow \\
& \Leftrightarrow 3 \sqrt[3]{(9-y)(7+y)} \times(\sqrt[3]{9-y}+\sqrt[3]{7+y})=48
\end{aligned}
$$
Since by the condition $\sqrt[3]{9-y}+\sqrt[3]{7+y}=4$, then
$$
12 \sqrt[3]{(9-y)(7+y)}=48 \Leftrightarrow(9-y)(7+y)=64, y^{2}-2 y+1=0,(y-1)^{2}=0
$$
from which $y_{1,2}=1$.
Then $\sqrt{x+1}=1, x=0$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.159. $\sqrt{x+2}-\sqrt[3]{3 x+2}=0$.
6.159. $\sqrt{x+2}-\sqrt[3]{3 x+2}=0$.
|
## Solution.
Domain of definition: $x+2 \geq 0, x \geq-2$.
$$
\begin{aligned}
& \text { From the condition } \sqrt{x+2}=\sqrt[3]{3 x+2} \Rightarrow(x+2)^{3}=(3 x+2)^{2} \\
& x^{3}+6 x^{2}+12 x+8=9 x^{2}+12 x+4 \Leftrightarrow x^{3}-3 x^{2}+4=0 \Leftrightarrow \\
& \Leftrightarrow(x+1)\left(x^{2}-x+1\right)-3(x-1)(x+1)=0 \Leftrightarrow(x+1)\left(x^{2}-4 x+4\right)=0 \\
& (x+1)(x-2)^{2}=0 . \text { Hence } x+1=0, x_{1}=-1, \text { or }(x-2)^{2}=0, x_{2,3}=2
\end{aligned}
$$
By substituting into the original equation, we verify that $x_{1}=-1$ is an extraneous root.
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.160. $\sqrt{\frac{20+x}{x}}+\sqrt{\frac{20-x}{x}}=\sqrt{6}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}\frac{20+x}{x} \geq 0, \\ \frac{20-x}{x} \geq 0,\end{array} \Leftrightarrow\left\{\begin{array}{l}x(x+20) \geq 0, \\ x(x-20) \geq 0, \\ x \neq 0,0<x \leq 20 .\end{array}\right.\right.$
By squaring both sides of the equation, we have
$$
\begin{aligned}
& \frac{20+x}{x}+2 \sqrt{\frac{(20+x)(20-x)}{x^{2}}}+\frac{20-x}{x}=6 \Leftrightarrow \frac{\sqrt{400-x^{2}}}{x}=\frac{3 x-20}{x} \Rightarrow \\
& \sqrt{400-x^{2}}=3 x-20 \text {, where } 3 x-20 \geq 0, x \geq \frac{20}{3} .
\end{aligned}
$$
Further: $400-x^{2}=9 x^{2}-120 x+400 \Leftrightarrow x(x-12)=0$, from which $x_{1}=0$, $x_{2}=12 ; x_{1}=0<\frac{20}{3}$ does not fit.
Answer: $x=12$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.164. $\sqrt{x+8+2 \sqrt{x+7}}+\sqrt{x+1-\sqrt{x+7}}=4$.
|
Solution.
Let $\sqrt{x+7}=y \geq 0, x+7=y^{2}, x=y^{2}-7$.
With respect to $y$, the equation takes the form
$$
\begin{aligned}
& \sqrt{y^{2}+2 y+1}+\sqrt{y^{2}-y-6}=4, \sqrt{(y+1)^{2}}+\sqrt{y^{2}-y-6}=4 \\
& |y+1|+\sqrt{y^{2}-y-6}=4
\end{aligned}
$$
Since $y \geq 0$, we have $y+1+\sqrt{y^{2}-y-6}=4, \sqrt{y^{2}-y-6}=3-y$, where $3-y \geq 0, y \leq 3$. Squaring both sides of the equation, we get $y^{2}-y-6=9-6 y+y^{2}, y=3$. Then $\sqrt{x+7}=3, x+7=9, x=2$.
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.169. $\sqrt{x}+\frac{2 x+1}{x+2}=2$.
6.169. $\sqrt{x}+\frac{2 x+1}{x+2}=2$.
|
## Solution.
Domain of definition: $x \geq 0$.
From the condition, we have $\sqrt{x}=2-\frac{2 x+1}{x+2} \Leftrightarrow \sqrt{x}=\frac{2 x+4-2 x-1}{x+2}, \sqrt{x}=\frac{3}{x+2}$.
Squaring both sides of the equation, we get $x=\frac{3}{x^{2}+4 x+4} \Leftrightarrow$ $\Leftrightarrow \frac{x^{3}+4 x^{2}+4 x-9}{x^{2}+4 x+4}=0$, from which $x^{3}+4 x^{2}+4 x-9=0$ for $x \neq-2$.
Rewrite the equation as $\left(x^{3}-1\right)+\left(4 x^{2}-4\right)+(4 x-4)=0$, $(x-1)\left(x^{2}+x+1\right)+4(x-1)(x+1)+4(x-1)=0 \Leftrightarrow(x-1)\left(x^{2}+5 x+9\right)=0$.
From this, $x-1=0$ or $x^{2}+5 x+9=0$. From the last two equations, we have $x_{1}=1 ;$ the second equation has no solutions, since $D<0$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.170. $\frac{\sqrt{x+4}+\sqrt{x-4}}{2}=x+\sqrt{x^{2}-16}-6$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}x+4 \geq 0, \\ x-4 \geq 0,\end{array} \Leftrightarrow x \geq 4\right.$.
By squaring both sides of the equation, we get
$$
\begin{aligned}
& \frac{x+4+2 \sqrt{(x+4)(x-4)}+x-4}{4}=\left(x+\sqrt{x^{2}-16}\right)^{2}-12\left(x+\sqrt{x^{2}-16}\right)+36 \\
& 2\left(x+\sqrt{x^{2}-16}\right)-25\left(x+\sqrt{x^{2}-16}\right)+72=0
\end{aligned}
$$
Let $x+\sqrt{x^{2}-16}=y$. The equation in terms of $y$ becomes
$$
2 y^{2}-25 y+72=0, \text { from which } y_{1}=\frac{9}{2}, y_{2}=8
$$
Then
$$
\text { 1) } x+\sqrt{x^{2}-16}=\frac{9}{2} \Leftrightarrow 2 \sqrt{x^{2}-16}=9-2 x, \text { where } 9-2 x \geq 0, x \leq 4.5
$$
After squaring the equation, we get
$$
4 x^{2}-64=81-36 x+4 x^{2}, 36 x=145, x_{1}=\frac{145}{36} ; \text { does not fit; }
$$
2) $x+\sqrt{x^{2}-16}=8, \sqrt{x^{2}-16}=8-x$, where $8-x \geq 0, x \leq 8$. After squaring the equation, we get $x^{2}-16=64-16 x+x^{2}, x=5$.
Answer: $x=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.173. $2 \sqrt{5 \sqrt[4]{x+1}+4}-\sqrt{2 \sqrt[4]{x+1}-1}=\sqrt{20 \sqrt[4]{x+1}+5}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x+1 \geq 0, \\ 2 \sqrt[4]{x+1}-1 \geq 0\end{array} \Leftrightarrow\left\{\begin{array}{l}x \geq-1, \\ 2 \sqrt[4]{x+1} \geq 1,\end{array} \Leftrightarrow x \geq-\frac{15}{16}\right.\right.$.
Let $\sqrt[4]{x+1}=y$, where $y \geq 0$. The equation in terms of $y$ becomes $2 \sqrt{5 y+4}-\sqrt{2 y-1}=\sqrt{20 y+5}$. Squaring both sides of the equation, we get
$$
\begin{aligned}
& 20 y+16-4 \sqrt{(5 y+4)(2 y-1)}+2 y-1=20 y+5 \Leftrightarrow \\
& \Leftrightarrow y+5=2 \sqrt{(5 y+4)(2 y-1)} \Leftrightarrow y^{2}+10 y+25=4\left(10 y^{2}+3 y-4\right) \Leftrightarrow \\
& \Leftrightarrow 39 y^{2}+2 y-41=0, \text { from which } y_{1}=-\frac{41}{39}, y_{2}=1 ; y_{1}=-\frac{41}{39}<0 \text { is not suitable. }
\end{aligned}
$$
Hence, $\sqrt[4]{x+1}=1 \Leftrightarrow x+1=1, x=0$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.176. $(\sqrt{x+1}+\sqrt{x})^{3}+(\sqrt{x+1}+\sqrt{x})^{2}=2$.
6.176. $(\sqrt{x+1}+\sqrt{x})^{3}+(\sqrt{x+1}+\sqrt{x})^{2}=2$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x+1 \geq 0, \\ x \geq 0\end{array} \Leftrightarrow x \geq 0\right.$.
Let $\sqrt{x+1}+\sqrt{x}=y$, where $y \geq 0$. The equation in terms of $y$ becomes
$$
\begin{aligned}
& y^{3}+y^{2}-2=0 \Leftrightarrow y^{3}-1+y^{2}-1=0 \Leftrightarrow \\
& \Leftrightarrow(y-1)\left(y^{2}+y+1\right)+(y+1)(y-1)=0 \Leftrightarrow \\
& \Leftrightarrow(y-1)\left(y^{2}+y+1+y+1\right)=0,(y-1)\left(y^{2}+2 y+2\right)=0
\end{aligned}
$$
The obtained equation is equivalent to two equations: $y-1=0$ and $y^{2}+2 y+2=0$, solving which, we find $y_{1}=1$; the second equation has no solutions, since $D<0$.
Then $\sqrt{x+1}+\sqrt{x}=1 \Leftrightarrow x+1+2 \sqrt{(x+1) x}+x=1, \sqrt{(x+1) x}=-x$, where $x \leq 0$. From the domain of definition, we get $\left\{\begin{array}{l}x \geq 0 \\ x \leq 0\end{array} \Leftrightarrow x=0\right.$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.177. $\sqrt[3]{x+7}-\sqrt{x+3}=0$.
6.177. $\sqrt[3]{x+7}-\sqrt{x+3}=0$.
|
## Solution.
Domain of definition: $x+3 \geq 0, x \geq-3$.
From the condition $\sqrt[3]{x+7}=\sqrt{x+3}$ and raising both sides to the sixth power, we get $(x+7)^{2}=(x+3)^{3} \Leftrightarrow x^{2}+14 x+49=x^{3}+9 x^{2}+27 x+27 \Leftrightarrow$
$\Leftrightarrow x^{3}+8 x^{2}+13 x-22=0$. By checking, we find that $x_{1}=1$, since $1+8+13-22=0$. We divide the left side of the equation by $x-1$:
$\frac{x^{3}+8 x^{2}+13 x-22}{x-1}=x^{2}+9 x+22$.
Then $(x-1)\left(x^{2}+9 x+22\right)=0$.
From this, $x-1=0, x_{1}=1$, or $x^{2}+9 x+22=0$, no solutions exist since $D<0$. Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.250. For what values of $a$ do the equations $x^{2}+a x+1=0$ and $x^{2}+x+a=0$ have a common root?
|
Solution.
If for some $a$ and $x$ the left parts of the equations are equal to 0, then they are equal to each other:
$$
\left\{\begin{array}{l}
x^{2}+a x+1=0 \\
x^{2}+x+a=0
\end{array}\right.
$$
Subtracting the second equation of the system from the first, we get
$a x-x+1-a=0,(a-1) x-(a-1)=0,(a-1)(x-1)=0$, from which:
1) if $a-1=0$, then $a=1$ and each equation will take the form $a^{2}+a+1=0$, i.e., it has no roots;
2) if $a-1 \neq 0$, then $x=1$, from which $1+a+1=0$, i.e., $a=-2$.
Answer: $a=-2$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.160. Simplify the expression $\log _{a+b} m+\log _{a-b} m-2 \log _{a+b} m \cdot \log _{a-b} m$, given that $m^{2}=a^{2}-b^{2}$.
|
Solution.
$\log _{a+b} m+\log _{a-b} m-2 \log _{a+b} m \cdot \log _{a-b} m=\log _{a+b} m+\frac{\log _{a+b} m}{\log _{a+b}(a-b)}-$
$-2 \frac{\log _{a+b} m \cdot \log _{a+b} m}{\log _{a+b}(a-b)}=\log _{a+b} m \cdot\left(1+\frac{1}{\log _{a+b}(a-b)}-\frac{2 \log _{a+b} m}{\log _{a+b}(a-b)}\right)=$
$=\frac{\log _{a+b} m\left(\log _{a+b}(a-b)+1-2 \log _{a+b} m\right)}{\log _{a+b}(a-b)}$.
Since $m=\sqrt{a^{2}-b^{2}}$, we have
$$
\begin{aligned}
& \frac{\log _{a+b} \sqrt{a^{2}-b^{2}}\left(\log _{a+b}(a-b)+1-2 \log _{a+b} \sqrt{a^{2}-b^{2}}\right)}{\log _{a+b}(a-b)}= \\
& =\frac{\log _{a+b} \sqrt{a^{2}-b^{2}}\left(\log _{a+b}(a-b)+1-\log _{a+b}(a-b)-1\right)}{\log _{a+b}(a-b)}= \\
& =\frac{\log _{a+b} \sqrt{a^{2}-b^{2}} \cdot 0}{\log _{a+b}(a-b)}=0
\end{aligned}
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.176. $2^{\log _{5} x^{2}}-2^{1+\log _{5} x}+2^{\log _{5} x-1}-1=0$.
7.176. $2^{\log _{5} x^{2}}-2^{1+\log _{5} x}+2^{\log _{5} x-1}-1=0$.
|
Solution.
Domain of definition: $x>0$.
Rewrite the equation as $2^{2 \log _{5} x}-2 \cdot 2^{\log _{5} x}+\frac{2^{\log _{5} x}}{2}-1=0 \Leftrightarrow$ $\Leftrightarrow 2 \cdot 2^{2 \log _{5} x}-3 \cdot 2^{\log _{5} x}-2=0$. Solving this equation as a quadratic equation in terms of $2^{\log _{5} x}$, we find $2^{\log _{5} x}=-\frac{1}{2}$ (not suitable) or $2^{\log _{5} x}=2$, from which $\log _{5} x=1, x=5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.177. $\frac{\log _{2}\left(9-2^{x}\right)}{3-x}=1$.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
7.177. $\frac{\log _{2}\left(9-2^{x}\right)}{3-x}=1$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}9-2^{x}>0, \\ 3-x \neq 0,\end{array} \Leftrightarrow 3 \neq x<\log _{2} 9\right.$.
## From the condition
$$
\log _{2}\left(9-2^{x}\right)=3-x \Leftrightarrow 9-2^{x}=2^{3-x} \Leftrightarrow 2^{2 x}-9 \cdot 2^{x}+8=0
$$
Solving it as a quadratic equation in terms of $2^{x}$, we find $\left(2^{x}\right)=1$, hence $x_{1}=0$ or $\left(2^{x}\right)_{2}=8$, hence $x_{2}=3 ; x_{2}=3$ does not satisfy the domain of definition.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.179. $\log _{a^{2}} x^{2}+\log _{a}(x-1)=\log _{a} \log _{\sqrt{5}} 5$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x>1, \\ 0<a \neq 1 .\end{array}\right.$
From the condition we have
$$
\log _{a} x+\log _{a}(x-1)=\log _{a} 2 \Rightarrow \log _{a} x(x-1)=\log _{a} 2
$$
from which $x^{2}-x-2=0 \Rightarrow x_{1}=2, x_{2}=-1 ; x_{2}=-1$ does not satisfy the domain of definition.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.186. $\log _{12}\left(4^{3 x}+3 x-9\right)=3 x-x \log _{12} 27$.
|
## Solution.
Domain of definition: $4^{3 x}+3 x-9>0$.
Rewrite the equation as
$$
\log _{12}\left(4^{3 x}+3 x-9\right)+\log _{12} 27^{x}=3 x \Rightarrow \log _{12} 27^{x}\left(4^{3 x}+3 x-9\right)=3 x
$$
from which $27^{x}\left(4^{3 x}+3 x-9\right)=12^{3 x} \Leftrightarrow 4^{3 x}+3 x-9=4^{3 x}, 3 x-9=0, x=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.187. $x^{2} \cdot \log _{x} 27 \cdot \log _{9} x=x+4$.
|
## Solution.
Domain of definition: $0<x \neq 1$.
Switch to base 3, then
$$
\frac{3 x^{2}}{\log _{3} x} \cdot \frac{\log _{3} x}{2}=x+4 \Leftrightarrow 3 x^{2}-2 x-8=0
$$
from which $x_{1}=2, x_{2}=-\frac{4}{3} ; x_{2}=-\frac{4}{3}$ does not satisfy the domain of definition.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.197. $5^{\frac{x}{\sqrt{x}+2}} \cdot 0.2^{\frac{4}{\sqrt{x}+2}}=125^{x-4} \cdot 0.04^{x-2}$.
|
## Solution.
Domain of definition: $x \geq 0$.
From the condition we have
$$
\begin{aligned}
& 5^{\frac{x}{\sqrt{x}+2}} \cdot 5^{-\frac{4}{\sqrt{x}+2}}=5^{3 x-12} \cdot 5^{-2 x+4} \Leftrightarrow 5^{\frac{x}{\sqrt{x}+2}-\frac{4}{\sqrt{x}+2}}=5^{3 x-12-2 x+4} \Leftrightarrow \\
& \Leftrightarrow \frac{x-4}{\sqrt{x}+2}=x-8 \Leftrightarrow x \sqrt{x}+x-8 \sqrt{x}-12=0
\end{aligned}
$$
Let $\sqrt{x}=y \geq 0$. The equation in terms of $y$ becomes $y^{3}+y^{2}-8 y-12=0,(y-3)(y+2)^{2}=0$, from which $y_{1}=3, y_{2,3}=-2 ; y_{2,3}=-2$ does not fit. Then $\sqrt{x}=3, x=9$.
Answer: 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.200. $\frac{1+2 \log _{9} 2}{\log _{9} x}-1=2 \log _{x} 3 \cdot \log _{9}(12-x)$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}0<x<12, \\ x \neq 1 .\end{array}\right.$
Switch to base 3. Then we get
$$
\begin{aligned}
& \frac{1+\frac{2 \log _{3} 2}{\log _{3} 9}}{\frac{\log _{3} x}{\log _{3} 9}}-1=\frac{2}{\log _{3} x} \cdot \frac{\log _{3}(12-x)}{\log _{3} 9} \Leftrightarrow \frac{2+2 \log _{3} 2}{\log _{3} x}-1=\frac{\log _{3}(12-x)}{\log _{3} x} \Leftrightarrow \\
& \Leftrightarrow \frac{2+2 \log _{3} 2-\log _{3} x}{\log _{3} x}=\frac{\log _{3}(12-x)}{\log _{3} x} \Leftrightarrow 2+2 \log _{3} 2-\log _{3} x=\log _{3}(12-x) \Leftrightarrow \\
& \Leftrightarrow 2+2 \log _{3} 2=\log _{3} x+\log _{3}(12-x) \Leftrightarrow \\
& \Leftrightarrow \log _{3} 9+\log _{3} 4=\log _{3} x+\log _{3}(12-x), \log _{3} 36=\log _{3} x(12-x)
\end{aligned}
$$
$$
\text { hence } 36=x(12-x) \text { or } x^{2}-12 x+36=0,(x-6)^{2}=0, x=6 \text {. }
$$
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.208. $2^{x-1}+2^{x-4}+2^{x-2}=6.5+3.25+1.625+\ldots$ (the expression on the right side is an infinite geometric progression).
|
Solution.
On the right side, we have the sum of the terms of an infinitely decreasing geometric progression $S$, where $b_{1}=6.5 ; q=\frac{3.25}{6.5}=0.5 \Rightarrow S=\frac{b_{1}}{1-q}=\frac{6.5}{1-0.5}=13$.
Rewrite the equation as $\frac{2^{x}}{2}+\frac{2^{x}}{16}+\frac{2^{x}}{4}=13 \Leftrightarrow \frac{13}{16} \cdot 2^{x}=13$, $2^{x}=16$, from which $x=4$.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.209. $49^{1+\sqrt{x-2}}-344 \cdot 7^{\sqrt{x-2}}=-7$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
7.209. $49^{1+\sqrt{x-2}}-344 \cdot 7^{\sqrt{x-2}}=-7$.
|
Solution.
Domain of definition: $x \geq 2$.
Rewrite the equation as $49 \cdot 7^{2 \sqrt{x-2}}-344 \cdot 7^{\sqrt{x-2}}+7=0$. Solving it as a quadratic equation in terms of $7^{\sqrt{x-2}}$, we get $\left(7^{\sqrt{x-2}}\right)=7^{-2}$ or $\left(7^{\sqrt{x-2}}\right)_{2}=7$, from which $(\sqrt{x-2})_{1}=-2$ (no solutions), or $(\sqrt{x-2})_{2}=1, x_{2}=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.212. $\frac{\log _{4 \sqrt{x}} 2}{\log _{2 x} 2}+\log _{2 x} 2 \cdot \log _{1 / 2} 2 x=0$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x>0, \\ x \neq \frac{1}{16}, \\ x \neq \frac{1}{2}, \\ x \neq 1 .\end{array}\right.$
Transition to base 2. We have
$\frac{\frac{\log _{2} 2}{\log _{2} 4 \sqrt{x}}}{\frac{\log _{2} 2}{\log _{2} 2 x}}+\frac{\log _{2} 2}{\log _{2} 2 x} \cdot \frac{\log _{2} 2 x}{\log _{2} \frac{1}{2}}=0 \Leftrightarrow \frac{1+\log _{2} x}{2+\frac{1}{2} \log _{2} x}-1=0$,
from which $\log _{2} x=2$ and $x=4$.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.214. $9^{x}+6^{x}=2^{2 x+1}$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
7.214. $9^{x}+6^{x}=2^{2 x+1}$.
|
Solution.
Rewrite the equation as $3^{2 x}+2^{x} \cdot 3^{x}-2 \cdot 2^{2 x}=0$ and divide it by $2^{2 x} \neq 0$. Then $\left(\frac{3}{2}\right)^{2 x}+\left(\frac{3}{2}\right)^{x}-2=0 \Rightarrow\left(\left(\frac{3}{2}\right)^{x}\right)=-2$ (no solutions) or $\left(\left(\frac{3}{2}\right)^{x}\right)_{2}=1 \Rightarrow x=0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.218. $\left(\frac{3}{5}\right)^{2 \log _{9}(x+1)} \cdot\left(\frac{125}{27}\right)^{\log _{27}(x-1)}=\frac{\log _{5} 27}{\log _{5} 243}$.
|
Solution.
Domain of definition: $x>1$.
From the condition we have
$\left(\frac{3}{5}\right)^{\log _{3}(x+1)} \cdot\left(\frac{3}{5}\right)^{\log _{3}(x-1)}=\frac{3}{5} \Leftrightarrow\left(\frac{3}{5}\right)^{\log _{3}(x+1)+\log _{3}(x-1)}=\frac{3}{5} \Rightarrow$
$\Rightarrow \log _{3}(x+1)+\log _{3}(x-1)=1 \Rightarrow \log _{3}\left(x^{2}-1\right)=1, x^{2}-1=3, x^{2}=4$.
From this, $x_{1}=-2, x_{2}=2 ; x_{1}=-2$ does not satisfy the domain of definition.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.219. $5^{1+x^{3}}-5^{1-x^{3}}=24$.
7.219. $5^{1+x^{3}}-5^{1-x^{3}}=24$.
|
Solution.
We have $5 \cdot 5^{x^{3}}-\frac{5}{5^{x^{3}}}-24=0 \Leftrightarrow 5 \cdot\left(5^{x^{3}}\right)^{2}-24 \cdot 5^{x^{3}}-5=0$. Solving this equation as a quadratic in terms of $5^{x^{3}}$, we get $5^{x^{3}}=-\frac{1}{5}$ (no solutions), or $5^{x^{3}}=5 \Rightarrow x^{3}=1, x=1$.
Answer: 1 .
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.220. $3^{2 x+4}+45 \cdot 6^{x}-9 \cdot 2^{2 x+2}=0$.
7.220. $3^{2 x+4}+45 \cdot 6^{x}-9 \cdot 2^{2 x+2}=0$.
(No change needed as the text is already in English and contains only a mathematical equation.)
|
Solution.
Rewrite the equation as $81 \cdot 3^{2 x}+45 \cdot 3^{x} \cdot 2^{x}-36 \cdot 2^{x}=0$. Dividing it by $9 \cdot 2^{2 x}$, we get $9 \cdot\left(\frac{3}{2}\right)^{2 x}+5 \cdot\left(\frac{3}{2}\right)^{x}-4=0 \Rightarrow\left(\frac{3}{2}\right)^{x}=-1$ (no solutions), or $\left(\frac{3}{2}\right)^{x}=\left(\frac{3}{2}\right)^{-2}$, from which $x=-2$.
Answer: -2 .
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.225. $\log _{3 x+7}(5 x+3)+\log _{5 x+3}(3 x+7)=2$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}0-\frac{3}{5}, x \neq-\frac{2}{5}\right.$.
Multiplying the equation by $\log _{3 x+7}(5 x+3) \neq 0$, we get
$$
\begin{aligned}
& \log _{3 x+7}^{2}(5 x+3)-2 \log _{3 x+7}(5 x+3)+1=0 \Leftrightarrow\left(\log _{3 x+7}(5 x+3)-1\right)^{2}=0 \Leftrightarrow \\
& \Leftrightarrow \log _{3 x+7}(5 x+3)=1 \Leftrightarrow 5 x+3=3 x+7, x=2 \\
& \text { Answer: } 2 .
\end{aligned}
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.227. $(\lg (x+20)-\lg x) \log _{x} 0.1=-1$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x+20>0, \\ 0<x \neq 1\end{array}\right.$ or $0<x \neq 1$.
Switch to base 10. We have $(\lg (x+20)-\lg x)\left(-\frac{1}{\lg x}\right)=-1 \Leftrightarrow$ $\Leftrightarrow \lg (x+20)-\lg x=\lg x \Leftrightarrow \lg (x+20)=2 \lg x \Leftrightarrow \lg (x+20)=\lg x^{2}$. Then $x+20=x^{2}, x^{2}-x-20=0$, from which $x_{1}=-4, x_{2}=5 ; x_{1}=-4$ does not satisfy the domain of definition.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.229. $27 \cdot 2^{-3 x}+9 \cdot 2^{x}-2^{3 x}-27 \cdot 2^{-x}=8$.
|
Solution.
Transform the equation:
$$
\begin{aligned}
& 27+9 \cdot 2^{4 x}-2^{6 x}-27 \cdot 2^{2 x}=8 \cdot 2^{3 x} \Leftrightarrow \\
& \Leftrightarrow 2^{6 x}-9 \cdot 2^{4 x}+8 \cdot 2^{3 x}+27 \cdot 2^{2 x}-27=0 \Leftrightarrow \\
& \Leftrightarrow 2^{6 x}-2^{4 x}-8 \cdot 2^{4 x}+8 \cdot 2^{3 x}+27 \cdot 2^{x}-27=0 \Leftrightarrow
\end{aligned}
$$
$$
\begin{aligned}
& \Leftrightarrow 2^{4 x}\left(2^{2 x}-1\right)-8 \cdot 2^{3 x}\left(2^{x}-1\right)+27\left(2^{x}-1\right)=0 \Leftrightarrow \\
& \Leftrightarrow 2^{4 x}\left(2^{x}-1\right)\left(2^{x}+1\right)-8 \cdot 2^{3 x}\left(2^{x}-1\right)+27\left(2^{x}-1\right)=0 \Leftrightarrow \\
& \Leftrightarrow\left(2^{x}-1\right)\left(2^{5 x}+2^{4 x}-8 \cdot 2^{3 x}+27\right)=0
\end{aligned}
$$
from which $2^{x}=1, x_{1}=0$. The equation $2^{5 x}+2^{4 x}-8 \cdot 2^{3 x}+27=0$ has no solutions.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.230. $\log _{x+1}(x-0.5)=\log _{x-0.5}(x+1)$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}0<x+1 \neq 1, \\ 0<x-0.5 \neq 1\end{array}\right.$ or $0.5<x \neq 1.5$.
Multiplying both sides of the equation by $\log _{x+1}(x-0.5) \neq 0$, we get
$$
\begin{aligned}
& \log _{x+1}^{2}(x-0.5)=1 \Rightarrow \log _{x+1}(x-0.5)=-1 \Rightarrow \\
& \Rightarrow x-0.5=\frac{1}{x+1}, 2 x^{2}+x-3=0, x_{1}=-\frac{3}{2} \text { (does not satisfy the domain of definition), }
\end{aligned}
$$
$x_{2}=1 ;$ or $\log _{x+1}(x-0.5)=1, x-0.5=x+1$, no solutions.
Answer: 1 .
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.235. $x \log _{x+1} 5 \cdot \log _{\sqrt[3]{1 / 5}}(x+1)=\frac{x-4}{x}$.
|
## Solution.
$$
\text { Domain: }\left\{\begin{array}{l}
0<x+1 \neq 1, \\
x \neq 0
\end{array} \Leftrightarrow-1<x \neq 0\right.
$$
Switch to base 5. We have $\frac{x}{\log _{5}(x+1)} \cdot(-3) \log _{5}(x+1)=\frac{x-4}{x}$,
$-3 x=\frac{x-4}{x}$ when $\log _{5}(x+1) \neq 0$. From here, $3 x^{2}+x-4=0, x_{1}=-\frac{4}{3}, x_{2}=1$; $x_{1}=-\frac{4}{3}$ does not satisfy the domain.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.241. $\frac{\log _{2}\left(x^{3}+3 x^{2}+2 x-1\right)}{\log _{2}\left(x^{3}+2 x^{2}-3 x+5\right)}=\log _{2 x} x+\log _{2 x} 2$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}x^{3}+3 x^{2}+2 x-1>0, \\ 0<x^{3}+2 x^{2}-3 x+5 \neq 1, \\ 0<x \neq \frac{1}{2} .\end{array}\right.$
By the formula for changing the base we have
$$
\begin{aligned}
& \log _{x^{3}+2 x^{2}-3 x+5}\left(x^{3}+3 x^{2}+2 x-1\right)=\log _{2 x} 2 x \Leftrightarrow \\
& \Leftrightarrow \log _{x^{3}+2 x^{2}-3 x+5}\left(x^{3}+3 x^{2}+2 x-1\right)=1 \Leftrightarrow
\end{aligned}
$$
$\Leftrightarrow x^{3}+3 x^{2}+2 x-1=x^{3}+2 x^{2}-3 x+5 \Leftrightarrow x^{2}+5 x-6=0 \Rightarrow x_{1}=1$, $x_{2}=-6 ; x_{2}=-6$ does not satisfy the domain of definition.
Answer: 1 .
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.242. $\left(16 \cdot 5^{2 x-1}-2 \cdot 5^{x-1}-0.048\right) \lg \left(x^{3}+2 x+1\right)=0$.
|
Solution.
Domain: $x^{3}+2 x+1>0$.
From the condition $16 \cdot 5^{2 x-1}-2^{x-1}-0.048=0$ or $\lg \left(x^{3}+2 x+1\right)=0$. Rewrite the first equation as
$\frac{16}{5} \cdot 5^{2 x}-\frac{2}{5} \cdot 5^{x}-0.048=0 \Leftrightarrow 16 \cdot 5^{2 x}-2 \cdot 5^{x}-0.24=0$.
Solving this equation as a quadratic in terms of $5^{x}$, we get $5^{x}=-\frac{3}{40}$ (no solutions), or $5^{x}=5^{-1} \Leftrightarrow x_{1}=-1$ (does not satisfy the domain). From the second equation, we have
$x^{3}+2 x+1=1 \Leftrightarrow x^{3}+2 x=0 \Leftrightarrow x\left(x^{2}+2\right)=0, x_{3}=0, x^{2}+2 \neq 0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.243. $5^{x} \cdot \sqrt[x]{8^{x-1}}=500$.
|
Solution.
Rewrite the equation as $5^{x} \cdot 8^{\frac{x-1}{x}}=500 \Leftrightarrow \frac{5^{x} \cdot 8}{8^{1 / x}}=500 \Leftrightarrow$ $\Leftrightarrow \frac{5^{x} \cdot 2}{8^{1 / x}}=125 \Leftrightarrow 5^{x-3}=2^{3 / x-1} \Rightarrow\left\{\begin{array}{l}x-3=0, \\ \frac{3}{x}-1=0,\end{array}\right.$ from which $x=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.245. $\log _{1+x}\left(2 x^{3}+2 x^{2}-3 x+1\right)=3$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}2 x^{3}+2 x^{2}-3 x+1>0, \\ -1<x \neq 0 .\end{array}\right.$
We have
$$
\begin{aligned}
& 2 x^{3}+2 x^{2}-3 x+1=(1+x)^{3} \Leftrightarrow 2 x^{3}+2 x^{2}-3 x+1=1+3 x+3 x^{2}+x^{3} \Leftrightarrow \\
& \Leftrightarrow x^{3}-x^{2}-6 x=0 \Leftrightarrow x\left(x^{2}-x-6\right)=0
\end{aligned}
$$
from which $x_{1}=0, x_{2}=-2, x_{3}=3 ; x_{1}=0, x_{2}=-2$ do not satisfy the domain of definition.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.246. $\log _{2} \sqrt[3]{x}+\sqrt[3]{\log _{2} x}=\frac{4}{3}$.
|
## Solution.
Domain of definition: $x>0$.
## From the condition we have
$$
\frac{1}{3} \log _{2} x+\sqrt[3]{\log _{2} x}=\frac{4}{3} \Leftrightarrow \log _{2} x+3 \sqrt[3]{\log _{2} x}-4=0
$$
Let $\sqrt[3]{\log _{2} x}=y$. The equation in terms of $y$ becomes
$$
\begin{aligned}
& y^{3}+3 y-4=0 \Leftrightarrow\left(y^{3}-1\right)+(3 y-3)=0 \Leftrightarrow \\
& \Leftrightarrow(y-1)\left(y^{2}+y+1\right)+3(y-1)=0 \Leftrightarrow(y-1)\left(y^{2}+y+4\right)=0
\end{aligned}
$$
from which $y-1=0$, since $y^{2}+y+4>0$. Therefore, $y=1, \sqrt[3]{\log _{2} x}=1$, $\log _{2} x=1, x=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.247. $\sqrt{\log _{5} x}+\sqrt[3]{\log _{5} x}=2$.
|
Solution.
Domain of definition: $\log _{5} x \geq 0$ or $x \geq 1$.
Rewrite the equation as $\sqrt[6]{\left(\log _{5} x\right)^{3}}+\sqrt[6]{\left(\log _{5} x\right)^{2}}-2=0$. Let $\sqrt[6]{\log _{5} x}=y$. The equation in terms of $y$ becomes
$$
y^{3}+y^{2}-2=0 \Leftrightarrow\left(y^{3}-1\right)+\left(y^{2}-1\right)=0 \Leftrightarrow
$$
$\Leftrightarrow(y-1)\left(y^{2}+y+1\right)+(y-1)(y+1)=0 \Leftrightarrow(y-1)\left(y^{2}+2 y+2\right)=0$, from which $y-1=0$, since $y^{2}+2 y+2>0$. We get $\sqrt[6]{\log _{5} x}=1, \log _{5} x=1$, $x=5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.252. $\frac{2}{15}\left(16^{\log _{9} x+1}-16^{\log _{3} \sqrt{x}}\right)+16^{\log _{3} x}-\log _{\sqrt{5}} 5 \sqrt{5}=0$.
|
## Solution.
Domain of definition: $x>0$.
Rewrite the equation as
$$
\begin{aligned}
& \frac{2}{15}\left(16 \cdot 16^{\frac{1}{2} \log _{3} x}-16^{\frac{1}{2} \log _{3} x}\right)+16^{\log _{3} x}-3=0 \Leftrightarrow \\
& \Leftrightarrow 16^{\log _{3} x}+2 \cdot 16^{\frac{\log _{3} x}{2}}-3=0
\end{aligned}
$$
Solving this equation as a quadratic in terms of $16^{\frac{\log _{3} x}{2}}$, we get $16^{\frac{\log _{3} x}{2}}=-3$ (no solutions), or $16^{\frac{\log _{3} x}{2}}=16^{0}$, from which $\frac{\log _{3} x_{2}}{2}=0$, $x=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.254. $\log _{2} \sqrt[3]{4}+\log _{8}\left(9^{x+1}-1\right)=1+\log _{8}\left(3^{x+1}+1\right)$.
|
## Solution.
Domain of definition: $9^{x+1}-1>0 \Leftrightarrow x>-1$.
Since $\log _{2} \sqrt[3]{4}=\frac{2}{3}$, we have
$$
\begin{aligned}
& \log _{8}\left(9 \cdot 3^{2 x}-1\right)-\log _{8}\left(3 \cdot 3^{x}+1\right)=\frac{1}{3} \Leftrightarrow \log _{8} \frac{9 \cdot 3^{2 x}-1}{3 \cdot 3^{x}+1}=\frac{1}{3} \Leftrightarrow \\
& \Leftrightarrow \frac{9 \cdot 3^{2 x}-1}{3 \cdot 3^{x}+1}=8^{\frac{1}{3}}=2 \Leftrightarrow 9 \cdot 3^{2 x}-6 \cdot 3^{x}-3=0
\end{aligned}
$$
Solving this equation as a quadratic in terms of $3^{x}$, we get $3^{x}=-\frac{1}{3}$ (no solutions), or $3^{x}=3^{0} \Rightarrow x=0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.255. $25^{\log _{4} x}-5^{\log _{16} x^{2}+1}=\log _{\sqrt{3}} 9 \sqrt{3}-25^{\log _{16} x}$.
|
## Solution.
Domain of definition: $x>0$.
Rewrite the equation as
$5^{\log _{2} x}-5 \cdot 5^{\frac{1}{2} \log _{2} x}=5-5^{\frac{1}{2} \log _{2} x} \Leftrightarrow 5^{\log _{2} x}-4 \cdot 5^{\frac{1}{2} \log _{2} x}-5=0$.
Solving this equation as a quadratic equation in terms of $5^{\frac{1}{\log _{2} x}}$, we get
$5^{\frac{1}{2} \log _{2} x}=-1$ (no solutions), or $5^{\frac{1}{2} \log _{2} x}=5 \Rightarrow \frac{1}{2} \log _{2} x=1, \log _{2} x=2$, $x=2^{2}=4$.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.111. Find the non-negative integer values of $x$ that satisfy the inequality $\frac{x+3}{x^{2}-4}-\frac{1}{x+2}<\frac{2 x}{2 x-x^{2}}$.
|
Solution.
Rewrite the inequality as $\frac{x+3}{x^{2}-4}-\frac{1}{x+2}+\frac{2 x}{x(x-2)}<0 \Leftrightarrow$
$$
\begin{aligned}
& \Leftrightarrow \frac{x+3}{(x-2)(x+2)}-\frac{1}{x+2}+\frac{2}{x-2}<0 \text { for } x \neq 0: \Leftrightarrow\left\{\begin{array}{l}
\frac{2 x+9}{(x-2)(x+2)}<0, \\
x \neq 0
\end{array} \Leftrightarrow\right. \\
& \Leftrightarrow\left\{\begin{array}{l}
(2 x+9)(x-2)(x+2)<0, \\
x \neq 0 .
\end{array}\right.
\end{aligned}
$$
Using the number line, we get $x=1$.
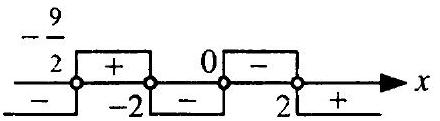
Answer: $x=1$.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.199. The bases of the trapezoid are 4 and 16 cm. Find the radii of the inscribed and circumscribed circles of the trapezoid, given that these circles exist.
|
Solution.
In trapezoid $ABCD$ (Fig. 10.9) $BC \| AD, BC=4$ cm, $AD=16$ cm. Since a circle is circumscribed around the given trapezoid, then $AB=CD$. Since a circle can be inscribed in the given trapezoid, then $AD+BC=AB+CD=2AB; AB=\frac{AD+BC}{2}=10$ cm. $BK$ is the height of the trapezoid. Then $AK=\frac{AD-BC}{2}=6$ cm. From $\triangle AKB \quad (\angle AKB=90^{\circ})$: $BK=\sqrt{AB^{2}-AK^{2}}=8$ cm. The radius of the inscribed circle $r=\frac{1}{2} BK=4$ cm.
The radius $R$ of the circumscribed circle will be found as the radius of the circle circumscribed around $\triangle ABD: R=\frac{AB \cdot BD \cdot AD}{4 S_{\triangle ABD}}, KD=AD-AK=10$ cm. From $\triangle BKD$ $\left(\angle BKD=90^{\circ}\right): BD=\sqrt{BK^{2}+KD^{2}}=2 \sqrt{41}$ cm. $S_{\triangle ABD}=\frac{1}{2} AD \cdot BK=64$ cm$^2$. Then $R=\frac{10 \cdot 2 \sqrt{41} \cdot 16}{4 \cdot 64}=\frac{5 \sqrt{41}}{4}$ (cm).
Answer: $4$ cm; $\frac{5 \sqrt{41}}{4}$ cm.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.206. What integers represent the sides of an isosceles triangle if the radius of the inscribed circle is $3 / 2 \mathrm{~cm}$, and the radius of the circumscribed circle is $25 / 8$ cm
|
Solution.
In $\triangle ABC$, $AB = BC$, $BD$ is the altitude, $O_1$ is the center of the inscribed circle, and $O_2$ is the center of the circumscribed circle (see Fig. 10.16). The radii of these circles are $r = \frac{3}{2}$ cm and $R = \frac{25}{8}$ cm, respectively. $E$ is the point of intersection of the ray $BD$ and the circumscribed circle. $AO_1$ is the bisector of $\angle BAC$. Let $\angle BAO_1 = \angle O_1AD = \alpha$. Then $\angle AO_1D = 90^\circ - \alpha$. Since $BE$ is the diameter of the circumscribed circle, $\angle BAE = 90^\circ$, $\angle O_1AE = 90^\circ - \alpha$, and $BE = 2R = \frac{25}{4}$ cm. Therefore, $AE = O_1E$. Let $DE = x$ cm. Then $AE = O_1E = O_1D + DE = r + x = \frac{3}{2} + x$. From $\triangle BAE$ ($\angle BAE = 90^\circ$, $AD$ is the altitude): $AE^2 = DE \cdot BE$; $\left(\frac{3}{2} + x\right)^2 = x \cdot \frac{25}{4}$; $x = \frac{9}{4}$ or $x = 1$. From $\triangle ADE$ ($\angle ADE = 90^\circ$): $AD = \sqrt{AE^2 - DE^2}$. When $x = \frac{9}{4}$: $AE = \frac{15}{4}$ cm, $AD = 3$ cm, $AC = 6$ cm. When $x = 1$: $AE = \frac{5}{2}$ cm, $AD = \frac{\sqrt{21}}{2}$ cm, and $AC$ is expressed as an irrational number. Therefore, $AC = 6$ cm, $AB = BC = \sqrt{BE^2 - AE^2} = 5$ cm.
Answer: 5 cm, 5 cm, 6 cm.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.208. Perpendiculars are drawn from the vertex of the acute angle of a rhombus to the lines containing the sides of the rhombus to which this vertex does not belong. The length of each perpendicular is 3 cm, and the distance between their bases is $3 \sqrt{3}$ cm. Calculate the lengths of the diagonals of the rhombus.
|
Solution.
Since $\triangle A E F$ is isosceles (Fig. 10.18), the bisector $A M$ is perpendicular to $E F$ and lies on the diagonal of the rhombus. We find $A M^{2}=A F^{2}-M F^{2}=9-\frac{27}{4}=\frac{9}{4}$, i.e., $A M=\frac{3}{2}$ (cm). In $\triangle A C F$, we have $\angle F=90^{\circ}$ and $F M \perp A C \Rightarrow A F^{2}=A C \cdot A M, 9=A C \cdot \frac{3}{2}, A C=6$ (cm).
Next, $\triangle A C D \sim \triangle A E F$ (the base angles are equal as angles with mutually perpendicular sides), so $\frac{A M}{O D}=\frac{E F}{A C} \Leftrightarrow \frac{3 / 2}{O D}=\frac{3 \sqrt{3}}{6}$, $O D=\sqrt{3}$ cm. We get $B D=2 \sqrt{3}$ cm, $A C=6$ cm.
Answer: 6 and $2 \sqrt{3}$ cm.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.211. On the larger leg of a right triangle, a circle is constructed with this leg as its diameter. Determine the radius of this circle if the smaller leg of the triangle is 7.5 cm, and the length of the chord connecting the vertex of the right angle with the point of intersection of the hypotenuse and the circle is 6 cm.
|
Solution.
In $\triangle ABC$ (Fig. 10.21) $\angle ACB=90^{\circ}, BC>AC, AC=7.5$ cm, $N$ is the intersection point of the circle mentioned in the condition and the hypotenuse $AB, CN=6$ cm. $\angle CNB$ is an inscribed angle and subtends the diameter. Therefore, $\angle CNB=90^{\circ}$. From $\triangle ANC \quad (\angle ANC=90^{\circ}): AN=\sqrt{AC^{2}-CN^{2}}=4.5$ cm. Since $CN$ is the altitude of the right $\triangle ACB$, $\triangle ANC \sim \triangle CNB$. Therefore, $\frac{AN}{AC}=\frac{CN}{BC}, BC=\frac{AC \cdot CN}{AN}=10$ cm. The desired radius $R=\frac{1}{2} BC=5$ cm.
Answer: 5 cm.
Fig. 10.22
Fig. 10.23
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.215. In a right-angled triangle, the medians of the legs are $\sqrt{52}$ and $\sqrt{73}$. Find the hypotenuse of the triangle.
|
## Solution.
In $\triangle A B C$ (Fig. 10.25) $\angle A C B=90^{\circ}, B P$ and $A E$ are medians, $B P=\sqrt{52}$, $A E=\sqrt{73}$. Let $B C=x, A C=y$. Then $A B=\sqrt{x^{2}+y^{2}}$.
From $\triangle A C E\left(\angle A C E=90^{\circ}\right):$
$$
A C^{2}+C E^{2}=A E^{2} ; y^{2}+\frac{x^{2}}{4}=73
$$
From $\triangle B C P\left(\angle B C P=90^{\circ}\right)$ :
$$
B C^{2}+C P^{2}=B P^{2} ; x^{2}+\frac{y^{2}}{4}=52
$$
Fig. 10.25
We have $\left\{\begin{array}{l}4 y^{2}+x^{2}=292, \\ 4 x^{2}+y^{2}=208 ;\end{array} 5 x^{2}+5 y^{2}=500 ; x^{2}+y^{2}=100\right.$. Therefore, $A B=\sqrt{x^{2}+y^{2}}=10$.
Answer: 10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.216. Two circles, with radii of 4 and 8, intersect at a right angle. Determine the length of their common tangent.
|
Solution.
Let $A$ be the point of intersection of the circles with centers $O$ and $O_{1}$ (Fig. 10.26), $O A=8 \text{ cm}, O_{1} A=4 \text{ cm}$, $M N$ - their common tangent. According to the problem, the circles intersect at a right angle, so the tangents to them at point $A$ are perpendicular to each other. Therefore, the radii drawn to the point of tangency are also perpendicular. From $\triangle O A O_{1}: O O_{1}^{2}=O A^{2}+O_{1} A^{2}=80$. Draw $O_{1} D \| M N$. Then $O_{1} D \perp O M, M N=O_{1} D, M D=N O_{1}=4, O D=$ $=O M-M D=4$. From $\triangle O D O_{1}: O_{1} D=\sqrt{O O_{1}^{2}-O D^{2}}=8$.
Answer: 8.
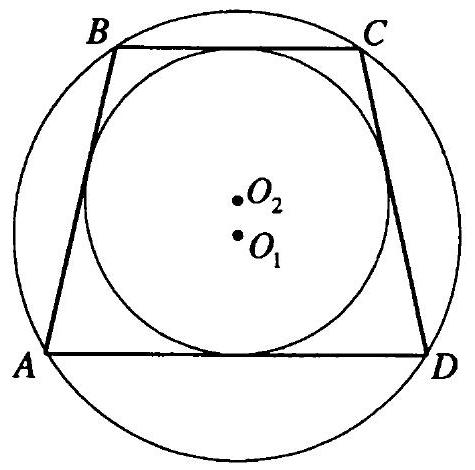
Fig. 10.27
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.218. A line parallel to the bases of a trapezoid passes through the point of intersection of its diagonals. Find the length of the segment of this line, enclosed between the lateral sides of the trapezoid, if the bases of the trapezoid are 4 and 12 cm.
|
## Solution.
In trapezoid $ABCD$ (Fig. 10.28) $BC \| AD, BC=4$ cm, $AD=12$ cm, $O$ is
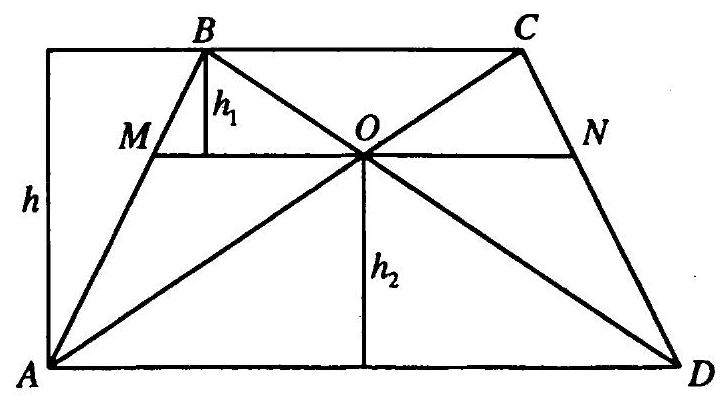
Fig. 10.28
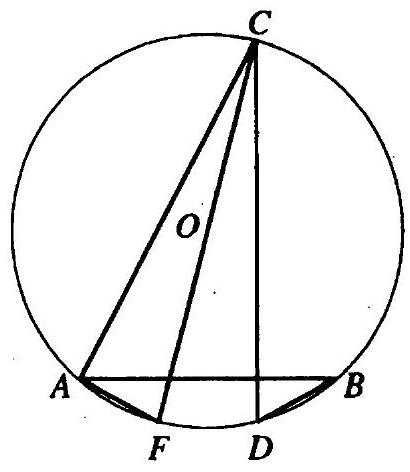
Fig. 10.29
the point of intersection of the diagonals, $MN$ is the segment of the desired length. Let $h_{1}$ be the distance between the lines $BC$ and $MN$, $h_{2}$ be the distance between $MN$ and $AD$, $h$ be the distance between $BC$ and $AD$, $h=h_{1}+h_{2}$. $\triangle MBO \sim \triangle ABD$. Then $\frac{MO}{AD}=\frac{h_{1}}{h}$ (1). $\triangle OCN \sim \triangle ACD$. Then $\frac{ON}{AD}=\frac{h_{1}}{h}$. Therefore, $MO=ON=\frac{1}{2} MN$. Let $MO=x$ cm. Then from (1) we have: $\frac{x}{12}=\frac{h_{1}}{h} \cdot \triangle MAO \sim \triangle BAC$. Then $\frac{MO}{BC}=\frac{h_{2}}{h} ; \frac{x}{4}=\frac{h_{2}}{h}$. Therefore, $\frac{x}{12}+\frac{x}{4}=\frac{h_{1}}{h}+\frac{h_{2}}{h} ; \frac{x}{3}=\frac{h_{1}+h_{2}}{h} ; x=3$. Thus, $MN=6$ cm.
Answer: 6 cm.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.224. Given an isosceles triangle with a base of 12 cm and a lateral side of $18 \mathrm{~cm}$. What segments need to be laid off from the vertex of the triangle on its lateral sides, so that by connecting their ends, a trapezoid with a perimeter of 40 cm is obtained?
|
## Solution.
By the condition in $\triangle A B C$ (Fig. 10.33) we have: $A B=B C=18, A C=12$. Let $B D=B E=x$. Then $A D=E C=18-x$. The perimeter of trapezoid $A D E C$ is: $P=A C+D E+2 A D=40$, from which $D E=40-(2 A D+A C)=2 x-8$. $\triangle A B C \sim$ $\sim \triangle D B E$, therefore, $\frac{B D}{D E}=\frac{A B}{A C}$ or $\frac{x}{2 x-8}=\frac{18}{12}, x=6$.
Answer: 6 cm.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.229. A parallelogram with sides of 3 cm and 5 cm and a diagonal of 6 cm is inscribed in a triangle. Find the sides of the triangle, given that the diagonals of the parallelogram are parallel to the lateral sides of the triangle, and the smaller of its sides lies on the base of the triangle.
|
Solution.
Let in $\triangle A B C D K=E F=3 \text{cm}, D E=5 \text{cm}, D F=6$ cm, $D K \| E F$, $O$ - the point of intersection of the diagonals $D F$ and $E K$ of the parallelogram $D E F K$ (Fig. 10.38). Let $E O=x$ cm. Then $D F^{2}+E K^{2}=2\left(D E^{2}+E F^{2}\right)$; $36+4 x^{2}=2(25+9) ; x=2 \sqrt{2}$. OEBF is a parallelogram. Then $B E=F O=3 \text{cm}, B F=E O=2 \sqrt{2} \text{cm}$. K E F C is a parallelogram. Then $F C=E K=4 \sqrt{2}$ cm, $K C=E F=3 \text{cm}$. A E F D is a parallelogram. Then $A E=D F=6$ cm, $A D=E F=3$ cm. Therefore, $A B=A E+E B=9$ cm, $B C=B F+F C=6 \sqrt{2} \text{cm}, A C=A D+D K+K C=9 \text{cm}$.
Answer: 9 cm; 9 cm; $6 \sqrt{2}$ cm.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.234. A circle with a radius of 13 cm touches two adjacent sides of a square with a side length of $18 \mathrm{~cm}$. Into which two segments does the circle divide each of the other two sides of the square?
|
## Solution.
Draw the radius $O K$ (Fig. 10.42); then $K L=\sqrt{K O^{2}-L O^{2}}$. $L O=B E=18-13=5(\mathrm{~cm}) \Rightarrow K L=\sqrt{13^{2}-5^{2}}=12$ (cm), $B K=13-12=1$ (cm). We have found that the side of the square is divided into segments of 1 and 17 cm.
Answer: 1 and 17 cm.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.255. Through point $A$ of a circle with a radius of 10 cm, two mutually perpendicular chords $A B$ and $A C$ are drawn. Calculate the radius of the circle that is tangent to the given circle and the constructed chords, if $A B=16$ cm.
|
Solution.
$O$ is the center of a circle with a radius of 10 cm (Fig. 10.60), $O_{1}$ is the center of a circle that touches the chords $A B$ and $A C$ and the given circle at points $M, D$, and $K$ respectively. Then $O_{1} D \perp A C, O_{1} M \perp A B$. $\angle B A C$ is an inscribed and right angle. Therefore, $B C$ is the diameter of the given circle, $B C=20 \text{ cm}$, $A C=\sqrt{B C^{2}-A B^{2}}=\sqrt{20^{2}-16^{2}}=12$ (cm). Drop perpendiculars $O L$ and $O N$ to $A C$ and $A B$ respectively. Then $A L=L C=\frac{1}{2} A C=6$ cm, $A N=N B=\frac{1}{2} A B=8$ cm. Let the desired radius $O_{1} K=O_{1} D=O_{1} M=$ $=x$ cm. $E$ is the point of intersection of $O L$ and $O_{1} M$. Then $\angle O E O_{1}=90^{\circ}$, $O E=O L-E L=A N-O_{1} D=(8-x) \text{ cm}, Q_{1} E=O_{1} M-M E=O_{1} M-A L=(x-6) \text{ cm}$.
$O Q_{1}=O K-Q_{1} K=(10-x)$ cm. From $\triangle O E Q\left(\angle O E Q=90^{\circ}\right): O E^{2}+E O_{1}^{2}=O O_{1}^{2} ;$ $(8-x)^{2}+(x-6)^{2}=(10-x)^{2} ; x=8$.
Answer: 8 cm.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.256. The lengths of two sides of an acute triangle are $\sqrt{13}$ and $\sqrt{10} \mathrm{~cm}$. Find the length of the third side, knowing that this side is equal to the height drawn to it.
|
Solution.
Let in $\triangle A B C$ (Fig. 10.61) $A B=\sqrt{10}$ cm, $B C=\sqrt{13}$ cm, height $B D=A C$. Since $\triangle A B C$ is an acute-angled triangle, point $D$ lies on the segment $A C$. Let $B D=A C=x$ cm. From $\triangle A D B\left(\angle A D B=90^{\circ}\right)$: $A D=\sqrt{A B^{2}-B D^{2}}=\sqrt{10-x^{2}} \cdot$ And from $\triangle C D B\left(\angle C D B=90^{\circ}\right): C D=\sqrt{B C^{2}-B D^{2}}=$ $=\sqrt{13-x^{2}} \cdot$ Therefore, $A D+D C=A C ; \sqrt{10-x^{2}}+\sqrt{13-x^{2}}=x$; $\sqrt{13-x^{2}}=x-\sqrt{10-x^{2}} ; 13-x^{2}=x^{2}-2 x \cdot \sqrt{10-x^{2}}+10-x^{2} ; 2 x \sqrt{10-x^{2}}=x^{2}-3$; $\left\{\begin{array}{l}4 x^{2}\left(10-x^{2}\right)=x^{2}-6 x^{2}+9 \\ x^{2} \geq 3 ;\end{array}\left\{\begin{array}{l}5 x^{4}-46 x^{2}+9=0, \\ x^{2} \geq 3 ;\end{array}\left\{\begin{array}{l}{\left[\begin{array}{l}x^{2}=9, \\ x^{2}=\frac{1}{5},\end{array} x^{2}=9\right.} \\ x^{2} \geq 3 ;\end{array}\right.\right.\right.$
From this, $A C=3 \text{ cm}$.
Answer: 3 cm.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.259. On the segment $A C$ of length 12 cm, a point $B$ is constructed such that $A B=4 \text{ cm}$. On the segments $A B$ and $A C$ as diameters, semicircles are constructed in the same half-plane with boundary $A C$. Calculate the radius of the circle that is tangent to the constructed semicircles and $A C$.
|
## Solution.
Points $O_{1}$ and $O_{2}$ are the centers of semicircles with diameters $A B$ and $A C$ and radii $R_{1}=2$ cm and $R_{2}=6$ cm, respectively (Fig. 10.64). $O_{3}$ is the center of the circle with the unknown radius $x$ cm, $x>0$. Then $O_{1} O_{3}=(x+2)$ cm,
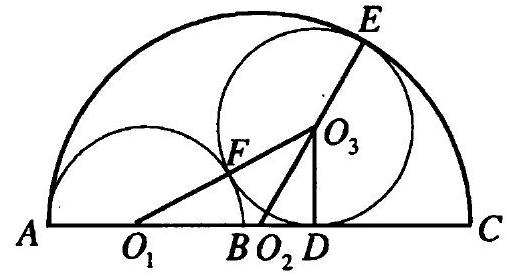
Fig. 10.64

Fig. 10.65
$O_{1} O_{2}=R_{2}-R_{1}=4 \text{ cm}, O_{2} O_{3}=(6-x) \text{ cm}$. $D$ is the point of tangency of the circle with center $O_{3}$ and $A C$. Then $O_{3} D \perp A C, O_{3} D=x$ cm. In $\Delta O_{1} O_{2} O_{3}$, the semiperimeter $p=\frac{O_{1} O_{3}+O_{2} O_{3}+O_{1} O_{2}}{2}=6$ cm. Then its area $S=\sqrt{p\left(p-O_{1} O_{3}\right)\left(p-O_{1} O_{2}\right)\left(p-O_{2} O_{3}\right)}=\sqrt{6(6-x-2)(6-4)(6-6+x)}=$ $=\sqrt{12 x(4-x)}$.
On the other hand, $S=\frac{1}{2} O_{1} O_{2} \cdot O_{3} D=2 x$. Then $\sqrt{12 x(4-x)}=2 x$; $3 x(4-x)=x^{2} ; x=3$.
Answer: 3 cm.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.281. A quadrilateral with angles of $120, 90, 60$, and $90^{\circ}$ is inscribed in a circle. The area of the quadrilateral is $9 \sqrt{3}$ cm $^{2}$. Find the radius of the circle, given that the diagonals of the quadrilateral are perpendicular to each other.
|
Solution.
Let $ABCD$ be the quadrilateral mentioned in the problem (Fig. 10.76), $\angle ABC = \angle ADC = 90^\circ$, $\angle BAD = 120^\circ$, $\angle BCD = 60^\circ$. $P$ is the intersection point of $AC$ and $BD$, and $AC \perp BD$. Since $\angle ABC = 90^\circ$, $AC$ is the diameter of the given circle. $BP$ is the height of the right triangle $\triangle ABC$. Therefore, $\angle ABD = \angle ACB$. $\angle ABD$ and $\angle ACD$ are inscribed angles subtending the chord $AD$. Thus, $\angle ABD = \angle ACD$. Consequently, $\angle ACB = \angle ACD = \frac{1}{2} \angle BCD = 30^\circ$. Therefore, $\triangle ABC = \triangle ADC$ (by hypotenuse and acute angle), $S_{\triangle ABC} = \frac{1}{2} S_{ABCD} = \frac{9\sqrt{3}}{2} \text{ cm}^2$. Let $AB = a$. Then $BC = AB \cot \angle ACB = a \sqrt{3}$ and $S_{\triangle ABC} = \frac{1}{2} AB \cdot BC = \frac{a^2 \sqrt{3}}{2}$. Therefore, $\frac{a^2 \sqrt{3}}{2} = \frac{9\sqrt{3}}{2}$, $a = 3$. The desired radius $R = \frac{1}{2} AC = AB = 3$ cm. Answer: 3 cm.
Fig. 10.77
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.283. The area of a right-angled triangle is $24 \mathrm{~cm}^{2}$, and the hypotenuse is 10 cm. Find the radius of the inscribed circle.
|
Solution.
Let $a$ and $b$ be the legs of the triangle. We have the system $\left\{\begin{array}{l}a b=48, \\ a^{2}+b^{2}=100,\end{array} \Rightarrow\right.$ $\Rightarrow a^{2}+2 a b+b^{2}=196, a^{2}-2 a b+b^{2}=4, \Rightarrow a+b=14, a-b=2$ and, consequently, $a=8$ (cm), $b=6$ (cm). Since $S=p r$, then $24=12 r, r=2$ (cm).
Answer: $2 \mathrm{~cm}$.
Fig. 10.78
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.309. The area of an isosceles trapezoid circumscribed about a circle is $32 \mathrm{~cm}^{2}$; the acute angle of the trapezoid is $30^{\circ}$. Determine the sides of the trapezoid.
|
## Solution.
Let the height $B H$ of the trapezoid be $h$ (Fig. 10.98). Then $A B=2 h$ (since $\angle A=30^{\circ}$), $B C+A D=4 h$ (since $B C+A D=A B+C D=2 A B$). The area of the trapezoid $S=\frac{(B C+A D) h}{2}=2 h^{2}=32\left(\mathrm{~cm}^{2}\right)$, from which $h=4$ cm. Therefore, $A B=C D=8 \mathrm{~cm}, B C+A D=16 \mathrm{~cm}$. But $B C+A D=2 B C+2 A H=$ $=2 B C+8 \sqrt{3}$. Thus, $A B=C D=8 \mathrm{~cm}, B C=8-4 \sqrt{3} \mathrm{~cm}, A D=8+4 \sqrt{3} \mathrm{~cm}$.
Answer: 8 cm; $8-4 \sqrt{3}$ cm; $8+4 \sqrt{3}$ cm.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.321. The medians of a triangle are 3, 4, and 5 cm. Find the area of the triangle.
|
## Solution.
Let $A N, B M, C P$ be the medians of $\triangle A B C$ (Fig. 10.110), $O$-the point of their intersection, $A N=3 \text{ cm}, B M=4 \text{ cm}, C P=5 \text{ cm}$. On the extension of segment $B M$ beyond point $M$, lay off segment $D M=O M$. Then $D O=B O=$ $=\frac{2}{3} B M=\frac{8}{3}$ cm. Drop a perpendicular $A K$ to $B M . S_{\triangle A D O}=$ $=\frac{1}{2} D O \cdot A K=\frac{1}{2} B O \cdot A K=S_{\triangle A B O}=\frac{1}{3} S_{\triangle A B C}$. Since $A O C D$ is a parallelogram, then $A D=O C=\frac{10}{3} \text{ cm} . A O=\frac{2}{3} A N=2 \text{ cm}$. Using Heron's formula, we find $S_{\triangle A D O}=\frac{8}{3} \text{ cm}^{2}$. Then $S_{\triangle A B C}=3 S_{\triangle 1 D O}=8 \text{ cm}^{2}$.
Answer: $8 \text{ cm}^{2}$.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.323. The diagonal of an isosceles trapezoid is $10 \mathrm{~cm}$, and the area is $48 \mathrm{~cm}^{2}$. Find the height of the trapezoid.
|
Solution.
In trapezoid $ABCD$ (Fig. 10.112) $AB=CD, AC=10$ cm, $CE$ is the height. Let $AE=x$ cm, $CE=y$ cm. Since $AE=\frac{AD+BC}{2}$, then by the condition $xy=48$ cm. From $\triangle AEC\left(\angle AEC=90^{\circ}\right): AE^{2}+CE^{2}=AC^{2} ; x^{2}+y^{2}=100$. We solve the system of equations: $\left\{\begin{array}{l}x^{2}+y^{2}=100 ; \\ xy=48 ;\end{array} ;\left\{\begin{array}{l}(x+y)^{2}-2xy=100 \\ xy=48 ;\end{array}\right.\right.$ $\left\{\begin{array}{l}(x+y)^{2}=196 ; \\ xy=48 .\end{array}\right.$ Since $x>0, y>0$, then $x+y=14$. Then $\left\{\begin{array}{l}x=8, \\ y=6,\end{array}\right.$ or $\left\{\begin{array}{l}x=6, \\ y=8 .\end{array}\right.$ Therefore, the height of the trapezoid is 6 cm or 8 cm.
Answer: 6 cm, 8 cm.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.346. A circle with center $O_{1}$ is divided by the diameter $A B$ into two semicircles. In one of them, two new semicircles are constructed, based on $O_{1} A$ and $O_{1} B$ as diameters. A circle is inscribed in the curvilinear figure bounded by the contours of these three semicircles. How many times smaller is its area compared to the area of the given circle?
|
## Solution.
Let $O_{2}$ be the midpoint of $A O_{1}$ - the center of one semicircle, $O_{3}$ be the midpoint of $B O_{1}$ - the center of the second semicircle, $O_{4}$ - the center of the circle inscribed in the curvilinear figure mentioned in the problem (Fig. 10.129).
Fig. 10.129
Let $R$ be the radius of the circle with center $O_{1}$, and $S_{1}$ be its area, $r$ be the radius of the circle with center $O_{4}$, and $S_{2}$ be its area. We have: $O_{1} O_{2}=O_{1} O_{3}=\frac{R}{2}$, $O_{2} O_{4}=O_{3} O_{4}=\frac{R}{2}+r, O_{1} O_{4}=R-r$. In triangle $O_{2} O_{4} O_{3}: O_{2} O_{4}=O_{3} O_{4}$, point $O_{1}$ is the midpoint of $O_{2} O_{3}$. Therefore, $O_{1} O_{4} \perp O_{2} O_{3}$, then
Fig. 10.130
Fig. 10.131
$O_{2} O_{4}^{2}=O_{1} O_{2}^{2}+O_{1} O_{4}^{2}$, i.e., $\left(\frac{R}{2}+r\right)^{2}=\left(\frac{R}{2}\right)^{2}+(R-r)^{2} . R^{2}=3 R r, R=3 r$.
Therefore, $\frac{S_{1}}{S_{2}}=\frac{R^{2}}{r^{2}}=9$.
Answer: 9 times.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.149. The base of a right parallelepiped is a parallelogram, one of the angles of which is $30^{\circ}$. The area of the base is 4 dm $^{2}$. The areas of the lateral faces of the parallelepiped are 6 and 12 dm ${ }^{2}$. Find the volume of the parallelepiped.
|
Solution.
The volume of the parallelepiped $V=S_{\text {base }} h$, where $h$ is the height of the parallelepiped. Since the parallelepiped is a right one, the heights of the lateral faces are also equal to $h$ (Fig. 11.44). According to the problem, $\angle B A D=30^{\circ}, A B \cdot h=6$ dm $^{2}, A D \cdot h=12$ dm $^{2}$, i.e., $A D=2 A B$. Let $B K \perp A D$; then $B K=\frac{1}{2} A B$.
Since $A D \cdot B K=4$ dm ${ }^{2}$, we have $2 A B \cdot \frac{1}{2} A B=4, A B=2$ (dm); therefore, $h=3$ dm. Finally, $V=4 \cdot 3=12$ dm $^{3}$.
Answer: 12 dm $^{3}$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.194. In a trapezoid, the smaller base is equal to 2, the adjacent angles are $135^{\circ}$ each. The angle between the diagonals, facing the base, is $150^{\circ}$. Find the area of the trapezoid.
Fig. 12.61
|
## Solution.
Let in trapezoid $A B C D$, $B C=2, \angle A B C=\angle D C B=135^{\circ}, O$ - the point of intersection of the diagonals, $\angle B O C=150^{\circ}$ (Fig. 12.61).
In $\triangle B O C: \angle A C B=\angle D B C=15^{\circ}$, then $\angle B A C=180^{\circ}-(\angle A B C+$ $+\angle A C B)=30^{\circ}$.
By the Law of Sines in $\triangle A B C$ :
$$
\begin{gathered}
\frac{A C}{\sin \angle A B C}=\frac{B C}{\sin \angle B A C} \Rightarrow A C=\frac{B C \sin \angle A B C}{\sin \angle A B C}=\frac{2 \sin 135^{\circ}}{\sin 30^{\circ}}=2 \sqrt{2} \\
S_{\triangle A B C D}=\frac{1}{2} A C \cdot B D \sin \angle B O C=\frac{1}{2} A C^{2} \sin \angle B O C=\frac{1}{2}(2 \sqrt{2})^{2} \sin 150^{\circ}=2
\end{gathered}
$$
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.223. Point $C$ is located 12 km downstream from point $B$. A fisherman set out from point $A$, located upstream from point $B$, to point $C$. After 4 hours, he arrived at $C$, and the return trip took 6 hours. On another occasion, the fisherman used a motorboat, thereby tripling his own speed relative to the water, and reached from $A$ to $B$ in 45 minutes. It is required to determine the speed of the current, assuming it is constant.
|
Solution.
Let $v_{T}$ km/h be the speed of the current; $v_{,}$ km/h be the speed of the boat; $a$ km/h be the distance between $A$ and $B$. Then, according to the problem,
$$
\left\{\begin{array}{l}
\left(v_{T}+v_{T}\right) \cdot 4=12+a, \\
\left(v_{L}-v_{T}\right) \cdot 6=12+a, \\
a=\left(3 v_{T}+v_{T}\right) \cdot 0.75
\end{array}\right.
$$
Answer: 1 km/h.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.225. A certain order takes 3.6 hours longer to complete in workshop No.1 compared to workshop No.2, and 10 hours longer compared to workshop No.3. If under the same conditions, workshops No.1 and No.2 combine to complete the order, the completion time will be the same as in workshop No.3 alone. By how many hours more or less than one seven-hour workday does the completion of the specified order in workshop No.3 take?
|
## Solution.
Let $x$ hours be the time to complete the order in Workshop No.3. Then in the 1st workshop, this time is $x+10$ hours, and in the 2nd workshop, it is $-x+6.4$ hours.
$$
\text { According to the condition } \frac{1}{x+10}+\frac{1}{x+6.4}=\frac{1}{x} \text {, from which } x=8 \text { hours. }
$$
This means that the completion of the order in Workshop No.3 takes 1 hour longer than the 7-hour workday.
Answer: longer by 1 hour.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.227. Two workers were assigned a task. The second one started working an hour later than the first. After 3 hours from the time the first one started, they had 9/20 of the entire work left to complete. By the end of the work, it turned out that each had completed half of the entire work. How many hours would each, working separately, need to complete the entire task?
|
Solution.
Let the 1st worker can complete the entire job in $x$ hours, the second in $y$ hours. The productivity of the 1st: $\frac{1}{x} ; 2$nd: $\frac{1}{y}$.
$$
\text { According to the condition }\left\{\begin{array}{l}
\frac{1}{x} \cdot 3+\frac{1}{y} \cdot 2=1-\frac{9}{20}, \\
\frac{x}{2}-\frac{y}{2}=1
\end{array} \text { from which } x=10 \text { hours, } y=8\right. \text { hours. }
$$
Answer: 10 and 8 hours.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.228. Two workers were assigned to manufacture a batch of identical parts. After the first worked for 2 hours and the second for 5 hours, it turned out that they had completed half of the entire work. Working together for another 3 hours, they found that they had 0.05 of the entire work left to complete. In what time interval can each of them, working separately, complete the entire work?
|
## Solution.
Let the 1st worker can complete the entire job in $x$ hours, the second - in $y$ hours.
Productivity of the 1st: $\frac{1}{x}$, the second $-\frac{1}{y}$.
According to the condition $\left\{\begin{array}{l}\frac{1}{x} \cdot 2+\frac{1}{y} \cdot 5=\frac{1}{2}, \\ \frac{1}{2}+\left(\frac{1}{x}+\frac{1}{y}\right) \cdot 3=1-0.05,\end{array}\right.$ from which $x=12$ hours; $y=15$ hours.
Answer: 12 and 15 hours.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.232. From the railway station to the beach is 4.5 km. A boy and a scheduled bus left the station for the beach simultaneously. After 15 minutes, the boy met the bus returning from the beach, and he managed to walk another $9 / 28$ km from the place of the first meeting with the bus, when he was caught up by the same bus, which had reached the station and set off to the beach again. Find the speeds of the boy and the bus, assuming they are constant and neither the boy nor the bus stopped en route, but the bus made stops of 4 minutes each at the beach and at the station.
|
## Solution.
Let $v_{\text {m }}, v_{\text{a}}$ be the speeds of the boy and the bus, respectively.
According to the problem, we have the system
$\left\{\begin{array}{l}\frac{15}{60} v_{M}+\frac{15-4}{60} v_{\text{a}}=2 \cdot 4.5, \\ \frac{9}{28 v_{M}}=\frac{4}{60}+\frac{2 \frac{15}{60} v_{M}+\frac{9}{28}}{v_{\text{a}}},\end{array}\right.$
from which $v_{\text{M}}=3 \text{ km/h}, v_{\text{a}}=45 \text{ km/h}$.
Answer: 3 and 45 km/h.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.233. A tourist was returning from vacation on a bicycle. On the first leg of the journey, which was 246 km, he traveled on average 15 km less per day than he did on the last leg of the journey, which was 276 km. He arrived home right on time at the end of his last vacation day. It is also known that it took him one day more than half the number of days remaining until the end of his vacation to complete the first leg of the journey. How many days before the end of his vacation did the tourist set out for home?
|
## Solution.
Let the tourist travel 267 km in $x$ days, and 246 km in $\frac{x}{2}+1$. On the first segment of 246 km, his speed was $v$ km/day, and on the second segment of 276 km, it was $(v+15)$ km/day.
Then $\left\{\begin{array}{l}\left(\frac{x}{2}+1\right) v=246, \\ x(v+15)=276,\end{array}\right.$
from which $x=2$.
Therefore, the tourist set off for home $x+\frac{x}{2}+1=4$ days before the end of the vacation.
Answer: 4 days.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.251. The hour and minute hands coincide at midnight, and a new day begins. At what hour of this new day will the hour and minute hands coincide again for the first time, assuming that the clock hands move without jumps?
|
## Solution.
Let's assume the speed of the minute hand is 1, then the speed of the hour hand is $-\frac{1}{12} \cdot$ The hands will coincide when $\frac{1}{12} \cdot t + 60 = t$, where $t$ is the time of movement of the hands.
Solving the equation, we find $t = \frac{720}{11}$ (min).
Answer: 1 hr $5 \frac{5}{11}$ min.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.262. It is known that a freely falling body travels 4.9 m in the first second, and in each subsequent second, it travels 9.8 m more than in the previous one. If two bodies start falling from the same height, one 5 seconds after the other, then after what time will they be 220.5 m apart?
|
## Solution.
Let $t \mathrm{c}$ be the required time. In this time, the first body will travel $4.9 t^{2} \mathrm{M}$, and the second body will travel $4.9(t-5)^{2}$ m.
According to the condition, $4.9 t^{2}-4.9(t-5)^{2}=220.5$, from which $t=7 \mathrm{c}$.
Answer: 7 seconds after the first body starts falling.
Fig. 13.7
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.264. To rise in an ordinary elevator to the top floor of an eight-story building (height 33 m) with two 6-second intermediate stops, it takes as much time as it would to rise in an elevator of a high-rise building with one 7-second intermediate stop at the 20th floor (height 81 m). Determine the lifting speed of the elevator in the high-rise building, knowing that it exceeds the speed of the ordinary elevator by $1.5 \mathrm{~m} / \mathrm{c}$, but does not reach $5 \mathrm{~m} / \mathrm{c}$.
|
## Solution.
Let $v_{1}$ m/s be the speed of a regular elevator ($v_{1} \leq 3.5 \text{ m/s}$), and $v_{2}$ m/s be the speed of the elevator in a high-rise building, $v_{2}=v_{1}+1.5 \text{ m/s}$.
According to the condition,
$$
\frac{33}{v_{1}}+2 \cdot 6=\frac{81}{v_{1}+1.5}+7 \text{, from which } v_{1}=1.5 \text{ m/s}, v_{2}=v_{1}+1.5=3 \text{ m/s}
$$
Answer: $3 \text{ m/s}$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.269. At the pier, two passengers disembarked from a steamship and headed to the same village. One of them walked the first half of the way at a speed of 5 km/h and the second half at a speed of 4 km/h. The other walked the first half of the time at a speed of 5 km/h and the second half at a speed of 4 km/h, arriving at the village 1 minute earlier than the first. How long did each of them take to cover the entire distance, and what is the distance between the pier and the village?
|
Solution.
Let $x$ km be the distance between the pier and the village, $t$ h be the time it took the second passenger to walk to the village.
According to the problem, $\left\{\begin{array}{l}\frac{x}{2 \cdot 5}+\frac{x}{2 \cdot 4}=t+\frac{1}{60}, \\ 5 \cdot \frac{t}{2}+4 \cdot \frac{t}{2}=x,\end{array}\right.$
from which $x=6$ km; $t=\frac{4}{3} \text{ h}=1 \text{ h } 20$ min.
Answer: 1 h 21 min; 1 h 20 min; 6 km.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.273. The ball is rolling perpendicular to the sideline of a football field. Suppose, moving uniformly decelerated, the ball rolled 4 m in the first second, and 0.75 m less in the next second. A football player, initially 10 m away from the ball, started running in the direction of the ball's movement to catch it. Moving uniformly accelerated, the player ran 3.5 m in the first second, and 0.5 m more in the next second. How long will it take for the player to catch the ball, and will he be able to catch it before the ball goes out of bounds, if the player needs to run 23 m to reach the sideline?
|
Solution.
Let $t$ be the desired time. In this time, the ball will roll $\frac{2 \cdot 4-0.75(t-1)}{2} \cdot t \mathrm{M}$, and the footballer will run $\frac{2 \cdot 3.5+0.5(t-1)}{2} \cdot t \mathrm{M}$. (The formula for the sum of $n$ terms of an arithmetic progression was used).
According to the condition,
$$
\frac{2 \cdot 3.5+0.5(t-1)}{2} \cdot t - \frac{2 \cdot 4-0.75(t-1)}{2} \cdot t = 10, \text{ from which } t = 5 \mathrm{s}
$$
The footballer will catch up with the ball, having run $\frac{2 \cdot 3.5+0.5 \cdot 4}{2} \cdot 5 = 22.5$ m, 0.5 m before the sideline.
Answer: in 5 s; 0.5 m before the line of the field.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.283. Two pedestrians set out towards each other simultaneously from two points, the distance between which is 28 km. If the first pedestrian had not stopped for 1 hour at a distance of 9 km from the starting point, the meeting of the pedestrians would have taken place halfway. After the stop, the first pedestrian increased their speed by $1 \mathrm{~km} / \mathrm{h}$, and the meeting occurred 4 km from the place where the first pedestrian had stopped. Find the speeds of the pedestrians.
|
Solution.
Since pedestrians could meet halfway, their speeds are equal. Let $V$ be the initial speed of one of the pedestrians.
According to the condition $\frac{9}{V}+\frac{4}{V+1}+1=\frac{28-(9+4)}{V}$, from which $V=3$ (km/h).
Answer: initially, both were walking at the same speed of 3 km/h.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.290. If both pipes are opened simultaneously, the pool will be filled in 2 hours and 24 minutes. In reality, however, only the first pipe was opened initially for $1 / 4$ of the time it takes the second pipe to fill the pool on its own. Then, the second pipe was opened for $1 / 4$ of the time it takes the first pipe to fill the pool on its own, after which it turned out that $11/24$ of the pool's full capacity remained to be filled. How much time is required for each pipe to fill the pool individually?
|
Solution.
Let's take the entire volume of the pool as 1. Let $x, y$ (liters) per hour leak through the first and second pipe, respectively. According to the conditions, we have the system
Then for the first pipe, it takes $\frac{1}{x}=4$ (hours) to fill the pool, and $\mathrm{a} \frac{1}{-}=6$ (hours) for the second.
Answer: 4 and $6$ hours.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.293. Two pipes of different cross-sections are connected to a swimming pool. One is a uniform water supply pipe, and the other is a uniform water discharge pipe, with the first pipe filling the pool 2 hours longer than the second pipe empties it. When the pool was filled to $1 / 3$ of its capacity, both pipes were opened, and the pool was found to be empty after 8 hours. How many hours, acting separately, does the first pipe take to fill, and the second pipe to empty the pool?
|
## Solution.
Let's write down the values of the sought and given quantities in the form of a table:
| Pipe | Time, h | Capacity | Productivity |
| :---: | :---: | :---: | :---: |
| Supply | $x+2$ | 1 | $\frac{1}{x+2}$ |
| Discharge | $x$ | 1 | $\frac{1}{x}$ |
| Both together | 8 | $\frac{1}{3}$ | $\frac{1}{24}$ |
According to the condition $\frac{1}{x}-\frac{1}{x+2}=\frac{1}{24}$, from which $x=6$.
Answer: in 8 and 6 hours.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.294. Two workers were assigned to manufacture a batch of identical parts; after the first worked for $a$ hours, and the second for $0.6 a$ hours, it turned out that they had completed $5 / n$ of the entire work. After working together for another $0.6 a$ hours, they found that they still had to manufacture $1 / n$ of the entire batch of parts. How many hours will each of them, working separately, need to complete the entire work? The number $n$ is a natural number; find it.
|
## Solution.
Let the entire volume of work be 1. Let $x, y$ be the labor productivity (the number of parts produced per hour) of the first and second workers, respectively. According to the conditions, we have the system
$$
\left\{\begin{array}{l}
a x+0.6 a y=\frac{5}{n} \\
a x+0.6 a y+0.6 a(x+y)=1-\frac{1}{n}
\end{array} \text {, from which } x=\frac{11-n}{0.4 a n}, y=\frac{n-9}{0.24 a n} .\right.
$$
Then the first worker will manufacture all the parts in $\frac{1}{x}=\frac{0.4 a n}{11-n}$ (hours), and the second worker will do so in $\frac{1}{y}=\frac{0.24 a n}{n-9}$ (hours). The value of $n$ must satisfy the system of inequalities
$$
\left\{\begin{array}{l}
11-n>0, \\
n-9>0,
\end{array} \text { i.e., } n=10\right.
$$
Answer: $\frac{0.4 a n}{11-n} ; \frac{0.24 a n}{n-9} ; n=10$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.299. Two points rotate uniformly along two concentric circles. One of them completes a full revolution 5 seconds faster than the other, and therefore manages to make two more revolutions per minute. Let the rays directed from the center of the circle to these points coincide at the beginning of the motion. Calculate the magnitude of the angle between the rays after $1 \mathrm{s}$.
|
Solution.
Let $V_{1}, V_{2}$ be the rotational speeds of the points, $l$ be the length of the circumference, and $x$ be the length of the arc between the points after 1 second of rotation. Then the angle between the rays will be $\alpha=\frac{x \cdot 360^{\circ}}{l}$ (1). According to the problem, we have the system $\left\{\begin{array}{l}\frac{l}{V_{2}}-\frac{l}{V_{1}}=5, \\ 60\left(V_{1}-V_{2}\right)=2 l,\end{array}\right.$ from which $V_{1}=\frac{l}{10}, V_{2}=\frac{l}{15}$.
If the points rotate in the same direction, then $x=V_{1}-V_{2}=\frac{l}{30}$ and $\alpha=12^{\circ}$; if in opposite directions, then $x=V_{1}+V_{2}=\frac{l}{6}$ and $\alpha=60^{\circ}$.
Answer: 12 or $60^{\circ}$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.300. The smaller arc between points $A$ and $B$, located on a circle, is 150 m. If the points start moving towards each other along the smaller arc, they will meet after $10 \mathrm{c}$, and if they move along the larger arc, the meeting will occur after $14 \mathrm{c}$. Determine the speeds of the points and the length of the circumference, given that point $A$ can run the entire circumference in the time it takes for $B$ to travel only $90 \mathrm{M}$.
|
## Solution.
Let $V_{a}$ and $V_{b}$ be the speeds of points $A$ and $B$, and $l$ be the length of the circumference. According to the conditions, we have the system $\left\{\begin{array}{l}10\left(V_{a}+V_{b}\right)=150, \\ 14\left(V_{a}+V_{b}\right)=l-150, \\ \frac{l}{V_{a}}=\frac{90}{V_{b}},\end{array}\right.$
from which $V_{a}=12(\mathrm{m} / \mathrm{s}), V_{b}=3(\mathrm{m} / \mathrm{s}), l=360(\mathrm{m})$.
Answer: 12 m $/$ s and 3 m $/ s ; 360$ m.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.302. Two points move uniformly in the same direction along a circle 60 m in circumference. One of them completes a full revolution 5 seconds faster than the other. At the same time, the points coincide every 1 minute. Determine the speeds of the points.
|
Solution.
Let $V_{1}, V_{2}$ be the speeds of the points. According to the problem, we have the system
$$
\left\{\begin{array}{l}
\frac{60}{V_{2}}-\frac{60}{V_{1}}=5, \\
60\left(V_{1}-V_{2}\right)=60,
\end{array} \text { from which } V_{1}=4(\mathrm{M} / \mathrm{c}), V_{2}=3(\mathrm{M} / \mathrm{c})\right.
$$
Answer: 3 and $4 \mathrm{~m} / \mathrm{c}$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.309. There are two gold and silver alloys. In one alloy, the quantities of these metals are in the ratio $1: 2$, in the other - $2: 3$.
How many grams should be taken from each alloy to obtain 19 g of an alloy in which gold and silver are in the ratio 7:12?
|
Solution.
Let $x$ (g) be the amount of the first alloy taken, which contains $\frac{1}{3} x$ gold and $\frac{2}{3} x$ silver. According to the problem, we have the system
$$
\left\{\begin{array}{l}
x+y=19 \\
\frac{1}{3} x+\frac{2}{5} y=\frac{7}{12}\left(\frac{2}{3} x+\frac{3}{5} y\right), \text{ from which } x=9(\mathrm{g}), y=10(\mathrm{g})
\end{array}\right.
$$
Answer: 9 and 10 g.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.317. One tourist set out at 6 a.m., and the second - towards him at 7 a.m. They met at 8 a.m. and, without stopping, continued their journey. How much time did each of them spend on the entire journey, if the first arrived at the place where the second started 28 minutes later than the second arrived at the place where the first started? It is assumed that each walked without stopping at a constant speed.
|
## Solution.
Let $V_{1}, V_{2}$ be the speeds of the first and second tourists, respectively, and $x$ be the time it takes for the second tourist to cover the distance that the first tourist covers in 2 hours. According to the problem, we have the system $\left\{\begin{array}{l}x V_{2}=120 V_{1}, \\ V_{2} x+60 V_{2}=120 V_{1}+V_{1}(x+28) .\end{array}\right.$ From the first equation, we express $\frac{V_{1}}{V_{2}}$ and substitute it into the second equation. From the resulting equation, we find $x=72$ (min). Then the first tourist spent a total of $120+72+28=220$ (min) on the entire journey, and the second tourist spent $-60+72=132$ (min).
Answer: 3 hours 40 minutes and 2 hours 12 minutes.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.319. A vessel with a capacity of 8 liters is filled with a mixture of oxygen and nitrogen, with oxygen accounting for $16 \%$ of the vessel's capacity. From this vessel, a certain amount of the mixture is released and an equal amount of nitrogen is added, after which the same amount of the mixture is released again and the same amount of nitrogen is added once more. In the new mixture, the oxygen content is $9 \%$. What amount of the mixture was released each time?
|
Solution.
Initially, the vessel contained $16 \cdot \frac{8}{100}=\frac{32}{25}$ liters of oxygen. The released $x$ liters of the mixture contain $\frac{16 x}{100}=\frac{4 x}{25}$ liters of oxygen. Now, for every 8 liters of the mixture in the vessel, there are $\frac{32-4 x}{25}$ liters of oxygen, which constitutes $(16-2 x) \%$. The second release of $x$ liters of the mixture contains $(16-2 x) \frac{x}{100}=(8-x) \frac{x}{50}$ liters of oxygen. According to the problem, $\frac{32-4 x}{25}-\frac{(8-x) x}{50}=9 \cdot \frac{8}{100}$, from which $x_{1}=2, x_{2}=14$.
Answer: 2 liters.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.320. Impurities constitute $20 \%$ of the total volume of the solution. What is the smallest number of filters through which the solution must be passed so that the final impurity content does not exceed $0.01 \%$, if each filter absorbs $80 \%$ of the impurities? (It is known that $\lg 2 \approx 0.30$.)
|
Solution.
Impurities constitute $\frac{1}{5}$ of the solution. After the first filtration, $\left(\frac{1}{5}\right)^{2}$ of the impurities will remain, and after the $k$-th filtration, $-\left(\frac{1}{5}\right)^{k+1}$. According to the condition, $\left(\frac{1}{5}\right)^{k+1} \leq 10^{-4} ;-(k+1) \lg 5 \leq-4$, from which $k \geq 4.7$.
Answer: 5 filters.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.325. 9000 parts can be manufactured on several new machines of the same design and one machine of the old design, which works twice as slowly as each of the new machines. The old machine can also be replaced by a new machine of the same design as the others. In this second option, each machine would produce 200 fewer parts than one new machine in the first option. How many machines were there in total?
|
Solution.
Let $x$ parts be manufactured on one new machine, $\frac{x}{2}$ - on the old one, $n$ - the number of machines. According to the condition, we have the system
$$
\left\{\begin{array}{l}
(n-1) x+\frac{x}{2}=9000, \\
\frac{9000}{n}=x-200, \quad \text { from which } n=5
\end{array}\right.
$$
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.330. Two trucks were supposed to transport a certain cargo in 6 hours. The second truck was delayed in the garage, and when it arrived at the loading site, the first truck had already transported $3 / 5$ of the total cargo; the remaining part of the cargo was transported by the second truck, and the entire cargo was transported in this way in 12 hours. How much time would each truck need separately to transport the cargo?
|
Solution.
Let's take the entire volume of work as 1. Let $x, y$ be the weight of cargo transported by each machine in one trip. According to the conditions, we have the system
$$
\left\{\begin{array}{l}
\frac{1}{x+y}=6, \\
\frac{3}{5 x}+\frac{2}{5 y}=12,
\end{array} \text { from which } x=\frac{1}{10}, y=\frac{1}{15} \text { or } x=y=\frac{1}{12} .\right. \text { Then the first ma- }
$$
chine will transport the entire cargo in 10 hours, and the second in 15 hours, or each in 12 hours.
Answer: 10 and 15 hours or 12 hours each.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.333. A ball falls from a height of 2 m 43 cm and, upon hitting the ground, bounces back up, each time reaching $2 / 3$ of the height from which it falls again. After how many bounces will the ball rise to a height of 32 cm?
|
Solution.
The numbers expressing the height to which the ball rises form a geometric progression with $b_{1}=243 q$ and $q=\frac{2}{3}$. According to the condition $q_{n}=32=b_{1} q^{n-1}$, from which $n=5$.
Answer: after 5 bounces.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.340. It is known that the difference between the variable quantities $z$ and $y$ is proportional to the quantity $x$, and the difference between the quantities $x$ and $z$ is proportional to the quantity $y$. The coefficient of proportionality is the same and is a positive integer $k$. A certain value of the quantity $z$ is $5 / 3$ times the difference of the corresponding values of $x$ and $y$. Find the numerical value of the coefficient $k$.
|
Solution.
From the condition, we have the system $\left\{\begin{array}{l}z-y=k x, \\ x-z=k y, \\ x-y=\frac{3}{5} z\end{array}\right.$
From the first two equations, we express $\frac{x}{z}$ and $\frac{y}{z}$ in terms of $k$, then substitute the obtained expressions for $\frac{x}{z}$ and $\frac{y}{z}$ into the third equation and find $k=3$.
## Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.346. The volume of substance A is half the sum of the volumes of substances B and C, and the volume of substance B is 1/5 of the sum of the volumes of substances A and C. Find the ratio of the volume of substance C to the sum of the volumes of substances A and B.
|
Solution.
Given that $2 V_{A}=V_{B}+V_{C}$ and $5 V_{B}=V_{A}+V_{C}$. Let $V_{A}=x V_{C}$ and $V_{B}=y V_{C}$. Then we get the system $\left\{\begin{array}{l}2 x-y=1, \\ -x+5 y=1,\end{array}\right.$ from which $x=\frac{2}{3}, y=\frac{1}{3}$. Therefore, $\frac{V_{C}}{V_{A}+V_{B}}=\frac{1}{x+y}=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.349. From post office $A$ to village $B$, one needs to walk 9 km. The postman walks the entire path there and back, without stopping in the village, in 3 hours and 41 minutes. The road from $A$ to $B$ goes uphill first, then on flat ground, and finally downhill. Over what distance does the road run on flat ground, if the postman walks uphill at a speed of 4 km/h, on flat ground at 5 km/h, and downhill at 6 km/h?
|
## Solution.
Let $x, y, z$ be the lengths of the road uphill, on flat ground, and downhill, respectively. According to the problem, we have the system
from which $y=4$ (km).
Answer: 4 km.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.362. A certain alloy consists of two metals in the ratio $1: 2$, while another contains the same metals in the ratio $2: 3$. How many parts of each alloy should be taken to obtain a third alloy containing the same metals in the ratio $17: 27?$
|
Solution.
Let $x$ parts of the first metal and $y$ parts of the second be taken. Then
$$
\frac{1}{3} x+\frac{2}{5} y=\frac{17}{44}(x+y), \text { hence } \frac{y}{x}=\frac{35}{9}
$$
Answer: 9 and 35 parts.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.369. Around the house, lindens and birches are planted, and their total number is more than 14. If the number of lindens is doubled and the number of birches is increased by 18, then the number of birches will be greater than the number of lindens. If, however, the number of birches is doubled without changing the number of lindens, then the number of lindens will now be greater than the number of birches. How many lindens and how many birches were planted?
Fig. 13.20
|
Solution.
Let $x, y$ be the number of lindens and birches, respectively. According to the condition, we have the system of inequalities $\left\{\begin{array}{l}x+y>14, \\ y+18>2 x, \\ x>2 y .\end{array}\right.$
Construct the lines $x+y=14$ (1), $y+18=2 x$ (2), $x=2 y$ (3). From Fig. 13.20, it is clear that the point ( $11 ; 5$ ) is the only point with natural coordinates that lies inside the triangle $A B C$, i.e., satisfies our system of inequalities.
Answer: 11 lindens and 5 birches.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$1.4 \frac{3 a^{2}+2 a x-x^{2}}{(3 x+a)(a+x)}-2+10 \frac{a x-3 x^{2}}{a^{2}+9 x^{2}}$.
$1.5\left(\left(\frac{x}{y-x}\right)^{-2}-\frac{(x+y)^{2}-4 x y}{x^{2}-x y}\right)^{2} \frac{x^{4}}{x^{2} y^{2}-y^{4}}$.
|
1.4 According to formula (1.8), we have $a^{2}-9 x^{2}=(a-3 x)(a+3 x)$. Simplify the fraction $\frac{a x-3 x^{2}}{(a-3 x)(a+3 x)}$ by canceling $a-3 x$, assuming $a \neq 3 x$; we get $\frac{x}{a+3 x}$. Next, using formula (1.15), factor the numerator of the first fraction:
$$
\begin{aligned}
& 3 a^{2}+2 a x-x^{2}=-\left(x^{2}-2 a x-3 a^{2}\right)=-(x-3 a)(x+a)= \\
& =(3 a-x)(x+a)
\end{aligned}
$$
Now, cancel the first fraction by $a+x$, where $a \neq -x$, and we find
$$
\frac{3 a-x}{3 x+a}-2+\frac{10 x}{a+3 x}=\frac{3 a-x-2(3 x+a)+10 x}{a+3 x}=\frac{a+3 x}{a+3 x}=1
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$1.6 \frac{\left(\frac{1}{a}+\frac{1}{b}-\frac{2 c}{a b}\right)(a+b+2 c)}{\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{2}{a b}-\frac{4 c^{2}}{a^{2} b^{2}}} ; a=7,4, b=\frac{5}{37}$.
|
1.6 Perform the following transformations in the numerator and denominator:
$$
\begin{aligned}
& \frac{1}{a}+\frac{1}{b}-\frac{2 c}{a b}=\frac{b+a-2 c}{a b} \\
& \frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{2}{a b}-\frac{4 c^{2}}{a^{2} b^{2}}=\frac{b^{2}+a^{2}+2 a b-4 c^{2}}{a^{2} b^{2}}= \\
& =\frac{(b+a)^{2}-(2 c)^{2}}{a^{2} b^{2}}=\frac{(b+a-2 c)(b+a+2 c)}{a^{2} b^{2}}
\end{aligned}
$$
Thus,
$$
\frac{(b+a-2 c)(b+a+2 c)}{a b} : \frac{(b+a-2 c)(b+a+2 c)}{a^{2} b^{2}}=a b
$$
When $a=7.4=\frac{37}{5}, b=\frac{5}{37}$, we get $a b=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$1.24 \frac{\sqrt{\frac{a b c+4}{a}+4 \sqrt{\frac{b c}{a}}}}{\sqrt{a b c}+2} ; a=0.04$.
|
1.24 Assuming $a b c \neq 0$, we have:
$$
\begin{aligned}
& \frac{a b c+4}{a}+4 \sqrt{\frac{b c}{a}}=b c+\frac{4}{a}+4 \sqrt{\frac{b c}{a}}= \\
& =(\sqrt{b c})^{2}+4 \sqrt{\frac{b c}{a}}+\left(\frac{2}{\sqrt{a}}\right)^{2}=\left(\sqrt{b c}+\frac{2}{\sqrt{a}}\right)^{2} \\
& \frac{\sqrt{\left(\sqrt{b c}+\frac{2}{\sqrt{a}}\right)^{2}}}{\sqrt{a b c}+2}=\frac{\sqrt{a b c}+2}{\sqrt{a}(\sqrt{a b c}+2)}=\frac{1}{\sqrt{a}}
\end{aligned}
$$
For $a=0.04$, we find $\frac{1}{\sqrt{0.04}}=5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.