problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
1.26 Given the expression
$$
\begin{aligned}
& \frac{x^{3}-a^{-\frac{2}{3}} \cdot b^{-1}\left(a^{2}+b^{2}\right) x+b^{\frac{1}{2}}}{b^{\frac{3}{2}} x^{2}} \\
& \text { Substitute } x=a^{\frac{2}{3} b}-\frac{1}{2} \text { and simplify the result }
\end{aligned}
$$
Eliminate the irrationality in the denominator of the fraction (1.27-1.28):
|
1.26 After performing the specified substitution, we find
$$
\begin{aligned}
& \frac{\left(a^{\frac{2}{3}} b^{-\frac{1}{2}}\right)^{3}-a^{-\frac{2}{3}+\frac{2}{3}} b^{-1-\frac{1}{2}}\left(a^{2}+b^{2}\right)+b^{\frac{1}{2}}}{b^{\frac{3}{2}}\left(a^{\frac{2}{3}} b^{\left.-\frac{1}{2}\right)^{2}}\right.}= \\
& =\frac{a^{2} b^{-\frac{3}{2}}-b^{-\frac{3}{2}} a^{2}-b^{\frac{1}{2}}+b^{\frac{1}{2}}}{a^{\frac{4}{3}} b^{\frac{1}{2}}}=0
\end{aligned}
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$1.53 \frac{\sqrt{7+4 \sqrt{3}} \cdot \sqrt{19-8 \sqrt{3}}}{4-\sqrt{3}}-\sqrt{3}=2$.
|
1.53 Consider the equality
$$
\frac{\sqrt{7+4 \sqrt{3}} \cdot \sqrt{19-8 \sqrt{3}}}{4-\sqrt{3}}=2+\sqrt{3}
$$
Obviously, if this equality is true, then the given equality is also true. Let
$$
a=\frac{\sqrt{7+4 \sqrt{3}} \cdot \sqrt{19-8 \sqrt{3}}}{4-\sqrt{3}}, b=2+\sqrt{3}
$$
It is easy to establish that $a>0$ and $b>0$. If in this case the equality $a^{2}=b^{2}$ holds, then $a=b$. We find
$$
\begin{aligned}
& a^{2}=\frac{(7+4 \sqrt{3})(19-8 \sqrt{3})}{(4-\sqrt{3})^{2}}= \\
& =\frac{(7+4 \sqrt{3})(19-8 \sqrt{3})}{19-8 \sqrt{3}}=7+4 \sqrt{3} \\
& b^{2}=(2+\sqrt{3})^{2}=7+4 \sqrt{3}
\end{aligned}
$$
Since $a^{2}=b^{2}$, then $a=b$, i.e., the given equality is valid.
This example can be solved faster if one guesses that both expressions under the square roots in the condition are squares of positive numbers, specifically:
$7+4 \sqrt{3}=(2+\sqrt{3})^{2}$ and $19-8 \sqrt{3}=(4-\sqrt{3})^{2}$.
Then the left side of the given equality is
$$
\frac{(2+\sqrt{3})(4-\sqrt{3})}{(4-\sqrt{3})}-\sqrt{3}=2+\sqrt{3}-\sqrt{3}=2 \text { and } 2=2
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$1.54 \sqrt[3]{38+\sqrt{1445}}+\sqrt[3]{38-\sqrt{1445}}=4$.
|
### 1.54 Let
$\sqrt[3]{38+\sqrt{1445}}+\sqrt[3]{38-\sqrt{1445}}=x$.
Cubing both sides of this equation, and using formula (1.11), we get
$38+\sqrt{1445}+38-\sqrt{1445}+3 \sqrt[3]{(38+\sqrt{1445})(38-\sqrt{1445})} x=x^{3}$,
or $x^{3}+3 x-76=0$. By substitution, we verify that $x=4$ is one of the roots of the resulting cubic equation: $64+12-76=0$.
Transform this cubic equation:
$$
\begin{aligned}
& x^{3}-64=3(4-x) ;(x-4)\left(x^{2}+4 x+16\right)+3(x-4)=0 \\
& (x-4)\left(x^{2}+4 x+19\right)=0
\end{aligned}
$$
But the factor $x^{2}+4 x+19$ has no real roots. Therefore, 4 is the only possible real value for $x$, which proves the required equality (since it is obvious that $\sqrt[3]{38+\sqrt{1445}}+\sqrt[3]{38-\sqrt{1445}}$ is a real number).
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.1 \quad \frac{2}{3-x}+\frac{1}{2}=\frac{6}{x(3-x)}$.
|
2.1 Let's move all terms of the equation to the left side and transform the obtained equation to the form
$$
\frac{x^{2}-7 x+12}{2 x(3-x)}=0
$$
From the equation $x^{2}-7 x+12=0$, we find $x_{1}=3, x_{2}=4$. When $x=3$, the denominator becomes zero; therefore, 3 is not a root. Thus, $x=4$.
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.13 \sqrt{x-2}=x-4$.
Translate the text above into English, keeping the original text's line breaks and format, and output the translation result directly.
$2.13 \sqrt{x-2}=x-4$.
|
2.13 Let's square both sides of the equation:
$$
\begin{aligned}
& (\sqrt{x-2})^{2}=(x-4)^{2} ; x-2=x^{2}-8 x+16 \\
& x^{2}-9 x+18=0 ; x_{1}=3 ; x_{2}=6
\end{aligned}
$$
Let's check the found roots by substituting them into the original equation. If $x=3$, we get $1=-1$ - an incorrect equality; if $x=6$, we get $2=2$ - a correct equality. Therefore, the given equation has a single root $x=6$.
Note that we could have first found the domain of the given equation. For this, we solve the system of inequalities
$\left\{\begin{array}{l}x-2 \geqslant 0, \\ x-4 \geqslant 0,\end{array}\right.$
from which $x \geqslant 4$. Then it is immediately clear that $x_{1}=3$ is an extraneous root of the original equation. By checking, we confirm that $x=6$ satisfies the given equation.
Answer: $x=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.14 \sqrt{15-x}+\sqrt{3-x}=6$.
|
2.14 We have $\sqrt{15-x}=6-\sqrt{3-x}$. Squaring both sides of the equation, we get $15-x=36-12 \sqrt{3-x}+3-x$; $\sqrt{3-x}=2 ; 3-x=4 ; x=-1$. Checking shows that this value is a root of the equation.
Omвem: $x=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.18 \frac{\sqrt[3]{x^{4}}-1}{\sqrt[3]{x^{2}}-1}-\frac{\sqrt[3]{x^{2}}-1}{\sqrt[3]{x}+1}=4$.
|
2.18 Reducing the fractions in the left part of the equation, we get
$\sqrt[3]{x^{2}}+1-\sqrt[3]{x}+1=4$, or $\sqrt[3]{x^{2}}-\sqrt[3]{x}-2=0$.
From this, $\sqrt[3]{x}=-1$ or $\sqrt[3]{x}=2$. Since $\sqrt[3]{x}$ cannot be equal to -1 (as this would make the denominators of the original fractions zero), then $x=8$.
Omeem: $x=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.20 \sqrt[7]{\frac{5-x}{x+3}}+\sqrt[7]{\frac{x+3}{5-x}}=2$.
|
2.20 Instruction. Use the substitution $\sqrt[7]{\frac{5-x}{x+3}}=z$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.49 \frac{x^{2}+1}{x+1}+\frac{x^{2}+2}{x-2}=-2$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
$2.49 \frac{x^{2}+1}{x+1}+\frac{x^{2}+2}{x-2}=-2$.
|
2.49 We have
$$
\left(x^{2}+1\right)(x-2)+\left(x^{2}+2\right)(x+1)=-2(x+1)(x-2)
$$
Performing the transformations, we get $2 x^{3}+x^{2}+x-4=0$. Since the sum of all coefficients is zero, then $x=1$. Let's write the last equation in the form
$2 x^{3}-2 x^{2}+3 x^{2}-3 x+4 x-4=0$,
or $(x-1)\left(2 x^{2}+3 x+4\right)=0$.
From this, $2 x^{2}+3 x+4=0$. Since the discriminant of this equation is negative, it has no roots.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.55 \sqrt{x+1}+\sqrt{4 x+13}=\sqrt{3 x+12}$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
$2.55 \sqrt{x+1}+\sqrt{4 x+13}=\sqrt{3 x+12}$.
|
2.55 By squaring both sides of the equation, we get
$$
\begin{aligned}
& x+1+4 x+13+2 \sqrt{(x+1)(4 x+13)}=3 x+12 \\
& \sqrt{(x+1)(4 x+13)}=-(x+1)
\end{aligned}
$$
Another squaring would eliminate the irrationality, but there is no need for this transformation here. We notice that the derived equation can have a solution only under the condition $x+1 \leqslant 0$. At the same time, one of the conditions for the existence of a solution to the original equation is the requirement $x+1 \geqslant 0$. Both these conditions are consistent in the unique case where $x+1=0$, from which $x=-1$. This value of $x$, as is easily verified, satisfies the original equation. Since the derived equation has no other roots, the original equation also has no other roots. Thus, $x=-1$.
Answer: $x=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.58 \sqrt{x}+\frac{2 x+1}{x+2}=2$.
Translate the text above into English, keeping the original text's line breaks and format, and output the translation result directly.
$2.58 \sqrt{x}+\frac{2 x+1}{x+2}=2$.
|
### 2.58 We have
$\sqrt{x}=2-\frac{2 x+1}{x+2}$, or $\sqrt{x}=\frac{3}{x+2}$.
After squaring and performing transformations, the equation will take the form $x^{3}+4 x^{2}+4 x-9=0$. Notice that the sum of the coefficients of the last equation is zero, which means it has a root $x=1$. Therefore,
$$
x^{3}-x^{2}+5 x^{2}-5 x+9 x-9=0
$$
or $(x-1)\left(x^{2}+5 x+9\right)=0$.
Since the equation $x^{2}+5 x+9=0$ has no roots, $x=1$ is the only root of the original equation.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.59 \sqrt{x+2}-\sqrt[3]{3 x+2}=0$.
Translate the text above into English, keeping the original text's line breaks and format, and output the translation result directly.
$2.59 \sqrt{x+2}-\sqrt[3]{3 x+2}=0$.
|
2.59 We have $\sqrt{x+2}=\sqrt[3]{3 x+2}$. After raising the equation to the sixth power, we get $(x+2)^{3}=(3 x+2)^{2}$, or $x^{3}-3 x^{2}+4=0$, or $(x+1)\left(x^{2}-4 x+4\right)=0$.
From this, $x_{1}=-1$ (extraneous root), $x_{2}=2$.
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.78 For what values of a do the equations $x^{2}+a x+1=0$ and $x^{2}+x+a=0$ have a common root?
|
2.78 Subtracting the second equation from the first, we get
$$
a x - x + 1 - a = 0, \text{ or } (a-1)(x-1) = 0
$$
$$
x^{2} + x + 1 = 0
$$
such an equation has no real roots. If $a \neq 1$, then $x = 1$ and, therefore, $1 + a + 1 = 2$, i.e., $a = -2$.
Answer: when $a = -2$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.8 The front wheel of a moving model makes 6 more revolutions than the rear wheel over a distance of 120 m. If the circumference of the front wheel is increased by $\frac{1}{4}$ of its length, and the circumference of the rear wheel is increased by $\frac{1}{5}$ of its length, then over the same distance, the front wheel will make 4 more revolutions than the rear wheel. Find the lengths of the circumferences of the front and rear wheels.
|
3.8 The circumference of a wheel $C$, the number of revolutions $n$, and the distance $s$ are related by the formula $C n=s$. We will fill in the table of values of these quantities in the order indicated by the numbers (1), (2), .., (12).
| Wheel | Before change | | | After change | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | $\bar{C}$ | $\boldsymbol{s}$ | $\bar{n}$ | $C$ | $s$ | $\boldsymbol{n}$ |
| Front | (1) ${ }^{x}$ | $(3)^{120}$ | (5) $\frac{120}{x}$ | (7) $\frac{5 x}{4}$ | $9^{120}$ | (11) $\frac{120 \cdot 4}{5 x}$ |
| Rear | (2) ${ }^{y}$ | (4) $^{120}$ | (6) $\frac{120}{y}$ | (8) $\frac{6 y}{5}$ | (10) $^{120}$ | (12) $\frac{120 \cdot 5}{6 y}$ |
According to the condition, we obtain the system
$$
\left\{\begin{array}{l}
\frac{120}{x}-\frac{120}{y}=6 \\
\frac{96}{x}-\frac{100}{y}=4
\end{array}\right.
$$
from which we find $x=4(m), y=5(m)$.
Answer: 4 and 5 m.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.14 A positive integer is thought of. To its representation, the digit 7 is appended on the right, and from the resulting new number, the square of the thought number is subtracted. The remainder is then reduced by $75\%$ of this remainder, and the thought number is subtracted again. In the final result, zero is obtained. What number was thought of?
## Motion: distance, speed, time
|
3.14 Let a number $x$ be thought of. Then, following the text of the condition, we get the numbers
$10 x+7, 10 x+7-x^{2}$ and the remainder $\frac{25}{100}\left(10 x+7-x^{2}\right)$.
Then $\frac{1}{4}\left(10 x+7-x^{2}\right)-x=0$, or $x^{2}-6 x-7=0$. Only the value $x=7$ works.
Answer: 7.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.18 The distance between points $A$ and $B$ is 270 m. A body moves uniformly from $A$ to $B$; upon reaching $B$, it immediately returns with the same speed. A second body, which leaves $B$ for $A$ 11 s after the first body leaves $A$, moves uniformly but more slowly. On its way from $\boldsymbol{B}$ to $\boldsymbol{A}$, it meets the first body twice: 10 and 40 s after its departure from $B$. Find the speed of each body.
|
3.18 A convenient model of the problem is a graph of uniform motion in the coordinate system "path" ($s$ - in meters), "time" ($t$ in seconds). Let $AC$ (Fig. 3.3) be the graph of the motion from $A$ to $B$ of the first body with speed $v_{1}=\operatorname{tg} \alpha$ (time axis $At$); $CD$ be the graph of the motion from $B$ to $A$ of the same body with the same speed $v_{1}=\operatorname{tg} \alpha$ (time axis $Bt$); $\boldsymbol{EF}$ be the graph of the motion of the second body from $B$ to $\boldsymbol{A}$ with speed $v_{2}=\operatorname{tg} \beta, \beta<\alpha$ (time axis $Bt$).
The time interval $BE=11$, the time interval to the first meeting $EH=10$, between the first and second meetings $HK=30$; then $NM=21 v_{1}, HM=10 v_{2}$, $KF=40 v_{2}, NM+HM=AB=270$, i.e.,
$21 v_{1}+10 v_{2}=270$
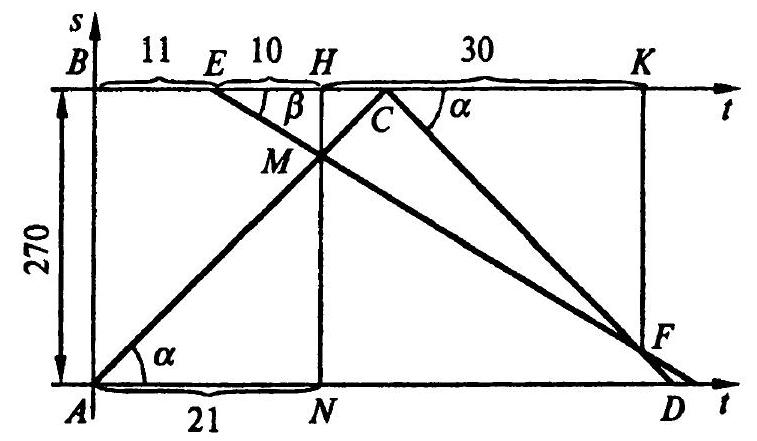
Fig. 3.3
The time interval $HC=\frac{HM}{v_{1}}=\frac{10 v_{2}}{v_{1}}$; the time interval $CK=\frac{KF}{v_{1}}=\frac{40 v_{2}}{v_{1}}$. Since $HC+CK=30$, then
$\frac{10 v_{2}}{v_{1}}+\frac{40 v_{2}}{v_{1}}=30$, hence
$5 v_{2}=3 v_{1}$.
Solving equations (1) and (2) simultaneously, we find $v_{1}=10 \mathrm{m} / \mathrm{s}$, $v_{2}=6 \mathrm{m} / \mathrm{s}$.
Answer: 10 and $6 \mathrm{~m} / \mathrm{s}$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.22 A pedestrian and a cyclist set off simultaneously towards each other from cities $A$ and $B$, the distance between which is $40 \mathrm{km}$, and meet 2 hours after departure. Then they continue their journey, with the cyclist arriving in $A$ 7 hours and 30 minutes earlier than the pedestrian in $B$. Find the speeds of the pedestrian and the cyclist, assuming that they remained constant throughout.
## Paboma
|
3.22 Fill in the table of speed, distance, and time values in the order indicated by the numbers (1), (2), .., (12):
| Tourist | Before Meeting | | | After Meeting | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | speed, km/h | time, h | distance, km | speed, km/h | time, h | distance, km |
| Pedestrian | (1) | $(3)^{2}$ | $5^{2 x}$ | $b^{x}$ | $\frac{40-2 x}{(1)}$ | $9^{40-2 x}$ |
| Cyclist | $\sqrt{20-x}$ | 4 | $40-2 x$ | $\sqrt[8]{20-x}$ | $\frac{2 x}{20-x}$ | $2 x$ |
By condition,
$$
\begin{aligned}
& \frac{40-2 x}{x}-\frac{2 x}{20-x}=\frac{15}{2} \\
& \text { from which } x=4(\text { km/h })
\end{aligned}
$$
Answer: 4 and 16 km/h.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.25 Two snow-clearing machines are working on snow removal. The first can clear a street in 1 hour, while the second can do it in $75\%$ of this time. Starting the cleaning simultaneously, both machines worked together for 20 minutes, after which the first machine stopped. How much more time is needed for the second machine to finish the work?
|
3.25 Let's accept the entire volume of work as a unit. The productivity of the first machine is 1 (per hour), and the second is $1: \frac{3}{4}=\frac{4}{3}$ (per hour). Working together for $\frac{1}{3}$ hour, they will complete $\frac{1}{3} \cdot 1 + \frac{1}{3} \cdot \frac{4}{3} = \frac{7}{9}$ of the entire work. Then, the remaining work for the second machine will be $\frac{2}{9}$, which will require $\frac{2}{9} : \frac{4}{3} = \frac{1}{6}(h)$.
Answer: 10 min.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.29 The volume of substance $A$ is half the sum of the volumes of substances $B$ and $C$, and the volume of substance $B$ is $\frac{1}{5}$ of the sum of the volumes of substances $A$ and $C$. Find the ratio of the volume of substance $C$ to the sum of the volumes of substances $A$ and $B$.
|
3.29 According to the condition, $2 V_{A}=V_{B}+V_{C}$ and $5 V_{B}=V_{A}+V_{C}$. Let $V_{A}=x V_{C}$ and $V_{B}=y V_{C}$. Then we get the system
$\left\{\begin{array}{l}2 x-y=1 \\ -x+5 y=1\end{array}\right.$
from which $x=\frac{2}{3}, y=\frac{1}{3}$. Therefore,
$\frac{V_{C}}{V_{A}+V_{B}}=\frac{1}{x+y}=1$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.30 It is known that the difference between the variable quantities $z$ and $y$ is proportional to the quantity $x$, and the difference between the quantities $x$ and $z$ is proportional to the quantity $y$. The coefficient of proportionality is the same and is equal to a positive integer $k$. A certain value of the quantity $z$ is $\frac{5}{3}$ times the difference of the corresponding values of $x$ and $y$. Find the numerical value of the coefficient $k$.
|
3.30 I n s t r u c t i o n. Write the condition as a system of three equations. From the first two equations, express $\frac{x}{y}$ and $\frac{y}{z}$ in terms of $k$, and then substitute the obtained expressions for $\frac{x}{y}$ and $\frac{y}{z}$ into the third equation and calculate the desired value of $k$.
A n s w e r: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.38 It is known that a freely falling body travels 4.9 m in the first second, and in each subsequent second, it travels 9.8 m more than in the previous one. If two bodies start falling from the same height, one 5 s after the other, then after what time will they be 220.5 m apart from each other?
|
3.38 Instruction. Use the well-known physics formula $s=4.9 t^{2}$.
Answer: 7 seconds after the start of the fall of the first body.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.48 A young man was returning home from vacation on a bicycle. At first, after traveling several kilometers, he spent one day more than half the number of days remaining after this until the end of his vacation. Now the young man has two options to travel the remaining distance to arrive home on time: to travel $h$ km more daily than originally planned, or to maintain the original daily travel distance, exceeding it only once - on the last day of the journey by $2 h$ km. How many days before the end of his vacation did the young man set out for home?
|
3.48 Let the segment $A B$ (Fig. 3.11) represent the entire journey of the young man and the number of days ($x$) it should take him to travel it at a rate of $v$ km per day. According to the problem, the time segment $A C$ is one unit more than half of the time segment $C B$; therefore,
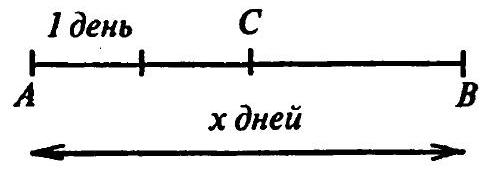
Fig. 3.11
$A C-1=\frac{C B}{2}$, or $x-C B-1=\frac{C B}{2}$,
from which $C B=\frac{2 x-2}{3}$ days. Let the distance represented by the segment $C B$ be taken as the unit. Then, according to the first option, $\frac{2 x-2}{3}(v+h)=1$, and according to the second, $\left(\frac{2 x-2}{3}-1\right) v+(v+2 h) \cdot 1=1$. By eliminating $v$ from these two equations, we find $x=4$.
Answer: $\quad$ in 4 days.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.56 Two pipes of different cross-sections are connected to a swimming pool, one uniformly supplying water, the other uniformly draining it, with the first pipe filling the pool 2 hours longer than the second pipe takes to empty it. When the pool was filled to $\frac{1}{3}$ of its capacity, both pipes were opened, and the pool was found to be empty after 8 hours. How many hours does it take for the first pipe to fill the pool and for the second pipe to empty it when acting separately?
## Mixtures, Alloys
A certain alloy consists of two metals in the ratio $1: 2$, while another contains the same metals in the ratio 2:3. How many parts of each alloy are needed to obtain a third alloy containing the same metals in the ratio 17:27?
A container with a capacity of 8 liters is filled with a mixture of oxygen and nitrogen, with oxygen accounting for $16 \%$ of the container's capacity. A certain amount of the mixture is released from this container and an equal amount of nitrogen is added, after which the same amount of the mixture is released again and the same amount of nitrogen is added. In the new mixture, the oxygen content is $9 \%$. What amount of the mixture was released from the container each time?
|
3.56 Let's write down the values of the required and given quantities in the form of a table:
| Pipe | Time, h | Capacity | Productivity |
| :---: | :---: | :---: | :---: |
| Supply | $x$ | 1 | $\frac{1}{x}$ |
| Discharge | $x+2$ | 1 | $\frac{1}{x+2}$ |
| Both together | 8 | 1 | $\frac{1}{24}$ |
According to the condition, $\frac{1}{x}-\frac{1}{x+2}=\frac{1}{24}$, from which $x=6$.
Answer: $\quad$ in 6 and 8 h.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.59 Impurities constitute $20 \%$ of the total volume of the solution. What is the smallest number of filters through which the solution must be passed so that the final impurity content does not exceed $0.01 \%$, if each filter absorbs $80 \%$ of the impurities? (It is known that $\lg 2 \approx 0.30$.)
|
3.59 Impurities constitute $\frac{1}{5}$ of the solution. After the first filtration, $\left(\frac{1}{5}\right)^{2}$ impurities remain, and after the $k$-th filtration, $-\left(\frac{1}{5}\right)^{k+1}$ impurities remain. According to the condition, $\left(\frac{1}{5}\right)^{k+1} \leqslant 10^{-4}$; $-(k+1) \lg 5 \leqslant-4$, from which $k \geqslant 4.7$.
Answer: 5 filters.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$4.35 \operatorname{tg} 435^{\circ}+\operatorname{tg} 375^{\circ}$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
$4.35 \tan 435^{\circ}+\tan 375^{\circ}$.
|
### 4.35 We have
$$
\begin{aligned}
& \tan 435^{\circ} + \tan 375^{\circ} = \tan 75^{\circ} + \tan 15^{\circ} = \frac{\sin 90^{\circ}}{\cos 75^{\circ} \cos 15^{\circ}} = \\
& = \frac{2}{\cos 90^{\circ} + \cos 60^{\circ}} = 4
\end{aligned}
$$
Here, reduction formulas, as well as (4.23) and (4.26), were used.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$4.47 \frac{\sin ^{2}\left(\frac{3 \pi}{2}-\alpha\right)\left(\tan^{2} \alpha-1\right) \cot\left(\alpha-\frac{5 \pi}{4}\right)}{\sin ^{2}\left(\frac{5 \pi}{4}+\alpha\right)}=2$.
|
4.47 Note that
$$
\begin{aligned}
& \sin ^{2}\left(\frac{3 \pi}{2}-\alpha\right)=\cos ^{2} \alpha \\
& \operatorname{tg}^{2} \alpha-1=\frac{\sin ^{2} \alpha-\cos ^{2} \alpha}{\cos ^{2} \alpha}=\frac{(\sin \alpha-\cos \alpha)(\sin \alpha+\cos \alpha)}{\cos ^{2} \alpha} \\
& \sin \alpha-\cos \alpha=\sqrt{2} \sin \left(\alpha-\frac{\pi}{4}\right) \\
& \sin \alpha+\cos \alpha=\sqrt{2} \sin \left(\frac{\pi}{4}+\alpha\right) \\
& \operatorname{ctg}\left(\alpha-\frac{5 \pi}{4}\right)=\operatorname{ctg}\left(\alpha-\frac{\pi}{4}\right)
\end{aligned}
$$
Then the left side of the identity can be written as:
$$
\frac{\cos ^{2} \alpha \cdot \sqrt{2} \sin \left(\alpha-\frac{\pi}{4}\right) \cdot \sqrt{2} \sin \left(\frac{\pi}{4}+\alpha\right) \cos \left(\alpha-\frac{\pi}{4}\right)}{\cos ^{2} \alpha \sin ^{2}\left(\frac{\pi}{4}+\alpha\right) \sin \left(\alpha-\frac{\pi}{4}\right)}=2
$$
$$
\text { since } \cos \left(\alpha-\frac{\pi}{4}\right)=\sin \left(\frac{\pi}{4}+\alpha\right) \text {. }
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$4.77 \operatorname{tg} 9^{\circ}+\operatorname{tg} 15^{\circ}-\operatorname{tg} 27^{\circ}-\operatorname{ctg} 27^{\circ}+\operatorname{ctg} 9^{\circ}+\operatorname{ctg} 15^{\circ}=8$.
|
### 4.77 We have
$$
\begin{aligned}
& \tan 9^{\circ} + \tan 81^{\circ} - (\tan 27^{\circ} + \tan 63^{\circ}) + \tan 15^{\circ} + \tan 75^{\circ} = \\
& = \frac{2}{\cos 90^{\circ} + \cos 72^{\circ}} - \frac{2}{\cos 90^{\circ} + \cos 36^{\circ}} + \frac{2}{\cos 90^{\circ} + \cos 60^{\circ}} = \\
& = \frac{2}{\cos 72^{\circ}} - \frac{2}{\cos 36^{\circ}} + 4 = \frac{2(\cos 36^{\circ} - \cos 72^{\circ}) \cdot 2}{\cos 36^{\circ} + \cos 108^{\circ}} + 4 = 8
\end{aligned}
$$
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.88 Prove that the expression
$$
\frac{1-2 \sin ^{2}\left(\alpha-\frac{3 \pi}{2}\right)+\sqrt{3} \cos \left(2 \alpha+\frac{3 \pi}{2}\right)}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}
$$
does not depend on $\alpha$, where $\alpha \neq \frac{\pi n}{2}+\frac{\pi}{12}$.
|
4.88 After applying the reduction formulas, we get
\[
\begin{aligned}
& \frac{1-2 \cos ^{2} \alpha+\sqrt{3} \sin 2 \alpha}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}=\frac{-2 \cos 2 \alpha+\sqrt{3} \sin 2 \alpha}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}= \\
& =\frac{2\left(\frac{\sqrt{3}}{2} \sin 2 \alpha-\frac{1}{2} \cos 2 \alpha\right)}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}=2 \frac{\sin \left(2 \alpha-\frac{\pi}{6}\right)}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}=-2
\end{aligned}
\]
|
-2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
6.7 The denominator of the geometric progression is $\frac{1}{3}$, the fourth term of this progression is $\frac{1}{54}$, and the sum of all its terms is $\frac{121}{162}$. Find the number of terms in the progression.
|
6.7 Since $b_{4}=b_{1} q^{3}$, then $\frac{1}{54}=b_{1} \cdot \frac{1}{27}$, from which $b_{1}=\frac{1}{2}$. Now, using formula (6.7a), we get the equation
$$
\frac{\frac{1}{2}\left(1-\frac{1}{3^{n}}\right)}{\frac{2}{3}}=\frac{121}{162}, \text { or } 1-\frac{1}{3^{n}}=\frac{121 \cdot 4}{162 \cdot 3}, \text { or } 1-\frac{1}{3^{n}}=\frac{242}{243}
$$
from which we find $n=5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.7 $\quad 2^{\log _{3} x^{2}} \cdot 5^{\log _{3} x}=400$.
|
7.7 The logarithmic function $y=\log _{3} x$ is defined for $x>0$. Therefore, according to formula (7.6), we have $\log _{3} x^{2}=2 \log _{3} x$. Consequently, $2^{2 \log _{3} x} \cdot 5^{\log _{3} x}=20^{2} ; 4^{\log _{3} x} \cdot 5^{\log _{3} x}=20^{2} ; 20^{\log _{3} x}=20^{2}$. From this, $\log _{3} x=2$, i.e., $x=3^{2}=9$.
Answer: $x=9$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.8 \quad 4^{\sqrt{x}}-9 \cdot 2^{\sqrt{x}-1}+2=0$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
$7.8 \quad 4^{\sqrt{x}}-9 \cdot 2^{\sqrt{x}-1}+2=0$.
|
7.8 Since $4^{\sqrt{x}}=2^{2 \sqrt{x}}$ and $2^{\sqrt{x}-1}=2^{\sqrt{x}} \cdot 2^{-1}=\frac{1}{2} \cdot 2^{\sqrt{x}}$, the given equation will take the form
$$
2^{2 \sqrt{x}}-\frac{9}{2} \cdot 2^{\sqrt{x}}+2=0
$$
Let's make the substitution $2^{\sqrt{x}}=y$, where $y>0$ due to the property of the exponential function $2^{0}$. Then we get the equation $y^{2}-\frac{9}{2} y+2=0$, the roots of which are $y_{1}=4$, $y_{2}=\frac{1}{2}$, both positive. From the equation $2^{\sqrt{x}}=4$ we have $2^{\sqrt{x}}=2^{2}, \sqrt{x}=2$, hence $x=4$. From the equation $2^{\sqrt{x}}=\frac{1}{2}$ we find $2^{\sqrt{x}}=2^{-1}$, hence $\sqrt{x}=-1$, which is impossible.
Thus, $x=4$.
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.9 \quad 3 \cdot 5^{2x-1}-2 \cdot 5^{x-1}=0.2$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
$7.9 \quad 3 \cdot 5^{2x-1}-2 \cdot 5^{x-1}=0.2$.
|
7.9 We have $5^{2 x-1}=5^{2 x} \cdot 5^{-1} ; 5^{x-1}=5^{x} \cdot 5^{-1} ; 0.2=5^{-1}$. After dividing all terms of the given equation by $5^{-1}$, it will take the form
$3 \cdot 5^{2 x}-2 \cdot 5^{x}=1$.
Let $5^{x}=y$, where $y>0$. Then we get the equation $3 y^{2}-2 y-1=0$, from which $y_{1}=1, y_{2}=-\frac{1}{3}$ (does not fit because the condition $y>0$ is not met). Therefore, $y=1$, from which $\boldsymbol{x}=\mathbf{0}$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.25 \lg (\sqrt{6+x}+6)=\frac{2}{\log _{\sqrt{x}} 10}$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
$7.25 \lg (\sqrt{6+x}+6)=\frac{2}{\log _{\sqrt{x}} 10}$.
|
7.25 From the definition of the logarithm, it follows that $\sqrt{x}>0, \sqrt{x} \neq 1$, i.e., $x>0, x \neq 1$. Applying formulas (7.8) and (7.6), we get $\lg (\sqrt{6+x}+6)=\lg x$. According to the hint $4^{0}$, we transition to an equivalent system of equations:
$\left\{\begin{array}{l}x>0, x \neq 1, \\ \sqrt{6+x}+6=x,\end{array}\right.$ or $\left\{\begin{array}{l}x>0, x \neq 1, \\ \sqrt{6+x}=x-6 .\end{array}\right.$
In the left part of the equation $\sqrt{6+x} \geq 0$, therefore $x-6 \geq 0$, i.e., $x \geq 6$, and both sides of the equation can be squared. We have
$$
\left\{\begin{array} { l }
{ x \geq 6 } \\
{ 6 + x = x ^ { 2 } - 1 2 x + 3 6 , }
\end{array} \text { or } \left\{\begin{array}{l}
x \geq 6 \\
x^{2}-13 x+30=0
\end{array}\right.\right.
$$
We find the roots of the equation: $x_{1}=3, x_{2}=10$; of these, only $x=10$ satisfies the inequality $x \geq 6$.
Answer: $x=10$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.27 \lg (3-x)-\frac{1}{3} \lg \left(27-x^{3}\right)=0$.
|
7.27 We have $\lg (3-x)^{3}=\lg \left(27-x^{3}\right)$, which is equivalent to the system
$$
\left\{\begin{array} { l }
{ 3 - x > 0 , } \\
{ ( 3 - x ) ^ { 3 } = 2 7 - x ^ { 3 } , }
\end{array} \text { or } \left\{\begin{array}{l}
x<3, \\
(3-x)^{3}=(3-x)\left(9+3 x+x^{2}\right)
\end{array}\right.\right.
$$
Further, we get
$$
(3-x)\left(9-6 x+x^{2}-9-3 x-x^{2}\right)=0, \text { or }(3-x)(-9 x)=0 \text {, }
$$
from which $x_{1}=0, x_{2}=3$ (does not satisfy the inequality $x<3$). Therefore, $x=0$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.28 \frac{2-\lg 4+\lg 0.12}{\lg (\sqrt{3 x+1}+4)-\lg 2 x}=1$.
$7.29 0.5\left(\lg \left(x^{2}-55 x+90\right)-\lg (x-36)\right)=\lg \sqrt{2}$.
|
7.28 Given the domains of the logarithmic function and the square root, we have the system of inequalities $3 x+1 \geq 0$ (under this condition $\sqrt{3 x+1}+4>0$), $x>0$, the solution of which is $\boldsymbol{x}>0$. This equation is equivalent to the system
$$
\left\{\begin{array}{l}
x>0 \\
\lg (\sqrt{3 x+1}+4)-\lg 2 x \neq 0 \\
2-\lg 4+\lg 0.12=\lg (\sqrt{3 x+1}+4)-\lg 2 x
\end{array}\right.
$$
Using the hint $5^{0}$, we transition to the equation
$$
\lg \frac{100 \cdot 0.12}{4}=\lg \frac{\sqrt{3 x+1}+4}{2 x}, \text{ or } 3=\frac{\sqrt{3 x+1}+4}{2 x}
$$
After multiplying both sides of the equation by $2 x$ (no extraneous roots will be introduced since $x>0$), we obtain the irrational equation
$$
\sqrt{3 x+1}=6 x-4
$$
Since $\sqrt{3 x+1} \geq 0$, then $6 x-4 \geq 0$, from which $x \geq \frac{2}{3}$.
Square both sides of equation (2):
$3 x+1=36 x^{2}-48 x+16$, or $36 x^{2}-51 x+15=0$.
From here, we find $x_{1}=1, x_{2}=\frac{5}{12}$ (does not satisfy the condition $x \geq \frac{2}{3}$). It remains to verify that for $x=1$, the second condition of system (1) is satisfied: $\lg (\sqrt{3 x+1}+4)-\lg 2 x=\lg 6-\lg 2=\lg 3 \neq 0$. Thus, $x=1$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.30 \lg (\lg x)+\lg \left(\lg x^{3}-2\right)=0$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
$7.30 \lg (\lg x)+\lg \left(\lg x^{3}-2\right)=0$.
|
7.30 For the existence of logarithms, it is necessary that the inequalities $x>0$, $\lg x>0$, $3 \lg x-2>0$ are satisfied simultaneously, i.e., $x>0, x>1, \lg x>\frac{2}{3}$. Hence, $\lg x>\frac{2}{3}$. Now we transition to the equivalent system of equations given by
$$
\left\{\begin{array}{l}
\lg x>\frac{2}{3} \\
\lg x(3 \lg x-2)=1
\end{array}\right.
$$
After substituting the variable $y=\lg x$, we obtain the equation $3 y^{2}-2 y-1=0$, whose roots are $y_{1}=1, y_{2}=-\frac{1}{3}$. Of these values, only the first satisfies the inequality $\lg x>\frac{2}{3}$. Therefore, $\lg x=1$, from which $x=10$.
Answer: $x=10$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.36 \quad 3 \log _{5} 2+2-x=\log _{5}\left(3^{x}-5^{2-x}\right)$.
$7.37 \quad 25^{\log _{2} \sqrt{x+3}-0.5 \log _{2}\left(x^{2}-9\right)}=\sqrt{2(7-x)}$.
|
7.36 Here
$3^{x}-5^{2-x}>0$.
Let's use the fact that $2-x=\log _{5} 5^{2-x}$, and write the equation in the form
$\log _{5}\left(2^{3} \cdot 5^{2-x}\right)=\log _{5}\left(3^{x}-5^{2-x}\right)$
Then we have
$2^{3} \cdot 5^{2-x}=3^{x}-5^{2-x} ; 5^{2-x}\left(2^{3}+1\right)=3^{x} ; 5^{2-x}=3^{x-2}$.
Finally, multiplying both sides of the equation by $3^{2-x} \neq 0$, we get
$(5 \cdot 3)^{2-x}=1 \Rightarrow 15^{2-x}=15^{0} \Rightarrow 2-x=0 \Rightarrow x=2$.
This root satisfies the inequality (1).
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.43 \quad 5^{x} \sqrt[x]{8^{x-1}}=500$.
$7.44 \quad 5^{\frac{x}{\sqrt{x}+2}} \cdot 0.2^{\frac{4}{\sqrt{x}+2}}=125^{x-4} \cdot 0.04^{x-2}$.
|
7.43 According to the definition of the root, $x \neq 0$. Let's write the equation as
$$
5^{x} \cdot 2^{\frac{3 x-3}{x}}=5^{3} \cdot 2^{2}
$$
Dividing both sides by $5^{3} \cdot 2^{2} \neq 0$, we get
$$
5^{x-3} \cdot 2^{\frac{3 x-3}{x}-2}=1, \text { or } 5^{x-3} \cdot 2^{\frac{x-3}{x}}=1, \text { or }\left(5 \cdot 2^{\frac{1}{x}}\right)^{x-3}=1
$$
Since $5 \cdot 2^{\frac{1}{x}}>0$ and $5 \cdot 2^{\frac{1}{x}} \neq 1$, then $x-3=0$, i.e., $x=3$.
Answer: $x=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1 $\quad A_{x}^{2} C_{x}^{x-1}=48$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
9.1 $\quad A_{x}^{2} C_{x}^{x-1}=48$.
|
9.1 According to formula (9.1), we find
$$
A_{x}^{2}=\frac{x!}{(x-2)!}=\frac{x(x-1)(x-2)!}{(x-2)!}=x(x-1)
$$
Further, using formulas (9.6) and (9.4), we have
$$
C_{x}^{x-1}=C_{x}^{x-(x-1)}=C_{x}^{1}=\frac{x!}{1!(x-1)!}=x
$$
Therefore, the given equation will take the form
$x^{2}(x-1)=48$, or $x^{2}(x-1)=4^{2} \cdot 3$.
Consequently, $x=4$.
Answer: $x=4$.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$9.2 \quad C_{x+1}^{x-2}+2 C_{x-1}^{3}=7(x-1)$.
|
9.2 Let's use formula (9.4):
$$
\frac{(x+1)!}{(x-2)!3!}+\frac{2(x-1)!}{(x-4)!3!}=7(x-1)
$$
from which, after simplifying the first fraction by $(x-2)!$ and the second fraction by $(x-4)!$, we get
$$
(x+1) x(x-1)+2(x-1)(x-2)(x-3)=42(x-1)
$$
Further, considering that $x \neq 1$, we arrive at the quadratic equation
$$
x^{2}+x+2\left(x^{2}-5 x+6\right)=42, \text{ or } x^{2}-3 x-10=0
$$
which has roots $x_{1}=5, x_{2}=-2$ (not suitable by the context of the problem).
Answer: $x=5$.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.7 For what value of $x$ is the fourth term of the expansion $\left(\sqrt{2^{x-1}}+\sqrt[3]{2^{-x}}\right)^{m}$ 20 times greater than $m$, if the binomial coefficient of the fourth term is to the binomial coefficient of the second term as $5: 1 ?$
|
9.7 The binomial coefficients of the fourth and second terms are $C_{m}^{3}$ and $m$, respectively. Therefore, $\frac{m(m-1)(m-2)}{3!m}=5$, or $(m-1)(m-2)=30$, from which $m=7$. Then the fourth term of the expansion has the form $T_{4}=C_{7}^{3} 2^{2(x-1)} \cdot 2^{-x}$, and we arrive at the equation $C_{7}^{3} 2^{x-2}=140$, from which we find $\frac{7 \cdot 6 \cdot 5}{6} \cdot 2^{x-2}=140$; $2^{x-2}=4 ; x=4$.
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$9.17 C_{x}^{x-1}+C_{x}^{x-2}+C_{x}^{x-3}+\ldots+C_{x}^{x-9}+C_{x}^{x-10}=1023$.
|
9.17 Obviously, when $x=10$ the left side of the equation is 1 less than the sum of the binomial coefficients in the expansion of the binomial $(a+b)^{10}$. This sum is 1024. Therefore, $x=10$ is a solution to the equation. There are no other solutions, as for $x>10$ the left side of the equation is greater than 1023.
Answer: $x=10$.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.21 The sum of the third from the beginning and the third from the end binomial coefficients in the expansion of $(\sqrt[4]{3}+\sqrt[3]{4})^{n}$ is 9900. How many rational terms are contained in this expansion?
|
9.21 The coefficients specified in the condition are equal to $C_{n}^{2}$. We have $2 \cdot \frac{n(n-1)}{2}=9900$, or $n(n-1)=100 \cdot 99$,
from which $n=100$. Then $T_{k+1}=C_{100}^{k} 3^{\frac{100-k}{4}} 4^{\frac{k}{3}} ;$ according to the condition, $\frac{k}{3}$ and $\frac{100-k}{4}$ are integers, i.e., $k$ is divisible by 12. For $n=100$, there are $\left[\frac{100}{12}\right]+1=9$ such numbers.
Answer: 9 terms.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3 Find the sum $A=i+i^{2}+i^{3}+\ldots+i^{15}$.
Translate the text above into English, keeping the original text's line breaks and format, and output the translation result directly.
|
10.3 Let's group the terms as follows:
$$
\begin{aligned}
& A=\left(i+i^{2}+i^{3}+i^{4}\right)+\left(i^{5}+i^{6}+i^{7}+i^{8}\right)+ \\
& +\left(i^{9}+i^{10}+i^{11}+i^{12}\right)+\left(i^{13}+i^{14}+i^{15}\right)
\end{aligned}
$$
from which
$$
A=\left(i+i^{2}+i^{3}+i^{4}\right)\left(1+i^{4}+i^{8}\right)+i^{13}+i^{14}+i^{15}
$$
Since
$$
\begin{aligned}
& i+i^{2}+i^{3}+i^{4}=i-1-i+1=0 \\
& A=i^{13}+i^{14}+i^{15}=i-1-i=-1
\end{aligned}
$$
Answer: -1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.36 Find the real number $b$ from the condition that the points representing the complex numbers $3-5 i, 1-i$ and $-2+b i$ lie on the same straight line.
|
10.36 The numbers $3-5i, 1-i$ and $-2+bi$ correspond to the points $A(3, -5), B(1, -1)$ and $C(-2, b)$ on the plane (Fig. 10.10). We find the coordinates of the vectors $\overline{A B}$ and $\overline{A C}$; we have $\overline{A B}(-2, 4), \overline{A C}(-5, b+5)$.
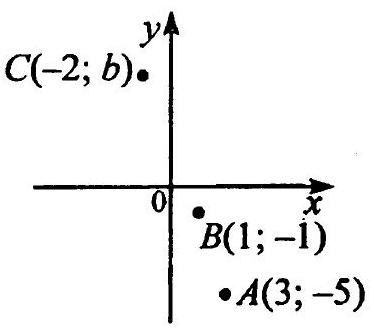
Fig. 10.10
Since these points lie on the same line, the equality $\overline{A C}=k \overline{A B}$ must hold,
i.e.
$$
\left\{\begin{array}{l}
-2k = -5 \\
4k = b + 5
\end{array}\right.
$$
From this system, we find $b=5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.47 Given complex numbers $z_{1}=1+a i$ and $z_{2}=2^{\frac{3}{4}}\left(\cos \frac{3 \pi}{8}+i \sin \frac{3 \pi}{8}\right)$. Find all real values of $a$ for which $z_{1}^{3}=z_{2}^{2}$.
|
10.47 We find
\[
\begin{aligned}
& z_{1}^{3}=(1+a i)^{3}=\left(1-3 a^{2}\right)+\left(3 a-a^{3}\right) i \\
& z_{2}^{2}=\left(2^{\frac{3}{4}}\left(\cos \frac{3 \pi}{8}+i \sin \frac{3 \pi}{8}\right)\right)^{2}= \\
& =2^{\frac{3}{2}}\left(\cos \frac{3 \pi}{4}+i \sin \frac{3 \pi}{4}\right)=2^{\frac{3}{2}}\left(-\frac{\sqrt{2}}{2}+i \frac{\sqrt{2}}{2}\right)=-2+2 i
\end{aligned}
\]
Since the numbers $z_{1}^{3}$ and $z_{2}^{2}$ are equal, we arrive at the system
\[
\left\{\begin{array}{l}
1-3 a^{2}=-2 \\
3 a-a^{3}=2
\end{array}\right.
\]
from which, considering that $a \in \boldsymbol{R}$, we obtain $a=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2 Solve the equation $|x+1|+|x-1|=2 x^{3}$.
|
11.2 We have $|x+1|=0$ when $x=-1$, and $|x-1|=0$ when $x=1$. We will solve the given equation in the intervals $(-\infty,-1)$, $[-1,1)$, $[1, \infty)$.
1) If $x<0$ for any $x$, then $x=0$; this value does not belong to the interval $(-\infty,-1)$.
2) If $-1 \leq x<1$, then $x+1-x+1=2 x^{3} ; 2 x^{3}=2 ; x^{3}=1$; $x=1 \notin[-1,1)$.
3) If $\quad x \geq 1, \quad$ then $\quad x+1+x-1=2 x^{3} ; \quad x^{3}-x=0$; $x\left(x^{2}-1\right)=0 ; x(x-1)(x+1)=0 ; \quad x_{1}=-1, x_{2}=0, x_{3}=1$. Only the value $x=1$ belongs to the interval $[1, \infty)$. Therefore: $x=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.16 For what value of $m$ does the system of equations
$$
\left\{\begin{array}{l}
2 x+(m-1) y=3 \\
(m+1) x+4 y=-3
\end{array}\right.
$$
have an infinite number of solutions? No solutions?
|
11.16 The system has an infinite number of solutions or no solutions if the coefficients of $x$ and $y$ are proportional. Therefore, $\frac{2}{m+1}=\frac{m-1}{4}$ (here $m+1 \neq 0$; it is easy to verify that when $m=-1$, the system has a unique solution). Further, we have $(m+1)(m-1)=8 ; m^{2}-1=8$, from which $m= \pm 3$. When $m=3$, we get $\frac{2}{4}=\frac{2}{4} \neq \frac{3}{-3}$, i.e., the system has no solutions. When $m=-3$, we get $\frac{2}{-2}=\frac{-4}{4}=\frac{3}{-3}$, i.e., the system has an infinite number of solutions.
Answer: an infinite number of solutions when $m=-3$; no solutions when $m=3$.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.36 Solve graphically the equation
$$
|x-1|+2x-5=0
$$
|
11.36 Let's write the equation as $|x-1|=5-2 x$. Since $|x-1| \geq 0$ for any $x$,
Fig. 11.11
and $\quad 5-2 x \geq 0$, i.e., $x \leq 2.5$.
Consider the functions $y_{1}=|x-1|, y_{2}=5-2 x$ and plot their graphs on the same diagram for $\quad x \leq 2.5 \quad$ (Fig.
11.12). The solution to the given equation is the points of intersection of these graphs. Using Fig. 11.12, we establish that $x=2$.
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.40 How many real solutions does the system of equations have
$\left\{\begin{array}{l}x^{2}+y=5 \\ x+y^{2}=3 ?\end{array}\right.$
|
11.40 The solutions of the system are the coordinates of the points of intersection of the graphs of the functions given by these equations. Let's write the original system in the form
$\left\{\begin{array}{l}y=5-x^{2}, \\ x=3-y^{2} .\end{array}\right.$
The graph of the first equation is a parabola with the axis of symmetry $O y$, and the graph of the second equation is a parabola with the axis of symmetry $O x$. By plotting these graphs (Fig. 11.14), we obtain four points of their intersection, i.e., the system has four real solutions.
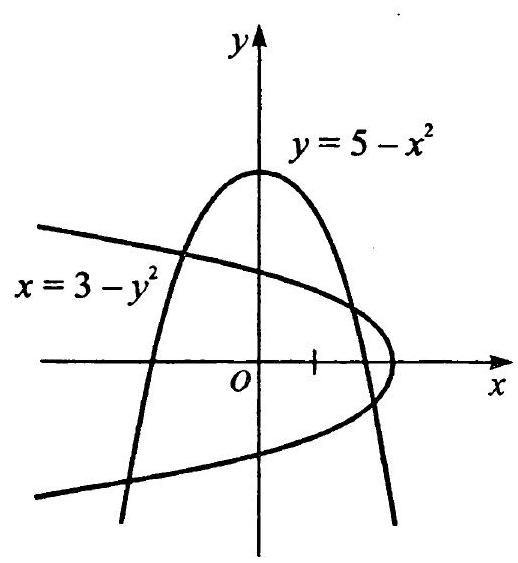
Fig. 11.14
Fig. 11.15
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.41 For what value of a is the sum of the squares of the roots of the equation $x^{2}+a x+a-2=0$ the smallest?
|
11.41 Let $x_{1}$ and $x_{2}$ be the roots of the equation. Then $x_{1} x_{2}=a-2$, $x_{1}+x_{2}=-a$. From this, we can express the sum of the squares of the roots:
$$
x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=a^{2}-2 a+4=f(a)
$$
Since $f(a)$ is a quadratic function with a positive leading coefficient, $f(a)$ attains its minimum value. This minimum value is achieved at $a=1$.
Answer: at $a=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.43 Solve the equation $x+\lg \left(1+4^{x}\right)=\lg 50$.
|
11.43 Let's write the equation as $x+\lg \left(1+4^{x}\right)=1+\lg 5$. It is not difficult to establish that the value $x=1$ satisfies the equation. The left side of the equation is $f(x)=x+\lg \left(1+4^{x}\right)$ - an increasing function; therefore, if $x<1$, then $f(x)<1+\lg 5$, and if $x>1$, then $f(x)>1+\lg 5$. This means the equation has a unique root $x=1$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.1 $\lim _{x \rightarrow 2} \frac{x^{3}-8}{2 x-4}$.
|
12.1 The function $f(x)=\frac{x^{3}-8}{2 x-4}$ is undefined at the point $x=2$. By factoring the numerator using formula (1.14), we can represent this function as
$f(x)=\frac{(x-2)\left(x^{2}+2 x+4\right)}{2(x-2)}$.
In the domain of the function $f(x)$, the expression $x-2 \neq 0$, so the fraction can be simplified by canceling out $x-2$. Then we get
$$
\lim _{x \rightarrow 2} f(x)=\lim _{x \rightarrow 2} \frac{x^{2}+2 x+4}{2}=f(2)=6
$$
Answer: 6.
|
6
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$12.3 \lim _{x \rightarrow-1} \frac{\sqrt{2 x+3}-1}{\sqrt{5+x}-2}$.
$12.3 \lim _{x \rightarrow-1} \frac{\sqrt{2 x+3}-1}{\sqrt{5+x}-2}$.
The above text is already in a mathematical expression format, so the translation is the same as the original text. If you need an explanation or solution for the limit, please let me know!
|
12.3 Multiplying the numerator and the denominator of the fraction by $(\sqrt{2 x+3}+1)(\sqrt{5+x}+2)$, we get $\lim _{x \rightarrow-1} \frac{(2 x+3-1)(\sqrt{5+x}+2)}{(5+x-4)(\sqrt{2 x+3}+1)}=\lim _{x \rightarrow-1} \frac{2(x+1)(\sqrt{5+x}+2)}{(x+1)(\sqrt{2 x+3}+1)}=$ $\lim _{x \rightarrow-1} \frac{2(\sqrt{5+x}+2)}{\sqrt{2 x+3}+1}=\frac{2 \cdot 4}{2}=4$.
Answer: 4.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.8 $f(x)=\sqrt{x^{2}+3}+\frac{2 x}{x+1} ; f^{\prime}(1)=?$
|
12.8 First, we find
$$
f^{\prime}(x)=\frac{x}{\sqrt{x^{2}+3}}+2 \frac{x+1-x}{(x+1)^{2}}=\frac{x}{\sqrt{x^{2}+3}}+\frac{2}{(x+1)^{2}}
$$
Now, setting $x=1$, we get $f^{\prime}(1)=\frac{1}{2}+\frac{2}{4}=1$.
Answer: 1.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.9 $f(x)=\sin 4 x \cos 4 x ; f^{\prime}\left(\frac{\pi}{3}\right)=$ ?
|
12.9 We have
$f^{\prime}(x)=4 \cos 4 x \cdot \cos 4 x+\sin 4 x(-4 \sin 4 x)=$ $=4\left(\cos ^{2} 4 x-\sin ^{2} 4 x\right)=4 \cos 8 x$.
At $x=\frac{\pi}{3}$ we find $f^{\prime}\left(\frac{\pi}{3}\right)=4 \cos \frac{8 \pi}{3}=4 \cos \frac{2 \pi}{3}=-2$.
Answer: -2.
|
-2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.11 $f(x)=\frac{(x-2)^{2}}{x^{2}}$.
|
12.11 The domain of the function is the entire number line, except for the point $x=0$. Using formula (12.4) and the table of derivatives, we find
$$
f^{\prime}(x)=\frac{2(x-2) x^{2}-(x-2)^{2} 2 x}{x^{4}}=\frac{4(x-2)}{x^{3}}
$$
$f^{\prime}(x)=0$ only at $x=2$. We will construct a table:
| Interval | $(-\infty, 0)$ | $(0,2)$ | 2 | $(2, \infty)$ |
| :---: | :---: | :---: | :---: | :---: |
| $f^{\prime}(x)$ | + | - | 0 | + |
| $f(x)$ | $\nearrow$ | $\searrow$ | $\min$ | $\nearrow$ |
Therefore, $x=2$ is a point of minimum; the function is increasing on $(-\infty, 0)$ and on $(2, \infty)$, and decreasing on $(0,2)$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.18 A pedestrian set out for a walk from point $A$ at a speed of $v$ km/h. After he had walked 6 km from $A$, a cyclist set out after him from $A$ at a speed 9 km/h greater than the pedestrian's speed. When the cyclist caught up with the pedestrian, they turned back and returned to $A$ together at a speed of 4 km/h. For what value of $v$ will the pedestrian's walking time be the shortest?
|
12.18 The time it takes for the cyclist to catch up with the pedestrian is $\frac{6}{9}=\frac{2}{3}$ (hours). Before the meeting, the pedestrian had been walking for $\frac{6}{v}+\frac{2}{3}$ (hours) and covered $v\left(\frac{6}{v}+\frac{2}{3}\right)$ (km). They covered this same distance on the way back at a constant speed of 4 km/h and spent $\frac{v\left(\frac{6}{v}+\frac{2}{3}\right)}{4}$ (hours). Therefore, the total time spent by the pedestrian on the walk can be expressed by the function
$$
t(v)=\frac{6}{v}+\frac{2}{3}+\frac{v\left(\frac{6}{v}+\frac{2}{3}\right)}{4}=\frac{6}{v}+\frac{2}{3}+\frac{3}{2}+\frac{v}{6}=\frac{v^{2}+13 v+36}{6 v}
$$
where $v>0$. We find
$$
t^{\prime}(v)=\frac{(2 v+13) v-\left(v^{2}+13 v+36\right)}{6 v^{2}}=\frac{v^{2}-36}{6 v^{2}}
$$
from which $t^{\prime}(v)=0$ when $v=6$. It is easy to verify that $v=6$ is a minimum point of the function $t(v)$. Therefore, the pedestrian will spend the least amount of time on the walk if they initially walk at a speed of 6 km/h.
Answer: 6 km/h
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$12.28 \int_{8}^{27} \frac{d x}{\sqrt[3]{x^{2}}}$
|
12.28 We have
$$
\int_{8}^{27} \frac{d x}{\sqrt[3]{x^{2}}}=\int_{8}^{27} x^{-2 / 3} d x=\left.\frac{x^{1 / 3}}{1 / 3}\right|_{8} ^{27}=3\left(27^{1 / 3}-8^{1 / 3}\right)=3
$$
Answer: 3.
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.35 $\lim _{x \rightarrow 4} \frac{x+\sqrt{x}-6}{x-5 \sqrt{x}+6}$.
|
12.35 The numerator and denominator of the given fraction are quadratic functions of $\sqrt{x}$. We have
$$
\lim _{x \rightarrow 4} \frac{(\sqrt{x}+3)(\sqrt{x}-2)}{(\sqrt{x}-3)(\sqrt{x}-2)}=\lim _{x \rightarrow 4} \frac{\sqrt{x}+3}{\sqrt{x}-3}=\frac{5}{-1}=-5
$$
Answer: -5.
|
-5
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
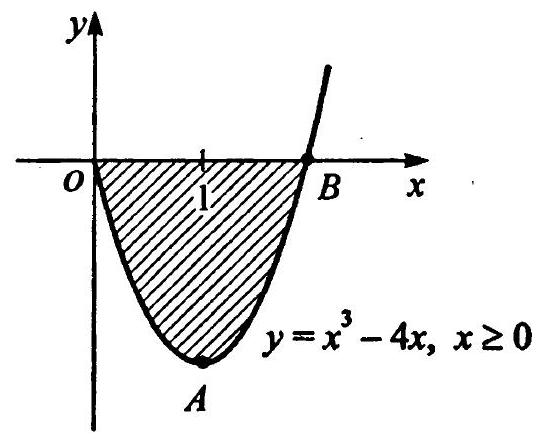
12.59 Find the area of the figure bounded by the lines $y=x^{3}-4 x$ and $y=0$ for $x \geq 0$.
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly.
|
12.59 First, let's construct the graph of the function $y=x^{3}-4 x$ for $x \geq 0$. We find the extrema:
$y^{\prime}=3 x^{2}-4$;
$3 x^{2}-4=0 ;$
$x= \pm \frac{2}{\sqrt{3}} \approx \pm 1.1$.
For
$x \geq 0$ the function is decreasing
on $\left(0, \frac{2}{\sqrt{3}}\right)$, increasing
Fig. 12.11
on $\left(\frac{2}{\sqrt{3}}, \infty\right)$, and $x=\frac{2}{\sqrt{3}}$ is a point of minimum, with $y_{\min }=-\frac{16}{3 \sqrt{3}} \approx-3$. Therefore, we need to find the area of the figure $O A B$ (Fig. 12.11). Since the function $y=x^{3}-4 x$ takes negative values on $(0,2)$, we have $S=\left|\int_{0}^{2}\left(x^{3}-4 x\right) d x\right|$. We get
$\int_{0}^{2}\left(x^{3}-4 x\right) d x=\left.\left(\frac{x^{4}}{4}-4 \frac{x^{2}}{2}\right)\right|_{0} ^{2}=-4$,
from which we obtain $S=4$ (sq. units).
Answer: 4 sq. units.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. The lengths of the sides of a right-angled triangle form an arithmetic progression with a common difference of 1 cm. Find the length of the hypotenuse.
|
1.1. Let $c$ be the length of the hypotenuse. Then the lengths of the legs are $c-1$ and $c-2$. We have
$$
(c-1)^{2}+(c-2)^{2}=c^{2}, \text { or } c^{2}-6 c+5=0
$$
from which $c=5$ (cm) (the second root of the equation does not satisfy the condition).
Answer: 5 cm.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.6. The legs of a right triangle are 9 and 12 cm. Find the distance between the point of intersection of its angle bisectors and the point of intersection of the medians.
|
1.6. In $\triangle A B C$ (Fig. 1.5), we have $A B=\sqrt{9^{2}+12^{2}}=15$ (cm); the median $C D$ is half the hypotenuse, i.e., $\frac{15}{2}$ cm. Let $E$ be the point of intersection of the medians; then $C E=\frac{2}{3} C D=\frac{2}{3} \cdot \frac{15}{2}=5$ (cm) (according to the additional relations, point $1^{\circ}$). Draw $D F \perp A C$; since $D F$ is the midline in $\triangle A B C$, we have $C F=6$ cm, $D F=\frac{9}{2}$ cm. Next, draw $E K \perp A C$; then $E K \| D F$ and $\triangle C E K \sim \triangle C D F$, from which
$$
E K=\frac{2}{3} D F=\frac{2}{3} \cdot \frac{9}{2}=3(\mathrm{~cm}), C K=\frac{2}{3} C F=\frac{2}{3} \cdot 6=4(\mathrm{~cm})
$$
Let $M$ be the point of intersection of the angle bisectors of $\angle C B A$ and $\angle B C A$,
Fig. 1.5
i.e., the center of the inscribed circle in $\triangle A B C$; then $M N \perp A C$, where $r=M N$ is the radius of this circle. By formula (1.4), we have $r=\frac{S}{p}$, where $S=\frac{1}{2} \cdot 9 \cdot 12=54\left(\mathrm{~cm}^{2}\right), p=\frac{1}{2}(9+12+15)=18$ (cm); thus, $r=\frac{54}{18}=3$ (cm). Finally, considering that $\angle M C N=45^{\circ}$, i.e., $C N=M N$, we get $N K=M E=C K-C N=4-3=1$ (cm).
Answer: 1 cm.

Fig. 1.6
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.9. Two circles touch each other externally. A tangent is drawn to the first circle, passing through the center of the second circle. The distance from the point of tangency to the center of the second circle is three times the radius of this circle. How many times greater is the length of the first circle compared to the length of the second circle?
|
1.9. Let $O_{1}$ and $O_{2}$ be the centers of the circles, and $A$ be the point of tangency (Fig. 1.8). Then $O_{1} A = R_{1}, O_{1} O_{2} = R_{1} + R_{2}, O_{2} A = 3 R_{2}$ (by the condition). We need to find the ratio $2 \pi R_{1} : 2 \pi R_{2} = R_{1} : R_{2}$. In the right triangle $O_{1} A O_{2} \left(\angle A = 90^{\circ}\right)$, we have
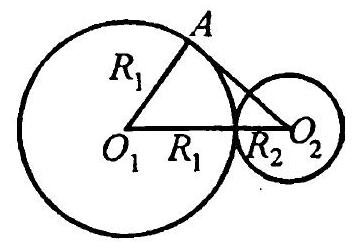
Fig. 1.8
$$
O_{1} O_{2}^{2} = O_{1} A^{2} + O_{2} A^{2}, \text{ or } \left(R_{1} + R_{2}\right)^{2} = R_{1}^{2} + \left(3 R_{2}\right)^{2}
$$
Simplifying this equation, we get $R_{1} = 4 R_{2}$, hence $R_{1} : R_{2} = 4$.
Answer: 4 times.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.20. A tangent, parallel to the base, is drawn to the circle inscribed in an isosceles triangle with a base of 12 cm and a height of 8 cm. Find the length of the segment of this tangent, enclosed between the sides of the triangle.
|
1.20. Let's find the length of the side $B C$ (Fig. 1.18); $B C=\sqrt{B M^{2}+M C^{2}}=\sqrt{6^{2}+8^{2}}=10$ (cm). Considering that $A O$ is the bisector of $\triangle A B M$, we have $\frac{M O}{O B}=\frac{A M}{A B}$, or $\frac{r}{8-r}=\frac{6}{10}$, from which $r=3$ (cm). Since $D E \| A C$, then $\triangle D B E \sim \triangle A B C$. That is, $\frac{D E}{A C}=\frac{B N}{B M}$, or $\frac{D E}{12}=\frac{8-2 r}{8}$, from which $D E=3 \text{ cm}$.
Answer: 3 cm.
Fig. 1.18
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.26. The area of an isosceles triangle is equal to $\frac{1}{3}$ of the area of the square constructed on the base of the given triangle. The lengths of the lateral sides of the triangle are shorter than the length of its base by 1 cm. Find the lengths of the sides and the height of the triangle, drawn to the base.
|
1.26. By the condition, $B C^{2}=$ $=3 \cdot \frac{1}{2} B C \cdot A H$ (Fig. 1.22), or $A H=$ $=\frac{2}{3} B C$. But $A H^{2}=A B^{2}-\left(\frac{1}{2} B C\right)^{2}$ and, therefore, $\frac{4}{9} B C^{2}=A B^{2}-\frac{1}{4} B C^{2}$, or $A B^{2}=\frac{25}{36} B C^{2}$, i.e., $A B=\frac{5}{6} B C$. Then we get $A B=\frac{5}{6}(A B+1)$, from which $A B=5$ (cm). Therefore, $B C=6 \mathrm{~cm}, A H=4 \mathrm{~cm}$.
Answer: 5 and 6 cm; 4 cm.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.28. One of the angles of the parallelogram is $60^{\circ}$, and the shorter diagonal is $2 \sqrt{31}$ cm. The length of the perpendicular dropped from the point of intersection of the diagonals to the longer side is $\frac{\sqrt{75}}{2}$ cm. Find the lengths of the sides and the longer diagonal of the parallelogram.
|
### 1.28. Let's conduct
Fig. 1.23 $B N \perp A D$ (Fig. 1.24); since $B N=2 O M$, then $B N=\sqrt{75}$ cm. Considering that in $\triangle A N B \angle A B N=30^{\circ}$, we have $A B=2 A N$ and, therefore, $4 A N^{2}=75+A N^{2}$, from which $A N=5$ cm and $A B=10$ cm. Further, from $\triangle B D N$ we get
Fig. 1.24 $N D^{2}=B D^{2}-B N^{2}=124-75=49$; hence, $N D=7$ cm and $A D=12$ cm. Finally, from the equality $A C^{2}+B D^{2}=2 A B^{2}+2 A D^{2}$ we find $A C^{2}=200+288-124=364$, i.e., $A C=2 \sqrt{91}$ cm.
Answer: 10 and 12 cm; $2 \sqrt{91}$ cm.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.30. The lengths of the parallel sides of the trapezoid are 25 and 4 cm, and the lengths of the non-parallel sides are 20 and 13 cm. Find the height of the trapezoid.
|
1.30. Given that $B C=$ $=4 \text{ cm}, A D=25 \text{ cm}, A B=20$ cm, $C D=13$ cm (Fig. 1.26). Draw $B E \perp A D$ and $C F \perp A D$. Let $B E=C F=$ $=h, A E=x, F D=y$. Then from $\triangle A B E$ and $\triangle C F D$ we find $h=\sqrt{20^{2}-x^{2}}=\sqrt{13^{2}-y^{2}}$. Considering that $y=25-4-$ $-x=21-x$, we have
$$
20^{2}-x^{2}=13^{2}-(21-x)^{2} \text {, or } 42 x=672 \text {, }
$$
from which $x=16$ (cm). Thus, $h=\sqrt{20^{2}-16^{2}}=12$ (cm).
Answer: $12 \text{ cm}$.
Fig. 1.27
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.44. In a circle with center $O$, a chord $A B$ is drawn, intersecting the diameter at point $M$ and forming an angle of $60^{\circ}$ with the diameter. Find $O M$, if $A M=10$ cm, and $B M=4$ cm.
|
1.44. Draw $O P \perp A B$ (Fig. 1.36). Then $A P=B P=7$ cm and, therefore, $M P=3$ cm. Since $\angle P M O=60^{\circ}$, then $\angle M O P=30^{\circ}$ and $O M=2 M P=6 \text{ cm}$.
Answer: 6 cm.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.49. The area of a right triangle is $24 \mathrm{~cm}^{2}$, and the hypotenuse is 10 cm. Find the radius of the inscribed circle.
|
1.49. I n d i c a t i o n. Denoting the legs of the triangle by $a$ and $b$, solve the system of equations
$$
\left\{\begin{array}{l}
a b=48 \\
a^{2}+b^{2}=100
\end{array}\right.
$$
and then use the formula $S=p r$.
Answer: 2 cm.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.43. Find the distance between the midpoints of two skew edges of a cube, the total surface area of which is $36 \mathrm{~cm}^{2}$.
|
2.43. Since the total surface area of the cube $S_{\text {full }}=36 \mathrm{~cm}^{2}$, the area of one face $S=6 \mathrm{~cm}^{2}$ and the edge of the cube
Fig. 2.37
$A D=a=\sqrt{6}$ cm (Fig. 2.37). The required distance
$$
\begin{gathered}
K M=\sqrt{A K^{2}+A M^{2}} \text {, where } A K=\frac{a}{2}=\frac{\sqrt{6}}{2}(\text { cm }), \\
A M=\sqrt{A D^{2}+D M^{2}}=\sqrt{a^{2}+\frac{a^{2}}{4}}=\frac{a \sqrt{5}}{2}=\frac{\sqrt{30}}{2} \text { (cm). }
\end{gathered}
$$
Finally, we get $K M=\sqrt{\frac{6}{4}+\frac{30}{4}}=3$ (cm).
Answer: 3 cm.
Fig. 2.38
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.67. In a trapezoid, the smaller base is equal to 2, the adjacent angles are $135^{\circ}$ each. The angle between the diagonals, facing the base, is $150^{\circ}$. Find the area of the trapezoid.
|
3.67. By the condition, $A D \| B C, B C=2, \angle A B C=\angle B C D=135^{\circ}$, $\angle A O D=150^{\circ}$ (Fig. 3.69). Since the angles at the base of the trapezoid are equal, the trapezoid is isosceles, i.e., $A B=C D$. We find
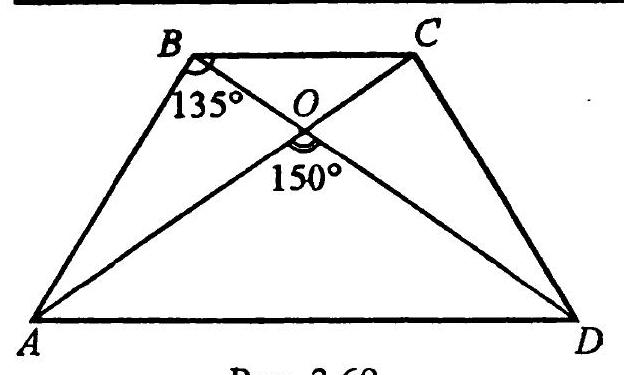
Fig. 3.69 $\angle A D C=180^{\circ}-135^{\circ}=45^{\circ} ;$
$\angle O D A=\frac{180^{\circ}-150^{\circ}}{2}=15^{\circ}$;
$\angle B D C=45^{\circ}-15^{\circ}=30^{\circ}$. From $\triangle B D C$ by the Law of Sines we have $\frac{B C}{\sin 30^{\circ}}=\frac{B D}{\sin 135^{\circ}}$, hence
$B D=\frac{2 \sin 45^{\circ}}{\sin 30^{\circ}}=2 \sqrt{2}$. Therefore,
$$
S_{A B C D}=\frac{1}{2} B D^{2} \sin 150^{\circ}=\frac{1}{2} \cdot 8 \cdot \frac{1}{2}=2
$$
(since the area of a convex quadrilateral is equal to $\frac{1}{2} d_{1} d_{2} \sin \alpha$, where $\alpha$ is the angle between the diagonals).
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.29. A regular $n$-sided polygon is inscribed in a circle of radius $R$, the area of which is equal to $3 R^{2}$. Find $n$.
|
4.29. We have $\angle A O B=\frac{360^{\circ}}{n}$ and, therefore, $S_{\triangle A O B}=\frac{R^{2}}{2} \sin \frac{360^{\circ}}{n}$ (Fig. 4.26). Thus, we obtain the equation $\frac{R^{2}}{2} \sin \frac{360^{\circ}}{n}=\frac{3 R^{2}}{n}$, which holds
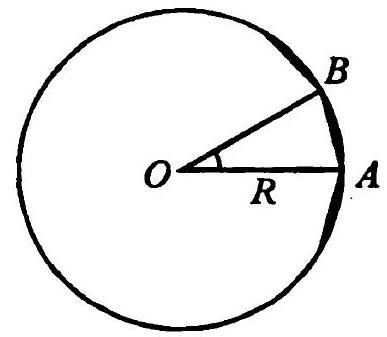
Fig. 4.26 for $n=12$.
Answer: $\boldsymbol{n}=12$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.8. Find the modulus of the projection of vector $\bar{a}(7; -4)$ onto the axis parallel to vector $\bar{b}(-8; 6)$.
untranslated text:
5.8. Найти модуль проекции вектора $\bar{a}(7 ;-4)$ на ось, параллельную вектору $\bar{b}(-8 ; 6)$.
|
5.8. We have $O K=$ proj $_{\bar{b}} \bar{a}=|\bar{a}| \cos \varphi$ (Fig. 5.5). From here, using
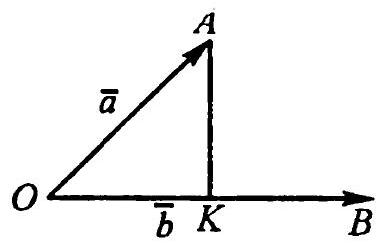
Fig. 5.5 the equality $\quad \bar{a} \bar{b}=|\bar{a}||\vec{b}| \cos \varphi, \quad$ we find proj $_{\bar{b}} \bar{a}=\frac{\bar{a} \bar{b}}{|\bar{b}|}$. Since $\bar{b}$ is the direction vector of the axis onto which the vector is projected,
$$
\operatorname{proj}_{\bar{b}} \bar{a}=\frac{7(-8)+(-4) 6}{\sqrt{64+36}}=\frac{-56-24}{10}=-8 \text {, i.e. }\left|\operatorname{proj}_{\bar{b}} \bar{a}\right|=8
$$
Answer: 8.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.18. In parallelogram $A B C D$, point $K$ is the midpoint of side $B C$, and point $M$ is the midpoint of side $C D$. Find $A D$, if $A K=6$ cm, $A M=3$ cm, and $\angle K A M=60^{\circ}$.
|
5.18. I n d i c a t i o n. Decompose the vector $\overline{A D}$ into vectors $\overline{A K}$ and $\overline{A M}$.
Answer: 4 cm.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.002. $\left(\left(\frac{7}{9}-\frac{47}{72}\right): 1.25+\left(\frac{6}{7}-\frac{17}{28}\right):(0.358-0.108)\right) \cdot 1.6-\frac{19}{25}$.
|
## Solution.
$$
\begin{aligned}
& \left(\left(\frac{7}{9}-\frac{47}{72}\right): 1.25+\left(\frac{6}{7}-\frac{17}{28}\right):(0.358-0.108)\right) \cdot 1.6-\frac{19}{25}= \\
& =\left(\frac{56-47}{72} \cdot \frac{4}{5}+\frac{24-17}{28}: 0.25\right) \cdot 1.6-\frac{19}{25}=(0.1+1) \cdot 1.6-\frac{19}{25}=1.76-0.76=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.005. $\frac{2 \frac{3}{4}: 1.1+3 \frac{1}{3}}{2.5-0.4 \cdot 3 \frac{1}{3}}: \frac{5}{7}-\frac{\left(2 \frac{1}{6}+4.5\right) \cdot 0.375}{2.75-1 \frac{1}{2}}$.
|
Solution.
$$
\frac{2 \frac{3}{4}: 1.1+3 \frac{1}{3}}{2.5-0.4 \cdot 3 \frac{1}{3}}: \frac{5}{7}-\frac{\left(2 \frac{1}{6}+4.5\right) \cdot 0.375}{2.75-1 \frac{1}{2}}=\frac{\frac{5}{2}+\frac{10}{3}}{\frac{5}{2}-\frac{4}{3}} \cdot \frac{7}{5}-\frac{\frac{20}{3} \cdot \frac{3}{8}}{1.25}=7-2=5
$$
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.006. $\frac{\left(13.75+9 \frac{1}{6}\right) \cdot 1.2}{\left(10.3-8 \frac{1}{2}\right) \cdot \frac{5}{9}}+\frac{\left(6.8-3 \frac{3}{5}\right) \cdot 5 \frac{5}{6}}{\left(3 \frac{2}{3}-3 \frac{1}{6}\right) \cdot 56}-27 \frac{1}{6}$.
|
## Solution.
$$
\begin{aligned}
& \frac{\left(13.75+9 \frac{1}{6}\right) \cdot 1.2}{\left(10.3-8 \frac{1}{2}\right) \cdot \frac{5}{9}}+\frac{\left(6.8-3 \frac{3}{5}\right) \cdot 5 \frac{5}{6}}{\left(3 \frac{2}{3}-3 \frac{1}{6}\right) \cdot 56}-27 \frac{1}{6}=\frac{\left(\frac{55}{4}+\frac{55}{6}\right) \cdot \frac{6}{5}}{(2.3-0.5) \cdot \frac{5}{9}}+\frac{\left(\frac{34}{5}-\frac{18}{5}\right) \cdot \frac{35}{6}}{\left(\frac{4}{6}-\frac{1}{6}\right) \cdot 56}- \\
& -\frac{163}{6}=\frac{11\left(1+\frac{3}{2}\right)}{\frac{18}{10} \cdot \frac{5}{9}}+\frac{\frac{16}{5} \cdot \frac{35}{6}}{28}-\frac{163}{6}=\frac{55}{2}+\frac{2}{3}-\frac{163}{6}=\frac{169}{6}-\frac{163}{6}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.008. $\left(\frac{3 \frac{1}{3}+2.5}{2.5-1 \frac{1}{3}} \cdot \frac{4.6-2 \frac{1}{3}}{4.6+2 \frac{1}{3}} \cdot 5.2\right):\left(\frac{0.05}{\frac{1}{7}-0.125}+5.7\right)$.
|
Solution.
$$
\begin{aligned}
& \left(\frac{3 \frac{1}{3}+2.5}{2.5-1 \frac{1}{3}} \cdot \frac{4.6-2 \frac{1}{3}}{4.6+2 \frac{1}{3}} \cdot 5.2\right):\left(\frac{0.05}{\frac{1}{7}-0.125}+5.7\right)= \\
& =\left(\frac{\frac{10}{3}+\frac{5}{2}}{\frac{5}{2}-\frac{4}{3}} \cdot \frac{\frac{23}{5}-\frac{7}{3}}{\frac{23}{5}+\frac{7}{3}} \cdot \frac{26}{5}\right):\left(\frac{\frac{1}{20}}{\frac{1}{7}-\frac{1}{8}}+\frac{57}{10}\right)= \\
& =\left(\frac{35}{7} \cdot \frac{34}{104} \cdot \frac{26}{5}\right):\left(\frac{28}{10}+\frac{57}{10}\right)=\frac{17}{2} \cdot \frac{2}{17}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.009.
$$
\frac{0.4+8\left(5-0.8 \cdot \frac{5}{8}\right)-5: 2 \frac{1}{2}}{\left(1 \frac{7}{8} \cdot 8-\left(8.9-2.6: \frac{2}{3}\right)\right) \cdot 34 \frac{2}{5}} \cdot 90
$$
|
Solution.
$$
\begin{aligned}
& \frac{0.4+8\left(5-0.8 \cdot \frac{5}{8}\right)-5: 2 \frac{1}{2}}{\left(1 \frac{7}{8} \cdot 8-\left(8.9-2.6: \frac{2}{3}\right)\right) \cdot 34 \frac{2}{5}} \cdot 90=\frac{\left(0.4+40-4-5 \cdot \frac{2}{5}\right) \cdot 90}{\left(\frac{15}{8} \cdot 8-\frac{89}{10}+\frac{13}{5} \cdot \frac{3}{2}\right) \cdot \frac{172}{5}}= \\
& =\frac{34.4 \cdot 90}{\left(\frac{150}{10}-\frac{89}{10}+\frac{39}{10}\right) \cdot \frac{172}{5}}=\frac{344 \cdot 9}{2 \cdot 172}=9 .
\end{aligned}
$$
Answer: 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.010. $\frac{\left(5 \frac{4}{45}-4 \frac{1}{6}\right): 5 \frac{8}{15}}{\left(4 \frac{2}{3}+0.75\right) \cdot 3 \frac{9}{13}} \cdot 34 \frac{2}{7}+\frac{0.3: 0.01}{70}+\frac{2}{7}$.
|
## Solution.
$$
\begin{aligned}
& \frac{\left(5 \frac{4}{45}-4 \frac{1}{6}\right): 5 \frac{8}{15}}{\left(4 \frac{2}{3}+0.75\right) \cdot 3 \frac{9}{13}} \cdot 34 \frac{2}{7}+\frac{0.3: 0.01}{70}+\frac{2}{7}=\frac{\left(\frac{229}{45}-\frac{25}{6}\right): \frac{83}{15}}{\left(\frac{14}{3}+\frac{3}{4}\right) \cdot \frac{48}{13}} \cdot \frac{240}{7}+\frac{30}{70}+\frac{2}{7}= \\
& =\frac{\frac{93}{90} \cdot \frac{15}{83}}{\frac{65}{12} \cdot \frac{48}{13}} \cdot \frac{240}{7}+\frac{5}{7}=\frac{1}{6 \cdot 20} \cdot \frac{240}{7}+\frac{5}{7}=\frac{2}{7}+\frac{5}{7}=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.011. $\frac{\left(\frac{3}{5}+0.425-0.005\right): 0.1}{30.5+\frac{1}{6}+3 \frac{1}{3}}+\frac{6 \frac{3}{4}+5 \frac{1}{2}}{26: 3 \frac{5}{7}}-0.05$.
|
## Solution.
$$
\frac{\left(\frac{3}{5}+0.425-0.005\right): 0.1}{30.5+\frac{1}{6}+3 \frac{1}{3}}+\frac{6 \frac{3}{4}+5 \frac{1}{2}}{26: 3 \frac{5}{7}}-0.05=
$$
$=\frac{(0.6+0.42) \cdot 10}{\frac{61}{2}+\frac{1}{6}+\frac{10}{3}}+\frac{12 \frac{1}{4} \cdot 26}{26 \cdot 7}-0.05=$
$=\frac{10.2}{34}+\frac{7}{4}-\frac{1}{20}=\frac{3}{10}+\frac{7}{4}-\frac{1}{20}=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.012. $\frac{3 \frac{1}{3} \cdot 1.9+19.5: 4 \frac{1}{2}}{\frac{62}{75}-0.16}: \frac{3.5+4 \frac{2}{3}+2 \frac{2}{15}}{0.5\left(1 \frac{1}{20}+4.1\right)}$.
|
## Solution.
$\frac{3 \frac{1}{3} \cdot 1.9 + 19.5 : 4 \frac{1}{2}}{\frac{62}{75} - 0.16} : \frac{3.5 + 4 \frac{2}{3} + 2 \frac{2}{15}}{0.5 \left(1 \frac{1}{20} + 4.1\right)} = \frac{\frac{10}{3} \cdot \frac{19}{10} + \frac{39}{2} \cdot \frac{2}{9}}{\frac{62}{75} - \frac{4}{25}} \cdot \frac{\frac{1}{2} \left(\frac{21}{20} + \frac{41}{10}\right)}{\frac{7}{2} + \frac{14}{3} + \frac{32}{15}}=$
$= \frac{\frac{19}{3} + \frac{13}{3}}{\frac{2}{3}} \cdot \frac{\frac{103}{40}}{\frac{103}{10}} = \frac{16}{4} = 4$.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.014. $\frac{\left(4.5 \cdot 1 \frac{2}{3}-6.75\right) \cdot \frac{2}{3}}{\left(3 \frac{1}{3} \cdot 0.3+5 \frac{1}{3} \cdot \frac{1}{8}\right): 2 \frac{2}{3}}+\frac{1 \frac{4}{11} \cdot 0.22: 0.3-0.96}{\left(0.2-\frac{3}{40}\right) \cdot 1.6}$.
|
## Solution.
$$
\begin{aligned}
& \frac{\left(4.5 \cdot 1 \frac{2}{3}-6.75\right) \cdot \frac{2}{3}}{\left(3 \frac{1}{3} \cdot 0.3+5 \frac{1}{3} \cdot \frac{1}{8}\right): 2 \frac{2}{3}}+\frac{1 \frac{4}{11} \cdot 0.22: 0.3-0.96}{\left(0.2-\frac{3}{40}\right) \cdot 1.6}=\frac{\left(\frac{9}{2} \cdot \frac{5}{3}-\frac{27}{4}\right) \cdot \frac{2}{3}}{\left(\frac{10}{3} \cdot \frac{3}{10}+\frac{16}{3} \cdot \frac{1}{8}\right) \cdot \frac{3}{8}}+ \\
& +\frac{\frac{15}{11} \cdot \frac{11}{50} \cdot \frac{10}{3}-\frac{24}{25}}{\left(\frac{1}{5}-\frac{3}{40}\right) \cdot \frac{8}{5}}=\frac{\left(\frac{30}{4}-\frac{27}{4}\right) \cdot \frac{2}{3}}{\left(1+\frac{2}{3}\right) \cdot \frac{3}{8}}+\frac{1-\frac{24}{25}}{\frac{1}{8} \cdot \frac{8}{5}}=\frac{1}{2} \cdot \frac{8}{5}+\frac{1}{5}=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.016. $\left(16 \frac{1}{2}-13 \frac{7}{9}\right) \cdot \frac{18}{33}+2.2\left(\frac{8}{33}-\frac{1}{11}\right)+\frac{2}{11}$.
|
## Solution.
$$
\begin{aligned}
& \left(16 \frac{1}{2}-13 \frac{7}{9}\right) \cdot \frac{18}{33}+2.2\left(\frac{8}{33}-\frac{1}{11}\right)+\frac{2}{11}=\left(\frac{33}{2}-\frac{124}{9}\right) \cdot \frac{6}{11}+ \\
& +\frac{22}{10}\left(\frac{8}{33}-\frac{3}{33}\right)+\frac{2}{11}=\frac{49}{18} \cdot \frac{6}{11}+\frac{1}{3}+\frac{2}{11}=\frac{49}{33}+\frac{17}{33}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.017. $\frac{0.128: 3.2+0.86}{\frac{5}{6} \cdot 1.2+0.8} \cdot \frac{\left(1 \frac{32}{63}-\frac{13}{21}\right) \cdot 3.6}{0.505 \cdot \frac{2}{5}-0.002}$.
|
## Solution.
$$
\begin{aligned}
& \frac{0.128: 3.2+0.86}{\frac{5}{6} \cdot 1.2+0.8} \cdot \frac{\left(1 \frac{32}{63}-\frac{13}{21}\right) \cdot 3.6}{0.505 \cdot \frac{2}{5}-0.002}=\frac{0.04+0.86}{1+0.8} \cdot \frac{\left(\frac{95}{63}-\frac{39}{63}\right) \cdot \frac{18}{5}}{0.202-0.002}= \\
& =\frac{9}{18} \cdot \frac{8}{9} \cdot \frac{18}{0.2 \cdot 5}=8
\end{aligned}
$$
Answer: 8.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.018. $\frac{3 \frac{1}{3}: 10+0.175: 0.35}{1.75-1 \frac{11}{17} \cdot \frac{51}{56}}-\frac{\left(\frac{11}{18}-\frac{1}{15}\right): 1.4}{\left(0.5-\frac{1}{9}\right) \cdot 3}$.
|
Solution.
$$
\begin{aligned}
& \frac{3 \frac{1}{3}: 10+0.175: 0.35}{1.75-1 \frac{11}{17} \cdot \frac{51}{56}}-\frac{\left(\frac{11}{18}-\frac{1}{15}\right): 1.4}{\left(0.5-\frac{1}{9}\right) \cdot 3}=\frac{\frac{1}{3}+\frac{1}{2}}{\frac{7}{4}-\frac{28}{17} \cdot \frac{51}{56}}-\frac{\frac{49}{90} \cdot \frac{5}{7}}{\frac{7}{18} \cdot 3}= \\
& =\frac{5}{6\left(\frac{7}{4}-\frac{3}{2}\right)}-\frac{7 \cdot 18}{18 \cdot 7 \cdot 3}=\frac{10}{3}-\frac{1}{3}=3 .
\end{aligned}
$$
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.019. $\frac{0.125: 0.25+1 \frac{9}{16}: 2.5}{(10-22: 2.3) \cdot 0.46+1.6}+\left(\frac{17}{20}+1.9\right) \cdot 0.5$.
|
## Solution.
$$
\begin{aligned}
& \frac{0.125: 0.25+1 \frac{9}{16}: 2.5}{(10-22: 2.3): 0.46+1.6}+\left(\frac{17}{20}+1.9\right) \cdot 0.5=\frac{\frac{1}{2}+\frac{5}{8}}{\left(10-\frac{220}{23}\right) \cdot \frac{23}{50}+\frac{8}{5}}+\frac{17}{40}+\frac{19}{20}= \\
& =\frac{\frac{9}{8}}{\frac{1}{5}+\frac{8}{5}}+\frac{17}{40}+\frac{38}{40}=\frac{5}{8}+\frac{11}{8}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.020. $\left(\left(1 \frac{1}{7}-\frac{23}{49}\right): \frac{22}{147}-\left(0.6: 3 \frac{3}{4}\right) \cdot 2 \frac{1}{2}+3.75: 1 \frac{1}{2}\right): 2.2$.
|
## Solution.
$$
\begin{aligned}
& \left(\left(1 \frac{1}{7}-\frac{23}{49}\right): \frac{22}{147}-\left(0.6: 3 \frac{3}{4}\right) \cdot 2 \frac{1}{2}+3.75: 1 \frac{1}{2}\right): 2.2= \\
& =\left(\left(\frac{8}{7}-\frac{23}{49}\right) \frac{147}{22}-0.16 \cdot 2.5+2.5\right): 2.2=\left(\frac{33}{49} \cdot \frac{147}{22}-0.4+2.5\right): 2.2= \\
& =(4.5-0.4+2.5) \cdot \frac{10}{22}=3
\end{aligned}
$$
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.022. $\frac{0.5+\frac{1}{4}+\frac{1}{6}+0.125}{\frac{1}{3}+0.4+\frac{14}{15}}+\frac{(3.75-0.625) \frac{48}{125}}{12.8 \cdot 0.25}$.
|
Solution.
$\frac{0.5+\frac{1}{4}+\frac{1}{6}+0.125}{\frac{1}{3}+0.4+\frac{14}{15}}+\frac{(3.75-0.625) \frac{48}{125}}{12.8 \cdot 0.25}=\frac{\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}}{\frac{1}{3}+\frac{2}{5}+\frac{14}{15}}+\frac{3.125 \cdot 48}{3.2 \cdot 125}=$
$=\frac{25}{24} \cdot \frac{3}{5}+\frac{1.2}{3.2}=0.625+0.375=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.024. $\frac{0.725+0.6+\frac{7}{40}+\frac{11}{20}}{0.128 \cdot 6 \frac{1}{4}-0.0345: \frac{3}{25}} \cdot 0.25$.
|
## Solution.
$$
\begin{aligned}
& \frac{0.725+0.6+\frac{7}{40}+\frac{11}{20}}{0.128 \cdot 6 \frac{1}{4}-0.0345: \frac{3}{25}} \cdot 0.25=\frac{1.325+\frac{29}{40}}{0.128 \cdot 6.25-0.0345: 0.12} \cdot 0.25= \\
& =\frac{1.325+0.725}{0.8-0.2875} \cdot 0.25=\frac{2.05}{0.5125} \cdot 0.25=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.025. $\left((520 \cdot 0.43): 0.26-217 \cdot 2 \frac{3}{7}\right)-\left(31.5: 12 \frac{3}{5}+114 \cdot 2 \frac{1}{3}+61 \frac{1}{2}\right)$.
|
Solution.
$$
\begin{aligned}
& \left((520 \cdot 0.43): 0.26-217 \cdot 2 \frac{3}{7}\right)-\left(31.5: 12 \frac{3}{5}+114 \cdot 2 \frac{1}{3}+61 \frac{1}{2}\right)= \\
& =\left(223.6: 0.26-217 \cdot \frac{17}{7}\right)-\left(\frac{63}{2} \cdot \frac{5}{63}+114 \cdot \frac{7}{3}+\frac{123}{2}\right)= \\
& =(860-527)-\left(\frac{5}{2}+266+\frac{123}{2}\right)=333-330=3
\end{aligned}
$$
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.026. $\frac{(3.4-1.275) \cdot \frac{16}{17}}{\frac{5}{18} \cdot\left(1 \frac{7}{85}+6 \frac{2}{17}\right)}+0.5\left(2+\frac{12.5}{5.75+\frac{1}{2}}\right)$.
|
Solution.
$$
\begin{aligned}
& \frac{(3.4-1.275) \cdot \frac{16}{17}}{\frac{5}{18} \cdot\left(1 \frac{7}{85}+6 \frac{2}{17}\right)}+0.5\left(2+\frac{12.5}{5.75+\frac{1}{2}}\right)=\frac{2.125 \cdot \frac{16}{17}}{\frac{5}{18}\left(\frac{92}{85}+\frac{104}{17}\right)}+\frac{1}{2}\left(2+\frac{12.5}{6.25}\right)= \\
& =\frac{\frac{17}{8} \cdot \frac{16}{17}}{\frac{5}{18} \cdot \frac{612}{85}}+1+1=1+2=3
\end{aligned}
$$
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.027. $\left(\frac{3.75+2 \frac{1}{2}}{2 \frac{1}{2}-1.875}-\frac{2 \frac{3}{4}+1.5}{2.75-1 \frac{1}{2}}\right) \cdot \frac{10}{11}$.
|
Solution.
$\left(\frac{3.75+2 \frac{1}{2}}{2 \frac{1}{2}-1.875}-\frac{2 \frac{3}{4}+1.5}{2.75-1 \frac{1}{2}}\right) \cdot \frac{10}{11}=\left(\frac{3.75+2.5}{2.5-1.875}-\frac{2.75+1.5}{2.75-1.5}\right) \cdot \frac{10}{11}=$
$=\left(\frac{6.25}{0.625}-\frac{4.25}{1.25}\right) \cdot \frac{10}{11}=\left(10-\frac{17}{5}\right) \cdot \frac{10}{11}=\frac{33}{5} \cdot \frac{10}{11}=6$.
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.028. $((21.85: 43.7+8.5: 3.4): 4.5): 1 \frac{2}{5}+1 \frac{11}{21}$.
|
## Solution.
$$
\begin{aligned}
& ((21.85: 43.7+8.5: 3.4): 4.5): 1 \frac{2}{5}+1 \frac{11}{21}=\left((0.5+2.5): 4 \frac{1}{2}\right): \frac{7}{5}+\frac{32}{21}= \\
& =\left(3 \cdot \frac{2}{9}\right) \cdot \frac{5}{7}+\frac{32}{21}=\frac{10}{21}+\frac{32}{21}=\frac{42}{21}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.029. $\left(1 \frac{2}{5}+3.5: 1 \frac{1}{4}\right): 2 \frac{2}{5}+3.4: 2 \frac{1}{8}-0.35$.
|
## Solution.
$$
\begin{aligned}
& \left(1 \frac{2}{5}+3.5: 1 \frac{1}{4}\right): 2 \frac{2}{5}+3.4: 2 \frac{1}{8}-0.35= \\
& =(1.4+3.5: 1.25): 2.4+3.4: 2.125-0.35=(1.4+2.8): 2.4+ \\
& +1.6-0.35=4.2: 2.4+1.25=1.75+1.25=3
\end{aligned}
$$
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.032. $\frac{\left(3^{-1}-\sqrt{1 \frac{7}{9}}\right)^{-2}: 0.25}{\frac{37}{300}: 0.0925}+12.5 \cdot 0.64$.
|
## Solution.
$$
\begin{aligned}
& \frac{\left(3^{-1}-\sqrt{1 \frac{7}{9}}\right)^{-2}: 0.25}{\frac{37}{300}: 0.0925}+12.5 \cdot 0.64=\frac{\left(\frac{1}{3}-\sqrt{\frac{16}{9}}\right)^{-2} \cdot 4}{\frac{37}{300} \cdot \frac{400}{37}}+8= \\
& =\frac{\left(\frac{1}{3}-\frac{4}{3}\right)^{-2} \cdot 4}{\frac{4}{3}}+8=3(-1)^{-2}+8=3+8=11
\end{aligned}
$$
Answer: 11.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.033. $\frac{\left(\frac{5}{8}+2 \frac{17}{24}\right): 2.5}{\left(1.3+\frac{23}{30}+\frac{4}{11}\right) \cdot \frac{110}{401}} \cdot 0.5$.
|
## Solution.
$\frac{\left(\frac{5}{8}+2 \frac{17}{24}\right): 2.5}{\left(1.3+\frac{23}{30}+\frac{4}{11}\right) \cdot \frac{110}{401}} \cdot 0.5=\frac{\left(\frac{5}{8}+\frac{65}{24}\right) \cdot \frac{2}{5} \cdot \frac{1}{2}}{\left(\frac{13}{10}+\frac{23}{30}+\frac{4}{11}\right) \cdot \frac{110}{401}}=\frac{\frac{10}{3} \cdot \frac{1}{5}}{\frac{401}{165} \cdot \frac{110}{401}}=\frac{2}{3}: \frac{2}{3}=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.039. $\left(\frac{(3.2-1.7): 0.003}{\left(\frac{29}{35}-\frac{3}{7}\right) \cdot 4: 0.2}-\frac{\left(1 \frac{13}{20}-1.5\right) \cdot 1.5}{\left(2.44+1 \frac{14}{25}\right) \cdot \frac{1}{8}}\right): 62 \frac{1}{20}+1.364: 0.124$.
|
Solution.
$$
\begin{aligned}
& \left(\frac{(3.2-1.7): 0.003}{\left(\frac{29}{35}-\frac{3}{7}\right) \cdot 4: 0.2}-\frac{\left(1 \frac{13}{20}-1.5\right) \cdot 1.5}{\left(2.44+1 \frac{14}{25}\right) \cdot \frac{1}{8}}\right): 62 \frac{1}{20}+1.364: 0.124= \\
& =\left(\frac{1.5: 0.003}{\frac{14}{35} \cdot 4 \cdot 5}-\frac{\frac{3}{20} \cdot \frac{3}{2}}{4 \cdot \frac{1}{8}}\right): \frac{1241}{20}+11=\left(\frac{500}{8}-\frac{9}{40} \cdot 2\right) \cdot \frac{20}{1241}+11= \\
& =\left(\frac{125}{2}-\frac{9}{20}\right) \cdot \frac{20}{1241}+11=\frac{1241}{20} \cdot \frac{20}{1241}+11=12
\end{aligned}
$$
Answer: 12.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.041. $\frac{\left(4-3.5 \cdot\left(2 \frac{1}{7}-1 \frac{1}{5}\right)\right): 0.16}{X}=\frac{3 \frac{2}{7}-\frac{3}{14}: \frac{1}{6}}{41 \frac{23}{84}-40 \frac{49}{60}}$.
|
## Solution.
$$
\begin{aligned}
& X=\frac{\left(4-3.5 \cdot\left(2 \frac{1}{7}-1 \frac{1}{5}\right)\right): 0.16 \cdot\left(41 \frac{23}{84}-40 \frac{49}{60}\right)}{3 \frac{2}{7}-\frac{3}{14}: \frac{1}{6}}= \\
& =\frac{\left(4-3.5 \cdot\left(\frac{15}{7}-\frac{6}{5}\right)\right): 0.16 \cdot \frac{16}{35}}{\frac{23}{7} \cdot \frac{9}{7}}=\frac{\left(4-\frac{7}{2} \cdot \frac{33}{35}\right): \frac{4}{25} \cdot \frac{16}{35}}{2} \\
& =\frac{\left(4-\frac{33}{10}\right): \frac{4}{25} \cdot \frac{16}{35}}{2}=\frac{\frac{7}{10} \cdot \frac{25}{4} \cdot \frac{16}{35}}{2}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.