problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
1.043. $\frac{0.125 X}{\left(\frac{19}{24}-\frac{21}{40}\right) \cdot 8 \frac{7}{16}}=\frac{\left(1 \frac{28}{63}-\frac{17}{21}\right) \cdot 0.7}{0.675 \cdot 2.4-0.02}$.
|
Solution.
$X=\frac{\left(1 \frac{28}{63}-\frac{17}{21}\right) \cdot 0.7 \cdot\left(\frac{19}{24}-\frac{21}{40}\right) \cdot 8 \frac{7}{16}}{(0.675 \cdot 2.4-0.02) \cdot 0.125}=\frac{\left(\frac{91}{63}-\frac{17}{21}\right) \cdot \frac{7}{10} \cdot \frac{4}{15} \cdot \frac{135}{16}}{(1.62-0.02) \cdot 0.125}=$ $=\frac{\frac{40}{63} \cdot \frac{63}{40}}{1.6 \cdot 0.125}=\frac{1}{0.2} 5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.046.
$$
\frac{\sqrt{6.3 \cdot 1.7} \cdot\left(\sqrt{\frac{6.3}{1.7}}-\sqrt{\frac{1.7}{6.3}}\right)}{\sqrt{(6.3+1.7)^{2}-4 \cdot 6.3 \cdot 1.7}}
$$
|
Solution.
$$
\begin{aligned}
& \frac{\sqrt{6.3 \cdot 1.7} \cdot\left(\sqrt{\frac{6.3}{1.7}}-\sqrt{\frac{1.7}{6.3}}\right)}{\sqrt{(6.3+1.7)^{2}-4 \cdot 6.3 \cdot 1.7}}=\frac{\sqrt{6.3 \cdot 1.7} \cdot\left(\sqrt{\frac{6.3}{1.7}}-\sqrt{\frac{1.7}{6.3}}\right)}{\sqrt{6.3^{2}+2 \cdot 6.3 \cdot 1.7+1.7^{2}-4 \cdot 6.3 \cdot 1.7}}= \\
& =\frac{\sqrt{6.3 \cdot 1.7} \cdot \frac{\sqrt{6.3^{2}}-\sqrt{1.7^{2}}}{\sqrt{6.3 \cdot 1.7}}}{\sqrt{6.3^{2}-2 \cdot 6.3 \cdot 1.7+1.7^{2}}}=\frac{6.3-1.7}{\sqrt{(6.3-1.7)^{2}}}=\frac{6.3-1.7}{6.3-1.7}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.049. $\frac{2^{-2}+5^{0}}{(0.5)^{-2}-5(-2)^{-2}+\left(\frac{2}{3}\right)^{-2}}+4.75$.
|
Solution.
$$
\begin{aligned}
& \frac{2^{-2}+5^{0}}{(0.5)^{-2}-5(-2)^{-2}+\left(\frac{2}{3}\right)^{-2}}+4.75=\frac{\frac{1}{2^{2}}+1}{-\frac{1}{(0.5)^{2}}-\frac{5}{(-2)^{-2}}+\left(\frac{3}{2}\right)^{2}}+4.75= \\
& =\frac{\frac{1}{4}+1}{\frac{1}{0.25}-\frac{5}{4}+\frac{9}{4}}+4.75=\frac{-\frac{4}{4}}{4+1}+4.75=\frac{1}{4}+4 \frac{3}{4}=5 .
\end{aligned}
$$
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.025. $\frac{a^{3}-a-2 b-b^{2} / a}{\left(1-\sqrt{\frac{1}{a}+\frac{b}{a^{2}}}\right) \cdot(a+\sqrt{a+b})}:\left(\frac{a^{3}+a^{2}+a b+a^{2} b}{a^{2}-b^{2}}+\frac{b}{a-b}\right) ;$
$a=23 ; b=22$.
|
Solution.
$$
\begin{aligned}
& \frac{a^{3}-a-2 b-b^{2} / a}{\left(1-\sqrt{\frac{1}{a}+\frac{b}{a^{2}}}\right) \cdot(a+\sqrt{a+b})}:\left(\frac{a^{3}+a^{2}+a b+a^{2} b}{a^{2}-b^{2}}+\frac{b}{a-b}\right)= \\
& =\frac{\frac{a^{4}-a^{2}-2 a b-b^{2}}{a}}{\left(1-\sqrt{\frac{a+b}{a^{2}}}\right) \cdot(a+\sqrt{a+b})}:\left(\frac{a^{2}(a+1)+a b(a+1)}{(a-b)(a+b)}+\frac{b}{a-b}\right)= \\
& =\frac{a^{4}-\left(a^{2}+2 a b+b^{2}\right)}{(a-\sqrt{a+b})(a+\sqrt{a+b})}:\left(\frac{a(a+1)(a+b)}{(a-b)(a+b)}+\frac{b}{a-b}\right)= \\
& =\frac{a^{4}-(a+b)^{2}}{a^{2}-a-b}:\left(\frac{a(a+1)}{a-b}+\frac{b}{a-b}\right)= \\
& =\frac{\left(a^{2}-a-b\right)\left(a^{2}+a+b\right)}{a^{2}-a-b}: \frac{a^{2}+a+b}{a-b}= \\
& =\frac{\left(a^{2}+a+b\right)(a-b)}{a^{2}+a+b}=a-b=23-22=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.030. $\sqrt{\frac{\sqrt{2}}{a}+\frac{a}{\sqrt{2}}+2}-\frac{a \sqrt[4]{2}-2 \sqrt{a}}{a \sqrt{2 a}-\sqrt[4]{8 a^{4}}}$.
2.030. $\sqrt{\frac{\sqrt{2}}{a}+\frac{a}{\sqrt{2}}+2}-\frac{a \sqrt[4]{2}-2 \sqrt{a}}{a \sqrt{2 a}-\sqrt[4]{8 a^{4}}}$.
(Note: The original text and the translation are identical as the expression is already in a mathematical form that does not require translation.)
|
Solution.
Domain of definition: $\left\{\begin{array}{l}a>0, \\ a \neq \sqrt{2} .\end{array}\right.$
$$
\sqrt{\frac{\sqrt{2}}{a}+\frac{a}{\sqrt{2}}+2}-\frac{a^{2} \sqrt[4]{2}-2 \sqrt{a}}{a \sqrt{2 a}-\sqrt[4]{8 a^{4}}}=\sqrt{\frac{a^{2}+2 a \sqrt{2}+(\sqrt{2})^{2}}{a \sqrt{2}}}-
$$
$$
\begin{aligned}
& -\frac{a^{2} \cdot 2^{1 / 4}-2 \cdot a^{1 / 2}}{a^{3 / 2} \cdot 2^{1 / 2}-2^{3 / 4} \cdot a}=\frac{\sqrt{(a+\sqrt{2})^{2}}}{\sqrt{a \sqrt{2}}}-\frac{2^{1 / 4} \cdot a^{1 / 2} \cdot\left(a^{3 / 2}-2^{3 / 4}\right)}{2^{1 / 2} \cdot a \cdot\left(a^{1 / 2}-2^{1 / 4}\right)}= \\
& =\frac{a+\sqrt{2}}{a^{1 / 2} \cdot 2^{1 / 4}}-\frac{2^{1 / 4} \cdot a^{1 / 2} \cdot\left(\left(a^{1 / 2}\right)^{3}-\left(2^{1 / 4}\right)^{3}\right)}{2^{1 / 2} \cdot a \cdot\left(a^{1 / 2}-2^{1 / 4}\right)}=\frac{a+2^{1 / 2}}{a^{1 / 2} \cdot 2^{1 / 4}}- \\
& -\frac{\left(a^{1 / 2}-2^{1 / 4}\right)\left(a+2^{1 / 4} \cdot a^{1 / 2}+2^{1 / 2}\right)}{a^{1 / 2} \cdot 2^{1 / 4} \cdot\left(a^{1 / 2}-2^{1 / 4}\right)}=\frac{a+2^{1 / 2}}{a^{1 / 2} \cdot 2^{1 / 4}}-\frac{a+2^{1 / 4} \cdot a^{1 / 2}+2^{1 / 2}}{a^{1 / 2} \cdot 2^{1 / 4}}= \\
& =\frac{a+2^{1 / 2}-a-2^{1 / 4} \cdot a^{1 / 2}-2^{1 / 2}}{a^{1 / 2} \cdot 2^{1 / 4}}=\frac{-2^{1 / 4} \cdot a^{1 / 2}}{a^{1 / 2} \cdot 2^{1 / 4}}=-1
\end{aligned}
$$
Answer: -1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.039. $\frac{9 b^{4 / 3}-\frac{a^{3 / 2}}{b^{2}}}{\sqrt{a^{3 / 2} b^{-2}+6 a^{3 / 4} b^{-1 / 3}+9 b^{4 / 3}}} \cdot \frac{b^{2}}{a^{3 / 4}-3 b^{5 / 3}} ; \quad b=4$.
|
Solution.
$$
\begin{aligned}
& \frac{9 b^{4 / 3}-\frac{a^{3 / 2}}{b^{2}}}{\sqrt{a^{3 / 2} b^{-2}+6 a^{3 / 4} b^{-1 / 3}+9 b^{4 / 3}}} \cdot \frac{b^{2}}{a^{3 / 4}-3 b^{5 / 3}}=\frac{\frac{9 b^{4 / 3} \cdot b^{2}-a^{3 / 2}}{b^{2}}}{\sqrt{\frac{a^{3 / 2}}{b^{2}}+\frac{6 a^{3 / 4}}{b^{+1 / 3}}+9 b^{4 / 3}}} \times \\
& \times \frac{b^{2}}{a^{3 / 4}-3 b^{5 / 3}}=\frac{9 b^{10 / 3}-a^{3 / 2}}{\sqrt{\frac{a^{3 / 2}+6 a^{3 / 4} b^{5 / 3}+9 b^{10 / 3}}{b^{2}}} \cdot\left(a^{3 / 4}-3 b^{5 / 3}\right)}= \\
& =\frac{-\left(\left(a^{3 / 4}\right)^{2}-\left(3 b^{5 / 3}\right)^{2}\right)}{\sqrt{\frac{\left(a^{3 / 4}\right)^{2}+6 a^{3 / 4} b^{5 / 3}+\left(3 b^{5 / 3}\right)^{2}}{b^{2}}} \cdot\left(a^{3 / 4}-3 b^{5 / 3}\right)}= \\
& =\frac{-\left(a^{3 / 4}-3 b^{5 / 3}\right)\left(a^{3 / 4}+3 b^{5 / 3}\right)}{\frac{\sqrt{\left(a^{3 / 4}+3 b^{5 / 3}\right)^{2}}}{b} \cdot\left(a^{3 / 4}-3 b^{5 / 3}\right)}=\frac{-\left(a^{3 / 4}+3 b^{5 / 3}\right) b}{a^{3 / 4}+3 b^{5 / 3}}=-b=-4 .
\end{aligned}
$$
Answer: -4.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.044. $\left(\frac{\sqrt{x-a}}{\sqrt{x+a}+\sqrt{x-a}}+\frac{x-a}{\sqrt{x^{2}-a^{2}}-x+a}\right): \sqrt{\frac{x^{2}}{a^{2}}-1} ; x>a>0$.
2.044. $\left(\frac{\sqrt{x-a}}{\sqrt{x+a}+\sqrt{x-a}}+\frac{x-a}{\sqrt{x^{2}-a^{2}}-x+a}\right): \sqrt{\frac{x^{2}}{a^{2}}-1} ; x>a>0$.
|
Solution.
$$
\begin{aligned}
& \left(\frac{\sqrt{x-a}}{\sqrt{x+a}+\sqrt{x-a}}+\frac{x-a}{\sqrt{x^{2}-a^{2}}-x+a}\right): \sqrt{\frac{x^{2}}{a^{2}}-1}= \\
& =\left(\frac{\sqrt{x-a}}{\sqrt{x+a}+\sqrt{x-a}}+\frac{(\sqrt{x-a})^{2}}{\sqrt{x-a}(\sqrt{x+a}-\sqrt{x-a})}\right): \sqrt{\frac{x^{2}-a^{2}}{a^{2}}}= \\
& =\left(\frac{\sqrt{x-a}}{\sqrt{x+a}+\sqrt{x-a}}+\frac{\sqrt{x-a}}{\sqrt{x+a}-\sqrt{x-a}}\right) \cdot \frac{a}{\sqrt{x^{2}-a^{2}}}= \\
& =\frac{\sqrt{x-a}(\sqrt{x+a}-\sqrt{x-a})+\sqrt{x-a}(\sqrt{x+a}+\sqrt{x-a})}{(\sqrt{x+a}+\sqrt{x-a})(\sqrt{x+a}-\sqrt{x-a})} \cdot \frac{a}{\sqrt{x^{2}-a^{2}}}= \\
& =\frac{\sqrt{x^{2}-a^{2}}-x+a+\sqrt{x^{2}-a^{2}}+x-a}{x+a-x+a} \cdot \frac{a}{\sqrt{x^{2}-a^{2}}}=\frac{2 \sqrt{x^{2}-a^{2}} \cdot a}{2 a \sqrt{x^{2}-a^{2}}}=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.046. $\frac{\sqrt{1-x^{2}}-1}{x} \cdot\left(\frac{1-x}{\sqrt{1-x^{2}}+x-1}+\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}\right)$
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}x \neq 0, \\ -1 \leq x<1 .\end{array}\right.$
$$
\begin{aligned}
& \frac{\sqrt{1-x^{2}}-1}{x} \cdot\left(\frac{1-x}{\sqrt{1-x^{2}}+x-1}+\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}\right)=\frac{\sqrt{1-x^{2}}-1}{x} \times \\
& \times\left(\frac{(\sqrt{1-x})^{2}}{\sqrt{1-x}(\sqrt{1+x}-\sqrt{1-x})}+\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}\right)=\frac{\sqrt{1-x^{2}}-1}{x} \times
\end{aligned}
$$
$$
\begin{aligned}
& \times\left(\frac{\sqrt{1-x}}{\sqrt{1+x}-\sqrt{1-x}}+\frac{\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}\right)=\frac{\sqrt{1-x^{2}}-1}{x} \cdot \frac{\sqrt{1-x}+\sqrt{1+x}}{\sqrt{1+x}-\sqrt{1-x}}=
\end{aligned}
$$
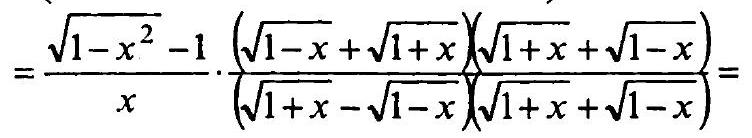
$$
\begin{aligned}
& =\frac{\sqrt{1-x^{2}}-1}{x} \cdot \frac{1-x+2 \sqrt{1-x^{2}}+1+x}{1+x-1+x}=\frac{\sqrt{1-x^{2}}-1}{x} \cdot \frac{2\left(\sqrt{1-x^{2}}+1\right)}{2 x}= \\
& =\frac{\left(\sqrt{1-x^{2}}-1\right)\left(\sqrt{1-x^{2}}+1\right)}{x^{2}}=\frac{1-x^{2}-1}{x^{2}}=\frac{-x^{2}}{x^{2}}=-1
\end{aligned}
$$
Answer: -1 .
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.051. $\frac{\left(a^{2}-b^{2}\right)\left(a^{2}+\sqrt[3]{b^{2}}+a \sqrt[3]{b}\right)}{a \sqrt[3]{b}+a \sqrt{a}-b \sqrt[3]{b}-\sqrt{a b^{2}}}: \frac{a^{3}-b}{a \sqrt[3]{b}-\sqrt[6]{a^{3} b^{2}}-\sqrt[3]{b^{2}}+a \sqrt{a}} ;$
$$
a=4.91 ; b=0.09
$$
|
Solution.
$$
\begin{aligned}
& \frac{\left(a^{2}-b^{2}\right)\left(a^{2}+\sqrt[3]{b^{2}}+a \sqrt[3]{b}\right)}{a \sqrt[3]{b}+a \sqrt{a}-b \sqrt[3]{b}-\sqrt{a b^{2}}}: \frac{a^{3}-b}{a \sqrt[3]{b}-\sqrt[6]{a^{3} b^{2}}-\sqrt[3]{b^{2}}+a \sqrt{a}}= \\
& =\frac{(a-b)(a+b)\left(a^{2}+a \sqrt[3]{b}+\sqrt[3]{b^{2}}\right)}{a(\sqrt{a}+\sqrt[3]{b})-b(\sqrt{a}+\sqrt[3]{b})}: \frac{a^{3}-b}{a(\sqrt{a}+\sqrt[3]{b})-\sqrt[3]{b}(\sqrt{a}+\sqrt[3]{b})}= \\
& =\frac{(a-b)(a+b)\left(a^{2}+a \sqrt[3]{b}+\sqrt[3]{b^{2}}\right)}{(\sqrt{a}+\sqrt[3]{b})(a-b)}: \frac{a^{3}-(\sqrt[3]{b})^{3}}{(\sqrt{a}+\sqrt[3]{b})(a-\sqrt[3]{b})}=
\end{aligned}
$$
$$
\begin{aligned}
& =\frac{(a+b)\left(a^{2}+a \sqrt[3]{b}+\sqrt[3]{b^{2}}\right)}{\sqrt{a}+\sqrt[3]{b}} \cdot \frac{(\sqrt{a}+\sqrt[3]{b})(a-\sqrt[3]{b})}{(a-\sqrt[3]{b})\left(a^{2}+a \sqrt[3]{b}+\sqrt[3]{b^{2}}\right)}= \\
& =a+b=4.91+0.09=5
\end{aligned}
$$
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.054. $\frac{3 a^{2}+2 a x-x^{2}}{(3 x+a)(a+x)}-2+10 \cdot \frac{a x-3 x^{2}}{a^{2}-9 x^{2}}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x \neq \pm \frac{a}{3}, \\ x \neq-a .\end{array}\right.$
$$
\begin{aligned}
& \frac{3 a^{2}+2 a x-x^{2}}{(3 x+a)(a+x)}-2+10 \cdot \frac{a x-3 x^{2}}{a^{2}-9 x^{2}}=\frac{-(x+a)(x-3 a)}{(3 x+a)(a+x)}-2+ \\
& +10 \cdot \frac{x(a-3 x)}{(a-3 x)(a+3 x)}=\frac{-x+3 a}{3 x+a}-2+\frac{10 x}{3 x+a}= \\
& =\frac{-x+3 a-6 x-2 a+10 x}{3 x+a}=\frac{3 x+a}{3 x+a}=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.058. $\left(\left(\frac{1}{a}+\frac{1}{b+c}\right):\left(\frac{1}{a}-\frac{1}{b+c}\right)\right):\left(1+\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)$;
$$
a=1 \frac{33}{40} ; b=0.625 ; c=3.2
$$
|
Solution.
$$
\begin{aligned}
& \left(\left(\frac{1}{a}+\frac{1}{b+c}\right):\left(\frac{1}{a}-\frac{1}{b+c}\right):\left(1+\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)=\right. \\
& =\left(\frac{a+b+c}{a(b+c)}: \frac{-a+b+c}{a(b+c)}\right): \frac{2 b c+b^{2}+c^{2}-a^{2}}{2 b c}= \\
& =\left(\frac{a+b+c}{a(b+c)} \cdot \frac{a(b+c)}{-a+b+c}\right): \frac{\left(b^{2}+2 b c+c^{2}\right)-a^{2}}{2 b c}= \\
& =\frac{a+b+c}{-a+b+c} \cdot \frac{2 b c}{(b+c)^{2}-a^{2}}=\frac{2(a+b+c) b c}{(-a+b+c)(b+c-a)(b+c+a)}= \\
& =\frac{2 b c}{(-a+b+c)^{2}}=\frac{2 \cdot 0.625 \cdot 3.2}{\left(-1 \frac{33}{40}+0.625+3.2\right)^{2}}=\frac{4}{(-1.825+3.825)^{2}}=\frac{4}{4}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.068. $\frac{\left(\frac{1}{a}+\frac{1}{b}-\frac{2 c}{a b}\right)(a+b+2 c)}{\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{2}{a b}-\frac{4 c^{2}}{a^{2} b^{2}}} ; \quad a=7.4 ; b=\frac{5}{37}$.
|
Solution.
$$
\begin{aligned}
& \frac{\left(\frac{1}{a}+\frac{1}{b}-\frac{2 c}{a b}\right)(a+b+2 c)}{\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{2}{a b}-\frac{4 c^{2}}{a^{2} b^{2}}}=\frac{\frac{a+b-2 c}{a b} \cdot(a+b+2 c)}{\frac{a^{2}+2 a b+b^{2}-4 c^{2}}{a^{2} b^{2}}}= \\
& =\frac{\frac{(a+b-2 c)(a+b+2 c)}{a b}}{\frac{(a+b)^{2}-(2 c)^{2}}{a^{2} b^{2}}}=\frac{(a+b-2 c)(a+b+2 c) a^{2} b^{2}}{\left((a+b)^{2}-(2 c)^{2}\right) a b}= \\
& =\frac{(a+b-2 c)(a+b+2 c) a b}{(a+b-2 c)(a+b+2 c)}=a b=7.4 \cdot \frac{5}{37}=\frac{37}{5} \cdot \frac{5}{37}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.073. $\frac{\sqrt{5-2 \sqrt{6}}}{(\sqrt[4]{3}+\sqrt[4]{2})(\sqrt[4]{3}-\sqrt[4]{2})}$.
|
Solution.
$$
\begin{aligned}
& \frac{\sqrt{5-2 \sqrt{6}}}{(\sqrt[4]{3}+\sqrt[4]{2})(\sqrt[4]{3}-\sqrt[4]{2})}=\frac{\sqrt{3-2 \sqrt{3 \cdot 2}+2}}{(\sqrt[4]{3})^{2}-(\sqrt[4]{2})^{2}}= \\
& =\frac{\sqrt{(\sqrt{3})^{2}-2 \sqrt{3} \cdot \sqrt{2}+(\sqrt{2})^{2}}}{\sqrt{3}-\sqrt{2}}= \\
& =\frac{\sqrt{(\sqrt{3}-\sqrt{2})^{2}}}{\sqrt{3}-\sqrt{2}}=\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}-\sqrt{2}}=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.078. $\left(\frac{1}{t^{2}+3 t+2}+\frac{2 t}{t^{2}+4 t+3}+\frac{1}{t^{2}+5 t+6}\right)^{2} \cdot \frac{(t-3)^{2}+12 t}{2}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}t \neq-3, \\ t \neq-2, \\ t \neq-1 .\end{array}\right.$
$$
\begin{aligned}
& \left(\frac{1}{t^{2}+3 t+2}+\frac{2 t}{t^{2}+4 t+3}+\frac{1}{t^{2}+5 t+6}\right)^{2} \cdot \frac{(t-3)^{2}+12 t}{2}= \\
& =\left(\frac{1}{(t+2)(t+1)}+\frac{2 t}{(t+3)(t+1)}+\frac{1}{(t+3)(t+2)}\right)^{2} \cdot \frac{t^{2}-6 t+9+12 t}{2}= \\
& =\left(\frac{t+3+2 t(t+2)+t+1}{(t+1)(t+2)(t+3)}\right)^{2} \cdot \frac{t^{2}+6 t+9}{2}=\left(\frac{2(t+2)+2 t(t+2)}{(t+1)(t+2)(t+3)}\right)^{2} \cdot \frac{(t+3)^{2}}{2}= \\
& =\frac{(2(t+2)(t+1))^{2}(t+3)^{2}}{2((t+1)(t+2)(t+3))^{2}}=\frac{4(t+2)^{2}(t+1)^{2}(t+3)^{2}}{2(t+2)^{2}(t+1)^{2}(t+3)^{2}}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.084. $\left(\frac{2-b}{b-1}+2 \cdot \frac{a-1}{a-2}\right):\left(b \cdot \frac{a-1}{b-1}+a \cdot \frac{2-b}{a-2}\right)$;
$a=\sqrt{2}+0.8 ; b=\sqrt{2}-0.2$.
|
Solution.
$$
\begin{aligned}
& \left(\frac{2-b}{b-1}+2 \cdot \frac{a-1}{a-2}\right):\left(b \cdot \frac{a-1}{b-1}+a \cdot \frac{2-b}{a-2}\right)=\frac{(2-b)(a-2)+2(a-1)(b-1)}{(b-1)(a-2)} \\
& \frac{b(a-1)(a-2)+a(2-b)(b-1)}{(b-1)(a-2)}=\frac{a b-2}{(b-1)(a-2)} \cdot \frac{(b-1)(a-2)}{a^{2} b-a b^{2}-2 a+2 b}= \\
& =\frac{a b-2}{a b(a-b)-2(a-b)}=\frac{a b-2}{(a-b)(a b-2)}=\frac{1}{a-b}=\frac{1}{\sqrt{2}+0.8-\sqrt{2}+0.2}=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.105. $\left(\frac{1+\sqrt{1-x}}{1-x+\sqrt{1-x}}+\frac{1-\sqrt{1+x}}{1+x-\sqrt{1+x}}\right)^{2} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}-1<x<1, \\ x \neq 0 .\end{array}\right.$
$$
\begin{aligned}
& \left(\frac{1+\sqrt{1-x}}{1-x+\sqrt{1-x}}+\frac{1-\sqrt{1+x}}{1+x-\sqrt{1+x}}\right)^{2} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}= \\
& \left.\left.=\left(\frac{1+\sqrt{1-x}}{\sqrt{1-x}(\sqrt{1-x}+1}\right)+\frac{1-\sqrt{1+x}}{\sqrt{1+x}(\sqrt{1+x}-1}\right)\right)^{2} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}= \\
& =\left(\frac{1}{\sqrt{1-x}}-\frac{1}{\sqrt{1+x}}\right)^{2} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}= \\
& =\left(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1-x^{2}}}\right)^{2} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}= \\
& =\frac{1+x-2 \sqrt{1-x^{2}}+1-x}{1-x^{2}} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}= \\
& =\frac{2\left(1-\sqrt{1-x^{2}}\right)}{1-x^{2}} \cdot \frac{x^{2}-1}{2}-\sqrt{1-x^{2}}= \\
& =-1+\sqrt{1-x^{2}}-\sqrt{1-x^{2}}=-1
\end{aligned}
$$
Answer: -1 .
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.123. $2 \sqrt{40 \sqrt{12}}+3 \sqrt{5 \sqrt{48}}-2 \sqrt[4]{75}-4 \sqrt{15 \sqrt{27}}$.
|
Solution.
$$
\begin{aligned}
& 2 \sqrt{40 \sqrt{12}}+3 \sqrt{5 \sqrt{48}}-2 \sqrt[4]{75}-4 \sqrt{15 \sqrt{27}}= \\
& =2 \sqrt{40 \sqrt{4 \cdot 3}}+3 \sqrt{5 \sqrt{16 \cdot 3}}-2 \sqrt[4]{25 \cdot 3}-4 \sqrt{15 \sqrt{9 \cdot 3}}= \\
& =2 \sqrt{40 \cdot 2 \sqrt{3}}+3 \sqrt{5 \cdot 4 \sqrt{3}}-2 \sqrt{\sqrt{25 \cdot 3}}-4 \sqrt{15 \cdot 3 \sqrt{3}}= \\
& =2 \sqrt{80 \sqrt{3}}+3 \cdot 2 \sqrt{5 \sqrt{3}}-2 \sqrt{5 \sqrt{3}}-4 \sqrt{45 \sqrt{3}}= \\
& =2 \sqrt{16 \cdot 5 \sqrt{3}}+6 \sqrt{5 \sqrt{3}}-2 \sqrt{5 \sqrt{3}}-4 \sqrt{9 \cdot 5 \sqrt{3}}= \\
& =2 \cdot 4 \sqrt{5 \sqrt{3}}+6 \sqrt{5 \sqrt{3}}-2 \sqrt{5 \sqrt{3}}-4 \cdot 3 \sqrt{5 \sqrt{3}}= \\
& =8 \sqrt{5 \sqrt{3}}+6 \sqrt{5 \sqrt{3}}-2 \sqrt{5 \sqrt{3}}-12 \sqrt{5 \sqrt{3}}=14 \sqrt{5 \sqrt{3}}-14 \sqrt{5 \sqrt{3}}=0 .
\end{aligned}
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.126. $(4+\sqrt{15})(\sqrt{10}-\sqrt{6}) \cdot \sqrt{4-\sqrt{15}}=2$.
|
## Решение.
Возведем обе части равенства в квадрат. Тогда
$$
\begin{aligned}
& (4+\sqrt{15})^{2}(\sqrt{10}-\sqrt{6})^{2}(4-\sqrt{15})=4 \\
& (4+\sqrt{15})(4-\sqrt{15})(4+\sqrt{15})(10-2 \sqrt{60}+6)=4 \\
& \left(4^{2}-(\sqrt{15})^{2}\right)(4+\sqrt{15})(16-2 \sqrt{60})=4 \\
& (16-15)(4+\sqrt{15}) \cdot 2 \cdot(8-\sqrt{60})=4, \quad(4+\sqrt{15})(8-\sqrt{4 \cdot 15})=2, \\
& (4+\sqrt{15})(8-2 \sqrt{15})=2, \quad(4+\sqrt{15}) \cdot 2 \cdot(4-\sqrt{15})=2, \\
& (4+\sqrt{15})(4-\sqrt{15})=1, \quad 4^{2}-(\sqrt{15})^{2}=1, \quad 16-15=1, \quad 1=1
\end{aligned}
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.129. $\frac{25 \cdot \sqrt[4]{2}+2 \sqrt{5}}{\sqrt{250}+5 \sqrt[4]{8}}-\sqrt{\frac{\sqrt{2}}{5}+\frac{5}{\sqrt{2}}+2}=-1$.
|
## Solution.
Let's set
$$
X=\frac{25 \cdot \sqrt[4]{2}+2 \sqrt{5}}{\sqrt{250}+5 \sqrt[4]{8}}=\frac{\sqrt[4]{5^{8} \cdot 2}+\sqrt[4]{5^{2} \cdot 2^{4}}}{\sqrt[4]{5^{6} \cdot 2^{2}}+\sqrt[4]{5^{4} \cdot 2^{3}}}=\frac{\sqrt[4]{5^{2} \cdot 2}\left(\sqrt[4]{5^{6}}+\sqrt[4]{2^{3}}\right)}{\sqrt[4]{5^{2} \cdot 2} \cdot \sqrt[4]{5^{2} \cdot 2}\left(\sqrt[4]{5^{2}}+\sqrt[4]{2}\right)}=
$$
$$
\begin{aligned}
& =\frac{\left(\sqrt[4]{5^{2}}\right)^{3}+(\sqrt[4]{2})^{3}}{\sqrt[4]{5^{2} \cdot 2}\left(\sqrt[4]{5^{2}}+\sqrt[4]{2}\right)}=\frac{\left(\sqrt[4]{5^{2}}+\sqrt[4]{2}\right)\left(\left(\sqrt[4]{5^{2}}\right)^{2}-\sqrt[4]{5^{2} \cdot 2}+(\sqrt[4]{2})^{2}\right)}{\sqrt[4]{5^{2} \cdot 2}\left(\sqrt[4]{5^{2}}+\sqrt[4]{2}\right)}= \\
& =\frac{\sqrt[4]{5^{4}}-\sqrt[4]{5^{2} \cdot 2}+\sqrt[4]{2^{2}}}{\sqrt[4]{5^{2} \cdot 2}}
\end{aligned}
$$
$Y=\sqrt{\frac{\sqrt{2}}{5}+\frac{5}{\sqrt{2}}+2}=\sqrt{\frac{2+2 \cdot 5 \sqrt{2}+25}{5 \sqrt{2}}}=\sqrt{\frac{(5+\sqrt{2})^{2}}{\sqrt{5^{2} \cdot 2}}}=\frac{5+\sqrt{2}}{\sqrt[4]{5^{2} \cdot 2}}$.
## Conclusion
$$
\begin{aligned}
& X-Y=\frac{5-\sqrt[4]{5^{2} \cdot 2}+\sqrt{2}}{\sqrt[4]{5^{2} \cdot 2}}-\frac{5+\sqrt{2}}{\sqrt[4]{5^{2} \cdot 2}}=\frac{5-\sqrt[4]{5^{2} \cdot 2}+\sqrt{2}-5-\sqrt{2}}{\sqrt[4]{5^{2} \cdot 2}}= \\
& =\frac{-\sqrt[4]{5^{2} \cdot 2}}{\sqrt[4]{5^{2} \cdot 2}}=-1
\end{aligned}
$$
We obtained $-1=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.130. $\frac{\sqrt{\sqrt[4]{27}+\sqrt{\sqrt{3}-1}}-\sqrt{\sqrt[4]{27}-\sqrt{\sqrt{3}-1}}}{\sqrt{\sqrt[4]{27}-\sqrt{2 \sqrt{3}}+1}}=\sqrt{2}$.
|
## Решение.
Возведем обе части равенства в квадрат. Тогда
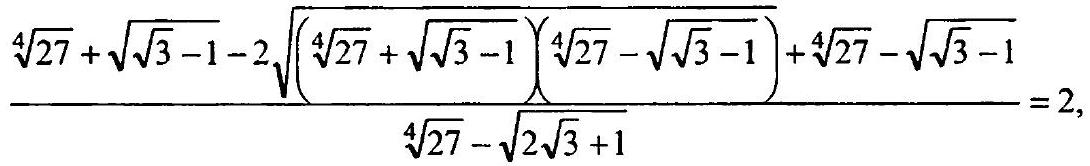
$$
\begin{aligned}
& \frac{2 \sqrt[4]{27}-2 \sqrt{(\sqrt[4]{27})^{2}-(\sqrt{\sqrt{3}-1})^{2}}}{\sqrt[4]{27}-\sqrt{2 \sqrt{3}+1}}=2, \frac{\sqrt[4]{27}-\sqrt{\sqrt{27}-\sqrt{3}+1}}{\sqrt[4]{27}-\sqrt{2 \sqrt{3}+1}}=1
\end{aligned}
$$
$\frac{\sqrt[4]{27}-\sqrt{3 \sqrt{3}-\sqrt{3}+1}}{\sqrt[4]{27}-\sqrt{2 \sqrt{3}+1}}=1, \quad \frac{\sqrt[4]{27}-\sqrt{2 \sqrt{3}+1}}{\sqrt[4]{27}-\sqrt{2 \sqrt{3}+1}}=1, \quad 1=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.135. $\frac{x^{3}-a^{-2 / 3} \cdot b^{-1}\left(a^{2}+b^{2}\right) x+b^{1 / 2}}{b^{3 / 2} \cdot x^{2}} ; x=a^{2 / 3} b^{-1 / 2}$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}a \neq 0, \\ b \neq 0 .\end{array}\right.$
$$
\begin{aligned}
& \frac{\left(a^{2 / 3} b^{-1 / 2}\right)^{3}-a^{2 / 3} \cdot b^{-1}\left(a^{2}+b^{2}\right)^{2 / 3} b^{-1 / 2}+b^{1 / 2}}{b^{3 / 2} \cdot\left(a^{2 / 3} b^{-1 / 2}\right)^{2}}= \\
& =\frac{a^{2} b^{-3 / 2}-a^{0} b^{-3 / 2}\left(a^{2}+b^{2}\right)+b^{1 / 2}}{b^{3 / 2} a^{4 / 3} b^{-1}}= \\
& =\frac{\frac{a^{2}}{b^{3 / 2}}-\frac{a^{2}+b^{2}}{b^{3 / 2}}+b^{1 / 2}}{b^{1 / 2} a^{4 / 3}}=\frac{\frac{a^{2}-a^{2}-b^{2}+b^{2}}{b^{3 / 2}}}{b^{1 / 2} a^{4 / 3}}=0
\end{aligned}
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.136. $\frac{1-b}{\sqrt{b}} \cdot x^{2}-2 x+\sqrt{b} ; \quad x=\frac{\sqrt{b}}{1-\sqrt{b}}$.
2.136. $\frac{1-b}{\sqrt{b}} \cdot x^{2}-2 x+\sqrt{b} ; \quad x=\frac{\sqrt{b}}{1-\sqrt{b}}$.
|
## Solution.
Domain of definition: $0<b \neq 1$.
$$
\begin{aligned}
& \frac{1-b}{\sqrt{b}} \cdot\left(\frac{\sqrt{b}}{1-\sqrt{b}}\right)^{2}-2 \cdot \frac{\sqrt{b}}{1-\sqrt{b}}+\sqrt{b}=\frac{(1-\sqrt{b})(1+\sqrt{b})}{\sqrt{b}} \cdot \frac{b}{(1-\sqrt{b})^{2}}-\frac{2 \sqrt{b}}{1-\sqrt{b}}+ \\
& +\sqrt{b}=\frac{(1+\sqrt{b}) \sqrt{b}}{1-\sqrt{b}}-\frac{2 \sqrt{b}}{1-\sqrt{b}}+\sqrt{b}=\frac{\sqrt{b}+b}{1-\sqrt{b}}-\frac{2 \sqrt{b}}{1-\sqrt{b}}+\sqrt{b}= \\
& =\frac{\sqrt{b}+b-2 \sqrt{b}+\sqrt{b}-b}{1-\sqrt{b}}=0 .
\end{aligned}
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.141. $\frac{(1-y)(y+2)}{y^{2}(y+1)^{2}} ; \quad y=\frac{\sqrt{3}-1}{2}$.
|
Solution.
$$
\begin{aligned}
& \frac{\left(1-\frac{\sqrt{3}-1}{2}\right) \cdot\left(\frac{\sqrt{3}-1}{2}+2\right)}{\left(\frac{\sqrt{3}-1}{2}\right)^{2} \cdot\left(\frac{\sqrt{3}-1}{2}+1\right)^{2}}=\frac{-\left(\frac{\sqrt{3}-1}{2}-1\right) \cdot\left(\frac{\sqrt{3}-1}{2}+2\right)}{\left(\frac{\sqrt{3}-1}{2} \cdot\left(\frac{\sqrt{3}-1}{2}+1\right)\right)^{2}}= \\
& =-\frac{\left(\frac{\sqrt{3}-1}{2}\right)^{2}+\frac{\sqrt{3}-1}{2}-2}{\left(\left(\frac{\sqrt{3}-1}{2}\right)^{2}+\frac{\sqrt{3}-1}{2}\right)^{2}}=-\frac{\frac{4-2 \sqrt{3}}{4}+\frac{\sqrt{3}-1}{2}-2}{\left(\frac{4-2 \sqrt{3}}{4}+\frac{\sqrt{3}-1}{2}\right)^{2}}= \\
& =-\frac{\frac{2-\sqrt{3}}{2}+\frac{\sqrt{3}-1}{2}-2}{\left(\frac{2-\sqrt{3}}{2}+\frac{\sqrt{3}-1}{2}\right)^{2}}=-\frac{\frac{2-\sqrt{3}+\sqrt{3}-1}{2}-2}{\left(\frac{2-\sqrt{3}+\sqrt{3}-1}{2}\right)^{2}}=6 .
\end{aligned}
$$
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.145. $\frac{1-a x}{1+a x} \cdot \sqrt{\frac{1+b x}{1-b x}} ; \quad x=\frac{1}{a} \cdot \sqrt{\frac{2 a-b}{b}} ; \quad 0<\frac{b}{2}<a<b$.
|
Solution.
$\frac{1-a \cdot \frac{1}{a} \cdot \sqrt{\frac{2 a-b}{b}}}{1+a \cdot \frac{1}{a} \cdot \sqrt{\frac{2 a-b}{b}}} \cdot \sqrt{\frac{1+b \cdot \frac{1}{a} \cdot \sqrt{\frac{2 a-b}{b}}}{1-b \cdot \frac{1}{a} \cdot \sqrt{\frac{2 a-b}{b}}}}=\frac{1-\sqrt{\frac{2 a-b}{b}}}{1+\sqrt{\frac{2 a-b}{b}}} \times$
$$
\begin{aligned}
& \times \sqrt{\frac{1+\frac{1}{a} \cdot \sqrt{\frac{b^{2}(2 a-b)}{b}}}{1-\frac{1}{a} \cdot \sqrt{\frac{b^{2}(2 a-b)}{b}}}}=\frac{1-\frac{\sqrt{2 a-b}}{\sqrt{b}}}{1+\frac{\sqrt{2 a-b}}{\sqrt{b}}} \cdot \sqrt{\frac{\frac{a+\sqrt{b(2 a-b)}}{a}}{\frac{a-\sqrt{b(2 a-b)}}{a}}}=\frac{\sqrt{b}-\sqrt{2 a-b}}{\sqrt{b}+\sqrt{2 a-b}} \times \\
& \times \sqrt{\frac{a+\sqrt{b(2 a-b)}}{a-\sqrt{b(2 a-b)}}}=\frac{(\sqrt{b}-\sqrt{2 a-b})(\sqrt{b}-\sqrt{2 a-b})}{(\sqrt{b}+\sqrt{2 a-b})(\sqrt{b}-\sqrt{2 a-b})} \times \\
& \times \sqrt{\frac{(a+\sqrt{b(2 a-b)})(a+\sqrt{b(2 a-b)})}{(a-\sqrt{b(2 a-b)})(a+\sqrt{b(2 a-b)})}}=\frac{b-2 \sqrt{b(2 a-b)}+2 a-b}{b-2 a+b} \times \\
& \times \sqrt{\frac{(a+\sqrt{b(2 a-b)})^{2}}{a^{2}-b(2 a-b)}}=\frac{2 a-2 \sqrt{b(2 a-b)}}{2 b-2 a} \cdot \sqrt{\frac{(a+\sqrt{b(2 a-b)})^{2}}{a^{2}-2 a b+b^{2}}}= \\
& =\frac{a-\sqrt{b(2 a-b)}}{b-a} \cdot \sqrt{\left(\frac{a+\sqrt{b(2 a-b)}}{a-b}\right)^{2}}=\frac{a-\sqrt{b(2 a-b)}}{b-a} \cdot \frac{a+\sqrt{b(2 a-b)}}{b-a}= \\
& =\frac{a^{2}-b(2 a-b)}{(b-a)^{2}}=\frac{a^{2}-2 a b+b^{2}}{(b-a)^{2}}=\frac{(b-a)^{2}}{(b-a)^{2}}=1 \text {. }
\end{aligned}
$$
Answer: 1.
Rationalize the denominator of the fraction (2.146-2.151):
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.154. What is the value of $\sqrt{25-x^{2}}+\sqrt{15-x^{2}}$, given that the difference $\sqrt{25-x^{2}}-\sqrt{15-x^{2}}=2$ (the value of $x$ does not need to be found)?
|
Solution.
Domain of definition: $\left\{\begin{array}{l}25-x^{2} \geq 0, \\ 15-x^{2} \geq 0\end{array} \Leftrightarrow-\sqrt{15} \leq x \leq \sqrt{15}\right.$.
Multiplying both sides of the equation by $\sqrt{25-x^{2}}+\sqrt{15-x^{2}}$, we have
$$
\begin{aligned}
& \left(\sqrt{25-x^{2}}-\sqrt{15-x^{2}}\right)\left(\sqrt{25-x^{2}}+\sqrt{15-x^{2}}\right)= \\
& =2\left(\sqrt{25-x^{2}}+\sqrt{15-x^{2}}\right) \Leftrightarrow \\
& \Leftrightarrow 25-x^{2}-15+x^{2}=2\left(\sqrt{25-x^{2}}+\sqrt{15-x^{2}}\right)
\end{aligned}
$$
from which $\sqrt{25-x^{2}}+\sqrt{15-x^{2}}=5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.040. $\frac{1-\cos 4 \alpha}{\cos ^{-2} 2 \alpha-1}+\frac{1+\cos 4 \alpha}{\sin ^{-2} 2 \alpha-1}=2$.
|
Solution.
$$
\begin{aligned}
& \frac{1-\cos 4 \alpha}{\cos ^{-2} 2 \alpha-1}+\frac{1+\cos 4 \alpha}{\sin ^{-2} 2 \alpha-1}=\frac{1-\cos 4 \alpha}{\frac{1}{\cos ^{2} 2 \alpha}-1}+\frac{1+\cos 4 \alpha}{\frac{1}{\sin ^{2} 2 \alpha}-1}= \\
& =\frac{(1-\cos 4 \alpha) \cos ^{2} 2 \alpha}{1-\cos ^{2} 2 \alpha}+\frac{(1+\cos 4 \alpha) \sin ^{2} 2 \alpha}{1-\sin ^{2} 2 \alpha}=\frac{(1-\cos 4 \alpha) \cos ^{2} 2 \alpha}{\sin ^{2} 2 \alpha}+ \\
& +\frac{(1+\cos 4 \alpha) \sin ^{2} 2 \alpha}{\cos ^{2} 2 \alpha}=\frac{\left(1-\left(1-\sin ^{2} 2 \alpha\right) \cos ^{2} 2 \alpha\right.}{\sin ^{2} 2 \alpha}+\frac{\left(1+2 \cos ^{2} 2 \alpha-1\right) \sin ^{2} 2 \alpha}{\cos ^{2} 2 \alpha}= \\
& =\frac{2 \sin ^{2} 2 \alpha \cos ^{2} 2 \alpha}{\sin ^{2} 2 \alpha}+\frac{2 \cos ^{2} 2 \alpha \sin ^{2} 2 \alpha}{\cos ^{2} 2 \alpha}=2 \cos ^{2} 2 \alpha+2 \sin ^{2} 2 \alpha= \\
& =2\left(\cos ^{2} 2 \alpha+\sin ^{2} 2 \alpha\right)=2 .
\end{aligned}
$$
The identity is proven.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.081. $\sin ^{2}\left(\alpha-\frac{3 \pi}{2}\right)\left(1-\operatorname{tg}^{2} \alpha\right) \operatorname{tg}\left(\frac{\pi}{4}+\alpha\right) \cos ^{-2}\left(\frac{\pi}{4}-\alpha\right)$.
|
Solution.
$$
\begin{aligned}
& \sin ^{2}\left(\alpha-\frac{3 \pi}{2}\right)\left(1-\operatorname{tg}^{2} \alpha\right) \operatorname{tg}\left(\frac{\pi}{4}+\alpha\right) \cos ^{-2}\left(\frac{\pi}{4}-\alpha\right)= \\
& =\left(\sin \left(\frac{3}{2} \pi-\alpha\right)\right)^{2}\left(1-\operatorname{tg}^{2} \alpha\right) \operatorname{tg}\left(\frac{\pi}{4}+\alpha\right) \cdot \frac{1}{\cos ^{2}\left(\frac{\pi}{4}-\alpha\right)}= \\
& =\cos ^{2} \alpha\left(1-\frac{1-\cos 2 \alpha}{1+\cos 2 \alpha}\right) \cdot \frac{1-\cos \left(\frac{\pi}{2}+2 \alpha\right)}{\sin \left(\frac{\pi}{2}+2 \alpha\right)} \cdot \frac{1}{\frac{1+\cos \left(\frac{\pi}{2}-2 \alpha\right)}{2}}= \\
& =\frac{1+\cos 2 \alpha}{2} \cdot \frac{1+\cos 2 \alpha-1+\cos 2 \alpha}{1+\cos 2 \alpha} \cdot \frac{1+\sin 2 \alpha}{\cos 2 \alpha} \cdot \frac{2}{1+\sin 2 \alpha}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.088. $\frac{\operatorname{ctg}\left(270^{\circ}-\alpha\right)}{1-\operatorname{tg}^{2}\left(\alpha-180^{\circ}\right)} \cdot \frac{\operatorname{ctg}^{2}\left(360^{\circ}-\alpha\right)-1}{\operatorname{ctg}\left(180^{\circ}+\alpha\right)}$.
|
## Solution.
$\frac{\operatorname{ctg}\left(270^{\circ}-\alpha\right)}{1-\operatorname{tg}^{2}\left(\alpha-180^{\circ}\right)} \cdot \frac{\operatorname{ctg}^{2}\left(360^{\circ}-\alpha\right)-1}{\operatorname{ctg}\left(180^{\circ}+\alpha\right)}=\frac{\operatorname{tg} \alpha}{1-\operatorname{tg}^{2} \alpha} \cdot \frac{\operatorname{ctg}^{2} \alpha-1}{\operatorname{ctg} \alpha}=\frac{2 \operatorname{tg} \alpha}{1-\operatorname{tg}^{2} \alpha} \times$ $\times \frac{\operatorname{ctg}^{2} \alpha-1}{2 \operatorname{ctg} \alpha}=\operatorname{tg} 2 \alpha \operatorname{ctg} 2 \alpha=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.098. $\sin \left(2 \alpha-\frac{3}{2} \pi\right)+\cos \left(2 \alpha-\frac{8}{3} \pi\right)+\cos \left(\frac{2}{3} \pi+2 \alpha\right)$.
|
## Solution.
Let
$$
\begin{aligned}
& X=\sin \left(2 \alpha-\frac{3}{2} \pi\right)+\cos \left(2 \alpha-\frac{8}{3} \pi\right)+\cos \left(\frac{2}{3} \pi+2 \alpha\right)= \\
& =-\sin \left(\frac{3}{2} \pi-2 \alpha\right)+\cos \left(\frac{8}{3} \pi-2 \alpha\right)+\cos \left(\frac{2}{3} \pi+2 \alpha\right) \\
& -\sin \left(\frac{3}{2} \pi-2 \alpha\right)=\cos 2 \alpha \\
& \cos \left(\frac{8}{3} \pi-2 \alpha\right)=\cos \left(\frac{9 \pi-\pi}{3}-2 \alpha\right)=\cos \left(3 \pi-\left(\frac{\pi}{3}+2 \alpha\right)\right)= \\
& =-\cos \left(\frac{\pi}{3}+2 \alpha\right)=-\cos \frac{\pi}{3} \cos 2 \alpha+\sin \frac{\pi}{3} \sin 2 \alpha=-\frac{1}{2} \cos 2 \alpha+\frac{\sqrt{3}}{2} \sin 2 \alpha
\end{aligned}
$$
$$
\cos \left(\frac{2}{3} \pi+2 \alpha\right)=\cos \frac{2}{3} \pi \cos 2 \alpha-\sin \frac{2}{3} \pi \sin 2 \alpha=-\frac{1}{2} \cos 2 \alpha-\frac{\sqrt{3}}{2} \sin 2 \alpha
$$
$$
X=\cos 2 \alpha-\frac{1}{2} \cos 2 \alpha+\frac{\sqrt{3}}{2} \sin 2 \alpha-\frac{1}{2} \cos 2 \alpha-\frac{\sqrt{3}}{2} \sin 2 \alpha=0
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.105. $\frac{\sin 6 \alpha}{\sin 2 \alpha}+\frac{\cos (6 \alpha-\pi)}{\cos 2 \alpha}$.
|
## Solution.
$\frac{\sin 6 \alpha}{\sin 2 \alpha}+\frac{\cos (6 \alpha-\pi)}{\cos 2 \alpha}=\frac{\sin 6 \alpha}{\sin 2 \alpha}+\frac{\cos (\pi-6 \alpha)}{\cos 2 \alpha}=\frac{\sin 6 \alpha}{\sin 2 \alpha}+\frac{\cos 6 \alpha}{\cos 2 \alpha}=$
$=\frac{\sin 6 \alpha \cos 2 \alpha-\cos 6 \alpha \sin 2 \alpha}{\sin 2 \alpha \cos 2 \alpha}=\frac{\sin 4 \alpha}{\sin 2 \alpha \cos 2 \alpha}=\frac{2 \sin 4 \alpha}{2 \sin 2 \alpha \cos 2 \alpha}=$
$=\frac{2 \sin 4 \alpha}{\sin 4 \alpha}=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.148. $\left(\sin 160^{\circ}+\sin 40^{\circ}\right)\left(\sin 140^{\circ}+\sin 20^{\circ}\right)+\left(\sin 50^{\circ}-\sin 70^{\circ}\right) \times$
$$
\times\left(\sin 130^{\circ}-\sin 110^{\circ}\right)=1
$$
|
Solution.
$\left(\sin 160^{\circ}+\sin 40^{\circ}\right)\left(\sin 140^{\circ}+\sin 20^{\circ}\right)+\left(\sin 50^{\circ}-\sin 70^{\circ}\right)\left(\sin 130^{\circ}-\sin 110^{\circ}\right)=$
$$
\begin{aligned}
& =\left(\sin \left(180^{\circ}-20^{\circ}\right)+\sin 40^{\circ}\right)\left(\sin \left(180^{\circ}-40^{\circ}\right)+\sin 20^{\circ}\right)+ \\
& +\left(\sin 50^{\circ}-\sin 70^{\circ}\right)\left(\sin \left(180^{\circ}-50^{\circ}\right)-\sin \left(180^{\circ}-70^{\circ}\right)\right)= \\
& =\left(\sin 20^{\circ}+\sin 40^{\circ}\right)\left(\sin 40^{\circ}+\sin 20^{\circ}\right)+\left(\sin 50^{\circ}-\sin 70^{\circ}\right)\left(\sin 50^{\circ}-\sin 70^{\circ}\right)= \\
& =\left(\sin 20^{\circ}+\sin 40^{\circ}\right)^{2}+\left(\sin 50^{\circ}-\sin 70^{\circ}\right)^{2}=\left(2 \sin 30^{\circ} \cos 10^{\circ}\right)^{2}+ \\
& +\left(2 \cos 60^{\circ} \sin 10^{\circ}\right)^{2}=\left(2 \cdot \frac{1}{2} \cos 10^{\circ}\right)^{2}+\left(2 \cdot \frac{1}{2} \sin 10^{\circ}\right)^{2}=\cos ^{2} 10^{\circ}+\sin ^{2} 10^{\circ}=1
\end{aligned}
$$
The equality holds.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3.153. $\sin ^{2} \frac{\pi}{8}+\cos ^{2} \frac{3 \pi}{8}+\sin ^{2} \frac{5 \pi}{8}+\cos ^{2} \frac{7 \pi}{8}$.
|
Solution.
$$
\begin{aligned}
& \sin ^{2} \frac{\pi}{8}+\cos ^{2} \frac{3 \pi}{8}+\sin ^{2} \frac{5 \pi}{8}+\cos ^{2} \frac{7 \pi}{8}= \\
& =\frac{1-\cos \frac{\pi}{4}}{2}+\frac{1+\cos \frac{3 \pi}{4}}{2}+\frac{1-\cos \frac{5 \pi}{4}}{2}+\frac{1+\cos \frac{7 \pi}{4}}{2}=
\end{aligned}
$$
$$
\begin{aligned}
& =\frac{4-\cos \frac{\pi}{4}+\cos \frac{4 \pi-\pi}{4}-\cos \frac{4 \pi+\pi}{4}+\cos \frac{8 \pi-\pi}{4}}{2}= \\
& =\frac{4-\cos \frac{\pi}{4}+\cos \left(\pi-\frac{\pi}{4}\right)-\cos \left(\pi+\frac{\pi}{4}\right)+\cos \left(2 \pi-\frac{\pi}{4}\right)}{2}= \\
& =\frac{4-\cos \frac{\pi}{4}-\cos \frac{\pi}{4}+\cos \frac{\pi}{4}+\cos \frac{\pi}{4}}{2}=\frac{4}{2}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.154. $\operatorname{tg} 435^{\circ}+\operatorname{tg} 375^{\circ}$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
3.154. $\operatorname{tan} 435^{\circ}+\operatorname{tan} 375^{\circ}$.
|
## Solution.
$$
\begin{aligned}
& \tan 435^{\circ}+\tan 375^{\circ}=\tan\left(450^{\circ}-15^{\circ}\right)+\tan\left(360^{\circ}+15^{\circ}\right)= \\
& =\cot 15^{\circ}+\tan 15^{\circ}=\frac{\cos 15^{\circ}}{\sin 15^{\circ}}+\frac{\sin 15^{\circ}}{\cos 15^{\circ}}=\frac{\cos ^{2} 15^{\circ}+\sin ^{2} 15^{\circ}}{\sin 15^{\circ} \cos 15^{\circ}}= \\
& =\frac{1}{\sin 15^{\circ} \cos 15^{\circ}}=\frac{2}{2 \sin 15^{\circ} \cos 15^{\circ}}=\frac{2}{\sin 30^{\circ}}=\frac{2}{\frac{1}{2}}=4
\end{aligned}
$$
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.177. Calculate $(1+\operatorname{ctg} \alpha)(1+\operatorname{ctg} \beta)$, if $\alpha+\beta=\frac{3 \pi}{4}$.
|
Solution.
$$
\begin{aligned}
& (1+\operatorname{ctg} \alpha)(1+\operatorname{ctg} \beta)=\left(1+\frac{\cos \alpha}{\sin \alpha}\right)\left(1+\frac{\cos \beta}{\sin \beta}\right)=\frac{\sin \alpha+\cos \alpha}{\sin \alpha} \times \\
& \times \frac{\sin \beta+\cos \beta}{\sin \beta}=\frac{\cos \alpha \cos \beta+\sin \alpha \sin \beta+\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\sin \alpha \sin \beta}= \\
& =\frac{\cos (\alpha-\beta)+\sin (\alpha+\beta)}{\frac{1}{2}(\cos (\alpha-\beta)-\cos (\alpha+\beta))}=\frac{2\left(\cos (\alpha-\beta)+\frac{\sqrt{2}}{2}\right)}{\cos (\alpha-\beta)+\frac{\sqrt{2}}{2}}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.178. Calculate $(1+\operatorname{tg} \alpha)(1+\operatorname{tg} \beta)$, if $\alpha+\beta=\frac{\pi}{4}$.
|
Solution.
$$
(1+\operatorname{tg} \alpha)(1+\operatorname{tg} \beta)=\left(1+\frac{\sin \alpha}{\cos \alpha}\right)\left(1+\frac{\sin \beta}{\cos \beta}\right)=\frac{\cos \alpha+\sin \alpha}{\cos \alpha} \times
$$
$$
\begin{aligned}
& \times \frac{\cos \beta+\sin \beta}{\cos \beta}=\frac{\cos \alpha \cos \beta+\sin \alpha \sin \beta+\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\cos \alpha \cos \beta}= \\
& =\frac{\cos (\alpha-\beta)+\sin (\alpha+\beta)}{\frac{1}{2}(\cos (\alpha-\beta)+\cos (\alpha+\beta))}=\frac{2\left(\cos (\alpha-\beta)+\frac{\sqrt{2}}{2}\right)}{\cos (\alpha-\beta)+\frac{\sqrt{2}}{2}}=2
\end{aligned}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.018. The denominator of the geometric progression is $1 / 3$, the fourth term of this progression is $1 / 54$, and the sum of all its terms is 121/162. Find the number of terms in the progression.
|
Solution.
From the condition we have $\left\{\begin{array}{l}b_{4}=\frac{1}{54}, \\ S_{n}=\frac{121}{162}\end{array}\right.$.
Using formulas (4.6) and (4.11), we get
$$
\begin{aligned}
& b_{4}=b_{1} q^{3}=b_{1}\left(\frac{1}{3}\right)^{3} ; \frac{b_{1}}{27}=\frac{1}{54}, b_{1}=\frac{1}{2} ; \\
& S_{n}=\frac{b_{1}\left(1-q^{n}\right)}{1-q} ; \frac{\frac{1}{2}\left(1-\left(\frac{1}{3}\right)^{n}\right)}{1-\frac{1}{3}}=\frac{121}{162} \Rightarrow 243\left(3^{n}-1\right)=242 \cdot 3^{n} \Rightarrow \\
& \Rightarrow 3^{n}=243, n=5
\end{aligned}
$$
Answer: $n=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.028. Find the number of terms in a finite geometric progression, where the first, second, and last terms are 3, 12, and 3072, respectively.
|
Solution.
From the condition we have $b_{1}=3, b_{2}=12, \ldots, b_{n}=3072$.
By formula (4.6) we get
$$
\left\{\begin{array} { l }
{ b _ { 1 } = 3 , } \\
{ b _ { 1 } q = 1 2 , } \\
{ b _ { 1 } q ^ { n - 1 } = 3 0 7 2 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
b_{1}=3, \\
q=4, \\
4^{n-1}=1024
\end{array} \Rightarrow 4^{n-1}=4^{5} \Leftrightarrow n-1=5 \Rightarrow n=6\right.\right.
$$
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.031. It is known that the interior angles of a certain convex polygon, the smallest of which is $120^{\circ}$, form an arithmetic progression with a difference of $5^{\circ}$. Determine the number of sides of the polygon.
|
Solution.
From the condition, we have $a_{1}=120^{\circ}, d=5^{\circ}$. Using the formulas for the sum of terms of an arithmetic progression (4.5) and the sum of the interior angles of an $n$-sided polygon $S_{n}=180^{\circ}(n-2)$, we get
$$
\frac{240^{\circ}+(n-1) 5^{\circ}}{2} \cdot n=180^{\circ}(n-2), n^{2}-25 n+144=0 \Rightarrow
$$
$\Rightarrow n_{1}=9, n_{2}=16$ (the latter does not fit, as in this case
$\Rightarrow a_{16}=120^{\circ}+5^{\circ} \cdot 15=195^{\circ}$, while the interior angle of a convex $n$-sided polygon is always less than $\left.180^{\circ}\right)$.
Answer: 9.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.012. $(x-1)\left(x^{2}-3\right)+(2 x-1)\left(x^{2}+2\right)=3$.
|
Solution.
Domain of definition: $x \in R$.
## We have
$$
\begin{aligned}
& x^{3}-x^{2}-3 x+3+2 x^{3}-x^{2}+4 x-2=3 \Leftrightarrow \\
& \Leftrightarrow 3 x^{3}-2 x^{2}+x-2=0 \Leftrightarrow 3 x^{3}-3 x^{2}+x^{2}-x+2 x-2=0 \Leftrightarrow \\
& \Leftrightarrow 3 x^{2}(x-1)+x(x-1)+2(x-1)=0 \Leftrightarrow(x-1)\left(3 x^{2}+x+2\right)=0 \\
& x-1=0, x_{1}=1 \text { or } 3 x^{2}+x+2=0, x_{2,3} \in \varnothing(D<0)
\end{aligned}
$$
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.014. $\frac{4}{x^{2}+4}+\frac{5}{x^{2}+5}=2$.
|
## Solution.
Domain: $x \in R$.
$\frac{2 x^{4}+9 x^{2}}{\left(x^{2}+4\right)\left(x^{2}+5\right)}=0 \Leftrightarrow 2 x^{4}+9 x^{2}=0 \Leftrightarrow x^{2}\left(2 x^{2}+9\right)=0$,
$x^{2}=0, x_{1}=0$ or $2 x^{2}+9=0, x_{2,3} \in \varnothing$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.031. $\sqrt{3 x+4}+\sqrt{x-4}=2 \sqrt{x}$.
|
## Solution.
Domain of definition: $3 x+4 \geq 0, x-4 \geq 0, x \geq 0 \Rightarrow x \geq 4$.
Squaring both sides of the equation, we get
$$
\begin{aligned}
& 3 x+4+2 \sqrt{(3 x+4)(x-4)}+x-4=4 x \Leftrightarrow \\
& \Leftrightarrow 2 \sqrt{(3 x+4)(x-4)}=0
\end{aligned}
$$
Squaring again, we get: $(3 x+4)(x-4)=0$. From this, we have $3 x+4=0$ or $x-4=0, x_{1}=-\frac{4}{3}, x_{2}=4 ; x_{1}=-\frac{4}{3}$ does not satisfy the domain of definition. Checking $x=4$ by direct substitution into the original equation, we get:
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.032. $\sqrt{x+\sqrt{x+11}}+\sqrt{x-\sqrt{x+11}}=4$.
6.032. $\sqrt{x+\sqrt{x+11}}+\sqrt{x-\sqrt{x+11}}=4$.
|
Solution.
Let $\sqrt{x+11}=y \geq 0$ or $x+11=y^{2}$, i.e., $x=y^{2}-11$. Then
$$
\sqrt{y^{2}+y-11}+\sqrt{y^{2}-y-11}=4 \text { or } \sqrt{y^{2}+y-11}=4-\sqrt{y^{2}-y-11}
$$
Squaring both sides of the equation, we get
$$
y^{2}+y-11=16-8 \sqrt{y^{2}-y-11}+y^{2}-y-11, 8 \sqrt{y^{2}-y-11}=16-2 y
$$
or $4 \sqrt{y^{2}-y-11}=8-y$. Squaring both sides of the equation again, we find
$$
\begin{aligned}
& 16 y^{2}-16 y-176=64-16 y+y^{2}, 0<y \leq 8 \Rightarrow \\
& \Rightarrow\left\{\begin{array}{l}
15 y^{2}=240, \\
0<y \leq 8
\end{array} \text { or } y=4 .\right.
\end{aligned}
$$
From this, we get $\sqrt{x+11}=4$ or $x+11=16, x=5$. Checking, we confirm that this is a root of the original equation.
Answer: $x=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.034. $1+\sqrt{1+x \sqrt{x^{2}-24}}=x$.
6.034. $1+\sqrt{1+x \sqrt{x^{2}-24}}=x$.
|
Solution.
Write the equation as $\sqrt{1+x \sqrt{x^{2}-24}}=x-1$. Squaring both sides of the equation, we get
$$
\begin{aligned}
& \left\{\begin{array} { l }
{ 1 + x \sqrt { x ^ { 2 } - 2 4 } = x ^ { 2 } - 2 x + 1 , } \\
{ x - 1 \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \sqrt{x^{2}-24}=x^{2}-2 x, \\
x \geq 1
\end{array}\right.\right. \\
& \Leftrightarrow\left\{\begin{array}{l}
\sqrt{x^{2}-24}=x-2, \\
x \geq 1
\end{array}\right. \\
& \Rightarrow x^{2}-24=x^{2}-4 x+4 \text { or } 4 x=28 ; x=7 .
\end{aligned}
$$
Checking $x=7$ by direct substitution into the original equation, we have:
Answer: $x=7$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.037. $\sqrt[3]{1+\sqrt{x}}+\sqrt[3]{1-\sqrt{x}}=2$.
|
Solution.
Domain of definition: $x \geq 0$.
Raising both sides of the equation to the third power, we get
$$
\begin{aligned}
& 1+\sqrt{x}+3 \sqrt[3]{(1+\sqrt{x})^{2}(1-\sqrt{x})}+3 \sqrt[3]{(1+\sqrt{x})(1-\sqrt{x})^{2}}+1-\sqrt{x}=8 \Leftrightarrow \\
& \Leftrightarrow 3 \sqrt[3]{(1+\sqrt{x})^{2}(1-\sqrt{x})}+3 \sqrt[3]{(1+\sqrt{x})(1-\sqrt{x})^{2}}=6 \Leftrightarrow \\
& \Leftrightarrow 3 \sqrt[3]{(1+\sqrt{x})(1-\sqrt{x})}(\sqrt[3]{1+\sqrt{x}}+\sqrt[3]{1-\sqrt{x}})=6
\end{aligned}
$$
Since $\sqrt[3]{1+\sqrt{x}}+\sqrt[3]{1-\sqrt{x}}=2$, the equation becomes:
$3 \sqrt[3]{(1+\sqrt{x})(1-\sqrt{x})} \cdot 2=6 \Leftrightarrow \sqrt[3]{(1+\sqrt{x})(1-\sqrt{x})}=1 \Leftrightarrow \sqrt[3]{1-x}=1 \Leftrightarrow$ $\Leftrightarrow 1-x=1, x=0$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.040. $\sqrt[3]{24+\sqrt{x}}-\sqrt[3]{5+\sqrt{x}}=1$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
6.040. $\sqrt[3]{24+\sqrt{x}}-\sqrt[3]{5+\sqrt{x}}=1$.
|
## Solution.
Domain of definition: $x \geq 0$.
Raising both sides of the equation to the third power, we get
$$
\begin{aligned}
& 24+\sqrt{x}-3 \sqrt[3]{(24+\sqrt{x})^{2}(5+\sqrt{x})}+3 \sqrt[3]{(24+\sqrt{x})(5+\sqrt{x})^{2}}-5-\sqrt{x}=1 \Leftrightarrow \\
& \Leftrightarrow-3 \sqrt[3]{(24+\sqrt{x})}(5+\sqrt{x})(\sqrt[3]{24+\sqrt{x}}-\sqrt[3]{5+\sqrt{x}})=-18
\end{aligned}
$$
Since $\sqrt[3]{24+\sqrt{x}}-\sqrt[3]{5+\sqrt{x}}=1$ by the condition, we obtain
$\sqrt[3]{(24+\sqrt{x})}(5+\sqrt{x})=6 \Leftrightarrow(24+\sqrt{x})(5+\sqrt{x})=216$,
$(\sqrt{x})^{2}+29 \sqrt{x}-96=0$.
From which $\sqrt{x}=3, \sqrt{x}=-3$ (not suitable). Therefore, $x=9$.
Answer: $x=9$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.049. $\sqrt{x^{3}+8}+\sqrt[4]{x^{3}+8}=6$.
6.049. $\sqrt{x^{3}+8}+\sqrt[4]{x^{3}+8}=6$.
|
## Solution.
Domain of definition: $x^{3}+8 \geq 0 \Leftrightarrow x^{3} \geq-8 \Leftrightarrow x \geq-2$.
Let $\sqrt[4]{x^{3}+8}=y, y>0$, and the equation becomes $y^{2}+y=6 \Leftrightarrow$ $\Leftrightarrow y^{2}+y-6=0$, from which $y_{1}=-3, y_{2}=2 ; y_{1}=-3$ is not suitable. Then $\sqrt[4]{x^{3}+8}=2, x^{3}+8=16, x^{3}=8, x=2$.
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.052.
$$
\frac{1}{x-\sqrt{x^{2}-x}}-\frac{1}{x+\sqrt{x^{2}-x}}=\sqrt{3}
$$
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}x^{2}-x \geq 0, \\ x \neq 0\end{array} \Leftrightarrow\left\{\begin{array}{l}x(x-1) \geq 0, \\ x \neq 0\end{array} \Leftrightarrow x \in(-\infty ; 0) \cup[1 ;+\infty)\right.\right.$.
From the condition we get
$$
\begin{aligned}
& \frac{x+\sqrt{x^{2}-x}-x+\sqrt{x^{2}-x}}{x^{2}-x^{2}+x}=\sqrt{3} \Leftrightarrow \frac{2 \sqrt{x^{2}-x}}{x}=\sqrt{3} \Leftrightarrow \\
& \Leftrightarrow \frac{2 \sqrt{x} \sqrt{x-1}}{x}=\sqrt{3} \Leftrightarrow \frac{2 \sqrt{x-1}}{\sqrt{x}}=\sqrt{3}(x \neq 0)
\end{aligned}
$$
Squaring both sides of the equation, we get $\frac{4 x-4}{x}=3$ or $x=4$. By verification, we confirm that $x=4$ is a root of the last equation with radicals.
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.053. $\frac{\sqrt[3]{x^{4}}-1}{\sqrt[3]{x^{2}}-1}-\frac{\sqrt[3]{x^{2}}-1}{\sqrt[3]{x}+1}=4$
|
## Solution.
Domain of definition: $x \neq \pm 1$.
Let $\sqrt[3]{x}=y, y \neq \pm 1$. The equation in terms of $y$ becomes
$$
\begin{aligned}
& \frac{y^{4}-1}{y^{2}-1}-\frac{y^{2}-1}{y+1}=4 \Leftrightarrow \frac{\left(y^{2}-1\right)\left(y^{2}+1\right)}{y^{2}-1}-\frac{(y-1)(y+1)}{y+1}=4 \Leftrightarrow \\
& \Leftrightarrow y^{2}+1-y+1=4 \Leftrightarrow y^{2}-y-2=0
\end{aligned}
$$
from which we find $y_{1}=-1, y_{2}=2$. Then $\sqrt[3]{x}=-1, x_{1}=-1$, or $\sqrt[3]{x}=2$, $x_{2}=8 ; x_{1}=-1$ does not satisfy the domain of definition.
Answer: $x=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.058. $\sqrt[3]{\frac{5-x}{x+3}}+\sqrt[7]{\frac{x+3}{5-x}}=2$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x \neq-3, \\ x \neq 5\end{array}\right.$
Let $\sqrt[7]{\frac{5-x}{x+3}}=z, z \neq 0$. The equation in terms of $z$ becomes $z+\frac{1}{z}=2 \Leftrightarrow z^{2}-2 z+1=0 \Leftrightarrow(z-1)^{2}=0 \Leftrightarrow z-1=0, z=1$.
Then $\sqrt[7]{\frac{5-x}{x+3}}=1 \Leftrightarrow \frac{5-x}{x+3}=1 ; x=1$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.064. $\sqrt{x+2}+\sqrt{3 x+8}=\sqrt{2 x+6}$.
6.064. $\sqrt{x+2}+\sqrt{3 x+8}=\sqrt{2 x+6}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x+2 \geq 0, \\ 3 x+8 \geq 0, \\ 2 x+6 \geq 0\end{array} \Leftrightarrow x \geq-2\right.$.
Write the equation in the form $\sqrt{x+2}-\sqrt{2 x+6}=-\sqrt{3 x+8}$ and square both sides:
$$
\begin{aligned}
& x+2-2 \sqrt{(x+2)(2 x+6)}+2 x+6=3 x+8 \Leftrightarrow \\
& \Leftrightarrow \sqrt{(x+2)(2 x+6)}=0
\end{aligned}
$$
from which $x+2=0, x_{1}=-2$, or $2 x+6=0, x_{2}=-3$ - does not satisfy the domain of definition. By checking, we confirm that $x=-2$ is a root of the given equation.
Answer: $x=-2$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.065. $\sqrt{2 x+5}+\sqrt{5 x+6}=\sqrt{12 x+25}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}2 x+5 \geq 0, \\ 5 x+6 \geq 0, \\ 12 x+25 \geq 0\end{array} \Leftrightarrow x \geq-\frac{6}{5}\right.$.
By squaring both sides of the equation, we have
$$
\begin{aligned}
& 2 x+5+2 \sqrt{(2 x+5)(5 x+6)}+5 x+6=12 x+25 \Leftrightarrow \\
& \Leftrightarrow 2 \sqrt{(2 x+5)(5 x+6)}=5 x+14 \Rightarrow \\
& \Rightarrow 4(2 x+5)(5 x+6)=25 x^{2}+140 x+196 \Leftrightarrow 15 x^{2}+8 x-76=0
\end{aligned}
$$
from which $x_{1}=-\frac{38}{15}, x_{2}=2 ; x_{1}=-\frac{38}{15}$ does not satisfy the domain of definition. By checking, we confirm that $x=2$ is a root of the equation.
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.126. For what integer value of $k$ is one of the roots of the equation $4 x^{2}-(3 k+2) x+\left(k^{2}-1\right)=0$ three times smaller than the other?
|
Solution.
From the condition, by Vieta's theorem, we have
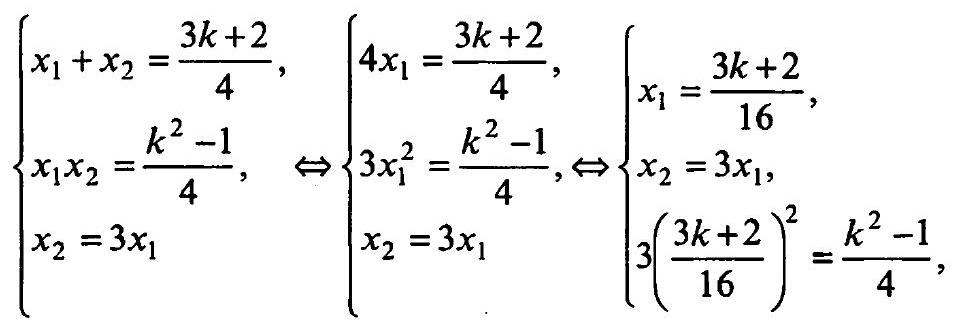
where $k \in \mathbb{Z}$. From this, $37 k^{2}-36 k-76=0, k_{1}=2, k_{2}=-\frac{38}{37} \notin \mathbb{Z}$ (does not fit).
Answer: $k=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.129. For what value of $a$ do the equations $x^{2}+a x+8=0$ and $x^{2}+x+a=0$ have a common root?
|
## Solution.
Let $x_{1}$ be the common root, then
$$
\left\{\begin{array}{l}
x_{1}^{2}+a x_{1}+8=0, \\
x_{1}^{2}+x_{1}+a=0
\end{array} \Rightarrow a x_{1}-x_{1}+8-a=0, x_{1}=\frac{a-8}{a-1}\right.
$$
From the second equation of the system, we have
$$
\begin{aligned}
& \left(\frac{a-8}{a-1}\right)^{2}+\left(\frac{a-8}{a-1}\right)+a=0, \frac{a^{3}-24 a+72}{(a-1)^{2}}=0 \Leftrightarrow\left\{\begin{array}{l}
a^{3}-24 a+72=0, \\
a \neq 1,
\end{array}\right. \\
& a^{3}+216-216-24 a+72=0,\left(a^{3}+216\right)-24 a-144=0, \\
& \left(a^{3}+6^{3}\right)-24(a+6)=0 \\
& (a+6)\left(a^{2}-6 a+36\right)-24(a+6)=0 \\
& (a+6)\left(a^{2}-6 a+12\right)=0
\end{aligned}
$$
from which $a=-6$. For the quadratic equation, $D<0, \varnothing$.
Answer: $a=-6$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.131. Without solving the equation $x^{2}-(2 a+1) x+a^{2}+2=0$, find the value of $a$ for which one of the roots is twice the other.
|
Solution.
From the condition, by Vieta's theorem, we have
$$
\left\{\begin{array} { l }
{ x _ { 1 } + x _ { 2 } = 2 a + 1 , } \\
{ x _ { 1 } \cdot x _ { 2 } = a ^ { 2 } + 2 , } \\
{ x _ { 2 } = 2 x _ { 1 } }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ 3 x _ { 1 } = 2 a + 1 , } \\
{ 2 x _ { 1 } ^ { 2 } = a ^ { 2 } + 2 } \\
{ x _ { 2 } = 2 x _ { 1 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x_{1}=\frac{2 a+1}{3} \\
x_{1}^{2}=\frac{a^{2}+2}{2} \\
x_{2}=2 x_{1}
\end{array}\right.\right.\right.
$$
From here,
$$
\begin{aligned}
& \left(\frac{2 a+1}{3}\right)^{2}=\frac{a^{2}+2}{2} \Leftrightarrow \frac{4 a^{2}+4 a+1}{9}=\frac{a^{2}+2}{2} \Leftrightarrow \\
& \Leftrightarrow a^{2}-8 a+16=0 \Leftrightarrow(a-4)^{2}=0
\end{aligned}
$$
Thus, $a=4$.
Answer: $a=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.134. For what integer value of $b$ do the equations $2 x^{2}+(3 b-1) x-3=0$ and $6 x^{2}-(2 b-3) x-1=0$ have a common root?
|
Solution.
Let $x_{1}$ be the common root. Then
$$
\begin{aligned}
& \left\{\begin{array} { l }
{ 2 x _ { 1 } ^ { 2 } + ( 3 b - 1 ) x _ { 1 } - 3 = 0 , } \\
{ 6 x _ { 1 } ^ { 2 } - ( 2 b - 3 ) x _ { 1 } - 1 = 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
6 x^{2}+(9 b-3) x-9=0, \\
6 x^{2}-(2 b-3) x_{1}-1=0
\end{array}\right.\right. \\
& \Leftrightarrow(9 b-3) x+(2 b-3) x-9+1=0, \quad x=\frac{8}{11 b-6} .
\end{aligned}
$$
From the first equation we have
$2\left(\frac{8}{11 b-6}\right)^{2}+(3 b-1)\left(\frac{8}{11 b-6}\right)-3=0,99 b^{2}-164 b-68=0$,
$b_{1}=-\frac{34}{99}, b_{2}=2$
$b_{1}=-\frac{34}{99}$ is not an integer value.
Answer: $b=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.001. $\sqrt{25^{\frac{1}{\log _{6} 5}}+49^{\frac{1}{\log _{8} 7}}}$
|
## Solution.
$$
\begin{aligned}
& \sqrt{\frac{1}{25^{\log _{6} 5}}+49^{\frac{1}{\log _{8} 7}}}=\sqrt{5^{2 \log _{5} 6}+7^{2 \log _{7} 8}}=\sqrt{5^{\log _{5} 6^{2}}+7^{\log _{7} 8^{2}}}= \\
& =\sqrt{6^{2}+8^{2}}=10
\end{aligned}
$$
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.003. $-\log _{2} \log _{2} \sqrt{\sqrt[4]{2}}$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
7.003. $-\log _{2} \log _{2} \sqrt{\sqrt[4]{2}}$.
|
Solution.
$$
-\log _{2} \log _{2} \sqrt{\sqrt[4]{2}}=-\log _{2} \log _{2} 2^{\frac{1}{8}}=-\log _{2} \frac{1}{8} \log _{2} 2=-\log _{2} 2^{-3}=3
$$
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.004. $-\log _{3} \log _{3} \sqrt[3]{\sqrt[3]{3}}$.
7.004. $-\log _{3} \log _{3} \sqrt[3]{\sqrt[3]{3}}$.
|
## Solution.
$-\log _{3} \log _{3} \sqrt[3]{\sqrt[3]{3}}=-\log _{3} \log _{3} 3^{\frac{1}{9}}=-\log _{3} \frac{1}{9} \log _{3} 3=-\log _{3} 3^{-2}=2$.
Answer: 2.
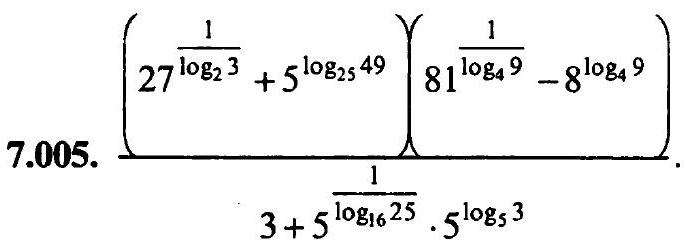
## Solution.
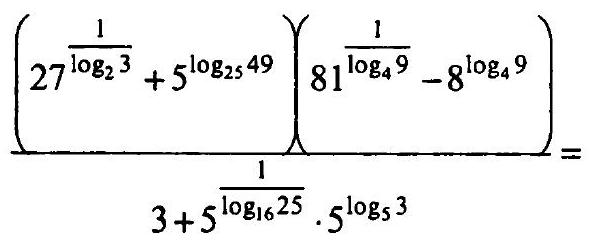
$=\frac{\left(\left(3^{3}\right)^{\log _{3} 2}+5^{\log _{5} 27^{2}}\right)\left(\left(9^{2}\right)^{\log _{9} 4}-\left(2^{3}\right)^{\log _{2} 23^{2}}\right)}{3+5^{\log _{5} 24^{2}} \cdot 3}=$
$=\frac{\left(3^{\log _{3} 2^{3}}+5^{\log _{5} 7}\right)\left(9^{\log _{9} 4^{2}}-2^{\log _{2} 3^{3}}\right)}{3+5^{\log _{5} 4} \cdot 3}=\frac{\left(2^{3}+7\right)\left(4^{2}-3^{3}\right)}{3+4 \cdot 3}=$
$=\frac{15 \cdot(-11)}{15}=-11$.
Answer: -11.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.008. $\frac{81^{\frac{1}{\log _{5} 9}}+3^{\frac{3}{\log _{\sqrt{6}} 3}}}{409} \cdot\left((\sqrt{7})^{\frac{2}{\log _{25} 7}}-125^{\log _{25} 6}\right)$
|
## Решение.
$$
\frac{81^{\frac{1}{\log _{5} 9}}+3^{\frac{3}{\log _{\sqrt{6}}}}}{409} \cdot\left((\sqrt{7})^{\frac{2}{\log _{25} 7}}-125^{\log _{25} 6}\right)=
$$
$=\frac{9^{2 \log _{9} 5}+3^{3 \log _{3} \sqrt{6}}}{409} \cdot\left(\left(7^{\frac{1}{2}}\right)^{2 \log _{7} 25}-5^{3 \log _{5} 26}\right)=\frac{9^{\log _{9} 5^{2}}+3^{\log _{3}(\sqrt{6})}}{409} \times$
$\times\left(7^{\log _{7} 25}-5^{\log _{5} 6^{\frac{3}{2}}}\right)=\frac{\left(25+6^{\frac{3}{2}}\right)\left(25-6^{\frac{3}{2}}\right)}{409}=\frac{625-216}{409}=1$.
Omвem: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.009. $\left(N^{\frac{1}{\log _{2} N}} \cdot N^{\frac{1}{\log _{4} N}} \cdot N^{\frac{1}{\log _{8} N}} \cdots N^{\frac{1}{\log _{64} N}}\right)^{\frac{1}{15}}$ (the bases of the logarithms are consecutive natural powers of the number 2).
|
## Solution.
$$
\begin{aligned}
& \left(N^{\frac{1}{\log _{2} N}} \cdot N^{\frac{1}{\log _{4} N}} \cdot N^{\frac{1}{\log _{8} N}} \cdots N^{\frac{1}{\log _{512} N}}\right)^{\frac{1}{15}}= \\
& =\left(N^{\log _{N} 2} \cdot N^{\log _{N} 4} \cdot N^{\log _{N} 8} \cdots N^{\log _{N} 512}\right)^{\frac{1}{15}}= \\
& =(2 \cdot 4 \cdot 8 \cdots 512)^{\frac{1}{15}}=\left(2^{1} \cdot 2^{2} \cdot 2^{3} \cdots 2^{9}\right)^{\frac{1}{15}}=\left(2^{1+2+3+\ldots+9}\right)^{\frac{1}{15}}
\end{aligned}
$$
The expression $S_{n}=1+2+3+\ldots+9$ is the sum of the terms of an arithmetic progression, where $a_{1}=1, d=1, a_{n}=9, n=9$. Then $S_{n}=\frac{a_{1}+a_{n}}{2} n=$ $=\frac{1+9}{2} \cdot 9=45$. Therefore, $\left(2^{45}\right)^{\frac{1}{15}}=2^{3}=8$.
Answer: 8.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.021. $3 \log _{5} 2+2-x=\log _{5}\left(3^{x}-5^{2-x}\right)$.
7.021. $3 \log _{5} 2+2-x=\log _{5}\left(3^{x}-5^{2-x}\right)$.
|
Solution.
Domain of definition: $3^{x}-5^{2-x}>0$.
$\log _{5} 8+2 \log _{5} 5-\log _{5}\left(3^{x}-25 \cdot 5^{-x}\right)=x \Leftrightarrow \log _{5} \frac{8 \cdot 25}{3^{x}-25 \cdot 5^{-x}}=x$,
from which $\frac{200}{3^{x}-25 \cdot 5^{-x}}=5^{x} \Leftrightarrow 15^{x}=15^{2}$. Therefore, $x=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.028. $5^{2\left(\log _{5} 2+x\right)}-2=5^{x+\log _{5} 2}$.
|
## Solution.
$\left(5^{x+\log _{5} 2}\right)^{2}-5^{x+\log _{5} 2}-2=0$; solving this equation as a quadratic equation in terms of $5^{x+\log _{5} 2}$, we find $5^{x+\log _{5} 2}=-1$ and $5^{x+\log _{5} 2}=2 ; 5^{x+\log _{5} 2}=-1$ has no solutions.
Thus,
$$
5^{x+\log _{5} 2}=2 \Rightarrow \log _{5} 5^{x+\log _{5} 2}=\log _{5} 2, x+\log _{5} 2=\log _{5} 2
$$
from which $x=0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.029. $0.25^{\log _{2} \sqrt{x+3}-0.5 \log _{2}\left(x^{2}-9\right)}=\sqrt{2(7-x)}$.
|
## Solution.
Domain of definition: $\quad\left\{\begin{array}{l}x+3>0, \\ x^{2}-9>0.33 . \Rightarrow x_{1}=5, x_{2}=-1 ; x_{2}=-1 \text{ does not fit the domain of definition.}\end{array}\right.$
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.031. $\log _{5}(x-2)+\log _{\sqrt{5}}\left(x^{3}-2\right)+\log _{0.2}(x-2)=4$.
|
## Solution.
Domain of definition: $\quad x-2>0, x>2$.
From the condition we have
$$
\log _{5}(x-2)+2 \log _{5}\left(x^{3}-2\right)-\log _{5}(x-2)=4, \log _{5}\left(x^{3}-2\right)=2
$$
from which $x^{3}-2=25, x^{3}=27$. Then $x=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.034. $\lg \left(3^{x}-2^{4-x}\right)=2+0.25 \lg 16-0.5 x \lg 4$.
|
Solution.
Domain of definition: $3^{x}-2^{4-x}>0$.
From the condition
$$
\begin{aligned}
& \lg \left(3^{x}-2^{4-x}\right)=\lg 100+\lg 2-\lg 2^{x} \Rightarrow \lg \left(3^{x}-2^{4-x}\right)=\lg \frac{100 \cdot 2}{2^{x}} \\
& 3^{x}-2^{4-x}=\frac{200}{2^{x}}
\end{aligned}
$$
From here $6^{x}=216$, hence $x=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.035. $\log _{3}\left(81^{x}+3^{2 x}\right)=3 \log _{27} 90$.
|
## Solution.
From the condition $\log _{3}\left(81^{x}+3^{2 x}\right)=\log _{3} 90, 9^{2 x}+9^{x}-90=0$, from which we find $9^{x}=-10$, which is not suitable, or $9^{x}=9$, from which we have $x=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.039. $\lg \left(10^{\lg \left(x^{2}-21\right)}\right)-2=\lg x-\lg 25$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}x^{2}-21>0, \\ x>0,\end{array} x>\sqrt{21}\right.$.
From the condition we have
$$
\lg \left(x^{2}-21\right)-\lg 100=\lg x-\lg 25, \lg \frac{x^{2}-21}{100}=\lg \frac{x}{25}, \quad \frac{x^{2}-21}{100}=\frac{x}{25}
$$
We obtain the quadratic equation $x^{2}-4 x-21=0$, the roots of which are $x_{1}=7, x_{2}=-3 ; x_{2}=-3$ does not satisfy the domain of definition.
Answer: 7.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.042. $x(\lg 5-1)=\lg \left(2^{x}+1\right)-\lg 6$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
7.042. $x(\lg 5-1)=\lg \left(2^{x}+1\right)-\lg 6$.
|
Solution.
$$
\begin{aligned}
& x(\lg 5-\lg 10)=\lg \left(2^{x}+1\right)-\lg 6, \quad x \lg \frac{5}{10}=\lg \frac{2^{x}+1}{6} \\
& \lg 2^{-x}=\lg \frac{2^{x}+1}{6}, 2^{-x}=\frac{2^{x}+1}{6}, 2^{2 x}+2^{x}-6=0
\end{aligned}
$$
Solving this equation as a quadratic in terms of $2^{x}$, we find $2^{x}=-3$ (not valid), $2^{x}=2$, from which we have $x=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.047. Find the natural number $n$ from the equation
$$
3^{2} \cdot 3^{5} \cdot 3^{8} \cdots 3^{3 n-1}=27^{5}
$$
|
## Solution.
$3^{2+5+8+\ldots+3 n-1}=3^{15}, 2+5+8+\ldots+3 n-1=15$.
On the left side of the equation, we have the sum of the terms of an arithmetic progression $S_{k}$, where $a_{1}=2, d=3, a_{k}=3 n-1, k=\frac{a_{k}-a_{1}}{d}+1=\frac{3 n-1-2}{3}+1=n$.
Then $S_{k}=\frac{a_{1}+a_{k}}{2} \cdot k=\frac{2+3 n-1}{2} \cdot n=\frac{3 n^{2}+n}{2}$, and the equation becomes $\frac{3 n^{2}+n}{2}=15,3 n^{2}+n-30=0$, from which $n=3$.
Answer: 3.
Solve the equations (7.048 - 7.127):
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.050. $\log _{2} \frac{x-5}{x+5}+\log _{2}\left(x^{2}-25\right)=0$.
|
## Solution.
Domain of definition: $\frac{x-5}{x+5}>0$ or $x \in(-\infty ;-5) \cup(5 ; \infty)$.
We have $\log _{2} \frac{(x-5)\left(x^{2}-25\right)}{x+5}=0,(x-5)^{2}=1$, from which $x-5=-1$ or $x-5=1$. Then $x_{1}=4, x_{2}=6 ; x_{1}=4$ does not fit the domain of definition.
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.053. $\lg (\lg x)+\lg \left(\lg x^{3}-2\right)=0$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
7.053. $\lg (\lg x)+\lg \left(\lg x^{3}-2\right)=0$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}\lg x>0, \\ \lg x^{3}-2>0,\end{array} \quad x>\sqrt[3]{100}\right.$.
From the condition we have
$\lg \left(\lg x \cdot\left(\lg x^{3}-2\right)\right)=0, \quad \lg x(3 \lg x-2)=1$,
$3 \lg ^{2} x-2 \lg x-1=0$.
Solving this equation as a quadratic equation in terms of $\lg x$, we find $(\lg x)_{1}=-\frac{1}{3}$, hence $x_{1}=\frac{1}{\sqrt[3]{10}}$, or $(\lg x)_{2}=1$, hence $x_{2}=10 ; x_{1}=\frac{1}{\sqrt[3]{10}}$ does not satisfy the domain of definition.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.055. $\log _{3}\left(3^{x}-8\right)=2-x$.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
7.055. $\log _{3}\left(3^{x}-8\right)=2-x$.
|
Solution.
Domain of definition: $3^{x}-8>0$.
By the definition of logarithm, we have $3^{x}-8=3^{2-x}, 3^{x}-8=\frac{9}{3^{x}}$, $3^{2 x}-8 \cdot 3^{x}-9=0$, from which, solving this equation as a quadratic equation in terms of $3^{x}$, we find $3^{x}=-1, \varnothing$; or $3^{x}=9$, from which $x=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.057. $5^{x+6}-3^{x+7}=43 \cdot 5^{x+4}-19 \cdot 3^{x+5}$.
|
Solution.
We have $5^{6} \cdot 5^{x}-43 \cdot 5^{4} \cdot 5^{x}=3^{7} \cdot 3^{x}-19 \cdot 3^{5} \cdot 3^{x},\left(\frac{5}{3}\right)^{x}=\left(\frac{5}{3}\right)^{-3}$, from which $x=-3$.
Answer: -3.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.066. $2^{\frac{1}{\sqrt{x}-1}} \cdot 0.5^{\frac{1}{\sqrt{x}+1}}=4^{\frac{\sqrt{x}}{x+\sqrt{x}}}$
|
Solution.
Domain of definition: $0<x \neq 1$.
We have: $2^{\frac{1}{\sqrt{x}-1}} \cdot 2^{-\frac{1}{\sqrt{x}+1}}=2^{\frac{2 \sqrt{x}}{x+\sqrt{x}}}, 2^{\frac{1}{\sqrt{x}-1}-\frac{1}{\sqrt{x}+1}}=2^{\frac{2 \sqrt{x}}{x+\sqrt{x}}}$.
Then $\frac{1}{\sqrt{x}-1}-\frac{1}{\sqrt{x}+1}=\frac{2 \sqrt{x}}{x+\sqrt{x}}, x-\sqrt{x}-2=0$. Solving this equation as a quadratic equation in terms of $\sqrt{x}$, we find $\sqrt{x}=-1, \varnothing$; or $\sqrt{x}=2$, from which we have $x=4$.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.069. $\log _{\sqrt{5}}\left(4^{x}-6\right)-\log _{\sqrt{5}}\left(2^{x}-2\right)=2$.
|
Solution.
Domain of Definition (DOD): $\left\{\begin{array}{l}4^{x}-6>0 \\ 2^{x}-2>0 .\end{array}\right.$
We have $\log _{\sqrt{5}} \frac{4^{x}-6}{2^{x}-2}=2, \frac{2^{2 x}-6}{2^{2}-2}=5,2^{2 x}-5 \cdot 2^{x}+4=0$. Solving this equation as a quadratic in terms of $2^{x}$, we find $\left(2^{x}\right)=1$, from which we get $x_{1}=0$, or $\left(2^{x}\right)_{2}=4$, from which we get $x_{2}=2 ; x_{1}=0$ does not satisfy the DOD.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.071. $3 \cdot 5^{2 x-1}-2 \cdot 5^{x-1}=0.2$.
|
## Solution.
From the condition $3 \cdot 5^{2 x}-2 \cdot 5^{x}=1,3 \cdot 5^{2 x}-2 \cdot 5^{x}-1=0$. Solving this equation as a quadratic in terms of $5^{x}$, we get $5^{x}=-\frac{1}{3}, \varnothing$; or $5^{x}=1$, from which $x=0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.076. $9^{\sqrt{x-5}}-27=6 \cdot 3^{\sqrt{x-5}}$.
7.076. $9^{\sqrt{x-5}}-27=6 \cdot 3^{\sqrt{x-5}}$.
|
Solution.
Domain of definition: $x-5 \geq 0, x \geq 5$.
$$
3^{2 \sqrt{x-5}}-6 \cdot 3^{\sqrt{x-5}}-27=0
$$
We solve the equation as a quadratic equation in terms of $3^{\sqrt{x-5}}$. We have $3^{\sqrt{x-5}}=-3$. (not suitable) or $3^{\sqrt{x-5}}=9$, from which $\sqrt{x-5}=2$, or $x-5=4$. Then $x=9$.
Answer: 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.080. $\lg (\sqrt{6+x}+6)=\frac{2}{\log _{\sqrt{x}} 10}$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}6+x \geq 0, \\ x>0, \\ x \neq 1,\end{array} \quad 0<x \neq 1\right.$.
We will switch to base 10. We have
$\lg (\sqrt{6+x}+6)=2 \lg \sqrt{x}, \quad \lg (\sqrt{6+x}+6)=\lg x$.
Then $\sqrt{6+x}+6=x, \sqrt{6+x}=x-6 \Rightarrow\left\{\begin{array}{l}x^{2}-13 x+30=0, \\ x \geq 6,\end{array}\right.$
from which $x=10$.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.084. $\frac{2^{x}+10}{4}=\frac{9}{2^{x-2}}$.
7.084. $\frac{2^{x}+10}{4}=\frac{9}{2^{x-2}}$.
|
## Solution.
From the condition
$$
\frac{2^{x}+10}{4}=\frac{9}{2^{x} \cdot 2^{-2}}, \frac{2^{x}+10}{4}=\frac{36}{2^{x}}, 2^{2 x}+10 \cdot 2^{x}-144=0 .
$$
Solving this equation as a quadratic in terms of $2^{x}$, we find $2^{x}=-18, \varnothing$, or $2^{x}=8$, from which $x=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.091. $\log _{2}\left(4 \cdot 3^{x}-6\right)-\log _{2}\left(9^{x}-6\right)=1$.
|
## Solution.
oDZ: $\left\{\begin{array}{l}4 \cdot 3^{x}-6>0 \\ 9^{x}-6>0\end{array}\right.$
We have $\log _{2} \frac{4 \cdot 3^{x}-6}{3^{2 x}-6}=1, \frac{4 \cdot 3^{x}-6}{3^{2 x}-6}=2 \Rightarrow 3^{2 x}-2 \cdot 3^{x}-3=0$. Solving it as a quadratic equation in terms of $3^{x}$, we find $3^{x}=-1, \varnothing$; or $3^{x}=3$, from which $x=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.098. $\lg \sqrt{x-3}+\lg \sqrt{x+3}=2-0.5 \lg 625$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x-3>0, \\ x+3>0\end{array} x>3\right.$.
## We have
$\lg \sqrt{x-3}+\lg \sqrt{x+3}=\lg 100-\lg 25, \lg \sqrt{x^{2}-9}=\lg 4, \sqrt{x^{2}-9}=4$, from which $x^{2}=25, x_{1}=-5, x_{2}=5, x_{1}=-5$ does not satisfy the domain of definition.
Answer: 5 .
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.099. $\lg (3-x)-\frac{1}{3} \lg \left(27-x^{3}\right)=0$.
|
## Solution.
Domain of definition: $3-x>0, x<3$.
## Rewrite the equation as
$$
3 \lg (3-x)=\lg \left(27-x^{3}\right), \lg (3-x)^{3}=\lg \left(27-x^{3}\right)
$$
Then $(3-x)^{3}=27-x^{3} \Rightarrow x^{2}-9 x=0$, from which $x_{1}=0, x_{2}=9 ; x_{2}=9$ does not satisfy the domain of definition.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.101. $\lg 8-\lg \sqrt{x+6}=\lg 16-\lg (x-2)$
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x+6>0, \\ x-2>0,\end{array} \quad x>2\right.$.
We have
$$
\lg \frac{8}{\sqrt{x+6}}=\lg \frac{16}{x-2}, \quad \frac{8}{\sqrt{x+6}}=\frac{16}{x-2}, \quad 2 \sqrt{x+6}=x-2, x^{2}-8 x-20=0
$$
from which $x_{1}=10, x_{2}=-2 ; x_{2}=-2$ does not satisfy the domain of definition.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.103. $\frac{\lg (2 x-19)-\lg (3 x-20)}{\lg x}=-1$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}2 x-19>0, \\ 3 x-20>0,\end{array} \quad x>\frac{19}{2}\right.$.
## From the condition
$$
\begin{aligned}
& \lg (2 x-19)-\lg (3 x-20)=-\lg x, \lg (2 x-19)+\lg x=\lg (3 x-20) \\
& x(2 x-19)=3 x-20, x^{2}-11 x+10=0 .
\end{aligned}
$$
From here $x_{1}=10, x_{2}=1 ; x_{2}=1$ does not satisfy the domain of definition.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.104. $\frac{\lg x^{2}}{\lg (6 x-5)}=1$.
|
Solution.
Domain of definition: $\left\{\begin{array}{l}x \neq 0, \\ 6 x-5>0,\end{array}, \frac{5}{6}<x \neq 1\right.$.
We have $\lg x^{2}=\lg (6 x-5)$, from which $x^{2}=6 x-5, x^{2}-6 x+5=0$, hence $x_{1}=5$ and $x_{2}=1 ; x_{2}=1$ does not satisfy the domain of definition.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.109. $5^{2 x-1}+2^{2 x}-5^{2 x}+2^{2 x+2}=0$.
|
Solution.
Write the equation as
$$
\begin{aligned}
& \frac{5^{2 x}}{5}-5^{2 x}=-2^{2 x}-4 \cdot 2^{2 x},-\frac{4}{5} \cdot 5^{2 x}=-5 \cdot 2^{2 x} \\
& \left(\frac{5}{2}\right)^{2 x}=\left(\frac{5}{2}\right)^{2}, x=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.110. $\log _{2}\left(9-2^{x}\right)=10^{\lg (3-x)}$.
7.110. $\log _{2}\left(9-2^{x}\right)=10^{\lg (3-x)}$.
|
## Solution.
Domain of definition: $\left\{\begin{array}{l}9-2^{x}>0, \\ 3-x>0,\end{array} \quad x<3\right.$.
We have $\log _{2}\left(9-2^{x}\right)=3-x, 9-2^{x}=2^{3-x}, 2^{2 x}-9 \cdot 2^{x}+8=0$. Solving this equation as a quadratic in terms of $2^{x}$, we get $\left(2^{x}\right)=1$ or $\left(2^{x}\right)_{2}=8$, hence $x_{1}=0, x_{2}=3 ; x_{2}=3$ does not satisfy the domain of definition.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.111. $\frac{1}{3} \lg \left(271+3^{2 \sqrt{x}}\right)+\lg 10=2$.
|
## Solution.
Domain: $x \geq 0$.
From the condition $\frac{1}{3} \lg \left(271+3^{2 \sqrt{x}}\right)+1=2, \lg \left(271+3^{2 \sqrt{x}}\right)=3$. Then $271+3^{2 \sqrt{x}}=$ $=1000,3^{2 \sqrt{x}}=3^{6}$, from which $\sqrt{x}=3, x=9$.
Answer: 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.112. $\left.(\sqrt[5]{27})^{\frac{x}{4}-\sqrt{\frac{x}{3}}}\right)^{\frac{x}{4}+\sqrt{\frac{x}{3}}}=\sqrt[4]{3^{7}}$.
|
## Solution.
Domain of definition: $x \geq 0$.
Rewrite the equation as $3^{\frac{3}{5}\left(\frac{x}{4}-\sqrt{\frac{x}{3}}\right)\left(\frac{x}{4}+\sqrt{\frac{x}{3}}\right)}=3^{\frac{7}{4}}$. Then
$$
\frac{3}{5}\left(\frac{x}{4}-\sqrt{\frac{x}{3}}\right)\left(\frac{x}{4}+\sqrt{\frac{x}{3}}\right)=\frac{7}{4}, 3 x^{2}-16 x-140=0
$$
from which $x_{1}=10, x_{2}=-\frac{14}{3} ; x_{2}=-\frac{14}{3}$ does not satisfy the domain of definition.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.114. $\lg (x(x+9))+\lg \frac{x+9}{x}=0$.
|
## Solution.
Domain of definition: $x(x+9)>0, x \in(-\infty ;-9) \cup(0 ; \infty)$.
We have $\lg \frac{x(x+9)(x+9)}{x}=0$, from which $(x+9)^{2}=1$. Then $(x+9)_{1}=-1$, $x_{1}=-10$ or $(x+9)_{2}=1, x_{2}=-8 ; x_{2}=-8$ does not fit the domain of definition.
Answer: -10.
|
-10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.117. $2^{\log _{3} x^{2}} \cdot 5^{\log _{3} x}=400$.
|
Solution.
Domain: $x>0$.
From the condition $4^{\log _{3} x} \cdot 5^{\log _{3} x}=400, 20^{\log _{3} x}=20^{2}$, hence $\log _{3} x=2$, $x=9$.
Answer: 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.121. $\log _{2}\left(4^{x}+4\right)=x+\log _{2}\left(2^{x+1}-3\right)$
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
7.121. $\log _{2}\left(4^{x}+4\right)=x+\log _{2}\left(2^{x+1}-3\right)$
|
## Solution.
Domain of definition: $2^{x+1}-3>0$.
Rewrite the equation as
$$
\begin{aligned}
& \log _{2}\left(2^{2 x}+4\right)-\log _{2}\left(2 \cdot 2^{x}-3\right)=x, \quad \log _{2} \frac{2^{2 x}+4}{2 \cdot 2^{x}-3}=x \\
& \frac{2^{2 x}+4}{2 \cdot 2^{x}-3}=2^{x}, 2^{2 x}-3 \cdot 2^{x}-4=0 .
\end{aligned}
$$
Solving this equation as a quadratic in terms of $2^{x}$, we get $2^{x}=-1, \varnothing$; or $2^{x}=4$, hence $x=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.127. $\log _{2}\left(25^{x+3}-1\right)=2+\log _{2}\left(5^{x+3}+1\right)$
|
Solution.
Domain of definition: $25^{x+3}-1>0, 25^{x+3}>25^{0}, x>-3$.
From the condition
$\log _{2}\left(25^{3} \cdot 25^{x}-1\right)=\log _{2} 4\left(5^{3} \cdot 5^{x}+1\right) 25^{3} \cdot 5^{2 x}-1=4 \cdot 5^{3} \cdot 5^{x}+4$, $3125 \cdot 5^{2 x}-100 \cdot 5^{x}-1=0$,
from which, solving this equation as a quadratic in terms of $5^{x}$, we have $5^{x}=-\frac{1}{125}, \varnothing ;$ or $5^{x}=5^{-2}$, from which $x=-2$.
Answer: -2.
Solve the systems of equations (7.128-7.149):
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.010. Find the positive integer values of $x$ that satisfy the inequality $\frac{5 x+1}{x-1}>2 x+2$.
|
Solution.
We have
$$
\begin{aligned}
& \frac{5 x+1}{x-1}-2 x-2>0 \Leftrightarrow \frac{5 x+1-2(x+1)(x-1)}{x-1}>0 \Leftrightarrow \frac{-2 x^{2}+5 x+3}{x-1}>0 \Leftrightarrow \\
& \Leftrightarrow\left(2 x^{2}-5 x-3\right)(x-1)<0 \Leftrightarrow 2\left(x+\frac{1}{2}\right)(x-3)(x-1)<0
\end{aligned}
$$
Using the number line, we find that $x=2$.
Answer: $\quad x=2$.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.012. Find the natural values of $x$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
\log _{\sqrt{2}}(x-1)<4 \\
\frac{x}{x-3}+\frac{x-5}{x}<\frac{2 x}{3-x}
\end{array}\right.
$$
|
Solution.
From the condition
$$
\begin{aligned}
& \left\{\begin{array} { l }
{ 0 0 \text { for } x \in R, \\
x(x-3)<0 .
\end{array}\right.
\end{aligned}
$$
Using the number line, we find the solution to the system $x=2$.
Answer: $x=2$.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.007. An isosceles trapezoid with a side length of 17 cm is circumscribed around a circle with a diameter of 15 cm. Find the bases of the trapezoid.
|
Solution.
According to the condition, $K Q=15 \mathrm{~cm}, A B=C D=17 \mathrm{~cm}, B C+A D=A B+C D=34$. In $\triangle C E D \angle C E D=90^{\circ}, C E=K Q$ (Fig. 10.7) We have $D E=\sqrt{289-225}=8 \mathrm{~cm}$, $A D=2 E D+B C=16+B C, B C+16+B C=34, B C=9 \mathrm{~cm}, A D=25 \mathrm{~cm}$.
Answer: 9 cm $; 25$ cm.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.013. Given a triangle with sides 12, 15, and \(18 \, \text{cm}\). A circle is drawn that touches both smaller sides and has its center on the larger side. Find the segments into which the center of the circle divides the larger side of the triangle.
|
## Solution.
Using the cosine theorem, from Fig. 10.13 we have:
$$
\begin{aligned}
& A B^{2}=B C^{2}+A C^{2}-2 \cdot B C \cdot A C \cdot \cos \alpha \Rightarrow \\
& \Rightarrow 12^{2}=15^{2}+18^{2}-2 \cdot 15 \cdot 18 \cos \alpha, \cos \alpha=\frac{3}{4}, \sin \alpha=\sqrt{1-\cos ^{2} \alpha}=\frac{\sqrt{7}}{4} \\
& B C^{2}=A B^{2}+A C^{2}-2 \cdot A B \cdot A C \cdot \cos \beta \Rightarrow \\
& \Rightarrow 15^{2}=12^{2}+18^{2}-2 \cdot 12 \cdot 18 \cdot \cos \beta, \cos \beta=\frac{9}{16}, \sin \beta=\sqrt{1-\cos ^{2} \beta}=\frac{5 \sqrt{7}}{16}
\end{aligned}
$$
$$
\begin{aligned}
& \sin \alpha=\frac{O M}{O C}=\frac{R}{18-x}, \sin \beta=\frac{O K}{A O}=\frac{R}{x} \text { and } \frac{\sin \alpha}{\sin \beta}=\frac{x}{18-x}=\frac{4}{5} \\
& 5 x=72-4 x, 9 x=72, x=8, y=10 . A O=8 \text{ cm}, O C=10 \text{ cm}
\end{aligned}
$$
Answer: 8 and 10 cm.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.017. Given a point $P$, which is 7 cm away from the center of a circle with a radius of $11 \mathrm{~cm}$. A chord of length 18 cm is drawn through this point. What are the lengths of the segments into which the chord is divided by point $P$?
|
## Solution.
Draw the diameter $C D$ through point $P$ (Fig. 10.17), which will divide it into segments $P D$ and $C P$ of lengths $11-7=4$ and $11+7=18$ (cm). Let $A P=x$; then $P B=18-x$. Since $A P \cdot P B=C P \cdot P D=4 \cdot 18$, we have $x(18-x)=72$ or $x^{2}-18 x+72=0$, from which $x_{1}=12, x_{2}=6$, i.e., the chord $A B$ is divided by point $P$ into segments of lengths 12 and 6 cm.
Answer: 12 and 6 cm.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.024. The lengths of the parallel sides of the trapezoid are 25 and 4 cm, and the lengths of the non-parallel sides are 20 and 13 cm. Find the height of the trapezoid.
|
## Solution.
Given $B C=4 \text{ cm}, A D=25 \text{ cm}, A B=20 \text{ cm}, C D=13 \text{ cm}$ (Fig. 10.24). Draw $B E \perp A D$ and $C F \perp A D$. Let $B E=C F=h, A E=x$, $F D=y$. Then from $\triangle A B E$ and $\triangle C F D$ we find $h^{2}=20^{2}-x^{2}=13^{2}-y^{2}$. Considering that $y=25-4-x=21-x$, we have $20^{2}-x^{2}=13^{2}-(21-x)^{2}$ or $42 x=672$, from which $x=16$ (cm). Therefore, $h=\sqrt{20^{2}-16^{2}}=12$ (cm).
Answer: 12 cm.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.033. A tangent, parallel to the base, is drawn to the circle inscribed in an isosceles triangle with a base of 12 cm and a height of 8 cm. Find the length of the segment of this tangent, enclosed between the sides of the triangle.
|
## Solution.
Let's find the length of the side $B C$ (Fig. 10.33): $B C=\sqrt{B M^{2}+M C^{2}}=$ $=\sqrt{6^{2}+8^{2}}=10$ (cm). Considering that $A O$ is the bisector of $\triangle A B M$, we have $M O / O B=A M / A B$ or $r /(8-r)=6 / 10$, from which $r=3$ (cm). Since $D E \| A C$, then $\triangle D B E \sim \triangle A B C$, i.e., $D E / A C=B N / B M$ or $D E / 12=(8-2 r) / 8$, from which $D E=3$ cm.
Answer: 3 cm.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.