problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
10.039. The lines containing the non-parallel sides of an isosceles trapezoid intersect at a right angle (Fig. 10.39). Find the lengths of the sides of the trapezoid if its area is \(12 \mathrm{~cm}^{2}\) and the height is \(2 \mathrm{~cm}\).
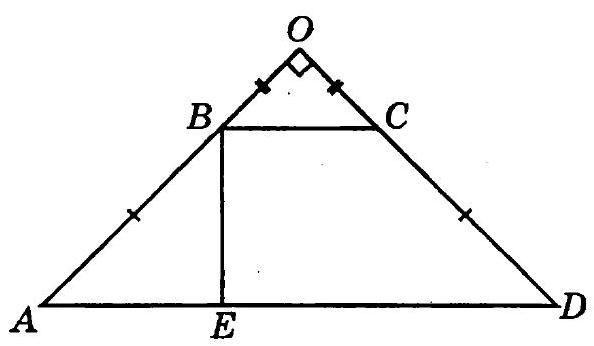
Fig. 10.39
Fig. 10.40
|
## Solution.
Given $S_{\triangle A B C D}=12 \mathrm{~cm}^{2}, B E=2 \mathrm{~cm} ; \angle O A D=\angle O D A=\frac{90^{\circ}}{2}=45^{\circ}$, $\frac{B E}{\sin 45^{\circ}}=A B, A B=\frac{2}{\sqrt{2}} \cdot 2=2 \sqrt{2}=C D, A E=B E=2, \frac{B C+A D}{2} \cdot B E=12$, $\frac{B C+A D}{2} \cdot 2=12, B C+A D=12$, then $2 B C+2 A E=12, B C+A E=6$, $B C+2=6, B C=4 \mathrm{~cm}, A D=4+4=8 \mathrm{~cm}$.
Answer: 4 and 8 cm; $2 \sqrt{2}$ and $2 \sqrt{2}$ cm.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.042. One of the angles of the trapezoid is $30^{\circ}$, and the lines containing the lateral sides of the trapezoid intersect at a right angle (Fig. 10.42). Find the length of the shorter lateral side of the trapezoid if its midline is 10 cm, and one of the bases is $8 \mathrm{~cm}$.
|
## Solution.
Given $\angle B C A=30^{\circ}, \angle A B C=90^{\circ}, K M=10$ cm, $D E=8$ cm, $\frac{8+A C}{2}=10, A C=12$ cm (since $K M$ is the midline). Since $\triangle D B E \sim \triangle A B C$, then $\frac{A B}{D B}=\frac{A C}{D E} ; \frac{x+D B}{D B}=\frac{12}{8}$ (where $A D=x$ ), $x=D B \cdot \frac{1}{2}$. In $\triangle D B E, \angle D B E=90^{\circ}, \angle B E D=\angle B C A=30^{\circ}, D B=D E \cdot \sin 30^{\circ}=8 / 2=4$, so, $x=4 \cdot \frac{1}{2}=2$ cm.
Answer: 2 cm.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.045. The common chord of two intersecting circles is seen from the centers at angles of $90^{\circ}$ and $60^{\circ}$. Find the radii of the circles if the distance between their centers is $\sqrt{3}+1$.
|
Solution.
Let $r$ be the radius of one circle, and $R$ be the radius of the other circle. According to the problem, $\angle A O_{1} B=90^{\circ}, \angle A O_{2} B=60^{\circ}, O_{1} O_{2}=\sqrt{3}+1 ; A B=r \sqrt{2} ;$ $O_{1} E=A B / 2 ; O_{1} E=r \frac{\sqrt{2}}{2}, A B=2 R \cdot \sin 30^{\circ}=R\left(\angle A O_{2} E=\frac{\angle A O_{2} B}{2}\right)$, therefore, $R=r \sqrt{2}, E O_{2}=R \frac{\sqrt{3}}{2}=r \frac{\sqrt{6}}{2}, O_{1} O_{2}=O_{1} E+O_{2} E=\frac{r \sqrt{6}}{2}+\frac{r \sqrt{2}}{2}=$ $=\sqrt{3}+1, r(\sqrt{6}+\sqrt{2})=(\sqrt{3}+1) \cdot 2, r=\sqrt{2} ; R=\sqrt{2} \cdot \sqrt{2}=2$ (Fig. 10.45).
Answer: 2 and $\sqrt{2}$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.051. Three circles of different radii touch each other pairwise. The segments connecting their centers form a right triangle. Find the radius of the smallest circle, if the radii of the largest and medium circles are 6 and 4 cm.
|
Solution.
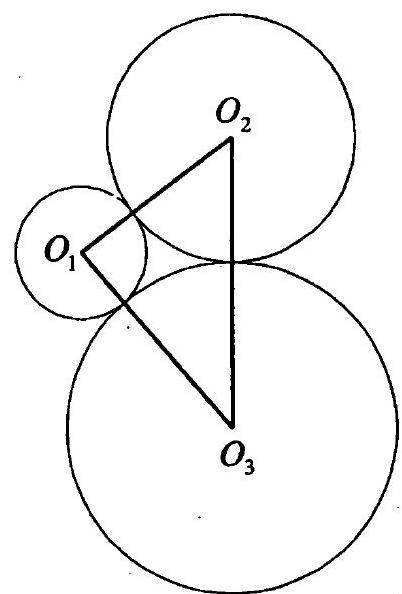
Fig. 10.51
Fig. 10.52
Let $r$ be the radius of the smaller circle. Then $O_{1} O_{2}=r+4$, $O_{1} O_{3}=r+6$ (Fig. 10.51). Since $O_{2} O_{3}^{2}=O_{1} O_{2}^{2}+O_{1} O_{3}^{2}$, we have $10^{2}=(r+4)^{2}+(r+6)^{2}, r^{2}+10 r-24=0$, from which $r=2$ cm (the root $r=-12$ does not satisfy the condition).
Answer: $2 \text{ cm}$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.064. The lateral side of an isosceles triangle is $10 \mathrm{~cm}$, and the base is $12 \mathrm{~cm}$. Tangents are drawn to the inscribed circle of the triangle, parallel to the height of the triangle, and cutting off two right triangles from the given triangle. Find the lengths of the sides of these triangles.
|
## Solution.
The area of the triangle is found using the formula (Fig. 10.63):
$$
S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{16(16-10)(16-10)(16-12)}=48
$$
The radius of the inscribed circle $r=\frac{S}{p}=\frac{48}{16}=3$ (cm); $r=D H . H C=D C-$ $-D H=6-3=3 \text{ cm} ; \triangle B C D$ and $\triangle F C H$ are similar, so $\frac{D C}{H C}=\frac{B C}{F C}$. Therefore, $F C=\frac{B C \cdot H C}{D C}=\frac{10 \cdot 3}{6}=5$ cm. From $\triangle F C H$ it follows that $F C^{2}=$ $=F H^{2}+H C^{2} ; F H=\sqrt{F C^{2}-H C^{2}}=\sqrt{5^{2}-3^{2}}=4$ (cm).
## Answer: 3 cm, 4 cm, 5 cm.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.096. The area of an isosceles trapezoid circumscribed around a circle is $32 \sqrt{3} \mathrm{~cm}^{2}$ (Fig. 10.92). Determine the lateral side of the trapezoid, given that the acute angle at the base is $\pi / 3$.
|
Solution.
$\triangle C E D-$ is a right triangle and $\sin 60^{\circ}=\frac{2 R}{C D}$. Therefore, $2 R=\frac{\sqrt{3}}{2} C D$, $C D=x \Rightarrow 2 R=\frac{\sqrt{3}}{2} x$. The area of the trapezoid $S=\frac{a+b}{2} h=2 R x=\frac{\sqrt{3}}{2} x^{2}$. According to the condition $\frac{\sqrt{3}}{2} x^{2}=32 \sqrt{3} \Rightarrow x^{2}=64, x=8$ (cm).
Answer: 8 cm.
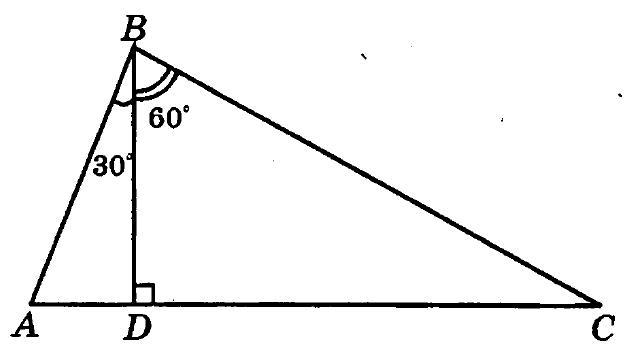
Fig. 10.93
Fig. 10.94
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.142. A circle is inscribed in an equilateral triangle, and a regular hexagon is inscribed in the circle. Find the ratio of the areas of the triangle and the hexagon.
|
## Solution.
Let the side of the equilateral triangle be $a$. Then its area $S_{1}=\frac{a^{2} \sqrt{3}}{4} \cdot$ The radius of the circle inscribed in the triangle, $r=\frac{a \sqrt{3}}{6}$.
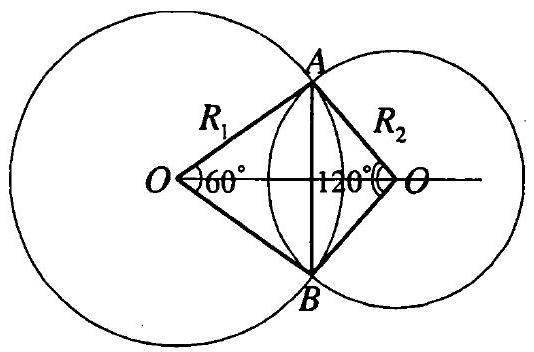
Fig. 10.128
Fig. 10.129
It will be equal to the side of the hexagon inscribed in this circle: $a_{6}=\frac{a \sqrt{3}}{6} \cdot$ And the radius of the circle inscribed in this hexagon:
$$
r=\frac{a_{6}}{2 \operatorname{tg} \frac{180^{\circ}}{6}}=\frac{a_{6} \sqrt{3}}{2}=\frac{a}{4}
$$
The area of the hexagon
$$
S_{2}=\frac{6 a_{5} r}{2}=\frac{a^{2} \sqrt{3}}{8} ; \frac{S_{1}}{S_{2}}=\frac{a^{2} \sqrt{3} \cdot 8}{4 a^{2} \sqrt{3}}=2
$$
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.147. In a parallelogram with a perimeter of 32 cm, the diagonals are drawn. The difference between the perimeters of two adjacent triangles is 8 cm. Find the lengths of the sides of the parallelogram.
|
Solution.
Let the sides of the parallelogram be denoted by $a$ and $b$. Then its perimeter is $p=2(a+b)=32$. The perimeter of one triangle is $p_{1}=b+\frac{d_{1}}{2}+\frac{d_{2}}{2}$, and the second is $p_{2}=a+\frac{d_{1}}{2}+\frac{d_{2}}{2}$, where $d_{1}, d_{2}$ are the diagonals of the parallelogram. The difference $p_{1}-p_{2}=b-a=8$. We obtain the system: $\left\{\begin{array}{l}a+b=16, \\ b-a=8 .\end{array}\right.$ Solving it, we find $a=4, b=12$.
Answer: 12 cm, 4 cm.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.157. Through points $R$ and $E$, belonging to sides $A B$ and $A D$ of parallelogram $A B C D$, and such that $A R=(2 / 3) A B, A E=(1 / 3) A D$, a line is drawn. Find the ratio of the area of the parallelogram to the area of the resulting triangle.
|
## Solution.
Let $h$ be the height of parallelogram $ABCD$, and $h_{1}$ be the height of triangle $ARE$ (Fig. 10.134). Then $S_{ABCD} = AD \cdot h$, and $S_{\triangle ARE} = \frac{1}{2} AE \cdot h_{1}$. But $\frac{h}{h_{1}} = \frac{AB}{AR} = \frac{3}{2}$. Therefore, $\frac{S_{ABCD}}{S_{\triangle ARE}} = \frac{AD \cdot h}{\frac{1}{2} AE \cdot h_{1}} = \frac{AD \cdot h}{\frac{1}{2} \cdot \frac{1}{3} AD \cdot \frac{2}{3} h} = 9$.
Answer: 9.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.189. A square is inscribed in a segment whose arc is $60^{\circ}$. Calculate the area of the square if the radius of the circle is $2 \sqrt{3}+\sqrt{17}$.
|
Solution.
Let $B C=C D=D A=A B=x$ (Fig. 10.156). Consider $\triangle O N C$,

Fig. 10.156
Fig. 10.157
$\angle O N C=90^{\circ}$. We have $O N^{2}+N C^{2}=O C^{2}$, where $O C=R=2 \sqrt{3}+\sqrt{17}$. $O N \doteq$ $=O M+M N=O M+x, N C=\frac{x}{2}$. In $\triangle O M F \quad \angle O M F=90^{\circ}, \angle M O F=$ $=\frac{\angle E O F}{2}=30^{\circ}$, then $O M=O F \cdot \frac{\sqrt{3}}{2}=R \cdot \frac{\sqrt{3}}{2}$, therefore, $O N=$ $=\frac{R \sqrt{3}}{2}+x$. Thus, we have $\left(\frac{R \sqrt{3}}{2}+x\right)^{2}+\frac{x^{2}}{4}=R^{2}$. Solving the quadratic equation, we get $x=\frac{2 R}{10}(\sqrt{17}-2 \sqrt{3}) ; S_{A B C D}=x^{2}$; $x=\frac{(2 \sqrt{3}+\sqrt{17})(\sqrt{17}-2 \sqrt{3})}{5}=1, S_{A B C D}=1$.
Answer: 1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.007. Find the ratio of the volume of a cube to the volume of a regular tetrahedron, the edge of which is equal to the diagonal of the face of the cube.
|
## Solution.
For a tetrahedron where all edges are equal, denote the edges as $a$. The radius of the circumscribed circle around the base of the tetrahedron is $R=\frac{a \sqrt{3}}{3}$. The foot of the height $H$ is the center of the circumscribed circle around $\triangle A B C$ (see Fig. 11.5). Therefore, $H=\sqrt{a^{2}-R^{2}}=\frac{\sqrt{2} a}{\sqrt{3}}$ and the volume $V_{1}=\frac{1}{3} S_{\text {base }} \cdot H$. Since $\triangle A B C$ is equilateral, $S_{\text {base }}=\frac{a^{2} \sqrt{3}}{4}$. Thus, $V_{1}=\frac{a^{3} \sqrt{2}}{12}$. Let the edge of the cube be $b$. The diagonal of the cube is $b \sqrt{2}$. It is equal to the edge of the tetrahedron $b \sqrt{2}=a$, hence $b=\frac{a}{\sqrt{2}}$. The volume of the cube $V_{2}=b^{3}=\frac{a^{3}}{2 \sqrt{2}}$. The ratio $\frac{V_{2}}{V_{1}}=\frac{a^{3} \cdot 12}{2 \sqrt{2} \cdot a^{3} \sqrt{2}}=3$.
Answer: 3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.073. The measurements of a rectangular parallelepiped are 2, 3, and 6 cm. Find the length of the edge of a cube such that the volumes of these bodies are in the same ratio as their surface areas.
|
Solution.
The volume of a rectangular parallelepiped is $V_{\text {par }}=2 \cdot 3 \cdot 6=36 \mathrm{~cm}^{3}$. The volume of a cube is $V_{\mathrm{x}}=a^{3}$. The area of the complete surface of a rectangular parallelepiped is calculated as follows: $S_{\text {par }}=S_{\text {side }}+2 S_{\text {base }}=P H+2 S_{\text {base }}=2(2+3) \cdot 6+$ $+2 \cdot 3 \cdot 2=72 \mathrm{~cm}^{2}$. The area of the complete surface of a cube is $S_{\mathrm{K}}=6 a^{2}$. From the condition $\frac{V_{\text {par }}}{V_{\mathrm{K}}}=\frac{S_{\text {par }}}{S_{\mathrm{K}}}$. Hence, $\frac{36}{a^{3}}=\frac{72}{6 a^{2}}$. We get $a=3$ cm.
Answer: 3 cm.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.011. Due to the reconstruction of equipment, the labor productivity of a worker increased twice during the year by the same percentage. By what percentage did the labor productivity increase each time, if during the same time a worker used to produce goods worth 2500 rubles, and now produces goods worth 2809 rubles?
|
Solution.
Let a worker produce a parts in 8 hours of work. Then the rate is $\frac{2500}{a}$ rubles per part, and the labor productivity is $\frac{a}{8}$ parts per hour. After the first increase in productivity by $x \%$, the worker started producing $\frac{a}{8}+\frac{x \cdot a}{100 \cdot 8}$ parts per hour; after the second increase in productivity by $x \% - \frac{a}{8}\left(1+\frac{x}{100}\right)\left(1+\frac{x}{100}\right)$ parts per hour. In 8 hours, he started producing $a\left(1+\frac{x}{100}\right)^{2}$ parts and earned $a\left(1+\frac{x}{100}\right)^{2} \cdot \frac{2500}{a}$ rubles. According to the condition, $a\left(1+\frac{x}{100}\right)^{2} \cdot \frac{2500}{a}=2809$, from which $x=6 \%$.
Answer: $6 \%$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.019. Two snow-clearing machines are working on snow removal. The first can clear the entire street in 1 hour, while the second can do it in $75\%$ of this time. Starting the cleaning simultaneously, both machines worked together for 20 minutes, after which the first machine stopped. How much more time is needed for the second machine to finish the work?
|
## Solution.
Let's consider the entire volume of work as 1. The productivity of the first machine is 1 (per hour), and the second machine's productivity is $1: \frac{3}{4}=\frac{4}{3}$ (per hour). Working together for $\frac{1}{3}$ of an hour, they will complete $\frac{1}{3} \cdot 1 + \frac{1}{3} \cdot \frac{4}{3} = \frac{7}{9}$ of the entire work. Then, the remaining work for the second machine will be $\frac{2}{9}$, which will require $\frac{2}{9} : \frac{4}{3} = \frac{1}{6}$ (hours).
Answer: 10 min.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.020. The sum of the first three terms of the proportion is 58. The third term is $2 / 3$, and the second term is $3 / 4$ of the first term. Find the fourth term of the proportion and write it down.
|
Solution.
Let the proportion be $\frac{a}{b}=\frac{c}{d}$. Given that $a+b+c=58$; $c=\frac{2}{3} a$; $b=\frac{3}{4} a$. Therefore, $a+\frac{3}{4} a+\frac{2}{3} a=58$, from which $a=24$; $c=16$; $b=18$. Thus, $d=\frac{b c}{a}=12$.
Answer: $12 ; \frac{24}{18}=\frac{16}{12}$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.021. One brigade can harvest the entire field in 12 days. The second brigade needs $75\%$ of this time to complete the same work. After the first brigade worked alone for 5 days, the second brigade joined, and together they finished the work. How many days did the brigades work together?
|
## Solution.
Let the teams work together for $x$ days. The productivity of the first team is $-\frac{1}{12}$; the productivity of the second team is $-\frac{1}{12 \cdot 0.75}=\frac{1}{9}$. According to the condition, $\frac{1}{12} \cdot 5+\left(\frac{1}{12}+\frac{1}{9}\right) \cdot x=1$, from which $x=3$ days.
Answer: 3 days.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.026. A tourist traveled 90 km by boat along the river and walked 10 km on foot. For the walking route, 4 hours less were spent compared to the river journey. If the tourist had walked for as long as he had rowed, and rowed for as long as he had walked, these distances would have been equal. How long did he walk and how long did he row?
|
## Solution.
Let $x$ be the number of hours the tourist walked. Then he spent $(x+4)$ hours on the boat. The tourist's walking speed is $\frac{10}{x}$ km/h; the speed on the boat is $-\frac{90}{x+4}$ km/h. According to the problem, $\frac{10}{x}(x+4)=\frac{90}{x+4} \cdot x$, from which $x=2$ hours.
Answer: 2 and 6 hours.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.032. In 3.5 hours of operation, one stamping press can produce $42\%$ of all ordered parts. The second press can produce $60\%$ of all parts in 9 hours, and the work speeds of the third and second presses are in the ratio of $6:5$. How long will it take to complete the entire order if all three presses work simultaneously?
|
Solution.
Let $x$ parts be the entire order. Then the working speed of the first press is $-\frac{0.42 x}{3.5}$ parts/hour; the second press is $\frac{0.6 x}{9}$ parts/hour; the third press is $\frac{6}{5} \cdot \frac{0.6 x}{9}$ parts/hour. Therefore, all three presses working simultaneously will complete the entire order in $\frac{x}{\frac{0.6 x}{9}+\frac{0.42 x}{3.5}+\frac{6}{5} \cdot \frac{0.6 x}{9}}=3.75$ (hours) $=3$ hours 45 minutes.
Answer: $i n ~ 3$ hours 45 minutes.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.033. Each of the two typists retyped a manuscript of 72 pages. The first typist retyped 6 pages in the same time it took the second to retype 5 pages. How many pages did each typist retype per hour, if the first finished the work 1.5 hours faster than the second?
|
Solution.
Let $x$ pages per hour be the typing speed of the first typist, then the second typist's speed is $\frac{5}{6} x$. The first typist worked $\frac{72}{x}$ hours; the second - $\frac{72}{5}$ hours. According to the problem, $\frac{72}{x}=\frac{72}{\frac{5}{6} x}-1.5$, from which $x=9.6($ pages/hour); the second typist typed $\frac{5}{6} \cdot 9.6=8$ pages/hour.
Answer: 8 and 9.6 pages/hour.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.051. Two cylinders roll down an inclined board 6 m long, one of which has a circumference of 3 dm, and the other 2 dm. Can the circumferences of both cylinders be increased by the same amount so that on the same path one of them makes 3 more revolutions than the other?
|
Solution.
Assume that the lengths of the circumferences can be increased by $x$ dm. Then the first cylinder will make $\frac{60}{3+x}$ revolutions, and the second will make $-\frac{60}{2+x}$. According to the condition, $\frac{60}{3+x}+3=\frac{60}{2+x}$, from which we get $x^{2}+5 x-14=0$. Solving this equation, we find that the lengths of the circumferences can be increased by $x=2$ dm.
Answer: can be increased by 2 dm.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.061. To pay for the delivery of four parcels, 4 different postage stamps were needed for a total of 84 kopecks. Determine the cost of the stamps purchased by the sender, if these costs form an arithmetic progression, and the most expensive stamp is 2.5 times more expensive than the cheapest one.
|
Solution.
Let $x$ kop. - the cost of the cheapest stamp, $x+d, x+2 d$, $x+3 d$ - the costs of the other stamps. By condition
$$
\left\{\begin{array}{l}
x+x+d+x+2 d+x+3 d=84, \\
x+3 d=2.5 x,
\end{array} \text { from which } x=12 ; d=6\right. \text {. Costs of the }
$$
stamps: 12 kop., 18 kop., 24 kop, 30 kop.
Answer: 12 kop., 18 kop., 24 kop, 30 kop.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.064. The hay reserve is such that 96 kg can be issued daily for all the horses. In fact, the daily portion for each horse could be increased by 4 kg because two horses were sold. How many horses were there originally?
|
Solution.
Let there initially be $x$ horses. The daily portion for each horse was $\frac{96}{x}$ kg. Since two horses were sold to another collective farm, the number of horses became $x-2$, and the daily portion for each horse became $\frac{96}{x}+4$ kg. According to the condition, $\left(\frac{96}{x}+4\right)(x-2)=96$, from which $x=8$.
Answer: 8.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.069. In one pool there are 200 m $^{3}$ of water, and in another - 112 m $^{3}$. Taps are opened, through which the pools are filled. After how many hours will the amount of water in the pools be the same, if 22 m $^{3}$ more water is poured into the second pool per hour than into the first?
|
Solution.
Let the amount of water in the pools become equal after $x$ hours. Let $y$ m$^{3}$ of water be added to the first pool per hour, and $y+22$ m$^{3}$ - to the second. According to the condition, $200+x y=112+x(y+22)$, from which $x=4$.
Answer: in 4 hours.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.082. Two groups of tourists must walk towards each other from tourist bases $A$ and $B$, the distance between which is 30 km. If the first group leaves 2 hours earlier than the second, they will meet 2.5 hours after the second group leaves. If the second group leaves 2 hours earlier than the first, the meeting will occur 3 hours after the first group leaves. At what average speed does each group walk?
|
Solution.
Let $x$ km/h be the speed of the first group, $y$ km/h be the speed of the second. If the first group starts earlier than the second, then $2.5 y + (2.5 + 2) x = 30$. If the second group starts earlier than the first, then $3 x + (3 + 2) y = 30$. Solving the system $\left\{\begin{array}{l}2.5 y + 4.5 x = 30, \\ 3 x + 5 y = 30,\end{array}\right.$ we find $x = 5$ km/h, $y = 3$ km/h.
Answer: 5 and 3 km/h.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.085. Two brothers took their bicycles and set off simultaneously with the intention of riding $42 \mathrm{km}$. The older brother maintained the same speed throughout the journey; while the younger brother fell behind by 4 km every hour. However, since the older brother rested for a whole hour during the trip, and the younger brother only rested for 20 minutes, they arrived at the finish line simultaneously. How long did the trip last?
|
## Solution.
Let $x$ km/h be the speed of the older brother, then $(x-4)$ km/h is the speed of the younger brother. The older brother was on the road for $t_{\text {old }}=\frac{42}{x}+1$, and the younger brother for $t_{\text {young }}=\frac{42}{x-4}+\frac{1}{3}$. According to the problem, $t_{\text {old }}=t_{\text {young }}$, that is, $\frac{42}{x}+1=\frac{42}{x-4}+\frac{1}{3}$, from which $x=18$ and $t=1+\frac{42}{18}=3 \frac{1}{3}$.
Answer: 3 hours 20 minutes.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.086. A positive integer is thought of. To its notation, the digit 7 is appended on the right, and from the resulting new number, the square of the thought number is subtracted. The remainder is reduced by $75\%$ of this remainder, and the thought number is subtracted again. In the final result, zero is obtained. What number was thought of?
|
Solution.
Let the number be $x$. Consider the numbers $10 x+7, 10 x+7-x^{2}$, and the remainder $\frac{25}{100}\left(10 x+7-x^{2}\right)$. Then $\frac{1}{4}\left(10 x+7-x^{2}\right)-x=0, x^{2}-6 x-7=0 \Rightarrow$ $\Rightarrow x=7$
Answer: 7.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.087. A positive integer is thought of. The digit 5 is appended to its right, and from the resulting new number, the square of the thought number is subtracted. The difference is divided by the thought number, and then the thought number is subtracted, and the result is one. What number is thought of?
|
## Solution.
Let $x$ be the number thought of. Then the new number can be represented as $10 x + 5$. According to the condition, $\frac{10 x + 5 - x^2}{x} - x = 1$, from which $x = 5$.
Answer: 5.
Fig. 13.6
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.098. A pedestrian and a cyclist set off simultaneously towards each other from cities $A$ and $B$, the distance between which is 40 km, and meet 2 hours after departure. Then they continue their journey, with the cyclist arriving in $A$ 7 hours and 30 minutes earlier than the pedestrian in $B$. Find the speeds of the pedestrian and the cyclist, assuming that they remained constant throughout.
|
Solution.
We will fill in the table of speed, distance, and time values in the order indicated by the numbers (1), (2), ..., (12):
| Tourist | Before Meeting | | | After Meeting | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | speed, km $/ \mathbf{4}$ | time, h | distance, | speed, km $/ \mathbf{4}$ | time, | distance, km |
| Pedestrian | (1) $x$ | (3) 2 | (5) $2 x$ | (7) $x$ | (11) $40-2 x$ | (9) $40-2 x$ |
| Cyclist | (2) $20-x$ | (4) 2 | (6) $40-2 x$ | (8) $20-x$ | (12) $\frac{2 x}{20-x}$ | (10) $2 x$ |
According to the condition $\frac{40-2 x}{x}-\frac{2 x}{20-x}=\frac{15}{2}$, from which $x=4$ (km/h).
Answer: 4 and 16 km/h.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.103. From the railway station to the tourist base, one can walk along the highway or a path, with the path being 5 km shorter. Two friends agreed that one would walk along the highway at a constant speed of $\mathrm{v}$ km/h, while the other would take the path at a speed of 3 km/h. The second one arrived at the tourist base 1 hour earlier than the first. Find the distance from the station to the tourist base along the highway and the speed $v$ of the first friend, given that $v$ is an integer.
|
Solution.
Let $x$ km be the distance from the station to the tourist base by road, and $x-5$ km by trail. According to the problem, $\frac{x}{v}-\frac{x-5}{3}=1$, from which $x=\frac{2 v}{v-3}$. The expression makes sense for $v>3$. By trial, we find: at $v=4$ km/h, $x=8$ km. Other solutions to this equation do not satisfy the condition $x-5>0$.
Answer: 8 km, 4 km/h.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.109. Two cyclists set off simultaneously towards each other from two places, the distance between which is 270 km. The second cyclist travels 1.5 km less per hour than the first, and meets him after as many hours as the first cyclist travels in kilometers per hour. Determine the speed of each cyclist.
|
## Solution.
Let $x$ km/h be the speed of the first cyclist, and $x-1.5$ km/h be the speed of the second cyclist. Before they meet, the first cyclist traveled $x \cdot x$ km, and the second cyclist traveled $x(x-1.5)$ km. According to the problem, $x^{2}+x(x-1.5)=270$, from which $x=12$ km/h; $12-1.5=10.5$ km/h.
Answer: 12 and 10.5 km/h.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.112. Two bodies move towards each other from two places, the distance between which is 390 km. The first body traveled 6 m in the first second, and in each subsequent second, it traveled 6 m more than in the previous one. The second body moved uniformly at a speed of $12 \mathrm{~m} / \mathrm{c}$ and started moving 5 seconds after the first. After how many seconds from the start of the first body will they meet?
|
## Solution.
Let $t$ s be the time of movement of the first body until the meeting; $t-5$ s of the second. The first traveled until the meeting $\frac{a t^{2}}{2}=\frac{6 t^{2}}{2}=3 t^{2}$ km; the second $12(t-5)$ km. According to the condition $3 t^{2}+12(t-5)=360$, from which $t=10$ s.
Answer: in $10 \mathrm{s}$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.148. A photograph measuring $12 \times 18$ cm is inserted into a frame of constant width. Determine the width of the frame if its area is equal to the area of the photograph itself.
|
## Solution.
Let $x$ cm be the width of the frame (Fig. 13.9). Then its area is $2 \cdot 12 x + 2(18 + 2 x) x$ cm. According to the condition, $2 \cdot 12 x + 2(18 + 2 x) x = 12 \cdot 18$, from
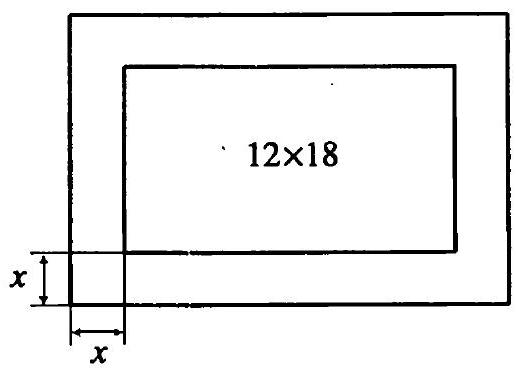
Fig. 13.9 where $x=3$ cm.
Answer: 3 cm.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.153. A plot in the shape of a rectangle with a diagonal of 185 m was allocated for a sports field. During construction, the length of each side was reduced by 4 m. The rectangular shape was maintained, but the area was reduced by \(1012 \mathrm{~m}^{2}\). What are the actual dimensions of the sports field?
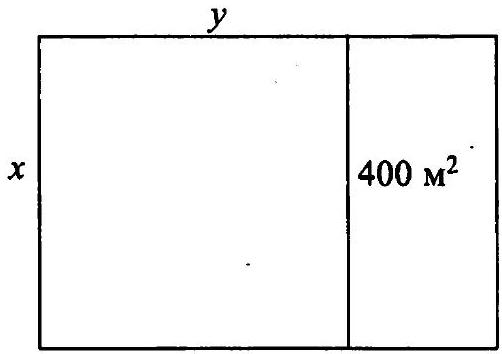
Fig. 13.10
|
Solution.
Let $x$ be the length and $y$ be the width of the plot. By the Pythagorean theorem, $x^{2}+y^{2}=185^{2}$. Additionally, $(x-4)(y-4)=x y-1012$, from which $x y-4(x+y)=$ $=x y-1028 ; x+y=257 ; y=257-x$. Solving the quadratic equation $x^{2}+(257-x)^{2}-185^{2}=0$, we find $x_{1}=104, x_{2}=153$.
Answer: $100 \times 149$ m.
13.154.3a 1 kg of one product and 10 kg of another cost 20 rubles. If, due to seasonal price changes, the first product increases in price by $15 \%$, and the second decreases in price by $25 \%$, then the same amount of these products will cost 18 rubles 20 kopecks. What is the cost of 1 kg of each product?
Solution.
Let $x$ rubles be the price of one product, and $y$ rubles be the price of the other. According to the problem, $x+10 y=20$. With the seasonal price changes, 1 kg of the first product will cost $1.15 x$ rubles, and 1 kg of the second product will cost $0.75 y$ rubles. Then $1.15 x+10 \cdot 0.75 y=18.2$. Solving the system $\left\{\begin{array}{l}1.15 x+0.75 \cdot 10 y=18.2, \\ x+10 y=20,\end{array}\right.$ we find $x=8$ rubles, $y=1.2$ rubles.
Answer: 8 rubles and 1 ruble 20 kopecks.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.156. A motorboat with a speed of 20 km/h traveled the distance between two points along the river and back without stopping in 6 hours and 15 minutes. The distance between the points is 60 km. Determine the speed of the river current.
|
Solution.
Let $v_{\text {r }}$ km/h be the speed of the river current; the boat traveled 60 km downstream in $\frac{60}{20+v_{\mathrm{r}}}$ hours, and upstream in $\frac{60}{20-v_{\mathrm{r}}}$ hours. According to the problem, $\frac{60}{20+v_{\mathrm{r}}}+\frac{60}{20-v_{\mathrm{r}}}=6.25$, from which $v_{\mathrm{r}}=4$ km/h.
Answer: 4 km/h.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.162. A certain product was purchased in the fall for 825 rubles. A kilogram of this product in the fall was 1 ruble cheaper than in the spring, and therefore, for the same amount in the spring, 220 kg less was purchased. How much does 1 kg of the product cost in the spring and how much of it was purchased in the fall?
|
## Solution.
Let $x$ kg of the product be purchased in the fall. In the spring, $x-220$ kg of the product was purchased for the same amount of money. The cost of 1 kg in the fall is $\frac{825}{x}$ rubles, and in the spring it is $\frac{825}{x-220}$ rubles. According to the condition, $\frac{825}{x-220}-\frac{825}{x}=1$, from which $x=550$ kg. The cost of 1 kg of the product in the spring is $\frac{825}{550-220}=2$ rubles 50 kopecks.
Answer: 2 rubles 50 kopecks; 550 kg.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.168. A one-digit number was increased by 10 units. If the resulting number is increased by the same percentage as the first time, the result is 72. Find the original number.
|
Solution.
Let $x$ be the number we are looking for, which was increased by $y \cdot 100\%$. Then $x+10=y x$, from which $y=\frac{x+10}{x}$. According to the condition $(x+10) \cdot \frac{x+10}{x}=72$, from which $x=2$.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.181. A team of workers was supposed to manufacture 7200 parts per shift, with each worker making the same number of parts. However, three workers fell ill, and therefore, to meet the entire quota, each of the remaining workers had to make 400 more parts. How many workers were in the team?
|
Solution.
Let there be $x$ workers in the team. Each worker made $\frac{7200}{x}$ parts. After the team size was reduced to $x-3$ workers, each worker started making $\frac{7200}{x}+400$ parts. According to the condition, $\left(\frac{7200}{x}+400\right)(x-3)=7200$, from which $x=9$.
## Answer: 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.191. Two forces are applied to a material point, the angle between which is $30^{\circ}$. The magnitude of one of the applied forces is $7 \sqrt{3}$ times the magnitude of the other, and the magnitude of the resultant force is $24 \mathrm{N}$ greater than the magnitude of the smaller force. Determine the magnitude of the smaller force and the resultant force.
|
## Solution.
Let $x \mathrm{H}$ be the modulus of the smaller force (Fig. 13.11). By the cosine rule: $\quad(24+x)^{2}=x^{2}+(7 \sqrt{3} x)^{2}-2 x \cdot 7 \sqrt{3} x \cdot \cos \left(180^{\circ}-30^{\circ}\right)$, from which $x=2 \mathrm{H}$ is the modulus of the smaller force; $24+2=26 \mathrm{H}$ is the modulus of the resultant force.
Answer: 2 and $26 \mathrm{H}$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.193. During exercises, a reconnaissance boat approached the lead ship of the squadron and received an order to conduct reconnaissance ahead of the squadron in the direction of its movement at a distance of 70 km. Determine how long it will take for the boat to return to the lead ship of the squadron, which continues to move forward, if it is known that the speed of the boat is 28 km/h, and the squadron must move at a speed of 14 km/h.
|
Solution.
Let the boat return to the lead ship after $x$ hours. In this time, the squadron will travel $14 x$ km. Therefore, the boat must travel $70+70-14 x$ km. According to the condition, $140-14 x=28 x$, from which $x=3 \frac{1}{3}$ hours.
Answer: in 3 hours 20 minutes.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.194. The front wheel of a moving model makes 6 more revolutions than the rear wheel over a distance of 120 m. If the circumference of the front wheel is increased by $1 / 4$ of its length, and the circumference of the rear wheel is increased by $1 / 5$ of its length, then over the same distance, the front wheel will make 4 more revolutions than the rear wheel. Find the lengths of the circumferences of the front and rear wheels.
|
Solution.
The circumference of the wheel $C$, the number of revolutions $n$, and the distance $s$ are related by the formula $\mathrm{Cn}=s$. We will fill in the table of values for these quantities in the order indicated by the numbers (1), (2), ..., (12):
| Wheel | Before change | | | After change | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | $C$ | $s$ | $n$ | $C$ | $s$ | $n$ |
| Front | (1) $x$ | (3) 120 | (5) $\frac{120}{x}$ | (7) $\frac{5 x}{4}$ | (9) 120 | (11) $\frac{120 \cdot 4}{5 x}$ |
| Rear | (2) $y$ | (4) 120 | (6) $\frac{120}{y}$ | (8) $\frac{6 y}{5}$ | (10) 120 | (12) $\frac{120 \cdot 5}{6 y}$ |
According to the problem, we have the system $\left\{\begin{array}{l}\frac{120}{x}-\frac{120}{y}=6, \\ \frac{96}{x}-\frac{100}{y}=4,\end{array}\right.$ from which $x=4$ (m), $y=5$ (m).
Answer: 4 and $5 \mathrm{m}$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.197. A cinema hall has two doors, a wide one and a narrow one. After a screening, the audience exits the hall through both doors in 3 minutes and 45 seconds. If the audience is let out through only the wide door, it takes 4 minutes less than if they are let out through only the narrow door. How much time is required for the audience to exit the cinema hall through each door separately?
|
## Solution.
Let $x$ min be necessary to release the audience only through the wide door, $(x+4)$ min - only through the narrow door. In one minute, $\frac{1}{x}$ people exit through the wide door, and $\frac{1}{x+4}$ people exit through the narrow door. According to the condition: $\frac{1}{x}+\frac{1}{x+4}=\frac{1}{3 \frac{3}{4}}$, from which $x=6$ min.
Answer: 6 and 10 min.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2.322 A=\sqrt{y^{2}-6 y+9}-|y-9|+2$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
$2.322 A=\sqrt{y^{2}-6 y+9}-|y-9|+2$.
|
Solution. $A=\sqrt{(y-3)^{2}}-|y-9|+2=|y-3|-|y-9|+2$.
Consider 3 cases.
1) $\left\{\begin{array}{l}y9, \\ A=y-3-(y-9)+2\end{array} \Leftrightarrow\left\{\begin{array}{l}y>9, \\ A=8 .\end{array}\right.\right.$
Answer: if $y>9$, then $A=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.275 $\frac{2+x}{2-x}+\sqrt{x}=1+x$
|
Solution. $\frac{2+x}{2-x}-1=x-\sqrt{x} \Leftrightarrow \frac{2 x}{2-x}=\sqrt{x}(\sqrt{x}-1)$. Let $y=\sqrt{x}$, then $\frac{2 y^{2}}{2-y^{2}}=y(y-1) \Leftrightarrow\left[\begin{array}{l}y=0, \\ y \neq \sqrt{2}, \\ y^{3}-y^{2}+2=0\end{array} \Leftrightarrow\right.$ $\Leftrightarrow\left[\begin{array}{l}y=0 . \\ (y+1)\left(y^{2}-2 y+2\right)=0\end{array} \Leftrightarrow \sqrt{x}=0\right.$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.277 \sqrt{x-1}+\sqrt{x+3}+2 \sqrt{(x-1)(x+3)}=4-2 x
$$
6.277 \sqrt{x-1}+\sqrt{x+3}+2 \sqrt{(x-1)(x+3)}=4-2 x
$$
|
Solution. Let $u=\sqrt{x-1}, v=\sqrt{x+3}$, then $u+v+2uv=-(u^2+v^2)+6 \Leftrightarrow$ $(u+v)^2+(u+v)-6=0 \Leftrightarrow\left[\begin{array}{l}u+v=-3, \\ u+v=2\end{array} \Leftrightarrow\left[\begin{array}{l}\varnothing, \\ \sqrt{x-1}+\sqrt{x+3}=2 .\end{array}\right.\right.$
Since $x \geq 1$, then $\sqrt{x+3} \geq 2 \Rightarrow x=1$ is the only solution to the last equation.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.278 \sqrt{2 x+3}+\sqrt{x+1}=3 x+2 \sqrt{2 x^{2}+5 x+3}-16$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
$6.278 \sqrt{2 x+3}+\sqrt{x+1}=3 x+2 \sqrt{2 x^{2}+5 x+3}-16$.
|
Solution. $\sqrt{2 x+3}+\sqrt{x+1}=3 x-16+2 \sqrt{(2 x+3)(x+1)}$.
Let $u=\sqrt{2 x+3}, v=\sqrt{x+1}$, then $u+\dot{v}=u^{2}+v^{2}-20+2 u v \Leftrightarrow$
$$
\Leftrightarrow(u+v)^{2}-(u+v)-20=0 . \Leftrightarrow\left[\begin{array}{l}
u+v=5, \\
u+v=-4
\end{array} \Leftrightarrow \sqrt{2 x+3}+\sqrt{x+1}=5 \Leftrightarrow\right.
$$
$$
\begin{aligned}
& \Leftrightarrow\left\{\begin{array} { l }
{ x \geq - 1 , } \\
{ 3 x + 4 + 2 \sqrt { ( 2 x + 3 ) ( x + 1 ) } = 2 5 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq-1, \\
x \leq 7, \\
4(2 x+3)(x+1)=9(7-x)^{2}
\end{array} \Leftrightarrow\right.\right. \\
& \Leftrightarrow\left\{\begin{array}{l}
-1 \leq x \leq 7, \\
x^{2}-146 x+429=0
\end{array} \Leftrightarrow x=3 .\right.
\end{aligned}
$$
Answer: $x=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.279 \sqrt[4]{x+8}-\sqrt[4]{x-8}=2$
|
Solution. Let $u=\sqrt[4]{x+8}, v=\sqrt[4]{x-8}$, then $\left\{\begin{array}{l}u-v=2, \\ u^{4}-v^{4}=16\end{array} \Rightarrow\right.$ $\Rightarrow(v+2)^{4}-v^{4}=16 \Leftrightarrow\left((v+2)^{2}-v^{2}\right)\left((v+2)^{2}+v^{2}\right)=16 \Leftrightarrow(v+1)(v+2 v+2)=2$.
Since $v \geq 0$, then $v+1 \geq 1, v^{2}+2 v+2 \geq 2 \Rightarrow v=0$ is the only solution to the last equation.
Answer: $x=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.280 \sqrt{x}-\sqrt{x+1}-\sqrt{x+4}+\sqrt{x+9}=0$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
$6.280 \sqrt{x}-\sqrt{x+1}-\sqrt{x+4}+\sqrt{x+9}=0$.
|
Solution. $\sqrt{x}+\sqrt{x+9}=\sqrt{x+1}+\sqrt{x+4} \Leftrightarrow$
$\Leftrightarrow\left\{\begin{array}{l}x \geq 0, \\ x+x+9+2 \sqrt{x(x+9)}=x+1+x+4+2 \sqrt{(x+1)(x+4)}\end{array} \Leftrightarrow\right.$
$\Leftrightarrow\left\{\begin{array}{l}x \geq 0, \\ 2+\sqrt{x(x+9)}=\sqrt{(x+1)(x+4)}\end{array} \Leftrightarrow\left\{\begin{array}{l}x \geq 0 \\ 4+x^{2}+9 x+4 \sqrt{x(x+9)}=x^{2}+5 x+4\end{array} \Leftrightarrow\right.\right.$ $\Leftrightarrow\left\{\begin{array}{l}x \geq 0, \\ x+\sqrt{x(x+9)}=0\end{array} \Leftrightarrow x=0\right.$.
Answer: $x=0$.
## $6.281 \sqrt[3]{x+5}+\sqrt[3]{x+6}=\sqrt[3]{2 x+11}$
Solution. Raise both sides to the third power:
$2 x+11+3 \sqrt[3]{(x+5)(x+6)} \cdot(\sqrt[3]{x+5}+\sqrt[3]{x+6})=2 x+11 \Leftrightarrow$
$\sqrt[3]{(x+5)(x+6)} \cdot(\sqrt[3]{x+5}+\sqrt[3]{x+6})=0 \Leftrightarrow \sqrt[3]{(x+5)(x+6)(2 x+11)}=0 \Rightarrow\left[\begin{array}{l}x=-5, \\ x=-6, \\ x=-\frac{11}{2} .\end{array}\right.$
By checking, we confirm that all these values are roots of the original equation.
Answer: $x_{1}=-6 ; x_{2}=-5.5 ; x_{3}=-5$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.282 \sqrt{x^{2}-x-1}+\sqrt{x^{2}+x+3}=\sqrt{2 x^{2}+8}, x>0$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
$6.282 \sqrt{x^{2}-x-1}+\sqrt{x^{2}+x+3}=\sqrt{2 x^{2}+8}, x>0$.
|
Solution. Raise both sides to the square:
$\left\{\begin{array}{l}x^{2}-x-1 \geq 0, ; \\ 2 x^{2}+2+2 \sqrt{\left(x^{2}-x-1\right)\left(x^{2}+x+3\right)}=2 x^{2}+8, \\ x>0\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}x^{2}-x-1 \geq 0, \\ \sqrt{\left(x^{2}-x-1\right)\left(x^{2}+x+3\right)} \\ x>0\end{array}, \Leftrightarrow\left\{\begin{array}{l}x>0, \\ \left(x^{2}-x-1\right)\left(x^{2}+x+3\right)=9\end{array} \Leftrightarrow\right.\right.$
$\Leftrightarrow\left\{\begin{array}{l}x>0, \\ x^{4}+x^{2}-4 x-12=0\end{array} \Leftrightarrow\left\{\begin{array}{l}x>0, \\ (x-2)\left(x^{3}+2 x^{2}+5 x+6\right)=0\end{array} \Leftrightarrow x=2\right.\right.$.
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.288 \frac{x^{2}}{\sqrt{2 x+15}}+\sqrt{2 x+15}=2 x$.
|
Solution.
$$
\begin{aligned}
& \frac{x^{2}}{\sqrt{2 x+15}}+\sqrt{2 x+15}-2 x=0 \Leftrightarrow\left(\frac{x}{\sqrt[4]{2 x+15}}-\sqrt[4]{2 x+15}\right)^{2}=0 \Leftrightarrow \\
& \Leftrightarrow \frac{x}{\sqrt[4]{2 x+15}}=\sqrt[4]{2 x+15} \Leftrightarrow x=\sqrt{2 x+15} \Leftrightarrow\left\{\begin{array}{l}
x \geq 0, \\
x^{2}=2 x+15
\end{array} \Leftrightarrow x=5 .\right.
\end{aligned}
$$
Answer: $x=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$6.290 \sqrt{x+2 \sqrt{x-1}}+\sqrt{x-2 \sqrt{x-1}}=x-1$.
|
Solution. $\sqrt{(x-1)+2 \sqrt{x-1}+1}+\sqrt{(x-1)-2 \sqrt{x-1}+1}=x-1 \Leftrightarrow$ $\Leftrightarrow \sqrt{(\sqrt{x-1}+1)^{2}}+\sqrt{(\sqrt{x-1}-1)^{2}}=x-1 \Leftrightarrow \sqrt{x-1}+1+|\sqrt{x-1}-1|=x-1 \Leftrightarrow$ $\Leftrightarrow \sqrt{x-1}+|\sqrt{x-1}-1|=x-2$.
Since $x \geq 2$, then $\sqrt{x-1} \geq 1$. Therefore, the last equation is equivalent to the system:
$\left\{\begin{array}{l}2 \sqrt{x-1}-1=x-2, \\ x \geq 2\end{array} \Leftrightarrow\left\{\begin{array}{l}2 \sqrt{x-1}=x-1, \\ x \geq 2\end{array} \Leftrightarrow\left\{\begin{array}{l}2=\sqrt{x-1}, \\ x \geq 2\end{array} \Leftrightarrow x=5\right.\right.\right.$.
Answer: $x=5$.
$6.2918,4 \sqrt[12]{x^{-7}}-0.2 \sqrt[4]{x^{-1} \cdot \sqrt[3]{x^{2}}}=\sqrt[12]{x^{11}}$
Solution. Note that $\sqrt[4]{x^{-1} \cdot \sqrt[3]{x^{2}}}=\sqrt[12]{x^{-1}}$. Multiply both sides of the equation by $\sqrt[12]{x}: \frac{8.4}{\sqrt{x}}-0.2=x$. Let $y=\sqrt{x}$, then $5 y^{3}+y-42=0 \Leftrightarrow$ $\Leftrightarrow(y-2)\left(5 y^{2}+10 y+21\right)=0 \Leftrightarrow y=2 \Leftrightarrow x=4$.
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.293
$$
\frac{\sqrt[7]{x-\sqrt{2}}}{2}-\frac{\sqrt[7]{x-\sqrt{2}}}{x^{2}}=\frac{x}{2} \cdot \sqrt[7]{\frac{x^{2}}{x+\sqrt{2}}}
$$
|
Solution. $\frac{\sqrt[7]{x^{2}-2}}{2}-\frac{\sqrt[7]{x^{2}-2}}{x^{2}}=\frac{x}{2} \cdot \sqrt[7]{x^{2}} \Leftrightarrow \sqrt[7]{x^{2}-2} \cdot\left(x^{2}-2\right)=x^{3} \cdot \sqrt[7]{x^{2}} \Leftrightarrow$ $\Leftrightarrow\left(x^{2}-2\right)^{8}=x^{23} \Leftrightarrow\left|x^{2}-2\right|=x^{\frac{23}{8}}$.
Consider two cases:
1) $\left\{\begin{array}{l}x^{2}-2=x^{\frac{23}{8}} \\ x \geq \sqrt{2}\end{array}, \Leftrightarrow \varnothing\right.$, since $x^{\frac{23}{8}} \geq x^{2}$ for $\dot{x}>1$.
2) $\left\{\begin{array}{l}2-x^{2}=x^{\frac{23}{8}} \\ 00$. Therefore, the equation $f(x)=2$ has a unique root $x=1$ for $0 \leqslant x<\sqrt{2}$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.300 \sqrt{x-2}+\sqrt{4-x}=x^{2}-6 x+11
|
Solution. $\sqrt{(x-3)+1}+\sqrt{1-(x-3)}=\left(x^{2}-6 x+9\right)+2$.
Let $y=x-3$, then $\sqrt{y+1}+\sqrt{1-y}=y^{2}+2 \Leftrightarrow$ $y^{4}+4 y^{2}+2\left(1-\sqrt{1-y^{2}}\right)=0$.
Since $1 \geq \sqrt{1-y^{2}}$, the last equation is equivalent to the system:
$$
\left\{\begin{array}{l}
y^{4}+4 y^{2}=0 \\
1=\sqrt{1-y^{2}}
\end{array} \Leftrightarrow y=0 .\right.
$$
Answer: $x=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.365 Solve the equation $\left(x^{3}+x^{-3}\right)+\left(x^{2}+x^{-2}\right)+\left(x+x^{-1}\right)=6$.
|
Solution. $\left(x^{3}-2+\frac{1}{x^{3}}\right)+\left(x^{2}-2+\frac{1}{x^{2}}\right)+\left(x-2+\frac{1}{x}\right)=0 \Leftrightarrow \frac{\left(x^{3}-1\right)^{2}}{x^{3}}+\frac{\left(x^{2}-1\right)^{2}}{x^{2}}+\frac{(x-1)^{2}}{x}=0$ $(x-1)^{2}\left(\left(x^{2}+x+1\right)^{2}+x(x+1)^{2}+x^{2}\right)=0 \Leftrightarrow$ $\Leftrightarrow(x-1)^{2}\left(\left(x^{2}+x+1\right)^{2}+x\left(x^{2}+2 x+1\right)+x^{2}\right)=0 \Leftrightarrow x=1$ or $\left(x^{2}+x+1\right)^{2}+x\left(x^{2}+x+1\right)+2 x^{2}=0$. Let $v=x, u=x^{2}+x+1$, then $\left[\begin{array}{l}x=1 \\ u^{2}+u v+2 v^{2}=0\end{array} \Leftrightarrow\left[\begin{array}{l}x=1 \\ x \in \varnothing\end{array} \Rightarrow x=1\right.\right.$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.370 Solve the equation $\sqrt[4]{x^{4}+x-2}+\sqrt{x^{4}+x-2}=6$ given that $\boldsymbol{x}>\mathbf{0}$.
|
Solution. Let $y=\sqrt[4]{x^{4}+x-2}$, then $y^{2}+y-6=0 \Leftrightarrow \sqrt[4]{x^{4}+x-2}=2 \Leftrightarrow$ $\Leftrightarrow x^{4}+x-18=0 \Leftrightarrow(x-2)\left(x^{3}+2 x^{2}+4 x+9\right)=0$.
Since $x>0$, then $x^{3}+2 x^{2}+4 x+9>0 \Rightarrow x=2$.
Answer: $x=2$.
## pRoGReSSiOnS
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.084 In a volleyball competition, $n$ teams participated. Each team played with all the others once. For each game, the winning team was awarded one point, and no points were awarded for a loss, as there are no draws in volleyball. At the end of the competition, it turned out that the points scored by the teams formed an arithmetic progression. How many points did the team that finished in last place score?
|
Solution. Let the points scored by the teams form a non-decreasing arithmetic progression $a_{1}, a_{2}, \ldots, a_{n}$ with a common difference $d$. A total of $\frac{n(n-1)}{2}$ games were played. Therefore, the total number of points scored by all teams is $\frac{n(n-1)}{2}$, from which we have $a_{1}+a_{2}+\ldots+a_{n}=\frac{n(n-1)}{2} \Rightarrow \frac{n}{2}\left(2 a_{1}+(n-1) d\right)=\frac{n(n-1)}{2} \Rightarrow 2 a_{1}=(n-1)(1-d)$.
Since $d$ and $a_{1}$ are integers, we have $\left[\begin{array}{l}d=1, \\ d=0 .\end{array}\right.$ However, according to the problem, there is a team that finished in the last place, so $d=1 \Rightarrow a_{1}=0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.296
$2 \log _{a}^{\frac{1}{2}} b \cdot\left(\left(\log _{a} \sqrt[4]{a b}+\log _{b} \sqrt[4]{a b}\right)^{\frac{1}{2}}-\left(\log _{a} \sqrt[4]{\frac{b}{a}}+\log _{b} \sqrt[4]{\frac{a}{b}}\right)^{\frac{1}{2}}\right), a, b>1$.
|
Solution.
1) $\left(\log _{a} \sqrt[4]{a b}+\log _{b} \sqrt[4]{a b}\right)^{\frac{1}{2}}=\left(\frac{1}{4}\left(\log _{a} b+1+\log _{b} a+1\right)\right)^{\frac{1}{2}}=$
$=\left(\frac{1}{4}\left(2+\log _{a} b+\frac{1}{\log _{a} b}\right)\right)^{\frac{1}{2}}=\frac{1}{2}\left(\frac{\left(\log _{a} b+1\right)^{2}}{\log _{a} b}\right)^{\frac{1}{2}}=\frac{\log _{a} b+1}{2 \sqrt{\log _{a} b}}$.
2) $\left(\log _{a} \sqrt[4]{\frac{b}{a}}+\log _{b} \sqrt[4]{\frac{a}{b}}\right)^{\frac{1}{2}}=\left(\frac{1}{4} \log _{a} b-\frac{1}{4}+\frac{1}{4} \log _{b} a-\frac{1}{4}\right)^{\frac{1}{2}}=\frac{1}{2}\left(\frac{\left(\log _{a} b-1\right)^{2}}{\log _{a} b}\right)^{\frac{1}{2}}=$
$$
=\frac{\left|\log _{a} b-1\right|}{2 \sqrt{\log _{a} b}} .
$$
3) $2 \log _{a}^{\frac{1}{2}} b \cdot\left(\frac{\log _{a} b+1}{2 \sqrt{\log _{a} b}}-\frac{\left|\log _{a} b-1\right|}{2 \sqrt{\log _{a} b}}\right)=\log _{a} b+1-\left|\log _{a} b-1\right|$.
Answer: 2, if $1<a \leq b ; 2 \log _{a} b$, if $1<b<a$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.308 \quad(\sqrt[3]{0.5}+\sqrt[3]{4})^{x}=13.5$.
|
## Solution.
$$
\left(\frac{1}{\sqrt[3]{2}}+\sqrt[3]{4}\right)^{x}=\frac{27}{2} \Leftrightarrow\left(\frac{3}{\sqrt[3]{2}}\right)^{x}=\frac{27}{2} \Leftrightarrow\left(\frac{27}{2}\right)^{\frac{x}{3}}=\left(\frac{27}{2}\right)^{1} \Leftrightarrow x=3
$$
Answer: $x=3$.
$$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3092 \log _{9}^{2} x=\log _{3} x \cdot \log _{3}(\sqrt{2 x+1}-1)
|
Solution. $\frac{\log _{3}^{2} x}{2}=\log _{3} x \cdot \log _{3}(\sqrt{2 x+1}-1) \Leftrightarrow \log _{3} x \cdot\left(\log _{3} x-2 \log _{3}(\sqrt{2 x+1}-1)\right)=0$
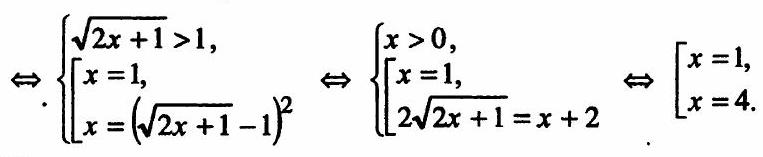
Answer: $x_{1}=1, x_{2}=4$.
$7.310\left(1+\log _{x} \frac{4-x}{10}\right) \lg x=\lg \lg 10^{3}-1$.
Solution. $\log _{x} \frac{(4-x) x}{10} \cdot \lg x=\lg 3-1 \Leftrightarrow \log _{x} \frac{(4-x) x}{10}=\frac{\lg \frac{3}{10}}{\lg x} \Leftrightarrow$ $\Leftrightarrow \log _{x} \frac{(4-x) x}{10}=\log _{x} \frac{3}{10} \Leftrightarrow\left\{\begin{array}{l}x>0, \\ x \neq 1, \\ (4-x) x=3\end{array} \Leftrightarrow x=3\right.$.
Answer: $x=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.313 \log _{x+1}\left(x^{3}-9 x+8\right) \cdot \log _{x-1}(x+1)=3$.
|
## Solution.
$\log _{x+1}\left((x-1)\left(x^{2}+x-8\right)\right) \cdot \log _{x-1}(x+1)=3 \Leftrightarrow$
$\Leftrightarrow\left\{\begin{array}{l}\log _{x+1}\left((x-1)\left(x^{2}+x-8\right)\right)=3 \log _{x+1}(x-1), \\ x \neq 2\end{array} \Leftrightarrow\left\{\begin{array}{l}x-1>0, \\ x \neq 2, \\ (x-1)\left(x^{2}+x-8\right)=(x-1)^{3}\end{array} \Leftrightarrow\right.\right.$
$\Leftrightarrow\left\{\begin{array}{l}x-1>0, \\ x \neq 2, \\ x^{2}+x-8=(x-1)^{2}\end{array} \Leftrightarrow x=3\right.$
Answer: $x=3$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.317 \log _{4} x+\log _{x} 2-\log _{4} \sqrt{x}=1$
|
Solution. $\frac{1}{2} \log _{2} x+\frac{1}{\log _{2} x}-\frac{1}{4} \log _{2} x=1 \Leftrightarrow \log _{2}^{2} x-4 \log _{2} x+4=0 \Leftrightarrow$ $\left(\log _{2} x-2\right)^{2}=0 \Leftrightarrow x=4$.
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$3.457 A=\operatorname{ctg}\left(\frac{1}{2} \arccos \frac{3}{5}-2 \operatorname{arcctg}\left(-\frac{1}{2}\right)\right)$
$3.457 A=\cot\left(\frac{1}{2} \arccos \frac{3}{5}-2 \operatorname{arcctg}\left(-\frac{1}{2}\right)\right)$
|
Solution. Let $\alpha=\arccos \frac{3}{5}, \beta=\operatorname{arcctg}\left(-\frac{1}{2}\right) \Rightarrow \cos \alpha=\frac{3}{5}, \sin \alpha=\frac{4}{5}$, $\operatorname{ctg} \frac{\alpha}{2}=\frac{1+\cos \alpha}{\sin \alpha}=2, \operatorname{ctg} \beta=-\frac{1}{2}, \operatorname{ctg} 2 \beta=\frac{\operatorname{ctg}^{2} \beta-1}{2 \operatorname{ctg} \beta}=\frac{3}{4} \Rightarrow A=\operatorname{ctg}\left(\frac{\alpha}{2}-2 \beta\right)=$
$$
=\frac{\operatorname{ctg} \frac{\alpha}{2} \cdot \operatorname{ctg} 2 \beta+1}{-\operatorname{ctg} \frac{\alpha}{2}+\operatorname{ctg} 2 \beta}=-2
$$
Answer: $A=-2$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.477 Find the minimum value of the expression
$$
A=\frac{\operatorname{ctg} 2 \alpha-\operatorname{tg} 2 \alpha}{1+\sin \left(\frac{5 \pi}{2}-8 \alpha\right)} \text { for } 0<\alpha<\frac{\pi}{8}
$$
|
## Solution.
$\operatorname{ctg} 2 \alpha-\operatorname{tg} 2 \alpha=\frac{\cos ^{2} 2 \alpha-\sin ^{2} 2 \alpha}{\sin 2 \alpha \cdot \cos 2 \alpha}=\frac{2 \cos 4 \alpha}{\sin 4 \alpha} \Rightarrow A=\frac{2 \cos 4 \alpha}{\sin 4 \alpha \cdot(1+\cos 8 \alpha)}=$ $=\frac{2 \cos 4 \alpha}{2 \sin 4 \alpha \cdot \cos ^{2} 4 \alpha}=\frac{2}{\sin 8 \alpha}$. Since $0<8 \alpha<\pi$, the minimum value of $A$ is achieved when $\sin 8 \alpha=1$, i.e., when $\alpha=\frac{\pi}{16}$.
Answer: 2 when $\alpha=\frac{\pi}{16}$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.481 Find the minimum value of the expression
$A=\frac{\operatorname{ctg} \alpha-\operatorname{tg} \alpha}{\cos 4 \alpha+1}$ for $0<\alpha<\frac{\pi}{4}$.
|
## Solution.
$\operatorname{ctg} \alpha-\operatorname{tg} \alpha=\frac{\cos ^{2} \alpha-\sin ^{2} \alpha}{\sin \alpha \cdot \cos \alpha}=\frac{2 \cos 2 \alpha}{\sin 2 \alpha} \Rightarrow A=\frac{2 \cos 2 \alpha}{\sin 2 \alpha \cdot 2 \cos ^{2} 2 \alpha}=\frac{2}{\sin 4 \alpha}$.
Since $0<\alpha<\frac{\pi}{4}$, the minimum value of $A$ is achieved when $\sin 4 \alpha=1$, i.e., when $\alpha=\frac{\pi}{8}$.
Answer: 2 when $\alpha=\frac{\pi}{8}$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
### 3.485 Find the maximum value of the expression
$$
A=\frac{1}{\sin ^{6} \alpha+\cos ^{6} \alpha} \text { for } 0 \leq \alpha \leq \frac{\pi}{2}
$$
|
## Solution.
$\sin ^{6} \alpha+\cos ^{6} \alpha=\sin ^{4} \alpha-\sin ^{2} \alpha \cdot \cos ^{2} \alpha+\cos ^{4} \alpha=1-3 \sin ^{2} \alpha \cdot \cos ^{2} \alpha=$ $=1-\frac{3}{4} \sin ^{2} 2 \alpha=\frac{1+3 \cos ^{2} 2 \alpha}{4} \Rightarrow A=\frac{4}{1+3 \cos ^{2} 2 \alpha}$.
From this, it is clear that $A$ takes its maximum value when $\cos 2 \alpha=0$, i.e., when $\alpha=\frac{\pi}{4}$.
Answer: 4 when $\alpha=\frac{\pi}{4}$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
### 3.486 Find the maximum value of the expression
$A=\frac{1}{\sin ^{4} \alpha+\cos ^{4} \alpha}$ for $0 \leq \alpha \leq \frac{\pi}{2}$.
|
Solution. $\sin ^{4} \alpha+\cos ^{4} \alpha=1-2 \sin ^{2} \alpha \cdot \cos ^{2} \alpha=1-\frac{\sin ^{2} 2 \alpha}{2}=\frac{1+\cos ^{2} 2 \alpha}{2} \Rightarrow$
$\Rightarrow A=\frac{2}{1+\cos ^{2} 2 \alpha}$. From this, it is clear that $A$ takes its maximum value when $1+\cos ^{2} 2 \alpha$ takes its minimum value, i.e., when $\cos 2 \alpha=0$ or $\alpha=\frac{\pi}{4}$.
Answer: 2 when $\alpha=\frac{\pi}{4}$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
### 9.303 Find integer values of $x$ that satisfy the inequality
$$
\log _{0.3}(\sqrt{x+5}-x+1)>0
$$
|
Solution. The inequality is equivalent to the system:
$\left\{\begin{array}{l}\sqrt{x+5}-x+10, \\ x-\text { integer }\end{array} \Leftrightarrow\left\{\begin{array}{l}\sqrt{x+5}x-1, \\ x-\text { integer. }\end{array}\right.\right.$
From this, $x>0$ and, consequently, $x \geq 1$ ( $x$ - integer). Therefore,
$\left\{\begin{array}{l}(x+5)(x-1)^{2}, \\ x-\text { integer, } \\ x \geq 1\end{array} \Leftrightarrow\left\{\begin{array}{l}\frac{1+\sqrt{21}}{2}<x<4, \\ x-\text { integer }\end{array} \Leftrightarrow x=3\right.\right.$.
Answer: $x=3$.
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.361 In triangle $A B C$, the measure of angle $A$ is twice the measure of angle $B$, and the lengths of the sides opposite these angles are 12 cm and 8 cm, respectively. Find the length of the third side of the triangle.
|
Solution.
A
Let $A K$ be the bisector of $\angle A$. Then
$\angle K A C = \angle A B C \Rightarrow \triangle A K C \sim \triangle A B C \Rightarrow$
$\Rightarrow \frac{A C}{B C} = \frac{K C}{A C} = \frac{A K}{A B} \Rightarrow K C = \frac{A C^2}{B C} = \frac{16}{3}$,
$A K = B K = B C - K C = 12 - \frac{16}{3}$, $A B = \frac{A K \cdot A C}{K C} = 10$.
Answer: 10 cm
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.368 Calculate the length of the angle bisector of angle $A$ in triangle $A B C$ with side lengths $a=18$ cm, $b=15$ cm, $c=12$ cm.
|
Solution. Let $A K$ be the bisector of $\angle A$ of the given $\triangle A B C$. By Theorem 4, $\frac{C K}{B K}=\frac{15}{12} \Rightarrow \frac{18-B K}{B K}=\frac{15}{12} \Rightarrow B K=8, C K=10$.
Applying the Law of Cosines to $\triangle A B K$ and $\triangle A C K$, we have:
$\left\{\begin{array}{l}8^{2}=12^{2}+A K^{2}-24 \cdot A K \cdot \cos \angle K A B, \\ 10^{2}=15^{2}+A K^{2}-30 \cdot A K \cdot \cos \angle K A B\end{array} \Leftrightarrow\right.$
$\Leftrightarrow\left\{\begin{array}{l}A K^{2}-24 \cdot A K \cdot \cos \angle K A B+80=0, \\ A K^{2}-30 \cdot A K \cdot \cos \angle K A B+125=0\end{array} \Rightarrow A K=10\right.$.
Answer: 10 cm
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
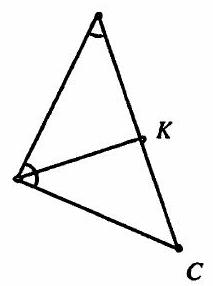
10.369 In a triangle with a perimeter of 20 cm, a circle is inscribed. The segment of the tangent, drawn parallel to the base and enclosed between the sides of the triangle, measures 2.4 cm. Find the base of the triangle.
|
## Solution.
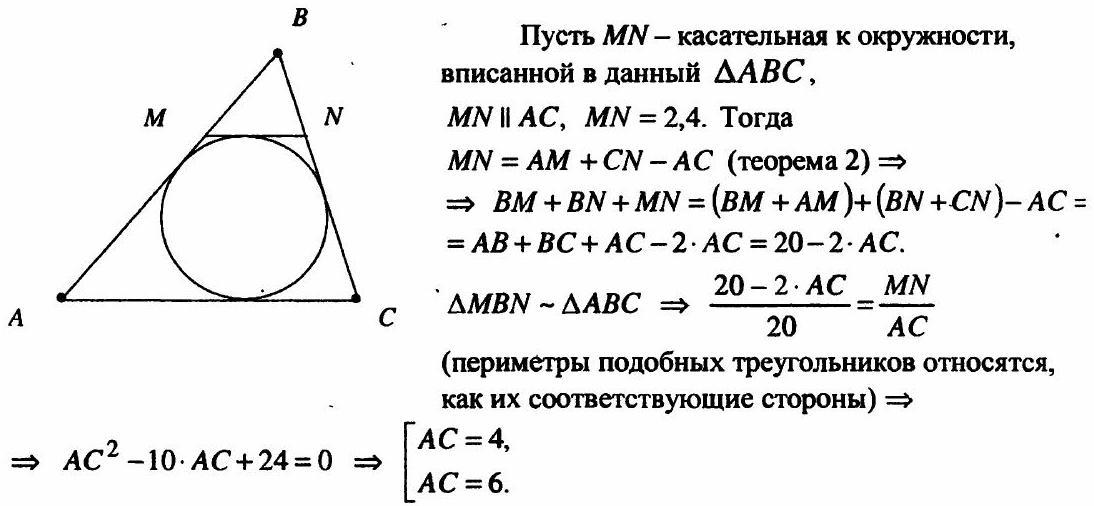
Answer: 4 cm or 6 cm.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.377 The bisector of a triangle's angle divides the opposite side into segments of length 4 and 2 cm, and the height drawn to the same side is $\sqrt{15}$ cm. What are the lengths of the sides of the triangle, given that they are expressed as integers?
|
Solution. Let the bisector of angle $A$ divide side $B C$ of the given $\triangle A B C$ into segments 2 and 4. Suppose $A Bh=\sqrt{15}(h$ - the height of $\triangle A B C) \Rightarrow \sqrt{15}<n<6 \Rightarrow 4 \leq n \leq 5$.
If $n=5$, then by Heron's formula $S_{A B C}=\sqrt{\frac{21}{2} \cdot \frac{11}{2} \cdot \frac{9}{2} \cdot \frac{1}{2}}=\frac{3 \sqrt{231}}{4}$.
But $S_{A B C}=B C \cdot \frac{h}{2}=3 \sqrt{15}$, which is impossible. Therefore, $n=4$.
Answer: 4 cm, 8 cm, 6 cm.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.391 On the segment $A C$ there is a point $B$, and $A B=14 \text{~cm}, B C=28 \text{~cm}$. On the segments $A B, B C$ and $A C$ as diameters, semicircles are constructed in the same half-plane relative to the boundary $\boldsymbol{A} \boldsymbol{B}$. Find the radius of the circle that is tangent to all three semicircles.
|
## Solution.
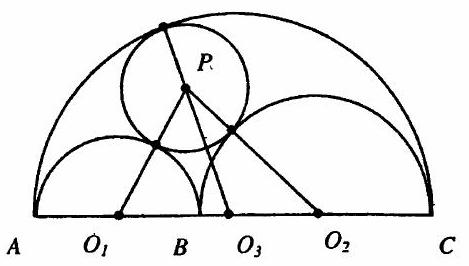
Let $O_{1}, O_{2}, O_{3}$ be the centers of semicircles with radii $r_{1}, r_{2}, r_{3}$ and diameters $A B, B C$, and $A C$ respectively; $P$ be the center of the circle with radius $x$ that touches all three semicircles. Then
$$
\begin{aligned}
& P O_{1}=x+r_{1}, P O_{2}=x+r_{2}, P O_{3}=r_{3}-x \\
& O_{1} O_{3}=r_{3}-r_{1}, O_{2} O_{3}=r_{3}-r_{2} ; r_{1}=7
\end{aligned}
$$
$r_{2}=14, r_{3}=21$ (by the problem statement). Applying the cosine rule to $\Delta O_{1} \mathrm{PO}_{3}$ and $\Delta O_{3} \mathrm{PO}_{2}$,
we have: $\left\{\begin{array}{l}(7+x)^{2}=14^{2}+(21-x)^{2}-28 \cdot(21-x) \cdot \cos \angle O_{1} O_{3} P, \\ \left(14+x^{2}\right)=7^{2}+(21-x)^{2}-14 \cdot(21-x) \cdot \cos \left(180^{\circ}-\angle O_{1} O_{3} P\right),\end{array} \Rightarrow\right.$
$\Rightarrow(7+x)^{2}+2(14+x)^{2}=14^{2}+2 \cdot 7^{2}+3(21-x)^{2} \Rightarrow x=6$.
Answer: $6 \mathrm{~cm}$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.403 In a right triangle $A B C$ ( $\angle C=90^{\circ}$ ), the altitude $CD$ is drawn. The radii of the circles inscribed in triangles $ACD$ and $BCD$ are 0.6 and 0.8 cm, respectively. Find the radius of the circle inscribed in triangle $\boldsymbol{A} \boldsymbol{\text { B }}$.
|
Solution. Let $x, r_{1}, r_{2}$ be the radii of the circles inscribed in $\triangle A B C$, $\triangle A C D, \triangle B C D$ respectively. $\triangle A C D \sim \triangle B C D \Rightarrow \frac{A C}{B C}=\frac{r_{1}}{r_{2}}=\frac{0.6}{0.8}$ (the radii of the circles inscribed in similar triangles are proportional to the corresponding sides) $\Rightarrow B C=\frac{4}{3} A C, \quad A B=\sqrt{A C^{2}+B C^{2}}=\frac{5}{3} A C$.
$$
\triangle A C D \sim \triangle A B C \Rightarrow \frac{r_{1}}{r}=\frac{A C}{A B} \Rightarrow r=1
$$
Answer: 1 cm.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
### 10.417
In a right triangle $ABC\left(\angle C=90^{\circ}\right)$, a circle is inscribed, touching its sides at points $A_{1}, B_{1}, C_{1}$. Find the ratio of the area of triangle $ABC$ to the area of triangle $A_{1} B_{1} C_{1}$, if $AC=4 \text{ cm}, BC=3 \text{ cm}$.
|
## Solution.
Let $O$ be the center of the circle with radius $r$ inscribed in the given $\triangle ABC$.
Then $AB=5, r=\frac{3+4-5}{2}=1$ (Theorem 1).
$S_{A_{1} B_{1} C_{1}}=S_{O A_{1} B_{1}}+S_{O A_{1} C_{1}}+S_{O B_{1} C_{1}}=$
$=\frac{1}{2} r^{2} \sin \angle A_{1} O B_{1}+\frac{1}{2} r^{2} \sin \angle A_{1} O C_{1}+$
$+\frac{1}{2} r^{2} \sin \angle C_{1} O B_{1}=\frac{r^{2}}{2}(\sin \angle C+\sin \angle A+\sin \angle B)=\frac{1}{2}\left(1+\frac{3}{5}+\frac{4}{5}\right)=\frac{6}{5} \Rightarrow \frac{S_{A B C}}{S_{A_{1} B_{1} C_{1}}}=5$.
## Answer: 5.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.373 A computing machine was given the task to solve several problems sequentially. Registering the time spent on the assignment, it was noticed that the machine spent the same multiple of time less on solving each subsequent problem compared to the previous one. How many problems were proposed and how much time did the machine spend solving all the problems, if the time spent on solving all the problems except the first one was 63.5 minutes, the time spent on solving all the problems except the last one was 127 minutes, and the time spent on solving all the problems except the first two and the last two was 30 minutes?
|
Solution. Let $n$ be the number of problems, $b$ be the time to solve the first problem, and $q$ be the common ratio of the geometric progression that represents the times to complete the problems. Using the formula for the sum of $k$ terms of a geometric progression, we have:
$$
\begin{aligned}
& \left\{\begin{array} { l }
{ b q \cdot \frac { q ^ { n - 1 } - 1 } { q - 1 } = \frac { 127 } { 2 } , } \\
{ b \cdot \frac { q ^ { n - 1 } - 1 } { q - 1 } = 127 , } \\
{ b q ^ { 2 } \cdot \frac { q ^ { n - 4 } - 1 } { q - 1 } = 30 }
\end{array} \Rightarrow \left\{\begin{array} { l }
{ q = \frac { 1 } { 2 } , } \\
{ b \cdot \frac { q ^ { n - 1 } - 1 } { q - 1 } = 127 , } \\
{ b \cdot \frac { q ^ { n - 2 } - q ^ { 2 } } { q - 1 } = 30 }
\end{array} \Rightarrow \left\{\begin{array}{l}
q=\frac{1}{2} \\
\frac{q^{n-1}-1}{q^{n-2}-q^{2}}=\frac{127}{30}
\end{array} \Rightarrow\right.\right.\right. \\
& \Rightarrow\left\{\begin{array}{l}
q=\frac{1}{2}, \\
q^{n-2}=\left(\frac{1}{2}\right)^{6}
\end{array} \Rightarrow n=8, \Rightarrow b=64, \Rightarrow 64+63.5=127.5\right. \text { (total time to solve all problems). }
\end{aligned}
$$
Answer: 8 problems; 127.5 minutes.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.384 Five people perform a certain job. The first, second, and third, working together, can complete the entire job in 327.5 hours; the first, third, and fifth together - in 5 hours; the first, third, and fourth together - in 6 hours; and the second, fourth, and fifth together - in 4 hours. In what time interval will all 5 people complete this job, working together?
|
Solution. Let $x_{i}$ be the productivity of the $i$-th worker, $y$ be the volume of work. Then, according to the problem,
$$
\left\{\begin{array}{l}
x_{1}+x_{2}+x_{3}=\frac{y}{7.5} \\
x_{1}+x_{3}+x_{5}=\frac{y}{5} \\
x_{1}+x_{3}+x_{4}=\frac{y}{6} \\
x_{2}+x_{4}+x_{5}=\frac{y}{4}
\end{array}\right.
$$
Multiplying the last equation by 2 and then adding all four equations, we get: $3\left(x_{1}+x_{2}+x_{3}+x_{4}+x_{5}\right)=y\left(\frac{1}{7.5}+\frac{1}{5}+\frac{1}{6}+\frac{1}{2}\right) \Rightarrow \frac{y}{x_{1}+x_{2}+x_{3}+x_{4}+x_{5}}=3$.
Answer: in 3 hours.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.389 From two pieces of alloy of the same mass but with different percentage content of copper, pieces of equal mass were cut off. Each of the cut pieces was melted with the remainder of the other piece, after which the percentage content of copper in both pieces became the same. How many times smaller is the cut piece than the whole?
|
Solution. Let $y$ be the mass of each alloy piece, $x$ be the mass of the cut-off piece, $p$ and $q$ be the concentration of copper in the first and second pieces of the alloy. Then $p x+q(y-x)$ and $q x+p(y-x)$ are the amounts of copper in the new alloys, respectively. According to the problem,
$$
\frac{p x+q(y-x)}{y}=\frac{q x+p(y-x)}{y} \Rightarrow(p-q) x=(y-x)(p-q) \Rightarrow x=y-x \Rightarrow y=2 x
$$
Answer: 2 times.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.391 Two cars start simultaneously from points A and B and meet at 12 o'clock noon. If the speed of the first car is doubled while the speed of the second car remains the same, the meeting will occur 56 minutes earlier. If, however, the speed of the second car is doubled while the speed of the first car remains the same, they will meet 65 minutes earlier. Determine the time of the meeting in the case where the speed of both was doubled.
|
Solution. Let $x$ and $y$ be the initial speeds (km/min) of the cars, and $2z$ be the time (in minutes) after which they met after leaving from A and B. Then $2z(x+y)$ is the distance between A and B, hence
\[
\left\{
\begin{array}{l}
2z(x+y) = (2z-56)(2x+y) \\
2z(x+y) = (2z-65)(x+2y)
\end{array}
\right.
\]
\[
\left\{
\begin{array}{l}
z x = 28(2x + y) \\
2 z y = 65(x + 2y)
\end{array}
\right.
\]
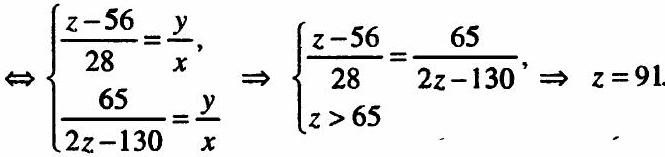
By the problem's context, $z$ is the time it would take for the cars to meet if their speed were twice as fast. Hence, $z = 91$ minutes.
Answer: The meeting time is 10 hours and 29 minutes.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.394 Two brothers had tickets to a stadium located 10 km from their home. At first, they planned to walk to the stadium, but they changed their mind and decided to use a bicycle, agreeing that one would go by bicycle while the other would walk at the same time. After covering part of the distance, the first brother would leave the bicycle, and the second, upon reaching the abandoned bicycle, would ride it and catch up with the first at the stadium entrance. How much time do the brothers save with this plan compared to their initial intention of walking the entire distance, if each of them on a bicycle covers each kilometer 12 minutes faster than on foot?
|
Solution. Since the brothers arrived at the stadium simultaneously (i.e., spent the same amount of time on the journey), they walked (and cycled) the same distance. But in total, they walked 10 km, so each of them walked 5 km. Therefore, the time gain will be $5 \cdot 12=60$ minutes.
Answer: 1 hour.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.395 A sportsman, walking along a highway, noticed that every 6 minutes a trolleybus catches up with him and every 3 minutes a trolleybus passes him in the opposite direction. Find the intervals at which trolleybuses depart from the terminal points and how many times slower the sportsman was walking compared to the trolleybus, assuming that trolleybuses depart in both directions at the same intervals, travel without stops, and maintain a constant and equal speed?
|
Solution. Let $x$ and $y$ be the speeds of the athlete and the trolleybuses, and $z$ be the interval of the trolleybuses' movement. Then $y z$ is the distance between the trolleybuses. According to the problem, $\left\{\begin{array}{l}y z=3(x+y), \\ y z=6(y-x),\end{array} \Rightarrow x=\frac{y}{3} ; z=4\right.$.
Answer: 4 min; 3 times.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.399 The train was delayed at the departure station for 1 hour 42 minutes. Upon receiving the departure signal, the driver followed this schedule: on the section constituting 0.9 of the entire route from the departure station to the destination station, he maintained a speed 20% higher than the usual speed, and on 0.1 of the route, he drove the train at a speed 25% higher than the usual speed. As a result, the train arrived at the destination station without being late. What is the duration of the train's journey between the stations at the usual speed?
|
Solution. Let $z$ be the distance between stations, $x$ be the usual speed of the train.
$$
\begin{aligned}
& \text { Then } \frac{0.9 z}{1.2 x}+\frac{0.1 z}{1.25 x}-\text { is the travel time of the train, hence } \\
& \frac{0.9 z}{1.2 x}+\frac{0.1 z}{1.25 x}=\frac{z}{x}-1 \frac{42}{60} \Rightarrow \frac{z}{x}=10 .
\end{aligned}
$$
Answer: 10 hours.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.405 Two pedestrians set out simultaneously from A to B and from B to A. When the first had walked half the distance, the second had 24 km left to walk to the end, and when the second had walked half the distance, the first had 15 km left to walk to the end. How many kilometers will the second pedestrian have left to walk after the first completes the transition?
|
Solution. Let $x$ be the distance between A and B, $y$ be the ratio of the speeds of the first and second pedestrians. Then
$\left(\frac{x}{2}\right):(x-24)=y,(x-15):\left(\frac{x}{2}\right)=y$, from which $\frac{x}{2(x-24)}=\frac{2(x-15)}{x} \Rightarrow x=40$ (the value $x=12$ is not suitable, as $x>24) \Rightarrow y=\frac{5}{4}$. Therefore, if the first pedestrian walks 40 km, the second pedestrian will walk 32 km.
Answer: 8 km.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.408 A material particle $m_{1}$ oscillates between points $A$ and $B$, which are 3.01 m apart. The particle's speed is constant, and it does not stop at the endpoints. After 11 s from the departure of particle $m_{1}$ from point $A$, another particle $m_{2}$ starts moving from point $B$ with a constant but lower speed. This particle, moving towards point $A$, meets particle $m_{1}$ twice, specifically 10 and 45 s after the departure of the second particle. Determine the speeds of the particles.
|
Solution. Let $x$ and $y$ be the speeds (cm/s) of particles $m_{1}$ and $m_{2}$. By the time particle $m_{2}$ exits, the distance between $m_{1}$ and $m_{2}$ is $301-11 x$ cm, hence $301-11 x=10(x+y)$. Let $C$ be the point of the first meeting of the particles. Then $B C=10 y$, and therefore, by the time of the second meeting (i.e., 35 s after the first), particle $m_{l}$ will have traveled a distance $C B+B C=20 y$ greater than particle $m_{2}$ (counting from the moment of the first meeting). Therefore, $\left\{\begin{array}{l}301-11 x=10(x+y), \\ 20 y=35(x-y)\end{array} \Rightarrow\left\{\begin{array}{l}x=11, \\ y=7 .\end{array}\right.\right.$
Answer: 11 cm/s, 7 cm/s.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.410 Along the sides of a right angle, towards the vertex, two spheres with radii of 2 and 3 cm are moving, with the centers of these spheres moving along the sides of the angle at unequal but constant speeds. At a certain moment, the center of the smaller sphere is 6 cm from the vertex, and the center of the larger sphere is 16 cm away. After 1 second, the distance between the centers became 13 cm, and after another 2 seconds, the spheres collided without reaching the vertex. Find the speeds of the spheres.
|
Solution. Let $x$ and $y$ be the speeds of the balls. After 1 second, the distances from the centers of the balls to the corner are $6-x$ and $16-y$, and after 3 seconds, they are $6-3x$ and $16-3y$. By the Pythagorean theorem, we have: $\left\{\begin{array}{l}(6-x)^{2}+(16-y)^{2}=13^{2}, \\ (6-3 x)^{2}+(16-3 y)^{2}=5^{2},\end{array}\right.$ (since at the moment of impact, the distance between the centers of the balls is 5 cm).
From this, $\left\{\begin{array}{l}x^{2}+y^{2}=32 y+12 x-123, \\ 3\left(x^{2}+y^{2}\right)=32 y+12 x-89\end{array} \Rightarrow\left\{\begin{array}{l}3(32 y+12 x-123)=32 y+12 x-89, \\ 2\left(x^{2}+y^{2}\right)=34\end{array} \Rightarrow\right.\right.$ $\Rightarrow\left\{\begin{array}{l}3 x+8 y=35, \\ x^{2}+y^{2}=17\end{array} \Rightarrow\left\{\begin{array}{l}x=1, \\ y=4 .\end{array}\right.\right.$
Answer: 1 cm/s, 4 cm/s.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.415 Two cyclists set out simultaneously from points $A$ and $B$ towards each other. Four hours after their meeting, the cyclist who had set out from $A$ arrived at $B$, and nine hours after their meeting, the cyclist who had set out from $B$ arrived at $A$. How many hours was each cyclist on the road?
|
Solution. Let $x$ and $y$ be the travel times of the first and second cyclists, respectively. Then $x-4=y-9$ is the time each of them traveled until they met. Since each of them traveled a distance after the meeting equal to the distance the other had traveled before the meeting, $\frac{4}{y-9}=\frac{x-4}{9}$.
$$
\text{Thus, }\left\{\begin{array} { l }
{ x = y - 5 } \\
{ \frac { 4 } { y - 9 } = \frac { x - 4 } { 9 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=10 \\
y=15
\end{array}\right.\right.
$$
Answer: 10 hours, 15 hours.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.426 Two pumps were installed to fill a swimming pool with water. The first pump can fill the pool 8 hours faster than the second one. Initially, only the second pump was turned on for a time equal to twice the amount of time it would take to fill the pool if both pumps were working simultaneously. Then, the first pump was also turned on, and 1.5 hours after the first pump was turned on, the pool was filled with water. How many hours does it take for each pump, working separately, to fill the pool?
|
Solution. Let $x$ and $y$ be the pump efficiencies, and $z$ be the volume of work. Then $\frac{z}{x+y}$ is the time it takes to fill the pool when both pumps are working simultaneously. According to the conditions of the problem,
$\left\{\begin{array}{l}\frac{z}{y}-\frac{z}{x}=8, \\ \frac{2 z}{x+y} \cdot y+1.5(x+y)=z\end{array} \Leftrightarrow\left\{\begin{array}{l}z(x-y)=8 x y, \\ \frac{3}{2}(x+y)=\frac{z(x-y)}{x+y}\end{array} \Rightarrow \frac{3}{2}(x+y)=\frac{8 x y}{x+y} \Leftrightarrow\right.\right.$
$\Leftrightarrow 3 x^{2}-10 x y+3 y^{2}=0 \Leftrightarrow\left[\begin{array}{l}x=3 y, \\ x=\frac{y}{3} .\end{array}\right.$
Since $x>y$, then $x=3 y$. Substituting this into the first equation of the system, we get
$\frac{z}{y}=12, \frac{z}{x}=4$.
Answer: 4 hours, 12 hours.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.428 A batch of identical parts was processed on three machines of different designs in the following sequence: first, only the first machine worked for as many hours as it would take for the second and third machines to complete the entire job together; then, only the second machine worked for as many hours as it would take for the first and third machines to complete the entire job together. The remaining part of the batch was processed on the third machine for as many hours as it would take for the first and second machines to complete the entire job together.
How many times faster would this work be completed if all three machines worked together?
|
Solution. Let $x, y, z$ be the efficiencies of the machines, and $V$ be the volume of work. According to the problem, $\frac{V}{y+z}$ is the time taken by the first machine, $\frac{V}{x+z}$ is the time taken by the second machine, and $\frac{V}{x+y}$ is the time taken by the third machine.
From this, $\frac{V x}{y+z}+\frac{V y}{x+z}+\frac{V z}{x+y}=V \Rightarrow \frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=1$.
Furthermore, $\frac{V}{x+y+z}$ is the time it would take to complete the work if all three machines worked simultaneously.
According to the question, we need to determine the following quantity $t$:
$t=\frac{\frac{V}{x+y}+\frac{V}{x+z}+\frac{V}{z+y}}{\frac{V}{x+y+z}}=\frac{x+y+z}{x+y}+\frac{x+y+z}{x+z}+\frac{x+y+z}{y+z}=$
$=\left(1+\frac{z}{x+y}\right)+\left(1+\frac{y}{x+z}\right)+\left(1+\frac{x}{y+z}\right)=3+\left(\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}\right)=4$.
Answer: 4 times.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.430 A passenger can travel from Moscow to city $N$ by train. In this case, he will be on the way for 20 hours. If, however, he waits for the departure of the plane (and he will have to wait more than 5 hours after the train departs), the passenger will reach city $N$ in 10 hours, including the waiting time. How many times faster is the speed of the plane compared to the speed of the train, if it is known that the plane will be over this train 8/9 hours after departure from the airport and will have flown as many kilometers by this moment as the train will have traveled?
|
Solution. Let $x$ and $y$ be the speeds (km/h) of the train and the airplane, respectively, and $z$ be the waiting time for the airplane to depart. Then $\frac{8}{9} y$ is the distance the airplane will fly until it meets the train. According to the problem, $\frac{8}{9} y = x \left(z + \frac{8}{9}\right)$. Additionally, $20 x = (10 - z) y' - $ is the distance to city $N$.
$$
\begin{gathered}
\text { If now } t = \frac{y}{x}, \text { then } \\
\left\{\begin{array}{l}
t = \frac{9}{8} \left(z + \frac{8}{9}\right), \\
t = \frac{20}{10 - z}, \\
z > 5.
\end{array} \Rightarrow \left\{\begin{array}{l}
z = \frac{8 t - 8}{9}, \\
z = \frac{10 t - 20}{t}, \\
\frac{10 t - 20}{t} > 5
\end{array} \Rightarrow \left\{\begin{array}{l}
4 t^{2} - 49 t + 9 = 0, \\
t > 4
\end{array} \Leftrightarrow t = 10 .\right.\right.\right.
\end{gathered}
$$
Answer: 10 times.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.437 What whole positive number should 180 be divided by, so that the remainder is $25\%$ of the quotient?
|
Solution. Let $n$ be the required number, $m$ be the remainder of the division of 180 by $n$, and $k$ be the quotient.
Then $\left\{\begin{array}{l}180=n \cdot k+m, \\ 4 m=k, \\ m4 m n>4 m^{2}$, i.e., $m^{2}<45 \Rightarrow m=4 \Rightarrow 4 n+1=45 \Rightarrow n=11$.
Answer: 11.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.438 By mixing $2 \mathrm{~cm}^{3}$ of three substances, 16 g of the mixture was obtained. It is known that $4 \mathrm{r}$ of the second substance occupies a volume that is $0.5 \mathrm{~cm}^{3}$ larger than $4 \mathrm{r}$ of the third substance. Find the density of the third substance, given that the mass of the second substance in the mixture is twice the mass of the first.
|
Solution. Let $x, y, z$ be the densities of three substances. Then, according to the condition $\left\{\begin{array}{l}2 x+2 y+2 z=16, \\ \frac{4}{y}-\frac{4}{z}=0.5, \quad \Rightarrow z=4 . \\ y=2 x\end{array}\right.$
Answer: 4 g $/ \mathrm{cm}^{3}$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13.450 If at the beginning of the time measurement there were $m_{0}$ g of substance $A$ and $2 m_{0}$ g of substance $B$, then after any number $t$ years, as a result of the radioactive decay of these substances, there will remain respectively $\boldsymbol{m}=\boldsymbol{m}_{0} \cdot 2^{-\lambda_{1} t}$ and $M=2 m_{0} \cdot 2^{-\lambda_{2} t}$, where $\lambda_{1}$ and $\lambda_{2}$ are constants depending on the nature of the substances. Calculate the half-life of each of these substances, i.e., find out after how many years only half of the initial amount of each substance will remain, if it is known that the half-life of substance $B$ is two times less than that of substance $A$, and that after 20 years the total mass of these substances decreases by 8 times.
|
Solution. Let $x$ and $2x$ be the half-lives of the second and first substances, respectively. According to the conditions,
$$
\left\{\begin{array}{l}
m_{0} \cdot 2^{-\lambda_{1} \cdot 2x} = \frac{m_{0}}{2}, \\
2m_{0} \cdot 2^{-\lambda_{2} \cdot x} = m_{0}, \\
m_{0} \cdot 2^{-\lambda_{1} \cdot 20} + 2m_{0} \cdot 2^{-\lambda_{2} \cdot 20} = \frac{3m_{0}}{8}
\end{array} \Leftrightarrow \left\{\begin{array}{l}
2^{-2\lambda_{1} x + 1} = 1 \\
2^{-\lambda_{2} \cdot x + 1} = 1 \\
8 \cdot 2^{-20\lambda_{1}} + 16 \cdot 2^{-20\lambda_{2}} = 3
\end{array}\right.\right.
$$
From the first two equations, it follows that $\lambda_{1} = \frac{1}{2x}, \lambda_{2} = \frac{1}{x}$.
Substituting these values into the third equation, we get: $16 \cdot 2^{-\frac{20}{x}} + 8 \cdot 2^{-\frac{10}{x}} - 3 = 0$.
Let $y = 2^{-\frac{10}{x}}$, then we have:
$16y^{2} + 8y - 3 = 0 \Rightarrow y = 2^{-2} \Rightarrow 2^{-\frac{10}{x}} = 2^{-2} \Rightarrow x = 5$.
Answer: 10 years, 5 years.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
### 5.080 Find the largest term in the expansion of $(\sqrt{5}+\sqrt{2})^{20}$.
|
Solution. Let $T_{k}$ be the $k$-th term in the expansion of $(\sqrt{5}+\sqrt{2})^{20}$.
Then $\frac{T_{k+1}}{T_{k}}=\frac{C_{20}^{k} \cdot(\sqrt{5})^{20-k} \cdot(\sqrt{2})^{k}}{C_{20}^{k-1} \cdot(\sqrt{5})^{21-k} \cdot(\sqrt{2})^{k-1}}=\frac{\sqrt{2}}{\sqrt{5}} \cdot \frac{21-k}{k}$.
The ratio $\frac{T_{k+1}}{T_{k}}>1 \Leftrightarrow \frac{\sqrt{2}}{\sqrt{5}} \cdot \frac{21-k}{k}>1 \Leftrightarrow k<\frac{21\sqrt{2}}{\sqrt{2}+\sqrt{5}} \approx 8.49$.
In other words, $\left\{\begin{array}{l}T_{1}<T_{2}<\ldots<T_{9} \\ T_{9}>T_{10}>T_{11}>\ldots T_{21} .\end{array}\right.$
Answer: The 9th term.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Senderovv B.A.
Find the smallest natural number that cannot be represented in the form $\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$, where $a, b, c, d$ are natural numbers.
|
$1=\frac{4-2}{4-2}, \quad 2=\frac{8-4}{4-2}, 3=\frac{8-2}{4-2}, 4=\frac{16-8}{4-2}, 5=\frac{32-2}{8-2}$
$6=\frac{16-4}{4-2}, 7=\frac{16-2}{4-2}, 8=\frac{32-16}{4-2}, 9=\frac{128-2}{16-2}, 10=\frac{64-4}{8-2}$.
Assume that $11=\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$. Without loss of generality, let $a>b, c>d$. Denote $m=a-b, n=c-d, k=b-d$. We get
$11\left(2^{n}-1\right)=2^{k}\left(2^{m}-1\right)$. Since the left side is an odd integer, $k=0$. Note that $n=1$ does not work. If $m>n>1$, then $2^{m}-1$ and $2^{n}-1$ give a remainder of 3 when divided by 4. Thus, the left and right sides give remainders of 1 and 3, respectively, when divided by 4. Contradiction.
## Answer
11.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Solve the system in positive numbers:
$$
\begin{cases}x^{y} & =z \\ y^{z} & =x \\ z^{x} & =y\end{cases}
$$
|
First, note that if one of the unknowns is equal to one, then the others are also equal to one.
Indeed, let $x=1$. Then $z=1^{\mathrm{y}}=1, y=z^{\mathrm{x}}=1^{1}=1$. Suppose there exists another solution besides $(1,1,1)$. Let's first consider $x>1$. Then $z=x^{\mathrm{y}}>1, y=z^{\mathrm{x}}>1$. Therefore, $z=x^{\mathrm{y}}>x^{1}=x, y=z^{\mathrm{x}}>z^{1}=z, x=y^{\mathrm{z}}>y^{1}=y$, which is impossible. Thus, this case is impossible. The case $x<1$ is impossible for the same reason by replacing all the ">" signs with "<" signs.
## Answer
$x=y=z=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Methods for solving problems with parameters]
[Investigation of a quadratic trinomial]
For what positive value of $p$ do the equations $3 x^{2}-4 p x+9=0$ and $x^{2}-2 p x+5=0$ have a common root?
|
The common root of the given equations must also be a root of the equation $\left(3 x^{2}-4 p x+9\right)-3\left(x^{2}-2 p x+5\right)=0 \Leftrightarrow$ $2 p x-6=0$. Therefore, it equals $3 / p$. Substituting, for example, into the second equation, we get $9 / p^{2}=1$, from which $p=3$.
## Answer
For $p=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Initially on the computer screen - some prime number. Every second, the number on the screen is replaced by the number obtained from the previous one by adding its last digit, increased by 1. What is the maximum time it will take for a composite number to appear on the screen?
#
|
Let the initial number on the screen be 2, then we get the following sequence: $2-5-11-13-17-25$. The sixth number is composite, so in this case, it will take 5 seconds. We will prove that in other cases, it will take no more than 5 seconds.
Indeed, if the number on the screen was an odd prime number not ending in 9, then its last digit will change in a cycle:
$1-3-7-5-1$. This means that no later than 4 seconds, a number ending in 5 will appear. Since it is not equal to 5, it is composite.
If the number on the screen was a prime number ending in 9, then 10 will be added every second. Since 10 gives a remainder of 1 when divided by 3, adding 10 once or twice will definitely result in a number divisible by 3. In this case, it will take no more than 2 seconds for a composite number to appear on the screen.
## Answer
In 5 seconds
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On the board after the class, there was a note left:
"Calculate $t(0)-t(\pi / 5)+t\left((\pi / 5)-t(3 \pi / 5)+\ldots+t\left({ }^{8 \pi} / 5\right)-t(9 \pi / 5)\right.$, where $t(x)=\cos 5 x+* \cos 4 x+* \cos 3 x+* \cos 2 x+$ $*^{\cos x}+* "$.
Seeing it, a math student told a friend that he could calculate this sum even without knowing the values of the coefficients erased from the board (denoted by * in our notation). Is he mistaken?
|
Let $t_{k}(x)=\cos k x$ for $k=0,1,2,3,4$. If we consider a similar sum for $t_{5}$ instead of $t$, we will get 10 as the result. We will check that for all other $t_{k}$ the sums are equal to 0. For $k=0$ this is obvious. For $k=1,2,3,4$ we arrive at the same equality
$\cos 0+\cos (2 \pi / 5)+\cos ((\pi / 5) \cos (6 \pi / 5)+\cos ((\pi / 5)=\cos (\pi / 5)+\cos (3 \pi / 5)+\cos (5 \pi / 5)+\cos (7 \pi / 5)+\cos ((\pi / 5)$. The expression on both the right and left sides is equal to 0. This follows from the fact that the sum of vectors going from the center of a regular pentagon to its vertices is 0 (see problem $\underline{55373}$ a or problem $\underline{85241}$ ).
## Answer
It is correct; the sum is 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bogosnov I.I.
Numbers, either red or blue, are arranged in a circle. Each red number is equal to the sum of its neighboring numbers, and each blue number is equal to the half-sum of its neighboring numbers. Prove that the sum of the red numbers is zero.
#
|
Let $a, b, c$ - be three consecutive numbers. If $b$ is red, then $b=a+c$, and if $b$ is blue, then $2 b=a+c$. We will write such equations for all triples of consecutive numbers and add them. On the right side, we will get twice the sum of all numbers, and on the left side - the sum of red numbers plus twice the sum of blue numbers. Then, if $R$ is the sum of all red numbers, and $B$ is the sum of all blue numbers, we get the equation $R+2 B=2(R+B)$, from which $R=0$.
Send a comment
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Rushkin C.
On the surface of a cube, a closed eight-segment broken line is drawn, the vertices of which coincide with the vertices of the cube.
What is the minimum number of segments of this broken line that can coincide with the edges of the cube?
#
|
The segments of the broken line are either edges of the cube or diagonals of its faces. To do this, let's color the vertices of the cube in two colors in a checkerboard pattern (see fig.). Note that an edge of the cube connects vertices of different colors, while a diagonal connects vertices of the same color. For the broken line to pass through all vertices, it must change color at some point, and to be closed, it must change color again. This means that the segments of the broken line must coincide with the edges of the cube at least twice.
This is sufficient, see the example in the figure.
## Answer
Two segments.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Rubanov I.S.
In five pots standing in a row, Rabbit poured three kilograms of honey (not necessarily into each and not necessarily equally). Winnie-the-Pooh can take any two adjacent pots. What is the maximum amount of honey that Winnie-the-Pooh can guarantee to eat?
#
|
Evaluation. Let's assume Winnie-the-Pooh cannot take at least a kilogram of honey. This means that in any pair of adjacent pots, there is less than a kilogram of honey. This is true for both the two rightmost pots and the two leftmost pots. However, then in the middle pot, there must be more than a kilogram of honey (otherwise, the total amount of honey would be less than 3 kg). This is a contradiction. Therefore, Winnie-the-Pooh will always be able to take at least a kilogram of honey.
Example. If the first, third, and fifth pots each contain 1 kg of honey, and the second and fourth pots are empty, then
Winnie-the-Pooh will not be able to eat more than a kilogram of honey.
## Answer
1 kg.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Auto: : Bogosnov I.I.
All integers from -33 to 100 inclusive were arranged in some order, and the sums of each pair of adjacent numbers were considered. It turned out that there were no zeros among them. Then, for each such sum, the number reciprocal to it was found. The obtained numbers were added. Could the result be an integer?
#
|
Let's consider an example of such an arrangement. Consider the sequence $100, -33, 99, -32, \ldots, 34, 33$. Then, if the first number of the pair is in an odd position, the sum is 67. If it is in an even position, the sum is 66. The reciprocals will be $\frac{1}{67}$ and $\frac{1}{66}$, respectively, with the first occurring -67 times, and the second -66 times. Therefore, the final sum is 2.
## Answer
it is possible.
Send a comment
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.