problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Yamenniko i.v.
The numbers 2, 3, 4, ..., 29, 30 are written on the board. For one ruble, you can mark any number. If a number is already marked, you can freely mark its divisors and numbers that are multiples of it. What is the minimum number of rubles needed to mark all the numbers on the board?
|
Let's mark the numbers $17, 19, 23$, and 29, spending four rubles. Then mark the number 2, spending another ruble. After this, we can freely mark all even numbers (since they are divisible by 2), and then all odd numbers not exceeding 15 - for any of them (let's say for the number $n$) the even number $2n$ is already marked, and we can mark $n$ as its divisor. It remains to mark 21, 25, and 27, and this is also done for free: 25 is divisible by the marked number 5, and 21 and 27 are divisible by the marked number 3. In any way of solving the problem, the prime numbers 17, 19, 23, and 29, which exceed 15, will have to be marked at a cost - they are not divisors or multiples of any numbers on the board. Thus, 4 rubles will be spent only on them. To mark anything else, we will have to spend a fifth ruble. Therefore, it is not possible to fulfill the conditions of the problem for less than five rubles.
Comment. In fact, after marking the "large" prime numbers, we could have marked any of the remaining numbers on the board instead of the number 2. Indeed, then we will freely mark its smallest prime divisor $p$. If $p=2$, we act according to the algorithm described above. If not, we mark $2p$ (this can be done since $p < 15$), then mark the number 2, and from there everything else is done in the known way.
A similar solution is applicable for an arbitrarily long set $2, 3, 4, \ldots, N$ - we are forced to mark all "large" prime numbers (exceeding $N / 2$) at a cost, and then mark any of the remaining numbers for a ruble. Then we freely mark the number 2 in the way described above, then all even numbers, then all "small" prime numbers (not exceeding $N / 2$), because any "small" $p$ will be a divisor of $2p$. Now we can mark all the remaining unmarked numbers: each of them will be divisible by its minimal prime divisor - a "small" prime number.
## Answer
For 5 rubles.
Submit a comment
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Evdokimov M.A.
16 cards with integers from 1 to 16 are laid face down in a $4 \times 4$ table so that cards with consecutive numbers are adjacent (touching by a side). What is the minimum number of cards that need to be flipped simultaneously to definitely determine the location of all numbers (regardless of how the cards are arranged)?
|
Evaluation. Let's number the cells as shown in Figure 1.
| 1 | 2 | 3 | 4 |
| :--- | :--- | :--- | :--- |
| 2 | 1 | 4 | 3 |
| 5 | 6 | 7 | 8 |
| 6 | 5 | 8 | 7 |
Fig. 1
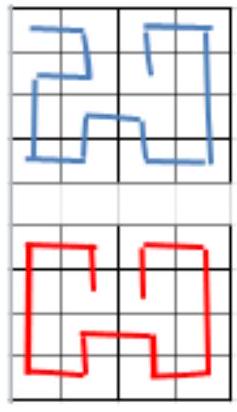
Fig. 2
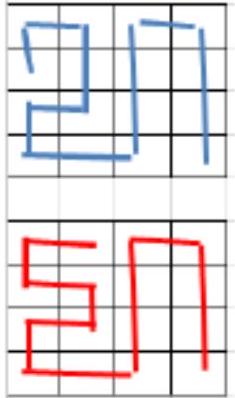
Fig. 3
Notice that one of the cells numbered 1 must be open, otherwise the red and blue ways of filling the table in Figure 2 would be indistinguishable. One of the cells numbered 2 must also be open, otherwise the red and blue ways of filling the table in Figure 3 would be indistinguishable.
Similarly, at least one of the cells numbered 3, 4, 5, 6, 7, 8 must be open, meaning that at least 8 cards must be open.
Example. We will prove that by seeing the numbers in the second and third columns, we can restore the numbers in the first and fourth columns. Notice that in the black cells of the chessboard coloring, all numbers have the same parity, and in the white cells, the other parity. By seeing the second and third columns, we understand the parity of the number in each cell.
From the open cells, we highlight those for which the number written in the cell does not have all neighboring numbers open. From each such cell, we draw an edge to the only unopened neighboring cell and uniquely restore the number in it.
Notice that if an edge leads to a corner, we will restore the number in it. If no edge leads to a corner cell, then it contains the extreme number, i.e., 1 or 16, and since we know the parity of the number in each cell, we can also restore the number in the corner. Thus, the numbers in the corners are definitely restored.
If there are corner cells for which not all neighboring numbers are open, we draw an edge from each such corner to the unopened neighboring cell and uniquely restore the number in it.
The numbers in the non-corner cells of the first and fourth columns may remain un-restored. Consider any of them. No edge leads to it from the neighboring column or from the corner, so in this cell, there is definitely an extreme number (since it has at most one neighboring cell with a number). By parity, it is easy to determine which extreme number should be there.
Thus, we have restored the numbers in all cells.
## [ Lengths of sides, heights, medians, and bisectors ] Problem $\underline{67255}$ Topics: [ Triangle inequality (other) $]$
Difficulty: $3+$
Grades: 8,9
Author: Bakayev E.V.
In triangle ABC, medians $\mathrm{BK}$ and $\mathrm{CN}$ intersect at point M. What is the maximum number of sides of quadrilateral ANMK that can have a length of 1?
## Solution
For example, any triangle where $\mathrm{AB}=\mathrm{AC}=2$ works. Let's prove that there cannot be three equal sides.
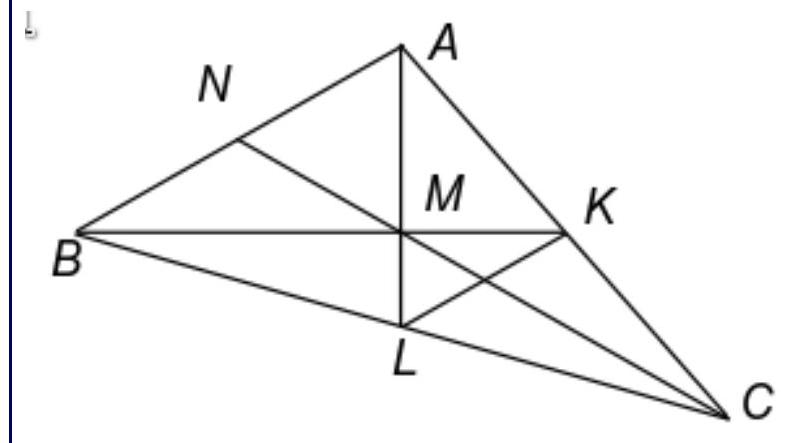
Method 1. Suppose that at least three sides of quadrilateral ANMK are equal to 1. There are only two fundamentally different cases. 1) $\mathrm{AN}=\mathrm{NM}=\mathrm{MK}=1$. Then $\mathrm{NB}=1, \mathrm{MB}=2$, so $\mathrm{MN}+\mathrm{NB}=\mathrm{MB}$. 2) $\mathrm{AN}=\mathrm{NM}=\mathrm{MK}=1$. Then $\mathrm{AC}=2, \mathrm{NC}=3$, so $\mathrm{NA}+\mathrm{AC}=\mathrm{NC}$. In both cases, a contradiction with the triangle inequality is obtained.
Method 2. If more than two sides of the quadrilateral are equal to 1, then either $\mathrm{AK}=\mathrm{NA}$ or $\mathrm{KM}=\mathrm{MN}$. In the first case, triangle ABC is isosceles. In the second case, $\mathrm{BK}=\mathrm{CN}=3$, so in this case, triangle ABC is also isosceles. From this, it follows that $\mathrm{AK}=\mathrm{KM}=\mathrm{MN}=\mathrm{NA}$, meaning that $\mathrm{AKMN}$ is a rhombus. Contradiction, since lines AK and NM are not parallel.
Method 3. Let $\mathrm{L}$ be the midpoint of side $\mathrm{BC}$. If $\mathrm{NM}=\mathrm{NA}=\mathrm{NB}$, then triangle AMB is a right triangle. Triangle LMK is similar to triangle AMB with a coefficient of 0.5, so MK = LM, and therefore the hypotenuse of triangle AMK is greater than the hypotenuse of triangle LMK, i.e., $\mathrm{AK}>\mathrm{LK}=\mathrm{NA}$. Thus, in quadrilateral ANMK, there are no three sides equal to each other.
The case when KM = KA is similar, and if $KM \neq KA$ and $NM \neq NA$, then among the segments NM, NA, KM, KA, there are also no three equal to each other.
## Answer
2 sides.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On a sheet of paper, points $A, B, C, D$ are marked. A recognition device can perform two types of operations with absolute accuracy: a) measure the distance in centimeters between two given points; b) compare two given numbers. What is the minimum number of operations this device needs to perform to definitely determine whether the quadrilateral $A B C D$ is a rectangle?
|
To determine whether $A B C D$ is a rectangle, it is sufficient to check the equalities $A B=C D$, $B C=A D$, and $A C=B D$ - a total of 9 operations (3 operations for each equality: two measurements and one comparison). The rectangle $A B C D$ will be a square if $A B=B C$ - for this, one more, the 10th, operation of comparing the lengths of segments $A B$ and $B C$ is needed. We will prove that a smaller number of operations will not suffice in both cases, i.e., that all the specified operations must be performed. Indeed, if we do not know that two opposite sides of a quadrilateral are equal, we cannot even assert that $A B C D$ is a parallelogram, since an isosceles trapezoid (its diagonals are equal) is also possible. Therefore, checking the equalities $A B=C D$ and $B C=A D$ is necessary. If, however, we do not know that $A C=B D$, then $A B C D$ can be any parallelogram. Thus, checking the equality of the diagonals is also necessary. Finally, in the case of a square, it is also necessary to check the equality of two adjacent sides.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a single-round-robin tournament, 10 chess players are participating. What is the minimum number of rounds after which a sole winner can be determined prematurely? (In each round, the participants are paired.
Win - 1 point, draw - 0.5 points, loss - 0).
#
|
Evaluation. After the sixth round, 30 points have been played, and the leader has no more than 6 points, while the other nine participants have collectively scored no less than 24 points. Therefore, among them, there is at least one who has no less than 3 points. Since there are still 3 rounds ahead, the winner is still unknown.
Example. Suppose in the first seven rounds, the leader won all their games, and the other games ended in draws. Then, two chess players who have not yet played against the leader have 3.5 points each, while the others have 3 points each. Since there are 2 rounds left until the end of the tournament, the winner is already determined.
## Answer
After 7 rounds.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bogdanov I.I.
In a store, 21 white and 21 purple shirts are hanging in a row. Find the smallest $k$ such that for any initial order of the shirts, it is possible to remove $k$ white and $k$ purple shirts so that the remaining white shirts hang together and the remaining purple shirts also hang together.
|
First, let's show that \( k \), equal to 10, is sufficient.
First method. We will walk along the row of shirts and count the white and purple shirts separately. As soon as we count 11 of one color - let's assume, without loss of generality, purple - shirts, we will stop. Now we will remove all the white shirts that we have passed (there are no more than 10), and all the purple shirts that we have not yet reached (there are exactly 10). If necessary, we will remove a few more white shirts. It is obvious that all 11 purple shirts are hanging in a row (all the white shirts that were between them have been removed). The remaining white shirts also hang in a row: all the remaining purple shirts have been removed.
Second method. We will stand between the 21st and 22nd shirt, then there will be 21 shirts on both the left and the right. Without loss of generality, we can assume that there are no more white shirts on the left than purple ones. Then there are no more than 10 white shirts on the left, and no more than 10 purple shirts on the right (because there should be as many purple shirts as there are white ones on the left). We will remove all the white shirts on the left and all the purple shirts on the right. After this, all the remaining purple shirts will be hanging on the left, and all the remaining white ones on the right. If we removed \( n \) shirts, the problem 64770 Topics: [ Proof by contradiction ] \([ \quad \underline{\text{ Induction (other) }} \quad]\) Difficulty: 4 Classes: 9, 10, 11 Author: Khrrabrov A. Given a function \( f \), defined on the set of real numbers and taking real values. It is known that for any \( x \) and \( y \), such that \( x > y \), the inequality \( (f(x))^2 \leq f(y) \) holds. Prove that the set of values of the function is contained in the interval \([0,1]\).
## Solution
By the condition \( f(y) \geq (f(y+1))^2 \geq 0 \) for any \( y \), so all values of the function are non-negative.
Now let \( f(x_0) = 1 + a > 1 \) for some \( x_0 \). We will prove by induction on \( n \) that \( f(y) > 1 + 2^n a \) for any \( y < x_0 \).
Base case. For \( n = 0 \), \( f(y) > 1 + 2^0 a = 1 + a \).
Inductive step. Assume \( f(y) > 1 + 2^n a \). Then \( f(y) \geq (f(\frac{1}{2}(x_0 + y)))^2 = 1 + 2^{n+1} a + (2^n a)^2 > 1 + 2^{n+1} a \).
Thus, for any fixed \( y < x_0 \), \( f(y) > 1 + 2^n a \) for any natural \( n \). But this is impossible, as \( 2^n a > f(y) \) for sufficiently large \( n \). Contradiction.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Gooovanovo A.C. Positive rational numbers $a$ and $b$ are written as decimal fractions, each of which has a minimal period consisting of 30 digits. The decimal representation of the number $a-b$ has a minimal period length of 15. For what smallest natural $k$ can the minimal period length of the decimal representation of the number $a+k b$ also be 15?
|
By multiplying, if necessary, the numbers $a$ and $b$ by a suitable power of ten, we can assume that the decimal representations of the numbers $a, b, a-b$, and $a+k b$ are purely periodic (i.e., the periods start immediately after the decimal point).
Then $a=\frac{m}{10^{30}-1}, b=\frac{n}{10^{30}-1}$. We also know that the numbers $a-b=\frac{m-n}{10^{30}-1}$ and $a+k b=\frac{m+k n}{10^{30}-1}$ can be written as decimal fractions with a period of length 15, i.e., they can be written as common fractions with the denominator $10^{15}-1$. Therefore, their difference $(k+1) b=\frac{(k+1) n}{10^{30}-1}$ can also be written this way. Thus, the number $(k+1) n$ is divisible by $10^{15}+1$, while the number $n$ is not (otherwise, $b$ would be written as a fraction with a period of length 15). Therefore, the number $k+1$ is divisible by some prime divisor of the number $10^{15}+1$. The smallest such divisor is 7. Indeed, the number $10^{15}+1$ is not divisible by 2 or 5 and gives a remainder of 2 when divided by 3. On the other hand, it is divisible by $10^{3}+1=7 \cdot 143$. Thus, $k+1 \geq 7$, i.e., $k \geq 6$.
Let $a-b=\frac{1}{10^{15}-1}, \quad a+6 b=\frac{2}{10^{15}-1}$. Then $a=\frac{8}{7\left(10^{15}-1\right)}, \quad b=\frac{1}{7\left(10^{15}-1\right)}$. It is clear that the lengths of the minimal periods of the numbers
$a-b$ and $a+6 b$ are 15. The lengths of the minimal periods of the numbers $a$ and $b$ are greater than 15 and are divisible by 15 (since $10^{T}-1$ must divide $10^{15}-1$). On the other hand, since $10^{30}-1$ is divisible by $7\left(10^{15}-1\right)$, the numbers $a$ and $b$ are periodic with a period length of 30. Therefore, the lengths of their minimal periods are 30.
## Answer
For $k=6$.
## [ Divisibility of numbers. General properties ] Problem 64817 Topics: $[$ Evenness and oddness $\quad]$ [ Examples and counterexamples. Constructions ]
Complexity: $4-$
Classes: 8,9
Author: Bakayev E.V.
Does there exist a number that is divisible by exactly 50 numbers from the set $1,2, \ldots, 100$?
## Solution
For example, the product of all odd numbers from 1 to 99 will work. Indeed, this product is divisible by all odd numbers from 1 to 100 - and there are exactly 50 of them, - and it is not divisible by any even number, as it is not even divisible by 2.
## Answer
Yes, such a number exists.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11 |
Let $x, y, z$ be positive numbers and $x y z(x+y+z)=1$. Find the minimum value of the expression $(x+y)(x+z)$.
|
Make the substitutions $x=p-a, y=p-b, z=p-c$.
## Solution
Let $a=y+z, b=x+z, c=x+y, p=x+y+z$. Consider a triangle with sides $a, b, c$ (the triangle inequalities are obviously satisfied). The perimeter of this triangle is $2 p$, and let the area be denoted by $S$. By Heron's formula,
$S^{2}=p(p-a)(p-b)(p-c)=(x+y+z) x y z=1$, so $(x+y)(x+z)=b c \geq 2 S=2$. Equality is achieved for a right triangle
(for example, respectively,
## Answer
2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bogdanov I.i.
Initially, there are 111 pieces of plasticine of the same mass on the table. In one operation, you can choose several groups (possibly one) with the same number of pieces and in each group, combine all the plasticine into one piece. What is the minimum number of operations required to get exactly 11 pieces, each of which has a different mass?
#
|
Let the mass of one original piece be 1. If in the first operation in each group there are $k$ pieces, then after it each piece will have a mass of 1 or $k$; therefore, it is impossible to get 11 pieces of different masses in one operation.
We will show that the required result can be achieved in two operations. For the first operation, choose 37 groups of 2 pieces each; after the operation, there will be 37 pieces with masses of 1 and 2. For the second operation, choose 9 groups of 8 pieces each: in the $i$-th group $(1 \leq i \leq 9)$, there will be $i-1$ pieces of mass 2 and $9-i$ pieces of mass 1. Two pieces of masses 1 and 2 will remain unused, and from the $i$-th group, a piece of mass $9-i+2(i-1)=7+i$ will be obtained. Thus, 11 pieces with masses 1, 2, 8, 9, ..., 16 will be obtained.
## Answer
In two operations.

Complexity: 3
Classes: 5,6
Arrange the numbers $1,2,3, \ldots, 9$ in the circles so that the sum of the numbers on each side of the triangle equals ..... 17.
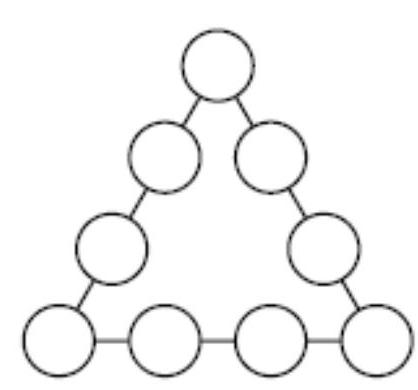
## Answer
See the diagram
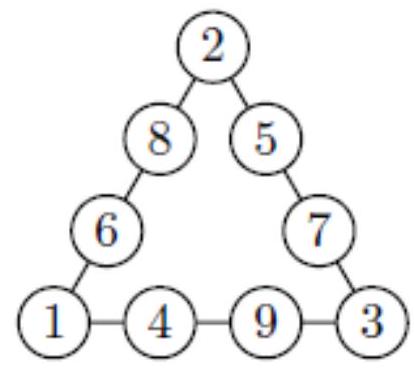
Submit a comment
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bakayev E.B.
A boy and a girl were sitting on a long bench. Twenty more children approached them one by one, and each of them sat between two of the already seated children. We will call a girl brave if she sat between two neighboring boys, and a boy brave if he sat between two neighboring girls. When everyone was seated, it turned out that the boys and girls were sitting on the bench, alternating. How many of them were brave?
|
The first method. Let's look at the number of pairs of adjacent boys and girls. Initially, it is equal to 1. Notice that if a boy sits between two boys, the number of such pairs does not change. If he sits between a boy and a girl, he "destroys" one such pair and "creates" one, so the number of such pairs does not change. Only in the case where the boy was brave, he increases the number of such pairs by two. Similar reasoning applies to girls. Since we end up with 21 such pairs, the number of brave children was $(21-1): 2=10$.
The second method. Each brave child reduces the number of same-sex pairs by 1. Each non-brave child increases the number of same-sex pairs by 1. At the beginning, there were no same-sex pairs, and at the end, there were none either. Therefore, the number of brave children is equal to the number of non-brave children.
The third method. Groups of boys alternate with groups of girls. Initially, there were two groups. When a non-brave child sat down, he joined a group, and the number of groups did not change. When a brave child sat down, he split a group of the opposite sex into two and formed a new group consisting of himself, increasing the total number of groups by 2. In the end, there were 22 groups. Therefore, the number of brave children was (22 - 2) : $2=10$.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For what value of $a$ does the polynomial $P(x)=x^{1000}+a x^{2}+9$ divide by $x+1$?
#
|
$P(-1)=1+a+9=a+10$. By the theorem of Bezout, this number should equal zero.
## Answer
For $a=-10$.
|
-10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The principle of the extreme (etc.). $\quad]$ Symmetry helps solve the task_ $\quad]$
There are thirty cards, each with a number: on ten cards - $a$, on ten others - $b$, and on the remaining ten - $c$ (the numbers $a, b, c$ are all different). It is known that for any five cards, it is possible to find another five such that the sum of the numbers on these ten cards is zero. Prove that one of the numbers $a, b, c$ is zero.
|
Let $a<b<c$. We will mark on the number line all possible sums of the numbers on five cards. For each of them, the opposite is also marked, so the marked points are symmetrically located relative to zero. In particular, the largest (5c) and the smallest (5a) sums are opposite, so $5 a+5 c=0$, which means $c=-a$. The sums closest to the "extreme" ones are also opposite: $(4 a+b)+(4 c+b)=0$. From this, it follows that $b=0$.
|
0
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Bakayev E.v.
10 children of different heights are standing in a circle. From time to time, one of them runs to another place (between some two children). The children want to stand in order of increasing height as quickly as possible, in a clockwise direction (from the shortest to the tallest). What is the minimum number of such moves they will definitely need, regardless of how they are initially standing?
#
|
Number the children in ascending order of height $-1, 2, \ldots, 10$.
Estimation. Suppose they initially stood in reverse order.
First method. If there were fewer than eight sprints, then some three children remained in their places, and their order is opposite to the required one.
Second method. Let's call the complexity the number of turns we make when walking counterclockwise from the 1st to the 2nd, then to the 3rd, ..., from the 10th to the 1st. Initially, the complexity is 1, and at the end, it is 9. It is not difficult to verify that when one child sprints, the complexity can change by no more than 1. Therefore, at least eight sprints are needed.
Example with eight sprints: the 1st and 2nd remain in their places, the 3rd sprints and stands behind the 2nd, then the 4th - behind the 3rd, and so on.
## Answer
8 sprints.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
The weight of each weight in the set is a non-integer number of grams. They can balance any integer weight from 1 g to 40 g (weights are placed on one pan of the scales, the weight to be measured - on the other). What is the smallest number of weights in such a set?
|
Example 1. Let's take weights of 1, 1, 3, 5, 11, 21, 43 g. The first two can measure any integer weight up to 2 g. Therefore, the first three can measure up to 5 g, the first four up to 10 g, the first five up to 21 g, the first six up to 42 g, and all seven up to 85 g. If we reduce the weight of each weight by half, all the weights will now be non-integer grams, and they can measure any integer or half-integer weight from 0.5 to 42.5 g.
Example 2. Weights of 1, 2, 4, 8, 16, 32, 64 g can measure any integer weight up to 127 g. If we leave only a third of each weight, the weights will become non-integer, and they can measure any integer weight up to 42 g.
Estimation. Suppose there are 6 weights in the set. There are $2^6 = 64$ different subsets. Let's paint one weight yellow and divide the subsets into pairs that differ only by the presence of the yellow weight. Since the weights of the paired subsets differ by the non-integer weight of the yellow weight, at most one of them can have an integer weight in grams. Therefore, there are no more than 32 subsets with an integer weight, and 40 different integer weights cannot be measured with this set of weights.
## Answer
7 weights.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The hostess made a pirog (a type of Russian pie) and wants to pre-cut it into such (not necessarily equal) pieces so that the pie can be evenly divided both among five and seven people. What is the minimum number of pieces she can manage with?
#
|
This task is a particular case of problem $\underline{98057 .}$
## Answer
11 pieces.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the minimum number of weights needed to be able to weigh any number of grams from 1 to 100 on a balance scale, if the weights can be placed on either pan of the scale?
#
|
When solving this problem, we need the following interesting property of the ternary numeral system: any natural number can be represented as the difference of two numbers, the ternary representation of which contains only 0 and 1.
To prove this, we need to write the original number in ternary notation and construct the required numbers digit by digit from right to left. If the resulting numbers have ones in the same positions, they can be replaced with zeros.
Now it is clear that it is sufficient to have 5 weights with masses of 1, 3, 9, 27, 81 (think about why a weight of 243 grams is not needed).
Four weights, however, are clearly insufficient, as they can measure no more than \(3^4-1=80\) different weights (each weight is either on the left pan, or on the right pan, or not involved in the weighing).
Send a comment
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ionin Yu.I.
a) Does there exist an infinite sequence of natural numbers with the following property: no number in the sequence divides another, but among any three numbers, one can choose two whose sum is divisible by the third?
b) If not, how many numbers can be in a set with such a property?
c) Solve the same problem under the additional condition: only odd numbers are allowed in the set. Here is an example of such a set of four numbers: \(3, 5, 7, 107\). In the triplet \(3, 5, 7\), the sum \(5 + 7\) is divisible by 3; in the triplet \(5, 7, 107\), the sum \(107 + 5\) is divisible by 7; in the triplet \(3, 7, 107\), the sum \(7 + 107\) is divisible by 3; finally, in the triplet \(3, 5, 107\), the sum \(3 + 107\) is divisible by 5.
|
b) To the sequence of four numbers $3,5,7,107$ given in the condition, we can add the fifth number 10693: 10693 + 5 is divisible by $3,10693+3$ is divisible by $7,10693+7$ is divisible by $5,10693+107$ is divisible by 3 and by $5,10693+7$ is divisible by 107.
We will show that it is impossible to form a sequence satisfying the condition of the problem from six odd numbers. Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}$ be such numbers. We will make several preliminary remarks.
1) If $a, b, c$ are three terms of our sequence, $a>b>c$, then $b+c$ does not divide $a$.
Indeed, if $b+c$ divided $a$, then $a$ would be equal to $b+c$, which contradicts the condition $a>b>c$.
2) If $a, b, c$ are three terms of our sequence, $a>b>c$, then $a+b$ is divisible by all terms of the sequence less than $b$, except possibly one.
Indeed, if $a+b$ is not divisible by two numbers $c$ and $d$, less than $b$, then $a+c$ and $a+d$ are divisible by $b$, but then $c-d$ is divisible by $b$, which is impossible.
3) If $a, b, c, d$ are four terms of our sequence, $a+b$ and $a+c$ are divisible by $d$, then $b+c$ does not divide $d$.
Indeed, since $a+b$ and $a+c$ are divisible by $d$, then $2a+(b+c)$ is divisible by $d$, while $2a$ is not divisible by $d$ (since $d$ is an odd number and $a$ is not divisible by $d$).
Let $a_{1}>a_{2}>a_{3}$ be the three largest of the six numbers $a_{1}, a_{2}, \ldots, a_{6}$.
Each of the numbers $a_{1}+a_{2}, a_{1}+a_{3}, a_{2}+a_{3}$, according to 2), is divisible by at least two of the numbers $a_{4}, a_{5}, a_{6}$. At the same time, 3) shows that these numbers do not have a common divisor among the numbers $a_{4}, a_{5}, a_{6}$. Therefore, each of the numbers $a_{1}+a_{2}, a_{1}+a_{3}, a_{2}+a_{3}$ is divisible by two of the numbers $a_{4}, a_{5}, a_{6}$ and does not divide the third.
Suppose $a_{1}+a_{2}$ is divisible by $a_{4}$ and $a_{5}$ and does not divide $a_{6} ; a_{1}+a_{3}$ is divisible by $a_{4}$ and $a_{6}$ and does not divide $a_{5} ; a_{2}+a_{3}$ is divisible by $a_{5}$ and $a_{6}$ and does not divide $a_{4}$. Then the numbers $a_{1}+a_{5}$ and $a_{2}+a_{4}$ are divisible by $a_{3}$. Therefore, the number $\left(a_{1}+a_{2}\right)+\left(a_{4}+a_{5}\right)$ is also divisible by $a_{3}$.
At the same time, $a_{1}+a_{2}$ is divisible by three of the numbers $a_{3}, a_{4}, a_{5}, a_{6}$, and since $a_{1}+a_{2}$ does not divide $a_{6}$, then $a_{1}+a_{2}$ divides $a_{3}$, from which it follows that $a_{4}+a_{5}$ divides $a_{3}$. This contradicts 1).
Thus, a sequence of odd numbers with the property we are interested in can consist of no more than five numbers.
b) If the sequence consists only of even numbers, then, without violating the condition, we can divide them all by 2. We will therefore assume that there are odd numbers in the sequence. By the result of part c), there are no more than five of them. Remarks 1) - 3) are now valid under some additional assumptions.
In 1) we need to require that $a$ does not equal $b+c$; 2) is valid if the number $a$ does not equal the sum of any two members of the sequence, and 3) is valid if $d$ is an odd number.
If the members of the sequence $a, b, c$ are even, and $d$ is odd, then the numbers $a+d, b+d$ and $c+d$ do not divide $a$, $b$, or $c$. Therefore, the numbers $a+b, a+c$ and $b+c$ divide $d$, which contradicts 3).
Thus, there are no more than two even numbers in our sequence. Let them be two: $a$ and $b(a>b)$. Then the number $a+b$ divides all odd members of the sequence, and therefore the number $a$ is the largest in the sequence.
If the number $a$ does not equal the sum of any two members of the sequence, then, by discarding the number $b$, we obtain a sequence for which remarks 1), 2), 3) are valid without any restrictions. The solution to part c) shows that such a sequence has no more than five members, that is, the original sequence has no more than six numbers.
Suppose now that the number $a$ equals the sum of some two odd members of the sequence. If $c$ is the larger of these odd numbers, then $a=c+d$ where $d$ is the smaller odd number. If $d > a/2$, then $c > a/2$, and $a = c + d > a$, which is a contradiction. If $d \leq a/2$, then $c \leq a/2$, and $a = c + d \leq a$, which is also a contradiction.
Thus, in any case, there are no more than six numbers in our sequence.
Here is an example of a six-member sequence: $2,3,5,7,107,10693$.
Submit a comment
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ CaseAnalysis ] $[$ Divisibility Rules (etc.) $]$ Author: Fomin S.B. A natural number $n$ is written in the decimal system. It is known that if a digit appears in this representation, then $n$ is divisible by this digit (0 does not appear in the representation). What is the maximum number of different digits that this representation can contain?
|
If the digit 5 is included in the representation of a number, then the number must end in 5. Therefore, it is odd and, consequently, contains only odd digits. Thus, it cannot have more than five digits. If 5 does not appear in the decimal representation of the number, then it can include all other 8 digits. For example: 1471963248. This number is divisible by $1,2,3,4,6,7,8,9$.
## [ Dirichlet's Principle (other). ] Problem 98031 Topics: [Proof by contradiction] $[$ Combinations and permutations $]$ Author: Folklore 10 friends sent each other holiday cards, with each sending five cards. Prove that there will be a pair who sent cards to each other. Solution Suppose this is not the case, that is, there is no pair of friends who sent cards to each other. Each friend sent cards to five others, so they could have received no more than four cards. Therefore, the total number of cards received is no more than 40, while 50 cards were sent ($5 \cdot 10=50$). This is a contradiction.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Text problems ] $[$ Case enumeration ]
In a box, there are blue, red, and green pencils. In total, there are 20. The number of blue pencils is 6 times the number of green pencils, and the number of red pencils is less than the number of blue pencils. How many red pencils are in the box?
|
Think about how many blue pencils there can be.
## Solution
Since there are 20 pencils in total, and blue and green pencils together make up 7 parts. This means there can be 6 or 12 blue pencils, and green and red pencils would then be 1 and 13 or 2 and 6, respectively. Since there are fewer red pencils than blue ones, only the second option is possible: 12 blue, 2 green, and 6 red.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Yashchenko I.V.
On a circular road, there are four gas stations: $A, B, C$, and $D$. The distance between $A$ and $B$ is 50 km, between $A$ and $C$ is 40 km, between $C$ and $D$ is 25 km, and between $D$ and $A$ is 35 km (all distances are measured along the circular road in the shortest direction).
a) Provide an example of the arrangement of the gas stations (with the distances between them) that satisfies the condition of the problem.
b) Find the distance between $B$ and $C$ (list all possibilities).
|
First, determine the arrangement of gas stations $A, C$, and $D$.
## Solution
The problem provides all three distances between $A, C$, and $D$. First, let's determine the arrangement of these three gas stations. Gas stations $A$ and $C$ divide the circular road into two arcs. If gas station $D$ were on the shorter arc, the sum of the distances from $A$ to $D$ and from $D$ to $C$ would be equal to the distance from $A$ to $C$. However, this is not the case.
Therefore, gas station $D$ must be on the longer arc, so the length of the longer arc between $A$ and $C$ is $A D + D C = 25 + 35 = 60$ km. Consequently, the length of the circular road is 60 km $+ A C = 100$ km.
Since $B A = 50$ km, $A$ and $B$ are diametrically opposite. Therefore, the distance from $B$ to $C$ is $50 - 40 = 10$ km (see the diagram).
## Answer
a) See the diagram; b) 10 km.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Pairing and grouping; bijections $]$ [ Decimal number system ]
Find the last digit of the number $1^{2}+2^{2}+\ldots+99^{2}$.
|
$1^{2}+2^{2}+\ldots+99^{2} \equiv 10\left(1^{2}+2^{2}+\ldots+9^{2}\right)=0(\bmod 10)$.
## Answer
0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Investigation of a quadratic trinomial ]
A quadratic trinomial $y=a x^{2}+b x+c$ has no roots and $a+b+c>0$. Determine the sign of the coefficient $c$.
#
|
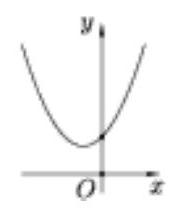
The quadratic polynomial has no roots, which means its graph does not intersect the x-axis. Since \( y(1) = a + b + c > 0 \), the graph is located in the upper half-plane (see the figure), therefore, \( c = y(0) > 0 \).
## Answer
\( c > 0 \).
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bakayev E.V.
In a circle, there are boys and girls (both are present), a total of 20 children. It is known that for each boy, the neighbor in the clockwise direction is a child in a blue T-shirt, and for each girl, the neighbor in the counterclockwise direction is a child in a red T-shirt. Can the number of boys in the circle be determined unambiguously?
|
The MHD (clockwise) arrangement cannot be due to the color of child X's T-shirt. Therefore, one boy should stand clockwise from the boy, one boy from him, and so on. This means that there are no fewer than half of all the children in the circle who are boys. By similar considerations, there are no fewer than half of the girls. Therefore, there are 10 boys and 10 girls.
## Answer
It can be.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V. A sequence of several natural numbers is written, with a sum of 20. No number and no sum of several consecutive numbers equals 3. Could there be more than 10 numbers written?
|
Example with 11 numbers: $1,1,4,1,1,4,1,1,4,1,1$.
## Answer
It could.
Send a comment
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ [Reverse Process ]
Lёnya thought of a number. He added 5 to it, then divided the sum by 3, multiplied the result by 4, subtracted 6, divided by 7, and got 2. What number did Lёnya think of?
Try to form an equation to determine the unknown number.
#
|
Let's denote the number thought of by Lёna as $x$. Then we can form the equation
$$
\{[((x+5): 3)-4]-6\}: 7=2
$$
By sequentially moving all numbers from the left side to the right, we get a new equation
$$
x=\{[((27)+6): 4] 3\}-5
$$
from which it is easy to determine that $x=10$. From this, it is also clear that to determine the thought number (which we denoted as $x$) we need to perform the inverse operations in reverse order on the number obtained by Lёna (i.e., 2).
## Answer
10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Dirichlet's Principle (continued).]
In a bag, there are balls of two different colors: black and white. What is the smallest number of balls that need to be taken out of the bag blindly so that among them there are definitely two balls of the same color?
#
|
We need to draw three balls in total, so the balls are the "rabbits," and the colors are the "cages." Since there are fewer cages than rabbits, by the Pigeonhole Principle, there will be a cage with at least two rabbits. That is, two balls of the same color. It is easy to notice that by drawing two balls, we might get balls of different colors.
## Answer
3 balls.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Sharygin I.F.
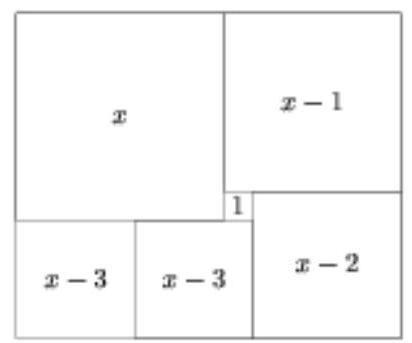
A rectangle is composed of six squares (see the right figure). Find the side of the largest square if the side of the smallest one is 1.
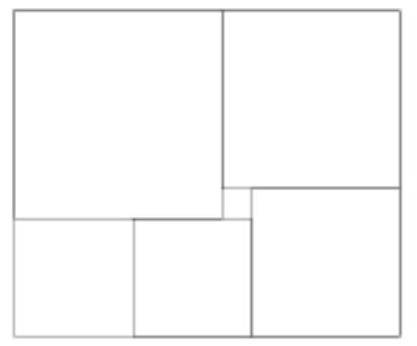
The side of the largest square is equal to the sum of the sides of two squares: the next one in the clockwise direction and the smallest one.
#
|
Notice that the side of the largest square is equal to the sum of the sides of two squares: the one following it clockwise and the smallest one. Denoting the side of the largest square as \( x \), we can sequentially express the sides of the other squares: \( x-1, x-2, x-3, x-3 \) (see the figure). Now notice that the length of the upper side of the rectangle is \( x+(x-1) \), and the length of the lower side is \( (x-2)+(x-3)+(x-3) \). But the opposite sides of the rectangle are equal. We get the equation
\[
x+(x-1)=(x-2)+(x-3)+(x-3)
\]
From this, \( 2x-1=3x-8 \) and, therefore, \( x=7 \).
## Answer
7.00
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Baranov d..V.
The hare bought seven drums of different sizes and seven pairs of sticks of different lengths for her seven baby hares. If a baby hare sees that both its drum is larger and its sticks are longer than those of one of its brothers, it starts to drum loudly. What is the maximum number of baby hares that can start drumming?
|
Not all the bunnies can play the drum, as the baby bunny that gets the smallest drum will not play it. On the other hand, if the same baby bunny is also given the shortest drumsticks, all the other bunnies will play the drum.
## Answer
6 bunnies.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Dirichlet's Principle (continued).]
A store received 25 boxes of three different types of apples (each box contains apples of only one type). Prove that among them, there are at least 9 boxes of apples of the same type.
#
|
25 boxes - "rabbits" will be distributed among 3 cells-sorts. Since $25=3 \cdot 8+1$, we apply the "generalized pigeonhole principle" for $N=3, k=8$ and obtain that in some cell-sort there will be no less than 9 boxes.
|
9
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
7,8
What is the maximum number of rooks that can be placed on an 8x8 chessboard so that they do not attack each other
#
|
Obviously, 8 rooks can be placed, for example, along the diagonal from a1 to h8. Let's prove that it is impossible to place 9 rooks that do not attack each other.
On one horizontal row, there cannot be more than one rook - otherwise, they would attack each other; therefore, the number of rooks that can be placed cannot exceed the number of rows on the board, which is eight. Consequently, it is impossible to place more than 8 rooks on the board.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[
Several points were marked on a line. After that, a point was added between each pair of adjacent points. This operation was repeated three times, and as a result, there were 65 points on the line. How many points were there initially?
#
|
If there were $n$ points on a line, then in one operation, $n-1$ points were added.
## Solution
If there were 65 points at the end, then there were 33 (and 32 were added) points before that. Similarly, there were 17 points after the first operation, and 9 before it.
## Answer
9 points.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Coordinate method on the plane $]$
Find the equation of the line passing through the intersection point of the lines $3 x+2 y-5=0$ and $x-3 y+2=0$ and parallel to the y-axis.
|
Solving the system of equations
$$
\left\{\begin{array}{l}
3 x+2 y-5=0 \\
x-3 y+2=0
\end{array}\right.
$$
we find the coordinates of the point $B\left(x_{0} ; y_{0}\right)$ of intersection of these lines: $x_{0}=1, y_{0}=1$.
Since the desired line is parallel to the y-axis and passes through the point $B\left(x_{0} ; y_{0}\right)$, its equation is of the form $x=$ $x_{0}$, i.e., $x=1$.
## Answer
$x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 [ Examples and counterexamples. Constructions ]
Can integers be written in the cells of a $4 \times 4$ table so that the sum of all the numbers in the table is positive, while the sum of the numbers in each $3 \times 3$ square is negative?
|
The central square of size $2 \times 2$ is contained in each square of size $3 \times 3$. If we place the number -9 in one of the cells of the central square, and fill the rest of the cells of this table with ones, then the sum of all numbers in the table is $15+(-9)=6$, and the sum of the numbers inside any $3 \times 3$ square is $8+(-9)=-1$.
## Answer
It is possible.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Multiplied several natural numbers and got 224, and the smallest number was exactly half of the largest. How many numbers were multiplied
#
|
$224=2^{5} \cdot 7$. Consider the two numbers mentioned in the condition: the smallest and the largest. If one of them is divisible by 7, then the other must also be divisible by 7. But 224 is not divisible by 7², so both of these numbers must be powers of two. From the condition, it also follows that these are two consecutive powers of the number 2. In addition, the largest number must be greater than 7. Therefore, it is $2^{3}=8$, and the smallest is $2^{2}=4$. The only remaining factor is seven, so the required numbers are three: 4, 7, and 8.
## Answer
Three numbers.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
It is known that ЖЖ + Ж = МЁД. What is the last digit of the product: В $\cdot И \cdot H \cdot H \cdot U \cdot \Pi \cdot У \cdot X$ (different letters represent different digits, the same letters represent the same digits)?
#
|
Since a two-digit number ЖЖ was added to a one-digit number Ж to get a three-digit number, then Ж $=9$, and МЁД = 108. Four digits have already been used. In the product $\mathrm{B} \cdot \mathrm{U}^{\prime} \cdot \mathrm{H} \cdot \mathrm{H} \cdot И \cdot П \cdot У \cdot \mathrm{X}$, six other digits are used.
Therefore, among them, there must be the digits 2 and 5, so this product ends in 0.
## Answer
Ends in 0.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Irrational Equations $]$ [ Monotonicity and Boundedness
Solve the equation $2017 x^{2017}-2017+x=\sqrt[2017]{2018-2017 x}$.
#
|
The function $f(x)=2017 x^{2017}-2017+x$ is increasing, while the function $g(x)=\sqrt[2017]{2018-2017 x}$ is decreasing. Therefore, the equation $f(x)=g(x)$ has no more than one root. However, it is obvious that $f(1)=g(1)$.
## Answer
$x=1$.
Author: Volienkov S.G.
A sheet of paper has the shape of a circle. Can five segments be drawn on it, each connecting two points on the boundary of the sheet, such that among the parts into which these segments divide the sheet, there are a pentagon and two quadrilaterals?
## Solution
For example, see the figure. Two quadrilaterals and a pentagon are highlighted in color.
## Answer
Yes, it is possible.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\begin{aligned} & {\left[\begin{array}{l}\text { Irrational Equations } \\ \text { [ Completing the Square. Sums of Squares }\end{array}\right]}\end{aligned}$
Solve the equation
$$
\left(x^{2}+x\right)^{2}+\sqrt{x^{2}-1}=0
$$
|
Since the numbers $\left(x^{2}+x\right)^{2}$ and $\sqrt{x^{2}-1}$ are non-negative, and their sum is zero, then both these numbers are equal to zero. On the other hand, if both these numbers are equal to zero, then their sum is zero. Therefore, the original equation is equivalent to the following system:
$$
\left\{\begin{array} { c }
{ ( x ^ { 2 } + x ) ^ { 2 } = 0 ; } \\
{ \sqrt { x ^ { 2 } - 1 } = 0 }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ x ^ { 2 } + x = 0 ; } \\
{ x ^ { 2 } - 1 = 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \in\{0,-1\} ; \\
x \in\{1,-1\}
\end{array} \Leftrightarrow x=-1\right.\right.\right.
$$
## Answer
$x=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Investigation of a quadratic trinomial ] [ Methods for solving problems with parameter $]
For the quadratic trinomial $f(x)=a x^{2}-a x+1$, it is known that $|f(x)| \leq 1$ for $0 \leq x \leq 1$. Find the greatest possible value of $a$.
|
Since $f(0)=f(1)=1$, the graph of the quadratic function is a parabola symmetric about the line $x=0.5$. From the condition $|f(x)| \leq 1$ for
$0 \leq x \leq 1$, it follows that the branches of the parabola are directed upwards. The minimum value of $f(x)$ is $f(0.5)=1-\frac{a}{4}$.
The maximum possible value of $a$ is achieved when this number is -1, that is, when $a=8$.
Send a comment
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9
The areas of the projections of a certain triangle onto the coordinate planes Oxy and Oyz are $\sqrt{6}$ and $\sqrt{7}$, respectively, and the area of the projection onto the plane $O x z$ is an integer. Find the area of the triangle itself, given that it is also an integer.
|
Let the vector perpendicular to the plane of the original triangle form angles $\alpha, \beta$, and $\gamma$ with the coordinate axes $O x, O y$, and $O z$ respectively. Then
$$
\cos 2 \alpha+\cos 2 \beta+\cos 2 \gamma=1
$$
Let the area of the original triangle be denoted by $S$, and the areas of the projections on the coordinate planes $O y z, O x z$, and $O x y$ be denoted by $S_{x}, S_{y}$, and $S_{z}$ respectively ( $S_{z}=\sqrt{6}, S_{x}=\sqrt{7}$ ). According to the theorem of the area of the projection of a plane figure onto a plane,
$$
\sqrt{7}=S_{x}=S|\cos \alpha|, S_{y}=S|\cos \beta|, \sqrt{6}=S_{z}=S|\cos \gamma|
$$
Then
$$
7+6+S_{y} 2=S 2 \cos 2 \alpha+S 2 \cos 2 \beta+S 2 \cos 2 \gamma=S 2(\cos 2 \alpha+\cos 2 \beta+\cos 2 \gamma)=S 2
$$
Therefore,
$$
S 2-S_{y} 2=13,\left(S-S_{y}\right)\left(S+S_{y}\right)=13
$$
Since both factors on the left side of the equation are positive integers, and the second factor is greater than the first, the equality is possible only in the case when
$$
\left\{\begin{array}{l}
S-S_{y}=1 \\
S+S_{y}=13
\end{array}\right.
$$
From this system, we find that $S_{y}=7$.
## Answer
On the edges $A 1 B 1, A B, A 1 D 1$, and $D D 1$ of the unit cube $A B C D A 1 B 1 C 1 D 1$, points $K, L, M$, and $N$ are taken respectively, such that $A 1 K=\frac{2}{3}, A L=\frac{1}{5}, A 1 M=\frac{1}{3}$. Determine which of the edges $A 1 D 1$ or $D 1 C 1$ is intersected by the plane parallel to the segment $M L$ and containing the segment $K N$. In what ratio does this edge divide the plane?
## Solution
Choose a coordinate system with the origin at point $A 1$. The $x$-axis is directed along the ray $A 1 D 1$, the $y$-axis along the ray $A 1 B 1$, and the $z$-axis along the ray $A 1 A$. Then the coordinates of points $K, L, M$, and $N$ are:
$$
K\left(0 ; \frac{2}{3} ; 0\right), L\left(0 ; \frac{1}{5} ; 1\right), M\left(\frac{1}{3} ; 0 ; 0\right), N(1 ; 0 ; t)
$$
where $0 \leqslant t \leqslant 1$. From point $L$, lay off the vector
$$
\overrightarrow{L P}=\overrightarrow{M K}=\left(0-\frac{1}{-3} ; 3-0 ; 0-0\right)=\left(-\frac{1}{3} ; \frac{2}{3} ; 0\right)
$$
Then point $P$ has coordinates $\left(-\frac{1}{3} ; \frac{13}{1} ; 1\right)$. The desired plane passes through points $K, P$, and $N$. We seek the equation of this plane in the form $a x+b y+c z=1$. Substituting the coordinates of points $K, P$, and $N$ into this equation, we find that
$$
c=\frac{1}{10(t+3)}, a=\frac{9+30}{10(t+3)}, b=\frac{3}{2}
$$
After obvious simplifications, we obtain the equation $(9 t+30) x+15(t+3) y+z=10(t+3)$. Substituting zeros for $y$ and $z$, we find the point of intersection of the plane with the line $A 1 D 1-x=\frac{10(t+3)}{3(3 t+10)}$, and since $0 \leqslant t \leqslant 1$, then $1 \leqslant x \leqslant \frac{40}{39}$. Therefore, the cutting plane does not intersect the edge $A 1 D 1$. Substituting $x=1$ and $z=0$ into the obtained equation, we find the point of intersection of the plane with the line $D 1 C 1-y=\frac{1}{15(t+3)}$, and since $0 \leqslant t \leqslant 1$, then $0 \leqslant y \leqslant \frac{1}{60}$. Therefore, the cutting plane intersects the edge $D 1 C 1$ and in this case, the point of intersection divides this edge in any ratio from 0 to $\frac{1}{59}$, counting from vertex $D 1$.
## Answer
$D 1 C 1$; in any ratio from 0 to $\frac{1}{59}$, counting from vertex $D 1$.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bakayev E.V.
At the beginning of the school year, Andrey started recording his math grades. Upon receiving a new grade (2, 3, 4, or 5), he called it unexpected if, up to that point, it had occurred less frequently than each of the other possible grades. (For example, if he had received the grades 3, 4, 2, 5, 5, 5, 2, 3, 4, 3 in sequence, the first 5 and the second 4 would have been unexpected.) Over the entire school year, Andrey received 40 grades - 10 fives, fours, threes, and twos (the order is unknown). Can we determine exactly how many grades were unexpected for him?
|
The first unexpected grade will be the last one received for the first time. The second unexpected grade will be the last one received for the second time, and so on. Therefore, there will be a total of 10 unexpected grades.
## Answer
It can be.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Mathematical logic (miscellaneous).] Case analysis $\quad]$
After a hockey game, Anton said that he scored 3 goals, and Ilya only one. Ilya said that he scored 4 goals, and Seryozha as many as 5. Seryozha said that he scored 6 goals, and Anton only two. Could it be that together they scored 10 goals, given that each of them told the truth once and lied once?
|
There are two cases.
1) Anton told the truth about himself, that is, he scored 3 goals. Then Seryozha lied about Anton, so he told the truth about himself, that is, he scored 6 goals. Therefore, Ilya lied about Seryozha and told the truth about himself, that is, he scored 4 goals. In this case, the boys scored a total of $3+6+4=13$ goals.
2) Anton lied about himself. Then he told the truth about Ilya, that is, Ilya scored 1 goal. Then Ilya also lied about himself and told the truth about Seryozha: Seryozha scored 5 goals. Therefore, Seryozha lied about himself and told the truth about Anton: the latter scored 2 goals. In this case, the boys scored a total of $1+5+2$ = 8 goals.
## Problem 64941 Topics: [ \[\begin{array}{l}\text { Equations in integers } \\ \text { [Proof by contradiction }]\end{array}\] \]
Can different natural numbers be placed in the circles (see figure) such that the sums of three numbers along each segment are equal?
## Solution
Suppose the required arrangement exists, $S$ - the sum of all the numbers placed, $a$ and $b$ - the numbers in the circles located at any two vertices of the triangle. Then for the vertex where the number $a$ is located, the sum of the numbers along the three segments containing this vertex is $S+2 a$. Similarly, for the vertex where the number $b$ is located, this sum is $S+2 b$. Since the sums of the numbers along each segment are equal, then $S+2 a=$ $S+2 b$, that is, $a=b$. But this contradicts the condition.
## Answer
No.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A set of several numbers, none of which are the same, has the following property: the arithmetic mean of some two numbers from this set is equal to the arithmetic mean of some three numbers from the set and is equal to the arithmetic mean of some four numbers from the set. What is the smallest possible number of numbers in such a set?
#
|
Let $C\left(a_{1}, \ldots, a_{k}\right)$ be the arithmetic mean of the numbers $\left(a_{1}, \ldots, a_{k}\right)$. Note that adding a number different from the arithmetic mean of a set changes the original arithmetic mean of the set.
Suppose that $(a, b, c, d)$ is a set of four numbers satisfying the condition, and $C(a, b, c, d)=C(a, b, c)=$ C. Then $d=C$.
A set of two different numbers with the same arithmetic mean cannot contain the number $d$. If these are, for example, the numbers $a$ and $b$, then $c=C=d$, which contradicts the condition.
Therefore, a set of four numbers satisfying the condition does not exist.
An example of a set of five numbers: $1,2,3,4,5$. Indeed, $C(2,4)=C(2,3,4)=C(1,2,4,5)=3$.
## Answer
5 numbers.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The Unified State Exam (USE) in mathematics in the magical country of Oz is organized as follows. Each paper is independently checked by three teachers, and each gives 0 or 1 point for each problem. Then the computer finds the arithmetic mean of the scores for that problem and rounds it to the nearest integer. The points received for all problems are then summed. It so happened that in one of the papers, each of the three experts gave 1 point for 3 problems and 0 points for all other problems. Find the highest possible total score for this paper.
|
It's easy to come up with a case where you get 4 points. To get 5 or more, there must be at least 10 units in total, but the teachers have only given 9 units in total. Therefore, it's impossible to get 5.
## Answer
4 points.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\begin{array}{ll}{\left[\begin{array}{l}\text { Common fractions } \\ \text { [Examples and counterexamples. Constructions ] }\end{array}\right]}\end{array}\right]$
Author: Akonn E, Kaminin D.
Can the stars in the equation $\frac{*}{*}+\frac{*}{*}+\frac{*}{*}+\frac{*}{*}=$ * be replaced with the digits from 1 to 9, each used once, so that the equation becomes true?
|
From the possible examples, let's give two: $7 / 4+6 / 8+5 / 1+3 / 2=9$, $5 / 4+6 / 8+9 / 3+2 / 1=7$.
## Answer
It can be done.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a theater troupe, there are 60 actors. Any two of them have at least once played in the same play. In each play, no more than 30 actors are involved.
What is the minimum number of plays the theater could have staged?
|
Example. Let's divide the troupe into four groups of 15 people and hold 6 performances, in each of which some two groups are involved. The number of ways to choose two groups out of four is 4$\cdot$3:2=6.
Estimate. In total, the actors played no more than $30 \cdot 5=150$ roles, so if there are five performances, there will be an actor who played no more than two roles. Then he played in one performance with no more than $29 \cdot 2=58$ colleagues from the remaining 59. Therefore, five performances are insufficient to meet the condition.
## Answer
6 performances.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Lobov A.
Let \( n \) be a natural number. We will call a sequence \( a_1, a_2, \ldots, a_n \) interesting if for each \( i = 1, 2, \ldots, n \), one of the equalities \( a_i = i \) or \( a_i = i + 1 \) holds. We will call an interesting sequence even if the sum of its terms is even, and odd otherwise. For each odd interesting sequence, we found the product of its terms and wrote it down on the first sheet. For each even sequence, we did the same and wrote it down on the second sheet. On which sheet is the sum of the numbers greater, and by how much? (Give the answer in terms of \( n \)).
|
Denoting the sum containing the term $2 \cdot 3 \cdot \ldots \cdot n(n+1)$ by $A_n$, and the other by $B_n$, we will prove the equality $A_n - B_n = 1$ by induction.
Base case. $A_1 - B_1 = 2 - 1 = 1$.
Inductive step. Represent the sum $A_n$ as $A' + A''$, where $A'$ contains all terms of the form
$a_1a_2...a_{n-1}(n + 1)$, and $A''$ contains all terms of the form $a_1a_2...a_{n-1}n$. Since the sum $A'$ contains
the term $2 \cdot 3 \cdot \ldots \cdot n(n+1)$, for each of its terms $a_1a_2...a_{n-1}(n + 1)$, the sequence $a_1, a_2, ..., a_{n-1}$ has the same parity as the sequence $2, 3, \ldots, n$. Therefore, $A' = (n+1)A_{n-1}$. Correspondingly, in the sum $A''$ for each of its terms $a_1a_2...a_{n-1}n$ the parity of the sequence $a_1, a_2, ..., a_{n-1}$ is opposite to the parity of the sequence
$2, 3, \ldots, n$. Then $A'' = nB_{n-1}$, from which $A_n = A' + A'' = (n + 1)A_{n-1} + nB_{n-1}$. Similarly, $B_n = nA_{n-1} + (n + 1)B_{n-1}$. Therefore, $A_n - B_n = (n + 1)A_{n-1} + nB_{n-1} - nA_{n-1} - (n + 1)B_{n-1} = A_{n-1} - B_{n-1} = 1$.
## Answer
When $n \equiv 0,1 \pmod{4}$, the sum on the second sheet is greater by 1; for other $n$, the opposite is true. In other words, the sum that contains the term $2 \cdot 3 \cdot \ldots \cdot n(n+1)$ is greater by 1.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Regular Polyhedra. Duality and Relationships ] [ Distance between_two points. Equation of a sphere ]
Authors: Rabzimiotskyl., Giadkih A.
Can an octahedron be inscribed in a cube such that the vertices of the octahedron lie on the edges of the cube?
#
|
In the figure, an octahedron is inscribed in a cube with an edge length of 4; the vertices of the octahedron divide the edges of the cube in the ratio $1: 3$. The square of the length of each edge of the octahedron is 18 (either $3^{2}+3^{2}$, or $4^{2}+1^{2}+$ $\left.1^{2}\right)$, that is, all its edges are equal.
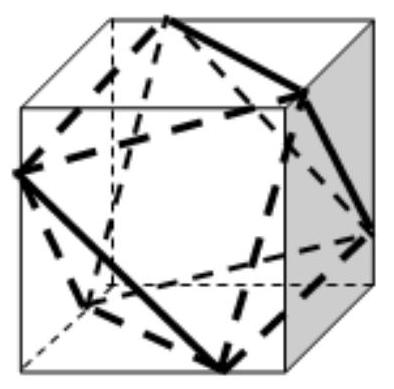
## Answer
It is possible.
| Problem 66183 Topics: | [ Chessboards and chess pieces ] | Difficulty: 3+ Grades: 7,8,9,10 |
| :---: | :---: | :---: |
| | [ Examples and counterexamples. Constructions ] | |
| | Dirichlet's principle (other). | |
| | Parity and oddity | |

What is the minimum number of rooks needed to place on an $8 \times 8$ chessboard so that all white cells are under attack by these rooks? (A cell is considered under attack by a rook if it is in the same row or column as the rook.)
## Solution
Estimate. Each rook attacks no more than two cells of the white diagonal.
Example. Place rooks on the fields a1, c3, e5, and g7.
| Problem 66186 Topics: | $\left[\begin{array}{l}\text { [ Chessboards and chess pieces ] }] \text { ] } \\ \text { Examples and counterexamples. Constructions }]\end{array}\right.$ | Difficulty: 3+ |
| :---: | :---: | :---: |
| | Dirichlet's principle (other). | Grades: 8,9,10,11 |
| | Parity and oddity | |
Author: Kenooarov. P.
The cells of a $9 \times 9$ board are colored in a checkerboard pattern in black and white (corner cells are white). What is the minimum number of rooks needed to place on this board so that all white cells are under attack by these rooks? (A cell is considered under attack by a rook if it is in the same row or column as the rook.)
## Solution
Estimate. A rook attacks no more than two cells of the white diagonal, so four rooks are insufficient.
Example. Place rooks on the fields indicated in the figure.
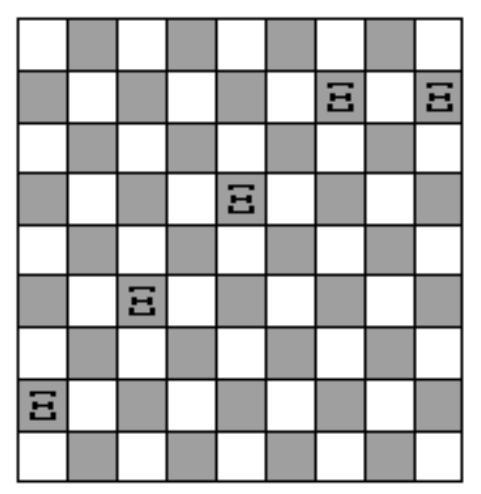
## Answer
5 rooks.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Evoikinov M.A.
A pirate has five bags of coins, each containing 30 coins. He knows that one bag contains gold coins, another contains silver coins, a third contains bronze coins, and each of the two remaining bags contains an equal number of gold, silver, and bronze coins. You can simultaneously take any number of coins from any of the bags and see what kind of coins they are (coins are taken out only once). What is the smallest number of coins that need to be taken to definitely determine the contents of at least one bag?
|
Example. Let's take one coin from each bag. Among these five coins, there are coins of all three types, so there is only one coin of a certain type. If it is, for example, a gold coin, then it was taken from the bag with gold coins. Indeed, for each coin from the "mixed" bag, there is a matching one from the corresponding "homogeneous" bag.
Evaluation. Suppose we took only 4 coins. Note that it makes no sense to take more than one coin from a bag, as they may turn out to be the same, and then we would not gain any additional information. Therefore, we can assume that we took one coin from each of four different bags. Then we could have taken coins 3, 3, S, B, and in this case, there are at least two possible distributions of the corresponding bags: 3, Mixed, S, Mixed, B and Mixed, 3, Mixed, B, S, which do not match in any of the positions (the last one indicates the bag from which no coins were taken).
## Answer
5 coins.
Send a comment
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
|
| | $[$ Chess Coloring $]$ | |
Author: Raskina I.V.
At the edge of a round rotating table, 30 cups of tea were placed at equal intervals. The March Hare and Alice sat down at the table and started drinking tea from two of the cups (not necessarily adjacent). When they finished their tea, the Hare turned the table so that each of them had a full cup in front of them again. When these cups were also emptied, the Hare turned the table again (possibly by a different angle), and once again each had a full cup in front of them. This continued until all the tea was drunk. Prove that if the Hare always turned the table so that his new cup was one cup away from the previous one, they would also have been able to drink all the tea (that is, each time both cups would have been full).
#
|
We will paint every other cup blue and red. Let the March Hare drink from a red cup at first. We will prove that Sonya drank from a blue cup at first. Indeed, if she drank from a red one, then after any rotation of the table, two cups of the same color would be emptied. Since there are 15 of each color, and they are emptied in pairs, at the end, two cups of different colors would remain, which could not be simultaneously placed in front of Sonya and the March Hare by any rotation of the table. Now it is clear why the Hare could always rotate
## [ Divisibility of numbers. General properties ] $\left.\begin{array}{rl}\text { Problem } 116209 \text { Topics: [ Text problems (miscellaneous) ] } \\ \text { [ Counting in two ways }\end{array}\right]$
Author: Khachatryan A.V.
Petr was born in the 19th century, and his brother Pavel - in the 20th century. Once, the brothers met to celebrate their common birthday. Petr said: "My age is equal to the sum of the digits of the year of my birth." - "Mine too," replied Pavel. How much younger is Pavel than Petr?
## Solution
Let Petr and Pavel be born in the years $\overline{18 x y}$ and $\overline{19 u v}$, respectively. At the time of their meeting, Petr and Pavel were $1 + 8 + x + y$ and $1 + 9 + u + v$ years old, respectively. We will determine the year of their meeting in two ways. Since Petr's age at that time was equal to the sum of the digits of his year of birth, the meeting took place in the year $1800 + 10 x + y + 9 + x + y$. On the other hand, since Pavel's age was also equal to the sum of the digits of his year of birth, the meeting took place in the year $1900 + 10 u + v + 10 + u + v$. Therefore, $1800 + 10 x + y + 9 + x + y = 1900 + 10 u + v + 10 + u + v$.
After simplification, the equation transforms to $11(x - u) + 2(y - v) = 101$. Rewrite it as $11(x - u) + 2(y - v - 1) = 99$.
From this, it is clear that $y - v - 1$ is divisible by 11. Since $-9 \leq y - v \leq 9$, then $y - v = 1$. Consequently, $x - u = 9$. Pavel is older than Petr by
$1900 + 10 u + v - 1800 - 10 x - y = 100 - 10(x - u) - (y - v) = 100 - 90 - 1 = 9$ years.
We need to consider two more cases: Petr could have been born in 1900 (which also belongs to the 19th century), or Pavel in 2000. In the first case, the meeting would have taken place in 1910, meaning Pavel was born no earlier than 1901 and no later than 1910, and he could not have been less than 11 years old at the time of the meeting. Contradiction. In the second case, the meeting would have taken place in 2002, and Petr would have been at least 102 years old at that time, which is also impossible, as the sum of the digits of any integer from 1801 to 1900 is no more than 27.
## Answer
9 years.
|
9
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Folklore
In a certain state, the airline system is arranged in such a way that each city is connected by air routes to no more than three other cities, and from any city, you can reach any other city with no more than one layover. What is the maximum number of cities that can be in this state?
|
Evaluation. From a fixed city $A$, one can directly reach no more than three cities, and with one transfer - no more than $3 \cdot 2=6$ additional cities. Thus, the total number of cities can be no more than ten. An example of a network of 10 cities is shown in the figure.
## Answer
10.
Submit a comment
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shaovalov A.v.
Fox Alice and Cat Basilio have grown 20 fake banknotes on a tree and are now filling in seven-digit numbers on them. Each banknote has 7 empty cells for digits. Basilio calls out one digit at a time, either "1" or "2" (he doesn't know any other digits), and Alice writes the called digit in any free cell of any banknote and shows the result to Basilio. When all cells are filled, Basilio takes as many banknotes with different numbers as possible (if there are several with the same number, he takes only one), and the rest go to Alice. What is the maximum number of banknotes Basilio can get, no matter how Alice acts?
|
Basilio can always get two banknotes: he knows where the last digit should be written and names it so that it differs from the digit in the same position on another banknote. Then the numbers on these two banknotes will be different, and the cat can take them.
Let's show how Alice can ensure that there are no more than two different numbers. She arranges the banknotes one on top of the other so that the cells for the digits form a table.
When the cat names a one, Alice writes it in the leftmost column where there is a free cell (in any of the cells), and when the cat names a two - in the rightmost column.
If both ones and twos start appearing in any column, then all other columns are already filled: ones on the left, twos on the right. This means there will be at most one column where both ones and twos appear. Therefore, if the numbers do differ, they will differ only by the digit in this column. Since there are only two digits, there will be no more than two different numbers.
## Answer
2.
Submit a comment
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Blinkov A.D:
The teams held a football tournament in a round-robin format (each team played one match against every other team, with 3 points for a win, 1 point for a draw, and 0 points for a loss). It turned out that the sole winner scored less than $50 \%$ of the maximum possible points for one participant. What is the minimum number of teams that could have participated in the tournament?
|
Let's prove that there could not have been fewer than six teams. If, for example, there were five teams in the tournament, then they played $5 \cdot 4: 2=10$ matches and scored a total of at least 20 points. Therefore, the sole winner scored more than $20: 5=4$ points. However, according to the condition, he scored no more than 5 points out of 12 possible. Thus, the winner scored exactly 5 points, and each of the other teams scored no more than 4. Therefore, the total points scored by all participants does not exceed $5+4 \cdot 4=21$. But the number of points scored by the winner means that he won at least once and lost at least once, which means that in this case, the total points scored by all teams cannot be less than 22. Contradiction.
The reasoning for a tournament with two, three, or four teams is similar.
Let's provide two possible examples for a tournament with six teams:
| Team | Total | 1 | 2 | 3 | 4 | 5 | 6 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | **7** | | 1 | 1 | 1 | 1 | 3 |
| 2 | **5** | 1 | | 1 | 1 | 1 | 1 |
| 3 | **5** | 1 | 1 | | 1 | 1 | 1 |
| 4 | **5** | 1 | 1 | 1 | | 1 | 1 |
| 5 | **5** | 1 | 1 | 1 | 1 | | 1 |
| 6 | **4** | 0 | 1 | 1 | 1 | 1 | |
| Team | Total | 1 | 2 | 3 | 4 | 5 | 6 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | **7** | | 3 | 3 | 0 | 0 | 1 |
| 2 | **6** | 0 | | 1 | 1 | 3 | 1 |
| 3 | **6** | 0 | 1 | | 3 | 1 | 1 |
| 4 | **6** | 3 | 1 | 0 | | 1 | 1 |
| 5 | **6** | 3 | 0 | 1 | 1 | | 1 |
| 6 | **5** | 1 | 1 | 1 | 1 | 1 | |
## Answer
6 teams.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7,8,9 |
In a deck of 16 cards, numbered from top to bottom. It is allowed to take a portion of the deck from the top, after which the removed and remaining parts of the deck, without flipping, are "interleaved" with each other. Can it happen that after several such operations, the cards end up numbered from bottom to top? If yes, in what minimum number of operations can this occur?
|
Let's consider a method that allows achieving the required order in four operations. Each time, we will take exactly half of the deck - 8 cards from the top and "interleave" the removed part into the remaining part "one by one". The transformation of the deck during such operations is shown in the diagram:
| Top | | 1 | 1 | | | | | | | | | Bottom | | | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 9 | 1 | 10 | 2 | 11 | 3 | 12 | 4 | 13 | 5 | 14 | 6 | 15 | 7 | 16 | 8 |
| 13 | 9 | 5 | 1 | 14 | 10 | 6 | 2 | 15 | 11 | 7 | 3 | 16 | 12 | 8 | 4 |
| 15 | 13 | 11 | 9 | 7 | 5 | 3 | 1 | 16 | 14 | 12 | 10 | 8 | 6 | 4 | 2 |
| 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Consider any three operations on the deck that satisfy the condition. During each operation, the deck is divided into two parts: the part that is removed and the part that remains. Since there are 16 cards in total, one of these parts contains at least eight cards. A similar reasoning shows that among these cards, there will be at least four cards that, during the second operation, were either all in the removed part of the deck or all in the remaining part. And among them, in turn, there will be two cards that ended up in the same part during the third operation. Thus, we have found two cards that, in all operations, were either removed or remained in
Submit a comment
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Linear Inequalities and Systems of Inequalities ] Evaluation + Example
Authors: Bogdanov I.I., Knop K.A.
King Hiero has 11 metal ingots that are indistinguishable in appearance; the king knows that their weights (in some order) are 1, 2, ..., 11 kg. He also has a bag that will tear if more than 11 kg is placed in it. Archimedes has learned the weights of all the ingots and wants to prove to Hiero that the first ingot weighs 1 kg. In one step, he can load several ingots into the bag and demonstrate to Hiero that the bag does not tear (the bag cannot be torn!). What is the minimum number of bag loadings Archimedes needs to achieve the required result?
|
Let Archimedes first put ingots weighing 1, 2, 3, and 5 kg into the bag, and then ingots weighing 1, 4, and 6 kg. In both cases, the bag does not tear.
We will prove that this could only happen if the 1 kg ingot was used twice. Indeed, if Archimedes used ingots weighing \( w_{1}, \ldots, w_{6} \) kg instead of ingots weighing 1, ..., 6 kg in these two cases, then these weights would satisfy the system of inequalities
\[ w_{1} + w_{2} + w_{3} + w_{5} \leq 11, \quad w_{1} + w_{4} + w_{6} \leq 11. \]
Adding these inequalities, we get
\[ w_{1} + (w_{1} + w_{2} + \ldots + w_{6}) \leq 22. \]
The sum in parentheses is the sum of six different natural numbers, which is at least \( 1 + 2 + \ldots + 6 = 21 \). Therefore, we have
\[ w_{1} \leq 22 - 21 = 1. \]
Thus, \( w_{1} = 1 \), meaning the 1 kg ingot is uniquely determined.
It remains to show that one loading is insufficient. If Archimedes loads only one ingot, the bag will not tear in any case, so no ingot can be identified. Suppose Archimedes loads more than one ingot, and the bag does not tear. If the 1 kg ingot is not loaded into the bag, then replacing it with any ingot in the bag will not change the result; in this case, Hiero will not be able to determine whether this ingot is in the bag. If the required ingot is in the bag, then Hiero will not be able to determine which of the (at least two) loaded ingots is the required one.
## Answer
In two loadings.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ $\left.\quad \begin{array}{lc}{\left[\begin{array}{l}\text { Processes and operations }\end{array}\right]} \\ {[} & \text { Semivariants }\end{array}\right]$
Authors: Fadin M. Kovalenko K.
Initially, a natural number $N$ is written on the board. At any moment, Misha can choose a number $a>1$ on the board, erase it, and write down all natural divisors of $a$, except for $a$ itself (the same numbers can appear on the board). After some time, it turned out that there are $N^{2}$ numbers on the board. For which $N$ could this have happened?
#
|
Let $N>1$, and $1=d_{1}<d_{2}<\ldots<d_{k}<d_{k+1}=N-$ be all the divisors of $N$.
Notice that $d_{i} d_{k+2-i}=N$. Therefore,
$d_{1}^{2}+d_{2}^{2}+\ldots+d_{k}^{2}=\frac{N^{2}}{d_{k+1}^{2}}+\frac{N^{2}}{d_{k}^{2}}+\ldots+\frac{N^{2}}{d_{2}^{2}} \leq N^{2}\left(\frac{1}{2^{2}}+\frac{1}{3^{2}}+\ldots+\frac{1}{N^{2}}\right)<N^{2}$ (the last inequality follows from problem $\underline{30898})$.
From this, it follows that
1) on the first step, the sum of the squares of the numbers written on the board decreases;
2) in the subsequent steps, it does not increase.
Thus, the sum of the squares of the numbers written on the board at all moments, except the initial one, is less than $N^{2}$. Since all numbers are natural, their quantity is also less than $N^{2}$.
## Answer
Only for $N=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapoveaov A.B.
The plan of the palace is a $6 \times 6$ square, divided into rooms of size $1 \times 1$. There is a door in the middle of each wall between the rooms. The Shah told his architect: "Knock down some walls so that all rooms become $2 \times 1$, no new doors appear, and the path between any two rooms passes through no more than $N$ doors." What is the smallest value of $N$ that the Shah should name to make it possible to carry out the order?
|
Consider an arbitrary route from the lower left corner of the palace to the upper right. Since one needs to "climb" 5 horizontal levels and "shift right" 5 vertical levels, one has to pass through at least 10 doors, visiting at least 11 rooms (including the starting and ending rooms).
11 rooms of size $1 \times 1$ could not have been transformed into 5 rooms of size $2 \times 1$. Therefore, the same route in the reconstructed palace must pass through at least 6 rooms, and thus through at least 5 doors. Such a reconstruction of the palace is indeed possible (see the figure).
| 2 | 2 | 2 | 2 | $\mid 2$ |
| :---: | :---: | :---: | :---: | :---: |
| | | 1 | | |
| | | 0 | | 1 |
| | | | | 1 |
| 2 | 9 | 1 | 2 | 19 |
| | | 2 | | |
In this case, it is indeed possible to get from any room to any other room by passing through no more than 5 doors. Let's denote the central rooms with the number 0, those connected to them by a door with the number 1, and those connected by a door to rooms of type 1 with the number 2. Since all rooms have been marked, one can get from any room to one of the central rooms by passing through no more than two doors. Therefore, one can get from any room to any other room by constructing a route through the central rooms and passing through no more than 5 doors (the fifth door is needed if one has to move from one central room to another).
## [Tournaments and tournament tables] Problem 116689 Topics: [Examples and counterexamples. Constructions] Difficulty: 4 [ $\underline{\text { Induction (other) }}$ ] Classes: 8,9,10
Author: Blyunkov A.d:
a) In a football tournament in a single round-robin format, 75 teams participated. A team received 3 points for a win, 1 point for a draw, and 0 points for a loss. It is known that every two teams scored a different number of points. Find the smallest possible difference in points between the teams that took first and last place.
b) The same question for $n$ teams.
## Solution
b) The minimum gap between the first and last place cannot be less than $n-1$. We will prove that for $n>3$ it is possible to construct a tournament schedule such that the gap is $n-1$ (if $n=2$ or 3, the minimum gap is obviously 3 points).
By induction, we will construct a table for $n$ teams, where the results are all integers from $n-2$ to $2n-3$. Base case $(n=4)$. An example of a tournament table for four teams:
| Team | 1 | 2 | 3 | 4 | Points |
| :--- | :---: | :---: | :---: | :---: | :--- |
| 1 | $\times$ | 3 | 1 | 1 | 5 |
| 2 | 0 | $\times$ | 1 | 3 | 4 |
| 3 | 1 | 1 | $\times$ | 1 | 3 |
| 4 | 1 | 0 | 1 | $\times$ | 2 |
Inductive step. By the inductive hypothesis, there is such a table for $n$ teams. We will divide the teams into triples based on the number of points they scored: the first triple consists of teams with $2n-3, 2n-4, 2n-5$ points, the second triple consists of teams with $2n-6, 2n-7, 2n-8$ points, and so on (the last triple may be incomplete). We will add one more team. Consider three cases.
1) $n=3k+1$. Let the new team win against the first team in the first triple and lose to the second and third. Then the first team will still have $2n-3$ points, the second team will have $2n-1$ points and move to the first place, and the third team will have $2n-2$ points. We will do the same for the other complete triples. Then all triples will shift "up" by two points. There will be one team left, which was in the last place with $n-2$ points, and the new team will have $n-1$ points. Let them play a draw and add one point each.
2) $n=3k+2$. The teams from $k$ triples play against the new team similarly to case 1). The last two teams had $n-1$ and $n-2$ points, and the new team has $n-2$ points. Let the last team win against the new team, and the second-to-last team play a draw with the new team.
3) $n=3k$. After the new team plays against the first $k-1$ triples, it will have $n-3$ points. The last three teams had $n, n-1$, and $n-2$ points. Let the second-to-last team win against the new team, the last team play a draw with the new team, and the team with $n$ points lose. Then the former last teams will have $n, n+2, n-1$ points, and the new team will have $n+1$ points.
## Answer
a) 74; b) $n-1$, if $n>3$; 3, if $n=2$ or 3.
Send a comment
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovadov A.V.
In a set of several weights, all of which have different masses. It is known that if any pair of weights is placed on the left pan, the scales can be balanced by placing one or several weights from the remaining ones on the right pan. Find the smallest possible number of weights in the set.
|
To balance a pair of the heaviest weights, at least three weights are needed, which means there are at least five weights in total. Suppose there are exactly five weights, and their weights are
$P_{1}2$, then a pair
$(m+1, n-1)$ weighs the same. If $m>3$ and $n<8$, then a pair ( $m-1, n+1$ ) weighs the same. The cases considered do not cover four pairs: $(3,4),(3,5),(6,8)$ and ( 7,8 ). They are balanced respectively by the sets (7), $(8),(3,4,7),(4,5,6)$.
## Answer
6 weights.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Schön D.…
On the island of knights and liars, a traveler came to visit his acquaintance, a knight, and saw him at a round table with five guests.
- I wonder, how many of you are knights? - he asked.
- Why don't you ask each of us a question and find out yourself, - one of the guests suggested.
- Alright. Tell me each: who are your neighbors? - the traveler asked.
To this question, everyone answered the same.
- Not enough data! - said the traveler.
- But today is my birthday, don't forget about that, - said one of the guests.
- Yes, today is his birthday! - said his neighbor.
And the traveler was able to figure out how many knights were at the table. Indeed, how many of them are there?
|
If everyone said, "Both of my neighbors are knights," it would be immediately clear that everyone sitting at the table is a knight. Indeed, the traveler's acquaintance, who is a knight, told the truth, meaning that both of his neighbors also told the truth, and so on, which means everyone told the truth.
If everyone said, "My neighbors are a knight and a liar," it would also be immediately clear how many knights there are. Indeed, the traveler's acquaintance told the truth, meaning his neighbors are a knight and a liar. The neighboring knight also told the truth, meaning the other neighbor is a liar. The neighboring liar lied, meaning both of his neighbors are knights. Continuing this way, we get that at the table: there are two pairs of knights sitting next to each other, and two liars between them.
Therefore, everyone said, "Both of my neighbors are liars." This is possible in two cases:
1) Knights and liars sat alternately;
2) The neighbors of the knights are liars, and the neighbors of the liars are a knight and a liar, meaning there are two knights and four liars at the table.
Since two people sitting next to each other said the same thing about their birthday, the first case is impossible. Therefore, there are two knights at the table.
## Answer
Two knights.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On a circle of radius 1, a point $O$ is marked, and from it, a notch is made to the right with a radius of $l$. From the resulting point $O_{1}$, another notch is made in the same direction with the same radius, and this is repeated 1968 times. After this, the circle is cut at all 1968 notches, resulting in 1968 arcs. How many different lengths of arcs can be obtained in this way?
|
We will prove by induction on $n$ that the number of different arcs after $n$ cuts does not exceed 3. For $n=2$, this is obvious. Let $A_{k}$ denote the cut with number $k$. Suppose $n$ cuts have been made and the point $A_{n}$ falls on the ARC $A_{k} A_{l}$. Then the point $A_{n-1}$ falls on the arc $A_{k-1} A_{l-1}$. Therefore, if $k, l \neq 1$, no new lengths will appear, and the required statement is proved. Now suppose, for example, that $l=1$. We will prove that then the length of any arc $A_{p} A_{q}$ between neighboring cuts is equal to the length of one of the arcs $A_{k} A_{1}, A_{n} A_{1}, A_{1} A_{s}$, where $A_{s}$ is the nearest cut to $A_{1}$, different from $A_{n}$. Indeed, if $p, q \neq 1$, the length of the arc $A_{p} A_{q}$ is equal to the length of the arc $A_{p-1} A_{q-1}$, and there are no other cuts between the cuts $A_{p-1}$ and $A_{q-1}$ except possibly $A_{n}$. Thus, in a finite number of steps, we arrive at one of the three considered arcs.
## Answer
no more than three.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
To glaze 15 windows of various sizes and shapes, 15 pieces of glass have been prepared exactly to fit the windows (the windows are such that each window should have one piece of glass). The glazier, not knowing that the glasses are matched, works as follows: he approaches the next window and tries the unused glasses until he finds one that is large enough (i.e., either exactly fitting or one from which a fitting piece can be cut), if no such glass is found, he moves to the next window, and so on, until he has gone through all the windows. It is not allowed to assemble a piece of glass from several parts. What is the maximum number of windows that can remain unglazed?
|
First, let's show that if at any moment there are no fewer than 8 windows (and, accordingly, no fewer than 8 panes), then a pane for one of the remaining windows can be found. Indeed, no more than seven panes have been used, so at least one of the eight panes, intended for the eight remaining windows, remains. This one can be inserted into its "own" window. Therefore, more than seven windows cannot remain unglazed.
Now, let's show that seven windows can remain unglazed. This will happen, for example, in the following case. The panes have such sizes that any one of them can be obtained from another by cutting (note that the problem statement does not require this). Thus, all panes can be ordered from the smallest to the largest so that any smaller one can be "cut" from a larger one.
The windows can be similarly ordered. Suppose the glazier approaches the windows in the order of increasing size (from the smallest to the largest), while selecting panes in the order of decreasing size. In this case, he will manage to glaze the 8 smallest windows, the eighth window will get its "own" pane. The 7 largest windows will remain unglazed, and the 7 smallest panes will remain unused.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Malkin M.I.
On the board, 101 numbers are written: $1^{2}, 2^{2}, \ldots, 101^{2}$. In one operation, it is allowed to erase any two numbers and write down the absolute value of their difference instead.
What is the smallest number that can result from 100 operations?
|
From four consecutive squares (in three operations), you can get the number 4: $(n+3)^{2}-(n+2)^{2}-((n+$ $\left.1)^{2}-n^{2}\right)=(2 n+5)-(2 n+1)=4$.
We can get 24 such fours from the numbers $6^{2}, 7^{2}, \ldots, 101^{2}$. 20 fours can be turned into zeros by pairwise subtraction. From the numbers $4,9,16,25$ we get
$14=(25-4)-(16-9)$. From the remaining numbers $(14,4,4,4,4,1)$ we get the unit: $4-(14-4-4-4)-1=1$. It is impossible to get 0, since the parity of the sum of all numbers is preserved.
## Answer
1.
## Problem
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Solve the equation $2^{\mathrm{x}}+3^{\mathrm{x}}=5^{\mathrm{x}}$.
#
The above text has been translated into English, preserving the original text's line breaks and format.
|
One solution is obvious - x=1. Prove that there are no other solutions using the monotonic increase of some functions.
## Solution
One of the solutions can be guessed immediately: $\mathrm{x}=1$. Now it is enough to show that this equation has no more than one solution. Transform the equation to the form $(2 / 5)^{\mathrm{x}}+(3 / 5)^{\mathrm{x}}=1$. On the left side, we have a function that is decreasing over the entire number line (as the sum of two decreasing functions). Therefore, this function takes each real value no more than once. Hence, for any number c, the equation $(2 / 5)^{\mathrm{x}}+(3 / 5)^{\mathrm{x}}=c$ has no more than one solution.
## Answer
$\mathrm{x}=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ [ Evaluation + example $\quad]$
In a corridor 100 meters long, 20 carpet strips with a total length of 1000 meters are laid. What is the maximum number of uncovered segments (the width of the strip is equal to the width of the corridor)?
#
|
First, let's provide an example: take eleven long paths, each 90.5 meters long, and the remaining nine short paths, each 0.5 meters long. Place the eleven long paths on top of each other, leaving a 0.5-meter gap from the edge of the corridor, and in the remaining 9 meters of the corridor, leave the first half empty and cover the second half with a short path. Thus, there are 9 uncovered segments before each short path and 1 before the long ones.
Now, let's show that it is impossible to achieve more uncovered segments. First, note that the difference between the number of uncovered segments and the number of covered segments, in absolute value, does not exceed one. Therefore, it is sufficient to prove that the number of covered segments cannot exceed ten.
For each covered segment, find the number of carpet paths used in that segment. Let the maximum of these numbers be \( N \). Then the number of covered segments does not exceed \( 1 + (20 - N) = 21 - N \). Thus, it remains to prove that \( N \geq 11 \). To do this, we need to show that there is a point covered by at least eleven paths. Suppose that each point is covered by no more than ten paths. Since the total length of the paths is exactly ten times the length of the corridor, the entire corridor is covered, and thus there are no uncovered segments, which is not the case we are interested in. Therefore, there is a point covered by at least eleven paths. Consequently, in the corresponding covered segment, at least eleven paths are used, so \( N \geq 11 \).
## Answer
11 segments.
Can 100,000 six-digit phone numbers be chosen such that when the \( k \)-th digit ( \( k=1,2, \ldots 6 \) ) is simultaneously erased from all these numbers, all five-digit numbers from 00000 to 99999 are obtained?
## Solution
We will prove that it is sufficient to choose all phone numbers for which the sum of the digits is divisible by ten. First, note that when the \( k \)-th digit is simultaneously erased from all these numbers, all five-digit numbers are obtained, and each exactly once. Indeed, the number \(\overline{a_{1} a_{2} a_{3} a_{4} a_{5}}\) is obtained by erasing the digit \( d \) if and only if the number \( d + s \), where \( s = a_{1} + \ldots + a_{5} \), is divisible by ten, and for any integer \( s \), there is exactly one digit \( d \) such that \( s + d \) is divisible by ten. Therefore, the total number of selected numbers is equal to the number of five-digit numbers, i.e., 100,000. Thus, we have found 100,000 numbers that meet the requirements of the problem.
## Answer
Yes, it is possible.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kazitsyna T.
Baba Yaga was given large sandglasses for 5 minutes and small ones for 2 minutes. The potion must boil continuously for exactly 8 minutes. When it started boiling, all the sand in the large sandglasses was in the lower half, and in the small sandglasses, some (unknown) part of the sand was in the upper half, and the rest was in the lower half. Help Baba Yaga measure exactly 8 minutes.
(The sand keeps flowing at a constant rate. No time is spent on flipping the sandglasses.)
#
|
Let at the beginning in the upper half of the small hourglass there was sand for $x$ minutes.
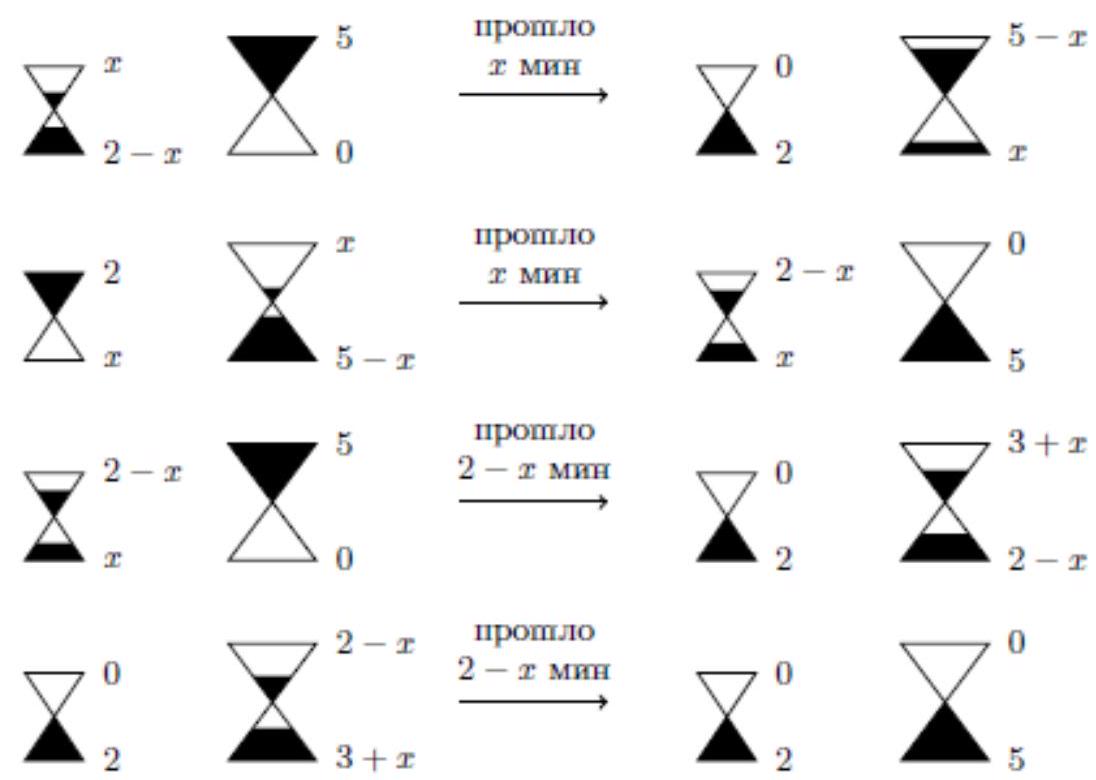
From the start of the process, $x+x+(2-x)+(2-x)=4$ minutes have passed, and the sand in both hourglasses is entirely in the lower half. It remains to measure 4 minutes - this can easily be done using the 2-minute hourglasses.
The solution is not unique. However, it can be shown that in any solution, it is necessary to immediately start the large hourglasses.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Izmeystiev I.V.
The network of bus routes in the suburb of Amsterdam is organized in such a way that:
a) each route has exactly three stops;
b) any two routes either have no common stops at all or have only one common stop. What is the maximum number of routes that can be in this suburb if there are a total of 9 stops?
|
Evaluation. Consider some stop A. Determine the maximum number of routes passing through it. Besides A, there are 8 other stops in the city. On each route passing through A, there are two more stops. Since no two of these routes can have common stops other than A, a total of no more than 8 / 2 = 4 routes can pass through A. Number all the stops and denote by \(a_{1}\) the number of routes passing through the first stop, by \(a_{2}\) the number of routes passing through the second stop, ..., and by \(a_{9}\) the number of routes passing through the ninth stop. Since each route has exactly 3 stops, \(a_{1} + \ldots + a_{9} = 3n\), where \(n\) is the total number of routes. According to the above proof, each term is no more than four. Therefore, \(3n < 4 \cdot 9 = 36\), which means \(n < 12\).
Example. The diagram below shows a scheme that satisfies the problem's conditions and contains 12 routes.

## Answer
12 routes.
Submit a comment
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[The Pigeonhole Principle (continued).]
In a photo studio, 20 birds flew in - 8 sparrows, 7 wagtails, and 5 woodpeckers. Each time the photographer clicks the camera shutter, one of the birds flies away (permanently). How many shots can the photographer take to be sure: he will have at least four birds of one species left, and at least three of another?
#
|
8 snapshots are dangerous: in this time, 3 woodpeckers and 5 wagtails may fly away, leaving only 2 of each.
Let's show that 7 snapshots can be made. Then, in the studio, there will be $20-7=13$ birds left. This means that the number of birds of one species is at least $13: 3$, that is, at least 5. On the other hand, their number is no more than 8, so the number of the two remaining species together is at least 5, and, therefore, the number of one of these species is at least three.
## Answer
7 snapshots.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Combinations and Permutations ] [ Directed Graphs ]
In the discussion, 15 deputies participated. Each of them, in their speech, criticized exactly $k$ of the remaining 14 deputies.
For what smallest $k$ can we assert that there will be two deputies who criticized each other?
|
Consider a directed graph where the vertices correspond to deputies, and an edge leading from $A$ to $B$ means that deputy $A$ has criticized deputy $B$.
## Solution
If each deputy has criticized 8 others, then the number of edges in the graph is $15 \cdot 8 = 120$, which is greater than the number of pairs $C_{15}^{2} = 105$ of its vertices. This proves that some two vertices are connected by at least two edges, meaning that there will be two deputies who have criticized each other.
On the other hand, suppose 15 deputies are sitting around a round table and each has criticized the seven deputies sitting next to them in a clockwise direction. It is easy to see that in this case, no two deputies have criticized each other.
## Answer
For $k=8$.
Submit a comment
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11
In the cube $A B C D A 1 B 1 C 1 D 1$, where $A A 1, B B 1, C C 1$ and $D D 1$ are parallel edges, the plane $P$ passes through point $D$ and the midpoints of edges $A 1 D 1$ and $C 1 D 1$. Find the distance from the midpoint of edge $A A 1$ to the plane $P$, if the edge of the cube is 2.
|
Let $M, N, K$ and $L$ be the midpoints of edges $A1D1, C1D1$, $AA1$ and $CC1$ respectively (Fig.1). The line $KL$ is parallel to the line $MN$, so the line $KL$ is parallel to the plane $P$. Moreover, the line $KL$ passes through the center $O$ of the cube $ABCD A1B1C1D1$. Therefore, the distance from the midpoint $K$ of edge $AA1$ to the plane $P$ is equal to the distance from point $O$ to this plane. Let $E$ be the intersection point of segments $MN$ and $B1D1$, and $F$ be the foot of the perpendicular dropped from point $O$ to line $DE$. Since line $MN$ is perpendicular to plane $BB1D1D$, then $MN \perp OF$. Therefore, $OF$ is perpendicular to plane $P$. Thus, the desired distance is equal to the length of segment $OF$. Consider the section of the given cube by plane $BB1D1D$ (Fig.2). Let the line passing through the midpoint $O$ of diagonal $BD1$ parallel to $BD$ intersect segment $DE$ at point $Q$, and segment $DD1$ at point $S$. Then $OS$ is the midline of triangle $BD1D$, and $QS$ is the midline of triangle $EDD1$. Therefore,
$$
OQ = OS - QS = \frac{1}{2} BD - \frac{1}{2} ED1 = \frac{1}{2}(BD - ED1) = \frac{1}{2}\left(2\sqrt{2} - \frac{\sqrt{2}}{2}\right) = \frac{3\sqrt{2}}{1}.
$$
Let $\angle FOQ = \alpha$. Then
$$
\angle EDD1 = \angle FOQ = \alpha, \cos \alpha = \frac{DD1}{DE} = \frac{DD1}{\sqrt{DD1^2 + ED1^2}} = \frac{2}{\sqrt{1 + \left(\frac{\bar{\Sigma}_2^2}{2}\right)^2}} = \frac{2\sqrt{2}}{3}.
$$
Therefore,
$$
OF = OQ \cos \alpha = \frac{3\sqrt{2}}{1} \cdot \frac{2\sqrt{2}}{3} = 1.
$$
Choose a rectangular coordinate system $D1xyz$, taking the origin at point $D1$ and directing the coordinate axes along the rays $D1A1, D1C1$, and $D1D$ respectively. The equation of plane $P$ will be
$$
\frac{x}{1} + \frac{y}{1} + \frac{z}{2} = 1
$$
(the equation of the plane in intercepts), or $2x + 2y + z - 2 = 0$. The distance from point $K(2; 0; 1)$ to this plane is
$$
\frac{2 \cdot 2 + 2 \cdot 0 + 1 - 2}{\sqrt{1 + 1 + 1}} = \frac{3}{3} = 1.
$$
## Answer
1.00
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Proizvolov V.V.
There are 19 weights of $1, 2, 3, \ldots, 19$ grams: nine iron, nine bronze, and one gold. It is known that the total weight of all iron weights is 90 grams more than the total weight of the bronze weights. Find the weight of the gold weight.
|
Prove that the nine lightest weights are bronze, and the nine heaviest are iron.
## Solution
The difference between the total weight of the nine heaviest weights and the total weight of the nine lightest weights is $(19+18+\ldots+11)-(9+8+\ldots+1)=90$ grams. Therefore, the iron weights are the heaviest, and the bronze weights are the lightest (otherwise, the difference between the total weight of the iron weights and the total weight of the bronze weights would be less). Thus, the gold weight weighs 10 grams.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Zhendarov R.G.
In the cells of a $4 \times 4$ table, numbers are written such that the sum of the neighbors of each number is 1 (cells are considered neighbors if they share a side).
Find the sum of all the numbers in the table.
#
|
Let's divide all cells into 6 groups (in the figure, cells of each group are marked with their own symbol). Each group consists of all neighbors of some one cell, so the sum of the numbers in it is 1. Therefore, the sum of all numbers is 6.

## Answer
6.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Evdokimov M.A.
Place 32 knights on a chessboard so that each of them attacks exactly two others.
#
|
In a $3 \times 3$ square, it is possible to visit all cells except the central one with a knight's move and return to the starting cell.
## Solution
If knights are placed on all cells of a $3 \times 3$ square except the central one, each knight will attack exactly two others. Now, place four such "squares" on the board far enough apart so that knights from different squares do not attack each other (see figure).
Author: Shapovalov A.V.
On the Moon, coins with denominations of 1, 15, and 50 ferthings are in circulation. Nезнайка paid for a purchase with several coins and received change - one more coin than he paid with. What is the smallest possible price of the purchase?
## Hint
The remainder when 1, 15, and 50 are divided by 7 is 1.
## Solution
The remainder when the denomination of each coin is divided by 7 is 1. Let Nезнайка pay with $k$ coins totaling $A$ and receive change $C$. Then $A \equiv k(\bmod 7)$, and
$C \equiv k+1(\bmod 7)$. Therefore, the price of the purchase $A-C \equiv 6(\bmod 7)$. Consequently, this price cannot be less than 6 ferthings.
An example where the purchase costs 6 ferthings: Nезнайка paid with two coins - 1 ferthing and 50 ferthings, and received change with three coins of 15 ferthings each.
## Answer
6 ferthings.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\begin{array}{l}\text { Substitution of variables (other) }\end{array}\right]$
$\left[\begin{array}{l}\text { Completing the square. Sums of squares }\end{array}\right]$
$\left[\begin{array}{l}\text { Polynomials (other) }\end{array}\right]$
Given the polynomial $x(x+1)(x+2)(x+3)$. Find its minimum value.
|
$x(x+3)(x+1)(x+2)=\left(x^{2}+3 x\right)\left(x^{2}+3 x+2\right)$. Let's denote $x^{2}+3 x$ by $z$. Then $\left(x^{2}+3 x\right)\left(x^{2}+3 x+2\right)=z(z+2)=(z+1)^{2}-1$. The minimum value -1 of this function is reached when $z=-1$. The equation $x^{2}+3 x+1=0$ has solutions (the discriminant is greater than zero), therefore, such an $x$ exists for which our function reaches the value 1.
## Answer
$-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 [ Coloring $\quad]$
Tom Sawyer has taken on the task of painting a very long fence, adhering to the condition: any two boards, between which there are exactly two, exactly three, or exactly five boards, must be painted in different colors. What is the minimum number of paints Tom will need for this job?
|
Two colors (let's say white and red) are not enough: painting board number 1 in white, Tom will be forced to paint boards with numbers 4, 5, and 7 in red. Then between the red boards numbered 4 and 7, there will be exactly two boards, which violates the condition.
Three colors are sufficient: Tom can paint three boards in a row white, then three boards blue, then three red, then three white again, and so on. In this way, between identically painted boards, there will be either no more than one board (if they are in the same triplet) or no fewer than six (if they are in different triplets), so the condition of the problem will be met.
## Answer
3 colors.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The function $f(x)$ is defined for all $x$, except 1, and satisfies the equation: $(x-1) f\left(\frac{x+1}{x-1}\right)=x+f(x)$. Find $f(-1)$.
#
|
Substitute the values $x=0$ and $x=-1$ into the given equation. We get: $\left\{\begin{array}{c}-f(-1)=f(0), \\ -2 f(0)=-1+f(-1)\end{array}\right.$. Therefore, $2 f(-1)=-1+f(-1)$, which means $f(-1)=-1$.
## Answer
$-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Agakhanov N.X.
At a round table, 30 people are sitting - knights and liars (knights always tell the truth, while liars always lie). It is known that each of them has exactly one friend at the same table, and a knight's friend is a liar, while a liar's friend is a knight (friendship is always mutual). When asked, "Is your friend sitting next to you?" every other person answered "Yes." How many of the rest could have also answered "Yes"?
|
All those sitting at the table are paired as friends, which means there are an equal number of knights and liars. Consider any pair of friends. If they are sitting next to each other, the knight will answer "Yes" to the given question, and the liar will answer "No." If they are not sitting next to each other, their answers will be opposite. In any case, exactly one of the pair of friends will answer "Yes." Therefore, all the other 15 answers will be "No."
## Answer
0.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Folklore }}$
Solve the equation: $2 \sqrt{x^{2}-16}+\sqrt{x^{2}-9}=\frac{10}{x-4}$.
|
Since the left, and therefore the right, part of the equation takes only positive values, then $x>4$. On the interval $(4,+\infty)$, the function
$f(x)=2 \sqrt{x^{2}-16}+\sqrt{x^{2}-9}$ is increasing, while the function $g(x)=\frac{10}{x-4}$ is decreasing, so the equation $f(x)=g(x)$ has no more than one root.
It remains to note that $f(5)=g(5)$.
## Answer
$x=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kosukhin O.n.
Sasha found that there were exactly $n$ working digit buttons left on the calculator. It turned out that any natural number from 1 to 99999999 can either be entered using only the working buttons, or obtained as the sum of two natural numbers, each of which can be entered using only the working buttons. What is the smallest $n$ for which this is possible?
|
Let's show that the conditions of the problem are met if the buttons with digits $0,1,3,4,5$ remain functional.
Indeed, any digit from 0 to 9 can be represented as the sum of some two "functional" digits. Let the number from 1 to 99999999 that we want to obtain consist of digits $a_{1}, a_{2}, \ldots, a_{8}$ (some of them, including the leading ones, may be zeros). Represent each of them as the sum of two "functional" digits: $a_{1} = b_{1} + c_{1}, a_{2} = b_{2} + c_{2}, \ldots, a_{8} = b_{8} + c_{8}$. Then the number composed of "functional" digits $b_{1}, b_{2}, \ldots, b_{8}$ and the number composed of "functional" digits $c_{1}, c_{2}, \ldots, c_{8}$ give the desired number when summed.
Suppose that the desired result can be achieved for some set of four "functional" digits. Let $a$ be some odd digit. Among the numbers from 1 to 99999999, there will be one that ends in $a$ and contains "non-functional" digits in its decimal representation. Then this number can be represented as the sum of two numbers, whose representations contain only "functional" digits. Therefore, for each odd digit $a$, there will be two "functional" digits (possibly the same) whose sum ends in $a$. On the other hand, it is not difficult to see that among all the sums of pairs of four "functional" digits, there can be no more than four odd numbers. Therefore, one of the digits $1,3,5,7,9$ will not appear at the end of such sums. Contradiction.
## Answer
5.

Author: Gasikov S.B., Folklore
Does there exist a quadratic trinomial $f(x) = a x^{2} + b x + c$ with integer coefficients and $a$ not divisible by 2014, such that all numbers $f(1), f(2), \ldots, f(2014)$ have different remainders when divided by 2014?
## Solution
Let $f(x) = 1007 x^{2} + 1008 x = 1007 x(x+1) + x$. Since the product $x(x+1)$ is an even number for all natural $x$, $1007 x(x+1)$ is divisible by 2014 for all such $x$. Therefore, $f(x)$ gives the same remainder when divided by 2014 as $x$. Thus, all numbers $f(1), f(2), \ldots, f(2014)$ have different remainders when divided by 2014.
## Answer
Exists.

Each of two regular polyhedra $P$ and $Q$ is cut by a plane into two parts. One part of $P$ and one part of $Q$ are attached to each other along the plane of the cut. Can the resulting polyhedron be a regular polyhedron different from the original ones, and if so, how many faces can it have?
## Solution
Let $R$ be the resulting polyhedron. Clearly, the part of polyhedron $P$ contains at least one vertex $A$ not lying in the plane of the cut. The polyhedral angle of polyhedron $P$ at this vertex will also be a polyhedral angle of polyhedron $R$; this means that polyhedra $P$ and $R$ are similar. Similarly, $Q$ is also similar to them. Moreover, if at least one edge of polyhedron $P$ emanating from $A$ does not intersect (even at another vertex!) the plane of the cut, then it will also be an edge in $R$. Then in similar polyhedra $P$ and $R$, the edges are equal, and therefore, the polyhedra are equal, which contradicts the condition.
Thus, the part of $P$ that entered $R$ is a pyramid with vertex $A$. Similarly, the part of $Q$ that entered $R$ is a pyramid with vertex $B$. Therefore, at least half of the faces in $R$ adjoin the same vertex. This excludes the dodecahedron and the icosahedron. If our polyhedra are cubes, then triangular pyramids are cut off from $P$ and $Q$, and the resulting polyhedron has no more than five vertices, which is impossible.
The remaining cases of the octahedron and the tetrahedron are possible, as shown in the figure.
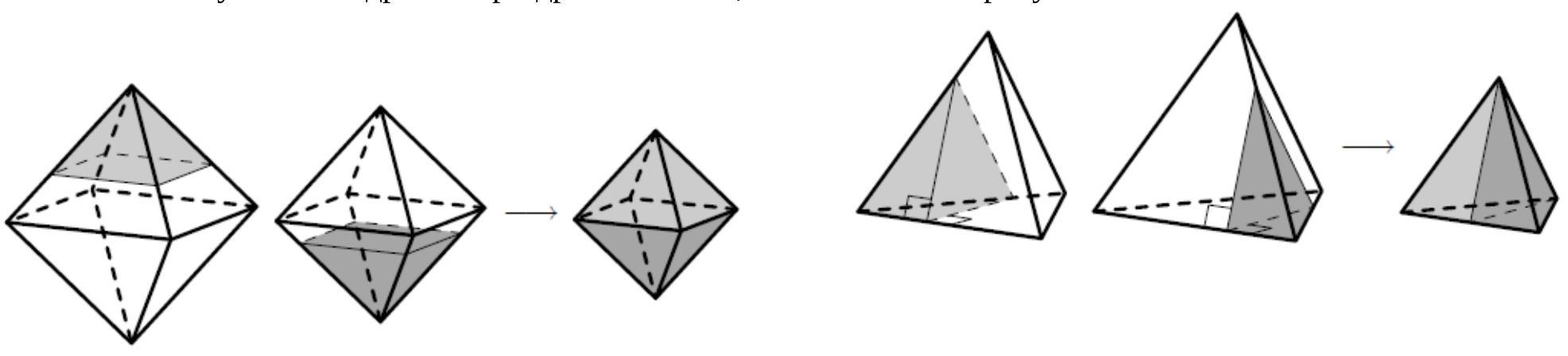
## Answer
Yes; 4 or 8 faces.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|

Authors: Shapovalov A.V., Yatsenno I.V.
At the "Come on, creatures!" competition, 15 dragons are standing in a row. The number of heads of neighboring dragons differs by 1. If a dragon has more heads than both of its neighbors, it is considered cunning; if it has fewer heads than both of its neighbors, it is considered strong; the rest (including those standing at the ends) are considered ordinary. In the row, there are exactly four cunning dragons with 4, 6, 7, and 7 heads, and exactly three strong dragons with 3, 3, and 6 heads. The first and last dragons have the same number of heads.
a) Provide an example of how this could be.
b) Prove that the number of heads of the first dragon is the same in all examples.
|
It is convenient to represent a row of dragons as a graph: instead of each dragon, we draw a point at a height corresponding to the number of heads the dragon has, and connect these points.
a) See the figure.
b) First, note that somewhere between every two cunning dragons stands a strong one. Indeed, if we walk along the row of dragons, after we pass a cunning dragon, the number of heads starts to decrease. At some point, it must start to increase again - this is the position where the strong dragon stands. Similarly, the increase will eventually end at a cunning dragon.
The first method. Let's look at the order in which strong and cunning dragons can stand. A strong dragon with six heads can only stand between two cunning dragons with seven heads. This gives rise to three cases: the two remaining strong dragons can stand either on the same side of this trio in one of two orders, or on opposite sides.
Case ... $43 \ldots 6 \ldots 3$... 767 ...
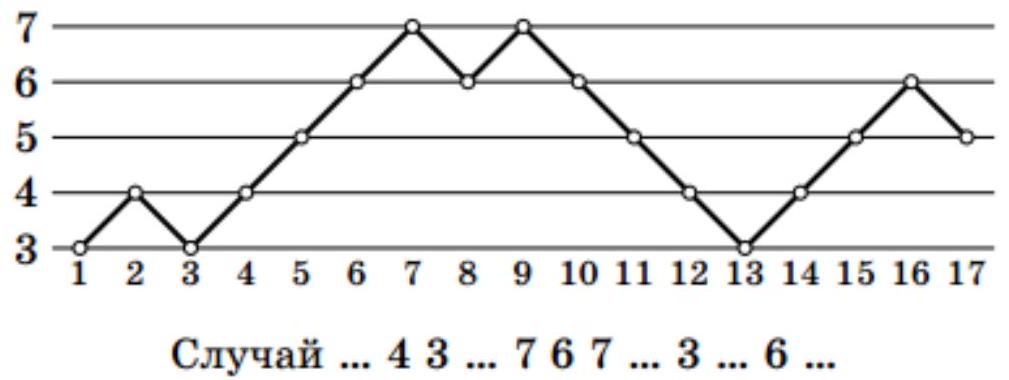
In the first case, 14 dragons are already uniquely determined, and the only way to ensure that the first and last dragons have the same number of heads is to add another dragon with five heads at the far right.
The second and third variants are impossible, as they require more than 15 dragons (even without considering the condition that the first and last dragons have the same number of heads).
The second method (sketch). We can manage without enumeration. Choose a segment of the graph between some strong dragon and the nearest cunning dragons to it and "straighten" it, replacing the "valley" with a "hill" (see the figure).
The number of heads of the dragons will change, and instead of two cunning dragons and one strong one in this segment, there will now be only one cunning dragon. Note that the number of heads of the new cunning dragon will be equal to the sum of the number of heads of the original two cunning dragons minus the number of heads of the former strong dragon. This means that the value "sum of the number of heads of all cunning dragons minus the sum of the number of heads of all strong dragons" does not change.
Note also that the number of heads of the extreme dragons in the row does not change with such an operation. Now repeat this operation until all strong dragons disappear. We will be left with one cunning dragon, which, by symmetry, will be exactly in the middle of the row. Let's calculate how many heads it will have. We know that initially, the sum of the number of heads of cunning dragons minus the sum of the number of heads of strong dragons is
$4+6+7+7-3-3-6=12$. But now this sum is equal to simply the number of heads of the single cunning dragon!
Knowing that it has 12 heads, we can easily restore that the extreme dragons (which are seven positions away from it in the row) each have five heads.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Folklore }}$
Among the actors of Karabas Barabas theater, a chess tournament was held. Each participant played exactly one game with each of the others. One solido was given for a win, half a solido for a draw, and nothing for a loss. It turned out that among any three participants, there would be a chess player who earned exactly 1.5 solido in games with the other two. What is the maximum number of actors that could have participated in such a tournament?
|
Example. Let's denote the participants with letters A, B, V, G, D. Suppose A won against B, B won against V, V won against G, G won against D, D won against A, and all other matches ended in a draw. The condition of the problem is satisfied.
Evaluation. From the condition, it follows that for this tournament, two statements must be true:
1) there are no three players, all matches between whom ended in a draw;
2) there are no players whose matches did not end in a draw.
Assume that there were at least six players in the tournament. Let's leave only them and draw a complete graph with six vertices (corresponding to these six players), where blue edges correspond to decisive matches, and red edges correspond to draws. According to problem $\underline{30815}$, there are three vertices in it, all edges between which are of the same color. But this contradicts the statements just formulated.
## Answer
5 players.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bogdanov I.I.
On a chessboard, 32 white and 32 black pawns are placed in all squares. A pawn can capture pawns of the opposite color by moving diagonally one square and taking the place of the captured pawn (white pawns can only capture to the right-up and left-up, while black pawns can only capture to the left-down and right-down). Pawns cannot move in any other way. What is the minimum number of pawns that can remain on the board?
|
Note that a pawn that stood on a black square will always move only on black squares. Then after each move (on black squares) there will always be at least one pawn on black squares - the one that made the move. Similarly, at least one pawn will remain on white squares, and there will be no less than two pawns in total. The diagrams show how to arrange the pawns on white squares and how to move them so that only one remains. The arrangement and actions on black squares are analogous.
## Answer
Two pawns.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bogdanov I.I.
The distance between two cells on an infinite chessboard is defined as the minimum number of moves in the path of a king between these cells. On the board, three cells are marked, the pairwise distances between which are 100. How many cells exist such that the distances from them to all three marked cells are 50?
|
Consider two arbitrary cells $A$ and $B$. Let the difference in the abscissas of their centers be $x \geq 0$, and the difference in the ordinates be $y \geq 0$. Then the distance $\rho(A, B)$ between these cells is $\max \{x, y\}$.
Let cells $A, B, C$ be marked. Then for each pair of cells, there exists a coordinate in which they differ by exactly 100. For two pairs of cells, this will be the same coordinate; for definiteness, let these be the pairs $(A, B)$ and $(A, C)$, differing horizontally. Then the abscissas of points $B$ and $C$ either differ by 200 or coincide. The first case is impossible, since $\rho(B, C)=100$. Therefore, their abscissas coincide, and their ordinates differ by 100. We can assume that the cells have coordinates $B(0,0), C(0,100), A(100, x)(0 \leq x \leq 100)$. Consider a point $X$ that is 50 units away from points $A, B$, and $C$. Its abscissa must be 50, otherwise $\rho(X, B)>50$ or $\rho(X, A)>50$. Similarly, the ordinate of $X$ is 50. Therefore, the coordinates of $X$ are $(50,50)$, and this cell fits. Thus, the sought cell is exactly one.
## Answer
One cell
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underset{\text { Tokarev } C . \text {. }}{ }$
Numbers $a, b$ and $c$ are such that $(a+b)(b+c)(c+a)=a b c,\left(a^{3}+b^{3}\right)\left(b^{3}+c^{3}\right)\left(c^{3}+a^{3}\right)=a^{3} b^{3} c^{3}$. Prove that $a b c=0$.
|
First, note that $x^{2}-x y+y^{2}>|x y|$ for any distinct numbers $x$ and $y$.
Assume that $a b c \neq 0$. Then, dividing the second equality by the first, we get $\left(a^{2}-a b+b^{2}\right)\left(b^{2}-b c+c^{2}\right)\left(c^{2}\right.$
$\left.-c a+a^{2}\right)=|a b| \cdot |b c| \cdot |a c|$.
All the parentheses on the left and all the factors on the right are positive; moreover, each factor on the left is not less than the corresponding factor on the right. Therefore, equality can only be achieved when all these three inequalities turn into equalities, that is, when $a=b=c$. In this case, the first equality from the condition becomes $8 a^{3}=a^{3}$, which is impossible for $a \neq 0$. Thus, our assumption is incorrect, and $a b c=0$.
Send a comment
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
B.R.'s Problem
The segments connecting an inner point of a convex non-equilateral $n$-gon with its vertices divide the $n$-gon into $n$ equal triangles.
For what smallest $n$ is this possible?
|
Let's prove that the specified situation is impossible for $n=3,4$.
The first method. For $n=3$, the angles of the triangles in the partition that meet at an internal point are equal, since the sum of any two different angles in them is less than $180^{\circ}$. But then the sides opposite to them, which are sides of the polygon, are also equal. Contradiction.
Suppose the quadrilateral $ABCD$ is cut into equal triangles by segments drawn from point $O$. Draw the broken line (or straight line) $AOC$. At point $O$, the sum of two angles on one side of $AOC$ is not less than $180^{\circ}$. Similarly to the case of $n=3$, we get that the corresponding sides are equal. Considering the broken line $BOD$, we get the equality of one of these sides and the third side. Let, for example, $AB = BC = CD = l$. Suppose $AD \neq l$. In triangle $AOD$, there is a side of length $l$, say $AO$. Thus, in triangle $AOB$ (and all equal to it), there are two sides of length $l$. As a result, $AO = DO = l$. In triangle $BOC$, there are two sides of length $l$. One of them is $BC$, and the other, say, $BO$. But then in triangle $AOB$, all sides are equal. Therefore, this is also true for triangle $AOD$, i.e., $AD = l$. Contradiction.
The second method. Since the triangles into which the given triangle is cut are equal, the radii of the circumcircles and the areas of these triangles are also equal. The first implies that the point defining the partition is the orthocenter of the triangle (see problem 56681a), and the second implies that it is the point of intersection of its medians (see problem 54992). However, the orthocenter and the point of intersection of the medians coincide only in an equilateral triangle (see problem $\underline{108458}$).
$\angle OAB = \angle OCB$, as angles opposite the same side of equal triangles. Similarly, $\angle OAD = \angle OCD, \angle OBC = \angle ODC, \angle OBA = \angle ODA$. Therefore, $\angle A = \angle C, \angle B = \angle D$, and $ABCD$ is a parallelogram. Since the segments from $O$ divide it into equal-area triangles, $O$ is the point of intersection of its diagonals, and then from the equality of the triangles, it follows that $ABCD$ is a rhombus.
For $n=5$, the specified situation is possible (see figure).
Answer
$n=5$
Send a comment
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Berdonikov A.
Let's call a natural number good if all its digits are non-zero. A good number is called special if it has at least $k$ digits and the digits are in strictly increasing order (from left to right).
Suppose we have some good number. In one move, it is allowed to append a special number to either end or insert it between any two of its digits, or, conversely, erase a special number from its representation. For what largest $k$ can any good number be transformed into any other good number using such moves?
|
Obviously, a special number does not have more than nine digits. If $k=9$, then with each operation, the number of digits changes by exactly 9, meaning the remainder of the number of its digits divided by 9 does not change, and a two-digit number cannot be made from a one-digit number.
Let $k=8$. Since all operations are reversible, it is sufficient to prove that any digit can be inserted.
We will prove by induction on $n$ that we can insert the digit $n$.
Base case. To insert 1, first insert 123456789, and then erase 23456789.
Inductive step. Suppose we can insert (and erase) digits from 1 to $n-1<9$. To insert $n$, first insert 123456789, erase $12 \ldots(n-1)$ one by one, then insert $12 \ldots(n-1)$ one by one to the right of $n$, and finally erase the number $12 \ldots(n-1)(n+1) \ldots 9$ (for $n=9$, the last two actions are not needed, and for $n=8$, the number 12...79 is erased).
## Answer
For $k=8$.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Senderov V.A.
Find all natural numbers $k$ such that the product of the first $k$ prime numbers, decreased by 1, is a perfect power of a natural number (greater than the first power).
#
|
Let $n \geq 2$, and $2=p_{1}1$; then $k>1$. The number $a$ is odd, so it has an odd prime divisor $q$. Then $q>p_{k}$, otherwise the left side of the equation (*) would be divisible by $q$, which is not the case. Therefore, $a>p_{k}$.
Without loss of generality, we can assume that $n$ is a prime number (if $n=s t$, then we can replace $n$ with $t$ and $a$ with $a^{s}$). Note that $n>2$, since
$a^{2}+1$ cannot be divisible by $3=p_{2}$.
We will show that $n>p_{k}$. Indeed, otherwise $n=p_{i}$, where $i \leq k$. Then $a^{p_{i}}+1$ is divisible by $p_{i}$; on the other hand, by Fermat's Little Theorem, $a^{p_{i}}-a$ is divisible by $p_{i}$. Since $a^{p_{i}}+1=(a+1)\left(a^{p_{i}-1}-a^{p_{i}-2}+\ldots-a+1\right)$, and $a+1=\left(a^{p_{i}}+1\right)-\left(a^{p_{i}}-a\right)$ is divisible by $p_{i}$, and $a^{p_{i}-1}-a^{p_{i}-2}+\ldots-a+1 \equiv 1+1+\ldots+1=p_{i} \equiv 0\left(\bmod p_{i}\right)$, then $a^{p_{i}}+1$ is divisible by $p_{i}^{2}$, which contradicts the condition.
Thus, $a>p_{k}$ and $n>p_{k}$, from which $a^{n}+1>p_{k}^{p_{k}}>p_{1} p_{2} \ldots p_{k}$, which contradicts the equation (*).
## Answer
$k=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2+$
John had a full basket of trempons. First, he met Anna and gave her half of his trempons and another half-trempon. Then he met Banna and gave her half of the remaining trempons and another half-trempon. After meeting Vanna and giving her half of the trempons and another half-trempon, the basket was empty. How many trempons did John have at the beginning? (It was not possible to determine what trempons are, as there were none left by the end of the problem.)
|
Notice that before meeting Vanna, John had one tremponch left, as half of this amount was half a tremponch. Before meeting Banna, he had 3 tremponchs, because half of this amount was one and a half tremponchs, that is, one and a half. Similarly, we get that initially there were 7 tremponchs.
## Answer
7 tremponchs.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $M$ be a finite set of numbers. It is known that among any three of its elements, there are two whose sum belongs to $M$.
What is the maximum number of elements that can be in $M$?
|
Consider either the four largest or the four smallest numbers.
## Solution
Example of a set of 7 elements: $\{-3,-2,-1,0,1,2,3\}$.
We will prove that the set $M=\left\{a_{1}, a_{1}, \ldots, a_{n}\right\}$ of $n>7$ numbers does not have the required property. We can assume that $a_{1}>a_{2}>a_{3}>\ldots>a_{n}$ and $a_{4}>0$ (changing the signs of all elements does not change our property). Then $a_{1}+a_{2}>a_{1}+a_{3}>a_{1}+a_{4}>a_{1}$, which means that none of the sums $a_{1}+a_{2}, a_{1}+a_{3}$, and $a_{1}+a_{4}$ belong to the set $M$. Moreover, the sums $a_{2}+a_{3}$ and $a_{2}+a_{4}$ cannot both belong to $M$, since $a_{2}+a_{3}>a_{2}+a_{4}>a_{2}$. Therefore, for at least one of the triples $\left(a_{1}, a_{2}, a_{3}\right)$ and $\left(a_{1}, a_{2}, a_{4}\right)$, the sum of any two of its elements does not belong to the set $M$.
## Answer
7 elements.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9,10,11 |
Author: S $\underline{\text { Saghafian M. }}$.
In the plane, five points are marked. Find the maximum possible number of similar triangles with vertices at these points.
|
Example. Vertices and the center of a square.
Evaluation. Let's describe all configurations of four points forming four similar triangles. Let $\$ \mathrm{~A} \$$, $\$ \mathrm{~B} \$$, \$C \$ \$ \$
1. Point $\$ \mathrm{~A} \$$ lies inside triangle $\$ B C D \$$. Let $\$ B \$$ be the largest angle of triangle $\$ B C D \$$. Then angle \$CAD is similar to
2.1. Diagonal \$AC\$ bisects angle \$ \$ \$ABCD\$ - a rhombus, and since the triangles \$
2.2. There will be a vertex for which the diagonal is not a bisector, let this vertex be \$A\$. Then angles \$BAC\$, \$CAD\$, and \$BAD\$ are pairwise different. Therefore, they are the three angles of each of the four similar triangles, i.e., their sum is $\$ 180 \wedge\{\backslash$ circ $\} \$$ and \$ \$angle BAD=90^\{|circ $\} \$$.
Among the angles formed by the given points, there are four right angles and eight acute angles. Angles $\$ \mathrm{ABD} \$$, \$CBD\$ and so on cannot be right angles, as then one of the angles of the quadrilateral would be obtuse. Therefore, the right angles are \$BAD\$, \$ABC\$, \$BCD\$, and \$ADC\$.
Thus, in both subcases, $\$ \mathrm{ABCD} \$$ is a rectangle.
Returning to the problem. Let's call a triangle bad if it is formed by any three of the given points and does not belong to the set of similar triangles. (In particular, a bad triangle is formed by three collinear points). We will show that there are at least two bad triangles.
Note that five points can form no more than one rectangle. As shown above, each of the other quadruples contains at least one bad triangle. Each bad triangle is defined by two quadruples, so the total number of bad triangles is no less than $4 / 2=2$.
## Answer
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Chessboards and chess pieces ] [ Examples and counterexamples. Constructions ]
What is the maximum number of queens that can be placed on an $8 \times 8$ chessboard without attacking each other?
|
You can place no more than eight queens that do not attack each other, as each queen controls one row.
Let's show how you can place eight queens:
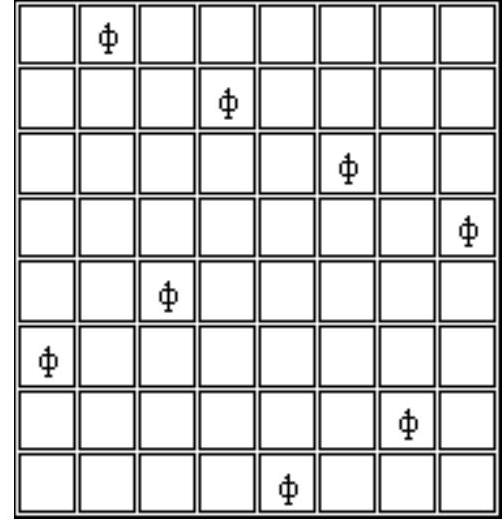
Send a comment
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3[ Examples and counterexamples. Constructions]
In the cells of a $5 \times 5$ square table, the numbers 1 and -1 are arranged. It is known that the number of rows with a positive sum is greater than the number of rows with a negative sum.
What is the maximum number of columns in this table that can have a negative sum?
|
Let's consider one of the possible examples (see the table). The sum of the numbers in each of the three upper rows is positive, while the sum of the numbers in each column is negative.
| 1 | 1 | 1 | -1 | -1 |
| :---: | :---: | :---: | :---: | :---: |
| 1 | -1 | 1 | -1 | 1 |
| -1 | 1 | -1 | 1 | 1 |
| -1 | -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 | -1 |
## Answer
5 columns.
Problem
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the minimum number of sportlotto cards (6 out of 49) you need to buy to ensure that at least one number is guessed correctly in at least one of them?
#
|
Let's fill eight cards as follows: in the first one, we will strike out numbers from 1 to 6, in the second one - from 7 to 12, and so on, in the last one - from 43 to 48. The number 49 will remain unstruck in any card. Therefore, at least five of the winning numbers will be struck out.
We will prove that seven cards may not be enough. Indeed, no more than 42 different numbers will be struck out in total. Therefore, at least seven numbers will not be struck out in any of the cards. It may happen that the winning numbers are exactly six of these seven.
## Answer
8 cards
Send a comment
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kostrikina I.A.
At a round table, pastries are placed at equal intervals. Igor walks around the table and eats every third pastry he encounters (each pastry can be encountered several times). When there were no pastries left on the table, he noticed that the last pastry he took was the first one he encountered, and he had walked exactly seven rounds around the table. How many pastries were there?
|
Since Igor passed an integer number of circles, he met the first pastry at the moment of approaching the table. In addition, the sequence of eating pastries will not change if we remove the requirement of "equal intervals". If there were four pastries, Igor would have walked exactly five circles (see the figure).
Let the number of pastries on the table be divisible by three. Then, in the first circle, Igor eats every third pastry and returns to the initial position. Thus, after one circle, the number of pastries becomes $2 / 3$ of the number that was on the table. Therefore, if there were six pastries, Igor would have walked exactly six circles, and if there were nine pastries, Igor would have walked exactly seven circles.
If there are more than nine pastries, then Igor will travel some distance before the number of pastries is exactly nine, reach the nearest pastry, and then make exactly seven circles. Thus, in total, he has walked more than seven circles.
If there are fewer than nine pastries, and the number of circles is also seven, then, as shown above, we prove that for nine pastries, the number of circles is more than seven. Contradiction.
## Answer
9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Three people are playing table tennis, with the player who loses a game giving way to the player who did not participate in it. In the end, it turned out that the first player played 10 games, the second - 21. How many games did the third player play?
|
The first player plays the rarest every second game.
## Solution
According to the condition, the second player played 21 games, so there were at least 21 games in total. Out of every two consecutive games, the first player must participate in at least one, so the number of games was no more than $2 \cdot 10 + 1 = 21$. Therefore, a total of 21 games were played, and the second player participated in each of them. In 10 games, he faced the first player, and in the remaining 11 games, he faced the third player.
## Answer
11 games.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Evaluation + example ] [ Combinatorial geometry (other).]
What is the minimum number of shots in the game "Battleship" on a 7*7 board needed to definitely hit a four-deck ship (a four-deck ship consists of four cells arranged in a row)?
#
|
If on a $7 * 7$ board, n non-overlapping four-deck ships can fit, this means that (n-1) shots would not be enough.
## Solution
In the first picture, an example sequence of 12 shots is provided, with which any four-deck ship would be hit. In the second picture, an example of the placement of twelve non-overlapping four-deck ships is shown. Thus, if we have made eleven shots, we would not be able to hit a ship that coincides with one of the twelve shown.
## Answer
12.00
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the maximum value that the expression $a e k-a f h+b f g-b d k+c d h-c e g$ can take if each of the numbers $a, b, c, d, e, f, g, h, k$ is equal to $\pm 1$.
#
|
Evaluation. The product of all addends equals - $(a b c d e f g h k)^{2}$, which is negative. Therefore, the number of minus ones among the addends is odd and thus not equal to zero. Consequently, the sum does not exceed 4.
Example. Let $a=c=d=e=g=h=k=1, b=f=-1$. Then the given expression equals 4.
## Answer
4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Ordering in ascending (descending) order. ] [ Classical combinatorics (other). $\quad]$
a) A traveler stopped at an inn, and the owner agreed to accept rings from a golden chain the traveler wore on his wrist as payment for lodging. However, he set a condition that the payment should be daily: each day the owner should have one more ring than the previous day. The chain, which was closed in a loop, contained 11 rings, and the traveler planned to stay exactly 11 days, so he agreed. What is the minimum number of rings he needs to cut to be able to pay the owner?
b) How many rings should the chain consist of so that the traveler can stay at the inn for the maximum number of days, given that he can only cut $n$ rings?
|
a) It is enough to cut two rings so that pieces of three and six rings are separated. On the third day, the traveler gives the piece of three rings and receives two rings as change, and on the sixth day, the piece of six rings and receives five rings as change.
b) Arrange the resulting pieces of the chain (not counting the cut rings) in increasing order of the number of rings in them: \(a_{1} \leq a_{2} \leq \ldots\) Clearly, \(a_{1} \leq n+1\) (otherwise, it would be impossible to pay for the \((n+1)\)-th day), \(a_{2} \leq a_{1}+n+1 \leq 2(n+1), \quad a_{3} \leq a_{2}+a_{1}+n+1 \leq 4(n+1), \ldots\) Moreover, the number of pieces does not exceed \(n\). Therefore, the chain contains no more than \(n+(n+1)\left(1+2+2^{2}+\ldots+2^{n-1}\right)=(n+1) 2^{n}-1\) rings.
By taking pieces of the maximum possible length \(\left(a_{k}=(n+1) 2^{k-1}, k=1, \ldots, n\right), \quad\) we obtain a chain of \((n+1) 2^{n}-1\) rings.
## Answer
a) 2 rings. b) From \((n+1) 2^{n}-1\) rings.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kanel-Belov A.Y.
Two numbers are written on the board in the laboratory. Every day, the senior researcher Petya erases both numbers on the board and writes down their arithmetic mean and harmonic mean instead. On the morning of the first day, the numbers 1 and 2 were written on the board. Find the product of the numbers written on the board in the evening of the 1999th day.
|
The product of the numbers on the board does not change. Indeed, $\frac{a+b}{2} \cdot \frac{2 a b}{a+b}=a b$. Therefore, the desired product is 2.
## Answer
2.
Send a comment
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kuuyggin A.K.
Among any five nodes of a regular square grid, there will always be two nodes such that the midpoint of the segment between them is also a node of the grid. What is the minimum number of nodes of a regular hexagonal grid that must be taken so that among them there will always be two nodes such that the midpoint of the segment between them is also a node of this grid?
|
Lemma. Among any five nodes of a grid of equilateral triangles, there will be two such that the midpoint of the segment between them is also a grid node.
Proof of the lemma. Introduce the origin at one of the grid nodes and denote by $\$ \mid v e c\{a\} \$$ and $\$ \mid v e c\{b\} \$$ the radius vectors to the two nearest nodes, as shown in the figure. Then the grid nodes are points of the form $\$ m \mid v e c\{a\}+ n \mid v e c\{b\} \$$ for integers \$m $\$$ and \$n $\$$. By the pigeonhole principle, among five points, there will be two points $\$m_1 \mid v e c\{a\}+ n_1 \mid v e c\{b\} \$$ and $\$m_2 \mid v e c\{a\}+ n_2 \mid v e c\{b\} \$$, for which the parity of \$m_1 and \$ \$m_2\$, and the parity of \$n_1 and \$n_2\$, coincide simultaneously. The midpoint of the segment connecting these two points is the point $\$ \backslash frac \left\{m \_1+m \_2\right\} 2 \backslash m k e r n 2 m u \operatorname{vec}\{a\}+\backslash f r a c\left\{n \_1+n \_2\right\} 2 \backslash m k e r n 2 m u \operatorname{vec}\{b\} \$$$. It is a grid node, since the numbers $\$ \backslash frac \left\{m \_1+m \_2\right\} 2 \$$ and $\$ \backslash frac \left\{n \_1+n \_2\right\} 2 \$$ are integers due to the same parity of \$ \mathrm{~m} \_1 \$$ and \$m_2\$, and \$n_1\$, and \$n_2\.
Solution. In the figure on the left, you can see an example of the placement of 8 grid nodes, among which there are no two such that the midpoint of the segment between them is a grid node. We will prove that nine nodes are sufficient. Note that the hexagonal grid is divided into the union of two triangular grids (see the figure on the right). By the pigeonhole principle, among any nine nodes, at least five will be in one of these two triangular grids. By the lemma, among these five nodes, there will be two of the required ones.
## Answer
9.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Coordinate method on the plane ] [Triangle inequality (other).]
Point $M$ lies on the line $3 x-4 y+34=0$, and point $N-$ lies on the circle $x^{2}+y^{2}-8 x+2 y-8=0$. Find the minimum distance between points $M$ and $N$.
|
Notice that
$$
x^{2}+y^{2}-8 x+2 y-8=0 \Leftrightarrow x^{2}-8 x+16+y^{2}+2 y+1=25 \Leftrightarrow(x-4)^{2}+(y+1)^{2}=5^{2}
$$
This means the center of the circle is the point $Q(4, -1)$, and the radius is 5.
Let $d$ be the distance from the point $Q$ to the line $3 x-4 y+34=0$. Then
$$
d=\frac{|3 \cdot 4-4 \cdot(-1)+34|}{\sqrt{3^{2}+4^{2}}}=\frac{50}{5}=10>5
$$
This means that all points on the given line lie outside the given circle. Therefore, for each point $M$ on the given line and each point $N$ on the given circle,
$$
M N>M Q-Q N=M Q-5>d-5=10-5=5
$$
and this distance equals 5 if $M$ is the projection of the point $Q$ onto the given line.
## Answer
5.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Klepitsyn V.A.
Cells of a $5 \times 5$ board are painted in a checkerboard pattern (corner cells are black). A figure, a mini-bishop, moves along the black cells of this board, leaving a trail on each cell it visits and not returning to that cell again. The mini-bishop can move either to free (diagonally) adjacent cells or jump (also diagonally) over one cell with a trail to a free cell beyond it. What is the maximum number of cells the mini-bishop can visit?
|
Let's first provide an example of the mini-elephant's route that ensures it visits twelve cells (see the figure, numbers from 1 to 12 show the order of cell visits).
| 1 | | 4 | | 6 |
| :--- | :--- | :--- | :--- | :--- |
| | 2 | | 5 | |
| 3 | | 7 | | 9 |
| | 11 | | 8 | |
| 12 | | 10 | | |
We will prove that the mini-elephant cannot visit all black cells. Consider the four corner cells. The mini-elephant can leave such a cell either to an adjacent cell or to the central cell. It can go to an adjacent cell from a corner cell only on the first move. Indeed, to enter a corner cell, the mini-elephant can either come from an adjacent cell or from the central cell, jumping over an already visited adjacent cell. In both cases, it cannot go to an adjacent cell again. The mini-elephant can go to the central cell from a corner cell no more than once. Thus, the mini-elephant will leave the corner cells no more than twice, meaning it will visit no more than three corner cells.
## Answer
12 cells.
Author: Berdnikov A.
An equilateral triangle has been cut out of the plane.
Can the remaining part of the plane be tiled with triangles, any two of which are similar but not homothetic?
## Solution
We will provide two examples of such tiling.
Example 1. On the extensions of the sides of the cut-out triangle, mark points \(A_1, B_1, C_1\) such that \(AA_1 = BB_1 = CC_1 = xAB\) (see the left figure). Triangles \(A_1AB_1, B_1BC_1\), and \(C_1CA_1\) are equal, and triangle \(A_1B_1C_1\) is equilateral. Now extend the sides of triangle \(A_1B_1C_1\) and mark points \(A_2, B_2, C_2\) such that \(A_1A_2 = B_1B_2 = C_1C_2 = xA_1B_1\). Triangles \(A_2A_1B_2, B_2B_1C_2\), and \(C_2C_1A_2\) are equal to each other and similar to triangle \(A_1A_2B_1\). Similarly, construct points \(A_3, B_3, C_3\) and so on. The sizes of triangles \(A_kB_kC_k\) grow in a geometric progression, so the entire plane will be covered. Thus, we have obtained a tiling of the plane into similar triangles of the form \(A_iB_{i-1}B_i, B_jB_{j-1}C_j\), and \(C_kC_{k-1}A_k\).
Consider the equilateral triangles \(A_kB_kC_k\). All of them have a common center, and the directions of the sides of adjacent triangles differ by a rotation of angle \(B_1C_1B\). To ensure that the triangles in the tiling are not homothetic, choose the value of \(x\) such that the angle \(B_1C_1B\) is irrational. Then, for any pair of triangles in the tiling, their long sides will not be parallel to each other, and thus the triangles will not be homothetic. Therefore, this tiling satisfies the condition.
Example 2. See the right figure. All triangles are equal. Equal triangles can be homothetic only with a coefficient of -1. But there are no centrally symmetric triangles in the figure.
## Answer
Yes.
Submit a comment
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Examples and counterexamples. Constructions]
A snail woke up, crawled from the mushroom to the spring, and fell asleep. The journey took six hours. The snail moved sometimes faster, sometimes slower, and stopped. Several scientists observed the snail. It is known that:
1) At every moment of the journey, the snail was observed by at least one scientist.
2) Each scientist observed the awake snail for one hour (continuously) and says that during this time the snail crawled exactly one meter.
What is the maximum possible distance from the mushroom to the spring?
|
Example. Let's divide the entire time of the snail's movement into 30 intervals of 12 minutes each. Suppose the snail crawls 1 m in each of the 10 intervals numbered $1, 6, 7, 12, 13, 18, 19, 24, 25$, and 30, and rests the rest of the time. Scientists observe it in intervals 1-5 (from 1st to 5th - exactly one hour), 2-6, 7-11, 8-12, 13-17, 14-18, 19-23, $20-24, 25-29, 26-30$.
See the estimate in problem 73652.
## Answer
$10 \text{ m}$.
a) 2000 chips are placed on a plane at the vertices of a convex 2000-gon. In one move, you can divide them into two groups and move the chips of the first group by some vector, leaving the other chips in place. Can it happen that after 9 moves all the chips end up on one line? b) And after 10 moves?
## Hint
If after the $\mathrm{n}$-th move the chips lie on $\mathrm{k}$ lines, then after the (n-1)-th move they must have lain on $2 \mathrm{k}$ lines.
## Solution
a) If after the n-th move the chips are on one line, then after the (n-1)-th move they must have been on two lines, after the (n-2)-th - on 4 lines, and so on, and initially - on $2^{\text {n }}$ lines. Since no three vertices of a convex polygon lie on one line, the smallest number of lines containing all vertices of a 2000-gon is 1000. Therefore, $2^{\mathrm{n}}$ is not less than 1000, which means n is not less than 10, solving part a). b) Consider 1024 parallel lines, the distances between adjacent ones of which are 1. Place the vertices of the convex 2000-gon on these lines. The vectors of displacement will be perpendicular to the lines, and we will use each move to merge pairs of adjacent lines so that after 10 moves only one line remains.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.