problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
|
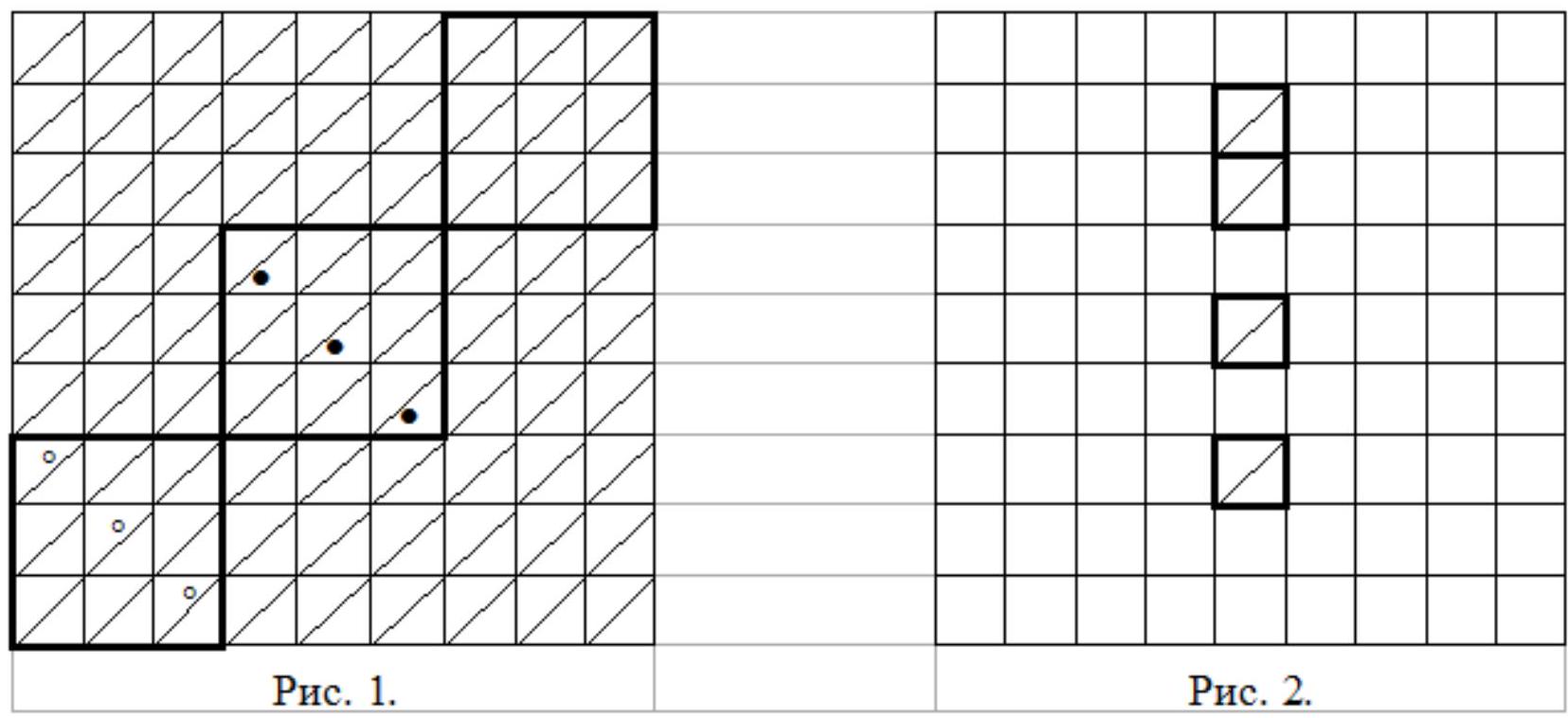
A city in the shape of a triangle is divided into 16 triangular blocks, and at the intersection of any two streets, there is a square (there are a total of 15 squares in the city). A tourist started touring the city from a certain square and ended the tour at a different square, visiting each square exactly once. Prove that during the tour, the tourist turned at least 4 times at $120^{0}$.
#
|
Paint the blocks in black and white in a checkerboard pattern. If a tourist has passed through two streets of one block, then he has made a turn of $120^{0}$.
## Solution
There are 15 areas in total, so the tourist has passed through 14 streets connecting pairs of adjacent areas. We will paint the blocks in black and white in a checkerboard pattern (see the picture), resulting in 10 black blocks, and each street is the boundary of exactly one black block. The tourist could not have passed through all three streets bounding a block. Therefore, there will be 14-10=4 black blocks for which the tourist passed through two streets. If the tourist passed through two streets of one block, it is not difficult to see that he made a turn of $120^{0}$ at one of the squares of this block. Thus, in at least four black blocks, a turn of $120^{0}$ was made.
|
4
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
[ Methods for solving problems with parameters ] [ Phase plane of coefficients ]
Plot on the phase plane $O p q$ the set of points $(p, q)$ for which the equation $x^{3}+p x+q=0$ has three distinct roots belonging to the interval $(-2,4)$.
|
See solutions of problems $\underline{61272}, \underline{61273}$.
## Answer
The set of points defined by the inequalities $4 p^{3}+27 q^{2}<0,-4 p-64<q<2 p+8$.[^0]
How many roots does the equation $8 x\left(1-2 x^{2}\right)\left(8 x^{4}-8 x^{2}+1\right)=1$ have on the interval $[0,1]$?
## Solution
Notice that $8 x^{4}-8 x^{2}+1=2\left(2 x^{2}-1\right)^{2}-1$. By making the substitution $x=\cos \varphi$, we get $8 \cos \varphi \cos 2 \varphi \cos 4 \varphi=-1$.
Multiplying by $\sin \varphi$, we obtain $\sin 8 \varphi=-\sin \varphi$,
from which $8 \varphi=-\varphi+2 k \pi$ or $8 \varphi=\pi+\varphi+2 k \pi$, that is, $x=\cos 2 k \pi / 9$ or $x=\cos (\pi / 7+2 k \pi / 7)$. On the interval $[0,1]$, there are four roots of the equation: $\cos 2 \pi / 9, \cos 4 \pi / 9, \cos \pi / 7$ and $\cos 3 \pi / 7$ (the root $x=1$ is extraneous, it arose from the multiplication by $\sin \varphi$).
## Answer
Four roots.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Franklin 5.
A convex $n$-gon $P$, where $n>3$, is cut into equal triangles by diagonals that do not intersect inside it.
What are the possible values of $n$, if the $n$-gon is cyclic?
|
Lemma. Let a convex $n$-gon be cut into equal triangles by diagonals that do not intersect inside it. Then, for each of the triangles in the partition, at least one side is a side (not a diagonal) of the $n$-gon.
Proof. Let a triangle in the partition have angles $\alpha \leq \beta \leq \gamma$ with vertices $A, B, C$ respectively, and $A C$ and $B C$ are diagonals of the $n$-gon. At vertex $C$, there are at least two more angles of the triangles in the partition. If at least one of these angles is greater than $\alpha$, then the sum of the angles at vertex $C$ is not less than $\gamma+\beta+\alpha=\pi>\angle C$. Contradiction. Therefore, all angles at vertex $C$, except $\angle A C B$, are equal to $\alpha$, and $\alpha<\beta$.
Consider the second triangle in the partition adjacent to $B C$. Since it is equal to triangle $A B C$, the angle opposite side $B C$ in it is equal to $\alpha$. But the angle at vertex $C$ in this triangle is also equal to $\alpha$. Contradiction.
Since the sum of the angles of the polygon $P$ is $\pi(n-2)$ and they are composed of all the angles of the triangles in the partition, the number of these triangles is $n-2$. By the lemma, in each of these triangles, at least one side is a side of $P$. From this, it follows that two of the triangles in the partition have two sides that are sides of $P$.
Let $K L M$ be one of these triangles, with $K L$ and $L M$ being sides of $P$. A side $K M$ is adjacent to another triangle in the partition $K M N$. One of its sides (for definiteness, $K N$) is a side of $P$. Since the triangles in the partition are equal, the angle $NKM$ is equal to either the angle $LKM$ or the angle $KML$. In the first case, $KM$ is the bisector of the angle of the described polygon $P$ and therefore contains the center $I$ of the inscribed circle. In the second case, $K N \parallel L M$. Then $I$ lies on the common perpendicular to these segments and therefore is contained (by convexity) in the parallelogram $K L M N$, and thus in at least one of the triangles $K L M, K M N$.
Let $K' L' M'$ be another triangle in the partition, two sides of which are sides of $P$. Similarly, $I$ is contained either in this triangle or in an adjacent triangle in the partition. If $I$ is contained in at least one of the triangles $K L M, K' L' M'$, then they have a common side, and then $n=4$. Otherwise, the triangle $K M N$ is adjacent to both of these triangles and contains $I$. In this case, the side $M N$ is common with the triangle $K' L' M'$; we can set $M=M'$, $N=K'$. Reasoning as above, we get that $L M, K N, L' M$ are parallel to each other. But then the adjacent sides $L M$ and $M L'$ lie on the same line. Contradiction.
## Answer
$n=4$.
Send a comment
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
All integers from 1 to 100 are written in a string in an unknown order. With one question about any 50 numbers, you can find out the order of these 50 numbers relative to each other. What is the minimum number of questions needed to definitely find out the order of all 100 numbers?
#
|
To find the desired order $a_{1}, a_{2}, \ldots, a_{100}$ of numbers in a row, it is necessary that each pair $\left(a_{i}, a_{i+1}\right), i=1,2, \ldots, 99$, appears in at least one of the sets about which questions are asked; otherwise, for two sequences $a_{1}, \ldots, a_{i}, a_{i+1}, \ldots, a_{100}$ and $a_{1}, \ldots, a_{i+1}, a_{i}, a_{100}$, all answers will be the same.
We will prove that after any two questions, a situation may arise where at least three more questions are needed to cover all pairs of adjacent numbers (not yet covered).
Let $k_{1}, k_{2}, \ldots, k_{50}$ be the order of the numbers about which the first question is asked, and $l_{1}, l_{2}, \ldots, l_{50}$ be the order of the numbers about which the second question is asked. We will construct a set $a_{1}, a_{2}, \ldots, a_{100}$ for which we cannot, by asking two more questions, uniquely determine the order of the numbers. Consider the situation where all numbers mentioned in both the first and second questions are in the same positions in the answers.
As the desired set, we will take the set where $k_{i}, l_{i} \in \{a_{2i-1}, a_{i}\}, i=1,2, \ldots, 50$, and, moreover, in each quartet $\left(a_{4m-3}, a_{4m-2}, a_{4m-1}, a_{4m}\right)$, $m=1,2, \ldots, 25$, there were no comparisons of adjacent pairs of numbers from this quartet in the first two questions. We will show that such a set exists.
Let $X$ be the set of numbers that did not appear in the first two questions. The following cases are possible:
$k_{2m-1}=l_{2m-1}, k_{2m}=l_{2m}$,
$k_{2m-1}=l_{2m-1}, k_{2m} \neq l_{2m}$,
$k_{2m-1} \neq l_{2m-1}, k_{2m} \neq l_{2m}$,
$k_{2m-1} \neq l_{2m-1}, k_{2m}=l_{2m}$,
For these cases, we will construct quartets $\left(a_{4m-3}, a_{4m-2}, a_{4m-1}, a_{4m}\right)$ as follows: $\left(k_{2m-1}, *, *, k_{2m}\right), \left(k_{2m-1}, *, k_{2m}, l_{2m}\right), \left(k_{2m-1}, l_{2m-1}, k_{2m}, l_{2m}\right)$
$\left(k_{2m-1}, l_{2m-1}, *, k_{2m}\right)$, where * can be any number from the set $X$ that did not appear in the questions and in the construction of previous quartets.
Thus, it is shown that after two questions, a situation is possible (regardless of the asker's desire) where no pair $(a_{i}, a_{i+1})$ for $i$ not divisible by 4 is covered. Each of the 100 numbers is part of at least one uncovered pair, and therefore, must appear in at least one of the subsequent questions.
Suppose that in this situation, all uncovered pairs can be covered in two questions; then each of the 100 numbers must appear in exactly one of such questions. Considering quartets of the form $(a_{4i-3}, a_{4i-2}, a_{4i-1}, a_{4i})$, $i=1,2, \ldots, 25$, we note that if one number from such a quartet appears in a question, then the other three must also (otherwise, not all pairs of adjacent numbers in this quartet will be covered). But then the number of numbers in the set about which the question is asked must be divisible by 4. Since 50 is not divisible by 4, we have a contradiction. Therefore, it is impossible to determine the order of the numbers $1,2, \ldots, 100$ in a row with four questions.
We will show how to do this in five questions. The first question is about the set $M_{1}=\{1,2, \ldots, 50\}$, the second is about the set $M_{2}=\{51,52, \ldots, 100\}$. The set $M_{3}$ will consist of the 25 leftmost numbers of the set $M_{1}$ and the 25 leftmost numbers of the set $M_{2}$, and the set $M_{4}$ will consist of the 25 rightmost numbers of the set $M_{1}$ and the 25 rightmost numbers of the set $M_{2}$. The answer to the question about the set $M_{3}$ will clearly determine the numbers $a_{1}, a_{2}, \ldots, a_{25}$, and the answer to the question about the set $M_{4}$ will determine the numbers $a_{76}, a_{77}, \ldots, a_{100}$. The fifth question will determine the order of the remaining 50 numbers in the desired row.
## Answer
In five questions.
Submit a comment
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ionin Yu.i.
In each cell of an infinite sheet of graph paper, a number is written such that the sum of the numbers in any square, the sides of which lie along the grid lines, does not exceed one in absolute value.
a) Prove the existence of a number $c$ such that the sum of the numbers in any rectangle, the sides of which lie along the grid lines, does not exceed $c$; in other words, prove that the sums of the numbers in rectangles are bounded.
b) Prove that you can take $c=4$.
c) Improve this estimate - prove that the statement is true for $c=3$.
d) Construct an example showing that the statement is false for $c>3$.
|
Suppose in a certain rectangle with sides $a$ and $b (a < b)$. We construct four squares, each of which has three sides along some three sides of this rectangle $a \times b$; then the lines on which the fourth sides of these squares lie form a new rectangle with sides $2b - a$ and $|2a - b|$ (see Fig. 1 and 2; the case $b = 2a$ is, of course, impossible).
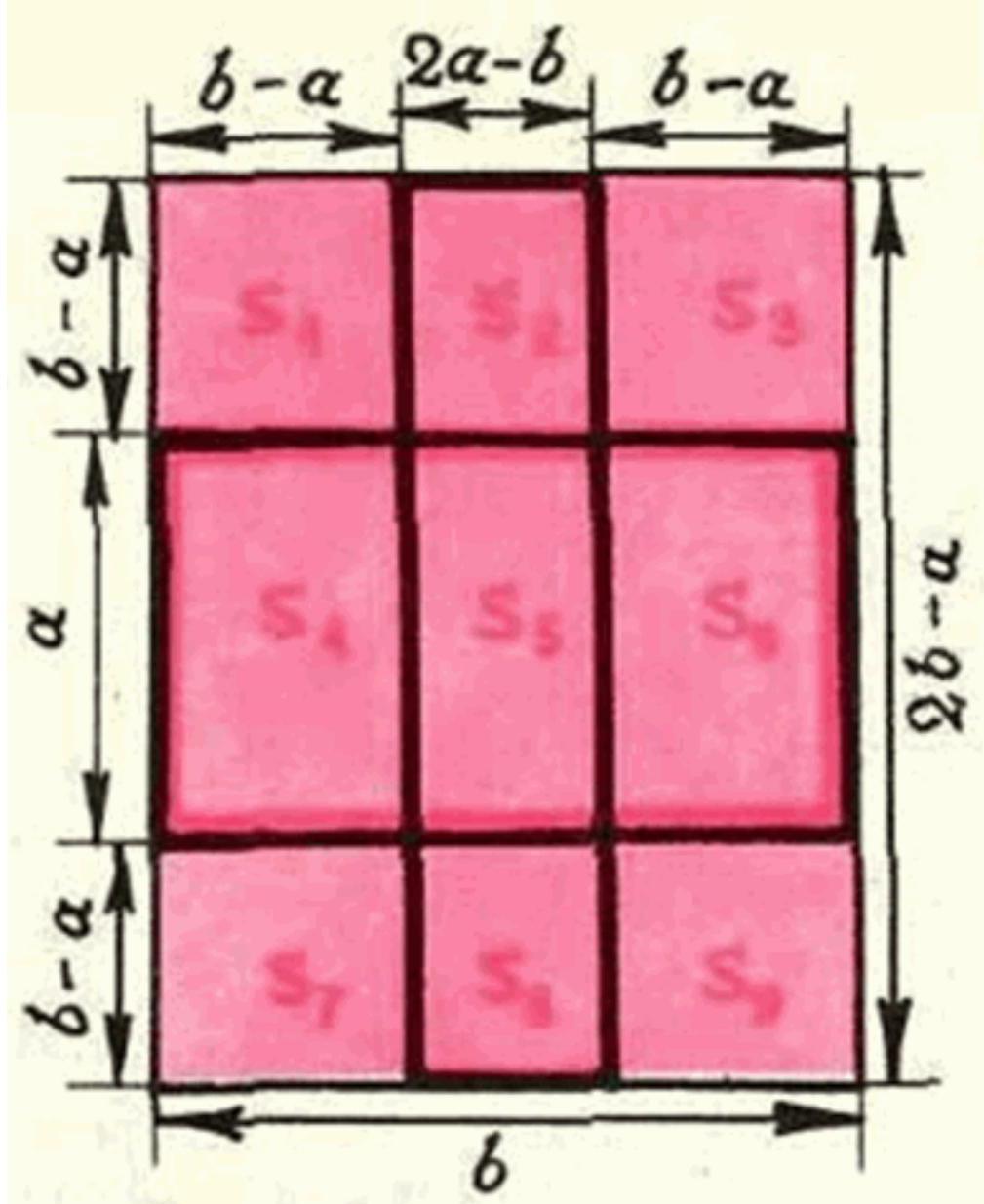
Fig. 1. $2a > b$.
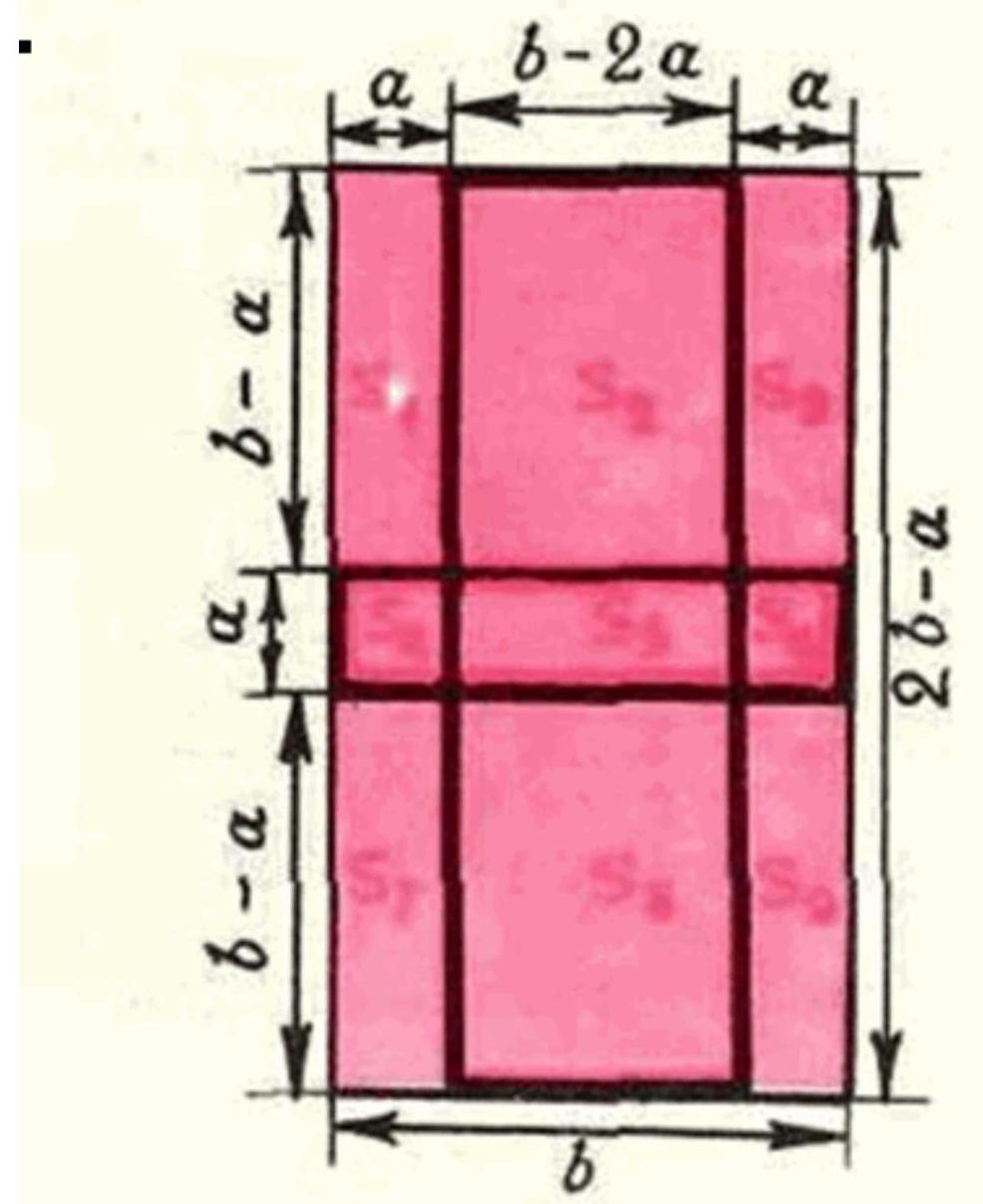
Fig. 2. $2a < b$.
If $2a > b$, then
$s_{5} = -s_{4} - s_{5} + (s_{4} + s_{5} + s_{6}) \leq -1 - 1 + 4 + \varepsilon \leq 2 + \varepsilon$
$s_{2} + s_{8} = (s_{1} + s_{2}) + (s_{2} + s_{3}) + (s_{7} + s_{8}) + (s_{8} + s_{9}) - (s_{1} + s_{2} + s_{3} + s_{4} + s_{5} + s_{6}) - (s_{4} + s_{5} + s_{6} + s_{7} + s_{8} + s_{9}) + 2(s_{4} + s_{5} + s_{6}) \geq 2 + 2 \varepsilon$
$s_{2} + s_{5} + s_{8} \geq 4 + 3 \varepsilon$
Thus, we have proved that if in the rectangle $a_{1} \times b_{1}$ the sum of the numbers in absolute value is greater than $4 + \varepsilon$, then in the new rectangle $a_{2} \times b_{2}$, where
$a_{2} = |2a_{1} - b_{1}|, b_{2} = 2b_{1} - a_{1}$, the sum of the numbers in absolute value is greater than $4 + 3 \varepsilon$. For the rectangle $a_{2} \times b_{2}$, we can construct a new rectangle $a_{3} \times b_{3}$ in the same way, in which the sum of the numbers will be greater than $4 + 3 \cdot 3 \varepsilon = 4 + 9 \varepsilon$, and so on - such a sequence of rectangles $a_{1} \times b_{1}, a_{2} \times b_{2}, \ldots, a_{n} \times b_{n}, \ldots$, that in the rectangle $a_{n} \times b_{n}$ the sum of the numbers in absolute value is greater than $4 + 3^{n-1} \varepsilon$.
We will prove that in this sequence all rectangles, starting from some, will belong to the second type, that is, for them
$b_{n} > 2a_{n}$. Indeed, first, it is easy to check that if $\frac{a_{n}}{b_{n}} < \frac{1}{2}$, then $\frac{1 - \frac{a_{n+1}}{1 - b_{n+1}}}{1 - \frac{a_{n}}{b_{n}}} = \frac{1 - \frac{2a_{n} - b_{n}}{2b_{n} - a_{n}}}{1 - \frac{a_{n}}{b_{n}}} = \frac{3b_{n}}{2b_{n} - a_{n}} > \frac{3b_{n}}{2b_{n} - \frac{b_{n}}{2}} = 2$; thus, the quantity $1 - \frac{a_{n}}{b_{n}}$ increases by at least a factor of two when transitioning from $n$ to $n+1$ until we reach a rectangle with $\frac{a_{n}}{b_{n}} \geq \frac{1}{2}$. Therefore, no matter how small $1 - \frac{a_{1}}{b_{1}}$ is, after several operations, we will always reach a rectangle of the second type, and further in our sequence, only such rectangles will appear.
Therefore, we can assume that already $\frac{a_{1}}{b_{1}} < \frac{1}{2}$; if $0 \leq k \leq \frac{1}{2}$, then $0 < f(k) < \frac{1}{2}$, and $f(f(k)) = k$, that is, the function $f$ on the interval $0 < k < \frac{1}{2}$ coincides with its inverse function, and its graph is symmetric with respect to the bisector of the angle between the coordinate axes.
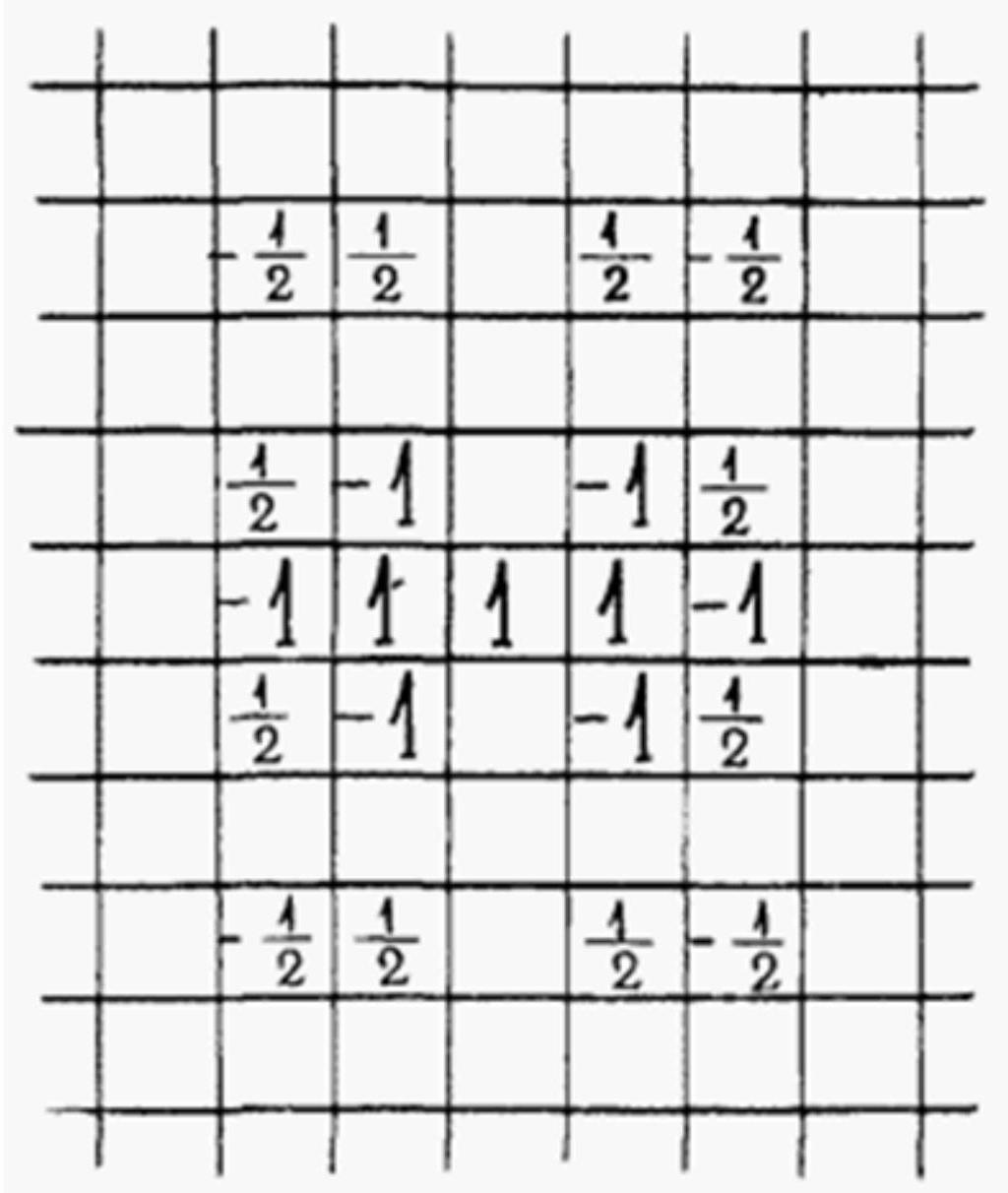
Fig. 4. All unfilled cells contain zeros.
g) Fig. 4 shows an example where the sum of the numbers in some rectangle is 3. Thus, for $c < 3$, the statement of the problem is false.
f) The solution to this problem is unknown. Moreover, it is quite plausible that the exact estimate $c = 4$. However, examples showing that $c$ can be greater than 3 are also unknown.
|
3
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Zaslavsky A.A.
In a single-round football tournament, $n>4$ teams played. For a win, 3 points were awarded, for a draw 1, and for a loss 0. It turned out that all teams scored the same number of points.
a) Prove that there will be four teams with the same number of wins, the same number of draws, and the same number of losses.
b) For what smallest $n$ might there not be five such teams?
|
a) If two teams have scored the same number of points, then the difference between the number of draws they have is a multiple of 3.
The number of draws a team has is between 0 and $n-1$. Therefore, the number of groups, each of which consists of teams with the same number of wins, draws, and losses, does not exceed $k=\left[\frac{n+2}{3}\right]$. This means there will be a group consisting of at least three teams.
Suppose all groups consist of three or fewer teams. Then there are exactly $k$ groups (otherwise, $n4$.
## Answer
b) For $n=10$.
|
10
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Chebotarev A.S.
On a plane, there is a circle. What is the minimum number of lines that need to be drawn so that, by symmetrically reflecting the given circle relative to these lines (in any order a finite number of times), it can cover any given point on the plane?
|
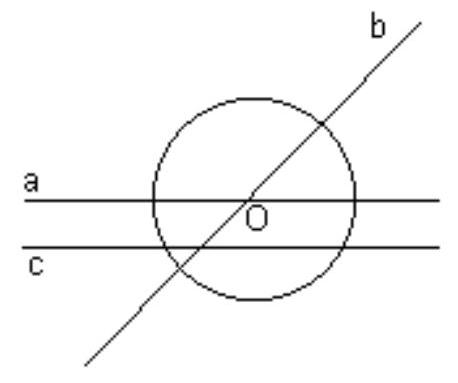
1) We will prove that three lines are sufficient. Let the horizontal line $a$ and line $b$, forming a $45^{\circ}$ angle with line $a$, contain the center $O$ of the circle, and let line $c$ be parallel to $a$ and be at a distance of $0.5R$ from it, where $R$ is the radius of the given circle (see figure).
The composition of axial symmetries with axes $a$ and $c$ is a parallel translation by a distance of $R$ (up or down, depending on the order of the symmetries). The composition of axial symmetries with axes $a$ and $b$ is a rotation around the center $O$ by an angle of $90^{\circ}$ (in either direction, depending on the order of the symmetries).
We will show that any point on the plane can be covered using the obtained transformations. For this, consider a Cartesian coordinate system with the origin at point $O$ and the $x$-axis coinciding with line $a$ (the $y$-axis passes through point $O$ perpendicular to $a$), where $R$ is the length of the unit segment. Let the point $M(x; y)$ need to be covered by the circle. The integers closest to $x$ and $y$ are denoted by $m$ and $n$ respectively, then $|x-m| \leq 0.5$ and $|y-n| \leq 0.5$.
If $m > 0$, then perform $m$ parallel translations upwards, then rotate around point $O$ by $-90^{\circ}$ and perform $n$ parallel translations upwards or downwards, depending on the sign of the number $n$. Similarly, if $m < 0$, then perform $|m|$ parallel translations downwards, then rotate around point $O$ by $-90^{\circ}$ and perform $n$ parallel translations upwards or downwards, depending on the sign of the number $n$. As a result of the performed transformations, the center of the circle will become point $O'(m; n)$, and
$$
O'M = \sqrt{(x-m)^2 + (y-n)^2} \leq \frac{\sqrt{2}}{2} < 1
$$
Therefore, point $M$ has been covered.
2) We will prove that two lines are insufficient. If the chosen lines are parallel, then the orthogonal projections of the circle onto these lines do not change when any number of reflections are performed. If the chosen lines intersect, then the distance from the point of intersection to the center of the circle does not change when any number of reflections are performed.
## Answer
3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ostrovsky $M$.
A number from 1 to 144 is guessed. You are allowed to select one subset of the set of numbers from 1 to 144 and ask whether the guessed number belongs to it. You have to pay 2 rubles for a "yes" answer and 1 ruble for a "no" answer. What is the minimum amount of money needed to surely guess the number?
|
Let $a_{1}=2, a_{2}=3, a_{i}=a_{i-} 1+a_{i-} 2$ for $i \geq 3$. Then $a 10=144$. We will prove by induction that among not less than $a_{i}$ numbers, the guessed number cannot be found by paying less than $i+1$ rubles.
For $i=1$ and $i=2$, this is true.
Suppose there are not less than $a_{i}$ numbers. Then either the set $M$ of numbers highlighted in the first question contains not less than $a_{i-} 2$ numbers (first case), or the set of numbers not in $M$ contains not less than $a_{i-1} 1$ numbers (second case). In the first case, if the guessed number is in $M$, then 2 rubles need to be paid for the answer, and, by the induction hypothesis, at least ( $i-2$ )+1 rubles are needed to guess the number, i.e., a total of at least $i+1$ rubles.
In the second case, if the guessed number is not in $M$, then 1 ruble needs to be paid for the answer and at least ( $i$ 1)+1 ruble for guessing the number, i.e., again a total of at least $i+1$ rubles.
The algorithm for guessing the number is clear from the previous reasoning: at each step, the set $M$ of $a_{i}$ numbers containing the guessed number should be divided into sets $M_{1}$ of $a_{i-} 2$ numbers and $M_{2}$ of $a_{i-} 1$ numbers, and ask whether the number belongs to the set $M_{1}$.
## Answer
11 rubles.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tamarkin D:
In the class, there are 16 students. Every month, the teacher divides the class into two groups.
What is the minimum number of months that must pass so that every two students end up in different groups at some point?
|
Example. The figure shows how to divide a class into two groups so that any two students are in different groups in at least one of the four months. Each student corresponds to a column in the table, and each month corresponds to a row. A zero in a cell of the table means that the student is in the first group, and a one means that the student is in the second group. Since there are no identical columns, any two students are in different groups at least one month out of the four.
| | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ | $\mathbf{7}$ | $\mathbf{8}$ | $\mathbf{9}$ | $\mathbf{1 0}$ | $\mathbf{1 1}$ | $\mathbf{1 2}$ | $\mathbf{1 3}$ | $\mathbf{1 4}$ | $\mathbf{1 5}$ | $\mathbf{1 6}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $\mathbf{1}$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| $\mathbf{2}$ | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| $\mathbf{3}$ | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| $\mathbf{4}$ | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Evaluation. We will prove that it is impossible to meet the condition in three months. We will construct a similar $3 \times 16$ table. In a column, zeros and ones can be arranged in only 8 ways, so there will be two identical columns. The students corresponding to these columns will be in the same group for all three months.
## Answer
4 months.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tokaeva I.
Let $F_{1}, F_{2}, F_{3}, \ldots$ be a sequence of convex quadrilaterals, where $F_{k+1}$ (for $k=1,2,3, \ldots$) is obtained by cutting $F_{k}$ along a diagonal, flipping one of the parts, and gluing it back along the cut line to the other part. What is the maximum number of different quadrilaterals that this sequence can contain? (Different polygons are those that cannot be made to coincide by a movement.)
|
Let $ABCD$ be the original quadrilateral $F_{1}$. We can assume that each time the half of the quadrilateral containing side $CD$ is flipped, while side $AB$ remains stationary. In this process, the sum of angle $A$ and the opposite angle does not change. Additionally, the set of side lengths does not change. However, the three lengths (sides other than $AB$) can be ordered in only six ways.
We will prove that if two resulting quadrilaterals $ABKL$ and $ABMN$ have the same ordered side lengths ($BK = BM$, $KL = MN$, $LA = NA$), then the quadrilaterals are equal. It is sufficient to prove the equality of the diagonals $AK$ and $AM$. Assuming, for example, that $AK > AM$, we get $\angle ABK > \angle ABM$, $\angle ALK > \angle ANM$, which contradicts the equality of the sums $\angle ABK + \angle ALK$ and $\angle ABM + \angle ANM$.
Six different quadrilaterals will result from any quadrilateral where all sides are different, the sums of opposite angles are also different, and the quadrilateral remains convex and does not degenerate into a triangle during transformations. Only quadrilaterals with the reverse order of sides might be suspected of being equal, but they are not equal either, since flipping one of them will not align the sums of opposite angles. The highlighted condition is satisfied, for example, for quadrilaterals whose area is greater than half the product of the two longest sides: this inequality is clearly not true for non-convex and degenerate quadrilaterals. A specific example: a right trapezoid with bases 3 and 6 and height 4.
## Answer
6 quadrilaterals.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tokarev S.I.
A set of five-digit numbers $\left\{N_{1}, N_{k}\right\}$ is such that any five-digit number, all digits of which are in non-decreasing order, coincides in at least one digit with at least one of the numbers $N_{1}, N_{k}$. Find the smallest possible value of $k$.
|
A set with the specified properties cannot consist of a single number. Indeed, for each $N=\overline{a b c d e}$, there is a number $G=\overline{\boldsymbol{g g 9 g g}}$ that differs from $N$ in all digits, where $g$ is a non-zero digit different from $a, b, c, d, e$. We will show that the numbers $N_{1}=13579$ and $N_{2}=12468$ form a set that satisfies the conditions of the problem.
Let $A=\overline{a_{1} a_{2} a_{3} a_{4} a_{5}}$ be an arbitrary number for which the digits satisfy the inequalities $1 \leq a_{1} \leq a_{2} \leq a_{3} \leq a_{4} \leq a_{5}$. Then, if $A$ does not match $N_{1}$ or $N_{2}$ in the units place, $a_{5} \leq 7$ and, consequently, $a_{4} \leq 7$; if there are no matches in the tens place either, then $a_{4} \leq 5$ and $a_{3} \leq 5$.
If, in addition, there are no matches in the hundreds place, then $a_{3} \leq 3$, from which it follows that $a_{2} \leq 3$; assuming further that $a_{2} \neq 2$ and $a_{2} \neq 3$, we arrive at the equality $a_{1}=1$, indicating that $A$ matches $N_{1}$ (and $N_{2}$) in the most significant digit.
## Answer
2.00
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
55 boxers participated in a tournament with a "loser leaves" system. The fights proceeded sequentially. It is known that in each match, the number of previous victories of the participants differed by no more than 1. What is the maximum number of fights the tournament winner could have conducted?
|
We will prove by induction that
a) if the winner has conducted no less than $n$ fights, then the number of participants is no less than $u_{n+2}$;
b) there exists a tournament with $u_{n+2}$ participants, the winner of which has conducted $n$ fights ( $u_{k}-$ Fibonacci numbers).
Base case $\left(n=1, u_{3}=2\right)$ is obvious.
Inductive step. a) Suppose the winner $A$ won the last fight against boxer $B$. The remaining fights effectively split into two tournaments: one won by $A$, and the other by $B$. In the first tournament, the winner $A$ conducted no less than $n-1$ fights, so the number of participants is no less than $u_{n+1}$. In the second tournament, the winner $B$ conducted no less than $n-2$ fights, so the number of participants is no less than $u_{n}$. Therefore, in the original tournament, the number of participants is no less than $u_{n+1} + u_{n} = u_{n+2}$.
b) It is sufficient to combine in the final fight the winner of a tournament with $u_{n+1}$ participants, who won $n-1$ fights, and the winner of a tournament with $u_{n}$ participants, who won $n-2$ fights.
Since $55 = u_{10}$, it follows from this that the answer is.
## Answer
8 fights.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A.K.
On the plane, there is an open non-intersecting broken line with 31 segments (adjacent segments do not lie on the same straight line). Through each segment, a line containing this segment was drawn. As a result, 31 lines were obtained, some of which may have coincided. What is the smallest number of different lines that could have resulted?
#
|
Evaluation. Except for the ends, the broken line has 30 vertices, and each is the intersection of two lines. If there are no more than eight lines, then there are no more than $7 \cdot 8: 2=28$ intersection points - a contradiction.
Example - in the figure.
## Answer
9 lines.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Gladkova E.B.
Computers $1,2,3, \ldots, 100$ are connected in a ring (the first with the second, the second with the third, ..., the hundredth with the first). Hackers have prepared 100 viruses, numbered them, and at different times, in a random order, they launch each virus on the computer with the same number. If a virus lands on an uninfected computer, it infects it and moves to the next computer in the chain with a higher number until it reaches an already infected computer (from computer 100, the virus moves to computer 1). Then the virus dies, and this computer is restored. No two viruses land on the same computer at the same time. How many computers will be infected as a result of the attack by these 100 viruses?
|
Let's prove several statements.
1) Every computer is infected by viruses at least twice.
Consider, for example, computer 1. If the first virus to infect it came from computer 100, then it will also be infected by virus 1. If the first virus to infect computer 1 is virus 1, then the virus that first infected computer 100 (which could be the same virus 1, having circled the entire network) will definitely move to computer 1.
2) All viruses will die.
Indeed, each computer is infected by at least two viruses, and the second virus dies by the condition. Therefore, at least one virus will die on each computer. Since there are as many viruses as there are computers, all viruses will die.
3) No computer can be infected by three viruses.
Consider the computer on which the last of all 100 viruses died (let's say it's computer 1; if several died simultaneously, consider any one of them). Then this virus arrived on it as the second one (otherwise, more than one virus would have died on it), and no more viruses arrived on it afterward. Thus, exactly two viruses arrived on computer 1. But then exactly two viruses also arrived on computer 2: one "native" and one from computer 1. Then exactly two viruses also arrived on computer 3. And so on.
Thus, each computer is infected exactly twice, and after that, the computer recovers. Therefore, after all viruses die, all computers will work normally!
## Answer
There will be no infected computers.
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Pairing and grouping; bijections] Proof by contradiction
What is the smallest number of weights in a set that can be divided into 3, 4, and 5 equal-mass piles?
|
Answer: 9. First, let's prove that the set cannot contain fewer than nine weights. Suppose this is not the case, that is, there are no more than eight. Let $60 m$ be the total mass of all the weights in the set. First, note that the set cannot contain weights with a mass greater than 12 t (since the set can be divided into five piles, each with a mass of $12 m$).
Therefore, each of the four piles with a mass of $15 m$ must contain at least two weights. Therefore, there are at least eight weights in total. This means there are exactly eight weights, and each of the four piles with a mass of 15 m consists of exactly two weights. When we distribute these eight weights into five piles, there will be at least two piles with only one weight each. Therefore, the set must contain at least two weights with a mass of $12 m$. We will prove that the set contains at least six weights with a mass of the form $3 k m$, where the number $k$ is a natural number. First, assume that the set contains at least three weights with a mass of $12 m$. Then it contains at least three weights with a mass of $3 m$, and therefore at least six weights with a mass of the form $3 \mathrm{~km}$. Now consider the case where the set contains exactly two weights with a mass of $12 m$. Then the set contains two weights with a mass of $3 m$. Therefore, the masses of the weights lying in the same piles as the weights with a mass of $3 m$ when divided into five piles are $9 m$. Therefore, the set contains at least six weights with a mass of the form $3 \mathrm{~km}$. Thus, in any case, the set contains at least six weights with a mass of the form $3 \mathrm{~km}$, where the number $k$ is a natural number. Then, when dividing into three piles, one of the piles must consist only of weights of this form, and therefore its mass cannot be $20 \mathrm{~m}$. It remains to prove that there exists a set of nine weights. For example, a set of weights with masses $3,4,5,6,6,7,8,9,12$ grams fits. We leave the verification that this set can be divided into 3, 4, and 5 piles of equal mass as an exercise for the reader.
|
9
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
|
Rabbits are sawing a log. They made 10 cuts. How many chunks did they get?
#
|
Into how many parts is a log divided by the first cut? How does the number of pieces change after each subsequent cut?
## Solution
The number of chunks is always one more than the number of cuts, since the first cut divides the log into two parts, and each subsequent cut adds one more chunk. Answer: 11 chunks.
## Answer
11 chunks.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Rabbits are sawing a log again, but now both ends of the log are secured. Ten middle chunks have fallen, while the two at the ends remain secured. How many cuts did the rabbits make?
#
|
How many logs did the rabbits get?
## Solution
The rabbits got 12 logs - 10 fallen and 2 secured. Therefore, there were 11 cuts.
## Answer
11 cuts.
## Problem
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Cutting (other).]
What is the maximum number of pieces into which a round pancake can be divided using three straight cuts?
#
|
Recall problem 11.
## Solution
If from three lines each pair intersects inside the pancake, it will result in 7 pieces (see Fig. 11.4). If, however, any two of these lines are parallel or intersect outside the pancake, there will be fewer pieces.
## Answer
7 pieces.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10 guests came to visit and each left a pair of galoshes in the hallway. All pairs of galoshes are of different sizes. The guests began to leave one by one, putting on any pair of galoshes that they could fit into (i.e., each guest could put on a pair of galoshes not smaller than their own). At some point, it was discovered that none of the remaining guests could find a pair of galoshes to leave. What is the maximum number of guests that could have remained?
|
If there are more than five guests left, then the guest with the smallest size of galoshes among the remaining guests can put on the largest of the remaining galoshes.
## Solution
Let's number the guests and their pairs of galoshes from 1 to 10 in ascending order of the size of the galoshes. Suppose there are 6 guests left (and accordingly 6 pairs of galoshes). Then the smallest number of the remaining guests is no more than 5, and the largest number of the remaining pairs of galoshes is no less than 6, so the guest with the smallest number can put on the galoshes with the largest number. Contradiction. On the other hand, if guests with numbers $1,2,3,4,5$ left sequentially and put on galoshes with numbers $10,9,8,7,6$ respectively, then none of the remaining five guests will be able to put on any of the remaining pairs of galoshes.
## Answer
5.00
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left.\quad \begin{array}{ll}{\left[\begin{array}{l}\text { Principles of divisibility by 3 and 9 } \\ \text { [Examples and counterexamples. Constructions] }\end{array}\right]}\end{array}\right]$
Write the number 2013 several times in a row so that the resulting number is divisible by 9.
|
The number 201320132013 is divisible by 9, since the sum of its digits is equal to $(2+0+1+3) \cdot 3=18$.
## Answer
Given a sheet of graph paper. Each node of the grid is marked with some letter. What is the smallest number of different letters needed to mark these nodes so that on any segment (going along the sides of the cells - ed.), connecting two nodes marked with the same letter, there is at least one node marked with one of the other letters?
## Solution
Answer: two letters. These letters should be arranged in a checkerboard pattern.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Chuk and Gek were decorating the Christmas tree with their mother. To prevent them from fighting, their mother gave each of them the same number of branches and the same number of ornaments. Chuk tried to hang one ornament on each branch, but he was short of one branch. Gek tried to hang two ornaments on each branch, but one branch was left empty. How many branches and how many ornaments do you think their mother gave to the boys?
|
Try to do as Chuk did - hang one toy on each branch.
## Solution
Let's try to do as Chuk did — hang one toy on each branch, then one toy will be left over. Now, let's take two toys — one that is left over, and another one from one of the branches. If we now hang these toys as the second ones on the branches that still have toys from the first time, then on two branches there will be toys and one branch will remain empty. If there were any other branches besides these three, then on these "extra" branches there would be one toy each, which contradicts the condition. Thus, there were 3 branches, and accordingly, 4 toys.
## Answer
3 branches, 4 toys.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The scent from a blooming lily-of-the-valley bush spreads in a radius of 20 m around it. How many blooming lily-of-the-valley bushes need to be planted along a straight 400-meter alley so that every point along it smells of lily-of-the-valley
#
|
Notice that to meet the conditions of the problem, the distance between adjacent lilies of the valley should not exceed $40 \mathrm{M}$.
## Solution
Let's mentally move the leftmost 20 m of the alley to the right end. Then we will have segments of the alley that are 40 m long, and to the right of each segment, a lily of the valley will grow. Thus, the number of lilies of the valley should be the same as the number of 40 m segments that can fit inside the alley. Since 10 such segments can fit, 10 bushes of lilies of the valley need to be planted.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Combinatorics (miscellaneous). ] [Principle of the extreme (miscellaneous) ]
How many ways are there to rearrange the numbers from 1 to 100 such that adjacent numbers differ by no more than 1?
#
|
Where can the number 1 be placed?
## Solution
Next to the number 1, only the number 2 can stand, so 1 must be at the edge. Suppose 1 is at the beginning. Then the next number is 2, the next is 3 (no other numbers can be next to 2), the next is 4, and so on. We get the arrangement $1, 2, \ldots, 99, 100$.
If 1 is at the end, then similarly, the arrangement is uniquely restored as 100, 99, ..., 2, 1.
## Answer
In two ways.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Case Analysis ] [ Proof by Contradiction ]
In the cells of a $3 \times 3$ table, numbers are arranged such that the sum of the numbers in each column and each row is zero. What is the smallest number of non-zero numbers that can be in this table, given that this number is odd?
#
|
## Example.
| 0 | -1 | 1 |
| :---: | :---: | :---: |
| -1 | 2 | -1 |
| 1 | -1 | 0 |
Evaluation. We will prove that it is impossible to use fewer non-zero numbers.
If the table contains exactly one non-zero number, then the sum of the numbers in the row containing this number is not zero. Suppose the table contains exactly three non-zero numbers. If all of them are in the same row, then the sum of the numbers in any column is not zero. If not all of them are in the same row, then in some row there is exactly one non-zero number, and the sum of the numbers in this row is not zero.
Suppose the table contains exactly five non-zero numbers. Then there are four zeros in the table, which means that some two zeros are in the same row. Since the sum of the numbers in this row is zero, all the numbers in this row are zeros.
It remains to note that in the column where the remaining zero is located, there are exactly two zeros, which is impossible.
## Answer
7 numbers.
A five-digit number is called irreducible if it cannot be factored into the product of two three-digit numbers.
What is the maximum number of consecutive irreducible five-digit numbers?
## Solution
Note that all numbers divisible by 100 are reducible. Therefore, more than 99 irreducible numbers in a row is impossible. On the other hand, between the numbers $100 \cdot 100$ and $100 \cdot 101$, all numbers are reducible, and there are exactly 99 of them.
## Answer
99.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Pe
In the country of Distant, a province is called large if more than $7 \%$ of the country's population lives in it. It is known that for each large province, there are two provinces with a smaller population such that their combined population is greater than that of this large province. What is the smallest number of provinces that can be in the country of Distant?
|
We will order the provinces by increasing population. The first and second provinces are not large, as for each of them, there will not be two provinces with a smaller population. In the third province, less than $14\%$ of the population lives, since in both provinces with a smaller population, the total is no more than $7\%+7\%$ $=14\%$. In the fourth province, less than $21\%$ of the population lives, as the population of any two smaller provinces is less than $7\%+14\%$ $=21\%$. For the same reasons, in the fifth province, less than $14\%+21\%$ $=35\%$ of the population lives. Therefore, in the first five provinces, less than $7\%+7\%+14\%+21\%+35\%$ $=84\%$ of the population lives. Consequently, there are more than 5 provinces.
Example of population distribution across six provinces: $7\%$, $7\%$, $11\%$, $16\%$, $25\%$, $34\%$ of the population.
## Answer
6 provinces.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Chessboards and chess pieces ] [ Examples and counterexamples. Constructions ]
Author: S. Preskova
Under one of the cells of an $8 \times 8$ board, a treasure is buried. Under each of the other cells, there is a sign indicating the minimum number of steps required to reach the treasure from that cell (one step allows moving to an adjacent cell by side). What is the minimum number of cells that need to be dug up to definitely retrieve the treasure?
|
Let's dig up the corner cell $U$. Suppose there is a sign there. All cells at the specified distance from $U$ form a diagonal perpendicular to the main diagonal drawn from $U$. Let's dig up the corner cell $W$ on the same side as $U$. If there is also a sign there, then another diagonal perpendicular to the first one is formed. The diagonals intersect at one cell, where the treasure is buried.
Two diggings may not be enough. For example, suppose we were unlucky and found a sign with the number 1 on the first try. Then the treasure is in the adjacent cell, but there are at least two such cells.
## Answer
3 cells.
Send a comment
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a company of 10 people, 14 pairwise arguments have occurred. Prove that it is still possible to form a group of three friends.
#
|
The total number of ways to choose a company of three people is $C_{10}^{3}=120$. Each quarrel destroys no more than eight such companies, so the number of destroyed companies is no more than $8 \cdot 14=112$. Therefore, at least 8 friendly companies remain.
|
8
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Laiko 0.
Around a round table, there is a company of thirty people. Each of them is either a fool or smart. Everyone sitting is asked: Is your right neighbor smart or a fool? In response, a smart person tells the truth, while a fool can say either the truth or a lie. It is known that the number of fools does not exceed $F$. For what maximum value of $F$ can one always, knowing these answers, point to a smart person in this company?
|
When $F=8$. If $F=0$, then one can point to any person sitting at the table. Let now $F \neq 0$. We divide all those sitting at the table into non-empty groups of consecutive smart and consecutive foolish people; the number of these groups is denoted by $2k$ ($k$ groups of smart people and $k$ groups of foolish people). The number of people in the $i$-th group of smart people is denoted by $w_i$, and the number of people in the $i$-th group of foolish people is denoted by $f_i$ ($1 \leq i \leq k$). Then $f_1 + f_2 + \cdots + f_k \leq F$. Consider the sequence of consecutive answers "smart" and the last person $x$ who is referred to as such. A group of $w_i$ smart people gives such a sequence of length not less than $w_i - 1$, and in this case, $x$ is indeed smart. If, however, $x$ is a fool and is in the $i$-th group of fools, then the length of such a sequence is no more than $f_i - 1$. Therefore, if $\max_i w_i > \max_i f_i$, then one can assert that the last person named smart in the longest sequence of answers "smart" is indeed smart. Since $\max_i w_i \geq \frac{30 - (f_1 + \cdots + f_k)}{k} \geq \frac{30 - F'}{k}$,
$$
\max_i f_i \leq (f_1 + \cdots + f_k) - k + 1 \leq F - k + 1,
$$
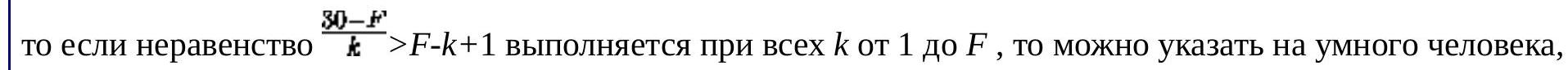
sitting at the table. This inequality is equivalent to:
$$
k^2 - (F + 1)k + 30 - F > 0
$$
It holds for all $k$ if $D = (F + 1)^2 + 4(F - 30) < 0$, i.e., when $F < -3 + \sqrt{128} < -3 + 12 = 9$. Thus, when $F \leq 8$, one can identify a smart person based on the given answers. When $F = 9$, this is not always possible. Indeed, consider a company sitting at the table as shown in Figure 104 (the answers are given next to the arrows: s - smart, f - fool; fools are represented by shaded circles). We will rotate this picture around the center by angles of $60^\circ, 120^\circ, 180^\circ, 240^\circ$, and finally $300^\circ$ clockwise. In this case, as one can easily verify, any place can be occupied by either a smart person or a fool, and the sequence of answers remains the same. Therefore, in such a company, it is impossible to identify a smart person based on the given answers.
## Answer
When $F=8$.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Fomin d:
Consider a set of weights, each weighing an integer number of grams, and the total weight of all weights is 200 grams. Such a set is called correct if any body with a weight expressed as an integer number of grams from 1 to 200 can be balanced by some number of weights from the set, and in a unique way (the body is placed on one pan of the scales, the weights - on the other; two balancing methods that differ only by the replacement of some weights with others of the same weight are considered the same).
a) Provide an example of a correct set where not all weights are one gram each.
b) How many different correct sets exist?
(Two sets are different if some weight participates in these sets a different number of times.)
|
The correct set should correspond to the factorization of the number 201 (see the solution of problem $\underline{98056}$), and it only factors into two factors: $201=3 \cdot 67$.
## Answer
a) Two weights of 67 g and 66 weights of 1 g or 66 weights of 3 g and two of 1 g.
b) 3 sets.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Fomin D:
Consider a set of weights, each weighing an integer number of grams, and the total weight of all weights is 500 grams. Such a set is called correct if any body with a weight expressed as an integer number of grams from 1 to 500 can be balanced by some number of weights from the set, and in a unique way (the body is placed on one pan of the scales, the weights - on the other; two balancing methods that differ only by the replacement of some weights with others of the same weight are considered the same).
a) Provide an example of a correct set where not all weights are one gram each.
b) How many different correct sets exist?
(Two sets are different if some weight participates in these sets a different number of times.)
|
Let the largest weight of a weight in some correct set be $M$ (grams). This means that any smaller weight can be balanced by smaller weights. Let the weight of all smaller weights be $m$. Clearly, $m \geq$ $M-1$. But if $m \geq M$, then we have two ways to balance the weight $M+r$, where $r$ is the remainder of the division of $m$ by $M$. Therefore, $m=M-1$.
Let there be $k$ weights of the maximum weight. Then the total weight of all weights $k M+m=500$, so 501 is divisible by $M$. By determining $M$, we can determine the weight of the second heaviest weight. Repeating the previous reasoning shows that it must be a divisor of $M$. But 501 has exactly two divisors other than 1 and 501: 3 and 167, each of which is a prime number. Therefore, there are exactly two correct sets, not counting the trivial set of 500 weights of 1 g: two weights of 167 g and 166 weights
of 1 g; 166 weights of 3 g and two weights of 1 g.
## Answer
a) Two weights of 167 g and 166 weights of 1 g or 166 weights of 3 g and two of 1 g.
b) 3 sets.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Rubanov I.S. }}$
Microcalculator MK-97 can perform only three operations on numbers stored in memory:
1) check if two selected numbers are equal,
2) add selected numbers,
3) find the roots of the equation $x^{2}+a x+b=0$ for selected numbers $a$ and $b$, or display a message if there are no roots.
The results of all actions are stored in memory. Initially, the memory contains a single number $x$. How can one use the MK-97 to determine if this number is equal to one?
|
By adding $x$ to itself, we get $2x$. We compare $x$ and $2x$. If they are equal, then $x=0$. Otherwise, we find the roots of the equation $y^{2}+2xy+x=0$. The discriminant of this equation is $4(x^{2}-x)$, so the roots are equal if and only if $x=1$.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11
The game board has the shape of a rhombus with an angle of $60^{\circ}$. Each side of the rhombus is divided into nine parts. Lines are drawn through the division points, parallel to the sides and the smaller diagonal of the rhombus, dividing the board into triangular cells. If a chip is placed on a certain cell, three lines are drawn through this cell, parallel to the sides and the smaller diagonal of the rhombus. The cells they intersect will be considered as being captured by the chip. What is the minimum number of chips needed to capture all the cells of the board?
|
Let's replace the board with an equivalent $9 \times 9$ square board, where diagonals of the same direction are drawn in all cells (see Fig. 1).
Six chips are sufficient to cover all cells (see Fig. 1).
Suppose there are only five chips. Consider one of the columns where no chip is placed. In this column, there are at least four squares that are not covered horizontally. These correspond to eight cells (see Fig. 2), none of which can be covered by a single chip diagonally.
Thus, at least three cells will not be covered by any chip.
## Answer
6 chips.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
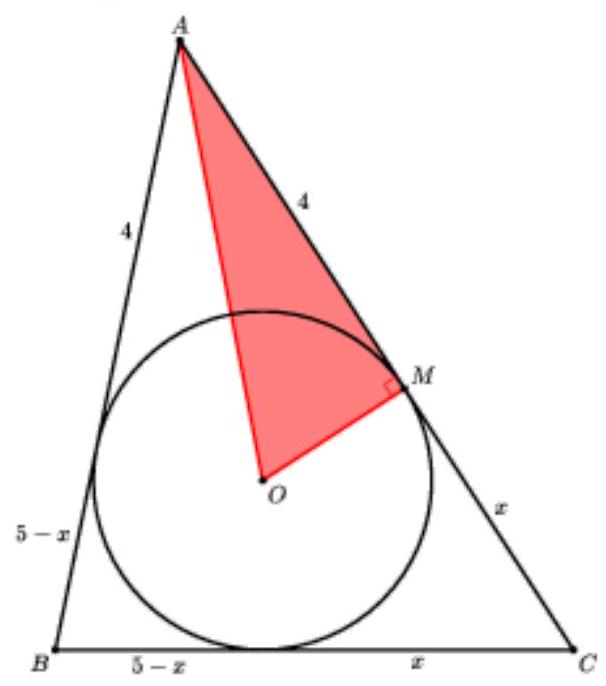
8,9 The area of a triangle is $6 \sqrt{6}$, its perimeter is 18, and the distance from the center of the inscribed circle to one of the vertices is $\frac{2 \sqrt{42}}{3}$. Find the smallest side of the triangle.
|
If the inscribed circle touches the side $A C$ of triangle $A B C$ at point $M$, and $p$ is the semiperimeter of the triangle, then $A M=p-B C$. Use this equality, and then apply the Law of Cosines.
## Solution
Let $O$ be the center of the circle inscribed in the given triangle $A B C$, $r$ its radius, $S=6 \sqrt{6}$ the area, $2 p=$ 18 the perimeter, and $M$ the point of tangency with side $A C$.
Since $S=p \cdot r$, then
$$
r=\frac{S}{p}=\frac{12 \sqrt{6}}{9}=\frac{2 \sqrt{6}}{3}
$$
From the right triangle $AOM$, we find that
$$
A M=\sqrt{A O^{2}-O M^{2}}=\sqrt{\left(\frac{2 \sqrt{42}}{3}\right)^{2}-\left(\frac{2 \sqrt{6}}{3}\right)^{2}}=\frac{2}{3} \cdot \sqrt{42-6}=4
$$
From the equality $A M=p-B C$, we find that $B C=9-4=5$. Let $C M=x$. From the equality $C M=p-A B$, we find that $A B=p-C M=9-x$.
By Heron's formula
$$
S=\sqrt{p(p-B C)(p-A C)(p-A B)} \text {, or } 6 \sqrt{6}=\sqrt{9 \cdot 4 \cdot(5-x) \cdot x} \text {. }
$$
From this equation, we find that $x=2$ or $x=3$. In the first case, $A B=7, A C=6$. In the second case, $A B=6, A C=7$. Therefore, in each of these cases, the side $B C=5$ is the smallest.
Answer
5. Send a comment
Problem
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Fon-err-Flaass problem: }}$
A square board is divided by a grid of horizontal and vertical lines into $n^{2}$ unit squares. For what largest $n$ can one mark $n$ cells so that every rectangle of area at least $n$ with sides along the grid lines contains at least one marked cell?
|
Evaluation. It is clear that if $n$ cells are marked in such a way that the condition of the problem is satisfied, then in each row and each column there is exactly one marked cell. Assuming that $n \geq 3$ (it is obvious that $n=2$ is not the largest), let's take row $A$, in which the leftmost cell is marked, row $B$, adjacent to $A$, and row $C$, adjacent either to $A$ (and not coinciding with $B$) or to $B$ (and not coinciding with $A$). Let $b$ be the number of the marked cell in row $B$. If $b \leq n-\left[\frac{n+1}{2}\right]$ or $b \geq\left[\frac{n+1}{2}\right]+2$, then in rows $A$ and $B$ there will be a rectangle of area not less than $n$ that does not contain marked cells, hence $b \leq n-\left[\frac{n+1}{2}\right]$. Consider two rectangles formed by the intersection of rows $A, B$ and $C$ with columns numbered $2,3, \ldots, n-\left[\frac{n+1}{2}\right]$ and columns numbered $2+\left[\frac{n+1}{2}\right], \ldots, n$. These rectangles do not contain the marked cells of rows $A$ and $B$. If $n > 7$, then the area of each of them is not less than $n$, but row $C$ contains only one marked cell, which means that one of these rectangles does not contain marked cells. Therefore, $n \leq 7$.
An example of a 7×7 board satisfying the condition of the problem is shown in the figure.
## Answer
For $n=7$.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Given $n$ sticks. From any three, an obtuse triangle can be formed. What is the largest possible value of $n$?
|
From three sticks of lengths $a \leq b \leq c$, a triangle can be formed if $a+b>c$. According to the cosine theorem, this triangle is obtuse if and only if $a^{2}+b^{2}<c^{2}$. For the given problem, we need to check if $a_{4}^{2}+a_{3}^{2} \geqslant 2 a_{3}^{2}>2 a_{2}^{2}+2 a_{1}^{2}$. On the other hand, $a_{5}<a_{1}+a_{2}$, from which $a_{5}^{2}<a_{1}^{2}+a_{2}^{2}+2 a_{1} a_{2}$. Comparing with the previous, we get $a_{1}^{2}+a_{2}^{2}<2 a_{1} a_{2}$, which is impossible.
An example for $n=4$ can be constructed as follows. Let $a_{1}=a_{2}=1$, choose $a_{3}$ slightly greater than $\sqrt{a_{1}^{2}+a_{2}^{2}}$, and $a_{4}$ slightly greater than $\sqrt{a_{2}^{2}+a_{3}^{2}}$. For example, the values $1 ; 1 ; 1.5 ; 1.9$ work.
## Answer
4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kondakov G.V.
Divide the segment $[-1,1]$ into black and white segments so that the integrals of any a) linear function;
b) quadratic trinomial over the white and black segments are equal.
#
|
Since the integral of a polynomial over an interval is equal to the increment of its antiderivative, our task is a special case of problem $\underline{98268}$.
## Answer
For example, a) intervals $[-1,-1 / 2],[1 / 2,1]$ - black, $[-1 / 2,1 / 2]-$ white.
b) intervals $[-1,-3 / 4],[-1 / 4,0],[1 / 4,3 / 4]$ - white, $[-3 / 4,-1 / 4],[0,1 / 4],[3 / 4,1]$ - black.

Author: Shestakov S.A.
In a convex quadrilateral $A B C D$, points $E$ and $F$ are the midpoints of sides $B C$ and $C D$ respectively.
The segments $A E, A F$, and $E F$ divide the quadrilateral into four triangles, the areas of which are (in some order) consecutive natural numbers. What is the greatest possible value of the area of triangle $A B D$?
## Solution
Author: $\underline{\text { Shestakov S.A. }}$
Let the areas of the triangles be $n, n+1, n+2$, and $n+3$. Then $S_{A B C D}=4 n+6$. Since $E F$ is the midline of triangle $B C D$, we have $S_{B C D}=4 S_{E C F} \geq 4 n$. Therefore, $S_{A B D}=S_{A B C D}-S_{B C D} \leq 6$.
We will show that this area can be equal to 6. Consider an isosceles trapezoid $A B C D$ with bases $A D=6, B C=4$ and height 2. Then
$S_{C F E}=1, S_{A B E}=2, S_{A D F}=3, S_{A E F}=S_{A B C D}-1-2-3=4$, and in this case $S_{A B D}=6$.
## Answer
6.
|
6
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Frankin B.R. }}$
Given a polynomial $P(x)$ with real coefficients. An infinite sequence of distinct natural numbers $a_{1}, a_{2}, a_{3}, \ldots$ is such that
$P\left(a_{1}\right)=0, P\left(a_{2}\right)=a_{1}, P\left(a_{3}\right)=a_{2}$, and so on. What degree can $P(x)$ have?
|
The constant clearly does not satisfy the condition.
For example, the polynomial $P(x)=x-1$ works.
Note that the leading coefficient of the polynomial $P$ is positive (otherwise, $P(x)x$ for each $x \in N$. Suppose the sequence exists. Starting from some index, the terms less than $N$ will end, that is, there will be an $n$ such that $a_{k} \geq N$ for all $k>n$. Then $a_{n}=P\left(a_{n+1}\right)$ $>a_{n+1}, a_{n+1}=P\left(a_{n+2}\right)>a_{n+2}, \ldots$, that is, $a_{n}>a_{n+1}>a_{n+2}>\ldots-$ an infinite decreasing sequence of natural numbers, which is impossible.
## Answer
Only the first degree
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shirov V.
On a circle, $2 N$ points are marked ($N$ is a natural number). It is known that through any point inside the circle, no more than two chords with endpoints at the marked points pass. We will call a matching a set of $N$ chords with endpoints at the marked points such that each marked point is the endpoint of exactly one of these chords. We will call a matching even if the number of points where its chords intersect is even, and odd otherwise. Find the difference between the number of even and odd matchings.
|
Let the marked points be $A_{1}, A_{2}, \ldots, A_{2 N}$ in the order of a clockwise traversal of the circle. We will prove by induction on $N$ that the number of even matchings is one more than the number of odd matchings. For $N=1$, the statement is obvious: there is only one matching, and it is even.
Inductive step. First method. Suppose in the matching, the chord $A_{1} A_{i}$ is involved and it is intersected by exactly $k$ chords. Consider the points $A_{2}, \ldots, A_{i-1}$; exactly $k$ of them are endpoints of chords intersecting $A_{1} A_{i}$. The remaining $i-2-k$ points are paired by chords that do not intersect $A_{1} A_{i}$. Thus, the number $i-2-k$ is even, meaning that $i$ and $k$ have the same parity.
We divide all matchings into $2 N-1$ groups $\Pi_{2}, \ldots, \Pi_{2 N}$: in group $\Pi_{i}$, the point $A_{1}$ is connected to $A_{i}$. Remove the chord $A_{1} A_{i}$ from each matching in $\Pi_{i}$; we obtain all possible matchings on the remaining $2 N-2$ points. By the inductive hypothesis, among them, there is one more even matching than odd. If $i$ is even, the parity of the matching does not change upon removal, and if $i$ is odd, the parity changes. Therefore, in each of the $N$ sets $\Pi_{2}, \ldots, \Pi_{2 N}$, there is one more even matching than odd, and in each of the $N-1$ sets $\Pi_{3}, \ldots, \Pi_{2 N-1}$, there is one more odd matching than even. In total, the number of even matchings is greater than the number of odd matchings by $N-(N-1)=1$.
Second method. Consider all matchings in which $A_{2 N-1}$ and $A_{2 N}$ are connected by a chord. This chord does not intersect any other. Thus, by removing it from each of the considered matchings, we obtain all matchings on the points $A_{1}, \ldots, A_{2 N-2}$, and the parity of each of them is preserved. By the inductive hypothesis, among our matchings, there is one more even matching than odd.
It remains to prove that among the remaining matchings, there are equally many even and odd. Consider any of them; suppose it contains chords $A_{2 N-1} A_{i}$ and $A_{2 N} A_{k}$. Replace these chords with $A_{2 N} A_{i}$ and $A_{2 N-1} A_{k}$. If the original chord intersected with some other chord, the new chord will also intersect with it. On the other hand, if the chords $A_{2 N-1} A_{i}$ and $A_{2 N} A_{k}$ did not intersect, the new chords will intersect, and vice versa. Thus, we have divided the remaining matchings into pairs of different parity.
## Answer
1.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ribamko A.V.
In the lower left corner of a $n \times n$ chessboard, there is a knight. It is known that the minimum number of moves it takes for the knight to reach the upper right corner is equal to the minimum number of moves it takes to reach the lower right corner. Find $n$.
#
|
Let $n$ be even. In this case, the left lower field has the same color as the right upper one, while the right lower field has a different color. After each move, the knight lands on a field of the opposite color. Therefore, any path from the left lower corner to the right upper one consists of an even number of moves, while the path to the right lower corner consists of an odd number of moves. Consequently, their lengths are different.
: Let $n=4 k+1$. Then, by making moves alternately along the fields of the two lower rows, the knight will reach the right lower corner in $2 k$ moves.
We will show that the path to the right upper corner is longer. Each move shifts the knight by a total of 3 fields horizontally and vertically. Even moving consistently to the right-up, the knight will move a total of $6 k$ fields in $2 k$ moves. The total distance horizontally and vertically from the left lower corner to the right upper one is $2 n-2 = 8 k > 6 k$. Therefore, the shortest path to the right upper field is longer.
Let $n=4 k-1$. Then, the right lower field can be reached in $2 k$ moves as follows: the first move is one field to the right and two up, the second move is one field to the right and two down, and then, as in the previous case, move alternately along the fields of the two lower rows. It is impossible to reach the destination in fewer moves.
Indeed, the knight needs to move $n-1=4 k-2$ cells to the right, and each move can shift it a maximum of two cells to the right. Therefore, the number of moves is at least $2 k-1$. But after $2 k-1$ moves, the knight will land on a field of the opposite color, while in our case, the right lower corner has the same color as the left lower corner, so at least one more move is needed, meaning the number of moves is at least $2 k$.
The maximum total shift to the right and up in $2 k$ moves remains $6 k$. The total distance horizontally and vertically from the left lower field to the right upper one is $2 n-2 = 8 k-4$. For $k>2$, this is greater than $6 k$. For $k=1 (n=3)$, it is easy to check all options and see that this case does not work. However, for $k=2 (n=7)$, both shortest paths consist of four moves, and this is also easy to verify.
## Answer
$n=7$.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Berov s.L.
Seryozha chose two different natural numbers $a$ and $b$. He wrote down four numbers in his notebook: $a, a+2, b$ and $b+2$. Then he wrote on the board all six pairwise products of the numbers from the notebook. What is the maximum number of perfect squares that can be among the numbers on the board?
|
Note that no two squares of natural numbers differ by 1: $x^{2}-y^{2}=(x-y)(x+y)$, and the second bracket is greater than one. Therefore, the numbers
$a(a+2)=(a+1)^{2}-1$ and $b(b+2)=(b+1)^{2}-1$ are not squares.
The numbers $a b$ and $a(b+2)$ cannot both be squares; otherwise, their product $a^2 b(b+2)$ would also be a square, and then the number $b(b+2)$ would be a square as well. Similarly, among the numbers $(a+2) b$ and $(a+2)(b+2)$, at most one can be a square. In total, there are no more than two squares on the board.
Two squares can be obtained, for example, with $a=2$ and $b=16$: then $a(b+2)=6^{2}$ and $(a+2) b=8^{2}$.
## Answer
Two squares.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Rubanov I.S.
For four different integers, all their pairwise sums and pairwise products were calculated.
The obtained sums and products were written on the board. What is the smallest number of different numbers that could end up on the board?
#
|
If we take the numbers $-1,0,1,2$, then, as is easy to check, each of the numbers written on the board will be equal to $-2,-1,0$, 1,2 or 3 - a total of 6 different values.
We will show that fewer than six different numbers on the board could not have occurred. Let the numbers taken be $ac+d$. If $ac+d$.
The second method. Let $u$ and $v$ be the two largest in absolute value among the numbers $a, b, c, d$, with $|u| \leq|v|$. If $|u| \geq 2$, then $|u v| \geq 2|v|$, which is greater than any sum. If, however, $|u| \leq 1$, then among the original numbers there must be $-1,0,1$. If $v>0$, at least 6 different numbers are written on the board: $-1,0,1, v,-v, v+1$.
The case $v<0$ is handled similarly.
## Answer
6 numbers.
Send a comment
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Combinatorics (miscellaneous).]
$[$ Estimation + example $]$
In a pond, 30 pikes were released, which gradually eat each other. A pike is considered full if it has eaten at least three pikes (full or hungry). What is the maximum number of pikes that can become full?
|
The number of pikes eaten is not less than three times the number of satiated ones.
## Solution
Let $s$ be the number of satiated pikes. Then they together have eaten no less than $3 s$ pikes. Since each pike can only be eaten once, and at least one pike remains at the end, $3 s<30$. Therefore, $s \leq 9$.
We will provide an example where exactly 9 pikes are satiated. Suppose 7 pikes (from the 3rd to the 9th) ate 21 pikes (from the 10th to the 30th; each ate 3 pikes). After this, 9 pikes remain. The first and second pikes can become satiated by eating 6 pikes (from the 4th to the 9th).
## Answer
9 pikes.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For what value of the parameter $m$ is the sum of the squares of the roots of the equation $x^{2}-(m+1) x+m-1=0$ the smallest?
#
|
The sum of the squares of the roots $\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=(m+1)^{2}-2(m-1)=m^{2}+3$ is minimal when $m=0$. Note that in this case, the equation
$x^{2}-x-1=0$ has roots.
## Answer
When $m=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bakayev E.V.
Cheburashka has a set of 36 stones with masses of 1 g, 2 g, ..., 36 g, and Shapoklyak has super glue, one drop of which can glue two stones together (thus, three stones can be glued with two drops, and so on). Shapoklyak wants to glue the stones in such a way that Cheburashka cannot select one or several stones from the resulting set with a total mass of 37 g. What is the minimum number of drops of glue she needs to achieve her goal?
|
Example. By gluing stones with masses 1 and 18, 2 and 17, ..., 9 and 10, respectively, Cheburashka will get a set where each stone weighs from 19 to 36 grams, so one stone will be too little, and two will be too many.
Another way. By gluing all the stones with odd masses in pairs, Cheburashka will get a set where all stones have even masses, and Cheburashka will not be able to form an odd mass.
Estimate. If Cheburashka uses only 8 drops, then no more than 16 of the original stones will be involved in the gluing. Therefore, at least one of the 18 pairs
$\{1,36\},\{2,35\}, \ldots,\{18,19\}$ will remain "untouched," and Cheburashka will be able to choose it.
## Answer
9 drops.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5,6 |
| :---: | :---: | :---: |
| | Classical combinatorics (miscellaneous). | |
| | Examples and counterexamples. Constructions | |
| | Estimation + example | |
Each of thirty sixth-graders has one pen, one pencil, and one ruler. After their participation in the Olympiad, it turned out that 26 students lost their pen, 23 - their ruler, and 21 - their pencil. Find the smallest possible number of sixth-graders who lost all three items.
|
From the condition, it follows that four sixth-graders have a pen, seven have a ruler, and nine have a pencil. Thus, at least one item can be owned by no more than $4+7+9=20$ people. Therefore, no fewer than $30-20=10$ people have lost all three items.
All three items will be lost by exactly 10 people if each of the other twenty loses exactly two items.
## Answer
10 sixth-graders.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Folklore }}$
Does there exist such an $N$ and $N-1$ infinite arithmetic progressions with differences $2,3,4, \ldots, N$, such that every natural number belongs to at least one of these progressions?
|
Let $N=12$. Each natural number can be written in the form $12 k+r$, where $r$ is one of the numbers $0,1, \ldots, 11$. All numbers for which $r$ is even belong to the progression $2,4,6, \ldots$; all numbers for which $r$ is a multiple of $3$ belong to the progression $3,6,9, \ldots$ The remaining numbers have $r=1,5,7$ and 11. They are covered by the progressions $4 k+1,6 k+7$ and $12 k+$ $11(k=0,1, \ldots)$ with differences 4,6 and 12.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tolony A.K.
In a certain kingdom, there were 32 knights. Some of them were vassals of others (a vassal could have only one suzerain, and a suzerain was always richer than his vassal). A knight who had at least four vassals bore the title of baron. What is the maximum number of barons that could be under these conditions?
(The kingdom had a law: "a vassal of my vassal is not my vassal".)
|
Evaluation. 8 barons should have 32 vassals, and the richest knight cannot be anyone's vassal. Example. Let 24 knights be vassals of six barons, and all these barons be vassals of the richest Baron. In total, 7 barons.
## Answer
7 barons.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Berlov S.L.
A natural number $n$ is called good if every its natural divisor, increased by 1, is a divisor of the number $n+1$.
Find all good natural numbers.
|
Clearly, $n=1$ satisfies the condition. Also, all odd prime numbers satisfy it: the divisors of such a number $p$, increased by 1, are 2 and
$p+1$; both of them divide $p+1$.
On the other hand, any number $n$ that satisfies the condition has a divisor 1; hence, $n+1$ is divisible by 1 +1, which means $n$ is odd.
Suppose some composite $n=ab$, where $a \geq b \geq 2$, satisfies the condition. Then the number $n+1$ is divisible by $a+1$ and the number $n+b=(a+1)b$ is also divisible by $a+1$. Therefore, the number $b-1=(n+b)-(n+1)$ is also divisible by $a+1$. Since $b-1>0$, we get that $b-1 \geq a+1$. But this contradicts the inequality $b \leq a$.
## Answer
One and all odd prime numbers.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On the plane, $n$ lines are drawn such that every two intersect, but no four pass through the same point. There are a total of 16 intersection points, and through 6 of them, three lines pass. Find $n$.
#
|
"Move" the given construction in such a way that any two lines still intersect, but no three lines pass through the same point. Then, if some three lines intersected at a certain point $O$, now instead of one point $O$, there will be three points of pairwise intersection of these lines. Therefore, as a result of "moving" the initial number of lines will not change, but the number of intersection points will increase by $2 \cdot 6=$ 12. In the end, all lines will intersect pairwise, and the number of intersection points will become $16+12=28$. Thus, $1 / 2 n(n-1)=28$, from which $n=8$.
## Answer
$n=8$.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bakayev E.V.
In a $10 \times 10$ square, all cells of the left upper $5 \times 5$ square are painted black, and the rest of the cells are white. Into what maximum number of polygons can this square be cut (along the cell boundaries) so that in each polygon, the number of black cells is three times less than the number of white cells? (Polygons do not have to be equal or even of equal area.)
|
In each polygon of the partition, there must be cells of both colors. This means that there must be a black cell adjacent to a white one. However, there are only 9 such cells. See the example of cutting into 9 polygons in the figure.

## Answer
Into 9 polygons.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Frankin B.R. }}$ 5.
A billiard table has the shape of a rectangle $2 \times 1$, with pockets located at the corners and at the midpoints of the longer sides. What is the smallest number of balls that need to be placed inside the rectangle so that each pocket lies on a line with some two balls?
|
Let there be only three balls. A line passing through a pair of balls inside a rectangle intersects the boundary of the rectangle exactly at two points. We have six pockets, so we need at least three lines. Three balls will give three lines only if these lines form a triangle. However, there are only seven lines passing through two pockets, and no three of them form a triangle with vertices inside the billiard table (see figure).
An example for four balls is indicated in the same figure.
## Answer
Four balls.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On the board, two-digit numbers are written. Each number is composite, but any two numbers are coprime.
What is the maximum number of numbers that can be written?
|
Evaluation. Since any two written numbers are coprime, each of the prime numbers 2, 3, 5, and 7 can appear in the factorization of no more than one of them. If there are five or more numbers on the board, then all prime factors in the factorization of one of them must be at least 11. But this is a composite number, so it must be at least 121. This contradicts the condition. Therefore, there are no more than four numbers on the board.
Example. 25, 26, 33, 49.
## Answer
4 numbers.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the expression $10: 9: 8: 7: 6: 5: 4: 3: 2: 1$, parentheses were placed such that the value of the expression is an integer.
What is the smallest number that could have been obtained?
#
|
In order for the value of the expression to be an integer, after placing the parentheses and writing the resulting expression as a common fraction, the number 7 must end up in the numerator. Therefore, the value of this expression is no less than 7. This can be achieved, for example, as follows:
$10: 9:(8: 7:(6:(5: 4:(3: 2: 1)))=(10 \cdot 7 \cdot 6 \cdot 4 \cdot 3):(9 \cdot 8 \cdot 5 \cdot 2 \cdot 1)=7$.
Send a comment
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Zaslavsky A.A.
In a volleyball tournament, each team met every other team once. Each match consisted of several sets - until one of the teams won three sets. If a match ended with a score of $3: 0$ or $3: 1$, the winning team received 3 points, and the losing team received 0. If the set score was
$3: 2$, the winner received 2 points, and the loser received 1 point. By the end of the tournament, it turned out that the team "Tricksters" scored the most points, while the team "Simples" scored the least. However, the "Tricksters" won fewer matches than they lost, while the "Simples" had more wins than losses. What is the smallest number of teams for which this is possible?
|
Evaluation. If there are no more than three teams, then the "Simpletons" won all the matches, which means they have the most points. Contradiction.
If there are four or five teams, then each team will play three or four matches. This means that the "Cunning" won no more than one match and scored a maximum of $5=3+1+1$ or $6=3+1+1+1$ points, respectively. The "Simpletons" won at least two matches with four participants and at least three matches with five participants, that is, they scored at least $4=2+2+0$ or $6=2+2+2+0$ points, respectively. Considering that the "Cunning" must score at least 2 points more than the "Simpletons," we get a contradiction.
Therefore, there are no fewer than six teams.
Example. See the table.
| Teams | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ | Points |
| :--- | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| "Cunning" | $\bullet$ | 1 | 1 | 1 | 3 | 3 | $\mathbf{9}$ |
| A | 2 | $\bullet$ | 2 | 2 | 1 | 1 | $\mathbf{8}$ |
| $\mathbf{\text { B }}$ | 2 | 1 | $\bullet$ | 2 | 2 | 1 | $\mathbf{8}$ |
| $\mathbf{B}$ | 2 | 1 | 1 | $\bullet$ | 2 | 1 | 7 |
| $\Gamma$ | 0 | 2 | 1 | 1 | $\bullet$ | 3 | 7 |
| "Simpletons" | 0 | 2 | 2 | 2 | 0 | $\bullet$ | $\mathbf{6}$ |
## Answer
With six teams.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bakayev E.V.
In each cell of a $1000 \times 1000$ square, a number is inscribed such that in any rectangle of area $s$ that does not extend beyond the square and whose sides lie along the cell boundaries, the sum of the numbers is the same. For which $s$ will the numbers in all cells necessarily be the same?
|
It is clear that when $s=1$, the numbers in all cells are the same.
Let $s>1$ and $p$ be a prime divisor of $s$. In cells where the sum of the coordinates is divisible by $p$, we write ones, and in the other cells, we write zeros. In any rectangle $T$ of area $s$, one of the sides is divisible by $p$, so it is divided into $s / p$ strips of length $p$. Each such strip contains exactly one one. Therefore, the sum of the numbers in $T$ is ${ }^{s} / p$, which does not depend on the choice of the rectangle.
## Answer
Only when $s=1$.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Andjans A.
$N$ friends simultaneously learned $N$ pieces of news, with each person learning one piece of news. They started calling each other and exchanging news.
Each call lasts 1 hour. Any number of news items can be shared in one call.
What is the minimum number of hours required for everyone to learn all the news? Consider three cases:
a) $N=64$,
b) $N=55$,
c) $N=100$.
|
a) A piece of news known to one of the friends will be known to no more than two (including the first) after 1 hour, no more than four after the second hour, ..., and no more than 32 after the fifth hour. Therefore, it will take no less than 6 hours.
We will show that 6 hours are sufficient. The conversations can proceed according to the following scheme. Number the participants with six-digit binary numbers. In the $k$-th hour, people whose numbers differ only in the $k$-th digit converse (for example, in the 3rd hour, $a b c 0 d e$ converses with $a b c 1 d e$). Each hour, the number of pieces of news known to each person doubles. (For example, after the 2nd hour, each person knows four pieces of news known to four participants whose numbers differ from his number in the first two digits.)
Remark. This method of conversation is only suitable for powers of two. Below is a method that works for any even numbers.
b) That 6 hours are insufficient is evident from a). We will show that 7 hours are sufficient. Number the participants with elements from $\mathbf{Z}_{50} \times\{-1,1\}$. In the 1st hour, the participant with number $(x, y)$ converses with $(x,-y)$, in the 2nd hour with $(x+1,-y)$, in the 3rd hour with $(x+3,-y)$, and so on. The number of pieces of news each friend knows doubles each hour (except the last). (Number the pieces of news the same way as the friends who know them at the beginning. After the 1st hour, the participant with number $(0,0)$ knows all pieces of news with $x=0$, after the 2nd hour, all pieces of news with $x=0,1$, after the 3rd hour, all pieces of news with $x=0,1,2,3$; and so on.)
b) In the first hour, one of the participants does not converse with anyone. As seen from a), the others will need at least 6 more hours to learn his news.
Divide the participants into two groups: 32 and 23 people. In the 1st hour, all members of the second group converse with members of the first. Over the next 5 hours, the members of the first group exchange news (according to the scheme from a) or b); as a result, each knows all the news). In the last hour, they inform the members of the second group of all the information.
## Answer
a) 6 hours, b) 7 hours, c) 7 hours. On the board, three functions are written: $f_{1}(x)=x+1 / x, f_{2}(x)=x^{2}, f_{3}(x)=(x-1)^{2}$. You can add, subtract, and multiply these functions (including squaring, cubing, ...), multiply them by any number, add any number to them, and perform these operations on the resulting expressions. Obtain the function $1 / x$.
Prove that if any of the functions $f_{1}, f_{2}, f_{3}$ is erased from the board, it is impossible to obtain $1 / x$.
## Solution
Since $f_{2}(x)-f_{3}(x)=2 x-1$, and since we can add 1 and multiply the resulting expression $2 x$ by $1 / 2$, we can obtain the function $x$. Subtracting it from $f_{1}(x)$, we get $1 / x = f_{1}(x) - 1 / 2 (f_{2}(x) - f_{3}(x) + 1)$.
Since the division operation is not allowed, it is impossible to express $1 / x$ using only the functions $f_{2}$ and $f_{3}$: if you multiply and add polynomials, you will get polynomials again, and the function $1 / x$ is not a polynomial. The derivatives of the functions $f_{1}$ and $f_{3}$ at the point $x=1$ are 0. If the derivatives of two functions at the point 1 are 0, then the derivative of both their sum and their product is 0. So, all functions that can be obtained using the specified operations from the functions $f_{1}$ and $f_{3}$ have a zero derivative at the point 1. The derivative of the function $1 / x$ at the point 1 is not 0.
All our functions are defined for all complex $x \neq 0$. If we substitute $x=i$ into $f_{1}$ and $f_{2}$, we get $i + i^{-1} = 0, i^{2} = -1$ - real numbers. This means that each of the functions obtained from $f_{1}$ and $f_{2}$ will have a real value at the point $i$. And it is impossible to express the imaginary number $f_{3}(i) = -2i$ using only real numbers.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On weekdays, the Absent-Minded Scientist travels to work on the ring line of the Moscow Metro from "Taganskaya" station to "Kievskaya" station, and in the evening - back (see diagram).
Upon entering the station, the Scientist boards the first arriving train. It is known that trains run in both directions with approximately equal intervals, and that the train traveling on the northern route (via "Belorusskaya") takes 17 minutes to travel from "Kievskaya" to "Taganskaya" or vice versa, while on the southern route (via "Paveletskaya") it takes 11 minutes. Out of habit, the Scientist always calculates everything. Once, he calculated that over many years of observation:
- the train traveling counterclockwise arrives at "Kievskaya" on average 1 minute and 15 seconds after the train traveling clockwise arrives. The same is true for "Taganskaya".
- on average, the Scientist spends 1 minute less on the trip from home to work than on the trip from work to home.
Find the expected interval between trains traveling in the same direction.
|
Let $p$ be the probability that the Scientist boards a train going clockwise. Then the expected travel time from "Taganskaya" to "Kievskaya" is $11 p + 17(1-p) = 17 - 6p$.
On the return journey from "Kievskaya" to "Taganskaya," the expected travel time is $17 p + 11(1-p) = 11 + 6p$.
According to the condition, $(11 + 6p) - (17 - 6p) = 1$, from which $p = \frac{7}{12}$. Let the interval between trains be $T$. Then $T(1-p) = Y$, where $Y$ is the time between the arrival of a clockwise train and the arrival of a counterclockwise train at the Scientist's favorite stations. Therefore, $\mathrm{ET} = \mathrm{EY}_{/ 1-p} = \frac{5}{4} \cdot \frac{12}{5} = 3$.
## Answer
## 3 minutes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the class, there are fewer than 30 people. The probability that a randomly chosen girl is an excellent student is $3 / 13$, and the probability that a randomly chosen boy is an excellent student is $4 / 11$. How many excellent students are there in the class?
|
The probability that a randomly chosen girl is an excellent student is the ratio of the number of excellent girl students to the total number of girls in the class. Therefore, the number of girls is divisible by 13, meaning it is either 13 or 26.
Similarly, the number of boys is either 11 or 22. Considering that there are fewer than 30 students in the class, we find that there are 13 girls (3 excellent students) and 11 boys (4 excellent students).
## Answer
7 excellent students.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The probability that a purchased light bulb will work is 0.95.
How many light bulbs need to be bought so that with a probability of 0.99, there will be at least five working ones among them?
#
|
Let's take 6 light bulbs. The probability that at least 5 of them will be working is the sum of the probabilities that exactly 5 of them will be working and that all 6 will be working, which is $6 \cdot 0.95^{5} \cdot 0.05 + 0.95^{6} = 0.9672$.
Let's take 7 light bulbs. The desired probability is $21 \cdot 0.95^{5} \cdot 0.05^{2} + 7 \cdot 0.95^{6} \cdot 0.05 + 0.95^{7} = 0.9962$.
## Answer
## 7 light bulbs.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
According to the conditions of the chess match, the winner is the one who outperforms the opponent by two wins. Draws do not count. The probabilities of winning for the opponents are equal. The number of decisive games in such a match is a random variable. Find its mathematical expectation.
|
Let $X$ be the number of decisive games. At the beginning of the match, the difference in the number of wins between the two participants is zero. Let's list the possible cases of two decisive games, denoting a win by the first participant as 1 and a win by the second participant as 2: 11, 12, 21, 22. Two of the four cases mean a win in the match, specifically, 11 and 22. The other two cases bring us back to the initial state with a zero difference in the number of wins.
Thus, with probability $1 / 2$ the number of wins is 2, and with the same probability $X=2+X^{\prime}$, where $X^{\prime}$ is distributed the same as $X$. Therefore,
$\mathrm{E} X=2 \cdot 1 / 2+(2+\mathrm{E} X) \cdot 1 / 2$, which means $\mathrm{E} X=4$.
Answer
## 4.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
At a familiar factory, they cut out metal disks with a diameter of 1 m. It is known that a disk with a diameter of exactly 1 m weighs exactly 100 kg. During manufacturing, there is a measurement error, and therefore the standard deviation of the radius is 10 mm. Engineer Sidorov believes that a stack of 100 disks will on average weigh 10000 kg. By how much is Engineer Sidorov mistaken?
|
Given $\mathrm{E} R=0.5 \mathrm{~m}, \mathrm{D} R=10^{-4} \mathrm{~m}^{2}$. Let's find the expected value of the area of one disk:
$\mathrm{ES}=\mathrm{E}\left(\pi R^{2}\right)=\pi \mathrm{E} R^{2}=\pi\left(\mathrm{D} R+\mathrm{E}^{2} R\right)=\pi\left(10^{-4}+0.25\right)=0.2501 \pi$.
Therefore, the expected value of the mass of the disk is ${ }^{0.2501 \pi} / 0.25 \pi \cdot 100=100.04$ kg. Thus, a stack of 100 disks on average will weigh 10004 kg.
## Answer
4 kg more.
Send a comment
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the Valley of Five Lakes, there are five identical lakes, some of which are connected by streams (on the diagram, dashed lines indicate possible "routes" of the streams). Small carp are born only in lake $S$. While growing up, a carp crosses from one lake to another exactly four times via some stream (the carp chooses a stream at random), and then stays to live in the lake where it ends up. Out of every thousand carp, on average 375 stay to live in lake $S$, and the rest stay to live in lake $B$, with no one staying to live in the other lakes. Determine how many streams there are in the Valley of Five Lakes.
|
The transition from one lake to another will be called a route of length $n$ if it passes through $n$ streams. Let's prove several statements.
1. There is no route of length 2 from $S$ to any of the lakes $A, C$, and $D$.
Proof. Suppose it is possible to sail from lake $S$ to lake $A$ through one intermediate lake (say $C$). Then the route $S-C-A-C-A$ would be possible. In this case, there would be a non-zero probability of reaching lake $A$ in four transitions. Therefore, there is no route of length 2 from $S$ to $A$.
2. Lake $S$ is connected to lake $B$ by a route of length 2.
Proof. Clearly, $S$ and $B$ are connected. Suppose they are connected by a common stream. Then there are no other exits from $B$, otherwise condition (1) would not be satisfied. This means one can only arrive at $B$ from $S$ on the first or third move. But then, after the fourth transition, the carp cannot end up in $B$. Contradiction.
Suppose $S$ and $B$ are connected by a route of length 3 or 4. But then there is a route of length 2 from $S$ to one of the lakes $A$, $C$, or $D$, which cannot exist.
Therefore, there is a route from $S$ to $B$ passing through one intermediate lake $A, C$, or $D$, and one is no better than the other. We can assume, for definiteness, that there is a route $S-A-B$.
From this and statement 1, it follows that there are no routes $A-C$ and $A-D$.
3. There is at least one of the routes $B-C$ or $B-D$.
Proof. Suppose there is neither a route $B-C$ nor $B-D$. We get one of the following diagrams:
In the first case, the carp makes the first transition to lake $A$, and it has three transitions left. Lakes $S$ and $B$ are equally positioned relative to $A$, so their chances should be equal. It is easy to see that in the other three cases, the probability of remaining in lake $S$ is greater than in $B$.
Therefore, one of the routes $B-C$ or $B-D$ must exist.
From this, it follows that there is no route $C-D$.
4. The constructed configuration of three streams satisfies the condition.
Proof. For the constructed configuration, the following routes of length 4 are possible:

Above each transition, the probability of this transition is indicated, and on the right, the probability of the entire route, obtained by multiplying the probabilities of transitions between lakes.
The probability that the carp, after four transitions, will end up in lake $S$ is $0.25 + 0.125 = 3/8$ - exactly what is needed.
Therefore, the probability that $B$ is the final point of the route is $1 - 3/8 = 5/8$.
5. There cannot be more streams.
Proof. By adding any streams $S-C, S-D, B-D$ individually or together, we will change the probabilities. This can be verified directly by making seven more diagrams corresponding to possible configurations and calculating the probabilities for each of the resulting schemes.
Thus, with the accuracy of the vertex labeling, the scheme shown in the last diagram is the only possible one, and the total number of streams is 3.
Send a comment
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Every day, the dog Patrick gnaws one slipper from the available supply in the house. With a probability of 0.5, Patrick wants to gnaw a left slipper and with a probability of 0.5 - a right slipper. If the desired slipper is not available, Patrick gets upset. How many pairs of identical slippers need to be bought so that with a probability of at least 0.8, Patrick does not get upset for a whole week (7 days)?
|
Let in a week Patrick wants to eat $S$ left and $7-S$ right slippers. We need to find such $k$ that the inequality $\mathrm{P}(S \leq k \cap 7-S \leq k) \geq 0.8$ holds. Rewrite the event in parentheses: $P(7-k \leq S \leq k)$. It is clear that $7-k \leq k$, that is, $k \geq 4$.
The probability on the left side of the inequality is the sum
$C_{7}^{7-k} \frac{1}{2^{7}}+C_{7}^{8-k} \frac{1}{2^{7}}+\ldots+C_{7}^{k} \frac{1}{2^{7}}=\frac{1}{128} \cdot\left(C_{7}^{7-k}+C_{7}^{8-k}+\ldots+C_{7}^{k}\right)=\frac{1}{64} \cdot\left(C_{7}^{4}+C_{7}^{5}+\ldots+C_{7}^{k}\right)$. Therefore,
$C_{7}^{4}+C_{7}^{5}+\ldots+C_{7}^{k} \geq 64 \cdot 0.8=51.2$
Note that $C_{4}^{7}=35, \quad C_{5}^{7}=21$, so the sum $C_{7}^{4}+C_{7}^{5}=35+21>52$. Therefore, the smallest $k$ is 5.
## Answer
## Problem
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On board an airliner, there are $2 n$ passengers, and the airline has loaded $n$ portions of chicken and $n$ portions of fish for them. It is known that a passenger prefers chicken with a probability of 0.5 and fish with a probability of 0.5. We will call a passenger dissatisfied if they are left with what they do not prefer.
a) Find the most probable number of dissatisfied passengers.
b) Find the expected value of the number of dissatisfied passengers.
c) Find the variance of the number of dissatisfied passengers.
|
a) The number of dissatisfied passengers can be any from 0 to $n$. In the case of $n=1$, everything is obvious: there is either no dissatisfied passenger or one, and both cases are equally likely. We will further assume that $n>1$.
Let us introduce the random variable $\xi$ "Number of dissatisfied passengers". $\xi=0$ only if exactly $n$ passengers prefer chicken, and the other $n$ prefer fish. We will consider a success the event "a passenger wants chicken". Then
$$
\mathrm{P}(\xi=0)=\mathrm{P}(\{\text { there are $n$ successes in a series of $2n$ trials }\})=C_{2 n}^{n} \frac{1}{2^{2 n}} \text {. }
$$
Exactly one passenger will be dissatisfied if the number of passengers preferring chicken differs from $n$ by one, that is, the number of successes is
$n \pm 1$. Therefore, $\mathrm{P}(\xi=1)=\mathrm{P}(\{n+1$ success in a series of $2n$ trials $\})+\mathrm{P}(\{n-1$ success in a series of $2n$ trials $\})=2 C_{2 n}^{n-1} \frac{1}{2^{2 n}}$.
Reasoning similarly, we find that $\mathrm{P}(\xi=k)=2 C_{2 n}^{n-k} \frac{1}{2^{2 n}}$, where $k=1,2, \ldots, n$.
In the sequence of numbers $C_{2 n}^{m}$, there are $2n+1$ numbers (this is the $2n$-th row of Pascal's triangle). These numbers first increase for $m=0,1, \ldots, n$, and then decrease for $m=n, n+1, \ldots, 2n$. The middle number $C_{2 n}^{n}$ is larger than the others, but smaller than twice the previous one: $C_{2 n}^{n}1 \quad \mathrm{P}(\xi=0)\mathrm{P}(\xi=2)>\ldots>\mathrm{P}(\xi=n)$.
The result is illustrated by the distribution diagram of the random variable $\xi$ for $n=5$. For comparison, the diagram of the binomial distribution $\frac{1}{2^{10}} C_{10}^{k}$ is given in a lighter color on the same graph.
Thus, the most probable number of dissatisfied passengers is one.
b) Let us find the expected value of the quantity $\xi+n$:
$$
\begin{aligned}
& \mathrm{E}(\xi+n)=n \mathrm{P}(\xi=0)+(n+1) \mathrm{P}(\xi=1)+(n+2) \mathrm{P}(\xi=2)+\ldots+2 n \mathrm{P}(\xi=n)= \\
& =n C_{2 n}^{n} \frac{1}{2^{2 n}}+\frac{1}{2^{2 n-1}}\left((n+1) C_{2 n}^{n-1}+(n+2) C_{2 n}^{n-2}+\ldots+(n+k) C_{2 n}^{n-k}+\ldots+2 n C_{2 n}^{0}\right)
\end{aligned}
$$
Notice that $(n+k) C_{2 n}^{n-k}=\frac{(n+k)(2 n)!}{(n-k)!(n+k)!}=2 n C_{2 n-1}^{n-k}$. Therefore, $\mathrm{E}(\xi+n)=$
$n C_{2 n}^{n} \frac{1}{2^{2 n}}+\frac{2 n}{2^{2 n-1}}\left(C_{2 n-1}^{n-1}+C_{2 n-1}^{n-2}+\ldots+C_{2 n-1}^{0}\right)$
In the parentheses, we have the sum of the first half of all numbers in the $(2n-1)$-th row of Pascal's triangle. The sum of all numbers in this row is $2^{2 n-1}$, so the sum in the parentheses is $2^{2 n-2}$. Thus, $\mathrm{E}(\xi+n)=n C_{2 n}^{n} \frac{1}{2^{2 n}}+n$, and $\mathrm{E} \xi=\mathrm{E}(\xi+n)-n=n C_{2 n}^{n} \frac{1}{2^{2 n}}$
Let us find this number approximately using Stirling's formula $\quad m!\approx \sqrt{2 \pi m} \cdot m^{m} e^{-m}$ :
$\mathrm{E} \xi \approx \frac{n}{2^{n}} \cdot \frac{\sqrt{4 \pi n} \cdot(2 n)^{2 n} e^{-2 n}}{\left(\sqrt{2 \pi n} \cdot n^{n} e^{-n}\right)^{2}}=\sqrt{\frac{n}{\pi}}$
c) $\mathrm{E} \xi^{2}=0^{2} \cdot \mathrm{P}(\xi=0)+1^{2} \cdot \mathrm{P}(\xi=1)+\ldots+n^{2} \mathrm{P}(\xi=n)=1^{2} \cdot \frac{C_{2 n}^{n-1}}{2^{2 n-1}}+2^{2} \cdot \frac{C_{2 n}^{n-2}}{2^{2 n-1}}+\ldots+n^{2} \cdot \frac{C_{2 n}^{0}}{2^{2 n-1}}=$
$$
=(0-n)^{2} \cdot \frac{C_{2 n}^{0}}{2^{2 n}}+(1-n)^{2} \cdot \frac{C_{2 n}^{1}}{2^{2 n}}+(2-n)^{2} \cdot \frac{C_{2 n}^{2}}{2^{2 n}}+\ldots+(2 n-n)^{2} \cdot \frac{C_{2 n}^{2 n}}{2^{2 n}}
$$
This expression is exactly equal to the variance of the random variable $\eta$ "number of successes in a series of $2n$ Bernoulli trials with a success probability of $0.5$". As is known, it is equal to $2n \cdot 0.5 \cdot 0.5=n / 2$.
Therefore, $\mathrm{D} \xi=\mathrm{E} \xi^{2}-(\mathrm{E} \xi)^{2}=\frac{n}{2}-\left(\frac{n C_{2 n}^{n}}{2^{2 n}}\right)^{2} \approx \frac{n}{2}-\frac{n}{\pi}=\frac{\pi-2}{2 \pi} n \approx 0.182 n$.
## Answer
a) If $n>1$, then the most probable number of dissatisfied passengers is one; if $n=1$, then with equal probability, there is either one dissatisfied passenger or none at all;
b) $\frac{n C_{2 n}^{n}}{2^{2 n}} \approx \sqrt{\frac{n}{\pi}} \approx 0.564 \sqrt{n}$
c) $\frac{n}{2}-\left(\frac{n C_{2 n}^{n}}{2^{2 n}}\right)^{2} \approx \frac{\pi-2}{2 \pi} n \approx 0.182 n$.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In Anchuria, a checkers championship is taking place in several rounds. The days and cities for the rounds are determined by a draw. According to the championship rules, no two rounds can take place in the same city, and no two rounds can take place on the same day. Among the fans, a lottery is organized: the main prize goes to the person who correctly guesses before the start of the championship in which cities and on which days all the rounds will take place. If no one guesses correctly, the main prize will go to the championship organizing committee. There are eight cities in Anchuria, and the championship is allocated a total of eight days. How many rounds should the championship have so that the organizing committee has the highest probability of getting the main prize?
|
In an $8 \times 8$ table, you need to select $k$ cells such that no more than one cell is selected in any row or column. The number of tours $k$ should be chosen so that the number $N k$ of possible selection options is maximized.
$$
N_{k}=C_{8}^{k} A_{8}^{k}=\frac{8!\cdot 8!}{(8-k)!(8-k)!k!}\left(C_{8}^{k}-\text { the number of ways to choose } k\right. \text { cities from eight without considering }
$$
the order, $A_{8}^{k}$ - the number of ways to choose $k$ days from eight considering the order, as each day must correspond to one of the cities).
Notice that $\frac{N_{k}}{N_{k-1}}=\frac{(9-k)^{2}}{k}=\frac{m^{2}}{9-m}$, where $m=9-k$. Since $m^{2}N_{7}>N_{8}$.
## Answer
6 tours.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ilya Muromets meets the three-headed Zmei Gorynych. And the battle begins. Every minute Ilya cuts off one of Zmei's heads. With a probability of $1 / 4$, two new heads grow in place of the severed one, with a probability of $1 / 3$ - only one new head, and with a probability of $5 / 12$ - no heads at all. The Zmei is considered defeated if he has no heads left. Find the probability that Ilya will eventually defeat the Zmei.
|
Strikes by Ilya Muromets, in which the number of heads changes, are called successful.
Let's find the probability that at some point there will be a last successful strike. This means that starting from this point, there will be no more successful strikes, that is, all strikes will be unsuccessful. The probability of this is $1 / 3 \cdot 1 / 3 \cdot 1 / 3 \cdot \ldots$ $=0$.
Thus, there will be no last successful strike, but there will be an infinite subsequence of successful strikes, which we will consider, ignoring all other strikes.
The probability of a successful strike is $2 / 3$. The conditional probability that the number of heads increases when a strike is successful is $1 / 4 : 2 / 3 = 3 / 8$.
Similarly, the conditional probability that the number of heads decreases when a strike is successful is $5 / 12 : 2 / 3 = 5 / 8$.
This leads to a standard one-dimensional random walk problem. Suppose that as a result of a certain series of successful strikes, the number of heads of the Serpent has decreased by one compared to what it was. Let's call this event $D$, and its probability $x$.
There are two possibilities.
1) As a result of the first successful strike, the number of heads decreased by one (event $M$, probability $5 / 8$). In this case, event $D$ has already occurred - its conditional probability is 1.
2) As a result of the first successful strike, the number of heads increases by one (event $N$, probability $3 / 8$). In this case, event $D$ will occur only if the number of heads decreases by 2 - by one, and then by another one. Therefore, the conditional probability of event $D$ in this case is $x^2$.
By the formula for total probability, $x = P(D) = P(D \mid M) \cdot P(M) + P(D \mid N) \cdot P(N) = 5 / 8 + 3 / 8 x^2$.
From this, $x = 1$ or $x = 5 / 3$. The second root is extraneous. Therefore, event $D$ is certain.
Thus, sooner or later, the number of heads will inevitably decrease from three to two. Then, for the same reason, the number of heads will decrease to one and, finally, to zero. The Serpent has no chance.
## Answer
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A deck of playing cards is laid out on the table (for example, in a row). On top of each card, a card from another deck is placed. Some cards may have matched. Find:
a) the expected value of the number of matches;
b) the variance of the number of matches.
#
|
a) Let's number the pairs from 1 to $N$ (we don't know how many there are) in the order they lie on the table. Let
the indicator $I_{k}$ be 1 if the two cards in the $k$-th pair are the same, and 0 if the cards in the $k$-th pair are different.
Obviously, $\mathrm{P}\left(I_{k}=1\right)=1 / N$. Therefore, $\mathrm{E}_{k}=1 / N$.
Let $S$ be the number of pairs with a match. It is equal to $I_{1}+I_{2}+\ldots+I_{N}$. Therefore, $\mathrm{E} S=\mathrm{E}I_{1}+\mathrm{E}I_{2}+\ldots+\mathrm{E}I_{N}=N \cdot{ }^{1} / N$ $=1$.
b) $S^{2}=\left(I_{1}+I_{2}+\ldots+I_{N}\right)^{2}=I_{1}^{2}+I_{2}^{2}+\ldots+I_{N}^{2}+2\left(I_{1} I_{2}+I_{1} I_{3}+\ldots+I_{j} I_{k}+\ldots+I_{N-1} I_{N}\right)$, where the sum of all possible different indicator products is in the parentheses.
Obviously, $I_{k}^{2}=I_{k}$, so $\mathrm{E} I_{k}^{2}=\frac{1}{N}$.
Now consider the quantity $I_{j} I_{k}$. It is 1 if the cards match in both the $j$-th and $k$-th pairs. The cards in the $j$-th pair match with probability $1 / N$. If this happens, the probability of the cards in the $k$-th pair matching is ${ }^{1}{ }_{N-1}$.
Therefore, $\mathrm{P}\left(I_{j} I_{k}=1\right)=1 / N(N-1)$. In all other cases, $I_{j} I_{k}=0$. Therefore, $\mathrm{E}\left(I_{j} I_{k}\right)=1 / N(N-1)$.
Thus, $\mathrm{E}S^{2}=N \cdot 1 /{ }_{N}+N(N-1) \cdot{ }^{1} / N(N-1)=1+1=2$, and therefore, $\mathrm{D}S=\mathrm{E}S^{2}-(\mathrm{E}S)^{2}=2-1=1$.
## Answer
a) 1 ; b) 1.
Submit a comment
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kanel-Belov A.Y.
The game takes place on a $9 \times 9$ grid of squared paper. Two players take turns. The player who starts the game places crosses in free cells, while his partner places noughts. When all cells are filled, the number of rows and columns $K$ in which there are more crosses than noughts, and the number of rows and columns $H$ in which there are more noughts than crosses, are counted. The difference $B=K-H$ is considered the win of the player who starts. Find such a value of $B$ that
1) the first player can ensure a win of at least $B$, no matter how the second player plays;
2) the second player can always achieve that the first player gets a win of no more than $B$, no matter how the first player plays.
|
One possible strategy for the first player: the first move is to the center of the board; thereafter, for each move the second player makes to any cell, the first player responds by moving to the cell symmetric to the center. This is possible because the second player always breaks the symmetry.
In the final position, in each pair of cells symmetric relative to the center, there is a cross and a nought. Therefore, in the central row and the central column, there are more crosses than noughts; and for each row (column) not passing through the center, there is a corresponding symmetric row (column), where in one of them there are more noughts, and in the other fewer, than crosses. Thus, with this strategy, the first player's win is 2.
Now let's indicate a strategy for the second player. If he has the opportunity to occupy the cell symmetric (relative to the center) to the cell just occupied by the first, he does so. Otherwise, he makes any move. With this strategy, after the second player's move, the set of occupied cells is either symmetric (until the first player occupies the center) or differs from the symmetric one by exactly one cell. In each pair of occupied symmetric cells, there will be one cross and one nought. With his last move, the first player is forced to create the position described in the previous paragraph, and his win is again 2.
## Answer
$\mathrm{B}=2$.
Submit a comment
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
Two players take turns coloring the sides of an $n$-gon. The first player can color a side that borders with zero or two colored sides, the second player - a side that borders with one colored side. The player who cannot make a move loses. For which $n$ can the second player win, regardless of how the first player plays?
|
For $n=3$, it is obvious that the first player wins, while for $n=4$, the second player wins. Let's show how the first player wins for $n>4$. After the first move of the second player, two adjacent sides are painted. The first player can paint a side "one apart" from them, creating an unpainted "hole" of one side. This is his sanctuary, which the second player cannot paint. The first player uses the sanctuary only if he has no other move. If such a moment comes (the second player may lose earlier), then (after "closing" the sanctuary) the unpainted part will consist of pairs of adjacent sides. From then on, the first player can always respond to the second player's move by painting a side from the same pair.
## Answer
Only for $n=4$.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.B.
The weight of each weight in the set is a non-integer number of grams. They can balance any integer weight from 1 g to 40 g (weights are placed on one pan of the scales, the weight to be measured - on the other). What is the smallest number of weights in such a set?
|
Example 1. Let's take weights of $1,1,3,5,11,21,43$ g. The first two can measure any integer weight up to 2 g. Therefore, the first three can measure up to 5 g, the first four up to 10 g, the first five up to 21 g, the first six up to 42 g, and all seven up to 85 g. If we reduce the weight of each weight by half, all the weights will now be non-integer grams, and they can measure any integer or half-integer weight from 0.5 to 42.5 g.
Example 2. Weights of 1, 2, 4, 8, 16, 32, 64 g can measure any integer weight up to 127 g. If we leave only a third of each weight, the weights will become non-integer, and they can measure any integer weight up to 42 g.
Estimate. Suppose there are 6 weights in the set. There are $2^{6}=64$ different subsets. Let's paint one weight yellow and divide the subsets into pairs that differ only by the presence of the yellow weight. Since the weights of the paired subsets differ by the non-integer weight of the yellow weight, at most one of them can have an integer weight in grams. Therefore, there are no more than 32 subsets with an integer weight, and 40 different integer weights cannot be achieved with this set of weights.
## Answer
7 weights.
Send a comment
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Fomin D:
Consider a set of weights, each weighing an integer number of grams, and the total weight of all weights is 200 grams. Such a set is called correct if any body with a weight expressed as an integer number of grams from 1 to 200 can be balanced by some number of weights from the set, and in a unique way (the body is placed on one pan of the scales, the weights - on the other; two balancing methods that differ only by the replacement of some weights with others of the same weight are considered the same).
a) Provide an example of a correct set where not all weights are 1 gram each.
b) How many different correct sets exist?
(Two sets are different if some weight participates in these sets a different number of times.)
|
The correct set should correspond to the factorization of the number 201 (see the solution to problem $\underline{98056}$), and it only factors into two factors: $201=3 \cdot 67$.
## Answer
a) Two weights of 67 grams and 66 weights of 1 gram or 66 weights of 3 grams and two of 1 gram.
b) 3 sets.
Author: Fomin D:
Given 103 coins of the same appearance. It is known that two of them are counterfeit, that all genuine coins weigh the same, and that the counterfeit coins also weigh the same but differ from the weight of the genuine coins. However, it is unknown whether the counterfeit coins are heavier or lighter than the genuine ones. How can this be determined using three weighings on a two-pan balance without weights? (It is not required to separate the counterfeit coins.)
## Solution
Suppose we have $6 k+1$ coins, two of which are counterfeit. Discard one coin, and divide the rest into three piles $-A, B, C$ - each containing $2 k$ coins. Note that among them, there will be exactly two piles with the same weight. Weigh $A$ against $B$ first, and then $B$ against $C$. Suppose, for example, that $A$ is heavier than $B$ and $C$. Then $B$ contains no more than one counterfeit coin (since the weights of $B$ and $C$ are equal). Divide $B$ into two equal parts and weigh them. If the weights are equal, then the counterfeit coin is heavier than the genuine one, otherwise, it is lighter.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Fomin }}$ D:
Consider a set of weights, each weighing an integer number of grams, and the total weight of all weights is 500 grams. Such a set is called correct if any body with a weight expressed as an integer number of grams from 1 to 500 can be balanced by some number of weights from the set, and in a unique way (the body is placed on one pan of the scales, the weights - on the other; two balancing methods that differ only by the replacement of some weights with others of the same weight are considered the same).
a) Provide an example of a correct set where not all weights are one gram each.
b) How many different correct sets exist?
(Two sets are different if some weight participates in these sets a different number of times.)
|
Let the largest weight of a weight in some correct set be $M$ (grams). This means that any smaller weight can be balanced by smaller weights. Let the weight of all smaller weights be $m$. Clearly, $m \geq M-1$. But if $m \geq M$, then we have two ways to balance the weight $M+r$, where $r$ is the remainder of the division of $m$ by $M$.
Therefore, $m=M-1$.
Let there be $k$ weights of the maximum weight. Then the total weight of all weights $k M+m=500$, so 501 is divisible by $M$. By determining $M$, we can determine the weight of the second heaviest weight. Repeating the previous reasoning shows that it must be a divisor of $M$. But 501 has exactly two divisors other than 1 and 501: 3 and 167, each of which is a prime number. Therefore, there are exactly two correct sets, not counting the trivial set of 500 weights of 1 g: two weights of 167 g and 166 weights
of 1 g; 166 weights of 3 g and two weights of 1 g.
## Answer
a) Two weights of 167 g and 166 weights of 1 g or 166 weights of 3 g and two of 1 g.
b) 3 sets.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Twelve chairs are arranged in a row. Sometimes a person sits on one of the free chairs. At this point, exactly one of his neighbors (if they were present) stands up and leaves. What is the maximum number of people that can be sitting at the same time, if initially all the chairs were empty?
#
|
Evaluation. It is impossible for all chairs to be occupied simultaneously, because at the moment when a person sits on the last unoccupied chair, one of his neighbors will stand up. Therefore, the number of people sitting simultaneously cannot exceed 11.
Example. Let's show how to seat 11 people. Number the chairs from 1 to 12. The first chair is easy to occupy. The second chair will be occupied in two stages. In the first stage, a person sits on the third chair, and in the second stage, we seat a person on the second chair, and the person sitting on the third chair stands up. We proceed similarly: if the chairs numbered from 1 to \( k \) are occupied, we first seat a person on the chair numbered \( k+2 \), and then seat a person on the chair numbered \( k+1 \), thereby freeing the chair numbered \( k+2 \). After this operation is performed for all \( k \) from 1 to 10, the chairs numbered from 1 to 11 will be occupied, and the twelfth chair will be free.
## Answer
11.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Evdokiyov M.A.
A pirate has five bags of coins, each containing 30 coins. He knows that one bag contains gold coins, another contains silver coins, a third contains bronze coins, and each of the two remaining bags contains an equal number of gold, silver, and bronze coins. You can simultaneously take any number of coins from any of the bags and see what kind of coins they are (coins are taken out only once). What is the smallest number of coins that need to be taken to definitely determine the contents of at least one bag?
|
Example. Let's take one coin from each bag. Among these five coins, there are coins of all three types, so there is only one coin of a certain type. If it is, for example, a gold coin, then it was taken from the bag with gold coins. Indeed, for each coin from the "mixed" bag, there is a matching one from the corresponding "homogeneous" bag.
Evaluation. Suppose we took only 4 coins. Note that it makes no sense to take more than one coin from a bag, as they may turn out to be the same, and then we would not gain any additional information. Therefore, we can assume that we took one coin from each of four different bags. Then we could have taken coins 3, 3, S, B, and in this case, there are at least two possible distributions of the corresponding bags: 3, Mixed, S, Mixed, B and Mixed, 3, Mixed, B, S, which do not match in any of the positions (the last one indicates the bag from which no coins were taken).
## Answer
5 coins.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Folkior
There is a set of tickets numbered from 1 to 30 (numbers can repeat). Each student drew one ticket. The teacher can perform the following operation: read out a list of several (possibly one) numbers and ask their owners to raise their hands. How many times does he need to perform this operation to find out the number of each student? (There are not necessarily 30 students.)
#
|
We will encode the tickets with binary numbers from 00001 to 11110. On the $k$-th stage, the teacher includes in the list all numbers whose $k$-th bit is one (for example, on the 3rd stage, the numbers are $4,5,6,7,12,13,14,15,20,21,22,23$, $28,29,30$). After the fifth stage, the teacher learns the binary code of the numbers from all students.
Four stages are insufficient even for one student: the number of their "possible" numbers after each stage (if the teacher is "unlucky") can decrease by no more than half.
## Problem
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the room, there are 12 people; some of them are honest, meaning they always tell the truth, while the rest always lie. "There is not a single honest person here," said the first. "There is no more than one honest person here," said the second. The third said that there are no more than two honest people, the fourth said no more than three, and so on until the twelfth, who said that there are no more than eleven honest people. How many honest people are actually in the room?
|
Note that if someone among those present lied, then all the previous ones lied as well. Such people are in the room; otherwise, the first one told the truth, and according to his words, there are no honest people in the room. For the same reason, there must be honest people in the room.
Let there be $x$ liars in the room. The last liar said that there are no more than ($x-1$) honest people in the room. Therefore, there are actually no fewer than $x$ honest people in the room. Next, the $(x+1)$-th person already told the truth about there being no more than $x$ honest people. Therefore, the number of honest people is exactly $x$, which is the same as the number of liars. Consequently, there are 6 honest people in the room.
## Answer
6 people.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Symmetric Strategy ]
There are two piles of stones: one has 30, the other has 20. On a turn, you are allowed to take any number of stones, but only from one pile. The player who cannot make a move loses.
#
|
The first one wins. With the first move, he equalizes the number of stones in the piles, after which he plays as in problem 10.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Combinatorics (miscellaneous) $]$ $[$ Estimation + example ]
In a pond, 30 pikes were released, which gradually eat each other. A pike is considered full if it has eaten at least three pikes (full or hungry). What is the maximum number of pikes that can become full?
|
The number of pikes eaten is not less than three times the number of satiated ones.
## Solution
Let $s$ be the number of satiated pikes. Then they together have eaten no less than $3 s$ pikes. Since each pike can only be eaten once, and at least one pike remains at the end, $3 s<30$. Therefore, $s \leq 9$.
We will provide an example where exactly 9 pikes are satiated. Suppose 7 pikes (from the 3rd to the 9th) ate 21 pikes (from the 10th to the 30th; each ate 3 pikes). After this, 9 pikes remain. The first and second pikes can become satiated by eating 6 pikes (from the 4th to the 9th).
## Answer
9 pikes.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On Uncle Fyodor's birthday, Postman Pechkin wants to find out how old he is. Sharik says that Uncle Fyodor is more than 11 years old, and cat Matroskin claims that he is more than 10 years old. How old is Uncle Fyodor, given that exactly one of them is wrong? Justify your answer.
|
Note that if Sharik did not make a mistake, then Matroskin did not make a mistake either, which contradicts the condition. Therefore, Sharik must have lied, while Matroskin told the truth. Thus, Uncle Fyodor is more than 10 years old, but not more than 11. Therefore, Uncle Fyodor is 11 years old.
## Problem
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
There are five chain links, each with 3 rings. What is the minimum number of rings that need to be unlinked and relinked to connect these links into one chain?
#
|
For connecting two links, one ring is required.
## Solution
Example: we unlock 3 rings from one link. The remaining 4 links are connected using the three unlocked rings.
Evaluation: if fewer than 3 rings are unlocked, at least 5 separate links will remain, which would require at least 4 unlocked rings to connect - a contradiction.
## Answer
3 rings.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
|
There are 85 balloons in the room - red and blue. It is known that: 1) at least one of the balloons is red; 2) in every arbitrarily chosen pair of balloons, at least one is blue. How many red balloons are in the room?
#
|
Think about whether there can be two red balls in the room.
## Solution
Since among any two balls, one is blue, there cannot be two red balls in the room. Therefore, there are 84 blue balloons and 1 red balloon in the room.
## Answer
1 ball.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How can you use a balance scale without weights to divide 24 kg of nails into two parts - 9 and 15 kg?
#
|
Try to weigh out 12 kg first, then -6 kg, and then -3 kg.
## Solution
Weigh out 12 kg of nails and set them aside. From the remaining 12 kg, weigh out 6 kg and set them aside in a different place. From the remaining 6 kg, weigh out 3 kg and combine them with the 6 kg that were set aside. We get the desired 9 kg of nails.
## Answer
Weigh out 12 kg; from them, weigh out 6 kg and set them aside; from the remaining 6 kg, weigh out 3 kg and combine them with the 6 kg that were set aside.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Five first-graders stood in a line and held 37 flags. All those to the right of Tanya had 14 flags, to the right of Yasha - 32, to the right of Vera - 20, and to the right of Maksim - 8. How many flags does Dasha have?
#
|
## Solution
Obviously, the more flags to the right of a first-grader, the "further left" their place in the line. Someone is standing to the right of Maksim (otherwise there would be no flags to his right). But everyone except Dasha is definitely standing to the left of Maksim. Therefore, Dasha is standing to the right of Maksim and holding 8 flags.
## Answer
8 flags.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\begin{aligned} & {[\text { Mathematical Logic (other) }]} \\ & {[\text { Arithmetic. Mental calculation, etc. }]}\end{aligned}$
Rabbits are sawing a log. They made 10 cuts. How many chunks did they get?
|
Into how many parts is a log divided by the first cut? How does the number of pieces change after each subsequent cut?
## Solution
The number of chunks is always one more than the number of cuts, since the first cut divides the log into two parts, and each subsequent cut adds one more chunk.
## Answer
11 chunks.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Mathematical logic (miscellaneous).]
In the wallet, there are 2 coins with a total value of 15 kopecks. One of them is not a five-kopeck coin. What are these coins?
#
|
Two coins can only be 5 kopecks and 10 kopecks. If one of them is not a five-kopeck coin, then it is a ten-kopeck coin, and the other one is a five-kopeck coin.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[
There are pan scales without weights and 3 visually identical coins, one of which is counterfeit: it is lighter than the genuine ones (the genuine coins weigh the same). How many weighings are needed to determine the counterfeit coin?
#
|
When searching for a counterfeit coin among three coins, try placing one coin on each pan of the balance.
## Solution
We will need only 1 weighing. Place one coin on each pan of the balance. If one of the pans is lighter, the counterfeit coin is on it. If the balance is even, the counterfeit coin is the one that was not placed on the balance.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Mathematical logic (other)]
In the room, there are 85 balloons - red and blue. It is known that: 1) at least one of the balloons is red, 2) in every arbitrarily chosen pair of balloons, at least one is blue. How many red balloons are in the room?
#
|
Think about whether there can be two red balls in the room.
## Solution
Since among any two balls, one is blue, there cannot be two red balls in the room. Therefore, there are 84 blue balloons and 1 red balloon in the room.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the garden of Anya and Vitya, there were 2006 rose bushes. Vitya watered half of all the bushes, and Anya watered half of all the bushes. It turned out that exactly three bushes, the most beautiful ones, were watered by both Anya and Vitya. How many rose bushes remained unwatered?
|
Vitya watered 1003 bushes, of which 1000 he watered alone, and three - together with Anya. Similarly, Anya watered 1003 bushes, of which 1000 she watered alone, and three - with Vitya. Therefore, together they watered $1000+1000+3=2003$ bushes. Thus, 2006 - 2003 = 3 rose bushes were left unwatered.
## Answer
3 bushes.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Golenischeva-Kumuzova T.I.
Yura has a calculator that allows multiplying a number by 3, adding 3 to a number, or (if the number is divisible by 3) dividing the number by 3. How can Yura use this calculator to get from the number 1 to the number 11?
|
Comment. Note that on Yura's calculator, any number can be increased by $1: (x \cdot 3+3): 3=x+1$. Therefore, in principle, from one, any natural number can be obtained on it.
## Answer
For example, $((1 \cdot 3 \cdot 3 \cdot 3)+3+3): 3=11$ or $(1 \cdot 3+3): 3+3+3+3=11$.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Zsspasii A.A.
The number of the current Olympiad (70) is formed by the last digits of the year of its holding, written in reverse order.
How many more times will such a situation occur in this millennium?
#
|
Let in some year the described coincidence occurred.
If the number of the Olympics is two-digit, then the sum of this number and the number formed by the last two digits of the year is divisible by 11 (the sum of two numbers consisting of digits $a$ and $b$ is $11(a+b)$). Since each year this sum increases by 2, the event can repeat no more often than every 11 years. Indeed, the 81st and 92nd Olympics will take place in 2018 and 2029.
If the number of the Olympics is three-digit, then the second-to-last digits of the number and the year coincide. Therefore, the second-to-last digit of their difference can only be 0 or 9. But the difference between the year of the Olympics and its number is always 1937. Contradiction.
If the number of the Olympics is four-digit, then the sums of the digits of the number and the year coincide. Since any number gives the same remainder when divided by 9 as the sum of its digits, the difference between the year and the number must be divisible by 9. But the remainder when 1937 is divided by 9 is 2. Contradiction.
Note that such a situation will not be observed in the future.
## Answer
Twice.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Rubanov I.S.
Microcalculator MK-97 can perform only three operations on numbers stored in memory:
1) check if two selected numbers are equal,
2) add two selected numbers,
3) find the roots of the equation $x^{2}+a x+b=0$ for selected numbers $a$ and $b$, and if there are no roots, display a message about it.
The results of all actions are stored in memory. Initially, one number $x$ is recorded in memory. How can you use MK-97 to determine if this number is equal to one?
|
By adding $x$ to itself, we get $2x$. We compare $x$ and $2x$. If they are equal, then $x=0$. Otherwise, we find the roots of the equation $y^{2}+2xy+x=0$. The discriminant of this equation is $4(x^{2}-x)$, so the roots are equal if and only if $x=1$.
Send a comment
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Anzhans A.
There are 100 silver coins, ordered by weight, and 101 gold coins, also ordered by weight. It is known that all coins have different weights. We have a two-pan balance that allows us to determine which of any two coins is heavier. How can we find the coin that ranks 101st in weight among all the coins with the fewest number of weighings?
|
Let's prove that if from $n$ silver and $n$ gold coins, the $n$-th by weight coin can be found in $k$ weighings, then the $2n$-th by weight coin can be found in $k+1$ weighings from $2n$ silver and $2n$ gold coins.
Indeed, suppose the $n$-th silver coin is heavier than the $n$-th gold coin. Then the $n$ first silver coins occupy places by weight above the $2n$-th, as they are heavier than
$n$ silver and $n+1$ gold coins. On the other hand, the $n$ last gold coins must occupy places below the $2n$-th, as they are lighter than $n$ gold and $n$ silver coins. Therefore, the sought coin is among the remaining $n$ lighter silver and $n$ heavier gold coins and occupies the $n$-th place among them; it can be found in the remaining $k$ weighings.
Example. One weighing can find the heavier coin from two, so in 8 weighings, the 128-th coin can be found from 128 silver and 128 gold coins.
Let's add 27 gold coins (14 very heavy and 13 very light) and 28 silver coins (14 heavy and 14 light) to our coins and apply the described algorithm to them. The 128-th coin from these 256 coins will be the 101-st from the original ones.
Estimate. Suppose the required coin can be determined in 7 weighings. Consider the flowchart of the algorithm that allows this to be done. This flowchart has the form of a tree, with a check [which of the two specified coins is lighter?] in each vertex (then from this vertex, there is a branch to two subsequent vertices); or an answer [such-and-such a coin is the 101-st by weight] (then this vertex is a terminal one). There are no more than seven branches on each path, so there are no more than $2^7 = 128$ terminal vertices. But a priori, any of the given coins can be in the 101-st place, so there should be no fewer than 201 terminal vertices. Contradiction.
## Answer
8 weighings.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Authors: Bogdanov I.Y., Knop K.A.
King Hiero has 11 metal ingots that are indistinguishable in appearance; the king knows that their weights (in some order) are 1, 2, ..., 11 kg. He also has a bag that will tear if more than 11 kg is placed in it. Archimedes has learned the weights of all the ingots and wants to prove to Hiero that the first ingot weighs 1 kg. In one step, he can load several ingots into the bag and demonstrate to Hiero that the bag does not tear (the bag cannot be torn!). What is the minimum number of bag loadings Archimedes needs to achieve the required result?
|
Let Archimedes first put ingots weighing 1, 2, 3, and 5 kg into the bag, and then put ingots weighing 1, 4, and 6 kg. In both cases, the bag will not tear.
We will prove that this could only happen if the 1 kg ingot was used twice. Indeed, if Archimedes used ingots weighing \( w_1, \ldots, w_6 \) kg instead of ingots weighing 1, ..., 6 kg in these two cases, then these weights would satisfy the system of inequalities:
\[ w_1 + w_2 + w_3 + w_5 \leq 11, \]
\[ w_1 + w_4 + w_6 \leq 11. \]
Adding these inequalities, we get:
\[ w_1 + (w_1 + w_2 + \ldots + w_6) \leq 22. \]
The expression in parentheses is the sum of six different natural numbers, which is at least \( 1 + 2 + \ldots + 6 = 21 \). Therefore, we have:
\[ w_1 \leq 22 - 21 = 1. \]
This means \( w_1 = 1 \), so the 1 kg ingot is uniquely determined.
It remains to show that one loading is insufficient. If Archimedes loads only one ingot, the bag will not tear in any case, so no ingot can be identified. Suppose Archimedes loads more than one ingot, and the bag does not tear. If the 1 kg ingot is not loaded into the bag, then replacing it with any ingot in the bag will not change the result; in this case, Hiero will not be able to determine whether this ingot is in the bag. If the required ingot is in the bag, then Hiero will not be able to determine which of the (at least two) loaded ingots is the required one.
## Answer
In two loadings.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11
There is a piece of chain consisting of 150 links, each weighing 1 g. What is the smallest number of links that need to be broken so that from the resulting parts, all weights of 1 g, 2 g, 3 g, ..., 150 g can be formed (a broken link also weighs 1 g)?
|
Answer: 4 links. According to the solution of problem 5 for grades $7-8$, for a chain consisting of $n$ links, where $64 \leq n \leq 159$, it is sufficient to unfasten 4 links.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tokarev S.i.
Among 2000 indistinguishable balls, half are aluminum with a mass of 10 g, and the rest are duralumin with a mass of 9.9 g. It is required to separate the balls into two piles such that the masses of the piles are different, but the number of balls in them is the same. What is the smallest number of weighings on a balance scale without weights that can achieve this?
#
|
Let's compare the mass of 667 balls with the mass of another 667 balls. If the masses of these two piles are not equal, the required condition is met.
Suppose the specified masses are equal. Then the mass of 666 balls that did not participate in the weighing is not equal to the mass of any 666 balls lying on one of the pans of the scales.
Indeed, if each of the weighed piles contains exactly $k$ aluminum balls, then among any 666 balls of any of these piles, the number of aluminum balls is $k$ or $k-1$. Meanwhile, among the 666 balls that did not participate in the weighing, there are exactly $1000-2k$ aluminum balls. It remains to note that neither the equality $k = 1000 - 2k$, nor the equality $k - 1 = 1000 - 2k$ can be satisfied for any integer $k$.
## Answer
In one weighing.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The Cantor Set. A segment of the number line from 0 to 1 is painted green. Then its middle part, the interval $(1 / 3 ; 2 / 3)$, is repainted red. Next, the middle part of each of the remaining green segments is also repainted red, and the same operation is performed on the remaining green segments, and so on to infinity. The points that remain green form the Cantor set.
a) Find the sum of the lengths of the red intervals.
b) Prove that the number $1 / 4$ will remain painted green.
c) From the sum
$$
\frac{2}{3}+\frac{2}{9}+\frac{2}{27}+\frac{2}{81}+\ldots
$$
arbitrarily chosen terms are erased. Prove that the sum of the remaining terms is a green number.
|
Numbers from 0 to 1 can conveniently be considered as infinite ternary fractions of the digits 0, 1, and 2. The numbers mentioned in point v) are those numbers whose ternary representation contains no 1.
| | Game Theory (Other) |
| :---: | :---: |
| | Similarity Criteria |
| | [ Auxiliary Similar Triangles |
| Problem $\underline{64723}$ Topics: | [ Symmetry Helps Solve the Problem |
| | [ Inscribed and Circumscribed Polygons |
| | Complex Numbers in Geometry |
| | Estimation + Example |
Author: Knop K.
Given a triangle with no equal angles, Petya and Vasya play the following game: in one move, Petya marks a point on the plane, and Vasya paints it either red or blue at his discretion. Petya wins if any three of the marked and painted points form a monochromatic triangle similar to the original. What is the minimum number of moves Petya needs to guarantee a win (regardless of the original triangle)?
## Solution
In 4 moves, Petya cannot guarantee a win: if Vasya paints two points red and two blue, there will be no monochromatic triangles.
We will show how to win in 5 moves. In the first three moves, Petya marks points on the plane that are the vertices of a triangle \(ABC\) similar to the original. If Vasya paints all the marked points the same color, then Petya has already won.
Suppose vertices \(A\) and \(B\) are painted red, and \(C\) is painted blue. Then, in the next two moves, Petya marks points \(P\) and \(Q\) in the same half-plane relative to the line \(AB\) as point \(C\), such that triangles \(ABC\), \(PAB\), and \(BQA\) are similar (see figure).
If Vasya paints at least one of the points \(P\) and \(Q\) red, then a triangle similar to the original, with all vertices red, will be formed. If Vasya paints both these vertices blue, then a "blue" triangle \(CPQ\) will be formed, which is also similar to the original. We will prove this.
First method. \(\angle CAQ = \angle CAB - \angle QAB = \angle CAB - \angle ACB = \angle QBA - \angle PBA = \angle PBQ\), and \(\frac{AC}{AQ} = \frac{AC}{AB} \cdot \frac{AB}{AQ} = \frac{AC}{AB} \cdot \frac{AC}{CB} = \frac{BA}{BQ} \cdot \frac{BP}{BA} = \frac{BP}{BQ}\). Therefore, triangles \(CAQ\) and \(PBQ\) are similar, with the similarity ratio equal to \(\frac{QB}{QA} = \frac{BA}{BC}\).
Thus, \(\angle CQP = \angle CQA + \angle AQP = \angle CQA + \angle AQB - \angle PQB = \angle AQB = \angle CBA\) and \(\frac{QP}{QC} = \frac{BA}{BC}\), which implies the similarity of triangles \(CQP\) and \(CBA\).
Second method. Mark points \(C'\), \(P'\), and \(Q'\), which are symmetric to points \(C\), \(P\), and \(Q\) with respect to the perpendicular bisector of \(AB\) (see figure).
From the equality of angles, it is clear that each triplet of points \(A, C, Q'\); \(A, P', Q\); \(A, P, C'\); \(B, P', C\); \(B, P, Q'\); \(B\), \(C', Q\) lies on a straight line.
\(\angle ACB = \angle QAB = \angle AQ Q'\), so quadrilateral \(CQ'QP'\) is cyclic. The perpendicular bisector of \(QQ'\) coincides with the perpendicular bisector of \(AB\) and passes through the center of the circumcircle of quadrilateral \(CQ'QP'\). Therefore, this circle is symmetric with respect to it, and thus it also contains points \(C'\) and \(P\).
From the cyclic nature of hexagon \(Q'Q C' P P' C\), it follows that \(\angle ACB = \angle Q'BA = \angle BQ'Q = \angle PCQ\) and \(\angle CBA = \angle BQ'A = \angle CQP\). We obtain the similarity of triangles \(ABC\) and \(PQC\) by two angles.
## Answer
In 5 moves.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Mathematical Logic (Miscellaneous).] $[$ Evenness and Oddness $]$
Author: Khaitumuren A.v.
13 children sat around a round table and agreed that boys would lie to girls, but tell the truth to each other, and girls, on the contrary, would lie to boys, but tell the truth to each other. One of the children said to their right neighbor: "The majority of us are boys." That child said to their right neighbor: "The majority of us are girls," and that one to their right: "The majority of us are boys," and so on, until the last child said to the first: "The majority of us are boys." How many boys were there at the table?
|
It is clear that there were both boys and girls at the table. A group of boys sitting next to each other is followed by a group of girls, then boys again, then girls, and so on (a group can consist of just one person). Groups of boys and girls alternate, so their number is even. Incorrect statements were made at the transitions from one group to another, so there are also an even number of them. Since the statement "most of us are boys" was made seven times, six of the statements "most of us are girls" were incorrect, and there were six groups.
The alternation of correct and incorrect statements means that there were two children in each group. Only the first and last child sitting next to each other said the same thing, so there are three people in their group. These are boys, as they are in the majority. In total, there were $2+2+2=6$ girls and $2+2+3=7$ boys at the table.
(On the diagram, it shows exactly how the children were seated at the table. The first speaker is outlined in a frame.)
## Answer
7 boys.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$:$ Folkiore
It is known that among 63 coins there are 7 counterfeit ones. All counterfeit coins weigh the same, all genuine coins also weigh the same, and a counterfeit coin is lighter than a genuine one. How can you determine 7 genuine coins in three weighings using a balance scale without weights?
|
1) Let's set aside one coin and put 31 coins on each pan of the scales. If the pans balance, then we have set aside the counterfeit coin, and there are 3 counterfeit coins on each pan. If one of the pans is heavier, then there are no more than three counterfeit coins on it. Thus, after the first weighing, we will be able to select 31 coins, among which there are no more than three counterfeit ones.
2) Take this group of coins and perform a similar operation: set aside one coin again and put 15 coins on each pan of the scales. After this weighing, we will be able to select 15 coins, among which there is no more than one counterfeit.
3) Repeating a similar operation for the third time, we will end up with 7 genuine coins.
At an international congress, 578 delegates from different countries arrived. Any three delegates can communicate with each other without the help of others (although one of them may have to translate the conversation between the other two). Prove that all delegates can be accommodated in double rooms of a hotel in such a way that any two living in the same room can communicate without external help.
## Solution
Take any three delegates; some two of them can definitely communicate with each other without a translator. We will house them in one room.
We will repeat this operation until only 4 delegates remain. As it is not difficult to verify by enumeration, they can always be divided into 2 rooms in such a way that those living in each room can communicate with each other without external help.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Mathematical logic (other).]
Several natives met (each one is either a liar or a knight), and each one declared to all the others: “You are all liars.” How many knights were among them?
#
|
Think, for example, could there have been 3 knights?
## Solution
Two (or more) knights cannot be, because then the statement made by the knight would not be true. It is also impossible to have no knights at all - then the statements of all liars would be true. The only possibility left is - 1 knight, the rest are liars.
Send a comment
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
At the end of the quarter, Vovochka wrote down his current grades for singing in a row and placed a multiplication sign between some of them. The product of the resulting numbers turned out to be 2007. What grade does Vovochka get for singing in the quarter? ("Kol" is not given by the singing teacher.)
#
|
$2007=3 \cdot 3 \cdot 223=9 \cdot 223=3 \cdot 669$. Since there is no grade 9, only the first option fits. Since Vovochka has more threes than twos, and the last grade, no matter how you rearrange the factors, is a three, we can hope that he will get a three for the quarter.
## Answer
Three.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.