problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
From the four inequalities $2x > 70$, $x < 25$, $x > 5$, and $x > 5$, two are true and two are false. Find the value of $x$, given that it is an integer.
|
Given that $x$ is an integer, the inequalities can be rewritten as: $x>35, x>6$ and $x>5$. If it is not true that $x>5, x>6$ and $x>35$ - one is true and two are false.
Since the third inequality implies the first two, and the second implies the first, there is only one option: the first inequality is true, and the other two are false. Therefore, $5<x \leq 6$, which means $x=6$.
## Answer
$x=6$.
|
6
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2+ $[$ Prime numbers and their properties $]$
Four kids were discussing the answer to a problem.
Kolya said: "The number is 9."
Roman: "It's a prime number."
Katya: "It's an even number."
And Natasha said that the number is divisible by 15.
One boy and one girl answered correctly, while the other two were wrong. What is the actual answer to the problem?
|
If Kolya answered correctly, then both girls were wrong, since the number 9 is odd and does not divide by 15. This means that Roman gave the correct answer. But a prime number does not divide by 15, and the only even prime number is 2.
## Answer
2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2+$
12 candidates for mayor were talking about themselves. After some time, one said: "They lied to me once." Another said: "Now it's twice." "Now it's three times" - said the third, and so on up to the 12th, who said: "Now they have lied 12 times." At this point, the host interrupted the discussion. It turned out that at least one candidate correctly counted how many times they had been lied to before them. So, how many times did the candidates lie in total?
|
## Solution
Assume that the first candidate lied. This means that before his statement, the number of false statements was not equal to 1. After his statement, this number increased by 1, so it became not equal to 2. Therefore, the second candidate also lied. Continuing this reasoning, we get that all candidates lied, which contradicts the condition of the problem. Therefore, the first candidate told the truth. Thus, the number of false statements was 1 both before and after his statement. Therefore, the second candidate lied. Continuing this reasoning, we get that all subsequent candidates also lied. Thus, all candidates except the first one lied, and one more lie was uttered before the described discussion. Therefore, the candidates lied a total of 12 times.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a physics class, the teacher set up the following experiment. He placed 16 weights with masses of $1, 2, 3, \ldots, 16$ grams on a balance scale so that one of the pans was heavier. Fifteen students took turns leaving the classroom and each took one weight, and after each student left, the balance changed its position and the opposite pan became heavier. Which weight could have remained on the scale?
|
Since at any given moment the masses on the scales differed by at least 1 gram, in order for the opposite scale to outweigh, it is necessary to remove a weight of no less than two grams. Therefore, no student could have taken a 1-gram weight when leaving the class.
## Answer
A 1-gram weight remained on the scales.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
In a row from left to right, there are 31 wallets, each containing 100 coins. From one of the wallets, some coins were moved: one coin to each of the wallets to the right of it. With one question, you can find out the total number of coins in any set of wallets. What is the minimum number of questions needed to reliably determine the "lightened" wallet?
|
It is enough to get an answer to the question "How many coins are there in total in the wallets with odd numbers?" Indeed, if the answer to it is " $1600+n$ " ( $n>0$ ), then the coins were moved from the wallet with an even number, to the right of which there were exactly $n$ wallets with odd numbers - that is, from the ( $2 n+1$ )-th wallet from the right. If, however, the answer to it is " $1600-n$ " ( $n>0$ ), then the coins were moved from the wallet with an odd number, to the right of which there were exactly $n$ wallets with even numbers - that is, from the $2 n$-th wallet from the right.
## Answer
In one question.
## Problem
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Fundamental Theorem of Arithmetic. Prime Factorization]
In the country of Anchuria, where President Miraflores is in power, the time for new presidential elections is approaching. The country has exactly 20 million voters, of which only one percent support Miraflores (the regular army of Anchuria). Miraflores, of course, wants to be elected, but on the other hand, he wants the elections to be "democratic." Miraflores defines a "democratic vote" as follows: all voters are divided into equal groups; each of these groups is then divided into some number of equal smaller groups, with larger groups potentially being divided into different numbers of smaller groups, and so on. In the smallest groups, a representative "elector" is chosen to vote in the larger group; the electors in this larger group choose an elector to vote in an even larger group, and so forth. Finally, the representatives of the largest groups choose the president. Miraflores divides the voters into groups at his discretion and instructs his supporters on how to vote. Can he organize "democratic" elections in such a way that he will be elected? (In each group, electors choose their representative by a simple majority. In the event of a tie, the opposition wins.)
|
We will divide the voters into groups of 5 people. In 66666 such groups, we can place 3 military personnel. As a result, we get 66666 military electors out of 4 million.
We will divide these 4 million electors into groups of 4 people, placing 3 military personnel in 22222 of them. As a result, we get 22222 military electors out of a million.
By repeating these two operations, we see that reducing the number of electors by 20 times, we reduce the number of military electors by 9 times. Sequentially, we get 2469 military electors out of 50000, 274 - out of 2500, 30 - out of 125. Further, dividing twice into groups of 5, we get three military electors out of five, which will allow the president to win.
## C
Can.
Send a comment
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tokarev S.i.
In a line, all integers from 1 to 100 are written in an unknown order. With one question about any 50 numbers, you can find out the order of these 50 numbers relative to each other. What is the minimum number of questions needed to definitely determine the order of all 100 numbers?
|
To find the desired order $a_{1}, a_{2}, \ldots, a_{100}$ of numbers in a row, it is necessary that each pair $\left(a_{i}, a_{i+1}\right), i=1,2, \ldots, 99$, appears in at least one of the sets about which questions are asked; otherwise, for two sequences $a_{1}, \ldots, a_{i}, a_{i+1}, \ldots, a_{100}$ and $a_{1}, \ldots, a_{i+1}, a_{i}, a_{100}$, all answers will be the same.
We will prove that after any two questions, a situation may arise where at least three more questions are needed to cover all pairs of adjacent numbers (not yet covered).
Let $k_{1}, k_{2}, \ldots, k_{50}$ be the order of the numbers about which the first question is asked, and $l_{1}, l_{2}, \ldots, l_{50}$ be the order of the numbers about which the second question is asked. We will construct a set $a_{1}, a_{2}, \ldots, a_{100}$ for which we cannot, by asking two more questions, uniquely determine the order of the numbers. Consider the situation where all numbers mentioned in both the first and second questions are in the same positions in the answers.
As the desired set, we will take the set where $k_{i}, l_{i} \in \{a_{2i-1}, a_{i}\}, i=1,2, \ldots, 50$, and, moreover, in each quartet $(a_{4m-3}, a_{4m-2}, a_{4m-1}, a_{4m})$,
$m=1,2, \ldots, 25$, no comparisons of adjacent pairs of numbers from this quartet were made in the first two questions. We will show that such a set exists.
Let $X$ be the set of numbers that did not appear in the first two questions. The following cases are possible:
$k_{2m-1}=l_{2m-1}, k_{2m}=l_{2m}$,
$k_{2m-1}=l_{2m-1}, k_{2m} \neq l_{2m}$,
$k_{2m-1} \neq l_{2m-1}, k_{2m} \neq l_{2m}$,
$k_{2m-1} \neq l_{2m-1}, k_{2m}=l_{2m}$,
For these cases, we will construct quartets $(a_{4m-3}, a_{4m-2}, a_{4m-1}, a_{4m})$ as follows: $(k_{2m-1}, *, *, k_{2m})$, $(k_{2m-1}, *, k_{2m}, l_{2m})$, $(k_{2m-1}, l_{2m-1}, k_{2m}, l_{2m})$,
$(k_{2m-1}, l_{2m-1}, *, k_{2m})$, where * can be any number from the set $X$ that did not appear in the questions and in the construction of previous quartets.
Thus, it is shown that after two questions, a situation is possible (regardless of the asker's desire) where no pair $(a_{i}, a_{i+1})$ for $i$ not divisible by 4 is covered. Each of the 100 numbers is part of at least one uncovered pair, and therefore, must appear in at least one of the subsequent questions.
Suppose that in this situation, all uncovered pairs can be covered in two questions; then each of the 100 numbers must appear in exactly one of such questions. Considering quartets of the form $(a_{4i-3}, a_{4i-2}, a_{4i-1}, a_{4i})$, $i=1,2, \ldots, 25$, note that if one number from such a quartet appears in a question, then the other three must also (otherwise, not all pairs of adjacent numbers in this quartet will be covered). But then the number of numbers in the set about which the question is asked must be divisible by 4. Since 50 is not divisible by 4, we have a contradiction. Therefore, it is impossible to determine the order of the numbers $1,2, \ldots, 100$ in a row with four questions.
We will show how to do this in five questions. The first question is about the set $M_{1}=\{1,2, \ldots, 50\}$, the second is about the set $M_{2}=\{51,52, \ldots, 100\}$. The set $M_{3}$ will consist of the 25 leftmost numbers of the set $M_{1}$ and the 25 leftmost numbers of the set $M_{2}$, and the set $M_{4}$ will consist of the 25 rightmost numbers of the set $M_{1}$ and the 25 rightmost numbers of the set $M_{2}$. The answer to the question about the set $M_{3}$ will clearly determine the numbers $a_{1}, a_{2}, \ldots, a_{25}$, and the answer to the question about the set $M_{4}$ will determine the numbers $a_{76}, a_{77}, \ldots, a_{100}$. The fifth question determines the order of the remaining 50 numbers in the desired row.
## Answer
In five questions.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|

7 wolves eat 7 sheep in 7 days. How many days will it take for 9 wolves to eat 9 sheep?
|
The number of wolves has increased by the same factor as the number of sheep, so the time of consumption will not change.
## Answer
In 7 days.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
I.v.
In the multiplication example written on the board, the hooligan Petya changed two digits. It became 4$\cdot$5$\cdot$4$\cdot$5$\cdot$4 = 2247. Restore the original example.
#
|
In the original example, at least one of the multipliers is even.
## Solution
In the resulting example, three multipliers are even, which means that at least one was even in the original example. Therefore, the product was an even number, meaning the last digit of the product was changed. Thus, no more than one digit on the left was changed. Therefore, in the original example, there were both fives and fours on the left, and the product ended in 0.
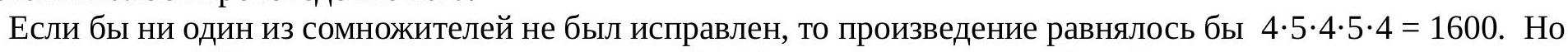
The number 1600 differs from the number 2240 by more than one digit. Therefore, exactly one of the multipliers was corrected, and the product is 2240. Therefore, one of the fives was corrected to a seven.

Author: Cherapanov.
Let $M$ be a finite set of numbers. It is known that among any three of its elements, there are two whose sum belongs to $M$.
What is the maximum number of elements that can be in $M$?
## Hint
Consider either the four largest or the four smallest numbers.
## Solution
An example of a set with 7 elements: $\{-3, -2, -1, 0, 1, 2, 3\}$.
We will prove that a set $M = \{a_1, a_2, \ldots, a_n\}$ with $n > 7$ numbers does not have the required property. We can assume that $a_1 > a_2 > a_3 > \ldots > a_n$ and $a_4 > 0$ (changing the signs of all elements does not change our property). Then $a_1 + a_2 > a_1 + a_3 > a_1 + a_4 > a_1$, which means that none of the sums $a_1 + a_2$, $a_1 + a_3$, and $a_1 + a_4$ belong to the set $M$. Moreover, the sums $a_2 + a_3$ and $a_2 + a_4$ cannot both belong to $M$, since $a_2 + a_3 > a_2 + a_4 > a_2$. Therefore, for at least one of the triples $(a_1, a_2, a_3)$ and $(a_1, a_2, a_4)$, the sum of any two of its elements does not belong to the set $M$.
## Answer
7 elements.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Kalinin }}$ D.:
In the room, there are 20 chairs of two colors: blue and red. On each chair sits either a knight or a liar. Knights always tell the truth, and liars always lie. Each of the seated individuals claimed that they were sitting on a blue chair. Then they somehow rearranged themselves, after which half of those seated said they were sitting on blue chairs, and the rest said they were sitting on red chairs. How many knights are now sitting on red chairs?
|
Initially, all knights sit on blue chairs, and all liars on red ones. Therefore, the number of knights who moved to red chairs is equal to the number of liars who moved to blue chairs. Both groups claimed they were sitting on red chairs. In total, 10 people said they were sitting on red chairs. Therefore, the number of knights sitting on red chairs is $10: 2=5$.
Answer
## 5.
Send a comment
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The kindergarten received cards for reading lessons: some have "MA" written on them, and others have "NYA". Each child took three cards and started forming words from them. It turned out that 20 children can form the word "MAMA", 30 children can form the word "NYANYA", and 40 children can form the word "MANYA". How many children have all three cards the same?
#
|
Notice that each child has three cards, and there are two different inscriptions on them.
## Solution
Since each child has three cards, and there are only two inscriptions in total, it is necessary that two inscriptions must match, meaning each can form either the word MAMA (20 such children) or the word NYANYA (30 such children). Therefore, the total number of children is 50. If a child has all three cards the same, they cannot form the word MANYA (there were 40 such cases). Therefore, three identical cards are held by $50-40=10$ children.
## Answer
10 children.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a certain kingdom, there were 32 knights. Some of them were vassals of others (a vassal could have only one suzerain, and a suzerain was always richer than his vassal). A knight who had at least four vassals bore the title of baron. What is the maximum number of barons that could be under these conditions?
(The kingdom had a law: "a vassal of my vassal is not my vassal".)
#
|
Evaluation. 8 barons should have 32 vassals, and the richest knight cannot be anyone's vassal. Example. Let 24 knights be vassals of six barons, and all these barons be vassals of the richest Baron. In total, 7 barons.
## Answer
7 barons.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Yashchenko I.V.
In Mexico, ecologists have succeeded in passing a law according to which each car must not be driven at least one day a week (the owner reports to the police the car's number and the "day off" for the car). In a certain family, all adults wish to drive daily (each for their own business!). How many cars (at a minimum) should the family have if there are
a) 5 adults? b) 8 adults?
|
b) If no more than one car "rests" each day, then there are no more than 7 cars in total.
## Solution
a) Five cars are not enough, because on the day when one of the cars is "resting," someone will have no car to ride in. Six cars, obviously, are enough.
b) If no more than one car "rests" each day, then the total number of cars is no more than the number of days in a week, which is seven. But this is obviously not enough. Therefore, on some day, two cars are resting, and on that day, at least 8 cars are needed. In total, 10 cars are required. We have proven that it is impossible to manage with fewer than ten cars.
Ten cars are sufficient: for example, each working day, two cars rest.
## Answer
a) 6 ; b) 10 cars.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Around a round table, 30 people are sitting - knights and liars (knights always tell the truth, while liars always lie). It is known that each of them has exactly one friend at the same table, and a knight's friend is a liar, while a liar's friend is a knight (friendship is always mutual). When asked "Is your friend sitting next to you?", those sitting every other person answered "Yes". How many of the others could have also answered "Yes"?
|
All those sitting at the table are paired as friends, which means there are an equal number of knights and liars. Consider any pair of friends. If they are sitting next to each other, the knight will answer "Yes" to the given question, and the liar will answer "No." If they are not sitting next to each other, their answers will be opposite. In any case, exactly one of the pair of friends will answer "Yes." Therefore, all the other 15 answers will be "No."
## Answer
0.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Mathematical logic (other) ] [ Divisibility of numbers. General properties ]
On a meadow, ladybugs gathered. If a ladybug has six spots on its back, it always tells the truth, and if it has four spots, it always lies, and there were no other ladybugs on the meadow. The first ladybug said: "Each of us has the same number of spots on our backs." The second said: "All of us together have 30 spots on our backs." - "No, all of us together have 26 spots on our backs," - the third ladybug objected. "Exactly one of these three told the truth," - each of the other ladybugs declared. How many ladybugs gathered on the meadow?
|
If the first ladybug tells the truth, then the second and third should also tell the truth, as they should have the same number of spots on their backs as the first. But the second and third ladybugs contradict each other, so at least one of them is lying. Therefore, the first ladybug is also lying.
Suppose each of the first three ladybugs lied, then all the others lied as well, since none of these three told the truth. This means all the ladybugs are liars. But in this case, the first ladybug actually told the truth, which cannot be. Therefore, the first three ladybugs cannot lie simultaneously, so either the second or the third told the truth, and the other two are liars. Thus, each of the other ladybugs told the truth.
Therefore, there are two ladybugs with four spots on their backs, and several ladybugs with six spots on their backs, and in total, the spots on the backs of all the ladybugs are either 30 or 26. But \(30 - 2 \cdot 4 = 22\), which is not divisible by 6, so the total number of spots is 26, and the number of honest ladybugs is \((26 - 2 \cdot 4) : 6 = 3\). Therefore, there are five ladybugs on the meadow.
## Answer
5 ladybugs.
Author: Zhenedarov R.G.
30 girls - 13 in red dresses and 17 in blue dresses - were dancing in a circle around a Christmas tree.
Later, each of them was asked if the girl to their right was in a blue dress. It turned out that those who answered correctly were exactly those standing between girls in dresses of the same color. How many girls could have answered affirmatively?
## Solution
Consider any girl. The colors of the dresses of her left and right neighbors could be: blue - blue, blue - red, red - blue, red - red. A girl answers "yes" only in the first two cases; that is, exactly when her left neighbor is in a blue dress.
But the left neighbor was in a blue dress for exactly 17 girls, so the answer "yes" was given 17 times.
## Answer
17 girls.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Raskin M.A.
On an island, there live chameleons of five colors. When one chameleon bites another, the color of the bitten chameleon changes according to some rule, and the new color depends only on the color of the biter and the color of the bitten. It is known that $\$ 2023 \$$ red chameleons can agree on a sequence of bites, after which all of them will turn blue. For what smallest $\$ \mathrm{k} \$$ can we guarantee that $\$ \mathrm{k} \$$ red chameleons can agree to turn blue?
For example, the rules might be such that if a red chameleon bites a green one, the bitten one changes to blue; if a green chameleon bites a red one, the bitten one remains red, i.e., "changes to red"; if a red chameleon bites a red one, the bitten one changes to yellow, and so on. (The specific rules for color changes may be different.)
#
|
Let's start with an example of rules under which at least 5 red chameleons would be necessary for the described recoloring. Let's number the colors so that red is the first color and blue is the last. Then, let the rules be as follows: a chameleon of color $k 1$ can reduce the number of its color by a bite from a chameleon of color $\$ \mathrm{l}<\mathrm{k} \$$$. In other words, chameleons of colors $\$ 1$, \dots, $\mathrm{k} \$$ can become colors $\$ 1, \backslash d o t s, \mathrm{k}-1 \$$$. By applying this reasoning several times, we get that our chameleons can all change their color to blue.
Comment. It is not hard to notice that for $\$ n \$$ colors, $\$ n \$$ chameleons will be needed. In fact, this problem is one of many questions around (in general) Petri nets. With even minor changes to the problem, the minimum size of the initial population can increase significantly.
For example, suppose that upon biting, both chameleons can change their color differently, and the goal is to reach a state with one green chameleon and many blue ones. In this case, the minimum number can grow faster than any polynomial in $\$ n \$$, and even any function of the form $\$ n \wedge\{n \wedge\{n \wedge\{\backslash d o t s\}\}\} \$$! This was proven quite recently; the so-called Ackermann function appears in the answer.
Fortunately, if all chameleons must be of one color both at the beginning and at the end, the situation simplifies significantly. The requirement that only one of the chameleons changes color upon biting further simplifies the situation. It corresponds to "immediate observation" or "one-way communication" in Petri nets (immediate observation, one-way communication). In this variant, it has been shown, for example, using combinatorial methods accessible to school students, that if there are two sets of chameleon colors and after adding the same number of blue chameleons to the first, it becomes possible to obtain the second, then it is sufficient to add $\$$ d $^{\prime} \wedge 3 \$$ chameleons.
## Answer
for $\$ \mathrm{k}=5 \$$\.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic operations. Numerical identities ] Joke problems
Calculate the product
$$
\left(100-1^{2}\right)\left(100-2^{2}\right)\left(100-3^{2}\right) \ldots\left(100-25^{2}\right)
$$
#
|
Pay attention to the factors hidden behind the ellipsis.
## Solution
The product is 0, since among the factors there will be (100 - $10^{2}$).
## Answer
0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ [equations in integers $]$ ]
In the room, there are three-legged stools and four-legged chairs. When people sat on all these seats, there were 39 legs in the room.
How many stools are in the room?
|
According to the condition, there are five- and six-legged creatures in the room, with a total of 39 legs. The number of legs of the five-legged creatures ends in 0 or 5. But it cannot end in 0: then the number of legs of the six-legged creatures would end in 9. In such a case, the number of five-legged creatures can be 1, 3, 5, or 7. By trial and error, we determine that there are 3 five-legged creatures and 4 six-legged creatures. That is, there are 4 chairs and 3 stools in the room.
## Answer
3 stools.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
|Rabbits sawed several logs. They made 10 cuts and got 16 chunks. How many logs did they saw
#
|
Recall problem 89914 - the problem about how the rabbits made 10 cuts to split one log.
## Solution
From each log, you get one more chunk than the number of cuts. Since there are 6 more chunks, it means there were 6 logs.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Text problems ] [Algorithm theory]
Pouring milk. From an 8-liter bucket filled with milk, you need to measure out 4 liters using empty 3-liter and 5-liter buckets.
|
Let's record the solution in a table.
| Eight-liter bucket | Five-liter bucket | Three-liter bucket |
| :---: | :---: | :---: |
| 8 | | |
| 3 | 5 | |
| | 5 | |
| 3 | 2 | 3 |
| :---: | :---: | :---: |
| 6 | 2 | |
| 6 | | 2 |
| 1 | 5 | 2 |
| 4 | 4 | 3 |
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Three mad painters started painting the floor each in their own color. One managed to paint 75% of the floor red, another 70% green, and the third 65% blue. What part of the floor is definitely painted with all three colors?
|
Evaluation. 25% of the floor is not painted red, 30% of the floor is not painted green, and 35% of the floor is not painted blue.
25+30+35=90. From this, it follows that at least 10% of the floor is painted with all three colors.
An example where exactly 10% is painted with all three colors is clear from the evaluation: 25% of the floor is painted in two colors: blue and green, 30% - in red and green, 35% - in red and blue.
## Answer
10%.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Andjans A.
In a table with $m$ rows and $n$ columns, a horizontal move is defined as a permutation of the elements in the table such that each element remains in the same row it was in before the permutation; similarly, a vertical move is defined ("row" in the previous definition is replaced with "column"). Determine such a $k$ that any permutation of the elements in the table can be achieved in $k$ moves (of any kind), but there exists a permutation that cannot be achieved in fewer moves.
|
The case $m=1$ or $n=1$ is trivial.
Let $m \neq 1$ and $n \neq 1$. We will show that two moves are insufficient. Suppose in the initial table, the top-left

square is \begin{tabular}{|l|l|}
\hline \& $b$
\cline { 1 - 3 } \& $c$
. In one move, $d$ cannot be converted to $a$, so $d$ must move on the first move, either to the position of $b$ or to the position of $c$. Due to symmetry, it makes no difference; suppose $d$ moves to the position of $c$. Then, by the same reasoning, $a$ moves to the position of $b$, so the top-left square becomes
$*$ \& $a$
\hline \& $*$
\cline { 1 - 3 }
\end{tabular} (where $*$ denotes any element). In this case, $c$ remains in the second row. The next, second move must be vertical to place $d$ and $a$ in their correct positions, but $c$ is not in the first column, so the required table cannot be achieved.
For further discussion, we need the
Marriage Theorem. Suppose there are $n$ young men, and for each $k \leq n$, the following condition is satisfied: for any group of $k$ young men, there are at least $k$ young women who are acquainted with these young men. Then each young man can be married to a young woman he knows.
Lemma. Suppose in an $m \times n$ table, the numbers from 1 to $m$ are arranged such that each number appears $n$ times. Then in each row, one can choose a number such that all chosen numbers are distinct.
Proof. We will consider that in the $j$-th row, the numbers represent the indices of the young women acquainted with the $j$-th young man (the fact that one number can appear multiple times is irrelevant). The condition of the Marriage Theorem is satisfied: in any $k$ rows, there are at least $k$ distinct numbers. Indeed, in $k$ rows, there are $k n$ positions, and $k-1$ distinct numbers in the table occupy $(k-1) n < k n$ positions.
We will now show that any permutation of the elements of the table in the problem can be achieved in three moves.
By the lemma, in each row, one can choose an element that, after the permutation, should end up in different rows. We will gather them in the first column with a horizontal move. Applying the lemma to the table without the first column, we will gather (with the same move) in the second column elements that should also end up in different rows, and so on.
The second move will rearrange the elements in each column so that all elements of the table end up in the rows where they should be after the permutation (in each column, the elements whose interests are distinct are gathered, so this is possible).
The third move will place the numbers in each row in their correct positions.
## Answer
If $m=1$ or $n=1$, then $k=1$; otherwise, $k=3$.
Send a comment
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Zkov G.
A bank serves a million customers, the list of whom is known to Ostap Bender. Each has a six-digit PIN code, and different customers have different codes. In one move, Ostap Bender can choose any customer he has not yet chosen and peek at the digits of the code at any $N$ positions (he can choose different positions for different customers). Ostap wants to find out the code of the millionaire Koreiko. For what smallest $N$ can he guarantee to do this?
|
It is not difficult to do when $N=3$. Since any combination of the first three digits occurs exactly 1000 times, by looking at these digits for everyone except Koreiko, Bender will know them for Koreiko as well. Then it is sufficient to look at the last three digits of Koreiko's code.
We will prove that when $N<3$, it is impossible to reliably determine Koreiko's code $K$. For each of the 6 positions, choose a code that differs from $K$ only in that position. The corresponding digit in the chosen code will be called bad. Suppose Bender is unlucky, and on the first check of a non-Koreiko code, he gets the chosen code, but does not check the bad digit (there are four unchecked positions, so a code with a bad digit in one of these positions could have been selected). Suppose the same happens on the second and third checks of non-Koreiko codes (there are four unchecked positions, and of the four chosen codes with bad digits in these positions, no more than two have been previously checked, so such a code could have been selected). When all codes have been checked, we will see which $N<3$ positions have been checked in code $K$. Among the four unchecked positions, at least one coincides with the position of the bad digit in one of the three checked chosen codes - code $L$. But if $L$ and $K$ are swapped, the results of all checks will not change. Therefore, Bender will not be able to distinguish $L$ from $K$.
## Answer
When $N=3$.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a box, there are cards numbered with natural numbers from 1 to 2006. On the card numbered 2006 lies the card numbered 2005, and so on down to 1. In one move, it is allowed to take one top card (from any box) and place it either at the bottom of an empty box, or on a card with a number one greater. How many empty boxes are needed to transfer all the cards to another box?
|
The answer follows from the general fact: let the number of cards be $n$, where $2^{\mathrm{k}-1} \leq n < 2^{\mathrm{k}}$. If we assume that all cards can be placed in $k$ boxes, then card $a$ still needs to be moved so that all cards end up in one box. For this, at some point, it will be necessary to occupy the "top" cards of $k$ other boxes. In these boxes, "bottom" cards cannot be present (since directly under a "top" card, there can only be card $a$, which is still in box $i$). This means that all "bottom" cards are already in one box -- a contradiction. Therefore, it will require at least $k+1$ boxes.
## Answer
11 boxes.
## Problem
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let's call a natural number "remarkable" if it is the smallest among all natural numbers with the same digit sum as it has.
How many three-digit remarkable numbers exist?
#
|
"Remarkable" numbers with the sum of digits from 1 to 18 are either single-digit or two-digit. Therefore, remarkable three-digit numbers have a sum of digits from 19 to 27. Each such sum corresponds to one remarkable number. Consequently, there are nine three-digit "remarkable" numbers.
## Answer
9 numbers.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the pond, 30 pikes were released, which gradually eat each other. A pike is considered full if it has eaten no less than three pikes (full or hungry). What is the maximum number of pikes that can become full?
|
The number of pikes eaten is not less than three times the number of satiated pikes.
## Solution
Let $s$ be the number of satiated pikes. Then they together have eaten no fewer than $3s$ pikes. Since each pike can only be eaten once, and at least one pike remains at the end, $3s < 30$. Therefore, $s \leq 9$.
We will provide an example where exactly 9 pikes are satiated. Suppose 7 pikes (from the 3rd to the 9th) ate 21 pikes (from the 10th to the 30th; each ate 3 pikes). After this, 9 pikes remain. The first and second pikes can become satiated by eating 6 pikes (from the 4th to the 9th).
## Answer
9 pikes.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Each of the thirty sixth-graders has one pen, one pencil, and one ruler. After their participation in the Olympiad, it turned out that 26 students lost a pen, 23 - a ruler, and 21 - a pencil. Find the smallest possible number of sixth-graders who lost all three items.
|
From the condition, it follows that four sixth-graders have a pen, seven have a ruler, and nine have a pencil. Thus, at least one item can be owned by no more than $4+7+9=20$ people. Therefore, no fewer than $30-20=10$ people have lost all three items.
All three items will be lost by exactly 10 people if each of the other twenty loses exactly two items.
## Answer
10 sixth-graders.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Lobanov M. S.
Around a round rotating table, on which there are 8 white and 7 black cups, 15 gnomes are sitting. They have put on 8 white and 7 black caps. Each gnome takes a cup whose color matches the color of their cap and places it in front of them, after which the table is rotated randomly. What is the maximum number of matches between the color of the cup and the cap that can be guaranteed after the table is rotated (the gnomes choose how to sit, but they do not know how the table will be rotated)?
|
Let's consider an arbitrary arrangement of cups and write down their colors in a row. Below this row, we will also write down all its different cyclic shifts — a total of 14. We will count how many color matches there will be in the same position in the original arrangement and in the arrangements obtained by shifts. For black cups, the color matches will be exactly in 6 shifts, and for white cups — in 7 shifts. Therefore, the total number of color matches for 14 shifts will be \(7 \cdot 6 + 8 \cdot 7 = 98\). This means there exists a shift in which there will be no more than \(98/14 = 7\) matches with the original arrangement.
Consider such an arrangement of cups: ббббчбчббччбччч. By direct verification, one can confirm that all its cyclic shifts have exactly 7 matches with it.
## Answer
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## In the city, there are 57 bus routes. It is known that:
1) from any stop, you can get to any other stop without transferring;
2) for each pair of routes, there is one, and only one, stop where you can transfer from one of these routes to the other
3) each route has no fewer than three stops.
How many stops does each of the 57 routes have?
|
Let there be $n$ stops on some route $a$. Take a stop $B$ that route $a$ does not pass through. From $B$, there is a route to each of the $n$ stops on route $a$, and there is exactly one such route, since two different routes cannot have two common stops. Each route passing through $B$ intersects route $a$. Therefore, exactly $n$ routes pass through $B$.
Now it is clear that any route $b$ that does not pass through stop $B$ has exactly $n$ stops.
Indeed, as above, the number of stops on it is equal to the number of routes passing through $B$. Consider an arbitrary point $A$ on route $a$, take a stop $C$ on route $A B$ different from $A$ and $B$, and draw a route $c$ through it, different from $A B$. Route $c$ does not pass through $B$, so it has $n$ stops. Stop $A$ does not lie on $c$, so, as shown above, $n$ routes (including $a$) pass through $A$. The same is true for each point on route $a$.
Thus, a total of $n(n-1)$ routes, different from $a$, pass through the points of route $a$, and there is also the route $a$ itself. These are all the routes in the city.
Solving the equation $n(n-1)+1=57$, we find that $n=8$.
## Answer
8 stops.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kalinin D.A.
Find the maximum number of colors in which the edges of a cube can be painted (each edge in one color) so that for each pair of colors there are two adjacent edges painted in these colors. Adjacent are considered edges that have a common vertex.
#
|
There are several ways to color the edges of a cube in six colors while satisfying the condition of the problem. Here is one of them:
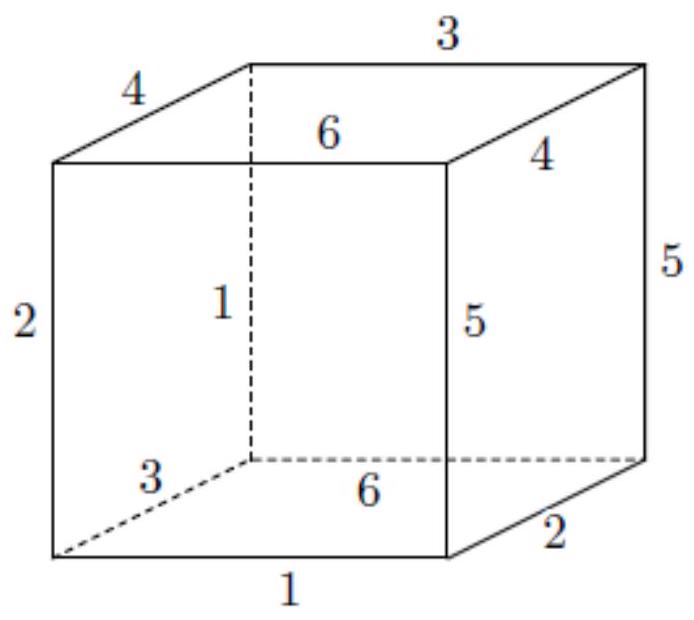
We will show that more than six colors are not possible.
Suppose we have colored the edges of the cube in seven or more colors. Since the cube has a total of 12 edges, there must be a color, for example, white, in which only one edge is painted. For each edge of the cube, there are exactly four adjacent edges. Therefore, the white color can be paired with no more than four other colors, which means there cannot be more than five different colors in total. This is a contradiction.
## Answer
6 colors.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Graph Traversal ]
There is a group of islands connected by bridges in such a way that from any island, you can reach any other island. A tourist visited all the islands, crossing each bridge exactly once. He visited the Triplet Island three times. How many bridges lead to the Triplet Island if the tourist
a) did not start or end on it?
b) started on it but did not end on it
c) started and ended on it?
|
a) If the Triple tourist entered the island 3 times and exited 3 times, that means he used 6 bridges.
b) In this case, the tourist entered the island twice, but exited three times.
## Answer
a) 6 bridges; b) 5 bridges; c) 4 bridges.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Pascal's Triangle and Newton's Binomial ]
How many times greater is the sum of the numbers in the 101st row of Pascal's Triangle compared to the sum of the numbers in the 100th row?
#
|
Let in the 100th row stand the numbers $c_{0}, c_{1}, \ldots, c_{100}$. Then in the 101st row stand the numbers $c_{0}, c_{0}+c_{1}, c_{1}+c_{2}, \ldots, c_{99}+$ $c_{100}, c_{100}$
their sum is $2 c_{0}+2 c_{1}+\ldots+2 c_{100}$.
## Otvet
Twice.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Graph Theory (Miscellaneous)]
Several Top Secret Objects are connected by an underground railway in such a way that each Object is directly connected to no more than three others, and from each Object, it is possible to reach any other by underground travel with no more than one transfer. What is the maximum number of Top Secret Objects?
#
|
Evaluation. From this Object, you can reach three Objects in one "move", and with a transfer - to another $2 \cdot 3=6$ Objects. Therefore, there are no more than 10 Objects.
An example with 10 Objects is shown in the figure.
## Task
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\begin{array}{l}[\text { Combinatorics (other) })] \\ [\text { Extreme Principle (other) })]\end{array}\right.$
In how many ways can the numbers from 1 to 100 be permuted so that adjacent numbers differ by no more than 1?
|
Where can the number 1 be placed?
## Solution
Next to the number 1, only the number 2 can stand, so 1 must be at the edge. Suppose 1 is at the beginning. Then the next number is 2, the next is 3 (no other numbers can be next to 2), the next is 4, and so on. We get the arrangement $1, 2, \ldots, 99, 100$.
If 1 is at the end, then similarly, the arrangement is uniquely restored as 100, 99, ..., 2, 1.
## Answer
In two ways.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Announce $A$.
$N$ friends simultaneously learned $N$ pieces of news, with each person learning one piece of news. They started calling each other and exchanging news.
Each call lasts 1 hour. Any number of news items can be shared in one call.
What is the minimum number of hours required for everyone to learn all the news? Consider three cases:
a) $N=64$,
b) $N=55$
c) $N=100$.
|
a) A piece of news known to one of the friends will be known to no more than two (including the first) after 1 hour, no more than four after the second hour, ..., and no more than 32 after the 5th hour. Therefore, it will take no less than 6 hours.
We will show that 6 hours are sufficient. The conversations can proceed according to the following scheme. We will number the participants with six-digit binary numbers. In the $k$-th hour, people whose numbers differ only in the $k$-th digit will converse (for example, in the 3rd hour, $a b c 0 d e$ will converse with $a b c 1 d e$). In this way, the number of pieces of news known to each person doubles every hour. (For example, after the 2nd hour, each person knows four pieces of news known to four participants whose numbers differ from his number in the first two digits.)
Remark. This method of conversation is only suitable for powers of two. Below is a method that works for any even numbers.
c) That 6 hours are insufficient is clear from a). We will show that 7 hours are sufficient. We will number the participants by elements of $\mathbf{Z}_{50} \times \{-1,1\}$. In the 1st hour, the participant with number $(x, y)$ will converse with $(x, -y)$, in the 2nd hour with $(x+1, -y)$, in the 3rd hour with $(x+3, -y)$, in the 4th hour with $(x+7, -y)$, in the 5th hour with $(x+15, -y)$, in the 6th hour with $(x+31, -y)$, and in the 7th hour with $(x+63, -y)$. In this way, the number of pieces of news each friend has doubles every hour (except the last). (We will number the pieces of news the same way as the friends who know them at the beginning. After the 1st hour, the participant with number $(0,0)$ knows all pieces of news with $x=0$, after the 2nd hour all pieces of news with $x=0,1$, after the 3rd hour all pieces of news with $x=0,1,2,3$; and so on.)
b) In the first hour, one of the participants does not converse with anyone. As seen from a), the others will need at least 6 more hours to learn his news.
We will divide the participants into two groups: 32 and 23 people. In the 1st hour, all members of the second group will converse with members of the first. Over the next 5 hours, the members of the first group will exchange news (according to the scheme from a) or c); as a result, each will know all the news). In the last hour, they will inform all the members of the second group with all the information.
## Answer
a) 6 hours, b) 7 hours, c) 7 hours.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Combinations and Permutations ]
[ $\underline{\text { Directed Graphs }}$ ]
In the discussion, 15 deputies participated. Each of them, in their speech, criticized exactly $k$ of the remaining 14 deputies.
For what smallest $k$ can we assert that there will be two deputies who criticized each other?
|
Consider a directed graph where the vertices correspond to deputies, and an edge leading from $A$ to $B$ means that deputy $A$ has criticized deputy $B$.
## Solution
If each deputy has criticized 8 others, then the number of edges in the graph is $15 \cdot 8 = 120$, which is greater than the number of pairs $C_{15}^{2} = 105$ of its vertices. This proves that some two vertices are connected by at least two edges, meaning that there will be two deputies who have criticized each other.
On the other hand, suppose 15 deputies are sitting around a round table and each has criticized the seven deputies sitting next to them in a clockwise direction. It is easy to see that in this case, no two deputies have criticized each other.
## Answer
For $k=8$.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Sorting in ascending (descending) order ] [ Classical combinatorics (other). $\quad]$
a) A traveler stopped at an inn, and the owner agreed to accept rings from a golden chain the traveler wore on his wrist as payment for his stay. However, he set a condition that the payment should be daily: each day the owner should have one more ring than the previous day. The chain, which was closed in a loop, contained 11 rings, and the traveler planned to stay exactly 11 days, so he agreed. What is the minimum number of rings he needs to cut to be able to pay the owner?
b) How many rings should the chain consist of so that the traveler can stay at the inn for the maximum number of days, given that he can only cut $n$ rings?
|
a) It is enough to cut two rings so that pieces of three and six rings are separated. On the third day, the traveler gives the piece of three rings and receives two rings as change, and on the sixth day, the piece of six rings and receives five rings as change.
b) Arrange the resulting pieces of the chain (not counting the cut rings) in increasing order of the number of rings in them: \(a_{1} \leq a_{2} \leq \ldots\) Clearly, \(a_{1} \leq n+1\) (otherwise, it would be impossible to pay for the \((n+1)\)-th day), \(a_{2} \leq a_{1}+n+1 \leq 2(n+1), a_{3} \leq a_{2}+a_{1}+n+1 \leq 4(n+1), \ldots\) Moreover, the number of pieces does not exceed \(n\). Therefore, the chain contains no more than \(n+(n+1)\left(1+2+2^{2}+\ldots+2^{n-1}\right)=(n+1) 2^{n}-1\) rings.
By taking pieces of the maximum possible length \(\left(a_{k}=(n+1) 2^{k-1}, k=1, \ldots, n\right)\), we obtain a chain of \((n+1) 2^{n}-1\) rings.
## Answer
a) 2 rings. b) From \((n+1) 2^{n}-1\) rings.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A kindergarten received cards for reading lessons: some have "MA" written on them, and others have "NYA".
Each child took three cards and started forming words from them. It turned out that 20 children could form the word "MAMA", 30 children could form the word "NYANYA", and 40 children could form the word "MANYA". How many children have all three cards the same?
#
|
Notice that each child has three cards, and there are two different inscriptions on them.
## Solution
Since each child has three cards, and there are only two inscriptions in total, it is necessary that two inscriptions must match, meaning each child can form either the word MAMA (20 such children) or the word NYANYA (30 such children). Therefore, the total number of children is 50. If a child has all three cards the same, they cannot form the word MANYA (there were 40 such cases). Therefore, three identical cards are held by $50-40=10$ children.
## Answer
10 children.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tompsongo A.K.
In a certain kingdom, there were 32 knights. Some of them were vassals of others (a vassal could have only one suzerain, and the suzerain was always richer than his vassal). A knight who had at least four vassals bore the title of baron. What is the maximum number of barons that could be under these conditions?
(The kingdom had a law: "a vassal of my vassal is not my vassal.")
#
|
Evaluation. 8 barons should have 32 vassals, and the richest knight cannot be anyone's vassal. Example. Let 24 knights be vassals of six barons, and all these barons be vassals of the richest Baron. In total, 7 barons.
## Answer
7 barons.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
|
| | $[$ Pigeonhole Principle (other) $)]$ | |
In a company of 10 people, 14 pairwise arguments have occurred. Prove that it is still possible to form a group of three friends.
|
The total number of ways to choose a company of three people is $C_{10}^{3}=120$. Each quarrel destroys no more than eight such companies, so the number of destroyed companies is no more than $8 \cdot 14=112$. Therefore, at least 8 friendly companies remain.
|
8
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
$\begin{aligned} & \text { [Systems of points and segments. Examples and counterexamples] } \\ & {[\quad \underline{\text { Classical combinatorics (other) }}]}\end{aligned}$
On a plane, 10 equal segments were drawn, and all their points of intersection were marked. It turned out that each point of intersection divides any segment passing through it in the ratio $3: 4$. What is the maximum possible number of marked points?
|
On each segment, there are no more than two points. On the other hand, each intersection point belongs to at least two segments. Therefore, there are no more than $10 \cdot 2: 10=10$ points. An example with 10 points is shown in the figure.
## Answer
10 points.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The probability that a purchased light bulb will work is $0.95$.
How many light bulbs need to be bought so that with a probability of $0.99$ there are at least five working ones among them?
#
|
Let's take 6 light bulbs. The probability that at least 5 of them will be working is the sum of the probabilities that exactly 5 of them will be working and that all 6 will be working, which is $6 \cdot 0.95^{5} \cdot 0.05 + 0.95^{6} = 0.9672$.
Let's take 7 light bulbs. The desired probability is $21 \cdot 0.95^{5} \cdot 0.05^{2} + 7 \cdot 0.95^{6} \cdot 0.05 + 0.95^{7} = 0.9962$.
## Answer
7 light bulbs.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Folklore }}$
At a chamber music festival, six musicians gathered. At each concert, some of the musicians perform, while the others listen from the audience. What is the minimum number of concerts required for each of the six musicians to have listened to (from the audience) all the others?
|
A total of $6 \cdot 5=30$ auditions are needed. No more than 9 auditions can take place in one concert. Therefore, there must be at least four concerts.
Example: Musicians with numbers (4,5,6), (2,3,6), (1,3,5), and (1,2,4) perform in the concerts.
## Answer
In 4 concerts.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Folkoro
In a certain state, the airline system is arranged in such a way that each city is connected by air routes
to no more than three other cities, and from any city, you can reach any other city with no more than one
transfer. What is the maximum number of cities that can be in this state?
|
Evaluation. From a fixed city $A$, one can directly reach no more than three cities, and with one transfer - no more than $3 \cdot 2=6$ additional cities. Thus, the total number of cities can be no more than ten. For an example of a network of 10 cities, see the figure below.
## Answer
10.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 [Pairings and Groupings; Bijections $]
Three people are playing table tennis, with the player who loses a game giving up their place to the player who did not participate in it. In the end, it turned out that the first player played 10 games, the second - 21. How many games did the third player play?
#
|
The first player plays the rarest every second game.
## Solution
According to the condition, the second player played 21 games, so there were at least 21 games in total. Out of every two consecutive games, the first player must participate in at least one, which means there were no more than $2 \cdot 10+1=21$ games. Therefore, a total of 21 games were played, and the second player participated in each of them. In 10 games, he faced the first player, and in the remaining 11 games, he faced the third player.
## Answer
11 games.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Around a round table, 10 boys and 15 girls sat down. It turned out that there were exactly 5 pairs of boys sitting next to each other.
How many pairs of girls sitting next to each other are there?
#
|
How many groups of boys sitting next to each other are there at the table?
## Solution
Groups of boys sitting next to each other alternate with groups of girls sitting next to each other. Let the number of groups of boys sitting next to each other be $k$. Then the number of groups of girls sitting next to each other is also $k$. In a group of $n$ boys sitting next to each other, there are exactly $n-1$ pairs of boys sitting next to each other. Since we have a total of 10 boys and $k$ groups, there are $10-k$ pairs of boys sitting next to each other. According to the problem, $k=5$. Therefore, the number of pairs of girls sitting next to each other is $15-5=10$.
## Answer
10 pairs.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $M$ - be a finite set of numbers. It is known that among any three of its elements, there will be two whose sum belongs to $M$.
What is the maximum number of elements that can be in $M$?
|
Consider either the four largest or the four smallest numbers.
## Solution
Example of a set of 7 elements: $\{-3,-2,-1,0,1,2,3\}$.
We will prove that the set $M=\left\{a_{1}, a_{1}, \ldots, a_{n}\right\}$ of $n>7$ numbers does not have the required property. We can assume that $a_{1}>a_{2}>a_{3}>\ldots>a_{n}$ and $a_{4}>0$ (changing the signs of all elements does not change our property). Then $a_{1} + a_{2} > a_{1} + a_{3} > a_{1} + a_{4} > a_{1}$, which means that none of the sums $a_{1} + a_{2}$, $a_{1} + a_{3}$, and $a_{1} + a_{4}$ belong to the set $M$. Moreover, the sums $a_{2} + a_{3}$ and $a_{2} + a_{4}$ cannot both belong to $M$, since $a_{2} + a_{3} > a_{2} + a_{4} > a_{2}$. Therefore, at least one of the triples $\left(a_{1}, a_{2}, a_{3}\right)$ and $\left(a_{1}, a_{2}, a_{4}\right)$ has the property that the sum of any two of its elements does not belong to the set $M$.
## Answer
7 elements.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$[$ Classical combinatorics (miscellaneous).]
In a dark room, on a shelf, there are four pairs of socks of two different sizes and two different colors lying in a random order. What is the smallest number of socks that need to be moved from the shelf to a suitcase, without leaving the room, to ensure that the suitcase contains two pairs of different sizes and colors?
#
|
First, note that seven socks are sufficient. Indeed, only one sock is not taken, which means all pairs of socks except one are taken. Therefore, in the suitcase, there are two pairs of different colors and sizes, specifically the pair that differs from the one not taken only by color, and the pair that differs from the one not taken only by size.
If one sock from each of the two pairs of the same color is left on the shelf, then there will not be two pairs of different colors in the suitcase. Therefore, six socks may not be enough.
## Answer
7 socks.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the number of zeros with which the number $11^{100}-1$ ends.
#
|
Use the binomial expansion of the expression $(10+1)^{100}$.
## Solution
$S=(10+1)^{100}-1=\ldots+(100 \cdot 99 \cdot 98: 6) \cdot 10^{3}+(100 \cdot 99: 2) \cdot 10^{2}+100 \cdot 10+1=\ldots+(33 \cdot 49) \cdot 10^{5}+495000+1000=A$ +496000, where all terms in place of the ellipsis are divisible by $10^{4}$, meaning $A$ ends with at least four zeros. Therefore, the number $S$ ends with three zeros (and the fourth last digit of the number $S$ is 6).
## Answer
Three zeros.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Planar graphs. Euler's formula ]
In the country of Lake, there are seven lakes connected by ten non-intersecting channels, such that one can sail from any lake to any other. How many islands are there in this country?
#
|
Consider a planar graph, where the vertices correspond to lakes, and the edges - to channels. Let it divide the plane into $F$ pieces. By Euler's formula (problem $\underline{30759}$) $7-10+F=2$, so $F=5$. One of these pieces is the mainland, and the rest are islands.
## Answer
4 islands.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Frankin B.R.
In a tournament with 20 athletes, 10 referees were involved. Each athlete played against each other once, and each match was officiated by exactly one referee. After each game, both participants took a photo with the referee. A year after the tournament, a stack of all these photos was found. It turned out that not everyone could be identified as either an athlete or a referee. How many such people could there be?
|
Let's call a person suspicious if we cannot determine whether they are an athlete or an referee. Note that each referee was only photographed with athletes, that is, no more than 20 people. On the other hand, each athlete was photographed with all other athletes and at least one referee, that is, no fewer than 20 people. Therefore, every suspicious person was photographed with exactly 20 people.
Note that if an athlete was photographed with exactly 20 people, then 19 of his games were judged by the same referee, meaning that the same person is present on all the photographs with him.
Let $X$ be some suspicious person. Since we can consider $X$ as an athlete, then, as mentioned above, there is some $Y$ present on all the photographs with him. These two were photographed together 19 times, so one of them must be a referee. Consequently, the third person on each of these photographs must be an athlete.
Thus, we can identify 19 athletes, and the remaining athlete is either $X$ or $Y$. All the others are referees. If we could determine the status of at least one of the pair $X$ and $Y$, we could determine the other as well, and there would be no suspicious people at all. Therefore, there are exactly two suspicious people - $X$ and $Y$.
## Answer
Two.
Submit a comment
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A.K.
In the plane, there is an open, non-self-intersecting broken line with 31 segments (adjacent segments do not lie on the same straight line). Through each segment, a line containing this segment was drawn. As a result, 31 lines were obtained, some of which may have coincided. What is the smallest number of different lines that could have resulted?
#
|
Evaluation. Except for the ends, the broken line has 30 vertices, and each is the intersection of two lines. If there are no more than eight lines, then there are no more than $7 \cdot 8: 2=28$ intersection points - a contradiction.
Example - in the figure.
## Answer
9 lines.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A.K. Tolpygo
A broken line consisting of 37 segments is given, which is not closed and does not intersect itself. A straight line has been drawn through each segment.
What is the smallest number of different lines that could result?
#
|
Suppose there are eight lines. Then they have no more than 28 intersection points, but the broken line cannot have vertices not at the intersection points of the lines, except for the initial and final points, meaning it cannot have more than 29 segments. An example for nine lines is shown in the figure.
(A circle is depicted, with the vertices of a regular nonagon marked on it. Each of them is connected to two others by a straight line. The broken line in question runs along these lines, marked in white in the figure.)
## Answer
9 lines.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Lifshits $\underline{\text { K. }}$.
Hydras consist of heads and necks (each neck connects exactly two heads). With one sword strike, one can cut all the necks coming out of some head $A$ of the hydra. But in this case, from head $A$, one neck will instantly grow to all heads with which $A$ was not connected. Heracles defeats the hydra if he manages to cut it into two parts not connected by necks. Find the smallest $N$ such that Heracles can defeat any hundred-necked hydra by striking no more than $N$ times.
|
Let's move on to a graph where heads are vertices, necks are edges, and a strike on the necks coming out of head $A$ is called inverting vertex $A$.
If there is a vertex $X$ of degree no more than 10, it is sufficient to invert its neighbors, and it will separate. If there is a vertex connected to all vertices except $n$ (where $n \leq 9$), then it is necessary to first invert this vertex, and then those $n$ vertices with which it was not initially connected, and then this vertex will separate.
If, however, each vertex is connected to at least 11 and not connected to at least 10 others, then there are at least 22 vertices, and at least $22 \cdot 11 / 2 > 100$ edges.
An example of a hydra that cannot be cut with fewer than nine strikes: two groups of 10 heads and 100 necks, connecting all pairs of heads from different groups.
Note that the state of the edge between vertices $A$ and $B$ does not change if and only if vertices $A$ and $B$ are inverted an even number of times in total. Therefore, the order of cutting vertices does not matter, and it is meaningless to invert a vertex twice.
Suppose no more than nine strikes have been made on our hydra. Then in each group, there is one non-inverted head left, and therefore there is a neck from one group to the other; moreover, all non-inverted heads form a connected set. On the other hand, each non-inverted head is connected to all inverted heads in its group. Therefore, if at least one head is inverted in each part, the hydra remains connected. If all inverted heads are in one part, the hydra also remains connected: each non-inverted head in this part is connected to the entire other part and to all inverted heads.
## Answer
$N=10$.
Submit a comment
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A cube with a side of 10 is divided into 1000 smaller cubes with an edge of 1. In each small cube, a number is written, and the sum of the numbers in each column of 10 cubes (in any of the three directions) is 0. In one of the cubes (denoted as $A$), the number 1 is written. Three layers, parallel to the faces of the cube (each layer having a thickness of 1), pass through cube A. Find the sum of all the numbers in the cubes that do not lie in these layers.
|
Through the given cube $A$ pass one horizontal layer $G$ and two vertical layers. The sum of all numbers in 81 vertical columns not included in the last two layers is 0. From this sum, we need to subtract the sum $S$ of the numbers lying in the cubes at the intersection of these columns with $G$ (there are 81 such cubes). These cubes are completely covered by nine columns lying in $G$. The sum of all numbers in these columns (which is 0) exceeds $S$ by the sum of nine numbers lying in a perpendicular column containing $A$. The latter sum is obviously -1. Hence, $S=1$. Finally, we have: $0-1=-1$.
## Answer
$-1$.
|
-1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In Anchuria, a unified state exam is taking place. The probability of guessing the correct answer to each question on the exam is 0.25. In 2011, to obtain a certificate, one needed to answer three questions correctly out of 20. In 2012, the School Administration of Anchuria decided that three questions were too few. Now, one needs to answer six questions correctly out of 40. The question is, if one knows nothing and simply guesses the answers, in which year is the probability of obtaining an Anchurian certificate higher - in 2011 or in 2012?
|
If a graduate guesses the answers, the Unified State Exam (EGE) can be considered a Bernoulli scheme with a success probability of $p=0.25$ and a failure probability of $q=0.75$. In 2011, to pass the exam, one needed to answer at least three questions correctly. It is more convenient to find the probability of the opposite event, i.e., the probability of answering fewer than three questions correctly. This is the sum of the probabilities of answering 0, 1, and 2 questions correctly, i.e., $\quad \sum_{k=0}^{2} C_{20}^{k} p^{k} q^{20-k} \approx 0.091$; therefore, the probability of passing the exam is approximately 0.909. Similarly, in 2012, the probability of failing the exam is
$$
\sum_{k=0}^{5} C_{40}^{k} p^{k} q^{40-k} \approx 0.043, \text { and }
$$
the probability of passing the exam is approximately 0.957.
## Answer

While waiting for customers, a watermelon seller sequentially weighed 20 watermelons (weighing 1 kg, 2 kg, 3 kg, ..., 20 kg), balancing the watermelon on one scale pan with one or two weights on the other pan (possibly identical). The seller recorded on a piece of paper the weights of the weights he used. What is the smallest number of different numbers that could have appeared in his records, if the weight of each weight is an integer number of kilograms?
## Solution
With one or two weights of 1 kg, 3 kg, 5 kg, 7 kg, 9 kg, and 10 kg, any of the given watermelons can be weighed. Indeed, $2=1+1, 4=3+1$, $6=5+1, 8=7+1, 11=10+1, 12=9+3, 13=10+3, 14=9+5, 15=10+5, 16=9+7, 17=10+7, 18=9+$ $9, 19=10+9, 20=10+10$. Thus, six different numbers could have been recorded.
We will show that five types of weights are insufficient for the required weighings. If there are five weights, then, generally speaking, twenty watermelons can be weighed. Specifically: five watermelons can be balanced with single weights, five with double weights, and the remaining $5 \cdot 4: 2=10$ watermelons with pairs of different weights. However, each combination of weights must be used exactly once.
Note that half of the watermelons have an odd mass. Let $k$ of the five weights have an odd mass, and $5-k$ have an even mass. Then the number of ways to weigh a watermelon with an odd mass is exactly $k+k(5-k)=6k-k^2$. However, for no $k=0,1,2,3,4,5$ does this expression equal 10 (this can be verified either by substitution or by solving the quadratic equation $\left.6k-k^2=10\right)$.
## Answer
6 numbers.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Coloring Vertex Degree
20 phones are connected by wires in such a way that each wire connects two phones, each pair of phones is connected by no more than one wire, and no more than two wires extend from each phone. It is necessary to color the wires (each wire entirely in one color) so that the wires extending from each phone are of different colors. What is the smallest number of colors sufficient for such a coloring?
|
We will represent phones as points and the wires connecting them as segments connecting these points. Since no more than two segments come out of each point, the resulting graph breaks down into open paths and simple cycles. Note that an open path can be painted with two colors, and a simple cycle with three. For this, it is enough to paint every other segment in an open path, and in a cycle, paint one segment in color 3, and the remaining ones alternately in colors 1 and 2. Additionally, note that if there is a triangle in the resulting graph, two colors will not be enough. Therefore, the number of colors needed is 3.
## Answer
Three colors.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[The product of the lengths of the segments of chords and the lengths of the segments of secants] [Properties and characteristics of an isosceles triangle.] [Thales' theorem and the theorem of proportional segments]
On the extension of side $A D$ of rhombus $A B C D$ beyond point $D$, point $K$ is taken. Lines $A C$ and $B K$ intersect at point $Q$. It is known that $A K=14$ and that points $A, B$ and $Q$ lie on a circle with radius 6, the center of which lies on segment $A A$. Find $B K$.
|
Let $O$ be the center of the circle. Use the similarity of triangles $K Q O$ and $K B A$.
## Solution
Let $O$ be the center of the circle, $F$ be the second intersection point of the circle with the line $A$. Since triangle $A O Q$ is isosceles $(O A=O Q=6)$, then
$\angle A Q O=\angle O A Q=\angle B A Q$. Therefore, $O Q \| A B$. Hence, $K Q: K B=K O: K A=4: 7,4 / 7 K B^{2}=K Q \cdot K B=K F \cdot K A=$ 28, from which $B K=7$.
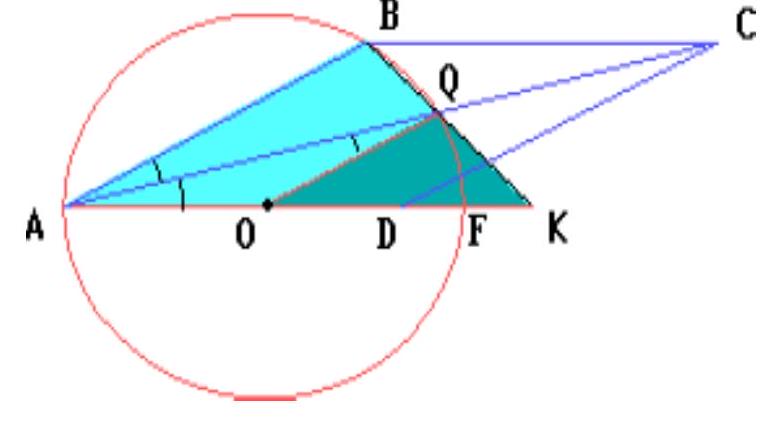
## Answer
7.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In triangle $A B C$, the bisector $C D$ of the right angle $A C B$ is drawn; $D M$ and $D N$ are the altitudes of triangles $A D C$ and $B D C$, respectively.
Find $A C$, given that $A M=4, B N=9$.
#
|
Note that $M C=M D=D N$. From the similarity of triangles $A M D$ and $D N B$, it follows that $A M: M D=D N: N B$, that is, $M C^{2}=A M \cdot N B=36$. Therefore,
$A C=A M+M C=4+6=10$.
## Answer
10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## [ Quadrilaterals (extreme properties).]
For what value of the height does a rectangular trapezoid with an acute angle of $30^{\circ}$ and a perimeter of 6 have the maximum area
#
|
Express the area of the given trapezoid through its height and apply the Cauchy inequality.
## Solution
Let $h$ be the height of the trapezoid, $3 x$ be the sum of the bases. Then the larger lateral side of the trapezoid is $2 h$, and the perimeter is $3 x + 3 h = 6$. The area of the trapezoid is $\frac{3 x h}{2} = \frac{3}{2} \left( \frac{x + h}{2} \right)^{2} = \frac{3}{2}$, and equality is achieved when $h = x = 2 - h$, that is, when $h = 1$.
## Answer
When $h = 1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the greatest possible number of rays in space emanating from a single point and forming obtuse angles with each other
#
|
Answer: 4. We will consider vectors instead of rays. We can assume that the first vector has coordinates (1, $0,0)$. Then the other vectors have coordinates ( $x_{i}, y_{i}, z_{i}$ ), where $x_{i}0$, and thus, $y_{\mathrm{i}}2$ the inequality $x_{\mathrm{i}} x_{\mathrm{j}}+y_{\mathrm{i}} y_{\mathrm{j}}+z_{\mathrm{i}} z_{\mathrm{j}}0$ and $y_{\mathrm{i}} y_{\mathrm{j}}>0$ holds, so $z_{\mathrm{i}} z_{\mathrm{j}}<0$, i.e., the numbers $z_{\mathrm{i}}$ and $z_{\mathrm{j}}$ have different signs. There cannot be more than two such numbers.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
From a point located outside a circle, two mutually perpendicular tangents are drawn to the circle. The radius of the circle is 10. Find the length of each tangent.
#
|
## Solution
The quadrilateral formed by the given tangents and radii drawn to the points of tangency is a square.
## Answer
10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left.\frac{\text { [Inscribed and Circumscribed Circles ]}}{\text { Rhombuses Properties and Characteristics }}\right]$
The side of the rhombus is 8 cm, and the acute angle is $30^{\circ}$. Find the radius of the inscribed circle.
|
The diameter of the inscribed circle is equal to the height of the rhombus.
## Solution
The diameter of the inscribed circle is equal to the height of the rhombus, and the height, dropped from a vertex to the opposite side, is the leg of a right triangle opposite the angle of $30^{\circ}$.
Therefore, the height of the rhombus is 4, and the desired radius is 2.
## Answer
2 cm.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A circle is inscribed in a right angle. A chord connecting the points of tangency is equal to 2. Find the distance from the center of the circle to this chord.
#
|
The diagonals of a square are equal.
## Solution
The quadrilateral formed by the tangents and radii drawn to the points of tangency is a square.
The desired segment is half the diagonal of this square, i.e., 1.
## Answer
1
Send a comment
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Frankin 5.
A billiard table has the shape of a $2 \times 1$ rectangle, with pockets located at the corners and at the midpoints of the longer sides. What is the minimum number of balls that need to be placed inside the rectangle so that each pocket lies on a line with some two balls?
|
Let there be only three balls. A line passing through a pair of balls inside a rectangle intersects the boundary of the rectangle exactly at two points. We have six pockets, so we need at least three lines. Three balls will give three lines only if these lines form a triangle. However, there are only seven lines passing through two pockets, and no three of them form a triangle with vertices inside the billiard table (see figure).
An example for four balls is indicated in the same figure.
## Answer
Four balls.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bakayev E.V.
On a line, four points are marked, and one more point is marked outside the line. In total, there are six triangles with vertices at these points.
What is the maximum number of them that can be isosceles?
|
Let's take an isosceles triangle with an angle of $108^{\circ}$. We will divide this angle into three equal parts (see figure). The six resulting triangles will be isosceles.
## Answer
All six.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Vassily H.S.
Consider all possible closed broken lines with six segments, all vertices of which lie on a circle.
a) Draw such a broken line that has the maximum possible number of self-intersections.
b) Prove that a broken line of this kind cannot have a greater number of self-intersections.
|
a) The figure shows a six-segment broken line with seven self-intersection points.
b) We will prove that such a broken line cannot have more than seven self-intersections. Let the total number of self-intersections be \( N \). For each segment, consider the number of self-intersection points that lie on this segment, and denote the sum of these numbers by \( S \). Then \( S \geq 2N \) (if two segments intersect at one point, this point is counted twice in the sum, if three or more - more than twice). On each segment, there can be no more than three self-intersection points, since besides this segment and the two adjacent to it, there are only three other segments that can intersect with it. Moreover, three points can only be on a "diagonal" segment: such that of the four vertices that are not its endpoints, two lie on one half-plane from it, and the other two - on the other. (If on one side of the segment there is only one vertex, then it is impossible to draw more than two segments to the vertices lying on the other side of the segment.) There can be at most three such "diagonal" segments. On each of the others, there are no more than two self-intersection points, so \( S \leq 3 \cdot 2 + 3 \cdot 3 = 15 \), that is, \( N \leq S / 2 \leq 7.5 \).
|
7
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
9
A point lying inside a circumscribed $n$-gon is connected by segments to all vertices and points of tangency. The triangles formed by this are alternately painted red and blue. Prove that the product of the areas of the red triangles is equal to the product of the areas of the blue triangles.
|
Let $h_{1}, \ldots, h_{n}$ be the distances from a given point to the corresponding sides, and $a_{1}, \ldots, a_{n}$ be the distances from the vertices of the polygon to the points of tangency. Then the product of the areas of both the red and blue triangles is $a_{1} \ldots a_{n} h_{1} \ldots h_{n} / 2^{n}$.
What is the maximum number of acute angles a convex polygon can have?
## Solution
Let a convex $n$-gon have $k$ acute angles. Then the sum of its angles is less than $k \cdot 90^{\circ} + (n-k) \cdot 180^{\circ}$. On the other hand, the sum of the angles of an $n$-gon is $(n-2) \cdot 180^{\circ}$. Therefore, $(n-2) \cdot 180^{\circ} < k \cdot 90^{\circ} + (n-k) \cdot 180^{\circ}$, i.e., $k < 4$. Since $k$ is an integer, $k \leq 3$.
For any $n \geq 3$, there exists a convex $n$-gon with three acute angles (see figure).
Submit a comment
|
3
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
[The triangle formed by the bases of two altitudes and a vertex]
The side of the triangle is $\sqrt{2}$, and the angles adjacent to it are $75^{\circ}$ and $60^{\circ}$.
Find the segment connecting the bases of the altitudes drawn from the vertices of these angles.
|
Let $B M$ and $C N$ be the altitudes of triangle $A B C$, $B C=\sqrt{2}$, $\angle B=75^{\circ}$, $\angle C=60^{\circ}$. Then $\angle A=45^{\circ}$.
Triangle $A M N$ is similar to triangle $A B C$ with a similarity coefficient of $\cos 45^{\circ}$. Therefore, $M N=$ $B C \cdot \cos 45^{\circ}=1$.
## Answer
1.
Problem
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Algebraic problems on the triangle inequality ]
In a triangle, two sides are equal to 3.14 and 0.67. Find the third side, given that its length is an integer.
#
|
Apply the triangle inequality.
## Solution
Let the integer $n-$ be the length of the third side. Then
$$
3.14-0.67<n<3.14+0.67
$$
From this, we find that $n=3$.
## Answer
3.
## Problem
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Homothetic Circles]
Inside an angle, there are three circles $\mathrm{S}_{1}, \mathrm{~S}_{2}, \mathrm{~S}_{3}$, each of which touches the two sides of the angle, and circle $S_{2}$ touches circles $S_{1}$ and $S_{3}$ externally. It is known that the radius of circle $S_{1}$ is 1, and the radius of circle $S_{3}$ is 9. What is the radius of circle $S_{2}$?
|
Homothety with the center at the vertex of the angle, translating circle $S_{1}$ to circle $S_{2}$, also translates circle $S_{2}$ to circle $S_{3}$.
## Solution
Consider the homothety $\mathrm{H}$ with the center at the vertex of the angle, translating circle $\mathrm{S}_{1}$ to circle $\mathrm{S}_{2}$. Circle $\mathrm{S}_{2}$, when this homothety is applied, transitions to a circle that is tangent to the sides of the angle and externally tangent to the circle $\mathrm{H}\left(\mathrm{S}_{1}\right)=\mathrm{S}_{2}$; thus, circle $\mathrm{S}_{2}$, when the homothety is applied, transitions to circle $S_{3}$. Denote the radius of circle $S_{i}$ by $R_{i}, i=1,2,3$, and the homothety coefficient of $H$ by $k$. Then $\mathrm{R}_{2}=\mathrm{kR}_{1}$ and $\mathrm{R}_{3}=\mathrm{kR} \mathrm{R}_{2}$, from which $\mathrm{R}_{2}{ }^{2}=\mathrm{R}_{1} \mathrm{R}_{3}$. Substituting the values $\mathrm{R}_{1}=1$ and $\mathrm{R}_{3}=9$, we finally get $\mathrm{R}_{2}{ }^{2}=9$ and $\mathrm{R}_{2}=3$.
## Answer
3.00
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ inscribed quadrilaterals]
Three consecutive sides of an inscribed quadrilateral are in the ratio 1:2:3. Find its sides if it is known that the perimeter is 24 m.
#
|
Since the sums of the opposite sides of a circumscribed quadrilateral are equal to each other, two parts fall on the fourth side. Therefore, the sides are $\frac{1}{8}, \frac{1}{4}, \frac{3}{8}$ and $\frac{1}{4}$ of the perimeter, i.e., 3, 6, 9, 6.
## Answer
3 cm, 6 cm, 9 cm, 6 cm.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Dirichlet's Principle (finite number of points, lines, etc.).] [ Central angle. Arc length and circumference length ]
On a circle of radius 1, a point $O$ is marked and a notch is made to the right with a compass of radius $l$. From the resulting point $O_{1}$, another notch is made in the same direction with the same radius, and this is done 1968 times. After this, the circle is cut at all 1968 notches, resulting in 1968 arcs. How many different arc lengths can result from this?
|
We will prove by induction on $n$ that the number of different arcs after $n$ cuts does not exceed 3. For $n=2$, this is obvious. Let $A_{k}$ denote the cut with number $k$. Suppose $n$ cuts have been made and the point $A_{n}$ falls on the ARC $A_{k} A_{l}$. Then the point $A_{n-1} 1$ falls on the arc $A_{k}-1 A_{l-} 1$. Therefore, if $k, l \neq 1$, no new lengths will appear, and the required statement is proved. Now suppose, for example, that $l=1$. We will prove that then the length of any arc $A_{p} A_{q}$ between neighboring cuts is equal to the length of one of the arcs $A_{k} A_{1}, A_{n} A_{1}, A_{1} A_{s}$, where $A_{s}$ is the nearest cut to $A_{1}$, different from $A_{n}$.
Indeed, if $p, q \neq 1$, the length of the arc $A_{p} A_{q}$ is equal to the length of the arc $A_{p-} 1 A_{q-}-1$, and there are no other cuts between the cuts $A_{p-} 1$ and $A_{q-} 1$ except possibly $A_{n}$. Thus, in a finite number of steps, we arrive at one of the three considered arcs.
## Answer
no more than three.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic. Mental calculation, etc.] [ Volume of a parallelepiped ]
A cube with a side of 1 m was sawn into cubes with a side of 1 cm and laid in a row (in a straight line). What length did the row turn out to be
#
|
We get $100 \times 100 \times 100=1000000$ (cm) or 10000 m = 10 km.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9}
On a ruler, three marks are made: 0, 2, and 5. How can you measure a segment equal to 6 using it?
#
|
$5-2=3$, so you can lay down a segment of length 3. Two such segments give a segment equal to 6.
Send a comment
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Sharygin I.F.
A rectangle is composed of six squares (see the right figure). Find the side of the largest square if the side of the smallest one is 1.
|
The side of the largest square is equal to the sum of the sides of two squares: the next one in the clockwise direction and the smallest one.
## Solution
Note that the side of the largest square is equal to the sum of the sides of two squares: the next one in the clockwise direction and the smallest one. Denoting the side of the largest square as $x$, we can sequentially express the sides of the other squares: $x-1, x-2, x-3, x-3$ (see the diagram). Now note that the length of the upper side of the rectangle is $x+(x-1)$, and the length of the lower side is $(x-2)+(x-3)+(x-3)$. But the opposite sides of the rectangle are equal. We get the equation
$$
x+(x-1)=(x-2)+(x-3)+(x-3)
$$
From this, $2x-1=3x-8$ and, therefore, $x=7$.
| $x$ | | $x-1$ |
| :---: | :---: | :---: |
| $x-3$ | $x-3$ | $x-2$ |
## Answer
7.00
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Prokopenko D:
Around triangle $A B C$, a circle $\Omega$ is described. Let $L$ and $W$ be the points of intersection of the angle bisector of angle $A$ with side $B C$ and circle $\Omega$, respectively. Point $O$ is the center of the circumcircle of triangle $A C L$. Restore triangle $A B C$ if the circle $\Omega$ and points $W$ and $O$ are given.
|
Let $O^{\prime}$ be the center of $\Omega$. Then the lines $O^{\prime} O$ and $O^{\prime} W$ are perpendicular to the sides $A C$ and $B C$, so the directions of these sides are known. Moreover,
$\angle C O L=2 \angle C A L=2 \angle L C W$ and, therefore, $\angle O C W=90^{\circ}$ (see the figure). Consequently, $C$ is the intersection point of the circle $\Omega$ and the circle with diameter $O W$.
Send a comment
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9 |
In triangle $A B C$, it is known that $\angle B A C=75^{\circ}, A B=1, A C=\sqrt{6}$. A point $M$ is chosen on side $B C$, such that $\angle$ ВАМ $=30^{\circ}$. Line $A M$ intersects the circumcircle of triangle $A B C$ at point $N$, different from $A$. Find $A N$.
|
Denote $A N$ as $x$, express $B N$ and $C N$ through the circumradius of triangle $A B C$, and apply the Law of Cosines to triangles $A B N$ and $A C N$ (or use Ptolemy's theorem).
## Solution
## First Method.
Let $A N=x, R$ be the circumradius of the triangle. Then
$$
B N=2 R \sin 30^{\circ}=R, C N=2 R \sin 45^{\circ}=R \sqrt{2}
$$
By the Law of Cosines in triangles $A B N$ and $A C N$, we find that
$$
\begin{gathered}
B N^{2}=R^{2}=A B^{2}+A N^{2}-2 A B \cdot A N \cos 30^{\circ}=1+x^{2}-x \sqrt{3} \\
C N^{2}=2 R^{2}=6+x^{2}-2 \sqrt{6} x \cdot \frac{1}{\sqrt{2}}=6+x^{2}-2 x \sqrt{3}
\end{gathered}
$$
From the resulting system of equations, we find that $x^{2}=4$. Therefore, $A N=x=2$.
## Second Method.
Let $R$ be the radius of the circle. In the inscribed quadrilateral $A B N C$, we have:
$$
D N=2 R \sin 30^{\circ}=R, C N=2 R \sin 45^{\circ}=R \sqrt{2}, D C=2 R \sin 75^{\circ}
$$
By Ptolemy's theorem,
$$
A B \cdot C N+A C \cdot B N=A N \cdot B C \text {, or } R \sqrt{2}+R \sqrt{6}=A N \cdot 2 R \sin 75^{\circ} \text {. }
$$
Therefore,
$$
A N=\frac{\sqrt{2}+\sqrt{6}}{2 \sin 75^{\circ}}=\frac{\sqrt{2}+\sqrt{6}}{2 \cdot \frac{\sqrt{2}+\sqrt{6}}{4}}=2
$$
## Answer
2.00
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Trapezoids Auxiliary similar triangles $]$
Point $M$ is located on the lateral side $A B$ of trapezoid $A B C D$, such that $A M: B M=2: 1$. A line passing through point $M$ parallel to the bases $A D$ and $B C$ intersects the lateral side $C D$ at point $N$. Find $M N$, if $A D=18, B C=6$.
|
Let's draw the diagonal $B D$. Suppose it intersects the segment $M N$ at point $P$. According to the theorem of proportional segments,
$B P: P D = C N: N D = B M: A M = 1: 2$. Triangle $B M P$ is similar to triangle $B A D$ with a similarity ratio of $B M / B A = 1 / 3$, and triangle $D N P$ is similar to triangle $D C B$ with a similarity ratio of $D N / N C = 2 / 3$, so $M P = 1 / 3 A D = 1 / 3 \cdot 18 = 6$, $N P = 2 / 3 B C = 4$, $M N = M P + N P = 6 + 4 = 10$.
## Answer
10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[
Thales' Theorem and the Theorem of Proportional Segments
] Difficulty [Ratio of Areas of Triangles with a Common Base or Common Height]
In triangle $ABC$, with an area of 6, a point $K$ is taken on side $AB$, dividing this side in the ratio $AK: BK = 2: 3$, and a point $L$ is taken on side $AC$, dividing $AC$ in the ratio $AL: LC = 5: 3$. The point $Q$, the intersection of lines $CK$ and $BL$, is 1.5 units away from line $AB$. Find the side $AB$.
#
|
Draw a line through point $K$ parallel to $BL$, until it intersects side $AC$ at point $M$. By Thales' theorem, $LM = 3/5 AL = CL$. Therefore, $CQ = KQ$.
## Answer
4. Send a comment
## Problem
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10}
Points $A, B, C, D$ are marked on a sheet of paper. A recognition device can perform two types of operations with absolute accuracy: a) measure the distance in centimeters between two given points; b) compare two given numbers. What is the minimum number of operations this device needs to perform to definitely determine whether the quadrilateral $A B C D$ is a rectangle?
|
To determine whether $A B C D$ is a rectangle, it is sufficient to check the equalities $A B=C D$, $B C=A D$, and $A C=B D$ - a total of 9 operations (3 operations for each equality: two measurements and one comparison).
A rectangle $ABCD$ will be a square if $A B=B C$ - for this, one more, the 10th, operation of comparing the lengths of segments $A B$ and $B C$ is needed. We will prove that a smaller number of operations will not suffice in both cases, i.e., that all the specified operations must be performed. Indeed, if we do not know that two opposite sides of a quadrilateral are equal, we cannot even assert that $A B C D$ is a parallelogram, since an isosceles trapezoid (its diagonals are equal) is also possible. Therefore, checking the equalities $A B=C D$ and $B C=A D$ is necessary. If we do not know that $A C=B D$, then $A B C D$ can be any parallelogram. Thus, checking the equality of the diagonals is also necessary. Finally, in the case of a square, it is also necessary to check the equality of two adjacent sides.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
On the table, there are 9 apples, forming 10 rows with 3 apples in each (see the figure).
It is known that the weights of nine rows are the same, while the weight of the tenth row differs from them. There are electronic scales, on which you can find out the weight of any group of apples for one ruble. What is the minimum number of rubles you need to pay to determine which row's weight differs?
#
|
Before spending money, let's think
Let $l_{1}, l_{2}, l_{3}$ be the weights of the three highlighted (see fig. a) diagonal rows, and $v_{1}, v_{2}, v_{3}$ be the weights of the three vertical rows. Then $l_{1}+l_{2}+l_{3}=v_{1}+v_{2}+v_{3}:$ both are simply the sum of the weights of all nine apples. But at least five of these six quantities are equal to the same value $t$, so all six are equal.
Similarly, we find that the weights of the other three diagonal rows are also equal to $t$. We have found nine rows, the weights of which are equal. Therefore, the weight of the remaining row, the horizontal one, is different.
## Answer
0 rubles.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Emelyanov L.A.
A square is cut into $n$ rectangles of size $a_{i} \times b_{i}, i=1, \ldots, n$.
For what smallest $n$ can all the numbers in the set $\left\{a_{1}, b_{1}, \ldots, a_{n}, b_{n}\right\}$ be distinct?
|
First, let's show that no rectangle (in particular, a square) can be cut into two, three, or four rectangles with different sides.
Obviously, if a rectangle is cut into two rectangles, they share a common side. Suppose the rectangle is cut into three rectangles. Then one of them contains two vertices of the original rectangle (since three rectangles must cover all four vertices of the original), and we reduce the problem to the previous case (the remaining part is a rectangle that needs to be divided into two).
Finally, assume that the rectangle is cut into four others. We have two possibilities - either one of the rectangles in the partition contains two vertices of the original (and we reduce the problem to cutting a rectangle into three parts), or each of the rectangles in the partition contains one vertex of the original.
In the latter case, consider the two rectangles containing the top vertices. They must touch (if there were a "gap" between them, it could not be covered by the two rectangles containing the other two vertices of the original). Suppose the height of the right rectangle is greater. Then the lower left rectangle has a common side with the upper left one (see the figure).
[^0]
## Answer
For $n=5$.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9
In a convex quadrilateral $A B C D$, diagonal $A C$ is drawn, $A D=7, B C=3, \angle A C D=60^{\circ}$. It is known that points $A, B, C, D$ lie on the same circle, and the perpendicular from point $A$ to side $C D$ bisects angle $\angle B A D$. Find the diagonal $A C$.
|
Find the sine of angle $A D C$.
## Solution
Let $A M$ be the perpendicular dropped from point $A$ to side $C D$. The ray $A C$ passes between the sides of angle $B A M$, so
$$
\angle B A M=\angle B A C+\angle C A M .
$$
Let $R$ be the radius of the circumscribed circle of quadrilateral $A B C D$. Then
$$
\begin{aligned}
R & =\frac{A D}{2 \sin \angle A C D}=\frac{7}{\sqrt{3}} \\
\sin \angle B A C & =\frac{B C}{2 R}=\frac{3 \sqrt{3}}{14}, \angle C A M=30^{\circ} .
\end{aligned}
$$
Therefore,
$$
\begin{aligned}
\sin \angle M A D= & \sin \left(\angle B A C+30^{\circ}\right)=\frac{3 \sqrt{3}}{14} \cdot \frac{\sqrt{3}}{2}+\frac{1}{2} \cdot \frac{13}{14}=\frac{11}{14} \\
& \sin \angle A D C=\cos \angle M A D=\frac{5 \sqrt{3}}{14}
\end{aligned}
$$
$$
A C=2 R \sin \angle A D C=\frac{2 \cdot 7}{\sqrt{3}} \cdot \frac{5 \sqrt{3}}{14}=5
$$
## Answer
5.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Rhombi. Properties and characteristics ] [Area of a triangle (using two sides and the angle between them).]
In an acute-angled triangle $A B C$, point $D$ is chosen on side $A B$ such that $\angle D C A=45^{\circ}$. Point $D_{1}$ is symmetric to point $D$ with respect to line $B C$, and point $D_{2}$ is symmetric to point $D_{1}$ with respect to line $A C$ and lies on the extension of segment $B C$ beyond point $C$. Find the area of triangle $A B C$, if $B C=\sqrt{3} C D_{2}, A B=4$.
|
$\angle B C D=30^{\circ}$, quadrilateral $D B D_{1} C-$ is a rhombus.
## Solution
Let $Q$ and $P$ be the points of intersection of segments $D D_{1}$ and $D_{1} D_{2}$ with lines $B C$ and $A C$. Denote $\angle A C B=\gamma$. Then
$$
\begin{gathered}
\angle D_{1} C P=\angle D_{2} C P=\angle A C B=\gamma \\
\angle Q C D_{1}=\angle Q C D=\angle A C B-\angle A C D=\gamma-45^{\circ}
\end{gathered}
$$
Since
$$
\angle Q C D_{1}+\angle D_{1} C P+\angle D_{2} C P=180^{\circ}
$$
From this, we find that $\gamma=75^{\circ}$, and $\angle D C B=30^{\circ}$.
Let $C D_{2}=x$. Then
$$
\begin{gathered}
D C=D_{1} C=D_{2} C=x, B C=x \sqrt{3} \\
Q C=D C \cos 30^{\circ}=\frac{x \sqrt{3}}{2}, B Q=B C-Q C=\frac{x \sqrt{3}}{2}=Q C
\end{gathered}
$$
Therefore, $D B D_{1} C-$ is a rhombus. Then
$$
\begin{gathered}
\angle A B C=\angle D C B=30^{\circ} \\
\angle B A C=180^{\circ}-\angle A B C-\angle A C B=180^{\circ}-30^{\circ}-75^{\circ}=75^{\circ} .
\end{gathered}
$$
Therefore, triangle $A B C-$ is isosceles, $B C=A B=4$. Consequently,
$$
S_{\triangle \mathrm{ABC}}=\frac{1}{2} A B \cdot B C \sin 30^{\circ}=\frac{1}{2} \cdot 4 \cdot 4 \cdot \frac{1}{2}=4
$$
## Answer
4.
Send a comment
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9 | |
A circle can be inscribed in quadrilateral $A B C D$. Let $K$ be the intersection point of its diagonals. It is known that $A B>B C>K C, B K=4+\sqrt{2}$, and the perimeter and area of triangle $B K C$ are 14 and 7, respectively.
Find $D C$.
|
Applying Heron's formula, find the sides of triangle $B K C$. Prove that $A C \perp B D$. Also prove that if the diagonals of a convex quadrilateral are perpendicular to each other, then the sums of the squares of the opposite sides are equal.
## Solution
Let $p=7$ be the semi-perimeter, $S=7$ be the area of triangle $B K C$; $L, M$ and $N$ are the points of tangency of the inscribed circle of this triangle with the sides $B C, K C$ and $B K$ respectively. Denote $K M=K N=x, B L=B N=$ $y$. Then
$$
\begin{gathered}
p-B K=7-(4+\sqrt{2})=3-\sqrt{2}, p-B C=K M=x \\
p-K C=B L=y, x+y=K N+B N=4+\sqrt{2}
\end{gathered}
$$
By Heron's formula $S=\sqrt{p(p-B K)(p-B C)(p-K C)}$, or $7=\sqrt{7(3-\sqrt{2}) x y}$. From this, we find that
$$
x y=\frac{7}{3-\sqrt{2}}=3+\sqrt{2}
$$
Since $x+y=4+\sqrt{2}$, the numbers $x$ and $y$ are the roots of the quadratic equation $t^{2}-(4+\sqrt{2}) t+3+\sqrt{2}=0$. Thus, $x=1, y=3+\sqrt{2}$ or $x=3+\sqrt{2}, y=1$.
In the first of these cases,
$$
\begin{gathered}
B C=B L+L C=B L+(p-B K)=y+7-(4+\sqrt{2})=3+\sqrt{2}+3-\sqrt{2}=6 \\
K C=K M+M C=K M+(p-B K)=x+7-(4+\sqrt{2})=1+3-\sqrt{2}=4-\sqrt{2}4-\sqrt{2}>B C
\end{gathered}
$$
which does not satisfy the condition of the problem. Therefore, $B C=6, K C=4-\sqrt{2}$.
Since
$$
B K^{2}+K C^{2}=(4+\sqrt{2})^{2}+(4-\sqrt{2})^{2}=36=B C^{2}
$$
triangle $B K C$ is a right triangle, $\angle B K C=90^{\circ}$. Thus, the diagonals of quadrilateral $A B C D$ are perpendicular.
We will prove that if the diagonals of a convex quadrilateral are perpendicular to each other, then the sums of the squares of the opposite sides are equal.
Indeed, let the diagonals $A C$ and $B D$ of such a quadrilateral $A B C D$ intersect at point $K$. By the Pythagorean theorem,
$$
A B^{2}+C D^{2}=\left(K A^{2}+K B^{2}\right)+\left(K C^{2}+K D^{2}\right)=\left(K A^{2}+K D^{2}\right)+\left(K B^{2}+K C^{2}\right)=A D^{2}+B C^{2}
$$
Let for quadrilateral $A B C D$ from our problem $A B=a, B C=b, C D=c$ and $A D=d$. Since a circle can be inscribed in it, then $a+c=b+d$. Moreover, as proven, $a^{2}+c^{2}=b^{2}+d^{2}$. Then
$$
\begin{aligned}
& \left\{\begin{array} { l }
{ a + c = b + d } \\
{ a ^ { 2 } + c ^ { 2 } = b ^ { 2 } + d ^ { 2 } } \\
{ a > b }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ a - b = d - c } \\
{ a ^ { 2 } - b ^ { 2 } = d ^ { 2 } - c ^ { 2 } } \\
{ a > b }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
a-b=d-c \\
(a-b)(a+b)=(d-c)(d+c) \\
a>b
\end{array} \Leftrightarrow\right.\right.\right. \\
& \left\{\begin{array} { l }
{ a - b = d - c } \\
{ ( a - b ) ( a + b ) = ( a - b ) ( d + c ) } \\
{ a > b }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ a - b = d - c } \\
{ a + b = d + c } \\
{ a > b }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
a=d \\
b=c \\
a>b
\end{array}\right.\right.\right.
\end{aligned}
$$
Therefore, $C D=c=b=B C=6$.
## Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ $\left.\begin{array}{l}\text { Inscribed quadrilaterals } \\ \text { [Quadrilateral: calculations, metric relations.] }\end{array}\right]$
In the quadrilateral $A B C D$, a circle can be inscribed. Let $K$ be the point of intersection of its diagonals. It is known that $B C>A B>B K, K C=\sqrt{7}-1$, the cosine of angle $K B C$ is $\frac{\sqrt{7}+1}{4}$, and the perimeter of triangle $B K C$ is $2 \sqrt{7}+4$. Find $D C$.
|
Let $\angle K B C=\alpha, B K=x, B C=y$. Let $P=2 \sqrt{7}+4$ be the perimeter of triangle $B K C$. Then
$$
x+y=P-K C=2 \sqrt{7}+4-(\sqrt{7}-1)=5+\sqrt{7}
$$
By the cosine rule,
$$
K C^{2}=B K^{2}+B C^{2}-2 \cdot B K \cdot B C \cdot \cos \alpha, \text { or }(\sqrt{7}-1)^{2}=x^{2}+y^{2}-2 x y \cdot \frac{\sqrt{7}+1}{4} .
$$
Since
$$
x^{2}+y^{2}=(x+y)^{2}-2 x y=(5+\sqrt{7})^{2}-2 x y=32+10 \sqrt{7}-2 x y
$$
from the second of the obtained equations, we find that
$$
x y=\frac{24(2+\sqrt{7})}{5+\sqrt{7}}=4(1+\sqrt{7})
$$
From the system
$$
\left\{\begin{array}{l}
x+y=5+\sqrt{7} \\
x y=4(1+\sqrt{7}) \\
x a }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ a - y = d - c } \\
{ a ^ { 2 } - y ^ { 2 } = d ^ { 2 } - c ^ { 2 } } \\
{ y > a }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
a-y=d-c \\
(a-y)(a+y)=(d-c)(d+c) \\
y>a
\end{array} \Leftrightarrow\right.\right.\right. \\
& \left\{\begin{array}{l}
a-y=d-c \\
(a-y)(a+y) \\
y>a
\end{array}=(a-y)(d+c) \Leftrightarrow\left\{\begin{array} { l }
{ a - y = d - c } \\
{ a + y = d + c } \\
{ y > a }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
a=d \\
y=c \\
y>a
\end{array}\right.\right.\right.
\end{aligned}
$$
Therefore, $C D=c=y=B C=4$.
Using the cosine rule, find the sides of triangle $B K C$. Prove that $A C \perp B D$. Also prove that if the diagonals of a convex quadrilateral are perpendicular, then the sums of the squares of the opposite sides are equal.
## Answer
4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In triangle $K L M$, the ratio of the radii of the circumscribed and inscribed circles is 3. The inscribed circle touches the sides of triangle $K L M$ at points $A, B$, and $C$. Find the ratio of the area of triangle $K L M$ to the area of triangle $A B C$.
#
|
Let $O$ be the center of the circle inscribed in triangle $KLM$. Then point $O$ lies inside triangle $ABC$ and
$$
S_{\triangle \mathrm{ABC}}=S_{\triangle \mathrm{BOC}}+S_{\triangle \mathrm{AOC}}+S_{\triangle \mathrm{AOB}}.
$$
Next, apply the Law of Sines and formulas for the area of a triangle.
## Solution
Let the vertices $A, B$, and $C$ of triangle $ABC$ lie on the sides $ML, KM$, and $KL$ of triangle $KLM$ respectively; $O$ be the center of the circle with radius $r$ inscribed in triangle $KLM$, and $R$ be the radius of the circumcircle of this triangle. Denote
$$
ML=a, KM=b, KL=c, \angle LKM=\alpha, \angle KLM=\beta, \angle LMK=\gamma
$$
Then
$$
\angle BAC=90^{\circ}-\frac{\alpha}{2}<90^{\circ}, \angle ABC=90^{\circ}-\frac{\beta}{2}<90^{\circ}, \angle ACB=90^{\circ}-\frac{\gamma}{2}<90^{\circ}.
$$
Since all angles of triangle $ABC$ are acute, the center $O$ of the circumcircle of triangle $ABC$ lies inside this triangle. Therefore,
$$
S_{\triangle \mathrm{ABC}}=S_{\triangle \mathrm{BOC}}+S_{\triangle \mathrm{AOC}}+S_{\triangle \mathrm{AOB}}=
$$
$$
\begin{gathered}
=\frac{1}{2} \cdot OB \cdot OC \cdot \sin \left(180^{\circ}-\alpha\right)+\frac{1}{2} \cdot OA \cdot OC \cdot \sin \left(180^{\circ}-\beta\right)+\frac{1}{2} \cdot OA \cdot OB \cdot \sin \left(180^{\circ}-\gamma\right)= \\
=\frac{1}{2}(r \cdot r \cdot \sin \alpha+r \cdot r \cdot \sin \beta+r \cdot r \cdot \sin \gamma)=\frac{1}{2} r^{2}(\sin \alpha+\sin \beta+\sin \gamma)
\end{gathered}
$$
Since
$$
S_{\Delta \mathrm{KLM}}=\frac{1}{2} \cdot KL \cdot KM \cdot \sin \angle LKM=\frac{1}{2} bc \sin \alpha
$$
then
$$
\begin{gathered}
\frac{S_{\triangle ABC}}{S_{\triangle KLM}}=\frac{\frac{1}{2} r^{2}(\sin \alpha+\sin \beta+\sin \gamma)}{\frac{1}{2} bc \sin \alpha}=\frac{r^{2}}{bc} \cdot\left(1+\frac{\sin \beta}{\sin \alpha}+\frac{\sin \gamma}{\sin \alpha}\right)= \\
=\frac{r^{2}}{bc} \cdot\left(1+\frac{b}{a}+\frac{c}{a}\right)=\frac{r^{2}(a+b+c)}{abc}
\end{gathered}
$$
Since
$$
S_{\Delta \mathrm{KLM}}=\frac{a+b+c}{2} \cdot r \text{ and } S_{\Delta \mathrm{KLM}}=\frac{abc}{4R}
$$
then
$$
a+b+c=\frac{2 S_{\Delta KLM}}{r}, \text{ and } abc=4 S_{\Delta \mathrm{KLM}} \cdot R
$$
Thus,
$$
\frac{S_{\triangle ABC}}{S_{\triangle KLM}}=\frac{r^{2} \cdot \frac{2 S_{\triangle KLM}}{r}}{S_{\triangle KLM} \cdot 4R}=\frac{r}{2R}=\frac{1}{6}
$$
Therefore, $\frac{S_{\triangle KLM}}{S_{\triangle ABC}}=6$.
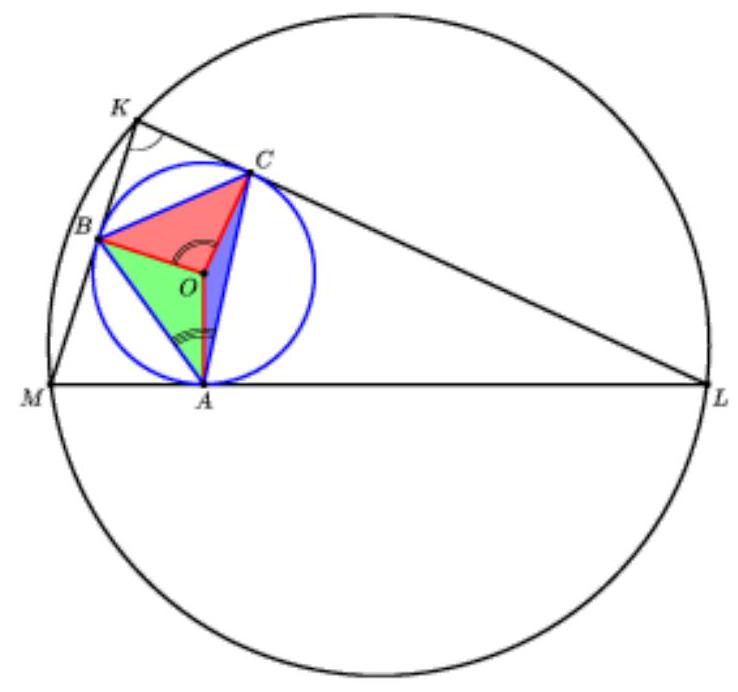
## Answer
6.00
## Answer
$40^{\circ}$.
The diagonals of the convex quadrilateral $ABCD$ intersect at point $E, BC=CD, AC$ is the angle bisector of $\angle A, \angle BCD=160^{\circ}, \angle CED=130^{\circ}$. Find the angle $\angle ABD$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Chords and secants (etc.). $]$
A chord subtends an arc of $90^{\circ}$ and is equal to 16. Find its distance from the center.
|
The foot of the perpendicular dropped from the center of the circle to the given chord bisects it.
## Solution
Let $M$ be the foot of the perpendicular dropped from the center $O$ of the circle to the chord $A B$. Then $M$ is the midpoint of $A B$ and the right triangle $O M A$ is isosceles. Therefore, $O M = M A = 8$.
## Answer
8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The radius of the circle is 13, the chord is 10. Find its distance from the center.
#
|
A diameter perpendicular to a chord bisects it. Therefore, the square of the desired distance is $13^{2}-5^{2}=$ $12^{2}$.
Answer
12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\begin{aligned} & \text { [ Congruent triangles. Criteria for congruence ] } \\ & \text { [Central symmetry helps solve the problem].] }\end{aligned}$
Segments $A B$ and $C D$ intersect at point $O$, which is the midpoint of each of them. What is the length of segment $B D$ if segment $A C=10$?
|
Triangle $B O D$ is equal to triangle $A O C$ by two sides and the included angle. Therefore, $B D=A C=10$.
## Answer
10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Properties and characteristics of an isosceles triangle. ]
The median $A M$ of triangle $A B C$ is perpendicular to its bisector $B K$. Find $A B$, if $B C=12$.
|
Let $P$ be the intersection point of $B K$ and $A M$. In triangle $A B M$, the bisector $B P$ is an altitude.
## Solution
Let $P$ be the intersection point of segments $B K$ and $A M$. In triangle $A B M$, the bisector $B P$ is an altitude, so triangle $A B M$ is isosceles. Therefore, $A B = B M = 1 / 2 B C = 6$.
## Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The area of an isosceles trapezoid is 32. The cotangent of the angle between the diagonal and the base is 2. Find the height of the trapezoid.
#
|
The projection of the diagonal of an isosceles trapezoid onto its base is equal to the midline of the trapezoid.
## Solution
Let $h$ be the height we are looking for. The projection of the diagonal of the trapezoid onto its larger base is $2h$. Therefore, the midline of the trapezoid is also $2h$. According to the problem, $2h^2 = 32$, from which we get $h = 4$.

## Answer
4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Properties and characteristics of tangents ] [ Pythagorean Theorem (direct and inverse) ]
Find the geometric locus of points from which tangents are drawn to a given circle, equal to a given segment.
#
|
Consider a right triangle with vertices at the considered point, the center of the given circle, and the point of tangency.
## Solution
Let the tangent line drawn from point $M$ to the given circle be $d$ (i.e., the segment with endpoints at point $M$ and the point of tangency is equal to the given length), and the radius of this circle be $r$. Then, point $M$ is at a distance of $\sqrt{r^{2}+d^{2}}$ from the center of the circle. Therefore, point $M$ is located on a circle with the same center as the given circle and a radius of $\sqrt{r^{2}+d^{2}}$.
On the other hand, if point $K$ lies on a circle with radius $\sqrt{r^{2}+d^{2}}$ and center at point $O$ (the center of the given circle), then the tangent line drawn from point $K$ to the given circle is equal to $d$.
## Answer
A circle concentric with the given one.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Tangent Circles [ Equilateral (Equiangular) Triangle ]
In a given circle with a radius of 3, six equal circles are inscribed, each touching the given circle; moreover, each of these six circles touches two adjacent ones. Find the radii of the circles.
#
|
Consider a triangle with vertices at the centers of the external and two adjacent internal circles.
## Solution
Let $r$ be the radius of one of the six internal circles. The triangle with vertices at the centers of the external and two adjacent internal circles is equilateral, so $3-r=2r$. Therefore, $r=1$.
## Answer
1.
Six equal circles touch externally a circle of radius 1 and, in addition, each of these six circles touches two adjacent ones. Find the radii of the circles.
## Hint
Consider a triangle with vertices at the centers of the internal and two adjacent external circles.
## Solution
Let $r$ be the radius of one of the six external circles. The triangle with vertices at the centers of the internal and two adjacent external circles is equilateral. Therefore, $1+r=2r$. Consequently, $r=1$.
## Answer
1. Submit a comment
Problem
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9
One of the angles of the trapezoid is $30^{\circ}$, and the lines containing the lateral sides of the trapezoid intersect at a right angle. Find the length of the shorter lateral side of the trapezoid if its midline is equal to 10, and one of the bases is equal to 8.
#
|
Draw a line through the vertex of the smaller base of the trapezoid, parallel to the lateral side.
## Solution
The second (larger) base $AD$ of trapezoid $ABCD$, according to the midline theorem, is 12. Through the vertex $C$ of the smaller base $BC$, draw a line parallel to the lateral side $AB$, until it intersects the base $AD$ at point $K$. Triangle $KCD$ is a right triangle ($\angle KCD=90^{\circ}$). Therefore,
$$
AB=KC=\frac{1}{2}KD=\frac{AD-AK}{2}=\frac{AD-BC}{2}=2
$$

## Answer
2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$C D$ is the median of triangle $A B C$. The circles inscribed in triangles $A C D$ and $B C D$ touch the segment $C D$ at points $M$ and $N$. Find $M N$, if $A C - B C = 2$.
|
If the circle inscribed in triangle $P Q R$ touches side $P Q$ at point $S$, then $P S=1 / 2(P Q+P R-R Q)$.
## Solution
Since $A D=D B$, and
$$
C M=1 / 2(A C+C D-A D) \text{ and } C N=1 / 2(B C+C D-B D)
$$
then
$$
\begin{aligned}
M N=|C M-C N| & =|1 / 2(A C+C D-A D)-1 / 2(B C+C D-B D)|= \\
& =1 / 2|A C-B C|=1 / 2 \cdot 2=1
\end{aligned}
$$
## Answer
1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Acute angle $A$ of rhombus $A B C D$ is $45^{\circ}$, the projection of side $A B$ on side $A D$ is 12. Find the distance from the center of the rhombus to side $C D$.
|
Use the theorem of the midline of a triangle.
## Solution
Let $M$ be the projection of vertex $B$ of the rhombus $A B C D$ onto side $A D$. According to the problem, $A M=12$. The acute angle at vertex $A$ of the right triangle $A M B$ is $45^{\circ}$, so $B M=A M$.
Let $P$ and $Q$ be the projections of the center $O$ of the rhombus $A B C D$ onto sides $A D$ and $C D$ respectively. From the equality of right triangles $O D P$ and $O D Q$ (by hypotenuse and acute angle), it follows that $O Q=O P$, and since $O P$ is the midline of triangle $A B M$, then
$$
O P=\frac{1}{2} B M=\frac{1}{2} A M=6
$$
## Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Inside triangle $A B C$, there are points $P$ and $Q$ such that point $P$ is at distances 6, 7, and 12 from the lines $A B, B C, C A$ respectively, and point $Q$ is at distances 10, 9, and 4 from the lines $A B, B C, C A$ respectively. Find the radius of the inscribed circle of triangle $A B C$.
|
Prove that the midpoint of segment $P Q$ is the center of the inscribed circle of triangle $A B C$.
## Solution
Let $D, E, F$ be the feet of the perpendiculars dropped from points $P, Q, O$ to line $A B$ respectively. By the given condition, $P D=6, Q E=10$. $O F$ is the midline of trapezoid $D P Q E$, so the length of $O F$ is $1 / 2(P D+Q E)=1 / 2(6+10)=8$. Therefore, point $O$ is 8 units away from line $A B$. Similarly, we find that $O$ is $1 / 2(7+9)=8$ units away from line $B C$ and $1 / 2(12+4)=8$ units away from line $C A$. Thus, $O$ is the center of the inscribed circle of triangle $A B C$, and the radius of this circle is 8.
## Answer
## Problem
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Construction on a projection drawing ]
The base of a right prism $A B C A 1 B 1 C 1$ is a right triangle $A B C\left(\angle B=90^{\circ}, A B=B C=10\right)$; $A A 1=B B 1=C C 1=12$. Point $M$ is the midpoint of the lateral edge $A A 1$. A plane is drawn through points $M$ and $B 1$, forming an angle of $45^{\circ}$ with the base plane and intersecting the edge $C C 1$ at point $E$. Find $C E$.
|
Let the lines $M E$ and $A 1 C 1$ intersect at point $P$. Then the plane of the section intersects the plane of the base $A 1 B 1 C 1$ along the line $B 1 P$ (Fig.1). Suppose that point $P$ lies on the extension of the edge $A 1 C 1$ beyond point $A 1$. Drop the perpendicular $A 1 K$ from point $A 1$ to the line $B 1 P$. By the theorem of three perpendiculars, $M K \perp B 1 P$, so $A 1 K M$ is the linear angle of the dihedral angle between the cutting plane and the base plane of the prism. According to the problem, $\angle A 1 K M=45^{\circ}$. From the right triangles $A 1 B 1 C 1$, $A 1 K M$, and $A 1 K B 1$, we find that
$$
A 1 C 1=10 \sqrt{2}, A 1 K=A 1 M=6, B 1 K=\sqrt{A_{1} B_{1}^{2}-A_{1} K^{2}}=\sqrt{100-36}=8
$$
Consider the triangle $P B 1 C 1$ (Fig.2). Let $\angle K A 1 B 1=\alpha$. Then
$$
\cos \alpha=\frac{A_{1} K}{A_{1} B_{1}}=\frac{6}{10}=\frac{3}{5}, \sin \alpha=\frac{4}{5}
$$
$$
\begin{gathered}
\angle P A 1 K=180^{\circ}-45^{\circ}-\alpha=135^{\circ}-\alpha \\
P A 1=\frac{K A_{1}}{\cos \angle P^{P} A_{1} K}=\frac{6}{\operatorname{css}\left(135^{\circ}-\operatorname{co}\right)}=\frac{6}{\cos 135^{\circ} \cos \left(2+\sin 135^{\circ} \sin \boldsymbol{r}\right.}= \\
\frac{6 \sqrt{2}}{-\sqrt{2}+\frac{1}{5}}=30 \sqrt{2}, P C 1=P A 1+A 1 C 1=30 \sqrt{2}+10 \sqrt{2}=40 \sqrt{2}
\end{gathered}
$$
From the similarity of triangles $P E C 1$ and $P M A 1$, we find that
$$
E C 1=M A 1 \cdot \frac{P C_{1}}{P A_{1}}=6 \cdot \frac{40 \sqrt{2}}{30 \sqrt{2}}=6 \cdot \frac{4}{3}=8
$$
Therefore,
$$
C E=C C 1-E C 1=12-8=4 .
$$
If point $P$ lies on the extension of the edge $A 1 C 1$ beyond point $C 1$, then, reasoning similarly, we get that
$$
\begin{aligned}
& \cos \alpha=\frac{4}{5}, \sin \alpha=\frac{3}{5}, \\
& \angle P A 1 K=45^{\circ}+90^{\circ}-\alpha=135^{\circ}-\alpha, \\
& P A 1=\frac{K A_{1}}{\cos \angle P^{\prime} A_{1} K}=\frac{6}{\cos \left(135^{\circ}-\operatorname{r}\right)}=\frac{6}{\cos 135^{\circ} \cos r 2+\sin 135^{\circ} \sin \boldsymbol{n} \boldsymbol{n}}=
\end{aligned}
$$
which is impossible.
## Answer
4.00
Send a comment
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.