problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
[ [Sphere touching the edges or sides of the pyramid]
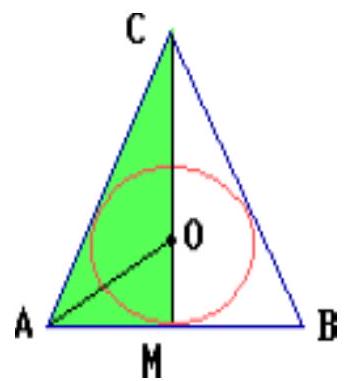
The base of the pyramid $S A B C$ is an equilateral triangle $A B C$ with side $2 \sqrt{2}$. Edges $S B$ and $S C$ are equal. A sphere touches the sides of the base, the plane of the face $S B C$, and the edge $S A$. What is the radius of the sphere if $S A=\frac{3 \sqrt{2}}{2}$?
|
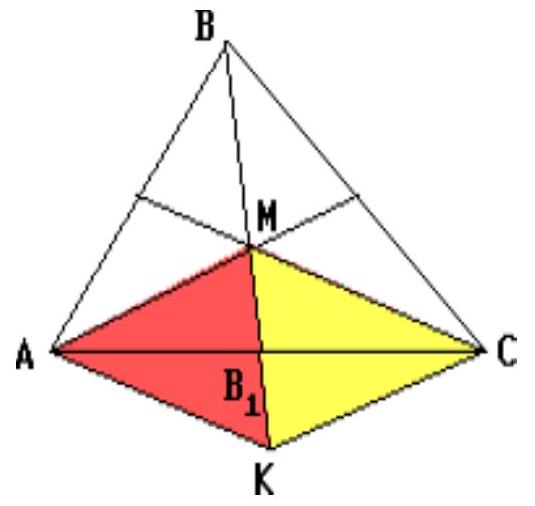
Let a sphere of radius $R$ touch the side $BC$ of the base at point $D$ (Fig.1). Then $D$ is the only common point of the sphere with the plane of the face $SBC$, i.e., the sphere touches this plane at point $D$. If the sphere touches the edges $AB$ and $AC$ at points $M$ and $N$ respectively, then the center $O$ of the sphere lies in the plane passing through the midpoint of segment $MN$ perpendicular to $MN$. Since triangle $ABC$ is equilateral, this plane is also perpendicular to edge $BC$ and passes through the midpoint of $BC$, and since point $S$ is equidistant from the ends of segment $BC$, vertex $S$ lies in this plane. Since $SD \perp BC$, point $D$ is the midpoint of $BC$. The section of the sphere by the plane of the base of the pyramid is a circle inscribed in the equilateral triangle $ABC$ with side $a=2\sqrt{2}$ (Fig.2). If $r$ is the radius of this circle, then
$$
r=\frac{a \sqrt{3}}{6}=\frac{2 \sqrt{2} \sqrt{3}}{6}=\frac{\sqrt{6}}{3}
$$
If $E$ is the point of intersection of the incircle of triangle $ABC$ with segment $AD$, then
$$
DE=2r=\frac{2\sqrt{6}}{3}, \quad AE=AD-DE=\frac{2\sqrt{3}}{2}-2r=\sqrt{6}-\frac{2\sqrt{6}}{3}=\frac{\sqrt{6}}{3}
$$
Let the sphere touch the edge $SA$ at point $K$. Consider the section of the pyramid and the sphere by the plane $SAD$ (Fig.3).
We obtain a circle with center $O$ and radius $R$, passing through points $D, K, E$ and touching $SD$ and $SA$ at points $D$ and $K$. By the tangent-secant theorem,
$$
AK=\sqrt{AE \cdot AD}=\sqrt{\frac{\sqrt{6}}{3} \cdot \sqrt{6}}=\sqrt{2}
$$
Then
$$
SD=SK=SA-AK=\frac{3\sqrt{2}}{2}-\sqrt{2}=\frac{\sqrt{2}}{2}
$$
The center of the circle inscribed in an angle lies on the bisector of this angle, so $SO$ is the bisector of angle $ASD$. Let $\angle ASO=\angle DSO=\alpha$. By the cosine rule,
$$
\begin{aligned}
& \cos 2\alpha=\cos \angle ASD=\frac{SA^2+SD^2-AD^2}{2SA \cdot SD}= \\
& =\frac{\left(\frac{3\sqrt{2}}{2}\right)^2+\left(\frac{\sqrt{2}}{2}\right)^2-(\sqrt{6})^2}{2 \cdot \frac{3\sqrt{2}}{2} \cdot \frac{\sqrt{2}}{2}}=\frac{\frac{9}{2}+\frac{1}{2}-6}{3}=-\frac{1}{3}
\end{aligned}
$$
From the equation
$$
\frac{1}{-3}=\cos 2\alpha=\frac{1-\tan^2 \alpha}{1+\tan^2 \alpha}
$$
we find that $\tan \alpha=\sqrt{2}$. Therefore,
$$
R=OD=SD \tan \angle OSD=\frac{\sqrt{2}}{2} \cdot \tan \alpha=\frac{\sqrt{2}}{2} \cdot \sqrt{2}=1
$$
## Answer
1.00
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In triangle $A B C$, it is known that $A B=10, B C=24$, and the median $B D$ is 13. The circles inscribed in triangles $A B D$ and $B D C$ touch the median $B D$ at points $M$ and $N$ respectively. Find $M N$.
|
Let's first prove the following statement. If a circle is inscribed in a triangle $X Y Z$, and $x$ is the distance from vertex $X$ to the point of tangency of the circle with side $X Y$, and $Y Z=a$, then $x=p-a$, where $p$ is the semiperimeter of the triangle.
Let the points of tangency of the inscribed circle with sides $X Y, Y Z$, and $X Z$ be denoted by $Z_{1}, X_{1}$, and $Y_{1}$, respectively. Let $X Z=b$ and $X Y=c$. Then,
\[
\begin{gathered}
Y X_{1}=Y Z_{1}=X Y-X Z_{1}=c-x, \quad Z X_{1}=Z Y_{1}=X Z-X Y_{1}=X Z-X Z_{1}=b-x, \\
Y Z=Y X_{1}+Z X_{1}=c-x+b-x=b+c-2 x .
\end{gathered}
\]
Therefore,
\[
x=\frac{b+c-a}{2}=\frac{b+c+a}{2}-a=p-a
\]
This completes the proof.
Now, let's return to our problem. The circle inscribed in triangle $A B D$ touches its side $B D$ at point $M$. By the proven statement,
\[
B M=\frac{A B+B D+A D}{2}-A D=\frac{A B+B D-A D}{2}=\frac{23-A D}{2}
\]
Similarly,
\[
B N=\frac{B C+B D-C D}{2}=\frac{37-C D}{2}
\]
Since $A D=C D$, we have
\[
M N=|B N-B M|=\left|\frac{37-C D}{2}-\frac{23-A D}{2}\right|=\frac{37-23}{2}=7
\]
## Answer
7.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[
$[$ Inscribed and Circumscribed Circles $]$
In an isosceles triangle, the height is 20, and the base is to the lateral side as $4: 3$. Find the radius of the inscribed circle.
#
|
Find the ratio in which the bisector of the angle at the base divides the height.
## Solution
Let $C M$ be the height of the given triangle $A B C$, $C M=20$, $A C=B C$, and $O$ be the center of the inscribed circle. Then $O M$ is the radius of this circle.
Since $A O$ is the bisector of angle $C A B$, then $\frac{O M}{O C}=\frac{A M}{A C}$, and since $\frac{A M}{A C}=\frac{2}{3}$, then
$$
O M=\frac{2}{5} C M=8
$$
## Answer
8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Properties and characteristics of tangents ] [ Pythagorean Theorem (direct and inverse) ]
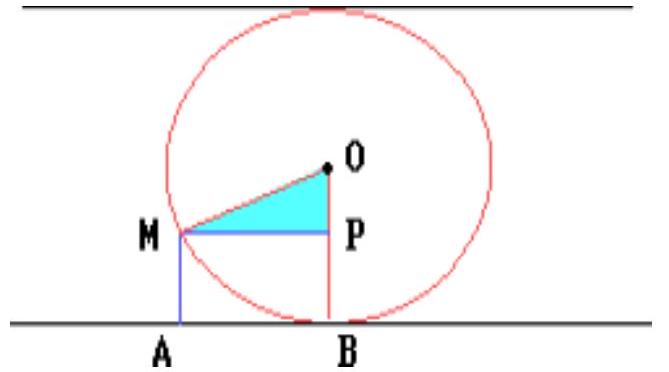
Given two parallel lines at a distance of 15 from each other; between them is a point $M$ at a distance of 3 from one of them. A circle is drawn through point $M$, touching both lines. Find the distance between the projections of the center and point $M$ on one of the given lines.
|
Drop a perpendicular from point $M$ to the radius of the circle, drawn to one of the points of tangency.
## Solution
Let $A$ and $B$ be the projections of point $M$ and the center $O$ of the circle onto one of the lines, with $M A=3$. Then $O B$ is the radius of the circle and $O B=\frac{15}{2}$.
Let $P$ be the projection of point $M$ onto $O B$. In the right triangle $M P O$, it is known that
$$
M O=\frac{15}{2}, O P=O B-P B=O B-M A=\frac{15}{2}-3=\frac{9}{2}
$$
Therefore,
$$
A B^{2}=M P^{2}=M O^{2}-O P^{2}=\left(\frac{15}{2}\right)^{2}-\left(\frac{9}{2}\right)^{2}=36
$$
## Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11
In a regular truncated quadrilateral pyramid, the height is 2, and the sides of the bases are 3 and 5. Find the diagonal of the truncated pyramid.
|
Let's make a section through the opposite lateral edges $A A_{1}$ and $C C_{1}$ of the given truncated pyramid $A B C D A_{1} B_{1} C_{1} D_{1}$ with bases $A B C D$ and $A_{1} B_{1} C_{1} D_{1}\left(A B=5, A_{1} B_{1}=3\right)$. Let $O$ and $O_{1}$ be the centers of the bases $A B C D$ and $A_{1} B_{1} C_{1} D_{1}$, respectively. The cutting plane passes through the height $O O_{1}$ of the truncated pyramid. In the section, we obtain an isosceles trapezoid $A A_{1} C_{1} C$ with bases $A C=5 \sqrt{2}$ and $A_{1} C_{1}=3 \sqrt{2}$. Let $A_{1} K$ be the height of the trapezoid. Then
$$
\begin{gathered}
A_{1} K=O O_{1}=2 \\
A K=\frac{1}{2}\left(A C-A_{1} C_{1}\right)=\frac{1}{2}(5 \sqrt{2}-3 \sqrt{2})=\sqrt{2} \\
C K=A C-A K=5 \sqrt{2}-\sqrt{2}=4 \sqrt{2}
\end{gathered}
$$
From the right triangle $A_{1}$ КС, we find that
$$
A_{1} C=\sqrt{A K^{2}+C K^{2}}=\sqrt{4+32}=6
$$
## Answer
6.
Submit a comment
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Zhendarov R.G.
Each side of an equilateral triangle is divided into $n$ equal segments, and lines parallel to the sides are drawn through all the division points. This triangle is divided into $n^{2}$ small triangular cells. Triangles located between two adjacent parallel lines form a strip.
a) What is the maximum number of cells that can be marked so that no two marked cells belong to the same strip in any of the three directions, if $n=10$?
b) The same question for $n=9$.
|
a) Examples are shown in the figures.
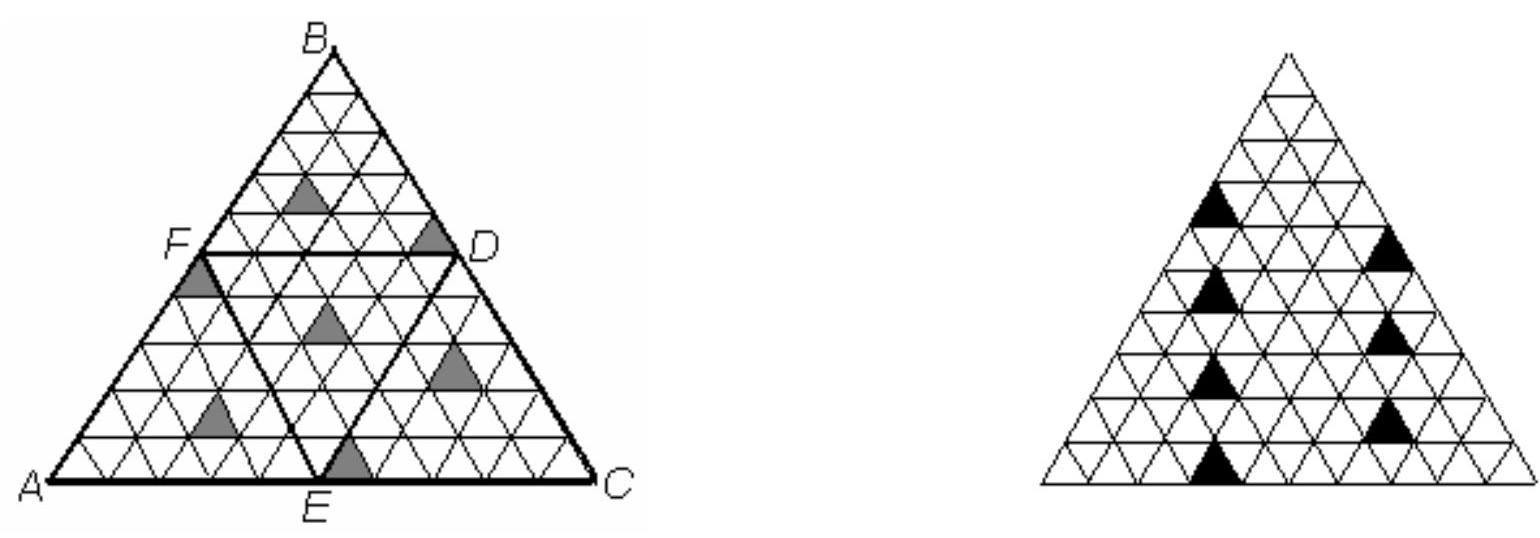
Estimate. First method. Cut the triangle into four equal triangles using the midlines (left figure). Suppose we managed to mark a certain number of cells, with $a, b, c$, and $d$ cells falling into triangles $A E F, B D F, C D E, D E F$ respectively. Note that trapezoid $A B D E$ is covered by five strips parallel to side $A B$. Therefore, it contains no more than five marked cells, i.e., $a+b+d \leq 5$. Similarly, $b+c+d \leq 5$, and $a+c+d \leq 5$. Adding these three inequalities, we get $2(a+b+c+d)+d \leq 15$. Therefore, the total number of marked cells $a+b+c+d$ is no more than 7.
Second method. Suppose we managed to mark $k$ cells. Draw all three strips through each marked cell and count the total number $M$ of cells that fall into these strips (if a cell falls into several strips, count it with the corresponding multiplicity).
On the one hand, each of the 30 possible strips participates in the count as many times as there are marked cells in it (i.e., no more than once). All strips, taken once, cover the triangle three times, so $M \leq 300$.
On the other hand, the three strips passing through one marked cell "cover" (with multiplicity) no fewer than 39 cells. (Indeed, if the marked cell is at the left vertex of the triangle, the corresponding strips cover $19+19+1=39$ cells. When the marked cell is shifted to the adjacent cell to the right, one of the strips extends by 2, and the other two remain unchanged; with the next shift, one of the strips shortens by 2, and so on. Since shifts parallel to the sides of the triangle can reach any cell, the number of cells covered by the corresponding three strips will always be 39 for triangles pointing upwards and 41 for triangles pointing downwards).
Therefore, the strips corresponding to all marked cells cover no fewer than $39k$ cells, i.e., $M \geq 39k$. Thus, $39k \leq 300$, so $k \leq 7$.
b) Examples are obtained from the examples in part a) by cutting off the bottom strip.
Estimate. First method. Suppose we managed to mark a certain number of cells while satisfying the conditions. Only one of the cells marked with black dots can be marked. Due to their symmetric placement, we can assume that the bottom one of these cells is not marked. Cut the remaining part of the triangle into four pieces (see figure).
The same reasoning we used in the first method of part a) shows that the number of marked cells is no more than $(4+4+5): 2=6.5<7$.
Second method. Repeating the reasoning of the second method in part a), we get the inequality $35k \leq 243$, from which $k \leq 6$.
## Answer
a) 7; b) 6 cells.
Submit a comment
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9}
The medians of a triangle are 3, 4, and 5. Find the area of the triangle.
#
|
Prove that the area of the triangle formed by the medians of a given triangle is $\frac{3}{4}$ of the area of the given triangle.
## Solution
Let $B_{1}$ be the midpoint of side $A C$ of triangle $A B C$, and $M$ be the point of intersection of its medians. On the extension of median $B B_{1}$ beyond point $B_{1}$, lay off segment $B_{1} K$ equal to $M B_{1}$. Then $A M C K$ is a parallelogram, $C K=A M$. The sides of triangle $K M C$ are $\frac{2}{3}$ of the corresponding medians of triangle $A B C$. Therefore, triangle $K M C$ is similar to the triangle whose sides are equal to the medians of triangle $A B C$. Thus, the area of triangle $K M C$ is $\frac{4}{9}$ of the area of the triangle with sides $3, 4, 5$, i.e., $\frac{4}{9} \cdot 6=\frac{8}{3}$. Therefore,
$$
S_{\Delta \mathrm{ABC}}=6 S_{\Delta \mathrm{B}_{1} \mathrm{MC}}=6 \cdot \frac{1}{2} S_{\Delta \mathrm{KMC}}=8
$$
## Answer
8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Given a circle with center $O$ and radius 1. From point $A$, tangents $A B$ and $A C$ are drawn to the circle. Point $M$, lying on the circle, is such that the quadrilaterals $O B M C$ and $A B M C$ have equal areas. Find $M A$.
|
Note that point $M$ lies on the smaller arc $BC$ (otherwise, $OBMC$ is either inside $ABMC$ or is not a quadrilateral at all). Then
$S_{OBMC} - S_{ABMC} = S_{OBC} + 2S_{MBC} - S_{ABC}$. Therefore, the geometric locus of points for which $S_{OBMC} = S_{ABMC}$ is the perpendicular bisector of segment $OA$. Hence, $AM = OM = 1$.
## Answer
1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The distance from a fixed point $P$ on the plane to two vertices $A, B$ of an equilateral triangle $A B C$ are $A P=2 ; B P=3$. Determine the maximum value that the segment $P C$ can have.
#
|
Let $A, B, C$ and $P$ be points on a plane such that $AB = BC = CA$, $AP = 2$, and $BP = 3$. Draw a ray $BM$ from point $B$ such that $\angle CBM = \angle ABP$, and mark a segment $BP' = PB$ on this ray. From the equality of angles: $\angle CBM = \angle ABP$, it follows that $\angle PBP' = \angle ABC = 60^\circ$, and therefore triangle $PBP'$ is equilateral (since $PB = BP'$). Hence, $PP' = PB = 3$. Furthermore, $\triangle PAB = \triangle P'CB$ (since $AB = BC$, $PB = P'B$, and $\angle ABP = \angle CBP'$).
Therefore, $P'C = PA = 2$. Thus, the broken line $PP'C$ has a length $PP' + P'C = 3 + 2 = 5$, and therefore the length of the segment $PC$ cannot be greater than 5. Choose point $A$ arbitrarily at a distance $AP = 2$ from the given point $P$.
Draw circles with radii $R_1 = 3$ and $R_2 = 5$ centered at point $P$ and rotate the second circle by an angle of $60^\circ$ relative to point $A$. Let $P'$ be the center of the new circle, $AP = AP' = 2$, and $\angle PAP' = 60^\circ$. Choose point $B$ as the intersection of the newly constructed circle with the circle of radius $R_1 = 3$ constructed earlier. Thus, the maximum possible distance from point $P$ to point $C$ is 5.
Submit a comment
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the smallest number of non-overlapping tetrahedra into which a cube can be divided?
#
|
Answer: 5. If a tetrahedron $A^{\prime} B C^{\prime} D$ is cut out from the cube $A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}$, the remaining part of the cube splits into 4 tetrahedra, i.e., the cube can be cut into 5 tetrahedra. We will prove that it is impossible to cut the cube into fewer than 5 tetrahedra. The face $A B C D$ cannot be a face of the tetrahedra into which the cube is divided, because at least two tetrahedra adjoin it. Consider all tetrahedra adjacent to the face $A B C D$. Their heights dropped onto this face do not exceed $a$, where $a$ is the edge of the cube, and the sum of the areas of their faces lying on $A B C D$ is equal to $a^{2}$. Therefore, the sum of their volumes does not exceed $a^{3} / 3$. Since the faces of one tetrahedron cannot lie on opposite faces of the cube, at least 4 tetrahedra adjoin the faces $A B C D$ and $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$, and the sum of their volumes does not exceed $2 a^{3} / 3 < a^{3}$. Therefore, there is still one more tetrahedron in the partition.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9
The volume of the pyramid $A B C D$ is 5. A plane is drawn through the midpoints of the edges $A D$ and $B C$, intersecting the edge $C D$ at point $M$. In this case, $D M: M C=2: 3$. Find the area of the section of the pyramid by the specified plane, if the distance from it to the vertex $A$ is 1.
|
Since the secant plane passes through the midpoints of opposite edges of the tetrahedron, it divides its volume in half. Let the secant plane intersect edge $AB$ at point $K$, and let $P$ and $Q$ be the midpoints of edges $AD$ and $BC$. Then the volume of the polyhedron $PMQKAC$ is $\frac{5}{2}$. On the other hand, it is equal to the sum of the volumes of the quadrilateral pyramid $APMKQ$ and the triangular pyramid $AMCQ$ with a common vertex $A$, and since
$$
V_{AMCQ}=\frac{CM}{CD} \cdot \frac{CQ}{CB} V_{ABCD}=\frac{3}{5} \cdot \frac{1}{2} V_{ABCD}=\frac{3}{5} \cdot \frac{1}{2} \cdot 5=\frac{3}{2}
$$
then
$$
V_{APMQK}=V_{PMQKAC}-V_{AMCQ}=\frac{5}{2}-\frac{3}{2}=1 .
$$
On the other hand, if $h$ is the distance from vertex $A$ to the secant plane, then
$$
V_{APMQK}=\frac{1}{3} S_{PMQK} \cdot h
$$
so $\frac{1}{3} S_{PMQK} \cdot h=1$, from which we find that
$$
S_{PMQK}=\frac{3}{h}=3
$$
## Answer
3.00
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$[$ [extension of a tetrahedron to a parallelepiped]
Segment $A B(A B=1)$, being a chord of a sphere with radius 1, is positioned at an angle of $60^{\circ}$ to the diameter $C D$ of this sphere. The distance from the end $C$ of the diameter to the nearest end $A$ of the chord $A B$ is $\sqrt{2}$. Find $B D$.
#
|
Complete the tetrahedron $ABCD$ to a parallelepiped $AKBLNDMC (AN\|KD\|BM\|LC)$ by drawing pairs of parallel planes through its opposite edges. Let $O$ and $Q$ be the centers of the faces $NDMC$ and $AKBL$ respectively. Then $O$ is the center of a sphere, $KL=CD=2, OQ \perp AB, OA=OB=1$ as radii of the sphere, $KL \| CD, QB$ $=QA=\frac{1}{2}, QL=QK=1$. Let $\angle BQL=60^{\circ}$. Then by the cosine theorem,
\[
BL=\sqrt{QB^2+QL^2-2 QB \cdot QL \cos 60^{\circ}}=\sqrt{\frac{1}{4}+1-2 \cdot \frac{1}{2} \cdot \frac{1}{2}}=\frac{1}{2} \sqrt{3}
\]
Therefore, triangle $BQL$ is a right triangle, $\angle QBL=90^{\circ}$. This means $AB \perp BL$, and since $BM \| OQ$ and $OQ \perp AB$, then $AB \perp BM$, hence the line $AB$ is perpendicular to the plane of the face $BMLC$. Then $AB \perp BC$, so in the right triangle $ABC$, the hypotenuse $AC$ is greater than the leg $BC$. But according to the condition $AC < BC$, so $\angle BQL$ $=120^{\circ}$. In this case $\angle BQK=60^{\circ}$. Then
\[
BK=\sqrt{QB^2+QK^2-2 QB \cdot QK \cos 60^{\circ}}=\sqrt{\frac{1}{4}+1-2 \cdot \frac{1}{2} \cdot \frac{1}{2}}=\frac{1}{2} \sqrt{3}
\]
\[
OQ^2=OA^2-QA^2=1-\frac{1}{4}=\frac{3}{4}
\]
Thus, $AN=CL=OQ=\frac{1}{2} \sqrt{3}$. In the parallelogram $ALCN$
\[
NL^2+AC^2=2AN^2+2AL^2
\]
Therefore,
\[
\begin{aligned}
& BD^2=NL^2=2AN^2+2AL^2-AC^2= \\
& =2AN^2+2BK^2-AC^2=\frac{3}{2}+\frac{3}{2}-2=1 .
\end{aligned}
\]
Thus, $BD=1$.
## Answer
1.00
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ $\underline{\text { Cone }}$
Through the edge $B C$ of the triangular pyramid $P A B C$ and the point $M$, the midpoint of the edge $P A$, a section $B C M$ is drawn. The vertex of the cone coincides with the vertex $P$ of the pyramid, and the circle of the base is inscribed in the triangle $B C M$, touching the side $B C$ at its midpoint. The points of tangency of the circle with the segments $B M$ and $C M$ are the points of intersection of the medians of the faces $A P B$ and $A P C$. The height of the cone is twice the radius of the base. Find the ratio of the lateral surface area of the pyramid to the area of the base of the pyramid.
#
|
Let $E$ and $D$ be the points of intersection of the medians of triangles $A P B$ and $A P C$, $K$ be the midpoint of $B C$, $O$ be the center of the circle inscribed in triangle $B M C$, and $r$ be the radius of the base of the cone, with $2 r$ being its height. Then
$$
P D=P E=P K=\sqrt{r^{2}+4 r^{2}}=r \sqrt{5}
$$
Let $M E=M D=x$. Then $B K=B E=2 x$, $C K=D C=2 x$, so triangle $B M C$ is isosceles. Then
$$
M K=\sqrt{9 x^{2}-4 x^{2}}=x \sqrt{5}
$$
If $p$ is the semiperimeter of the triangle and $S$ is its area, then
$$
S=p r=5 x r, S=\frac{1}{2} B C \cdot M K=2 \times 2 \sqrt{5}
$$
from which we find that $x=\frac{\sqrt{5}}{2}$. Let $P F$ be the median of triangle $A P B$. Since $O E \perp B M$, by the theorem of three perpendiculars, $P F \perp B M$, so
$$
S_{\triangle A P B}=2 S_{\triangle B M P}=2 \cdot \frac{1}{2} M B \cdot P E=3 x \cdot r \sqrt{5}=3 r \cdot \frac{\sqrt{5}}{2} \cdot r \sqrt{5}=\frac{15 r^{2}}{2}
$$
Similarly, $S_{\triangle A P C}=\frac{15 r^{2}}{2}$. Additionally,
$$
S_{\triangle B P C}=\frac{1}{2} B C \cdot P K=2 x \cdot r \sqrt{5}=r \sqrt{5} \cdot r \sqrt{5}=5 r 2
$$
Therefore, the lateral surface area of the pyramid $P A B C$ is $20 r 2$. From the right triangle $B E F$, we find that
$$
\begin{aligned}
B F & =\sqrt{B E^{2}+F E^{2}}=\sqrt{B E^{2}+\left(\frac{1}{2} P E\right)^{2}}= \\
& =\sqrt{4 x^{2}+\left(\frac{r \sqrt{5}}{2}\right)^{2}}=\sqrt{5 r^{2}+\frac{5 r^{2}}{4}}=\frac{5}{2} r .
\end{aligned}
$$
$A B=2 B F=5 r$. Similarly, $A C=5 r$. Then
$$
\begin{aligned}
& A K=\sqrt{A B^{2}-B K^{2}}=\sqrt{25 r^{2}-5 r^{2}}=2 r \sqrt{5} \\
& S_{\triangle A B C}=\frac{1}{2} B C \cdot A K=2 x \cdot 2 r \sqrt{5}=r \sqrt{5} \cdot 2 r \sqrt{5}=10 r 2
\end{aligned}
$$
Therefore, the desired ratio is 2.
## Answer
2.00
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
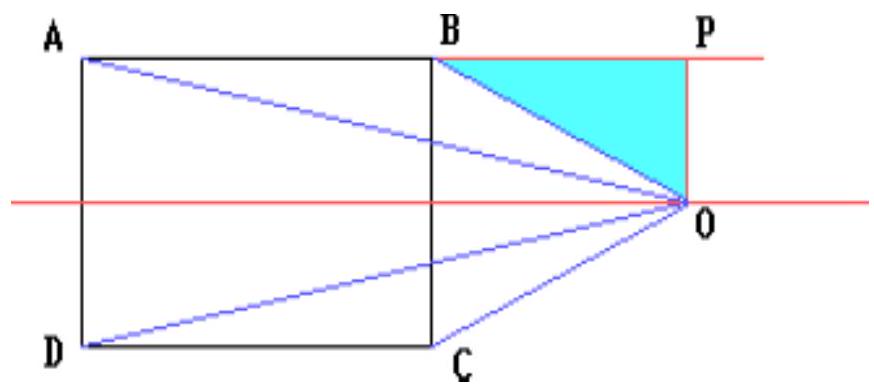
[ Distance between skew lines]
On the line $l$ in space, points $A, B$ and $C$ are sequentially located, with $A B=18$ and $B C=14$. Find the distance between the lines $l$ and $m$, if the distances from points $A, B$ and $C$ to the line $m$ are 12, 15 and 20, respectively.
#
|
Let $A 1, B 1$ and $C 1$ be the feet of the perpendiculars dropped from points $A, B$ and $C$ to the line $m$ respectively (Fig.1). According to the problem,
$$
A A 1=12, B B 1=15, C C 1=20 .
$$
Assume that lines $l$ and $m$ lie in the same plane. It is clear that they cannot be parallel. If the intersection point of lines $l$ and $m$ lies outside the segment $A 1 C 1$ (Fig.2), then by dropping perpendiculars $A D$ and $B E$ from points $A$ and $B$ to lines $B B 1$ and $C C 1$ respectively, we obtain similar triangles $A D B$ and $B E C$, which is impossible, since
$$
\frac{B D}{A B}=\frac{3}{18}=\frac{1}{6} \neq \frac{5}{14}=\frac{C E}{B C}
$$
Similarly for the case when the intersection point of lines $l$ and $m$ lies on the segment $A 1 C 1$. Thus, $l$ and $m$ are skew lines. Consider the orthogonal projection of lines $l$ and $m$ onto the plane $\alpha$, perpendicular to the line $m$ (Fig.3). Let points $P, Q$ and $R$ be the orthogonal projections of points $A$, $B$ and $C$ respectively, and $M$ be the projection of points $A 1, B 1$ and $C 1$. By the property of parallel projection, and since segments $A A 1, B B 1$ and $C C 1$ are perpendicular to the line $m$, they are parallel to the plane $\alpha$. Therefore,
$$
P M=A A 1=12, Q M=B B 1=15, M R=C C 1=20 .
$$
Let $P Q=9 x, Q R=7 x, \angle M R P=\phi$. From triangles $M Q R$ and $M P R$ using the cosine theorem, we find that
$$
\cos \phi=\frac{400+47 x^{2}-225}{2 \cdot 20 \cdot 7 x}
$$
$$
\cos \phi=\frac{400+256 x^{2}-144}{2 \cdot 20 \cdot 16 x} .
$$
From the equation
$$
\frac{400+47 x^{2}-225}{2 \cdot 20 \cdot 7 x}=\frac{400+256 x^{2}-144}{2 \cdot 20 \cdot 16 x}
$$
we find that $x=1$. Therefore, $P R=16 x=16$. Since $M P 2+P R 2=144+256=400=M R 2$, triangle $M P R$ is a right triangle, with $\angle M P R=90^{\circ}$. Therefore, $P M$ is perpendicular to the projection $P R$ of the inclined line $l$ on the plane $\alpha$. By the theorem of three perpendiculars, $M P \perp l$, and since the line $P M$ lies in the plane $\alpha$, perpendicular to the line $m$, then $M P \perp m$. It remains to note that the segment $MP$ is the orthogonal projection on the plane $\alpha$ of the common perpendicular of lines $l$ and $m$. Since this common perpendicular is parallel to the plane $\alpha$, it is equal to the segment $MP$. Therefore, the distance between the lines $l$ and $m$ is 12.
## Answer
12.00
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
S. Rukhin
A closed eight-segment broken line is drawn on the surface of a cube, with its vertices coinciding with the vertices of the cube.
What is the minimum number of segments of this broken line that can coincide with the edges of the cube?
#
|
The segments of the broken line are either edges of the cube or diagonals of its faces. To do this, let's color the vertices of the cube in two colors in a checkerboard pattern (see fig.). Note that an edge of the cube connects vertices of different colors, while a diagonal connects vertices of the same color. For the broken line to pass through all vertices, it must change color at some point, and to be closed, it must change color again. This means that the segments of the broken line must coincide with the edges of the cube at least twice.
This is sufficient, see the example in the figure.
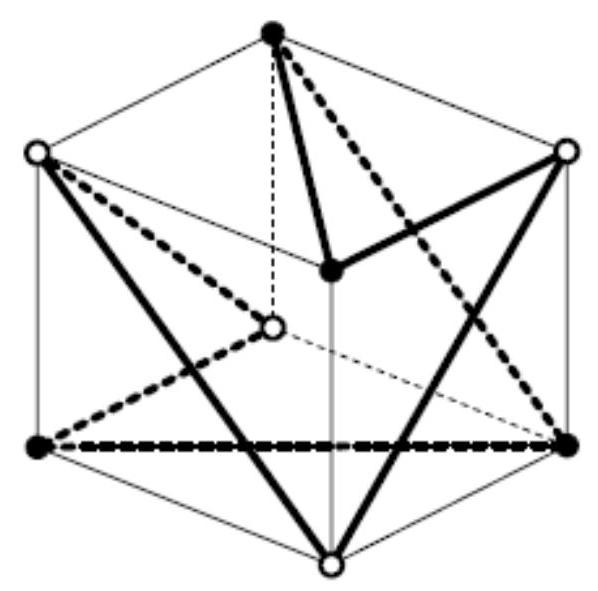
## Answer
Two segments.
Send a comment
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$3+$ [ The transfer helps solve the task_ ]
On the side AB of the square ABCD, an equilateral triangle AKB was constructed (outside). Find the radius of the circle circumscribed around triangle CKD, if $\mathrm{AB}=1$.
#
|
Construct an equilateral triangle on side $\mathrm{CD}$ inside the square $\mathrm{ABCD}$.
## Solution
Construct an equilateral triangle CDM on side CD inside the square ABCD. Then CM=1 and DM=1. Moreover, triangle ABK is obtained from triangle CDM by a parallel translation by vector CB, the length of which is 1. Therefore, KM equals 1. Thus, point M is at a distance of 1 from points C, D, and K. This means that M is the center of the circumcircle of triangle CDK, and the radius of this circle is 1.
## Problem
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[
Diameter, main properties
On the leg $B C$ of the right triangle $A B C$ as a diameter, a circle is constructed, intersecting the hypotenuse at point $D$ such that $A D: B D=1: 3$. The height dropped from the vertex $C$ of the right angle to the hypotenuse is 3. Find the leg $B C$.
#
|
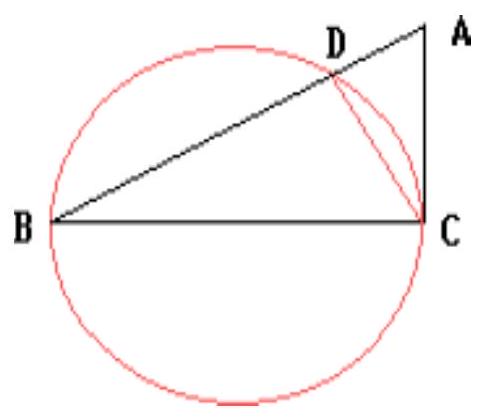
$C D$ - the height of triangle $A C D$.
## Solution
Since angle $B D C$ is inscribed in the given circle and rests on its diameter $B C$, then $\angle B D C=90^{\circ}$. Therefore, $C D$ is the height of triangle $A B C$.
Let $A D=x, B D=3 x$. Since $C D^{2}=A D \cdot D B$, then $3 x^{2}=9$. From this, we find that $x^{2}=3$. Therefore,
$$
B C^{2}=C D^{2}+B D^{2}=9+9 x^{2}=9+27=36
$$
and $B C=6$.
Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\begin{array}{l}{[\text { Inscribed quadrilaterals }]} \\ \text { Area of a trapezoid }]\end{array}\right.$
The midline of an isosceles trapezoid is 5. It is known that a circle can be inscribed in the trapezoid.
The midline of the trapezoid divides it into two parts, the ratio of the areas of which is $\frac{7}{13}$. Find the height of the trapezoid.
|
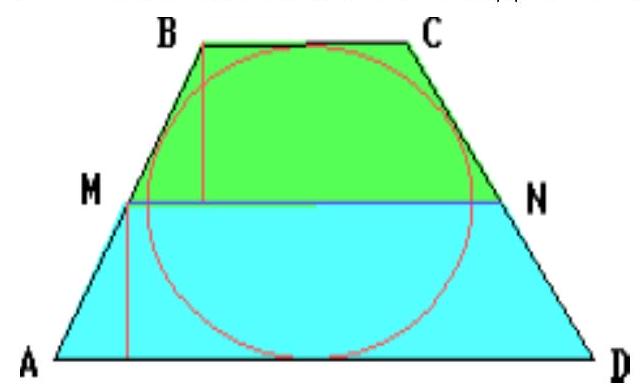
Solve the system of equations with two unknowns - the lengths of the bases of the trapezoid.
## Solution
Let $x$ and $y$ be the bases of the trapezoid. Then
$$
\left\{\begin{array}{l}
x+y=10 \\
\frac{x+5}{y+5}=\frac{7}{13}
\end{array}\right.
$$
From this, we find that $x=2$ and $y=8$. Therefore, the lateral side of the trapezoid is 10.
Drop a height from the vertex of the upper base to the lower base and find it using the Pythagorean theorem.
## Answer
4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11
In the pyramid $ABCD$, the edges are given: $AB=7, BC=8, CD=4$. Find the edge $DA$, if it is known that the lines $AC$ and $BD$ are perpendicular.
|
Let's draw the height $B K$ of triangle $A B C$. The line $A C$ is perpendicular to two intersecting lines $B K$ and $B D$ in the plane $B D K$. Therefore, the line $A C$ is perpendicular to each line in this plane, particularly to the line $D K$. Hence, $D K$ is the height of triangle $A D C$. We can apply the Pythagorean theorem to the right triangles $A B K$, $C B K$, $A D K$, and $C D K$:
$$
A B^2 - A K^2 = B C^2 - C K^2, \quad A D^2 - A K^2 = D C^2 - C K^2.
$$
Subtracting these equations term by term, we get the equation
$$
A B^2 - A D^2 = B C^2 - D C^2, \text{ or } 49 - A D^2 = 64 - 16
$$
from which we find that $A D^2 = 1$. Therefore, $A D = 1$.
## Answer
1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Sum of interior and exterior angles of a polygon]
Find the number $n$ of sides of a convex $n$-gon if each of its interior angles is not less than $143^{\circ}$ and not more than $146^{\circ}$.
#
|
The sum of the interior angles of a convex $n$-gon is $180^{\circ}(n-2)$, therefore
from which we find that $9 \frac{27}{37} \leqslant n \leqslant 10 \frac{20}{27}$. This inequality is satisfied by the unique natural number 10.
## Answer
10.00
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Given points $A, B, C$, and $D$ such that segments $A C$ and $B D$ intersect at point $E$. Segment $A E$ is 1 cm shorter than segment $A B$, $A E = D C$, $A D = B E$,
$\angle A D C = \angle D E C$. Find the length of $E C$.
|
$\angle B E A=\angle D E C=\angle A D C$, therefore triangles $A D C$ and $B E A$ are equal by two sides and the included angle. Thus, $A B=A C$. Therefore,
$E C=A C-A E=A B-A E=1$.
## Answer
1 cm.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[
Find the height of a right triangle dropped to the hypotenuse, given that the base of this height divides the hypotenuse into segments of 1 and 4.
#
|
Let $A B C$ be a right triangle with hypotenuse $A B$, and $C H$ be its altitude, $B H=1, A H=4$.
According to the altitude theorem of a right triangle drawn from the vertex of the right angle,
$$
C H^2=B H \cdot A H=1 \cdot 4=4
$$
Therefore, $C H=2$.
## Answer
2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Ratio of areas of triangles with a common angle]
On the sides $AB$ and $AC$ of triangle $ABC$, whose area is 50, points $M$ and $K$ are taken such that $AM: MB=1: 5$, and $AK: KC=3: 2$. Find the area of triangle $AMK$.
#
|
$$
S_{\triangle A M K}=\frac{A M}{A B} \cdot \frac{A K}{A C} S_{\triangle A B C}=\frac{1}{6} \cdot \frac{3}{5} \cdot 50=5
$$
## Answer
5.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$[$ Theorem on the lengths of a tangent and a secant; the product of the entire secant and its external part
A point $M$ is connected to a circle by two lines. One of them touches the circle at point $A$, while the other intersects the circle at points $B$ and $C$, with $B C=7$ and $B M=9$. Find $A M$.
#
|
Use the Tangent-Secant Theorem. Consider two cases.
## Solution
Let point $B$ lie between points $M$ and $C$. According to the Tangent-Secant Theorem,
$$
A M^{2}=M C \cdot M B=(9+7) 9=16 \cdot 9=12^{2}
$$
Therefore, $A M=12$.
If point $C$ lies between points $B$ and $M$, then similarly we get $A M=3 \sqrt{2}$.
## Answer
12 or $3 \sqrt{2}$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Rectangles and Squares. Properties and Characteristics ]
In a plane, there is a square with vertices $A, B, C, D$ in sequence and a point $O$ outside the square. It is known that $A O=O B=5$ and $O D=\sqrt{13}$. Find the area of the square.
|
Compose an equation with respect to the side of the square. One of the solutions of this equation contradicts the condition of the problem.
## Solution
Let $x$ be the side of the square. Let $P$ be the projection of point $O$ onto the line $A D$. From the condition of the problem, it follows that points $O$ and $A$ lie on opposite sides of the line $C D$.
Since point $O$ is equidistant from points $A$ and $B$, point $O$ lies on the perpendicular bisector of segments $A B$ and $C D$. Therefore, $O P = C D / 2 = x / 2$.
By the Pythagorean theorem in right triangles $A R O$ and $D P O$:
$$
A P = \sqrt{A O^{2} - O P^{2}} = \sqrt{25 - x^{2} / 4} ; D P = \sqrt{O D^{2} - O P^{2}} = \sqrt{13 - x^{2} / 4}
$$
Since $A D + D P = A P$, then $x + \sqrt{13 - x^{2} / 4} = \sqrt{25 - x^{2} / 4}$.
From the obtained equation, we find that $x^{2} = 2$ or $x^{2} = 36$. In the second case, $A D = 6$, which is impossible, since
$$
A P = A D + D P = 6 + D P > 5 = A O
$$
## Answer
2.
Let $A, B, C, D$ be the consecutive vertices of the square, and point $O$ is located inside the square. It is known that $O C = O D = \sqrt{10}$ and $O B = \sqrt{26}$. Find the area of the square.
## Solution
See the given problem.
## Answer
32.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$[$ Theorem on the lengths of a tangent and a secant; the product of the entire secant and its external part
From a point $M$, located outside the circle at a distance of $\sqrt{7}$ from the center, a secant is drawn, the internal part of which is half the external part and equal to the radius of the circle.
Find the radius of the circle.
|
Apply the tangent-secant theorem.
## Solution
Let $r$ be the radius of the circle. According to the tangent-secant theorem, $2 r \cdot 3 r = (\sqrt{7} - r)(\sqrt{7} + r) = 7 - r^2$, from which we get $r = 1$.
## Answer
1. Send a comment
Point $B$ lies on segment $AC$, which is equal to 5. Find the distance between the midpoints of segments $AB$ and $BC$.
## Hint
The distance between the midpoints of the given segments is half the length of segment $AC$.
## Solution
Let $M$ and $N$ be the midpoints of segments $AB$ and $BC$, respectively. Then segment $MN$ is composed of half of segments $AB$ and $BC$, and since $AB + BC = 5$, we have
$MN = \frac{1}{2} AB + \frac{1}{2} BC = \frac{1}{2} AC = \frac{5}{2}$.
## Answer
2.5.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Measurement of segment lengths and angle measures. Adjacent angles.]
On a straight line, points $A, B, C$ and $D$ are marked sequentially, and $A B=B C=C D=6$.
Find the distance between the midpoints of segments $A B$ and $C D$.
#
|
Let $M$ and $N$ be the midpoints of segments $AB$ and $CD$ respectively. Then $MN = MB + BC + CN = 3 + 6 + 3 = 12$.
## Answer
12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Measuring lengths of segments and measures of angles. Adjacent angles.] [Arithmetic operations. Numerical identities]
On a ruler 9 cm long there are no divisions.
Mark three intermediate divisions on it so that it can measure distances from 1 to 9 cm with an accuracy of 1 cm
#
|
It is sufficient to make intermediate divisions at the points 1 cm, 4 cm, 7 cm. Then we have 4 segments: 1 cm, 3 cm, 3 cm, and 2 cm. It is not difficult to verify that with such a ruler, one can measure any whole distance from 1 to 9 cm.
Send a comment
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Inscribed and Circumscribed Circles ]
The hypotenuse of a right triangle is 4 m. Find the radius of the circumscribed circle.
#
|
The center of the circle circumscribed around a right triangle coincides with the midpoint of the hypotenuse.
## Solution
The center of the circle circumscribed around a right triangle coincides with the midpoint of the hypotenuse. Therefore, the radius of the circle is half the hypotenuse, i.e., 2 m.
## Answer
Problem
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the maximum number of planes of symmetry a tetrahedron can have?
#
|
Show that each plane of symmetry must pass through an edge of the tetrahedron.
## Solution
In a regular tetrahedron, there are 6 planes of symmetry: each of them passes through one of the edges and bisects the edge that intersects it. We will show that there cannot be more than six planes of symmetry. Immediately note that a plane of symmetry passes through an even number of vertices of the tetrahedron, as the remaining vertices must be divided into pairs that are symmetric with respect to this plane of symmetry. Suppose a plane of symmetry does not pass through any of the vertices of the tetrahedron. Then the 4 vertices of the tetrahedron must be divided into two pairs of vertices that are symmetric with respect to the plane of symmetry. Consequently, the lines passing through these pairs of vertices must be perpendicular to the plane of symmetry, i.e., parallel to each other. Thus, the four vertices of the tetrahedron must lie in the same plane, which is impossible. It is clear that all four vertices of the tetrahedron cannot lie in the plane of symmetry. Therefore, the plane of symmetry must pass through exactly two of the vertices (i.e., through an edge) of the tetrahedron. Suppose a plane of symmetry passes through one of the edges of the tetrahedron. Then the remaining two vertices are symmetric with respect to this plane, so this plane must pass through the midpoint of the edge connecting the remaining two vertices. The previous
arguments show that there is no more than one plane of symmetry passing through a given edge of the tetrahedron. Thus, the total number of planes of symmetry is no greater than the number of edges of the tetrahedron, i.e., no more than six.
## Answer
6.00
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Median line of a triangle ]
Points $M$ and $N$ are located on sides $A B$ and $A C$ of triangle $A B C$, respectively, such that $B M=3 A M$ and $C N=$ $3 A N$. Prove that $M N \| B C$ and find $M N$, if $B C=12$.
#
|
Connect the midpoints of $A B$ and $A C$.
## Solution
Let $K$ and $L$ be the midpoints of sides $A B$ and $A C$. Then $K L$ is the midline of triangle $A B C$, and $M N$ is the midline of triangle $A K L$. Therefore,
$$
M N\|K L\| B C \text{ and } M N=\frac{1}{2} K L=\frac{1}{2} \cdot \frac{1}{2} B C=\frac{1}{4} B C=3 .
$$
## Answer
3.
|
3
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
[ Cutting (other).]
Two people had two square cakes. Each made 2 straight cuts from edge to edge on their cake. As a result, one ended up with three pieces, and the other with four. How could this happen?
|
Note: Cuts can intersect.
## Solution
This could happen if in the first case the cuts did not intersect each other, while in the second case they did. For example, if in the first case the cuts were parallel to each other, and in the second case they were perpendicular.
## Answer
In the first case, the cuts were parallel to each other, and in the second case, they were perpendicular.
How many pieces can a round pancake be divided into with three straight cuts?
## Hint
Recall problem 11.
## Solution
If each of the three lines intersects the other two inside the pancake, it will result in 7 pieces (see Fig. 11.4). If any two of these lines are parallel or intersect outside the pancake, there will be fewer pieces.
## Answer
7 pieces.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Angles between angle bisectors $\quad]$
In triangle $ABC$, the angle bisectors of the angles at vertices $A$ and $C$ intersect at point $D$. Find the radius of the circumcircle of triangle $ABC$, if the radius of the circumcircle of triangle $ADC$ with center at point $O$ is $R=6$, and $\angle ACO=30^{\circ}$.
|
Prove that $\angle A D C=90^{\circ}+\frac{1}{2} \angle B$.
## Solution
Since $\angle B A C+\angle A C B=180^{\circ}-\angle B$, then $\angle D A C+\angle A C D=90^{\circ}-\frac{1}{2} \angle B$. Therefore,
$$
\angle A D C=180^{\circ}-\left(90^{\circ}-\frac{1}{2} \angle B=90^{\circ}+\frac{1}{2} \angle B>90^{\circ}-\angle B,\right.
$$
i.e., angle $A D C$ is obtuse. Therefore, points $D$ and $O$ lie on opposite sides of the line $A C$. From the isosceles triangle $A O C$, we find that
$$
A C=2 O C \cos 30^{\circ}=2 R \cdot \frac{\sqrt{3}}{2}=6 \sqrt{3}
$$
Since $\angle A O C$ is a central angle of the circle with center $O$ and $\angle A O C=120^{\circ}$, the inscribed angle $\angle A D C$ is half the arc $A C$ not containing point $D$, i.e., $\angle A D C=\frac{1}{2} \cdot 240^{\circ}=120^{\circ}$. From the equality $\angle A D C=90^{\circ}+\frac{1}{2} \angle B$, we find that
$$
\angle B=2\left(\angle A D C-90^{\circ}\right)=2\left(120^{\circ}-90^{\circ}\right)=60^{\circ}
$$
Let $r$ be the radius of the circumcircle of triangle $A B C$. By the Law of Sines,
$$
r=\frac{A C}{2 \sin \angle B}=\frac{6 \sqrt{3}}{2 \cdot \frac{\sqrt{3}}{2}}=6
$$

## Answer
6.00
Submit a comment
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Triangle Inequality
Point $C$ divides the chord $A B$ of a circle with radius 6 into segments $A C=4$ and $C B=5$. Find the minimum distance from point $C$ to the points on the circle.
#
|
Let $O$ be the center of the circle. Extend the segment $OC$ beyond point $C$ to intersect the circle at point $M$, and using the triangle inequality, prove that the length of the segment $CM$ is the smallest of the distances from point $C$ to the points on the circle.
## Solution
Let $O$ be the center of the circle. Extend the segment $OC$ beyond point $C$ to intersect the circle at point $M$. We need to prove that the length of the segment $CM$ is the smallest of the distances from point $C$ to the points on the circle.
Indeed, let $X$ be any point on the circle, different from $M$. Then
$$
OC + CM = OM = OX < OC + CX
$$
(triangle inequality for triangle $OCX$). From this, it follows that $CM < CX$, which is what we needed to prove. Extend the segment $CO$ beyond point $O$ to intersect the circle at point $N$. By the theorem of the products of the segments of intersecting chords, $CM \cdot CN = AC \cdot CB$, or $CM \cdot (12 - CM) = 4 \cdot 5$. Considering the condition $CM < OM = 6$, from the obtained equation, we find that $CM = 2$.
## Answer
The problem
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Mutual Position of Two Circles]
What is the mutual position of two circles if:
a) the distance between the centers is 10, and the radii are 8 and 2;
b) the distance between the centers is 4, and the radii are 11 and 17;
c) the distance between the centers is 12, and the radii are 5 and 3?
|
Let $O_{1}$ and $O_{2}$ be the centers of the circles, $R$ and $r$ be their radii, and $R \geqslant r$.
If $R+r=O_{1} O_{2}$, then the circles touch.
If $R+r<O_{1} O_{2}$, then one circle is located outside the other.
If $O_{1} O_{2}<R-r$, then one circle is located inside the other.
## Answer
a) touch; b) one inside the other; c) one outside the other.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bogov and I.I.
The distance between two cells on an infinite chessboard is defined as the minimum number of moves in the path of a king between these cells. On the board, three cells are marked, the pairwise distances between which are 100. How many cells exist such that the distances from them to all three marked cells are 50?
|
Consider two arbitrary cells $A$ and $B$. Let the difference in the abscissas of their centers be $x \geq 0$, and the difference in the ordinates be $y \geq 0$. Then the distance $\rho(A, B)$ between these cells is $\max \{x, y\}$.
Let cells $A, B, C$ be marked. Then for each pair of cells, there exists a coordinate in which they differ by exactly 100. For two pairs of cells, this will be the same coordinate; for definiteness, let these be the pairs $(A, B)$ and $(A, C)$, differing horizontally. Then the abscissas of points $B$ and $C$ either differ by 200 or coincide. The first case is impossible, since $\rho(B, C)=100$. Therefore, their abscissas coincide, and their ordinates differ by 100. We can assume that the cells have coordinates $B(0,0), C(0,100), A(100, x)(0 \leq x \leq 100)$. Consider a point $X$ that is 50 units away from points $A, B$, and $C$. Its abscissa must be 50, otherwise $\rho(X, B)>50$ or $\rho(X, A)>50$. Similarly, the ordinate of $X$ is 50. Therefore, the coordinates of $X$ are $(50,50)$, and this cell fits. Thus, the sought cell is exactly one.
## Answer
One cell.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
Segments connecting an inner point of a convex non-equilateral $n$-gon with its vertices divide the $n$-gon into $n$ equal triangles.
For what smallest $n$ is this possible?
|
Let's prove that the specified situation is impossible for $n=3,4$.
The first method. For $n=3$, the angles of the triangles in the partition that meet at an internal point are equal, since the sum of any two different angles in them is less than $180^{\circ}$. But then the sides opposite to these angles, which are sides of the polygon, are also equal. This is a contradiction.
Suppose the quadrilateral $ABCD$ is divided into equal triangles by segments drawn from point $O$. Draw the broken line (or straight line) $AOC$. At point $O$, the sum of two angles on one side of $AOC$ is not less than $180^{\circ}$. Similarly to the case of $n=3$, we get that the corresponding sides are equal. Considering the broken line $BOD$, we get the equality of one of these sides and the third side. Let, for example, $AB = BC = CD = 1$. Suppose $AD \neq l$. In triangle $AOD$, there is a side of length $l$, say $AO$. Thus, in triangle $AOB$ (and all equal to it), there are two sides of length $l$. As a result, $AO = DO = l$. In triangle $BOC$, there are two sides of length $l$. One of them is $BC$, and the other, say, $BO$. But then in triangle $AOB$, all sides are equal. Therefore, this is also true for triangle $AOD$, i.e., $AD = l$. This is a contradiction.
The second method. Since the triangles into which the given triangle is divided are equal, the radii of the circumscribed circles around them and their areas are equal. The first implies that the point defining the division is the orthocenter of the triangle (see problem 56681a), and the second implies that it is the point of intersection of its medians (see problem 54992). However, the orthocenter and the point of intersection of the medians coincide only in an equilateral triangle (see problem 108458).
$\angle OAB = \angle OCB$, as angles opposite the same side of equal triangles. Similarly, $\angle OAD = \angle OCD$, $\angle OBC = \angle ODC$, $\angle OBA = \angle ODA$. Therefore, $\angle A = \angle C$, $\angle B = \angle D$, and $ABCD$ is a parallelogram. Since the segments from $O$ divide it into equal-area triangles, $O$ is the point of intersection of its diagonals, and then from the equality of the triangles, it follows that $ABCD$ is a rhombus.
For $n=5$, the specified situation is possible (see figure).
## Answer
$n=5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The diagonals of the trapezoid are 3 and 5, and the segment connecting the midpoints of the bases is 2. Find the area of the trapezoid.
#
|
Through the vertex of the smaller base of the trapezoid, draw a line parallel to the diagonal.
## Solution
Let $M$ and $K$ be the midpoints of the bases $BC$ and $AD$ of trapezoid $ABCD$. Through vertex $C$ of the smaller base $BC (AC=3, BD=5)$, draw a line parallel to diagonal $BD$, intersecting line $AD$ at point $P$, and draw a line parallel to $MK$, intersecting line $AD$ at point $Q$. Then
$$
\begin{gathered}
A Q=A K+K Q=A K+M C=\frac{1}{2} A D+\frac{1}{2} B C= \\
=\frac{1}{2}(A D+B C)=\frac{1}{2}(A D+D P)
\end{gathered}
$$
Therefore, $CQ$ is the median of triangle $ACP$,
$$
C Q=M K=2, A C=3, C P=B D=5, S_{\mathrm{ABCD}}=S_{\triangle \mathrm{ACP}}
$$
Extend median $CQ$ beyond point $Q$ and lay off segment $QF$ equal to $CQ$. The sides of triangle $CFP$ are:
$$
C F=2 C Q=4, C P=B D=5, F P=A C=3 .
$$
This triangle is right-angled ( $C P^{2}=C F^{2}+P F^{2}$ ). Therefore,
$$
S_{\triangle \mathrm{CFP}}=\frac{1}{2} C F \cdot P F=6
$$
Thus,
$$
S_{\mathrm{ABCD}}=S_{\triangle \mathrm{ACP}}=S_{\triangle \mathrm{CFP}}=6
$$
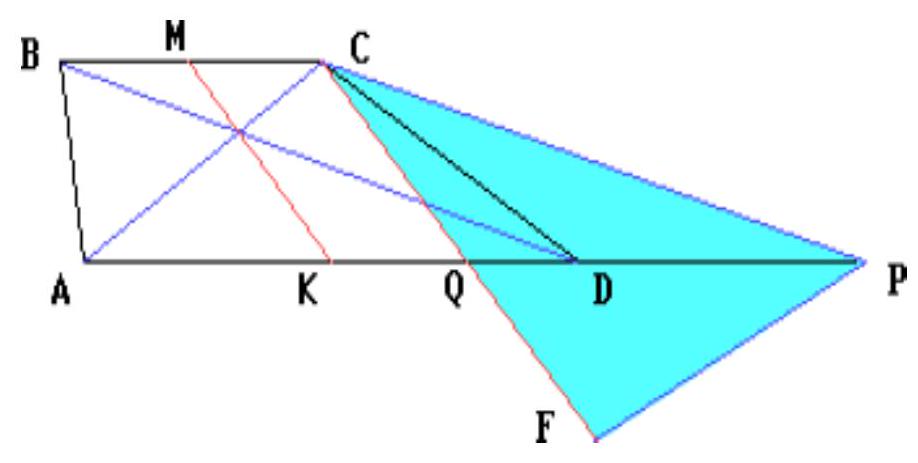
## Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A circle with radius $\frac{2}{\sqrt{3}}$ is inscribed in an isosceles trapezoid. The angle between the diagonals of the trapezoid, subtending the larger base, is $2 \operatorname{arctg} \frac{2}{\sqrt{3}}$. Find the segment connecting the points of tangency of the circle with the larger base of the trapezoid and one of its lateral sides.
|
Denote the halves of the bases of the trapezoid as $x$ and $y$; find $x, y$ and the angle between the lateral side and the larger base.
## Solution
Let $Q$ be the point of intersection of the diagonals $A C$ and $B D$ of trapezoid $A B C D$; $N, M$, and $K$ be the points of tangency of the inscribed circle with the smaller base $A D$, the lateral side $A B$, and the larger base $B C$ respectively; $O$ be the center of the circle. Denote $A N=x, B K=y$. Then,
$$
x y=O M^{2}=\frac{4}{3}, \quad x+y=A N+B K=(N Q+Q K) \operatorname{tg} \angle A N Q=\frac{8}{3}
$$
From the obtained system, we find that $x=\frac{2}{3}$ and $y=2$. Therefore,
$$
\cos \angle A B K=\frac{y-x}{y+x}=\frac{1}{2}, \quad \angle A B K=60^{\circ}, \quad M K=y=2
$$
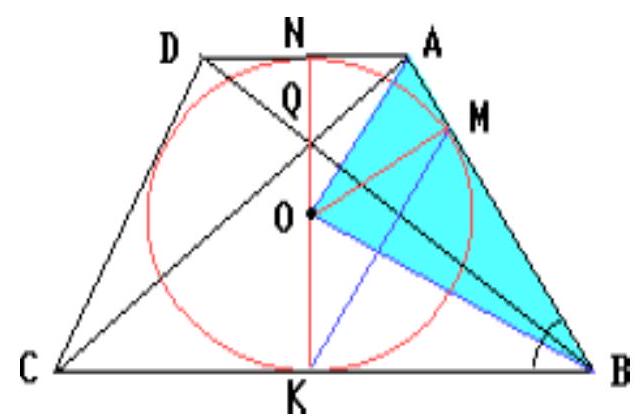
## Answer
2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ [tangents drawn from one point] [ Midline of a triangle $\quad$]
A circle of radius 1 is inscribed in triangle $ABC$, where $\cos \angle B=0.8$. This circle touches the midline of triangle $ABC$, parallel to side $AC$. Find the side $AC$.
|
The distance from the vertex of a triangle to the nearest point of tangency with the inscribed circle is equal to the difference between the semiperimeter and the opposite side.
## Solution
Let $O$ be the center of the inscribed circle, and $K$ be its point of tangency with side $AB$. Then
$$
\operatorname{tg} \frac{1}{2} \angle B = \frac{\sin \angle B}{1 + \cos \angle B} = \frac{0.6}{1 + 0.8} = \frac{1}{3}
$$
Therefore,
$$
B K = \frac{O K}{\operatorname{tg} \frac{1}{2} \angle B} = 3
$$
On the other hand, the segment $BK$ is equal to the semiperimeter of the cut-off triangle, which is similar to the given triangle with a similarity coefficient of $\frac{1}{2}$. Therefore, the semiperimeter of the given triangle is 6. Consequently, $AC = 6 - BK = 3$.
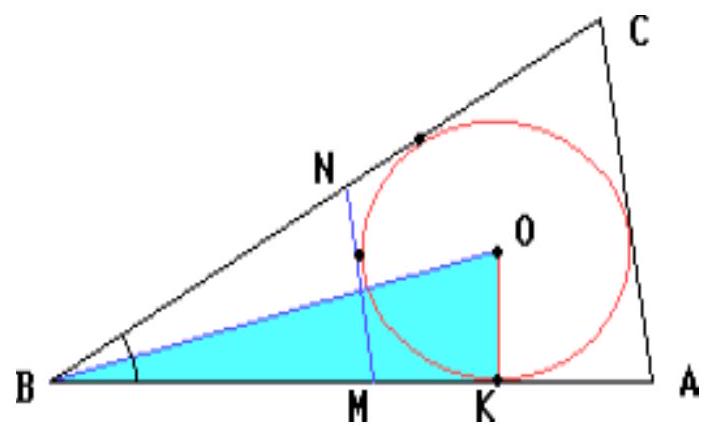
Answer
3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Measuring lengths of segments and measures of angles. Adjacent angles.] Unusual constructions (miscellaneous). $\quad]$
On a wooden ruler, three marks are made: 0, 7, and 11 centimeters. How can you measure with it a segment equal to: a) 8 cm $;$ b) 5 cm
#
|
a) Using divisions of 7 and 11, you can measure 4 cm. Doing this twice, you will get a segment of 8 cm.
b) First method. Knowing how to measure 8 and 7, you can measure 1 cm. Doing this 5 times, you will get 5 cm.
Second method. $5=3 \cdot 11-4 \cdot 7$, so it is enough to measure 3 times 11 cm and then 4 times 7 in the opposite direction.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Measuring lengths of segments and measures of angles. Adjacent angles.] Extreme properties (miscellaneous).
In a village, along a straight road, there are two houses $A$ and $B$ located 50 meters apart from each other.
At what point on the road should a well be dug so that the sum of the distances from the well to the houses is minimized?
|
Any point $X$ on the road segment between $A$ and $B$ is equally good, since the segments $A X$ and $B X$ together total 50 m. If a point is taken outside this segment, then the sum of the distances from it to points $A$ and $B$ will be greater than $50 \mathrm{M}$.
## Answer
At any point on the segment $A B$.
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a square with an area of 18, a rectangle is inscribed such that one vertex of the rectangle lies on each side of the square. The sides of the rectangle are in the ratio $1: 2$.
Find the area of the rectangle.
|
Let the vertices $K, L, M$ and $N$ of the rectangle $K L M N$ be located on the sides $A B, B C, C D$ and $A D$ of the square $A B C D$, respectively, such that $K N=2 K L$. Let $K L=x, \angle A K N=\alpha$. Then
$M N=x, L M=K N=2 x, \angle C M L=\angle B L K=\angle A K N=\alpha, A K=2 x \cos \alpha, B K=x \sin \alpha, B L=x \cos \alpha, C L=L M \sin \alpha=$ $2 x \sin \alpha$.
Since $A B=A K+B K$ and $B C=B L+C L$, we have $2 x \cos \alpha+x \sin \alpha=x \cos \alpha+2 x \sin \alpha$, from which $\sin \alpha=\cos \alpha$, and since $\alpha<90^{\circ}$, then $\alpha=45^{\circ}$.
Since $2 x \cos 45^{\circ}+x \sin 45^{\circ}=A B=\sqrt{18}=3 \sqrt{2}$, then $x=2$, and $S_{K L M N}=2 x^{2}=8$.
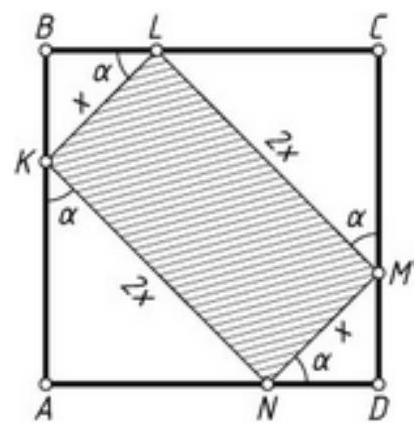
## Answer
8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 ( A square with an area of 24 has a rectangle inscribed in it such that one vertex of the rectangle lies on each side of the square. The sides of the rectangle are in the ratio $1: 3$.
Find the area of the rectangle.
#
|
## Answer
9.
## Problem
Translate the text above into English, please retain the original text's line breaks and format, and output the translation result directly.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
Each face of a cube $6 \times 6 \times 6$ is divided into $1 \times 1$ cells. The cube is covered with $2 \times 2$ squares such that each square covers exactly four cells, no squares overlap, and each cell is covered by the same number of squares. What is the maximum value that this identical number can take? (Squares can be bent over the edge.)
|
Evaluation. A cell in the corner of a face can be covered in three ways (entirely within the face, with a fold over one edge of the corner, with a fold over the other edge of the corner). This means that each cell is covered by no more than three squares.
Example. Consider the usual covering of a cube with squares, where each face is covered by nine squares. From the usual covering, we can obtain a rotated one: leave two opposite faces untouched, and on the other four faces, shift all the squares in a ring by one cell. Since a pair of opposite faces can be chosen in three ways, there will be exactly three rotated coverings.
We will show that no two squares on coverings rotated differently coincide. Indeed, consider one face. On the diagram, the centers of the squares covering it are marked: with crosses if this face was not shifted, with black and white dots - if it was shifted in one or the other direction. It is clear that no centers, and therefore no squares, coincide.

## Answer
3.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Triangle Inequality (other).]
At vertex $A$ of a unit square $A B C D$, there is an ant. It needs to reach point $C$, where the entrance to the ant hill is located. Points $A$ and $C$ are separated by a vertical wall, which has the shape of an isosceles right triangle with hypotenuse $B D$. Find the length of the shortest path the ant must travel to reach the ant hill.
|
Let $K$ be the vertex of the right angle of triangle $B K D$ (a vertical wall). The path of the ant consists of four segments: $A M, M P, P M$, and $M C$, where point $M$ lies on line $B D$, and point $P$ lies on segment $D K$ or $B K$. Clearly, $A M = M C$, so it is sufficient to specify points $M$ and $P$ such that the path $A M P$ is minimal.
Place the wall so that vertex $K$ coincides with $C$. Then point $P$ will coincide with some point $P_{1}$ on segment $C D$ (or $B C$), and
$$
A M + M P = A M + K P_{1} \geqslant A P_{1} \geqslant A D
$$
and this inequality becomes an equality only in the case where points $P_{1}$ and $D$ coincide. Therefore, the shortest path of the ant passes along sides $A D$ and $C D$ (or $A B$ and $B C$). The length of this path is 2.
## Second Method.
Let $K$ be the vertex of the right angle of triangle $B K D$ (a vertical wall). Suppose the ant's path intersects the leg $B K$. Consider the triangle $B A D$ as a paper fold: the fold lines are $B D$ (twice) and $B K$ (see figure). By unfolding this fold, we get that the ant's path will be a straight line segment. Thus, the length of the shortest path is 2, and the shortest path is along the sides of the square, bypassing the obstacle.
## Answer
2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
C
[Median line of a triangle
[ Trigonometric ratios in a right-angled triangle ]
In triangle $ABC$, the median $BM$ and the altitude $AH$ are drawn. It is known that $BM = AH$. Find the angle $MBC$.
#
|
Drop a perpendicular from point $M$ to line $B C$.
## Solution
Drop the perpendicular $M K$ to line $B C$. Then $M K$ is the midline of triangle $A H C$. Therefore, $M K = 1/2 A H = 1/2 B M$, which means $\angle M B K = 30^{\circ}$. Consequently, $\angle M B C = 30^{\circ}$ or $150^{\circ}$.
## Answer
Inside the triangle, there are two points. The distances from one of them to the sides of the triangle are 1, 3, and 15, and from the other (in the same order) are 4, 5, and 11.
Find the radius of the inscribed circle of the given triangle.
## Hint
Let $M_{1}$ and $M_{2}$ be the given points. On the line $M_{1} M_{2}$, take a point $O$ such that $O M_{2} = M_{2} M_{1}$. Then $O$ is the center of the inscribed circle of the given triangle.
## Solution
Let $M_{1}$ and $M_{2}$ be the given points; $O$ be the point for which $M_{2}$ is the midpoint of $O M_{1}$. By the property of the midline of a trapezoid, the distances from point $O$ to the sides of the triangle are respectively $2 \cdot 4 - 1 = 7, 2 \cdot 5 - 3 = 7, 2 \cdot 11 - 15 = 7$.
Since the segment $O M_{1}$ cannot intersect any of the sides of the triangle, $O$ is the center of the inscribed circle, and its radius is 7.

## Answer
7. Send a comment
## 3
Problem
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Given an isosceles triangle with a base of 12 and a side length of 18. What segments need to be marked off from the vertex of the triangle on its sides so that connecting their ends forms a trapezoid with a perimeter of 40?
#
|
The smaller base of the trapezoid cuts off a similar triangle from the given triangle.
## Solution
Let $ABC$ be the given triangle, $AB=BC=18, AC=12$. Denote the sought segments $BM$ and $BN$ by $x$. Then $AM=CN=18-x$.
From the similarity of triangles $MBN$ and $ABC$, we find that $MN=\frac{BM \cdot AC}{AB}=2x / 3$.
The perimeter of trapezoid $AMNC$ is $2AM + AC + MN = 2(18 - x) + 12 + 2x / 3 = 40$. From this, $x=6$.
Answer

Inside a right angle, a point $M$ is given, the distances from which to the sides of the angle are 4 and 8. A line passing through point $M$ cuts off a triangle from the right angle with an area of 100. Find the legs of the triangle.
## Solution
Denote the sought legs by $x$ and $y$. Then $xy=200$. Moreover, from the similarity of right triangles, it follows that $8 / y - 4 = x / y$. Hence, $x = 8y / (y - 4)$.
Substituting $x$ into the first equation, we get $8y^2 / (y - 4) = 200, y^2 = 25y - 100, y^2 - 25y + 100 = 0$.
Therefore, $y_1 = 20, x_1 = 10$ or $y_2 = 5, x_2 = 40$.
Answer
20, 10 or $5, 40$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left.\frac{\text { Auxiliary similar triangles }}{[\quad \text { Law of Cosines }}\right]$
In triangle $ABC$, a point $D$ is taken on side $AC$, such that $AD=3$, $\cos \angle BDC=13/20$, and $\angle B+\angle ADB=180^{\circ}$. Find the perimeter of triangle $ABC$ if $BC=2$.
|
Triangles $A B C$ and $B D C$ are similar.
## Solution
Since $\angle B=180^{\circ}-\angle A D B=\angle B D C$, triangles $A B C$ and $B D C$ are similar by two angles. Therefore, $B C$ : $A C=D C: B C$, or $\frac{2}{3+D C}=1 / 2 D C$. From this, we get $D C=1, A C=4$. By the cosine rule, $A C^{2}=A B^{2}+B C^{2}-$
$2 A B \cdot B C \cos \angle B$, or $16=A B^{2}+4-2 \cdot 2 A B \cdot 13 / 20$.
From this, we find that $A B=5$. Therefore, the perimeter of triangle $A B C$ is $A C+B C+A B=4+2+5=$ 11.
## Answer
11.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\begin{aligned} & {\left[\begin{array}{l}\text { Sum of the angles of a triangle. Theorem about the exterior angle. } \\ \text { [ Criteria and properties of an isosceles triangle. }\end{array}\right]}\end{aligned}$
In triangle $ABC$, angle $B$ is $20^{\circ}$, angle $C$ is $40^{\circ}$. The bisector $AD$ is 2. Find the difference between sides $BC$ and $AB$.
|
On side $B C$, lay off segment $B M$ equal to $A B$.
## Solution
On side $B C$, we lay off segment $B M$ equal to $A B$. In the isosceles triangle $A B M$, the angles at the base $A M$ are each $80^{\circ}$, so
$\angle C A M = \angle A M D - \angle A C B = 40^{\circ} = \angle A C M$.
Moreover, $\angle A D M = \angle A B C + \angle B A D = 80^{\circ} = \angle A M D$.
Thus, triangles $A M C$ and $A M D$ are isosceles. Therefore, $B C - A B = C M = A M = A D = 2$.
## Answer
2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$3+$ [Properties and characteristics of an isosceles triangle.]
On each side of a square, one point was taken. It turned out that these points are the vertices of a rectangle, the sides of which are parallel to the diagonals of the square. Find the perimeter of the rectangle if the diagonal of the square is 6.
#
|
Let the vertices $K, L, M$ and $N$ of the rectangle $K L M N$ be located on the sides $A B, B C, C D$ and $A D$ of the square $A B C D$, respectively, such that $K N \| B D$ and
$K L \| A C$, and the segments $K L$ and $M N$ intersect the diagonal $B D$ of the square at points $P$ and $Q$, respectively. Then $K P=B P$, $N Q=D Q, K N=P Q$.
## Answer
12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shestakov C.A.
In a convex quadrilateral $ABCD$, points $E$ and $F$ are the midpoints of sides $BC$ and $CD$ respectively.
Segments $AE$, $AF$, and $EF$ divide the quadrilateral into four triangles, the areas of which are (in some order) consecutive natural numbers. What is the greatest possible value of the area of triangle $ABD$?
|
Author: Shestakov S.A.
Let the areas of the triangles be $n, n+1, n+2$, and $n+3$. Then $S_{A B C D}=4 n+6$. $E F$ is the midline of triangle $B C D$, so $S_{B C D}=4 S_{E C F} \geq 4 n$. Therefore, $S_{A B D}=S_{A B C D}-S_{B C D} \leq 6$.
We will show that this area can equal 6. Consider an isosceles trapezoid $A B C D$ with bases $A D=6, B C=4$ and height 2. Then
$S_{C F E}=1, S_{A B E}=2, S_{A D F}=3, S_{A E F}=S_{A B C D}-1-2-3=4$, and in this case $S_{A B D}=6$.
## Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Sergeev I.N.
At the base $A_{1} A_{2} \ldots A_{n}$ of the pyramid $S A_{1} A_{2} \ldots A_{n}$ lies a point $O$, such that $S A_{1}=S A_{2}=\ldots=S A_{n}$ and $\angle S A_{1} O=\angle S A_{2} O=$ $\ldots=\angle S A_{n} O$.
For what least value of $n$ does it follow from this that $S O$ is the height of the pyramid?
|
By the Law of Sines for triangles $S A_{k} O (k=1,2, \ldots, n)$, we have $\sin \angle S O A_{k} = \frac{S A_{k}}{S O} \cdot \sin \angle S A_{k} O$.
Since the right-hand side of this equality does not depend on the choice of $k=1,2, \ldots, n$, the value of $\sin \angle S O A_{k}$ also does not depend on this choice. Therefore, for different choices of $k$, the angle $S O A_{k}$ can take no more than two different values, each of which, together with the lengths $S O, S A_{k}$, and the angle $S O A_{k}$, uniquely determines the triangle $S A O$.
If $n \geq 5$, then among the triangles $S A_{k} O (k=1,2, \ldots, 5)$, there are at least three identical ones. Let these, for definiteness, be the triangles $S A_{1} O, S A_{2} O$, and $S A_{3} O$. Since $O A_{1} = O A_{2} = O A_{3}$, the point $O$ is the center of the circumscribed circle of the triangle $A_{1} A_{2} A_{3}$. Let $S H$ be the height of the pyramid $S A_{1} A_{2} A_{3}$. Then the point $H$ is also the center of the circumscribed circle around $A_{1} A_{2} A_{3}$, i.e., $H = O$.
For $n=4$, it does not follow from the condition that $S O$ is the height of the pyramid. For example, if $A_{1} A_{2} A_{3} A_{4}$ is an isosceles trapezoid, $O$ is the intersection point of its diagonals, and $H$ is the center of the circumscribed circle around it, then for the pyramid $S A_{1} A_{2} A_{3} A_{4}$, where $S H$ is the height to the base, all the conditions of the problem are satisfied. Indeed, first, $S A_{1} = S A_{2} = S A_{3} = S A_{4}$ due to the equality (by two legs) of triangles $S H A_{1}, S H A_{2}, S H A_{3}$, and $S H A_{4}$, and secondly,
$\angle S A_{1} O = \angle S A_{2} O = \angle S A_{3} O = \angle S A_{4} O$ due to the equality (by three sides) of isosceles triangles $S A_{1} A_{3}$ and $S A_{2} A_{4}$. In this case, $H \neq O$. For $n \leq 4$, it also does not follow from the condition that $S O$ is the height of the pyramid (the corresponding example is obtained from the previous one by considering its part - the pyramid $S A_{1} A_{2} A_{3}$).
## Answer
For $n=5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Parallelism of lines and planes $]$ [ Systems of segments, lines, and circles ]
In space, there are $n$ segments, no three of which are parallel to the same plane. For any two segments, the line connecting their midpoints is perpendicular to both segments. What is the largest $n$ for which this is possible?
|
Answer: $n=2$.
Suppose that $n \geq 3$. Take three segments $a, b$, and $c$ and draw three lines connecting the midpoints of each pair. Each of the segments $a, b, c$ is perpendicular to the two lines emanating from its midpoint, and therefore it is perpendicular to the plane passing through all three drawn lines. Thus, the three segments $a, b, c$ are parallel to one plane, which contradicts the condition. (Article XXX "Problems XL MMO - answers, hints, solutions", Kvant 1978 issue 2 p. 64, problem 10)
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
For what largest $n$ can one choose $n$ points on the surface of a cube so that not all of them lie in the same face of the cube and are vertices of a regular (planar) $n$-gon.
|
On one face of a cube, no more than two vertices of a polygon can lie (otherwise, the entire polygon would lie in this face). Therefore, the polygon cannot have more than 12 vertices.
To obtain a 12-sided polygon, recall that there exists a section of the cube by a plane that forms a regular hexagon. This section passes through the midpoints of six edges of the cube (see the left figure).
Indeed, the "large" diagonals of the section—segments connecting the midpoints of opposite edges of the cube—obviously pass through the center of the cube and, therefore, lie in the same plane. The regularity of the hexagon follows from the symmetry of the picture.
By taking two points on each side of the regular hexagon that divide it in the ratio $1: \sqrt{3}: 1$, we, as it is easy to verify, obtain the vertices of a regular 12-sided polygon (see the right figure).
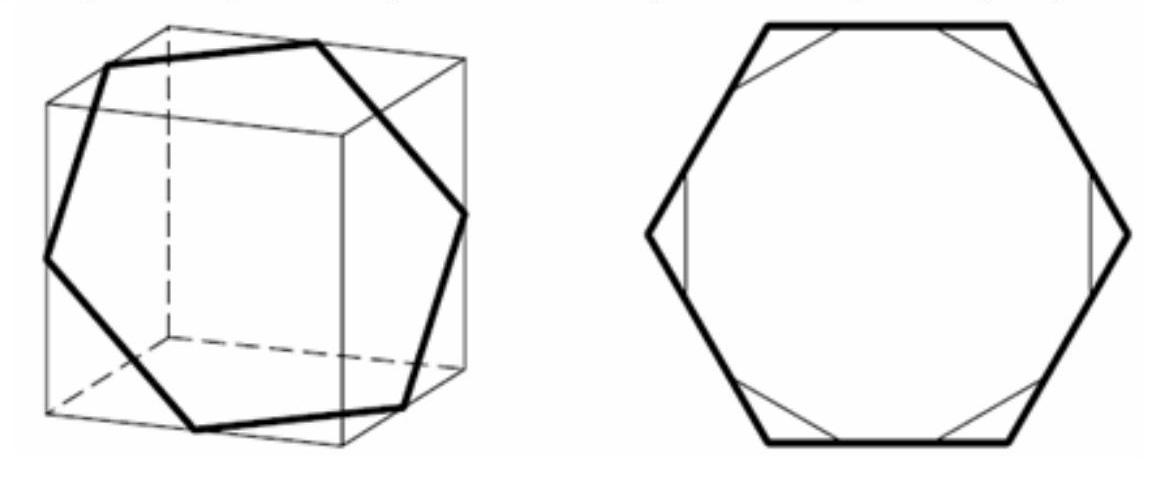
Answer
$n=12$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Inscribed Quadrilaterals (Miscellaneous) ]
Quadrilateral $ABCD$ is inscribed in a circle. Point $X$ lies on its side $AD$, such that $BX \parallel CD$ and $CX \parallel BA$. Find $BC$, if $AX = 3/2$ and $DX = 6$.
#
|
Triangles $A B C, B X C$ and $X C D$ are similar.
## Solution
Let the angles at vertices $A, B$, and $X$ of triangle $A B X$ be denoted as $\alpha, \beta$, and $\gamma$ respectively. Since $C X \| B A$ and $B X \| C D$, then
$\angle D C X = \angle B X C = \angle A B X = \beta, \quad \angle C D X = \angle B X A = \gamma$ and $\angle C X D = \angle B A X = \alpha$.
$\angle C B A = 180^{\circ} - \angle C D A = 180^{\circ} - \gamma = \alpha + \beta$, and since $\angle A B X = \beta$, then $\angle C B X = \alpha$. Therefore, triangles $A B C, B X C$ and $X C D$ are similar. Multiplying the equalities $B C: A X = C X: B X$ and $B C: D X = B X: C X$ term by term, we get $B C^2 = A X \cdot D X = 9$.
## Answer
3.
Send a comment
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Sum of angles in a triangle. Theorem about the exterior angle. ] [ Lengths of sides, heights, medians, and angle bisectors ]
In triangle $A B C \angle A=40^{\circ}, \angle B=20^{\circ}$, and $A B-B C=4$. Find the length of the angle bisector of angle $C$.
|
Let's set aside segment $BD$ on side $AB$, equal to $BC$. Then triangle $BCD$ is isosceles with the angle at the vertex $20^{\circ}$, so the angles at the base are $80^{\circ}$ (see the figure). Let $CE$ be the bisector of angle $C$. Then $\angle BCE = 60^{\circ}$, so $\angle AEC = 20^{\circ} + 60^{\circ} = 80^{\circ}$. Thus, in triangle $DEC$, two angles are equal, so it is isosceles. The angle at its vertex $C$ is $20^{\circ}$, so $\angle ACD = 40^{\circ}$. Therefore, triangle $ACD$ is also isosceles, hence $CE = CD = AD = AB - BC = 4$.
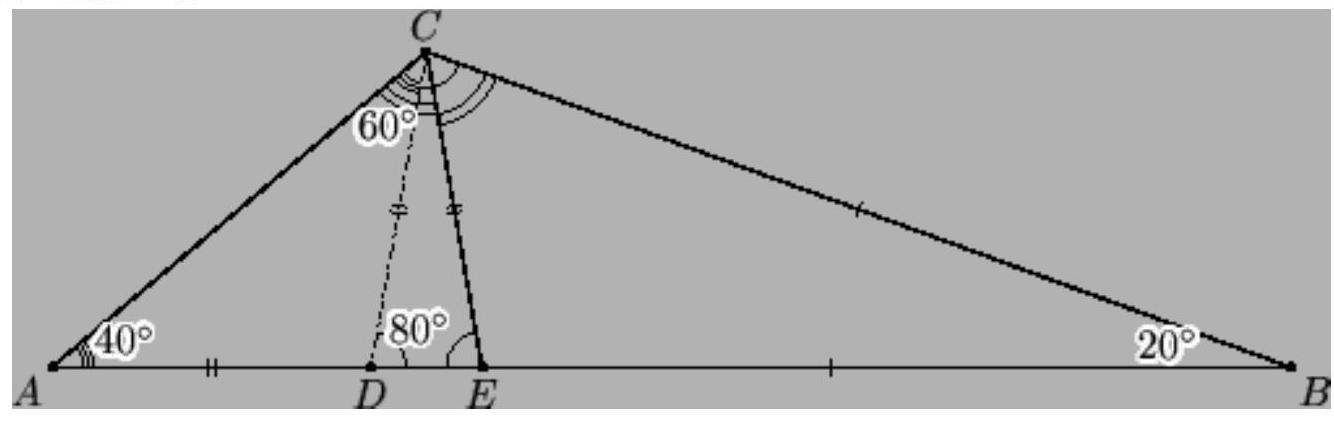
## Answer
4
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Examples and counterexamples. Constructions ]
Six identical parallelograms of area 1 were used to cover a cube with an edge of 1. Can we assert that all parallelograms are squares? Can we assert that all of them are rectangles?
|
Examples of such cube nets are shown in Figure 1.
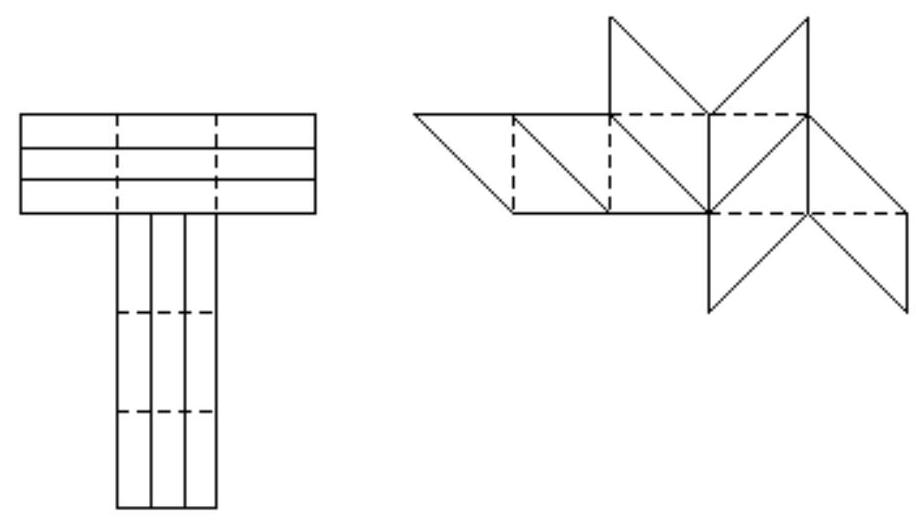
Fig. 1
## [Elementary (basic) constructions with a compass and straightedge] Problem 107725 Topics: [ Construction of triangles by various elements $]$ Difficulty: $3+$ Grades: $7,8,9,10$
Given a line and a point outside it, how can you construct a line parallel to the given line and passing through the given point using a compass and straightedge, while drawing the fewest possible lines (circles and lines), so that the last line drawn is the desired line? What is the minimum number of lines you were able to achieve?
## Solution
Given a line $a$ and a point $O$ (notations). Mark two arbitrary points $A$ and $B$ on the line. Draw a circle with center at point $B$ and radius $AO$, and a circle with center at point $O$ and radius $AB$. They will intersect at point $X$. The quadrilateral $AOXB$ is a parallelogram because its opposite sides are equal. Now we can draw the desired line $OX$.
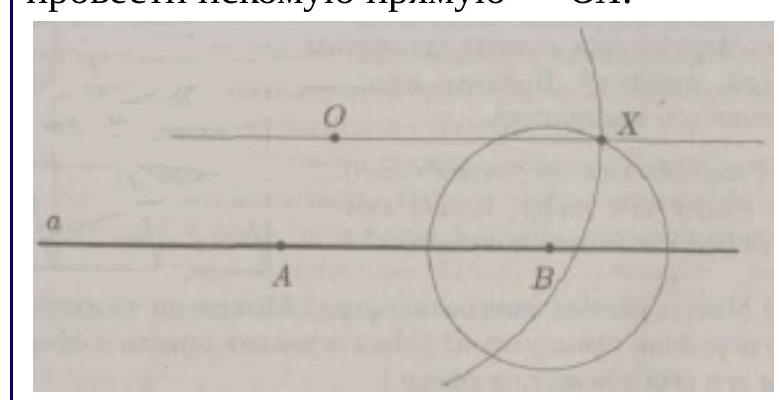
Fig. 1
Expressing this solution in different words, we can say that we constructed the triangle $BOX$ in the standard way by two vertices ($B$ and $O$) and the lengths of two sides, equal to the lengths of segments $AO$ and $AB$. Clearly, $\triangle ABO = \triangle XOB$ (by three sides). Therefore, $\angle ABO = \angle XOB$, which are alternate interior angles for lines $a$ and $OX$ and the transversal $BO$. From the equality of these angles, it follows that $a$ and $OX$ are parallel. Another solution. Mark an arbitrary point $A$ on the line and draw a circle with center at point $A$ and passing through point $O$. This circle intersects the line at two points; denote them as $M$ and $N$. Next, measure (see explanation at the end of the problem) the segment $MO$ with the compass and draw a circle with center at point $N$ and radius $MO$. The desired line passes through point $O$ and point $B$, the intersection of the two constructed circles.
Fig. 2
$\triangle MAO = \triangle NAB$ by three sides, so the heights of these triangles, drawn from vertices $O$ and $B$, are equal. The bases of these triangles ($MA$ and $NA$) lie on line $a$, so points $O$ and $B$ are at the same distance from line $a$.
A disadvantage of this solution is that if point $A$ happens to be the foot of the perpendicular dropped from point $O$, then points $O$ and $B$ coincide and do not define the required line. This same issue is "masked" in the first solution in the statement "Mark two arbitrary points $A$ and $B$ on the line." If the points are arbitrary, they can accidentally coincide (and then the construction will not work), and to mark two non-coincident points on the line, additional lines will need to be drawn.
Now let's prove that it is impossible to achieve the construction with only two lines. The second line must be the desired line. To draw it, we need to obtain a second point that is at the same distance from line $a$ as point $O$. However, after drawing one line, all points on this line, except for the points of intersection with line $a$, will be indistinguishable, and it is impossible to find a second point at the required distance from line $a$ by drawing only one line.
Explanation. In the solution, we mentioned a parallelogram, triangles, the transversal $BO$, and angles. However, for the construction, we only needed the points (vertices of the parallelogram and triangles, endpoints of the transversal segment, and endpoints of the segments forming the angles). The segments themselves were not needed for the construction, so we did not draw them and, of course, did not count them when tallying the number of lines drawn.
Clarification for the problem. In classical works on geometry, the question of which constructions with a compass and straightedge are possible in principle is discussed, but not the number of operations required for a particular construction. However, differences of opinion can arise on this issue. For example, in Euclid's "Elements," it is considered impossible to measure a distance with a compass and transfer it to construct a circle with an arbitrary center. However, in Theorem 2 of this book, it is proven that transferring a measured distance is possible, but not in one step, but through a certain construction performed in several steps.
After this theorem, one can forget about how the distance is transferred—whether in one step or several—unless the question is about the principle of the construction's possibility, not the number of necessary constructions. In modern geometry textbooks, it is generally accepted that no special constructions are required to transfer a distance. For example, in the well-known textbook by Pogorelov, it is stated that if the center and radius are given, the circle is considered constructed. In this case, the authors of the problem proceed from this point of view.
## Answer
3 lines.
Submit a comment
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Two tangents drawn from one point $]$
Given a circle of radius 1. From an external point $M$, two perpendicular tangents $MA$ and $MB$ are drawn to the circle. Between the points of tangency $A$ and $B$ on the smaller arc $AB$, a point $C$ is taken, and a third tangent $KL$ is drawn through it, forming a triangle $KLM$ with the tangents $MA$ and $MB$. Find the perimeter of this triangle.
|
Tangents drawn from a single point to a circle are equal to each other.
## Solution
Since $KA = KC$ and $BL = LC$, then
$$
\begin{gathered}
ML + LK + KM = ML + (LC + CK) + KM = \\
= (ML + LC) + (CK + KM) = (ML + LB) + (AK + KM) = \\
= MB + AM = 1 + 1 = 2.
\end{gathered}
$$
## Answer
2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9The legs of a right triangle are 15 and 20. Find the distance from the center of the inscribed circle to the height dropped to the hypotenuse.
#
|
The desired distance is equal to the distance between the base of the given height and the point of tangency of the inscribed circle with the hypotenuse.
## Solution
Let $O$ be the center of the inscribed circle, $Q$ and $P$ be the points of tangency with the smaller leg $BC$ and the hypotenuse $AB$, $CM$ be the height of the triangle, and $OK$ be the desired distance. If $r$ is the radius of the inscribed circle, then
$$
r=\frac{BC + AC - AB}{2}=\frac{20 + 15 - 25}{2}=5
$$
Therefore,
$$
\begin{gathered}
CQ = r = 5, \quad BP = BQ = BC - CQ = 15 - 5 = 10, \\
BM = \frac{BC^2}{AB} = \frac{225}{25} = 9, \\
OK = PM = BP - BM = 10 - 9 = 1.
\end{gathered}
$$
## Answer
1.
In a right triangle, a height is drawn from the vertex of the right angle. A circle is constructed on this height as a diameter. It is known that this circle intercepts segments of 12 and 18 on the legs. Find the legs.
## Hint
Connect the endpoints of the specified segments with the bases of the perpendicular.
## Solution
Let the given circle intersect the legs $AC$ and $BC$ of triangle $ABC$ at points $D$ and $E$, respectively, different from point $C$, with $CD = 12$ and $CE = 18$. If $M$ is the foot of the perpendicular dropped from vertex $C$ to $AB$, then
$$
\angle MDC = \angle MEC = 90^\circ, \quad DM = CE = 18, \quad ME = CD = 12.
$$
From the right triangles $AMC$ and $BMC$, we find that
$$
DM^2 = AD \cdot DC, \quad ME^2 = BE \cdot EC
$$
Thus,
$$
AD = \frac{DM^2}{DC} = \frac{18^2}{12} = 27, \quad BE = \frac{ME^2}{EC} = \frac{12^2}{18} = 8
$$
Therefore,
Answer
39 and 26.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Diagonal $M P$ of the convex quadrilateral $M N P Q$, inscribed in a circle, is the bisector of angle $N M Q$ and intersects diagonal $N Q$ at point $T$. Find $N P$, if $M T=5, T P=4$.
#
|
Triangles $M N P$ and NTP are similar.
## Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Two circles with radii 5 and 3 touch each other internally. A chord of the larger circle touches the smaller circle and is divided by the point of tangency in the ratio $3: 1$. Find the length of this chord.
|
Let $O_{1}$ and $O_{2}$ be the centers of circles with radii 5 and 3, respectively. $AB$ is a given chord, $C$ is the point of tangency with the smaller circle ($AC: BC=1: 3$), and $P$ is the projection of point $O_{1}$ onto the radius $O_{2}C$ of the smaller circle.
If $AC = x$, then $BC = 3x$. Drop a perpendicular $O_{1}K$ to the chord $AB$. Then $AK = KB = 2x$, $CK = x$, $O_{1}P = CK = x$, $O_{1}O_{2} = 2$, $O_{2}C = 3$, and $O_{1}K^2 = O_{1}B^2 - KB^2 = 25 - 4x^2$.
By the Pythagorean theorem, $O_{1}O_{2}^2 = O_{2}P^2 + O_{1}P^2$, or $4 = \left(3 - \sqrt{25 - 4x^2}\right)^2 + x^2$, from which $x^2 = 4$. Therefore, $AB = 4x = 8$.

## Answer
8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Two circles with radii 5 and 4 touch each other externally. A line tangent to the smaller circle at point $A$ intersects the larger circle at points $B$ and $C$, and
$A B = B C$. Find $A C$.
|
Let a circle of radius 4 with center $O_{1}$ and a circle of radius 5 with center $O_{2}$ touch each other externally at point $D$ (see the left figure). Then
$O_{1} O_{2}=O_{1} D+O_{2} D=9$
Drop perpendiculars $O_{2} M$ to the chord $B C$ and $O_{1} F$ to the line $O_{2} M$. Then $A O_{1} F M$ is a rectangle, so $M F=4$ and $O_{1} F=A M$.
Let $B M=M C=x$. Then $A B=B C=2 x, A M=3 x$. By the Pythagorean theorem, $O_{2} M^{2}=25-x^{2}, O_{1} F^{2}+O_{2} F^{2}=81$, or $9 x^{2}+\left(\sqrt{25-4 x^{2}}-4\right)^{2}=81$. From this, $x^{2}=9$. Therefore, $A C=4 x=12$.

## Answer
12.
Send a comment
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The height of a right triangle, dropped to the hypotenuse, is 1, and one of the acute angles is $15^{\circ}$.
Find the hypotenuse.
|
Draw the median from the vertex of the right angle.
## Solution
Let $C H$ be the height of the right triangle $A B C$, drawn from the vertex of the right angle $C, \angle A=15^{\circ}$. Draw the median $C M$. The angle $C M H$ as the external angle of the isosceles triangle $A M C$ is $30^{\circ}$. From the right triangle $C M H$, we find that $C M=2 C H=2$. Therefore, $A B=2 C M=4$.
## Answer
4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Each face of the cube was divided into four equal squares and these squares were painted in three colors so that squares sharing a side were painted in different colors. Prove that 8 squares were painted in each color.
|
Three squares meeting at a vertex of a cube are painted with different colors. Therefore, each color is used 8 times.
|
8
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
| ethics. Mental arithmetic, etc. |
| :---: |
On a straight line, ten points were placed at equal intervals, and they occupied a segment of length $a$. On another straight line, one hundred points were placed at the same intervals, and they occupied a segment of length $b$. How many times is $b$ greater than $a$?
|
On a segment of length $a$, 9 intervals fit, and on a segment of length $b-99$. Therefore, $b=11a$.

Author: Folkpor
In a hexagon, five angles are $90^{\circ}$, and one angle is $-270^{\circ}$ (see the figure). Using a ruler without divisions, divide it into two equal-area polygons.

## Solution
First method. Extend the hexagon $A B C D E F$ to a rectangle $A B M F$ (see Fig. a). We use the fact that any line passing through the center of symmetry of a figure divides it into two equal parts. Therefore, if we draw a line through the points of intersection of the diagonals of rectangles $A B M F$ and $C M E D$, it will divide each of these rectangles into two equal-area parts. Consequently, this line will divide the given hexagon into two equal-area polygons.
Comment. Another possible "solution" (see Fig. b). But for the figure given in the problem, this division results in 3 parts.
Since the problem does not specify that the cut must be a straight line, this "solution" can be easily corrected as follows.
Fig. a
Fig. b

Fig. c
Second method. Extend $C D$ to intersect $A F$ at point $G$ (see Fig. c), and extend $E D$ to intersect $A B$ at point $H$. Find the center $O$ of rectangle $D E F G$ by drawing its diagonals. Similarly, find the center $O_{1}$ of rectangle $A G D H$. The line $O O_{1}$ intersects $D G$ at some point $P$. It remains to find the center $O_{2}$ of rectangle $A B C G$ and draw the line $P O_{2}$. By the reasoning outlined in the first solution, segment $X P$ divides rectangle $A B C G$ into two equal parts, and therefore, the broken line $X P Y$ will divide the given hexagon into two equal-area parts.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Folklore
What is the smallest value that the perimeter of a scalene triangle with integer side lengths can take?
#
|
Let $a, b$ and $c$ be the integer lengths of the sides of a triangle and $a>b>c$. According to the triangle inequality, $c>a-b$. Since $a$ and $b$ are different natural numbers, $c \geq 2$, thus $b \geq 3$ and $a \geq 4$. Therefore, $a+b+c \geq 9$. Equality is achieved for a triangle with sides 2, 3, and 4.
## Otвет
9.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
One side of the rectangle was increased by 3 times, and the other side was reduced by 2 times, resulting in a square.
What is the side of the square if the area of the rectangle is 54 m²
#
|
Let's reduce one side of the given rectangle by half. Then the area of the resulting rectangle will be $27 \mathrm{~m}^{2}$. Next, we will triple the other side. The area of the resulting figure will become $27 \cdot 3=81$ ( $\mathrm{m}^{2}$ ). Since, by the condition, a square is formed, its side is 9 m.
## Answer
9 m.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the minimum number of three-cell corners that can be placed in an $8 \times 8$ square so that no more such corners can be placed in this square?
|
In each $2 \times 2$ square, at least two cells must be covered by corners (otherwise, another corner can fit into such a square).
A $8 \times 8$ square can be divided into 16 squares of size $2 \times 2$ each, meaning that at least 32 cells must be covered by corners, which requires no fewer than 11 corners.

## Answer
11.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9
Angle $A$ at the vertex of isosceles triangle $A B C$ is $100^{\circ}$. On ray $A B$, segment $A M$ is laid off, equal to the base $B C$. Find angle $B C M$.
|
On the ray $B M$, we lay off the segment $B N$ equal to $A M$. Let $A C = A B = a, B N = A M = B C = b$. The angles at the base $C N$ of the isosceles triangle $C B N$ are each $20^{\circ}$. Then
$$
B M = A M - A B = b - a, \quad M N = B N - B M = b - (b - a) = a, \quad C N = 2 B C \cos 20^{\circ} = 2 b \cos 20^{\circ},
$$
$$
\frac{B M}{M N} = \frac{b - a}{a} = \frac{b}{a} - 1 = \frac{\sin 100^{\circ}}{\sin 40^{\circ}} - 1, \quad \frac{C B}{C N} = \frac{b}{2 b \cos 20^{\circ}} = \frac{1}{2 \cos 20^{\circ}}.
$$
We will prove that $\frac{B M}{M N} = \frac{C B}{C N}$. From this it will follow that $C M$ is the angle bisector of triangle $B C N$, and then
$$
\angle B C M = \frac{1}{2} \angle B C N = \frac{1}{2} \cdot 20^{\circ} = 10^{\circ}
$$
Indeed,
$$
\begin{gathered}
\frac{B M}{M N} = \frac{C B}{C N} \Leftrightarrow \frac{\sin 100^{\circ}}{\sin 40^{\circ}} - 1 = \frac{1}{2 \cos 20^{\circ}} \Leftrightarrow \\
\Leftrightarrow \frac{\sin 100^{\circ} - \sin 40^{\circ}}{\sin 40^{\circ}} = \frac{1}{2 \cos 20^{\circ}} \Leftrightarrow \frac{2 \sin 30^{\circ} \cos 70^{\circ}}{2 \sin 20^{\circ} \cos 20^{\circ}} = \frac{1}{2 \cos 20^{\circ}} \Leftrightarrow \\
\Leftrightarrow \frac{\cos 70^{\circ}}{\sin 20^{\circ}} = 1 \Leftrightarrow \frac{\sin 20^{\circ}}{\sin 20^{\circ}} = 1
\end{gathered}
$$
Which is what we needed to prove.
## Answer
$10^{\circ}$.
It is known that for some internal point $K$ of the median $B M$ of triangle $A B C$, the angles $B A K$ and $B C K$ are equal. Prove that triangle $A B C$ is isosceles.
## Solution
It is sufficient to prove that $B K \perp A C$. Suppose this is not the case. Let $\angle B M C < 90^{\circ}$, and let $T$ be the point symmetric to vertex $C$ with respect to the line $B M$. Then triangle $A M T$ is isosceles, and $M B$ is the bisector of its external angle at the vertex, so $A T \parallel B K$ and $\angle B T K = \angle B C K = \angle B A K$.
From points $A$ and $T$, lying on the same side of the line $B K$, the base $B K$ of the trapezoid $A T B K$ is seen at the same angle, meaning that this trapezoid is inscribed, and therefore, isosceles. The perpendicular bisector of its base $A T$ passes through the midpoint of the base $B K$, which is impossible, since the perpendicular bisector of the base $A T$ of the isosceles triangle $A M T$ passes through the point $M$, distinct from $K$.
Submit a comment
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Touching Circles $\quad$ [
Two circles touch each other externally at point $A$, and a third circle at points $B$ and $C$. The extension of chord $A B$ of the first circle intersects the second circle at point $D$, the extension of chord $A C$ intersects the first circle at point $E$, and the extensions of chords $B E$ and $C D$ intersect the third circle at points $F$ and $G$ respectively. Find $B C$, if $B F=12$ and $B G=15$.
#
|
Let $S 1, S 2$ and $S 3$ be the first, second, and third circles, respectively. Draw the common tangents $l_{a}, l_{b}, l_{c}$ through points $A, B$ and $C$ to the circles $S 1$ and $S 2, S 1$ and $S 3, S 2$ and $S 3$ respectively. Then the tangents $l_{a}$ and $l_{b}$ form equal angles with the chord $A B$. Denote these angles by $\gamma$. Similarly, the equal angles formed by the tangents $l_{a}$ and $l_{c}$ with the chord $A C$ are denoted by $\beta$, and the equal angles formed by the tangents $l_{b}$ and $l_{c}$ with the chord $B C$ are denoted by $\alpha$. The sum $2 \alpha+2 \beta+2 \gamma$ is the sum of the angles of triangle $A B C$, so $\alpha+\beta+\gamma=90^{\circ}$. On the tangent $I_{a}$, mark point $P$ inside angle $D A E$ and point $Q$ inside angle $B A C$. From the theorem about the angle between a tangent and a chord, it follows that
$$
\angle B E C=\angle B E A=\angle B A Q=\angle P A D=\angle A C D=\angle E C D
$$
Thus, $B E \| C D$, and since
$$
\angle B C D=\angle A C B+\angle A C D=\alpha+\beta+\gamma=90^{\circ}
$$
then $\angle B C G=90^{\circ}$, so quadrilateral $B C G F$ is a rectangle. Therefore,
$$
B C=\sqrt{B G^{2}-C G^{2}}=\sqrt{B G^{2}-B F^{2}}=\sqrt{15^{2}-12^{2^{2}}}=9
$$
## Answer
9.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4 [ Sphere inscribed in a dihedral angle ]
Point $O$ is located in the section $A A^{\prime} C^{\prime} C$ of a rectangular parallelepiped $A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ with dimensions $2 \times 6 \times 9$ such that $\angle O A B + \angle O A D + \angle O A A^{\prime} = 180^{\circ}$. A sphere with center at point $O$ touches the planes $A^{\prime} B^{\prime} C^{\prime}, A A^{\prime} B$ and does not intersect the plane $A A^{\prime} D$. Find the distance from point $O$ to this plane.
|
Let $\angle O A B=\alpha, \angle O A D=\beta, \angle O A A^{\prime}=\gamma$. According to the problem, $\alpha+\beta+\gamma=180^{\circ}$.
We mark a segment $A E=1$ on the ray $A O$ (Fig.1). Then the projections of point $E$ onto the lines $A B, A D$, and $A A^{\prime}$ are $\cos \alpha, \cos \beta$, and $\cos \gamma$ respectively. By the theorem of the square of the diagonal of a rectangular parallelepiped, $\cos 2 \alpha+\cos 2 \beta+\cos 2 \gamma=1$. Since $\gamma=180^{\circ}-\alpha-\beta$, we have
\[
\begin{gathered}
\cos 2 \alpha+\cos 2 \beta+\cos 2\left(180^{\circ}-\alpha-\beta\right)=1, \cos 2 \alpha+\cos 2 \beta+\cos 2(\alpha+\beta)=1 \\
2 \cos 2 \alpha+2 \cos 2 \beta+2 \cos 2(\alpha+\beta)=2, 1+\cos 2 \alpha+1+\cos 2 \beta+2 \cos 2(\alpha+\beta)=2 \\
\cos 2 \alpha+\cos 2 \beta+2 \cos 2(\alpha+\beta)=0, 2 \cos (\alpha+\beta) \cos (\alpha-\beta)+2 \cos 2(\alpha+\beta)=0 \\
\cos (\alpha+\beta)(\cos (\alpha-\beta)+\cos (\alpha+\beta))=0, \cos (\alpha+\beta) \cos \alpha \cos \beta=0, \cos \gamma \cos \alpha \cos \beta=0
\end{gathered}
\]
Therefore, either $\gamma=90^{\circ}$, or $\beta=90^{\circ}$, or $\cos \alpha=90^{\circ}$.
If $\alpha=90^{\circ}$, then point $O$ lies in the plane $A A^{\prime} D$, which is impossible because the sphere with center $O$ does not have common points with this plane. If $\beta=90^{\circ}$, then point $O$ lies in the plane $A A^{\prime} B$, which is also impossible because the sphere with center $O$ touches this plane. Therefore, $\gamma=90^{\circ}$, so point $O$ lies in the plane $A B C D$, and thus on the line $A C$ at the intersection of the planes $A A^{\prime} C^{\prime} C$ and $A B C D$.
According to the problem, point $O$ lies in the section $A A^{\prime} C^{\prime} C$, so it is located on the segment $A C$. The sphere with center $O$, lying in the plane $A B C$, touches the planes $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ and $A A^{\prime} B$, so its radius is equal to the length of the edge $A A^{\prime}$ and is less than the length of the edge $A D$. Since the sphere does not have common points with the face $A A^{\prime} D$, its radius $r$ is less than the length of the edge $A B$. Therefore, $A A^{\prime}$ is the smallest edge of the parallelepiped, i.e., $r=A A^{\prime}=2$.
The distance from the center of the sphere to the plane $A A^{\prime} D$ (Fig.2) is equal to the distance from point $O$, lying on the diagonal $A C$ of the rectangle $A B C D$, to the side $A D$, so $A B>A D$. Therefore, $A B=9$ and $A D=6$. Let $H$ be the projection of point $O$ onto the side $A B$. Then the desired distance is the length of the segment $A H$. From the similarity of the right triangles $A O H$ and $A C B$, we find that
\[
A H=A B \cdot \frac{O H}{B C}=9 \cdot \frac{2}{6}=3
\]
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Rectangular parallelepipeds ] [ Sphere inscribed in a dihedral angle ]
Point $O$ is located in the section $A C C^{\prime} A^{\prime}$ of a rectangular parallelepiped $A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ with dimensions $2 \times 3 \times 6$ such that $\angle O C B + \angle O C D + \angle O C C^{\prime} = 180^{\circ}$. A sphere with center at point $O$ touches the planes $A^{\prime} B^{\prime} C^{\prime}, C C^{\prime} D$ and does not intersect the plane $B B^{\prime} C$. Find the distance from point $O$ to this plane.
|
Let $\angle O C B=\alpha, \angle O C D=\beta, \angle O C C^{\prime}=\gamma$. According to the problem, $\alpha+\beta+\gamma=180^{\circ}$.
We mark a segment $C E=1$ on the ray $C O$. Then the projections of point $E$ on the lines $C B, C D$, and $C C^{\prime}$ are $\cos \alpha, \cos \beta$, and $\cos \gamma$ respectively. By the theorem of the square of the diagonal of a rectangular parallelepiped, $\cos 2 \alpha+\cos 2 \beta+\cos 2 \gamma=1$. Since $\gamma=180^{\circ}-\alpha-\beta$, we have
\[
\begin{gathered}
\cos 2 \alpha+\cos 2 \beta+\cos 2\left(180^{\circ}-\alpha-\beta\right)=1, \cos 2 \alpha+\cos 2 \beta+\cos 2(\alpha+\beta)=1 \\
2 \cos 2 \alpha+2 \cos 2 \beta+2 \cos 2(\alpha+\beta)=2,1+\cos 2 \alpha+1+\cos 2 \beta+2 \cos 2(\alpha+\beta)=2 \\
\cos 2 \alpha+\cos 2 \beta+2 \cos 2(\alpha+\beta)=0,2 \cos (\alpha+\beta) \cos (\alpha-\beta)+2 \cos 2(\alpha+\beta)=0 \\
\cos (\alpha+\beta)(\cos (\alpha-\beta)+\cos (\alpha+\beta))=0, \cos (\alpha+\beta) \cos \alpha \cos \beta=0, \cos \gamma \cos \alpha \cos \beta=0 .
\end{gathered}
\]
Therefore, either $\gamma=90^{\circ}$, or $\beta=90^{\circ}$, or $\cos \alpha=90^{\circ}$.
If $\beta=90^{\circ}$, then point $O$ lies in the plane $B B^{\prime} C$, which is impossible because the sphere with center $O$ does not have common points with this plane. If $\alpha=90^{\circ}$, then point $O$ lies in the plane $C C^{\prime} D$, which is also impossible because the sphere with center $O$ touches this plane. Therefore, $\gamma=90^{\circ}$, so point $O$ lies in the plane $A B C D$, and thus on the line $A C$ at the intersection of the planes $A A^{\prime} C^{\prime} C$ and $A B C D$.
According to the problem, point $O$ lies in the section $A A^{\prime} C^{\prime} C$, so it is located on the segment $A C$. The sphere with center $O$, lying in the plane $A B C$, touches the planes $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ and $C C^{\prime} D$, so its radius is equal to the length of the edge $C C^{\prime}$ and is less than the length of the edge $A B$. Since the sphere does not have common points with the face $B B^{\prime} C$, its radius $r$ is less than the length of the edge $A B$. Therefore, $C C^{\prime}$ is the smallest edge of the parallelepiped, i.e., $r=C C^{\prime}=2$.
The distance from the center of the sphere to the plane $B B^{\prime} C$ is equal to the distance from point $O$, lying on the diagonal $A C$ of the rectangle $A B C D$, to the side $B C$, so $C D>B C$. Therefore, $C D=6$ and $B C=3$. Let $H$ be the projection of point $O$ on the side $C D$. Then the desired distance is the length of the segment $C H$. From the similarity of the right triangles $C O H$ and $C A D$, we find that
\[
C H=C D \cdot \frac{O H}{A D}=6 \cdot \frac{2}{3}=4 .
\]
| pedeы й ] й angle ] | |
| :---: | :---: |
| | |
| | |
| | |
## Answer
4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kalinin A.
Anya and Borya, whose speeds are constant but not necessarily the same, simultaneously set out from villages A and B towards each other. If Anya had set out 30 minutes earlier, they would have met 2 km closer to village B. If Borya had set out 30 minutes earlier, the meeting would have taken place closer to village A. By how much?
|
Let Kolya (half an hour after Borya) and Tolya (half an hour before Borya) also leave from B at the same speed, and from A - Tanya (half an hour before Anya).
First method. Anya meets Tolya, Borya, and Kolya sequentially at equal time intervals. Therefore, the distances between the adjacent meeting points are also equal. It is clear that Anya's meeting with Kolya happened half an hour later, and at the same point where Tanya met Borya, as mentioned in the condition. Thus, the distances between the adjacent meeting points of Anya with the three boys are 2 km, and, in particular, the meeting point of Anya with Tolya is 2 km closer to A than the meeting point of Anya with Borya.
Second method. Consider the graphs of the movements of Anya, Borya, Tanya, and Tolya. These are two pairs of parallel lines, so the points of their intersections are the vertices of a parallelogram. Two opposite vertices have the same ordinate (the meeting point of Anya with Borya coincides with the meeting point of Tanya with Tolya), which means that this point is the arithmetic mean of the ordinates of the other two vertices. Therefore, the other two meeting points lie on opposite sides but at the same distance of 2 km from this point.
## Answer
2 km.
## [ Rectangles and Squares. Properties and Criteria ] Problem 65570 Topics: [ Ratios of Linear Elements of Similar Triangles ] [ Criteria for Equality of Right Triangles ] Difficulty: $3+$ Grades: $8,9,10,11$ Author: Akoyan A.V. Given a square $A B C D$, $M$ and $N$ are the midpoints of sides $B C$ and $A D$. On the extension of diagonal $A C$ beyond point $A$, point $K$ is taken. Segment $K M$ intersects side $A B$ at point $L$. Prove that angles $K N A$ and $L N A$ are equal.
## Solution
Let line $A B$ intersect segment $K N$ at point $T$. Note that segment $K C$ intersects segment $M N$ at its midpoint. Since segment $L T$ is parallel to $M N$, it cuts off a similar triangle $L K T$ from triangle $M K N$, and therefore $K C$ intersects $L T$ at its midpoint as well. Consequently, right triangles $A N T$ and $A N L$ are equal by two legs. Therefore, $\angle L N A = \angle T N A = \angle K N A$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
|
At a familiar factory, they cut out metal disks with a diameter of 1 m. It is known that a disk with a diameter of exactly 1 m weighs exactly 100 kg. During manufacturing, there is a measurement error, and therefore the standard deviation of the radius is 10 mm. Engineer Sidorov believes that a stack of 100 disks will on average weigh 10000 kg. By how much is Engineer Sidorov mistaken?
#
|
Given $\mathrm{E} R=0.5 \mathrm{~m}, \mathrm{D} R=10^{-4} \mathrm{M}^{2}$. Let's find the expected value of the area of one disk:
$\mathrm{E} S=\mathrm{E}\left(\pi R^{2}\right)=\pi \mathrm{E} R^{2}=\pi\left(\mathrm{D} R+\mathrm{E}^{2} R\right)=\pi\left(10^{-4}+0.25\right)=0.2501 \pi$.
Therefore, the expected value of the mass of the disk is $0.2501 \pi / 0.25 \pi \cdot 100=100.04$ kg. Thus, a stack of 100 disks on average will weigh 10004 kg.
## Answer
4 kg.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11 | |
A right circular cone with base radius $R$ and height $H=3 R \sqrt{7}$ is laid on its side on a plane and rolled so that its vertex remains stationary. How many revolutions will the base make before the cone returns to its original position?
|
The base circle rolls along the circumference of a circle of radius $L$, where $L$ is the slant height of the cone. Therefore, the number of revolutions is $\frac{2 \pi L}{2 \pi R}=\frac{\sqrt{H^{2}+R^{2}}}{R}=8$.
## Answer
8 revolutions.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The altitudes $A D$ and $B E$ of an acute-angled triangle $A B C$ intersect at point $H$. The circumcircle of triangle $A B H$ intersects sides $A C$ and $B C$ at points $F$ and $G$ respectively. Find $F G$, if $D E=5$ cm.
|
Let $\angle F A H = \angle H B F = \alpha$. Right triangles $A D C$ and $E C B$ share the common angle $C$, so $\angle E B C = \alpha$.
Thus, $B E$ is both the altitude and the angle bisector of triangle $F B C$, which means this triangle is isosceles and $B E$ is its median, i.e.,
$F E = E C$. Similarly, $C D = D G$. Therefore, $E D$ is the midline of triangle $F C G$. Hence, $F G = 2 D E$.
Answer
10 cm.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On a circle of radius 5, circumscribed around an equilateral triangle, a point $D$ is taken. It is known that the distance from point $D$ to one of the vertices of the triangle is 9. Find the sum of the distances from point $D$ to the other two vertices of the triangle.
|
Let the distance from vertex $A$ of triangle $A B C$ to point $D$ be 9. Prove that point $D$ lies on the smaller arc $B C$ and $B D + C D = A D$.
## Solution
Let the distance from vertex $A$ of triangle $A B C$ to point $D$ be 9. Note that $B C = 5 \sqrt{3}$. Since
$A D = 9 > B C$, point $D$ lies on the smaller arc $B C$.
Construct a segment $A K$ on ray $A D$ equal to $B D$. Then triangle $A K C$ is congruent to triangle $B D C$ by two sides and the included angle
( $\angle K A C = \angle D A C = \angle D B C$ as inscribed angles subtending the same arc). Therefore, $C K = C D$, and since $\angle K D C = \angle A D C = \angle B = 60^{\circ}$, triangle $C K D$ is equilateral, meaning $D K = D C$. Since $A K = B D < B C < A D$, point $K$ lies on segment $A D$. Therefore, $B D + C D = A K + K D = A D = 9$.
## Answer
9.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9 |
In an acute triangle $A B C$, altitudes $A L$ and $B M$ are drawn. Then, the line $L M$ is extended to intersect the extension of side $A B$.
What is the maximum number of pairs of similar triangles that can be counted on this diagram, if no pairs of congruent triangles are formed on it?
|
Points $A, B, M$ and $L$ lie on the same circle.
## Solution
Right triangles $C A L$ and $C B L$ are similar by two angles.
Let $H$ be the orthocenter of triangle $A B C$. Right triangles $A M H$ and $B L H$ are similar by two angles.
Right triangles $A M H$ and $A L C$ are similar by two angles.
Right triangles $B L H$ and $B M C$ are similar by two angles.
Therefore, right triangles $A M H$ and $B M C$ are similar, as well as right triangles $B L H$ and $A L C$.
Points $M$ and $L$ lie on the circle with diameter $A B$. Therefore, triangles $M H L$ and $A H B$ are similar by two angles.
Triangles $C L M$ and $C A B$ are also similar.
Let the lines $A B$ and $M L$ intersect at point $D$. Similarly, triangles $D B L$ and $D M A$ are similar by two angles.
Finally, from the equality $\angle B M L = \angle B A L$, it follows that triangles $D B M$ and $D L A$ are similar.
Answer
10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Dolmatov $C$.
Point $M$ lies on the side $A C$ of an acute-angled triangle $A B C$. Circles are circumscribed around triangles $A B M$ and $C B M$. For what position of point $M$ will the area of the common part of the circles bounded by them be the smallest?
|
The angles under which the segment $BM$ is seen from the centers of the circles have a constant magnitude.
## Solution
Let $O$ and $O_{1}$ be the centers of the circumcircles of triangles $ABM$ and $CBM$. The common part of the specified circles is the union of two segments with a common chord $BM$.
Since
$$
\angle BOM = 2 \angle BAC, \angle BO_{1}M = 2 \angle BCA,
$$
the magnitudes of the angles $BOM$ and $BO_{1}M$ are constant. Therefore, the area of each segment is smaller the shorter the chord $BM$. Consequently, the area of the common part of the circles is minimal when $BM$ is the altitude of triangle $ABC$.
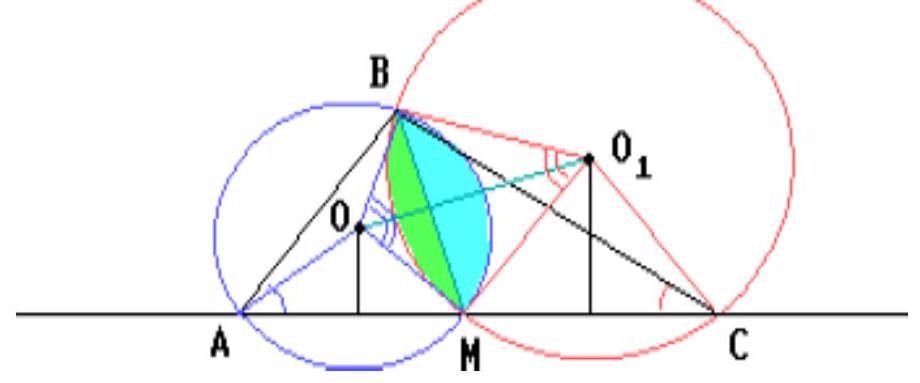
## Answer
The point $M$ is the foot of the altitude of triangle $ABC$.
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In quadrilateral $A B C D$, it is known that $D O=4, B C=5, \angle A B D=45^{\circ}$, where $O$ is the point of intersection of the diagonals. Find $B O$, if the area of quadrilateral $A B C D$ is equal to $\frac{1}{2}(A B \cdot C D+B C \cdot A D)$.
|
Prove that $ABCD$ is a cyclic quadrilateral with mutually perpendicular diagonals.
## Solution
Let $C_{1}$ be the point symmetric to vertex $C$ with respect to the perpendicular bisector of diagonal $BD$. Then
$$
\begin{gathered}
S_{\triangle \mathrm{ABCD}}=S_{\Delta \mathrm{ABC}_{1} \mathrm{D}}=S_{\Delta \mathrm{ABC}_{1}}+S_{\Delta \mathrm{AC}_{1} \mathrm{D}}= \\
=\frac{1}{2} \cdot A B \cdot B C_{1} \sin \angle A B C_{1}+\frac{1}{2} \cdot A D \cdot D C_{1} \sin \angle A D C_{1} \leqslant \\
\leqslant \frac{1}{2}\left(A B \cdot B C_{1}+A D \cdot D C_{1}\right)=\frac{1}{2}(A B \cdot D C+A D \cdot B C)
\end{gathered}
$$
with equality only when
$$
\angle A B C_{1}=\angle A D C_{1}=90^{\circ}
$$
Therefore, quadrilateral $A B C_{1} D$ is cyclic and $A C_{1}$ is the diameter of its circumscribed circle.
The perpendicular bisector of diagonal $BD$ is the axis of symmetry of this circle. Therefore, vertex $C$ also lies on the circle. Hence, quadrilateral $A B C D$ is cyclic. Since $A C_{1}$ is the diameter of its circumscribed circle, $\angle A C C_{1}=90^{\circ}$. Therefore, diagonal $A C$ is parallel to the perpendicular bisector of diagonal $B D$. Consequently, diagonals $A C$ and $B D$ of quadrilateral $A B C D$ are mutually perpendicular. Then in triangle $COD$:
$$
O D=4, \angle C O D=90^{\circ}, \angle O C D=\angle A C D=\angle A B D=45^{\circ}
$$
Therefore, $O C=O D=4$. By the Pythagorean theorem in right triangle $COB$, we find that
$$
O B=\sqrt{B C^{2}-O C^{2}}=\sqrt{5^{2}-4^{2}}=3
$$
## Answer
3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Trigonometric ratios in a right triangle [ Theorem of the length of a tangent and a secant; the product of the entire secant and its external part [ Two tangents drawn from the same point
In parallelogram $K L M N$, side $K L$ is equal to 8. A circle, tangent to sides $N K$ and $N M$, passes through point $L$ and intersects sides $K L$ and $M L$ at points $C$ and $D$ respectively. It is known that $K C: L C=4: 5$ and $L D: M D=8: 1$. Find side $K N$.
|
Apply the tangent-secant theorem.
## Solution
Let $A B$ be the hypotenuse of the right triangle $A B C$. Then $A B=2 R$. If $\angle C A B=\boldsymbol{\alpha}$, then
$$
B C=A B \sin \alpha=2 R \sin \alpha .
$$
If $C D$ is the height of the triangle $A B C$, then
$$
C D=B C \cos \angle D C B=B C \cos \alpha=2 R \sin \alpha \cos \alpha=R \sin 2 \alpha
$$
Let $P$ and $Q$ be the points of tangency of the given circle with the sides $K N$ and $M N$ of the parallelogram $K L M N$. By the tangent-secant theorem,
$$
K P^{2}=K L \cdot K C=8 \cdot \frac{4}{9} \cdot 8=\frac{256}{9} .
$$
Therefore, $K P=\frac{16}{3}$.
Let $K N=M L=x$. Then
$$
Q N=N P=K N-K P=x-\frac{16}{3}, D M=\frac{1}{9} M L=\frac{x}{9}
$$
By the tangent-secant theorem,
$$
M Q^{2}=M D \cdot M L, \text { or }\left(8-x+\frac{16}{3}\right)^{2}=\frac{x^{2}}{9}, \text { or } \frac{40}{3}-x=\frac{x}{3}
$$
From this, we find that $x=10$.
[ GMT - circle or arc of a circle ]
Problem
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Malkin M.i.
On the board, 101 numbers are written: $1^{2}, 2^{2}, \ldots, 101^{2}$. In one operation, it is allowed to erase any two numbers and write down the absolute value of their difference instead.
What is the smallest number that can result from 100 operations?
|
From four consecutive squares (in three operations), the number 4 can be obtained: $(n+3)^{2}-(n+2)^{2}-((n+$ $\left.1)^{2}-n^{2}\right)=(2 n+5)-(2 n+1)=4$.
We can get 24 such fours from the numbers $6^{2}, 7^{2}, \ldots, 101^{2}$. 20 fours can be turned into zeros by pairwise subtraction. From the numbers $4,9,16,25$ we get
$14=(25-4)-(16-9)$. From the remaining numbers $(14,4,4,4,4,1)$ we get the unit: $4-(14-4-4-4)-1=1$. It is impossible to get 0, since the parity of the sum of all numbers is preserved.
## Answer
1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9 | |
In parallelogram $A B C D$, the diagonals $A C=15, B D=9$ are known. The radius of the circle circumscribed around triangle $A D C$ is 10. Find the radius of the circle circumscribed around triangle $A B D$.
|
Apply the formula $a=2 R \sin \boldsymbol{\alpha}$.
## Solution
Let $R=10$ be the radius of the circumcircle of triangle $A D C$. Then
$$
\sin \angle A D C=\frac{A C}{2 R}=\frac{15}{20}=\frac{3}{4}
$$
Since $\angle B A D=180^{\circ}-\angle A D C$, then
$$
\sin \angle B A D=\sin \angle A D C=\frac{3}{4}
$$
If $R_{1}$ is the radius of the circumcircle of triangle $A B D$, then
$$
R_{1}=\frac{B D}{2 \sin \angle B A D}=\frac{B D}{2 \sin \angle A D C}=\frac{9 \cdot 2}{3}=6
$$
## Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Given a triangle with sides $A B=2, B C=3, A C=4$. A circle is inscribed in it, and the point $M$ where the circle touches side $B C$ is connected to point $A$. Circles are inscribed in triangles $A M B$ and $A M C$. Find the distance between the points where these circles touch the line $A M$.
|
Since $K$ is the point of tangency of the incircle inscribed in triangle $AMB$ with side $AM$, $AK = (AB + AM - BM) / 2$.
Similarly, expressing $AL$ and subtracting the obtained expressions from each other, we get
$KL = (AB - AC - BM + MC) / 2$.
| 3 Topics: | $\left[\begin{array}{lc}\text { [ Cube } & \text { [ } \\ \text { [ Unfolding helps solve the problem }\end{array}\right]$ | Difficulty: 3+ |
| :---: | :---: | :---: |
Substituting the expression $BM = (BC + AB - AC) / 2$ into this equation, we get $KL = 0$.
Answer: 0.
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Zaslavsky A.A.
Given a circle with center $O$ and a point $P$ not lying on it. Let $X$ be an arbitrary point on the circle, $Y$ the intersection point of the bisector of angle $P O X$ and the perpendicular bisector of segment $P X$. Find the geometric locus of points $Y$.
|
Let $K, L$ be the projections of point $Y$ onto $O P$ and $O X$. From the definition of point $Y$, it follows that $Y P = Y X$ and $Y K = Y L$. Therefore, triangles $Y K P$ and $Y L X$ are equal, which means
$X L = P K$. Moreover, $O L = O K$. Since the lengths of segments $O P$ and $O X$ are not equal, one of them is equal to the sum of the lengths of segments $O K$ and $K P$, and the other is their difference. Consequently, $O K = 1 / 2(O P + O X)$ (see figure), which means point $K$ is fixed. It is obvious that any point on the perpendicular dropped from point $K$ to line $O P$ belongs to the desired locus of points.
## Answer
The line perpendicular to ray $O P$ and intersecting it at a point that is a distance of ½ ( $O P + O X$) from $O$. Send a comment
Problem
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Systems of points and segments. Examples and counterexamples ]
$$
\text { [ Combinatorial geometry (miscellaneous). ] }
$$
The grandfather called his grandson to visit him in the village:
- You'll see what an extraordinary garden I've planted! There are four pears growing there, and there are also apple trees, planted in such a way that exactly two pears are 10 meters away from each apple tree.
- So what's so interesting about that, - the grandson replied. - You only have two apple trees.
- And you're wrong, - the grandfather smiled. - I have more apple trees than pears in my garden.
Draw how the apple trees and pears could have grown in the grandfather's garden. Try to place as many apple trees as possible on the drawing without violating the conditions.
|
Various arrangements of apple and pear trees are possible, for example, as shown in the figure on the left. The maximum number of apple trees can be placed if the pears grow densely enough. For instance, if pears are planted in a row every 5 meters, there will be room for 12 apple trees (figure in the center).
Let's prove that more than twelve apple trees are not possible. Consider any two pear trees. At a distance of 10 meters from them, there can be only two apple trees - one on one side of the line of pears, and the other on the opposite side (figure on the right). Therefore, each pair of pears "serves" no more than two apple trees. Since there are six pairs of pears, the maximum number of apple trees is 12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Place as many points as possible on a plane so that any three points do not lie on the same line and are vertices of an isosceles triangle.
#
|
The maximum number of points is six: a regular pentagon and its center (see figure).

|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How to cut a square into unit squares a) $4 \times 4$ b) $5 \times 5$ with the fewest number of cuts. (Parts can be stacked on top of each other during cutting).
#
|
a) 4 cuts; b) 6 cuts.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Geometry (miscellaneous).]
A sphere of radius $\sqrt{5}$ with center at point $O$ touches all sides of triangle $ABC$. The point of tangency $N$ bisects side $AB$. The point of tangency $M$ divides side $AC$ such that $AM=\frac{1}{2} MC$. Find the volume of the pyramid $OABC$, given that $AN=NB=1$.
|
The radius of the circle inscribed in a triangle is equal to the area of the triangle divided by its semi-perimeter.
## Solution
Let the given sphere touch the side $BC$ of triangle $ABC$ at point $K$. Then
$$
BK = BN = 1, AM = AN = 1, CM = 2 \cdot AM = 2, CK = CM = 2
$$
The section of the sphere by the plane of triangle $ABC$ is the circle inscribed in triangle $ABC$, and the center $O_1$ of this circle is the orthogonal projection of the center $O$ of the sphere onto the plane of triangle $ABC$. Therefore, $OO_1$ is the height of the pyramid $OABC$.
Let $r$ be the radius of the circle inscribed in triangle $ABC$, $p$ be the semi-perimeter of the triangle, and $s$ be the area. Since triangle $ABC$ is isosceles, the segment $CN$ is its height. Then
$$
\begin{gathered}
CN = \sqrt{AC^2 - AN^2} = \sqrt{9 - 1} = 2\sqrt{2}, \\
s = \frac{1}{2} AB \cdot CN = 2\sqrt{2}, \quad r = s / p = 2\sqrt{2} / 4 = \sqrt{2} / 2
\end{gathered}
$$
From the right triangle $OO_1N$, we find that
$$
OO_1 = \sqrt{ON^2 - ON^2} = \sqrt{5 - 1/2} = 3 / \sqrt{2} \text{.}
$$
Therefore,
$$
V(OABC) = \frac{1}{3} s \cdot OO_1 = \frac{1}{3} 2\sqrt{2} \cdot 3 / \sqrt{2} = 2
$$
## Answer
2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Geometry (other) ]
A sphere with radius $3 / 2$ has its center at point $N$. From point $K$, located at a distance of $3 \sqrt{5} / 2$ from the center of the sphere, two lines $K L$ and $K M$ are drawn, touching the sphere at points $L$ and $M$ respectively. Find the volume of the pyramid $K L M N$, given that $M L=2$.
|
From the right triangle $K L N$, we find that
$$
K L=\sqrt{K N^{2}-L N^{2}}=\sqrt{45 / 4-9 / 4}=3
$$
Therefore, $K M=K L=3$. In the isosceles triangles $L N M$ and $L K M$, the medians $N P$ and $K P$ are altitudes, so
$$
\begin{gathered}
N P^{2}=\sqrt{N L^{2}-L P^{2}}=\sqrt{9 / 4-1}=\sqrt{5} / 2 \\
K P^{2}=\sqrt{K L^{2}-L P^{2}}=\sqrt{9-1}=\sqrt{8} / 2
\end{gathered}
$$
Thus, $S(L N M)=\frac{1}{2} L M \cdot N P=\frac{1}{2} 2 \cdot \sqrt{5} / 2=\sqrt{5} / 2$.
Let $K H$ be the height of the pyramid $K L M N$. Since $K L=K M$, point $H$ is equidistant from points $L$ and $M$. Therefore, point $H$ lies on the line $N P$, and $K H$ is the height of triangle $K N P$. Let $P H=x$. By the Pythagorean theorem,
$$
K N^{2}-N H^{2}=K P^{2}-P H^{2}, \text { or } 45 / 4-(\sqrt{5} / 2+x)^{2}=8-x^{2},
$$
from which $x=2 / \sqrt{5}$. Therefore,
$$
K H=\sqrt{K P^{2}-P H^{2}}=\sqrt{8-4 / 5}=6 / \sqrt{5}
$$
Thus,
$$
V(K L M N)=\frac{1}{3} S(L N M) \cdot K H=\frac{1}{3}(\sqrt{5} / 2) \cdot 6 / \sqrt{5}=1 .
$$
## Answer
1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Plane, divided by lines ]
How many maximum parts can 5 segments divide a plane into?
#
|
Each subsequent segment intersects with p already drawn segments in no more than p points.
## Solution
Let $\mathrm{n}$ segments have already been drawn, and they divide the plane into K(n) parts. Draw the ( $\mathrm{n}+1$ )-th segment. It intersects with the n already drawn segments in no more than n points, which can divide it into no more than (n-1) segments. Each of these segments can divide an existing part of the plane into two. Thus, drawing the $(\mathrm{n}+1)$-th segment adds no more than (n-1) new parts to the plane, i.e., K(n+1) does not exceed K(n)+n-1 (for $\mathrm{n}>1$). From this, it is easy to see (since K(2)=1) that K(5) does not exceed $1+(1+2+3)=7$. An example with seven parts of the plane can be constructed as follows. Draw 5 lines in general position and take 5 segments on these lines, containing all pairwise intersection points of these lines.
## Answer
7.00
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Law of Cosines ]
Find the sum of the squares of the distances from a point $M$, taken on the diameter of a certain circle, to the ends of any chord parallel to this diameter, if the radius of the circle is $R$, and the distance from the point $M$ to the center of the circle is $a$.
|
Apply the Law of Cosines.
## Solution
Let $O$ be the center of the circle. $AB$ is an arbitrary chord parallel to the given diameter. Denote $\angle BOM = \varphi$. Then $\angle AOM = 180^\circ - \varphi$.
By the Law of Cosines in triangles $BOM$ and $AOM$, we find that
\[
\begin{gathered}
BM^2 = a^2 + R^2 - 2aR \cos \varphi \\
AM^2 = a^2 + R^2 - 2aR \cos (180^\circ - \varphi) = a^2 + R^2 + 2aR \cos \varphi
\end{gathered}
\]
Adding these equations term by term, we get
Answer
$2(a^2 + R^2)$
The bisector $AE$ of angle $A$ divides the quadrilateral $ABCD$ into an isosceles triangle $ABE (AB = BE)$ and a rhombus $AEC D$. The radius of the circle circumscribed around triangle $ECD$ is 1.5 times the radius of the circle inscribed in triangle $ABE$. Find the ratio of the perimeters of these triangles.
## Hint
Denote $\angle BAE = \angle EAD = \angle ECD = \angle AEB = 2\alpha$ and set up an equation in terms of $\alpha$.
## Solution
Let $AE = x$, $\angle BAE = 2\alpha$. Then $DC = EC = x$, $\angle EAD = \angle ECD = \angle AEB = 2\alpha$. Let $r$ be the radius of the circle inscribed in triangle $ABE$. Then $r = (x / 2) \cdot \tan \alpha$. Let $R$ be the radius of the circle circumscribed around triangle $ECD$. Then
\[
R = \frac{EC}{2 \cdot \sin \angle EDC} = \frac{x}{2 \cdot \sin (90^\circ - \alpha)} = \frac{x}{2 \cdot \cos \alpha}
\]
According to the problem,
\[
\frac{R}{r} = \frac{3}{2}, \text{ i.e., } \frac{x}{2 \cdot \cos \alpha} = \left(\frac{x}{2} \cdot \tan \alpha \right) \cdot \frac{3}{2}
\]
Then
\[
\tan \alpha \cdot \cos \alpha = \frac{2}{3}, \sin \alpha = \frac{2}{3}, \cos \alpha = \frac{\sqrt{5}}{3}, \cos 2\alpha = \frac{1}{9}
\]
In triangle $ABE$, $AB = BE = \frac{x}{2 \cdot \cos 2\alpha} = \frac{9x}{2}$. Therefore, its perimeter is $\frac{9x}{2} + \frac{9x}{2} + x = 10x$.
In triangle $ECD$, $DE = 2x \cdot \sin \alpha = \frac{4x}{3}$. Therefore, its perimeter is $x + x + \frac{4x}{3} = \frac{10x}{3}$.
Thus, the ratio of the perimeters is $\frac{10x}{\frac{10x}{3}} = 3$.
## Answer
3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ The product of the lengths of the chord segments and the lengths of the secant segments ]
On a line, points $A, B, C$, and $D$ are arranged in the given order. It is known that $B C = 3, A B = 2 \cdot C D$. A circle is drawn through points $A$ and $C$, and another circle is drawn through points $B$ and $D$. Their common chord intersects segment $B C$ at point $K$. Find $B K$.
#
|
Apply the theorem of intersecting chords twice.
## Solution
Let $C D=a, A B=2 a$. Denote $B K=x$. Then
$$
K C=3-x, K D=D C+K C=a+3-x, A K=A B+B K=2 a+x
$$
Let $M N$ be the common chord of the specified circles. Then
$$
A K \cdot K C=M K \cdot N K=B K \cdot K D
$$
from which
From this equation, we find that $x=2$.
## Answer
2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A circle of radius $1+\sqrt{2}$ is circumscribed around an isosceles right triangle. Find the radius of the circle that touches the legs of this triangle and internally touches the circle circumscribed around it.
|
Let $M$ and $N$ be the points of tangency of the desired circle with the legs $A C$ and $B C$ of triangle $A B C$, and $Q$ be the center of this circle. Then the quadrilateral $Q M C N$ is a square.
## Solution
Let $r$ be the radius of the desired circle, $Q$ its center, $M, N$ the points of tangency with the legs $A C$ and $B C$ of triangle $A B C$, $O$ the center of the circumscribed circle, and $P$ the point of tangency of the circles. Then the points $O$ and $Q$ lie on the diameter $C P$, and the quadrilateral $Q M C N$ is a square with side $r$. Therefore,
$$
C Q = r \sqrt{2}, \quad C Q + Q P = C P, \quad r \sqrt{2} + r = 2(1 + \sqrt{2})
$$
From this, we find that
$$
r = \frac{2(1 + \sqrt{2})}{\sqrt{2} + 1} = 2
$$
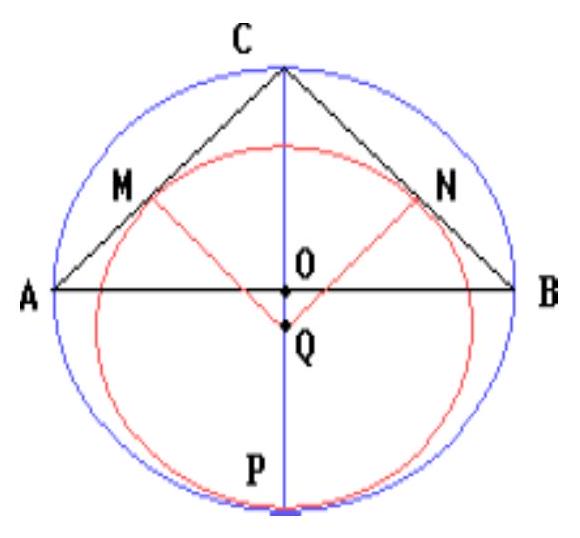
## Answer
2.
## Problem
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Common tangent to two circles [ Trigonometric ratios in a right triangle ]
On the plane, there are two circles with radii 12 and 7, centered at points $O_{1}$ and $O_{2}$, touching a certain line at points $M_{1}$ and $M_{2}$ and lying on the same side of this line. The ratio of the length of the segment $M_{1} M_{2}$ to the length of the segment $O_{1} O_{2}$ is $\frac{2 \sqrt{5}}{5}$. Find $M_{1} M_{2}$.
|
Consider the right triangle $O_{1} P O_{2}$, where $P$ is the projection of point $O_{2}$ onto $O_{1} M_{1}$.
## Solution
Let $P$ be the projection of point $O_{2}$ onto the line $O_{1} M_{1}$. Denote $\angle O_{1} O_{2} P=\alpha$. Then
$$
\begin{gathered}
\cos \alpha=\frac{O_{2} P}{O_{1} O_{2}}=\frac{M_{1} M_{2}}{O_{1} O_{2}}=\frac{2 \sqrt{5}}{5} \\
\sin \alpha=\frac{\sqrt{5}}{5}, \operatorname{ctg} \alpha=\frac{\cos \alpha}{\sin \alpha}=2
\end{gathered}
$$
In the right triangle $O_{1} \mathrm{PO}_{2}$:
$$
\begin{gathered}
O_{1} P=O_{1} M_{1}-P M_{1}=O_{1} M_{1}-O_{2} M_{2}=12-7=5 \\
M_{1} M_{2}=O_{2} P=O_{1} P \cdot \operatorname{ctg} \alpha=5 \cdot 2=10
\end{gathered}
$$
Answer
10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\begin{array}{l}{[\text { Equilateral (regular) triangle }]} \\ {[\quad \text { Area of a circle, sector, and segment }}\end{array}\right]$
In an equilateral triangle $ABC$, a circle is drawn passing through the center of the triangle and touching side $BC$ at its midpoint $D$. A line is drawn from point $A$, tangent to the circle at point $E$, and $\angle BAE < 30^{\circ}$. Find the area of triangle $ABE$ if the area of triangle $ABC$ is $\frac{10}{4-\sqrt{2}}$.
|
Find $\sin \angle D A E$ from the right triangle $E A Q(Q$ - the center of the given circle).
## Solution
Let $O$ be the center of triangle $A B C, Q$ be the center of the given circle. Denote the side of triangle $A B C$ by $a$. Then
$$
O D=\frac{1}{3} A D=\frac{a \sqrt{3}}{6}, O Q=Q D=\frac{a \sqrt{3}}{12}
$$
$$
A Q=A D-Q D=\frac{a \sqrt{3}}{2}-\frac{a \sqrt{3}}{12}=\frac{5 a \sqrt{3}}{12}
$$
From the right triangle $A E Q$, we find that
$$
\begin{gathered}
\sin \angle E A Q=\frac{E Q}{A Q}=\frac{1}{5}, \cos \angle E A Q=\frac{2 \sqrt{6}}{5} \\
A E=E Q \tan \angle E A Q=\frac{a \sqrt{2}}{2}
\end{gathered}
$$
Therefore,
$$
\begin{aligned}
& S_{\triangle \mathrm{ABE}}=\frac{1}{2} A E \cdot A B \sin \left(30^{\circ}-\angle E A Q\right)= \\
= & \frac{a^{2}}{\sqrt{2}} \cdot \frac{\frac{\sqrt{6}}{5}-\frac{\sqrt{3}}{15}}{4}=\frac{a^{2} \sqrt{6}(2 \sqrt{2}-1)}{40}
\end{aligned}
$$
According to the problem statement
$$
S_{\triangle \mathrm{ABC}}=\frac{10}{4-\sqrt{2}}=\frac{a^{2} \sqrt{3}}{4}
$$
Solving for $a^{2}$ from this equation and substituting it into the previous one, we get: $S_{\Delta \mathrm{ABE}}=1$
## Answer
1.
## Problem
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## In a convex quadrilateral $A B C D$, the length of the segment connecting the midpoints of sides $A B$ and $C D$ is 1. Lines
$B C$ and $A D$ are perpendicular. Find the length of the segment connecting the midpoints of diagonals $A C$ and $B D$.
|
Prove that the midpoints of sides $AB$ and $CD$ and the midpoints of diagonals $AC$ and $BD$ are the vertices of a rectangle.
## Solution
Let $M$ and $N$ be the midpoints of sides $AB$ and $CD$ of quadrilateral $ABCD$, and $P$ and $Q$ be the midpoints of its diagonals $AC$ and $BD$, respectively. Then $MP$ is the midline of triangle $ABC$, and $QN$ is the midline of triangle $DBC$. Therefore,
$$
MP = \frac{1}{2} BC = QN, \quad MP \| BC \| QN
$$
Thus, quadrilateral $MPNQ$ is a parallelogram. Its adjacent sides $MP$ and $MQ$ are parallel to lines $BC$ and $AD$, respectively, so $MP \perp MQ$. Therefore, quadrilateral $MPNQ$ is a rectangle. The diagonals of a rectangle are equal, so
$$
PQ = MN = 1
$$

## Answer
1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9 | |
The height $B K$ of the rhombus $A B C D$, dropped to the side $A D$, intersects the diagonal $A C$ at point $M$. Find $M D$, if it is known that $B K=4, A K: K D=1: 2$.
|
## Solution
Since $AC$ is the perpendicular bisector of diagonal $BD$, then $MD = MB$. Since $AM$ is the angle bisector of triangle $BAK$, then
$$
\frac{BM}{MK} = \frac{AB}{AK} = \frac{AD}{AK} = 3
$$
Therefore,
$$
MD = BM = \frac{3}{4} BK = 3
$$
Answer
3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Auxiliary area. The area helps to solve the problem_] Heron's formula
The sides of the triangle are 13, 14, and 15. Find the radius of the circle that has its center on the middle side and touches the other two sides.
|
Let the center $O$ of the given circle be located on the side $AB$ of triangle $ABC$. The area of triangle $ABC$ is equal to the sum of the areas of triangles $AOC$ and $BOC$.
## Solution
Let $AC=13$, $AB=14$, $BC=15$, $O$ be the center of the given circle (with $O$ on side $AB$), $R$ be its radius, and $P$ and $Q$ be the points of tangency of the circle with sides $AC$ and $BC$ respectively. Using Heron's formula,
$$
S_{\triangle \mathrm{ABC}}=\sqrt{21(21-13)(21-14)(21-15)}=\sqrt{21 \cdot 8 \cdot 7 \cdot 6}=84
$$
Since $OP$ and $OQ$ are the heights of triangles $AOC$ and $BOC$, respectively, we have
$$
S_{\triangle \mathrm{ABC}}=S_{\triangle \mathrm{AOC}}+S_{\triangle \mathrm{BOC}}=\frac{1}{2} AC \cdot OP + \frac{1}{2} BC \cdot OQ = \frac{1}{2}(AC + BC) R = 14 R
$$
Therefore,
$$
R=\frac{S_{\triangle ABC}}{14}=\frac{84}{14}=6
$$
Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.