problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
[Theorem of the tangent and secant; the product of the entire secant and its external part [Pythagorean Theorem (direct and inverse).
One of the two lines passing through point $M$ touches the circle at point $C$, while the second intersects this circle at points $A$ and $B$, with $A$ being the midpoint of segment $B M$. It is known that $M C=2$ and $\angle B M C=45^{\circ}$. Find the radius of the circle.
#
|
Prove that triangle $B M C$ is a right triangle.
## Solution
Let $A M=A B=x$. By the tangent-secant theorem, $B M \cdot A M=M C^{2}$, or $2 x^{2}=4$, from which $x=\sqrt{2}$.
In triangle $B M C$, the sides $M C=2, B M=2 x=2 \sqrt{2}$ and the angle between them $\angle B M C=45^{\circ}$ are known. Consider a right triangle with a leg equal to 2 and an acute angle equal to $45^{\circ}$. Its hypotenuse is $2 \sqrt{2}$, so this triangle is congruent to triangle $B M C$ by two sides and the included angle. Therefore, triangle $B M C$ is a right triangle, $\angle B C M=90^{\circ}$. Then $B C$ is the diameter of the circle and $B C=M C=2$.
## Answer
1.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kovaldji A.K.
Vladimir is running on a circular track at a constant speed. There are two photographers standing at two points on the track. After the start, Vladimir was closer to the first photographer for 2 minutes, then closer to the second photographer for 3 minutes, and then closer to the first photographer again. How long did it take Vladimir to run the entire circle?
|
Let's mark the first and second photographers on the circle with points $A$ and $B$ respectively, and points $C$ and $D$ will denote the midpoints of the arcs connecting $A$ and $B$. Then on the semicircle $C A D$, Vasya is closer to the first photographer, and on the semicircle $C B D$ (marked in bold on the diagram) - closer to the second photographer. According to the problem, he was closer to the second photographer for 3 minutes. Therefore, he runs the entire circle in 6 minutes.
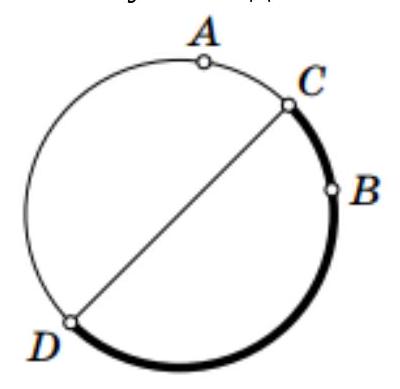
Answer
In 6 minutes.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Zaytsev C.A.
A checkerboard paper square $8 \times 8$ was folded several times along the cell lines so that a $1 \times 1$ square was obtained. It was then cut along a segment connecting the midpoints of two opposite sides of the square. Into how many pieces could the square have split as a result?
|
Let the cut be vertical. Draw vertical segments in all $1 \times 1$ squares, connecting the midpoints of opposite sides. When folding along the lines of the cells, these segments overlap with each other. Therefore, when cutting, only these segments are cut. As a result, 9 parts are obtained.

## Answer
Into 9 parts.
Send a comment
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9
In a sphere of radius 9, three equal chords $A A 1, B B 1$, and $C C 1$ are drawn through a point $S$ such that $A S=4, A 1 S=8, B S < B 1 S, C S < C 1 S$. Find the radius of the sphere circumscribed about the pyramid $S A B C$.
|
The products of the segments of intersecting chords are equal, so $B S \cdot S B 1=A S \cdot S A 1=4 \cdot 8=32$. In addition, $B B 1=A A 1=A S+S A 1=4+8=12$. From the system
$$
\left\{\begin{array}{l}
B S \cdot S B_{1}=32 \\
B S+S B_{1}=12
\end{array}\right.
$$
and the condition $B S<B 1 S$, we find that $B S=4$ and $S B 1=8$. Similarly, $C S=4$ and $S C 1=8$. Let $A 2, B 2$, and $C 2$ be the feet of the perpendiculars dropped from the center $O$ of the sphere to the chords $A A 1, B B 1$, and $C C 1$, respectively. Then the points $A 2, B 2$, and $C 2$ are the midpoints of these chords. Note that the triangular pyramid $S A B C$ is similar to the triangular pyramid $S A 2 B 2 C 2$, since these pyramids are homothetic with the center of homothety $S$ and the coefficient
$$
k=\frac{A S}{S A_{2}}=\frac{A S}{-A A_{2}-A S}=-\frac{4}{-6-4}=-2
$$
Therefore, the radius $R$ of the sphere circumscribed around the pyramid $S A B C$ is twice the radius $r$ of the sphere circumscribed around the pyramid $S A 2 B 2 C 2$. The segment $O S$ is seen from the points $A 2, B 2$, and $C 2$ at a right angle, meaning that these points lie on the sphere with diameter $O S$, i.e., $O S$ is the diameter of the sphere circumscribed around the pyramid $S A 2 B 2 C 2$. From the right triangles $A O A 2$ and $O S A 2$, we find that
$$
\begin{gathered}
O A 22=O A 2-A A 22=O A 2-\left(\frac{1}{2} A A 1\right) 2=92-62=45 \\
2 r=O S=\sqrt{S A_{2}^{2}+O A_{2}^{2}}=\sqrt{4+45}=7 \\
\text { Therefore, } R=2 r=7
\end{gathered}
$$
## Answer
7.00
Submit a comment
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Right triangle with an angle in ]
The hypotenuse $AB$ of the right triangle $ABC$ is 2 and is a chord of a certain circle. The leg $AC$ is 1 and lies inside the circle, and its extension intersects the circle at point $D$, with $CD=3$. Find the radius of the circle.
|
The leg $A C$ is equal to half the hypotenuse $A B$, so $\angle A=60^{\circ}$. In addition, $A D=2 A B$, so the angle $A B D-$ is a right angle. Therefore, $A D$ is the diameter of the circle.
## Answer
2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
\[
\begin{aligned} & {\left[\begin{array}{l}\text { Angle between the tangent and the chord }\end{array}\right]} \\ & \text { [Inscribed angle is half of the central angle]}\end{aligned}
\]
Secant $A B C$ intercepts arc $B C$, which contains $112^{\circ}$; tangent $A D$ at point of tangency $D$ divides this arc in the ratio $7: 9$. Find $\angle B A D$.
|
Consider the exterior angle of triangle $A D C$, adjacent to angle $A D C$.
## Solution
Let $K$ be a point lying on the extension of the tangent $A D$ beyond point $D$. The angle $K D C$ is an exterior angle for triangle DAC. Therefore,
$\angle A=\angle K D C-\angle D C B=1 / 2-C D-1 / 2-D B=1 / 2\left(9 / 16-{ }^{7} / 16\right) \cdot 112^{\circ}=7^{\circ}$.
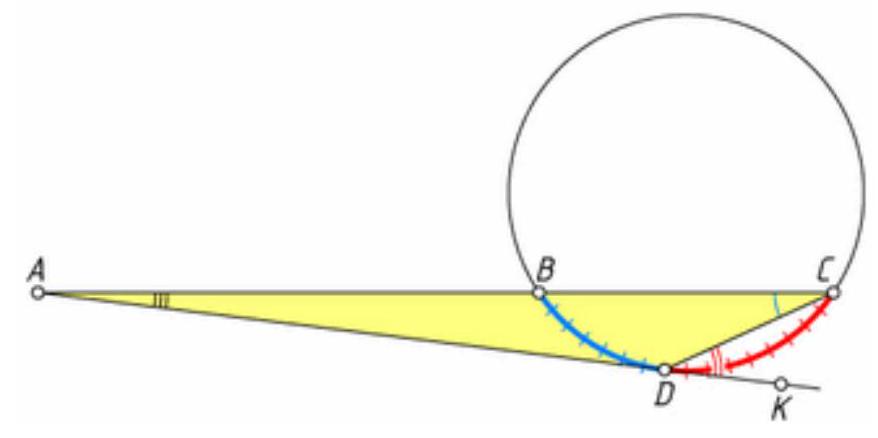
## Answer
$7^{\circ}$.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 [Pythagorean Theorem (direct and inverse)]
Three circles of different radii touch each other externally. The segments connecting their centers form a right triangle. Find the radius of the smallest circle if the radii of the largest and medium circles are 6 and 4.
#
|
Let $x$ be the radius of the smaller circle. The sides of the resulting triangle are $10, 6+x$, and $4+x$. Since 10 is the largest side, it is the hypotenuse. Therefore, $(x+6)^{2}+(x+4)^{2}=100$, from which $x=2$.
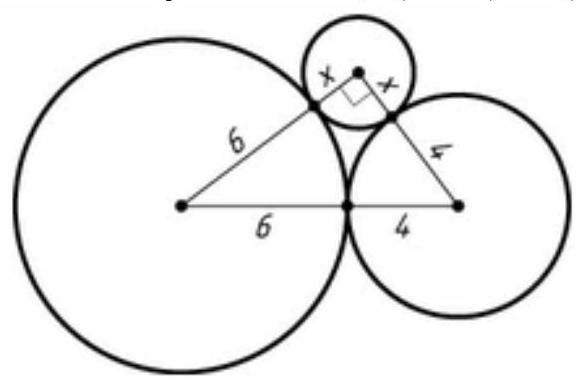
## Answer
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
\left.\begin{array}{l}{[\text { Angles subtending equal arcs and equal chords }]} \\ {[\text { Inscribed angle subtending the diameter }]\end{array}\right]
A circle passes through vertices $A$ and $C$ of triangle $ABC$, intersecting side $AB$ at point $E$ and side $BC$ at point $F$. Angle $AEC$ is five times the angle $BAF$, and angle $ABC$ is $72^{\circ}$. Find the radius of the circle if $AC=6$.
|
Let $\angle B A F=\alpha$. Then $\angle A E C=5 \alpha$. Inscribed angles $E C F$ and $E A F$ subtend the same arc, so $\angle B C E=\angle E C F=\angle E A F=\angle B A F=\alpha$.
By the exterior angle theorem of a triangle, $\angle A B C+\angle B C E=\angle A E C$, or $72^{\circ}+\alpha=5 \alpha$, from which we find that $\alpha=\frac{1}{4} \cdot 72^{\circ}=18^{\circ}$, hence $\angle A E C=5 \alpha=5 \cdot 18^{\circ}=90^{\circ}$.
The center of the circle circumscribed around the right triangle $A E C$ is the midpoint of the hypotenuse $A C$, so the radius of the circle is half of $A C$, i.e., 3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9 | |
Find the radius of the smallest circle in which a triangle with sides 7, 9, and 12 can be placed.
|
The given triangle is obtuse.
## Solution
$7^{2}+9^{2}<127^{2}$, therefore the given triangle is obtuse. Consequently, the circle constructed with the largest side of the triangle as its diameter contains the triangle.
## Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Linear element relationships of similar triangles] [Rectangles and squares. Properties and characteristics]
In a triangle with a base of 30 and a height of 10, an isosceles right triangle is inscribed such that its hypotenuse is parallel to the base of the given triangle, and the vertex of the right angle lies on this base. Find the hypotenuse.
|
Use the equality of the ratios of corresponding heights to the bases in similar triangles.
## Solution
Let the vertices $M$ and $N$ of the hypotenuse lie on the sides $A C$ and $B C$ of triangle $A B C$, respectively, and the vertex of the right angle $K$ lies on the base $A B$. Denote by $x$ the height of triangle $M N K$ drawn from vertex $K$. Then $M N = 2x$.
The heights of similar triangles $M C N$ and $A C B$, drawn from vertex $C$, are in the same ratio as the bases $M N$ and $A B$, that is, $(10 - x) / 10 = 2x / 30$. Therefore, $x = 6$, and $M N = 2x = 12$.
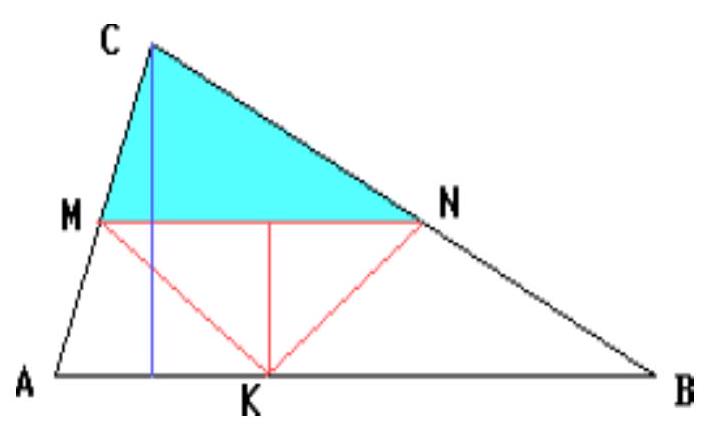

$A B C$ is the given triangle; $C D$ is the angle bisector of angle $C$; point $E$ lies on side $B C$, and $D E \parallel A C$. Find $D E$ if $B C = a$ and $A C = b$.
## Hint
The angle bisector of a triangle divides the opposite side into segments proportional to the other two sides.
## Solution
By the property of the angle bisector of a triangle, $B D / A B = a / (a + b)$.
From the similarity of triangles $D B E$ and $A B C$, it follows that $D E : A C = B D : A B$, hence $D E = ab / (a + b)$.
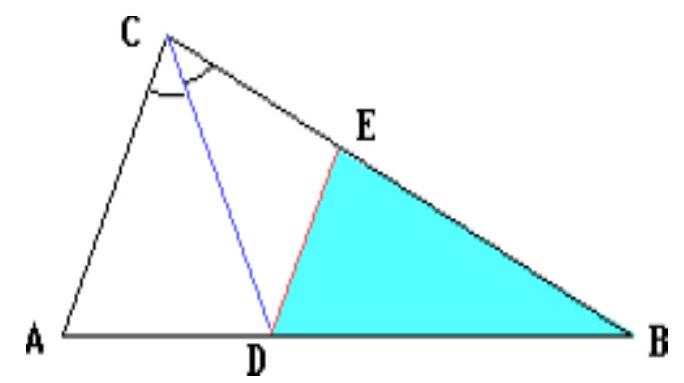
Answer
$ab / (a + b)$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On the plane, there are 16 points (see the figure).
a) Show that it is possible to erase no more than eight of them so that no four of the remaining points lie at the vertices of a square.
b) Show that it is possible to manage with erasing six points.
c) Find the minimum number of points that need to be erased for this.
|
b) All these points form 20 squares: 9 with side 1, 4 with side 2, 1 with side 3, 4 with side $\sqrt{2}$, and 2 with side $\sqrt{5}$. Let's denote the points with letters (Fig. 1) and count how many squares each point is a vertex of (Fig. 2).
| $A$ | $B$ | $C$ | $D$ |
| :--- | :--- | :--- | :--- |
| $E$ | $F$ | $G$ | $H$ |
| $I$ | $J$ | $X$ | $L$ |
| $M$ | $N$ | $O$ | $P$ |
Fig. 1
| 3 | 5 | 5 | 3 |
| :--- | :--- | :--- | :--- |
| 5 | 6 | 6 | 5 |
| 5 | 6 | 6 | 5 |
| 3 | 5 | 5 | 3 |
Fig. 2
| 2 | 3 | 3 | 3 |
| :--- | :--- | :--- | :--- |
| 3 | $F$ | 4 | 3 |
| 3 | 4 | 4 | 5 |
| 3 | 3 | 5 | 3 |
Fig. 3
| 2 | 3 | 2 | 2 |
| :--- | :--- | :--- | :--- |
| 2 | $F$ | $G$ | 1 |
| 3 | 3 | 3 | 3 |
| 2 | 3 | 3 | 3 |
Fig. 4
| 2 | 2 | 2 | 2 |
| :--- | :--- | :--- | :--- |
| 3 | $F$ | 2 | 3 |
| 3 | 2 | 2 | $L$ |
| 3 | 2 | 3 | 3 |
Fig. 5
$F G J K$ is a square, so one of its vertices is erased. We can assume it is $F$. As a result, 6 squares are "destroyed." In Fig. 3, it is indicated how many squares remain "sitting" on each point.
$G L O J$ is a square, so one of its vertices is erased. We can assume it is $G$ or $L$.
In the first case, 4 more squares are "destroyed." 10 remain. But on each of the remaining points, no more than three of the remaining squares "sit" (Fig. 4). Therefore, at least 4 more points need to be erased.
In the second case, 5 more squares are "destroyed." 9 remain. If we want to erase only 3 more points, then on each of them, 3 squares must "sit," and all these 9 squares must be different. But it is not difficult to check that no matter which three of the six "three-square" points we take (Fig. 5), there will be two of them that are vertices of the same square. Therefore, in this case, we will also have to erase 4 more points.
## Answer
a) For example, see the left figure. b) For example, see the right figure. c) 6 points.

Author: Khachatryan A.v.
There is a chocolate bar in the shape of an equilateral triangle with side $n$, divided by grooves into equilateral triangles with side 1. Two players play. On a turn, a player can break off a triangular piece from the chocolate bar along a groove, eat it, and pass the remainder to the opponent. The player who gets the last triangular piece with side 1 is the winner. For each $n$, determine who of the players can always win, regardless of how the opponent plays.
## Solution
A broken off or formed triangle (obviously, equilateral) with side length $m$ will be called an $m$-triangle.
The cases $n=1,2$ are obvious. Let's consider two cases for $n>2$.
1) $n$ is prime. Suppose the first move breaks off a $k$-triangle. A trapezoid with sides $k, n-k, n, n-k$ remains. Let $a$ be the larger of the numbers $k, n-k$, and $b$ be the smaller (they are not equal: $\mathrm{GCD}(a, b)=\mathrm{GCD}(n, n-k)=1$). The second player breaks off a piece so that a parallelogram with sides $a$ and $b$ remains. The first player will have to break off a $b$-triangle (otherwise, the second player will prematurely win by breaking off a 1-triangle from the remaining acute angle and leaving the first player with a hexagon, all of whose angles are obtuse). A trapezoid with sides $a-b, b, a, b$ will remain, where $\mathrm{GCD}(a-b, b)=\mathrm{GCD}(a, b)=1$, meaning the game will return to the same situation as one move back, but the trapezoid will be smaller. The game will continue until $a$ and $b$ become 1 (a trapezoid with sides $0,1,1,1$ is a 1-triangle!), which means the second player wins.
2) $n$ is composite. The first player fixes $p$ - one of the prime divisors of the number $n$ - and breaks off a $p$-triangle. The second player must break off an $(n-p)$-triangle (otherwise, the first player will break off a 1-triangle from the remaining acute angle and prematurely win). A parallelogram with sides $p$ and $n-p$ (this number is divisible by $p$) will remain. The first player again breaks off a $p$-triangle, and so on. Eventually, after the first player's move, a $p$-triangle will remain. Since it is the second player's turn, according to 1), he will lose.
## Answer
If the number $n$ is prime, then the second player wins; otherwise, the first player wins.
|
6
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
$\left.\begin{array}{l}\text { [ Homothety helps solve the problem. } \\ \text { [Two tangents drawn from one point] }\end{array}\right]$
On the sides $A C$ and $B C$ of triangle $A B C$, points $P$ and $Q$ are marked, respectively. It turned out that $A B=A P=B Q=1$, and the point of intersection of segments $A Q$ and $B P$ lies on the inscribed circle of triangle $A B C$. Find the perimeter of triangle $A B C$.
|
Let the incircle of triangle $ABC$ touch its sides $AB, BC$, and $AC$ at points $S, R$, and $T$; $M$ is the intersection point of segments $AQ$ and $BP$. We can observe that point $P$ lies on segment $CT$, and point $Q$ lies on segment $CR$. Then segments $AM$ and $BM$ intersect the circle again. Let the points of intersection be $K$ and $L$ respectively. If $I$ is the center of the circle, then $BI$ is the angle bisector of $\angle BAC$. Under symmetry with respect to line $BI$, point $S$ maps to $R$, point $A$ maps to $Q$ (since $BQ = BA$), and the circle maps to itself. Therefore, arcs $KS$ and $MR$ are equal. Similarly, we can prove that arcs $SL$ and $MT$ are equal. Since $BI \perp AM$ and $AI \perp BM$, $T$ is the orthocenter of triangle $ABM$. Therefore, $MI \perp AB$, and $MS$ is the diameter of the circle. Hence, arcs $KT$ and $RL$ are equal. Consequently, arc $KTMR$ is $180^\circ$, meaning $KR$ is the diameter of the circle. Under a homothety centered at $A$, which maps the incircle to the excircle of triangle $ABC$, the tangent $l$ at point $K$ to the incircle will map to a parallel tangent to the excircle, i.e., to line $BC$, and ray $AK$ will map to itself. Therefore, $Q$ is the point of tangency of the excircle with side $BC$. Then, if $p$ is the semiperimeter of triangle $ABC$, we have
$$
1 = BQ = p - AB = p - 1
$$
From this, we find that $p = 2$. Therefore, the perimeter of triangle $ABC$ is 4.
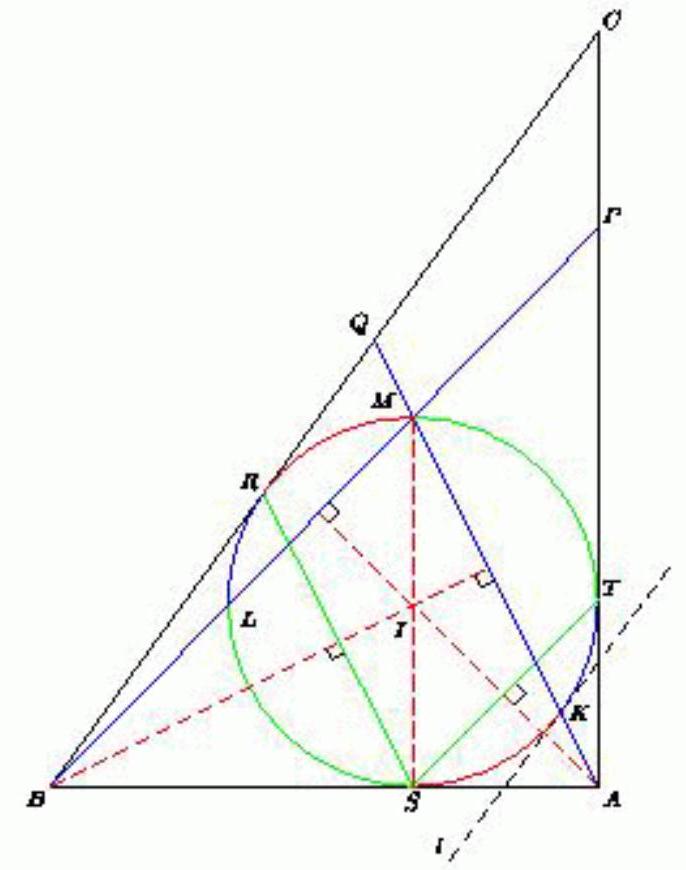
## Answer
4.00
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Coordinate method in space ] [Area and orthogonal projection]
The areas of the projections of a certain triangle onto the coordinate planes Oxy and Oyz are $\sqrt{6}$ and $\sqrt{7}$, respectively, and the area of the projection onto the plane $O x z$ is an integer. Find the area of the triangle itself, given that it is also an integer.
|
Let the vector perpendicular to the plane of the original triangle form angles $\alpha, \beta$, and $\gamma$ with the coordinate axes $O x, O y$, and $O z$ respectively. Then
$$
\cos 2 \alpha+\cos 2 \beta+\cos 2 \gamma=1
$$
Let the area of the original triangle be denoted by $S$, and the areas of the projections on the coordinate planes $O y z, O x z$, and $O x y$ be denoted by $S_{x}, S_{y}$, and $S_{z}$ respectively ($S_{z}=\sqrt{6}, S_{x}=\sqrt{7}$). According to the theorem of the area of the projection of a plane figure onto a plane,
$$
\sqrt{7}=S_{x}=S|\cos \alpha|, S_{y}=S|\cos \beta|, \sqrt{6}=S_{z}=S|\cos \gamma|
$$
Then
$$
7+6+S_{y} 2=S 2 \cos 2 \alpha+S 2 \cos 2 \beta+S 2 \cos 2 \gamma=S 2(\cos 2 \alpha+\cos 2 \beta+\cos 2 \gamma)=S 2
$$
Therefore,
$$
S 2-S_{y} 2=13,\left(S-S_{y}\right)\left(S+S_{y}\right)=13
$$
Since both factors on the left side of the equation are positive integers, and the second factor is greater than the first, the equality is possible only in the case when
$$
\left\{\begin{array}{l}
S-S_{y}=1 \\
S+S_{y}=13
\end{array}\right.
$$
From this system, we find that $S_{y}=7$.

On the edges $A 1 B 1, A B, A 1 D 1$, and $D D 1$ of the unit cube $A B C D A 1 B 1 C 1 D 1$, points $K, L, M$, and $N$ are taken, respectively, such that $A 1 K=\frac{2}{3}, A L=\frac{1}{5}, A 1 M=\frac{1}{3}$. Determine which of the edges $A 1 D 1$ or $D 1 C 1$ is intersected by the plane parallel to the segment $M L$ and containing the segment $K N$. In what ratio does this edge divide the plane?
## Solution
Choose a coordinate system with the origin at point $A 1$. The $x$-axis is directed along the ray $A 1 D 1$, the $y$-axis along the ray $A 1 B 1$, and the $z$-axis along the ray $A 1 A$. Then the coordinates of points $K, L, M$, and $N$ are:
$$
K\left(0 ; \frac{2}{3} ; 0\right), L\left(0 ; \frac{1}{5} ; 1\right), M\left(\frac{1}{3} ; 0 ; 0\right), N(1 ; 0 ; t)
$$
where $0 \leqslant t \leqslant 1$. From point $L$, lay off the vector
$$
\overrightarrow{L P}=\overrightarrow{M K}=\left(0-\frac{1}{3} ; \frac{2}{3}-0 ; 0-0\right)=\left(-\frac{1}{3} ; \frac{2}{3} ; 0\right)
$$
$1 \underline{13}$
Then point $P$ has coordinates $\left(-\frac{1}{3} ; \frac{13}{15} ; 1\right)$. The desired plane passes through points $K, P$, and $N$. We seek the equation of this plane in the form $a x+b y+c z=1$. Substituting the coordinates of points $K, P$, and $N$ into this equation, we find that
$$
c=\frac{1}{10(t+3)}, a=\frac{9 t+30}{10(t+3)}, b=\frac{3}{2}
$$
After obvious simplifications, we obtain the equation $(9 t+30) x+15(t+3) y+z=10(t+3)$. Substituting zeros for $y$ and $z$, we find the point of intersection of the plane with the line $A 1 D 1-x=\frac{10(t+3)}{3(t+10)}$, and since $0 \leqslant t \leqslant 1$, then $1 \leqslant x \leqslant \frac{40}{89}$. Therefore, the cutting plane does not intersect the edge $A 1 D 1$. Substituting $x=1$ and $z=0$ into the obtained equation, we find the point of intersection of the plane with the line $D 1 C 1-y=\frac{1}{15(t+3)}$, and since $0 \leqslant t \leqslant 1$, then $0 \leqslant y \leqslant \frac{1}{60}$. Therefore, the cutting plane intersects the edge $D 1 C 1$ and in this case, the point of intersection divides this edge in any ratio from 0 to $\frac{1}{59}$, counting from vertex $D 1$.
## Answer
$D 1 C 1$; in any ratio from 0 to $\frac{1}{59}$, counting from vertex $D 1$.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a triangular pyramid PABC, the sums of the three plane angles at each of the vertices A and B are both $180^{\circ}$ and $PC = AB$. Inside the pyramid, a point $D$ is taken, the sum of the distances from which to the three lateral faces PAB, PAC, and PBC is 7. Find the distance from the center of the circumscribed sphere to the face PAB, if the volumes of the pyramids PABC and BABC are in the ratio of $8: 1$.
#
|
Consider the unfolding P1AP2CP3BP1 of the tetrahedron ABCD onto the plane of triangle ABC (Fig.1), where points P1, P2, and P3 are the vertices of triangles with bases AB, AC, and BC, respectively. Since the sums of the three plane angles at each of the vertices A and B of the tetrahedron PABC are $180^{\circ}$, point A lies on the segment P1P2, and point B lies on the segment P1P3, and A and B are the midpoints of these segments. Therefore, AB is the midline of triangle P1P2P3. This means that $P2P3 = 2AB$, and since $PC = AB$, then $CP2 = CP3 = AB$, so $CP2 + CP3 = P2P3$. This implies that point C lies on the segment P2P3, and C is the midpoint of this segment (Fig.2). Thus, AC, AB, and BC are the midlines of triangle P1P2P3. Therefore,
$$
BC = AP1 = AP, \quad AC = BP1 = BP
$$
i.e., the opposite edges of the tetrahedron ABCD are pairwise equal. This means that all faces of the tetrahedron are equal triangles (by three sides). We will prove that the center of the inscribed sphere of this tetrahedron coincides with the center of the inscribed sphere. Let O be the center of the sphere of radius R circumscribed around the given tetrahedron (Fig.3). Perpendiculars dropped from point O to the faces of the tetrahedron pass through the centers of the circumscribed circles of these faces, and since the tetrahedron is equifacial, all its faces are equal acute-angled triangles. Therefore, the radii of their circumscribed circles are equal, and the centers of these circles are located inside the faces. Denote them by R1. Then the distances from point O to the planes of the faces are equal to $\sqrt{R^2 - R_1} = r$. This means that point O is equidistant from all the faces of the tetrahedron at a distance of $r$. Therefore, O is the center of the inscribed sphere, and $r$ is the radius of this sphere. Let S be the area of each of the four faces of the tetrahedron PABC, H be the height of the tetrahedron drawn from vertex P, and x, y, z, and t be the heights of the pyramids DABP, DACP, DBCP, and DABC, respectively, drawn from their common vertex D (Fig.4). From the problem statement, it follows that $H = 8t$, and since
$$
V_{DABP} + V_{DACP} + V_{DBCP} + V_{DABC} = V_{PABC}
$$
we have
$$
\begin{gathered}
\frac{1}{3} S \cdot x + \frac{1}{3} S \cdot y + \frac{1}{3} S \cdot y + \frac{1}{3} S \cdot z = \\
= \frac{1}{3} S \cdot (x + y + z + t) = \frac{1}{3} S \cdot (7 + t) = \frac{1}{3} S \cdot H
\end{gathered}
$$
from which
$$
7 + t = H = 8t, \quad t = 1, \quad H = 8.
$$
Thus,
$$
V_{PABC} = \frac{1}{3} S \cdot H = \frac{1}{3} \cdot 8S.
$$
and since $V_{PABC} = \frac{1}{3} \cdot 4S \cdot r$, then
$$
r = \frac{3 V_{PABC}}{4S} = 2
$$
## Answer
2.00
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Coverings ]
It is known that a set $M$ of points on a line can be covered by three segments of length 1.
What is the smallest number of segments of length 1 that can certainly cover the set of midpoints of segments with endpoints in the points of the set $M$?
#
|
If point $A$ is covered by the segment $[a, a+1]$, and point $B$ by the segment $[b, b+1]$, then the midpoint of segment $A B$ is covered by the segment $\left[a+b / 2, a+b / 2+1\right]$.
## Solution
Let two points $A$ and $B$ be covered by one unit segment. Then the midpoint of segment $A B$ is also covered by this segment. If point $A$ is covered by the unit segment $[a, a+1]$, and point $B$ by the segment $[b, b+1]$, then the midpoint of segment $A B$ is covered by the unit segment $\left[a+b / 2, a+b / 2+1\right]$.
Example. Let $[a, a+1],[b, b+1],[c, c+1]$ be three segments covering the given set $M$. As shown above, the set of midpoints of segments with endpoints in the points of set $M$ is covered by six segments $[a, a+1],[b, b+1],[c, c+1],\left[a+b / 2, a+b / 2+1\right],\left[a+c / 2, a+c / 2+1\right],\left[b+c / 2, b+c / 2+1\right]$.
Estimate. Let $M=[0,1] \cup[2,3] \cup[6,7]$. Then the set of midpoints of segments with endpoints in the points of set $M$ is $[0,5] \cup [6,7]$. Therefore, it is impossible to cover with fewer than six segments of length 1.
## Answer
Six segments.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Two pairs of similar triangles]
Through a point taken inside an arbitrary triangle, segments are drawn parallel to its sides with endpoints on the sides of the triangle.
Prove that the sum of the three ratios of these segments to the sides of the triangle parallel to them is equal to 2.
|
Consider similar triangles.
## Solution
Let $O$ be an arbitrary point taken inside triangle $A B C ; A_{1} A_{2} \| B C, B_{1} B_{2} \| A C, C_{1} C_{2} \| A B$ (see figure).
Denote $A_{2} C = O B_{2} = x, A_{2} C_{1} = y$,
$A C_{1} = O B_{1} = z$. Then $\frac{C_{1} C_{2}}{A B} = \frac{x + y}{A C}, \frac{A_{1} A_{2}}{B C} = \frac{z + y}{A C}, \frac{B_{1} B_{2}}{A C} = \frac{x + z}{A C}$. Therefore, $\frac{A_{1} A_{2}}{B C} + \frac{B_{1} B_{2}}{A C} + \frac{C_{1} C_{2}}{A B} = \frac{2(x + y + z)}{A C} = 2$
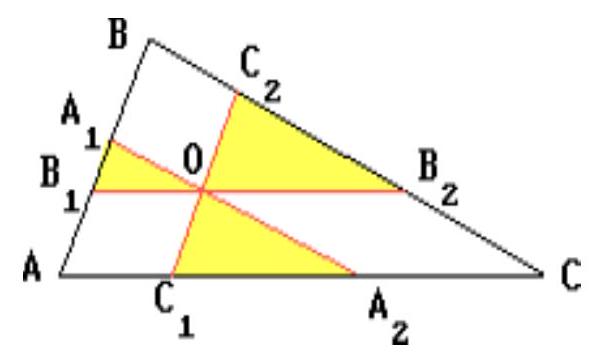
Submit a comment
|
2
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
[ Product of the lengths of the chord segments and the lengths of the secant segments ]
A line passing through point $A$, located outside the circle at a distance of 7 from its center, intersects the circle at points $B$ and $C$. Find the radius of the circle, given that $AB=3$, $BC=5$.
#
|
The product of the entire secant and its external part for a given point and a given circle is constant.
## Solution
Since $A B<B C$, point $B$ lies between points $A$ and $C$. Let $O$ be the center of the circle, $R$ its radius, and the line $A O$ intersects the circle at points $D$ and $E$ (with $D$ between $A$ and $O$). Then
$$
A D \cdot A E=A B \cdot A C, (7-R)(7+R)=3 \cdot 8, 49-R^{2}=24
$$
$R^{2}=25$. Therefore, $R=5$.
## Answer
5.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Systems of points and segments. Examples and counterexamples ] [ Classical combinatorics (miscellaneous). ]
On a plane, 10 equal segments were drawn, and all their points of intersection were marked. It turned out that each point of intersection divides any segment passing through it in the ratio $3: 4$. What is the maximum possible number of marked points?
|
On each segment, there are no more than two points. On the other hand, each intersection point belongs to at least two segments. Therefore, there are no more than $10 \cdot 2: 10=10$ points. An example with 10 points is shown in the figure.
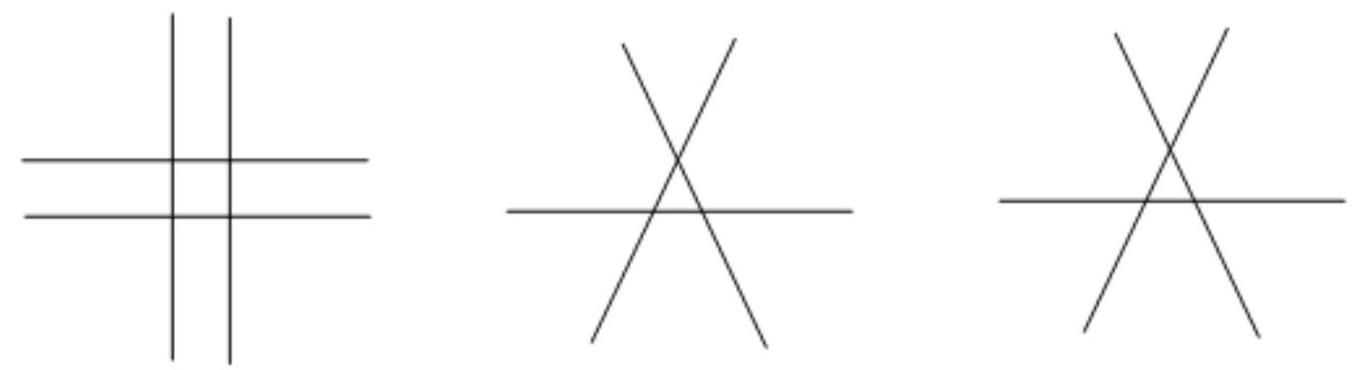
Answer
10 points.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bakayev E.V.
A secret base is surrounded by a transparent winding fence in the shape of a non-convex polygon, with a swamp outside. A straight power line consisting of 36 poles runs through the swamp, some of which are outside the base, and some are inside. (The power line does not pass through the vertices of the fence.) A spy walks around the base along the fence from the outside, keeping the fence always to his right. Each time he reaches the power line, he counts how many poles are to his left (he can see all of them). By the time the spy has walked around the entire fence, he has counted a total of 2015 poles. How many poles are inside the base?
|
A straight power line crosses the territory of the base in several segments. When the spy is at the end of one of these segments, he counts the poles. Consider one of them ($AB$). When the spy is at point $A$, he counts the poles on one side of $AB$, and when he is at point $B$, he counts the poles on the other side of $AB$. If the poles inside $AB$ are added to these, a total of 36 poles are obtained. Summing these equations for all segments, we get that 2015 plus the number $n$ of poles inside the base is divisible by 36. Since $n \leq 36$ and 2016 is divisible by 36, then $n=1$.
## Answer
## Problem
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shaovalov A.v.
Two players take turns coloring the sides of an $n$-gon. The first player can color a side that borders with zero or two colored sides, the second player - a side that borders with one colored side. The player who cannot make a move loses. For which $n$ can the second player win, regardless of how the first player plays?
|
For $n=3$, it is obvious that the first player wins, while for $n=4$, the second player wins. Let's show how the first player wins when $n>4$. After the first move of the second player, two adjacent sides are painted. The first player can paint a side "one apart" from them, creating an unpainted "hole" of one side. This is his sanctuary, which the second player cannot paint. The first player uses the sanctuary only if he has no other move. If such a moment comes (the second player may lose earlier), then (after "closing" the sanctuary) the unpainted part will consist of pairs of adjacent sides. From then on, the first player can always respond to the second player's move by painting a side from the same pair.
## Answer
Only for $n=4$.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Similar auxiliary triangles $]$ [ Right triangle with an angle at ]
On the cathetus $A C$ of the right triangle $A B C$, a circle is constructed with $A C$ as its diameter. It intersects side $A B$ at point $E$. A point $G$ is taken on side $B C$ such that segment $A G$ intersects the circle at point $F$, and segments $E F$ and $A C$ are parallel, $B G=2 C G$ and $A C=2 \sqrt{3}$. Find $G F$.
|
Triangles $A B C$ and $G A C$ are similar.
## Solution
Let $C G=t, \angle C A G=\alpha$. Then $B C=3 t$, and since $C E$ is the height, $\angle B=\angle A C E$. Since trapezoid $A E F C$ is inscribed in a circle, it is isosceles, so $\angle A C E=\alpha$. Therefore, $\angle B=\alpha$. Consequently, right triangles $A B C$ and $G A C$ are similar by two angles. Thus,
$C G: A C=A C: B C$, which means $A C^{2}=C G \cdot B C$, or $12=3 t^{2}$, from which $t=2$. $\operatorname{tg} \alpha=C G / A C=\frac{1}{\sqrt{3}}$, so $\alpha=30^{\circ}$.
Therefore, $A G=2 C G=4$. By the tangent-secant theorem, $G F=C G^{2} / G A=1$.
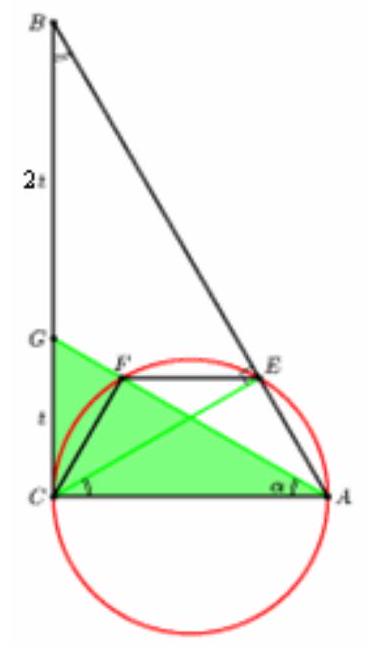
## Answer
1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[The ratio of the areas of triangles with a common base or common height $]$ Complex Trapezoids (other)
The area of trapezoid $A B C D$ with bases $A D$ and $B C (A D > B C)$ is 48, and the area of triangle $A O B$, where $O-$ is the point of intersection of the diagonals of the trapezoid, is 9. Find the ratio of the bases of the trapezoid $A D: B C$.
|
$S_{\triangle \mathrm{AOD}}=\frac{D O}{O B} \cdot S_{\triangle \mathrm{AOB}}$
## Solution
Notice that triangles $A B D$ and $A C D$ are equal in area, as they share the same base and have equal heights. Therefore, triangles $C O D$ and $A O B$ are also equal in area.
Let $\frac{A D}{B C}=x>1$. From the similarity of triangles $A O D$ and $C O B$, it follows that $\frac{A O}{O C}=\frac{D O}{O B}=\frac{A D}{B C}=x$. Then,
$$
S_{\triangle \mathrm{AOD}}=\frac{D O}{O B} \cdot S_{\triangle \mathrm{AOB}}=9 x, \quad S_{\triangle \mathrm{BOC}}=\frac{C O}{O A} \cdot S_{\triangle \mathrm{AOB}}=\frac{9}{x}
$$
and since
$$
S_{\triangle \mathrm{AOD}}+S_{\triangle \mathrm{BOC}}=S_{\mathrm{ABCD}}-S_{\triangle \mathrm{AOB}}-S_{\triangle \mathrm{COD}}=48-2 \cdot 9=30
$$
we obtain the equation $9 x+\frac{9}{x}=30$, the larger root of which $(x=3)$ satisfies the condition $x>1$.
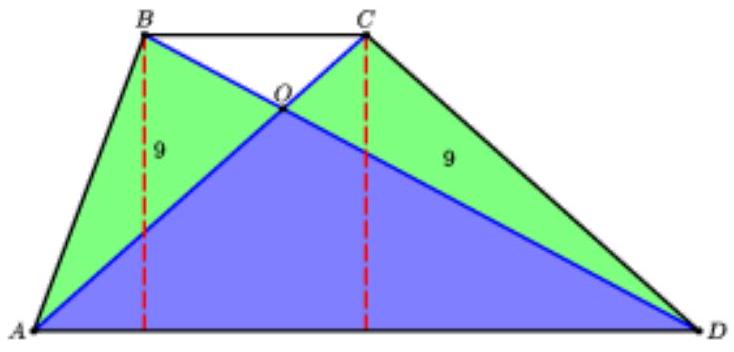
## Answer
3. Send a comment
Problem
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the greatest number of acute angles that can occur in a convex polygon?
#
|
The sum of all exterior angles of a convex polygon is $360^{\circ}$. Therefore, a convex polygon cannot have more than three obtuse exterior angles, i.e., it cannot have more than three acute interior angles. Three acute angles can be found, for example, in a triangle.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The sides of the blue and green equilateral triangles are respectively parallel. The perimeter of the blue triangle is 4, and the perimeter of the green triangle is 5. Find the perimeter of the hexagon formed by the intersection of these triangles.
#
|
The sum of the perimeters of the blue and green triangles is equal to the sum of the perimeters of the six small triangles surrounding the hexagon.
## Solution
Notice that the sum of the perimeters of the blue and green triangles is equal to the sum of the perimeters of the six small equilateral triangles surrounding the hexagon. Each side of the hexagon is $1 / 3$ of the perimeter of the corresponding triangle. Therefore, the perimeter of the hexagon is one third of the sum of the perimeters of the blue and green triangles, i.e., it is 3.
## Answer
## Problem
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Two equal circles touch the inside of a third circle and touch each other. By connecting the three centers, a triangle with a perimeter of 18 is obtained. Find the radius of the larger circle.
|
The line connecting the centers of two tangent circles passes through their point of tangency.
## Solution
Let the radii of the given circles be $r, r$ and $R (r < R)$. Then the sides of the specified triangle are $R - r, R - r$, and $2r$. Therefore,
Consequently, $R = 9$.
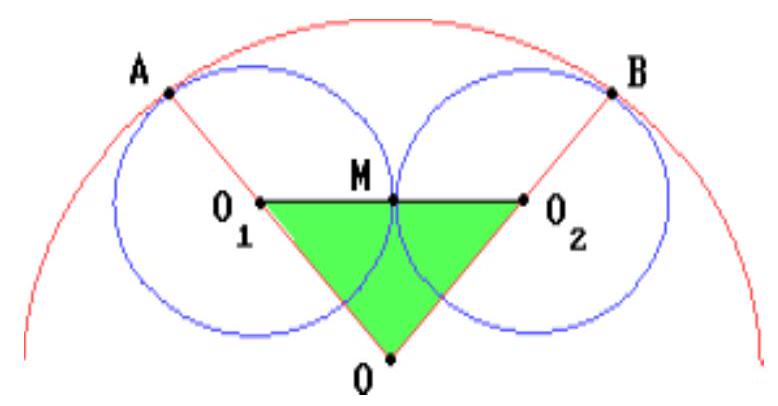
Answer
9.
Send a comment
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a right-angled triangle, the medians drawn from the vertices of the acute angles are equal to $\sqrt{52}$ and $\sqrt{73}$. Find the hypotenuse of the triangle.
|
Let the legs be denoted by $x$ and $y$. Then, by the Pythagorean theorem, $x^{2} + y^{2} / 4 = 52$, and $y^{2} + x^{2} / 4 = 73$.
Adding these equations, we get $5 / 4\left(x^{2} + y^{2}\right) = 125 \Rightarrow x^{2} + y^{2} = 100$.
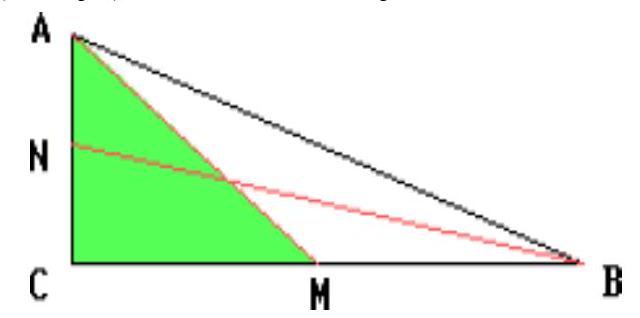
## Answer
10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kustarev A.A.
The faces of a cube are numbered from 1 to 6. The cube was rolled twice. The first time, the sum of the numbers on the four side faces was 12, the second time it was 15. What number is written on the face opposite the one where the digit 3 is written?
|
The sum of the numbers on all faces of the cube is 21.
## Solution
Notice that the sum of all numbers written on the cube is 21. The sum of the numbers on the top and bottom faces in the first and second cases is 9 and 6, respectively.
After the first roll, it is clear that either 3 is opposite 6, or 4 is opposite 5. Suppose 4 is opposite 5. But after the second roll, it is clear that either 1 is opposite 5, or 2 is opposite 4. This is a contradiction, so 3 is opposite 6.
## Answer
6.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Groovitz $\mathbf{B . M}$.
A regular polygon is drawn on the board. Vova wants to mark $k$ points on its perimeter so that there is no other regular polygon (not necessarily with the same number of sides) that also contains the marked points on its perimeter.
Find the smallest $k$ sufficient for any initial polygon.
#]
|
Example. Let's prove that five points are sufficient. Let $A, B, C, D$ be four consecutive vertices of the polygon (possibly $A=D$). Mark points $A, B$, an arbitrary point $X$ on side $AB$, point $Y$ on side $BC$, sufficiently close to $B$, and point $Z$ on side $CD$, sufficiently close to $C$.
Let $P$ be the original polygon, $Q$ be some regular polygon containing our five points on its perimeter, $\alpha$ and $\beta$ be the angles of these polygons. The line $AB$ must contain a side of polygon $Q$, as it contains three marked points. Let this side be $A'B'$. Further, let the side of $Q$ containing $Y$ lie on line $l$; then points $B$ and $Z$ must lie on the same side of it (see figure).
Since $Z$ is close to $C$, this means that the angle between lines $l$ and $BC$ is small. On the other hand, $\alpha = \angle ABY \geq \angle A'B'Y \geq \beta$, i.e., the number of sides of $Q$ is not greater than that of $P$. Therefore, the angle between $l$ and $BC$ can be sufficiently small only when these lines coincide. Thus, the line $BC$ also contains a side of $Q$, and point $B$ is then its vertex. Hence, $P$ and $Q$ are homothetic with center at point $B$, and the contour of $Q$ can contain $Z$ only when $P$ coincides with $Q$.
Estimate. Let's prove that for a sufficiently large number of sides $n$ of a regular polygon $P$, four points are not enough to determine it. Suppose that three of these points lie on one side $AB$ of the polygon $P$. The equilateral triangle constructed on $AB$ lies entirely inside $P$, so the fourth marked point lies outside it. Therefore, by applying a homothety to our triangle with center at the midpoint of $AB$ and a suitable coefficient greater than 1, we can ensure that the fourth marked point also lies on its contour. This means that in this case, the polygon is not uniquely determined. If our assumption is incorrect, then the marked points form a convex quadrilateral $ABCD$ "sufficiently close" to an inscribed one. Specifically, we will show that $\angle A + \angle C \geq 180^\circ - 360^\circ / n$. Let points $B$ and $C$ lie on sides $KL$ and $MN$ of the polygon $P$, and points $A$, $K$, and $N$ lie on the same side of $BD$ (see figure).
Describe a circle $\omega$ with center $O$ around $P$. Then $\angle A + \angle C \geq \angle LAM + \angle KCN = 1/2(\angle LOM + \angle KON) = 180^\circ - 360^\circ / n$. Similarly,
$\angle B + \angle D \geq 180^\circ - 360^\circ / n$, so $\angle A + \angle C \leq 180^\circ + 360^\circ / n$.
We will show that $ABCD$ can be inscribed either in a square or in an equilateral triangle. Let angle $A$ be the largest angle of the quadrilateral $ABCD$, and $B \geq \angle D$. There are several cases.
1) $\angle B \geq 90^\circ$. Then it is clear that $ABCD$ can be inscribed in a square such that points $A, B$ fall on one of the sides - in one of the ways shown in the figure, depending on whether the projection of $CD$ on $AB$ or the projection of $ABCD$ on the line perpendicular to $AB$ is larger.
2) $\angle B \geq 240^\circ$ (since angle $A$ is the largest, $\angle B + \angle C < 240^\circ$). We will show that in this case, $ABCD$ can be inscribed in a square as shown in the figure.
Let $X$ and $Y$ be the projections of points $C$ and $D$ on $AB$; it is sufficient to check that $YB \leq CX$. But $\angle DCX = 270^\circ - (\angle A + \angle D) \leq 30^\circ$, so $XY \leq CX \tan 30^\circ \leq CX / \sqrt{3}$; on the other hand, $\angle B \geq 1/2(\angle B + \angle D) \geq 90^\circ - 180^\circ / n$, so for large $n$, $\tan \angle B \geq 10$; thus,
$XB = CX \cot \angle B \leq CX / 10$, and $YB \leq CX / \sqrt{3} + CX / 10 < CX$, as required.
## Answer
$k=5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ [sphere touching the edges of a tetrahedron]
A sphere touches the edges $A S, B S, B C$ and $A C$ of the triangular pyramid $S A B C$ at points $K, L, M$ and $N$ respectively.
Find the segment $K L$, if $M N=7, N K=5, L N=2 \sqrt{29}$ and $K L=L M$.
#
|
Let's prove that points $K, L, M$, and $N$ lie in the same plane (Fig.1). Denote
$$
A K=A N=a, B L=B M=b, C M=C N=c, S K=S L=d .
$$
If $c=d$, then lines $K N$ and $L M$ are parallel to line $S C$, so $K N \| L M$. Therefore, points $K, L, M$, and $N$ lie in the same plane. Let $c \neq d$. Therefore, points $K, L, M$, and $N$ lie in the same plane. Consider the section of the pyramid and the sphere by this plane (Fig.2). We obtain a quadrilateral $K L M N$ inscribed in a circle. Denote $K L=L M=x, \angle N K L=\alpha$. Then $\angle N M L=180^{\circ}-\alpha$. Further, we have:
$$
\left\{\begin{array} { l }
{ N L ^ { 2 } = K N ^ { 2 } + K L ^ { 2 } - 2 K N \cdot K L \operatorname { c o s } \alpha } \\
{ N L ^ { 2 } = M N ^ { 2 } + M L ^ { 2 } - 2 M N \cdot M L \operatorname { c o s } ( 1 8 0 ^ { \beta } - \alpha ) }
\end{array} \left\{\begin{array}{l}
116=25+x^{2}-10 x \cdot \cos \alpha \\
116=49+x^{2}+14 x \cdot \cos \alpha
\end{array}\right.\right.
$$
Subtracting the first equation from the second term by term, we get $x \cos \alpha=-1$. Then from the first equation, we find that
$$
x^2=116-25-10=81
$$
Therefore, $K L=x=9$.
## Answer
9.00
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the quadrilateral pyramid $S A B C D$, the base $A B C D$ has its axis of symmetry as the diagonal $A C$, which is equal to 9, and the point $E$ of intersection of the diagonals of the quadrilateral $A B C D$ divides the segment $A C$ such that the segment $A E$ is smaller than the segment $E C$. A plane is drawn through the midpoint of the lateral edge of the pyramid $S A B C D$, parallel to the base and intersecting the edges $S A, S B, S C, S D$ at points $A 1, B 1, C 1, D 1$ respectively.
The polyhedron $A B C D A 1 B 1 C 1 D 1$, which is part of the pyramid $S A B C D$, intersects the plane $\alpha$ in a regular hexagon with a side length of 2. Find the area of the triangle $A B D$, if the plane $\alpha$ intersects the segments $B B 1$ and $D D 1$.
|
From the condition, it follows that the diagonals $A C$ and $B D$ of the quadrilateral $A B C D$ are perpendicular, and the triangles $A B D$ and $C B D$ are isosceles. Since the truncated pyramid $A B C D A 1 B 1 C 1 D 1$ has 6 faces, the plane $\alpha$ intersects each face along a segment, the ends of which do not coincide with the vertices of the polyhedron. Let the vertices of the hexagon lying on the sides of the base $A B C D$ be denoted by $K$ and $M$, on the sides of the quadrilateral $A 1 B 1 C 1 D 1$ by $K 1$ and $M 1$, and on the lateral edges $D D 1$ and $B B 1$ by $P$ and $T$ respectively (for definiteness, we assume that the vertex $P$ is adjacent to the vertices $K$ and $K1$). Since $K M T M 1 K 1 P$ is a regular hexagon, the line $P T$ is parallel to the lines $K M$ and $K 1 M 1$ and, consequently, parallel to the planes $A B C D$ and $A 1 B 1 C 1 D 1$ and equidistant from them. Therefore, the points $P$ and $T$ are the midpoints of the edges $D D 1$ and $B B 1$ respectively, and $P T$ is the midline of the trapezoid $B B 1 D 1 D$, so the lines $K M, K 1 M 1, P T, D 1 B 1$, and $D B$ are parallel. Let $E 1$ be the point of intersection of the diagonals of the quadrilateral $A 1 B 1 D 1 C 1$, $H$ be the point of intersection of the side $K M$ with the diagonal $A C$, and $H 1$ be the point of intersection of the side $K 1 M 1$ with the diagonal $A 1 C 1$. There are two possible cases for the position of the plane $\alpha$: in the first case, the point $H$ lies between $A$ and $E$, and in the second case, between $E$ and $C$. We will prove that only the first case is possible. Let $O$ be the point of intersection of the plane $A A 1 C 1 C$ with the diagonal $P T$. The triangles $H E O$ and $H 1 E 1 O$ are equal by two sides and the angle between them. Therefore, $H E = H 1 E 1$. Thus, the trapezoids $B D K M$ and $B 1 D 1 K 1 M 1$ have equal heights $H E$ and $H 1 E 1$ and smaller bases $K M$ and $K 1 M 1$. Since these trapezoids are isosceles (they are symmetric with respect to the diagonals $A C$ and $A 1 C 1$ respectively) and $B D > B 1 D 1$, then $\angle K D B < \angle K 1 D 1 B 1$. Therefore, the second case is impossible (otherwise, $\angle C D B < \angle A D B$, which contradicts the condition $A E < C E$). Let $\frac{\sigma E}{A E} = m$. Since the triangle $B C D$ is similar to the triangle $K 1 C 1 M 1$, and the triangle $B A D$ is similar to the triangle $K A M$, then
$$
\frac{C_{1} H_{1}}{G E} = \frac{K_{1} M M_{1}}{B D} = \frac{K M}{B D} = \frac{A B}{A E}
$$
Therefore, $\frac{C_{1} H_{1}}{A B} = m$. Then
$$
A H + H E = A E = \frac{\square E}{m} = \frac{2 C_{l} H_{1}}{m} = \frac{2\left(C_{l} H_{l} + H_{l} E_{l}\right)}{m} = 2 A H + \frac{2 E H}{m}.
$$
From this, it follows that $A H = \frac{m-2}{2 m-2} \cdot A E \cdot$ Therefore,
$$
\frac{K M}{B D} = \frac{A H}{A E} = \frac{m-2}{2 m-2}
$$
On the other hand,
$$
K M = \frac{1}{2} P T = \frac{1}{1}(B 1 D 1 + B D) = \frac{3}{\frac{3}{8}} B D
$$
Therefore, $\frac{m-2}{2 m-2} = \frac{3}{3}$, from which $m = 5$, and $A E = \frac{1}{6} A C = \frac{3}{2}$. Therefore,
$$
S_{\triangle A B D} = \frac{1}{2} A E \cdot B D = \frac{1}{2} \cdot \frac{3}{2} \cdot \frac{16}{3} = 4
$$
## Answer
4.00
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
At the base of the pyramid lies an isosceles triangle $ABC$ with base $AC=2$ and lateral side $\sqrt{7}$. The face $ACD$ is perpendicular to the base plane and is an equilateral triangle. Find the edge $BD$, as well as the areas of all sections of the pyramid that are squares.
|
Let $DM$ be the height of the equilateral triangle $ADC$. Then $M$ is the midpoint of $AC$ and
$$
DM = AD \cdot \frac{\sqrt{3}}{2} = \sqrt{3}
$$
Since the plane of the face $ADC$ is perpendicular to the plane of the base $ABC$, the line $DM$ is perpendicular to the plane of the base. Therefore, $DM$ is the height of the pyramid $ABCD$. The median $BM$ of the isosceles triangle $ABC$ is its height. The line $BM$ is the orthogonal projection of the inclined line $DB$ on the plane of the base of the pyramid. Since $BM \perp AC$, by the theorem of three perpendiculars, $DB \perp AC$. From the right triangle $ACM$ we find that
$$
BM = \sqrt{BC^2 - CM^2} = \sqrt{7 - 1} = \sqrt{6}
$$
Therefore,
$$
BD = \sqrt{DM^2 + BM^2} = \sqrt{3 + 6} = 3
$$
Consider the section of the pyramid by a plane intersecting the edges $AB$, $CB$, $CD$, and $AD$ at points $P$, $Q$, $R$, and $T$ respectively. Suppose that $PQ \parallel RT$. Then through the parallel lines $PQ$ and $RT$ there are two planes $ABC$ and $ADC$, intersecting along the line $AC$. Thus, the lines $PQ$ and $RT$ are parallel to the line $AC$. Similarly, we can prove that if $PT \parallel QR$, then the lines $PT$ and $QR$ are parallel to the line $BD$. From the previously proven $AC \perp BD$. Therefore, if the plane intersecting the edges $AB$, $CB$, $CD$, and $AD$ gives a parallelogram in the section of the pyramid, then this parallelogram is a rectangle. Let $\frac{BP}{BA} = k$. Then
$$
PQ = kAC = 2k, \quad PT = (1-k)BD = 3(1-k).
$$
From the equation $2k = 3(1-k)$ we find that $k = \frac{3}{5}$. Thus, if the specified section is a square, then $PQ = PT = \sqrt{3}$.
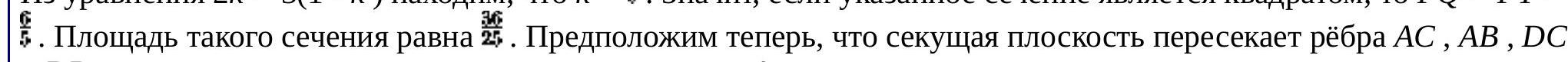
and $DB$, and in the section, a parallelogram is obtained. Similarly, we can prove that one pair of opposite sides of the parallelogram is parallel to the edge $AD$, and the other pair is parallel to the edge $BC$. Therefore, if a rectangle were obtained in the section, then the opposite edges $AD$ and $BC$ of the given pyramid would be perpendicular. We will prove that this is not the case. Suppose that $AD \perp BC$. Since the line $AC$ is the orthogonal projection of the inclined line $AD$ on the plane of the base of the pyramid, by the theorem of three perpendiculars, $AC \perp BC$, which is impossible ($\angle ACB < 90^\circ$). Similarly, we can prove that in the section of the pyramid $ABCD$ by a plane intersecting the edges $CA$, $CB$, $DA$, and $DB$, a square cannot be obtained.
## Answer
$3;$ 活
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The area of the triangle is $4 \sqrt{21}$, the perimeter is 24, and the segment of the bisector from one of the vertices to the center of the inscribed circle is $\frac{\sqrt{30}}{3}$. Find the largest side of the triangle.
|
If the inscribed circle touches the side $A C$ of triangle $A B C$ at point $M$, and $p$ is the semiperimeter of the triangle, then $A M=p-B C$.
## Solution
Let $O$ be the center of the circle inscribed in the given triangle $A B C, r$ be its radius, $S=4 \sqrt{21}$ be the area, $2 p$
$=24$ be the perimeter, and $M$ be the point of tangency with side $A C$.
Since $S=p \cdot r$, then
$$
r=\frac{2 S}{P}=\frac{8 \sqrt{21}}{24}=\frac{\sqrt{21}}{3}
$$
From the right triangle $A O M$, we find that
$$
A M=\sqrt{A O^{2}-O M^{2}}=\sqrt{\left(\frac{\sqrt{30}}{3}\right)^{2}-\left(\frac{\sqrt{21}}{3}\right)^{2}}=1
$$
Let $\angle B A C=\alpha$. Then
$$
\operatorname{tg} \frac{\alpha}{2}=\frac{O M}{A M}=\frac{\sqrt{21}}{3}
$$
Therefore,
$$
\cos \alpha=\frac{1-\operatorname{tg}^{2} \frac{\alpha}{2}}{1+\operatorname{tg}^{2} \frac{\alpha}{2}}=\frac{1-\frac{21}{9}}{1+\frac{21}{9}}=-\frac{2}{5}
$$
From the equality $A M=p-B C$, we find that $B C=12-1=11$.
Since $\cos \angle B A C=\cos \alpha=-\frac{2}{5}<0$, the angle $B A C$ is obtuse, and therefore the side $B C$ $=11$ is the largest side of triangle $A B C$.
## Answer
11.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Concerning the Homothety of Tangent Circles helps to solve the problem, $\quad]$
In a right triangle $ABC$, angle $C$ is a right angle, and side $CA=4$. A point $D$ is taken on the leg $BC$, such that $CD=1$. A circle with radius $\frac{\sqrt{5}}{2}$ passes through points $C$ and $D$ and is tangent at point $C$ to the circumcircle of triangle $ABC$. Find the area of triangle $ABC$.
|
Since point $D$ lies inside the circumcircle of triangle $A B C$, the given circles touch internally. If $M$ is the point of intersection of the first circle with the leg $A C$ other than $C$, then $M D$ is the diameter of this circle,
$$
M C=\sqrt{M C D^{2}-C D^{2}}=\sqrt{5-1}=2
$$
Let $Q$ and $O$ be the midpoints of the diameters $M D$ and $A B$ of the given circles. Since $\angle C M D=\angle O C A=\angle B A C$, triangles $M C D$ and $A C B$ are similar with a ratio of $\frac{M I C}{C A}=\frac{1}{2}$. Therefore,
$$
B C=2 C D=2, S_{\triangle A B C}=\frac{1}{2} B C \cdot A C=4
$$
## Answer
4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Zassovstiy A.A.
Given a square sheet of paper with a side length of 2016. Is it possible, by folding it no more than ten times, to construct a segment of length 1?
|
Note that we can bisect any segment by overlapping its ends. In addition, we can fold the paper along a line passing through a given point, perpendicular to a given line. In other words, we can construct the midpoints of segments and a perpendicular to a given line passing through a given point.
We will use these constructions in solving the problem, along with the fact that $2016=32 \cdot 63$.
Fold the square $A B C D$ along the diagonal $B D$, and then six times along lines perpendicular to it so that this diagonal is divided into 64 equal parts. Let $X_{1}$ and $X_{2}$ lie on the diagonal $B D$, such that $B X_{1}=X_{1} X_{2}=1 / 64 B D$ (see the figure).
Let the line $A X_{1}$ intersect $B C$ at point $Y$. Then $B Y: B C=B Y: A D=B X_{1}: X_{1} D=1: 63$, so $B Y=32$. Considering the point $Z$ - the projection of $X_{2}$ onto $B C$, we get that $B Z: B C=B X_{2}: B D=1: 32$, so $B Z=63$. Therefore, by folding along the lines $A X_{1}$ and $X_{2} Z$, and then along the line passing through $Y$ and perpendicular to $B C$, we obtain a segment of length $2 B Y - B Z = 1$.
## Answer
It is possible.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Tangents touching circles $\quad$]
A circle of radius 2 touches another circle externally at point A. The common tangent to both circles, drawn through point $A$, intersects with another common tangent at point $B$. Find the radius of the second circle if $A B=4$.
|
If $r$ and $R$ are the radii of the circles, then $A B=\sqrt{r R}$.
## Solution
First method.
Let $r$ and $R$ be the radii of the circles ($r=2$), and $C$ and $D$ be the points of tangency of the circles with the second (external) tangent. Then
$$
B C=A B=B D=4
$$
Since $C D=2 \sqrt{r R}$, we have $\sqrt{2 R}=4$. From this, we find that $R=8$.
## Second method.
If $O_{1}$ and $O_{2}$ are the centers of the circles, then $B A$ is the altitude of the right triangle $O_{1} B O_{2}$, dropped from the vertex of the right angle to the hypotenuse $O_{1} O_{2}$. Therefore,
$$
O_{1} A \cdot O_{2} A=A B^{2}=16
$$
From this, we find that $O_{2} A=8$.
## First method.
Let $r$ and $R$ be the radii of the circles ($r=2$), and $C$ and $D$ be the points of tangency of the circles with the second (external) tangent. Then
$$
B C=A B=B D=4
$$
Since $C D=2 \sqrt{r R}$, we have $\sqrt{2 R}=4$. From this, we find that $R=8$.
## Second method.
If $O_{1}$ and $O_{2}$ are the centers of the circles, then $B A$ is the altitude of the right triangle $O_{1} B O_{2}$, dropped from the vertex of the right angle to the hypotenuse $O_{1} O_{2}$. Therefore,
$$
O_{1} A \cdot O_{2} A=A B^{2}=16
$$
From this, we find that $O_{2} A=8$.
## Answer
8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In parallelogram $A B C D$, diagonal $B D$ is equal to 2, angle $C$ is $45^{\circ}$, and line $C D$ is tangent to the circumcircle of triangle $A B D$. Find the area of parallelogram $A B C D$.
|
Prove that $B D \perp B C$.
## Solution
It is clear that $\angle A=\angle C=45^{\circ}$. Angle $\angle B A D$ is inscribed in the circle, and $\angle B D C$ is the angle between the tangent and the chord $B D$, therefore,
$$
\angle B D C=\angle A=45^{\circ}
$$
Thus, $\angle C B D=90^{\circ}$. Therefore,
## Answer
4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left.\begin{array}{c}\text { Circle, sector, segment, etc. } \\ {\left[\begin{array}{l}{[\text { Pythagorean Theorem (direct and inverse) }}\end{array}\right]}\end{array}\right]$
In a segment, the arc of which is $60^{\circ}$, a square is inscribed. Find the area of the square if the radius of the circle is $2 \sqrt{3}+$ $\sqrt{17}$.
|
Let $x$ be the side of the square and apply the Pythagorean theorem to the triangle with vertices: at the center of the circle, at the midpoint of the side of the square, and at the vertex of the square belonging to this side.
## Solution
Let $O$ be the center of the circle, $R$ its radius ($R=2 \sqrt{3}+\sqrt{17}$), and $x$ the side of the square $ABCD$, with points $C$ and $D$ lying on the chord $PQ$ of the given segment.
Draw a line through the center of the circle perpendicular to $PQ$. Let $K$ and $M$ be the points of intersection of this line with the chords $PQ$ and $AB$. Then
$$
O K=\frac{R \sqrt{3}}{2}, M B=\frac{x}{2}, K M=x
$$
Consider the right triangle $OMB$. By the Pythagorean theorem,
$$
(O K+K M)^{2}+M B^{2}=O B^{2}, \text { or }\left(\frac{R \sqrt{3}}{2}+x\right)^{2}+\frac{x^{2}}{4}=R^{2}
$$
From this, we find that
$$
x=\frac{R(\sqrt{17}-2 \sqrt{3})}{5}=\frac{(2 \sqrt{3}+\sqrt{17})(\sqrt{17}-2 \sqrt{3})}{5}=1
$$
Therefore, $S_{\mathrm{ABCD}}=1$.
## Problem
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A certain line intersects parallel lines $a$ and $b$ at points $A$ and $B$ respectively. The bisector of one of the angles formed with vertex $B$ intersects line $a$ at point $C$. Find $A C$, if $A B=1$.
#
|
Prove that triangle $ABC$ is isosceles.
## Solution
Let $D$ be a point on line $b$, lying on the same side of line $AB$ as point $C$. Then $\angle ACB = \angle DBC = \angle ABC$, so triangle $ABC$ is isosceles. Therefore, $AC = AB$.
## Answer
1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tomong A.K.
On the plane, there is an open non-intersecting broken line with 31 segments (adjacent segments do not lie on the same straight line). Through each segment, a line containing this segment was drawn. As a result, 31 lines were obtained, some of which may have coincided. What is the smallest number of different lines that could have resulted?
#
|
Evaluation. Except for the ends, the broken line has 30 vertices, and each is the intersection of two lines. If there are no more than eight lines, then there are no more than $7 \cdot 8: 2=28$ intersection points - a contradiction.
## Answer
9 lines.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Regular pyramid ] [ Sections, unfoldings, and other frameworks. ]
On the extension of edge $S T$ beyond point $T$ of the regular quadrilateral pyramid $S P Q R T$ with vertex $S$, a point $B$ is taken such that the distance from it to the plane $S P Q$ is $\frac{9 \sqrt{7}}{2}$. Find the segment $B T$, if $Q R=12$, and $S R=10$.
|
Consider the section of the given pyramid by a plane passing through the vertex $S$ and the midpoints $A$ and $K$ of the sides $R T$ and $P Q$ of the square $P Q R T$, respectively. Let $S O$ be the height of the pyramid. Then $O$ is the center of the base $P Q R T$. From the right triangles $P K S$ and $K O S$, we find that
$$
\begin{gathered}
S K=\sqrt{S P^{2}-P K^{2}}=\sqrt{100-36}=8 \\
S O=\sqrt{S K^{2}-O K^{2}}=\sqrt{64-36}=\sqrt{28}=2 \sqrt{7}
\end{gathered}
$$
Let $A M$ be the height of the isosceles triangle $A K S$, dropped to the side $K S$. Then the line $A M$ is perpendicular to the plane of the face $P Q C$ and
$$
A M=\frac{A K \cdot S O}{K S}=\frac{12 \cdot 2 \sqrt{7}}{B}=3 \sqrt{7}
$$
Let $C$ and $D$ be the orthogonal projections of points $T$ and $B$ respectively onto the plane of the face $P Q S$. Since the line $R T$ is parallel to the plane of the face $P Q S$, the distances from all points of the line $R T$ to this plane are equal, so $T C=A M=3 \sqrt{7}$, and since the lines $T C$ and $B D$ are perpendicular to the plane of the face $P Q S$, $T C \| B D$. Therefore, the points $S, T, B, C$ and $D$ lie in the same plane. From the similarity of triangles $S T C$ and $S B D$, we find that
$$
B S=S T \cdot \frac{B D}{C t^{\prime}}=10 \cdot \frac{\frac{9 \sqrt{7}}{}}{3 \sqrt{7}}=15
$$
Therefore, $B T=B S-A S=15-10=5$.
## Answer
5.00
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The area of the base of a right triangular prism is 4, the areas of the lateral faces are 9, 10, and 17. Find the volume of the prism.
#
|
Let $V$ be the volume of the prism; $h$ be its height; $a, b$, and $c$ be the sides of the base of the prism; $p$ be the semi-perimeter of the base, and $S$ be the area of the base. According to the problem,
$$
a h=9, b h=10, c h=17
$$
from which
$$
a=\frac{9}{h}, b=\frac{19}{h}, c=\frac{17}{h} .
$$
Then
$$
p=\frac{1}{2}\left(\frac{9}{h}+\frac{19}{h}+\frac{17}{h}\right)=\frac{18}{h}, S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{\frac{18}{h} \cdot \frac{9}{h} \cdot \frac{8}{h} \cdot \frac{1}{h}}=\frac{3 \frac{1}{h}}{h}=4
$$
from which we find that $h=3$. Therefore,
$$
V=S h=4 \cdot 3=12 .
$$
## Answer
12.00
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 $[\quad$ Volume of a parallelepiped $\quad]$
The base of a right parallelepiped is a parallelogram, one of the angles of which is $30^{\circ}$. The area of the base is 4. The areas of two lateral faces of the parallelepiped are 6 and 12. Find the volume of the parallelepiped.
|
Let $a$ and $b$ be the sides of the parallelogram, $c$ be the height of the parallelepiped, and $V$ be its volume. From the problem statement, we have:
$$
a b \sin 30^{\circ}=\frac{1}{2} a b=4, a c=6, b c=12
$$
Therefore,
$$
a b c 2=6 \cdot 12=72, c 2=\frac{\frac{T 2}{\alpha b}}{\alpha i}=\frac{72}{8}=9
$$
from which $c=3$. Therefore,
$$
V=\frac{1}{2} a b c=4 \cdot 3=12 .
$$
## Answer
12.00
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the maximum area that a triangle with sides \(a\), \(b\), and \(c\) can have, given the following constraints:
\[
0 < a \leq 1 \leq b \leq 2 \leq c \leq 3 \text{ ? }
\]
|
First, assume that the length of the third side c is not subject to any conditions. The area of a triangle with sides a and b and the angle $\alpha$ between them is determined by the formula $1 / 2$ ab sin $\alpha$. If a and b are subject to the conditions 0 , then the product ab $\sin \alpha$ will be maximal when each of the factors is maximal, i.e., when $a=1, b=2, \sin \alpha=1\left(\alpha=90^{\circ}\right)$. Thus, the triangle with the largest area is a right triangle with legs 1 and 2. The third side of this triangle $c=\sqrt{5}$ satisfies the conditions 2 with 3 . Therefore, among all triangles whose sides are subject to the condition $0<a<=1<=b<=2<=c<=3$, the one with the maximum area will be the same right triangle. This area is equal to 1.
## Omвem
1.00
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the volume of a triangular pyramid, five edges of which are equal to 2, and the sixth is equal to $\sqrt{6}$.
#
|
Let $A B C D$ be a triangular pyramid, in which
$$
A D=B D=C D=A B=A C=2, B C=\sqrt{6} \text {. }
$$
If $D O$ is the height of the pyramid, then $O$ is the center of the circumcircle of triangle $A B C$ (since $A D=B D=C D$). Let $R$ be the radius of this circle, $M$ be the midpoint of $B C$, and $\angle A B C=\alpha$. Then
$$
\begin{gathered}
A M=\sqrt{A B^{2}-B M^{2}}=\sqrt{2^{2}-\left(\frac{\sqrt{6}}{2}\right)^{2}}=\sqrt{4-\frac{3}{2}}=\frac{\sqrt{5}}{\sqrt{2}} \\
\sin \alpha=\frac{A M}{A B}=\frac{\sqrt{5}}{2 \sqrt{2}}, R=\frac{A C}{2 \sin \alpha}=\frac{2 \sqrt{2}}{\sqrt{5}} \\
D O=\sqrt{A D^{2}-R^{2}}=\sqrt{4-\frac{8}{5}}=\sqrt{\frac{12}{5}} \\
V=\frac{1}{3} S_{\triangle A B C} \cdot D O=\frac{1}{3} \cdot \frac{1}{2} B C \cdot A M \cdot D O=\frac{1}{6} \cdot \sqrt{6} \cdot \frac{\sqrt{5}}{\sqrt{2}} \cdot \sqrt{\frac{12}{5}}=1
\end{gathered}
$$
Find the volume of a regular triangular pyramid with side length $a$ and radius $R$ of the circumscribed sphere.
## Answer
$\frac{a^{2}\left(R \sqrt{3}+\sqrt{3 R^{2}-a^{2}}\right)}{12}$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the height of a regular tetrahedron with edge $a$.
#
|
Let $A B C D$ be a regular tetrahedron, $D O$ its height, and $M$ the midpoint of $B C$. Since $A M$ is the height of the equilateral triangle $A B C$, and $O$ is the center of this triangle, we have
$$
A M = a^{\frac{\sqrt{3}}{2}}, \quad O A = \frac{2}{3}, \quad A M = \frac{a \sqrt{3}}{3}
$$
From the right triangle $O A D$, we find that
$$
D O = \sqrt{D A^{2} - O A^{2}} = \sqrt{a^{2} - \left(\frac{a \sqrt{3}}{3}\right)^{2}} = a \sqrt{1 - \frac{1}{3}} = a \sqrt{\frac{2}{3}}
$$

How many different pyramids exist, all of whose edges are equal to 1?
## Solution
Consider the $n$-sided angle at the vertex of a regular $n$-sided pyramid, all of whose edges are equal to 1. The lateral faces of such a pyramid are equilateral triangles with side length 1. Therefore, all the plane angles of the considered $n$-sided angle are $60^{\circ}$. Since the sum of the plane angles of a convex polyhedral angle is less than $360^{\circ}$, we have $60^{\circ} \cdot n < 360^{\circ}$. Thus, $n < 6$. Therefore, the condition of the problem can only be satisfied by three pyramids: a triangular pyramid (regular tetrahedron), a quadrilateral pyramid, and a pentagonal pyramid. It is possible to construct a quadrilateral and a pentagonal pyramid, all of whose edges are equal to 1.
## Answer
Three.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11 |
The lateral surface development of a cylinder is a square with a side length of $2 \sqrt[3]{\pi}$. Find the volume of the cylinder.
|
Let the generating line of the cylinder be $h$, and the radius of the base be $r$, the volume of the cylinder be $V$. Since the development of the lateral surface of the cylinder is a square with side $2 \sqrt[3]{\pi}$, the length of the circumference of the base and the generating line of the cylinder are also equal to $2 \sqrt[3]{\pi}$, i.e.,
$$
2 \pi r=2 \sqrt[3]{\pi}, h=2 \sqrt[3]{\pi}
$$
Therefore,
$$
V=\pi r^2 h=\pi \cdot\left(\frac{\sqrt[3]{\pi}}{\pi}\right)^2 \cdot(2 \sqrt[3]{\pi})=2
$$
## Answer
2.00
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On the diagonal $B D$ of the rectangular trapezoid $A B C D\left(\angle D=90^{\circ}, B C \| A D\right)$, a point $Q$ is taken such that $B Q: Q D=1: 3$. A circle with center at point $Q$ touches the line $A D$ and intersects the line $B C$ at points $P$ and $M$. Find the length of the side $A B$, if $B C=9, A D=8, P M=4$.
|
Let $E$ be the point of tangency of the circle with the line $A D$, and $F$ be the projection of the center $Q$ of the circle onto the line $B C$. Then the points $E, Q$, and $F$ lie on the same line, and $F$ is the midpoint of $P M$. Therefore, $F P = F M = 2$. Let $Q E = Q P = Q M = R$. Suppose that the point $P$ lies between $C$ and $M$. From the similarity of triangles $Q F B$ and $Q E D$, we find that $Q F = \frac{O B}{O D} \cdot Q E = \frac{R}{3}$. By the Pythagorean theorem, $Q P^{2} = Q F^{2} + F P^{2}$, or $R^{2} = \frac{1}{9} R^{2} + 4$, from which $R = \frac{3}{\sqrt{2}}$,
$E F = Q E + Q F = \frac{4 R}{3} = 2 \sqrt{2}$.
Let $H$ be the projection of point $A$ onto the line $B C$. Then $B H = B C - C H = B C - A D = 1, A H = E F = 2 \sqrt{2}$.
From the right triangle $A B H$, we find that $A B^{2} = A H^{2} + B H^{2} = 9$.
## Answer
3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ $\quad \underline{\text { Tangents to Spheres }}$]
In a regular hexagonal pyramid $\operatorname{SABCDEF}$ ( $S$ - apex) the side of the base is $2 \sqrt{3}$, and the height of the pyramid $S H$ is 6. A plane passes through point $E$ perpendicular to line $A S$ and intersects segment $S H$ at point $O$. Points $P$ and $Q$ are located on lines $A S$ and $C E$ respectively, such that line $P Q$ is tangent to a sphere of radius $\frac{\sqrt{5}}{2}$ centered at point $O$. Find the minimum length of segment $P Q$.
|
Let the diagonals $A D$ and $C E$ of the regular hexagon $A B C D E F$ intersect at point $N$. From the properties of a regular hexagon, it follows that $N$ is the midpoint of segments $D H$ and $C E$, and $A D \perp C E$. Then, by the theorem of three perpendiculars, $C E \perp S A$, which means that the line $C E$ lies in the plane passing through point $E$ and perpendicular to the line $S A$. Let this plane intersect the line $S A$ at point $K$. Then
\[
\begin{gathered}
A H=A B=2 \sqrt{3}, N H=\frac{1}{2} D H=\sqrt{3}, A N=N H+A H=3 \sqrt{3}, \\
\operatorname{tg} \angle S A H=\frac{S_{H}}{A H}=\frac{6}{2 \sqrt{3}}=\sqrt{3}, \angle S A H=60^{\circ}, N K=A N \sin 60^{\circ}=3 \sqrt{3} \cdot \frac{\sqrt{3}}{2}=\frac{9}{2}, \\
O N=\frac{O N}{\text { con } N 30^{\circ}}=\frac{\sqrt{3}}{\sqrt{3}}=2, O K=N K-O N=\frac{\frac{9}{2}}{2}-2=\frac{5}{2}.
\end{gathered}
\]
Let the line passing through points $P$ and $Q$ be tangent to the sphere at point $M$. Then $O M \perp P Q$. Denote $P K=x$, $N Q=y$. From the right triangles $N P K, K O P, M O P, Q N O$, and $N P Q$, we find that
\[
\begin{gathered}
O P 2=P K 2+O K 2=x 2+\frac{25}{4}, N P 2=P K 2+N K 2=x 2+\frac{81}{4} \\
M P 2=O P 2-O M 2=\left(x 2+\frac{25}{4}\right)-\frac{5}{4}=x 2+5, \\
Q O 2=N Q 2+N O 2=y 2+4, Q M 2=Q O 2-O M 2=(y 2+4)-\frac{5}{4}=y 2+\frac{\mathbf{1 1}}{4} \\
P Q 2=N P 2+N Q 2=\left(x 2+\frac{81}{4}\right)+y 2=x 2+y 2+\frac{81}{4}
\end{gathered}
\]
Since $P Q=P M+M Q$, we get the equation
\[
\sqrt{x^{2}+5}+\sqrt{y^{2}+\frac{11}{4}}=\sqrt{x^{2}+y^{2}+\frac{81}{4}}
\]
from which we find that $y 2=\frac{625}{16\left(x^{2}+5\right)}-\frac{11}{4}$. Then
\[
\begin{gathered}
P Q 2=x 2+y 2+\frac{81}{4}=x 2+\frac{625}{16\left(x^{2}+5\right)-4}+\frac{11}{4}+x 1 \\
=x 2+5+\frac{625}{16\left(x^{2}+5\right)}+\frac{81}{4}-5= \\
=x 2+5+\frac{625}{16\left(x^{2}+5\right)}+\frac{35}{2}-5 \geqslant 2 \sqrt{\left(x^{2}+5\right) \cdot \frac{625}{16\left(x^{2}+5\right)}}+\frac{25}{2}=\frac{25}{2}+\frac{25}{2}=25
\end{gathered}
\]
with equality achieved when
\[
x 2+5=\frac{625}{16\left(x^{2}+5\right)} \Leftrightarrow(x 2+5) 2=\frac{625}{16} \Leftrightarrow x 2=\frac{5}{4}.
\]
Therefore, the minimum length of the segment $P Q$ is 5.
## Answer
$P Q=5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9 [
In triangle $ABC$, angle $B$ is equal to $\arccos \frac{15}{17}$. On side $AC$, a point $K$ is taken such that $AK=12$, $KC=4$. Find the radius of the circle passing through vertex $B$, touching side $AC$ at point $K$, and touching the circumcircle of triangle $ABC$.
#
|
## Answer
12.00
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9}
In triangle $A B C$, angle $A$ is equal to $\arccos \frac{5}{13}$, side $B C$ is equal to 12. On the extension of $C B$ beyond point $C$, a point $M$ is taken such that $C M=6$. Find the radius of the circle passing through vertex $A$, tangent to line $B C$ at point $M$, and tangent to the circumcircle of triangle $A B C$.
|
## Answer
6.00
Send a comment
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Trapezoids $A B C D$ and $A C D E$ with equal larger bases $A D$ and $A C$ respectively are inscribed in a circle. What is the radius of this circle if the area of triangle $A D E$ is $1+\sqrt{3}$, and the angle $C O D$ is $60^{\circ}$, where $O$ is the point of intersection of the diagonals of trapezoid $A B C D$?
|
$\angle C O D=\frac{U C D+U A B}{2}$.
## Solution
Arcs enclosed between parallel chords are equal. Therefore, $\cup A B=\cup C D=\cup A E$. Since chords $A C$ and $A D$ are equal, then
$$
\cup A B+\cup B C=\cup A E+\cup E D
$$
Thus, $\cup B C=\cup E D$.
Let $\cup A B=\alpha, \cup B C=\beta$. Then
$$
\angle C O D=\frac{\cup C D+\cup A B}{2}=\alpha=60^{\circ}, 2 \beta=360^{\circ}-3 \alpha=180^{\circ}
$$
Therefore, $\beta=90^{\circ}$. Hence,
$$
\angle A D E=\frac{1}{2} \cup A E=\frac{\alpha}{2}=30^{\circ}, \angle D A E=\frac{1}{2} \cup E D=\frac{\beta}{2}=45^{\circ}
$$
Let $R$ be the desired radius. Then
$$
S_{\triangle \mathrm{ADE}}=\frac{1}{2} A E \cdot D E \sin \angle A E D=\frac{1}{2} \cdot 2 R \sin 30^{\circ} \cdot 2 R \sin 45^{\circ} \cdot \sin 75^{\circ}=\frac{R^{2}(\sqrt{3}+1)}{4}=\sqrt{3}+1
$$
Therefore, $R^{2}=4$.
## Answer
2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Rearrangement of areas]
a) Four vertices of a regular dodecagon are located at the midpoints of the sides of a square (see figure). Prove that the area of the shaded part is 12 times smaller than the area of the dodecagon. b) Prove that the area of a dodecagon inscribed in a circle of radius 1 is 3.
#
|
a) Let's cut the original square into four squares and consider one of them (see figure). Let point $B^{\prime}$ be symmetric to point $B$ with respect to the line $P Q$. We will prove that $\triangle A P B = \triangle O B^{\prime} P$. Triangle $A P B$ is isosceles, and the angle at its base is $15^{\circ}$, so triangle $B P Q$ is equilateral. Therefore, $\angle O P B^{\prime} = \angle O P Q - \angle B^{\prime} P Q = 75^{\circ} - 60^{\circ} = 15^{\circ}$ and $\angle P O B^{\prime} = \angle P O Q / 2 = 15^{\circ}$. Additionally, $A B = O P$. Similarly, it can be shown that $\triangle B Q C = \triangle O B^{\prime} Q$. Therefore, the area of the shaded part in the figure is equal to the area of triangle $O P Q$.
b) Let the area of the regular dodecagon inscribed in a circle of radius 1 be $12 x$. According to part a), the area of the square circumscribed around this circle is $12 x + 4 x = 16 x$; on the other hand, the area of this square is 4, so $x = 1 / 4$ and $12 x = 3$.
Send a comment
|
3
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Given a triangle $A B C$. On its sides $A B$ and $B C$, points $C_{1}$ and $A_{1}$ are fixed, respectively. Find a point $P$ on the circumcircle of triangle $A B C$ such that the distance between the centers of the circumcircles of triangles $A P C_{1}$ and $C P A_{1}$ is minimized.
|
Let $K$ be the second intersection point of the circumcircles of triangles $A P C_{1}$ and $C P A_{1}$ (see the left figure). We will prove that $K$ lies on the line $A_{1} C_{1}$.
Let point $P$ lie on the arc $A C$. Quadrilaterals $A C_{1} K P$ and $K A_{1} C P$ are cyclic, hence $\angle C_{1} K P = 180^{\circ} - \angle C_{1} A P$ and $\angle A_{1} K P = 180^{\circ} - \angle A_{1} C P$. On the other hand, from the cyclic quadrilateral $A B C P$, we get that $\angle C_{1} K P + \angle A_{1} C P = 180^{\circ}$. Therefore, $\angle C_{1} K P + \angle A_{1} K P = 180^{\circ}$, which means that point $K$ lies on the line $A_{1} C_{1}$. (Note that the proven statement is equivalent to problem $\underline{56623}$ a).
When point $P$ lies on the arc $A B$ or $B C$, the proof is analogous.
Let $M_{A}$ and $M_{C}$ be the midpoints of segments $C_{1} K$ and $A_{1} K$, and $O_{1}$ and $O_{2}$ be the centers of the circumcircles of triangles $A P C_{1}$ and $C P A_{1}$, respectively. Then $O_{1} M_{A}$ is the perpendicular bisector of $C_{1} K$, and $O_{2} M_{C}$ is the perpendicular bisector of $A_{1} K$. Therefore, $M_{A} M_{C} = \frac{1}{2} A_{1} C_{1}$, and $O_{1} O_{2} \geq M_{A} M_{C}$, with equality holding if and only if $O_{1} O_{2} \| A_{1} C_{1}$.
The line of centers $O_{1} O_{2}$ is perpendicular to the common chord $K P$, so we need to find the position of point $P$ such that lines $K P$ and $A_{1} C_{1}$ are perpendicular. In this case, $\angle C_{1} K P = 90^{\circ}$. Quadrilateral $A C_{1} K P$ is cyclic, hence $\angle B A P = 90^{\circ}$. Therefore, the distance between the centers of the circumcircles of triangles $A P C_{1}$ and $C P A_{1}$ is minimal when point $P$ is diametrically opposite to point $B$.
## Answer
$P$ is diametrically opposite to point $B$.
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The base of the pyramid is an equilateral triangle with a side length of 6. One of the lateral edges is perpendicular to
the base plane and equals 4. Find the radius of the sphere circumscribed around the pyramid.
#
|
Let $A B C D$ be a given triangular pyramid, the base of which is an equilateral triangle $A B C$, and the lateral edge $C D$ is perpendicular to the plane of the base. $O$ is the center of the sphere circumscribed around the pyramid $A B C D$, and $R$ is the radius of the sphere. Since point $O$ is equidistant from points $A, B$, and $C$, it lies on the line perpendicular to the plane of triangle $A B C$ passing through the center $M$ of the circumscribed circle of the triangle. On the other hand, point $O$ is equidistant from points $C$ and $D$, so it lies in the plane perpendicular to edge $C D$ and passing through its midpoint $P$. Since planes perpendicular to the same line are parallel, the quadrilateral $M O P C$ is a rectangle. We then find:
$$
\begin{gathered}
O P=M C=A B^{\frac{\sqrt{3}}{3}}=2 \sqrt{3}, C P=\frac{1}{2} C D=2, \\
R=O C=\sqrt{O P^{2}+C P^{2}}=\sqrt{12+4}=4
\end{gathered}
$$
## Answer
4.00
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the cube $A B C D A 1 B 1 C 1 D 1$, where $A A 1, B B 1, C C 1$ and $D D 1$ are parallel edges, the plane $P$ passes through point $D$ and the midpoints of edges $A 1 D 1$ and $C 1 D 1$. Find the distance from the midpoint of edge $A A 1$ to the plane $P$, if the edge of the cube is 2.
|
Let $M, N, K$ and $L$ be the midpoints of edges $A1D1, C1D1$, $AA1$ and $CC1$ respectively (Fig.1). The line $KL$ is parallel to the line $MN$, so the line $KL$ is parallel to the plane $P$. Moreover, the line $KL$ passes through the center $O$ of the cube $ABCD A1B1C1D1$. Therefore, the distance from the midpoint $K$ of edge $AA1$ to the plane $P$ is equal to the distance from point $O$ to this plane. Let $E$ be the intersection point of segments $MN$ and $B1D1$, and $F$ be the foot of the perpendicular dropped from point $O$ to line $DE$. Since line $MN$ is perpendicular to the plane $BB1D1D$, then $MN \perp OF$. Therefore, $OF$ is the perpendicular to the plane $P$. Thus, the desired distance is equal to the length of segment $OF$. Consider the section of the given cube by the plane $BB1D1D$ (Fig.2). Let the line passing through the midpoint $O$ of diagonal $BD1$ parallel to $BD$ intersect segment $DE$ at point $Q$, and segment $DD1$ at point $S$. Then $OS$ is the midline of triangle $BD1D$, and $QS$ is the midline of triangle $EDD1$. Therefore,
$$
OQ = OS - QS = \frac{1}{2} BD - \frac{1}{2} ED1 = \frac{1}{2}(BD - ED1) = \frac{1}{2}\left(2\sqrt{2} - \frac{\sqrt{2}}{2}\right) = \frac{3\sqrt{2}}{1}
$$
Let $\angle FOQ = \alpha$. Then
$$
\angle EDD1 = \angle FOQ = \alpha, \cos \alpha = \frac{DD1}{DE} = \frac{DD1}{\sqrt{DD1^2 + ED1^2}} = \frac{2}{\sqrt{1 + \left(\frac{\left(\bar{V}_2^2\right.}{2}\right)^2}} = \frac{2\sqrt{2}}{3}
$$
Therefore,
$$
OF = OQ \cos \alpha = \frac{3\sqrt{2}}{1} \cdot \frac{2\sqrt{2}}{3} = 1
$$
Choose a rectangular coordinate system $D1xyz$, taking the origin at point $D1$ and directing the coordinate axes along the rays $D1A1, D1C1$, and $D1D$ respectively. The equation of the plane $P$ will be
$$
\frac{x}{1} + \frac{y}{1} + \frac{z}{2} = 1
$$
(the equation of the plane in intercept form), or $2x + 2y + z - 2 = 0$. The distance from point $K(2; 0; 1)$ to this plane is
$$
\frac{2 \cdot 2 + 2 \cdot 0 + 1 - 2}{\sqrt{1 + 1 + 1}} = \frac{3}{3} = 1
$$
## Answer
1.00
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Perpendicularity of a line and a plane (other).]
In the pyramid $A B C D$, the edges $A D, B D$ and $C D$ are equal to 5, the distance from point $D$ to the plane $A B C$ is 4. Find the radius of the circle circumscribed around triangle $A B C$.
|
Let $R$ be the radius of the circle circumscribed around triangle $ABC$. Since the lateral edges of the pyramid $ABCD$ with vertex $D$ are equal, the height $DO$ of the pyramid passes through the center $O$ of the circle circumscribed around the base $ABC$. The line $DO$ is perpendicular to the plane of the base $ABC$, and therefore it is perpendicular to the line $OA$. From the right triangle $AOD$, we find that
$$
OA = \sqrt{DA^2 - DO^2} = \sqrt{25 - 16} = 3
$$
## Answer
Prove that if a line $p$ forms equal angles with three pairwise intersecting lines in a plane, then the line $p$ is perpendicular to this plane.
## Solution
Let the line $p$ intersect the plane $\alpha$, containing the given lines $k, m$, and $n$, at point $O$. Draw through point $O$ lines $k_1, m_1$, and $n_1$, respectively parallel to lines $k, m$, and $n$. Then the line $p$ forms equal angles with lines $k_1, m_1$, and $n_1$. Therefore, any point $A$ on the line $p$, different from $O$, is equidistant from these lines. Hence, the orthogonal projection $A_1$ of point $A$ onto the plane $\alpha$ is also equidistant from lines $k_1, m_1$, and $n_1$. Therefore, point $A_1$ lies on the bisector of one of the angles formed by lines $k_1$ and $m_1$, on the bisector of one of the angles formed by lines $k_1$ and $n_1$, and on the bisector of one of the angles formed by lines $m_1$ and $n_1$. Since lines $k_1, m_1$, and $n_1$ are distinct, the specified bisectors have only one common point $O$. Therefore, point $A_1$ coincides with point $O$. Then the line $p$ coincides with the line $AA_1$.
Therefore, the line $p$ is perpendicular to the plane $\alpha$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the greatest number of axes of symmetry that a spatial figure consisting of three lines, none of which are parallel or coincident, can have?
#
|
A spatial figure consisting of two non-parallel and non-coincident lines $l_{1}$ and $l_{2}$ has exactly three axes of symmetry. Indeed, consider the plane $\Pi$, parallel to the lines $l_{1}$ and $l_{2}$ and equidistant from them (in the case of intersecting lines, this will be the plane containing them). The axes of symmetry will be the two bisectors of the angles formed by the orthogonal projections of the lines $l_{1}$ and $l_{2}$ onto the plane $\Pi$, and the line perpendicular to the plane $\Pi$ and passing through the point of intersection of the projections. An axis of symmetry of a figure consisting of three lines is also an axis of symmetry of some two of these lines. From three lines, three pairs of lines can be chosen. Therefore, the number of axes of symmetry of a figure consisting of three lines does not exceed 9. It is also clear that a figure consisting of three mutually perpendicular lines passing through one point has exactly 9 axes of symmetry.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Authors: Feldman G. Baranov D.V.
An angle is drawn, and only a compass is available.
a) What is the minimum number of circles that need to be drawn to definitely determine whether the given angle is acute?
b) How can one determine if the given angle is $31^{\circ}$ (any number of circles can be drawn)?
|
a) Let's draw a circle with its center on one side of the angle, passing through its vertex $O$. If it intersects the other side of the angle, the angle was acute.
b) Let's draw a circle with center $O$. Suppose it intersects the sides of the angle at points $A$ and $B$. Starting from point $A$, we will lay off chords equal to $AB$ on this circle. If by laying off 360 such chords, we circle the circumference exactly 31 times, then the angle $AOB$ is $31^{\circ}$.
## Answer
a) One.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Sorrelkova N.P.
Under one of the cells of an $8 \times 8$ board, a treasure is buried. Under each of the other cells, there is a sign indicating the minimum number of steps required to reach the treasure from that cell (one step allows moving from a cell to an adjacent cell by side). What is the minimum number of cells that need to be dug up to definitely retrieve the treasure?
|
Let's dig up the corner cell $U$. Suppose there is a sign there. All cells at the specified distance from $U$ form a diagonal perpendicular to the main diagonal drawn from $U$. Let's dig up the corner cell $W$ on the same side as $U$. If there is also a sign there, then another diagonal perpendicular to the first one is formed. The diagonals intersect at one cell, where the treasure is buried.
Two diggings may not be enough. For example, suppose we were unlucky and found a sign with the number 1 on the first try. Then the treasure is in the adjacent cell, but there are at least two such cells.
## Answer
3 cells.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Yashchenko I.V.
On a grid sheet of paper, several cells were colored in such a way that the resulting figure had no axes of symmetry. Vanya colored one more cell. Could the resulting figure have four axes of symmetry?
|
To construct an example, one needs to take a figure with four axes of symmetry and remove a cell that does not lie on any of these axes. For example, a square has four axes of symmetry (see the left image). This results in the example in the center.
There are other examples as well (for example, on the right image).
\section*{[ Polyhedra and Polygons (Miscellaneous) $]$
 Difficulty: 3 Grades: 10,11}
Author: $\underline{\text { Folklore }}$
What is the maximum number of triangular faces a pentahedron can have?
## Solution
A quadrilateral pyramid has four triangular faces.
We will prove that all five faces of a pentahedron cannot be triangles. Indeed, suppose such a pentahedron exists. Each of its edges is shared by two faces, so it should have $5 \cdot 3$ : 2 edges, which is impossible.
## Answer
4 faces.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
In triangle $A B C$, a point $K$ is chosen on side $A B$, and the bisector $K E$ of triangle $A K C$ and the altitude $K H$ of triangle $B K C$ are drawn. It turns out that angle $E K H$ is a right angle. Find $B C$, if $H C=5$.
|
Since angles $A K C$ and $B K C$ are adjacent, their bisectors are perpendicular. Therefore, the bisector of angle $B K C$ coincides with $K H$.
Thus, in triangle $B K C$, segment $K H$ is both an altitude and a bisector. This means the triangle is isosceles, and $K H$ is its median to the base. Therefore, $B C = 2 H C = 10$.
## Answer
10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 [
From one point, two tangents are drawn to a circle. The length of each tangent is 12, and the distance between the points of tangency is 14.4. Find the radius of the circle.
#
|
The angle between the given chord and the radius drawn to the point of tangency is equal to half the angle between the tangents.
## Solution
Let $A$ be the given point, $B$ and $C$ be the points of tangency, and $O$ be the center of the circle. Since the line $O A$ is perpendicular to the segment $B C$ and passes through its midpoint $M$, then
$$
\angle O C B = \angle O A C, \sin \angle O A C = \frac{C M}{A C} = \frac{7.2}{12} = \frac{3}{5}
$$
Therefore, $\cos \angle O A C = \frac{4}{5}$. From triangle $OCM$, we find that
$$
O C = \frac{C M}{\cos \angle O C M} = 9
$$
## Answer
9.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\begin{array}{l}\text { [Mutual position of two circles] } \\ \text { Triangle inequality }\end{array}\right]$
One circle is inside the other. Their radii are 28 and 12, and the shortest distance between points on these circles is 10. Find the distance between the centers.
|
Determine the location of the center of the larger circle relative to the smaller circle.
## Solution
It is known that the shortest distance between points of two such circles is the smallest of the two segments of the line of centers enclosed between the circles. Let $O$ and $O_{1}$ be the centers of the larger and smaller circles, respectively. Draw the diameter of the larger circle so that it passes through the center of the smaller circle. Denote the points of intersection with the circles sequentially as $A, B, C$, and $D$. If $D C=10$, then
$$
A B=56-24-10=22, A O_{1}=12+22=34, O A=28
$$
thus,
$$
O O_{1}=34-28=6 .
$$
## Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Inscribed, circumscribed, and exscribed circles; their radii $]$
[ Auxiliary area. The area helps to solve the task_ ]
In an isosceles triangle, the base is 30, and the lateral side is 39. Find the radius of the inscribed circle.
|
The radius of the circle inscribed in a triangle is equal to the area of the triangle divided by its semi-perimeter.
## Solution
First method.
Let's find the height of the triangle dropped to the base:
$$
h^{2}=39^{2}-15^{2}=24 \cdot 54=36^{2}, h=36
$$
The desired radius is equal to the area of the triangle divided by its semi-perimeter:
$$
r=\frac{S}{p}=\frac{15 \cdot 36}{18}=10
$$
Second method.
Since the triangle is isosceles, the center $O$ of its inscribed circle lies on the height $A M$ dropped to the base $B C$. Let $K$ be the point of tangency of the inscribed circle with the lateral side $A C$. Then
$$
K C=C M=15, A K=39-15=24, A M=36 .
$$
The radius $O K$ of the inscribed circle will be found from the similarity of triangles $A O K$ and $A C M$.
$$
\text { Third method. }
$$
By the property of the angle bisector of a triangle $A O: O M=A B: B M$. Therefore,
$$
r=O M=\frac{15 \cdot 36}{15+39}=10
$$
## Answer
10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9
In an isosceles trapezoid, the height is 10, and the diagonals are perpendicular to each other. Find the midline of the trapezoid.
|
Through the vertex of the smaller base of the trapezoid, draw a line parallel to the diagonal.
## Solution
First method.
Through the vertex $C$ of the smaller base $BC$ of trapezoid $ABCD$, draw a line parallel to diagonal $BD$. Let $M$ be the point of intersection of this line with the extension of base $AD$, and $CK$ be the height of the trapezoid.
Since $CM = BD = AC$ and $\angle ACM = 90^{\circ}$, then $\angle CMK = 45^{\circ}$ and $KM = CK$. Therefore, the midline of the trapezoid is equal to
$$
\frac{BC + AD}{2} = \frac{AD + DM}{2} = \frac{1}{2} AM = MK = CK = 10
$$
Second method.
Let $P$ and $Q$ be the midpoints of the bases $BC$ and $AD$, respectively, and $R$ and $S$ be the midpoints of the lateral sides $AB$ and $CD$ of trapezoid $ABCD$. The sides of quadrilateral $PSQR$ are parallel to the diagonals of the trapezoid as the midlines of the corresponding triangles, so $PSQR$ is a rectangle. Its diagonal $PQ$ is equal to the height of the trapezoid, and diagonal $RS$ is the midline of the trapezoid. Since the diagonals of a rectangle are equal, then $RS = PQ = 10$.
## Answer
10.
Send a comment
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The base of an isosceles triangle is $4 \sqrt{2}$, and the median drawn to the lateral side is 5.
Find the lateral sides.
|
Complete the given triangle to a parallelogram.
## Solution
Let $x$ be the side $A B$ of the isosceles triangle $A B C (B C=4 \sqrt{2})$. On the extension of the median $B M$ beyond point $M$, we lay off the segment $D M$ equal to $B M$. Then $B A D C$ is a parallelogram. Therefore,
$$
A C^{2}+B D^{2}=2\left(A B^{2}+B C^{2}\right), \text { or } x^{2}+10^{2}=2(4 \sqrt{2})^{2}+2 x^{2}
$$
From this, we find that $x^{2}=36$.
Answer
6. Send a comment
Problem
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
\begin{aligned} & {[\text { Law of Cosines }]} \\ & {[\text { Law of Sines }]}\end{aligned}
Find the radius of the circle if an inscribed angle with sides of lengths 1 and 2 subtends an arc of $120^{\circ}$.
|
Apply the Law of Cosines.
## Solution
Let $A$ be the vertex of the given angle, $AC$ and $AB$ be the sides of the angle, and points $B$ and $C$ lie on the circle, with $AC=1$ and $AB=2$. By the inscribed angle theorem, $\angle BAC = \frac{1}{2} \cdot 120^{\circ} = 60^{\circ}$. By the Law of Cosines,
$$
BC = \sqrt{AC^2 + AB^2 - 2 \cdot AC \cdot AB \cdot \cos \angle BAC} = \sqrt{1 + 4 - 2 \cdot 1 \cdot 2 \cdot \cos 60^{\circ}} = \sqrt{5 - 2} = \sqrt{3}
$$
If $R$ is the desired radius, then
$$
R = \frac{BC}{2 \cdot \sin 60^{\circ}} = \frac{\sqrt{3}}{\sqrt{3}} = 1
$$
## Answer
$R=1$.
A obtuse angle with sides of lengths 3 and 6 is inscribed in a circle of radius $\sqrt{21}$. Determine the measure of the arc on which it subtends.
## Answer
$240^{\circ}$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a right triangle $A B C$, the leg $A B$ is 21, and the leg $B C$ is 28. A circle with center $O$ lying on the hypotenuse $A C$ touches both legs.
Find the radius of the circle.
|
Let $P$ be the point of tangency of the circle with the leg $B C$. Consider similar triangles $C P O$ and $C B A$.
## Solution
Let $R$ be the radius of the circle.
First method. Let $P$ be the point of tangency of the circle with the leg $B C$. From the similarity of triangles $C P O$ and $C B A$, it follows that ${ }^{28-R} /{ }^{R}=28 / 21$.
From this, $R=12$.
Second method. $S_{A O B}=1 / 2 A B \cdot R=21 R / 2, S_{C O B}=1 / 2 B C \cdot R=14 R$.
Since $S_{A O B}+S_{C O B}=S_{A B C}=1 / 2 A B \cdot B C=1 / 2 \cdot 21 \cdot 28$, we have the equation $21 R+28 R=21 \cdot 28$, from which $R=12$.
## Answer
12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The diagonals of a trapezoid are perpendicular to each other. One of them is equal to 6, and the second one forms an angle of $30^{\circ}$ with the base. Find the midline of the trapezoid.
|
Through the vertex of the trapezoid, draw a line parallel to the first diagonal.
## Solution
Let the diagonal $AC$ of trapezoid $ABCD$ be 6, and the diagonal $BD$ forms an angle of $30^{\circ}$ with the larger base $AD$. Let the line drawn through vertex $B$ parallel to $AC$ intersect the extension of base $AD$ at point $K$. Then $KBD$ is a right triangle with the leg $BK$ opposite the $30^{\circ}$ angle. Therefore, $BC + AD = AK + AD = 2 BK = 2 AC = 12$, and the midline of the trapezoid is half the sum of the bases.
Answer
## 6.
Find the height of an isosceles triangle drawn to the lateral side if the base is $a$ and the lateral side is $b$.
## Hint
The product of the desired height and the lateral side is equal to the product of the base and the height drawn to it.
## Solution
The height dropped to the base is $\frac{\sqrt{4 b^{2} - a^{2}}}{2}$ (see problem $\underline{\text{54199}}$). Therefore, twice the area of the triangle is $\frac{a \sqrt{4 b^{2} - a^{2}}}{2}$. Dividing it by the lateral side, we get the height drawn to it.
## Answer
$\frac{a \sqrt{4 b^{2} - a^{2}}}{2 b}$
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ The area of a figure is equal to the sum of the areas of the figures into which it is divided ]

A circle with its center on side $AC$ of isosceles triangle $ABC$ ($AB = BC$) touches sides $AB$ and $BC$, and divides side $AC$ into three equal parts. Find the radius of the circle if the area of triangle $ABC$ is $9 \sqrt{2}$.
|
Let a circle of radius $r$ with center $O$ on the base $A C$ of an isosceles triangle $A B C$ touch the lateral sides $A B$ and $A C$ at points $M$ and $N$ respectively and intersect the base $A C$ at points $P$ and $Q$, such that $A P=P Q=Q C$. Then $O M$ and $O N$ are the altitudes of triangles $A O B$ and $C O B$, $A P=P Q=2 r$, $A O=3 r$. By the Pythagorean theorem in the right triangle $A O M$, we find that
$$
A M=\sqrt{A O^{2}-O M^{2}}=\sqrt{9 r^{2}-r^{2}}=2 r \sqrt{2}
$$
$$
M B=\frac{O M^{2}}{A M}=\frac{r^{2}}{2 r \sqrt{2}}=\frac{r \sqrt{2}}{4}, A B=A M+M B=2 r \sqrt{2}+\frac{r \sqrt{2}}{4}=\frac{9 r \sqrt{2}}{4}
$$
$$
9 \sqrt{2}=S_{\triangle A B C}=S_{\triangle A O B}+S_{\triangle C O B}=\frac{1}{2} A B \cdot O M+\frac{1}{2} B C \cdot O N=A B \cdot O M=\frac{9 r \sqrt{2}}{4} \cdot r=\frac{9 r^{2} \sqrt{2}}{4} .
$$
From which we find that $r^2=4$. Therefore, $r=2$.
## Answer
2.00
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Circle inscribed in an angle Area of a trapezoid
A circle with a radius of 3 is inscribed in a right trapezoid, the smaller base of which is 4. Find the larger base of the trapezoid.
|
Let $O$ be the center of a circle with radius 3, inscribed in trapezoid $ABCD$ with bases $AD$ and $BC=4$, $\angle C = \angle D = 90^\circ$, and the circle touching sides $CD$, $BC$, $AB$, and $AD$ at points $K$, $L$, $M$, and $N$ respectively. The quadrilaterals $ONDK$ and $OKCL$ are squares, so
$$
DN = OK = 3, \quad CL = OK = 3, \quad BM = BL = BC - CL = 4 - 3 = 1.
$$
The rays $AO$ and $BO$ are the angle bisectors of the angles at the lateral side of the trapezoid. The sum of these angles is $180^\circ$, and the sum of their halves is $90^\circ$. Therefore, $\angle AOB = 90^\circ$, which means $OM = 3$ is the altitude of the right triangle $AOB$ drawn from the vertex of the right angle, so $OM^2 = BM \cdot AM$, from which we find that
$$
\begin{gathered}
AM = \frac{OM^2}{BM} = \frac{9}{1} = 9 \\
\text{Then} \\
AN = AM = 9, \quad AD = AN + DN = 9 + 3 = 12
\end{gathered}
$$
## Answer
12.00
Submit a comment
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Projections of the bases, sides, or vertices of a trapezoid ] $[\quad$ The midline of a trapezoid $\quad]$
It is known that a circle can be inscribed in an isosceles trapezoid $A B C D$ with bases $A D>B C$; $C H-$ is the height of the trapezoid, $A H=7$. Find the lateral side of the trapezoid.
|
Isosceles trapezoid $A B C D$ is circumscribed around a circle, so $2 A B=A B+A B=A B+C D=A D+B C$, which means $A B=\frac{1}{2}(A D+B C)$. On the other hand, the projection of the diagonal of an isosceles trapezoid onto the larger base is equal to half the sum of the bases, i.e., $A H=\frac{1}{2}(A D+B C)$, and the half-sum of the bases of any trapezoid is equal to its midline. Therefore, the midline of trapezoid $A B C D$ is equal to the lateral side, i.e., 7.
## Answer
7.00
Send a comment
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Folklore
Find the maximum value of the expression $x^{2}+y^{2}$, if $|x-y| \leq 2$ and $|3 x+y| \leq 6$.
|
The set of points satisfying the system of inequalities $|x-y|<2$ and $|3x+y|<6$ forms the intersection of two strips, and thus represents the boundary and interior of a parallelogram $ABCD$, where $A(1,3), B(2, 0), C(-1,-3), D(-2,0)$ (see figure).
We need to find the maximum square of the distance from a point in this parallelogram to the origin $O$. Clearly, this is $OA^2 = 1^2 + 3^2 = 10$.
## Answer
10.
Submit a comment
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Properties of bisectors, concurrency ] [ The ratio in which the bisector divides the side $]$ [ Properties of bisectors, concurrency ]
In triangle $A B C$, points $M$ and $N$ are marked on sides $A B$ and $B C$ respectively, such that $B M=B N$. A line is drawn through point $M$ perpendicular to $B C$, and a line through point $N$ perpendicular to $A B$. These lines intersect at point $O$. The extension of segment $B O$ intersects side $A C$ at point $P$ and divides it into segments $A P=5$ and $P C=4$. Find the length of segment $B P$, given that $B C=6$.
|
The altitudes of triangle $B M N$, drawn from vertices $M$ and $N$, intersect at point $O$, which means that the altitude from vertex $B$ also passes through point $O$. Since triangle $B M N$ is isosceles, ray $B O$ is the angle bisector of $\angle M B N$, and $B P$ is the angle bisector of triangle $A B C$. By the angle bisector theorem, $\frac{B C}{A B} = \frac{C P}{A P}$, from which we find that
$$
A B = \frac{B C \cdot A P}{C P} = \frac{6 \cdot 5}{4} = \frac{15}{2}
$$
Using the formula for the angle bisector of a triangle,
$$
B P^2 = B C \cdot A B - C P \cdot A P = 6 \cdot \frac{15}{2} - 4 \cdot 5 = 45 - 20 = 25 \text{.}
$$
Therefore, $B P = 5$.
## Answer
5.
| Problem 107711 Topics: | Quadrilateral Pyramid Perpendicular and Oblique | Difficulty |
| :---: | :---: | :---: |
| | [The larger angle lies opposite the larger side] | Grades: 10,11 |
| | Inequalities with Angles | |
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9 |
Given a trapezoid $A B C D$ with bases $A D=3$ and $B C=18$. Point $M$ is located on diagonal $A C$, such that $A M$ : $M C=1: 2$. A line passing through point $M$ parallel to the bases of the trapezoid intersects diagonal $B D$ at point $N$. Find $M N$.
|
Let $K$ be the point of intersection of the given line with the side $A B$. By the theorem of proportional segments, $A K: K B = A M: M C = 1: 2$. Similarly, $B N: N D = B K: A K = 2: 1$. From the similarity of triangles $A K M$ and $A B C$, we find that $M K = B C \cdot A M / A C = 1 / 3 B C = 6$, and from the similarity of triangles $B K N$ and $B A D$, $N K = A D \cdot B N / N D = 2 / 3 A D = 2$. Therefore, $M N = M K - N K = 6 - 2 = 4$.
## Answer
4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7,8,9,1 |
Avor: Kuyygin A.K:
Among any five nodes of a regular square grid, there will definitely be two nodes such that the midpoint of the segment between them is also a node of the grid. What is the minimum number of nodes of a regular hexagonal grid that must be taken so that among them there are definitely two nodes such that the midpoint of the segment between them is also a node of this grid?
|
Lemma. Among any five nodes of a grid of equilateral triangles, there will be two such that the midpoint of the segment between them is also a grid node.
Proof of the lemma. Introduce the origin at one of the grid nodes and denote by $\operatorname{lvec}\{a\}$ and $\operatorname{lvec}\{b\}$ the radius vectors to the two nearest nodes, as shown in the figure. Then the grid nodes are points of the form $m \operatorname{lvec}\{a\} + n \operatorname{lvec}\{b\}$ for integers $m$ and $n$. By the pigeonhole principle, among five points, there will be two points $m_1 \operatorname{lvec}\{a\} + n_1 \operatorname{lvec}\{b\}$ and $m_2 \operatorname{lvec}\{a\} + n_2 \operatorname{lvec}\{b\}$, for which the parity of $m_1$ and $m_2$ and the parity of $n_1$ and $n_2$ coincide simultaneously. The midpoint of the segment connecting these two points is the point $\frac{m_1 + m_2}{2} \operatorname{lvec}\{a\} + \frac{n_1 + n_2}{2} \operatorname{lvec}\{b\}$. This point is a grid node, since the numbers $\frac{m_1 + m_2}{2}$ and $\frac{n_1 + n_2}{2}$ are integers due to the same parity of $m_1$ and $m_2$, $n_1$ and $n_2$.
Solution. In the figure on the left, you can see an example of the placement of 8 grid nodes, among which there are no two such that the midpoint of the segment between them is a grid node. We will prove that nine nodes are sufficient. Note that the hexagonal grid is divided into the union of two triangular grids (see the figure on the right). By the pigeonhole principle, among any nine nodes, at least five will be in one of these two triangular grids. By the lemma, among these five nodes, there will be two of the required ones.
## Answer
9.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9
On a circle, a point $A$ is taken, on the diameter $B C$ - points $D$ and $E$, and on its extension beyond point $B$ - point $F$. Find $B C$, if $\angle B A D=\angle A C D, \angle B A F=\angle C A E, B D=2, B E=5$ and $B F=4$.
|
Let $\angle B A D=\angle A C D=\alpha, \angle B A F=\angle C A E=\beta$. Since point A lies on the circle with diameter $B C$, then $\angle B A C=90^{\circ}$. Therefore,
$$
\begin{gathered}
\angle A D C=180^{\circ}-\angle A C D-\angle C A D=180^{\circ}-\alpha-\left(90^{\circ}-\alpha\right)=90^{\circ}, \\
\angle F A E=\angle F A B+\angle B A E=\beta+\left(90^{\circ}-\beta\right)=90^{\circ} .
\end{gathered}
$$
Then $A D$ is the common altitude of the right triangles $B A C$ and $F A E$. By the theorem of the altitude of a right triangle drawn from the vertex of the right angle,
$$
F D \cdot D E=AD^2=B D \cdot D C \text{. }
$$
Let $E C=x$, we get the equation
$$
(4+2) 3=2(3+x)
$$
from which we find that $x=6$. Therefore,
$$
B C=B E+E C=5+6=11 .
$$
## Answer
11.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kaiibhanov A.K:
The audience has the shape of a regular hexagon with a side of 3 m. In each corner, a snoremeter is installed, determining the number of sleeping students at a distance not exceeding 3 m. How many sleeping students are there in total in the audience, if the sum of the snoremeter readings is 7?
#
|
Each student is "seen" by 2, 3, or 6 snorometers (see fig). Therefore, 7 can be broken down into a sum of terms, each of which is equal to 2, 3, or 6. It is easy to see that 7 can be represented as such a sum in only one way: \(7 = 3 + 2 + 2\). The number of terms is equal to the number of students.
## Problem
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The area of the triangle is 16. Find the area of the trapezoid that is cut off from the triangle by its midline.
#
|
The median line of a triangle cuts off a similar triangle from it, with a similarity coefficient of $\frac{1}{2}$. Therefore, the area of the cut-off triangle is one-fourth of the area of the original triangle, i.e., $\frac{1}{\mathbf{4}} 16=4$. Consequently, the area of the remaining trapezoid is $16-4=12$.
## Answer
12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[
[ Tangent Circles $]$
Two circles touch each other internally. A line passing through the center of the smaller circle intersects the larger circle at points $A$ and $D$, and the smaller circle at points $B$ and $C$. Find the ratio of the radii of the circles if $A B: B C: C D=2: 4: 3$.
#
|
Apply the theorem of the products of segments of intersecting chords.
## Solution
Let $M$ be the point of tangency of the circles, $r$ and $R (r < R)$ be their radii, and $O$ be the center of the smaller one. Denote: $AB = 2x, BC = 4x, CD = 3x$. Then
$$
r = OB = OC = 2x, DO \cdot OA = MO(2R - MO), \text{ or } 5x \cdot 4x = 2x(2R - 2x).
$$
Therefore,
$$
5x = R - x, R = 6x, \frac{R}{r} = \frac{6x}{2x} = 3
$$
Let $M$ be the point of tangency of the circles, $r$ and $R (r < R)$ be their radii, and $O$ be the center of the smaller one. Denote: $AB = 2x, BC = 4x, CD = 3x$. Then
$$
r = OB = OC = 2x, DO \cdot OA = MO(2R - MO), \text{ or } 5x \cdot 4x = 2x(2R - 2x).
$$
Therefore,
$$
5x = R - x, R = 6x, \frac{R}{r} = \frac{6x}{2x} = 3
$$
Let $M$ be the point of tangency of the circles, $r$ and $R (r < R)$ be their radii, and $O$ be the center of the smaller one. Denote: $AB = 2x, BC = 4x, CD = 3x$. Then
$$
r = OB = OC = 2x, DO \cdot OA = MO(2R - MO), \text{ or } 5x \cdot 4x = 2x(2R - 2x)
$$
Therefore,
$$
5x = R - x, R = 6x, \frac{R}{r} = \frac{6x}{2x} = 3
$$
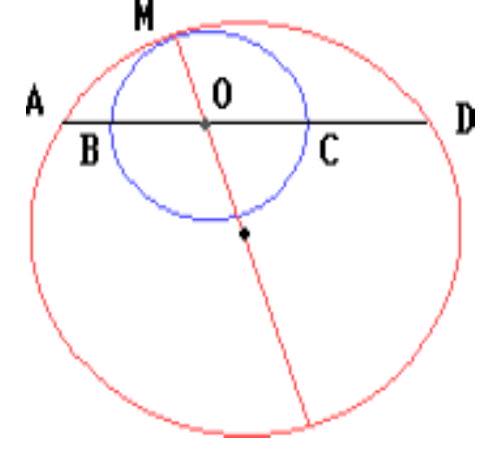
## Answer
3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11
Construct a circle equidistant from four points on a plane. How many solutions does the problem have?
|
Answer: 7 solutions (in the non-degenerate case). Let $A, B, C, D$ be the given points, and $S$ be the sought circle. On one side of $S$, there are $k$ given points, and on the other side, there are 4 - $k$ given points. We will assume that the given points do not lie on the same circle (otherwise, $S$ can be any circle with the same center, resulting in infinitely many solutions). Thus, $1 \leq k \leq 3$. We obtain two significant
perpendicular bisectors of segments $A B$ and $C D$. The radius of circle $S$ is the arithmetic mean of the lengths of segments $O A$ and $O C$. The four points can be paired in three ways, so we get 3 solutions. Now let points $A, B$, and $C$ lie on one side of circle $S$, and point $D$ lie on the other side. Draw a circle through points $A, B$, and $C$. Let $O$ and $R$ be its center and radius. Point $O$ is the center of the sought circle, and the radius of the sought circle is the arithmetic mean of $R$ and $O D$. One point out of four can be chosen in four ways, so we get 4 solutions.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tokaeva I.
Let $F_{1}, F_{2}, F_{3}, \ldots$ be a sequence of convex quadrilaterals, where $F_{k+1}$ (for $k=1,2,3, \ldots$) is obtained by cutting $F_{k}$ along a diagonal, flipping one of the parts, and gluing it back along the cut line to the other part. What is the maximum number of different quadrilaterals that this sequence can contain? (Quadrilaterals are considered different if they cannot be made to coincide by a movement.)
|
Let $ABCD$ be the original quadrilateral $F_{1}$. We can assume that each time the half of the quadrilateral containing side $CD$ is flipped, while side $AB$ remains stationary. In this process, the sum of angle $A$ and the opposite angle does not change. Additionally, the set of side lengths does not change. However, the three lengths (sides other than $AB$) can be ordered in only six ways.
We will prove that if two resulting quadrilaterals $ABKL$ and $ABMN$ have the same ordered side lengths ($BK = BM$, $KL = MN$, $LA = NA$), then the quadrilaterals are equal. It is sufficient to prove the equality of the diagonals $AK$ and $AM$. Assuming, for example, that $AK > AM$, we get $\angle ABK > \angle ABM$, $\angle ALK > \angle ANM$, which contradicts the equality of the sums $\angle ABK + \angle ALK$ and $\angle ABM + \angle ANM$.
Six different quadrilaterals will result from any quadrilateral where all sides are different, the sums of opposite angles are also different, and the quadrilateral remains convex and does not degenerate into a triangle during transformations. Only quadrilaterals with the reverse order of sides might be suspected of being equal, but they are not equal either, since flipping one of them will not align the sums of opposite angles. The highlighted condition is satisfied, for example, for quadrilaterals whose area is greater than half the product of the two longest sides: this inequality is clearly not true for non-convex and degenerate quadrilaterals. A specific example: a right trapezoid with bases 3 and 6 and height 4.
## Answer
6 quadrilaterals.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Pythagorean Theorem (direct and inverse). ] [ Properties and characteristics of an isosceles triangle. ]
In an isosceles triangle \(ABC\), the side \(AB\) is 10, and the base \(AC\) is 12. The angle bisectors of angles \(A\) and \(C\) intersect at point \(D\). Find \(BD\).
|
If $M$ is the midpoint of $A C$, then $B D: D M=B C: C M$.
## Solution
Since the angle bisectors of a triangle intersect at one point, $B D$ is the bisector of angle $B$. Extend $B D$ to intersect $A C$ at point $M$. Then $M$ is the midpoint of $A C, B M \perp A C$. Therefore, $B M^{2}=B C^{2}-M C^{2}=64$.
Since $C D$ is the bisector of triangle $B M C$, then $B D: D M=B C: C M=5: 3$.
Therefore, $B D=5 / 8 B M=5$.
Answer
## [ Properties and characteristics of isosceles triangles. ] $\left.\begin{array}{l}\text { Problem } 54303 \text { Topics: [Trigonometric ratios in a right triangle }] \\ \text { [ area of a triangle (using height and base). }]\end{array}\right]$
The base of an isosceles triangle is $b$, and the height dropped to the lateral side is $h$. Find the area of the triangle.
## Solution
Let $\alpha$ be the angle at the base, $H$ be the height dropped to the base of the triangle. Then
$$
\sin \alpha=\frac{h}{b}, \quad H=\frac{1}{2} b \operatorname{tg} \alpha=\frac{b h}{2 \sqrt{b^{2}-h^{2}}}, \quad S=\frac{1}{2} b h=\frac{b^{2} h}{4 \sqrt{b^{2}-h^{2}}}
$$
## Answer
$$
\frac{b^{2} h}{4 \sqrt{b^{2}-h^{2}}}
$$
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9
[ Rectangles and Squares. Properties and Characteristics]
The side of the square is 1. A line is drawn through its center. Calculate the sum of the squares of the distances from
the four vertices of the square to this line.
|
Let a line passing through the center $O$ of the square $A B C D$ intersect the side $A B$. Drop perpendiculars $A P$ and $B Q$ to this line. Triangles $A P O$ and $O Q B$ are equal by hypotenuse and acute angle. Therefore, $A P^{2}+B Q^{2}=$ $A P^{2}+O P^{2}=A O^{2}=1 / 2$
## Answer
1.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On weekdays, the Absent-Minded Scientist travels to work on the ring line of the Moscow Metro from "Taganskaya" station to "Kievskaya" station, and in the evening - back (see diagram).
Upon entering the station, the Scientist boards the first arriving train. It is known that trains run in both directions with approximately equal intervals, and that the train traveling on the northern route (via "Belorusskaya") takes 17 minutes to travel from "Kievskaya" to "Taganskaya" or vice versa, while on the southern route (via "Paveletskaya") it takes 11 minutes. Out of habit, the Scientist always calculates everything. Once, he calculated that over many years of observation:
- the train traveling counterclockwise arrives at "Kievskaya" on average 1 minute and 15 seconds after the train traveling clockwise arrives. The same is true for "Taganskaya".
- the trip from home to work takes the Scientist on average 1 minute less than the trip from work to home. Find the expected interval between trains traveling in the same direction.
|
Let $p$ be the probability that the Scientist boards a train going clockwise. Then the expected travel time from "Taganskaya" to "Kievskaya" is $11 p + 17(1-p) = 17 - 6p$.
On the return trip from "Kievskaya" to "Taganskaya," the expected travel time is $17 p + 11(1-p) = 11 + 6p$.
By the condition $(11 + 6p) - (17 - 6p) = 1$, from which $p = 7 / 12$. Let the interval between trains be $T$. Then $T(1-p) = Y$, where $Y$ is the time between the arrival of a train "clockwise" and the arrival of a train "counterclockwise" at the Scientist's favorite stations. Therefore, $\mathrm{ET} = \mathrm{EY}_{1-p} = 5 / 4 \cdot 12 / 5 = 3$.
## Answer
3 minutes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11
In triangle $ABC$, it is known that $AC=12, AB=BC=3\sqrt{10}$. Two spheres touch the plane of triangle $ABC$ at points $A$ and $C$ and are located on opposite sides of this plane. The distance between the centers of these spheres is 15. The center of a third sphere is at point $B$, and this sphere externally touches the two given spheres. Find the radius of the third sphere.
|
Let $O_1$ and $O_2$ be the centers of the spheres that touch the plane of triangle $ABC$ at points $A$ and $C$ respectively, with radii $x$ and $y$. Let $z$ be the radius of the third sphere. Through the lines $O_1A$ and $O_2C$, which are perpendicular to the plane $ABC$, we draw a plane. In this plane, we drop a perpendicular $O_2P$ from point $O_2$ to the line $O_1A$. In the right triangle $O_1O_2P$, it is known that
$$
O_1O_2 = 15, \quad O_1P = O_1A + AP = O_1A + O_2C = x + y, \quad O_2P = AC = 12.
$$
By the Pythagorean theorem,
$$
(x + y)^2 + 144 = 225
$$
from which we get $x + y = 9$. From the right triangles $ABO_1$ and $CBO_2$, we find that
$$
(x + z)^2 = x^2 + 90, \quad (y + z)^2 = y^2 + 90
$$
from which we get
$$
z^2 + 2xz = 90, \quad z^2 + 2yz = 90
$$
Adding these two equations term by term, we get
$$
2z^2 + 2z(x + y) = 180
$$
and since $x + y = 9$, we have
$$
z^2 + 9z - 90 = 0
$$
from which we find that $z = 6$.
## Answer
6.00
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8
How many sides can a convex polygon have if all its diagonals are of the same length?
|
Let's prove that the number of sides of such a polygon does not exceed 5. Suppose that all diagonals of the polygon $A_{1} \ldots A_{n}$ have the same length and $n \geq 6$. Then the segments $A_{1} A_{4}, A_{1} A_{5}, A_{2} A_{4}$, and $A_{2} A_{5}$ have the same length, as they are diagonals of this polygon. However, in the convex quadrilateral $A_{1} A_{2} A_{4} A_{5}$, the segments $A_{1} A_{5}$ and $A_{2} A_{4}$ are opposite sides, while $A_{1} A_{4}$ and $A_{2} A_{5}$ are diagonals.
Therefore, $A_{1} A_{5} + A_{2} A_{4} < A_{1} A_{4} + A_{2} A_{5}$. This leads to a contradiction.
It is also clear that a regular pentagon and a square satisfy the required condition.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9
In trapezoid $ABCD$, points $K$ and $M$ are the midpoints of the bases $AB=5$ and $CD=3$. Find the area of the trapezoid if triangle $AMB$ is a right triangle and $DK$ is the height of the trapezoid.
|
Draw the height of the trapezoid from point $M$.
## Solution
Notice that in triangle $A M B \angle M=90^{\circ}$ (otherwise, $M A$ or $M B$ would be perpendicular to $A B$, which is impossible).
Let $M P$ be another height of the trapezoid. Then
\[
\begin{gathered}
K P=D M=\frac{1}{2} D C=\frac{3}{2}, B P=K B-K P=\frac{5}{2}-\frac{3}{2}=1 \\
A P=A K+K P=\frac{5}{2}+\frac{3}{2}=4, M P^{2}=A P \cdot P B=4
\end{gathered}
\]
Therefore,
\[
S_{\mathrm{ABCD}}=\frac{A B+D C}{2} \cdot M P=8
\]
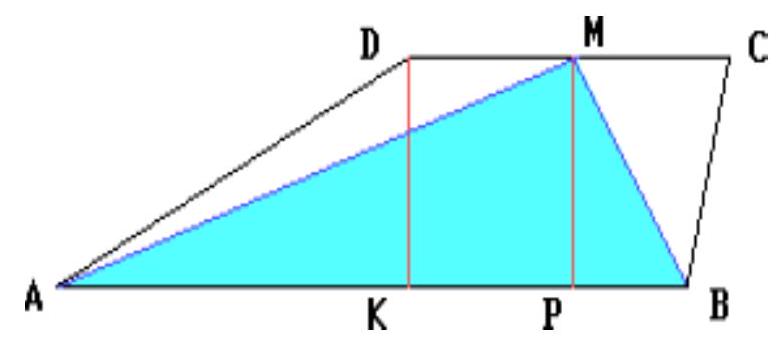
Answer
8. Send a comment
Problem
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Khachaturyan A.V.
Bus stop B is located on a straight highway between stops A and C. After some time following departure from A, the bus found itself at a point on the highway such that the distance from this point to one of the three stops is equal to the sum of the distances to the other two. After the same amount of time, the bus was again at a point with this property, and after another 25 minutes, it arrived at B. How much time does the bus need for the entire journey from A to C, if its speed is constant and it stops at B for 5 minutes?
|
At both moments in time mentioned in the problem, the sum will obviously be the distance from the bus to the farthest stop from it. This cannot be $B$, as it is closer than $C$. Therefore, these were $C$ (before the bus had traveled halfway from $A$ to $C$) and $A$ (after this moment).

In the first case, the bus was at point $X$ and the distance from it to $C$ was equal to the sum of the distances to $A$ and to $B$. But this distance is also equal to the sum of the distance to $B$ and the distance $BC$. Therefore, the bus had traveled exactly the distance $BC$. On the diagram, we marked equal distances with arcs.
By the second moment, the bus had traveled another distance $BC$ and arrived at point $Y$. The sum of the distances from it to $B$ and to $C$ is $BC$ plus $YB$, counted twice. According to the problem, this is the distance to $A$, so $YB$ is half the length of $BC$.

Since $YB$ was traveled by the bus in 25 minutes, $BC$ will be traveled in 50 minutes, and the entire journey will take $3 \cdot 50 + 25 + 5 = 180$ minutes, which is three hours.
## Answer
3 hours.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bakayev E.V.
In triangle $\mathrm{ABC}$, medians $\mathrm{BK}$ and $\mathrm{CN}$ are drawn, intersecting at point M. What is the maximum number of sides of quadrilateral ANMK that can have a length of 1?
|
Method 1. Suppose that at least three sides of the quadrilateral ANMK are equal to 1. There are only two fundamentally different cases. 1) $\mathrm{AN}=\mathrm{NM}=\mathrm{MK}=1$. Then $\mathrm{NB}=1, \mathrm{MB}=2$, so $\mathrm{MN}+\mathrm{NB}=\mathrm{MB}$. 2) $\mathrm{KA}=\mathrm{AN}=\mathrm{NM}=1$. Then $\mathrm{AC}=2, \mathrm{NC}=3$, so $\mathrm{NA}+\mathrm{AC}=\mathrm{NC}$. In both cases, a contradiction with the triangle inequality is obtained.
Method 2. If more than two sides of the quadrilateral are equal to 1, then either $\mathrm{AK}=\mathrm{NA}$ or $\mathrm{KM}=\mathrm{MN}$. In the first case, triangle ABC is isosceles. In the second case, $\mathrm{BK}=\mathrm{CN}=3$, so in this case, triangle ABC is also isosceles. From this, it follows that $\mathrm{AK}=\mathrm{KM}=\mathrm{MN}=\mathrm{NA}$, meaning that $AKMN$ is a rhombus. This is a contradiction, as lines AK and NM are not parallel.
Method 3. Let $\mathrm{L}$ be the midpoint of side $\mathrm{BC}$. If $\mathrm{NM}=\mathrm{NA}=\mathrm{NB}$, then triangle AMB is a right triangle.
Triangle LMK is similar to triangle AMB with a similarity ratio of 0.5, so MK $=\mathrm{LM}$. Therefore, in triangle AMK, the hypotenuse is larger than in triangle LMK, meaning $\mathrm{AK}>\mathrm{LK}=\mathrm{NA}$. Thus, in the quadrilateral ANMK, there are no three sides equal to each other.
The case when $\mathrm{KM}=\mathrm{KA}$ is analogous, and if $\mathrm{KM} \neq \mathrm{KA}$ and $\mathrm{NM} \neq \mathrm{NA}$, then among the segments NM, NA, KM, and KA, there are also no three equal to each other.
## Answer
2 sides.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\begin{array}{l}\text { The ratio in which the bisector divides the side. } \\ {[\underline{\text { Properties of bisectors, concurrency }}]}\end{array}\right]$
In triangle $ABC$, points $M$ and $N$ are marked on sides $AB$ and $BC$ respectively, such that $BM = BN$. A line is drawn through point $M$ perpendicular to $BC$, and a line through point $N$ perpendicular to $AB$. These lines intersect at point $O$. The extension of segment $BO$ intersects side $AC$ at point $P$ and divides it into segments $AP = 5$ and $PC = 4$. Find the length of segment $BP$, given that $BC = 6$.
|
Prove that $B P$ is the bisector of triangle $A B C$, apply the bisector theorem of a triangle and the formula for the square of the bisector of a triangle: $B P^{2}=A B \cdot B C-A P \cdot P C$.
## Solution
In the isosceles triangle $B M N$, point $O$ is the intersection of the altitudes. Therefore, $B P$ is the bisector of triangle $B M N$ and triangle $A B C$. According to the bisector theorem of a triangle, $A B: B C=A P: P C$, so
$$
A B=\frac{A P \cdot B C}{P C}=\frac{5 \cdot 6}{4}=\frac{15}{2}
$$
By the formula for the square of the bisector of a triangle,
$$
B P^{2}=A B \cdot B C-A P \cdot P C=\frac{15}{2} \cdot 6-5 \cdot 4=25
$$
Therefore, $B P=5$.
Answer
5.00
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$[\underline{C}$ Tangent Circles
Two circles touch each other externally at point $A$. Their common tangent touches the first circle at point $B$ and the second circle at point $C$. A line passing through points $A$ and $B$ intersects the second circle at point $D$. It is known that $A B=5$ cm, $A D=4$ cm. Find $C D$.
|
Prove that $C A$ is the altitude of the right triangle $B C D$, drawn from the vertex $C$ of the right angle.
## Solution
Let the common tangent, drawn to the given circles at point $A$, intersect the segment $B C$ at point $K$. Then $B K=K A=K C$. Therefore, $\angle B A C=90^{\circ}$. This means that the chord $C D$ of the second circle is seen from point $A$ of this circle at a right angle. Therefore, $C D$ is the diameter of the second circle, and since $B C$ is a tangent, $\angle B C D=90^{\circ}$. Thus, the segment $A D$ is the projection of the leg $C D$ of the right triangle $B C D$ onto the hypotenuse $B D$. Therefore,
$$
C D^{2}=A D \cdot B D=4 \cdot 9=36 \Rightarrow C D=6
$$
## Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In triangle $ABC$, the lines containing the altitudes $AP$, $CR$, and $BQ$ (points $P$, $R$, and $Q$ lie on the lines containing the corresponding sides of triangle $ABC$) intersect at point $O$. Find the areas of triangles $ABC$ and $POR$, given that $RP$ is parallel to $AC$, $AC=4$, and $\sin \angle ABC=\frac{24}{25}$.
|
Prove that the given triangle is isosceles. Consider two cases: $\angle A B C = 90^{\circ}$.
## Solution
Since from points $P$ and $R$ the segment $A C$ is seen at a right angle, these points lie on a circle with diameter $AC$. Therefore, the trapezoid ACPR (Fig.1) (or ACRP (Fig.2)) is isosceles. Hence, triangle $ABC$ is also isosceles. Its equal angles at the base $AC$ are acute, and $BQ$ is both a median and an angle bisector.
Let $\angle A B C = \beta$. Suppose $\beta = 90^{\circ}$ (Fig. 2). Then
$$
\begin{gathered}
\cos \beta = -\frac{7}{25}, \operatorname{ctg} \frac{\beta}{2} = \frac{1 + \cos \beta}{\sin \beta} = \frac{1 - \frac{7}{25}}{\frac{24}{25}} = \frac{18}{24} = \frac{3}{4} \\
\operatorname{tg} \frac{\beta}{2} = \frac{4}{3}, \cos \frac{\beta}{2} = \frac{1}{\sqrt{1 + \left(\frac{4}{3}\right)^{2}}} = \frac{3}{5}.
\end{gathered}
$$
From the right triangle $AQB$, we find that
$$
BQ = AQ \cdot \operatorname{ctg} \angle ABQ = 2 \cdot \operatorname{ctg} \frac{\beta}{2} = 2 \cdot \frac{3}{4} = \frac{3}{2}
$$
Therefore,
$$
S_{\triangle ABC} = \frac{1}{2} \cdot AC \cdot BQ = \frac{1}{2} \cdot 4 \cdot \frac{3}{2} = 3
$$
From the right triangles OQC and ORC, we find that
$$
OC = \frac{CQ}{\cos \angle OCQ} = \frac{2}{\cos \frac{\beta}{2}} = \frac{2}{\frac{3}{5}} = \frac{10}{3},
$$
$$
PC = OC \cdot \sin \angle COP = OC \cdot \sin \beta = \frac{10}{3} \cdot \frac{24}{25} = \frac{16}{5}
$$
$$
OP = OC \cdot \cos \angle COP = OC \cdot \cos (180^{\circ} - \beta) = -OC \cdot \cos \beta = -\frac{10}{3} \cdot \left(-\frac{7}{25}\right) = \frac{14}{15}
$$
Therefore,
$$
S_{\triangle POC} = \frac{1}{2} \cdot PC \cdot OP = \frac{1}{2} \cdot \frac{16}{5} \cdot \frac{14}{15} = \frac{112}{75}
$$
## Answer
$\frac{16}{3}$ and $\frac{21}{25}$ or 3 and $\frac{112}{75}$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The area of the right triangle ABC ( $\angle C=90^{\circ}$ ) is 6, and the radius of the circumscribed circle around it is $\frac{5}{2}$. Find the radius of the circle inscribed in this triangle.
#
|
The radius of the circle inscribed in a right-angled triangle with legs $a, b$ and hypotenuse $c$ is $\frac{a+b-c}{2}$.
## Solution
It is known that the radius $r$ of the circle inscribed in a right-angled triangle with legs $a, b$ and hypotenuse $c$ is $\frac{a+b-c}{2}$, and the area is $\frac{ab}{2}$.
Since the center of the circle circumscribed around a right-angled triangle coincides with the midpoint of the hypotenuse, then $c=5$. By the Pythagorean theorem, $a^{2}+b^{2}=25$. Therefore,
$$
(a+b)^{2}=a^{2}+b^{2}+2ab=25+4 \cdot 6=49, a+b=7
$$
Thus,
$$
r=\frac{a+b-c}{2}=\frac{7-5}{2}=1
$$
## Answer
1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Angles subtended by equal arcs and equal chords]
## Law of Sines
The lengths of three sides of a cyclic quadrilateral inscribed in a circle of radius $2 \sqrt{2}$ are equal and each is 2. Find the fourth side.
|
Prove that the given quadrilateral is an isosceles trapezoid. Then apply the Law of Sines.
## Solution
Let the quadrilateral $A B C D$ be inscribed in a circle with radius $R=2 \sqrt{2}$, and $A B=B C=C D=2$. Let $\angle C A D=\alpha$. Since equal chords subtend equal arcs, and inscribed angles subtending equal chords are equal, $\angle A C B=\angle C A D$. Therefore, $B C \| A D$. Hence, $A B C D$ is an isosceles trapezoid.
From the Law of Sines, it follows that
$$
\sin \alpha=\sin \angle C A D=\frac{C D}{2 R}=\frac{2}{4 \sqrt{2}}=\frac{1}{2 \sqrt{2}}
$$
Since $\angle B A C=\angle C A D=\alpha$, then $\angle B A D=2 \alpha$
Let $P$ be the projection of point $B$ onto the larger base $A D$ of the trapezoid $A B C D$. From the right triangle $A B P$, we find that
$$
A P=A B \cos 2 \alpha=2\left(1-2 \sin ^{2} \alpha\right)=2\left(1-2 \cdot \frac{1}{8}\right)=\frac{3}{2}
$$
By the property of an isosceles trapezoid, $A P=\frac{A D-B C}{2}$. From this, we find that
$$
A D=2 A P+B C=2 \cdot \frac{3}{2}+2=3+2=5
$$
## Answer
5.
## Problem
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Quadrilateral $ABCD$ is inscribed in a circle. It is known that $AC \perp BD$. Find the length of $BC$, if the distance from the center of the circle to side $AD$ is 2.
|
Draw the diameter $B B_{1}$. Then $C B_{1}=A D$.
## Solution
Let $B_{1}$ be the point diametrically opposite to point $B$. Since $B_{1} D \perp B D\left(B B_{1}\right.$ - the diameter of the circle) and $A C \perp B D$, then $B_{1} D \| A C$. Therefore, $C B_{1}=A D$, and since equal chords are equidistant from the center of the circle, the distance $O M$ from the center $O$ of the circle to the chord $B_{1} C$ is also 2.
Since $O M \perp B_{1} C, B C \perp B_{1} C$ and $O$ is the midpoint of $B B_{1}$, then $O M$ is the midline of the right triangle $B C B_{1}$. Therefore, $B C=2 \cdot O M=2 \cdot 2=4$.
## Answer
4.
Send a comment
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 [ [sphere, circumscribed around a pyramid]
A regular quadrilateral pyramid is inscribed in a sphere. The radius of the sphere is 1. The plane angle at the vertex of the pyramid is $45^{\circ}$. Find the lateral surface area of the pyramid.
#
|
The center $O$ of the sphere is equidistant from the vertices of the base $A B C D$ of the regular pyramid $P A B C D$, so the point $O$ lies on the height $P Q$ of the pyramid (Fig.1). Let
$$
A B=B C=C D=A D=a, P A=P B=P C=P D=l
$$
By the cosine theorem,
$$
A B 2=P A 2+P B 2-2 P A \cdot P B \cos \angle A P B
$$
or
$$
a 2=2 l 2-2 l 2 \cos 45^{\circ}=12(2-\sqrt{2})
$$
from which $a=I \sqrt{2-\sqrt{2}}$. Then
$$
A C=a \sqrt{2}=\sqrt{4-2 \sqrt{2}}, A Q=\frac{1}{2} A C=\frac{1}{2} / \sqrt{4-2 \sqrt{2}}
$$
Let $\angle P A Q=\alpha$. From the right triangle $P A Q$, we find that
$$
\begin{gathered}
\cos \alpha=\frac{A Q}{A P}=\frac{1}{2} \cdot \frac{l \sqrt{1-2 \sqrt{2}}}{i}=\frac{1}{2} \sqrt{4-2 \sqrt{2}}=\sqrt{1-\frac{\sqrt{2}}{2}} \\
\sin \alpha=\sqrt{1-\cos ^{2} \alpha}=\sqrt{1-1+\frac{\sqrt{2}}{2}}=\sqrt{\frac{\sqrt{2}}{2}}
\end{gathered}
$$
Consider the section of the pyramid and the sphere by a plane passing through the points $A, P$ and $C$ (Fig.2). We obtain an isosceles triangle $A P C$ inscribed in a circle with center $O$ and radius $R=1$. By the sine theorem,
$$
A P=2 R \sin \angle A C P, \text { or } l=2 \sin \alpha=2 \sqrt{\frac{\sqrt{2}}{2}} \text {. }
$$
If $S$ is the lateral surface of the given pyramid, then
$$
\begin{aligned}
S & =4 S_{\triangle A P B}=4 \cdot \frac{1}{2} A P \cdot B P \sin \angle A P B= \\
& =212 \sin 45^{\circ}=2\left(2 \sqrt{\frac{\sqrt{2}}{2}}\right) 2 \cdot \frac{\sqrt{2}}{2}=4
\end{aligned}
$$
## Answer
4.00
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11
The edge of a regular tetrahedron is $4 \sqrt{6}$. Find the radius of the sphere that touches the lateral faces of the tetrahedron at points lying on the sides of the base.
|
Let the sphere with center $O$ touch the planes of the faces $A B D, B C D$, and $A C D$ of the given regular tetrahedron $A B C D$ at points $N, M$, and $K$, respectively, which lie on the sides $A B, B C$, and $A C$ of the base $A B C$. Then the section of the sphere by the plane of the base $A B C$ is a circle inscribed in the equilateral triangle $A B C$. Therefore, points $N$, $M$, and $K$ are the midpoints of the sides of the base $A B C$ of the tetrahedron $A B C D$. The radii $O N, O M$, and $O K$ of the sphere are perpendicular to the planes of the faces $A B D, B C D$, and $A C D$, respectively, and pass through the midpoints of the segments $A B, B C$, and $A C$. Thus, point $O$ is equidistant from points $A, B$, and $C$. Therefore, point $O$ lies on the line $D Q$, where $Q$ is the center of the equilateral triangle $A B C$. Let $\angle M D O=\phi, A B=A D=a$. Then
$$
\begin{aligned}
& D M=A M=\frac{a \sqrt{3}}{2}, Q M=\frac{1}{3} A M=\frac{a \sqrt{3}}{6}, \sin \phi=\frac{Q M}{D M}=\frac{\frac{\alpha \sqrt{3}}{\frac{\pi}{2}}}{2}=\frac{1}{3},
\end{aligned}
$$
Therefore,
$$
O M=D M \operatorname{tg} \angle M D O=\frac{a \sqrt{3}}{2} \cdot \operatorname{tg} \phi=\frac{a \sqrt{3}}{2} \cdot \frac{1}{2 \sqrt{2}}=\frac{a \sqrt{6}}{8}=4 \sqrt{6} \cdot \frac{\sqrt{6}}{8}=3
$$
## Answer
3.00
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 [ Perpendicularity of a line and a plane (other).]
The base of the pyramid is an equilateral triangle with a side length of 6. One of the lateral edges is perpendicular to the base plane and equals 4. Find the radius of the sphere circumscribed around the pyramid.
#
|
Let $Q$ be the center of the base $ABC$ of the triangular pyramid $ABCD$, where the lateral edge $AD$ is perpendicular to the plane of the base, and $AB = BC = AC = a = 6$, $AD = h = 4$. The center $O$ of the sphere with radius $R$, circumscribed around the pyramid $ABCD$, lies on the line perpendicular to the plane of the base $ABC$ passing through the point $Q$, and also in the plane perpendicular to the line $AD$ and passing through the midpoint $P$ of the segment $AD$. The lines $AP$ and $OQ$ are parallel (since they are perpendicular to the same plane), and the quadrilateral $APOQ$ is a rectangle. In the right triangle $AOQ$, it is known that
$$
AQ = \frac{a \sqrt{3}}{3}, OQ = AP = \frac{h}{2}
$$
Therefore,
$$
R = OA = \sqrt{AQ^2 + OQ^2} = \sqrt{\left(\frac{a \sqrt{3}}{3}\right)^2 + \left(\frac{h}{2}\right)^2} = \sqrt{12 + 4} = 4
$$
## Answer
4.00
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A sphere with a radius of 1 is inscribed in a cone, the height of which is twice the diameter of the sphere. Find the ratio of the total surface area of the cone to the surface area of the sphere.
|
Consider the axial section of a cone with vertex $A$. We obtain an isosceles triangle $A B C$ with vertex $A$, in which a circle is inscribed, the center $O$ of which coincides with the center of the sphere inscribed in the cone. Let $M$ and $K$ be the points of tangency of the circle with the sides $B C$ and $A B$, respectively, and $P$ be the point of intersection of the circle with the height $A M$. Clearly, $M$ is the center of the base of the cone. Additionally,
$$
O K=O M=1, A P=P M=2, A O=A P+O P=2+1=3
$$
Let $\angle A B M=\angle A O K=\alpha$. Then
$$
\begin{gathered}
B M=\frac{A M}{\operatorname{kg} \angle A B M}=\frac{1}{B_{B 2}}=\frac{1}{2 \sqrt{2}}=\sqrt{2} \\
A B=\frac{B M}{m \angle A B M}=\frac{\sqrt{2}}{m \times B \Delta}=\frac{\sqrt{2}}{3}=3 \sqrt{2}
\end{gathered}
$$
Let $S$ be the total surface area of the cone, $l$ be the slant height of the cone, $r$ be the radius of the base, $R$ be the radius of the sphere, and $s$ be the surface area of the sphere. Then
$$
\begin{gathered}
S=\pi r l+\pi r 2=\pi r(l+r)=\pi \cdot B M \cdot(A B+B M)=\pi \cdot \sqrt{2}(3 \sqrt{2}+\sqrt{2})=8 \pi \\
s=4 \pi R 2=4 \pi \cdot O M 2=4 \pi
\end{gathered}
$$
Therefore, $\frac{\stackrel{5}{\Delta}}{\Delta}=\frac{8 \pi}{1 \pi}=2$.
## Answer
2.00
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.