problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
A metallic sphere with a radius of $\sqrt[z]{16}$ is recast into a cone, the lateral surface area of which is three times the area of the base. Find the height of the cone.
|
Let $R=\sqrt[3]{16}$ be the radius of the sphere, $V$ its volume, $r$ the radius of the base of the cone, $l$ the slant height, $h$ the height of the cone, $S$ the lateral surface area of the cone, and $s$ the area of its base. According to the problem,
$$
S=3 s, \text { or } \pi r l=3 \pi r^2 \text {, }
$$
$$
l=3 r, h^2=l^2-r^2=9 r^2-r^2=8 r^2, r^2=\frac{h^2}{8}
$$
According to the problem, the volume of the cone is equal to the volume of the sphere. Therefore,
$$
\begin{aligned}
& V=\frac{1}{3} \pi(\sqrt[3]{16})^3=\frac{1}{3} \cdot 16 \pi=\frac{16 \pi}{3} \\
& V=\frac{1}{3} \pi r^2 h=\frac{1}{3} \pi \cdot \frac{h^2}{8} \cdot h=\frac{\pi h^3}{24}
\end{aligned}
$$
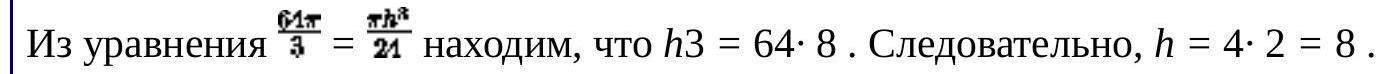
# Answer
8.00
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Khachaturyan A.V.
A rectangular sheet of paper was folded, aligning a vertex with the midpoint of the opposite shorter side (see figure). It turned out that triangles I and II are equal. Find the longer side of the rectangle if the shorter side is 8.

#
|
Let's mark the equal segments (see fig. - here we used the fact that in congruent triangles, sides opposite equal angles are equal).
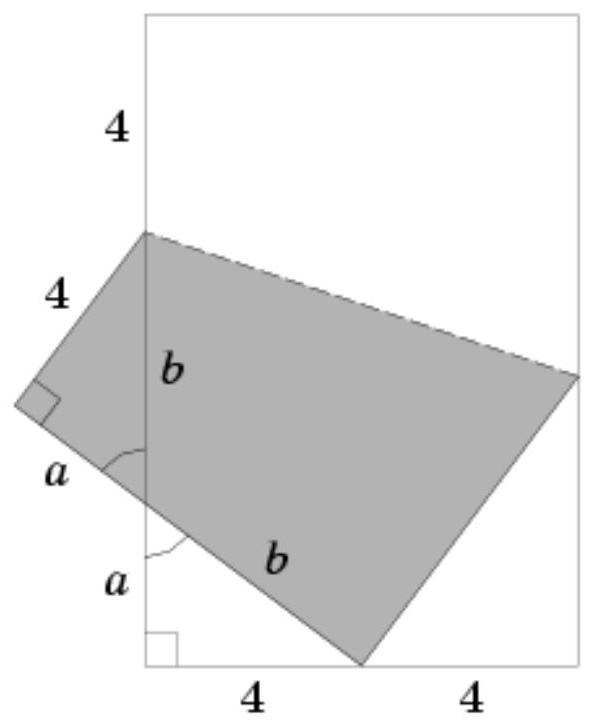
We see that the length of the smaller side is $a+b$. Therefore, $a+b=8$ and the larger side has a length of $a+b+4=$ $8+4=12$.
## Answer
12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On side $A B$ of triangle $A B C$, a point $K$ is marked. Segment $C K$ intersects the median $A M$ of the triangle at point $P$. It turns out that $A K = A P$.
Find the ratio $B K: P M$.
|
The first method. Draw a line through point $M$ parallel to $C K$, which intersects $A B$ at point $D$ (left figure). By Thales' theorem, $B D=K D$. By the theorem of proportional segments, $P M=K D=1 / 2 B K$.
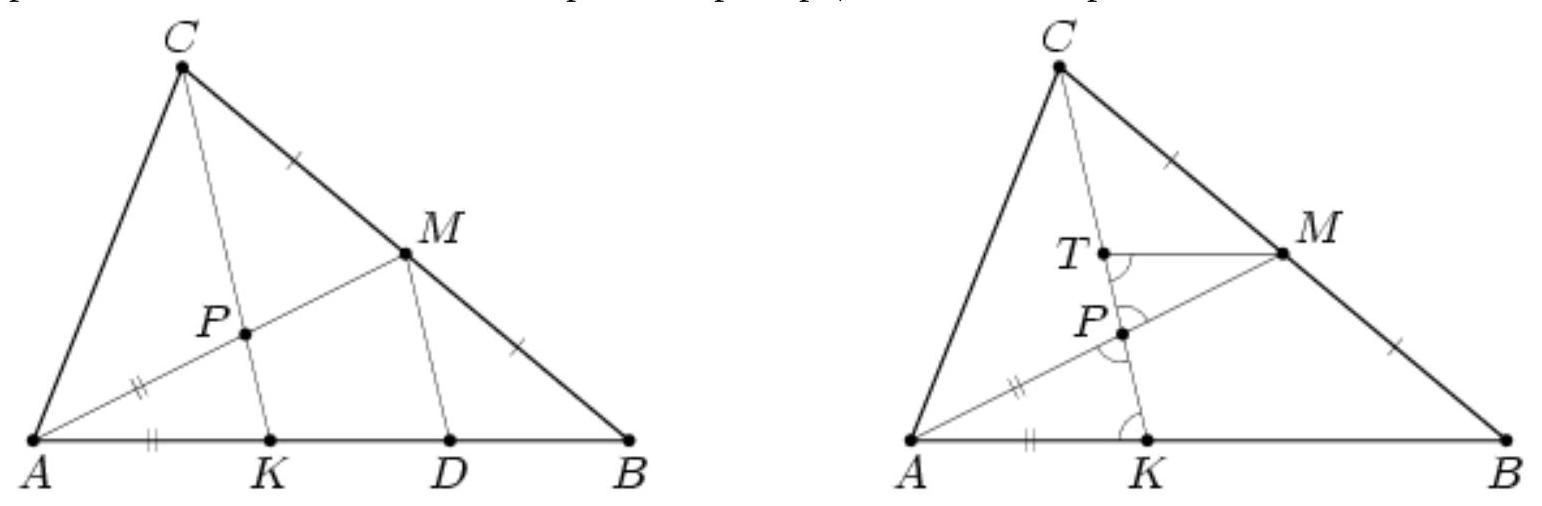
The second method. Let $T$ be the midpoint of segment $C K$ (right figure). $M T$ is the midline of triangle $C B K$, hence $M T \| B K$ and $B K=2 M T$. Triangles $K A P$ and $T M P$ are obviously similar, so $M P=M T=1 / 2 B K$.
## Answer
$B K: P M=2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a quadrilateral pyramid $S A B C D$, the base is a trapezoid $A B C D (B C \| A D), B C=\frac{4}{5} A D, \angle A S D=\angle$ $C D S=\frac{\pi}{2}$. All vertices of the pyramid lie on the circles of the bases of a cylinder, the height of which is 2, and the radius of the base is $\frac{\frac{5}{3}}{3}$. Find the volume of the pyramid.
|
If vertices $A$ and $D$ are located on different bases of the cylinder, then by the theorem of the intersection of two parallel planes by a third plane, $A B \| C D$, i.e., $A B C D$ is a parallelogram, not a trapezoid. Let vertices $A$ and $D$ be located on the circumference of one base of the cylinder. Then the median $S M$ of the right triangle $A S D$ is equal to half the hypotenuse $A D$, and thus is less than the radius of the base circle of the cylinder, i.e., $S M < \frac{5}{3}$. If $S M > \frac{5}{3}$, then point $S$ cannot lie on the circumference of the other base. Therefore, in this case, the right triangle $A S D$ is inscribed in the base circle of the cylinder, and then $A D$ is the diameter of the circle. In this case, points $B$ and $C$ lie on the circumference of the other base of the cylinder. Let $B_1$ and $C_1$ be the orthogonal projections of points $B$ and $C$ onto the plane of the base of the cylinder containing points $A, D$, and $S$.
Since $C D \perp S D$, by the theorem of three perpendiculars, $C_1 D \perp S D$, and since $A S \perp S D$, then $C_1 D \| A S$, so $A S D C_1$ is a rectangle. Since $B_1 C_1 \| B C$, the quadrilateral $A B_1 C_1 D$ is an isosceles trapezoid, so $A B_1 = D C_1 = S A$, which means the diameter $A D$ is perpendicular to the chord $S B_1$ and passes through its midpoint $K$. The segment $S C_1$ is the diagonal of the rectangle $A S D C_1$, so $S C_1$ is the diameter of the base circle of the cylinder, $S C_1 = A D = \frac{10}{3}$, and since
$$
B_1 C_1 = B C = \frac{4}{5} A D = \frac{4}{5} \cdot \frac{10}{3} = \frac{8}{3}
$$
then
$$
S K = \frac{1}{2} S B_1 = \frac{1}{2} \sqrt{S C_1^2 - B_1 C_1^2} = \frac{1}{2} \sqrt{\left(\frac{10}{3}\right)^2 - \left(\frac{8}{3}\right)^2} = 1
$$
By the theorem of three perpendiculars, $B K \perp A D$, i.e., $B K$ is the height of the trapezoid $A B C D$. From the right triangle $B K B_1$, we find that
$$
B K = \sqrt{B B_1^2 + K B_1^2} = \sqrt{4 + 1} = \sqrt{5}
$$
Therefore,
$$
S_{A B C D} = \frac{1}{2} (A D + B C) \cdot B K = \frac{1}{2} \left(\frac{10}{3} + \frac{8}{3}\right) \cdot \sqrt{5} = 3 \sqrt{5}
$$
Let $H$ be the foot of the perpendicular dropped from point $S$ to the line $B K$. Then $S H$ is the height of the pyramid $S A B C D$, since $S H \perp B K$ and $S H \perp A D$. Writing the area of triangle $B K S$ in two ways, we get
$$
S H = \frac{S K \cdot B B_1}{B K} = \frac{1 \cdot 2}{\sqrt{5}} = \frac{2}{\sqrt{5}}
$$
Therefore,
$$
V_{S A B C D} = \frac{1}{3} S_{A B C D} \cdot S H = \frac{1}{3} \cdot 3 \sqrt{5} \cdot \frac{2}{\sqrt{5}} = 2
$$
## Answer
2.00
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Angle Bisectors, Concurrency Problem $\underline{115562}$ topics: [Area of a Triangle (using semiperimeter and radius of inscribed or exscribed circle [ Inscribed, circumscribed, and exscribed circles; their radii
A circle with center $O$, inscribed in triangle $A B C$, touches its sides $A B$ and $A C$ at points $M$ and $N$. A circle with center $Q$ is inscribed in triangle $A M N$. Find $O Q$, if $A B=13, B C=15$ and $A C=14$.
#
|
Let $r$ be the radius of the circle inscribed in triangle $ABC$, and $p$ be the semiperimeter of triangle $ABC$. Then,
$$
p=\frac{AB+BC+AC}{2}=\frac{13+14+15}{2}=21
$$
By Heron's formula,
$$
S_{\triangle ABC}=\sqrt{p(p-AB)(p-BC)(p-AC)}=\sqrt{21 \cdot 8 \cdot 6 \cdot \bar{i}}=84
$$
Thus,
$$
r=\frac{S_{\triangle A}+BC}{p}=\frac{84}{21}=4
$$
We will prove that the center $Q$ of the circle inscribed in triangle $AMN$ lies on the inscribed circle of triangle $ABC$. Indeed, let $Q'$ be the midpoint of the smaller arc $MN$ of the inscribed circle of triangle $ABC$. From the theorem about the angle between a tangent and a chord, it follows that
$$
\angle AMQ'=\angle MNQ'=\angle NMQ'
$$
Therefore, $MQ'$ is the angle bisector of $\angle AMN$. Similarly, $NQ'$ is the angle bisector of $\angle ANM$, so $Q'$ is the point of intersection of the angle bisectors of triangle $AMN$, i.e., the center of the inscribed circle of this triangle. Thus, point $Q'$ coincides with point $Q$.
Therefore, $OQ=r=4$.
Answer
## 4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$[$ Properties of Sections $]$ $[$ Tetrahedron and Pyramid $]$
The base of a quadrilateral pyramid $S A B C D$ is a parallelogram $A B C D$. 1) Construct the section of the pyramid by a plane passing through the midpoint of edge $A B$ and parallel to the plane $S A D$. 2) Find the area of the resulting section if the area of face $S A D$ is 16.
|
1) Let $M$ be the midpoint of edge $A B$. According to the theorem of the intersection of two parallel planes by a third intersecting plane, the intersecting plane intersects the plane of face $A S B$ along a line parallel to $A S$, i.e., along the midline $M N$ of triangle $A S B$. Similarly, the intersecting plane intersects the faces $A B C D$ and $C S D$ along lines parallel to $A D$ and $S D$ respectively. Therefore, the points $N, L$, and $K$ where the intersecting plane intersects the edges $S B, C D$, and $S C$ are the midpoints of segments $S B, C D$, and $S C$ respectively, and the desired section is the trapezoid $M N K L$. 2) Let the lines $M N$ and $L K$, lying in the intersecting plane, intersect at point $Q$. Then point $Q$ lies on the line of intersection of the planes $A S B$ and $C S D$, drawn through two parallel lines $A B$ and $C D$, i.e., on the line passing through point $S$ parallel to lines $A B$ and $C D$. Triangle $M Q L$ is equal to triangle $A S D$ (by three sides), and $N K$ is the midline of triangle $M Q L$ (since $N K \| M L$ and $N K=\frac{1}{2} B C=\frac{1}{2} M L$). Triangle $N Q K$ is similar to triangle $M Q L$ with a similarity ratio of $\frac{1}{2}$, so
$$
S_{\triangle N Q K}=\frac{1}{\mathbf{4}} S_{\triangle M Q L}=\frac{1}{\mathbf{4}} S_{\triangle A S D}=\frac{16}{4}=4 .
$$
$$
S_{M N K L}=S_{\triangle M Q L}-S_{\triangle N Q K}=16-4=12
$$
## Answer
12.00
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Area and Volume (Extremum Problems).]
Consider all possible rectangular parallelepipeds whose bases are squares and each of whose lateral faces has a perimeter of 6. Find among them the parallelepiped with the greatest volume and calculate this volume.
|
Let's denote the side of the base of the rectangular parallelepiped by $x$. Then its lateral edge is $\frac{1}{2}(6-2 x) = 3 - x$. If $V(x)$ is the volume of the parallelepiped, then
$$
V(x) = x^2 (3 - x),
$$
so the problem reduces to finding the maximum value of the function $V(x) = x^2 (3 - x)$ on the interval $(0 ; 3)$.
Let's find the critical points of the function $V(x) = x^2 (3 - x)$ on the interval $(0 ; 3)$. For this, we solve the equation
$$
V'(x) = (3x^2 - x^3)' = 6x - 3x^2 = 3x(2 - x) = 0
$$
The interval $(0 ; 3)$ contains the only root of this equation, $x = 2$. On this interval, $V'(x)$ is positive for $x < 2$ and negative for $x > 2$, so the function $V(x)$ is increasing on the interval $(0 ; 2)$ and decreasing on the interval $(2 ; 3)$. Therefore, $x = 2$ is the point of maximum of the function. Consequently, $V(2) = 4$ is the maximum volume of the parallelepiped.
## Second Method.
Applying the Cauchy inequality for three numbers, we get
$$
\begin{aligned}
V(x) & = x^2 (3 - x) = 4 \cdot \frac{1}{2} x \cdot \frac{1}{2} x \cdot (3 - x) \leq \\
& \leq 4 \cdot \left( \frac{\frac{1}{2} x + \frac{1}{2} x + (3 - x)}{3} \right)^3 = 4
\end{aligned}
$$
with equality if $\frac{1}{2} x = 3 - x$, i.e., when $x = 2$. Therefore, the maximum volume of the parallelepiped is 4.
## Answer
4.00
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\begin{array}{l}{[\text { Problems on maximum and minimum (miscellaneous). }} \\ {[\quad \underline{\text { Rectangular parallelepipeds }}]}\end{array}\right]$
Consider all possible rectangular parallelepipeds, each with a volume of 4, and whose bases are squares. Find among them the parallelepiped with the smallest perimeter of the lateral face and calculate this perimeter.
|
Let $x$ be the side of the base of a rectangular parallelepiped. Then its lateral edge is $\frac{4}{x^{2}}$. If $P(x)$ is the perimeter of the lateral face of the parallelepiped, then
$$
P(x)=\frac{B}{x^{2}}+2 x
$$
Thus, the problem reduces to finding the minimum value of the function $P(x)=\frac{8}{x^{2}}+2 x$ on the ray $(0 ;+\infty)$.
## First Method.
We find the critical points of the function $P(x)=\frac{8}{x^{2}}+2 x$ on the ray $(0 ;+\infty)$.
$$
P^{\prime}(x)=-\frac{16}{x^{3}}+2=\frac{2\left(-x^{3}\right)}{x^{3}}=0
$$
The ray $(0 ;+\infty)$ contains the unique root of this equation $x=2$. On this ray, when $x>2$, the derivative is positive, so the function $P(x)$ decreases on the interval $(0 ; 2)$ and increases on the interval $(2; +\infty)$. Therefore, $x=2$ is a point of minimum of the function. Consequently, $P(2)=6$ is the minimum value of the perimeter of the lateral face of the parallelepiped.
## Second Method.
Applying the Cauchy inequality to three numbers, we get that
$$
P(x)=\frac{8}{x^{2}}+2 x=\frac{8}{x^{2}}+x+x \geqslant 3 \sqrt[3]{\frac{8}{x^{2}} \cdot x \cdot x}=6
$$
with equality if $\frac{8}{x^{2}}=x$, i.e., when $x=2$. Therefore, the minimum value of the perimeter of the lateral face of the parallelepiped is 6.
## Answer
The parallelepiped, whose base side is 2, has a lateral edge of 1; the sought perimeter is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11 Find the volume of a rectangular parallelepiped, the areas of the diagonal sections of which are equal to $\sqrt{13}, 2 \sqrt{10}$ and $3 \sqrt{5}$
|
Let $A B C D A 1 B 1 C 1 D 1$ be a rectangular parallelepiped, and
$$
S_{B B} 1 D 1 D=\sqrt{13}, S_{C D A} 1 B 1=2 \sqrt{10}, S_{A D C} 1 B 1=3 \sqrt{5}
$$
Denote $A B=x, B C=y, A A 1=z$. Then
$$
B D 2=x 2+y 2, A 1 D 2=y 2+z 2, A B 1=x 2+z 2
$$
Since $B B 1 D 1 D, C D A 1 B 1$, and $A D C 1 B 1$ are rectangles with areas $\sqrt{13}, 2 \sqrt{10}$, and $3 \sqrt{5}$, respectively, we have
$$
\begin{aligned}
& \sqrt{13}=S(B B 1 D 1 D)=B D \cdot B B 1=\sqrt{x^{2}+y^{2}} \cdot z \\
& 2 \sqrt{10}=S(C D A 1 B 1)=C D \cdot A 1 D=\sqrt{y^{2}+z^{2}} \cdot x \\
& 3 \sqrt{5}=S(A D C 1 B 1)=A B 1 \cdot A D=\sqrt{x^{2}+z^{2}} \cdot y
\end{aligned}
$$
From this, we obtain the system of equations
$$
\left\{\begin{array}{l}
\left(x^{2}+y^{2}\right) z^{2}=13 \\
\left(y^{2}+z^{2}\right) x^{2}=40 \\
\left(x^{2}+z^{2}\right) y^{2}=45
\end{array}\right.
$$
or
$$
\left\{\begin{array}{l}
x^{2} z^{2}+y^{2} z^{2}=13 \\
x^{2} y^{2}+x^{2} z^{2}=40 \\
x^{2} y^{2}+z^{2} y^{2}=45
\end{array}\right.
$$
Adding the first and second equations term by term and subtracting the third, we get
$$
2 x 2 z 2=8, x 2 z 2=4, x z=2 \text {. }
$$
Similarly, $x y=6$ and $y z=3$. Therefore,
$$
V 2_{A B C D A} 1 B 1 C 1 D 1=x 2 y 2 z 2=x y \cdot y z \cdot x z=6 \cdot 3 \cdot 2=36
$$
$$
V_{A B C D A} 1 B 1 C 1 D 1=6
$$
## Answer
6.00
## Problem
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The center of a circle touching the legs $A C$ and $B C$ of a right triangle $A B C$ lies on the hypotenuse $A B$. Find the radius of the circle, if it is six times smaller than the sum of the legs, and the area of triangle $A B C$ is 27.
|
Let $O$ be the center of the circle, $M$ and $N$ be the points of tangency with the legs $A C$ and $B C$ respectively. Then $O M$ and $O N$ are the altitudes of triangles $A O C$ and $B O C$. Let $B C=a, A C=b, O M=O N=r$. According to the problem, $a+b=6 r$. Then
$$
27=S_{\triangle A B C}=S_{\triangle A O C}+S_{\triangle B O C}=\frac{1}{2} a r+\frac{1}{2} b r=\frac{1}{2}(a+b) r=3 r 2,
$$
from which we find that
$$
r 2=\frac{27}{3}=9, r=3
$$
## Answer
3.00
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On the side $A D$ of the inscribed quadrilateral $A B C D$, there is the center of the circle that touches the other three sides of the quadrilateral. Find $A D$, if $A B=2$ and $C D=3$.
#
|
Prove that $A D=A B+C D$.
## Answer
5.
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Sum of angles in a triangle. Theorem about the exterior angle. ] [ Criteria and properties of an isosceles triangle. ]
In triangle $A B C$, angle $C$ is three times angle $A$. A point $D$ is taken on side $A B$ such that $B D=B C$.
Find $C D$, if $A D=4$.
|
Let $\angle A=\alpha, \angle A C D=\varphi$, then $\angle C=3 \alpha, \angle B C D=\alpha+\varphi$. Therefore, $\varphi+(\alpha+\varphi)=3 \alpha$, that is, $\varphi=\alpha$. Thus, triangle $A D C$ is isosceles with base $A C$. Therefore, $C D=A D=4$.
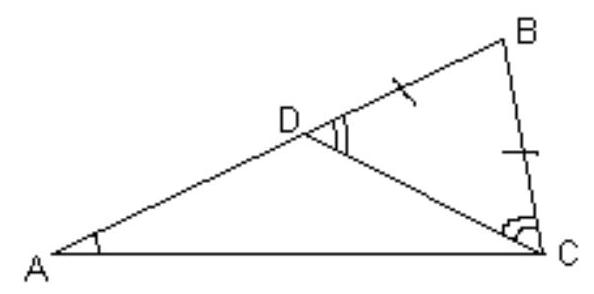
Answer
$C D=4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9 | |
Segments $A M$ and $B H$ are the median and altitude of an acute triangle $A B C$, respectively. It is known that $A H=1$ and $2 \angle M A C=\angle M C A$. Find the side $B C$.
|
Let $\angle M A C=\alpha$. Then $\angle M C A=2 \alpha$. Segment $H M$ is the median of the right triangle $B H C$, drawn from the vertex of the right angle. Therefore, $H M=M C$. Triangle $C M H$ is isosceles, so $\angle C H M=\angle M C H=2 \alpha$.
By the external angle theorem of a triangle, $\angle A H M=\angle C H M-\angle M A C=\alpha$.
Therefore, triangle $A H M$ is also isosceles, $H M=A H=1$. Consequently, $B C=2 H M=2$.
## Answer
2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11
Find the length of the shortest path on the surface of a unit regular tetrahedron between the midpoints of its opposite edges.
#
|
Let $M$ and $N$ be the midpoints of the opposite edges $A B$ and $C D$ of a regular tetrahedron $A B C D$ (Fig.1), and the path between $M$ and $N$ intersects the edge $A C$. Consider the net of the tetrahedron, consisting of four equilateral triangles: $A B C, D_1 A B, D_2 A C$, and $D_3 B C$ (Fig.2). Then the shortest path sought is the shortest path between the midpoint $M$ of segment $A B$ and the midpoint $N'$ of segment $D_2 C$. The length of this path is 1. Similarly, for the shortest paths intersecting the edges $A D, C D$ or $B D$. All other possible paths are obviously longer.
## Answer
1.00
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9
[ Ratio in which the bisector divides the side ]
In an isosceles triangle $A B C$, a rhombus $D E C F$ is inscribed such that vertex $E$ lies on side $B C$, vertex $F$ on side $A C$, and vertex $D$ on side $A B$. Find the length of the side of the rhombus if $A B=B C=12, A C=6$.
|
Let $x$ be the side of the rhombus. Since $D E \| A C$, triangles $D B E$ and $A B C$ are similar. Therefore, $B E: B C=D E: A C$, or $12-x / 12=x / 6$. From this, $x=4$.
## Answer
4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the square $A B C D$ with side 1, point $F$ is the midpoint of side $B C$, and $E$ is the foot of the perpendicular dropped from vertex $A$ to $D F$.
Find the length of $B E$.
#
|
Extend segment $D F$ to intersect line $A B$ at point $K$ (see figure). Right triangles $K B F$ and $D C F$ are equal (by leg and acute angle), so $K B = D C$. Therefore, $E B$ is the median of the right triangle $A E K$, drawn to the hypotenuse, hence $B E = 1 / 2 A K = 1$.
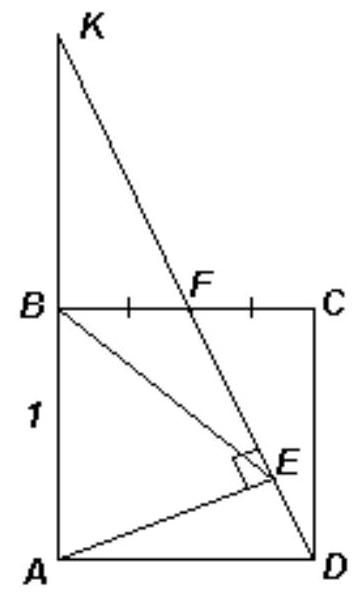
## Answer
1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$:$ Folkpor
In trapezoid $A B C D(A D \| B C)$, from point $E$ - the midpoint of $C D$, a perpendicular $E F$ to line $A B$ is drawn. Find the area of the trapezoid if $A B=5, E F=4$.
|
It is sufficient to prove that the area of the trapezoid is twice the area of triangle $ABE$ (which is 10). The first method. Draw a line through point $E$ parallel to the side $AB$, and mark the points $P$ and $Q$ where it intersects the lines $AD$ and $BC$ respectively (see figure).
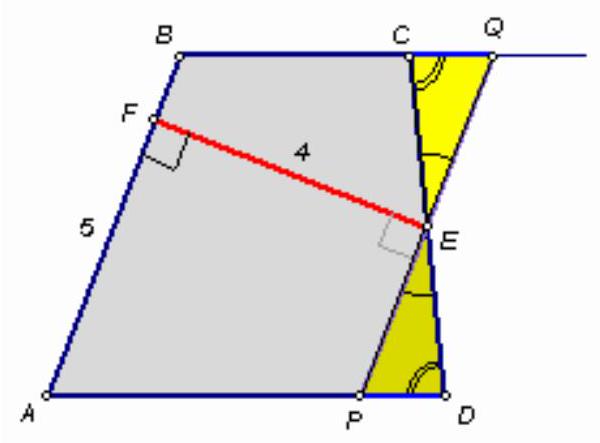
$ABQP$ is a parallelogram. Moreover, triangles $PED$ and $QEC$ are equal (by side and two adjacent angles), so their areas are equal. Thus, $S_{ABCD}=S_{ABQP}=2S_{ABE}$.
The second method. Let $G$ be the intersection point of the lines $BE$ and $AD$. Triangles $BEC$ and $GED$ are equal, so $S_{ABCD}=S_{ABG}=2S_{ABE}$.
The third method. See the solution to problem 54964.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The area of a triangle is $6 \sqrt{6}$, its perimeter is 18, and the distance from the center of the inscribed circle to one of the vertices is $\frac{2 \sqrt{42}}{3}$. Find the smallest side of the triangle.
|
If the inscribed circle touches the side $A C$ of triangle $A B C$ at point $M$, and $p$ is the semiperimeter of the triangle, then $A M=p-B C$. Use this equality, and then apply the Law of Cosines.
## Solution
Let $O$ be the center of the circle inscribed in the given triangle $A B C$, $r$ its radius, $S=6 \sqrt{6}$ the area, $2 p=$ 18 the perimeter, and $M$ the point of tangency with side $A C$.
Since $S=p \cdot r$, then
$$
r=\frac{S}{p}=\frac{12 \sqrt{6}}{9}=\frac{2 \sqrt{6}}{3}
$$
$$
A M=\sqrt{A O^{2}-O M^{2}}=\sqrt{\left(\frac{2 \sqrt{42}}{3}\right)^{2}-\left(\frac{2 \sqrt{6}}{3}\right)^{2}}=\frac{2}{3} \cdot \sqrt{42-6}=4
$$
From the equality $A M=p-B C$, we find that $B C=9-4=5$. Let $C M=x$. From the equality $C M=p-A B$, we find that $A B=p-C M=9-x$.
By Heron's formula
$$
S=\sqrt{p(p-B C)(p-A C)(p-A B)} \text {, or } 6 \sqrt{6}=\sqrt{9 \cdot 4 \cdot(5-x) \cdot x} \text {. }
$$
From this equation, we find that $x=2$ or $x=3$. In the first case, $A B=7, A C=6$. In the second case, $A B=6, A C=7$. Therefore, in each of these cases, the side $B C=5$ is the smallest.
Answer
5. Send a comment
Problem
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { by Banov I.S }}$
The height and the radius of the base of a cylinder are equal to 1. What is the smallest number of spheres with a radius of 1 that can completely cover this cylinder?
|
We will inscribe an equilateral triangle in the cylinder with its vertices at the midpoints of the generators and consider three unit spheres with centers at the midpoints of its sides. Taking the base of the cylinder, our spheres intersect it in three circles of radius $\sqrt{3} / 2$ with centers at the midpoints of the sides of the inscribed equilateral triangle. It is easy to verify that these three circles completely cover the base.
Thus, the cylinder is entirely covered by three cylinders of height 1 built on these circles, and consequently, by our spheres containing these cylinders.
To show that the cylinder cannot be covered by two spheres, it is sufficient to note that if the center of a sphere does not coincide with the center of the base, then the circle where the sphere intersects the base plane intersects the boundary of the base along an arc less than $180^{\circ}$, and two such arcs cannot cover the circumference.
If the centers of the two spheres coincide with the centers of the bases, then the lateral surface of the cylinder remains uncovered.
## Answer
Three.
Send a comment
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Completion of a Tetrahedron to a Parallelepiped]
On the faces of a regular tetrahedron with edge $a$, equal regular pyramids are constructed. The plane angles at the vertices of these pyramids, opposite to the faces of the tetrahedron, are right angles. Consider the polyhedron formed by the tetrahedron and the constructed pyramids. How many faces does this polyhedron have? What is it called?
|
Consider the cube $A B C D A 1 B 1 C 1 D 1$. All edges of the triangular pyramid $A C B 1 D 1$ are equal. Therefore, this pyramid is a regular tetrahedron. On the lateral faces of the regular tetrahedron $A C B 1 D 1$ as bases, regular triangular pyramids $D A C D 1$ with vertex $D$, $A 1 A B 1 D 1$ with vertex $A 1$, $B A B 1 C$ with vertex $B$, and $C 1 C B 1 D 1$ with vertex $C 1$ are constructed. The planar angles at the vertices of these four pyramids are each $90^{\circ}$. Conversely, for any regular tetrahedron, there exists a unique cube, the intersecting diagonals of opposite faces of which are the edges of the given regular tetrahedron (it is sufficient to draw three pairs of parallel planes through the intersecting diagonals of opposite faces of the tetrahedron). On the lateral face of this tetrahedron as a base, an external unique regular triangular pyramid can be constructed, the planar angles at the vertex of which are right angles. It is clear that the lateral faces of such a pyramid lie in the faces of the cube.
## Answer
6 faces; cube.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Inscribed Quadrilaterals (Miscellaneous)]
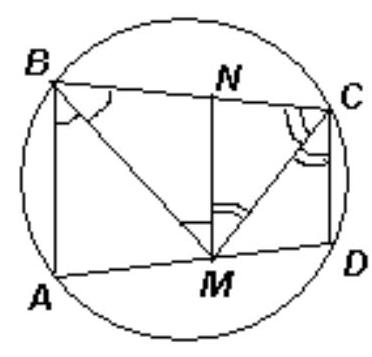
Quadrilateral $ABCD$ is inscribed in a circle. The bisectors of angles $B$ and $C$ intersect at a point lying on the segment $AD$.
Find $AD$, if $AB=5, CD=3$.
|
Let $M$ be the point of intersection of the bisectors of angles $B$ and $C$.
First method. Denote: $\angle A B C=2 \alpha, \angle B C D=2 \beta$, then $\angle A D C=180^{\circ}-2 \alpha, \angle B A D=180^{\circ}-2 \beta$ (see fig.).
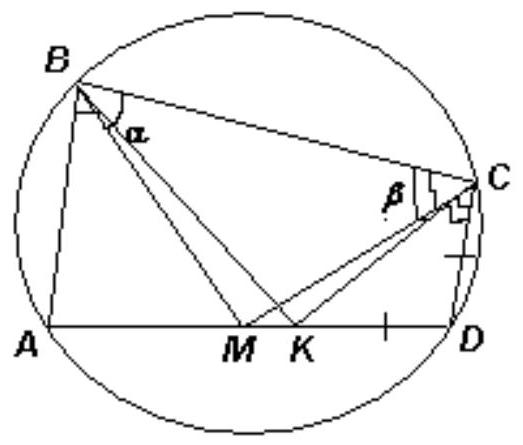
If $\alpha \beta$, a similar reasoning can be applied by marking a segment $A K$ on ray $A D$ equal to $A B$. The case $\alpha=\beta$ is impossible, otherwise $A B C D$ would be an isosceles trapezoid ($A B=D C$), which contradicts the condition.
Second method. Consider two cases.
1) $A B \| D C$. Then $A B C D$ is an isosceles trapezoid ($B C=A D$, see fig.). Draw $M N \| A B$. From the equality of alternate interior angles, we get:
$B N=N M=N C$, so $M N$ is the midline of the trapezoid, that is, $M N=1 / 2(A B+D C)$. Therefore, $A D=B C=$ $2 M N=A B+C D=8$.
2) $A B$ intersects $D C$ at point $T$. Then $M$ is either the center of the inscribed circle of triangle $B T C$, or the center of the excircle of this triangle (see fig.). Since the reasoning in both cases is completely analogous, we will consider only the second one.
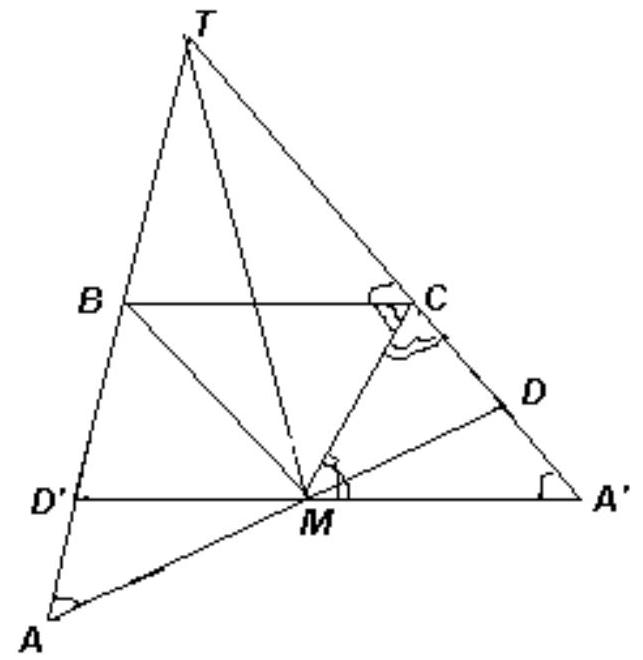
Let segment $A^{\prime} D^{\prime}$ be symmetric to side $A D$ with respect to the bisector $T M$ of angle $B T C$. Then $\angle D A^{\prime} M=\angle D^{\prime} A M$ $=\angle T C B$: since $A B C D$ is a cyclic quadrilateral, $A^{\prime} D^{\prime} \| B C$. From the equality of alternate interior angles, we get that $A^{\prime} M^{\prime}=A^{\prime} C$. Similarly, $D^{\prime} M=D^{\prime} B$, and also $A D^{\prime}=A^{\prime} D$ (from symmetry). Thus, $A D$ $=A^{\prime} D^{\prime}=A^{\prime} M+D^{\prime} M=A^{\prime} C+D^{\prime} B=A B+C D=8$.
## Answer
$A D=8$.
## Author: Lopatnikov A.A.
Can all cells of an infinite grid be colored in white and black so that each vertical line and each horizontal line intersect a finite number of white cells, and each slanted line intersects a finite number of black cells?
## Solution
Introduce a coordinate system $Oxy$ such that the vertical and horizontal grid lines have equations $x=n$ and $y=m$ ($n$ and $m$ are integers). Color black those and only those cells, all points of which satisfy one of the inequalities $|y| \geq x^{2}$ or $|x| \geq y^{2}$ (see fig.), and color the remaining cells white.
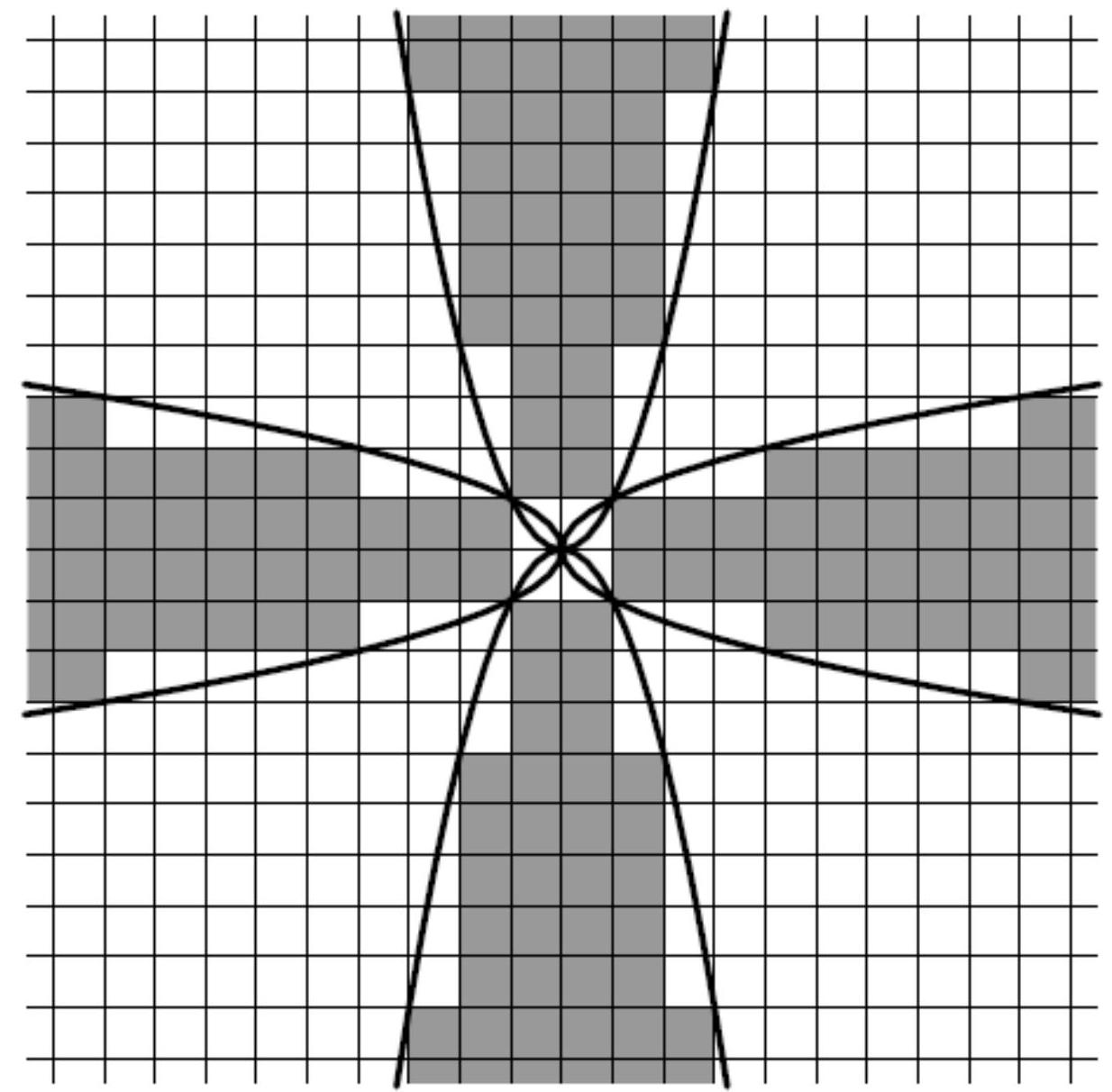
Every vertical line will intersect a finite number of white cells between the parabolas $y= \pm x^{2}$, and every horizontal line will intersect a finite number of white cells between the parabolas $y= \pm x^{2}$. Every slanted line will intersect only a finite number of black cells, as its intersection with each of the four "black" regions can be either empty, a point, or a segment.
## Answer
Yes, it is possible.
Submit a comment
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shmarov V.
On a circle, $2 N$ points are marked ($N$ is a natural number). It is known that through any point inside the circle, no more than two chords with endpoints at the marked points pass. We will call a matching a set of $N$ chords with endpoints at the marked points such that each marked point is the endpoint of exactly one of these chords. We will call a matching even if the number of points where its chords intersect is even, and odd otherwise. Find the difference between the number of even and odd matchings.
|
Let the marked points be $A_{1}, A_{2}, \ldots, A_{2 N}$ in the order of clockwise traversal of the circle. We will prove by induction on $N$ that the number of even matchings is one more than the number of odd matchings. For $N=1$, the statement is obvious: there is only one matching, and it is even.
Inductive step. First method. Suppose in the matching there is a chord $A_{1} A_{i}$ and it is intersected by exactly $k$ chords.
Consider the points $A_{2}, \ldots, A_{i-1}$; exactly $k$ of them are endpoints of chords intersecting $A_{1} A_{i}$. The remaining $i-2-k$ points are paired by chords that do not intersect $A_{1} A_{i}$. Thus, the number $i-2-k$ is even, meaning that the numbers $i$ and $k$ have the same parity.
We divide all matchings into $2 N-1$ groups $\Pi_{2}, \ldots, \Pi_{2 N}$: the group $\Pi_{i}$ will contain those matchings in which point $A_{1}$ is connected to $A_{i}$. Remove the chord $A_{1} A_{i}$ from each matching in $\Pi_{i}$; we will get all possible matchings on the remaining $2 N-2$ points. By the inductive hypothesis, among them, there are one more even matchings than odd ones. If $i$ is even, the parity of the matching does not change upon removal, and if $i$ is odd, it changes. Therefore, in each of the $N$ sets $\Pi_{2}, \ldots, \Pi_{2 N}$, there are one more even matchings than odd ones, and in each of the $N-1$ sets $\Pi_{3}, \ldots, \Pi_{2 N-1}$, there are one more odd matchings than even ones. In total, there are one more even matchings than odd ones, $N-(N-1)=1$.
Second method. Consider all matchings in which $A_{2 N-1}$ and $A_{2 N}$ are connected by a chord. This chord does not intersect any other. Therefore, by removing it from each of the considered matchings, we will get all matchings on the points $A_{1}, \ldots, A_{2 N-2}$, and the parity of each of them will be preserved. By the inductive hypothesis, among our matchings, there are one more even matchings than odd ones.
It remains to prove that among the remaining matchings, there are an equal number of even and odd ones. Consider any of them; suppose it contains chords $A_{2 N-1} A_{i}$ and $A_{2 N} A_{k}$. Replace these chords with $A_{2 N} A_{i}$ and $A_{2 N-1} A_{k}$. In this case, if the original chord intersected with some other, then the new chord will also intersect with it. On the other hand, if the chords $A_{2 N-1} A_{i}$ and $A_{2 N} A_{k}$ did not intersect, then the new chords will intersect, and vice versa. Thus, we have divided the remaining matchings into pairs of different parities.
## Answer
1.
Submit a comment
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
The plan of the palace of the Shah is a $6 \times 6$ square, divided into rooms of size $1 \times 1$. In the middle of each wall between the rooms, there is a door. The Shah said to his architect: "Knock down some of the walls so that all rooms become $2 \times 1$, no new doors appear, and the path between any two rooms passes through no more than $N$ doors." What is the smallest value of $N$ that the Shah should name to make it possible to fulfill the order?
|
Consider an arbitrary path from the bottom-left corner of the palace to the top-right corner. Since one needs to "climb" 5 horizontal levels and "move right" 5 vertical levels, one has to pass through at least 10 doors, visiting at least 11 rooms (including the starting and ending rooms).
11 rooms of size $1 \times 1$ could not have been transformed into 5 rooms of size $2 \times 1$. Therefore, the same path in the reconstructed palace must pass through at least 6 rooms, and thus through at least 5 doors. Such a reconstruction of the palace is indeed possible (see the diagram).
| 2 | 2 | 2 | 2 | 2 |
| :---: | :---: | :---: | :---: | :---: |
| | | 1 | | |
| | | | | 1 |
| | | | | 1 |
| 2 | 9 | 1 | 2 | 19 |
| | | 2 | | |
In this case, it is indeed possible to get from any room to any other room by passing through no more than 5 doors. Let's denote the central rooms with the number 0, the rooms connected to them by a door with the number 1, and the rooms connected by a door to the rooms of "type" 1 with the number 2. Since all rooms have been labeled, one can get from any room to one of the central rooms by passing through no more than two doors. Therefore, one can get from any room to any other room by constructing a path through the central rooms and thus passing through no more than 5 doors (the fifth door would be needed if one has to move from one central room to another).
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Rubaev I.S.
There is a square grid paper with a size of $102 \times 102$ cells and a connected figure of unknown shape, consisting of 101 cells. What is the maximum number of such figures that can be guaranteed to be cut out from this square? A figure composed of cells is called connected if any two of its cells can be connected by a chain of its cells, in which any two adjacent cells share a common side.
|
Lemma. Any connected figure composed of 101 cells can be enclosed in a rectangle with sides \(a\) and \(b\) such that \(a + b = 102\).
Take two cells of our figure that share a common side. They form a rectangle \(1 \times 2\), the sum of whose sides is 3. Due to the connectivity of the given figure, there will be a cell in it that is adjacent to this rectangle along a side. Attach this cell to the rectangle. The resulting configuration of three cells can be enclosed in a rectangle with the sum of sides equal to 4, if one of the sides of the rectangle \(1 \times 2\) is extended by 1. We will repeat this procedure until the configuration includes all the cells of the figure. The procedure will be performed no more than 99 times, so the sum of the sides of the rectangle in which the figure will eventually be enclosed will be no more than 102.
From the lemma, it immediately follows that four figures equal to the given one can always be cut out: for this, it is sufficient to enclose it in a rectangle with the sum of sides 102, and then cut out four such rectangles from the given square as shown in the figure. Now consider a figure in the shape of a cross, each arm of which consists of 25 cells. It contains \(4 \times 25 + 1 = 101\) cells.
If such a cross is cut out from a square, its center must lie outside a border 25 cells wide, adjacent to the boundary of the square. This means that this center must lie within a square of side 52, obtained after removing the border. Divide this square into four equal squares with side 26.
It is easy to see that if several non-overlapping crosses are cut out from a sheet of paper, then in each of these four squares, the center of only one cross can be located (otherwise, two crosses will overlap).
Therefore, it is impossible to cut out more than four crosses from the sheet, which completes the proof.
## Answer
4.00
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Eveokkimov $M$.
A polyhedron is circumscribed around a sphere. We will call a face of the polyhedron large if the projection of the sphere onto the plane of the face is entirely contained within the face. Prove that there are no more than 6 large faces.
|
The first solution. If two large faces are not parallel, then the dihedral angle containing these faces cannot be obtuse (in Fig. 1, projections of the sphere and these two faces onto a plane perpendicular to their line of intersection are shown, with the projections of the large faces highlighted). Therefore, if we erect a perpendicular to each large face, pointing outward from the polyhedron, then the angle between any two such perpendiculars ($\alpha$ in Fig. 1) will be non-acute.
Suppose the statement of the problem is false and there are at least 7 large faces. Then we obtain 7 vectors $\vec{n}_1, \ldots, \vec{n}_7$, the angles between which are not less than $90^\circ$ (for parallel faces, such an angle is $180^\circ$).
Let us place all vectors from one point $P$ and draw a plane $\beta$ passing through $P$ and not containing any of the 7 vectors. Then on one side of it, at least 4 vectors will be placed (for example, $\vec{n}_1, \ldots, \vec{n}_4$).
We decompose each of them into the sum of two:
$\vec{n}_i = \vec{a}_i + \vec{b}_i$, where $\vec{a}_i \in \beta, \vec{b}_i \perp \beta$ (see Fig. 2).
In this case, we can assume that $\vec{b}_1 = \vec{b}_2 = \vec{b}_3 = \vec{b}_4 = \vec{b}$, where $|\vec{b}| = 1$. According to our assumption, $(\vec{n}_i, \vec{n}_j) \leq 0$, since the angles between the vectors are not acute.
Fig. 1
Fig. 2
On the other hand, $(\vec{n}_i, \vec{n}_j) = (\vec{a}_i + \vec{b}_i, \vec{a}_j + \vec{b}_j) = (\vec{a}_i, \vec{a}_j) + 1$, since $(\vec{a}_i, \vec{b}_j) = (\vec{a}_j, \vec{b}_i) = 0, (\vec{b}_i, \vec{b}_j) = \vec{b}^2 = 1$. Thus, for the four vectors $\vec{a}_1, \ldots, \vec{a}_4$ lying in the plane $\beta$, $(\vec{a}_i, \vec{a}_j) < 0$, which is impossible, as the angle between at least two of them is not obtuse. This contradiction means that our assumption about the polyhedron having 7 large faces is false. A cube has 6 large faces.
The second solution. Let $R$ be the radius of the sphere. We associate with each large face a part of the boundary sphere of the sphere, located in the cone whose vertex is the center of the sphere and whose base is the projection of the sphere onto this face. The specified part of the sphere is a spherical cap (i.e., a part of the sphere lying on one side of a plane intersecting the sphere) of height $h = R(1 - \sqrt{2}/2)$. By a known formula, the area of such a cap is $2\pi Rh = \pi R^2(2 - \sqrt{2})$. Since the specified caps do not overlap, the sum of their areas does not exceed the area of the sphere. Denoting the number of large faces by $n$, we get $n(2 - \sqrt{2}) \leq 4$, i.e., $n \leq \frac{4}{2 - \sqrt{2}}$. The solution ends with checking that $\frac{4}{2 - \sqrt{2}} < 7$.
|
6
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Quadrilateral $ABCD$, whose diagonals are perpendicular to each other, is inscribed in a circle.
Perpendiculars dropped from vertices $B$ and $C$ to side $AD$ intersect diagonals $AC$ and $BD$ at points $E$ and $F$ respectively. Find $EF$, if $BC=1$.
|
Prove that BCFE is a parallelogram.
## Solution
First method.
Let $\angle C B D=\alpha$. Then
$$
\angle C A D=\alpha, \angle B E C=90^{\circ}-\alpha, \angle D B E=\alpha
$$
Therefore, $B E=B C$.
Let $\angle A C B=\beta$. Similarly, we can prove that $\angle A C F=\beta$. Therefore, $C F=B C$. Hence, $B E=C F$, and since $B E \| C F$ (perpendiculars to the same line $A D$), $B C F E$ is a parallelogram (even a rhombus). Therefore, $E F=$ $B C=1$.
Let $Q$ be the point of intersection of the diagonals. Note that $E$ is the point of intersection of the altitudes of triangle $A B D$. By a known property of the orthocenter of a triangle, $E Q=Q C$. Similarly, $F Q=Q B$. Since the diagonals of quadrilateral $B C F E$ are perpendicular and bisected by the point of intersection $Q$, $B C F E$ is a rhombus. Therefore, $E F=B C=1$.
## Answer
1. Post a comment
Problem
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Segment $K L$ is the diameter of a certain circle. Through its endpoints $K$ and $L$, two lines are drawn, intersecting the circle at points $P$ and $Q$, respectively, lying on the same side of the line $K L$. Find the radius of the circle if $\angle P K L=60^{\circ}$ and the point of intersection of the lines $K P$ and $Q L$ is 1 unit away from points $P$ and $Q$.
|
Triangle $K M L-$ is equilateral ( $M$ - the intersection point of lines $K P$ and $L Q$).
## Solution
Let $M$ be the intersection point of lines $K P$ and $L Q$. Point $M$ cannot lie on the circle. If $M$ is inside the circle, then $K M \cdot M P = L M \cdot M Q$. Therefore, $K M = M L$, which is impossible.
If point $M$ is outside the circle, then $M P \cdot M K = M Q \cdot M L$. Therefore, $K M = M L$. Then triangle $K M L-$ is equilateral. Its height $K Q$ is also a median. Therefore,
$$
K L = M L = 2 M Q = 2,
$$
and the desired radius is 1.
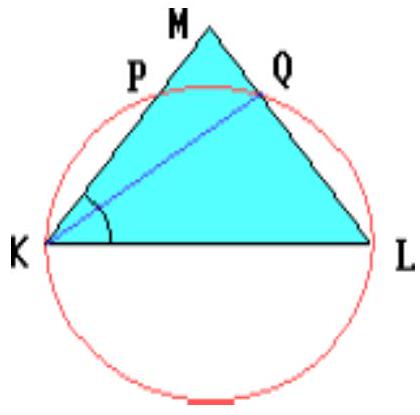
## Answer
1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In trapezoid $A B C E$ base $A E$ is equal to $16, C E=8 \sqrt{3}$. The circle passing through points $A, B$ and $C$ intersects line $A E$ again at point $H ; \angle A H B=60^{\circ}$. Find $A C$.
|
Apply the Law of Cosines.
## Solution
Let $O_{1}$ be the center of the given circle, $N$ be its point of tangency with the line $A C$, and $K$ be with the side $B C$.
From the right triangle $A O_{1} N$, we find that
$$
A N=O_{1} N \operatorname{ctg} 30^{\circ}=\sqrt{3}
$$
On the other hand, $A N$ is equal to the semiperimeter $p$ of triangle $A B C$. The radius of the inscribed circle of triangle $A B C$ is
$$
\frac{S_{\triangle A B C}}{p}=\frac{2 \sqrt{3}-3}{\sqrt{3}}=2-\sqrt{3} \text {. }
$$
If $O$ is the center of this circle, and $P$ is the point of tangency with the side $A C$, then
$$
O_{1} O=A O_{1}-A O=2 O_{1} N-2 O P=2(\sqrt{3}-1)
$$
Let $F$ be the foot of the perpendicular dropped from point $O$ to the extension of segment $O_{1} K$. Then
$$
\cos \angle O O_{1} F=\frac{O_{1} F}{O_{1} O}=\frac{1+2-\sqrt{3}}{2(\sqrt{3}-1)}=\frac{\sqrt{3}}{2}
$$
Therefore, $\angle O O_{1} F=30^{\circ}$. If segments $O O_{1}$ and $B C$ intersect at point $Q$, then
$$
\angle A Q B=\angle O_{1} Q K=60^{\circ}
$$
Thus,
$$
\angle B C A=\angle A Q B-\angle Q A C=60^{\circ}-30^{\circ}=30^{\circ}
$$
## Answer
8.
The trapezoid $A B C H$ is inscribed in a circle, so it is isosceles. Therefore, $\angle C A H=\angle A H B=60^{\circ}$. Let $A C=x$ and apply the Law of Cosines to triangle $A C E$:
$$
(8 \sqrt{3})^{2}=x^{2}+16^{2}-16 x
$$
From this, we find that $x=8$.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Based on the base $AB$ of isosceles triangle $ABC$, a point $D$ is taken such that $BD - AD = 4$. Find the distance between the points where the incircles of triangles $ACD$ and $BCD$ touch the segment $CD$.
|
If the circle inscribed in triangle $P Q R$ touches side $P Q$ at point $S$, then $P S=\frac{P Q+P R-R Q}{2}$.
## Solution
Let the circles inscribed in triangles $A C D$ and $B C D$ touch segment $C D$ at points $M$ and $N$ respectively. Since $A C=B C$, and
$$
C M=\frac{A C+C D-A D}{2}, C N=\frac{B C+C D-B D}{2},
$$
then
$$
\begin{aligned}
M N=|C M-C N|=\mid & \left.\frac{A C+C D-A D}{2}-\frac{B C+C D-B D}{2} \right\rvert\,= \\
& =\frac{|B D-A D|}{2}=\frac{4}{2}=2
\end{aligned}
$$
## Answer
2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9
A regular octagon with side 1 is cut into parallelograms. Prove that among them there are at least two rectangles, and the sum of the areas of all rectangles is 2.
#
|
Let's highlight two mutually perpendicular pairs of opposite sides in a regular octagon and consider, as in problem 25.1, chains of parallelograms connecting opposite sides. At the intersections of these chains, there are rectangles. By considering two other pairs of opposite sides, we will obtain at least one more rectangle.
The parallelograms of each chain can be further cut so that the chain splits into several paths, where in each path, adjacent parallelograms touch each other with entire sides, not parts of sides. The union of rectangles in the new partition coincides with the union of rectangles in the original partition, so the proof is sufficient to conduct for the new partition. Each path has a constant width; therefore, the length of one side of each rectangle in the path is equal to the width of the path, and the sum of the lengths of all other sides is equal to the sum of all widths of paths corresponding to the second pair of sides. Consequently, the area of all rectangles in one path is equal to the product of the width of the path by the length of the side of the polygon, i.e., numerically equal to the width of the path. Therefore, the area of all rectangles corresponding to two perpendicular pairs of opposite sides is 1, and the area of all rectangles in general is 2.
|
2
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Find the distance between the points of tangency of the circles inscribed in triangles $A B C$ and $C D A$ with side $AC$, if
a) $A B=5, B C=7, C D=D A$;
b) $A B=7, B C=C D, D A=9$.
|
The distance from the vertex of a triangle to the nearest point of tangency with the inscribed circle is equal to the difference between the semiperimeter and the opposite side of the triangle ($x = p - a$).
## Solution
a) Let the inscribed circle of triangle $ABC$ touch side $AC$ at point $K$, and the inscribed circle of triangle $CDA$ touch at point $M$. Since the distance from the vertex of a triangle to the point of tangency with the inscribed circle is equal to the difference between the semiperimeter and the opposite side of the triangle, then
$$
A K = \frac{A B + A C - B C}{2}, A M = \frac{A C + A D - D C}{2}
$$
Then
$$
K M = |A K - A M| = \frac{|A B + D C - B C - A D|}{2} = |7 - 9| = 1.
$$
## Answer
a) 1; b) 1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{53619}$ topics:
In an isosceles triangle $ABC$ with base $AB$, the bisector $BD$ is drawn. A point $E$ is taken on the line $AB$ such that $\angle EDB=90^{\circ}$.
Find $BE$, if $AD=1$.
|
Connect point $D$ with the midpoint of segment $C E$.
## Solution
Let $M$ be the midpoint of $B E$. Then $D M$ is the median of the right triangle $E D C$, drawn to the hypotenuse $E B$, so $D M=1 / 2 B E=B M$. Therefore,
$\angle D M A=2 \angle M B D=\angle B=\angle A=\angle D A M$. Hence, $D M=D A=1, B E=2 D M=2$.
## Answer
2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ $\left[\begin{array}{l}\text { The ratio in which the bisector divides the side } \\ {[\text { Law of Cosines }}\end{array}\right]$
In triangle $ABC$, the bisectors $BL$ and $AE$ of angles $ABC$ and $BAC$ respectively are drawn, intersecting at point $O$. It is known that $AB=BL$, the perimeter of triangle $ABC$ is $28$, and $BO=2OL$. Find $AB$.
|
Use the property of the bisector of a triangle and the cosine theorem.
## Solution
Let $O L=2 a, B O=4 a$. Then $A B=B L=6 a$. Since $A O$ is the bisector of triangle $A B L$, then $\frac{A B}{A L}=\frac{B O}{O L}=2$, so $A L=\frac{1}{2} A B=3 a$.
Let $C L=b$. Since $B L$ is the bisector of triangle $A B C$, then $\frac{B C}{C L}=\frac{A B}{A L}=2$, so $B C=2 C L=2 b$.
The height $B K$ of the isosceles triangle $A B L$ bisects the base $A L$, so $\cos \angle B A C=\frac{A K}{A B}=\frac{1}{4}$. By the cosine theorem,
$$
\begin{gathered}
B C^{2}=A B^{2}+A C^{2}-2 A B \cdot A C \cos \angle B A C, \text { or } \\
4 b^{2}=36 a^{2}+(3 a+b)^{2}-3 a(3 a+b) .
\end{gathered}
$$
After obvious transformations, we get the equation
$$
b^{2}-a b-12 a^{2}=0
$$
from which we find that $b=4 a$. Then the perimeter of triangle $A B C$ is
$$
A B+B C+A C=6 a+8 a+7 a=21 a=28
$$
from which $a=\frac{4}{3}$. Therefore, $A B=6 a=8$.
## Answer
8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Radii of the inscribed, circumscribed, and exscribed circles (other) [ Area of a triangle (through the semiperimeter and the radius of the inscribed or exscribed circle).
Through the center $O$ of the inscribed circle $\omega$ of triangle $A B C$, a line parallel to side $B C$ is drawn, intersecting sides $A B$ and $A C$ at points $M$ and $N$, respectively. $S_{A B C}=\sqrt{15}, B C=2$, and segment $A O$ is four times the radius of $\omega$. Find the perimeter of triangle $A M N$.
#
|
Let $r$ be the radius of $\omega, p$ be the semiperimeter of triangle $ABC, P$ be the point of tangency of $\omega$ with side $AB$. Then $AP^2 = AO^2 - OP^2 = 15r^2$, $AP = p - BC = AP = r\sqrt{15} + 2$,
$\sqrt{15} = S_{ABC} = pr = (r\sqrt{15} + 2)r$, from which $AP = r\sqrt{15} = 3, p = 5$.
The perimeter of triangle $AMN$ is $AB + AC$ (see the solution of problem $\underline{54896}$), that is, $2p - BC = 8$.
## Answer
8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## angle between the tangent and the chord [Angles subtended by equal arcs and equal chords]
A circle touches the sides $A C$ and $B C$ of triangle $A B C$ at points $A$ and $B$ respectively. On the arc of this circle, lying inside the triangle, there is a point $K$ such that the distances from it to the sides $A C$ and $B C$ are 6 and 24, respectively. Find the distance from point $K$ to the side $A B$.
|
Let $M, H$ and $N$ be the feet of the perpendiculars dropped from point $K$ to $AC, AB$ and $BC$ respectively. Points $M$ and $H$ lie on the circle with diameter $AK$. From the theorem about the angle between a tangent and a chord, $\angle K M H = \angle K A H = \angle K A B = \angle K B N$.
Points $N$ and $H$ lie on the circle with diameter $BK$, so $\angle K H N = \angle K B N = \angle K M H$.
Similarly, $\angle K H M = \angle K N H$, hence triangles $K M H$ and $K H N$ are similar by two angles. Therefore, $K H : K N = K M : K H$, from which
$K H^{2} = K N \cdot K M = 144$
## Answer
12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9 [ Properties and characteristics of an isosceles triangle.]
Quadrilateral \(ABCD\) is inscribed in a circle, \(M\) is the intersection point of its diagonals, \(O_1\) and \(O_2\) are the centers of the inscribed circles of triangles \(ABM\) and \(CMD\) respectively, \(K\) is the midpoint of the arc \(AD\) not containing points \(B\) and \(C\), \(\angle O_1 K O_2 = 60^\circ\), \(K O_1 = 10\). Find \(O_1 O_2\).
|
Point $K$ is the midpoint of arc $AD$, so $BK$ is the bisector of the inscribed angle $ABD$, which means point $O_{1}$ lies on segment $BK$. Similarly, point $O_{2}$ lies on segment $CK$. The rays $MO_{1}$ and $MO_{2}$ are the bisectors of the vertical angles
$AMB$ and $CMD$, so point $M$ lies on segment $O_{1}O_{2}$ and $\angle BMO_{1} = \angle DMO_{2} = \angle CMO_{2}$.
The inscribed angles $ABD$ and $ACD$ are equal. Therefore, $\angle MBO_{1} = \angle MCO_{2}$.
By the exterior angle theorem of a triangle, $\angle KO_{1}O_{2} = \angle MBO_{1} + \angle BMO_{1} = \angle MCO_{2} + \angle CMO_{2} = \angle KO_{2}O_{1}$, so triangle $O_{1}K_{2}$ is isosceles, and since one of its angles is $60^{\circ}$, this triangle is equilateral. Therefore, $O_{1}O_{2} = KO_{1} = 10$.
## Answer
10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The radii of two circles are 2 and 4. Their common internal tangents are perpendicular to each other. Find the length of each of them.
|
For each of the given circles, the quadrilateral formed by the indicated tangents and radii drawn to the points of tangency is a square.
## Solution
For each of the given circles, the quadrilateral formed by the tangents and radii drawn to the points of tangency is a square. Therefore, the length of the desired tangent is equal to the sum of the radii, i.e., the sides of the squares.
## Answer
6.
3 Problem $\underline{52637}$ Topics: [ $\frac{\text { Inscribed quadrilaterals (other) }}{\text { Diameter, basic properties }}$ [Inscribed quadrilateral with perpendicular diagonals]
In the inscribed quadrilateral $A B C D$, diagonal $A C$ is perpendicular to diagonal $B D$ and bisects it. Find the angles of the quadrilateral if $\angle B A D=\alpha$.
## Hint
The perpendicular bisector of a chord passes through the center of the circle.
## Solution
Since diagonal $A C$ is a diameter, then
$$
\angle A B C=\angle A D C=90^{\circ}
$$
Since $\angle B A D$ and $\angle B C D$ are opposite angles of the inscribed quadrilateral, then
$$
\angle B C D=90^{\circ}-\angle B A D=90^{\circ}-\alpha
$$
[Inscribed angle subtending a diameter]
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Pythagorean Theorem (direct and inverse).] [Tangent properties and criteria]
Circles with radii 8 and 3 touch each other internally. A tangent is drawn from the center of the larger circle to the smaller circle. Find the length of this tangent.
|
The line connecting the centers of two tangent circles passes through their point of tangency.
## Solution
Let $O$ and $O_{1}$ be the centers of circles with radii 8 and 3, respectively, and $A$ be the point of tangency, $O M-$ be the desired tangent. Then
$$
O O_{1}=O A-O O_{1}=8-3=5
$$
Therefore,
$$
O M^{2}=O O^{2}_{1}-O_{1} M^{2}=25-9=16, O M=4
$$
## Answer

How many parts do $n$ planes divide space when they all pass through one point, and no three have a common line?
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Properties and signs of tangents ] [ Rectangles and squares. Properties and signs ]
Two circles are given. Their common internal tangents are perpendicular to each other. The chords connecting the points of tangency are 3 and 5. Find the distance between the centers of the circles.
|
For each of the circles, the quadrilateral formed by the tangents and radii drawn to the points of tangency is a square.
## Solution
For each of the circles, the quadrilateral formed by the tangents and radii drawn to the points of tangency is a square. The segment connecting the point of intersection of the tangents with the center of the circle is the diagonal of the square. The sum of these segments is the distance between the centers.

## Answer
8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The perimeter of triangle $ABC$ is 8. An incircle is inscribed in the triangle, and a tangent is drawn to it, parallel to side $AB$. The segment of this tangent, enclosed between sides $AC$ and $CB$, is equal to 1. Find the side $AB$.
#
|
The truncated triangle is similar to the given one with a coefficient equal to the ratio of their perimeters.
## Solution
Let the points of intersection of the tangent with sides $A C$ and $C B$ be $M$ and $N$, and the points of tangency of these sides with the inscribed circle be $P$ and $Q$. Then the semiperimeter of triangle $C M N$ is $C P = C Q = 4 - A B$. From the similarity of triangles $C M N$ and $C A B$, it follows that ${ }^{M N} / A B = 1 / 4(4 - A B)$, or ${ }^{1 /}{ }_{A B} = 1 - { }^{A B} / 4$. From this, $A B = 2$.
## Answer
2.
Send a comment
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Right triangle $A B C$ is divided by the height $C D$, drawn to the hypotenuse, into two triangles: $B C D$ and $A C D$. The radii of the circles inscribed in these triangles are 4 and 3, respectively. Find the radius of the circle inscribed in triangle $A B C$.
|
Let $r$ be the desired radius, $r_{1}$ and $r_{2}$ be the radii of the given circles. From the similarity of triangles $A C D$, $C B D$, and $A B C$, it follows that $r_{1}: r_{2}: r = A C: B C: A B$. Therefore, $r^{2} = r_{1}^{2} + r_{2}^{2} = 25$.
## Answer
5.
Send a comment
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On the segment $A C$ there is a point $B$, and $A B=14, B C=28$. On the segments $A B, B C, A C$ as diameters, semicircles are constructed in the same half-plane relative to the line $A B$. Find the radius of the circle that is tangent to all three semicircles.
|
Apply Heron's formula or the Pythagorean theorem.
## Solution
Let points $O_{1}, O_{2}$, and $O$ be the centers of the given semicircles with diameters $A B, B C, A C$ respectively, $x$ be the radius of the desired circle, and $O_{3}$ be its center. Then
$O O_{1}=14, O O_{2}=7, O_{1} O_{3}=7+x, O O_{3}=21-x, O_{2} O_{3}=14+x$.
First method. By Heron's formula, $S_{\mathrm{OO}_{1} \mathrm{O}_{3}}=\sqrt{21 \cdot 7 x(14-x)}, S_{\mathrm{OO}_{2} \mathrm{O}_{3}}=\sqrt{21 \cdot 14 x(7-x)}$. Since $S_{O O_{1} O_{3}}: O O_{2} O_{3}=O O_{1}: O O_{2}=2: 1$, then $\frac{\sqrt{14-x}}{\sqrt{2(7-x)}}=2$. From this equation, we find that $x=6$.
Let $K$ be the projection of point $O_{3}$ onto $A C, O K=u$. Then $(21-x)^{2}-(7+x)^{2}=u^{2}-(14-u)^{2}, 28(14-2 x)=14(2 u-14), 2(14-2 x)=2 u-14$, $(14+x)^{2}-(21-x)^{2}=(7+u)^{2}-u^{2}, 35(2 x-7)=7(2 u+7), 5(2 x-7)=2 u+7$. Subtracting, we get $14 x-63=21$, from which $x=6$.
## Answer
6.
Given a triangle with sides 10, 24, and 26. The two smaller sides are tangents to a circle, the center of which lies on the larger side.
Find the radius of the circle.
## Hint
The area of the given triangle is equal to the sum of the areas of the triangles into which it is divided by the segment connecting the vertex of the largest angle to the center of the given circle.
## Solution
Note that the given triangle is a right triangle $\left(12^{2}+5^{2}=13^{2}\right)$. Let $r$ be the desired radius.
The segment connecting the vertex of the right angle to the center of the given circle divides the triangle into two triangles. The radii of the circle, drawn to the points of tangency, are the heights of these triangles. The sum of the areas of the resulting triangles is equal to the area of the given triangle, that is, $5 r+12 r=120$. From this, $r=120 / 17$.

## Answer
$120 / 17$
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Evdokimov M.A.
A convex polyhedron with vertices at the midpoints of the edges of a certain cube is called a cuboctahedron. When a cuboctahedron is intersected by a plane, a regular polygon is obtained. What is the maximum number of sides it can have?
|
Let the edge of the original cube, from which the cuboctahedron is obtained, be 1. Consider the sections of the cuboctahedron by a plane parallel to the base of the cube at a distance of $08$. Then the vertices of this $n$-gon must lie on the edges of the cuboctahedron, and no edge can have more than two vertices of the $n$-gon.
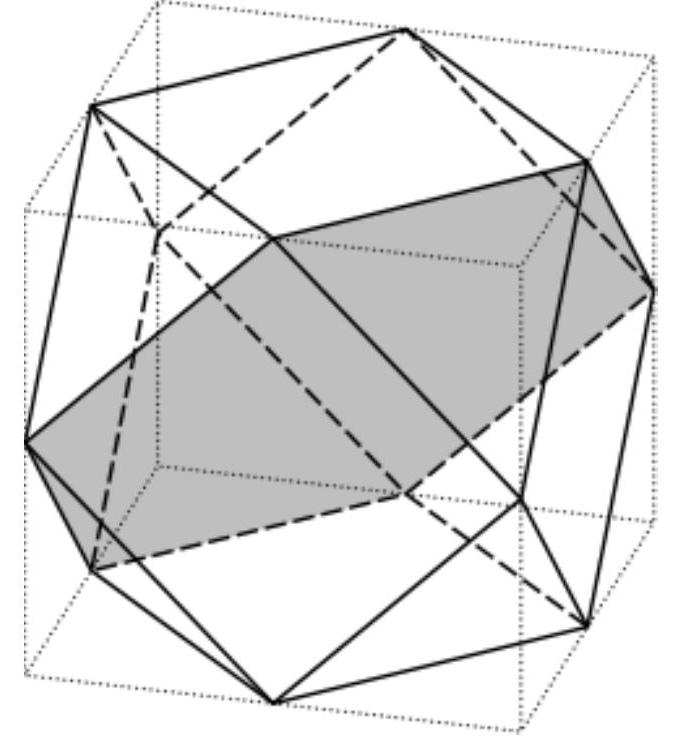
Consider the section of the original cube, which is a regular hexagon (shaded gray in the figure), as well as the sections obtained from this by rotating $90^\circ$, $180^\circ$, and $270^\circ$ about the vertical axis of the cube. Note that the union of the sides of these four regular hexagons is the union of all the edges of the cuboctahedron. We will show that on the sides of one of these four selected regular hexagons, there lie at least 3 vertices of the $n$-gon. Indeed, if on the sides of each such hexagon there are no more than two vertices, then the total number of vertices will not exceed eight. Therefore, the plane of the $n$-gon section coincides with the plane of this hexagon, and a hexagon is obtained in the section of the cuboctahedron. This leads to a contradiction.
## Omвem
8.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In an acute-angled triangle, two altitudes are equal to 3 and $2 \sqrt{2}$, and their point of intersection divides the third altitude in the ratio 5:1, counting from the vertex of the triangle. Find the area of the triangle.
|
Let $\alpha$ and $\beta$ be the acute angles of a triangle, from the vertices of which the given altitudes are drawn. Formulate a system of trigonometric equations in terms of $\alpha$ and $\beta$.
## Solution
Let $A A_{1}, B B_{1}$, and $C C_{1}$ be the altitudes of triangle $ABC$, and $H$ be their point of intersection; $A A_{1}=3, B B_{1}=2 \sqrt{2}$.
Denote
$$
\angle C A B=\alpha, \angle A B C=\beta, H C_{1}=x
$$
Then
$$
C C_{1}=6 x, \angle A H C_{1}=\beta, \angle B H C_{1}=\alpha .
$$
From the right triangles $A A_{1} B$ and $B B_{1} A$, we find that
$$
A B=\frac{3}{\sin \beta}=\frac{2 \sqrt{2}}{\sin \alpha}
$$
Therefore, $\sin \beta=\frac{3 \sin \alpha}{2 \sqrt{2}}$. From the right triangles $B C_{1} C$ and $B C_{1} H$, we find that
$$
B C_{1}=\frac{6 x}{\tan \beta}=x \tan \alpha .
$$
Therefore
$$
\tan \alpha \tan \beta=6 \Rightarrow \sin \alpha \sin \beta=6 \cos \alpha \cos \beta \Rightarrow \sin ^{2} \alpha \sin ^{2} \beta=36 \cos ^{2} \alpha \cos ^{2} \beta
$$
Substitute into the last equation
$$
\sin ^{2} \beta=\frac{9 \sin ^{2} \alpha}{8}, \cos ^{2} \beta=1-\sin ^{2} \beta=1-\frac{9 \sin ^{2} \alpha}{8}, \cos ^{2} \alpha=1-\sin ^{2} \alpha
$$
We get the equation
$$
35 \sin ^{4} \alpha-68 \sin ^{2} \alpha+32=0
$$
from which we find that $\sin \alpha=\frac{2}{\sqrt{5}}$ ( $\alpha$ and $\beta$ are less than 90° ). Therefore,
$$
\cos \alpha=\frac{1}{\sqrt{5}}, \sin \beta=\frac{3}{\sqrt{10}}, \cos \beta=\frac{1}{\sqrt{10}}, A B=\frac{3}{\sin \beta}=\sqrt{10}
$$
From triangle $ABC$, we find by the sine rule:
$$
A C=\frac{A B \sin \beta}{\sin (\alpha+\beta)}=3 \sqrt{2}
$$
Therefore,
$$
S_{\triangle A B C}=\frac{1}{2} A B \cdot A C \sin \alpha=\frac{1}{2} \cdot \sqrt{10} \cdot 3 \sqrt{2} \cdot \frac{2}{\sqrt{5}}=6
$$
## Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The height of the isosceles trapezoid $ABCD$ with bases $AD$ and $BC$ is $4 \sqrt{3}$, the diagonals of the trapezoid intersect at point $O, \angle AOD=120^{\circ}$. Find the midline of the trapezoid.
|
The diagonals of an isosceles trapezoid form equal angles with the base, therefore
$$
\angle O A D=\angle O D A=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}
$$
Let $H$ be the foot of the perpendicular dropped from vertex $C$ to $A D$. Then $A H=\frac{1}{2}(A D+B C)$, i.e., segment $A H$ is equal to the midline of the trapezoid. From the right triangle $A C H$, we find that
$$
A H=C H \operatorname{ctg} \angle C A H=C H \operatorname{ctg} 30^{\circ}=4 \sqrt{3} \cdot \sqrt{3}=12
$$
Therefore, the midline of trapezoid $A B C D$ is 12.
## Answer
12.00
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The circle constructed on the larger lateral side $AB$ of the right trapezoid $ABCD$ as its diameter intersects the base $AD$ at its midpoint. It is known that $AB=10, CD=6$. Find the midline of the trapezoid.
|
Let $M$ be the midpoint of $A D$. Then $\angle A M B=90^{\circ}$, so the quadrilateral $M B C D$ is a rectangle, $B M=C D=6$. From the right triangle $A B M$ we find that
$$
A M=\sqrt{A B^{2}-B M^{2}}=\sqrt{100-36}=8
$$
Then $B C=M D=A M=8$. Therefore, the midline of the trapezoid $A B C D$ is
$$
\frac{1}{2}(A D+B C)=\frac{1}{2}(16+8)=12
$$
## Answer
12.00
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Isosceles, inscribed, and circumscribed trapezoids ] [ Projections of the bases, sides, or vertices of a trapezoid ]
The height of an isosceles trapezoid, dropped from the vertex of the smaller base to the larger base, divides the larger base into segments that are in the ratio 2:3. How does the larger base relate to the smaller one?
|
Let $CH$ be the height of the isosceles trapezoid $ABCD$, dropped from the vertex $C$ of the smaller base $BC$ to the larger base $AD$. Let $DH = 2t$, $AH = 3t$. Drop a perpendicular $BQ$ from vertex $B$ to the base $AD$. From the equality of the right triangles $AQB$ and $DHC$, it follows that $AQ = DH = 2t$, and since $BCHQ$ is a rectangle, then
$$
BC = HQ = AD - DH - AQ = 5t - 2t - 2t = t
$$
Therefore, $\frac{AD}{BC} = \frac{5t}{t} = 5$.
## Answer
5.00
Problem
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Isosceles, inscribed and circumscribed trapezoids]
The perimeter of a trapezoid circumscribed about a circle is 40. Find the midline of the trapezoid.
|
Since the trapezoid is circumscribed around a circle, the sums of its opposite sides are equal, meaning the sum of the bases is equal to the semiperimeter of the trapezoid, i.e., 20, and the midline of the trapezoid is equal to the half-sum of the bases, i.e., 10.
## Answer
10.00
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{115625}$ topics: [ Tangent circles [Mean proportionals in a right triangle]
Two circles touch each other externally at point $C$. A line is tangent to the first circle at point $A$ and to the second circle at point $B$. The line $A C$ intersects the second circle at point $D$, different from $C$. Find $B C$, if $A C=9$, $C D=4$.
#
|
Let the common tangent to the circles passing through point $C$ intersect segment $A B$ at point $M$. Then $M A = M C = M B$, i.e., the median $C M$ of triangle $A B C$ is equal to half of side $A B$, which means $\angle A C B = 90^{\circ}$.
The adjacent angle to $\angle A C B$, $\angle B C D$, is also $90^{\circ}$, so $B D$ is the diameter of the second circle. Since $A B$ is tangent to this circle, $B D \perp A B$.
In the right triangle $A B D$, segment $B C$ is the altitude dropped to the hypotenuse, therefore,
$$
B C = \sqrt{A C \cdot C D} = \sqrt{3 \cdot 4} = 6
$$
## Answer
6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Folklore
Points $K$ and $L$ are the midpoints of sides $A B$ and $B C$ of a regular hexagon $A B C D E F$. Segments $K D$ and $L E$ intersect at point $M$. The area of triangle $D E M$ is 12. Find the area of quadrilateral KBLM.
|
Since quadrilateral $K B C D$ is the image of quadrilateral $L C D E$ under a rotation around the center of $A B C D E F$ by an angle of $60^{\circ}$, these quadrilaterals are equal, and therefore, have the same area (see figure). By subtracting the area of quadrilateral $L C D M$ from each of them, we get that $S_{K B L M}=S_{D E M}=12$.
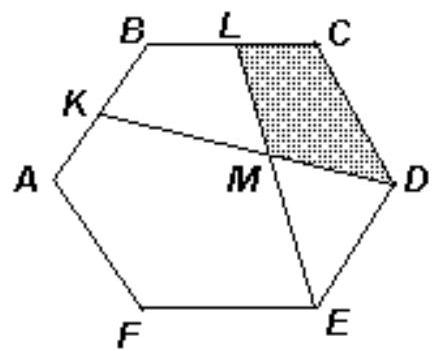
Answer
12.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $A$ be the following.
A numerical sequence is defined by the conditions: $a_{1}=1, a_{n+1}=a_{n}+\left[\sqrt{a_{n}}\right]$.
How many perfect squares occur among the first terms of this sequence, not exceeding
1000000?
|
According to the solution of problem $\underline{9152}$, all perfect squares in this sequence have the form $4^{m}$. There are exactly 10 numbers of this form within the specified limits
$\left(4^{10}=1024^{2}>10^{6}\right)$.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Boodanov I.I.
On the board, nine quadratic trinomials are written: $x^{2}+a_{1} x+b_{1}, x^{2}+a_{2} x+b_{2}, \ldots, x^{2}+a_{9} x+b_{9}$. It is known that the sequences $a_{1}, a_{2}, \ldots, a_{9}$ and $b_{1}, b_{2}, \ldots, b_{9}$ are arithmetic progressions. It turned out that the sum of all nine trinomials has at least one root. What is the maximum number of the original trinomials that can have no roots?
|
Let $P_{i}(x)=x^{2}+a_{i} x+b_{i}, P(x)=P_{1}(x)+\ldots+P_{9}(x)$. Note that $P_{i}(x)+P_{10-i}(x)=2 P_{5}(x)$. Therefore, $P(x)=$ $9 P_{5}(x)$, and the condition is equivalent to $P_{5}(x)$ having at least one root.
Let $x_{0}$ be one of its roots. Then $P_{i}\left(x_{0}\right)+P_{10-i}\left(x_{0}\right)=2 P_{5}\left(x_{0}\right)$, which means either $P_{i}\left(x_{0}\right) \leq 0$ or $P_{10-i}\left(x_{0}\right) \leq 0$. This implies that in each of the pairs $\left(P_{1}, P_{9}\right),\left(P_{2}, P_{8}\right),\left(P_{3}, P_{7}\right),\left(P_{4}, P_{6}\right)$, at least one of the quadratic polynomials has a root. Therefore, there are at least five quadratic polynomials that have roots, meaning there are no more than four quadratic polynomials without roots.
An example where exactly five quadratic polynomials have at least one root: $x^{2}-4, x^{2}-3, x^{2}-2, \ldots, x^{2}+4$.
## Answer
4 quadratic polynomials.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For the numbers $1000^{2}, 1001^{2}, 1002^{2}, \ldots$, the last two digits are discarded. How many of the first terms of the resulting sequence form an arithmetic progression?
|
The general term of the original sequence is: $a_{n}=\left(10^{3}+n\right)^{2}=10^{6}+2 n \cdot 10^{3}+n^{2}$ ( $a_{0}-$ the first term).
Let the general term of the resulting sequence be denoted by $b_{n}$, then
$b_{n}=\left[\frac{a_{n}}{100}\right]=\left[\frac{10^{6}+2 \cdot n \cdot 10^{3}+n^{2}}{100}\right]=10^{4}+20 n+\left[\frac{n^{2}}{100}\right]$
Therefore, the difference between consecutive terms of the new sequence will be 20 as long as
$\left[\frac{n^{2}}{100}\right]=0$, that is, if $n^{2}<100$. Considering that $n-$ is a natural number or zero, we get: $0 \leq n \leq 9$. Thus,
the first 10 terms of the new sequence form an arithmetic progression.
## Answer
10.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$2+$ $[$ higher degree equations (miscellaneous). ]
Solve the equation $\left[x^{3}\right]+\left[x^{2}\right]+[x]=\{x\}-1$.
#
|
The number on the left is an integer, and, consequently, the number on the right is also an integer, that is, $\{x\}=0$. Therefore, $x$ is an integer, so the equation can be rewritten as $x^{3}+x^{2}+x=-1$, or $(x+1)\left(x^{2}+1\right)=0$.
## Answer
$x=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Folklore
The function $f(x)$ is defined for all $x$, except 1, and satisfies the equation: $(x-1) f\left(\frac{x+1}{x-1}\right)=x+f(x)$. Find $f(-1)$.
|
Substitute the values $x=0$ and $x=-1$ into the given equation. We get: $\left\{\begin{array}{c}-f(-1)=f(0), \\ -2 f(0)=-1+f(-1)\end{array}\right.$. Therefore, $2 f(-1)=-1+f(-1)$, which means $f(-1)=-1$.
## Answer
-1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[
For all real $x$ and $y$, the equality $f\left(x^{2}+y\right)=f(x)+f\left(y^{2}\right)$ holds. Find $f(-1)$.
#
|
Substituting $x=0, y=0$, we get $f(0)=f(0)+f(0)$, that is, $f(0)=0$.
Substituting $x=0, y=-1$, we get $f(-1)=f(0)+f(1)$, that is, $f(-1)=f(1)$.
Substituting $x=-1, y=-1$, we get $f(0)=f(-1)+f(1)$. Therefore, $2 f(-1)=0$.
## Answer
0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Monotonicity, boundedness $\quad$ ]
Find the maximum value of the expression $a+b+c+d-ab-bc-cd-da$, if each of the numbers $a, b, c$ and $d$ belongs to the interval $[0,1]$.
#
|
Notice that $a+b+c+d-a b-b c-c d-d a=(a+c)+(b+d)-(a+c)(b+d)$. Let $a+c=x, b+d=y, 0$ $\leq x \leq 2$ and $0 \leq y \leq 2$.
$x+y-x y=(x-1)(1-y)+1$, where $|x-1| \leq 1$ and $|1-y| \leq 1$. Therefore, $(x-1)(1-y) \leq 1$, and $x+y-x y \leq 2$.
The value 2 is achieved, for example, if $a=c=1, b=d=0$.
## Answer
2
Solve the system of equations: $\left\{\begin{array}{c}\sin y-\sin x=x-y \\ \sin y-\sin z=z-y \\ x-y+z=\pi\end{array}\right.$.
## Solution
Write the system in the form $\left\{\begin{array}{c}\sin y+y=\sin x+x \\ \sin y+y=\sin z+z \\ x-y+z=\pi\end{array}\right.$. Notice that the function $f(t)=\sin t+t$ is strictly increasing.
Indeed, $f^{\prime}(t)=\cos t+1 \geq 0$; moreover, the derivative takes the value 0 at $t=\pi+2 k \pi, k \in \mathbf{Z}$, that is, there are no intervals where $f^{\prime}(t)=0$. Therefore, each value of the function $f(t)$ is taken only at one value of the variable. This means that $x=y=z, x-y+z=\pi$, from which $x=y=z=\pi$.
## Answer
$(\pi, \pi, \pi)$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Does there exist a natural number $n$ such that $\sqrt[n]{17 \sqrt{5}+38}+\sqrt[n]{17 \sqrt{5}-38}=2 \sqrt{5}$?
|
Note that $(\sqrt{5} \pm 2)^{3}=5 \sqrt{5} \pm 30+12 \sqrt{5} \pm 8=17 \sqrt{5} \pm 38$. Therefore, the given equality is true for $n=3$.
## Answer
It exists.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Rybnikov I.g.
A store received 20 kg of cheese, and a queue formed. After selling cheese to the next customer, the saleswoman accurately calculates the average weight of the purchase for all the cheese sold and informs how many people the remaining cheese will last if everyone buys exactly this average weight. Could the saleswoman have reported after each of the first 10 customers that the cheese would last exactly 10 more people? If so, how much cheese was left in the store after the first 10 customers?
#
|
Let $s_{k}$ be the average weight of cheese sold to the first $k$ customers. According to the condition, $20 - k s_{k} = 10 s_{k}$, hence $s_{k} = \frac{20}{k+10}$ kg, and after the $k$-th customer, there remains
200
$k+10$
message after each customer (not limited to the first ten). After the 10th customer, exactly half of the cheese remained - 10 kg.
## Answer
It could; 10 kg.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$4-$ [Increasing and Decreasing. Function Analysis]
Solve the equation $2 \sin \pi x / 2 - 2 \cos \pi x = x^{5} + 10 x - 54$.
#
|
Transferring all terms to one side, we get the equation $x^{5}+10 x-54-2 \sin \pi x / 2+2 \cos \pi x=0$. Consider the function
$f(x)=x^{5}+10 x-54-2 \sin ^{\pi x} / 2+2 \cos \pi x$. Note that $f^{\prime}(x)=5 x^{4}+10-\pi \cos \pi x / 2-2 \sin \pi x>5 x^{4}+10-3 \pi>0$. Therefore, $f(x)$ is an increasing function, so the equation $f(x)=0$ has no more than one root.
Since $f(2)=32+20-54-2 \sin \pi+2 \cos 2 \pi=0$, then $2$ is a root of the original equation.
Answer
## 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ilya Muromets meets the three-headed Zmei Gorynych. And the battle begins. Every minute Ilya cuts off one of Zmei's heads. With a probability of $1 / 4$, two new heads grow in place of the severed one, with a probability of $1 / 3$ only one new head grows, and with a probability of $5 / 12$ - no heads grow. The Zmei is considered defeated if he has no heads left. Find the probability that Ilya will eventually defeat the Zmei.
|
Blows by Ilya Muromets, in which the number of heads changes, are called successful.
Let's find the probability that at some point there will be a last successful blow. This means that starting from this point, there will be no more successful blows, that is, all blows will be unsuccessful. The probability of this is $1 / 3 \cdot 1 / 3 \cdot 1 / 3 \cdot \ldots=0$.
Thus, there will be no last successful blow, but there will be an infinite subsequence of successful blows, which we will consider, ignoring all other blows.
The probability of a successful blow is $2 / 3$. The conditional probability that the number of heads increases when a successful blow occurs is $1 / 4: 2 / 3=3 / 8$.
Similarly, the conditional probability that the number of heads decreases when a successful blow occurs is $5 / 12: 2 / 3=5 / 8$.
A standard one-dimensional random walk problem arises. Suppose that as a result of a certain series of successful blows, the number of the Dragon's heads has decreased by one compared to what it was. Let's call this event $D$, and its probability $x$.
There are two possibilities.
1) As a result of the first successful blow, the number of heads decreased by one (event $M$, probability $5 / 8$). In this case, event $D$ has already occurred - its conditional probability is 1.
2) As a result of the first successful blow, the number of heads increases by one (event $N$, probability $3 / 8$). In this case, event $D$ will occur only if the number of heads decreases by 2 - by one, and then by another one. Therefore, the conditional probability of event $D$ in this case is $x^{2}$.
By the formula of total probability $x=\mathrm{P}(D)=\mathrm{P}(D \mid M) \cdot \mathrm{P}(M)+\mathrm{P}(D \mid N) \cdot \mathrm{P}(N)=5 / 8+3 / 8 x^{2}$.
From this, $x=1$ or $x=5 / 3$. The second root is extraneous. Therefore, event $D$ is certain.
Thus, sooner or later, the number of heads will inevitably decrease from three to two. Then, for the same reason, the number of heads will decrease to one and, finally, become zero. The Dragon has no chance.
## Answer
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Sequence $A$.
The sequence of numbers $x_{1}, x_{2}, \ldots$ is such that $x_{1}=1 / 2$ and $x_{k+1}=x_{k}^{2}+x_{k}$ for any natural number $k$.
Find the integer part of the sum $\frac{1}{x_{1}+1}+\frac{1}{x_{1}+1}+\ldots+\frac{1}{x_{100}+1}$.
|
Note that $\frac{1}{x_{k+1}}=\frac{1}{x_{k}}-\frac{1}{x_{k}+1}$, which means $\frac{1}{x_{k}+1}=\frac{1}{x_{k}}-\frac{1}{x_{k+1}}$. Therefore,
$\frac{1}{x_{1}+1}+\frac{1}{x_{2}+1}+\ldots+\frac{1}{x_{100}+1}=\frac{1}{x_{1}}-\frac{1}{x_{2}}+\frac{1}{x_{2}}-\frac{1}{x_{3}}+\ldots+\frac{1}{x_{100}}-\frac{1}{x_{101}}=\frac{1}{x_{1}}-\frac{1}{x_{101}}=2-\frac{1}{x_{101}}$. The sequence is increasing, so $x_{101}>x_{3}>1$, hence the integer part of the desired sum is 1.
## Answer
1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Given natural numbers $M$ and $N$, both greater than ten, consisting of the same number of digits, and such that $M = 3N$. To obtain the number $M$, one of the digits in $N$ must be increased by 2, and each of the other digits must be increased by an odd digit. What digit could the number $N$ end with?
|
The number $A=M-N=2 N$ is even. However, by the condition, the number $A$ is composed of odd digits and the digit 2. Therefore, $A$ ends in 2. Thus, the number $N$, which is half of $A$, ends in either 1 or 6.
If $N$ ends in 1, then when it is doubled, there is no carry from the last digit to the second last digit. This means the second last digit of the number $A=2 N$ would be even, but it must be odd. This is a contradiction.
## Answer
The digit is 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
A bag of seeds was passed around the table. The first person took 1 seed, the second took 2, the third took 3, and so on: each subsequent person took one more seed than the previous one. It is known that in the second round, the total number of seeds taken was 100 more than in the first round. How many people were sitting at the table?
|
Let there be $n$ people sitting at the table. Then on the second round, each took $n$ more seeds than on the first, and all together took $n \cdot n=n^{2}$ more seeds than on the first. Since $n^{2}=100$, then $n=10$.
## Answer
10 people.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$3+$
$p$ and $8 p^{2}+1$ are prime numbers. Find $p$.
|
If $p \neq 3$, then $8 p^{2}+1$ is divisible by 3.
Answer
$p=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Decimal numeral system ] [ Divisibility rules for 3 and 9 ]
For the number $2^{100}$, the sum of its digits was found, then the sum of the digits of the result, and so on. Eventually, a single-digit number was obtained. Find it.
|
$2^{100}=\left(2^{6}\right)^{16} \cdot 2^{4} \equiv 1^{16} \cdot 16 \equiv 7(\bmod 9)$.
## Answer
7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the greatest common divisor of the numbers $9 m+7 n$ and $3 m+2 n$, if the numbers $m$ and $n$ have no common divisors other than one?
#
|
Any common divisor of the numbers $9 m+7 n$ and $3 m+2 n$ must also be a divisor of the numbers $(9 m+7 n)-3(3 m+2 n) = n$ and $7(3 m+2 n)-2(9 m+7 n) = 3 m$. Since the numbers $m$ and $n$ are coprime, any common divisor of the numbers $n$ and $3 m$ must be a divisor of the number 3, that is, it cannot be greater than 3.
This value is possible: for $m=1, n=3$ GCD $(9 m+7 n, 3 m+2 n)=$ GCD(30,9$)=3$.
## Answer
3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tokoroiev $C$. $\mathbf{L}$.
Numbers $a, b$ and $c$ are such that $(a+b)(b+c)(c+a)=a b c,\left(a^{3}+b^{3}\right)\left(b^{3}+c^{3}\right)\left(c^{3}+a^{3}\right)=a^{3} b^{3} c^{3}$. Prove that $a b c=0$.
|
First, note that $x^{2}-x y+y^{2}>|x y|$ for any distinct numbers $x$ and $y$.
Assume that $a b c \neq 0$. Then, dividing the second equality by the first, we get $\left(a^{2}-a b+b^{2}\right)\left(b^{2}-b c+c^{2}\right)\left(c^{2}-c a+a^{2}\right)=|a b| \cdot|b c| \cdot|a c|$
All the brackets on the left and all the factors on the right are positive; moreover, each factor on the left is not less than the corresponding factor on the right. Therefore, equality can only be achieved when all these three inequalities turn into equalities, that is, when $a=b=c$. In this case, the first equality from the condition takes the form $8 a^{3}=a^{3}$, which is impossible for $a \neq 0$. Thus, our assumption is incorrect, and $a b c=0$.
Send a comment
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Berdnikov A.
Let's call a natural number good if all its digits are non-zero. A good number is called special if it has at least $k$ digits and the digits are in strictly increasing order (from left to right).
Suppose we have some good number. In one move, it is allowed to append a special number to either end or insert it between any two of its digits, or, conversely, erase a special number from its representation. For what largest $k$ can any good number be transformed into any other good number using such moves?
|
Obviously, a special number does not have more than nine digits. If $k=9$, then with each operation, the number of digits changes by exactly 9, meaning the remainder of the number of its digits divided by 9 does not change, and a single-digit number cannot be turned into a two-digit number.
Let $k=8$. Since all operations are reversible, it is sufficient to prove that any digit can be inserted. We will prove by induction on $n$ that we can insert the digit $n$.
Base case. To insert 1, first insert 123456789, and then erase 23456789.
Inductive step. Suppose we can insert (and erase) digits from 1 to $n-1<9$. To insert $n$, first insert 123456789, erase 12...( $n-1$ ) one by one, then insert 12... $(n-1)$ one by one to the right of $n$, and finally erase the number $12 \ldots(n-1)(n+1) \ldots 9$ (for $n=9$, the last two actions are not needed, and for $n=8$, the number 12...79 is erased).
## Answer
For $k=8$.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Sindarov V.A.
Find all such natural $k$ that the product of the first $k$ prime numbers, decreased by 1, is a perfect power of a natural number (greater than the first power).
#
|
Let $n \geq 2$, and $2=p_{1}1$; then $k>1$. The number $a$ is odd, so it has an odd prime divisor $q$. Then $q>p_{k}$, otherwise the left side of the equation (*) would be divisible by $q$, which is not the case. Therefore, $a>p_{k}$.
Without loss of generality, we can assume that $n$ is a prime number (if $n=s t$, then we can replace $n$ with $t$ and $a$ with $a^{S}$). Note that $n>2$, since
$a^{2}+1$ cannot be divisible by $3=p_{2}$.
We will show that $n>p_{k}$. Indeed, otherwise $n=p_{i}$, where $i \leq k$. Then $a^{p_{i}}+1$ is divisible by $p_{i}$; on the other hand, by Fermat's Little Theorem, $a^{p_{i}}-a$ is divisible by $p_{i}$. Since $a^{p_{i}}+1=(a+1)\left(a^{p_{i}-1}-a^{p_{i}-2}+\ldots-a+1\right)$, and $a+1=\left(a^{p_{i}}+1\right)-\left(a^{p_{i}}-a\right)$ is divisible by $p_{i}$ and $a^{p_{i}-1}-a^{p_{i}-2}+\ldots-a+1 \equiv 1+1+\ldots+1=p_{i} \equiv 0\left(\bmod p_{i}\right)$, then $a^{p_{i}}+1$ is divisible by $p_{i}^{2}$, which contradicts the condition.
Thus, $a>p_{k}$ and $n>p_{k}$, from which $a^{n}+1>p_{k}^{p_{k}}>p_{1} p_{2} \ldots p_{k}$, which contradicts the equation $(*)$.
## Answer
$k=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
Three square paths with a common center are spaced 1 m apart from each other (see figure). Three ants start simultaneously from the lower left corners of the paths and run at the same speed: Mu and Ra counterclockwise, and Wei clockwise. When Mu reaches the lower right corner of the largest path, the other two, not yet having completed a full circle, are on the right sides of their paths, and all three are on the same straight line. Find the sides of the squares.
|
The lengths of the sides of two adjacent paths differ by 2 meters. Therefore, at the moment when Mu reached the corner, Ra had run 2 meters along the right side of the path and was at a distance of $2+1=3$ meters from the "lower" side of the outer path. Since Ra is halfway between Mu and Vey, Vey is at twice the distance from this side, which is 6 meters. This means Vey still has to run $6-1-1=4$ meters along the side.
But if Vey had run counterclockwise, he would have run the entire lower side and an additional 4 meters along the right side (since this side is 4 meters shorter than the side of the outer square), thus ending up at the same point. Since Vey ends up at the same point whether he runs clockwise or counterclockwise, this point is the upper right corner of the square. Therefore, the side of this square is 4 meters. Accordingly, the sides of the other two squares are $4+2=6$ meters and $6+2=8$ meters.
## Answer
4 meters, 6 meters, 8 meters.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Дубанов И.С.
In five pots standing in a row, Rabbit poured three kilograms of honey (not necessarily into each and not necessarily equally). Winnie-the-Pooh can take any two adjacent pots. What is the maximum amount of honey that Winnie-the-Pooh can guarantee to eat?
#
|
Evaluation. Let's assume Winnie-the-Pooh cannot take at least a kilogram of honey. This means that in any pair of adjacent pots, there is less than a kilogram of honey. This is true for both the two rightmost pots and the two leftmost pots. However, then in the middle pot, there must be more than a kilogram of honey (otherwise, the total amount of honey would be less than 3 kg). This is a contradiction. Therefore, Winnie-the-Pooh will always be able to take at least a kilogram of honey. Example. If the first, third, and fifth pots each contain 1 kg of honey, and the second and fourth pots are empty, then Winnie-the-Pooh will not be able to eat more than a kilogram of honey.
## Answer
1 kg.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Xichaturyan A.V.
Bus stop B is located on a straight highway between stops A and C. At some point after leaving A, the bus found itself at a point on the highway such that the distance from it to one of the three stops is equal to the sum of the distances to the other two. After the same amount of time, the bus was again at a point with this property, and then after another 25 minutes, it arrived at B. How much time does the bus need for the entire journey from A to C, if its speed is constant, and it stops for 5 minutes at stop B?
|
At both moments in time mentioned in the problem, the sum will obviously be the distance from the bus to the farthest stop from it. This cannot be $B$, as it is closer than $C$. Therefore, these were $C$ (before the bus had traveled halfway from $A$ to $C$) and $A$ (after this moment).

In the first case, the bus was at point $X$ and the distance to $C$ was equal to the sum of the distances to $A$ and to $B$. But it is also equal to the sum of the distance to $B$ and the distance $BC$. Therefore, the bus had traveled exactly the distance $BC$. On the diagram, we marked equal distances with arcs.
By the second moment, the bus had traveled another distance $BC$ and was at point $Y$. The sum of the distances from it to $B$ and to $C$ is $BC$ plus $YB$, counted twice. According to the problem, this is the distance to $A$, so $YB$ is half the length of $BC$.

Since $YB$ was traveled by the bus in 25 minutes, $BC$ will be traveled in 50 minutes, and the entire journey will take $3 \cdot 50 + 25 + 5 = 180$ minutes, which is three hours.
## Answer
3 hours.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Yashchenko I.V.
The numbers 2, 3, 4, ... 29, 30 are written on the board. For one ruble, you can mark any number. If a number is already marked, you can freely mark its divisors and numbers that are multiples of it. What is the minimum number of rubles needed to mark all the numbers on the board?
|
Let's mark the numbers $17, 19, 23$, and 29, spending four rubles. Then mark the number 2, spending another ruble. After this, we can freely mark all even numbers (since they are divisible by 2), and then all odd numbers not exceeding 15 - for any of them (let's say for the number $n$) the even number $2n$ is already marked, and we can mark $n$ as its divisor. It remains to mark 21, 25, and 27, and this is also done for free: 25 is divisible by the marked number 5, and 21 and 27 are divisible by the marked number 3. In any way of solving the problem, the prime numbers 17, 19, 23, and 29, which exceed 15, will have to be marked at a cost - they are not divisors or multiples of any numbers on the board. Thus, 4 rubles will be spent only on them. To mark anything else, we will have to spend a fifth ruble. Therefore, it is not possible to fulfill the conditions of the problem for less than five rubles.
Comment. In fact, after marking the "large" prime numbers, we could have marked any of the remaining numbers on the board instead of the number 2. Indeed, then we will freely mark its smallest prime divisor $p$. If $p=2$, we act according to the algorithm described above. If not, we mark $2p$ (this can be done since $p < 15$), then mark the number 2, and from there everything else is done in the known way.
A similar solution is applicable for an arbitrarily long set $2, 3, 4, \ldots, N$ - we are forced to mark all "large" prime numbers (exceeding $N / 2$) at a cost, and then mark any of the remaining numbers for a ruble. Then we freely mark the number 2 in the way described above, then all even numbers, then all "small" prime numbers (not exceeding $N / 2$), because any "small" $p$ will be a divisor of $2p$. Now we can mark all the remaining unmarked numbers: each of them will be divisible by its minimal prime divisor - a "small" prime number.
## Answer
For 5 rubles.
Submit a comment
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Work problem. $]$
The bathtub fills up in 23 minutes from the hot water tap, and in 17 minutes from the cold water tap. Masha first turned on the hot water tap. After how many minutes should she turn on the cold water tap so that by the time the bathtub is full, 1.5 times more hot water is used than cold water?
|
To have 1.5 times more hot water than cold water in the bathtub, the cold water tap should fill 2/5 of the bathtub, and the cold water $-3 / 5$. Then the hot water tap should be open for $3 / 5 \cdot 23=69 / 5$ minutes, and the cold water tap for $2 / 5 \cdot 17=34 / 5$ minutes. Therefore, the cold water tap should be opened after $69 / 5-34 / 5=7$ minutes.
## Answer
After 7 minutes.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On a straight line, ten points were placed at equal intervals, and they occupied a segment of length $a$. On another straight line, one hundred points were placed at the same intervals, and they occupied a segment of length $b$. How many times is $b$ greater than $a$?
|
On a segment of length $a$, 9 intervals fit, and on a segment of length $b-99$. Therefore, $b=11a$.
C
11 times.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
It is known that $\operatorname{tg} A+\operatorname{tg} B=2$ and $\operatorname{ctg} A+\operatorname{ctg} B=3$. Find $\operatorname{tg}(A+B)$.
|
$\frac{2}{\operatorname{tg} A \operatorname{tg} B}=\frac{\operatorname{tg} A+\operatorname{tg} B}{\operatorname{tg} A \operatorname{tg} B}=\operatorname{ctg} A+\operatorname{ctg} B=3$, hence $\operatorname{tg} A \operatorname{tg} B=2 / 3$. Therefore,
$\operatorname{tg}(A+B)=\frac{\operatorname{tg} A+\operatorname{tg} B}{1-\operatorname{tg} A \operatorname{tg} B}=\frac{2}{1-\frac{2}{3}}=6$.
## Answer
6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic. Mental calculation, etc.]
It is known that 9 cups of tea cost less than 10 rubles, and 10 cups of tea cost more than 11 rubles. How much does a cup of tea cost
#
|
Write the condition in the form of inequalities and use the fact that the cost of a glass of tea is expressed as an integer number of kopecks.
## Solution
Let the cost of a glass of tea, expressed in kopecks, be \( x \). Then, according to the condition, \( 9x \leq 1100 \).
Therefore, \( 9x \) does not exceed 999, and \( x \) does not exceed 111. \( x = 111 \) fits - in this case, \( 10x = 1110 > 1100 \). If, however, \( x < 111 \), then \( x \) does not exceed 110, and in this case, \( 10x \) does not exceed 1100. Thus, there is only one possibility: \( x = 111 \).
## Answer
1 ruble 11 kopecks
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Absolute value ]
Solve the equation $|x-2|+|x-1|+|x|+|x+1|+|x+2|=6$.
#
|
The number |x-a| is equal to the distance from the point on the number line with coordinate x to the point with coordinate a.
## Solution
Consider a point on the number line with coordinate x. The sum $|\mathrm{x}-2|+|\mathrm{x}-1|+|\mathrm{x}|+|\mathrm{x}+1|+|\mathrm{x}+2|$ is equal to the sum of the distances from the point x to the points with coordinates $2,1,0,-1,-2$. Note that the sum of the distances from any point to points A and B is not less than the length of the segment AB (and equality is achieved if and only if the point is located on the segment AB). From this, we get that |x-2|+|x+2| is not less than 4, and |x-1|+|x+1| is not less than 2 for any
| x. Therefore, for the sum $|x-2|+|x-1|+|x|+|x+1|+|x+2|$ to be equal to 2+4=6, it is necessary that |x|=0. Thus, x must be equal to 0. It is easy to verify that the value $x=0$ is indeed a solution to the given equation.
## Answer
$\mathrm{x}=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Text problems] [Case enumeration]
In a box, there are blue, red, and green pencils. In total, there are 20 pieces. The number of blue pencils is 6 times the number of green pencils, and the number of red pencils is less than the number of blue pencils. How many red pencils are in the box?
|
Think about how many blue pencils there can be.
## Solution
Since there are 20 pencils in total, and blue and green pencils together make up 7 parts. This means there can be 6 or 12 blue pencils, and green and red pencils would then be 1 and 13 or 2 and 6, respectively. Since there are fewer red pencils than blue ones, only the second option is possible: 12 blue, 2 green, and 6 red.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Fedorov P.M.
It is known that $a+\frac{b^{2}}{a}=b+\frac{a^{2}}{b}$. Is it true that $a=b$?
|
Let's bring the left side to a common denominator: $a+\frac{b^{2}}{a}=\frac{a^{2}+b^{2}}{a}$. Similarly, we will do the same for the right side.
We obtain the equality:
$$
\frac{a^{2}+b^{2}}{a}=\frac{a^{2}+b^{2}}{b}
$$
From the condition, it is clear that $a \neq 0, b \neq 0$. Therefore, $a^{2}+b^{2}>0$ (see comment). Thus, both sides of the equality can be divided by $a^{2}+b^{2}$. We get $\frac{1}{a}=\frac{1}{b}$, from which $a=b$.
Comment. The following obvious statements are often used in solving problems (and in mathematics in general): 1) the square of a non-zero number is positive, 2) the sum of squares of several numbers is non-negative. If this sum is zero, then each of the numbers is zero.
Find the minimum value of the expression $x+\frac{1}{4 x}$ for positive values of $x$.
## Solution
$x+\frac{1}{4 x} \geq 2 \sqrt{x \cdot \frac{1}{4 x}}=1$. Equality is achieved when $x=\frac{1}{2}$.
## Answer
1. Send a comment
Problem
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9,10,11 |
Solve the equation $x^{3}+x-2=0$ by trial and error and using Cardano's formula.
|
The equation has an obvious root $x=1$. Dividing by $x-1$, we obtain the quadratic equation $x^{2}+x+2=0$, which has no real roots.
Cardano's formula gives $x=\sqrt[3]{-1+\sqrt{\frac{28}{27}}}+\sqrt[3]{-1-\sqrt{\frac{28}{27}}}$.
From this, it follows that $\sqrt[3]{-1+\sqrt{\frac{28}{27}}}+\sqrt[3]{-1-\sqrt{\frac{28}{27}}}=1$.
## Answer
$x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\begin{array}{l}{[\text { Identical Transformations }]} \\ {[\text { Factorization }]}\end{array}\right]$
For different numbers $a$ and $b$, it is known that $\frac{a}{b}+a=\frac{b}{a}+b$. Find $\frac{1}{a}+\frac{1}{b}$.
|
The given equality can be written as $\frac{a}{b}-\frac{b}{a}=b-a$, from which $\frac{a^{2}-b^{2}}{a b}=b-a$ or $\frac{(a-b)(a+b)}{a b}=b-a$. Since the numbers $a$ and $b$ are different, we can divide both sides of the equation by $a-b$, after which we get: $\frac{a+b}{a b}=-1$. This is the desired value, since $\frac{a+b}{a b}=\frac{1}{a}+\frac{1}{b}$.
## Answer
$-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\begin{array}{l}\text { [Rectangles and squares. Properties and characteristics } \\ \text { Word problems (miscellaneous). }\end{array}\right]$
A frame for three square photographs has the same width everywhere (see figure). The perimeter of one opening is 60 cm, and the perimeter of the entire frame is 180 cm. What is the width of the frame?
|
From the condition, it follows that the length of the side of the opening is 15 cm. Let $d$ cm be the width of the frame, then the perimeter of the rectangle is
$8 \cdot 15 + 12 d = 120 + 12 d = 180$. Therefore, $d=5$.
## Answer
5 cm.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the nearest integer to the number $x$, if $x=\frac{1}{\sqrt[4]{\frac{5}{4}+1}-\sqrt[4]{\frac{5}{4}-1}}$.
|

If the inequalities are verified by squaring, then \(1.9 < \frac{\sqrt{6} + \sqrt{2}}{2} < 2\).
## Answer
2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Gukhanov $H . X$.
Given quadratic trinomials $f_{1}(x), f_{2}(x), \ldots, f_{100}(x)$ with the same coefficients for $x^{2}$, the same coefficients for $x$, but different constant terms; each of them has two roots. From each trinomial $f_{i}(x)$, one root was chosen and denoted as $x_{i}$. What values can the sum $f_{2}\left(x_{1}\right)+$ $f_{3}\left(x_{2}\right)+\ldots+f_{100}\left(x_{99}\right)+f_{1}\left(x_{100}\right)$ take?
|
Let the $i$-th quadratic polynomial have the form $f_{i}(x)=a x^{2}+b x+c_{i}$. Then $f_{2}\left(x_{1}\right)=f_{1}\left(x_{1}\right)+\left(c_{2}-c_{1}\right)=c_{2}-c_{1}$, since $f_{1}\left(x_{1}\right)=$ 0. Similarly, we obtain the equalities
$f_{3}\left(x_{2}\right)=c_{3}-c_{2}, \ldots, f_{100}\left(x_{99}\right)=c_{100}-c_{99}$ and $f_{1}\left(x_{100}\right)=c_{1}-c_{100}$.
By adding, we get $f_{2}\left(x_{1}\right)+f_{3}\left(x_{2}\right)+\ldots+f_{1}\left(x_{100}\right)=\left(c_{2}-c_{1}\right)+\ldots+\left(c_{1}-c_{100}\right)=0$.
## Answer
Only 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kalinin D.A.
In the room, there are 20 chairs of two colors: blue and red. On each chair sits either a knight or a liar. Knights always tell the truth, and liars always lie. Each of the seated individuals claimed that they were sitting on a blue chair. Then they somehow rearranged themselves, after which half of those seated said they were sitting on blue chairs, and the rest said they were sitting on red chairs. How many knights are now sitting on red chairs?
|
Initially, all knights sit on blue chairs, and all liars on red ones. Therefore, the number of knights who moved to red chairs is equal to the number of liars who moved to blue chairs. Both groups claimed they were sitting on red chairs. In total, 10 people said they were sitting on red chairs. Therefore, the number of knights sitting on red chairs is $10: 2=5$.
## Answer
5.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
Several natural numbers are written in a row with a sum of 20. No number and no sum of several consecutive numbers equals 3. Could there be more than 10 numbers written?
|
Example with 11 numbers: $1,1,4,1,1,4,1,1,4,1,1$.
## Answer
It could.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shnop D.
In the park, there were lindens and maples. Maples made up $60 \%$ of them. In the spring, lindens were planted in the park, after which maples accounted for $20 \%$. In the fall, maples were planted, and maples again made up $60 \%$. By what factor did the number of trees in the park increase over the year?
|
At first, there were 1.5 times fewer lindens than maples, and in the summer, there became 4 times more. At the same time, the number of maples did not change. Therefore, the number of lindens became $1.5 \cdot 4=6$ times more.
By the end of the year, the ratio of the number of lindens to the total number of trees became the same as it was at the beginning. But in the fall, the number of lindens did not change, so the total number of trees (compared to the initial) increased by six times.
## Answer
6 times.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$3-$ $[$ Algorithm Theory (miscellaneous). $\quad]$
Author: Berdikov A.
Sasha writes a sequence of natural numbers on the board. The first number $N>1$ is written in advance. New natural numbers he gets by subtracting from or adding to the last written number any of its divisors greater than 1. Can Sasha, for any natural $N>1$, eventually write the number 2011 on the board at some point?
|
The first method. By adding $N$ each time, we get 2011N. By subtracting 2011 each time, we get 2011.
The second method. If $N$ is odd, add $N$ and get an even number. By adding or subtracting twos from it, we get 4022. By subtracting 2011, we get 2011.
## Answer
In any case.
Author: $\underline{\text { Folklore }}$
In the cells of a $5 \times 5$ square table, the numbers 1 and -1 are arranged. It is known that the number of rows with a positive sum is greater than the number of rows with a negative sum.
What is the maximum number of columns in this table that can have a negative sum?
## Solution
Let's provide one possible example (see the table). The sum of the numbers in each of the top three rows is positive, while the sum of the numbers in each column is negative.
| 1 | 1 | 1 | -1 | -1 |
| :---: | :---: | :---: | :---: | :---: |
| 1 | -1 | 1 | -1 | 1 |
| -1 | 1 | -1 | 1 | 1 |
| -1 | -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 | -1 |
## Answer
5 columns.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Folkopr }}$
Three companies $A, B$, and $C$ decided to jointly build a road 16 km long, agreeing to finance this project equally. In the end, $A$ built 6 km of the road, $B$ built 10 km, and $C$ contributed her share in money - 16 million rubles. How should companies $A$ and $B$ divide this money between themselves?
|
Each company was supposed to build $51 / 3$ km of road. Instead of company $C$, company $A$ built $6-5 \frac{1}{3}=2 / 3$ km of road, and company $B$ built
$10-5 \frac{1}{3}=14 / 3$ km. Therefore, 16 million rubles should be divided between them in the ratio $2: 14$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Folklore
In the class, there are 17 people. It is known that among any ten, there is at least one girl, and there are more boys than girls. How many girls are there in this class?
|
Since there are more boys than girls in the class, there are no fewer than nine boys. If there are more than nine boys, the condition that among any ten people there is at least one girl will not be met. Therefore, there are exactly 9 boys and 8 girls.
## Answer
8.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Processes and operations [ Examples and counterexamples. Constructions ]
Several boxes together weigh 10 tons, and each of them weighs no more than one ton. How many three-ton trucks are definitely enough to haul this cargo?
#
|
We will load the trucks with boxes in any order, only ensuring that the "overloading" of the truck does not occur. As a result, more than 2 tons will be loaded onto each truck. Therefore, five trucks will definitely be enough. Four trucks may not be enough. For example, let's say we have 13 boxes, each weighing ${ }^{10} / 13$ tons. Then one truck can carry no more than three such boxes (4 boxes weigh more than 3 tons), and all four trucks will carry no more than 12 boxes.
## Otvet
5 three-ton trucks
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Covering with percentages and ratios ] [ Inclusion-exclusion principle ]
Three crazy painters started painting the floor each in their own color. One managed to paint $75 \%$ of the floor red, another $70 \%$ green, and the third $65 \%$ blue. What part of the floor is definitely painted with all three colors?
|
Evaluation. 25% of the floor is not painted red, 30% of the floor is not painted green, and 35% of the floor is not painted blue.
25+30+35=90. From this, it follows that at least 10% of the floor is painted with all three colors.
An example where exactly 10% of the floor is painted with all three colors is clear from the evaluation: 25% of the floor is painted in two colors: blue and green, 30% - in red and green, 35% - in red and blue.
## Answer
Problem
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Prove that $M . \mathbf{B}$.
The sequence of numbers $a_{1}, a_{2}, \ldots$ is defined by the conditions $a_{1}=1, a_{2}=143$ and $a_{n+1}=5 \cdot \frac{a_{1}+a_{2}+\ldots+a_{n}}{n}$ for all $n$ $\geq 2$.
Prove that all members of the sequence are integers.
|
The number $a_{3}=5 \cdot 72=360$ is an integer. For $n \geq 4$
$$
a_{n}=5 \cdot \frac{a_{1}+\ldots+a_{n-1}}{n-1} \text { and } a_{n-1}=5 \cdot \frac{a_{1}+\ldots+a_{n-2}}{n-2} \text {, hence } a_{n}=\frac{5}{n-1}\left(\frac{n-2}{5} a_{n-1}+a_{n-1}\right)=\frac{n+3}{n-1} a_{n-1} \text {. Therefore, if } n \geq
$$
$$
\text { 4, }
$$
$$
a_{n}=\frac{(n+3)(n+2) \ldots \cdot 7}{(n-1)(n-2) \ldots \cdot 3} \cdot a_{3}=\frac{(n+3)(n+2)(n+1) n}{6 \cdot 5 \cdot 4 \cdot 3} \cdot 360=(n+3)(n+2)(n+1) n
$$
\section*{[ Parity and Imparity $]$ [ GCD and LCM. Mutual Primality ] Problem 116592 Topics:
[ Factorization $]$
Author: Podlipsky O.K.
Petya chose a natural number $a>1$ and wrote down fifteen numbers $1+a, 1+a^{2}, 1+a^{3}, \ldots, 1+a^{15}$ on the board. Then he erased several numbers so that any two of the remaining numbers are coprime. What is the maximum number of numbers that could remain on the board?
## Solution
Notice that if $k$ is odd, then the number $1+a^{n k}$ is divisible by $1+a^{n}$. Each of the numbers $1,2, \ldots, 15$ can be expressed as $k, 2 k, 4 k, 8 k$, where $k$ is odd. Thus, each of the written numbers is divisible by either $1+a$, or $1+a^{2}$, or $1+a^{4}$, or $1+a^{8}$. Therefore, if we take at least five numbers, there will be two among them that are divisible by the same number greater than 1; hence, they will not be coprime. Thus, the number of remaining numbers cannot exceed four.
Four numbers could remain: if $a=2$, then the numbers $1+2=3,1+2^{2}=5,1+2^{4}=17$ and $1+2^{8}=$ 257 can be left. All of them are pairwise coprime.
## Answer
4 numbers.
|
4
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Martynova } H}$.
To play the game of Hat, Nadya wants to cut a sheet of paper into 48 identical rectangles. What is the minimum number of cuts she will have to make if she can rearrange any pieces of paper but cannot fold them, and Nadya can cut as many layers of paper at once as she likes? (Each cut is a straight line from edge to edge of the piece.)
#
|
With each cut, the number of paper pieces can increase by no more than twice. Therefore, after five cuts, you can get no more than 32 pieces, which is not enough.
Six cuts will suffice. For example, you can cut the sheet in half, align the two rectangular pieces and cut them in half again (resulting in four equal rectangles). By continuing to align the obtained parts and cutting them in half, you can get 16 equal rectangles with four cuts. Then, by dividing the entire stack into three equal parts with two cuts, you will get 48 equal rectangles.
## Answer
6 cuts.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Senderov V.A.
At the vertices of a cube, numbers from 1 to 8 were written, and on each edge - the absolute difference of the numbers at its ends. What is the smallest number of different numbers that can be written on the edges?
#
|
Three numbers must be necessarily present: for this, it is sufficient to consider the three edges of the cube coming out of the vertex where the number 1 (or 8) is written. Let's prove that there will be an arrangement of numbers for which exactly three numbers will be required. Consider 2 squares. In the vertices of the first, place the numbers $1,2,3,4$ clockwise, and in the vertices of the second, also clockwise, place the numbers $5,6,7,8$. So far, we have used two different numbers: 1 and 3. Now place the first square below the second: 1 below 5, 2 below 6, and so on.
## Answer
$$
3.00
$$
Send a comment
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Examples and Counterexamples. Constructions] [ Proof by Contradiction ]
## Auto: Zassavsiy A.A.
In a volleyball tournament, each team met every other team once. Each match consisted of several sets - until one of the teams won three times. If a match ended with a score of $3: 0$ or $3: 1$, the winning team received 3 points, and the losing team received 0. If the set score was
$3: 2$, the winner received 2 points, and the loser received 1 point. By the end of the tournament, it turned out that the team "Cunning" scored the most points, while the team "Simpletons" scored the least. However, "Cunning" won fewer matches than they lost, while "Simpletons" had more wins than losses. What is the smallest number of teams for which this is possible?
|
Evaluation. If there are no more than three teams, then the "Simpletons" won all the matches, which means they have the most points. Contradiction.
If there are four or five teams, then each team will play three or four matches. This means that the "Cunning" won no more than one match and scored a maximum of $5=3+1+1$ or $6=3+1+1+1$ points, respectively. The "Simpletons," however, won at least two matches with four participants and at least three matches with five participants, meaning they scored at least $4=2+2+0$ or $6=2+2+2+0$ points, respectively. Considering that the "Cunning" must score at least 2 points more than the "Simpletons," we get a contradiction.
Therefore, there must be no fewer than six teams.
Example. See the table.
| Teams | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ | Points |
| :--- | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| "Cunning" | $\bullet$ | 1 | 1 | 1 | 3 | 3 | $\mathbf{9}$ |
| A | 2 | $\bullet$ | 2 | 2 | 1 | 1 | $\mathbf{8}$ |
| B | 2 | 1 | $\bullet$ | 2 | 2 | 1 | $\mathbf{8}$ |
| $\mathbf{B}$ | 2 | 1 | 1 | $\bullet$ | 2 | 1 | 7 |
| $\Gamma$ | 0 | 2 | 1 | 1 | $\bullet$ | 3 | 7 |
| "Simpletons" | 0 | 2 | 2 | 2 | 0 | $\bullet$ | 6 |
## Answer
With six teams.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Glibov A. }}$.
Let $n$ be a natural number. We call a sequence $a_{1}, a_{2}, \ldots, a_{n}$ interesting if for each $i=1,2$, $\ldots, n$ one of the equalities $a_{i}=i$ or $a_{i}=i+1$ holds. We call an interesting sequence even if the sum of its terms is even, and odd otherwise. For each odd interesting sequence, we found the product of its terms and wrote it on the first sheet. For each even sequence, we did the same and wrote it on the second sheet. On which sheet is the sum of the numbers greater and by how much? (Give the answer in terms of $n$.)
|
Denoting the sum containing the term $2 \cdot 3 \cdot \ldots \cdot n(n+1)$ by $A_{n}$, and the other by $B_{n}$, we will prove the equality $A_{n}-B_{n}=1$ by induction.
Base case. $A_{1}-B_{1}=2-1=1$.
Inductive step. Represent the sum $A_{n}$ as $A^{\prime}+A^{\prime \prime}$, where $A^{\prime}$ contains all terms of the form $a_{1} a_{2} \ldots a_{n-1}(n+1)$, and $A^{\prime \prime}$ contains all terms of the form $a_{1} a_{2} \ldots a_{n-1} n$. Since the sum $A^{\prime}$ contains the term $2 \cdot 3 \cdot \ldots \cdot n(n+1)$, for each term $a_{1} a_{2} \ldots a_{n-1}(n+1)$ in it, the sequence $a_{1}, a_{2}, \ldots, a_{n-1}$ has the same parity as the sequence $2,3, \ldots, n$. Therefore, $A^{\prime}=(n+1) A_{n-1}$. Correspondingly, in the sum $A^{\prime \prime}$, for each term $a_{1} a_{2} \ldots a_{n-1}$, the parity of the sequence $a_{1}, a_{2}, \ldots, a_{n-1}$ is opposite to the parity of the sequence $2,3, \ldots, n$. Then $A^{\prime \prime}=n B_{n-1}$, from which $A_{n}=A^{\prime}+A^{\prime \prime}=(n+1) A_{n-1}+n B_{n-1}$. Similarly, $B_{n}=n A_{n-1}+(n+1) B_{n-1}$. Therefore, $A_{n}-B_{n}=(n+1) A_{n-1}+n B_{n-1}-n A_{n-1}-(n+1) B_{n-1}=A_{n-1}-B_{n-1}=1$.
## OTBet
When $n \equiv 0,1(\bmod 4)$, the sum on the second sheet is greater by 1, and for other $n$ - the opposite. In other words, the sum that contains the term $2 \cdot 3 \cdot \ldots \cdot n(n+1)$ is greater by 1.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
\left.\begin{array}{l}{[\text { Systems of exponential equations and inequalities] }} \\ {[\quad \text { Monotonicity and boundedness }}\end{array}\right]
Solve the system in positive numbers:
$$
\begin{cases}x^{y} & =z \\ y^{z} & =x \\ z^{x} & =y\end{cases}
$$
|
First, note that if one of the unknowns is equal to one, then the others are also equal to one. Indeed,
Answer
$x=y=z=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.