problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Avor: frankin 5.
A natural number $\$ \mathrm{k} \$$ is called interesting if the product of the first $\$ \mathrm{k} \$$ prime numbers is divisible by $\$ \mathrm{k} \$$ (for example, the product of the first two prime numbers is $2 \cdot 3=6$, and 2 is an interesting number).
What is the maximum number of interesting numbers that can occur consecutively?
|
Evaluation. Obviously, a number that is a multiple of 4 is not interesting.
Examples. $1,2,3 ; 5,6,7$.
## Answer
3 numbers.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9,10
In the tournament, each chess player scored half of all their points in matches against the participants who took the last three places.
How many people in total participated in the tournament
#
|
For brevity, let's call the players who took the last three places "bad," and all others "good." The bad players played three games among themselves, and in these games, a total of three points were scored. According to the condition, this is half of all the points scored by the bad players; therefore, in games with the good players, the bad players scored another 3 points. However, a total of \(3(n-3)\) games were played between the bad and good players, and the same number of points were distributed (\(n\) is the total number of players). Of these, 3 points were taken by the bad players, and the rest by the good players. Therefore, in games with the bad players, the good players won \(3(n-3) - 3 = 3(n-4)\) points, and thus, the good players scored (in total) \(3(n-4)\) points in games with each other. Between the good players, there were \(\frac{1}{2}(n-3)(n-4)\) games and the same number of points were distributed. Therefore, \((n-3)(n-4) = 6(n-4)\), from which \(n=4\) or \(n=9\). The first option should be excluded, as in this case, the only good player would have scored 0 points, meaning he would not have been the first. The only solution left is \(n=9\). For nine players, this could have happened: an example of the corresponding tournament table is given below.
## Answer
9 people.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 [Chessboards and Chess Pieces]
Avoris A. Anjanis
What is the minimum number of cells that need to be marked on a chessboard so that
1) among the marked cells, there are no adjacent cells (having a common side or a common vertex),
2) adding any one cell to these cells would violate point 1?
#
|
Evaluation. Let's divide the board into nine parts (see the figure). In each of them, a cell must be marked, otherwise the black cell contained in it can be added.
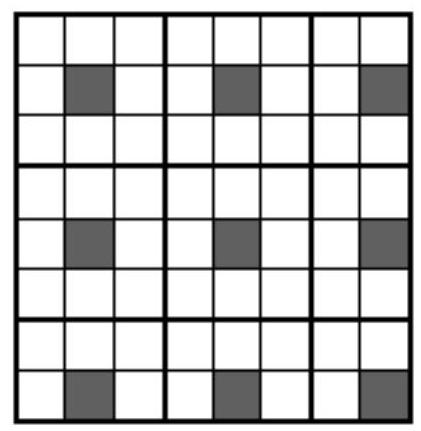
Example. The nine black cells in the figure satisfy both conditions.
## Answer
9 cells
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Senderov V.A.
1999 numbers stand in a row. The first number is 1. It is known that each number, except the first and the last, is equal to the sum of its two neighbors.
Find the last number.
#
|
Let's denote our numbers as $a_{1}, a_{2}, \ldots, a_{1999}$. By adding the equations $a_{n+1}=a_{n+2}+a_{n}$ and $a_{n+2}=a_{n+3}+a_{n+1}$, we get $a_{n+3}+a_{n}=0$, or $a_{n+3}=-a_{n}$. From this, $a_{n+6}=-a_{n+3}=a_{n}$, which means the sequence has a period of 6. Therefore, $a_{1999}=a_{6 \cdot 333+1}=a_{1}=1$.
## Answer
1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shaovalov A.v.
For which $n>2$ can the integers from 1 to $n$ be arranged in a circle so that the sum of any two adjacent numbers is divisible by the next number in the clockwise direction?
|
Just like in solving the problem $\underline{98454}$, we prove that there is no more than one even number. Therefore, there are no more than three numbers in total. The numbers 1, 2, 3 can be placed in any order.
## Answer
Only when $n=3$
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
There are six children in the family. Five of them are respectively 2, 6, 8, 12, and 14 years older than the youngest, and the age of each child is a prime number.
How old is the youngest?
|
Can the age of the youngest child be an even number?
## Solution
The age of the youngest child cannot be an even number, as otherwise the ages of the older children would not be prime numbers. It cannot end in $1,3,7,9$ - otherwise the age of one of the older children would be divisible by 5. The only prime number that meets these conditions is 5. Checking shows that if the age of the youngest child is 5 years, the ages of all the older ones will be expressed as prime numbers.
## Answer
5 years.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3Among the unseen beasts that left tracks on unknown paths, there was a herd of one-headed Thirty-four-legged creatures and three-headed Dragons. In total, the herd has 286 legs and 31 heads. How many legs does a three-headed Dragon have?
#
|
Think about how many Thirty-four-legged creatures can be in a herd.
## Solution
In the herd, there are 286 legs, which means that the number of Thirty-four-legged creatures cannot be more than 8, since $34 \cdot 9 > 286$. In the herd, there are 31 heads, and each Dragon has three heads, so the number of Thirty-four-legged creatures, when divided by 3, should leave a remainder of 1. Therefore, the number of Thirty-four-legged creatures can be either 1, 4, or 7. Knowing the total number of heads, we can determine the number of Dragons - which is either 10, 9, or 8, respectively.
In the first case, 10 Dragons have 252 legs, in the second case, 9 Dragons have 150 legs, and only in the third case does each Dragon have an integer number of legs, specifically 6 (48 legs for 8 Dragons). Thus, each Dragon has 6 legs.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Kaibhanov A.K. }}$
The auditorium has the shape of a regular hexagon with a side length of 3 meters. In each corner, there is a snore meter that determines the number of sleeping students within a distance of no more than 3 meters. How many sleeping students are there in the auditorium if the sum of the readings of the snore meters is 7?
|
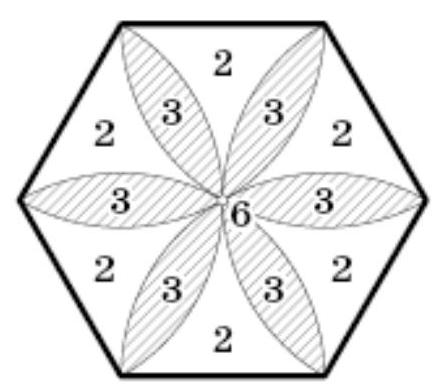
Each student is "seen" by 2, 3, or 6 snorometers (see fig). Therefore, 7 can be broken down into a sum of terms, each of which is 2, 3, or 6. It is easy to see that 7 can be represented as such a sum in only one way: \(7 = 3 + 2 + 2\). The number of terms is equal to the number of students.
## Answer
3 students.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kuyna A.K.
Among any five nodes of a regular grid paper, there will definitely be two nodes, the midpoint of the segment between which is also a node of the grid paper. What is the minimum number of nodes of a grid made of regular hexagons that need to be taken so that among them there will definitely be two, the midpoint of the segment between which is also a node of this grid?
#
|
Lemma. Among any five nodes of a grid of equilateral triangles, there will be two such that the midpoint of the segment between them is also a grid node.
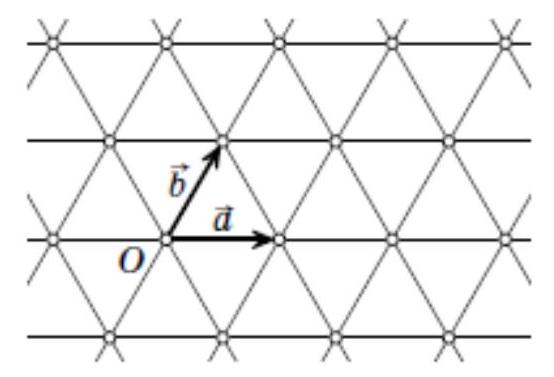
Proof of the lemma. Introduce the origin at one of the grid nodes and denote by $\$ \mid vec\{a\} \$$ and $\$ \operatorname{vec}\{b\} \$$ the radius vectors to the two nearest nodes, as shown in the figure. Then the grid nodes are points of the form $\$ m \mid vec\{a\} + n \mid vec\{b\} \$$ for integers \$m $\$$ and \$n\$. By the pigeonhole principle, among five points, there will be two points $\$ m_1 \mid vec\{a\} + n_1 \mid vec\{b\} \$$ and $\$ m_2 \mid vec\{a\} + n_2 \mid vec\{b\} \$$, for which the parity of \$m_1 \$$ and \$m_2 \$$ and the parity of \$n_1 \$$ and \$n_2 \$$ coincide simultaneously. The midpoint of the segment connecting these two points is the point $\$ \frac{m_1 + m_2}{2} \mid vec\{a\} + \frac{n_1 + n_2}{2} \mid vec\{b\} \$$, which is a grid node because the numbers $\$ \frac{m_1 + m_2}{2} \$$ and $\$ \frac{n_1 + n_2}{2} \$$ are integers due to the same parity of \$m_1 \$$ and \$m_2 \$$ and \$n_1 \$$ and \$n_2 \$$.
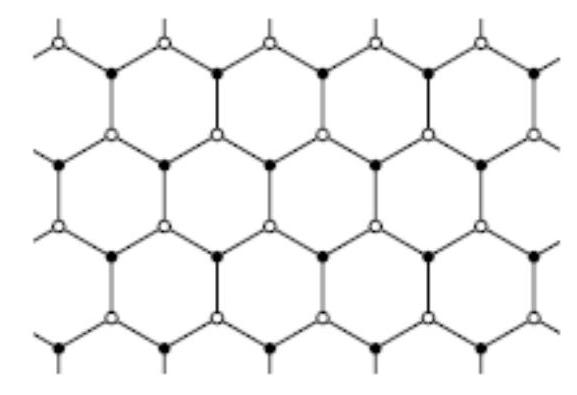
Solution. In the figure on the left, you can see an example of the placement of 8 grid nodes, among which there are no two such that the midpoint of the segment between them is a grid node. We will prove that nine nodes are sufficient. Notice that the hexagonal grid can be divided into the union of two triangular grids (see the figure on the right). By the pigeonhole principle, among any nine nodes, at least five will be in one of these two triangular grids. By the lemma, among these five nodes, there will be two of the required ones.
# Answer
9.
Submit a comment
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
|
| $[$ Decimal numeral system $]$ | | |
Find the last digit of the number $7^{7}$.
#
|
$7^{2} \equiv-1(\bmod 10)$, so, $7^{4} \equiv 1(\bmod 10). 7^{7} \equiv(-1)^{7}=-1(\bmod 4)$, therefore $7^{7^{7}} \equiv 7^{3}=343(\bmod 10)$.
## Answer
3.
Prove that the sum of the squares of five consecutive natural numbers is not a perfect square.
## Solution
First method. The remainder of the division by 4 of the square of an odd number is 1, and the remainder of the square of an even number is 0. Therefore, the specified sum when divided by 4 gives a remainder of 2 or 3, that is, it is not a square.
Second method. $(n-2)^{2}+(n-1)^{2}+n^{2}+(n+1)^{2}+(n+2)^{2}=5 n^{2}+10=5\left(n^{2}+2\right)$, and $n^{2}+2$ is not divisible by 5.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
}
For which $n>3$ can a set of weights with masses $1,2,3, \ldots, n$ grams be divided into three equal-mass piles?
#
|
Six weights, whose masses are six consecutive numbers, can easily be divided into three equal mass piles.
## Solution
Let's call a number $n$ good if a set of weights with masses $1,2,3, \ldots, n$ can be divided into three equal mass piles. For a good $n$, the total mass of the weights, which is $1 / 2 n(n+1)$, is divisible by 3. Therefore, $n$ can only give remainders of 0 or 2 when divided by 3.
If the number $n$ is good, then the number $n+6$ is also good, since the weights with masses $n+1, n+2, \ldots, n+6$ can easily be divided into three equal mass piles.
It is easy to check that the numbers 5, 8, 9 are good: $1+4=2+3=5 ; 1+2+3+6=4+8=5+7 ; 1+2+3+4+5=6$ $+9=7+8$. That 6 is a good number is shown above. Therefore, good numbers are all numbers of the form $3 k(k \geq 3)$ and $3 k+2(k \geq 1)$.
## [Inscribed and Circumscribed Circles] Problem $\underline{35074}$ Topics: [ Midline of a Trapezoid ] [ Systems of Linear Equations ]
Difficulty: $3+$
Grades: $9,10,11$
Inside triangle $A B C$, there are points $P$ and $Q$ such that point $P$ is at distances 6, 7, and 12 from the lines $A B, B C, C A$ respectively, and point $Q$ is at distances 10, 9, and 4 from the lines $A B, B C, C A$ respectively. Find the radius of the inscribed circle of triangle $A B C$.
## Hint
Prove that the midpoint of segment $P Q$ is the center of the inscribed circle of triangle $A B C$.
## Solution
Let $D, E, F$ be the feet of the perpendiculars dropped from points $P, Q, O$ to the line $A B$ respectively. By the problem's condition, $P D=6, Q E=10$. $O F$ is the midline of trapezoid $D P Q E$, so the length of $O F$ is $1 / 2(P D+Q E)=1 / 2(6+10)=8$. Therefore, point $O$ is at a distance of 8 from the line $A B$. Similarly, we find that $O$ is at a distance of $1 / 2(7+9)=8$ from the line $B C$ and at a distance of $1 / 2(12+4)=8$ from the line $C A$. Thus, $O$ is the center of the inscribed circle of triangle $A B C$, and the radius of this circle is 8.
## Answer
8.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the remainder from dividing the polynomial $P(x)=x^{81}+x^{27}+x^{9}+x^{3}+x$ by
a) $x-1$;
b) $x^{2}-1$.
#
|
a) $P(1)=5$.
b) First method. Let $P(x)=(x^2-1)Q(x) + ax + b$. Substituting $x=-1$, we get $b-a=-5$; substituting $x=1$, we get $a+b=5$.
From this, $b=0, a=5$.
Second method. $P(x)=x(x^{80}+x^{26}+x^{8}+x^{2}+1)$. By substituting $t=x^2$, the second factor transforms into the polynomial $Q(t)=t^{40}+t^{13}+t^{4}+t+1$, which, when divided by $t-1$, gives a remainder of $Q(1)=5$. Therefore, $P(x)$, when divided by $x^2-1$, gives a remainder of $x \cdot 5$.
## Answer
a) 5; b) $5x$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For what positive value of $p$ do the equations $3 x^{2}-4 p x+9=0$ and $x^{2}-2 p x+5=0$ have a common root?
#
|
The common root of the given equations must also be a root of the equation $\left(3 x^{2}-4 p x+9\right)-3\left(x^{2}-2 p x+5\right)=0 \quad \Leftrightarrow$ $2 p x-6=0$. Therefore, it equals $3 / p$. Substituting, for example, into the second equation, we get $9 / p^{2}=1$, from which $p=3$.
## Answer
For $p=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3+ [Inequalities. Case Analysis] Pinocchio buried two ingots - a golden one and a silver one - on the Field of Wonders. On good weather days, the golden ingot increases by $30\%$, and the silver ingot by $20\%$. On bad weather days, the golden ingot decreases by $30\%$, and the silver ingot by $20\%$. After a week, it turned out that one of the ingots had increased, while the other had decreased. How many days was the weather good?
|
Increasing a number by $20 \%$ is equivalent to multiplying it by 1.2, and decreasing a number by $20 \%$ is equivalent to multiplying it by 0.8 (for $30 \%$ - by 1.3 and 0.7, respectively). Therefore, the result does not depend on the sequence of good and bad weather, but only on the number of good and bad days.
After one good and one bad day, both ingots decrease: $1.2 \cdot 0.81$, while $1.3^{4} \cdot 0.7^{3}<1$. On the other hand, after two good and one bad day, the gold ingot increases. Therefore, it also increases after four good and two bad days, and even more so after five good and two bad days. Thus, if there are five or more good days, the gold ingot grows. Therefore, only when there are four good days does one ingot grow while the other decreases.
## Answer
4 days.
|
4
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Berlov S.L. }}$.
A natural number $n$ is called good if each of its natural divisors, increased by 1, is a divisor of the number $n+1$.
Find all good natural numbers.
|
Clearly, $n=1$ satisfies the condition. Also, all odd prime numbers satisfy it: the divisors of such a number $p$, increased by 1, are 2 and
$p+1$; both of them divide $p+1$.
On the other hand, any number $n$ that satisfies the condition has a divisor 1; hence, $n+1$ is divisible by $1+$ 1, which means $n$ is odd.
Suppose some composite $n=ab$, where $a \geq b \geq 2$, satisfies the condition. Then the number $n+1$ is divisible by $a+1$ and the number $n+b=(a+1)b$ is also divisible by $a+1$. Therefore, the number $b-1=(n+b)-(n+1)$ is also divisible by $a+1$. Since $b-1>0$, we get that $b-1 \geq a+1$. But this contradicts the inequality $b \leq a$.
## Answer
One and all odd prime numbers.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## [ Non-Convex Polygons Division with Remainder $\quad]$
A secret base is surrounded by a transparent winding fence in the shape of a non-convex polygon, with a swamp outside. A straight power line with 36 poles runs through the swamp, some of which are outside the base, and some are inside. (The power line does not pass through the vertices of the fence.) A spy walks around the base along the fence from the outside, keeping the fence always to his right. Each time he reaches the power line, he counts how many poles are to his left (he can see all of them). By the time the spy has walked around the entire fence, he has counted a total of 2015 poles. How many poles are inside the base?
#
|
A straight power line crosses the territory of the base in several segments. When the spy is at the end of one of these segments, he counts the poles. Consider one of them ($A B$). When the spy is at point $A$, he counts the poles on one side of $A B$, and when he is at point $B$, he counts the poles on the other side of $A B$. If the poles inside $A B$ are added to these, the total is 36 poles. Summing these equations for all segments, we get that 2015 plus the number $n$ of poles inside the base is divisible by 36. Since $n \leq 36$ and 2016 is divisible by 36, then $n=1$.
## Answer
One pole.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Frankin B.R.
On three red and three blue cards, six positive numbers are written, all of them are different. It is known that on the cards of one color, the pairwise sums of some three numbers are written, and on the cards of the other color - the pairwise products of the same three numbers. Can these three numbers always be guaranteed to be determined?
#
|
All the sought numbers are distinct, otherwise some numbers on the cards would be equal. Since their pairwise products are positive, all numbers have the same sign, and since their pairwise sums are positive, this sign is positive.
Let the sought numbers be \( x < y < z \).
First method. For the cards of each color, consider the ratio of the largest number on them to the smallest. In one case, this is \(\frac{y+z}{x+y}\), in the other \(\frac{x+y}{x}\). Since the first ratio is less than the second, it is clear on which cards the sums are written and on which the products.
Knowledge of the pairwise sums of three numbers determines these numbers, for example, \( x = \frac{1}{2}((x+y) + (x+z) - (y+z)) \).
Second method. Notice that \( x+y < x+z < y+z \) and \( xy < xz < yz \). Let \( a < b < c \) be the numbers on the cards of one color, and \( A < B < C \) be the numbers on the cards of the other color. Then \( x = \sqrt{\frac{(a+A+1)(b+B+1)}{c+C+1}} - 1 \). Similarly, \( y \) and \( z \) can be calculated.
## Answer
Always.
Author: \(\underline{\text{Mukhin}}\) D.G.
On the graph of the function \( y = \frac{1}{x} \), Misha marked all points with abscissas \( 1, 2, 3, \ldots \) until he got tired. Then Masha came and colored all rectangles, one of whose vertices is a marked point, another is the origin, and the other two lie on the axes (the figure shows which rectangle Masha would have colored for the marked point \( P \)). Then the teacher asked the students to calculate the area of the figure consisting of all points colored exactly once. What did they get?
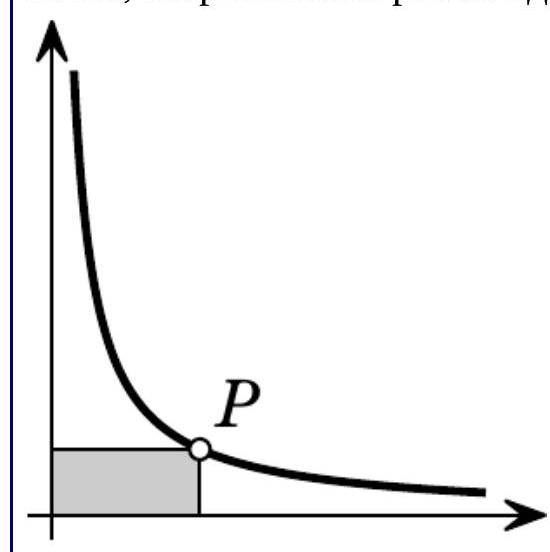
## Solution
Suppose Misha got tired after marking the point with abscissa \( n \). Let's see how the figure consisting of all points colored exactly once is structured. On the segment of abscissas \([i-1, i]\), where \( i = 1, \ldots, n-1 \), this is a rectangle of width \( 1 \) and height \( h_i = \left| \frac{1}{i} - \frac{1}{i+1} \right| \). On the segment \([n-1, n]\), this is a rectangle of width \( 1 \) and height \( h_n = \frac{1}{n} \). Then the area of the figure \( S = 1 \cdot h_1 + 1 \cdot h_2 + \cdots + 1 \cdot h_n = \left(1 - \frac{1}{2}\right) + \left(\frac{1}{2} - \frac{1}{3}\right) + \cdots + \left(\frac{1}{n-1} - \frac{1}{n}\right) + \frac{1}{n} = 1 \).
## Comments
1. One can conduct a proof by induction. Suppose Masha colors the rectangle immediately after Misha marks a point. When Misha marks the point \( (1, 1) \), Masha colors a rectangle of area \( 1 \). Next, when Misha marks a point with abscissa \( n \), Masha colors a rectangle of area \( \frac{1}{n} \) for the first time and a rectangle of area \( \frac{1}{n} \) for the second time (the rest will be points already colored more than once). Thus, the area of the figure consisting of all points colored exactly once does not change.
2. This fact can be seen visually by "shifting" all rectangles to the y-axis.
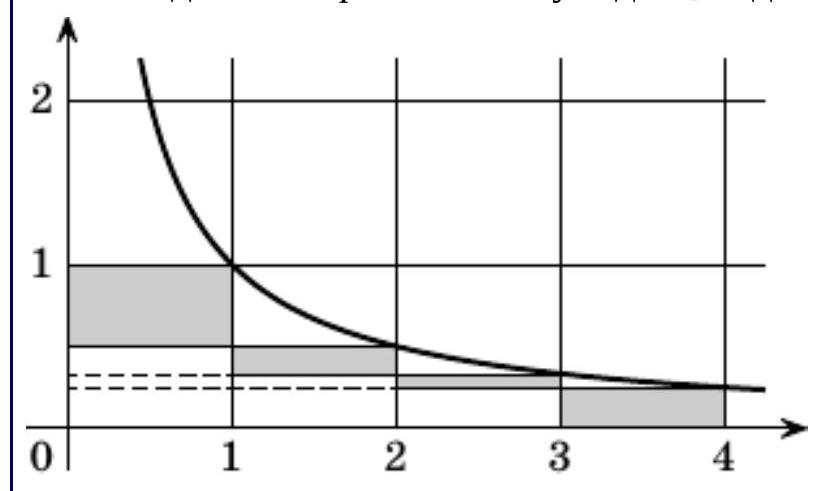
## Answer
Submit a comment
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Zhendarov P.G
In the cells of a $4 \times 4$ table, numbers are written such that the sum of the neighbors of each number is 1 (cells are considered neighbors if they share a side).
Find the sum of all the numbers in the table.
#
|
Let's divide all cells into 6 groups (in the figure, cells of each group are marked with their own symbol). Each group consists of all neighbors of a single cell, so the sum of the numbers in it is 1. Therefore, the sum of all numbers is 6.

## Answer
6.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Motion Problems ]
Two pedestrians set out at dawn. Each walked at a constant speed. One walked from $A$ to $B$, the other from $B$ to $A$. They met at noon and, without stopping, arrived: one - in $B$ at 4 PM, and the other - in $A$ at 9 PM. At what hour of the day was dawn?
|
After noon, the first pedestrian walked as much as the second did before noon.
## Solution
Let $x$ be the number of hours from dawn to noon. The first pedestrian walked $x$ hours before noon and 4 after, while the second walked $x$ hours before noon and 9 after. The ratio of the times is equal to the ratio of the lengths of the paths before and after the meeting point, so ${ }^{x} / 4=9 / x$. From this proportion, we find that $x=6$.
## Answer
At 6 a.m.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Five football teams held a tournament - each team played against each other once. 3 points were awarded for a win, 1 point for a draw, and no points for a loss. Four teams scored 1, 2, 5, and 7 points respectively. How many points did the fifth team score?
#
|
Each team played 4 games. It is clear that the first team drew once and lost the rest of the games. The second team has two draws and two losses. The third team could not have scored five points with draws alone, so it must have won once, in addition to having two draws and one loss. The fourth team won twice (otherwise, it would have scored no more than 6 points). This team also has one draw and one loss. In the end, the first four teams won 3 times and lost 7 times. However, the number of wins should equal the number of losses. Therefore, they lost 4 times to the fifth team, and that team has 12 points.
Example of a tournament with such a distribution of points: the fifth team won against everyone, the fourth team won against the first and second, the third team won against the first, and all other games ended in draws.
## Answer
12 points.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Case Analysis $]$ [ Proof by Contradiction ]
In the cells of a $3 \times 3$ table, numbers are arranged such that the sum of the numbers in each column and each row is zero. What is the smallest number of non-zero numbers that can be in this table, given that this number is odd?
|
Example.
| 0 | -1 | 1 |
| :---: | :---: | :---: |
| -1 | 2 | -1 |
| 1 | -1 | 0 |
Evaluation. We will prove that it is impossible to get by with fewer non-zero numbers.
If the table contains exactly one non-zero number, then the sum of the numbers in the row containing this number is not zero. Suppose the table contains exactly three non-zero numbers. If all of them are in the same row, then the sum of the numbers in any column is not zero. If not all of them are in the same row, then in some row there is exactly one non-zero number, and the sum of the numbers in this row is not zero.
Suppose the table contains exactly five non-zero numbers. Then there are four zeros in the table, which means that some two zeros are in the same row. Since the sum of the numbers in this row is zero, all the numbers in this row are zeros.
It remains to note that in the column where the remaining zero stands, there are exactly two zeros, which is impossible.
## Answer
7 numbers.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Problems on Mixtures and Concentrations]
From two pieces of alloys (with different lead content) weighing 6 and 12 kg, pieces of equal mass were cut. Each of the cut pieces was melted with the remainder of the other piece, after which the percentage of lead in both alloys became the same. What are the masses of each of the cut pieces?
|
In each of the received pieces, the ratio of the first alloy to the second should be the same (namely $1: 2$, since the second alloy is twice as much). This means the cut piece constitutes $1 / 3$ of 12 kg (and $2 / 3$ of 6 kg).
## Answer
4 kg.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ [Divisibility of numbers. General properties]
Authors: Binkov A.d,, Raskina I.v.
Several whole heads of cheese were stored in the warehouse. At night, rats came and ate 10 heads, and all of them ate equally. Several rats got sick from overeating. The remaining seven rats the next night finished off the remaining cheese, but each rat was able to eat only half as much cheese as the night before. How much cheese was originally in the warehouse?
#
|
Let there be $k$ rats in total ($k>7$), then each rat ate $10 / k$ pieces of cheese on the first night. On the second night, each rat ate half as much, i.e., $5 / k$ pieces. Seven rats thus ate $35 / k$ pieces. This is an integer.
The only divisor of the number 35 that exceeds 7 is the number 35 itself. Therefore,
$35 / k=1$, and there were $10+1=11$ pieces of cheese in the warehouse before the rat invasion.
## Answer
11 pieces of cheese
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A pedestrian set out from point $A$ to point $B$. At the same time, a cyclist set out from $B$ to $A$. After one hour, the pedestrian found himself exactly halfway between point $A$ and the cyclist. Another 15 minutes later, they met, and each continued on their way.
How much time did the pedestrian spend on the journey from $A$ to $B$? (The speeds of the pedestrian and the cyclist are constant.)
#
|
Let one hour after the start of the movement, the pedestrian be at point $C$, and the cyclist at point $D$. Then the segment $A C$ is equal to the segment $C D$ (see figure). Let them meet at point $E$ after 15 minutes.
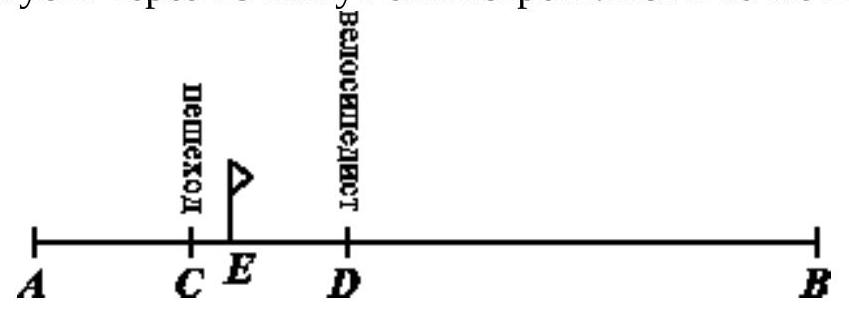
The pedestrian spent 60 minutes on the path $A C$, so he also spent 60 minutes on the path $C D$. Therefore, the path $E D$ took the pedestrian $60-15=45$ minutes, and the cyclist 15 minutes. Consequently, the pedestrian's speed is 3 times less than the cyclist's speed.
The cyclist traveled the path $B D$ in one hour, so it took the pedestrian 3 hours to travel this path. The pedestrian spent 2 hours on the path $A D$, so the total time for the entire journey was 5 hours.
## Answer
5 hours.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Folklore
Solve the equation: $2 \sqrt{x^{2}-16}+\sqrt{x^{2}-9}=\frac{10}{x-4}$.
|
Since the left, and therefore the right, part of the equation takes only positive values, then $x>4$. On the interval $(4,+\infty)$, the function
$f(x)=2 \sqrt{x^{2}-16}+\sqrt{x^{2}-9}$ is increasing, while the function $g(x)=\frac{10}{x-4}$ is decreasing, so the equation $f(x)=g(x)$ has no more than one root.
It remains to note that $f(5)=g(5)$.
## Answer
$x=5$
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A sowing plot for rye has a rectangular shape. As part of the restructuring of the collective farm lands, one side of the plot was increased by $20\%$, and the other side was reduced by $20\%$. Will the rye yield change as a result, and if so, by how much?
|
Let $a$ and $b$ be the original sides of the rectangle. The new area is equal to $1.2 a \cdot 0.8 b = 0.96 a b$, which means the area has decreased by $4\%$.
## Answer
It will decrease by $4\%$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Folklore }}$
Find the largest natural $n$, for which $n^{200}<5^{300}$.
|
Let's rewrite the inequality as: $\left(n^{2}\right)^{100}<\left(5^{3}\right)^{100}$. Therefore, it is sufficient to find the greatest natural solution to the inequality $n^{2}<125$.
## Answer
$n=11$.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Formulas for abbreviated multiplication (other).]
Calculate: $\frac{(2001 \cdot 2021+100)(1991 \cdot 2031+400)}{2011^{4}}$
|
$2001 \cdot 2021+100=(2011-10)(2011+10)+100=2011^{2}-10^{2}+100=2011^{2}, 1991 \cdot 2031=2011^{2}-20^{2}+400=$ 20112. Thus, the numerator is equal to the denominator.
## Answer
1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic. Mental arithmetic, etc. ]
[Mathematical logic (other)]
The rabbits sawed several logs. They made 10 cuts and got 16 chunks. How many logs did they saw?
|
Recall the problem $\underline{89914}$ - the problem about how the rabbits made 10 cuts to split one log.
## Solution
From each log, you get one more piece than the number of cuts. Since there are 6 more pieces, it means there were 6 logs.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic operations. Numerical identities ]
Malvina asked Buratino to multiply a number by 4 and add 15 to the result, but Buratino multiplied the number by 15 and then added 4, and yet, the answer was correct. What was the number?
|
Try to form an equation
## Solution
Let the unknown number be $x$ and write the equation: $4 x + 15 = 15 x + 4$. Solving this equation, we get: $11 = 11 x$, or $x = 1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Word problems ]
In a pet store, they sell large and small birds. A large bird costs twice as much as a small one. One lady bought 5 large birds and 3 small ones, while another bought 5 small birds and 3 large ones. In this case, the first lady paid 20 rubles more. How much does each bird cost?
#
|
Try to express the difference in purchases of two ladies "in small birds".
## Solution
The first lady paid for her purchase as if for 13 small birds (let's recall that a large bird is twice as expensive as a small one), while the second lady paid as if for 11 small birds. That is, the difference in purchases is 2 small birds, and the difference in price is 20 rubles. Therefore, a small bird costs 10 rubles, and a large bird costs 20 rubles.
Send a comment
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ [Evenness and Oddness]
All the dominoes were laid out in a chain. At one end, there were 5 dots. How many dots are at the other end?
#
|
The number five on half of the dominoes appears 8 times. Inside the chain, all fives are paired. The unpaired five is at one end. Therefore, the remaining five is at the other end.
## Answer
5 points.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the remainder of $4^{18}+5^{17}$ when divided by 3.
#
|
$4^{18}+5^{17} \equiv 1^{18}+(-1)^{17}=0(\bmod 3)$.
Answer
0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Residue arithmetic (other).]
Find the remainder of $\left(116+17^{17}\right)^{21} \cdot 7^{49}$ when divided by 8.
#
|
$\left(116+17^{17}\right)^{21} \cdot 7^{49} \equiv\left(4+1^{17}\right)^{21} \cdot 7 \cdot 49^{24} \equiv 5^{21} \cdot(-1) \cdot 1^{24}=-5 \cdot 25^{10} \equiv-5 \cdot 1^{10} \equiv 3(\bmod 8)$.
Answer
## 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Inequalities Problems. Case Analysis]
9 kg of candies cost less than 10 rubles, and 10 kg of the same candies cost more than 11 rubles. How much does 1 kg of these candies cost?
|
The first condition is equivalent to the statement that 1 kg of candies costs less than $10 / 9$ rubles $= 1$ ruble $11_{1}^{1} / 9$ kopecks. Similarly, the second condition is equivalent to the statement that 1 kg of candies costs more than ${ }^{11} / 10$ rubles = 1 ruble 10 kopecks. Therefore, the answer to the problem is any amount greater than 1 ruble 10 kopecks and less than 1 ruble $11^{1 / 9}$ kopecks. Therefore, the answer is unambiguous: 1 ruble 11 kopecks.
## Answer
1 ruble 11 kopecks.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Rabbits are sawing a log. They made 10 cuts. How many chunks did they get?
|
Into how many parts is a log divided by the first cut? How does the number of pieces change after each subsequent cut?
# Solution
The number of chunks is always one more than the number of cuts, since the first cut divides the log into two parts, and each subsequent cut adds one more chunk. Answer: 11 chunks.
## Answer
11 chunks.
Problem
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Decimal numeral system]
How many two-digit numbers have a sum of digits equal to 10?
#
|
There are nine such numbers: $19,28,37, \ldots 91$.
## Answer
There are 9 numbers.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Rabbits sawed several logs. They made 10 cuts and got 16 chunks. How many logs did they saw?
#
|
Recall problem 4.
## Solution
From each log, you get one more chunk than the number of cuts made. Since there are 6 more chunks, it means there were 6 logs.
## Answer
6 logs.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic. Mental calculation, etc.]
$[\quad$ Invariants $]$
The rabbits are sawing the log again, but now both ends of the log are secured. Ten middle pieces fell, while the two end pieces remained secured. How many cuts did the rabbits make?
|
How many logs did the hares receive
## Solution
The hares received 12 logs - 10 fallen and 2 secured. Therefore, there were 11 cuts.
## Answer
The problem
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic. Mental calculation, etc.]
How many times longer is the staircase to the fourth floor of a house compared to the staircase to the second floor of the same house?
|
Think about how many floors you need to go up to reach the second floor?
## Solution
To get to the 2nd floor, you need to go up 1 floor, and to get to the 4th floor, you need to go up three floors. Therefore, the answer is: 3 times (and not 2, as it might seem at first).
## Answer
3 times.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic. Mental calculation, etc.]
Malvina asked Buratino to multiply a number by 4 and add 15 to the result, but Buratino multiplied the number by 15 and then added 4, and yet the answer was correct. What was the number?
|
Try to form an equation
## Solution
Let the unknown number be x and write the equation: $4 x + 15 = 15 x + 4$. Solving this equation, we get: $11 = 11 x$, or $x = 1$.
## Answer
This number is 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic. Mental calculation, etc.]
On the mailbox, it is written: "Mail is collected five times a day from 7 to 19 hours." Indeed, the first time the postman collects the mail is at 7 in the morning, and the last time is at 7 in the evening. At what intervals are the letters taken out of the box?
|
How many intervals will there be between mail pickups? Recall problem 4.
## Solution
If the mail is picked up 5 times within the specified time, there will be 4 intervals, i.e., the duration of one interval will be 3 hours.
## Answer
Every 3 hours.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the last digit of the product of all odd numbers from 1 to 99? And from 1 to 199?
#
|
Notice that among the numbers involved in the product, there are those ending in 5.
## Solution
The product of any sequence of numbers, among which there are numbers ending in 5, will end in either 0 (if there is at least one even number in the sequence) or 5 (if all numbers are odd). In both cases here, there are no even numbers, but there are numbers ending in 5, so the last digit in both products will be 5.
## Answer
## $5 ; 5$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic. Mental calculation, etc.]
A full milk barrel weighs 34 kg, and one filled to half - 17.5 kg. How much does the empty barrel weigh?
#
|
How much greater is the doubled weight of a bucket filled halfway compared to the weight of a full bucket?
## Solution
The weight of the bucket is equal to the difference between the doubled weight of the bucket filled halfway (i.e., the weight of the contents + twice the weight of the bucket) and the weight of a full bucket (i.e., the weight of the bucket + the weight of the contents). Therefore, the weight of the bucket is 1 kg.
## Answer
1 kg.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Rational Equations]
Solve the equation:
$$
x+\frac{x}{x}+\frac{x}{x+\frac{x}{x}}=1
$$
|
On the domain of definition, the equation can be reduced to $\mathrm{x}+1+\mathrm{x} /(\mathrm{x}+1)=1$. Multiply both sides of the equation by $\mathrm{x}+1$. After simplification, we get: $\mathrm{x}^{2}+2 \mathrm{x}=0$, that is, $\mathrm{x}=0$ or $\mathrm{x}=-2$. The root of the equation is only $\mathrm{x}=$ $-2$.
Answer
$-2$
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A cube with a side of 1 m was sawn into cubes with a side of 1 cm and laid in a row (in a straight line). What length did the row turn out to be
#
|
We get $100 \times 100 \times 100=1000000$ (cm) or 10000 m $=10$ km.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ [ divisibility rules for 3 and 9 ]
It is known that $35!=10333147966386144929 * 66651337523200000000$. Find the digit replaced by the asterisk.
The number 35! is divisible by 9.
#
|
Since 35! is divisible by 9, the sum of the digits of this number is also divisible by 9. It is not difficult to calculate that the sum of the digits (excluding the asterisk) of the written number gives a remainder of 3 when divided by 9. Therefore, the digit replaced by the asterisk is 6.
## Answer
6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
In a sequence of natural numbers, each number, except the first, is obtained by adding to the previous one its largest digit.
What is the maximum number of consecutive odd terms that can occur in the sequence?
|
Let $a_{1}, \ldots, a_{5}$ be consecutive odd terms of a sequence. The last digits of these numbers are odd, and the largest digits of the numbers $a_{1}, \ldots, a_{4}$ are even and, therefore, not the last. When moving to the next number, the largest digit of the previous number does not change (otherwise, it would increase by 1 and become odd), so $a_{1}, \ldots, a_{5}$ form an arithmetic progression with a non-zero even digit $d$ as the common difference. The numbers $0, d, 2d, 3d, 4d$ end in different digits (since they give different remainders when divided by 5). By adding these numbers to $a_{1}$, we see that $a_{1}, \ldots, a_{5}$ also end in different digits. Therefore, one of the numbers must end in
9. But this can only be $a_{5}$, and thus, the next term in the sequence is an even number.
Five consecutive odd terms can be found, for example, in the sequence: 807, 815, 823, 831, 839.
## Answer
5 terms.
The area of triangle $ABC$ is $10 \text{ cm}^2$. What is the smallest value that the radius of the circumscribed circle of triangle $ABC$ can take, given that the midpoints of the heights of this triangle lie on the same line?
## Solution
According to the solution of problem 102505, triangle $ABC$ is a right triangle. Let its legs be $a$ and $b$, the hypotenuse be $c$, and the radius of the circumscribed circle be $R$. We can reason in different ways.
First method. $4R^2 = c^2 = a^2 + b^2 \geq 2ab = 40$. Therefore, $R^2 \geq 10$.
Second method. From the solution of problem 102505, we see that $10 = S_{ABC} \leq R^2$.
Equality is achieved for an isosceles right triangle.
## Answer
$\sqrt{10}$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Systems of linear equations]
Seven coins (weighing 1, 2, ... 7 grams) are laid out in a row in some order. For each coin (except the outermost ones), the sum of the weights of its neighbors is known.
What is the maximum number of coins whose weight can be guaranteed to be known?
#
|
Make sure that the weights of the second, fourth, and sixth coins can be expressed through known weights.
## Solution
Let the weights of the coins in the order of their arrangement be: $x_{1}, x_{2}, \ldots, x_{7}$. From the condition, we have:
$x_{1}+x_{3}=a_{2}, x_{2}+x_{4}=a_{3}, x_{3}+x_{5}=a_{4}, x_{4}+x_{6}=a_{5}, x_{5}+x_{7}=a_{6}, x_{1}+x_{2}+x_{3}+x_{4}+x_{5}+x_{6}+x_{7}=28$, where $a_{k}$ is the sum of the weights of the neighbors of the $k$-th coin $(k=2,3,4,5)$. Therefore, $x_{4}=a_{3}+a_{5}-\left(28-a_{2}-a_{6}\right)$. This means the weight of the fourth coin can be determined. Since $x_{2}=a_{3}-x_{4}, x_{6}=a_{5}-x_{4}$, the weights of the second and sixth coins can also be determined.
On the other hand, if the coins in the row have weights $2,1,5,7,3,6,4$ or $4,1,3,7,5,6,2$, then the sums of the weights of the neighbors of each coin are the same in both cases, so it is impossible to reliably determine the weights of the first, third, fifth, and seventh coins.
## Answer
For three coins.
Children are throwing red, white, and blue balls. Each child threw and caught a total of three balls, and these are balls of different colors. Additionally, some three balls were thrown but not caught by anyone. Prove that these three balls are of three different colors.
## Hint
Show that the number of balls of each color that were thrown but not caught has the same parity.
## Solution
Let the number of children be $k$, and the number of red balls that were thrown but not caught be $m$. Then the number of red balls that were thrown and caught is $1 / 2(k-m)$ (since each of these balls was thrown by one child and caught by another). Thus, $k$ and $m$ have the same parity. Similarly, the number of balls of each color that were thrown but not caught has the same parity as $k$. The sum of these three numbers is 3. Since they are non-negative, they must all be equal to 1.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ equations in integers ]
A combination ( $x, y, z$ ) of three natural numbers, lying in the range from 10 to 20 inclusive, is an unlocking combination for a code lock if
$3 x^{2}-y^{2}-7 z=99$. Find all the unlocking combinations.
|
Note that $3 x^{2}-y^{2} \equiv 1(\bmod 7)$. There are 8 such pairs of remainders: $(1,3),(1,4),(2,2),(2,5),(5,2),(5,5),(6,3),(6,4)$. Considering the range of values for $x$ and $y$, we get 19 possible pairs: $(15,10),(15,17),(16,16),(16,12),(16,19)$, $(12,16),(19,16),(12,12),(12,19),(19,12),(19,19),(13,10),(13,17),(20,10),(20,17)$, $(13,11),(13,18),(20,11),(20,18)$. For each pair $(x, y)$, we find the corresponding value of $z$. Only three options fall within the range $[10,20]$:

For what value of the height does a rectangular trapezoid with an acute angle of $30^{\circ}$ and a perimeter of 6 have the maximum area?
## Hint
Express the area of the given trapezoid in terms of its height and apply the Cauchy inequality.
## Solution
Let $h$ be the height of the trapezoid, and $3x$ be the sum of the bases. Then the larger lateral side of the trapezoid is $2h$, and the perimeter is $3x + 3h = 6$. The area of the trapezoid is $\frac{3xh}{2} = \frac{3}{2}\left(\frac{x+h}{2}\right)^2 = \frac{3}{2}$, and equality is achieved when $h = x = 2 - h$, i.e., when $h = 1$.
## Answer
At $h = 1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For what value of $a$ does the polynomial $P(x)=x^{1000}+a x^{2}+9$ divide by $x+1$?
|
$P(-1)=1+a+9=a+10$. By the theorem of Bezout, this number should equal zero.
## Answer
For $a=-10$.
|
-10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Bezout's Theorem. Factorization]
For what values of the parameter $a$ does the polynomial $P(x)=x^{n}+a x^{n-2}(n \geq 2)$ divide by $x-2$?
|
$P(2)=2^{n}+a \cdot 2^{n-2}=2^{n-2}(4+a)$.
## Answer
For $a=-4$.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the remainder when the number $10^{10}+10^{10^{2}}+10^{10^{3}}+\ldots+10^{10^{10}}$ is divided by 7.
#
|
$10^{6} \equiv 1(\bmod 7)$, since $10^{3}+1$ is divisible by 7, and $10^{k} \equiv 4(\bmod 6)$ for $k \geq 1$, since the number $9 \ldots . .96$ is even and divisible by 3. Therefore,
## Methods for solving problems with parameters
$$
\text { }
$$

$10^{10^{k}} \equiv 10^{4}(\bmod 7)$ for $k \geq 1$. Therefore, the required remainder is the remainder of the division of the number $10 \cdot 10^{4} \equiv 3^{5} \equiv 2$
$(\bmod 7)$.
## Answer
5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Solve the equation $x^{2 y-1}+(x+1)^{2 y-1}=(x+2)^{2 y-1}$ in natural numbers.
#
|
$x^{2 y-1} \equiv 1(\bmod x+1)$. Since the number $2 y-1$ is odd, then $x^{2 y-1}=-1(\bmod x+1)$. Therefore, $0=(x+2)^{2 y-1}-x^{2 y-1}$ $-(x+1)^{2 y-1}=1+1=2(\bmod x+1)$, that is, $x+1=2$. Hence, $1+2^{2 y-1}=3^{2 y-1} \Leftrightarrow 2 y-1=1 \Leftrightarrow y=1$.
## Answer
$x=y=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let's consider the sum of the digits of all numbers from 1 to 1000000 inclusive. For the resulting numbers, we will again consider the sum of the digits, and so on, until we get a million single-digit numbers. Which are more numerous among them - ones or twos?
|
The sum of the digits of a number gives the same remainder when divided by 9 as the number itself. Therefore, units are obtained from numbers of the form $9k+1$, and twos from numbers of the form $9k+2$. All numbers from 1 to 999999 are divided into consecutive nines, each of which contains one number of each kind. The remaining number 1000000 is of the form $9k+1$, so a one is obtained from it. Thus, there is one more one than two.
## Answer
There is one more one
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tokarev S.I
In a row, 10 integers are written. The second row is constructed as follows: under each number $A$ in the first row, a number is written that is equal to the count of numbers in the first row that are greater than $A$ and are located to the right of $A$. The third row is constructed similarly from the second row, and so on.
a) Prove that all rows, starting from some point, are zero (consist entirely of zeros).
b) What is the maximum possible number of non-zero rows (containing at least one number different from zero)?
|
a) In all rows starting from the second, all numbers are non-negative integers. In the second row, the tenth number (the rightmost) is 0, as there is nothing to the right of it. In the third row, the tenth number is also 0, and the ninth number is also 0, because in the second row, the ninth number is non-negative, and the tenth is 0. Reasoning this way, we arrive at the conclusion that in the eleventh row, all numbers are zeros. Thus, the number of non-zero rows is no more than 10.
b) Here is an example of the first row, from which 10 non-zero rows, including the first, are obtained:
| 1st row: | 0 | 5 | 0 | 4 | 0 | 3 | 0 | 2 | 0 | 1 |
| ---: | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 2nd row: | 5 | 0 | 4 | 0 | 3 | 0 | 2 | 0 | 1 | 0 |
| 3rd row: | 0 | 4 | 0 | 3 | 0 | 2 | 0 | 1 | 0 | 0 |
| 4th row: | 4 | 0 | 3 | 0 | 2 | 0 | 1 | 0 | 0 | 0 |
| 5th row: | 0 | 3 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 0 |
| 6th row: | 3 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 7th row: | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8th row: | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9th row: | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10th row: | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
## Answer
10 rows.
|
10
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
[Inequality problems. Case analysis]
A student passed 31 exams over 5 years of study. In each subsequent year, he passed more exams than in the previous year, and in the fifth year, he passed three times as many exams as in the first year. How many exams did he pass in the fourth year?
#
|
Try to determine the number of exams taken in the first (and, respectively, fifth) year.
## Solution
It is easy to determine that three exams were taken in the first year and, accordingly, nine in the fifth year. There are two possible distributions of the number of exams in the other years: $4+7+8$ and $5+6+8$. Thus, the student took 8 exams in the fourth year; in the third year, 6 or 7 exams.
## Answer
8 exams.
|
8
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Trigonometric Inequalities]
Find the maximum value of the expression $\sin x \sin y \sin z + \cos x \cos y \cos z$.
|
What is the greatest value of the expression $\sin x \sin y+\cos x \cos y$?
## Solution
When $x=y=z=0$, the expression $\sin x \sin y \sin z+\cos x \cos y \cos z$ equals 1. We will show that a value greater than 1 cannot be achieved. The expression $\sin x \sin y \sin z+\cos x \cos y \cos z_{\text {does not }}$ exceed
$|\sin x\|\sin y|+| \cos x\| \cos y| \cdot$ There exist angles $x^{\prime}, y^{\prime}$ from the interval $[0, \pi / 2]$ such that $\sin x^{\prime}=|\sin x|_{\text {and }} \sin y^{\prime}=|\sin y|$. Then $|\sin x\|\sin y|+| \cos x\| \cos y|=\sin x^{\prime} \sin y^{\prime}+\cos x^{\prime} \cos y^{\prime}=\cos \left(x^{\prime}-y^{\prime}\right)$, which obviously does not exceed 1.
## Answer
1.00
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A group of tourists was supposed to arrive at the train station at 5 o'clock. By this time, a bus was supposed to come from the tourist base to pick them up. However, arriving at the train station at 3:10, the tourists started walking to the tourist base. Meeting the bus on the road, they got on and arrived at the tourist base 20 minutes earlier than the scheduled time. At what speed did the tourists walk before meeting the bus, if the bus's speed was 60 km/h?
|
Tourists saved 20 minutes, during which the bus would have traveled the distance they walked twice.
Therefore, on the way to the station, the bus saved 10 minutes, meaning it met the tourists at 4:50. This means the tourists walked the distance from the station to the meeting point in 100 minutes, which is 10 times slower than the bus.
## Answer
6 km/h.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
a) A traveler stopped at an inn, and the owner agreed to accept rings from a golden chain the traveler wore on his wrist as payment for lodging. However, he set a condition that the payment should be daily: each day the owner should have one more ring than the previous day. The closed chain contained 11 rings, and the traveler planned to stay exactly 11 days, so he agreed. What is the minimum number of rings he needs to cut to be able to pay the owner?
b) How many rings should the chain consist of so that the traveler can stay at the inn for the maximum number of days, given that he can only cut $n$ rings?
|
a) It is enough to cut two rings so that pieces of three and six rings are separated. On the third day, the traveler gives the piece of three rings and receives two rings as change, and on the sixth day, the piece of six rings and receives five rings as change.
b) Arrange the resulting pieces of the chain (not counting the cut rings) in increasing order of the number of rings in them: $a_{1} \leq a_{2} \leq \ldots$ Clearly, $a_{1} \leq n+1$ (otherwise, it would be impossible to pay for the ( $n+1$ )-th day), $a_{2} \leq a_{1}+n+1 \leq 2(n+1), a_{3} \leq$ $a_{2}+a_{1}+n+1 \leq 4(n+1), \ldots$ Moreover, the number of pieces does not exceed $n$. Therefore, the chain contains no more than $n+(n+1)\left(1+2+2^{2}+\ldots+2^{n-1}\right)=(n+1) 2^{n}-1$ rings.
Taking pieces of the maximum possible length $\left(a_{k}=(n+1) 2^{k-1}, k=1, \ldots, n\right), \quad$ we get a chain of $(n+1) 2^{n}-1$ rings.
## Answer
a) 2 rings. b) From $(n+1) 2^{n}-1$ rings.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Ordinary fractions ]
How many representations does the fraction $\frac{2 n+1}{n(n+1)}$ admit as a sum of two positive fractions with denominators $n$ and $n+1$?
|
$\frac{2 n+1}{n(n+1)}=\frac{1}{n}+\frac{1}{n+1}$. Since both terms are the smallest fractions with the specified denominators, there are no other representations
## Answer
One.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Folklore
In Italy, they produce clocks where the hour hand makes one revolution in a day, and the minute hand makes 24 revolutions, with the minute hand being longer than the hour hand (in regular clocks, the hour hand makes two revolutions in a day, and the minute hand makes 24). Consider all positions of the two hands and the zero mark on the Italian clocks that also occur on regular clocks. How many such positions exist on the Italian clocks in a day? (The zero mark indicates 24 hours on Italian clocks and 12 hours on regular clocks.)
#
|
Let some position of the hour hand of ordinary clocks before noon be taken at time $t$ (counting from the beginning of the day; $0 \leq t<12$ : we measure time in hours). Since the hour hand of Italian clocks moves twice as slowly as the hour hand of ordinary clocks, it will coincide with the considered position of the hour hand of ordinary clocks at the moment $2 t$. The minute hands (of ordinary and Italian clocks) occupy the same position if the difference in times is an integer number of hours. Thus, the condition for "coincidence of positions" is that the number $2 t-t=t$ is an integer. In the specified interval, there are exactly 12 integer values - from 0 to 11 (which correspond to the moments $0,1, \ldots, 11$ o'clock exactly on ordinary clocks).
## Answer
12 positions.
## Problem
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Rynbniov i...
In the store, 20 kg of cheese was delivered, and a queue formed. After selling cheese to the next customer, the saleswoman accurately calculates the average weight of the purchase for all the cheese sold and informs how many people the remaining cheese will last if everyone buys exactly this average weight. Could the saleswoman have reported after each of the first 10 customers that the cheese would last exactly 10 more people? If so, how much cheese was left in the store after the first 10 customers?
#
|
Let $s_{k}$ be the average weight of cheese sold to the first $k$ customers. By the condition $20-k s_{k}=10 s_{k}$, hence
$s_{k}=\frac{20}{k+10}$ kg, and after the $k$-th customer, there remains
200
$k+10$
kg of cheese. Since the obtained sequence is decreasing, the seller can make such a statement after each customer (not limited to the first ten). After the 10th customer, exactly half of the cheese remains - 10 kg.
## [ Problem 98538 Topics: [ Continuity considerations ] [ Examples and counterexamples. Constructions ] Difficulty: $3+$ Grades: $9,10,11$
Author: G. Talperin $[$. .
There exist 1000 consecutive natural numbers, none of which are prime (for example, $1001!+2, 1001!+3, \ldots, 1001!+1001$ ).
But do there exist 1000 consecutive natural numbers, among which there are exactly five prime numbers?
## Solution
Let $P_{n}$ denote the number of prime numbers among a thousand consecutive numbers from $n$ to $n+999$. Note that $P_{n+1}$ differs from $P_{n}$ by no more than one. However, $P_{1}>5$, and $P_{1001!+2}=0<5$, so when $n$ changes from 1 to $1001!+2$, the value of $P_{n}$ will be equal to 5 for some $n$.
## Answer
They exist.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ equations in integers ]
A shepherd was tending a herd of 100 heads. For this, he was paid 200 r. For each bull, he was paid 20 r, for each cow - 10 r, and for each calf - 1 r.
How many bulls, how many cows, and how many calves are in the herd?
|
The number of calves is a multiple of 10.
## Solution
From the condition, it follows that the number of calves is a multiple of 10. Let the number of bulls be $a$, cows be $b$, and calves be $10 c$. Then $a+b+10 c=100$ and $20 a+10 b+10 c=200$, which simplifies to $2 a+b+c=20$.
From the first equation, it is clear that $a+b$ is a multiple of 10. From the second equation, $-a+b<20$. Therefore, $a+b=10, c=9, 2 a+b=11$. From this, we get $a=1, b=9, c=9$.
## Answer
1 bull, 9 cows, and 90 calves.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The distance between points $A$ and $B$ is 40 km. A pedestrian left $A$ at 4 o'clock. When he had walked half the distance, he was caught up by a cyclist who had left $A$ at 7:20. An hour after this, the pedestrian met another cyclist who had left $B$ at 8:30. The speeds of the cyclists are the same. Determine the speed of the pedestrian.
|
The second cyclist was on the road for $11 / 6$ hours less than the first (by the time of the second cyclist's meeting with the pedestrian). If he had set out simultaneously with the first cyclist, he would have been halfway through his journey one hour earlier than the moment of his meeting with the pedestrian. Therefore, it took him $1 / 6$ of an hour to travel the distance from the meeting point with the pedestrian to the halfway point. This same distance the pedestrian covers in one hour. Therefore, the speed of the cyclist is 6 times the speed of the pedestrian.
The pedestrian spent $7 \frac{1}{3}-4=10 / 3$ hours more on 20 km than the first cyclist. Thus, he covered 20 km in $6 / 5.10 / 3=4$ hours.
## Answer
5 km/h.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Golovanov A.S.
The numbers from 1 to 10 are divided into two groups such that the product of the numbers in the first group is divisible by the product of the numbers in the second group.
What is the smallest value that the quotient of the first product divided by the second can have?
|
Among the numbers from 1 to 10, only the number 7 is divisible by 7. Therefore, it must be included in the first group, and the quotient is no less than 7.
For example, when it equals $7:(3 \cdot 5 \cdot 6 \cdot 7 \cdot 8):(1 \cdot 2 \cdot 4 \cdot 9 \cdot 10)$.
## Answer
7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Percentage and Ratio Problems ]
Joe knows that to convert from pounds to kilograms, you need to divide the weight in pounds by 2 and then decrease the resulting number by $10 \%$. From this, Joe concluded that to convert from kilograms to pounds, you need to multiply the weight in kilograms by 2 and then increase the resulting number by $10 \%$. By what percentage of the correct value of the weight in pounds will he be wrong?
|
According to the condition, 1 pound equals $0.5 - 0.05 = 0.45$ kg. When converting 0.45 kg to pounds using John's method, he will get $0.9 + 0.09 = 0.99$ pounds, which is $1\%$ less.
## Answer
By $1\%$ less.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the maximum number of cells that can be marked on a chessboard so that from each of them, it is possible to move to any other marked cell in exactly two moves of a chess knight?
#
|
Let the knight be on a square of a certain color, then after two moves it will be on a square of the same color. Therefore, the marked squares should be of the same color (let's say black).
We will divide all the black squares of the board into eight four-square figures of two types (striped and gray), as shown in the image.
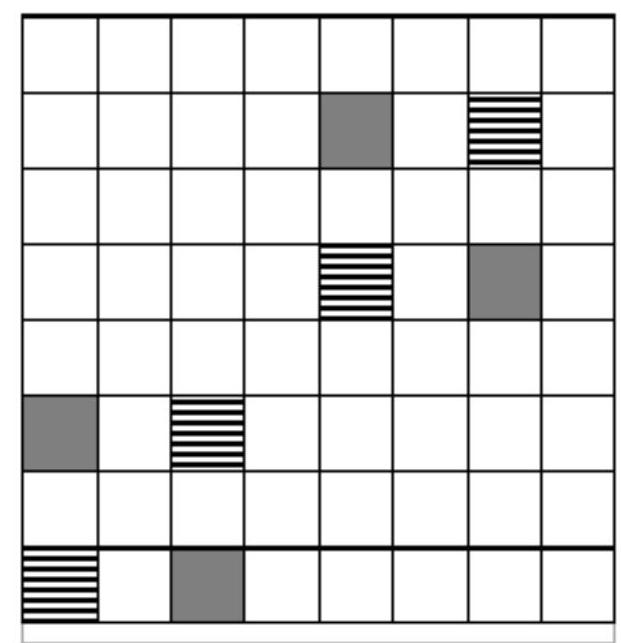
The distance between any two squares of each such figure is at least four knight moves. Therefore, each of these figures can contain no more than one marked square. Consequently, no more than eight squares can be marked. An example for eight marked squares is shown in the image.

## Answer
## [ Ordinary fractions $]$ Problem 116612 Topics: [ Case enumeration $\quad]$ [Mathematical logic (other) $]$
Author: Shapovalov A.V.
Vasya wrote a true statement:
"In this phrase, $1 / 3$ of all digits are the digit 3, and $1 / 2$ of all digits are the digit $1$."
And Kolya wrote the phrase:
"In this phrase, 1/... of all digits are the digit *, the fractions of digits * and * are the same and equal to 1/..., and the fraction of all other digits is $1 / \ldots$."
Insert three different digits in place of the asterisks, and three different numbers in place of the ellipses so that the statement is true.
## Solution
If any of the numbers replaced by ellipses is at least three digits, then there are at least 100 digits in this phrase, which is impossible (then one of the numbers consists of at least 30 characters, but then there are at least $10^{30}$ digits in total, and so on, it is clear that this cannot be). Therefore, all numbers are either single-digit or double-digit, and there are between 9 and 12 digits in total.
The digit "1" is not less than 4, and its fraction is not less than $4 / 12 = 1 / 3$, so the denominator of the first fraction is a single-digit number, meaning there are fewer than 12 digits.
All denominators are divisors of the number of digits, greater than one. Therefore, there cannot be 11 digits (the number 11 has no single-digit divisors other than one), nor 9 digits (four terms of the form $1 / 3$ and $1 / 9$ do not sum to 1). Therefore, there are 10 digits in total, and the fraction of the digit "1" is $1 / 2$. The other fractions can be $1 / 5$ and $1 / 10$. The sum of the fractions must be equal to 1: $1 / 2 + 1 / 5 + 1 / 5 + 1 / 10$.
In the denominators, the digits 0, 2, and 5 appear once each. Any two can be mentioned explicitly, then their fraction will be $1 / 5$, and the fraction of the only remaining digit will be $1 / 10$.
## Answer
"In this phrase, 1/2 of all digits are the digit 1, the fractions of digits 2 and 5 are the same and equal to 1/5, and the fraction of all other digits is $1 / 10$"
(or "...the fractions of digits 0 and 2 are the same..." or "...the fractions of digits 0 and 5 are the same...").
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Nazarov $\Phi$.
15 elephants are standing in a row, each weighing an integer number of kilograms. If you take any elephant except the one on the far right and add twice the weight of its right neighbor, the result is 15 tons (for each of the 14 elephants). Find the weight of each of the 15 elephants.
|
Number the elephants from left to right from 1 to 15. Denote the weight of the elephant with number $i$ as $5000 + x_{i}$ kg ($i=1, \ldots, 15$). Then $\left(5000 + x_{i}\right) + 2\left(5000 + x_{i+1}\right) = 15000$, which means $x_{i} = -2 x_{i+1}$. Therefore, $x_{1} = -2 x_{2} = 2^{2} x_{3} = -2^{3} x_{4} = \ldots = 2^{14} x_{15}$.
If $x_{15} > 0$, then $x_{15} \geq 1, x_{1} \geq 2^{14} = 16384$, and the weight of the first elephant exceeds 15 tons. Similarly, we reach a contradiction if $x_{15} < 0$. Therefore, $x_{15} = 0$, which means $x_{1} = x_{2} = \ldots = x_{15} = 0$, and the weight of each elephant is 5 tons.
## Answer
The weight of each elephant is 5 tons.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all such natural numbers $p$, that $p$ and $2 p^{2}+1$ are primes.
#
|
If $p$ is not divisible by 3, then $2 p^{2}+1$ is divisible by 3.
## Answer
$p=3$.
## Problem
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
It's very boring to look at a black-and-white clock face, so Clive painted the number 12 red at exactly noon and decided to paint the current hour red every 57 hours.
a) How many numbers on the clock face will end up being painted?
b) How many red numbers will there be if Clive paints them every 1913 hours?
|
a) Since GCD $(12,57)=3$, every third hour will be red: 12, 3, 6, and 9 o'clock.
b) Since GCD $(12,1913)=1$, all numbers on the clock will turn red. (This will happen, however, almost after 3 years.)
## Answer
a) 4 numbers; b) all 12 numbers.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the sum of the coefficients of the even powers in the polynomial that results from the expression $f(x)=(x^{3} - x + 1)^{100}$ after expanding the brackets and combining like terms.
#
|
What will be the result if we substitute $x=1$ and $x=-1$ into the given expression?
## Solution
If we substitute $x=1$ into the polynomial $f(x)$, we get the sum of all coefficients of $x^{k}$. If we substitute $x=-1$, we get the difference between the sums of coefficients of even and odd powers. Therefore, the sum of the coefficients of even powers is $1 / 2(f(1)+f(-1))=1$.
## Answer
1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
\[
\begin{aligned} & {\left[\begin{array}{c}\text { Cryptography } \\ {[\underline{\text { Evenness and Oddness }}]}\end{array}\right]}\end{aligned}
\]
Suppose we need to transmit a message consisting of \( n^2 \) zeros and ones. Write it as an \( n \times n \) square table. Append to each row the sum of its elements modulo 2. This will result in an additional column of height \( n \). Similarly, do the same for each column (including finding the sum of the elements of the added column). For example, if the message 0111 needs to be transmitted, the \( 2 \times 2 \) table (left) will be extended to a \( 3 \times 3 \) table (right).
| 0 | 1 | 1 |
| :--- | :--- | :--- |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
a) Prove that if one error occurs during the transmission of the extended table \((n+1) \times (n+1)\), this error can be found and corrected.
b) What is the minimum number of errors that must occur so that it cannot be detected?
#
|
a) In the extended table, the sum of elements in any column and any row is even. If one element is changed, the sums for one row and one column will become odd. To correct such an error, the element at the intersection of the row and column with odd sums needs to be changed.
b) The minimum number of errors that cannot be detected is 4. For example, all four digits in the message 0111 can be changed. In this case, the sums in all rows and columns will remain even.
## Answer
b) 4 errors.
|
4
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
[ [ $\left[\begin{array}{l}\text { Divisibility of numbers. General properties } \\ \text { p }\end{array}\right]$
Find such an $n$ that the number $10^{n}-1$ is divisible by a) 7 ; b) 13 ; c) 91 ; d) 819.
|
$10^{6}-1$ is divisible by $10^{3}+1=1001=7 \cdot 11 \cdot 13$, and therefore, by 7, and 13, and $91=7 \cdot 13$. In addition, $10^{6}-1=$ 999999 is divisible by 9, and therefore, by
$819=9 \cdot 91$.
## Answer
$n=6$.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Quadratic equations. Vieta's theorem ] [ Methods for solving problems with parameters ]
For what value of the parameter $m$ is the sum of the squares of the roots of the equation $x^{2}-(m+1) x+m-1=0$ the smallest?
|
The sum of the squares of the roots $\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=(m+1)^{2}-2(m-1)=m^{2}+3$ is minimal when $m=0$. Note that in this case, the equation
$x^{2}-x-1=0$ has roots.
## Answer
When $m=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovavov A.B.
10 children were standing in a row. The total number of nuts that the girls and boys had was equal. Each child gave one nut to each of the children standing to their right. After this, the girls had 25 more nuts than they originally had. How many girls are in the row?
|
The first child from the left gave away 9 nuts, which means he had 9 fewer nuts; the second child gave away 8 nuts and received 1, which means he had 7 fewer nuts. Continuing with similar reasoning, we notice that the first five children had 9, 7, 5, 3, and 1 fewer nuts, respectively, while the next five had 1, 3, 5, 7, and 9 more nuts, respectively. Since \(1+3+5+7+9=25\), the girls could only have been the last five children.
## Answer
5 girls.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
nine (not necessarily distinct) nine-digit numbers have been formed; each digit has been used in each number exactly once. What is the maximum number of zeros that the sum of these nine numbers can end with
#
|
Evaluation. Let the sum end with nine zeros. Each of the numbers formed is divisible by 9, since the sum of its digits is divisible by 9. Therefore, their sum is also divisible by 9. The smallest natural number that is divisible by 9 and ends with nine zeros is $9 \cdot 10^{9}$, so the sum of our numbers is no less than $9 \cdot 10^{9}$. This means that one of them is no less than $10^{9}$. Contradiction.
Example with eight zeros: $8 \cdot 987654321 + 198765432 = 81 \cdot 10^{8}$.
## Answer
To 8 zeros.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9
Let $N$ be an even number that is not divisible by 10. Find the tens digit of the number $N^{20}$.
|
From the condition, it follows that $N$ is not divisible by 5. Therefore, according to Fermat's Little Theorem, $N^{4} \equiv 1(\bmod 5)$. Therefore, $N^{20}-1=\left(N^{4}-1\right)\left(N^{16}+N^{12}+N^{8}+N^{4}+1\right)$ is divisible by $5^{2}$. Since the number $N^{20}$ is even, it ends in 26 or 76. But a number ending in 26 is not divisible by 4.
## Answer
7

It is known that in the decimal representation of the number $2^{29}$, all digits are different. Is there a digit 0 among them?
## Solution
Notice that $2 \cdot 2^{29}=2^{30}=(1024)^{3}5 \cdot 10^{8}$. Therefore, the number $2^{29}$ has exactly nine digits.
If there is no zero among them, then the sum of the digits in the decimal representation of this number is $1+2+\ldots+9=45$. From this, it follows that $2^{29}$ is divisible by 3, which is not true. Contradiction.
## Answer
There is.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\stackrel{\text { Ceнгероов V... }}{ }$.
$a, b, c$ are the sides of a triangle. Prove the inequality $\frac{a^{2}+2 b c}{b^{2}+c^{2}}+\frac{b^{2}+2 a c}{c^{2}+a^{2}}+\frac{c^{2}+2 a b}{a^{2}+b^{2}}>3$.
|
Given the triangle inequality $a^{2}>(b-c)^{2}$. Hence, $a^{2}+2 b c>b^{2}+c^{2}$. Therefore, the first term on the left side of the inequality to be proven is greater than 1. The same is true for the other two. Therefore, their sum is greater than 3.
Author: $\underline{\text { Kuznetsov }} \underline{\text { R.M. }}$
Solve the equation $(x+1)^{63}+(x+1)^{62}(x-1)+(x+1)^{61}(x-1)^{2}+\ldots+(x-1)^{63}=0$.
## Solution
Multiplying both sides of the equation by $(x+1)-(x-1)=2$, we get $(x+1)^{64}-(x-1)^{64}=0$. Hence, $(x+1)= \pm(x-$ $1)$, that is, $x=0$.
## Answer
$x=0$.
|
0
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
At the "Lukomorye" station, they sell cards for one, five, and twenty rides. All cards cost a whole number of gold coins. Five cards for one ride are more expensive than one card for five rides, and four cards for five rides are more expensive than one card for twenty rides. It turned out that the cheapest way for 33 bogatyrs to travel is to buy cards for 35 rides, spending 33 gold coins on this. How much does a card for five rides cost?
|
Since 5, 20, and 35 are all divisible by 5, the number of tickets bought for a single ride is also divisible by 5. However, it is more cost-effective to replace every five such tickets with one ticket for five rides. Therefore, there is no need to buy tickets for a single ride. For the same reason, it is most cost-effective to buy three tickets for five rides and one ticket for 20 rides, which costs exactly 33 coins, while seven tickets for five rides cost more. Therefore, a ticket for five rides costs no less than 5 coins.
On the other hand, according to the condition, it is more cost-effective to pay for 35 rides than to buy two tickets for 20 rides, meaning that three tickets for five rides are cheaper than one for 20. Therefore, six tickets for five rides cost less than 33 coins, meaning that one such ticket costs no more than five coins.
## Answer
5 coins.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 Products and factorials $\quad$ K
Determine the highest natural power of the number 2007 that divides 2007!
|
$2007=3^{2} \cdot 223$. In the prime factorization of the number 2007!, the exponent of the number 3 will be quite large, as the factor 3 is included in the factorization of every third number. The factor 223 is only included in the factorization of numbers of the form 223 p, where $p$ is a natural number not exceeding 9. Thus, in the prime factorization of the number 2007!, the number 223 will enter with an exponent of 9. Therefore, the number 2007! will be divisible by $2007^{9}$, but will not be divisible by $2007^{10}$.
## Answer
To the ninth power
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3 [Arithmetic. Mental arithmetic, etc.]
Having walked $4 / 9$ of the length of the bridge, the pedestrian noticed that a car was catching up to him, which had not yet entered the bridge. Then he turned back and met it at the beginning of the bridge. If he had continued his movement, the car would have caught up with him at the end of the bridge. Find the ratio of the car's speed to the pedestrian's speed.
|
From the condition, it follows that the time it takes for the car to approach the bridge is equal to the time it takes for the pedestrian to walk $4 / 9$ of the bridge. Therefore, if the pedestrian continues moving, by the time the car reaches the bridge, he will have walked ${ }^{8} / 9$ of the bridge. This means that in the time it takes for the car to drive across the bridge, the pedestrian manages to walk one-ninth of the bridge, so the speed of the car is 9 times greater than the speed of the pedestrian.
## Answer
9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Factorization] [Exponential Equations]
Find all positive roots of the equation $x^{x}+x^{1-x}=x+1$.
#
|
Since $x>0$, we have $0=x^{2x}+x-x^{x+1}-x^{x}=x^{x}(x^{x}-1)-x(x^{x}-1)=x(x^{x}-1)(x^{x-1}-1)$. Therefore, $x=1$.
## Answer
$x=1$.
## [ Numerical tables and their properties ]
Problem
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Binkov A. D:
After the lesson, the graph of the function $y=k / x$ and five lines parallel to the line $y=k x$ ( $k \neq 0$ ) remained on the board. Find the product of the abscissas of all ten intersection points.
|
A line parallel to the line $y=k x$ has the equation $y=k x+b$. The abscissas of the points of its intersection with the hyperbola are both roots of the equation $k / x=k x+b \quad \Leftrightarrow \quad k x^{2}+b x-k=0$. The product of the roots of this equation is -1. Multiplying five such products, we get the answer.
## Answer
$-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Raskina I.V.
At the exchange office, two types of operations are carried out:
1) give 2 euros - get 3 dollars and a candy as a gift;
2) give 5 dollars - get 3 euros and a candy as a gift.
When the wealthy Pinocchio came to the exchange office, he only had dollars. When he left, he had fewer dollars, no euros appeared, but he received 50 candies. How much did such a "gift" cost Pinocchio in dollars?
|
Since Buratino received 50 candies, he performed exactly 50 operations. During this time, he exchanged all the euros he received back into dollars. Therefore, for every two operations of the second type, there were three operations of the first type, and on these five operations, Buratino lost $2 \cdot 5 - 3 \cdot 3 = 1$ dollar. Thus, he spent $50 : 5 = 10$ dollars.
## Answer
10 dollars.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Folklore }}$
Find the smallest natural $n$, for which the number $A=n^{3}+12 n^{2}+15 n+180$ is divisible by 23.
|
$n^{3}+12 n^{2}+15 n+180=n^{2}(n+12)+15(n+12)=(n+12)\left(n^{2}+15\right)$. The smallest value of $n$ for which the first factor is divisible by 23 is 11, and for the second factor, such $n$ is 10. This can be verified by direct enumeration or by noting that
$n^{2}+15 \equiv n^{2}-100=(n-10)(n+10)(\bmod 23)$.
## Answer
$n=10$
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the class, there are a teacher and several students. It is known that the teacher's age is 24 years older than the average age of the students and 20 years older than the average age of all present in the class. How many students are in the class?
#
|
The assumption that all students are of the same age does not affect the average age and, therefore, the answer. Under this assumption, the age of the student is 4 years less than the average age of all present. To "balance" the 20 years "excess" of the teacher, the number of students should be $20: 4=5$.
## Answer
5 students.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Twelve toddlers went out to the yard to play in the sandbox. Each one who brought a bucket also brought a shovel. Nine toddlers forgot their bucket at home, and two forgot their shovel. By how many fewer toddlers brought a bucket than those who brought a shovel but forgot their bucket?
|
3 kids brought a bucket, which means. and a spade. 10 kids brought a spade. So, 7 kids brought a spade without a bucket. $7-3=4$.
## Answer
It's 4.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bogdanov I.I.
A number not less than 10 digits, in its notation only two different digits are used, and identical digits do not stand next to each other.
By what highest power of two can such a number be divisible?
#
|
Let's cut off the "tail" of the last 8 digits from the number in the condition. The remaining number ends with 8 zeros, so it is divisible by $2^{8}$. The "tail" has the form $\frac{a b a b a b a b}{}=\overline{a b} \cdot 1010101$, where $a$ and $b$ are digits. It is clear that the twos in the prime factorization of the "tail" come only from the number $\overline{a b}$. The highest power of two by which it can be divisible is no more than the sixth ( $2^{7}$ is already three-digit). Then the original number is divisible by no more than the sixth power of two. This is achieved for the number 6464646464.
## Answer
By $2^{6}$.
## [Divisibility of numbers. General properties]
Little Man gave 111 candies to Karlson. Some of them they ate together, $45 \%$ of the remaining candies went to Karlson for lunch, and a third of the candies left after lunch were found by Fröken Bok during cleaning. How many candies did she find?
## Solution
$45 \%$ is $9 / 20$ of the number of candies remaining before Karlson's lunch. Therefore, this number is a multiple of 20. Let's denote it as 20n. Note that
$n \leq 5$. After lunch, 11n candies remained, and Fröken Bok found a third of this amount. Therefore, $n$ is a multiple of 3.
Thus, $n=3$, and Fröken Bok found 11 candies.
## Answer
11 candies.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On a clearing, ladybugs gathered. If a ladybug has six spots on its back, it always tells the truth, and if it has four spots, it always lies, and there were no other ladybugs on the clearing. The first ladybug said: "Each of us has the same number of spots on our backs." The second said: "All of us together have 30 spots on our backs." - "No, all of us together have 26 spots on our backs," - the third one objected. "Exactly one of these three told the truth," - each of the other ladybugs declared. How many ladybugs gathered on the clearing?
|
If the first ladybug tells the truth, then the second and third ones should also tell the truth, as they should have the same number of spots on their backs as the first one. But the second and third ladybugs contradict each other, so at least one of them is lying. Therefore, the first ladybug is also lying.
Suppose each of the first three ladybugs lied, then all the others lied as well, since none of these three told the truth. This means all the ladybugs are liars. But in this case, the first ladybug did tell the truth, which cannot be. Therefore, the first three ladybugs cannot lie simultaneously, so either the second or the third told the truth, while the other two are liars. Thus, each of the other ladybugs told the truth.
Therefore, there are two ladybugs with four spots on their backs, and several ladybugs with six spots on their backs, and in total, the spots on the backs of all the ladybugs are either 30 or 26. But \(30 - 2 \cdot 4 = 22\), which is not divisible by 6, so the total number of spots is 26, and the number of honest ladybugs is \((26 - 2 \cdot 4) : 6 = 3\). Therefore, there are five ladybugs on the meadow.
## Answer
5 ladybugs.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Number of divisors and sum of divisors of a number ] equations in integers $\quad]$
Find a natural number $n$, knowing that it has two prime divisors and satisfies the conditions $\tau(n)=6$, $\sigma(n)=28$.
|
According to the formulas from problem $\underline{60537} n=p^{2} q,\left(p^{2}+p+1\right)(q+1)=28=22 \cdot 7$, where $p$ and $q-$ are prime numbers. From this, $q$ $=3, p=2$.
## Answer
$n=12$.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ $\underline{\text { Modular Arithmetic (other). ] }}$ [Periodicity and Non-periodicity ] Find the remainder of the division by 17 of the number $2^{1999}+1$.
|
$2^{1999}+1=8 \cdot 16^{499} \equiv 8 \cdot(-1)^{499}=-8 \equiv 9(\bmod 17)$.
## Answer
9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Prove that the sum $\cos \alpha+\cos \left(72^{\circ}+\alpha\right)+\cos \left(144^{\circ}+\alpha\right)+\cos \left(216^{\circ}+\alpha\right)+\cos \left(288^{\circ}+\alpha\right)$ does not depend on $\alpha$.
#
|
Apply the formula for the sum of cosines:
$$
\begin{gathered}
\cos \alpha + \left(\cos \left(72^{\circ} + \alpha\right) + \cos \left(288^{\circ} + \alpha\right)\right) + \left(\cos \left(144^{\circ} + \alpha\right) + \cos \left(216^{\circ} + \alpha\right)\right) = \\
= \cos \alpha + 2 \cos \left(180^{\circ} + \alpha\right) \cos 108^{\circ} + 2 \cos \left(180^{\circ} + \alpha\right) \cos 36^{\circ} = \\
= \cos \alpha + 2 \cos \alpha \cos 72^{\circ} - 2 \cos \alpha \cos 36^{\circ} = \cos \alpha \left(1 + 2 \left(\cos 72^{\circ} - \cos 36^{\circ}\right)\right) = \\
= \cos \alpha \left(1 - 2 \sin 54^{\circ} \sin 18^{\circ}\right) = \cos \alpha \left(1 - 4 \cos 36^{\circ} \sin 18^{\circ}\right) = \\
= \cos \alpha \left(1 - \sin 72^{\circ} / \cos 18^{\circ}\right) = 0
\end{gathered}
$$
Problem
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Ribamko A.v.
In the lower left corner of a $n \times n$ chessboard, there is a knight. It is known that the minimum number of moves it takes for the knight to reach the upper right corner is equal to the minimum number of moves it takes to reach the lower right corner. Find $n$.
#
|
Let $n$ be even. In this case, the lower left field has the same color as the upper right, while the lower right has a different color. After each move, the knight lands on a field of the opposite color. Therefore, any path from the lower left corner to the upper right consists of an even number of moves, and to the lower right - of an odd number.
Thus, their lengths are different.
: Let $n=4 k+1$. Then, by moving alternately along the fields of the two lower rows, the knight will reach the lower right corner in $2 k$ moves.
We will show that the path to the upper right corner is longer. Each move shifts the knight by a total of 3 fields horizontally and vertically. Even moving consistently to the right-up, the knight will move $6 k$ fields in $2 k$ moves. The total distance horizontally and vertically from the lower left corner to the upper right is $2 n-2 = 8 k > 6 k$. Therefore, the shortest path to the upper right field is longer.
Let $n=4 k-1$. Then the lower right field can be reached in $2 k$ moves as follows: the first move is one field to the right and two up, the second is one to the right and two down, and then, as in the previous case, move alternately along the fields of the two lower rows. It is impossible to get there in fewer moves.
Indeed, the knight needs to move $n-1=4 k-2$ cells to the right, and each move shifts it a maximum of two cells to the right. Therefore, the number of moves is at least $2 k-1$. But after $2 k-1$ moves, the knight will land on a field of the opposite color, and in our case, the lower right corner has the same color as the lower left, so at least one more move is needed, meaning the number of moves is at least $2 k$.
The maximum total shift to the right and up in $2 k$ moves remains $6 k$. The total distance horizontally and vertically from the lower left field to the upper right is $2 n-2 = 8 k-4$. For $k>2$, this is more than $6 k$. For $k=1 (n=3)$, it is easy to check all options and see that this case does not work. However, for $k=2 (n=7)$, both shortest paths consist of four moves, and this is also easy to verify.
## Answer
$n=7$.
Send a comment
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The numbers $x, y$ and $z$ are such that $\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}=1$. What values can the expression $\frac{x^{2}}{y+z}+\frac{y^{2}}{z+x}+\frac{z^{2}}{x+y}$ take?
|
$\frac{x^{2}}{y+z}+\frac{y^{2}}{z+x}+\frac{z^{2}}{x+y}+(x+y+z)=\frac{x^{2}}{y+z}+x+\frac{y^{2}}{z+x}+y+\frac{z^{2}}{x+y}+z=$
$=\frac{x^{2}+xy+xz}{y+z}+\frac{y^{2}+yz+yx}{z+x}+\frac{z^{2}+zx+zy}{x+y}=$
$\left(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}\right)(x+y+z)=x+y+z$.
From this, it is clear that the desired sum is zero.
## Answer
0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a single-round-robin tournament, 10 chess players are participating. After what minimum number of rounds can it happen that a sole winner has already been determined prematurely? (In each round, the participants are divided into pairs. Win - 1 point, draw - 0.5 points, loss - 0).
|
Evaluation. After the sixth round, 30 points have been played, and the leader has no more than 6 points, while the other nine participants have collectively scored no less than 24 points. Therefore, among them, there is at least one who has no less than 3 points. Since there are still 3 rounds ahead, the winner is still unknown.
Example. Suppose in the first seven rounds, the leader won all their games, and the other games ended in draws. Then, two chess players who have not yet played against the leader have 3.5 points each, while the others have 3 points each. Since there are 2 rounds left until the end of the tournament, the winner is already determined.
## Answer
After 7 rounds.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Berpow S.l.
Seryozha chose two different natural numbers $a$ and $b$. He wrote down four numbers in his notebook: $a, a+2, b$ and $b+2$. Then he wrote on the board all six pairwise products of the numbers from the notebook. What is the maximum number of perfect squares that can be among the numbers on the board?
|
Note that no two squares of natural numbers differ by 1: $x^{2}-y^{2}=(x-y)(x+y)$, and the second bracket is greater than one. Therefore, the numbers
$a(a+2)=(a+1)^{2}-1$ and $b(b+2)=(b+1)^{2}-1$ are not squares.
The numbers $a b$ and $a(b+2)$ cannot both be squares; otherwise, their product $a^2 b(b+2)$ would also be a square, and then the number
$b(b+2)$ would be a square as well. Similarly, among the numbers $(a+2) b$ and $(a+2)(b+2)$, at most one can be a square. Therefore,
Two squares can be obtained, for example, when $a=2$ and $b=16$: then $a(b+2)=6^{2}$ and $(a+2) b=8^{2}$.
## Answer
Two squares.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kuzneuov A.
Sasha chose a natural number $N>1$ and wrote down in ascending order all its natural divisors: $d_{1}<\ldots<d_{s}$ (so that $d_{1}=1$ and $d_{s}=N$). Then for each pair of adjacent numbers, he calculated their greatest common divisor; the sum of the resulting $s-1$ numbers turned out to be
$N-2$. What values could $N$ take?
|
Note that $d_{s+1-i}=N / d_{i}$ for all $i=1,2,3, \ldots, s$.
The number $d_{i+1}-d_{i}$ is divisible by $\left(d_{i}, d_{i+1}\right)$, so $\left(d_{i}, d_{i+1}\right) \leq d_{i+1}-d_{i}$. For $i=1,2, s-1$, let $r_{i}=\left(d_{i+1}-d_{i}\right)$
$-\left(d_{i}, d_{i+1}\right) \geq 0$. By the condition
$\left(d_{2}-d_{1}\right)+\left(d_{3}-d_{2}\right)+\ldots+\left(d_{s}-d_{s-1}\right)=d_{s}-d_{1}=N-1$, and $\left(d_{1}, d_{2}\right)+\left(d_{2}, d_{3}\right)+\ldots+\left(d_{s-1}, d_{s}\right)=N-2$.
Subtracting, we get $r_{1}+r_{2}+\ldots+r_{s-1}=1$. This means that $r_{k}=1$ for some $k$, and all other $r_{i}$ are zero.
The left side of the equation $\left(d_{k+1}-d_{k}\right)-\left(d_{k}, d_{k+1}\right)=1$ is divisible by $\left(d_{k}, d_{k+1}\right)$, so $\left(d_{k}, d_{k+1}\right)=1$ and $d_{k+1}-d_{k}=2$. This is possible only if both $d_{k}$ and $d_{k+1}$ are odd.
Since $d_{k}$ and $d_{k+1}$ are two consecutive divisors of $N$, then ${ }^{N} / d_{k+1}$ and ${ }^{N} / d_{k}$ are also two consecutive divisors of $N$: if ${ }^{N} / d_{k+1}=d_{m}$, then
$N / d_{k}=d_{m+1}$. In this case, $\left(d_{m}, d_{m+1}\right)=N /\left[d_{k}, d_{k+1}\right]=N\left(d_{k}, d_{k+1}\right) / d_{k} d_{k+1}0$, which is possible only when $k=m$ (and, consequently, $s=2 k$ ).
Thus, $d_{k+1}=N / d_{k}$, meaning the number $N=d_{k} d_{k+1}$ is odd. But then $d_{s-1} \leq N / 3$, from which $\left(d_{s-1}, d_{s}\right) \leq d_{s-1} \leq N / 3$.
Therefore, $1 \geq r_{s-1} \geq 2 N / 3-N / 3=N / 3$, so $N \leq 3$. Since $N>1$, we get the only possible value $N=3$, which, as is easy to verify, satisfies the condition.
## Answer
$N=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Fomin $D$ d.
Consider a set of weights, each weighing an integer number of grams, and the total weight of all weights is 200 grams. Such a set is called correct if any body with a weight expressed as an integer number of grams from 1 to 200 can be balanced by some number of weights from the set, and in a unique way (the body is placed on one pan of the scales, the weights - on the other; two ways of balancing, differing only in the replacement of some weights with others of the same weight, are considered the same).
a) Provide an example of a correct set where not all weights are 1 gram each.
b) How many different correct sets exist?
(Two sets are different if some weight participates in these sets a different number of times.)
|
The correct set must correspond to the factorization of the number 201 (see the solution to problem $\underline{98056}$), and it only factors into two factors: $201=3 \cdot 67$.
## Answer
a) Two weights of 67 grams each and 66 weights of 1 gram each, or 66 weights of 3 grams each and two of 1 gram each.
b) 3 sets.
## Author: Fomin D:
Consider a set of weights, each weighing an integer number of grams, with the total weight of all weights being 500 grams. Such a set is called correct if any object with a weight expressed as an integer number of grams from 1 to 500 can be balanced by some number of weights from the set, and in a unique way (the object is placed on one pan of the scales, the weights on the other; two ways of balancing, differing only in the replacement of some weights with others of the same weight, are considered the same).
a) Provide an example of a correct set where not all weights are 1 gram each.
b) How many different correct sets exist?
(Two sets are different if a certain weight participates in these sets a different number of times.)
## Solution
Let the largest weight of a weight in some correct set be $M$ (grams). This means that any smaller weight can be balanced by smaller weights. Let the weight of all smaller weights be $m$. Clearly, $m \geq M-1$. But if $m \geq M$, then we have two ways to balance the weight $M+r$, where $r$ is the remainder of the division of $m$ by $M$. Therefore, $m=M-1$.
Let there be $k$ weights of the maximum weight. Then the total weight of all weights $k M+m=500$, which means 501 is divisible by $M$. Determining $M$, we can determine the weight of the second heaviest weight. Repeating the previous reasoning shows that it must be a divisor of $M$. But 501 has exactly two divisors other than 1 and 501: 3 and 167, each of which is a prime number. Therefore, there are exactly two correct sets, not counting the trivial set of 500 weights of 1 gram each: two weights of 167 grams each and 166 weights of 1 gram each; 166 weights of 3 grams each and two weights of 1 gram each.
## Answer
a) Two weights of 167 grams each and 166 weights of 1 gram each, or 166 weights of 3 grams each and two of 1 gram each.
b) 3 sets
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Zhendarov R.G.
Find all such prime numbers $p$ that the number $p^{2}+11$ has exactly six distinct divisors (including one and the number itself).
|
Note that $p^{2}+11=(p-1)(p+1)+12$. If $p \geq 5$ and is prime, then the numbers $p-1$ and $p+1$ are even, and one of them is divisible by 3. Therefore, the product $(p-1)(p+1)$ is divisible by 12, hence $p^{2}+11$ is also divisible by 12, which means it has at least seven divisors (6 divisors of the number 12 and the number $p^{2}+11>12$ itself). It remains to check $p=2$ and $p=3$. For $p=2$, the number $p^{2}+11=2^{2}+11=15$ has four divisors $(1,3,5,15)$; for $p=3$, the number $p^{2}+$ $11=3^{2}+11=20$ has six divisors $(1,2,4,5,10,20)$.
## Answer
$p=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.