problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
[ Decimal numeral system]
A 1992-digit number is written. Each two-digit number formed by adjacent digits is divisible by 17 or 23. The last digit of the number is 1. What is the first?
#
|
Let's consider all two-digit numbers divisible by 17 or 23. Recall problem 41.
## Solution
List all two-digit numbers divisible by 17 or 23. These are 17, 34, 51, 68, 85, 23, 46, 69, 92. The last digits of all these numbers are different, so the number can be uniquely restored. The last digit is 1, which means the corresponding two-digit number is 51, so the previous digit in the number is 5. This digit 5 corresponds to the two-digit number 85, so the digit before it is 8. Reasoning similarly, we get a sequence of the last nine digits of the number: 692346851. The sequence 92346 will now repeat. In total, there are 1992 digits, including: 3 last digits, our 5 digits from the period, appearing 397 times, and 4 more digits - the last 4 digits of the period, which are also the first 4 digits of the number. Thus, the first digit of the desired number is 2.
## Answer
The digit 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic. Mental calculation, etc.]
In a row, 37 numbers are written such that the sum of any six consecutive numbers is 29. The first number is 5. What can the last number be?
#
|
The sum of the first 36 numbers is $6 \cdot 29$, the sum of the last 36 numbers is also $6 \cdot 29$. Therefore, the last number is equal to the first.
## Answer
5.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
After Clive assembled and wound his clock (see problem $\underline{32798}$), setting it by his grandfather's, it started running backward. How many times a day will it show the correct time?
|
The hour hands on Clive's clock and the correct clock will first coincide at the moment of setting the "correct" time. The next time this will happen is 6 hours after setting, when each of them will have made half a rotation. Of course, the minute hands will coincide then as well. And so on.
## Answer
4 times.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the minimum value of the fraction $\frac{x^{2}-1}{x^{2}+1}$.
#
|
$\frac{x^{2}-1}{x^{2}+1}=1-\frac{2}{x^{2}+1}$. The right side is the smallest when the denominator of the fraction is the smallest, that is, when $x=0$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$3-$ [Methods for solving problems with parameters] The quadratic trinomial $y=a x^{2}+b x+c$ has no roots and $a+b+c>0$. Determine the sign of the coefficient $c$.
#
|
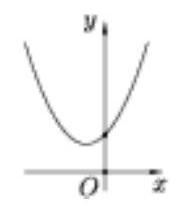
The quadratic polynomial has no roots, which means its graph does not intersect the x-axis. Since \( y(1) = a + b + c > 0 \), the graph is located in the upper half-plane (see the figure), therefore, \( c = y(0) > 0 \).
## Answer
\( c > 0 \).
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Inequalities Problems. Case Analysis]
Long, long ago, nine identical books cost 11 rubles and some kopecks, and thirteen such books cost 15 rubles and some kopecks.
How much did one book cost
#
|
From the first condition, it follows that one book cost more than ${ }^{11} / 9=1.222 \ldots$ rubles, and from the second - that it cost less than ${ }^{16} / 15=1.2307 \ldots$ rubles.
## Answer
1 rub. 23 kop.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[
The Tale of the Dead Princess and the Seven Bogatyrs. Once, returning home in the evening, the bogatyrs gave the princess their prey - 29 gray ducks. Each brother shot at least one duck. All of them hunted a different number of ducks: the older the brother, the more game he shot. What was the catch of the eldest brother?
#
|
Let's consider the seven smallest natural numbers.
## Solution
The youngest brother cannot shoot fewer than 1 duck, the next one fewer than 2, the next one fewer than 3, and finally, the oldest brother cannot shoot fewer than 7 ducks. This means that the minimum total number of ducks shot by the brothers is \(1+2+\ldots+7=28\) ducks. According to the problem, the brothers shot 29 ducks. Therefore, one of the brothers must have shot exactly one more duck. (If he had shot more than one, then someone else would have to shoot fewer than they currently did, which is impossible.) But only the oldest brother can shoot one more duck, because if anyone else did, there would be two brothers who shot the same number of ducks. Therefore, the oldest brother's catch is 8 ducks.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Decimal numeral system ]
Top student Polycarp has formed a huge number by writing down natural numbers from 1 to 500 in a row:
123...10111213...499500. Poor student Kolya erased the first 500 digits of this number. What do you think, with which digit does the remaining number start?
#
|
Note: Kolya was erasing digits, while Polycarp was writing down numbers - single-digit, two-digit, and three-digit.
## Solution
Out of the 500 digits erased by Kolya, 9 digits will be used for single-digit numbers, leaving 491 digits. For two-digit numbers, $90 \times 2 = 180$ digits will be used, leaving 311 digits. From this number of digits, 103 three-digit numbers can be formed, with 2 digits left over from the 104th number. This means that the digit we are interested in is the 3rd digit of the 104th three-digit number. This number is 203, so the digit we are looking for is 3.
## Answer
3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic. Mental calculation, etc.]
Gena went to the shooting range with his dad. They agreed that Gena would make 5 shots and for each hit, he would get the right to make 2 more shots. In total, Gena made 17 shots. How many times did he hit the target?
#
|
How many shots did Gena earn by hitting the target?
## Solution
It was predetermined that Gena would have 5 shots, and the additional 12 shots were earned by hitting the target - 2 shots for each hit. Therefore, the number of hits was 6.
## Answer
6 times.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic. Mental calculation, etc.]
What is the value of the expression $\left(10^{2}+11^{2}+12^{2}+13^{2}+14^{2}\right) / 365$ ?
|
Notice that one can simply "calculate directly," i.e., compute each of the squares, add them all up, and finally divide; or one can recall the formula for the square of a sum and make some transformations.
## Solution
Let's outline the steps that can quite easily be done mentally.
$$
10^{2}+11^{2}+12^{2}+13^{2}+14^{2}=10^{2}+(10+1)^{2}+(10+2)^{2}+(10+3)^{2}+(10+4)^{2}=5 \times 10^{2}+2 \times 10 \times(1+2+3+4)+1^{2}+2^{2}
$$
$+3^{2}+4^{2}=500+200+1+4+9+16=730$.
Now it's easy to figure out that the answer to the problem is 2. The problem can also be solved differently:
$10^{2}+11^{2}+12^{2}+13^{2}+14^{2}=(12-2)^{2}+(12-1)^{2}+12^{2}+(12+1)^{2}+(12+2)^{2}=5 \times 12^{2}+2 \times 10 \times(1+2-1-2)+2 \times\left(1^{2}+2^{2}\right)=$ $60 \times 12+0+2 \times 5=720+10=730$.
And now it's also easy to figure out that the answer to the problem is 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Word Problems ]
Chuk and Gek were decorating the Christmas tree. To prevent them from fighting, their mother gave each of them the same number of branches and the same number of toys. Chuk tried to hang one toy on each branch, but he was short of one branch. Gek tried to hang two toys on each branch, but one branch remained empty. How many branches and how many toys do you think their mother allocated to the boys?
#
|
Try to do as Chuk did - hang one toy on each branch.
## Solution
Let's try to do as Chuk did - hang one toy on each branch, then one toy will be left over. Now, take two toys - one that is left over, and another one from one of the branches. If we now hang these toys as the second ones on the branches that still have toys from the first time, then on two branches there will be toys, and one branch will remain empty. If there were other branches besides these three, then on these "extra" branches there would be one toy each, which contradicts the condition. Thus, there were 3 branches, and there were 4 toys, respectively.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Yatsenko I.V.
Vanya thought of a simple three-digit number, all digits of which are different.
What digit can it end with if its last digit is equal to the sum of the first two?
|
Use the divisibility rules for 2, $2,3$.
## Solution
Obviously, the last digit is greater than 1. A three-digit prime number cannot end in an even digit (i.e., $0,2,4,6$ or 8), nor in the digit 5. If the last digit is 3 or 9, then the sum of all the digits of the number, which is twice the last digit, is divisible by 3, and thus the number itself is divisible by 3. Therefore, the only remaining digit is seven.
## Answer
By 7.
## Problem
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ GCD and LCM. Mutual simplicity ]
Candies "Sweet Mathematics" are sold in boxes of 12, and candies "Geometry with Nuts" - in boxes of 15.
What is the smallest number of boxes of candies of both types that need to be bought so that there are an equal number of each type of candy?
#
|
$\operatorname{HOK}(12,15)=60$.
## Answer
5 boxes of "Sweet Mathematics" and 4 boxes of "Geometry with Nuts".
Send a comment
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Prove the equality $\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}=1$.
|
Let $u=\sqrt[3]{2+\sqrt{5}}, v=\sqrt[3]{2-\sqrt{5}}$. Then $u^{3}+v^{3}=4, u v=\sqrt[3]{4-5}=-1$. From the equality $(u+v)^{3}$ $=u^{3}+v^{3}+3 u v(u+v)$ it is clear that $u+v$ is a root of the equation $x^{3}+3 x-4=0$. This equation has an obvious root $x=1$, and it has no other roots (see problem $\underline{61252}$ a).
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Shnol D.e.
In the morning, a dandelion blooms, it flowers yellow for three days, on the fourth morning it turns white, and by the evening of the fifth day, it withers. On Monday afternoon, there were 20 yellow and 14 white dandelions on the meadow, and on Wednesday - 15 yellow and 11 white. How many white dandelions will there be on the meadow on Saturday?
|
A dandelion that has bloomed can be white on the fourth and fifth day. This means that on Saturday, the dandelions that bloomed on Tuesday or Wednesday will be white. Let's determine how many there are. The dandelions that were white on Monday had flown away by Wednesday, and 20 yellow ones had definitely survived until Wednesday (perhaps turning white).
On Wednesday, there were $15+11=26$ dandelions on the meadow. We know that 20 of them were on the meadow on Monday, and the remaining $26-20=6$ had just bloomed on Tuesday and Wednesday.
## Answer
6.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Average values ]
Three pirates divided the diamonds they had obtained during the day in the evening: twelve each for Bill and Sam, and the rest for John, who could not count. At night, Bill stole one diamond from Sam, Sam stole one from John, and John stole one from Bill. As a result, the average weight of Bill's diamonds decreased by one carat, Sam's decreased by two carats, but John's increased by four carats. How many diamonds did John get?
|
The number of diamonds each pirate had did not change over the night. Since Bill had 12 diamonds, and their average weight decreased by 1 carat, the total weight of his diamonds decreased by 12 carats. Similarly, the total weight of Sam's diamonds decreased by 24 carats. Since the total weight of Bill's and Sam's diamonds decreased by 36 carats, the weight of John's diamonds increased by the same 36 carats. Since the average weight of his diamonds increased by 4 carats, he had $36: 4=9$ diamonds.
## Answer
9 diamonds.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A set of several numbers, none of which are the same, has the following property: the arithmetic mean of some two numbers from this set is equal to the arithmetic mean of some three numbers from the set and is equal to the arithmetic mean of some four numbers from the set. What is the smallest possible number of numbers in such a set?
#
|
Let $C\left(a_{1}, \ldots, a_{k}\right)$ be the arithmetic mean of the numbers $\left(a_{1}, \ldots, a_{k}\right)$. Note that adding a number to the set that is different from its arithmetic mean changes the original arithmetic mean of the set.
Suppose that $(a, b, c, d)$ is a set of four numbers satisfying the condition, and $C(a, b, c, d)=C(a, b, c)=$
C. Then $d=C$.
A set of two different numbers with the same arithmetic mean cannot contain the number $d$. If, for example, these are the numbers $a$ and $b$, then $c=C=d$, which contradicts the condition.
Therefore, a set of four numbers satisfying the condition does not exist.
An example of a set of five numbers: $1,2,3,4,5$. Indeed, $C(2,4)=C(2,3,4)=C(1,2,4,5)=3$.
## Answer
5 numbers.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Authors: Vysokiy I. Raskina I.V.
In the aquarium, there are three types of fish: gold, silver, and red. If the cat eats all the gold fish, the number of fish will be one less than $2 / 3$ of the original number. If the cat eats all the red fish, the number of fish will be four more than $2 / 3$ of the original number. Which fish, gold or silver, are there more of, and by how many?
|
From the first condition, it is clear that the number of goldfish is 1 more than a third. From the second condition, it follows that the number of red fish is 4 less than a third. Therefore, the number of silver fish is 3 more than a third.
## Answer
The number of silver fish is 2 more
Authors: Baksueva E.V., Khachatryan A.V.
The Smeshariki live on the shores of a pond in the shape of an equilateral triangle with a side length of 600 meters. Krysh and Barash live on the same shore, 300 meters apart. In the summer, it is 900 meters for Losyash to walk to Krysh, and 900 meters for Barash to walk to Nyusha. Prove that in the winter, when the pond freezes and it is possible to walk directly on the ice, the distance for Losyash to walk to Krysh will again be the same number of meters as for Barash to walk to Nyusha.
## Solution
Let Krysh live at a distance of $x$ from the nearest corner of the pond: $A K=x$. Then the distance $B V$ from Barash to his corner of the pond is $300-x$.
According to the condition, $V L=900-B K=300+x$ (since 900 is exactly half the perimeter of the pond, it does not matter which of the two paths Losyash takes to get to Krysh),
$A H=900-A B=600-x$. It remains to note that triangles AHB and VKL are equal by angle and two sides adjacent to it $(A B=300+x=B L$,
$A H=B K)$. Therefore, their corresponding sides LK and BN are also equal.
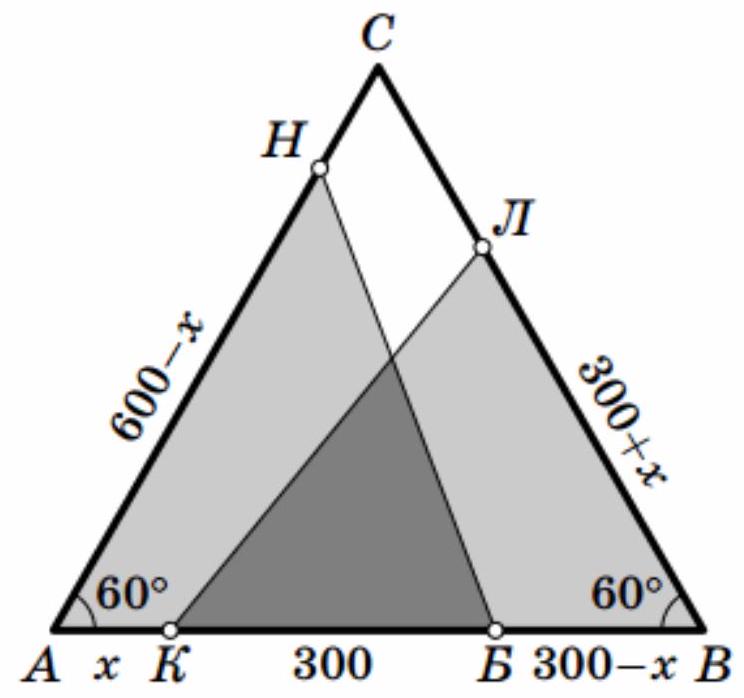
Send a comment
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.V.
In a small town, there is only one tram line. It is a circular line, and trams run in both directions. There are stops called Circus, Park, and Zoo on the loop. The journey from Park to Zoo via Circus is three times longer than the journey not via Circus. The journey from Circus to Zoo via Park is half as short as the journey not via Park. Which route from Park to Circus is shorter - via Zoo or not via Zoo - and by how many times?
|
Let's get on the tram at the Zoo stop and travel through the Circus to the Park, and then, without leaving the tram, return to the Zoo. The second part of the journey is three times shorter than the first, meaning the first part takes up three-quarters of the full circle, and the second part takes up one-quarter. Mark the Zoo and the Park on the diagram, and somewhere on the longer arc between them, mark the Circus (see the figure). Now, on the same tram, let's travel from the Circus to the Zoo (passing the Park, as shown on the diagram).
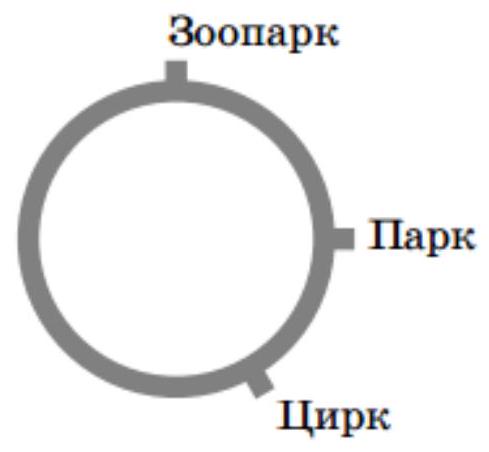
Upon arriving at the Zoo, we will return to the Circus on the same tram, completing a full circle. The first part of the journey is half as long as the second, meaning it takes up one-third of the circle. This means that the journey from the Circus to the Park will not pass through the Zoo and will constitute \( \frac{1}{3} - \frac{1}{4} = \frac{1}{12} \) of the full circle. The journey through the Zoo, on the other hand, is \( 1 - \frac{1}{12} = \frac{11}{12} \) of the circle, which is 11 times longer.
## Answer
The path not passing through the Zoo is 11 times shorter.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Zhendarov R.G.
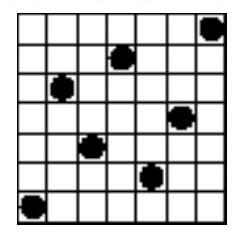
Cells of a $9 \times 9$ board are painted in a checkerboard pattern with black and white colors (corner cells are white). What is the minimum number of rooks needed to be placed on this board so that all white cells are under attack by these rooks? (A rook attacks all cells in the row and column where it is placed.)
|
Evaluation. A rook attacks no more than two cells of a white diagonal, so four rooks are insufficient.
Example. Let's place the rooks on the squares indicated in the figure.
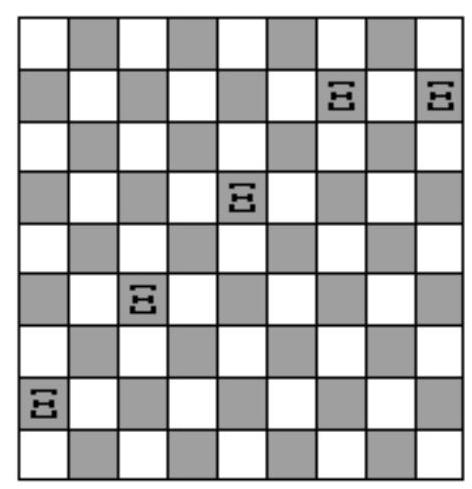
## Answer
5 rooks.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
##
Side $A B$ of parallelogram $A B C D$ is equal to $2, \angle A=45^{\circ}$. Points $E$ and $F$ are located on diagonal $B D$, such that
$\angle A E B=\angle C F D=90^{\circ}, B F=\frac{3}{2} B E$.
Find the area of the parallelogram.
|
Let $E F=x$, then $B E=2 x$. Since the right triangles $A B E$ and $C D F$ are equal, $F D=2 x$, $B D=5 x$.
The height $B K$ of the parallelogram is $\sqrt{2}$. By the Pythagorean theorem, $D K^{2}=25 x^{2}-2, D A^{2}-9 x^{2}=A E^{2}=4-4 x^{2}$, so $A D^{2}=5 x^{2}+4$. Moreover, from the similarity of triangles $E D K$ and $A D B$, it follows that $D A \cdot D K=D B \cdot D E=15 x^{2}$.
Therefore, $(5 D A-D K)^{2}=25 D A^{2}-10 D A \cdot D K+D K^{2}=100-2=98$, from which $5 D A-D K=7 \sqrt{2}$. Since $D A-D K=\sqrt{2}$, then $4 D A=6 \sqrt{2}$, and
$S_{A B C D}=A D \cdot B K=3$.
## Answer
3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The angle formed by the rays $y=x$ and $y=2x$ for $x \geq 0$ cuts two arcs on the parabola $y=x^{2}+p x+q$. These arcs are projected onto the $Ox$ axis. Prove that the projection of the left arc is 1 unit shorter than the projection of the right arc.
|
The abscissas $x_{1}$ and $x_{2}$ of the points of intersection of the parabola and the line $y=x$ satisfy the equation $x^{2}+(p-1) x+q=0$. By Vieta's theorem, $x_{1}+x_{2}=1-p$. Similarly, we obtain that the abscissas $x_{3}$ and $x_{4}$ of the points of intersection of the parabola and the line $y=2 x$ are related by $x_{3}+x_{4}=2-p$. If $x_{1}<x_{2}$, and
$x_{3}<x_{4}$, then the projection of the left arc is $x_{1}-x_{3}$, and the right arc is $-x_{4}-x_{2}$ (see figure). The difference between them is $\left(x_{4}-x_{2}\right)-\left(x_{1}-x_{3}\right)=\left(x_{3}+x_{4}\right)-\left(x_{1}+x_{2}\right)=(2-p)-(1-p)=1$.
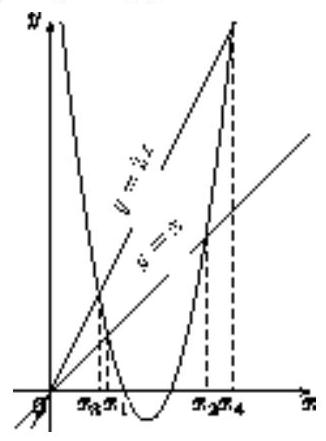
Send a comment
|
1
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Kenodarov R.G.
Prove that if $a, b, c$ are positive numbers and $ab + bc + ca > a + b + c$, then $a + b + c > 3$.
#
|
According to the problem $30865(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2(a b+b c+c a) \geq 3(a b+b c+c a)>3(a+b+c)$. Since $a+b$ $+c>0$, we get $a+b+c>3$
|
3
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Khachaturyan A.V.
Petr was born in the 19th century, and his brother Pavel - in the 20th century. Once, the brothers met to celebrate their shared birthday. Petr said: "My age is equal to the sum of the digits of the year of my birth." - "Mine too," replied Pavel. How much younger is Pavel than Petr?
|
Let Peter and Pavel be born in the years $\overline{18 x y}$ and $\overline{19 u v}$, respectively. At the time of their meeting, Peter and Pavel were $1 + 8 + x + y$ and $1 + 9 + u + v$ years old, respectively. We can determine the year of their meeting in two ways. Since Peter's age at that time was equal to the sum of the digits of his birth year, the meeting took place in the year $1800 + 10 x + y + 9 + x + y$. On the other hand, Pavel's age was also equal to the sum of the digits of his birth year, so the meeting took place in the year $1900 + 10 u + v + 10 + u + v$. Therefore, $1800 + 10 x + y + 9 + x + y = 1900 + 10 u + v + 10 + u + v$.
After simplifications, the equation transforms to $11(x - u) + 2(y - v) = 101$. We can rewrite it as $11(x - u) + 2(y - v - 1) = 99$.
From this, it is clear that $y - v - 1$ is divisible by 11. Since $-9 \leq y - v \leq 9$, then $y - v = 1$. Consequently, $x - u = 9$. Pavel is older than Peter by
$1900 + 10 u + v - 1800 - 10 x - y = 100 - 10(x - u) - (y - v) = 100 - 90 - 1 = 9$ years.
We need to consider two more cases: Peter could have been born in 1900 (which also belongs to the 19th century), or Pavel in 2000. In the first case, the meeting would have taken place in 1910, meaning Pavel was born no earlier than 1901 and no later than 1910, and he could not have been less than 11 years old at the time of the meeting. This is a contradiction. In the second case, the meeting would have taken place in 2002, and Peter would have been at least 102 years old at that time, which is also impossible, as the sum of the digits of any integer from 1801 to 1900 is no more than 27.
## Answer
9 years.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[formulas for abbreviated multiplication (other)] [Problems on maximum and minimum]
On the board, 101 numbers are written: $1^{2}, 2^{2}, \ldots, 101^{2}$. In one operation, it is allowed to erase any two numbers and write down the absolute value of their difference instead.
What is the smallest number that can result after 100 operations?
|
From four consecutive squares (in three operations), the number 4 can be obtained: $(n+3)^{2}-(n+2)^{2}-((n+$ $\left.1)^{2}-n^{2}\right)=(2 n+5)-(2 n+1)=4$.
We can get 24 such fours from the numbers $6^{2}, 7^{2}, \ldots, 101^{2}$. 20 fours can be turned into zeros by pairwise subtraction. From the numbers $4,9,16,25$ we get
$14=(25-4)-(16-9)$. From the remaining numbers $(14,4,4,4,4,1)$ we get the unit: $4-(14-4-4-4)-1=1$. It is impossible to get 0, since the parity of the sum of all numbers is preserved.
## Answer
1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Beroov S.L.
The numbers $a$ and $b$ are such that each of the two quadratic trinomials $x^{2} + a x + b$ and $x^{2} + b x + a$ has two distinct roots, and the product of these trinomials has exactly three distinct roots. Find all possible values of the sum of these three roots.
|
From the condition, it follows that the quadratic polynomials $x^{2}+a x+b$ and $x^{2}+b x+a$ have a common root $x_{0}$, as well as roots $x_{1}$ and $x_{2}$ different from it, respectively; in particular, $a \neq b$. The common root is also a root of the difference of these quadratics, that is, $(a-b)\left(x_{0}-1\right)=0$. Thus, $x_{0}=1$. Substituting this root into any quadratic, we get $1+a+b=0$. By Vieta's formulas, $x_{0}+x_{1}=-a, x_{0}+x_{2}=-b$, from which $x_{0}+x_{1}+x_{2}=-x_{0}-a-b=-(1+a+b)=0$.
Answer
## 0
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ [trigonometric inequalities ]
Solve the inequality $\sin \frac{x}{x^{2}+1}+\frac{x^{2}+1}{x} \cos \frac{x}{x^{2}+1}>0$
|
1) Note that $x \neq 0$ and $t=\frac{x}{x^{2}+1}=\frac{1}{x+\frac{1}{x}}$. Since $|x+1 / x| \geq 2$, then $|t| \leq 1 / 20$, so $00$ and $\cos t>0$. Moreover, $1 / t>0$, which means $\sin t+1 / t \cos t>0$. Therefore, for all $x>0$, the original inequality holds.
3) If $x>0$, then $-1 / 2 \leq t0.1 / t [ [various and GMT on the coordinate plane $]$ [ Properties and characteristics of a parallelogram ] Author: Kalinin A. At the same time, Anya and Borya (their speeds are constant but not necessarily the same) walked out from villages A and B towards each other. If Anya had left 30 minutes earlier, they would have met 2 km closer to village B. If Borya had left 30 minutes earlier, the meeting would have taken place closer to village A. By how much?
## Solution
Suppose Kolya (30 minutes later than Borya) and Tolya (30 minutes earlier than Borya) also left from B with the same speed, and Tanya (30 minutes earlier than Anya) left from A.
First method. Anya meets Tolya, Borya, and Kolya sequentially at equal time intervals. Therefore, the distances between the meeting points of Anya with the three boys are equal. It is clear that the meeting of Anya with Kolya happened 30 minutes later, and at the same point where the meeting of Tanya with Borya mentioned in the condition took place. Thus, the distances between the meeting points of Anya with the three boys are 2 km, and, in particular, the meeting point of Anya with Tolya is 2 km closer to A than the meeting point of Anya with Borya.
Second method. Consider the graphs of the movements of Anya, Borya, Tanya, and Tolya. These are two pairs of parallel lines, so the points of their intersections are the vertices of a parallelogram. Two opposite vertices have the same ordinate (the meeting point of Anya with Borya coincides with the meeting point of Tanya with Tolya), which means that this point is the arithmetic mean of the ordinates of the other two vertices. Therefore, the other two meeting points lie on opposite sides but at the same distance of 2 km from this point.
## Answer
By 2 km.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ $\quad$ Arithmetic progression $\quad]$ [Integer and fractional parts. Archimedes' principle ]
For the numbers $1000^{2}, 1001^{2}, 1002^{2}, \ldots$, the last two digits are discarded. How many of the first terms of the resulting sequence form an arithmetic progression?
|
The general term of the original sequence is: $a_{n}=\left(10^{3}+n\right)^{2}=10^{6}+2 n \cdot 10^{3}+n^{2}\left(a_{0}-\right.$ the first term $)$.
Let the general term of the resulting sequence be denoted by $b_{n}$, then
$b_{n}=\left[\frac{a_{n}}{100}\right]=\left[\frac{10^{6}+2 \cdot n \cdot 10^{3}+n^{2}}{100}\right]=10^{4}+20 n+\left[\frac{n^{2}}{100}\right]$
Therefore, the difference between consecutive terms of the new sequence will be 20 as long as $\left[\frac{n^{2}}{100}\right]=0$, which is if $n^{2}<100$. Considering that $n$ is a natural number or zero, we get: $0 \leq n \leq 9$. Thus, the first 10 terms of the new sequence form an arithmetic progression.
## Answer
10.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Average values $\quad]$ [ Area of a circle, sector, and segment ]
At a familiar factory, metal disks with a diameter of 1 m are cut out. It is known that a disk with a diameter of exactly 1 m weighs exactly 100 kg. During manufacturing, there is a measurement error, and therefore the standard deviation of the radius is 10 mm. Engineer Sidorov believes that a stack of 100 disks will on average weigh 10000 kg. By how much is Engineer Sidorov mistaken?
|
Given $\mathrm{E} R=0.5 \mathrm{~m}, \mathrm{D} R=10^{-4} \mathrm{~M}^{2}$. Let's find the expected value of the area of one disk: $\mathrm{E} S=\mathrm{E}\left(\pi R^{2}\right)=\pi \mathrm{E} R^{2}=\pi\left(\mathrm{D} R+\mathrm{E}^{2} R\right)=\pi\left(10^{-4}+0.25\right)=0.2501 \pi$.
Therefore, the expected value of the mass of the disk is $0.2501 \pi / 0.25 \pi \cdot 100=100.04$ kg. Thus, a stack of 100 disks on average will weigh 10004 kg.
## Answer
4 kg.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Sedrakyan $H$.
Two parabolas with different vertices are the graphs of quadratic trinomials with leading coefficients $p$ and $q$. It is known that the vertex of each parabola lies on the other parabola. What can $p+q$ be?
|
We can assume that the vertex of the first parabola is the point $(0,0)$. Let the vertex of the second be $(a, b)$. Then the equations of the parabolas are: $y=p x^{2}$ and $y=q(x-a)^{2}+b$, with $b=p a^{2}$ and $0=q a^{2}+b$. From this, $(p+q) a^{2}=0$. If $a=0$, then $b=$ 0, but the vertices are different. Therefore, $p+q=0$.
## Answer
0.
Submit a comment
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A kangaroo jumps along a straight line. Pushing off with its left foot, it jumps 3 meters, with its right foot - 5 meters, and with both feet - 7 meters.
How can it cover exactly 200 meters in 30 jumps?
|
If all 30 jumps are 7 m, then the kangaroo will cover 10 m more than needed. Replacing a 7 m jump with a 5 m jump reduces this distance by 2 m, and replacing it with a 3 m jump reduces it by 4 m. The number 10 can be represented as the sum of twos and fours in three ways: $2+2+2+2+2$, $2+2+2+4$, and $2+4+4+4$. Hence, the first three answers.
A 7 (5) m jump backward reduces the distance by 14 (12) m, which is too much. However, a 3 m jump backward reduces the distance by exactly 10 m. Hence, the last answer.
## Answer
You can make 25 jumps of 7 m and 5 jumps of 3 m, or 26 jumps of 7 m, three jumps of 5 m, and one jump of 3 m, or 27 jumps of 7 m, one jump of 5 m, and two jumps of 3 m, or 29 jumps of 7 m and one jump of 3 m backward.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ $[$ graphs and GMT on the coordinate plane $]$ Cauchy's Inequality $\quad]$
The graph of the linear function $y=k x+k+1$, where $k>0$, intersects the coordinate axes at points $A$ and $B$.
What is the smallest possible area of triangle $A B O$ ( $(O$ - the origin)?
|
The abscissa of the point of intersection of the graph with the $O X$ axis is $-\left(1+\frac{1}{k}\right)$. The ordinate of the point of intersection with the $O Y$ axis is $k+1$. Therefore,
$S_{A B O}=1 / 2 O A \cdot O B=1 / 2(k+1)(1+1 / k)=1 / 2(2+k+1 / k)$. The minimum value of the expression $k+1 / k$ is achieved when $k$ $=1$, hence, the smallest possible area of triangle $A B O$ is 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Evdokimov M.A.
In the Country of Fools, coins of 1, 2, 3, ..., 19, 20 soldo (no others) are in circulation. Buratino had one coin. He bought an ice cream and received one coin as change. He bought the same ice cream again and received change in three different coins. Buratino wanted to buy a third such ice cream, but he did not have enough money. How much does the ice cream cost?
|
Paying with three different coins amounts to no less than $1+2+3=6$ soldos. Since this amount was not enough to buy the ice cream, it must cost no less than 7 soldos.
The ice cream cannot cost more than 7 soldos; otherwise, two ice creams would cost no less than $8+8=$ 16 soldos. However, Buratino had only one coin, which is no more than 20 soldos, and he would not have been able to get 6 soldos in change. Therefore, the ice cream can only cost 7 soldos.
The payment process for the ice cream looked like this: $20-7=13, 13-7=6=1+2+3$.
## Answer
7 soldos.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A team of several workers can complete a task in 7 full days. The same team, without two people, can complete the same task in several full days, and the same team, without six people, can also complete the same task in several full days. How many workers are in the team? (The productivity of the workers is the same.)
#
|
Let there be $n$ workers in the team. The daily productivity of one worker is called the norm.
Over 7 days, the reduced teams will fall short by 14 and 42 norms, respectively. This means that $n-2$ is a divisor of 14, and $n-6$ is a divisor of 42. Since $n>6$, then $n-2=7$ or 14, that is, $n=9$ or 15. Since 42 is divisible by $9-6=3$, but not by $15-6=9$, then $n=9$.
## Otvet
9 workers.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Text problems (other).]
Kolya and Katya study in the same class. There are twice as many boys as girls in this class. Kolya has 7 more classmates than classmates of the opposite gender. How many female classmates does Katya have?
|
Since Kolya has 7 more classmates who are boys than classmates who are girls, there are 8 more boys than girls in this class. In addition, there are twice as many of them as there are girls. Therefore, there are 16 boys and 8 girls.
## Answer
7 girl classmates.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Inequalities. Case Analysis ]
A magical moment is when the number of minutes on a digital clock matches the number of hours. To brew a magical potion, it must be put on the fire and taken off the fire at magical moments. To make it taste good, it must be cooked for 1.5 to 2 hours. How long does it take to cook a delicious magical potion?
#
|
The number of hours on digital clocks equals the number of minutes 23 times a day: 00:00, 01:01, 02:02, .., 21:21, 22:22, 23:23.
If we are within one day, the difference between these numbers is either 1 hour 1 minute, or 2 hours 2 minutes, and so on. That is, if the potion is brewed without crossing midnight, it cannot be tasty. When crossing midnight, there are two ways to get a time difference of between one and a half to two hours: start at 22:22 and finish at 00:00, or start at 23:23 and finish at 01:01. In both cases, the potion needs to be brewed for 1 hour and 38 minutes.
## Answer
1 hour 38 minutes.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Fermat's Little Theorem ]
Find the remainder when $2^{100}$ is divided by 101.
#
|
According to Fermat's little theorem, it is equal to 1.
## Answer
1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Fermat's Little Theorem]
Find the remainder when $8^{900}$ is divided by 29.
#
|
$8^{900}=8^{32 \cdot 28+4} \equiv 8^{4}=64^{2} \equiv 6^{2} \equiv 7(\bmod 29)$.
## Answer
7.
Send a comment
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Residue arithmetic (other).]
How many zeros does the number $9^{999}+1$ end with?
#
|
$9^{999}+1=(9+1)\left(9^{998}-9^{997}+\ldots-9+1\right), 9^{998}-9^{997}+\ldots-9+1 \equiv(-1)^{998}-(-1)^{997}+\ldots-(-1)+1=999(\bmod 10)$. Therefore, $9^{999}+1$ is divisible by 10, but not by 100.
## Answer
By one.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Font der Flasch D:
A square board is divided by a grid of horizontal and vertical lines into $n^{2}$ cells with a side length of 1. For what largest $n$ can $n$ cells be marked so that every rectangle of area at least $n$ with sides along the grid lines contains at least one marked cell?
|
Evaluation. It is clear that if $n$ cells are marked in such a way that the condition of the problem is satisfied, then in each row and each column there is exactly one marked cell. Assuming that $n \geq 3$ (it is obvious that $n=2$ is not the largest), let's take row $A$, in which the leftmost cell is marked, row $B$, adjacent to $A$, and row $C$, adjacent either to $A$ (and not coinciding with $B$) or to $B$ (and not coinciding with $A$). Let $b$ be the number of the marked cell in row $B$. If $b \leq n-\left[\frac{n+1}{2}\right]$ or $b \geq\left[\frac{n+1}{2}\right]+2$, then in rows $A$ and $B$ there will be a rectangle of area not less than $n$ that does not contain marked cells, hence $b \leq n-\left[\frac{n+1}{2}\right]$. Consider two rectangles formed by the intersection of rows $A, B$ and $C$ with columns numbered $2,3, \ldots, n-\left[\frac{n+1}{2}\right]$ and columns numbered $2+\left[\frac{n+1}{2}\right], \ldots, n$. These rectangles do not contain the marked cells of rows $A$ and $B$. If $n > 7$, then the area of each of them is not less than $n$, but row $C$ contains only one marked cell, which means that one of these rectangles does not contain marked cells. Therefore, $n \leq 7$.
An example of a $7 \times 7$ board that satisfies the condition of the problem is shown in the figure.
## Answer
For $n=7$.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalov A.B.
55 boxers participated in a tournament with a "loser leaves" system. The fights proceeded sequentially. It is known that in each match, the number of previous victories of the participants differed by no more than 1. What is the maximum number of fights the tournament winner could have conducted?
|
We will prove by induction that
a) if the winner has conducted no less than $n$ battles, then the number of participants is no less than $u_{n+2}$;
b) there exists a tournament with $u_{n+2}$ participants, the winner of which has conducted $n$ battles ( $u_{k}-$ Fibonacci numbers).
Base case $\left(n=1, u_{3}=2\right)$ is obvious.
Inductive step. a) Let the winner $A$ win the last battle against boxer В. The remaining battles effectively split into two tournaments: one won by $A$, and the other by В. In the first tournament, the winner $A$ has conducted no less than $n-1$ battles, so the number of participants is no less than $u_{n+1}$. In the second tournament, the winner $B$ has conducted no less than $n-2$ battles, so the number of participants is no less than $u_{n}$. Therefore, in the original tournament, the number of participants is no less than $u_{n+1} + u_{n} = u_{n+2} \cdot$
b) It is sufficient to combine in the final battle the winner of a tournament with $u_{n+1}$ participants, who has won $n-1$ battles, and the winner of a tournament with $u_{n}$ participants, who has won $n-2$ battles.
Since $55=u_{10}$, it follows from this that the answer is.
## Answer
8 battles.
## Motion Problems
Problem
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Properties of polynomial coefficients]
Find the sum of all coefficients of the polynomial $\left(x^{2}-3 x+1\right)^{100}$ after expanding the brackets and combining like terms.
#
|
The sum of the coefficients of a polynomial is equal to the value of the polynomial at $x=1$.
## Solution
This sum is equal to the value of the polynomial at $x=1$, that is, $(1-3 \cdot 1+1)^{100}=1$.
## Answer
1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ [ Linear inequalities and systems of inequalities] ]
The number x is natural. Among the statements
1) $2 x>70$,
2) $x>100$,
3) $3 x>25$,
4) $x \geq 10.5$,
5) $x>5$ three are true and two are false. What is the value of $x$?
|
Write down all inequalities with respect to $x$.
## Solution
Let's write the first and third inequalities as $x>35, x>25 / 3$. We will mark the numbers $5, 25 / 3, 10, 35$, 100 on the number line; these points divide the line into six intervals (two of which are infinite). It remains to consider all intervals and find the one that satisfies the condition of the problem.
## Answer
$x=9$.
|
9
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Text problems (other) $)]$
The scale's needle is off. When one bunch of bananas was placed on the scale, it showed 1.5 kg. When a larger bunch of bananas was placed on the scale, it showed 2.5 kg. When both bunches of bananas were weighed together, the scale showed 3.5 kg. What is the actual weight of the bunches of bananas?
|
The pointer shifts twice for the total weight of $1.5+2.5=4$ kg, but only once for the weight of 3.5 kg. Therefore, the pointer shift is $4-3.5=0.5$ kg. Consequently, the correct weight of the bundles is half a kilogram less than what the scales show.
## Answer
1 and 2 kg.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ [motion problems ]
A swimmer is swimming upstream against the current of the Neva River. Near the Palace Bridge, he lost an empty flask. After swimming another 20 minutes against the current, he noticed the loss and turned back to catch up with the flask; he caught up with it near the Lieutenant Schmidt Bridge. What is the speed of the current of the Neva River, if the distance between the bridges is 2 km?
#
|
Relative to the flask, the swimmer moves at a constant speed in both directions, so he will catch up with the flask in 20 minutes. Therefore, the current "travels" 2 km in 40 minutes.
## Answer
3 km $/$ h.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
To assemble a car, Leonid needed to buy several screws and dowels. When he approached the cash register, it turned out that the store was running a promotional offer, offering customers either a $15\%$ discount on the entire purchase or a $50\%$ discount on dowels. It turned out that the cost of the purchase with the discount did not depend on the chosen discount option. How much money did Leonid initially plan to spend on dowels, if he planned to spend 7 rubles on screws?
#
|
According to the condition, $15\%$ of the total purchase cost constitutes $50\%$ of the cost of the dowels. Therefore, the cost of the dowels is $30\%$ of the total purchase cost. Consequently, the (planned) costs of the screws and dowels are in the ratio of $7:3$.
## Answer
3 rubles.
Does there exist such an $x$ that $\sqrt{x+9}+\sqrt{x}+\sqrt{x-9}=7$?
## Solution
The left side of the equation makes sense for $x \geq 9$. Therefore, $\sqrt{x} \geq 3, \sqrt{x+9} \geq \sqrt{9+9}=3\sqrt{2}$. Thus, $\sqrt{x+9}+\sqrt{x}+\sqrt{x-9} \geq 3\sqrt{2}+3 > 3 \cdot 3.14 = 7.2 > 7$.
## Answer
No such $x$ exists.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Average values $]$
Professor Tester conducts a series of tests, based on which he assigns the test subject an average score. After finishing his answers, John realized that if he had received 97 points for the last test, his average score would have been 90; and if he had received only 73 points for the last test, his average score would have been 87. How many tests are in Professor Tester's series
#
|
A change of 24 points in the score changes the average by 3 points. This means there are $24 : 3 = 8$ tests.
## Answer
8 tests.
## Problem
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tokarev S.i.
A natural number \$N\$ is divisible by 2020. In its decimal representation, all digits are distinct, and if any two of them are swapped, the resulting number is not divisible by 2020. For how many digits in the decimal representation of \$N\$ is this possible?
|
If the seventh digit from the right in a number is $\$ 2 \$$, and the third from the right is $\$ \mathrm{~b} \$$, then by swapping them, we change the number by \$b|cdot10^6-alcdot10^6+a|cdot10^2-blcdot10^2=(b-a)\} \backslash \operatorname { c d o t } ( 1 0 \wedge 4 - 1 ) \backslash \operatorname { c d o t } 1 0 0 \$ . Therefore, with such a swap,
the divisibility by \$2020 = 20\cdot101\$ will not be affected, since \$10^4 - 1\$ is divisible by 101, and 100 is divisible by 20.
Thus, the number $\$ N \$$ cannot have more than 6 digits.
Six digits are possible. For example, the number 351480 works (0 must remain at the end, swapping 3 and 8 would ruin divisibility by 4, and swapping adjacent digits or digits separated by one or two positions would ruin divisibility by 101, since the numbers $\$ 10-1 \$, \$ 10 \wedge 2$ - 1 $\$$ and $\$ 10 \wedge 3$ - 1 are not divisible by 101). There are other examples, such as 531260. A five- or four-digit number divisible by 2020 is obtained by multiplying 2020 by a number $\$ 10 a+b \$$ less than 50. In the number $\$ 2020 b \$$, the second and fourth digits are equal, and in the number $\$ 20200$ a they are zero, so in the sum these digits are equal, which is not what we want.
## Answer
with 6 digits.
Submit a comment
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the maximum number of a) rooks; b) queens that can be placed on an $8 \times 8$ chessboard so that each of these pieces is attacked by no more than one of the others?
|
a) Let $k$ rooks be placed while satisfying the condition. On each field where a rook stands, we write the number 0. In each of the $n$ columns, we perform the following operation: if there are two numbers in the column, we add 1 to both; if there is one number, we add 2 to it (we do nothing in an empty column). Then we perform the same operation for each row. Clearly, on the position of each of the $k$ rooks, the result will be either 3 or 4, so the sum $S$ of all written numbers is at least $3k$; on the other hand, since in each of the eight columns and then in each of the eight rows we added no more than 2, we have $S \leq 32$. Therefore, $3k \leq S \leq 4n$, from which $k \leq 10$.
An example of placing 10 rooks that satisfy the condition is shown in the left figure.
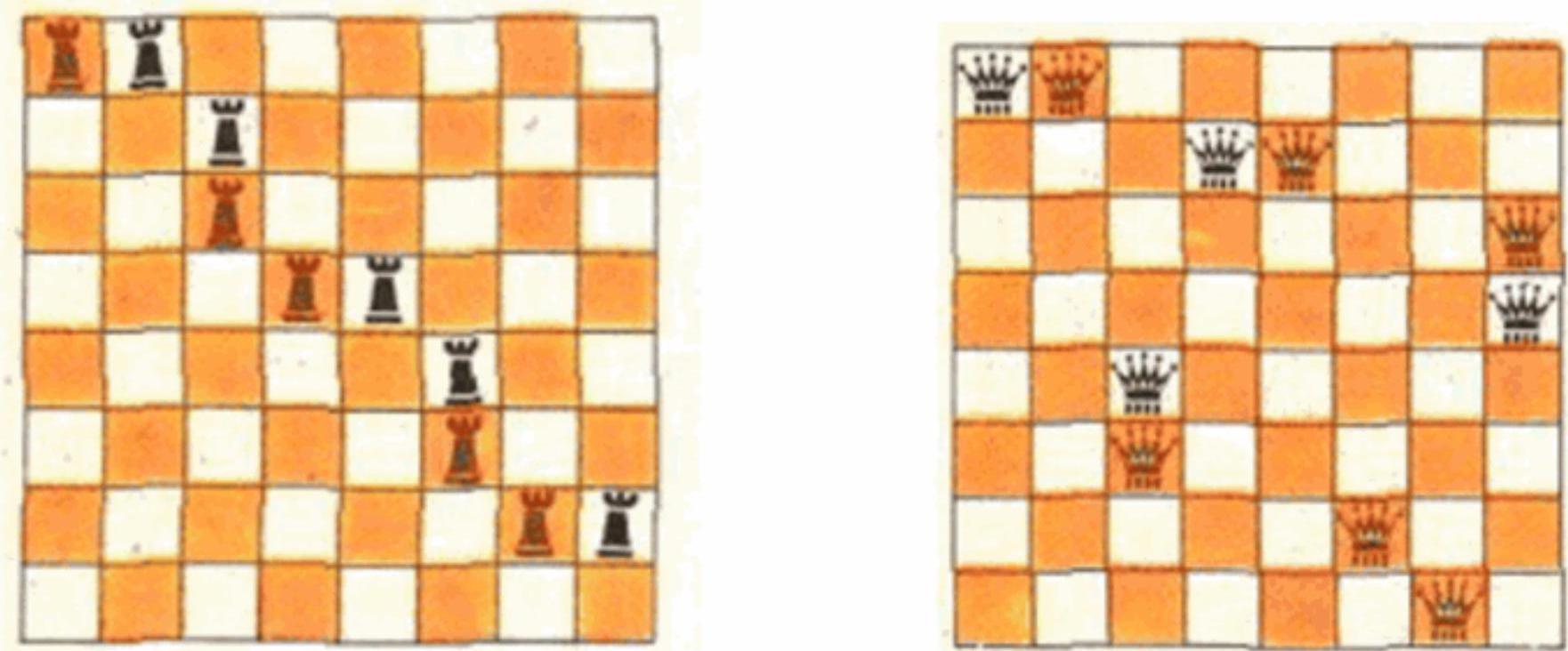
b) Clearly, the number of queens that can be placed is no more than the number of rooks. The right figure shows how to place 10 queens.
## Answer
a) 10 rooks, b) 10 queens.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
All integers are written in a row, starting from one. Determine which digit stands at the 206788th position.
#
|
Answer: the digit 7. There are exactly 9 single-digit numbers, 99 - 9 = 90 two-digit numbers, 999 - 99 - 9 = 900 three-digit numbers, 9000 four-digit numbers, and so on. Single-digit numbers will occupy the first 9 positions in the written sequence, two-digit numbers 90 * 2 = 180 positions, three-digit numbers 900 * 3 = 2700 positions, four-digit numbers 9000 * 4 = 36000 positions, and five-digit numbers 90000 * 5 = 450000 positions. Therefore, the digit we are interested in belongs to a five-digit number. The digits belonging to numbers with no more than four digits have numbers from 1 to 9 + 180 + 2700 + 36000 = 38,889. The difference 206788 - 38889 = 167899 needs to be divided by 5 with a remainder: 167899 = 5 * 33579 + 4. The digit we are interested in belongs to the 33,580th five-digit number, i.e., the number 43579 (the first five-digit number is the number 10,000). In this number, the digit we are interested in is in the 4th position.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10,11
The game board has the shape of a rhombus with an angle of $60^{\circ}$. Each side of the rhombus is divided into nine parts. Lines are drawn through the division points, parallel to the sides and the short diagonal of the rhombus, dividing the board into triangular cells. If a chip is placed on a certain cell, three lines are drawn through this cell, parallel to the sides and the short diagonal of the rhombus. The cells they intersect will be considered as being captured by the chip. What is the minimum number of chips needed to capture all the cells of the board?
|
Let's replace the board with an equivalent $9 \times 9$ square board, where diagonals of the same direction are drawn in all cells (see Fig. 1).
Six chips are sufficient to cover all cells (see Fig. 1).
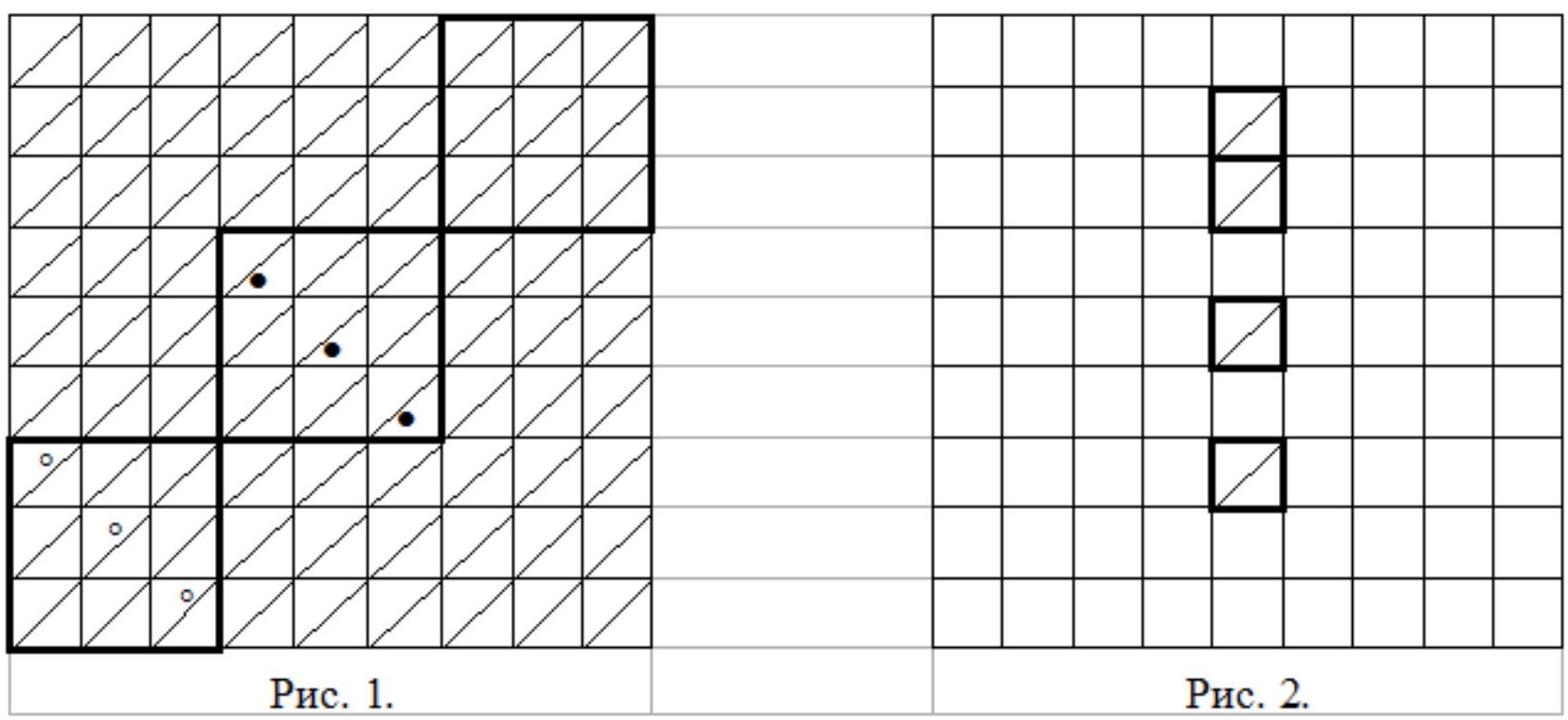
Suppose there are only five chips. Consider one of the columns where no chip is placed. In this column, there are at least four squares that are not covered horizontally. These correspond to eight cells (see Fig. 2), none of which can be covered by a single chip diagonally.
Thus, at least three cells will not be covered by any chip.
## Answer
6 chips.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Systems of nonlinear algebraic equations ]
Given the system of equations:
$$
\left\{\begin{aligned}
& x_{1} x_{2} \cdot \ldots \cdot x_{1962}=1 \\
& x_{1}-x_{2} x_{3} \cdot \cdots \cdot x_{1962}=1 \\
& x_{1} x_{2}-x_{3} x_{4} \cdot \cdots \cdot x_{1962}=1 \\
& \cdots \cdots \cdots \cdots \cdots \\
& x_{1} x_{2} \cdot \ldots \cdot x_{1961}-x_{1962}=1
\end{aligned}\right.
$$
What values can $x_{25}$ take?
#
|
Note that the product $x_{1} \ldots x_{k}$ satisfies the equation $x+1 / x^{\prime}=1 \Rightarrow x^{2}-x-1=0$. Therefore, $x_{1} \ldots x_{k}=$ $\frac{1 \pm \sqrt{5}}{2}$. On the other hand, for the same reason, $x_{1} \ldots x_{k+1}=\frac{1 \pm \sqrt{5}}{2}$. From this, we get that $x_{k+1}=\frac{1+\varepsilon_{1} \sqrt{5}}{1+\varepsilon_{2} \sqrt{5}}$, where $\varepsilon_{1,2}= \pm 1$. Therefore, $x_{25}=1$ or $-\frac{3 \pm \sqrt{5}}{2}$. In the first case, the example fits:
$$
x_{1}=\frac{1+\sqrt{5}}{2}, x_{2}=x_{3}=\ldots=x_{1961}=1, x_{1962}=\frac{\sqrt{5}-1}{2} . \text { In the second case, the example fits }
$$
$$
x_{1}=-x_{1962}=\frac{1 \pm \sqrt{5}}{2}, x_{2}=x_{3}=\ldots=x_{24}=x_{26}=\ldots=x_{1961}=1, x_{25}=-\frac{3 \mp \sqrt{5}}{2}
$$
## Answer
1 and $-\frac{3 \pm \sqrt{5}}{2}$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let's denote the sequence as $A$.
The numerical sequence is defined by the conditions: $a_{1}=1, a_{n+1}=a_{n}+\left[\sqrt{a_{n}}\right]$.
How many perfect squares are there among the first terms of this sequence, not exceeding $1000000$?
|
According to the solution of problem $\underline{98152}$, all perfect squares in this sequence have the form $4^{m}$. There are exactly 10 numbers of this form within the specified limits
$\left(4^{10}=1024^{2}>10^{6}\right)$.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Identical Transformations ]
Knowing that $x^{2}+x+1=0$, determine $x^{14}+1 / x^{14}$.
#
|
Given $x < 0$. Dividing the given equation term by term by $x$, we get $x+1 / x=-1$. Multiplying the given equation term by term by $x: x^{3}+x^{2}+x=0$, from which $x^{3}=-\left(x^{2}+x\right)=1$ (due to our equation).
$$
\begin{aligned}
x^{14}+1 / x^{14} & =\left(x^{3}\right)^{4} x^{2}+1 /\left(x^{3}\right)^{4} x^{2}=x^{2}+1 / x^{2}= \\
& =(x+1 / x)^{2}-2=1-2=-1
\end{aligned}
$$
## Answer
-1 .
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\stackrel{\text { Senderov B.A. }}{ }$.
Find the smallest natural number that cannot be represented in the form $\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$, where $a, b, c, d$ are natural numbers.
|
$1=\frac{4-2}{4-2}, 2=\frac{8-4}{4-2}, 3=\frac{8-2}{4-2}, 4=\frac{16-8}{4-2}, 5=\frac{32-2}{8-2}$
$6=\frac{16-4}{4-2}, \quad 7=\frac{16-2}{4-2}, 8=\frac{32-16}{4-2}, 9=\frac{128-2}{16-2}, \quad 10=\frac{64-4}{8-2}$.
Assume that $11=\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$. Without loss of generality, let $a>b, c>d$. Denote $m=a-b, n=c-d, k=b-d$. We get
$11\left(2^{n}-1\right)=2^{k}\left(2^{m}-1\right)$. Since the left side is an odd integer, $k=0$. Note that $n=1$ does not work.
If $m>n>1$, then $2^{m}-1$ and $2^{n}-1$ give a remainder of 3 when divided by 4. Thus, the left and right sides give remainders of 1 and 3, respectively, when divided by 4. This is a contradiction.
## Answer
11.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left.\begin{array}{ll}{\left[\begin{array}{l}\text { Averages }\end{array}\right]} \\ {[\text { Pascal's Triangle and the Binomial Theorem }]}\end{array}\right]$
[ Products and Factorials $\quad]$
On board an airliner, there are $2 n$ passengers, and the airline has loaded $n$ portions of chicken and $n$ portions of fish for them. It is known that a passenger prefers chicken with a probability of 0.5 and fish with a probability of 0.5. We will call a passenger dissatisfied if they are left with what they do not prefer.
a) Find the most probable number of dissatisfied passengers.
b) Find the expected value of the number of dissatisfied passengers.
c) Find the variance of the number of dissatisfied passengers.
|
a) The number of dissatisfied passengers can be any from 0 to $n$. In the case of $n=1$, everything is obvious: there is either no dissatisfied passenger or one, and both cases are equally likely. We will further assume that $n>1$.
Let us introduce the random variable $\xi$ "Number of dissatisfied passengers". $\xi=0$ only if exactly $n$ passengers prefer chicken, and the other $n$ prefer fish. We will consider a success the event "a passenger wants chicken". Then
$$
\mathrm{P}(\xi=0)=\mathrm{P}(\{\text { there are $n$ successes in a series of $2n$ trials }\})=C_{2 n}^{n} \frac{1}{2^{2 n}} \text {. }
$$
Exactly one passenger will be dissatisfied if the number of passengers preferring chicken differs from $n$ by one, that is, the number of successes is
$n \pm 1$. Therefore, $\mathrm{P}(\xi=1)=\mathrm{P}(\{n+1$ success in a series of $2n$ trials $\})+\mathrm{P}(\{n-1$ success in a series of $2n$ trials $\})=2 C_{2 n}^{n-1} \frac{1}{2^{2 n}}$.
Reasoning similarly, we find that $\mathrm{P}(\xi=k)=2 C_{2 n}^{n-k} \frac{1}{2^{2 n}}$, where $k=1,2, \ldots, n$.
In the sequence of numbers $C_{2 n}^{m}$, there are $2n+1$ numbers (this is the $2n$-th row of Pascal's triangle). These numbers first increase for $m=0,1, \ldots, n$, and then decrease for $m=n, n+1, \ldots, 2n$. The middle number $C_{2 n}^{n}$ is larger than the others, but smaller than twice the previous one: $C_{2 n}^{n}1 \mathrm{P}(\xi=0)\mathrm{P}(\xi=2)>\ldots>\mathrm{P}(\xi=n)$.
The result is illustrated by the distribution diagram of the random variable $\xi$ for $n=5$. For comparison, the diagram of the binomial distribution $\frac{1}{2^{10}} C_{10}^{k}$ is given in a lighter color on the same graph.
Thus, the most probable number of dissatisfied passengers is one.
b) Let us find the expected value of the quantity $\xi+n$:
$$
\begin{aligned}
& \mathrm{E}(\xi+n)=n \mathrm{P}(\xi=0)+(n+1) \mathrm{P}(\xi=1)+(n+2) \mathrm{P}(\xi=2)+\ldots+2 n \mathrm{P}(\xi=n)= \\
& =n C_{2 n}^{n} \frac{1}{2^{2 n}}+\frac{1}{2^{2 n-1}}\left((n+1) C_{2 n}^{n-1}+(n+2) C_{2 n}^{n-2}+\ldots+(n+k) C_{2 n}^{n-k}+\ldots+2 n C_{2 n}^{0}\right)
\end{aligned}
$$
Notice that $(n+k) C_{2 n}^{n-k}=\frac{(n+k)(2 n)!}{(n-k)!(n+k)!}=2 n C_{2 n-1}^{n-k}$. Therefore, $\mathrm{E}(\xi+n)=$
$n C_{2 n}^{n} \frac{1}{2^{2 n}}+\frac{2 n}{2^{2 n-1}}\left(C_{2 n-1}^{n-1}+C_{2 n-1}^{n-2}+\ldots+C_{2 n-1}^{0}\right)$
In the parentheses, we have the sum of the first half of all numbers in the $(2n-1)$-th row of Pascal's triangle. The sum of all numbers in this row is $2^{2 n-1}$, so the sum in the parentheses is $2^{2 n-2}$. Thus, $\mathrm{E}(\xi+n)=n C_{2 n}^{n} \frac{1}{2^{2 n}}+n$, and $\mathrm{E} \xi=\mathrm{E}(\xi+n)-n=n C_{2 n}^{n} \frac{1}{2^{2 n}}$
Let us find this number approximately using Stirling's formula $\quad m!\approx \sqrt{2 \pi m} \cdot m^{m} e^{-m}$ :
$\mathrm{E} \xi \approx \frac{n}{2^{n}} \cdot \frac{\sqrt{4 \pi n} \cdot(2 n)^{2 n} e^{-2 n}}{\left(\sqrt{2 \pi n} \cdot n^{n} e^{-n}\right)^{2}}=\sqrt{\frac{n}{\pi}}$.
c) $\mathrm{E} \xi^{2}=0^{2} \cdot \mathrm{P}(\xi=0)+1^{2} \cdot \mathrm{P}(\xi=1)+\ldots+n^{2} \mathrm{P}(\xi=n)=1^{2} \cdot \frac{C_{2 n}^{n-1}}{2^{2 n-1}}+2^{2} \cdot \frac{C_{2 n}^{n-2}}{2^{2 n-1}}+\ldots+n^{2} \cdot \frac{C_{2 n}^{0}}{2^{2 n-1}}=$
$$
=(0-n)^{2} \cdot \frac{C_{2 n}^{0}}{2^{2 n}}+(1-n)^{2} \cdot \frac{C_{2 n}^{1}}{2^{2 n}}+(2-n)^{2} \cdot \frac{C_{2 n}^{2}}{2^{2 n}}+\ldots+(2 n-n)^{2} \cdot \frac{C_{2 n}^{2 n}}{2^{2 n}}
$$
This expression is exactly equal to the variance of the random variable $\eta$ "number of successes in a series of $2n$ Bernoulli trials with a success probability of $0.5$". As is known, it is equal to $2n \cdot 0.5 \cdot 0.5=n / 2$.
Therefore, $\mathrm{D} \xi=\mathrm{E} \zeta^{2}-(\mathrm{E} \xi)^{2}=\frac{n}{2}-\left(\frac{n C_{2 n}^{n}}{2^{2 n}}\right)^{2} \approx \frac{n}{2}-\frac{n}{\pi}=\frac{\pi-2}{2 \pi} n \approx 0.182 n$.
## Answer
a) If $n>1$, then the most probable is one dissatisfied; if $n=1$, then with equal probabilities either there is one dissatisfied, or there are no dissatisfied at all;
b) $\frac{n C_{2 n}^{n}}{2^{2 n}} \approx \sqrt{\frac{n}{\pi}} \approx 0.564 \sqrt{n}$; c) $\frac{n}{2}-\left(\frac{n C_{2 n}^{n}}{2^{2 n}}\right)^{2} \approx \frac{\pi-2}{2 \pi} n \approx 0.182 n$.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Akulich I.F. }}$
There are 40 identical gas cylinders, the pressure values in which are unknown to us and may be different. It is allowed to connect any cylinders to each other in a quantity not exceeding a given natural number $k$, and then disconnect them; in this case, the gas pressure in the connected cylinders is set equal to the arithmetic mean of the pressures in them before connection. For what smallest $k$ does there exist a way to equalize the pressures in all 40 cylinders regardless of the initial distribution of pressures in the cylinders?
#
|
When $k=5$, the following method of equalizing pressures is suitable. By dividing the cylinders into 8 groups of 5 cylinders each, we equalize the pressures in the cylinders of each of these groups. Then we form 5 new groups, each consisting of 8 cylinders that previously belonged to different groups. We achieve equal pressures in the cylinders of each of the new groups (and thus in all 40 cylinders) by first connecting the cylinders in groups of four, and then in pairs, taking cylinders from different quartets in each pair.
We will show that when $k \leq 4$, the required method does not exist.
Suppose the pressure value in one of the cylinders is 2, and in each of the others, it is 1; then after equalization, the pressure value in each cylinder should be $(2+39): 40 = 41 / 40$.
However, after each connection, all values will be expressed as irreducible fractions, the denominators of which are not divisible by 5.
Indeed, if before any connection, none of the denominators were divisible by 5, then the denominator of the arithmetic mean of the corresponding two, three, or four fractions, being double, triple, or quadruple the least common multiple of their denominators, cannot be a multiple of 5.
Since 40 is a multiple of 5, we cannot equalize the pressure with the specified initial values.
## Answer
When $k=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a single-round football tournament, $n>4$ teams played. For a win, 3 points were awarded, for a draw 1, and for a loss 0. It turned out that all teams scored the same number of points.
a) Prove that there will be four teams with the same number of wins, the same number of draws, and the same number of losses.
b) For what smallest $n$ might there not be five such teams?
|
a) If two teams have scored the same number of points, then the difference in the number of draws between them is a multiple of 3.
The number of draws for a team is between 0 and $n-1$. Therefore, the number of groups, each of which consists of teams with the same number of wins, draws, and losses, does not exceed $k=\left[\frac{n+2}{3}\right]$. This means there will be a group consisting of at least three teams.
Suppose all groups consist of three or fewer teams. Then there are exactly $k$ groups (otherwise, $n4$.
## Answer
b) For $n=10$.
## Problem
|
10
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Find the remainder of the division of the polynomial $P(x)=x^{6 n}+x^{5 n}+x^{4 n}+x^{3 n}+x^{2 n}+x^{n}+1$ by $Q(x)=x^{6}+x^{5}+x^{4}+x^{3}+x^{2}$ $+x+1$, given that $n$ is a multiple of 7.
|
The difference $x^{k n}-1$ is divisible by $x^{7}-1$, and therefore also by $Q(x)$. Therefore, $P(x)-7=\left(x^{6 n}-1\right)+\left(x^{5 n}-1\right)+\ldots+\left(x^{n}-1\right)$ is divisible by $Q(x)$.
## Answer
7.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Kosukhin O.N. }}$
Sasha found that there were exactly $n$ working number buttons left on the calculator. It turned out that any natural number from 1 to 99999999 can either be entered using only the working buttons, or obtained as the sum of two natural numbers, each of which can be entered using only the working buttons. What is the smallest $n$ for which this is possible?
|
Let's show that the conditions of the problem are met if the buttons with digits 0, 1, 3, $4, 5$ remain functional. Indeed, any digit from 0 to 9 can be represented as the sum of some two "working" digits. Let the number from 1 to 99999999 that we want to obtain consist of digits $a_{1}, a_{2}, \ldots, a_{8}$ (some of them, including the leading ones, may be zeros). Represent each of them as the sum of two "working" digits: $a_{1} = b_{1} + c_{1}, a_{2} = b_{2} + c_{2}, \ldots, a_{8} = b_{8} + c_{8}$. Then the number composed of "working" digits $b_{1}, b_{2}, \ldots, b_{8}$ and the number composed of "working" digits $c_{1}, c_{2}, \ldots, c_{8}$ give the desired number when summed.
Suppose that the desired result can be achieved for some set of four "working" digits. Let $a$ be some odd digit. Among the numbers from 1 to 99999999, there will be one that ends in $a$ and contains "non-working" digits in its decimal representation. Then this number can be represented as the sum of two numbers, whose representations contain only "working" digits. Therefore, for each odd digit $a$, there will be such two "working" digits (possibly the same) whose sum ends in $a$. On the other hand, it is not difficult to see that among all the sums of pairs of four "working" digits, there can be no more than four odd numbers. Therefore, one of the digits $1, 3, 5, 7, 9$ will not appear at the end of such sums. Contradiction.
## Answer
5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Golovnov A.S.
Positive rational numbers $a$ and $b$ are written as decimal fractions, each of which has a minimal period consisting of 30 digits. The decimal representation of the number $a-b$ has a minimal period length of 15. For what smallest natural $k$ can the minimal period length of the decimal representation of the number $a+k b$ also be 15?
|
By multiplying, if necessary, the numbers $a$ and $b$ by a suitable power of ten, we can assume that the decimal representations of the numbers $a, b, a-b$, and $a+k b$ are purely periodic (i.e., the periods start immediately after the decimal point).
Then $a=\frac{m}{10^{30}-1}, \quad b=\frac{n}{10^{30}-1}$. We also know that the numbers $a-b=\frac{m-n}{10^{30}-1}$ and
$a+k b=\frac{m+k n}{10^{30}-1}$ can be written as decimal fractions with a period of length 15, meaning they can be written as common fractions with the denominator $10^{15}-1$. Therefore, their difference
$(k+1) b=\frac{(k+1) n}{10^{30}-1}$ can also be written this way. Thus, the number $(k+1) n$ is divisible by $10^{15}+1$, while the number $n$ is not (otherwise, $b$ would be written as a fraction with a period of length 15). Therefore, the number $k+1$ is divisible by some prime divisor of the number $10^{15}+1$. The smallest such divisor is 7. Indeed, the number $10^{15}+1$ is not divisible by 2 or 5 and gives a remainder of 2 when divided by 3. On the other hand, it is divisible by $10^{3}+1=7 \cdot 143$. Thus, $k+1 \geq 7$, i.e., $k \geq 6$.
Let $a-b=\frac{1}{10^{15}-1}, \quad a+6 b=\frac{2}{10^{15}-1}$. Then $a=\frac{8}{7\left(10^{15}-1\right)}, \quad b=\frac{1}{7\left(10^{15}-1\right)}$. It is clear that the lengths of the minimal periods of the numbers
$a-b$ and $a+6 b$ are 15. The lengths of the minimal periods of the numbers $a$ and $b$ are greater than 15 and are divisible by 15 (since $10^{T}-1$ must divide $10^{15}-1$). On the other hand, since $10^{30}-1$ is divisible by $7\left(10^{15}-1\right)$, the numbers $a$ and $b$ are periodic with a period length of 30. Therefore, the lengths of their minimal periods are 30.
## Answer
For $k=6$.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Evenness and Oddness ] [ Monotonicity, Boundedness ]
Integers $a_{1}, a_{2}, \ldots, a_{n}$ are such that the equality
$$
a_{1}+\frac{1}{a_{2}+\frac{1}{a_{3}+\cdots+\frac{1}{a_{n}+\frac{1}{x}}}}=x
$$
is satisfied for all integer values of $x$ that belong to the domain of the fraction on the left side.
a) Prove that the number $n$ is even.
b) For what smallest $n$ do such numbers exist?
|
a) Let $n$ be odd. Consider the interval ( $b,+\infty$ ), where the number $b$ is greater than all the points of discontinuity of the function on the left side. The function $a_{n}+1 / x$ decreases on this interval, the function $a_{n-1}+\frac{1}{a_{n}+\frac{1}{x}}$ increases, ..., the function on the left side of the given equation decreases. And the function on the right side increases. Contradiction.
b) For $n=2$, such an equality is impossible. Indeed, the function $a_{1}+\frac{1}{a_{2}+\frac{1}{x}}$ is fractional-linear (with the denominator $a_{2} x+1$), and the line $y=x$ intersects its graph in no more than two points.
For $n=4$, the equality is already possible. For example,
$-1+\frac{1}{2+\frac{1}{-1+\frac{1}{2+\frac{1}{x}}}}=-1+\frac{1}{2+\frac{1}{-1+\frac{x}{2 x+1}}}=-1+\frac{1}{2+\frac{2 x+1}{-x-1}}=x$
## Answer
b) For $n=4$.
|
4
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Golovanov A.S. $^{2}$
Given three reduced quadratic trinomials: $P_{1}(x), P_{2}(x)$, and $P_{3}(x)$. Prove that the equation $\left|P_{1}(x)\right|+\left|P_{2}(x)\right|=$ $\left|P_{3}(x)\right|$ has no more than eight roots.
|
Each root of the given equation is a root of one of the quadratic trinomials $\pm P_{1} \pm P_{2} \pm P_{3}$ with some set of signs. There are 8 such sets, and all of them yield genuine quadratic trinomials, since the coefficient of $x^{2}$ is odd. However, two opposite sets of signs correspond to quadratic equations that have the same roots. Therefore, all solutions of the equation $\left|P_{1}(x)\right|+\left|P_{2}(x)\right|=\left|P_{3}(x)\right|$ are contained among the roots of four quadratic equations. Hence, there are no more than eight of them.
|
8
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Shapovalovo $A . B$. The numbers from 1 to 37 were written in a row such that the sum of any initial segment of numbers is divisible by the next number in the sequence.
What number is in the third position if the first position is occupied by the number 37, and the second by 1? #
|
Let the last place in the line be occupied by the number $x$. The sum of all numbers in the line, except for $x$, is divisible by $x$; therefore, the sum of all numbers in the line, which is
$1+2+\ldots+37=37 \cdot 19$, is also divisible by $x$. Hence, $x=19$, since 37 is already placed in the first position. The third position is occupied by a divisor of the number
$37+1=38=19 \cdot 2$, different from 1 and 19, which are in other positions.
## Answer
2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Chkhhanov N.X.
In the natural number $A$, the digits were rearranged to obtain the number $B$. It is known that $A-B=\underbrace{1 \ldots 1}_{n}$. Find the smallest possible value of $n$.
#
|
Numbers obtained from each other by rearranging digits have the same remainder when divided by 9, which means their difference is divisible by 9. Therefore, the sum of the digits of the difference, equal to $n$, is also divisible by 9, hence $n \geq 9$.
The value $n=9$ can be obtained, for example, as follows: $9012345678-8901234567=111111111$.
Answer
## 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
We took three numbers $x, y, z$. We calculated the absolute values of the pairwise differences $x_{1}=|x-y|, y_{1}=|y-z|, z_{1}=|z-x|$. In the same way, from the numbers $x_{1}, y_{1}, z_{1}$, we constructed the numbers $x_{2}, y_{2}, z_{2}$, and so on. It turned out that for some $n$, $x_{\mathrm{n}}=x, y_{\mathrm{n}}=y, z_{\mathrm{n}}=z$. Knowing that $x=1$, find $y$ and $z$.
|
Answer: $y=z=0$. The numbers $x_{n}, y_{\mathrm{n}}, z_{\mathrm{n}}$ are non-negative, so the numbers $x, y, z$ are also non-negative. If all the numbers $x, y, z$ were positive, then the largest of the numbers $x_{1}, y_{1}, z_{1}$ would be strictly less than the largest of the numbers $x, y$, $z$, and then the largest of the numbers $x_{\mathrm{n}}, y_{\mathrm{n}}, z_{\mathrm{n}}$ would be strictly less than the largest of the numbers $x, y, z$. Therefore, among the numbers $x, y, z$ there is a 0. Similarly, it is proved that among the numbers $x_{1}, y_{1}, z_{1}$ there is a 0 (for $n=1$ there is nothing to prove, because then $x_{1}=x, y_{1}=y, z_{1}=z$). This means that two of the numbers $x, y, z$ are equal. In the end, we get that the unordered set of numbers $x, y, z$ can be either $0,0,1$ or $0,1,1$. Obviously, the second set does not have the required property.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tokorevev. S.
Among 2000 indistinguishable balls, half are aluminum with a mass of 10 g, and the rest are duralumin with a mass of 9.9 g. It is required to separate the balls into two piles such that the masses of the piles are different, but the number of balls in them is the same. What is the smallest number of weighings on a balance scale without weights that can achieve this?
|
Let's compare the mass of 667 balls with the mass of another 667 balls. If the masses of these two piles are not equal, the required condition is achieved.
Suppose the specified masses are equal. Then the mass of 666 balls that did not participate in the weighing is not equal to the mass of any 666 balls lying on one of the pans of the scales.
Indeed, if each of the weighed piles contains exactly $k$ aluminum balls, then among any 666 balls of any of these piles, the number of aluminum balls is $k$ or $k-1$. Meanwhile, among the 666 balls that did not participate in the weighing, there are exactly $1000-2k$ aluminum balls. It remains to note that neither the equality $k = 1000 - 2k$, nor the equality $k - 1 = 1000 - 2k$ can be satisfied for any integer $k$.
Answer
In one weighing.
Send a comment
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8,9,10 | |
What is the minimum number of weights needed to be able to weigh any number of grams from 1 to 100 on balance scales, if the weights can be placed on both pans of the scales?
|
When solving this problem, we need the following interesting property of the ternary numeral system: any natural number can be represented as the difference of two numbers, the ternary representation of which contains only 0 and 1.
To prove this, we need to write the original number in ternary notation and construct the required numbers digit by digit from right to left. If the resulting numbers have ones in the same positions, they can be replaced with zeros.
Now it is clear that it is sufficient to have 5 weights with masses of 1, 3, 9, 27, 81 (think about why a weight of 243 grams is not needed).
Four weights, however, are clearly insufficient, as they can measure no more than \(3^4-1=80\) different weights (each weight is either on the left pan, or on the right pan, or not involved in the weighing).
|
5
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
KOVSHIN=BOTTLE+GLASS; $\quad$ TWO KOVSHINS=SEVEN GLASSES; BOTTLE=CUP+TWO GLASSES; $\quad$ BOTTLE=how many CUPS?
|
Try to replace the BOTTLE in the first line with its equivalent in CUPS and GLASSES (see the third line).
## Solution
Let's restate the conditions of the problem:
JUG = BOTTLE + GLASS; TWO JUGS = SEVEN GLASSES; BOTTLE = CUP + TWO GLASSES; BOTTLE = how many CUPS?
From the 1st and 3rd lines, it follows that the capacity of a jug is equal to the capacity of a cup and three glasses. Comparing this equality with the 2nd line, we get that a glass contains two cups. Considering now the 3rd line, we determine that the capacity of a bottle is five cups.
## Answer
5 cups.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic operations. Numerical identities ] Common fractions
Half of half of a number is equal to half. What is this number?
#
|
Half of half is a quarter.
## Solution
If half of half (i.e., a quarter) of a given number is 0.5, then the number itself is $0.5 \times 4 = 2$.
## Answer
2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A natural number A, when divided by 1981, gave a remainder of 35, and when divided by 1982, it also gave a remainder of 35. What is the remainder when the number $A$ is divided by 14?
#
|
Let $A=1981 k+35=1982 l+35$. Then $1981 k=1982 l$; in particular, $k$ is even. Therefore, the number $1981 k$ is divisible by 14. Hence, when divided by 14, the number A gives the same remainder as 35.
## Answer
7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left.\begin{array}{ll}{\left[\begin{array}{l}\text { Irrational Equations } \\ \text { [Completing the Square. Sums of Squares] }\end{array}\right]}\end{array}\right]$
Solve the equation
$$
\left(x^{2}+x\right)^{2}+\sqrt{x^{2}-1}=0
$$
|
Since the numbers $\left(x^{2}+x\right)^{2}$ and $\sqrt{x^{2}-1}$ are non-negative, and their sum is zero, then both these numbers are equal to zero. On the other hand, if both these numbers are equal to zero, then their sum is zero. Therefore, the original equation is equivalent to the following system:
$$
\left\{\begin{array} { c }
{ ( x ^ { 2 } + x ) ^ { 2 } = 0 ; } \\
{ \sqrt { x ^ { 2 } - 1 } = 0 }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ x ^ { 2 } + x = 0 ; } \\
{ x ^ { 2 } - 1 = 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \in\{0,-1\} ; \\
x \in\{1,-1\}
\end{array} \Leftrightarrow x=-1\right.\right.\right.
$$
## Answer
$x=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Divisibility of numbers. General properties ]
On a bus rode Andrey
To the circle and back home,
Paying 115 rubles,
He bought himself a pass.
In January he didn't get it,
And therefore for several days
He bought a ticket from the driver
For 15 rubles for himself.
And on another day the conductor
Took only 11 rubles from him.
Returning from his circle
Every time he walked home our Andrey.
For January, how much money was spent,
The thrifty Andrey calculated:
To his surprise, he got
Exactly 115 rubles!
Calculate now as quickly as you can,
How many times the circle was in January
#
|
The amount of rubles spent by Andrey on the days when he bought a ticket from the driver is divisible by 5; the total amount of rubles spent by him in January is also divisible by 5. Therefore, the total amount of money spent on other days is also divisible by 5. Hence, the number of days when Andrey bought a ticket from the conductor is divisible by 5. The numbers 0 and 10 are not suitable; numbers greater than 10 are even less suitable, so the only possible option is 5 days. Then the number of other days is $(115-11 \cdot 5): 15=4$, and the circle was 9 times.
## Answer
9 times.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Investigation of a quadratic trinomial ] [ Methods for solving problems with parameters ]
For the quadratic trinomial $f(x)=a x^{2}-a x+1$, it is known that $|f(x)| \leq 1$ for $0 \leq x \leq 1$. Find the greatest possible value of $a$.
|
Since $f(0)=f(1)=1$, the graph of the quadratic polynomial is a parabola symmetric with respect to the line $x=0.5$. From the condition $|f(x)| \leq 1$ for
$0 \leq x \leq 1$, it follows that the branches of the parabola are directed upwards. The minimum value of $f(x)$ is $f(0.5)=1-a / 4$.
The maximum possible value of $a$ is achieved when this number equals -1, that is, when $a=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6,7,8 |
In 2 seconds, the kangaroo mother makes three jumps, and the joey makes five jumps. The length of the mother kangaroo's jump is 6 meters, while the length of the joey's jump is three times less. The mother and joey are playing tag: the joey jumps ahead by 12 jumps, after which the mother starts to chase him, and he continues to jump. How long will it take for the mother to catch up?
|
In two seconds, the mother kangaroo makes 3 jumps, which means she jumps 9 jumps of the joey. Therefore, in two seconds, the distance between the mother and the joey decreases by 4 jumps of the joey. Initially, there were 12 jumps of the joey between them, so it will take the mother 6 seconds to catch up.
## Answer
In 6 seconds.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Folklore
What values can the expression $(x-y)(y-z)(z-x)$ take if it is known that $\sqrt{x-y+z}=\sqrt{x}-\sqrt{y}+\sqrt{z}$?
|
Let $\sqrt{x}=a, \sqrt{y}=b, \sqrt{z}=c, \sqrt{x-y+z}=d$, we get the system $a-b+c=d$ $a^{2}-b^{2}+c^{2}=d^{2}$, or
$a-b=d-c$
$a^{2}-b^{2}=d^{2}-c^{2}$.
If $a=b$, then $x=y$. Otherwise, dividing the second equation by the first, we get $a+b=d+c$.
Subtracting the first equation from this, we get $b=c$, that is, $y=z$.
In any case, $(x-y)(y-z)(z-x)=0$.
Answer
## 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\begin{array}{ll}{[\text { Arithmetic. Mental calculation, etc. }]} \\ {[\text { Word problems (miscellaneous) }]}\end{array}\right]$
The length of the crocodile from head to tail is three times less than ten ken, and from tail to head it is three ken and two shaku. It is known that one shaku is equal to 30 cm. Find the length of the crocodile in meters. (Ken and shaku are Japanese units of length.)
|
According to the condition, the tripled length of the crocodile is 9 ken and 6 shaku or 10 ken. Therefore, 1 ken = 6 shaku = 180 cm. The length of the crocodile is 3 ken 2 shaku, which is 600 cm.
## Answer
6 m.
|
6
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35298 topics: [ Equations in integers ] [Products and factorials]
Find all natural integer solutions of the equation $(n+2)!-(n+1)!-n!=n^{2}+n^{4}$.
#
|
The equation can be written as $n!((n+2)(n+1)-(n+1)-1)=n^{2}\left(n^{2}+1\right)$, or $n!(n+2) n=n^{2}\left(n^{2}+1\right)$.
Checking shows that $n=1$ is not a solution.
Let $n>1$. Write the equation as $(n-2)!(n+2)(n-1)=\left(n^{2}+1\right)$. From this, $n^{2}+1 \geq(n+2)(n-1)$.
Expanding the brackets, we get $n \leq 3$. Checking shows that $n=2$ does not work, but $n=3$ is a solution.
## Answer
$n=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Algebra and arithmetic (miscellaneous).] $[$ Sequences (miscellaneous) ]
Find the value of the expression $1!* 3-2!* 4+3!* 5-4!* 6+\ldots-2000!* 2002+2001!$.
|
Start simplifying the given expression from the end.
## Solution
Let's denote the given expression by S and start transforming it from the end: -2000!*2002 + 2001! = 2000! * (-2002 + 2001) = -2000!. Thus, S = 1!*3 - 2!*4 + 3!*5 - 4!*6 + ... + 1999!*2001 - 2000!. Next, 1999!*2001 - 2000! = 1999!(2001 - 2000) = 1999!. Therefore, S = 1!*3 - 2!*4 + 3!*5 - 4!*6 + ... - 1998!*2000 + 1999!. By continuing to simplify the sum S in this manner, we will arrive at S = 1! = 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a chess tournament, sports masters and candidates for masters are participating. What is the smallest number of people that can participate in this tournament if it is known that among them, masters are less than half, but more than $45 \%$.
#
|
Let $n$ chess players participate in a tournament, and $k$ of them are masters. According to the condition, $0.9 n2 k$ $-n>0.2 k-n$ is an integer, so it is at least 1. Therefore, $0.1 n>1, n>10$.
The case $n=11$ works: in the tournament, 5 masters and 6 candidates can play.
## Answer
11.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Dirichlet's Principle (miscellaneous). ] $[\quad$ Tables and tournaments (miscellaneous). $\quad]$
On each cell of a $9 \times 9$ board, there is a beetle. When a whistle is blown, each beetle moves to one of the diagonally adjacent cells. As a result, some cells may end up with more than one beetle, while some cells may remain unoccupied.
Prove that in this case, there will be at least 9 unoccupied cells.
|
Paint the vertical lines of the board in black and white, alternating. Then, from a black cell, the beetle moves to a white one, and from a white one - to a black one.
## Solution
We will paint the vertical lines of the board in black and white, alternating. As a result, $5 \times 9$ $=45$ cells will be painted black (5 columns), and only 36 will be painted white. Note that from a black cell, the beetle can only move to a white one, and from a white one - only to a black one. Consequently, after the beetles have moved to adjacent diagonal cells, 36 beetles are on 45 black cells. This means that at least 9 black cells remained unoccupied.
|
9
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
[ Examples and counterexamples. Constructions ]
In the cells of a $3 \times 3$ table, the digits from 1 to 9 were placed. Then, the sums of the digits in each row were found. What is the maximum number of these sums that can be perfect squares?
#
|
The smallest possible sum of digits in a row is $1+2+3=6$, and the largest is $7+8+9=24$. Therefore, if the sum is a perfect square, it must be 9 or 16. Suppose that in each row, the sum is 9 or 16, which means it gives a remainder of 2 when divided by 7. Then the sum of all digits in the table, when divided by 7, will give a remainder of 6. However, the sum of the numbers from 1 to 9 is 45, which gives a remainder of 3 when divided by 7. Therefore, it is impossible to have three such sums.
Two such sums are possible, for example, see the table:

## Answer
Two sums.
## [ Arithmetic Progression ]
Problem
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For an arbitrary number $x$, consider the sum $Q(x)=\lfloor x \rfloor + \left\lfloor \frac{x}{10000} \right\rfloor$.
Find the difference $Q(2023) - Q(2022)$. (Here $\lfloor x \rfloor$ denotes the integer part of $x$, that is, the greatest integer not exceeding $x$.)
#
|
\$ \left\lfloor \left| \frac{\mathrm{x}-1}{\mathrm{k}} \right| \right\rfloor < \left\lfloor \left| \frac{\mathrm{x}}{\mathrm{k}} \right| \right\rfloor = m \$ means that \$ \mathrm{x}-1 < \mathrm{k} \mathrm{m} \leq \mathrm{x} \$, from which \$ x = k m \$, that is, \$ x \$
\$\left\lfloor \frac{x}{k} \right\rfloor\$
This means that among the numbers \$ \left\lfloor 2023 \right\rfloor - \left\lfloor 2022 \right\rfloor, \left\lfloor \frac{2023}{2} \right\rfloor - \left\lfloor \frac{2022}{2} \right\rfloor, \ldots, \left\lfloor \frac{2023}{10000} \right\rfloor - \left\lfloor \frac{2022}{10000} \right\rfloor \$, there are as many ones as the number of natural divisors of 2023 that do not exceed 2023, and the rest of the numbers are zero. The difference \$ Q(2023) - Q(2022) \$ is equal to the sum of the above numbers, which is the number of natural divisors of the number \$ 2023 = 7 \cdot 17^2 \$, which is 6.
Answer
## 6.
Send a comment
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How many three-digit numbers exist in which the digits 1, 2, 3 appear exactly once each?
#
|
We can place any of the three digits in the first position, any of the two remaining digits in the second position, and the last remaining digit in the third position. Thus, we get a total of 6 numbers.
## Answer
$3!=6$ numbers.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the box, there are blue, red, and green pencils. In total, there are 20 pieces. Blue pencils are 6 times more than green ones, and there are fewer red pencils than blue ones.
How many red pencils are in the box?
#
|
The total number of blue and green pencils is divisible by 7. Therefore, they are either 7 or 14. In the first case, the number of red pencils is 13 more than the blue ones. Therefore, only the second option is possible: 6 red pencils.
## Answer
6 red pencils.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
There are nuts in three boxes. In the first box, there are 6 kg fewer nuts than in the other two together. And in the second box, there are 10 kg fewer nuts than in the other two together. How many nuts are in the third box?
|
Let's combine both given conditions and obtain the following statement: "In the first and second boxes, there are $6+10$ kg fewer nuts than in the first, second, and two-thirds of the third box." From this, it follows that in two-thirds of the third box, there are 16 kg of nuts, which means that in the third box, there are 8 kg of nuts.
## Answer
8 kg.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ $[$ Divisibility of numbers. General properties $]$
Vovochka had more nuts than Pavlik. If Vovochka had given Pavlik as many nuts as Pavlik had, both boys would have had an equal number of nuts. But instead, Vovochka gave Pavlik a few nuts (no more than five), and divided the rest equally among three squirrels. How many nuts did Vovochka give to Pavlik?
#
|
Initially, Volodya had 3 times more nuts than Pavlik.
## Solution
From the condition, it follows that Volodya had 3 times more nuts than Pavlik. After giving some nuts to Pavlik, the number of his nuts remained a multiple of 3—otherwise, he wouldn't have been able to divide them among three squirrels. The only number that is a multiple of 3 and less than 5 is 3. Therefore, Volodya gave Pavlik 3 nuts.
## Answer
[ Measurement of segment lengths and angles. Adjacent angles.]
Problem
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bootin D. ..
Several guard brigades of the same size slept for the same number of nights. Each guard slept more nights than there are guards in a brigade, but fewer than the number of brigades. How many guards are in a brigade if all the guards together slept for 1001 person-nights?
|
$1001=7 \cdot 11 \cdot 13$.
## Solution
Let $s$ be the number of guards in a squad, $b$ be the number of squads, and $n$ be the number of nights one guard slept. Then $2 b n=1001$.
But $1001=7 \cdot 11 \cdot 13$, and the numbers $7,11,13$ are prime. Considering that $s<n<b$, we get $s=7$.
Answer
7 guards.
Submit a comment
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2 [ Inequalities problems. Case analysis ]
Sasha invited Petya to visit, saying that he lives in the 10th entrance in apartment No. 333, but forgot to mention the floor. Approaching the building, Petya noticed that the building is nine-story. Which floor should he go to? (The number of apartments on each floor is the same, apartment numbers in the building start from one.)
#
|
If there are no more than three apartments on a floor, then in ten entrances, there will be no more than $10 \cdot 9 \cdot 3=270$ apartments, which means apartment № 333 will not be in the 10th entrance. If there are no fewer than five apartments on a floor, then already in nine entrances, there will be no fewer than $9 \cdot 9 \cdot 5=405$ apartments, which means Sasha's apartment will not be in the 10th entrance. Therefore, there are 4 apartments on each floor, and in the first nine entrances, there are $9 \cdot 9 \cdot 4=324$ apartments. Then in the 10th entrance, the apartments start from 325. On the second floor, they will start from 329, and on the third floor, from 333. Thus, Petya needs to go up to the third floor.
## Answer
To the 3rd floor.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left.\begin{array}{l}\text { [Inclusion-Exclusion Principle]} \\ {[\quad \text { Word Problems (Miscellaneous). }}\end{array}\right]$
In the garden, Anya and Vitya had 2006 rose bushes. Vitya watered half of all the bushes, and Anya watered half of all the bushes. It turned out that exactly three bushes, the most beautiful ones, were watered by both Anya and Vitya. How many rose bushes were left unwatered?
|
Vitya watered 1003 bushes, of which 1000 he watered alone, and three - together with Anya. Similarly, Anya watered 1003 bushes, of which 1000 she watered alone, and three - with Vitya. Therefore, together they watered $1000+1000+3=2003$ bushes. Thus, $2006-2003=3$ rose bushes remained unwatered.
## Answer
3 bushes.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kolya and his sister Masha went to visit someone. After walking a quarter of the way, Kolya remembered that they had forgotten the gift at home and turned back, while Masha continued on. Masha arrived at the visit 20 minutes after leaving the house. How many minutes later did Kolya arrive at the visit, given that they walked at the same speed the whole time?
|
Kolya walked an "extra" half of the distance. This means the delay time is equal to half of the time spent on the entire journey, which is 10 minutes.
## Answer
10 minutes.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Folklore
Find the smallest natural value of $n$ for which the number $n!$ is divisible by 990.
|
The number $11!=1 \cdot 2 \cdot \ldots \cdot 9 \cdot 10 \cdot 11$ is divisible by $9 \cdot 10 \cdot 11=990$.
For $n!<11$, the number $n!$ is not even divisible by 11.
## Answer
$n=11$.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2+ |
| :---: | :---: |
Find the remainder when $6^{100}$ is divided by 7.
|
$6^{100} \equiv(-1)^{100}=1(\bmod 7)$
## Answer
1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Factorization ] [ Equations in integers ]
In how many ways can the number 1979 be represented as the difference of squares of natural numbers?
|
Let $1979=x^{2}-y^{2}=(x-y)(x+y)$. Since $1979-$ is a prime number, there is a unique representation of it as a product of two natural numbers $1979=1 \cdot 1979$. Since $x-y<x+y$, then $x-y=$ $1, x+y=1979$, from which $x=990, y=989$.
## Answer
One way.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\begin{array}{l}\text { Factorization } \\ {[\underline{\text { Modular Arithmetic (other) })]}]}\end{array}\right.$
What remainders can be obtained when dividing $n^{3}+3$ by $n+1$ for a natural number $n>2$?
|
Find a number close to $n^{3}+3$ that is divisible by $n+1$.
## Solution
$n^{3}+3=(n+1)\left(n^{2}-n+1\right)+2$.
## Answer
Only 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Tournaments and tournament tables ] [ Problems on percentages and ratios ]
In a volleyball tournament, which was held in a round-robin format, $20 \%$ of all teams did not win a single game. How many teams were there
#
|
Can it happen that two teams did not win a single game?
## Solution
Note that there cannot be two teams that did not win a single game. Indeed, in the match between these teams, one of them won. Thus, $20 \%$ (that is, $1 / 5$) of the total number of teams is one team.
## Answer
5 teams.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tokarev S.i.
The set of five-digit numbers $\{N_1, \dots, N_k\}$ is such that any five-digit number, all of whose digits are in increasing order, coincides in at least one digit with at least one of the numbers $N_1, \dots, N_k$. Find the smallest possible value of $k$.
|
Let's prove that the condition is satisfied by the set consisting of a single number $13579$. Indeed, let
$\overline{a_1a_2a_3a_4a_5}$ be a five-digit number, the digits of which satisfy the inequalities $a_1 < a_2 < a_3 < a_4 < a_5$. Then, if $a_1 \ne 1$, we have $2 \leq a_1 < a_2$. If at the same time $a_2 \ne 3$, then $4 \le a_2 < a_3$.
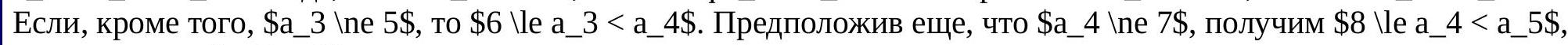
i.e., the equality $a_5 = 9$, meaning the digits in the units place coincide.
## Answer
$\$ \mathrm{k}=1 \$$.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Folklore }}$
For different positive numbers $a$ and $b$, the equality $\frac{1}{1+a}+\frac{1}{1+b}=\frac{2}{1+\sqrt{a b}}$ holds. Prove that $a$ and $b$ are reciprocal numbers.
|
$0=\frac{1}{1+a}-\frac{1}{1+\sqrt{a b}}+\frac{1}{1+b}-\frac{1}{1+\sqrt{a b}}=\frac{1}{1+\sqrt{a b}}\left(\frac{\sqrt{a b}-a}{1+a}-\frac{\sqrt{a b}-b}{1+b}\right)=$
$\frac{\sqrt{b}-\sqrt{a}}{1+\sqrt{a b}}\left(\frac{\sqrt{a}}{1+a}-\frac{\sqrt{b}}{1+b}\right)$
Therefore, $0=\frac{\sqrt{a}}{1+a}-\frac{\sqrt{b}}{1+b}=\frac{\sqrt{a}+b \sqrt{a}-\sqrt{b}-a \sqrt{b}}{(1+a)(1+b)}=\frac{(\sqrt{a}-\sqrt{b})(1-\sqrt{a b})}{(1+a)(1+b)}$. Hence, $a b=1$.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
[ Fermat's Little Theorem ]
Find the remainder when $3^{102}$ is divided by 101.
#
|
Since $101$ is a prime number, then $3^{100} \equiv 1(\bmod 101)$. Therefore, $3^{102}=9 \cdot 3^{100} \equiv 9(\bmod 101)$.
Send a comment
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Trigonometric substitutions $]$
How many roots does the equation $8 x\left(1-2 x^{2}\right)\left(8 x^{4}-8 x^{2}+1\right)=1$ have on the interval $[0,1]$?
|
Note that $8 x^{4}-8 x^{2}+1=2\left(2 x^{2}-1\right)^{2}-1$. By making the substitution $x=\cos \varphi$, we get $8 \cos \varphi \cos 2 \varphi \cos 4 \varphi=-1$. Multiplying by $\sin \varphi$, we obtain $\sin 8 \varphi=-\sin \varphi$, from which $8 \varphi=-\varphi+2 k \pi$ or $8 \varphi=\pi+\varphi+2 k \pi$, that is, $x=\cos 2 k \pi / 9$ or $x=\cos (\pi / 7+2 k \pi / 7)$. On the interval $[0,1]$, there are four roots of the equation: $\cos 2 \pi / 9, \cos 4 \pi / 9, \cos \pi / 7$ and $\cos 3 \pi / 7$ (the root $x=1-$ is extraneous, it arose from the multiplication by $\sin \varphi)$.
## Answer
Four roots.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.