problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Blinkov A. A:
The teams held a football tournament in a round-robin format (each team played one match against every other team, with 3 points for a win, 1 point for a draw, and 0 points for a loss). It turned out that the sole winner scored less than $50 \%$ of the maximum possible points for one participant. What is the minimum number of teams that could have participated in the tournament?
|
Let's prove that there could not have been fewer than six teams. If, for example, there were five teams in the tournament, then they played $5 \cdot 4: 2=10$ matches and scored a total of at least 20 points. Therefore, the sole winner scored more than $20: 5=4$ points. However, according to the conditions, he scored no more than 5 points out of 12 possible. Thus, the winner scored exactly 5 points, and each of the other teams scored no more than 4. Therefore, the total points scored by all participants does not exceed $5+4 \cdot 4=21$. But the number of points scored by the winner means that he won at least once and lost at least once, which means that in this case, the total points scored by all teams cannot be less than 22. Contradiction.
The reasoning for a tournament with two, three, or four teams is similar.
Let's provide two possible examples for a tournament with six teams:
| Team | Total | 1 | 2 | 3 | 4 | 5 | 6 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | **7** | | 1 | 1 | 1 | 1 | 3 |
| 2 | **5** | 1 | | 1 | 1 | 1 | 1 |
| 3 | **5** | 1 | 1 | | 1 | 1 | 1 |
| 4 | **5** | 1 | 1 | 1 | | 1 | 1 |
| 5 | **5** | 1 | 1 | 1 | 1 | | 1 |
| 6 | **4** | 0 | 1 | 1 | 1 | 1 | |
| Team | Total | **1** | 2 | 3 | 4 | 5 | 6 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | **7** | | 3 | 3 | 0 | 0 | 1 |
| 2 | **6** | 0 | | 1 | 1 | 3 | 1 |
| 3 | **6** | 0 | 1 | | 3 | 1 | 1 |
| 4 | **6** | 3 | 1 | 0 | | 1 | 1 |
| 5 | **6** | 3 | 0 | 1 | 1 | | 1 |
| 6 | **5** | 1 | 1 | 1 | 1 | 1 | |
## Answer
6 teams.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9,10,11 |
| :---: | :---: | :---: |
King Hiero has 11 metal ingots that are indistinguishable in appearance; the king knows that their weights (in some order) are $1, 2, \ldots, 11$ kg. He also has a bag that will tear if more than 11 kg is placed in it.
Archimedes has learned the weights of all the ingots and wants to prove to Hiero that the first ingot weighs
1 kg. In one step, he can load several ingots into the bag and demonstrate to Hiero that the bag does not tear (the bag cannot be torn!). What is the minimum number of bag loadings Archimedes can use to achieve
the required result?
|
Let Archimedes first put ingots weighing 1, 2, 3, and 5 kg into the bag, and then put ingots weighing 1, 4, and 6 kg. In both cases, the bag does not tear.
We will prove that this could only happen if the 1 kg ingot was used twice. Indeed, if Archimedes used ingots weighing \( w_{1}, \ldots, w_{6} \) kg instead of ingots weighing 1, ..., 6 kg in these two cases, then these weights would satisfy the system of inequalities
\[ w_{1} + w_{2} + w_{3} + w_{5} \leq 11, \quad w_{1} + w_{4} + w_{6} \leq 11. \]
Adding these inequalities, we get
\[ w_{1} + (w_{1} + w_{2} + \ldots + w_{6}) \leq 22. \]
The sum in parentheses is the sum of six different natural numbers, which is at least \( 1 + 2 + \ldots + 6 = 21 \). Therefore, it follows that
\[ w_{1} \leq 22 - 21 = 1. \]
Thus, \( w_{1} = 1 \), meaning the 1 kg ingot is uniquely determined.
It remains to show that one loading is insufficient. If Archimedes loads only one ingot, the bag will not tear in any case, so no ingot can be identified. Suppose Archimedes loads more than one ingot, and the bag does not tear. If the 1 kg ingot is not loaded into the bag, then replacing it with any ingot in the bag will not change the result; in this case, Hiero will not be able to determine whether this ingot is in the bag. If the required ingot is in the bag, then Hiero will not be able to determine which of the (at least two) loaded ingots is the required one.
## Answer
In two loadings.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ten dogs and cats were fed 56 biscuits. Each cat received 5 biscuits, and each dog - 6. How many
were dogs and how many were cats?
|
How many biscuits would be needed if all the animals were dogs?
## Solution
If only dogs were being fed, 106=60 biscuits would be needed. The extra 4 biscuits are required because a dog eats one more biscuit than a cat. This means there were 4 cats, and consequently, 6 dogs.
## Answer
6 dogs and 4 cats.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Sabin A. }}$.
Ofenya bought a batch of pens at a wholesale market and offers customers either one pen for 5 rubles or three pens for 10 rubles. From each customer, Ofenya makes the same profit. What is the wholesale price of a pen?
|
According to the condition, the difference $10-5=5$ is the wholesale price of two pens.
## Answer
2 rubles 50 kopecks.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$[$ Arithmetic of residues (other). ]
Find the remainder of the division of $2^{100}$ by 3.
|
$2^{100}=4^{50} \equiv 1^{50}=1(\bmod 3)$.
## Answer
1.
In a class of 30 people, can it be that 9 of them have 3 friends (in this class), 11 have 4 friends, and 10 have 5 friends?
## Solution
In the corresponding graph, there would be 30 vertices, 9 of which would have a degree of 3, 11 a degree of 4, and 10 a degree of 5. However, such a graph would have 19 vertices with odd degrees, which contradicts problem 87972 b).
## Answer
It cannot.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left.\frac{[\text { Prime numbers and their properties }]}{[\underline{\text { Evenness and oddness }}]}\right]$
Find all such natural numbers $p$, that $p$ and $3 p^{2}+1$ are primes.
|
If $p$ is odd, then $3 p^{2}+1$ is even.
## Answer
$p=2$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic operations. Numerical identities ]
Find the sum of the digits in the decimal representation of the number $4^{12} \cdot 5^{21}$.
#
|
Let's transform: $4^{12} \cdot 5^{21}=2^{3} \cdot 10^{21}=80 \ldots 0$.
## Answer
8.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7 chocolates are more expensive than 8 packs of cookies. What is more expensive - 8 chocolates or 9 packs of cookies?
#
|
Think about what is more expensive: $7 \cdot 8$ chocolate bars or $8 \cdot 8$ packs of cookies.
## Solution
7 chocolate bars are more expensive than 8 packs of cookies. Therefore, 56 chocolate bars cost more than 64 packs of cookies and even more than 63 packs of cookies. Hence,
8 chocolate bars cost more than 9 packs of cookies.
## Answer
8 chocolate bars.
|
8
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Mathematical logic (miscellaneous).] $[$ Arithmetic. Mental arithmetic, etc. ]
In the room, there are 85 balloons — red and blue. It is known that: 1) at least one of the balloons is red; 2) in every arbitrarily chosen pair of balloons, at least one is blue. How many red balloons are in the room?
|
Think about whether there can be two red balls in the room.
## Solution
Since among any two balls, one is blue, there cannot be two red balls in the room. Therefore, there are 84 blue balloons and 1 red balloon in the room.
## Answer
1 ball.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Decimal number system ] [ Divisibility of numbers. General properties ]
In a 100-digit number 12345678901234...7890, all digits standing at odd positions were erased; in the resulting 50-digit number, all digits standing at odd positions were erased again, and so on. The erasing continued until there was nothing left to erase. What was the last digit to be erased?
|
What characterizes the ordinal numbers of the digits that remain after the first deletion? And after the second?
## Solution
After the first deletion, only those digits will remain whose initial numbers are even, after the second, those whose initial numbers are divisible by 4, after the third - by 8, and so on. Before the last deletion, a digit will remain whose initial number is equal to the greatest possible power of 2, that is, 64. This digit is 4.
## Answer
## 4
Numbers greater than three natural numbers are written in a circle, the sum of which is 37. It is known that the sums of any three consecutive numbers are equal. What numbers are written in the circle?
## Hint
Try to consider two cases: a) the number of written numbers is not a multiple of 3; b) the number of written numbers is a multiple of 3.
## Solution
Since the sums of any three consecutive numbers written in a circle are equal to each other, every third number is equal to each other. Consider two cases: a) the number of written numbers is not a multiple of 3; b) the number of written numbers is a multiple of 3. In the first case, all numbers will be equal to each other, and in the second - the sum of them will be a multiple of 3. The second case is impossible since 37 is not divisible by 3. In the first case, the only possibility is to write 37 ones in a circle.
## Answer
Ones.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Mathematical logic (miscellaneous).] [ Arithmetic. Mental arithmetic, etc. ]
Rabbits are sawing a log. They made 10 cuts. How many chunks did they get?
#
|
Into how many parts is a log divided by the first cut? How does the number of pieces change after each subsequent cut?
## Solution
The number of chunks is always one more than the number of cuts, since the first cut divides the log into two parts, and each subsequent cut adds one more chunk.
## Answer
11 chunks.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2 [Arithmetic. Mental arithmetic, etc.]
There are nuts in the boxes. In the first box, there are 6 kg fewer nuts than in the other two together. And in the second box, there are 10 kg fewer nuts than in the other two together. How many nuts are in the third box?
|
Of course, we can set up a system of equations, but let's try to do without it.
## Solution
Let's combine both given conditions and obtain the following statement: "In the first and second boxes, there are 6 kg + 10 kg fewer nuts than in the first, second, and two-thirds of the third box." From this, it follows that in two-thirds of the third box, there are 16 kg of nuts, i.e., in the third box, there are 8 kg of nuts.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left.\begin{array}{l}\text { The ratio of volumes } \\ {[\text { Arithmetic. Mental calculation, etc. ]] }\end{array}\right]$
When Gulliver arrived in Lilliput, he found that everything there was exactly 12 times shorter than in his homeland. Can you tell how many Lilliputian matchboxes would fit into Gulliver's matchbox?
|
Notice that 12 Lilliputian matchboxes should fit into a Gulliver's matchbox in width, 12 - in length, and 12 - in height.
## Solution
In a Gulliver's matchbox, 12 Lilliputian matchboxes should fit in width, 12 - in length, and 12 - in height. In total, $12 \cdot 12 \cdot 12=1728$ matchboxes.
$$
\text { Send a comment }
$$
Outstanding student Polikarp composed a huge number by writing down natural numbers from 1 to 500: 123...1011... 499500. Poor student Kolya erased the first 500 digits of this number. What do you think, with which digit does the remaining number start?
## Hint
Kolya was erasing digits, while Polikarp was writing down numbers - single-digit, two-digit, and three-digit.
## Solution
Out of the 500 digits erased by Kolya, 9 digits will be used for single-digit numbers, so 491 digits will remain. For two-digit numbers, $90 \times 2=180$ digits will be used, so 311 digits will remain. From this number of digits, 103 three-digit numbers and two more digits from the 104th number will be obtained. This means that the digit we are interested in is the 3rd digit of the 104th three-digit number. This number is 203, so the desired digit is 3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Yashchenko I.v.
In all entrances of the house, there is the same number of floors, and on each floor, there is the same number of apartments. The number of floors in the house is greater than the number of apartments per floor, the number of apartments per floor is greater than the number of entrances, and the number of entrances is greater than one. How many floors are there in the house if there are a total of 105 apartments?
|
$105=3 \cdot 5 \cdot 7$.
## Solution
Let $p$ denote the number of entrances in the building, $f$ the number of floors, and $k$ the number of apartments per floor. Then $p \cdot f \cdot k=105=3 \cdot 5 \cdot 7$, where the numbers $3,5,7-$ are prime. Considering that $1<p<k<f$, we get $f=7$.
## Answer
7 floors.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Andjensss A.
$N$ friends simultaneously learned $N$ pieces of news, with each person learning one piece of news. They started calling each other and exchanging news.
Each call lasts 1 hour. Any number of news items can be shared in one call.
What is the minimum number of hours required for everyone to learn all the news? Consider three cases:
a) $N=64$,
b) $N=55$,
c) $N=100$.
|
a) The news known to one of the friends will be known to no more than two (including the first) after 1 hour, no more than four after the second hour, ..., and no more than 32 after the 5th hour. Therefore, it will take no less than 6 hours.
We will show that 6 hours are sufficient. The conversations can proceed according to the following scheme. Number the participants with six-digit binary numbers. In the $k$-th hour, people whose numbers differ only in the $k$-th digit converse (for example, in the 3rd hour, $a b c 0 d e$ converses with $a b c 1 d e$). Each hour, the number of news items known to each person doubles. (For example, after the 2nd hour, each person knows four news items known to four participants whose numbers differ from his number in the first two digits.)
Remark. This method of conversation is only suitable for powers of two. Below is a method that works for any even numbers.
c) That 6 hours are insufficient is clear from a). We will show that 7 hours are sufficient. Number the participants by elements from
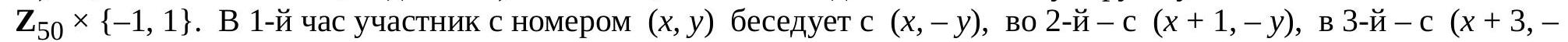
$y$), in the 4th hour with $(x+7, -y)$, in the 5th hour with $(x+15, -y)$, in the 6th hour with $(x+31, -y)$, and in the 7th hour with $(x+63, -y)$. Each hour (except the last), the number of news items each friend knows doubles. (Number the news items the same way as the friends who know them at the beginning. After the 1st hour, the participant with the number $(0,0)$ knows all news items with $x=0$, after the 2nd hour, all news items with $x=0,1$, after the 3rd hour, all news items with $x=0,1,2,3$; and so on.)
b) In the first hour, one of the participants does not converse with anyone. As seen from a), the others will need at least 6 more hours to learn his news.
Divide the participants into two groups: 32 and 23 people. In the 1st hour, all members of the second group converse with members of the first. Over the next 5 hours, the members of the first group exchange news (according to the scheme from a) or c); as a result, each knows all the news). In the last hour, they inform all the information to the members of the second group.
## Answer
a) 6 hours,
b) 7 hours,
c) 7 hours.
Submit a comment
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A number is guessed from 1 to 144. You are allowed to select one subset of the set of numbers from 1 to 144 and ask whether the guessed number belongs to it. For an answer of "yes," you have to pay 2 rubles, and for an answer of "no" - 1 ruble. What is the smallest amount of money needed to surely guess the number?
#
|
Let $a_{1}=2, a_{2}=3, a_{i}=a_{i-1}+a_{i-2}$ for $i \geq 2$. Then $a_{10}=144$. We will prove by induction that among no fewer than $a_{i}$ numbers, the guessed number cannot be found by paying less than $i+1$ rubles.
For $i=1$ and $i=2$, this is true.
Suppose there are no fewer than $a_{i}$ numbers. Then either the set $M$ of numbers highlighted in the first question contains no fewer than $a_{i-2}$ numbers (first case), or the set of numbers not in $M$ contains no fewer than $a_{i-1}$ numbers (second case). In the first case, if the guessed number is in $M$, then 2 rubles need to be paid for the answer, and by the induction hypothesis, at least $(i-2)+1$ rubles are needed to guess the number, i.e., a total of at least $i+1$ rubles.
In the second case, if the guessed number is not in $M$, then 1 ruble needs to be paid for the answer and at least $(i-1)+1$ rubles for guessing the number, i.e., again a total of at least $i+1$ rubles.
The algorithm for guessing the number is clear from the previous reasoning: at each step, the set $M$ of $a_{i}$ numbers containing the guessed number should be divided into sets $M_{1}$ of $a_{i-2}$ numbers and $M_{2}$ of $a_{i-1}$ numbers, and ask whether the number belongs to the set $M_{1}$.
## Answer
11 rubles.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Similar triangles (other). $\quad[$ [Ratio of areas of triangles with a common base or common height] $]$ Difficult [The area of a figure is equal to the sum of the areas of the figures into which it is divided Cauchy's inequality
The diagonals of a convex quadrilateral $ABCD$ intersect at point $E$. It is known that the area of each of the triangles $ABE$ and $DCE$ is 1, the area of the entire quadrilateral does not exceed 4, and $AD=3$. Find the side $BC$.
#
|
Prove that $B C \| A D$.
## Solution
According to problem 35162, $B C \| A D$.
Let $B C = x$. From the similarity of triangles $B E C$ and $D E A$, it follows that $S_{B E C} = \frac{B E}{E D} \cdot S_{D C E} = \frac{x}{3}, S_{D E A} = \frac{D E}{B E} \cdot S_{A B E} = \frac{3}{x}$.
By the condition $S_{A B C D} \leq 4$, therefore $\frac{x}{3} + \frac{3}{x} \leq 2$.
On the other hand, according to the Cauchy inequality, this sum is not less than 2, and equality is achieved if and only if each of these numbers is 1. Therefore, $\frac{x}{3} + \frac{3}{x} = 2, x = 3$.
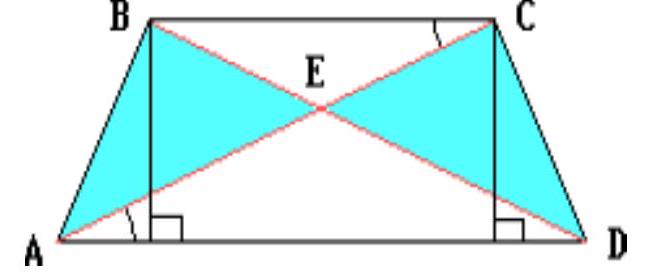
## Answer
3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Chessboards and chess pieces $]$ [ Examples and counterexamples. Constructions ] [ Evenness and oddness
Authors: Pechkovsky A.N., Itenberg I.
Given an infinite grid paper with a cell side equal to one. The distance between two cells is defined as the length of the shortest path of a rook from one cell to another (the path of the center of the rook is considered). What is the minimum number of colors needed to color the board (each cell is colored with one color) so that two cells, located at a distance of 6, are always colored differently?
#
|
An example of coloring a square grid in four colors, such that any two cells at a distance of 6 are colored differently, is shown in the figure on the left.
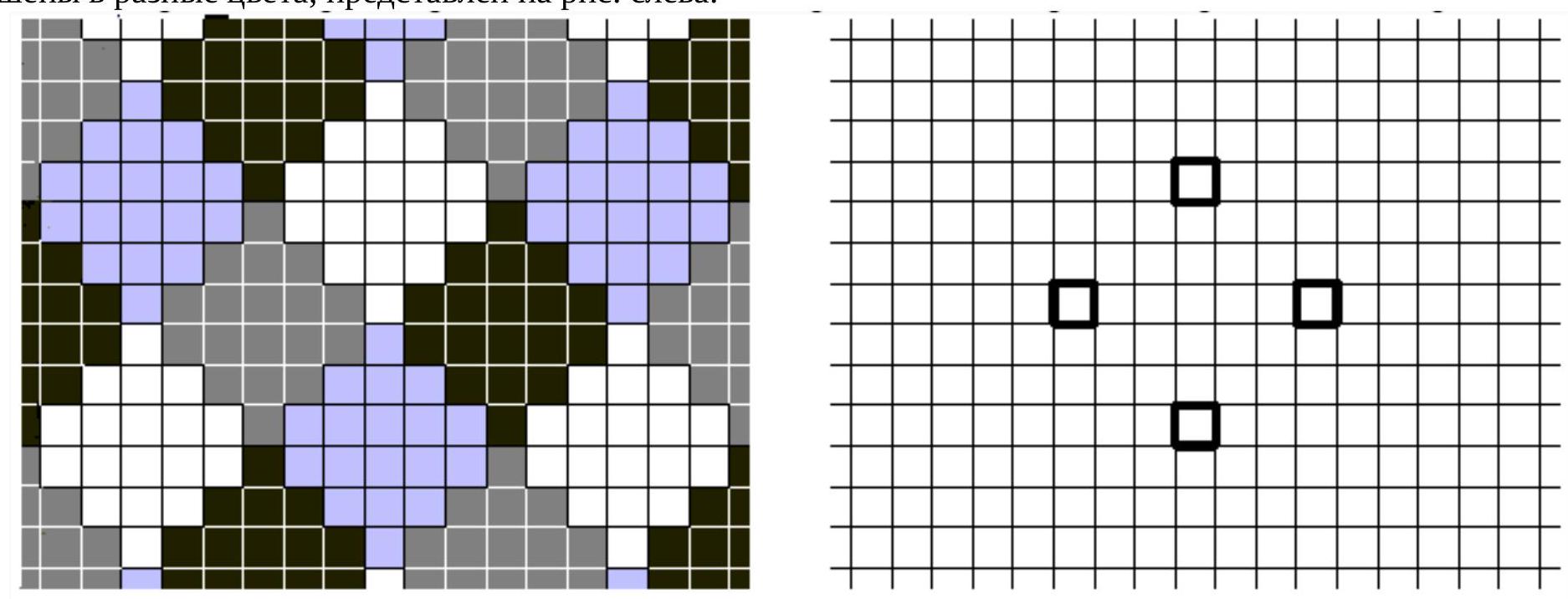
Another example. Introduce a coordinate system on the square grid. It is sufficient to color the cells with even coordinate sums (the coloring of the remaining cells can be obtained from this by shifting 1 to the right). Points with coordinate sums divisible by 4 will be colored in two colors: if both coordinates are even - blue, if both are odd - red. Points with even but not divisible by 4 coordinate sums will be similarly colored in the remaining two colors. To prove that fewer colors cannot suffice, it is enough to consider the four cells shown in the figure on the right. Any two of them are located at a distance of 6 from each other, and therefore, all of them must be colored differently.
## Answer
In 4 colors.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tokarev S.i.
A set of five-digit numbers $\left\{N_{1}, N_{k}\right\}$ is such that any five-digit number, all digits of which are in non-decreasing order, coincides in at least one digit with at least one of the numbers $N_{1}, N_{k}$. Find the smallest possible value of $k$.
|
A set with the specified properties cannot consist of a single number. Indeed, for each $N=\overline{a b c d e}$, there is a number $G=\overline{g g g 9 g}$ that differs from $N$ in all digits, where $g$ is a non-zero digit different from $a, b, c, d, e$. We will show that the numbers $N_{1}=13579$ and $N_{2}=12468$ form a set that satisfies the conditions of the problem.
Let $A=\overline{a_{1} a_{2} a_{3} a_{4} a_{5}}$ be an arbitrary number for which the digits satisfy the inequalities $1 \leq a_{1} \leq a_{2} \leq a_{3} \leq a_{4} \leq a_{5}$. Then, if $A$ does not match $N_{1}$ or $N_{2}$ in the units place, $a_{5} \leq 7$ and, consequently, $a_{4} \leq 7$; if there are no matches in the tens place either, then $a_{4} \leq 5$ and $a_{3} \leq 5$.
If, in addition, there are no matches in the hundreds place, then $a_{3} \leq 3$, from which it follows that $a_{2} \leq 3$; assuming further that $a_{2} \not=2$ and $a_{2} \not= 3$, we arrive at the equality $a_{1}=1$, indicating that $A$ matches $N_{1}$ (and $N_{2}$) in the most significant digit.
## Answer
2.00
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Blinkov A.d:
a) In a football tournament in a round-robin format, 75 teams participated. A team received 3 points for a win, 1 point for a draw, and 0 points for a loss. It is known that every two teams scored a different number of points. Find the smallest possible difference in points between the teams that took first and last place.
b) The same question for $n$ teams.
|
b) The minimum gap between the first and last place cannot be less than $n-1$. We will prove that for $n>3$ it is possible to construct a tournament scheme to achieve a gap of $n-1$ (if $n=2$ or 3, the minimum gap is obviously 3 points).
By induction, we will construct a table for $n$ teams, where the results are all integers from $n-2$ to $2n-3$. Base case ($n=4$). Example of a tournament table for four teams:
| Team | 1 | 2 | 3 | 4 | Points |
| :--- | :---: | :---: | :---: | :--- | :--- |
| 1 | $\times$ | 3 | 1 | 1 | 5 |
| 2 | 0 | $\times$ | 1 | 3 | 4 |
| 3 | 1 | 1 | $\times$ | 1 | 3 |
| 4 | 1 | 0 | 1 | $\times$ | 2 |
Inductive step. By the inductive hypothesis, there is such a table for $n$ teams. We will divide the teams into triples based on the number of points they have: the first triple consists of teams with $2n-3, 2n-4, 2n-5$ points, the second triple consists of teams with $2n-6, 2n-7, 2n-8$ points, and so on (the last triple may be incomplete). Add one more team. Consider three cases.
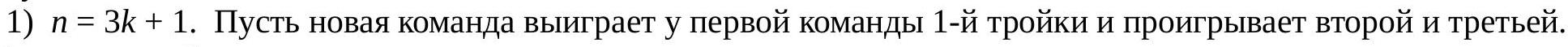
Then the first team will have
$2n-3$ points, the second team will have $2n-1$ points and will move to the first place. The third team will have $2n-2$ points. Similarly, we will proceed with the other complete triples. Then all triples will shift "up" by two points. There will be one team left that was in the last place with $n-2$ points, and the new team will have $n-1$ points. Let them play a draw against each other and add one point each.
2) $n=3k+2$. Teams from $k$ triples play against the new team similarly to case 1). The last two teams had $n-1$ and $n-2$ points, and the new team has $n-2$ points. Let the last team win against the new team, and the second-to-last team play a draw with the new team:
3) $n=3k$. After the new team plays against the first $k-1$ triples, it will have $n-3$ points. The last three teams had $n, n-1$,
$n-2$ points. Let the second-to-last team win against the new team, the last team play a draw with the new team, and the team with $n$ points lose. Then the former last teams will have $n, n+2, n-1$ points, and the new team will have $n+1$ points.
## Answer
a) 74; b) $n-1$, if $n>3$; 3, if $n=2$ or 3.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The equation with integer coefficients $x^{4}+a x^{3}+b x^{2}+c x+d=0$ has four positive roots, counting multiplicities.
Find the smallest possible value of the coefficient $b$ under these conditions.
|
Let $x_{1}, x_{2}, x_{3}, x_{4}$ be the roots of the equation (some of them may coincide). By Vieta's theorem, $b=x_{1} x_{2}+x_{1} x_{3}$ $+x_{1} x_{4}+x_{2} x_{3}+x_{2} x_{4}+x_{3} x_{4}$
$d=x_{1} x_{2} x_{3} x_{4}$, hence $b$ and $d$ are positive. Notice that
$$
\frac{b}{\sqrt{d}}=\left(\sqrt{\frac{x_{1} x_{2}}{x_{3} x_{4}}}+\sqrt{\frac{x_{3} x_{4}}{x_{1} x_{2}}}\right)+\left(\sqrt{\frac{x_{1} x_{3}}{x_{2} x_{4}}}+\sqrt{\frac{x_{2} x_{4}}{x_{1} x_{3}}}\right)+\left(\sqrt{\frac{x_{1} x_{4}}{x_{2} x_{3}}}+\sqrt{\frac{x_{2} x_{3}}{x_{1} x_{4}}}\right) \geq 2+2+2 \text { (inequality }
$$
of Koshi). Therefore, $b \geq 6$ ( $d$ is an integer, so $d \geq 1$ ). Equality is achieved when the equation has four repeated roots, all equal to 1. In this case, the polynomial has the form
$(x-1)^{4}=x^{4}-4 x^{3}+6 x^{2}-4 x+1$
## Answer
$b=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$[\underline{\text { equations in integers }}]$
Solve the equation $\underbrace{\sqrt{n+\sqrt{n+\ldots \sqrt{n}}}}_{1964 \text { times }}=m$ in integers
#
|
Let's solve the more general equation $A_{y}(x)=z$ in integers, where $A_{y}(x)=\underbrace{\sqrt{x+\sqrt{x+\ldots \sqrt{x}}}}_{y \text { times }}$. Clearly, $x+A_{y-1}(x)=z^{2}$, or $A_{y-1}(x)=z^{2}-x$.
Thus, if the number $A_{y}(x)=z$ is an integer, then the number $A_{y-1}(x)=\left(z^{2}-x\right)$ is also an integer; but then the number $A_{y-2}(x)=\left(z^{2}\right.$ $-x)^{2}-x$ is also an integer, and $A_{y-3}$ is an integer, ..., and $A_{1}(x)=\sqrt{x}$ is an integer. Therefore, $x=t^{2}$ is an integer (where $t$ is an integer).
On the other hand, for any integer $t\left(t^{2}, 1, t\right)$ is a solution to our equation.
Let $y>1$. In this case, the numbers $A_{1}(x)=\sqrt{x}=t$ and $A_{2}(x)=\sqrt{x+\sqrt{x}}=\sqrt{t^{2}+t}=\sqrt{t(t+1)}$ must be integers. But the numbers $t$ and $t+1$ are coprime, which implies that $t$ and $t+1$ are perfect squares, i.e., $t=0$. Thus, $x=0$ and $A_{y}(x)=0$ for any $y$.
## Answer
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Khachaturyan A.V. }}$
13 children sat at a round table and agreed that boys would lie to girls, but tell the truth to each other, and girls, on the contrary, would lie to boys, but tell the truth to each other. One of the children said to their right neighbor: "The majority of us are boys." That child said to their right neighbor: "The majority of us are girls," and that one to their right neighbor: "The majority of us are boys," and so on, until the last child said to the first: "The majority of us are boys." How many boys were at the table?
|
It is clear that there were both boys and girls at the table. A group of boys sitting next to each other is followed by a group of girls, then boys again, then girls, and so on (a group can consist of one person). Groups of boys and girls alternate, so their number is even. The incorrect statements were made at the transitions from one group to another, so there are also an even number of them. Since the statement "most of us are boys" was made seven times, six of the statements "most of us are girls" were incorrect, and there were six groups.
The alternation of correct and incorrect statements means that there were two children in each group. Only the first and last child sitting next to each other said the same thing, so there are three people in their group. These are boys, as they are in the majority. In total, there were $2+2+2=6$ girls and $2+2+3=7$ boys at the table.
(The diagram shows exactly how the children were seated at the table. The first speaker is outlined in a frame.)
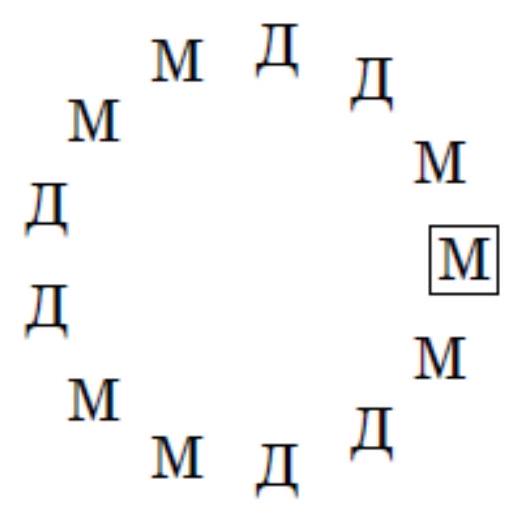
## Answer
7 boys.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Evdokimov M.A.
16 cards with integers from 1 to 16 are laid face down in a \(4 \times 4\) table so that cards with consecutive numbers are adjacent (touching by a side). What is the minimum number of cards that need to be flipped simultaneously to definitely determine the location of all numbers (regardless of how the cards are arranged)?
|
Evaluation. Number the cells as shown in Figure 1.
| 1 | 2 | 3 | 4 |
| :--- | :--- | :--- | :--- |
| 2 | 1 | 4 | 3 |
| 5 | 6 | 7 | 8 |
| 6 | 5 | 8 | 7 |
Fig. 1
Fig. 2
Fig. 3
Notice that one of the cells numbered 1 must be open, otherwise the red and blue ways of filling the table in Figure 2 would be indistinguishable. One of the cells numbered 2 must also be open, otherwise the red and blue ways of filling the table in Figure 3 would be indistinguishable.
Similarly, at least one cell from each of the numbers 3, 4, 5, 6, 7, 8 must be open, meaning that at least 8 cards must be open.
Example. We will prove that by seeing the numbers in the second and third columns, we can restore the numbers in the first and fourth columns. Notice that in the black cells of the chessboard coloring, all numbers have the same parity, and in the white cells, the other parity. By seeing the second and third columns, we understand the parity of each cell.
From the open cells, we highlight those for which not all adjacent numbers are open. From each such cell, we draw an edge to the only unopened adjacent cell and uniquely restore the number in it.
Notice that if an edge leads to a corner, we will restore the number in it. If no edge leads to a corner cell, then it contains the extreme number, i.e., 1 or 16, and since we know the parity of the number in each cell, we can also restore the number in this case. Thus, the numbers in the corners are definitely restored.
If there are corner cells among the corners for which not all adjacent numbers are open, we draw an edge from each such corner to the unopened adjacent cell and uniquely restore the number in it.
The numbers in the non-corner cells of the first and fourth columns may remain unrecovered. Consider any of them. No edge leads to it from the adjacent column or from the corner, then in this cell there is definitely an extreme number (since it has at most one cell with an adjacent number). By parity, it is easy to determine which extreme number should be there.
Thus, we have restored the numbers in all cells.
## Answer
Eight cards.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the maximum value of the expression
$$
x \sqrt{1-y^{2}}+y \sqrt{1-x^{2}}
$$
|
Answer: The maximum value of the expression is 1. Since the expression $\sqrt{1-x^{2}}$ is defined, $|x| \leq 1$, which means there exists an angle $\varphi$ such that $x=\cos \varphi, \sqrt{1-x^{2}}=\sin \varphi$. Similarly, $y=\cos \psi, \sqrt{1-y^{2}}=\sin \psi$.
Therefore,
$$
x \sqrt{1-y^{2}}+y \sqrt{1-x^{2}}=\cos \varphi \sin \psi+\sin \varphi \cos \psi=\sin (\varphi+\psi) \leq 1
$$
On the other hand, when $x=1, y=0$, the value 1 is achieved.
There are balance scales, any weights, and ten bags of coins. All coins in all bags look the same, but in one of the bags, all the coins are counterfeit and each weighs 15 g, while in the other nine bags, all the coins are genuine and each weighs 20 g. How can you determine with one weighing which bag contains the counterfeit coins?
## Hint
Try taking 1 coin from the first bag, 2 from the second, 3 from the third, ..., 10 from the last and weigh them.
## Solution
Take 1 coin from the first bag, 2 from the second, 3 from the third, ..., 10 from the last. In total, there will be $1+2+3+\ldots+10=55$ coins. Weigh them. If all of them were genuine, they would weigh (55×20) = 1100 g, but in our case, they will weigh less. If there is one counterfeit coin, there will be a shortage of 5 g, if two 10 g, ... if ten counterfeit coins, there will be a shortage of 50 g. Thus, knowing how much is missing from 1100 g, we can immediately determine the number of counterfeit coins. The number of counterfeit coins, in turn, will show us the number of the bag in which they are located.
## Answer
Take 1 coin from the first bag, 2 from the second, 3 from the third, ..., 10 from the last. Weigh them. If the counterfeit coin is in the first bag, there will be a shortage of 5 g, if in the second 10 g, ... if in the last 50 g.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Tasks with inequalities. Case analysis Examples and counterexamples. Constructions
Author: Shapovosov A.B.
The plan of the shah's palace is a $6 \times 6$ square, divided into rooms of size $1 \times 1$. There is a door in the middle of each wall between the rooms. The shah told his architect: "Knock down some walls so that all rooms become $2 \times 1$, no new doors appear, and the path between any two rooms passes through no more than $N$ doors." What is the smallest value of $N$ that the shah should name to make the order executable?
|
Consider an arbitrary path from the bottom-left corner of the palace to the top-right corner. Since it is necessary to "climb" 5 horizontal levels and "shift to the right" 5 vertical levels, one would have to pass through at least 10 doors, visiting at least 11 rooms (including the starting and ending rooms).
11 rooms of size $1 \times 1$ could not have been transformed into 5 rooms of size $2 \times 1$. Therefore, the same path in the reconstructed palace must pass through at least 6 rooms, and thus through at least 5 doors. Such a reconstruction of the palace is indeed possible (see the diagram).
| 2 | 2 | 2 | 2 | 2 |
| :---: | :---: | :---: | :---: | :---: |
| | | 1 | | |
| | 1 | 0 | 1 | |
| | 1 | | 1 | |
| 2 | 6 | 1 | 2 | 2 |
| | | 2 | | |
In this case, it is indeed possible to get from any room to any other room by passing through no more than 5 doors. Let's denote the central rooms with the number 0, the rooms connected to them by a door with the number 1, and the rooms connected by a door to the rooms "of type" 1 with the number 2. Since all rooms have been labeled, it is possible to get from any room to one of the central rooms by passing through no more than two doors. Therefore, it is possible to get from any room to any other room by constructing a path through the central rooms and thus passing through no more than 5 doors (the fifth door would be needed if it is necessary to move from one central room to another).
## Answer
$N=5$.
Submit a comment
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $A$ be the sum of the digits of the number $4444^{4444}$, and $B$ be the sum of the digits of the number $A$. Find the sum of the digits of the number $B$.
#
|
The sum of the digits is comparable to $4444^{4444} \equiv (-2)^{4444} = (2^6)^{740} \cdot 2^4 \equiv 1^{740} \cdot 7 \pmod{9}$. Moreover, $4444^{4444} < 10^{4 \cdot 5000}$, meaning this number has no more than 20000 digits. Therefore, $A \leq 180000, B \leq 45$, and the sum of the digits of the number $B$ is no more than 14.
## Answer
7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $\Phi$.
On the board, $N \geq 9$ different non-negative numbers, each less than one, are written. It turns out that for any eight different numbers on the board, there is a ninth, different from them, such that the sum of these nine numbers is an integer. For which $N$ is this possible?
|
Clearly, when $N=9$, the required is possible - it is sufficient to write 9 different positive numbers with a unit sum on the board. We will show that when $N>9$, the required is impossible.
Assume the contrary; let $S$ be the sum of all numbers on the board. Choose any numbers $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{7}$ with sum $T$; let $A$ be the set of all other numbers on the board. By the condition, for any number $\beta \in A$, there exists a number $\gamma \in A$ different from it such that the number $T+\beta+\gamma$ is an integer. We say that the number $\gamma$ corresponds to the number $\beta$. Note that such a number is unique. Indeed, if there were another number $\gamma^{\prime} \in A$ for which the sum $T+\beta+\gamma^{\prime}$ is an integer, then the number $\gamma-\gamma^{\prime}=(T+\beta+\gamma)-\left(T+\beta+\gamma^{\prime}\right)$ would also be an integer. But this is impossible, since $0 < \gamma - \gamma^{\prime} < 1$, as $N=7+2 l>9$.
Consider the sum $\Sigma=\left(T+\beta_{1}+\gamma_{1}\right)+\left(T+\beta_{2}+\gamma_{2}\right)+\ldots+\left(T+\beta_{l}+\gamma_{l}\right)$. $\Sigma$ is an integer. On the other hand, each number from $A$ appears in $\Sigma$ exactly once; hence, $\Sigma=I T+(S-T)=S+(l-1) T$, from which $T=\frac{\Sigma-S}{\ell-1}$.
Now, choosing the numbers $\alpha_{2}, \alpha_{3}, \ldots, \alpha_{8}$ on the board and denoting their sum by $T^{\prime}$, we similarly obtain that $T^{\prime}=\frac{\Sigma^{\prime}-S}{\ell-1}$ for an integer $\Sigma^{\prime}$. Therefore, $\alpha_{1}-\alpha_{8}=\frac{\Sigma-S}{\ell-1}-\frac{\Sigma^{\prime}-S}{\ell-1}=\frac{\Sigma-\Sigma^{\prime}}{\ell-1}$.
Since $\alpha_{1}$ and $\alpha_{8}$ could be any two numbers on the board, we get that the difference between any two numbers on the board is of the form $\frac{k}{l-1}$ for an integer $k$.
Let $\mu$ be the smallest number on the board. Then the board can only contain the numbers $\mu, \mu+\frac{1}{\ell-1}, \ldots, \mu+\frac{\ell-2}{\ell-1}$ (all larger numbers would already be at least 1) - a total of $l$ numbers. However, the total number of numbers on the board is $N=7+2 l>l$; hence, they cannot all be distinct. Contradiction.
## Answer
Only when $N=9$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Solve the equation $2 \sin \pi x / 2 - 2 \cos \pi x = x^{5} + 10 x - 54$.
#
|
Transferring all terms to one side, we get the equation $x^{5}+10 x-54-2 \sin \pi x / 2+2 \cos \pi x=0$. Consider the function
$f(x)=x^{5}+10 x-54-2 \sin \pi x / 2+2 \cos \pi x$. Note that $f^{\prime}(x)=5 x^{4}+10-\pi \cos \pi x / 2-2 \sin \pi x>5 x^{4}+10-3 \pi>0$. Therefore, $f(x)$ is an increasing function, so the equation $f(x)=0$ has no more than one root.
Since $f(2)=32+20-54-2 \sin \pi+2 \cos 2 \pi=0$, then $2$ is a root of the original equation.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Numerical tables and their properties ]
Each cell of a $7 \times 8$ table (7 rows and 8 columns) is painted in one of three colors: red, yellow, or green. In each row, the number of red cells is not less than the number of yellow cells, and not less than the number of green cells, while in each column, the number of yellow cells is not less than the number of red cells, and not less than the number of green cells. How many green cells can there be in such a table?
|
1) In each row of the table, there are no fewer red cells than yellow ones, so in the entire table, there are no fewer red cells than yellow ones.
In each column of the table, there are no fewer yellow cells than red ones, so in the entire table, there are no fewer yellow cells than red ones.
Thus, in the table, there are an equal number of red and yellow cells.
2) Suppose in some column there are more yellow cells than red ones. Since in each of the other columns there are no fewer yellow cells than red ones, then in the entire table, there will be more yellow cells than red ones, but this is not the case (see 1). Therefore, in each of the eight columns, there are an equal number of red and yellow cells.
3) Since in each column there are no fewer yellow cells than green ones, the cases where in each column: a) 1 yellow, 1 red, 5 green cells and b) 2 yellow, 2 red, 3 green cells are excluded.
The only remaining case is when in each column there are 3 red, 3 yellow, and 1 green cell. Thus, in the entire table, there are 8 green cells.
This case is possible. For example, see the table.
| 3 | 3 | Y | **R** | WR | R | Y | **R** |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| R | ऊ | 3 | 3 | **R** | $\overleftarrow{X}^{\prime}$ | **R** | $\aleph_{\mathrm{F}}$ |
| Y | **R** | R | ऊ | 3 | 3 | $\aleph^{\Im}$ | **R** |
| R | Y | Y | **R** | WR | R | 3 | 3 |
| Y | **R** | R | ऊ | **R** | $\Psi_{1}$ | **R** | $\aleph_{\mathrm{F}}$ |
| **R** | Y | R | $\mathscr{W}^{2}$ | **R** | Y | **R** | Y |
| $\varlimsup^{*}$ | **R** | Y | R | WR | R | Y | **R** |
## Answer
8.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Folklore }}$Among the actors of Karabas Barabas theater, a chess tournament was held. Each participant played exactly one game with each of the others. One solido was given for a win, half a solido for a draw, and nothing for a loss. It turned out that among any three participants, there would be a chess player who earned exactly 1.5 solido in games with the other two. What is the maximum number of actors that could have participated in such a tournament?
|
Example. Let's denote the participants with letters A, B, V, G, D. Suppose A won against B, B won against V, V won against G, G won against D, D won against A, and all other matches ended in a draw. The condition of the problem is satisfied.
Evaluation. From the condition, it follows that for this tournament, two statements must be true:
1) there are no three players, all matches between whom ended in a draw;
2) there are no players whose matches did not end in a draw.
Assume that there were at least six players in the tournament. Let's leave only them and draw a complete graph with six vertices (corresponding to these six players), where blue edges correspond to decisive matches, and red edges correspond to draws. According to problem 30815, there are three vertices in it, all edges between which are of the same color. But this contradicts the statements just formulated.
## Answer
5 players.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Decimal numeral system ] [Arithmetic. Mental calculation, etc.]
Given the number: $123456789101112 \ldots$. What digit is in the 2000th place?
|
Let's find out from which point the decimal representation of the given number will start to include three-digit numbers: 2000 - $9 \cdot 1$ $90 \cdot 2=1811$.
$1811: 3$ = 603 (remainder 2), which means that the 2000th position is the second digit of the 604th three-digit number. This number is 703, so the required digit is 0.
## Answer
The required digit is 0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The bathtub fills with cold water in 6 minutes 40 seconds, and with hot water in 8 minutes. In addition, if the plug is removed from a full bathtub, the water will drain in 13 minutes 20 seconds. How long will it take to fill the bathtub completely, given that both taps are open, but the bathtub is not plugged?
#
|
Let's replace the time in seconds with time in minutes: 6 minutes 40 seconds will be replaced by $62 / 3$, or $20 / 3$, and 13 minutes 20 seconds by $40 / 3$. In one minute, the cold water will fill $3 / 20$ of the bathtub, the hot water will fill $-1 / 8$ of the bathtub, and $3 / 40$ of the bathtub will drain. Therefore, in one minute, the bathtub will fill by
$3 / 20 + 1 / 8 - 3 / 40 = 1 / 5$ of the bathtub. Thus, the entire bathtub will fill in
5 minutes.
## Answer
5 minutes.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the books of Novgorod scribes of the $X V$ century, such measures of liquid are mentioned: barrel, nozzle, and bucket. From these same books, it became known that a barrel and 20 buckets of kvass are equal to three barrels of kvass, and 19 barrels, a nozzle, and 15.5 buckets are equal to twenty barrels and eight buckets. Can historians determine from these data how many nozzles are contained in a barrel based on this information?
|
From the first condition, it follows that the barrel's capacity is 10 buckets, and from the second condition, that 7.5 buckets and one nozzle can fit into the barrel. Therefore, one nozzle holds 2.5 buckets, or a quarter of the barrel, meaning that 4 nozzles can fit into the barrel.
## Answer
They can.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7 wolves eat 7 sheep in 7 days. How many days will it take for 9 wolves to eat 9 sheep?
#
|
The number of wolves has increased by the same factor as the number of sheep, so the time of consumption will not change.
## Answer
In 7 days.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\right.$ Arithmetic. Mental calculation, etc.] $\left[\begin{array}{l}\text { Work problems. }\end{array}\right]$
Three diggers dug three holes in three hours. How many holes will six diggers dig in five hours?
|
First, calculate how many pits 6 diggers will dig in 3 hours.
## Solution
Six diggers in 3 hours will dig $2 \cdot 3=6$ pits. And in 5 hours, they will dig $5 / 3 \cdot 6=10$ pits.
## Answer
10 pits.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Several gnomes, loading their luggage onto a pony, set off on a long journey. They were spotted by trolls, who counted 36 legs and 15 heads in the caravan. How many gnomes and how many ponies were there?
#
|
There were 15 creatures in the caravan. If all of them were gnomes, they would have $15 \cdot 2=30$ legs; but in reality, there are 6 more legs, which means there were $6:(4-2)=3$ ponies and $15-3=12$ gnomes.
## Answer
12 gnomes and 3 ponies.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Text problems (miscellaneous) ] [Arithmetic. Mental calculation, etc.]
In response to a question about the age of his children, the mathematician answered:
- My wife and I have three children. When our first child was born, the total age of the family members was 45 years, a year ago, when the third child was born - 70 years, and the current total age of the children is 14 years.
How old is each child, given that all family members have their birthdays on the same day? #
|
A year ago, the total age of the children was 11 years, which means the parents' total age was 59 years. And on the day of the first child's birth, this sum was 45. Therefore, the time between these two events is (59 - 45) : $2=7$ years. Thus, the first child was 7 years old a year ago, and the second was 4.
## Answer
8 years, 5 years, 1 year
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The graphs of the functions $y=k x+b$ and $y=b x+k$ intersect. Find the abscissa of the point of intersection.
#
|
First method. The desired abscissa is the solution to the equation $k x + b = b x + k$. This equation can be simplified to: $(k - b) x = k - b$. Since the given graphs intersect (do not coincide), $k \neq b$, therefore $x = 1$.
Second method. Notice that $x = 1$ is a solution to the problem: when $x = 1$, both given linear functions take the same value $y = k + b$. Since their graphs intersect, meaning these lines have exactly one common point, there are no other solutions.
## Answer
$x = 1$.
## Problem
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic. Mental calculation, etc. ] [ Problems on percentages and ratios ]
Author: Raskina I.V.
Children went to the forest to pick mushrooms. If Anya gives half of her mushrooms to Vitya, all the children will have the same number of mushrooms, and if instead Anya gives all her mushrooms to Sasha, Sasha will have as many mushrooms as all the others combined. How many children went to pick mushrooms?
|
Let Anya give half of her mushrooms to Vitya. Now all the kids have the same number of mushrooms (this means Vitya had no mushrooms of his own). For Sasha to get all of Anya's mushrooms, he needs to take the mushrooms from Vitya and Anya. Then he will have the mushrooms of three kids - Vitya's, Anya's, and his own. The others will have just as many, which means that besides Vitya, Anya, and Sasha, three more children went to the forest.
## Answer
6 children.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The sum of the three smallest distinct divisors of some number $A$ is 8. How many zeros can the number $A$ end with?
#
|
The number 8 can be represented as the sum of three different natural numbers in two ways: $8=1+2+5=$ $1+3+4$. The numbers 1, 3, and 4 cannot be the three smallest divisors of the number $A$: if $A$ is divisible by 4, then it is also divisible by 2. Therefore, the three smallest divisors of $A$ are 1, 2, and 5. Thus, $A$ is divisible by 10, but not by 4. Consequently, the number $A$ ends with exactly one zero.
## Answer
One zero.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Proovvoov v.V.
A chess king has traversed the entire $8 \times 8$ board, visiting each square exactly once and returning to the starting square on the last move.
Prove that he made an even number of diagonal moves.
|
At each non-diagonal move, the color of the field the king stands on changes; at a diagonal move - it does not change. Since the king has toured the entire board and returned, the color of the field changed from white to black as many times as from black to white, which means the king made an even number of non-diagonal moves. The number of diagonal moves is 64 minus the number of non-diagonal moves - also an even number.
The monkeys - Masha, Dasha, Glasha, and Natasha - ate 16 bowls of semolina porridge for lunch. Each monkey got something. Glasha and Natasha together ate 9 portions. Masha ate more than Dasha, more than Glasha, and more than Natasha. How many bowls of porridge did Dasha get?
## Hint
Notice that either Glasha or Natasha got at least 5 portions of porridge.
## Solution
Glasha and Natasha together ate 9 bowls, so one of them must have eaten at least 5 bowls. But then Masha, who ate more than each of them, must have eaten at least 6 bowls. In total, these 3 monkeys ate at least $9+6=15$ bowls. Therefore, Dasha got only one bowl.
## Answer
One bowl.
|
1
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Booin D.A.
The whole family drank a full cup of coffee with milk, and Katya drank a quarter of all the milk and a sixth of all the coffee. How many people are in the family?
|
Let $n$ be the number of cups (the number of people in the family), and $x$ be the amount of milk consumed (in cups). Then the amount of coffee consumed is $n-x$. Katya drank one cup of coffee with milk, which consisted of one quarter of all the milk $(x / 4)$ and one sixth of all the coffee $((n-x) / 6)$. We get
$$
\begin{gathered}
\frac{x}{4}+\frac{(n-x)}{6}=1 \\
3 x+2(n-x)=12 \\
x+2 n=12
\end{gathered}
$$
Since $n$ is an integer, it follows from the last equation that $x$ is an integer, and even ($x=12 - 2 n$). Moreover, $x \leq n$, since the amount of milk consumed is certainly no more than the total amount of the drink.
By a small enumeration, we find that the last equation has three solutions:
$$
n=6, x=0 ; \quad n=5, x=2 ; \quad n=4, x=4 .
$$
The first and last solutions correspond to the case where everyone drank just milk or just coffee, while the second solution corresponds to the case where they drank coffee with milk.
## Answer
5 people.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Inclusion-Exclusion Principle] [Arithmetic. Mental calculation, etc.]
In a group of 50 children, some know all the letters except "r", which they simply skip when writing, while others know all the letters except "k", which they also skip. One day, the teacher asked 10 students to write the word "кот" (cat), 18 other students to write the word "рот" (mouth), and the rest to write the word "крот" (mole). It turned out that the words "кот" and "рот" were each written 15 times. How many children wrote their word correctly?
|
The word "крот" was not written correctly by anyone, because no one can write both the letter "p" and the letter "к" at the same time. The word "рот" or "кот" should have been written by $10+18=28$ people. Note that only
| the words "рот", "кот", and "от" were written. The first two words were written 15 times each, so the word "от" was written by 50 - 15 - 15
$=20$ kids out of 28. Therefore, only 8 kids managed to complete their task.
## Answer
8 kids.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Tiling with domino bones and tiles $]$ [ Text problems (other). $]$
A square $8 \times 8$ was cut into squares $2 \times 2$ and rectangles $1 \times 4$. As a result, the total length of the cuts was 54.
How many figures of each type were obtained?
|
In an $8 \times 8-64$ square, there are 64 cells, and each of the resulting figures has 4 cells. Therefore, there are 16 figures in total.
Let's find the sum of the perimeters of all the resulting figures. Since each cut boundary is part of the perimeter of two figures, we add to the perimeter of the square twice the length of the cuts: $32 + 2 \cdot 54 = 140$.
The perimeter of a $2 \times 2$ square is 8, and the perimeter of a rectangle is 2 more. If all 16 figures were squares, their total perimeter would be $16 \cdot 8 = 128$, which is 12 less than the actual total. To increase the total perimeter by 12, 6 squares need to be replaced with rectangles. Therefore, there were 6 rectangles and 10 squares.
## Answer
10 squares and 6 rectangles.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A chess player played 20 games in a tournament and scored 12.5 points. How many more games did he win than he lost?
#
|
If a chess player had an equal number of wins and losses, he would have scored 10 points (the same as if he had drawn all 20 games). Since in reality he scored 2.5 points more, five draws need to be replaced by five wins, meaning the chess player has 5 more wins than losses.
## Answer
By 5 games.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\underline{\text { Folklore }}$
The sequence $a_{n}$ is defined by the condition: $a_{n+1}=a_{n}-a_{n-1}$. Find $a_{100}$, if $a_{1}=3, a_{2}=7$.
|
Note that $a_{n+3}=a_{n+2}-a_{n+1}=-a_{n}$. Therefore, $a_{n+6}=a_{n}$, which means the terms of the sequence repeat with a period of 6. Since 100 divided by 6 leaves a remainder of 4, we have $a_{100}=a_{4}=-a_{1}$.
## Answer
$-3$.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$\left[\begin{array}{l}{[\text { Prime numbers and their properties }} \\ {[\underline{\text { Arithmetic of residues (other) })]}}\end{array}\right.$
a) $p, p+10, p+14$ - prime numbers. Find $p$.
b) $p, 2 p+1,4 p+1$ - prime numbers. Find $p$.
|
Consider the remainders when dividing by 3. One of these numbers is divisible by 3.
## Answer
$p=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Prove that for any $n$
a) $7^{2 n}-4^{2 n}$ is divisible by 33;
b) $3^{6 n}-2^{6 n}$ is divisible by 35.
|
a) $7^{2 n}-4^{2 n}$ is divisible by $7^{2}-4^{2}=33$.
b) First method. $3^{6 n}-2^{6 n}$ is divisible by $3^{6}-2^{6}=665=19 \cdot 35$.
Second method. $3^{6 n}-2^{6 n}=(-2)^{6 n}-2^{6 n}=0(\bmod 5), 27^{2 n}-8^{2 n}=(-1)^{2 n}-1^{2 n}=0(\bmod 7)$.
$a \equiv 68(\bmod 1967), \quad a \equiv 69(\bmod 1968)$. Find the remainder of the division of $a$ by 14.
## Solution
$1967=7 \cdot 281$.
First method. Notice that $a+1899$ is divisible by both 1967 and 1968, which means it is divisible by $14.1899 \equiv 9(\bmod 14)$, so $a+9$ is divisible by 14, which means
$a \equiv 5(\bmod 14)$.
Second method. From the first congruence, it follows that $a \equiv 5(\bmod 7)$, and from the second, that $a$ is odd. Therefore, $a \equiv 5(\bmod 14)$
## Answer
5.
|
5
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
9,10 Can integers be written in the cells of a $4 \times 4$ table so that the sum of all the numbers in the table is positive, while the sum of the numbers in each $3 \times 3$ square is negative?
|
The central square of size $2 \times 2$ is contained in each square of size $3 \times 3$. Place the number -9 in one of the cells of the central square, and fill the rest of the cells in this table with ones. Then the sum of all numbers in the table is $15+(-9)=6$, and the sum of the numbers inside any $3 \times 3$ square is $8+(-9)=-1$.
## Answer
It is possible.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Multiplied several natural numbers and got 224, and the smallest number was exactly half of the largest.
How many numbers were multiplied?
#
|
$224=2^{5} \cdot 7$. Consider the two numbers mentioned in the condition: the smallest and the largest. If one of them is divisible by 7, then the other must also be divisible by 7. But 224 is not divisible by $7^{2}$, so both of these numbers must be powers of two. From the condition, it also follows that these are two consecutive powers of the number 2. In addition, the largest number must be greater than 7. Therefore, it is $2^{3}=8$, and the smallest is $2^{2}=4$. The only remaining factor is seven, so the required numbers are three: 4, 7, and 8.
## Answer
Three numbers.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
When it is noon in Bratsk - it is 6 a.m. in Gusev, and 2 p.m. in Komsomolsk-on-Amur. When it is noon in Zlatoust - it is 6 p.m. in Elizovo, and 9 a.m. in Gusev. What time is it in Komsomolsk-on-Amur when it is noon in Elizovo?
|
When it is noon in Elizovo, it is 3 o'clock in Gusev (from the second condition). And when it is 3 o'clock in Gusev, it is 11 o'clock in Komsomolsk-on-Amur (from the first condition).
## Otвет
11 o'clock in the morning.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Text problems (other).]
In a seven-story building, house spirits live. The elevator travels between the first and the last floors, stopping at each floor. On each floor, starting from the first, one house spirit entered the elevator, but no one exited. When the thousandth house spirit entered the elevator, the elevator stopped. On which floor did this happen?
|
Let's find out how many house elves ended up in the elevator for a trip from the first to the seventh floor and back, until the elevator returned to the first floor. One house elf entered on the first and seventh floors, and two house elves entered on all other floors. Thus, 12 house elves enter the elevator in one trip.
$1000=83 \cdot 12+4$. This means that after 83 trips, 4 more house elves will be able to enter the elevator: on the first, second, third, and fourth floors.
## Answer
On the fourth floor
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[The Fundamental Theorem of Arithmetic. Prime Factorization]
## Authors: Raskina I.V., Fedumin L.E.
A hunter told a friend that he saw a wolf with a meter-long tail in the forest. That friend told another friend that a wolf with a two-meter-long tail had been seen in the forest. Passing on the news further, ordinary people doubled the length of the tail, while creative people tripled it. As a result, the TV reported about a wolf with a tail 864 meters long. How many ordinary and how many creative people "grew" the wolf's tail?
|
Each storyteller either doubled or tripled the length of the tail, so 864 is the product of a certain number of twos and threes. Since
$864=2^{5} \cdot 3^{3}$, the wolf's tail was "lengthened" by five ordinary people and three creative individuals.
## Answer
5 ordinary people and 3 creative individuals.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Each of the artists in the creative association "Patience and Labor" has their own work schedule. Six of them paint one picture every two days, another eight artists - one picture every three days, and the rest never paint pictures. From September 22 to 26, they painted a total of 30 pictures. How many pictures will they paint on September 27?
|
Let's see how many paintings the artists will create from September 22 to 27 inclusive. Each of the six artists, who paint one painting every two days, will create three paintings (one for each pair of days 22-23, 24-25, and 26-27), and each of the eight artists, who paint one painting every three days, will create two paintings. Thus, the artists will collectively create \(6 \cdot 3 + 8 \cdot 2 = 34\) paintings. Since they created 30 paintings from the 22nd to the 26th, they will create \(34 - 30 = 4\) paintings on the 27th.
## Answer
4 paintings.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Identical Transformations ]
It is known that $a^{2}+b=b^{2}+c=c^{2}+a$. What values can the expression $a\left(a^{2}-b^{2}\right)+b\left(b^{2}-c^{2}\right)+c\left(c^{2}-\right.$ $\left.a^{2}\right)$ take?
|
From the condition, it follows that $a^{2}-b^{2}=c-b, b^{2}-c^{2}=a-c$ and $c^{2}-a^{2}=b-a$. Therefore, $a\left(a^{2}-b^{2}\right)+b\left(b^{2}-c^{2}\right)+$ $c\left(c^{2}-a^{2}\right)=a(c-b)+b(a-c)+c(b-a)=0$.
## Answer
0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Text problems (other) ]
At each of the four math club sessions, 20 schoolchildren were present. Nine students attended exactly three out of these four sessions, five students - exactly two sessions, and three students only attended one session. How many schoolchildren attended all sessions?
|
Let's fill in the "attendance record" for this club. In total, for the specified four sessions, there will be $20 \cdot 4=80$ attendance marks. Each student who attended three sessions is marked three times in the record, so nine such students are marked a total of $9 \cdot 3=27$ times. Similarly, those who attended twice are marked a total of $5 \cdot 2=10$ times. Three students who attended once are marked a total of three times in the record. The remaining $80-(27+10+3)=40$ attendance marks are for those who attended all four sessions, with each of them marked four times. Therefore, the number of students who attended all sessions is $40: 4=10$.
## Answer
## Problem
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic operations. Numerical identities ]
In a test, each of the 25 students received one of the grades "3", "4", or "5". By how many more were there fives than threes, if the sum of all grades is 106?
#
|
Let $a$ students received a grade of 3, $b$ students received a grade of 4, and $c$ students received a grade of 5. From the problem, we have $a+b+c=25$ and $3a+4b+5c=106$.
Multiply both sides of the first equation by 4: $4a+4b+4c=100$. Now subtract the obtained equation from the second equation, then $c-a=6$.
## Answer
6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Arithmetic. Mental calculation, etc.]
Prosperous Mole in autumn dug up 8 bags of grain. For each winter month, he needs either 3 bags of grain or 1 bag of grain and 3 bags of millet. Mole can trade with other moles 1 bag of grain for 2 bags of millet. But his burrow cannot hold more than 12 bags, and in winter Mole does not leave his burrow and cannot engage in trading. Help him make provisions for three months.
#
|
A mole can exchange 3 bags of grain for 6 bags of millet, then in its burrow there will be 11 bags: 5 bags of grain and 6 bags of millet. For one month, it will spend 3 bags of grain, and for each of the other two - 1 bag of grain and 3 bags of millet.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[ Motion problems ]
A cyclist rode from point A to point B, where he stayed for 30 minutes, and then returned to A. On the way to B, he overtook a pedestrian, and 2 hours later met him on the return trip. The pedestrian arrived in B at the same time the cyclist returned to A. How much time did it take the pedestrian to travel from A to B, if his speed is four times less than the cyclist's speed?
|
The first method. The distance that the pedestrian covers in 2 hours, we will take as a unit. Then the cyclist covers this same distance in 30 minutes. From the moment of their first meeting, the pedestrian has walked one unit, while the cyclist has traveled three units (he rested for half an hour in point B). Therefore, the distance from the point of their second meeting to point B is one unit. Then, after the second meeting, the pedestrian will walk another unit, while the cyclist will travel 4 units in the same time. Therefore, the distance between A and B is 5 units, so it took the pedestrian 10 hours to travel from A to B.
The second method. Let $v$ km/h be the speed of the pedestrian, then the speed of the cyclist is $4v$ km/h. Let the first meeting of the cyclist and the pedestrian occur at a distance of $x$ km from point B. Then in 2 hours, which passed until the second meeting, the pedestrian walked $2v$ km and was at a distance of $x-2v$ km from point B, while the cyclist traveled a distance of $1.5 \times 4v = 6v$ (km) and was at a distance of $6v-x$ km from point B.
Therefore, $x-2v=6v-x$, from which $x=4v$. This means that the point of the first meeting is at a distance from point B that the cyclist covers in one hour, and the point of the second meeting is at a distance that the cyclist covers in half an hour. Since 2 hours after the second meeting, the pedestrian will be at point B, and the cyclist will be at point A, it took the cyclist 2.5 hours to travel from B to A. Therefore, it will take the pedestrian 4 times longer, that is, 10 hours, to travel from A to B.
## Answer
10 hours.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the last digit of the number $2^{50}$.
#
|
$2^{50}=(16)^{3} \cdot 4.6$ any power of 6 ends in 6, so $2^{50}$ ends with the same digit as $6 \cdot 4=24$.
## Answer
4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
[Periodicity and Non-periodicity] [
Find the last digit of the number $7^{1988}+9^{1988}$.
#
|
$7^{1988}+9^{1988}=49^{994}+9^{1988} \equiv(-1)^{994}+(-1)^{1988}=2(\bmod 10)$.
## Answer
2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
| Reverse Process |
| :---: | :---: |
| | [ Arithmetic. Mental calculation, etc.] |
| | [ Word problems (miscellaneous). [ Iterations |
John had a full basket of trampolines. First, he met Anna and gave her half of his trampolines and another half trampoline. Then he met Banna and gave her half of the remaining trampolines and another half trampoline. After meeting Vanna and giving her half of the trampolines and another half trampoline, the basket was empty. How many trampolines did John have at the beginning? (It was not possible to find out what trampolines are, as there were none left by the end of the problem.)
#
|
Notice that before meeting Vanna, John had one tremponch left, as half of this amount was half a tremponch. Before meeting Banna, he had 3 tremponchs, because half of this amount was one and a half tremponchs, that is, one and a half. Similarly, we get that initially there were 7 tremponchs.
## Answer
7 tremponchs.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Fomin S.B.
A natural number $n$ is written in the decimal system. It is known that if any digit is included in this representation, then $n$ is divisible by this digit (0 does not appear in the representation). What is the maximum number of different digits that this representation can contain?
|
If the digit 5 is included in the number, then the number must end in 5. Thus, it is odd and, consequently, contains only odd digits. Therefore, it cannot have more than five digits. If 5 does not appear in the decimal representation of the number, then it can include all the other 8 digits. Here is an example: 1471963248. This number is divisible by $1,2,3,4,6,7,8,9$.
## Answer
8 digits.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7,8,9 |
| $[\underline{\text { Modular Arithmetic (other) }}]$ | | |
Find all prime numbers that are equal to the sum of two prime numbers and the difference of two prime numbers.
|
The given prime number $p$ is odd, so the sum and difference involve numbers of different parity. Thus, $p=q+2=r-2$. From this, it is clear that the numbers give different remainders when divided by 3, meaning one of them is divisible by 3, and since it is prime, it equals 3.
## Answer
5.

Difficulty: 3 [ Residue arithmetic (other) $]$
In a right-angled triangle, the lengths of the sides are natural coprime numbers.
Prove that the length of the hypotenuse is an odd number, and the lengths of the legs have different parity.
## Hint
If $a$ and $b$ are odd numbers, then the equation $a^{2}+b^{2}=c^{2}$ is impossible, since $c^{2}$ cannot give a remainder of 2 when divided by 4.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Dasha and Tanya live in the same entrance. Dasha lives on the 6th floor. Leaving Dasha's place, Tanya went up instead of down as she needed to. Reaching the top floor, Tanya realized her mistake and went down to her floor. It turned out that Tanya walked one and a half times more than if she had gone down immediately. How many floors are there in the building?
|
From Dasha to Tanya is no more than 5 floors, so the extra path was no more than two floors, and the path upwards was no more than one. Therefore, Tanya went up exactly one floor.
## Answer
7 floors.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. How many pairs $(m, n)$ of positive integers with $m<n$ fulfill the equation
$$
\frac{3}{2008}=\frac{1}{m}+\frac{1}{n} ?
$$
## Answer: 5.
|
Let $d$ be the greatest common divisor of $m$ and $n$, and let $m=d x$ and $n=d y$. Then the equation is equivalent to
$$
3 d x y=2008(x+y) \text {. }
$$
The numbers $x$ and $y$ are relatively prime and have no common divisors with $x+y$ and hence they are both divisors of 2008. Notice that $2008=8 \cdot 251$ and 251 is a prime. Then $x$ and $y$ fulfil:
1) They are both divisors of 2008 .
2) Only one of them can be even.
3) The number 251 can only divide none or one of them.
4) $x<y$.
That gives the following possibilities of $(x, y)$ :
$$
(1,2),(1,4),(1,8),(1,251),(1,2 \cdot 251),(1,4 \cdot 251),(1,8 \cdot 251),(2,251),(4,251),(8,251) \text {. }
$$
The number 3 does not divide 2008 and hence 3 divides $x+y$. That shortens the list down to
$$
(1,2),(1,8),(1,251),(1,4 \cdot 251),(4,251) \text {. }
$$
For every pair $(x, y)$ in the list determine the number $d=\frac{2008}{x y} \cdot \frac{x+y}{3}$. It is seen that $x y$ divides 2008 for all $(x, y)$ in the list and hence $d$ is an integer. Hence exactly 5 solutions exist to the equation.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $N$ be a positive integer. Two persons play the following game. The first player writes a list of positive integers not greater than 25 , not necessarily different, such that their sum is at least 200 . The second player wins if he can select some of these numbers so that their sum $S$ satisfies the condition $200-N \leqslant S \leqslant 200+N$. What is the smallest value of $N$ for which the second player has a winning strategy?
Answer: $N=11$.
|
If $N=11$, then the second player can simply remove numbers from the list, starting with the smallest number, until the sum of the remaining numbers is less than 212. If the last number removed was not 24 or 25 , then the sum of the remaining numbers is at least $212-23=189$. If the last number removed was 24 or 25 , then only 24 -s and 25 -s remain, and there must be exactly 8 of them since their sum must be less than 212 and not less than $212-24=188$. Hence their sum $S$ satisfies $8 \cdot 24=192 \leqslant S \leqslant 8 \cdot 25=200$. In any case the second player wins.
On the other hand, if $N \leqslant 10$, then the first player can write 25 two times and 23 seven times. Then the sum of all numbers is 211 , but if at least one number is removed, then the sum of the remaining ones is at most 188 - so the second player cannot win.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all integers $n>1$ such that any prime divisor of $n^{6}-1$ is a divisor of $\left(n^{3}-1\right)\left(n^{2}-1\right)$.
|
Clearly $n=2$ is such an integer. We will show that there are no others.
Consider the equality
$$
n^{6}-1=\left(n^{2}-n+1\right)(n+1)\left(n^{3}-1\right) \text {. }
$$
The integer $n^{2}-n+1=n(n-1)+1$ clearly has an odd divisor $p$. Then $p \mid n^{3}+1$. Therefore, $p$ does not divide $n^{3}-1$ and consequently $p \mid n^{2}-1$. This implies that $p$ divides $\left(n^{3}+1\right)+\left(n^{2}-1\right)=n^{2}(n+1)$. As $p$ does not divide $n$, we obtain $p \mid n+1$. Also, $p \mid\left(n^{2}-1\right)-\left(n^{2}-n+1\right)=n-2$. From $p \mid n+1$ and $p \mid n-2$ it follows that $p=3$, so $n^{2}-n+1=3^{r}$ for some positive integer $r$.
The discriminant of the quadratic $n^{2}-n+\left(1-3^{r}\right)$ must be a square of an integer, hence
$$
1-4\left(1-3^{r}\right)=3\left(4 \cdot 3^{r-1}-1\right)
$$
must be a squareof an integer. Since for $r \geqslant 2$ the number $4 \cdot 3^{r-1}-1$ is not divisible by 3 , this is possible only if $r=1$. So $n^{2}-n-2=0$ and $n=2$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A lattice point in the plane is a point whose coordinates are both integral. The centroid of four points $\left(x_{i}, y_{i}\right), i=1,2,3,4$, is the point $\left(\frac{x_{1}+x_{2}+x_{3}+x_{4}}{4}, \frac{y_{1}+y_{2}+y_{3}+y_{4}}{4}\right)$. Let $n$ be the largest natural number with the following property: There are $n$ distinct lattice points in the plane such that the centroid of any four of them is not a lattice point. Prove that $n=12$.
|
To prove $n \geq 12$, we have to show that there are 12 lattice points $\left(x_{i}, y_{i}\right)$, $i=1,2, \ldots, 12$, such that no four determine a lattice point centroid. This is guaranteed if we just choose the points such that $x_{i} \equiv 0(\bmod 4)$ for $i=1, \ldots, 6, x_{i} \equiv 1(\bmod 4)$ for
$i=7, \ldots, 12, y_{i} \equiv 0(\bmod 4)$ for $i=1,2,3,10,11,12, y_{i} \equiv 1(\bmod 4)$ for $i=4, \ldots, 9$.
Now let $P_{i}, i=1,2, \ldots, 13$, be lattice points. We have to show that some four of them determine a lattice point centroid. First observe that, by the Pigeonhole Principle, among any five of the points we find two such that their $x$-coordinates as well as their $y$-coordinates have the same parity. Consequently, among any five of the points there are two whose midpoint is a lattice point. Iterated application of this observation implies that among the 13 points in question we find five disjoint pairs of points whose midpoint is a lattice point. Among these five midpoints we again find two, say $M$ and $M^{\prime}$, such that their midpoint $C$ is a lattice point. Finally, if $M$ and $M^{\prime}$ are the midpoints of $P_{i} P_{j}$ and $P_{k} P_{\ell}$, respectively, $\{i, j, k, \ell\} \subseteq\{1,2, \ldots, 13\}$, then $C$ is the centroid of $P_{i}, P_{j}, P_{k}, P_{\ell}$.
|
12
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
. Let $\Gamma$ be a circle in the plane and $S$ be a point on $\Gamma$. Mario and Luigi drive around the circle $\Gamma$ with their go-karts. They both start at $S$ at the same time. They both drive for exactly 6 minutes at constant speed counterclockwise around the track. During these 6 minutes, Luigi makes exactly one lap around $\Gamma$ while Mario, who is three times as fast, makes three laps.
While Mario and Luigi drive their go-karts, Princess Daisy positions herself such that she is always exactly in the middle of the chord between them. When she reaches a point she has already visited, she marks it with a banana.
How many points in the plane, apart from $S$, are marked with a banana by the end of the race?
|
. Without loss of generality, we assume that $\Gamma$ is the unit circle and $S=(1,0)$. Three points are marked with bananas:
(i) After 45 seconds, Luigi has passed through an arc with a subtended angle of $45^{\circ}$ and is at the point $\left(\sqrt{2} / 2, \sqrt{2} / 2\right.$ ), whereas Mario has passed through an arc with a subtended angle of $135^{\circ}$ and is at the point $(-\sqrt{2} / 2, \sqrt{2} / 2)$. Therefore Daisy is at the point $(0, \sqrt{2} / 2)$ after 45 seconds. After 135 seconds, Mario and Luigi's positions are exactly the other way round, so the princess is again at the point $(0, \sqrt{2} / 2)$ and puts a banana there.
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
(ii) Similarly, after 225 seconds and after 315 seconds, Princess Daisy is at the point $(0,-\sqrt{2} / 2)$ and puts a banana there.
(iii) After 90 seconds, Luigi is at $(0,1)$ and Mario at $(0,-1)$, so that Daisy is at the origin of the plane. After 270 seconds, Mario and Luigi's positions are exactly the other way round, hence Princess Daisy drops a banana at the point $(0,0)$.
We claim that no other point in the plane, apart from these three points and $S$, is marked with a banana. Let $t_{1}$ and $t_{2}$ be two different times when Daisy is at the same place. For $n \in\{1,2\}$ we write Luigis position at time $t_{n}$ as a complex number $z_{n}=\exp \left(i x_{n}\right)$ with $\left.x_{n} \in\right] 0,2 \pi[$. At this time, Mario is located at $z_{i}^{3}$ and Daisy at $\left(z_{i}^{3}+z_{i}\right) / 2$. According to our assumption we have $\left(z_{1}^{3}+z_{1}\right) / 2=\left(z_{2}^{3}+z_{2}\right) / 2$ or, equivalently, $\left(z_{1}-z_{2}\right)\left(z_{1}^{2}+z_{1} z_{2}+z_{2}^{2}+1\right)=0$. We have $z_{1} \neq z_{2}$, so that we must have $z_{1}^{2}+z_{1} z_{2}+z_{2}^{2}=-1$.
We proceed with an observation of the structure of $\Gamma$ as a set of complex numbers. Suppose that $z \in \Gamma \backslash\{S\}$. Then $z+1+z^{-1} \in \Gamma$ if and only if $z \in\{i,-1,-i\}$. For a proof of the observation note that $z+1+z^{-1}=z+1+\bar{z}$ is a real number for every $z \in \mathbb{C}$ with norm $|z|=1$. So it lies on the unit circle if and only if it is equal to 1 , in which case the real part of $z$ is equal to 0 , or it is equal to -1 , in which case the real part of $z$ is equal to -1 . We apply the observation to the number $z=z_{1} / z_{2}$, which satisfies the premise since $z+1+\bar{z}=-\overline{z_{1}} \cdot \overline{z_{2}} \in \Gamma$. Therefore, one of the following cases must occur.
(i) We have $z= \pm i$, that is, $z_{1}= \pm i z_{2}$. Without loss of generality we may assume $z_{2}=i z_{1}$. It follows that $-1=z_{1}^{2}+z_{1} z_{2}+z_{2}^{2}=i z_{1}^{2}$, so that $z_{1}=\exp (i \pi / 4)$ or $z_{1}=\exp (5 i \pi / 4)$. In the former case $\left(z_{1}, z_{2}\right)=(\exp (i \pi / 4), \exp (3 i \pi / 4))$, which matches case (1) above. In the latter case $\left(z_{1}, z_{2}\right)=(\exp (5 i \pi / 4), \exp (7 i \pi / 4))$, which matches case (2) above.
(ii) We have $z=-1$, that is, $z_{2}=-z_{1}$. It follows that $-1=z_{1}^{2}+z_{1} z_{2}+z_{2}^{2}=z_{1}^{2}$, so that $z_{1}=i$ or $z_{1}=-i$. This matches case (3) above.
Depiction of the path Daisy takes
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. Distinct positive integers $a, b, c, d$ satisfy
$$
\left\{\begin{array}{l}
a \mid b^{2}+c^{2}+d^{2}, \\
b \mid a^{2}+c^{2}+d^{2}, \\
c \mid a^{2}+b^{2}+d^{2}, \\
d \mid a^{2}+b^{2}+c^{2},
\end{array}\right.
$$
and none of them is larger than the product of the three others. What is the largest possible number of primes among them?
|
At first we note that the given condition is equivalent to $a, b, c, d \mid a^{2}+b^{2}+c^{2}+d^{2}$.
It is possible that three of the given numbers are primes, for example for $a=2, b=3, c=13$ and $d=26$. In this case $2^{2}+3^{2}+13^{2}+26^{2}=13 \cdot 66$ which is divisible by all four given numbers. Furthermore we will show that it is impossible that all four of them are primes.
Let us assume that $a, b, c$ and $d$ are primes. As the sum $a^{2}+b^{2}+c^{2}+d^{2}$ is divisible by each of them then it is divisible also by their product $a b c d$. If one of the primes is equal to 2 , then we obtain a contradiction: the sum of four squares is odd, but its divisor $a b c d$ is even. Therefore all four primes are odd, and $a^{2}+b^{2}+c^{2}+d^{2}=0(\bmod 4)$. Hence $a^{2}+b^{2}+c^{2}+d^{2}$ is divisible by $4 a b c d$ which leads to a contradiction as it is easy to see that $a^{2}+b^{2}+c^{2}+d^{2}<4 a b c d$. Indeed, this is equivalent to
$$
\frac{a}{b c d}+\frac{b}{a c d}+\frac{c}{a b d}+\frac{d}{a b c}<4
$$
which is true as none of the numbers exceed the product of three three other and equality can hold only for the largest of the four.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. Find all real numbers $x, y, z$ so that
$$
\begin{aligned}
x^{2} y+y^{2} z+z^{2} & =0 \\
z^{3}+z^{2} y+z y^{3}+x^{2} y & =\frac{1}{4}\left(x^{4}+y^{4}\right)
\end{aligned}
$$
|
Answer: $x=y=z=0$.
$y=0 \Longrightarrow z^{2}=0 \Longrightarrow z=0 \Longrightarrow \frac{1}{4} x^{4}=0 \Longrightarrow x=0 . x=y=z=0$ is a solution, so assume that $y \neq 0$. Then $z=0 \Longrightarrow x^{2} y=0 \Longrightarrow x=0 \Longrightarrow \frac{1}{4} y^{4}=0$, which is a contradiction. Hence $z \neq 0$. Now we solve the quadratic (first) equation w.r.t. $x, y$, and $z$.
$$
\begin{aligned}
& x= \pm \frac{\sqrt{-4 y^{3} z-4 y z^{2}}}{2 y} \\
& y=\frac{-x^{2} \pm \sqrt{x^{4}-4 z^{3}}}{2 z} \\
& z=\frac{-y^{2} \pm \sqrt{y^{4}-4 x^{2} y}}{2}
\end{aligned}
$$
The discriminants must be non-negative.
$$
\begin{gathered}
-4 y^{3} z-4 y z^{2} \geqslant 0 \\
x^{4}-4 z^{3} \geqslant 0 \\
y^{4}-4 x^{2} y \geqslant 0
\end{gathered}
$$
Adding the inequalities we get
$$
\begin{gathered}
y^{4}-4 x^{2} y+x^{4}-4 z^{3}-4 y^{3} z-4 y z^{2} \geqslant 0 \\
\frac{1}{4}\left(x^{4}+y^{4}\right) \geqslant z^{3}+z^{2} y+z y^{3}+x^{2} y
\end{gathered}
$$
But equation 2 says that $\frac{1}{4}\left(x^{4}+y^{4}\right)=z^{3}+z^{2} y+z y^{3}+x^{2} y$. This is only possible if all of the inequalities are in fact equalities, so we have
$$
\begin{gathered}
-4 y^{3} z-4 y z^{2}=0 \\
x^{4}-4 z^{3}=0 \\
y^{4}-4 x^{2} y=0
\end{gathered}
$$
This means that $x= \pm \frac{\sqrt{0}}{2 y}=0 \Longrightarrow y=\frac{-0^{2} \pm \sqrt{0}}{2 z}=0$, which is a contradiction. Hence the only solution is $x=y=z=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. Let $n>2$ be a given positive integer. There are $n$ guests at Georg's bachelor party and each guest is friends with at least one other guest. Georg organizes a party game among the guests. Each guest receives a jug of water such that there are no two guests with the same amount of water in their jugs. All guests now proceed simultaneously as follows. Every guest takes one cup for each of his friends at the party and distributes all the water from his jug evenly in the cups. He then passes a cup to each of his friends. Each guest having received a cup of water from each of his friends pours the water he has received into his jug. What is the smallest possible number of guests that do not have the same amount of water as they started with?
|
Answer: 2 .
If there are guests $1,2, \ldots, n$ and guest $i$ is friends with guest $i-1$ and $i+1$ modulo $n$ (e.g. guest 1 and guest $n$ are friends). Then if guest $i$ has $i$ amount of water in their jug at the start of the game, then only guest 1 and $n$ end up with a different amount of water than they started with.
To show that there always will be at least two guests with a different amount of water at the end of the game than they started with, let $x_{i}$ and $d_{i}$ be the amount of water and number of friends, respectively, that guest $i$ has. Define $z_{v}=x_{v} / d_{v}$ and assume without loss of generality that the friendship graph of the party is connected. Since every friend has at least one friend, there must exist two guests $a$ and $b$ at the party with the same number of friends by the pigeonhole principle. They must satisfy $z_{a} \neq z_{b}$. Thus, the sets
$$
S=\left\{c \mid z_{c}=\min _{d} z_{d}\right\} \text { and } T=\left\{c \mid z_{c}=\max _{d} z_{d}\right\}
$$
are non-empty and disjoint. Since we assumed the friendship graph to be connected, there exists a guest $c \in S$ that has a friend $d$ not in $S$. Let $F$ be the friends of $c$ at the party. Then the amount of water in $c$ 's cup at the end of the game is
$$
\sum_{f \in F} z_{f} \geqslant z_{d}+\left(d_{c}-1\right) z_{c}>d_{c} \cdot z_{c}=x_{c}
$$
Thus, $c$ ends up with a different amount of water at the end of the game. Similarly, there is a guest in $T$ that ends up with a different amount of water at the end of the game than what they started with.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On a $16 \times 16$ torus as shown all 512 edges are colored red or blue. A coloring is good if every vertex is an endpoint of an even number of red edges. A move consists of switching the color of each of the 4 edges of an arbitrary cell. What is the largest number of good colorings such that none of them can be converted to another by a sequence of moves?
#
|
Answer: 4. Representatives of the equivalence classes are: all blue, all blue with one longitudinal red ring, all blue with one transversal red ring, all blue with one longitudinal and one transversal red ring.
First, show that these four classes are non equivalent. Consider any ring transversal or longitudinal and count the number of red edges going out from vertices of this ring in the same halftorus. This number can not be changed mod 2.
Now we show that each configuration can be transformed to one of these four classes. We suggest two independent reasoning.
Scanning of the square.
Cut the torus up in a square $16 \times 16$. In order to restore the initial torus we will identify the opposite sides of the square, but we will do it in the end of solution. Now we will work with the square. It is clear that during all recolorings each vertex of torus has even red degree. The same is true for the degrees of the inner vertices of the $16 \times 16$ square when we deal with it instead of the torus.
Scan all cells of this square one by one from left to right and from bottom to top. For convenience we may think that in each moment the scanned area is colored grey. First we take bottom left corner cell ( $a 1$ in chess notations) and color it grey. Then we consider the next cell ( $b 1$ in chess notations) color it grey and if the edge between the cells $a 1$ and $b 1$ is red, change the colors of the cell $b 1$ edges.
We obtain a grey area with no red edges in its interior. After that when we scan each new cell we append this cell to the grey figure and if it is necessary change the colors of edges of the new cell to make the color of all new edges in the grey area blue.
The latter is always possible because the new cell have either one common edge with the grey figure (as in the case " $a 1-b 1$ " above) or two common edges. For example let grey figure consist of the first row of the square and $a 2$ cell. When we append the cell $b 2$ to the grey figure two edges of its lower left corner vertex already belong to the grey figure, they are blue. Therefore the other two edges $a 2-b 2$ and $b 1-b 2$ have the same color and we can make them both blue (if they are not) by recoloring the edges of cell $b 2$.
So by doing that with all cells of the square we obtain $16 \times 16$ square with blue edges inside it. Now its time to recall that the sides of the square should be identified, and the red degree of each vertex of torus is even. It follows that the whole (identified) vertical sides of the square are either red or blue, and the same for horizontal sides.
Deformations of red loops (sketch).
To see that any configuration can be made into one of the above four configurations it is most clear to cut the torus up in a square with opposite edges identified.
Since the red degree of each vertex is even we can always find a loop consisting of red edges only. Now, suppose that one can make a (simple) red loop that does not cross the boundary of the square. We can change the color of this loop by changing one by one the colors of unit squares inside it. In the remaining configuration every vertex is still an endpoint of an even number of red edges and we can repeat the operation. So by doing that to every red loop we are left with a configuration where one can not make red loops that do not intersect the boundary. Second, any red loop left that passes through more than one boundary vertex can be deformed into a loop containing only one boundary vertex. Finally, any two loops crossing the same side of the square can be removed by changing colors of all unit squares between these loops. Thus, we are left with only the four possibilities mentioned.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a forest each of $n$ animals $(n \geqslant 3)$ lives in its own cave, and there is exactly one separate path between any two of these caves. Before the election for King of the Forest some of the animals make an election campaign. Each campaign-making animal visits each of the other caves exactly once,
uses only the paths for moving from cave to cave, never turns from one path to another between the caves and returns to its own cave in the end of its campaign. It is also known that no path between two caves is used by more than one campaign-making animal.
a) Prove that for any prime $n$, the maximum possible number of campaign-making animals is $\frac{n-1}{2}$;
b) Find the maximum number of campaign-making animals for $n=9$.
|
Answer: b) 4 .
a) As each campaign-making animal uses exactly $n$ paths and the total number of paths is $\frac{n(n-1)}{2}$, the number of campaign-making animals cannot exceed $\frac{n-1}{2}$. Labeling the caves by integers $0,1,2, \ldots, n-1$, we can construct $\frac{n-1}{2}$ non-intersecting campaign routes as follows:
$$
\begin{aligned}
& 0 \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow \ldots \rightarrow n \rightarrow 0 \\
& 0 \rightarrow 2 \rightarrow 4 \rightarrow 6 \rightarrow \ldots \rightarrow n-1 \rightarrow 0 \\
& 0 \rightarrow 3 \rightarrow 6 \rightarrow 9 \rightarrow \ldots \rightarrow n-2 \rightarrow 0 \\
& \ldots \ldots \ldots+\cdots \\
& 0 \rightarrow \frac{n-1}{2} \rightarrow n-1 \rightarrow \ldots \rightarrow \frac{n+1}{2} \rightarrow 0
\end{aligned}
$$
(As each of these cyclic routes passes through any cave, the $\frac{n-1}{2}$ campaign-making animals can be chosen arbitrarily).
b) As noted above, the number of campaign-making animals cannot exceed $\frac{9-1}{2}=4$. The 4 non-intersecting campaign routes can be constructed as follows:
$$
\begin{aligned}
& 0 \rightarrow 1 \rightarrow 2 \rightarrow 8 \rightarrow 3 \rightarrow 7 \rightarrow 4 \rightarrow 6 \rightarrow 5 \rightarrow 0 \\
& 0 \rightarrow 2 \rightarrow 3 \rightarrow 1 \rightarrow 4 \rightarrow 8 \rightarrow 5 \rightarrow 7 \rightarrow 6 \rightarrow 0 \\
& 0 \rightarrow 3 \rightarrow 4 \rightarrow 2 \rightarrow 5 \rightarrow 1 \rightarrow 6 \rightarrow 8 \rightarrow 7 \rightarrow 0 \\
& 0 \rightarrow 4 \rightarrow 5 \rightarrow 3 \rightarrow 6 \rightarrow 2 \rightarrow 7 \rightarrow 1 \rightarrow 8 \rightarrow 0
\end{aligned}
$$
Remark. In fact it can be proved that the maximal number of nonintersecting Hamiltonian cycles in a complete graph on $n$ vertices (that is what the problem actually asks for) is equal to $\left\lfloor\frac{n-1}{2}\right\rfloor$ for any integer $n$. The proof uses a construction similar to the one shown in part b) of the above solution.
|
4
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Twelve cards lie in a row. The cards are of three kinds: with both sides white, both sides black, or with a white and a black side. Initially, nine of the twelve cards have a black side up. The cards 1-6 are turned, and subsequently four of the twelve cards have a black side up. Now cards $4-9$ are turned, and six cards have a black side up. Finally, the cards 1-3 and 10-12 are turned, after which five cards have a black side up. How many cards of each kind are there?
## Solutions
|
Answer: there are 9 cards with one black and one white side and 3 cards with both sides white.
Divide the cards into four types according to the table below.
| Type | Initially up | Initially down |
| :---: | :---: | :---: |
| $A$ | black | white |
| $B$ | white | black |
| $C$ | white | white |
| $D$ | black | black |
When the cards 1-6 were turned, the number of cards with a black side up decreased by 5 . Hence among the cards 1-6 there are five of type $A$ and one of type $C$ or $D$. The result of all three moves is that cards $7-12$ have been turned over, hence among these cards there must be four of type $A$, and the combination of the other two must be one of the following:
(a) one of type $A$ and one of type $B$;
(b) one of type $C$ and one of type $D$;
(c) both of type $C$;
(d) both of type $D$.
Hence the unknown card among the cards 1-6 cannot be of type $D$, since this would make too many cards having a black side up initially. For the same reason, the alternatives (a), (b) and (d) are impossible. Hence there were nine cards of type $A$ and three cards of type $C$.
Alternative solution. Denote by $a_{1}, a_{2}, \ldots, a_{12}$ the sides of each card that are initially visible, and by $b_{1}, b_{2}, \ldots, b_{12}$ the initially invisible sides each of these is either white or black. The conditions of the problem imply the following:
(a) there are 9 black and 3 white sides among $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}$, $a_{7}, a_{8}, a_{9}, a_{10}, a_{11}, a_{12}$
(b) there are 4 black and 8 white sides among $b_{1}, b_{2}, b_{3}, b_{4}, b_{5}, b_{6}, a_{7}$, $a_{8}, a_{9}, a_{10}, a_{11}, a_{12}$;
(c) there are 6 black and 6 white sides among $b_{1}, b_{2}, b_{3}, a_{4}, a_{5}, a_{6}, b_{7}$, $b_{8}, b_{9}, a_{10}, a_{11}, a_{12}$;
(d) there are 5 black and 7 white sides among $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}, b_{7}$, $b_{8}, b_{9}, b_{10}, b_{11}, b_{12}$.
Cases (b) and (d) together enumerate each of the sides $a_{i}$ and $b_{i}$ exactly once - hence there are 9 black and 15 white sides altogether. Therefore, all existing black sides are enumerated in (a), implying that we have 9 cards with one black and one white side, and the remaining 3 cards have both sides white.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The graph of the function $f(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$ (where $n>1$ ), intersects the line $y=b$ at the points $B_{1}, B_{2}, \ldots, B_{n}$ (from left to right), and the line $y=c(c \neq b)$ at the points $C_{1}, C_{2}, \ldots, C_{n}$ (from left to right). Let $P$ be a point on the line $y=c$, to the right to the point $C_{n}$. Find the sum $\cot \angle B_{1} C_{1} P+\cdots+\cot \angle B_{n} C_{n} P$.
|
Let the points $B_{i}$ and $C_{i}$ have the coordinates $\left(b_{i}, b\right)$ and $\left(c_{i}, c\right)$, respectively, for $i=1,2, \ldots, n$. Then we have
$$
\cot \angle B_{1} C_{1} P+\cdots+\cot \angle B_{n} C_{n} P=\frac{1}{b-c} \sum_{i=1}^{n}\left(b_{i}-c_{i}\right)
$$
The numbers $b_{i}$ and $c_{i}$ are the solutions of $f(x)-b=0$ and $f(x)-c=0$, respectively. As $n \geq 2$, it follows from the relationships between the roots and coefficients of a polynomial (Viète's relations) that $\sum_{i=1}^{n} b_{i}=$ $\sum_{i=1}^{n} c_{i}=-a_{n-1}$ regardless of the values of $b$ and $c$, and hence $\cot \angle B_{1} C_{1} P+\cdots+\cot \angle B_{n} C_{n} P=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Consider the sequence $a_{k}$ defined by $a_{1}=1, a_{2}=\frac{1}{2}$,
$$
a_{k+2}=a_{k}+\frac{1}{2} a_{k+1}+\frac{1}{4 a_{k} a_{k+1}} \quad \text { for } k \geq 1
$$
Prove that
$$
\frac{1}{a_{1} a_{3}}+\frac{1}{a_{2} a_{4}}+\frac{1}{a_{3} a_{5}}+\cdots+\frac{1}{a_{98} a_{100}}<4
$$
|
Note that
$$
\frac{1}{a_{k} a_{k+2}}a_{k}+\frac{1}{2} a_{k+1}
$$
which is evident for the given sequence. Now we have
$$
\begin{aligned}
\frac{1}{a_{1} a_{3}}+\frac{1}{a_{2} a_{4}} & +\frac{1}{a_{3} a_{5}}+\cdots+\frac{1}{a_{98} a_{100}} \\
& <\frac{2}{a_{1} a_{2}}-\frac{2}{a_{2} a_{3}}+\frac{2}{a_{2} a_{3}}-\frac{2}{a_{3} a_{4}}+\cdots \\
& <\frac{2}{a_{1} a_{2}}=4
\end{aligned}
$$
|
4
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Let $m=30030=2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13$ and let $M$ be the set of its positive divisors which have exactly two prime factors. Determine the minimal integer $n$ with the following property: for any choice of numbers from $M$, there exist three numbers $a, b, c$ among them satisfying $a \cdot b \cdot c=m$.
Answer: $n=11$.
|
Taking the 10 divisors without the prime 13 shows that $n \geq 11$. Consider the following partition of the 15 divisors into five groups of three each with the property that the product of the numbers in every group equals $m$.
$$
\begin{array}{ll}
\{2 \cdot 3,5 \cdot 13,7 \cdot 11\}, & \{2 \cdot 5,3 \cdot 7,11 \cdot 13\}, \\
\{2 \cdot 11,3 \cdot 5,7 \cdot 13\}, & \{2 \cdot 13,3 \cdot 11,5 \cdot 7\} .
\end{array}
$$
If $n=11$, there is a group from which we take all three numbers, that is, their product equals $m$.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the smallest number of circles of radius $\sqrt{2}$ that are needed to cover a rectangle
(a) of size $6 \times 3$ ?
(b) of size $5 \times 3$ ?
Answer: (a) Six circles, (b) five circles.
|
(a) Consider the four corners and the two midpoints of the sides of length 6 . The distance between any two of these six points is 3 or more, so one circle cannot cover two of these points, and at least six circles are needed.
On the other hand one circle will cover a $2 \times 2$ square, and it is easy to see that six such squares can cover the rectangle.
(b) Consider the four corners and the centre of the rectangle. The minimum distance between any two of these points is the distance between the centre and one of the corners, which is $\sqrt{34} / 2$. This is greater than the diameter of the circle $(\sqrt{34 / 4}>\sqrt{32 / 4})$, so one circle cannot cover two of these points, and at least five circles are needed.
Partition the rectangle into three rectangles of size $5 / 3 \times 2$ and two rectangles of size $5 / 2 \times 1$ as shown on the right. It is easy to check that each has a diagonal of length less than $2 \sqrt{2}$, so five circles can cover the five small rectangles and hence the $5 \times 3$ rectangle.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A set of 8 problems was prepared for an examination. Each student was given 3 of them. No two students received more than one common problem. What is the largest possible number of students?
|
Answer: 8 .
Denote the problems by $A, B, C, D, E, F, G, H$, then 8 possible problem sets are $A B C, A D E, A F G, B D G, B F H, C D H, C E F, E G H$. Hence, there could be 8 students.
Suppose that some problem (e.g., $A$ ) was given to 4 students. Then each of these 4 students should receive 2 different "supplementary" problems, and there should be at least 9 problems - a contradiction. Therefore each problem was given to at most 3 students, and there were at most $8 \cdot 3=24$ "awardings" of problems. As each student was "awarded" 3 problems, there were at most 8 students.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $f$ be a real-valued function defined on the positive integers satisfying the following condition: For all $n>1$ there exists a prime divisor $p$ of $n$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)
$$
Given that $f(2001)=1$, what is the value of $f(2002)$ ?
|
Answer: 2.
For any prime $p$ we have $f(p)=f(1)-f(p)$ and thus $f(p)=\frac{f(1)}{2}$. If $n$ is a product of two primes $p$ and $q$, then $f(n)=f(p)-f(q)$ or $f(n)=f(q)-f(p)$, so $f(n)=0$. By the same reasoning we find that if $n$ is a product of three primes, then there is a prime $p$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=-f(p)=-\frac{f(1)}{2} .
$$
By simple induction we can show that if $n$ is the product of $k$ primes, then $f(n)=(2-k) \cdot \frac{f(1)}{2}$. In particular, $f(2001)=f(3 \cdot 23 \cdot 29)=1$ so $f(1)=-2$. Therefore, $f(2002)=f(2 \cdot 7 \cdot 11 \cdot 13)=-f(1)=2$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Two positive integers are written on the blackboard. Initially, one of them is 2000 and the other is smaller than 2000. If the arithmetic mean $m$ of the two numbers on the blackboard is an integer, the following operation is allowed: one of the two numbers is erased and replaced by $m$. Prove that this operation cannot be performed more than ten times. Give an example where the operation can be performed ten times.
|
Each time the operation is performed, the difference between the two numbers on the blackboard will become one half of its previous value (regardless of which number was erased). The mean value of two integers is an integer if and only if their difference is an even number. Suppose the initial numbers were $a=2000$ and $b$. It follows that the operation can be performed $n$ times if and only if $a-b$ is of the form $2^{n} u$. This shows that $n \leqslant 10$ since $2^{11}>2000$. Choosing $b=976$ so that $a-b=1024=2^{10}$, the operation can be performed 10 times.
|
10
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Let's call a positive integer "interesting" if it is a product of two (distinct or equal) prime numbers. What is the greatest number of consecutive positive integers all of which are "interesting"?
|
The three consecutive numbers $33=3 \cdot 11,34=2 \cdot 17$ and $35=5 \cdot 7$ are all "interesting". On the other hand, among any four consecutive numbers there is one of the form $4 k$ which is "interesting" only if $k=1$. But then we have either 3 or 5 among the four numbers, neither of which is "interesting".
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Solve the system of equations:
$$
\left\{\begin{array}{l}
x^{5}=y+y^{5} \\
y^{5}=z+z^{5} \\
z^{5}=t+t^{5} \\
t^{5}=x+x^{5} .
\end{array}\right.
$$
|
Adding all four equations we get $x+y+z+t=0$. On the other hand, the numbers $x, y, z, t$ are simultaneously positive, negative or equal to zero. Thus, $x=y=z=t=0$ is the only solution.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
An equilateral triangle $A B C$ is divided into 100 congruent equilateral triangles. What is the greatest number of vertices of small triangles that can be chosen so that no two of them lie on a line that is parallel to any of the sides of the triangle $A B C$ ?
|
An example for 7 vertices is shown in Figure 2. Now assume we have chosen 8 vertices satisfying the conditions of the problem. Let the height of each small triangle be equal to 1 and denote by $a_{i}, b_{i}, c_{i}$ the distance of the $i$ th point from the three sides of the big triangle. For any $i=1,2, \ldots, 8$ we then have $a_{i}, b_{i}, c_{i} \geq 0$ and $a_{i}+b_{i}+c_{i}=10$. Thus, $\left(a_{1}+a_{2}+\cdots+a_{8}\right)+\left(b_{1}+b_{2}+\cdots+b_{8}\right)+\left(c_{1}+c_{2}+\cdots+c_{8}\right)=80$. On the other hand, each of the sums in the brackets is not less than $0+1+\cdots+7=28$, but $3 \cdot 28=84>80$, a contradiction.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A square is divided into 16 equal squares, obtaining the set of 25 different vertices. What is the least number of vertices one must remove from this set, so that no 4 points of the remaining set are the vertices of any square with sides parallel to the sides of the initial square?
Remark. The proposed solution to this problem claimed that it is enough to remove 7 vertices but the example to demonstrate this appeared to be incorrect. Below we show that removing 6 vertices is not sufficient but removing 8 vertices is. It seems that removing 7 vertices is not sufficient but we currently know no potential way to prove this, apart from a tedious case study.
|
The example in Figure 3a demonstrates that it suffices to remove 8 vertices to "destroy" all squares. Assume now that we have managed to do that by removing only 6 vertices. Denote the horizontal and vertical lines by $A, B, \ldots, E$ and $1,2, \ldots, 5$ respectively. Obviously, one of the removed vertices must be a vertex of the big square - let this be vertex $A 1$. Then, in order to "destroy" all the squares shown in Figure $3 \mathrm{~b}-\mathrm{e}$ we have to remove vertices $B 2, C 3, D 4, D 2$ and $B 4$. Thus we have removed 6 vertices without having any choice but a square shown in Figure $3 \mathrm{f}$ is still left intact.
12345
$\mathrm{a}$
$\mathrm{b}$
c
d
e
f
Figure 3
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $\mathbb{N}$ denote the set of positive integers. Let $\varphi: \mathbb{N} \rightarrow \mathbb{N}$ be a bijective function and assume that there exists a finite limit
$$
\lim _{n \rightarrow \infty} \frac{\varphi(n)}{n}=L
$$
What are the possible values of $L$ ?
|
In this solution we allow $L$ to be $\infty$ as well. We show that $L=1$ is the only possible value. Assume that $L>1$. Then there exists a number $N$ such that for any $n \geq N$ we have $\frac{\varphi(n)}{n}>1$ and thus $\varphi(n) \geq n+1 \geq N+1$. But then $\varphi$ cannot be bijective, since the numbers $1,2, \ldots, N-1$ cannot be bijectively mapped onto $1,2, \ldots, N$.
Now assume that $L1,
$$
i.e., $\lim _{n \rightarrow \infty} \frac{\varphi^{-1}(n)}{n}>1$, which is a contradiction since $\varphi^{-1}$ is also bijective. (When $L=0$ we interpret $\frac{1}{L}$ as $\infty$ ).
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
We say that an integer $m$ covers the number 1998 if $1,9,9,8$ appear in this order as digits of $m$. (For instance, 1998 is covered by 215993698 but not by 213326798 .) Let $k(n)$ be the number of positive integers that cover 1998 and have exactly $n$ digits $(n \geqslant 5)$, all different from 0 . What is the remainder of $k(n)$ in division by 8 ?
## Solutions
|
Answer: 1.
Let $1 \leqslant g<h<i<j \leqslant n$ be fixed integers. Consider all $n$-digit numbers $a=\overline{a_{1} a_{2} \ldots a_{n}}$ with all digits non-zero, such that $a_{g}=1, a_{h}=9, a_{i}=9$, $a_{j}=8$ and this quadruple 1998 is the leftmost one in $a$; that is,
$$
\begin{cases}a_{l} \neq 1 & \text { if } l<g ; \\ a_{l} \neq 9 & \text { if } g<l<h ; \\ a_{l} \neq 9 & \text { if } h<l<i \\ a_{l} \neq 8 & \text { if } i<l<j\end{cases}
$$
There are $k_{g h i j}(n)=8^{g-1} \cdot 8^{h-g-1} \cdot 8^{i-h-1} \cdot 8^{j-i-1} \cdot 9^{n-j}$ such numbers $a$. Obviously, $k_{g h i j}(n) \equiv 1(\bmod 8)$ for $g=1, h=2, i=3, j=4$, and $k_{g h i j}(n) \equiv 0(\bmod 8)$ in all other cases. Since $k(n)$ is obtained by summing up the values of $k_{g h i j}(n)$ over all possible choicecs of $g, h, i, j$, the remainder we are looking for is 1 .
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Prove that there exists a number $\alpha$ such that for any triangle $A B C$ the inequality
$$
\max \left(h_{A}, h_{B}, h_{C}\right) \leq \alpha \cdot \min \left(m_{A}, m_{B}, m_{C}\right)
$$
holds, where $h_{A}, h_{B}, h_{C}$ denote the lengths of the altitudes and $m_{A}, m_{B}, m_{C}$ denote the lengths of the medians. Find the smallest possible value of $\alpha$.
|
Let $h=\max \left(h_{A}, h_{B}, h_{C}\right)$ and $m=\min \left(m_{A}, m_{B}, m_{C}\right)$. If the longest height and the shortest median are drawn from the same vertex, then obviously $h \leq m$. Now let the longest height and shortest median be $A D$ and $B E$, respectively, with $|A D|=h$ and $|B E|=m$. Let $F$ be the point on the line $B C$ such that $E F$ is parallel to $A D$. Then $m=|E B| \geq|E F|=\frac{h}{2}$, whence $h \leq 2 m$. For an example with $h=2 m$, consider a triangle where $D$ lies on the ray $C B$ with $|C B|=|B D|$. Hence the smallest such value is $\alpha=2$.
|
2
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
For a sequence $a_{1}, a_{2}, a_{3}, \ldots$ of real numbers it is known that
$$
a_{n}=a_{n-1}+a_{n+2} \quad \text { for } n=2,3,4, \ldots
$$
What is the largest number of its consecutive elements that can all be positive?
Answer: 5.
|
The initial segment of the sequence could be $1 ; 2 ; 3 ; 1 ; 1 ;-2 ; 0$. Clearly it is enough to consider only initial segments. For each sequence the first 6 elements are $a_{1} ; a_{2}$; $a_{3} ; a_{2}-a_{1} ; a_{3}-a_{2} ; a_{2}-a_{1}-a_{3}$. As we see, $a_{1}+a_{5}+a_{6}=a_{1}+\left(a_{3}-a_{2}\right)+\left(a_{2}-a_{1}-a_{3}\right)=$ 0 . So all the elements $a_{1}, a_{5}, a_{6}$ can not be positive simultaneously.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a, b, c, d, e, f$ be non-negative real numbers satisfying $a+b+c+d+e+f=6$. Find the maximal possible value of
$$
a b c+b c d+c d e+d e f+e f a+f a b
$$
and determine all 6-tuples $(a, b, c, d, e, f)$ for which this maximal value is achieved.
Answer: 8 .
|
If we set $a=b=c=2, d=e=f=0$, then the given expression is equal to 8 . We will show that this is the maximal value. Applying the inequality between arithmetic and geometric mean we obtain
$$
\begin{aligned}
8 & =\left(\frac{(a+d)+(b+e)+(c+f)}{3}\right)^{3} \geq(a+d)(b+e)(c+f) \\
& =(a b c+b c d+c d e+d e f+e f a+f a b)+(a c e+b d f),
\end{aligned}
$$
so we see that $a b c+b c d+c d e+d e f+e f a+f a b \leq 8$ and the maximal value 8 is achieved when $a+d=b+e=c+f$ (and then the common value is 2 because $a+b+c+d+$ $e+f=6)$ and $a c e=b d f=0$, which can be written as $(a, b, c, d, e, f)=(a, b, c, 2-a, 2-$ $b, 2-c)$ with $a c(2-b)=b(2-a)(2-c)=0$. From this it follows that $(a, b, c)$ must have one of the forms $(0,0, t),(0, t, 2),(t, 2,2),(2,2, t),(2, t, 0)$ or $(t, 0,0)$. Therefore the maximum is achieved for the 6 -tuples $(a, b, c, d, e, f)=(0,0, t, 2,2,2-t)$, where $0 \leq t \leq 2$, and its cyclic permutations.
|
8
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine all positive integers $n$ such that $3^{n}+1$ is divisible by $n^{2}$.
Answer: Only $n=1$ satisfies the given condition.
|
First observe that if $n^{2} \mid 3^{n}+1$, then $n$ must be odd, because if $n$ is even, then $3^{n}$ is a square of an odd integer, hence $3^{n}+1 \equiv 1+1=2(\bmod 4)$, so $3^{n}+1$ cannot be divisible by $n^{2}$ which is a multiple of 4 .
Assume that for some $n>1$ we have $n^{2} \mid 3^{n}+1$. Let $p$ be the smallest prime divisor of $n$. We have shown that $p>2$. It is also clear that $p \neq 3$, since $3^{n}+1$ is never divisible by 3. Therefore $p \geq 5$. We have $p \mid 3^{n}+1$, so also $p \mid 3^{2 n}-1$. Let $k$ be the smallest positive integer such that $p \mid 3^{k}-1$. Then we have $k \mid 2 n$, but also $k \mid p-1$ by Fermat's theorem. The numbers $3^{1}-1,3^{2}-1$ do not have prime divisors other than 2 , so $p \geq 5$ implies $k \geq 3$. This means that $\operatorname{gcd}(2 n, p-1) \geq k \geq 3$, and therefore $\operatorname{gcd}(n, p-1)>1$, which contradicts the fact that $p$ is the smallest prime divisor of $n$. This completes the proof.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. In a club with 30 members, every member initially had a hat. One day each member sent his hat to a different member (a member could have received more than one hat). Prove that there exists a group of 10 members such that no one in the group has received a hat from another one in the group.
|
Let $S$ be the given group of 30 people. Consider all subsets $A \subset S$ such that no member of $A$ received a hat from a member of $A$. Among such subsets, let $T$ be a subset of maximal cardinality. The assertion of the problem is that $|T| \geq 10$.
Let $U \subset S$ consist of all people that have received a hat from a person belonging to $T$. Now consider any member $x \in S \backslash(T \cup U)$. Since $x \notin U$, no member of $T$ sent his hat to $x$. It follows that no member of $T$ sent a hat to a person from $T \cup\{x\}$. But the maximality of $T$ implies that some person from $T \cup\{x\}$ sent his hat to a person from the same subset. This means that $x$ sent his hat to a person from $T$. Consequently, all members of the subset $S \backslash(T \cup U)$ sent their hats to people in $T$. In particular, $S \backslash(T \cup U)$ has the property described in the beginning. The maximality of $T$ gives $|S \backslash(T \cup U)| \leq|T|$. Finally, we obviously have $|U| \leq|T|$, so
$$
|T| \geq|S \backslash(T \cup U)|=|S|-|T|-|U| \geq|S|-2|T|,
$$
or $|T| \geq \frac{1}{3}|S|=10$, as desired.
|
10
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
. For a positive integer $k$, let $d(k)$ denote the number of divisors of $k$ (e.g. $d(12)=6$ ) and let $s(k)$ denote the digit sum of $k$ (e.g. $s(12)=3$ ). A positive integer $n$ is said to be amusing if there exists a positive integer $k$ such that $d(k)=s(k)=n$. What is the smallest amusing odd integer greater than 1 ?
|
The answer is 9 . For every $k$ we have $s(k) \equiv k(\bmod 9)$. Calculating remainders modulo 9 we have the following table
| $m$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $m^{2}$ | 0 | 1 | 4 | 0 | 7 | 7 | 0 | 4 | 1 |
| $m^{6}$ | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
If $d(k)=3$, then $k=p^{2}$ with $p$ a prime, but $p^{2} \equiv 3(\bmod 9)$ is impossible. This shows that 3 is not an amusing number. If $d(k)=5$, then $k=p^{4}$ with $p$ a prime, but $p^{4} \equiv 5(\bmod 9)$ is impossible. This shows that 5 is not an amusing number. If $d(k)=7$, then $k=p^{6}$ with $p$ a prime, but $p^{6} \equiv 7(\bmod 9)$ is impossible. This shows that 7 is not an amusing number. To see that 9 is amusing, note that $d(36)=s(36)=9$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. For which $k$ do there exist $k$ pairwise distinct primes $p_{1}, p_{2}, \ldots, p_{k}$ such that
$$
p_{1}^{2}+p_{2}^{2}+\cdots+p_{k}^{2}=2010 ?
$$
|
We show that it is possible only if $k=7$.
The 15 smallest prime squares are:
$$
4,9,25,49,121,169,289,361,529,841,961,1369,1681,1849,2209
$$
Since $2209>2010$ we see that $k \leq 14$.
Now we note that $p^{2} \equiv 1 \bmod 8$ if $p$ is an odd prime. We also have that $2010 \equiv 2 \bmod 8$. If all the primes are odd, then writing the original equation modulo 8 we get
$$
k \cdot 1 \equiv 2 \bmod 8
$$
so either $k=2$ or $k=10$.
$k=2:$ As $2010 \equiv 0 \bmod 3$ and $x^{2} \equiv 0$ or $x^{2} \equiv 1 \bmod 3$ we conclude that $p_{1} \equiv p_{2} \equiv 0$ mod 3. But that is impossible.
$k=10$ : The sum of first 10 odd prime squares is already greater than $2010(961+841+$ $529+\cdots>2010)$ so this is impossible.
Now we consider the case when one of the primes is 2 . Then the original equation modulo 8 takes the form
$$
4+(k-1) \cdot 1 \equiv 2 \quad \bmod 8
$$
so $k \equiv 7 \bmod 8$ and therefore $k=7$.
For $k=7$ there are 4 possible solutions:
$$
\begin{aligned}
4+9+49+169+289+529+961 & =2010 \\
4+9+25+121+361+529+961 & =2010 \\
4+9+25+49+121+841+961 & =2010 \\
4+9+49+121+169+289+1369 & =2010
\end{aligned}
$$
Finding them should not be too hard. We are already asuming that 4 is included. Considerations modulo 3 show that 9 must also be included. The square 1681 together with the 6 smallest prime squares gives a sum already greater than 2010 , so only prime squares up to $37^{2}=1369$ can be considered. If 25 is included, then for the remaining 4 prime squares considerations modulo 10 one can see that 3 out of 4 prime squares from $\{121,361,841,961\}$ have to be used and two of four cases are successful. If 25 is not included, then for the remaining 5 places again from considerations modulo 10 one can see, that 4 of them will be from the set $\{49,169,289,529,1369\}$ and two out of five cases are successful.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
If the price of a product increased from $R \$ 5.00$ to $R \$ 5.55$, what was the percentage increase?
|
The increase in reais was $5.55-5=0.55$; so the percentage increase was
$$
\frac{0.55}{5}=\frac{0.55 \times 20}{5 \times 20}=\frac{11}{100}=11 \%
$$
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A factory produced an original calculator that performs two operations:
- the usual addition +
- the operation $\circledast$
We know that for any natural number $a$ we have:
$$
\text { (i) } a \circledast a=a \quad \text { and (ii) } a \circledast 0=2 a
$$
and, for any four naturals $a, b, c$ and $d$
$$
\text { (iii) }(a \circledast b)+(c \circledast d)=(a+c) \circledast(b+d) \text {. }
$$
What are the results of the operations $(2+3) \circledast(0+3)$ and $1024 \circledast 48$?
|
To calculate $(2+3) \circledast(0+3)$, we will use property (iii), and we have:
$$
(2+3) \circledast(0+3)=(2 \circledast 0)+(3 \circledast 3)
$$
Now, by (i) we have $2 \circledast 0=2 \times 2=4$, and by (ii) we have $3 \circledast 3=3$. Therefore,
$$
(2+3) \circledast(0+3)=4+3=7
$$
Now, to calculate $1024 \circledast 48$ we will use the same strategy as above. For this, note that $1024=976+48$ and $48=0+48$.
$$
\begin{aligned}
1024 \circledast 48 & =(976+48) \circledast(0+48) \\
& =(976 \circledast 0)+(48 \circledast 48) \\
& =2 \times 976+48 \\
& =1952+48=2000
\end{aligned}
$$
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the figure below, $D$ is the midpoint of side $A B, C E: D E=5: 3 \text{ and } B F: E F=1: 3$. If the area of triangle $A B C$ is $192 \text{ cm}^2$, determine the area of triangle $B D F$.
|
Solution
Denote the lengths of $B D, B F$ and $D E$ by $x, z$ and $3 y$, respectively. Given the proportions, it follows that $E F=3 z, C E=5 y$ and $A D=x$. Therefore,
$$
\begin{aligned}
& \frac{A_{B D F}}{A_{B D E}}=\frac{z}{3 z+z} \\
& \frac{A_{B D E}}{A_{C D B}}=\frac{3 y}{3 y+5 y} \\
& \frac{A_{C D B}}{A_{A B C}}=\frac{x}{x+x}
\end{aligned}
$$
Multiplying these equations, we have
$$
\frac{A_{B D F}}{A_{A B C}}=\frac{1}{4} \cdot \frac{3}{8} \cdot \frac{1}{2}
$$
Thus,
$$
A_{B D F}=\frac{192 \cdot 3}{64}=9
$$
Note: We are denoting the area of triangle $X Y Z$ by $A_{X Y Z}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.