problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
In the right isosceles triangle $A O B$, the points $P, Q$, and $S$ are chosen on the sides $O B, O A$, and $A B$, respectively, such that $P Q R S$ is a square. If the lengths of $O P$ and $O Q$ are $a$ and $b$, respectively, and the area of the square $P Q R S$ is $2 / 5$ of the area of the triangle $A O B$, determine the value of $a / b$.
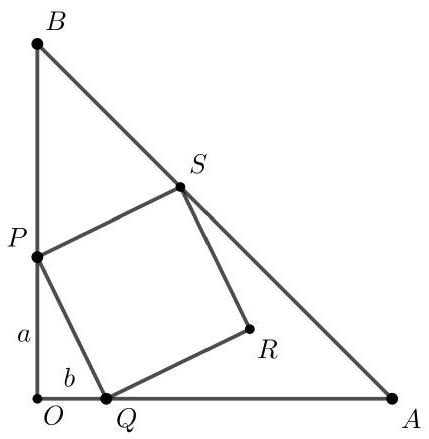
|
Solution
Let $C$ be the foot of the perpendicular from point $S$ to segment $O B$. The triangles $S P C$ and $P Q O$ have the same angles, since
$$
\begin{aligned}
\angle C P S & =\angle 180^{\circ}-\angle S P Q-\angle O P Q \\
& =90^{\circ}-\angle O P Q \\
& =\angle P Q O
\end{aligned}
$$
Since $P S=P Q$, these triangles are congruent by the A.L.A. case. Thus $P C=b, C S=a$. Since $B S C$ is an isosceles right triangle, we get $O B=2 a+b$. Consequently, the area of triangle $A O B$ is $(2 a+b)^{2} / 2$. By the Pythagorean Theorem, the area of square $P Q R S$ is $P Q^{2}=a^{2}+b^{2}$. Therefore,
$$
\begin{aligned}
\frac{A_{P Q R S}}{A_{O A B}} & =\frac{2}{5} \\
5\left(a^{2}+b^{2}\right) & =(2 a+b)^{2} \\
a^{2}+4 b^{2} & =4 a b \\
(a-2 b)^{2} & =0
\end{aligned}
$$
Thus, $a=2 b$ and the desired ratio is $a / b=2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
If $n$ is a positive integer, what is the smallest value that the sum of the digits in the decimal representation of $3 n^{2}+n+1$ can take?
#
|
Solution
If $n=8$, we have that $3 n^{2}+n+1=201$ and the sum of its digits is 3. We will now verify that the sum of the digits of $3 n^{2}+n+1$ cannot be 1 or 2 and conclude that the smallest possible value is 3. Since $n(n+1)$ is the product of two consecutive numbers, it is even, and thus $3 n^{2}+n+1=2 n^{2}+n(n+1)+1$ is an odd number. For the sum of the digits to be 1, we must have $3 n^{2}+n+1=10^{k}$. This is impossible, as $3 n^{2}+n+1>1$ and $10^{k}$ is even for $k>1$. For the sum of the digits to be 2, we must have $3 n^{2}+n+1=10^{i}+10^{j}$, with $i>j$ or $3 n^{2}+n+1=2 \cdot 10^{k}$. The second option is invalid, as $2 \cdot 10^{k}$ is even. In the first option, since $10^{i}+10^{j}$ needs to be odd, we must have $j=0$, that is,
\[
\begin{aligned}
3 n^{2}+n+1 & =10^{i}+1 \\
n(3 n+1) & =10^{i} \\
n(3 n+1) & =2^{i} \cdot 5^{i}
\end{aligned}
\]
If a prime number $p$ divides $n$, then it divides $3 n$ and, consequently, cannot divide its successor $3 n+1$. Thus, $n$ and $3 n+1$ do not have common prime factors. Since $n4^{i}>3 \cdot 2^{i}+1=3 n+1
\]
When $i=1$, there is no solution, as $5 \neq 3 \cdot 2+1$. This concludes our analysis and shows that the minimum sum of the digits is 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the following drawing, the chords $D E$ and $B C$ are perpendicular, with $B C$ being a diameter of the circle with center at $A$. Additionally, $\angle C G F=40^{\circ}$ and $G H=2 \text{~cm}$.
a) Determine the value of the angle $\angle C H F$.
b) Find the length of $H J$.
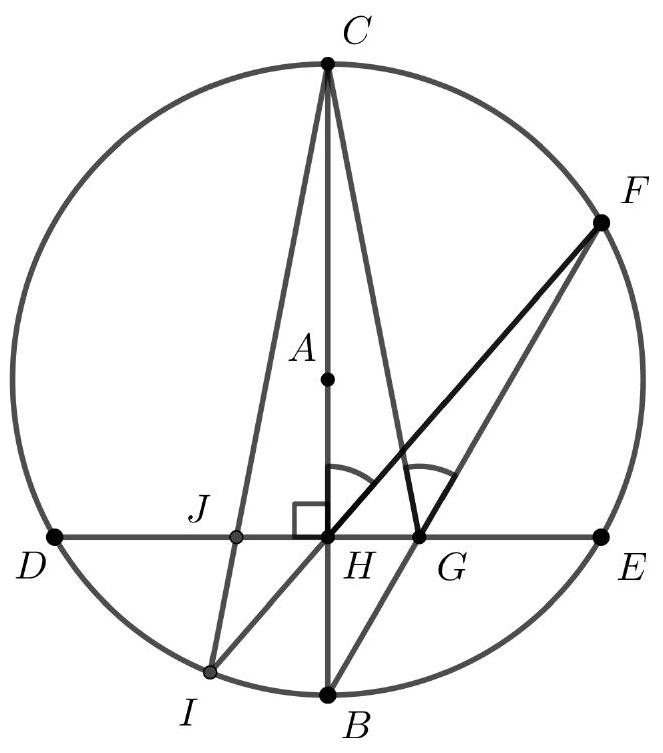
|
Solution
a) Since $BC$ is a diameter, it follows that $\angle BFC=90^{\circ}$. Thus, as we also have $\angle CHG=90^{\circ}$, the circle $\Gamma$ with diameter $CG$ passes through $F$ and $H$. In this circle, the angles $\angle CGF$ and $\angle CHF$ are inscribed in the same arc $CF$, so $\angle CHF = \angle CGF = 40^{\circ}$.
b) Observing the circle $\Gamma$ again, we can conclude that $\angle HCG = \angle HFG$, as both are inscribed in the arc $GH$. Considering now the circle with diameter $BC$, we have $\angle ICB = \angle IFB$, because both are inscribed in the arc $IB$. Thus, $\angle ICH = \angle BFH = \angle HFG = \angle HCG$. Therefore, since the right triangles $CHG$ and $CHJ$ have the same angles and a common leg, they are congruent, resulting in $HJ = GH = 2 \text{ cm}$.
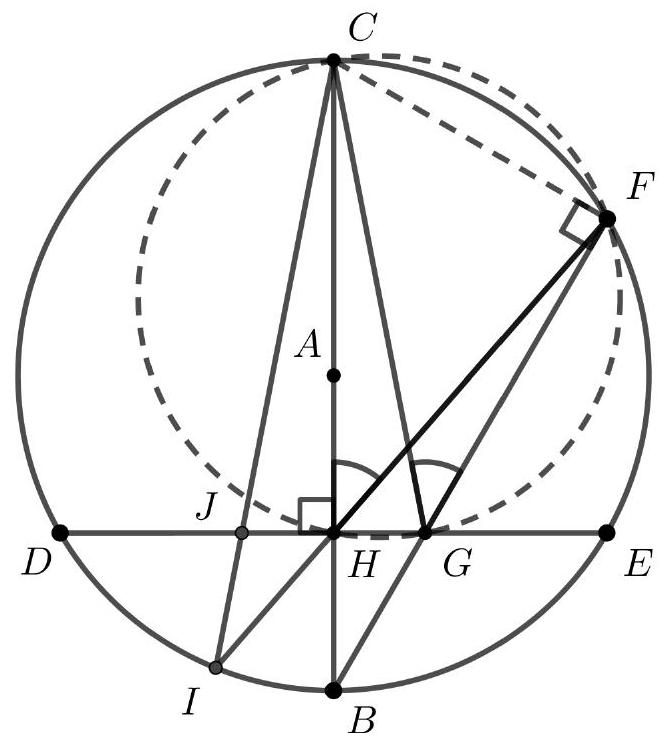
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Two precocious students from Level 3 participated in a university chess tournament. Each participant plays against all the others exactly once. A win is worth 1 point, a draw is worth 0.5 points, and a loss is worth 0 points. The sum of the scores of the two Level 3 students is 6.5. All university students scored the same. How many university students participated in the competition?
|
Solution
Let $x$ be the number of college students and $p$ the common score of all of them. Since exactly 1 point is contested in each game, it follows that the total score of the tournament, which is $6.5 + p x$, coincides with the number of games, which is $\frac{(x+2)(x+1)}{2}$. In addition, the score of each participant is an integer multiple of 0.5, so we can write $p = k / 2$, for some positive integer $k$. Therefore:
$$
\begin{aligned}
\frac{(x+2)(x+1)}{2} & = 6.5 + p x \\
(x+2)(x+1) & = 13 + k x \\
x^2 + 3x + 2 & = 13 + k x \\
x(x + 3 - k) & = 11
\end{aligned}
$$
Since $x$ and $x + 3 - k$ are integers, we can conclude that $x$ is a positive divisor of 11, that is, $x = 1$ or $x = 11$. We cannot have $x = 1$, because in that case the tournament would have only 3 participants, and it would not be possible for two students to score 6.5 points. To show that $x = 11$ is a solution, consider the tournament formed by the college students $U_1, U_2, \ldots, U_{11}$ and the Level 3 students $E_1$ and $E_2$ with the following results:
I) All games between two college students ended in a draw.
II) $E_1$ lost to $U_1, U_2, \ldots, U_{11}$ and $E_2$.
III) $E_2$ drew with $U_1, U_2, \ldots, U_{11}$.
The tournament with these results satisfies the statement.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
a) Verify that for any positive integer $a, \operatorname{with} a>1$, the equation
$$
\frac{1}{x}+\frac{1}{y}=\frac{1}{a}
$$
has at least three solutions of the form $(x, y)$, with $x$ and $y$ positive integers. For example, for $a=3$, the pairs $(6,6),(4,12)$ and $(12,4)$ are solutions.
b) Find the number of pairs of positive integers $(x, y)$ that are solutions to this equation when $a=2019$.
Hint: If the prime factorization of the positive integer $n$ is $p_{1}^{\alpha_{1}} \cdot p_{2}^{\alpha_{2}} \cdot \ldots \cdot p_{k}^{\alpha_{k}}$, then it has $\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right) \ldots\left(\alpha_{k}+1\right)$ positive divisors.
|
Solution
a) We can find an equivalent equation:
$$
\begin{aligned}
\frac{1}{x}+\frac{1}{y} & =\frac{1}{a} \Leftrightarrow \\
(x-a)(y-a) & =a^{2}
\end{aligned}
$$
Since $1 / x$ and $1 / y$ are less than $1 / a$, it follows that $x-a$ and $y-a$ are positive. To find solutions to the last equation, consider the following systems:
$$
\left\{\begin{array} { l }
{ x - a = 1 } \\
{ y - a = a ^ { 2 } }
\end{array} \quad \left\{\begin{array} { l }
{ x - a = a } \\
{ y - a = a }
\end{array} \quad \left\{\begin{array}{l}
x-a=a^{2} \\
y-a=1
\end{array}\right.\right.\right.
$$
The solutions $(x, y)$ of them are, respectively, $\left(a+1, a+a^{2}\right),(2 a, 2 a)$ and $\left(a+a^{2}, a+1\right)$. If $a>1$, these solutions are distinct and satisfy the given equation.
b) In general, if $d$ is any divisor of $a^{2}$, there always exists a solution in positive integers for the system
$$
\left\{\begin{array}{l}
x-a=d \\
y-a=\frac{a^{2}}{d}
\end{array}\right.
$$
which is given by $(x, y)=\left(a+d, a+\frac{a^{2}}{d}\right)$. There is a correspondence between the pairs $(x, y)$ that are solutions to the original equation and the positive divisors of $a^{2}$, since for each solution the integer $x-a$ corresponds to some positive divisor $d$ of $a^{2}$. Since $2019^{2}=3^{2} \cdot 673^{2}$, the number of positive divisors is $(2+1) \cdot(2+1)=9$. Therefore, the number of solutions is 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
An empty swimming pool was filled with water by two faucets $A$ and $B$, both with constant flow rates. For 4 hours, both faucets were open and filled $50 \%$ of the pool. Then, faucet B was turned off and for 2 hours faucet A filled $15 \%$ of the pool's volume. After this period, faucet A was turned off and faucet $\mathrm{B}$ was turned on. For how long did this faucet have to remain open for it to fill the pool by itself?
|
Since taps A and B pour water into the pool at a constant flow rate, the volume of water poured by each tap is proportional to the time it is open. Therefore, if tap A fills $15 \%$ of the pool's volume in 2 hours, then in 4 hours it will fill $30 \%$ of the pool's volume.
However, when taps A and B are both open for 4 hours, they manage to fill $50 \%$ of the pool's volume. From this, we can deduce that tap B fills $50 \%-30 \%=20 \%$ of the pool's volume in 4 hours.
To find out how long tap B needs to be open to fill the remaining $35 \%$ of the pool's volume, we can use the proportion:
$$
\begin{array}{ccc}
\text { hours } & \rightarrow & \text { percentage } \\
4 & \rightarrow & 20 \% \\
x & \rightarrow & 35 \%
\end{array}
$$
Therefore, tap B will take $x=\frac{35 \times 4}{20}=7$ hours to fill the remaining $35 \%$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Davi has a very original calculator; it performs only two operations: the usual addition $(+)$ and another operation, denoted by $*$, which satisfies:
(i) $a * a=a$
(ii) $a * 0=2a$
(iii) $(a * b) + (c * d) = (a * c) + (b * d)$
What are the results of the operations $(2+3) * (0+3)$ and $1024 * 48$?
|
To calculate $(2 * 3)+(0 * 3)$, we use properties (i), (ii), and (iii). Then
$$
\begin{aligned}
& (2 * 3)+(0 * 3) \quad \stackrel{(\mathrm{iii})}{=} \quad(2 * 0)+(3 * 3) \\
& \text { (i) (ii) } 2 \times 2+3=7 \text {. }
\end{aligned}
$$
To calculate $1024 * 48$, observe that $1024=976+48$. We have:
$$
\begin{aligned}
1024 * 48 & =(976+48) *(0+48) \\
& =(976 * 0)+(48 * 48) \\
& =976 \times 2+48 \\
& =1952+48=2000
\end{aligned}
$$
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The rectangular grid in the figure is made of 31 segments of $0.5 \mathrm{~cm}$ and comprises 12 squares. Rosa drew on a rectangular sheet of $21 \mathrm{~cm}$ by $29.7 \mathrm{~cm}$, grid-lined with squares of side $0.5 \mathrm{~cm}$, a large rectangular grid made with 1997 segments. How many squares does this rectangle have?

|
Let $m$ and $n$ be, respectively, the number of segments of $0.5 \, \text{cm}$ on two consecutive sides of the rectangle. We know that the total number of segments of $0.5 \, \text{cm}$ in the division of the rectangle into $m \times n$ squares of side $0.5 \, \text{cm}$ is: $m(n+1) + n(m+1)$ (prove this). Thus,
$$
m(n+1) + n(m+1) = 1997 \Rightarrow n = \frac{1997 - m}{2m + 1}
$$
Moreover, one of the sides considered is less than or equal to the other, say: $m \leq n$. In this case, we can conclude that $m \leq 31$, because
$$
n \geq m \Rightarrow n(m+1) + m(n+1) \geq 2m(m+1)
$$
Thus, $1997 \geq 2m(m+1)$ and since $1998 > 1997$, it follows that
$$
1998 > 2m(m+1) \Rightarrow 999 > m(m+1)
$$
From this, we conclude that $m < 32$.
On the other hand, we have
$$
n = \frac{1997 - m}{2m + 1} \Rightarrow 2n = \frac{3994 - 2m}{2m + 1} = \frac{3995 - (2m + 1)}{2m + 1} \Rightarrow 2n = \frac{3995}{2m + 1} - 1
$$
Thus, the problem now reduces to investigating the divisors of $3995 = 5 \times 17 \times 47$. The only values of $m$ that satisfy the condition $1 \leq m \leq 31$ are $m = 2$, $m = 8$, and $m = 23$, which correspond, respectively, to the divisors 5, 17, and 47. For these values of $m$, we have $n = 399$, $n = 117$, and $n = 42$ respectively. The other divisors will give equivalent configurations (by swapping $m$ and $n$).
Therefore, Rosa could have constructed 3 different configurations with the 1997 segments. The first with $2 \times 399$ squares, the second with $8 \times 117$ squares, and the third with $23 \times 42$ squares.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A triangle has vertex $A=(3,0), B=(0,3)$ and $C$, where $C$ is on the line $x+y=7$. What is the area of the triangle?
|
Observe that the height $h$, relative to the side $A B$, of all triangles $A B C$ that have the vertex $C$ on the line $x+y=7$, is the same, since the latter line is parallel to the line passing through $A$ and $B$. Therefore, these triangles all have the same area, namely:
$$
\frac{A B \times h}{2}
$$
We need to determine $A B$ and $h$. Since $A B$ is the hypotenuse of a right triangle that has both legs equal to $7-4=3$, it follows from the Pythagorean Theorem that:
$$
A B=\sqrt{3^{2}+3^{2}}=\sqrt{18}=3 \sqrt{2}
$$
It remains to calculate $h$, which is the distance between the parallel lines. The line $x+y=7$ is determined by the points $C=(7,0)$ and $D=(0,7)$. The line $x=y$ is perpendicular to the parallel lines above and forms a $45^{\circ}$ angle with the $O Y$ axis. Let $M$ be the foot of the perpendicular from $B$ to the line $x+y=7$. Therefore, the triangle $B M C$ is a right isosceles triangle with legs equal to $h$ and hypotenuse $7-3=4 \text{ cm}$.
From the Pythagorean Theorem it follows that:
$$
4^{2}=h^{2}+h^{2} \Rightarrow h=2 \sqrt{2}
$$
Finally, the area sought is:
$$
\frac{3 \sqrt{2} \times 2 \sqrt{2}}{2}=6
$$
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Three circles with radii $1 \mathrm{~cm}, 2 \mathrm{~cm}$, and $3 \mathrm{~cm}$ are pairwise externally tangent, as shown in the figure below.
Determine the radius of the circle that is externally tangent to the three circles.
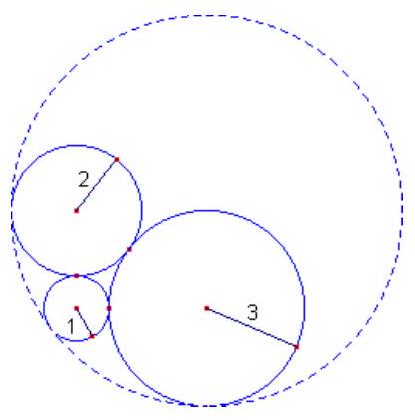
|
By connecting the centers of the three circles, we obtain the triangle $\triangle A B C$ with sides $A B=3 \mathrm{~cm}, A C=4 \mathrm{~cm}$, and $B C=5 \mathrm{~cm}$. Since $3^{2}+4^{2}=5^{2}$, this triangle is a right triangle with hypotenuse $B C$.
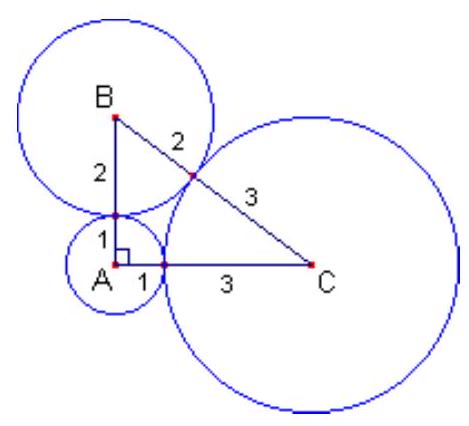
Construct the rectangle $A B D C$ by making a copy $\triangle B C D$, congruent to the triangle $\triangle A B C$ and with a common side $B C$.
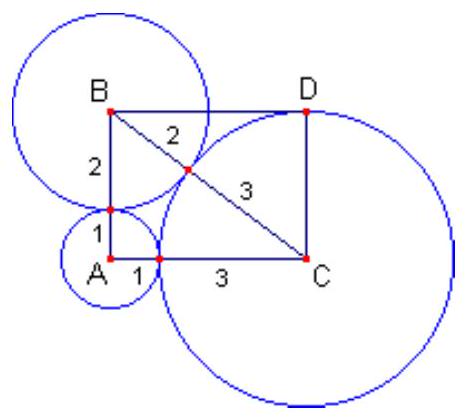
Since $D C=A B=3$ and the circle centered at $C$ also has a radius of $3 \mathrm{~cm}$, we see that point $D$ lies on this circle.
By connecting point $D$ to each vertex of the triangle $\triangle A B C$ and extending these segments until they intersect the circles, we obtain the points $P_{1}, P_{2}$, and $P_{3}$.
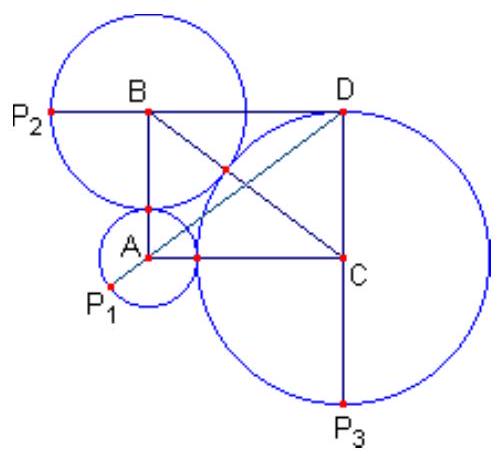
We have:
- $D P_{2}=D B+B P_{2}=C A+B P_{2}=4+2=6$.
- $D P_{1}=D A+A P_{1}=5+1=6$.
- $D P_{3}=D C+C P_{3}=3+3=6$.
Thus, $D P_{1}=D P_{2}=D P_{3}=6$. Therefore, if we consider the circle centered at $D$ with a radius of $6 \mathrm{~cm}$, we see that this circle passes through $P_{1}, P_{2}$, and $P_{3}$. Additionally, since the points $\left\{D, A, P_{1}\right\}$, $\left\{D, B, P_{2}\right\}$, and $\left\{D, C, P_{3}\right\}$ are collinear, it follows that the circle centered at $D$ with a radius of $6 \mathrm{~cm}$ is tangent to the three given circles with centers at $A, B$, and $C$.

|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $A B C D$ be a right trapezoid with bases $A B$ and $C D$, and right angles at $A$ and $D$. Given that the shorter diagonal $B D$ is perpendicular to the side $B C$, determine the smallest possible value for the ratio $\frac{C D}{A D}$.
|
Let $A \widehat{B} D=B \widehat{D} C=\alpha$. Then we have that $D C=\frac{B D}{\cos \alpha}$ and $A D=B D \sin \alpha$, hence
$\frac{D C}{A D}=\frac{\frac{B D}{\cos \alpha}}{B D \sin \alpha}=\frac{1}{\sin \alpha \cos \alpha}=\frac{2}{\sin 2 \alpha} \geq 2$.
Equality occurs when $\sin 2 \alpha=1$, that is, when $\alpha=45^{\circ}$.
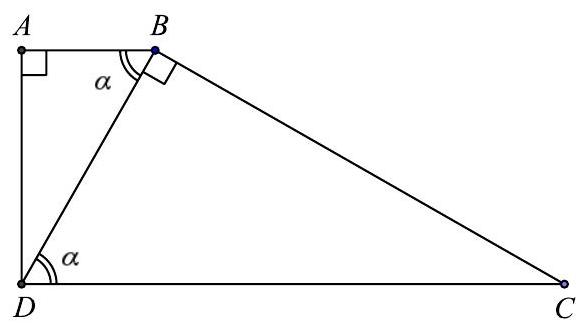
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let's denote by $s(n)$ the sum of the digits of the number $n$. For example, $s(2345) = 2 + 3 + 4 + 5 = 14$. Observe that:
$40 - s(40) = 36 = 9 \times 4; 500 - s(500) = 495 = 9 \times 55; 2345 - s(2345) = 2331 = 9 \times 259$.
(a) What can we say about the number $n - s(n)$?
(b) Using the previous item, calculate $s\left(s\left(s\left(2^{2009}\right)\right)\right)$.
HINT: Show that the number sought is less than 9.
## Solutions of Level 3
## List 1
|
(a) Observe these two examples:
$$
\underbrace{2000}_{2 \cdot 10^3}-\underbrace{s(2000)}_{2}=1998, \underbrace{60000}_{6 \cdot 10^4}-\underbrace{s(60000)}_{6}=59994
$$
From these, it is easy to understand that if $a$ is a digit between 1 and 9, then $s\left(a \cdot 10^{k}\right)=a$.
Thus, we have:
$$
a \cdot 10^{k}-s\left(a \cdot 10^{k}\right)=a \cdot 10^{k}-a=a\left(10^{k}-1\right)=a \times \underbrace{9 \cdots 9}_{k \text { nines }}=a \times 9 \times \underbrace{1 \cdots 1}_{k \text { ones }}
$$
Since every number can be decomposed into units, tens, hundreds, etc., that is, every number can be written in the form:
$$
n=a_{0}+a_{1} \cdot 10+a_{2} \cdot 10^{2}+\cdots+a_{k} \cdot 10^{k}
$$
we have that
$$
n-s(n)=a_{1} \times 9+a_{2} \times 99+\cdots a_{k} \times \underbrace{9 \cdots 9}_{k \text { nines }}
$$
Therefore, the difference $n-s(n)$ is always divisible by 9.
(b) Following the same reasoning, we have that $s(n)-s(s(n))$ and $s(s(n))-s(s(s(n)))$ are divisible by 9, so $n-s(s(s(n)))$ is divisible by 9. In particular, $2^{2009}-s(s(s(2^{2009})))$ is divisible by 9, or equivalently, $2^{2009}$ and $s(s(s(2^{2009})))$ leave the same remainder when divided by 9.
Since $2^{6}-1=63$ is divisible by 9, then $\left(2^{6}\right)^{334}-1=2^{2004}-1$ is divisible by 9, and therefore, $2^{2009}-2^{5}$ is divisible by 9. Since $2^{5}=32$ leaves a remainder of 5 when divided by 9, we have that $2^{2009}$ leaves a remainder of 5 when divided by 9.
On the other hand,
$$
2^{2009}<\left(2^{9}\right)^{224}<\left(10^{3}\right)^{224}=10^{672}
$$
Thus, $2^{2009}$ has fewer than 672 digits, and therefore,
$$
\begin{aligned}
s\left(2^{2009}\right) & <9 \times 672=6048 \\
s\left(s\left(2^{2009}\right)\right) & \leq 5+9+9+9=32 \\
s\left(s\left(s\left(2^{2009}\right)\right)\right) & \leq 2+9=13
\end{aligned}
$$
Since the only number less than or equal to 13 that leaves a remainder of 5 when divided by 9 is 5, we have that $s(s(s(2^{2009})))=5$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A number is framed when, by adding it to the number obtained by reversing the order of its digits, the result is a perfect square. For example, 164 and 461 are framed, since 164+461 = $625=25^{2}$. How many framed numbers are there between 10 and 100?
A) 5
B) 6
C) 8
D) 9
E) 10
|
Solution
## ALTERNATIVE C
Let $n$ be a number between 10 and 100, $a$ its tens digit, and $b$ its units digit; note that $1 \leq a \leq 9$ and $0 \leq b \leq 9$. Then $n=10a+b$ and the number obtained by reversing the digits of $n$ is $10b+a$. Since $n$ is a framed number, we have that $(10a+b) + (10b+a) = 11a + 11b = 11(a+b)$ is a perfect square.
First, we note that if $b=0$, then it is not possible for $11(a+b)$ to be a perfect square, since $11a$ is never a perfect square for $a$ taking values from 1 to 9. Therefore, we have $b \neq 0$. With this, we see that $2 \leq a+b \leq 18$; among these possible values for $a+b$, the only one that makes $11(a+b)$ a perfect square is 11. Thus, $a+b=11$ and the possibilities for $n$ are then 29 and 92, 38 and 83, 47 and 74, and 56 and 65, for a total of 8.
Observation: We can also conclude that $b \neq 0$ by directly verifying that 10, 20, $30, \ldots, 90$ are not framed numbers.
|
8
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
In the figure, triangles $A B C$ and $D E F$ are equilateral with sides $14 \mathrm{~cm}$ and $13 \mathrm{~cm}$, respectively, and sides $B C$ and $E F$ are parallel.
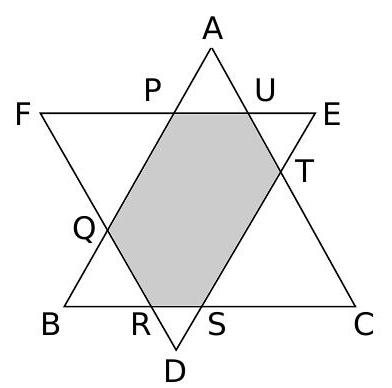
a) Calculate the measure of angle EÛT.
b) Calculate the perimeter of polygon $P Q R S T U$.
c) If segment $P Q$ measures $6 \mathrm{~cm}$, what is the measure of segment $S T$?
|
Solution
a) Since $BC$ and $EF$ are parallel, the angles $EUT$ and $ACB$ are alternate interior angles, hence $E \hat{U} T = A \hat{C} B = 60^{\circ}$. b) From item a) we can conclude that all triangles in the figure are equilateral. Thus, we have $QP = FP$, $UT = UE$, $TS = CS$, and $RQ = RB$. Therefore, the perimeter of $PQRSTU$ is
\[
\begin{gathered}
QP + PU + UT + TS + SR + RQ = (FP + PU + UE) + (CS + SR + RB) \\
= FE + CB = 13 \text{ cm} + 14 \text{ cm} = 27 \text{ cm}
\end{gathered}
\]
c) From $PQ = 6 \text{ cm}$ it follows that $FP = 6 \text{ cm}$, since triangle $QFP$ is equilateral, and we conclude that $PE = FE - EP = 13 \text{ cm} - 6 \text{ cm} = 7 \text{ cm}$. Since $BC$ is parallel to $EF$ and $AB$ is parallel to $DE$, the quadrilateral $PESB$ is a parallelogram, hence $BS = PE = 7 \text{ cm}$. Finally, we have $SC = BC - BS = 14 \text{ cm} - 7 \text{ cm} = 7 \text{ cm}$; thus $ST = SC = 7 \text{ cm}$, since triangle $TCS$ is equilateral.

A similar solution can be given starting from the parallelogram QDTA.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A board of size $2013 \times 5$ (i.e., with 2013 rows and 5 columns) must be painted with the colors $A, B, C, D$. Some squares in the first row have already been painted, as shown in the figure below (the squares not represented in the figure have not been painted yet). To continue painting the board, we must follow this rule: adjacent squares (those that share a side or a vertex) cannot have the same color.
a) Describe the ways we can complete the painting of the first two rows.
b) In how many ways can we paint the entire board?
c) Describe the possible paintings for the 2013th row.
|
Solution
a) The house that is missing painting in the first row has neighbors painted with $B$ and $C$. Therefore, it can only be painted with $A$ or $D$. Let's analyze the case where it is painted with $A$, as shown in the figure below.

In this case, the house directly below the one we painted with $A$ can only be painted with $D$, as it has neighboring houses of colors $A, B$, and $C$. Painting it with $D$, we arrive at:
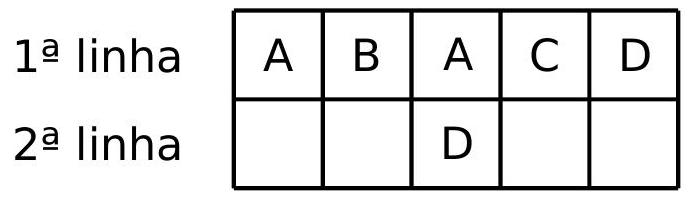
The house to the left of the house we painted with $D$, having neighbors of colors $B, A$, and $D$, can only be painted with $C$. The house to the right can only be painted with $B$. Thus, we arrive at:
1st row
2nd row
| $\mathrm{A}$ | $\mathrm{B}$ | $\mathrm{A}$ | $\mathrm{C}$ | $\mathrm{D}$ |
| :--- | :--- | :--- | :--- | :--- |
| | $\mathrm{C}$ | $\mathrm{D}$ | $\mathrm{B}$ | |
Finally, painting the remaining houses, we arrive at the painting:
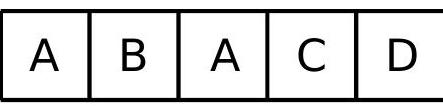
1st row
2nd row
| $A$ | $B$ | $A$ | $C$ | $D$ |
| :---: | :---: | :---: | :---: | :---: |
| $D$ | $C$ | $D$ | $B$ | $A$ |
And if we had started with the color $D$ in the first house we painted? In that case, we would have arrived at
| 1st row | A | B | D | C | D |
| :--- | :---: | :---: | :---: | :---: | :---: |
| 2nd row | D | C | A | B | A |
| | | | | | |
Thus, these are the two possible paintings of the first two rows.
b) Continuing the painting we started in the previous item, we arrive at the two paintings for the first eight rows:
| 1st row | $\mathrm{A}$ | B | $\mathrm{D}$ | C | $\mathrm{D}$ | 1st row | A | $B$ | $A$ | $\mathrm{C}$ | $\mathrm{D}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 2nd row | $\mathrm{D}$ | $\mathrm{C}$ | A | B | A | 2nd row | $D$ | C | $\mathrm{D}$ | $\mathrm{B}$ | A |
| 3rd row | $\mathrm{A}$ | B | $\mathrm{D}$ | C | $\mathrm{D}$ | 3rd row | A | $B$ | A | $\mathrm{C}$ | $\mathrm{D}$ |
| 4th row | $\mathrm{D}$ | c | A | B | A | 4th row | $D$ | C | $D$ | $\mathrm{~B}$ | A |
| 5th row | $\mathrm{A}$ | B | $\mathrm{D}$ | C | $\mathrm{D}$ | 5th row | A | $B$ | A | $\mathrm{c}$ | $D$ |
| 6th row | $\mathrm{D}$ | $\mathrm{c}$ | A | B | A | 6th row | $\mathrm{D}$ | C | $\mathrm{D}$ | B | A |
| 7th row | $\mathrm{A}$ | B | $\mathrm{D}$ | C | $\mathrm{D}$ | 7th row | A | $B$ | A | C | $\mathrm{D}$ |
| 8th row | $\mathrm{D}$ | c | A | B | A | 8th row | $D$ | C | $\mathrm{D}$ | $\mathrm{B}$ | A |
Note that the pattern repeats every two rows. Following each of the cases, we conclude that there are only two possible paintings for the entire board.
c) As mentioned in the previous item, in each of the two possible cases, the painting of the rows repeats every two rows. Therefore, dividing 2013 by 2, we get $2013 = 1006 \times 2 + 1$. Thus, we conclude that the painting of the 2013th row is the same as the painting of the first row. Therefore, the two paintings that can appear in the 2013th row are:
and
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The figure below contains a square and two congruent right triangles.

Using these polygons, we form a rectangle and a trapezoid as shown in the following figure:
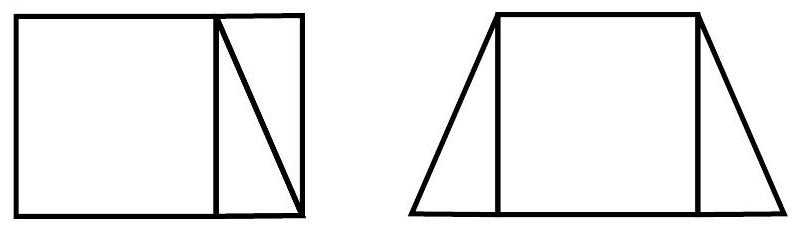
Knowing that the perimeter of the rectangle is 58, and that the perimeter of the trapezoid is 60, calculate the side of the square.
Note: A triangle is said to be right if one of its angles measures $90^{\circ}$. Two triangles are said to be congruent when both have sides of the same lengths.
#
|
Solution
It is clear from the figure in the statement of this exercise that the length of the side of the square must coincide with the length of one of the legs of the triangles. Let's call this length $a$. In addition, let's call the length of the hypotenuse $b$ and the length of the other leg $x$. From the figure below, we see that the perimeter of the trapezoid is given by $2a + 2b + 2x$.

Therefore, for the perimeter of the trapezoid to be equal to 60, the following equation must be satisfied:
$$
2a + 2b + 2x = 60
$$
From this, we conclude that
$$
x = \frac{60 - 2a - 2b}{2} = 30 - a - b
$$
Note that the perimeter of the rectangle is given by $4a + 2x$, as we can observe below.
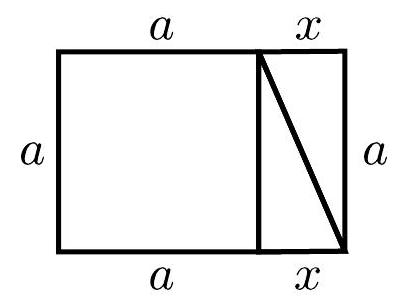
Thus, using the expression for $x$ obtained above, we get that this perimeter is equal to:
$$
2(30 - a - b) + 4a
$$
which must coincide with 58 according to the problem statement. Therefore, the following equation must be satisfied:
$$
2(30 - a - b) + 4a = 58
$$
Simplifying the equation above, we get $b = a + 1$. Substituting this expression for $b$ into the expression $x = 30 - a - b$, we obtain $x = 29 - 2a$.
Thus, the lengths of the legs of each triangle are $a$ and $29 - 2a$, while the length of the hypotenuse is $b = a + 1$, as illustrated in the figure below:
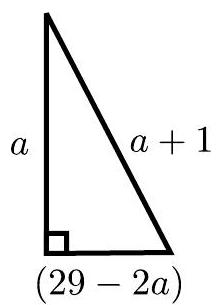
Using the Pythagorean Theorem, we have the equation
$$
a^2 + (29 - 2a)^2 = (a + 1)^2
$$
Simplifying the equation above, we get that $a$ satisfies
$$
4a^2 - 118a + 840 = 0
$$
Factoring the polynomial in $a$ on the left side, we can rewrite the equation above as
$$
2(a - 12)(2a - 35) = 0
$$
Thus, we obtain the solutions of the quadratic equation as the numbers 12 and 35/2. But if $a$ were equal to $35 / 2$, the length $x = 29 - 2a$ would be negative. Therefore, the only valid solution is $a = 12$.
#
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine um valor de $n$ para o qual o numero $2^{8}+2^{11}+2^{n}$ seja um quadrado perfeito.
|
Observe que
$$
2^{8}+2^{11}+2^{n}=\left(2^{4}\right)^{2}+2 \times 2^{4} \times 2^{6}+\left(2^{\frac{n}{2}}\right)^{2}
$$
Logo, se $n=12$, temos
$$
2^{8}+2^{11}+2^{12}=\left(2^{4}+2^{6}\right)^{2}
$$
Logo $n=12$ é uma solução.
Solução Geral: $\operatorname{Se} 2^{8}+2^{11}+2^{n}=k^{2}$, então:
$$
\begin{aligned}
2^{8}+2^{3} \times 2^{8}+2^{n} & =k^{2} \\
9 \times 2^{8}+2^{n} & =k^{2} \\
2^{n} & =k^{2}-\left(3 \times 2^{4}\right)^{2} \\
2^{n} & =\left(k-3 \times 2^{4}\right)\left(k+3 \times 2^{4}\right)
\end{aligned}
$$
Logo, $\left(k-3 \times 2^{4}\right)$ e $\left(k+3 \times 2^{4}\right)$ são potências de 2 , ou seja:
$$
k+3 \times 2^{4}=2^{a}, k-3 \times 2^{4}=2^{b} \text { e } a+b=n
$$
Temos:
$$
2^{a}-2^{b}=\left(k+3 \times 2^{4}\right)-\left(k-3 \times 2^{4}\right)=3 \times 2^{5}=96
$$
Examinemos a lista das potências de 2:
$$
1,4,8,16,32,64,128,256, \cdots
$$
Constatamos que $128-32=96$. Logo, $a=7, b=5$ e $n=12$.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The reverse of a two-digit integer is the number obtained by reversing the order of its digits. For example, 34 is the reverse of 43. How many numbers exist such that when added to their reverse, they give a perfect square?
|
Let's denote by $a b \mathrm{e}$ ba the number and its reverse. We have that
$$
a b+b a=10 a+b+10 b+a=11(a+b)
$$
On the other hand, $a \leq 9$ and $b \leq 9$, so, $a+b \leq 18$. Since 11 is a prime number and $a+b \leq 18$, for $11(a+b)$ to be a perfect square, we can only have $a+b=11$.
Thus, we have 8 numbers satisfying the condition of
Reminder: two-digit numbers where $a$ is the tens digit and $b$ is the units digit are of the form
$10 \times a+b$.
Ex: $47=4 \times 10+7$
problem: 29, 38, 47, 56, 65, 74, 83 and 92.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a warehouse, a dozen eggs and 10 apples had the same price. After a week, the price of eggs fell by $2 \%$ and the price of apples rose by 10\%. How much more will be spent on the purchase of a dozen eggs and 10 apples?
(a) $2 \%$
(b) $4 \%$
(c) $10 \%$
(d) $12 \%$
(e) $12.2 \%$
|
We can assume that the initial price of a dozen eggs is $R \$ 1.00$, so 10 apples also cost $R \$ 1.00$. Since the price of eggs has dropped by $2 \%$, the new price of a dozen eggs is $R \$ 0.98$. The price of apples has increased by $10 \%$, so the new price of 10 apples is $R \$ 1.10$. Thus, before it cost $R \$ 2.00$ to buy eggs and apples, and now it costs $0.98+1.10=2.08$ reais. Therefore, the increase was $R \$ 0.08$, which corresponds to $\frac{0.08}{2} \times 100 \% = 4 \%$. The correct option is (b).
|
4
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
The number
$$
A=(\sqrt{6}+\sqrt{2})(\sqrt{3}-2) \sqrt{\sqrt{3}+2}
$$
is equal to:
(a) $-\sqrt{3}$
(b) $-\sqrt{2}$
(c) -2
(d) 1
(e) 2
|
(c) Like
$$
\begin{aligned}
A^{2} & =[(\sqrt{6}+\sqrt{2})(\sqrt{3}-2) \sqrt{\sqrt{3}+2}]^{2} \\
& =(\sqrt{6}+\sqrt{2})^{2}(\sqrt{3}-2)^{2}(\sqrt{\sqrt{3}+2})^{2} \\
& =(\sqrt{6}+\sqrt{2})^{2}(\sqrt{3}-2)^{2}(\sqrt{3}+2) \\
& =(\sqrt{6}+\sqrt{2})^{2}(\sqrt{3}-2)[(\sqrt{3}-2)(\sqrt{3}+2)] \\
& =(6+2 \sqrt{12}+2)(\sqrt{3}-2)\left((\sqrt{3})^{2}-2^{2}\right) \\
& =(6+2 \sqrt{12}+2)(\sqrt{3}-2)(-1) \\
& =(8+4 \sqrt{3})(2-\sqrt{3}) \\
& =4(2+\sqrt{3})(2-\sqrt{3}) \\
& =4\left(2^{2}-(\sqrt{3})^{2}\right)=4 \times 1=4
\end{aligned}
$$
Thus $A^{2}=4$ and therefore, $A$ can be 2 or -2. Since $\sqrt{3}-2$ is negative, $A$ must be negative, and thus $A=-2$.
|
-2
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Five points lie on the same line. When we list the ten distances between any two of these points, from smallest to largest, we get $2,4,5,7,8, k, 13,15,17,19$. What is the value of $k$?
|
Solution 1: - This solution is a bit difficult to write because it is based on "trial and error." We start by drawing a number line and placing the points 0 and 19. Since the first distance is 2, we mark our first three points:

Since we need a distance of 7, we place the point 7 on the number line. This gives us distances that are not incompatible with the problem:

The distances between these 4 points are: 2, 7, 19, 5, 17, and 12. Finally, placing the point 15 on the number line, we get the following:

With these points, the distances are: \(2, 7, 15, 19, 5, 13, 17, 8, 12, 4\), which are compatible with the data in the problem. Therefore, \(k=12\).
Note that we also have another distribution of the numbers, namely:

In this distribution, we also get \(k=12\).
Solution 2: Since the largest distance is 19, we can assume that one point is 0 and the other is 19.
If \(a\) is another point, then in the list of distances, we have the numbers: \(a-0 = a\) and \(19-a\). Indeed, in the list, we have the pairs 2 and 17, so we can assume that the number 2 is another point on the number line.
Similarly, since 4 and 15 are in the list of distances, 4 or 15 is another point on the number line. However, 4 cannot be one of the points because the distance 2 did not appear twice. Therefore, 15 is another point on the number line.
Finally, the fifth point must be 5 units away from one of the points and 7 units away from another, so the missing point is the point 7, and the unknown distance is \(k=19-7=12\).
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A class has 22 boys and 18 girls. During the holidays, $60\%$ of the students in this class went to do community work. At least, how many girls participated in this work?
(A) 1
(B) 2
(C) 4
(D) 6
(E) 8
|
The correct answer is (B).
Of the total number of students in this class, $60 \%$ went to do community work, that is, $0.6 \times 40=24$. The minimum number of female students who participated in this work is obtained when the number of male students who participated is maximum, that is, when 22 male students are involved in the work, leaving a minimum of 2 spots for the female students.
|
2
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
In the luminous mechanism of the figure, each of the eight buttons can light up in green or blue. The mechanism works as follows: when turned on, all buttons light up blue, and if we press a button, that button and its neighbors switch colors. If we turn on the mechanism and successively press buttons 1, 3, and 5, how many green lights will be on at the end?
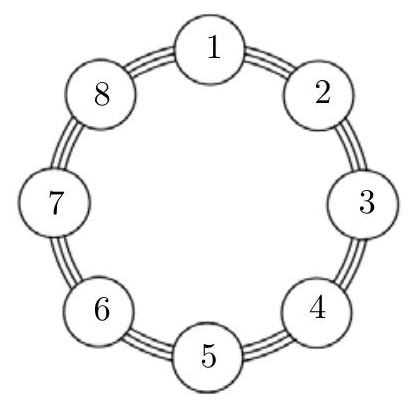
(A) 3
(B) 4
(C) 5
(D) 6
(E) 7
|
The correct answer is (C).
The table shows the color of each button at each step.
| | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ | $\mathbf{7}$ | $\mathbf{8}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| start | blue | blue | blue | blue | blue | blue | blue | blue |
| pressing button 1 | green | green | blue | blue | blue | blue | blue | green |
| pressing button 3 | green | blue | green | green | blue | blue | blue | green |
| pressing button 5 | green | blue | green | blue | green | green | blue | green |
Therefore, the buttons that ended up with green lights on are $1,3,5,6$ and 8, giving us a total of 5 buttons.
|
5
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Is the number $3^{444}+4^{333}$ divisible by 5?
## List 5
|
There is a pattern for the unit digit of a power of 3: it has a period of 4, as it repeats every 4 times.
$$
\begin{aligned}
& 3 \\
& 3^{2}=9 \\
& 3^{3}=27 \\
& 3^{4}=81 \\
& 3^{5}=243 \\
& 3^{6}=\ldots 9 \\
& 3^{7}=\ldots 7 \\
& 3^{8}=\ldots 1
\end{aligned}
$$
Since 444 is a multiple of 4, the unit digit of $3^{444}$ is 1.
Similarly, the unit digit of powers of 4 has a period of 2. Indeed, we have:
$$
\begin{array}{ll}
4^{1}=4 & ; \quad 4^{3}=64 \\
4^{2}=16 \quad & ; \quad 4^{4}=256
\end{array}
$$
Since 333 is odd, the unit digit of $4^{333}$ is 4. Therefore, the unit digit of $3^{444}+4^{333}$ is $1+4=5$, and thus it is divisible by 5.
REMEMBER: Numbers divisible by 5 end in 0 or 5.
## List 5
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Fill in the squares with the numbers $1,2,3,5,6$.
$$
(\square+\square-\square) \times \square \div \square=4
$$
|
The operation is equivalent to
$$
(\square+\square-\square) \times \square=4 \times
$$
Therefore, the left side of the equality is a multiple of 4, so the only possibilities are:
$$
(\square+\square-\square) \times \square=4 \times \square \quad \text { or } \quad(\square+\square-\square) \times \square=4 \times \square
$$
From this, we can conclude that:
$$
(\boxed{3}+5-\square) \times \square=4 \times \square \quad \text { or } \quad(6+5-\square) \times \square=4 \times \square
$$
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Writing successively the natural numbers, we obtain the sequence:
$$
12345678910111213141516171819202122 \ldots
$$
Which digit is in the $2009^{th}$ position of this sequence?
|
- the numbers 1 to 9 occupy 9 positions;
- the numbers 10 to 99 occupy $2 \times 90=180$ positions;
- the numbers 100 to 199 occupy $3 \times 100=300$ positions; the numbers 200 to 299 occupy $3 \times 100=300$ positions; the numbers 300 to 399 occupy $3 \times 100=300$ positions; etc.
$$
\underbrace{100, \ldots 199}_{3 \times 100=300}, \underbrace{200, \ldots, 299}_{3 \times 100=300}, \underbrace{300, \ldots, 399}_{3 \times 100=300}, \underbrace{400, \ldots, 499}_{3 \times 100=300}, \underbrace{500, \ldots, 599}_{3 \times 100=300}, \underbrace{600, \ldots, 699}_{3 \times 100=300}
$$
Thus, the digits used to write from 1 to 699 occupy $9+180+6 \times 300=1989$ positions, so we are missing $2009-1989=20$ positions. Since $20=3 \times 6+2$ we still need to write from 700 to 706, obtaining 21 positions, with the digit 6 occupying the 21st position. Therefore, the digit 0 is the one that occupies the 2009th position.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Elisa has 24 science books and others of mathematics and literature. If Elisa had one more mathematics book, then $\frac{1}{9}$ of her books would be mathematics and one quarter literature. If Elisa has fewer than 100 books, how many mathematics books does she have?
## List 10
|
Let $N$ be the total number of books Elisa has. Since $N+1$ is a multiple of 9 and 4, it follows that it is a multiple of 36. Therefore, $N+1$ is 36 or 72, as Elisa has fewer than 100 books. If $N=35$, then the number of math books is $36 \div 9-1=3$ and the number of literature books is $36 \div 4=9$. Thus, Elisa would have: $24+3+9=36$ books, which is impossible because 36 is greater than 35.
Therefore, $N=71$ and the number of math books is $72 \div 9-1=7$.
## List 10
#
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$O$ double of a number divided by 5 leaves a remainder of 1. What is the remainder of the division of this number by 5?
Translating the text as requested, while preserving the original line breaks and format.
|
According to the data from the problem, double the number is a multiple of 5 plus 1. Since multiples of 5 end in 0 or 5, the double ends in 1 or 6. But the double is an even number, so it ends in 6. Thus, the number ends in 3 or 8, therefore when divided by 5, it leaves a remainder of 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
At a circular table, 5 people are sitting: Arnaldo, Bernaldo, Cernaldo, Dernaldo, and Ernaldo, each in a chair. Analyzing in a clockwise direction, we have:
I. Between Arnaldo and Bernaldo there is 1 empty chair;
II. Between Bernaldo and Cernaldo are 5 chairs;
III. Between Dernaldo and Ernaldo are 4 chairs, almost all empty;
IV. Between Dernaldo and Cernaldo are 2 chairs;
V. Between Ernaldo and Bernaldo are 3 chairs, not all empty.
How many chairs are there around the table?
|
Solution
Let's position Arnaldo in the chair we will call 1, and by information $I$, Bernaldo should sit in chair 3, and consequently, by information $II$, Cernaldo should sit in chair 9. Since there are 6 chairs between Dernaldo and Ernaldo and 2 chairs between Dernaldo and Cernaldo, Cernaldo is between Dernaldo and Ernaldo, with Dernaldo sitting in chair 6 and Ernaldo in chair 11. Since there are 3 chairs between Ernaldo and Bernaldo, Arnaldo is between them, with one empty chair between Ernaldo and Arnaldo, which is chair 12, the last chair. Therefore, there are 12 chairs in total.
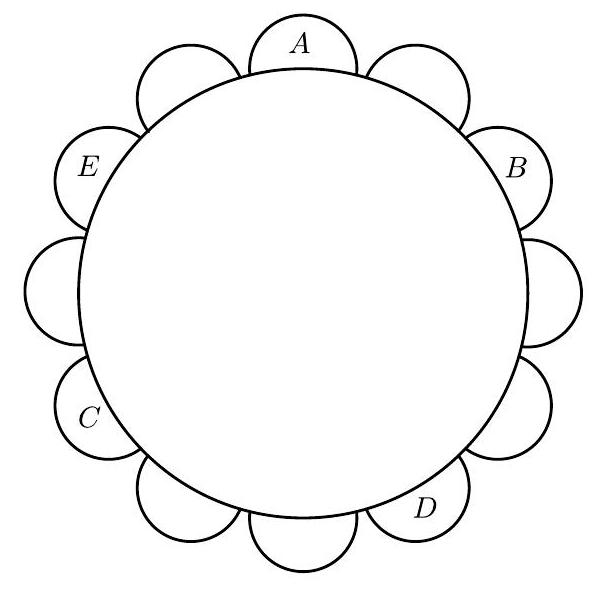
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Mario bought some sweets at the market, where 3 chocolates cost the same as 2 popsicles and 2 lollipops cost the same as 5 chocolates.
a) Mario decided to return to the market with money to buy exactly 3 lollipops but decided to buy popsicles instead. How many popsicles did he manage to buy?
b) If he had used the money for 3 chocolates, 2 popsicles, and 2 lollipops to buy the maximum number of sweets possible, how many would he have bought?
|
Solution
a) 15 chocolates cost the same as 10 popsicles and the same as 6 lollipops. Therefore, 10 popsicles are worth the same as 6 lollipops, and consequently, 5 popsicles the same as 3 lollipops. Thus, with the money for 3 lollipops, Mario can buy 5 popsicles.
b) From the previous item, we saw that the largest number of sweets Mario can buy with the same amount of money is chocolates. If 2 popsicles are equivalent to 3 chocolates and 2 lollipops are equivalent to 5 chocolates, then the maximum number of sweets is $3+3+5=11$ chocolates.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Jonas wrote a sequence with the positive multiples of 13 in ascending order.
## $1326395265 \ldots$
a) What is the $2,019^{\text{th}}$ digit of Jonas's sequence?
b) Will the number 2,019 appear in this sequence?
|
Solution
a) There are 7 multiples of 13 with 2 digits (14 digits); with 3 digits, there are 69 multiples of $13(3 \cdot 69=207$ digits). Already, there are $14+207=221$ digits, so $2,019-221=1,798$ are still needed. Dividing 1,798 by 4, we get 449 and a remainder of 2, that is, the first multiple of 13 with 4 digits is $13 \cdot 77=1001$, so $13(449+76)=6,825$. Since the remainder of the division is 2 and the next multiple is 6,838, then the $2,019^{\text{th}}$ digit is 8.
b) Yes. Dividing 20,190 by 13, we find the quotient is 1,553 and the remainder is 1, so 20,189 and 20,202 are multiples of 13, which means there is no multiple of 13 between 20,190 and 20,199. But, dividing 201,900 by 13, we find the quotient is 15,530 and the remainder is 10, so 201,903 is a multiple of 13 and, consequently, 2,019 appears in the sequence.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The owner of a clothing factory is a math enthusiast and organizes his products into packages whose number of items is a prime number. For example, the green-colored pieces, he organizes into packages of 2 pieces each; the blue-colored pieces, into packages of 3 pieces each; the pink-colored pieces, into packages of 5 pieces each; the white-colored pieces, into packages of 7 pieces each; and so on. In a large box, the factory owner decides to place only packages of green, blue, and pink colors (it can have all three colors or just one, including only one color). The box must contain exactly 20 pieces. In how many different ways can he organize this box?
#
|
Solution
The colors green, blue, and pink have 2, 3, and 5 pieces per pack, respectively. We can take various quantities of packs of each color, including not taking any, as long as the total number of pieces is exactly 20. Let's create a table to list the possibilities:
| Green | Blue | Pink |
| :---: | :---: | :---: |
| 10 | 0 | 0 |
| 7 | 2 | 0 |
| 6 | 1 | 1 |
| 5 | 0 | 2 |
| 4 | 4 | 0 |
| 3 | 3 | 1 |
| Green | Blue | Pink |
| :---: | :---: | :---: |
| 2 | 2 | 2 |
| 1 | 6 | 0 |
| 1 | 1 | 3 |
| 0 | 5 | 1 |
| 0 | 0 | 4 |
Therefore, there are 11 different ways.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The sums of the three columns and the three rows of the table are equal.
| 4 | 9 | 2 |
| :--- | :--- | :--- |
| 8 | 1 | 6 |
| 3 | 5 | 7 |
What is the minimum number of cells in the table that need to be changed so that all the new six sums are different from each other?
|
Solution
If three or fewer cells are changed, there will either be two rows without any changed cells or one cell is the only one changed in its row and column. In the first case, these two rows without any changed cells have the same sum. In the second case, if only one cell is the only one changed in its row and column, they also have the same sum. The table below represents an example with only 4 changes and all 6 row and column sums are distinct.
| $\mathbf{5}$ | $\mathbf{9}$ | $\mathbf{7}$ |
| :--- | :--- | :--- |
| 8 | $\mathbf{3}$ | $\mathbf{9}$ |
| 3 | 5 | 7 |
Therefore, the minimum number of changes is 4.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a class with 35 students, a survey was conducted on preferences for mathematics and literature, and it was found that:
- 7 men like mathematics;
- 6 men like literature;
- 5 men and 8 women said they do not like either;
- there are 16 men in the class;
- 5 students like both; and
- 11 students like only mathematics.
a) How many men like both mathematics and literature?
b) How many women like only literature?
|
Solution
Let $H$ be the set of men and $U$ the total set of people, so $U-H$ is the set of women. In addition, consider the sets Mat and $L$ of people who like mathematics and literature, respectively. If $x$ represents the number of men who like both mathematics and literature and $y$ the number of women who like only literature, we have the following diagram:
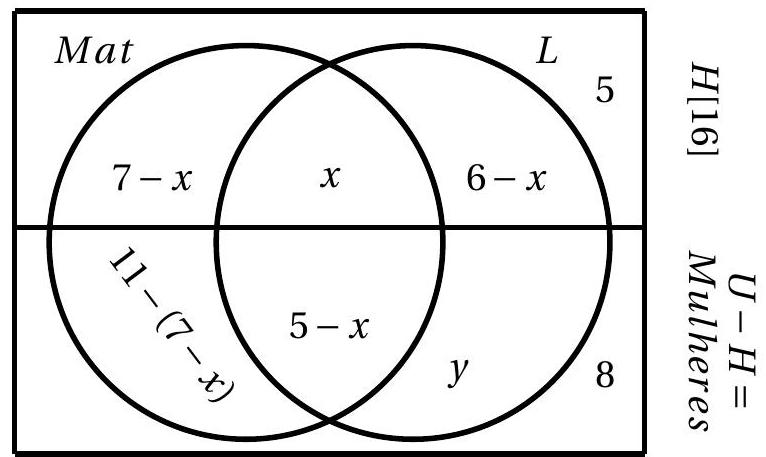
a) Since there are 16 men in the room,
$$
\begin{aligned}
5+7-x+x+6-x & =16 \\
x & =2
\end{aligned}
$$
b) Since the room is composed of 35 students
$$
\begin{aligned}
|H|+|U-H| & =35 \\
16+4+x+5-x+y+8 & =35 \\
y & =2
\end{aligned}
$$
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the triangle $ABC$ below, there is a point $D$ on its side $AB$, such that $AB=CD$, $\widehat{ABC}=100^{\circ}$, and $\widehat{DCB}=40^{\circ}$.
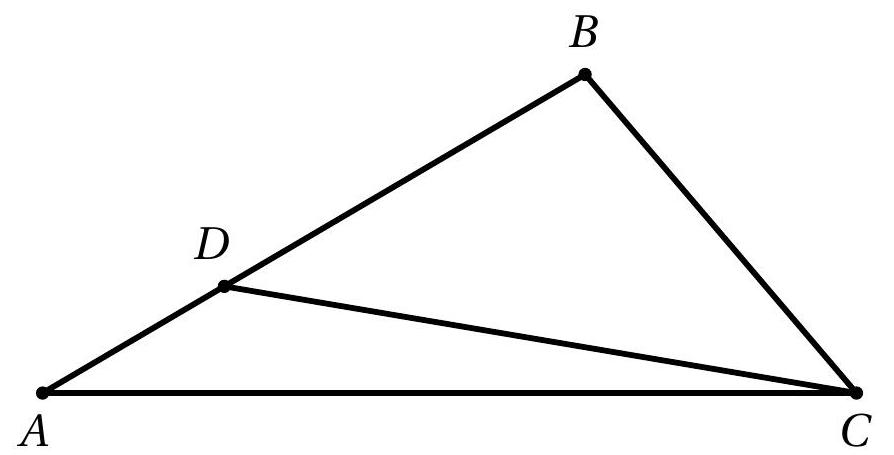
a) What is the measure of the angle $\widehat{BDC}$?
b) What is the measure of the angle $\widehat{ACD}$?
#
|
Solution
a) Analyzing the sum of the internal angles of the triangle $\triangle B D C$, we have $100^{\circ}+40^{\circ}+\angle B D C=180^{\circ}$, that is, $\angle B D C=40^{\circ}$.
b) Due to the previous item, $\triangle B D C$ is isosceles with base $C D$ and thus $B C=B D$. Construct the auxiliary triangle $\triangle B C E$, equilateral, and denote $\angle A C D=\alpha$.
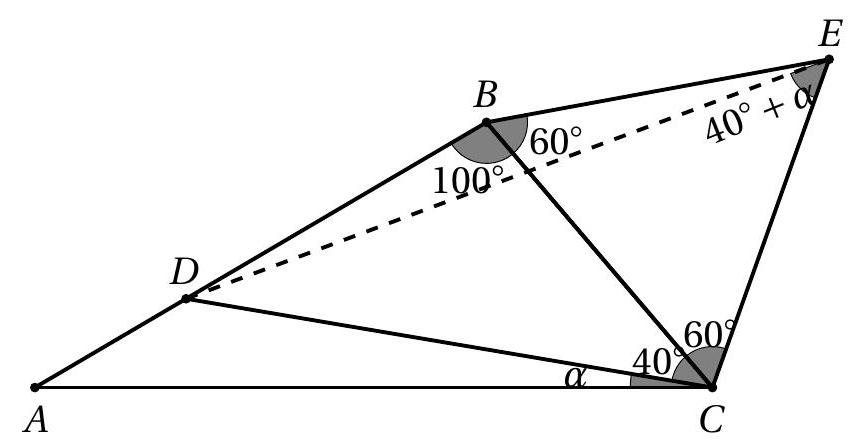
By construction, $\angle D C E=100^{\circ}$ and $C E=B C$. From $A B=D C$ and $\angle A B C=\angle D C E$, we can write $\triangle A B C \equiv \triangle D C E$, by the $L A L$ case. Thus, we arrive at
$$
\angle A C B=\angle D E C=40^{\circ}+\alpha
$$
Since $\triangle B C E$ is equilateral ($B C=C E=E B$); and $\triangle B C D$ is isosceles ($B C=B D$), we conclude that $\triangle B D E$ is isosceles with $B E=B D$ and base $D E$. Therefore, its base angles are equal to $10^{\circ}$. Finally, since $\angle B E C=60^{\circ}=10^{\circ}+40^{\circ}+\alpha$, we conclude that $\alpha=10^{\circ}$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
a) Consider a prime $p$ that divides $10^{n}+1$ for some positive integer $n$. For example, $p=7$ divides $10^{3}+1$. By analyzing the principal period of the decimal representation of $\frac{1}{p}$, verify that the number of times the digit $i$ appears is equal to the number of times the digit $9-i$ appears for each $i \in\{0,1,2, \ldots, 9\}$.
b) Consider a prime number $p$ that does not divide 10 and suppose that the period of the decimal representation of $\frac{1}{p}$ is $2 k$. Is it always possible to break the period into two numbers that sum to $10^{k}-1$? For example, the period of $\frac{1}{7}$ has length $6=2 k$, as it is equal to 142857. Notice that $142+857=999=10^{3}-1=10^{k}-1$.
c) Given
$$
x=\frac{1}{1998}+\frac{1}{19998}+\frac{1}{199998}+\ldots
$$
when writing $2 x$ as a decimal number, what will be the $59^{\text{th}}$ digit after the decimal point?
|
Solution
a) We can write $10^{n}+1=p \cdot a$ where $a$ is a number with no more than $n$ digits in base 10, say $a=a_{1} a_{2} \ldots a_{n}$. We mean by this that each number $a_{i}$ is one of the digits of $a$. Even if it has strictly fewer than $n$ digits, we can place some $a_{i}$'s on the left as being 0. We have
$$
\begin{aligned}
\frac{1}{p} & =\frac{a}{a \cdot p} \\
& =\frac{a}{10^{n}+1} \\
& =\frac{a\left(10^{n}-1\right)}{10^{2 n}-1} \\
& =\frac{\left[10^{n}(a-1)+\left(10^{n}-1\right)-(a-1)\right]}{10^{2 n}-1}
\end{aligned}
$$
The number $10^{n}-1$ consists of $n$ numbers all equal to 9 and the difference $\left(10^{n}-1\right)-(a-1)$ reduces each of these 9 digits by a digit of $a$. Thus, the decimal representation of the numerator is:
$$
a_{1} a_{2} \ldots a_{n-1}\left(a_{n}-1\right)\left(9-a_{1}\right)\left(9-a_{2}\right) \ldots\left(9-a_{n-1}\right)\left(10-a_{n}\right)
$$
The previous number represents the period of the decimal representation of $\frac{1}{p}$ and each digit $i$ can be paired with another digit of the form $9-i$. Thus, the quantities of appearances of such digits are equal. In the example from the statement, the period of 1/7 is 142857 and we have the following pairings:
$$
\begin{aligned}
& 1 \rightarrow 8 \\
& 4 \rightarrow 5 \\
& 2 \rightarrow 7
\end{aligned}
$$
b) Since $10^{2 k}-1=\left(10^{k}-1\right)\left(10^{k}+1\right)$ and $p$ is prime, one of $10^{k}-1$ and $10^{k}+1$ is a multiple of $p$. We cannot have $10^{k}-1$ as a multiple of $p$, because otherwise we could write $\frac{1}{p}=$ $\frac{\left(10^{k}-1\right) / p}{10^{k}-1}$ and obtain a periodic decimal with a period smaller than $2 k$. Therefore, $p$ divides $10^{k}+1$ and we can repeat the solution from the previous item to conclude that the period of the decimal representation of $1 / p$ is of the form:
$$
a_{1} a_{2} \ldots a_{k-1}\left(a_{k}-1\right)\left(9-a_{1}\right)\left(9-a_{2}\right) \ldots\left(9-a_{k-1}\right)\left(10-a_{k}\right)
$$
By adding the number formed by the first $k$ digits to the number formed by the last $k$ digits, we get $\underbrace{99 \ldots 9}_{k \text { times }}=10^{k}-1$.
c) Notice that
$$
\begin{aligned}
2 x & =\frac{1}{999}+\frac{1}{9999}+\frac{1}{99999}+\ldots \\
& =0, \overline{001}+0, \overline{0001}+0, \overline{00001}+\ldots
\end{aligned}
$$
In the first term, the 1 appears in multiples of three, in the second, in multiples of four, in the third, in multiples of five, and so on. When we add the first two decimals $0, \overline{001}$ and $0, \overline{0001}$, we get the periodic decimal
$$
0,001101011002 \ldots
$$
In positions that are multiples of only one of the numbers in the set $\{3,4\}$, we will have the number 1. In those that are simultaneously multiples of 3 and 4, we will have 2, and in the others, the number 0. In addition, the representation will be periodic with a period of length 12. To find the digits in a given position in the sum, we need to study how many divisors greater than 2 the position has. Among the natural numbers less than 60, none have more than 8 positive integer divisors greater than 2. Thus, in the sum of decimals:
$$
0, \overline{001}+0, \overline{0001}+0, \overline{00001}+\ldots+\overline{0,00 \ldots 01}
$$
there will be no "carry over" in the first 59 places and the digit in the 59th position will be 1, as 59 has only one divisor greater than 2. The other positions will have numbers less than or equal to 8, as 48 is the natural number less than 60 that has the most positive divisors and only 8 of them are greater than 2. Since 60 has 10 positive divisors greater than 2, namely, $3,4,5,6,10,12,15,20,30$ and 60, the "carry over" will occur when we add this decimal to the previous ones and thus the 59th place will have an increment of one unit and will become 2. It remains to verify the contribution of the other decimals in positions of order greater than 60, taking into account the "carry over" in the addition algorithm. The other places of these decimals and the remaining ones that have not yet been accounted for can contribute through the "carry over" in the sum algorithm with an estimated number of
$$
\begin{aligned}
& \frac{60}{10^{61}}+0, \underbrace{\overline{00 \ldots 01}}_{61 \text { digits }}+0, \underbrace{\overline{00 \ldots 01}}_{62 \text { digits }}+\ldots< \\
& \frac{60}{10^{61}}+\frac{1}{9 \cdot 10^{60}}+\frac{1}{9 \cdot 10^{61}}+\ldots= \\
& \frac{60}{10^{61}}+\frac{1}{81 \cdot 10^{59}}< \\
& \frac{1}{10^{59}}
\end{aligned}
$$
Therefore, we will not need to account for other contributions in the 59th position after the decimal point and its digit in the sum is 2.
[^0]: ${ }^{2}$ There are tournaments with the "Bilbao Scoring" or "Sofia Rule", which, among other conditions, set a win to be worth 3 points, a draw to be worth 1 point, and a loss to be worth zero points.
${ }^{3}$ As each game, regardless of the outcome, adds 1 to the total points of the tournament (in a win by the player with the white pieces, he will gain one point and vice versa, and in a draw, both gain half a point).
${ }^{4}$ If he wins all the games he plays.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the figure below, the sides of rectangle $A B C D$ have been extended so that $E B=2 A B$, $A H=3 A D$, $D G=2 D C$, and $F C=3 B C$. Find the ratio between the areas of quadrilateral $E H G F$ and rectangle $A B C D$.
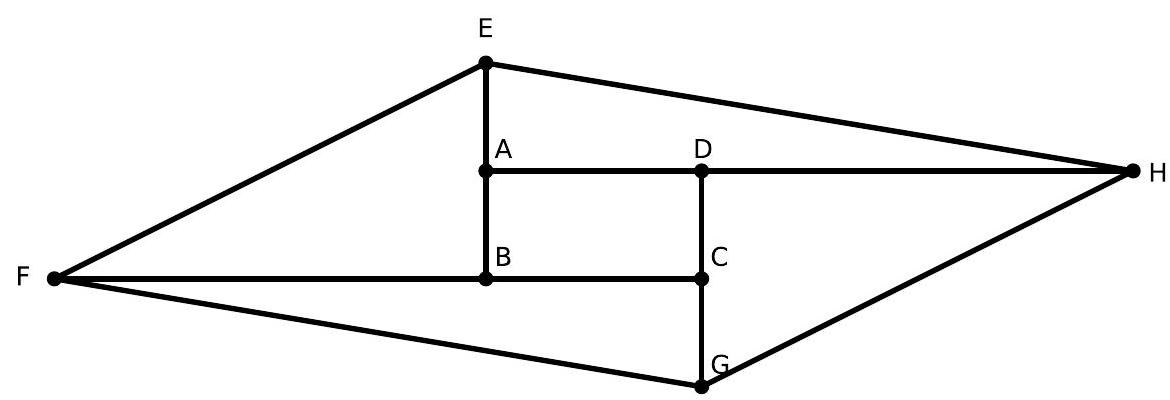
|
Solution
The area of quadrilateral $E F G H$ can be decomposed into four triangles and one rectangle. If $S=A_{A B C D}$, we have
$$
\begin{aligned}
A_{E A H} & =(E A \cdot A H) / 2 \\
& =(A B \cdot 3 A D) / 2 \\
& =3 S / 2 \\
A_{D H G} & =(D H \cdot D G) / 2 \\
& =(2 A D \cdot 2 D C) / 2 \\
& =2 S \\
A_{F C G} & =(F C \cdot C G) / 2 \\
& =(3 B C \cdot D C) / 2 \\
& =3 S / 2 \\
A_{F B E} & =(F B \cdot B E) / 2 \\
& =(2 B C \cdot 2 A B) / 2 \\
& =2 S
\end{aligned}
$$
Therefore,
$$
\begin{aligned}
\frac{A_{E F G H}}{A_{A B C D}} & =\frac{3 S / 2+2 S+3 S / 2+2 S+S}{S} \\
& =8
\end{aligned}
$$
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
During the FIFA World Cup, several mathematicians were called upon to speak about the teams' chances of qualification. In the group stage, each group is formed by four teams, and each team faces each of the other teams exactly once. In case of a win, a team earns 3 points; in case of a draw, 1 point; and in case of a loss, 0 points. It is known that the top two teams qualify for the next round. If two teams tie with the same number of points, the tiebreaker is the goal difference. What is the minimum number of points for a team to qualify without depending on the results of other matches?
Note: Remember that to show that the number $k$ found is indeed the minimum, in addition to showing that such a quantity is sufficient to guarantee victory, you must also ensure that there are examples of scores where teams can total no more than $k-1$ points and not advance to the next round.
|
Solution
The minimum number of points is 7 points. First, let's see that with 6 points a team may not qualify. Let $A, B, C$ and $D$ be the teams in a certain group and consider the following table of results:
| Winner | Result | Loser |
| :---: | :---: | :---: |
| $A$ | $2 \times 0$ | $D$ |
| $B$ | $1 \times 0$ | $D$ |
| $C$ | $1 \times 0$ | $D$ |
| $A$ | $2 \times 0$ | $B$ |
| $B$ | $2 \times 0$ | $C$ |
| $C$ | $1 \times 0$ | $A$ |
Note that $C$ scored 6 points and finished in third place because its goal difference is 0, placing it behind $A$ and $B$ who have the same number of points but goal differences of 3 and 1, respectively. Therefore, with 6 points, a team may not qualify.
If a team $A$ scores 7 points, then it has won against two teams. These two teams can only reach a maximum of 6 points since they have lost at least one game. Therefore, $A$ will, in the worst case, be ahead of these two teams, and its qualification is guaranteed.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A cricket can jump two distances: 9 and 8 meters. It competes in a 100-meter race to the edge of a cliff. How many jumps must the cricket make to reach the end of the race without going past the finish line and falling off the cliff?
#
|
Solution
First solution: Suppose the cricket only jumps 9 meters. On its twelfth jump, it would fall off the cliff, since $9 \cdot 12 = 108 \, \text{m}$. Since it can also jump 8 meters, it is enough to "exchange" 8 jumps of 9 meters for jumps of 8 meters. Thus, we have 4 jumps of 9 meters and 8 jumps of 8 meters, for a total of $4 + 8 = 12$ jumps.
This is the only combination of jumps possible, because if the cricket makes fewer than 4 jumps of 9 meters, the maximum distances it can travel without falling off the cliff are: $3 \cdot 9 + 9 \cdot 8 = 99 \, \text{m}, 2 \cdot 9 + 10 \cdot 8 = 98 \, \text{m}, 1 \cdot 9 + 11 \cdot 8 = 97 \, \text{m}, \text{and} 0 \cdot 9 + 12 \cdot 8 = 96 \, \text{m}$. Furthermore, if the cricket makes more than 4 jumps of 9 meters, it must make fewer than 8 jumps of 8 meters, and thus the maximum distances it can travel without falling off the cliff are: $5 \cdot 9 + 6 \cdot 8 = 93 \, \text{m}, 6 \cdot 9 + 5 \cdot 8 = 94 \, \text{m}, 7 \cdot 9 + 4 \cdot 8 = 95 \, \text{m}, 8 \cdot 9 + 3 \cdot 8 = 96 \, \text{m}, 9 \cdot 9 + 2 \cdot 8 = 97 \, \text{m}, 10 \cdot 9 + 1 \cdot 8 = 98 \, \text{m}, \text{and} 11 \cdot 9 + 0 \cdot 8 = 99 \, \text{m}$. Since none of these distances equal 100, there is no other combination.
Second solution: Let $x$ be the number of 9-meter jumps and $y$ be the number of 8-meter jumps. We want to determine $x + y$, knowing that:
$$
\begin{aligned}
100 & = 9x + 8y \\
& = 8(x + y) + x
\end{aligned}
$$
Since 100 leaves a remainder of 4 when divided by 8, the same must be true for the number $8(x + y) + x$. That is, $x$ must leave a remainder of 4 when divided by 8, since $8(x + y)$ is already a multiple of 8. If $x > 4$, we know that $x$ is at least $8 \cdot 1 + 4 = 12$, which is the next number that leaves a remainder of 4 when divided by 8 after 4. If the cricket makes 12 jumps of $9 \, \text{m}$, it will reach $9 \cdot 12 = 108 \, \text{m}$ and fall off the cliff. Therefore, $x = 4$, and after substituting $x$ into the equation above, we can conclude that $y = (100 - 9 \cdot 4) / 8 = 8$. Thus, the cricket must make $4 + 8 = 12$ jumps.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The king is a chess piece that can move only one square vertically, one horizontally, or one diagonally. We say that a king attacks a square if it can occupy it with a single move. For example, a king placed in the central squares of a $6 \times 6$ board attacks 8 squares, a king placed on the side squares attacks 5 squares, and a king positioned in one of the four corners of the board attacks only 3 squares.
a) Consider a $6 \times 6$ board. What is the minimum number of kings that can be placed on the board so that all the squares of the board are either occupied or attacked by one of the kings?
b) Still considering the $6 \times 6$ board, what is the maximum number of kings that can be placed on the board so that they do not attack each other?
#
|
Solution
a) Divide the $6 \times 6$ board into 4 $3 \times 3$ boards. If one of these four regions does not have a king, the central cell of that region will not be occupied or attacked by any king. Therefore, at least 4 kings are needed. If we place a king in the central cell of each $3 \times 3$ board, then all cells of the board will be attacked. Thus, the minimum number of kings is 4.
b) Divide the $6 \times 6$ board into 9 $2 \times 2$ boards. If two kings are in the same $2 \times 2$, then they will be attacking each other. Therefore, we can have at most 9 kings. If we place a king in the top-left corner of each of these $2 \times 2$ boards, we will have 9 kings that do not attack each other.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all values of $x$ satisfying
$$
\frac{x+\sqrt{x+1}}{x-\sqrt{x+1}}=\frac{11}{5}
$$
|
Solution
The equation can be rewritten as
$$
\begin{aligned}
\frac{x+\sqrt{x+1}}{x-\sqrt{x+1}} & =\frac{11}{5} \\
5 x+5 \sqrt{x+1} & =11 x-11 \sqrt{x+1} \\
16 \sqrt{x+1} & =6 x \\
8 \sqrt{x+1} & =3 x
\end{aligned}
$$
Squaring both sides of the last equation, we get
$$
\begin{aligned}
9 x^{2} & =64(x+1) \\
9 x^{2}-64 x-64 & =0
\end{aligned}
$$
The roots of this equation are $x=8$ and $x=-\frac{8}{9}$. Of these solutions, only $x=8$ satisfies the given equation.
#
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Consider a square $ABCD$ with center $O$. Let $E, F, G$, and $H$ be points on the interiors of sides $AB, BC, CD$, and $DA$, respectively, such that $AE = BF = CG = DH$. It is known that $OA$ intersects $HE$ at point $X$, $OB$ intersects $EF$ at point $Y$, $OC$ intersects $FG$ at point $Z$, and $OD$ intersects $GH$ at point $W$. Let $x$ and $y$ be the lengths of $AE$ and $AH$, respectively.
a) Given that Area $(EFGH) = 1 \text{ cm}^2$, calculate the value of $x^2 + y^2$.
b) Verify that $HX = \frac{y}{x+y}$. Then, conclude that $X, Y, Z$, and $W$ are vertices of a square.
c) Calculate
Area $(ABCD) \cdot$ Area $(XYZW)$.
|
Solution
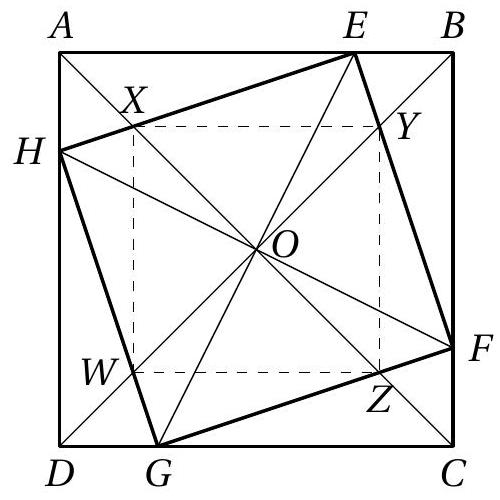
a) Let $x$ and $y$ be the lengths of $A E$ and $A H$, respectively. Given that $A H = E B$, $A E = B F$, and $\angle H A E = \angle E B F$, it follows that triangles $A E H$ and $E B F$ are congruent. Therefore,
$$
\angle H E F = 180^{\circ} - \angle H E A - \angle B E F = 180^{\circ} - \angle E F B - \angle B E F = 90^{\circ}
$$
Similarly, we can conclude that $\angle E F G = \angle F G H = \angle G H E = 90^{\circ}$. By the Pythagorean Theorem, $H E^{2} = x^{2} + y^{2}$. The same applies to the other sides of the rectangle $H E F G$, i.e., $E H = E F = F G = G H = 1$. Therefore, its area is $1 = A_{H E F G} = x^{2} + y^{2}$.
b) Since $A C$ is the angle bisector of $\angle H A E$, it follows from the Angle Bisector Theorem that
$$
\begin{aligned}
\frac{H X}{E X} & = \frac{A H}{A E} \\
\frac{H X}{H X + E X} & = \frac{A H}{A H + A E} \\
H X & = \frac{y}{x + y}
\end{aligned}
$$
Similarly, $E X = \frac{x}{x + y}$. The diagonal $B D$ is also the angle bisector of $\angle E B F$ and $\triangle E B F \equiv A H E$. Therefore, $E Y = H X = \frac{y}{x + y}$, and by analogy with the initial argument, now applied to the square $H E F G$, we can conclude that the points $X, Y, Z$, and $W$ are vertices of a square.
c) Applying the Pythagorean Theorem to triangle $E X Y$, we get
$$
\begin{aligned}
X Y^{2} & = E X^{2} + E Y^{2} \\
& = \frac{x^{2}}{(x + y)^{2}} + \frac{y^{2}}{(x + y)^{2}}
\end{aligned}
$$
Therefore, the area of the quadrilateral $X Y Z W$ is Area $(X Y Z W) = \frac{x^{2} + y^{2}}{(x + y)^{2}}$. Since Area $(E F G H) = 1$, it follows that $x^{2} + y^{2} = 1$ and that
$$
\text{Area}(A B C D) \cdot \text{Area}(X Y Z W) = (x + y)^{2} \cdot \frac{x^{2} + y^{2}}{(x + y)^{2}} = 1
$$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a school, $n$ clubs must be formed, with $n \geq 3$ and each with 3 members, such that for each pair of clubs there is exactly one student who is a member of both.
a) Give an example of a distribution of 7 clubs that satisfy the mentioned conditions.
b) Verify that if a student belongs to 4 clubs, then he must belong to all the others.
c) Determine the minimum value of $n$ such that for any set of clubs that satisfy these conditions, it is mandatory for one student to be in all of them.
|
Solution
a) Naming the students as $A, B, C, D, E$ and $F$, the following sets represent 7 clubs that meet the conditions stated:
$$
\{A, B, C\},\{A, D, E\},\{A, F, G\},\{B, E, F\},\{B, D, G\},\{C, D, F\},\{C, E, G\}
$$
b) Suppose student $A$ belongs to the following 4 clubs:
$$
\{A, B, C\},\{A, D, E\},\{A, F, G\},\{A, H, I\}
$$
Suppose there exists a club $K$ formed by students $\{M, N, P\}$ of which $A$ is not a part. Then, $K$ must have at least one element from each of the following 4 disjoint sets:
$$
\{B, C\},\{D, E\},\{F, G\},\{H, I\}
$$
This is a contradiction, because for this to happen, $K$ would need to have at least 4 elements. Therefore, $A$ must belong to all clubs.
c) We claim that the minimum value is $n=8$. From the previous item, it suffices to verify that in this case some student must belong to at least 4 clubs. Suppose this does not happen, that is, that each student belongs to at most 3 clubs and consider a generic club $w$ formed by students $\{X, Y, Z\}$. Each of the elements of $w$ can be in at most 2 more clubs. Since any other club must share a student in common with $w$, counting the other clubs that contain $X, Y$ or $Z$, we conclude that there can be at most $2+2+2=6$ other distinct clubs besides $w$. Thus, the total number of clubs would be at most $6+1=7$, which is a contradiction.
Comment: It is possible to construct the example from item a) by considering the segments and the circle of the Fano diagram, as illustrated below. In it, each segment passing through 3 marked points and the central circle represent a club. Note that these segments and the central circle have a point of intersection.

|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $A B C$ be a right triangle with $\angle B A C=90^{\circ}$ and $I$ the point of intersection of its angle bisectors. A line through $I$ intersects the sides $A B$ and $A C$ at $P$ and $Q$, respectively. The distance from $I$ to the side $B C$ is $1 \mathrm{~cm}$.
a) Find the value of $P M \cdot N Q$.
b) Determine the minimum possible value for the area of triangle $A P Q$.
Hint: If $x$ and $y$ are two non-negative real numbers, then $x+y \geq 2 \sqrt{x y}$.
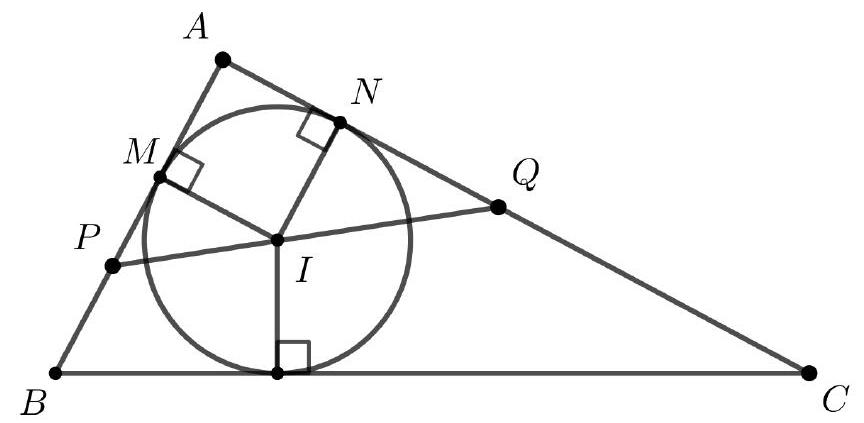
|
Solution
a) If $\angle A P Q=\alpha$, it follows that $\angle M I P=90^{\circ}-\alpha$ and
$$
\angle N I Q=180^{\circ}-\angle M I N-\angle M I P=\alpha
$$
Therefore, triangles $I M P$ and $N I Q$ are similar, and thus
$$
\frac{I M}{N Q}=\frac{P M}{I N} \Rightarrow P M \cdot N Q=I M \cdot I N=1
$$
b) Let $x=M P$ and $y=N Q$. Since $A M I N$ is a square with a side length of $1 \mathrm{~cm}$, the area of triangle $A P Q$ is given by
$$
\begin{aligned}
\frac{A P \cdot A Q}{2} & =\frac{(1+x)(1+y)}{2} \\
& =\frac{1+x y+x+y}{2}
\end{aligned}
$$
From the previous item, $x y=1$. Additionally, by the inequality presented in the hint, $x+y \geq 2 \sqrt{1}=2$. Thus, the minimum area is $\frac{1+1+2}{2}=2$ and can be achieved by setting $A P=A Q=2$. Note: The inequality presented as a hint is a special case of the arithmetic mean-geometric mean inequality $(M A \geq M G)$. To verify this case, from $(\sqrt{x}-\sqrt{y})^{2} \geq 0$, it follows that
$$
x-2 \sqrt{x y}+y \geq 0 \Rightarrow x+y \geq 2 \sqrt{x y}
$$
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be an odd function, that is, a function that satisfies $-f(x)=f(-x)$ for all $x \in \mathbb{R}$. Suppose that $f(x+5)=f(x)$ for all $x \in \mathbb{R}$ and that $f(1 / 3)=1$. Determine the value of the sum:
$$
f(16 / 3)+f(29 / 3)+f(12)+f(-7)
$$
#
|
Solution
We have
$$
\begin{aligned}
f\left(\frac{1}{3}\right) & =1 \\
f\left(\frac{1}{3}+5\right) & =1 \\
f\left(\frac{16}{3}\right) & =1
\end{aligned}
$$
Since $f$ is an odd function, i.e., $f(-x)=-f(x)$, it follows that
$$
\begin{aligned}
f\left(-\frac{1}{3}\right) & =-1 \\
f\left(-\frac{1}{3}+5+5\right) & =-1 \\
f\left(\frac{29}{3}\right) & =-1
\end{aligned}
$$
and
$$
\begin{aligned}
f(-7) & =f(-12+5) \\
& =f(-12) \\
& =-f(12)
\end{aligned}
$$
Finally,
$$
\begin{aligned}
f(16 / 3)+f(29 / 3)+f(12)+f(-7) & = \\
1+(-1)+f(12)-f(12) & =0
\end{aligned}
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the following figure, $\angle C A B=2 \cdot \angle C B A, A D$ is an altitude and $M$ is the midpoint of $A B$. If $A C=2 \text{ cm}$, find the length of the segment $D M$.
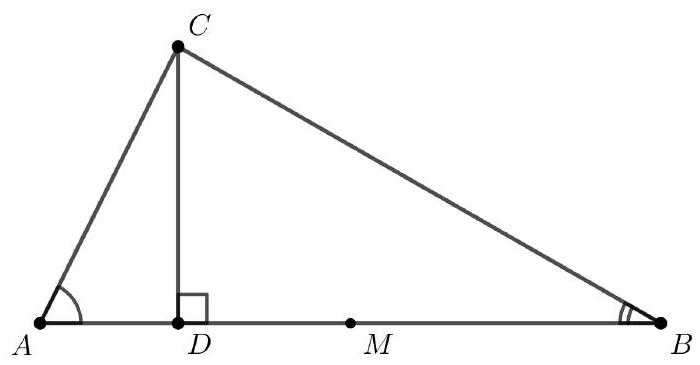
#
|
Solution
Let $K$ be the midpoint of $A C$. Since the circle with center $K$ and diameter $A C$ passes through $D$, it follows that $C K=A K=D K=1 \mathrm{~cm}$. From this last equality, it follows that triangle $A D K$ is isosceles and thus $\angle K D A=\angle K A D$. The segment $K M$ is the midline of triangle $A B C$, implying that $K M \| B C$ and thus $\angle K M D=\angle C B A$. By the Exterior Angle Theorem,
$$
\angle D K M=\angle A D K-\angle D M K=\angle D M K
$$
Finally, since the last equalities show that triangle $D K M$ is isosceles, it follows that $D M=D K=1 \mathrm{~cm}$.
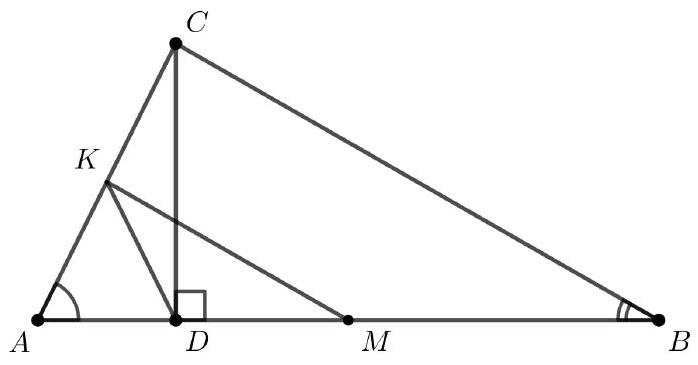
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $A B C D$ be a rectangle such that $A B=\sqrt{2} B C$. Let $E$ be a point on the semicircle with diameter $A B$, as indicated in the following figure. Let $K$ and $L$ be the intersections of $A B$ with $E D$ and $E C$, respectively. If $A K=2 \mathrm{~cm}$ and $B L=9 \mathrm{~cm}$, calculate, in $\mathrm{cm}$, the length of the segment $K L$.
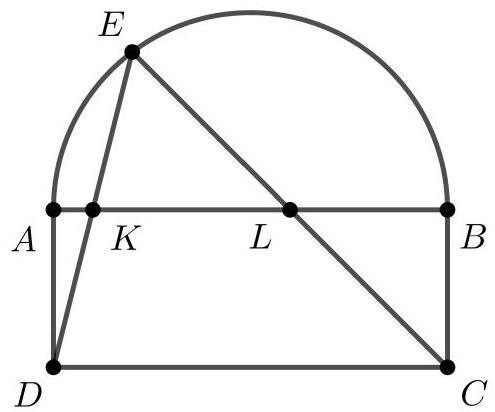
|
Solution
Let $x$ and $y$ be the lengths of the orthogonal projections of segments $E K$ and $E L$ onto segment $A B$, and $P$ be the orthogonal projection of $E$ onto $A B$. Also, let $h = E P$. By the similarity of triangles, we have
$$
\frac{2}{x} = \frac{B C}{h} \text{ and } \frac{9}{y} = \frac{B C}{h}
$$
Therefore,
$$
\begin{aligned}
K L & = x + y \\
& = \frac{11 h}{B C}
\end{aligned}
$$
Since $E A B$ is a right triangle at $E$, it follows from the metric relations of right triangles that
$$
\begin{aligned}
h^{2} & = A P \cdot P B \\
& = (2 + x)(9 + y) \\
& = \left(2 + \frac{2 h}{B C}\right)\left(9 + \frac{9 h}{B C}\right) \\
& = 18\left(1 + \frac{h}{B C}\right)^{2}
\end{aligned}
$$
Therefore,
$$
1 + \frac{h}{B C} = \frac{h}{3 \sqrt{2}}
$$
Moreover, from
it follows that
$$
\sqrt{2} B C = A K + K L + L B = 11\left(1 + \frac{h}{B C}\right)
$$
$$
\frac{h}{3 \sqrt{2}} = \frac{\sqrt{2} B C}{11}
$$
That is, $\frac{h}{B C} = \frac{6}{11}$ and $K L = \frac{11 h}{B C} = 6 \text{ cm}$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On planet $X$, there are 100 alien countries in conflict with each other. To prevent a world war, these countries organize themselves into military alliance groups for mutual protection. We know that the alliances follow these rules:
1) No alliance contains more than 50 countries.
2) Any two countries belong to at least one alliance.
a) Is it possible for a country to participate in fewer than three military alliances?
b) What is the minimum number of alliances possible for these two conditions to be satisfied?
|
Solution
a) It is not possible. Suppose that country $A$ belongs to at most two alliances. In this case, since each alliance has at most 50 countries, country $A$ is a member of the same alliance with at most $49+49=98$ countries. Since there are 99 countries distinct from $A$, at least one of them will not be in an alliance with $A$, which conflicts with rule (2).
b) Since each country participates in at least 3 alliances, if we sum the number of participations of all countries in all alliances, we will get at least the number $3 \cdot 100=300$. On the other hand, each alliance accounts for at most 50 participations. Thus, the minimum number of alliances cannot be less than $\frac{300}{50}=6$. To verify that this number is indeed the smallest possible, it suffices to exhibit an example of a configuration in which it is achieved. Divide the 100 countries into 4 groups of 25 countries: $A$, $B, C, D$. Now, form the alliances of 50 countries consisting of all 6 combinations of two of these groups:
$$
A \cup B, A \cup C, A \cup D, B \cup C, B \cup D \text { and } C \cup D
$$
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the drawing to the side, triangle $ABC$ is equilateral and $BD = CE = AF = \frac{AB}{3}$. The ratio $\frac{EG}{GD}$ can be written in the form $\frac{m}{n}, \operatorname{gcd}(m, n)=1$. What is the value of $m+n$?
#
|
Solution
Notice that $\frac{E G}{G D}=\frac{[E B G]}{[B G D]}$. Now, $\frac{[E B G]}{[B C F]}=\frac{\frac{1}{2} E B \cdot B G \cdot \sin(\angle E B G)}{\frac{1}{2} B C \cdot B F \cdot \sin(\angle C B F)}$. Since $\angle E B G=\angle C B F$, we have
$$
\frac{[E B G]}{[B C F]}=\frac{E B \cdot B G}{B C \cdot B F}
$$
Similarly,
$$
\frac{[B G D]}{[A B F]}=\frac{B G \cdot B D}{B A \cdot B F}
$$
Dividing (1) by (2), we get $\frac{[E B G]}{[B G D]} \cdot \frac{[A B F]}{[B C F]}=\frac{E B \cdot B A}{B C \cdot B D}$. Finally, since $\frac{[A B F]}{[B C F]}=$ $\frac{A F}{C F}=\frac{1}{2}$, we have
$$
\frac{[E B G]}{[B G D]}=\frac{E B \cdot B A \cdot C F}{B C \cdot B D \cdot A F}=\frac{2}{3} \cdot 3 \cdot 2=4
$$
Therefore, $\frac{E G}{G D}=\frac{4}{1}$ and, hence, $m+n=5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the greatest result we can find when we divide a two-digit number by the sum of its digits?
|
We are looking for the maximum value of $\frac{10 a+b}{a+b}$, where $a$ and $b$ represent digits, with at least one different from 0. We have
$$
\frac{10 a+b}{a+b}=\frac{10 a+10 b-9 b}{a+b}=\frac{10 a+10 b}{a+b}-\frac{9 b}{a+b}=10-\frac{9 b}{a+b} \leq 10
$$
Therefore, if we can find $a$ and $b$ such that $\frac{10 a+b}{a+b}=10$, we will have the maximum result. Note that this occurs when $b=0$, that is:
$$
\frac{10}{1}=\frac{20}{2}=\frac{30}{3}=\frac{40}{4}=\frac{50}{5}=\frac{60}{6}=\frac{70}{7}=\frac{80}{8}=\frac{90}{9}=10 .
$$
Therefore, the answer is 10.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Pedro decided to take all his children, boys and girls, for ice cream at the Ice Cream Math parlor. At the parlor, there are 12 different ice cream flavors, and each child ordered a combo with 3 scoops of ice cream. After leaving the parlor, Pedro realized that exactly two scoops of each available flavor were ordered in total.
a) Knowing that Pedro did not have ice cream, what is the total number of his children (girls and boys)?
b) Pedro looked more closely at the flavors each one ordered and noticed that no flavor was chosen by both a boy and a girl, that is, if a boy chose a flavor, no girl chose that same flavor. Knowing that at least one of his children is a boy and that he has more daughters than sons, determine the number of his daughters.
|
Solution
a) Let $n$ be the number of Pedro's children. In total, $3 n$ scoops of ice cream were ordered. Since each of the 12 flavors was ordered twice, we have $3 n=2 \cdot 12$, that is, $n=8$. Therefore, Pedro has 8 children.
b) Let $x$ be the number of boys and $y$ be the number of girls. From the previous item, we know that $x+y=8$. Since there is at least one child and there are more girls than boys, we know that: $0<x<y$. Given that no flavor was ordered simultaneously by boys and girls, the flavors can be separated into boys' flavors and girls' flavors. Thus, $3 x$ is equal to twice the number of boys' flavors, as exactly two scoops of each flavor were ordered and no girl could order one of the boys' flavors. Consequently, $x$ is even. Similarly, $y$ is also even. Since $0<x<y$ and $x+y=8$, we can conclude that $x=2$ and $y=6$. Therefore, Pedro has 6 daughters.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a$ and $b$ be any positive real numbers. Determine the value of the expression
$$
\frac{\sqrt{\frac{a b}{2}}+\sqrt{8}}{\sqrt{\frac{a b+16}{8}+\sqrt{a b}}}
$$
|
Solution
Let $x=\sqrt{\frac{a b}{2}}+\sqrt{8}$. Then:
$$
\begin{aligned}
x^{2} & =\frac{a b}{2}+4 \sqrt{a b}+8 \\
& =4\left(\frac{a b+16}{8}+\sqrt{a b}\right) \\
& =4\left(\sqrt{\frac{a b+16}{8}+\sqrt{a b}}\right)^{2}
\end{aligned}
$$
Thus, the value of the desired expression is
$$
\begin{aligned}
\frac{\sqrt{\frac{a b}{2}}+\sqrt{8}}{\sqrt{\frac{a b+16}{8}+\sqrt{a b}}} & =\frac{x}{x / 2} \\
& =2
\end{aligned}
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $D$ be a point on side $A B$ of triangle $\triangle A B C$ and $F$ the intersection of $C D$ and the median $A M$. If $A F=A D$, find the ratio between $B D$ and $F M$.
|
Solution
Let $E$ be the intersection point of the line parallel to side $AB$, passing through point $M$, with segment $CD$. Since $ME \| AB$, it follows that $\angle MED = \angle EDA$. Moreover, since $\angle AFD = \angle EFM$ and triangle $\triangle AFD$ is isosceles, we can conclude that $\triangle EFM$ is also isosceles with $EM = FM$. Given that $M$ is the midpoint of $BC$ and $EM \| BD$, segment $EM$ is a midsegment of triangle $\triangle CDB$. Thus,
$$
\frac{BD}{FM} = \frac{BD}{EM} = 2
$$
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Augusto has a wire that is $10 \mathrm{~m}$ long. He makes a cut at a point on the wire, obtaining two pieces. One piece has a length of $x$ and the other has a length of $10-x$ as shown in the figure below:
Augusto uses the two pieces of wire to make two squares.
a) What is the length of the side of each of the squares? What is the area of each?
b) What is the length of each of the two pieces of wire so that the sum of the areas of the squares obtained is minimized?
c) Suppose Augusto cuts the wire into ten pieces and uses each one to make a square. What should be the size of each piece so that the sum of the areas of the squares obtained is minimized?
|
Solution
In this problem, all lengths are given in meters and areas in square meters.
a) A piece of rope has length $x$ and another piece of rope has length $10-x$. Since a square has four sides of equal length, one square will have a side length of $\frac{x}{4}$ and the other square will have a side length of $\frac{10-x}{4}$.
The area of a square with side length $\ell$ is $\ell^{2}$. Therefore, one square will have an area of $\left(\frac{x}{4}\right)^{2}=\frac{x^{2}}{16}$, while the other square will have an area of $\left(\frac{10-x}{4}\right)^{2}=\frac{100-20 x+x^{2}}{16}$.
b) Let $S(x)$ be the sum of the areas of the two squares. From the previous part, we have
$$
S(x)=\frac{x^{2}}{16}+\frac{100-20 x+x^{2}}{16}=\frac{100-20 x+2 x^{2}}{16}=\frac{1}{8} x^{2}-\frac{5}{4} x+\frac{25}{4}
$$
which is a quadratic function. The minimum of a function of the form
$$
f(x)=a x^{2}+b x+c
$$
with $a>0$ is achieved at $x=\frac{-b}{2 a}$. Thus, the minimum area will be achieved if
$$
x=-\frac{\left(-\frac{5}{4}\right)}{2 \frac{1}{8}}=5
$$
In other words, if the rope is cut exactly in the middle!
c) From the previous part, we know that to minimize the sum of the areas, it is necessary to cut the rope exactly in the middle. Well, we claim that to minimize the area with nine cuts (i.e., creating ten squares), it is necessary that all pieces of rope be equal. To show this, consider the following argument: if two of the ten pieces of rope were different, it would be possible to reduce the area by cutting the pieces of rope so that these two were equal (we are using the previous part). Therefore, any two pieces of rope must be equal. Hence, all must be equal!
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Julian trains on a $3 \mathrm{~km}$ track. He walks the first kilometer, runs the second, and cycles the third. If he had cycled the entire track, it would have taken him 10 minutes less. Julian runs at twice the speed he walks, and cycles at three times the speed he walks. How long does Julian take to run $1 \mathrm{~km}$?
|
Solution
Let $t$ be the time, in minutes, that Julian takes to cycle one kilometer. Since he cycles at three times the speed he walks, he walks one kilometer in $3 t$ minutes, and since he runs at twice the speed he walks, he runs one kilometer in $3 t / 2$ minutes. Thus, he took
$$
t+3 t+\frac{3 t}{2}=\frac{11 t}{2}
$$
minutes to cover the three kilometers of the track. If he had covered the three kilometers of the track by bicycle, he would have taken $3 t$ minutes. Thus, according to the problem statement, we have (in minutes)
$$
\frac{11 t}{2}-3 t=10
$$
and solving the above equation, we get $t=4$ minutes. Finally, Julian runs one kilometer in $3 t / 2=6$ minutes.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Carla wrote on the blackboard the integers from 1 to 21. Diana wants to erase some of them so that the product of the remaining numbers is a perfect square.
a) Show that Diana must necessarily erase the numbers 11, 13, 17, and 19 to achieve her goal.
b) What is the minimum number of numbers that Diana must erase to achieve her goal?
#
|
Solution
a) If Diana decides not to erase the number 11, then the product of the remaining numbers will be of the form $P=11 \times A$. Since 11 is the only multiple of 11 among the numbers written by Carla, $A$ is the product of numbers not divisible by 11, and thus $A$ is not a multiple of 11. Therefore, $P$ would be a multiple of 11 but not a multiple of $11^{2}$, so $P$ would not be a perfect square. Similarly, we can see that Diana must also erase the numbers 13, 17, and 19.
b) If Diana erases only the numbers 11, 13, 17, and 19, the product of the remaining 17 numbers would be
$$
1 \times 2 \times 3 \times \cdots \times 10 \times 12 \times 14 \times 15 \times 16 \times 18 \times 20 \times 21=\left(2^{9} \times 3^{4} \times 5^{2} \times 7\right)^{2} \times 21
$$
This number is not a perfect square, so she needs to erase at least one more number. From the factorization above, it is easy to see that if Diana also erases the number 21, she will achieve her goal. Therefore, the smallest number of numbers that Diana must erase is 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The squares of the natural numbers from 1 to 99 were written one after another, forming the number 14916253649 ... What is the digit that occupies the $100^{th}$ position? (The positions are counted from left to right: the $1^{st}$ position is the 1, the $2^{nd}$ is the 4, etc.)
|
Separating the numbers whose squares have 1, 2, and 3 digits, we have:
1 digit: $1, 2, 3$
2 digits: $4, 5, 6, 7, 8, 9$
3 digits: $10, 11, 12, \ldots, 31$
Up to $31^{2}$, the sequence has $3+12+66=81$ digits.
$$
\underbrace{1^{2}, 2^{2}, 3^{2}}_{1 \times 3 \text { digits }}, \underbrace{4^{2}, \ldots, 9^{2}}_{2 \times 6=12 \text { digits }}, \underbrace{10^{2}, \ldots, 31^{2}}_{3 \times 22=66 \text { digits }}
$$
Thus, we are missing $100-81=19$ digits to reach the $100^{\text{th}}$ digit. Since $19=4 \times 4+3$, we will have 4 more numbers, each with 4 digits, which are $32^{2}, 33^{2}, 34^{2}$, and $35^{2}$, plus the first 3 digits (thousands, hundreds, tens) of the number: $36^{2}=1296$.
$$
\underbrace{1^{2}, 2^{2}, 3^{2}}_{1 \times 3 \text { digits }}, \underbrace{4^{2}, \ldots, 9^{2}}_{2 \times 6=12 \text { digits }}, \underbrace{10^{2}, \ldots, 31^{2}}_{3 \times 22=66 \text { digits }}, \underbrace{32^{2}, 33^{2}, 34^{2}, 35^{2}}_{4 \times 4=16 \text { digits }}, 12 \underbrace{9}_{100^{2} \text { digit }} 6
$$
Therefore, the number is 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the figure, we have a target at which darts are thrown. The inner circle is worth 10 points, the intermediate ring is worth 5 points, the outer ring is worth 3 points, and the external area is worth 0 points. If a dart hits a line, the score will be the average of the points of the regions divided by the line. In each turn, the player throws 4 darts.
a) The marks on the target in the following figure indicate the darts thrown by Leo. How many points did he score?
b) How many different points can be obtained by throwing the 4 darts, without any of them hitting any line?
c) William intends to score 30 points in his 4 throws. In how many different ways can he achieve this sum, regardless of the sequence of the darts, i.e., the sequences $(10,10,10,0)$ and $(0,10,10,10)$ are considered the same way to sum 30 points $(3 \cdot 10=30)$?
|
Solution
a) Leo scored $10+5+\frac{5+3}{2}+\frac{3+0}{2}=20.5$ points.
b) The minimum score is 0 and the maximum is 40. Therefore, it is enough to verify for each of the natural numbers in this interval the possibility of being a possible sum. Let's construct a table, showing an example for each possible sum.
| $1^{\text{st}}$ dart | $2^{\text{nd}}$ dart | $3^{\text{rd}}$ dart | $4^{\text{th}}$ dart | Sum |
| :---: | :---: | :---: | :---: | :---: |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 3 | 3 |
| 0 | 0 | 0 | 5 | 5 |
| 0 | 3 | 3 | 0 | 6 |
| 5 | 0 | 0 | 3 | 8 |
| 3 | 3 | 0 | 3 | 9 |
| 5 | 5 | 0 | 0 | 10 |
| 5 | 3 | 3 | 0 | 11 |
| 3 | 3 | 3 | 3 | 12 |
| 10 | 3 | 0 | 0 | 13 |
| 5 | 3 | 3 | 3 | 14 |
| 5 | 0 | 0 | 10 | 15 |
| 5 | 3 | 5 | 3 | 16 |
| 10 | 5 | 0 | 3 | 18 |
| 3 | 3 | 10 | 3 | 19 |
| 10 | 10 | 0 | 0 | 20 |
| 10 | 5 | 3 | 3 | 21 |
| 10 | 3 | 10 | 0 | 23 |
| 10 | 0 | 10 | 5 | 25 |
| 10 | 3 | 3 | 10 | 26 |
| 10 | 10 | 5 | 3 | 28 |
| 10 | 10 | 10 | 0 | 30 |
| 10 | 10 | 3 | 10 | 33 |
| 10 | 10 | 10 | 5 | 35 |
| 10 | 10 | 10 | 10 | 40 |
| | | | | |
Therefore, there are 25 different scores.
c) In addition to the scores of 0, 3, 5, and 10, we have the scores of the lines which can be 1.5 or 4 or 7.5. To achieve 30 points without hitting the region worth 7.5, we must hit at least two darts in the region worth 10 points, that is, $(10; 10; 5; 5)$ or $(10; 10; 10; 0)$. In addition to these possibilities, we also have $(10; 7.5; 7.5; 5)$ and $(7.5; 7.5; 7.5; 7.5)$, totaling 4 possibilities altogether.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a fruit shop, Jaime noticed that an orange costs the same as half an apple plus half a real, and he also noticed that a third of an apple costs the same as a quarter of an orange plus half a real. With the value of 5 oranges plus 5 reals, how many apples can Jaime buy?
#
|
Solution
If an orange costs the same as half an apple plus half a real, then, 2 oranges cost the same as 1 apple plus 1 real; we also have that if a third of an apple costs the same as a quarter of an orange plus half a real, then, multiplying each part by 12, we have that 4 apples cost the same as 3 oranges plus 6 reals. Combining the two pieces of information, we conclude that 5 oranges plus 5 reals cost the same as 5 apples. We can solve this problem using the system of equations:
$$
\left\{\begin{array} { c }
{ L = \frac { M } { 2 } + \frac { 1 } { 2 } } \\
{ \frac { M } { 3 } = \frac { L } { 4 } + \frac { 1 } { 2 } }
\end{array} \rightarrow \left\{\begin{array} { c }
{ 2 L = M + 1 } \\
{ 4 M = 3 L + 6 }
\end{array} \rightarrow \left\{\begin{array}{llc}
2 L-1= & M \\
3 L+6= & 4 M
\end{array}\right.\right.\right.
$$
Adding the equations of the last system, we arrive at $5 L+5=5 M$, that is, 5 oranges plus 5 reals cost the same as 5 apples.
#
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Joseane's calculator has gone crazy: for each digit she presses, its double appears on the screen. The addition, subtraction, multiplication, and division operation keys work normally and cannot be pressed twice in a row. For example, a permitted sequence of operations is to write $2 \rightarrow \times \rightarrow 3$, which generates the number $4 \cdot 6=24$.
a) How can she make 80 appear by pressing 3 keys?
b) How can she make 50 appear by pressing 3 digit keys and two operation keys alternately?
c) What is the minimum number of keys she must press to obtain the number 23?
|
Solũ̧̧̃o
a) By pressing the digits, the numbers that can appear on the screen are $0, 2, 4, 6, 8$, 10, 12, 14, 16, and 18. One way to make 80 appear on the display is to press the sequence $4 \rightarrow \times \rightarrow 5$, which results in $8 \times 10=80$.
b) The sequence should be: digit - operation - digit - operation - digit. One way is $5 \rightarrow \times \rightarrow 5 \rightarrow \div \rightarrow 1$, which results in the operation $(10 \times 10) \div 2=50$.
c) One way to get 23 is to press 4 keys: $2 \rightarrow 3 \rightarrow \div \rightarrow 1$, which results in $46 \div 2 = 23$. Since all the digits entered generate even numbers, if we use only the keys +, -, or $\times$, the result will be even, and thus she will not obtain 23. Therefore, the symbol $\div$ will be used at least once. If she uses another operation key, as they cannot be pressed twice in a row, at least 5 keys will need to be pressed. On the other hand, using only one operation, we will need at least two more keys with digits. Since no admissible division between the digits in the set $\{0, 2, \ldots, 18\}$ produces 23, the minimum number of keys she must use is 4.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A school with 862 students will participate in a scavenger hunt, whose rules are:
I) The number of registrants must be a number between $\frac{2}{3}$ and $\frac{7}{9}$ of the total number of students in the school.
II) Since the students will be divided into groups of 11, the number of registrants must be a multiple of 11.
How many are the possible numbers of registrants for this school?
#
|
Solution
Since $\frac{2}{3} \cdot 862=574, \overline{6}$ and $\frac{7}{9} \cdot 862=670, \overline{4}$, the number of students must be a multiple of 11 in the interval $[575,670]$. The smallest multiple in the interval is $53 \cdot 11=583$ and the largest is $60 \cdot 11=660$. Therefore, there are $60-52=8$ possible different numbers of students from this school participating in the scavenger hunt.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On a table are 10 coins, all with "heads" facing up. A move consists of flipping exactly 4 coins.
a) What is the minimum number of moves required for all to be "tails" facing up?
b) If there were 11 coins, would it be possible to have all of them with tails facing up?
|
Solution
a) With 2 moves it is not possible, as we can only change $2 \cdot 4=8$ coins and we need to change 10. We will now show that it is possible with 3 moves, analyzing the sequence in the figure, where $k$ represents heads and $C$, tails.
b) We always flip 4 coins (an even number) with each move. Initially, the number of heads (10) and tails (0) is even. Each time we flip 4 coins, the number is either even in both heads and tails or odd in both, since the sum of the quantities flipped is even (4). Thus, after each move, the number of heads and tails has the same parity (both even or both odd). Therefore, we conclude that it is not possible to have all 11 coins with "tails" facing up, as the number of tails (11) would be odd and the number of heads (0) would be even.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the figure, each of the 5 letters has a certain number of circles. We have 3 colors (blue, red, orange) to paint the circles (each one in a single color).
a) In how many different ways can we paint the circles of the letter "O", not necessarily using all 3 colors?
b) In how many different ways can we paint the circles of the letter "E" using all 3 colors?
c) In how many different ways can we paint the letter "B" such that circles connected by a segment must have different colors? (The three circles aligned vertically have TWO segments separating them).
#
|
Solution
a) There are 3 color possibilities for each of the circles. Therefore, we can paint it in $3 \cdot 3 \cdot 3 \cdot 3=81$ ways.
b) Without considering the restriction (using all 3 colors necessarily), the total number of possibilities, according to the reasoning from the previous item, is $3^{6}=729$. Now let's subtract from this result the possibilities where we use only 1 or 2 colors. For example, if we choose only 2 colors, such as blue and red, we have $2^{6}-2=62$ possibilities of painting with 2 colors (we subtract 2 to discount the two possibilities where we paint only blue and only red. Don't worry! We will put them back later). If we choose blue and orange, as well as orange and red, we also have 62 possibilities in each case. Remembering that in 3 possibilities all the circles are the same color, we have, therefore, a total of $729-3 \cdot 62-3=540$ ways to paint the circles of the letter $E$ using all the colors.
c) Let's paint the circle at the midpoint of the vertical segment right away, as it has a common segment with all the others: there are 3 possibilities. Now, there are 2 colors left to paint the 2 circles at the top and the same 2 colors for the ones at the bottom. Assuming the first circle was painted blue, we can paint the top circles red - orange or orange - red, that is, 2 possibilities, as well as the 2 at the bottom. Therefore, there are $3 \cdot 2 \cdot 2=12$ ways.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How many positive integers $n$ exist such that $\frac{2 n^{2}+4 n+18}{3 n+3}$ is an integer?
|
As
$$
\frac{2 n^{2}+4 n+18}{3 n+3}=\frac{2}{3} \frac{\left(n^{2}+2 n+1\right)+8}{n+1}=\frac{1}{3}\left(2 n+2+\frac{16}{n+1}\right)
$$
it follows that $n+1$ must divide 16. Thus, $n$ must belong to the set $\{1,3,7,15\}$. In each of these cases, we have
| $n$ | $\frac{2 n^{2}+4 n+18}{3 n+3}$ |
| :---: | :---: |
| 1 | 4 |
| 3 | 4 |
| 7 | 6 |
| 15 | 11 |
Therefore, for the four values of $n$, 1, 3, 7, and 11, $\frac{2 n^{2}+4 n+18}{3 n+3}$ is an integer.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The five cards below are on a table, and each one has a number on one side and a letter on the other. Simone must decide whether the following statement is true: "If a card has a vowel on one side, then it has an even number on the other." What is the minimum number of cards she needs to turn over to decide correctly?

## Solutions from List 3
|

She does not need to turn over the card with the number 2, because whether it is a vowel or a consonant, it meets the condition in the same way. She also does not need to turn over the card with the letter M. The card with the number 3 must be turned over to verify that the other side has a consonant, and the cards with the letters **A** and **E** must be turned over to check that the numbers on the other side are even. Therefore, she only needs to turn over 3 cards.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A number is even and has 10 digits, and the sum of these digits is 89. What is the unit digit of this number?
A) 0
B) 2
C) 4
D) 6
E) 8
|
Solution
## Alternative E
The greatest possible sum of ten digits is $10 \times 9=90$, which occurs when we have ten digits 9. To get a sum of 89, we just need to reduce one unit from one of the digits, that is, replace a 9 with an 8. Therefore, the number has nine digits 9 and one digit 8. Since it is even, its units digit can only be 8, that is, the number is 9999999998.
|
8
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
By placing addition signs between some of the digits of the number 123456789, we can obtain various sums. For example, we can obtain 279 with four addition signs: $123+4+56+7+89=279$. How many addition signs are needed to obtain the number 54 in this way?
A) 4
B) 5
C) 6
D) 7
E) 8
|
Solution
## ALTERNATIVE D
Since we want to obtain the sum of 54, we must place addition signs between all the digits starting from 5, that is, $1 ? 2 ? 3 ? 4 ? 5 + \underbrace{6+7+8+9}_{30} = 54$. Therefore, we need $1 ? 2 ? 3 ? 4 ? 5 = 24$.
Using the same argument as before, we see that this can only be done as $12 + 3 + 4 + 5$. Thus, $12 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 54$ is the desired expression, for which we need 7 addition signs.
|
7
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Using matchsticks, we form digits as shown in the figure. In this way, to write the number 188, we use 16 matchsticks.
César wrote the largest number possible using exactly 13 matchsticks. What is the sum of the digits of the number that César wrote?
A) 8
B) 9
C) 11
D) 13
E) 15
#
|
Solution
## ALTERNATIVE B
A number with a certain number of digits, where the first digit from the left is not zero, is always greater than any number that has one less digit. For example, 1000 (with 4 digits) is greater than 999 (which has only 3 digits).
Thus, with exactly 13 sticks, we should form a number that has the maximum possible number of digits, with the first digit from the left being different from 0. Since, among all the digits, the digit 1 is the one formed with the fewest sticks, we see that to obtain the largest possible number with 13 sticks, we should use as many 1s as possible.
It is not possible to use the digit 1 six times, as in this case we would already have used 12 sticks and there is no digit that can be formed with only one stick. For the same reason, it is not possible to use the digit 1 five times; there is no digit formed by 3 sticks.
But it is possible to use the digit 1 four times; in this case, we use 8 sticks and can complete the number with one of the digits 2 or 5, which are formed by 5 sticks. In this case, we should choose the 5, which allows us to form the number 51111 with 13 sticks. The sum of the digits of this number is \(5+1+1+1+1=9\).
|
9
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A farmer asked his son: How many feet can I count when I am milking a cow? The boy replied: There are 6, 4 from the cow and 2 from you. The father then said: Actually, there are 9, because you forgot to count the 3 from the stool I sit on. Following this, the father proposed another problem to his son: In a corral, there are some people, cows, and stools, at least one of each. The total number of feet is 22 and the number of heads is 5. How many cows are there in the corral? The boy solved the problem correctly. What was his answer?
A) 1
B) 2
C) 3
D) 4
E) 5
|
Solution
## ALTERNATIVE C
The table below represents all possibilities for the number of heads to be 5 (we remember that stools do not have heads and there is at least one person and one cow).
| Heads | | Feet | Feet of stools |
| :---: | :---: | :---: | :---: |
| Cows | People | | (22 - feet, cows and people) |
| 1 | 4 | 12 | 10 |
| 2 | 3 | 14 | 8 |
| 3 | 2 | 16 | 6 |
| 4 | 1 | 18 | 4 |
The last column represents the possibilities for the number of feet of stools in the corral. Since each stool has 3 feet, the total number of feet of stools must be a multiple of 3. The
only multiple of 3 that appears in the last column is 6, corresponding to 2 stools. Therefore, in the corral there were 3 cows, 2 people, and 2 stools.
|
3
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Pedrinho wrote all the integers between 100 and 999 whose sum of digits is 12. For example, the numbers 129 and 750 appear among the numbers written.
a) How many of the written numbers have only two equal digits?
b) How many of the written numbers are formed only by odd digits?
|
Solution
a) The digit 1 cannot be repeated because it is not possible to write 12 as a sum of the form $1+1+x$ where $x$ is a digit; indeed, since $x$ is at most 9, this sum will be at most 11. The digit 4 also cannot be repeated, as in this case the number would have to be 444, which has three identical digits and does not comply with the statement. Finally, the digits 7, 8, and 9 cannot be repeated, as in this case the sum of the digits would exceed 12. Therefore, the repeated digit can only be 2, 3, 5, or 6. With 2, 3, and 5, we can form 9 numbers: 228, 282, 822, 336, 363, 633, 552, 525, and 255. With the digit 6, we can form 2 numbers: 606 and 660. Therefore, the total number of numbers written is $9+2=11$.
b) The sum of three odd numbers is an odd number. Since 12 is even, we see that it is impossible to find three odd digits whose sum is 12. Therefore, none of the numbers written have all three digits odd.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Four teams competed in a football tournament where each played once against each of the others. When a match ended in a draw, each team received one point; otherwise, the winner received three points and the loser, zero. The table shows the final score of the tournament. How many were the draws?
| Team | Points |
| :--- | :---: |
| Cruzínthians | 5 |
| Flameiras | 3 |
| Nauritiba | 3 |
| Greminense | 2 |
A) 2
B) 3
C) 4
D) 5
E) 6
|
Solution
## ALTERNATIVE D
$1^{st}$ solution: Each team played three times. With 5 points, Cruzinthians could only have won one match and drawn two, because if they had won two matches, they would have at least 6 points, and if they hadn't won any, they would have a maximum of 3 points. Greminense did not win any matches, as they only scored 2 points; thus, they drew two matches and lost one. Flameiras, in second place with 3 points, did not win any matches, because if this had happened, they would have had to lose two; since Greminense did not win any and Cruzinthians only one, they would have lost to Nauritiba. But the same reasoning shows that then Nauritiba, having won the match against Flameiras, should have lost to Flameiras! Since this cannot happen, we conclude that Flameiras and Nauritiba drew all three of their matches. Therefore, the number of draws was $3+3-1=5; the -1$ appears in this expression because the draw between Flameiras and Nauritiba should be counted only once. The table below shows the championship scoring.
| | Cruzinthians | Flameiras | Nauritiba | Greminense |
| :---: | :---: | :---: | :---: | :---: |
| Points scored by Cruzinthians | | 1 | 1 | 3 |
| Points scored by Flameiras | 1 | | 1 | 1 |
| Points scored by Nauritiba | 1 | 1 | | 1 |
| Points scored by Greminense | 0 | 1 | 1 | |
$2^{nd}$ solution: Another solution is to note that in each match played, 2 points are distributed in the case of a draw or 3 points if there is no draw. Since each of the four teams played once against each of their three opponents, a total of six matches were played, in which $5+3+3+2=13$ points were distributed. The only way to partition 13 into six parts of 2 or 3 is $13=3+2+2+2+2+2$; thus, five of the six matches ended in a draw.
|
5
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Dona Benta divided the Sítio do Picapau Amarelo among six characters, keeping a part of the Sítio as a forest reserve. The division is indicated in the figure, where the area of each character is given in hectares and the shaded area is the forest reserve. The Sítio has a rectangular shape and $AB$ is a diagonal.
a) What is the area of the forest reserve?
b) To prepare the lands for planting, each of the six characters spent an amount proportional to the area of their land. Quindim and Cuca together spent $R \$ 2.420,00$. How much did the Saci spend?
#
|
Solution
a) A rectangle is divided into two regions of the same area by its diagonal. Therefore, the lands of Quindim, Visconde de Sabugosa, and Cuca together have an area equal to half the area of the Sítio. The area of these lands, in hectares, totals $4+7+12=23$. The other half of the Sítio has the same area and is equal to the sum of the areas of the lands of Saci, Narizinho, Rabicó, and the forest reserve. Therefore, $6+5+10+$ (area of the reserve) $=23$, which means the area of the reserve is equal to 23ha $-21 \mathrm{ha}=2$ ha.
b) Quindim and Cuca together own 4ha +7 ha $=11 \mathrm{ha}$. Thus, they spent $\frac{2420}{11}=220$ reais per hectare. Since Saci's land is 6ha, he spent $6 \times 220=1320$ reais.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Mário built a cube with twelve equal sticks and wants to paint them so that no vertex has sticks of the same color meeting there. What is the minimum number of colors he needs to use?
A) 2
B) 3
C) 4
D) 6
E) 8
|
Solution
## ALTERNATIVE B
Each vertex is the endpoint of three edges and, therefore, at least three different colors are needed. On the other hand, three different colors are enough; we can see this in the figure, where three different colors are indicated by solid, dashed, and dotted lines.
#
|
3
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
What is the unit digit of the number $3^{1}+3^{2}+3^{3}+3^{4}+\cdots 3^{2013}$?
Remember, for example, that $3^{2}=3 \times 3=9$. And $3^{3}=3 \times 3 \times 3=27$. Also remember that the unit digit of a number is the last one on the right. For example, the unit digit of 376564534539 is 9.
|
Solution
## Note that
$3^{1}=3$, whose unit digit is 3.
$3^{2}=9$, whose unit digit is 9.
$3^{3}=27$, whose unit digit is 7.
$3^{4}=81$, whose unit digit is 1.
$3^{5}=243$, whose unit digit is 3.
$3^{6}=729$, whose unit digit is 9.
$3^{7}=2187$, whose unit digit is 7.
$3^{8}=6561$, whose unit digit is 1.
We can already notice that every four powers, the unit digits repeat (always 3, 9, 7, and 1, in that order). And also that, since $3+7=10$ and $1+9=10$, these groups of four numbers do not affect the unit digit, because adding a number that ends in zero does not change the unit digit.
Dividing 2013 by 4, we notice that the remainder is 1. Therefore, the unit digit of $3^{1}+3^{2}+3^{3}+3^{4}+\cdots+3^{2013}$ is 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Aline received as a gift a cube composed of $4 \times 4 \times 4$ small white cubes, as shown in the following figure.
Without separating the small cubes, Aline decided to paint all the faces of her cube red.
a) How many small cubes ended up with exactly one of their faces painted red?
b) How many small cubes ended up with exactly two of their faces painted red?
Some time later, Aline asked her father for an even larger cube to paint in the same way she had done with the previous cube.
c) After painting, Aline separated the small cubes. She noticed that the number of small cubes that remained with no faces painted red was equal to three times the number of small cubes that had two faces painted red. Determine the size of the new cube Aline received.
|
Solution
a) On each face of the cube, the small cubes that end up with one face painted red are the four that are in the center, that is, those that do not have any edge contained in an edge of the large cube. The figure below illustrates which these cubes are.

Since the cube has six faces, and each face has four of these cubes, we have, in total, $4 \times 6=24$ small cubes with only one face painted red.
b) On each face of the cube, the small cubes that end up with two faces painted red are the eight that have only one edge contained in some edge of the large cube. The figure below illustrates which these cubes are.
Note that these small cubes are counted twice, once for each face of the large cube to which they belong. Therefore, we have a quantity of $\frac{8 \times 6}{2}=24$ small cubes that end up with two faces painted red.
c) In a cube of side $n$, the cubes that will end up with no face painted red are those that are part of the sub-cube of side $n-2$ that remains when we remove all the small cubes from the surface of the original cube. Since the sub-cube of side $n-2$ is made up of $(n-2)^{3}$, we then have that the number of small cubes with no face painted is equal to $(n-2)^{3}$.
Following the same reasoning as in item $b$), we have that, on each face of the cube of side $n$, there are $4 \times(n-2)$ small cubes with exactly two faces painted red. Again, they are counted twice, once for each face of the cube of side $n$ to which they belong. Thus, there are $\frac{4 \times(n-2) \times 6}{2}$ small cubes with exactly two faces painted red.
Since the number of small cubes that ended up with no face painted red is equal to three times the number of small cubes that ended up with two faces painted red, we have that
$$
(n-2)^{3}=3 \times\left[\frac{4 \times(n-2) \times 6}{2}\right]
$$
Since the new cube that Aline has is larger than the cube she had previously, it holds that $n>2$, so we can simplify the equation to get:
$$
(n-2)^{2}=\frac{3 \times 4 \times 6}{2}=36
$$
Taking the square root of both sides, we get $n-2=6$, so we have $n=8$.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Bruno and Pedro play billiards on a strange table. It contains two walls that meet forming an angle of $20^{\circ}$. They observed that the reflections of the ball against the walls are perfect, that is, if the trajectory of incidence makes an angle of $x^{\circ}$ with the wall, then the angle that the reflected trajectory makes with the wall will also be equal to $x^{\circ}$. The figure below illustrates this reflection rule.
Playing with the ball, they noticed that it is possible that, after reflecting several times off the wall of the table, the ball's trajectory intersects itself. For example, Bruno launched a ball in such a way that, after 3 reflections, its trajectory intersected itself, as illustrated in the figure below.
After Bruno, Pedro launched the ball as shown in the following figure:
Say how many reflections the ball sent by Pedro suffered before its trajectory intersected itself.
|
Solution
After the third bounce, we will observe the following drawing:
From the drawing, we see that $\measuredangle B A O=20^{\circ}$, since the bounces are perfect.
Let's recall that the sum of the interior angles of a triangle is $180^{\circ}$. Consequently, the sum of the interior angles at two vertices of a triangle coincides with the exterior angle at the third vertex. We will use this fact systematically.
Applying this fact to triangle $A B O$, we have $\angle A B P=\measuredangle B A O+\measuredangle A O B=40^{\circ}$. Using the fact that the bounce is perfect, we conclude that $\measuredangle C B D=\measuredangle A B P=40^{\circ}$.
We can now use the previously mentioned fact in triangle $B C O$, and thus conclude that $\measuredangle B C A=\measuredangle C B O+\measuredangle B O C=40^{\circ}+20^{\circ}=60^{\circ}$. Knowing that the bounce is perfect, we have $\measuredangle B C A=\measuredangle D C O=60^{\circ}$. Therefore, in triangle $C D O$, we have $\measuredangle C D B=$ $\measuredangle D C O+\measuredangle C O D=60^{\circ}+20^{\circ}=80^{\circ}$. The fourth bounce is perfect, so $\measuredangle E D O=$ $\measuredangle C D B=80^{\circ}$, where $E$ is the point shown in the following figure.
Since the sum of the interior angles in triangle $E D O$ must be $180^{\circ}$, then $\measuredangle D E O=$ $80^{\circ}$. It follows that after the fifth bounce (at point $E$), the trajectory will return and intersect itself.
Therefore, the answer is 5 bounces.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A symmetric ring with $m$ regular polygons, each with $n$ sides, is formed according to the rules:
i) each polygon in the ring meets two others;
ii) two adjacent polygons share only one side;
iii) the perimeter of the region inside the ring consists of exactly two sides of each polygon.
The example in the following figure shows a ring with $m=6$ and $n=9$. For how many different values of $n$ is it possible to construct this ring?
|
Solution
Let $\alpha=\frac{360^{\circ}}{n}$ be the measure of each exterior angle of a regular polygon $A B C D E \ldots$. Suppose that the path $B C D$ is part of the perimeter of some internal region of a ring. If $O$ is the intersection of the extensions of $A B$ and $D E$, by symmetry, it is the center of the internal region. Since there are $m$ regular polygons, we conclude that $\angle B O D=\frac{360^{\circ}}{m}$. Now, the sum of the interior angles of $B C D O$ is
$$
\begin{aligned}
360^{\circ} & =\frac{360^{\circ}}{m}+\alpha+(180+\alpha)+\alpha \\
360^{\circ} & =\frac{360^{\circ}}{m}+\frac{3 \cdot 360^{\circ}}{n}+180^{\circ} \\
1 & =\frac{2}{m}+\frac{6}{n}
\end{aligned}
$$
Thus, multiplying the above equation by $m n$ and factoring the resulting expression, we have
$$
\begin{aligned}
m n & =6 m+2 n \\
(m-2)(n-6) & =12
\end{aligned}
$$
For the ring to exist, we need $m>2$. Additionally, $(m-2)$ and $(n-6)$ must divide 12 and $n>0$, so $(n-6) \in\{1,2,3,4,6,12\}$, which means $n \in\{7,8,9,10,12,18\}$, giving 6 different possible values for $n$. To verify that all of them are solutions, it suffices to consider the following examples of rings:
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The figure below shows a segment $AB$, its midpoint $C$, and the semicircles with diameters $AB$ and $AC$. A circle with center $P$ is tangent to both semicircles and also to the segment $AB$. Given $AB=8 \text{ cm}$, and $O$, the midpoint of $AC$, the questions are:
a) What is the measure of the perimeter of triangle $OCP$?
b) What is the measure of the radius of the circle with center $P$?
|
Solution
a) Let $x$ be the radius of the circle centered at $P$. We draw $OP$, which passes through the point of tangency $D$; $CP$, which passes through the point of tangency $F$; and $PE$, perpendicular to $AB$ (and a radius of the circle highlighted in the figure). We have $CP=4-x$ and $OP=2+x$. The perimeter of triangle $OCP$ is
$$
\begin{aligned}
2 p & =O P+C P+C O \\
& =(2+x)+(4-x)+2 \\
& =8 \text{ cm}
\end{aligned}
$$
b) Now, we will calculate the area of $\triangle OCP$ in two ways: using Heron's formula, which uses the semi-perimeter $p=4 \text{ cm}$, and as half the product of the base by the height.
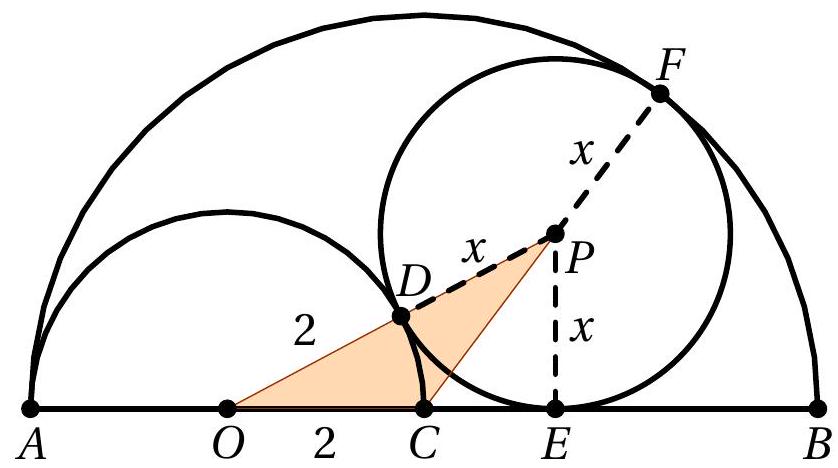
Thus,
$$
\sqrt{4 \cdot(4-2)(4-(2+x))(4-(4-x))}=\frac{2 \cdot x}{2}
$$
Solving the equation above, we get $x=\frac{16}{9} \text{ cm}$.
Note: A triangle with perimeter $2 p$ and side lengths $a, b$, and $c$, by Heron's Formula, has an area given by
$$
A=\sqrt{p(p-a)(p-b)(p-c)}
$$
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine the minimum term of the sequence
$$
\sqrt{\frac{7}{6}}+\sqrt{\frac{96}{7}}, \sqrt{\frac{8}{6}}+\sqrt{\frac{96}{8}}, \sqrt{\frac{9}{6}}+\sqrt{\frac{96}{9}}, \ldots, \sqrt{\frac{95}{6}}+\sqrt{\frac{96}{95}}
$$
|
Solution
Remember that $(x-y)^{2} \geq 0$ for all real numbers $x$ and $y$. Thus, we can rewrite the inequality as $\frac{x^{2}+y^{2}}{2} \geq x y$, and by substituting $x=\sqrt{a}$ and $y=\sqrt{b}$, with $a$ and $b$ being non-negative real numbers, we have $\frac{a+b}{2} \geq \sqrt{a b}$. Now, observe that all terms are of the form $\sqrt{\frac{n}{6}}+\sqrt{\frac{16 \cdot 6}{n}}=$ $\sqrt{\frac{n}{6}}+4 \sqrt{\frac{6}{n}}$, with $n$ being an integer and greater than or equal to 7. Taking $a=\sqrt{\frac{n}{6}}$ and $b=4 \sqrt{\frac{6}{n}}$, we can do
$$
\begin{aligned}
\frac{\sqrt{\frac{n}{6}}+4 \sqrt{\frac{6}{n}}}{2} & \geq \sqrt{\sqrt{\frac{n}{6}} \cdot 4 \sqrt{\frac{6}{n}}} \\
\sqrt{\frac{n}{6}}+4 \sqrt{\frac{6}{n}} & \geq 2 \cdot 2 \cdot \sqrt{\sqrt{\frac{n}{6} \cdot \frac{6}{n}}} \\
& =4
\end{aligned}
$$
The minimum value of each term is 4 and occurs when $\sqrt{\frac{n}{6}}=4 \sqrt{\frac{6}{n}}$, that is, $n=24$. The term we are looking for is $\sqrt{\frac{24}{6}}+\sqrt{\frac{96}{24}}$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Some students from a school were divided into teams satisfying the following conditions:
i) Any 2 different teams have exactly 2 members in common.
ii) Every team has exactly 4 members.
iii) For any 2 students, there is a team of which neither is a member.
a) Explain why any pair of students can participate in at most 3 teams.
b) What is the maximum number of teams?
#
|
Solution
a) Suppose there are students $A$ and $B$ participating in 4 teams called $E_{1}, E_{2}$, $E_{3}$, and $E_{4}$:
$$
\begin{aligned}
E_{1} & =\{A, B, C, D\} \\
E_{2} & =\{A, B, E, F\} \\
E_{3} & =\{A, B, G, H\} \\
E_{4} & =\{A, B, I, J\}
\end{aligned}
$$
By condition (iii), there exists a team $E_{5}$ that does not simultaneously have students $A$ and $B$. By condition (i), team $E_{5}$ must have exactly two members in common with $E_{1}, E_{2}, E_{3}$, and $E_{4}$. If $E_{5}$ does not have $A$ and $B$, then it must have elements from the following 4 disjoint sets $\{C, D\},\{E, F\},\{G, H\}$, and $\{I, J\}$. This forces $E_{5}$ to have more than 4 elements. Suppose $E_{5}$ does not have student $A$ but has student $B$ (since $A$ and $B$ play the same role in this analysis, the study we will do for $A$ is the same for $B$). Thus, $E_{5}$ must have at least one student from each of the same 4 sets mentioned earlier, and again this team will be forced to have more than 4 elements. This absurdity shows that any pair of students cannot participate in 4 teams.
b) Consider a pair of students ($A, B$) that participates in more than one team, whose existence is guaranteed by item (i), and study the following possibilities based on the information from the previous item.
1) The pair ($A, B$) participates in exactly three other teams called $E_{1}$, $E_{2}$, and $E_{3}$:
$$
\begin{aligned}
& E_{1}=\{A, B, C, D\} \\
& E_{2}=\{A, B, E, F\} \\
& E_{3}=\{A, B, G, H\}
\end{aligned}
$$
We will show that in this case, there cannot be more than 4 other teams. Repeating the argument from the previous item, if a team does not have $A$ and $B$, it will have all the elements of the set $\{C, D, E, F, G, H\}$, which produces an absurdity with condition (i). Therefore, all other teams must have $A$ or $B$, and by condition (i), any other team must have exactly one element from each of the three sets: $\{C, D\},\{E, F\}$, and $\{G, H\}$. Analyzing the possible combinations of the remaining 3 elements, in principle, we would have at most $2 \cdot 2 \cdot 2=8$ choices associated with the sets mentioned earlier. However, there are some pairs of choices that cannot be present simultaneously to satisfy condition (i):
$$
\begin{array}{ccc}
\{C, E, G\} & \text { and } & \{D, F, H\} \\
\{C, E, H\} & \text { and } & \{D, F, G\} \\
\{C, F, G\} & \text { and } & \{D, E, H\} \\
\{C, F, H\} & \text { and } & \{D, E, G\}
\end{array}
$$
Thus, there can be at most 4 more teams in addition to $E_{1}, E_{2}$, and $E_{3}$.
2) The pair $(A, B)$ participates in exactly two other teams called $E_{1}$ and $E_{2}$:
$$
\begin{aligned}
& E_{1}=\{A, B, C, D\} \\
& E_{2}=\{A, B, E, F\}
\end{aligned}
$$
Due to condition (i), the only team that cannot simultaneously have $A$ and $B$ is $\{C, D, E, F\}$. Considering a team distinct from it, again by item (i), one element from each of the sets $\{A, B\},\{C, D\}$, and $\{E, F\}$ must be present. This again generates $2 \cdot 2 \cdot 2=8$ choices that can be divided into the following pairs:
$$
\begin{array}{lcc}
\{A, C, E\} & \text { and } & \{B, D, F\} \\
\{A, C, F\} & \text { and } & \{B, D, E\} \\
\{A, D, E\} & \text { and } & \{B, C, F\} \\
\{A, D, F\} & \text { and } & \{B, C, E\}
\end{array}
$$
From each pair, only one choice can be present in the teams of students, and this shows that there can be at most 4 more teams that contain $A$ or $B$. Considering the two teams that contain $\{A, B\}$, the potential team $\{C, D, E, F\}$, and the possible 4 other teams, we have a total of at most $2+1+4=7$ teams.
In both cases, the maximum number of teams is 7. To show that it is possible to satisfy all three conditions with this number, it is sufficient to consider the following example:
$$
\{A, B, C, H\},\{A, D, F, H\},\{A, E, G, H\},\{B, D, G, H\},\{B, E, F, H\},\{C, D, E, H\},\{C, F, G, H\}
$$
where each letter, as before, represents a certain student.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the sum below, the same letters represent the same digits and different letters represent different digits.
$$
\begin{array}{ccc}
& & X \\
+ & & X \\
& Y & Y \\
\hline Z & Z & Z
\end{array}
$$
What digit does the letter $X$ represent?
#
|
Solution
Initially note that $X+X+Z \leq 2 \cdot 9+8=26$. Therefore, at most 2 units will be added to the tens place. Since $Y \neq Z$, when we add 1 or 2 units to $Y$, we should obtain the two-digit number $\overline{Z Z}$. As $Y+2 \leq 9+2=11$, the only possibility is to have $\overline{Z Z}=11$, thus, $Y=9$. For the sum $2 X+Y$ to end in 1 and have $X \neq 1$, we must have $X=6$. Indeed, these values satisfy the sum:
$$
\begin{array}{r}
\\
6 \\
+\quad 6 \\
\\
99 \\
\hline 119
\end{array}
$$
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A regular icosahedron is a geometric solid with 20 faces, which are equilateral triangles. By drawing the numbers from 1 to 20 on the faces of a regular icosahedron, it is transformed into a die. Luísa and Mathias invented a game in which each of them rolls the icosahedral die 5 times and records the numbers drawn in sequence, forming a single number. For example, Luísa rolled the sequence $5,11,7,20,17$, so she wrote down the number 51,172,017.
a) In the first game, Luísa won with the largest possible difference. What is this difference?
b) In the second game, Luísa scored 162,012,510 points and Mathias rolled the die four times, drawing 14, 11, 8, and 19. Is it possible for Mathias to win this game with his last roll?
c) In the third game, Luísa scored 12,111,813 points. How many sequences are possible to achieve this score?
|
Solution
a) 2,020,190,909. For this to happen, Luísa scored 20 in her 5 throws and Mathias scored 1 in his 5 throws, making the difference equal to 2,020,202,020 - 11,111 = 2,020,190,909.
b) No. The highest possible score would be by scoring 20 on the last throw, resulting in 141,181,920, which is less than 162,012,510.
c) 10. Let's use a diagram to check all the possibilities:
Counting the total number of possibilities, we arrive at 10.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
King Arthur had to fight the Three-Headed and Three-Tailed Dragon (known as $D T C T C$). His task was made easier when he managed to obtain a magical sword that could deliver the following strikes (one at a time):
A) cut off one head;
C) cut off one tail;
B) cut off two heads;
D) cut off two tails.
Moreover, the Fairy Morgana revealed the dragon's secret to him:
i) if one head is cut off, a new one will grow;
ii) if two heads are cut off, no new heads or tails will grow immediately after the strike;
iii) in place of a cut tail, two new tails will grow;
iv) if two tails are cut off, a new head will grow;
v) the dragon dies if it loses all three heads and three tails.
a) Is it possible for the dragon to end up with 4 heads and 4 tails?
b) To kill the $D T C T C$, what is the minimum number of strikes King Arthur will need to deliver?
|
Solution
a) Yes, it is enough for the King to use, for example, the sequence of strikes $D \rightarrow C \rightarrow C \rightarrow C$.
b) From a practical standpoint, the only strike that reduces the number of heads is $B$, but we need two of them to perform it (the same applies to tails and the strike $D$), unless some strike leaves it without a head and a tail, in which case it dies before regenerating. Due to parity, the number of heads will need to increase at least once. Moreover, no strike eliminates more than 2 members, so we will need at least 3 more strikes. Below is a sequence with this minimum of $1+3=4$ strikes.
| $n$ | Strike | Head | Tail |
| :---: | :---: | :---: | :---: |
| 0 | - | 3 | 3 |
| 1 | After $D$ | 4 | 1 |
| 2 | After $B$ | 2 | 1 |
| 3 | After $B$ | 0 | 1 |
| 4 | After $C$ | 0 | 0 |
[*] Notice that when cutting the tails, as there are no more heads at the moment, the DTCTC both loses its regenerative power and dies. Therefore, 4 is the minimum number of strikes.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A tournament will take place with 100 competitors, all with different skill levels. The most skilled competitor always wins against the least skilled competitor. Each participant plays exactly twice, with two randomly drawn opponents (once against each). A competitor who wins two matches receives a medal. Determine the minimum number of medals that can be distributed in the tournament.
|
Solution
Let's denote that a player $A$ is more skilled than a player $B$ by $A \rightarrow B$. Suppose that
$$
L_{1} \rightarrow L_{2} \rightarrow L_{3} \rightarrow \ldots \rightarrow L_{100}
$$
are the 100 players in the tournament. Since $L_{1}$ is the most skilled of all, he will certainly win a medal by winning his two matches. We will show that this is the minimum number of medals by providing an example of a tournament where he is the only one to win it. In the first round of the tournament, consider the matches:
$$
L_{100} \times L_{99}, L_{98} \times L_{97}, \ldots, L_{2} \times L_{1}
$$
Thus, all players with odd numbers have lost at least one match. In the second round, consider the matches:
$$
L_{100} \times L_{1}, L_{99} \times L_{98}, \ldots, L_{3} \times L_{2}
$$
Thus, all players with even numbers have lost at least one match. In this situation, only $L_{100}$ will win a medal.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Consider the set $A=\{1,2,3, \ldots, 2011\}$. How many subsets of $A$ exist such that the sum of their elements is 2023060?
|
Observe that the sum $1+2+\cdots+2011=\frac{2011 \times 2012}{2}=$ 2023066. Therefore, to obtain a subset of $A$ that has a sum of its elements equal to 2023060, it suffices to remove from $A$ the elements whose sum is 6. The possible cases are:
- Subsets with one element: $\{6\}$.
- Subsets with two elements: $\{2,4\}$ and $\{1,5\}$.
- Subsets with three elements: $\{1,2,3\}$.
Therefore, there are four subsets of $A$ whose sum of elements is 6, and consequently, there are also four subsets of $A$ whose sum of elements is 2023060.
Suggestion: Observe that the ant is always at 1 in the odd seconds.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The 2,019 lockers of 2,019 students in a school are numbered with the squares of the first 2,019 positive natural numbers, that is, the first locker has the number $1^{2}=1$, the second locker has the number $2^{2}=4$, the third locker has the number $3^{2}=9$, and so on until the last locker which has the number $2,019^{2}=4,076,361$.
a) How many digits were used to paint the numbers on the first hundred lockers?
b) Adding all the numbers on the lockers, what is the units digit of this result?
#
|
Solution
a) Let's divide into groups by the number of digits:
I) 1 digit: 3 lockers $\left(1^{2}, 2^{2}, 3^{2}\right)$;
II) 2 digits: $9-3=6$ lockers ( $4^{2}$ to $9^{2}$ );
III) 3 digits: $31-9=22$ lockers $\left(10^{2}\right.$ to $\left.31^{2}\right)$;
IV) 4 digits: $99-31=68$ lockers $\left(32^{2}\right.$ to $\left.99^{2}\right)$;
V) 5 digits: only the locker $100^{2}$.
Therefore, $3+2 \cdot 6+3 \cdot 22+4 \cdot 68+5 \cdot 1=358$ digits were painted on the first hundred lockers.
b) The unit digit of the squares of the first 10 lockers are
$$
1,4,9,6,5,6,9,4,1,0
$$
This sequence of digits repeats every 10. Since the sum of one of these sequences ends in 5 and there are, up to $2020^{2}$ (let's consider $2020^{2}$ to have a whole number of sequences and as its unit digit is zero, it does not affect the result) 202 sums that end in 5, when added together, the result ends in 0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
At the edge of a circular lake, there are stones numbered from 1 to 10, in a clockwise direction. Frog starts from stone 1 and jumps only on these 10 stones in a clockwise direction.
a) If Frog jumps 2 stones at a time, that is, from stone 1 to stone 3, from stone 3 to stone 5, and so on, on which stone will Frog be after 100 jumps?
b) If on the first jump, Frog goes to stone 2, on the second jump to stone 4, on the third jump to stone 7, that is, in each jump he jumps one more stone than in the previous jump. On which stone will Frog be after 100 jumps?
|
Solution
a) After 5 jumps, Frog returns to stone 1 and starts the same sequence. Since 100 is a multiple of 5, on the $100^{\text{th}}$ jump, he goes to stone 1.
b) On the $1^{\text{st}}$ jump, he moves 1 stone; on the $2^{\text{nd}}$, 2 stones; on the $3^{\text{rd}}$, 3 stones, and so on until the last jump when he moves 100 stones. The total number of movements is $\frac{(1+100) \cdot 100}{2}=$ 5,050. Since every 10 movements, he returns to stone 1 and 5,050 is a multiple of 10, after 100 jumps, Frog returns to stone 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On a line $r$, points $A$ and $B$ are marked, and on a line $s$, parallel to $r$, points $C$ and $D$ are marked, such that $A B C D$ is a square. Point $E$ is also marked on the segment $C D$.
a) What is the ratio between the areas of triangles $A B E$ and $B C D$, if $E$ is the midpoint of $C D$?
b) What is the ratio $\frac{D E}{E C}$, so that the area of triangle $B F E$ is double the area of $D F E$, where $F$ is the intersection of segments $A E$ and $B D$?
|
Solution
a) Let $2 k$ be the area of square $A B C D$, then the area of triangle $A B E$ is equal to $k$ and the area of triangle $B C D$ is also equal to $k$, therefore, the ratio between the areas is 1.
b) If $\frac{A_{B F E}}{A_{D F E}}=2$, then $\frac{B F}{F D}=2$. If $r / / s$, then $\triangle A B F \sim \triangle D E F$, with a ratio of 2, and consequently, $\frac{A B}{D E}=2$, it follows that $E$ is the midpoint of segment $C D$, that is, $\frac{D E}{E C}=1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The table shows the final standings of the Quixajuba football championship. In this championship, each team played against each of the other teams four times. Each team earns 3 points for a win, 1 point for a draw, and no points for a loss.
| Team | Points |
| :---: | :---: |
| Bissetriz | 22 |
| Primo | 19 |
| Potência | 14 |
| MDC | 12 |
(a) How many matches were played in the championship?
(b) How many matches ended in a draw?
##
|
(a) There are 6 possible matches between the four teams: (Bissetriz vs Primo), (Bissetriz vs Potência), (Bissetriz vs MDC), (Primo vs Potência), (Primo vs MDC), and (Potência vs MDC). Each of these matches occurred 4 times, so the number of matches is equal to $4 \times 6 = 24$.
(b) The maximum number of points in the championship is 3 times the number of games, that is, $3 \times 24 = 72$. Each time a draw occurs, this number decreases by one unit. Since the total number of points at the end of the championship was $22 + 19 + 14 + 12 = 67$, the number of matches that ended in a draw is $72 - 67 = 5$.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Guilherme wrote 0 or 1 in each cell of a $4 \times 4$ board. He placed the numbers in such a way that the sum of the numbers in the neighboring cells of each cell on the board was equal to 1.
For example, in Figure 40.1, considering the cell marked with $\bullet$, the sum of the numbers in the shaded cells is equal to 1.
Determine the sum of all 16 numbers on the board.
|
Each house can only have one neighbor with a number 1, and the other neighbors must be zeros, since the sum of the neighbors is 1.
Starting from the top left corner, we can assume without loss of generality that we fill the board as shown in Figure 40.2.
In the following steps, the filled cells are the neighbors of the marked cell.
In each step, the numbers filled in are unique to respect the conditions of the problem.
The sum of the numbers in the filled cells is 3. By making a similar analysis, starting from the bottom left corner or the top right corner, we conclude that the sum of the numbers in the other cells is also equal to 3.
Therefore, the sum of the numbers placed on the board is always equal to 6.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A game starts with 7 coins aligned on a table, all with the head side facing up. To win the game, you need to flip some coins so that in the end, two adjacent coins are always with different sides facing up. The rule of the game is: in each move, you have to flip two adjacent coins. What is the minimum number of moves required to win the game?

|
If we assign the value of 1 to heads and -1 to tails and sum the results after each flip, the game starts with a sum of 7 and we need to reach alternating heads and tails, so the game ends at 1 or -1. We observe that at each step of the game, we have the following possibilities: we swap two heads for two tails and the sum decreases by 4; we swap one head and one tail for one tail and one head and the sum remains unchanged; or we swap two tails for two heads and the sum increases by 4. Therefore, it is impossible to go from an initial sum of 7 to 1, but it is possible to reach -1, which is 4 tails and 3 heads. Since we need to obtain 4 non-consecutive tails, we need at least 4 moves. The 4 moves are illustrated in the following diagram:
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The price of a kilogram of chicken was $R \$ 1.00$ in January 2000 and began to triple every 6 months. When will it reach $R \$ 81.00$?
(a) 1 year
(b) 2 years
(c) $21 / 2$ years
(d) 13 years
(e) $131 / 2$ years
|
As $81=3^{4}$, then the value of the franc has tripled 4 times, the number of months elapsed is $4 \times 6=24$ months, that is, 2 years, meaning that in January 2002 the chicken will reach the proposed price. The correct option is (b).
|
2
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
What is the unit digit of the product
$$
(5+1)\left(5^{3}+1\right)\left(5^{6}+1\right)\left(5^{12}+1\right) ?
$$
(a) 0
(b) 1
(c) 2
(d) 5
(e) 6
|
The unit digit of any power of 5 is 5, so the unit digit of each factor of the product is $5+1=6$. But, $6 \times 6=36$, that is, the product of two numbers ending in 6 is also a number that ends in 6. Therefore, the unit digit of this product is 6. The correct option is (e).
|
6
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
In a warehouse, a dozen eggs and 10 apples had the same price. After a week, the price of eggs dropped by $10 \%$ and the price of apples increased by $2 \%$. How much more will be spent on the purchase of a dozen eggs and 10 apples?
(a) $2 \%$
(b) $4 \%$
(c) $10 \%$
(d) $12 \%$
(e) $12.2 \%$
## Solutions to List 3
|
Suppose, initially, that a dozen eggs cost $R \$ 1.00$. Thus, 10 apples also cost $R \$ 1.00$. Since the price of eggs increased by $10 \%$, the new price of eggs is $R \$ 1.10$. The price of apples decreased by $2 \%$, so the new price of apples is $R \$ 0.98$.
Thus, before it cost 2 reais to buy 1 dozen eggs and 10 apples, now it costs $1.10+0.98=2.08$. Therefore, the increase was $R \$ 0.08$, which corresponds to the percentage:
$$
\frac{0.08}{2}=0.04=\frac{4}{100}=4 \%
$$
The correct option is (b).
|
4
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
What is the digit $a \mathrm{in}$
$$
a 000+a 998+a 999=22997 ?
$$
|
Performing the addition
$$
\begin{array}{r}
a \\
a \\
a 998 \\
+\quad a 999 \\
\hline \square 997
\end{array}
$$
we find $\square 997=22997$, where $\square=a+a+a+1$.
Therefore, $22=a+a+a+1$. Thus, $a=7$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A magic square is a square table in which the sum of the numbers in any row or column is constant. For example,
| 1 | 5 | 9 |
| :--- | :--- | :--- |
| 8 | 3 | 4 |
| 6 | 7 | 2 |
is a magic square, which uses the numbers from 1 to 9. As the reader can verify, the sum in any row or column is always equal to 15.
a) The square below is part of a magic square that uses the odd numbers between 1 and 17. Determine which number $X$ should be.
| | 1 | |
| :---: | :---: | :---: |
| 5 | | 13 |
| $X$ | | 3 |
b) A magic square is said to be hypermagic when the sum in any row, column, or diagonal is constant. Write the numbers from 1 to 9 in the square below so that it becomes hypermagic.
|
Solution
a) The sum of all odd numbers from 1 to 17 is 81. Since there are three columns in the square, and all columns (and rows) have the same sum, the sum in each column must be $81 / 3 = 27$. From this, we deduce that the missing number in the third column (the one with the numbers 13 and 3) is the number 11, because then we will have $11 + 13 + 3 = 27$. Similarly, we deduce that the central number is 9. In the first row, we already have the 1 and the 11. Therefore, the missing number in the top-left corner is 15. Following the argument with the remaining cells, we arrive at the table
| 15 | 1 | 11 |
| :---: | :---: | :---: |
| 5 | 9 | 13 |
| 7 | 17 | 3 |
from which we conclude that $X=7$.
b) There are several possible solutions. One, for example, would be
| 8 | 1 | 6 |
| :--- | :--- | :--- |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Arnaldo, Bernaldo, Cernaldo, Dernaldo, and Ernaldo are students from different parts of Brazil who were chosen to represent their country in international olympiads. After several weeks of training, some friendships were formed. We then asked each of them how many friends they had made in the group. Arnaldo, Bernaldo, Cernaldo, and Dernaldo answered, respectively, that they had made 1, 2, 3, and 4 friends within the group. How many of the group members are friends with Ernaldo?
|
Solution
Suppose Ernaldo has $x$ friends within the group. Since Dernaldo has 4 friends and the group has 5 members, everyone is a friend of Dernaldo. Let's remove Dernaldo from the group. Thus, Arnaldo, Bernaldo, Cernaldo, and Ernaldo now have $0, 1, 2$, and $x-1$ friends within the subgroup, respectively. Since Arnaldo no longer has any friends within the subgroup, we can ignore him. The following table shows the number of friends each member has within the subgroup.
| Member | Number of friends |
| :--- | :---: |
| Bernaldo | 1 |
| Cernaldo | 2 |
| Ernaldo | $x-1$ |
Obviously, the two friends of Cernaldo within the subgroup are Bernaldo and Ernaldo. Moreover, since Bernaldo has only one friend within the group, Cernaldo must be that friend. In particular, Ernaldo and Bernaldo are not friends. Therefore, Cernaldo is also the only friend of Ernaldo within the subgroup, i.e., $x-1=1$. We conclude that Cernaldo and Dernaldo are the only friends of Ernaldo. The answer is 2.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Show that $M=\sqrt[3]{\sqrt{5}+2}-\sqrt[3]{\sqrt{5}-2}$ is an integer.
|
Let $a=\sqrt[3]{\sqrt{5}+2}$ and $b=\sqrt[3]{\sqrt{5}-2}$. Thus, $M=a-b$ and we have:
$$
M^{3}=(a-b)^{3}=a^{3}-b^{3}-3 a b(a-b)
$$
We know that $a^{3}-b^{3}=4$ and $a b=1$. Therefore, $M^{3}+3 M-4=0$, which means the number $M$ is a root of the polynomial $x^{3}+3 x-4$.
In turn, the number 1 is a root of the polynomial $x^{3}+3 x-4$. Factoring this polynomial, we get $(x-1)\left(x^{2}+x+4\right)$. However, the quadratic $x^{2}+x+4$ has a negative discriminant. Consequently, 1 is the only real root of $x^{3}+3 x-4$. Therefore, $M=1$.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
The squared rectangle in the figure is made of 31 segments of $0.5 \mathrm{~cm}$, and comprises 12 squares. Rosa drew on a rectangular sheet of $21 \mathrm{~cm}$ by $29.7 \mathrm{~cm}$, quadriculated with squares of side $0.5 \mathrm{~cm}$, a large squared rectangle made with 1997 segments. How many squares does this rectangle have?

|
Let $m$ and $n$ be, respectively, the number of segments of $0.5 \, \text{cm}$ on two consecutive sides of the rectangle. We know that the total number of segments of $0.5 \, \text{cm}$ in the division of the rectangle into $m \times n$ squares of side $0.5 \, \text{cm}$ is: $m(n+1) + n(m+1)$ (prove this). Thus,
$$
m(n+1) + n(m+1) = 1997 \Rightarrow n = \frac{1997 - m}{2m + 1}
$$
Moreover, one of the sides considered is less than or equal to the other, say: $m \leq n$. In this case, we can conclude that $m \leq 31$, because
$$
n \geq m \Rightarrow n(m+1) + m(n+1) \geq 2m(m+1)
$$
Thus, $1997 \geq 2m(m+1)$ and since $1998 > 1997$, it follows that
$$
1998 > 2m(m+1) \Rightarrow 999 > m(m+1)
$$
From this, we conclude that $m < 32$.
On the other hand, we have:
$$
n = \frac{1997 - m}{2m + 1} \Rightarrow 2n = \frac{3994 - 2m}{2m + 1} = \frac{3995 - (2m + 1)}{2m + 1} \Rightarrow 2n = \frac{3995}{2m + 1} - 1
$$
Thus, the problem now reduces to investigating the divisors of $3995 = 5 \times 17 \times 47$. The only values of $m$ that satisfy the condition $1 \leq m \leq 31$ are $m = 2$, $m = 8$, and $m = 23$, which correspond, respectively, to the divisors 5, 17, and 47. For these values of $m$, we have $n = 399$, $n = 117$, and $n = 42$ respectively. The other divisors will give equivalent configurations (by swapping $m$ and $n$).
Therefore, Rosa could have constructed 3 different configurations with the 1997 segments. The first with $2 \times 399$ squares, the second with $8 \times 117$ squares, and the third with $23 \times 42$ squares.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Draw two circles with the same center, one with a radius of $1 \mathrm{~cm}$ and the other with a radius of $3 \mathrm{~cm}$. In the region outside the circle with a radius of $1 \mathrm{~cm}$ and inside the circle with a radius of $3 \mathrm{~cm}$, draw circles that are simultaneously tangent to both circles, as shown in the figure below.
(a) What should be the radius of these circles?
(b) What is the maximum number of these circles, assuming they do not overlap?
|
(a) Since the circles with radii $1 \mathrm{~cm}$ and $3 \mathrm{~cm}$ are concentric, the other circles shown in the figure must have a radius equal to $1 \mathrm{~cm}$.
(b) The centers of the 3 circles with radius $1 \mathrm{~cm}$ shown in the figure form an equilateral triangle with side length $2 \mathrm{~cm}$. Therefore, their internal angles measure $60^{\circ}$.
Since $\frac{360}{60}=6$, we conclude that up to 6 circles can be arranged under the given conditions.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.