problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
In triangle $\triangle A B C$, point $F$ is on side $A C$ and $F C=2 A F$. If $G$ is the midpoint of segment $B F$ and $E$ is the intersection point of the line passing through $A$ and $G$ with segment $B C$, calculate the ratio $\frac{E C}{E B}$.
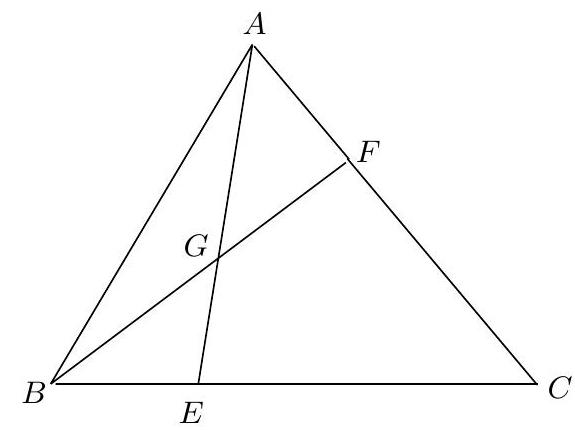
|
We have $\frac{F C}{A F}=2$. Now, draw the segment $F H$, parallel to the segment $A E$ where $H$ is on the segment $B C$, as shown in the following figure.
The triangles $\triangle A E C$ and $\triangle F H C$ are similar because they have parallel sides. This implies that $C H=2 E H$.
On the other hand, the triangles $\triangle B F H$ and $\triangle B G E$ are also similar, as they have parallel sides. From this similarity and the fact that $G$ is the midpoint of the segment $B F$, we conclude that $E$ is the midpoint of the segment $B H$.
Thus, $B E=E H$ and, therefore, $E C=E H+C H=E H+2 E H=3 E H=3 E B$. Consequently, $\frac{E C}{E B}=3$.
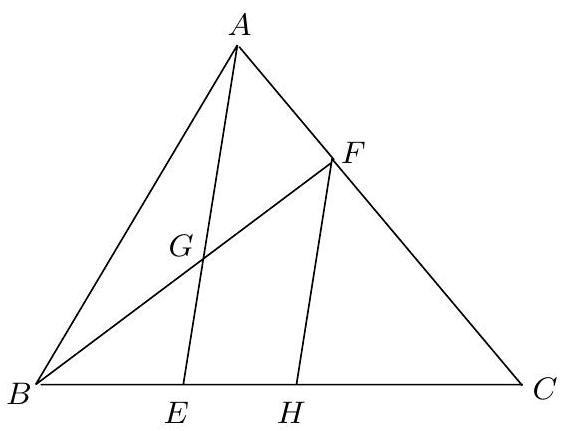
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine all solutions of the equation $\sqrt{x}=x-2$.
untranslated text has been directly translated while preserving the original formatting and structure.
|
By squaring both sides of the equation, we obtain $x=x^{2}-4 x+4$, which is equivalent to $x^{2}-5 x+4=0$. The roots of this quadratic equation are $x=1$ and $x=4$. However, when substituting $x=1$ into the original equation $\sqrt{x}=x-2$, we get $\sqrt{1}=-1$, which is false. However, when substituting $x=4$, we get $\sqrt{4}=2$, which is true. Therefore, the given equation has $x=4$ as its only solution.
Note: The appearance of the "strange solution" $x=1$ is due to the fact that the implication
$$
a^{2}=b^{2} \Rightarrow a=b
$$
is not generally true. The correct statement is
$$
a^{2}=b^{2} \Rightarrow a= \pm b
$$
Thus, when we square both sides of an equation, we obtain a new equation that may, eventually, contain more solutions than the original equation. You can also see this clearly, for example, in the equations: $x=1 \mathrm{and}$ $x^{2}=1^{2}$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A number is said to be a palindrome if reading from right to left is the same as reading from left to right. For example, the numbers 23432 and 18781 are palindromes. How many 4-digit palindrome numbers are divisible by 9?
|
A 4-digit palindrome number is of the form: $a b b a$, where $a$ is a digit between 1 and 9 and $b$ is a digit between 0 and 9. Since the number is divisible by 9, the sum of its digits: $2a + 2b = 2(a + b)$ is divisible by 9, which means $a + b$ is divisible by 9. If $a + b = 9$, we have the 9 solutions:
$a=1$ and $b=8 \quad ; \quad a=2$ and $b=7 \quad ; \quad a=3$ and $b=6 \quad ; \quad a=4$ and $b=5$
$a=5$ and $b=4 \quad ; \quad a=6$ and $b=3 \quad ; \quad a=7$ and $b=2 \quad ; \quad a=8$ and $b=1$
$a=9$ and $b=0$.
If $a + b = 18$, then the only solution is: $a = b = 9$.
Therefore, the number of 4-digit palindromes divisible by 9 is 10, they are: 1881, 2772, 3663, 4554, 8118, 7227, 6336, 5445, 9009, and 9999.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the sequence $1,3,2, \ldots$ each term after the first two is equal to the preceding term subtracted from the term that precedes it, that is: if $n>2$ then $a_{n}=a_{n-1}-a_{n-2}$. What is the sum of the first 100 terms of this sequence?
|
Let's initially write some terms:
$$
1,3,2,-1,-3,-2,1,3,2, \ldots
$$
The 7th and 80th terms are, respectively, equal to the 10th and 2nd terms. This means that the sequence repeats every 6 terms. The sum of the first 6 terms is $1+3+2-1-3-2=0$, and therefore, the sum of the first 96 terms is also 0. Thus, the sum of the first 100 terms of this sequence is equal to the sum of the last 4 terms, that is, $1+3+2-1=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Consider two drums of sufficiently large capacity, one of them empty and the other full of liquid.
a) Determine if it is possible to place exactly one liter of liquid from the full drum into the empty one, using two buckets, one with a capacity of 5 liters and the other with a capacity of 7 liters.
b) Determine if it is possible to place exactly one liter of liquid from one of the drums into the other using two buckets, one with a capacity of $2-\sqrt{2}$ liters and the other with a capacity of $\sqrt{2}$ liters.
|
Solution
a) It is enough to fill the empty drum with 15 liters ($3 \times 5$ liters) using the 5-liter bucket three times, and then remove 14 liters ($2 \times 7$ liters) using the 7-liter bucket twice. This way, we transport $3 \times 5 - 2 \times 7 = 1$ liter.
b) The amount $a$ that we can transport from the full drum to the empty one is of the form $k(2-\sqrt{2}) + l(\sqrt{2})$ liters, where $k$ and $l$ are integers indicating how many times we remove or add liquid using each of the buckets. If $l - k \neq 0$, we can write:
$$
\begin{aligned}
a & = k(2-\sqrt{2}) + l \sqrt{2} \\
a - 2k & = \sqrt{2}(l - k) \\
\frac{a - 2k}{l - k} & = \sqrt{2}
\end{aligned}
$$
Thus, the number $\sqrt{2}$ would be the quotient of two integers, which would result in a rational number. We know that this cannot happen because $\sqrt{2}$ is irrational. We still need to analyze what happens when $l = k$. The equation transforms into:
$$
\begin{aligned}
a & = k(2-\sqrt{2}) + l \sqrt{2} \\
& = k(2-\sqrt{2}) + k \sqrt{2} \\
& = 2k
\end{aligned}
$$
Notice that $2k$ is even, and thus we cannot carry an odd value like $a = 1$. In any case, it is not possible to place exactly 1 liter using the buckets with the given capacities in this item.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Some Christmas lights are arranged using magical wires. Each light can be green or yellow. Each wire is connected to two lights and has a magical property: when someone touches a wire connecting two lights, each of them changes color from green to yellow or from yellow to green.
a) In the arrangement below, each point represents a light and the segments represent the magical wires. At the beginning, all of them are yellow. What is the minimum number of wires we need to touch so that all the lights turn green? Show an example of how to make this change with the minimum number of wires.
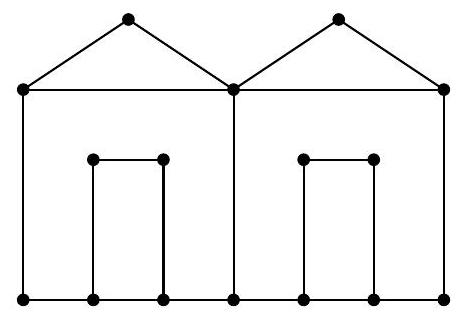
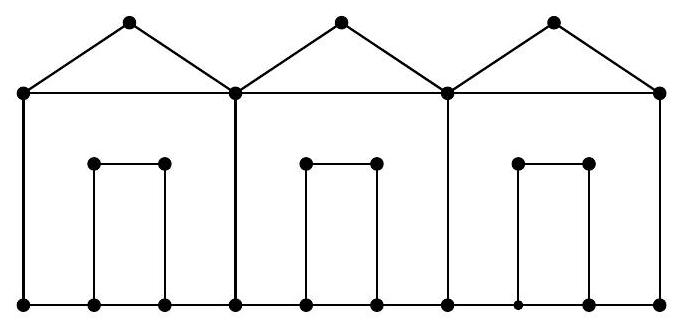
b) Consider the arrangement in the following figure where all the lights are yellow. Show that it is not possible to touch some magical wires and change the color of all the lights to green.
|
Solution
a) Each wire we touch changes the color of exactly two lamps. Since there are 16 yellow lamps, we must touch at least 8 wires. The figure below shows an example of wire choices that make this possible:
b) Note that the configuration given in part b) has exactly 23 lamps. Observe that when we touch a magic wire, there are three possible changes in the lamps:
i) Two green lamps can turn into two yellow lamps.
ii) Two yellow lamps can turn into two green lamps.
iii) One green and one yellow lamp can turn into one yellow and one green lamp.
Thus, the number of green lamps either decreases by 2, increases by 2, or remains the same. Therefore, if we start with 0 green lamps, we will always have an even number of green lamps. Since 23 is odd, it is not possible to turn all 23 lamps green.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Given an $8 \times 8$ board.
a) What is the minimum number of squares we need to mark on this board so that each of its $3 \times 3$ subboards has at least one marked square?
b) What is the minimum number of squares we need to mark on this board so that each of its $3 \times 3$ subboards has at least three marked squares?
|
Solution
a) Consider the figure below.

Each of the four $3 \times 3$ sub-boards marked in the figure must have at least one cell marked. Additionally, with the four marked cells in the figure above, we have the desired property. Therefore, the minimum is 4.
b) Consider the figure below.

Notice that each of the six $3 \times 3$ pieces must have at least three cells marked. Also, there are two cells that can be counted for two pieces. With this, we will have a minimum of $6 \times 3 - 2 = 16$ marked cells. Observe also that with the 16 marked cells in the figure, we have the desired property.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
João managed to paint the squares of an $n \times n$ board in black and white such that the intersections of any two rows and any two columns were not made up of squares of the same color. What is the maximum value of $n$?
#
|
Solution
An example $\operatorname{with} n=4$ is given in the figure below:

We want to show now that, if $n \geq 5$, such a coloring is not possible. Consider then an $n \times n$ board with $n \geq 5$.
Analyzing the squares of the first row, at least three of them will be of the same color. Let's say this color is black (if it were white, it would make no difference to our subsequent analysis) and observe now the columns $A, B$, and $C$ that contain these three black squares. The second row must intersect these three columns in at least two white squares, otherwise, we would have four black intersections between the first two rows and two of these three columns.
Now suppose that the columns containing two black squares in the first row and two white squares in the second are columns $A$ and $B$ (if they were $A$ and $C$ or $B$ and $C$, the subsequent analysis would be the same). Starting from the third row, since we cannot have squares of the same color simultaneously in columns $A$ and $B$, the color distributions can only be the following two options: black and white or white and black. Thus, among rows 3, 4, or 5, two of them will have exactly the same color distribution. These two rows with the same color distribution intersect column $C$ in two squares, neither of which can be black or white, and this prevents the existence of a coloring satisfying the conditions of the problem.
#
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
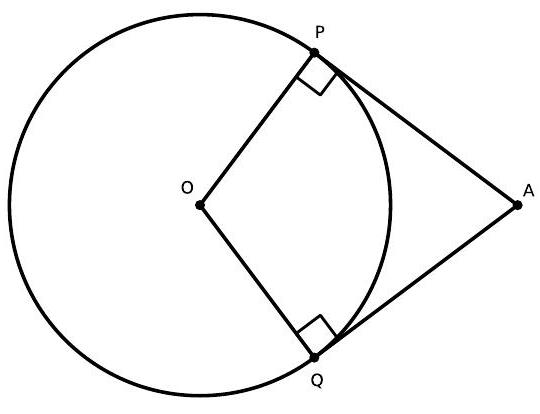
In this problem, we will learn and use the famous Beak Theorem, which is named so because the figure formed really resembles the head and beak of a bird.
a) The Beak Theorem states that the distances from an external point to the points where its tangents touch the circle are equal. In the following figure, $A P$ and $A Q$ are tangents to the circle. Show that $A P = A Q$.
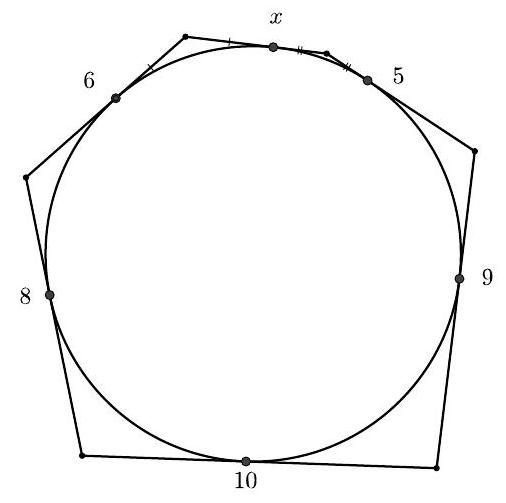
b) Consider the hexagon in the following figure, where all sides are tangent to the circle. Determine the value of the unknown side $x$.
Note: Do not confuse this with the Beaks Theorem from problem 13. In both cases, these are the popular names for the mentioned results.
|
Solution
a) Draw $O A$. Observe that the triangles $\triangle O P A$ and $\triangle O Q A$ are congruent because they are right triangles with the same hypotenuse and one of the legs of the same length. Therefore, $A P=A Q$.
b) Each of the sides is divided by the point of tangency into two segments, as shown in the figure. From the previous item, two of these segments, which share a vertex of the hexagon, are equal. Thus,
$$
\begin{aligned}
6+5+10 & =\left(x_{6}+x_{1}\right)+\left(x_{2}+x_{3}\right)+\left(x_{5}+x_{4}\right) \\
& =\left(x_{1}+x_{2}\right)+\left(x_{3}+x_{4}\right)+\left(x_{5}+x_{6}\right) \\
& =x+9+8
\end{aligned}
$$
Therefore, $x=21-17=4$.
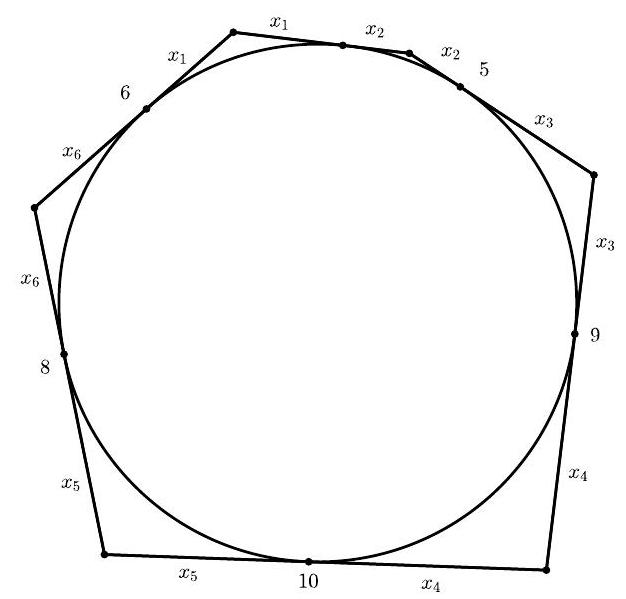
|
4
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Amanda drew the following figure:
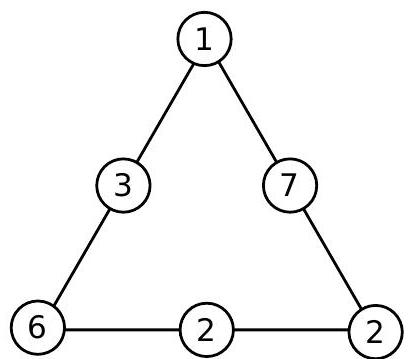
Observe that the sum along any side of the triangle above is always the same, as we can verify,
$$
1+3+6=6+2+2=1+7+2
$$
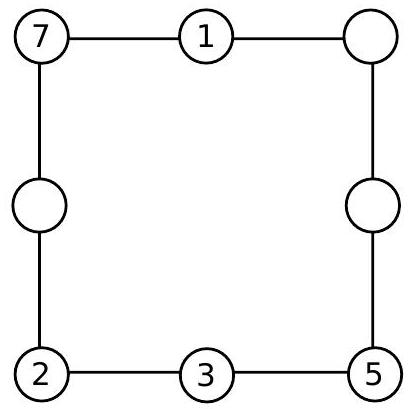
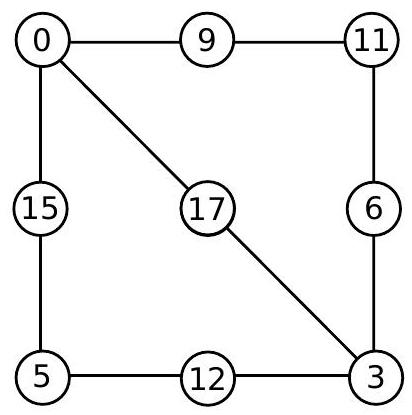
a) Complete the numbers that are missing in the circles of the figure below so that the sums along any side of the square are always the same.
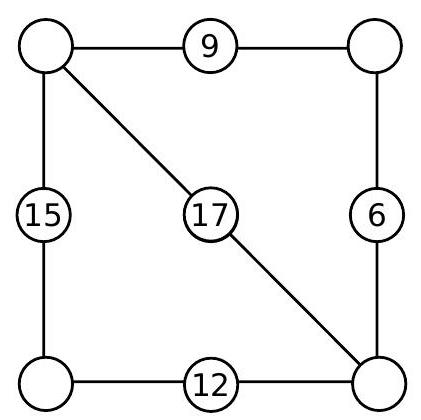
b) Find a way to place the numbers in the circles so that the sums along any line are always the same. Is there more than one solution?
c) In the figure below, which was only partially drawn (due to lack of space!), it is also true that the sum along each segment is always the same. However, Amanda erased all the numbers except the two numbers shown in the figure (3 and 4). It is known that there are 40 circles in the drawing. Is it possible to determine which numbers were in the circles shaded light gray and dark gray?

|
Solution
a) In the bottom row, the sum is $2+3+5=10$. Since the sums along any side are equal, the missing number in the top right corner of the square must be equal to 2, as shown in the following figure:
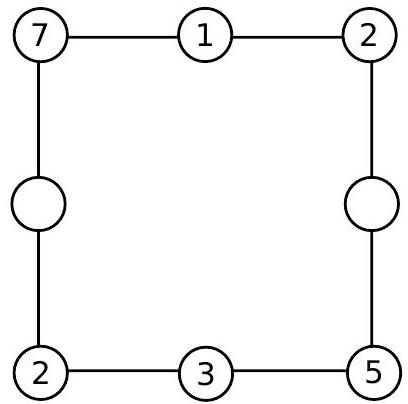
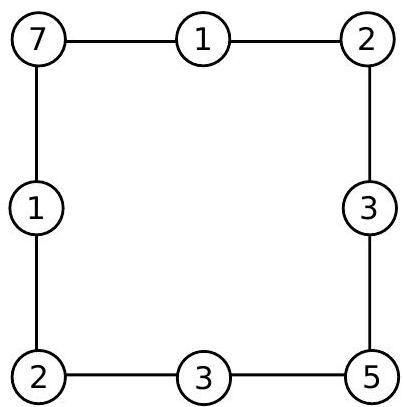
Two more numbers are missing. Again, since the sum must be 10 along any side, the missing numbers are 1 and 3, as shown in the following figure:
b) Let's call the numbers to be placed in the top corners of the square $x$ and $y$, as shown in the following figure:
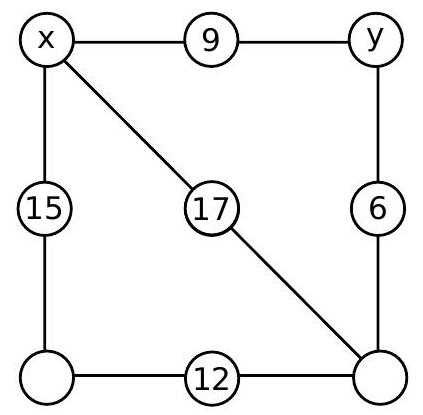
The sums must be constant along any side or diagonal drawn. The sum along the top side is $x+9+y$, so all sums must be equal to $x+9+y$. Observing the sums along the vertical sides, we deduce that the bottom corners must be equal to $y-6$ and $x+3$, as shown in the following figure:
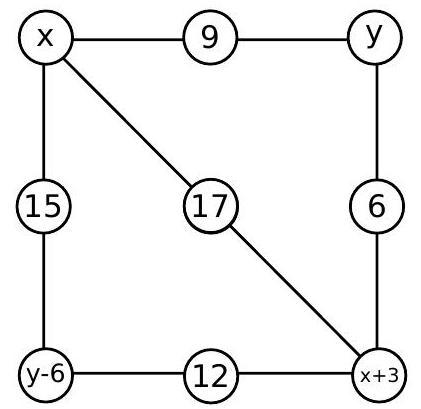
We need to verify the sum along the drawn diagonal and the bottom horizontal side. The sum along the bottom horizontal side is equal to
$$
(y-6)+12+(x+3)=x+9+y
$$
verifying the desired sum. Verifying the sum along the drawn diagonal, we get
$$
x+17+(x+3)=x+9+y
$$
from which we conclude that $y=x+11$. Therefore, any solution will be of the form
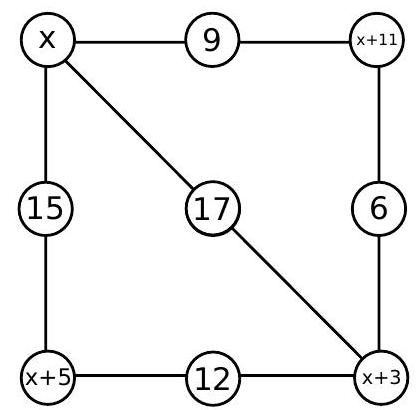
Since the value of $x$ has not been fixed, we can obtain many solutions! For example, taking $x=0$, we get the solution:
c) Let's call the numbers adjacent to the numbers 3 and 4 $x$ and $y$, as shown in the following figure:

Since the sum along each segment is constant, the next two numbers must be equal to 3 and 4:

Since there are 40 circles in the drawing, there are 20 circles in the top row and 20 circles in the bottom row. Continuing the process above, we will get:

Notice the $x$ at the top right corner. This $x$ is connected to the $4$ and the $y$. Since $x+4=x+y$, we conclude that $y=4$. Therefore, the numbers in the two gray circles are equal to 4.
#
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
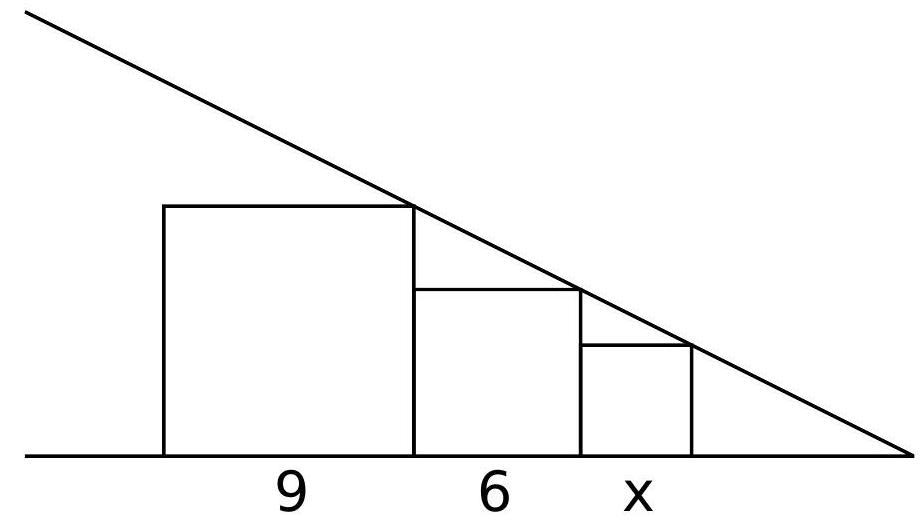
a) In the figure below, there are three squares with sides 9, 6, and $x$. Determine the value of $x$.
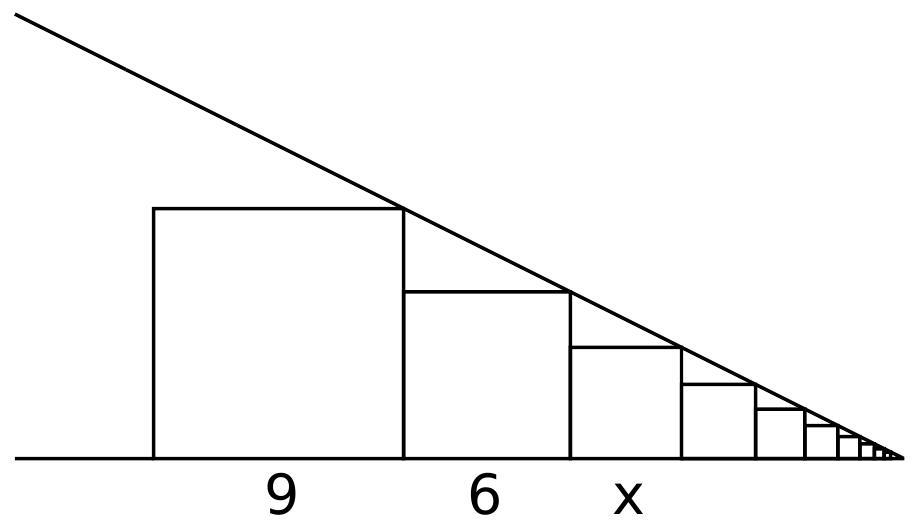
b) Marcelo continues the drawing above and draws more squares (many!). Since these became too small, they cannot be seen, but we show some in the figure below. What is the length of the side of the $2014^{\circ}$ square, counting from left to right?
#
|
Solution
a) Observe the figure:
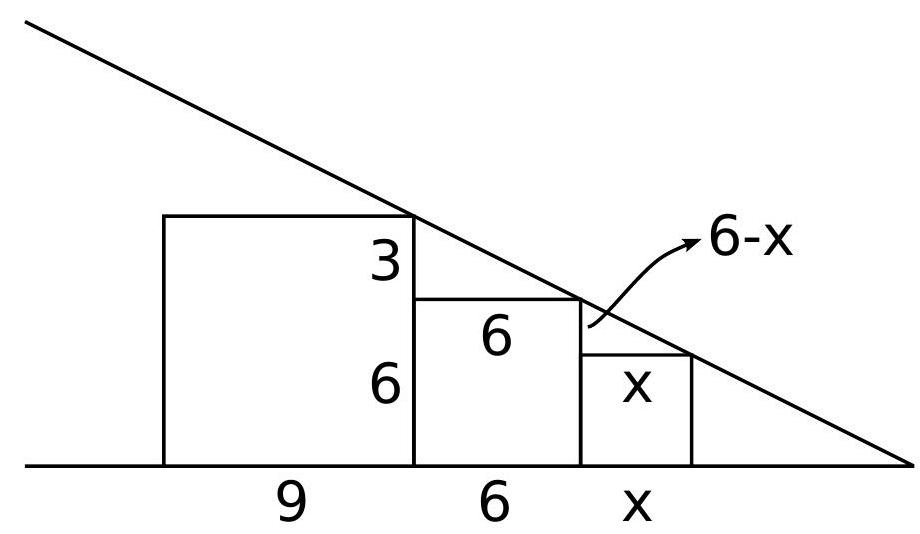
By similarity of triangles, we have
$$
\frac{6-x}{x}=\frac{3}{6}
$$
Therefore, $x=4$.
b) We have that the squares are similar in a ratio of $\frac{2}{3}$. That is, each new square has a side length equal to $\frac{2}{3}$ of the previous side. Thus, the $2014^{\varrho}$ square will have a side equal to
$$
9\left(\frac{2}{3}\right)^{2013}
$$
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $A B C D$ and $E F G H$ be squares with side lengths 33 and 12, respectively, with $E F$ lying on side $D C$ (as shown in the figure below). Let $X$ be the intersection point of segments $H B$ and $D C$. Suppose that $\overline{D E}=18$.
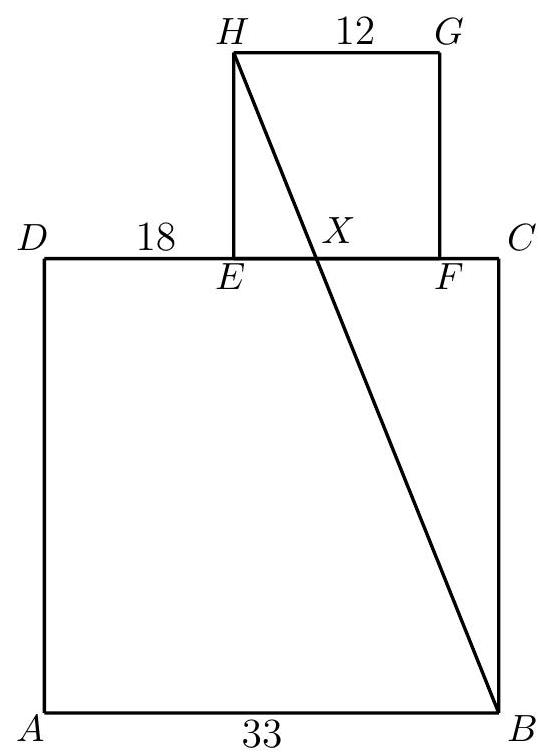
a) Calculate the length of the segment $\overline{E X}$.
b) Prove that the points $A, X$, and $G$ are collinear.
|
Solution
a) Denote $\overline{E X}=x$. We have that $|\overline{C X}|=33-18-x=15-x$.
Now note that the triangles $E X H$ and $C X B$ are similar, so:
$$
\frac{|\overline{E H}|}{|\overline{C B}|}=\frac{|\overline{E X}|}{|\overline{C X}|} \Rightarrow \frac{12}{33}=\frac{x}{15-x}
$$
Now we find $x$ :
$$
\begin{aligned}
12(15-x) & =33 x \\
4(15-x) & =11 x \\
60-4 x & =11 x \\
15 x & =60 \\
x & =4
\end{aligned}
$$
Therefore, $|\overline{E X}|=4$.
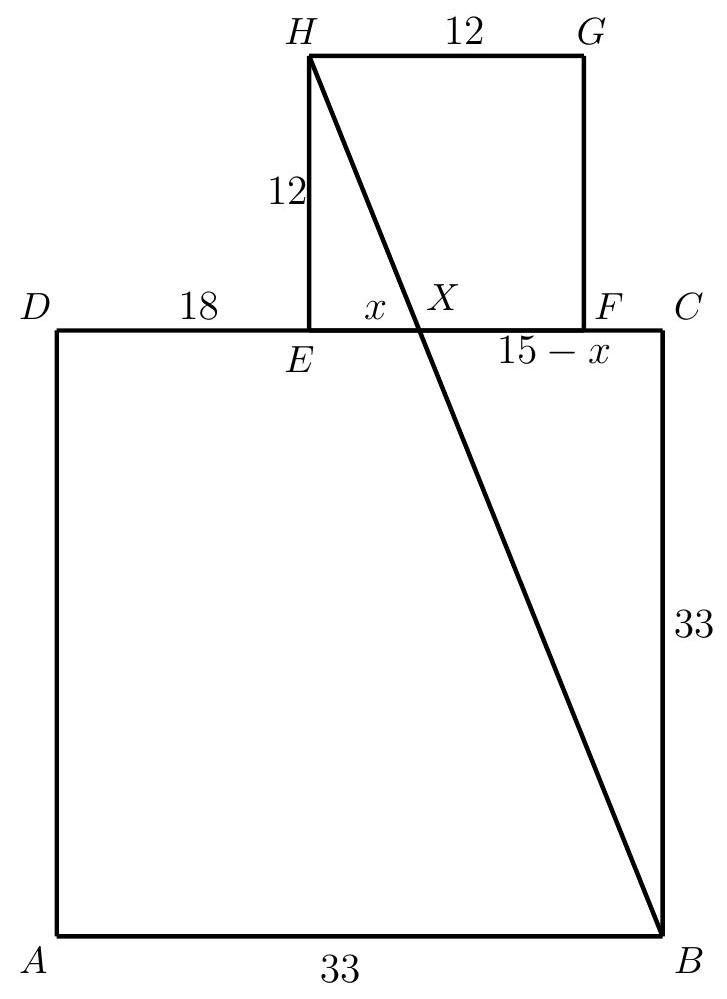
b) Let $Y$ be the intersection of the line $A G$ with the segment $D C$. To prove that $A, X$ and $G$ are collinear, it suffices to show that $Y=X$. And for that, we will calculate $|\overline{E Y}|$, and then see that this is equal to $|\overline{E X}|$. Denote $|\overline{E Y}|=y$. Therefore, $|\overline{F Y}|=12-y$.
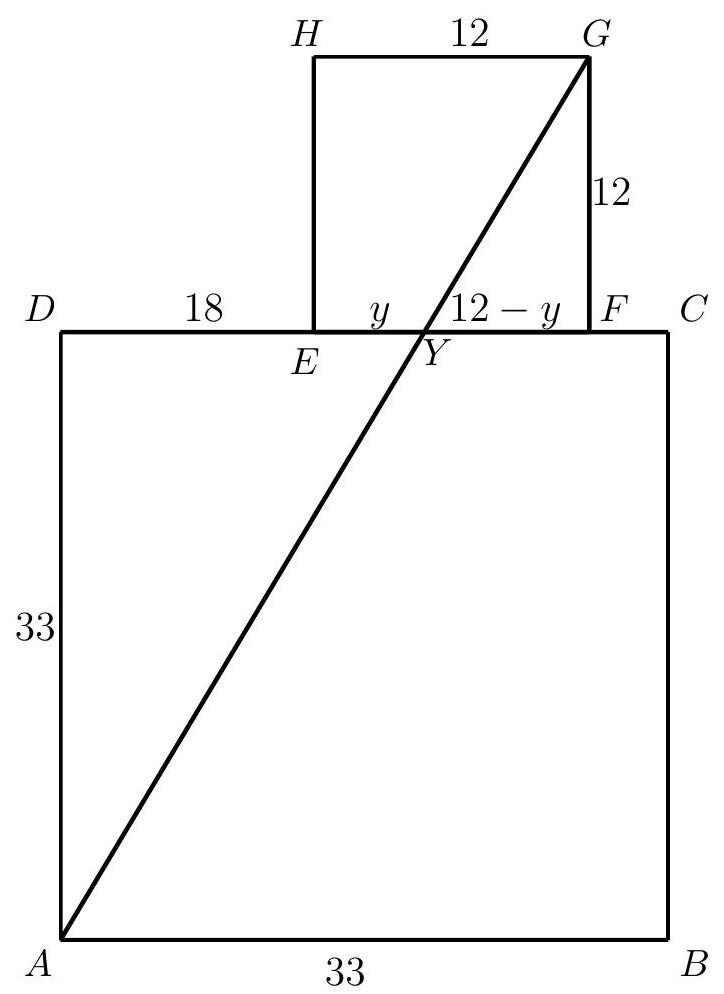
Analogously to the previous case, we see that the triangles $F Y G$ and $D Y A$ are similar. Therefore:
$$
\frac{|\overline{F G}|}{|\overline{D A}|}=\frac{|\overline{F Y}|}{|\overline{D Y}|} \quad \Rightarrow \frac{12}{33}=\frac{12-y}{18+y}
$$
Now we find $y$ :
$$
\begin{array}{ccc}
12(18+y) & = & 33(12-y) \\
4(18+y) & = & 11(12-y) \\
72+4 y & = & 132-11 y \\
15 y & = & 60 \\
y & = & 4 .
\end{array}
$$
Therefore, $|\overline{E Y}|=|\overline{E X}|$. Thus, $X=Y$, and we conclude that the points $A, X$ and $G$ are collinear.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A group of boys and girls went out to eat pizza for two consecutive days. At the restaurant they went to, the pizzas are cut into twelve equal slices. Maria observed that on the first day, each boy ate 7 slices, and each girl 3 slices. On the second day, each boy ate 6 slices, and each girl 2 slices. Interestingly, on both days they ordered four pizzas that were completely consumed, and then ordered another one, from which some slices were left (that is, at least one slice was eaten and at least one slice was left). How many boys and girls went to the pizzeria?
|
Solution
Let $x$ and $y$ be the number of boys and girls, respectively. We know that the total number of slices consumed was at least 49 (4 pizzas and one slice of the last pizza) and at most 59 (4 pizzas plus 11 slices, remember that at least one slice of the last pizza was left). On the other hand,
$$
\begin{aligned}
& 7 x+3 y \leq 59 \\
& 6 x+2 y \geq 49
\end{aligned}
$$
Multiplying the last equation by -1, we need to switch the inequality, resulting in
$$
\begin{aligned}
7 x+3 y & \leq 59 \\
-6 x-2 y & \leq-49
\end{aligned}
$$
Adding the two inequalities, we get
$$
x+y \leq 10
$$
Substituting into the second inequality, we have
$$
4 x+10+10 \geq 4 x+(x+y)+(x+y)=6 x+2 y \geq 49
$$
Thus, $4 x \geq 29$, and therefore $x \geq 8$. On the other hand, from the first equation, we have
$$
7 x \leq 7 x+3 y \leq 59
$$
Therefore, $7 x \leq 59$, which implies $x \leq 8$. Hence, $x=8$ and substituting, we get
$$
3 y \leq 3 \quad \text { and } \quad 2 y \geq 1
$$
This gives us $y=1$. Therefore, there were 8 boys and 1 girl at the pizzeria.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a class, there are 70 students, such that:
I) 14 boys passed in Mathematics;
II) 12 boys passed in Physics;
III) 10 boys and 16 girls did not pass in Mathematics or Physics;
IV) 32 are boys;
V) 10 passed in both subjects;
VI) 22 passed only in Mathematics.
How many girls passed only in Physics?
|
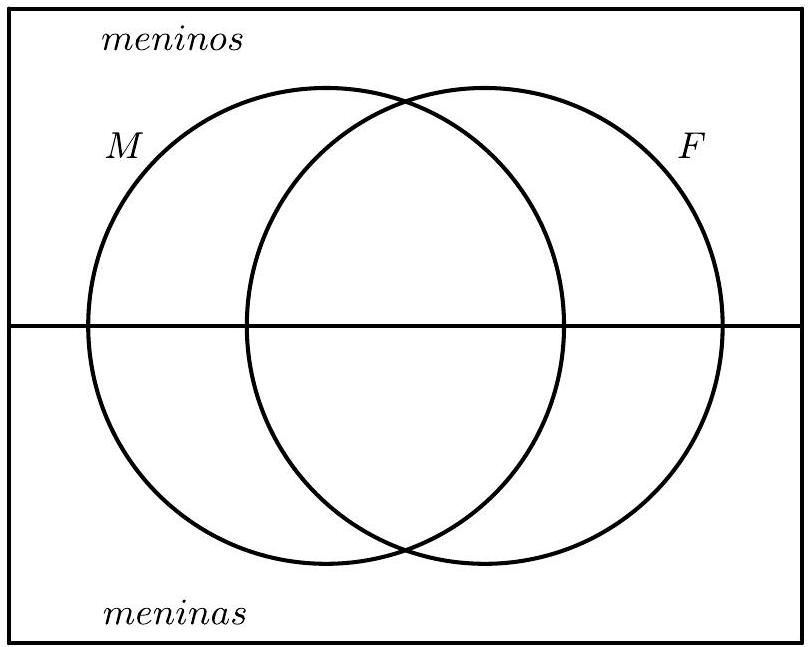
Solution
To solve the problem, we will use the diagram below, where the upper rectangle represents the quantities of boys in each case and the lower one the quantities of girls; in the left circle, the number of students who passed in mathematics, while in the right one, the number who passed in physics, and in the intersection, the number who passed in both.
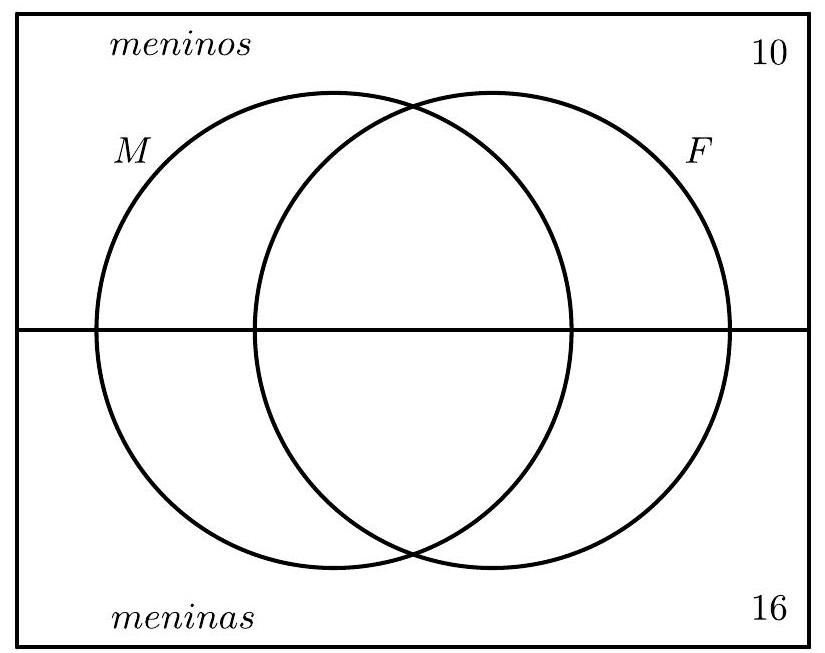
Now, let's fill in the diagram using the information, in a convenient sequence. By $I I I$, we have:
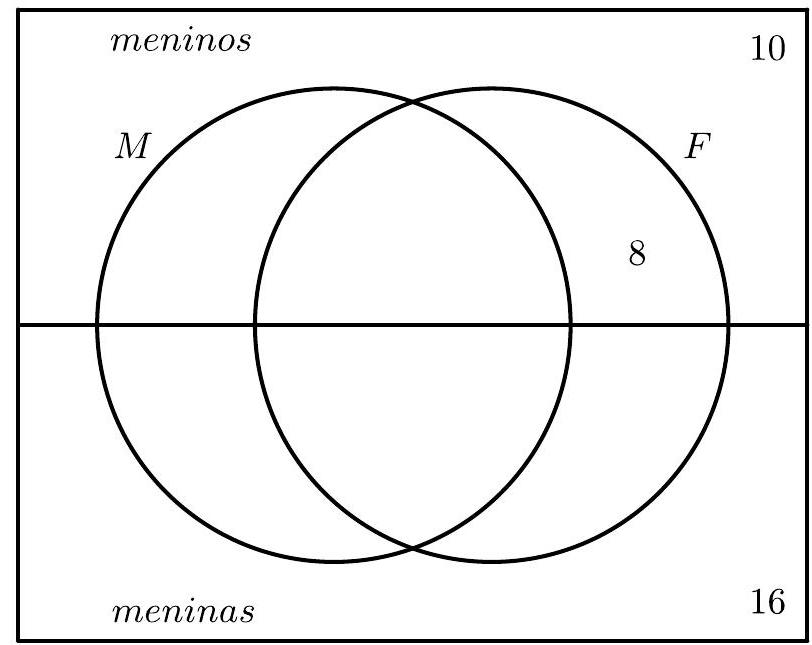
By $I V$ and $I$, since 32 are boys and 14 of them passed in mathematics, then $32-14=18$ did not pass in mathematics, which means that $18-10=8$ of them passed only in physics.
By $I I$, since 12 boys passed in physics, then $12-8=4$ of them also passed in mathematics.
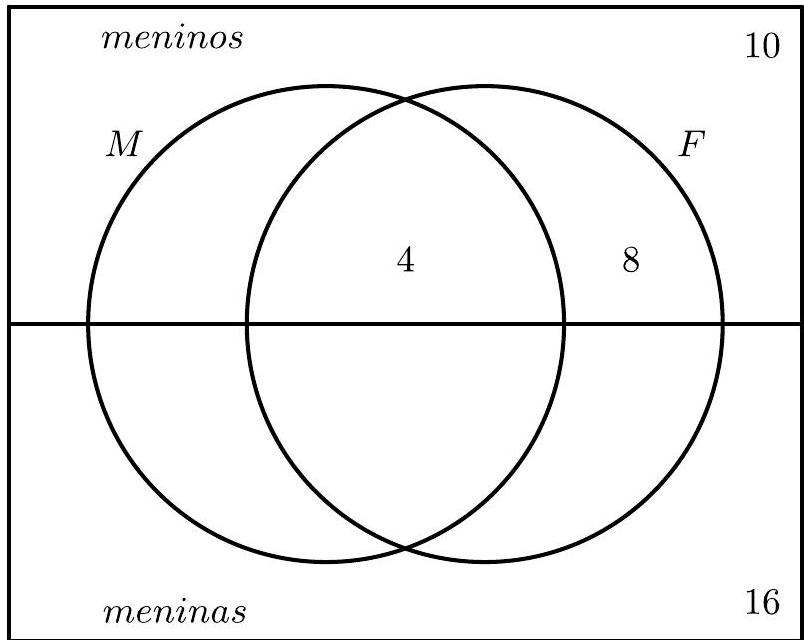
By $I$, since 14 boys passed in mathematics, then $14-4=10$ of them passed only in mathematics. With this, we have determined all the quantities related to the boys.
| | boys | | |
| :---: | :---: | :---: | :---: |
By $V$, since 10 students passed in both subjects, then $10-4=6$ girls passed in both.
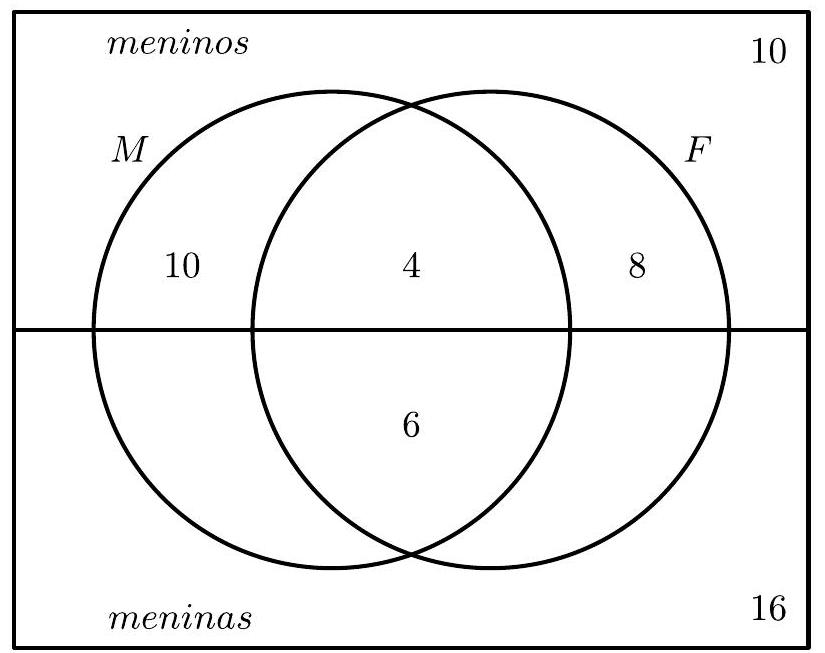
By $V I$, since 22 passed only in mathematics, then $22-10=12$ girls passed only in mathematics.
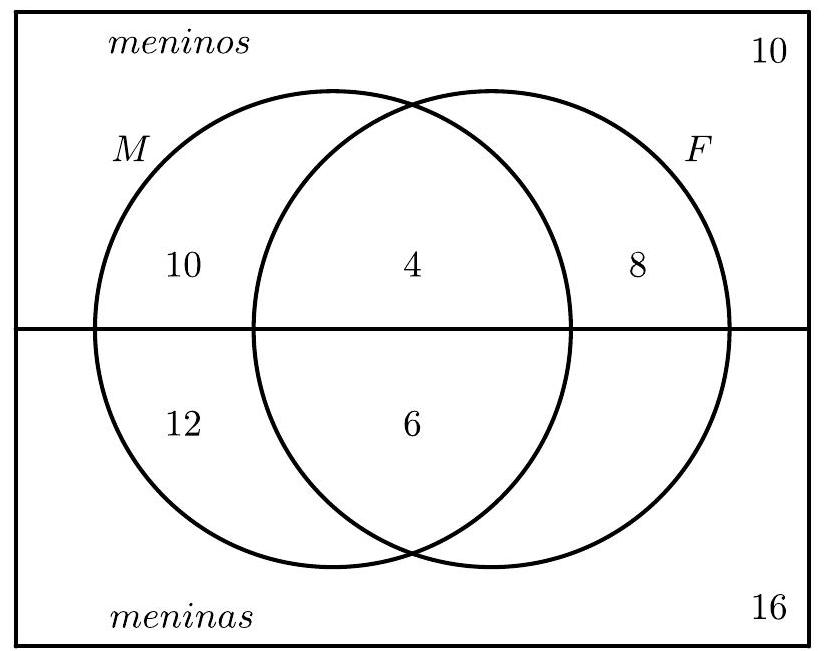
Since we already have $10+10+4+8+12+6+16=66$ students in the diagram, the number of girls who passed only in physics is $70-66=4$.
#
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Using 5 non-zero digits, we can form 120 numbers, without repeating a digit within the same number. Let $S$ be the sum of all these numbers. Determine the sum of the digits of $S$, where:
a) 1, 3, 5, 7, and 9 are the 5 digits;
b) 0, 2, 4, 6, and 8 are the 5 digits, remembering that 02468 is a number with 4 digits and, therefore, we will not have 120 numbers in this case.
|
Solution
a) There are 120 numbers in total, with all possible combinations. Thus, in each of the positions (units, tens, hundreds, thousands, ten thousands), each digit appears the same number of times, that is, $\frac{120}{5}=24$. For example, in the units place, the digit 1 appears 24 times, as does 3, 5, 7, and 9. Therefore, the sum of all the units is:
$$
\begin{aligned}
24 \cdot 1+24 \cdot 3+24 \cdot 5+24 \cdot 7+24 \cdot 9 & = \\
24(1+3+5+7+9) & = \\
24 \cdot 25 & =600
\end{aligned}
$$
Thus, the sum $S$ is:
$$
\begin{aligned}
S & =600+600 \cdot 10+600 \cdot 100+600 \cdot 1.000+600 \cdot 10.000 \\
& =600(1+10+100+1.000+10.000) \\
& =600 \cdot 11.111 \\
& =6.666 .600
\end{aligned}
$$
Finally, the sum of the digits of $S$ is $6+6+6+6+6+0+0=30$.
b) We will use the same reasoning as in the previous item, also counting the numbers that start with 0, that is, those that have only 4 digits. Calling this sum of the 120 numbers $S^{\prime}$, we have:
$$
\begin{aligned}
S^{\prime} & =24 \cdot(0+2+4+6+8) \cdot 11.111 \\
& =24 \cdot 20 \cdot 11.111 \\
& =5.333 .280
\end{aligned}
$$
We now need to subtract the numbers that start with 0, which is the sum of all 4-digit numbers that can be formed with 2, 4, 6, and 8 (120-24 = 96 in total). This sum is $24 \cdot(2+4+6+8) \cdot 1.111=533.280$. Therefore, $S=S^{\prime}-533.280=4.800 .00$, and the sum of its digits is $4+8+0+0+0+0+0=12$.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On a $4 \times 4$ board, the numbers from 1 to 16 must be placed in the cells without repetition, such that the sum of the numbers in each row, column, and diagonal is the same. We call this sum the Magic Sum.
a) What is the Magic Sum of this board?
b) If the sum of the cells marked with $X$ in the board below is 34, what is the sum of the cells marked with $Y$?
| $Y$ | | | $Y$ |
| :--- | :--- | :--- | :--- |
| | $X$ | $X$ | |
| | $X$ | $X$ | |
| $Y$ | | | $Y$ |
c) If we fill in with consecutive natural numbers from $k$ to $(k+15)$, such that the Magic Sum is 50, what is the value of $k$?
|
Solution
a) Since there are 4 rows (as well as 4 columns), the Magic Sum is:
$$
\frac{1+2+3+\ldots+16}{4}=34
$$
b) If we add the two diagonals, we will have exactly the sum of the cells marked with $X$ and with $Y$. Thus, the sum of the cells marked with $Y$ is $2 \cdot 34-34=34$.
c) We have:
$$
\begin{aligned}
\frac{k+(k+1)+(k+2)+\ldots+(k+15)}{4} & =50 \\
16 k+(1+2+3+\ldots+15) & =200 \\
16 k+\frac{(1+15) 15}{2} & =200 \\
16 k+120 & =200 \\
16 k & =80 \\
k & =5
\end{aligned}
$$
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The numbers $a$ and $b$ are positive integers and satisfy $96 a^{2}=b^{3}$. What is the smallest value of $a$?
|
Factoring 96 we have: $2^{5} \times 3 \times a^{2}=b^{3}$. For $2^{5} \times 3 \times a^{2}$ to be a cube, the number $a$ must be of the form: $a=2^{n} \times 3^{m}$. Thus,
$$
2^{5} \times 3 \times a^{2}=2^{5} \times 3 \times\left(2^{n} \times 3^{m}\right)^{2}=2^{5+2 n} \times 3^{1+2 m}=b^{3}
$$
Therefore, $5+2 n$ and $1+2 m$ are multiples of 3. The smallest values of $n$ and $m$ are: $n=2$ and $m=1$. Therefore, $a=2^{2} \times 3=12$.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Twelve points are marked on a sheet of graph paper, as shown in the figure. What is the maximum number of squares that can be formed by connecting four of these points?
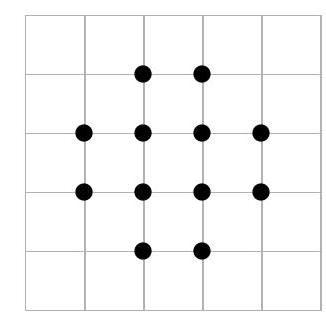
|
In total, we have 11 possible squares as shown below.
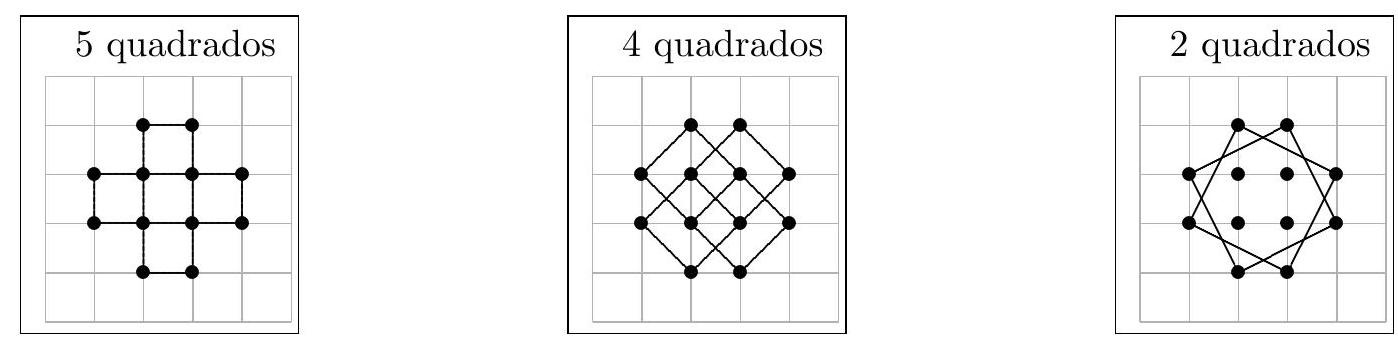
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the map of Figure 21.1, the curve XY is one of the boundaries. Countries like I and II share a common border. Point $Y$ is not considered a border, that is, countries like I and V do not share a common border. You must color the map such that countries with a common border have different colors.
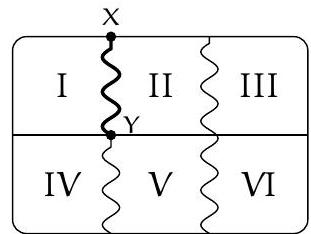
Figure 21.1
(a) What is the minimum number of colors needed to color the map? Show how to color it.
(b) Draw another map of 6 countries that requires at least 4 colors to be painted. Show how to color it with colors A, B, C, and D.
|
(a) At a minimum, two colors are necessary, as shown in Figure 21.2.
(b) Figures 21.3 and 21.4 display two maps with six countries that require at least four colors to be painted.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The cities of Coco da Selva and Quixajuba are connected by a bus line. Buses leave Coco da Selva for Quixajuba every hour, with the first one departing at midnight on the dot. Buses leave Quixajuba for Coco da Selva every hour, with the first one departing at half past midnight. The bus journey takes exactly 5 hours.
If a bus leaves Coco da Selva at noon, how many buses coming from Quixajuba does it encounter during the journey?
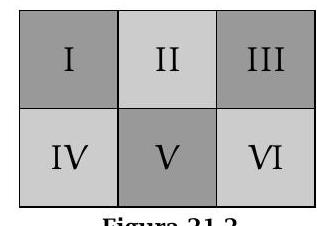
Figure 21.2
Figure 21.3
Figure 21.4
|
Let's observe that the bus departing from Coco da Selva to Quixajuba meets the buses that, at the time of its departure, are
Suggestion: Divide the coins into three groups of 16 coins. on the way from Quixajuba to Coco da Selva and the buses that depart in the next five hours.
The buses that are on the road are those that departed up to 5 hours before this bus, while the buses that are yet to depart must do so within 5 hours after. Thus, the bus will meet all those that departed from Quixajuba between 7:30 AM and 4:30 PM, which are 10.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
pongue
Some students from the seventh and eighth grades of a school participate in a ping pong tournament, where each student plays against all the others exactly once, receiving 1 point for a win and 0 points for a loss. There are ten times as many eighth-grade students as seventh-grade students. The total score of the eighth-grade students is 4.5 times the total score of the seventh-grade students.
a) Verify that if there are $k$ students in the tournament, then the number of games is $\frac{k(k-1)}{2}$.
b) What is the sum of the scores obtained by all the seventh-grade students?
|
pongue - Solution
a) Each of the $k$ students will play $k-1$ times. Summing the number of games each one plays, we get $k(k-1)$. However, we will have counted each game twice, once for each of the participants in the match. Therefore, the number of games is $\frac{k(k-1)}{2}$.
b) Let $n$ be the number of seventh-grade students and suppose this group of students scored $m$ points. Then the number of eighth-grade students is $10 n$ and the score obtained by them is $4.5 \mathrm{~m}$. Since the total number of participants in the tournament is $n+10 n=11 n$ and each match is worth exactly 1 point, the number of points contested is $\frac{11 n(11 n-1)}{2}$. On the other hand, we know that $m+4.5 m$ corresponds to all the points contested, thus
$$
\begin{aligned}
\frac{11 n(11 n-1)}{2} & =5.5 m \\
n(11 n-1) & =m
\end{aligned}
$$
Since each participant played $11 n-1$ games and each game is worth 1 point, the sum of the points obtained by the seventh-grade students is at most $n(11 n-1)$. Since this number coincides with the score obtained by this group of participants, we can conclude that there are no two seventh-grade students who played against each other, otherwise we must subtract from $n(11 n-1)$ the double counting of such a match. This is only possible if there is only one seventh-grade student. Therefore, $n=1 \mathrm{~and} m=1 \cdot 10=10$.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A group of 10 students participates in a mathematics competition formed by teams of 4 students. We know that any two of the teams have exactly one student in common.
a) What is the maximum number of teams a student can participate in? Provide an example of a distribution of 10 students where this maximum number can be verified.
b) Can the competition have 8 teams?
|
Solution
a) Consider a student $A$ who is part of the most teams and say that he is in a team with three other students $B, C$ and $D$. Any other team that also includes $A$ must contain three other students who are not in the set $\{B, C, D\}$. Since there are only $10-1=9$ students different from $A$, the maximum number of teams that can include $A$ is $9 / 3=3$. An example of distributing 10 students, represented by the letters of the set $\{A, B, C, D, E, F, G, H, I, J\}$, is
| A | B | C | D |
| :--- | :--- | :--- | :--- |
| A | E | F | G |
| A | H | I | J. |
Each row indicates a team, and all of them have only student $A$ in common.
b) Suppose, for the sake of contradiction, that there could be 8 teams. Since each team has 4 students, we would have at least $8 \cdot 4=32$ student participations, counted with repetitions. Given that there are only 10 students and $32 / 10>3$, at least one student would have to participate in 4 teams. This contradicts the previous item, and this contradiction shows that we cannot have 8 teams.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Sérgio chooses two positive integers $a$ and $b$. He writes 4 numbers in his notebook: $a, a+2, b$ and $b+2$. Then, all 6 products of two of these numbers are written on the board. Let $Q$ be the number of perfect squares written on it, determine the maximum value of $Q$.
#
|
Solution
Initially, we will prove that the product $a(a+2)$ is not a perfect square for any choice of $a$. We have two cases to consider:
i) If $a$ is odd, then no prime that divides $a$ can divide $a+2$. Therefore, $a$ and $a+2$ must each be a perfect square. This clearly has no solution for $a \geq 1$, as the difference between two perfect squares is at least 3.
ii) If $a$ is even, we have $a=2k$ for some positive integer $k$. Thus, $a(a+2)=2k(2k+2)=(2k+1)^2-1$. This is also not possible, as in this case we would have a perfect square between two consecutive perfect squares: $(2k)^2 < a(a+2) < (2k+1)^2$.
Therefore, the product $a(a+2)$ cannot be a perfect square. Moreover, $ab$ and $b(a+2)$ cannot both be perfect squares simultaneously, because in that case $ab \cdot b(a+2) = b^2 \cdot a(a+2)$ would be a perfect square, implying that $a(a+2)$ is also a perfect square, which contradicts the previous lemma. Similarly, $a(b+2)$ and $(a+2)(b+2)$ cannot both be perfect squares simultaneously. By symmetry, $(a+2)b$ and $(a+2)(b+2)$ cannot both be perfect squares at the same time.
Thus, the possible squares would be $ab, b(a+2), a(b+2)$, and $(a+2)(b+2)$. Excluding the products $a(a+2), b(b+2)$, and noting that in the pairs $(ab, b(a+2))$ and $(ab, a(b+2))$, only one of their members can be a perfect square, we can conclude that $Q \leq 3$. To have $Q=3$, $b(a+2), a(b+2), (a+2)(b+2)$ must all be squares. This is absurd, as we have already seen that $b(a+2)$ and $(a+2)(b+2)$ cannot be perfect squares simultaneously. Note that $Q=2$ can be achieved, for example, with $a=b=1$, since $ab=1^2$ and $(a+2)(b+2)=3^2$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A chessboard is an $8 \times 8$ square where the squares are arranged in 8 rows and 8 columns.
A rook on a chessboard attacks all pieces that are in its row or column. Knowing this, determine:
a) What is the maximum number of rooks that can be placed on a chessboard so that no two attack each other?
b) What is the maximum number of rooks that can be placed on a chessboard so that each rook is threatened by at most one of the other rooks?
|
Solution
a) Below, we have an example with 8 towers, none of which are attacking each other.
If we place 9 or more towers, since there are only 8 rows, there will be two in the same row, and one can attack the other. Therefore, the maximum number is 8.
b) Below, we have an example with 10 towers, each of which is attacked by at most one other tower.
Now we need to show that if we place 11 or more towers, there will be a tower threatened by at least two others. Consider a distribution of towers where each is threatened by at most one other. We can classify them into two groups: those that are not threatened by other towers, called solitary towers, and those that are threatened by exactly one other tower, called towers with enemies. For each solitary tower, we can place a label on its row and column. This uses exactly two labels. For each tower that is threatened by exactly one other, we can place a label on the rows and columns that contain it and its enemy. This uses exactly three labels in this case. If \( x \) is the number of solitary towers and \( 2y \) is the number of towers with enemies, where \( y \) is the number of pairs of enemy towers, then the number of labels used is \( 2x + 3y \). Additionally, since each row and column, totaling 16, received only one label, we have:
\[
\begin{aligned}
16 & \geq 2x + 3y \\
32 & \geq 4x + 6y \\
& \geq 3x + 6y
\end{aligned}
\]
Thus, \( 32 / 3 \geq x + 2y \). Since the number of towers, given by \( x + 2y \), is an integer and \( 32 / 3 < 11 \), it follows that there can be at most 10 towers on the board satisfying the conditions of the second item.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the number $6 a 78 b$, $a$ is the digit of the thousands place and $b$ is the digit of the units place. If $6 a 78 b$ is divisible by 45, then the value of $a+b$ is:
(a) 5
(b) 6
(c) 7
(d) 8
(e) 9
|
The number is divisible by 5 and 9.
Every number divisible by 5 ends in 0 or 5. Thus, $b=0$ or $b=5$.
Every number divisible by 9 has the sum of its digits as a multiple of 9.
Therefore, we have that $6+a+7+8+0=21+a$ or $6+a+7+8+5=26+a$ are multiples of 9. Hence, $a=6$ or $a=1$, respectively. From this, we get: $a+b=6+0=6 \quad$ or $a+b=1+5=6$.
|
6
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
In 13 boxes, 74 pencils were packed. If the maximum capacity of each box is 6 pencils, what is the minimum number of pencils that can be in a box?
(a) 1
(b) 2
(c) 3
(d) 4
(e) 6
|
Let's see in how many boxes we can place the maximum number of pencils, which is 6 per box. In 13 boxes it is not possible, because $13 \times 6=78$, which is greater than the number of pencils 74. In 12 boxes we would have: $12 \times 6=72$. Thus, there would be one box with $74-72=2$ pencils. Therefore, the correct option is (b).
|
2
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Imagine as 2015 fractions:
$$
\frac{2}{2016}, \frac{3}{2015}, \frac{4}{2014}, \ldots, \frac{2014}{4}, \frac{2015}{3}, \frac{2016}{2}
$$
Is it possible to choose three of these fractions with a product equal to 1?
|
Solution
Yes. See that each fraction is of the form $\frac{x}{2018-x}$. Thus, for $x=1009$, the fraction $\frac{1009}{1009}=1$ is part of the list. It then suffices to multiply the fractions:
$$
\frac{2}{2016} \cdot \frac{1009}{1009} \cdot \frac{2016}{2}=1
$$
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Carlinhos likes to write numbers in his notebook. One day he wrote the numbers from 1 to 999, one after the other, to form the giant number:
$$
123456789101112 \ldots 997998999
$$
About this number, the following questions are asked:
(a) How many digits were written?
(b) How many times does the digit 1 appear?
(c) Considering that 1 occupies position 1, 2 occupies position 2, and 0 appears for the first time occupying position 11, which digit occupies position 2016?
|
Solution
(a) Observe that we have 9 numbers with one digit each, $99-9=90$ numbers with two digits each, and $999-99=900$ numbers with three digits each. Therefore, the number of digits written is:
$$
9 \cdot 1 + 90 \cdot 2 + 900 \cdot 3 = 2889
$$
(b) Note that the digit 1 appears once among the one-digit numbers. Among the two-digit numbers, the digit 1 appears 10 times as the tens place and 9 times as the units place, totaling 19 times among the two-digit numbers. Among the three-digit numbers, the digit 1 appears 100 times as the hundreds place. Additionally, for each of the 9 different hundreds, the digit 1 appears 10 times as the tens place and 10 times as the units place. Thus, in these numbers, it appears $9 \cdot (10 + 10) = 180$ times. We conclude that the number of appearances of the digit 1 is:
$$
1 + 19 + 100 + 180 = 300
$$
(c) Note that $2016 > 9 + 90 \cdot 2 = 189$, so the digit at position 2016 will appear among the three-digit numbers. Indeed, we can look for the digit $2016 - 189 = 1827$ from the numbers $100101102103 \ldots$... Since $1827 = 3 \cdot 609$, then, being 100 the first number, the last digit of the number in the 609th position will be the digit we are looking for. The number in the 609th position is
$$
100 + 609 - 1 = 708
$$
Thus, we conclude that the digit at position 2016 in this sequence is 8.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The figure below shows a "staircase" formed by two squares, one with a side of $8 \mathrm{~cm}$ and one with a side of $6 \mathrm{~cm}$. The task is to cut the figure into three pieces and reassemble them to form a square without any gaps.
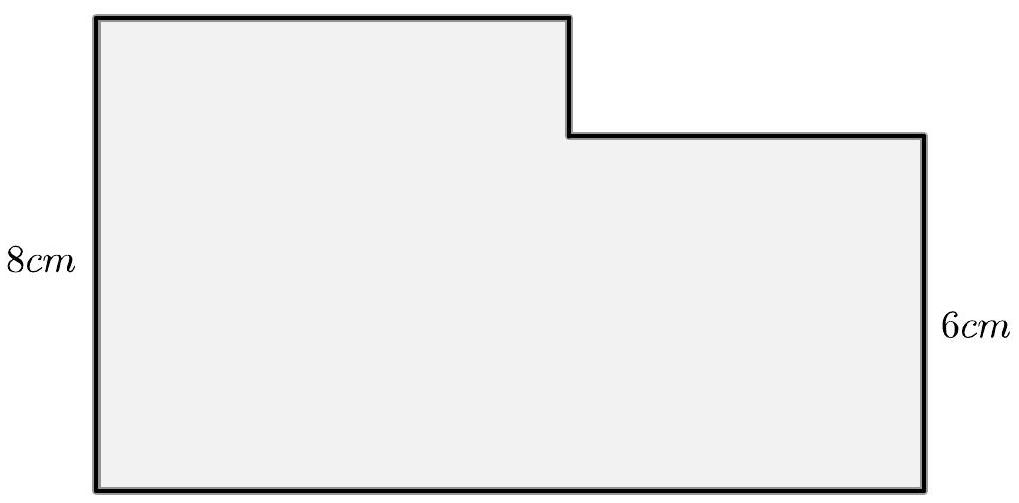
(a) What is the side length of the square that should be formed at the end?
(b) Using only a pencil, a $20 \mathrm{~cm}$ ruler with markings every $1 \mathrm{~cm}$, and a pair of scissors that can only cut along a straight line, show how to perform the desired task.
|
Solution
Cutting the staircase to form a square
(a) Since the square should not have any holes, the final area must be equal to the original area. If we call $L$ the side of the square, we have:
$$
\begin{aligned}
L^{2} & =8^{2}+6^{2} \\
L^{2} & =64+36 \\
L^{2} & =100 \\
L & =10
\end{aligned}
$$
(b) By the Pythagorean Theorem, 8, 6, and 10 are the sides of a right triangle, since $6^{2}+8^{2}=10^{2}$. Taking the longest side of the figure above, which has a length of $8+6=14$, mark the point $R$ that divides it into pieces of lengths 6 and 8. This can be done with a ruler. With a pencil, draw segments from this point to the opposite left and right ends, denoted by $P$ and $Q$, as shown in the following figure. Using the Pythagorean Theorem, we have $P R=Q R=10$. These segments separate the figure into pieces $A, B$, and $C$. Pieces $A$ and $C$ are congruent triangles, and using the sums of their internal angles, we can conclude that $\angle P R Q=90^{\circ}$.
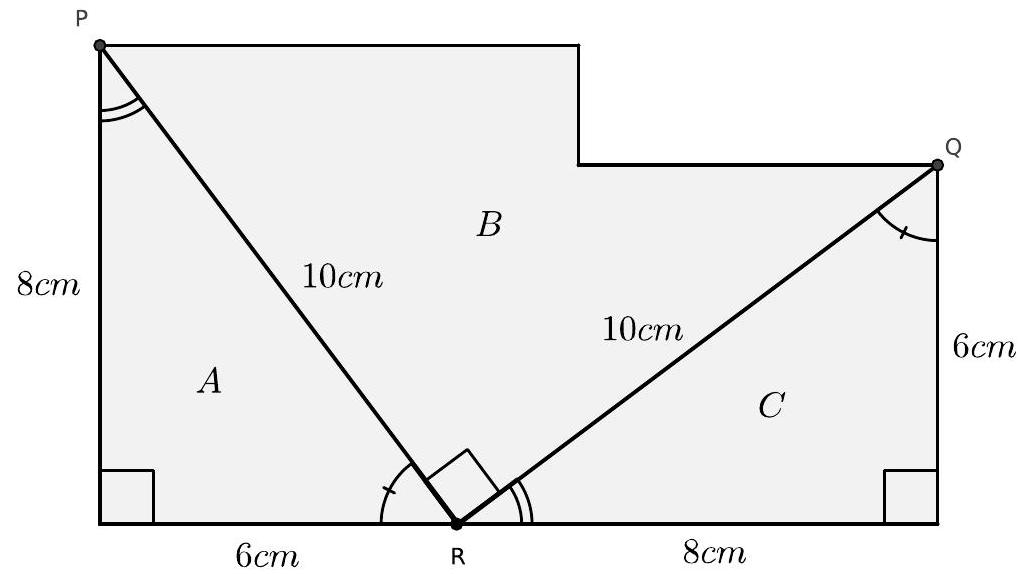
With scissors, the figure is separated into pieces $A, B$, and $C$. Then, they are rearranged to form the square with side 10 as shown in the following figure:
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The 9 squares of a $3 \times 3$ board, as shown in the figure below, must be painted in such a way that in each row, each column, and each of its two diagonals, there are no squares of the same color. What is the minimum number of colors needed for this painting?
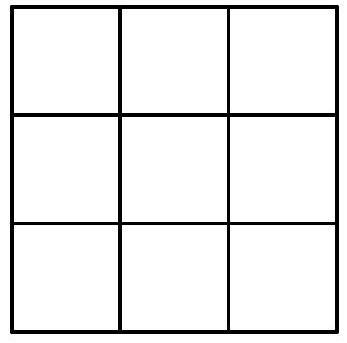
#
|
Solution
Let's denote the colors of the main diagonal by the numbers 1, 2, and 3, as shown in the first figure.
| 1 | | $X$ |
| :--- | :--- | :--- |
| | 2 | |
| $Y$ | | 3 |
Now consider the colors of the two corner squares of the secondary diagonal, denoted by $X$ and $Y$ in the first figure. Since $X$ is in a row that contains the color 1, a diagonal with the color 2, and a column with the color 3, the color $X$ is not in the set $\{1,2,3\}$. By the same argument, the color $Y$ is also not in this set. Moreover, since $X$ and $Y$ are on the same diagonal, they must represent different colors. Therefore, we need at least $3+2=5$ colors. To ensure that 5 is the minimum number, it suffices to exhibit a configuration with this number of colors. This is done in the next figure, where each number represents a color.
| 1 | 3 | 5 |
| :--- | :--- | :--- |
| 3 | 2 | 1 |
| 4 | 1 | 3 |
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
At the end of a day of activities, an amusement park collected 100 reais from the tickets of 100 people. We know that each adult had to pay 3 reais to enter, each young person 2 reais, and each child 30 cents. What is the minimum number of adults who entered the park on that day?
#
|
Solution
To find the minimum number of adults, we will divide the problem into cases:
a) Suppose it is possible to have 0 adults. Thus, the sum of the quantities of young people and children is 100. Consequently, if each child pays 1.70 more to match the contribution of the young people, we will have $2 \cdot 100=200$ reais. Since the actual contribution of these people was 100, the difference $200-100=100$ corresponds to the extra contribution of the children. Therefore, the number of children is $\frac{100}{1.7}$, which is not an integer. This shows that it is not possible to have 0 adults.
b) Suppose it is possible to have 1 adult. Thus, the sum of the quantities of young people and children is 99. Again, if each child pays 1.70 more to match the contribution of the young people, we will have $2 \cdot 99=198$ reais. Since the actual contribution of these people was $100-3 \cdot 1=97$, the difference $198-97=101$ corresponds to the extra contribution of the children. Therefore, the number of children is $\frac{101}{1.7}$, which is not an integer. This shows that it is not possible to have only 1 adult.
c) To show that the minimum number of adults required is 2, it suffices to exhibit compatible quantities of young people and children with the data from the problem. Repeating the strategy from the previous cases of simulating the extra payment of 1.70 by each child, we can conclude that the number of children needed with 2 adults is
$$
\frac{2 \cdot (100-2)-(100-2 \cdot 3)}{1.7}=60
$$
Thus, with 2 adults, the quantities of young people and children are $100-2-60=38$ and 60, respectively. Note that $3 \cdot 2+2 \cdot 38+0.3 \cdot 60=100$.
Therefore, at least 2 adults are necessary.
Observation: Assuming that $x, y$, and $z$ represent the quantities of adults, young people, and children, respectively, we can obtain another solution by writing:
$$
x+y+z=100 \text{ and } 3x+2y+0.3z=100
$$
Then, it suffices to multiply the first equation by 20 and subtract it from the second equation multiplied by 10, obtaining $10x-17z=-1000$. From this, 17 divides $10(x+100)$. Since 100 leaves a remainder of 15 when divided by 17 and $\text{gcd}(10,17)=1$, $x$ must leave a remainder of 2 when divided by 17. The smallest non-negative integer that leaves a remainder of 2 when divided by 17 is 2. It then suffices to follow the final steps of the previous solution to exhibit an example with 2 adults.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the board below, in each row and in each column, exactly one number from the set $\{1,2,3,4\}$ is written. Which number is in the square with the symbol $\star$?
| 1 | 2 | | |
| :--- | :--- | :--- | :--- |
| | 1 | 2 | |
| 2 | | $\star$ | 1 |
| 3 | | 1 | |
|
Solution
Consider the positions indicated by the letters: $A, B, C$ and $D$. Whenever a row or column already has three numbers written, its fourth element is completely determined and is equal to the number that has not yet appeared in it. Thus, $C=4$. Analyzing the numbers in the second row, we have $D=3$. The cell in the top right corner cannot be any number in the set $\{1,2,3\}$, as these have already appeared in the first row and last column. Therefore, $B=4$. Analyzing the numbers in the first row, we can conclude that $A=3$. Finally, observing the third column, we can conclude that $\star=4$.
| 1 | 2 | $A$ | $B$ |
| :---: | :---: | :---: | :---: |
| $C$ | 1 | 2 | $D$ |
| 2 | | $\star$ | 1 |
| 3 | | 1 | |
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Around a circular table, 18 girls are sitting, 11 dressed in blue and 7 dressed in red. Each of them is asked if the girl to their right is dressed in blue, and each one answers yes or no. It is known that a girl tells the truth only when her two neighbors, the one on the right and the one on the left, are wearing clothes of the same color. How many girls will answer yes? If there is more than one possibility, state all of them.
|
Solution
Let's analyze the possibilities. If the two neighbors of a certain girl are wearing blue, then she answers yes, and if they both wear red, she answers no, because in these cases she tells the truth. If the neighbor on the right is wearing red and the one on the left is wearing blue, the answer is yes, and if the one on the right is wearing blue and the one on the left is wearing red, the answer is no, because in these cases she lies. Observing the possibilities, we conclude that a girl answers yes when her left neighbor is wearing blue. Since there are 11 girls wearing blue, there are 11 girls who have their left neighbor wearing blue, and we can conclude that exactly 11 girls will answer yes.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A round table has a diameter of $1.40 \, \text{m}$. For a party, the table is expanded by adding three planks, each $40 \, \text{cm}$ wide, as shown in the figure. If each person at the table should have a space of $60 \, \text{cm}$, how many guests can sit at the table?
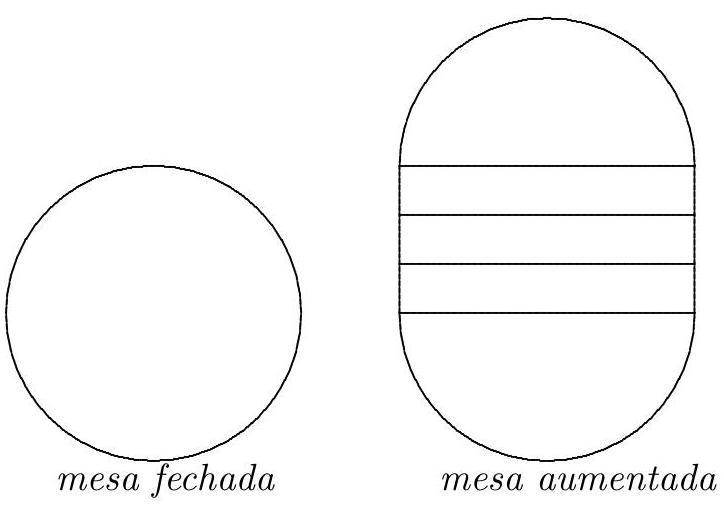
|
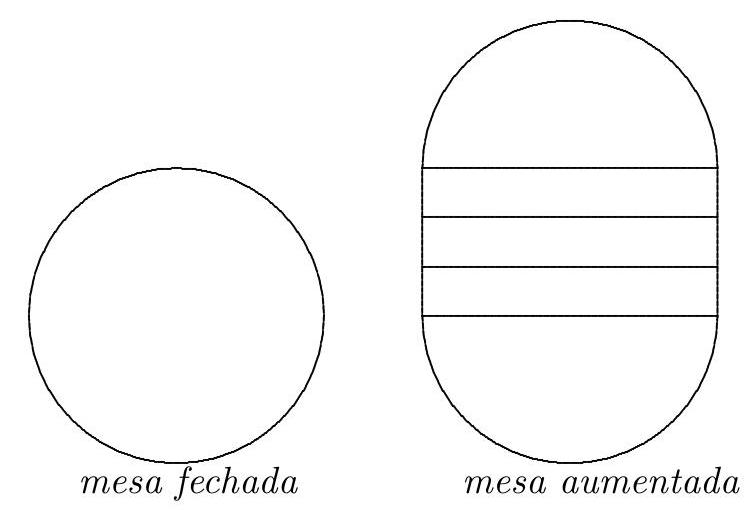
The perimeter of the enlarged table is
$$
140 \times \pi + 40 \times 6 \simeq 140 \times 3.14 + 240 = 679.60 \mathrm{~cm}
$$
If each guest needs $60 \mathrm{~cm}$ to sit around the table and
$$
\frac{679.60}{60} \simeq 11.3
$$
Then, 11 guests can be accommodated.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A surveillance service is to be installed in a park in the form of a network of stations. The stations must be connected by telephone lines so that any of the stations can communicate with all the others, either by a direct connection or through at most one other station. Each station can be directly connected by a cable to at most 3 other stations.
The diagram shows an example of such a network connecting 7 stations. What is the maximum number of stations that can be connected in this way?
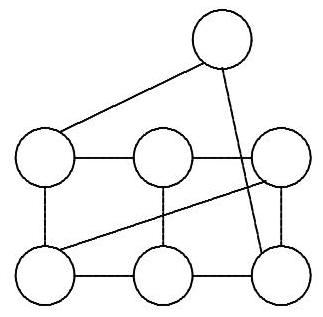
|
The example shows that we can connect at least 7 stations under the proposed conditions. We start with a particular station, and think of it as the base of the network. It can be connected to 1, 2, or 3 stations as shown in the diagram.
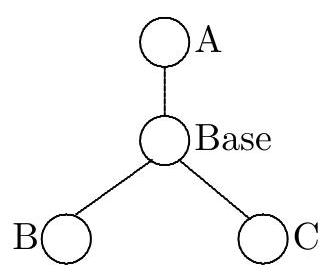
Now, stations A, B, and C still have two unused lines, so they can be connected to two other stations as follows:
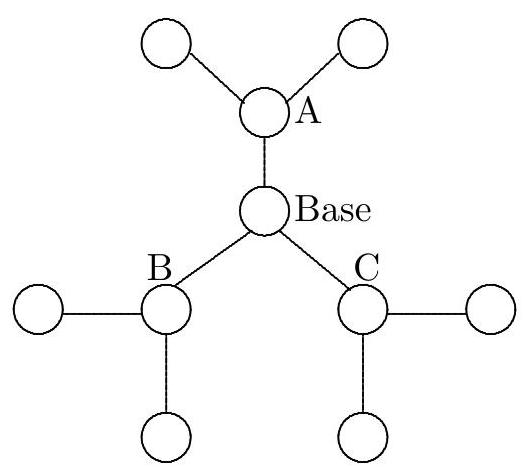
Now, it is impossible to add more stations because any additional one would not be able to connect to the base while satisfying the conditions of the problem. This shows that we cannot have more than 10 stations. Let's now check if we can build the network with these 10 stations. Observe in the diagram above that only the Base is connected to all other stations (either directly or via a connection through another station). The stations at the ends still have two unused lines, and now we will use them to "close" the network; see the following diagram.
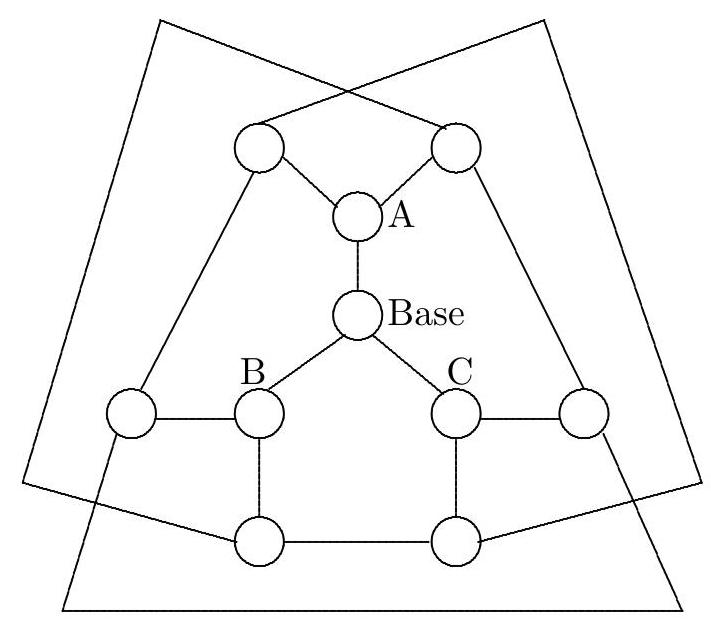
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A box has exactly 100 black balls and 100 white balls. Repeatedly, 3 balls are removed from the box and replaced by other balls that are in a bag as follows:
## BALLS REMOVED REPLACED BY
3 black $\Longrightarrow 1$ black
2 black and 1 white $\Longrightarrow 1$ black and 1 white
1 black and 2 white $\Longrightarrow 2$ white
3 white $\Longrightarrow 1$ black and 1 white
What can be the content of the box after repeated applications of this procedure?
(a) 2 black
(b) 2 white
(c) 1 black
(d) 1 black and 1 white
(e) 1 white.
|
Initially observe that after each replacement, the number of white balls either remains the same or decreases by 2. Therefore, the number of white balls remains even. On the other hand, each group of balls removed that contains at least 1 white ball is replaced by another that also contains 1 white ball, so the number of white balls is never zero. Now observe that option (b) is the only one including at least 2 white balls, so it is the correct option. One way to achieve this result is to remove 3 white balls 49 times until you have 149 black and 2 white balls, and then, remove 1 black and 2 white balls 149 times.
|
2
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
(a) In how many ways can the number 105 be written as the difference of two perfect squares?
(b) Show that it is not possible to write the number 106 as the difference of two perfect squares.
##
|
(a) Let $x$ and $y$ be two positive integers such that the difference between their squares is equal to 105, that is, $x^{2}-y^{2}=105$. Factoring, we get $(x-y)(x+y)=105$, and therefore, $x+y$ and $x-y$ must be divisors of 105, with $x+y > x-y$. Note that $1 \cdot 105 = 3 \cdot 35 = 5 \cdot 21 = 7 \cdot 15$ are all the ways to write the number 105 as a product of two positive integers. Thus, we have four cases:
$$
\begin{aligned}
& \left\{\begin{array}{l}
x+y=105 \\
x-y=1
\end{array} \Longleftrightarrow x=53 \text { and } y=52 .\right. \\
& \left\{\begin{array}{l}
x+y=35 \\
x-y=3
\end{array} \Longleftrightarrow x=19 \text { and } y=16\right. \\
& \left\{\begin{array}{l}
x+y=21 \\
x-y=5
\end{array} \Longleftrightarrow x=13 \text { and } y=8\right.
\end{aligned}
$$
Therefore, it is possible to write 105 as the difference of two squares in four ways, namely: $53^{2}-52^{2}, 19^{2}-16^{2}, 13^{2}-8^{2}$, and $11^{2}-4^{2}$.
(b) Observe that for any integers $x$ and $y$, the numbers $x+y$ and $x-y$ are both even or both odd, since the sum of the two numbers is equal to $2x$, which is even, so we cannot have one even and the other odd.
From this, we conclude that the product $(x+y)(x-y)=x^{2}-y^{2}$ is a multiple of 4 (if $x+y$ and $x-y$ are even) or an odd number (if $x+y$ and $x-y$ are odd).
Since 106 is even but not divisible by 4, it cannot be written as the difference of two squares.
Facts that Help: The difference between the squares of two numbers is equal to the product of the sum of these numbers by the difference of the same numbers. Algebraically:
$$
m^{2}-n^{2}=(m+n)(m-n)
$$
Suggestion: Verify that the sequence that remains on the board after the entire process is periodic.
Facts that Help: A number and the sum of its digits leave the same remainder when divided by 9.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
If $(x+y)^{2}-(x-y)^{2}=20$, then $x y$ is equal to:
(a) 0
(b) 1
(c) 2
(d) 5
(e) 10
|
As $(x+y)^{2}=x^{2}+2 x y+y^{2}$ and $(x-y)^{2}=$ $x^{2}-2 x y+y^{2}$, we have:
$$
(x+y)^{2}-(x-y)^{2}=x^{2}+2 x y+y^{2}-x^{2}+2 x y-y^{2}=4 x y=20
$$
it follows that $x y=5$. The correct option is (d).
|
5
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
feira 13 - What is the maximum number of Friday the 13ths that can occur in a non-leap year? In this case, what is the $10^{\text{th}}$ day of the year?
|
Feira 13 - Given that the days of the week repeat every 7 days, the difference between the days of the week is given by the remainder when dividing by 7 the number of days that have passed.
$\mathrm{In}$ the following table:
- in the first row, the number of days between the 13th of one month and the 13th of the next month;
- in the second row, the remainder when we divide this number by 7;
- in the third row, the remainder when we divide by 7 the number of days between the 13th of January and the 13th of the corresponding month, that is, it is obtained by summing the results obtained in the previous row from January to the corresponding month and then calculating the remainder when dividing by 7.
| J-F | F-M | M-A | A-M | M-J | J-J | J-A | A-S | S-O | O-N | N-D |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 |
| 3 | 0 | 3 | 2 | 3 | 2 | 3 | 3 | 2 | 3 | 2 |
| 3 | 3 | 6 | 1 | 4 | 6 | 2 | 5 | 0 | 3 | 5 |
The equal values in the last row mean that in these months the 13th fell on the same day of the week. In particular, this last row tells us that the 13th of February, the 13th of March, and the 13th of November correspond to the same day of the week. Therefore, we have at most three Friday the 13ths.
In this case, the 13th of January occurred 3 days before Friday, that is, on a Tuesday, and the 10th of January occurred 3 days before, that is, on a Saturday.
Note: The 6th Friday the 13th occurs only when the 1st day of the month is a Sunday. Thus, another way, perhaps simpler, to solve the problem is to determine the maximum number of times the 1st day of the month is a Sunday in a non-leap year.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How many triangles exist whose sides are integers and the perimeter is 12?
(a) 1
(b) 3
(c) 5
(d) 7
(e) 9
|
For three numbers $a, b, c$ to be the lengths of the sides of a triangle, each of them must be greater than the difference and less than the sum of the other two.
Let $a \leq b \leq c$ be the lengths of the sides of the triangle. Thus, $c < a + b$.
Now, adding $c$ to both sides, we have: $2c < a + b + c = 12$, that is, $2c < 12$, $\log c < 6$.
Moreover, since $3c \geq a + b + c = 12$, we have: $c \geq 4$. Therefore, $4 \leq c < 6$.
In the case of $c = 5$, we have $a + b = 7$. The possible values of $a$ and $b$ are: $a = 2$ and $b = 5$ or $a = 3$ and $b = 4$.
In the case of $c = 4$, we have $a + b = 8$, and thus we have only the solution $a = b = 4$.
Thus, we have 3 possible triangles. The correct option is (b).
|
3
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Archaeologists found a gold necklace made of plates in the shape of regular pentagons. Each of these plates is connected to two other plates, as illustrated in the figure.
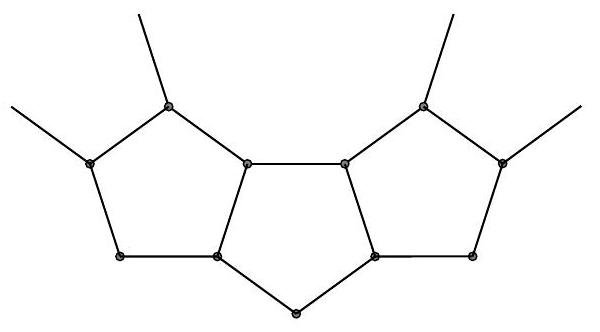
Figure 51.1
How many plates form the necklace?
|
The internal angle of a regular pentagon measures $108^{\circ}$. Therefore, the internal angle of the polygon determined by the necklace measures $360^{\circ}-108^{\circ}-108^{\circ}=144^{\circ}$. We must then find $n$ such that
$$
\frac{180^{\circ}(n-2)}{n}=144^{\circ}
$$
Solving this equation, we get $n=10$. Therefore, ten plates form the necklace.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The sum of 3 numbers is 100, two are prime and one is the sum of the other two.
(a) What is the largest of the 3 numbers?
(b) Give an example of these 3 numbers.
(c) How many solutions exist for this problem?
|
(a) Initially observe that:
- the largest number is the sum of the other two;
- the largest number cannot exceed 50, otherwise the sum of the three would be greater than 100;
- the largest number cannot be less than 50, otherwise the sum of the three would be less than 100.
Therefore, the largest number can only be 50.
(b) The numbers 3, 47, and 50 form a solution to the problem.
(c) There are as many solutions as there are pairs of primes that sum to 50. The table shows all the solutions. Therefore, this problem has 4 solutions.
| 3 | 47 | 50 |
| :---: | :---: | :---: |
| 7 | 43 | 50 |
| 13 | 37 | 50 |
| 19 | 31 | 50 |
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the digit of the $1997^{\mathrm{th}}$ decimal place of:
(a) $\frac{1}{22}$
(b) $\frac{1}{27}$
## Level 1 Solutions
## List 1
#
|
(a) Dividing 1 by 22 we get: $\frac{1}{22}=0.0454545 \ldots$ We observe that the digit 4 is in the even positions: $2,4,6, \ldots$ and the digit 5 in the odd positions: $3,5,7 \ldots$ Since 1997 is an odd number, the digit in the $1997^{\text{th}}$ decimal place is 5.
(b) Dividing 1 by 27 we get: $\frac{1}{27}=0.037037037 \ldots$
We observe that the digits 0, 3, and 7 repeat, successively, every three decimal places, with the digit:
- 0 in the positions: $1,4,7, \ldots$, that is, when divided by three, they leave a remainder of 1;
- 3 in the positions: $2,5,8, \ldots$, that is, when divided by three, they leave a remainder of 2;
- 7 in the positions: $3,6,9, \ldots$, that is, they are multiples of 3.
Since the division $1997 \div 3$ leaves a remainder of 2, the digit in the $1997^{\text{th}}$ decimal place is 3.
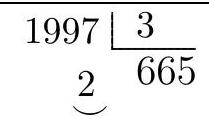
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In how many ways can the 6 faces of a cube be colored black or white? Two colorings are the same if one can be obtained from the other by a rotation.
|
Let's observe that it suffices to count how many colorings exist that have exactly 0, 1, 2, and 3 black faces, because the other cases are symmetric. With one or no black face, there is a unique coloring for each case. When we have two black faces, we have two possible colorings: when these faces are opposite and when they are not. Lastly, with three black faces, we also have two cases: when two of these black faces are opposite and when there are no opposite black faces. Thus, in total, we have $1+1+2+2+2+1+1=10$ possible colorings.
## Related Problem
In how many ways can the 12 edges of a cube be colored white or black? Two colorings are considered the same if one can be obtained from the other by a rotation.
#
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Each person in a group of ten people calculates the sum of the ages of the other nine members of the group. The ten sums obtained are $82, 83, 84, 85, 87, 89, 90, 90, 91$ and 92.
Determine the age of the youngest person.
|
Observe that the age of each person appears as a term in 9 of the 10 numbers. Thus, if we sum the 10 numbers, we will get nine times the sum of all the ages. Therefore, the sum of the ages of the ten people is
$$
\frac{82+83+84+85+87+89+90+90+91+92}{9}=\frac{873}{9}=97
$$
The youngest person obtained the highest sum, which corresponds to the sum of the ages of the nine oldest, so their age is $97-92=5$ years.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The unit digit of the number $1 \times 3 \times 5 \times 79 \times 97 \times 113$ is
(a) 1
(b) 3
(c) 5
(d) 7
(e) 9
|
The correct option is (c).
The given product has one of its factors equal to 5, therefore, it is a multiple of 5, which always has the unit digit equal to 0 or 5. Moreover, since all the factors are odd numbers, the product is an odd number. Thus, its unit digit is 5.
|
5
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
See the promotions of two supermarkets:
| Supermarket A | Supermarket B |
| :---: | :---: |
| 6 cans of 3 liters of QUOTE ice cream | QUOTE ice cream - can of 3 liters |
| $\mathrm{R} \$ 24.00$ | 4 cans - only $\mathrm{R} \$ 14.00$ |
Joana wants to buy 12 cans of ice cream for her birthday party. In which supermarket should she buy and why?
(a) At A, because she will save $R \$ 7.00$ compared to $B$.
(b) At A, because she will save $R \$ 6.00$ compared to $B$.
(c) At B, because she will save $\mathrm{R} \$ 8.00$ compared to $\mathrm{A}$.
(d) At B, because she will save $\mathrm{R} \$ 6.00$ compared to $\mathrm{A}$.
(e) It doesn't matter, because the price is the same in both supermarkets.
|
The correct option is (d).
If Joana buys at supermarket A, she will spend $2 \times 24=48$ reais. If she buys at supermarket B, she will spend $3 \times 14=42$ reais. Therefore, at supermarket B, she will save 6 reais compared to A.
|
6
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Seven teams, divided into two groups, participated in the football tournament in my neighborhood. Group 1 consisted of the teams Avaqui, Botágua, and Corinense. Group 2 consisted of the teams Dinossaurs, Esquisitos, Flurinthians, and Guaraná.
$\mathrm{In}$ the first round of the tournament, each team played against each of the other teams in its group exactly once. In the second round of the tournament, each team played against each of the teams in the other group exactly once.
(a) How many matches were played in the first round in Group 1?
(b) How many matches were played in the first round in Group 2?
(c) How many matches were played in the second round?
|
Let's denote the seven teams by their initial letter.
(a) In the first round of Group 1, three matches were played: $\mathrm{A} \times \mathrm{B}, \mathrm{B} \times \mathrm{C}$, and $\mathrm{C} \times \mathrm{A}$.
(b) In the first round of Group 2, six matches were played: $\mathrm{D} \times \mathrm{E}, \mathrm{D} \times \mathrm{F}$, $\mathrm{D} \times \mathrm{G}, \mathrm{E} \times \mathrm{F}, \mathrm{E} \times \mathrm{G}$, and $\mathrm{F} \times \mathrm{G}$.
(c) In the second round, each team in Group 1 played four matches, one against each team in Group 2. Since Group 1 has three teams, in the second round, $3 \times 4=12$ matches were played.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Have you seen a numeric trick? Here are the steps of a numeric trick:
(i) Choose any number.
(ii) Multiply it by 6.
(iii) Subtract 21 from the result.
(iv) Divide this new result by 3.
(v) Subtract twice the number you chose from this last result.
(a) Try this sequence of five steps three times, starting each time with a different number. What was the result of your experiment?
(b) Next, using the letter $x$ to represent the number you chose in the first step, show why the results from part (a) are not just a coincidence, but a mathematical fact.
|
(a) Let's do the experiment with the numbers 0, 5, and -4.
$$
\begin{aligned}
& 0 \xrightarrow[\times 6]{ } 0 \xrightarrow[-21]{ }-21 \xrightarrow[\div 3]{ }-7 \xrightarrow[-(0 \times 2)=0]{ }-7 \\
& 5 \xrightarrow[\times 6]{ } 30 \xrightarrow[-21]{ } 9 \xrightarrow[\div 3]{ } 3 \underset{-(5 \times 2)=-10}{\longrightarrow}-7 \\
& -4 \xrightarrow[\times 6]{\longrightarrow}-24 \xrightarrow[-21]{ }-45 \xrightarrow[\div 3]{-15 \xrightarrow[-(-4 \times 2)=+8]{\longrightarrow}}-7
\end{aligned}
$$
The final result is always -7.
(b) It is reasonable, then, to conjecture that for any initial number chosen, the final result of this procedure will always be -7. Let $x$ be the initial number. We then have the following operations.
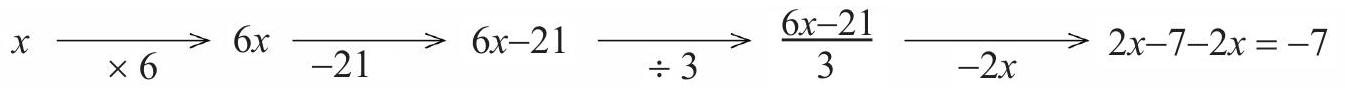
Therefore, the result of this "magic" will always be equal to -7, regardless of the number initially chosen.
|
-7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
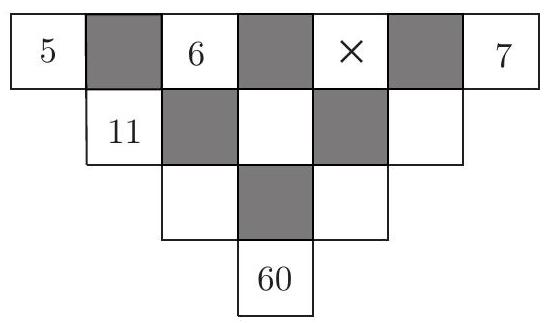
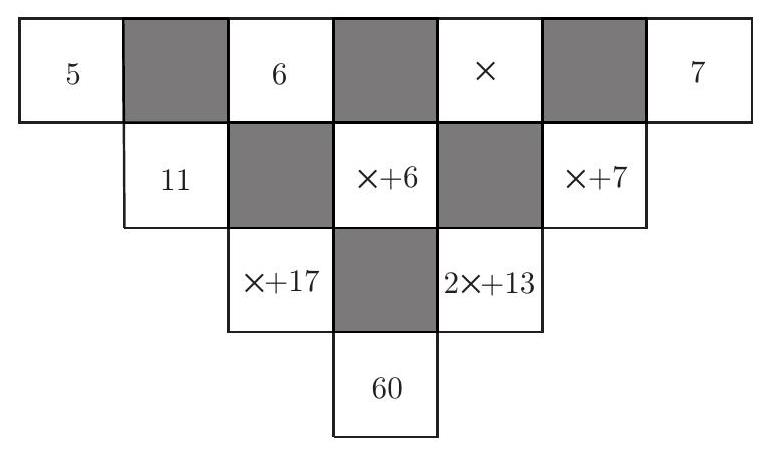
The blank squares in the figure must be filled with numbers in such a way that each number, starting from the second row, is equal to the sum of the two adjacent numbers in the immediately preceding row. For example, the number in the first cell of the second row is 11, because $11=5+6$. What number will appear in the square marked with $\times$?
(a) 4
(b) 6
(c) 9
(d) 15
(e) 10
|
The correct option is (e).
Filling the board according to the rules of the problem, it follows that $60=(x+17)+(2x+13)=3x+30$, from which $x=10$.
|
10
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
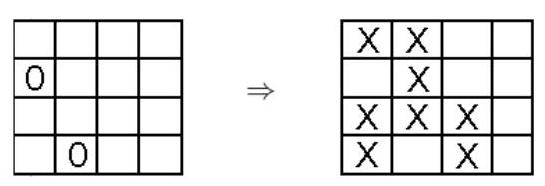
Camila and Lara each have a $4 \times 4$ board. Starting with both boards blank, they play a game with the following sequence of events.
- Camila, hidden from Lara, paints some squares on her board black.
- Still on her board, Camila writes in each square the number of adjacent squares that are painted black (two distinct squares are adjacent if they share a side or a vertex).
- Camila copies the numbers written on her board onto Lara's board.
- Lara must guess, based on the numbers written on her board, how many squares on Camila's board are black.
For example, if Camila paints her board as shown in the left figure, then she places the numbers on Lara's board as shown in the right figure.
| 1 | 1 | 3 | 1 |
| :--- | :--- | :--- | :--- |
| 2 | 3 | 2 | 2 |
| 1 | 3 | 1 | 1 |
| 1 | 2 | 0 | 0 |
How many squares did Camila paint if Lara's board has the numbers from the following board?
(a) 3
(d) 6
(b) 4
(e) 7
(c) 5
| 1 | 2 | 1 | 1 |
| :--- | :--- | :--- | :--- |
| 0 | 2 | 1 | 2 |
| 2 | 3 | 3 | 1 |
| 1 | 0 | 2 | 1 |
|
The correct option is (b).
First, we note that if a cell has the digit 0, then none of its neighboring cells can be painted. Therefore, the cells marked with an $\times$ in the figure on the right were not painted.
Now, consider the cell in the upper right corner, which has the number 1. It has three neighbors, and we already know that two of them were not painted.
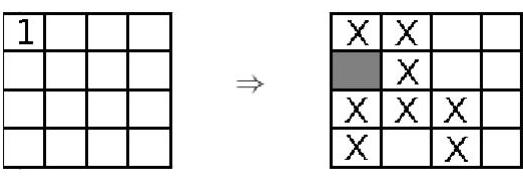
Therefore, the remaining neighbor (the cell immediately below) was painted. We can apply the same argument to the cells in the lower left and lower right corners.
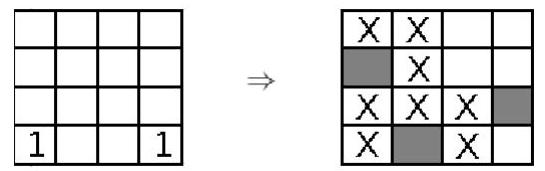
Now, we look at the 2 in the last row. Since this cell already has two painted neighbors, all its other neighbors were not painted.
The same argument applies to the cell in the second row and third column, as it has a 1 and already has one of its neighbors painted. Therefore, its other three neighbors were not painted.
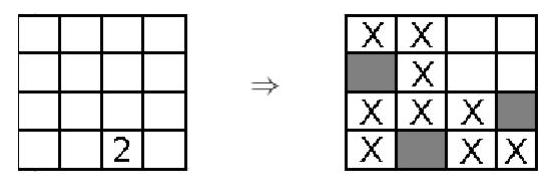
Finally, we use the 3 that appears in the cell in the third row and third column. This cell already has two painted neighbors, so there must be one more of its neighbors painted.
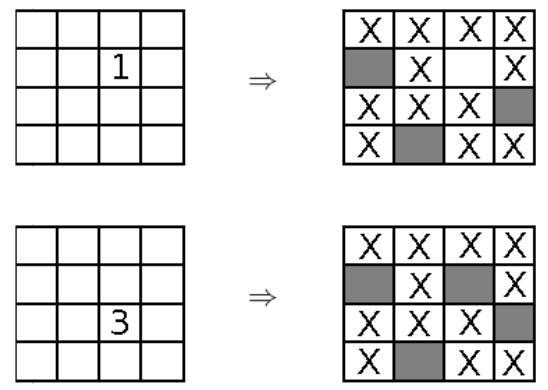
This neighbor can only be the blank cell in the figure above, and we can complete the table. We conclude that the number of painted cells is 4.
|
4
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A teacher has 237 candies to give to her 31 students. What is the minimum number of additional candies she needs to ensure that all her students receive the same number of candies, with none left over?
(a) 11
(b) 20
(c) 21
(d) 31
(e) 41
|
The correct option is (a).
Dividing 237 by 37, we get $237=7 \times 31+20$. Therefore, 237 is not divisible by 31. This means the teacher really needs to buy more candies so that all the students can receive the same number of candies. We need to add to the expression $7 \times 31+20$ the smallest positive integer $x$ such that $7 \times 31+20+x$ is a multiple of 31. Since $20+11=31$, the teacher only needs to buy 11 additional candies.
|
11
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
If $m$ and $n$ are integers greater than zero and $m < n$, we define $m \nabla n$ as the sum of the integers between $m$ and $n$, including $m$ and $n$. For example, $5 \nabla 8 = 5 + 6 + 7 + 8 = 26$. What is the value of $\frac{22 \nabla 26}{4 \nabla 6}$?
(a) 4
(b) 6
(c) 8
(d) 10
(e) 12
|
The correct option is (c).
By definition, we obtain $\frac{22 \nabla 26}{4 \nabla 6}=\frac{22+23+24+25+26}{4+5+6}=\frac{120}{15}=8$.
|
8
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Which is the greatest among the given numbers?
(a) $2 \times 0 \times 2006$
(c) $2+0 \times 2006$
(e) $2006 \times 0+0 \times 6$
(b) $2 \times 0+6$
(d) $2 \times(0+6)$
|
The correct option is (d).
Remember that if one of the factors in a product is zero, then the product is also zero. We have $2 \times 0 \times 2006=0$, $2 \times 0+6=0+6=6$, $2+0 \times 2006=2+0=2$, $2 \times(0+6)=2 \times 6=12$ and $2006 \times 0+0 \times 6=0+0=0$. Therefore, the largest number is $2 \times(0+6)=12$.
|
12
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
If two sides of a triangle measure 5 and 7 cm, then the third side cannot measure how many centimeters?
(a) 11
(b) 10
(c) 6
(d) 3
(e) 1
|
The correct option is (e).
Remember that, in a triangle, the sum of any two sides must be greater than the third side. Since $1+5$ is not greater than 7, the third side cannot measure $1 \mathrm{~cm}$.
|
1
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
If I give two chocolate bars to Tião, he will lend me his bicycle for 3 hours. If I give him 12 chocolates, he will lend me the bicycle for 2 hours. Tomorrow, I will give him one chocolate bar and 3 chocolates. For how many hours will he lend me the bicycle?
(a) $1 / 2$
(b) 1
(c) 2
(d) 3
(e) 4
|
The correct option is (c).
Given $\left\{\begin{array}{l}2 \text { bars give } 3 \text { hours} \\ 12 \text { chocolates give } 2 \text { hours}\end{array}\right.$, it follows that $\left\{\begin{array}{l}1 \text { bar gives } 1.5 \text { hours }=1 \text { hour } 30 \text { minutes} \\ 3 \text { chocolates give } 0.5 \text { hours }=30 \text { minutes}\end{array}\right.$
Thus, Tião will lend me the bicycle for $1 \text { hour } 30 \text { minutes } + 30 \text { minutes } = 2$ hours.
|
2
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
How many positive integers satisfy the double inequality $2000<\sqrt{n(n-1)}<2005$?
(a) 1
(b) 2
(c) 3
(d) 4
(e) 5
|
The correct option is (e).
Since the numbers that appear are all positive, we can square them while maintaining the direction of the inequalities, obtaining
$$
2000 \times 2000=2000^{2}<n(n+1)<2005^{2}=2005 \times 2005
$$
Notice that $n$ and $n+1$ are consecutive integers, so the only options are the following.
- $2000^{2}<2000 \times 2001<2005^{2}$
- $2000^{2}<2001 \times 2002<2005^{2}$
- $2000^{2}<2002 \times 2003<2005^{2}$
- $2000^{2}<2003 \times 2004<2005^{2}$
- $2000^{2}<2004 \times 2005<2005^{2}$
Therefore, we have five possibilities for $n$, namely, 2000, 2001, 2002, 2003, and 2004.
|
5
|
Inequalities
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
If $(x+y)^{2}-(x-y)^{2}=20$, then $x y$ is equal to:
(a) 0 ;
(b) 1 ;
(c) 2 ;
(d) 5 ;
(e) 10 .
|
The correct option is (d).
Since $(x+y)^{2}=x^{2}+2 x y+y^{2}$ and $(x-y)^{2}=x^{2}-2 x y+y^{2}$, we have
$$
20=(x+y)^{2}-(x-y)^{2}=x^{2}+2 x y+y^{2}-x^{2}+2 x y-y^{2}=4 x y
$$
therefore $x y=5$.
|
5
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
feira treze - What is the maximum number of Friday the 13ths that can occur in a non-leap year? In this case, what day of the week does the tenth day of the year fall on?
|
feira treze - Since the days of the week repeat every 7 days, the difference between the days of the week is given by the remainder when the number of days that have passed is divided by 7. In the table below,
(a) in the first row, the number of days between the 13th of one month and the 13th of the following month;
(b) in the second row, the remainder obtained when this number is divided by 7;
(c) in the third row, the remainder obtained when dividing by 7 the number of days between the 13th of January and the 13th of the corresponding month; thus, this number is obtained by summing the results obtained in the first row, from January to the corresponding month, and then calculating the remainder of the division by 7.
| J-F | F-M | M-A | A-M | M-J | J-J | J-A | A-S | S-O | O-N | N-D |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 |
| 3 | 0 | 3 | 2 | 3 | 2 | 3 | 3 | 2 | 3 | 2 |
| 3 | 3 | 6 | 1 | 4 | 6 | 2 | 5 | 0 | 3 | 5 |
The equal values in the last row mean that, in those months, the 13th fell on the same day of the week. In particular, the last row tells us that the 13th of February, the 13th of March, and the 13th of November correspond to the same day of the week. Thus, at most, we have three Fridays the 13th.
In the case of three Fridays the 13th in the same year, the 13th of January occurred 3 days before Friday, that is, on a Tuesday, and the 10th of January occurred 3 days before, that is, on a Saturday.
Note: A Friday the 13th occurs only when the first day of the month falls on a Sunday. Thus, another, perhaps simpler, way to solve the problem is to determine the maximum number of times the first day of the month falls on a Sunday in a non-leap year.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How many triangles exist whose sides are integers and the perimeter measures 12 units?
(a) 1
(b) 3
(c) 5
(d) 7
(e) 9
|
The correct option is (b).
For three numbers $a, b$, and $c$ to be the lengths of the sides of a triangle, each of them must be greater than the difference and less than the sum of the other two. Let $a \leq b \leq c$ be the lengths of the sides of the triangle, so that $c < a + b$. Now, adding $c$ to both sides, we have $2c < a + b + c = 12$, that is, $2c < 12$, so $c < 6$. Moreover, since $3c \geq a + b + c = 12$, we have that $c \geq 4$, so $4 \leq c < 6$.
In the case $c = 5$, we have $a + b = 7$ and the possible values of $a$ and $b$ are $a = 2$ and $b = 5$, or $a = 3$ and $b = 4$. In the case $c = 4$, we have $a + b = 8$, and therefore, the only solution is $a = b = 4$. Conclusion: we have 3 possible triangles.
|
3
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
The number $(\sqrt{6}+\sqrt{2})(\sqrt{3}-2) \sqrt{\sqrt{3}+2}$ is equal to:
(a) $-\sqrt{3}$;
(b) $-\sqrt{2}$;
(c) -2 ;
(d) 1 ;
(e) 2.
|
The correct option is (c).
Observe that, denoting by $A$ the given expression, we have
$$
\begin{aligned}
A^{2} & =[(\sqrt{6}+\sqrt{2})(\sqrt{3}-2) \sqrt{\sqrt{3}+2}]^{2} \\
& =(\sqrt{6}+\sqrt{2})^{2}(\sqrt{3}-2)^{2}(\sqrt{\sqrt{3}+2})^{2} \\
& =(\sqrt{6}+\sqrt{2})^{2}(\sqrt{3}-2)^{2}(\sqrt{3}+2) \\
& =(\sqrt{6}+\sqrt{2})^{2}(\sqrt{3}-2)[(\sqrt{3}-2)(\sqrt{3}+2)] \\
& =(6+2 \sqrt{12}+2)(\sqrt{3}-2)\left((\sqrt{3})^{2}-2^{2}\right) \\
& =(6+2 \sqrt{12}+2)(\sqrt{3}-2)(-1) \\
& =(8+4 \sqrt{3})(2-\sqrt{3})=4(2+\sqrt{3})(2-\sqrt{3}) \\
& =4\left(2^{2}-(\sqrt{3})^{2}\right)=4 \times 1=4
\end{aligned}
$$
Thus, $A^{2}=4$ and, therefore, $A$ can be 2 or -2. Since $\sqrt{3}-2$ is negative and the other two factors of $A$ are positive, we have that $A$ must be negative, that is, $A=-2$.
|
-2
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Five points lie on the same line. When we list the 10 distances between any two of these points, from smallest to largest, we find $2,4,5$, $7,8, k, 13,15,17$ and 19. What is the value of $k$?
|
Solution 1: Since the greatest distance between two points is 19 and the smallest is 2, we draw a number line with the two points 0 and 19 at the ends and the point 2 two units from 0, obtaining the first three points in the figure.

Next, we place two other points to try to meet the required distances. Since we need distances of 5 and 7, we place the point 7 on the line, which gives us distances that are not incompatible with the problem data, as the distances between these 4 points are 2, 5, 7, 12, 17, and 19, as shown in the figure.

Thus, if our attempt to place all the points is successful, $k$ must necessarily be 12. We are lucky because to obtain the distances 4, 8, 13, and 15, it is enough to place the point 15 on the line, obtaining all the distances 2, 4, 5, 7, 8, 12, 13, 15, 17, and 19, as shown in the figure.

Choosing 4 as the third point, we obtain another distribution of points with the same distances between them, as in the following figure, where again, $k=12$.

Solution 2: Since the greatest distance is 19, we can assume that one point is 0 and the other is 19. If a third point is equal to $a$, we will have the distances $a-0=a$ and $19-a$ in the given list of distances. Since the pairs 2 and 17, as well as 4 and 15, appear in this list of distances, we can choose the number $a=2$ or $a=4$ as the third point. Let's choose the point 2. Since 4 and 15 are in the list of distances, 4 or 15 is another point on the line; but, 4 cannot be one of the points because the distance 2, between 2 and 4, does not appear twice. Therefore, 15 is the fourth point on the line. Finally, the fifth point must be 5 units from one of the points and 7 units from another. Thus, the missing point is the point 7 and the unknown distance is $k=19-7=12$.
Choosing 4 as the third point, we would obtain the points 12 and 14 as the fourth and fifth points, and again, the unknown distance is $k=12$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine a value of $n$ for which the number $2^{8}+2^{11}+2^{n}$ is a perfect square.
|
Solution 1: Observe that $2^{8}+2^{11}+2^{n}=\left(2^{4}\right)^{2}+2 \times 2^{4} \times 2^{6}+\left(2^{\frac{n}{2}}\right)^{2}$. Therefore, for $n=12$, we have $2^{8}+2^{11}+2^{12}=\left(2^{4}+2^{6}\right)^{2}$. Thus, $n=12$ is a solution.
Solution 2: If $2^{8}+2^{11}+2^{n}=k^{2}$, then
$$
\begin{aligned}
2^{8}+2^{3} \times 2^{8}+2^{n} & =k^{2} \\
9 \times 2^{8}+2^{n} & =k^{2} \\
2^{n} & =k^{2}-\left(3 \times 2^{4}\right)^{2} \\
2^{n} & =\left(k-3 \times 2^{4}\right)\left(k+3 \times 2^{4}\right)
\end{aligned}
$$
Therefore, $\left(k-3 \times 2^{4}\right)$ and $\left(k+3 \times 2^{4}\right)$ are powers of 2, that is, $k+3 \times 2^{4}=2^{a}$ and $k-3 \times 2^{4}=2^{b}$, with $a+b=n$ and
$$
2^{a}-2^{b}=\left(k+3 \times 2^{4}\right)-\left(k-3 \times 2^{4}\right)=3 \times 2^{5}=96
$$
Let's examine the list of powers of 2:
$$
2,4,8,16,32,64,128,256, \ldots
$$
We observe that the difference between these powers is only 96 between $128=2^{7}$ and $32=2^{5}$. Therefore, $a=7$ and $b=5$. Thus, $n=7+5=12$ is the only solution.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The reverse of a two-digit integer is the number obtained by reversing the order of its digits. For example, 34 is the reverse of 43. How many numbers exist that, when added to their reverse, give a perfect square?
|
Let's recall that two-digit numbers $ab$, where $a$ is the tens digit and $b$ is the units digit, are given by $ab = a \times 10 + b$. For example, $47 = 4 \times 10 + 7$.
If $ab$ is a two-digit number, then its reverse is $ba$. We have that
$$
ab + ba = a \times 10 + b + b \times 10 + a = (a + b) \times 11
$$
On the other hand, $a, b \leq 9$, so $a + b \leq 18$. Since 11 is a prime number and $a + b \leq 18$, 11 does not divide $a + b$ and, therefore, the product $(a + b) \times 11$ is only a perfect square if $a + b = 11$. Thus, we have 8 numbers satisfying the condition of the problem: $29, 38, 47, 56, 65, 74, 83$ and 92.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a warehouse, a dozen eggs and 10 apples had the same price. After a week, the price of eggs dropped by $2 \%$ and the price of apples increased by $10 \%$. How much more will be spent on the purchase of a dozen eggs and 10 apples?
(a) $2 \%$
(b) $4 \%$
(c) $10 \%$
(d) $12 \%$
(e) $12.2 \%$
|
The correct option is (b).
Since the statement and the answer are in percentages, we can, in this case, set any price and any currency unit, and the answer will always be the same. The simplest approach, therefore, is to assume that initially, a dozen eggs cost 100 and that 10 apples also cost 100. Since the price of eggs increased by 10%, the new price of eggs is 110. The price of apples decreased by 2%, so the new price of 10 apples is 98. Thus, while it used to cost 200 to buy a dozen eggs and 10 apples, it now costs $110+98=208$. Therefore, the increase was 8 out of 200, which corresponds to the percentage of
$$
\frac{8}{200}=\frac{4}{100}=4 \%
$$
|
4
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
The numbers $a$ and $b$ are positive integers that satisfy $96 a^{2}=b^{3}$. What is the smallest possible value of $a$?
|
Factoring 96, we have $2^{5} \times 3 \times a^{2}=b^{3}$. For $2^{5} \times 3 \times a^{2}$ to be a cube, the number $a$ must have, at least, the factorization $2^{n} \times 3^{n}$. To find the smallest value of $a$, we take $a=2^{n} \times 3^{n}$, and thus,
$$
2^{5} \times 3 \times a^{2}=2^{5} \times 3 \times\left(2^{n} \times 3^{m}\right)^{2}=2^{5+2 n} \times 3^{1+2 m}
$$
Therefore, $5+2 n$ and $1+2 m$ are multiples of 3. The smallest values of $n$ and $m$ are $n=2$ and $m=1$. Hence, $a=2^{2} \times 3=12$.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Twelve points are marked on a sheet of graph paper, as shown in the figure. What is the maximum number of squares that can be formed by connecting four of these points?
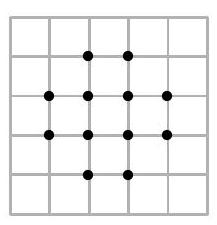
|
In total, we have 11 possible squares, shown in the following figures.
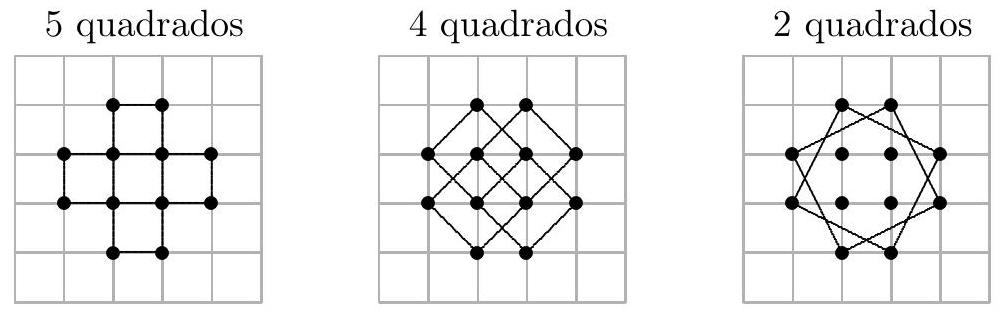
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Professor Newton divided his students into groups of 4 and 2 were left over. He divided his students into groups of 5 and one student was left out. If 15 students are women and there are more women than men, the number of male students is:
(a) 7 ;
(b) 8 ;
(c) 9 ;
(d) 10 ;
(e) 11 .
|
The correct option is (c).
Since the number of male students is less than 15 and the number of female students is 15, we have $15<$ male students + female students $<15+15=30$, which means the total number of students is between 15 and 30.
Solution 1: When we divide the number of students by 4, there are 2 students left, so the number of students is even. When we divide by 5, there is a remainder of 1, so the last digit of the number of students is 1 or 6; being even, it can only be 6. Thus, we have only two possible values, 16 or 26. We discard 16 because it is divisible by 4, so the number of students is 26. Consequently, we have $26-15=9$ male students.
Solution 2: Observe that the number 6, when divided by 4, leaves a remainder of $2 \text{ and }$, when divided by 5, leaves a remainder of 1. Therefore, if we add 6 to a common multiple of 4 and 5, the resulting number will also have this property. The least common multiple of 4 and 5 is 20, so the possible values for the number of students are $6, 26, 46, 66, \ldots$ Since the number of students is between 15 and 30, this number is 26, and it follows that we have $26-15=9$ male students.
|
9
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
The surface of the Earth consists of $70\%$ water and $30\%$ land. Two fifths of the land are deserts or covered by ice and one third of the land is pasture, forest, or mountain; the rest of the land is cultivated. What is the percentage of the total surface of the Earth that is cultivated?
|
The fraction of land that is cultivated is
$$
1-\frac{2}{5}-\frac{1}{3}=\frac{15-6-5}{15}=\frac{4}{15}
$$
Since land occupies 3/10 of the total surface area of the Earth, it follows that the cultivated area is $\frac{4}{15} \times \frac{3}{10}=\frac{2}{25}$, that is, $\frac{2}{25}=\frac{2}{25} \times \frac{4}{4}=\frac{8}{100}=8\%$ of the Earth's surface.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A store was selling each unit of a toy for $R \$ 13.00$. To sell its entire stock, which was not more than 100 units, the store management decided to lower the price by an integer number of reais, thus obtaining $\mathrm{R} \$ 781.00$ for the entire stock. What was the price reduction, per unit?
|
If $x$ denotes the discount in reais and $y$ the total number of pieces, then $(13-x) \times y=781$. Thus, $(13-x)$ and $y$ are divisors of 781, and since $781=11 \times 71$, the only divisors of 781 are $1, 11, 71$, and 781. The divisor $13-x$ of 781 cannot be equal to 1, as we know that $y \leq 100$. The only option, then, is $13-x=11$ and $y=71$, so the reduction was $x=\mathrm{R} \$ 2.00$ per unit.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
If the price of a product increased from 5.00 to 5.55 reais, what was the percentage increase?
|
In reais, the increase was $5.55 - 5 = 0.55$ and, therefore, the percentage increase was
$$
\frac{0.55}{5}=\frac{0.55 \times 20}{5 \times 20}=\frac{11}{100}=11 \%
$$
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A factory produced an original calculator that performs two operations,
(a) the usual addition, denoted by $+\mathrm{e}$
(b) an operation denoted by $\circledast$.
We know that, for any natural number $a$, the following hold
$$
\text { (i) } \quad a \circledast a=a \quad \text { and } \quad \text { (ii) } \quad a \circledast 0=2 a
$$
and, for any four natural numbers $a, b, c$ and $d$, the following holds
$$
\text { (iii) } \quad(a \circledast b)+(c \circledast d)=(a+c) \circledast(b+d)
$$
What are the results of the operations $(2+3) \circledast(0+3)$ and $1024 \circledast 48$?
|
To calculate $(2+3) \circledast(0+3)$, we will use property (iii), obtaining $(2+3) \circledast(0+3)=(2 \circledast 0)+(3 \circledast 3)$. Now, by (ii), we have $2 \circledast 0=2 \times 2=4$ and, by (i), we have $3 \circledast 3=3$. Therefore, $(2+3) \circledast(0+3)=4+3=7$.
To calculate $1024 \circledast 48$ we will use the same strategy, noting that $1024=976+48$ and $48=0+48$. Thus,
$$
\begin{aligned}
1024 \circledast 48 & =(976+48) \circledast(0+48) \\
& =(976 \circledast 0)+(48 \circledast 48) \\
& =2 \times 976+48=1952+48=2000 .
\end{aligned}
$$
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Joana wrote a sequence in 10 lines using the digits from 0 to 9, following the pattern below.
$$
\begin{array}{lllllllllll}
0 & & & & & & & & & \\
1 & 1 & 0 & & & & & & & \\
2 & 2 & 2 & 1 & 1 & 0 & & & & \\
3 & 3 & 3 & 3 & 2 & 2 & 2 & 1 & 1 & 0
\end{array}
$$
Which digit was used the most? How many times was this digit used?
|
According to the pattern of the sequence, we have

Thus,
one digit 0 in each line gives \(1 \times 10 = 10\) digits 0 in total; two digits 1 in nine lines give \(2 \times 9 = 18\) digits 1 in total; three digits 2 in eight lines give \(3 \times 8 = 24\) digits 2 in total; four digits 3 in seven lines give \(4 \times 7 = 28\) digits 3 in total,
and so on. Therefore, it is a matter of finding which is the largest of the following products, where each represents how many digits, from 0 to 9, appear in the sequence.
Since the largest product is 30, the most used digits were 4 and 5, 30 times each.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The measures of the sides of a rectangle are even numbers. How many rectangles of this type exist with an area equal to 96?
|
If $a$ and $b$ denote the length and width of the rectangle, we have $a \times b=96$. Therefore, $a$ and $b$ are even divisors of 96, and thus we have four rectangles satisfying the given conditions, namely, rectangles with sides measuring 2 and 48; 4 and $24 ; 6$ and 16 and 8 and 12.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine the nearest integer to
(a) $\frac{19}{15}+\frac{19}{3}$
(b) $\frac{85}{42}+\frac{43}{21}+\frac{29}{14}+\frac{15}{7}$
(c) $-\frac{11}{10}-\frac{1}{2}-\frac{7}{5}+\frac{2}{3}$
|
(a) We have:
$$
\frac{19}{15}+\frac{19}{3}=1+\frac{4}{15}+6+\frac{1}{3}=7+\frac{9}{15}=7+\frac{3}{5}
$$
Thus, the given sum is between 7 and 8. Since $\frac{3}{5}>\frac{1}{2}$, the nearest integer is 8.
(b) We have:
$$
\begin{aligned}
\frac{85}{42}+\frac{43}{21} & +\frac{29}{14}+\frac{15}{7}=2+\frac{1}{42}+2+\frac{1}{21}+2+\frac{1}{14}+2+\frac{1}{7} \\
& =8+\frac{1}{42}+\frac{1}{21}+\frac{1}{14}+\frac{1}{7}=8+\frac{1}{7}\left(\frac{1}{6}+\frac{1}{3}+\frac{1}{2}+1\right)=8+\frac{2}{7}
\end{aligned}
$$
Thus, the given sum is between 8 and 9. Since $\frac{2}{7}<\frac{1}{2}$, the nearest integer is 8.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
An ant starts from a vertex of a cube, walking only along the edges, until it returns to the initial vertex, without passing through any vertex twice. What is the longest walk that this ant can make?
|
In the figure, we have a path consisting of eight edges that the ant can take starting from the vertex identified as 1.
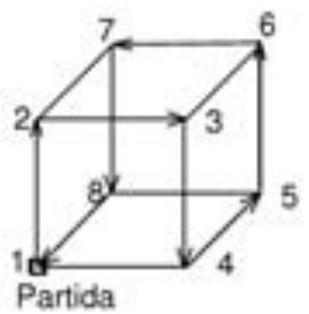
Would it be possible for her to make a path passing through nine edges? To make this path, she would have to pass through nine vertices, as the arrival vertex is the same as the starting vertex, since the little ant returns to the initial vertex.
Since the cube only has eight vertices, this walk is not possible. Therefore, the longest walk covers eight edges.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a promotion, Joana bought blouses for $\mathrm{R} \$ 15.00$ each and pants for $\mathrm{R} \$ 17.00$ each, spending a total of $\mathrm{R} \$ 143.00$. How many blouses and pants did Joana buy?
|
Let $b$ and $c$ be the number of blouses and pants bought, respectively. Therefore, we have $15 b + 17 c = 143$, where $b$ and $c$ are positive integers. Note that $b < 10$ and $c < 9$, because both $15 \times 10$ and $17 \times 9$ are greater than 143. From this point, we present two possible solutions.
Solution 1: We have $15 b = 143 - 17 c$, so $143 - 17 c$ is a multiple of 15, meaning that $143 - 17 c$ ends in 0 or 5. This means that $17 c$ ends in 3 or 8. Therefore, $c = 9$ or $c = 4$. Since $c < 9$, the only solution is $c = 4$, and therefore,
$$
b = \frac{143 - 17 \times 4}{15} = 5
$$
Thus, Joana bought five blouses and four pants.
Solution 2: We have
$$
b = \frac{143 - 17 c}{15} = 9 - c + \frac{8 - 2 c}{15}
$$
Note that $c$ is a positive integer, so $8 - 2 c$ must be a multiple of 15. If $8 - 2 c \geq 15$, $c$ results in a negative number, so $8 - 2 c = 0$, that is, $c = 4$. From this, we obtain that $b = 5$. Thus, Joana bought five blouses and four pants.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the figure, $O$ is the center of the semicircle with diameter $P Q, R$ is a point on the semicircle, and $R M$ is perpendicular to $P Q$. If the measure of arc $\widehat{P R}$ is twice the measure of arc $\overparen{R Q}$, what is the ratio between $P M$ and $M Q$?
|
If the arc $\widehat{P R}$ is twice the arc $\overparen{R Q}$, the same relationship holds for the central angles, that is, $P \widehat{O} R=2 R \widehat{O} Q$. Since $P \widehat{O} R+R \widehat{O} Q=180^{\circ}$, it follows that
$$
180^{\circ}=2 R \widehat{O} Q+R \widehat{O} Q=3 R \widehat{O} Q
$$
from which $R \widehat{O} Q=60^{\circ}$. But, $O R=O Q$ is the radius of the circle, so the triangle $\triangle O R Q$ is equilateral. Thus, its height $R M$ is also the median, that is, $O M=M Q$. If $r$ is the radius of the circle, then $O M=M Q=\frac{1}{2} r$ and
$$
\frac{P M}{M Q}=\frac{P O+O M}{M Q}=\frac{r+\frac{1}{2} r}{\frac{1}{2} r}=3
$$
that is, the ratio between $P M$ and $M Q$ is 3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How many triangles exist that have a perimeter of 15 units and sides measuring integers?
|
Let's assume that $a, b$ and $c$ are the lengths of the sides of the triangle. Without loss of generality, we can assume that $a \leq b \leq c$, so that $a+b+c \leq 3 c$. Since each side of a triangle is less than the sum of the other two, we have $c<a+b$ and, therefore, we get $2 c<a+b+c \leq 3 c$. But, $a+b+c=15$, so $2 c<15 \leq 3 c$ and, since $c$ is an integer, 5, 6, or 7 are the only options for $c$.
If $c=5$, then $a+b=10$ and we have one possibility, $a=b=c=5$. If $c=6$, then $a+b=9$ and we have two possibilities for $a$, 3 or 4, in which case, necessarily, $b$ is 6 or 5, respectively. If $c=7$, then $a+b=8$ and we have four possibilities for $a, 1, 2, 3$ or 4. In these cases, necessarily, $b$ is $7, 6, 5$ or 4, respectively. Thus, in total, we have seven such triangles.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Draw two circles with the same center, one with a radius of $1 \mathrm{~cm}$ and the other with a radius of $3 \mathrm{~cm}$. In the region outside the circle with a radius of $1 \mathrm{~cm}$ and inside the circle with a radius of $3 \mathrm{~cm}$, draw circles that are simultaneously tangent to both circles, as shown in the given figure.
(a) What should be the radius of these circles?
(b) What is the maximum number of these circles that can be drawn without overlapping?
|
(a) Since the circles with radii of 1 and $3 \mathrm{~cm}$ are concentric, the new circles tangent to the original ones must also have a radius of $1 \mathrm{~cm}$.
(b) The centers of the three circles with a radius of $1 \mathrm{~cm}$ shown in the figure form an equilateral triangle with a side length of 2 $\mathrm{cm}$. Therefore, their internal angles measure $60^{\circ}$. Since 360/60 = 6, we conclude that a maximum of six circles can be arranged without overlapping, under the given conditions.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In triangle $\triangle A B C$, point $F$ is on side $A C$ and $F C=2 A F$. If $G$ is the midpoint of segment $B F$ and $E$ is the intersection point of the line passing through $A$ and $G$ with segment $B C$, calculate the ratio $E C / B E$.
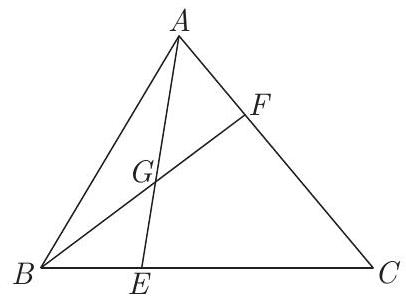
|
Let's choose point $H$ on segment $B C$ such that segment $F H$ is parallel to segment $A E$, as shown in the given figure. It follows that triangles $\triangle A E C$ and $\triangle F H C$ are similar, as they have parallel sides.

Since $F C=2 A F$, it follows from the similarity that $H C=2 E H$. On the other hand, triangles $\triangle B H F$ and $\triangle B E G$ are also similar, as they have parallel sides. From this similarity and the fact that $G$ is the midpoint of segment $B F$, we conclude that $E$ is the midpoint of segment $B H$. Thus, $B E=E H$ and, therefore,
$$
E C=E H+H C=E H+2 E H=3 E H=3 B E
$$
Consequently, $E C / B E=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the sequence 1, 3, 2, .. each term after the first two is equal to the preceding term, subtracted from the term that precedes it, that is, if $n>2$, then $a_{n}=a_{n-1}-a_{n-2}$. What is the sum of the first hundred terms of this sequence?
|
Initially, we write the first terms of this sequence as follows.
$$
1,3,2,-1,-3,-2,1,3,2, \ldots
$$
The seventh and eighth terms are, respectively, equal to the first and second. This means that the sequence repeats every six terms. The sum of the first six terms is $1+3+2-1-3-2=0$ and, therefore, the sum of the first 96 terms is also 0. Thus, the sum of the first 100 terms of this sequence is equal to the sum of the last four terms, that is, $1+3+2-1=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
40 - 120
In triangle $ABC$, the angle $A \hat{B C}$ measures $20^{\circ}$ and the angle $A \hat{C} B$ measures $40^{\circ}$. Let $E$ be a point on $BC$ such that $BE = BA$.
(a) Show that triangle CEA is isosceles.
(b) Knowing that the length of the angle bisector of angle BÂC is 2, determine $\mathrm{BC}-\mathrm{AB}$.
|
(a) We have $C \hat{A B}=180^{\circ}-20^{\circ}-40^{\circ}=120^{\circ}$. Since triangle $A B E$ is isosceles, it follows that
$$
A \hat{E} B=E \hat{A} B=\frac{180^{\circ}-20^{\circ}}{2}=80^{\circ}
$$
Thus, $\mathrm{CA} E=120^{\circ}-80^{\circ}=40^{\circ}$ and triangle ACE has two angles of $40^{\circ}$, and therefore, is isosceles with $C E=E A$.
(b) Let $\mathrm{D}$ be the foot of the angle bisector of angle BÂC. The bisector divides angle CÂB into two angles of $60^{\circ}$. Therefore, the angle
$$
\mathrm{CDA}=180^{\circ}-40^{\circ}-60^{\circ}=80^{\circ}
$$
Since AÊB also measures $80^{\circ}$, triangle $A D E$ is isosceles. Finally,
$$
\mathrm{BC}-\mathrm{AB}=\mathrm{BC}-\mathrm{BE}=\mathrm{CE}=\mathrm{EA}=\mathrm{AD}=2
$$
## Related Problem
The triangle $A B C$ is isosceles with base $B C$ and $B \hat{A C}=48^{\circ}$. Points $D$ and $E$ are on sides $A B$ and $A C$, respectively, such that $D \hat{C A}=9^{\circ}$ and $E \hat{B C}=33^{\circ}$. Determine the measure of angle CDE.
Hint: Use the Pythagorean theorem.
Figure 102.1
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The square of 13 is 169, which has the digit 6 in the tens place. The square of another number has the digit 7 in the tens place. What are the possible values for the digit in the units place of this square?
|
Suppose the number is $10a + b$, with $b$ being a digit. When we square it, we get
$$
(10a + b)^2 = 100a^2 + 20ab + b^2
$$
which has three terms: $100a^2$, $20ab$, and $b^2$.
The first term ends in 00, while the second term ends in an even number followed by zero. For the tens digit to be 7, which is odd, it is necessary that the tens digit of $b^2$ be odd, which only happens when $b = 4$ or $b = 6$. In each of these cases, $4^2 = 16$ and $6^2 = 36$, the units digit of the square is 6.
## Related Problem
Is there a perfect square number consisting only of the digits 0 and 6?
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The fractions of the form $\frac{n}{n+1}$, with $n$ a positive integer are:
$$
\underbrace{\frac{1}{2}}_{n=1} ; \quad \underbrace{\frac{2}{3}}_{n=2} ; \quad \underbrace{\frac{3}{4}}_{n=3} ; \quad \underbrace{\frac{4}{5}}_{n=4} ; \quad \underbrace{\frac{5}{6}}_{n=5} \cdots
$$
Observe that this sequence of fractions is increasing, that is: $\frac{1}{2}<\frac{2}{3}<\frac{3}{4}<\frac{4}{5}<\frac{5}{6} \cdots$
To find the fractions of the form $\frac{n}{n+1}$ that are less than $\frac{7}{9}$, we can compare $\frac{4}{5}$ and $\frac{7}{9}$:
$$
\frac{4}{5}=\frac{36}{45} \quad \text{and} \quad \frac{7}{9}=\frac{35}{45}
$$
Therefore, $\frac{4}{5}>\frac{7}{9}$
Thus, 4/5 is greater than 7/9, and since the sequence is increasing, from $4 / 5$ onwards all the fractions in this sequence are greater than 7/9. Therefore, the fractions of the form $\frac{n}{n+1}$ that are less than $\frac{7}{9}$ are $\frac{1}{2}, \frac{2}{3}, \frac{3}{4}$. Hence, the answer is 3.
|
2 - Converting to decimal numbers we have: $7 / 9=0.777 \ldots$ and $1 / 2=0.5$; $2 / 3=0.666 \ldots ; 3 / 4=0.75 ; 4 / 5=0.8 ; 5 / 6=0.8333 \ldots$
Therefore, the sequence is increasing and only $1 / 2=0.5 ; 2 / 3=0.666 \ldots ; 3 / 4=0.75$ are less than $7 / 9=0.777 \ldots$
Solution 3 - If $\frac{n}{n+1}<\frac{7}{9}$, we must have $2 n-7<0$, that is $n<\frac{7}{2}=3.5$. Therefore, $n=1,2,3$ and thus, the fractions are $\frac{1}{2}, \frac{2}{3} \text{ and } \frac{3}{4}$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Comment: Note that:
the units digit of $\left(9867^{3}-9867^{2}\right)=$ the units digit of $\left(7^{3}-7^{2}\right)$
|
2: $n^{3}-n^{2}=n^{2}(n-1)$. Thus, $n^{2}=(9867)^{2}$ ends in 9 and $n-1=9866$ ends in 6. Since, $9 \times 6=54$, the last digit of the result is 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
As $96 \div 8=12$, we have $8 \times 12=96$.
Notice that the solution is equivalent to solving the equation $8 x=96$, whose root is $x=\frac{96}{8}=12$.
|
2 - We must find among the list of five options which number, when multiplied by 8, gives 96. The unit digit of this number can only be 2 or 7.
Therefore, it can only be the number 12.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The figures show that the volumes occupied by the liquids correspond, approximately to more than half in bottle A, half in bottle B, and less than half in bottle C.
The only group of fractions that corresponds to these estimates is: $\frac{2}{3}$ (more than half); $\frac{1}{2}$ (half); $\frac{1}{4}$ (less than half).
|
2 - The figures show that the volumes occupied by the liquids are decreasing numbers. The only possible options are B and E. Since $\frac{3}{3}=1$ and none of the flasks are full, the answer is B.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the following figure, the circle with center $B$ is tangent to the circle with center $A$ at $X$. The circle with center $C$ is tangent to the circle with center $A$ at $Y$. Additionally, the circles with centers $B$ and $C$ are also tangent. If $A B=6, A C=5$ and $B C=9$, what is the measure of $A X$?
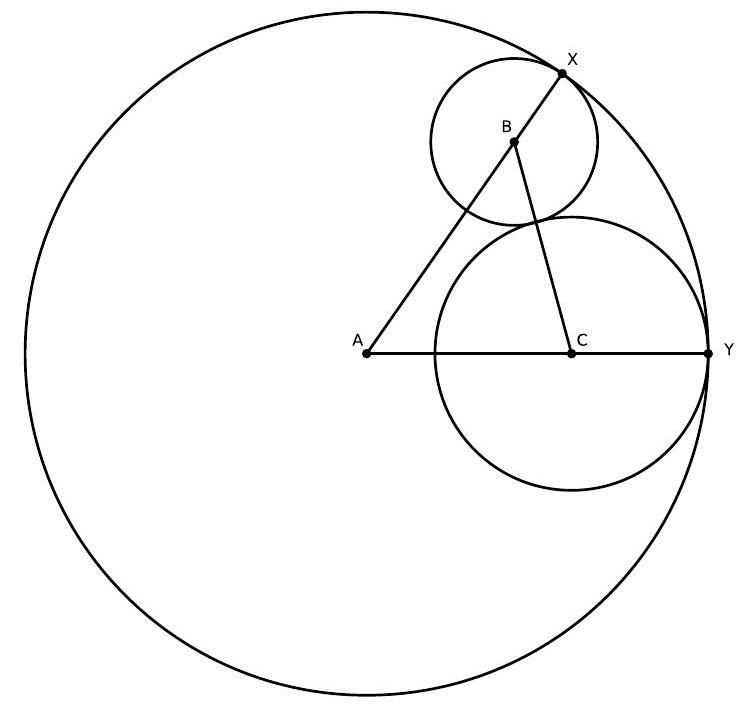
#
|
Solution
Let $r_{a}, r_{b}$, and $r_{c}$ be the radii of the circles centered at $A, B$, and $C$, respectively. If $Z$ is the point of tangency of the circles centered at $B$ and $C$, the data from the problem allows us to set up the following system of equations:
$$
\begin{aligned}
A B & =A X-B X \\
6 & =r_{a}-r_{b} \\
A C & =A Y-C Y \\
5 & =r_{a}-r_{c} \\
B C & =B Z+Z C \\
9 & =r_{b}+r_{c}
\end{aligned}
$$
Then
$$
\begin{aligned}
6+5 & =\left(r_{a}-r_{b}\right)+\left(r_{a}-r_{c}\right) \\
& =2 r_{a}-\left(r_{b}+r_{c}\right) \\
& =2 r_{a}-9 \\
r_{a} & =10
\end{aligned}
$$
Therefore, $A X=10$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
a) João arranged 13 sticks in the shape of a rectangular fence $1 \times 4$ as shown in the figure below. Each stick is the side of a $1 \times 1$ square, and inside each of these squares, he placed an ant. What is the minimum number of sticks we need to remove to ensure that all 4 ants can escape and return to their anthills?
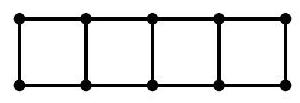
b) João now arranged 24 sticks in the shape of a square fence $4 \times 4$ as shown in the figure below, and inside each of these squares, he placed an ant. What is the minimum number of sticks we need to remove to ensure that all 9 ants can escape and return to their anthills?
|
Solution
a) It is possible to free all the ants by removing 4 matchsticks as indicated in the following figure.

Since each matchstick is shared by at most two squares and each square must have at least one open side for the ant inside to escape, to use 3 or fewer matchsticks, we are forced to remove at least one interior matchstick that is a side of two squares. The removal of one of these interior matchsticks merges the interiors of two small squares into a larger compartment and, from a practical standpoint, transforms the problem of freeing 4 ants in a $1 \times 4$ enclosure into the problem of freeing 3 ants in a $1 \times 3$ enclosure. If it is possible to remove 3 or fewer matchsticks in the $1 \times 4$ enclosure, it should also be possible to free the ants in a $1 \times 3$ enclosure using 2 or fewer matchsticks. By the same initial argument, this forces us to remove at least one interior matchstick, and thus the problem is again transformed into freeing 2 ants in a $1 \times 2$ enclosure by removing only one matchstick. This is clearly impossible, whether by removing the single interior matchstick or a matchstick from the edge of such an enclosure. Therefore, the minimum number of matchsticks that must be removed in this case is 4.
b) It is possible to free all the ants by removing 9 matchsticks as indicated in the example on the left of the following figure.
During the successive removal of matchsticks to free the ants, let's call any moment a compartment any closed polygonal line of matchsticks that does not have another closed polygonal line of matchsticks inside it. For example, in the figure on the right above, where 6 matchsticks have been removed, we have 3 compartments indicated by three different types of fillings. Note that the removal of a matchstick reduces the number of compartments by at most one unit. Therefore, since we initially have 9 compartments and want to ensure that no ant remains trapped in any type of compartment at the end, we must remove at least 9 matchsticks.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the figure, line $t$ is parallel to segment $E F$ and tangent to the circle. If $A E=12, A F=10$ and $F C=14$, determine the length of $E B$.
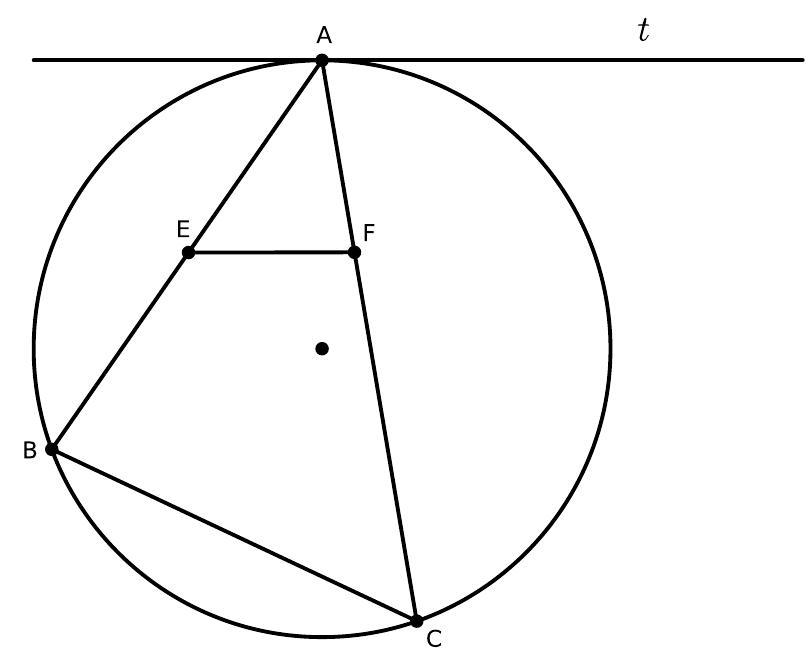
|
Solution
Since the line $t$ is tangent to the circle, we have $\angle X A E=\angle A C B$. Furthermore, since $t$ and $E F$ are parallel, we have $\angle X A E=\angle A E F$. Similarly, we have $\angle Y A F=\angle A F E=\angle A B C$. Therefore, $\triangle A F E \simeq \triangle A B C$. Thus,
$$
\begin{aligned}
\frac{A E}{A C} & =\frac{A F}{A B} \\
\frac{12}{10+14} & =\frac{10}{12+E B} \\
12+E B & =20 \\
E B & =8
\end{aligned}
$$
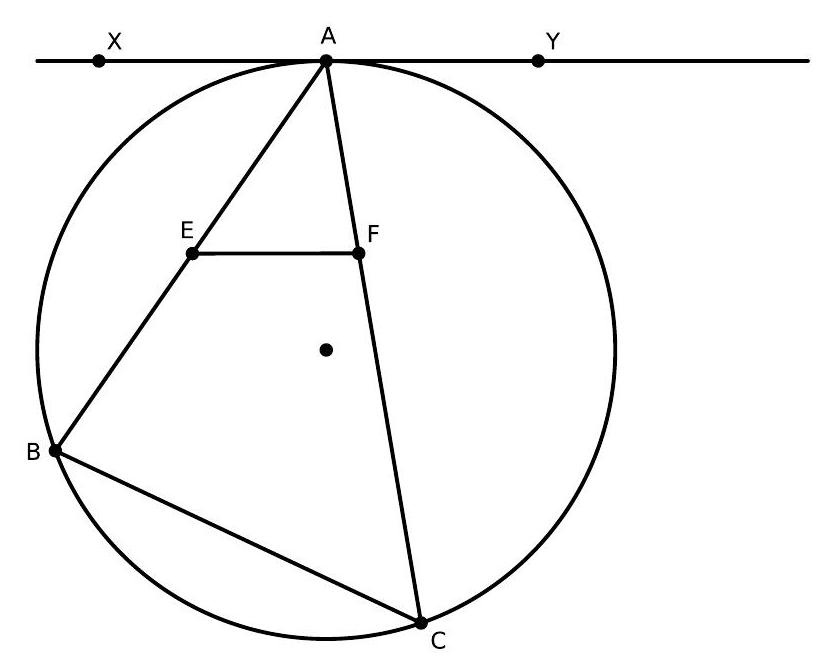
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the figure below, triangle $A B C$ is a right triangle at $C$ and both $B C D E$ and $C A F G$ are squares. If the product of the areas of triangles $E A B$ and $B F A$ is 64, determine the area of triangle $A B C$.
|
Solution
Since $D A$ is parallel to $E B$, the area of triangle $A E B$ is $\frac{E B \cdot B C}{2}=\frac{B C^{2}}{2}$. Similarly, the area of triangle $A B F$ is $\frac{A C^{2}}{2}$. Therefore,
$$
\begin{aligned}
{[A B E] \cdot[A B F] } & =\frac{B C^{2}}{2} \cdot \frac{A C^{2}}{2} \\
64 \cdot 4 & =B C^{2} \cdot A C^{2} \\
16 & =B C \cdot A C
\end{aligned}
$$
Thus, the area of triangle $A B C$ is $\frac{B C \cdot A C}{2}=\frac{16}{2}=8$.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the city of Oropis, there is a triangular lake with each of its three sides being part of the perimeter of a square-shaped land with areas of $370 \mathrm{~m}^{2}$, $116 \mathrm{~m}^{2}$, and $74 \mathrm{~m}^{2}$, as shown in the first figure below. The mayor of Oropis, Arnaldo, wants to calculate the area of the lake but doesn't know how. The mayor's assistant, Bernaldo, has an idea. He says that it is enough to find integer values of $a, b, c$, and $d$ that satisfy the geometric conditions of the second figure, where the shaded area is congruent to the lake. He claims that after this, the task will become much simpler.
(a) Determine integer values of $a, b, c$, and $d$ that satisfy the geometric conditions of Bernaldo's figure.
(b) Determine the area of the lake.
|
Solution
(a) See that the sides of the lake squared result in 74, 116, and 370. The conditions that must be met are the equations derived from three applications of the Pythagorean Theorem:
$$
\begin{aligned}
a^{2}+c^{2} & =74 \\
b^{2}+d^{2} & =116 \\
(a+b)^{2}+(c+d)^{2} & =370
\end{aligned}
$$
We can limit the tests of the first equation to numbers less than 9, since $9^{2}>74$. After a case analysis, we obtain $a=5$ and $c=7$ or $a=7$ and $c=5$ as the only possibilities. In the second equation, also after a case analysis, we have $b=4$ and $d=10$ or $b=10$ and $d=4$, and consequently, $a+b=5+4=9$ and $c+d=7+10=17$, since $(5+10)^{2}+(7+4)^{2} \neq 370$. Therefore, $a=5, b=4, c=7$, and $d=10$.
(b) Thus, the area of the lake is the area of the larger triangle minus two triangles and one rectangle. That is, the area of the lake, in $m^{2}$, is
$$
\begin{aligned}
\frac{17 \cdot 9}{2}-\frac{7 \cdot 5}{2}-\frac{10 \cdot 4}{2}-7 \cdot 4 & =\frac{118}{2}-20-28 \\
& =11
\end{aligned}
$$
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
We know that
$$
\frac{8^{x}}{2^{x+y}}=64 \text{ and } \frac{9^{x+y}}{3^{4 y}}=243
$$
Determine the value of $2 x y$.
#
|
Solution
Since $8=2^{3}$ and $9=3^{2}$, we have
$$
\begin{aligned}
64 & =\frac{8^{x}}{2^{x+y}} \\
2^{6} & =2^{3 x-(x+y)} \\
& =2^{2 x-y}
\end{aligned}
$$
$$
\begin{aligned}
243 & =\frac{9^{x+y}}{3^{4 y}} \\
3^{5} & =3^{(2 x+2 y)-4 y} \\
& =3^{2 x-2 y}
\end{aligned}
$$
Thus, we have the following system:
$$
\left\{\begin{array}{l}
2 x-y=6 \\
2 x-2 y=5
\end{array}\right.
$$
Subtracting the second equation from the first, we get $y=1$. Substituting this value into the first equation, we get $x=7 / 2$. Therefore, $2 x y=2 \cdot \frac{7}{2} \cdot 1=7$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
triminos and I-triminós
We want to cover a grid board with certain pieces without overlap and so that no part of them is outside the board. We will use pieces, formed by squares, called L-triminós and I-triminós, which can be rotated into the positions described in the following figure.

To prove that it is possible to achieve a covering, it suffices to show a way to position the pieces. On the other hand, to prove that it is not possible to achieve some covering, it is not always convenient to test all possible configurations of pieces, and often we need to sketch clever arguments. For example, we will prove that it is not possible to cover a $3 \times 3$ board using only L-triminós.
Observe the shaded squares in the figure. There are 4 squares, and it is not possible to cover two of them using a single L-triminó. Thus, to cover the 4 squares, we would need at least 4 L-triminós, but this would result in $4 \cdot 3 = 12$ squares covered, which clearly exceeds the total of 9 squares of the entire board. Therefore, it is not possible to cover the $3 \times 3$ board with L-triminós.
a) Show a way to cover a $3 \times 4$ board using only L-triminós.
b) Prove that it is not possible to cover a $3 \times 5$ board using only L-triminós.
c) It is possible to cover the $3 \times 5$ board using exactly one I-triminó and some L-triminós. Determine the positions that the I-triminó can occupy so that the rest of the board can be covered with L-triminós.
|
triminós and I-triminós - Solution
a) The figure below shows a way to cover the $3 \times 4$ board using only L-triminós.
b) Consider the $3 \times 5$ board below with the 6 shaded squares.
Since an L-triminó cannot cover two of these shaded squares, if it were possible to cover the entire board, we would need at least 6 L-triminós. However, these 6 L-triminós would cover a total of $6 \cdot 3 = 18$ squares, which exceeds the total of $3 \cdot 5 = 15$ squares on the board. Therefore, it is not possible to achieve this coverage.
c) Note that an I-triminó can cover 0, 1, or 2 of the shaded squares in the previous figure. If it covers 0 or 1, we can use the argument from the previous item to show that it will not be possible to complete the coverage, as 5 L-triminós already cover 15 squares. Therefore, the only possibility is that the I-triminó covers 2 squares. Indeed, if the I-triminó covers two shaded squares, it is always possible to complete the coverage with the L-triminós as indicated in the next figure:
There are 4 horizontal positions, two in the first row and two in the third row, and 3 vertical positions, covering the first, third, and fifth columns. In total, the I-triminó can occupy 7 positions.
|
7
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
How many fractions of the form $\frac{n}{n+1}$ are less than $7 / 9$, knowing that $n$ is a positive integer?
(a) 1
(b) 2
(c) 3
(d) 4
(e) 5
|
The correct option is (c).
Solution 1: The fractions of the form $\frac{n}{n+1}$, with $n$ a positive integer, are
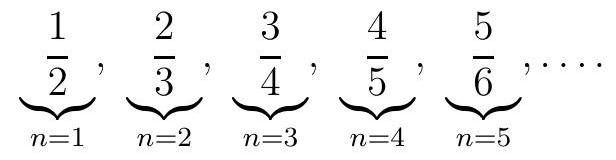
Observe that we have $\frac{1}{2} \cdot \frac{35}{45} = \frac{7}{9}$. Therefore, $\frac{4}{5}$ is greater than $\frac{7}{9}$, and since the sequence is increasing, from $\frac{4}{5}$ onwards, all fractions in this sequence are greater than $\frac{7}{9}$. Thus, there are only three fractions of the form $\frac{n}{n+1}$ that are less than $\frac{7}{9}$, namely, $\frac{1}{2}, \frac{2}{3}$, and $\frac{3}{4}$.
Solution 2: Converting everything to decimal numbers, we have $7 / 9 = 0.777 \ldots$ and $1 / 2 = 0.5, 2 / 3 = 0.666 \ldots, 3 / 4 = 0.75, 4 / 5 = 0.8, 5 / 6 = 0.8333 \ldots$ Therefore, the sequence is increasing, and only $1 / 2 = 0.5, 2 / 3 = 0.666 \ldots$, and $3 / 4 = 0.75$ are less than $7 / 9 = 0.777 \ldots$
|
3
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
The absolute value $|a|$ of any number $a$ is defined by
$$
|a|=\left\{\begin{array}{cl}
a & \text { if } a>0 \\
0 & \text { if } a=0 \\
-a & \text { if } a<0
\end{array}\right.
$$
For example, $|6|=6,|-4|=4$ and $|0|=0$. What is the value of $N=|5|+|3-8|-|-4|$?
(a) 4
(b) -4
(c) 14
(d) -14
(e) 6
|
The correct option is (e).
We have: $|5|=5,|3-8|=|-5|=5$ and $|-4|=4$. Therefore, $N=5+5-4=6$.
|
6
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
The vertices of a cube are numbered from 1 to 8, such that one of the faces has the vertices $\{1,2,6,7\}$ and the other five have the vertices $\{1,4,6,8\},\{1,2,5,8\}$, $\{2,3,5,7\},\{3,4,6,7\}$ and $\{3,4,5,8\}$. Which is the number of the vertex that is farthest from the vertex numbered 6?
(a) 1
(b) 3
(c) 4
(d) 5
(e) 7
|
The correct option is (d).
Solution 1: By drawing the cube and numbering its vertices according to the question statement, we obtain a figure in which we can see that vertex 5, being diametrically opposite, is the farthest from vertex 6.
Solution 2: Vertex 6 is on the faces $\{1,2,6,7\},\{1,4,6,8\}$, and $\{3,4,6,7\}$. Since the only vertex not appearing in these faces is 5, it follows that this is the vertex diagonally opposite to 6, that is, 5 is the vertex farthest from 6.
|
5
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Given two real numbers $a$ and $b$, consider $ab = a^2 - ab + b^2$. What is the value of 1?
(a) 1
(b) 0
(c) 2
(d) -2
(e) -1
|
The correct option is (a).
By setting $a=1$ and $b=0$ in $a=a^{2}-a b+b^{2}$, we obtain $1 \times 1^{2}-1 \times 0+0^{2}=1$.
|
1
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
In the given figure, $ABCD$ is a rectangle and $\triangle ABE$ and $\triangle CDF$ are right triangles. The area of triangle $\triangle ABE$ is $150 \mathrm{~cm}^{2}$ and the segments $AE$ and $DF$ measure, respectively, 15 and $24 \mathrm{~cm}$. What is the length of the segment $CF$?
|
The segment $C F$, whose length we want to calculate, is a leg of the right triangle $\triangle C D F$. The Pythagorean Theorem, applied to this triangle, states that $(C D)^{2}=(C F)^{2}+(F D)^{2}=(C F)^{2}+24^{2}$, and from this, we get $(C F)^{2}=(C D)^{2}-24^{2}$. In other words, to find $C F$, it is enough to know $C D$. Since the opposite sides of a rectangle (and more generally, of a parallelogram) are equal, we have $C D=A B$. Our goal, then, becomes the calculation of $A B$. For this, let's look at the triangle $\triangle A B E$. Its area is
$$
\frac{1}{2}(A E \times B E)=\frac{1}{2}(15 \times B E)=150
$$
from which we get $B E=20$. The Pythagorean Theorem applied to this triangle gives us $(A B)^{2}=(A E)^{2}+(B E)^{2}=15^{2}+20^{2}=625=25^{2}$, from which $A B=25$. Therefore, $C D=$ $A B=25$ and, according to our previous observation, we obtain
$$
(C F)^{2}=(C D)^{2}-24^{2}=25^{2}-24^{2}=(25+24)(25-24)=49
$$
Thus, $C F=7$.
Notice that the solution is independent of the measures of the sides $A D$ and $B E$.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.