problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Using only the digits 1, 2, 3, 4, and 5, Peri constructed the sequence
$$
1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,1,1,1,1,1,1,2,2,2,2,2,2,2, \ldots
$$
starting with one 1, followed by two 2s, three 3s, four 4s, five 5s, six 1s, seven 2s, and so on. What is the hundredth term of this sequence?
|
We group the sequence into consecutively numbered blocks, each block formed by consecutive equal terms, as shown below.
$$
\begin{aligned}
& \underbrace{1}_{\text {block } 1}, \underbrace{2,2}_{\text {block } 2}, \underbrace{3,3,3}_{\text {block } 3}, \underbrace{4,4,4,4}_{\text {block } 4}, \underbrace{5,5,5,5,5}_{\text {block } 5}, \underbrace{1,1,1,1,1,1}_{\text {block } 6}, \underbrace{2,2,2,2,2,2,2}_{\text {block } 7} \\
& \underbrace{3,3,3,3,3,3,3,3}_{\text {block } 8}, \underbrace{4,4,4,4,4,4,4,4,4}_{\text {block } 9}, \underbrace{5,5,5,5,5,5,5,5,5,5}_{\text {block } 10} \\
& \underbrace{1,1,1,1,1,1,1,1,1,1}_{\text {block } 11}, \ldots, \underbrace{k, k, k, k, k, k, k, k, k, k, k, k, k, \ldots, k}_{\text {block } n, \operatorname{with} k \in\{1,2,3,4,5\}}, \cdots
\end{aligned}
$$
Notice that the numbering of each block coincides with the number of terms it contains: block 1 has one term, block 2 has two terms, block 3 has three terms, and so on, up to block $n$, which has $n$ terms. The position in the sequence of the last term of each block is obtained by summing all the numbers from 1 to the number assigned to the block. For example, as can be counted in the enumeration above,
- the last 3 in block 8 is the $36^{\text{th}}$ term, since $1+2+3+4+5+6+7+8=36$.
- the last 1 in block 11 is the $66^{\text{th}}$ term, since $1+2+3+\cdots+10+11=66$.
In general, the last term of the $n$-th block is in the position $1+2+3+\cdots+n$. To calculate the value of this sum, we recall that $1,2,3, \ldots, n$ is an arithmetic progression with a common difference of 1, the first term $a_{1}=1$, and the $n$-th term $a_{n}=n$. The sum of its first $n$ terms is then,
$$
1+2+3+4+\cdots+n=\frac{n\left(a_{1}+a_{n}\right)}{2}=\frac{n(n+1)}{2}
$$
Now we need to determine in which block the hundredth term of the sequence is located. Assuming it is in the $n$-th block, its position will be, at most, that of the last term of this block. Since it will not be in the $(n+1)$-th block, we conclude that $n$ is the smallest integer such that $100 \leq \frac{1}{2} n(n+1)$, or equivalently, $200 \leq n(n+1)$.
To determine this value of $n$, we need to solve this inequality and choose, among its solutions, the smallest integer. Since the expression is quite simple, it is easier to solve it by trial. Doing so, we see that $n=14$. Indeed, $13 \times (13+1) = 182 < 200$. Thus, the hundredth term of the sequence is in block 14. The numbers that appear in the blocks repeat every five, in the order 1, 2, 3, 4, and 5. Since $14 = 5 \times 2 + 4$, block 14 is formed by the number 4. Therefore, the hundredth term of the sequence is 4.
Note: The above solution to the inequality $200 \leq n(n+1)$, although correct, would not serve if the problem asked, for example, to determine the 10000th term of the sequence. In that case, we would have to deal with the inequality $20000 \leq n(n+1)$, and, of course, finding its smallest integer solution by trial does not seem promising (unless with a lot, a lot of luck!). Therefore, let's solve the inequality $200 \leq n(n+1)$ in a way that works in general.
We start by writing $200 \leq n(n+1)$ as $n^{2}+n-200 \geq 0$.
This leads us to the study of the sign of the quadratic function $f(x)=x^{2}+x-200$, whose graph is illustrated in the figure. The roots of $f(x)$ are
$$
\begin{aligned}
& x_{1}=\frac{-1-\sqrt{1+800}}{2} \\
& x_{2}=\frac{-1+\sqrt{1+800}}{2}
\end{aligned}
$$
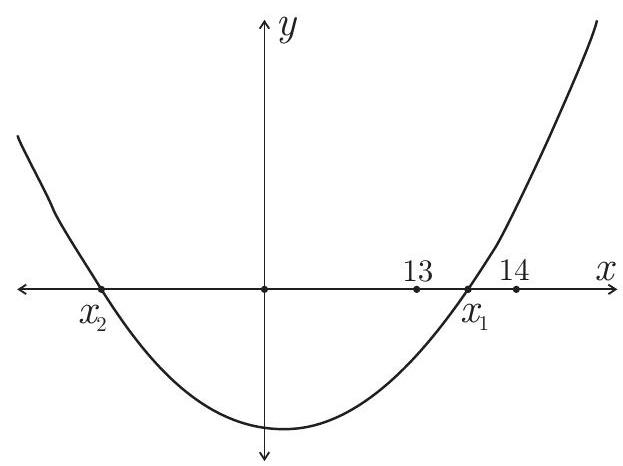
Notice that $x_{1}$ is negative and $x_{2}$ is approximately equal to 13.6. Since $f(x) \geq 0$ for $x \leq x_{1}$ and $x \geq x_{2}$, it follows that the $n$ we are looking for is the smallest integer that is greater than or equal to $x_{2}$, i.e., $n=14$.
Now, if we wanted to determine the 10000th term of the sequence, we could simply repeat the above procedure, finding $x_{2}=\frac{1}{2}[-1+\sqrt{1+80000}]$, which is approximately equal to 140.9. Therefore, $n=141$ and the 10000th term of the sequence is in the 141st block. Since $141=28 \times 5+1$, it follows that the 10000th term is 1.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A point $P$ is at the center of a square with a side length of $10 \mathrm{~cm}$. How many points on the edge of the square are $6 \mathrm{~cm}$ away from $P$?
(a) 1
(b) 2
(c) 4
(d) 6
(e) 8
|
The correct option is (e).
The points that are $6 \mathrm{~cm}$ away from point $P$ form a circle with center $P$ and radius $R=6$ $\mathrm{cm}$. If $d$ denotes the diagonal of the square, by the Pythagorean Theorem we have
$$
d=\sqrt{10^{2}+10^{2}}=\sqrt{2 \times 10^{2}}=10 \sqrt{2}
$$
The circle with radius $L / 2=5 \mathrm{~cm}$ touches the square at four points.

The circle with radius $D / 2$ touches the square at four points, specifically at the vertices of the square. We have $L=10, R=6$ and $D=10 \sqrt{2}$, therefore
$$
\underbrace{5}_{L / 2}<\underbrace{6}_{R}<\underbrace{5 \sqrt{2}}_{D / 2}
$$
(Observe that $1.2<\sqrt{2}, 5 \times 1.2<5 \times \sqrt{2}$ and, therefore, $6<5 \sqrt{2}$). Thus, the circle with radius $R=6$ is "between" the two circles with radii 5 and $5 \sqrt{2}$. Therefore, it intersects the square at eight points.
|
8
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
If $2\left(2^{2 x}\right)=4^{x}+64$, what is the value of $x$?
(a) -2
(b) -1
(c) 1
(d) 2
(e) 3
|
The correct option is (e).
Solution 1: We observe that the terms on the right side of the given equation can be written as powers of 2. Indeed, $4^{x}=\left(2^{2}\right)^{x}=2^{2 x}$ and $64=2^{6}$. Thus, the equation becomes $2\left(2^{x}\right)=2^{2 x}+2^{3}$. We then have $2\left(2^{2 x}\right)-2^{2 x}=2^{6}$, which simplifies to $2^{2 x}(2-1)=2^{6}$, or $2^{2 x}=2^{6}$. Therefore, $2 x=6$ and it follows that $x=3$.
Solution 2: $4^{x}+4^{x}=2\left(4^{x}\right)=2\left(2^{2 x}\right)=4^{x}+4^{3}$, hence $4^{x}=4^{3}$ and it follows that $x=3$.
|
3
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
In the figure, the number 8 was obtained by adding the two numbers directly below its position. By doing the same to fill in the blank spaces, one gets 42 in the indicated position. What is the value of $x$?
(a) 7
(b) 3
(c) 5
(d) 4
(e) 6
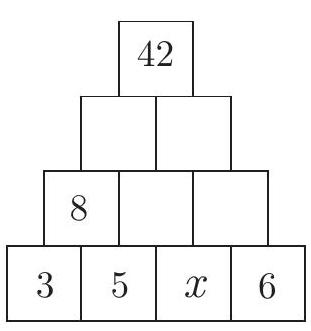
|
The correct option is (e).
Using the given rule, we fill in the empty cells starting from the second row from the bottom and obtain the figure. Therefore,
$$
(13+x)+(11+2 x)=42
$$
and thus, $24+3 x=42$, which means $x=6$.
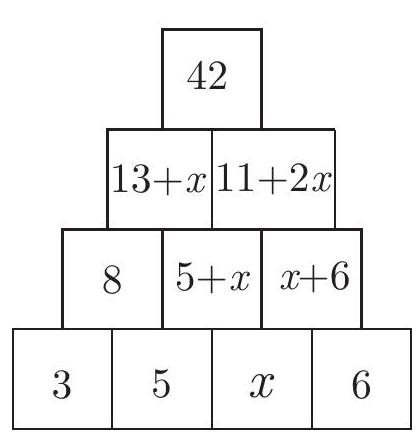
|
6
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Let $n=9867$. If you calculated $n^{3}-n^{2}$, what would be the unit digit found?
(a) 0
(b) 2
(c) 4
(d) 6
(e) 8
|
The correct option is (c).
Solution 1: The last digit of $9867^{3}$ is the same as that of $7^{3}=343$, which is 3. The last digit of $9867^{2}$ is the same as that of $7^{2}=49$, which is 9. If we subtract a number ending in 9 from another ending in 3, the last digit of the result is 4.
Note: Observe that the last digit of the difference $9867^{3}-9867^{2}$ is the same as the last digit of $\left(7^{3}-7^{2}\right)$.
Solution 2: $n^{3}-n^{2}=n^{2}(n-1)$, with $n^{2}=9867^{2}$ ending in 9 and $n-1=9866$ ending in 6. Since $9 \times 6=54$, the last digit of $n^{2}(n-1)$ is 4.
|
4
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
The function $f$ is given by the table
| $x$ | 1 | 2 | 3 | 4 | 5 |
| :---: | :--- | :--- | :--- | :--- | :--- |
| $f(x)$ | 4 | 1 | 3 | 5 | 2 |
For example, $f(2)=1$ and $f(4)=5$. What is the value of $\underbrace{f(f(f(f(\ldots f}_{2004 \text { times }}(4) \ldots)))$ ?
(a) 1
(b) 2
(c) 3
(d) 4
(e) 5
|
The correct option is (d).
From the table
| $x$ | 1 | 2 | 3 | 4 | 5 |
| :---: | :--- | :--- | :--- | :--- | :--- |
| $f(x)$ | 4 | 1 | 3 | 5 | 2 |
we obtain
$$
\begin{aligned}
& f(4)=5, f(\underbrace{f(4)}_{5})=f(5)=2, f(f(\underbrace{f(4)}_{5}))=f(\underbrace{f(5)}_{2})=f(2)=1 \text{ and} \\
& \underbrace{f(f(f(f(4)}_{4 \text { times }})))=f(f(f(\underbrace{f(4)}_{5})))=f(f(\underbrace{f(5)}_{2}))=f(\underbrace{f(2)}_{1})=f(1)=4
\end{aligned}
$$
Since 2004 is a multiple of 4, it follows that $\underbrace{f(f(f(f(\ldots f}_{2004 \text { times }}(4) \ldots)))=4$. The diagram below illustrates this statement.
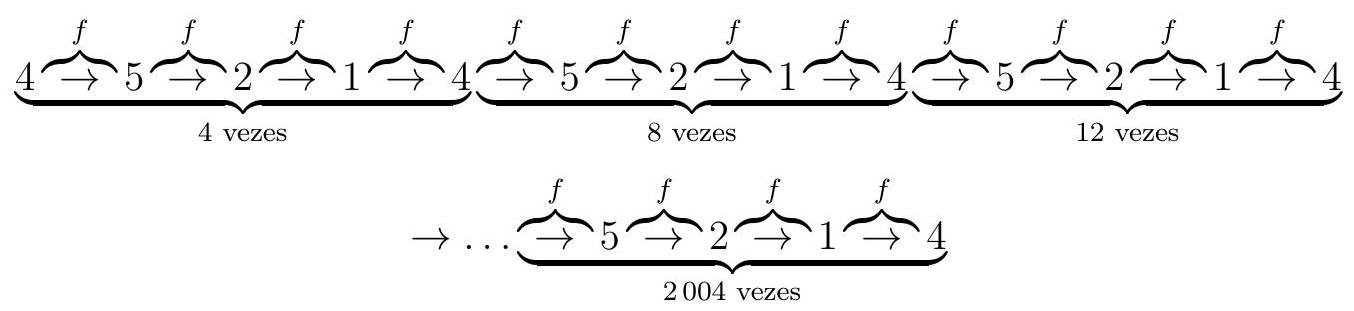
|
4
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A bus, a train, and a plane depart from city A to city B at the same time. If I take the bus, which has an average speed of 100 $\mathrm{km} / \mathrm{h}$, I will arrive in city B at 8 PM. If I take the train, which has an average speed of $300 \mathrm{~km} / \mathrm{h}$, I will arrive in city B at 2 PM. What will be the arrival time of the plane if its average speed is $900 \mathrm{~km} / \mathrm{h}$?
|
Let $d$ be the distance between the two cities and $h$ be the common departure time of the bus, the train, and the airplane. Since distance $=$ speed $\times$ time, we have $d=100 \times(20-h)$ and $d=300 \times(14-h)$. Therefore, $100 \times(20-h)=300 \times(14-h)$, from which $h=11$. Thus, the distance between the two cities is $d=100 \times(20-11)=900 \mathrm{~km}$. Therefore, the airplane takes 1 hour from city $\mathrm{A}$ to city $\mathrm{B}$ and, thus, the airplane arrives at 12 o'clock.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How many different pairs of positive integers $(a, b)$ are there such that $a+b \leq 100$ and $\frac{a+\frac{1}{b}}{\frac{1}{a}+b}=13$?
(a) 1
(b) 5
(c) 7
(d) 9
(e) 13
|
The correct option is (c).
We have
$$
13=\frac{a+\frac{1}{b}}{\frac{1}{a}+b}=\frac{\frac{a b+1}{b}}{\frac{1+a b}{a}}=\frac{(a b+1) \times a}{(1+a b) \times b}=\frac{a}{b}
$$
Thus, $a=13 b$. Since $a+b \leq 100$, it follows that $14 b \leq 100$ and, therefore, $b \leq 7.14$. Since $b$ is an integer, we must have $b \leq 7$. Therefore, the pairs are seven in number, namely,
$$
(13,1),(26,2),(39,3),(52,4),(65,5),(78,6) \text { and }(91,7)
$$
|
7
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
In the figure, the three circles are concentric, and the area of the smallest circle coincides with the area of the largest ring, highlighted in gray. The radius of the smallest circle is $5 \mathrm{~cm}$ and of the largest $13 \mathrm{~cm}$. What is the radius (in cm) of the intermediate circle?
(a) 12
(c) $10 \sqrt{65}$
(e) $12 \sqrt{2}$
(b) 11
(d) $5 \sqrt{3}$
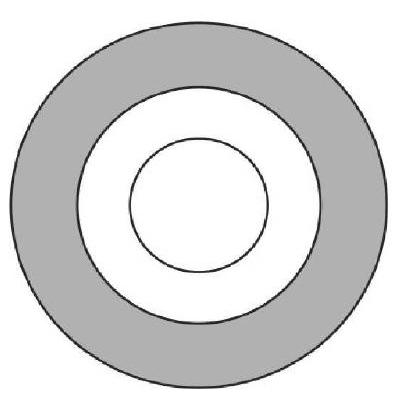
|
The correct option is (a).
The area of the largest circle is $13^{2} \pi=169 \pi$ and that of the smallest is $5^{2} \pi=25 \pi$, which is also the area of the largest ring. Let $r$ be the radius of the intermediate circle. Then, the area of the largest ring is $169 \pi-\pi r^{2}$. Therefore, $169 \pi-\pi r^{2}=25 \pi$, that is, $\pi r^{2}=169 \pi-25 \pi=144 \pi$, from which $r^{2}=144$ and $r=12 \text{ cm}$.
|
12
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
How many of the numbers $-5,-4,-3,-2,-1,0$, $1,2,3$ satisfy the inequality $-3 x^{2}<-14$?
(a) 1
(b) 2
(c) 3
(d) 4
(e) 5
|
The correct option is (d).
If $-3 x^{2}14$, or $x^{2}>\frac{1}{3} 14=4 \frac{2}{3}$. Since we are only looking at integer values of $x$, then $x^{2}$ is also an integer. Given that $x^{2}>4 \frac{2}{3}$, we conclude that $x^{2}$ is at least 5. Among the numbers $-5,-4,-3,-2,-1,0,1,2,3$ only four, namely, $-5,-4,-3$ and 3 satisfy $x^{2} \geq 5$.
|
4
|
Inequalities
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
If $S_{n}=1-2+3-4+5-6+\cdots+(-1)^{n+1} n$ for each positive integer $n$, then $S_{1992}+S_{1993}$ is equal to
(a) -2 ;
(b) -1 ;
(c) 0 ;
(d) 1 ;
(e) 2 .
|
The correct option is (d).
The expression $(-1)^{n+1}$ in the definition of $S_{n}$ has a value of 1 if $n$ is even and a value of -1 if $n$ is odd.
Solution 1: By associating consecutive terms in pairs, we obtain a sum of several terms equal to -1: $(1-2)+(3-4)+(5-6)+\cdots$. Therefore,
$$
S_{1992}=\underbrace{(1-2)+(3-4)+\cdots+(1991-1992)}_{1992 \div 2=996 \text{ terms}}=(-1) \times 996=-996
$$
and
$$
S_{1993}=(1-2)+(3-4)+\cdots+(1991-1992)+1993=-996+1993=997
$$
Thus, $S_{1992}+S_{1993}=-996+997=1$.
Solution 2: Since
$$
S_{2 n}=\underbrace{(1-2)+(3-4)+(5-6)+\cdots+[2 n-(2 n+1)]}_{n \text{ terms equal to }-1}
$$
we get $S_{2 n}=-n$ and $S_{2 n+1}=S_{2 n}+(2 n+1)=-n+2 n+1=n+1$. Therefore, $S_{2 n}+S_{2 n+1}=$ 1.
|
1
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
How many positive integers $n$ exist such that the quotient $\frac{2 n^{2}+4 n+18}{3 n+3}$ is an integer?
|
As
$$
\frac{2 n^{2}+4 n+18}{3 n+3}=\frac{2}{3}\left[\frac{\left(n^{2}+2 n+1\right)+8}{n+1}\right]=\frac{1}{3}\left(2 n+2+\frac{16}{n+1}\right)
$$
it follows that the expression in parentheses must be a multiple of 3 and, in particular, $n+1$ must divide 16. Thus, $n$ can be $1, 3, 7$ or 15. From the table below, in each of these four cases, that is, for $n$ equal to 1, 3, 7, or 15, the given quotient results in an integer.
| $n$ | $\frac{2 n^{2}+4 n+18}{3 n+3}$ |
| :---: | :---: |
| 1 | 4 |
| 3 | 4 |
| 7 | 6 |
| 15 | 11 |
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Four mayors decide to build a circular highway that passes within the boundaries of their cities. Since the four cities are not on the same circle, the mayors hire a company to develop a project for the construction of a circular highway equidistant from the four cities. What is the maximum number of geographically distinct projects that the company can develop?
|
The number of highways is equal to the number of points that can be the center of a circle (highway) that is equidistant from four given points (cities). Since no circle passes through all four points, if any circle is equidistant from the four points, this circle cannot leave all four points on the inside or all on the outside, so it must divide the set of four points into two, without passing through any of them. Thus, we can only have three types of configurations, depending on the number of points inside and outside the circle. In the first type, the equidistant circle leaves three points inside and one outside; in the second type, two inside and two outside; and in the third type, one inside and two outside.
In the figures below, the continuous circle is the equidistant one.
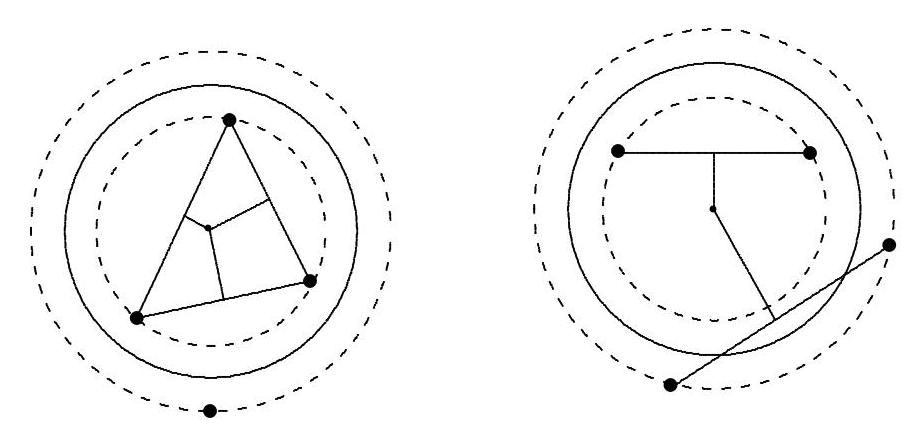
In the first figure, the center of the equidistant circle coincides with the center of the circumcircle of the triangle formed by the three internal points. This same configuration occurs in the third type, where the center of the equidistant circle coincides with the center of the circumcircle of the triangle formed by the three external points. Thus, in these two types, the number of equidistant circles is equal to the number of triangles that can be formed with three of the four points, which is four.
In the second figure, the center of the equidistant circle is on the perpendicular bisector of the two internal points and also on the perpendicular bisector of the two external points. Thus, in this type, the number of equidistant circles is equal to the number of ways to divide the set of four points into two sets of two points each, which is three.
Therefore, the number of possible circular highway projects equidistant from the four cities is \(4 + 3 = 7\).
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Five cards are on a table, and each has a number on one side and a letter on the other. Simone must decide whether the following statement is true: "If a card has a vowel on one side, then it has an even number on the other." What is the minimum number of cards she needs to turn over to make a correct decision?

|
Simone doesn't need to turn over the card that has the number $\mathbf{2}$ because the other side, whether a vowel or a consonant, will satisfy the condition "If a card has a vowel on one side, then it has an even number on the other."

She also doesn't need to turn over the card with the letter $\mathbf{M}$, since, on the other side, the number can be even or odd and the condition is still satisfied. However, the card with the number 3 needs to be turned over to verify that the other side has a consonant, as well as the cards with the letters $\mathbf{A}$ and $\mathbf{E}$, to verify that the other side has an even number. Therefore, Simone needs to turn over only 3 cards.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A surveillance service is to be installed in a park in the form of a network of stations. The stations must be connected by telephone lines so that any of the stations can communicate with all the others, either by a direct connection or through, at most, one other station.
Each station can be directly connected by a cable to, at most, three other stations. The diagram shows an example of such a network, connecting seven stations. What is the largest number of stations that can be connected in this way?
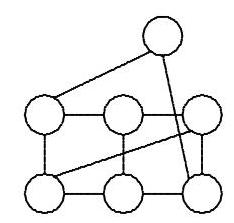
|
The example shows that we can connect at least seven stations under the proposed conditions. We start with a particular station, and think of it as the base of the network. It can be connected to one, two, or three stations, as shown in the first of the two diagrams below. Stations A, B, and C still have two unused lines, so they can be connected to two other stations, as shown in the second of the two diagrams below.
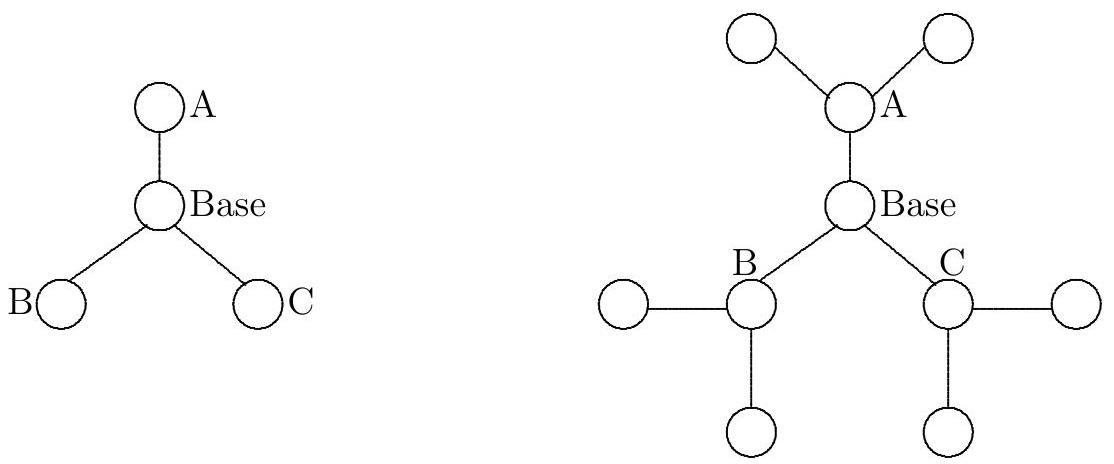
Now, it is impossible to add more stations, as any additional one would not be able to connect to the base while satisfying the conditions of the problem. This shows that we cannot have more than 10 stations.
Let's now see if it is possible to build a network with these 10 stations. Observe, in the diagram above, that only the base is connected to all other stations (either directly or via a connection through another station). The stations at the ends still have two unused lines, and now we will use them to close the network. See the diagram below.
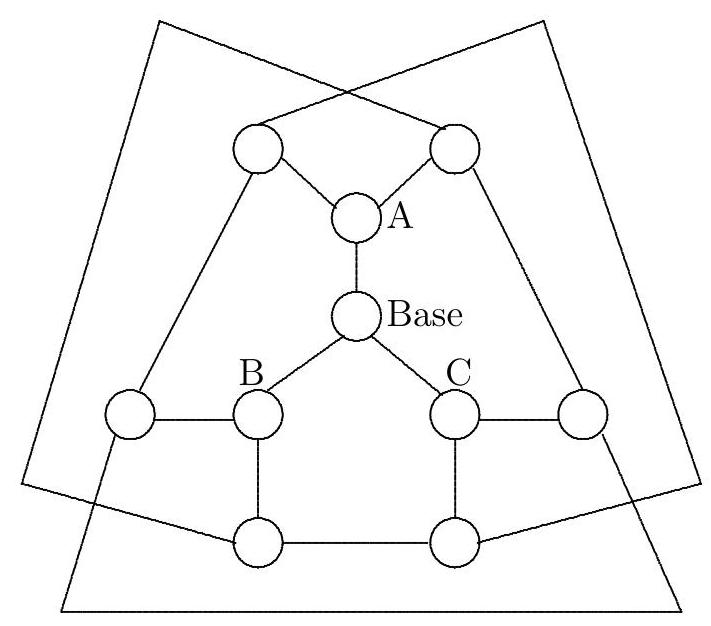
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A round table has a diameter of 1.40 meters.
For a party, the table is expanded by adding three planks, each 40 cm wide, as shown in the figure. If each person at the table should have 60 cm of space, how many guests can sit at the table?
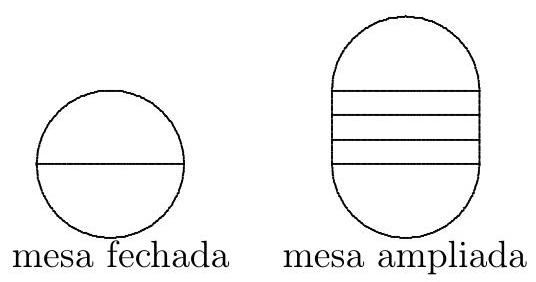
|
The perimeter of the expanded table is
$$
140 \times \pi + 40 \times 6 \approx 140 \times 3.14 + 240 = 679.60 \text{ cm}
$$
If each guest needs $60 \text{ cm}$ of space, the maximum number of guests that can sit at the table is
$$
\frac{679.60}{60} \approx 11.3
$$
that is, 11 guests.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the given figure, we have 16 points forming a square grid and two lines, $r$ and $s$, which are perpendicular to each other.
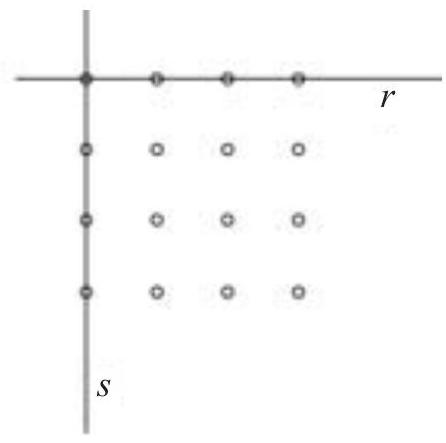
(a) How many squares can we construct such that their vertices belong to the grid, but none of their sides are parallel to either line $r$ or line $s$?
(b) How many right-angled isosceles triangles can we construct such that their vertices belong to the grid, but none of their sides are parallel to either line $r$ or line $s$?
|
(a) The only squares that do not have any of their sides parallel to line $r$ or line $s$ are those of type 1 and type 2 (see figures).
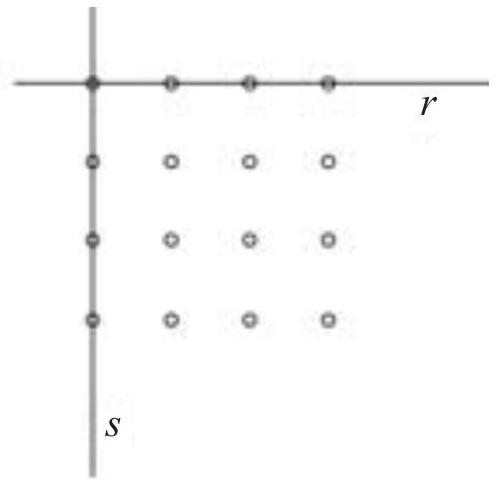
Thus, there are a total of six squares, four of type 1 and two of type 2.
(b) Suppose the vertical or horizontal distance between two adjacent points on the grid is equal to one unit. The total of these triangles is sixteen, each with legs equal to $\sqrt{5}$ units and a hypotenuse of $\sqrt{10}$ units. Indeed, each of the squares of type 2, as seen in (a), gives us four triangles, by dividing along each of the two diagonals, thus obtaining eight triangles. The remaining eight triangles are obtained through a single horizontal or vertical translation of each of the previous ones. In the figure, we illustrate the only possible translation of one of the four triangles obtained from a square of type 2.
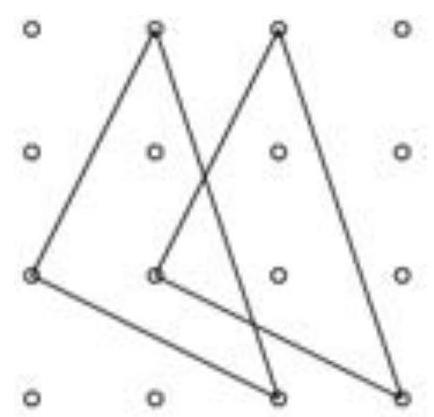
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
All natural numbers starting from 1 were written consecutively, forming a sequence of digits, as follows.
$$
1234567891011121314151617181920212223 \ldots
$$
What is the digit that appears in the 206788th position?
|
The numbers with one digit form the first 9 terms of the sequence. The 90 two-digit numbers form the next 180 terms. Then come the 2700 terms corresponding to the three-digit numbers, followed by the 36000 terms corresponding to the four-digit numbers, and finally, the 450000 terms corresponding to the five-digit numbers. Thus, enumerating the terms of the sequence, we get 488889 terms.
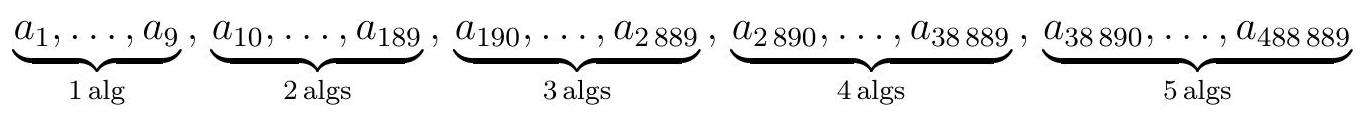
To write all the terms of 1, 2, 3, and 4 digits, we reach the $38889^{\text{th}}$ position of the sequence. Therefore, the digit at the $206788^{\text{th}}$ position is part of a five-digit number, i.e., it is in the block
$$
\underbrace{a_{38890}, \ldots, a_{488889}}_{5 \text{ digits}}
$$
This block is of the form 10000, 10001,.. 99 999. To see how many five-digit numbers exist from position 38889 to position 206788, we divide this difference by 5. Thus, $206788-38889=167899$ and $167899=5 \times 33579+4$. Therefore, we need 33579 five-digit numbers, plus the first four digits of the $33580^{\text{th}}$ five-digit number, which is 43579, to reach the digit at position 206788.
Since the fourth digit of the number 43579 is 7, the digit we are looking for is 7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How many zeros are there at the end of the number $9^{2007}+1$?
|
Initially, we verify how the powers of 9 end, that is, we list the last two digits, the tens and units, of the powers $9^{n}$, in order.
| If $n$ is | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $9^{n}$ ends with | 01 | 09 | 81 | 29 | 61 | 49 | 41 | 69 | 21 | 89 | 01 | 09 | 81 |
Thus, we see that the last two digits of $9^{10}, 9^{11}$, and $9^{12}$ are the same as those of $9^{0}, 9^{1}$, and $9^{2}$. Starting from $9^{10}$, the last two digits of the powers begin to repeat, forming a periodic sequence with a period of 10. Since $2007=10 \times 200+7$ and the last two digits of $9^{10 \times 200}$ are 01, it follows that the last two digits of $9^{2007}$ are the last two digits of $9^{7}$, which are 69. Therefore, the last two digits of $9^{2007}+1$ are equal to $69+1=70$. Thus, there is a single zero at the end of the number $9^{2007}+1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
When Isabel was born, her mother was turning 20 years old. If Isabel and her mother live for another 100 years, how many times will their ages be multiples of each other?
|
When Isabel is $a$ years old, her mother is $20+a$ years old. If $a$ is a divisor of $20+a$, then $(20+a) / a=(20 / a)+1$ is an integer, and consequently, $20 / a$ is also an integer. Therefore, $a$ is a divisor of 20, and thus $a$ can be 1, 2, 4, 5, 10, or 20. So, there are a total of 6 times when their ages are multiples of each other.
| Isabel | 1 | 2 | 4 | 5 | 10 | 20 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| Mother | 21 | 22 | 24 | 25 | 30 | 40 |
Notice that, after Isabel turns 20, her mother's age will never again be a multiple of Isabel's age.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
An empty swimming pool was filled with water by two faucets A and B, both with constant flow rates. For four hours, both faucets were open and filled $50 \%$ of the pool. Then, faucet B was turned off and, for two hours, faucet A filled $15 \%$ of the pool's volume. After this period, faucet A was turned off and faucet B was turned on. For how long did this faucet have to remain open for it to fill the pool by itself?
|
Given that taps A and B pour water into the pool at a constant flow rate, the volume of water poured by each tap is proportional to the time it is open. Therefore, if tap A fills $15 \%$ of the pool volume in two hours, then in four hours it will fill $30 \%$ of the pool volume.
However, when taps A and B are both open simultaneously for four hours, they manage to fill $50 \%$ of the pool volume. Thus, tap B fills $50 \% - 30 \% = 20 \%$ of the pool volume in four hours.
To determine how long tap B needs to be open to fill the remaining $35 \%$ of the pool volume, we can use the rule of three.
$$
\begin{array}{ccc}
\text { hours } & \rightarrow & \text { percentage } \\
4 & \rightarrow & 20 \% \\
x & \rightarrow & 35 \%
\end{array}
$$
Therefore, tap B will take $x=\frac{35 \times 4}{20}=7$ hours to fill the remaining $35 \%$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A triangle has vertices $A=(3,0), B=(0,3)$, and $C$, where $C$ lies on the line with equation $x+y=7$. What is the area of this triangle?
|
Observe that the height $h$ relative to side $AB$ of all triangles $\triangle ABC$ that have vertex $C$ on the line $x+y=7$ is always the same, since the line $x+y=7$ is parallel to the line $x+y=3$ that passes through $A$ and $B$. Therefore, all these triangles have the same area, namely,
$$
\frac{1}{2}(AB \times h)
$$
It remains, therefore, to determine $AB$ and $h$. Since $AB$ is the hypotenuse of a right triangle that has both legs equal to 3, it follows from the Pythagorean Theorem that
$$
AB=\sqrt{3^{2}+3^{2}}=\sqrt{18}=3 \sqrt{2}
$$
On the other hand, $h$ is the distance between the parallel lines $x+y=3$ determined by points $A$ and $B$ and $x+y=7$. The line $x=y$ is perpendicular to these parallel lines and forms a $45^{\circ}$ angle with the $Ox$ axis. Let $M$ be the foot of the perpendicular to the line $x+y=7$ drawn from $A$ and $D=(7,0)$ the point of intersection of the line $x+y=7$ with the $Ox$ axis. The triangle $\triangle AMD$ thus formed is a right isosceles triangle, with two legs equal to $h$ and hypotenuse $7-3=4$. By the Pythagorean Theorem, it follows that $4^{2}=h^{2}+h^{2}=2 h^{2}$, that is, $h=\sqrt{8}=2 \sqrt{2}$. Thus, the area sought is given by
$$
\frac{1}{2}(3 \sqrt{2} \times 2 \sqrt{2})=6
$$
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
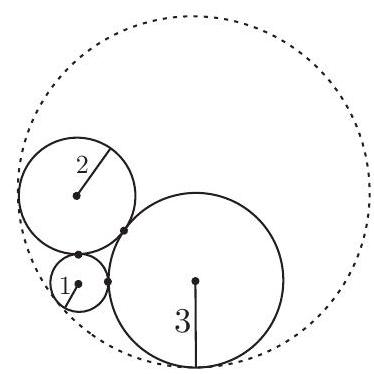
Three circles, with radii measuring 1, 2, and $3 \mathrm{~cm}$, are pairwise externally tangent, as shown in the given figure. Determine the radius of the circle that is externally tangent to the three circles.
|
By connecting the centers of the three circles, we obtain the triangle $\triangle ABC$ with sides $AB=3, AC=4$, and $BC=5$. Since $3^{2}+4^{2}=5^{2}$, this triangle is a right triangle with hypotenuse $BC$.
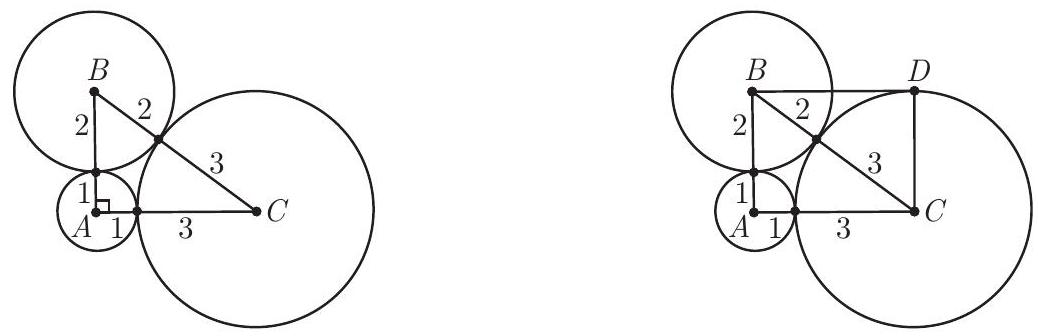
Now we construct the rectangle $ADCB$ with a congruent copy of the triangle $\triangle ABC$ and a common hypotenuse $BC$, as shown in the figure. Since $DC=AB=3$ and the circle centered at $C$ also has a radius of 3, we see that point $D$ lies on the circle. Finally, we connect point $D$ to each of the vertices of the triangle $\triangle ABC$ and extend these segments until they intersect the circles centered at $A, B$, and $C$, obtaining the points $P_{1}, P_{2}$, and $P_{3}$, as shown in the figure.
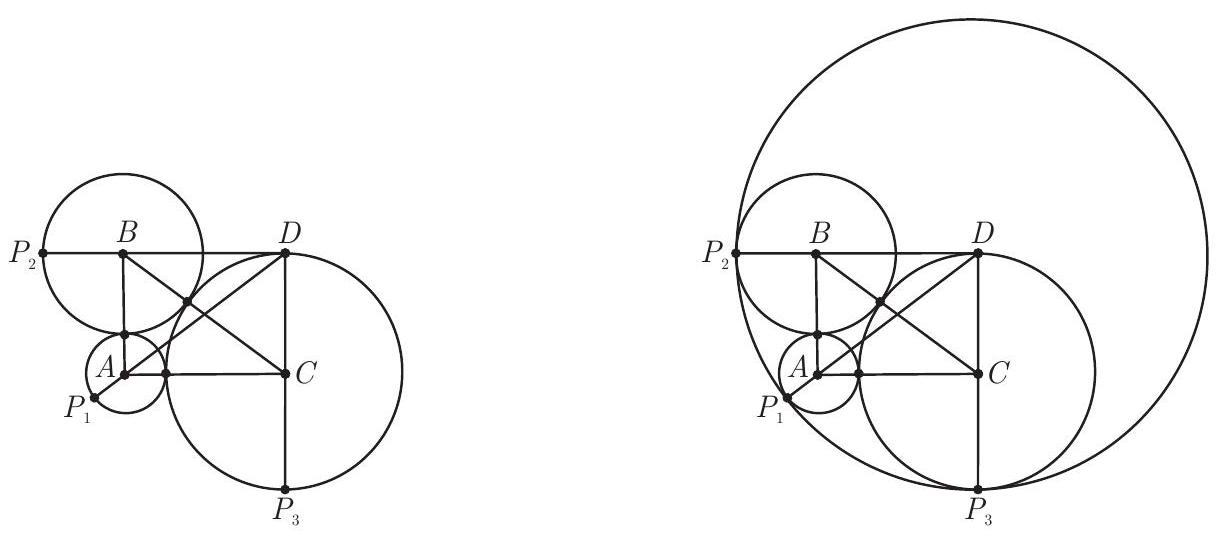
Observe that
- $DP_{2}=DB+BP_{2}=CA+BP_{2}=4+2=6$,
- $DP_{1}=DA+AP_{1}=5+1=6$, and
- $DP_{3}=DC+CP_{3}=3+3=6$.
Thus, $DP_{1}=DP_{2}=DP_{3}=6$, and therefore, the circle centered at $D$ with radius 6 passes through $P_{1}, P_{2}$, and $P_{3}$. Furthermore, since the points $\{D, A, P_{1}\}, \{D, B, P_{2}\}$, and $\{D, C, P_{3}\}$ are collinear, it follows that the circle centered at $D$ with radius 6 is externally tangent to the given circles centered at $A, B$, and $C$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $A B C D$ be a right trapezoid with bases $A B$ and $C D$, and right angles at $A$ and $D$. Given that the shorter diagonal $B D$ is perpendicular to the side $B C$, determine the smallest possible value for the ratio $C D / A D$.
|
Let $A \widehat{B} D = B \widehat{D} C = \alpha$, as shown in the given figure. Then we have $C D = \frac{B D}{\cos \alpha}$ and $A D = B D \sin \alpha$, hence
$$
\begin{aligned}
\frac{C D}{A D} & = \frac{\frac{B D}{\cos \alpha}}{B D \sin \alpha} = \frac{1}{\sin \alpha \cos \alpha} \\
& = \frac{2}{\sin 2 \alpha} \geq 2
\end{aligned}
$$
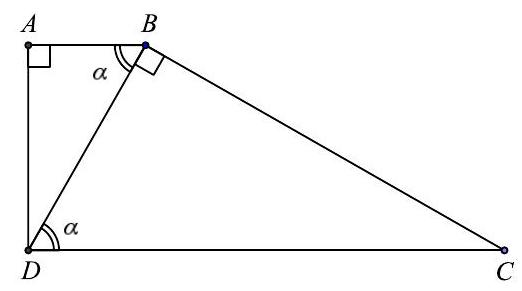
Thus, the smallest value of the ratio $C D / A D$ is 2, which occurs when $\sin 2 \alpha = 1$, i.e., when $\alpha = 45^{\circ}$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let's denote by $s(n)$ the sum of the digits of the number $n$. For example, $s(2345) = 2 + 3 + 4 + 5 = 14$. Observe that:
\[
\begin{gathered}
40 - s(40) = 36 = 9 \times 4; \quad 500 - s(500) = 495 = 9 \times 55 \\
2345 - s(2345) = 2331 = 9 \times 259
\end{gathered}
\]
(a) What can we say about the number $n - s(n)$?
(b) Using the previous item, calculate $s\left(s\left(s\left(2^{2009}\right)\right)\right)$.
HINT: Show that the number sought is less than 9.
|
(a) It is immediate that if $a$ is a digit between 1 and 9, then $s\left(a \cdot 10^{k}\right)=a$, since the number $a \cdot 10^{k}$ is formed by the digit $a$ followed by $k$ zeros. Therefore, we have
$$
a \cdot 10^{k}-s\left(a \cdot 10^{k}\right)=a \cdot 10^{k}-a=a\left(10^{k}-1\right)=a \times \underbrace{9 \cdots 9}_{k \text { nines }}=a \times 9 \times \underbrace{1 \cdots 1}_{k \text { ones }}.
$$
Since every number can be decomposed into units, tens, hundreds, etc., that is, every positive integer $n$ can be written, uniquely, in the form
$$
n=a_{0}+a_{1} \cdot 10+a_{2} \cdot 10^{2}+\cdots+a_{k} \cdot 10^{k}
$$
we have that
$$
n-s(n)=a_{1} \cdot 9+a_{2} \cdot 99+\cdots+a_{k} \cdot \underbrace{9 \cdots 9}_{k \text { nines }}
$$
Thus, the difference $n-s(n)$ is always divisible by 9.
(b) Following the same reasoning, we have that both $s(n)-s(s(n))$ and $s(s(n))-s(s(s(n)))$ are divisible by 9, therefore, $n-s(s(s(n)))$ is divisible by 9. In particular, $2^{2009}-s\left(s\left(s\left(2^{2009}\right)\right)\right)$ is divisible by 9 or, equivalently, $2^{2009}$ and $s\left(s\left(s\left(2^{2009}\right)\right)\right)$ leave the same remainder when divided by 9.
Since $2^{6}-1=63$ is divisible by 9, then substituting $x=2^{6}$ and $m=334$ in the identity
$$
x^{m}-1=(x-1)\left(x^{m-1}+x^{m-2}+\cdots+x^{2}+x+1\right)
$$
we conclude that $\left(2^{6}\right)^{334}-1=2^{2004}-1$ is divisible by 9 and, therefore, $2^{2009}-2^{5}$ is divisible by 9. Since $2^{5}=32$ leaves a remainder of 5 when divided by 9, we have that $2^{2009}$ leaves a remainder of 5 when divided by 9. On the other hand,
$$
2^{2009}<\left(2^{9}\right)^{224}<\left(10^{3}\right)^{224}=10^{672}
$$
Thus, $2^{2009}$ has fewer than 672 digits and, therefore,
$$
\begin{aligned}
s\left(2^{2009}\right) & <9 \times 672=6.048 \\
s\left(s\left(2^{2009}\right)\right) & \leq 5+9+9+9=32 \text{ and} \\
s\left(s\left(s\left(2^{2009}\right)\right)\right) & \leq 2+9=13
\end{aligned}
$$
Since the only number less than or equal to 13 that leaves a remainder of 5 when divided by 9 is 5, it follows that
$$
s\left(s\left(s\left(2^{2009}\right)\right)\right)=5
$$
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
If $S_{n}=1-2+3-4+5-6+\ldots+(-1)^{n+1} n$, where $n$ is a positive integer, then $S_{1992}+S_{1993}$ is:
(a) -2
(b) -1
(c) 0
(d) 1
(e) 2
|
Solution 1: Remember that
$(-1)^{n+1}= \begin{cases}1 & \text { if } n \text { is odd } \\ -1 & \text { if } n \text { is even }\end{cases}$
Observe that by grouping consecutive terms in pairs,
$$
(1-2)+(3-4)+(5-6)+\cdots
$$
we get a sum of $n$ terms all equal to -1. Therefore,
$S_{1992}=\underbrace{(1-2)+(3-4)+(5-6)+\cdots+(1991-1992)}_{1992 \div 2=996 \text { terms }}=(-1) \times 996=-996$.
$S_{1993}=(1-2)+(3-4)+(5-6)+\cdots+(1991-1992)+1993=-996+1993=997$.
Thus, $S_{1992}+S_{1993}=-996+997=1$. The correct option is (d).
Solution 2: Note that
$$
S_{2 n}=\underbrace{(1-2)+(3-4)+(5-6)+\cdots+[2 n-(2 n+1)]}_{n \text { terms equal to }-1}
$$
We obtain that $S_{2 n}=-n$ and $S_{2 n+1}=S_{2 n}+(2 n+1)=-n+2 n+1=n+1$. Therefore, $S_{2 n}+S_{2 n+1}=1$.
|
1
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Ester goes to a stationery store to buy notebooks and pens. In this stationery store, all notebooks cost $\mathrm{R} \$ 6.00$. If she buys three notebooks, she will have R \$4.00 left. If, instead, her brother lends her an additional $\mathrm{R} \$ 4.00$, she will be able to buy two notebooks and seven pens, all the same.
(a) How much does each pen cost?
(b) If she buys two notebooks and does not borrow money, how many pens can Ester buy?
|
By buying three notebooks at 6 reais each, Ester still has 4 reais left, so the amount she has is $3 \times 6 + 4 = 22$ reais.
(a) If her brother lends her 4 reais, she then has $22 + 4 = 26$ reais and can buy 2 notebooks at 6 reais each, leaving her with $26 - 2 \times 6 = 26 - 12 = 14$ reais for 7 pens. We conclude that the price of each pen is $14 \div 7 = 2$ reais.
(b) Since Ester has 22 reais, if she buys 2 notebooks, she will have $22 - 2 \times 6 = 22 - 12 = 10$ reais left. Since each pen costs 2 reais, she can buy $10 \div 2 = 5$ pens.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Diamantino put three liters of water and one liter of soft drink in a container. The soft drink is composed of $20 \%$ orange juice and $80 \%$
water. After mixing everything, what percentage of the final volume represents the orange juice?
(a) $5 \%$
(b) $7 \%$
(c) $8 \%$
(d) $20 \%$
(e) $60 \%$
|
The correct option is (a).
The refreshment is composed of $20 \%$ of a liter, that is, 0.2 liters of juice and $80 \%$ of a liter, that is, 0.8 liters of water. Therefore, the final mixture has 0.2 liters of juice and $3+0.8=3.8$ liters of water. The percentage of juice in relation to the volume of the mixture is then,
$$
\frac{\text { volume of juice }}{\text { total volume }}=\frac{0.2}{4}=\frac{2}{40}=\frac{5}{100}=5 \%
$$
|
5
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
What is the value of $2^{6}+2^{6}+2^{6}+2^{6}-4^{4}$?
(a) 0
(b) 2
(c) 4
(d) $4^{2}$
(e) $4^{4}$
|
The correct option is (a).
We have $2^{6}+2^{6}+2^{6}+2^{6}-4^{4}=4 \times 2^{6}-4^{4}$. There are several ways to calculate this.
Solution 1: $4 \times 2^{6}-4^{4}=4 \times\left(2^{2}\right)^{3}-4^{4}=4 \times 4^{3}-4^{4}=4^{4}-4^{4}=0$.
Solution 2: $4 \times 2^{6}-4^{4}=4\left(2^{6}-4^{3}\right)=4\left[2^{6}-\left(2^{2}\right)^{3}\right]=4\left[2^{6}-2^{6}\right]=0$.
Solution 3: $4 \times 2^{6}-4^{4}=2^{2} \times 2^{6}-\left(2^{2}\right)^{4}=2^{8}-2^{8}=0$.
|
0
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
In a year, at most how many months have five Sundays?
(a) 3
(b) 4
(c) 5
(d) 6
(e) 7
|
The correct option is (c).
A common year has 365 days and a leap year has 366. From the division of 365 by 7, we get $365=52 \times 7+1$ and from the division of 366 by 7 we get $366=52 \times 7+2$. Therefore,
$$
\begin{aligned}
\text { common year } & =52 \text { weeks }+1 \text { day } \\
\text { leap year } & =52 \text { weeks }+2 \text { days }
\end{aligned}
$$
Thus, a common or leap year has, at a minimum, 52 and, at a maximum, 53 Sundays (one Sunday for each of the 52 weeks and, perhaps, one additional Sunday for the day or the two days that complete the year).
Each of the 12 months of the year has, at a minimum, 28 days and, at a maximum, 31 days, therefore, it has, at a minimum, 4 Sundays and, at a maximum, 5 Sundays. Considering that $12 \times 4=48$, we conclude that
i) In a year with 52 Sundays, there are still $52-48=4$ Sundays left. Each of these will be in a different month, because no month can have six Sundays; thus, we have four months with 5 Sundays.
ii) Analogously, in a year with 53 Sundays, there are 5 Sundays left, which will be in different months. Therefore, in this case, we will have five months with 5 Sundays.
|
5
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
What is the unit digit of the number
$$
1 \times 3 \times 5 \times \cdots \times 97 \times 99 ?
$$
(a) 1
(b) 3
(c) 5
(d) 7
(e) 9
|
The correct option is (c).
The last digit of a multiple of 5 is 0 or 5; those ending in 0 are even and those ending in 5 are odd. Since $1 \times 3 \times 5 \times \cdots \times 97 \times 99$ is odd, being a product of odd numbers, and is a multiple of 5, it follows that its units digit is 5.
|
5
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
The figure shows the map of a country (imaginary) consisting of five states. It is desired to color this map with the colors green, blue, and yellow, so that two adjacent states do not have the same color. In how many different ways can the map be painted?
(a) 12
(b) 6
(c) 10
(d) 24
(e) 120
|
The correct option is (b).
State A can be painted in three ways: green, blue, or yellow. For any neighboring state, for example, state $\mathrm{B}$, we have two possibilities, and the colors of the other states are determined. Therefore, we can color the map in $3 \times 2=6$ ways.
Below we illustrate two of these ways to paint the map; in both, state A has the same color.
|
6
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
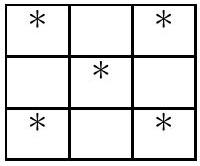
In a $3 \times 3$ board, nine houses must be painted such that in each column, each row, and each of the two diagonals, there are no two houses of the same color. What is the minimum number of colors needed for this?
(a) 3
(b) 4
(c) 5
(d) 6
(e) 7
|
The correct option is (c).
To satisfy the conditions of the problem, the five houses on the diagonals, marked with *, must have different colors. Therefore, we will need at least five distinct colors. Let's denote these five distinct colors by 1, 2, 3, 4, and 5, and determine how we can choose the colors for the remaining four houses to satisfy the given conditions. One way is shown on the right, as follows.
| 1 | | 4 |
| :--- | :--- | :--- |
| | 3 | |
| 2 | | 5 |$\rightarrow$| 1 | 2 | 4 |
| :--- | :--- | :--- |
| 4 | 3 | 1 |
| 2 | 4 | 5 |
Thus, it is possible to paint the remaining four houses without using more colors. Therefore, five colors are sufficient. Below, we show three other ways to color the houses.
| 2 | | 3 |
| :--- | :--- | :--- |
| | 1 | |
| 5 | | 4 |$\rightarrow$| 2 | 4 | 3 |
| :--- | :--- | :--- |
| 4 | 1 | 2 |
| 5 | 2 | 4 |$\quad$| 1 | | 2 |
| :--- | :--- | :--- |
| | 4 | |
| 3 | | 5 |$\rightarrow$| 1 | 3 | 2 |
| :--- | :--- | :--- |
| 2 | 4 | 1 |
| 3 | 2 | 5 |
| 1 | | 5 |
| :--- | :--- | :--- |
| | 2 | |
| 4 | | 3 |$\rightarrow$| 1 | 3 | 5 |
| :--- | :--- | :--- |
| 3 | 2 | 4 |
| 4 | 1 | 2 |
|
5
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
If $\frac{n}{24}$ is a number between $\frac{1}{6}$ and $\frac{1}{4}$, who is $n$?
(a) 5
(b) 6
(c) 7
(d) 8
(e) 9
|
The correct option is (a).
Since $\frac{1}{6}=\frac{4}{24}$ and $\frac{1}{4}=\frac{6}{24}$, then $n$ can only be equal to 5.
|
5
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
What is the smallest natural number $n$ for which $10^{n}-1$ is a multiple of 37?
(a) 6
(b) 5
(c) 4
(d) 3
(e) 2
|
The correct option is (d).
Observe that $10^{n}-1$ is a number that has all its digits equal to 9. Note, also, that a multiple of 37, of the form $37 \times n$, only ends in 9 if $n$ ends in 7. Therefore, the smallest multiples of 37 ending in 9 are $37 \times 7=259$, $37 \times 17=629$, and $37 \times 27=999$. Since $999=10^{3}-1$, it follows that $n=3$.
|
3
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
What is the value of $2-2\{2-2[2-2(4-2)]\}$?
(a) 0
(b) 2
(c) -2
(d) 4
(e) -10
|
The correct option is (e).
The order of precedence for solving an expression is
$$
\underbrace{\text { parentheses }}_{1 \varrho} \rightarrow \underbrace{\text { brackets }}_{2 \varrho} \rightarrow \underbrace{\text { braces }}_{3 \propto}
$$
and
$$
\underbrace{\text { multiplications and divisions }}_{1 \varrho} \rightarrow \underbrace{\text { additions and subtractions }}_{2 \varrho}
$$
Thus,
$$
\begin{aligned}
2 & -2\{2-2[2-2(\underbrace{4-2}_{2})]\}=2-2\{2-2[2-\underbrace{2 \times 2}_{4}]\} \\
& =2-2\{2-2[\underbrace{2-4}_{-2}]\}=2-2\{2-\underbrace{2 \times(-2)}_{-4}\} \\
& =2-2\{2-(-4)\}=2-2\{\underbrace{2+4}_{6}\}=2-\underbrace{2 \times 6}_{12}=2-12=-10
\end{aligned}
$$
|
-10
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
What is the digit $a$ in $a 000+a 998+a 999=22$ 997?
|
Performing the addition
| 111 |
| ---: |
| $a 000$ |
| $a 998$ |
| $+a 999$ |
| $\square 997$ |
we find $\square 997=22997$, where $\square=a+a+a+1$. Therefore, $22=a+a+a+1$, and thus, $a=7$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
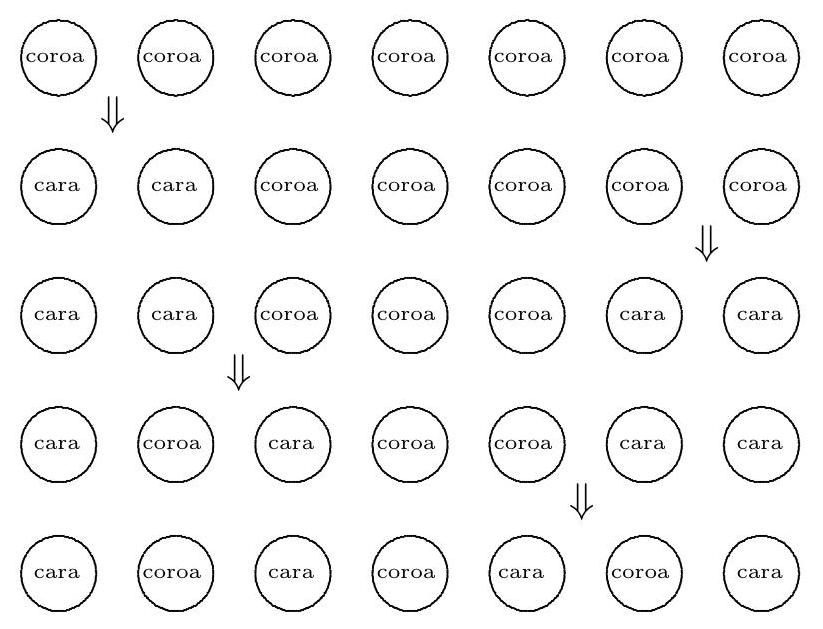
A game starts with seven coins aligned on a table, all with the crown face up. To win the game, you need to flip some coins in such a way that, in the end, two adjacent coins always have different faces up. The rule of the game is to flip two adjacent coins in each move. What is the minimum number of moves required to win the game?

|
Assigning the value 1 to heads and -1 to tails and summing the results after each flip, the game starts with a sum of 7 and we want to reach alternating heads and tails, so that the game ends at 1 or -1. We observe that, in each step of the game, we have the following possibilities: we exchange two heads for two tails and the value of the sum decreases by 4; we exchange one head and one tail for one tail and one head and the value of the sum remains unchanged; or we exchange two tails for two heads and the value of the sum increases by 4. Therefore, it is impossible to start from 7 as the initial sum and reach 1, but let's see that, indeed, it is possible to reach -1, that is, four tails and three heads. Since we want to obtain four non-consecutive tails, we need at least four moves.
The four moves, which make the sum go from 7 to 3, from 3 to -1, and then remain at -1, are illustrated in the figure.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The price of a kilogram of chicken was $R \$ 1.00$ in January 2000, when it started to triple every 6 months. How long will it take for the price to reach $\mathrm{R} \$ 81.00$?
(a) 1 year
(b) 2 years
(c) $2 \frac{1}{2}$ years
(d) 13 years
(e) $13 \frac{1}{2}$ years
|
The correct option is (b).
Since $81=3^{4}$, the value of the chicken has tripled four times. The number of months that have passed is $4 \times 6=24$ months, that is, two years, meaning that in January 2002, the chicken will reach a price of R\$ 81.00.
|
2
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
In a certain warehouse, a dozen eggs and 10 apples had the same price. After a week, the price of eggs dropped by $10 \%$ and the price of apples increased by $2 \%$ How much more will be spent on the purchase of a dozen eggs and 10 apples?
(a) $2 \%$
(b) $4 \%$
(c) $10 \%$
(d) $12 \%$
(e) $12.2 \%$
|
The correct option is (b).
Since the statement and the answer are in percentages, we can, in this case, assume any price and any currency unit, and the answer will always be the same. The simplest approach, therefore, is to assume that initially, a dozen eggs cost 100 and that ten apples also cost 100. Since the price of eggs increased by $10 \%$, the new price of eggs is 110. The price of apples decreased by $2 \%$, so the new price of ten apples is 98. Thus, while previously one would spend 200 on a dozen eggs and ten apples, now one spends $110+98=208$. Therefore, the increase was 8 out of 200, which corresponds to the percentage of
$$
\frac{8}{200}=\frac{4}{100}=4 \%
$$
|
4
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
The squares of the natural numbers from 1 to 99 were written one after another, forming the number 14916253649... What is the digit that occupies the 100th position? (The positions are counted from left to right, so the $1^{\underline{a}}$ position is the 1, the $2^{\underline{a}}$ is the 4, and so on.)
|
Separating the numbers whose squares have 1, 2, and 3 digits, we have,
$$
\begin{array}{ll}
\text { with } 1 \text { digit: } & 1,2,3 \\
\text { with } 2 \text { digits: } & 4,5,6,7,8,9 \\
\text { with } 3 \text { digits: } & 10,11,12, \ldots, 31
\end{array}
$$
Up to $31^{2}$, the number already has $3+12+66=81$ digits. Abbreviating digit by "dgs", we have
$$
\underbrace{1^{2}, 2^{2}, 3^{2}}_{1 \times 3 \text { dgs }}, \underbrace{4^{2}, \ldots, 9^{2}}_{2 \times 6=12 \text { dgs }}, \underbrace{10^{2}, \ldots, 31^{2}}_{3 \times 22=66 \text { dgs }}
$$
Thus, we are short of $100-81=19$ digits to reach 100. Since only $100^{2}$ has 5 digits, and since $19=4 \times 4+3$, we will have 4 more numbers, each with 4 digits, which are $32^{2}$, $33^{2}$, $34^{2}$, and $35^{2}$, plus the 3 digits (thousands, hundreds, tens) of the number $36^{2}=1296$, as follows.
$$
\underbrace{1^{2}, 2^{2}, 3^{2}}_{1 \times 3 \text { dgs }}, \underbrace{4^{2}, \ldots, 9^{2}}_{2 \times 6=12 \text { dgs }}, \underbrace{10^{2}, \ldots, 31^{2}}_{3 \times 22=66 \text { dgs }}, \underbrace{32^{2}, 33^{2}, 34^{2}, 35^{2}}_{4 \times 4=16 \text { dgs }}, 12 \underbrace{9}_{100^{\text{th}} \text { dgs }} 6
$$
Thus, we see that the digit 9 occupies the 100th position.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Seventy-four pencils were packed into 13 boxes. If the maximum capacity of each box is six pencils, what is the minimum number of pencils that can be in a box?
(a) 1
(b) 2
(c) 3
(d) 4
(e) 6
|
The correct option is (b).
Let's see in how many boxes we can place the maximum number of pencils, which is 6 per box. In 13 boxes it is not possible, because $13 \times 6=78$ is greater than the total number of pencils, which is 74. In 12 boxes we can have $12 \times 6=72$, leaving one box with $74-72=2$ pencils.
|
2
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
In the number $6 a 78 b$, $a$ represents the thousands digit and $b$ represents the units digit. If $6 a 78 b$ is divisible by 45, then the value of $a+b$ is:
(a) 5 ;
(b) 6 ;
(c) 7 ;
(d) 8 ;
(e) 9 .
|
The correct option is (b).
The number is divisible by $45=5 \times 9$, so it is divisible by 5 and 9. Every number divisible by 5 ends in 0 or 5. Thus, $b=0$ or $b=5$. Every number divisible by 9 has the sum of its digits as a multiple of 9. Therefore, $6+a+7+8+b=21+a+b$ is a multiple of 9. Since $a \leq 9$, and $b=0$ or $b=5$, we have $21 \leq 21+a+b \leq 21+9+5=35$. But the only multiple of 9 between 21 and 35 is 27. Thus, $21+a+b=27$. We conclude that $a+b=6$ and the number sought is 61785 or 66780.
|
6
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Henrique bought chocolate bars for $\mathrm{R} \$ 1.35$ each. He paid with a $\mathrm{R} \$ 10.00$ bill and received change less than $\mathrm{R} \$ 1.00$. How many bars did he buy?
|
As $8 \times 1.35 = 10.8$ is greater than 10, Henrique bought 7 chocolate bars and received $10 - 7 \times 1.35 = 0.55$ dollars, or 55 cents, in change.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The sum of three numbers is 100, two are prime and one is the sum of the other two.
(a) What is the largest of the three numbers?
(b) Give an example of such three numbers.
(c) How many solutions exist for this problem?
|
(a) Initially observe that, since the sum of the three numbers is 100 and the largest of them is equal to the sum of the other two, then twice the largest number is 100, that is, the largest number is 50.
(b) Since 50 is not a prime number, the other two numbers are primes and their sum is 50. For example, 3 and 47 are primes and $3+47=50$. Therefore, the numbers 3, 47, and 50 form a solution to the problem.
(c) There are other solutions to the problem. To find them, we write down the list of all primes between 1 and 50, that is, $2,3,5,7,11,13,17,19,23,29,31,37,41,43$ and 47, and for each of these numbers, we check if the difference from 50 is also a prime. We find a total of four solutions.
| Solution 1 | 3 | 47 | 50 |
| :--- | :---: | :---: | :---: |
| Solution 2 | 7 | 43 | 50 |
| Solution 3 | 13 | 37 | 50 |
| Solution 4 | 19 | 31 | 50 |
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Antônio has a parrot that performs fantastic calculations with integers. When Antônio whispers certain numbers into its ear, the parrot multiplies that number by 5, then adds 14, divides the result by 6, and finally subtracts 1, shouting the result afterward. However, the parrot knows nothing about decimals, so sometimes it cannot shout out an answer.
(a) If Antônio whispers the number 8, what number will the parrot shout?
(b) If the parrot shouted 3, what number did Antônio whisper into its ear?
(c) Why does the parrot never shout the number 7?
(d) Which numbers, when whispered by Antônio, elicit a response from the parrot?
|
(a) We have $8 \xrightarrow{\times 5} 40 \xrightarrow{+14} 54 \xrightarrow{\dot{\circ} 6} 9 \xrightarrow{-1} 8$. Therefore, the parrot shouts 8.
(b) We should perform the inverse operation of what the parrot did, starting from the last operation, that is, add 1 to the number, multiply the number by 6, then subtract 14, and finally divide the result by 5:
$$
3 \xrightarrow{+1} 4 \xrightarrow{\times 6} 24 \xrightarrow{-14} 10 \xrightarrow{\div 5} 2.
$$
Therefore, Antônio whispered 2 into the parrot's ear.
(c) Observe that $7 \xrightarrow{+1} 8 \xrightarrow{\times 6} 48 \xrightarrow{-14} 34 \xrightarrow{\dot{* 5}} 6.8$. Since 6.8 is not an integer, Antônio will not whisper it into the parrot's ear, and even if he did, the parrot would not know how to perform the first operation, which would be to multiply $6.8 \times 5$.
(d) When Antônio whispers a number $n$, the parrot performs the operations
$$
n \xrightarrow{\times 5} 5 n \xrightarrow{+14} 5 n+14 \xrightarrow{\dot{\circ}} \frac{5 n+14}{6} \xrightarrow{-1} \frac{5 n+14}{6}-1.
$$
The parrot will only know how to calculate the answer if $5 n+14$ is divisible by 6, that is, if it is of the form $6 k$, with $k$ a non-negative integer. If $5 n+14=6 k$, then $5 n+2=6(k-2)$ and, multiplying both sides by 5, we get $25 n+10=6(5 k-10)$, which simplifies to $n+24 n=25 n=6(5 k-10)-12+2$, or $n=6(5 k-12)+2-24 n=6(5 k-12-4 n)+2$. Thus, if Antônio whispers a number $n$ of the form $6 m+2$, the parrot performs the operations
$$
6 m+2 \xrightarrow{\times 5} 30 m+10 \xrightarrow{+14} 30 m+24 \xrightarrow{\dot{\circ} 6} 5 m+4 \xrightarrow{-1} 5 m+3
$$
and shouts the number $5 m+3$. If $n$ is not of this form, the parrot remains silent. Therefore, Antônio can only whisper the numbers
$$
2,8,14,20,26,32,38, \ldots
$$
and the parrot can only respond, respectively,
$$
3,8,13,18,23,28,33, \ldots
$$
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Roberto wants to write the number 111111 as a product of two numbers, neither of which ends in 1. Is this possible? Why?
|
Factoring 111111, we obtain $111111=3 \times 7 \times 11 \times 13 \times 37$. It follows that it is indeed possible to write the number 111111 as a product of two factors, neither of which ends in 1. For example, $111111=3 \times 37037$. But there are other possibilities, such as, for example, $111111=7 \times 15873$.
In fact, it is possible to list all the possibilities. They are
$$
\begin{array}{lllll}
3 \times 37037, & 7 \times 15873, & 13 \times 8547, & 33 \times 3367, & 37 \times 3003 \\
39 \times 2849, & 77 \times 1443, & 143 \times 777, & 259 \times 429 \quad \text { and } & 273 \times 407
\end{array}
$$
Therefore, Roberto has 10 options to write 111111 in the desired form.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A class has 22 male students and 18 female students. During the holidays, $60 \%$ of the students in this class went to do community work. At a minimum, how many female students participated in this work?
(a) 1
(b) 2
(c) 4
(d) 6
(e) 8
|
The correct answer is (b).
The total number of students in this class is $22+18=40$, of which $60\%$ went to do community work, that is, $0.6 \times 40=24$. The minimum number of female students who participated in this work is obtained when the number of male students who participated is maximum, that is, when all 22 male students are involved in the work, leaving a minimum of two spots for the female students.
|
2
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
The sum on the side is incorrect. To correct it, it is enough to replace a certain digit in all the places where it appears in the equation with another digit. Which is the incorrect digit and what is its correct substitute?
|
At first inspection, we can admit that the three digits to the right of the numbers are correct, that is, the digits $0,1,3,4,5$, 6 and 8 are correct. Therefore, among the digits 2, 7, and 9, one of them is wrong. The digit 9 is correct, because if we change it, the sum with 2 will not be correct. Thus, only 2 and 7 remain. If the 7 were wrong, then the 2 would be correct, but this is not possible, because $1+4+2=7$. Therefore, it is the 2 that is wrong and must be replaced. Looking again at the sum $1+4+2$, we see that the result is a number with the unit digit equal to 1. Therefore, the digit 2 must be replaced four times by 6. By making this replacement, we verify that the sum is correct.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the luminous mechanism of the figure, each of the eight buttons can light up in green or blue. The mechanism works as follows: when turned on, all buttons light up blue, and if we press a button, that button and its two neighbors change color. If we turn on the mechanism and successively press buttons 1, 3, and 5, how many green lights will be on at the end?
1 8 2
7 3 6 4 5
(a) 3
(b) 4
(c) 5
(d) 6
(e) 7
|
The correct answer is (c).
The table shows the color of each button at each step.
| | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ | $\mathbf{7}$ | $\mathbf{8}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| start | blue | blue | blue | blue | blue | blue | blue | blue |
| pressing button 1 | green | green | blue | blue | blue | blue | blue | green |
| pressing button 3 | green | blue | green | green | blue | blue | blue | green |
| pressing button 5 | green | blue | green | blue | green | green | blue | green |
Therefore, the buttons that ended up with green lights on are $1,3,5,6$ and 8, giving us a total of five buttons.
|
5
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Will the number $3^{444}+4^{333}$ be divisible by 5?
|
There is a pattern for the unit digit of a power of 3: it has a period of 4, as it repeats every four times. Indeed, we have
$$
\begin{array}{ll}
3 & 3^{5}=243 \\
3^{2}=9 & 3^{6}=\ldots 9 \\
3^{3}=27 & 3^{7}=\ldots 7 \\
3^{4}=81 & 3^{8}=\ldots 1
\end{array}
$$
Since 444 is a multiple of 4, the unit digit of $3^{444}$ is 1.
Analogously, the unit digit of powers of 4 has a period of 2. Indeed, we have
$$
\begin{array}{ll}
4^{1}=4 & 4^{3}=64 \\
4^{2}=16 & 4^{4}=256
\end{array}
$$
Since 333 is odd, the unit digit of $4^{333}$ is 4. Therefore, the unit digit of $3^{444}+4^{333}$ is $1+4=5$, which means it is divisible by 5.
REMINDER: Any number ending in 0 or 5 is divisible by 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Writing successively the natural numbers, we obtain the sequence
$$
12345678910111213141516171819202122 \ldots
$$
What is the digit that is in the $2009^{th}$ position of this sequence?
|
Observe that:
- the numbers from 1 to 9 occupy nine positions;
- the numbers from 10 to 99 occupy $2 \times 90=180$ positions;
- the numbers from 100 to 199 occupy $3 \times 100=300$ positions;
- the numbers from 200 to 299 occupy $3 \times 100=300$ positions;
- the numbers from 300 to 399 occupy $3 \times 100=300$ positions; etc.
$\underbrace{100, \ldots 199}_{3 \times 100=300}, \underbrace{200, \ldots, 299}_{3 \times 100=300}, \underbrace{300, \ldots, 399}_{3 \times 100=300}, \underbrace{400, \ldots, 499}_{3 \times 100=300}, \underbrace{500, \ldots, 599}_{3 \times 100=300}, \underbrace{600, \ldots, 699}_{3 \times 100=300}$
Thus, the digits used to write from 1 to 699 occupy $9+180+6 \times 300=1989$ positions, so we are missing $2009-1989=20$ positions. Since $20=3 \times 6+2$, we still need to write from 700 to 706, obtaining 21 positions, with the digit 6 occupying the 21st position. Therefore, it is the digit 0 that occupies the $2009^{th}$ position.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
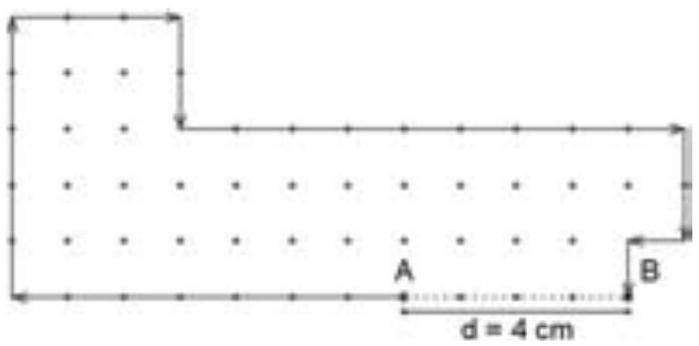
An ant leaves point $A$, walks $7 \mathrm{~cm}$ to the left, $5 \mathrm{~cm}$ up, $3 \mathrm{~cm}$ to the right, $2 \mathrm{~cm}$ down, $9 \mathrm{~cm}$ to the right, $2 \mathrm{~cm}$ down, $1 \mathrm{~cm}$ to the left, and $1 \mathrm{~cm}$ down, arriving at point $B$. What is the distance, in cm, between $A$ and $B$?
(a) 0
(b) 1
(c) 4
(d) 5
(e) 7
|
The correct answer is (c).
|
4
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Elisa has 24 science books and others of mathematics and literature. If Elisa had one more mathematics book, then one ninth of her books would be mathematics and one quarter literature. If Elisa has fewer than 100 books, how many mathematics books does she have?
|
Let $N$ be the total number of books Elisa has. Since $N+1$ is a multiple of 9 and 4, it follows that $N+1$ is a multiple of 36. Therefore, $N+1$ is 36 or 72, as Elisa has fewer than 100 books. If $N=35$, then the number of math books is $36 \div 9-1=3$ and the number of literature books is $36 \div 4=9$. However, this would mean Elisa has $24+3+9=36$ books, which is impossible because 36 is greater than 35. Thus, $N=71$ and Elisa has $72 \div 9-1=7$ math books.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
O dobro de um número dividido por 5 deixa resto 1. Qual é o resto da divisão desse número por 5 ?
The double of a number divided by 5 leaves a remainder of 1. What is the remainder of the division of this number by 5?
|
Solution 1: The double of the number sought is a multiple of 5 increased by 1. Since multiples of 5 end in 0 or 5, the double ends in 1 or 6. But the double is an even number, so it ends in 6. Thus, the number ends in 3 or 8 and, therefore, when divided by 5, leaves a remainder of 3.
Solution 2: We know that the integer $n$ sought satisfies $2 n=5 m+1$, for some integer $m$. Then the product $5 m=2 n-1$ of 5 by $m$ is odd, which implies that $m$ is odd. Thus, $m=2 k+1$, for some integer $k$ and, therefore,
$$
2 n=5 m+1=5(2 k+1)+1=10 k+6=2(5 k+3)
$$
that is, $n=5 k+3$ leaves a remainder of 3 when divided by 5.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. $V$ each of the four rooms there are several items. Let $n \geqq 2$ be a natural number. We move one $n$-th of the items from the first room to the second. Then, one $n$-th of the (new) number of items is moved from the second room to the third. Similarly, from the third room to the fourth, and from the fourth back to the first. (Each time, we move whole items.) If you know that at the end there was the same number of items in each room, determine the least number of items that could have been in the second room at the beginning. For which $n$ can this happen?
|
SOLUTION. When analyzing the number of items after individual steps, we will proceed "backwards." First, let's show how the numbers of items in two rooms before the transfer can be determined from the numbers of items in the rooms after the transfer. Let's say that before the transfer from room $A$ to room $B$, there are $a$ and $b$ items in rooms $A$ and $B$, respectively. Let these numbers after the transfer be denoted by $a^{\prime}, b^{\prime}$. According to the problem statement, we have
$$
a^{\prime}=\frac{n-1}{n} a, \quad b^{\prime}=b+\frac{1}{n} a .
$$
From the first equation and then from the relation $a+b=a^{\prime}+b^{\prime}$, we find
$$
a=\frac{n}{n-1} a^{\prime}, \quad b=b^{\prime}-\frac{1}{n-1} a^{\prime} .
$$
Now, let $M$ be the number of items found in each of the four rooms at the end. By repeatedly applying the derived relation $\left(a^{\prime}, b^{\prime}\right) \rightarrow(a, b)$, we can work our way back to express the initial counts in terms of $M$ and $n$:
$$
\begin{array}{crrrr}
\text { At the end: } & M, & M, & M ; \\
\text { Before } 4 \rightarrow 1: & \frac{n-2}{n-1} M, & M, & M, & \frac{n}{n-1} M ; \\
\text { Before } 3 \rightarrow 4: & \frac{n-2}{n-1} M, & M, & \frac{n}{n-1} M, & M ; \\
\text { Before } 2 \rightarrow 3: & \frac{n-2}{n-1} M, & \frac{n}{n-1} M, & M, & M ; \\
\text { Before } 1 \rightarrow 2: & \frac{n(n-2)}{(n-1)^{2}} M, & \frac{(n-1)^{2}+1}{(n-1)^{2}} M, & M, & M .
\end{array}
$$
Since the number of items in the first room at the beginning was positive, we must have $n \geqq 3$. Now we can easily determine the minimum possible value of the expression
$$
V_{2}=\frac{(n-1)^{2}+1}{(n-1)^{2}} M
$$
The numerator and the denominator of the fraction differ by one, so the fraction cannot be simplified. For the result to be an integer, $M$ must be $k \cdot(n-1)^{2}$ for some $k$, and thus $V_{2}=k\left((n-1)^{2}+1\right)$.
For $n \geqq 3$, however, $(n-1)^{2}+1 \geqq 5$, so $V_{2} \geqq 5$. By choosing $n=3, k=1$, and $M=4$, we achieve the value $V_{2}=5$, and we can easily verify that the corresponding quadruple $(3,5,4,4)$ satisfies the conditions of the problem: after individual transfers from it, we get the quadruple $(2,6,4,4)$, then $(2,4,6,4)$, then $(2,4,4,6)$, and finally $(4,4,4,4)$. The sought minimum number of items $v$ in the second room is thus indeed 5 and can be achieved only for $n=3$, because for $n \geqq 4$, $V_{2} \geqq 3^{2}+1=10$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Nela and Jana choose a natural number $k$ and then play a game with a $9 \times 9$ table. Starting with Nela, each player, on their turn, selects an empty cell and writes a zero in it. Jana, on her turn, writes a one in some empty cell. Additionally, after each of Nela's moves, Jana makes $k$ moves. If at any point during the game, the sum of the numbers in each row and each column is odd, Jana wins. If the girls fill the entire table without this happening, Nela wins. Find the smallest value of $k$ for which Jana has a winning strategy.
|
SOLUTION. Let's first show that in the case $k=3$, Jana wins. We will work with squares $A_{1}, A_{2}$, and $A_{3}$ of size $3 \times 3$ (Fig. 3). A $3 \times 3$ square is considered covered if there is exactly one one in each of its rows and columns. If Jana covers the squares $A_{1}, A_{2}$, and $A_{3}$ without playing into other squares, she ensures her victory, as all row and column sums will be equal to the odd number 1.
Fig. 3
It is clear that if after Nela's move there is at most one zero (and no one) in some $3 \times 3$ square, Jana can cover this square with a triplet of her moves thanks to the value $k=3$. Jana's strategy is therefore as follows: If Nela plays into one of the uncovered squares $A_{1}, A_{2}$, or $A_{3}$, Jana will immediately cover this square. Otherwise, Jana will cover any of the still uncovered squares $A_{1}, A_{2}$, and $A_{3}$. After the first three triplets of moves, Jana will always win this way.
We claim that in the cases $k \in \{1,2\}$, Nela has a winning strategy. First, note that if a move offers Jana a win (let's call it a winning move), it means that before it is played, the sum is odd in exactly eight columns and eight rows, and that winning move is Jana's move at the intersection of the single "even" row and the single "even" column. This implies that if Jana ever has a winning move, there is exactly one such move.
Now it is clear how Nela can achieve victory in the case $k=1$. If Jana has a winning move after her turn, Nela writes a zero on that cell, and Jana thus loses her (only) chance to win in the next turn. If, on the other hand, Jana does not have a winning move after her turn, Nela writes a zero anywhere. This does not change the sums in the rows or columns, so Jana will not win with the next move. This way, Nela will achieve the filling of the entire table without allowing Jana to win.
In the case $k=2$, Nela will play according to the same strategy as for $k=1$, thus preventing Jana from ever winning after the first move of her pair. In the second move, however, Jana can never win, because after it is played, there will be an even number of ones in the table, and it will be impossible for an odd number of ones to be in each of the (odd number of) nine rows.
Answer. The smallest value of $k$ for which Jana has a winning strategy is $k=3$.
GUIDING AND ADDITIONAL PROBLEMS:
N1. Solve the given game first in a $3 \times 3$ table.
N2. On a magic tree, 25 lemons and 30 oranges grew. The gardener picks two fruits every day, and overnight, one new fruit grows on the tree, an orange (respectively, a lemon) if the picked fruits were the same (respectively, different). What fruit will grow on the tree last? [Lemon — their number is odd after each night.]
D1. Simona and Lenka play a game. For a given integer $k$ such that $0 \leq k \leq 64$, Simona selects $k$ cells of an $8 \times 8$ chessboard and marks each with a cross. Lenka then fills the chessboard with thirty-two domino tiles in some way. If the number of tiles covering two crosses is odd, Lenka wins; otherwise, Simona wins. Determine, depending on $k$, which of the girls has a winning strategy. [64-C-I-3]
D2. In the top-left corner of an $8 \times 8$ chessboard stands a king figure. Two players take turns making moves, each moving the figure (with a legal chess move) to a place where it has not stood before. The player who cannot make a move loses. Show that the player who moves first has a winning strategy. [Divide the chessboard into $2 \times 1$ rectangles and find a strategy for the first player in which they do not move into any rectangle first.]
D3. In the top-left corner of an $8 \times 8$ chessboard stands a knight figure. Two players take turns making moves, each moving the figure (with a legal chess move) to a place where it has not stood before. The player who cannot make a move loses. Show that the starting player has a winning strategy. [Divide the chessboard into $2 \times 4$ rectangles and divide the cells within them into pairs with the same intention as in problem D2.]
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. For positive real numbers $a, b, c$ it holds that
$$
a b+b c+c a=16, \quad a \geqq 3 .
$$
Find the smallest possible value of the expression $2 a+b+c$.
|
3. Let's modify the square of the expression $V=2a+b+c$, which is clearly positive. We will conveniently use the given relationship $ab+bc+ca=16$:
$$
\begin{aligned}
V^{2} & =(2a+b+c)^{2}=4a^{2}+b^{2}+c^{2}+4ab+4ac+2bc= \\
& =4a^{2}+b^{2}-2bc+c^{2}+4(ab+bc+ca)=4a^{2}+(b-c)^{2}+4 \cdot 16 .
\end{aligned}
$$
According to the problem, $a^{2} \geq 9$ and clearly $(b-c)^{2} \geq 0$, so $V^{2} \geq 4 \cdot 9 + 4 \cdot 16 = 100$. Therefore, $V \geq 10$.
Let's try to find numbers $a, b, c$ that satisfy the conditions and for which $V=10$. For the derived inequalities to become equalities, $b$ must equal $c$ and $a$ must equal 3, so then $ab+bc+ca=6b+b^{2}$. We need to find $b>0$ such that $6b+b^{2}=16$. This quadratic equation has roots $2$ and $-8$. The suitable triplet $(a, b, c)$ is thus $(3,2,2)$, and the minimum possible value of the given expression is indeed 10.
Another solution. From the given equation $ab+bc+ca=16$, we express $c=(16-ab)/(a+b)$ and substitute it into the expression $V$, whose minimum value we are looking for:
$$
\begin{aligned}
V=2a+b+c & =2a+b+\frac{16-ab}{a+b}= \\
& =a+b+\frac{16+a^{2}}{a+b} \geq 2 \sqrt{16+a^{2}} \geq 2 \sqrt{16+3^{2}}=10 .
\end{aligned}
$$
In the first inequality, we used the well-known inequality between the arithmetic and geometric means of two positive numbers $a+b$ and $(16+a^{2})/(a+b)$.
The triplet for which $V=10$ can be found as easily as in the first solution; the equality of the two averaged numbers occurs precisely when $a+b=\sqrt{16+a^{2}}$, which for $a=3$ immediately leads to the value $b=2$, so from the formula $c=(16-ab)/(a+b)$ we also get $c=2$.
Note. The key inequality $V \geq 10$ can also be obtained by the following manipulation:
$$
\begin{aligned}
& V=2a+b+c=(a+b)+(a+c) \geq \\
& \quad \geq 2 \sqrt{(a+b)(a+c)}=2 \sqrt{a^{2}+(ab+bc+ca)} \geq 2 \sqrt{3^{2}+16}=10
\end{aligned}
$$
in which we used the inequality between the arithmetic and geometric means of two positive numbers $a+b$ and $a+c$.
For a complete solution, award 6 points, of which 4 points for proving that $V \geq 10$, and 2 points for finding a corresponding triplet of numbers $a, b, c$ (even by guessing - it was not the task to find all such triplets), which satisfy the conditions and for which $V=10$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Determine the largest integer $n$, for which it is possible to fill a square table $n \times n$ with natural numbers from 1 to $n^{2}$ in such a way that in every $3 \times 3$ square part of it, at least one square of an integer is written.
|
SOLUTION. It will be easy for us to fill the $11 \times 11$ table in the required way; it is enough to choose nine out of the 11 squares of integers $1^{2}, 2^{2}, \ldots, 11^{2}$ and place them on nine cells of the table with coordinates
$$
(3,3),(3,6),(3,9), \quad(6,3),(6,6),(6,9), \quad(9,3),(9,6),(9,9)
$$
and fill the remaining cells with other numbers in any way. Since in each $3 \times 3$ part of the given table there is one of the nine mentioned cells, the number $n=11$ has the required property.
We will show that no $n \geq 12$ satisfies the problem. For any $n \geq 12$, let $k$ be the integer quotient of the number $n$ when divided by three with a remainder, so that $3 k \leq n \leq 3 k+2$ and $k \geq 4$. In the $n \times n$ table, we can then find $k^{2}$ non-overlapping (disjoint) $3 \times 3$ squares, but we have only $n$ squares of integers $1^{2}, 2^{2}, \ldots, n^{2}$ available, and it is clear that
$$
n \leq 3 k+2 < 4 k \leq k^{2}
$$
For $n \geq 12$, it is therefore impossible to fill the given table in the required way.
Answer. The largest $n$ sought is 11.
GUIDING PROBLEMS:
N1. Find all natural numbers $n$ for which it is possible to fill a square table $n \times n$ with natural numbers from 1 to $n^{2}$ such that in each row and each column there is at least one square of an integer. [It can be done for any $n$ - the squares $1^{2}, 2^{2}, \ldots, n^{2}$ can be written on the diagonal.]
N2. Determine the largest integer $n$ for which it is possible to fill a square table $n \times n$ with natural numbers from 1 to $n^{2}$ such that in each of its $2 \times 2$ square parts there is at least one square of an integer. $[n=5]$
D1. We wrote the natural numbers $1,2, \ldots, 121$ into a square table $11 \times 11$ in sequence by rows from left to right and from top to bottom. We covered exactly 16 cells with a $4 \times 4$ square tile in all possible ways. How many times was the sum of the covered numbers a square of an integer? [65-B-I-2]
D2. We will fill a square table $6 \times 6$ with all integers from 1 to 36.
a) Give an example of such a table filling where the sum of any two numbers in the same row or column is greater than 11.
b) Show that in any filling of the table, there will be two numbers in some row or column whose sum does not exceed 12. [66-C-II-2]
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On the board, there are several (not necessarily distinct) prime numbers such that their product is $2020$ times greater than their sum. Determine their smallest possible number. (Patrik Bak)
|
SOLUTION. Let the prime numbers on the board be denoted as $p_{1}, p_{2}, \ldots, p_{n}$. According to the problem statement, we have
$$
2020 \cdot\left(p_{1}+p_{2}+\ldots+p_{n}\right)=p_{1} p_{2} \ldots p_{n}
$$
The left side of equation (1) is divisible by the number $2020=2 \cdot 2 \cdot 5 \cdot 101$. Therefore, the prime numbers $2,2,5,101$ must appear in the prime factorization on the right side of (1). Without loss of generality, assume that $p_{1}=2, p_{2}=2, p_{3}=5, p_{4}=101$. If only these 4 prime numbers were on the board (case $n=4$), then equation (1) would clearly not hold $(2020 \cdot 110 \neq 2020)$. Therefore, it must be that $n \geqq 5$.
By substituting the already known prime numbers $p_{1}=2, p_{2}=2, p_{3}=5, p_{4}=101$ into equation (1) and dividing by 2020, we get the equation
$$
110+p_{5}+p_{6}+\ldots+p_{n}=p_{5} \cdot p_{6} \cdot \ldots \cdot p_{n}
$$
Since we are looking for the smallest possible $n \geqq 5$ for which there exist prime numbers $p_{5}, p_{6}, \ldots, p_{n}$ satisfying equation (2), we will further analyze the smallest possible values of $n=5,6, \ldots$, until we find the first suitable $n$.
- Case $n=5$. Equation (2) is of the form $110+p_{5}=p_{5}$, which is not satisfied by any prime number $p_{5}$.
- Case $n=6$. The corresponding equation is
$$
p_{5} p_{6}=p_{5}+p_{6}+110
$$
which we rearrange into the product form
$$
\left(p_{5}-1\right)\left(p_{6}-1\right)=111
$$
Both factors on the left side must be odd, so the numbers $p_{5}$ and $p_{6}$ must both be even.* The only even prime numbers $p_{5}=p_{6}=2$ do not satisfy equation (3).
- Case $n=7$. Equation (2) has the form
$$
p_{5} p_{6} p_{7}=p_{5}+p_{6}+p_{7}+110 .
$$
Let us emphasize that our task is only to determine whether there exists a triplet of prime numbers that satisfies equation (4). It is not difficult to guess the triplet $p_{5}=p_{6}=p_{7}=5$:
$$
5^{3}=125=5+5+5+110 .
$$
This completes the solution of the problem. Let us add that other triplets of prime numbers that satisfy equation (4) are $(2,5,13)$ and $(2,3,23)$.** Therefore, if we do not guess the triplet $(5,5,5)$, we can complete the solution by substituting the smallest existing prime number $p_{5}=2$ into equation (4). For the prime numbers $p_{6}$ and $p_{7}$, we then get the equation, which, when converted to the product form $\left(2 p_{6}-1\right)\left(2 p_{7}-1\right)=225$, yields two prime number solutions $(3,23)$ and $(5,13)$.
Summarizing our findings: At least 7 prime numbers were written on the board, an example of such a septet (arranged in ascending order) is $2,2,5,5,5,5,101$.
Conclusion. The smallest possible number of prime numbers on the board is 7. [^0]NOTES.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. If a, b, c are distinct non-negative real numbers, what is the smallest possible number of distinct numbers among the numbers $a+b, b+c, c+a, a^{2}+b^{2}, b^{2}+c^{2}, c^{2}+a^{2}$? (Patrik Bak)
|
SOLUTION. The problem is symmetric in the variables $a, b, c$: changing their order only changes the order of the six numbers being examined. In the first part of the solution, we will assume that $a < b < c$ and $a > 1$. Then it will hold that
$$
11$ will satisfy the condition $a^{2}=a+1$. A simple calculation reveals that this number is
$$
a=\frac{1+\sqrt{5}}{2}
$$
known as the golden ratio, not only in mathematics but also in art.
Conclusion. The smallest possible number of different numbers in the given sextet is 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Along a circle, 16 real numbers are arranged with a sum of 7.
a) Prove that there exists a segment of five consecutive numbers with a sum of at least 2.
b) Determine the smallest $k$ such that in the described situation, one can always find a segment of $k$ consecutive numbers with a sum of at least 3.
|
2. a) Among 16 numbers written along a circle, there are exactly 16 segments of five consecutive numbers (if we select any of the written numbers and mark the numbers along the circle sequentially as the first, second, ..., sixteenth, the first segment will consist of the first to fifth numbers, the second segment will consist of the second to sixth numbers, ... and the last sixteenth segment will consist of the sixteenth, first, second, third, and fourth numbers).
We can prove the statement by contradiction. Assume that the statement in question is false, i.e., that the sum of the numbers in each of the 16 segments is less than 2. The total sum $S_{5}$ of all 16 sums of the numbers in the individual quintets is thus less than $16 \cdot 2 = 32$. However, each number on the circle is part of exactly five segments of five consecutive numbers, so each of the 16 numbers is counted exactly five times in the mentioned sum. Therefore, the sum $S_{5}$ is also equal to five times the sum of all the numbers on the circle, which is 35. This is in contradiction with the derived inequality $S_{5} < 32$. Therefore, there must exist five consecutive numbers on the circle whose sum is at least 2 (in fact, more than 2).
b) First, let's show that $k \leq 6$ cannot be true. It is sufficient to place 16 identical numbers along the circle with a sum of 7. The sum of the numbers in any segment of $k$ numbers is then
$$
k \cdot \frac{7}{16} \leq \frac{42}{16} < 3
$$
Now let $k=7$. By repeating the reasoning from part a), we can prove that the desired segment already exists: Assume, on the contrary, that the sum of any seven consecutive numbers (from the given sixteen) is less than three. There are sixteen such segments along the circle (their number does not depend on $k$!), so the sum $S_{7}$ of all 16 sums of the numbers in the individual septets is less than $16 \cdot 3 = 48$. Each of the given 16 numbers is counted seven times in the sum $S_{7}$, so $S_{7} = 7 \cdot 7 = 49$, which contradicts the previous estimate $S_{7} < 48$.
The sought number $k$ is 7.
For a complete solution, award 6 points. For the proof of each part a) and b), award 3 points each. If part b) lacks only the example that $k \leq 6$ does not work, deduct 2 points.
|
7
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. On the table lie 54 piles of stones with $1,2,3, \ldots, 54$ stones. In each step, we select any pile, say with $k$ stones, and remove it from the table along with $k$ stones from each pile that has at least $k$ stones. For example, after the first step, if we select the pile with 52 stones, the piles remaining on the table will have $1,2,3, \ldots, 51,1$ and 2 stones. Suppose that after a certain number of steps, only one pile remains on the table. Justify how many stones can be in it.
|
1. If in each step we choose the pile with the most stones, we will gradually remove piles with $54, 53, 52, \ldots$ stones, and after 53 steps, only one pile with one stone will remain on the table.
We can prove that regardless of the procedure, the last pile will always contain a single stone. We will show that after each step, as long as there is at least one pile left on the table, the number of stones in each pile will always form the entire set $\{1, 2, \ldots, n\}$ for some natural number $n$ (we do not exclude the possibility that some numbers may correspond to multiple piles with the same number of stones). This means that there will always be at least one pile with exactly one stone on the table.
At the beginning, the number of stones in the piles forms the set $\{1, 2, \ldots, 54\}$. Suppose that after a certain number of steps, the number of stones in the piles forms the set $\{1, 2, \ldots, n\} (n \geq 2)$. If we now choose a pile with $n$ stones or a pile with one stone, the number of stones in the piles in the next step will form the set $\{1, 2, \ldots, n-1\}$. If we choose a pile with $m$ stones, where $m \notin \{1, n\}$, the number of stones in the piles in the next step will form the set $\{1, 2, \ldots, m-1\} \cup \{1, 2, \ldots, n-m\} = \{1, 2, \ldots, p\}$, where $p = \max \{m-1, n-m\}$. This proves the statement about the number of stones in the piles.
Answer: The last pile will always contain a single stone, regardless of the chosen procedure.
For a complete solution, award 6 points, of which 4 points for formulating the hypothesis that after each step, the number of stones in the piles forms the entire set $\{1, 2, \ldots, n\}$.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a rectangle $A B C D$ with perimeter $o$. In its plane, find the set of all points whose sum of distances from the lines $A B, B C, C D, D A$ is equal to $\frac{2}{3} o$.
|
SOLUTION. The required value of the sum of four distances can be written in the form
$$
\frac{2}{3} o=\frac{1}{6} o+\frac{1}{2} o=\frac{1}{6} o+|A B|+|B C| \text {. }
$$
For any point in the strip determined by the lines $A B$ and $C D$, it holds that the sum of its distances from these two parallel lines is equal to their distance, i.e., $|B C|$. For any point outside this strip, the sum of the two considered distances is equal to the sum of the value $|B C|$ and twice the distance from the closer of the two parallel lines. Similar two statements hold for the sum of distances of any point from the parallel lines $B C$ and $A D$ in relation to their distance $|A B|$. With regard to the expression (1), we can make the first two conclusions.
(1) In the strip between the lines $A B$ and $C D$, the sought points are precisely those whose sum of distances from the lines $B C$ and $A D$ is equal to $\frac{1}{6} o+|A B|$. These are the points that lie outside the strip determined by the lines $B C$ and $A D$ and have a distance from the closer of them equal to $\frac{1}{6} o: 2=\frac{1}{12} o$. The set of sought points in the strip between $A B$ and $C D$ thus consists of two segments $B_{1} C_{1}$ and $A_{1} D_{1}$ as shown in Fig. 1. Their endpoints $A_{1}, B_{1}$ lie on the line $A B$ outside the segment $A B$ such that $\left|A A_{1}\right|=\left|B B_{1}\right|=\frac{1}{12} o$; the endpoints $C_{1}, D_{1}$ lie on the line $C D$ outside the segment $C D$ such that $\left|C C_{1}\right|=\left|D D_{1}\right|=\frac{1}{12} o$.
Fig. 1
(2) In the strip between the lines $B C$ and $A D$, the sought points are precisely those whose sum of distances from the lines $A B$ and $C D$ is equal to $\frac{1}{6} o+|B C|$. These are the points that lie outside the strip determined by the lines $A B$ and $C D$ and have a distance from the closer of them equal to $\frac{1}{12} o$. The set of sought points in the strip between $B C$ and $A D$ thus consists of two segments $A_{2} B_{2}$ and $C_{2} D_{2}$, with the endpoints $B_{2}, C_{2}$ lying on the line $B C$ outside the segment $B C$ such that $\left|B B_{2}\right|=\left|C C_{2}\right|=\frac{1}{12} o$ and the endpoints $A_{2}, D_{2}$ lying on the line $A D$ outside the segment $A D$ such that $\left|A A_{2}\right|=\left|D D_{2}\right|=\frac{1}{12} o$.
It remains to find the sought points outside the union of the two considered strips, i.e., points lying in one of the four right angles $A_{1} A A_{2}, B_{1} B B_{2}, C_{1} C C_{2}$, or $D_{1} D D_{2}$. From the above considerations, it follows that in each of these angles, we are looking for precisely those points whose sum of distances from both sides of the angle is equal to the value $\frac{1}{12} o$. Considering the symmetry, we will only show that such points in the angle $A_{1} A A_{2}$ fill the segment $A_{1} A_{2}$; in the other three angles, they will be the segments $B_{1} B_{2}, C_{1} C_{2}, D_{1} D_{2}$ (Fig. 1).
First, note that the points $A_{1}, A_{2}$ are the only points on the sides of the angle $A_{1} A A_{2}$ that have the required property. For any interior point $X$ of the angle $A_{1} A A_{2}$, let $d_{1}, d_{2}$ be the distances of point $X$ from the sides $A A_{1}$ and $A A_{2}$, respectively. We are looking for precisely those points $X$ for which $d_{1}+d_{2}=\frac{1}{12} o$ (Fig. 2). We will solve this "equation" by considering the area $S$ of the figure $A A_{1} X A_{2}$, which is either a triangle or a convex or concave quadrilateral.
Fig. 2 The area $S$ is always equal to the sum of the areas of two triangles $A A_{1} X$ and $A A_{2} X$:
$$
S=S_{A A_{1} X}+S_{A A_{2} X}=\frac{1}{2}\left|A A_{1}\right| d_{1}+\frac{1}{2}\left|A A_{2}\right| d_{2}=\frac{1}{2} \cdot \frac{1}{12} o \cdot\left(d_{1}+d_{2}\right) .
$$
The equation $d_{1}+d_{2}=\frac{1}{12} o$ is satisfied precisely when the area $S$ has the same value as the area $S_{0}$ of the right triangle $A A_{1} A_{2}$, whose both legs have the same length $\frac{1}{12} o$.
The sought points $X$ are thus precisely those for which the figure $A A_{1} X A_{2}$ is a triangle; if $A A_{1} X A_{2}$ is a convex or concave quadrilateral, it is clear that $S>S_{0}$ or $S<S_{0}$. The sought points $X$ of the angle $A A_{1} A_{2}$ therefore indeed form the segment $A_{1} A_{2}$.
Answer: The sought set is the union of eight segments that form the boundary of the octagon $A_{1} A_{2} B_{2} B_{1} C_{1} C_{2} D_{2} D_{1}$.
Note. From Fig. 2, it is also clear that the equation $d_{1}+d_{2}=c$, where $c=\left|A A_{1}\right|=\left|A A_{2}\right|$, will be satisfied precisely when $\left|X_{1} A_{1}\right|=d_{1}$ and $\left|X_{2} A_{2}\right|=d_{2}$, i.e., precisely when both triangles $X X_{1} A_{1}$ and $X X_{2} A_{2}$ are isosceles. This clearly happens precisely when the angle $A_{1} X A_{2}$ is right, because $\left|\nless A A_{1} A_{2}\right|=45^{\circ}$.
GUIDING AND ADDITIONAL PROBLEMS:
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. An unconventional piece, which we will call the "sick lady," threatens any square in the row and column where it stands, while on the diagonal, it only threatens the adjacent squares. How many "sick ladies" do we need to place on an $8 \times 8$ chessboard so that they threaten all unoccupied squares?
(Tomáš Bárta, Josef Tkadlec)
|
Solution. Fields threatened by a sick queen (we will not consider other queens further) are called directly threatened if they lie in the column or row where the queen stands; threatened fields that are not directly threatened are called indirectly threatened. Each queen thus threatens 15 fields directly (including the field on which she stands) and at most 4 fields indirectly.
First, we will show that for any placement of up to four queens on the chessboard, there is at least one field not threatened by any queen, in other words, that four queens do not threaten the entire chessboard. It is clear from this that fewer queens also do not threaten all fields of the chessboard.
Assume that the required placement of four queens exists. We can certainly find 4 rows and 4 columns of the chessboard where none of the four queens stand. These rows and columns intersect at 16 fields, which must all be indirectly threatened. Since each queen indirectly threatens at most 4 fields, each of the four given queens must indirectly threaten exactly 4 fields. Moreover, no two of them stand in the same row or column, because otherwise the number of fields indirectly threatened by our four queens would have to be even greater than 16 (there would be a fifth row or column where no queen stands).
No queen that indirectly threatens 4 fields can apparently stand in the edge row or edge column of the chessboard. The four corner fields of the entire chessboard are thus indirectly threatened in our situation, each by a different one of the four queens, which must necessarily stand on fields diagonally adjacent to the corner fields. They thus stand in pairs in the same rows (and in pairs in the same columns), which contradicts the conclusion of the first paragraph. This proves that up to four queens are not enough to threaten all fields of the chessboard.
As we can see from the following images, 5 queens can be placed on an $8 \times 8$ chessboard so that every field of the chessboard is threatened by at least one queen.
The smallest number of (sick) queens needed is five.
Fig. 2
Note. From the professional literature, it is known that the smallest number of "normal queens" that can be placed on an $8 \times 8$ chessboard so that they threaten all its fields (the so-called domination number for the queens' graph $Q(8)$) is 5. Thus, the number of "sick queens" must be at least 5, because these queens threaten fewer fields than "normal queens." Furthermore, we can determine by computer simulation that there are only 8 suitable placements of 5 sick queens, all of which arise from the two placements mentioned above by rotation (or symmetry).
For a complete solution, award 6 points. Of this, award 3 points for proving the inequality $n>4$ (including the possibility that a knowledgeable solver declares this inequality for normal queens as known) (tolerate the absence of a mention of values $n<4$). Award 3 points for an example of a correct placement of 5 queens. Award 1 point for just an example of a correct placement of 6 queens.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The average of Pažout's grades is exactly 3. If we did not include three of Pažout's fives in the average, the average of his grades would be exactly 2. Determine the maximum number of ones that Pažout could have received. (Possible grades are 1, 2, 3, 4, 5.)
|
SOLUTION. Let $s$ be the sum of all Pážout's grades and $p$ their count. We do not know either of these numbers, but we know that
$$
\frac{s}{p}=3 \quad \text { or } \quad s=3 p .
$$
According to the second sentence of the problem, we set up another equation for the unknowns $s, p$ and immediately simplify it:
$$
\frac{s-3 \cdot 5}{p-3}=2 \quad \Leftrightarrow \quad s-15=2 p-6 \quad \Leftrightarrow \quad s=2 p+9
$$
From this, by substituting $s=3 p$, we get the equation $3 p=2 p+9$ with the only solution $p=9$. The sum of the grades is thus equal to $s=3 p=27$.
Besides the three fives, Pážout therefore received another six grades with a sum equal to $27-3 \cdot 5=12$. It could not have been six ones (with a sum of only 6), nor five ones, because the sixth grade would then be $12-5 \cdot 1=7$. However, Pážout could have received four ones, his remaining two grades with a sum of $12-4=8$ would then be either two fours, or a three and a five.
Conclusion. The maximum possible number of Pážout's ones is 4.
For a complete solution, award 6 points. In case of incomplete solutions, evaluate partial steps as follows:
A0. Stating the correct answer without justification: 0 points.
A1. Stating the correct answer along with a suitable example of a set of grades: 1 point.
A2. Translating the verbal problem into mathematical notation (most likely into a system of two equations with two unknowns): 1 point.
A3. Solving the mathematical problem from point A2 or other justification leading to the conclusion that Pážout received 9 grades (or 6 grades, if the three fives are not considered): 4 points.
A4. Justification why Pážout could not have received more than 4 ones: 5 points.
In total, then award $\max (\mathrm{A} 2, \mathrm{~A} 3, \mathrm{~A} 4)+\mathrm{A} 1$ points. In a complete solution, it must be justified that the situation with four ones can actually occur (most likely by an example of a set of grades, as stated in point A1).
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Consider any $3 \times 3$ table filled with positive integers such that the sum of the numbers $v$ in each row and each column is 10. How many numbers $v$ in such a table can be: a) the same, b) different?
(Ján Mazák)
|
SOLUTION. a) Six identical numbers can be found, for example, in the following table that meets the conditions of the problem:
| 8 | 1 | 1 |
| :--- | :--- | :--- |
| 1 | 8 | 1 |
| 1 | 1 | 8 |
If the table contained at least seven identical numbers, one of the rows would contain three of these seven identical numbers. The sum of three identical integers, however, cannot be equal to 10.
Conclusion. The largest possible number of identical numbers in the table is 6.
b) The table can contain six different numbers, one of many examples* looks like this:
| 7 | 1 | 2 |
| :--- | :--- | :--- |
| 1 | 6 | 3 |
| 2 | 3 | 5 |
We will further justify that the table cannot contain more than six different numbers.
In the table, only integers from 1 to 8 can be present. If there were a number greater than 8, the sum of the numbers in the row containing this number would be at least $9+1+1$, which is more than 10.
We know, therefore, that if the table contained at least seven different numbers, one of them must be either 7 or 8. We will evaluate both possibilities separately.
* The presence of the number $8$ in the table means that in the row and column with the number 8, there are two 1s, so there can be at most 6 different numbers in the entire table (besides 8 and 1, there can only be numbers from the 4 remaining cells outside the mentioned row and column).
* The presence of the number $7$ in the table means that in the row and column with the number 7, there are two 1s and 2s in both cases. Of the other four numbers in the table, we denote as $x$ the one that lies in the row of one of the two mentioned 1s and in the column of the other, as shown in the figure, where the other three numbers are marked with dots.
| 1 | 7 | 2 |
| :--- | :--- | :--- |
| $\bullet$ | 2 | $\circ$ |
| $x$ | 1 | $\bullet$ |
In the row and column with the numbers $x$ and 1, the third number must be $9-x$. The two black dots in the figure thus represent the same number, so there are again at most six different numbers in the table.
Conclusion. The largest possible number of different numbers in the table is 6.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all real numbers $p$ for which the system of inequalities
$$
\begin{aligned}
& 25+2 x^{2} \leqq 13 y+10 z-p \\
& 25+3 y^{2} \leqq 6 z+10 x \\
& 25+4 z^{2} \leqq 6 x+5 y+p
\end{aligned}
$$
with unknowns $x, y, z$ has a solution in the set of real numbers.
|
1. By adding all three inequalities, we obtain the inequality
$$
75+2 x^{2}+3 y^{2}+4 z^{2} \leqq 16 x+18 y+16 z
$$
from which, after "completing the square," we get
$$
2(x-4)^{2}+3(y-3)^{2}+4(z-2)^{2} \leqq 0 .
$$
This inequality, which is a consequence of the given system of inequalities, clearly holds only when the bases of all three squared terms on the left side of the inequality are zero, i.e., when $x=4$, $y=3$, $z=2$. Therefore, the given system has at most one solution for a given $p$, and that is the triplet of numbers written above. We will now determine for which value of the parameter $p$ this is indeed a solution. By substituting the values $x=4, y=3, z=2$ into the given system, we obtain the triplet of inequalities
$$
57 \leqq 59-p, \quad 52 \leqq 52, \quad 41 \leqq 39+p
$$
From the first inequality, we get the condition $p \leqq 2$, and from the third, the condition $p \geqq 2$. The number $p=2$ is therefore the only value of $p$ for which the given system has a solution in the set of real numbers.
For a complete solution, 6 points are awarded, 4 points for determining the unknowns $x, y, z$ and 2 points for determining the value of $p$.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the greatest natural number $d$ that has the property that for any natural number $n$, the value of the expression
$$
V(n)=n^{4}+11 n^{2}-12
$$
is divisible by the number $d$.
|
SOLUTION. First, let's calculate the values of $V(n)$ for the smallest natural numbers $n$ and write their prime factorizations in a table:
| $n$ | 1 | 2 | 3 | 4 |
| :---: | :---: | :---: | :---: | :---: |
| $V(n)$ | 0 | $48=2^{4} \cdot 3$ | $168=2^{3} \cdot 3 \cdot 7$ | $420=2^{2} \cdot 3 \cdot 5 \cdot 7$ |
From this, we see that the sought divisor $d$ of all numbers $V(n)$ must be a divisor of the number $2^{2} \cdot 3=12$, satisfying the inequality $d \leqq 12 .{ }^{1}$ If we can show that the number $d=12$ meets the conditions, i.e., that $V(n)$ is a multiple of 12 for every natural $n$, we will be done with the solution.
Transformation
$$
V(n)=n^{4}+11 n^{2}-12=\left(12 n^{2}-12\right)+\left(n^{4}-n^{2}\right),
$$
where we have "factored out" the binomial $12 n^{2}-12$ from the expression $V(n)$, which is clearly a multiple of 12, reducing our task to verifying the divisibility of the binomial $n^{4}-n^{2}$ by 12 (i.e., by 3 and 4). For this, we use its factorization
$$
n^{4}-n^{2}=n^{2}\left(n^{2}-1\right)=(n-1) n^{2}(n+1) .
$$
For any integer $n$, the expression $n^{4}-n^{2}$ is certainly divisible by three (since one of the three consecutive integers $n-1, n, n+1$ is divisible by three) and simultaneously by four (which is guaranteed by the factor $n^{2}$ in the case of even $n$, and by the two even factors $n-1$ and $n+1$ in the case of odd $n$).
Let's add that the divisibility of the expression $V(n)$ by 12 can also be proven in other ways, for example, by using the factorization
$$
V(n)=n^{4}+11 n^{2}-12=\left(n^{2}+12\right)\left(n^{2}-1\right)
$$
or by working with the binomial $n^{4}+11 n^{2}$ and similarly.
Answer. The sought number $d$ is equal to 12.
## GUIDING AND SUPPLEMENTARY PROBLEMS:
N1. Prove that in the infinite sequence of numbers
$$
1 \cdot 2 \cdot 3,2 \cdot 3 \cdot 4,3 \cdot 4 \cdot 5,4 \cdot 5 \cdot 6, \ldots
$$
the first number is a divisor of all subsequent numbers. [Use the fact that among two, or three consecutive numbers, there is always a number divisible by two, or three, respectively.]
N2. Find all integers $d>1$ such that the values of the expressions $U(n)=n^{3}+17 n^{2}-1$ and $V(n)=$ $=n^{3}+4 n^{2}+12$ give the same remainders when divided by $d$, regardless of the integer $n$ chosen. [Only $d=13$ satisfies. The sought $d$ are precisely those that divide the difference $U(n)-V(n)=13 n^{2}-13=13(n-1)(n+1)$ for every integer $n$. To show that (apparently suitable) $d=13$ is the only one, substitute the value $n=d$ into the difference $U(n)-V(n)$: the number $d$ is coprime with the numbers $d-1$ and $d+1$, so it divides the product $13(d-1)(d+1)$ only if it divides the factor 13, i.e., when $d=13$.]
D1. For which natural numbers $n$ is the expression $V(n)=n^{4}+11 n^{2}-12$ not a multiple of eight? [The expression $V(n)=(n-1)(n+1)\left(n^{2}+12\right)$ is certainly a multiple of eight in the case of odd $n$, because $n-1$ and $n+1$ are two consecutive even numbers, so one of them is divisible by four, and the product of both is thus a multiple of eight. Since the product $(n-1)(n+1)$ is odd for even $n$, we are looking for those $n$ of the form $n=2 k$ for which the expression $n^{2}+12=4\left(k^{2}+3\right)$ is not divisible by eight, which occurs precisely when $k$ is even. The sought $n$ are therefore precisely those that are divisible by four.]
D2. Prove that for any integers $n$ and $k$ greater than 1, the number $n^{k+2}-n^{k}$ is divisible by twelve. $[59-\mathrm{C}-\mathrm{II}-1]$
D3. Prove that the expressions $23 x+y$ and $19 x+3 y$ are divisible by 50 for the same pairs of natural numbers $x$ and $y$. $[60-\mathrm{C}-\mathrm{I}-2]$
D4. Determine all integers $n$ for which $2 n^{3}-3 n^{2}+n+3$ is a prime number. $[62-C-I-5]$
D5. Prove that for every odd natural number $n$, the sum $n^{4}+2 n^{2}+2013$ is divisible by 96. $[63-\mathrm{C}-\mathrm{I}-5]$
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On the board, five different positive numbers are written. Determine the maximum number of ways in which pairs can be formed from them, the sum of which equals one of the five numbers written on the board.
|
1. Let $a_{1}<a_{2}<a_{3}<a_{4}<a_{5}$ be positive numbers written on the board. The smallest numbers $a_{1}$ and $a_{2}$ clearly cannot be the sum of any two numbers written on the board. The number $a_{3}$ can be obtained as the sum of some pair in at most one way, namely $a_{3}=a_{1}+a_{2}$. The number $a_{4}$ can theoretically be obtained in three ways: $a_{1}+a_{2}$, $a_{2}+a_{3}$, or $a_{1}+a_{3}$, but since $a_{1}+a_{2}<a_{1}+a_{3}<a_{2}+a_{3}$, $a_{4}$ can be the sum of at most one of the pairs $\left\{a_{1}, a_{2}\right\}$, $\left\{a_{1}, a_{3}\right\}$, $\left\{a_{2}, a_{3}\right\}$. Finally, the number $a_{5}$ can be obtained in at most two ways. If $a_{5}$ could be obtained in three ways as the sum of two numbers written on the board, at least one of the numbers $a_{1}, a_{2}, a_{3}, a_{4}$ would be a summand in two different sums, which is not possible.
In total, we have found that the number of suitable pairs never exceeds the sum $0+0+1+1+2$, which equals four.
An example of five numbers written on the board, for which the sums of four (of the pairs formed from them) are also listed on the board, is $a_{i}=i$ for $i \in\{1,2,3,4,5\}$, where $1+2=3$, $1+3=4$, $1+4=5$, and $2+3=5$.
Conclusion. From the given five different positive numbers, at most four pairs with the required property can be formed.
For a complete solution, award 6 points. For obtaining the estimate that there are no more than four suitable pairs, award 4 points. (For the estimate that there are no more than six pairs, because the largest number cannot be in a pair, do not award points.) For an example of five numbers with four suitable pairs, award 2 points, even if the solver fails to prove the upper estimate.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Consider the expression
$$
V(x)=\frac{5 x^{4}-4 x^{2}+5}{x^{4}+1} .
$$
a) Prove that for every real number $x$, $V(x) \geq 3$.
b) Find the maximum value of $V(x)$.
|
1. The expression $V$ is apparently defined for all real numbers $x$.
a) Since $x^{4}+1>0$ for every $x$, the inequality $V(x) \geqq 3$ is equivalent to the inequality $5 x^{4}-4 x^{2}+5 \geqq 3\left(x^{4}+1\right)$ or $2 x^{4}-4 x^{2}+2 \geqq 0$. The expression on the left side is equal to $2\left(x^{2}-1\right)^{2}$, so it is non-negative for every $x$.
b) Let's use the following transformation:
$$
V(x)=\frac{5 x^{4}-4 x^{2}+5}{x^{4}+1}=\frac{5\left(x^{4}+1\right)}{x^{4}+1}-\frac{4 x^{2}}{x^{4}+1}=5-\frac{4 x^{2}}{x^{4}+1} .
$$
Since the fraction $\frac{4 x^{2}}{x^{4}+1}$ is non-negative for any real number $x$ due to the even powers of the variable $x$, the expression $V$ attains its maximum value $V_{\max }$ precisely when $\frac{4 x^{2}}{x^{4}+1}=0$, i.e., precisely when $x=0$. This gives us $V_{\max }=V(0)=5$.
For a complete solution, award 6 points, of which 2 points for solving part a), 4 points for a complete solution of part b): 3 points for proving the inequality $V(x) \leqq 5$ and 1 point for determining the equality for $x=0$. Algebraic manipulation of the fraction for $V(x)$ by partial division of the numerator by the denominator without further successful evaluation should be awarded 1 point.
|
5
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the smallest positive number $x$, for which the following holds: If $a, b, c, d$ are any positive numbers whose product is 1, then
$$
a^{x}+b^{x}+c^{x}+d^{x} \geqq \frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}
$$
(Pavel Novotný)
|
Solution. Let $a, b, c, d$ be any positive numbers whose product equals 1. According to the inequality between the arithmetic and geometric means of the triplet of numbers $a^{x}, b^{x}, c^{x}$ for any $x>0$, we have
$$
\frac{a^{x}+b^{x}+c^{x}}{3} \geqq \sqrt[3]{a^{x} b^{x} c^{x}}=\sqrt[3]{\frac{1}{d^{x}}}
$$
By choosing $x=3$, we get the inequality $\frac{1}{3}\left(a^{3}+b^{3}+c^{3}\right) \geqq 1 / d$. Similarly, we have
$$
\frac{1}{3}\left(a^{3}+b^{3}+d^{3}\right) \geqq 1 / c, \quad \frac{1}{3}\left(a^{3}+c^{3}+d^{3}\right) \geqq 1 / b, \quad \frac{1}{3}\left(b^{3}+c^{3}+d^{3}\right) \geqq 1 / a
$$
By adding the above four inequalities, we get
$$
a^{3}+b^{3}+c^{3}+d^{3} \geqq \frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}
$$
so for $x=3$ the inequality in the problem statement always holds.
We will show that $x=3$ is the smallest value sought, i.e., that for any positive $x<3$ (dependent on the given $x$),
$$
4 t^{x} < 4^{\frac{1}{3-x}}
$$
which is indeed satisfied for sufficiently large $t$.
Conclusion. The sought smallest positive number is $x=3$.
Note. Not only $x=3$ but also any $x \geqq 3$ (and any $x \leqq-1$) has the required property. We explain this by replacing the ones in the denominators of the fractions on the right-hand side of the considered inequality with the expression $(a b c d)^{\frac{x+1}{4}}$; we then obtain the homogeneous inequality
$$
a^{x}+b^{x}+c^{x}+d^{x} \geqq a^{\frac{x-3}{4}}(b c d)^{\frac{x+1}{4}}+b^{\frac{x-3}{4}}(a c d)^{\frac{x+1}{4}}+c^{\frac{x-3}{4}}(a b d)^{\frac{x+1}{4}}+d^{\frac{x-3}{4}}(a b c)^{\frac{x+1}{4}},
$$
which is Muirhead's inequality for the quadruples of exponents
$$
(x, 0,0,0) \text { and }\left(\frac{x+1}{4}, \frac{x+1}{4}, \frac{x+1}{4}, \frac{x-3}{4}\right),
$$
whose application in the case $x>0$ is subject to the single condition $\frac{x-3}{4} \geqq 0$ or $x \geqq 3$ (while in the case $x<0$ the only condition is $\frac{x+1}{4} \leqq 0$ or $x \leqq-1$).
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In a $11 \times 11$ square grid, we sequentially wrote the numbers $1,2, \ldots, 121$ from left to right and from top to bottom. Using a $3 \times 3$ square tile, we covered exactly nine cells in all possible ways. In how many cases was the sum of the nine covered numbers a perfect square of an integer?
|
2. Let $n$ be the number covered by the middle cell of the square tile. Then the first row of this tile covers the numbers $n-12, n-11, n-10$, its second row covers the numbers $n-1, n$ and $n+1$, and finally the third row covers the numbers $n+10, n+11$ and $n+12$. The sum of all numbers covered by the tile is thus $9n$.
The sum of the numbers covered by the square tile will be a perfect square of an integer if and only if the number $n$ covered by its center is itself a perfect square of an integer. Among the numbers $1, 2, \ldots, 121$, only the numbers in the set $\{1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121\}$ have this property, but the numbers $1, 4, 9, 100$, and 121 lie on the edge row or edge column of the $11 \times 11$ grid and cannot be covered by the center of the $3 \times 3$ square tile.
Of all possible coverings of the grid, 6 coverings have the desired property, where the center of the tile covers one of the numbers $16, 25, 36, 49, 64$, and 81.
For a complete solution, award 6 points, of which up to 2 points for expressing the sum of the numbers under the square tile in terms of some (covered) cell, up to 2 more points for a correct discussion of when this sum is a perfect square of an integer. Award one point for finding at least three valid coverings of the grid, deduct 1 point if the solver incorrectly specifies any position of the tile, and deduct 2 points if the solver incorrectly specifies at least three positions of the tile.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Determine all integers greater than 1 by which some fraction of the form
$$
\frac{3 p-q}{5 p+2 q}
$$
can be divided, where $p$ and $q$ are coprime integers.
The written part of the school round in category A takes place
## on Tuesday, December 2, 2008
so that it starts in the morning and the contestants have 4 hours of pure time to solve the problems. For each problem, a contestant can earn 6 points, and a successful solver is a student who scores 10 points or more. Allowed aids are writing and drawing supplies, school MF tables, and calculators without a graphical display. These details will be communicated to the students before the start of the competition.
## 58th Mathematical Olympiad
## Solutions to the problems of the written part of the school round in category $A$
|
3. A fraction can be reduced by an integer $d>1$ if and only if the number $d$ is a common divisor of the numerator and the denominator of the considered fraction. Let us assume, therefore, that $d \mid 3 p-q$ and at the same time $d \mid 5 p+2 q$, where $p$ and $q$ are coprime integers. By adding suitable multiples of the binomials $3 p-q$ and $5 p+2 q$, we get
$$
2(3 p-q)+(5 p+2 q)=11 p \quad \text { and } \quad 3(5 p+2 q)-5(3 p-q)=11 q
$$
Since both numbers $3 p-q$ and $5 p+2 q$ are multiples of the number $d$ by assumption, the constructed numbers $11 p$ and $11 q$ are also its multiples. In other words, the number $d$ is a common divisor of the numbers $11 p$ and $11 q$. However, the numbers $p$ and $q$ are coprime and the number 11 is a prime number, so the numbers $11 p$ and $11 q$ have only one common divisor greater than 1, and that is the number 11. Therefore, it must be $d=11$.
The solution is not yet complete: we must show that the number 11 can indeed reduce some of the considered fractions. How, then, to find a pair of coprime numbers $p$ and $q$ such that $11 \mid 3 p-q$ and at the same time $11 \mid 5 p+2 q$? With a little patience, we can find such values of $p$ and $q$ by trial substitution; however, it is sufficient to write the system of equations
$$
3 p-q=11 m \quad \text { and } \quad 5 p+2 q=11 n
$$
find its solution $(p, q)=(2 m+n, 3 n-5 m)$ and then conveniently substitute: we will certainly get a pair of coprime numbers $p$ and $q$ when $q=3 n-5 m=1$, i.e., for example, for $n=2$ and $m=1$, when $(p, q)=(4,1)$ and the considered fraction is $11 / 22$.
Answer. The only integer greater than 1 by which some of the given fractions can be reduced is the number 11.
For a complete solution, award 6 points, of which 1 point for converting to the relations $d \mid 3 p-q$ and $d \mid 5 p+2 q$, another 2 points for deriving the relations $d \mid 11 p$ and $d \mid 11 q$, another point for the conclusion $d=11$ and the remaining 2 points for providing a suitable example of a pair of coprime numbers $p$ and $q$.
[^0]: $1 \mathrm{~V}$ in the given solution, the equality $|C U|=c|\cos \gamma| / \sin \gamma$ was derived using standard notation, where $U$ is the intersection of the altitudes of triangle $A B C$.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find all positive integers $n$ for which the number $n^{2}+6 n$ is a perfect square of an integer.
|
2. Clearly $n^{2}+6 n>n^{2}$ and at the same time $n^{2}+6 n<n^{2}+6 n+9=(n+3)^{2}$. In the given range, there are only two squares of integers: $(n+1)^{2}$ and $(n+2)^{2}$.
In the first case, we have $n^{2}+6 n=n^{2}+2 n+1$, thus $4 n=1$, but no integer $n$ satisfies this.
In the second case, we have $n^{2}+6 n=n^{2}+4 n+4$, thus $2 n=4$. We get the only solution $n=2$.
Another solution. We will examine the factorization $n^{2}+6 n=n(n+6)$. The greatest common divisor of both numbers $n$ and $n+6$ must divide their difference, so their greatest common divisor can only be 1, 2, 3, or 6. We will analyze these four possibilities.
If the numbers $n$ and $n+6$ were coprime, each of them would have to be a square. However, the difference between two squares of natural numbers is never 6. For small numbers, this is easily verified, and for $k \geq 4$, the difference between even consecutive squares $k^{2}$ and $(k-1)^{2}$ is at least 7. The property that 1, 3, 5, and 7 are the four smallest differences between two squares will be used further.
If the greatest common divisor of the numbers $n$ and $n+6$ is 2, then $n=2 m$ for some $m$, which is not divisible by three. If $n(n+6)=4 m(m+3)$ is a square, then $m(m+3)$ must also be a square. The numbers $m$ and $m+3$ are coprime, so each must be a square of a natural number. This occurs only for $m=1$ or $n=2$. We can easily verify that $n(n+6)$ is indeed a square of an integer in this case.
If the greatest common divisor of the numbers $n$ and $n+6$ is 3, then $n=3 m$ for some odd $m$. If $n(n+6)=9 m(m+2)$ is a square, then the coprime numbers $m$ and $m+2$ must also be squares. However, such two squares do not exist.
If the greatest common divisor of the numbers $n$ and $n+6$ is 6, then $n=6 m$ for some $m$. If $n(n+6)=36 m(m+1)$ is a square, then the coprime numbers $m$ and $m+1$ must also be squares, which occurs only for $m=0$, but we are looking for positive numbers $n$.
The problem is satisfied only by $n=2$.
For a complete solution, award 6 points. If the solver reduces the problem to a manageable finite number of possibilities for $n$ (as in the first solution), award 4 points. For an argument of the type "if $n$ and $n+6$ are coprime for $n$ not divisible by 2 and 3, then they must be squares" without reducing to a finite number of possibilities, award no more than 3 points. For discovering the solution $n=2$ without proof, do not award any points.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all prime numbers $p$ for which there exists a natural number $n$ such that $p^{n}+1$ is a cube of some natural number.
|
SOLUTION. Let's assume that for a natural number $a$ the following holds: $p^{n}+1=a^{3}$ (obviously $a \geq 2$). We will rearrange this equation to make it possible to factor one side:
$$
p^{n}=a^{3}-1=(a-1)\left(a^{2}+a+1\right) \text {. }
$$
From this factorization, it follows that if $a>2$, both numbers $a-1$ and $a^{2}+a+1$ are powers of the prime number $p$ (with positive integer exponents).
In the case $a>2$, we have $a-1=p^{k}$ or $a=p^{k}+1$ for a positive integer $k$, which, when substituted into the trinomial $a^{2}+a+1$, gives the value $p^{2 k}+3 p^{k}+3$. Since $a-1=p^{k}2$ no prime number $p$ satisfies the equation $p^{n}+1=a^{3}$, regardless of the choice of the exponent $n$.
For $a=2$, we get the equation $p^{n}=7$, so $p=7$ is the only prime number that satisfies the equation.
SUPPLEMENTARY AND ADDITIONAL PROBLEMS:
N1. Determine all triples $(a, b, c)$ of natural numbers for which the following holds:
$$
2^{a}+4^{b}=8^{c} \text {. }
$$
$[62-\mathrm{B}-\mathrm{I}-1]$
N2. Find all pairs of natural numbers $a, b$ such that $a b=a+b$. [We move all terms to the left side and factor it: $(a-1)(b-1)=1$. There is only one way to write the number 1 on the right side as a product of two non-negative integers, so $a=b=2$.]
N3. Find all prime numbers $p$ for which there exists a natural number $x$ such that $p^{5}+4=x^{2}$. [Clearly $x>2$ and from the rearranged equation $p^{5}=(x-2)(x+2)$, considering $x+2>x-2>0$, it follows that the pair $(x+2, x-2)$ is either $\left(p^{5}, 1\right),\left(p^{4}, p\right)$, or $\left(p^{3}, p^{2}\right)$. In the first case, $p^{5}-1=4$, in the second $p^{4}-p=4$, but neither of these equations has a prime solution. The remaining possibility is $p^{3}-p^{2}=4$, which gives $p=2$ and $x=6$.]
D1. Find all pairs of prime numbers $p, q$ for which there exists a natural number $a$ such that
$$
\frac{p q}{p+q}=\frac{a^{2}+1}{a+1}
$$
$[62-\mathrm{A}-\mathrm{I}-1]$
D2. Find all pairs of natural numbers $x, y$ such that
$$
\frac{x y^{2}}{x+y}
$$
is a prime number. [58-A-I-3]
D3. Prove that for no natural number $n$ is the number $27^{n}-n^{27}$ a prime number. [Slovak version $57-$ A-III-4, https://skmo.sk/dokument.php?id=215]
D4. Find all integers $n$ for which $n^{4}-3 n^{2}+9$ is a prime number. [61-A-III-1]
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Determine the values that the expression
$$
\frac{a+b c}{a+b}+\frac{b+c a}{b+c}+\frac{c+a b}{c+a}
$$
can take if \( a \), \( b \), and \( c \) are positive real numbers with a sum of 1. (Michal Rolínek, Pavel Calábek)
|
SOLUTION. The fractions in the given expression make sense because their denominators are positive numbers according to the problem statement. Thanks to the condition $a+b+c=1$, for the first fraction we have
$$
\frac{a+b c}{a+b}=\frac{(a+b)+(b c-b)}{a+b}=1-b \cdot \frac{1-c}{a+b}=1-b \cdot \frac{a+b}{a+b}=1-b.
$$
Similarly, the second and third fractions take the values $1-c$ and $1-a$, respectively. Therefore,
$$
\frac{a+b c}{a+b}+\frac{b+c a}{b+c}+\frac{c+a b}{c+a}=(1-b)+(1-c)+(1-a)=3-(a+b+c)=2,
$$
which is the only possible value of the given expression under the conditions of the problem.
## GUIDING AND SUPPLEMENTARY PROBLEMS:
N1. Let $a, b, c$ be non-zero real numbers whose sum is 0. Determine the values that the expression
$$
\frac{(a-b)^{2}+(b-c)^{2}+(c-a)^{2}}{3(a b+b c+c a)}
$$
can take.
[Use the identity $a^{2}+b^{2}+c^{2}=(a+b+c)^{2}-2(a b+b c+c a)$. The value of the given expression is -2.]
N2. Let $a, b, c$ be non-zero real numbers whose sum is 0. Prove that
$$
\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}=\frac{a^{2}+b^{2}+c^{2}}{2 a b c}.
$$
[Replace the denominators of the fractions on the left side with $-c, -a, -b$ and after adding the thus modified fractions, apply the same identity as in the solution of N1.]
N3. Let $x, y, z$ be positive real numbers whose product is 1. Prove that the equality
$$
\frac{1}{1+x+x y}+\frac{1}{1+y+y z}+\frac{1}{1+z+z x}=1
$$
holds.
[Expand the first fraction by $z$, the second by $x z$, and use the condition $x y z=1$ three times.]
D1. If real numbers $a, b, c$ satisfy the equation
$$
a^{3}+b^{3}+c^{3}-3 a b c=0,
$$
then $a+b+c=0$ or $a=b=c$. Prove it. $[18-\mathrm{B}-\mathrm{I}-1]$
D2. Determine the smallest possible value of the expression $\left(1+a_{1}\right)\left(1+a_{2}\right)\left(1+a_{3}\right)$, where $a_{1}, a_{2}, a_{3}$ are positive real numbers whose product is 1. [Prove and then multiply the inequalities $1+a_{i} \geqq 2 \sqrt{a_{i}}$ for $\left.i=1,2,3.\right]$
D3. For non-negative real numbers $a, b, c$ such that $a+b+c=1$, find the greatest and smallest possible values of the expression
$$
(a+b)^{2}+(b+c)^{2}+(c+a)^{2}.
$$
$[69-\mathrm{C}-\mathrm{II}-4]$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In the plane, there is a right-angled triangle $ABC$, on whose hypotenuse $AB$ we consider an arbitrary point $K$. The circle constructed over the segment $CK$ as a diameter intersects the legs $BC$ and $CA$ at internal points, which we denote by $L$ and $M$ respectively. Determine for which point $K$ the quadrilateral $ABLM$ has the smallest possible area.
|
2. Since the angles $KLC$, $KMC$, and $LCM$ are right angles (Fig. 1), the quadrilateral $KLCM$ is a rectangle and triangles $AKM$ and $KBL$ are similar to triangle $ABC$. Let us denote
Fig. 1
as usual, $a = |BC|$, $b = |AC|$, $c = |AB|$, and let $|AK| = kc$, where $0 < k < 1$. If $|AK| > \frac{1}{2}|AB|$, we will use the similar trapezoid $BK'M'C$ (Fig. 2b) and conclude that
$$
S_{KLCM} = \frac{1}{2} S_{BK'M'C} < \frac{1}{2} S_{ABC}
$$
This proves the statement about the maximum area of $S_{KLCM}$.
a)
b)
Fig. 2
Answer: The quadrilateral $ABLM$ has the smallest possible area when point $K$ lies at the midpoint of the hypotenuse $AB$.
For a complete solution, award 6 points. If the solver only derives a functional expression for one of the areas $S_{ABLM}$, $S_{LMC}$, or $S_{KLCM}$, which would allow finding its extreme value, award 3 points. Award 1 point if the correct answer is only guessed or completely incorrectly justified.
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Consider the 2022 fractions
$$
\frac{0}{2022}, \frac{1}{2021}, \frac{2}{2020}, \ldots, \frac{2021}{1}
$$
in the form of the ratio of two non-negative integers, whose sum for each fraction is equal to 2022. How many of them take integer values?
(Jaroslav Zhouf)
|
SOLUTION. The denominators of the given fractions are natural numbers from 1 to 2022. The numerator $c$ of the fraction with a given denominator $j$ is determined by the equation $c+j=2022$, i.e., $c=2022-j$. Therefore, our fractions can be expressed, and we will immediately simplify this expression:
$$
\frac{2022-j}{j}=\frac{2022}{j}-1, \quad \text { where } \quad j=2022,2021, \ldots, 1
$$
(The values of the denominators $j$ are listed in descending order, as they are in the problem statement.)
According to the problem, our task is to determine how many of all the denominators $j$ divide the corresponding numerator $2022-j$. The simplification we performed makes our task easier: we need to find the number of $j$ from 1 to 2022 that are divisors of the number 2022.
Since the number 2022 has the prime factorization $2022=2 \cdot 3 \cdot 337$, its divisors are precisely the numbers 1, 2, 3, 6, 337, 674, 1011, and 2022, of which there are eight in total. These are the denominators $j$ of all the considered fractions with integer values. Their numerators $c=2022-j$ are, in order, the numbers 2021, 2020, 2019, 2016, 1685, 1348, 1011, and 0.
Conclusion. Exactly eight of the given fractions have integer values, specifically
$$
\frac{0}{2022}, \frac{1011}{1011}, \frac{1348}{674}, \frac{1685}{337}, \frac{2016}{6}, \frac{2019}{3}, \frac{2020}{2}, \frac{2021}{1}
$$
## NOTES.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the real domain, consider the system of equations
$$
\begin{aligned}
& x^{4}+y^{2}=\left(a+\frac{1}{a}\right)^{3}, \\
& x^{4}-y^{2}=\left(a-\frac{1}{a}\right)^{3}
\end{aligned}
$$
with a non-zero real parameter $a$.
a) Find all values of $a$ for which the given system has a solution.
b) Prove that for any solution $(x, y)$ of this system, $x^{2}+|y| \geqq 4$. When does equality hold in this inequality?
(Ján Mazák)
|
SOLUTION. We solve the system as a linear system of equations with unknowns $x^{4}$ and $y^{2}$. By adding both equations and dividing by two, we get
$$
x^{4}=\frac{1}{2}\left(\left(a+\frac{1}{a}\right)^{3}+\left(a-\frac{1}{a}\right)^{3}\right)=a^{3}+\frac{3}{a} .
$$
Similarly, by subtracting the second equation from the first and dividing by two, we get
$$
y^{2}=\frac{1}{2}\left(\left(a+\frac{1}{a}\right)^{3}-\left(a-\frac{1}{a}\right)^{3}\right)=3 a+\frac{1}{a^{3}} \text {. }
$$
a) If the given system of equations has a solution in the set of real numbers, it is necessary that $y^{2} \geq 0$. From equation (2), we see that $a>0$ must hold. Conversely, if $a>0$, both right-hand sides of equations (1) and (2) are positive, and by taking their square roots, we find real numbers $x$ and $y$ that are solutions to both the system $(1) \wedge(2)$ and the original system of equations.
b) For a positive real number $a$, according to the inequality between the arithmetic and geometric means of two positive numbers $x^{2}$ and $|y|$, and due to equations (1) and (2), we have
$$
x^{2}+|y| \geq 2 \sqrt{x^{2}|y|}=2 \sqrt[4]{x^{4} y^{2}}=2 \sqrt[4]{\left(a^{3}+\frac{3}{a}\right)\left(3 a+\frac{1}{a^{3}}\right)}=2 \sqrt[4]{3\left(a^{4}+\frac{1}{a^{4}}\right)+10}
$$
According to the same inequality between means of positive real numbers $a^{4}$ and $1 / a^{4}$, we further have
$$
a^{4}+\frac{1}{a^{4}} \geq 2 \sqrt{a^{4} \cdot \frac{1}{a^{4}}}=2
$$
Together, we get
$$
x^{2}+|y| \geq 2 \sqrt[4]{3\left(a^{4}+\frac{1}{a^{4}}\right)+10} \geq 2 \sqrt[4]{16}=4
$$
which we were to prove.
The two means (arithmetic and geometric) we referred to (even twice) are generally equal only when the two averaged values are equal (see the introductory problem N3).
Equality in the proven inequality occurs precisely when $x^{2}=|y|$ and simultaneously $a^{4}=1 / a^{4}$. From the second equality, considering $a>0$, we get $a=1$, which, when substituted into (1) and (2), gives $x^{4}=4$ and $y^{2}=4$, so the first equality $x^{2}=|y|=2$ is also satisfied. Equality in the proven inequality thus occurs precisely when $a=1$.
Note. If the solvers know the inequality between the arithmetic and geometric means of four non-negative numbers, they can prove part b) as follows. We have
$$
x^{4}=a^{3}+\frac{3}{a}=a^{3}+\frac{1}{a}+\frac{1}{a}+\frac{1}{a} \geq 4 \sqrt[4]{a^{3} \cdot \frac{1}{a} \cdot \frac{1}{a} \cdot \frac{1}{a}}=4,
$$
with equality occurring precisely when $a=1$. Similarly, we can prove the inequality
$$
y^{2}=3 a+\frac{1}{a^{3}} \geq 4
$$
again with the addition that equality occurs precisely when $a=1$. Then we easily get
$$
x^{2}+|y|=\sqrt{x^{4}}+\sqrt{y^{2}} \geq \sqrt{4}+\sqrt{4}=4 .
$$
GUIDING AND ADDITIONAL PROBLEMS:
N1. For which values of the real parameter $a$ does the system of equations
$$
\begin{aligned}
x^{2}+y^{2} & =a \\
2 x^{2}+y^{2} & =a^{2}
\end{aligned}
$$
have a solution in the set of real numbers? [We solve it as a linear system of equations with unknowns $x^{2}$, $y^{2}$, we get $x^{2}=a^{2}-a=a(a-1), y^{2}=2 a-a^{2}=a(2-a)$. From $x^{2} \geq 0$ we get $a \in \mathbb{R} \backslash(0 ; 1)$, from $y^{2} \geq 0$ we have $a \in\langle 0 ; 2\rangle$, both conditions are satisfied by $a \in\{0\} \cup\langle 1 ; 2\rangle$.]
N2. Solve the system of equations in the set of real numbers
$$
\begin{aligned}
x+y-z & =2 a \\
x-y+z & =2 b \\
-x+y+z & =2 c
\end{aligned}
$$
with real parameters $a, b, c[x=a+b, y=a+c, z=b+c$.
N3. For non-negative real numbers $a, b$, the so-called inequality between the arithmetic and geometric means (AG-inequality) holds
$$
\sqrt{a b} \leq \frac{a+b}{2}
$$
Prove it. When does equality occur? [We rearrange the inequality to $(\sqrt{a}-\sqrt{b})^{2} \geq 0$, which clearly holds. Equality occurs only when $a=b$.]
N4. Prove that for any positive numbers $a, b, c, d$,
$$
(a b+c d)\left(\frac{1}{a c}+\frac{1}{b d}\right) \geq 4
$$
[We expand the expression on the left side and use the inequality $x+1 / x \geq 2$ (valid $\forall x>0$) for $x=a / d$ and for $x=b / c$.]
D1. For any numbers $a, b$ from the interval $\langle 1,+\infty)$, the inequality holds
$$
\left(a^{2}+1\right)\left(b^{2}+1\right)-(a-1)^{2}(b-1)^{2} \geq 4
$$
Prove it and determine when equality occurs. $559-\mathrm{C}-\mathrm{II}-2$
D2. Find all real numbers $x$ and $y$ for which the expression $2 x^{2}+y^{2}-2 x y+2 x+4$ attains its minimum value. [65-C-I-3, part a)]
D3. Prove that for any positive real numbers $a, b$,
$$
\sqrt{a b} \leq \frac{2\left(a^{2}+3 a b+b^{2}\right)}{5(a+b)} \leq \frac{a+b}{2}
$$
and for each of the two inequalities, determine when equality occurs. [59-C-I-5]
D4. Find the smallest possible value of the expression
$$
3 x^{2}-12 x y+y^{4} \text {, }
$$
where $x$ and $y$ are any non-negative integers. 65-C-II-1
D5. Determine the minimum value of the expression
$$
V=x^{2}+\frac{2}{1+2 x^{2}}
$$
where $x$ is any real number. For which $x$ does the expression $V$ attain this value? [64-B-1I-2] D6. Determine all pairs $(x, y)$ of real numbers that satisfy the inequality
$$
(x+y)\left(\frac{1}{x}+\frac{1}{y}\right) \geq\left(\frac{x}{y}+\frac{y}{x}\right)^{2} .
$$
## $63-\mathrm{B}-\mathrm{I}-2$
D7. Determine all real numbers $p$ such that for any positive numbers $x, y$ the inequality
$$
\frac{x^{3}+p y^{3}}{x+y} \geq x y
$$
holds. $50-\mathrm{B}-\mathrm{II}-1$
D8. Find all possible values of the sum $x+y$, where real numbers $x, y$ satisfy the equation $x^{3}+y^{3}=3 x y$. $48-\mathrm{B}-\mathrm{I}-6$
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. On the board, the numbers $1,2, \ldots, 33$ are written. In one step, we choose several numbers written on the board (at least two), whose product is a square of a natural number, erase the chosen numbers, and write the square root of their product on the board. We continue this process until only such numbers remain on the board that the product of any of them is not a square. What is the minimum number of numbers that can remain on the board?
The written part of the school round in category A takes place
on Tuesday, December 1, 2009
so that it starts in the morning and the contestants have 4 hours of pure time to solve the problems. For each problem, a contestant can earn 6 points, and a successful solver is a student who scores 10 points or more. Allowed aids are writing and drawing supplies, school MF tables, and calculators without a graphical display. These details will be communicated to the students before the start of the competition.
## Solutions to the written part of the school round in category $A$
|
3. The product of all numbers written on the board is equal to
$$
S=2^{31} \cdot 3^{15} \cdot 5^{7} \cdot 7^{4} \cdot 11^{3} \cdot 13^{2} \cdot 17 \cdot 19 \cdot 23 \cdot 29 \cdot 31 .
$$
The presence of odd exponents means that $S$ is not a perfect square. Therefore, we cannot erase all the numbers in the first step, and the prime numbers 17, 19, 23, 29, and 31 will never be erased. From all the other numbers that can participate in the modifications, a non-empty set of numbers will always be formed, so there will always be at least $5+1=6$ numbers on the board. We will show that 6 is the smallest possible number by describing one of the possible procedures.
Due to the odd exponents of the prime numbers $2, 3, 5$, and 11, we first select the group of numbers $A=\{2,9,11,22,25\}$ and place all other numbers different from 17, 19, 23, 29, and 31 into the group
$$
B=\{3,4,5,6,7,8,10,12,13,14,15,16,18,20,21,24,26,27,28,30,32,33\} .
$$
In the first step, we select all numbers from $A$ and replace them with the number
$$
n=\sqrt{2 \cdot 9 \cdot 11 \cdot 22 \cdot 25}=\sqrt{2^{2} \cdot 3^{2} \cdot 5^{2} \cdot 11^{2}}=2 \cdot 3 \cdot 5 \cdot 11 .
$$
Since the product of all numbers in $B$ is $2^{31-2} \cdot 3^{15-2} \cdot 5^{7-2} \cdot 7^{4} \cdot 11^{3-2} \cdot 13^{2}=2^{29} \cdot 3^{13} \cdot 5^{5} \cdot 7^{4} \cdot 11 \cdot 13^{2}$, in the second step, we select the number $n$ along with all numbers from $B$ and replace them with the number
$$
\sqrt{(2 \cdot 3 \cdot 5 \cdot 11) \cdot\left(2^{29} \cdot 3^{13} \cdot 5^{5} \cdot 7^{4} \cdot 11 \cdot 13^{2}\right)}=2^{15} \cdot 3^{7} \cdot 5^{3} \cdot 7^{2} \cdot 11 \cdot 13
$$
Then, only six numbers will remain on the board, which, as we have explained, is the smallest possible number.
For a complete solution, award 6 points, of which 1 point for the consideration of the prime numbers 17, 19, 23, 29, and 31, 2 points for identifying the odd exponents of the prime numbers 2, 3, 5, and 11, and 3 points for describing the procedure leading to the target six numbers (the sixth number different from 17, 19, 23, 29, and 31 may vary depending on different procedures).
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. To each vertex of a regular 63-gon, we assign one of the numbers 1 or -1. To each of its sides, we append the product of the numbers at its vertices and sum all the numbers next to the individual sides. Find the smallest possible non-negative value of such a sum.
|
SOLUTION. Let $S$ be the value we are examining, i.e., the sum of the numbers on the sides of the 63-gon. If we assign the number 1 to each vertex of the 63-gon, we get $S=63$, because each of its sides will be assigned the number 1. It is clear that for any chosen numbering of the vertices, it can be reached by gradually changing 1 to -1.
Now let's examine how the value of $S$ will change when we change the value at some vertex of the 63-gon from 1 to -1. Let's denote the values at the neighboring vertices as $a$ and $b$ (their order does not matter). By performing this change, we will obviously change the numbers on the two sides that emanate from this vertex (and on no others). In the calculation of the value of $S$, the values of exactly two addends will change.
If $a=b=1$, the sum $S$ will decrease by 4 (before the change, the numbers $a, b$ contributed $a+b=1 \cdot 1+1 \cdot 1=2$, and after the change, their contribution will be $1 \cdot(-1)+(-1) \cdot 1=-2$). Similarly, we can analyze the other possibilities:
| $a$ | $b$ | change in $a+b$ | difference in the value of $S$ |
| ---: | ---: | :---: | :---: |
| 1 | 1 | $2 \rightarrow-2$ | -4 |
| 1 | -1 | $0 \rightarrow 0$ | 0 |
| -1 | 1 | $0 \rightarrow 0$ | 0 |
| -1 | -1 | $-2 \rightarrow 2$ | 4 |
We see, therefore, that changing one number at a vertex does not change the remainder of the number $S$ when divided by four. At the beginning, we found that one of the achievable values is $S=63$, which gives a remainder of 3 when divided by four, so the smallest non-negative value must also give the same remainder of 3, hence we will look for the smallest possible value of the sum $S$ among the numbers $\{3,7,11, \ldots\}$.
As we can easily verify, the value $S=3$ can be achieved: it is enough to place the following 63 numbers in the vertices of the 63-gon in the given order
$$
\underbrace{1,1,-1,-1,1,1,-1,-1, \ldots, 1,1,-1,-1}_{60 \text { numbers }}, 1,1,1
$$
and we get $S=3$. However, the same sum can be achieved with a different choice of numbers.
GUIDING AND ADDITIONAL PROBLEMS:
N1. In the vertices of a regular 63-gon, we write 32 units and 31 zeros in any order, with one number in each vertex. To each of its sides, we write the product of the numbers in its vertices and sum all the numbers on the individual sides. Find the smallest value that this sum can take. [The sum is non-negative, and since there are more units than zeros, there will be at least two units next to each other on the perimeter, so each sum is at least 1, and such a sum can be achieved by regularly alternating the numbers 1 and 0 in the vertices of the sides: starting with a one in any vertex and ending with a one in the adjacent vertex from the opposite side.]
N2. To each vertex of a regular $n$-gon, we assign the number -1. In one step, it is allowed to change two adjacent numbers to their opposites. Determine for which values of $n$ it is possible to achieve, by repeating the steps, that all numbers are +1? [For even $n$ it is possible, for odd $n$ it is not. When changing two numbers, the remainder of the sum of all numbers when divided by four does not change, and the difference between the sum of all numbers in the desired and initial positions is $2 n$.]
D1. On each face of a cube, exactly one integer is written. In one step, we choose any two adjacent faces of the cube and increase the numbers written on them by 1. Determine the necessary and sufficient condition for the numbering of the faces of the cube at the beginning, so that after a finite number of suitable steps, the same numbers can be on all faces of the cube. [60-A-I-5]
D2. In each vertex of a regular 2008-gon $A_{1} A_{2} \ldots A_{n}$, there is one coin. We select two coins and move each of them to an adjacent vertex, one in the direction and the other against the direction of the clock hands. Decide whether it is possible in this way to gradually move all the coins a) into 8 piles of 251 coins each, b) into 251 piles of 8 coins each. [58-A-I-5]
D3. In each of the vertices of a regular $n$-gon $A_{1} A_{2} \ldots A_{n}$, there is a certain number of coins: in vertex $A_{k}$ there are exactly $k$ coins, $1 \leqq k \leqq n$. We select two coins and move each of them to an adjacent vertex, one in the direction and the other against the direction of the clock hands. Decide for which $n$ it is possible to achieve, after a finite number of such moves, that for any $k, 1 \leqq k \leqq n$, there will be $n+1-k$ coins in vertex $A_{k}$. $[58-\mathrm{A}-\mathrm{III}-5]$
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Dana wrote a three-digit number on paper, which when divided by seven gives a remainder of 2. By swapping the first two digits, a three-digit number was formed that when divided by seven gives a remainder of 3. The number formed by swapping the last two digits of the original number gives a remainder of 5 when divided by seven. What remainder will the number, which is formed by swapping the first and last digits of Dana's number, have when divided by seven?
|
SOLUTION. Let's denote the digits of Dana's number as $a, b, c$. The information about the remainders when divided by seven from the problem can be rewritten into equations
$$
\begin{aligned}
& 100 a+10 b+c=7 x+2, \\
& 100 b+10 a+c=7 y+3, \\
& 100 a+10 c+b=7 z+5 .
\end{aligned}
$$
The digits $a$ and $b$ cannot be zero, because both the first and the second number in the problem are three-digit numbers; thus, $a, b \in\{1,2, \ldots, 9\}, c \in\{0,1,2, \ldots, 9\}$ and $x, y$ and $z$ are integers.
Now we will try to find the remainders of the digits $a, b, c$ when divided by seven. This will give us at most two possibilities for each digit. Looking at the coefficients in equations (1)-(3), we see that by a suitable subtraction, we can eliminate two digits $a$ and $c$ at once if we subtract equation (3) from ten times equation (2). We will then simplify the result step by step to find the remainder of the digit $b$ when divided by seven
$$
\begin{aligned}
10(100 b+10 a+c)-(100 a+10 c+b) & =10(7 y+3)-(7 z+5), \\
999 b & =70 y-7 z+25, \\
5 b & =70 y-7 z-7 \cdot 142 b+7 \cdot 3+4, \\
15 b & =3(70 y-7 z-7 \cdot 142 b+7 \cdot 3)+3 \cdot 4, \\
b & =3(70 y-7 z-7 \cdot 142 b+7 \cdot 3)-7 \cdot 2 b+12 .
\end{aligned}
$$
Since all terms on the right side of the last equation are divisible by seven except for the number 12, $b$ gives the same remainder when divided by seven as the number 12, and the only suitable digit $b$ is $b=5$.
By subtracting equation (3) from equation (1), we get the equation $9 c-9 b=7(z-x)+3$, and after substituting $b=5$ we get
$$
\begin{aligned}
9 c-9 \cdot 5 & =7(z-x)+3, \\
2 c & =7(z-x-c)+48, \\
8 c & =4 \cdot 7(z-x-c+6)+4 \cdot 6, \\
c & =4 \cdot 7(z-x-c+6)-7 c+7 \cdot 3+3 .
\end{aligned}
$$
From the divisibility of individual terms by seven, we get $c=3$.
Finally, by substituting $b=5$ and $c=3$ into the first equation, we can easily calculate the value of $a$:
$$
\begin{aligned}
100 a+10 b+c & =7 x+2, \\
100 a+53 & =7 x+2 \quad(53=7 \cdot 8-3,98=7 \cdot 14), \\
2 a & =7 x+2-7 \cdot 8+3-7 \cdot 14 a, \\
a & =4(7 x-7 \cdot 8-7 \cdot 14 a)+4 \cdot 5-7 a,
\end{aligned}
$$
from which it follows that the digit $a$ gives the same remainder when divided by seven as the number $20=7 \cdot 2+6$, and thus $a=6$.
Dana therefore wrote the number 653 on the paper, so the number formed by swapping the first and last digit is $356=7 \cdot 50+6$ and gives a remainder of 6 when divided by seven.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. We have a certain number of boxes and a certain number of balls. If we put exactly one ball in each box, we will have n balls left. However, if we set aside exactly n boxes, we can distribute all the balls so that there are exactly $n$ balls in each of the remaining boxes. How many boxes and how many balls do we have?
|
SOLUTION. If we denote $x$ as the number of boxes and $y$ as the number of balls, the problem leads to the system of equations
$$
x+n=y \quad \text { and } \quad(x-n) \cdot n=y
$$
with unknowns $x$, $y$, and $n$ from the set of natural numbers. By eliminating the unknown $y$, we get the equation $x+n=(x-n) \cdot n$, which has no solution for $n=1$. For $n \geqq 2$, we obtain
$$
x=\frac{n^{2}+n}{n-1}=n+2+\frac{2}{n-1},
$$
from which we see that the (natural) number $n-1$ must be a divisor of the number 2. Thus, $n \in\{2,3\}$. Substituting the permissible values of $n$ into (1) and solving the system (or using the last relation), for $n=2$ we get $x=6, y=8$ and for $n=3$ we determine $x=6$ and $y=9$.
Verification: Suppose we have six boxes and eight balls. If we put exactly one ball in each box, $n=2$ balls will remain. However, if we remove two boxes, we can distribute the balls into the remaining four boxes, each getting exactly two balls. The conditions of the problem are thus satisfied. For six boxes and nine balls, the verification is equally straightforward.
Conclusion: We either have six boxes and eight balls, or six boxes and nine balls.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Construct a trapezoid, given the lengths of its diagonals $9 \mathrm{~cm}$ and $12 \mathrm{~cm}$, the length of the midline $8 \mathrm{~cm}$, and the distance between the midpoints of the diagonals $2 \mathrm{~cm}$.
|
SOLUTION. Let's choose the notation according to Fig. $1, K P$ is the midline in triangle $A C D$,
Fig. 1
thus $|K P|=\frac{1}{2}|D C|$, similarly $|Q L|=\frac{1}{2}|D C|,|P L|=\frac{1}{2}|A B|$, so $|P Q|=\frac{1}{2}(a-c)=$ $=2 \text{ cm}$. Since $|K L|=\frac{1}{2}(a+c)=8 \text{ cm}$, we have $a=10 \text{ cm}, c=6 \text{ cm}$. First, we construct triangle $A E C$ according to the $s s s$ theorem, then on segment $A E$ we place point $B$, through which we draw a line parallel to $C E$. This line intersects the line drawn through point $C$ parallel to $A E$ at point $D$.
Solvers should recall the concept of the midline of a trapezoid, whose length is equal to the arithmetic mean of the lengths of the bases.
AUXILIARY PROBLEMS:
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find all pairs of natural numbers $a, b$ for which
$$
n(a, b)+D(a, b)=63
$$
where $n(a, b)$ denotes the least common multiple and $D(a, b)$ the greatest common divisor of the numbers $a, b$.
|
SOLUTION. We will use what we stated in the 1st problem. Let $a=D p, b=D q, n=D p q$, where $D$ is the greatest common divisor, $n$ is the least common multiple of the numbers $a, b$, and the numbers $p, q$ are coprime. According to the problem statement, $D(1+p q)=63$ must hold, so we have the following options (without loss of generality, we assume that $a \leqq b$):
| $D$ | $p q$ | $(p, q)$ | | $(a, b)$ | |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | 62 | $(1,62)$, | $\overline{(2,31)}$ | $(1,62)$, | $\overline{(2,31)}$ |
| 3 | 20 | $(1,20)$, | $(4,5)$ | $(3,60)$, | $(12,15)$ |
| 7 | 8 | $(1,8)$ | | $(7,56)$ | |
| 9 | 6 | $(1,6)$, | $(2,3)$ | $(9,54)$ | $(18,27)$ |
| 21 | 2 | $(1,2)$ | | $(21,42)$ | |
The problem has 8 solutions, not distinguishing the order of the numbers $a, b$.
AUXILIARY PROBLEMS:
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the board, one or several different two-digit natural numbers are written. We will call a digit c on the board good if the sum of those numbers on the board that contain the digit c is equal to the number 71. (Sometimes it may be a "sum" of a single number with the given digit)
a) Which of the digits 0 to 9 can be good?
b) How many digits can be good at the same time?
(Josef Tkadlec)
|
SOLUTION. a) The following examples of one or two numbers written on the board show that the digits 1, 2, 3, 4, 5, 7 can be good:
$$
\begin{array}{ll}
\text { 1: } & \{71\}, \\
\text { 2: } & \{29,42\}, \\
\text { 3: } & \{32,39\}, \\
\text { 4: } & \{24,47\}, \\
\text { 5: } & \{15,56\}, \\
\text { 7: } & \{71\} .
\end{array}
$$
Let's show that none of the remaining digits $0, 6, 8$, and 9 can ever be good. We will prove this for each of them individually, always speaking about the occurrences of the given digit in the numbers on the board.
- The digit 0 can only appear in the units place. But the sum of such numbers always ends in the digit 0, and not the required digit 1.
- If the digit 6 were only in the units place, the sum of the numbers with the digit 6 would be even, and thus different from 71. So let's assume we have at least one number of the form $6 \sqcup$. For these, however, $6 \sqcup 7171$.
Conclusion of part a). The digits that can be good are precisely 1, 2, 3, 4, 5, or 7.
b) First, we will prove that all the digits $1, 2, 3, 4, 5$, and 7, of which there are 6 in total, cannot be good simultaneously. It is enough to show that the digits 4 and 7 cannot be good at the same time.
Let's examine when the digit 4 is good. Since the number 71 is odd, all the numbers being added cannot have the digit 4 in the units place. At least one number, therefore, has the digit 4 in the tens place, and clearly, there cannot be two such numbers. So we have exactly one number starting with 4 and at least one number ending with 4. However, this number is also unique, as $41+14+24>71$. Therefore, we must have (on the board) exactly two numbers with the digit 4, namely $4 \sqcup$ and $\quad 4$, and their sum is 71. These are certainly the numbers 47 and 24.
Now, let's assume that the digit 7 is good. If it appeared only in the units place, it would have to be in at least 3 numbers to make the sum end in 1, but $17+27+37>71$. Therefore, the good digit 7 must appear in the tens place somewhere - then there is clearly only one number with the digit 7 on the board, namely the number 71.
From the last two paragraphs, it follows what we promised to show: the digits 4 and 7 cannot be good at the same time - on the board, there would have to be the numbers 47, 24, and 71 simultaneously, so the digit 7 would not be good. According to the introduction to part b), this means that the maximum number of good digits on the board is always at most 5 and that the candidates for a set of five simultaneously good digits are only the sets $(1,2,3,4,5)$ and $(1,2,3,5,7)$. To solve the problem, we need to provide an example of numbers on the board with five good digits. For interest, we will provide four such examples, all for the first set $(1,2,3,4,5)$:
$$
\begin{aligned}
& \{10,11,15,16,19\} \cup\{20,24,27\} \cup\{33,38\} \cup\{24,47\} \cup\{15,56\}, \\
& \{10,11,15,17,18\} \cup\{20,24,27\} \cup\{33,38\} \cup\{24,47\} \cup\{15,56\}, \\
& \quad\{15,16,19,21\} \cup\{21,24,26\} \cup\{33,38\} \cup\{24,47\} \cup\{15,56\}, \\
& \quad\{15,17,18,21\} \cup\{21,24,26\} \cup\{33,38\} \cup\{24,47\} \cup\{15,56\} .
\end{aligned}
$$
Conclusion of part b). The maximum number of simultaneously good digits is 5.
Note. First, we will explain why no example of numbers with the set of five good digits $(1,2,3,5,7)$ exists. In the second part of the note, we will at least hint at how to find an example with the set of five good digits $(1,2,3,4,5)$. (Without proof, we leave the fact that in the conclusion of our solution, we have listed all four possible examples.)
It is not difficult to prove that the digit 5 is good only if it appears in two numbers, namely 15 and 56. If the digit 7 is also good, then the numbers 15, 56, and 71 are on the board, so the digit 1 is not good, and the first goal is achieved.
For constructing an example for the set $(1,2,3,4,5)$: We already know that the numbers with the digits 4 or 5 on the board are exactly 24, 47, 15, and 65. By analyzing the numbers with the digit 3, we can find five possible sets: $\{32,39\},\{33,38\},\{34,37\},\{35,36\},\{13,23,35\}$. The last three of these can be immediately ruled out due to the presence of the digits 4 or 5. The first possibility $\{32,39\}$ leads to a problem with the digit 2 - expressing its "deficit" $71-24-32=15$ is not possible. Therefore, the digit 3 must be represented exactly in the numbers 33 and 38. Subsequent analysis of the representation of the digit 2 leads to two possibilities: adding $\{20,27\}$ or $\{21,26\}$ to the number 24. In both cases, the representation of the digit 1 remains to be analyzed, and adding $\{21,26\}$ is simpler - there we are looking for an expression of the "deficit" $71-21-15=35$, for which we can easily find both valid possibilities $16+19$ and $17+18$.
For a complete solution, award 6 points, 3 points for part a) and 3 points for part b). In incomplete solutions, evaluate partial steps as follows.
A1. Determining all six digits $1,2,3,4,5,7$ that can be good, together with providing valid examples - 1 point. Do not award this point if one digit or example is missing, or if an incorrect digit is included.
A2. Determining all four digits $0,6,8,9$ that cannot be good, supported by appropriate justifications - 2 points. A partial 1 point can be awarded if only one of the four digits is omitted.
B1. Proof of the statement that the digits 4 and 7 cannot be good at the same time - 1 point. (No other pair of digits from the set $\{1,2,3,4,5,7\}$ has this negative property.) This point can also be awarded for proving that the digits 1, 5, 7 cannot be good at the same time, or any other statement leading to the same necessary conclusion that there cannot be more than five good digits simultaneously.
B2. Finding one (of the four possible) examples of numbers with five good digits - 2 points.
In total, award $\mathrm{A} 1+\mathrm{A} 2+\mathrm{B} 1+\mathrm{B} 2$ points. If the student does not follow the given scheme but achieves relevant findings, up to 2 points can be awarded (for example, if it is justified which of the digits 4, 5, 6, 7, 8, and 9 can be good and additionally what numbers on the board with each of these good digits must be present). For a mere hypothesis that the maximum number of good numbers on the board is 5, no points should be awarded.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A $10 \times 10$ table is filled with numbers 1 and -1 such that the sum of the numbers in each row, except one, is equal to 0, and the sum of the numbers in each column, except one, is equal to the same number s. Determine the largest possible value of s and show that it cannot be larger. Also, provide an example of a table with the determined largest value of s.
(Josef Tkadlec)
|
SOLUTION. In the first part of the solution, we will show that the value of $s$ never exceeds the number 2. For the value $s=2$, we will provide an example of a suitable table in the second part.
Let us consider any $10 \times 10$ table filled according to the problem statement and, in addition to the number $s$, let us also consider the sum $S$ of all the numbers in this table. Since the sum of the numbers in each row, except one, is equal to 0, the value of $S$ is equal to the sum of 10 numbers in this one row, which is always at most 10. Therefore, $S \leqq 10$.
On the other hand, when calculating the sum $S$ by columns of our table, we get a value of $9s$ for nine columns according to the problem statement. To this, we must add the sum of 10 numbers in the remaining tenth column, which is always at least -10. Therefore, $S \geqq 9s - 10$.
By combining the inequalities $S \leqq 10$ and $S \geqq 9s - 10$, we get $10 \geqq S \geqq 9s - 10$, which simplifies to $10 \geqq 9s - 10$ or $9s \leqq 20$. Since the number $s$ is an integer, the last inequality leads to the announced estimate $s \leqq 2$.
The promised example of a table that will satisfy the problem statement for $s=2$ is based on the trick of "shifting the diagonal," known from the sample solutions of the previous two competition rounds. Dark cells contain the number -1, and white cells contain the number 1. Only in the tenth row is the sum of the numbers different from 0 (it is equal to 10), and only in the first column is the sum of the numbers different from 2 (it is equal to -8).
Conclusion. The largest possible value of $s$ is equal to the number 2.
NOTE. It is clear that each row and column sum of the filled $10 \times 10$ table is an even number (equal to the number $2j - 10$, where $j$ is the number of represented ones). Therefore, the sought maximum value of $s$ is also an even number. This can be used to derive the estimate $s \leqq 2$ by sequentially examining the largest even values $s=10,8,6,4$ and reasoning about the number of ones in the entire table, which always easily leads to a contradiction. Let's show how the entire discussion of possible numbers of ones can be conducted more efficiently.
Information about the row sums tells us that in some nine rows there are exactly 5 ones. Since in the remaining tenth row there are at most 10 ones, there are at most $9 \cdot 5 + 10 = 55$ ones in the entire table. However, if $s \geqq 3$, then in each of the nine columns with sum $s$ there must be at least 7 ones - in total, there would be at least $7 \cdot 9 = 63$ ones, which is a contradiction. Therefore, it must be that $s \leqq 2$.
For a complete solution, award 6 points, with 3 points for proving the estimate $s \leqq 2$ and 3 points for constructing the table for the value $s=2$. For partial solutions, award:
- 1 point for excluding all odd $s \in \{3,5,7,9\}$, for example, by a more general observation that any possible $s$ must be even (which can be considered obvious, i.e., stated without explanation).
- 2 points for excluding all even $s \in \{4,6,8,10\}$, with 1 point for excluding both values $s \in \{8,10\}$ and 1 point for excluding both values $s \in \{4,6\}$.
- 1 point in the case of merely guessing the answer $s=2$ (without an example of the table), provided that the total score does not exceed 3 points.
Do not award any points for the trivial inequality $s \leqq 10$. Therefore, values $s > 10$ are not mentioned in the scoring criteria.
[^0]: ? It can be proven that for the digits 1, 2, and 3, there are 43, 11, and 5 examples of suitable sets of two-digit numbers with the respective digit. For the other listed digits 4, 5, and 7, the examples given are the only possible ones. We will justify this for digits 4 and 7 in part b) of the solution, and for digit 5, it can be done similarly easily.
|
2
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
2. Let's examine whether it is possible to fill an $n \times n$ square table with natural numbers from 1 to $n^{2}$ such that in every $2 \times 2$ square part, at least one multiple of five is written.
a) Prove that for no even $n$ is this possible.
b) Find the largest odd $n$ for which this is possible.
|
2. For even $n=2k$, divide the table into non-overlapping $2 \times 2$ squares. There will be exactly $k^2$ of these, and in each of them, a different multiple of five must be written. For this, we need $k^2$ multiples of five, the smallest of which are the numbers $5, 10, \ldots, 5k^2$. However, the last of these numbers cannot be found among the natural numbers from 1 to $n^2 = (2k)^2 = 4k^2$. This completes the proof of part a).
For odd $n=2k+1$, we select $k^2$ non-overlapping $2 \times 2$ squares in the table in a similar manner, for example, by omitting its last row and last column. To fill the table in the required way, it must again hold that $5k^2 \leq n^2 = (2k+1)^2 = 4k^2 + 4k + 1$ or $k^2 \leq 4k + 1$. However, the last inequality cannot hold for $k \geq 5$, because for such $k$, we have $k^2 \geq 5k > 4k + 1$.
The largest odd $n$ for which we have enough multiples of five among the numbers from 1 to $n^2$ is thus $n=9$. We will write all 16 multiples of five into the individual $2 \times 2$ parts, and then fill the remaining numbers into the empty cells arbitrarily:
| | | | | | | | | |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | 5 | | 10 | | 15 | | 20 | |
| | | | | | | | | |
| | 25 | | 30 | | 35 | | 40 | |
| | | | | | | | | |
| | 45 | | 50 | | 55 | | 60 | |
| | | | | | | | | |
| | 65 | | 57 | | 75 | | 80 | |
| | | | | | | | | |
The largest odd $n$ for which the table can be filled in the required way is nine.
For a complete solution, award 6 points. For the idea of dividing the table into $k^2$ non-overlapping $2 \times 2$ parts, award 3 points, for completing the proof of part a) award 1 point, for deriving the condition $n \leq 9$ in part b) award another point, and 1 point for providing an example of the filling.
|
9
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the bases $z$ of all number systems in which the four-digit number $(1001)_{z}$ is divisible by the two-digit number $(41)_{z}$.
|
1. Since the digit 4 appears in the notation of a two-digit number, it necessarily follows that $z \geq 5$. From the expanded notations $(1001)_z = z^3 + 1$ and $(41)_z = 4z + 1$, we are looking for exactly those natural numbers $z \geq 5$ for which the number $z^3 + 1$ is a multiple of the number $4z + 1$. Using the Euclidean algorithm, we can find their greatest common divisor. We can proceed by first dividing both expressions as polynomials and then eliminating the fractions:
$$
\begin{aligned}
z^3 + 1 & = \left(\frac{1}{4} z^2 - \frac{1}{4^2} z + \frac{1}{4^3}\right)(4z + 1) + \frac{63}{4^3}, \quad / \cdot 4^3 \\
4^3 (z^3 + 1) & = (16z^2 - 4z + 1)(4z + 1) + 63
\end{aligned}
$$
Since the numbers 4 and $4z + 1$ are coprime, we see from this that the number $4z + 1$ divides the number $z^3 + 1$ if and only if it divides the number 63, i.e., if and only if $4z + 1 \in \{1, 3, 7, 9, 21, 63\}$. From the condition $z \geq 5$, however, it follows that $4z + 1 \geq 21$, so $4z + 1 = 21$ (the equation $4z + 1 = 63$ has no integer solution) and $z = 5$.
Note. The factorization (1) can also be easily revealed by using the known formula $a^3 + b^3 = (a + b)(a^2 - ab + b^2)$: according to this, we can write directly
$$
4^3 (z^3 + 1) = (4^3 z^3 + 1) + 63 = (4z + 1)(16z^2 - 4z + 1) + 63.
$$
For a complete solution, award 6 points. If the solver neglects the condition $z \geq 5$ and considers the number $z = 2$ from the equation $4z + 1 = 9$ as a solution, deduct 2 points. Also deduct 1 point if the check for the solution $z = 5$ is missing and the condition $(4z + 1) \mid 63$ is derived only as necessary (not sufficient as in our solution). Award 4 points for the derivation of this condition. Award no more than 1 point in total for merely setting up the condition $(4z + 1) \mid (z^3 + 1)$ or for merely guessing the solution $z = 5$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Prove that there exists a unique digit $c$, for which there is a unique natural number $n$ ending in the digit $c$ and having the property that the number $2n+1$ is the square of a prime number.
|
SOLUTION. Let the (odd) number $2n+1$ be the square of a prime number $p$, then $p$ is also an odd number. From the relation $p^2 = 2n + 1$, it follows that $n = \frac{1}{2}(p^2 - 1) = \frac{1}{2}(p - 1)(p + 1)$. Let's create a table of the first few odd prime numbers $p$ and their corresponding numbers $n$:
| $p$ | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 |
| ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: |
| $n$ | 4 | 12 | 24 | 60 | 84 | 144 | 180 | 264 | 420 | 480 | 684 | 840 | 924 |
The number $n$ is clearly even, and indeed (as the table shows for several values of $p$) it is divisible by four. This is evident from the fact that the product $(p-1)(p+1)$ of two consecutive even numbers is always divisible by eight. From the table, we also see that among the digits by which $n$ ends, the digits 0 and 4 appear multiple times, the digit 2 appears only once, and the digits 6 and 8 do not appear at all.
Let's look at what digit $n$ ends with depending on the digit $a$ by which $p$ ends. If $p = 10k + a$, where $k$ is a non-negative integer and $a$ is an odd digit, then for each possible $a$ we get:
- If $a = 1$, then $n = 10k(5k + 1)$, so the number $n$ ends with the digit 0.
- If $a = 3$, then $n = 10k(5k + 4) + 4$, so the number $n$ ends with the digit 4.
- If $a = 5$, then $n = 10(5k^2 + 5k + 1) + 2$, so the number $n$ ends with the digit 2.
- If $a = 7$, then $n = 10(5k^2 + 7k + 2) + 4$, so the number $n$ ends with the digit 4.
- If $a = 9$, then $n = 10(k + 1)(5k + 4)$, so the number $n$ ends with the digit 0.
If $2n + 1$ is the square of an odd prime number (odd number), the number $n$ can only end with the digits 0, 2, or 4. The only candidate for the desired digit is 2.
If $2n + 1$ is the square of a prime number and $n$ ends with the digit 2, the prime number $p$ can be expressed in the form $10k + 5 = 5(2k + 1)$, which means it is divisible by five. The only prime number that is divisible by five is the number 5.
The desired digit is therefore $c = 2$; for this digit, there is only one natural number $n = 12$ that ends with the digit $c$, and $2n + 1$ is the square of a prime number.
|
2
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. Each cell of a $68 \times 68$ table is to be colored with one of three colors (red, blue, white). In how many ways can this be done so that every triplet of adjacent cells in each row and each column contains cells of all three colors?
(Josef Tkadlec)
|
Solution. Once we determine the colors of some two adjacent fields in a row or column of the table, the coloring of all its other fields is uniquely determined by the requirements of the problem. The colors in each row and column thus alternate regularly with a period of 3.
Let's say that $a b c a b c .$. is the coloring of the fields of the first row. Out of the six possible colorings of the fields of any row
abcabc...,
bcaacb...,
cababc...,
acbacb...,
bacacb...,
cbacba...
clearly, only the second and third are suitable for the second row. Once we choose one of them for the second row, the other must be the coloring of the fields of the third row. The fourth row will then be colored the same as the first, the fifth as the second, etc., with a period of 3.
Let's summarize our considerations. For the coloring $a b c a b c .$. of the first row, we have $3 \cdot 2=6$ possibilities (3 for choosing $a$, 2 for choosing $b$). For the coloring of the second row, as we have found, we then have two possibilities. The coloring of the subsequent rows is already uniquely determined. The number of all valid colorings of the entire table is thus equal to $6 \cdot 2=12$.
For a complete solution, award 6 points. For noting that the colors in each row alternate regularly with a period of 3 (even without a detailed explanation), award 2 points and another point for justifying that the number of ways to color one row is thus equal to 6. Award another 2 points for justifying why, after coloring one row, the next row can be colored in two ways, and the final point for concluding that the number of colorings is equal to 12. For merely guessing the correct result, award 1 point. (The same considerations obviously apply to columns as well.)
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In how many ways can a $3 \times 3$ square table be filled with the numbers $2,2,3,3,3,4,4,4,4$ so that the sum of the numbers in each $2 \times 2$ square of this table is equal to 14?
|
ANOTHER SOLUTION. Just like in the previous solution, we will show that the number 14 can be obtained from the given numbers as a sum of four numbers only as $4+4+4+2$ or $4+4+3+3$. It follows from this that in any $2 \times 2$ square that contains the number 2 (or 3), no other 2 can be present. In the central square (which is part of four $2 \times 2$ squares), there cannot be a 2 (there would be no room for the threes), nor a 3 (there would be no room for the twos). Therefore, the number 4 must be in the central square.
From the previous solution, we know that in the square adjacent to the central square, there cannot be a 2, because both $2 \times 2$ squares containing this 2 would already contain only fours, and we do not have enough of them. Therefore, the central square must contain a 4, and one of the corners must contain a 2. This determines the numbers in the corresponding $2 \times 2$ square of the table:
| 2 | | |
| :--- | :--- | :--- |
| | 4 | |
| | | |$\rightarrow$| 2 | 4 | |
| :--- | :--- | :--- |
| 4 | 4 | |
| | | |
We have five unfilled squares left, which must contain the numbers $2,3,3,3,4$. The number 3 must appear in at least one of the two $2 \times 2$ squares that share two squares with the already filled square (and this must happen twice). Let's choose one of them (choosing the other one would result in the same process and a symmetrical situation). The other numbers can then be written in only one way, because the 2 cannot be in the same $2 \times 2$ square as the 3:
| 2 | 4 | 3 |
| :--- | :--- | :--- |
| 4 | 4 | 3 |
| | | |$\longrightarrow$| 2 | 4 | 3 |
| :--- | :--- | :--- |
| 4 | 4 | 3 |
| 2 | | |$\rightarrow$| 2 | 4 | 3 |
| :--- | :--- | :--- |
| 4 | 4 | 3 |
| 2 | 4 | |$\rightarrow$| 2 | 4 | 3 |
| :--- | :--- | :--- |
| 4 | 4 | 3 |
| 2 | 4 | 3 |
By rotating by a multiple of $90^{\circ}$, we get three more distinct fillings. It is easy to see that these are all the possibilities that can be obtained by choosing a different initial corner with a 2 and choosing an adjacent square with two threes. The table can therefore be filled in four ways.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let $a, b, c$ be positive real numbers such that $a b + b c + c a = 1$. Determine the values that the expression
$$
\frac{a\left(b^{2}+1\right)}{a+b}+\frac{b\left(c^{2}+1\right)}{b+c}+\frac{c\left(a^{2}+1\right)}{c+a}
$$
can take.
(Josef Tkadlec \& Patrik Bak)
|
SOLUTION. Given the condition $a b+b c+c a=1$, we first modify the first of the three addends of the expression under consideration, similarly to problem 4 from the homework round,
$$
\frac{a\left(b^{2}+1\right)}{a+b}=\frac{a\left(b^{2}+a b+b c+c a\right)}{a+b}=\frac{a(b+a)(b+c)}{a+b}=a(b+c)=a b+c a .
$$
Similarly, the remaining two addends have the expressions
$$
\frac{b\left(c^{2}+1\right)}{b+c}=b c+a b \quad \text{and} \quad \frac{c\left(a^{2}+1\right)}{c+a}=c a+b c
$$
Together, we get for the sum of all three given fractions
$\frac{a\left(b^{2}+1\right)}{a+b}+\frac{b\left(c^{2}+1\right)}{b+c}+\frac{c\left(a^{2}+1\right)}{c+a}=(a b+c a)+(b c+a b)+(c a+b c)=2(a b+b c+c a)=2$,
where we have again used the equality $a b+b c+c a=1$ from the problem statement.
Conclusion. The given expression always takes the value 2 for any positive real numbers $a, b, c$ that satisfy the condition $a b+b c+c a=1$.
For a complete solution to the problem, award 6 points, of which: 3 points for the necessary modification of any of the three addends of the given expression; 2 points for adding the three modified addends (fractions); 1 point for providing the correct answer.
For an unproven hypothesis that the given expression always takes the value 2, award 1 point, even if it is supported by specific numerical calculations.
[^0]: * These known facts do not need to be proven in the solution. Nevertheless, we note that they follow from the properties of the medians $S K$ and $L S$ in triangles $A B C$ and $A B D$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Determine the largest natural number $k$ for which it is possible to place $k$ rooks and $k$ bishops on an $8 \times 8$ chessboard such that no piece threatens another. (A bishop threatens any square on the same diagonal, and a rook threatens any square on the same row or column.)
(Josef Tkadlec)
|
Solution. Consider any valid placement of $k$ rooks and $k$ archers. We will prove that the inequality $k \leqq 5$ holds.
If a rook is placed in any row (or column) of the chessboard, it must be the only piece in that row (or column). Therefore, for the number $k$ of placed rooks, it must be true that $k \leqq 8$, and additionally, a total of $8-k$ rows and $8-k$ columns of the chessboard are not occupied by rooks. The $k$ archers can then stand on any of the $(8-k)^{2}$ squares where these rows and columns intersect. Therefore, the inequality
$$
k \leqq (8-k)^{2}
$$
must hold. From this, it follows that $k \leqq 5$, because the derived inequality does not hold for any $k \in \{6,7,8\}$, as can be easily verified by substitution.
As we can see from the following figure, 5 rooks and 5 archers can be placed on the chessboard in such a way that they do not threaten each other, so the largest possible $k$ with the given property is $k=5$.
Fig. 2
Note. The derivation of the inequality $k \leqq 5$ can be presented more concisely as follows: first, we rule out the value $k=6$ (6 archers would have to stand on 4 squares, which lie in two rows and two columns not occupied by 6 rooks), and then we observe that if there were a valid placement for $k>6$, removing any $k-6$ rooks and $k-6$ archers would yield a valid placement for $k=6$.
For a complete solution, award 6 points. Of these, 1 point for ruling out the possibilities $k>6$ and 2 points for ruling out the possibility $k=6$. Finally, award 3 points for constructing a correct example of a valid placement for $k=5$. Do not award additional points for stating that no more rooks can be added to the found example for $k=5$—a complete solution to the problem would require testing all valid placements for $k=5$. If a correct example of a valid placement is given only for $k=4$, award 1 point.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let's have an $8 \times 8$ chessboard and for each "edge" that separates two of its squares, write a natural number that indicates the number of ways the entire chessboard can be cut into $2 \times 1$ rectangles such that the given edge is part of the cut. Determine the last digit of the sum of all such written numbers.
(Michal Rolínek)
|
Solution. There are $7 \cdot 8=56$ vertical edges and the same number of horizontal edges, making a total of $56 \cdot 2=112$. When the chessboard is cut in any way, 32 rectangles of $2 \times 1$ are formed, so each such cut touches exactly $112-32=80$ edges, contributing the number 80 to the total sum. Therefore, the resulting sum is divisible by 80, meaning its decimal representation ends in zero.
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A cinema received 234 visitors. Determine for which $n \geqq 4$ it could have happened that the visitors could be seated in $n$ rows such that each visitor in the $i$-th row knew exactly $s_j$ visitors in the $j$-th row for any $i, j \in\{1,2, \ldots, n\}, i \neq j$. (The relationship of knowing is symmetric.)
(Tomáš Jurík)
|
Solution. For each $k \in\{1,2, \ldots, n\}$, let $p_{k}$ be the number of viewers in the $k$-th row. The condition of the problem for given $i$ and $j$ means that the number of acquaintances between viewers in the $i$-th and $j$-th rows is equal to $j p_{i}$. By swapping the roles of the numbers $i$ and $j$, we find that the same number must equal $i p_{j}$. Therefore, it must hold that $j p_{i}=i p_{j}$, or $p_{i}: p_{j}=i: j$. We thus arrive at the conclusion that the numbers $p_{k}$ of viewers in the individual rows necessarily satisfy the condition
$$
p_{1}: p_{2}: \ldots: p_{n}=1: 2: \ldots: n
$$
Let us show that this is also a sufficient condition, that is, that for counts $p_{k}=k d$ for a suitable integer $d$, the viewers could have known each other in such a way that the condition of the problem is satisfied. For $d=1$, this is certainly the case when all viewers in the cinema know each other; for a general $d$, it suffices that the viewers are divided into $d$ groups of mutually acquainted viewers and that the viewers from each such group are seated in the rows in the same way as in the case $d=1$.
Our task is thus to determine for which $n \geqq 4$ there exists a positive integer $d$ satisfying the equation
$$
d+2 d+\ldots+n d=234 \quad \text { or } \quad d n(n+1)=468
$$
We are thus looking for all divisors of the number $468=2^{2} \cdot 3^{2} \cdot 13$ that are of the form $n(n+1)$. Since $22 \cdot 23>468$, it must hold that $n<22$, i.e., $n \in\{4,6,9,12,13,18\}$. We see that only $n=12$ (with the corresponding $d=3$) satisfies this.
Answer. The described situation could have occurred only with the seating of viewers in 12 rows.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Determine the maximum possible area of triangle $ABC$, whose medians satisfy the inequalities $t_{a} \leqq 2, t_{b} \leqq 3, t_{c} \leqq 4$.
(Pavel Novotný)
|
Solution. Let $T$ be the centroid of triangle $ABC$ and $K, L, M$ the midpoints of sides $BC, CA, AB$. The medians divide triangle $ABC$ into six smaller triangles of equal area: For example, triangle $AMT$ has side $|AM|=\frac{1}{2} c$ and its height to side $AM$ has a length of $\frac{1}{3} v_{c}$, so $S_{AMT}=\frac{1}{2} \cdot \frac{1}{2} c \cdot \frac{1}{3} v_{c}=\frac{1}{6} \cdot \frac{1}{2} c \cdot v_{c}=\frac{1}{6} S_{ABC}$, and we get the same result analogously for the remaining five triangles.
The given problem is thus equivalent to determining the maximum possible area of one of the six smaller triangles - the result just needs to be multiplied by six.
Fig. 1
Consider, for example, triangle $ATL$ (Fig. 1). For its two sides, we have
$$
|AT|=\frac{2}{3} t_{a} \leqq \frac{4}{3}, \quad|TL|=\frac{1}{3} t_{b} \leqq 1
$$
Therefore, for its area, we get
$$
S_{ATL}=\frac{1}{2}|AT| \cdot|TL| \cdot \sin |\angle ATL| \leqq \frac{1}{2} \cdot \frac{4}{3}=\frac{2}{3} .
$$
This proves that the area of triangle $ABC$, whose medians satisfy the given inequalities, cannot be greater than $6 \cdot \frac{2}{3}=4$. Moreover, the equality $S_{ATL}=\frac{2}{3}\left(\text{i.e., } S_{ABC}=4\right)$ occurs precisely when $t_{a}=2, t_{b}=3$ and $|\angle ATL|=90^{\circ} .{ }^{1}$
We can construct a triangle $ABC$ with these properties: First, we draw a right triangle $ATL$ in which we know the lengths of both legs $|AT|=\frac{4}{3},|TL|=1$, and then we construct point $C$ as the image of point $A$ under central symmetry with center $L$ and point $B$ as the image of point $L$ under a homothety with center $T$ and coefficient -2 (Fig. 2). It remains to verify that in such a triangle $ABC$, $t_{c} \leqq 4$.
Fig. 2
The length $t_{c}$ can be calculated in various ways. For example, in the right triangle $ABT$, the hypotenuse $AB$ has a length, according to the Pythagorean theorem,
$$
|AB|=\sqrt{|AT|^{2}+|TB|^{2}}=\sqrt{\frac{16}{9}+4}=\sqrt{\frac{52}{9}}=\frac{2}{3} \sqrt{13},
$$
so the radius of the Thales circle over the diameter $AB$ is
$$
|MT|=\frac{1}{2}|AB|=\frac{1}{3} \sqrt{13} .
$$
Thus, $t_{c}=3|MT|=\sqrt{13}<4 .^{2}$
Answer. The maximum possible area of triangle $ABC$ is 4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let's consider 20 statements:
| "I have exactly one sister." | "I have exactly one brother." |
| :--- | :--- |
| "I have exactly two sisters." | "I have exactly two brothers." |
| "I have exactly ten sisters." | "I have exactly ten brothers." |
a) Each of the four siblings made a different one of these 20 statements. Is it possible that all four were telling the truth?
b) Find the largest natural number $n$ such that each of the $n$ siblings can make a different one of these 20 statements and be telling the truth.
(Josef Tkadlec)
|
SOLUTION. a) Yes, it is possible. In the case where the four siblings are two brothers and two sisters, they can truthfully make four mutually different statements. One brother says: "I have exactly one brother" and the other: "I have exactly two sisters," one sister says: "I have exactly one sister" and the other: "I have exactly two brothers."
b) For $n=4$, we have found that each of the four siblings can make a different true statement.
In the case of $n \geqq 5$, there are at least three siblings of the same gender. Suppose each of them truthfully states the number of their sisters or brothers. Then, however, at least two of these statements will be the same (those about the number of sisters, or those about the number of brothers). Therefore, no integer $n \geqq 5$ has the required property.
Conclusion. The largest suitable $n$ is 4.
COMMENT. In part b) of the given solution, we used a fact known as the **Dirichlet principle** or the **pigeonhole principle**. It states, for example, that if we distribute 13 items into 2 containers, at least one container will have at least 7 items. Or if we distribute 13 items into 3 containers, at least one container will have at least 5 items. Or when distributing $2n+1$ items into 2 containers, at least one container will have at least $n+1$ items. Generally, when distributing at least $kn+1$ items into $k$ containers, at least one container will have at least $n+1$ items (we wrote this above for $k=2$ and $n=6$, as well as for $k=3$ and $n=4$, and for $k=2$ and general $n$). The "items" can be numbers, geometric shapes, people, statements, essentially anything. The containers can then represent any properties of the individual items. For example, we often divide integers into 2 containers based on whether they are even or odd (see introductory problem N2).
In our solution, we used the Dirichlet principle twice, each time for 2 containers. In the first case, the siblings played the role of "items" and gender (male/female) played the role of "containers". In the second case, the "items" were the statements and the "containers" were statements about sisters and statements about brothers.
NOTE. Let's show that the explanation of part b) of the solution can also be presented differently. If in a given group of $n$ siblings there are exactly $B$ brothers and exactly $S$ sisters, each of them can truthfully make only one of the following four statements (the first two are statements by brothers, the remaining two are statements by sisters):
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 4. Find the smallest value of the fraction
$$
V(n)=\frac{n^{3}-10 n^{2}+17 n-4}{n^{2}-10 n+18}
$$
$where\ n$ is any natural number greater than 2.
|
SOLUTION. First, let's calculate the values of the expression $V(n)$ for several natural numbers $n \geq 3:$
| $n$ | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $V(n)$ | $5 \frac{1}{3}$ | $5 \frac{1}{3}$ | $6 \frac{2}{7}$ | $7 \frac{2}{3}$ | $10 \frac{2}{3}$ | 2 | $7 \frac{5}{9}$ | $9 \frac{2}{9}$ | $10 \frac{14}{29}$ | $11 \frac{13}{21}$ | $12 \frac{40}{57}$ | $13 \frac{28}{37}$ |
From the table, we see that $V(n) \geq 2$ for all $n \in\{3,4, \ldots, 14\}$, with $V(8)=2$. We will show that for all $n \geq 9$, it holds that $V(n)>2$.
By successive manipulation of the expression $V(n)-2$, we get (we know that $V(8)-2=0$)
\[
\begin{aligned}
V(n)-2 & =\frac{n^{3}-10 n^{2}+17 n-4}{n^{2}-10 n+18}-2=\frac{n^{3}-12 n^{2}+37 n-40}{n^{2}-10 n+18}= \\
& =\frac{(n-8)\left(n^{2}-4 n+5\right)}{(n-5)^{2}-7}=\frac{(n-8)\left((n-2)^{2}+1\right)}{(n-5)^{2}-7} .
\end{aligned}
\]
For $n \geq 9$, both the numerator and the denominator of the last fraction are positive numbers. Therefore, $V(n)-2>0$ for every $n \geq 9$.
Answer: The smallest value of the fraction $V(n)$ for all natural numbers $n>2$ is 2; this value is attained by the expression $V(n)$ for $n=8$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.