problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
4. Let $a, b$ be any positive real numbers such that $a^{2}+b^{2}=1$. Find the smallest possible value of the expression
$$
\frac{a^{2}\left(a+b^{3}\right)}{b-b^{3}}+\frac{b^{2}\left(b+a^{3}\right)}{a-a^{3}}
$$
and determine for which pairs $(a, b)$ this value is achieved. (Tomáš Bárta)
|
SOLUTION. Using the condition $a^{2}+b^{2}=1$, we first simplify the first fraction of the given expression:
$$
\frac{a^{2}\left(a+b^{3}\right)}{b-b^{3}}=\frac{a^{2}\left(a+b^{3}\right)}{b\left(1-b^{2}\right)}=\frac{a^{2}\left(a+b^{3}\right)}{b \cdot a^{2}}=\frac{a+b^{3}}{b}=\frac{a}{b}+b^{2} .
$$
Similarly, for the second fraction we have
$$
\frac{b^{2}\left(b+a^{3}\right)}{a-a^{3}}=\frac{b}{a}+a^{2}
$$
By adding the expressions of both fractions, we get for the given expression $V$:
$$
V=\left(\frac{a}{b}+b^{2}\right)+\left(\frac{b}{a}+a^{2}\right)=\left(\frac{a}{b}+\frac{b}{a}\right)+\left(a^{2}+b^{2}\right)=\left(\frac{a}{b}+\frac{b}{a}\right)+1,
$$
where we have again used the condition $a^{2}+b^{2}=1$.
Notice that for the sum of the fractions in the last parentheses, we have
$$
\frac{a}{b}+\frac{b}{a}=\frac{a^{2}+b^{2}}{a b}=\frac{(a-b)^{2}+2 a b}{a b}=\frac{(a-b)^{2}}{a b}+2 \geqq 2 \text {, since } \quad \frac{(a-b)^{2}}{a b} \geqq 0 \text {. }
$$
From the derived expression for $V$, it follows that the lower bound is $V \geqq 2+1=3$. Moreover, in the used inequality $a / b+b / a \geqq 2$, equality holds if and only if $a=b$. Therefore, the equality $V=3$ holds if and only if the positive numbers $a, b$ satisfy both conditions $a^{2}+b^{2}=1$ and $a=b$, i.e., if and only if $a=b=\frac{1}{2} \sqrt{2}$. The number 3 is thus the smallest value of the given expression $V$ and is achieved for the unique pair of numbers $a, b$ (determined at the end of the previous sentence).
For a complete solution, award 6 points, of which: 2 points for the necessary simplification of at least one of the two given fractions; 1 point for simplifying their sum to a form suitable for minimizing the sum $a / b+b / a$ or maximizing the product $a b$; 2 points for justifying the lower bound of 3 (one can refer to the AM-GM inequality as in the footnote); 1 point for determining (not just guessing) when the minimum value is achieved.
For an incomplete solution, award 1 point for guessing the minimum value 3 only if the corresponding pair $a=b=\frac{1}{2} \sqrt{2}$ is provided. This point can be added to the first 2 or 3 points awarded according to the instructions in the previous paragraph. Without a complete proof of the inequality $V \geqq 3$, even with other methods, no more than 4 points can be awarded.[^1]
[^0]: * The first step in such a justification might be the consideration of the pair of segments $B C$ and $F G$ from the introductory paragraph of the solution.
[^1]: * The proof of this result can also use the AM-GM inequality $\frac{1}{2}(u+v) \geqq \sqrt{u v}$ for values $u=a / b$ and $v=b / a$. It is also possible to use the equality $a / b+b / a=1 /(a b)$ due to the condition $a^{2}+b^{2}=1$ and then maximize the product $a b$, for example, by using the mentioned AM-GM inequality for $u=a^{2}$ and $v=b^{2}$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A $3 \times 3$ table is filled with distinct natural numbers such that in each row and column, the sum of the outer numbers equals the number written between them. Determine the smallest number that can be written in the center of the table.
(Tomáš Jurík)
|
Solution. Let's denote the numbers in the corners of the table as $a, b, c, d$ (from left to right, top to bottom). These four numbers uniquely determine all other numbers in the table, as we can sequentially calculate the numbers between them and finally the number $a+b+c+d$ in the center of the table.
| $a$ | | $b$ |
| :---: | :---: | :---: |
| | | |
| $c$ | $d$ | |
| $a+c$ | | $b+d$ |
| $c$ | $c+d$ | $d$ |
| $a$ | $a+b$ | $b$ |
| $a+c$ | $a+b+c+d$ | $b+d$ |
| $c$ | $c+d$ | $d$ |
For the values $a=1, b=3, c=6$ and $d=2$, we get the table of different numbers
| 1 | 4 | 3 |
| :---: | :---: | :---: |
| 7 | 12 | 5 |
| 6 | 8 | 2 |
with the number $a+b+c+d=12$ in the center.
Now we will show that the number in the center of the table cannot be smaller than 12. A number smaller than 12 can be obtained as the sum of four different natural numbers in only two ways: as $1+2+3+4$ or $1+2+3+5$.
In both cases, the numbers 1, 2, and 3 are among the numbers written in the corners of the table. Let's try to see if they can be written in the corners of the table in such a way that we can fill the entire table as required.
The numbers 1 and 2 cannot be written in the same row or column, because then the number 3 would be written between them as their sum, and we need to have the number 3 in one of the corners of the table. Therefore, the numbers 1 and 2 must be in opposite corners of the table. For the number 3, we only have two possible corner positions in the table, and no matter which one we choose, we will have to write the number 4 between 3 and 1 and the number 5 between 3 and 2, so we will not be able to have either the number 4 or the number 5 in the last corner. Therefore, we cannot write the numbers $1,2,3,4$ or $1,2,3,5$ in the corners of the table, and thus the number $a+b+c+d$ in the center of the table, satisfying the conditions of the problem, always has a value of at least 12.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find all tetrahedra that have a net in the shape of a deltoid and exactly four edges of a given length a. (A deltoid is understood to be a convex quadrilateral symmetric with respect to only one of its diagonals; thus, neither a square nor a rhombus is considered a deltoid.)
|
SOLUTION. In the first (more significant) part of the solution, we will find all tetrahedra that have a net in the shape of a kite; then it will be relatively easy to determine which of the found tetrahedra have exactly four equal edges.
Consider, therefore, an arbitrary tetrahedron $ABCD$ and describe the lengths of its edges with the letters $x, y, z, u, v, w$ as shown in Fig. 3. We will divide all nets of the tetrahedron $ABCD$ into two groups. The first group will include those nets in which one face of the tetrahedron is adjacent to the other three faces;
the second group will include the remaining nets, in which each face is adjacent to at most two other faces. Since we have not specified the labeling of the tetrahedron's vertices in advance, we will further consider only one net from each of the two groups, namely the nets depicted in Figs. 4 and 5. We will deal with each of them separately.
The net in Fig. 4 is (in general) a hexagon $AD_3BD_1CD_2$, it will be a quadrilateral only if two of its angles at the vertices $A, B, C$ are right (i.e., have a size of $180^\circ$). It is clear that a right angle cannot be at any of the vertices $D_1, D_2, D_3$. Considering the already mentioned arbitrariness of labeling, let us assume that the angles $D_2AD_3$ and $D_3BD_1$ (marked in Fig. 4) are right. Our net is then a quadrilateral $D_2D_3D_1C$, whose sides (in the order in which they cyclically follow each other) have lengths $2u, 2v, w$, and $w$. If this quadrilateral is a kite (and not a rhombus), it must certainly be true that $u=v$ and $2u \neq w$ (Fig. 6a). From the axial symmetry with respect to the line $D_3C$, we then find that $y=x$; the tetrahedron with the "kite-shaped" net from Fig. 6a is shown in Fig. 6b. It is a tetrahedron symmetric with respect to the plane of symmetry of the edge $AB$. Let us add that
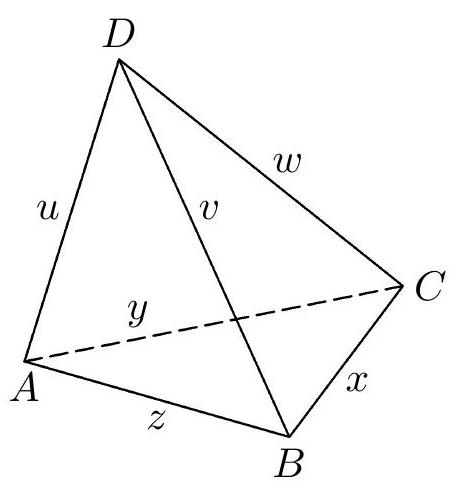
Fig. 3 in addition to the inequality $2u \neq w$, the inequality $z \neq x$ must also hold; in the net from Fig. 7a, it must be true that $2u = x + v$ and $x = v$, hence $x = u = v$. In the triangle $D_2D_1C$, the segment $AB$ is the midline (Fig. 7a), so $w = |D_2C| = 2|AB| = 2z$. The corresponding tetrahedron is shown in Fig. 7b.
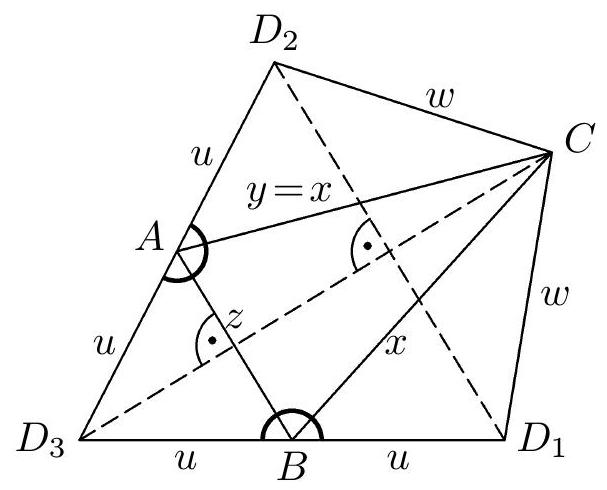
Fig. 6a
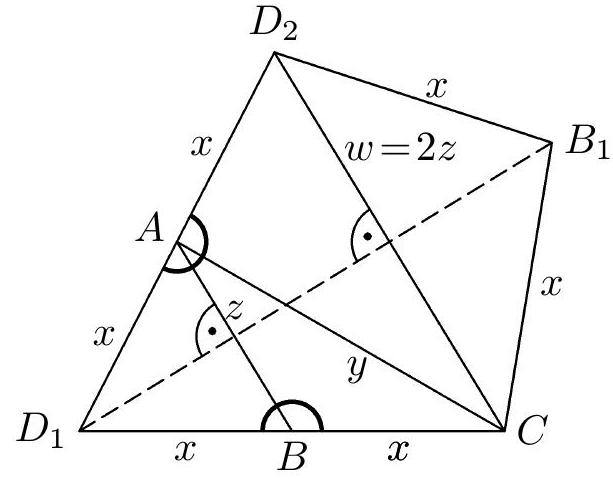
Fig. 7a
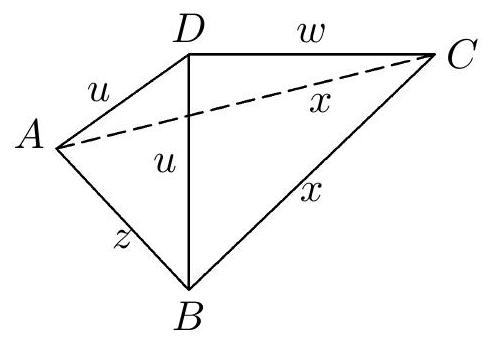
Fig. 6b
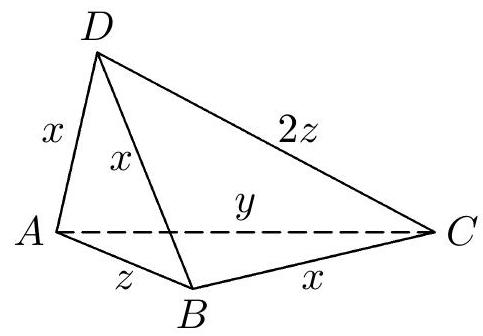
Fig. 7b
Let's summarize the results of our previous considerations: Only two types of tetrahedra (Figs. 6b and 7b) have a net in the shape of a kite. Our task is now to determine when these tetrahedra have exactly four equal edges (of a given length $a$). Let's first consider the tetrahedron from Fig. 6b, whose edges have lengths $x, x, z, u, u, w$. Suppose, therefore, that exactly four of them are equal to $a$, which ones are they? First, it must be true that $x = a$, otherwise it would have to be true that $a = z = u = w$, which is in contradiction with the inequality $z < 2u$, hence $x > z$. In the same net, the triangle $ABC$ has an obtuse interior angle at vertex $B$, because its exterior angle $ABD_1$ is the interior angle at the base $AB$ of the isosceles triangle $ABD_1$, so it is necessarily acute. Therefore, the longest side of the triangle $ABC$ is the side $AC$, which we can write as: $y > \max \{x, z\}$. Together, we get $y > x > z$, with respect to the equality $x = a$, it follows that $2z = a$. The tetrahedron $ABCD$ is thus uniquely (up to congruence) determined by the found conditions. The length of the last edge $AC$ we calculate as the median to the side $D_1D_2$ of the triangle $CD_1D_2$ with sides $2a, 2a, a$. We get $y = \frac{1}{2}a\sqrt{6}$. The solution to our problem is the unique tetrahedron from Fig. 8a, and its net in the shape of a kite is in Fig. 8b.
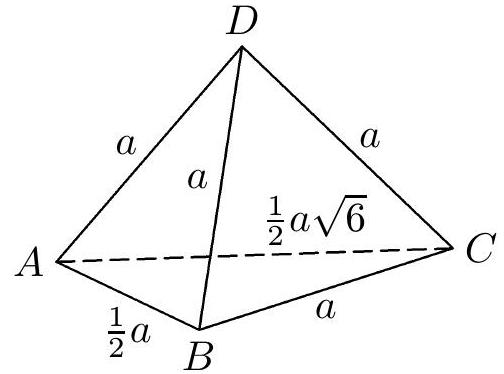
Fig. 8a
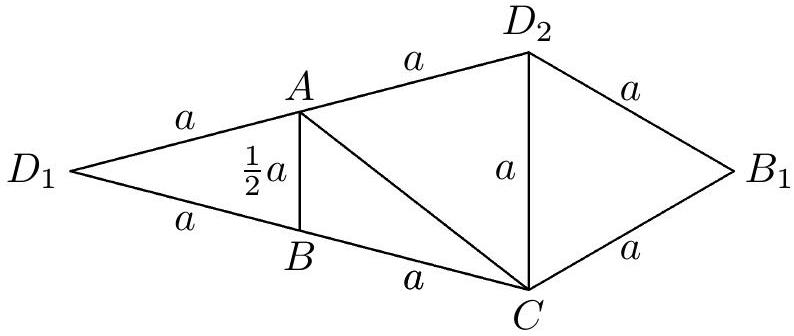
Fig. 8b
Answer. The sought tetrahedron is unique: its three edges of length $a$ emanate from one vertex, the edges of the opposite face have lengths $a, \frac{1}{2}a, \frac{1}{2}a\sqrt{6}$. One of the nets of this tetrahedron has the shape of a kite with sides $a, a, 2a, 2a. ^{6}$[^0]
[^0]: 5 In the case $w = z$, the "kite-shaped" net from Fig. 6a has a right angle at vertex $C$, so it is not a kite but a triangle.
6 We recommend that solvers cut out such a kite from paper and then fold the model of the tetrahedron.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Assume that for positive real numbers $a, b, c, d$ the following holds:
$$
a b+c d=a c+b d=4 \quad \text { and } \quad a d+b c=5 .
$$
Find the smallest possible value of the sum $a+b+c+d$ and determine which quadruples $a, b, c, d$ achieve it.
The regional round of category A takes place
## on Tuesday, January 17, 2012
so that it starts in the morning and contestants have 4 hours of clean time to solve the problems. Contestants can earn 6 points for each problem, and a successful solver is a student who scores 10 points or more. Allowed aids are writing and drawing supplies and school MF tables. Calculators, laptops, and any other electronic aids are not allowed. These details will be communicated to the students before the start of the competition.
|
4. Since the given equations contain mixed products of variables, it will be advantageous to examine the square of the sum $a+b+c+d$. By rearrangement and substitution of the given equations, we get
$$
\begin{aligned}
(a+b+c+d)^{2} & =a^{2}+b^{2}+c^{2}+d^{2}+2(ab+cd+ac+bd+ad+bc)= \\
& =a^{2}+b^{2}+c^{2}+d^{2}+2(4+4+5)=a^{2}+d^{2}+b^{2}+c^{2}+26 .
\end{aligned}
$$
Now we will use the known inequalities $a^{2}+d^{2} \geqq 2ad, b^{2}+c^{2} \geqq 2bc$, where equality holds if and only if $a=d$ and $b=c$. Based on this, from (1) we get
$$
(a+b+c+d)^{2} \geqq 2ad+2bc+26=2 \cdot 5+26=36 .
$$
Therefore, for such positive numbers $a, b, c, d$, we have $a+b+c+d \geqq \sqrt{36}=6$, with equality holding if and only if $a=d$ and $b=c$. Substituting into the original equations, we get the system
$$
2ab=4, \quad a^{2}+b^{2}=5 .
$$
This can be solved in several ways. For example, we can express
$$
(a+b)^{2}=a^{2}+b^{2}+2ab=5+4=9
$$
thus $a+b=3$ (since $a, b>0$). According to Vieta's formulas, $a, b$ are the roots of the quadratic equation $x^{2}-3x+2=0$, hence $\{a, b\}=\{1,2\}$. It is easy to verify that the quadruples $a=d=1$, $b=c=2$, or $a=d=2, b=c=1$ indeed satisfy the given equations and for them $a+b+c+d=6$.
Answer. The smallest possible value of the sum $a+b+c+d$ is 6, and it is achieved only by the quadruples $(1,2,2,1)$ and $(2,1,1,2)$.
Alternative Solution. From the equation $ab+cd=ac+bd$ it follows that $a(b-c)=d(b-c)$, so either $a=d$ or $b=c$. Considering the symmetry, we can only consider the quadruples $(a, b, c, d)$ where $d=a$, and find the smallest value of the sum $S=2a+b+c$ under the assumption that the positive numbers $a, b, c$ satisfy the equations $a(b+c)=4$ and $a^{2}+bc=5$.
According to Vieta's formulas, the positive numbers $b, c$ are the roots of the quadratic equation
$$
x^{2}-\frac{4}{a}x+(5-a^{2})=0
$$
This equation has two positive (not necessarily distinct) roots if and only if its discriminant
$$
D=\frac{16}{a^{2}}-4(5-a^{2})=\frac{4(a^{2}-1)(a^{2}-4)}{a^{2}}
$$
is non-negative and if, in addition to the inequality $a>0$, we also have $a^{2} \leq 1$ or $a^{2} \geq 4$. This means that $\min S=6$ and that $(1,2,2,1)$ and $(2,1,1,2)$ are the only quadruples providing the found minimum (since in both of them $b=c$, no other such quadruples - given the restriction of our considerations to the first of the possibilities $a=d, b=c$ - exist). From the expression for the difference $S-6$ in the form
$$
S-6=2a+b+c-6=2a+\frac{4}{a}-6=\frac{2(a-1)(a-2)}{a}
$$
we see that the desired inequality $S>6$ indeed holds for every $a \in (0,1) \cup (2, \sqrt{5})$.
For a complete solution, award 6 points, of which 4 points for estimating $a+b+c+d \geqq 6$ and 2 points for determining the quadruples for which equality holds.
If the solver uses the AG-inequalities $a^{2}+b^{2} \geqq 2ab, c^{2}+d^{2} \geqq 2cd$ in (1) and thus derives the weaker estimate $a+b+c+d \geqq \sqrt{34}$, award 2 points.
In the case of the second solution, award 1 point for deriving the equation $(a-d)(b-c)=0$, 1 point for transitioning to solving the system of two unknowns $b, c$ with parameter $a$, 2 points for finding the set of admissible values of $a$ (or at least deriving the necessary condition $a \leqq 1 \vee a \geqq 2$), 1 point for proving the inequality $2a+4/a \geqq 6$ for all admissible $a$, and 1 point for determining both sought quadruples.
If the student only guesses the result and finds the quadruples $(1,2,2,1)$ and $(2,1,1,2)$, award 1 point (this point should only be awarded if the student does not earn any other points in the problem).
[^0]: 1 Numbers having only twos and threes on the remaining $n-1$ places will be counted, as they already have the required at least one digit 1 in the units place.
2 When filling in the table, we do not need to laboriously divide $10^{n}-1$ by seven. It is sufficient to use the fact that $10^{n+1}$ gives the same remainder when divided by seven as 10 times the remainder of $10^{n}$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On the board, we will write ten different natural numbers. In each step, we first underline each number that is not the sum of any two different numbers written on the board, and then erase all underlined numbers. For example:
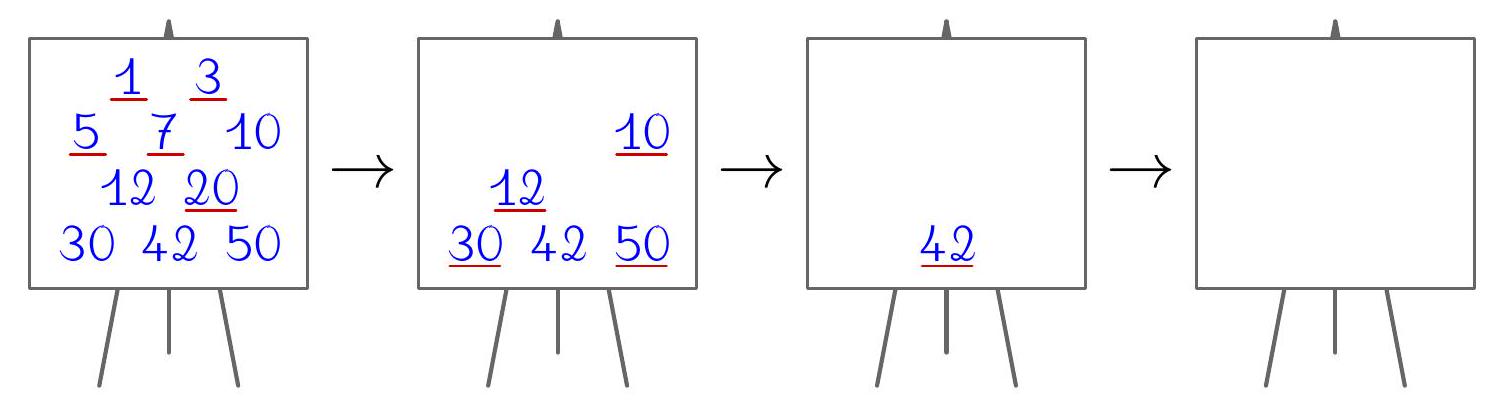
a) Prove that for any ten written numbers, the board will be empty after a finite number of steps.
b) Determine the maximum number of steps after which the board may still not be empty. Provide an example of ten numbers for which this maximum is achieved.
(Patrik Bak)
|
SOLUTION. a) According to the problem statement, all numbers on the board are positive and distinct. In each step, we will certainly underline the smallest number on the board, and - if it is not the only one - also the second smallest number, as it cannot equal the sum of two different numbers on the board. Since we erase at least one number in each step, after a finite number of steps, the board will be empty, as we were to prove.
b) First, note that the board will be empty after no more than 5 steps. This is evident from part a) if in no step only one number is erased. A step $\mathrm{s}$ with one erased number, however, can only be the last one; there can then be no more than 4 previous steps.
Now we will provide an example of ten initial numbers for which the board will not be empty after the fourth step. This will certainly happen if in each of the four steps only two numbers are erased (the smallest ones). For this to happen, each larger number (i.e., from the third smallest onward) must always equal the sum of two different (smaller) numbers that are still on the board. This motivates us to consider a sequence of natural numbers where each subsequent number equals the sum of the two preceding numbers. If we choose, for example, 1 and 2 as the first two numbers, the third number will be $1+2=3$, the fourth $2+3=5$, etc. Let's write down the first ten of these numbers (which are called Fibonacci numbers and play a significant role in various areas of mathematics and its applications):
$$
1,2,3,5,8,13,21,34,55,89
$$[^0]
If these numbers are written on the board at the beginning, then in each of the four steps, we will clearly erase only two numbers. Let's confirm this with the steps written out:
$$
\begin{aligned}
(\underline{1}, \underline{2}, 3,5,8,13,21,34,55,89) & \rightarrow(\underline{3}, \underline{5}, 8,13,21,34,55,89) \rightarrow \\
& \rightarrow(\underline{8}, \underline{13}, 21,34,55,89) \rightarrow(\underline{21}, \underline{34}, 55,89) \rightarrow(\underline{55}, \underline{89}) .
\end{aligned}
$$
This solves part b) as well: The largest number of steps is 4.
## GUIDING AND ADDITIONAL PROBLEMS:
We will only deal with the topic of the competition problem.
N1. After how many steps will the board be empty if the five smallest natural numbers are written on it at the beginning? [After two steps. In the first step, we erase the numbers 1 and 2, in the second step, the remaining numbers $3,4,5$.]
N2. What is the minimum number of natural numbers that can be written on the board if we want the board to be empty only after two steps? [If there are no more than two numbers on the board, it will clearly be empty after the first step. Three written numbers sometimes lead to two steps in general, this is the triplet $(a, b, c)$, where $c=a+b$. In more detail: If we want the board to not be empty after the first step, one of the written numbers $c$ must be the sum of some other numbers $a$ and $b$ satisfying $a \neq b$. Since all numbers in the equation $c=a+b$ are positive, we have in addition to $a \neq b$ also $c>a$ and $c>b$. Therefore, at least three numbers must be written on the board, such as $(1,2,3)$.]
N3. Solve the variant of the competition problem where we will underline and subsequently erase exactly those numbers that are not the product of any two different numbers written on the board. [If the number 1 is on the board, it will be erased as the only one in the first step. Otherwise, in each step, the two smallest numbers will be among the erased ones - the only exception can be the last step, if at that time there is only one number on the board. From the mentioned observations, it follows that the board will be empty after no more than 6 steps. After 5 steps, it does not have to be empty, as shown by the example of initial numbers $1,2,3,6,18, \ldots$, where each number starting from the fourth is equal to the product of two preceding numbers. The largest number of steps is therefore 5.]
D1. At the beginning, we can write any seven different natural numbers on the board, including the numbers 1 and 2. Find all such sevens for which the board will not be empty after three steps. [Such sevens are four: $(1,2,3,4,7,10,17),(1,2,3,4,7,11,18)$, $(1,2,3,5,8,11,19)$ and $(1,2,3,5,8,13,21)$. In each step, we must erase only the two smallest numbers. Let's arrange the numbers in ascending order. The third number must then be $1+2=3$, the fourth $1+3=4$ or $2+3=5$. Similarly, after the numbers 3,4, the numbers 7,10 or 7,11 must follow, and after the numbers 3,5, the numbers 8,11 or 8,13. The last seventh number must be the sum of the fifth and sixth numbers.]
D2. How would the conclusions of the competition problem change if any ten different integers were written on the board at the beginning? [Even the statement from part a) would no longer hold, consider, for example, the ten numbers $(-3,-2,-1,0,1,2,3,4,5,6)$, in which no number will be underlined, and thus not erased.]
D3. Suppose we have some initial ten different natural numbers for which the board will not be empty after four steps. Can the largest number in such a ten be equal to 35? [It can:
$$
\begin{aligned}
(\underline{1}, \underline{2}, 3,4,7,10,11,17,18,35) & \rightarrow(\underline{3}, \underline{4}, 7,10,11,17,18,35) \rightarrow \\
& \rightarrow(\underline{7}, \underline{10}, \underline{11}, 17,18,35) \rightarrow(\underline{17}, \underline{18}, 35) \rightarrow(\underline{35}) .]
\end{aligned}
$$
|
4
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. Find all integers $n>2$ such that the number $n^{n-2}$ is the $n$-th power of an integer.
(Patrik Bak)
|
SOLUTION. We will show that only $n=4$ satisfies the condition. For brevity, we will use "n-th power" instead of "n-th power of an integer" throughout the solution.
A positive integer is an $n$-th power if and only if each prime number in its prime factorization appears with an exponent that is a multiple of $n$. Therefore, if two integers are both $n$-th powers and their quotient is an integer, then this quotient must also be an $n$-th power. Applying this statement to the $n$-th powers $n^{n}$ and $n^{n-2}$ (as given in the problem), we get that the number $n^{n} / n^{n-2}=n^{2}$ is also an $n$-th power.
Below, we will prove that for every integer $n \geqq 5$, the inequalities $1^{n} < 2^{n-1}$ and $2^{n-1} < 3^{n-2}$ hold (the first inequality is obvious for $n \geqq 2$). We will prove the second inequality by mathematical induction.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. If a, b, c are distinct positive real numbers, what is the smallest possible number of distinct numbers among the numbers $a+b, b+c, c+a, ab, bc, ca, abc$?
(Patrik Bak)
|
SOLUTION. Since $a, b, c$ are distinct positive numbers, so are the numbers $a b, b c, c a$, because, for example, from $a b=b c$ it follows that $a=c$ (thanks to $b \neq 0$). We see, then, that in the examined septet of numbers $a+b, b+c, c+a, a b, b c, c a, a b c$ there are at least 3 different values. We will first prove by contradiction that exactly 3 values can never be. Then we will provide an example of the examined septet, which is composed of only 4 different values.
First, let us assume that in some septet there are exactly 3 different values. We know that these are the values of the three products $a b, b c, c a$, and so the product $a b c$ must equal one of them. This means that one of the numbers $a, b, c$ is equal to 1, because, for example, from $a b c=a b$ it follows that $c=1$.
Without loss of generality, we will further limit ourselves to the case $c=1$. The septet in question with three different values can then be reduced to a sextet of the same property, which is composed of the numbers
$$
a+b, a+1, b+1, a b, a, b
$$
(we have substituted $c=1$ and omitted the number $a b c$ equal to $a b$). Since the equalities $a=1$ and $b=1$ have already been ruled out, the three different values are represented both in the first triplet $a+b, a+1, b+1$ and in the second triplet $a b, a, b$. Both numbers $a, b$ from the second triplet, therefore, must lie in the set $\{a+b, a+1, b+1\}$. This can only be achieved if $a=b+1$ and simultaneously $b=a+1$, which is impossible. The proof by contradiction is complete.
As we have promised, in the second part of the solution, we will provide an example of the examined septet, which is composed of 4 different values. According to the previous observations, it is worthwhile to examine the situation where, for example, $c=1$ and at the same time $b=a+1$. Then we have
$(a+b, b+c, c+a)=(2 a+1, a+2, a+1) \quad$ and $\quad(a b, b c, c a, a b c)=\left(a^{2}+a, a+1, a, a^{2}+a\right)$.
It is enough to find such a positive number $a \neq 1$ so that in the quintet of numbers
$$
a, a+1, a+2,2 a+1, a^{2}+a
$$
there are only four different values. Considering the obvious inequalities that hold between these five numbers for the considered $a$, the requirement can be met in exactly two ways. They are expressed by the equations
$$
a^{2}+a=2 a+1, \quad \text { resp. } \quad a^{2}+a=a+2 .
$$
Both actually lead to suitable triplets, which are of the form
$$
(a, b, c)=\left(\frac{1+\sqrt{5}}{2}, \frac{3+\sqrt{5}}{2}, 1\right), \quad \text { resp. } \quad(a, b, c)=(\sqrt{2}, 1+\sqrt{2}, 1) \text {. }
$$
Conclusion. The smallest possible number of different numbers in the examined septet is equal to 4.
Note. If we do not distinguish triplets $(a, b, c)$ that differ only in the order of their elements, there are two more admissible triplets for which only 4 different values can be found in the examined septet. The first of them is the triplet
$$
(a, b, c)=\left(a, \frac{a}{a-1}, \frac{a}{(a-1)^{2}}\right)
$$
where $a>0$ is the only real root of the cubic equation $a^{3}-4 a^{2}+4 a-2=0$. The second suitable triplet is
$$
(a, b, c)=\left(a, \frac{a}{a^{2}-a-1}, \frac{a(a-1)}{a^{2}-a-1}\right)
$$
where $a$ is the larger of the two positive roots of the equation $a^{4}-2 a^{3}-2 a^{2}+2 a+2=0$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. For any four-element subset $\mathrm{P}$ of the set $\{1,2,3, \ldots, 12\}$, denote
$$
\mathrm{Q}=\{3 x: x \in \mathrm{P}\} \quad \text { and } \quad \mathrm{R}=\{4 x: x \in \mathrm{P}\} \text {. }
$$
Determine the number of such sets $P$ for which the numbers from $P, Q, R$ give all possible non-zero remainders when divided by 13.
(Jaromír Šimša)
|
Solution. We will calculate with all numbers modulo 13, i.e., as remainders upon division by 13. Furthermore, it is clear that not only the set $P$, but also the derived sets $Q$ and $R$ are four-element sets. Therefore, if the three mentioned sets are to contain all non-zero remainders modulo 13, of which there are twelve, they must be mutually disjoint.
Let $\mathrm{P}$ be any set satisfying the conditions of the problem and let $x \in \mathrm{P}$. Then from the incidences $3 x \in \mathrm{Q}$ and $4 x \in \mathrm{R}$ it follows that the number $12 x=3 \cdot 4 x=4 \cdot 3 x$ does not belong to $\mathrm{Q}$ nor to $\mathrm{R}$, because $4 x$ and $3 x$ do not belong to $\mathrm{P}$ and every two different numbers have different triplets and different quadruplets. Therefore, $12 x \in \mathrm{P}$ and also
$$
3 \cdot 12 x=10 x \in \mathrm{Q} \quad \text { and } \quad 4 \cdot 12 x=9 x \in \mathrm{R} .
$$
The six numbers $(x, 4 x, 3 x, 12 x, 9 x, 10 x)$, arranged as ( $\mathrm{P}, \mathrm{R}, \mathrm{Q}, \mathrm{P}, \mathrm{R}, \mathrm{Q})$, have the additional property, which is easy to verify, that each of its subsequent members is (modulo 13) the quadruple of the previous number, which is also true cyclically, i.e., for the last and the first member.
All numbers from 1 to 12 form two cyclic sextets of the described type
$$
(1,4,3,12,9,10) \quad \text { and } \quad(2,8,6,11,5,7)
$$
and to determine a suitable set $\mathrm{P}$, it is sufficient to specify which of the three used colors the numbers in $\mathrm{P}$ have - independently in each of the two sextets. The sought number is therefore equal to $3 \times 3=9$.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Determine the number of all triples of two-digit natural numbers $a, b, c$, whose product $abc$ has a representation in which all digits are the same. Triples differing only in the order of the numbers are considered the same, i.e., they are counted only once.
|
SOLUTION. For two-digit numbers $a, b, c$, the product $abc$ is a four-digit, five-digit, or six-digit number. If all the digits of the number $abc$ are equal to the same digit $k$, one of the equalities $abc = k \cdot 1111, abc = k \cdot 11111$, or $abc = k \cdot 111111, k \in \{1,2, \ldots, 9\}$ holds.
The numbers $1111 = 11 \cdot 101$ and $11 \cdot 111 = 41 \cdot 271$ have three-digit prime numbers in their factorization, so they cannot be the product of two-digit numbers. Therefore, the only remaining possibility is:
$$
abc = k \cdot 111111 = k \cdot 3 \cdot 7 \cdot 11 \cdot 13 \cdot 37
$$
Let's see how the prime numbers $3, 7, 11, 13, 37$ can be distributed among the individual factors $a, b, c$. Since the products $37 \cdot 3$ and $3 \cdot 7 \cdot 11$ are greater than 100, the prime number 37 must be a factor on its own, and the remaining four prime numbers $3, 7, 11, 13$ must be divided into pairs. Since the product $11 \cdot 13$ is also greater than 100, the only possible distributions are the factors $3 \cdot 11, 7 \cdot 13$, and 37, or the factors $3 \cdot 13, 7 \cdot 11$, and 37. We then add the possible factors from the factorization of the digit $k$ and get two types of solutions:
$$
\begin{array}{ll}
a = 33k_1, b = 91, c = 37k_2, & \text{where } k_1 \in \{1,2,3\}, k_2 \in \{1,2\}, \\
a = 39k_1, b = 77, c = 37k_2, & \text{where } k_1 \in \{1,2\}, k_2 \in \{1,2\},
\end{array}
$$
The number of triples of numbers $a, b, c$ we are looking for is therefore $3 \cdot 2 + 2 \cdot 2 = 10$.
GUIDING PROBLEMS:
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
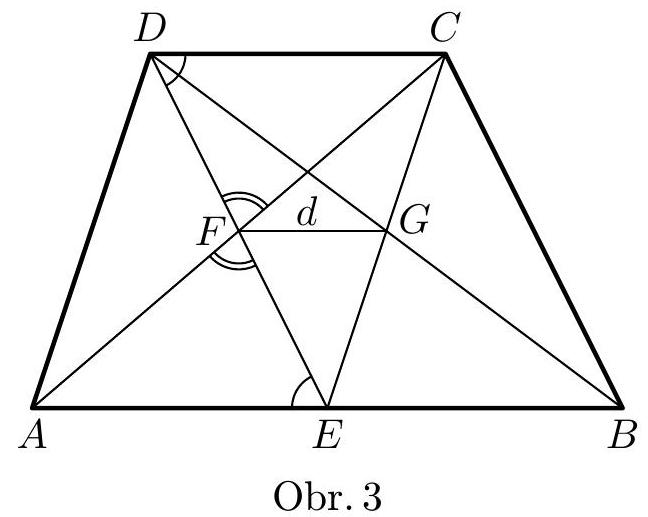
3. Given a trapezoid $A B C D$ with bases $A B$ and $C D$. Let $E$ be the midpoint of side $A B$, $F$ the midpoint of segment $D E$, and $G$ the intersection of segments $B D$ and $C E$. Express the area of trapezoid $A B C D$ in terms of its height $v$ and the length of segment $F G$, assuming that points $A, F, C$ lie on a straight line.
|
SOLUTION. According to the problem, angles $E F D$ and $A F C$ are right angles, so we have (Fig. 3)
$$
\begin{aligned}
& |\Varangle C D F|=|\Varangle A E F| \quad \text { (alternate interior angles), } \\
& |\Varangle C F D|=|\Varangle A F E| \quad \text { (vertical angles). }
\end{aligned}
$$
Furthermore, point $F$ bisects segment $D E$, so $|D F|=|E F|$ and triangles $C D F$ and $A E F$ are congruent by the SAS (Side-Angle-Side) theorem. Therefore, $|C D|=|A E|$, and together with the equality $|A E|=|E B|$, it follows that $E B$ and $D C$ are two congruent and parallel segments. This means that quadrilateral $E B C D$ is a parallelogram. The intersection $G$ of its diagonals therefore bisects each of them. Points $F$ and $G$ are the midpoints of sides $A C$ and $E C$ of triangle $A E C$, so segment $F G$ is its midline and $|A E|=2|F G|$. Therefore:
$$
|A B|=2|A E|=4 d \quad \text { and } \quad|C D|=|A E|=2 d \text {. }
$$
The area of trapezoid $A B C D$ is $S=\frac{1}{2}(|A B|+|C D|) v=3 d v$.
## PRACTICE PROBLEMS:
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. For any natural number $n$, let us form all possible "words" of length $n$ from the letters $A$ and $B$, and let $p_{n}$ denote the number of those words that do not contain the quadruple $AAAA$ of consecutive letters $A$, nor the triple $BBB$ of consecutive letters $B$. Determine the value of the expression
$$
\frac{p_{2004}-p_{2002}-p_{1999}}{p_{2001}+p_{2000}}
$$
(R. Kučera)
|
Solution. Let the number of suitable words of length $n$ ending with the letter $A$, respectively $B$, be denoted by $a_{n}$, respectively $b_{n}$. Then
$$
p_{n}=a_{n}+b_{n} \text {. }
$$
Let $n \geqq 4$. A suitable word ending with the letter $A$ has one of the endings $B A, B A A$, or $B A A A$. The number of words of the first type is $b_{n-1}$, of the second type $b_{n-2}$, and of the third type $b_{n-3}$. Therefore,
$$
a_{n}=b_{n-1}+b_{n-2}+b_{n-3} .
$$
Similarly, for $n \geqq 3$, a suitable word ending with the letter $B$ has one of the endings $A B$, $A B B$, thus
$$
b_{n}=a_{n-1}+a_{n-2} .
$$
Now let $n \geqq 6$; each of the numbers $b_{i}$ in relation (2) can be expressed using (3), giving us
$$
\begin{aligned}
a_{n} & =b_{n-1}+b_{n-2}+b_{n-3}= \\
& =\left(a_{n-2}+a_{n-3}\right)+\left(a_{n-3}+a_{n-4}\right)+\left(a_{n-4}+a_{n-5}\right)= \\
& =a_{n-2}+2 a_{n-3}+2 a_{n-4}+a_{n-5} .
\end{aligned}
$$
Similarly, we get
$$
\begin{aligned}
b_{n} & =a_{n-1}+a_{n-2}= \\
& =\left(b_{n-2}+b_{n-3}+b_{n-4}\right)+\left(b_{n-3}+b_{n-4}+b_{n-5}\right)= \\
& =b_{n-2}+2 b_{n-3}+2 b_{n-4}+b_{n-5} .
\end{aligned}
$$
By adding equations (4) and (5), we get from (1)
$$
p_{n}=p_{n-2}+2 p_{n-3}+2 p_{n-4}+p_{n-5} \text {. }
$$
Therefore, for any natural number $n \geqq 6$,
$$
\frac{p_{n}-p_{n-2}-p_{n-5}}{p_{n-3}+p_{n-4}}=2,
$$
thus the given fraction has the value 2 even for $n=2004$.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a segment $A B$. Construct a point $C$ such that the area of triangle $A B C$ equals $1 / 8$ of the area $S$ of a square with side $A B$, and the sum of the areas of squares with sides $A C$ and $B C$ equals $S$. How many solutions does the problem have for a given placement of segment $A B$ in the plane?
The school-based written part of the first round of category C takes place
on Tuesday, January 25, 2005
so that it starts in the morning and the contestants have 4 hours of clean time to solve the problems. Contestants can earn 6 points for each problem, and a successful solver is a student who scores 10 points or more. These details will be communicated to the students before the competition begins. Allowed aids are writing and drawing tools, school MF tables, and calculators without a graphical display.
|
3. The condition that the area of triangle $ABC$ is to equal $\frac{1}{8}$ of the area $S$ of the square with side $AB$ means that the height of triangle $ABC$ to side $AB$ has a length of $\frac{1}{4}|AB|$, so point $C$ must lie on one of the two lines parallel to line $AB$ and at a distance of $\frac{1}{4}|AB|$ from line $AB$.
The condition that the sum of the areas of the squares with sides $AC$ and $BC$ is to equal the area of the square with side $AB$ means, according to the Pythagorean theorem for triangle $ABC$, that this triangle is a right triangle with hypotenuse $AB$, so point $C$ must lie on the circle with center at the midpoint of hypotenuse $AB$ and radius $\frac{1}{2}|AB|$.
The construction of point $C$ is therefore simple. Both mentioned parallel lines will intersect the circle above the diameter $AB$ at four points (Fig. 1). Since this is a positional problem, the problem has four solutions.
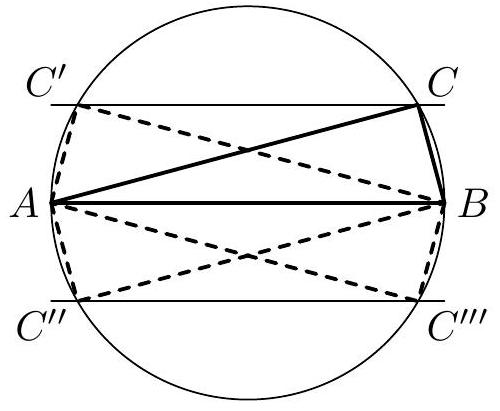
Fig. 1
For a complete solution, 6 points are awarded, of which 2 points are for correctly determining the number of solutions. For identifying that point $C$ lies on the specified parallel lines to line $AB$, award 2 points. For proving that point $C$ lies on the Thales' circle above the diameter $AB$, award 2 points. For stating that the problem has two solutions, award 1 point; for stating that the problem has four solutions, award 2 points. If no number of solutions is given, do not award the 2 points designated for this purpose.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Let $\tau(k)$ denote the number of all positive divisors of a natural number $k$, and suppose the number $n$ is a solution to the equation $\tau(1.6 n)=1.6 \tau(n)$. Determine the value of the ratio $\tau(0.16 n): \tau(n)$.
|
SOLUTION. If the prime factorization of the number $n$ is $n=\prod_{i=1}^{k} p_{i}^{s_{i}},$ where $p_{1}, \ldots, p_{k}$ are distinct primes and $s_{1}, \ldots, s_{k}$ are non-negative integers, the number of its positive divisors is $\tau(n)=\prod_{i=1}^{k}\left(s_{i}+1\right)$. If $n=2^{\alpha} 5^{\beta} n^{\prime}$ where $\beta \geqq 1$ and $n^{\prime}$ is coprime with $2 \cdot 5$, we can rewrite the given equation as
$$
(\alpha+4) \beta \tau\left(n^{\prime}\right)=\frac{8}{5}(\alpha+1)(\beta+1) \tau\left(n^{\prime}\right),
$$
which, after simplification, gives the equation
$3 \beta(\alpha-4)+8(\alpha+1)=3 \beta(\alpha-4)+8(\alpha-4)+40=(3 \beta+8)(\alpha-4)+40=0$.
From this, it follows that
$$
(3 \beta+8)(4-\alpha)=40=1 \cdot 40 .
$$
However, given that $3 \beta+8 \geqq 11$ and the number $3 \beta+8$ gives a remainder of 2 when divided by 3, the only factorization of the number 40 that satisfies this is
$$
3 \beta+8=20, \quad 4-\alpha=2
$$
thus $\alpha=2, \beta=4, n=2^{2} \cdot 5^{4} n^{\prime}$.
For the ratio $\tau(0.16 n): \tau(n)$, we get
$$
\frac{\tau\left(\frac{4}{25} n\right)}{\tau(n)}=\frac{\tau\left(2^{4} \cdot 5^{2}\right)}{\tau\left(2^{2} \cdot 5^{4}\right)}=\frac{5 \cdot 3}{3 \cdot 5}=1
$$
GUIDING PROBLEMS:
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let a regular n-gon be denoted as $A_{1} A_{2} \ldots A_{n}$. The point $A_{3}$ is reflected over the axis $A_{2} A_{4}$, resulting in the point $A_{3}^{\prime}$. Then, the point $A_{3}^{\prime}$ is reflected over the axis $A_{1} A_{3}$, resulting in the point $A_{3}^{\prime \prime}$. For which $n \geqq 4$ is the point $A_{3}^{\prime \prime}$ identical to the intersection of the lines $A_{1} A_{2}$ and $A_{3} A_{4}$?
(Jaroslav Zhouf)
|
SOLUTION. Let $S$ be the center of the circle circumscribed around the $n$-gon $A_{1} A_{2} \ldots A_{n}$. Since the central angle $A_{i} S A_{i+1}$ is equal to $\frac{360^{\circ}}{n}$ for each $i=1, \ldots, n-1$, all the acute inscribed angles over the chords $A_{i} A_{i+1}$ have a size of $\frac{180^{\circ}}{n}$. Four of them are marked in red in the diagram. For $n=4$, the sum of the sizes of these 4 red angles is $180^{\circ}$, and thus the lines $A_{1} A_{2}$ and $A_{3} A_{4}$ are parallel, which excludes the smallest value $n=4$. For further considered $n \geq 5$, the sum of the sizes of the four red angles is less than $180^{\circ}$, so the intersection of the lines $A_{1} A_{2}$ and $A_{3} A_{4}$ lies on the "converging" rays $A_{1} A_{2}$ and $A_{4} A_{3}$ as shown in Figure 1.
According to the two congruent red angles at vertex $A_{4}$, the ray $A_{4} A_{2}$ is the angle bisector of $\angle A_{3} A_{4} A_{1}$, and thus the point $A_{3}^{\prime}$ (the image of $A_{3}$ under reflection over $A_{4} A_{2}$) lies on the ray $A_{4} A_{1}$, and, as suggested by Figure 1 and as will be further utilized, inside the segment $A_{4} A_{1}$. Indeed, the necessary inequality $\left|A_{3} A_{4}\right| < \left|A_{1} A_{4}\right|$ follows from triangle $A_{1} A_{3} A_{4}$, in which, due to our assumption $n \geq 5$, we have
$$
\left|\angle A_{4} A_{1} A_{3}\right| = \frac{180^{\circ}}{n} < (n-3) \cdot \frac{180^{\circ}}{n} = 180^{\circ} - \frac{3 \cdot 180^{\circ}}{n} = \left|\angle A_{1} A_{3} A_{4}\right| .
$$
Similarly, from the congruent angles at vertex $A_{1}$, it follows that the point $A_{3}^{\prime \prime}$ (the image of $A_{3}^{\prime}$ under reflection over $A_{1} A_{3}$) lies on the ray $A_{1} A_{2}$. Since this holds for any $n \geq 5$, our task is to determine when the point $A_{3}^{\prime \prime}$ also lies on the ray $A_{4} A_{3}$, or when the angle $\angle A_{3}^{\prime \prime} A_{3} A_{4}$ is a right angle.
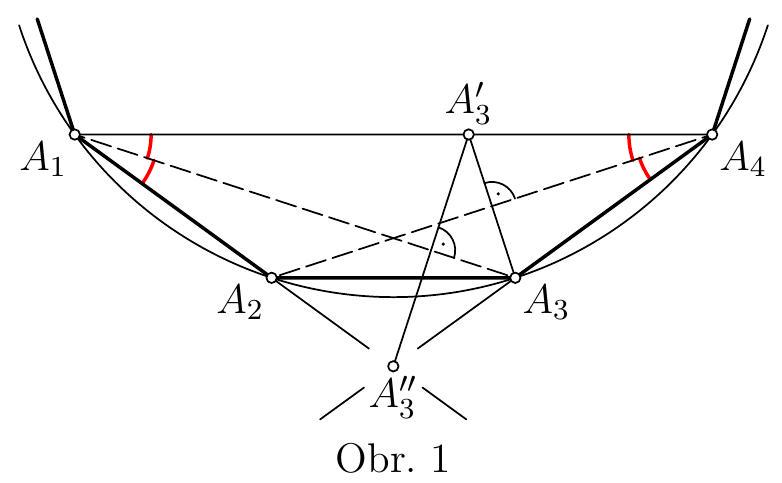
From the isosceles triangle $A_{3} A_{3}^{\prime} A_{4}$, we have $\left|\angle A_{3}^{\prime} A_{3} A_{4}\right| = 90^{\circ} - \frac{180^{\circ}}{n}$, and thus
$$
\begin{aligned}
\left|\angle A_{1} A_{3} A_{3}^{\prime}\right| & = \left|\angle A_{1} A_{3} A_{4}\right| - \left|\angle A_{3}^{\prime} A_{3} A_{4}\right| = \\
& = \left(180^{\circ} - \frac{3 \cdot 180^{\circ}}{n}\right) - \left(90^{\circ} - \frac{180^{\circ}}{n}\right) = 90^{\circ} - \frac{360^{\circ}}{n} .
\end{aligned}
$$
The determined angle $\angle A_{1} A_{3} A_{3}^{\prime}$ is congruent to the symmetrically associated angle $\angle A_{1} A_{3} A_{3}^{\prime \prime}$, so the angle $\angle A_{3}^{\prime \prime} A_{3} A_{3}^{\prime}$ has twice the size. We now have everything prepared for the necessary expression of the angle $\angle A_{3}^{\prime \prime} A_{3} A_{4}$:
$$
\begin{aligned}
& \left|\angle A_{3}^{\prime \prime} A_{3} A_{4}\right| = \left|\angle A_{3}^{\prime \prime} A_{3} A_{3}^{\prime}\right| + \left|\angle A_{3}^{\prime} A_{3} A_{4}\right| = 2 \cdot \left|\angle A_{1} A_{3} A_{3}^{\prime}\right| + \left|\angle A_{3}^{\prime} A_{3} A_{4}\right| = \\
& \quad = 2 \cdot \left(90^{\circ} - \frac{360^{\circ}}{n}\right) + \left(90^{\circ} - \frac{180^{\circ}}{n}\right) = 3 \cdot 90^{\circ} - \frac{5 \cdot 180^{\circ}}{n} = \frac{(3 n - 10) \cdot 180^{\circ}}{2 n} .
\end{aligned}
$$
The last expression clearly has the required value of $180^{\circ}$ if and only if $3 n - 10 = 2 n$ or $n = 10$. Thus, only for this $n$ does the point $A_{3}^{\prime \prime}$ lie on both lines $A_{1} A_{2}$ and $A_{3} A_{4}$.
Conclusion. The only number $n$ that satisfies the condition is 10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. For the sequence $\left(a_{n}\right)_{n=1}^{\infty}$, we know that for all natural numbers $n$,
$$
a_{n+1}=\frac{a_{n}^{2}}{a_{n}^{2}-4 a_{n}+6} .
$$
a) Find all values of $a_{1}$ for which this sequence is constant.
b) Let $a_{1}=5$. Determine the greatest integer not exceeding $a_{2018}$. (Vojtech Bálint)
|
SOLUTION. a) Suppose the sequence $\left(a_{n}\right)_{n=1}^{\infty}$ is constant. Then it must hold that $a_{2}=a_{1}$, which we can write using the relation from the problem as
$$
a_{1}=\frac{a_{1}^{2}}{a_{1}^{2}-4 a_{1}+6}
$$
We can easily rearrange this equation to $a_{1}\left(a_{1}-2\right)\left(a_{1}-3\right)=0$. From this, we get that $a_{1} \in\{0,2,3\}$. It is clear that for these values of $a_{1}$, the sequence $\left(a_{n}\right)_{n=1}^{\infty}$ is indeed constant and all its terms are equal to $a_{1}$. Formally, we could prove this by mathematical induction.
b) Let $a_{1}=5$. We will compute a few more terms of the sequence $\left(a_{n}\right)$. We get $a_{2} \approx 2.27, a_{3} \approx 2.49, a_{4} \approx 2.77$, etc. From this, we can infer that for all $n \geqq 2$ it holds that $20 \\
& a_{n+1}-2=\frac{a_{n}^{2}}{a_{n}^{2}-4 a_{n}+6}-2=\frac{\left(6-a_{n}\right)\left(a_{n}-2\right)}{\left(a_{n}-2\right)^{2}+2}>0
\end{aligned}
$$
This proves both inequalities $2<a_{n+1}<3$, so the proof by mathematical induction is complete. It follows that $2<a_{2018}<3$, from which it follows that the greatest integer not exceeding $a_{2018}$ is 2.
GUIDING AND SUPPLEMENTARY PROBLEMS:
N1. For the sequence $\left(b_{n}\right)_{n=1}^{\infty}$, we know that for all natural numbers $n$ it holds that $b_{n+1}=b_{n}^{2}-2$. Find all values of $b_{1}$ for which all terms of $\left(b_{n}\right)_{n=1}^{\infty}$ are equal to $b_{1}$. [From the relation for $n=1$ we get $b_{1}=b_{1}^{2}-2$, from which $b_{1} \in\{-1,2\}$. We then verify that these values satisfy the condition.]
N2. For the sequence $\left(b_{n}\right)_{n=1}^{\infty}$, we know that $b_{1}=1$ and that for all natural numbers $n$ it holds that $b_{n+1}=3 b_{n} /\left(b_{n}+1\right)$. Prove that all terms of the sequence are in the interval $\langle 1,2)$. [Verify by mathematical induction that for all natural $n$ the inequalities $1 \leqq b_{n}<2$ hold.]
D1. For the sequence $\left(b_{n}\right)_{n=1}^{\infty}$, it is known that for all natural numbers $n$ it holds that $b_{n+1}=$ $=2 b_{n}^{2} /\left(b_{n}^{2}-3\right)$. Find all values of $b_{1}$ such that the sequence $b_{2}, b_{3}, b_{4}, \ldots$ is constant. [Derive that $b_{n+1}=b_{n}$ if and only if $b_{n} \in\{-1,0,3\}$, so $b_{2}$ must be equal to one of these values. We then compute the corresponding values of $b_{1}$. The result is $b_{1} \in\{-3,-1,0,1,3\}$.]
D2. Derive the explicit expression for the sequence $\left(b_{n}\right)_{n=1}^{\infty}$ from problem N2. [Rearrange the given relation to $3 \cdot 1 / b_{n+1}=1+1 / b_{n}$. The sequence $c_{n}=1 / b_{n}$ thus satisfies the equation $3 c_{n+1}=c_{n}+1$. By substituting $c_{n}=d_{n}+1 / 2$, we eliminate the constant term and get $3 d_{n+1}=d_{n}$. The sequence $d_{n}$ is thus geometric, so we can determine its explicit form. By reverse substitution, we can find the expression for $b_{n}$. The result is $b_{n}=2 \cdot 3^{n-1} /\left(3^{n-1}+1\right)$.]
D3. The most famous recursively defined sequence is the Fibonacci sequence. It is given by the relations $f_{1}=1, f_{2}=1$ and the recursive relation $f_{n}=f_{n-1}+f_{n-2}$ for every $n \geqq 3$. Prove that $\sum_{i=1}^{n} f_{i}=f_{n+2}-1$ and $\sum_{i=1}^{n} f_{i}^{2}=f_{n} \cdot f_{n+1}$. [Proceed by mathematical induction on $n$.]
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. For any three-digit number, we determine its remainders when divided by the numbers 2, 3, 4, ..., 10 and then sum the nine resulting numbers. Find the smallest possible value of such a sum.
|
SOLUTION. Let $S(n)$ denote the sum of the mentioned remainders of the three-digit number $n$. We will explain why $S(n) \geqq 3$.
- For odd $n$, $S(n) \geqq 5$ (consider the remainders when dividing by even numbers $2,4,6,8$, 10). Hence, let $n$ be even from now on.
- If $4 \nmid n$, then $S(n) \geqq 4$ ( $n$ gives a remainder of at least 2 when divided by 4 and 8). Let $n$ be divisible by 4 from now on.
- If $8 \nmid n$, then $S(n) \geqq 4$ (remainder 4 when divided by 8). Therefore, let $n$ be divisible by 8 from now on.
- If $3 \nmid n$, then $S(n) \geqq 3$ ( $n$ gives a remainder of at least 1 when divided by $3,6,9$). Let $n$ be divisible by 8 and 3 from now on.
- If $9 \nmid n$, then $S(n) \geqq 3$ (remainder of at least 3 when divided by 9). Let $8 \mid n$ and $9 \mid n$ from now on.
- If $5 \nmid n$, then $S(n) \geqq 3$ (remainder of at least 1 when divided by 5 and at least 2 when divided by 10).
Therefore, assume that $5|n$, $8| n$, and $9 \mid n$. Then only the numbers 360 and 720 come into consideration, for which $S(360)=3$ and $S(720)=9$. This proves the inequality $S(n) \geqq 3$. At the same time, we have found that $S(n)=3$ for example for $n=360$. (It is also $S(840)=3$.)
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Determine the real number $p$ such that the equation
$$
x^{2}+4 p x+5 p^{2}+6 p-16=0
$$
has two distinct roots $x_{1}, x_{2}$ and the sum $x_{1}^{2}+x_{2}^{2}$ is minimized.
|
1. For the roots $x_{1}, x_{2}$ of the given quadratic equation (if they exist), according to Vièta's formulas, the following equalities hold:
$$
x_{1}+x_{2}=-4 p \quad \text { and } \quad x_{1} x_{2}=5 p^{2}+6 p-16
$$
from which we can compute the desired sum
$$
\begin{aligned}
x_{1}^{2}+x_{2}^{2} & =\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=(-4 p)^{2}-2\left(5 p^{2}+6 p-16\right)= \\
& =6 p^{2}-12 p+32=6(p-1)^{2}+26 .
\end{aligned}
$$
From this, the inequality $x_{1}^{2}+x_{2}^{2} \geqq 26$ follows, with equality possible only when $p=1$. We will therefore check whether for $p=1$ the given equation indeed has two distinct solutions: it is the equation $x^{2}+4 x-5=0$ with roots $x_{1}=-5$ and $x_{2}=1$. This solves the problem.
Let us add that most solvers would likely first determine for which $p$ the given equation has two distinct solutions. Since for its discriminant $D$ we have
$$
D=(4 p)^{2}-4\left(5 p^{2}+6 p-16\right)=-4 p^{2}-24 p+64=-4(p+8)(p-2),
$$
such $p$ are precisely the numbers in the interval $(-8,2)$.
Answer: The maximum value of the sum $x_{1}^{2}+x_{2}^{2}$ (equal to 26) corresponds to the single number $p=1$.
For a complete solution, 6 points are awarded, of which 4 points for expressing the sum $x_{1}^{2}+x_{2}^{2}$ as a quadratic function $6 p^{2}-12 p+32$, 1 point for finding its minimum, and 1 point for verifying that at the minimum point $p=1$ the equation indeed has two distinct roots (for example, by finding the interval $p \in(-8,2)$ from the inequality $D>0$).
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Determine the smallest values that the expression $V=(a-b)^{2}+(b-c)^{2}+(c-a)^{2}$ can take, given that the real numbers $a$, $b$, $c$ satisfy the pair of conditions
$$
\begin{aligned}
a+3 b+c & =6 \\
-a+b-c & =2
\end{aligned}
$$
|
SOLUTION. By adding both equations, we find that $b=2$. Substituting $b$ into one of them yields $c=-a$. Therefore, $V=(a-2)^{2}+(2+a)^{2}+(-2 a)^{2}$. After squaring and adding, we find that $V=6 a^{2}+8 \geqq 8$. Equality occurs precisely when $a=0, b=2$ and $c=0$.
The sought minimum value of the expression $V$ is thus equal to 8.
GUIDING AND SUPPLEMENTARY PROBLEMS:
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On the board, there is a positive integer $n$. In one step, we can erase the number on the board and write either its double, or its double increased by 1. For how many initial numbers $n$ different from 2019 can we achieve that the number 2019 appears on the board after a finite number of steps?
(Josef Tkadlec)
|
1. In one step, the current natural number $k$ is increased either to the even number $m=2k$, or to the odd number $m=2k+1$. Depending on the parity of the new number $m$, we can reconstruct the previous number $k$: either $k=m/2$, or $k=(m-1)/2$ — depending on whether $m$ is even or odd.
The odd number 2019 will thus appear on the board only after the number $(2019-1)/2=1009$. Since this is again an odd number, after two steps we will reach the target number 2019 only from the number $(1009-1)/2=504$. This is an even number, so after three steps we get 2019 only from the number $504/2=252$, etc. The entire process of determining all suitable numbers from the final 2019 leads to the following result:
$$
2019 \leftarrow 1009 \leftarrow 504 \leftarrow 252 \leftarrow 126 \leftarrow 63 \leftarrow 31 \leftarrow 15 \leftarrow 7 \leftarrow 3 \leftarrow 1 .
$$
(The number 1 is the smallest natural number, so we do not continue further.)
Answer. There are ten such initial values of the number $n$ (they are $1, 3, 7, 15, 31, 63, 126, 252, 504$, and 1009).
Alternative Solution. If we write the numbers on the board in binary, each modification of the current number $n$ consists in not erasing the number at all, but simply appending a zero (changing $n$ to $2n$) or a one (changing $n$ to $2n+1$) to the right of its representation. The number 2019 will thus be obtained after a certain number of steps precisely from such numbers whose binary representation is formed by the first few digits of the binary representation of the number 2019. Since $2^{10}=1024<2019<2048=2^{11}$, the binary representation of the number 2019 has exactly 11 digits, so there are a total of 10 initial numbers $n$ from which we get the number 2019 after one or more steps. (The smallest of these numbers is the number 1, which corresponds to the first digit of the binary representation of the number 2019; the problem does not ask for the other nine numbers.)
Note. The binary representation of the number 2019 itself does not concern us; we usually find it precisely by the sequence of modifications described in the first solution. Thus, the binary representation 11111100011 of the number 2019 is obtained when in the obtained sequence of numbers $1, 3, 7, \ldots, 1009$, 2019 we replace each odd number with a one and each even number with a zero.
For a complete solution, award 6 points, of which 4 points for a general justification that each previous number is determined by the following number, 1 point for finding all numbers down to the unit, and 1 point for formulating the correct conclusion.
The general description in the first paragraph of the solution is not necessary (nor is the final note about the smallest natural number 1); the solver can start the backward process directly by determining the number 1009 from the number 2009 and continue further. However, if they make a numerical error in the step-by-step calculations, do not award more than 4 points. If they make multiple errors, award no more than 3 points. For solutions that found 1009 but did not continue searching for other numbers, award 1 point.
In the case of the second solution, award 1 point for describing the behavior of the operation $\times 2$ and 1 point for describing the behavior of the operation $\times 2+1$ in binary. Another 2 points for explaining which numbers correspond to the sought ones, 1 point for determining the number of digits of the number 2019 in binary (either by estimation or manual conversion), and finally 1 point for the conclusion itself.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
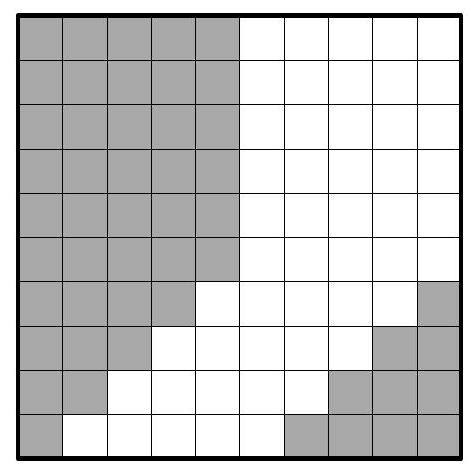
4. A $10 \times 10$ table is filled with numbers 1 and -1 such that the sum of the numbers in each row, except one, is equal to zero, and the sum of the numbers in each column, except one, is also equal to zero. Determine the maximum possible sum of all the numbers in the table.
(Patrik Bak)
|
SOLUTION. If we add up all the numbers in the considered table row by row, we will conclude that the total sum is equal to the sum of the numbers in the exceptional row where it is not zero. This sum is at most 10, and it equals 10 if all the numbers in the given row are ones. (We reach the same conclusion if we add up all the numbers in the table column by column.)
If we now provide an example of a filled $10 \times 10$ table that meets the conditions and where the sum of all the numbers is indeed 10, we will be done with solving the problem. We know that in such a table, there must be a row and a column filled entirely with ones. We place them in the first column from the left and the last row from the top. Then our task is to fill the remaining $9 \times 9$ square (in the top right corner of the table) with the numbers 1 and -1 so that in each of its rows and columns, there are exactly $5k$ times the number -1 (and thus 4 times the number 1).
The following images show three of the possible ways to accomplish the described task. For clarity, the numbers are not listed in the $10 \times 10$ tables. Instead, the cells with the number 1 are white (as is the case, for example, in the entire first column and the entire last row), and the cells with the number -1 are colored.
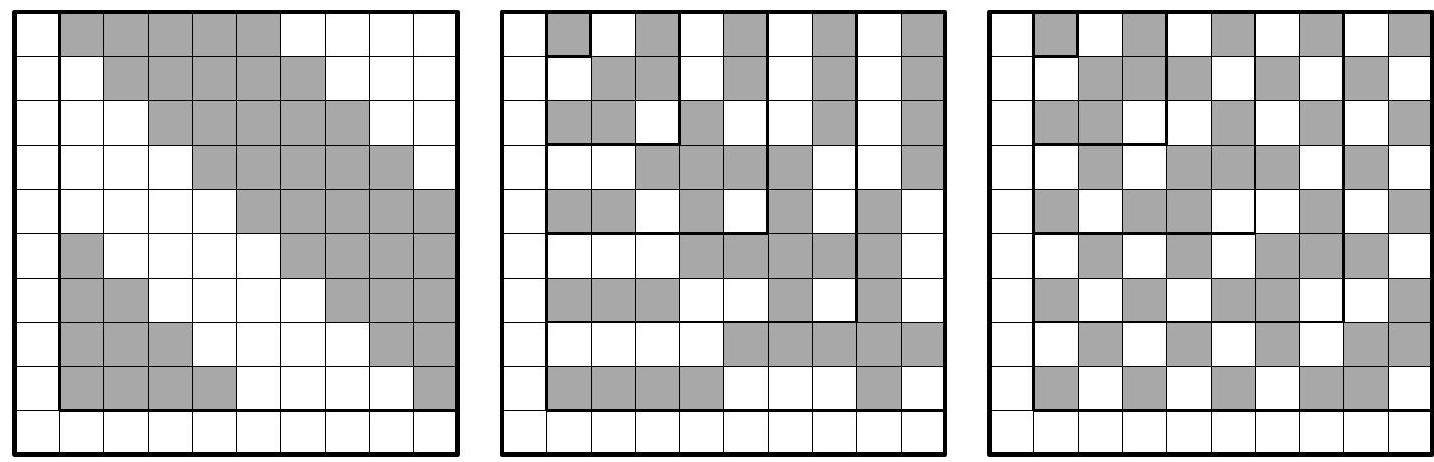
In the left image, a traditional construction with "cyclic shifting" of the colored group of cells along the rows of the "remaining" $9 \times 9$ table is used. The middle and right images are also not constructed randomly but by using a general method called mathematical induction. The way of coloring the cells on both images can be understood when we look at the parts $1 \times 1, 3 \times 3, 5 \times 5$, and $7 \times 7$ in the top left corner of the relevant $9 \times 9$ table.
Conclusion. The largest possible sum of all the numbers in the table is 10.
## GUIDING AND ADDITIONAL PROBLEMS:
N1. In one row, 71 numbers are written. Each of them is 1 or -1, and the sum of any ten consecutive numbers is 0. Prove that the first number is equal to the last number, and determine the largest possible sum of all the numbers. [The first 70 numbers can be divided into 7 tens with a sum of zero. The sum of all the numbers is therefore equal to the last number. Similarly, we find that the sum of all the numbers is equal to the first number when we consider the division into 7 tens of the last 70 numbers. The first and last numbers are therefore equal, and that is the sum of all the numbers, which is at most 1. The example of 71 numbers $1, -1, 1, \ldots, -1, 1$ satisfies the condition of the problem and their total sum is 1, which is the sought maximum possible sum.][^0]
N2. A $5 \times 4$ table is filled with the numbers 1 and -1 such that the sum of the numbers in each $2 \times 2$ square is 0. Determine the largest possible sum of all the numbers in the table. [The largest possible sum is 4. The given $5 \times 4$ table (with five rows and four columns) can be divided into the top row $1 \times 4$ and four $2 \times 2$ squares with zero sums of the written numbers. The sum of all the numbers in the table is therefore equal to the sum of the numbers in the first row, so it is at most 4. A sum of 4 can be achieved if the table is filled such that the first, third, and fifth rows contain only 1, while the second and fourth rows contain only -1.]
N3. For which $d \in \{0,1,2,3,4,5,6\}$ is it possible to color some cells of a $6 \times 6$ table so that in each row and each column there are exactly $d$ colored cells? [For each such $d$: For a given $d$, for example, the cells can be colored that contain numbers no greater than $d$ on the image.
| 1 | 2 | 3 | 4 | 5 | 6 |
| :--- | :--- | :--- | :--- | :--- | :--- |
| 6 | 1 | 2 | 3 | 4 | 5 |
| 5 | 6 | 1 | 2 | 3 | 4 |
| 4 | 5 | 6 | 1 | 2 | 3 |
| 3 | 4 | 5 | 6 | 1 | 2 |
| 2 | 3 | 4 | 5 | 6 | 1 |
D1. Is it possible to fill a square table with the numbers 1 and -1 so that the sum of the numbers in some column is even and in another column is odd? [No. In a square table $n \times n$, there are $n$ numbers in each column. If $a$ of them are 1, the others are $n-a$ and equal to -1, so the sum of the numbers in that column is $a - (n-a) = 2a - n$. This number is even, respectively odd, precisely when the number $n$ is. Thus, all the sums of the numbers in the individual columns have the same parity. Another explanation: The parity of the sum of the numbers in a given column does not change if each -1 in it is replaced by 1.]
D2. Is it possible to fill a $10 \times 10$ table with the numbers 1 and -1 so that the sum of the numbers in each row is the same and in each column is different? [Yes, see the image, where the cells with the number 1 are colored.
D3. A $10 \times 10$ table is filled with the numbers 1 and -1 such that the sum of the numbers is positive in at least 9 rows. a) Prove that the sum of the numbers is positive in at least one column. b) Does the same conclusion hold under the weaker assumption that the sum of the numbers is positive in at least 8 rows? [a) The smallest possible positive sum in a row is 2. The sum of all the numbers in the table is therefore at least $9 \times 2 - 10$, which is a positive number. Therefore, it is impossible for the sum of the numbers in each column to be non-positive. b) The conclusion does not hold in general, see the example in the image, where the cells with the number 1 are colored.
D4. Determine for which natural numbers $n$ it is possible to fill a $n \times n$ table with the numbers
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In a square table $11 \times 11$, we have written the natural numbers $1,2, \ldots, 121$ sequentially from left to right and from top to bottom. Using a square tile $4 \times 4$, we covered exactly 16 cells in all possible ways. How many times was the sum of the 16 covered numbers a perfect square?
|
SOLUTION. Let the number covered by the top left corner of the tile be denoted as $z$. The entire tile must lie within the given table, so the values of $z$ can only be the numbers written in the first eight rows and the first eight columns of the table (for example, if $z=10$, the tile would protrude, and thus could not cover 16 numbers in the table).
The first 8 rows of the table contain numbers from 1 to 88, from which we must exclude the numbers in the last three columns. Notice that the numbers in each column give the same remainder when divided by eleven. The last three columns from the left (the first three from the right) thus contain numbers that give remainders of 9, 10, and 0 when divided by eleven; these are the numbers 9, 10, 11 (first row), 20, 21, 22 (second row), and so on up to 86, 87, 88 (eighth row).
With this preparation, we can calculate the sum of the numbers that the tile will cover. The covered numbers are $z, z+1, z+2, z+3$ (first row of the tile), $z+11, z+12, z+13, z+14$ (second row of the tile), $z+22, z+23, z+24, z+25$ (third row of the tile), and $z+33, z+34, z+35, z+36$ (fourth row of the tile), and their sum is
$$
16 z+288=16(z+18)=4^{2}(z+18)
$$
If this sum is a perfect square of some integer, then $z+18$ must be a perfect square of some integer $n$. We already know that $1 \leqq z \leqq 88$, and thus $19 \leqq z+18=$ $=n^{2} \leqq 18+88=106$. This ensures that the top left corner of the tile is placed on a cell in the first eight rows. For the natural number $n$, where $19 \leqq n^{2} \leqq 106$, the possible values are $n \in\{5,6,7,8,9,10\}$. By calculating the values $z=n^{2}-18$, we get the corresponding $z \in\{7,18,31,46,63,82\}$.
We must also check whether any of these $z$ values lie in the last three columns of the table. Therefore, we calculate the remainders of these numbers when divided by eleven and find that we must additionally exclude the value $z=31$ with a remainder of 9.
The tile can be placed in five different positions as required, characterized by the number covered by the top left corner of the tile, which is $z \in\{7,18,46,63,82\}$. In these cases, the sum of the numbers covered by the tile will be $16(z+18) \in\{16 \cdot 25,16 \cdot 36,16 \cdot 64, 16 \cdot 81,16 \cdot 100\}$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a $4 \times 4$ table, positive real numbers are written such that the product in each pentad of the shape 母 is equal to 1. Determine the maximum number of different numbers written in the table.
Note: The shape 母 refers to a specific arrangement of five cells in the table, resembling the Chinese character 母. For clarity, it typically involves a central cell surrounded by four adjacent cells.
|
SOLUTION. Let $a, b, c, d, e, f, g, h, i$ be the numbers inscribed in the left upper $3 \times 3$ square of the table (Fig. 1). By comparing the products for pentads of the form $\mathbb{\text { a }}$ and placed in this part of the table, we must have $a b c d e=b d e f g$, or $a c=f g$. Similarly, for pentads $\mathrm{a}$ and $\mathrm{a}$, we get $a h f d i=c i g d h$, or $a f=c g$. Since all these are positive numbers, it follows from both equalities that $f=c$ and $g=a$. At the same time, we realize that this property (i.e., the equality of numbers in opposite corners of the $3 \times 3$ square) must hold for each of the four such squares that exist in the table. We will use this property for further completion of the given table.
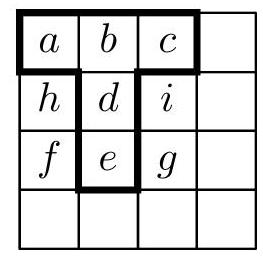
| $a$ | $b$ | $c$ | |
| :--- | :--- | :--- | :--- |
| $h$ | $d$ | $i$ | |
| $f$ | $e$ | $g$ | |
| | | | |
Fig. 1
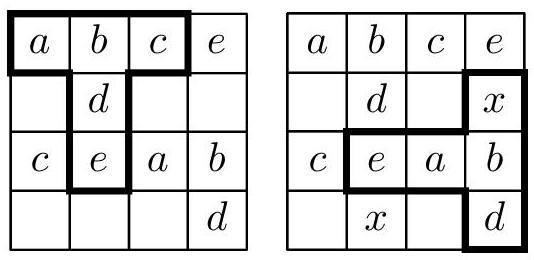
Fig. 2
Consider again the placement $\mathbb{\mathrm { v }} \mathrm{v}$ in the upper left corner of the given table $\mathrm{s}$ with the inscribed numbers $a, b, c, d, e$, and complete the other numbers according to the property just proven, and let $x$ be the missing number in the pentad 团 (Fig. 2). By comparing both identical products, we get $a b c d e=a b d e x$, or $x=c$. If we perform the same reasoning for the pentads of fields $\mathbb{Q}$ and $\boxminus$, which we get by flipping the considered pentads along the vertical axis of the table, we get an analogous equality for two more pairs of fields in the table (Fig. 3).
Fig. 3
| $a$ | $b$ | $c$ | $e$ |
| :--- | :--- | :--- | :--- |
| $b$ | $d$ | $y$ | $c$ |
| $c$ | $e$ | $a$ | $b$ |
| $y$ | $c$ | $b$ | $d$ |
Fig. 4
Now we have the table almost completely filled, except for two cells, into which we will write the number $y$ (Fig. 4). By comparing the products in both marked pentads, we get $a b c d e=a b c d y$, or $y=e$. The same equality must, however, also hold for the other two central fields of the table lying on the other diagonal, i.e., $d=a$. It is enough to repeat the entire reasoning for the pentads of fields that arise from the considered pentads by flipping them along the vertical axis of the table.
Now notice in the filled table the pentads of fields marked in Fig. 5. Clearly, we must have $a^{2} b c e=a b c e^{2}$, or $a=e$. We see that the table contains at most three different numbers $a, b, c$ (Fig. 6), with $a^{3} b c=1$. Now it remains to verify that the same product $a^{3} b c$ has every pentad of fields of the form $\$$, which can be placed in the table. Since the filled table is symmetric with respect to both diagonals, and thus also centrally symmetric, it is enough to verify this for only four possible positions of identically oriented pentads (e.g., 母 in the usual position of the letter $\mathrm{T}$ ).
| $a$ | $b$ | $c$ | $e$ |
| :--- | :--- | :--- | :--- |
| $b$ | $a$ | $e$ | $c$ |
| $c$ | $e$ | $a$ | $b$ |
| $e$ | $c$ | $b$ | $a$ |
Fig. 5
| $a$ | $b$ | $c$ | $a$ |
| :--- | :--- | :--- | :--- |
| $b$ | $a$ | $a$ | $c$ |
| $c$ | $a$ | $a$ | $b$ |
| $a$ | $c$ | $b$ | $a$ |
Fig. 6
Answer. The table contains at most three different positive numbers $a, b, c$, with $a^{3} b c=1$.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Determine how many numbers we can select $z$ from the set $\{1,2,3, \ldots, 75599,75600\}$ such that the set includes the number 75600 and for any two selected numbers $a$, $b$, it holds that $a$ is a divisor of $b$ or $b$ is a divisor of $a$. (List all possibilities.)
|
SOLUTION. Let's consider a set M that satisfies the conditions given in the problem. Since M contains the number 75600, it must be at least a one-element set. Further, notice that if we remove some number $a \neq 75600$ from the set M, we get a set $\mathrm{M}^{\prime} \subset \mathrm{M}$, which also satisfies the given conditions. Let's verify this. The set $\mathrm{M}^{\prime}$ still contains the number 75600. If $x, y$ are any two numbers from the set $\mathrm{M}^{\prime}$, it automatically holds that $x \mid y$ or $y \mid x$, because this holds for them as elements of the set $\mathrm{M}$.
By this, we have essentially proven that if we find a set with $m$ elements that satisfies the conditions of the problem, then there exists a $k$-element set with the required properties for any $k, 1 \leqq k \leqq m$. Therefore, it is sufficient to find a suitable set that has the maximum possible number of elements.
If $a$ is any element of the set M, it is primarily $a \leqq 75600$. If $a<75600$, according to the problem, it must hold that $a \mid 75600$. The set M therefore contains only divisors of the number 75600.
The prime factorization of the number 75600 is $75600=2^{4} \cdot 3^{3} \cdot 5^{2} \cdot 7$. Every divisor of the number 75600 thus has the form $2^{\alpha} \cdot 3^{\beta} \cdot 5^{\gamma} \cdot 7^{\delta}$, where $0 \leqq \alpha \leqq 4,0 \leqq \beta \leqq 3,0 \leqq \gamma \leqq 2,0 \leqq \delta \leqq 1$. Each element of $\mathrm{M}$ is therefore characterized by an ordered quadruple $(\alpha, \beta, \gamma, \delta)$ of the corresponding exponents in the given prime factorization. If $p$ and $p^{\prime}$ are two different elements of $\mathrm{M}$ and, for example, $p<p^{\prime}$, then according to the problem, it must simultaneously hold that $\alpha \leqq \alpha^{\prime}, \beta \leqq \beta^{\prime}, \gamma \leqq \gamma^{\prime}, \delta \leqq \delta^{\prime}$, and at least one inequality must be strict (otherwise it would hold that $p=p^{\prime}$), from which the inequality $\alpha+\beta+\gamma+\delta<\alpha^{\prime}+\beta^{\prime}+\gamma^{\prime}+\delta^{\prime}$ follows. Since in our case $0 \leqq \alpha+\beta+\gamma+\delta \leqq 10$, the set $M$ can contain at most 11 elements. Such a set is, for example,
$$
\mathrm{D}=\left\{1,2,2^{2}, 2^{3}, 2^{4}, 2^{4} \cdot 3,2^{4} \cdot 3^{2}, 2^{4} \cdot 3^{3}, 2^{4} \cdot 3^{3} \cdot 5,2^{4} \cdot 3^{3} \cdot 5^{2}, 2^{4} \cdot 3^{3} \cdot 5^{2} \cdot 7\right\}
$$
By this, we have proven that from the given set, we can select the required number of elements $1,2, \ldots, 11$ (including the number 75600).
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the board, the numbers 1, 2, .., 33 are written. In one step, we choose two numbers on the board, one of which is a divisor of the other, erase both, and write their (integer) quotient on the board. We continue this process until only numbers remain on the board, none of which is a divisor of another. (In one step, we can also erase two identical numbers and replace them with the number 1.) How few numbers can remain on the board?
|
SOLUTION. The numbers on the board will likely remain only from the set $M=\{1,2, \ldots, 33\}$. The prime numbers 17, 19, 23, 29, and 31 will always be written, each exactly once, because they have no divisors other than 1, and the set $M$ does not contain any of their multiples (so they can never disappear from the board, nor appear in another instance).
We will now explain why, in addition to the five mentioned primes, there will always be at least two more numbers on the board. The product $S$ of all numbers written on the board is initially equal to
$$
S=33 !=2^{31} \cdot 3^{15} \cdot 5^{7} \cdot 7^{4} \cdot 11^{3} \cdot 13^{2} \cdot 17 \cdot 19 \cdot 23 \cdot 29 \cdot 31
$$
In each step, we choose a pair of numbers $(x, y)$ with the property $x \mid y$, i.e., numbers of the form $x=a$ and $y=k a$, and replace them with a single number $y / x=k$. The product of all numbers on the board will then change from its previous value $S$ to a new value $S / a^{2}$, because two factors $x, y$ with a product $x y=k a^{2}$ will transition to one new factor $k$ (and the other factors will remain unchanged). It is clear that when changing $S \rightarrow S / a^{2}$, the exponent of any prime factor $p$ in the factorization of $S$ will either remain the same (if $p \nmid a$) or decrease by an even number (equal to the exponent of $p$ in the factorization of $a^{2}$). In no case will the parity (even-odd) of the exponent of any prime factor change. Therefore, each of the primes that initially had an odd exponent in the factorization (1) will have an odd exponent in the changing $S$ after any number of steps. These include (in addition to 17, 19, 23, 29, and 31) the primes $2,3,5$, and 11. This means that there will always be numbers on the board (not necessarily four different ones) that are divisible by these four individual primes. However, it cannot be just one number (since $2 \cdot 3 \cdot 5 \cdot 11>33$), so it must be at least two numbers, for example, 10 and 33 (or 11 and 30, or 15 and 22; other possibilities do not exist with a total of seven numbers on the board). Thus, we have proven that there will indeed always be at least 7 numbers on the board.
It remains to describe a sequence of steps that will leave 7 numbers on the board. There are many possibilities; for example, we can "set aside" the primes $17,19,23,29,31$ and the numbers 10 and 33, and with the remaining numbers perform the following steps:
$$
\begin{gathered}
32,16 \rightarrow 2, \quad 30,15 \rightarrow 2, \quad 28,14 \rightarrow 2, \quad 26,13 \rightarrow 2, \quad 24,12 \rightarrow 2, \quad 22,11 \rightarrow 2, \\
27,9 \rightarrow 3, \quad 21,7 \rightarrow 3, \quad 18,6 \rightarrow 3, \quad 25,5 \rightarrow 5, \quad 20,4 \rightarrow 5, \quad 8,2 \rightarrow 4, \\
5,5 \rightarrow 1, \quad 4,2 \rightarrow 2, \quad 3,3 \rightarrow 1, \quad 3,3 \rightarrow 1, \quad 2,2 \rightarrow 1, \quad 2,2 \rightarrow 1, \quad 2,2 \rightarrow 1 .
\end{gathered}
$$
After these steps, there are already 7 ones on the board (in addition to the seven numbers set aside), which we all remove in six steps $1,1 \rightarrow 1$ and the last step, for example, $10,1 \rightarrow 10$.
## GUIDING AND ADDITIONAL PROBLEMS:
N1. Determine how many zeros the decimal representation of the number 33! ends with. [Seven zeros. It is sufficient to determine the exponents of the prime numbers 2 and 5 in the factorization of the given factorial into prime factors. This can be done by a detailed analysis of the product $1 \cdot 2 \cdot 3 \cdot \ldots \cdot 33$, or by using a known rule: the number of occurrences of a prime number $p$ in the factorization of the number $n$! into prime factors is equal to the sum
$$
\left\lfloor\frac{n}{p^{1}}\right\rfloor+\left\lfloor\frac{n}{p^{2}}\right\rfloor+\left\lfloor\frac{n}{p^{3}}\right\rfloor+\ldots
$$
where $\lfloor x\rfloor$ denotes the integer part of the number $x$ and the summation continues as long as the power $p^{k}$ in the denominator of the fraction does not exceed the numerator $n$. The complete factorization of the number 33! is given in the solution to the competition problem.]
N2. Prove that the number $N=46 ! \cdot 47 ! \cdot 48 ! \cdot 49$! is not a perfect square, and then find its largest divisor that is a perfect square. [The number $N$ is not a perfect square because the prime number $47$ appears with an odd exponent 3 in its factorization into prime factors. From the expression $N=(46 !)^{4} \cdot 47 \cdot(47 \cdot 48) \cdot(47 \cdot 48 \cdot 49)=(46 !)^{4} \cdot 47^{3} \cdot\left(48^{2}\right) \cdot 7^{2}$, it follows that the largest perfect square that is a divisor of the number $N$ is the number $(46 !)^{4} \cdot 47^{2} \cdot 48^{2} \cdot 7^{2}=N / 47$.]
N3. Find the smallest positive integer $
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The quadratic equation $x^{2}-35 x+334=0$, whose coefficients are written in a number system with base $z(z \geqq 6)$, has two distinct real roots. Determine $z$ and both roots.
School - the written part of the 1st round of category B takes place
## on Tuesday, January 26, 1999
so that it starts in the morning and the contestants have 4 hours of pure time to solve the problems. For each problem, a contestant can earn 6 points, and a successful solver is a student who scores 10 points or more. These details will be communicated to the students before the start of the competition.
|
## 3. Given equation
$$
x^{2}-(3 z+5) x+\left(3 z^{2}+3 z+4\right)=0
$$
has two distinct real roots if and only if its discriminant $D$ is positive,
$$
\begin{aligned}
D & =(3 z+5)^{2}-4\left(3 z^{2}+3 z+4\right)=-3 z^{2}+18 z+9= \\
& =-3\left(z^{2}-6 z-3\right)=-3\left((z-3)^{2}-12\right)>0
\end{aligned}
$$
from which $z0 \mathrm{v}$ in the domain of integers $z \geqq 6,1$ point for calculating the roots $x_{1,2} \mathrm{v}$ in the case $z=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the smallest natural number $k$ such that every $k$-element set of pairwise coprime three-digit numbers contains at least one prime number.
|
SOLUTION. For constructing a set of two-by-two coprime three-digit composite numbers with a large number of elements, we can use the fact that powers of two different prime numbers are coprime. The set
$$
\left\{2^{7}, 3^{5}, 5^{3}, 7^{3}, 11^{2}, 13^{2}, 17^{2}, 19^{2}, 23^{2}, 29^{2}, 31^{2}\right\}
$$
contains 11 two-by-two coprime three-digit numbers, and there is no prime number in it. For the next prime number 37, it holds that $37^{2}>1000$, so every composite three-digit number is divisible by at least one prime number less than 37.
We will prove that every set of at least twelve two-by-two coprime three-digit numbers already contains a prime number. The set of all composite three-digit numbers can be divided into 11 subsets $A_{2}, A_{3}, A_{5}, A_{7}, A_{11}, A_{13}, A_{17}, A_{19}, A_{23}, A_{29}, A_{31}$, where $A_{i}$ contains the numbers whose smallest prime factor is the number $i$. Any two different numbers from the same set $A_{i}$ are coprime. Let the set $B$ of three-digit two-by-two coprime numbers have at least 12 elements. If $B$ contained only composite numbers, by the Dirichlet principle, $B$ would contain two numbers from the same set $A_{i}$; these numbers would, however, be coprime. Therefore, the set $B$ must contain at least one prime number.
The sought smallest number $k$ is thus 12.
## GUIDING AND SUPPLEMENTARY PROBLEMS:
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A right-angled triangle has integer lengths of sides. Its perimeter is the square of a natural number. We also know that one of its legs has a length equal to the square of a prime number. Determine all possible values of this length.
(Patrik Bak)
|
SOLUTION. We are looking for all prime numbers $p$ for which there exists a described triangle with one leg of length $p^{2}$. Let the length of its other leg be $b$ and the length of the hypotenuse $c$. Then, according to the Pythagorean theorem, the equation $c^{2}=p^{4}+b^{2}$ holds, which we rearrange into a product form
$$
p^{4}=c^{2}-b^{2}=(c+b)(c-b) .
$$
Since $c>b>0$ (the hypotenuse is longer than the leg), the right side of (1) is the product of two natural numbers $c+b$ and $c-b$, with $c+b>c-b$. The number $p^{4}$ on the left side of (1), however, can be factored into the product of two different natural numbers in exactly two ways (when the larger factor is written first): $p^{4} \cdot 1$ and $p^{3} \cdot p$. Thus the sum $c+b$ is equal to either $p^{4}$ or $p^{3}$. In the first case, the perimeter $o=p^{2}+b+c$ of our triangle has the value $o=p^{2}+p^{4}$, in the second case it is $o=p^{2}+p^{3}$.
According to the problem, the perimeter is a square of a natural number. If the value $p^{2}+p^{4}=p^{2}\left(p^{2}+1\right)$ were such, then with regard to the factor $p^{2}$, the factor $p^{2}+1$ one greater would also have to be a square, which is clearly impossible - it is a number $2 p$ less than the square $(p+1)^{2}$, which follows the square $p^{2}$.*
Therefore, the second case must occur, when the value $o=p^{2}+p^{3}=$ $=p^{2}(p+1)$ is a square. This happens precisely when the factor $p+1$ is a square, which, as we will immediately show, is satisfied by only one prime number $p=3$. Indeed, from the equality $p+1=k^{2}$ for integer $k>1$ we have $p=(k-1)(k+1)$, given that $\mathrm{k} 0$ are coprime natural numbers. Now from the equalities
$$
2 p^{2}=\left(c+p^{2}\right)-\left(c-p^{2}\right)=d u^{2}-d v^{2}=d\left(u^{2}-v^{2}\right)
$$
we see that $d$ is a divisor of the number $2 p^{2}$, which is at the same time less than $p^{2}$, since certainly $u^{2}-v^{2}>2$. We thus necessarily have $d \in\{1,2, p, 2 p\}$. These values can be individually evaluated by substituting into the equality[^1]$2 p^{2}=d(u+v)(u-v)$. From this, we then determine the factors $u+v$ and $u-v \cdot *$ We will write this here only for the value $d=2 p$ (which is the only one that does not lead to a contradiction): For it we get $(u+v)(u-v)=p$, so $u-v=1$ and $u+v=p$. When the resulting values of $u$, $v$ are substituted together $\mathrm{s} d=2 p$ into the formula $o=d u(u+v)$, we get after rearrangement $o=p^{2}(p+1)$ and the process can be easily completed as in the original solution.
For a complete solution, award 6 points. In incomplete solutions, evaluate partial steps as follows.
A1. Derivation of equation (1) (in product form!): 1 point.
A2. Derivation of the conclusion that $b+c \in\left\{p^{4}, p^{3}\right\}: 1$ point.
A3. Exclusion of the case $b+c=p^{4}$ : 1 point.
A4. Derivation that in the case $b+c=p^{3}$ it holds $p=3: 2$ points.
A5. Verification that the value $p=3$ (even if guessed) satisfies: 1 point.
B1. Derivation of the equation $b^{2}=\left(c+p^{2}\right)\left(c-p^{2}\right): 0$ points.
B2. Observation that the greatest common divisor of the factors $c+p^{2}, c-p^{2}$ (from equation in B1) is a divisor of the number $2 p^{2}$, i.e., one of the values $1,2, p, 2 p, p^{2}, 2 p^{2}: 1$ point.
B3. Exclusion of the values 1, 2, p, $p^{2}, 2 p^{2}$ from point B2: 3 points
B4. Solving the case with the value $2 p$ from point B2 (including verification): 2 points
In total, then award $\max (\mathrm{A} 1+\mathrm{A} 2+\mathrm{A} 3+\mathrm{A} 4+\mathrm{A} 5, \mathrm{~B} 2+\mathrm{B} 3+\mathrm{B} 4)$ points.
A solution that does not contain the required conclusion that the only possible length of the tangent leg is 9, can be rated no higher than 5 points.[^2]
[^0]: * The solution can also be concluded without mentioning the isosceles trapezoid: According to the common axis of segments $A E$ and $G H$, the segments $H A$ and $G E$ are symmetrically conjugate, and thus congruent.
[^1]: * The obvious statement that two consecutive natural numbers cannot both be squares does not need to be proven by solvers in their protocols.
** Verification of these two properties of $v$ in the mentioned process is not necessary: we have the equality from the Pythagorean theorem guaranteed and we know that the perimeter $p^{2}(p+1)$ is a square, because there is such a number $p+1=4$.
[^2]: * For the values $d=1$ and $d=2$, we will use the fact that due to the coprimality of the numbers $u$, $v$, the numbers $u+v, u-v$ can have only one common divisor greater than 1, namely the number 2.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Natural numbers $a$, $b$, $c$ are placed in a circle as shown in the figure, with each number being a divisor of the sum of the two numbers adjacent to it. How many of the numbers $a$, $b$, $c$ can be different? (Josef Tkadlec)
|
SOLUTION. We will prove that necessarily $b=c$, thus among the numbers $a, b, c$ there can be at most two different ones. The count of 2 can be achieved, for example, in the case of numbers $a=2$ and $b=c=1$, which clearly have the required property.
Let us assume, therefore, that the natural numbers $a, b, c$ satisfy the conditions of the problem. This can be expressed by three conditions:
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. For non-negative real numbers $a, b, c$ it holds that $a+b+c=1$. Find the greatest and the smallest possible value of the expression
$$
(a+b)^{2}+(b+c)^{2}+(c+a)^{2} .
$$
|
Solution. Notice that the expression $a+b+c$ contains only the first powers of the variables, and the expression we need to work with further contains their second powers. By expanding and rearranging the expression $V$ from the problem statement, we get
$$
\begin{aligned}
V & =(a+b)^{2}+(b+c)^{2}+(c+a)^{2}=2\left(a^{2}+b^{2}+c^{2}\right)+2(a b+b c+c a)= \\
& =a^{2}+b^{2}+c^{2}+1
\end{aligned}
$$
since
$$
a^{2}+b^{2}+c^{2}+2(a b+b c+a c)=(a+b+c)^{2}=1 \text {. }
$$
The numbers $a, b, c$ are non-negative, so the expression $a b+b c+a c$ is also non-negative, and from equation (2) we get the estimate
$$
a^{2}+b^{2}+c^{2} \leqq a^{2}+b^{2}+c^{2}+2(a b+b c+a c)=1 .
$$
Substituting this into equation (1), we find that the maximum possible value of the expression $V$ is 2, which is achieved for $a=1, b=c=0$.
From the problem in the home round, we know that the inequality
$$
a b+b c+a c \leqq a^{2}+b^{2}+c^{2},
$$
is obtained by expanding and rearranging the obvious inequality
$$
0 \leqq(a-b)^{2}+(b-c)^{2}+(c-a)^{2}
$$
Substituting twice the inequality (3) into equation (2), we get the estimate
$$
1=a^{2}+b^{2}+c^{2}+2(a b+b c+a c) \leqq 3\left(a^{2}+b^{2}+c^{2}\right) .
$$
From this, for the value of the expression $V$, we get the estimate
$$
V=a^{2}+b^{2}+c^{2}+1 \geqq \frac{1}{3}+1=\frac{4}{3},
$$
which is achieved by the given expression for $a=b=c=\frac{1}{3}$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Determine the values that the expression $V=a b+b c+c d+d a$ can take, given that the real numbers $a, b, c, d$ satisfy the following conditions:
$$
\begin{aligned}
& 2 a-5 b+2 c-5 d=4, \\
& 3 a+4 b+3 c+4 d=6 .
\end{aligned}
$$
|
1. For the given expression $V$, we have
$$
V=a(b+d)+c(b+d)=(a+c)(b+d).
$$
Similarly, we can modify both given conditions:
$$
2(a+c)-5(b+d)=4 \quad \text { and } \quad 3(a+c)+4(b+d)=6
$$
If we choose the substitution $m=a+c$ and $n=b+d$, we get the solution of the system (1) as $m=2$ and $n=0$. For the given expression, we then have $V=m n=0$.
Conclusion. Under the given conditions, the expression $V$ takes only the value 0.
Alternative solution. We can interpret the conditions of the problem as a system of equations with unknowns $a, b$ and parameters $c, d$. By solving this system (using the addition or substitution method), we find $a=2-c, b=-d$ (where $c, d \in \mathbb{R}$), and substituting into the expression $V$ gives
$$
V=(2-c)(-d)-d c+c d+d(2-c)=0.
$$
For a complete solution, award 6 points. For the first solution, award 2 points for factoring the expression $V$ into a product, 2 points for transforming the conditions into the system (1), 1 point for solving the system, and 1 point for calculating the value of $V$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On a $7 \times 7$ board, we are playing a game of battleships. There is one ship of size $2 \times 3$ on it. We can ask about any square on the board, and if we hit the ship, the game ends. If not, we ask again. Determine the smallest number of questions we need to ask to be sure to hit the ship.
|
SOLUTION. According to Fig. 2, we can place 8 disjoint rectangles $2 \times 3$ on the board (the middle cell of the board will remain empty). To definitely hit the ship, we need to ask about at least one cell in each of the eight marked rectangles, so the necessary number of questions is at least 8.
In Fig. 3, an example of selecting eight cells is given, asking about which is enough to ensure that no ship $2 \times 3$ can be placed on the board outside of them. Therefore, these 8 questions are always sufficient to hit the ship.

Fig. 2

Fig. 3
From both of the above considerations, the following conclusion follows.
Answer. The smallest number of questions we need to definitely hit the ship is exactly 8.
## GUIDING AND SUPPLEMENTARY PROBLEMS:
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Let A, B be sets of positive integers such that the sum of any two different numbers from $A$ belongs to $B$ and the quotient of any two different numbers from $B$ (the larger divided by the smaller) lies in $A$. Determine the maximum possible number of elements in the set $A \cup B$.
|
2. First, we will prove that the set $\mathrm{A}$ can contain at most two numbers. Assume that $\mathrm{A}$ contains three numbers $a < b < c$. Then the set $\mathrm{B}$ contains the numbers $a+b < a+c < b+c$, and thus the set $\mathrm{A}$ must contain the number
$$
\frac{b+c}{a+c}=1+\frac{b-a}{a+c}
$$
which is not an integer, since $0 < b-a < a+c$.
If the set $\mathrm{B}$ contained four numbers $k < l < m < n$, then the set $\mathrm{A}$ would contain three different numbers $n / k, n / l, n / m$. Therefore, the set $\mathrm{B}$ has at most three elements, and $\mathrm{A} \cup \mathrm{B}$ cannot have more than five elements.
This number is achieved precisely when $\mathrm{A}=\{a, b\}, \mathrm{B}=\{k, l, m\}$, where $a < b$ and $l / k = m / l = a, m / k = b$. Then $b = a^2 (a \geq 2)$ and one of the elements of the set $\mathrm{B}$ is $a + a^2$; the other two are then either $a^2 + a^3$ and $a^3 + a^4$, or $1 + a$ and $a^2 + a^3$. For example, the sets $\mathrm{A}=\{2,4\}, \mathrm{B}=\{3,6,12\}$ together have five elements.
For a complete solution, award 6 points. Award 3 points for proving the inequality $|A| \leq 2$, 1 point for proving the inequality $|B| \leq |A| + 1$, and 2 points for finding (one is sufficient) examples of sets $\mathrm{A}$ and $\mathrm{B}$ such that $|A \cup B| = 5$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. We need to fill a $3 \times 3$ table with nine given numbers such that in each row and column, the largest number is the sum of the other two. Determine whether it is possible to complete this task with the numbers
a) 1, 2, 3, 4, 5, 6, 7, 8, 9;
b) 2, 3, 4, 5, 6, 7, 8, 9, 10.
If yes, find out how many ways the task can be completed such that the largest number is in the center of the table.
(Jaromír Šimša)
|
SOLUTION. The sum of the numbers in each row (and in each column) is even, equaling twice the largest of the three written numbers. Therefore, the sum of all the numbers in the table must also be even. Since in case a) the sum of the numbers is 45, the task cannot be completed.
Since the sum of the numbers in case b) is even $(10 \cdot 11 / 2 - 1 = 54)$, we will try to fill the table in the required manner. Among the nine given numbers, there are five even numbers (which we will denote by the symbol $S$) and four odd numbers (which we will denote by the symbol $L$). Symbolically, then, in each row and column, one of the equations $S = L + L$, $S = S + S$, or $L = S + L$ must hold. If we look at the number of even and odd numbers used in these equations and also consider that we must use more even numbers than odd ones, we conclude that at least one row and one column must be of the type $S = S + S$.
We can swap the rows of our table among themselves without violating the condition given in the problem. The same applies to the columns. We can therefore assume that both the first row and the first column contain only even numbers (they are of the type $S = S + S$). Let's look at their common cell (the top left corner of the table), in which one of the numbers $2, 4, 6, 8$, or $10$ must be written.
We will list for each of the five candidates all the suitable equations to meet the condition of the problem for the first column and the first row:
$$
\begin{gathered}
2 = 6 - 4 = 8 - 6 = 10 - 8, \quad 4 = 6 - 2 = 10 - 6, \quad 6 = 2 + 4 = 8 - 2 = 10 - 4, \\
8 = 2 + 6 = 10 - 2, \quad 10 = 8 + 2 = 6 + 4 .
\end{gathered}
$$
We see that only the numbers 4 and 8 cannot be written in two "disjoint" ways, so in the common cell, one of the numbers 2, 6, or 10 must be written, and the table must then be (up to the order of rows, columns, and possibly flipping along the diagonal) filled with even numbers in one of three ways (asterisks here denote the four odd numbers $3, 5, 7, 9$ written in some order), which we will further examine:
| 2 | 8 | 10 |
| :---: | :---: | :---: |
| 4 | $*$ | $*$ |
| 6 | $*$ | $*$ |
Type A
| 6 | 2 | 8 |
| :---: | :---: | :---: |
| 4 | $*$ | $*$ |
| 10 | $*$ | $*$ |
Type B
| 10 | 4 | 6 |
| :---: | :---: | :---: |
| 2 | $*$ | $*$ |
| 8 | $*$ | $*$ |
Type C
In the table of type A, we would have to have $8 = 3 + 5$ and $10 = 3 + 7$ in the 2nd and 3rd columns, but the number 3 cannot be in both columns, so the required filling of the table of type A does not exist.
In the table of type B, we have the numbers 8 and 10 again in the 3rd row and 3rd column, and from the already mentioned equations, we see that the table can be completed in only one suitable way
| 6 | 2 | 8 |
| :---: | :---: | :---: |
| 4 | 9 | 5 |
| 10 | 7 | 3 |$\rightarrow$| 2 | 6 | 8 |
| :---: | :---: | :---: |
| 7 | 10 | 3 |
| 9 | 4 | 5 |
We have already transformed the table (by first swapping the first column with the second and then the second row with the third) into one of the possible forms where the number 10 stands in the middle of the table, as required by the problem.
Finally, in the table of type C, we have only one way to express $8 = 5 + 3$ in the 3rd row and $6 = 9 - 3$ in the 3rd column. This determines the position of not only the numbers 3, 5, and 9, but also the remaining number 7. The resulting table clearly does not meet the problem's requirements.
It remains to determine the number of different tables that can be created from the filled table of type B so that the number 10 is in the middle. In the middle row or column, along with 10, there must be the numbers 6 and 4, or 7 and 3, respectively, so we have a total of $4 \cdot 2 = 8$ possibilities (we place the 6 in one of the four fields adjacent to the middle 10, the 4 will then be in the opposite field, the 7 will be placed in one of the two remaining fields adjacent to the 10; the numbers in the corner fields are then uniquely determined).
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the largest possible number of elements in the set $\mathrm{M}$ of integers, which has the following property: for every triple of distinct numbers $z \mathrm{M}$, it is possible to select some two of them whose sum is a power of 2 with an integer exponent.
|
SOLUTION. Let us note at the outset that the mentioned power as an integer sum must have a non-negative exponent. We will only consider such powers of the number 2 further on.
We will prove that the set M can have at most 6 elements, as does, for example, the suitable (as we will verify immediately) set
$$
\{-1,3,5,-2,6,10\} \text {. }
$$
The sum of any two numbers from the triplet $-1,3,5$ is indeed a power of two, and the same is true for the triplet $-2,6,10$. Whenever we select three numbers from the mentioned set, some two of them will belong to one of the two mentioned triplets, and these two numbers will thus have a sum equal to a power of two.
Now, let us assume that there exists a suitable set with more than six elements. If the set M contained three non-positive numbers, the sum of any two of them would be negative, while every power of two is positive. Therefore, the set M contains at most two non-positive numbers, and thus at least five positive numbers. Let $x$ be the largest of them and $a, b, c, d$ some four other positive numbers from M.
Consider the four sums $x+a, x+b, x+c, x+d$. All of them are greater than $x$ and less than $2 x$. However, in the interval $(x, 2 x)$, there can be at most one power of two, so at most one of these four sums is equal to a power of two, and the remaining three (without loss of generality, $x+a, x+b, x+c$) are not powers of two. By applying the condition of the problem to the triples $(a, b, x)$, $(a, c, x)$, and $(b, c, x)$, we find that all three sums $a+b, a+c$, and $b+c$ must be powers of two. Without loss of generality, let $a=\max \{a, b, c\}$. Similarly as above, let us focus on the open interval $(a, 2 a)$. In it, there can be at most one power of two, but at the same time, it contains both (different) numbers $a+b$ and $a+c$, which we have already concluded must be powers of two. Thus, we have reached the desired contradiction.
Answer. The largest possible number of elements in the set $\mathrm{M}$ is 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. At the party, 10 boys and 10 girls gathered. Each boy likes a different positive number of girls. Each girl likes a different positive number of boys. Determine the largest integer n with the following property: It is always possible to form n disjoint pairs where both individuals like each other.
(Josef Tkadlec)
|
SOLUTION. We will show that the largest $n$ sought is equal to 1.
In the first part of the solution, we will show that one suitable pair can always be formed. According to the problem statement, the numbers of girls liked by individual boys are all the numbers from 1 to 10 (in some order). The same applies to the numbers of boys liked by individual girls. One boy likes all 10 girls, and one girl likes all 10 boys, so this boy and this girl form a suitable pair.
In the second part of the solution, we will provide an example of a party that meets the conditions of the problem, in which there do not exist two disjoint pairs with mutual attraction. For its construction, arrange the boys in the top row and the girls below them in the bottom row as shown in the figure.
Assume that what is marked with arrows for the sixth boy and the sixth girl from the left is true: Each boy likes exactly the girl directly below him and all the girls to the right of her, while each girl likes exactly the boy first from the left and all the boys to the right of the boy above her. Then, clearly, each boy likes a different number of girls and each girl likes a different number of boys, but in all (ten) pairs with mutual attraction, only one boy is represented - the first one from the left. Therefore, no two such pairs are disjoint.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the greatest real number $k$ such that the inequality
$$
\frac{2\left(a^{2}+k a b+b^{2}\right)}{(k+2)(a+b)} \geqq \sqrt{a b}
$$
holds for all pairs of positive real numbers $a, b$.
|
SOLUTION. For $k=2$, the inequality can be simplified to $\frac{1}{2}(a+b) \geqq \sqrt{a b}$, which is the well-known inequality between the arithmetic and geometric means, valid for any positive numbers $a, b$. The largest $k$ we are looking for is therefore at least 2. Let's further examine the given inequality under the assumption $k \geqq 2$.
By equivalent manipulation (since $k+2>0$), we get
$$
2\left(a^{2}+k a b+b^{2}\right) \geqq(k+2)(a+b) \sqrt{a b}
$$
and by dividing both sides by the positive number $b^{2}$, we have
$$
2\left(\frac{a^{2}}{b^{2}}+k \frac{a}{b}+1\right) \geqq(k+2)\left(\frac{a}{b}+1\right) \sqrt{\frac{a}{b}} .
$$
Let $\sqrt{a / b}=x$. By a suitable choice of positive numbers $a, b$, $x$ can take any positive value. Therefore, it suffices to consider the inequality
$$
2\left(x^{4}+k x^{2}+1\right) \geqq(k+2)\left(x^{2}+1\right) x
$$
and find the largest $k$ such that the above inequality holds for every positive $x$. After simple equivalent manipulations aimed at isolating $k$, we get
$$
\begin{aligned}
k\left(\left(x^{2}+1\right) x-2 x^{2}\right) & \leqq 2\left(x^{4}+1-\left(x^{2}+1\right) x\right), \\
k\left(x^{3}-2 x^{2}+x\right) & \leqq 2\left(x^{4}-x^{3}-x+1\right), \\
k x\left(x^{2}-2 x+1\right) & \leqq 2\left(x^{3}(x-1)-(x-1)\right), \\
k x(x-1)^{2} & \leqq 2(x-1)^{2}\left(x^{2}+x+1\right) .
\end{aligned}
$$
For $x=1$, the last inequality is always satisfied. For $x \neq 1$, we divide the inequality by the positive expression $x(x-1)^{2}$ and obtain a direct estimate for $k$:
$$
k \leqq \frac{2\left(x^{2}+x+1\right)}{x}=2+2\left(x+\frac{1}{x}\right)
$$
For positive $x$, $x+1 / x \geqq 2$ with equality only for $x=1$. For $x \neq 1$, the expression $x+1 / x$ takes all values in the interval $(2, \infty)$, and the right-hand side (1) thus takes all values in the interval $(6, \infty)$. From this, it is clear that the largest $k$ such that (1) holds for all positive $x \neq 1$ is $k=6$.
|
6
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For real numbers $a, b, c$ it holds that
$$
\frac{a}{b+c}=\frac{b}{c+a}=\frac{c}{a+b}
$$
Determine all possible values of the expression
$$
\frac{a^{3}+b^{3}+c^{3}}{(b+c)^{3}+(c+a)^{3}+(a+b)^{3}}.
$$
(Michal Rolínek)
|
SOLUTION. From the problem statement, it follows that the numbers $a, b, c$ satisfy the conditions
$$
b+c \neq 0, \quad c+a \neq 0, \quad a+b \neq 0 .
$$
Under the assumptions $(\mathrm{P})$, we equivalently transform the first of the given equalities:
$$
\begin{gathered}
\frac{a}{b+c}=\frac{b}{c+a}, \\
a(c+a)=b(b+c), \\
a c+a^{2}=b^{2}+b c \\
(a-b)(a+b)+c(a-b)=0, \\
(a-b)(a+b+c)=0 .
\end{gathered}
$$
By similar transformations of the second equality and also the equality of the third fraction with the first fraction, we get
$$
(b-c)(a+b+c)=0 \quad \text { and } \quad(c-a)(a+b+c)=0
$$
We see that under the assumptions $(\mathrm{P})$, the real numbers $a, b, c$ satisfy the problem statement if and only if $a+b+c=0$ or $a=b=c$.
In the case where $a+b+c=0$, for the given expression we have
$$
\frac{a^{3}+b^{3}+c^{3}}{(b+c)^{3}+(c+a)^{3}+(a+b)^{3}}=\frac{a^{3}+b^{3}+c^{3}}{(-a)^{3}+(-b)^{3}+(-c)^{3}}=-1,
$$
provided that $a^{3}+b^{3}+c^{3} \neq 0$, otherwise the expression makes no sense.
In the second case, where $a=b=c$, we have
$$
\frac{a^{3}+b^{3}+c^{3}}{(b+c)^{3}+(c+a)^{3}+(a+b)^{3}}=\frac{a^{3}+a^{3}+a^{3}}{(2 a)^{3}+(2 a)^{3}+(2 a)^{3}}=\frac{1}{8},
$$
but this time under the condition that $a^{3} \neq 0$.
It remains to show that each of the two found values is achievable.
The conditions $(\mathrm{P})$ and the equality $a+b+c=0$ are satisfied, for example, by the triplet $(a, b, c)=$ $=(1,1,-2)$, for which the expression $a^{3}+b^{3}+c^{3}$ (indeed non-zero) has the value 6.
The conditions $(\mathrm{P})$ and the equality $a=b=c$ are satisfied, for example, by the triplet $(a, b, c)=$ $=(1,1,1)$, for which the expression $a^{3}$ (indeed non-zero) has the value 1.
Conclusion. The given expression has only two possible values: -1 and $1 / 8$.
Comment. Without verifying the condition $a^{3}+b^{3}+c^{3} \neq 0$ for the chosen triplet $(1,1,-2)$, the provided solution would not be complete. Although more laborious, but ultimately more interesting, is to show that under the conditions $(\mathrm{P})$ never both equalities $a+b+c=0$ and $a^{3}+b^{3}+c^{3}=0$ hold. If the first of them holds, we can substitute $c=-a-b$ into the second equality and further transform its left side:
$a^{3}+b^{3}+c^{3}=a^{3}+b^{3}+(-a-b)^{3}=-3 a^{2} b-3 a b^{2}=-3 a b(a+b)=-3(b+c)(c+a)(a+b)$,
where in the last step we replaced the factors $a, b$ with $-b-c$, resp. $-c-a$. It remains to add that due to the conditions $(\mathrm{P})$, the product $(b+c)(c+a)(a+b)$ is not equal to zero.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Consider two quadratic equations
$$
x^{2}-a x-b=0, \quad x^{2}-b x-a=0
$$
with real parameters $a, b$. Determine the smallest and the largest values that the sum $a+b$ can take, given that there exists exactly one real number $x$ that satisfies both equations simultaneously. Also, determine all pairs $(a, b)$ of real parameters for which the considered sum of these values is achieved.
|
1. By subtracting the given equations, we obtain the equality $(b-a) x+a-b=0$ or $(b-a)(x-1)=0$, from which it follows that $b=a$ or $x=1$.
If $b=a$, both equations take the form $x^{2}-a x-a=0$. Exactly one solution exists if and only if the discriminant $a^{2}+4 a$ is zero. This holds for $a=0$ and for $a=-4$. Since $b=a$, the sum $a+b$ is 0 in the first case and -8 in the second case.
If $x=1$, we get from the given equations $a+b=1$, thus $b=1-a$. The equations then take the form
$$
x^{2}-a x+a-1=0 \quad \text { and } \quad x^{2}+(a-1) x-a=0 .
$$
The first has roots 1 and $a-1$, the second has roots $1$ and $-a$. Exactly one common solution is obtained in all cases except when $a-1=-a$ or $a=\frac{1}{2}$, in which case there are two common solutions.
Conclusion. The smallest value of the sum $a+b$ is -8 and is achieved for $a=b=-4$. The largest value of the sum $a+b$ is 1; this value is achieved for all pairs $(a, 1-a)$, where $a \neq \frac{1}{2}$ is any real number.
For a complete solution, award 6 points. Award one point for deriving the condition $(b=a) \vee(x=1)$, two points for solving the case $b=a$, two points for solving the case $x=1$, and one point for the correct conclusion.
|
-8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the plane containing the segment $B D$, find the set of all vertices $A$ of convex quadrilaterals $A B C D$ for which the following conditions are simultaneously satisfied:
a) the center $O_{C}$ of the incircle of triangle $B C D$ lies on the circumcircle of triangle $A B D$,
b) the center $O_{A}$ of the incircle of triangle $A B D$ lies on the circumcircle of triangle $B C D$.
|
Solution: Let $\alpha=|\angle B A D|$ and $\gamma=|\angle B C D|$. We have
$$
\left|\angle B O_{C} D\right|=180^{\circ}-\left(\left|\angle O_{C} B D\right|+\left|\angle O_{C} D B\right|\right)=
$$
$$
=180^{\circ}-\frac{1}{2}(|\angle C B D|+|\angle C D B|)=90^{\circ}+\frac{1}{2}
$$
Similarly, $\left|\angle B O_{A} D\right|=90^{\circ}+\frac{1}{2} \alpha$. Since points $A$ and $O_{C}$ lie in opposite half-planes with the boundary line $B 1$, condition a) of the problem is equivalent to the sum of the magnitudes of angles $B A D$ and $B O_{C} D$ being $180^{\circ}$, i.e., $\alpha+\left(90^{\circ}+\frac{1}{2} \gamma\right)=180^{\circ}$. Similarly, we conclude that condition b) is satisfied if and only if $\gamma+\left(90^{\circ}+\frac{1}{2} \alpha\right)=180^{\circ}$. The found pair of equations has a unique solution $\alpha=\gamma=60^{\circ}$. Therefore, points $A$ and $C$ lie on two different circular arcs from which the segment $B D$ is seen at an angle of $60^{\circ}$. On the other hand, if we choose any interior point $A$ of one of these arcs, we can choose a point $C$ on the other arc such that $A B C D$ is a convex quadrilateral (it suffices to complete the triangle $A B D$ to a parallelogram $A B C D$).
Answer: The set of vertices $A$ consists of the interior points of two circular arcs from which the segment $B D$ is seen at an angle of $60^{\circ}$.
Grading instructions: If the solver does not explain why every point $A$ in the found set is a vertex of some suitable quadrilateral $A B C D$, award no more than 5 points.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Mr. Kutil wanted to paint star ornaments on 20 tiles in the bathroom. On the can of paint, it was written that the paint would cover $750 \mathrm{~cm}^{2}$. How many cans of paint did Mr. Kutil have to buy at least, if one square of the grid has an area of $1 \mathrm{~cm}^{2}$? The ornament on one tile is shown in the picture.
(L. Hozová)
|
The tile is a square with a side of $12 \mathrm{~cm}$, its area is $(12 \mathrm{~cm})^{2}=144 \mathrm{~cm}^{2}$.
Let's calculate the area of the parts that will not be colored:
4 pentagons in the corners have a total area of $4 \cdot 15 \mathrm{~cm}^{2}=60 \mathrm{~cm}^{2}$,
4 isosceles triangles in the middle of the sides have a total area of $4 \cdot \frac{4 \cdot 6}{2} \mathrm{~cm}^{2}=$ $=48 \mathrm{~cm}^{2}$.
The total uncolored area of the tile is $(60+48) \mathrm{~cm}^{2}=108 \mathrm{~cm}^{2}$.
The colored part of the tile has an area of $(144-108) \mathrm{~cm}^{2}=36 \mathrm{~cm}^{2}$.
The colored area of 20 tiles is $(36 \cdot 20) \mathrm{~cm}^{2}=720 \mathrm{~cm}^{2}$,
$$
720 \mathrm{~cm}^{2}<750 \mathrm{~cm}^{2} \quad \text { (1 can). }
$$
Mr. Kutil will have enough with one can of paint to color the ornaments on 20 tiles.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Anička has 50 Kč, Anežka has 46 Kč, and they want to buy snacks for a family celebration with all their money. They are deciding between cupcakes and windmills: a windmill is 4 Kč more expensive than a cupcake, and with all their money, they could buy a third more cupcakes than windmills.
How much does each snack cost?
(M. Volfová)
Hint. In how many ways can Anička and Anežka spend all their money without any remainder?
|
Anička and Anežka together have 96 Kč. This amount can only be spent in a few ways, which are derived from expressing the number 96 as a product of two natural numbers:
$$
96=1 \cdot 96=2 \cdot 48=3 \cdot 32=4 \cdot 24=6 \cdot 16=8 \cdot 12 \text {. }
$$
The price of a kite and the price of a cake should correspond to numbers with a difference of 4. Such pairs of numbers are only three among the given factors (marked in bold):
$$
\mathbf{2} \cdot 48=\mathbf{6} \cdot 16, \quad \mathbf{4} \cdot 24=\mathbf{8} \cdot 12, \quad 6 \cdot \mathbf{1 6}=8 \cdot \mathbf{1 2} .
$$
In the first case, the girls would choose between 48 cakes at 2 Kč each and 16 kites at 6 Kč each; however, 48 is not one third more than 16, so this option does not work.
In the second case, the girls would choose between 24 cakes at 4 Kč each and 12 kites at 8 Kč each; however, 24 is not one third more than 12, so this option also does not work.
In the third case, the girls would choose between 8 cakes at 12 Kč each and 6 kites at 16 Kč each; 8 is one third more than 6, so this is the only viable option.
One cake costs 12 Kč, and one kite costs 16 Kč.
Another solution. For the same amount of money, one can buy one third more cakes than kites, meaning that for the price of 3 kites, one can buy 4 cakes. A kite is 4 Kč more expensive than a cake, so 3 kites cost 12 Kč more than 3 cakes. From this, it follows that 12 Kč plus the price of 3 cakes equals the price of 4 cakes. Therefore, a cake costs 12 Kč. A kite costs 4 Kč more, so 16 Kč.
(For verification: for 96 Kč, the girls can buy $96: 16=6$ kites or $96: 12=8$ cakes.)
Note. For those who can express the conditions from the problem using variables, we add:
If we denote the price of a cake by $d$ (Kč), then a kite costs $d+4$ (Kč). If the number of kites that can be bought with all the money is denoted by $k$, then the number of cakes that can be bought for the same amount of money is $\frac{4}{3} k$. From the problem, we know that
$$
k \cdot(d+4)=\frac{4}{3} k \cdot d
$$
From this, it follows that $3 d+12=4 d$, so $d=12$, and $d+4=16$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine for how many natural numbers greater than 900 and less than 1001 the digital sum of the digital sum of their digital sum is equal to 1.
(E. Semerádová)
Hint. What is the largest digital sum of numbers from 900 to 1001?
|
Among the numbers 900 and 1001, the number with the greatest digit sum is 999, which is 27; we don't need to consider larger sums.
Among the numbers 1 and 27, the number with the greatest digit sum is 19, which is 10; we don't need to consider larger sums.
Among the numbers 1 and 10, the digit sum of 1 is only found in the numbers 1 and 10; we don't need to consider other numbers.
Now, working backwards, we can determine all solutions (the first column is 1, and in each subsequent column are the numbers whose digit sum equals the number in the previous column):
| 1 | 1 | 1 | 1000 |
| :---: | :---: | :---: | :---: |
| | | 10 | 901 |
| | | | 910 |
| | 10 | 19 | 919 |
| | | | 928 |
| | | | 937 |
| | | | 946 |
| | | | 955 |
| | | | 964 |
| | | | 973 |
| | | | 982 |
| | | | 991 |
There are a total of 12 numbers with the specified properties.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
King Pan was distributing ducats to his sons. He gave a certain number of ducats to his eldest son, one ducat less to the next younger son, and continued this pattern until he reached the youngest. Then he returned to the eldest son, giving him one ducat less than he had just given to the youngest, and continued distributing in the same manner as in the first round. In this round, the youngest son received one ducat. The eldest son received a total of 21 ducats.
Determine how many sons the king had and how many ducats he distributed in total.
(K. Pazourek)
Hint. How many ducats would the eldest son receive if the king distributed them in the same manner to, for example, four sons?
|
For a specific number of sons, one can vividly test the king's method of distributing ducats. It's enough to proceed from the back: the youngest received one ducat in the second round, the second youngest received two ducats, etc. For example, for two, three, and four sons, the number of ducats in individual rounds would look as follows (arranged from top to bottom according to rounds, from left to right according to age):
The eldest son would receive 6 ducats in the first case, 9 ducats in the second case, and 12 ducats in the third case. In this way, one can gradually find the situation where the eldest son received 21 ducats:
$$
\begin{array}{rrrrrrr}
14 & 13 & 12 & 11 & 10 & 9 & 8 \\
\hline 7 & 6 & 5 & 4 & 3 & 2 & 1
\end{array}
$$
Thus, the king had 7 sons and distributed a total of 105 ducats to them.
Notes. Instead of trial and error, one can notice that the following follows from the problem statement: the eldest son will receive exactly as many ducats in the second round as there are sons, and in the first round, twice as many, making a total of three times the number of sons. For this number to be 21, there must be 7 sons, and the total number of ducats is \(1+2+\ldots+14=105\).
The sum of the distributed ducats can be determined in various ways, see for example the following shortcut:
$$
(1+14)+(2+13)+\ldots+(7+8)=7 \cdot 15=105
$$
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Mom brought 10 snacks of three types: there were fewer coconut snacks than lollipops, and the most were caramel chews. Josef chose two different types of snacks, Jakub did the same, and for Jan, only snacks of the same type were left.
How many coconut snacks, lollipops, and caramel chews did Mom bring?
Hint. Which type of snack was left for Jan?
|
When Jan received $\mathrm{k}$ snacks, there were 6 of the same kind, and they were caramel chews - if they were coconuts or laskonky, there would have to be more than 6 chews and more than 10 snacks in total. Therefore, there were at least 6 caramel chews originally, and mom brought
- either 1 coconut, 3 laskonky, and 6 chews,
- or 1 coconut, 2 laskonky, and 7 chews.
The first option is not suitable - for Josef and Jakub to each have two different kinds of snacks, at least one of them would have to choose a chew as well, and then there wouldn't be 6 left for Jan.
The second option is suitable - one of the first two boys chose a coconut and a laskonka, the other chose a laskonka and a chew, leaving 6 chews for Jan.
Mom brought 1 coconut, 2 laskonky, and 7 caramel chews.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Adam and Eve were playing chess.
Adam won and comforted Eve: "You know, I've been playing chess for a long time, twice as long as you!" Eve got upset: "But last time you said you've been playing three times longer!"
Adam was surprised: "Did I say that? And when was that?"
"Two years ago!"
"Well, then I was telling the truth - and I am today as well."
How long has Adam been playing chess?
(M. Volfová)
|
Let's assume that Eva has been playing chess for $x$ years. Then the time data appearing in the problem can be briefly expressed in the following table:
| | last year | today |
| :---: | :---: | :---: |
| Eva | $x-2$ | $x$ |
| Adam | $2 x-2$ | $2 x$ |
Last year, Adam played chess three times longer than Eva, which we can express with the equation:
$$
\begin{aligned}
2 x-2 & =3(x-2), \\
2 x-2 & =3 x-6, \\
4 & =x .
\end{aligned}
$$
Thus, $2 x=8$, which means Adam has been playing chess for 8 years.
Evaluation. 2 points for data corresponding to our table; 2 points for setting up and solving the equation; 2 points for the correct conclusion.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Grandma had a square garden. She bought a few neighboring plots, thus obtaining a square plot whose side was three meters longer than the side of the original garden. The area of the new plot was nine square meters larger than twice the original area.
How long was the side of the original garden?
(K. Buzáková)
|
Let $a$ be the length of the side of the original square garden. After the purchase, a new square plot was formed, with the side length of $a+3$. According to the areas of the plots given in the problem, we have
$$
(a+3)^{2}=2 a^{2}+9 \text {. }
$$
By equivalent transformations, we get
$$
\begin{aligned}
a^{2}+6 a+9 & =2 a^{2}+9 \\
6 a & =a^{2} \\
0 & =a(a-6)
\end{aligned}
$$
The given equation has two solutions: $a=0$ and $a=6$.
The original garden had non-zero dimensions, so its side was six meters long.
Note. Although we do not know what the purchased plots looked like, we can illustrate the areas of the gardens (and their auxiliary divisions) as follows:
The large square is composed of two squares and two congruent rectangles, or one square and four congruent rectangles. This visual representation reveals the result $a=3+3=6$.
Evaluation. 2 points for formulating the conditions from the problem using one variable; 2 points for equivalent transformations; 2 points for excluding the zero solution and concluding.
Solutions based on graphical representation should be evaluated according to the quality of the accompanying commentary.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the picture, there is a structure composed of twelve identical cubes. To how many different places can we move the dark cube so that the surface area of the assembled body does not change?
Just like in the original structure, the cubes in the new structure must touch each other with entire faces. The positions of the light cubes cannot be changed.
(D. Reichmann)
Hint. How will the surface area of the body change after removing the dark cube?
|
Originally, on the surface of the assembled body, there are three dark cube walls, and the other three walls touch light cubes. After removing the dark cube, the total surface area of the body does not change (three dark walls are replaced by three light ones).
In order for the surface area of the body to remain unchanged even after moving the dark cube, it must touch exactly three light cubes (three light walls will be replaced by three dark ones). By trial, we quickly find that the dark cube can only be moved to the following three places:
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Eva wrote down consecutive natural numbers: 1234567891011. . What digit did she write on the 2009th place?
(M. Volfová)
|
There are 9 single-digit numbers (1 to 9) and it takes 9 digits to write them. There are 90 two-digit numbers (10 to 99) and it takes 180 digits to write them. There are 900 three-digit numbers (100 to 999) and it takes a total of 2700 digits to write them. To write all single-digit and two-digit numbers, 189 digits are needed; the 2009th digit was used in some three-digit number.
The number of digits used to create three-digit numbers is $2009-189=1820$. Since $1820: 3=606$ (remainder 2), the 2009th digit in the sequence is the second digit of the 607th three-digit number. The first three-digit number is 100, the second three-digit number is $101=100+1$, the third three-digit number is $102=100+2 \ldots$ Similarly, the 607th three-digit number is $100+606=706$ and its second digit is 0. Therefore, Eva wrote 0 at the 2009th position.
Scoring. 1 point for determining the number of digits needed to write single-digit and two-digit numbers (i.e., 189); 3 points for determining that the sought digit is in the 607th three-digit number; 2 points for finding the digit 0 in the number 706.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
When Bořek was painting the garage door, he accidentally painted over the scale of the outdoor wall thermometer. However, the mercury tube remained undamaged, so Bořek covered the original scale with a homemade strip. On it, he carefully marked divisions, all of the same size and labeled with numbers. His division, however, had a different size than the original division, which represented one degree Celsius, and he also placed the zero differently than where $0{ }^{\circ} \mathrm{C}$ was. Thus, Bořek began measuring temperature in his own units: borcs. When the thermometer should have indicated a temperature of $11^{\circ} \mathrm{C}$, it showed 2 borcs. When it should have indicated $-4{ }^{\circ} \mathrm{C}$, it showed -8 borcs. What is the temperature in degrees Celsius if Bořek sees a temperature of -2 borcs on his thermometer?
(L. Simünek)
|
At $11^{\circ} \mathrm{C}$, the thermometer shows 2 boroks. When the temperature drops to $-4{ }^{\circ} \mathrm{C}$, which is a decrease of $15^{\circ} \mathrm{C}$, the thermometer shows -8 boroks, which is 10 boroks less than in the first case. A change of 10 boroks corresponds to a change of $15^{\circ} \mathrm{C}$, so a change of 1 borok represents a change of $1.5^{\circ} \mathrm{C}$. The temperature of -2 boroks, which the problem asks for, is 4 boroks less than the temperature given at the beginning of our solution. Therefore, the temperature of -2 boroks in degrees Celsius is
$$
11-4 \cdot 1.5=5
$$
Another solution. The problem can also be solved graphically, for example, on graph paper:
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Jirka drew a square grid with 25 squares, see the image. Then he wanted to color each square so that squares of the same color do not share any vertex.
How many colors did Jirka need at least?
(M. Dillingerová)
Hint. Start in one of the corner squares.
|
If the top-left square is colored with some color, the surrounding three squares must be colored with mutually different colors. Jirka had to use at least 4 colors, which we will denote by the digits from 1 to 4:
| 1 | 2 | | | |
| :--- | :--- | :--- | :--- | :--- |
| 4 | 3 | | | |
| | | | | |
| | | | | |
| | | | | |
Now we need to determine whether four colors are sufficient to color the rest of the grid according to the given rules, or not. We will gradually find out that four colors are indeed sufficient:
| 1 | 2 | 1 | 2 | 1 |
| :--- | :--- | :--- | :--- | :--- |
| 4 | 3 | 4 | 3 | 4 |
| 1 | 2 | 1 | 2 | 1 |
| 4 | 3 | 4 | 3 | 4 |
| 1 | 2 | 1 | 2 | 1 |
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Mom was going to bake rolls, all from the same pieces of dough. If she baked three rolls for each child, she would have dough left for two more rolls. If she wanted to bake four rolls for each child, she would be short of dough for one roll.
For how many children was Mom baking rolls?
(L. Hozová)
|
We will gradually examine the possibilities based on the number of children:
- If she had 1 child, then the dough should yield $1 \cdot 3 + 2 = 5$ and simultaneously $1 \cdot 4 - 1 = 3$ rolls. These values are different, so she did not have 1 child.
- If she had 2 children, then the dough should yield $2 \cdot 3 + 2 = 8$ and simultaneously $2 \cdot 4 - 1 = 7$ rolls. These values are different, so she did not have 2 children.
- If she had 3 children, then the dough should yield $3 \cdot 3 + 2 = 11$ and simultaneously $3 \cdot 4 - 1 = 11$ rolls. These values are the same, so she had 3 children.
For larger numbers of children, equality will not occur, and the difference between the compared values will gradually increase. The mother baked rolls for 3 children.
Note. The previous examination of possibilities can be clearly written as follows ($d$ represents the number of children):
| $d$ | 1 | 2 | $\mathbf{3}$ | 4 | 5 | $\ldots$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $3 d + 2$ | 5 | 8 | $\mathbf{1 1}$ | 14 | 17 | $\ldots$ |
| $4 d - 1$ | 3 | 7 | $\mathbf{1 1}$ | 15 | 19 | $\ldots$ |
The correct possibility can be reached by solving the equation
$$
3 d + 2 = 4 d - 1
$$
Evaluation. 3 points for examining the possibilities for different numbers of children or setting up the equation; 3 points for the correct result.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Inside the rectangle $A B G H$ are two identical squares $C D E F$ and $I J K L$. The side $C F$ of the first square lies on the side $B G$ of the rectangle, and the side $I L$ of the second square lies on the side $H A$ of the rectangle. The perimeter of the octagon $A B C D E F G H$ is $48 \, \text{cm}$, and the perimeter of the dodecagon $A B C D E F G H I J K L$ is $58 \, \text{cm}$. This dodecagon is symmetric with respect to a horizontal axis, and the lengths of all its sides are expressed in whole numbers of centimeters.
Determine the lengths of the sides of the rectangle $A B G H$.
(L. Šimůnek)
|
Significant parts of the perimeters of the octagon $A B C D E F G H$ and the dodecagon $A B C D E F G H I J K L$ are common to both figures. On the other hand, the segments $I J, J K$, and $K L$ are part of only the perimeter of the dodecagon, and the segment $I L$ is part of only the perimeter of the octagon. These four segments are congruent to each other, and their length is denoted by $a$. The difference in the perimeters of the figures, $58-48=10(\mathrm{~cm})$, corresponds to two $a$; i.e., $a=5 \mathrm{~cm}$.
Similarly, the difference between the perimeter of the octagon $A B C D E F G H$ and the perimeter of the rectangle $A B G H$ is equal to two $a$, or $10 \mathrm{~cm}$. Therefore, the perimeter of the rectangle is $48-10=38(\mathrm{~cm})$, and the sum of the lengths of its sides is $38: 2=19(\mathrm{~cm})$.
Given that the figure is symmetric with respect to a horizontal axis, the segments $A L, B C, F G$, and $I H$ must be congruent. Since the lengths of all sides of the dodecagon are expressed in whole numbers in centimeters, the lengths of the sides of the rectangle $A B G H$ can only take the following values (in cm):
$$
\begin{aligned}
|A B| & =11,12,13, \ldots \\
|B G| & =7,9,11, \ldots
\end{aligned}
$$
For the sum of these lengths to be 19, the lengths of the sides of the rectangle $A B G H$ must be $12 \mathrm{~cm}$ and $7 \mathrm{~cm}$.
Note. If the length of the congruent segments $A L, B C, F G$, and $I H$ is denoted by $b$ and the length of the congruent segments $K D$ and $E J$ is denoted by $c$, then the perimeter of the dodecagon can be expressed as follows:
$$
\begin{aligned}
10 a+4 b+2 c & =58 \\
4 b+2 c & =8 .
\end{aligned}
$$
Since the lengths of all sides of the dodecagon (in cm) are integers, $b$ and $c$ must also be integers and positive. Therefore, the problem has a unique solution: $b=1$ and $c=2$. The lengths of the sides of the rectangle $A B G H$ are $2 a+c=12(\mathrm{~cm})$ and $2 b+a=7(\mathrm{~cm})$.
Scoring suggestion. 3 points for the length of the side of the square $a$ (1 point for justification); 2 points for the relationship $|A B|+|B G|=19 \mathrm{~cm}$ or its equivalent (e.g., $4 b+2 c=8$); 1 point for calculation and correct conclusion.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
I want to construct a triangle $ABC$ with sides $|AB|=3 \text{~cm}$ and $|BC|=4 \text{~cm}$. Furthermore, I want to construct all circles, each of which will have its center at one of the vertices of the triangle and will pass through another vertex.
How long must the side $AC$ be so that there are exactly five such circles? Determine all possibilities.
(V. Hucíková)
|
If sides $AB$ and $AC$ were of the same length, then the circle centered at point $A$ passing through point $B$ would also pass through point $C$. In such a case, Ema would construct only one circle centered at point $A$.
If sides $AB$ and $AC$ were of different lengths, then the circle centered at point $A$ passing through one of the points $B$ and $C$ would not pass through the other. In such a case, Ema would construct two circles centered at point $A$.
Similar cases can occur for circles centered at point $C$. Circles centered at point $B$ will certainly be two, because from the problem statement we know that sides $BA$ and $BC$ are of different lengths.
If the sides of triangle $ABC$ were all different, then Ema would construct $2+2+2=6$ circles. If side $AC$ were equal to one of the remaining two sides, then Ema would construct $1+2+2=5$ circles. Therefore, side $AC$ must be either $3 \text{ cm}$ or $4 \text{ cm}$.
Scoring suggestion. 1 point for each of the two valid options; 3 points for the correct justification of the number of circles; 1 point for explaining that no other options are possible.
Justification of the correct number of circles for only one of the two valid options is considered sufficient.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Mrs. Teacher needed to come up with examples of equations for a written test. Therefore, she wrote down all equations of the form
$$
a \cdot x + b = 13
$$
where $a$ and $b$ are one-digit natural numbers. From all of them, she selected the equations whose root $x$ was 3. She put one equation into each group. What is the maximum number of groups there could be?
(K. Pazourek)
|
We know that $x=3$ is a solution to the given equation, so the equality
$$
a \cdot 3 + b = 13 \text{.}
$$
holds. For $a$ and $b$ to be natural numbers, $a$ must be either $1, 2, 3$, or $4$ (for $a=5$, we get $5 \cdot 3 = 15 > 13$ and $b$ would have to be negative, which is not possible). Now we substitute the individual values of $a$ into the equation and calculate the corresponding $b$:
- $a=1, b=10$,
- $a=2, b=7$,
- $a=3, b=4$,
- $a=4, b=1$.
We see that the case $a=1, b=10$ does not satisfy the conditions given in the problem. Therefore, there are exactly three pairs $(a, b)$ that solve the problem: $(2,7)$, $(3,4)$, and $(4,1)$. The teacher could thus form a maximum of three groups.
Grading. 1 point for substituting the root into the equation; 2 points for finding all three solutions; 3 points for explaining why there are no more solutions.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
We received a cube, the length of whose edge was expressed in centimeters as an integer greater than 2. We painted all its faces yellow and then cut it into smaller cubes, each with an edge length of $1 \mathrm{~cm}$. We sorted these small cubes into four piles. The first pile contained cubes with one yellow face, the second pile contained cubes with two yellow faces, and the third pile contained cubes with three yellow faces. The fourth pile contained cubes with no yellow faces. Determine the length of the edge of the original cube, given that at least one of the following statements is true:
- The numbers of cubes in the first and fourth piles were in the ratio $4: 9$.
- There were three times as many cubes in the first pile as in the second.
|
Let the length of the edge of the original cube in centimeters be denoted by $a+2$, where $a$ is a natural number. Each face of the original cube corresponds to $a^{2}$ small cubes with exactly one colored face, so there are a total of $6 a^{2}$ such small cubes. On each edge of the original cube, we have $a$ small cubes with exactly two colored faces. Since the original cube had 12 edges, there are a total of $12 a$ such small cubes. The number of small cubes that have no colored faces is $a^{3}$.
The first statement in the problem is expressed by this equation:
$$
\frac{6 a^{2}}{a^{3}}=\frac{4}{9}
$$
After simplifying the fraction by the non-zero expression $a^{2}$, we get
$$
\frac{6}{a}=\frac{4}{9},
$$
thus $a=13.5$. The problem assumes an integer length of the cube's edge, but here the length of the edge comes out to be $13.5+2=15.5(\mathrm{~cm})$. We see that the given ratio of the number of small cubes can never be obtained by cutting any cube.
The first statement in the problem is not true, so the second one must be true, which is expressed by the equation
$$
\frac{6 a^{2}}{12 a}=\frac{3}{1}
$$
After simplifying the fraction by the non-zero expression $6 a$, we get
$$
\frac{a}{2}=\frac{3}{1}
$$
thus $a=6$. The length of the edge of the original cube was $6+2=8(\mathrm{~cm})$.
Scoring. 3 points for expressing the number of small cubes in the first, second, and fourth piles; 2 points for the edge lengths according to the first and second statements; 1 point for the correct conclusion.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Two pairs of parallel lines $A B \| C D$ and $A C \| B D$ are given. Point $E$ lies on line $B D$, point $F$ is the midpoint of segment $B D$, point $G$ is the midpoint of segment $C D$, and the area of triangle $A C E$ is $20 \mathrm{~cm}^{2}$.
Determine the area of triangle $D F G$.
(V. Semeráková)
Hint. Compare the areas of triangles $A C E$ and $A B C$.
|
The area of a triangle depends on the length of its side and the height to this side. Since lines $A C$ and $B D$ are parallel and point $E$ lies on line $B D$, the area of triangle $A C E$ is always the same for any chosen point $E$. In particular, the area of triangle $A C E$ is the same as the area of triangle $A C D$. For the same reason, the area of triangle $A C D$ is the same as the area of triangle $B C D$. Therefore,
$$
S_{A C E}=S_{A C D}=S_{B C D}=20 \mathrm{~cm}^{2}
$$
Now let's compare the areas of triangles $B C D$ and $D F G$:
Triangles $D F G$ and $F B G$ have a common height from vertex $G$ and point $F$ is at the midpoint of side $B D$, so these triangles have the same area. Triangles $D F G$ and $F B G$ together form triangle $D B G$, so $S_{D F G}=\frac{1}{2} S_{D B G}$. For the same reason, $S_{D B G}=\frac{1}{2} S_{D B C}$. Therefore,
$$
S_{D F G}=\frac{1}{4} S_{D B C}=\frac{1}{4} \cdot 20=5\left(\mathrm{~cm}^{2}\right)
$$
Note. The previous expression of the ratio of the areas of triangles $D F G$ and $D B C$ implicitly refers to their similarity, which can also be used in the reasoning ( $F G$ is the midline of triangle $D B C$, so all corresponding sides are proportional in the ratio $1: 2$ ). Without referring to the concept of similarity, it is possible to directly compare, for example, the bases $D F$ and $D B$ and the corresponding heights (both in the ratio $1: 2$ ). This can also be considered for triangles $D F G$ and $A C E$ with any $E \in B D$ (i.e., without the transformations used above).
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Pat wrote on the board the example:
$$
589+544+80=2013 .
$$
Mat wanted to correct the example so that both sides would actually be equal, and he searched for an unknown number which he then added to the first addend on the left side, subtracted from the second addend, and multiplied the third addend by. After performing these operations, the example was numerically correct. What number did Mat find?
(L. Hozová)
|
By adding an unknown number to the first addend and subtracting the same number from the second addend on the left side, the sum of these two numbers will not change and is equal to $589+544=$ $=1133$. This intermediate sum is $2013-1133=880$ less than the number on the right side of the equation. Therefore, the product of 80 and the unknown number Mat found should be equal to 880. The number Mat found was $880: 80=11$.
Evaluation. 2 points for recognizing that the first two operations have no effect on the result; 2 points for expressing the difference 2013 - $1133=880$ and explaining its significance; 2 points for expressing the unknown number.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Jiřka constructed two congruent equilateral triangles as shown in the figure. She further wants to construct all circles that will have their center at one of the vertices and will pass through another vertex of one of the triangles.
Construct and calculate all circles that meet Jiřka's requirements.
(K. Pazourek)
Hint. Start with the vertices that are common to both triangles.
|
Let's name the vertices as shown in the following image and note that points $A$ and $C$ are always equidistant from the remaining three points (the corresponding segments form the sides of equilateral triangles). Therefore, the circle centered at point $A$ passing through point $B$ also passes through points $C$ and $D$. The circle centered at point $A$ that meets Jiřčin's requirements is thus unique. Similarly, there is a unique circle centered at point $C$ that meets the requirements.
The circle centered at point $B$ passing through point $A$ also passes through point $C$, and another circle passes through point $D$. Therefore, there are two circles centered at point $B$ that meet Jiřčin's requirements. Similarly, there are two circles centered at point $D$ that meet the requirements.
In total, there are six circles that meet the requirements:
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine which digit is in the 1000th place after the decimal point in the decimal expansion of the number $\frac{9}{28}$.
(M. Krejčová)
Hint. What does the decimal expansion of the given number look like?
|
The decimal expansion of the rational number $\frac{9}{28}$ is
$$
0.32 \overline{142857}
$$
where the repeating part, consisting of six digits, is marked with a bar.
Six goes into a thousand 166 times with a remainder of four $(1000 = 166 \cdot 6 + 4)$. There are two digits between the decimal point and the repeating part. Therefore, the digit in the 1000th place after the decimal point is the same as the second digit of the repeating part, which is the digit 4.
Note. In the solution, only the remainder of dividing 1000 by 6 is significant, and this can be determined without complete division as follows: The largest number divisible by 6 (i.e., divisible by 2 and 3) that is less than 1000 is 996. The remainder of $1000 \div 6$ is $1000 - 996 = 4$.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A subtraction pyramid is a pyramid formed by non-negative integers, each of which is the difference between the two nearest numbers from the previous level (read from bottom to top). Here is an example of a subtraction pyramid:
## 1
2
2
5 7
4
3
5
8
A significant number is the largest number in the subtraction pyramid. An excellent pyramid is a subtraction pyramid that has a 0 at the top and at least one level consisting of distinct numbers.
1. How many levels must an excellent pyramid have at a minimum?
2. What is the smallest significant number that can be contained in an excellent pyramid with the minimum number of levels?
(K. Jasenčáková)
Hint. What does the level below the apex look like?
|
If it is 0 at the top, there must be two identical numbers in the previous row. Each excellent pyramid must have at least three floors.
An excellent pyramid with the smallest number of floors and the smallest possible numbers looks like this (except for the order of the numbers on the third line):
## 0
1
0 ..... 2
The largest number in this pyramid is 2, and that is also the answer to the second question in the problem statement.
Note. The top three floors of a subtraction pyramid with zero at the top look like this (except for the order of the numbers on the third line):
$$
b-a
$$
b
$b+a$
#
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In Mr. Goat's garden, several cherry trees were in bloom. On each cherry tree, three sparrows were sitting, and one more was sitting on the fence. Mr. Goat's dog scared them away and the sparrows flew off. After a while, they all returned and settled on the cherry trees. The cherry tree under which the dog was sleeping remained empty, and on each of the others, four sparrows settled. How many cherry trees does Mr. Goat have and how many sparrows were there in the garden?
|
Let $x$ be the number of cherries in the garden and $y$ be the number of sparrows. If we know that all the sparrows perched on the cherries in groups of three and one remained on the fence, we can set up the following equation:
$$
y=3 x+1
$$
After the sparrows returned to the cherries, they occupied all the cherries except one, where a dog was lying, in groups of four. Again, we can set up the equation:
$$
y=4(x-1) \text {. }
$$
Since the number of sparrows remains the same, $y$ must be equal to the same number in both equations. Then we get:
$$
\begin{aligned}
3 x+1 & =4(x-1), \\
5 & =x .
\end{aligned}
$$
By substituting into $y=3 x+1$, we calculate that there were 16 sparrows.
Mr. Goat has a total of 5 cherries and 16 sparrows flew into the garden.
[1 point for setting up each equation, 2 points for solving the equation, 2 points for the correct answer]
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In Zverimex, they were selling fish from one aquarium. Ondra wanted half of all the fish, but to avoid cutting any fish, he received half a fish more than he requested. Matěj wished for half of the remaining fish, but like Ondra, he received half a fish more than he requested. Finally, Petr wanted half of the remaining fish, and he also received half a fish more than he requested. After that, the aquarium was empty.
How many fish were originally in the aquarium, and how many did Ondra, Matěj, and Petr get?
(M. Volfová)
|
Let's consider it from the end:
Petr got half a fish more than half of all the fish that remained after Matej. Since the aquarium was then empty, that half a fish more was exactly half of what remained after Matej. Therefore, after Matej's purchase, one fish remained in the aquarium.
Matej got half a fish more than half of all the fish that remained after Ondřej. Since one fish remained in the aquarium after Matej's purchase, this fish and the half a fish more were exactly half of what remained after Ondřej. After Ondřej's purchase, three fish remained in the aquarium.
Ondřej got half a fish more than half of all the fish that were originally in the aquarium. Since three fish remained in the aquarium after Ondřej's purchase, these three fish and the half a fish more were exactly half of the original number of fish. Originally, there were seven fish in the aquarium. Thus, Ondřej got four fish, Matej got two, and Petr got one fish.
Scoring suggestion. 1 point for determining the remainder after Matej; 2 points for determining the remainder after Ondřej; 3 points for determining the original number and the number of fish each boy took.
Another solution. If we denote the original number of fish in the aquarium as $x$, then we can express the subsequent numbers as follows:
| | got | remained |
| :---: | :---: | :---: |
| Ondřej | $\frac{x+1}{2}$ | $\frac{x-1}{2}$ |
| Matej | $\frac{x+1}{4}$ | $\frac{x-3}{4}$ |
| Petr | $\frac{x+1}{8}$ | $\frac{x-7}{8}$ |
From this, it is clear that the aquarium could be empty after Petr's purchase only if $x=7$. By substitution, we can easily determine the number of fish each boy took.
Scoring suggestion. 2 points for the second-to-last row of the table; 2 points for the last row of the table; 1 point for solving the unknown; 1 point for the number of fish for each boy.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The encryption games involved 168 players in 50 teams, which had two to five members. The most were four-member teams, there were 20 three-member teams, and the games were attended by at least one five-member team. How many two-member, four-member, and five-member teams were there? (M. Mach)
|
There were 20 three-member teams, which represents 60 players. The remaining 108 players from the total number need to be divided into 30 teams of two, four, and five players. Four-member teams were the most, i.e., at least 21, which represents at least 84 players. The remaining 24 players need to be divided into 9 teams of two, four, and five players.
There was at least one five-member team. Additionally, from 24 players, a maximum of four five-member teams can be formed. Now let's consider all the cases that may arise:
- If there was exactly 1 five-member team, then 19 players remain to be divided into 8 teams of two and four players. This is not possible because 19 is an odd number.
- If there were 2 five-member teams, then 14 players remain to be divided into 7 teams of two and four players. This can only be realized in one way - all these players will be in two-member teams, and no additional four-member team will be formed.
- If there were 3 five-member teams, then 9 players remain to be divided into 6 teams of two and four players. This is not possible because at least 12 players are needed for 6 teams.
- If there were 4 five-member teams, then 4 players remain to be divided into 5 teams of two and four players. This is not possible because at least 10 players are needed for 5 teams.
From the above discussion, the only possibility is that the game was attended by 7 two-member, 20 three-member, 21 four-member teams, and 2 five-member teams.
Evaluation. 2 points for considering that it is sufficient to divide 24 players into 9 teams of 2, 4, and 5 players; 3 points for justifying that there could only be two five-member teams; 1 point for the correct result.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The teacher wrote the following numbers on the board:
$$
1,4,7,10,13,16,19,22,25,28,31,34,37,40,43
$$
Any two adjacent numbers differ by the same value, in this case, 3. Then she erased all the numbers from the board except for 1, 19, and 43. She further added several integers between these three numbers such that any two adjacent numbers again differed by the same value, and no number was written more than once.
In how many ways could the teacher have completed the numbers?
(K. Pazourek)
Hint. Could 5 be among the added numbers?
|
One way to fill in the numbers is, of course, the one the teacher erased (in this case, the difference between consecutive numbers is 3). Another possible, and probably the simplest, way is to fill in all natural numbers from 1 to 43 (in this case, the difference is 1).
Each filling according to the task is completely determined by the difference between consecutive numbers, which we denote as $d$. Therefore, all possible fillings can be determined by considering all possible differences $d$ and checking whether the corresponding sequence (starting with 1) contains the numbers 19 and 43.
However, for a number 19 to be included in such a sequence, the difference $19-1=18$ must be some multiple of the determining constant $d$. Similarly, for the number 43 to be included in such a sequence, the difference $43-19=24$ must be some multiple of the number $d$. In other words, $d$ must be a common divisor of the numbers 18 and 24. Therefore, all possible fillings correspond to all common divisors of the numbers 18 and 24, which are precisely the numbers $1, 2, 3$, and 6. The teacher could have filled in the numbers on the board in four ways.
Note. The previous considerations can be appropriately supported by a visual representation on a number line; here, the division $s$ by the largest possible difference $d=6$ is highlighted:

|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
We have a square grid with 77 nodal points. Two of them are marked as $A$ and $B$ as shown in the figure. Let $C$ be one of the remaining nodal points. Find all possible positions of point $C$ such that triangle $ABC$ has an area of 6 square units.
(E. Novotná)
Hint. Try points first such that one side of the triangle lies on one of the lines forming the square grid.
|
If we are looking for a solution by trial, we will most likely start testing the nodal points as indicated by the hint. Let's first consider the nodal points on the horizontal line passing through point $A$; the position of point $C$ is calculated from $A$ to the left:
1. the triangle is right-angled and its area is clearly 2 squares, which is too small,
2. the height from point $B$ divides the triangle into two (congruent) right-angled triangles, the area is $2+2=4$ squares, which is still too small,
3. the height from point $B$ divides the triangle into two (non-congruent) right-angled triangles, the area is $4+2=6$ squares, and we have our first valid solution, which we denote as $C_{1}$.
The same point can also be found without trial if we realize in time that the area of each discussed triangle is equal to half the area of a rectangle, one side of which is $A C$ and the other is 4 units (the height from point $B$), see the figure. We are looking for a nodal point on the considered line such that the area of the corresponding rectangle is
12 squares. Point $C$ must therefore be $12: 4=3$ units from $A$, and to stay within the marked area, we must go to the left.

In a very similar way, we can justify the other solution on the horizontal line passing through point $B$, which we denote as $C_{2}$. (The symmetric point with respect to $B$ again falls outside the marked area.) The line $C_{1} C_{2}$ is parallel to $A B$, so every triangle $A B C$ whose vertex $C$ lies on this line has the same height to the side $A B$, and thus the same area. We are therefore looking for nodal points that simultaneously lie on the line $C_{1} C_{2}$. This way we find the point marked as $C_{3}$.
By similar reasoning in the opposite half-plane defined by the line $A B$, we find that the remaining solutions are precisely those nodal points that simultaneously lie on the marked unnamed line. This way we find the last valid point, which is marked as $C_{4}$.
The problem has a total of 4 solutions, which we have sequentially marked as $C_{1}, C_{2}, C_{3}$, and $C_{4}$.
Notes. In the given solution, we assume knowledge of the fact that the area of any triangle is equal to half the area of a rectangle that has one side in common with the triangle and the other side equal to the height to this side. A simple justification of this statement is essentially shown in the solution to problem Z6-I-2.
Even without this knowledge, the problem can be solved by trial, as we indicated at the beginning. The area of any triangle $A B C$ with vertices at nodal points can always be expressed as follows:
- we circumscribe a rectangle around the triangle $A B C$, whose sides lie on the lines forming the square grid,
- if necessary, we divide the supplementary areas to the triangle in the circumscribed rectangle into right-angled triangles, or right-angled rectangles,
- we express the area of the triangle as the difference between the area of the circumscribed rectangle and the areas of the individual supplementary parts from the previous step.
The calculation of the areas of some triangles would look like this according to this guide (see the figures above):
$$
\begin{aligned}
& S_{A B C_{1}}=3 \cdot 4-\frac{2 \cdot 4}{2}-\frac{1 \cdot 4}{2}=12-6=6, \\
& S_{A B C_{2}}=4 \cdot 4-\frac{4 \cdot 4}{2}-\frac{1 \cdot 4}{2}=16-10=6, \\
& S_{A B C_{3}}=5 \cdot 8-\frac{5 \cdot 8}{2}-\frac{4 \cdot 4}{2}-1 \cdot 4-\frac{1 \cdot 4}{2}=40-34=6, \\
& S_{A B C_{4}}=2 \cdot 8-\frac{1 \cdot 4}{2}-\frac{2 \cdot 4}{2}-\frac{1 \cdot 8}{2}=16-10=6 .
\end{aligned}
$$
Note that even with this method, it is not necessary to exhaust all possibilities: for example, if we have found that point $C_{2}$ is a solution, we certainly do not need to consider such nodal points where the corresponding triangle either contains triangle $A B C_{2}$ or is part of it (in the first case, the resulting triangle would have a larger than required area, in the second case a smaller area).
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Eliška was placing cakes into boxes, from which she then built a pyramid as shown in the picture. Each box in a higher row contained as many cakes as the two adjacent boxes below it combined. In the three boxes marked with stars, there were three, five, and six cakes.
Eliška noticed that if she were to swap the marked boxes (and adjust the number of cakes in the other boxes according to the previous rule), the total number of cakes would not be less.
How many cakes were in the marked box in the second row from the bottom?
(L. Hozová)
|
Let's denote the number of cakes in the lower row of the pyramid as $a, b, c, d$, and from there, we can express the numbers in the other boxes:
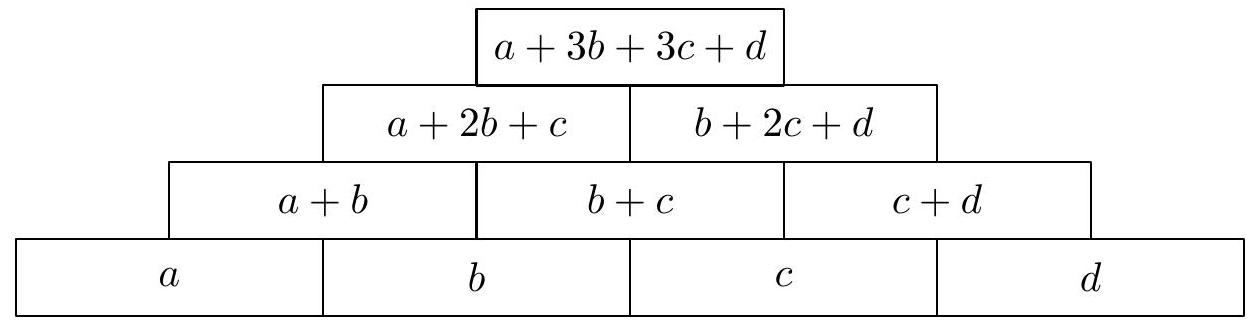
The sum of all the given numbers is
$$
4 a + 9 b + 9 c + 4 d = 4(a + d) + 9(b + c)
$$
The numbers in the boxes marked with stars are $a, d$, and $b+c$, which are (in some order) the numbers 3, 5, and 6. The total sum is the smallest possible when the number $b+c$ (which contributes the most to the sum) is the smallest possible, i.e., 3.
There were three cakes in the marked box in the second row from the bottom.
Note. The problem can also be solved by examining all possible distributions of the known numbers of cakes. Given the evident symmetries, it suffices to consider three cases:
- $a=3, d=5, b+c=6$, which gives a total sum of 86,
- $a=3, d=6, b+c=5$, which gives a total sum of 81,
- $a=5, d=6, b+c=3$, which gives a total sum of 71.
The smallest sum occurs in the third case, which agrees with the previous conclusions.
Evaluation. 3 points for the general completion of the pyramid, or for the analysis of possibilities; 3 points for solving the problem.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Vojta bought 24 identical square tiles. The side of each tile measured $40 \mathrm{~cm}$. Vojta wanted to create a rectangular platform in front of the cottage with the smallest possible perimeter. How many meters did the perimeter of the paved rectangle measure, given that no tiles were left over? Vojta did not cut or break any tiles in any way.
(L. Hozová)
|
Let's go through all the possibilities; for each, we will provide the dimensions of such a rectangle in "tiles" and further the perimeter in "tiles," resp. in "sides of tiles":
- dimensions: $1 \times 24$, perimeter: $2 \cdot(1+24)=50$,
- dimensions: $2 \times 12$, perimeter: $2 \cdot(2+12)=28$,
- dimensions: $3 \times 8$, perimeter: $2 \cdot(3+8)=22$,
- dimensions: $4 \times 6$, perimeter: $2 \cdot(4+6)=20$.
It is clear that the smallest perimeter expressed in centimeters/meters must also be the smallest when expressed in "tiles." The smallest perimeter is obtained in the fourth case, which is 20 tiles. If the side of one tile is $40 \mathrm{~cm}$ long, then 20 such sides measure a total of $20 \cdot 40=800(\mathrm{~cm})$. The perimeter of the paved rectangle measured 8 meters.
Evaluation. 1 point for the idea of the solution; 1 point for each correctly stated and analyzed possibility; 1 point for the result.
If the solver does not list all possibilities and does not explain why some of them were omitted (e.g., in the first possibility, that the perimeter is too long compared to the other perimeters), they can receive a maximum of 4 points, even if they provide the correct result.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Káta wants to give presents to her friends and is thinking: if I bought each of them a hair clip for 28 Kč, I would still have 29 Kč left, but if it were a teddy bear for 42 Kč, I would be short of 13 Kč. How many friends does Káta have and how much money does she have for gifts?
(M. Volfová)
|
The difference in the price of a gift for one friend is $42-28=14$ (CZK). The difference in the total price that Káta would pay for gifts for all her friends is $29+13=42$ (CZK). If we multiply the difference in the price of a gift for one friend by the number of friends, we get the difference in the total price. Therefore, the number of friends is determined as the result of dividing the difference in the total price by the difference in the price of both gifts, i.e., $42: 14=3$. Káta has 3 friends.
If she bought a hair clip for 28 CZK for each of them, she would have 29 CZK left, so she has $3 \cdot 28+29=84+29=113$ (CZK).
Note. The final calculation can also be done as follows: if she bought a teddy bear for 42 CZK for each of them, she would be short by 13 CZK, so she would have $3 \cdot 42-13=126-13=113$ (CZK).
The problem can also be solved by experimenting or using equations.
Evaluation. 1 point for the difference in the price of gifts for one friend (i.e., 14 CZK); 2 points for the total difference for all friends (i.e., $42 \mathrm{CZK}); 2$ points for determining and justifying the number of friends; 1 point for determining the amount of money Káta has for gifts.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Šárka declared:
"I am the youngest of three sisters. Líba is three years older, and Eliška is eight years older. Our mom loves to hear that the average age of all of us (including her) is 21. When I was born, mom was already 29."
How many years ago was Šárka born?
(M. Volfová)
|
If we denote Śárka's age in years by $x$, then Líbě is $x+3$, Eliška is $x+8$, and the mother is $x+29$ years old. The average age of all of them is 21 years, i.e.,
$$
(x+(x+3)+(x+8)+(x+29)): 4=21,
$$
after rearrangement
$$
\begin{aligned}
4 x+40 & =84, \\
x & =11 .
\end{aligned}
$$
Śárka was born 11 years ago.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the figure, squares $ABCD$, $EFCA$, $GHEC$, and $IJHE$ are depicted. Points $S$, $B$, $F$, and $G$ are the centers of these squares, respectively. Segment $AC$ is $1 \, \text{cm}$ long.
Determine the area of triangle $IJS$.
(E. Semerádová)
Hint. The area of the triangle is half the area of some rectangle.
|
The area of triangle $I J S$ is equal to half the area of the rectangle with sides $I J$ and $I A$. Side $I J$ is a side of the square $I J H E$, and side $I A$ is the sum of the side of the square $I J H E$ and the side of the square $E F C A$.
Square $I J H E$ has a side that is twice the side of square $E F C A$, and that measures $1 \mathrm{~cm}$. Therefore, side $I J$ measures $2 \mathrm{~cm}$ and side $I A$ measures $3 \mathrm{~cm}$. The area of triangle $I J S$ is equal to
$$
\frac{1}{2} \cdot 2 \cdot 3=3\left(\mathrm{~cm}^{2}\right)
$$
Note. By more finely dividing the indicated square grid, the same result can be achieved through visual counting of the squares, or triangular segments.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the picture, there is a cube with an edge of $2 \mathrm{~cm}$ made up of eight smaller cubes with an edge of $1 \mathrm{~cm}$. Eight faces of the smaller cubes are painted black, and the rest are white. From them, a cube can be assembled whose surface is white. In how many ways can the smaller cubes be painted? Assume that identically painted smaller cubes cannot be distinguished and can therefore be interchanged.

(K. Pazourek)
|
From the task, it follows that each of the eight small cubes, from which the large cube is composed, has three white faces that share a common vertex. The remaining faces of each small cube are either black or white. In total, eight faces should be black, regardless of how we arrange the small cubes; what matters is only how many faces are colored. Moreover, it doesn't matter if we color, for example, the first and second faces or the first and third faces - we can rotate the small cube to convert one case to another and vice versa. Let's list the possible colorings of the small cubes. The rows record the number of black faces on each of the small cubes, always from the highest number $\mathrm{k}$ to the lowest:
- $3,3,2,0,0,0,0,0$,
$\bullet 3,3,1,1,0,0,0,0$,
- $3,2,2,1,0,0,0,0$,
- $3,2,1,1,1,0,0,0$,
- $3,1,1,1,1,1,0,0$,
- $2,2,2,2,0,0,0,0$,
- $2,2,2,1,1,0,0,0$
- $2,2,1,1,1,1,0,0$,
- 2, 1, 1, 1, 1, 1, 1, 0,
- $1,1,1,1,1,1,1,1$.
This gives us a total of 10 different colorings of the small cubes.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
From the right pocket of my pants, I moved 4 five-crown coins to the left pocket, and from the left pocket, I moved 16 two-crown coins to the right pocket. Now I have 13 crowns less in the left pocket than in the right. In which pocket did I have more crowns at the beginning, and by how much?
(Bednářová)
|
We solve the example from the end, using the $\mathrm{k}$ table:
state at the end
left pocket (L) right pocket $(\mathrm{P}) \quad$ difference
move 16 two-crowns from $\mathrm{P}$ to $\mathrm{L}$
32
13
13
move 4 five-crowns from $\mathrm{L}$ to $\mathrm{P}$
12
owe 19
51
1
Conclusion: I had 11 crowns more in the left pocket than in the right.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Karolína wrote all three-digit numbers formed by the digits 1, 2, and 3, in which no digit was repeated and 2 was in the tens place. Nikola wrote all three-digit numbers formed by the digits 4, 5, and 6, in which no digit was repeated. Kuba chose one number from Karolína and one number from Nikola so that the sum of these two numbers was even.
What was the digit in the units place of the product of the numbers chosen by Kuba? Determine all possibilities.
(L. Hozová)
|
Karolína wrote the numbers
$$
123, \quad 321 .
$$
Nikola wrote the numbers
$$
456, \quad 465, \quad 546, \quad 564, \quad 645, \quad 654 .
$$
Both of Karolína's numbers are odd. For an even sum, Kuba had to choose an odd number from Nikola. The even sums are given by the following cases:
$$
123+465, \quad 123+645, \quad 321+465, \quad 321+645
$$
In all cases, the digit in the units place of the product is determined by an odd multiple of 5, which can only be 5.
Evaluation. 1 point for Karolína's and Nikola's numbers; 2 points for Kuba's choice of an even sum; 2 points for determining the last digit of the product.
Note. It is not necessary to list the products to reach the correct conclusion. However, for the quartet of possibilities in $(*)$, these products are, in order,
$$
57195, \quad 79335, \quad 149265, \quad 207045 .
$$
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In rectangle $A B C D$ with side $A D$ of length $5 \mathrm{~cm}$, point $P$ is located such that triangle $A P D$ is equilateral. Ray $A P$ intersects side $C D$ at point $E$, and segment $C E$ measures $5 \mathrm{~cm}$.
How long is segment $A E$ and what is the measure of angle $A E B$?
(L. Hozová)
|
Triangle $A P D$ is equilateral, so the lengths of all its sides are $5 \mathrm{~cm}$ and the measures of all its internal angles are $60^{\circ}$.
The internal angles of rectangle $A B C D$ are right angles, so the measures of angles $P D E$ and $P A B$ are $30^{\circ}$. Angle $P E D$ is the third angle of triangle $A E D$ (or also the alternate angle to angle $E A B$), so its measure is $30^{\circ}$. Angles $P D E$ and $P E D$ are congruent, thus triangle $D E P$ is isosceles and $|P D|=|P E|=5 \mathrm{~cm}$. Segment $A E$ is
$$
|A E|=|A P|+|P E|=5+5=10(\mathrm{~cm}) \text {. }
$$
Segment $C E$ is congruent to segment $C B$, so triangle $E B C$ is isosceles with a right angle at vertex $C$. The remaining two internal angles are therefore congruent with a measure of $45^{\circ}$. The measure of angle $A E B$ is
$$
|\angle A E B|=180^{\circ}-|\angle A E D|-|\angle B E C|=180^{\circ}-30^{\circ}-45^{\circ}=105^{\circ} .
$$
Scoring suggestion. 1 point for recognizing the isosceles nature of triangles $D P E$ and $E B C$; 1 point for calculating the length of segment $A E$ and the measure of angle $A E B$; 2 points based on the quality of the commentary.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Mice have built an underground house consisting of chambers and tunnels:
- each tunnel leads from one chamber to another (i.e., none are dead ends),
- from each chamber, exactly three tunnels lead to three different chambers,
- from each chamber, one can reach any other chamber via tunnels,
- the house has exactly one tunnel such that its collapse would divide the house into two separate parts.
What is the minimum number of chambers the mouse house could have? Sketch how the chambers could be connected.
(K. Jasenčáková)
Hint. Start with the critical tunnel.
|
We will denote cells with circles and tunnels with lines. We start with a critical tunnel, whose collapse divides the house into two separate parts. If we denote the cells at the ends of this tunnel as $A$ and $B$, then each cell belongs to exactly one of the following two groups:
a) cell $A$ and all cells that can be reached from it without using the tunnel $A B$,
b) cell $B$ and all cells that can be reached from it without using the tunnel $B A$.
This means that no cell from one group is connected by a tunnel to any cell from the other group. Now we will determine the minimum number of cells that can be in one group while satisfying the other conditions:
- For there to be three tunnels from cell $A$, there must be at least two more cells in group a), which we will denote as $C$ and $D$. However, three cells in the group are not enough - only $C$ and $D$ can be connected, and this would mean that only two tunnels lead from $C$ and $D$.
- Therefore, there must be at least one more cell in group a), which we will denote as $E$. However, four cells are still not enough - $E$ can only be connected to $C$ and $D$, and this would mean that only two tunnels lead from $E$.
- Therefore, there must be at least one more cell in group a), which we will denote as $F$. Five cells in one group are sufficient - the cells can be connected, for example, as follows:
The house had at least 10 cells.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
At the tournament, teams Akouska, Bovenska, Colska, and Demecka met. Each team played against each other exactly once. The winning team received three points, the losing team received no points, and in the event of a draw, each of the drawing teams received one point. After all six matches were played, Akouska had 7 points, Bovenska had 4 points, Colska had 3 points, and Demecka had 2 points.
a) How many matches ended in a draw?
b) What was the result of the match between Bovenska and Colska?
(J. Tkadlec)
|
The team names are abbreviated to A, B, C, and D. Each team played three matches against the remaining teams, and could earn 0, 1, or 3 points per match. The distribution of points for teams A, B, and D is therefore uniquely determined, while for team C there are two possibilities:
$$
7=3+3+1, \quad 4=3+1+0, \quad 3=3+0+0=1+1+1, \quad 2=1+1+0 .
$$
One point is always awarded to two teams, so the total number of ones in the above decompositions must be even. In the decompositions of 7, 3, and 2 (i.e., the points of teams A, B, and D), there are a total of four ones. Therefore, team C must have earned its 3 points as follows:
$$
3=3+0+0 \text{. }
$$
From this, it also follows that two matches ended in a draw.
Team D drew twice, and teams A and B each drew once. Therefore, team D drew with teams A and B.
Team A drew once and won twice. Since it drew with team D, it must have won against teams B and C.
Team B lost once, drew once, and won once. Since it lost to team A and drew with team D, it must have won against team C.
Note. From the above, we can construct a table of all matches:
| | A | B | C | D | total |
| :---: | :---: | :---: | :---: | :---: | :---: |
| A | - | 3 | 3 | 1 | 7 |
| B | 0 | - | 3 | 1 | 4 |
| C | 0 | 0 | - | 3 | 3 |
| D | 1 | 1 | 0 | - | 2 |
The answer to question a) can also be derived as follows: In total, 16 points were awarded in the tournament: \(7 + 4 + 3 + 2 = 16\). If no match had ended in a draw, a total of \(6 \times 3 = 18\) points would have been awarded. Each draw contributes two points to the total (i.e., one point less than a win), so two matches ended in a draw.
Evaluation. 2 points for the answer to each of the questions a) and b); 2 points for the quality of the commentary.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The worm consists of a white head and several segments, see the image.
When the worm is born, it has a head and one white segment. Each day, the worm gains a new segment in one of the following ways:
- either a white segment splits into a white and a gray segment:
- or a gray segment splits into a gray and a white segment:
(In both cases, we describe the situation when looking at the worm from the head.) On the fourth day, the worm matures and stops growing - its body consists of a head and four segments.
How many different color variants of mature worms of this species can exist?
(E. Novotná)
Hint. What can a two-day-old worm look like?
|
On the first day of its life, a worm has only one white segment (and a head):
On the second day, it can grow a new segment only in the first of the mentioned ways; all worms that are two days old therefore look the same:
On the third day, either the first (white) or the second (gray) segment can split, so there are two possibilities:

On the fourth day, any of the three segments of both types of worms from the previous day can split, so we need to check a total of six possibilities:
By comparing all six adult worms, we find that there are two pairs of identical worms, and the remaining two are different from all others. Therefore, there are exactly four different color variants of adult worms of this interesting species.
#
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Iveta gradually listed natural numbers composed of the digits 1, 3, 5, 7. She used no other digits, proceeded in ascending order from the smallest number, and did not omit any number. She wrote the numbers immediately after each other, thus forming one extraordinarily long number:
$$
1357111315173133 \ldots
$$
Which digit is in the 1286th place of this number?
(E. Novotná)
|
From the given digits, Iveta created 4 one-digit numbers. All these numbers occupy 4 places in Iveta's long number.
$Z$ from the given digits, Iveta created $4^{2}=16$ two-digit numbers. All these numbers occupy $2 \cdot 16=32$ places in Iveta's long number. The last digit of the last two-digit number is at the 36th place $(4+32=36)$.
From the given digits, Iveta created $4^{3}=64$ three-digit numbers. All these numbers occupy $3 \cdot 64=192$ places in Iveta's long number. The last digit of the last three-digit number is at the 228th place $(36+192=228)$.
From the given digits, Iveta created $4^{4}=256$ four-digit numbers. All these numbers occupy $4 \cdot 256=1024$ places in Iveta's long number. The last digit of the last four-digit number is at the 1252nd place $(228+1024=1252)$.
To reach the 1286th place, 34 places are missing, and these are occupied by five-digit numbers. Since $34: 5$ is 6 with a remainder of 4, the sought digit is the 4th digit in the 7th five-digit number that Iveta created. These numbers, arranged in ascending order, are:
$$
11111,11113,11115,11117,11131,11133,111 \underline{3} 5 .
$$
In Iveta's long number, the 1286th place is occupied by the digit 3.
Evaluation. 2 points for the counts of one-, two-, three-, and four-digit numbers; 2 points for the counts of places these numbers occupy in Iveta's long number; 2 points for determining the sought digit and the quality of the commentary.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In five bags, there are 52 balls in total. In no two bags is the number of balls the same, and some bags may be empty. All the balls from any (non-empty) bag can be moved to the other four bags so that they will have the same number of balls.
a) Find some distribution of balls into the bags that has all the mentioned properties.
b) Show that in any distribution $s$ with the mentioned properties, there is exactly 12 balls in one of the bags.
(J. Zhouf)
|
After moving the balls, one bag is empty and the other four contain the same number. In total, there are 52 balls, so after moving, there are 13 balls in each non-empty bag $(52: 4=13)$. Therefore, originally, there could not have been more than 13 balls in any bag.
a) Possible original numbers of balls in the bags correspond to possible expressions of the number 52 as the sum of five distinct non-negative integers, none of which are greater than 13. By trial, the following possibilities can be found:
$$
52=13+12+11+10+6=13+12+11+9+7=13+12+10+9+8 .
$$
b) If there were no more than 12 balls in any bag, then there would be at most $12+11+10+9+8=50$ balls in total. Therefore, there must have been 13 balls in one of the bags.
If there were no 12 balls in any bag, then there would be at most $13+11+10+9+8=51$ balls in total. Therefore, there must have been 12 balls in one of the bags.
Note. The distributions listed in part a) are the only possible ones. This can be justified by systematically substituting successively decreasing distinct addends no greater than 13 and checking their sum. In each of the listed possibilities, the number 12 indeed appears.
Evaluation. 1 point for any valid distribution; 2 points for justifying that there were no more than 13 balls in any bag; 3 points for justifying that there were 12 balls in one of the bags. Solutions based on the note in part a) can be awarded full points depending on the completeness of the comment on part a). Solutions containing all possible options without justification are worth 2 points.
|
12
|
Logic and Puzzles
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Half of the children in 5.A attend a dance club. All girls attend and one third of the 18 boys attend.
a) How many children are in 5.A?
b) How many girls are in 5.A?
|
All girls and one third of 18 boys, i.e., 6 boys, attend the dance club, which is half of the students in 5.A. 12 boys, who do not attend the dance club, make up the other half of the class.
a) There are thus 24 children in class $V$.
b) $24-18=6$. There are 6 girls.
[ 6 boys ... 1 point, 12 boys are half ... 1 point, 24 children in the class ... 2 points, 6 girls ... 2 points]
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Matěj and his friends went caroling. In addition to apples, walnuts, and gingerbread, each of the boys also received an orange. Jarda got one orange, Milan too. Radek, Patrik, Michal, and Dušan each got two oranges. Matěj got as many as four oranges, which was the most of all the boys. The other boys each got three oranges. How many boys went caroling if they received a total of 23 oranges?
(M. Volfová)
|
Boys whose names we know received a total of $1+1+2+2+2+2+4=14$ oranges. For the boys whose names we do not know, there are $23-14=9$ oranges left. Since each of these boys received three oranges, there must have been $9: 3=3$ of them. We know the names of seven boys, and three more boys whose names we do not know, so in total, 10 boys went caroling.
Evaluation. 2 points for determining the number of oranges received by boys with known names; 1 point for determining the number of oranges received by boys with unknown names; 2 points for determining the number of boys with unknown names; 1 point for determining the total number of boys.
#
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Friends Jarda, Premek, and Robin were playing marbles. Jarda wasn't doing well, so after the game, he had the fewest marbles of all. The boys felt sorry for him, so Robin gave Jarda half of all his marbles, and Premek gave him a third of his. Then Jarda had the most marbles, so he returned seven marbles to each of his friends. After these exchanges, they all had the same number, which was 25 marbles.
How many marbles did Jarda have after the game (before the exchanges)?
(M. Petrová)
|
We can solve the task advantageously from the end:
- Before the second (last) exchange round, Premek and Robin had seven marbles less, while Jarda had 14 more. So Premek and Robin had $25-7=18$ marbles, while Jarda had $25+14=39$.
- Before the first exchange round, Robin had double the number of marbles (he gave half to Jarda, leaving him with half), and Premek had three halves of the marbles (he gave a third to Jarda, leaving him with two-thirds). So Robin had $2 \cdot 18=36$ marbles and Premek had $\frac{3}{2} \cdot 18=27$ marbles.
- The total number of marbles remained constant throughout the redistribution. The sum after the second, respectively, first exchange was $25+25+25=18+18+39=75$ marbles. Before the first exchange (after the game), Robin had 36 and Premek had 27 marbles. So after the game, Jarda had
$$
75-36-27=12 \text { marbles. }
$$
Note. The visualization of the previous considerations, or the verification of the results, might look like this:
| states | Robin | Premek | Jarda | exchanges |
| ---: | :---: | :---: | :---: | :--- |
| after 2nd exchange | 25 | 25 | 25 | |
| | | $\uparrow 7$ | $\downarrow 7$ | Jarda to Premek |
| | $\uparrow 7$ | | $\downarrow 7$ | Jarda to Robin |
| after 1st exchange | 18 | 18 | 39 | |
| | $\downarrow 18$ | | $\uparrow 18$ | Robin to Jarda |
| | | $\downarrow 9$ | $\uparrow 9$ | Premek to Jarda |
| after the game | 36 | 27 | 12 | |
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Péta constructed several plane figures from identical triangles, see the image. The perimeters of the first three are $8 \mathrm{~cm}, 11.4 \mathrm{~cm}$, and $14.7 \mathrm{~cm}$, respectively.
Determine the perimeter of the fourth figure.
(E. Semerádová)
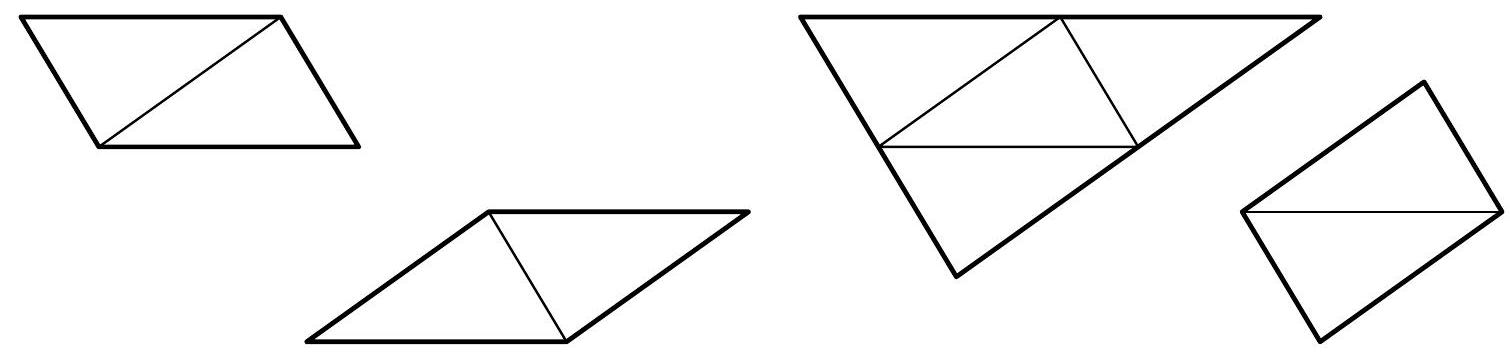
Note: the image is for illustration only.
|
In the perimeters of the first, second, and fourth figures, two out of the three sides of the basic triangle are always included, such that each of the two sides is counted twice, and in the perimeters of different figures, different pairs of sides are included.
In the perimeter of the third figure, all sides of the basic triangle are included, and again each is counted twice.
Thus, the sum of the perimeters of the first, second, and fourth figures is equal to twice the perimeter of the third figure. This means that the unknown perimeter of the fourth figure is equal to the difference between the perimeters of the first and second figures and twice the perimeter of the third:
$$
2 \cdot 14.7 - 8 - 11.4 = 29.4 - 19.4 = 10(\mathrm{~cm}).
$$
Notes. From the problem statement, the lengths of the sides of the basic triangle, which we will denote as \(a, b, c\), can be derived:
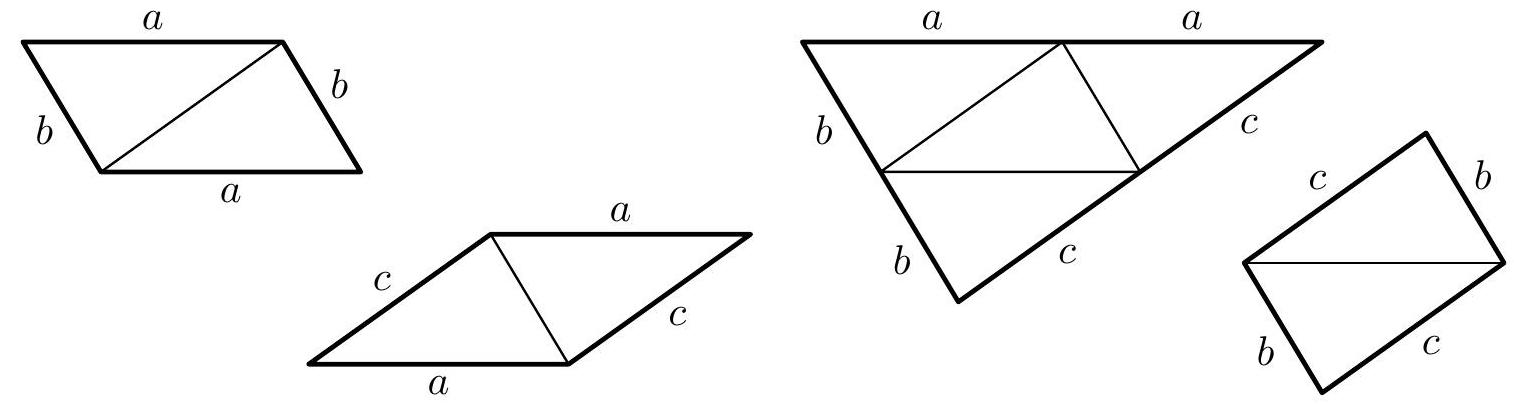
The difference in the perimeters of the third and first figures is equal to twice \(c\), thus
$$
c = \frac{1}{2}(14.7 - 8) = 3.35(\mathrm{~cm})
$$
The difference in the perimeters of the third and second figures is equal to twice \(b\), thus
$$
b = \frac{1}{2}(14.7 - 11.4) = 1.65(\mathrm{~cm})
$$
From this and the known perimeters of the first three figures, the length of the last side of the basic triangle can be expressed:
$$
a = \frac{8}{2} - 1.65 = \frac{11.4}{2} - 3.35 = \frac{14.7}{2} - 1.65 - 3.35 = 2.35(\mathrm{~cm}).
$$
The values of \(a, b, c\) satisfy the triangle inequalities \((1.65 + 2.35 > 3.35\) etc.), so a triangle with sides of these lengths actually exists and (up to scale) looks like this:
From the above, we can derive the perimeter of the fourth figure for verification:
$$
2(b + c) = 2(1.65 + 3.35) = 10(\mathrm{~cm}).
$$
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For how many positive numbers less than 1000 is it true that among the numbers $2,3,4,5,6,7,8$ and 9 there is exactly one that is not its divisor?
(E. Semerádová)
|
If a number is not divisible by 2, then it is also not divisible by 4, 6, and 8. If a number is not divisible by 3, then it is also not divisible by 6 and 9. If a number is not divisible by 4, then it is also not divisible by 8. If a number is not divisible by 6, then it is not divisible by 2 or 3. Therefore, none of the numbers 2, 3, 4, and 6 can be the only number from the given list that is not a divisor of the sought number.
A number divisible by all numbers from the given list except 5 must be a multiple of $7 \cdot 8 \cdot 9 = 504$, which is the least common multiple of the remaining numbers. The positive number less than $1000$ with this property is unique, and that is 504.
A number divisible by all numbers from the given list except 7 must be a multiple of $5 \cdot 8 \cdot 9 = 360$. The positive numbers less than 1000 with this property are two, and they are 360 and 720.
A number divisible by all numbers from the given list except 8 must be a multiple of $4 \cdot 5 \cdot 7 \cdot 9 = 1260$. There is no positive number less than 1000 with this property.
A number divisible by all numbers from the given list except 9 must be a multiple of $3 \cdot 5 \cdot 7 \cdot 8 = 840$. The positive number less than 1000 with this property is unique, and that is 840.
The numbers with the given properties are exactly four.
Evaluation. 2 points for the four correct options; 4 points for excluding other options and the quality of the commentary.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Dwarves painted cubic dice with green and white colors so that each face was entirely painted in one of these two colors. After a while, they noticed that some of the painted dice looked exactly the same after a suitable rotation and began to sort them into groups (in the same group are identically painted dice).
What is the maximum number of groups they could thus obtain?
(I. Jančigová)
Hint. What relationships can pairs of cube faces have?
|
A cube has six faces, with each face adjacent to four other faces (they share an edge) and parallel to one face (they share no points).
We can categorize the colorings based on the number of green (or white) faces. This gives us seven possibilities, for each of which we will analyze different types of coloring.
- No green faces (all white): all such cubes look the same, so we have only one type.
- One green face (five white): likewise, only one type.
- Two green faces (four white): we distinguish two types based on whether the green faces are adjacent or not.
- Three green faces (three white): we distinguish two types, depending on whether the green faces are adjacent in pairs or all mutually adjacent.
- Other cases do not need to be listed: the discussion for options with swapped numbers of green and white faces is the same.
In total, we get $1+1+2+2+2+1+1=10$ types of coloring. The dwarves could receive a maximum of 10 groups of colored cubes.
#
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the parking lot, there were cars and bicycles. If one more car arrived, there would be as many of them as there are bicycles. If five more bicycles arrived, all the bicycles would have as many wheels as all the cars.
How many cars and how many bicycles were in the parking lot?
(M. Dillingerová)
Hint. Imagine a situation where the number of wheels of the cars and bicycles is the same.
|
A car has four wheels, a bicycle has two; one car has the same number of wheels as two bicycles.
There was one more bicycle than cars in the parking lot. Consider the situation where there would be five more bicycles in the parking lot than originally, that is, the situation where the number of wheels would match. In such a case, there would be six more bicycles than cars.
Six more bicycles mean 12 more wheels. This difference corresponds to exactly six cars (a car has two more wheels than a bicycle and $2 \cdot 6=12$). Therefore, there were six cars and seven bicycles (one more than cars) in the parking lot.
Notes. The reasoning in the last paragraph can be replaced by testing possibilities, where the numbers of vehicles are gradually increased and their difference is checked:
| cars | 3 | 4 | 5 | 6 | $\ldots$ |
| :---: | :---: | :---: | :---: | :---: | :---: |
| bicycles | 6 | 8 | 10 | 12 | $\ldots$ |
| difference | 3 | 4 | 5 | $\mathbf{6}$ | $\ldots$ |
The observed difference keeps increasing, so the problem has no other solution.
If we assume that each car also has one spare wheel, then by similar reasoning we would conclude that there were four cars and five bicycles in the parking lot.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ivan and Mirka were sharing pears from a plate. Ivan always took two pears, and Mirka took half of what was left on the plate. They proceeded in this manner: Ivan, Mirka, Ivan, Mirka, and finally Ivan, who took the last two pears.
Determine who ended up with more pears and by how many.
(M. Dillingerová)
Hint. How many pears did Mirka take the second time?
|
Ivan took three times two pears, in the end, he had 6 pears. To determine how many pears Mirka ended up with, we will trace back the changes in the number of pears step by step. $\mathrm{K}$ to do this, it is enough to realize that before each of Ivan's takings, there were two more pears on the plate, and before each of Mirka's takings, there were twice as many pears on the plate.
Ivan took the last 2 pears during his third taking.
Mirka took 2 pears during her second taking, before that, there were 4 pears on the plate. Ivan took 2 pears during his second taking, before that, there were 6 pears on the plate.
Mirka took 6 pears during her first taking, before that, there were 12 pears on the plate. Ivan took 2 pears during his first taking, originally, there were 14 pears on the plate. Mirka took a total of 8 pears, so in the end, she had two more pears than Ivan.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Arnošt cut out a $4 \times 4$ square from graph paper. Kristián cut out two holes in it, see the two black squares in the picture. Arnošt tried to cut this shape along the marked lines into two identical parts.
Find at least four different ways Arnošt could have done this. (Two cuttings are considered different if the parts created by one cutting are not congruent to the parts created by the other cutting.)
(A. Bohiniková)

Hint. Notice a certain symmetry.
|
One of the simplest possible divisions is indicated in the following figure:
The newly created parts are — like the original shape — symmetric with respect to the center of the bounding square. The previous division can be gradually modified so that the centrally symmetric squares belong to different parts. By adding or removing squares in the first column, we get the following possible divisions:

Note. Any further modification leads either to a division identical to one of the previous ones, or to a division that consists of multiple disconnected parts. The four solutions mentioned thus represent all different ways of division.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In triangle $ABC$, we denote the midpoints of sides $CB$ and $CA$ by the letters $K$ and $L$. We know that the quadrilateral $ABKL$ has a perimeter of $10 \text{ cm}$ and triangle $KLC$ has a perimeter of $6 \text{ cm}$. Calculate the length of segment $KL$.
(J. Mazák)
|
Segment $K L$ is the midline of triangle $A B C$ parallel to $A B$, since $K$ and $L$ are the midpoints of sides $B C$ and $A C$. Therefore, $2|K L|=|A B|$ and also $|A L|=|L C|$ and $|C K|=|K B|$.
The perimeter of triangle $K L C$ is $|C K|+|K L|+|L C|=6$. The perimeter of quadrilateral $A B K L$ is
$$
|A B|+|B K|+|K L|+|L A|=10 \text {. }
$$
The sum on the left side of the aforementioned equality can be expressed according to previous observations as $2|K L|+(|C K|+|K L|+|L C|)$, or $2|K L|+6$. The mentioned equality thus takes the form
$$
2|K L|+6=10
$$
from which we get $2|K L|=4$, i.e., $|K L|=2(\mathrm{~cm})$.
Evaluation. 2 points for identifying and justifying that $|A B|=2|K L| ; 2$ points for considerations about perimeters; 2 points for calculating $|K L|$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Adam, Borrek, and Cenda were comparing how many kilograms of chestnuts they had collected. They found that the arithmetic mean of what Adam and Borrek collected is 10 kg more than Cenda's contribution. And the arithmetic mean of what Adam and Cenda collected is 3 kg less than Borrek's contribution.
Determine the difference between the arithmetic mean of what Borrek and Cenda collected and Adam's contribution.
(M. Petrová)
Hint. Express the relationships from the problem using unknowns.
|
The amount of chestnuts ( $\mathrm{vg}$ ) collected by Adam, Borek, and Cenda will be denoted by $a, b$, and $c$ respectively. According to the problem statement, the following equations hold:
$$
\frac{a+b}{2}=c+10, \quad \frac{a+c}{2}=b-3 .
$$
We want to determine the difference between $\frac{b+c}{2}$ and $a$. To do this, it is sufficient to add the two equations and simplify:
$$
\begin{gathered}
a+\frac{b+c}{2}=b+c+7, \\
a-7=\frac{b+c}{2} .
\end{gathered}
$$
Adam's contribution is 7 kg greater than the arithmetic mean of what Borek and Cenda collected.
Notes. If we denote the desired difference by $x$ and add the equation $\frac{b+c}{2}=a-x$ to the initial two equations, then the sum of all three equations (and a simple rearrangement) gives $x=7$.
The initial pair of equations is equivalent to the pair
$$
a+b-2 c=20, \quad a-2 b+c=-6 \text {. }
$$
From these, two of the unknowns can be expressed in terms of the third, for example:
$$
b=\frac{26}{3}+c, \quad a=\frac{34}{3}+c
$$
The desired difference then becomes
$$
a-\frac{b+c}{2}=\frac{34}{3}+c-\frac{26}{6}-c=\frac{21}{3}=7 .
$$
Without additional information, it is not possible to determine how much each boy collected (fewer equations than unknowns). However, it is clear from the above process that the problem is feasible: regardless of what Cenda collected, as long as $c$ is non-negative, the contributions of the other boys, $a$ and $b$, are also non-negative according to the expressions (*).
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A group of children organized a tic-tac-toe tournament. Everyone played with everyone else, and a total of 136 games were played. Out of these, exactly 66 games were of the type girl-girl or boy-boy. How many boys and how many girls were in the group?
(Bednářová)
|
Let's consider a group of $n$ players. Each one plays a match with every other, and we are interested in the total number of matches. Each player will play $\mathrm{s} n-1$ opponents, and there are $n$ players, so in total we have $n \cdot(n-1)$. Now we must realize that we have counted each match twice. Therefore, we have proven that the total number of matches in a group of $n$ players is $\frac{1}{2} n \cdot(n-1)$.
We will create a table from which we can easily determine the solution.
| number of players $n$ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| :--- | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| number of matches | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | 66 | 78 | 91 | 105 | 120 | 136 |
From the table, it is clear that there were a total of 17 children in the group. Now we can easily calculate the solution - it could be 7 boys and 10 girls, or 10 boys and 7 girls.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The average age of the Kebulov family, consisting of a father, a mother, and several children, is 18 years. When the father, who is 38 years old, is not included, the average age of the family is 14 years. How many children do the Kebulovs have?
(L. Hozová)
|
Let the number of members in this family be $n$. The sum of the ages of all members is equal to the product of the average age of the family and the number of members, that is, $18 \cdot n$. The family without the father has $n-1$ members, and the sum of the ages of these members is $14 \cdot(n-1)$. We know that this sum is 38 less than the sum of the ages of all members. Therefore, we arrive at the equation
$$
18 \cdot n=14 \cdot(n-1)+38
$$
after rearrangement, we get
$$
\begin{aligned}
4 n & =24 \\
n & =6 .
\end{aligned}
$$
The entire family has 6 members, so the Kebulovis have 4 children.
Evaluation. 2 points for setting up the equation; 2 points for justifying this setup; 1 point for solving the equation; 1 point for the correct conclusion.
Alternative solution. Ignoring the fact that there must be a certain age gap between children and parents, after reading the first sentence in the problem, one can imagine a family consisting only of 18-year-old members. After reading the second sentence, we can adjust our imagination and see a 38-year-old father and the rest of the members being 14 years old. The father's age has been increased by 20, and the age of the other members has been reduced by 4 each. To keep the sum of the ages of all family members the same when adjusting our imagination, the number of family members without the father must be $20: 4=5$. One of them is the mother, so the children must be 4.
Evaluation. 6 points.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Honzík received his pocket money and wants to buy something nice with it. If he bought four rolls, he would have 5 Kč left. If he wanted to buy five rolls, he would be short of 6 Kč. If he bought two rolls and three pretzels, he would spend his entire pocket money without any remainder.
How much does one pretzel cost?
(L. Dedková)
Hint. How much does one roll cost?
|
Honzík's pocket money can be expressed in three ways, namely as
- the sum of the price of 4 cakes plus 5 Kč,
- the sum of the price of 5 cakes minus 6 Kč,
- the sum of the prices of 2 cakes and 3 pretzels.
From the first two expressions, it follows that one cake costs $5+6=11$ Kč. From this, we also find that Honzík's pocket money was $4 \cdot 11+5=5 \cdot 11-6=49$ Kč. From the third expression, it follows that for three pretzels, Honzík would pay $49-2 \cdot 11=27$ Kč. Therefore, one pretzel costs $27: 3=9$ Kč.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the homework for calculating the value of the expression
$$
2-3+4-5+6-7+8-9+10=
$$
Radek forgot to write two parentheses, so he got a result that was 18 greater than what he would have obtained if he had written the parentheses. Add the parentheses in two ways and write down what number Radek got and what number he should have gotten.
(M. Dillingerová)
|
Radek calculated
$$
2-3+4-5+6-7+8-9+10=6 \text {. }
$$
He got a result 18 more than it should have been. The result should have been $6-18=-12$. To get a smaller number, it is necessary to subtract a larger value, i.e., place the parentheses after the minus sign. Two required solutions:
$$
\begin{aligned}
& 2-3+(4-5)+6-(7+8-9+10)=-12 \\
& 2-3+4-(5+6-7)+8-(9+10)=-12
\end{aligned}
$$
Another correct solution is, for example,
$$
(2-3)+4-5+6-(7+8-9+10)=-12,
$$
etc. Each additional student solution must always be checked to ensure it is correct.
|
-12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Mom cooked homemade currant syrup and poured it into bottles. The bottles were of two types: small with a volume of $500 \mathrm{ml}$ and large with a volume of $750 \mathrm{ml}$. In the end, she had 12 empty small bottles left, and all other bottles were completely filled. Then Mom realized that she could have poured the syrup so that only large bottles would be left empty and all others would be completely filled.
How many empty bottles would she have in such a case?
(M. Petrová)
Hint. How much syrup did Mom lack to fill all the bottles?
|
Mom has 12 unfilled bottles, each with a volume of $500 \mathrm{ml}$. They could hold $6000 \mathrm{ml}$ of syrup $(12 \cdot 500=6000)$.
The same amount would fit into 8 large bottles $(6000: 750=8)$. If Mom were to pour the syrup the second way, she would be left with 8 empty large bottles.
Note. One large bottle has the same volume as one and a half small bottles, i.e., two large bottles have the same volume as three small ones. According to this guide, bottles can be appropriately exchanged to avoid dealing with large numbers: 12 small bottles have the same volume as 8 large ones.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Míša has five candies. Vojta has fewer candies than Míša. Vendelín has as many candies as Míša and Vojta together. All three of them together have seven times more candies than Vojta.
How many candies does Vendelín have?
(L. Hozová)
Hint. How few and how many candies can they have together at minimum and maximum?
|
Vojta has fewer candies than Míša, so he can have
$$
0,1,2,3 \text {, or } 4
$$
candies. Vendelín has five more candies than Vojta, so he can have
$$
5,6,7,8, \text { or } 9
$$
candies. All three together have twice as many as Vendelín, so they can have
$$
10,12,14,16 \text {, or } 18
$$
candies.
Among these numbers, only 14 is a multiple of seven, $14=7 \cdot 2$. Therefore, Vojta has 2 candies and Vendelín has $2+5=7$ candies.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Two guards are overseeing the order in a room whose shape and dimensions are shown in the diagram. Each two adjacent walls are perpendicular to each other, and the dimensions are given in meters. The guards stand close to the wall at the locations marked with squares. Together, they can oversee the entire room, but only a part of the room can be overseen by both at the same time.
a) Mark the part of the room that both guards can oversee in the diagram.
b) How many times larger is the entire room compared to the part that both guards can oversee.
(K. Pazourek)
|
The entire room can be divided into squares with a side of 10 meters as shown in the image. The parts of the room visible to each guard are marked with two types of hatching. The part that both guards can see is thus doubly hatched:
This part consists of 4 squares, while the entire room consists of 16 squares. Therefore, the entire room is four times larger than the part that both guards can see.
Evaluation. 2 points for correctly depicting the part visible to both guards; 2 points for the auxiliary division of the room; 2 points for solving the problem and providing the result.
Note. The entire room can be divided into coarser parts based on whether they are under the control of one or both guards. These are rectangles with dimensions $30 \times 20$, $20 \times 30$, and a square $20 \times 20$ (all in meters). The entire room corresponds to a rectangle with dimensions $80 \times 20$, and the doubly hatched part has dimensions $20 \times 20$, which is exactly one quarter of the whole.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In the magical bazaar, wizards exchanged wizard hats, wands, and cloaks among themselves. For 4 wands, there are 6 cloaks and for 5 wands, there are 5 hats. How many cloaks are there for 5 wands and 1 hat?
( $V$. Hucíková)
|
For 5 sticks, there are 5 hats. For 1 stick, there is therefore 1 hat, and thus 5 sticks and 1 hat have the same value as 6 sticks.
Furthermore, we know that for 4 sticks, there are 6 coats. For 2 sticks, there are therefore 3 coats, and thus 6 sticks have the same value as 9 coats.
In total, we can see that 5 sticks and 1 hat have the same value as 9 coats.
Grading suggestion. 2 points for deriving the relationship 5 sticks + 1 hat = 6 sticks; 3 points for deriving the relationship 6 sticks = 9 coats; 1 point for the answer.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Grandpa keeps geese, pigs, goats, and chickens - a total of 40 animals. For every goat, there are 3 geese. If there were 8 fewer chickens, there would be as many as geese and pigs combined. If Grandpa traded a quarter of the geese for chickens at a ratio of 3 chickens for 1 goose, he would have a total of 46 animals.
How many of each animal does Grandpa keep?
(M. Volfová)
|
Let's denote the quantities of each type of animal by their initial letters. The information from the problem can be written step by step as follows:
\[
\begin{aligned}
h + p + k + s & = 40, \\
h & = 3k, \\
s - 8 & = h + p, \\
40 - \frac{1}{4}h + \frac{3}{4}h & = 46.
\end{aligned}
\]
From the last equation, we get \(\frac{1}{2}h = 6\), so \(h = 12\). From the second equation, we find that \(k = 4\). Substituting these values into the remaining two equations, we get
\[
\begin{aligned}
& 12 + p + 4 + s = 40, \quad \text{so} \quad p + s = 24, \\
& s - 8 = 12 + p, \quad \text{so} \quad s = p + 20.
\end{aligned}
\]
From this, we further derive
\[
\begin{aligned}
p + (p + 20) & = 24, \\
2p & = 4, \\
p & = 2, \quad \text{and thus} \quad s = 22.
\end{aligned}
\]
The grandfather keeps 12 geese, 2 pigs, 4 goats, and 22 chickens.
Scoring suggestion. 2 points for determining the number of geese; 1 point for determining the number of goats; 3 points for determining the number of pigs and chickens.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Adam wrote the numbers from 1 to 9 into a $3 \times 3$ table as shown in the image:
| 7 | 6 | 4 |
| :--- | :--- | :--- |
| 1 | 2 | 8 |
| 9 | 3 | 5 |
For this filling, the sum of the numbers in the three cells along each side is always the same. Adam found that the numbers can be filled into the table in other ways without breaking the property of having the same sums along the sides.
What is the smallest value that this sum can have? Provide an example of a table with the smallest sum along the sides and explain why it cannot be smaller.
(J. Tkadlec)
|
Given that each corner cell appears in two sums, we try to place the smallest possible numbers in these cells and somehow fill in the rest. After some trial and error, the following filling can be revealed, where the sum of the numbers along each side is 12:
| 1 | 9 | 2 |
| :--- | :--- | :--- |
| 8 | 7 | 6 |
| 3 | 5 | 4 |
Filling with smaller sums is not possible, because it is not feasible. The smallest possible sum along a side with the addend 9 is $1+2+9=12$. Thus, the number 9 would have to be in the center of the table, and the remaining numbers would be along the sides. The smallest possible sum along a side with the addend 8 is $1+2+8=11$. Thus, a smaller sum cannot be achieved, and we consider filling the table such that the numbers 1, 2, and 8 are along one side. Along the opposite side, there would be three of the remaining five numbers. The smallest possible numbers are 3, 4, and 5, whose sum is $3+4+5=12$, not 11.
The smallest possible value of the sum in Adam's table is 12.
Note. Each of the four corner cells contributes to two sums, and each of the remaining four cells along the sides contributes to one sum. Therefore, the sum of all four sums along the sides is at least
$$
2 \cdot(1+2+3+4)+(5+6+7+8)=46.
$$
The requirement for the sums along the sides to be equal means that the previous sum must be divisible by four. The nearest larger number divisible by four is 48. Thus, the smallest possible value of the sum in Adam's table is $48: 4=12$. The table above shows that such a filling is possible.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.