problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Determine the number of ways to write the numbers $1,2,3,4,5,6,7,8$ and 9 in the individual cells of the triangle in the picture so that the sum in each four-cell triangle is 23 and so that the given number is written in one of the cells in the direction of each arrow.
(E. Novotná)
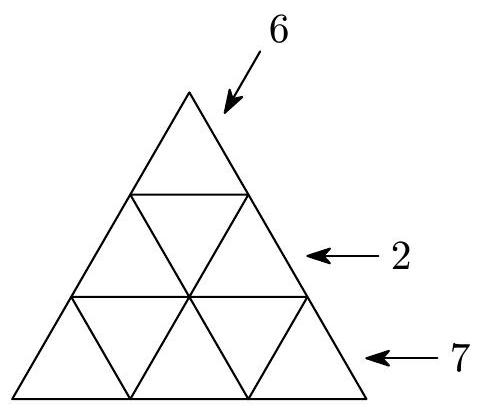
|
The sum of all the numbers written is $1+2+3+4+5+6+7+8+9=45$. In the figure, there are exactly three four-cell triangles, and the sum of the quadruples of numbers written in these triangles is $3 \cdot 23=69$. However, in this sum, the numbers on the gray cells are counted twice (each belongs to two four-cell triangles), while the other numbers are counted once. Therefore, the sum of the numbers on the three gray cells must be $69-45=24$.
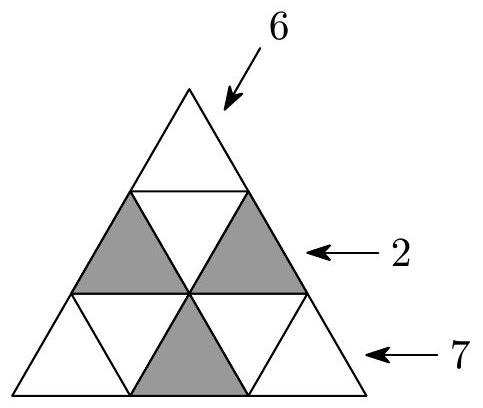
Since the largest possible sum of three written numbers is $9+8+7=24$, the numbers 7, 8, and 9 must be in the gray cells. From the problem statement, we know that 7 must be in the bottom row, so the numbers 8 and 9 must be in the outer cells of the second row.
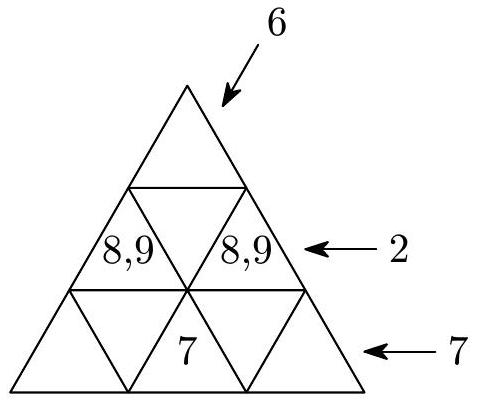
The number 2 then has only one free spot, as shown in the figure. In the top four-cell triangle, only one number is missing, which we can now fill in: $23-8-9-2=4$.
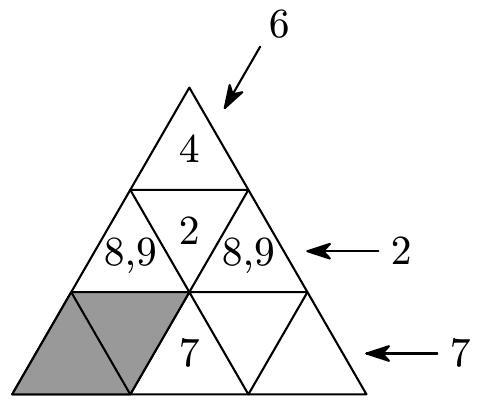
The number 6 must be in one of the gray cells in the previous figure, so it belongs to the left four-cell triangle. If this triangle contained the number 8, the last free cell would contain the number $23-8-7-6=2$, which is not possible (2 is already placed in the second row). Therefore, the left four-cell triangle has the number 9 in its top cell, and in the last unoccupied cell, it is $23-9-7-6=1$. Thus, the numbers in the gray cells are 1 and 6, which can be placed in two ways.
In the unoccupied spots in the right four-cell triangle, only the numbers 3 and 5 can be placed; the sum in this triangle is indeed $8+7+3+5=23$. The numbers 3 and 5 can be filled in two ways. Therefore, the problem has a total of $2 \cdot 2=4$ solutions:
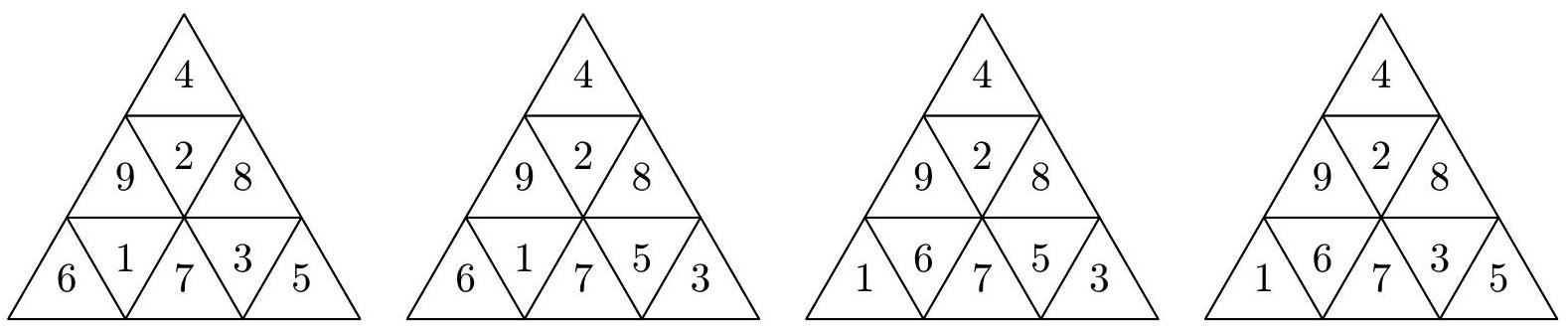
Grading. 3 points for explaining where the numbers 7, 8, and 9 are located; 1 point for filling in the numbers 2 and 4; 1 point for filling in the numbers 6 and 1; 1 point for the correct number of solutions.
If the solver finds one correct solution randomly (without a gradable explanation), award 1 point; for two solutions, 2 points; for three and four solutions, 3 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Mr. Rychlý and Mr. Louda set out on the same hiking tour at the same time, but Mr. Rychlý started from the mountain hut and Mr. Louda from the bus at the bottom of the town, heading up to the hut. They met on the trail at 10 o'clock. Mr. Rychlý was in a hurry and reached his destination by 12 o'clock. On the other hand, Mr. Louda moved slowly and did not arrive at the hut until 18 o'clock. At what time did the gentlemen set out on their journey, knowing that each of them walked at a constant speed the whole time?
(M. Volfová)
|
Let's denote the speed (in $\mathrm{km} / \mathrm{h}$) of Mr. Rychlý as $v_{R}$ and Mr. Louda as $v_{L}$. The time (in hours) from their departure until their meeting is denoted as $x$. Up to the meeting, Mr. Rychlý walked $x \cdot v_{R}(\mathrm{~km})$ from the cabin, and Mr. Louda walked $x \cdot v_{L}(\mathrm{~km})$ from the bus. After the meeting, Mr. Rychlý walked for another $2 \mathrm{~h}$ to the bus, covering $2 \cdot v_{R}(\mathrm{~km})$, while Mr. Louda walked for another $8 \mathrm{~h}$ to the cabin, covering $8 \cdot v_{L}(\mathrm{~km})$.
By comparing the corresponding distances, we obtain two equations: the distance from the meeting point to the bus is $x \cdot v_{L}=2 \cdot v_{R}(\mathrm{~km})$, and the distance to the cabin is $8 \cdot v_{L}=x \cdot v_{R}(\mathrm{~km})$. From this, we can express
$$
\frac{v_{L}}{v_{R}}=\frac{2}{x}=\frac{x}{8}
$$
thus $x^{2}=16$ and $x=4$. From departure to the meeting, both gentlemen walked for 4 hours, and the total journey time was $10 \mathrm{~h}$. Therefore, they set out at 6 o'clock.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Petr and Pavel were picking apples and pears in the orchard. On Monday, Petr ate 2 more pears than Pavel and 2 fewer apples than Pavel. On Tuesday, Petr ate 4 fewer pears than on Monday. Pavel ate 3 more pears than Petr and 3 fewer apples than Petr on Tuesday. Pavel ate 12 apples over the two days and the same number of apples as pears on Tuesday. In the evening on Tuesday, both boys found out that the number of apples they had eaten together over the two days was the same as the number of pears they had eaten together. How many apples did Petr eat on Monday and how many pears did Pavel eat on Tuesday?
|
Let $x, y$ be the corresponding numbers of pears and apples that Pavel ate on Monday. According to the problem, we will patiently construct the following table:
| | Monday | Tuesday |
| :---: | :---: | :---: |
| Pavel pears | $x$ | $x+1$ |
| Pavel apples | $y$ | $12-y$ |
| Petr pears | $x+2$ | $x-2$ |
| Petr apples | $y-2$ | $15-y$ |
However, while filling out the table, we have not yet used the following information:
a) On Tuesday, Pavel ate the same number of apples as pears,
b) the total number of apples eaten together is the same as the number of pears eaten.
According to information b), we set up an equation, and after its rearrangement, we obtain the value of $x$:
$$
\begin{aligned}
y+(12-y)+(y-2)+(15-y) & =x+(x+1)+(x+2)+(x-2), \\
25 & =4 x+1, \\
x & =6 .
\end{aligned}
$$
According to information a), we also set up an equation, rearrange it, and substitute:
$$
\begin{aligned}
x+1 & =12-y, \\
y & =11-x=5 .
\end{aligned}
$$
By substituting into the relevant fields of the table, we find that Petr ate 3 apples on Monday and Pavel ate 7 pears on Tuesday.
For verification, we provide the table with all substituted values:
| | Monday | Tuesday |
| :---: | :---: | :---: |
| Pavel pears | 6 | $\mathbf{7}$ |
| Pavel apples | 5 | 7 |
| Petr pears | 8 | 4 |
| Petr apples | $\mathbf{3}$ | 10 |
Note. When compiling the data in the table, we can certainly proceed in different ways and the unused information may differ from that in the previous procedure. With the same notation of unknowns, we can thus obtain two different equations, which, when calculated correctly, lead to the same solution. Moreover, the unknowns can also be chosen differently, but at least two are always needed. The same number of unused information then determines the system of equations, which we subsequently solve.
Another solution. If we denote $x$ as the number of apples that Petr ate on Monday, and $y$ as the number of pears that Pavel ate on Tuesday, then the table might look like this:
| | Monday | Tuesday |
| :---: | :---: | :---: |
| Pavel pears | $y-1$ | $y$ |
| Pavel apples | $12-y$ | $y$ |
| Petr pears | $y+1$ | $y-3$ |
| Petr apples | $x$ | $y+3$ |
In this case, we have not used the following information:
a) On Monday, Petr ate 2 apples fewer than Pavel,
b) the total number of apples eaten together is the same as the number of pears eaten.
The corresponding equations (after simple rearrangement) are:
$$
\begin{aligned}
x+y & =10, \\
-x+3 y & =18,
\end{aligned}
$$
and the only solution to this system is $x=3$ and $y=7$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On July 1, 2010, Mrs. Hovorkova had a credit of 157.0 Kč on her mobile phone. The credit is gradually debited for calls, with 4.5 Kč deducted for each started minute. Mrs. Hovorkova does not send text messages and does not use any other paid services. She tops up her credit as needed, always by an amount of 400 Kč. On December 31, 2010, her credit was 353.0 Kč. How many times at least did Mrs. Hovorkova top up her credit during the mentioned half-year?
(L. Simünek)
|
The amount in crowns that Mrs. Hovorkova called during the period from July 1 to December 31 is a whole number because the initial and final credit balances and the top-up amounts are always whole numbers. For each minute started, 4.5 Kč is charged, and to reach a whole number, an even number of minutes must have been charged. Therefore, the amount called during this period is divisible by nine without a remainder.
Since the initial credit is less than the final credit, Mrs. Hovorkova must have topped up at least once during the observed period. If she topped up only once, the amount called would be \(157 + 400 - 353 = 204\) (Kč). By the digit sum of the number 204, we see that it is not a multiple of nine, so we reject this option. If she topped up twice, the amount called would be 400 Kč more, i.e., 604 Kč. We reject this option as well because 604 is not a multiple of nine. Similarly, we reject the option of three top-ups leading to an amount of 1004 Kč. If she topped up four times, the amount called would be 1404 Kč. This is possible because 1404 is a multiple of nine. Therefore, Mrs. Hovorkova topped up at least four times during the observed period.
Another solution. It is clear that Mrs. Hovorkova topped up her credit at least once. In the table, we will consider different numbers of top-ups: each time we will determine the amount called during the observed period and the number of minutes this amount corresponds to. We will continue until the number of charged minutes is a whole number.
| number of top-ups | amount called in Kč | number of charged minutes |
| :---: | :---: | :---: |
| 1 | \(157 + 400 - 353 = 204\) | \(204 \div 4.5 \approx 45.3\) |
| 2 | \(157 + 2 \cdot 400 - 353 = 604\) | \(604 \div 4.5 \approx 134.2\) |
| 3 | \(157 + 3 \cdot 400 - 353 = 1004\) | \(1004 \div 4.5 \approx 223.1\) |
| 4 | \(157 + 4 \cdot 400 - 353 = 1404\) | \(1404 \div 4.5 = 312\) |
Mrs. Hovorkova topped up at least four times during the observed period.
Evaluation. 4 points for verifying the options 204, 604, 1004, 1404; 1 point for explaining why the options are rejected; 1 point for the correct conclusion.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Kluci found an old minefield plan, see the picture. The numbers are on the fields where there are no mines, and they indicate the number of adjacent mined fields. Determine how many mines there are in the field and where they are. (Fields are adjacent if they share a vertex or a side.)
| 1 | | 2 | | 2 |
| :--- | :--- | :--- | :--- | :--- |
| | 3 | | 3 | |
| 3 | | | | 3 |
| | 2 | | | |
| | | | 2 | |
|
We can start unambiguously filling in the plan from the cell with the number $3 \mathrm{v}$ in the first column or from the cell with the number $2 \mathrm{v}$ in the upper right corner. In both cases, all unmarked adjacent cells must contain mines (marked as 丸):
| 1 | | 2 | $\star$ | 2 |
| :---: | :---: | :---: | :---: | :---: |
| $\star$ | 3 | | 3 | $\star$ |
| 3 | $\star$ | | | 3 |
| $\star$ | 2 | | | |
| | | | 2 | |
Then we can fill in all other cells, for example, in the following way:
| 1 | - | 2 | $\star$ | 2 |
| :---: | :---: | :---: | :---: | :---: |
| $\star$ | 3 | | 3 | $\star$ |
| 3 | $\star$ | | | 3 |
| $\star$ | 2 | | | |
| - | - | - | 2 | |
| 1 | - | 2 | $\star$ | 2 |
| :---: | :---: | :---: | :---: | :---: |
| $\star$ | 3 | | 3 | $\star$ |
| 3 | $\star$ | - | | 3 |
| $\star$ | 2 | - | | |
| - | - | - | 2 | |
| 1 | - | 2 | $\star$ | 2 |
| :---: | :---: | :---: | :---: | :---: |
| $\star$ | 3 | $\star$ | 3 | $\star$ |
| 3 | $\star$ | - | | 3 |
| $\star$ | 2 | - | | |
| - | - | - | 2 | |
| 1 | - | 2 | $\star$ | 2 |
| :---: | :---: | :---: | :---: | :---: |
| $\star$ | 3 | $\star$ | 3 | $\star$ |
| 3 | $\star$ | - | - | 3 |
| $\star$ | 2 | - | | |
| - | - | - | 2 | |
| 1 | - | 2 | $\star$ | 2 |
| :---: | :---: | :---: | :---: | :---: |
| $\star$ | 3 | $\star$ | 3 | $\star$ |
| 3 | $\star$ | - | - | 3 |
| $\star$ | 2 | - | $\star$ | $\star$ |
| - | - | - | 2 | |
| 1 | - | 2 | $\star$ | 2 |
| :---: | :---: | :---: | :---: | :---: |
| $\star$ | 3 | $\star$ | 3 | $\star$ |
| 3 | $\star$ | - | - | 3 |
| $\star$ | 2 | - | $\star$ | $\star$ |
| - | - | - | 2 | - |
There are a total of 8 mines on the plan, their placement is highlighted in the following image:
| | | | $\star$ | |
| :--- | :--- | :--- | :--- | :--- |
| $\star$ | | $\star$ | | $\star$ |
| | $\star$ | | | |
| $\star$ | | | $\star$ | $\star$ |
| | | | | |
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Consecutive natural numbers are added and subtracted according to the following guide:
$$
1+2-3-4+5+6-7-8+9+10-11-12+\ldots,
$$
that is, two positive and two negative addends always repeat.
Determine the value of such an expression whose last term is 2015.
(L. Hozová)
|
The sums of pairs of adjacent numbers with opposite signs are either -1 or 1. These values also alternate regularly. In the considered expression, several adjacent numbers thus cancel each other out:
$$
\begin{aligned}
& 1+2-3-4+5+6-7-8+9+10-11-12+13+\ldots \\
= & {[1+(2-3)]+[(-4+5)+(6-7)]+[(-8+9)+(10-11)]+[(-12+13)+\ldots} \\
= & {[1-1]+[1-1]+[1-1]+[1-\ldots} \\
= & 0+0+0+\ldots
\end{aligned}
$$
The first zero is obtained as the sum of the first triplet of numbers, and the other zeros are obtained as the sums of consecutive quadruplets of numbers. The sum of the given expression would thus be zero if it ended with the number 3, 7, 11, 15, etc. More generally, the sum of such an expression is zero precisely when it ends with a number that has a remainder of 3 when divided by four. Since the number 2015 has this property, the value of the given expression is zero.
Suggested scoring: 1 point for noticing that the sums of pairs of adjacent numbers with opposite signs are alternately -1 and 1; 2 points for noticing that the sums of consecutive quadruplets, or the first triplet of numbers, are equal to 0; 3 points for correctly determining and justifying the overall sum.
Note. The initial observations can be utilized in various ways, leading to a more detailed discussion of the signs of the numbers at the end of the given expression. From the given solution, it follows that this expression ends as follows:
$$
\ldots+[(-2012+2013)+(2014-2015)].
$$
The addends of the given expression can also be grouped, for example, as follows:
$$
[1+2-3-4]+[5+6-7-8]+[9+10-11-12]+\ldots=-4-4-4-\ldots
$$
Such quadruplets can be formed at most 503 times (2015 = 503 * 4 + 3). The overall sum is expressed according to this method as follows:
$$
503 \cdot(-4)+2013+2014-2015=-2012+2013+2014-2015=0.
$$
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ludvík noticed for a certain division example that if he doubles the dividend and increases the divisor by 12, he gets his favorite number as the result. He would get the same number if he reduced the original dividend by 42 and halved the original divisor.
Determine Ludvík's favorite number.
(M. Petrová)
|
If we denote the actors in the original example as $a: b$, then Ludvík's observation can be written as:
$$
2 a:(b+12)=(a-42): \frac{b}{2} .
$$
This is a double expression of Ludvík's favorite number, which we will denote as $\ell$ for subsequent modifications.
From the expression on the left, we get
$$
2 a=b \ell+12 \ell,
$$
from the expression on the right, we get
$$
\begin{aligned}
a-42 & =\frac{b}{2} \cdot \ell \\
2 a & =b \ell+84
\end{aligned}
$$
By comparing these two expressions, we find that $12 \ell=84$, so Ludvík's favorite number is $\ell=7$.
Evaluation. 3 points for writing down the relationships from the problem and auxiliary modifications; 3 points for the calculation, result, and quality of the commentary.
Notes. There is an infinite number of pairs of numbers $a$ and $b$ that satisfy Ludvík's equation. Randomly discovered possibilities leading to the correct result (e.g., $a=49$ and $b=2$) cannot be considered a complete solution to the problem - such processing should be evaluated no higher than 3 points.
Without additional notation of the ratio, we can modify the initial equality:
$$
\begin{aligned}
2 a \cdot \frac{b}{2} & =(a-42)(b+12), \\
a b & =a b-42 b+12 a-12 \cdot 42, \\
42(b+12) & =12 a .
\end{aligned}
$$
From this, after simplification, we get $2 a=7(b+12)$, so the desired ratio is $2 a:(b+12)=7$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In front of Honza sat three veiled princesses, one of whom was Goldilocks. Honza's task was to find out which one she was.
The princess in the first chair said: "Goldilocks is not sitting in the third chair."
The princess in the second chair said: "I am not Goldilocks."
The princess in the third chair said: "I am Goldilocks."
The magical fairy revealed to Honza how many princesses were lying. Only with this advice was Honza able to identify the real Goldilocks.
Which of the princesses was Goldilocks?
(M. Volfová)
|
We can distinguish three cases depending on where Blondie could have been sitting:
1. If Blondie was sitting in the first chair, then
- the princess in the first chair would be telling the truth,
- the princess in the second chair would be telling the truth,
- the princess in the third chair would be lying.
2. If Blondie was sitting in the second chair, then
- the princess in the first chair would be telling the truth,
- the princess in the second chair would be lying,
- the princess in the third chair would be lying.
3. If Blondie was sitting in the third chair, then
- the princess in the first chair would be lying,
- the princess in the second chair would be telling the truth,
- the princess in the third chair would be telling the truth.
In the first and third cases, one princess would be lying, while in the second case, two princesses would be lying. Since the mouse council helped Honza identify Blondie, the mouse must have revealed that two princesses were lying. This corresponds to the second case, which means that Blondie was sitting in the second chair. (If the mouse had claimed that one princess was lying, Honza would not have been able to decide between the first and third cases.)
Suggested grading. 4 points for analyzing all cases; 2 points for determining the only possible case and placing Blondie.
Note. The previous analysis of possibilities can also be approached in reverse, i.e., based on the truth or falsity of individual statements, deduce where Blondie should be sitting. This would require discussing a total of eight cases:
- The statements of the princesses in the first and third chairs are contradictory, so these two princesses cannot both be telling the truth at the same time - this eliminates two cases.
- For the same reason, the princesses in the first and third chairs cannot both be lying at the same time - this eliminates another two cases.
- It is not possible for the princess in the second chair to be lying and the princess in the third chair to be telling the truth at the same time (that would mean there are two Blondies) - this eliminates another case.
The remaining three cases correspond precisely to the cases in the given solution.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The commander summoned the other defenders of the castle and decided how to divide their reward:
"The first will take one gold coin and a seventh of the remainder, the second will take two gold coins and a seventh of the new remainder, and so on. That is, the $n$-th defender will take $n$ gold coins and in addition a seventh of the remaining amount, until there are any left."
This way, all the gold coins were distributed, and all the defenders received the same amount.
How many defenders shared the reward?
(M. Volfová)
|
Let the number of defenders be $p$ and consider from the back. The last $p$-th defender took $p$ gold coins, and thus all the gold coins were taken. The second-to-last $(p-1)$-th defender took $p-1$ gold coins and a seventh of the current remainder, which we denote as $z$. Since both defenders received the same amount, we have
$$
p-1+\frac{1}{7} \cdot z=p
$$
From this, we get $\frac{1}{7} \cdot z=1$, hence $z=7$. At the same time, it follows that the last defender had $\mathrm{k}$ of the remaining six sevenths available. This means that
$$
p=\frac{6}{7} \cdot z
$$
thus $p=6$. If the defenders divided all the gold coins equally and each received the same amount, there must have been six defenders, each receiving six gold coins, so the total number of gold coins was $6 \cdot 6=36$. Since we have only considered some of the information from the problem so far, it is necessary to verify that such a division is indeed possible:
| | took | remained |
| :---: | :---: | :---: |
| first | $1+\frac{1}{7}(36-1)=6$ | $36-6=30$ |
| second | $2+\frac{1}{7}(30-2)=6$ | $30-6=24$ |
| third | $3+\frac{1}{7}(24-3)=6$ | $24-6=18$ |
| fourth | $4+\frac{1}{7}(18-4)=6$ | $18-6=12$ |
| fifth | $5+\frac{1}{7}(12-5)=6$ | $12-6=6$ |
| sixth | $6+\frac{1}{7}(6-6)=6$ | $6-6=0$ |
The reward was divided among six defenders.
Suggested scoring. 3 points for the relationship (1) and determining $z=7$; 2 points for the relationship (2) and the result $p=6$; 1 point for verification.
Another solution. Let the total number of gold coins be $l$ and consider from the beginning. The first defender took one gold coin and a seventh of the remainder, so he took
$$
1+\frac{1}{7}(l-1)=\frac{1}{7}(l+6)
$$
gold coins, and the number of gold coins was reduced to $\frac{6}{7}(l-1)$. The second defender took two gold coins and a seventh of the new remainder, so he took
$$
2+\frac{1}{7}\left(\frac{6}{7}(l-1)-2\right)=\frac{1}{49}(6 l+78)
$$
gold coins. Since both defenders received the same amount, we have
$$
\frac{1}{7}(l+6)=\frac{1}{49}(6 l+78)
$$
From this, we get
$$
\begin{aligned}
7 l+42 & =6 l+78 \\
l & =36 .
\end{aligned}
$$
By expanding as in the table for the previous method, it can be verified that we have found a valid solution and that there were six defenders.
Suggested scoring. 1 point each for the relationships (3) and (4) and their possible simplification; 2 points for setting up and solving the equation (5); 2 points for verification and the result.
Another solution. Let the number of defenders be $p$. The last $p$-th defender took $p$ gold coins, and thus all the gold coins were taken. Since all defenders received the same amount, each received $p$ gold coins. The defenders therefore shared a total of $p^{2}$ gold coins.
The first defender took one gold coin and a seventh of the remainder, so
$$
1+\frac{1}{7}\left(p^{2}-1\right)=p
$$
thus
$$
p^{2}-1=7(p-1) \text {. }
$$
The left side of this equation can be expressed as $p^{2}-1=(p+1)(p-1)$. From the problem, it follows that $p>1$, so $p-1>0$ and the previous equation is equivalent to
$$
p+1=7 \text {, }
$$
thus $p=6$. By expanding as in the table for the first method, it can be verified that we have found a valid solution. The reward was divided among six defenders.
Suggested scoring. 2 points for expressing the total number of gold coins in terms of $p$; 3 points for setting up and solving the equation (6); 1 point for verification.
With the knowledge of the total number of gold coins, it can be determined by trial that the smallest $p$ for which the gold coins can be divided according to the given rules is $p=6$. Such a solution without justification that it is the only possibility should be rated no more than 4 points. Award an additional 2 points for the quality of the justification.
Another solution. Let the total number of gold coins be $l$. The first defender took one gold coin and a seventh of the remainder, so the remainder $l-1$ must be divisible by seven. The number $l$ is therefore of the form
$$
l=7 k+1
$$
for some positive integer $k$. The first defender thus took
$$
1+\frac{1}{7}(l-1)=1+k
$$
gold coins. Since all defenders received the same amount and the last one received exactly as many gold coins as his ordinal number, there were $k+1$ defenders, and each received $k+1$ gold coins, so they shared a total of
$$
l=(k+1)^{2}=k^{2}+2 k+1
$$
gold coins. By comparing (7) and (8), we get the equation
$$
7 k+1=k^{2}+2 k+1
$$
or $5 k=k^{2}$. From the problem, it follows that there were at least two defenders, so $k>0$ and the previous equation is equivalent to $k=5$. By expanding as in the table for the first method, it can be verified that we have found a valid solution. The reward was divided among six defenders.
Suggested scoring. 1 point for the relationship (7); 2 points for the relationship (8); 2 points for setting up and solving the equation (9); 1 point for verification.
With the knowledge (7), it can be determined by trial that the smallest $k$ for which the gold coins can be divided according to the given rules is $k=5$. Such a solution without justification that it is the only possibility should be rated no more than 4 points. Award an additional 2 points for the quality of the justification.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
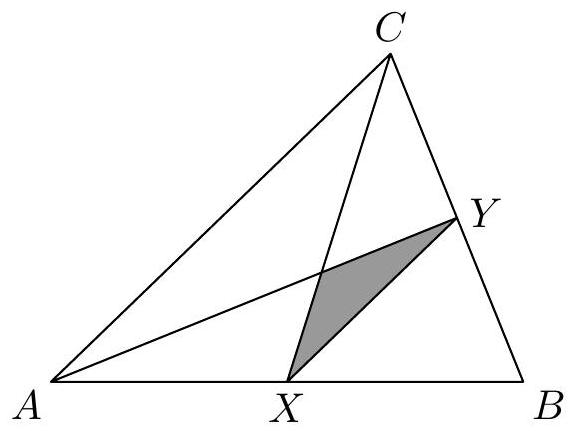
Given a triangle $ABC$. On side $AB$ lies point $X$ and on side $BC$ lies point $Y$ such that $CX$ is a median, $AY$ is an altitude, and $XY$ is a midline of triangle $ABC$. Calculate the area of the shaded triangle in the figure, given that the area of triangle $ABC$ is $24 \, \text{cm}^2$.
(M. Dillingerová)
|
Since $X Y$ is the midline of triangle $A B C$, $Y$ must be the midpoint of side $B C$, and thus segment $A Y$ is not only an altitude but also a median. The intersection of medians $C X$ and $A Y$ is the centroid of triangle $A B C$, which we will denote as $T$.
Each median divides the triangle into two triangles of equal area (the triangles thus formed have a common altitude to the same length sides): $A Y$ is a median of triangle $A B C$, therefore
$$
S_{A B Y}=S_{A C Y}=\frac{1}{2} S_{A B C}=\frac{24}{2}=12\left(\mathrm{~cm}^{2}\right),
$$
and similarly $X Y$ is a median of triangle $A B Y$, therefore
$$
S_{A X Y}=S_{B X Y}=\frac{1}{2} S_{A B Y}=\frac{12}{2}=6\left(\mathrm{~cm}^{2}\right) .
$$
Triangle $A X Y$, whose area we know, consists of triangles $A X T$ and $Y X T$. These two triangles have a common altitude from point $X$, so their areas are in the same ratio as the lengths of sides $A T$ and $T Y$, i.e., in the ratio $2: 1$ (the centroid divides the median in the ratio $2: 1$). The area of triangle $Y X T$ is therefore one-third of the area of triangle $A X Y$, so it is
$$
S_{Y X T}=\frac{1}{3} S_{A X Y}=\frac{6}{3}=2\left(\mathrm{~cm}^{2}\right) .
$$
Evaluation. 2 points for the observation (including justification) that $A Y$ is a median in triangle $A B C$; 1 point each for the areas of triangles $A B Y$ and $A X Y$; 2 points for the final area of triangle $Y X T$ (including its derivation or justification).
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a laboratory, on a shelf stands a closed glass container in the shape of a cuboid. It contains 2.4 liters of distilled water, but the volume of the container is larger. The water reaches a height of $16 \mathrm{~cm}$. When the cuboid container is placed on another of its sides, the water level will be at a height of $10 \mathrm{~cm}$. If we place it on yet another side, the water will reach a height of $9.6 \mathrm{~cm}$. Determine the dimensions of the container.
|
Let the dimensions of the container be denoted by $a, b, c$. For each position of the container, we will set up an equation expressing the volume of water:
$$
\begin{aligned}
a \cdot b \cdot 16 & =2400 \\
a \cdot c \cdot 10 & =2400 \\
b \cdot c \cdot 9.6 & =2400
\end{aligned}
$$
We solve the system of three equations with three unknowns:
$$
\begin{aligned}
a \cdot b & =150 \\
a \cdot c & =240, \\
b \cdot c & =250 .
\end{aligned}
$$
From equation (1), we calculate $b$, from equation (2) we calculate $c$, and substitute into equation (3), resulting in the equation
$$
\frac{150}{a} \cdot \frac{240}{a}=250 \text {. }
$$
This equation has a unique solution (in the set of positive numbers) $a=12$. By substituting into the above relationships, we calculate $b, c$.
The dimensions of the container are therefore $12 \text{ cm}, 12.5 \text{ cm}$, and $20 \text{ cm}$.
[setting up the system of equations - 1 pt., calculating one unknown - 2 pts., calculating the second and third unknowns $-1+1$ pt., correct answer - 1 pt.]
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Mommy preserves plums in jars so that the plums from one jar are enough for either 16 cups, or 4 pies, or half a sheet of fruit slices.
In the pantry, she has 4 such jars and wants to bake one sheet of fruit slices and 6 pies. $\mathrm{On}$ how many cups will the remaining plums be enough?
(M. Petrová)
|
First, we will determine how many of each type of delicacy can be prepared from all the plums:
- Four cups of plums are enough for $4 \cdot \frac{1}{2}=2$ whole trays of fruit slices.
- Four cups of plums are enough for $4 \cdot 4=16$ small cakes.
- Four cups of plums are enough for $4 \cdot 16=64$ small pastries.
In terms of plum consumption, the following equalities hold:
$$
2 \text{ trays} = 16 \text{ small cakes} = 64 \text{ small pastries.}
$$
When the mother uses the plums for one tray of fruit slices, she consumes half of all the plums. Thus, the remaining plums are enough for
$$
1 \text{ tray} = 8 \text{ small cakes} = 32 \text{ small pastries.}
$$
When she uses the plums for 6 small cakes, the remaining plums are only enough for 2 small cakes, which is a quarter of the previous amount. Therefore, from the remaining plums, she can bake
$$
2 \text{ small cakes} = 8 \text{ small pastries.}
$$
Scoring suggestion. 2 points for expressing the amount of each type of delicacy that can be baked from all the plums; 1 point each for expressing the consumption of plums for 1 tray and 6 small cakes; 2 points for expressing the consumption of plums for small pastries and the conclusion.
Note. The initial conversion ratios can also be written as follows:
$$
1 \text{ tray} = 8 \text{ small cakes, } 1 \text{ small cake} = 4 \text{ small pastries.}
$$
The previous considerations can then be simplified as follows:
After baking a tray of fruit slices, the remaining plums are enough for 1 tray, i.e., 8 small cakes. After baking 6 more small cakes, the remaining plums are enough for 2 small cakes, i.e., 8 small pastries.
For such a procedure, score 2 points for each of the three steps mentioned.
Another solution. We will calculate the consumption of plums in cups:
Since one cup of plums is enough for half a tray of fruit slices, one tray requires two cups. For further use, 2 cups remain.
Since one cup is enough for 4 small cakes, 6 small cakes require one and a half cups. For further use, half a cup remains.
Since one cup is enough for 16 small pastries, from the remaining half cup, 8 small pastries can be baked.
Scoring suggestion. 2 points for the observation that after baking a tray, 2 cups remain; 2 points for the observation that after baking 6 more small cakes, half a cup remains; 2 points for the calculation and conclusion.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a greyhound race, 36 dogs participated. The number of dogs that finished before Punta was four times smaller than the number of those who finished after him.
What was Punta's position?
(L. Hozová)
|
All the dogs without Punto was $36-1=35$. One fifth of this number is $35: 5=7$; before Punto, 7 dogs ran, behind Punto, $7 \cdot 4=28$ dogs ran. Punto ran eighth.
Evaluation. 3 points for dividing 35 dogs without Punto into fifths; 3 points for dividing the dogs before/behind Punto and placing Punto.
#
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Anička set out from the hotel for a walk, walked $5 \mathrm{~km}$ north, then $2 \mathrm{~km}$ east, $3 \mathrm{~km}$ south, and finally $4 \mathrm{~km}$ west. Thus, she arrived at a pond where she took a bath. Vojta set out from the camp, walked $3 \mathrm{~km}$ south, $4 \mathrm{~km}$ west, and $1 \mathrm{~km}$ north. Thus, he arrived at a rock which was $5 \mathrm{~km}$ west of the pond where Anička had bathed.
Another day, Anička set out from her hotel and Vojta from his camp, both wanting to reach the pond where Anička had bathed earlier, and both proceeded only in the directions of the four cardinal points.
Determine how many kilometers Anička and Vojta had to walk at a minimum. (E. Semerádová)

|
According to the task, we will sequentially illustrate Anička's route, Vojta's route, and their mutual relationship (each marked tile represents $1 \mathrm{~km}$):
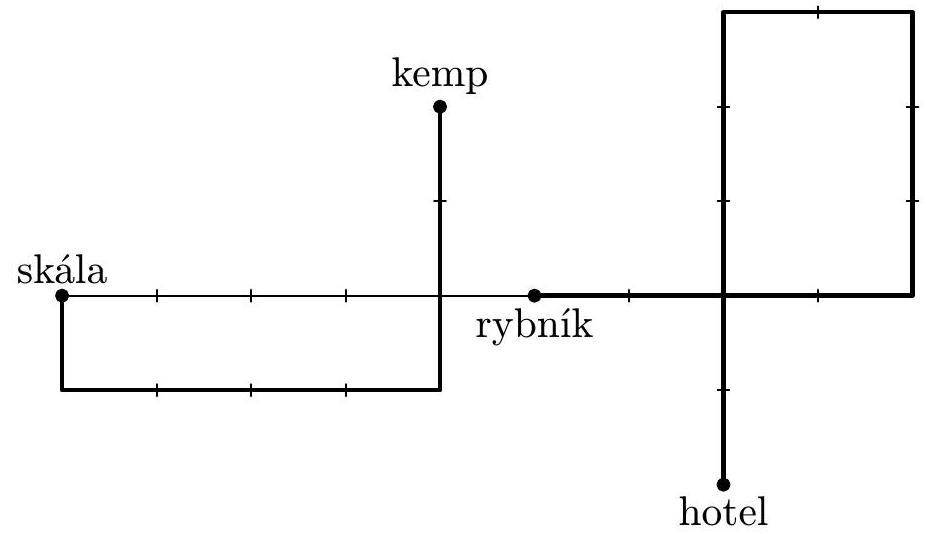
Now we see that Anička has at least $4 \mathrm{~km}$ from the hotel to the pond, for example, $2 \mathrm{~km}$ north and $2 \mathrm{~km}$ west. Vojta has at least $3 \mathrm{~km}$ from the camp to the pond, for example, $2 \mathrm{~km}$ south and $1 \mathrm{~km}$ east.
Evaluation. 1 point for illustrating Anička's and Vojta's routes; 2 points for their mutual relationship; 1 point for the shortest distances of Anička and Vojta to the pond.
Note on the second part. Routes of the same length between two places are not unique according to the given rules and can be devised in many ways (for example, Anička could have walked her $4 \mathrm{~km}$ from the hotel to the pond as follows: $1.5 \mathrm{~km}$ west, $2 \mathrm{~km}$ north, and $0.5 \mathrm{~km}$ west). We do not expect such an analysis from the solver, but a complete solution must include some specific realization.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a given group of numbers, one number is equal to the average of all, the largest number is 7 greater than the average, the smallest is 7 less than the average, and most of the numbers in the group have below-average values.
What is the smallest number of numbers that can be in the group?
(K. Pazourek)
Hint. What is the average of the three more closely described numbers from the group?
|
Let's denote the average of the numbers in the group as $p$. The smallest number in the group is $p-7$, and the largest is $p+7$. The average of these three numbers is $p$, so the average of the remaining numbers in the group must also be $p$.
Therefore, some of the remaining numbers must be less than $p$, and some must be greater than $p$. To ensure that the majority of the numbers are below average, there must be at least two more numbers that are less than $p$ than those that are greater than $p$.
The group contains at least seven numbers, arranged schematically as follows:
$$
p-7, \quad *, \quad *, \quad *, \quad p, \quad *, \quad p+7 .
$$
Notes. There are infinitely many sets of seven numbers that satisfy the conditions; they can be described, for example, as follows:
$$
p-7, \quad p-a, \quad p-b, \quad p-c, \quad p, \quad p+d, \quad p+7
$$
where $0 < a, b, c, d \leq 7$ and $a+b+c=d$. (An example could be the set $-7, -4, -1, -1, 0, 6, 7$.)
The formal justification for the initial observation follows from the definition of (arithmetic) average: if the number of remaining numbers in the group is $n$ and their sum is $s$, then their average is $\frac{s}{n}$, while the average of all numbers is $\frac{s+3p}{n+3}=p$. By manipulating the second expression, we get $\frac{s}{n}=p$.
The problem can be solved by incrementally increasing the number of numbers in the group and verifying all the given conditions.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A natural number $N$ is called bombastic if it does not contain any zero in its representation and if no smaller natural number has the same product of digits as the number $N$.
Karel first became interested in bombastic prime numbers and claimed that there are not many of them. List all two-digit bombastic prime numbers.
Then Karel chose one bombastic number and revealed to us that it contains the digit 3 and that only one of its other digits is even. Which even digit could it be?
(M. Rolinek)
Hint (for the second part). Find non-bombastic numbers containing the digit 3.
|
All two-digit prime numbers are listed in the first row of the following table. In the second row, the digit products of the individual numbers are listed. In the third row, the smallest natural numbers with the corresponding digit products are listed (these numbers can be determined by comparing the factorizations with all divisors less than 10). There are seven two-digit bombastic prime numbers, and they are marked in bold in the table.
| 11 | 13 | 17 | 19 | 23 | $\mathbf{2 9}$ | 31 | $\mathbf{3 7}$ | 41 | 43 | $\mathbf{4 7}$ | 53 | $\mathbf{5 9}$ | 61 | $\mathbf{6 7}$ | 71 | 73 | $\mathbf{7 9}$ | 83 | $\mathbf{8 9}$ | 97 |
| ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: |
| 1 | 3 | 7 | 9 | 6 | 18 | 3 | 21 | 4 | 12 | 28 | 15 | 45 | 6 | 42 | 7 | 21 | 63 | 24 | 72 | 63 |
| 1 | 3 | 7 | 9 | 6 | 29 | 3 | 37 | 4 | 26 | 47 | 35 | 59 | 6 | 67 | 7 | 37 | 79 | 38 | 89 | 79 |
In the previous list, we can notice several things related to the second part of the problem. The number 23 is not bombastic because 6 is a smaller number with the same digit product. More generally, no number containing the digits 2 and 3 can be bombastic, because by removing these two digits and adding 6 at any position, we get a smaller number with the same digit product (for example, for $\underline{2} 7 \underline{3} 7$, one of such numbers is $\underline{6} 77$).
Similarly, the number 34 is not bombastic because 26 is a smaller number with the same digit product. Therefore, no number containing the digits 3 and 4 can be bombastic (see, for example, the numbers $\underline{3} 8 \underline{4}$ and $28 \underline{6}$). Thirdly, the number 36 is not bombastic because 29 is a smaller number with the same digit product. Therefore, no number containing the digits 3 and 6 can be bombastic (see, for example, the numbers $2 \underline{3} 4 \underline{6}$ and $2 \underline{29} 4$).
On the other hand, we see that the number 38 is bombastic. The only even digit that can be with 3 in Karl's bombastic number is therefore 8.
Note. In the table in the first part of the problem, it was not necessary to consider numbers containing the digit 1 or numbers that have a larger digit in the tens place than in the units place—such numbers are never bombastic. With this insight, it was sufficient to test only eight of the listed numbers.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Pan Stříbrný uspořádal výstavu. Vystavoval 120 prstenů, které ležely na stolech podél stěn sálu a tvořily tak jednu velkou kružnici. Prohlídka začínala u vchodových dveří v označeném směru. Odtud každý třetí prsten v řadě byl zlatý, každý čtvrtý prsten byl starožitný a každý desátý prsten měl diamant. Prsten, který neměl žádnou z těchto tří vlastností, byl padělek.
Kolik bylo na výstavě zlatých prstenů, které byly starožitné a zároveň měly diamant? Kolik vystavil pan Stříbrný padělků?
(L. Hozová)
Nápověda. Podle jakých pravidel byly rozmístěny prsteny s různými kombinacemi třech zmiňovaných vlastností?
Mr. Silver organized an exhibition. He displayed 120 rings, which were placed on tables along the walls of the hall, forming one large circle. The tour started at the entrance door in a marked direction. From there, every third ring in the row was gold, every fourth ring was antique, and every tenth ring had a diamond. A ring that did not have any of these three properties was a counterfeit.
How many gold rings were on display that were also antique and had a diamond? How many counterfeits did Mr. Silver display?
(L. Hozová)
Hint. According to what rules were the rings with different combinations of the three mentioned properties placed?
|
Every 3rd ring was golden, every 4th was antique, and every 10th had a diamond. Thus,
- the number of golden rings was $120: 3=40$,
- the number of antique rings was $120: 4=30$,
- the number of rings with a diamond was $120: 10=12$.
When counting rings with multiple properties, we first determine the regularity with which they appeared at the exhibition: every 12th ring was both golden and antique, every 30th ring was golden with a diamond, and every 20th ring was antique with a diamond (here, 20 is the least common multiple of the numbers 4 and 10). Thus,
- the number of golden antique rings was $120: 12=10$,
- the number of golden rings with a diamond was $120: 30=4$,
- the number of antique rings with a diamond was $120: 20=6$.
Furthermore, every 60th ring had all three properties (60 is the least common multiple of the numbers 3, 4, and 10), thus
- the number of golden antique rings with a diamond was $120: 60=2$.
When counting rings with any of the mentioned properties, we must be cautious: 10 rings were both golden and antique, 2 of which also had a diamond, so the number of golden antique rings without a diamond was $10-2=8$. Similarly, the number of golden non-antique rings with a diamond was $4-2=2$ and the number of non-golden antique rings with a diamond was $6-2=4$.
The number of golden rings with some additional property was $2+8+2=12$, while the total number of golden rings was 40, so the number of golden non-antique rings without a diamond was $40-12=28$. Similarly, the number of non-golden antique rings without a diamond was $30-(2+8+4)=16$ and the number of non-golden non-antique rings with a diamond was $12-(2+2+4)=4$.
The previous counts and relationships can be illustrated using a Venn diagram as follows:
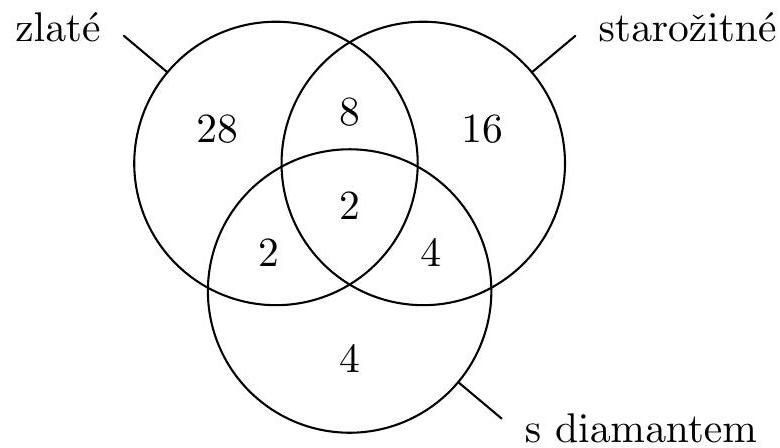
The number of rings with any of the three properties (i.e., rings that were not fakes) was $2+8+4+2+28+16+4=64$. Therefore, the number of fakes was $120-64=56$.
Note. If we denote the three basic sets of rings as $Z, S$, and $D$, the initial part of the solution can be summarized as follows:
$$
\begin{gathered}
|Z|=40, \quad|S|=30, \quad|D|=12 \\
|Z \cap S|=10, \quad|Z \cap D|=4, \quad|S \cap D|=6, \\
|Z \cap S \cap D|=2 .
\end{gathered}
$$
In the next part, we determined the number of elements in the union $Z \cup S \cup D$ by gradually expressing the number of elements in mutually disjoint* subsets $(Z \cap S) \backslash(Z \cap S \cap D)$, $(Z \cap D) \backslash(Z \cap S \cap D)$, etc., which we then summed. More concisely, the same result can be obtained by the following calculation:
$$
\begin{aligned}
|Z \cup S \cup D| & =|Z|+|S|+|D|-|Z \cap S|-|Z \cap D|-|S \cap D|+|Z \cap S \cap D|= \\
& =40+30+12-10-4-6+2=64 .
\end{aligned}
$$
This relationship is known as the principle of inclusion and exclusion. To justify it generally (or to further generalize it), it suffices to verify that each of the disjoint parts of the Venn diagram is counted exactly once.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Robots Robert and Hubert assemble and disassemble coffee grinders. Each of them assembles a coffee grinder four times faster than the other disassembles it. When they came to the workshop in the morning, there were already some assembled coffee grinders there.
At 9:00, Hubert started assembling and Robert disassembling, and precisely at 12:00, Hubert finished assembling a coffee grinder and Robert disassembling another one. In total, 27 coffee grinders were added during this shift.
At 13:00, Robert started assembling and Hubert disassembling, and precisely at 19:00, Robert finished assembling the last coffee grinder and Hubert disassembling another one. In total, 120 coffee grinders were added during this shift.
How long does it take for Hubert to assemble a coffee grinder? How long does it take for Robert to assemble one?
(K. Pazourek)
Hint. How many coffee grinders are added per hour in each shift?
|
In the morning three-hour shift, 27 coffee mugs were added, which corresponds to $27: 3=9$ coffee mugs per hour. Since Robert disassembles four times slower than Hubert assembles, Hubert alone would assemble 9 coffee mugs in $\frac{3}{4}$ of an hour, i.e., 45 minutes. Therefore, Hubert assembles one coffee mug in $45: 9=5$ minutes.
In the afternoon six-hour shift, 120 coffee mugs were added, which corresponds to $120: 6=20$ coffee mugs per hour. This time, Robert assembles and Hubert disassembles, so Robert alone would assemble 20 coffee mugs in $\frac{3}{4}$ of an hour, i.e., 45 minutes. Therefore, Robert assembles one coffee mug in $45: 20=2.25$ minutes, i.e., 2 minutes and 15 seconds.
Another solution. If $h$ represents the number of coffee mugs Hubert assembles per hour, and $r$ represents the number of coffee mugs Robert assembles per hour, then in one hour Hubert disassembles $\frac{1}{4} r$ coffee mugs and Robert disassembles $\frac{1}{4} h$ coffee mugs. The information from the problem leads to the equations:
$$
\begin{aligned}
& 3\left(h-\frac{1}{4} h\right)=27 \\
& 6\left(r-\frac{1}{4} r\right)=120 .
\end{aligned}
$$
The solution to the first equation is $h=12$, so Hubert assembles 12 coffee mugs per hour, i.e., 60 minutes. Hubert assembles one coffee mug in $60: 12=5$ minutes. The solution to the second equation is $r=\frac{80}{3}$, so Robert assembles 80 coffee mugs in 3 hours, i.e., 180 minutes. Robert assembles one coffee mug in $180: 80=2.25$ minutes.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Given an isosceles right triangle $A B S$ with the base $A B$. On the circle with center at point $S$ and passing through points $A$ and $B$, there is a point $C$ such that triangle $A B C$ is isosceles.
Determine how many points $C$ satisfy the given conditions, and construct all such points.
(K. Pazourek)
Hint. What is an isosceles triangle?
|
Side $AB$ of the isosceles triangle $ABC$ can be either its base or one of its legs. Depending on this, we divide the solution into two parts.
a) Side $AB$ is the base of the isosceles triangle $ABC$. In this case, $C$ is the main vertex of the triangle $ABC$ and lies on its axis of symmetry. The axis of symmetry of the triangle $ABC$ is the perpendicular bisector of segment $AB$. This line intersects the given circle at two points, which are two possible solutions to the problem, denoted as $C_{1}$ and $C_{2}$.
b) Side $AB$ is a leg of the isosceles triangle $ABC$. In this case, the main vertex of the triangle $ABC$ can be either point $A$ or point $B$. If the main vertex were point $A$, then side $AC$ would be a leg and point $C$ would be equidistant from point $A$ as point $B$. Therefore, point $C$ would lie on the circle centered at point $A$ passing through point $B$. This circle intersects the given circle at one additional point, which we denote as $C_{3}$.
Similarly, if the main vertex were point $B$, then the remaining vertex of the triangle would lie on the circle centered at point $B$ passing through point $A$. The corresponding intersection with the given circle is denoted as $C_{4}$.
On the given circle, there are four points $C_{1}, C_{2}, C_{3}, C_{4}$ that satisfy the conditions of the problem. The construction of all points follows from the previous description: points $C_{3}$ and $C_{4}$ are the intersections of the given circle with two auxiliary circles; the perpendicular bisector of segment $AB$, and thus points $C_{1}$ and $C_{2}$, is determined by the common points of these two auxiliary circles.
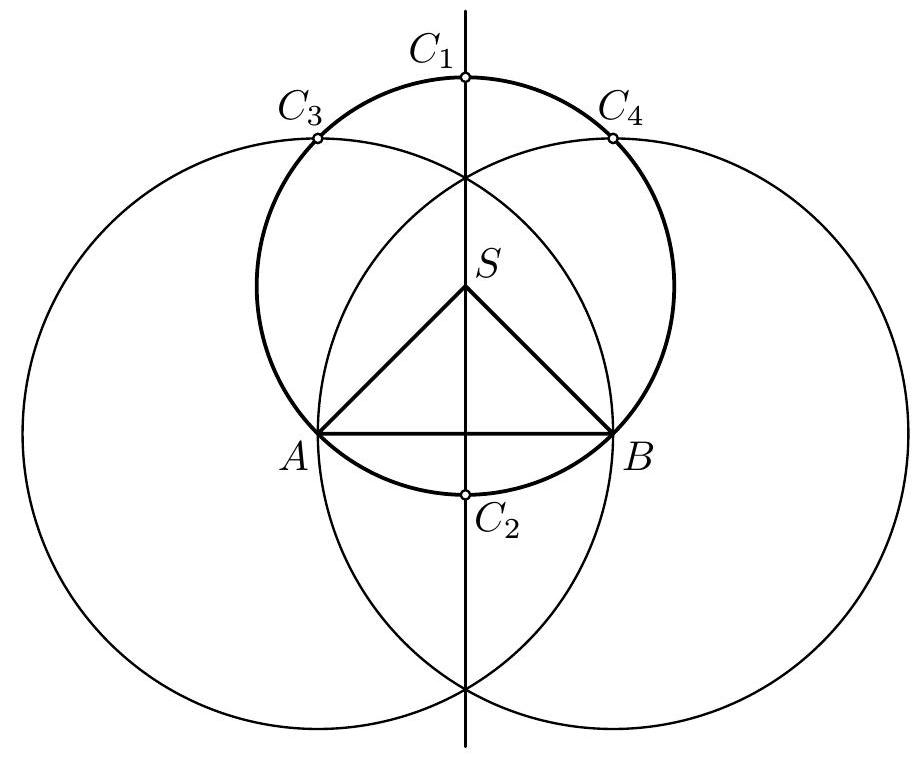
Note. The right-angled triangle $ABS$ implies that points $A, B, C_{3}, C_{4}$ form the vertices of a square. From this, alternative constructions of the relevant points can be derived.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
An arithmetic sequence is a sequence of numbers in which the difference between each number and the one preceding it is always the same; this difference is called the common difference. (For example, 2, 8, 14, 20, 26, 32 is an arithmetic sequence with a common difference of 6.)
Bolek and Lolek each had their own arithmetic sequence. Both Bolk's and Lolek's sequences started with the number 2023 and ended with the number 3023. These two sequences had 26 common numbers. The ratio of Bolk's to Lolek's common difference was $5:2$.
Determine the difference between Bolk's and Lolek's common difference.
(E. Novotná)
Hint. Bolk's and Lolek's common differences can be expressed using one variable.
|
The ratio of Bolko's and Lolko's difference was $5: 2$. Thus, Bolko's difference was $5k$ and Lolko's $2k$, where $k$ is an unknown number that we will soon determine from other information. The difference between Bolko's and Lolko's difference can then be expressed as $5k - 2k = 3k$.
Bolko's, respectively, Lolko's sequence was
$$
\begin{aligned}
& \text { 2023, } \quad 2023+5k, \quad 2023+10k, \ldots \text {, } \\
& 2023, \quad 2023+2k, \quad 2023+4k, \quad 2023+6k, \quad 2023+8k, \quad 2023+10k, \quad \ldots,
\end{aligned}
$$
the common numbers of both sequences were
$$
2023, \quad 2023+10k, \quad 2023+20k, \quad 2023+30k, \quad \ldots
$$
There were 26 common numbers, and the last one was 3023. The 26th number in the sequence (*) is of the form $2023 + 250k$, so it must have been $k=4 (2023 + 250 \cdot 4 = 3023)$.
The difference between Bolko's and Lolko's difference was 12.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine the last digit of the product of all even natural numbers less than 100 that are not multiples of ten.
(M. Volfová)
|
The last digit of the product is determined exclusively by the last digits of the factors. Therefore, in solving the problem, we will consider only the last digits in the calculations. According to the problem, we multiply ten sets of four factors, and in each set, the factors end with the digits 2, 4, 6, and 8. The product $2 \cdot 4 \cdot 6 \cdot 8$ ends with the digit 4. To determine the last digit of the result of multiplying ten such sets, it is sufficient to multiply ten fours and, in the multiplication, track only the last digit:
The product $4 \cdot 4$ ends with the digit 6, so instead of multiplying ten fours, it is sufficient to multiply five sixes. The number 6 multiplied by itself again gives a number ending with the digit 6, and therefore the product of five sixes, and thus also of ten fours, ends with the digit 6. The sought digit is 6.
Another solution. Again, we consider only the last digits in the products. We are given ten factors ending with the digit 2, ten ending with the digit 4, ten ending with the digit 6, and ten ending with the digit 8. We will consider each set of ten factors in turn:
When multiplying $2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2$, we track only the digits in the units place and find that the result ends with the digit 4. Similarly, we find that the product $4 \cdot 4 \cdot 4 \cdot 4 \cdot 4 \cdot 4 \cdot 4 \cdot 4 \cdot 4 \cdot 4$ ends with the digit 6, the product $6 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 6$ ends with the digit 6, and the product $8 \cdot 8 \cdot 8 \cdot 8 \cdot 8 \cdot 8 \cdot 8 \cdot 8 \cdot 8 \cdot 8$ ends with the digit 4. The last digit of the sought product will be determined by multiplying the digits just found, i.e., $4 \cdot 6 \cdot 6 \cdot 4$. This product ends with the digit 6, so the sought digit is 6.
Suggested evaluation. 1 point for realizing that it is sufficient to consider only the last digits of the factors; 4 points for intermediate results and their justification (e.g., 2 points for the last digit of the product $2 \cdot 4 \cdot 6 \cdot 8$ and 2 points for the last digit of the power $4^{10}$); 1 point for the sought digit 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On a fairy-tale island, dragons and cyclopes live. All dragons are red, three-headed, and two-legged. All cyclopes are brown, one-headed, and two-legged. Cyclopes have one eye in the middle of their forehead, and dragons have two eyes on each head. Together, the cyclopes and dragons have 42 eyes and 34 legs.
How many dragons and how many cyclopes live on the island?
(M. Petrová)
|
Since both cyclopes and dragons are bipedal, the total number of these creatures is $17(34: 2=17)$.
If all the creatures were cyclopes, they would have a total of 17 eyes. This is 25 fewer than the actual number $(42-17=25)$.
Each dragon has 5 more eyes than any cyclops, so there are 5 dragons among the creatures $(25: 5=5)$. The remaining 12 creatures are cyclopes $(17-5=12)$.
Another solution. The problem can also be solved by trying out possibilities: there are a total of 17 creatures on the island $(34: 2=17)$, among which there are at most 7 dragons $(42: 6=7)$.
In the following table, we list the number of cyclopes $(k=17-d)$ and the total number of their eyes $(6d+k=5d+17)$, which should be 42, depending on the number of dragons $(d)$:
| dragons | 1 | 2 | 3 | 4 | $\mathbf{5}$ | 6 | 7 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| cyclopes | 16 | 15 | 14 | 13 | $\mathbf{12}$ | 11 | 10 |
| total eyes | 22 | 27 | 32 | 37 | 42 | 47 | 52 |
The only solution that fits is marked in bold.
Note. With the notation used in the description of the above table, the number of dragons can be determined as the solution to the equation $5d+17=42$ (which also corresponds to the reasoning in the first solution to the problem).
Testing can also be based on a different principle, without needing to know the number of creatures on the island (but considering the number of legs).
Evaluation. 2 points for partial insights (e.g., the total number of creatures or the maximum number of dragons); 3 points for solving the problem; 1 point for completeness and quality of the commentary.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
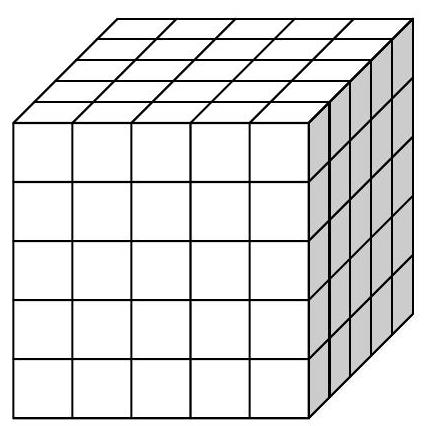
Danka and Janka received two identical white cubes for their birthdays, each made up of 125 small cubes as shown in the picture. To distinguish the cubes, they decided to paint them. Danka took a brush and painted three of the six faces of her cube red. Janka painted three faces of her cube green. After some time, both cubes were cut into the individual small cubes they were made of. When they did this, they were surprised to find that the number of small cubes with at least one red face differed from the number of small cubes with at least one green face. Determine this difference.
(E. Novotná)
|
We know that both Danka and Janka painted three sides of the cube. This can only be done in two ways:
1. Two opposite sides are painted, and then one side between them is also painted; consider, for example, the top, bottom, and one side.
2. No two opposite sides are painted, so the three painted sides share a common vertex; consider, for example, the top, front, and side.
If the number of painted small cubes in each case is different, the girls must have painted the cubes in different ways. For each way of painting, we will determine how many small cubes have at least one side painted. We will proceed layer by layer, counting layers from the bottom:
1. In the first and fifth layers, all 25 small cubes have at least one side painted, in the second, third, and fourth layers, 5 small cubes are painted each time; in total, in this case, $25+5+5+5+25=65$ small cubes are painted.
2. In the first four layers, 9 small cubes have at least one side painted each time, in the fifth layer, all 25 small cubes are painted; in total, in this case, $9+9+9+9+25=61$ small cubes are painted.
The sought difference in the number of painted small cubes is $65-61=4$.
Evaluation. 1 point for determining the possible ways of painting; 4 points for determining the number of painted small cubes in each case; 1 point for the difference.
Note. The difference can also be determined without calculating the total number of painted small cubes in each case. In such a solution, evaluate the second part of the task with 1 to 5 points based on the quality of the justification (the first point is the same).
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On a night march, the Wolf and Fox patrols each received one identical candle. They lit the candles together at the start and set off. Each member of the patrol carried the candle for the duration it took for its length to be halved. The Wolves reached the finish line at the moment when the sixth carrier was passing the candle to the seventh. After that, their candle burned for another three minutes. The Foxes reached the finish line in two hours and 57 minutes.
- Which patrol reached the finish line first?
- By how many minutes did the winning patrol finish earlier than the other patrol?
(The candle burns evenly: it always burns the same amount in the same time.)
(M. Dillingerová)
|
First, we will determine how long the Wolves ran. The sixth carrier passed the candle to the seventh at the moment when it still had 3 minutes left to burn. He, therefore, carried it for 3 minutes and received it from the fifth carrier at the moment when it still had $3+3=6$ minutes left to burn. The fifth carrier, therefore, carried it for 6 minutes and received it from the fourth carrier at the moment when it still had $6+6=12$ minutes left to burn. We can proceed this way up to the first carrier:
| carrier no. | carried the candle (min) |
| :---: | :---: |
| 7 | 0 |
| 6 | 3 |
| 5 | 6 |
| 4 | 12 |
| 3 | 24 |
| 2 | 48 |
| 1 | 96 |
The march of the Wolves lasted $96+48+24+12+6+3=189$ minutes. (Alternatively, it can be calculated as $96+96-3=189$.)
The march of the Foxes lasted $120+57=177$ minutes.
Therefore, the Foxes were the first to reach the finish, and they were ahead by $189-177=12$ minutes.
Scoring. 1 point for recognizing that each carrier carried the candle for as long as it had left to burn when they passed it to the next; 2 points for filling out the table or its equivalent; 1 point for determining the duration of the Wolves' march; 1 point for each answer to the questions in the assignment.
Do not award any points for a solution that only has an unjustified conclusion that the Foxes were the first to reach the finish.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Filoména has a mobile phone with the following button layout:
| 1 | 2 | 3 |
| :--- | :--- | :--- |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 0 | | |
| | | |
| | | |
The nine-digit phone number of her best friend Kunhuta has the following properties:
- all digits in Kunhuta's phone number are different,
- the first four digits are arranged in ascending order from smallest to largest, and the centers of their buttons form a square,
- the centers of the buttons of the last four digits also form a square,
- the phone number is divisible by three and five.
How many different nine-digit numbers could be Kunhuta's phone number?
(K. Pazourek)
Idea. Which digits can form the last and which the first quartet?
|
First, let's find all quadruples of buttons whose centers form a square. These are the buttons with the following digits:
$$
\begin{array}{ll}
1,2,4,5 & 1,3,7,9 \\
2,3,5,6 & 2,4,6,8 \\
4,5,7,8 & 5,7,9,0 \\
5,6,8,9 &
\end{array}
$$
The quadruples in the left column, however, cannot be used because, besides the square formed by the relevant buttons, we cannot form another square with the remaining buttons. Since the phone number is divisible by five, it must end in 5 or 0; therefore, the last four digits of the phone number are 5, 7, 9, 0 (their order will be discussed later). Since we have already used the digits 7 and 9, the first four digits of the phone number must be 2, 4, 6, 8 (in this order, they are arranged by size).
The digits that have not yet been used and can be in the middle of the phone number are 1 and 3. The phone number must be divisible by three, so let's determine the possible digit sums. The sum of all digits on the keypad is 45. If the phone number contains 1, i.e., the phone number includes all digits except 3, the digit sum would be $45-3=42$. If the phone number contains 3, the digit sum would be $45-1=44$. The number 42 is divisible by 3, while 44 is not; therefore, the middle digit is 1.
Since we have not overlooked any of the requirements in the problem, the sought phone number is
$$
24681 * * * *
$$
where the last four digits are $5,7,9,0$ in an unknown order, but we know that the last digit must be 5 or 0. To determine the number of all possible Kunhut's phone numbers, we will not list them all but use this idea: The last digit can be chosen in two ways, the second-to-last digit can then be chosen from the three remaining digits, the preceding one from the two remaining, and the last unfilled position will always have one remaining digit. Altogether, we get
$$
2 \cdot 3 \cdot 2=12
$$
possible orders for the last four digits, and thus 12 possible Kunhut's phone numbers.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On the meadow, there were 45 sheep and several shepherds. After half of the shepherds and a third of the sheep left, the remaining shepherds and sheep together had 126 legs. All the sheep and shepherds had the usual number of legs.
How many shepherds were originally on the meadow?
(L. Hozová)
Hint. How many sheep were left on the meadow after the departure?
|
After one third of the sheep left, two thirds of the original number remained on the meadow, which is 30 sheep $\left(\frac{2}{3} \cdot 45=30\right)$. These have a total of 120 legs $(30 \cdot 4=120)$.
The shepherds who remained on the meadow had a total of 6 legs $(126-120=6)$, so 3 shepherds remained $(6: 2=3)$. Since half of the shepherds left, there were originally $6(3 \cdot 2=6)$ shepherds.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
I am Ivan and I am three times younger than my father. I have brothers Vincent and Jakub, who are 11 and 9 years old. My age is equal to five times the third of the age of the younger of the brothers. A peculiarity of our family is that we were all born on April 12th, so today we are celebrating our birthdays.
How many years will it take for the age of our father to be equal to the sum of the ages of the three of us? (L. Hozová)
|
The younger of the brothers is 9 years old, so I am 15 years old $\left(\frac{9}{3} \cdot 5=15\right)$. I am three times younger than my father, so my father is 45 years old $(3 \cdot 15=45)$. The sum of the ages of the three of us brothers is 35 years $(11+9+15=35)$.
The father's age is 10 years older than the sum of the ages of the three of us brothers, and this difference decreases by 2 each year (the father gains 1 year, while the sum of our ages gains 3 years). The father's age will be the same as the sum of the ages of the three of us brothers in 5 years $(10: 2=5)$.
Evaluation. 3 points for partial results; 3 points for the calculation and quality of the commentary.
Note. The problem can be solved by successively adding years $k$ to the father's age and the sum of the brothers' ages until the difference is zero. Symbolically: in $r$ years, the father's age will be $45+r$, while the sum of the brothers' ages will be $35+3r$. The required equality, after rearrangement, gives
$$
\begin{aligned}
35+3 r & =45+r, \\
2 r & =10, \\
r & =5 .
\end{aligned}
$$
#
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For the sequence of numbers starting
$$
1,3,4,7,11,18, \ldots
$$
it holds that each number starting from the third is the sum of the two preceding ones.
What is the last digit of the 2023rd number in this sequence?
Hint. Use the sequence formed by the last digits to help yourself.
|
The last digit of each number corresponds to the remainder of that number when divided by ten. Therefore, it is sufficient to deal with the sequence of corresponding remainders:
$$
1,3,4,7,1,8, \ldots
$$
which means the sequence where each number starting from the third is the remainder of the sum of the previous two when divided by ten. This sequence repeats every 12 terms:
$$
1,3,4,7,1,8,9,7,6,3,9,2 ; 1,3, \ldots
$$
Thus, for example, the 1st, 13th, 25th, 145th, or 2017th term of the sequence consists of the same numbers.
The number 2023, when divided by 12, gives 168 with a remainder of 7. Therefore, the 2023rd term of this sequence is the same as the 7th term, which is the number 9.
The 2023rd number in the given sequence ends with the digit 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a certain polygon, the ratio of the sum of the magnitudes of its interior angles to the sum of the magnitudes of $\mathrm{k}$ supplementary angles is $3: 5$. (To explain: a supplementary angle complements a given angle to a full angle.)
How many vertices does that polygon have?
(I. Jančigová)
|
The sum of the sizes of the interior angles in every triangle is $180^{\circ}$, in every quadrilateral $360^{\circ}$, etc. Generally, it is true that every $n$-sided polygon can be composed of $n-2$ triangles, so the sum of its interior angles is $(n-2) \cdot 180^{\circ}$.

The sum of the sizes of the exterior angles of a general $n$-sided polygon is
$$
n \cdot 360^{\circ}-(n-2) \cdot 180^{\circ}=(n+2) \cdot 180^{\circ}.
$$
The ratio of these two values is $(n-2):(n+2)$, which is supposed to be $3: 5$. By rearranging, we get:
$$
\begin{aligned}
\frac{n-2}{n+2} & =\frac{3}{5}, \\
5 n-10 & =3 n+6, \\
2 n & =16, \\
n & =8.
\end{aligned}
$$
The unknown polygon is an octagon.
Another solution. The sums of the sizes of the interior and exterior angles are the same in all polygons with the same number of vertices. Therefore, it is sufficient to consider (for example) only regular polygons.
A regular $n$-sided polygon can be composed of $n$ congruent isosceles triangles. The interior angle at the main vertex of the triangle has a size of $\frac{1}{n} 360^{\circ}$, the sum of the interior angles at the base is equal to the interior angle of the regular $n$-sided polygon and has a size of $180^{\circ}-\frac{1}{n} \cdot 360^{\circ}$. The exterior angle of the regular $n$-sided polygon thus has a size of $360^{\circ}-\left(180^{\circ}-\frac{1}{n} \cdot 360^{\circ}\right)=180^{\circ}+$ $+\frac{1}{n} \cdot 360^{\circ}$.
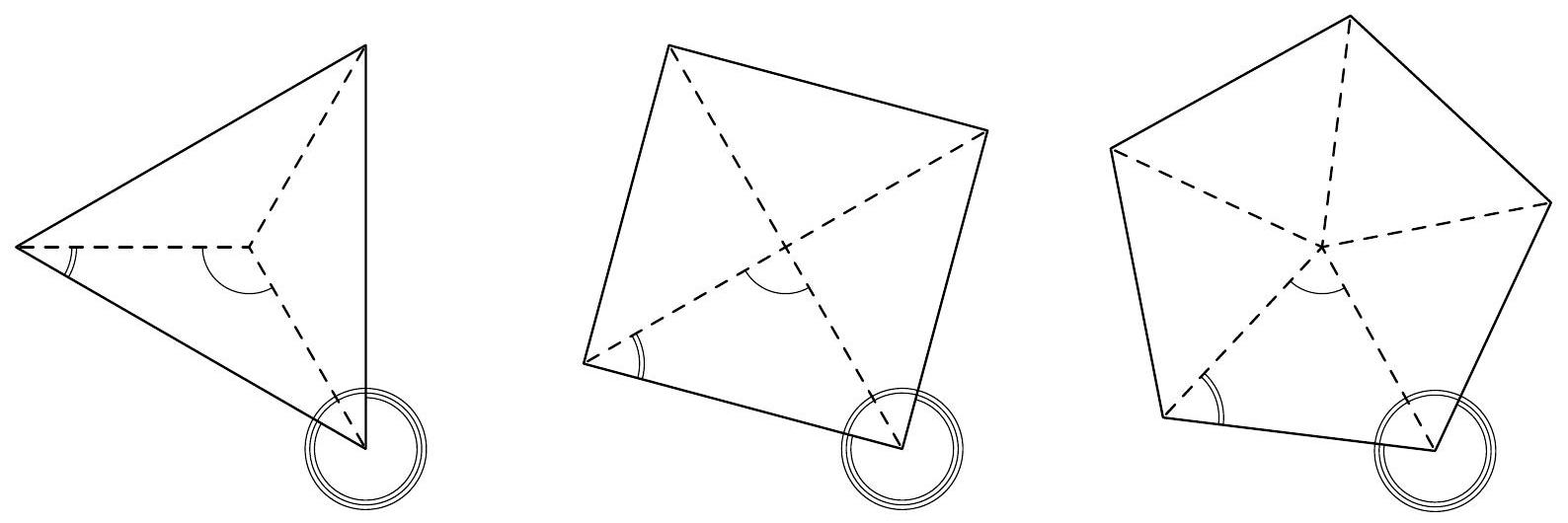
The sums of the sizes of the interior and exterior angles are, respectively,
$$
\begin{aligned}
& n\left(180^{\circ}-\frac{1}{n} \cdot 360^{\circ}\right)=(n-2) \cdot 180^{\circ}, \\
& n\left(180^{\circ}+\frac{1}{n} \cdot 360^{\circ}\right)=(n+2) \cdot 180^{\circ}.
\end{aligned}
$$
The ratio of these two values is $(n-2):(n+2)$, which is supposed to be $3: 5$. From this, by the same rearrangements as above, we get $n=8$. The unknown polygon is an octagon.
Evaluation. 2 points for preparatory expressions in terms of $n$; 2 points for setting up and solving the equation; 2 points for the quality of the commentary.
Another solution. Similarly to the previous solution, we focus only on regular polygons, or their division into congruent isosceles triangles, see the illustration above.
In a regular polygon, the ratio of the sums of the sizes of the interior and exterior angles is the same as the ratio of the sizes of these angles at each vertex. This ratio is $3: 5$, precisely when the interior angle of the unknown polygon has a size of
$$
\frac{3}{8} \cdot 360^{\circ}=135^{\circ}
$$
$(3+5=8$ parts correspond to a full angle). The angle at the main vertex of the auxiliary isosceles triangle, i.e., the central angle of the polygon, is $45^{\circ}$ (so that the sum of the interior angles of the triangle is $180^{\circ}$). This angle is one-eighth of a full angle. The unknown polygon is an octagon.
Note. The previous idea can be processed by successively expressing the central, interior, and exterior angles of a regular $n$-sided polygon in terms of $n$ and checking the required ratio:
| $n$ | 3 | 4 | 5 | 6 | 7 | 8 | $\ldots$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| central | $120^{\circ}$ | $90^{\circ}$ | $72^{\circ}$ | $60^{\circ}$ | $\frac{1}{7} 360^{\circ}$ | $45^{\circ}$ | $\ldots$ |
| interior | $60^{\circ}$ | $90^{\circ}$ | $108^{\circ}$ | $120^{\circ}$ | $\frac{1}{7} 900^{\circ}$ | $135^{\circ}$ | $\ldots$ |
| exterior | $300^{\circ}$ | $270^{\circ}$ | $252^{\circ}$ | $240^{\circ}$ | $\frac{1}{7} 1620^{\circ}$ | $225^{\circ}$ | $\ldots$ |
| ratio | $1: 5$ | $1: 3$ | $3: 7$ | $1: 2$ | $5: 9$ | $\mathbf{3 : 5}$ | $\ldots$ |
From the geometric intuition, it follows that for increasing $n$, the value of the ratio of the interior and exterior angles gradually increases to $1: 1$. Thus, if the problem has a solution, it is the only solution.
Evaluation. 2 points each for the sizes of the interior and central angles of a regular polygon; 2 points for solving and the quality of the commentary.
When checking step by step, consider the completeness of the commentary. A randomly discovered unexplained solution should be rated 2 points.
[^0]: The district round of the Z9 category takes place on January 25, 2023, starting no later than 10:00 AM, and participants have 4 hours of clean time to solve the problems. Each problem can earn a participant 6 points, and a successful solver is a student who earns 12 or more points. Allowed aids are writing and drawing tools, school mathematical tables. Calculators and other electronic aids are not allowed.
If a student solves the district round remotely, they may use a computer (tablet, phone) only to display the problem, or to ask a teacher a question and receive an answer. The student must submit their scanned or photographed solutions within 4 hours and 20 minutes after the start of the competition, but no later than 14:20. To be recognized, numerical results must be accompanied by supporting calculations in the submitted solution.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On a secret island, there live two kinds of natives: one kind always speaks the truth (honest ones), and the other always lies (liars). Researchers there encountered several groups of natives and asked each member of the groups how many honest ones were in their group.
- From one four-member group, they received the same number from everyone.
- From another group, they received the numbers $0,1,3,3,3,4$.
How many honest ones could there be in one group and how many in the other? Determine all possibilities.
(M. Volfová)
|
If the first group consisted only of honest people, the researchers would receive the numbers 4, 4, 4, 4 as answers. If the group had three, two, or one honest person, the researchers could not receive four identical numbers as answers. If the group consisted only of liars, the researchers could receive any set of four numbers that do not include 0 as answers. Therefore, in the first group, there could either be four honest people or none.
Since all honest people in the group must (unlike liars) answer the same, the number $k$ can represent the answer of an honest person only if it repeats $k$ times. Therefore, the number of honest people in the second group could be either one or three. (If the group consisted only of liars, then the answer 0 would be true, which is not possible for liars.)
Evaluation. 2 points for determining the possibilities for each group; 2 points for completeness and quality of the commentary.
#
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Vítek has written down two numbers, 541 and 293. From the six digits used, he first needs to strike out two such that the sum of the two resulting numbers is the largest possible. Then, he needs to strike out two digits from the original six digits such that the difference between the two resulting numbers is the smallest possible (subtracting the smaller number from the larger one). Which digits should he strike out?
(M. Petrová)
|
First, we will be crossing out digits so that the sum is as large as possible. We can either cross out two digits from the first number, or we can cross out two digits from the second, or we can cross out one digit from each number. In each case, we cross out digits so that the resulting sum is as large as possible. We get the following numbers:
- cross out 4 and 1, leaving 5 and 293: sum 298,
- cross out 2 and 3, leaving 541 and 9: sum 550,
- cross out 1 and 2, leaving 54 and 93: sum 147.
We see that the largest sum (550) is obtained by crossing out the digits 2 and 3 from the second number.
Now we will look for the smallest difference. Again, we can cross out two digits from one number, or two digits from the other, or one digit from each number. If we were to cross out two digits from one number, the difference would always be a three-digit number. When we cross out one digit from each number, we get the following numbers:
- cross out 5 and 2, leaving 41 and 93: difference 52,
- cross out 5 and 9, leaving 41 and 23: difference 18,
- cross out 5 and 3, leaving 41 and 29: difference 12,
- cross out 4 and 2, leaving 51 and 93: difference 42,
- cross out 4 and 9, leaving 51 and 23: difference 28,
- cross out 4 and 3, leaving 51 and 29: difference 22,
- cross out 1 and 2, leaving 54 and 93: difference 39,
- cross out 1 and 9, leaving 54 and 23: difference 31,
- cross out 1 and 3, leaving 54 and 29: difference 25.
We see that the smallest difference (12) is obtained by crossing out 5 from the first number and 3 from the second number.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Four friends Adam, Mojmír, and twins Petr and Pavel earned a total of 52 smileys in math class, each getting at least 1. The twins together have 33, but the most successful was Mojmír. How many did Adam get?
(M. Volfová)
|
All smileys amount to 52, while the twins got 33 and Adam at least one. For Mojmír, there are at most $52-33-1=18$ smileys left. For him to have the most of all, each of the twins can have at most 17 smileys. This means that Petr got exactly 17 and Pavel 16, or vice versa. If one had less than 16, the other would have to have more than 17 to make a total of 33. From this, it also follows that Mojmír could not have gotten less than 18 smileys to have more than each of the twins. Therefore, Mojmír got exactly 18 smileys, and one smiley is left for Adam :-).
Another solution. We know that the twins got a total of 33 smileys, and each got at least one. If Petr got 32 smileys and Pavel one, Mojmír would have to get at least 33 to have the most. Then, all together with Adam, they would have at least $33+33+1=67$ smileys, which is not possible because from the problem statement we know they have 52 in total. Similarly, if Petr got 31 smileys and Pavel 2, Mojmír would have to have at least 32, together with Adam then $33+32+1=66$, which is still too much. ... By the same reasoning, all possibilities for the distribution of smileys between the twins can be excluded except for the following case: Petr 17, Pavel 16 (or vice versa), then Mojmír 18 and Adam 1.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Mrs. Siroka was expecting guests in the evening. First, she prepared 25 sandwiches for them. Then she calculated that each guest could take two, but three would not be enough for everyone. She thought that if she made another 10 sandwiches, each guest could take three, but not four. This still seemed too little to her. In the end, she prepared a total of 52 sandwiches. Each guest could then take four sandwiches, but five would not be enough for everyone. How many guests was Mrs. Siroka expecting? She herself is on a diet and never eats in the evening.
|
First, let's work with the part of the problem where 25 sandwiches are considered. According to this, Mrs. Siroka expected no more than 12 guests, because $25: 2=12$, remainder 1, which means that 12 people could take two sandwiches each, but only one would be left. Here we also find out that Mrs. Siroka expected more than 8 guests, because $25: 3=8$, remainder 1, which means that with 8 guests, everyone could take three sandwiches. So far, it is plausible that she expected 9, 10, 11, or 12 guests.
Now let's consider only the part of the problem that talks about 35 sandwiches. We determine that Mrs. Siroka expected at most 11 guests, since $35: 3=11$, remainder 2, and more than 8 guests, since $35: 4=8$, remainder 3. Therefore, Mrs. Siroka could have expected 9, 10, or 11 guests.
Next, let's work only with the consideration of 52 sandwiches. According to this, Mrs. Siroka expected at most 13 guests, because $52: 4=13$, and more than 10 guests, because $52: 5=10$, remainder 2. She therefore expected 11, 12, or 13 guests.
We see that the only number of guests that fits all the data in the problem is 11.
Another solution. Just as in the first paragraph of the previous solution, we determine that Mrs. Siroka could have expected 9, 10, 11, or 12 guests. For each number, we will check whether it corresponds to the other data in the problem.
9 guests: With 35 sandwiches, everyone could take three sandwiches, not four, because $9 \cdot 3 < 35$. With 52 sandwiches, everyone could take four sandwiches, but even five, because $9 \cdot 4 < 52$. With 52 sandwiches, everyone could take four sandwiches, but even five, because $10 \cdot 4 < 52$. With 52 sandwiches, everyone could take four sandwiches, but not five, because $11 \cdot 4 \leq 52$. This number of guests fits the entire problem.
12 guests: With 35 sandwiches, everyone could not take three sandwiches, because $12 \cdot 3 > 35$. This number of guests is rejected.
Mrs. Siroka expected 11 guests.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Some objects are in each of four rooms. Let $n \geqslant 2$ be an integer. We move one $n$-th of objects from the first room to the second one. Then we move one $n$-th of (the new number of) objects from the second room to the third one. Then we move similarly objects from the third room to the fourth one and from the fourth room to the first one. (We move the whole units of objects only.) Finally the same number of the objects is in every room. Find the minimum possible number of the objects in the second room. For which $n$ does the minimum come?
(Vojtech Bálint, Michal Rolínek)
|
Solution. Let us compute backwards. Firstly we find the number of the objects in two rooms before the move. Let $a$ and $b$ be number of the objects in the rooms $A$ and $B$ before the move. This number after the move we denote by $a^{\prime}$ and $b^{\prime}$. By the conditions
$$
a^{\prime}=\frac{n-1}{n} a, \quad b^{\prime}=b+\frac{1}{n} a
$$
holds. From the first equation and an identity $a+b=a^{\prime}+b^{\prime}$ we obtain
$$
a=\frac{n}{n-1} a^{\prime}, \quad b=b^{\prime}-\frac{1}{n-1} a^{\prime}
$$
Now let $M$ be the final number of the objects in every room after the fourth move. By this identity we can compute the initial number of objects in every room in terms of $M$ and $n$ :
Finally: $\quad M \quad M \quad M \quad M \quad M$
| before $4 \rightarrow 1:$ | $\frac{n-2}{n-1} M$, | $M$, | $M$, | $\frac{n}{n-1} M ;$ |
| :--- | ---: | ---: | ---: | ---: |
| before $3 \rightarrow 4:$ | $\frac{n-2}{n-1} M$, | $M$, | $\frac{n}{n-1} M$, | $M ;$ |
| before $2 \rightarrow 3:$ | $\frac{n-2}{n-1} M$, | $\frac{n}{n-1} M$, | $M$, | $M ;$ |
| before $1 \rightarrow 2:$ | $\frac{n(n-2)}{(n-1)^{2}} M$, | $\frac{(n-1)^{2}+1}{(n-1)^{2}} M$, | $M$, | $M$. |
Since the number of objects in the first room was positive, $n \geqslant 3$ holds. Now we can easily find the minimum of
$$
V_{2}=\frac{(n-1)^{2}+1}{(n-1)^{2}} M
$$
The difference between numerator and denominator is 1 , so the fraction is irreducible. Since $V_{2}$ is integer it must be $M=k(n-1)^{2}$ for proper $k$, therefore $V_{2}=k\left((n-1)^{2}+1\right)$. For $n \geqslant 3$ we can estimate $(n-1)^{2}+1 \geqslant 5$, so $V_{2} \geqslant 5$ too. Using $n=3, k=1$ and $M=4$ we obtain $V_{2}=5$ and we can easily check that the quadruple $(3,5,4,4)$ satisfies the problem: it transforms to quadruple $(2,6,4,4)$, then $(2,4,6,4)$, after that $(2,4,4,6)$ and finally $(4,4,4,4)$. So the minimal numbers of objects in the second room is 5 and we can obtain it only for $n=3$ because for $n \geqslant 4$ is $V_{2} \geqslant 3^{2}+1=10$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Nela and Jane choose positive integer $k$ and then play a game with a $9 \times 9$ table. Nela selects in every of her moves one empty unit square and she writes 0 to it. Jane writes 1 to some empty (unit) square in every her move. Furthermore $k$ Jane's moves follows each Nela's move and Nela starts. If sum of numbers in each row and each column is odd anytime during the game, Jane wins. If girls fill out the whole table (without Jane's win), Nela wins. Find the least $k$ such that Jane has the winning strategy.
(Michal Rolínek)
|
Solution. Let us show at first that Jane wins for $k=3$. Let us assume $3 \times 3$ squares $A_{1}, A_{2}$ and $A_{3}$ (see the picture). We will call the $3 \times 3$ square covered if just one 1 is in each its row and column. If Jane covers squares $A_{1}, A_{2}$ and $A_{3}$ without writing to other squares, she wins, because sums in all rows and columns are odd number 1.
Fig. 3
It is obvious that if at most one 0 (and no 1 ) is written in any $3 \times 3$ square after Nela's move, Jane can cover this square because of $k=3$. Jane has the following strategy: If Nela writes 0 to any uncovered square $A_{1}, A_{2}$ or $A_{3}$, Jane covers it immediately. In the opposite case Jane covers any of the uncovered $3 \times 3$ squares. Jane thus wins after three her triples of moves.
We will show that Nela has winning strategy for $k \in\{1,2\}$. Let us realize that if Jane has some winning move, just 8 rows and 8 columns have odd sum before Jane's move, and the winning Jane's move is writing 1 to the intersection of the only one "even" row with the only one "even" column. This implies that if Jane has winning move, this move is unique.
Now it is obvious Nela's winning strategy for $k=1$. If Jane has winning move after her move, Nela writes 0 to this square and Jane looses her unique chance for win. In the opposite case Nela writes 0 to some empty square. This move doesn't change parity of sums in rows and columns and Jane still hasn't winning move. This strategy allows Nela to fill out whole table without giving Jane chance to win.
In the case $k=2$ Nela will use the same strategy as for $k=1$. This strategy doesn't give Jane chance to win in her first move. In the second move Jane can't win because after that move the table contains even number of 1 's which excludes possibility to be odd number 1's in every of (odd number) nine rows.
Conclusion. The least value $k$, for which Jane has winning strategy, is $k=3$.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Let $\left(a_{n}\right)_{n=1}^{\infty}$ be an infinite sequence such that for all positive integers $n$ we have
$$
a_{n+1}=\frac{a_{n}^{2}}{a_{n}^{2}-4 a_{n}+6}
$$
a) Find all values $a_{1}$ for which the sequence is constant.
b) Let $a_{1}=5$. Find $\left\lfloor a_{2018}\right\rfloor$.
(Vojtech Bálint)
|
Solution. a) Assume $\left(a_{n}\right)_{n=1}^{\infty}$ is constant. Then $a_{2}=a_{1}$, hence
$$
a_{1}=\frac{a_{1}^{2}}{a_{1}^{2}-4 a_{1}+6}
$$
which rewrites as $a_{1}\left(a_{1}-2\right)\left(a_{1}-3\right)=0$. It follows that $a_{1} \in\{0,2,3\}$. On the other hand, once $a_{2}=a_{1}$, the sequence is clearly constant (formally e.g. by mathematical induction), thus any such $a_{1}$ indeed works.
b) Let $a_{1}=5$. Using the recurrence, we obtain $a_{2} \approx 2.27, a_{3} \approx 2.49, a_{4} \approx 2.77$, and so on. This leads to the following conjecture: For any $n \geqslant 2$ we have $20, \\
& a_{n+1}-2=\frac{a_{n}^{2}}{a_{n}^{2}-4 a_{n}+6}-2=\frac{\left(6-a_{n}\right)\left(a_{n}-2\right)}{\left(a_{n}-2\right)^{2}+2}>0 .
\end{aligned}
$$
This proves $2<a_{n+1}<3$, hence the proof of the conjecture is complete. In particular, $2<a_{2018}<3$ and the answer is $\left\lfloor a_{2018}\right\rfloor=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the maximal value of $a^{2}+b^{2}+c^{2}$ for real numbers $a, b, c$ such that $a+b$, $b+c, c+a$ all lie in the interval $[0,1]$.
(Ján Mazák)
|
Solution. By symmetry of the problem, we can WLOG suppose $a \geqslant b \geqslant c$.
Then both $b-c$ and $b+c$ are non-negative (by our assumptions), hence their product will also be non-negative and $b^{2} \geqslant c^{2}$. Analogously, both $1-b-a$ and $1-b+a$ are non-negative and $(1-b)^{2} \geqslant a^{2}$.
Thus we have $a^{2}+b^{2}+c^{2} \leqslant(1-b)^{2}+2 b^{2}=1-b(2-3 b)$. The original restrictions on $a, b, c$ also impose certain restrictions on $b$ : we must have $1 \geqslant a+b \geqslant 2 b$ and $2 b \geqslant b+c \geqslant 0$, hence $b \in\left[0, \frac{1}{2}\right]$. But for $b$ in this interval it is clearly true that $b(2-3 b) \geqslant 0$, hence $a^{2}+b^{2}+c^{2} \leqslant 1$. This value is attained e.g. for $(a, b, c)=(1,0,0)$.
Remark. Note that we are maximizing a convex function on a convex set, therefore it is sufficient only to consider the boundary values where $a+b, b+c, c+a \in\{0,1\}$.
## Final Round of the 68th Czech and Slovak Mathematical Olympiad (March 24-27, 2019)

|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let us call by an "edge" any segment of length 1 which is common to two adjacent fields of a given chessboard $8 \times 8$. Consider all possible cuttings of the chessboard into 32 pieces $2 \times 1$ and denote by $n(e)$ the total number of such cuttings that involve the given edge $e$. Determine the last digit of the sum of the numbers $n(e)$ over all the edges $e$.
(Michal Rolínek)
|
Solution. The total number of the vertical edges is $7 \cdot 8=56$ as well as the total number of the horizontal edges. Thus the number of all the edges under consideration is $56 \cdot 2=112$.
The number of edges, which are not involved in a given cutting, is equal to 32, because each of these edges must coincide with the common segment of the two fields forming one of the 32 resulting pieces $2 \times 1$. Thus each cutting gives a contribution $112-32=80$ to the sum $S$ of all the numbers $n(e)$. Consequently, the sum $S$ is a multiple of 80 and thus its last digit is zero.
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. There are 234 visitors in a cinema auditorium. The visitors are sitting in $n$ rows, where $n \geqslant 4$, so that each visitor in the $i$-th row has exactly $j$ friends in the $j$-th row, for any $i, j \in\{1,2, \ldots, n\}, i \neq j$. Find all the possible values of $n$. (Friendship is supposed to be a symmetric relation.)
(Tomáš Jurík)
|
Solution. For any $k \in\{1,2, \ldots, n\}$ denote by $p_{k}$ the number of visitors in the $k$-th row. The stated condition on given $i$ and $j$ implies that the number of friendly pairs $(A, B)$, where $A$ and $B$ are from the $i$-th row and from $j$-th row respectively, is equal to the product $j p_{i}$. Interchanging the indices $i$ and $j$, we conclude that the same number of friendly pairs $(A, B)$ equals $i p_{j}$. Thus $j p_{i}=i p_{j}$ or $p_{i}: p_{j}=i: j$, and therefore, all the numbers $p_{k}$ must be proportional as follows:
$$
p_{1}: p_{2}: \cdots: p_{n}=1: 2: \cdots: n \text {. }
$$
Let us show that under this proportionality the visitors can be friendly in such a way which ensures the property under consideration. Thus assume that for some positive integer $d$, the equality $p_{k}=k d$ holds with any $k \in\{1,2, \ldots, n\}$. Let us
start with the case $d=1$ when the numbers of visitors in single rows are successively $1,2, \ldots, n$. Then the stated property holds true if (and only if) any two visitors taken from distinct rows in the whole auditorium - are friends. In the case when $d>1$, let us divide all the visitors into $d$ groups $G_{1}, G_{2}, \ldots, G_{d}$ so that for arbitrary $k=1,2, \ldots, d$, the numbers of visitors from the group $G_{k}$ in single rows are successively $1,2, \ldots, n$. It is evident that the stated property holds true under the following condition: two visitors are friends if and only if they belong to the same group $G_{k}$.
It follows from the preceding that our task is to find such integer values of $n$, $n \geqslant 4$, for which there exists a positive integer $d$ satisfying the equation
$$
d+2 d+\cdots+n d=234 \quad \text { or } \quad d n(n+1)=468 \text {. }
$$
Thus we look for all divisors $468=2^{2} \cdot 3^{2} \cdot 13$ which are of the form $n(n+1)$. Inequality $22 \cdot 23>468$ implies that $n<22$ and hence $n \in\{4,6,9,12,13,18\}$. It is easy to see that the only satisfactory $n$ equals 12 (which corresponds to $d=3$ ).
Answer. The unique solution is $n=12$.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Let $A, B$ be sets of positive integers such that a sum of arbitrary two different numbers from $A$ is in $B$ and a ratio of arbitrary two different numbers from $B$ (greater one to smaller one) is in $A$. Find the maximum number of elements in $A \cup B$.
(Martin Panák)
|
Solution. Initially we will prove that the set $A$ consists from at most two numbers. Suppose that three numbers $a<b<c$ belongs to the set $A$. Then the numbers $a+b<a+c<b+c$ are in $B$ and therefore the number
$$
\frac{b+c}{a+c}=1+\frac{b-a}{a+c}
$$
have to be in $A$. This is contradiction because $0<b-a<a+c$ and the number is not integer.
If the set $B$ contains four numbers $k<l<m<n$, then the set $A$ will contain three different numbers $n / k, n / l, n / m$. So the set $B$ has at most three elements and $A \cup B$ has at most five elements.
We achieve the number 5 of elements if $A=\{a, b\}, B=\{k, l, m\}$, where $a<b$ and $l / k=m / l=a, m / k=b$. Then $b=a^{2}(a \geqslant 2)$ and $a+a^{2}$ is one of the elements of $B$; the next two elements are either $a^{2}+a^{3}$ and $a^{3}+a^{4}$ or $1+a$ and $a^{2}+a^{3}$. Eg. sets $A=\{2,4\}, B=\{3,6,12\}$ have five elements together.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Determine all triples $(x, y, z)$ of positive numbers satisfying the system of equations
$$
\begin{aligned}
& 2 x^{3}=2 y\left(x^{2}+1\right)-\left(z^{2}+1\right), \\
& 2 y^{4}=3 z\left(y^{2}+1\right)-2\left(x^{2}+1\right), \\
& 2 z^{5}=4 x\left(z^{2}+1\right)-3\left(y^{2}+1\right) .
\end{aligned}
$$
|
Solution. For any integer $k \geqslant 3$ and any $x \geqslant 0$ we have
$$
2 x^{k} \geqslant[(k-1) x-(k-2)]\left(x^{2}+1\right) .
$$
To see this, observe that, by AM-GM inequality,
$$
x^{k}+x^{k}+\underbrace{x+x+\ldots+x}_{(k-3) \text { times }} \geqslant(k-1) x^{3}
$$
and add it to
$$
(k-2)\left(x^{2}-2 x+1\right) \geqslant 0 \text {. }
$$
Note that we have equality if and only if $x=1$.
Therefore, for $x, y, z$ satisfying the system of equations, we have
$$
\begin{aligned}
2 y\left(x^{2}+1\right)-\left(z^{2}+1\right) & \geqslant(2 x-1)\left(x^{2}+1\right), \\
3 z\left(y^{2}+1\right)-2\left(x^{2}+1\right) & \geqslant(3 y-2)\left(y^{2}+1\right), \\
4 x\left(z^{2}+1\right)-3\left(y^{2}+1\right) & \geqslant(4 z-3)\left(z^{2}+1\right),
\end{aligned}
$$
or
$$
\begin{array}{r}
2(y-x)\left(x^{2}+1\right)+(x-z)(x+z) \geqslant 0, \\
3(z-y)\left(y^{2}+1\right)+2(y-x)(y+x) \geqslant 0, \\
4(x-z)\left(z^{2}+1\right)+3(z-y)(z+y) \geqslant 0 .
\end{array}
$$
Now suppose $x \geqslant \max \{y, z\}$. Then from the second inequality of (1) we infer that $y \leqslant z$ and
$$
\begin{aligned}
2(y-x)\left(x^{2}+1\right)+(x-z)(x+z) & \leqslant(z-x)\left(2\left(x^{2}+1\right)-(x+z)\right) \\
& \leqslant(z-x)\left(2 x^{2}-2 x+2\right) \leqslant 0,
\end{aligned}
$$
which, by the first inequality in (1), implies $x=y=z$.
If $y \geqslant \max \{x, z\}$, then $z \leqslant x$ by the third inequality in (1) and
$$
\begin{aligned}
3(z-y)\left(y^{2}+1\right)+2(y-x)(y+x) & \leqslant(x-y)\left(3\left(y^{2}+1\right)-2 y-2 x\right) \\
& \leqslant(x-y)\left(3 y^{2}-4 y+3\right) \leqslant 0,
\end{aligned}
$$
hence, by the second inequality in (1), $x=y=z$. ously,
Finally, if $z \geqslant \max \{x, y\}$, then $x \leqslant y$ by the first estimate in (1) and, as previ-
$$
4(x-z)\left(z^{2}+1\right)+3(z-y)(z+y) \leqslant(y-z)\left(4 z^{2}-6 z+4\right) \leqslant 0
$$
which again implies $x=y=z$. Thus we have equality in (0) and hence $x=y=z=1$. We easily check that this is the solution to the system.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the largest possible size of a set $\mathbb{M}$ of integers with the following property: Among any three distinct numbers from $\mathbb{M}$, there exist two numbers whose sum is a power of 2 with non-negative integer exponent.
(Ján Mazák)
|
Solution. The set $\{-1,3,5,-2,6,10\}$ attests that $\mathbb{M}$ can have 6 elements: The sum of any two numbers from the triplet $(-1,3,5)$ is a power of two and the same is true for triplet $(-2,6,10)$. For the sake of contradiction, assume that some set $\mathbb{M}$ has more than 6 elements.
Clearly, $\mathbb{M}$ can't contain three (or more) non-positive numbers. Hence it contains at least five positive numbers. Denote by $x$ the largest positive number in $\mathbb{M}$ and by $a, b, c, d$ some four other positive numbers in $\mathbb{M}$. Consider pairs $x+a, x+b, x+c$, $x+d$. They are all larger than $x$ and less than $2 x$. The open interval $(x, 2 x)$ contains at most one power of two, hence at least three of the four sums are not a power of two. Without loss of generality, assume those are $x+a, x+b, x+c$. Considering the triplets $(a, b, x),(a, c, x),(b, c, x)$ we infer that all $a+b, a+c, b+c$ are powers of two. However, this is impossible. Without loss of generality, let $a=\max \{a, b, c\}$. Then $a+b$ and $a+c$ both lie in $(a, 2 a)$, hence at least one of them is not a power of two, a contradiction.
## First Round of the 67th Czech and Slovak Mathematical Olympiad (December 12th, 2017) $\mathbb{N} / /(10)$
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the greatest real $k$ such that
$$
\frac{2\left(a^{2}+k a b+b^{2}\right)}{(k+2)(a+b)} \geqslant \sqrt{a b}
$$
holds for any positive real $a$ and $b$.
(Ján Mazák)
|
Solution. If $k=2$ then the inequality is equivalent to $\frac{1}{2}(a+b) \geqslant \sqrt{a b}$ (which holds), therefore $k \geqslant 2$. For $k>2$ we have $k+2>0$
$$
2\left(a^{2}+k a b+b^{2}\right) \geqslant(k+2)(a+b) \sqrt{a b},
$$
the division by $b^{2}$ gives
$$
2\left(\frac{a^{2}}{b^{2}}+k \frac{a}{b}+1\right) \geqslant(k+2)\left(\frac{a}{b}+1\right) \sqrt{\frac{a}{b}} .
$$
Denote $\sqrt{a / b}=x$. The value of $x$ can be any positive number. Thus the problem is equivalent to find greatest $k$, such that
$$
2\left(x^{4}+k x^{2}+1\right) \geqslant(k+2)\left(x^{2}+1\right) x
$$
holds for any positive $x$. We get
$$
\begin{aligned}
k\left(\left(x^{2}+1\right) x-2 x^{2}\right) & \leqslant 2\left(x^{4}+1-\left(x^{2}+1\right) x\right), \\
k\left(x^{3}-2 x^{2}+x\right) & \leqslant 2\left(x^{4}-x^{3}-x+1\right), \\
k x\left(x^{2}-2 x+1\right) & \leqslant 2\left(x^{3}(x-1)-(x-1)\right), \\
k x(x-1)^{2} & \leqslant 2(x-1)^{2}\left(x^{2}+x+1\right) .
\end{aligned}
$$
For $x=1$ the inequality holds. If $x \neq 1$ then the division by positive number $x(x-1)^{2}$ gives
$$
k \leqslant \frac{2\left(x^{2}+x+1\right)}{x}=2+2\left(x+\frac{1}{x}\right) .
$$
If $x \neq 1$ then the values of $x+1 / x$ fill the whole interval $(2, \infty)$, the RHS can be any number in $(6, \infty)$, consequently $k \geqslant 6$.
|
6
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find all positive integers $n$ such that $\left(2^{n}+1\right)\left(3^{n}+2\right)$ is divisible by $5^{n}$.
(Ján Mazák)
|
Solution. The following table shows $2^{n}+1$ and $3^{n}+2$ modulo 5 (we know, that both sequences modulo 5 have to be periodic):
| $n$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | $\ldots$ |
| ---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $2^{n}+1$ | 3 | 5 | 9 | 17 | 33 | 65 | 129 | 257 | $\ldots$ |
| modulo 5 | 3 | 0 | 4 | 2 | 3 | 0 | 4 | 2 | $\ldots$ |
| $3^{n}+2$ | 5 | 11 | 29 | 83 | 245 | 731 | 2189 | 6563 | $\ldots$ |
| modulo 5 | 0 | 1 | 4 | 3 | 0 | 1 | 4 | 3 | $\ldots$ |
Both sequences modulo 5 are periodic with period 4 . But $2^{n}+1$ is divisible by 5 iff $n$ is 2 modulo 4 , and $3^{n}+2$ is divisible by 5 iff $n$ is 1 modulo 4 . Thus if $5^{n}$ should divide $\left(2^{n}+1\right)\left(3^{n}+2\right)$, it has to divide one of the factors. But for $n \geqslant 2$ obviously $5^{n}>3^{n}+2$ and $5^{n}>2^{n}+1$ and $5^{n}$ cannot divide any of the factors. For $n=1$ we have $5^{1} \mid\left(2^{1}+1\right)\left(3^{1}+2\right)=15$, thus $n=1$ is the unique solution of the problem.
## Second Round of the 61st Czech and Slovak Mathematical Olympiad (January 17th, 2012)
$\mathbb{N} /$ 行
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Among real numbers $a, b, c$, and $d$ which satisfy
$$
a b+c d=a c+b d=4 \quad a \quad a d+b c=5
$$
find these, for which the value of $a+b+c+d$ is the least possible. Find this (the least) value as well.
(Jaromír Šimša)
|
Solution. We have
$$
\begin{aligned}
(a+b+c+d)^{2} & =a^{2}+b^{2}+c^{2}+d^{2}+2(a b+c d+a c+b d+a d+b c)= \\
& =a^{2}+b^{2}+c^{2}+d^{2}+2(4+4+5)=a^{2}+d^{2}+b^{2}+c^{2}+26 .
\end{aligned}
$$
Now $a^{2}+d^{2} \geqslant 2 a d, b^{2}+c^{2} \geqslant 2 b c$ where the equality holds iff $a=d$ and $b=c$ and from (1) we get
$$
(a+b+c+d)^{2} \geqslant 2 a d+2 b c+26=2 \cdot 5+26=36 .
$$
Thus among reals which satisfy the conditions we always have $a+b+c+d \geqslant 6$, where the equality holds iff $a=d$ and $b=c$, or
$$
2 a b=4, \quad a^{2}+b^{2}=5,
$$
thus $\{a, b\}=\{1,2\}$.
Conclusion. The sought $a, b, c, d$ are the quadruples $(1,2,2,1)$ and $(2,1,1,2)$ with the least value of $a+b+c+d=6$.
Final Round of the 61st Czech and Slovak
Mathematical Olympiad
(March 26-27, 2012)
$\mathbb{N} / /$ (6)
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the greatest possible area of a triangle ABC with medians satisfying $t_{a} \leqslant 2$, $t_{b} \leqslant 3, t_{c} \leqslant 4$.
(Pavel Novotný)
|
Solution. Let $T$ be the centroid of $A B C$ and $K, L, M$ be the midpoints of $B C$, $C A, A B$. Medians cut $A B C$ into six smaller triangles, each with the same area: for example in the triangle $A M T$ we have $A M=\frac{1}{2} c$, its altitude through $T$ is $\frac{1}{3} v_{c}$ long, that is $S_{A M T}=\frac{1}{2} \cdot \frac{1}{2} c \cdot \frac{1}{3} v_{c}=\frac{1}{6} \cdot \frac{1}{2} c \cdot v_{c}=\frac{1}{6} S_{A B C}$. Analogously for the other triangles.
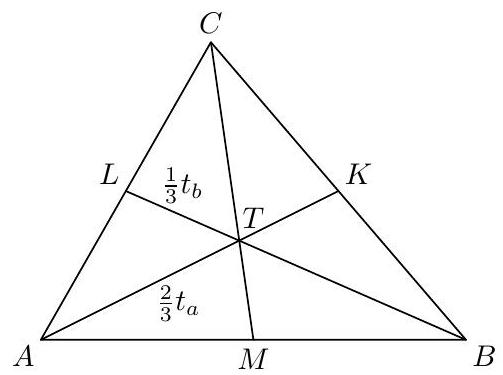
Fig. 1
Thus we will seek for the greatest possible area of one of the triangles, say $A T L$ (Fig. 1), and then we multiply the result by six. There is
$$
A T=\frac{2}{3} t_{a} \leqslant \frac{4}{3}, \quad T L=\frac{1}{3} t_{b} \leqslant 1
$$
Therefore we can constrain the area:
$$
S_{A T L}=\frac{1}{2} A T \cdot T L \cdot \sin \angle A T L \leqslant \frac{1}{2} \cdot \frac{4}{3}=\frac{2}{3} .
$$
Thus the area of the $A B C$ can be at most $6 \cdot \frac{2}{3}=4$, where the equality holds iff $t_{a}=2, t_{b}=3$ and $\angle A T L=90^{\circ}$.
There is a triangle satisfying the conditions with the area 6 indeed: first we construct right triangle $A T L$ with the legs $A T=\frac{4}{3}$ and $T L=1$. Then $C$ is the symmetric image of $A$ with respect to $L$ and $B$ is the image of $L$ under the homothety with center $T$ and coefficient -2 (Fig. 2). It is easy to count the length of $A B$. For
Fig. 2
example the theorem of Pythagoras in $A B T$ gives
$$
A B=\sqrt{A T^{2}+T B^{2}}=\sqrt{\frac{16}{9}+4}=\sqrt{\frac{52}{9}}=\frac{2}{3} \sqrt{13} .
$$
Since $M$ is on the Thales' circle with the diameter $A B$, there is $M T=\frac{1}{2} A B=\frac{1}{3} \sqrt{13}$. Then $t_{c}=3 \cdot M T=\sqrt{13}<4$.
Conclusion. The greatest possible area of the triangle $A B C$ is 4 .
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. There are numbers 1,2,.., 33 written on a blackboard. In one step we choose two numbers on the blackboard such that one of them divides the other one, we erase the two numbers and write their integer quotient instead. We proceed in this manner until no number on the blackboard divides another one. What is the least possible amount of numbers left on the blackboard?
|
Solution. In the process, apparently only numbers from the set $M=\{1,2, \ldots, 33\}$ can be on the blackboard. Prime numbers 17, 19,23, 29 a 31 are going to stay on the blackboard, in one copy each, because they have no other divisor than the number 1 and the set $M$ does not contain any other of their multiples.
We explain now, why there must always be two other numbers on the blackboard. the product of all numbers is
$$
S=33 !=2^{31} \cdot 3^{15} \cdot 5^{7} \cdot 7^{4} \cdot 11^{3} \cdot 13^{2} \cdot 17 \cdot 19 \cdot 23 \cdot 29 \cdot 31
$$
at the beginning.
In each step we choose a pair $(x, y)$ with $x \mid y$, that is numbers of the form $x=a, y=k a$ and we replace them with the number $y / x=k$. the product $S$ of all the numbers on the blackboard changes to the new value $S / a^{2}$. It is evident, that the parity of the exponent of each prime number divisor in the prime number factorization of $S$ is preserved. Especially the four primes 2, 3, 5, and 11 divide the product $S$ throughout the process. Since $2 \cdot 3 \cdot 5 \cdot 11>33$ it follows that on the table there always must be at least two numbers which product is divisible by $2 \cdot 3 \cdot 5 \cdot 11$. On the whole, there must always be at least seven numbers on the blackboard.
The sequence of steps
$$
\begin{gathered}
32,16 \rightarrow 2, \quad 30,15 \rightarrow 2, \quad 28,14 \rightarrow 2, \quad 26,13 \rightarrow 2, \quad 24,12 \rightarrow 2, \quad 22,11 \rightarrow 2 \\
27,9 \rightarrow 3, \quad 21,7 \rightarrow 3, \quad 18,6 \rightarrow 3, \quad 25,5 \rightarrow 5, \quad 20,4 \rightarrow 5, \quad 8,2 \rightarrow 4 \\
5,5 \rightarrow 1, \quad 4,2 \rightarrow 2, \quad 3,3 \rightarrow 1, \quad 3,3 \rightarrow 1, \quad 2,2 \rightarrow 1, \quad 2,2 \rightarrow 1, \quad 2,2 \rightarrow 1
\end{gathered}
$$
leaves numbers $17,19,23,29,31,10,33$, and seven numbers 1 on the blackboard. The 1s can be eliminated in seven further steps, which leaves just seven numbers on the blackboard.
Conclusion: the least amount of numbers which can be left on the blackboard is seven.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all real solutions of the system
$$
\begin{aligned}
& \sqrt{x-y^{2}}=z-1, \\
& \sqrt{y-z^{2}}=x-1, \\
& \sqrt{z-x^{2}}=y-1 .
\end{aligned}
$$
|
Solution. The square roots and their arguments have to be positive, therefore $x, y, z \geqslant 1, x \geqslant y^{2}, y \geqslant z^{2}$, and $z \geqslant x^{2}$. The last three inequalities imply $x \geqslant$ $y^{2} \geqslant y \geqslant z^{2} \geqslant z \geqslant x^{2}$, and since $x \geqslant 1$, the inequality $x \geqslant x^{2}$ forces $x=1$, and all the values in the given chain of inequalities are equal, especially $x=y=z=1$, which is indeed a solution.
Conclusion. There is a unique solution $x=y=z=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. There are numbers $1,2, \ldots, 33$ written on the blackboard. In one step we choose a group of numbers on the blackboard (at least two) such that their product is a square, we erase them and write the square root of their product instead. We proceed until no group can be chosen. What is the least amount of numbers left on the blackboard?
|
Solution. The product of all the numbers written on the blackboard is
$$
S=2^{31} \cdot 3^{15} \cdot 5^{7} \cdot 7^{4} \cdot 11^{3} \cdot 13^{2} \cdot 17 \cdot 19 \cdot 23 \cdot 29 \cdot 31 .
$$
Apparently, the numbers $17,19,23,29$, and 31 can never be erased and can never be a part of any change. In any step, there is always left at least one other number, which gives in total $5+1=6$ numbers. Six numbers on the blackboard are achievable indeed: because of the odd exponents of primes 2, 3, 5, and 11 in $S$ we allocate the set $A=\{2,9,11,22,25\}$ and we put all the other numbers with exception of 17,19 , 23, 29 a 31 into set
$$
B=\{3,4,5,6,7,8,10,12,13,14,15,16,18,20,21,24,26,27,28,30,32,33\} .
$$
In the first step we choose the group $A$ and replace it by the number
$$
n=\sqrt{2 \cdot 9 \cdot 11 \cdot 22 \cdot 25}=\sqrt{2^{2} \cdot 3^{2} \cdot 5^{2} \cdot 11^{2}}=2 \cdot 3 \cdot 5 \cdot 11 .
$$
Because the product of all the numbers from $B$ is $2^{31-2} \cdot 3^{15-2} \cdot 5^{7-2} \cdot 7^{4} \cdot 11^{3-2}$. $13^{2}=2^{29} \cdot 3^{13} \cdot 5^{5} \cdot 7^{4} \cdot 11 \cdot 13^{2}$, in the second step we choose $n$ together with all the numbers from $B$ and replace it by
$$
\sqrt{(2 \cdot 3 \cdot 5 \cdot 11) \cdot\left(2^{29} \cdot 3^{13} \cdot 5^{5} \cdot 7^{4} \cdot 11 \cdot 13^{2}\right)}=2^{15} \cdot 3^{7} \cdot 5^{3} \cdot 7^{2} \cdot 11 \cdot 13,
$$
which leaves just six numbers on the blackboard.
Conclusion. The sought least amount is six.
## Second Round of the 59th Czech and Slovak Mathematical Olympiad (January 20th, 2010)

|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find all integers greater than 1 by which a cancellation can be made in some fraction of the form
$$
\frac{3 p-q}{5 p+2 q}
$$
where $p$ and $q$ are mutually prime integers.
|
Solution. The fraction admits cancellation by an integer $d>1$ if and only if $d$ is a common divisor of its numerator and its denominator. Let us thus assume that $d \mid 3 p-q$ and at the same time $d \mid 5 p+2 q$, where $p$ and $q$ are mutually prime integers. Adding up the appropriate multiples of the two binomials $3 p-q$ and $5 p+2 q$, we get
$$
2(3 p-q)+(5 p+2 q)=11 p \quad \text { and } \quad 3(5 p+2 q)-5(3 p-q)=11 q
$$
Since both $3 p-q$ and $5 p+2 q$ are assumed to be divisible by $d$, the two numbers $11 p$ and $11 q$ must also be multiples of $d$. However, $p$ and $q$ are mutually prime by hypothesis and 11 is a prime, thus the numbers $11 p$ and $11 q$ have only one common divisor greater than 1 , namely the number 11. Thus $d=11$.
We now need to show that it is indeed possible to make a cancellation by 11 in some fraction of the given form. That is, we need to find a pair of mutually prime integers $p$ and $q$ so that $11 \mid 3 p-q$ and at the same time $11 \mid 5 p+2 q$. Solving the system of equations
$$
3 p-q=11 m \text { and } \quad 5 p+2 q=11 n
$$
we get $(p, q)=(2 m+n, 3 n-5 m)$, and $p, q$ will certainly be prime if we choose them so that $q=3 n-5 m=1$, thus e.g. for $n=2$ and $m=1$, when $(p, q)=(4,1)$ and the corresponding fraction is $11 / 22$.
Answer. The only integer greater than 1 , which can be cancelled in some fraction of the given form, is the number 11 .
## Second Round of the 58th Czech Mathematical Olympiad (January 20th, 2009)

|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the least positive number $x$ with the following property: if $a, b, c, d$ are arbitrary positive numbers whose product is 1 , then
$$
a^{x}+b^{x}+c^{x}+d^{x} \geqslant \frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d} .
$$
|
Solution. Let $a, b, c, d$ be positive numbers whose product equals 1 . From the inequality between the arithmetic and geometric mean of the three numbers $a^{x}, b^{x}$, $c^{x}$, with arbitrary $x>0$, we obtain
$$
\frac{a^{x}+b^{x}+c^{x}}{3} \geqslant \sqrt[3]{a^{x} b^{x} c^{x}}=\sqrt[3]{\frac{1}{d^{x}}}
$$
Choosing $x=3$ gives the inequality $\frac{1}{3}\left(a^{3}+b^{3}+c^{3}\right) \geqslant 1 / d$. Similarly,
$$
\frac{1}{3}\left(a^{3}+b^{3}+d^{3}\right) \geqslant 1 / c, \quad \frac{1}{3}\left(a^{3}+c^{3}+d^{3}\right) \geqslant 1 / b, \quad \frac{1}{3}\left(b^{3}+c^{3}+d^{3}\right) \geqslant 1 / a .
$$
Adding up these four inequalities we obtain
$$
a^{3}+b^{3}+c^{3}+d^{3} \geqslant \frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}
$$
so for $x=3$ the given inequality always holds.
We now show that $x=3$ is the smallest number with this property, that is, that for any positive $x1$ (depending on $xt^{3} .
$$
Thus if we can choose $t$ so that $4 t^{x}4^{\frac{1}{3-x}}
$$
which is certainly fulfilled for $t$ large enough.
Conclusion. The least number with the desired property is $x=3$.
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers satisfies $a_{1}>5$ and $a_{n+1}=5+6+\cdots+a_{n}$ for all positive integers $n$. Determine all prime numbers $p$ such that, regardless of the value of $a_{1}$, this sequence must contain a multiple of $p$.
#
|
We claim that the only prime number of which the sequence must contain a multiple is $p=2$. To prove this, we begin by noting that
$$
a_{n+1}=\frac{a_{n}\left(a_{n}+1\right)}{2}-10=\frac{\left(a_{n}-4\right)\left(a_{n}+5\right)}{2} .
$$
Let $p>2$ be an odd prime, and choose $a_{1} \equiv-4(\bmod p)$, so $2 a_{2} \equiv(-4-4)(-4+5) \equiv-8(\bmod p)$, whence $a_{2} \equiv-4(\bmod p)$, since $p$ is odd. By induction, $a_{n} \equiv-4(\bmod p) \not \equiv 0(\bmod p)$ for all $n$, and so the sequence need not contain a multiple of $p$.
We are left to show that the sequence must contain an even number. Suppose to the contrary that $a_{n}$ is odd for $n=1,2, \ldots$ We observe that
$$
a_{n+1}-a_{n}=\frac{a_{n}\left(a_{n}+1\right)}{2}-\frac{a_{n-1}\left(a_{n-1}+1\right)}{2}=\frac{a_{n}-a_{n-1}}{2}\left(a_{n}+a_{n-1}+1\right) .
$$
By assumption, $a_{n}+a_{n-1}+1$ is odd for $n=1,2, \ldots$, so this shows that $v_{2}\left(a_{n+1}-a_{n}\right)=v_{2}\left(a_{n}-a_{n-1}\right)-1$, and so there exists $N$ such that $v_{2}\left(a_{N+1}-a_{N}\right)=0$. This is a contradiction, because $a_{n+1}-a_{n}$ is even for $n=1,2, \ldots$ by assumption, and thus completes the proof.
#
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the smallest possible value of the expression
$$
\left\lfloor\frac{a+b+c}{d}\right\rfloor+\left\lfloor\frac{b+c+d}{a}\right\rfloor+\left\lfloor\frac{c+d+a}{b}\right\rfloor+\left\lfloor\frac{d+a+b}{c}\right\rfloor,
$$
in which $a, b, c$ and $d$ vary over the set of positive integers.
(Here $\lfloor x\rfloor$ denotes the biggest integer which is smaller than or equal to $x$.)
#
|
The answer is 9 .
Notice that $\lfloor x\rfloor>x-1$ for all $x \in \mathbb{R}$. Therefore the given expression is strictly greater than
$$
\frac{a+b+c}{d}+\frac{b+c+d}{a}+\frac{c+d+a}{b}+\frac{d+a+b}{c}-4,
$$
which can be rewritten as
$$
\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{a}{d}+\frac{d}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{b}{d}+\frac{d}{b}\right)+\left(\frac{c}{d}+\frac{d}{c}\right)-4 .
$$
Since $t+\frac{1}{t} \geq 2$ for $t>0$, we get that $6 \cdot 2-4=8$ is a strict lower bound for the given expression; since it takes integral values only, we actually get that 9 is a lower bound.
It remains to check that 9 can be attained; this happens for $a=b=c=5$ and $d=4$.
#
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. A finite set of integers is called bad if its elements add up to 2010. A finite set of integers is a Benelux-set if none of its subsets is bad. Determine the smallest integer $n$ such that the set $\{502,503,504, \ldots, 2009\}$ can be partitioned into $n$ Benelux-sets.
(A partition of a set $S$ into $n$ subsets is a collection of $n$ pairwise disjoint subsets of $S$, the union of which equals $S$.)
|
As $502+1508=2010$, the set $S=\{502,503, \ldots, 2009\}$ is not a Benelux-set, so $n=1$ does not work. We will prove that $n=2$ does work, i.e. that $S$ can be partitioned into 2 Benelux-sets.
Define the following subsets of $S$ :
$$
\begin{aligned}
A & =\{502,503, \ldots, 670\}, \\
B & =\{671,672, \ldots, 1005\}, \\
C & =\{1006,1007, \ldots, 1339\}, \\
D & =\{1340,1341, \ldots, 1508\}, \\
E & =\{1509,1510, \ldots, 2009\} .
\end{aligned}
$$
We will show that $A \cup C \cup E$ and $B \cup D$ are both Benelux-sets.
Note that there does not exist a bad subset of $S$ of one element, since that element would have to be 2010. Also, there does not exist a bad subset of $S$ of more than three elements, since the sum of four or more elements would be at least $502+503+504+505=2014>2010$. So any possible bad subset of $S$ contains two or three elements.
Consider a bad subset of two elements $a$ and $b$. As $a, b \geq 502$ and $a+b=2010$, we have $a, b \leq 2010-502=1508$. Furthermore, exactly one of $a$ and $b$ is smaller than 1005 and one is larger than 1005. So one of them, say $a$, is an element of $A \cup B$, and the other is an element of $C \cup D$. Suppose $a \in A$, then $b \geq 2010-670=1340$, so $b \in D$. On the other hand, suppose $a \in B$, then $b \leq 2010-671=1339$, so $b \in C$. Hence $\{a, b\}$ cannot be a subset of $A \cup C \cup E$, nor of $B \cup D$.
Now consider a bad subset of three elements $a, b$ and $c$. As $a, b, c \geq 502, a+b+c=2010$, and the three elements are pairwise distinct, we have $a, b, c \leq 2010-502-503=1005$. So $a, b, c \in A \cup B$. At least one of the elements, say $a$, is smaller than $\frac{2010}{3}=670$, and at least one of the elements, say $b$, is larger than 670 . So $a \in A$ and $b \in B$. We conclude that $\{a, b, c\}$ cannot be a subset of $A \cup C \cup E$, nor of $B \cup D$.
This proves that $A \cup C \cup E$ and $B \cup D$ are Benelux-sets, and therefore the smallest $n$ for which $S$ can be partitioned into $n$ Benelux-sets is $n=2$.
Remark. Observe that $A \cup C \cup E_{1}$ and $B \cup D \cup E_{2}$ are also Benelux-sets, where $\left\{E_{1}, E_{2}\right\}$ is any partition of $E$.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 4. Let $n \geqslant 3$ be an integer. For each pair of prime numbers $p$ and $q$ such that $p<q \leqslant n$, Morgane has written the sum $p+q$ on the board. She then notes $\mathcal{P}(n)$ as the product of all these sums. For example, $\mathcal{P}(5)=(2+3) \times(2+5) \times(3+5)=280$.
Find all values of $n \geqslant 3$ for which $n$ ! divides $\mathcal{P}(n)$.
Note: If two sums $p+q$ formed from two different pairs are equal to each other, Morgane writes them both. For example, if $n=13$, she writes both sums $3+13$ and $5+11$.
|
Solution to Exercise 4 Let $n$ be a potential solution, and let $r$ be the largest prime number such that $r \leqslant n$. Since $r$ divides $n$!, it divides $\mathcal{P}(n)$, so there exist two prime numbers $p$ and $q$ such that $p<q \leqslant n$ and $r$ divides $p+q$. By the maximality of $r$, we know that $p+q<2 r$, so $p+q=r$. Since $q$ and $r$ are odd, $p$ is therefore even, and $p=2$.
Similarly, there exist two prime numbers $s$ and $t$ such that $s<t \leqslant n$ and $q$ divides $s+t$. We will prove that $q-2$ is prime. Indeed, if $t \leqslant q$, then $s+t=q$, so $s=2$ and $t=q-2$. Otherwise, $t=r=q+2$, so $q<t+s<2 q+2<3 q$, which means $t+s=2 q$ and $s=q-2$.
In particular, 3 divides one of the three prime numbers $q-2, q$ and $q+2$; it must necessarily be $q-2$, which means that $q-2=3$ and $q+2=r=7$. Thus, $n \geqslant 7$, and $n$! divides
$$
\mathcal{P}(n)=(2+3) \times(2+5) \times(2+7) \times(3+5) \times(3+7) \times(5+7)=2^{6} \times 3^{3} \times 5^{2} \times 7
$$
Since $2 \times 4 \times 6 \times 8=2^{7} \times 3$ does not divide $\mathcal{P}(n)$, we must have $n=7$.
Conversely, $n=7$ is indeed a solution, as $7!=2^{4} \times 3^{2} \times 5 \times 7$.
Graders' Comments The exercise was rarely attempted; it's a pity, as a number of students had good ideas. However, as mentioned in the comments on Problem 5, the writing was problematic: do not hesitate to look at the comments on Problem 5 to see various recurring errors.
## Senior Problems
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 1. Let $x$ and $y$ be two real numbers. We define
$$
M=\max \{x y+1, x y-x-y+3,-2 x y+x+y+2\}
$$
Prove that $M \geqslant 2$, and determine the cases of equality.
|
Solution to Exercise 1 Among the three numbers $x y+1, x y-x-y+3$ and $-2 x y+x+y+2$, we denote $K$ as the smallest, $L$ as the second smallest, and $M$ as the largest. Therefore, $K \leqslant L \leqslant M$ and
$$
3 M \geqslant K+L+M=(x y+1)+(x y-x-y+3)+(-2 x y+x+y+2)=6
$$
which means that $M \geqslant 2$.
Furthermore, if $M=2$, the inequalities $K \leqslant L \leqslant M$ are in fact equalities, which means that
$$
x y+1=x y-x-y+3=-2 x y+x+y+2=2
$$
Let $p$ be the product $x y$ and $s$ be the sum $x+y$. The equalities in equation (1) are satisfied if and only if $p=1$ and $s=2$.
The arithmetic-geometric mean inequality generally indicates that
$$
\frac{s^{2}}{4}=\left(\frac{x+y}{2}\right)^{2} \geqslant x y=p
$$
with equality if and only if $x=y$. This result can also be seen if we note that
$$
\left(\frac{x+y}{2}\right)^{2}=\left(\frac{x-y}{2}\right)^{2}+x y
$$
Here, since we want $s^{2} / 4=1=p$, we must also have $x=y$, so that $x=y=1$.
Finally, conversely, if $x=y=1$, we easily verify that
$$
x y+1=x y-x-y+3=-2 x y+x+y+2=2
$$
so that $M=2$ as well.
|
2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 6. Find the largest integer $n \geqslant 3$ for which there exists a set $\mathcal{S}$ of $n$ points in the plane with the following property: every triangle (even degenerate) whose vertices belong to $\mathcal{S}$ is isosceles but not equilateral.
|
Solution to Exercise 6 We say that a set $\mathcal{S}$ having the required property is cute. We will prove that any cute set contains at most 6 elements. Furthermore, we will denote by $\omega_{A, B}$ the circle centered at $A$ passing through $B$, and by $\ell_{A, B}$ the perpendicular bisector of the segment $[A B]$.
First, if $\mathcal{S}$ consists of the five vertices $P_{1}, \ldots, P_{5}$ of a regular pentagon and its center $O$, it is easily verified that $\mathcal{S}$ is cute.
Conversely, let $\mathcal{S}$ be a cute set with $n \geqslant 6$ points: we will prove that $n=6$. For any points $X, Y$, and $Z$ in $\mathcal{S}$, we know that $Z$ belongs to one of the three sets $\omega_{X, Y}, \omega_{Y, X}$, or $\ell_{X, Y}$. This observation already allows us to prove the following result.
Lemma 1. Any three points in $\mathcal{S}$ are never collinear.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 6. For any integer $k \geqslant 0$, we denote $F_{k}$ as the $k^{\text{th}}$ Fibonacci number, defined by $F_{0}=0$, $F_{1}=1$, and $F_{k}=F_{k-2}+F_{k-1}$ when $k \geqslant 2$. Let $n \geqslant 2$ be an integer, and let $S$ be a set of integers with the following property:
For every integer $k$ such that $2 \leqslant k \leqslant n$, the set $S$ contains two integers $x$ and $y$ such that $x-y=F_{k}$.
What is the smallest possible number of elements in such a set $S$?
|
Solution to Exercise 6 First, let $m=\lceil n / 2\rceil$, and let $S$ be the set $\left\{F_{2 \ell}: 0 \leqslant \ell \leqslant m\right\}$. For any integer $k$ such that $2 \leqslant k \leqslant n$, we choose $x=F_{k}$ and $y=F_{0}=0$ if $k$ is even, or $x=F_{k+1}$ and $y=F_{k-1}$ if $k$ is odd. In both cases, $x$ and $y$ are two elements of $S$ such that $x-y=F_{k}$.
Conversely, let $S$ be a set as described in the statement. We will prove that $|S| \geqslant m+1$. To do this, we construct a weighted, undirected graph $G$ as follows. The vertices of our graph are the elements of the set $S$. Then, for every odd integer $k$ such that $1 \leqslant k \leqslant n$, and recalling that $F_{1}=F_{2}$, we choose two elements $x$ and $y$ of $S$ such that $x-y=F_{k}$. We then insert the edge $\{x, y\}$ into our graph $G$, assigning it the weight $F_{k}$.
The graph thus obtained has $m$ edges. Furthermore, suppose it contains a cycle $c=x_{0} x_{1} \ldots x_{\ell}$, with $x_{0}=x_{\ell}$, which we choose to have minimal length $\ell$. Without loss of generality, we assume that $x_{0}>x_{1}$, and that $\left\{x_{0}, x_{1}\right\}$ is the edge of $c$ with the maximum weight. We denote this weight by $F_{2 k+1}$. The cumulative weight of the other edges does not exceed $F_{1}+F_{3}+\ldots+F_{2 k-1}$ and, by construction, it is equal to
$$
\left|x_{1}-x_{2}\right|+\left|x_{2}-x_{3}\right|+\ldots+\left|x_{\ell-1}-x_{\ell}\right| \geqslant\left|x_{\ell}-x_{1}\right|=F_{2 k+1}
$$
However, a straightforward induction on $k$ shows that $F_{1}+F_{3}+\ldots+F_{2 k-1}=F_{2 k}<F_{2 k+1}$. Consequently, our graph is acyclic, and since it has $m$ edges, it has at least $m+1$ vertices.
The minimal cardinality sought is therefore equal to $m+1$.
|
+1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 1. Morgane and Bosphore are playing the following game. Morgane has written the integers from 1 to 8 on the vertices of a regular octagon: each integer is written on one of the eight vertices of the octagon. Bosphore then chooses a vertex and calculates the sum of the numbers written on that vertex and its two neighbors. He notes this sum as $s$, and gives $s$ candies to Morgane.
Bosphore chooses a vertex to give the fewest candies to Morgane, and Morgane writes the integers from 1 to 8 to receive as many candies as possible. Prove that Bosphore will give her 12 candies.
|
Solution to Exercise 1 First, if Morgane distributes the integers from 1 to 8 as follows, we indeed observe that Bosphore will have to give her at least 12 candies; next to each vertex, we have indicated the sum $s$ that Bosphore would calculate if he chose this vertex.
Conversely, regardless of the distribution Morgane chooses, Bosphore can proceed as follows to avoid giving her 13 or more candies. Below, each vertex is identified with the integer that Morgane wrote on it.
If the two neighbors of vertex 8 are vertices 1 and 2, Bosphore only needs to choose vertex 8, and he will give only 11 candies to Morgane. Otherwise, one of the two neighbors of vertex 8 is an integer $k \geqslant 3$. Bosphore divides the remaining six vertices into two groups of three consecutive vertices, as illustrated below. The sum of the values of these two groups of vertices is $(1+2+\ldots+8)-(k+8)=28-k \leqslant 25$, so one of the two groups has a sum $s \leqslant 12$. Bosphore ensures that he gives at most 12 candies to Morgane by choosing the vertex in the middle of this group.

|
12
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 2. Let $x, y$ and $z$ be three real numbers such that $0 \leqslant x \leqslant y \leqslant z$ and $x+y+z=1$. Find the maximum value that the expression
$$
(x-y z)^{2}+(y-z x)^{2}+(z-x y)^{2}
$$
can take.
|
Solution to Exercise 2 The quantity we wish to maximize can be rewritten as
$$
\begin{aligned}
\mathcal{S} & =\left(x^{2}+y^{2}+z^{2}\right)+\left((x y)^{2}+(y z)^{2}+(z x)^{2}\right)-6 x y z \\
& =(x+y+z)^{2}-2(x y+y z+z x)+(x y+y z+z x)^{2}-2 x y z(x+y+z)-6 x y z \\
& =1-2(x y+y z+z x)+(x y+y z+z x)^{2}-8 x y z \\
& =(x y+y z+z x-1)^{2}-8 x y z
\end{aligned}
$$
Since $0 \leqslant x y+y z+z x \leqslant(x+y+z)^{2} / 2=1 / 2$, we deduce that $\mathcal{S} \leqslant 1$. Conversely, if $x=y=0$ and $z=1$, we have $\mathcal{S}=1$, which concludes the proof.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 6. Let $n \geqslant 1$ be an integer. Morgane initially has $n$ piles, each containing one coin. She then allows herself operations of the following form: she chooses two piles, takes as many coins from the first pile as from the second, and forms a new pile with the coins she has taken.
Determine, as a function of $n$, the smallest number of non-empty piles that Morgane can obtain from such operations.
|
Solution to Exercise 6 If $n$ is a power of 2, Morgane can manage to end up with only one pile by proceeding as follows: she merges the $n$ piles of size 1 into $n / 2$ piles of size 2, then merges these $n / 2$ piles into $n / 4$ piles of size 4, and so on.
Conversely, when Morgane extracts $k$ pieces from two piles originally containing $a$ and $b$ pieces to form three piles (possibly empty) of $a-k, b-k$, and $2k$ pieces, we observe that $\operatorname{PGCD}(a-k, b-k, 2k)$ divides $2a$ and $2b$, and thus divides $2 \operatorname{PGCD}(a, b)$. Consequently, an immediate induction shows that if Morgane has $k$ piles of sizes $t_{1}, t_{2}, \ldots, t_{k}$, the number $\operatorname{PGCD}(t_{1}, t_{2}, \ldots, t_{k})$ is a power of 2. In particular, if Morgane manages to have only one pile, which will contain $n$ pieces, then $n$ must be a power of 2.
Finally, here is how, for any value of $n$, Morgane can proceed to end up with only two piles. She writes $n$ as a sum of increasing powers of 2, that is, numbers $2^{a_{1}} < 2^{a_{2}} < \cdots < 2^{a_{k}}$ such that $n = 2^{a_{1}} + 2^{a_{2}} + \cdots + 2^{a_{k}}$. For each $i \leq k$, and proceeding as in the case where $n$ is a power of 2, Morgane groups $2^{a_{i}}$ of her pieces into a single pile, thus obtaining $k$ piles.
Morgane then distinguishes her pile of size $2^{a_{1}}$, which she calls the target, and her pile of size $2^{a_{k}}$, which she calls the reserve. The $k-2$ other piles are seen as normal piles. Then Morgane sets out to double the size of her target pile while ensuring it will never be larger than a normal pile, proceeding as follows:
$\triangleright$ if the target pile is the same size as a normal pile, Morgane merges these two piles into a new target pile; a normal pile disappears during this operation;
$\triangleright$ otherwise, the target pile is of size $2^{a}$ strictly smaller than each normal pile, and Morgane then extracts $2^{a}$ pieces from the reserve to integrate them into the target pile, which is now of size $2^{a+1}$.
After $\ell$ such steps, the target pile is now of size $2^{a_{1}+\ell}$, and it has absorbed the piles of sizes $2^{a_{i}} < 2^{a_{1}+\ell}$, as well as at most $2^{a_{k-1}}$ pieces from the reserve, which is therefore still not empty. Thus, after $a_{k-1}+1-a_{1}$ steps, the target pile is now of size $2^{a_{k-1}+1}$, and it has absorbed all the normal piles, which means that there are now only two piles.
In conclusion, the minimum number of piles Morgane can end up with is 1 if $n$ is a power of 2, and it is 2 otherwise.
Graders' Comments The exercise was of progressive difficulty. Like many combinatorial exercises, it rewarded students who tested small cases. Indeed, by testing small cases, such as 2 and 4, one sees that if $n$ is a power of 2, then one can form a single pile. By continuing with small cases such as 3, 5, and 6, one sees that if $n$ is a sum of $k$ powers of 2, then one can form $k$ piles. But $k$ is not necessarily the minimum: for 7, one can obtain a pile of 4, one of 2, and one of 1; then one can obtain a pile of 3, and two of 2, thus a pile of 4 and one of 3. Thus, one can do better than the number of 1s in the binary representation of $n$.
By testing numbers from 8 to 16, one sees that one can obtain 2 piles for numbers that are not powers of 2, but not better, and that the good strategy is to form a large pile of a power of 2, then to slightly empty it to form 2 piles. After that, it only remains to formalize this argument to show that one can obtain two piles.
The most difficult part of the exercise remained: why, if $n$ is not a power of 2, one cannot obtain a single pile. Unfortunately, some misread the statement and thought they had to remove as many pieces from the first pile as there were in the second: this is not stated in the statement. Some tried to proceed by induction to show that several steps before the end, there was a pile of size $n / 2^{k}$ (or even $2^{k}$ such piles). This is not true for $k=3$: indeed, one can imagine having a pile of $5n / 8$ and one of $3n / 8$, taking $n / 8$ pieces from each to have a pile of $n / 2$ and two of $n / 4$, and in two merges obtaining a single pile.
The argument was more subtle: the simplest was to write $n = 2^{k} \times y$ with $y$ odd, and to show by induction that $k$ steps before the end, each pile had a size divisible by $y$. Alternatively, to show that the piles had a size of the form $k n / 2^{j}$ with $k$ odd, and thus could never be of size 1.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 3. Consider 2017 lines in the plane, which intersect pairwise at distinct points. Let $E$ be the set of these intersection points.
We want to assign a color to each point in $E$ such that any two points on the same line, whose segment connecting them contains no other point of $E$, are of different colors.
How many colors are needed at a minimum to achieve such a coloring?
|
Solution to Exercise 3 The minimum $m$ sought is $m=3$ and, with what follows, it will be quite evident that the result remains true for $n \geq 3$ lines.
First, we note that, in the obtained configuration, there is at least one non-subdivided region that is a triangle. Indeed, three non-concurrent lines and two never parallel lines form a triangle. Now, any line that crosses a triangle divides it into two polygons, at least one of which is a triangle. Therefore, starting from three of the given lines and "adding" the other 2014 one by one, we are assured of the existence of such a triangular region in the final configuration. The three vertices of such a triangle must be of different colors, which implies that $m \geq 3$.
To conclude, we will construct an adequate coloring with three colors. We start by noting that, since there is only a finite number of intersection points, we can choose an orthogonal coordinate system in which these points have distinct x-coordinates. We then number the points $M_{1}, M_{2}, \ldots, M_{k}$ according to increasing x-coordinates (where $k=\frac{2017 \times 2016}{2}$). For any $i$, the point $M_{i}$ has at most four neighbors, and if it belongs to a segment joining two of its neighbors, only one of these two neighbors has an x-coordinate less than that of $M_{i}$. This ensures that, for any $i \leq k$, among the neighbors of $M_{i}$, at most two have indices less than $i$. We can then color the $M_{i}$ in the order of the numbering according to the following procedure: we color $M_{1}$ green and $M_{2}$ red. And, for all $i$ such that $2 \leq i \leq k-1$, if we assume that the points $M_{1}, M_{2}, \ldots, M_{i}$ have been colored either green, red, or blue so that no two adjacent points are (yet) the same color, then, according to the previous remark, at most two neighbors of $M_{i+1}$ have already been colored, leaving one color free for $M_{i+1}$.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 4. We want to color the three-element subsets of $\{1,2,3,4,5,6,7\}$ such that if two of these subsets have no element in common, then they must be of different colors. What is the minimum number of colors needed to achieve this goal?
|
## Solution to Exercise 4
Consider the sequence of sets $\{1,2,3\},\{4,5,6\},\{1,2,7\},\{3,4,6\},\{1,5,7\},\{2,3,6\},\{4,5,7\}, \{1,2,3\}$.
Each set must have a different color from the next, so there must be at least two colors. If there were exactly two colors, then the colors would have to alternate, which is impossible because the last set is the same as the first and should be of the opposite color.
Conversely, let's show that three colors suffice:
- We color blue the sets that contain at least two elements from $\{1,2,3\}$.
- We color green the sets not colored blue and that contain at least two elements from $\{4,5,6\}$.
- We color red the sets not colored blue or green.
It is clear that two blue sets have an element in common among $\{1,2,3\}$; similarly, two green sets have an element in common among $\{4,5,6\}$. Finally, any red set contains three elements, and necessarily includes the element 7: thus, two red sets also have an element in common.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 1. Determine the maximum value of $\sqrt{x}+\sqrt{2 y+2}+\sqrt{3 z+6}$ when $x, y, z$ are strictly positive real numbers satisfying $x+y+z=3$.
|
Solution to Exercise 1 According to the Cauchy-Schwarz inequality, we have
$$
\sqrt{x} \sqrt{1}+\sqrt{y+1} \sqrt{2}+\sqrt{z+2} \sqrt{3} \leqslant \sqrt{x+y+1+z+2} \sqrt{1+2+3}=6
$$
Equality is achieved when $x=y=z=1$. Therefore, the maximum value is 6.
|
6
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 3. Let $x, y$ and $z$ be three real numbers such that $x^{2}+y^{2}+z^{2}=1$. Find the minimum and maximum possible values of the real number $x y+y z-z x$.
|
Solution to Exercise 3 According to the identity
$$
(x-y+z)^{2}=x^{2}+y^{2}+z^{2}-2(x y+y z-z x)=1-2(x y+y z-z x)
$$
the goal here is to find the extreme values that the number $(x-y+z)^{2}$ can take.
First, since $(x-y+z)^{2} \geqslant 0$, with equality when $x=y=1 / \sqrt{2}$ and $z=0$, we have
$$
x y+y z-z x=\frac{1-(x-y+z)^{2}}{2} \leqslant \frac{1}{2}
$$
with equality when $x=y=1 / \sqrt{2}$ and $z=0$.
Furthermore, the Cauchy-Schwarz inequality indicates that
$$
(x-y+z)^{2} \leqslant\left(x^{2}+y^{2}+z^{2}\right) \times\left(1^{2}+(-1)^{2}+1^{2}\right)=3
$$
with equality if and only if the triplets $(x, y, z)$ and $(1,-1,1)$ are collinear. Therefore, we have
$$
(x y+y z-z x)=\frac{1-(x-y+z)^{2}}{2} \geqslant \frac{1-3}{2}=-1
$$
with equality when $x=-y=z=1 / \sqrt{3}$.
In conclusion, the sought extreme values are -1 and $1 / 2$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 1. Determine all real numbers $x, y, z$ satisfying the following system of equations: $x=\sqrt{2 y+3}, y=\sqrt{2 z+3}, z=\sqrt{2 x+3}$.
|
Solution to Exercise 1 It is clear that the numbers $x, y, z$ must be strictly positive. The first two equations give $x^{2}=2 y+3$ and $y^{2}=2 z+3$. By subtracting them, we get $x^{2}-y^{2}=2(y-z)$. We deduce that if $x \leqslant y$ then $y \leqslant z$, and similarly if $y \leqslant z$ then $z \leqslant x$. Therefore, if $x \leqslant y$, we have $x \leqslant y \leqslant z \leqslant x$, which implies that $x=y=z$.
We similarly show that if $x \geqslant y$ then $x=y=z$. Therefore, in all cases, $x, y, z$ are equal, and their common value satisfies the equation $x^{2}=2 x+3$, which can also be written as $(x-3)(x+1)=0$. Since $x$ is strictly positive, it must be that $x=y=z=3$. Conversely, it is immediately verified that $x=y=z=3$ is indeed a solution to the system.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 2. The real numbers $a, b, c$ are distinct and non-zero, and we assume that there exist two real numbers $x$ and $y$ such that $a^{3} + a x + y = 0, b^{3} + b x + y = 0$ and $c^{3} + c x + y = 0$.
Prove that $a + b + c = 0$.
|
## Solution.
On a
$$
\left\{\begin{array}{l}
a^{3}+a x+y=0 \\
b^{3}+b x+y=0 \\
c^{3}+c x+y=0
\end{array}\right.
$$
Subtract the first and the third equation: $\left(a^{3}-c^{3}\right)+(a-c) x=0$. Since $a^{3}-c^{3}=(a-c)\left(a^{2}+\right.$ $\left.a c+c^{2}\right)$, we have $(a-c)\left(a^{2}+a c+c^{2}+x\right)=0$. Given that $a-c \neq 0$, it follows that
$$
a^{2}+a c+c^{2}+x=0
$$
Similarly, we show that $\mathrm{b}^{2}+\mathrm{bc}+\mathrm{c}^{2}+\mathrm{x}=0$. By subtracting the last two equations, we get $0=a^{2}-b^{2}+a c-b c=(a-b)(a+b+c)$. Since $a-b \neq 0$, we conclude that $a+b+c=0$.
$$
\text { \%ி }
$$
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 1. The integers $1,2, \ldots, 2018$ are written on the board. Then 2017 operations are performed as follows: choose two numbers $a$ and $b$, erase them, and write $a+b+2ab$ in their place. At the end, only one integer remains on the board.
What are the possible values that the units digit of this integer can take?
|
Solution to Exercise 1 Since there are 1009 odd numbers between 1 and 2018, we know that the sum of the integers initially written on the board is odd. Furthermore, one of these integers is congruent to $2(\bmod 5)$. An immediate induction then shows that, after each operation, the sum of the integers written on the board remains odd, and one of these integers is congruent to 2 $(\bmod 5)$. Consequently, the last integer written on the board is congruent to $1(\bmod 2)$ and to 2 $(\bmod 5)$, that is, to $7(\bmod 10)$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 3. Maena and Théodore are playing a game. They play on a square grid consisting of $99 \times 99$ cells. Two cells are considered adjacent if they share a vertex or a side.
Initially, Maéna numbers the cells of the grid from 1 to $99^{2}$, in an arbitrary manner. Théodore then places a token on one of the cells of the square, and he allows himself moves of the following form: he can move the token from one cell to another only if these cells are adjacent and if the new cell on which the token lands has a strictly greater number than the old cell.
How many moves can Théodore guarantee at a minimum, regardless of how Maena placed her integers?
|
Solution to Exercise 3 First, Théodore can always manage to perform at least three moves. To do this, he just needs to select a $2 \times 2$ square inside the $99 \times 99$ square, then traverse its four cells, which are necessarily adjacent since they share a vertex.
Conversely, here is how Maena can proceed to prevent Théodore from performing more than three moves. She numbers the rows and columns from 1 to 99, then groups the $99 \times 99$ cells of the square into four categories:
$\triangleright$ Category 1 contains the cells located in an odd row and an odd column;
$\triangleright$ Category 2 contains the cells located in an odd row and an even column;
$\triangleright$ Category 3 contains the cells located in an even row and an odd column;
$\triangleright$ Category 4 contains the cells located in an even row and an even column.
Two cells in the same category are never adjacent.
Next, Maena places her integers, in ascending order, in cells of category 1, then category 2, then category 3, and finally category 4. Thus, Théodore can never move between two cells of the same category, and even less so decrease the category. Therefore, every move increases the category of the cell in which Théodore's token is located, thereby limiting him to performing at most three moves.
Comment from the graders In a problem like this, there are two things to do:
1. Propose a strategy that Maena can use to prevent Théodore from making too many moves;
2. Propose a strategy that Théodore can use to make at least $k$ moves (with $k$ to be chosen) regardless of Maena's strategy.
Among the students who looked for a strategy for Maena, many concluded that she could prevent Théodore from making more than three moves. Among those who looked for a strategy for Théodore, many concluded that he could always make at least three moves.
Unfortunately, few students thought to look for strategies for both Maena and Théodore. In particular, proving that Théodore can always make at least three moves when Maena follows the strategy she chose is almost useless, since Maena still has $\left(99^{2}\right)!-1 \approx 10^{34864}$ alternative ways to number the grid, and it remains to prove that Théodore can also make at least three moves in each of these $\left(99^{2}\right)!-1$ cases.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 5. Martin is trying to fill each cell of a rectangular grid with 8 rows and $\mathrm{n}$ columns with one of the four letters $\mathrm{P}, \mathrm{O}, \mathrm{F}$, and $\mathrm{M}$ such that for any pair of distinct rows, there is at most one column where the intersections of the two rows are cells with the same letter. What is the largest integer $n$ for which this is possible?
|
Solution to Exercise 5 In this problem, we are looking for the largest integer satisfying a certain property. Suppose we want to show that the largest integer sought is the integer c. To show that c is indeed the largest integer, we will on the one hand show that if an integer n satisfies the property, then n ≤ c, and on the other hand we will show that we can find a table with exactly c columns.
The statement provides an assumption about the rows and columns of a table.
We start by looking at the information we have about the rows of this table. There are 8 rows, so there are \(\binom{8}{2} = 28\) pairs of rows.
We then look at the information we have about the columns of the table. Since the statement's hypothesis mentions identical letters within the same column, we will count how many pairs of identical letters can belong to the same column. We fix a column of the table and see how many pairs of identical letters we can form at a minimum. After several trials on a column of size 8, we conjecture that there are always at least 4 pairs of identical letters within the same column. Indeed, in a column there are 8 letters, so a letter appears at least 2 times.
- If each letter appears at most 2 times, then each letter appears exactly 2 times since there are 8 cells in the column and 4 possible letters. We thus have 4 pairs of identical letters in the column.
- If a letter appears exactly 3 times, say the letter P, then we can form 3 pairs of letters P. Among the 5 remaining letters, at least one of the letters O, F, and M appears twice according to the pigeonhole principle, which gives us a fourth pair of identical letters.
- If a letter appears at least 4 times in the column, say the letter P, we can form 4 pairs of letters P.
Thus, in a column, we can always find 4 pairs of identical letters. Therefore, for each column, there are at least 4 pairs of rows such that the intersections with the column have the same letter. But according to the statement's hypothesis, a pair of rows can be associated with at most one column such that its intersections with the two rows are two cells containing the same letter. We deduce that there are at most \(4 \times n\) pairs of rows. Therefore, \(4n \leq 28\) and \(n \leq 7\).
Conversely, there exists a configuration with the following 7 columns:
| P | P | P | P | P | P | P |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| O | O | O | O | O | P | O |
| F | F | F | F | O | O | P |
| M | M | M | M | P | O | O |
| P | M | F | O | F | F | F |
| O | F | M | P | M | F | M |
| F | P | P | M | M | M | F |
| M | O | O | F | F | M | M |
The largest integer \(\mathfrak{n}\) of columns is therefore \(\mathfrak{n} = 7\).
Graders' Comments
The exercise is generally well done; students have understood that the constraint is that each column adds 4 pairs of identical letters, but few have provided a fully rigorous proof of this fact. Some have given a set of 7 columns and justified that 7 is optimal because it is not possible to add a column to what they have done. However, this justification is not sufficient. Indeed, just because the construction cannot be enlarged does not mean that its size is maximal: one can imagine that there exists a larger and very different construction from the one given.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 12. Martin is trying to fill each cell of a rectangular grid with 8 rows and $n$ columns with one of the four letters $\mathrm{P}, \mathrm{O}, \mathrm{F}$, and $\mathrm{M}$ such that for any pair of distinct rows, there is at most one column where the intersections of the two rows are cells with the same letter. What is the largest integer $\mathrm{n}$ for which this is possible?
|
Solution to Exercise 12 In this problem, we are looking for the largest integer satisfying a certain property. Suppose we want to show that the largest integer sought is the integer c. To show that c is indeed the largest integer, we will on the one hand show that if an integer n satisfies the property, then n ≤ c, and on the other hand we will show that we can find a table with exactly c columns.
The statement presents a hypothesis concerning the rows and columns of a table.
We start by looking at the information we have about the rows of this table. There are 8 rows, so there are \(\binom{8}{2} = 28\) pairs of rows.
We then look at the information we have about the columns of the table. Since the hypothesis in the statement mentions identical letters within the same column, we will count how many pairs of identical letters belong to the same column. We fix a column of the table and see how many pairs of identical letters we can form at a minimum. After several trials on a column of size 8, we conjecture that there are always at least 4 pairs of identical letters within the same column. Indeed, in a column there are 8 letters, so a letter appears at least 2 times.
- If each letter appears at most 2 times, then each letter appears exactly 2 times since there are 8 cells in the column and 4 possible letters. We thus have 4 pairs of identical letters in the column.
- If a letter appears exactly 3 times, say the letter P, then we can form 3 pairs of letters P. Among the 5 remaining letters, at least one of the letters O, F, and M appears twice according to the pigeonhole principle, which gives us a fourth pair of identical letters.
- If a letter appears at least 4 times in the column, say the letter P, we can form 4 pairs of letters P.
Thus, in a column, we can always find 4 pairs of identical letters. Therefore, for each column, there are at least 4 pairs of rows such that the intersections with the column have the same letter. But according to the hypothesis in the statement, a pair of rows can be associated with at most one column such that its intersections with the two rows are two cells containing the same letter. We deduce that there are at most \(4 \times n\) pairs of rows. Therefore, \(4n \leq 28\) and \(n \leq 7\).
Conversely, there exists a configuration with the following 7 columns:
| P | P | P | P | P | P | P |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| O | O | O | O | O | P | O |
| F | F | F | F | O | O | P |
| M | M | M | M | P | O | O |
| P | M | F | O | F | F | F |
| O | F | M | P | M | F | M |
| F | P | P | M | M | M | F |
| M | O | O | F | F | M | M |
The largest integer n of columns is therefore n = 7.
Comment from the graders
Many students managed to find the answer n = 7 and provided an example. Most propose a correct argument to show that it is optimal, but sometimes this reasoning is written in a somewhat unclear manner.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 1. Let $x$ be a strictly positive real number. Show that $x^{3}+\frac{1}{x} \geqslant 2 x$ and find the cases of equality.
|
Solution to Exercise 1 Given that $x$ is a strictly positive real number, the same is true for $x^{3}$ and $\frac{1}{x}$. The arithmetic-geometric mean inequality then indicates that
$$
x^{3}+\frac{1}{x} \geqslant 2 \sqrt{\frac{x^{3}}{x}}=2 \sqrt{x^{2}}=2 x
$$
To determine the case of equality, one must look at the equality case of the means. Indeed, if equality holds, this means that $x^{3}=\frac{1}{x}$. Therefore, $x^{4}=1$, which implies that $x^{2}=1$ or $x^{2}=-1$. Since $x$ is real, $x^{2} \geqslant 0$, so we have $x^{2} \stackrel{2}{=}$. This implies that $x=1$ or $x=-1$. Since $x$ is positive, we must have $x=1$.
Conversely, if $x=1$, then $x^{3}+\frac{1}{x}=2=2 x$
Comment from the graders: The exercise is largely successful. However, a number of students retain $x=-1$ as a case of equality, even though they implicitly use that $x>0$ (stated in the problem) to prove the inequality.
|
1
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 6. Determine all sequences $\left(a_{n}\right)_{n \geqslant 1}$ of real numbers such that $a_{i}=a_{i+2020}$ for all integers $i \geqslant 1$, and such that
$$
a_{j}+2 a_{j+2} \geqslant a_{j+1}^{2}+a_{j+1}+1
$$
for all integers $\mathrm{j} \geqslant 1$.
|
Solution to Exercise 6: Here, the terms $a_{j+1}^{2}$ and 1 in the inequality seem a bit troublesome, as they are not of degree 1 like the other terms in the inequality. We would like to reduce it to a homogeneous inequality, that is, an inequality that remains true if we multiply the different terms by the same factor $k$. Therefore, we will use the inequality $x^{2}+1 \geqslant 2 x$, which is true for all real $x$, since $(x-1)^{2} \geqslant 0$. Applying this inequality to the relation gives
$$
a_{j}+2 a_{j+2} \geqslant a_{j+1}+a_{j+1}^{2}+1 \geqslant 3 a_{j+1}
$$
This relation is already more manageable. Now we would like to use the fact that the sequence is 2020-periodic. We will therefore consider an integer $j \geqslant 1$ such that $a_{j}$ is maximal. This is possible given that the sequence takes a finite number of distinct values because it is periodic. Without loss of generality, we assume that $j \geqslant 2$.
Thus, we have $3 a_{j} \leqslant a_{j-1}+2 a_{j+1} \leqslant a_{j}+2 a_{j}=3 a_{j}$ by the maximality of $a_{j}$. In particular, to have equality, we must have $a_{j-1}=a_{j}=a_{j+1}$. An immediate induction shows that if $k \geqslant 0, a_{j+k}=a_{j}$ and that if $k \leqslant j-1, a_{j-k}=a_{j}$. The sequence is therefore constant and equals $a_{j}$. The inequality then becomes $a_{j}+2 a_{j} \geqslant a_{j}^{2}+a_{j}+1$ or $a_{j}^{2}-2 a_{j}+1=\left(a_{j}-1\right)^{2} \leqslant 0$, so $a_{j}=1$.
Conversely, if $a_{k}=1$ for all $k \geqslant 1$, then for any positive integer $j, a_{j}+2 a_{j+2}=3 \geqslant 3=a_{j+1}^{2}+a_{j+1}+1$, so the constant sequence equal to 1 is a solution. The only sequence that is a solution is therefore the constant sequence equal to 1.
Comment from the graders: The exercise is generally well done, by various methods. However, few students thought to verify that the sequence obtained at the end is indeed a solution: even though it was very easy to verify here, it is important to at least mention a verification. Indeed, when asked to find all solutions to a problem, it is always necessary to verify that the solutions obtained are indeed solutions.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 18. We say that a set $A$ of polynomials with real coefficients is beautiful if, whenever $P$ and $Q$ are two distinct elements of $A$, there exist positive integers $a_{1}>\cdots>a_{2020}$ such that
$$
P Q=\sum_{i=1}^{2020} i X^{a_{i}}
$$
What is the maximal cardinality of a beautiful set?
|
Solution to Exercise 18 Let $A$ be a magnificent set. Suppose that $A$ has 3 distinct elements, which we denote as $P, Q, R$.
Since $\mathrm{P}^{2}=\frac{(\mathrm{PQ}) \times(\mathrm{PR})}{\mathrm{QR}}, \mathrm{P}^{2}$ is the product of two polynomials with integer coefficients, divided by a polynomial with integer coefficients. Therefore, it is a polynomial with rational coefficients that is also unitary. Indeed, the Euclidean algorithm for computing the GCD of two polynomials with rational coefficients yields a quotient and a remainder with rational coefficients, because the set of rationals is stable under division, multiplication, addition, and subtraction.
Thus, $P^{2}$ is a unitary polynomial with rational coefficients. Let $P=\sum_{n=0}^{d} a_{n} X^{n}$ with $a_{d} \neq 0$. We have $a_{d}^{2}=1$, so $a_{d}= \pm 1$. We will prove by strong downward induction that $a_{i}$ is rational for all $i$ between 0 and $n$.
The base case comes from the fact that $a_{n}= \pm 1$. For the inductive step, let $i \in\{0, n-1\}$ such that $a_{i+1}, \ldots, a_{n}$ are rational. The coefficient of degree $i+n$ of $P^{2}$ is $\sum_{j=i}^{n} a_{j} a_{n+i-j}=2 a_{i} a_{n}+\sum_{j=i+1}^{n-1} a_{j} a_{n+i-j}$.
If $i+1 \leqslant j \leqslant n-1, a_{j}$ and $a_{n+i-j}$ are rational, so $\sum_{j=i+1}^{n-1} a_{j} a_{n+i-j}$ is rational. Since the coefficient of degree $i+n$ of $P^{2}$ is rational, $2 a_{i} a_{n}$ is also rational. Since $a_{n}= \pm 1$, $a_{i}$ is rational, which concludes the induction.
Now, $P^{2}(1)=1+\cdots+2020=\frac{2020 \times 2021}{2}=1010 \times 2021$ which is divisible by 2 but not by 4. In particular, since $P_{i}$ has rational coefficients, there exists $(p, q) \in \mathbb{Z} \times \mathbb{N}^{*}$ such that $P(1)=\frac{p}{q}$. Therefore, $p^{2}=1010 \times 2021 \times q^{2}$. We obtain that $p \neq 0$, and that $V_{2}\left(p^{2}\right)=2 V_{2}(p)=V_{2}\left(1010 \times 2021 \times q^{2}\right)=$ $1+2 V_{2}(q)$. We conclude that $2 V_{2}(p)=2 V_{2}(q)+1$. Since the left term is even and the right term is odd, we obtain a contradiction.
Thus, we cannot have $|A| \geqslant 3$. However, we can have $|A|=2$ by taking $A=\left\{1, \sum_{i=1}^{2019} i X^{2019-i}\right\}$, which works well. We conclude that the maximum cardinality of a magnificent set is 2.
Alternative Solution $n^{\circ} 1$ This solution is essentially the same as the previous one but presented from a different angle. The first solution proved that the coefficients of the polynomials are rational. The additional idea is to notice that the same can be said about the polynomials divided by $\sqrt{2020}$. Suppose $A \supseteq\{P, Q, R\}$ is magnificent. Since $P^{2} \cdot Q R=P Q \cdot R P$ and $P Q, Q R, R P$ are unitary polynomials with rational coefficients, $\mathrm{P}^{2}$ is also unitary and has rational coefficients.
Let $\tilde{P}$ be the polynomial obtained by reversing the coefficients of $P$. Precisely, if $P=\sum_{i=0}^{n} p_{i} X^{i}$ with $p_{n} \neq 0$, then $\tilde{P}=\sum_{\tilde{i}=0}^{n} p_{n-i} X^{i}$. Reversing the coefficients is compatible with multiplication, i.e., $\tilde{\mathrm{PQ}}=\tilde{\mathrm{P}} \tilde{\mathrm{Q}}$.
In our case, we notice that $\frac{\mathrm{PQ}}{2020}, \frac{\text { RR }}{2020}, \frac{\tilde{\mathrm{RP}}}{2020}$ are also unitary and have rational coefficients because
$$
\frac{\tilde{P Q}}{2020}=\sum_{i=1}^{2020} \frac{i}{2020} X^{a_{1}-a_{i}}=X^{a_{1}-a_{2020}}+\frac{2019}{2020} X^{a_{1}-a 2019}+\cdots+\frac{1}{2020}
$$
Thus, repeating the argument, since $\left(\frac{\tilde{\mathrm{P}}}{\sqrt{2020}}\right)^{2} \cdot \frac{\tilde{\mathrm{QR}}}{2020}=\frac{\tilde{\mathrm{P}}}{2020} \cdot \frac{\tilde{\mathrm{RP}}}{2020}$ and $\frac{\tilde{\mathrm{PQ}}}{2020}, \frac{\tilde{\mathrm{Q} R}}{2020}, \frac{\tilde{\mathrm{RP}}}{2020}$ are unitary polynomials with rational coefficients, $\left(\frac{\tilde{\mathrm{P}}}{\sqrt{2020}}\right)^{2}$ is also unitary and has rational coefficients.
As proven in Solution 1, from $\mathrm{P}^{2} \in \mathbb{Q}[\mathrm{X}]$ and $\mathrm{P}^{2}$ being unitary, we get $\mathrm{P} \in \mathbb{Q}[\mathrm{X}]$. From $\left(\frac{\tilde{\mathrm{P}}}{\sqrt{2020}}\right)^{2} \in \mathbb{Q}[\mathrm{X}]$ and $\left(\frac{\tilde{\mathrm{P}}}{\sqrt{2020}}\right)^{2}$ being unitary, we get $\frac{\tilde{\mathrm{P}}}{\sqrt{2020}} \in \mathbb{Q}[\mathrm{X}]$. Contradiction, since $\mathrm{P} \neq 0$.
Comment from the graders: The exercise was rarely attempted. The ideas provided by the students who tried the problem are excellent and demonstrate a good understanding of the exercise. There are few actual errors, and the only remark to make is that certain concepts (degree, Viète's formulas) were doomed to fail given that one could replace $\mathrm{P} \in A$ with $XP$ and that the degrees of the elements of $A$ are poorly understood, an observation that can sometimes be salvaging.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 8. In a tournament organized between 6 teams, each team plays against each other team exactly once. When a team wins, it gets 3 points, and the losing team receives 0 points. If the game is a draw, both teams receive 1 point. Determine the values of \( a \) for which it is possible that the final scores of the teams can be the six consecutive numbers \( a, a+1, \ldots, a+5 \)?
|
Solution to Exercise 8: In each match, between two and three points are awarded in total. Given that there are 15 matches in total, there must have been between 30 and 45 points distributed among the teams. Therefore, we must have:
$$
\begin{aligned}
& 30 \leqslant a+(a+1)+(a+2)+\cdots+(a+5) \leqslant 45 \\
& 30 \leqslant 6 a+15 \leqslant 45
\end{aligned}
$$
This means that \(a\) can only be 3, 4, or 5.
If \(a=5\), no match could have ended in a draw, so all scores are multiples of 3. It is therefore not possible to have 6 consecutive numbers for the scores, and this case is not possible.
If \(a=3\), the scores are 3, 4, 5, 6, 7, 8. The teams with 6 and 7 points have each won at least one match, and the team with 8 points has won at least 2 matches, so at least 4 matches did not end in a draw. Thus, the total number of points distributed among the teams is at least 34, but \(3+4+5+6+7+8=33\), so this case is not possible.
The case \(a=4\) is possible. The scores are 4, 5, 6, 7, 8, 9. Here is a table that works:
| $\mathrm{X}$ | 3 | 1 | 0 | 0 | 0 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | $\mathrm{X}$ | 1 | 0 | 3 | 1 |
| 1 | 1 | $\mathrm{X}$ | 3 | 0 | 1 |
| 3 | 3 | 0 | $\mathrm{X}$ | 1 | 0 |
| 3 | 0 | 3 | 1 | $\mathrm{X}$ | 1 |
| 3 | 1 | 1 | 3 | 1 | $\mathrm{X}$ |
The number written in the j-th column of the i-th row is the score obtained by team \(i\) in its match against team \(j\).
Comment from the graders: The exercise was very well done by the students who attempted it.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 16. Consider a circular necklace with 2021 beads. Each bead can be colored either white or green. A coloring of the necklace is said to be chic if, among any 21 consecutive beads, there is always at least one green bead. Show that the number of chic colorings of the necklace is odd.
|
Solution to Exercise 16 Let's consider a slightly different problem, which involves calculating, for a given integer $\mathrm{N}$, the parity of the number of lines of $\mathrm{N}$ pearls where each pearl is either white or green, and such that among 21 consecutive pearls there is always one green. Let $a_{N}$ be this number modulo 2. We thus have a problem where we have a line, whereas previously we had a necklace. As we will see later, calculating $\mathrm{a}_{\mathrm{N}}$ for any integer $\mathrm{N}$ is quite easy, because the line is well-suited to a reasoning by recurrence. Let's now see how to solve the initial problem from the knowledge of the $\mathrm{a}_{\mathrm{N}}$.
Number the pearls on our necklace of 2021 pearls. The goal is to "break the necklace" to reduce it to a line. For a given chic coloring $\mathrm{c}$, let $k$ be the number of the first pearl after (in the broad sense) pearl 1 that is green and $\ell$ the number of the first pearl before (in the strict sense) pearl 1 that is green. Since $\mathrm{c}$ is chic, we have $1 \leqslant \mathrm{k} \leqslant 21$, and $2001 \leqslant \ell \leqslant 2021$. Moreover, there are at most 20 white pearls between pearl $\ell$ and pearl $k$, so $2021-\ell+k \leqslant 21$, hence $\ell \geqslant 2000+k$. Conversely, given these three conditions on $\ell$ and $k$, for the necklace $c$ to be chic, it suffices that the line of pearls $k+1, k+2, \ldots, \ell-1$ be chic. Therefore, the parity of the number of chic necklaces is
$$
P=\sum_{1 \leqslant k \leqslant 21} \sum_{2000+k \leqslant \ell \leqslant 2021} a_{\ell-k-1}
$$
To calculate $a_{N}$, we note that $a_{0}=1$ and $a_{i}=0$ for $1 \leqslant i \leqslant 20$. Moreover, we have the recurrence formula $a_{i+21}=\sum_{j=0}^{20} a_{i+j}$ because if we call $i+j+1$ the number of the last green pearl on a chic line of size $i+21$, then $0 \leqslant j \leqslant 20$ and it remains to choose a chic line of size $i+j$. This recurrence formula immediately shows that $\mathrm{a}_{N}=1$ if and only if $\mathrm{N} \equiv 0$ or $-1(\bmod 22)$.
Finally, we calculate (still modulo 2)
$$
P=\sum_{k=1}^{21} \sum_{N=1999}^{2020-k} a_{N}=a_{1999}+a_{2001}+\ldots+a_{2019}=1
$$
because $2001 \equiv-1(\bmod 22)$.
Graders' Comment: The exercise was approached by very few students and was not solved.
|
1
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 3. Let E be a finite set of strictly positive real numbers such that, for any strictly positive real number $x$, E contains as many elements strictly greater than $x$ as elements strictly less than $\frac{1}{x}$. Determine the product of all elements of $E$.
|
## Solution.
Let $x_{0} \in E$ such that $x_{0}>1$. Then, by hypothesis,
- the sets $E \cap]-\infty, \frac{1}{x_{0}}[$ and $E \cap] x_{0},+\infty[$ have cardinals of the same parity,
- the sets $E \cap]-\infty, x_{0}[$ and $E \cap] \frac{1}{x_{0}},+\infty[$ have cardinals of the same parity.
Consequently, the two sets
$$
\begin{aligned}
\left.E \cap] \frac{1}{x_{0}}, x_{0}\right] & =(E \cap] \frac{1}{x_{0}},+\infty[) \backslash(E \cap] x_{0},+\infty[) \\
E \cap\left[\frac{1}{x_{0}}, x_{0}[\right. & =(E \cap]-\infty, x_{0}[) \backslash(E \cap]-\infty, \frac{1}{x_{0}}[)
\end{aligned}
$$
have cardinals of the same parity. These sets are composed of the same elements, except possibly $x_{0}$ and $\frac{1}{x_{0}}$: the first set contains $x_{0}$ but not $\frac{1}{x_{0}}$; thus, the second set contains one and only one element of $\left\{\frac{1}{x_{0}}, x_{0}\right\}$ but cannot contain $x_{0}$: it therefore contains $\frac{1}{x_{0}}$.
We have thus established that if $x_{0} \in E$, then $\frac{1}{x_{0}} \in E$. The product of all elements of $E$ is therefore 1.

## Common Exercises
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 2. Find all real numbers $x, y$ such that
$$
x(x-2 y)+y(2 y-4)+4=0
$$
|
## Solution to Exercise 2
Let's develop the equation to obtain
$$
x^{2}-2 x y+2 y^{2}-4 y+4=0
$$
The terms $x^{2}-2 x y$ remind us of the remarkable identity $x^{2}-2 x y+y^{2}=(x-y)^{2}$. We then separate the $2 y^{2}$ into $y^{2}+y^{2}$ to write
$$
(x-y)^{2}+y^{2}-4 y+4=0
$$
But we then recognize a second remarkable identity $y^{2}-4 y+4=(y-2)^{2}$. Factoring this, we get
$$
(x-y)^{2}+(y-2)^{2}=0
$$
However, the sum of squares of real numbers is always non-negative, and can only be zero if both squares are zero. Thus, if $x$ and $y$ are solutions to the equation, we must have
$$
x-y=0 \quad \text{and} \quad y-2=0
$$
Therefore, the only possible solution to the equation is $x=y=2$. We can verify conversely that this is indeed a solution, so it is the only one.
Graders' Comment: Students generally found the solution using the method presented in the solution. Unfortunately, most of them forget to verify that the solution they found is indeed a solution to the problem. It is indeed sufficient that at one step, the equivalence is not justified for the verification to be necessary. Some considered the expression as a polynomial in $x$, whose roots need to be found, which only exist for certain values of $y$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 7. An integer $k>1$ is said to be superb if there exist $m, n$, and $a$, three strictly positive integers such that
$$
5^{\mathrm{m}}+63 \mathrm{n}+49=\mathrm{a}^{\mathrm{k}}
$$
Determine the smallest superb integer.
|
## Solution to Exercise 7
Suppose $k=2$ is superb: there exist three strictly positive integers $m, n$, and $a$ such that $5^{m} + 63n + 49 = a^{2}$. By looking modulo 3, we have $5^{m} + 1 \equiv 2^{m} + 1 \equiv a^{2} \pmod{3}$. The powers of 2 modulo 3 alternate between 2 if $m$ is odd and 1 if $m$ is even, so $2^{m} + 1$ is either 2 or 0 modulo 3. Since the squares modulo 3 are 0 and 1, we deduce that $2^{m} + 1$ must be 0 modulo 3, hence $m$ is odd. By looking modulo 7, we get $5^{m} \equiv a^{2} \pmod{7}$. The squares modulo 7 are $0, 1, 2, 4$, and the powers of 5 modulo 7 alternate between $1, 5, 4, 6, 2, 3$. Thus, $5^{m}$ is 0, 1, 2, or 4 if and only if $m$ is 0, 2, or 4 modulo 6, which is impossible since $m$ is odd. Therefore, $k \neq 2$.
Suppose $k=3$ is superb: there exist three strictly positive integers $m$, $n$, and $a$ such that $5^{m} + 63n + 49 = a^{3}$. By looking modulo 7, we have $5^{m} \equiv a^{3} \pmod{7}$. The cubes modulo 7 are $0, 1, 6$. The powers of 5 modulo 7 alternate between $1, 5, 4, 6, 2, 3$. Thus, we get that $m \equiv 0 \pmod{6}$ or $m \equiv 3 \pmod{6}$; in all cases, 3 divides $m$. We then look modulo 9: we have $5^{m} + 4 \equiv a^{3} \pmod{9}$. Since $m$ is divisible by 3, $5^{m}$ and $a^{3}$ are cubes. The cubes modulo 9 are $0, 1, 8$. Thus, $5^{m} - a^{3}$ can be 0, 1, 2, 7, 8 modulo 9, but not 4, which is contradictory. Therefore, $k \neq 3$.
Suppose $k=3$ is superb: there exist three strictly positive integers $m, n$, and $a$ such that $5^{m} + 63n + 49 = a^{4} = (a^{2})^{2}$. In particular, 2 is superb, which is contradictory.
Note that 5 is superb: by taking $a=3$, we have $a^{k} = 3^{5} = 243 = 5^{1} + 63 \times 3 + 49$, so 5 is superb. Thus, 5 is the smallest superb integer.
Comment from the graders: The exercise was attempted by few students, who solved it well.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 11. Félix wishes to color the integers from 1 to 2023 such that if $a, b$ are two distinct integers between 1 and 2023 and $a$ divides $b$, then $a$ and $b$ are of different colors. What is the minimum number of colors Félix needs?
|
## Solution to Exercise 11
We can try to color the numbers greedily: 1 can be colored with a color we denote as $a$, 2 and 3 with the same color $b$ (but not color $a$), then 4 and 6 with color $c$ (we can also color 5 and 7 with color $c$), etc. It seems that an efficient coloring is to color all numbers $n$ such that $2^k \leq n < 2^{k+1}$ with color $k+1$, as long as $n \leq 2023$. Thus, we color $[1,2[$ with color 1, $[2,4[$ with color 2, ..., $[1024,2023]$ with color 11. If $a \neq b$ are of the same color $k \in \{1, \ldots, 11\}$, then $0 < \frac{a}{b} < \frac{2^{k+1}}{2^k} = 2$, so if $b$ divides $a$, then $\frac{a}{b}$ is an integer and must be 1. Thus, $a = b$, which is a contradiction. Therefore, our coloring satisfies the condition of the problem and requires 11 colors.
Conversely, if a coloring satisfies the problem statement, the numbers $2^0 = 1, 2^1, \ldots, 2^{10}$ are between 1 and 2023, and if we take $a \neq b$ among these 11 numbers, either $a$ divides $b$ or $b$ divides $a$. Thus, these 11 numbers must be of different colors. Therefore, at least 11 colors are needed.
Thus, the minimum number of colors required is 11.
Comment from the graders: The exercise is very well done. As in any problem where we need to find the minimum number such that, it is important to split the proof into two parts: why $n=11$ colors are sufficient, and why if $n \leq 10$, $n$ colors are not sufficient.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 3. Alice puts 100 balls in a bag. On each ball she has written the square of an integer. Bob wants to find two balls such that the difference of the numbers is a multiple of 7. How many balls does he need to draw at a minimum to be sure to achieve his goal, regardless of the numbers chosen by Alice at the beginning?
|
## Solution to Exercise 3
A congruence table modulo 7 shows that the square of an integer can only take the values $0, 1, 2,$ or $4$ modulo 7. Thus, if Bob draws 5 balls, he will have two that have the same remainder modulo 7, according to the pigeonhole principle. The difference in the numbers on these two balls will therefore be a multiple of 7. Conversely, if he draws only 4 balls, he could have one ball with a number congruent to 0 modulo 7, one with a number congruent to 1, one with a number congruent to 2, and one with a number congruent to 4, so he would not achieve his goal. Therefore, Bob must draw 5 balls.
Grader's Comment: The exercise is very well done. However, there are quite a few confusions about the pigeonhole principle. Since there are 4 squares modulo 7, the pigeonhole principle ensures that if you take 5 balls, then two will have the same congruence modulo 7. However, it should be explained why taking 4 balls does not guarantee having two with the same congruence modulo 7 (by providing a counterexample).
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 3. Let $x, y, z$ be non-zero real numbers such that $x+y+z=0$. Suppose that
$$
\frac{x}{y}+\frac{y}{z}+\frac{z}{x}=\frac{x}{z}+\frac{z}{y}+\frac{y}{x}+1
$$
Determine the value of $\frac{x}{y}+\frac{y}{z}+\frac{z}{x}$.
|
Solution to Exercise 3 Let \( a \) be the common value of \( \frac{x}{y} + \frac{y}{z} + \frac{z}{x} \) and \( \frac{x}{z} + \frac{z}{y} + \frac{y}{x} + 1 \) so that
\[
\frac{x}{y} + \frac{y}{z} + \frac{z}{x} = a
\]
and
\[
\frac{x}{z} + \frac{z}{y} + \frac{y}{x} + 1 = a
\]
Let's add these two equations:
\[
2a = \frac{x}{y} + \frac{y}{z} + \frac{z}{x} + \frac{x}{z} + \frac{z}{y} + \frac{y}{x} + 1 = 1 + \frac{x+z}{y} + \frac{x+y}{z} + \frac{y+z}{x} = 1 - \frac{y}{y} - \frac{z}{z} - \frac{x}{x} = -2
\]
In particular, \( a = -1 \), so \( \frac{x}{y} + \frac{y}{z} + \frac{z}{x} \) is -1.
Graders' Comment: The exercise is very well solved. Some students propose different proofs from the solution, but often these require more calculations.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 1. Find all integers $p$ such that $p, p+2$ and $p+4$ are all three prime?
A prime number is an integer $\geqslant 2$ that is divisible only by 1 and itself.
|
Solution to Exercise 1 First, we can expect there to be very few. We wish to obtain information about these prime numbers.
Note that a prime number divisible by 3 is necessarily equal to 3. We consider 3 cases based on the remainder of the division of $p$ by 3 (modulo 3):
- $p=3k: p$ is divisible by 3, so $p=3$. $\{3,5,7\}$ is indeed a triplet of prime numbers.
- $p=3k+1: p+2$ is divisible by 3 and prime, so $p=1$ (impossible).
- $p=3k+2: p+4$ is divisible by 3 and prime, so $p=-1$ (impossible).
Hence $p=3$.
Comment from the graders The exercise is generally very well handled, except for some attempts modulo 10, the argument modulo 3 was well understood. Be careful not to forget the case $p=2$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 5. In a grid of size $n \times n$, some cells are white and some are black. We assume that for any pair of columns and any pair of rows, the 4 cells formed by the intersections of these two columns and these two rows are never all the same color. Find the largest value of $n$ for which this is possible.
|
Solution to Exercise 5: We will show that it is not possible for \( n \geqslant 5 \), and that it is possible for \( n \leqslant 4 \).
To do this, we first observe that if it is possible for an \( n \), it is possible for all \( k \leqslant n \). Indeed, if we take an \( n \times n \) grid satisfying the hypotheses, and then restrict ourselves to the sub-grid formed by the first \( k \) rows and columns, this sub-grid also satisfies the hypotheses. Therefore, to conclude, it suffices to show that it is not possible for \( n=5 \) and to provide a construction for \( n=4 \).
In the case \( n=5 \), consider a \( 5 \times 5 \) colored grid. For each column, there is at least one color present at least 3 times, according to the pigeonhole principle. Therefore, there are 3 columns for which this color is the same (by symmetry, let's say 3 columns containing at least 3 white cells), for the same reason. Let's call these columns \( a \), \( b \), and \( c \). There are at least 3 white cells in column \( a \), and we call the rows \( x \), \( y \), and \( z \). If column \( b \) or column \( c \) contains at least 2 white cells in rows \( x \), \( y \), and \( z \), then (for example, if cells \((b, x)\) and \((b, y)\) are white) the intersections of rows \( x \) and \( y \) with columns \( a \) and \( b \) are all white. Otherwise, on each of the two columns \( b \) and \( c \), the cells in the last two rows are white, and thus by considering these two rows and columns \( b \) and \( c \), we find that the grid does not satisfy the hypothesis.
For the case \( n=4 \), the following construction works:

Grader Comments: For this exercise, the writing is often unclear. Some students overuse the phrase "without loss of generality" to consider a very specific case. However, often students do not identify enough symmetries in the problem to reduce it to a single case. A tip to avoid mistakes is to specify which generality is preserved before using the phrase, to ensure that one has not overused the formula. For example, in the case \( n=5 \): "There are three cells of the same color in the first column. Without loss of generality, and by swapping the color of each cell in the grid, we can assume that these three cells are white." However, after writing this, we are no longer allowed to make the same assumption for the three cells of the same color in the second column.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 7. Let $n$ be a strictly positive integer. Domitille has a rectangular grid divided into unit squares. Inside each unit square is written a strictly positive integer. She can perform the following operations as many times as she wishes:
- Choose a row and multiply each number in the row by $n$.
- Choose a column and subtract $n$ from each integer in the column.
Determine all values of $n$ for which the following property is satisfied:
Regardless of the dimensions of the rectangle and the integers written in the cells, Domitille can end up with a rectangle containing only 0s after a finite number of operations.
|
Solution to Exercise 7 For $\mathrm{n}=1$, if we start from a configuration with one column of two rows, with different integers on these two rows, the difference between the two integers remains invariant when one of the two operations is performed. Consequently, it cannot be canceled. In particular, Domitille cannot arrive at a rectangle containing only 0s in a finite number of steps.
We now assume that $n>2$. Consider the rectangle with one column of two rows with values 1 and 0. By looking at what happens modulo $n-1$, we see that multiplication by $n$ has no effect, and the second operation preserves the difference between the two values. Thus, the difference between the two values modulo $n-1$ is an invariant, initially non-zero. Consequently, it is impossible to make the two numbers equal $\bmod n-1$, and in particular to make them both zero.
Now let's show that Domitille can always reach 0 in the case $n=2$.
First, reduce the problem. If Domitille can handle the case where there is only one column, it is sufficient for her to deal with the columns one by one. Once a column is brought to 0, the only operation that its cells will undergo when processing the other columns will be the multiplication of a row by $\mathrm{n}$. But since the elements of the column are zero, this actually has no effect.
We can therefore assume that the rectangle is in fact composed of only one column. Then, if we can make two cells of the column equal, we can merge them, that is, each time we multiply the row of the first by $\mathrm{n}$, we do the same for the second. In this case, the two cells will always contain the same value. We can therefore restrict ourselves to the case where the column contains 2 cells with the integers $a$ and $b$. By multiplying each of the rows by 2, we can actually assume that $a$ and $b$ are even. We then subtract 2 from the smallest until it is 2. This is possible because neither $a$ nor $b$ is zero. Then we apply the "double then subtract" operation: we double the one that is 2, then subtract 2 from the column, until both numbers are 2. We have thus reduced to a configuration where all the numbers in the column are 2. We then subtract 2 from the column, and we have thus nullified the column, which concludes. Note also that the integers in all the other columns remain non-zero during all these manipulations.
Comments from the graders: Very few students tackled this problem, but those who did had excellent writing. Too bad some forgot the case $n=1$. One student attempted a proof by the principle of the minimum, which unfortunately did not lead to a conclusion.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 13. Let $\mathrm{n}$ be a strictly positive integer. Domitille has a rectangular grid divided into unit squares. Inside each unit square is written a strictly positive integer. She can perform the following operations as many times as she wishes:
- Choose a row and multiply each number in the row by $n$.
- Choose a column and subtract $n$ from each integer in the column.
Determine all values of $n$ for which the following property is satisfied:
Regardless of the dimensions of the rectangle and the integers written in the cells, Domitille can end up with a rectangle containing only 0s after a finite number of operations.
|
Solution to Exercise 13 For $n=1$, if we start from a configuration with one column of two rows, with different integers on these two rows, the difference between the two integers remains invariant when one of the two operations is performed. Consequently, it cannot be canceled. In particular, Domitille cannot arrive at a rectangle containing only 0s in a finite number of steps.
We now assume that $n>2$. Consider the rectangle with one column of two rows, with values 1 and 0. By looking at what happens modulo $n-1$, we see that multiplication by $n$ has no effect, and the second operation preserves the difference between the two values. Thus, the difference between the two values modulo $n-1$ is an invariant, initially non-zero. Consequently, it is impossible to make the two numbers equal $\bmod n-1$, and in particular to make them both zero.
Now let's show that Domitille can always reach 0 in the case $n=2$.
First, reduce the problem. If Domitille can handle the case where there is only one column, it is sufficient for her to deal with the columns one by one. Once a column is brought to 0, the only operation that its cells will undergo when processing the other columns will be the multiplication of a row by $n$. But since the elements of the column are zero, this actually has no effect.
We can therefore assume that the rectangle is in fact composed of only one column. Then, if we can make two cells of the column equal, we can merge them, that is, each time we multiply the row of the first by $n$, we do the same for the second. In this case, the two cells will always contain the same value. We can therefore restrict ourselves to the case where the column contains 2 cells with the integers $a$ and $b$. By multiplying each of the rows by 2, we can actually assume that $a$ and $b$ are even. We then subtract 2 from the smallest until it is 2. This is possible because neither $a$ nor $b$ is zero. Then we apply the "double then subtract" operation: we double the one that is 2, then subtract 2 from the column, until both numbers are 2. We have thus reduced to a configuration where all the numbers in the column are 2. We then subtract 2 from the column, and we have thus nullified the column, which concludes. Note also that the integers in all the other columns remain non-zero during all these manipulations.
Comments from the graders: The problem mainly involved two parts: handling the case $n>2$ and handling the case $n=2$ (without forgetting $\mathrm{n}=1$). The problem was widely addressed and often at least one of the two parts is well handled. The writing of the case $n=2$ is, however, often quite messy.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 5. Let $x, y, z$ be strictly positive real numbers such that
$$
x+\frac{y}{z}=y+\frac{z}{x}=z+\frac{x}{y}=2
$$
Determine all possible values that the number $x+y+z$ can take.
|
Solution to Exercise 5 In such a problem, it is necessary to examine each equation separately but also to relate them. In practice, this involves looking at the equation obtained when performing the sum or product of two or more equations. Another idea is to apply known inequalities on one side or the other of the equation. Indeed, often the equalities present in the problems are only possible when the variables satisfy the equality case of a well-known inequality.
Let's start with a separate examination. We consider the first equation $x+\frac{y}{z}=2$. According to the inequality of means, we have
$$
2=x+\frac{y}{z} \geqslant 2 \sqrt{x \cdot \frac{y}{z}}
$$
which means $\sqrt{\frac{x y}{z}} \leqslant 1$. Similarly, the second equation $y+\frac{z}{x}=2$ gives $\sqrt{\frac{y z}{x}} \leqslant 1$. By multiplying these two inequalities, we obtain
$$
1 \geqslant \sqrt{\frac{x y}{z}} \cdot \sqrt{\frac{y z}{x}}=y
$$
Thus $y \leqslant 1$, and similarly we find that $x \leqslant 1$ and $z \leqslant 1$. We now seek to apply these estimates or to prove inverse estimates (for example, $y \geqslant 1$, which would imply that $y=1$).
Note that the relation $x+\frac{y}{z}=2$ can be rewritten as $x z+y=2 z$. Similarly, we get $y x+z=2 x$ and $y z+x=2 y$. By summing these three relations, we find that $x z+y x+y z+x+y+z=2(x+y+z)$, or equivalently $x y+y z+z x=x+y+z$. But then
$$
x+y+z=x y+y z+z x \leqslant x \cdot 1+y \cdot 1+z \cdot 1=x+y+z
$$
Our inequality is actually an equality. And since $x, y$, and $z$ are non-zero, each of the inequalities used in the line above is actually an equality. Therefore, we have $x=y=z=1$ and $x+y+z=3$. This value is indeed achievable since the triplet $(1,1,1)$ satisfies the system given in the problem, which completes our problem.
## Comments from the graders:
The exercise was quite well done. The methods of solving are extremely varied. Some students made the mistake of considering the problem symmetric, whereas it is only cyclic.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 9. Determine the smallest integer $n \geqslant 2$ such that there exist strictly positive integers $a_{1}, \ldots, a_{n}$ such that
$$
a_{1}^{2}+\ldots+a_{n}^{2} \mid\left(a_{1}+\ldots+a_{n}\right)^{2}-1
$$
|
Solution to Exercise 9 Let's analyze the problem. In this problem, we are looking for the smallest integer $\mathrm{n}$ satisfying a certain property. Suppose we want to show that the smallest integer sought is the integer $c$. To show that it is indeed the smallest integer, we must on the one hand show that if an integer $n$ satisfies the property, then $\mathrm{n} \geqslant \mathrm{c}$, and on the other hand, we must show that we can find $\mathrm{c}$ integers satisfying the divisibility relation.
Since there is a divisibility relation, we can expect to use various ideas:
- If $a \mid \mathrm{b}$ then $a$ divides the linear combinations of $\mathrm{a}$ and $\mathrm{b}$
- If $a \mid b$ and $a$ and $b$ are strictly positive, then $a \mid b$
- If $a \mid \mathrm{b}$, the divisors of $a$ also divide $b$
Once this initial analysis is done, we can start by looking for integers $a_{i}$ satisfying the property for small values of $n$, for example for $n=2,3$ or even 4 if we are brave, before realizing that this method will not allow us to determine $n$.
However, having searched for $a_{i}$ for small values of $n$ allows us to find potential properties that the $a_{i}$ must satisfy. For example, we may have noticed that the integers $a_{i}$ cannot all be even, since in that case the sum of the $a_{i}^{2}$ would be even but $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ is odd. We then realize that what matters in this argument is not the parity of the $a_{i}$ but the parity of the sum.
We obtain that $a_{1}+a_{2}+\ldots+a_{n}$ is odd. Otherwise, since $a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2} \equiv a_{1}+a_{2}+\ldots+a_{n} \bmod 2, a_{1}+\ldots+a_{n}$ is also even, but then $a_{1}^{2}+\ldots+a_{n}^{2}$ is even and divides $\left(a_{1}+a_{2}+\ldots+a_{n}\right)^{2}-1$ which is odd, which is absurd.
We deduce that $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ is even. The previous parity argument invites us to refine this study. We will therefore look to see if $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ is divisible by $4,8 \ldots$ The presence of multiple squares invites us to look at each term with well-chosen moduli.
For example, modulo $4,\left(a_{1}+\ldots+a_{n}\right)^{2} \equiv 1$ so 4 divides $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$. Let's not stop here; we also know that the squares of odd numbers can only be 1 modulo 8. Thus, $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ is divisible by 8. Since 8 is coprime with $a_{1}^{2}+\ldots+a_{n}^{2}$ which is odd, we deduce from all this that
$$
8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \mid\left(a_{1}+\ldots+a_{n}\right)^{2}-1
$$
Another remark that we can make about the statement is that it involves the sum of squares of numbers on one side and the square of the sum of numbers on the other side. This makes one think of the Cauchy-Schwarz inequality, or the inequality of arithmetic and quadratic means. We can therefore try to compare the quantities $8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)$ and $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$.
This idea of comparing the terms is consistent with what we are trying to show. The divisibility obtained gives that $8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \leqslant\left(a_{1}+\ldots+a_{n}\right)^{2}-1$. In the arithmetic and quadratic means inequality, the square of the sum is smaller than the sum of the squares of the elements multiplied by the number of variables. We therefore suspect that the inequality obtained will be false for $n$ too small, which will provide the desired bound. More precisely,
$$
8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \leqslant\left(a_{1}+\ldots+a_{n}\right)^{2}-1 \leqslant n\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)-18$ so $\mathrm{n} \geqslant 9$.
Conversely, we are looking for 9 integers satisfying the property. We can expect that small integers will work. We can therefore look for $a_{i}$ equal to 1 or 2. Finally, we find that by taking $a_{1}=\cdots=a_{7}=1$ and $a_{8}=a_{9}=2$, we indeed have 15 dividing $11^{2}-1=120=15 \times 8$.
The expected answer is therefore $\mathrm{n}=9$.
Comment from the graders: The problem was solved by only one student. This is an instructive and very complete exercise, involving both arithmetic arguments and inequalities.
## Senior Exercises
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 4. Let $A B C D$ be a rectangle with area 4. Let I be the midpoint of $[A D]$ and let $J$ be the midpoint of $[B C]$. Let $X$ be the point of intersection of (AJ) and (BI), and let $Y$ be the point of intersection of (DJ) and (CI). What is the area of the quadrilateral IXJY?
|
Solution to exercise 4 Let's cut the rectangle $A B C D$ into isometric right triangles, as shown below. All triangles have the same area, and the rectangle is made up of 16 triangles in total: each triangle therefore has an area of $1 / 4$. The quadrilateral IXJY is formed of 4 triangles. Its area is therefore equal to 1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 10. I have socks of two different colors: 6 blue socks and 6 red socks. I take several socks at random. How many should I take, at a minimum, to be sure of having two socks of different colors?
|
Solution to Exercise 10: I must take, at a minimum, 7 socks to be sure of having two socks of different colors. Indeed, if I take 6 socks or fewer, it is possible that these socks are all blue. Conversely, if I take 7 socks, they cannot all be blue (so I will have taken at least one red sock), and they cannot all be red either (so I will have taken at least one blue sock). Thus, I will have taken two socks of different colors.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 11. Let $A B C D$ be a rectangle with area 4. Let I be the midpoint of $[A D]$ and let $J$ be the midpoint of $[B C]$. Let $X$ be the point of intersection of (AJ) and (BI), and let Y be the point of intersection of (DJ) and (CI). What is the area of the quadrilateral IXJY?
|
Solution to Exercise 11 Let's cut the rectangle $A B C D$ into isometric right triangles, as shown below. All the triangles have the same area, and the rectangle is made up of 16 triangles in total: each triangle therefore has an area of $1 / 4$. The quadrilateral IXJY is formed of 4 triangles. Its area is therefore equal to 1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 8. Calculate
$$
\sqrt{7+\sqrt{1+\sqrt{7+\sqrt{1+\sqrt{7+\sqrt{1+\sqrt{7+\sqrt{3+\sqrt{1}}}}}}}}}
$$
Only a numerical answer is expected here.
|
Solution to exercise 8 We notice the following chain of simplifications: $\sqrt{3+\sqrt{1}}=2$ then $\sqrt{7+\sqrt{3+\sqrt{1}}}=\sqrt{7+2}=3$ then $\sqrt{1+\sqrt{7+\sqrt{3+\sqrt{1}}}}=\sqrt{1+3}=2$, and so on...
Step by step, we deduce that any expression of the type $\sqrt{1+\sqrt{7+\sqrt{1+\sqrt{\cdots}}}}$ equals 2 and that any expression of the type $\sqrt{7+\sqrt{1+\sqrt{7+\sqrt{\cdots \cdots}}}}$ equals 3, regardless of the number of square roots, provided that $4=3+\sqrt{1}$ is under the last radical.
Since a 7 is found in the sum under the first radical, the answer is therefore 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 11. The integers $1,2, \ldots, 20$ have been arranged around a circle, in some order. For each of these integers $k$, Matthieu counts how many integers are less than $k$ among the 9 integers that follow $k$ when traversing the circle clockwise; he counts $A(k)$. He also counts how many integers are less than $k$ among the 9 integers that follow $k$ when traversing the circle counterclockwise; he counts $B(k)$. Matthieu then notes that $A(k)=B(k)$ for all $k$. What is the number diametrically opposite to 11 on the circle?
|
Solution to Exercise 11 From now on, to simplify the terms used, when we talk about a number "before" (or "after") another number, it means that the first number is among the 9 numbers preceding (or following) the second number, looking in the clockwise direction.
In the following, we denote $o(a)$ as the number diametrically opposite to the integer $a$ on the circle.
Let's start with some useful observations.
- First, the only number that does not appear before or after $a$ is the number $a$ itself.
- Furthermore, if two numbers $a$ and $b$ are opposite each other on the circle, then $a$ is before and $b$ is after (or $a$ after and $b$ before) any number on the circle other than $a$ and $b$.
After these general observations, let's look at which number can be the opposite of each number on the circle.
Since $A(2)=B(2)$, there are as many numbers less than 2 before and after 2. Since 1 is the only integer less than 2 among the integers on the circle, we deduce that $A(2)=B(2)=0$ and $o(2)=1$.
We can repeat this same reasoning step by step to show that the numbers $2k$ and $2k-1$ are diametrically opposite on the circle.
Indeed, if we already know that $o(2i)=2i-1$ for all $1 \leq i < k$, we can prove that $2k$ and $2k-1$ are also diametrically opposite.
To do this, suppose by contradiction that $o(2k) \neq 2k-1$. Then $2k-1$ is either before or after $2k$. Considering the pairs of opposite numbers $(2i-1, 2i)$ for $1 \leq i \leq k-1$, we get $k-1$ numbers before $2k$ and $k-1$ numbers after $2k$ on the circle. Considering the number $2k-1$, which is either before or after $2k$ on the circle, and since all other numbers on the circle are greater than $2k$, we get $A(2k)=k-1$ and $B(2k)=k$ or $A(2k)=k$ and $B(2k)=k-1$, which is impossible. Thus, $o(2k)=2k-1$ as claimed.
Finally, we have shown that the numbers $2k$ and $2k-1$ are always diametrically opposite on the circle for $1 \leq k \leq 10$. In particular, the number diametrically opposite to 11 on the circle is 12.
Remark: We could have provided a very similar solution by noting with the same reasoning that the number diametrically opposite to 19 on the circle is necessarily 20, and then descending step by step to 11 instead of ascending to 11.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 2. Let $\mathrm{ABC}$ be a triangle, $\mathrm{O}$ a point inside this triangle. The line parallel to (BC) passing through $O$ intersects $[C A]$ at $D$, the line parallel to $(C A)$ passing through $O$ intersects $[A B]$ at $E$, and the line parallel to $(A B)$ passing through $O$ intersects $[\mathrm{BC}]$ at $\mathrm{F}$. What is the value of the following sum of ratios:
$$
\frac{B F}{B C}+\frac{A E}{A B}+\frac{C D}{A C} ?
$$
|
## Solution to Exercise 2 First Solution:
Let $|A B C|$ denote the area of triangle $A B C$. We observe that
$$
\frac{B F}{B C}=\frac{|A B F|}{|A B C|}=\frac{|A B O|}{|A B C|}
$$
because triangles $A B F$ and $A B C$ have the same height and bases $B F$ and $B C$, and $A B O$ and $A B F$ have the same base $A B$ and two parallel heights of the same length (if $O'$ and $F'$ are the feet of the heights, then $OO'F'F$ is a rectangle).
From this, we deduce that
$$
\frac{B F}{B C}+\frac{A E}{A B}+\frac{C D}{A C}=\frac{|A B O|}{|A B C|}+\frac{|A O C|}{|A B C|}+\frac{|O C B|}{|A B C|}=1
$$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 4. We are given five numbers in ascending order, which are the lengths of the sides of a quadrilateral (not crossed, but not necessarily convex, meaning a diagonal is not necessarily inside the polygon) and one of its diagonals $D$. These numbers are 3, 5, 7, 13, and 19. What can be the length of the diagonal $D$?
|
Solution to exercise 4 We can rephrase the problem: let $a, b, c, d$ be the lengths of the sides of the quadrilateral, and $e$ the length of the diagonal that separates, on one side, the sides of length $a$ and $b$, and on the other side, the sides of length $d$ and $e$. It is necessary and sufficient that the triplets $(a, b, e)$ and $(c, d, e)$ satisfy the triangle inequality.
If $e=3$ or $e=5$, the triplet containing 19 will not work because $19-3>13$ and $19-5>13$: the side of length 19 is too large.
If $e=13$, it is necessary simultaneously that $a+b>13$ and $c+d>19$. However, if $a$ or $b=19$, then $c+d \leq 5+7<13$, and similarly if $c$ or $d=19$. Therefore, we cannot have $e=13$. We verify that the same applies for $e=19$.
Thus, only $e=7$ remains. In this case, we can have $a=3, b=5, c=13, d=19$ for example.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 5. A number has been written on the board. At each step, we add to it the largest of its digits (for example, if 142 is written, the next number will be 146). What is the maximum number of odd numbers that can be written consecutively by proceeding in this way?
|
Solution to Exercise 5 The answer is 5. Suppose we start with an odd number $n$. We denote $n_{i}$ as the $i$-th number written, with $n_{1}=n$. Let $c_{i}$ and $d_{i}$ be the largest digit and the units digit of $n_{i}$. If $c_{1}$ is odd, then $n_{2}=n_{1}+c_{1}$ is even, and we have only written one odd number. Note also that $c_{1}$ cannot be equal to 0.
If $c_{1}=2$, then $d_{1}=1$. We have $n_{2}=n_{1}+2$, so $c_{2}=3$ and $d_{2}=3$, and $n_{3}=n_{2}+3$ is even. The third number written is therefore even.
If $c_{1}=4$, then $d_{1}$ can be 1 or 3. If $d_{1}=1$, then $n_{2}=n_{1}+4$ so $c_{2}=5$ and $d_{2}=5$, so $n_{3}=n_{2}+5$ is even. If $d_{1}=3$, then $n_{2}=n_{1}+4$ so $c_{2}=7$ and $d_{2}=7$, so $n_{3}=n_{2}+7$ is even.
If $c_{1}=6$, then $d_{1}$ can be 1, 3, or 5. In the first two cases, we get $n_{3}$ even as before. If $d_{1}=5$, then $n_{2}=n_{1}+6$ so $d_{2}=1$. Moreover, the largest digit either remains the same $\left(c_{2}=6\right)$ or increases by 1 $\left(c_{2}=7\right)$. In the second case, $n_{3}=n_{2}+7$ is even. In the first case, $n_{3}=n_{2}+6$ so $d_{3}=7$ and $c_{3}=7$ so $n_{4}=n_{3}+7$ is even.
If $c_{1}=8$, then $d_{1}$ can be 1, 3, 5, or 7.
- if $d_{1}=1$, we get $c_{2}=d_{2}=9$ so $n_{3}$ is even.
- if $d_{1}=3$, then $d_{2}=1$ and $c_{2}$ can be 8 or 9. In the second case $n_{3}$ is even, and in the first we are reduced to the previous case $\left(c=8, d=1\right)$ so $n_{4}$ is even.
- if $d_{1}=5$, then $d_{2}=3$ and $c_{2}$ can be 8 or 9. In the second case $n_{3}$ is even, and in the first we are reduced to the previous case $(c=8, d=3)$ so $n_{4}$ or $n_{5}$ is even.
- if $d_{1}=7$, then $d_{2}=5$ and $c_{2}$ can be 8 or 9. In the second case $n_{3}$ is even, and in the first we are reduced to the previous case $(c=8, d=5)$ so $n_{4}$ or $n_{5}$ or $n_{6}$ is even.
It is therefore impossible to write 6 consecutive odd integers. However, if we start with 807, we will write successively $807, 815, 823, 831$, and 839, so we can write 5 consecutive odd integers.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 4. Let ABCD be a rectangle with area 4. Let I be the midpoint of $[A D]$ and let J be the midpoint of $[B C]$. Let $X$ be the point of intersection of (AJ) and (BI), and let $Y$ be the point of intersection of (DJ) and (CI). What is the area of the quadrilateral IXJY?
|
Solution to Exercise 4: Let's cut the rectangle ABCD into isometric right triangles, as shown below. All triangles have the same area, and the rectangle is made up of 16 triangles in total: each triangle therefore has an area of $1 / 4$. The quadrilateral IXJY is formed of 4 triangles. Its area is therefore equal to 1.
Grader's Comment: The exercise was generally well done. However, a significant number of submissions presented reasoning without any supporting figures, which hinders grading and often leads to multiple confusions. An explicit figure was sometimes worth more than a long discourse.
Furthermore, a surprising number of students immediately considered the special case where the rectangle is a square or has dimensions $4 \times 1$, which is a pity because the solution to this special case is the same as the general case.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 11. Let $A B C D$ be a rectangle with area 4. Let I be the midpoint of $[A D]$ and let $J$ be the midpoint of $[B C]$. Let $X$ be the point of intersection of (AJ) and (BI), and let $Y$ be the point of intersection of (DJ) and (CI). What is the area of the quadrilateral IXJY?
|
Solution to Exercise 11 Let's cut the rectangle ABCD into isometric right triangles, as shown below. All triangles have the same area, and the rectangle is made up of 16 triangles in total: each triangle therefore has an area of $1 / 4$. The quadrilateral IXJY is formed of 4 triangles. Its area is therefore equal to 1.
Grader's Comment Exercise was generally well done. However, a significant number of papers propose a reasoning without any supporting figure, which hinders grading and is often accompanied by several confusions. An explicit figure was sometimes worth more than a long discourse.
Moreover, a surprising number of students immediately consider the special case where the rectangle is a square or has dimensions $4 \times 1$, which is a pity because the solution to this case is the same as the general case.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 5. In a football tournament, each team plays exactly twice against each of the others. There are no draws; a win earns two points, and a loss earns none. It turns out that only one team won the tournament with 26 points, and there are two teams tied for last with 20 points each. Determine the number of teams, and provide an example of a tournament where such results occur.
|
Solution to Exercise 5 Let $n$ be the number of teams.
Each team wins a number of matches between 10 and 13. Since there are $n(n-1)$ matches, each team wins on average $n-1$ matches. The winning team and the two last teams tied win on average 11 matches, while the other teams win on average between 11 and 12 matches. Therefore, the average number of matches won per team is $\geqslant 11$ and $<12$. Since $n-1$ is an integer, we must have $n-1=11$, that is, $n=12$.
Let's show that such a tournament is possible. For the sake of clarity, let's say that the 12 teams belong to 12 different cities. Each pair of cities plays two matches, one in the city of one of the teams and the other in the city of the other team. We will say that a team plays at home if the match takes place in its city, and away otherwise.
Here is an example of a suitable tournament: when two of the teams $2, \ldots, 12$ meet, the team playing at home wins. In addition, team 1 wins all its matches against teams 2 and 3, and wins only at home against teams $4, \ldots, 12$.
Alternative solution for the first part. Let $a$ be the number of teams that win 11 matches and $b$ be the number of teams that win 12 matches. The total number of teams is $n=3+a+b$. On the other hand, the number of matches won is $n(n-1)=10 \times 2+11 a+12 b+13=33+11 a+12 b=11(3+a+b)+b=11 n+b$. We deduce that $b=n(n-1)-11 n=n(n-12)$. Since $0 \leqslant b<n$, we have $0 \leqslant n(n-12)<n$. Dividing by $n$, we get $0 \leqslant n-12<1$, hence $n=12$.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 6. Given a point $P$ and a circle $\mathcal{C}$ in the plane, the distance from $P$ to $\mathcal{C}$ is defined as the minimum length $PM$ between $P$ and a point $M$ on the circle $\mathcal{C}$. For example, if $P$ lies on the circle, then the distance from $P$ to $\mathcal{C}$ is zero, and if $P$ is the center of the circle, then the distance from $P$ to $\mathcal{C}$ is equal to the radius of $\mathcal{C}$.
Given four non-cyclic points $A, B, C, D$, what is the maximum number of circles that pass at equal distance from these four points?
|
Solution to Exercise 6: Let $\mathcal{C}$ be a circle passing at equal distance from $A, B, C, D$. The four points cannot all be inside the circle, otherwise they would be equidistant from the center, and thus would be concyclic. Similarly, they cannot all be outside.
Determine the number of circles $\mathcal{C}$ passing at equal distance from $A, B, C, D$ such that $A, B, C$ are on the same side of the circle. Suppose $A, B, C$ are not collinear. Let $\Omega$ be the center of the circumcircle of $A, B, C$ and $R$ its radius. Let $r$ be the radius of $\mathcal{C}$ and $d = \Omega D$. The fact that $A, B, C, D$ are equidistant from $\mathcal{C}$ can be written as $|r - R| = |r - d|$. Moreover, $r - R$ and $r - d$ cannot be equal, otherwise we would have $d = R$ and $A, B, C, D$ would be concyclic. The equality $|r - R| = |r - d|$ is therefore equivalent to $r - R = d - r$, or $r = \frac{R + d}{2}$, which proves the existence and uniqueness of the circle $\mathcal{C}_{D}$ such that $A, B, C$ are on one side and $D$ on the other side of the circle.
(If $A, B, C$ are collinear, no point is equidistant from $A, B, C$, so there does not exist a circle passing at equal distance from $A, B, C$ such that $A, B, C$ are all on the same side of the circle.)
We similarly define the circles $\mathcal{C}_{A}, \mathcal{C}_{B}$, and $\mathcal{C}_{C}$ if they exist.
Determine the number of circles $\mathcal{C}$ passing at equal distance from $A, B, C, D$ such that $A, B$ are on one side and $C, D$ on the other. The center of $\mathcal{C}$ must be equidistant from $A$ and $B$, so it lies on the perpendicular bisector of $[A B]$. Similarly, it lies on the perpendicular bisector of $[C D]$.
Suppose that $(A B)$ and $(C D)$ are not parallel. Then the perpendicular bisectors of $[A B]$ and $[C D]$ intersect at a point $\Omega$. Let $R_{1} = \Omega A$ and $R_{2} = \Omega C$. Then $R_{1} \neq R_{2}$ because $A, B, C, D$ are not concyclic. As in the previous case, we see that the circle with center $\Omega$ and radius $\frac{R_{1} + R_{2}}{2}$ is the unique circle equidistant from $A$ and $B$ such that $A$ and $B$ are on one side and $C, D$ on the other. Denote it by $\mathcal{C}_{A B}$.
Suppose that the perpendicular bisectors of $[A B]$ and $[C D]$ are parallel but not coincident. Then there does not exist a circle equidistant from $A, B, C, D$ such that $A, B$ are on one side and $C, D$ on the other.
Suppose that the perpendicular bisectors of $[A B]$ and $[C D]$ are coincident. If $A, B, C, D$ are not collinear, then the perpendicular bisectors of $[A B]$ and $[A C]$ intersect at a point $\Omega$ which is equidistant from $A, B, C, D$, which contradicts the fact that $A, B, C, D$ are not concyclic.
Suppose that $A, B, C, D$ are collinear such that the midpoints of $[A B]$ and $[C D]$ are coincident. Then there are infinitely many circles passing at equal distance from $A, B, C, D$, with centers on the common perpendicular bisector.
The discussion above shows that, except in the special case where the four points are collinear such that the midpoint of two points is equal to the midpoint of the other two, there are at most 7 circles passing at equal distance from $A, B, C, D$: these are $\mathcal{C}_{A}, \mathcal{C}_{B}, \mathcal{C}_{C}, \mathcal{C}_{D}, \mathcal{C}_{A B}, \mathcal{C}_{A C}, \mathcal{C}_{A D}$. Equality holds when any two of the six lines determined by $A, B, C, D$ are not parallel.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.