problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Exercise 2. Let $\mathrm{ABC}$ be a triangle, $\mathrm{O}$ a point inside this triangle. The line parallel to $(\mathrm{BC})$ passing through $O$ intersects $[C A]$ at $D$, the line parallel to $(C A)$ passing through $O$ intersects $[A B]$ at $E$, the line parallel to $(A B)$ passing through $\mathrm{O}$ intersects $[\mathrm{BC}]$ at $\mathrm{F}$. What is the value of the following sum of ratios:
$$
\frac{\mathrm{BF}}{\mathrm{BC}}+\frac{\mathrm{AE}}{\mathrm{AB}}+\frac{C D}{\mathrm{AC}} ?
$$
|
## Solution to Exercise 2 First Solution:
Let $|A B C|$ denote the area of triangle $A B C$. We observe that
$$
\frac{\mathrm{BF}}{\mathrm{BC}}=\frac{|\mathrm{ABF}|}{|\mathrm{ABC}|}=\frac{|\mathrm{ABO}|}{|\mathrm{ABC}|}
$$
because triangles $A B F$ and $A B C$ with bases $B F$ and $B C$ have the same height, and $A B O$ and $A B F$ have the same base $A B$ and two parallel heights of the same length (since, if $\mathrm{O}^{\prime}, \mathrm{F}^{\prime}$ are the feet of the heights, $\mathrm{OO}^{\prime} \mathrm{F}^{\prime} \mathrm{F}$ is a rectangle).
We deduce that
$$
\frac{B F}{B C}+\frac{A E}{A B}+\frac{C D}{A C}=\frac{|A B O|}{|A B C|}+\frac{|A O C|}{|A B C|}+\frac{|O C B|}{|A B C|}=1 .
$$
Second Solution:
Here we will use a slightly more general result than Thales' theorem: the fact that two triangles with the same angles have proportional side lengths (such triangles are called similar).
Let $F^{\prime}$ be the intersection of $[A C]$ and (OF).
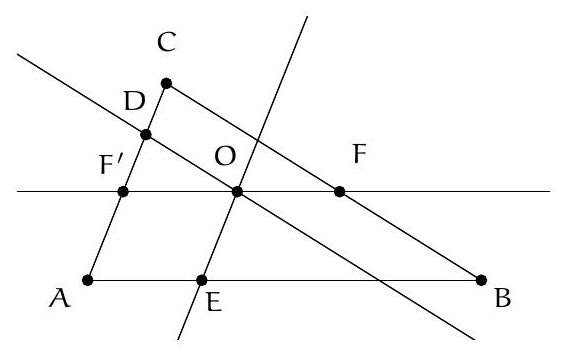
For example, triangles $\mathrm{ABC}$ and $\mathrm{F}^{\prime} \mathrm{CF}$ in the exercise have parallel sides, so they have the same angles and are similar, hence $\frac{B F}{B C}=\frac{A F^{\prime}}{A C}$. (But this can also be shown using Thales' theorem.)
However, triangles $A B C$ and $F^{\prime} O D$ are also similar, so $\frac{F^{\prime} D}{A C}=\frac{F^{\prime} O}{A B}$.
Moreover, $A F O^{\prime} E$ is a parallelogram, so $\mathrm{F}^{\prime} \mathrm{O}=A E$, and finally:
$$
\frac{B F}{B C}+\frac{A E}{A B}+\frac{C D}{A C}=\frac{A F^{\prime}}{A C}+\frac{F^{\prime} D}{A C}+\frac{C D}{A C}=1
$$
Exercise 3. Consider a number $N$ that can be written in the form $30 x 070 y 03$, where $x$ and $y$ are digits between 0 and 9. For which values of $(\mathrm{x}, \mathrm{y})$ is the integer $N$ divisible by 37?
Solution to Exercise 3 We can write $N=300070003+1000000 x+100 y$. Since $100=37 \times 3-11$ and $1000=37 \times 30-110=37 \times 27+1$, we have $1000000=1000^{2}=37 \times (37 \times 27^{2}+2 \times 27)+1$ (by double distributivity).
Since 37 divides $N$, 37 also divides $300070003+x-11 y$. By performing the Euclidean division of 300070003 by 37, we find that $300070003=37 \times 8110000+3$.
In short, 37 divides $N$ if and only if it divides $3+x-11 y$, which is an integer between 12 (if $x=9$ and $y=0$) and -96 (if $x=0$ and $y=9$). Therefore, there are three possibilities:
- We have $3+x-11 y=0$, i.e., $y=1$ and $x=8$;
- We have $3+x-11 y=-37$, so $y=4$ and $x=4$;
- We have $3+x-11 y=-74$, so $y=7$ and $x=0$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Exercise 8. Calculate
$$
\sqrt{7+\sqrt{1+\sqrt{7+\sqrt{1+\sqrt{7+\sqrt{1+\sqrt{7+\sqrt{3+\sqrt{1}}}}}}}}}
$$
Only a numerical answer is expected here.
|
Solution to exercise 8 We notice the following chain of simplifications: $\sqrt{3+\sqrt{1}}=2$ then $\sqrt{7+\sqrt{3+\sqrt{1}}}=\sqrt{7+2}=3$ then $\sqrt{1+\sqrt{7+\sqrt{3+\sqrt{1}}}}=\sqrt{1+3}=2$, and so on...
Step by step, we deduce that any expression of the type $\sqrt{1+\sqrt{7+\sqrt{1+\sqrt{\cdots}}}}$ equals 2 and that any expression of the type $\sqrt{7+\sqrt{1+\sqrt{7+\sqrt{\cdots}}}}$ equals 3, regardless of the number of square roots, provided that $4=3+\sqrt{1}$ is under the last radical.
Since a 7 is found in the sum under the first radical, the answer is therefore 3.
Comment from the graders: Overall, students were not misled by the nesting of all the square roots and performed very well on this exercise. However, it is worth noting that many students wrote down the result without any justification: as mentioned in the instructions, this risks a direct 0 in case of an incorrect answer, it is better to justify the answer to some extent to avoid disappointment in case of a calculation error.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 4. A number appears on a computer screen. It is known that if $x$ appears on the screen, the number $x^{2}-2 x+1$ appears right after. If the first number to appear is 2, what is the 2020th number to appear?
|
Solution to Exercise 4 Let's start by looking at the first values displayed by the computer:
$\triangleright$ The first number is 2.
$\triangleright$ The second number is $2^{2}-2 \times 2+1=1$
$\triangleright$ The third number is $1^{2}-2 \times 1+1=1-2+1=0$
$\triangleright$ The fourth number is $0^{2}-2 \times 0+1=1$
$\triangleright$ The fifth number is $1^{2}-2 \times 1+1=1-2+1=0$
$\triangleright$ The sixth number is $0^{2}-2 \times 0+1=1$
$\triangleright$ The seventh number is $1^{2}-2 \times 1+1=1-2+1=0$
We see that the numbers that appear are in the order $2,1,0,1,0,1,0$. Since after a 0 there is necessarily $0^{2}-2 \times 0+1=1$ and after a 1 there is necessarily $1^{2}-2 \times 1+1=1-2+1=0$, we will have an alternation of 0 and 1. Since 1 appears in second place, all the numbers appearing at an even rank will be 1s, so the 2020th number is 1.
Comment from the graders We congratulate the students who have largely succeeded in this exercise. The few errors observed are mainly calculation errors or rank shifts in the numbers displayed. For example, some students considered that the rank of the first number to appear on the screen was rank 0, while it is rank 1. To avoid this mistake, some students used a table, which was greatly appreciated. We invite students to be vigilant about this kind of error, which has sometimes caused a lot of damage, and not to rush through the exercises, always checking the reasoning used.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Exercise 6.
1) Alice wants to color the integers between 2 and 8 (inclusive) using $k$ colors. She wishes that if $m$ and $n$ are integers between 2 and 8 such that $m$ is a multiple of $n$ and $m \neq n$, then $m$ and $n$ are of different colors. Determine the smallest integer $k$ for which Alice can color the integers $2,3, \ldots, 8$ using $k$ colors.
2) Alice wants to color the integers between 2 and 31 (inclusive) using $k$ colors. She wishes that if $m$ and $n$ are integers between 2 and 31 such that $m$ is a multiple of $n$ and $m \neq n$, then $m$ and $n$ are of different colors. Determine the smallest integer $k$ for which Alice can color the integers $2,3, \ldots, 31$ using $k$ colors.
|
Solution alternative $n^{\circ} 1$ We show, as in the previous case, that for the first question, at least 3 colors are needed and at least 4 in the second.
We propose here to generalize the previous coloring: we construct a coloring with the optimal number of colors to color the integers from 2 to $r$, with $r \geqslant 2$. Let $n \geqslant 2$, and let $n=p_{1}^{a_{1}} \times \cdots \times p_{k}^{a_{k}}$ be its prime factorization. We will color $n$ with the color $a_{1}+\cdots+a_{k}$ (note that since $n \geqslant 2$, we have $a_{1}+\cdots+a_{k} \geqslant 1$). Let's show that this coloring is correct: let $m \neq n$ be two integers such that $m$ divides $n$. Let $n=p_{1}^{a_{1}} \times \cdots \times p_{k}^{a_{k}}$ be its prime factorization. $m$ can necessarily be written in the form $m=p_{1}^{b_{1}} \times \cdots \times p_{k}^{b_{k}}$ with $b_{1} \leqslant a_{1}, \ldots b_{k} \leqslant a_{k}$. Since $m \neq n$, there must exist some $i$ such that $a_{i} \neq b_{i}$, hence $a_{i}>b_{i}$. Thus, we must have $a_{1}+\cdots+a_{k}>b_{1}+\cdots+b_{k}$, so $m$ and $n$ are indeed of different colors.
If $n \leqslant 8$ and $n=p_{1}^{a_{1}} \times \cdots \times p_{k}^{a_{k}}$, then $2^{3}=8 \geqslant n \geqslant 2^{a_{1}+\cdots+a_{k}}$ so $a_{1}+\cdots+a_{k} \leqslant 3$. The coloring uses at most 3 colors for the integers from 2 to 8, so for the first question, the minimal $k$ is 3.
If $n \leqslant 31$ and $n=p_{1}^{a_{1}} \times \cdots \times p_{k}^{a_{k}}$, then $2^{5}=32>n \geqslant 2^{a_{1}+\cdots+a_{k}}$ so $a_{1}+\cdots+a_{k}<5$ and since $a_{1}+\cdots+a_{k}$ is an integer, we have $a_{1}+\cdots+a_{k} \leqslant 4$. The coloring uses at most 4 colors for the integers from 2 to 31, so for the second question, the minimal $k$ is 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Exercise 11.
1) Alice wants to color the integers between 2 and 8 (inclusive) using $k$ colors. She wishes that if $m$ and $n$ are integers between 2 and 8 such that $m$ is a multiple of $n$ and $m \neq n$, then $m$ and $n$ are of different colors. Determine the smallest integer $k$ for which Alice can color the integers $2,3, \ldots, 8$ using $k$ colors.
2) Alice wants to color the integers between 2 and 31 (inclusive) using $k$ colors. She wishes that if $m$ and $n$ are integers between 2 and 31 such that $m$ is a multiple of $n$ and $m \neq n$, then $m$ and $n$ are of different colors. Determine the smallest integer $k$ for which Alice can color the integers $2,3, \ldots, 31$ using $k$ colors.
|
Solution alternative $n^{\circ} 1$ We show, as in the previous case, that for the first question, at least 3 colors are needed and at least 4 in the second.
We propose here to generalize the previous coloring: we construct a coloring with the optimal number of colors to color the integers from 2 to $r$, with $r \geqslant 2$. Let $n \geqslant 2$, and let $n=p_{1}^{a_{1}} \times \cdots \times p_{k}^{a_{k}}$ be its prime factorization. We will color $n$ with the color $a_{1}+\cdots+a_{k}$ (note that since $n \geqslant 2$, we have $a_{1}+\cdots+a_{k} \geqslant 1$). Let's show that this coloring is correct: let $m \neq n$ be two integers such that $m$ divides $n$. Let $n=p_{1}^{a_{1}} \times \cdots \times p_{k}^{a_{k}}$ be its prime factorization. $m$ can necessarily be written in the form $m=p_{1}^{b_{1}} \times \cdots \times p_{k}^{b_{k}}$ with $b_{1} \leqslant a_{1}, \ldots b_{k} \leqslant a_{k}$. Since $m \neq n$, there must exist some $i$ such that $a_{i} \neq b_{i}$, hence $a_{i}>b_{i}$. Thus, we must have $a_{1}+\cdots+a_{k}>b_{1}+\cdots+b_{k}$, so $m$ and $n$ are indeed of different colors.
If $n \leqslant 8$ and $n=p_{1}^{a_{1}} \times \cdots \times p_{k}^{a_{k}}$, then $2^{3}=8 \geqslant n \geqslant 2^{a_{1}+\cdots+a_{k}}$ so $a_{1}+\cdots+a_{k} \leqslant 3$. The coloring uses at most 3 colors for the integers from 2 to 8, so for the first question, the minimal $k$ is 3.
If $n \leqslant 31$ and $n=p_{1}^{a_{1}} \times \cdots \times p_{k}^{a_{k}}$, then $2^{5}=32>n \geqslant 2^{a_{1}+\cdots+a_{k}}$ so $a_{1}+\cdots+a_{k}<5$ and since $a_{1}+\cdots+a_{k}$ is an integer, we have $a_{1}+\cdots+a_{k} \leqslant 4$. The coloring uses at most 4 colors for the integers from 2 to 31, so for the second question, the minimal $k$ is 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 2. In a deck of cards consisting only of red cards and black cards, there are 2 times as many black cards as red cards. If 4 black cards are added, there are then 3 times as many black cards as red cards. How many cards did the deck have before adding the 4 black cards?
Only a numerical answer is expected here.
|
Solution to Exercise 2 Let $r$ be the number of red cards and $n$ be the number of black cards in the initial deck. By hypothesis, we have $n=2 r$. After adding 4 black cards, there are $n+4$ black cards in the deck, and by hypothesis, we have $n+4=3 r$. Thus, $4=3 r-n=3 r-2 r=r$ and $n=2 \times 4=8$. Initially, the deck contains $r+n=4+8=12$ cards.
Graders' Comment: Very well solved exercise! However, be sure to read the instructions carefully: the question here was the total number of cards and not the number of black cards...
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 9. In a deck of cards consisting only of red cards and black cards, there are 2 times as many black cards as red cards. If 4 black cards are added, there are then 3 times as many black cards as red cards. How many cards did the deck have before adding the 4 black cards?
Only a numerical answer is expected here.
|
Solution to Exercise 9 Let $r$ be the number of red cards and $n$ be the number of black cards in the initial deck. By hypothesis, we have $n=2 r$. After adding 4 black cards, there are $n+4$ black cards in the deck, and by hypothesis, we have $n+4=3 r$. Thus, $4=3 r-n=3 r-2 r=r$ and $n=2 \times 4=8$. Initially, the deck contains $r+n=4+8=12$ cards.
Graders' comments: The exercise was generally very well done. It's a pity that some students only found the number of black cards or made mistakes in their conclusion.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 4. Consider a large square grid with side length 10, divided into small squares with side length 1. Two small squares are said to be neighbors if they share a common side. On each of the small squares, a positive real number is inscribed. Furthermore, 5 frogs move on the grid and can cover one small square each. Two frogs never cover the same square. Between two moments, each frog jumps from the square where it is to a neighboring square.
It is assumed that the sum of the visible numbers is 10 at time 1, then $10^{2}$ at time 2, then $10^{3}$ at time 3, and so on until time $k$ where the sum is $10^{k}$. What is the largest possible value of $\mathrm{k}$?
|
Solution to Exercise 4: We will show that the largest possible value of $k$ is 6. First, let's verify that 6 is indeed achievable. For this, we isolate a $2 \times 3$ rectangle in the top left corner of the grid. On all the cells that are not in this rectangle, we write the number 0. On the cells of the rectangle, we write the numbers $10, 100, \ldots, 10^{6}$ as follows:
| $10^{3}$ | $10^{4}$ |
| :--- | :--- |
| $10^{2}$ | $10^{5}$ |
| 10 | $10^{6}$ |
At time 1, the frogs occupy the 5 cells bearing the numbers $10^{2}, \ldots, 10^{6}$, so only the number 10 is visible (along with all the 0s). Then at time 2, the frogs rotate clockwise, so $10^{2}$ is visible (along with the 0s), and so on... We then have a configuration as desired with $k=6$.
Now let's show that $k>6$ is impossible. Suppose $k \geq 7$. When moving from time 1 to time 2, at most 5 new numbers are revealed (the 5 that were covered at time 1), and the sum of the visible numbers increases by $10^{2}-10=90$. Therefore, the sum of the numbers discovered between time 1 and time 2 is at least 90. Since there are at most 5 numbers discovered, at least one is greater than $90 / 5=18$. On the other hand, the sum of the visible numbers at time 2 is 100, so the discovered numbers do not exceed 100, meaning there is a cell bearing a number between 18 and 100. By reasoning similarly between times 2 and 3, then 3 and 4, and so on until 6 and 7, we find a cell bearing a number between 180 and 1000, then between 1800 and 10000, and so on up to $18 \times 10^{5}$ and $10^{7}$. We have thus found 6 cells greater than 18. Since there are only 5 frogs at time 1, at least one of these cells was visible at time 1, so the sum was at least 18, leading to a contradiction.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 1. Fred and Sarah are the eldest of the same large family. Fred has twice as few brothers as sisters, while Sarah has as many sisters as brothers.
How many children are there in this family?
|
Solution to Exercise 1 Let $\mathrm{f}$ be the number of girls and $\mathrm{g}$ be the number of boys in this family.
Fred therefore has $g-1$ brothers and $f$ sisters, and the text states that $f=2(g-1)$. On the other hand, Sarah has $\mathrm{f}-1$ sisters and $\mathrm{g}$ brothers, and the statement tells us that $\mathrm{f}-1=\mathrm{g}$.
By substituting $g$ with $\mathrm{f}-1$ in the first equation, we get $\mathrm{f}=2 \cdot(\mathrm{f}-2)$, which leads to $\mathrm{f}=4$ and then $\mathrm{g}=\mathrm{f}-1=3$, resulting in a total of 7 children.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 6. For any strictly positive integer $m$, we call the first digit of $m$ the leftmost digit in its decimal representation. Let $n$ be a strictly positive integer. Suppose that the two integers $2^{n}$ and $5^{n}$ have the same first digit. Show that this same first digit is 3.
|
Solution to Exercise 6 Let $a$ be the first digit common to the decimal representation of $2^{n}$ and $5^{n}$.

verified.
The hypothesis of the statement can then be translated as follows: we have an integer $k \geqslant 0$ and an integer $\ell \geqslant 1$ satisfying the two inequalities:
$$
\begin{aligned}
& a \times 10^{k} \leqslant 2^{n} < (a+1) \times 10^{k} \\
& a \times 10^{\ell} \leqslant 5^{n} < (a+1) \times 10^{\ell}
\end{aligned}
$$
On the other hand, we verify that, since $a \leqslant 9$, we have $(a+1)^{2} \leqslant(9+1)^{2}=100$. Thus, $10^{n-k-\ell}$ is a power of 10 strictly less than 100 and strictly greater than 1. We deduce that $10^{n-k-\ell}=10$. Since $a^{2}0$.
The idea of this solution is to look at the product $\left(a \times 10^{k}+x\right)\left(a \times 10^{\ell}+y\right)=2^{n} \times 5^{n}=10^{n}$ and to control the carry generated by $x$ and $y$. Indeed, we have:
$$
10^{n}=a^{2} \times 10^{k+\ell}+x \times a \times 10^{\ell}+y \times a \times 10^{k}+x y
$$
We are interested in the first digit of the right-hand side. This is 1 on the one hand since the right-hand side is a power of 10. On the other hand, since $1 \leqslant a \leqslant 9$, we have $x \times a \times 10^{\ell}0$. The interval $\llbracket 10^{k+\ell}+1,28 \times 10^{k+\ell+1} \rrbracket$ contains a unique power of 10, namely $10^{k+\ell+1}$. But if $a \in\{1,2\}$, then
$10^{k+\ell+1}=\left(a \times 10^{k}+x\right)\left(a \times 10^{\ell}+y\right)<a^{2} \times 10^{k+\ell}+2 x \times 10^{\ell}+2 y \times 10^{k}+x y<4 \times 10^{k+\ell}+5 \times 10^{k+\ell}=9 \times 10^{k+\ell}$
which is absurd. Therefore, we have $a=3$ as desired.
Comment from the graders The exercise was difficult and was solved by few students. Many students were content to find an example of a value of $n$ (for example $n=5$) where $2^{n}$ and $5^{n}$ had the same first digit, and to note that it was 3. This is by no means sufficient, the statement required a proof valid for all $n$ satisfying the condition. Students who attempted to set up inequalities were appreciated, but they still needed to be careful with the various inequalities given.
|
3
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 7. A set of $n$ non-zero and distinct real numbers is said to be regular if, when these numbers are written on the board in ascending order, the difference between two adjacent numbers is always the same, regardless of the two adjacent numbers chosen. For example, the set $\{4,18,-3,11\}$ is regular because if the numbers are written in ascending order, $18-11=11-4=4-(-3)$. A set $A$ of non-zero and distinct real numbers is said to be super-regular if it is regular and the set formed by the inverses of the numbers in set $A$ is also regular.
What is the largest integer $n$ such that there exists a super-regular set of $n$ non-zero and distinct real numbers?
|
## Solution to Exercise 7
Answer: $n=4$
In this exercise, we aim to demonstrate that 4 is the largest integer satisfying the property stated in the problem. The solution necessarily consists of two parts. First, we show that if a super-regular set has size $k$, then $k \leqslant 4$; this step is called the analysis. Second, we show that there indeed exists a super-regular set of size 4; this step is called the construction or synthesis.
In the following, we call the common difference of a regular set the difference between the largest number and the second largest number in that set.
## Analysis:
Step 1: We start by showing that there does not exist a super-regular set of size 3 where all elements have the same sign.
By contradiction, we assume a super-regular set $A=\{a, b, c\}$ such that $a < b < c$ and all elements are strictly positive. Let $r = b - a > 0$ be the common difference of $A$. Then $c - b = r$, so $c = b + r$ and $b = a + r$.
We define $B=\left\{\frac{1}{a}, \frac{1}{a+r}, \frac{1}{a+2r}\right\}$ as the set composed of the inverses of the elements of $A$. We verify that $\frac{1}{a+2r} < \frac{1}{a+r} < \frac{1}{a}$. The common difference of $B$ is given by:
$$
\frac{1}{a} - \frac{1}{a+r} = \frac{1}{a+2r} - \frac{1}{a+r}
$$
After simplification, this gives the relation $2a + 3r = 0$. Taking $a = -1$, we obtain the set $A = \{-3, -1, 1, 3\}$, which we verify is regular with a common difference of 2, and the set $B = \left\{-\frac{1}{3}, -1, 1, \frac{1}{3}\right\}$ composed of the inverses of the elements of $A$ is also regular with a common difference of $\frac{2}{3}$. Therefore, the set $A$ is super-regular, providing an example of a super-regular set of size 4.
Remark: The reasoning presented above may seem difficult to intuit if one does not already know the value of $n$. Here, a strategy to tackle the problem is to look for a super-regular set of size 3, and then a super-regular set of size 4. Generally, looking for small configurations that satisfy the properties of a problem is a good way to approach it and make conjectures.
Comment from the graders: Very few students had the time to tackle the problem and score points: only about ten students scored at least one point, and no one solved it entirely. It was relevant to consider the case where all the real numbers in the set have the same sign, as long as one kept in mind that this was not the only case. Note that many students confuse inverse and opposite: the opposite of 2 is -2, and its inverse is $\frac{1}{2}$.
High school exercises
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 12. For any strictly positive integer $m$, we call the first digit of $m$ the leftmost digit in its decimal representation. Let $n$ be a strictly positive integer. Suppose that the two integers $2^{n}$ and $5^{n}$ have the same first digit. Show that this same first digit is 3.
|
Solution to Exercise 12 Let $a$ be the first digit common to the decimal representation of $2^{n}$ and $5^{n}$.

verified.
The hypothesis of the statement can then be translated as follows: we have an integer $k \geqslant 0$ and an integer $\ell \geqslant 1$ satisfying the two inequalities:
$$
\begin{aligned}
& a \times 10^{k} \leqslant 2^{n} < (a+1) \times 10^{k} \\
& a \times 10^{\ell} \leqslant 5^{n} < (a+1) \times 10^{\ell}
\end{aligned}
$$
On the other hand, we verify that, since $a \leqslant 9$, we have $(a+1)^{2} \leqslant (9+1)^{2} = 100$. Thus, $10^{n-k-\ell}$ is a power of 10 strictly less than 100 and strictly greater than 1. We deduce that $10^{n-k-\ell} = 10$. Since $a^{2} \leqslant 81$, we have:
$$
a^{2} \times 10^{k+\ell} \leqslant 81 \times 10^{k+\ell} < 100 \times 10^{k+\ell} = 10^{k+\ell+2}
$$
The idea of this solution is to look at the product $\left(a \times 10^{k} + x\right)\left(a \times 10^{\ell} + y\right) = 2^{n} \times 5^{n} = 10^{n}$ and control the carry generated by $x$ and $y$. We indeed have:
$$
10^{n} = a^{2} \times 10^{k+\ell} + x \times a \times 10^{\ell} + y \times a \times 10^{k} + x y
$$
We are interested in the first digit of the right-hand side. This digit is 1 on the one hand since the right-hand side is a power of 10. On the other hand, since $1 \leqslant a \leqslant 9$, we have $x \times a \times 10^{\ell} < 10 \times 9 \times 10^{\ell} = 90 \times 10^{\ell}$ and $y \times a \times 10^{k} < 10 \times 9 \times 10^{k} = 90 \times 10^{k}$. Therefore, the first digit of the right-hand side is determined by $a^{2} \times 10^{k+\ell}$, which must be 1. This implies that $a^{2} = 1$ or $a^{2} = 9$. Since $a \leqslant 9$, the only possible value for $a$ is 3.
The interval $\llbracket 10^{k+\ell} + 1, 28 \times 10^{k+\ell+1} \rrbracket$ contains a unique power of 10, namely $10^{k+\ell+1}$. But if $a \in \{1, 2\}$, then
$$
10^{k+\ell+1} = \left(a \times 10^{k} + x\right)\left(a \times 10^{\ell} + y\right) < a^{2} \times 10^{k+\ell} + 2 x \times 10^{\ell} + 2 y \times 10^{k} + x y < 4 \times 10^{k+\ell} + 5 \times 10^{k+\ell} = 9 \times 10^{k+\ell}
$$
which is absurd. Therefore, $a = 3$ as required.
Comment from the graders: Many students had the right intuition for this problem: to look at the product of the two numbers and hope that the product of the first digits corresponds to the first digit of the product. We expected students to quantify this reasoning and make it rigorous. Those who made an effort in this direction were rewarded. A significant number of students who understood the problem also lost points for being too quick in the case where the first common digit of $2^{n}$ and $5^{n}$ is 1. Finally, a large number of students were content to note that the statement is verified for $n=5$. While it is a good idea to look at small cases, it does not constitute a relevant argument for treating the general case.
|
3
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 13. A set of $n$ non-zero and distinct real numbers is said to be regular if, when these numbers are written on the board in ascending order, the difference between two adjacent numbers is always the same, regardless of the two adjacent numbers chosen. For example, the set $\{4,18,-3,11\}$ is regular because if the numbers are written in ascending order, $18-11=11-4=4-(-3)$. A set $A$ of non-zero and distinct real numbers is said to be super-regular if it is regular and the set formed by the inverses of the numbers in set $A$ is also regular.
What is the largest integer $n$ such that there exists a super-regular set of $n$ non-zero and distinct real numbers?
|
## Solution to Exercise 13
Answer: $n=4$
In this exercise, we aim to demonstrate that 4 is the largest integer satisfying the property stated in the problem. The solution necessarily includes two parts. First, we show that if a super-regular set has size $k$, then $k \leqslant 4$; this step is called the analysis. Second, we show that there indeed exists a super-regular set of size 4; this step is called the construction or synthesis.
In the following, we call the common difference of a regular set the difference between the largest number and the second largest number in that set.
## Analysis:
We start by showing that there does not exist a super-regular set of size 3 whose elements are all of the same sign.
By contradiction, we assume a super-regular set $A=\{a, b, c\}$ such that $a0$, meaning all three elements are strictly positive. We set $r=b-a>0$ as the common difference of $A$. Then, $c-b=r$, so $c=a+2r$ and $b=a+r$.
We set $B=\left\{\frac{1}{a}, \frac{1}{a+r}, \frac{1}{a+2r}\right\}$ as the set composed of the inverses of the elements of $A$. We verify that $\frac{1}{a+2r}0$ and $a1 / b>1 / c$. Moreover, the inequality $1 / a>1 / b>1 / c$ is false precisely when the reals are not of the same sign: if $a=-1, b=1, c=3$, it does not hold.
Therefore, many students used $b-a=c-b$ and $1 / b-1 / a=1 / c-1 / b$ to obtain $a=c$, and received 2 points if the inequality $1 / a>1 / b>1 / c$ was mentioned, 1 point otherwise, as they missed the difficulty of the problem.
In fact, it was necessary to use the previous reasoning for a super-regular set of any size and show that having three consecutive elements of the same sign was impossible. Very few students understood this part of the problem, and those who did were often able to complete the exercise.
Note that many students confuse inverse and opposite: the opposite of 2 is -2, its inverse is $1 / 2$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 14. Let $A B C D$ be a rectangle and $M$ the midpoint of the segment $[C D]$. A line parallel to $(A B)$ intersects the segments $[A D],[A M],[B M],[B C]$ at points $P, Q, R$ and $S$, respectively. The line $(D R)$ intersects the segment $[A M]$ at $X$ and the segment $[B C]$ at $Y$. If $D X=6$ and $X R=4$, what is the length of the segment $[R Y]$?
|
## Solution alternative $n^{\circ} 1$
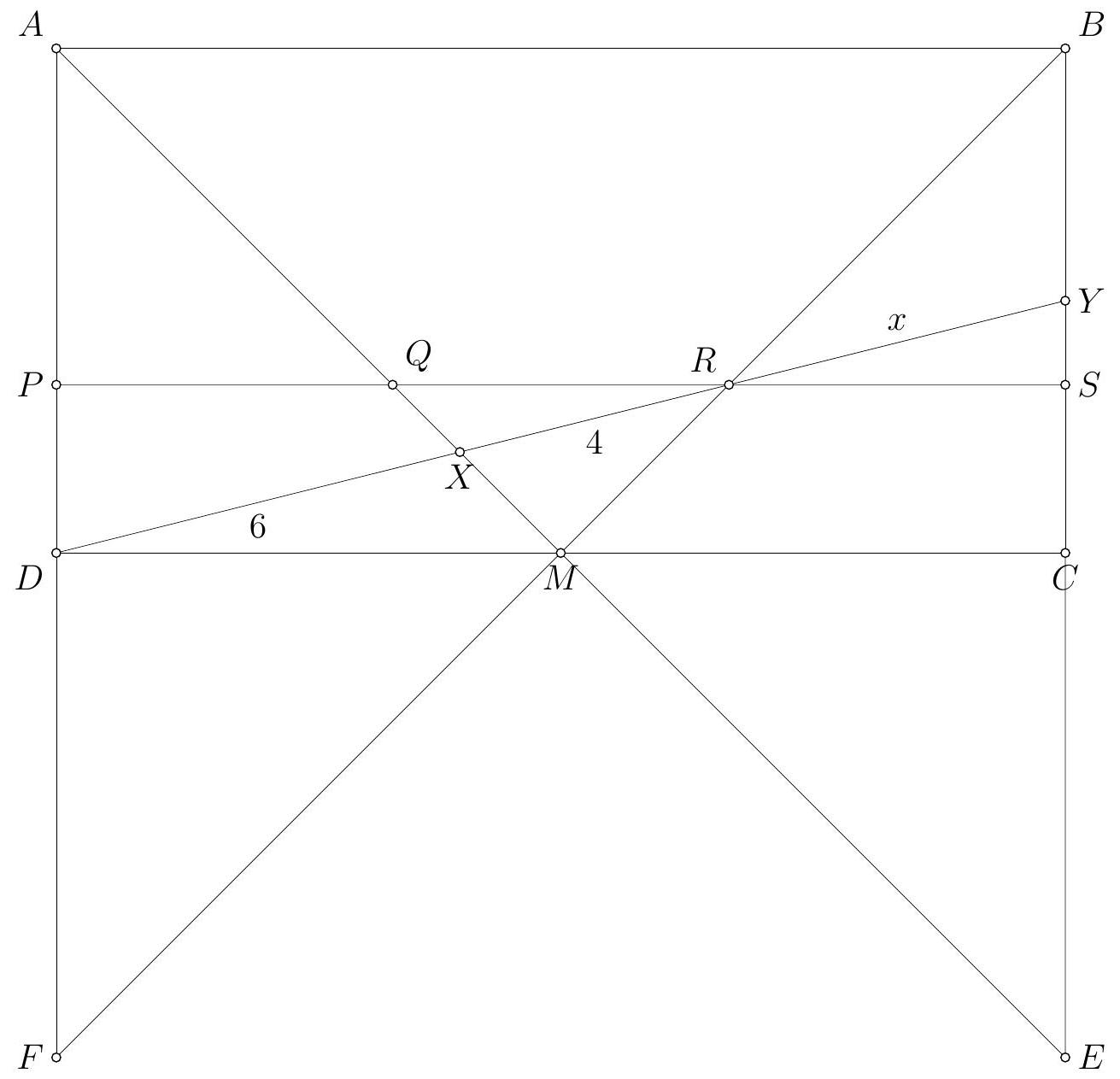
We propose a solution using Thales' theorem in two other "butterflies."
We introduce $E$ as the intersection point of the lines $(A M)$ and $(B C)$, and $F$ as the intersection point of the lines $(B M)$ and $(A D)$. Since $M C = \frac{1}{2} A B$, the line $(M C)$ is a midline for the triangle $A B E$. Thus, $B C = C E$ and $A M = M E$. Similarly, $A D = D F$ and $B M = M F$.
We now set $x = R Y$ and will seek two equations involving $X$. On the one hand, according to Thales' theorem in the butterfly $B Y R D F$, we have
$$
\frac{x}{10} = \frac{R Y}{R D} = \frac{B Y}{D F} = \frac{B Y}{A D}
$$
On the other hand, according to Thales' theorem in the butterfly $A D X Y E$, we find
$$
\frac{4 + x}{6} = \frac{X Y}{D X} = \frac{Y E}{A D} = \frac{B E - B Y}{A D} = 2 - \frac{B Y}{A D}
$$
By combining these two equations, we get
$$
\frac{2}{3} + \frac{x}{6} = 2 - \frac{x}{10}
$$
which has the solution $x = 5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 6. Determine all integers $n \geqslant 3$ such that it is possible to place $n$ distinct real numbers on a circle so that each of these numbers is the product of its two neighbors.
|
Solution to Exercise 6: Let $a_{1}, a_{2}, \ldots, a_{n}$ be these numbers, with the convention that $a_{n+1}=a_{1}, a_{n+2}=$ $a_{2}$, etc. By hypothesis, we have $a_{i} a_{i+2}=a_{i+1}$ and $a_{i+1} a_{i+3}=a_{i+2}$ for all $i$. Multiplying these two equalities, we get $a_{i} a_{i+1} a_{i+2} a_{i+3}=a_{i+1} a_{i+2}$, hence $a_{i} a_{i+3}=1$. Similarly, $a_{i+3} a_{i+6}=1$, so $a_{i}=a_{i+6}$. Since the integers are all distinct, this implies that 6 is a multiple of $n$, so $n=3$ or $n=6$.
If $n=3$, then $a_{i} a_{i+3}=1$ gives that $a_{i}^{2}=1$ for all $i$, so $a_{i}= \pm 1$. Therefore, at least two of these three numbers are equal, either to 1 or to -1. This contradicts the fact that the numbers are all distinct.
If $\mathrm{n}=6$ then it is possible, for example, with the numbers $2,3, \frac{3}{2}, \frac{1}{2}, \frac{1}{3}, \frac{2}{3}$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 8. Determine the number of natural numbers $n>2015$ such that $n$ is divisible by $n-2015$.
|
Solution to exercise 8 Let's write $n=2015+k$. We are looking for the number of positive integers $k$ such that $2015+k$ is divisible by $k$. This is equivalent to $k$ dividing $2015=5 \times 13 \times 31$. The divisors of 2015 are numbers of the form $5^{a} 13^{b} 31^{c}$ with $a, b, c$ equal to 0 or 1: there are 8 of them.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 5. In a country, there are 10 cities. Any two cities are always directly connected by exactly one one-way road. The roads never cross, with some passing over others using bridges.
Unfortunately, the officials at the Ministry of Traffic Direction, apparently distracted, have oriented the roads in such a way that if one leaves any city, it is then impossible to return to it, even by passing through several other cities and roads.
a) Prove that there exists a city from which one cannot leave.
b) Prove that there exists a city from which one can directly reach all other cities (i.e., without passing through other cities).
c) How many, at a minimum, road orientations need to be changed so that one can travel from any city to any other (possibly in several steps)?
|
Solution to exercise 5 a) Starting from any city $V_{1}$. We visit successive cities $V_{2}, V_{3}$, etc. Since we can never return to a city already visited, after a maximum of 10 steps, we are inevitably stuck in a city.
b) Starting from any city $V_{1}$. We visit successive cities $V_{2}, V_{3}$, etc., but only by going against the one-way streets. It is impossible to return to a city already visited, otherwise by retracing the path in the opposite direction, we could visit the same city twice while respecting the direction of traffic. After a maximum of 10 steps, we reach a city from which we cannot go against any one-way street, hence from which we can directly reach all other cities.
c) Let A be a city from which we cannot leave, and B a city from which we can directly reach all others. We change the direction of the road between B and $A$.
Let $X$ and $Y$ be two cities.
If $X=B$ and $Y \neq A$, there is a direct road from $X$ to $Y$.
If $X=B$ and $Y=A$, we can go from $X$ to $Y$ by taking any path $X \rightarrow Z \rightarrow Y$.
If $X=A$ and $Y=B$, there is a direct road from $X$ to $Y$.
If $X=A$ and $Y \neq B$, then there is a path $X \rightarrow B \rightarrow Y$.
If $X \neq A, X \neq B$ and $Y=A$ then there is a direct road between $X$ and $Y$.
If $X \neq A, X \neq B$ and $Y=B$ then there is a path $X \rightarrow B \rightarrow Y$.
If $X$ and $Y$ are different from $A$ and $B$ then there is a path $X \rightarrow A \rightarrow B \rightarrow Y$.
|
1
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 10. 22 cards bearing the numbers $1,2, \ldots, 22$ are on the table. Alcindor and Benoît take turns removing a card of their choice from the table, until there are none left. Alcindor goes first. Then each calculates the units digit of the sum of their cards. The winner is the one with the highest result.
Does one of the two players have a sure way to win? If so, determine which one.
|
Solution to Exercise 10: Let's show that Alcindor can win for sure.
First, we note that the outcome of the game is not affected if we replace the values of the cards with their units digit. All cards are then in pairs, except for the cards 1 and 2, which are in triples.
Alcindor chooses the following strategy: he starts by drawing the card 2. Then, each time Benoît takes a card, he chooses a card of the same value if possible; if none are left, he chooses any card.
The game proceeds as follows, from the second move: Benoît and Alcindor take turns picking cards of the same value, until Benoît draws the last 1. Then Alcindor draws a card of any value $v$. Benoît and Alcindor take turns picking cards of the same value, until Benoît draws the last $v$, and so on.
At the end, Alcindor has two "2" cards and one card of each of the other values, while Benoît has two "1" cards and one card of each of the other values. They obtain respective scores of 7 and 6, so Alcindor wins.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 10. Using the numbers from 1 to 22 exactly once each, Antoine writes 11 fractions: for example, he can write the fractions $\frac{10}{2}, \frac{4}{3}, \frac{15}{5}, \frac{7}{6}, \frac{8}{9}, \frac{11}{19}, \frac{12}{14}, \frac{13}{17}, \frac{22}{21}, \frac{18}{16}$, and $\frac{20}{1}$.
Antoine wishes to have as many fractions with integer values as possible among the fractions written: in the previous example, he wrote three fractions with integer values: $\frac{10}{2}=5, \frac{15}{5}=3$, and $\frac{20}{1}=20$. What is the maximum number of fractions that can have integer values?
|
Solution to Exercise 10 First, it is possible to form 10 whole numbers with the fractions
$$
\left\{\frac{22}{11}, \frac{20}{10}, \frac{18}{9}, \frac{16}{8}, \frac{14}{7}, \frac{12}{6}, \frac{21}{3}, \frac{19}{1}, \frac{15}{5}, \frac{4}{2}, \frac{17}{13}\right\}
$$
Furthermore, it is impossible to have 11 whole fractions. Indeed, there are 3 prime numbers that have no smaller multiples than 22: 19, 17, and 13. Thus, the only way for any of these three numbers to form a whole fraction is with the number 1, which can only be used with one of these three numbers.
Graders' Comments: The exercise was generally very well done. However, some students, although noting the importance of 13, 17, and 19, did not think to combine two of them in the same fraction, and therefore only obtained 9 whole fractions, which is a pity. Other students were content with a configuration of 10 fractions without justifying that it is optimal. Finally, we remind you that $\frac{19}{8}$ is definitely not an integer.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 2. Over a certain number of days, it was observed that on each day it rained in the morning, it was sunny in the afternoon, and that on each day it rained in the afternoon, it had been sunny in the morning.
During the observation period, it rained on 15 days, and it was sunny 8 mornings and 13 afternoons.
How many mornings did it rain?
|
## Solution to Exercise 2
According to the statement, it did not rain for a full day during the period in question. Since it rained for 15 half-days and was sunny for 21 half-days, this gives a total of 36 half-days, and allows us to assert that we are in fact considering a period of 18 days.
Since it was sunny on 8 of the 18 mornings, there were therefore 10 rainy mornings.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 8. Let a be a strictly positive integer, such that $a^{3}$ has 5 times more positive divisors than a.
How many positive divisors does $a$ have?
|
Solution to Exercise 8
Since the divisors of $1^{3}$ are exactly the same as those of 1, we must have $a \geqslant 2$. Let then $a=p_{1}^{\alpha_{1}} \cdots p_{k}^{\alpha_{k}}$ be the prime factorization of $a$, with $\alpha_{i} \geqslant 1$ for all $i$. The number of positive divisors of $a$ is therefore $\left(\alpha_{1}+1\right) \times \cdots \times\left(\alpha_{k}+1\right)$. Moreover, the prime factorization of $a^{3}$ is then $a^{3}=p_{1}^{3 \alpha_{1}} \cdots p_{k}^{3 \alpha_{k}}$, and the number of positive divisors of $a^{3}$ is therefore $\left(3 \alpha_{1}+1\right) \times \cdots \times\left(3 \alpha_{k}+1\right)$. Thus, the condition in the statement translates to
$$
\left(3 \alpha_{1}+1\right) \times \cdots \times\left(3 \alpha_{k}+1\right)=5\left(\alpha_{1}+1\right) \times \cdots \times\left(\alpha_{k}+1\right)
$$
It is easy to verify that if $x \geqslant 1$, then $3 x+1 \geqslant 2(x+1)$. Therefore, $\left(3 \alpha_{1}+1\right) \times \cdots \times\left(3 \alpha_{k}+1\right) \geqslant 2^{k}\left(\alpha_{1}+1\right) \times \cdots \times\left(\alpha_{k}+1\right)$, and to achieve (1), we need $2^{k} \leqslant 5$. Since $k$ is a strictly positive integer, this means $k=1$ or $k=2$.
For $k=1$, equation (1) reduces to $3 \alpha_{1}+1=5 \alpha_{1}+5$, which is clearly impossible.
For $k=2$, equation (1) becomes $\left(3 \alpha_{1}+1\right)\left(3 \alpha_{2}+1\right)=5\left(\alpha_{1}+1\right)\left(\alpha_{2}+1\right)$, which, after expansion, leads to $2 \alpha_{1}+2 \alpha_{2}-4 \alpha_{1} \alpha_{2}+4=0$, or $\left(2 \alpha_{1}-1\right)\left(2 \alpha_{2}-1\right)=5$. Each of the two factors on the left-hand side are strictly positive integers and 5 is prime. Without loss of generality, we can assume that $\alpha_{1} \leqslant \alpha_{2}$, and it follows that $2 \alpha_{1}-1=1$ and $2 \alpha_{2}-1=5$, or $\alpha_{1}=1$ and $\alpha_{2}=3$.
Finally, $a$ has exactly 8 positive divisors.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 5. In a classroom, there are ten students. Aline writes ten consecutive integers on the board. Each student chooses one of the ten integers written on the board, such that any two students always choose two different integers. Each student then calculates the sum of the nine integers chosen by the other nine students. Each student whose result is a perfect square then receives a gift.
What is the maximum number of students who will receive a gift?
A perfect square is an integer of the form $n^{2}$, where $n$ is a natural number.
|
Solution to Exercise 5 The exercise asks to determine the maximum value of a certain quantity. The reasoning therefore consists of two steps, called analysis and synthesis.
Step 1, the analysis: We show that the number of students receiving a gift is necessarily less than or equal to four, regardless of the numbers chosen by Aline.
Let $n, n+1, \ldots, n+9$ be the ten numbers written on the board and let $S$ be their sum. If one of the integers is erased from the board, the sum of the remaining nine numbers is one of the integers:
$$
S-n, S-n-1, \ldots, S-n-9
$$
which are ten consecutive integers.
We then seek the maximum number of integers that can be perfect squares among ten consecutive integers.
First, since perfect squares are positive integers, a set of ten consecutive integers containing a negative integer has fewer perfect squares than the set $\{0, \ldots, 9\}$. Next, note that among the integers from 0 to 9, there are four perfect squares, which are the integers $0,1,4$ and 9. Suppose there exist ten consecutive positive integers such that at least five of them are perfect squares. Then there exists a positive integer $a$ such that the numbers $a^{2},(a+1)^{2},(a+2)^{2},(a+3)^{2}$ and $(a+4)^{2}$ are among the ten consecutive integers. We then have $9 \geqslant(a+4)^{2}-a^{2}=8 a+16>9$, which is absurd.
Thus, the maximum number of integers that can be perfect squares among the ten integers $S-n, \ldots, S-n-9$ is 4, which means that at most four students will receive a gift.
Step 2, the synthesis: We show that the bound obtained in the analysis is achievable, that is, there exist ten consecutive integers for which the students can arrange to receive four gifts.
For this, we observe that the sum of nine of the ten integers $n, n+1, \ldots, n+9$ is always between
$$
n+(n+1)+\ldots+(n+8)=9 n+36 \quad \text { and } \quad(n+1)+(n+2)+\ldots+(n+9)=9 n+45
$$
Thus, the perfect squares chosen by the students are integers between $9 n+36$ and $9 n+45$. We saw during the analysis that the set $\{0, \ldots, 9\}$ contains 4 perfect squares. We therefore seek $n$ satisfying $9 n+36=0$ and $9 n+45=9$, which leads to $n=-4$.
Thus, if Aline writes the integers
$$
-4,-3,-2,-1,0,1,2,3,4,5
$$
the students can choose the integers $5,4,1$ or -4, so that the sum of the remaining nine integers will be respectively $0,1,4$ and 9.
The largest number of students who can receive a gift is four.
Comment from the graders: The exercise was difficult for many students and was often only partially solved. It consisted of two parts: an analysis to show that it is not possible to do better than 4 gifts, and a synthesis in which it is necessary to explicitly state with which initial integers on the board it is actually possible to obtain 4 gifts. Many students did not take into account the fact that the integers written on the board were relative, i.e., positive or negative, and limited themselves to the positive case. Many students overlooked key arguments, such as the fact that the sums obtained are consecutive, which justifies looking for squares in an interval of size 10. Some attempt to invoke arguments of "density" of squares to try to justify that one must look at small integers to find many squares, but this argument is insufficient. Finally, a surprising proportion of students forget that 0 is a perfect square, which was ultimately not penalized.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 11. In a classroom, there are ten students. Aline writes ten consecutive integers on the board. Each student chooses one of the ten integers written on the board, such that any two students always choose two different integers. Each student then calculates the sum of the nine integers chosen by the other nine students. Each student whose result is a perfect square then receives a gift.
What is the maximum number of students who will receive a gift?
A perfect square is an integer of the form $n^{2}$, where $n$ is a natural number.
|
Solution to Exercise 11 The exercise asks to determine the maximum value of a certain quantity. The reasoning therefore consists of two steps, called analysis and synthesis.
Step 1, the analysis: We show that the number of students receiving a gift is necessarily less than or equal to four, regardless of the numbers chosen by Aline.
Let $n, n+1, \ldots, n+9$ be the ten numbers written on the board and let $S$ be their sum. If one of the integers is erased from the board, the sum of the remaining nine numbers is one of the integers:
$$
S-n, S-n-1, \ldots, S-n-9
$$
which are ten consecutive integers.
We then seek the maximum number of integers that can be perfect squares among ten consecutive integers.
First, since perfect squares are positive integers, a set of ten consecutive integers containing a negative integer contains fewer perfect squares than the set $\{0, \ldots, 9\}$. Next, note that among the integers from 0 to 9, there are four perfect squares, which are the integers $0,1,4$ and 9. Suppose there exist ten consecutive positive integers such that at least five of them are perfect squares. Then there exists a positive integer $a$ such that the numbers $a^{2},(a+1)^{2},(a+2)^{2},(a+3)^{2}$ and $(a+4)^{2}$ are among the ten consecutive integers. We then have $9 \geqslant(a+4)^{2}-a^{2}=8 a+16>9$, which is absurd.
Thus, the maximum number of integers that can be perfect squares among the ten integers $S-n, \ldots, S-n-9$ is 4, which means that at most four students will receive a gift.
Step 2, the synthesis: We show that the bound obtained in the analysis is achievable, that is, there exist ten consecutive integers for which the students can arrange to receive four gifts.
For this, we observe that the sum of nine of the ten integers $n, n+1, \ldots, n+9$ is always between
$$
n+(n+1)+\ldots+(n+8)=9 n+36 \quad \text { and } \quad(n+1)+(n+2)+\ldots+(n+9)=9 n+45
$$
Thus, the perfect squares chosen by the students are integers between $9 n+36$ and $9 n+45$. We saw during the analysis that the set $\{0, \ldots, 9\}$ contains 4 perfect squares. We therefore seek $n$ satisfying $9 n+36=0$ and $9 n+45=9$, which leads to $n=-4$.
Thus, if Aline writes the integers
$$
-4,-3,-2,-1,0,1,2,3,4,5
$$
the students can choose the integers $5,4,1$ or -4, so that the sum of the remaining nine integers will be respectively $0,1,4$ and 9.
The largest number of students who can receive a gift is four.
Comment from the graders: This exercise was approached by most students, who generally understood the substance of it, but it was surprisingly not well done. Most students (more than two-thirds) managed to find the configuration allowing 4 winning students - many students forgot to count 0 as a perfect square.
However, very few students managed to rigorously justify that the interval from 0 to 9 was the interval of 10 consecutive integers containing the most perfect squares. If the grading had taken more account of the ideas than the way they were written, we still expected more care in the justification of the arguments. Thus, the majority of the solutions were incomplete, even though they were awarded 7 points, and few students produced a truly rigorous proof of their assertion. It is a pity to see phrases such as "the squares get further and further apart," "the square function is increasingly increasing," "the squares are increasingly dispersed" replacing calculations, which are the only source of rigor here. We also note vocabulary problems, notably when students claimed that the square function was exponential, to cite just one example.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 1. Seven people dine together every Saturday evening around a round table.
How many times is it possible to dine if everyone wants to have two new neighbors each time?
What is the result for eight people?
|
Solution: Under the conditions stated, at each dinner, a given person has two new neighbors. Therefore, after the second dinner, they will have had four different neighbors, six different neighbors after the third, and eight different neighbors after the fourth, which is not possible: if there are seven people in total, each can only have six different neighbors, which limits the number of dinners that can be organized under the stated conditions to three. The result is the same if there are eight people in total.
It remains to prove that three dinners can be organized so that each person has two new neighbors at each dinner. At the first dinner, the seven people are numbered in order from 1 to 7: 1234567. At the second dinner, compared to the first, they are placed "one person apart": 1357246, and at the third, "one person apart every three": 1473625. It is easy to verify that such a placement works, but it is not the only one.
If an eighth person is added, it is sufficient to insert them so that they also have two new neighbors each time, for example: 12834567 then 13587246 and finally 18473625. Thus, the following pairs will never have been neighbors: 2 and 3, 5 and 7, 1 and 4, as well as 8 and 6.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 5. Seventeen people dine every Saturday evening around a round table.
How many times is it possible to dine if everyone wants to have two new neighbors each time?
What is the result for eighteen people?
Note: This exercise is the same as Exercise 1 (middle school students had to solve 1, high school students 5), but in a less specific case. The proposed solution below is very general, but difficult for an average high school student to access. This exercise was therefore intended to identify students who are best able to tackle formidable Olympic problems.
|
Solution: The first thing to notice is the following. Let $n$ be the number of guests (17 or 18), and $k$ be the number of dinners; we are interested in a particular guest among the $n$. Knowing that he has two neighbors at each dinner, and that he must never meet the same person more than once, he will therefore meet $2 k$ different people in total. Since there are only $n-1$ people he can meet, we have $2 k \leq n-1$, which means - in both cases - that there are at most 8 possible dinners.
Now let's show that there indeed exist 8 arrangements such that two people are never neighbors more than once. We number the guests and the seats from 0 to $n-1$ (since the table is round, the $(n-1)$-th seat is therefore next to the 0-th), and the arrangements from 1 to 8.
For $n=17$, we can proceed as follows: at the $i$-th dinner, we place the $j$-th person at the $i j$-th seat modulo 17. (The complete scheme of arrangements is presented a bit further down. In a less abstract, but longer and vaguer way, we can say that
on the first Saturday, we place all guests in order; on the second Saturday, we place one out of two; on the third, one out of three; and so on; knowing that when the numbers exceed 17, we "return to 0".) We need to verify two things.
First, let's verify that this is a valid arrangement. Each guest receives one and only one seat, because between 0 and 16, there is one and only one number congruent to a given residue modulo 17. No seat is occupied by two guests: indeed, let $j$ and $j^{\prime}$ be two guests who occupy the same seat at the $i$-th dinner. Then we have $i j \equiv i j^{\prime}(\bmod 17)$, or $17 \mid i j-i j^{\prime}$, or $17 \mid i\left(j-j^{\prime}\right)$. Since 17 is prime and $0<i<17$, $i$ is coprime with 17, so $17 \mid j-j^{\prime}$. Therefore, $j \equiv j^{\prime}(\bmod 17)$, which means $j=j^{\prime}$. And since there are as many seats as guests, all seats are necessarily occupied.
Now let's verify that this is indeed a solution to the problem. Since the difference between the numbers of two adjacent seats is congruent to $\pm 1$ modulo 17, this means that at the $i$-th dinner, the difference between the numbers of two adjacent people is congruent to $\pm i$ modulo 17. The numbers $\pm 1, \pm 2, \ldots, \pm 8$ are all different modulo 17: two given people can therefore be neighbors only once.
We could also have explicitly presented the scheme of arrangements:
| Place $\quad 012345678910111213141516$ |
| :--- |
| 1st dinner 012345678910111213141516 |
| 2nd dinner 024681012141613579111315 |
| 3rd dinner 036912151471013162581114 |
| 4th dinner 048121637111526101415913 |
| 5th dinner 051015381316111649142712 |
| 6th dinner 061217132814391541016511 |
| 7th dinner 071441118155122916613310 |
| 8th dinner 081671561451341231121019 |
and verify that each guest appears once and only once in each row and has different neighbors in each row. But such a solution, although less abstract, would be much more laborious (366 checks to make in total!), and has the drawback of being "parachuted": one can see that it works, but one does not understand very well why it works.
For $n=18$, a possible solution is to start from the previous arrangement and to intercalate the new person each time. Since we already know that the first 17 people are well placed as required, it is enough to ensure that the last person (who, in this case, bears the number 17: this is not an error, as we numbered from 0) has different neighbors each time. We can, for example, place her between 3 and 4 at the first dinner, between 11 and 13 at the second, then between 2 and 5, between 10 and 14, between 1 and 6, between 9 and 15, between 0 and 7, and finally between 8 and 16 at the eighth dinner: each number between 0 and 16 appears at most once in this list. The complete arrangement is therefore as follows:
```
Place \(\quad 01234567891011121314151617\)
1st dinner 01231745678910111213141516
2nd dinner 02468101214161357911171315
3rd dinner 03691215147101316217581114
4th dinner 04812163711152610171415913
5th dinner 05101538131176111649142712
6th dinner 06121713281439171541016511
7th dinner 01771441118155122916613310
8th dinner 08171671561451341231121019 .
```
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Exercise 4. Determine the number of natural numbers that are multiples of 8 and 50, and that are divisors of 10000.
|
Solution to exercise 4 An integer is a multiple of 200. It all comes down to finding the number of divisors of $10000 / 200=50=2 \times 5^{2}$. There are 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4
Find all integers $n \geqslant 0$ such that $20 n+2$ divides $2023 n+210$.
## $\S$
|
Solution $\mathbf{n}^{\circ} 1$
Let $n \geqslant 0$ be any solution. The integer $20 n+2$ divides
$$
20 \times(2023 n+210)-2023 \times(20 n+2)=4200-4046=154=2 \times 7 \times 11
$$
whose divisors are $1,2,7,11,14,22,77$ and 154. Thus, $20 n+2$ is 2 or 22, so $n$ is 0 or 1.
Conversely, $n=0$ is a solution, because 210 is even, but $n=1$ is not a solution, because $2023+210$ is odd while $20+2$ is even. In conclusion, $n=0$ is the only solution.
## $\S$
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the smallest integer $n \geqslant 1$ such that the equation
$$
a^{2}+b^{2}+c^{2}-n d^{2}=0
$$
admits the only integer solution $a=b=c=d=0$.
## Solutions
|
Solution 1 First, we check that no integer $n \leqslant 6$ works. Indeed, the quintuplets $(a, b, c, d, n)$ equal to
$$
(1,0,0,1,1),(1,1,0,1,2),(1,1,1,1,3),(2,0,0,1,4),(2,1,0,1,5) \text { and }(2,1,1,1,6)
$$
are solutions to the equation.
We will now show that $n=7$ is the integer we are looking for. Indeed, let $(a, b, c, d)$ be a solution to the equation in the statement, such that $|d|$ is minimal.
If $d$ is odd,
$$
0 \equiv a^{2}+b^{2}+c^{2}-n d^{2} \equiv a^{2}+b^{2}+c^{2}+1 \quad(\bmod 8)
$$
However, the only squares modulo 8 are 0, 1, and 4. The above relation is therefore impossible.
Thus, $d$ is even and
$$
0 \equiv a^{2}+b^{2}+c^{2}-n d^{2} \equiv a^{2}+b^{2}+c^{2} \quad(\bmod 4)
$$
However, the only squares modulo 4 are 0 and 1. Consequently, $a^{2} \equiv b^{2} \equiv c^{2} \equiv 0(\bmod 4)$, so $a, b$, and $c$ are all even.
In conclusion, $(a / 2, b / 2, c / 2, d / 2)$ is also a solution to the problem. Since $|d| / 2 \geqslant|d|$, we conclude that $d=0$, and therefore $a=b=c=0$ as well. Thus, $n=7$ is indeed the integer we are looking for.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Calculate the sums: $a=99+999, b=99+999+9999$ and $c=99+999+9999+99999$.
2. Consider the number $N$ defined as the sum:
$$
N=99+999+9999+\cdots+9999999 \ldots 999
$$
The first term of this sum is written with two nines; then we add the numbers written with three, four nines, etc. The last term of the sum is written with one hundred nines. We perform the sum and write $N$ in ordinary decimal notation. How many times does the digit 1 appear in this notation?
3. Same question for the number $M=11+111+1111+\cdots+1111111 \ldots 111$ where the last term of the sum is written with one hundred ones.
|
1. The answers are $a=1098, b=11097$ and $c=111096$.
2. Let $N=99+999+\cdots+\overbrace{99 \ldots 9}^{100}$. This sum has 99 terms. We write each term differently:
$$
99=100-1,999=1000-1 \ldots \text {, and } \overbrace{99 \ldots 9}^{100}=1 \overbrace{00 \ldots 0}^{100}-1
$$
$$
\begin{aligned}
N & =(100-1)+(1000-1)+\cdots+1 \overbrace{00 \ldots 0}^{100}-1 \\
& =\overbrace{11 \ldots 11}^{99} 00-99 \\
& =\overbrace{11 \ldots 1}^{98} 001
\end{aligned}
$$
The digit 1 appears 99 times.
3. We first notice that $M=N / 9$. Therefore, we need to divide this large number by 9.
$$
\begin{aligned}
& \overbrace{111111111}^{9} \div 9=012345679, \text { so } \\
& \overbrace{1111111111111111111 \ldots 1111}^{99} \div 9= \\
& 012345679012345679 \ldots 5679
\end{aligned}
$$
where the sequence 012345679 is repeated 11 times.
$$
\begin{aligned}
M & =(\overbrace{111111111111111111 \ldots 11}^{99} 00-99) \div 9 \\
& =012345679012345679 \ldots 567900-11 \\
& =012345679012345679 \ldots 567889
\end{aligned}
$$
The digit 1 is written 11 times.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $I$ be the center of the circle inscribed in triangle $A B C$. Suppose that: $C A+A I=$ $B C$. Determine the value of the ratio $\frac{\widehat{B A C}}{\widehat{C B A}}$
|
When two segments are not end-to-end on the same line, we cannot say much about the sum of their lengths. Therefore, to use the hypothesis \( CA + AI = BC \), we need to construct a segment \( AJ \) on the line \((CA)\) such that: \( AJ = AI \) and \( CJ = CA + AJ \) (so \( C \) and \( J \) are on opposite sides of \( A \)). The relation \( AJ = AI \) implies that triangle \( AJI \) is isosceles, so \(\widehat{AJI} = \widehat{AIJ}\): let's call this angle \(\alpha\). \(\widehat{IAC} = \widehat{AJI} + \widehat{AIJ} = 2\alpha\). Since \((AI)\) is the bisector of \(\widehat{BAC}\), \(\widehat{IAC} = \frac{\widehat{BAC}}{2}\). Furthermore, triangles \(IJC\) and \(IBC\) have one equal angle: \(\widehat{ICJ} = \widehat{ICB}\) located between two equal sides, \(CI\) and \(CJ = CB\), so they are congruent (they have all their sides and all their angles equal), hence in particular: \(\alpha = \widehat{IJC} = \widehat{IBC} = \frac{\widehat{CBA}}{2}\). Therefore, ultimately: \(\widehat{CBA} = 2\alpha\) while \(\widehat{BAC} = 4\alpha\), so \(\widehat{CAC} = 2\).
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How many Friday the 13ths can there be in a year? (What is the maximum? What is the minimum?) And if the year is a leap year?
|
We only consider the case of a non-leap year (the case of a leap year is treated in exactly the same way). Having a Friday the 13th is equivalent to having a Monday the 1st, so we will count the Mondays the 1st. Furthermore, $31 \equiv 3(\bmod 7)$, thus we obtain the shift in the week between January 1st and February 1st (it is 3 days: if January 1st is a Monday, then February 1st will be a Thursday). We then do this for all the months:
$$
3+28 \equiv 3(\bmod 7) \text { for March }
$$
$$
\begin{gathered}
3+31 \equiv 6 \quad(\bmod 7) \text { for April } \\
6+30 \equiv 1 \quad(\bmod 7) \text { for May } \\
1+31 \equiv 4 \quad(\bmod 7) \text { for June } \\
4+30 \equiv 6 \quad(\bmod 7) \text { for July } \\
6+31 \equiv 2 \quad(\bmod 7) \text { for August } \\
2+31 \equiv 5 \quad(\bmod 7) \text { for September } \\
5+30 \equiv 0 \quad(\bmod 7) \text { for October } \\
0+31 \equiv 3 \quad(\bmod 7) \text { for November } \\
3+30 \equiv 5 \quad(\bmod 7) \text { for December }
\end{gathered}
$$
We thus get 2 times 0 modulo 7, 1 time 1, 1 time 3, 3 times 3, 1 time 4, 2 times 5, and 2 times 6. Therefore, there will be only one Friday the 13th if the year starts on a Sunday (day -1 of the week which results in only one 1 in the residues modulo 7), a Saturday, or a Thursday. There will be 2 if the year starts on a Monday, a Tuesday, or a Wednesday, and finally, there will be 3 if the year starts on a Friday. Note that if the year is a leap year, there can be 4 Fridays the 13th.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The first term of a sequence is equal to $3^{2012}$. Each subsequent term is equal to the sum of the digits of the previous term. Find the 10th term.
|
From the correction of the previous exercise, we know that all terms are divisible by 9. On the other hand, $a_{1}=3^{2012}=9^{1006}<10^{1006}$, so the number of digits of $a_{1}$ is less than 1005, and since each digit is less than 10, we have $a_{2} \leq 9 \cdot 1005 < 10000$. Similarly, $a_{3}<40$, $a_{4}<13$, and $a_{5}<10$. Therefore, from $a_{5}$ onwards, the sequence is constant and equal to 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all integers $n$ such that $2^{n}+3$ is a perfect square. The same question with $2^{n}+1$.
|
A square is never congruent to 3 modulo 4 (if you don't believe me, try it and see!), so $2^{n}+3$ cannot be a square if $n \geq 2$. And if $n=1$ then $2^{1}+3=5$ is not a square and if $n=0$ then $2^{0}+2=3$ is not a square. The second question is less easy. We are looking for $n$ and $x$, two integers, such that $2^{n}+1=x^{2}$. In other words:
$$
2^{n}=x^{2}-1=(x-1)(x+1)
$$
so $x+1$ and $x-1$ are both powers of 2. The only powers of 2 that are 2 units apart are 2 and 4, so $2^{n}=(x-1)(x+1)=2 \cdot 4=8$ thus $n=3$ is the only solution.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
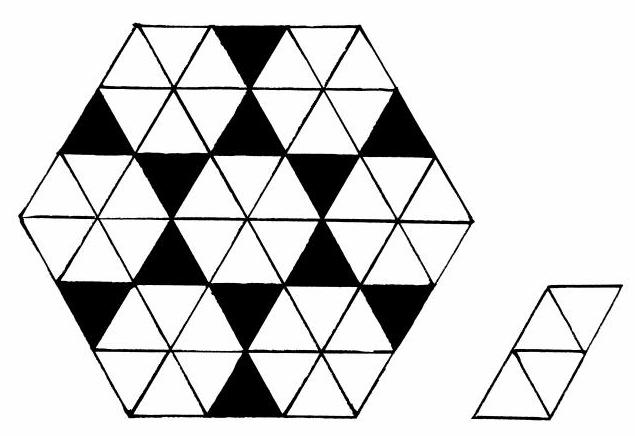
How many parallelograms with sides 1 and 2, and angles $60^{\circ}$ and $120^{\circ}$, can be placed at most in a regular hexagon with side 3?
|
Let $s$ be the area of an equilateral triangle with side 1. A regular hexagon can be divided into 6 equilateral triangles with sides of 3, thus each having an area of $9s$: its total area is $54s$. Now, each parallelogram has an area of $4s$: since $\frac{54s}{4s} > 13$, one might think it is possible to place 13 parallelograms. However, this is not possible: it suffices to color the hexagon with 12 black triangles and 42 white triangles such that any parallelogram, regardless of the four cells it occupies, will necessarily cover one and only one black triangle. Therefore, the maximum number of parallelograms that can be placed is 12, but it still needs to be proven that 12 can indeed be placed (for example, by not covering the white hexagon at the center at all).
## 2 TD
## - Statements -
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all integer solutions $x$ of the equation: $x^{3}+(x+1)^{3}+(x+2)^{3}=(x+3)^{3}$
|
By developing the left-hand side, we have: $3 x^{3}+9 x^{2}+15 x+9=(x+3)^{3}$. It follows that $x+3$ is divisible by 3, and thus $x$ is also divisible by 3, and we can set: $x=3 t$, which leads us to: $81 t^{3}+81 t^{2}+45 x+9=27\left(t^{3}+3 t^{2}+3 t+1\right)$, or, after simplifications:
$3 t^{3}-2 t-1=0$. 1 is an obvious root, and we can factorize: $3 t^{3}-2 t-1=(t-1)\left(3 t^{2}+3 t+1\right)$. The term $3 t^{2}+3 t+1$ being always strictly positive, this equation admits for its unique root (integer or not): $t=1$, so the initial equation admits for its unique root, a fortiori for its unique integer root: $x=3$. The relation; $3^{3}+4^{3}+5^{3}=6^{3}$ is classic.
## - Reminder on congruences -
Two integers $a$ and $b$ are congruent modulo $n: a \equiv b(\bmod n)$ if their difference is divisible by $n$. This is an equivalence relation, allowing all integers to be divided into $n$ congruence classes: those of the form $n k, n k+1, \ldots n k+(n-1)$. These classes can be manipulated almost like numbers, with additional properties, notably Fermat's (little) theorem: if $p$ is a prime number and $a$ is an integer not divisible by $p, a^{p-1} \equiv 1(\bmod p)$. This can be proven by noting that modulo $p, a, 2 a, \ldots(p-1) a$ are each in a different class, so $a \times 2 a \times \ldots \times(p-1) a \equiv 1 \times 2 \times \ldots \times(p-1)$ (since on both sides, we find all non-zero classes modulo $p$), which simplifies.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
a) Show that for all $a \in \mathbb{N}$, the equation $x^{2}+y^{2}+z^{2}=8 a+7$ has no solutions in $\mathbb{Q}^{3}$.
b) Find all natural numbers $n$ such that $7^{n}+8$ is a perfect square.
|
a) To reduce to an equation with integer unknowns, we set $x=\frac{X}{T}, y=\frac{Y}{T}$ and $z=\frac{Z}{T}$, where $X, Y, Z \in \mathbb{Z}$, and where $T \in \mathbb{N}^{*}$ is the minimal integer allowing this writing (in other words, $T$ is the LCM of the denominators of $x, y$, and $z$ written in irreducible form). We then have $X^{2}+Y^{2}+Z^{2}=(8 a+7) T^{2}$. Motivated by the presence of squares, we look modulo 8 (to which a square can be congruent to 0, 1, or 4 only). The equation then becomes $X^{2}+Y^{2}+Z^{2}+T^{2} \equiv 0 \bmod 8$.
At least one of the integers $X, Y, Z$ and $T$ is odd, otherwise we could replace them respectively by $\frac{X}{2}, \frac{Y}{2}, \frac{Z}{2}$ and $\frac{T}{2}$, which would contradict the minimality of $T$. Without loss of generality, we can assume that it is $X$. We then have $X^{2} \equiv 1 \bmod 8$, hence $1+Y^{2}+Z^{2}+T^{2} \equiv 0 \bmod 8$. By looking at the values that $X^{2}, Y^{2}$ and $Z^{2}$ can take modulo 8, we see that this equality cannot be satisfied.
b) We need to solve the Diophantine equation $7^{n}+8=x^{2}$ (in which we can consider, without loss of generality, that $x \geqslant 0$). The presence of the square encourages us to look modulo 4. $x^{2}$ can be congruent to 0 or 1, and $7^{n} \equiv(-1)^{n} \equiv \pm 1 \bmod 4$. We therefore necessarily have $7^{n} \equiv(-1)^{n} \equiv 1 \bmod 4$, so $n$ is even; we can write $n=2 m$, with $m \in \mathbb{N}^{*}$. We then have $8=x^{2}-\left(7^{m}\right)^{2}=\left(x-7^{m}\right)\left(x+7^{m}\right)$, so $x+7^{m} \leqslant 8$ and a fortiori, $7^{m} \leqslant 8$. Therefore, $m=0$ or 1, and we verify reciprocally that $m=0$ is the only solution. The only integer $n$ such that $7^{n}+8$ is a perfect square is therefore 0.
|
0
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Nine cells of a $10 \times 10$ diagram are infected. At each step, a cell becomes infected if it was already infected or if it had at least two infected neighbors (among the 4 adjacent cells).
(a) Can the infection spread everywhere?
(b) How many initially infected cells are needed to spread the infection everywhere?
|
(a) No, this is not possible. Note that the perimeter of the area delimited by the infected cells decreases in a broad sense at each step. Initially, it is at most $9 \times 4=36$, and cannot reach 40.
(b) According to question (a), at least 10 cells must already be infected. We place 10 cells along a diagonal. We verify that then the infection can spread everywhere.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all integers $n \geq 1$ such that $3^{n-1}+5^{n-1}$ divides $3^{n}+5^{n}$.
|
(Algebraic manipulations, using the fact that if $a \mid b$, then $a \mid b+k a$ for any integer $k$)
Let $n \geq 1$ such that $3^{n-1}+5^{n-1} \mid 3^{n}+5^{n}$. Then
$$
3^{n-1}+5^{n-1} \mid 5\left(3^{n-1}+5^{n-1}\right)-3^{n}+5^{n}=2 \cdot 3^{n-1}
$$
But $3^{n-1}+5^{n-1}>2 \cdot 3^{n-1}$ for $n \geq 2$, so $3^{n-1}+5^{n-1}$ does not divide $2 \cdot 3^{n-1}$ for $n \geq 2$. Conversely, we verify that $n=1$ works.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Calculate the value of
$$
\frac{2014^{4}+4 \times 2013^{4}}{2013^{2}+4027^{2}}-\frac{2012^{4}+4 \times 2013^{4}}{2013^{2}+4025^{2}}
$$
|
For better readability, let $n=2013$. Our expression can be rewritten as
$$
\frac{(n+1)^{4}+4 n^{4}}{n^{2}+(2 n+1)^{2}}-\frac{(n-1)^{4}+4 n^{4}}{n^{2}+(2 n-1)^{2}}=\frac{5 n^{4}+4 n^{3}+6 n^{2}+4 n+1}{5 n^{2}+4 n+1}-\frac{5 n^{4}-4 n^{3}+6 n^{2}-4 n+1}{5 n^{2}-4 n+1}
$$
To simplify (because we always need to simplify!), let's try to factorize the numerator of each fraction by its denominator. For example, we want to write $5 n^{4}+4 n^{3}+6 n^{2}+4 n+1 = (5 n^{2}+4 n+1)(\ldots)$. In the parenthesis $(\ldots)$, we can only have terms in $n^{2}$, $n$, or $n^{0}$. Indeed, if we had a power of $n$ greater than 3, the expansion would give a power greater than 5, which is not present in the numerator. After some trial and error, we find that $5 n^{4}+4 n^{3}+6 n^{2}+4 n+1 = (5 n^{2}+4 n+1)(n^{2}+1)$ and similarly that $5 n^{4}-4 n^{3}+6 n^{2}-4 n+1 = (5 n^{2}-4 n+1)(n^{2}+1)$, hence the answer we are looking for is zero.
Remark: To find the parenthesis ( ... ) systematically, we can use the concept of polynomial division. This involves performing a Euclidean division exactly as we learn in elementary school, but replacing numbers with polynomials, i.e., expressions of the form $\sum a_{i} x^{i}$. Here, this gives:
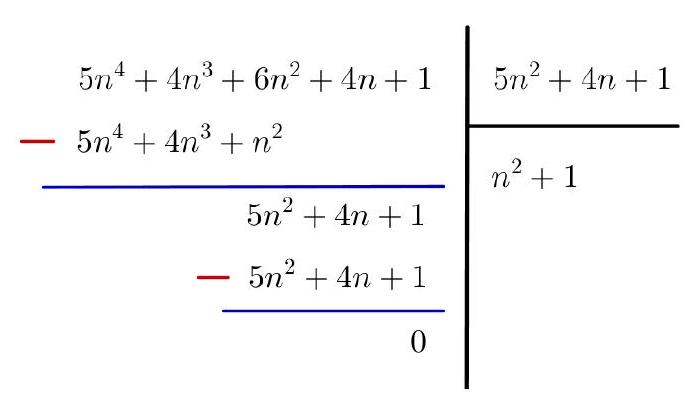
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $\alpha, \beta, \gamma$ be the three roots of $x^{3}-x-1$. What is the value of $\frac{1-\alpha}{1+\alpha}+\frac{1-\beta}{1+\beta}+\frac{1-\gamma}{1+\gamma}$?
|
A safe method, even if in this case, one can find a faster one, is to look for the equation having roots $\frac{1-\alpha}{1+\alpha}, \frac{1-\beta}{1+\beta}, \frac{1-\gamma}{1+\gamma}$ and to calculate the sum of the roots of this equation from its coefficients. If $x$ is a root of $x^{3}-x-1$, what equation is $y=\frac{1-x}{1+x}$ a root of? We note that $x=\frac{1-y}{1+y}$ (the function is involutive), so $\left(\frac{1-y}{1+y}\right)^{3}-\left(\frac{1-y}{1+y}\right)-1=0$, which gives: $(1-y)^{3}-(1-y)(1+y)^{2}-(1+y)^{3}=0$. The equation in $y$ is therefore: $-y^{3}+y^{2}-7 y-1$, the sum of its roots is 1.
Another method: we could also have put everything over a common denominator, expanded the numerator and the denominator, and expressed everything in terms of elementary symmetric polynomials.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(IMO 1959) Show that for all $n \in \mathbb{Z}$, the fraction $\frac{21 n+4}{14 n+3}$ is irreducible.
|
Here is a one-line solution:
$$
(21 n+4,14 n+3)=(7 n+1,14 n+3)=(7 n+1,7 n+2)=(1,2)=1
$$
|
1
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Let $p$ be a prime number. Show that $\binom{2 p}{p} \equiv 2[p]$.
|
According to the Vandermonde convolution formula
$$
\binom{2 p}{p}=\sum_{0 \leqslant n \leqslant p}\binom{p}{n}^{2}
$$
Now, $p \left\lvert\,\binom{ p}{n}\right.$ for $1 \leqslant n \leqslant p-1$, so $\binom{2 p}{p} \equiv\binom{p}{0}+\binom{p}{p} \equiv 2$ modulo $p$.
|
2
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Find all $n \in \mathbb{N}^{*}$ such that $n$ divides $2^{n}-1$.
|
Let $n>1$ such that $n$ divides $2^{n}-1$, and $p$ be the smallest prime divisor of $n$. We denote $d$ as the order of 2 modulo $p$: we know that $d$ divides $p-1$, and on the other hand, from the statement $p \mid 2^{n}-1$ so $d$ divides $n$, thus $d$ divides $\text{GCD}(n, p-1)$.
However, since $p$ is minimal, $p-1$ is smaller than all prime divisors of $n$, so $n$ and $p-1$ have no common prime divisors, thus their $\text{GCD}$ is 1, so $d=1$. In other words, $2 \equiv 1(\bmod p)$, so $p=1$, which is absurd, so the only solution is $n=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all $n \in \mathbb{N}^{*}$ odd such that $n$ divides $3^{n}+1$.
untranslated text remains unchanged:
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
First, $n=1$ is a solution.
Moreover, let $q$ be the smallest prime divisor of $n$ and $d$ the order of 3 modulo $q$: $n$ is odd, so $q>2$. On one hand, $d \mid q-1$ and on the other hand $3^{n} \equiv-1(\bmod q)$, so $3^{2 n} \equiv 1(\bmod n)$, thus $d \mid 2 n$.
Therefore, $d$ divides the GCD of $2 n$ and $q-1$, which is 2 for the same reasons as in the previous exercise, so $d$ is 1 or 2, thus $q \mid 3^{2}-1=8$ so $q=2$, which is absurd since $n$ is odd.
Therefore, $n=1$ is the only solution.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Check that 2 is a solution of the equation:
$$
(x+1)^{3}+(x+2)^{3}+(x+3)^{3}=(x+4)^{3}
$$
Does this equation have any other integer solutions?
|
$3^{3}+4^{3}+5^{3}=27+64+125=216=6^{3}$. Several techniques can be used to solve the equation: setting $x=2+k$, which, when expanded, gives a third-degree equation in $k$ of which one root is zero (this equation does not admit any other real root). But one can also expand directly: $(x+1)^{3}+(x+2)^{3}+(x+3)^{3}-(x+4)^{3}=$ $2 x^{3}+6 x^{2}-6 x-28$ : for this to be zero, it is necessary that $2 x$ divide the constant term -28, which limits the number of cases to study. One can also see that for $x \geq 3,2 x^{3}>28$ and $6 x^{2}>6 x$, so $(x+1)^{3}+(x+2)^{3}+(x+3)^{3}-(x+4)^{3}>0$ and for $x \leq-2,(x+1)^{3}+(x+2)^{3}<0$ and $(x+3)^{3}-(x+4)^{3}<0$, so $(x+1)^{3}+(x+2)^{3}+(x+3)^{3}-(x+4)^{3}<0$ : there remain four simple cases to study. Finally, one can note that modulo 3, as for any integer $n$, $n^{3} \equiv n$ $(\bmod 3),(x+1)^{3}+(x+2)^{3}+(x+3)^{3}-(x+4)^{3} \equiv(x+1)+(x+2)+(x+3)-(x+4)=2 x+2$, so $x$ must be congruent to 2 modulo 3.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Consider 2015 lines in the plane, no two of which are parallel and no three of which are concurrent. Let $E$ be the set of their intersection points.
We want to assign a color to each point in $E$ such that any two points on the same line, whose segment connecting them contains no other point of $E$, are of different colors.
How many colors are needed at a minimum to achieve such a coloring?
|
The configuration contains at least one triangle. This can be proven, for example, by induction on the number of lines: three lines form a triangle, and if you add a line, it either leaves the triangle intact or splits it into a triangle and a quadrilateral. Consequently, it is impossible to perform a coloring with two colors.
We will now show that a coloring with three colors is possible: we order the points by increasing abscissa as before, and color them in this order. When it is time to color a point $P=\left(d_{i}\right) \cap\left(d_{j}\right)$, we have already colored at most one of its neighbors on $\left(d_{i}\right)$ (the one to the left) and one on $\left(d_{j}\right)$ (also the one to the left). Therefore, we have at most two forbidden colors and can always choose the third. The answer is therefore 3 colors.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all positive integers $n$ such that $2^{n}+3$ is a perfect square.
|
It is about solving $2^{n}+3=a^{2}$ with $a$ being a natural integer. If $2 \leq n$, then we have $a^{2} \equiv 3 \bmod 4$, which is not possible according to what we have seen earlier. Therefore, the only possibilities are $n=0$ and $n=1$, which, after verification, gives $n=0$ as the only solution.
Solution to the exercise $4 n-1 \mid 3 n+4$ so $n-1 \mid(3 n+4)-3(n-1)=7$. Since $n-1$ is positive and the only positive divisors of 7 are 1 and 7, we have $n-1=1$ or $n-1=7$, that is, $n=2$ or $n=8$. Conversely, for $n=2$, we have $1 \mid 7=3 \times 1+4$, and for $n=8$, we have $7 \mid 28=3 \times 8+4$. Solution to the exercise $5 n+2 \mid n^{2}+3 n$ so $n+2 \mid\left(n^{2}+3 n\right)-n(n+2)=n$, thus $n+2 \leq n$ that is $2 \leq 0$ which is impossible, hence there is no solution to the proposed equation.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all positive integers $a$ such that $a^{2}+2 a$ is a perfect square.
|
There are two cases. If $a>0$, we note that $a^{2}<a^{2}+2a<$ $a^{2}+2a+1=(a+1)^{2}$. Therefore, $a^{2}+2a$ cannot be a perfect square. If $a=0$, we find $a^{2}+2a=0$ which is a perfect square. This is thus the only one.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all integers $x$ such that $x^{3}+(x+1)^{3}+(x+2)^{3}=(x+3)^{3}$.
|
Let's develop both sides of the equality:
$$
x^{3}+x^{3}+3 x^{2}+3 x+1+x^{3}+6 x^{2}+12 x+8=x^{3}+9 x^{2}+27 x+27
$$
, so
$x^{3}-6 x-9=0$. We deduce that $x$ divides 9, so $x$ is $-9,-3,-1,1,3$ or 9. Of all these possibilities, only 3 is correct. The solution to this equation is therefore 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For which positive integers $n$, does the number $n^{2}+1$ divide $n+1$?
|
If $n^{2}+1$ divides $n+1$, we must have $n^{2}+1 \leq n+1$, or equivalently $n^{2} \leq n$, that is, $n \leq 1$. The only possibility is therefore $n=1$. Conversely, $n=1$ does work.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all natural numbers $n$ such that $2^{n}+3$ is a perfect square.
|
For $n=0,2^{n}+3=2^{2}$ is a perfect square. We verify that $n=1$ is not a solution. Therefore, we can assume $n \geq 2$ and then $2^{n}+3 \equiv 3[4]$. However, a square is congruent to 0 or 1 modulo 4, so for $n \geq 2, 2^{n}+3$ is not a perfect square.
Proposition 150. If $n$ is an integer, then $n^{3} \equiv -1, 0$ or $1[7]$.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What are the last two digits of $7^{9^{9^{9}}}$?
|
We look at the remainders of the powers of 7 modulo 100. It is a cycle of length 4. Since $9 \equiv 1(\bmod 4)$, the last two digits are 07.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Show that if $0 \leqslant a, b, c \leqslant 1$ then
$$
\frac{a}{b c+1}+\frac{b}{a c+1}+\frac{c}{a b+1} \leqslant 2
$$
|
The left member is twice differentiable in each variable with positive second derivatives. Therefore, the function is convex in each variable. However, the global maximum of a convex function defined on a closed and bounded space is attained at an extremal point. Note that here we only know that the function is convex in each variable (which is strictly weaker). We can still deduce that the maximum is attained at the boundary, and even, since the domain is a cube with sides parallel to the axes, the maximum is attained at one of the vertices. These vertices have coordinates, in some order of the coordinates, $(0,0,0),(0,0,1),(0,1,1)$, and $(1,1,1)$. The values at these points are respectively $0,1,2$, and $3/2$, which concludes.
|
2
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Calculate $\frac{1}{3}$ in $\mathbb{Z}_{5}$.
untranslated text:
Calculer $\frac{1}{3}$ dans $\mathbb{Z}_{5}$.
|
We find the Bézout coefficients (using, for example, the extended Euclidean algorithm) to progress from decimal to decimal:
$$
1=3 \times 2-5 \times 1
$$
so
$$
\frac{1}{3}=2+5 \times \frac{-1}{3}
$$
We know that $\frac{-1}{3}$ is a $p$-adic integer, so the first decimal of $\frac{1}{3}$ is 2. Similarly,
$$
\begin{aligned}
& -1=3 \times 3-5 \times 2 \text { so } \frac{-1}{3}=3+5 \times \frac{-2}{3} \\
& -2=3 \times 1-5 \times 1 \text { so } \frac{-2}{3}=1+5 \times \frac{-1}{3}
\end{aligned}
$$
We have already encountered $\frac{-1}{3}$, so we have a periodicity.
We deduce: $\frac{1}{3}=\ldots 13 \ldots 13132$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the maximum number of angles less than $150^{\circ}$ that a non-crossing 2017-sided polygon can have, all of whose angles are strictly less than $180^{\circ}$?
## 3 High School Eliminators: Statements
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly.
|
Answer: 11. If the angles are $180-x_{i}$, then we have $x_{i}>0$ and $x_{1}+\cdots+x_{2017}=360$, so at most 11 of the $x_{i}$ can be greater than 30. We can verify that conversely there exists such a polygon.
## 5 High School Eliminatory: Solutions
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $x, y, z$ be integers such that for any triangle $ABC$ we have $16 H N^{2} = x BC^{2} + y CA^{2} + z AB^{2}$, where $H$ is the foot of the altitude from $A$, $M$ is the midpoint of $[BC]$, and $N$ is the midpoint of $[AM]$. Determine $x^{2} + y^{2} + z^{2}$.
|
Answer: 9. Since $A H M$ is a right triangle at $H$, $N$ is the center of the circumcircle of $A H M$ so $H N=A M / 2$. The median theorem then gives $16 H N^{2}=$ $4 A M^{2}=-A C^{2}+2\left(A B^{2}+B C^{2}\right)$, thus $x=2, y=2, z=-1$, and consequently $x^{2}+y^{2}+z^{2}=9$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Five numbers are given in ascending order, which are the lengths of the sides of a quadrilateral (not crossed, but not necessarily convex, meaning a diagonal is not necessarily inside the polygon) and one of its diagonals $D$. These numbers are $3, 5, 7, 13$ and 19. What can be the length of the diagonal $D$?
|
We can rephrase the problem: let $a, b, c, d$ be the lengths of the sides of the quadrilateral, and $e$ be the length of the diagonal that separates, on one side, the sides of lengths $a$ and $b$, and on the other side, the sides of lengths $d$ and $e$. It is necessary and sufficient that the triplets $(a, b, e)$ and $(c, d, e)$ satisfy the triangle inequality.
If $e=3$ or $e=5$, the triplet containing 19 will not work because $19-3>13$ and $19-5>13$: the side of length 19 is too large.
If $e=13$, it is required simultaneously that $a+b>13$ and $c+d>19$. However, if $a$ or $b=19$, then $c+d \leq 5+7<13$, and similarly if $c$ or $d=19$. Therefore, we cannot have $e=13$. We verify that the same applies for
$e=19$.
Thus, only $e=7$ remains. In this case, we can have $a=3, b=5, c=13, d=19$ for example.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A number was written on the board. At each step, we add to it the largest of its digits (for example, if we have written 142, the next number will be 146). What is the maximum number of odd numbers that can be written consecutively by proceeding in this way?
## High school statements
|
The answer is 5. Suppose we start from an odd number $n$. We denote $n_{i}$ as the $i$-th number written, with $n_{1}=n$. Let $c_{i}$ and $d_{i}$ be the largest digit and the units digit of $n_{i}$, respectively. If $c_{1}$ is odd, then $n_{2}=n_{1}+c_{1}$ is even, and we have written only one odd number. Note also that $c_{1}$ cannot be equal to 0.
If $c_{1}=2$, then $d_{1}=1$. We have $n_{2}=n_{1}+2$, so $c_{2}=3$ and $d_{2}=3$, and $n_{3}=n_{2}+3$ is even. The third number written is therefore even.
If $c_{1}=4$, then $d_{1}$ can be 1 or 3. If $d_{1}=1$, then $n_{2}=n_{1}+4$ so $c_{2}=5$ and $d_{2}=5$, and $n_{3}=n_{2}+5$ is even. If $d_{1}=3$, then $n_{2}=n_{1}+4$ so $c_{2}=7$ and $d_{2}=7$, and $n_{3}=n_{2}+7$ is even.
If $c_{1}=6$, then $d_{1}$ can be 1, 3, or 5. In the first two cases, we get $n_{3}$ even as before. If $d_{1}=5$, then $n_{2}=n_{1}+6$ so $d_{2}=1$. Moreover, the largest digit either remains the same ($c_{2}=6$) or increases by 1 ($c_{2}=7$). In the latter case, $n_{3}=n_{2}+7$ is even. In the former, $n_{3}=n_{2}+6$ so $d_{3}=7$ and $c_{3}=7$ so $n_{4}=n_{3}+7$ is even.
If $c_{1}=8$, then $d_{1}$ can be 1, 3, 5, or 7.
$\nabla$ if $d_{1}=1$, we get $c_{2}=d_{2}=9$ so $n_{3}$ is even.
$\triangleright$ if $d_{1}=3$, then $d_{2}=1$ and $c_{2}$ can be 8 or 9. In the latter case, $n_{3}$ is even, and in the former, we are reduced to the previous case ($c=8, d=1$) so $n_{4}$ is even.
$\triangleright$ if $d_{1}=5$, then $d_{2}=3$ and $c_{2}$ can be 8 or 9. In the latter case, $n_{3}$ is even, and in the former, we are reduced to the previous case ($c=8, d=3$) so $n_{4}$ or $n_{5}$ is even.
$\triangleright$ if $d_{1}=7$, then $d_{2}=5$ and $c_{2}$ can be 8 or 9. In the latter case, $n_{3}$ is even, and in the former, we are reduced to the previous case ($c=8, d=5$) so $n_{4}$ or $n_{5}$ or $n_{6}$ is even.
It is therefore impossible to write 6 consecutive odd integers. However, if we start with 807, we will write successively $807, 815, 823, 831$, and 839, so we can write 5 consecutive odd integers.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the last digit of $2017 7^{2017}$?
|
It is enough to look at the last digit of $7^{2017}$. We notice that the powers of 7 are periodic modulo 10 (i.e., the value of the last digit of $7^{n}, n \geq 1$, is periodic), with a period of 4: the last digit is successively $7,9,3,1,7,9,3,1$, etc. 2016 is a multiple of 4, so the last digit of $7^{2016}$ is a 1. Therefore, that of $7^{2017}$ is a 7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Show that if $a, b, c$ and $d$ are four positive real numbers such that $a b c d=1$, then
$$
a^{2}+b^{2}+c^{2}+d^{2}+a b+a c+a d+b c+b d+c d \geq 10
$$
|
We have a sum of 10 terms, let's try to apply the AM-GM inequality which suggests
Sum of 10 terms $\geq 10 \sqrt[10]{\text{ Product of these } 10 \text{ terms }}$
which gives us here
$$
\begin{aligned}
a^{2}+b^{2}+c^{2}+d^{2}+a b+a c+a d+b c+b d+c d & \geq 10 \sqrt[10]{a^{2} \cdot b^{2} \cdot c^{2} \cdot d^{2} \cdot a b \cdot a c \cdot a d \cdot b c \cdot b d \cdot c d} \\
& =10 \sqrt[10]{(a b c d)^{5}}=10 \text{ given that } a b c d=1
\end{aligned}
$$
|
10
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
We have 21 pieces of type $\Gamma$ (formed of three small squares). We are allowed to place them on an $8 \times 8$ chessboard (without overlapping, so that each piece covers exactly three squares). An arrangement is said to be maximal if no additional piece can be added while respecting this rule. What is the smallest $k$ such that there exists a maximal arrangement of $k$ pieces of type $\Gamma$?
|
On pave the chessboard with 16 squares $2 \times 2$. Each square contains two cells of the arrangement, so it covers at least 32 cells, which requires a minimum of 11 pieces. Conversely, we can construct such an arrangement:
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all natural numbers $n$ such that $n \mid 2^{n}-1$.
|
We see that $n$ must be odd. Since $n=1$ is a solution, we now assume $n>1$. Let $p$ be its smallest prime divisor, which is therefore odd, and $\omega$ the order of 2 modulo $p$. Then, according to the statement, $\omega \mid n$, and by Fermat's little theorem, $\omega \mid p-1$. However, $p-1$ has only prime divisors strictly smaller than $p$, and thus does not divide $n$ by the minimality of $p$. Therefore, $n \wedge (p-1)=1$ and thus $\omega=1$. Hence, $2 \equiv 1 \pmod{p}$, which is absurd. Therefore, $n=1$ is the only natural number such that $n \mid 2^n - 1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine the smallest integer $n$ such that for any configuration of $n$ points with integer coordinates, there exist two of these points whose midpoint also has integer coordinates.
Recall that if we denote $\left(x_{m} ; y_{m}\right)$ as the coordinates of the midpoint between $\left(x_{1} ; y_{1}\right)$ and $\left(x_{2} ; y_{2}\right)$, then we have $x_{m}=\frac{x_{1}+x_{2}}{2}$ and $y_{m}=\frac{y_{1}+y_{2}}{2}$.
|
We are interested in the midpoint $\left(x_{m} ; y_{m}\right)$ of a segment between $\left(x_{1} ; y_{1}\right)$ and $\left(x_{2} ; y_{2}\right)$. For this midpoint to have integer coordinates, it is necessary that $x_{m}$ AND $y_{m}$ are integers, which means that $x_{1}+x_{2}$ AND $y_{1}+y_{2}$ must be even numbers.
If we look at a point, we have 4 possibilities:
$\triangleright x$ even and $y$ even;
$\Delta x$ even and $y$ odd;
$\Delta x$ odd and $y$ even;
$\Delta x$ odd and $y$ odd.
These possibilities will be our drawers: indeed, if two points are in the same category, $x_{1}$ and $x_{2}$ have the same parity, and also $y_{1}$ and $y_{2}$ have the same parity; therefore, $x_{1}+x_{2}$ AND $y_{1}+y_{2}$ are even numbers.
We want to place two points in the same drawer.
Since we have 4 drawers, we need at least 5 points by the pigeonhole principle.
Thus, $n=5$ allows us to have a midpoint with integer coordinates.
It remains to show that $n<5$ does not work: indeed, for example, for $n=4$, by taking the points $(0 ; 0),(1 ; 0),(0 ; 1)$ and $(1 ; 1)$, we have six midpoints and none of them have integer coordinates.
From this, the smallest integer $n$ satisfying the property is $n=5$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(warm-up)
Let $x>0$. Show that
$$
x+\frac{1}{x} \geq 2
$$
For which $x$ do we have equality?
|
Let $x>0$. We have:
$$
x+\frac{1}{x} \geq 2 \Longleftrightarrow x^{2}-2 x+1 \geq 0 \Longleftrightarrow(x-1)^{2} \geq 0
$$
The last assertion is true, which concludes the proof.
Case of equality:
$$
x+\frac{1}{x}=2 \Longleftrightarrow x^{2}-2 x+1=0 \Longleftrightarrow(x-1)^{2}=0
$$
Therefore, equality is only achieved for $x=1$.
|
1
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Let $a$ and $b$ be two distinct roots of the polynomial $X^{3}+3 X^{2}+X+1$. Calculate $a^{2} b+a b^{2}+3 a b$.
|
Let $c$ be the third root of this polynomial. The relations between coefficients and roots give:
$$
\left\{\begin{aligned}
\sigma_{1}=a+b+c & =-3 \\
\sigma_{2}=a b+b c+c a & =1 \\
\sigma_{3}=a b c \quad & =-1
\end{aligned}\right.
$$
Thus $a^{2} b+a b^{2}+3 a b=a^{2} b+a b^{2}-(a+b+c) a b=-a b c=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $P(x)=x^{3}-3 x-1$. Denote $x_{1}, x_{2}$ and $x_{3}$ as its three real roots. Evaluate the quantity $x_{1}^{3}+x_{2}^{3}+x_{3}^{3}$.
|
A first solution is to use the Gauss identity
$$
x_{1}^{3}+x_{2}^{3}+x_{3}^{3}-3 x_{1} x_{2} x_{3}=\left(x_{1}+x_{2}+x_{3}\right)\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}-x_{1} x_{2}-x_{2} x_{1}-x_{1} x_{3}\right)
$$
which leads to
$$
x_{1}^{3}+x_{2}^{3}+x_{3}^{3}=3 \sigma_{3}+\sigma_{1}\left(\sigma_{1}^{2}-3 \sigma_{2}\right)=3
$$
since $\sigma_{1}=0$ and $\sigma_{3}=1$ according to the relations between coefficients and roots.
Alternatively, a more ingenious solution is to exploit the fact that $P\left(x_{1}\right)=P\left(x_{2}\right)=P\left(x_{3}\right)=0$, so for $i \in\{1,2,3\}$, we have $x_{i}^{3}=3 x_{i}+1$. We deduce that $x_{1}^{3}+x_{2}^{3}+x_{3}^{3}=3\left(x_{1}+x_{2}+\right.$ $\left.x_{3}\right)+3=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all rational numbers $x$ such that $x^{3}+(x+1)^{3}+(x+2)^{3}=(x+3)^{3}$.
|
After simplification, it is a matter of finding the rational roots of the polynomial $P(x)=x^{3}-6 x-9$. We notice that 3 is a root of $P$. By polynomial division, $P(x)=(x-3)\left(x^{2}+3 x+3\right)$. Since $x^{2}+3 x+3$ has no real solutions $(\Delta=-3), P$ has no other rational roots than 3.
Another idea is to exploit the following lemma:
Lemma 95. Let $P(X)=a_{n} X^{n}+\cdots+a_{1} X+a_{0}$ be a polynomial with integer coefficients for which we are looking for rational roots in the form $x=\frac{r}{s}$, with $r$ and $s$ coprime. Then:
$$
s \mid a_{n} \text { and } r \mid a_{0}
$$
## Proof.
$P(x)=0 \Leftrightarrow a_{n} \frac{r^{n}}{s^{n}}+a_{n-1} \frac{r^{n-1}}{s^{n-1}}+\cdots+a_{1} \frac{r}{s}+a_{0}=0 \Leftrightarrow a_{n} r^{n}+a_{n-1} r^{n-1} s+\cdots+a_{1} r s^{n-1}+a_{0} s^{n}=0$ Since $s \mid 0$, we have $s \mid a_{n} r^{n}+a_{n-1} r^{n-1} s+\cdots+a_{1} r s^{n-1}+a_{0} s^{n}$. Thus, $s \mid a_{n} r^{n}$. Since $s$ and $r$ are coprime, it follows that $s \mid a_{n}$. We similarly show that $r \mid a_{0}$.
According to our lemma, if $x=\frac{r}{s}$ is a rational root of $x^{3}-6 x-9$, then $s$ divides the leading coefficient of this polynomial, that is, $s \mid 1$ and thus $s=1$. In other words, all solutions to the problem are integers. And we even know that $r \mid 9$, hence $x \in\{-9,-3,-1,1,3,9\}$. We then easily verify that $x=3$ is the only value that works.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all odd integers $y$ such that there exists an integer $x$ satisfying
$$
x^{2}+2 y^{2}=y x^{2}+y+1
$$
## 2 Solution
|
We rewrite the equation in the form
$$
(y-1) x^{2}=2 y^{2}-y-1
$$
since $2 y^{2}-y-1=(y-1)(2 y+1)$, therefore if $y \neq 1$, we can divide by $y-1$, and the equation becomes $x^{2}=2 y+1$. Since $y$ is odd, it can be written in the form $y=2 k+1$. In this case, $x^{2}=4 k+3$, but a table of congruences shows that $x^{2}$ can only be 0 or 1 modulo 4, and thus cannot be of the form $4 k+3$. It remains to handle the case $y=1$, and we easily notice that it leads to a solution for all $x$. The only integer $y$ that is a solution to this problem is therefore $y=1$.
## 2 Group B
## 1 Statement
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine all complex numbers $z$ such that $|z|+|\bar{z}|=|z+\bar{z}|$.
|
We note $z=a+i b$. We observe that $z+\bar{z}=a+i b+a-i b=2 a$ and the equality becomes $\sqrt{a^{2}+b^{2}}+\sqrt{a^{2}+b^{2}}=\sqrt{4 a^{2}}$. However, $2 \sqrt{a^{2}+b^{2}}=\sqrt{4 a^{2}+4 b^{2}} \geq \sqrt{4 a^{2}}$ with equality if and only if $b=0$. The complex solutions are therefore the complexes whose imaginary part is zero, that is, the real numbers.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For any real number $x$, we denote $\lfloor x\rfloor$ as the integer part of $x$, that is, the greatest integer less than or equal to $x$. We denote $\{x\}$ as its decimal part, that is, $\{x\}=x-\lfloor x\rfloor$. For example, we have $\lfloor 3.1\rfloor=3$ and $\{3.1\}=3.1-3=0.1$. We also have $\lfloor-2.7\rfloor=-3$ and $\{-2.7\}=-2.7-(-3)=0.3$.
Find all real numbers $x$ such that $\lfloor x\rfloor \times\{x\}=2019 \times x$.
|
Let $x$ be a solution to the problem. We denote $n=\lfloor x\rfloor$ and $y=\{x\}$. Then $n$ is an integer and $0 \leqslant y < 1$. We have $n+y=x$ and $n-2019y=n-2019\{x\}=n-2019(x-n)=2019n-x$.
If $n>0$, then $2019 n>n$, so $n-2019>0$, thus $y>1$, which is impossible. If $0<n<2019$, then $0>n-2019$, so $y<0$, which is also impossible. Therefore, we must have $n \leqslant 0$, so we set $n=-n'$ with $n' \geqslant 0$. Then we have $y=\frac{-2019 n'}{-n'-2019}=\frac{2019 n'}{n'+2019}$.
But we also have $y<1$, so $2019 n'<n'+2019$, which simplifies to $2018 n'<2019$, thus $n'<\frac{2019}{2018}$, so $n'$ is 0 or 1, hence $n$ is 0 or -1. In the first case, we have $y=0$ so $x=0$. In the second case, we have $y=\frac{2019}{2020}$, so $x=-1+\frac{2019}{2020}=-\frac{1}{2020}$. Therefore, there are two solutions, which are 0 and $-\frac{1}{2020}$.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Consider a large square grid with side length 10, divided into small squares with side length 1. Two small squares are said to be neighbors if they share a common side. On each of the small squares, a positive real number is inscribed. Furthermore, 5 frogs move on the grid and can each cover a small square. Two frogs never cover the same square. Between two moments, each frog jumps from the square where it is to a neighboring square.
It is assumed that the sum of the visible numbers is 10 at instant 1, then $10^{2}$ at instant 2, then $10^{3}$ at instant 3, and so on until instant $k$ where the sum is $10^{k}$. What is the largest possible value of $k$?
|
We will show that the largest possible value of $k$ is 6. First, let's verify that 6 is indeed achievable. For this, we isolate a $2 \times 3$ rectangle in the top left corner of the grid. On all the cells that are not in this rectangle, we write the number 0. On the cells of the rectangle, we write the numbers $10, 100, \ldots, 10^{6}$ as follows:
| $10^{3}$ | $10^{4}$ |
| :---: | :---: |
| $10^{2}$ | $10^{5}$ |
| 10 | $10^{6}$ |
At instant 1, the frogs occupy the 5 cells bearing the numbers $10^{2}, \ldots, 10^{6}$, so only the number 10 is visible (along with all the 0s). Then at instant 2, the frogs rotate clockwise, so that $10^{2}$ is visible (along with the 0s), and so on... We then have a configuration as desired with $k=6$.
Now let's show that $k>6$ is impossible. Suppose $k \geqslant 7$. When moving from instant 1 to instant 2, at most 5 new numbers are revealed (the 5 that were covered at instant 1), and the sum of the visible numbers increases by $10^{2}-10=90$. Therefore, the sum of the numbers discovered between instant 1 and instant 2 is at least 90. Since there are at most 5 numbers discovered, at least one is greater than $90 / 5=18$. On the other hand, the sum of the visible numbers at instant 2 is 100, so the discovered numbers do not exceed 100, hence there is a cell bearing a number between 18 and 100. By reasoning similarly between instants 2 and 3, then 3 and 4, and so on until 6 and 7, we find a cell bearing a number between 180 and 1000, then between 1800 and 10000, and so on until $18 \times 10^{5}$ and $10^{7}$. We have thus found 6 cells greater than 18. Since there are only 5 frogs at instant 1, at least one of these cells was visible at instant 1, so the sum was at least 18, leading to a contradiction.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
- Show that for any strictly positive real number $x: x+\frac{1}{x} \geq 2$. Find the case of equality.
- Show that for all strictly positive real numbers $a$ and $b: \frac{a}{b}+\frac{b}{a} \geq 2$. Find the case of equality.
- Determine the minimum for $a$ and $b$ two non-zero real numbers of:
$$
\frac{a^{6}}{b^{6}}+\frac{a^{4}}{b^{4}}+\frac{a^{2}}{b^{2}}+\frac{b^{6}}{a^{6}}+\frac{b^{4}}{a^{4}}+\frac{b^{2}}{a^{2}}
$$
and find where it is achieved.
|
- Since $x$ must be strictly positive, the inequality is equivalent to $x^{2}-2 x+1 \geq 0$, which is $(x-1)^{2} \geq 0$ and this is always true, with equality if and only if $x=1$.
- It suffices to apply the previous question to $x=\frac{a}{b}$, and we have equality if and only if $a=b$.
- We have $\frac{a^{6}}{b^{6}}+\frac{b^{6}}{a^{6}} \geq 2, \frac{a^{4}}{b^{4}}+\frac{b^{4}}{a^{4}} \geq 2$ and $\frac{a^{2}}{b^{2}}+\frac{b^{2}}{a^{2}} \geq 2$ so by summing all of these, the minimum value of the expression is 6, with equality if and only if $a=b$.
|
6
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
What are the integers $k$ such that the following identity is always true for any real numbers $a, b$, and $c$?
$$
(a+b)(b+c)(c+a)=(a+b+c)(a b+b c+c a)+k a b c
$$
|
By developing:
$$
\begin{aligned}
(a+b)(b+c)(c+a) & =a b c+a b a+a c c+a c a+b b c+b b a+b c c+b c a \\
(a+b+c)(a b+b c+c a) & =a a b+a b c+a c a+b a b+b b c+b c a+c a b+c b c+c c a
\end{aligned}
$$
By substituting the two equalities, we get $2 a b c=3 a b c-k a b c$ which gives $k=-1$. The calculation ensures that this solution works.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How many integers must one select from the set $\{1,2, \ldots, 20\}$ to ensure that this selection includes two integers $a$ and $b$ such that $a-b=2$?
|
Consider the drawers of the form $\{1,3\},\{2,4\},\{5,7\},\{6,8\},\{9,11\},\{10,12\},\{13,15\}$, $\{14,16\},\{17,19\},\{18,20\}$. By choosing 11 integers, by the pigeonhole principle, there will be two that are in the same drawer, and thus have a difference of 2. This quantity is indeed minimal because the set $\{1,2,5,6,9,10,13,14,17,18\}$ is of size 10 and does not contain such integers $a$ and $b$.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Paris has two million inhabitants. A human being has, at most, 600000 hairs on their head. What is the largest number of Parisians that we can hope to find who have exactly the same number of hairs on their head?
|
Here, the drawers are the numbers of hairs and the socks will be the Parisians. We then have 2000000 socks for 600001 drawers (we don't forget the bald Parisians): the pigeonhole principle assures us that it is possible to find $\left\lceil\frac{2000000}{600001}\right\rceil=4$ Parisians who have exactly the same number of hairs.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A fly and $\mathrm{k}$ spiders move on a $2019 \times 2019$ grid. On their turn, the fly can move 1 square and the $k$ spiders can each move 1 square. What is the minimal $k$ for which the spiders are sure to catch the fly.
|
We show that 2 spiders suffice: when the fly moves to a coordinate, the spider on that coordinate replicates the movement, the other approaches.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all non-negative integers $x, y$ such that:
$$
2^{x}=y^{2}+y+1
$$
|
The left side of the equation is even if $x>0$. The right side is always odd: indeed $y$ and $y^{2}$ have the same parity, their sum is therefore even, so $1+y+y^{2}$ is always odd.
If $x=0$, then it is necessary and sufficient that $1+y+y^{2}=1$ with $y \geqslant 0$ so the only solution is $x=y=0$.
## Congruences
Definition, compatibility with addition and multiplication.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $\mathrm{a}, \mathrm{b}$ be two positive real numbers such that $a b \geqslant 1$. Show that:
$$
\frac{1}{1+a}+\frac{1}{1+b} \leqslant 1
$$
Determine the case of equality.
|
$\frac{1}{1+a}+\frac{1}{1+b} \leqslant 1 \Longleftrightarrow \frac{1+b+1+a}{(1+a)(1+b)} \leqslant 1 \Longleftrightarrow 2+a+b \leqslant 1+a+b+a b \Longleftrightarrow 1 \leqslant a b$ The inequality is therefore satisfied by assumption, the case of equality is thus $a b=1$.
|
1
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
A permutation of $\{1, \ldots, n\}$ is drawn at random. On average, how many fixed points does it have?
|
Consider an $n \times n$ table, where the rows correspond to the elements of $\{1, \ldots, n\}$ and the columns to permutations. We mark a 1 in position $(i, s)$ if the element $i$ is a fixed point of the permutation $s$. The number of 1s is counted:
- by rows: each element $i$ is a fixed point of $(n-1)!$ permutations,
- by columns: this is the total number of fixed points of all permutations.
Thus, a permutation of $\{1, \ldots, n\}$ has on average $\frac{n \cdot (n-1)!}{n!} = 1$ fixed point.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
If $\alpha, \beta, \gamma$ are the three roots of $x^{3}-x+1$, determine the value of
$$
\frac{1-\alpha}{1+\alpha}+\frac{1-\beta}{1+\beta}+\frac{1-\gamma}{1+\gamma}
$$
|
Given that $x$ is a root of $x^{3}-x+1$, we wonder about the polynomial for which $y=\frac{1-x}{1+x}$ is a root. We find $x=\frac{1-y}{1+y}$ and substitute it into the polynomial. We then find that $y$ is a root of $-y^{3}+y^{2}-7 y-1$. By Viète's formulas, we conclude that the desired sum is 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a, b$ and $c$ be strictly positive real numbers such that $a^{2}+b^{2}+c^{2}=\frac{1}{2}$. Show that
$$
\frac{1-a^{2}+c^{2}}{c(a+2 b)}+\frac{1-b^{2}+a^{2}}{a(b+2 c)}+\frac{1-c^{2}+b^{2}}{b(c+2 a)} \geqslant 6
$$
|
We note that $1-a^{2}+c^{2}=2\left(a^{2}+b^{2}+c^{2}\right)-a^{2}+c^{2}=a^{2}+2 b^{2}+3 c^{2}$ using the hypothesis. On the other hand, by the inequality of means, we have $a c \leqslant \frac{1}{2}\left(a^{2}+c^{2}\right)$ and $2 b c \leqslant b^{2}+c^{2}$, so
$$
c(a+2 b)=a c+2 b c \leqslant \frac{1}{2}\left(a^{2}+c^{2}\right)+b^{2}+c^{2}=\frac{1}{2}\left(a^{2}+2 b^{2}+3 c^{2}\right)
$$
We deduce that
$$
\frac{1-a^{2}+c^{2}}{c(a+2 b)} \geqslant \frac{a^{2}+2 b^{2}+3 c^{2}}{\frac{1}{2}\left(a^{2}+2 b^{2}+3 c^{2}\right)}=2
$$
Similarly, we find $\frac{1-b^{2}+a^{2}}{a(b+2 c)} \geqslant 2$ and $\frac{1-c^{2}+b^{2}}{b(c+2 a)} \geqslant 2$. By summing the three terms, we get
$$
\frac{1-a^{2}+c^{2}}{c(a+2 b)}+\frac{1-b^{2}+a^{2}}{a(b+2 c)}+\frac{1-c^{2}+b^{2}}{b(c+2 a)} \geqslant 2+2+2=6
$$
|
6
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
(N1 2002) Find the smallest integer $t$ such that there exist strictly positive integers $x_{1}, \ldots, x_{t}$, satisfying $x_{1}^{3}+\ldots+x_{t}^{3}=2002^{2002}$.
|
Let's show that $t \geq 4$. We are looking for an integer $n$ such that $3 \mid \varphi(n)$, so that cubes take on only a few values modulo $n$. This is the case for 9, for which cubes can only be 0, 1, or -1. We observe that $2002^{2002} \equiv 4 \pmod{9}$, so we have $t \geq 4$. It suffices to find $x_{1}, x_{2}, x_{3}, x_{4}$ that work to conclude. We have $2002 = 3 \cdot 667 + 1$, so $2002^{2002} = 2002 \cdot (2002^{667})^3$. It suffices to show that 2002 can be written as the sum of 4 cubes, which is easy to notice: $2002 = 1000 + 1000 + 1 + 1$.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the smallest integer $n$ such that there exist polynomials $f_{1}, f_{2}, \ldots, f_{n}$ such that:
$$
f_{1}(x)^{2}+f_{2}(x)^{2}+\ldots+f_{n}(x)^{2}=x^{2}+7
$$
|
We show that the equation $a^{2}+b^{2}+c^{2}=7 d^{2}$ has no non-trivial solutions, which concludes the cases for $n=1,2,3$ by looking at the constant coefficient. Moreover, the $f_{i}$ are affine since otherwise the degree would be too high, so there exists an $i$ and a $t$ such that $f_{i}(t)= \pm t$ for $n=4$, reducing it to the case $n=3$ that has been studied. Therefore, $n \geq 5$ and $\left(f_{1}, f_{2}, f_{3}, f_{4}, f_{5}\right)=(1,1,1,2, x)$ work.
Key ideas: When dealing with polynomials, look at the degree, and try to fix particular values when there is a lot of freedom. :
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A triangle has side lengths: 3, 4, 5. Calculate the radius of the inscribed circle (circle inside the triangle and tangent to all three sides of the triangle).
|
Let's call $A, B, C$ the vertices of the triangle, $a=BC, b=CA, c=AB$ the lengths of the three sides, $I$ and $r$ the center and the radius of the inscribed circle. The heights from $I$ to the triangles $IAB, IBC$, and $ICA$ are all equal to $r$, so the areas of these three triangles are: area $(IAB)=\frac{rc}{2}$, area $(IBC)=\frac{ra}{2}$, area $(ICA)=\frac{rb}{2}$. From this, we deduce: area $(ABC)=\frac{r(a+b+c)}{2}$. The triangle with sides $3, 4, 5$ is a right triangle, and its area is: $\frac{3 \times 4}{2}=6=\frac{r(3+4+5)}{2}$. It follows that $r=1$.
The given triangle, with sides $3, 4, 5$, being a right triangle, we can also reason as follows. Let $D, E, F$ be the projections of $I$ onto the sides $BC, CA, AB$. These are the points of tangency of the inscribed circle with the sides of the triangle. If $A$ is the vertex of the right angle, $AEIF$ is a square, and $r=IE=IF=AE=AF$. The lengths $AE$ and $AF$ are easy to calculate: if we set $u=AE=AF, v=BF=BD$, $w=CD=CE, u+v=c, v+w=a, w+u=b$, then by adding: $2(u+v+w)=a+b+c$ or finally $u=\frac{-a+b+c}{2}, v=\frac{a-b+c}{2}, w=\frac{a+b-c}{2}$. We deduce: $r=u=\frac{-5+4+3}{2}=1$.
The two methods are very different, but the results are the same. Indeed, $\frac{r(a+b+c)}{2}=\left(\frac{-a+b+c}{2}\right)\left(\frac{a+b+c}{2}\right)=\frac{-a^{2}+(b+c)^{2}}{4}=\frac{bc}{2}=$ area $(ABC)$ because the square of the hypotenuse $a^{2}=b^{2}+c^{2}$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
We write on the board the integers from 1 to 2013. At each step, we erase two of them and write their difference instead. The number of integers thus decreases by 1. Can the last integer obtained at the two thousand and twelfth step be equal to 0?
|
This is still an argument of parity that allows us to conclude. Since the difference of two integers has the same parity as their sum, the sum of all integers on the board retains the same parity at each step of the process. Initially, it is: $1+2+\ldots+2011=\frac{2011 \times 2012}{2}$, which is even. This sum will therefore remain even, and the last number obtained will be an even number, it cannot be 1.
To prove that it can be 0 (although this is not required), a completely different reasoning would be needed. We would group the numbers as follows: $(1,2,3),(4,5,6,7), \ldots(2008,2009,2010,2011)$. The first triplet can be reduced to 0 by replacing $(2,3)$ with 1 and then $(1,1)$ with 0. Similarly, for each of the following quadruplets, by replacing $(4n, 4n+2)$ with 2, $(4n+1, 4n+3)$ with 2, and then $(2,2)$ with 0. Proving that the answer is "yes" or that the answer is "no" requires completely different reasoning, so it is imperative to guess the correct answer as quickly as possible because a lot of time is lost when one goes in the wrong direction. The technique of invariants is useful for proving an impossibility. To prove that something is possible, usually one shows that it can be constructed explicitly.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
On each cell of a $9 \times 9$ grid, there is a chip. At a certain signal, each chip jumps to one of the cells touching diagonally the one it is in. Find the minimum number of empty cells after this move.
|
We color the columns of the table alternately in black and white. There are then $9 \times 5=45$ black squares, and $9 \times 4=36$ white squares. During the movement, each chip changes the color of its column. Thus, there are more than 36 chips on the 45 black squares after the signal, and therefore at least 9 empty squares. On the other hand, it is easy to find a configuration where there are exactly 9.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a deck of cards consisting only of red and black cards, there are 2 times as many black cards as red cards. If 4 black cards are added, there are then 3 times as many black cards as red cards. How many cards were in the deck before adding the 4 black cards?
Only a numerical answer is expected here.
|
Let $r$ be the number of red cards and $n$ be the number of black cards in the initial deck. By hypothesis, we have $n=2 r$. After adding 4 black cards, there are $n+4$ black cards in the deck, and by hypothesis, we have $n+4=3 r$. Thus, $4=3 r-n=3 r-2 r=r$ and $n=2 \cdot 4=8$. Initially, the deck contains $r+n=4+8=12$ cards.
Comment from the graders: The exercise is very well solved! However, be sure to carefully read the instructions: the question here was the total number of cards and not the number of black cards...
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all integers $n$ such that $4 n^{4}+1$ is a prime number.
|
By the Sophie-Germain identity:
$1+4 n^{4}=\left(1-2 n+2 n^{2}\right)\left(1+2 n+2 n^{2}\right)$ Therefore, it is necessary that $1-2 n+2 n^{2}=1$, so $n=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find $k$ such that, for all real $a, b, c$,
$$
(a+b)(b+c)(c+a)=(a+b+c)(a b+b c+c a)+k \cdot a b c
$$
|
In the development, we find $k=-1$
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all even primes.
|
If a prime is even, then it is divisible by 2, and 2 is a divisor. Therefore, since $2 \neq 1$, it must be 2. Conversely, 2 is indeed prime.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all primes of the form $a^{2}-1$, with $a \geqslant 2$ natural.
|
3 is the only prime of this form. Indeed, if a prime $p$ is of the form $a^{2}-1=(a-1)(a+1)$, it is divisible by $a-1$ and $a+1$. Therefore, these must be 1 and $p$. Since they are distinct and $a-1$ is the smallest of them, $a-1=1$ and $p=a^{2}-1=2^{2}-1=3$. Conversely, $2^{2}-1=3$ is indeed prime.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What are the prime numbers $p$ such that $p+2$ and $p+4$ are also prime?
|
It is known that among three consecutive numbers, one of them will be a multiple of 3. The idea here is the same, and we will reason as we would for consecutive numbers. We know that $p$ can be written in the form $3k$, $3k+1$, or $3k+2$. Let's consider these three cases:
- If $p=3k$, $p$ is divisible by 3 and is prime, so $p=3$. Conversely, 3, 5, and 7 are prime.
- If $p=3k+1$, $p+2$ is divisible by 3, so $p+2=3$ and $p=1$, which is not prime.
- If $p=3k+2$, $p+4$ is divisible by 3, so $p+4=3$ and $p=-1$, which is not prime.
Thus, $p=3$ is the only value that works.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For which strictly positive integers $n$ do we have $5^{n-1}+3^{n-1} \mid 5^{n}+3^{n}$?
|
If $5^{n-1}+3^{n-1} \mid 5^{n}+3^{n}$, then $5^{n-1}+3^{n-1} \mid 5^{n}+3^{n}-5\left(5^{n-1}+3^{n-1}\right)=-2 \cdot 3^{n-1}$. Thus, $5^{n-1}+3^{n-1} \leqslant 2 \cdot 3^{n-1}$, hence $5^{n-1} \leqslant 3^{n-1}$ and we deduce that $n=1$. Conversely, for $n=1,2$ divides 8 and $n=1$ is our only solution.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine the set of natural numbers $n$ such that $5^{n}+4$ is a square.
|
We are therefore looking for the $n$ such that the equation
$$
5^{n}+4=a^{2}
$$
This can be rewritten as
$$
5^{n}=a^{2}-4
$$
By recognizing a notable identity, this is equivalent to
$$
(a-2)(a+2)=5^{n}
$$
Consequently, since 5 is prime, we deduce that $a-2$ and $a+2$ are powers of 5, i.e., there exist integers $r$ and $s$ such that
$$
\begin{aligned}
& a+2=5^{r} \\
& a-2=5^{s}
\end{aligned}
$$
Their difference is therefore, assuming without loss of generality that $r \geq s$,
$$
\begin{aligned}
(a+2)-(a-2)=4 & =5^{r}-5^{s} \\
& =5^{s}\left(5^{r-s}-1\right)
\end{aligned}
$$
The only possibility is therefore $s=0$ and $r-s=1$.
We deduce that if $n$ is a solution, then $5^{n}+4=9$.
We verify that $5^{2}+4=9$.
Consequently, there is a unique solution which is
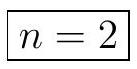
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Show that if $n \geqslant 2$ divides $2^{n}+1$, then $n$ is a multiple of 3.
|
As $n \geqslant 2$, consider one of its prime divisors $p$. Then $2^{n} \equiv-1[p]$ so $2^{2 n} \equiv 1[p]$. We deduce that $p$ divides $2^{2 n}-1 \wedge 2^{p-1}-1$ by Fermat's little theorem. A classical lemma (which we will reprove later) ensures that $p$ divides $2^{(2 n) \wedge(p-1)}-1$. Suppose then that $p$ is the smallest prime divisor of $n$, so that $p-1 \wedge n=1$. Then $p \mid 2^{2}-1=3$ hence $p=3$.
|
3
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Find all integers $n$ such that $n^{3}-3 n^{2}+n+2$ is a power of 5.
## More exercises
|
We then have: $(n-2)\left(n^{2}-n-1\right)=5^{a}$. Thus, we have: $n-2=5^{x}$ and $n^{2}-n-1=5^{y}$. It follows that $5^{y}-5^{2 x}-3 \cdot 5^{x}=1$. Therefore, if $x, y \geqslant 1$ then $0 \equiv 1[5]$, which is absurd. Therefore, $x=0$ or $y=0$. If $x=0$, then $y=1$, which gives $n=3$. If $y=0$, then $5^{2 x}+3 \cdot 5^{x}=0$, which is absurd. The only solution is thus $n=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine the non-zero real numbers $x$ such that $x+\frac{1}{x}=2$.
|
We could just multiply by $x$ (non-zero) to obtain $(x-1)^{2}=0$ and that's it, but that's not fun, we need to use Viète!
Let's take a polynomial whose roots are $x$ and $\frac{1}{x}$. Their sum is 2 and their product is 1, so they are roots of $X^{2}-2 X+1$, hence $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that for all real numbers $x$ and $y$:
$$
f\left(x^{2022}+y\right)=f\left(x^{1747}+2 y\right)+f\left(x^{42}\right)
$$
|
For complicated exponents, we will try to simplify them. For a given $x$, we have $x^{2022} + y = x^{1747} + 2y$ if and only if $y = x^{2022} - x^{1747}$, so we take this $y$. We then have $f\left(2 x^{2022} - x^{1747}\right) = f\left(2 x^{2022} - x^{1747}\right) + f\left(x^{42}\right)$, from which: $f\left(x^{42}\right) = 0$, thus $f$ is zero on the positives. Considering $y = 0$, we then have for all negative $x$, $f\left(x^{1747}\right) = 0$, hence $f = 0$. This function works $(0 + 0 = 0)$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A sequence $a_{1}, a_{2}, a_{3}, \ldots$ of strictly positive integers satisfies $a_{1}>5$ and $a_{n+1}=5+6+\cdots+a_{n}$ for all strictly positive integers $n$. We assume that, regardless of the value of $a_{1}$, this sequence always contains a multiple of $p$. Show that $p=2$.
Bonus: Show that $p=2$ satisfies the statement.
|
Suppose $p \neq 2$, note that by immediate induction $a_{n} \geq 5$ so the statement is well-posed. We have $a_{n+1}=\frac{a_{n}\left(a_{n}+1\right)}{2}-10$
We would ideally like no term to be divisible by $p$. The simplest case would be for all $a_{n}$ to be congruent to $a_{0}$ modulo $p$, and for $a_{1}$ not to be divisible by $p$.
We are thus looking to solve the equation $x \equiv \frac{x(x+1)}{2}-10(\bmod p)$ which is equivalent to $2 x \equiv$ $x^{2}+x-20(\bmod p)$, or to $x^{2}-x-20 \equiv 0(\bmod p)$. Now, $x^{2}-x-20=(x-5)(x+4)$ (which can be found by applying the formulas for solving a quadratic polynomial modulo $p$). In particular, if $a_{1} \equiv 5 p$ or $a_{1} \equiv-4(\bmod p)$, then $a_{n} \equiv 5(\bmod p)$ for all $n \geq 1$, or $a_{n} \equiv-4(\bmod p)$ for all $n \geq 1$. By taking $a_{1}=10 p-4>5, a_{n}$ is not divisible by $p$ because $p \neq 2$ for all $n \geq 1$. Thus, we have $p=2$.
For $p=2$, suppose there exists $a_{1}$ such that the sequence $\left(a_{n}\right)_{n \geq 1}$ contains no even terms. In this case, let $a_{1}=5+2^{l} k$ with $l \geq 1$ (since $a_{1}$ is odd) and $k$ odd.
Then, if $a_{n}$ is of the form $5+2^{b} c$ with $c$ odd and $b \geq 1$,
$$
a_{n+1}=\frac{\left(5+2^{b} c\right)\left(6+2^{b} c\right)}{2}-10=\left(5+2^{b} c\right)\left(3+2^{b-1} c\right)-10=5+2^{b-1}\left(5 c+6 c+2^{b-1} c\right)
$$
$a_{n+1}$ is of the form $5 \times 2^{b-1} c^{\prime}$ with $c^{\prime}$ odd (equal to $\left(5 c+6 c+2^{b-1} c\right)$ ).
By immediate induction, we get that $a_{m+1}=5+2^{l-m} c_{m}$ for $0 \leq m \leq l$ with $c_{m}$ an odd integer. Thus $a_{l+1}$ is even, which gives the desired result.
|
2
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Determine all prime numbers $p$ for which there exists a unique $a$ in $\{1, \ldots, p\}$ such that $a^{3}-3 a+1$ is divisible by $p$.
---
The translation maintains the original formatting and structure of the source text.
|
Let $p$ satisfy the statement, and $a$ be the unique solution of $a^{3}-3 a+1 \equiv 0(\bmod p)$. Note that $a \neq 0$, so by setting $b \equiv \frac{1}{a}(\bmod p), b^{3}-3 b^{2}+1 \equiv 0$ thus $(b-1)^{3}-3 b+2 \equiv 0$ thus $(b-1)^{3}-3(b-1)-$ $1 \equiv 0$. In particular, $-(b-1)$ is also a root modulo $p$ of $X^{3}-3 X+1$, so $a \equiv-(b-1)$, thus $a^{2} \equiv-(a b-a) \equiv a-1$ thus $a^{2}-a+1 \equiv 0(\bmod p)$. Now, $a^{3}-3 a+1=\left(a^{2}-a+1\right)(a+1)-3 a$, so modulo $p, 3 a \equiv 0(\bmod p)$. Clearly, $a$ cannot be zero modulo $p$, so $p=3$.
Conversely, if $p=3$, there is a unique solution to $a^{3}+1 \equiv 0(\bmod 3): a \equiv 2$. Thus $p=3$ is the only prime number that fits.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.