problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
(BXMO 2014)
() Let $a, b, c$ and $d$ be strictly positive integers. Determine the smallest value that the expression:
$$
S=\left\lfloor\frac{a+b+c}{d}\right\rfloor+\left\lfloor\frac{a+b+d}{c}\right\rfloor+\left\lfloor\frac{a+c+d}{b}\right\rfloor+\left\lfloor\frac{b+c+d}{a}\right\rfloor
$$
can take.
|
With integer parts, there is not much to do: we apply the inequality $\lfloor x\rfloor>x-1$ to find, by rearranging the terms
$$
S>\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{a}{d}+\frac{d}{a}\right)+\left(\frac{c}{b}+\frac{b}{c}\right)+\left(\frac{d}{b}+\frac{b}{d}\right)+\left(\frac{c}{d}+\frac{d}{c}\right)-4
$$
and each term in parentheses is bounded below by 2 by IAG. Therefore, we have $S>8$, which means $S \geqslant 9$.
By trial and error, we find the construction $(5,5,5,4)$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a, b>1$ be odd such that $a+b=2^{l}$. Find the $k \in \mathbb{N}^{*}$ such that $k^{2} \mid a^{k}+b^{k}$.
|
Let's start by eliminating the case $k=1$ which works. Already $k$ is odd, because if $k$ were even, we would have a contradiction since $a^{k}+b^{k} \equiv 2[4]$. Next, take $p$ to be the minimal prime divisor of $k$ (possible since we have eliminated the case $k=1$). Since it is necessary that $a$ and $b$ are coprime, we have
$$
\left(\frac{a}{b}\right)^{2 k} \equiv 1[p]
$$
so by setting $\omega$ the order of $\frac{a}{b}$ modulo $p, \omega \mid 2 k$ and $\omega \mid p-1$ hence $\omega=1$ or 2. We study each of these cases and end up with a contradiction in each one.
The only $k$ that works is therefore 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Consider 2021 lines in the plane, no two of which are parallel and no three of which are concurrent. Let E be the set of their intersection points. We want to assign a color to each point in E such that any two points on the same line, and whose connecting segment contains no other point of E, are of different colors.
How many colors are needed at a minimum to achieve such a coloring?
|
First, note that it is necessary to have at least 3 colors to obtain such a coloring. Indeed, it is easily shown by induction on the number of lines that the configuration contains at least one triangle formed by the lines (this is true for $n=3$, and if we add a line, either it leaves the triangle intact or it separates it into a quadrilateral and a triangle).
Let us show that 3 colors suffice. As in many other exercises, we perform a rotation of the plane so that no line is vertical, we sort the intersection points by increasing abscissa $A_{1}, \ldots, A_{n}$ (where $n=\binom{2021}{2}$) and we color them in the same order. At each step, we can always color the point in question with a valid color since if it is the intersection point of $(d)$ and $\left(d^{\prime}\right)$, the only constraints on the color of the point are those given by the point to its left on $(d)$ and the one to its left on $\left(d^{\prime}\right)$, and in all cases we can choose a color that fits.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(IMO 1995, P3) Find all integers $n>3$ for which there exist $n$ points $A_{1}, \ldots, A_{n}$ in the plane and real numbers $r_{1}, \ldots, r_{n}$ such that:
1. no three of the points are ever collinear.
2. for all $i, j, k$, the area of the triangle $A_{i} A_{j} A_{k}$ is equal to $r_{i}+r_{j}+r_{k}$.
|
If we have four points $A_{i}, A_{j}, A_{k}, A_{l}$ that form a convex quadrilateral in this order, denoting $\mathcal{A}$ as the area, we have
$$
\mathcal{A}\left(A_{i} A_{j} A_{k} A_{l}\right)=\mathcal{A}\left(A_{i} A_{j} A_{k}\right)+\mathcal{A}\left(A_{k} A_{l} A_{i}\right)=\mathcal{A}\left(A_{j} A_{k} A_{l}\right)+\mathcal{A}\left(A_{l} A_{i} A_{j}\right)
$$
which can be rewritten as $r_{i}+r_{k}=r_{j}+r_{l}$. Now, if $A_{i} A_{j} A_{k} A_{l} A_{m}$ is a convex pentagon, the previous result applied to the convex quadrilaterals $A_{i} A_{j} A_{k} A_{l}$ and $A_{j} A_{k} A_{l} A_{m}$ gives $r_{i}+r_{k}=r_{j}+r_{l}=r_{k}+r_{m}$, hence $r_{i}=r_{m}$. Similarly, by iterating, we have $r_{i}=r_{j}=r_{k}=r_{l}=r_{m}$. Therefore, the triangles $A_{i} A_{j} A_{k}, A_{i} A_{j} A_{l}$, and $A_{i} A_{j} A_{m}$ have the same area $3 r_{i}$, and the points $A_{k}, A_{l}, A_{m}$ are at the same distance from the line $(A_{i} A_{j})$. Since the pentagon $A_{i} A_{j} A_{k} A_{l} A_{m}$ is convex, they are also on the same side of this line and are therefore collinear, which is absurd. Thus, there does not exist a convex pentagon among the points $A_{i}$. Notably, the convex hull of these points contains at most 4 points, without loss of generality, it is of the form $A_{1}, A_{2}, \ldots, A_{m}(m \leqslant 4)$.
Now, if $A_{i}$ does not belong to this convex hull (i.e., $i>m$), we have
$$
\begin{gathered}
\mathcal{A}\left(A_{1} A_{2} \ldots A_{m}\right)=\mathcal{A}\left(A_{1} A_{2} A_{i}\right)+\mathcal{A}\left(A_{2} A_{3} A_{i}\right)+\ldots+\mathcal{A}\left(A_{m-1} A_{m} A_{i}\right)+\mathcal{A}\left(A_{m} A_{1} A_{i}\right) \\
=2\left(r_{1}+r_{2}+\ldots+r_{m}\right)+m r_{i}
\end{gathered}
$$
and thus all $r_{i}$ for $i>m$ are equal. Then, if $i, i^{\prime}$ are of this form, for all $k, l \leqslant m$, the areas of $A_{k} A_{l} A_{i}$ and $A_{k} A_{l} A_{i^{\prime}}$ are equal, and $(A_{i} A_{i^{\prime}})$ is parallel to $(A_{k} A_{l})$. Since this is true for any pair of points in the convex hull (of which there are at least 3), we must have $i=i^{\prime}$. With the inequality $m \leqslant 4$, we must have $n \leqslant 5$. For $n=4$, we can simply take a square and all $r_{i}$ equal. It remains to show that the case $n=5$ is impossible.
In this case, we have $m=4$. The point $A_{5}$ is inside two triangles $A_{i} A_{j} A_{k}$ with $i, j, k \leqslant 4$, for example, $A_{1} A_{2} A_{3}$ and $A_{2} A_{3} A_{4}$. We write
$$
\mathcal{A}\left(A_{1} A_{2} A_{3}\right)=\mathcal{A}\left(A_{5} A_{2} A_{3}\right)+\mathcal{A}\left(A_{1} A_{5} A_{3}\right)+\mathcal{A}\left(A_{1} A_{2} A_{5}\right)
$$
which gives $r_{1}+r_{2}+r_{3}+3 r_{5}=0$. Similarly, we have $r_{2}+r_{3}+r_{4}+3 r_{5}=0$, hence $r_{1}=r_{4}$. We deduce that $(A_{1} A_{4})$ is parallel to $(A_{2} A_{3})$ and to $(A_{2} A_{5})$, so $A_{2}, A_{3}, A_{5}$ are collinear, which is absurd.
The only value of $n$ that works is therefore $n=4$.
|
4
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
In a room, there are ten students. Aline writes ten consecutive integers on the board. Each student chooses one of the ten integers written on the board, such that any two students always choose two different integers. Each student then calculates the sum of the nine integers chosen by the other nine students. Each student whose result is a perfect square then receives a gift.
What is the maximum number of students who will receive a gift?
A perfect square is an integer of the form $n^{2}$, where $n$ is a natural number.
|
The exercise requires determining the maximum value of a certain quantity. The reasoning therefore consists of two steps, called analysis and synthesis.
Step 1, the analysis: We show that the number of students receiving a gift is necessarily less than or equal to four, regardless of the numbers chosen by Aline.
Let $n, n+1, \ldots, n+9$ be the ten numbers written on the board, and let $S$ be their sum. If one of the integers is erased from the board, the sum of the remaining nine numbers is one of the integers:
$$
S-n, S-n-1, \ldots, S-n-9
$$
which are ten consecutive integers.
We then seek the maximum number of integers that can be perfect squares among ten consecutive integers.
First, since perfect squares are positive integers, a set of ten consecutive integers containing a negative integer contains fewer perfect squares than the set $\{0, \ldots, 9\}$. Next, note that among the integers from 0 to 9, there are four perfect squares, which are the integers $0, 1, 4,$ and $9$. Suppose there exist ten consecutive positive integers such that at least five of them are perfect squares. Then there exists a positive integer $a$ such that the numbers $a^{2}, (a+1)^{2}, (a+2)^{2}, (a+3)^{2},$ and $(a+4)^{2}$ are among the ten consecutive integers. We then have $9 \geqslant (a+4)^{2} - a^{2} = 8a + 16 > 9$, which is absurd.
Thus, the maximum number of integers that can be perfect squares among the ten integers $S-n, \ldots, S-n-9$ is 4, which means that at most four students will receive a gift.
Step 2, the synthesis: We show that the bound obtained in the analysis is achievable, i.e., there exist ten consecutive integers for which the students can arrange to receive four gifts.
For this, we observe that the sum of nine of the ten integers $n, n+1, \ldots, n+9$ is always between
$$
n + (n+1) + \ldots + (n+8) = 9n + 36 \quad \text{and} \quad (n+1) + (n+2) + \ldots + (n+9) = 9n + 45
$$
Thus, the perfect squares chosen by the students are integers between $9n + 36$ and $9n + 45$. We have seen in the analysis that the set $\{0, \ldots, 9\}$ contains 4 perfect squares. We seek $n$ satisfying $9n + 36 = 0$ and $9n + 45 = 9$, which leads to $n = -4$.
Thus, if Aline writes the integers
$$
-4, -3, -2, -1, 0, 1, 2, 3, 4, 5
$$
the students can choose the integers $5, 4, 1,$ or $-4$, so that the sum of the remaining nine integers will be $0, 1, 4,$ and $9$, respectively.
The largest number of students who can receive a gift is four.
Comment from the graders: The exercise was difficult for many students and was often only partially solved. It consisted of two parts: an analysis to show that it is not possible to do better than 4 gifts, and a synthesis in which it is necessary to explicitly state with which initial integers on the board it is actually possible to obtain 4 gifts. Many students did not take into account the fact that the integers written on the board were relative, i.e., positive or negative, and limited themselves to the positive case. Many students overlooked key arguments, such as the fact that the sums obtained are consecutive, which justifies looking for squares in an interval of size 10. Some tried to invoke arguments about the "density" of squares to try to justify that one should look at small integers to find many squares, but this argument is insufficient. Finally, a surprising proportion of students forgot that 0 is a perfect square, which was ultimately not penalized.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
In a room, there are ten students. Aline writes ten consecutive integers on the board. Each student chooses one of the ten integers written on the board, such that any two students always choose two different integers. Each student then calculates the sum of the nine integers chosen by the other nine students. Each student whose result is a perfect square then receives a gift.
What is the maximum number of students who will receive a gift?
A perfect square is an integer of the form $n^{2}$, where n is a natural number.
|
The exercise requires determining the maximum value of a certain quantity. The reasoning therefore consists of two steps, called analysis and synthesis.
Step 1, the analysis: We show that the number of students receiving a gift is necessarily less than or equal to four, regardless of the numbers chosen by Aline.
Let $n, n+1, \ldots, n+9$ be the ten numbers written on the board and let $S$ be their sum. If one of the integers is erased from the board, the sum of the remaining nine numbers is one of the integers:
$$
S-n, S-n-1, \ldots, S-n-9
$$
which are ten consecutive integers.
We then seek the maximum number of integers that can be perfect squares among ten consecutive integers.
First, since perfect squares are positive integers, a set of ten consecutive integers containing a negative integer has fewer perfect squares than the set $\{0, \ldots, 9\}$. Next, note that among the integers from 0 to 9, there are four perfect squares, which are the integers $0, 1, 4,$ and $9$. Suppose there exist ten consecutive positive integers such that at least five of them are perfect squares. Then there exists a positive integer $a$ such that the numbers $a^{2}, (a+1)^{2}, (a+2)^{2}, (a+3)^{2},$ and $(a+4)^{2}$ are among the ten consecutive integers. We then have $9 \geqslant (a+4)^{2} - a^{2} = 8a + 16 > 9$, which is absurd.
Thus, the maximum number of integers that can be perfect squares among the ten integers $S-n, \ldots, S-n-9$ is 4, which means that at most four students will receive a gift.
Step 2, the synthesis: We show that the bound obtained in the analysis is achievable, i.e., there exist ten consecutive integers for which the students can arrange to receive four gifts.
For this, we observe that the sum of nine of the ten integers $n, n+1, \ldots, n+9$ is always between
$$
n + (n+1) + \ldots + (n+8) = 9n + 36 \quad \text{and} \quad (n+1) + (n+2) + \ldots + (n+9) = 9n + 45
$$
Thus, the perfect squares chosen by the students are integers between $9n + 36$ and $9n + 45$. We have seen in the analysis that the set $\{0, \ldots, 9\}$ contains 4 perfect squares. We seek $n$ satisfying $9n + 36 = 0$ and $9n + 45 = 9$, which leads to $n = -4$.
Thus, if Aline writes the integers
$$
-4, -3, -2, -1, 0, 1, 2, 3, 4, 5
$$
the students can choose the integers $5, 4, 1,$ or $-4$, so that the sum of the remaining nine integers will be $0, 1, 4,$ and $9$, respectively.
The largest number of students who can receive a gift is four.
Comment from the graders: This problem was approached by most students, who generally understood the essence of it, but it was surprisingly not well done. Most students (more than two-thirds) managed to find the configuration that allows four students to win - many students forgot to count 0 as a perfect square.
However, very few students managed to rigorously justify that the interval from 0 to 9 is the interval of ten consecutive integers containing the most perfect squares. If the grading had placed more emphasis on the ideas rather than the way they were written, we would have expected more care in the justifications of the arguments. Thus, the majority of the solutions were incomplete, even though they were awarded 7 points, and few students produced a truly rigorous proof of their assertion. It is unfortunate to see phrases such as "squares get further and further apart," "the square function is increasingly increasing," "squares are increasingly dispersed" substituting for calculations, which are the only source of rigor here. We also note vocabulary issues, particularly when students claimed that the square function was exponential, to give just one example.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Knowing that $a b c=8$, with $a, b, c$ positive, what is the minimum value of $a+b+c$?
|
By the Arithmetic Mean-Geometric Mean Inequality (AM-GM Inequality): $\frac{a+b+c}{3} \geqslant \sqrt[3]{a b c}$.
Therefore, $a+b+c \geqslant 3 \cdot \sqrt[3]{8}=6$. This bound is indeed achieved with $a=b=c=2$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What are the integers $k$ such that for all real numbers $a, b, c$,
$$
(a+b+c)(a b+b c+c a)+k a b c=(a+b)(b+c)(c+a)
$$
|
Suppose the equation is verified for an integer $k$. By taking $a=b=c=1$, we get $3 \times 3 + k = 2^{3}$, so $k = 8 - 9 = -1$.
It remains to verify that $(a+b+c)(ab+bc+ca) - abc = (a+b)(b+c)(c+a)$ for all real numbers $a, b, c$. Now,
$$
(a+b+c)(ab+bc+ca) - abc = a^2b + a^2c + abc + b^2c + b^2a + abc + c^2a + c^2b + abc - abc
$$
so
$$
(a+b+c)(ab+bc+ca) - abc = a^2b + a^2c + b^2a + b^2c + c^2a + c^2b + 2abc
$$
and
$$
(a+b)(b+c)(a+c) = (ab + b^2 + ac + bc)(a+c) = a^2b + ab^2 + a^2c + abc + abc + b^2c + ac^2 + bc^2
$$
so
$$
(a+b)(b+c)(a+c) = a^2b + a^2c + b^2a + b^2c + c^2a + c^2b + 2abc
$$
For $k = -1$, we indeed have for all real numbers $a, b, c$,
$$
(a+b+c)(ab+bc+ca) + kabc = (a+b)(b+c)(c+a)
$$
The unique solution is therefore $k = -1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $x>0$. Show that $x+\frac{1}{x} \geqslant 2$. Find the cases of equality.
|
Let $c=x, d=\frac{1}{x}$ and apply proposition 4. We obtain $c+d=x+\frac{1}{x} \geqslant 2 \sqrt{c d}=2 \sqrt{\frac{x}{x}}=$ 2. We have equality if and only if $c=d$ that is $x=\frac{1}{x}$ if and only if $x^{2}=1$. The case of equality is thus achieved for $x=1$.
|
1
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Alice wants to color the integers between 2 and 31 (inclusive) using $k$ colors. She wishes that if $m$ and $n$ are integers between 2 and 31 such that $m$ is a multiple of $n$ and $m \neq n$, then $m$ and $n$ are of different colors. Determine the smallest integer $k$ for which Alice can color the integers $2,3, \ldots, 31$ using $k$ colors.
|
We show that $k \geqslant 4$. Consider the numbers 2, 4, 8, and 16. 2 divides the other 3, so 2 is not the same color as any of the others. Similarly, 4 divides 8 and 16, so it does not share a color with any of the others. And 8 divides 16, so they each have a different color. We have thus $k \geqslant 4$. Construction: We color the numbers from 2 to 3 in red, from 4 to 7 in blue, from 8 to 15 in green, and from 16 to 31 in yellow. We can verify that the construction works (This is because for $m$ divides $n$ and $m \neq n$, we have that $n \geqslant 2 m$).
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How many integers must one select from the set $\{1,2, \ldots, 20\}$ to ensure that this selection includes two integers $a$ and $\mathrm{b}$ such that $a-b=2$?
|
Consider the drawers of the form $\{1,3\},\{2,4\},\{5,7\},\{6,8\},\{9,11\},\{10,12\},\{13,15\}$, $\{14,16\},\{17,19\},\{18,20\}$. By choosing 11 integers, by the pigeonhole principle, there will be two that are in the same drawer, and thus have a difference of 2. This quantity is minimal because the set $\{1,2,5,6,9,10,13,14,17,18\}$ is of size 10 and does not contain such integers $a$ and $b$.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $n$ be an integer greater than 1.
Show that
$$
\sum_{k=0}^{n}(-1)^{k}\binom{n}{k}=0
$$
|
We have the binomial formula
$$
\sum_{k=0}^{n}(-1)^{k}\binom{n}{k}=(1-1)^{n}=0^{n}=0
$$
|
0
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Let $a>0$. Show that
$$
a+\frac{1}{a} \geq 2
$$
When do we have equality?
|
By applying the inequality of Theorem 1 to $\sqrt{a}$ and $\frac{1}{\sqrt{a}}$, we have $\frac{a+\frac{1}{a}}{2} \geq 1$, which gives us the desired inequality.
We have equality for $\sqrt{a}=\frac{1}{\sqrt{a}}$, that is, $a=1$.
|
1
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
What is the last digit of $2019^{2020^{2021}}$?
|
$2020^{2021}$ is even, and since $2019 \equiv-1(\bmod 10)$, we get $2019^{2020^{2021}} \equiv 1(\bmod 10)$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the last digit of $2023^{2024^{2025}}$?
|
We notice that $3^{2} \equiv 9 \equiv -1(\bmod 10)$, so $3^{4} \equiv 1(\bmod 10)$. Moreover, $2024^{2025}$ is a multiple of 4, so we have once again $2023^{2024^{2025}} \equiv 1(\bmod 10)$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the remainder of the Euclidean division of $2022^{2022^{2022}}$ by 11?
|
By Fermat's Little Theorem, we have \(2022^{10} \equiv 1 \pmod{11}\). Thus, if we know the value of \(2022^{2022} \mod 10\), we would be very happy.
We look at the powers of 2 modulo 10: they have a period of 4: 2, 4, 6, 8, 2, ... Since 2022 is congruent to \(2 \pmod{4}\), we get \(2022^{2022} \equiv 2^{2022} \equiv 4 \pmod{10}\).
Moreover, \(2024 = 184 \times 11\), so \(2022 \equiv -2 \pmod{11}\).
Finally, \(2022^{2022^{2022}} \equiv 2022^{10k} \times (-2)^{4} \equiv 16 \equiv 7 \pmod{11}\).
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The integers $a$ and $b$ have the following property: for any natural number $n$, the integer $2^{n} a+b$ is a perfect square. Show that $a$ is zero.
|
For all $n \in \mathbb{N}$ we write $x_{n}^{2}=2^{n} a+b$ with $x_{n} \in \mathbb{N}$. Then $x_{n+2}^{2}=2^{n+2} a+b$ and $\left(2 x_{n}\right)^{2}=$ $4 \cdot\left(2^{n} a+b\right)=2^{n+2} a+4 b$ are perfect squares and we have: $\left(2 x_{n}\right)^{2}-x_{n+2}^{2}=3 b$.
But as soon as $\left(2 x_{n}\right)>2|b|$ the distance between two consecutive squares (and thus between $\left(2 x_{n}\right)^{2}$ and any other square) is at least $4|b|+1>3 b$.
Thus, when $b \neq 0,\left(x_{n}\right)_{n \geq 0}$ is bounded (by $\left.|b|\right)$ and therefore $\left(2^{n} a+b\right)_{n \geq 0}$ is bounded: $a=0$.
If on the contrary $b=0$, we have $x_{1}^{2}=2 x_{0}^{2}$ or $x_{1}=x_{0} \sqrt{2}$. Since $\sqrt{2}$ is irrational, we have $a=x_{0}^{2}=0$.
|
0
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
$P$ is a polynomial of degree 4. $P(0)=P(1)=1, P(2)=4, P(3)=9, P(4)=16$. Calculate $P(-1)$
|
$P$ looks a lot like $X^{2}$, so we will study $P(X)-X^{2}$. This polynomial has 4 roots $(1,2,3,4)$. Thus $P(X)-X^{2}=(X-1)(X-2)(X-3)(X-4) Q(X)$, where $Q$ is a polynomial. Let's study the degrees:
$\operatorname{deg}\left(P(X)-X^{2}\right)=4=\operatorname{deg}((X-1)(X-2)(X-3)(X-4) Q(X))=4+\operatorname{deg}(Q) \Longleftrightarrow \operatorname{deg}(Q)=0$ Therefore $Q$ is a constant $c$, which we will determine with $P(0) . P(0)-0^{2}=c(0-$ $1)(0-2)(0-3)(0-4) \Longleftrightarrow c=\frac{1}{4!}=\frac{1}{24}$. So $P(-1)=(-1)^{2}+\frac{(-2) \cdot(-3) \cdot(-4) \cdot(-5)}{4!} \Longleftrightarrow P(-1)=$ $1+5=6$
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Consider 2022 lines in the plane, no two of which are parallel and no three of which are concurrent. Let $E$ be the set of their intersection points. We want to assign a color to each point in $E$ such that any two points on the same line, whose segment connecting them contains no other point of $E$, are of different colors. How many colors are needed at a minimum to achieve such a coloring?
|
The configuration contains at least one triangle. This can be proven, for example, by induction on the number of lines: three lines form a triangle, and if you add a line, it either leaves the triangle intact or splits it into a triangle and a quadrilateral. Consequently, it is impossible to perform a coloring with two colors.
We will now show that a coloring with three colors is possible: we order the points by strictly increasing abscissa, and color them in this order. When it is time to color a point \( P = (d_i) \cap (d_j) \), we have already colored at most one of its neighbors on \((d_i)\) (the one to the left) and one on \((d_j)\) (also the one to the left). Therefore, we have at most two forbidden colors and can always choose the third. The answer is therefore 3 colors.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(A1 IMO 1996)
Let $a, b, c>0$ such that $a b c=1$. Show that
$$
\sum_{c y c} \frac{a b}{a b+a^{5}+b^{5}} \leq 1
$$
|
By IAG, we have
$$
\sum_{c y c} \frac{a b}{a b+a^{5}+b^{5}} \leq \sum_{c y c} \frac{a b}{a b+a^{2} b^{2}(a+b)}=\sum_{c y c} \frac{c}{c+a+b}=1
$$
|
1
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
(Infinite Solitaire)(^) You all know the rules of solitaire: there are marbles on a board, and you eliminate marbles by jumping over them with another marble, etc. Now consider the plane and place marbles on all integer points of the negative half-plane. The goal of the game is to place a marble as high as possible in a finite number of moves. The drawing shows how to place a marble at height 1. What is the maximum height that can be reached?
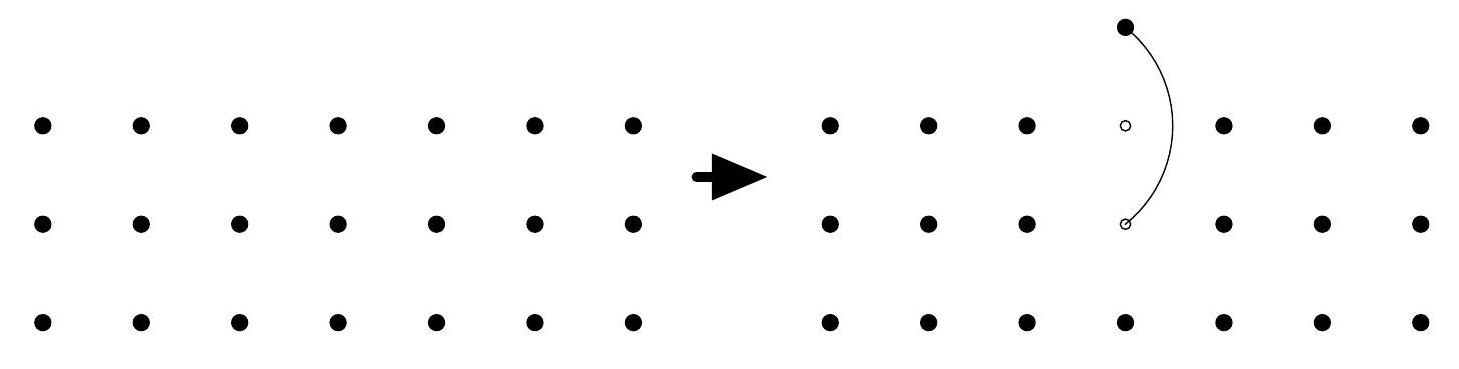
- Solutions to the exercises -
|
It is easy to raise a ball to height 1, 2, and 3, and with a bit of patience, one can raise a ball to height 4, but that is the limit. Let $\varphi$ be the golden ratio, which satisfies $\varphi^{2}=\varphi+1$:
$$
\varphi=\frac{1+\sqrt{5}}{2}
$$
Then, we need to sum over all points with coordinates $(x, y)$ on which there are balls of $\varphi^{y-|x|}$. I leave it to the reader to verify that this quantity remains constant or decreases when the balls are moved, and that in the initial position, it is equal to $\varphi^{5}$. This proves that it is impossible to raise a ball to height 5 or more.
## 2 Course/TD on Basic Strategies
## - Recurrence -
The principle of recurrence is fundamentally linked to the notion of integers: every time one needs to prove that a result is true for all integers from a certain rank, whether in arithmetic, geometry, algebra... one can be led to reason by recurrence.
The proof by recurrence is based on the fact that every integer $n$ has a successor $n+1$, and that if one "climbs step by step" the set $\mathbb{N}$ of natural numbers, starting from 0, going from one integer to the next, and repeating indefinitely, one thus fully traverses $\mathbb{N}$.
We will therefore prove that a property is true for the integer $n=0$ (initialization), and then that if it is true for any integer $n \geqslant 0$, it is still true for the next integer $n+1$ (induction): we deduce from this that the property is true for all natural numbers $n$. This is the reasoning by recurrence.
It should be noted that both parts of the proof are important, even if the first is often quite obvious. One must not forget to initialize the recurrence, that is, to prove that the property is true for $n=0$. One can start the recurrence at a value other than 0, for example, at $1, 2, \cdots$ or $K$; it will then be necessary to prove (initialization) that the property is true for $n=K$, and then (induction) that for $n \geqslant K$, if it is true for $n$, it is still true for $n+1$.
It should also be noted that induction has some variants. For example, it sometimes happens that one has to prove that if the property is true for all integers $k \leqslant n$, then it is true for $n+1$.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all odd integers $n \geqslant 1$ such that $n$ divides $3^{n}+1$.
untranslated text remains unchanged.
|
Let $n>1$ such that $n$ divides $3^{n}+1$. Another way to say this is that $3^{n} \equiv-1(\bmod n)$, so we are dealing with a purely multiplicative problem. We would like to use Fermat's theorem, but it is difficult to exploit because we have poor control over $\varphi(n)$. Let $p$ be a prime factor of $n$, which is odd. We have $3^{2 n} \equiv 1(\bmod p)$. Let $\omega$ be the order of 3 modulo $p$. Then $\omega$ divides $2 n$. On the other hand, by Fermat's little theorem, $3^{p-1} \equiv 1$ $(\bmod p)$. Thus $\omega$ divides $p-1$. We deduce that $\omega$ divides $\operatorname{GCD}(2 n, p-1)$. If we further impose that $p$ is the smallest prime factor of $n$, then necessarily $\omega=1$ or 2 (since a prime factor of $p-1$ cannot divide $n$ by minimality). In the first case, $3 \equiv 1(\bmod p)$ and thus $p=2$, which is excluded. In the second case, $3^{2} \equiv 1(\bmod p)$ and thus $p$ divides 8, which is also excluded. We conclude that $n=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find $k$ such that $(a+b)(b+c)(c+a)=(a+b+c)(a b+b c+c a)+k a b c$.
.
|
It is enough to develop the two members: $(a+b)(b+c)(c+a)=(a b+$ $\left.a c+b^{2}+b c\right)(c+a)=a^{2} b+a^{2} c+a b^{2}+a c^{2}+b^{2} c+b c^{2}+2 a b c,(a+b+c)(a b+b c+c a)+k a b c=$ $a^{2} b+a^{2} c+a b^{2}+a c^{2}+b^{2} c+b c^{2}+3 a b c+k a b c$ so $k=-1$.
## - Notable identities of degree 2 -
Proposition 1.3 (Notable identities of degree 2).
$$
\begin{aligned}
& (a+b)^{2}=a^{2}+2 a b+b^{2} \\
& (a-b)^{2}=a^{2}-2 a b+b^{2} \\
& a^{2}-b^{2}=(a+b)(a-b)
\end{aligned}
$$
## Proof.
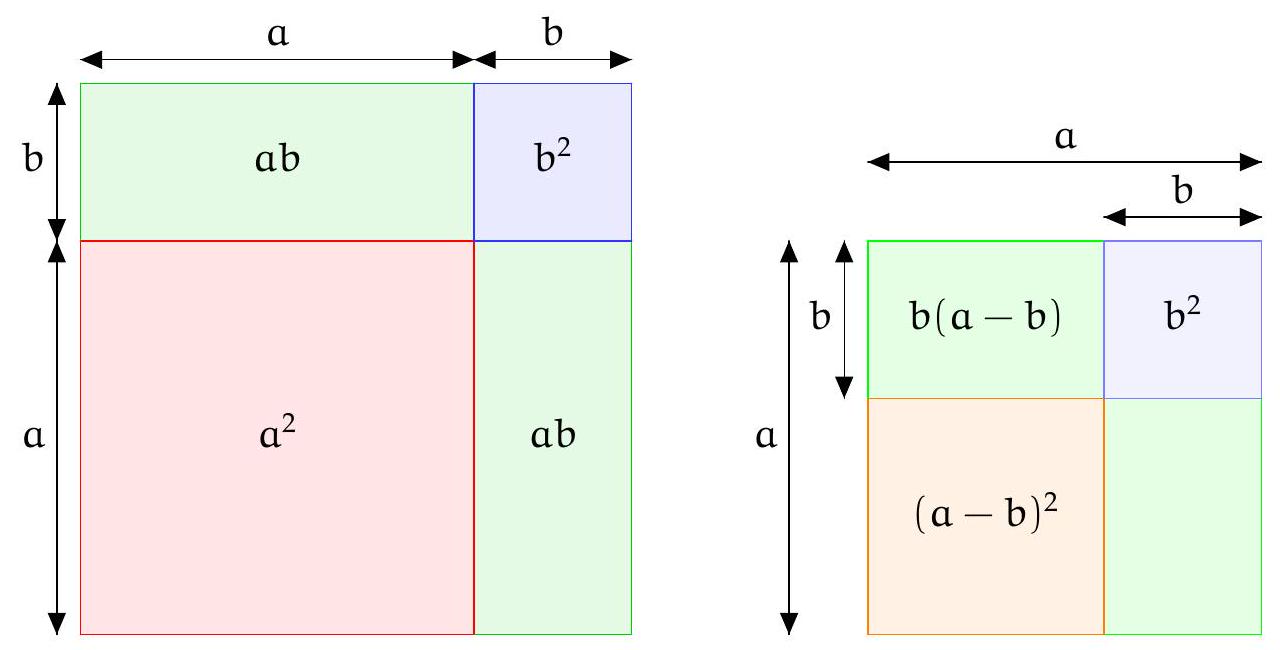
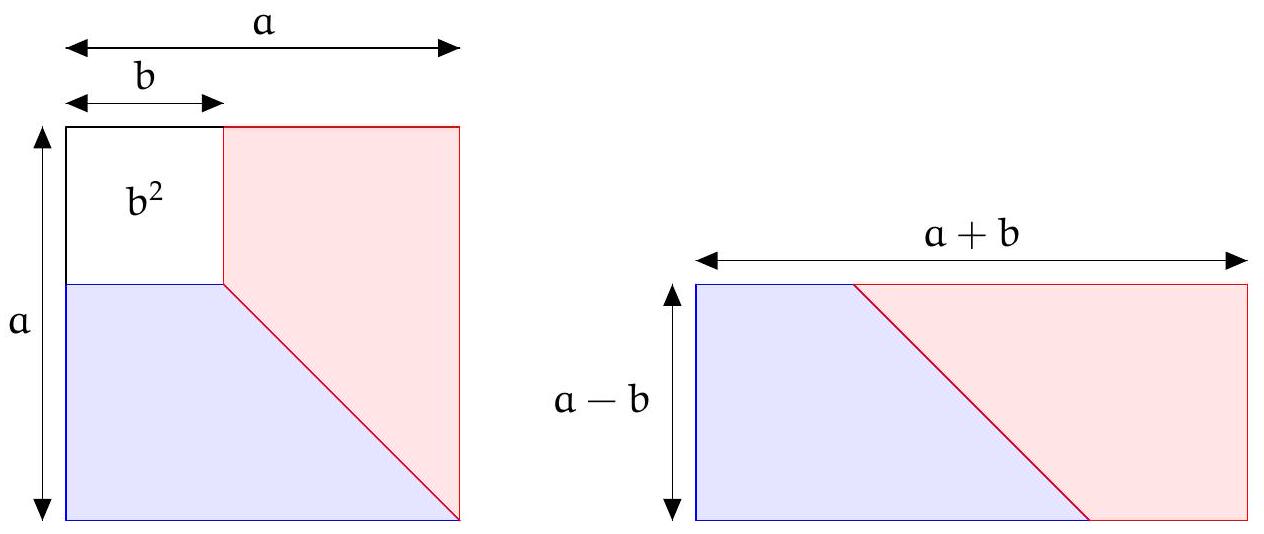
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$$
\binom{n}{0}-\binom{n}{1}+\binom{n}{2}-\ldots+(-1)^{k}\binom{n}{k}+\ldots+(-1)^{n}\binom{n}{n}=?
$$
|
As for the previous exercise, it involves recognizing a binomial of Newton but this time with $a=1$ and $b=-1$. We therefore find $(1-1)^{\mathfrak{n}}=0$.
## Corollary 1.14.
$$
\binom{n}{k}=\binom{n}{n-k}
$$
Proposition 1.15 (Pascal's Formula).
$$
\binom{n}{k}=\binom{n-1}{k}+\binom{n-1}{k-1}
$$
Proof. We want to choose $k$ elements from $n$. We isolate one element. Either this element is part of the chosen ones, or it is not. In the first case, we still need to choose $k-1$ elements from the remaining $n-1$, and in the second case, we need to choose $k$ elements from the remaining $n-1$. Thus,
$$
\binom{n}{k}=\binom{n-1}{k}+\binom{n-1}{k-1}
$$
Corollary 1.16. To find the value of $\binom{n}{k}$ for small $n$, we write Pascal's triangle:

It is sufficient to write "1" on the sides of the triangle, then each number is equal to the sum of the two numbers above it, according to the previous proposition. This easily provides the values of the binomial coefficients.
## 2 Algebra TD
## - Combinatorics -
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $x, y$ and $z$ be three strictly positive real numbers. Show that
$$
\frac{x}{y}+\frac{y}{z}+\frac{z}{x}+\frac{x}{z}+\frac{z}{y}+\frac{y}{x} \geqslant 6
$$
|
We group a term and its inverse, and apply the previous exercise, to obtain $\frac{x}{y}+\frac{y}{x}+\frac{z}{x}+\frac{x}{z}+\frac{z}{y}+\frac{y}{z} \geqslant 2+2+2=6$
|
6
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Study the sequence defined by $\mathfrak{u}_{0}=0$ and $\mathfrak{u}_{n+1}=\sqrt{12+\mathfrak{u}_{n}}$ for all $\mathfrak{n} \in \mathbb{N}$.
Regarding the second type of equations:
Definition 2.11. Let $\left(u_{n}\right)$ be a real sequence. We say it satisfies a recurrence equation of order $\mathbf{k}$ (linear) if there exists $k \in \mathbb{N}^{*}$ and real numbers $a_{0}, \cdots, a_{k-1}$ such that for all natural numbers $n$,
$$
u_{n+k}+a_{k-1} u_{n+k-1}+\cdots+a_{0} u_{n}=0
$$
Definition 2.12. The equation $X^{k}+a_{k-1} X^{k-1}+\cdots+a_{0}=0$ is called the characteristic equation.
Example 2.13. For an arithmetic sequence with common difference $a, u_{n+1}-u_{n}=u_{n+2}-u_{n+1}=a$, so $u_{n+2}-2 u_{n+1}+u_{n}=0$ is a recurrence equation satisfied by $u_{n}$.
For a geometric sequence with common ratio $a, u_{n+1}-a u_{n}=0$.
An arithmetico-geometric sequence satisfies a relation of the form: $\mathfrak{u}_{n+1}=a u_{n}+b$, and we obtain the recurrence equation $u_{n+2}-(a+1) u_{n+1}+a u_{n}=0$.
The general solution of such a recurrence equation (whose proof is unnecessary and tedious in our context) uses the concept of polynomials, discussed in the following section. Let's focus on orders 1 and 2 here.
Proposition 2.14. If for all $n \in \mathbb{N}, u_{n+1}-a u_{n}=0$, then $u_{n}=u_{0} a^{n}$.
Proposition 2.15. If for all $n \in \mathbb{N}, u_{n+2}+a_{1} u_{n+1}+a_{0} u_{n}=0$, we solve the quadratic characteristic equation $X^{2}+a_{1} X+a_{0}=0$.
- If it has two distinct solutions $r_{1}$ and $r_{2}$, then: $u_{n}=c_{1} r_{1}^{n}+c_{2} r_{2}^{n}$, where $c_{1}$ and $c_{2}$ are determined using, for example, the values of $\mathfrak{u}_{0}$ and $\mathfrak{u}_{1}$.
- If it has a double root $r$, then: $\mathfrak{u}_{n}=(a n+b) r^{n}$, and again $\mathfrak{u}_{0}$ and $\mathfrak{u}_{1}$ allow us to determine $a$ and $b$.
Would you be able to find in the previous property where the arithmetic, geometric, and arithmetico-geometric sequences are hidden?
Example 2.16. A geometric sequence corresponds to a recurrence equation of order 1. An arithmetic sequence corresponds to a recurrence equation of order 2 with 1 as a double root.
An arithmetico-geometric sequence with common ratio $a$ corresponds to a recurrence equation of order 2 whose solutions are 1 and $a$.
So much promising theory only calls out more strongly for exercises allowing us to apply these new knowledge victoriously.
|
We observe, by a quick induction, that the sequence is bounded by 4. We also show by induction on $n$ that $\mathfrak{u}_{n+1}>\mathfrak{u}_{n}:$ the initialization holds with $\mathfrak{u}_{1}=\sqrt{12}>0=\mathfrak{u}_{0}$. If we assume $a_{n+1}>a_{n}$, it follows that $a_{n+2}=\sqrt{12+a_{n+1}} \geq a_{n+1}$, which completes the induction.
The sequence is increasing and bounded, so it has a limit $l$. The function $x \rightarrow \sqrt{12+x}$ is continuous, so $l=\sqrt{12+l}$, which gives $l^{2}-l-12=0$. The unique positive solution to this equation is 4, which is therefore the limit of the sequence.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $x$ and $y$ be two non-zero numbers such that $x^{2} + x y + y^{2} = 0$ (where $x$ and $y$ are complex numbers, but that's not too important). Find the value of
$$
\left(\frac{x}{x+y}\right)^{2013} + \left(\frac{y}{x+y}\right)^{2013}
$$
|
Clearly, $x /(x+y)+y /(x+y)=1$ and
$$
\frac{x}{x+y} \cdot \frac{y}{x+y}=\frac{x y}{x^{2}+2 x y+y^{2}}=1
$$
Thus, $x /(x+y)$ and $y /(x+y)$ are the roots of $t^{2}-t+1=0$, so the sums $S_{k}=(x /(x+y))^{k}+(y /(x+y))^{k}$ satisfy $S_{0}=2, S_{1}=1$ and
$$
S_{k+2}=S_{k+1}-S_{k}
$$
for $k \geqslant 0$. We deduce that the sequence $\left(S_{k}\right)$ is periodic with period 6, its values being successively $2,1,-1,-2,-1,1,2,1,-1, \ldots$. We deduce that $S_{2013}=-2$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all real numbers $x, y, z$ such that
$$
x+y+z=3, \quad x^{2}+y^{2}+z^{2}=3, \quad x^{3}+y^{3}+z^{3}=3
$$
## - Polynomials with integer coefficients -
We now present some specific properties of polynomials with integer coefficients:
* We have already seen that if $P, Q \in \mathbb{Z}[X]$ and $\operatorname{deg} Q \geqslant 1$, we can always perform the Euclidean division of $P$ by $Q$ provided that the leading coefficient of $Q$ is equal to 1.
* An extremely useful property is that if $P \in \mathbb{Z}[X]$, then for all integers $a \neq b, a-b$ divides $P(a)-P(b)$. This is a simple consequence of the fact that $a-b$ divides $a^{n}-b^{n}$ for $n \geqslant 1$.
$\star$ If $P(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0} \in \mathbb{Z}[X]$, and if $p / q$ is a rational root of $P$ in irreducible form, then $p$ divides $a_{0}$ and $q$ divides $a_{n}$. This simple fact allows us to restrict the search for rational roots of a polynomial with integer coefficients.
* A polynomial $P \in \mathbb{Q}[X]$ satisfies $P(k) \in \mathbb{Z}$ for all $k \in \mathbb{Z}$ if and only if there exist integers $a_{0}, a_{1}, \ldots a_{n}$ such that
$$
P(x)=a_{0}\binom{x}{0}+a_{1}\binom{x}{1}+\cdots+a_{n}\binom{x}{n}
$$
where we denote $\binom{x}{k}=\frac{x(x-1) \cdots(x-k+1)}{k!}$ if $k \neq 0$ and $\binom{x}{0}=1$. This property follows from Exercise $10(2)$.
Example 3.42. Let's find all real numbers $x, y, z$ such that
$$
x+y+z=17, \quad x y+y z+x z=94, \quad x y z=168
$$
According to Viète's formulas, $x, y, z$ are roots of $P(x)=x^{3}-17 x^{2}+94 x-168=0$. Let's look for "obvious" roots of $P$. It is natural to first look for integer roots, which must be divisors of 168 (to test if, for example, 2 is a root, we perform the Euclidean division of $P$ by $x-2$ and check if the remainder is zero). We notice that $x=4$ is a root, and without difficulty, we find that $x=6$ and $x=7$ are roots of the polynomial $P(x) /(x-4)$. Thus, the solutions $(x, y, z)$ are the six possible permutations of $(4,6,7)$.
|
We write Newton's relations:
$$
S_{1}-\sigma_{1}=0, \quad S_{2}-\sigma_{1} S_{1}+2 \sigma_{2}=0, \quad S_{3}-\sigma_{1} S_{2}+\sigma_{2} S_{1}-3 \sigma_{3}=0
$$
Thus, $\sigma_{1}=3, \sigma_{2}=3, \sigma_{3}=1$. From this, we deduce that $x, y, z$ are roots of $t^{3}-3 t^{2}+3 t-1=0$. Now, $t^{3}-3 t^{2}+3 t-1=(t-1)^{3}$. Therefore, $x=y=z=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a, b, c, d$ be the four roots of $X^{4}-X^{3}-X^{2}-1$. Calculate $P(a)+P(b)+P(c)+$ $P(d)$, where $P(X)=X^{6}-X^{5}-X^{4}-X^{3}-X$.
|
First, note that $P(X)=X^{2}\left(X^{4}-X^{3}-X^{2}-1\right)-X^{3}+X^{2}-X$. Using the recurrence formula for symmetric polynomials, it suffices to compute $-S_{3}+S_{2}-S_{1}$. Now, $\sigma_{1}=1, \sigma_{2}=-1$ and $\sigma_{3}=0$. Therefore, $S_{1}=\sigma_{1}=1, S_{2}=\sigma_{1} S_{1}-2 \sigma_{2}=3$ and $\mathrm{S}_{3}=\sigma_{1} \mathrm{~S}_{2}-\sigma_{2} \mathrm{~S}_{1}+3 \sigma_{3}=4$, and the desired sum is -2.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $A, B, C, D$ and $E$ be five points in the plane in general position (that is, such that no three of them are collinear, and no four of them are concyclic). A separator is defined as a circle passing through three of these points, such that one of the two remaining points is located inside the circle, and the other outside. How many separators are there?
|
We quickly realize that if we try to tackle the problem naively, we will soon end up with perfectly sordid case studies. So we stop for a minute to think about how to simplify this case study as much as possible. To do this, we would like to get rid of as many circles as possible, which encourages us to invert through one of our points, say $A$. Another way to say the same thing is that these separation questions will be simpler with a point at infinity, as it will always be clear whether this point is separated from the others or not.
Throughout the following, I will call $ABC$ the circle passing through the three points $A, B$, and $C$, and the same for other circles. Let's therefore look at the effect of our inversion on the separators. We check that the inversion sends a separator passing through $A$, say $ABC$, to a line $B^{\prime} C^{\prime}$ separating $D^{\prime}$ and $E^{\prime}$: the segment $DE$, which intersects $ABC$ at exactly one point (distinct from $A$), is sent to an arc of a circle intersecting the line $B^{\prime} C^{\prime}$ at exactly one point. Conversely, we check in the same way that such a line is sent back to a separator.
The second case is that of separators not passing through $A$. Suppose then that $BCD$ separates $A$ and $E$. The segment $AE$ intersects $BCD$ at exactly one point (distinct from $A$), so the image of the segment, which is a ray starting from $E$, intersects the circle $B^{\prime} C^{\prime} D^{\prime}$ at exactly one point: $E^{\prime}$ is therefore inside this circle (whether $E$ is inside or outside $BCD$). Conversely, if $B^{\prime} C^{\prime} D^{\prime}$ contains $E^{\prime}$, we check in the same way that $BCD$ is a separator.
We have therefore reduced the problem to the following: we consider four points in the plane in general position, and we want to count the number of lines separating two of these points, as well as the number of circles passing through 3 points containing the 4th. There are two cases to consider. Case 1: if one of the points, say $D$, is inside the triangle $ABC$, then there are three such lines, $AD, BD$, and $CD$, and one such circle, $ABC$ (it is the only one by an angle argument). Case 2: if the points are the vertices of a convex quadrilateral. Then there are two lines that work, the diagonals, and two circles: there must be two vertices, say $A^{\prime}$ and $C^{\prime}$, such that the sum of the angles at these two vertices is strictly greater than $180^{\circ}$ (since the points are not cocyclic), and by an angle argument the only circles that work are $A^{\prime} B^{\prime} D^{\prime}$ and $C^{\prime} B^{\prime} D^{\prime}$.
Bonus! An exercise not done in class, but already typed before the session, so I leave it here.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a, b, c, d$ be real numbers defined by
$$
a=\sqrt{4-\sqrt{5-a}}, b=\sqrt{4+\sqrt{5-b}}, c=\sqrt{4-\sqrt{5+c}}, d=\sqrt{4+\sqrt{5+d}}
$$
Calculate their product.
## 2 Solutions
|
It would be wonderful if the four reals $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ were roots of the same polynomial, whose constant term would be their product. Fortunately, this is almost true. Indeed, by squaring each equality twice (taking care to isolate the root each time), we find that $a, b, -c, -d$ are roots of the polynomial $P(X) = X^4 - 8X^2 - X + 11$. And it is clear that $a, b > 0$ and $-c, -d < 0$ (the reals $a, b, c, d$ are non-zero, since $P(0) \neq 0$). Furthermore, if $a = b$, $\sqrt{4 - \sqrt{5 - a}} = \sqrt{4 + \sqrt{5 - a}}$ so $5 - a = 0$, hence $5 = \sqrt{4 - 0} = 2$, which is absurd. Similarly, we verify that $c \neq d$.
Thus $P$ has four distinct roots $a, b, -c, -d$, so $abcd = 11$ by Vieta's formulas.
## 3 Group C
## 1 Statements
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all natural numbers $n$ such that $n$ divides $2^{n}-1$.
|
The number 1 works. Let $p$ be the smallest prime divisor of $n \neq 1$. Since $2^{n} \equiv 1 \pmod{n}$, we also have $2^{n} \equiv 1 \pmod{p}$, and by Fermat's Little Theorem, $2^{p-1} \equiv 1 \pmod{p}$, so the order of 2 modulo $p$ divides the GCD of $n$ and $p-1$, hence it is 1 because $p-1$ is smaller than the smallest prime number dividing $n$, and is coprime with $n$. Thus $2 \equiv 1 \pmod{p}$, so $p=1$, which is absurd. Therefore, 1 is the only solution.
## 2 Arithmetic TD
## - Exercise Statements -
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine all strictly positive integers that are coprime with all numbers of the form $2^{n}+3^{n}+6^{n}-1$, for $n$ a natural number.
|
We are looking for prime numbers that do not divide any of the $2^{n}+3^{n}+6^{n}-1$ for $n$ a natural integer.
2 is not one of them, because it divides $2+3+6-1$.
Let $p \geqslant 5$ be a prime. 2, 3, and 6 are coprime with $p$, so $2^{p-1} \equiv 3^{p-1} \equiv 6^{p-1} \equiv 1(\bmod p)$.
$6\left(2^{p-2}+3^{p-2}+6^{p-2}-1\right)=3 \times 2^{p-1}+2 \times 3^{p-1}+6^{p-1}-6 \equiv 3+2+1-6=0(\bmod p)$. Therefore, $p$ divides $6\left(2^{p-2}+3^{p-2}+6^{p-2}-1\right)$, and since $p$ is coprime with 6, $p$ divides $2^{p-2}+3^{p-2}+6^{p-2}-1$.
There does not exist a prime number that does not divide any of the $2^{n}+3^{n}+6^{n}-1$ for $n$ a natural integer, so the only integer prime with all numbers of this form is 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $p$ be a prime number. Under what condition does there exist an integer $k$ such that $k^{2} \equiv-1$ $(\bmod p) ?$
|
Finding a necessary and sufficient condition requires mathematical tools that you do not have, but you can at least find a necessary condition. If $k^{2} \equiv -1 \pmod{p}$, then $k^{4} \equiv 1 \pmod{p}$, so the order of $k$ - the smallest exponent $n$ such that $k^n \equiv 1 \pmod{p}$ - divides 4. If $-1 \neq 1 \pmod{p}$, therefore if $p \neq 2$ (for $p=2$, the condition is satisfied), this order is not 2 because $k^{2} \equiv -1 \pmod{p}$, and it is certainly not 1 because if $k \equiv 1 \pmod{p}$, we would have $k^{2} \equiv 1 \pmod{p}$, so it is necessarily 4. Any other $n$ such that $k^n \equiv 1 \pmod{p}$ is divisible by the order 4 of $k$: otherwise, we would have $n = 4k + r$ with $0 \leq r < 4$ and $k^r \equiv 1 \pmod{p}$, which would contradict the minimality. Furthermore, by Fermat's theorem, since $k$ is not divisible by $p$ (otherwise we would have $k^{2} \equiv 0 \pmod{p}$), $k^{p-1} \equiv 1 \pmod{p}$, which implies that $p-1$ is divisible by 4. A necessary condition is therefore that $p=2$ or $p \equiv 1 \pmod{4}$.
Let's give an overview of the proof that this condition is sufficient. We work in the set of congruence classes modulo $p$: $a$ and $b$ are in the same class if $a \equiv b \pmod{p}$. This set of classes, $\mathbb{Z} / p \mathbb{Z}$, is equipped with addition and multiplication, because if $a \equiv b \pmod{p}$ and $a' \equiv b' \pmod{p}$, then $a + a' \equiv b + b' \pmod{p}$ and $aa' \equiv bb' \pmod{p}$. The elements $k$ and $-k$ have the same square: the "perfect squares" (we call them: quadratic residues) of $\mathbb{Z} / p \mathbb{Z}$ are therefore 0 and at most half of the other $p-1$ elements. In reality, it is exactly half of the other $p-1$ elements, and a given integer, for example -1, has "a one in two chance" of being a quadratic residue (for about half of the prime numbers, -1 is a quadratic residue). Because - and this is where it would be appropriate to delve deeper - the equation $x^2 = a$ cannot have more than two distinct roots, and more generally a polynomial of degree $d$ cannot have more than $d$ distinct roots, just as in the set of reals, for example. However, in $\mathbb{Z} / p \mathbb{Z}$, the equation $x^{p-1} = 1$ has $p-1$ distinct roots: all the non-zero elements of $\mathbb{Z} / p \mathbb{Z}$. If $p$ is odd and $x$ is non-zero, $x^{\frac{p-1}{2}}$ has a square of 1, so it is equal to either 1 or -1. If $x$ is a quadratic residue, there exists $y$ such that $y^2 = x$, so $x^{\frac{p-1}{2}} = y^{p-1} = 1$: all quadratic residues are roots of $x^{\frac{p-1}{2}} = 1$. But since there are $\frac{p-1}{2}$ quadratic residues, and this equation of degree $\frac{p-1}{2}$ cannot have more than $\frac{p-1}{2}$ roots, all its roots are quadratic residues. Therefore, if $(-1)^{\frac{p-1}{2}} = 1$, -1 is a quadratic residue. If $p \equiv 1 \pmod{4}$, $(-1)^{\frac{p-1}{2}} = 1$, hence the result.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How many triplets $(a, b, c)$ of integers satisfy the equation $a+b+c=6$ as well as the conditions $-1 \leqslant a \leqslant 2$ and $1 \leqslant b, c \leqslant 4$?
|
We start by generalizing the problem by looking for the generating series of the sequence of the number of solutions to the equation $a+b+c=n$ with the same conditions on $a, b, c$ (of course, this will actually be a polynomial). Since $-1 \leqslant a \leqslant 2$, the contribution of the variable $a$ is a factor $x^{-1}+x^{0}+x^{1}+x^{2}$. As for $b$ and $c$, each gives a factor $x^{1}+x^{2}+x^{3}+x^{4}$. The generating series we are looking for is therefore
$$
f(x)=\left(x^{-1}+x^{0}+x^{1}+x^{2}\right)\left(x^{1}+x^{2}+x^{3}+x^{4}\right)^{2}=x\left(1+x+x^{2}+x^{3}\right)^{3}
$$
What we are interested in is the coefficient of $x^{6}$ in this polynomial. Directly expanding the expression above is a bit lengthy and almost returns to the original combinatorial problem. It is always advantageous to rewrite things in a form that involves terms of the highest possible degree. Thus, here, we can write
$$
f(x)=x\left(\frac{1-x^{4}}{1-x}\right)^{3}=x\left(1-3 x^{4}+3 x^{8}-x^{12}\right)(1-x)^{-3}
$$
The terms of degree 6 come from choosing either 1 or $-3 x^{4}$ in the first parenthesis, and therefore the term of degree 5 or the term of degree 1 in the second parenthesis. According to the binomial formula, the coefficient we are looking for is therefore
$$
1 \times\left(-\binom{-3}{5}\right)+(-3) \times\left(-\binom{-3}{1}\right)=\binom{7}{5}-3\binom{3}{1}=21-9=12
$$
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Calculate $\sum_{i=1}^{n} \prod_{j \neq i} \frac{x-a_{j}}{a_{i}-a_{j}}$ for $a_{1}, \ldots, a_{n} \in \mathbb{R}$ pairwise distinct.
|
This polynomial is of degree at most $n-1$ and is equal to 1 at $a_{i}$, hence it is identically equal to 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For which positive integers $n$ does the number $n^{2}+1$ divide $n+1$?
|
The integers considered are strictly positive. Thus, if $\mathfrak{n}^{2}+1$ divides $n+1$, then $n^{2}+1 \leqslant n+1$, hence $n^{2} \leqslant n$. And since $n>0, n \leqslant 1$. Finally, $n$ being an integer, the only candidate left is $n=1$, and we verify that it works: 2 divides 2. It's good!
The following exercises aim to show the importance of factorization in exercises involving divisibility.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all values of $n \in \mathbb{N}$ such that $3^{2 n}-2^{n}$ is prime.
|
The expression we are discussing in terms of primality can be rewritten as $3^{2 n}-2^{n}=\left(3^{2}\right)^{n}-2^{n}=9^{n}-2^{n}=(9-2)\left(9^{n-1}+9^{n-2} \cdot 2+9^{n-3} \cdot 2^{2}+\cdots+2^{n-1}\right)$.
For $n \geqslant 2$, the right factor is at least $9^{1}$, so it is different from 1. The left factor is itself different from 1, so we conclude that $3^{2 n}-2^{n}$ is composite.
It suffices to handle the remaining cases by hand: for $n=1,9-2=7$ is prime, for $n=0$, $0-0=0$ is not prime.
The set we are looking for is therefore $\{1\}$.
Remark 1.1. Factoring an expression $n$ as $n=a b$ is a very classic method to show that a number is not prime. But be careful, the factorization represents only half of the work. It remains to verify that the two factors are strict divisors. This can be done by checking that $a>1$ and $b>1$ as we did earlier, or by checking that $1<a<n$, or even by checking that $\mathrm{a}<\mathrm{n}$ and $\mathrm{b}<\mathrm{n}$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all positive integers $a$ such that $a^{2}+2a$ is a perfect square.
|
There are two cases. If $a>0$, we notice that $a^{2}<a^{2}+2 a<$ $a^{2}+2 a+1=(a+1)^{2}$. Therefore, $a^{2}+2 a$ cannot be a perfect square. If $a=0$, we find $a^{2}+2 a=0$ which is a perfect square. This is therefore the only one.
## 2 Arithmetic Course
This session discussed congruences. The main points covered during the session are addressed in the course on the Animath website, in chapter 3. I will not repeat the entire course, but just provide a summary, referring to the course for more details. The address of this course is at http ://www.animath.fr/spip.php ?article255.
I started by defining congruences (definition 3.1.1), comparing congruences modulo an integer 12 with the hours written on a 12-hour clock, and then by analogy comparing congruences modulo any integer $n$ with the hours written around a hypothetical clock with $n$ hours.
I then emphasized the last property of the course: one can "add" and "multiply" modulo. Intuitively, the property of addition can be visualized by noting that advancing 15 hours from a given position on a 12-hour clock is the same as advancing 3 hours. To visualize the property of multiplication, an idea is to look modulo 10: a number is congruent to its last digit modulo 10, and we know well that to find the last digit of the product of two numbers, it suffices to examine the product of the last two digits.
I then moved on to section 3.2, on divisibility criteria. If an integer is written as $\overline{\text { abcde }}$ in base 10, then it is worth $\mathrm{a} \cdot 10^{4}+\mathrm{b} \cdot 10^{3}+\mathrm{c} \cdot 10^{2}+\mathrm{d} \cdot 10+\mathrm{e}$. If we know the values taken by the sequence $(10)^{n}$ modulo $k$, then we will have a quick method to find the value of $\overline{\mathrm{abcde}}$ modulo $k$.
For example, with $k=7$, we verify that $10 \equiv 3[7], 10^{2} \equiv 2[7], 10^{3} \equiv-1[7]$, and $10^{4} \equiv-3[7]$. Thus, we will have
$$
\begin{aligned}
\overline{\mathrm{abcde}} & \equiv a \cdot(-3)+b \cdot(-1)+c \cdot 2+d \cdot 3+e[7] \\
& \equiv-3 a-b+2 c+3 d+e[7]
\end{aligned}
$$
A concrete example: $\overline{17255} \equiv-3-7+4+15+5[7]$, and therefore it is divisible by 7. We can create as many such criteria as we want.
We see from this example the great strength of the notion of congruence: it allows replacing calculations on large numbers with calculations on much smaller numbers, which are therefore easier. A spectacular example is given by the following exercise. It uses a classic trick, due to the fact that 10 is congruent to 1 modulo 9: a number is always congruent to the sum of its digits modulo 9.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Calculate the sum of the digits of the sum of the digits of the sum of the digits of $A:=4444^{4444}$.
|
Let $S(n)$ denote the sum of the digits of an integer $n$. Then our trick says that for all $n, S(n) \equiv n[9]$. Thus, $S(S(S(A))) \equiv A[9]$. Let's calculate $A$ modulo 9. We have $4444 \equiv 4+4+4+4 \equiv -2$ [9], so we need to calculate $(-2)^{4444}$ modulo 9. We notice that $(-2)^{3} \equiv 1[9]$. We deduce that $(-2)^{3 k+i} \equiv\left((-2)^{3}\right)^{k} \cdot(-2)^{i} \equiv(-2)^{i}[9]$. In particular, since $4444 \equiv 4+4+4+4 \equiv 1[3]$, then $(-2)^{4444} \equiv(-2) \equiv 7[9]$.
Thus, we know $S(S(S(A)))$ modulo 9. To find its actual value, the idea is that $S(n)$ is generally much smaller than $n$. Thus, $S(S(S(A)))$ is much, much, much smaller than $A$, and with a bit of luck, it will be small enough to determine. We write that $A \leqslant\left(10^{4}\right)^{5000}=10^{20000}$, so $A$ has at most 20000 digits, so
$S(A) \leqslant 20000 \cdot 9 \leqslant 200000$. Thus, $S(S(A)) \leqslant 1+9 \cdot 5=46$, and then $S(S(S(A))) \leqslant 3+9=12$. Since it is 7 modulo 9, it must necessarily be 7.
The second part of the session was devoted to the study of linear equations modulo $n$. We examined the equations $5 x \equiv 10$ [16] and $5 x \equiv 10$ [15]. In each case, we are tempted to "divide by 5". THIS MAKES NO SENSE, AND YOU MUST NOT DO IT. The only operations we are allowed to perform modulo $n$ are addition and multiplication; do not invent other rules like a possible division by 5, as in most cases, it will be wrong.
Let's solve these systems explicitly. For the first one, the equation can be rewritten as $5 x=16 k+10$. In particular, 5 must divide 16k, but since it is coprime with 16, it must divide $k$ by Gauss's lemma: we write $k=5 k^{\prime}$ and then divide by 5, leaving $x=16 k^{\prime}+2$. Conversely, we verify that the $x \equiv 2$ [16] are solutions: in this case, the "division by 5" would have given the correct result.
For the second one, it can be rewritten as $5 x=15 k+10$: we divide by 5 and get $x=3 k+2$. Conversely, the $x \equiv 2$ [3] are solutions. In this case, the "division by 5" would not have worked.
The results 3.1.2 and 3.1.3 of the course specify all of this. In fact, the "division by 5" that we want to perform can be seen as a multiplication by $1 / 5$, and Theorem 3.1.2 precisely states that, in certain cases, we have a notion of an inverse modulo $n$. Thus, 5 has an inverse modulo 16 (for example, -3), so we can multiply the equation $5 x \equiv 10$ [16] by -3, yielding $x \equiv 5 \cdot(-3) \cdot x \equiv 10 \cdot(-3) \equiv 2[16]$. This is the essence of Proposition 3.1.3. On the other hand, 5 does not have an inverse modulo 15 (if you want to prove it, start from the fact that $5 \cdot 3 \equiv 0$ [15]). When we examine the proof of these results, we notice that it is just an application of Bézout's theorem. In particular, if we know a Bézout pair for the integers $c$ and $N$ (i.e., $x$ and $y$ such that $x c+y N=1$), then we know an inverse of $c$ modulo $N: x$. The part 2.3 of the course is therefore fundamental: it explains how, from the Euclidean division, we can construct Bézout pairs. Thus, we have a very practical algorithm for determining inverses modulo $N$.
I then moved on to systems of several equations, giving the example of the system $\left\{\begin{array}{l}x \equiv 5[7] \\ x \equiv 8[11]\end{array}\right.$. We can solve this system explicitly, so the first equation allows us to write $x$ in the form $7 k+5$, and then we need $7 k+5 \equiv 8$ [11], i.e., $7 k \equiv 3[11]$ and then $k \equiv 2[11]$ by multiplying by the inverse 8 of 7 modulo 11. Thus, $k$ is of the form $11 k^{\prime}+2$, and then $x$ is of the form $7(11 k^{\prime}+2)+5$, i.e., $77 k^{\prime}+19$. Conversely, these numbers are indeed solutions.
In fact, a theorem, called the Chinese theorem, 3.4.1 in the course, states that this kind of method is very general: if $m$ and $n$ are two coprime numbers, if $u m+v n=1$ is a Bézout relation between these two integers, then the solutions of the system $\left\{\begin{array}{l}x \equiv a[m] \\ x \equiv b[n]\end{array}\right.$ are exactly the numbers congruent to $s:=u m b+v n a$ modulo $m n$. Indeed, this number is clearly a solution (note that $u m \equiv 1[n]$, which is the meaning of the Bézout relation), and if $x$ is another solution, then $m$ and $n$ divide $x-s$, so their product divides $x-s$ (since $m$ and $n$ are coprime), so $x \equiv s[m n]$. Note again the great usefulness of the Euclidean algorithm: it allows us to find the Bézout coefficients, and thus to solve such systems of equations directly.
## 3 Arithmetic TD
## - Exercise statements -
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Show that the fraction $\frac{12 n+1}{30 n+2}$ is always irreducible.
|
According to the Euclidean algorithm, $\operatorname{gcd}(30 n+2,12 n+1)=\operatorname{gcd}(12 n+$ $1,6 n)=\operatorname{gcd}(6 n, 1)=1$.
|
1
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Let $A=2012^{2012}$, B the sum of the digits of $A$, C the sum of the digits of $B$, and D the sum of the digits of $C$.
What is the value of $\mathrm{D}$?
|
On a $2012 \equiv 5(\bmod 9)$ hence $2012^{2012} \equiv 5^{2012}(\bmod 9)$. We therefore study the powers of 5 modulo $9: 5^{2} \equiv 7$ so $5^{3} \equiv-1$ and $5^{6} \equiv 1$. Now, we can write $2012=$ $2+6 \times 335$, hence:
$$
2012^{2012} \equiv 5^{2012} \equiv 5^{2} \times\left(5^{6}\right)^{335} \equiv 5^{2} \equiv 7 \quad(\bmod 9)
$$
thus $\mathrm{D} \equiv \mathrm{C} \equiv \mathrm{B} \equiv \mathrm{A} \equiv 7(\bmod 9)$.
On the other hand, $A<\left(10^{4}\right)^{2012}=10^{8048}$ so $A$ has at most 8048 digits, so $B \leqslant 9 \times 8048=72432$, so $\mathrm{B}$ has at most 5 digits, so $\mathrm{C} \leqslant 45$, and $\mathrm{D} \leqslant 13$. The only possibility is therefore $\mathrm{D}=7$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all non-negative integers $x, y, z$ such that $x^{3}+4 y^{3}=16 z^{3}+4 x y z$.
## 2 Solutions
|
Let $x, y, z$ be a solution. We notice that $4 y^{3}, 16 z^{3}$, and $4 x y z$ are even, so $x^{3}$ must be even, and thus $x$ must be even. We set $x^{\prime}=x / 2$. The equation becomes $8 x^{13}+4 y^{3}=16 z^{2}+8 x^{\prime} y z$, or equivalently $2 x^{\prime 3}+y^{3}=4 z^{2}+2 x^{\prime} y z$. We notice that $y$ is even: we write $y=2 y^{\prime}$, and the equation becomes $x^{\prime 3}+4 y^{\prime 3}=2 z^{2}+2 x^{\prime} y^{\prime} z$. We notice that $x^{\prime}$ is even: we write $x^{\prime}=2 x^{\prime \prime}$, and the equation becomes $4 x^{\prime \prime 3}+2 y^{\prime 3}=z^{2}+2 x^{\prime \prime} y^{\prime} z$. We notice that $z$ is even: we write $z=2 z^{\prime}$, and the equation becomes $2 x^{\prime \prime 3}+y^{\prime 3}=4 z^{\prime 2}+2 x^{\prime \prime} y^{\prime} z^{\prime}$. We notice that this fifth equation is identical to the second! We have thus proven that, if $\left(x^{\prime}, y, z\right)$ is a solution to the equation $2 x^{\prime 3}+y^{3}=4 z^{2}+2 x^{\prime} y z$, which we will call (E), then $\left(x^{\prime} / 2, y / 2, z / 2\right)$ is also a solution. By the principle of infinite descent, the only solution to equation (E) is $(0,0,0)$. Since we had that, if $(x, y, z)$ is a solution to the original equation, $(x / 2, y, z)$ is a solution to (E). Thus, $(x / 2, y, z)=(0,0,0)$, and therefore $x=y=z=0$ as required.
## 2 Group B
## 1 Statements
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $\mathrm{a}<\mathrm{b}<\mathrm{c}<\mathrm{d}$ be odd natural integers such that $\mathrm{ad}=\mathrm{bc}, \mathrm{a}+\mathrm{d}$ and $\mathrm{b}+\mathrm{c}$ are powers of 2. Show that $a=1$.
## 2 Solutions
|
The nerve of the war is to find adequate factorizations, to have divisibility relations.
We set $a+d=2^{k}$ and $b+c=2^{l}$. We then have $a\left(2^{k}-a\right)=b\left(2^{l}-b\right)$, an identity in which two squares appear. One must immediately think of making their difference appear: $b^{2}-a^{2}=(b-a)(b+a)=2^{l} b-2^{k} a$. To factorize the powers of two, one must know which is the largest. We know that we must find $k>l$ because if $a=1, d=b c$ and $d+1$ is greater than $b+c$.
To verify this, we consider $2^{k}-2^{l}$, and we make the product $ad$ appear by multiplying by $a: a\left(2^{k}-2^{l}\right)=a(a+d-b-c)=a d-b a+a^{2}-a c=b c-b a+a(a-c)=(b-a)(c-a)>0$, hence $k>l$.
We take up the previous equation: $(b-a)(b+a)=2^{l}\left(b-2^{k-l} a\right)$. In particular, $2^{l}$ divides $(b-a)(b+a)$. Now, since $a$ and $b$ are odd, one of the two factors is congruent to 2 modulo 4, so $2^{l-1}$ divides $b-a$ or $b+a$. Thus, $2^{l-1} \leqslant b+a<b+c=2^{l}$, so $2^{l-1}$ is equal to the factor it divides. In particular, $a$ and $b$ are coprime, because if a prime $p$ divided both, it would divide their sum and their difference, hence $2^{l-1}$, so $p=2$, which is impossible since $a$ and $b$ are odd.
We similarly obtain that $a$ and $c$ are coprime. Now, $a$ divides $b c$. Therefore, $a=1$.
## 4 Group $D$
## 1 Statements
|
1
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Draw a few trees. How many edges at least need to be removed from the graph $\mathrm{K}_{4}$ to make it a tree?
## - Degree of a vertex, Handshaking Lemma -
The degree of a vertex is the number of edges emanating from that vertex. If we sum the degrees of all vertices, each edge is counted twice, since it always connects two vertices. Therefore, we have the following result:
Lemma 1.1. (Handshaking Lemma) The sum of the degrees of all vertices of a graph $G$ is equal to twice the number of edges of the graph.
|
At least one side must be removed because if we keep all four sides, it forms a cycle. Next, if we keep the two diagonals, we need to remove two more sides. Indeed, if we keep two adjacent sides, they will form a triangle with one of the diagonals, which results in a cycle. If we keep two opposite sides, they form a cycle with the two diagonals. In this case, we need to remove a total of 3 edges to obtain a tree. We get, up to rotation:
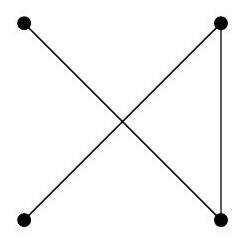
If we remove one of the diagonals but keep three sides, we will have a triangle formed by the remaining diagonal and two of the remaining sides. Therefore, we need to remove one of the sides. We get, up to rotation, one of the following drawings:
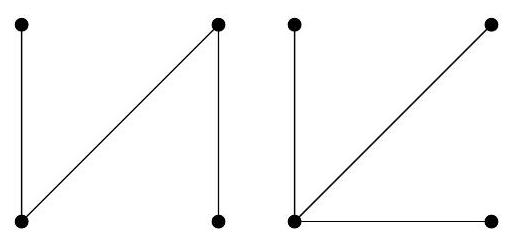
If we remove both diagonals, we get, up to rotation:
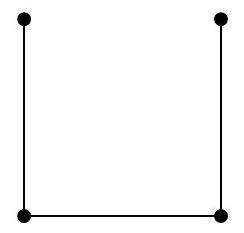
Thus, 3 is the minimum number of edges that need to be removed. Note that, up to deformation, we have obtained only two different types of trees.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $E=\{a, b, c, d\}$ be a set. How many functions $f$ from $E$ to $E$ satisfy, for all $x$ in $E, f(f(f(x)))=x$?
|
The identity, defined for all $x$ by $f(x)=x$, is obviously a solution. If one of the elements has an image distinct from itself, for example $f(x)=y$, what can $f(y)$ be equal to? If we had $f(y)=x$, we would have: $f(f(f(x)))=f(f(y))=f(x)=y$, the relation from the hypothesis would not be satisfied. Similarly, if we had $f(y)=y$. It follows that $f(y)=z$ distinct from $x$ and $y$, and $f(z)=f(f(f(x)))=x$. The function cyclically permutes three of the elements $x, y, z$ of the set, and leaves the last one $t$ invariant. Indeed, if we had $f(t) \in\{x, y, z\}$, we would also have $f(f(f(t))) \in\{x, y, z\}$, which would contradict $f(f(f(t)))=t$. To define one of these functions, it suffices to determine its "fixed point" (element $t$ such that $f(t)=t$), and then the direction of the cyclic permutation of the other three elements, which gives $4 \times 2=8$ functions, plus the identity, for a total of 9.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(i) Find all integers $n \geq 1$ such that $n$ divides $2^{n}-1$.
(ii) Find all odd integers $n \geq 1$ such that $n$ divides $3^{n}+1$.
|
(i) Let $n>1$ such that $n$ divides $2^{n}-1$. It is clear that $n$ is odd. Let $p$ be the smallest prime factor of $n$, which is therefore odd. Then $2^{n} \equiv 1 \bmod p$. Let $\omega$ be the order of 2 modulo $p$. Then $\omega$ divides $n$. On the other hand, by Fermat's Little Theorem, $2^{p-1} \equiv 1 \bmod p$. Thus $\omega$ divides $p-1$. Given the condition on $p$, we necessarily have $\omega=1$. Then $2 \equiv 1 \bmod p$, which is absurd. Therefore, we must have $n=1$.
(ii) Let $n>1$ such that $n$ divides $3^{n}+1$. Let $p$ be the smallest prime factor of $n$, which is therefore odd, and thus $p>3$. Then $3^{2 n} \equiv 1 \bmod p$. Let $\omega$ be the order of 3 modulo $p$. Then $\omega$ divides $2 n$. On the other hand, by Fermat's Little Theorem, $3^{p-1} \equiv 1 \bmod p$. Thus $\omega$ divides $p-1$. We deduce that $\omega$ divides $\operatorname{gcd}(2 n, p-1)$. Given the condition on $p$, we necessarily have $\omega=1$ or 2. In the first case, $3 \equiv 1 \bmod p$ and thus $p=2$, which is excluded. In the second case, $3^{2} \equiv 1 \bmod p$ and thus $p$ divides 8, which is also excluded. We conclude that $n=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the $a, n \geq 1$ such that $\left((a+1)^{n}-a^{n}\right) / n$ is an integer.
|
Suppose $n>2$. Let $p$ be the smallest prime factor of $n$. Then $p$ divides $(a+1)^{n}-a^{n}$. In other words, $((a+1) / a)^{n} \equiv 1 \bmod p$. Let $\omega$ be the order of $(a+1) / a$ modulo $p$. Then $\omega$ divides $n$. On the other hand, by Fermat's little theorem, $((a+1) / a)^{p-1} \equiv 1 \bmod p$ so that $\omega$ divides $p-1$. Given the condition on $p$, necessarily $\omega=1$. This implies $a+1 \equiv a \bmod p$, which is absurd.
The solutions are therefore $n=1$ and $a$ arbitrary.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a$ be a strictly positive integer. Suppose that $4\left(a^{n}+1\right)$ is the cube of an integer for all positive integers $n$. Find $a$.
Soit $a$ un entier strictement positif. On suppose que $4\left(a^{n}+1\right)$ est le cube d'un entier pour tout entier positif $n$. Trouver $a$.
(Note: The second line is kept in French as per your request to preserve the original text's line breaks and format.)
|
It is clear that $a=1$ works. Let's show that it is the only one. Suppose therefore $a>1$. Choose $n=2 m$ and note that $a^{2}+1$ is not a power of 2 since it is congruent to 1 or 2 modulo 4. Let $p$ be an odd prime such that $p$ divides $a^{2}+1$. Then, according to LTE:
$$
v_{p}\left(4\left(a^{n}+1\right)\right)=v_{p}\left(a^{2}+1\right)+v_{p}(m)
$$
We choose $m$ so that the latter term is congruent to 1 modulo 3. Then $4\left(a^{n}+1\right)$ cannot be a cube, contradiction.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all functions $f$ from $\mathbb{R}_{+}^{*}$ to $\mathbb{R}_{+}^{*}$ satisfying the following condition:
$$
\forall x, y \in \mathbb{R}_{+}^{*}, \quad f(x+f(y))=f(x+y)+f(y)
$$
## - Correction -
|
Let $g$ be the application $f$ - Id.
The equation in the statement can be rewritten after simplification in the following form:
$$
\forall x, y \in \mathbb{R}_{+}^{*}, \quad g(x+y+g(y))=g(x+y)+y
$$
First, note that this equation implies that $g$ is injective. Indeed, if $y_{1}$ and $y_{2}$ are strictly positive real numbers satisfying the condition $g\left(y_{1}\right)=g\left(y_{2}\right)$, we deduce from the equation that:
$$
g\left(y_{1}+y_{2}\right)+y_{2}=g\left(y_{1}+y_{2}+g\left(y_{2}\right)\right)=g\left(y_{2}+y_{1}+g\left(y_{1}\right)\right)=g\left(y_{2}+y_{1}\right)+y_{1}
$$
After simplification, we conclude that $y_{1}=y_{2}$, which proves that $g$ is indeed injective.
Next, note that, by setting $a=x+y$ and $b=y$, the functional equation can be rewritten as:
$$
\forall a, b \in \mathbb{R}_{+}^{*}: a>b, g(a+g(b))=g(a)+b
$$
By taking a sufficiently large strictly positive real number $c$, we can then perform the following calculation:
$$
\forall a, b \in \mathbb{R}_{+}^{*}, g(c+g(a)+g(b))=g(c+g(a))+b=g(c)+a+b=g(c+g(a)+g(b))
$$
Using the injectivity of $g$ and then simplifying by $c$, we see that $g$ satisfies the Cauchy equation.
Finally, since $f$ takes strictly positive values, we know that $g>-\mathrm{Id}$, which shows that the graph of $g$ is not dense (there are no points in the triangle bounded by the line with equation $y=-x$ and the y-axis). Thus, the course assures us that $g$ is linear. We immediately deduce that $g$ is also linear.
After verification, we conclude that the unique solution to this functional equation is 2Id.
## V. Third Period
## 1 Inevitable: Geometry
## 1 Course
We refer to the geometry courses downloadable from the Animath website.
## 2 First TD
|
2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Seven people dine around a round table every Saturday evening. How many times is it possible to have dinner if everyone wants to have two new neighbors each time? What is the result for eight people?
|
Under the conditions stated, at each dinner, a given person has two new neighbors. Therefore, after the second dinner, they will have had four different neighbors, six different neighbors after the third, and eight different neighbors after the fourth, which is not possible: if there are seven people in total, each can only have six different neighbors, which limits the number of dinners that can be held under the conditions stated to three. The same result applies if there are eight people in total. It remains to prove that three dinners can be organized so that each person has two new neighbors at each dinner. At the first dinner, the seven people are numbered in order from 1 to 7: 1234567. At the second dinner, compared to the first, they are placed "one person out of two": 1357246, and at the third, "one person out of three": 1473625. It is easy to verify that such a placement works, but it is not the only one. If an eighth person is added, it is sufficient to insert them so that they also have two new neighbors each time, for example: 12834567 then 13587246 and finally 1847362. Thus, the following pairs will never have been neighbors: 2 and 3, 5 and 7, 1 and 4, as well as 8 and 6.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Seventeen people dine around a round table every Saturday evening. How many times is it possible to dine if everyone wants to have two new neighbors each time? What is the result for eighteen people?
|
Note: This exercise is the same as Exercise 1 (middle school students were to solve 1, high school students 5), but in a less particular case. The proposed solution below is very general, but difficult for an average high school student to access. This exercise was therefore intended to identify the students best equipped to tackle formidable Olympic problems.
Solution: The first thing to notice is the following. We call $n$ the number of guests (17 or 18), and $k$ the number of dinners; we are interested in a particular guest among the $n$. Knowing that he has two neighbors at each dinner, and that he must never meet the same person more than once, he will therefore meet $2 k$ different people in total. But there are only $n-1$ people he can meet; we therefore have $2 k \leq n-1$, which means - in both cases - that there are at most 8 possible dinners. Let's now show that there indeed exist 8 arrangements such that two people are never neighbors more than once. We number the guests and the seats from 0 to $n-1$ (since the table is round, the $(n-1)$-th seat is therefore next to the 0-th), and the arrangements from 1 to 8. For $n=17$, we can proceed as follows: at the $i$-th dinner, we place the $j$-th person at the $i j$-th seat modulo 17. (The complete scheme of arrangements is presented a little further down. In a less abstract, but longer and vaguer way, we can say that the first Saturday, we place all the guests in order; the second Saturday, we place one out of two; the third, one out of three; and so on; knowing that when the numbers exceed 17, we "return to 0".) We must verify two things. First, let's verify that it is a valid arrangement. Each guest receives one and only one seat, because between 0 and 16, there is one and only one number congruent to a given residue modulo 17. No seat is occupied by two guests: indeed, let $j$ and $j^{\prime}$ be two guests who occupy the same seat at the $i$-th dinner. Then we have $i j \equiv i j^{\prime}(\bmod 17)$, or $17 \mid i j-i j^{\prime}$, or again $17 \mid i\left(j-j^{\prime}\right)$. Since 17 is prime and $0<i<17, i$ is coprime with 17, so $17 \mid j-j^{\prime}$. We therefore have $j \equiv j^{\prime}(\bmod 17)$, which means $j=j^{\prime}$. And since there are as many seats as guests, all seats are necessarily occupied. Now let's verify that it is indeed a solution to the problem. Since the difference between the numbers of two adjacent seats is congruent to $\pm 1$ modulo 17, this means that at the $i$-th dinner, the difference between the numbers of two adjacent people is congruent to $\pm i$ modulo 17. But the numbers $\pm 1, \pm 2, \ldots, \pm 8$ are all different modulo 17: two given people can therefore be neighbors only once. We could also have explicitly presented the scheme of arrangements:
Place $\quad 012345678910111213141516$
1st dinner 012345678910111213141516
2nd dinner 024681012141613579111315
3rd dinner 036912151471013162581114
4th dinner 048121637111526101415913
5th dinner 051015381316111649142712
6th dinner 061217132814391541016511
7th dinner 071441118155122916613310
8th dinner 081671561451341231121019
and verify that each guest appears once and only once in each row and has different neighbors in each row. But such a solution, although less abstract, would be much more laborious (366 checks to be made in total!), and has the drawback of being "parachuted": one can see that it works, but one does not understand very well why it works. For $n=18$, a possible solution is to start from the previous arrangement and to intercalate the new person somewhere each time. Since we already know that the first 17 people are well placed as required, it is enough to make sure that the last person (who, however, bears the number 17: this is not an error, as we numbered from 0) has different neighbors each time. We can, for example, place him between 3 and 4 at the first dinner, between 11 and 13 at the second, then between 2 and 5, between 10 and 14, between 1 and 6, between 9 and 15, between 0 and 7, and finally between 8 and 16 at the eighth dinner: each number between 0 and 16 appears well at most once in this list. The complete arrangement is therefore as follows:
| Place 01234567891011121314151617 |
| :--- |
| 1st dinner 01231745678910111213141516 |
| 2nd dinner 02468101214161357911171315 |
| 3rd dinner 03691215147101316217581114 |
| 4th dinner 04812163711152610171415913 |
| 5th dinner 05101538131176111649142712 |
| 6th dinner 06121713281439171541016511 |
| 7th dinner 01771441118155122916613310 |
| 8th dinner 08171671561451341231121019. |
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. The sequence $\left(x_{n}\right)$ is defined recursively by $x_{0}=1, x_{1}=1$, and:
$$
x_{n+2}=\frac{1+x_{n+1}}{x_{n}}
$$
for all $n \geqslant 0$. Calculate $x_{2007}$.
|
. We start by calculating the first terms of the sequence $\left(x_{n}\right)$. We find:
$$
x_{2}=2 \quad ; \quad x_{3}=3 \quad ; \quad x_{4}=2 \quad ; \quad x_{5}=1 \quad ; \quad x_{6}=1
$$
and we find two consecutive terms equal to 1. From this point on, the calculations repeat, which proves that the sequence $\left(x_{n}\right)$ is periodic, in this case with a period of 5. Thus $x_{2007}=x_{2}=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Using the numbers from 1 to 22 exactly once each, Antoine writes 11 fractions: for example, he can write the fractions $\frac{10}{2}, \frac{4}{3}, \frac{15}{5}, \frac{7}{6}, \frac{8}{9}, \frac{11}{19}, \frac{12}{14}, \frac{13}{17}, \frac{22}{21}, \frac{18}{16}$, and $\frac{20}{1}$.
Antoine wishes to have as many fractions as possible with integer values among the fractions written: in the previous example, he wrote three fractions with integer values: $\frac{10}{2}=5, \frac{15}{5}=3$, and $\frac{20}{1}=20$. What is the maximum number of fractions that can have integer values?
|
First, it is possible to make 10 integers with the fractions
$$
\left\{\frac{22}{11}, \frac{20}{10}, \frac{18}{9}, \frac{16}{8}, \frac{14}{7}, \frac{12}{6}, \frac{21}{3}, \frac{19}{1}, \frac{15}{5}, \frac{4}{2}, \frac{17}{13}\right\}
$$
Furthermore, it is impossible to have 11 integer fractions. Indeed, there are 3 prime numbers that have no multiple smaller than 22: 19, 17, and 13. Thus, the only way for one of these three numbers to form an integer fraction is with the number 1, which can only be used with one of these three numbers.
Comment from the graders: The exercise was generally very well done. However, some students, although they noticed the importance of 13, 17, and 19, did not think to associate two of them in the same fraction, and therefore only obtain 9 integer fractions, which is a pity. Other students were content with a configuration of 10 fractions without justifying that it is optimal. Finally, we remind you that $\frac{19}{8}$ is definitely not an integer.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a, b, c$ be positive real numbers such that $a b c=8$. Find the minimum value that the expression $a+b+c$ can take.
|
The form of this exercise is a bit different from the previous ones, but we should not be destabilized by it. To find the minimum value that $a+b+c$ can take, we need to lower-bound this expression, that is, find an inequality of the form $a+b+c \geqslant x$ where $x$ will be a real number, and then find a case of equality for this inequality (since we are looking for the minimum value, an inequality alone is not enough). Given that we have a hypothesis on the product, it is natural to apply the AM-GM inequality to see what it yields. We get $a+b+c \geqslant 3 \sqrt[3]{a b c}=3 \cdot 2=6$. Be careful, this does not suffice to conclude that 6 is the minimum value; our inequality might be too crude, so we still need to show that this value can be achieved! Fortunately, we know that the AM-GM inequality has an equality case when $a=b=c$. This equality can be achieved while still satisfying the hypothesis $a b c=8$ by choosing $a=b=c=2$, and we verify that we indeed get $a+b+c=2+2+2=6$, so 6 is indeed the minimum value sought.
|
6
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the inverse of 11 modulo 54
|
## 5
Translate the text above into English, please retain the original text's line breaks and format, and output the translation result directly.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(Exercise 3.9 from the course notes)
Find the inverse of 37 modulo 53
Proposition 11 (Inverse of a product).
Proposition 12 (Proper inverse).
|
Sometimes, trial and error is enough, but here we proceed with certainty. We start by performing the Euclidean algorithm
\[
\begin{aligned}
& 53=37+16 \\
& 37=16 * 2+5 \\
& 16=5 * 3+1
\end{aligned}
\]
From this, we deduce a Bézout's identity
\[
\begin{array}{r}
16-5 * 3=1 \\
16-(37-16 * 2) * 3=1 \\
53-37-(37-(53-37) * 2) * 3=1 \\
7 * 53-10 * 37=1
\end{array}
\]
We look modulo 53: 10 is the inverse of 37 modulo 53.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A person has between 0 and 300,000 hairs on their head. The urban area of Marseille contains 2,000,000 inhabitants. How many Marseillais have the same number of hairs at a minimum?
|
Here, we need to apply the generalized pigeonhole principle. The socks are the Marseillais, and the possible number of hairs are the drawers. There are 300001 drawers for 2000000 Marseillais. By the generalized pigeonhole principle, $300001 \times 6 + 199994 = 2000000$, so there are at least 7 people who have the same number of hairs.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all functions $f: \mathbb{R} \mapsto \mathbb{R}$ such that for all $x, y \in \mathbb{R}$,
$$
f(x+y)=x f(x)+y f(y)
$$
|
We guess (and at the same time verify) that the null function is a solution. Let's show that it is the only one. By setting $y=f(0)$ we have $f(x)=x f(x)$. In other words, for all $x \in \mathbb{R}$,
$$
(x-1) f(x)=0 \text {. }
$$
Thus, by substituting $x$ with any value different from 1, we obtain that the function is zero except possibly at 1. We are not done yet! Indeed, there still exists an infinity of such functions. Let's show that $f(1)=0$. For example, with $x=y=\frac{1}{2}$ we have
$$
f(1)=f\left(\frac{1}{2}+\frac{1}{2}\right)=\frac{1}{2} f\left(\frac{1}{2}\right)+\frac{1}{2} f\left(\frac{1}{2}\right)=0
$$
since $f\left(\frac{1}{2}\right)=0$. Therefore, 0 is the only function solution.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What are the $p$ such that $p, p+2, p+4$ are all primes?
|
Necessarily $p, p+2$ or $p+4$ is a multiple of 3, hence equal to 3. Since $p \geqslant 2$, we have $p=3$. Conversely, $p=3$ is a solution.
## Lemma 3.
Let $n \geqslant 2$, and let $p$ be the smallest divisor of $n$ that is greater than or equal to 2. Then $p$ is prime.
Proof. Let $d$ be a positive divisor of $p$. If $d \neq 1$, then $d \geqslant 2$ (since $d$ is not zero, as $d$ divides $n$, and $n$ is not zero). Since $d$ divides $p$ and $p$ is not zero, we have $d \leqslant p$. But on the other hand, $d$ divides $p$, so $d$ divides $n$. The choice of $p$ ensures that $d \geqslant p$, hence $d=p$. Therefore, $p$ is prime.
In particular, this implies that every integer greater than or equal to 2 has a prime divisor!
## Theorem 4.
There are infinitely many prime numbers.
Proof. Suppose, for the sake of contradiction, that there are only finitely many prime numbers, say $p_{1}, \ldots, p_{n}$, and let $N=p_{1} \ldots p_{n}+1$. Let $p$ be a prime divisor of $N$. It is clear that $p$ cannot be any of $p_{1}, \ldots, p_{n}$, which provides the desired contradiction.
There is (at least to date) no formula to find prime numbers. In general, to show that a number is prime, one simply checks that it has no other prime divisor than itself...
## Example 5.
Is 127 prime? It is not divisible by 2, 3, 5, or 11. It is easy to verify that it is not divisible by 7 either. In fact, there is no need to perform further checks! Indeed, if 127 were not prime, it would have a divisor $a$ strictly between 1 and 127. We could write $127=a \cdot b$, with $1<a, b<127$. But then $a \leqslant \sqrt{127}$ or $b \leqslant \sqrt{127}$. By symmetry, we can assume $a \leqslant \sqrt{127}$. Then $a$ has a prime divisor $p$, which is in turn less than or equal to $\sqrt{127}$. Therefore, it is sufficient to check that no prime number less than or equal to $\sqrt{127}$ divides 127, and since $\sqrt{127}<12$, it is enough to test all prime numbers less than or equal to 11.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Calculate the remainder of the Euclidean division of $2022^{2023^{2024}}$ by 19.
|
On a $2022 \equiv 8[19]$.
Moreover, we observe that $8^{6} \equiv 1[19]$.
With $q$ and $r$ such that $2023^{2024}=6 q+r$ we therefore have
$$
\begin{aligned}
2022^{2023^{2024}} & \equiv 8^{2023^{2024}} \\
& \equiv 8^{q 6} 8^{r} \\
& \equiv 8^{r}
\end{aligned}
$$
it is therefore sufficient to determine the remainder of the Euclidean division of $2023^{2024}$ by 6.
We proceed in the same way. Since $2023 \equiv 1[6]$ we have $2023^{2024} \equiv 1[6]$ and thus we conclude that
$$
2022^{2023^{2024}} \equiv 8^{1}[19]
$$
which means that the remainder of the Euclidean division is 8 (since $0 \leqslant 8 \leqslant 18$).
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(AHSME 1990, P9)
Consider a cube whose edges are colored either red or black such that each face of the cube has at least one black edge. What is the minimum number of black edges?
|
Of course, we will solve this problem in two steps:
- We need at least 3 black edges. Indeed, each edge is shared between 2 faces, and since there are 6 faces, we need at least $\frac{6}{2}=3$ black edges.
- 3 is indeed sufficient: it is enough that no pair of edges shares a vertex.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the last digit of $2023^{2024^{00252^{206^{2027}}}}$
|
On a $2023^{2024^{2005^{20252^{2027}}}} \equiv 3^{2024^{20255^{206^{2027}}}} \equiv 3^{(4 \cdot 506)^{n>0}} \equiv\left(3^{4}\right)^{506^{n}} \equiv 1[10]$ with $n=2025^{2026^{2027}}$
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the set of positive integers $n$ such that $5^{n}+4$ is a perfect square
untranslated text kept the same format and line breaks.
|
Let $a>0$ such that $5^{n}+4=a^{2}$, which gives us $5^{n}=(a-2)(a+2)$. Therefore, the two terms on the right must be powers of 5. However, they are not congruent modulo 5, so one of them must be a zero power. Thus, $a-2=1 \Rightarrow a=3$. We then have $5^{n}+4=9 \Rightarrow n=1$. The only solution is therefore $n=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the real numbers $x, y$ and $z$ such that
$$
\left\{\begin{array}{l}
x+y+z=3 \\
x^{2}+y^{2}+z^{2}=3 \\
x^{3}+y^{3}+z^{3}=3
\end{array}\right.
$$
|
First, by trial and error, we find that $x=y=z=1$ works. We will now prove that this is the only solution. To do this, 1 the idea is to obtain several polynomials of the degrees that interest us, in order to get expressions that we can use.
For example, $(x+y+z)^{2}=\left(x^{2}+y^{2}+z^{2}\right)+2(x y+y z+z x)$, so
$$
x y+y z+z x=\frac{(x+y+z)^{2}-\left(x^{2}+y^{2}+z^{2}\right)}{2}=\frac{3^{2}-3}{2}=3
$$
Similarly,
$$
\begin{aligned}
& (x+y+z)^{3}=\left(x^{3}+y^{3}+z^{3}\right)+3\left(x^{2} y+x^{2} z+y^{2} x+y^{2} z+z^{2} x+z^{2} y\right)+6 x y z \text { and } \\
& (x+y+z)\left(x^{2}+y^{2}+z^{2}\right)=\left(x^{3}+y^{3}+z^{3}\right)+\left(x^{2} y+x^{2} z+y^{2} x+y^{2} z+z^{2} x+z^{2} y\right) .
\end{aligned}
$$
We deduce that
$$
\begin{aligned}
x y z & =\frac{(x+y+z)^{3}-\left(x^{3}+y^{3}+z^{3}\right)-3(x+y+z)\left(x^{2}+y^{2}+z^{2}\right)+3\left(x^{3}+y^{3}+z^{3}\right)}{6} \\
& =\frac{3^{3}-3-3^{3}+3^{2}}{6} \\
& =1
\end{aligned}
$$
We conclude that
$$
(t-x)(t-y)(t-z)=t^{3}-3 t^{2}+3 t-1=(t-1)^{3}
$$
and therefore that $x=y=z=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the non-zero real numbers $x$ such that $x+\frac{1}{x}=2$.
|
Let $x$ be a real number such that $x+\frac{1}{x}=2$. It suffices to consider the polynomial
$$
P(t)=(t-x)\left(t-\frac{1}{x}\right)=t-2 x+1=(t-1)^{2}
$$
to deduce that $x=1$. Conversely, $x=1$ indeed works.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all integers $n>0$ such that $n \mid 2^{n}-1$.
|
First, $n=1$ is a solution.
Suppose now $n>1$ such that $n \mid 2^{n}-1$ and $p$ the smallest prime divisor of $n$.
$$
2^{n} \equiv 1 \quad(\bmod p)
$$
Thus the order $\omega$ of 2 modulo $p$ divides $n$. Moreover,
$$
\omega \leq \phi(p)<p
$$
so $\omega$ is smaller than any prime divisor of $n$, yet $\omega \mid n$ so $\omega=1$. Therefore,
$$
2 \equiv 1 \quad(\bmod p) \Longrightarrow p=1
$$
Impossible, hence $n$ cannot have a smallest prime divisor, thus the only solution to the equation is 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all odd integers $n>0$ such that $n \mid 3^{n}+1$.
|
First, $n=1$ is a solution. Now, consider the case $n \geqslant 2$: $n$ therefore has at least one prime divisor, let $p$ be the smallest of them. We have
$$
3^{n} \equiv-1 \quad(\bmod p)
$$
We know how to manipulate the order and Fermat's theorem, and we have just seen in exercise 7 that these manipulations can solve exercises of this type. The only problem is having a -1 instead of a 1. The trick is to square our equality to make the 1 appear! Thus,
$$
\begin{gathered}
\left(3^{n}\right)^{2} \equiv(-1)^{2} \quad(\bmod p) \\
3^{2 n} \equiv 1 \quad(\bmod p)
\end{gathered}
$$
Now, let $\omega$ be the order of 3 modulo $p$. We have
$$
1 \leqslant \omega<p
$$
Then, $3^{2 n} \equiv 1(\bmod p)$ gives
$$
\omega \mid 2 n
$$
Finally, $3^{n} \equiv-1 \not \equiv 1(\bmod p)$. Indeed, otherwise we would have $p=2$ but $n$ is odd. Thus,
$$
\omega \nmid n
$$
Then, $\omega \mid 2 n$ implies that if there exists a prime number $q$ other than 2 dividing $\omega$, we would have $q|\omega| 2 n$
$$
q \mid 2 n
$$
But $\operatorname{pgcd}(q, 2)=1$ so by Gauss's lemma, $q \mid n$. Therefore, $q$ is a prime divisor of $n$ strictly less than $p$ ( $q$ divides $\omega$ so it is less than $\omega$, which is itself strictly less than $p$), which is absurd!
Thus, it follows that $\omega$ is a power of two. On the other hand, $n$ is odd, so the largest power of 2 dividing $2 n$ is 1: thus,
$$
\omega=2^{1}=2 \text { or } \omega=2^{0}=1
$$
$\omega=1$ does not work since $1 \mid n$ but $\omega \nmid n$.
Thus, $\omega=2$.
Therefore,
$$
\begin{aligned}
3^{2} & \equiv 1 \quad(\bmod p) \\
8 & \equiv 0 \quad(\bmod p)
\end{aligned}
$$
Hence $p=2$, but $n$ is odd: absurd. In conclusion, the only solution is $n=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a, b, c$ be three strictly positive real numbers such that $a+b+c+a b+b c+c a+a b c=7$. Show that:
$$
\sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} \geq 6
$$
|
Given that the constraint is quite ugly, we try to simplify it. We almost have the product $(1+a)(1+b)(1+c)$. Let's calculate this product: $(1+a)(1+b)(1+c)=1+a+b+c+ab+bc+ca+abc=1+7=8$ by hypothesis. Therefore, we need to try to make $1+a, 1+b, 1+c$ appear in the inequalities. Note that by the QM-AM inequality, $a^{2}+b^{2}+2=\left(a^{2}+1\right)+\left(b^{2}+1\right) \geqslant \frac{(a+1)^{2}+(b+1)^{2}}{2}$, thus by QM-AM:
$$
\sqrt{a^{2}+b^{2}+2} \geqslant \sqrt{\frac{(a+1)^{2}+(b+1)^{2}}{2}} \geqslant \frac{(a+1)+(b+1)}{2}
$$
We thus obtain
$$
\sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} \geqslant \frac{(a+1)+(b+1)+(b+1)+(c+1)+(c+1)+(a+1)}{2}
$$
so by AM-GM
$$
\sqrt{a^{2}+b^{2}+2}+\sqrt{b^{2}+c^{2}+2}+\sqrt{c^{2}+a^{2}+2} \geqslant(a+1)+(b+1)+(c+1) \geqslant 3 \sqrt[3]{8}=6
$$
|
6
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
(treatise)
For what condition on $y \in \mathbb{N}$ is $y^{2}+5 y+12$ a square?
|
We know that $(y+2)^{2}=y^{2}+4 y+4y^{2}+5 y+12$ if and only if $6 y+9>5 y+12$, if and only if $y>3$.
Therefore, for $y \geq 4, (y+2)^{2}<y^{2}+5 y+12<(y+3)^{2}$, under these conditions $y^{2}+5 y+12$ cannot be a square.
Finally, the only potential solutions are $0 \leq y \leq 3$. We test:
| $y$ | $y^{2}+5 y+12$ | Perfect square? |
| :---: | :---: | :---: |
| 0 | 12 | no |
| 1 | 18 | no |
| 2 | 26 | no |
| 3 | $36=6^{2}$ | YES |
In the end, there is a unique solution $y=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(unprocessed)
Find all positive integers $x$ satisfying $x!=x^{3}-11 x+4$.
|
Intuitively, the factorial grows faster than the cube, so quite quickly $x^{3}-11 x+40$. Therefore, for $x \geq 5$, we have $x! > x^{3}-11 x+4$, so we cannot have equality. We need to test the values $0 \leq x \leq 4$:
| $x$ | $x!$ | $x^{3}-11 x+4$ | Equality? |
| :---: | :---: | :---: | :---: |
| 0 | 1 | 4 | no |
| 1 | 1 | -6 | no |
| 2 | 2 | -10 | no |
| 3 | 6 | -2 | no |
| 4 | 24 | 24 | YES |
Finally, there is a unique solution $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What are the $n$ such that $4^{n}+5^{n}$ is a perfect square?
|
Let $k, n$ be such that $4^{n}+5^{n}=k^{2}$.
Then $5^{n}=k^{2}-2^{2 n}=\left(k-2^{n}\right)\left(k+2^{n}\right)$. If 5 divides each of the two factors, 5 also divides their difference, namely $2^{n+1}$, which is a contradiction. Thus $k+2^{n}=5^{n}$, and $k-2^{n}=1$. By taking the difference again, we find $2^{n+1}=5^{n}-1$. This equation has a solution when $n=1$, and if $n \geq 2$ we have $5^{n}>2^{n+1}+1$ (by induction, for example). Therefore, $n=1$ is the only potential solution, and it is indeed a solution.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
( Inspired by USAMO 2014, P1 )
Let $P \in \mathbb{R}[X]$ be a monic polynomial of degree 2. Suppose that $P(1) \geq P(0)+3$, and that $P$ has two real roots (not necessarily distinct) $x_{1}$ and $x_{2}$. Find the smallest possible value for $\left(x_{1}^{2}+1\right)\left(x_{2}^{2}+1\right)$.
|
Let's write $P=X^{2}+a X+b$ with $a, b \in \mathbb{R}$. The condition in the statement becomes $1+a+b \geq b+3$ thus $a \geq 2$. Furthermore, by Vieta's formulas, $x_{1}+x_{2}=-a$ and $x_{1} x_{2}=b$. We write:
$$
\begin{aligned}
\left(x_{1}^{2}+1\right)\left(x_{2}^{2}+1\right) & =x_{1}^{2} x_{2}^{2}+x_{1}^{2}+x_{2}^{2}+1 \\
& =\left(x_{1} x_{2}\right)^{2}+\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}+1 \\
& =b^{2}+(-a)^{2}-2 b+1 \\
& =(b-1)^{2}+a^{2} \\
& \geq 0^{2}+2^{2} \\
& =4
\end{aligned}
$$
Thus, $\left(x_{1}^{2}+1\right)\left(x_{2}^{2}+1\right) \geq 4$. Moreover, we have equality for $a=2, b=1$, that is, for $P=$ $X^{2}+2 X+1=(X+1)^{2}$, which indeed satisfies $P(1)=4 \geq 4=3+P(0)$. The minimum value is therefore 4.
Alternative method: we apply the Cauchy-Schwarz inequality.
$$
\left(x_{1}^{2}+1\right)\left(x_{2}^{2}+1\right)=\left(x_{1}^{2}+1^{2}\right)\left(1^{2}+x_{2}^{2}\right) \underset{\substack{\text { Cauchy-Schwarz } \\ \text { inequality }}}{\geq}\left(x_{1} \times 1+1 \times x_{2}\right)^{2}=(-a)^{2}=a^{2} \geq 4
$$
Moreover, we have equality for $x_{1}=x_{2}=-1$, and we conclude similarly.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A polyhedron has 20 triangular faces. Determine its number of vertices and edges.
|
Let's perform a double counting between the faces and the edges, using the notations $S, A, F$ from the previous exercise. Let $N$ be the number of pairs $(f, a)$ where $f$ is a face and $a$ is an edge that is a side of $f$. On one side, if we fix $f$, there are three edges that work because all the faces of the polyhedron are triangular, and thus $N=3 F$. On the other side, if we fix $a$, there are 2 faces that work because an edge is the side of exactly two triangles. We therefore get $N=2 A$, and thus
$$
A=\frac{3}{2} F=30
$$
Now, the number $S$ of vertices is obtained by Euler's formula
$$
S=A-F+2=12
$$
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the integers $n \geqslant 1$ for which $n$ divides $2^{n}-1$.
|
First, $n=1$ is a solution. We now look for a potential solution $n \geqslant 2$.
Let $p$ be the smallest prime factor of such an integer $n$. Since $2^{n} \equiv 1(\bmod p)$, we know that $p$ is odd and that $\omega_{p}(2)$ divides $n$. However, $\omega_{p}(2)$ also divides $p-1$. But, by the minimality of $p$, the integers $p-1$ and $n$ are coprime. This means that $\omega_{p}(2)=1$, that is, $p$ divides $2-1=1$. Faced with such an absurdity, we conclude that no integer $n \geqslant 2$ is a solution, and therefore that $n=1$ is the unique solution to the problem.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $p$ be a prime number. Find the integers $k \geqslant 0$ for which $p$ divides $1^{k}+2^{k}+\cdots+p^{k}$.
|
When $k=0$, our sum is equal to $p$. The integer $k=0$ is therefore a solution, and we now focus on the cases where $k \geqslant 1$.
Let $x$ be an element of $\mathbb{Z} / p \mathbb{Z}$ of order $p-1$. The first $p-1$ powers of $x$ coincide with the invertibles modulo $p$, so that
$$
1^{k}+2^{k}+\cdots+(p-1)^{k}+p^{k} \equiv 1^{k}+2^{k}+\cdots+(p-1)^{k} \equiv x^{0 k}+x^{k}+x^{2 k}+\cdots+x^{(p-2) k}
$$
This is the sum of a geometric sequence with common ratio $x^{k}$. If $x^{k} \equiv 1(\bmod p)$, that is, if $p-1$ divides $k$, this sum is $p-1$. Otherwise, it is
$$
\frac{x^{(p-1) k}-1}{x-1} \equiv 0 \quad(\bmod p)
$$
In conclusion, the integers $k$ we are looking for are $k=0$ and the non-zero integers that are not divisible by $p-1$.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(BXMO 2014) Let $a, b, c$ and $d$ be strictly positive integers. Determine the smallest value that the expression:
$$
S=\left\lfloor\frac{a+b+c}{d}\right\rfloor+\left\lfloor\frac{a+b+d}{c}\right\rfloor+\left\lfloor\frac{a+c+d}{b}\right\rfloor+\left\lfloor\frac{b+c+d}{a}\right\rfloor
$$
can take.
|
With integer parts, there is not much to do: we apply the inequality $\lfloor x\rfloor>x-1$ to find, by rearranging the terms
$$
S>\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{a}{d}+\frac{d}{a}\right)+\left(\frac{c}{b}+\frac{b}{c}\right)+\left(\frac{d}{b}+\frac{b}{d}\right)+\left(\frac{c}{d}+\frac{d}{c}\right)-4
$$
and each term in parentheses is bounded below by 2 by AM-GM. Therefore, we have $S>8$, which means $S \geqslant 9$. By trial and error, we find the construction $(5,5,5,4)$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(IMO SL 2020 A3) Let $a, b, c, d$ be strictly positive real numbers satisfying $(a+c)(b+d)=a c+b d$. Determine the smallest value that
$$
\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}
$$
can take.
|
The hypothesis suggests grouping the terms in $a$ and $c$ on one side, and the terms in $b$ and $d$ on the other. We can thus group as follows (and this preserves a certain symmetry in $a$ and $c$ and in $b$ and $d$):
$$
\left(\frac{a}{b}+\frac{c}{d}\right)+\left(\frac{b}{c}+\frac{d}{a}\right)
$$
To make factors $a c$ and $b d$ appear, we use the AM-GM inequality (IAG):
$$
\left(\frac{a}{b}+\frac{c}{d}\right)+\left(\frac{b}{c}+\frac{d}{a}\right) \geqslant 2 \sqrt{\frac{a c}{b d}}+2 \sqrt{\frac{b d}{a c}}
$$
We would then like to use the AM-GM inequality again by recognizing a term of the form $x + 1/x$. However, this is very demanding: we have not yet used the hypothesis from the statement, and a small reasoning shows that there do not exist real numbers $a, b, c, d$ satisfying $a c = b d$ and $(a+c)(b+d) = a c + b d$. However, we can still set $x = \sqrt{a c / b d}$ and determine the smallest value that $x + 1/x$ can take. The function in $x$ being convex, it suffices to determine the set of values that $x$ can take to be able to bound $f$ from below.
According to the AM-GM inequality and the hypothesis,
$$
a c + b d = (a+c)(b+d) \geqslant 2 \sqrt{a c} \cdot 2 \sqrt{b d} \geqslant 4 \sqrt{a c b d}
$$
By dividing both sides by $\sqrt{a c b d}$, we obtain that $x + \frac{1}{x} \geqslant 4$. Thus, the sum is always greater than or equal to 8.
To verify that the value is indeed attainable, we use the equality cases established previously. We see that we need $a = c$ and $b = d$. Substituting into the hypothesis, this gives $4 a b = a^2 + b^2$. We derive a quadratic equation in $a / b$, which gives the solution $a / b = 2 \pm \sqrt{3}$. The value 8 is therefore attained, for example, for $b = d = 1$ and $a = c = 2 + \sqrt{3}$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all $n>1$ such that $n^{2} \mid 2^{n}+1$.
|
(P3 IMO 1990)
First, $n$ must be odd, so $2^{n}+1$ must be divisible by 3, which means $n$ must be a multiple of 3. Let's find the 3-adic valuation of $2^{n}+1: v_{3}\left(2^{n}+1\right)=v_{3}(2+1)+v_{3}(n)$. On the other hand,
$v_{3}\left(n^{2}\right)=2 v_{3}(n)$ and by divisibility we should have $2 v_{3}(n) \leqslant 1+v_{3}(n)$, which imposes $v_{3}(n)=1$ so $n=3 m$ where $m$ is not a multiple of 3.
The problem then becomes equivalent to $m^{2} \mid 8^{m}+1$. Suppose $m \geqslant 2$, and let $p$ be the smallest prime divisor of $m$ (hence odd). It satisfies $8^{2 m} \equiv 1$ modulo $p$, so the order of 8 divides $p-1$ and $2 m$. But $m$ and $p-1$ have no common factors given the properties of $p$, and thus $p \mid 2$, so $p=2$, and $p$ divides $8^{2}-1=63$, so $p=7$ (since $p \neq 3$). However, $2^{n}+1$ is never divisible by 7 according to a study of powers modulo 7, so $m=1$, and we deduce that the only $n$ that works is $n=3$, which is indeed a solution.
## 6 Functional Equations (Benoît)
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $N \in \mathbb{N}$.
Discriminant the cat proposes the following game to you:
- You choose a finite sequence (of your choice and kept secret) of integers $\left(a_{0}, \ldots, a_{n}\right) \in \mathbb{N}^{n+1}$
- At each turn of the game, Discriminant gives you a real number $\beta \in \mathbb{N}$ and you respond with the value of $\sum_{k=0}^{n} a_{k} \beta^{k}$.
- The game continues until Discriminant has guessed the sequence of integers or until fewer than $N$ turns have taken place.
- If at the end of the game Discriminant has guessed the sequence of integers, he wins; otherwise, he loses.
If Discriminant wins, you owe him a can of cat pate.
For which values of $N$ would you accept to play this game?
|
Discriminant can always win in 1 turn.
It is enough to evaluate at an algebraic number.
For example, to be explicit, at the Liouville number
$$
\sum_{k=1}^{+\infty} \frac{1}{10^{k!}}
$$
(meditate on the link with the previous exercise).
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(British MO 1998)
Solve for $x, y, z \in \mathbb{R}^{+}$ real positive numbers the following system of equations:
$$
\begin{aligned}
& x y + y z + z x = 12 \\
& x y z = 2 + x + y + z
\end{aligned}
$$
|
This exercise is a disguised inequality problem. We notice that $(2,2,2)$ is a solution, so we would like to show that we are in the case of equality of an inequality.
Indeed, by AM-GM we have
$$
12 \geq x y+y z+z x \geq 3 \sqrt[3]{x^{2} y^{2} z^{2}}
$$
as well as
$$
x y z=2+x+y+z \geq 2+3 \sqrt[3]{x y z}
$$
We see that if we let $X=\sqrt[3]{x y z}$, both $X^{2} \leq 4$ and $X^{3}-3 X-2 \geq 0$, which means $X \leq 2$ and $(X-2)(X+1)^{2} \geq 0$, which is equivalent to saying that $X=2$. Thus, all the inequalities are equalities, and we quickly obtain $x=y=z=2$, the only solution.
The following exercises have not been covered in class.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Solve the equation $x^{4}-3 x^{3}+4 x^{2}-3 x+1=0$.
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly.
|
Let $y=x+1 / x$. We have $0=\frac{x^{4}-3 x^{3}+4 x^{2}-3 x+1}{x^{2}}=$ $\left(x^{2}+\frac{1}{x^{2}}\right)-3\left(x+\frac{1}{x}\right)+4=\left(y^{2}-2\right)-3 y+4=y^{2}-3 y+2$.
The roots of the polynomial $y^{2}-3 y+2$ are 1 and 2, so $y^{2}-3 y+2=(y-1)(y-2)$. Therefore, the equation is equivalent to $y=1$ or $y=2$.
If $y=2$ then $x+1 / x=2$, so $x^{2}+1=2 x$, which can be rewritten as $(x-1)^{2}=0$. This is equivalent to $x=1$.
If $y=1$ then $x+1 / x=1$, so $x^{2}-x+1=0$. However, $x^{2}-x+1=(x-1 / 2)^{2}+3 / 4>0$, so the equation has no solution.
Conclusion: the unique solution is $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Solve $1-4^{x}+2^{x+1}=2^{x}+2^{-x}$.
|
Let $t=2^{x}$. The equation is equivalent to $1-t^{2}+2 t=t+1 / t$, which simplifies to $1-t^{2}+t-1 / t=0$. By multiplying by $t$, we get $t(1-t^{2})+t^{2}-1=0$, or equivalently $0=(1-t^{2})(t-1)=(1-t)(1+t)(t-1)=-(t+1)(t-1)^{2}$.
Therefore, $t=1$ or $t=-1$. Since $t=2^{x}>0$, we necessarily have $t=1$, hence $x=0$.
Conversely, we verify that $x=0$ is indeed a solution.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all integers $n$ that are coprime with every number of the form $2^{m} + 3^{m} + 6^{m} - 1, m \in \mathbb{N}$.
|
We will show that only 1 is suitable. For this, it suffices to establish that for any prime $p$, there exists an integer $m$ such that $p \mid 2^{m}+3^{m}+6^{m}-1$. For $p=2$, any $m$ works. For $p=3$, any even $m$ (for example, 2) works. For $p \geq 5, p$ is coprime with $2,3,6$. We leave it to the reader to study the cases $p=5, p=7, p=11$ (by calculating the residues of $2^{m}+3^{m}+6^{m}-1$ modulo $p$) and note that in these cases $p \mid 2^{p-2}+3^{p-2}+6^{p-2}-1$. Let's show that this result is general.
For $p$ prime greater than $5,2^{p-2}+3^{p-2}+6^{p-2} \equiv 6^{p-2} * 3 * 2 * 2^{p-2}+6^{p-2} * 2 * 3 * 3^{p-2}+6^{p-2} \pmod{p}$, according to Fermat's Little Theorem, and the second term is congruent modulo $p$ (still by Fermat's Little Theorem) to $6^{p-2}(3 * 1+2 * 1+1) \equiv 6 * 6^{p-2} \equiv 1 \pmod{p}$, which is what we wanted to prove and concludes the proof.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(not treated in class) Determine the minimum of $x^{2}+y^{2}+z^{2}$ under the condition $x^{3}+y^{3}+z^{3}-3 x y z=1$.
|
We calculate that $S_{3}=\sigma_{1} S_{2}-\sigma_{1} \sigma_{2}+3 \sigma_{3}$, so $S_{3}-3 \sigma_{3}=\sigma_{1}\left(S_{2}-\frac{3 S_{2}-\sigma_{1}^{2}}{2}\right)$. We must therefore minimize $S_{2}$ under the condition that $\sigma_{1}\left(3 S_{2}-\sigma_{1}^{2}\right)=2$.
Now, $3 S_{2}=\frac{2}{\sigma_{1}}+\sigma_{1}^{2} \geqslant 3$ by the AM-GM inequality (or by a function study), so $S_{2} \geqslant 1$. The bound is achieved when $\sigma_{1}=1$ (for example, when $x=1$ and $y=z=0$).
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine all integers $n>1$ such that $\frac{2^{n}+1}{n^{2}}$ is an integer.
|
This exercise is a classic: it is problem 3 of the 1990 International Olympiad, held in Beijing, where France placed 5th with three gold medals, notably thanks to Vincent Lafforgue (younger brother of Fields Medalist Laurent Lafforgue), who achieved perfect scores of 42/42 in 1990 and 1991. It is worth noting, however, that there were half as many participating countries then as there are today: several European countries subsequently split up.
This exercise uses reasoning techniques that have become classic and useful for a wide range of problems. First, the idea is to look for the smallest prime factor \( p \) of \( n \), using the concept of the order of 2 modulo \( p \). Since \( n \) is odd, \( p \geq 3 \). The order of 2 modulo \( p \) is the smallest non-zero exponent \( b \) such that \( 2^b \equiv 1 \pmod{p} \), and it is shown that \( b \) divides any other exponent \( a \) such that \( 2^a \equiv 1 \pmod{p} \). It suffices to write the Euclidean division \( a = bq + r \) and note that \( 2^{bq} \equiv 1 \pmod{p} \) to deduce \( 2^r \equiv 1 \pmod{p} \), with \( 0 \leq r < b \). Since \( b \) is the smallest positive integer satisfying this relation, necessarily \( r = 0 \) so \( a = bq \).
According to Fermat's theorem, \( 2^{p-1} \equiv 1 \pmod{p} \), which implies that the order of 2 divides \( p-1 \). And since \( p \) divides \( n \), and thus \( 2^n + 1 \), and \( 2^{2n} - 1 = (2^n + 1)(2^n - 1) \), the order of 2 also divides \( 2n \). It is coprime with \( n \), since it is strictly less than \( p \) and \( p \) is, by hypothesis, the smallest divisor of \( n \) other than 1 (the order of 2 cannot obviously be 1, as for no prime \( p \neq 2 \) is 1 congruent to 1 modulo \( p \)). Therefore, by Gauss's theorem, it divides 2: it can only be 2, so \( p \) divides \( 2^2 - 1 = 3 \), and the smallest prime factor \( p \) of \( n \) is necessarily 3.
If we were to look for integers \( n \) such that \( n \) divides \( 2^n + 1 \), there would be many, and their prime factors could be numerous, even if the smallest of them is necessarily 3. For example, if \( n \) divides \( 2^n + 1 = nq \), \( 2^n + 1 \) divides \( 2^{nq} + 1 = 2^{2^n + 1} \) because \( q \) is odd, so \( 2^n + 1 \) is also a solution. 3, 9, but also \( 513 = 2^9 + 1 \) and even one-third of 513, \( 171 = 9 \times 19 \), are solutions. Only these numbers do not satisfy \( 2^n + 1 \) being divisible by \( n^2 \), because, for example, \( 2^9 + 1 = 3^3 \times 19 \) is not divisible by \( 9^2 = 3^4 \).
The second step of the proof is to show that \( n \) cannot be divisible by 9. Let \( n = 3^k d \), with \( k \geq 1 \) and \( d \) odd and not divisible by 3. We will prove by induction on \( k \) that the highest power of 3 dividing \( 2^n + 1 \) is \( 3^{k+1} \). For \( k = 1 \), \( 2^{3d} + 1 = (2^3 + 1)(2^{3(d-1)} - 2^{3(d-2)} + \cdots - 2^3 + 1) \). The second parenthesis contains a sum of \( d \) terms all congruent to 1 modulo 9, since \( 2^3 \equiv -1 \pmod{9} \), so it is congruent to \( d \) modulo 9, which implies that it is not a multiple of 3, and the first parenthesis is precisely 9, which initializes the induction by proving the result for \( k = 1 \), regardless of the factor \( d \). Now if the result is true for a given \( k \geq 1 \), since \( 2^{3n} + 1 = (2^n + 1)(2^{2n} - 2^n + 1) \) and \( 2^n \equiv -1 \pmod{3^{k+1}} \), \( 2^{2n} - 2^n + 1 \equiv 1 + 1 + 1 = 3 \pmod{9} \) is divisible by 3 but not by 9, which completes the proof. It follows that if \( k \geq 2 \) and \( n = 3^k d \), the highest power of 3 dividing \( 2^n + 1 \) is \( 3^{k+1} \), while \( n^2 \) is divisible by \( 3^{2k} \). Therefore, a solution to our problem must be a multiple of 3 and not a multiple of 9.
This result generalizes by an analogous proof: for a given prime \( p \), if we denote \( v_p(n) \) the exponent of the highest power of \( p \) dividing \( n \), and if \( a \) and \( b \) are integers such that \( p \) divides \( a - b \) but does not divide \( a \) or \( b \), then:
\[
v_p(a^n - b^n) = v_p(a - b) + v_p(n)
\]
This is the LTE (Lifting The Exponent) theorem, which allows solving many exercises. In the present problem, we apply this LTE theorem for \( p = 3 \), \( a = 2 \), and \( b = -1 \).
What can we say now about the factor \( d \)? For which values of \( d \) not multiples of 3 is \( 2^n + 1 \) divisible by \( n^2 \) with \( n = 3d \)? Let \( p \) be the smallest prime factor of \( d \) (\( p \geq 5 \)). The order of 2 modulo \( p \) divides \( p-1 \) by Fermat's theorem, but it also divides \( 2n = 6d \) since \( 2^{2n} \equiv 1 \pmod{p} \), and it does not divide \( n \) since \( 2^n \equiv -1 \pmod{p} \), so it is even. Since it is strictly less than \( p \), the smallest prime factor of \( d \), it is coprime with \( d \). Therefore, it divides 6 (by Gauss's theorem). The only even divisors of 6 are 2 and 6, but 2 cannot be the order of 2 because \( 2^2 - 1 = 3 \) has no prime factor other than 3, and it cannot be the order of 6 because \( 2^6 - 1 = 3^2 \times 7 \) has \( p = 7 \) as its only prime factor different from 3, but 7 is not of order 6 but of order 3 (it divides \( 2^3 - 1 \), so it also divides \( 2^{3d} - 1 \) and not \( 2^{3d} + 1 \)). Since \( d \) cannot have a smallest prime factor, \( d = 1 \), so the only integer \( n \) such that \( \frac{2^n + 1}{n^2} \) is an integer, besides the trivial solution \( n = 1 \), is \( n = 3 \).
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all odd integers $n \geq 1$ such that $n$ divides $3^{n}+1$.
|
Let $n>1$ such that $n$ divides $3^{n}+1$. Let $p$ be the smallest prime factor of $n$, which is therefore odd, and satisfies $p>3$. Then $3^{2 n} \equiv 1 \pmod{p}$. Let $\omega$ be the order of 3 modulo $p$. Then $\omega$ divides $2 n$. On the other hand, by Fermat's Little Theorem, $3^{p-1} \equiv 1 \pmod{p}$. Thus $\omega$ divides $p-1$. We deduce that $\omega$ divides $\gcd(2 n, p-1)$. Given the condition on $p$, we necessarily have $\omega=1$ or 2. In the first case, $3 \equiv 1 \pmod{p}$ and thus $p=2$, which is excluded. In the second case, $3^{2} \equiv 1 \pmod{p}$ and thus $p$ divides 8, which is also excluded. We conclude that $n=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Calculate the gcd of $21 n+4$ and $14 n+3$.
|
We apply the Euclidean algorithm.
$$
\begin{aligned}
21 n+4 & =(14 n+3) \cdot 1+7 n+1 \\
14 n+3 & =2 \cdot(7 n+1)+1 \\
7 n+1 & =1 \cdot(7 n+1)+0
\end{aligned}
$$
Therefore, this gcd is 1, and this holds for all $n \in \mathbb{N}$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the integers $n \in \mathbb{N}^{*}$ such that the function $x \mapsto x^{n}$ is convex.
|
The second derivative of the function $x \mapsto x^{n}$ is $x \mapsto n(n-1) x^{n-2}$, which is positive on $\mathbb{R}$ if and only if $n=1$ or if $n$ is even. Consequently, $x \mapsto x^{n}$ is convex if and only if $n=1$ or if $n$ is even.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the largest constant $\mathrm{C}$ such that for all $x, y, z \geq 0,(y z+z x+$ $x y)^{2}(x+y+z) \geq C x y z\left(x^{2}+y^{2}+z^{2}\right)$.
|
By setting $y=z=1, \frac{(y z+z x+x y)^{2}(x+y+z)}{x y z\left(x^{2}+y^{2}+z^{2}\right)}=\frac{(2 x+1)^{2}(x+2)}{x\left(x^{2}+2\right)}$. This quantity tends to 4 as $x$ tends to $+\infty$, so we will try to prove the inequality with $C=4$.
By expanding, we need to show that $\left(x^{3} y^{2}+x^{2} y^{3}+y^{3} z^{2}+y^{2} z^{3}+z^{3} x^{2}+z^{2} x^{3}\right)+5\left(x^{2} y^{2} z+y^{2} z^{2} x+z^{2} x^{2} y\right) \geq 2\left(x^{3} y z+y^{3} z x+z^{3} x y\right)$.
We then draw the triangle:
And we see that it suffices to apply the AM-GM inequality three times with the extreme black points $\left(x^{2} z^{3}+z^{3} y^{2} \geq 2 z^{3} x y\right.$, etc.) to conclude.
|
4
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(*) We call $I$ the set of points in the plane such that their abscissa and ordinate are irrational numbers, and $R$ the set of points whose both coordinates are rational. How many points of $R$ at most can lie on a circle of irrational radius whose center belongs to $I$?
|
(Solved by Yakob Kahane)
If we have two points on a circle, then the center of said circle lies on the perpendicular bisector of the two points. If the said two points have rational coordinates, their perpendicular bisector has an equation with rational coefficients.
We assume henceforth that there exist $A, B, C$ three points with rational coordinates on the same circle $\Gamma$ whose center is not at rational coordinates. We denote $L_{1}, L_{2}$ the equations of the perpendicular bisectors of $[A B]$ and $[A C]$ with rational coefficients:
\[
\begin{aligned}
& L_{1}: a_{1} x+b_{1} y=c_{1} \\
& L_{2}: a_{2} x+b_{2} y=c_{2}
\end{aligned}
\]
Their point of intersection is the solution to a system of two equations with two unknowns and rational coefficients; the calculation of the solution (i.e., the point of intersection) remains within $\mathbb{Q}$; but this point $O$ of intersection is the center of the circumcircle of $A B C$ and thus of $\Gamma$, which contradicts the hypothesis.
It remains to find two rational points on a circle with a center of irrational coordinates. The reader will verify that a circle with center $O(\sqrt{2} ; 1-\sqrt{2})$ passes through $A(0 ; 0)$ and $B(1 ; 1)$, which concludes the proof.
## X. Memorable Quotes
- Matthieu L "The problem is not that there is a problem"
- "It's a bit like being a fakir"
- Étienne M "Arithmetic is simpler when it's easy"
- Lucie W "Do sharp angles exist?"
- Victor "You can use it for drafts... like this course"
- Antoine: "If you are the Queen of England, I am the Prime Minister. Are you the Queen of England?" Olivine: "Yes!"
- Matthieu L: "An airplane is like an elevator, just a bit more complicated"
- Noémie: "François, how many ears do you have?"
- "Does François have a cut ear?"
- Victor: "Clara? Is she one of the two Chinese girls downstairs?"
- Clara B: "There are two players who are not playing"
- Antoine: "God created the world and prime factorization"
- Savinien: "Let $a_{1}, a_{2}, \ldots, a_{4}$ be real numbers"
- Thomas: "We need to check that it works with any value of 2016"
- Mathias: $" \sqrt{4} \equiv 3[5] "$ (convinced of what he is saying)
- Clara: "I would be willing to live my whole life with Lucie but not with a child"
Lucie: "I would live with a child, but not with Clara"
- Clément: "I don't know the Knights of the Round Table, except for D'Artagnan"
- Clara B: "My circle has a radius of 0 and I am supposed to place 4 distinct points on it"
- Rémi: "The blue circle has seven points of intersection with the red line"
Pierre-Alexandre: "Which one? The one with the loops?"
- Lucie W: "Who is motivated to drink Toblerone?"
- Lucie W: "A photo without us is of no interest"
- Savinien, in a copy: "We choose the endpoint of the side of the other side of the side of the triangle which is the $3^{rd}$ vertex of the triangle"
- Vincent J: "Bézout is the one who invented the bézounours"
- Vincent J: "Are we, in our group, Swiss? No? So we are not a group because we don't have a neutral element"
- Vincent J (during his lecture): "What is a positive braid, apart from a braid that has participated in the Tour de France?"
- Sébastien: "He shows us how to prove that"
- Tanguy: "It's trivialong"
Clément: "Ah, yeah, it's a bit like a triathlon"
[^0]: 1. For the attention of the geometric reader: here, unless otherwise stated, a geometric transformation is considered as a function $t$ associating a geometric figure with another figure and satisfying a certain number of properties. However, the fact that the ambient spaces of departure and arrival are the same up to isomorphism (and therefore that $t$ can be considered by its action within a given figure) is not taken into account.
2. We do not specify here the distinction between direct and indirect transformations, so we only consider direct transformations that, if they preserve angles, also preserve oriented angles.
[^1]: 8. Strictly speaking, on a trilateral.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Consider a $4 \times 4$ grid consisting of 16 cells. What is the minimum number of cells that need to be blackened so that by eliminating any two columns and any two rows, we are sure that at least one black cell remains?
## 2 Solution
|
We will show that at least 7 squares must be blackened. First, if we color the squares as follows:

then we verify the hypothesis of the statement. Indeed, let's try to erase two rows and two columns so that the four remaining squares are white. We need to erase the square in the top left corner, so let's erase the first row (erasing the first column would be the same). I leave it to you to verify that afterwards it is impossible to erase one row and two columns such that there are four remaining white squares.
Now suppose we have blackened 6 squares or fewer. We will erase the two rows with the most black squares. How many black squares remain in the remaining rows? Already, there are fewer than half, so 3 or fewer. But there cannot be 3 left, otherwise it would be one row of 2 and one row of 1, and in those we erased there were 3, so one row of 2 and one row of 1, and we would have had to erase the two rows of 2. Therefore, there are at most 2 black squares left in the remaining rows, and we can erase the two columns corresponding to these two squares, and the remaining squares will all be white.
It is therefore impossible to have a configuration that satisfies the condition of the statement if we color only 6 squares. We must indeed have at least 7 squares.
## IV. Beginners
## 1 Tuesday: Combinatorics
## 1 Morning: Irène Marcovici
## Pigeonhole Principle
PIGEONHOLE PRINCIPLE - If at least \( n+1 \) objects are placed in \( n \) drawers, at least one drawer (at least) will contain at least two objects. More generally, if at least \( k n+1 \) objects are placed in these same \( n \) drawers, at least one drawer (at least) will contain at least \( k+1 \) objects.
A very simple example: among 13 people, we can find 2 who were born in the same month of the year.
One of the first mathematical results that can be deduced from this is that the decimal expansion of the fraction \(\frac{p}{q}\) is periodic, with a period strictly less than \( q \). Indeed, when performing the division, each new decimal corresponds to a new remainder. Among \( q \) consecutive remainders, either one is zero (and the division stops, which corresponds to a period of 1, since from a certain rank, all the decimals are equal to 0), or these \( q \) remainders are all between 1 and \( q-1 \), which proves that at least two of them, \( r_i \) and \( r_j \), are equal. Since each remainder determines the entire sequence of the division, \( r_{i+1} = r_{j+1}, r_{i+2} = r_{j+2} \ldots \) therefore the decimal expansion will be periodic, with a period of at most \( |i-j| < q \).
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the GCD of all numbers of the form $i \times(i+1) \times(i+2)$ with $i \geq 1$ (we are looking for the greatest common divisor of all these numbers).
|
For $i=1$ we have $i \times(i+1) \times(i+2)=6$. Therefore, the GCD must be less than 6.
But among three consecutive numbers, there is always a multiple of 2 and a multiple of 3, so $i \times(i+1) \times(i+2)$ is always a multiple of 6.
The GCD of the numbers $i \times(i+1) \times(i+2)$ for $i \geq 1$ is exactly 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
The act of adding the digits of a number is called addichiffre. For example, when we addichiffre 124, we get $1+2+4=7$.
What do we get when we addichiffre $1998^{1998}$, then addichiffre the result obtained, and so on, three times in a row?
|
1998 and $1998^{1998}$ are multiples of 9, and therefore their digit sums are also multiples of 9. By induction, all digit sums obtained by repeated digit sum operations starting from $1998^{1998}$ are multiples of 9.
Moreover:
$$
1998^{1998} \leq 2000^{1998}=(2 \cdot 1000)^{1998}=2^{1998} \cdot 10^{3 \cdot 1998}=2^{1998} \cdot 10^{5994}
$$
and we know that $2^{9}=512<10^{3}$ and therefore $2^{1998}=2^{9 \cdot 222}<10^{3 \cdot 222}=10^{666}$ and thus $1998^{1998} < 10^{5994+666}=10^{6660}$. Therefore, the digit sum of $1998^{1998}$ is less than $9 \cdot 6660 = 59940$. The digit sum of a number less than 59940 is necessarily less than $5 + 9 \cdot 4 = 41$. The digit sum of a number less than 41 is less than $4 + 9 = 13$ and since this digit sum is a multiple of 9 and non-zero, this number must be 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Twelve candidates for the position of mayor are participating in a televised debate. After a while, one of them declares, "Up until now, we have lied once." A second then says, "Now, it's twice." A third exclaims, "Three times, now," and so on until the twelfth, who asserts that before him, there were twelve lies. The host then stops the discussion. Knowing that at least one of the candidates correctly announced how many times they had lied before their turn to speak, determine how many candidates lied in total.
|
We denote $C_{1}, \ldots, C_{12}$ as the candidates in the order of their speaking. Since at least one of them told the truth, we can consider the smallest integer $k$ such that $C_{k}$ told the truth (i.e., $C_{k}$ is the first to tell the truth). By the minimality of $k$, all those who spoke before him lied. Furthermore, since $C_{k}$ told the truth, there were exactly $k$ lies before his turn, and thus exactly $k$ lies after. Therefore, $C_{k+1}$ lied by saying there were $k+1$ lies before his turn, and there were indeed $k+1$ lies after $C_{k+1}$ spoke. Consequently, $C_{k+2}$ lied by saying there were $k+2$ lies before his turn, and there were indeed $k+2$ lies after $C_{k+2}$ spoke, and so on. Thus, all candidates who spoke after $C_{k}$ lied.
And, finally, only $C_{k}$ told the truth. Therefore, there were 11 liars.
Remark. In fact, we can specify the situation a bit more. Indeed, if $k \geq 2$, then with the above notation, we know that $C_{k}$ told the truth and that there were exactly $k$ lies before his turn. Taking into account the lie of $C_{k-1}$, it means there were exactly $k-1$ lies before $C_{k-1}$ spoke. But then, $C_{k-1}$ told the truth, which contradicts the minimality of $k$. Therefore, we must have $k=1$, which means that the first candidate to speak is the only one who told the truth.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Consider the graph $\mathcal{G}_{n}$ whose vertices are the integers from 1 to $n$. Two points $a$ and $b$ are connected if and only if $a+b$ is prime. For which $n$ is the graph $\mathcal{G}_{n}$ planar?
## Paths on graphs
Definition 3. A graph is said to be Eulerian if there exists a path that passes through each edge exactly once. A graph is said to be Hamiltonian if there exists a path that passes through each vertex exactly once.
## Theorem
A graph is Eulerian if and only if the number of vertices of odd degree is either 0 or 2.
|
It is possible to draw $\mathcal{G}_{8}$ in the plane, but arranging $\mathcal{G}_{9}$ can result in the graph of the three houses and three factories, which is not planar.

|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a$ and $b$ be strictly positive integers such that $ab$ divides $a^{2}+b^{2}+1$. Calculate the quotient.
|
As before, we denote $k=\frac{a^{2}+b^{2}+1}{a b}$ and consider a pair $(\alpha, \beta)$ of minimal sum among the pairs $(a, b)$ satisfying this equality. If $\alpha=\beta$, then $\alpha^{2}$ divides $2 \alpha^{2}+1$ so $\alpha^{2}=1$ and $k=3$. Otherwise, we can assume without loss of generality that $\alpha>\beta \geq 0$. We solve the equation $x^{2}+\beta^{2}+1=k x \beta$. The solutions are $\alpha$ and
$$
\alpha^{\prime}=k \beta-\alpha=\frac{\beta^{2}+1}{\alpha}
$$
$\alpha^{\prime}$ is a strictly positive integer (otherwise, $\alpha^{\prime 2}-k \beta \alpha^{\prime}+\beta^{2}+1 \geq 1>0$) and $\alpha^{\prime}<\alpha$ (since $\left.\beta^{2}+1 \leq \alpha^{2}\right):$ contradiction.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. A triangle has side lengths: 3, 4, 5. Calculate the radius of the inscribed circle (circle inside the triangle and tangent to all three sides of the triangle).
|
. Let $r$ be the radius of the inscribed circle. We start by drawing a figure.
The triangle $ABC$ with side lengths $3, 4, 5$ is a right triangle. We can calculate its area $S$ in two different ways: on the one hand, $S = \frac{4 \times 3}{2} = 6$; on the other hand, $S$ is the sum of the areas of triangles $IAB$, $IAC$, and $IBC$. The area of triangle $IAB$ is $\frac{r \times AB}{2} = 2r$, that of triangle $IAC$ is $\frac{r \times AC}{2} = \frac{3}{2}r$, and that of triangle $IBC$ is $\frac{r \times BC}{2} = \frac{5}{2}r$. We deduce that $6 = S = r \times \left(2 + \frac{3}{2} + \frac{5}{2}\right) = 6r$ and thus $r = 1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. For what value of $k$ do we have the identity (true for all $a, b, c$):
$$
(a+b)(b+c)(c+a)=(a+b+c)(a b+b c+c a)+k a b c ?
$$
|
. It suffices to develop each of the two members. All terms are identical except the terms in $a b c$ which appear twice on the left and $3+k$ times on the right. Therefore, $k=-1$. We note that for $a=b=c=1$, we get: $8=9+k$, so the only possible value of $k$ is -1, but this does not dispense with doing the calculation to prove the identity when $k=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Show that: $\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\ldots+\frac{1}{\sqrt{99}+\sqrt{100}}=9$.
## 2 Test Solution
Translate the text above into English, keep the original text's line breaks and format, and directly output the translation result.
|
The main idea of the exercise is to use the relation $a^{2}-b^{2}=(a-b)(a+b)$ to write: $1=(\sqrt{k+1}+\sqrt{k}) \cdot(\sqrt{k+1}-\sqrt{k})$, or equivalently $\frac{1}{\sqrt{k+1}+\sqrt{k}}=\sqrt{k+1}-\sqrt{k}$.
In other words, $\frac{1}{\sqrt{1}+\sqrt{2}}=\sqrt{2}-\sqrt{1}, \frac{1}{\sqrt{2}+\sqrt{3}}=\sqrt{3}-\sqrt{2} \cdots \frac{1}{\sqrt{99}+\sqrt{100}}=\sqrt{100}-\sqrt{99}$. This leads to:
$$
\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\cdots+\frac{1}{\sqrt{99}+\sqrt{100}}=(-\sqrt{1}+\sqrt{2})+(-\sqrt{2}+\sqrt{3})+\cdots
$$
$\cdots+(-\sqrt{k}+\sqrt{k+1})+(-\sqrt{99}+\sqrt{100})=-\sqrt{1}+\sqrt{100}=9$ because all the other square roots cancel out ("telescoping simplifications").
Whenever we see square roots in a sum in the denominator, we should have the reflex to eliminate them using this same technique, by multiplying the numerator and the denominator by what is called the "conjugate expression."
|
9
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.