problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
In a football tournament, each team plays exactly twice against each of the others. There are no draws, a win earns two points, and a loss earns nothing. It turns out that only one team won the tournament with 26 points, and there are two teams tied for last with 20 points each. Determine the number of teams, and provide an example of a tournament where such results occur.
|
Let $n$ be the number of teams.
Each team wins a number of matches between 10 and 13. Since there are $n(n-1)$ matches, each team wins on average $n-1$ matches. The winning team and the two last teams in a tie win on average 11 matches, while the other teams win on average between 11 and 12 matches. Therefore, the average number of matches won by each team is $\geqslant 11$ and $<12$. Since $n-1$ is an integer, we must have $n-1=11$, i.e., $n=12$.
Let's show that such a tournament is possible. For the sake of clarity, let's say that the 12 teams belong to 12 different cities. Each pair of cities plays two matches, one in the city of one team and the other in the city of the other team. We will say that a team plays at home if the match takes place in its city, and away otherwise.
Here is an example of a suitable tournament: when two of the teams $2, \ldots, 12$ meet, the team playing at home wins. In addition, team 1 wins all its matches against teams 2 and 3, and wins only at home against teams $4, \ldots, 12$.
Another solution for the first part. Let $a$ be the number of teams that win 11 matches and $b$ be the number of teams that win 12 matches. The total number of teams is $n=3+a+b$. On the other hand, the number of matches won is $n(n-1)=10 \times 2+11 a+12 b+13=33+11 a+12 b=11(3+a+b)+b=11 n+b$.
We deduce that $b=n(n-1)-11 n=n(n-12)$. Since $0 \leqslant b<n$, we have $0 \leqslant n(n-12)<n$. Dividing by $n$, we get $0 \leqslant n-12<1$, hence $n=12$.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
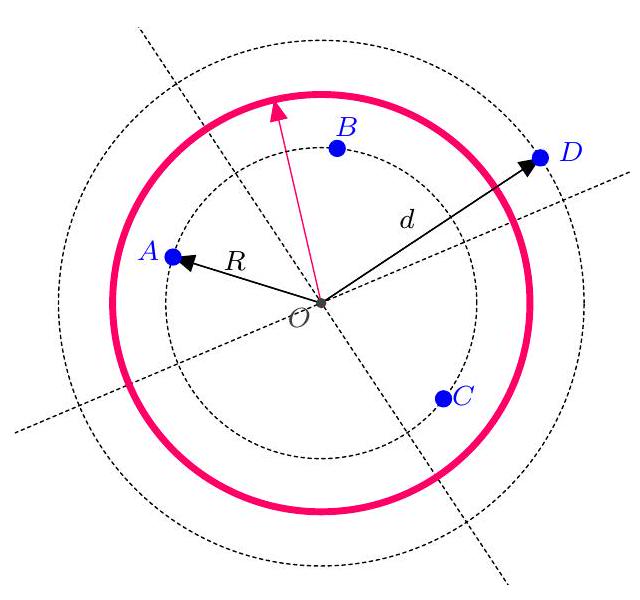
Given a point $P$ and a circle $\mathcal{C}$ in the plane, the distance from $P$ to $\mathcal{C}$ is defined as the minimum length $PM$ between $P$ and a point $M$ on the circle $\mathcal{C}$. For example, if $P$ lies on the circle, then the distance from $P$ to $\mathcal{C}$ is zero, and if $P$ is the center of the circle, then the distance from $P$ to $\mathcal{C}$ is equal to the radius of $\mathcal{C}$.
Given four non-cyclic points $A, B, C, D$, what is the maximum number of circles that pass at equal distance from these four points?
|
Let $\mathcal{C}$ be a circle passing at equal distance from $A, B, C, D$. The four points cannot all be inside the circle, otherwise they would be equidistant from the center, and thus would be concyclic. Similarly, they cannot all be outside.
Determine the number of circles $\mathcal{C}$ passing at equal distance from $A, B, C, D$ such that $A, B, C$ are on the same side of the circle. Suppose $A, B, C$ are not collinear. Let $\Omega$ be the center of the circumcircle of $A, B, C$ and $R$ its radius. Denote $r$ the radius of $\mathcal{C}$ and $d=\Omega D$. The fact that $A, B, C, D$ are equidistant from $\mathcal{C}$ can be written as $|r-R| = |r-d|$. Moreover, $r-R$ and $r-d$ cannot be equal, otherwise we would have $d=R$ and $A, B, C, D$ would be concyclic. The equality $|r-R| = |r-d|$ is equivalent to $r-R = d-r$, or equivalently $r = \frac{R+d}{2}$, which proves the existence and uniqueness of the circle $\mathcal{C}_{D}$ such that $A, B, C$ are on one side and $D$ on the other side of the circle.
(If $A, B, C$ are collinear, no point is equidistant from $A, B, C$, so there does not exist a circle passing at equal distance from $A, B, C$ such that $A, B, C$ are all on the same side of the circle.)
We similarly define the circles $\mathcal{C}_{A}, \mathcal{C}_{B}$, and $\mathcal{C}_{C}$ if they exist.
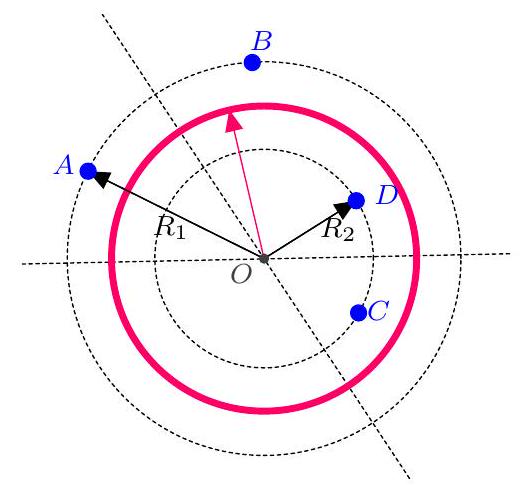
Determine the number of circles $\mathcal{C}$ passing at equal distance from $A, B, C, D$ such that $A, B$ are on one side and $C, D$ on the other. The center of $\mathcal{C}$ must be equidistant from $A$ and $B$, so it lies on the perpendicular bisector of $[A B]$. Similarly, it lies on the perpendicular bisector of $[C D]$.
Suppose that $(A B)$ and $(C D)$ are not parallel. Then the perpendicular bisectors of $[A B]$ and $[C D]$ intersect at a point $\Omega$. Let $R_{1} = \Omega A$ and $R_{2} = \Omega C$. Then $R_{1} \neq R_{2}$ because $A, B, C, D$ are not concyclic. As in the previous case, we see that the circle with center $\Omega$ and radius $\frac{R_{1} + R_{2}}{2}$ is the unique circle equidistant from $A$ and $B$ such that $A$ and $B$ are on one side and $C, D$ on the other. Denote it by $\mathcal{C}_{A B}$.
Suppose that the perpendicular bisectors of $[A B]$ and $[C D]$ are parallel but not coincident. Then there does not exist a circle equidistant from $A, B, C, D$ such that $A, B$ are on one side and $C, D$ on the other.
Suppose that the perpendicular bisectors of $[A B]$ and $[C D]$ are coincident. If $A, B, C, D$ are not collinear, then the perpendicular bisectors of $[A B]$ and $[A C]$ intersect at a point $\Omega$ which is equidistant from $A, B, C, D$, which contradicts the fact that $A, B, C, D$ are not concyclic.
Suppose that $A, B, C, D$ are collinear such that the midpoints of $[A B]$ and $[C D]$ are coincident. Then there are infinitely many circles passing at equal distance from $A, B, C, D$, with centers on the common perpendicular bisector.
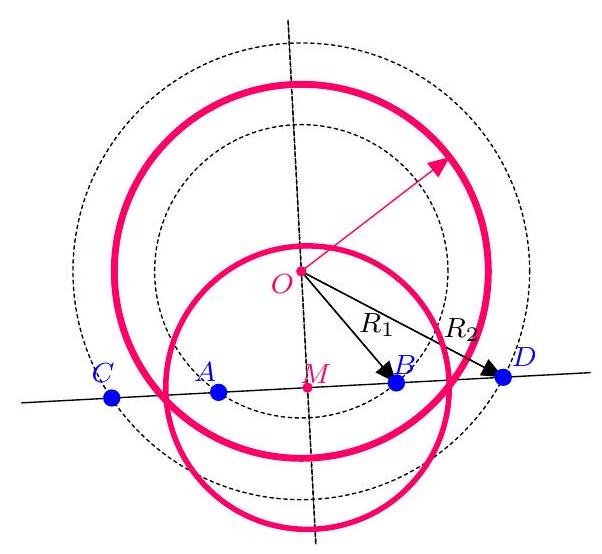
The discussion above shows that, except in the special case where the four points are collinear such that the midpoint of two points is equal to the midpoint of the other two, there are at most 7 circles passing at equal distance from $A, B, C, D$: these are $\mathcal{C}_{A}, \mathcal{C}_{B}, \mathcal{C}_{C}, \mathcal{C}_{D}, \mathcal{C}_{A B}, \mathcal{C}_{A C}, \mathcal{C}_{A D}$. Equality holds when any two of the six lines determined by $A, B, C, D$ are not parallel.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(French-Slovak Competition 1996) Find all strictly positive integers $x, y, p$ such that $p^{x}-y^{p}=1$ with $p$ prime.
|
Let's rewrite the equation in the form $y^{p}+1^{p}=p^{x}$. If $y=1$, we see that $p=2$ and $x=1$. If $p=2$, it readily follows that necessarily $x, y=1$. Therefore, we assume $p$ is odd so that $y+1$ divides $y^{p}+1$.
If the conditions of Zsigmondy's theorem are satisfied, there exists a prime factor of $y^{p}+1$ that does not divide $y+1$, so $y^{p}+1$ cannot be a power of a prime number. It remains to handle the case $(y, p)=(2,3)$, which gives the solution $x=2$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all strictly positive numbers $a, p, n$ such that $p^{a}-1=$ $2^{n}(p-1)$, where $p$ is a prime number.
|
It is clear that $p>2$. Suppose by contradiction that $a=$ $uv$ is composite. Then according to Zsigmondy's theorem, $p^{u}-1$ has a prime factor $q$ that does not divide $p-1$. But $p^{u}-1$ divides $p^{a}-1=2^{n}(p-1)$. Therefore, $q=2$. However, $p-1$ is even, which is a contradiction. Therefore, $a$ is prime.
If $a=2$, we find that $p=2^{n}-1$.
If $a>2$, similarly, Zsigmondy's theorem implies that $2^{n}(p-1)=p^{a}-1$ has a prime factor $r$ that does not divide $p-1$. This implies that $r=2$, which is absurd because $p-1$ is even.
The solutions are therefore $a=2$ and $n$ such that $2^{n}-1$ is prime.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine (without doing heavy calculations) the value of
$$
\binom{6}{0}-\binom{6}{1}+\binom{6}{2}-\binom{6}{3}+\binom{6}{4}-\binom{6}{5}+\binom{6}{6}
$$
Generalize by replacing 6 with $n$.
|
By taking $n=6, a=1$ and $b=-1$ in the proposition, since $(-1)^{k}$ is 1 if $k$ is even and -1 if $k$ is odd, we obtain that the first expression is $(1-1)^{6}=0$. More generally, we obtain for any $n$ that
$$
\binom{n}{0}-\binom{n}{1}+\binom{n}{2}-\binom{n}{3}+\ldots+(-1)^{n-1}\binom{n}{n-1}+(-1)^{n}\binom{n}{n}=0
$$
We can summarize the result of the previous exercise by saying that the alternating sum of the coefficients of Pascal's triangle is 0.
## Inequalities
This section is an introduction to inequalities, which represent a significant class of exercises in olympiads. It always involves showing that a certain quantity depending on one or more variables is greater than another quantity, when the variables in question take values in a certain set (which can be $\mathbb{R}$, or $\mathbb{R}^{+}$, or something else). Often, it is also necessary to determine the equality cases, that is, the values of the variables for which these two quantities are equal. To prove inequalities, one is allowed to use certain known inequalities.
The simplest and most well-known inequality is the one that states a square is always non-negative:
Proposition 116. For all $x \in \mathbb{R}$, we have $x^{2} \geq 0$. Moreover, equality holds if and only if $x=0$.
Despite its seemingly harmless appearance, this inequality is very useful and allows us to prove many things.
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $x$ and $y$ be two non-zero numbers such that $x^{2} + x y + y^{2} = 0$ ($x$ and $y$ are complex numbers, but that's not too important). Find the value of
$$
\left(\frac{x}{x+y}\right)^{2013} + \left(\frac{y}{x+y}\right)^{2013}
$$
|
Clearly, $x /(x+y)+y /(x+y)=1$ and
$$
\frac{x}{x+y} \cdot \frac{y}{x+y}=\frac{x y}{x^{2}+2 x y+y^{2}}=1
$$
Thus, $x /(x+y)$ and $y /(x+y)$ are the roots of $t^{2}-t+1=0$, so the sums $S_{k}=(x /(x+y))^{k}+(y /(x+y))^{k}$ satisfy $S_{0}=2, S_{1}=1$ and
$$
S_{k+2}=S_{k+1}-S_{k}
$$
for $k \geq 0$. We deduce that the sequence $\left(S_{k}\right)$ is periodic with period 6, its values being successively $2,1,-1,-2,-1,1,2,1,-1, \ldots$. We deduce that $S_{2013}=$ -2.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all real numbers $x, y, z$ such that
$$
x+y+z=3, \quad x^{2}+y^{2}+z^{2}=3, \quad x^{3}+y^{3}+z^{3}=3
$$
Distinction between polynomial and polynomial function Here, we explain why it is necessary to make this distinction, starting by defining a polynomial in another way. Here, $\mathbb{K}=\mathbb{Q}, \mathbb{R}, \mathbb{C}$ or $\mathbb{Z} / p \mathbb{Z}$ equipped with the usual addition and multiplication laws.
Definition. A polynomial with coefficients in $\mathbb{K}$ is an infinite sequence of elements of $\mathbb{K}$ that is zero from a certain rank.
Example. For example, $(0,1,2,3,0,0, \ldots, 0, \ldots)$ is a polynomial, as is $(0,0, \ldots, 0, \ldots)$. However, $(1,1, \ldots, 1, \ldots)$ is not one.
Definition. Let $P=\left(u_{n}\right)_{n}$ and $Q=\left(v_{n}\right)_{n}$ be two polynomials. We define the polynomial $P+Q$ by the sequence $w_{n}=u_{n}+v_{n}$ (which is indeed zero from a certain rank) and the polynomial $P \times Q$ by the sequence $\left(z_{n}\right)$, where $z_{n}=\sum_{i+j=n} u_{n} v_{n}$ (verify that $\left(z_{n}\right)$ is zero from a certain rank). We identify the elements of $\mathbb{K}$ with the constant polynomials via the application that associates to an element $\lambda \in \mathbb{K}$ the polynomial $(\lambda, 0,0, \ldots, 0, \ldots)$. Note that this is consistent with the intuitive notion of multiplying a polynomial by an element of $\mathbb{K}$: if $\left(u_{n}\right)$ is a polynomial and $\lambda \in \mathbb{K}$, then the polynomial $\lambda \times\left(u_{n}\right)$ is the polynomial $\left(\lambda u_{n}\right)$.
We now introduce the indeterminate $X$.
Definition. Let us denote by $X$ the polynomial $(0,1,0,0, \ldots)$.
Proposition. Every polynomial $P$ can be expressed in the form $P=\sum_{i=0}^{n} a_{n} X^{n}$. We denote $P$ or $P(X)$ indifferently to remind that we denote $X$ the indeterminate (we could very well denote it $Y!$ ).
Proof. If $P=\left(a_{0}, a_{1}, a_{2}, \ldots\right)$, let $N$ be an integer such that $i \geq N$ implies $a_{i}=0$. Then $P(X)=a_{0}+a_{1} X+\cdots+a_{N} x^{N}$. This is an immediate consequence of the definition of $X$ and the multiplication between polynomials.
Here is now the link between polynomial and associated polynomial function. Recall that, for now, a polynomial is just a sequence of numbers that is zero from a certain rank and is not seen as an application.
Proposition. Let $P(X)=a_{0}+a_{1} X+\cdots+a_{n} X^{n} \in \mathbb{K}[X]$ be a polynomial. We denote by $\widetilde{P}$ the application defined by $\widetilde{P}(x)=a_{0}+a_{1} x+\cdots+a_{n} x^{n}$ for $x \in \mathbb{K}$, which we call the polynomial function associated with $P$. The application $P \mapsto \widetilde{P}$ is injective if $\mathbb{K}$ is infinite. If $\mathbb{K}$ is finite, this application is not necessarily injective.
Proof. First, consider the case where $\mathbb{K}$ is infinite. Let $P, Q \in \mathbb{K}[X]$ such that $\widetilde{P}=\widetilde{Q}$. Write $P(X)=\sum_{i} a_{i} X^{i}$ and $Q(X)=\sum_{i} b_{i} X^{i}$. Then the polynomial $P(x)-Q(x)$, in the sense of the previous sections, has an infinite number of roots, so it is zero. Therefore, $a_{i}=b_{i}$ for all $i$.
However, in the case where $\mathbb{K}$ is finite, the previous reasoning does not apply. Moreover, let us exhibit a counterexample. Consider $\mathbb{K}=\mathbb{Z} / p \mathbb{Z}$ and $P(X)=X^{p}-X$. According to Fermat's little theorem, for all $x \in \mathbb{K}$, we have $P(x)=0$. Thus, $P$ is not the zero polynomial, but the two associated polynomial functions are the same.
In other words, when $\mathbb{K}$ is infinite (for example, $\mathbb{K}=\mathbb{Q}, \mathbb{R}, \mathbb{C}$, which explains why we did not lose generality in the first sections), we can talk without distinction about a polynomial or the associated polynomial function. However, in other cases, one must be very careful!
Elements of the answer to the exercises
|
We write Newton's relations:
$$
S_{1}-\sigma_{1}=0, \quad S_{2}-\sigma_{1} S_{1}+2 \sigma_{2}=0, \quad S_{3}-\sigma_{1} S_{2}+\sigma_{2} S_{1}-3 \sigma_{3}=0
$$
Thus, $\sigma_{1}=3, \sigma_{2}=3, \sigma_{3}=1$. From this, we deduce that $x, y, z$ are roots of $t^{3}-3 t^{2}+3 t-1=0$. Now, $t^{3}-3 t^{2}+3 t-1=(t-1)^{3}$. Therefore, $x=y=z=1$.
## 2 Thursday afternoon, February 21: Guillaume Conchon-Kerjan
## Exercises
Warning: The present sheet has a purely mathematical interest and is not intended to provide dietary advice.
## Aperitif
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a=\sqrt{4+\sqrt{5-a}}, b=\sqrt{4+\sqrt{5+b}}, c=\sqrt{4-\sqrt{5-c}}$ and $d=\sqrt{4-\sqrt{5+d}}$.
Calculate $a b c d$.
|
Since we are dealing with polynomials, let's honor them by getting rid of those nasty roots. $a, c, -b, -d$ are roots of $X^{4}-8 X^{2}+X+11$. So $a b c d = b d \times(-a) \times(-c)=11$ and we are done... no! To be sure we have the four roots of the polynomial (the product of the opposites of which gives the constant term) without any multiplicity issues, it would be good to show that these four roots are distinct. $a, c$ are positive, $-b, -d$ are negative. If $a=c$, $\sqrt{5-a}=-\sqrt{5-a}=0$. So $a=5$, and from the statement, $a=\sqrt{4}=2$, contradiction. Therefore, $a \neq c, b \neq d$ similarly, and we have the desired result.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
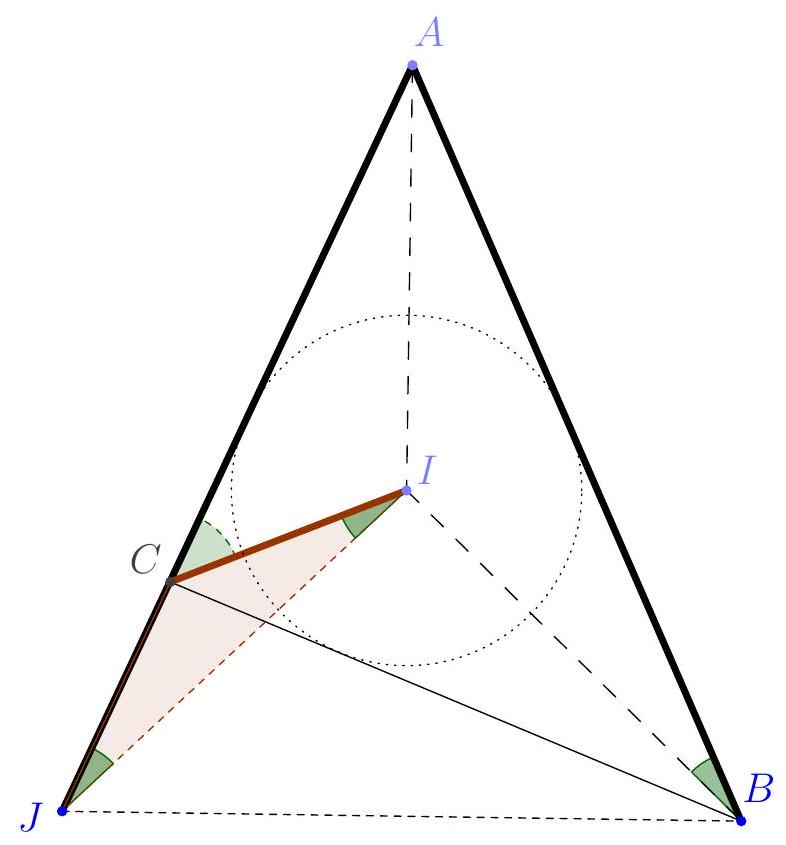
Let $I$ be the center of the circle inscribed in triangle $ABC$. Suppose that: $AB = AC + CI$. Determine the value of the ratio $\frac{\widehat{ACB}}{\widehat{ABC}}$.
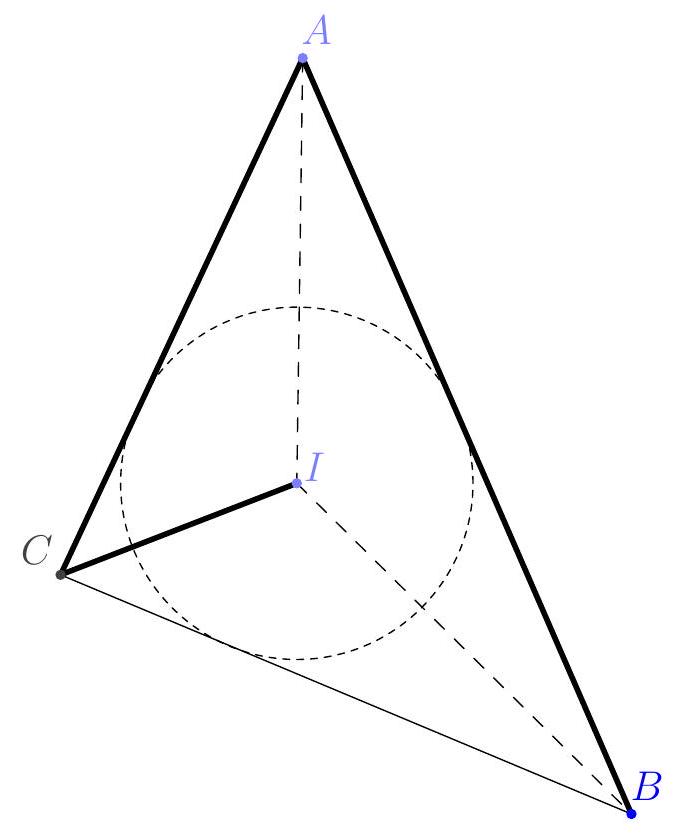
Recall that the bisector of an angle divides it into two equal angles. Points on the bisector are equidistant from the two sides of the angle. It follows that the three bisectors of a triangle $ABC$ intersect at a point generally called $I$, which is equidistant from the three sides of the triangle. This is therefore the center of a circle tangent to the three sides of the triangle, called the "circle inscribed in triangle $ABC$".
|
When two segments are not end-to-end on the same line, we cannot say much about the sum of their lengths. Therefore, to use the hypothesis $A B = A C + C I$, we need to construct a segment $C J$ on the line $(A C)$ such that: $C J = C I$ and $A J = A C + C I$ (so $A$ and $J$ are on opposite sides of $C$). The relation $C J = C I$ implies that the triangle $C J I$ is isosceles, so $\widehat{C J I} = \widehat{C I J}$: let's call this angle $\alpha$. $\widehat{I C A} = \widehat{C J I} + \widehat{C I J} = 2 \alpha$. Since $\widehat{I C A} = \frac{\widehat{B C A}}{2}$ because $(C I)$ is the bisector of $\widehat{B C A}$. Furthermore, the triangles $I J A$ and $I B A$ have an equal angle: $\widehat{I A J} = \widehat{I A B}$ situated between two equal sides, $A I$ and $A J = A B$, so they are congruent (they have all their sides and all their angles equal), hence in particular: $\alpha = \widehat{I J A} = \widehat{I B A} = \widehat{\frac{A B C}{2}}$. Therefore, ultimately: $\widehat{A B C} = 2 \alpha$ while $\widehat{B C A} = 4 \alpha$, hence $\widehat{\widehat{A C A}} = 2$.
## Inscribed Angles
If $B$ and $C$ are two fixed points on a circle, and we vary a third point $A$ on the same circle, the inscribed angle $\widehat{B A C}$ does not depend on the position of point $A$.
There are several ways to state this theorem: if four points $A, B, C, D$ are on the same circle, the angles $\widehat{B A C}$ and $\widehat{B D C}$ are equal if $A$ and $D$ are on the same side of the line $(B C)$, and supplementary if they are on opposite sides of $(B C)$. Conversely, any four points in the plane, $A, B, C, D$, satisfying: $\widehat{B A C} = \widehat{B D C}$ if $A$ and $D$ are on the same side of $(B C)$ or $\widehat{B A C} + \widehat{B D C} = 180^{\circ}$ if $A$ and $D$ are on opposite sides of $(B C)$ are "cyclic," meaning they lie on the same circle. The proof must consider all cases, but the key idea is that if $A$ and $B$ are on a circle with center $O$, the triangle $A O B$ is isosceles. If the line $(A O)$ intersects the circle again at $A'$, since the sum of the three angles of the triangle $A O B$ is $180^{\circ}$, $\widehat{B O A'} = \widehat{B A O} + \widehat{A B O} = 2 \cdot \widehat{B A O}$, from which we deduce that the central angle $\widehat{B O C}$, which does not depend on $A$, is twice the inscribed angle $\widehat{B A C}$.
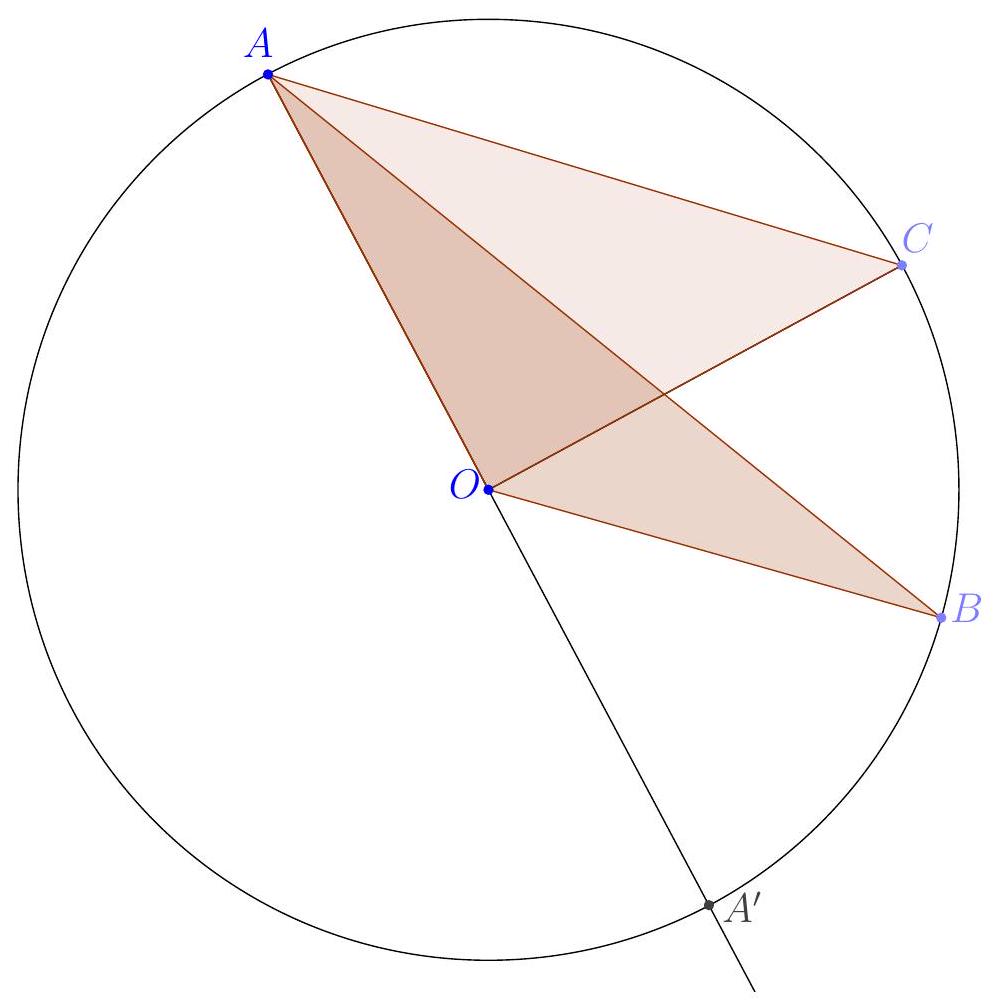
If we want a theorem that does not depend on the cases, we need to introduce angles of lines: the angle $(A B, A C)$ is the oriented angle through which the line $(A B)$ must be rotated to coincide with $(A C)$. Therefore, $(A B, A C) = -(A C, A B)$ and more generally: $(A B, A C) + (A C, A D) = (A B, A D)$ (Chasles' relation) for any points $A, B, C$, and $D$. Using these angles of lines, the inscribed angle theorem can be written: four points $A, B, C, D$ are on the same circle if and only if $(A B, A C) = (D B, D C)$.
An important special case of this theorem: the angle $\widehat{B A C}$ is a right angle if and only if $A$ is located on the circle with diameter $[B C]$ (so the central angle is a straight angle).
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. Determine the units digit of $1789^{1789}$.
.
|
. On a: $1789 \equiv 9(\bmod 10) \Rightarrow 1789^{1789} \equiv 9^{1789}(\bmod 10)$.
Let's look at the powers of 9 modulo 10. We have: $9^{0} \equiv 1(\bmod 10), 9^{1} \equiv 9$ $(\bmod 10), 9^{2} \equiv 1(\bmod 10), 9^{3} \equiv 9(\bmod 10)$, etc. Then for any natural number $k$, $9^{2 k} \equiv 1(\bmod 10)$ (indeed, $9^{2 k}=81^{k}$ and $81 \equiv 1(\bmod 10)$) and $9^{2 k+1} \equiv 9$ $(\bmod 10)$ (indeed, $9^{2 k+1}=9^{2 k} \times 9$ and $9^{2 k} \equiv 1(\bmod 10)$). Since 1789 is odd, we deduce that: $9^{1789} \equiv 9(\bmod 10)$. Thus, the units digit of $1789^{1789}$ is 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. Determine the units digit of $2^{49}$.
.
|
. On a $: 2^{1} \equiv 2(\bmod 10), 2^{2} \equiv 4(\bmod 10), 2^{3} \equiv 8(\bmod 10)$, $2^{4} \equiv 6(\bmod 10)$ and $2^{5} \equiv 2(\bmod 10)$.
We can then prove that $\forall k \in \mathbb{N}^{*}, 2^{4 k} \equiv 6(\bmod 10)$. Let's reason by induction on $k \in \mathbb{N}^{*}$. For $k=1$, we have: $2^{4 k}=2^{4} \equiv 6(\bmod 10)$. Suppose that: $2^{4 k} \equiv 6(\bmod 10)$ for $k \in \mathbb{N}^{*}, 2^{4(k+1)}=2^{4 k} \times 2^{4} \equiv 6(\bmod 10)$, which completes the induction. It follows that $\forall k \in \mathbb{N}, 2^{4 k+1} \equiv 2(\bmod 10)$ (indeed, for $k=0,2^{1} \equiv 2(\bmod 10)$ and for $k \in \mathbb{N}^{*}, 2^{4 k+1}=2^{4 k} \times 2$ and for $k \in \mathbb{N}^{*}$, $\left.2^{4 k} \equiv 6(\bmod 10)\right), 2^{4 k+2} \equiv 4(\bmod 10)$ and $2^{4 k+3} \equiv 8(\bmod 10)$. Perform the Euclidean division of 49 by 4. We have: $49=4 \times 12+1=4 k+1$ with $k=12$. Thus, $2^{49} \equiv 2(\bmod 10)$. Therefore, the units digit of $2^{49}$ is 2.
We could have reasoned more simply by writing that $2^{49}=2^{10} \times 2^{10} \times 2^{10} \times$ $2^{10} \times 2^{9}$. Since $2^{10}=\left(2^{5}\right)^{2}$ and $2^{5} \equiv 2(\bmod 10)$, we have: $2^{10} \equiv 4(\bmod 10)$. Furthermore, $2^{4} \equiv 6(\bmod 10)$, so $2^{9} \equiv 2(\bmod 10)\left(\right.$ by writing that $\left.2^{9}=\left(2^{4}\right)^{2} \times 2\right)$. Thus,
$2^{10} \times 2^{10} \equiv 6(\bmod 10)$ and $2^{10} \times 2^{10} \times 2^{10} \times 2^{10} \times 2^{9} \equiv 2(\bmod 10)$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $f$ be the function that associates with a positive integer the sum of its digits when it is written in base 10. For example, $f(537)=15$. Calculate $f\left(f\left(f\left(4444^{4444}\right)\right)\right)$.
|
Let $n \in \mathbb{N}$. We notice that $f(n) \equiv n[9]$. With $n=4444^{4444}$ and using an easy induction, we get $f(f(f(n))) \equiv 4444^{4444} \equiv 7^{4444}[9]$. Since $7^{3} \equiv 1[9]$, we have $7^{4444} \equiv\left(7^{3}\right)^{1481} \times 7 \equiv 1^{1481} \times 7 \equiv 7[9]$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine the gcd of all numbers of the form
$$
(a-b)(b-c)(c-d)(d-a)(b-d)(a-c)
$$
where $a, b, c, d$ range over $\mathbb{Z}$.
|
If we calculate the product in question for $a=0, b=1, c=2, d=3$, we find -12, so the gcd in question must divide $12=3 \times 4$.
Conversely, we will show that this gcd is 12, by showing that all numbers of this form are divisible by 3 and by 4.
An integer $n$ divides the difference between two of the integers among $a, b, c, d$ if these integers have the same remainder in the Euclidean division by $n$. Since there are only 3 possible remainders modulo 3, there must be two integers among $a, b, c, d$ that have the same remainder. All the products considered in the statement are therefore divisible by 3.
Now let's look at the remainders modulo 4: there are then two cases to consider. If there exist two integers among $a, b, c, d$ that have the same remainder in the Euclidean division by 4, the difference between these two integers will be divisible by 4. If $a, b, c, d$ all have different remainders modulo 4, this means that the 4 possible remainders in the Euclidean division by 4 are represented. Thus, there are among $a, b, c, d$ two even integers and two odd integers. The difference between two integers of the same parity being even, we have shown that in this case too all the products considered are divisible by $2 \times 2=4$.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. Let $\left(u_{n}\right)_{n \in \mathbb{N}^{*}}$ be the sequence such that $: \forall n \in \mathbb{N}^{*}, u_{n}=\frac{2 n+\cos (n)}{n \sin \left(\frac{1}{n}\right)+\sqrt{(n+1)(n+2)}}$.
Determine the limit of the sequence $\left(u_{n}\right)_{n \in \mathbb{N}^{*}}$.
|
. We write: $\forall n \in \mathbb{N}^{*}, u_{n}=\frac{2+\frac{\cos (n)}{n}}{\sin \left(\frac{1}{n}\right)+\sqrt{\left(1+\frac{1}{n}\right)\left(1+\frac{2}{n}\right)}}$.
Since we have: $\lim _{n \rightarrow+\infty} \frac{\cos (n)}{n}=0, \lim _{n \rightarrow+\infty} \sin \left(\frac{1}{n}\right)=0$ and $\lim _{n \rightarrow+\infty} \sqrt{\left(1+\frac{1}{n}\right)\left(1+\frac{2}{n}\right)}=1$, we deduce that the sequence $\left(u_{n}\right)$ converges to 2.
Definition 6. Given a sequence $\left(u_{n}\right)$, we call the supremum and infimum of $\left(u_{n}\right)$ the quantities, if they exist: $\sup \left\{u_{n}, n \in \mathbb{N}\right\}$ and $\inf \left\{u_{n}, n \in \mathbb{N}\right\}$. The supremum, if it exists, of the set $\left\{u_{n}, n \in \mathbb{N}\right\}$ is the smallest of the upper bounds of this set, and its infimum, if it exists, is the largest of the lower bounds of this set.
Remark. Every non-empty and bounded above (resp. bounded below) subset of $\mathbb{R}$ has a finite supremum (resp. a finite infimum).
Theorem 2.
1. Every increasing and bounded above sequence converges to its supremum.
2. Every increasing and unbounded above sequence tends to $+\infty$.
3. Every decreasing and bounded below sequence converges to its infimum.
4. Every decreasing and unbounded below sequence tends to $-\infty$.
## Proof.
1. Let $\left(u_{n}\right)$ be an increasing and bounded above sequence.
The set $\left\{u_{n}, n \in \mathbb{N}\right\} \subset \mathbb{R}$ is bounded above, so it has a finite supremum, which we denote by $\ell$. Since $\ell$ is the smallest of the upper bounds of the sequence $\left(u_{n}\right)$, for all $\varepsilon>0, \ell-\varepsilon$ is not an upper bound of the sequence $\left(u_{n}\right)$, so there exists $N_{\varepsilon} \in \mathbb{N}$ such that: $u_{N_{\varepsilon}}>\ell-\varepsilon$. Furthermore, the sequence $\left(u_{n}\right)$ is increasing, so $\forall n \geq N_{\varepsilon}, u_{n} \geq u_{N_{\varepsilon}}$. We finally have, $\forall \varepsilon>0, \exists N_{\varepsilon} \in \mathbb{N}, \forall n \geq N_{\varepsilon}, \ell-\varepsilon < u_{n} \leq \ell$.
The sequence $\left(v_{n}\right)$ is increasing, so $\forall n \geq n_{0}, v_{n} \geq v_{n_{0}}$ and thus $\forall n \geq n_{0}, v_{n}>A$. This proves that the sequence $\left(v_{n}\right)$ tends to $+\infty$. Points 3 and 4 are proven by applying points 1 and 2 and are left as exercises.
Definition 7. Let $\left(u_{n}\right)$ and $\left(v_{n}\right)$ be two real sequences. We say that the sequences $\left(u_{n}\right)$ and $\left(v_{n}\right)$ are adjacent if:
1. $\left(u_{n}\right)$ is increasing.
2. $\left(v_{n}\right)$ is decreasing.
3. $\lim _{n \rightarrow+\infty}\left(v_{n}-u_{n}\right)=0$.
Property 2. Two adjacent sequences converge to the same limit.
Proof. $\left(u_{n}\right)$ is increasing and $\left(v_{n}\right)$ is decreasing, so the sequence $\left(v_{n}-u_{n}\right)$ is decreasing. Furthermore, the sequence $\left(v_{n}-u_{n}\right)$ converges to 0, so $\forall n \in \mathbb{N}$, $v_{n}-u_{n} \geq 0$. Therefore, we have: $u_{0} \leq u_{n} \leq v_{n} \leq v_{0}$.
The sequence $\left(u_{n}\right)$ is increasing and bounded above by $v_{0}$, so it converges, and the sequence $\left(v_{n}\right)$ is decreasing and bounded below by $u_{0}$, so it converges. Since $\lim _{n \rightarrow+\infty}\left(v_{n}-u_{n}\right)=0$, we have: $\lim _{n \rightarrow+\infty} u_{n}=\lim _{n \rightarrow+\infty} v_{n}$.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. Let $\left(u_{n}\right)$ be the sequence defined on $\mathbb{N}$ by $: \forall n \in \mathbb{N}, u_{n}=\frac{n+(-1)^{n}}{n+2}$.
Show that the sequence $\left(u_{n}\right)$ converges and determine its limit.
|
. On has: $\forall n \in \mathbb{N},-1 \leq(-1)^{n} \leq 1$ thus $\forall n \in \mathbb{N}, \frac{n-1}{n+2} \leq$ $u_{n} \leq \frac{n+1}{n+2}$, hence, by the squeeze theorem, we deduce that the sequence $\left(u_{n}\right)$ tends to 1.
Theorem 4. Let $\left(u_{n}\right)$ and $\left(v_{n}\right)$ be two sequences of real numbers such that: $\forall n \in \mathbb{N}, u_{n} \leq v_{n}$.
1. If $\lim _{n \rightarrow+\infty} u_{n}=+\infty$ then $\lim _{n \rightarrow+\infty} v_{n}=+\infty$.
2. If $\lim _{n \rightarrow+\infty} v_{n}=-\infty$ then $\lim _{n \rightarrow+\infty} u_{n}=-\infty$.
The proof of this theorem is almost immediate, so it is left as an exercise.
III) Training exercises.
|
1
|
Calculus
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
. Consider the sequence $\left(u_{n}\right)$ defined by $u_{0}=3$ and for all $n \in \mathbb{N}^{*}$, $u_{n}=\frac{u_{n-1}+2 n^{2}-2}{n^{2}}$
Show that the sequence $\left(u_{n}\right)$ converges to 2.
|
. The trick in this kind of exercise (very open!) is to calculate the first terms of the sequence $\left(u_{n}\right)$ to conjecture its direction of variation. Then, according to the conjectured direction of variation, we can try to bound the sequence $\left(u_{n}\right)$ from below or above! We start by showing by induction that $\forall n \in \mathbb{N}$, $u_{n} \geq 2$.
For $n=0$, it is clear! Suppose that at rank $n \in \mathbb{N}$, we have: $u_{n} \geq 2$. Then: $u_{n}-2 \geq 0 \Rightarrow u_{n}+2(n+1)^{2}-2 \geq 2(n+1)^{2} \Rightarrow u_{n+1} \geq 2$, which completes the induction. Next, we show that the sequence $\left(u_{n}\right)$ is decreasing on $\mathbb{N}$, indeed: we have $\forall n \in \mathbb{N}^{*}, u_{n}-u_{n-1}=\frac{\left(n^{2}-1\right)\left(2-u_{n-1}\right)}{n^{2}} \leq 0$. Thus, the sequence $\left(u_{n}\right)$ is decreasing and bounded below, so it converges. Finally, since $\left(u_{n}\right)$ is decreasing on $\mathbb{N}$ and $u_{0}=3$, we have: $\forall n \in \mathbb{N}^{*}, u_{n-1} \leq 3 \Rightarrow u_{n} \leq \frac{1+2 n^{2}}{n^{2}}$. We finally have: $2 \leq u_{n} \leq \frac{1}{n^{2}}+2$ and using the squeeze theorem, we conclude that the sequence $\left(u_{n}\right)$ converges to 2.
|
2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
. Let $\left(u_{n}\right)$ be the sequence defined recursively by $u_{0}=1$ and $\forall n \in \mathbb{N}$, $u_{n+1}=\frac{u_{n}}{u_{n}^{2}+1}$.
Show that the sequence $\left(u_{n}\right)$ converges and determine its limit.
|
. After calculating $u_{1}$ and $u_{2}$, we conjecture that the sequence $\left(u_{n}\right)$ is decreasing and that it is bounded below by 0.
Showing that $\left(u_{n}\right)$ is bounded below by 0 is an immediate induction. To show that $\left(u_{n}\right)$ is decreasing, we calculate: $\forall n \in \mathbb{N}, u_{n+1}-u_{n}=\frac{-u_{n}^{2}+u_{n}-1}{u_{n}^{2}+1}$. We notice that the quadratic: $-x^{2}+x-1$ is strictly negative for all real $x$ because its discriminant is strictly negative and the coefficient of $x^2$ is strictly negative. Thus, we have: $\forall n \in \mathbb{N}, u_{n+1}-u_{n}<0$ so the sequence $\left(u_{n}\right)$ is decreasing on $\mathbb{N}$ (and even strictly decreasing on $\mathbb{N}$!). The sequence $\left(u_{n}\right)$ is decreasing and bounded below, so it converges to a real number $\ell$.
To find $\ell$, we can notice that: $\forall n \in \mathbb{N}, u_{n+1}=f\left(u_{n}\right)$ where $f$ is the function defined on $\mathbb{R}$ by: $f(x)=\frac{x}{x^{2}+1}$. This function is a rational function whose denominator does not vanish on $\mathbb{R}$, so it is continuous on $\mathbb{R}$. We can then apply the property from Exercise 11 and we deduce that $\ell$ is a fixed point of $f$ i.e.: $f(\ell)=\ell$. We have: $f(\ell)=\ell \Leftrightarrow \frac{\ell}{\ell^{2}+1}=\ell \Leftrightarrow \ell=\ell\left(\ell^{2}+1\right)$ (these logical equivalences make sense because $\ell^{2}+1 \neq 0$). We finally obtain: $f(\ell)=\ell \Leftrightarrow \ell^{3}=0 \Leftrightarrow \ell=0$.
Conclusion: the sequence $\left(u_{n}\right)$ converges to 0.
## 2 Wednesday, 27th afternoon: combinatorics, Joon Kwon
## Combinatorial exercises
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Let $F=\left\{(x, y, z) \in \mathbb{R}^{3}: x+y+z=0\right\}$ be a subspace of $\mathbb{R}^{3}$. Determine a basis of $F$ and then the dimension of $F$.
|
. We write: $F=\left\{(x, y, z) \in \mathbb{R}^{3}: x=-y-z, y=y, z=z\right\}=$ $\{(-y-z, y, z), y, z \in \mathbb{R}\}=\{(-y, y, 0)+(-z, 0, z), y, z \in \mathbb{R}\}=\operatorname{Vect}\{(-1,1,0),(-1,0,1)\}$. This writing allows us to deduce that the family $\{(-1,1,0),(-1,0,1)\}$ is a generating set of $F$. We also notice that this family is linearly independent. Thus, it is a basis of $F$. Since it contains 2 elements, we conclude that $F$ is of dimension 2 (it is then a vector plane).
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
We consider the sequence $u_{n}$ as follows: $u_{0}=2010^{2010}$, and $u_{n+1}=u_{n}+7$ if $u_{n}$ is odd, and $\frac{u_{n}}{2}$ if it is even. What is the smallest integer that this sequence will reach?
|
First, it is evident that the $u_{n}$ are always strictly positive. Next, let's look at the possible minima: if $u_{n}$ is even, then $u_{n+1}=\frac{u_{n}}{2}$ is strictly less than $u_{n}$. If $u_{n}$ is odd and greater than 7, then $u_{n+2}=\frac{u_{n}+7}{2}$ is strictly less than $u_{n}$. It remains to consider 1, 3, 5, and 7.
- if $u_{n}=7$, then the subsequent terms are $14,7,14,7, \ldots$ and the sequence loops
- if $u_{n}=1$, then the subsequent terms are $8,4,2,1,8,4, \ldots$
- if $u_{n}=3$, then the subsequent terms are $10,5,12,6,3,10, \ldots$, the same for $u_{n}=5$
Therefore, there are three possible minima: 1, 3, or 7. It is easy to verify that $7 \mid u_{n+1}$ if and only if $7 \mid u_{n}$. Since $2010^{2010}$ is not divisible by 7, the sequence never passes through 7. We try to use the same idea to separate the last two cases: we separate the residues modulo 7 into $A=\{1,2,4\}$ and $B=\{3,5,6\}$. I leave it to you to verify that $u_{n+1} \in A$ if and only if $u_{n} \in A \bmod 7$, and similarly for $B$. It remains to determine which of the two $2010^{2010}$ belongs to. The integer 2010 is divisible by 6, so by Fermat's Little Theorem, $2010^{2010} \equiv 1 \pmod{7}$, and the minimum value of the sequence is 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all positive integers $n$ such that $2^{n}+3$ is a perfect square. The same question with $2^{n}+1$.
|
For $n=0,2^{n}+3=2^{2}$ is a perfect square. We verify that $n=1$ is not a solution. Therefore, we can assume $n \geq 2$ and $2^{n}+3 \equiv 3 \pmod{4}$, but a square is congruent to 0 or 1 modulo 4, so for $n \geq 2, 2^{n}+3$ is not a perfect square.
Suppose that $2^{n}+1=x^{2}$. Then $(x-1)(x+1)=2^{n}$. Therefore, $x-1=2^{k}$ and $x+1=2^{n-k}$. Hence, $2^{k}+1=2^{n-k}-1$. Therefore, $2=2^{n-k}-2^{k}$, so $2^{k}$ divides 2, thus $k=0$ or $k=1$. We then get $x=2$ or $x=3$, which gives $(n, x)=(3,3)$ as the only solution.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the minimum of the function
$$
f(x)=\frac{\cos (x)^{3}}{\sin (x)}+\frac{\sin (x)^{3}}{\cos (x)}
$$
on $] 0, \pi / 2[$.
Theorem 1.70 (Tchebycheff's Inequality). With the same notations as before, if the $a_{i}$ and the $b_{i}$ are arranged in the same order, then
$$
\sum a_{i} b_{i} \geq \frac{1}{n}\left(\sum a_{i}\right)\left(\sum b_{i}\right)
$$
Proof. We use the rearrangement inequality to find the following $n$ relations
$$
\begin{aligned}
a_{1} b_{1}+a_{2} b_{2}+\cdots+a_{n} b_{n} & \geq a_{1} b_{1}+a_{2} b_{2}+\cdots+a_{n} b_{n} \\
a_{1} b_{1}+a_{2} b_{2}+\cdots+a_{n} b_{n} & \geq a_{1} b_{2}+a_{2} b_{3}+\cdots+a_{n} b_{1} \\
a_{1} b_{1}+a_{2} b_{2}+\cdots+a_{n} b_{n} & \geq a_{1} b_{3}+a_{2} b_{4}+\cdots+a_{n} b_{2} \\
\cdots & \cdots \\
a_{1} b_{1}+a_{2} b_{2}+\cdots+a_{n} b_{n} & \geq a_{1} b_{n}+a_{2} b_{1}+\cdots+a_{n} b_{n-1}
\end{aligned}
$$
And by adding these relations we obtain the desired inequality.
|
Let's use this exercise to recall how to determine the minimum of a function $f$ is $m$. This involves two steps: first, show that $f(x) \geq m$ for all $x$, and then find an $x_{0}$ where this minimum is achieved. Consider the function of interest,
$f(x)=\frac{\cos \left(x^{3}\right)}{\sin (x)}+\frac{\sin (x)^{3}}{\cos (x)}$. It is easy to see that the sequences $\left(\cos (x)^{3}, \sin (x)^{3}\right)$ and $(1 / \sin (x), 1 / \cos (x))$ are in the same order. The rearrangement inequality gives
$$
\begin{aligned}
\frac{\cos (x)^{3}}{\sin (x)}+\frac{\sin (x)^{3}}{\cos (x)} \geq f(x) & \geq \frac{\cos (x)^{3}}{\cos (x)}+\frac{\sin (x)^{3}}{\sin (x)} \\
& =\cos (x)^{2}+\sin (x)^{2}=1
\end{aligned}
$$
For the last step, we just note that $f(\pi / 4)=1$, which completes the proof.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $a, b, c, d$ be such that $a b c d=1$. Show that
$$
a^{2}+b^{2}+c^{2}+d^{2}+a b+a c+a d+b c+b d+c d \geq 10
$$
|
We use the arithmetic-geometric inequality:
$$
a^{2}+b^{2}+c^{2}+d^{2}+a b+a c+a d+b c+b d+c d \geq 10 \sqrt[10]{a^{5} b^{5} c^{5} d^{5}}=10
$$
|
10
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
How many Friday the 13ths can there be in a year (non-leap year)?
|
In the days of the year, the 13th of each month occupies the ranks: 13, 44, $72, 103, 133, 164, 194, 225, 256, 286, 317, 347$. To determine which day of the week each day corresponds to, it is sufficient to take these values modulo $7: 6,2,2,5,0,3,5,1,4,6,2,4$. If day 1 of the year (January 1st) is a Friday, then there will only be one Friday the 13th in August. If day 4 is a Friday, there will be 2 Friday the 13ths, in September and December. If day 2 is a Friday, there will be 3 Friday the 13ths. On the other hand, it is noted that it is impossible for there to be no Friday the 13th or more than 3.
Solution to the exercise \& Let's look at the equation modulo 4. If $x$ and $y$ are odd, then we would have $1+1=z^{2}(\bmod 4)$, which is impossible because a square cannot be congruent to 2 modulo 4.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A triangle has side lengths: 3, 4, 5. Calculate the radius of the inscribed circle (the circle inside the triangle and tangent to all three sides of the triangle).
|
Let's call $A, B, C$ the vertices of the triangle, $a=BC, b=CA, c=AB$ the lengths of the three sides, $I$ and $r$ the center and the radius of the inscribed circle. The heights from $I$ to the triangles $IAB, IBC$, and $ICA$ are all equal to $r$, so the areas of these three triangles are: area $(IAB)=\frac{rc}{2}$, area $(IBC)=\frac{ra}{2}$, area $(ICA)=\frac{rb}{2}$, from which we deduce: $\operatorname{area}(ABC)=\frac{r(a+b+c)}{2}$. The triangle with sides $3,4,5$ is a right triangle, its area is: $\frac{3 \times 4}{2}=6=\frac{r(3+4+5)}{2}$. It follows that $r=1$.
The given triangle, with sides $3,4,5$, being a right triangle, we can also reason as follows. Let $D, E, F$ be the projections of $I$ onto the sides $BC, CA, AB$. These are the points of contact of the inscribed circle with the sides of the triangle. If $A$ is the vertex of the right angle, $AEIF$ is a square, and $r=IE=IF=AE=AF$. Now, $AE$ and $AF$ are easy to calculate: if we set $u=AE=AF, v=BF=BD$, $w=CD=CE, u+v=c, v+w=a, w+u=b$, then by adding: $2(u+v+w)=a+b+c$ or finally $u=\frac{-a+b+c}{2}, v=\frac{a-b+c}{2}, w=\frac{a+b-c}{2}$. We deduce: $r=u=\frac{-5+4+3}{2}=1$.
The two methods are very different, but the results are the same. Indeed, $\frac{r(a+b+c)}{2}=\left(\frac{-a+b+c}{2}\right)\left(\frac{a+b+c}{2}\right)=\frac{-a^{2}+(b+c)^{2}}{4}=\frac{bc}{2}=$ area $(ABC)$ because the square of the hypotenuse $a^{2}=b^{2}+c^{2}$.
Let's call $M$ and $N$ the midpoints of $[AB]$ and $[CD]$. Suppose first that $(AD)$ and $(BC)$ intersect at a point $S$, and consider the line $(SM)$, which intersects $(CD)$ at $P$. Using Thales' theorem and the fact that $MA=MB$, we have: $\frac{PD}{PS}=\frac{MA}{MS}=\frac{MB}{MS}=\frac{PC}{PS}$, which implies: $PC=PD$. Therefore, $P$ is the midpoint $N$ of $[CD]$, and the line $(SM)$ is none other than $\Delta: \Delta, (AD)$ and $(BC)$ are indeed concurrent at $S$.
Now suppose that $(AD)$ and $(BC)$ are parallel, and draw the line parallel to $(AD)$ and $(BC)$ passing through $M$. Let $P$ be the intersection of this parallel with $(CD)$. $DPM A$ and $CPMB$ are parallelograms, so $DP=MA=MB=CP$. Once again, $P$ is the midpoint of $[CD]$, so $(MP)$, parallel to $(AD)$ and $(BC)$, is none other than $(MN)=\Delta$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(JBMO 1998 - Problem 2), discussed in class
Let $A B C D E$ be a convex pentagon such that $A B=A E=C D=B C+D E=1$ and $\widehat{A B C}=\widehat{D E A}=90^{\circ}$. Calculate the area of $A B C D E$.
|
Let $P$ be the point on the ray $[D E)$ such that $D P=1$. Since $\widehat{A E P}=\widehat{A B C}=$ $90^{\circ}$, $A B=A E=1$ and $B C=1-D E=E P$, the triangles $A E P$ and $A B C$ are directly isometric. It follows that $A P=A C$ and that the polygons $A B C D E$ and $A C D P$ have the same area.
Furthermore, since $A P=A C$ and $C D=D P=1$, the line $(A D)$ is the axis of symmetry of $A C D P$, so the area of $A C D P$ is 2 times the area of the triangle $A D P$. Finally, the triangle $A D P$ has base $P D=1$ and height $A E=1$, so its area is $\frac{1}{2}$, and thus the area of $A C D P$ and $A B C D E$ is 1.

|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A permutation of $\{1,2, \ldots, n\}$ is drawn at random. What is the average number of fixed points
|
Let $X$ be the set of pairs $(x, \sigma)$ where $x$ is a fixed point of the permutation $\sigma$. For every $x$, there are $(n-1)!$ permutations that fix $x$, so $|X|=n \times(n-1)!=n!$
On the other hand, we have $|X|=\sum_{\sigma}|Fix(\sigma)|$, so the average number of fixed points is equal to 1.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How many parallelograms can be placed at most in a regular hexagon with a side length of 3?
|
Let's call \( s \) the area of an equilateral triangle with side 1. The regular hexagon can be divided into 6 equilateral triangles with sides 3, thus each having an area of \( 9s \): its total area is \( 54s \). Now, each parallelogram has an area of \( 4s \): since \( \frac{54s}{4s} > 13 \), we should be able to place 13 of them. However, this is not possible: it suffices to color the hexagon with 12 black triangles and 42 white triangles such that any parallelogram, regardless of the four cells it occupies, will necessarily cover one and only one black triangle. Therefore, we can place a maximum of 12 parallelograms, but we still need to prove that it is indeed possible to place 12, which is relatively easy (by not covering the central white hexagon at all, for example).

|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let ABC be a triangle with side lengths 3, 4, 5. Calculate the radius of the inscribed circle.
|
If you didn't already know, by drawing the $3,4,5$ triangle you will realize that it is a right triangle:
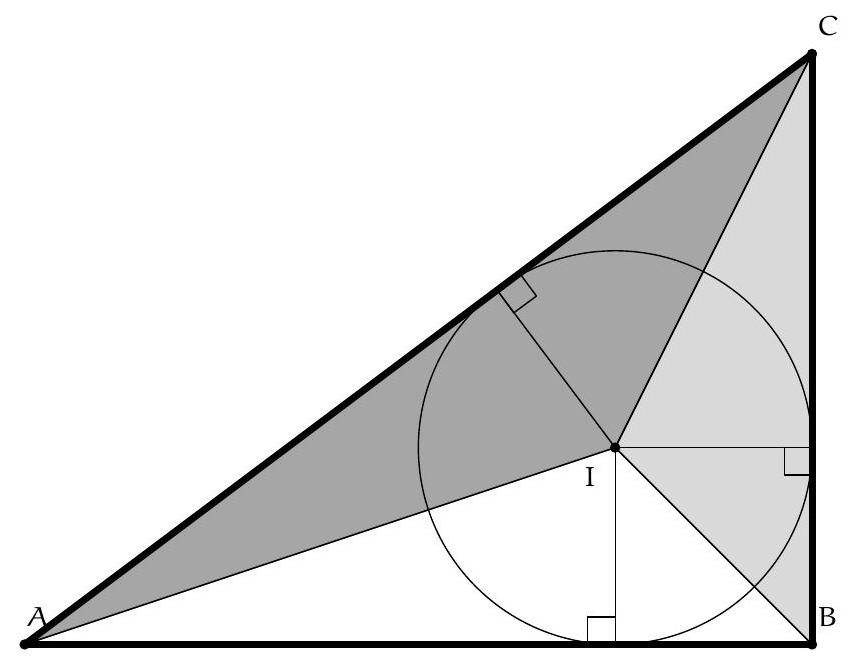
To calculate the radius $r$ of the inscribed circle, we will calculate the area $\mathcal{A}$ of the triangle in two different ways. First, $\mathcal{A}=\frac{3 \times 4}{2}=6$. Then, if we calculate the areas of the three differently colored triangles separately, we get:
$$
\mathcal{A}=\frac{5 \times \mathrm{r}}{2}+\frac{4 \times \mathrm{r}}{2}+\frac{3 \times \mathrm{r}}{2}=6 \mathrm{r}
$$
From this, we deduce that $r=1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $0 \leqslant a, b, c \leqslant 1$. Show that $\frac{a}{b c+1}+\frac{b}{a c+1}+\frac{c}{a b+1} \leqslant 2$.
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly.
|
The function $f(a, b, c)$ on the left-hand side is convex in each variable, so it reaches its maximum at one of the 8 points $\left(\epsilon_{1}, \epsilon_{2}, \epsilon_{3}\right)$ with $\epsilon_{i} \in\{0,1\}$ (indeed, we use the fact that if a function $g:[u, v] \rightarrow \mathbb{R}$ is convex, then $g$ reaches its maximum at $u$ or $v$). We verify that the maximum corresponds to ( $1,1,0$ ) and is 2.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $0 \leqslant a, b, c \leqslant 1$. Show that $\frac{a}{b+c+1}+\frac{b}{a+c+1}+\frac{c}{a+b+1}+(1-a)(1-b)(1-c) \leqslant 1$.
|
The function $f(a, b, c)$ on the left-hand side is convex in each variable, so it attains its maximum at one of the 8 points $\left(\epsilon_{1}, \epsilon_{2}, \epsilon_{3}\right)$ with $\epsilon_{i} \in\{0,1\}$. We verify that the maximum is 1.
|
1
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
We write the numbers $1,2,3, \ldots, 100000$ on a sheet of paper, then replace each number by the sum of its digits, and so on, until each number consists of only one digit. What is the most frequent digit in the resulting list?
## - Counting and Inclusion-Exclusion -
PRINCIPLE OF INCLUSION-EXCLUSION - We denote by $|A|$ the number of objects in a set $A$. If $A, B, C$ are sets, then we have:
$$
\begin{gathered}
|A \cup B|=|A|+|B|-|A \cap B| \\
|A \cup B \cup C|=|A|+|B|+|C|-|A \cap B|-|A \cap C|-|B \cap C|+|A \cap B \cap C|
\end{gathered}
$$
To prove these formulas, the simplest way is to draw potatoes!
|
Here, it is noted that for any integer $n$, the sum of the digits of $n$ is congruent to $n$ modulo 9. The resulting sequence is therefore periodic: $1,2,3,4,5,6,7,8,9,1,2,3,4, \ldots$ and it ends with a 1, so it is the one that appears most often.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
How many pairs $n$, $m$ exist such that $n \wedge m=50$ and $n \vee m=75$?
And such that $n \wedge m=50$ and $n \vee m=600$?
|
For the first one, the answer is 0! Indeed, a bit of reflection shows that we must always have $n \wedge m \mid n \vee m$, but $50 \nmid 75$.
For the second, we start by decomposing into prime factors: $50=2 \times 5^{2}$ and $600=2^{3} \times 3 \times 5^{2}$. We also know that if $n$, $m$ are solutions, then $n m=50 \times 600=2^{4} \times 3 \times 5^{4}$. Finally, $50 \mid n$ and $50 \mid m$.
In conclusion, the solutions will be exactly of the form $m=50 \times 2^{a} \times 3^{b}$ and $\mathfrak{n}=50 \times 2^{2-a} \times 3^{1-b}$, with $0 \leqslant a \leqslant 2$ and $0 \leqslant b \leqslant 1$. In conclusion, we have 3 choices for $a$ and 2 for $b$, making a total of 6 pairs of solutions.
We conclude this section with a fundamental result due to Gauss, hence its name.
Gauss's Lemma: Let three integers $a$, $b$, and $c$ be such that $a \mid b \times c$. If $a \wedge b=1$, then $a \mid c$.
With what we have seen previously, this result is quite intuitive. The hypothesis $a \mid b \times c$ can be translated as the fact that we find all the elements of the prime factorization of $a$ in the product $b \times c$. But since $a \wedge b=1$, none of these elements appear in the decomposition of $b$. They must therefore all come from $c$, hence the conclusion.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine the gcd of all numbers of the form
$$
(a-b)(b-c)(c-d)(d-a)(a-c)(b-d)
$$
where $a, b, c, d$ are integers.
|
We will show that the gcd sought is 12. Indeed, by the pigeonhole principle, among $a, b, c, d$ there are two numbers congruent modulo 3, and thus their difference is divisible by 3. Now if we look modulo 4, there are two possibilities: either there are two numbers among $a, b, c, d$ congruent modulo 4, and at that moment their difference is divisible by 4, or $a, b, c, d$ are distinct modulo 4. But in the latter case, two of them are even and two are odd, so the product of interest has two even factors. Thus, in all cases, this product is divisible by 3 and by 4, hence by 12.
On the other hand, taking $a=0, b=1, c=2, d=3$, the product obtained is -12, so the divisor we have found is indeed the gcd.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find an integer $x$ such that $x \equiv 2(\bmod 3), x \equiv 3(\bmod 4)$ and $x \equiv 1(\bmod 5)$.
|
First, the Chinese Remainder Theorem indicates that such an $x$ does indeed exist, as 3, 4, and 5 are pairwise coprime. Furthermore, it also indicates that there exists a unique natural number $a < 3 \times 4 \times 5 = 60$ such that $x \equiv 2(\bmod 3)$, $x \equiv 3(\bmod 4)$, and $x \equiv 1(\bmod 5)$ if and only if $x \equiv a(\bmod 60)$.
Let us then find such an integer $a$. We know that $a \equiv 2(\bmod 3)$ and that $a \equiv 3(\bmod 4)$. Therefore, we can write $a = 3k + 2$. It is then required that $k$ satisfy the equation $3k + 2 \equiv 3(\bmod 4)$, or equivalently $3k \equiv 1(\bmod 4)$.
Since 3 is invertible modulo 4 and its inverse is 3, this means that $k \equiv 3(\bmod 4)$. We can thus write $k = 4l + 3$, and therefore $a = 12l + 11$.
We then want $l$ to satisfy the equation $12l + 11 \equiv 1(\bmod 5)$, or equivalently $12l \equiv 0(\bmod 5)$. Since 12 is invertible modulo 5, it follows that $l \equiv 0(\bmod 5)$. We can thus write $l = 5m$ and $a = 60m + 11$.
We have thus shown that $a = 11$. In particular, it follows that $x = 11$ satisfies simultaneously the three equations $x \equiv 2(\bmod 3)$, $x \equiv 3(\bmod 4)$, and $x \equiv 1(\bmod 5)$.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine the number of ten-thousands in $A=5^{5^{5^{5^{5}}}}$.
Determine the number of ten-thousands in $A=5^{5^{5^{5^{5}}}}$.
|
We are going to determine the remainder of the Euclidean division of A by $10000=$ $2^{5} \times 5^{5}$. We start by dividing by $2^{5}$. Since $\varphi\left(2^{5}\right)=16$, it suffices to determine the remainder of the Euclidean division of $5^{5^{5^{5}}}$ by 16 and finally, since $\varphi(16)=8$, it is necessary to determine the remainder of $5^{5^{5}}$ by 8. And finally $5^{5}$ by 4, which is 1.
So we go back up: $5^{5^{5}} \equiv 5[8], 5^{5^{5^{5}}} \equiv 5^{5} \equiv 13[16]$. And finally, $A \equiv 5^{13} \equiv 5^{5}\left[2^{5}\right]$.
Phew, it turns out that we don't have to redo all the work for $5^{5}$, we immediately have $A \equiv 5^{5}=3125[10000]$. Thus, the ten-thousands digit of A is 0.
Let's return to our pair $(a, n)$ with $a \wedge n=1$. A pertinent question now is to determine for which integers $k \in \mathbb{N}$ we have $a^{k} \wedge 1[n]$. The solution uses the notion of the order of $a$.
The order of $a$ modulo $n$ is the smallest integer $k_{0}$ such that $a^{k_{0}} \wedge 1[n]$. The set of integers $k$ such that $a^{k} \wedge 1[n]$ is exactly the set of multiples of $k_{0}$. Finally, it follows from Euler's theorem that $k_{0} \mid \varphi(n)$.
Indeed, if $k$ satisfies $a^{k} \wedge 1[n]$, we perform the Euclidean division of $k$ by $k_{0}: k=l k_{0}+r$ and we find that
$$
a^{k} \equiv a^{l k_{0}+r} \equiv a^{r} \equiv 1[n]
$$
Thus, by the minimality of $k_{0}$, we must have $r=0$.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let A be the sum of the digits of 2012 ${ }^{2012}$. We define B as the sum of the digits of A, and $\mathrm{C}$ as the sum of the digits of $B$. Determine $C$.
|
We start by crudely bounding C. Since $2012^{2012} \leqslant 10000^{2012}$, it has fewer than $4 \times 2012 + 1 < 10000$ digits, so $A < 9 \times 10000 = 90000$. Similarly, $B < 9 \times 5 = 45$ and finally $C \leqslant 13$.
Now we look modulo 9 because we know that the operation of taking the sum of the digits leaves this congruence invariant. Thus,
$$
2012^{2012} \equiv 5^{2012} \equiv 5^{2} \equiv 7 \pmod{9}
$$
Thus, $C=7$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(i) Find all integers $n \geqslant 1$ such that $n$ divides $2^{n}-1$.
(ii) Find all odd integers $n \geqslant 1$ such that $n$ divides $3^{n}+1$.
## - Solution -
|
(i) Let $n>1$ such that $n$ divides $2^{n}-1$. It is clear that $n$ is odd. Let $p$ be the smallest prime factor of $n$, which is therefore odd. Then $2^{n} \equiv 1 \bmod p$. Let $\omega$ be the order of 2 modulo $p$. Then $\omega$ divides $n$. On the other hand, by Fermat's Little Theorem, $2^{p-1} \equiv 1 \bmod p$. Thus $\omega$ divides $p-1$. Given the condition on $p$, we necessarily have $\omega=1$. Then $2 \equiv 1 \bmod p$, which is absurd. Therefore, we must have $n=1$.
(ii) Let $n>1$ such that $n$ divides $3^{n}+1$. Let $p$ be the smallest prime factor of $n$, which is therefore odd, and thus $p>3$. Then $3^{2 n} \equiv 1 \bmod p$. Let $\omega$ be the order of 3 modulo $p$. Then $\omega$ divides $2 n$. On the other hand, by Fermat's Little Theorem, $3^{p-1} \equiv 1 \bmod p$. Thus $\omega$ divides $p-1$. We deduce that $\omega$ divides $\operatorname{gcd}(2 n, p-1)$. Given the condition on $p$, we necessarily have $\omega=1$ or 2. In the first case, $3 \equiv 1 \bmod p$ and thus $p=2$, which is excluded. In the second case, $3^{2} \equiv 1 \bmod p$ and thus $p$ divides 8, which is also excluded. We conclude that $n=1$.
## 3 Intermediate: Algebra
We refer to the polynomial course available on the Animath website for details and complements (see the links at the top of page 14).
## 1 First TD on Polynomials
## - Statements -
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For which values of $m \in \mathbb{R}$ does the equation:
$$
\left(x^{2}-2 m x-4\left(m^{2}+1\right)\right)\left(x^{2}-4 x-2 m\left(m^{2}+1\right)\right)=0
$$
have exactly three distinct roots?
|
The first quadratic $x^{2}-2 m x-4\left(m^{2}+1\right)$ always admits two distinct real roots. Therefore, either the second quadratic must admit a double root, or it must share a root with the first.
It admits a double root when $-2 m\left(m^{2}+1\right)=4$, which simplifies to $\mathfrak{m}^{3}+m+2=0$. This polynomial has an obvious root $\mathfrak{m}=-1$, so it can be factored as: $(\mathfrak{m}+1)\left(\mathfrak{m}^{2}-\mathfrak{m}+2\right)$, and $\mathfrak{m}^{2}-\mathfrak{m}+2$ has no real roots. For $m=-1$, the double root 2 of $x^{2}-4 x-2 m\left(m^{2}+1\right)$ is also a root of $x^{2}-2 m x-4\left(m^{2}+1\right)$, so the equation in the statement has only two distinct roots (one of which is a triple root).
If $x^{2}-2 m x-4\left(m^{2}+1\right)$ and $x^{2}-4 x-2 m\left(m^{2}+1\right)$ share a common root, this root is a root of their difference: $(4-2 m)\left(x-\left(m^{2}+1\right)\right)$. Either $m=2$, in which case the two quadratics are identical, equal to $x^{2}-4 x-20$, and the equation has only two distinct roots (two double roots), or $x=m^{2}+1$, in which case each quadratic is equal to $\left(m^{2}+1\right)\left(m^{2}-2 m-3\right)$ and $s'$ vanishes if $m=-1$ or $m=3$. $m=-1$ is excluded (it is the triple root already seen), leaving $m=3$ for which the equation $\left(x^{2}-6 x-40\right)\left(x^{2}-4 x-60\right)$ indeed has three roots: $-4, -6$, and 10 (a double root). This is therefore the unique solution to the exercise.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $\alpha, \beta, \gamma$ be the three roots of $x^{3}-x-1$, calculate: $\frac{1-\alpha}{1+\alpha}+\frac{1-\beta}{1+\beta}+\frac{1-\gamma}{1+\gamma}$
|
A safe method, even if in this case we can find a faster one, is to look for the equation whose roots are $\frac{1-\alpha}{1+\alpha}, \frac{1-\beta}{1+\beta}, \frac{1-\gamma}{1+\gamma}$ and to calculate the sum of the roots of this equation from its coefficients. If $x$ is a root of $x^{3}-x-1$, what equation is $y=\frac{1-x}{1+x}$ a root of? We note that $x=\frac{1-y}{1+y}$ (the function is involutive), so $\left(\frac{1-y}{1+y}\right)^{3}-\left(\frac{1-y}{1+y}\right)-1=$ 0, which means: $(1-y)^{3}-(1-y)(1+y)^{2}-(1+y)^{3}=0$. The equation in $y$ is therefore: $-y^{3}+y^{2}-7 y-1$, the sum of its roots is 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $\left(a_{n}\right)$ be the sequence defined by $a_{1}=1$ and $a_{n+1}=1+a_{1} a_{2} \ldots a_{n}$. Determine $\sum_{n=1}^{+\infty} \frac{1}{a_{n}}$.
|
It is clear that for all $n \geqslant 2$, we have $a_{n+1}-1=a_{n}\left(a_{n}-1\right)$, and by inverting this relation, we get $\frac{1}{a_{n+1}-1}=\frac{1}{a_{n}-1}-\frac{1}{a_{n}}$, in other words $\frac{1}{a_{n}}=\frac{1}{a_{n}-1}-\frac{1}{a_{n+1}-1}$. By summing, we obtain $\sum_{k=1}^{n} \frac{1}{a_{k}}=1+\frac{1}{a_{2}-1}-\frac{1}{a_{n+1}-1}=2+\frac{1}{a_{n+1}-1}$. To conclude that $\sum_{n=1}^{+\infty} \frac{1}{a_{n}}=2$, it suffices to show that $\frac{1}{a_{n+1}-1} \underset{n \rightarrow+\infty}{ } 0$, in other words that $a_{n} \xrightarrow[n \rightarrow+\infty]{ }+\infty$. But this is clear because the definition of $\left(a_{n}\right)$ shows that $a_{n+1} \geqslant 1+a_{n}$, hence that $a_{n} \geqslant n$ for all $n$.
## 4 Test
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine all integers $n \geqslant 1$ such that $n$ divides $2^{n}-1$.
## - Polynomials in $\mathbb{Z} / p \mathbb{Z}-$
Unless otherwise stated, throughout the following, $p$ will denote a prime number, and we will work in the field $\mathbb{Z} / \mathrm{p} \mathbb{Z}$.
If $A$ is an integral domain, many results that are true in $\mathbb{Z}[X]$ remain true in $A[X]$. In particular, there exists a Euclidean division by unitary polynomials, if $r \in A$ is a root of $P \in A[X]$, then $P(X)$ is divisible by $X-r$, and a polynomial of degree $n$ has at most $n$ roots, counted with multiplicities. Consequently, if a polynomial $P$ is of degree $n$, has leading coefficient $\lambda$, has roots $r_{1}, \ldots, r_{k}$ with respective multiplicities $\alpha_{1}, \ldots, \alpha_{k}$ such that $\alpha_{1}+\ldots+\alpha_{k}=n$, then $P(X)=\lambda\left(X-r_{1}\right)^{\alpha_{1}} \ldots\left(X-r_{k}\right)^{\alpha_{k}}$. If, moreover, $A$ is a field, then there is a Euclidean division by any non-zero polynomial, and in $A[X]$ there is a GCD, an LCM, Bézout's theorem, and Gauss's theorem, and the existence and uniqueness of the decomposition into a product of irreducibles. In particular, all these properties are true in $\mathbb{Z} / p \mathbb{Z}[X]$.
|
$n=1$ works, and we will show that it is the only solution. Let $n \geqslant 2$, and suppose that $n \mid 2^{n}-1$. It is clear that $n$ is odd, since $2^{n}-1$ is. Let $p$ be the smallest prime divisor of $n$, and set $n=k p$. We have $p \mid\left(2^{n}-1\right)$ and by Fermat's Little Theorem, $2^{n}=\left(2^{k}\right)^{p} \equiv 2^{k} \bmod p$, so $2^{k} \equiv 1 \bmod p$. Therefore, $\omega_{p}(2) \mid k$ and $\omega_{p}(2) \mid(p-1)$. From this last divisibility relation, we deduce that all prime divisors of $\omega_{p}(2)$ are strictly less than $p$. Now, $\omega_{p}(2)>1$ since $p \geqslant 3$, and since $\omega_{p}(2) \mid k$, we conclude that $k$ has a prime divisor strictly less than $p$, and thus $n$ does as well. This contradicts the minimality of $p$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Calculate $\left(\frac{37}{97}\right)$.
To translate the text into English, I have kept the format and line breaks as in the original text.
|
Let's apply quadratic reciprocity:
$$
\begin{array}{rlrl}
\left(\frac{37}{97}\right) & =\left(\frac{97}{37}\right) & & \text{since }\left(\frac{37}{97}\right)\left(\frac{97}{37}\right)=1 \\
& =\left(\frac{23}{37}\right) & & \text{since only the class of } 97 \text{ mod } 37 \text{ matters } \\
& =\left(\frac{37}{23}\right)=\left(\frac{14}{23}\right) & & \text{since }\left(\frac{37}{23}\right)\left(\frac{23}{37}\right)=1 \\
& =\left(\frac{2}{23}\right)\left(\frac{7}{23}\right) \\
& =\left(\frac{2}{23}\right) \cdot-\left(\frac{23}{7}\right) & & \text{since the Legendre symbol is multiplicative } \\
& =-1 & & \text{since }\left(\frac{7}{23}\right)\left(\frac{23}{7}\right)=-1 \\
& =1 \text{ and }\left(\frac{2}{7}\right)=1
\end{array}
$$
|
-1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(given to Jean-Denis Zafar). Let $m$ and $n$ be two integers that are coprime. Calculate the GCD of $5^{m}+7^{m}$ and $5^{n}+7^{n}$.
|
. We denote $S_{k}=5^{k}+7^{k}$. We will show that the GCD of $S_{n}$ and $S_{m}$ is 12 if $m$ and $n$ are odd, and 2 otherwise. We denote $\delta$ as the GCD we wish to calculate. For $m=n=1$, we directly have $\delta=12$. We assume $m>n$ and set $m=n+a$; $a$ and $n$ are coprime. Let $U_{a}=7^{a}-5^{a}$. Then $S_{m}-5^{a} S_{n}=7^{n} U_{a}$. Now, we have $\operatorname{GCD}(\delta, 7)=\operatorname{GCD}(\delta, 5)=1$, hence $\delta=\operatorname{GCD}\left(U_{a}, S_{n}\right)$. If $a$ is odd, we set $S_{n}=\delta \ell$ and $U_{a}=\delta k$ with $k$ and $\ell$ coprime. Then $7^{a n}=\left(\delta \ell-5^{n}\right)^{a}$ can be written as $\delta L-5^{a n}$ using the binomial formula. Similarly, $7^{a n}=\delta K+5^{a n}$ for some integer $K$. Thus $\delta(K-L)=2 \times 5^{a n}$. According to Gauss's theorem, $\delta$ is a divisor of 2. It is 2 because the two numbers are even. If $a$ is even, we set $a=2 b$ so that $\operatorname{GCD}(b, n)=1$ and $n$ is odd. Then $\delta$ divides $\left(7^{n}-5^{n}\right)\left(7^{n}+5^{n}\right)=7^{2 n}-5^{2 n}$ as well as $U_{a}=7^{2 b}-5^{2 b}$. It therefore divides their GCD, which is $7^{2}-5^{2}=24$. Furthermore, since $m$ and $n$ are odd, we have $7^{m} \equiv-1(\bmod 8)$ and $5^{m} \equiv 5(\bmod 8)$, and thus $S_{m} \equiv 4$ (mod 8). Similarly, $S_{n} \equiv 4(\bmod 8)$. Consequently, $S_{n}$ and $S_{m}$ are divisible by 4 but not by 8. Similarly, we show that they are divisible by 3. The value of $\delta$ is therefore 12 as announced.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(solved by François Caddet, Marc Coiffier, and Jean-Alix David). Let $\left(a_{n}\right)$ be defined by $a_{1}=3$, $a_{2}=2$, and for $n \geqslant 1, a_{n+2}$ is the remainder of the Euclidean division of $a_{n}+a_{n+1}$ by 100. Calculate the remainder of the Euclidean division of:
$$
a_{1}^{2}+a_{2}^{2}+\cdots+a_{2007}^{2}
$$
by 8.
|
. Consider the sequence $\left(b_{n}\right)$ such that $0 \leqslant b_{n} \leqslant 3$ and $b_{n} \equiv a_{n}(\bmod 4)$. Since 4 divides 100, $\left(b_{n}\right)$ satisfies the recurrence relation $b_{n+2} \equiv b_{n}+b_{n+1}(\bmod 4)$. We notice that the sequence $\left(b_{n}\right)$ is periodic, with the sequence $3,2,1,3,0,3$ repeating 334 times up to 2004. Furthermore, if $a \equiv b$ $(\bmod 4)$, then $a^{2} \equiv b^{2}(\bmod 8)$. Indeed, writing $a=b+4 k$, we have $a^{2}=(b+4 k)^{2}=b^{2}+8 k b+16 k^{2}$. We deduce that $a_{1}^{2}+a_{2}^{2}+\cdots+a_{2007}^{2} \equiv 334(1+4+1+1+0+1)+1+4+1 \equiv 6(\bmod 8)$. The answer to the question is therefore 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
. In the decimal writing of $A$, the digits appear in (strictly) increasing order from left to right. What is the sum of the digits of $9 A$?
|
. Let $A=\overline{a_{1} a_{2} \cdots a_{k}}$ be the decimal representation of $A$. By performing the subtraction
$$
\begin{aligned}
& \begin{array}{cccccc}
a_{1} & a_{2} & a_{3} & \cdots & a_{k} & 0
\end{array} \\
& \begin{array}{llllll}
- & a_{1} & a_{2} & \cdots & a_{k-1} & a_{k} \\
\hline
\end{array}
\end{aligned}
$$
we find that the digits of $9 A=10 A-A$ are $a_{1}, a_{2}-a_{1}, a_{3}-a_{2}, \ldots, a_{k-1}-a_{k-2}, a_{k}-a_{k-1}-1,10-a_{k}$. Their sum is $10-1=9$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find $k$ such that, for all real $a, b$ and $c$:
$$
(a+b)(b+c)(c+a)=(a+b+c)(a b+b c+c a)+k a b c
$$
|
$k=-1$ works.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find $k$ such that, for all $n$, the following quantity is a square:
$$
4 n^{2}+k n+9
$$
|
$k=12$ works.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Calculate the greatest common divisor of 15 and 70.
## - Prime numbers and the Sieve of Eratosthenes - Group A only -
Some integers in particular play a role of primary importance: these are the integers whose GCD is 1.
Definition 2.2.11.
Let $a$ and $b$ be two integers. We say that $a$ and $b$ are coprime if $a \wedge b=1$.
For example, 2 and 3 are coprime, whereas 4 and 6 are not, since they are both even.
|
It is enough to apply Euclid's algorithm: it is easily verified that $70=15 \times 4+10$, then
that $15=10 \times 1+5$, and finally that $10=5 \times 2+0$. This shows that $70 \wedge 15=5$, which was not really surprising anyway.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Among the pairs of integers $(a, b)$ such that $1 \leqslant a \leqslant b \leqslant 5$, how many are there for which $a$ and $b$ are coprime?
Moreover, there are also other numbers, much better known to the general public, which have remarkable divisibility properties: these are the prime numbers.
## Definition 2.2.12.
We say that an integer $n$ is prime if $n$ has exactly 2 positive divisors, which are 1 and $n$. Otherwise, we say that $n$ is composite.
## Remark 2.2.13.
The integer 1 is therefore not prime!
From the definition of prime numbers, the following crucial results quickly follow.
## Theorem 2.2.14.
Let $n$ be an integer and $p$ a prime number. Either $p$ divides $n$, or $p$ is coprime with $n$, these two cases being mutually exclusive.
Proof. First, if $p$ divides $n$, then $p$ is a common divisor of $p$ and $n$, so $p \wedge n \neq 1$, which shows that $p$ and $n$ are not coprime. Now suppose that $p$ does not divide $n$, and let $d = p \wedge n$. Since $d$ divides $p$, we know that $d = 1$ or $d = p$. Since $d$ divides $n$, it follows that $d \neq p$, and therefore $d = 1$.
## Theorem 2.2.15.
Let $n$ be an integer such that $n \geqslant 2$, and let $p$ be the smallest divisor of $n$ such that $p \geqslant 2$. Then the integer $p$ is a prime number.
Proof. Since $p \geqslant 2$, we already know that 1 and $p$ are two distinct divisors of $p$. Now let $d$ be a divisor of $p$. According to Theorem 2.2.3, and since $p$ divides $n$, we know that $d$ also divides $n$. By the minimality of $p$, we deduce that $d = 1$ or $d = p$, which means that $p$ is prime.
It is therefore very important to be able to detect whether an integer $n$ is prime or not. Achieving this efficiently is a difficult question, which will be the subject of the course on "primality tests" given to group D. However, there is already an ancient and relatively efficient method when $n$ is small: it is the Sieve of Eratosthenes, which allows identifying the set of prime numbers less than or equal to $n$.
Like the Euclidean algorithm, it is important to show that the Sieve of Eratosthenes returns the correct list of prime numbers $p \leqslant n$.
## Theorem 2.2.16.
The list of integers returned by the Sieve of Eratosthenes is indeed the list of prime numbers $p \leqslant n$.
```
Algorithm 2: Sieve of Eratosthenes
Argument(s): \(n \quad \triangleright\) We want to identify the prime numbers \(p \leqslant n\)
write all integers from 2 to \(n\)
as we go, we will either cross them out or circle them
while there is an integer \(p \leqslant \sqrt{n}\) that is neither crossed out nor circled:
choose the smallest such integer \(p\) and circle it
cross out all multiples of \(p\) between \(p^{2}\) and \(n\) that were not already crossed out
return the list of integers that were not crossed out (even those that are not circled)
```
Proof. Our proof will proceed by induction on $n$. First, if $n = 1$, the result is obvious. We therefore assume that $n \geqslant 2$ and that, if we run the Sieve of Eratosthenes with $n-1$ as the argument, it returns the correct list of prime numbers $p \leqslant n-1$. Let's then see how it behaves when we give it $n$ as the argument.
Already, it is clear that the integers $k \leqslant n-1$ that we will cross out are the same, whether the argument of the algorithm is $n-1$ or $n$. It remains to show that we will cross out $n$ if it is composite, but not if it is prime.
If $n$ is prime, we will clearly never cross it out. We therefore treat the case where $n$ is composite. Let $p$ then be its smallest divisor such that $p \geqslant 2$. Theorem 2.2.15 shows that $p$ is prime. Moreover, since $n = p \times (n / p)$ and $p < n$, we know that $n / p$ is a divisor of $n$ greater than or equal to 2, so $n / p \geqslant p$. This shows that $p \leqslant \sqrt{n}$.
Since $p$ is prime, we will never cross it out, so we will eventually circle it. By doing so, and since $n \geqslant p^{2}$, we will necessarily cross out $n$. This concludes the proof of the theorem.
|
It suffices to list the positive divisors of each integer between 1 and 5: each integer $n \in\{1,2,3,5\}$ is only divisible by 1 and itself, whereas 4 is divisible by 1, 2, and 4. Consequently, if $1 \leqslant a \leqslant b \leqslant 5$, the integer $a \wedge b$ is different from 1 if and only if $a=b \geqslant 2$ or if $(a, b)=(2,4)$.
Now, there are $5+4+3+2+1=15$ pairs $(a, b)$ such that $1 \leqslant a \leqslant b \leqslant 5$. Out of these 15 pairs, we have just counted 5 such that $a \wedge b \neq 1$. Therefore, there are 10 pairs such that $a$ and $b$ are coprime.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
( JBMO 2018 )
$n$ numbers are written on a board, satisfying the following properties:
- all the numbers have 3 digits
- none of them contain a 0
- two different numbers never have the same hundreds digit, or the same tens digit, or the same units digit
- the sum of the digits of each number is 9
What is the maximum possible value for $n$?
|
We already observe that $n \leqslant 7$, because we cannot use digits larger than 7 and we must use $n$ different unit digits. The sum of the $3 n$ digits used must be equal to $9 n$. The sum of the unit digits, for example, is at least: $1+\ldots+n=\frac{n(n+1)}{2}$. Hence the inequality satisfied by $n$:
$$
9 n \geqslant \frac{3 n(n+1)}{2}
$$
We have: $9 \times 7=63<\frac{3 \times 7 \times 8}{2}=84$ and $9 \times 6=54<\frac{3 \times 6 \times 7}{2}=63$, but we observe that 5 satisfies the inequality, and it is even an equality in this case: $9 \times 5=45=\frac{3 \times 5 \times 6}{2}$
If it is possible with 5 numbers, we then know that only the digits 1, 2, 3, 4, 5 are used. We arrive, for example, at the following 5 numbers, which allows us to verify that 5 is indeed the maximum (attained): $135,252,324,441,513$.
## 4 Geometry
## 1 Angle Hunting
The course partly reviewed the angle hunting course given to group B during the Montpellier olympic stage in 2016 (available here). The concepts actually covered are:
- Alternate interior angles, corresponding angles
- Sum of the angles of a triangle, of a quadrilateral (with proof)
- Isosceles triangle
- Central angle theorem (with proof)
- Inscribed angle theorem (with proof, without limit cases)
- Right triangle, English Thales' theorem (with proof)
- Cyclic points, Fifi's theorem (proof of the direct sense)
## - Exercises covered -
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the limit of the following sequence:
$$
u_{n}=\sum_{i=1}^{n} \frac{1}{F_{i} F_{i+2}}
$$
|
We find that $\frac{1}{F_{k} F_{k+2}}=\frac{1}{F_{k} F_{k+1}}-\frac{1}{F_{k+1} F_{k+2}}$. Therefore,
$$
u_{n}=\sum_{i=0}^{n} \frac{1}{F_{i} F_{i+2}}=\sum_{i=0}^{n}\left(\frac{1}{F_{i} F_{i+1}}-\frac{1}{F_{i+1} F_{i+2}}\right)=1-\frac{1}{F_{n+1} F_{n+2}}
$$
by telescoping sum.
Since $F_{k}$ tends to infinity, the limit of $u_{n}$ is 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A number is called sympathetic if, for each divisor $d$ of $n, d+2$ is a prime number. Find the maximum number of divisors of a sympathetic number.
## - Solutions -
|
Let $n$ be a fixed friendly integer, and let $d$ be a divisor of $n$. If $d \equiv 1(\bmod 3)$, then $d+2 \equiv 0$ $(\bmod 3)$, and since $d+2$ is prime, this means that $d+2=3$, so $d=1$.
Now suppose there exist two primes $p$ and $q$, distinct from 3, which both divide $n$. Then $p \equiv q \equiv 2(\bmod 3)$, so $p q \equiv 1(\bmod 3)$, and $p q$ does not divide $n$. We conclude that $n$ must necessarily be of the form $3^{k}$ or $3^{k} p^{\alpha}$, with $k \in \mathbb{N}, \alpha \in\{0,1\}$ and $p$ a prime such that $p \equiv 2(\bmod 3)$. The integer $n$ will then have $\sigma_{0}(n)=(k+1)(\alpha+1)$ divisors.
We will now show that $\sigma_{0}(n) \leqslant 8$. First, since $3^{5}+2=245$ is not prime, we know that $k \leqslant 4$. Consequently, if $\alpha=0$, we know that $\sigma_{0}(n)=k+1 \leqslant 5$, and if $k \leqslant 3$, then $\sigma_{0}(n) \leqslant 2(k+1) \leqslant 8$ as well. We therefore need to show that the pair $(k, \alpha)$ cannot be equal to $(4,1)$.
To do this, proceed by contradiction, and suppose that $n=3^{4} p$. Since $3^{4} \times 5+2=$ $407=11 \times 37$, we know that $p \neq 5$, so $p$ is invertible modulo 5. Now, since $3^{2} \equiv-1$ $(\bmod 5)$, the integer 3 has order 4 modulo 5. Therefore, there must necessarily be an integer $\ell$ between 1 and 4 such that $3^{\ell} \equiv-2 p^{-1}(\bmod 5)$, and then $3^{\ell} p+2$ is not prime. $^{2}$.
We have therefore shown that $\sigma_{0}(n) \leqslant 8$. Conversely, if $n=3^{3} \times 5=135$, then $n$ of course has 8 divisors, which are $1,3,5,9,15,27,45$ and 135 itself. It is easily verified that $3,5,7,11,17$, 29, 47 and 137 are all prime numbers, for example because they have no prime factor $p \leqslant 12=\sqrt{144}$ other than themselves.
Therefore, the integer $n=135$ is friendly, and the maximum number of divisors sought is therefore equal to 8.
## V. Group C
## Content of this section
1 Algebra ..... 170
1 Functional equations ..... 170
2 Polynomials - 1st part ..... 176
3 Polynomials - $2^{\text {nd }}$ part ..... 189
4 Inequalities ..... 193
2 Arithmetic ..... 201
1 Various exercises ..... 201
2 Multiplicative order and Fermat's little theorem ..... 202
3 Combinatorics ..... 211
1 Game theory ..... 211
2 Monovariants and invariants ..... 216
3 Groups ..... 224
4 Countability ..... 227
4 Geometry ..... 228
1 Inscribed angle and South Pole theorems, power of a point ..... 228
2 Geometric transformations - $1^{\text {st }}$ part ..... 233
3 Midpoints and parallelograms ..... 235
4 Geometric transformations $-2^{\text {nd }}$ part ..... 249
5 Training exercises ..... 266
1 Mid-training exercise ..... 266
2 Final training exercise ..... 269
## 1 Algebra
## 1 Functional equations
The notion of an equation can be generalized to the search for mathematical objects of any form, satisfying a given relation.
Functional equations, whose unknown is a function, most often from $\mathbb{N}$ to $\mathbb{N}$ or $\mathbb{Z}$, or from $\mathbb{R}$ to $\mathbb{R}$, are notably present in an olympic context.
A problem of a functional equation often aims to determine the exact set of solutions, but can sometimes be limited to finding a given property of the solutions, such as periodicity or continuity, or to finding the solutions that satisfy a given condition: $f(0)=0, f$ continuous, and so on.
We will cover here the most classic strategies for solving the different types of functional equations, and will notably mention Cauchy's equation in its various forms.
## - Types of problems and classic resolution methods -
The strategies to apply in the face of a functional equation most often rely on the idea of progressively acquiring information: by knowing certain elements of the behavior of $f$, one can manipulate the functional equation so as to get closer to an equation of the form $f(x)=\ldots$, where the right-hand side does not depend on $f$. However, a bold symmetry argument, for example, can sometimes allow one to bypass this long process (but, alas!, these arguments are rarely applicable outside a particular case...)
## Before starting the resolution
Even before thinking about a resolution path, the first reaction is always to look for obvious solutions, such as:
$-x \mapsto 0$
$-x \mapsto 1$
$-x \mapsto a$
$-x \mapsto x$
$-x \mapsto x^{2}$
$-x \mapsto 1 / x$
$-x \mapsto \frac{e^{x}+e^{-x}}{2} 1$
In the vast majority of cases, the functional equation has one or more solutions of this form, which are generally the only ones. Having an idea of what one is looking for can indeed be useful when one is looking to prove it.
In parallel, proving that a functional equation admits only "simple" solutions (or, more generally, solutions of a certain form) is generally not enough to conclude: it remains to verify that all candidate solutions are (or are not!) valid, which avoids, for example, going from $7 / 7$ to $5 / 7$ on a functional equation exercise.
Also, keep in mind that a solution function is not necessarily simple (polynomial, continuous, differentiable...), but can on the contrary be a highly pathological object (we will notably see a little later functions that cover, in a certain sense, the entire plane!)
## Substitution
The first reflex to have in front of a functional equation is to substitute one of the unknowns with a value that is easily manageable, such as 0, 1, or $f(0)$. This technique has several advantages:
- It allows simplifying the functional equation, allowing, for example, to manipulate $f(x)$ instead of $f(x+f(y))$ by taking $(x, y) \leftarrow(x-f(y), y)$
- It allows obtaining information about the behavior of $f$ at particular values, thus allowing more effective substitutions (for example by simplifying the expression obtained even more).
This strategy is particularly useful in the case of expressions of the form $x+f(y)$ and $f(x \cdot f(y))$, which both simplify to $f(0)$ by taking $(x, y) \leftarrow(0,0)$; or similarly $x \cdot f(y)$ and $f(y \cdot f(x))$, which simplify to $f(0)$ by taking $(x, y) \leftarrow(1,0)$.
1. Or at least if exercise 136 of the wall seems trivial to you!
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
For any natural number $n$, we denote $\mathbf{S}(n)$ as the sum of the digits of $n$. Calculate $\mathbf{S}^{5}\left(2018^{2018^{2018}}\right)$.
|
It is clear that $A \equiv B \equiv C \equiv D \equiv E(\bmod 9)$. Since 2 has order 6 modulo 9, we then find
$$
2018^{2018} \equiv 2^{2018} \equiv 0 \quad(\bmod 2) \text { and } 2018^{2018} \equiv 2^{2018} \equiv(-1)^{2018} \equiv 1 \quad(\bmod 3)
$$
so $2018^{2018} \equiv 4(\bmod 6)$, which means that
$$
E \equiv 2018^{2018^{2018}} \equiv 2^{2018^{2018}} \equiv 2^{4} \equiv 7 \quad(\bmod 9)
$$
On the other hand, $A<10^{4 \times 2018^{2018}}$ so $B<9 \times 4 \times 2018^{2018}<10^{2+4 \times 2018}$, then $C<9 \times 2+9 \times 4 \times 2018<73000$, so $D<6+4 \times 9=42$. Consequently, $E<3+9=12$ and, since $E \equiv 7$ $(\bmod 9)$, we deduce that $E=7$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Seven cases of a chessboard $(8 \times 8)$ are on fire. At each step, a case catches fire if at least two of its neighbors (by a side, not a corner) are on fire. Is it possible for the fire to spread everywhere? If not, how many cases initially on fire are needed at a minimum for the fire to be able to spread everywhere?
|
We can show that the perimeter of the burning area decreases at each step. Therefore, the fire cannot spread to the entire chessboard (perimeter of 32 if the squares have a side of 1) from seven burning squares (maximum perimeter of 28). At least eight squares are needed: if all the squares of a major diagonal are initially burning, the fire will be able to spread everywhere.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the smallest non-zero natural number $n$ such that 2016 divides $20^{n}-16^{n}$.
|
We start by factoring 2016 into a product of prime factors: $2016=2^{5} \times 3^{2} \times 7$. We need to find the integers $n \geqslant 1$ such that the integer $20^{n}-16^{n}=2^{2 n}\left(5^{n}-4^{n}\right)$ is divisible by $2^{5}, 3^{2}$, and 7. This is exactly the set of integers such that $2 n \geqslant 5$, $5^{n} \equiv 4^{n}\left(\bmod 3^{2}\right)$, and $2^{n} \equiv 4^{n}(\bmod 7)$.
Since $4 \times 7 \equiv 1\left(\bmod 3^{2}\right)$ and $4 \times 2(\bmod 7)$, this is equivalent to $n \geqslant 3$, $(-1)^{n} \equiv (5 \times 7)^{n} \equiv (4 \times 7)^{n} \equiv 1^{n} \equiv 1\left(\bmod 3^{2}\right)$, and $3^{n} \equiv (5 \times 2)^{n} \equiv (4 \times 2)^{n} \equiv 1^{n} \equiv 1(\bmod 7)$.
Let $\omega$ be the order of -1 modulo $3^{2}$ and $\omega^{\prime}$ be the order of 3 modulo 7. The integer $n$ we are looking for is the smallest multiple of $\omega$ and $\omega^{\prime}$ such that $n \geqslant 3$. Now, $(-1)^{1} \not \equiv 1\left(\bmod 3^{2}\right)$ and $(-1)^{2} \equiv 1$ $\left(\bmod 3^{2}\right)$, so $\omega=2$.
Similarly, $3^{1} \not \equiv 1(\bmod 7)$, $3^{2} \equiv 2 \not \equiv 1(\bmod 7)$, and $3^{3} \equiv-1 \not \equiv 1(\bmod 7)$, so $\omega^{\prime}>3$, and the little Fermat theorem ensures that $\omega^{\prime}$ divides 6. This means that $\omega^{\prime}=6$. The smallest integer $n$ we are looking for is therefore $n=6$.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Consider 2018 lines in the plane, no two of which are parallel and no three of which are concurrent. Let $E$ be the set of their intersection points. We want to assign a color to each point in $E$ such that any two points on the same line, whose segment connecting them contains no other point of $E$, are of different colors.
How many colors are needed at a minimum to achieve such a coloring?
|
The configuration contains at least one triangle. This can be proven, for example, by induction on the number of lines: three lines form a triangle, and if you add a line, it either leaves the triangle intact or splits it into a triangle and a quadrilateral. Consequently, it is impossible to perform a coloring with two colors.
We will now show that a coloring with three colors is possible: we order the points by increasing abscissa as in the previous exercise, and color them in this order. When it is time to color a point $P=\left(d_{i}\right) \cap\left(d_{j}\right)$, we have already colored at most one of its neighbors on $\left(d_{i}\right)$ (the one to the left) and one on $\left(d_{j}\right)$ (also the one to the left). Therefore, we have at most two forbidden colors and can always choose the third. The answer is therefore 3 colors.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $S$ be a finite set of points in the plane, no three of which are collinear. Each point in $S$ is colored either blue or red. Suppose that every triangle whose three vertices are blue contains at least one red point, and every triangle whose three vertices are red contains at least one blue point.
Determine the largest possible value of $|S|$.
|
The answer is 8. We will in fact show that there are at most 4 blue points and at most 4 red points. Suppose there are at least 5 blue points. By performing a rotation if necessary, we can assume that the points have distinct x-coordinates. We denote $\mathcal{B}$ as the set of 5 blue points with the smallest x-coordinates.
If the convex hull of $\mathcal{B}$ is a pentagon, this pentagon contains no blue points. The pentagon can be divided into 3 triangles, each containing a red point. These three red points form a triangle, which contains no blue points, which is impossible.
If the convex hull of $\mathcal{B}$ is a quadrilateral $B_{1} B_{2} B_{3} B_{4}$, let $B_{5}$ be the last point of $\mathcal{B}$. The triangles $B_{5} B_{1} B_{2}, B_{5} B_{2} B_{3}, B_{5} B_{3} B_{4}$, and $B_{5} B_{4} B_{1}$ each contain a red point, so we have 4 red points $R_{1}, R_{2}, R_{3}$, and $R_{4}$ within the convex hull of $\mathcal{B}$, and only one blue point $B_{5}$. This blue point must therefore be inside all triangles formed by $R_{1}, R_{2}, R_{3}$, and $R_{4}$, which is impossible.
Finally, if the convex hull of $\mathcal{B}$ is a triangle $B_{1} B_{2} B_{3}$, we can draw segments connecting the five points of $\mathcal{B}$ to divide the convex hull into 5 triangles, which therefore contain 5 red points. By the pigeonhole principle, we can find 3 of these points on the same side of $\left(B_{4} B_{5}\right)$. These three points form a red triangle that does not contain any blue vertex, which is also impossible.
Therefore, the total number of vertices cannot exceed 8. Finally, $|S|=8$ is achievable, as shown in the figure below.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A number appears on a computer screen. We know that if $x$ appears on the screen, the number $x^{2}-2 x+1$ appears right after. If the first number to appear is 2, what is the 2020-th number to appear
|
Let's start by looking at the first values displayed by the computer:
- The first number is 2.
- The second number is $2^{2}-2 \times 2+1=1$
- The third number is $1^{2}-2 \times 1+1=1-2+1=0$
- The fourth number is $0^{2}-2 \times 0+1=1$
- The fifth number is $1^{2}-2 \times 1+1=1-2+1=0$
- The sixth number is $0^{2}-2 \times 0+1=1$
- The seventh number is $1^{2}-2 \times 1+1=1-2+1=0$
We see that the numbers that appear are in the order $2,1,0,1,0,1,0$. Since after a 0 there is always $0^{2}-2 \times 0+1=1$ and after a 1 there is always $1^{2}-2 \times 1+1=1-2+1=0$, we will have an alternation of 0 and 1. Since 1 appears in second place, all the numbers appearing at an even rank will be 1, so the 2020th number is 1.
Comment: We congratulate the students who successfully completed this exercise. The few errors observed were mainly calculation errors or rank shifts of the numbers displayed. For example, some students considered that the rank of the first number to appear on the screen was rank 0, while it is rank 1. To avoid this mistake, some students used a table, which was greatly appreciated. We invite students to be vigilant about this kind of error, which has sometimes caused a lot of damage, and not to rush through the exercises, always checking the reasoning used.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1) Alice wants to color the integers between 2 and 8 (inclusive) using $k$ colors. She wishes that if $m$ and $n$ are integers between 2 and 8 such that $m$ is a multiple of $n$ and $m \neq n$, then $m$ and $n$ are of different colors. Determine the smallest integer $k$ for which Alice can color the integers $2,3, \ldots, 8$ using $k$ colors.
2) Alice wants to color the integers between 2 and 31 (inclusive) using $k$ colors. She wishes that if $m$ and $n$ are integers between 2 and 31 such that $m$ is a multiple of $n$ and $m \neq n$, then $m$ and $n$ are of different colors. Determine the smallest integer $k$ for which Alice can color the integers $2,3, \ldots, 31$ using $k$ colors.
|
In this problem, we are looking for the smallest integer $k$ satisfying a certain property. Suppose we want to show that the smallest integer sought is the integer $c$. There will then be two parts to the proof. On the one hand, it is necessary to show that if an integer $k$ satisfies the property, then $k \geqslant c$, on the other hand, it is necessary to show that we can indeed find a coloring of the integers with $c$ colors.
1) First, let's try to color the integers as we go in a naive way:
- We color 2 with the first color
- We also color 3 with the first color (it is possible because 2 does not divide 3).
- 4 is divisible by 2, so we cannot color it with the same color as 2, we therefore color it with another color (the second color).
- We can color 5 with the first color.
- 6 being divisible by 2 and 3, we color it with the second color.
- We can color 7 with the first color.
- But 8 is divisible by 2 and 4, it must therefore be colored with a third color.
We have thus obtained a coloring with 3 colors of the integers from 2 to 8. It is now necessary to verify that 3 colors are necessarily required in a coloring satisfying the property of the statement. In the previous construction, the problem was to color 8. Indeed, 8 is a multiple of 4 and 2 and 4 is a multiple of 2. Thus 4 cannot have the same color as 2 and 8 cannot have the same color as 2 or 4. Therefore, at least 3 different colors are needed to color $2,4,8$, so the smallest number of colors necessary is $k=3$.
2) Here, let's be inspired by the first question. We saw that $2,4,8$ were the numbers bringing a constraint in the coloring. We notice that these are powers of 2. We can therefore conjecture that the powers of 2 play an important role in the problem. Among the integers from 2 to 32, there are 5 powers of $2: 2,4,8$ and 16. As 2 divides $4,8,16,2$ must necessarily be of a different color from the other 3. As 4 divides $8,16,4$ must necessarily be of a different color from the other 2. Similarly, as 8 divides 16, $2,4,8,16$ must necessarily have different colors from each other. Therefore, at least 4 different colors are needed.
Conversely, we are looking for a coloring of the integers from 2 to 32 using exactly 4 colors. We can in fact continue the previous coloring by coloring each integer as we go with the smallest possible color. We get the following coloring:
1. The numbers colored with color 1 are $2,3,5,7,11,13,17,19,23,29,31$
2. The numbers colored with color 2 are $4,6,9,10,14,15,21,22,25,26$
3. The numbers colored with color 3 are $8,12,18,20,27,28,30$
4. The numbers colored with color 4 are 16,24
We do indeed have a correct coloring with 4 colors, so the minimum number of colors is 4.
Alternative solution: As in the previous case, we show that for the first question, at least 3 colors are needed and at least 4 in the second.
Here we propose to generalize the previous coloring: we construct a coloring with the optimal number of colors to color the integers from 2 to $r$, with $r \geqslant 2$. Let $n \geqslant 2$, and let $n=p_{1}^{a_{1}} \times \cdots \times p_{k}^{a_{k}}$ be its prime factorization. We will color $n$ with the color $a_{1}+\cdots+a_{k}$ (note that since $n \geqslant 2$, we indeed have $a_{1}+\cdots+a_{k} \geqslant 1$). Let's show that this coloring is correct: let $m \neq n$ be two integers such that $m$ divides $n$. Let $n=p_{1}^{a_{1}} \times \cdots \times p_{k}^{a_{k}}$ be its prime factorization. $m$ necessarily writes as $m=p_{1}^{b_{1}} \times \cdots \times p_{k}^{b_{k}}$ with $b_{1} \leqslant a_{1}, \ldots b_{k} \leqslant a_{k}$. Since $m \neq n$, there must necessarily be an $i$ such that $a_{i} \neq b_{i}$, so $a_{i}>b_{i}$. Thus we must have $a_{1}+\cdots+a_{k}>b_{1}+\cdots+b_{k}$, so $m$ and $n$ are indeed of different colors.
If $n \leqslant 8$ and $n=p_{1}^{a_{1}} \times \cdots \times p_{k}^{a_{k}}$ then $2^{3}=8 \geqslant n \geqslant 2^{a_{1}+\cdots+a_{k}}$ so $a_{1}+\cdots+a_{k} \leqslant 3$, the coloring uses at most 3 colors for the integers from 2 to 8, so for the first question, the minimal $k$ is 3.
If $n \leqslant 31$ and $n=p_{1}^{a_{1}} \times \cdots \times p_{k}^{a_{k}}$ then $2^{5}=32>n \geqslant 2^{a_{1}+\cdots+a_{k}}$ so $a_{1}+\cdots+a_{k}n$. Let $j$ be an integer such that $2 \leqslant j \leqslant n$. Let $l$ be the largest integer such that $2^{l} \leqslant j$ and similarly $2^{l+1}>j$. Since $2 \leqslant j \leqslant n<2^{k+1}$, we have $1 \leqslant l<k+1$, so $1 \leqslant l \leqslant k$. We will color $j$ with the color $l$.
Note that since $1 \leqslant l \leqslant k$, this coloring uses at most $k$ colors. Since $2 \leqslant 2 \leqslant 4 \leqslant \cdots \leqslant 2^{k} \leqslant n$, the $2^{j}$ for $1 \leqslant j \leqslant k$ are between 2 and $n$, and since $2^{j}$ is colored with the color $j$, the coloring uses exactly $j$ colors.
This coloring also satisfies the property of the statement: let $m, n$ such that $m$ divides $n$ and $m \neq n$. Let $j$ be the color of $m$, we have $m \geqslant 2^{j}$. Since $m$ divides $n$ and $m \neq n, n \geqslant 2 m \geqslant 2^{j+1}$, so $n$ cannot be colored with the color $j$, otherwise we would have $n<2^{j+1}$.
In particular for $n=8$, since $2^{3}=8<2^{4}$, the proposed coloring uses 3 colors and for $n=31$, since $2^{4} \leqslant n<2^{5}$, the coloring uses 4 colors. Thus for the first question, the minimal $k$ is 3, for the second it is 4.
Comment: In this exercise, each question contained two parts. For example, for question 2), it was necessary to show on the one hand that we can color the integers with 4 colors, on the other hand, it is necessary to show that, whatever the coloring, it always uses at least 4 colors. It is only by treating each point separately that one could get the maximum score. Moreover, a large part of the students made good progress on the problem and provided a valid coloring with the right number of colors.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $x>0$. Show that
$$
x+\frac{1}{x} \geq 2
$$
For which $x$ do we have equality?
|
This inequality is equivalent to $\left(\sqrt{x}-\frac{1}{\sqrt{x}}\right)^{2} \geq 0$.
Therefore, equality is obtained for $x=\frac{1}{x}$, i.e., for $x=1$.
|
1
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
How many positive common divisors do $10^{100}$ and $10^{121}+10^{813}+10$ have?
|
The number of common divisors is equal to the number of divisors of the GCD of these two numbers. Indeed: a common divisor of the two numbers will be a divisor of the GCD.
$$
\begin{aligned}
10^{813}+10^{121}+10 & =\left(10^{713}+10^{21}\right) \times 10^{100}+10 \\
10^{100} & =10^{99} \times 10+0
\end{aligned}
$$
The GCD of these two numbers is then 10, which has 4 positive divisors: $1, 2, 5$, and 10.
The number of common divisors sought is therefore 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine the GCD of 1000000000 and 1000 000, 005.
|
$$
\begin{aligned}
P G C D(1000000000,1000000005) & =P G C D(1000000005,1000000005-1000000000) \\
& =P G C D(1000000005,5) \\
& =5
\end{aligned}
$$
since $5 \mid 1000005$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
We write down all the numbers from 1 to one million successively. Then we replace each number with the sum of its digits. Then we repeat this process until only single-digit numbers remain. Which digit appears most frequently?
|
Among the integers from 1 to 999,999, there are exactly 111,111 that are congruent to 1 modulo 9, 111,111 to 2, ..., 111,111 to 9. Since an integer is congruent to the sum of its digits modulo 9, we conclude that the digit 1 will be written 111,111 times, the digit 2 will be written 111,111 times, ..., and the digit 9 will be written 111,111 times. The number 1,000,000 will be written at the end as a 1: there will then be 111,112 times the digit 1 written, making it the most frequent digit.
## Remark 2.
Invariance is not limited to divisibility. We can easily imagine that a sum or a difference might be preserved, or even that a point remains unchanged through various geometric transformations!
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
65 people are lined up in the central column of a 17-column grid. At each step, each person takes a random step either to the left or to the right (all steps are of the same magnitude).
Show that there is always at least one column that contains at least 8 people.
|
Color every other column pink, every other column green, starting with pink. Initially, everyone is on a pink column. Then, with each operation, everyone changes color. Thus, everyone is always on the same color at any given time. Therefore, either all the pink columns are empty, or all the green columns are empty. There are always at least 8 columns that are empty.
The 65 people are distributed in at most 9 columns. By the pigeonhole principle, at least one column contains at least $\left\lceil\frac{65}{9}\right\rceil=8$ people.
|
8
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
For which natural numbers $n$ is the integer $n^{2}+n+1$ a perfect square?
|
If $n=0$, we have $n^{2}+n+1=1$ which is a perfect square. Otherwise, we have
$$
n^{2}<n^{2}+n+1<n^{2}+2 n+1=(n+1)^{2}
$$
thus $n^{2}+n+1$ is strictly between two consecutive squares and cannot be one.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all positive integers $n$ such that $n+1$ divides $2n^2 + 5n$. Be sure to verify that the $n$ found are solutions.
|
- We factorize: $n+1$ divides $2n^2 + 5n = n(2n + 5)$. Since $\text{GCD}(n+1, n) = \text{GCD}(n+1-n, n) = \text{GCD}(1, n) = 1$, by Gauss's lemma, since $n+1$ and $n$ are coprime, $n+1$ divides $2n + 5 = 2(n+1) + 3$, so $n+1$ divides 3. Therefore, $n+1 = 1$ or 3, so $n = 0$ or 2.
Conversely, $n=0$ works because 1 divides 0, and $n=2$ works because 3 divides $2 \times 4 + 5 \times 2 = 18$.
- We use the fact that $n+1$ divides $(n+1)(n-1) = n^2 - 1$. In particular, $n+1$ divides $2n^2 + 5n = 2(n^2 - 1) + 2 + 5n$, so $n+1$ divides $5n + 2$. Thus, $n+1$ divides $5(n+1) - 5 + 2$, so $n+1$ divides -3, so $n+1$ divides 3. Therefore, $n+1 = 1$ or 3, so $n = 0$ or 2.
Conversely, $n=0$ works because 1 divides 0, and $n=2$ works because 3 divides $2 \times 4 + 5 \times 2 = 18$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all integers $k \geqslant 1$ such that there exists a pair of integers $(n, m)$ such that $9 n^{6}=2^{k}+$ $5 m^{2}+2$.
|
Given that we have squares $\left(n^{6}\right.$ and $\left.m^{2}\right)$, we look at the equation modulo 4. To look at it modulo 4, suppose $k \geqslant 2$, the equation becomes $n^{6} \equiv m^{2}+2(\bmod 4)$. Since a square is either 0 or 1, the left-hand side is 0 or 1, and the right-hand side is 2 or 3.
It remains to handle the case $k=1$: for $k=0, (n, m)=(1,1)$ is a solution. The only $k$ that works is $k=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all natural numbers $n$ such that: $n^{5}-2 n^{4}-7 n^{2}-7 n+3=0$
|
Let $n \in \mathbb{N}$. We notice that $n \mid n^{5}-2 n^{4}-7 n^{2}-7 n=-3$ thus $n \in\{-3,-1,1,3\}$. Only 3 works.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine all positive integers $n$ such that:
$$
5^{n-1}+3^{n-1} \mid 5^{n}+3^{n}
$$
|
Let $n \in \mathbb{N}$. We have:
$$
5^{n-1}+3^{n-1} \mid\left(5^{n}+3^{n}\right)-5\left(5^{n-1}+3^{n-1}\right)
$$
Then
$$
5^{n-1}+3^{n-1} \mid 3^{n}-5 \times 3^{n-1}
$$
i.e.
$$
5^{n-1}+3^{n-1} \mid 3^{n-1}(3-5)
$$
. We also have $\operatorname{gcd}\left(5^{n-1}+3^{n-1}, 3^{n}-1\right)=1$: let $d$ be a common divisor of $5^{n-1}+3^{n-1}$ and $3^{n-1}$, then $d \mid 3^{n-1}$ and $d \mid 5^{n-1}$, so $d$ is both a power of 3 and of 5, i.e., $d=1$.
Next, by Gauss's lemma,
$$
5^{n-1}+3^{n-1} \mid 2
$$
and thus $5^{n-1}+3^{n-1}=2$ and $n=1$.
Conversely, $n=1$ works.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What are the integers $p$ such that $p, p+2$ and $p+4$ are all prime?
|
We look modulo 3:
If $p \equiv 0(\bmod 3):$ then $p=3$.
If $p \equiv 1(\bmod 3): p+2 \equiv 0(\bmod 3)$ and thus $3 \mid p+2$ which is prime i.e. $p+2=3:$ impossible.
If $p \equiv 2(\bmod 3): p+4 \equiv 0(\bmod 3)$ and thus $3 \mid p+4$ which is prime i.e. $p+4=3:$ impossible.
Conversely, $p=3$ works: 3, 5, and 7 are indeed prime.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine the $gcd$ of all numbers of the form $(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)$ where $a, b, c, d$ range over the integers.
## Solutions
|
We denote $P G C D$ as the integer sought.
We only have 4 numbers at our disposal and thus no chance to certify that a prime number $p \geqslant 5$ always divides integers of this form: $\forall p \geqslant 5$, prime, $p \nmid P G C D$. Therefore, we must stick to the factors 2 and 3 that would be present in all these integers.
Regarding the factor 3, by the pigeonhole principle, we always have two of the four numbers that are congruent modulo 3, thus ensuring a factor of 3: $3 \mid P G C D$. However, we cannot ensure a second factor of 3: $9 \nmid P G C D$.
Now, modulo 4, we can have each of the 4 possible remainders, and thus only two factors congruent to 2 modulo 4: $4 \mid P G C D$ but $8 \nmid P G C D$.
For any other possibility modulo 4, the integers obtained are at least multiples of 4.
Hence:
$$
P G C D=12
$$
## 3 Pigeonhole Principle and Extremum Principle (Pierre-Marie)
This course mainly reviewed the exercises given to group B of the 2019 summer camp.
## Pigeonhole Principle
The pigeonhole principle is a simple logical observation, but despite its apparent simplicity, it allows solving very complex situations.
Proposition 1 (Simple Pigeonhole Principle).
Given $n$ drawers and $n+1$ socks placed in these drawers, there exists at least one drawer containing at least two socks.
## Example 2.
A drawer contains 2019 distinct pairs of socks. What is the minimum number of socks to be taken out to be sure of having taken out at least one pair of identical socks? Note that the drawer is so messy that it is not possible to search inside. Proof: It is a matter of finding a minimum, so we need to show both that the proposed number is a solution and that any smaller number is not a solution.
By the pigeonhole principle, if 2020 socks are taken out, then we are sure to have taken out two identical socks. On the other hand, it is possible to take out 2019 distinct socks: the number sought is 2020.
## Notation.
We denote $\lceil x\rceil$ the unique integer satisfying $x \leqslant\lceil x\rceil<x+1$. Thus, $\lceil 3\rceil=3,\lceil 1.7\rceil=2,\lceil\pi\rceil=4$ and $\lceil-2.7\rceil=-2$.
Proposition 3 (Precise Pigeonhole Principle).
Given $n$ drawers and $l$ socks placed in these drawers, there exists at least one drawer containing at least $\left\lceil\frac{k}{n}\right\rceil$ socks.
## Example 4.
Paris has two million inhabitants. A human being has, at most, 600,000 hairs on their head. What is the largest number of Parisians that can be found who have exactly the same number of hairs on their head?
Proof: Here, the drawers are the numbers of hairs and the socks are the Parisians. We then have 2,000,000 socks for 600,001 drawers (don't forget the bald Parisians, at the risk of having trouble with the SPPC, the Society for the Protection of Bald Parisians): the pigeonhole principle ensures that it is possible to find $\left\lceil\frac{2000000}{600001}\right\rceil=4$ Parisians who have exactly the same number of hairs.
Proposition 5 (Infinite Pigeonhole Principle).
Given $n$ drawers and an infinite number of socks, there exists at least one drawer containing an infinite number of socks.
## Example 6.
Show that there are infinitely many numbers composed only of 0 and 1 in decimal notation that are divisible by 2019.
Proof: Consider the set of integers consisting only of the digit 1 in decimal notation: $\{1,11,111,1111, \ldots\}$. By the pigeonhole principle, since the set of possible remainders by Euclidean division by 2019 is finite, there exists an integer $0 \leq r<2019$ such that there are infinitely many integers written only with 1s such that the remainder in the Euclidean division by 2019 is $r$. But then the difference between two of these numbers will be composed entirely of 0s and 1s in decimal notation and will be divisible by 2019. Moreover, the consideration of the number of digits ensures that we have an infinite number of such integers. We could have also simply multiplied such a number by a power of 10 to have an infinite number.
Now, we need to learn to recognize the drawers and the socks...
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the remainder of the Euclidean division of $2018^{2019^{2020}}$ by 11.
|
We know that $2018^{10} \equiv 1(\bmod 11)$, so we seek to calculate the value of $2019^{2020}$ modulo
10. Since $2019 \equiv -1(\bmod 10)$ and 2020 is even, we have $2019^{2020} \equiv 1(\bmod 10)$. Therefore, $2018^{2019^{2020}} \equiv 2018^{1} \equiv 5(\bmod 11)$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(CMC 2020) Let $n$ be an integer. We call $C_{n}$ the grid of side $n$ from which one diagonal has been removed. For which integers $n \geqslant 2$ can $C_{n}$ be tiled with tiles consisting of three adjacent squares in the shape of an $\mathrm{L}$ (tiles can be flipped in any direction, but must not overlap or extend outside of $C_{n}$ or onto the diagonal).
|
It is necessary that the number of cells in $C_{n}$ is a multiple of 3, in other words, $n(n-1)$ is divisible by 3. For this, $n \equiv 0[3]$ or $n \equiv 1[3]$. Then, we notice that if we know how to tile $C_{n}$, then:
- we can tile $C_{n+6}$ if $n$ is even
- we can tile $C_{n+6}$ if $n$ is odd
- we can tile $C_{n+2}$ if $n \equiv 1[3]$
It remains to exhibit the tilings of $C_{3}$, $C_{7}$, $C_{10}$, and to show that $C_{4}$ and $C_{6}$ are impossible to tile. The suitable integers $n$ are therefore 3 and all those of the form $6k+i$ with $k \in \mathbb{N}^{*}$ and $i \in \{1,3,4,6\}$.
## Strategic Coloring and Tiling Problems
When a problem takes place on a grid or a graph, coloring the points in a clever way often reveals useful properties. For example, in chess, a bishop always stays on the same color of square, while a knight changes color with each move.
Coloring techniques are used to solve certain tiling problems, with a well-chosen coloring (in a checkerboard pattern, in stripes, etc).
## Example 3.
Consider an $n \times n$ chessboard for $n \in \mathbb{N}^{*}$. We remove the two opposite corners. Can it be tiled with $2 \times 1$ dominoes?
If $n$ is odd, it is clear that the answer is no.
If $n$ is even, we observe that the two removed squares are of the same color. However, a domino, regardless of where and how it is placed, always covers one black and one white square. Therefore, it is impossible.
Now, we remove two adjacent corners. This time, we can exhibit a construction that works for all even $n$.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(EGMO 2017) Find the smallest positive integer $k$ for which there exists a $k$-coloring of the positive integers and a function $f: \mathbb{N}^{*} \rightarrow \mathbb{N}^{*}$ such that
1. $\forall n, m \in \mathbb{N}^{*}$ of the same color, $f(n+m)=f(n)+f(m)$
2. $\exists n, m \in \mathbb{N}^{*}$ such that $f(n+m) \neq f(n)+f(m)$
|
Obviously, at least two colors are needed to satisfy point (2). Moreover, we notice that 3 colors suffice: we color in blue the integers congruent to 0 modulo 3, in red those congruent to 1, and in yellow those congruent to 2 modulo 3, and the function
$$
f: n \in \mathbb{N}^{*} \mapsto \begin{cases}n & \text { if } n \equiv 0[3] \\ 2 n & \text { otherwise }\end{cases}
$$
It remains to show that two colors are not enough. For this, we assume that there exists a two-color coloring (black and white) and a suitable function $f$. Let $n$ be the smallest integer such that $f(n) \neq n f(1)$. $n$ is odd, otherwise $f(n)=2 f\left(\frac{n}{2}\right)$; we assume that $n$ is black. For all $i \in \llbracket 1, \frac{n-1}{2} \rrbracket, i$ and $n-i$ are of different colors. If there exists an odd integer $j \in \llbracket 1, n-1 \rrbracket$ that is black, $f(n+j)=f(n)+f(j) \neq(n+j) f(1)$ and $f(n+j)=2 f\left[\frac{n+j}{2}\right]=(n+j) f(1)$, which is impossible. Since there are only two colors, all even integers are black and all odd integers are white. We then have two possibilities for the color of $n+1$, knowing that $f(n+1)=f(2+(n-1))=2 f(1)+(n-1) f(1)=(n+1) f(1)$:
- If $n+1$ is white like $n-1, f(2 n)=f((n+1)+(n-1))=f(n+1)+f(n-1)=$ $(n+1) f(1)+(n-1) f(1)=2 n f(1)$. But we also have $f(2 n)=2 f(n) \neq 2 n f(1)$.
- If $n+1$ is black like $1, f(n+2)=f(n+1)+f(1)=(n+2) f(1)$. But we also have $f(n+2)=f(n)+f(2) \neq(n+2) f(1)$.
Thus, we cannot color $n+1$ either white or black, which is absurd.
The minimum number of colors possible for a satisfying coloring is therefore indeed 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find the positive integers $n$ such that $2^{n}+1$ is a perfect square.
|
We already see that 3 is a solution: let's show that it is the only one.
Let $n$ be such an integer: there exists $a \geq 0$ such that $2^{n}+1=a^{2}$. Clearly $a \neq 0$. But then $2^{n}=(a-1)(a+1)$, so $a+1$ and $a-1$ are positive divisors of a power of 2, hence they are powers of 2. Since they differ by 2, they can only be 2 and 4 (indeed, if $2^{x}+2=2^{y}$, then $y \geq 2$ because $2^{y}>2$ and $x \leq 1$ because $2^{y}-2^{x} \neq 0[4]$ and $x \neq 0$ so $x=1$ and $y=2$) so $a=3$ and $n=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all integers $n$ such that $n^{3}-3 n^{2}+n+2$ is a power of 5.
|
We then have: $(n-2)\left(n^{2}-n-1\right)=5^{a}$. Thus, we have: $n-2=5^{x}$ and $n^{2}-n-1=5^{y}$. It follows that $5^{y}-5^{2 x}-3 \cdot 5^{x}=1$. Therefore, if $x, y \geqslant 1$ then $0 \equiv 1[5]$, which is absurd. Therefore, $x=0$ or $y=0$. If $x=0$, then $y=1$, which gives $n=3$. If $y=0$, then $5^{2 x}+3 \cdot 5^{x}=0$, which is absurd. The only solution is thus $n=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all integers $x$ such that $x^{4}+x^{3}+x^{2}+x+1$ is a perfect square. (Bounding)
|
Let $A=x^{4}+x^{3}+x^{2}+x+1$. We have $x^{2}-x+1>0$ (quadratic with a strictly negative discriminant) and by immediate induction, for $x \geqslant 2, x^{3}>x+1$. We then have: $\left(x^{2}+x\right)^{2}=x^{4}+2 x^{3}+x^{2}>$ $A>x^{4}+2 x^{2}+1=\left(x^{2}+1\right)^{2}$. Therefore, there is no solution for $x \geqslant 2$. We notice that $x=1$ does not work and that $x=0$ works.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(factorisation) Find all natural numbers $n$ such that $n^{4}+4^{n}$ is prime.
|
For $n \geqslant 1, n^{4}+4^{n}=n^{4}+4 \cdot\left(2^{n-1}\right)^{2}=\left(n^{2}-n 2^{n}+2 \cdot 4^{n-1}\right)\left(n^{2}+n 2^{n}+2 \cdot 4^{n-1}\right)$ Thus, since $n^{2}+n 2^{n}+2 \cdot 4^{n-1} \geqslant 2$, if $n^{4}+4^{n}$ is prime, then $n^{2}+n 2^{n}+2=n^{4}+4^{n}$, and $n^{2}-n 2^{n}+2 \cdot 4^{n-1}=1$. Hence $\left(n-2^{n-1}\right)^{2}+4^{n-1}=1$, but $\left(n-2^{n-1}\right)^{2} \geqslant 0$, so since $4^{n-1} \geqslant 1$, it is necessarily true that $n=1$. And for $n=1$, we indeed have $n^{4}+4^{n}=5$ which is prime. And for $n=0, n^{4}+4^{n}=1$ and is therefore not prime.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all integers $n \geq 1$ such that $n$ divides $2^{n}-1$.
|
We notice that $n=1$ works. Let $p$ be a prime divisor of $n$. Then $2^{n} \equiv 1 \pmod{p}$ and $2^{p-1} \equiv 1 \pmod{p}$ by Fermat's little theorem. Therefore, considering $p$ minimal, $p \mid 2^{\gcd(n, p-1)}-1=2-1=1$, which is absurd. The answer is therefore 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
What is the multiplicity of the root 1 of $X^{2 n}-n X^{n+1}+n X^{n}-X^{2}$ for $n \in \mathbb{N}_{\geq 2}$?
|
1 is at least a root of multiplicity 1. We derive the polynomial and obtain: $2 n X^{2 n-1}-n(n+1) X^{n}+n^{2} X^{n-1}-2 X$. 1 is a root if and only if $n=2$. We derive once more if $n=2$: $12 X^{2}-12 X+4$ for which 1 is not a root. Therefore, 1 is always a simple root except if $n=2$ and then $c'$ is a double root.
Another way to determine the existence of a root of a polynomial is to use continuity: a continuous function is such that if $x$ approaches $a$, then $f(x)$ will be close to $f(a)$ for all $x$ and $a$. A polynomial satisfies the intermediate value property: if $a_{1}<a_{2}$ are real numbers and $P\left(a_{1}\right)$ and $P\left(a_{2}\right)$ have different signs, then $P$ has a root in $\left[a_{1} ; a_{2}\right]$.
Suppose that $P$ is of degree $d$ and leading coefficient $a$. When $x$ tends to $\pm \infty, P(x)$ will behave the same way as $a \cdot x^{d}$ (the ratio of $P(x)$ and $a \cdot x^{d}$ approaches 1 indefinitely as $|x|$ becomes very large).
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $P=X^{3}-3 X-1$. Calculate the sum of the inverses of the squares of the roots (real or complex) of $P$.
Soit $P=X^{3}-3 X-1$. Calculer la somme des inverses des carrés des racines (réelles ou complexes) de $P$.
(Note: The second line is kept in French as per the original text, but the first line is translated to English.)
|
Let's denote $r_{1}, r_{2}, r_{3}$ as these roots. Then by Viète's formulas:
$$
\begin{aligned}
\frac{1}{r_{1}^{2}}+\frac{1}{r_{2}^{2}}+\frac{1}{r_{3}^{2}} & =\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}+\frac{1}{r_{3}}\right)^{2}-2 \cdot\left(\frac{1}{r_{2} r_{3}} \frac{1}{r_{1} r_{2}} \frac{1}{r_{1} r_{3}}\right) \\
& =\left(\frac{r_{1} r_{2}+r_{1} r_{3}+r_{2} r_{3}}{r_{1} r_{2} r_{3}}\right)^{2}-2 \cdot\left(\frac{r_{1}+r_{2}+r_{3}}{r_{1} r_{2} r_{3}}\right) \\
& =(-3)^{2}-2 \cdot 0=9
\end{aligned}
$$
However, it is not possible to express the roots simply in terms of the coefficients in the general case (only for degrees $1,2,3,4$, and it is impossible for degrees greater than 5 (Galois groups)).
The Lagrange interpolation polynomial answers the question: can we find a polynomial whose graph passes through certain points?
Take $n$ distinct real numbers $x_{1}, \ldots, x_{n}$ and $n$ real numbers $y_{1}, \ldots, y_{n}$.
The initial idea is to start by solving an easier problem: find a polynomial $L_{k}$ of degree $n-1$ that vanishes at $n-1$ distinct real numbers $x_{1}, \ldots, x_{k-1}, x_{k+1}, \ldots, x_{n}$ and takes a certain value $y_{k}$ at $x_{k}: L_{k}=y_{k} \cdot \prod_{i \neq k} \frac{X-x_{i}}{x_{k}-x_{i}}$ works. It suffices to sum these polynomials to obtain the desired result.
The interpolation polynomial of degree $n-1$ is unique. It follows that the polynomial solutions are exactly the
$$
Q(X) \cdot \prod_{k=1}^{n}\left(X-x_{k}\right)+\sum_{k=1}^{n} L_{k}(X)
$$
with $Q(X)$ any polynomial.
All these results also hold for rationals and complexes.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $P$ be a polynomial with integer coefficients such that: $P(-1)=-4, P(-3)=-40$ and $P(-5)=$
$-156$.
What is the maximum number of integers $x$ for which: $P(P(x))=x^{2}$?
|
On a : $P(x) \equiv P(x \bmod 3) \bmod 3$ for all integer $x$. For each of the cases $x \equiv 0,1,2 \bmod 3$, we find $P(P(x)) \equiv 2 \bmod 3$ but a square is congruent to 0 or $1 \bmod 3:$ there are therefore none.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Determine the gcd of all numbers of the form
$$
(b-a)(c-b)(d-c)(d-a)(c-a)(d-b)
$$
where $a, b, c, d$ range over $\mathbb{Z}$.
## Bézout's Theorem and Euclidean Algorithm
|
Let $D$ be the gcd of all these numbers.
If we take $a=0, b=1, c=2$ and $d=3$, the product is
$$
1 \cdot 1 \cdot 1 \cdot 3 \cdot 2 \cdot 2=12
$$
Therefore, by the definition of gcd, $D \mid 12$.
Now let's check that 12 divides all numbers of this form. Let $a, b, c, d$ be four integers, and $n$ the corresponding product. By the pigeonhole principle, two of the numbers among $a, b, c$ and $d$ are congruent modulo 3. Therefore, their difference is divisible by 3. In particular, $3 \mid n$.
Now, let's look at modulo 2. Either three of the numbers among $a, b, c$ and $d$ have the same parity, or two of the numbers are even and the other two are odd. In the first case, say for example it is $a, b$ and $c$. Then $b-a$ and $c-a$ are divisible by 2, so $4 \mid n$. In the second case, we can say without loss of generality that $a$ and $b$ are even and $c$ and $d$ are odd. In this case, $b-a$ and $d-c$ are divisible by 2, so $4 \mid n$.
In all cases, $3 \mid n$ and $4 \mid n$. Since 3 and 4 are coprime, $12=3 \cdot 4 \mid n$. Finally, 12 divides each of the products, and 12 is one of the products, so $D=12$.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(IMO 2016 P4) A set of natural numbers is said to be fragrant if it contains at least two elements and if each of its elements has a prime factor in common with at least one of the other elements. Let $P(n)=n^{2}+n+1$. Determine the smallest positive integer $b$ for which there exists a positive integer $a$ such that the set
$$
\{P(a+1), P(a+2), \ldots, P(a+b)\}
$$
is fragrant.
|
Here it is natural to think that $b$ is likely to be relatively small, otherwise the problem risks being very complicated. We quickly calculate the $P(n)$ for $n$ between 1 and 20, and factorize them into prime factors to understand a bit how the problem works. Let's look at $b=2$: the question comes down to whether $P(n)$ and $P(n+1)$ are coprime. For this, we calculate $d$ their gcd. We have $d$ which divides $P(n+1)-P(n)=n^{2}+3 n+3-n^{2}-n-1=2 n+2=2(n+1)$. Moreover, $d$ is odd because $P(n)=n(n+1)+1$ is odd, so $d$ divides $(n+1$ and $n(n+1)+1$ so $d$ divides $1, d=1$.
Now what does this allow us to say about $b$? If $b=2$, let $a$ be an integer satisfying the statement. Since $P(a+1)$ and $P(a+2)$ are coprime for any integer $a$, the set is not fragranced. We have $b \geqslant 3$. If $b=3$, let $a$ satisfy the statement, $P(a+2)$ is coprime with $P(a+1)$ and $P(a+3)$ for any integer $a$, so necessarily $b \geqslant 4$.
Now we can ask ourselves if $P(n)$ and $P(n+2)$ are coprime. Let $d$ be their gcd, then $d$ divides $P(n+2)-P(n)=4 n+4+2=2(2 n+3)$. Thus $d$ divides $2 n+3$ so since $d$ divides $(2 n)^{2}+2 \times 2 n+4, d$ divides $9-6+4=7$. Thus either $d=1$, or $d=7$ and 7 divides $2 n+3$, so 7 divides $8 n+12$, so 7 divides $n-2$. In particular, since $P(2)$ and $P(4)$ are 7 and 21 and are indeed divisible by 7, we deduce that $P(7 k+2)$ and $P(7 k+4)$ are always divisible by 7. Thus $P(n)$ and $P(n+2)$ are not coprime if and only if $n \equiv 2(\bmod 7)$.
We ask the same question for $P(n)$ and $P(n+3)$: let $d$ be their gcd, we have $d$ which divides $P(n+3)-P(n)=6 n+12$ so $d$ divides $3(n+2)$. Now $P(1)$ is divisible by $3, P(0)$ and $P(2)$ are not, so we deduce that $P(3 k+2)$ and $P(3 k)$ are not divisible by 3 and $P(3 k+1)$ is. Thus if $n \equiv 1(\bmod 3), P(n)$ and $P(n+3)$ are both divisible by 3. If $n \not \equiv 1$ ( $\bmod 3$ ), we then have $d$ which divides $n+2$ and $n^{2}+n+1$, so $d$ divides $(-2)^{2}-2+1=3$, contradiction. Thus $P(n)$ and $P(n+3)$ are coprime if and only if $n \not \equiv 1(\bmod 3)-$.
Now let's return to the problem: if $b=4$, let $a$ be an integer satisfying the statement. Since $P(a+2)$ is coprime with $P(a+3)$ and $P(a+1)$, then it is not coprime with $P(a+4)$. Similarly, $P(a+3)$ is not coprime with $P(a+1)$. We then have $a+2 \equiv a+3 \equiv 2(\bmod 7)$, contradiction. If $b=5$, let $a$ be an integer satisfying the statement.
Now let's return to the problem: suppose that $b=5$, let $a$ be an integer satisfying the statement. Since $P(a+3)$ is coprime with $P(a+2)$ and $P(a+4)$, it must necessarily not be coprime with $P(n+1)$ or $P(n+5)$, and they are both divisible by 7. In particular, $P(n+2)$ and $P(n+4)$ are not divisible by 7, so they are coprime. Necessarily $P(n+2)$ and $P(n+5)$ are not coprime, same for $P(n+1)$ and $P(n+4)$, so $n+1 \equiv n+2 \equiv 1$ $(\bmod 3)$ contradiction.
Now we can ask ourselves if $P(n)$ and $P(n+4)$ are coprime. Let $d$ be their gcd, then $d$ divides $P(n+4)-P(n)=8 n+16+4=4(2 n+5)$. Thus $d$ divides $2 n+5$ so since $d$ divides $(2 n)^{2}+2 \times 2 n+4, d$ divides $25-10+4=19$. Thus either $d=1$, or $d=7$ and 19 divides $2 n+5$, so 19 divides $20 n+50$. Thus 19 divides $n-7$. Now we notice that $P(7)$ and
$P(11)$ are divisible by 19, so $P(n)$ and $P(n+4)$ are coprime if and only if $n \not \equiv 7(\bmod 19)$.
Now let's look at $b=6$, try to pair the different $P(a+1), P(a+2), \ldots, P(a+$ 6) to have potentially non-coprime pairs: thus the difference of the arguments of $p$ must be 2, 3 or 4, but not the same thing twice. We can then pair them as follows: $\{P(a+1), P(a+4)\},\{P(a+2), P(a+6)\},\{P(a+3), P(a+5)\}$. It is enough to have $a+1 \equiv 1(\bmod 3), a+2 \equiv 7(\bmod 19)$ and $a+3 \equiv 2(\bmod 7)$ and $a$ strictly positive, which is possible via the Chinese remainder theorem, so that the 3 different sets above consist of non-coprime integers. The set is then fragranced, so $b=6$ is the minimum value satisfying the statement.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Find all integers $n \geqslant 1$ such that $n$ divides $2^{n}-1$.
|
First, $n=1$ works. Conversely, suppose we have a solution $n \geqslant 2$. Let $p$ be the smallest prime factor of $n$. Since $2^{n}-1$ is odd, $n$ is also odd, hence $p \geqslant 3$.
Let $\omega$ be the multiplicative order of 2 modulo $p$. Since $\omega$ divides $n$ and divides $p-1$, it also divides $n \wedge(p-1)=1$, so $p$ divides $2^{1}-1=1$.
This impossibility shows that $n=1$ is the only solution.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
(F-M) Let $f: \mathbb{R} \rightarrow \mathbb{R}$ such that $x+f(x)=f(f(x))$ determine the solutions of $f(f(x))=0$.
|
We have the injectivity of $f$ and since $f(x)+f^{2}(x)=f^{3}(x)=f(x+f(x))$ we have $f(f(x))=0$ if and only if $f(x)=f(x+f(x))$ if and only if $x=x+f(x)$ if and only if $f(x)=0$ and thus $x+f(x)=f(f(x))=x=0$ so the only potential solution is 0. Furthermore, since $f(0)=f(f(0))$ we have $f(0)=0$ and thus $f(f(0))=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Consider the sequence $\left(a_{n}\right)_{n \in \mathbb{N}}$ defined by $a_{0}=2$ and $a_{n+1}=\sqrt{2 a_{n}-1}$ for all $n \geq 0$.
- Show that $a_{n}$ is irrational for all $n \geq 1$.
- Is the limit of $\left(a_{n}\right)$ irrational (if it exists)?
|
(solved by Pierre-Andréa Silvente)
First, the sequence is well-defined: indeed, we have $a_{n}>1$ for all integers $n \geqslant 0$. We show this by induction: we have $a_{0}>1$. Let $n$ be a positive integer, suppose $a_{n}>1$, then $a_{n+1}>$ $\sqrt{2 \times 1-1}=1$. Thus, by the principle of induction, $a_{n}>1$ for all $n \geqslant 0$.
Let's show by induction that $a_{n}$ is irrational for $n \geqslant 1$. For $n=1, a_{1}=\sqrt{3}$ which is irrational. Let $n$ be a positive integer, suppose $a_{n}$ is irrational. Since $a_{n}=\frac{1+a_{n+1}^{2}}{+} 1$, if $a_{n+1}$ is rational, then $a_{n}$ is also rational, so $a_{n+1}$ is irrational. Thus $a_{n}$ is irrational for all $n \geq 1$.
Let's show that $\left(a_{n}\right)$ is decreasing: indeed, by the positivity of $\left(a_{n}\right), a_{n+1} \leqslant a_{n}$ is equivalent to $2 a_{n}-1 \leqslant a_{n}^{2}$, which is equivalent to $\left(a_{n}-1\right)^{2} \geqslant 0$ which is true. Thus the sequence $\left(a_{n}\right)$ is decreasing and bounded below by 1, so it converges to a limit $l$ satisfying $l \geqslant 1$. By the continuity of $x \mapsto \sqrt{2 x-1}$ and the fixed point theorem, we have $l=\sqrt{2 l-1}$, so $l^{2}-2 l+1=0$, thus $(l-1)^{2}=0$: we have $l=1$ which is rational.
|
1
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Find the polynomials with integer coefficients $P$ such that:
$$
\forall n, n \text { divides } P\left(2^{n}\right)
$$
|
(let solved by Brieux Madeline-Derou)
Let $k$ be a positive integer and $q$ an odd prime integer. Set $n=2^{k} q$, then $n$ divides $P\left(2^{n}\right)$. Now $2^{n}=2^{(} 2^{k} \times 2^{q}$. By Fermat's Little Theorem, we have $0 \equiv P\left(2^{n}\right) \equiv P\left(2^{2^{k}} 2^{q}\right) \equiv P\left(2^{2^{k}} \times 2\right) \equiv P\left(2^{2^{k}+1}\right)$ $(\bmod q)$. Thus, every odd prime integer $q$ divides $P\left(2^{2^{k}}+1\right)$, and since it has an infinite number of prime factors, $P\left(2^{2^{k}+1}\right)=0$ for all positive integers $k$. Therefore, $P$ has an infinite number of zeros, and by rigidity, $P=0$. Conversely, $P=0$ works because for any positive $n$, $n$ divides 0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $n$ be a natural number. Consider $2 n+1$ tickets, each having a number which is a positive integer. Suppose that the sum of the numbers on the $2 n+1$ tickets does not exceed 2330 but that the sum of the numbers on any group of $n$ tickets is always greater than 1165.
Determine the maximum value of $n$.
|
(solved by Yaël Dillies)
Let $a_{1}<\cdots<a_{2 n+1}$ be the numbers written on the tickets.
We directly have $a_{i} \leqslant a_{j}+(i-j)$ for all $1 \leqslant i \leqslant j \leqslant 2 n+1$. Therefore, for all $i \in \llbracket 1, n+1 \rrbracket$,
$$
a_{i}=\frac{n a_{i}}{n} \leqslant \frac{1}{n} \sum_{j=n+2}^{2 n+1}\left(a_{j}+i-j\right)=\frac{a_{n+2}+\cdots+a_{2 n+1}}{n}+i-\frac{3}{2} n(n+1)
$$
Applying this to $i=1, \ldots, n+1$, we get:
$$
\begin{aligned}
2330 & \leqslant \sum_{i=1}^{2 n+1} a_{i} \\
& =\sum_{i=1}^{n} a_{i}+\sum_{i=n+1}^{2 n+1} a_{i} \\
& \leqslant \sum_{i=1}^{n+1}\left(\frac{a_{n+2}+\cdots+a_{2 n+1}}{n}+i-\frac{3}{2}(n+1)\right)+a_{n+2}+\cdots+a_{2 n+1}
\end{aligned}
$$
$\leqslant 1165\left(2+\frac{1}{n}\right)+-(2 n+1) \frac{n+1}{2}$
From this, we derive $n\left(n+\frac{1}{2}\right)(n+1) \leqslant 1165$, and thus $n \leqslant 10$ since $1165<1331=11^{3}<11$. $\left(11+\frac{1}{2}\right)(11+1)$ and the quantity $n\left(n+\frac{1}{2}\right)(n+1)$ is increasing in $n$. Conversely, $n=10$ is possible by taking $a_{i}=100+i$ for all $i \in \llbracket 1,21 \rrbracket$:
$-a_{1}+\cdots+a_{21}=21 a_{11}=21 \cdot 111=2331 \geqslant 2330$
$-a_{i_{1}}+\cdots+a_{i_{10}} \leqslant a_{12}+\cdots+a_{21}=10 \cdot \frac{121+112}{2}=1165$
The maximum sought is therefore 10.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Let $\sigma(n)$ be the sum of the prime divisors of $n$ (counted without multiplicity). Find all $n$ such that:
$$
\sigma\left(2^{n}+1\right)=\sigma(n)
$$
|
(Solved by Elias Caeiro)
Let us note that by Zsigmondy, if $n \neq 3, 2^{n}+1$ admits a primitive prime factor which is therefore congruent to 1 modulo $2n$. Indeed, if we denote $q$ this factor, $q \neq 2$ and the order of 2 modulo $q$ divides $2n$, but does not divide $n$. In particular, the order can be written as $2a$ with $a$ dividing $n$. We know that $p$ divides $\frac{2^{2a}-1}{2^{a}-1}=2^{a}+1$ so we must have $a=n$ because $q$ is primitive.
In particular, $\sigma\left(2^{n}+1\right)>2n$. Now, if we denote $p_{1}, \ldots, p_{k}$ the prime factors of $n$, we have $n \geqslant p_{1} \ldots p_{k}$ and $\sigma(n)=p_{1}+\cdots+p_{k} \leqslant 2 p_{1} \times \cdots \times p_{k}$ (we can easily show this by induction on $k$ since all the $p_{i}$ are at least 2).
It remains to consider the case $n=3$: we have $2^{n}+1=9$ so $\sigma\left(2^{n}+1\right)=\sigma(n)=3$. Thus, only $n=3$ is a solution.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A triangle has sides of length 3, 4, and 5. Determine the radius of the inscribed circle (circle inside the triangle and tangent to all three sides).
|
If we call $I$ the center of the inscribed circle, and $r$ the radius of the inscribed circle, since $r$ is the height of each of the triangles $I A B, I B C$ and $I C A$, the area of these triangles is: $\frac{1}{2} r \times A B$, $\frac{1}{2} r \times B C, \frac{1}{2} r \times C A$, so their sum is $r p$ by calling $p$ the semi-perimeter $\frac{1}{2}(A B+B C+C A)$.
## II. FIRST DAY
1. WARM-UP EXERCISES
The sum of these three areas is precisely the area $S$ of the triangle $A B C$, regardless of the point I inside the triangle, and by the Pythagorean theorem, since $3^{2}+4^{2}=5^{2}$, this triangle is right-angled. Its area is $S=\frac{1}{2}(3 \times 4)=6$, its semi-perimeter, $p=\frac{1}{2}(3+4+5)=6$, so the radius of its inscribed circle is: $r=\frac{S}{p}=1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. The natural number $n$ and the real number $a$ satisfy the relation
$$
n-\left(\frac{a-1}{a+1517}+\frac{\sqrt{|a|-2023}+\sqrt{2023-|a|}}{a-2023}\right)^{2024}=0
$$
Determine the last digit of the number $n$.
|
## Solution.
From the existence conditions of $\sqrt{|a|-2023}$ and $\sqrt{2023-|a|}$, we obtain $|a|-2023 \geq 0$ and $2023-|a| \geq 0$, which are equivalent to $|a| \geq 2023$ and $|a| \leq 2023$. From the last two inequalities, we get $|a|=2023$, or $a= \pm 2023$.
Since the denominator of the fraction $\frac{\sqrt{|a|-2023}+\sqrt{2023-|a|}}{a-2023}$ cannot be zero, we get $a \neq 2023$. For $a=-2023$, we obtain
$n-\left(\frac{-2023-1}{-2023+1517}+\frac{\sqrt{|-2023|-2023}+\sqrt{2023-|-2023|}}{-2023-2023}\right)^{2024}=0, n-4^{2024}=0, n=4^{2024}$. Since $n=4^{2024}=\left(4^{2}\right)^{1012}=16^{1012}$, we get that the last digit of the number $n$ is 6.
Answer: The last digit of the number $n$ is 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Determine all natural numbers $n$, which have exactly four positive divisors, knowing that the sum of all positive divisors of the number $n$ is twice as large as $n$.
|
## Solution:
Since the natural number $n$ has exactly four positive divisors, it follows that the number has the form $n=p \cdot q$, $p \neq q$ or $n=p^{3}$, where $p$ and $q$ are prime numbers.
Assume that $n=p \cdot q$. Then the positive divisors of the number $n$ are $1, p, q$, and $p \cdot q$. From the problem data, we obtain the equation $1+p+q+p q=2 p q$, which is equivalent to
$p q-p-q=1 \quad \Leftrightarrow p(q-1)-q+1=2 \Leftrightarrow(q-1)(p-1)=2$.
The last relation can only hold in two cases: 1) $q-1=1$ and $p-1=2$ or 2) $q-1=2$ and $p-1=1$. Thus, $q=2, p=3$ or $q=3, p=2$. In both cases, we get $n=6$.
Assume that $n=p^{3}$. Then the positive divisors of the number $n$ are $1, p, p^{2}$, and $p^{3}$. From the problem data, we obtain the equation $1+p+p^{2}+p^{3}=2 p^{3}$. Since $2 p^{3} \vdots p$ and $\left(p+p^{2}+p^{3}\right) \vdots p$, it follows that $1 \vdots p$. Contradiction since $p \geq 2$.
Answer: $n=6$.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.6. Consider the numbers: $a=2^{2}+4^{2}+6^{2}+\cdots+2020^{2} ; b=1^{2}+3^{2}+5^{2}+\cdots+2019^{2}$; $c=1 \cdot 2+2 \cdot 3+3 \cdot 4+\cdots+2019 \cdot 2020$. Calculate the value of the expression $E=\frac{a-b}{a+b-c}$.
|
## Solution:
$a-b=2^{2}+4^{2}+6^{2}+\cdots+2020^{2}-\left(1^{2}+3^{2}+5^{2}+\cdots+2019^{2}\right)=\left(2^{2}-1^{2}\right)+\left(4^{2}-3^{2}\right)+$ $\left(6^{2}-5^{2}\right)+\ldots .+\left(2020^{2}-2019^{2}\right)=3+7+11+\ldots .+4039=4042 \cdot 505$. $a+b-c=1^{2}+2^{2}+3^{2}+$. . $+2020^{2}-(1 \cdot 2+2 \cdot 3+3 \cdot 4+\ldots .+2019 \cdot 2020)=1+$ $\left(2^{2}-1 \cdot 2\right)+\left(3^{2}-2 \cdot 3\right)+\left(4^{2}-3 \cdot 4\right)+\ldots+\left(2020^{2}-2019 \cdot 2020\right)=1+2+$ $3+$. . . $+2020=2021 \cdot 1010=4042 \cdot 505$.
Therefore, $E=1$.
Answer: $E=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.3. Let the complex number $z=\frac{1}{2}-\frac{\sqrt{3}}{4}+\frac{1}{4} i$. Show that the value of the ratio $\sqrt{3} \cdot \frac{\operatorname{Re}\left(z^{2024}\right)}{\operatorname{Im}\left(z^{2024}\right)}$ is a rational number.
|
Solution 1. $z=\frac{1}{2}\left(1-\frac{\sqrt{3}}{2}+\frac{1}{2} i\right)=\frac{1}{2}\left(1-\cos \frac{\pi}{6}+i \sin \frac{\pi}{6}\right)=\frac{1}{2}\left(2 \sin ^{2} \frac{\pi}{12}+2 i \sin \frac{\pi}{12} \cos \frac{\pi}{12}\right)=$
$$
\begin{gathered}
=\sin \frac{\pi}{12}\left(\sin \frac{\pi}{12}+i \cos \frac{\pi}{12}\right)=i \sin \frac{\pi}{12}\left(\cos \left(-\frac{\pi}{12}\right)+i \sin \left(-\frac{\pi}{12}\right)\right) \\
z^{2024}=\sin ^{2024} \frac{\pi}{12}\left(\cos \left(-\frac{506 \pi}{3}\right)+i \sin \left(-\frac{506 \pi}{3}\right)\right)= \\
=\sin ^{2024} \frac{\pi}{12}\left(\cos \left(-168 \pi-\frac{2 \pi}{3}\right)+i \sin \left(-168 \pi-\frac{2 \pi}{3}\right)\right)=\sin ^{2024} \frac{\pi}{12}\left(-\frac{1}{2}-i \frac{\sqrt{3}}{2}\right)
\end{gathered}
$$
Then $\sqrt{3} \cdot \frac{\operatorname{Re}\left(z^{2024}\right)}{\operatorname{Im}\left(z^{2024}\right)}=\sqrt{3} \cdot \frac{-\frac{1}{2} \sin ^{2024} \frac{\pi}{12}}{-\frac{\sqrt{3}}{2} \sin ^{2024} \frac{\pi}{12}}=1 \in \mathbb{Q}$.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
11.2. Calculate the limit $\lim _{n \rightarrow \infty}\left(\left(1+\frac{1}{2}\right) \cdot\left(1+\frac{1}{2+3}\right) \cdot \ldots \cdot\left(1+\frac{1}{2+3+\ldots+n}\right)\right)$.
|
Solution.
Let $P_{n}=\left(1+\frac{1}{2}\right) \cdot\left(1+\frac{1}{2+3}\right) \cdots \cdot\left(1+\frac{1}{2+3+\ldots+n}\right)$.
$$
\begin{aligned}
& S_{n}=1+2+\ldots+n=\frac{n(n+1)}{2}, \forall n \in \mathbb{N}^{*} \Rightarrow \\
& S_{n}-1=2+3+\ldots+n=\frac{n(n+1)}{2}-1=\frac{n^{2}+n-2}{2}=\frac{(n-1)(n+2)}{2}, \forall n \in \mathbb{N}^{*} \Rightarrow \\
& P_{n}=\frac{S_{2}}{S_{2}-1} \cdot \frac{S_{3}}{S_{3}-1} \cdot \ldots \cdot \frac{S_{n}}{S_{n}-1}=\prod_{k=2}^{n} \frac{S_{k}}{S_{k}-1}=\prod_{k=2}^{n} \frac{k(k+1)}{(k-1)(k+2)}=
\end{aligned}
$$
$$
\begin{gathered}
=\frac{\left(\prod_{k=2}^{n} k\right) \cdot\left(\prod_{k=3}^{n+1} k\right)}{\left(\prod_{k=1}^{n-1} k\right) \cdot\left(\prod_{k=4}^{n+2} k\right)}=\frac{n!\cdot \frac{(n+1)!}{1 \cdot 2}}{(n-1)!\cdot \frac{(n+2)!}{1 \cdot 2 \cdot 3}}=\frac{3 \cdot n!\cdot(n+1)!}{(n-1)!\cdot(n+2)!}=\frac{3 \cdot n}{n+2}, \forall n \in \mathbb{N}^{*} \Rightarrow \\
\lim _{n \rightarrow \infty} P_{n}=\lim _{n \rightarrow \infty} \frac{3 \cdot n}{n+2}=3 .
\end{gathered}
$$
11. 3. Determine all continuous functions $f: \mathbb{R}_{+}^{*} \rightarrow \mathbb{R}$, which satisfy the relation
$$
f\left(\frac{x}{y}\right)=\frac{f(x)}{y}-\frac{f(y)}{x}, \quad \forall x, y \in \mathbb{R}_{+}^{*}
$$
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.4. Let $I_{n}=\int_{1}^{n} \frac{[x]}{x^{2}+1} d x, n \in \mathbb{N}, n \geq 2$. Calculate: $\lim _{n \rightarrow \infty} \frac{I_{n}}{\ln n}$.
|
## Solution:
According to the Stolz-Cesàro lemma, we obtain
$$
\begin{gathered}
\lim _{n \rightarrow \infty} \frac{I_{n}}{\ln n}=\lim _{n \rightarrow \infty} \frac{I_{n+1}-I_{n}}{\ln (n+1)-\ln n} \\
I_{n+1}-I_{n}=\int_{n}^{n+1} \frac{[x]}{x^{2}+1} d x=n \int_{n}^{n+1} \frac{d x}{x^{2}+1}= \\
=n(\operatorname{arctg}(n+1)-\operatorname{arctg} n)= \\
=n \cdot \operatorname{arctg} \frac{(n+1)-n}{1+(n+1) n}=n \cdot \operatorname{arctg} \frac{1}{n^{2}+n+1}
\end{gathered}
$$
Then
$$
\lim _{n \rightarrow \infty} \frac{I_{n+1}-I_{n}}{\ln \left(1+\frac{1}{n}\right)}=\lim _{n \rightarrow \infty} \frac{n \cdot \operatorname{arctg} \frac{1}{n^{2}+n+1}}{\ln \left(1+\frac{1}{n}\right)}=\lim _{n \rightarrow \infty} \frac{n \cdot \frac{1}{n^{2}+n+1}}{\frac{1}{n}}=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.6. Let the function $f: \mathbb{R} \rightarrow \mathbb{R}, f(x)=a x+b, a, b \in \mathbb{R}^{*}$. If $m, n$ are distinct natural numbers such that
$$
\begin{gathered}
n>2, m>2, f(1)+f(2)+\cdots+f(m)=-n \text { and } f(1)+f(2)+\cdots+f(n)=-m \text {, calculate } \\
\frac{f(1)+f(2)+\cdots+f(m+n)}{m+n}
\end{gathered}
$$
|
Solution: $f(1)+f(2)+\cdots+f(m)=a \cdot \frac{m(m+1)}{2}+m b$, similarly $f(1)+f(2)+\cdots+f(n)=$ $a \cdot \frac{n(n+1)}{2}+n b \Rightarrow a m^{2}+a m+2 m b+2 n=0$ and $a n^{2}+a n+2 n b+2 m=0 \Rightarrow$ $a m^{2}+a m+2 m b+2 n-a n^{2}-a n-2 n b-2 m=0 \Leftrightarrow a(m+n+1)=2(1-b)$ $(m \neq n)$.
$f(1)+f(2)+\cdots+f(m+n)=a \cdot \frac{(m+n)(m+n+1)}{2}+b(m+n)$. However, $a(m+n+1)=$
$2(1-b) \Rightarrow f(1)+f(2)+\cdots+f(m+n)=\frac{(m+n) 2(1-b)}{2}+b(m+n)=m+n \Rightarrow$ $\frac{f(1)+f(2)+\cdots+f(m+n)}{m+n}=1$.
Answer: 1
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Solve in $\mathbb{R}$ the equation $\sqrt{8 x^{2}+10 x-3}-\sqrt{8 x+12}=3+\sqrt{4 x+8}-\sqrt{4 x^{2}+7 x-2}$.
|
## Solution.
The equation from the statement is equivalent to the equation $\sqrt{(4 x-1)(2 x+3)}+\sqrt{(4 x-1)(x+2)}-2 \sqrt{2 x+3}-2 \sqrt{x+2}=3$.
We will have $D V A=\left[\frac{1}{4} ;+\infty\right)$.
Next, we write the equation in the form
$\sqrt{4 x-1}(\sqrt{2 x+3}+\sqrt{x+2})-2(\sqrt{2 x+3}+\sqrt{x+2})=3 \Leftrightarrow(\sqrt{4 x-1}-2)(\sqrt{2 x+3}+\sqrt{x+2})=3$.
Since $\sqrt{2 x+3}+\sqrt{x+2}>0$ for any $x \in D V A$, it follows from (1) that $\sqrt{4 x-1}-2>0$, i.e., $x>\frac{5}{4}$. Therefore, the equation from the statement can have solutions only on the interval $\left(\frac{5}{4} ;+\infty\right)$.
The sum of two strictly increasing functions is a strictly increasing function. Therefore, the function $f(x)=\sqrt{2 x+3}+\sqrt{x+2}$ is strictly increasing on $\left(\frac{5}{4} ;+\infty\right)$, and it is also positive. The function $g(x)=\sqrt{4 x-1}-2$ is also a strictly increasing and positive function on $\left(\frac{5}{4} ;+\infty\right)$.
The product of two positive and strictly increasing functions is a strictly increasing function, which represents the left-hand side of equation (1), while the right-hand side of equation (1) is a constant. Therefore, equation (1) has at most one solution on the interval $\left(\frac{5}{4} ;+\infty\right)$.
We observe that for $x=2 \in\left(\frac{5}{4} ;+\infty\right)$ in (1) we have $(\sqrt{7}-2)(\sqrt{7}+2)=3$, which is true.
Thus, the only solution is $x=2$.
Answer: $S=\{2\}$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. Let the set $M=\{f: \mathbb{R} \rightarrow \mathbb{R} \mid f(2 f(x)+x)+f(x)=4 x-4\}$.
a) Show that the set $M$ is not empty.
b) Find all numbers $a \in \mathbb{R}$ such that $f(a)=0$ holds for at least one function $f \in M$.
c) Find all numbers $a \in \mathbb{R}$ such that $f(a)=0$ holds for all functions $f \in M$.
|
Solution. a) Let's show that the function $f: \mathbb{R} \rightarrow \mathbb{R}, f(x)=x-1$ belongs to the set $M$. Indeed, $f(2 f(x)+x)+f(x)=f(3 x-2)+x-1=4 x-4$. Therefore, $M \neq \varnothing$.
b) We will show that the set of these values $a$ is not empty, i.e., there exists a zero for at least one function in $M$. For this, we choose a function $f$ from $M$, namely $f(x)=x-1$. This function has the zero $x=1$.
We will now show that any function in $M$ can have a zero only at $x=1$.
Let $f \in M$ and $x_{0}$ be a zero of $f$, i.e., $f\left(x_{0}\right)=0$. In the relation $f(2 f(x)+x)+f(x)=4 x-4$, substituting $x$ with $x_{0}$, we get $4 x_{0}-4=f\left(2 f\left(x_{0}\right)+x_{0}\right)+f\left(x_{0}\right)=f\left(x_{0}\right)+0=0 \Rightarrow x_{0}=1$. Therefore, any function $f \in M$ can have at most one zero, namely $x_{0}=1$, i.e., $a=1$.
Answer: $a=1$.
c) We will show that $x=1$ is a zero for any function $f \in M$, i.e., the equality $f(1)=0$ holds.
Let $f \in M$. Denote $f(1)=b$. Then $f(2 f(1)+1)+f(1)=4-4 \Leftrightarrow f(2 b+1)=-b$.
In the relation $f(2 f(x)+x)+f(x)=4 x-4$, substituting $x$ with $2 b+1$, we get:
$f(2 f(2 b+1)+2 b+1)+f(2 b+1)=4(2 b+1)-4 \Leftrightarrow f(-2 b+2 b+1)+f(2 b+1)=8 b \Leftrightarrow$ $\Leftrightarrow b-b=8 b \Leftrightarrow b=0$.
Thus, we have shown that the functions $f \in M$ have a unique zero, $x=1$. Therefore, $a=1$.
Answer: $a=1$.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.