_id
stringlengths 1
6
| text
stringlengths 0
5.02k
| title
stringlengths 0
170
|
|---|---|---|
83882
|
شاید این یک سوال احمقانه باشد، اما در نسبیت من مقدار زیادی ${g^{i}}_j$ برای یک تانسور متریک $g$ می بینم. آیا این فقط $$\delta^i_j ~=~ g(dx^i \sharp, \partial_{ x^j})~ است؟$$
|
منظور فیزیکدانان از ${g^{i}}_j$ چیست؟
|
123861
|
من از سرعت Verlet در دینامیک مولکولی استفاده می کنم. آیا فقط یک سوال ساده، اگر یک شبیه سازی با استفاده از فمتوثانیه مرحله زمانی، در سرعت Verlet فقط $dt = 10^{-15}$ برای استفاده از فمتوثانیه ضروری است؟
|
مرحله زمانی Verlet
|
134207
|
یک تاجر از نیروی 12 نیوتن [یا بیشتر] برای حمل کیف خود برای فاصله افقی 200 متری استفاده می کند. او چقدر روی کیف کار می کند؟ من سعی کردم نیرو را در فاصله ضرب کنم اما پاسخی که گرفتم با پاسخ در پاسخنامه متفاوت است. پاسخ صحیح 0 است. نمی دانم چرا باید از این فرمول استفاده کنیم: W = F * D
|
کار و انتقال انرژی
|
24796
|
در تصور من، انرژی هستهای میتواند از بین برود وقتی که ما تمام برق تولیدکننده اورانیوم را مصرف کنیم یا بمبهای هستهای را منفجر کنیم. آیا اورانیوم یک منبع تجدیدپذیر است؟ اگر نه، آیا می توانیم ثابت کنیم که این عنصر نمی تواند با پرتاب نوترون ها و پروتون ها به هم ایجاد شود؟
|
آیا اورانیوم قابل تجدید است یا این سناریوی علمی تخیلی به واقعیت تبدیل خواهد شد؟
|
83888
|
آیا راندمان گرمایش اجاق مایکروویو به حالت ماده ای که گرم می کند بستگی دارد؟ اگر بله، چگونه؟
|
امواج مایکروویو و حالت ماده
|
83880
|
آیا حالت پایه $| 0 \rangle$ نوسانگر هارمونیک یک حالت منسجم است فقط به این دلیل که محصول عدم قطعیت را به حداقل می رساند؟ شهود این چیست. من کاملاً اهمیت وضعیت پایه بودن یک حالت منسجم را درک نمی کنم. هر توضیحی قدردانی خواهد شد
|
چرا حالت پایه $| 0 \rangle$ نوسانگر هارمونیک یک حالت منسجم است؟
|
41624
|
این بیشتر برای روشنایی شخصی من است و مستقیماً با هیچ مدرسه یا پروژه کاری مرتبط نیست. من فقط سه نشانگر لیزری (قرمز، سبز و آبی) را برداشتم و متوجه شدم که وقتی آنها را به نمایش می گذارم، قرمز و آبی در چشم من از رنگ سبز تیره تر به نظر می رسد. من یک سوء ظن زودگذر داشتم که شاید این اثری از وجود آبی و قرمز در حاشیه مقیاس نور بصری باشد، اما صادقانه بگویم نمی دانم که آیا این چنین است یا اینکه فقط چشمانم مرا فریب می دهند. در این مورد، هر سه لیزر دارای قدرت اسمی یکسانی هستند.
|
چرا لیزرهای سبز روشن تر و قوی تر از لیزرهای قرمز و آبی به نظر می رسند؟
|
23024
|
چرا وقتی موسیقی در هدفون دارم و آنها را روی میز میگذارم، صدای موسیقی متفاوت است، مانند زمانی که من واقعاً از آنها استفاده میکنم، توناژ/حجم متفاوتی دارد؟
|
چرا وقتی موسیقی از گوشی دورتر شنیده می شود تونالیته متفاوتی دارد؟
|
41626
|
سلام، من روی آزمایشی کار می کردم که در آن LED ها را در نیتروژن مایع فرو می برم و تغییر رنگ را یادداشت می کنم. همه منابع آنلاینی که دیده ام پیش بینی می کنند که طول موج نور ساطع شده توسط LED با غوطه ور شدن کاهش می یابد. مشاهده شده است، با این حال، کاهش ناگهانی در طول موج و به دنبال آن افزایش قطعی در طول موج است، به عنوان مثال، یک LED زرد در ابتدا سبز شد، و سپس به سرعت به زرد-نارنجی تغییر یافتم. به نقل از Re: افزایش طول موج LED غوطه ور در نیتروژن مایع
|
افزایش طول موج LED غوطه ور در نیتروژن مایع
|
41625
|
سوال خیلی سریع، در نسبیت عام آیا تار و پود فضا، بافت فضا-زمان یا هر دو ذکر شده است؟
|
آیا تار و پود فضا است یا پارچه فضا-زمان؟
|
123866
|
من یک برد مدار چاپی دارم که یک خازن الکترولیتی نصب روی سطح به آن لحیم شده است. این قوطی دو پایه دوکی دارد که این قوطی را نگه میدارند، بنابراین میتواند کمی روی محور پاها به جلو و عقب حرکت کند. این برای جدا شدن از برد در حین تست ارتعاش کافی است.  آزمایش با نصب پیچ و مهره PCB روی سورتمه فلزی انجام می شود که سپس به طور تصادفی با شتاب کنترل شده به جلو و عقب می لرزد. و من کاهش سرعت را فرض می کنم) که از 3 گرم تجاوز نمی کند. خازن من با شتاب بسیار کمتری نسبت به آنچه که داده های تست سازندگان نشان می دهد، لیدهای خود را قطع کرد. این من را به سوال فیزیک واقعی من می رساند. از آنجایی که شتاب سورتمه ثابت نگه داشته می شود، کنجکاو هستم که آیا جرم سورتمه استفاده شده تفاوتی در نیروی احساس شده توسط خازن ایجاد می کند. اگر خانه آزمایش 1 از سورتمه 1 پوندی استفاده می کرد اما خانه آزمایش 2 از سورتمه 40 پوندی استفاده می کرد، آیا نیرویی که توسط خازن احساس می شود در خانه آزمایش 2 بیشتر خواهد بود زیرا جرم سورتمه برای رسیدن به آن شتاب به نیروی بیشتری نیاز دارد؟
|
نیرویی که توسط خازن نصب شده روی برد مدار چاپی احساس می شود
|
129777
|
کتابی را تصور کنید که ما آن را با نیرویی که دقیقاً برابر با نیروی گرانش است بلند می کنیم تا نیروها خنثی شوند و کتاب با سرعت ثابت حرکت کند. وضعیت پس از برداشته شدن کتاب را در نظر بگیرید، و یک بار دیگر آرام گرفت. با توجه به قوانین کار و انرژی جنبشی $\Delta W = \Delta K$ این به نظر می رسد در اینجا برقرار است، زیرا هر دو صفر هستند. اشکالی ندارد، اما افزایش انرژی پتانسیل از کجا آمده است؟ آیا انرژی ذخیره نمی شود؟
|
مفهوم انرژی بالقوه
|
43959
|
این دانش نسبتاً رایج است که وقتی کسی فوتبال را پا می زند، اگر به عقب متمایل شود توپ معمولاً بالاتر می رود و اگر کمی به جلو متمایل شود، در ارتفاع مطلوب تری می رود. چرا تکیه دادن به عقب باعث می شود توپ بالاتر برود؟ من حدس میزنم که میتواند به مرکز جرم یا تکانه زاویهای مربوط باشد.
|
چرا تکیه دادن به عقب باعث می شود توپی که پا زده شده بالاتر برود؟
|
74462
|
من سعی می کنم آزمایش دو شکاف یانگ را در خانه انجام دهم. توجه داشته باشید که من لیزر ندارم فقط مشعل دارم. من میتوانم یک لامپ تهیه کنم یا از یک شمع استفاده کنم، اگر کمک میکند شکافها را با برش دادن کاغذ نمودار سیاه با چاقو ایجاد کنم. من سعی کردم با قرار دادن یک شکاف تک، شکاف های دوتایی و یک صفحه نمایشگر یکی پس از دیگری یک راه اندازی ایجاد کنم و یک مشعل را از طریق شکاف تک بتابانم. من فاصله بین تک شکاف/دو شکاف و دو شکاف/صفحه نمایش را امتحان کردم که کمکی نکرد. **_من هیچ الگوی تداخلی را رعایت نکردم._** تنها چیزی که به دست آوردم دو حاشیه روشن موازی بود، مانند آنهایی که با تابیدن یک مشعل از طریق دو شکاف بسیار ضخیم به دست می آورید. > فکر میکنم مشکل دقیقاً همین است، این که شکافها بسیار ضخیم هستند. > ** عرض شکاف بهینه ای که باید برای مشاهده تداخل > الگو داشته باشم چقدر است؟ چگونه می توانم آن را با یک کاغذ نمودار بسازم؟** من ویدیوهایی از این آزمایش را به صورت آنلاین دیده ام، که در آن افراد از سرب های مداد و مو (!!) استفاده می کنند، اما هر دو از لیزر استفاده می کنند. _من نمیخوام از لیزر استفاده کنم_(فقط به این دلیل که لیزر ندارم و احتمالا خیلی تنبلم که برم و بگیرم!). توجه داشته باشید که ممکن است استفاده از مواد دیگری که ممکن است به راحتی در خانه در دسترس باشد را پیشنهاد کنید.
|
عرض شکاف بهینه در آزمایش دو شکاف یانگ
|
123867
|
من می خواهم یک عبارت برای سرعت انتهای یک رشته باز که به دلیل کشش آن منقبض می شود داشته باشم. نه نوسانات عرضی، که به نظر سرعت نور است، بلکه نوسانات یک پایان در فضازمان است. **وظیفه**: در ابتدا من یک رشته Nambu-Goto باز به طول $\sigma_0$ دارم. من آن را از $\sigma_0$ به $\sigma_l$ کشش دادم و اجازه دادم استراحت کند. از آنجا که با کشش $T_0$ تحت فشار قرار می گیرد، می خواهد طول ist را کاهش دهد. **سوال**: وابستگی $X(t)$ نقاط انتهایی رشته (t-time، X-مختصات) چیست؟ آیا می توانم کشش $T_0$ را به عنوان نیروی ثابتی در نظر بگیرم که بر روی بارها در انتهای رشته عمل می کند (چان-پاتون شارژ می کند)؟ اگر اینطور باشد، میتوانم حرکت رشتهها را به عنوان حرکت یک ذره نسبیتی توصیف کنم: $X(t)=\frac{c^2}{F/m}(\sqrt{1+\frac{( t-t_0)F/m}{c}})^2-1)$؟ یا جایز نیست؟
|
وابستگی X(t) انتهای رشته کشیده شده Nambu-Goto چیست؟
|
68851
|
بیایید با مشکلی مانند این برخورد کنیم: > فرض کنید یک A دوقلو در سیستم مختصات $x'y'$ داریم که **دور** > سفر به ستاره ای که 12 دلار سال نوری از ما فاصله دارد و او با آن سفر می کند، انجام می دهد. a > سرعت $u=0.6c$. دوقلو B با سیستم مختصات $xy$ روی زمین می ماند. چند > سال می گذرد تا دوقلو B تا یک دوقلو A برگردد. چند سال > برای Twin B می گذرد؟ * * * **در این صورت من خودم را در یک سیستم مختصات $xy$** قرار می دهم زمان $\Delta t$ را محاسبه می کنم (این آسان است زیرا $u$ یک ثابت است): $$u = \frac{ \Delta x}{\Delta t} \longrightarrow \Delta t = \frac{\Delta x}{u} = \frac{2 \cdot 12~l.y.}{0.6c}=\frac{2\cdot 12\cdot c \cdot 1 y}{0.6c} = 40y$$ بنابراین برای دوقلو B 40 سال میگذرد. **با توجه به اتساع زمان، هر ساعتی که در سیستم انتخاب شده در حالت استراحت نباشد، زمان مناسب را اندازه گیری نمی کند**. در سیستم مختصات انتخاب شده فعلی $xy$ فقط ساعت ناظر B در حالت استراحت است، بنابراین زمان مناسبی مانند $\boxed{\Delta t \equiv \tau}$ را انتخاب میکنیم. از این نتیجه میشود که: \begin{align} \Delta t' = \gamma \Delta t = 1.25 \cdot 40y = 50y \end{align} بنابراین ناظر در سیستم مختصات $xy$ میگوید که برای برادرش چنین است. 50 سال گذشت اکنون سعی می کنم همان نتیجه را با استفاده از تبدیل های لورنتس برای سیستم مختصات $xy$ محاسبه کنم: \begin{align} \Delta t' &= \gamma \left(\Delta t - \Delta x \frac{u}{c ^2}\راست)\\\ \Delta t' &= 1.25\left(40y - 2\cdot 12 \cdot c \cdot 1y \frac{0.6c}{c^2}\right)\\\ \Delta t' &= 1.25\left(40y - 2\cdot 12 \cdot 1y\cdot 0.6\right)\\\ \Delta t' & = 32y \end{align} **نتیجه یکسان نیست...** * * * اگر زمان مناسب را متفاوت انتخاب کنم نتایج یکسان خواهد بود $\boxed{\Delta t' \equiv \tau}$ از این پس، به دنبال آن خواهد بود: $$\Delta t = \gamma \Delta t \longrightarrow \Delta t' = \frac{1}{\gamma} \Delta t = \frac{1}{1.25}40y = 32y$$ اما من نمی توانم این کار را انجام دهم زیرا ساعتی که زمان $\Delta t'$ را اندازه می گیرد در سیستم مختصات $xy$ در حالت استراحت نیست. * * * **پس ما مشکل داریم.** من واقعاً نمی دانم چه اشتباهی کردم. آیا برداشت من از زمان مناسب اشتباه است یا تبدیل لورنتس اشتباه است. برای درک کامل این موضوع چه چیزی را از دست داده ام؟
|
دگرگونی های لورنتس و اتساع زمانی نتیجه یکسانی را بر نمی گرداند
|
87643
|
ویکی پدیا: > _نیروی محافظه کار نیرویی است با این ویژگی که کار انجام شده در > حرکت یک ذره بین دو نقطه مستقل از مسیر طی شده است. > به طور معادل، اگر یک ذره در یک حلقه بسته حرکت کند، کار خالص انجام شده (مجموع نیروی وارده در طول مسیر ضرب در مسافت طی شده) > در یک نیروی محافظه کار صفر است. _ آیا کار انجام شده توسط نیرو باقی می ماند. 0 حتی اگر در تمام نقاط حلقه متفاوت باشد؟ از تعریف ارائه شده در ویکی پدیا به نظر می رسد که برای کار انجام شده توسط یک نیروی محافظه کار ثابت تعریف شده است. آیا کار روی یک حلقه 0 برای نیروهای متغیر نیز انجام می شود؟ آیا می توان آن را برای یک نیروی متغیر به نوعی اثبات کرد؟
|
کاری که توسط یک نیروی محافظه کار انجام شده است
|
44102
|
بنابراین من شروع به بررسی کتاب مکانیک کوانتومی برای ریاضیدانان L. Takhatajan کردم و فرمول ریاضی QM را که او استفاده می کند دیدم (صفحه 51). (فایل پی دی اف در اینجا موجود است.) من فقط یک کلاس مکانیک کوانتومی به سبک فیزیک پایه گذرانده ام و می خواستم ببینم آیا کسی می تواند توضیح دهد که چگونه تعریف عملگر حالت ها (Axiom 3) با آنچه معمولاً در کلاس فیزیک تدریس می شود مطابقت دارد ( به عنوان مثال، توابع $L^{2}$). من اخیراً پست مربوط به فرمول فضایی هیلبرت تقلبی QM را دیدم و همچنین علاقه مند به مقایسه این بدیهیات با تاخاتجان هستم. آیا تعریف تاختاجان از حالت ها به نحوی شامل (یا می توان با آن) توابع ویژه عملگرهای موقعیت و حرکت را در بر می گیرد؟
|
فرمولبندی ریاضی مکانیک کوانتومی تاخاتجان
|
33371
|
میخواهم بدانم آیا جرم سیاهچالهای که از یک ستاره متولد شده، شبیه ستاره مادرش است یا خیر؟ آیا سیاهچاله متولد شده در مقایسه با ستاره مادرش جرم زیادی خواهد داشت یا کم. آیا سیاهچاله در طول عمر خود با خوردن ستاره های همسایه جرم خود را افزایش می دهد؟ پیشاپیش از کمک شما متشکرم
|
آیا جرم ستاره مادر برابر با جرم سیاهچاله متولد شده است
|
23341
|
به نظر می رسد که سرعت فاز نور می تواند بزرگتر از $c$ باشد، اگر $\sqrt{\epsilon \mu} <1/c$ باشد، یعنی برای پراکندگی غیرعادی. 1. آیا نمونه هایی از این گونه رسانه ها وجود دارد؟ برای دیامغناطیس از $\mu < \mu_0$ ممکن به نظر می رسد. 2. و معنای فیزیکی سرعت فاز در این حالت علاوه بر سرعت سطح موج چیست؟ چرا نمی توان آن را به عنوان یک موجود فیزیکی دید که سریعتر از نور حرکت می کند؟
|
چرا پراکندگی غیرعادی اجازه انتشار سریعتر از نور را نمی دهد؟
|
92965
|
من یک پست قبلی در این مورد خوانده بودم، اما پاسخ به اندازه کافی کامل نبود یا متوجه نشدم! بگذارید واضح تر بگویم، من تفاوت بین وزن و جرم را می دانم. همچنین روش مرسوم نشان دادن Kg و Kgf را به عنوان واحد وزن در برخی کشورها می شناسم. سوال من این است که مثلا ماشین را بگویم. گفته می شود که تویوتا کرولا وزنی معادل 2800 پوند یا 1270 کیلوگرم دارد. آیا مشخصات فوق واقعاً وزن (جرم x گرم) یا جرم ماشین را نشان می دهد؟
|
وقتی وزن یک جسم ذکر می شود، آیا واقعاً جرم است یا وزن؟
|
15540
|
> یک پل یکنواخت با وزن 1200 کیلونیوتن و طول 17 متر بر روی تکیه گاه های > هر انتها که عرض آنها 1 متر است قرار دارد. یک کامیون ثابت با وزن 60 کیلو نیوتن دارای مرکز جرم > 3 متر از مرکز پل است. > > نیروی تکیه گاه روی پل را در هر انتها محاسبه کنید. من جواب 642N و 618N را گرفتم. در حالی که جواب کتاب میگه 640 و 620. من فاصله بین دو ساپورت رو 15 گرفتم، باید 17 متر بگیرم، اگه هست چرا؟
|
چگونه مکان نیروها را هنگام محاسبه گشتاورها انتخاب می کنید؟
|
83776
|
به نظر می رسد تلفن های همراه مدرن دارای فیلترهای IR بر روی دوربین خود هستند. من می خواهم آزمایشی انجام دهم تا بفهمم این فیلترها چه طول موج هایی را می گذارند و کدام را مسدود می کنند. چگونه می توانم این کار را انجام دهم؟ همچنین، چه نوع تجهیزاتی نیاز دارم؟ من یک دانشجوی دانشگاه هستم بنابراین به یک آزمایشگاه فیزیک که به خوبی عرضه شده است دسترسی دارم. با تشکر
|
چگونه فرکانس قطع فیلتر IR را روی دوربین تست کنیم؟
|
128371
|
اگر من یک سنگ کوچک (1 کیلوگرم) را به یک سنگ بزرگ (100 کیلوگرم) پرتاب کنم، سنگ کوچک منعکس می شود. فرض کنید وزن من 80 کیلوگرم است - اگر به جای انعکاس در یک سنگ بزرگ بپرم، در همان جهت یک سنگ بزرگ حرکت می کنم. سنگ بزرگ سنگین تر است اما من را بازتاب نمی دهد - چرا اینطور است؟
|
چه چیزی نشان می دهد که آیا شی منعکس خواهد شد - مثال خاص
|
47664
|
جهانشمول بودن در مکانیک آماری به خوبی با تئوری گروه های عادی سازی مجدد توضیح داده شده است. با این حال، مقادیر کافی از مطالعات عددی و نظری وجود دارد که نشان میدهد در مدلهایی مانند مدل Ising، شیشه چرخشی، زنجیره پلیمری و نفوذپذیری قابل نقض است (مرجع مثال: 1، 2، 3، 4، 5، 6، 7) و برخی از تخلفات بسیار قوی هستند. بنابراین، سؤال من این است: * دلایل کلی نقض عمومیت چیست؟ * همچنین، چرا نمی توان آنها را با تئوری گروه های عادی سازی مجدد و فرضیه مقیاس بندی توضیح داد؟ * آیا همیشه درست است که برخی از عناصر اصلی برای هر کلاس جهانی وجود دارد؟ هر زمان که آنها غایب باشند، به طور قطع می توان گفت که در یک کلاس جهانی بودن نیستند. * آیا نمونهای از کلاس جهانی شناخته شده (مانند مدل دوبعدی Ising) وجود دارد که با تغییر جزئیات میکروسکوپی، شارحان بحرانی مختلف را نشان میدهد؟ توجه داشته باشید، با تعریف کلاس جهانی بودن نباید اتفاق بیفتد، اما هیچ مدرکی برای همه کلاس های جهانی وجود ندارد. من پاسخ هایی را می پذیرم که در مورد مثال های محکمی برای برخی از کلاس های جهانی در مورد این سؤالات بحث می کنند. * * * توجه: جهانی بودن به دسته بزرگی از سیستم های مختلف اطلاق می شود که بدون توجه به جزئیات میکروسکوپی آن مانند نوع شبکه (شبکه های مربع، شش ضلعی، مثلثی و کاگوم)، خواص یکسانی را از خود نشان می دهند. در مکانیک آماری، کلاس جهانی بودن معمولاً با تقارن پارامتر ترتیب (مانند تقارن بالا به پایین در مدل آیزینگ و تقارن کروی در مدل هایزنبرگ) و ساختار توپولوژیکی (مانند ابعاد) تعیین می شود.
|
دلایل نقض جهانی بودن در مکانیک آماری
|
8264
|
من 2 سوال دارم، به عنوان یک پدر و مادر مهاجر و جدید ساکن شانگهای (2000 کیلومتری فوکوشیما) جایی که ما اکنون در حال تجربه ریزش رادیواکتیو از نیروگاه هستهای فوکوشیما (ژاپن) هستیم، نمیتوانیم هیچ اطلاعات واقعی درباره محدودیتهای ایمن برای آن به دست آوریم. غذا و هوا ما به سادگی گزارشهایی را که به ما داده میشود درک نمیکنیم، و نه توضیحات ضعیفی را که همراه با گزارشها هستند، که با طراحی نوشته شدهاند تا سعی کنند مردم احساس امنیت کنند و وحشت نکنند. در واقع، ما هیچ ایده ای نداریم که آیا اعداد منتشر شده حتی درست هستند یا خیر. چیزی که به ما گفته می شود این است که بله، ریزش وجود دارد و برخی از سبزیجات 1-3 Bq/Kg روی آنها شناسایی شده است، یعنی اسفناج. و برای هوا در شانگهای امروز (mBq/m(3)) 131-I (0.58)، 137Cesium (0.17) و 134Cesium (0.16). اکنون می دانم - با توجه به آموخته هایم - هیچ کس نمی تواند جزئیات و قطعیت هایی را با این همه به من بدهد، اما ما در اینجا به چه چیزی نگاه می کنیم؟ آیا هر یک از شما نابغه های این جامعه - و من این را با احترام می گویم - می تواند به من بگوید که آیا این سطوح خطرناک هستند؟ از راهنمایی شما سپاسگزارم...
|
آیا این ذرات رادیواکتیو و انتشارات هوا در فاصله 2000 کیلومتری فوکوشیما خطرناک هستند؟
|
122116
|
با این دو عنصر چگونه می توان نیمه عمر ایزوتوپ را با استفاده از سینتیک مرتبه اول تعیین کرد؟ نیمه عمر nobelium-259 ثبت شد @ 58 دقیقه نیمه عمر fermium-253 ثبت شد @ 3 روز اگرچه من نمی دانم، احتمالاً غلظت اولیه متوسطی وجود دارد که احتمالاً می توان با نام عنصر تعیین کرد. شاید در نظرات کسی بتواند من را با برخی از میانگین های تخمینی مرتبط کند تا بسط ریاضی در پاسخ آورده شود.
|
با این دو عنصر چگونه می توان نیمه عمر ایزوتوپ را با استفاده از سینتیک مرتبه اول تعیین کرد؟
|
47662
|
M2-9 نمونه ای از یک سحابی دوقطبی است که شبیه دو نازل موشک پشت به پشت است. آیا ممکن است این شکل (تا حدی برای انفجار غیرعادی) نتیجه یک گرادیان زمانی باشد؟ یک ستاره نوترونی در حال چرخش که سقوط کرده و تکانه زاویهای خود را با سرعت استوایی با نسبتهای نسبیتی حفظ کرده باشد، در زمان بسیار متفاوتی با قطبهای ستاره خواهد بود. کشیدن فریم این اثر را از استوا به فضای همسایه گسترش می دهد. نواختری که تحت این شرایط منفجر میشود، در قطبها به سمت بیرون محدود میشود، زیرا گرادیان زمان نسبیتی، فضا را در آینده نزدیک به استوا، نسبت به قطبها، قرار میدهد و همان «اکنون» را به اشتراک نمیگذارد، و آن فضا را برای فضاهای در حال گسترش غیرقابل دسترس میکند. انفجار چیزی که با سرعت بسیار کمتری بچرخد به شکل کروی تری منفجر می شود. آیا این دلیل قابل قبولی برای شکل سحابی های دوقطبی است؟
|
آیا یک سحابی دوقطبی می تواند با گرادیان زمانی تولید شود؟
|
9012
|
پارادوکسی که من تصور می کنم شامل دو جسم است که در پتانسیل های گرانشی بسیار متفاوت وجود دارند -- یکی بسیار بالا (مثلاً: نزدیک به یک سیاهچاله) و دیگری بسیار پایین (مثلاً: دور از سیاهچاله). حال، تصور کنید این اجرام در واقع سفینههای فضایی کوچکی هستند که موتورهای خود را منفجر میکنند تا در فاصله ثابتی از سیاهچاله باقی بمانند. همچنین تصور کنید که آنها با یکدیگر ردیف شده اند (سیاهچاله، سفینه فضایی نزدیک و سفینه فضایی دور یک خط را تشکیل می دهند). آیا می توان رشته ای را از سفینه فضایی دیگر به سفینه فضایی که نزدیکتر است پایین آورد؟ **یعنی فاصله بین دو سفینه ثابت اندازه گیری می شود؟** _اگر نیست.._ لطفا این را توضیح دهید! عجیب به نظر می رسد که فاصله بین دو کشتی ثابت نباشد. _اگر هست_، به نظر می رسد که یک پارادوکس وجود دارد. ابتدا بیایید سفینه فضایی نزدیکتر به سیاهچاله را A و سفینه دیگر را B بگذاریم. بعد، فرض کنید طول رشته دقیقاً 1 ثانیه نوری باشد. حالا بیایید یک ساعت نوری بین A و B شروع کنیم -- A یک پالس نوری به B می فرستد، و با دریافت آن، B یک پالس نور را به A می فرستد، و به همین ترتیب. به پیش. از آنجایی که A و B هر دو می دانند که فاصله آنها 1 ثانیه نوری است، هر بار که پالس را دریافت می کنند، 2 ثانیه به ساعت خود اضافه می کنند. در حالی که ما در آن هستیم، آنها ممکن است زمان ضبط شده خود را با پالس نور ارسال کنند. تناقض این است که از منظر B که A را مشاهده می کند، A باید در حرکت آهسته به نظر برسد - همه چیز به قرمز منتقل می شود و همه چیز کندتر اتفاق می افتد. از منظر A در حال مشاهده B، B به رنگ آبی تغییر می کند و در حرکت سریع حرکت می کند. با این حال، این مورد نمی تواند باشد، زیرا هر دو در فواصل 2 ثانیه ای تیک دریافت می کنند و هر تیک نشان دهنده 2 ثانیه زمان سپری شده در طرف مقابل است. بنابراین، چه چیزی می دهد؟ من فرض میکنم که اگر پتانسیلهای گرانشی دو جسم متفاوت باشد، نمیتوان فاصله ثابتی بین دو جسم داشت. اما این خیلی عجیب به نظر می رسد. با تشکر ویرایش: بسیار مفید خواهد بود اگر پاسخها بتوانند مثالی از نحوه حضور در A و B. اگر روی A هستید و نبض را ارسال میکنید، قبل از شنیدن چقدر زمان میسنجید. از B برگشته؟ اگر روی B هستید و نبض را ارسال می کنید، قبل از اینکه از A بشنوید چقدر زمان می سنجید؟
|
پارادوکس نسبیت عام: نگه داشتن یک رشته در طول یک گرادیان گرانشی
|
134201
|
کتاب درسی من می گوید که با یک بار خالص اتم سدیم یونیزه شده +e داریم و اگر سطح کروی را با مرکزیت یون انتخاب کنیم و به اندازه ای بزرگ باشد که همه آن را در خود جای دهد، نیازی به دانستن توزیع بار درون یون نداریم. و با استفاده از قانون گاوس می توان میدان الکتریکی خارج از شعاع کره R را به صورت $E(R)=-\frac{e}{4\pi \varepsilon_0R^2}$ پیدا کرد. مشکل من اینجاست حتما باید بدانیم که شارژ به طور مساوی در اطراف مرکز توزیع می شود؟ اگر ما اینطور نبودیم، تمام بار می تواند مثلاً همه در یک طرف کره باشد و بنابراین میدان الکتریکی در آن طرف بزرگتر از میدان الکتریکی در طرف دیگر کره خواهد بود؟
|
قانون و یون های گاوس؟
|
44105
|
برای درک نقش تئوری بازنمایی در QM/QFT به کمک نیاز دارم. درک من از نظریه بازنمایی در این زمینه به شرح زیر است: سیستمی که ما در حال مطالعه آن هستیم تقارن های فیزیکی وجود دارد. این مجموعه از تقارن ها یک گروه $G$ را تشکیل می دهد. با این حال، فضاهای هیلبرت متعددی وجود دارد که میتوانیم از آنها برای نمایش سیستم مذکور استفاده کنیم. بنابراین میخواهیم $G$ را بهعنوان مجموعهای از همشکلها در هر فضای هیلبرت که برای استفاده انتخاب میکنیم، نشان دهیم. و برای انجام این کار، از یک نمایندگی استفاده می کنیم. اولاً آیا این تفسیر درستی است؟ آیا چیز بیشتری برای آن وجود دارد؟ ثانیاً، نمایشها معمولاً هممورفیسمهای گروهی هستند، نه لزوماً هممورفیسمها. آیا می توانیم گروهی (در فیزیک) را با نمایشی که هم شکلی نیست نشان دهیم؟ و اگر بتوانیم این کار را انجام دهیم از نظر فیزیکی چه معنایی دارد؟
|
نقش نظریه بازنمایی در QM/QFT؟
|
23342
|
> شبیه سازی مورد اشاره در box2d است. یک جسم به حداکثر ارتفاع $h$ با گرانش $g$ پرتاب می شود، سرعت اولیه آن چقدر است؟ من موارد زیر را امتحان کردم: $v = v_0 - g t$ $0 = v_0 - g t$ $t = \frac{v_0}{g}$ $h = v_0 * t - \frac{1}{2}g * t^2 $ $v_0 = \sqrt{2 * g * h}$ اما با قرار دادن آن در شبیهسازی فیزیکی، حداکثر ارتفاع متفاوتی به دست میآید، آیا معادله اشتباه است یا یک مصنوع شبیهسازی است؟
|
چگونه می توانم سرعت اولیه یک جسم پرتاب شده را با استفاده از حداکثر ارتفاع بدانم؟
|
128372
|
(این تکلیف نیست، من سعی می کنم برای مقاله ای که دارم می نویسم تصویری بسازم.) فرض کنید من یک نوار مستطیلی نازک با رسانایی یکنواخت دارم و در جاهای مختلف پروب های نقطه ای دارم: 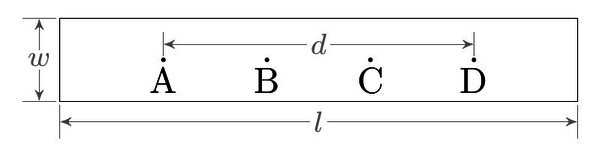 نوار دارای عرض است $w$ و ضخامت $t$ که در آن $t \ll w $. من قصد دارم بین نقاط $\boldsymbol A$ و $\boldsymbol D$ جریان را به نوار تزریق کنم. (فقط فرض کنید 1 آمپر در نقطه $\boldsymbol A$ وارد می شود و در نقطه $\boldsymbol D$ خارج می شود) اینها در امتداد عرض میله قرار دارند و فاصله $d$ از هم دارند. چگونه خطوط هم پتانسیل و چگالی جریان را بفهمم؟ * * * ویرایش: خاطرات مبهم از الکترواستاتیک کالج در حال بازگشت هستند - معادله لاپلاس است که در اینجا مرتبط است، من باید راه حلی برای $\nabla^2 V = 0$ پیدا کنم، سپس میدان های الکتریکی فقط گرادیان $V هستند. $ بنابراین $J = \sigma E = \sigma \nabla V$، و میدانم که شرایط مرزی در خارج مستطیل این است که جزء عمود بر $E$ $0$ است، اما من مطمئن نیستم که در مرحله بعد چه کنم.
|
محاسبه خطوط هم پتانسیل و چگالی جریان در یک هادی مستطیلی
|
15547
|
تفسیر کپنهاگ توسط نیلز بور اصرار دارد که سیستمهای کوانتومی مستقل از دستگاه اندازهگیری وجود ندارند، بلکه فقط توسط خود فرآیند اندازهگیری به وجود میآیند. فقط از طریق دستگاه است که می توان در مورد سیستم هر چیزی گفت. بر حسب ضرورت، دستگاه باید خارج از سیستم باشد. یک سیستم کوانتومی باز آیا مکانیک کوانتومی را می توان در سیستم های بسته ای که دستگاه اندازه گیری خود بخشی از سیستم است به کار برد؟ آیا یک دستگاه اندازه گیری می تواند خود را بسنجد و خود را به وجود آورد؟
|
باز کردن سیستم های کوانتومی و دستگاه های اندازه گیری
|
120056
|
متن من می گوید که سیگنال های ساطع شده در اندازه فیزیکی افق $l_{H}(t)$ به ناظر در زمان $t$ با یک انتقال بی نهایت به قرمز می آیند. چگونه این را از نظر ریاضی نشان دهم؟ رویکرد من به شرح زیر است: \begin{equation}l_H(t)=a(t)\eta(t)=a(t)\int_0^t\frac{dt'}{a(t')}=\frac {1}{1+z(t)}\int_0^t(1+z(t'))dt'.\end{equation} اکنون نمیدانم چگونه این را نتیجهگیری کنم. کسی میتونه لطفا کمکم کنه؟
|
انتقال بی نهایت به قرمز
|
72950
|
من یک تابع موج دارم ($a=1nm$): $$\psi=Ax\exp\left[\tfrac{-x^2}{2a}\right]$$ که قبلاً ضریب نرمالسازی را برای آن محاسبه کردهام. موضوع دیگر): $$A = \sqrt{\frac{2}{a\sqrt{\pi a}}} = 1.06\frac{1}{nm\sqrt{nm}}$$ چیزی که میخواهم بدانم نحوه محاسبه مقدار انتظار برای انرژی جنبشی است. من سعی کردم آن را به صورت تحلیلی محاسبه کنم اما در ادغام گم شدم: \begin{align} \langle E_k \rangle &= \int\limits_{-\infty}^{\infty} \overline\psi\hat{T} \psi \,dx = \int\limits_{-\infty}^{\infty} Axe \exp \left[{-\tfrac{x^2}{2a}}\right]\left(-\tfrac{\hbar^2}{2m}\tfrac{d^2}{dx^2}Ax \exp \ left[{-\tfrac{x^2}{2a}}\right]\right)\,dx =\dots \end{align} در این مرحله میروم و مشتق_دومین را حل میکنم و ادامه میدهم. بعد از این: \begin{align} &\phantom{=}\tfrac{d^2}{dx^2}Ax \exp \left[{-\tfrac{x^2}{2a}}\right] = A \tfrac{d^2}{dx^2}x \exp \left[{-\tfrac{x^2}{2a}}\right]= A\tfrac{d}{dx}\left(\exp \left[{-\tfrac{x^2}{2a}}\right]-\tfrac{2x^2}{2a}\exp \left[{ -\tfrac{x^2}{2a}}\right]\right)= \\\ &=A \left(-\tfrac{2x}{2a}\exp \left[{-\tfrac{x^2}{2a}}\right] - \tfrac{1}{a}\tfrac{d}{dx}x^2\exp \left[{-\tfrac{x ^2}{2a}}\right]\right) = \\\ &=A \left(-\tfrac{x}{a}\exp \left[{-\tfrac{x^2}{2a}}\right] - \tfrac{2x}{a}\exp \left[{-\tfrac{x^2}{2a}}\right] + \tfrac{x^3}{a^2}\exp \left[{-\tfrac{x^2}{2a}}\right]\right) = \\\ &= A \left(-\tfrac{3x}{a}\exp \left[{-\tfrac{x^2}{2a}}\right] + \tfrac{x^3}{a^2}\exp \left [{-\tfrac{x^2}{2a}}\right]\right) \end{align} بسیار خوب، اکنون میتوانم ادغام را ادامه دهم: \begin{align} \dots &= \int\limits_{-\infty}^{\infty} Axe \exp \left[{-\tfrac{x^2}{2a}}\right]\left(-\tfrac{\hbar^2}{2 دقیقه } \left(-\tfrac{3x}{a}\exp \left[{-\tfrac{x^2}{2a}}\right] + \tfrac{x^3}{a^2}\exp \left[{-\tfrac{x^2}{2a}}\right]\right)\right)\,dx = \\\ &= \int \limits_{-\infty}^{\infty} -\frac{A^2\hbar^2}{2m}x\exp\left[-\tfrac{x^2}{2a}\right] \left(-\tfrac{3x}{a}\exp \left[{-\tfrac{x^2}{2a}}\right] + \tfrac{x^3}{a^2}\exp \left [{-\tfrac{x^2}{2a}}\right]\right) \,dx\\\ &= \int\limits_{-\infty}^{\infty} \frac{A^2\hbar^2}{2m}\left(\tfrac{3x^2}{a}\exp \left[{-\tfrac{x^2}{a}}\right] - \ tfrac{x^4}{a^2}\exp \left[{-\tfrac{x^2}{a}}\right]\right) \,dx\\\ &= \frac{A^2\hbar^2}{2m} \underbrace{\int\limits_{-\infty}^{\infty}\left(\tfrac{3x^2}{a}\exp \left[{ -\tfrac{x^2}{a}}\right] - \tfrac{x^4}{a^2}\exp \left[{-\tfrac{x^2}{a}}\right]\right) \,dx}_{\text{چگونه این مشکل را حل کنم؟}}=\dots\\\ \end{align} این همان نقطه ای است که من به خودم اعتراف کردم که در یک انتگرال گم شده ام و از WolframAlpha برای کمک به خودم استفاده کردم. خب نتیجه عجیبی گرفتم استاد من به نوعی این را دریافت کرده است ($m$ جرم یک الکترون است) اما من نمی دانم چگونه: \begin{align} \dots = \frac{\hbar^2}{2m}\cdot\frac{3} {2a} = \frac{3\hbar^2}{4ma} = 0.058eV \end{align} آیا کسی میتواند به من کمک کند تا آخرین انتگرال را بفهمم؟ چگونه می توانم آن را حل کنم؟ آیا از نظر تحلیلی امکان پذیر است (به نظر می رسد استاد این کار را انجام داده است، اما من در مورد آن مطمئن نیستم)؟
|
محاسبه مقدار انتظار برای انرژی جنبشی $\langle E_k \rangle$ برای یک تابع موج شناخته شده
|
133263
|
من فکر می کنم این بدون داشتن نقطه مرجع قابل پاسخگویی نیست که زمین با چه سرعتی در فضا حرکت می کند، اما اگر اشتباه می کنم لطفاً فاصله مطلق را بیان کنید. با توجه به اینکه زمین به دور محور خود می چرخد و به دور خورشید و منظومه شمسی به دور مرکز کهکشان می چرخد. محیط زمین در خط استوا 25000 مایل است. زمین در حدود 24 ساعت می چرخد. بنابراین، اگر بخواهید بدون حرکت در بالای سطح زمین در استوا آویزان شوید، طی 24 ساعت 25000 مایل را می بینید، با سرعت 25000/24 یا کمی بیش از 1000 مایل در ساعت. زمین همچنین با سرعتی در حدود 67000 مایل در ساعت به دور خورشید در حال حرکت است. با استفاده از اندازه گیری سرعت گاز در فواصل مختلف از مرکز کهکشان، به نظر می رسد خورشید با سرعت 200 کیلومتر در ثانیه در حال حرکت است و تکمیل مدار بزرگ به دور کهکشان 240 میلیون سال طول می کشد. من مطمئن نیستم که فقط جمع کردن اعداد درست است یا باید از فرمولی استفاده کرد زیرا همه حرکات چرخشی هستند. **اگر یک فرد به طور متوسط 80 سال عمر کند، در طول عمرش چه مسافتی را طی می کند؟** ویرایش: نقطه مرجع باید مرکز کهکشان ما باشد، مگر اینکه معتقد باشید نقطه مرجع بهتری ممکن است وجود داشته باشد. EDIT2: آیا این محاسبه جمع آوری است یا چیزی را گم کرده ام. > 1000 مایل در ساعت = 447.04 متر بر ثانیه، 67000 مایل در ساعت = 29951.68 متر بر ثانیه > 447.04 + 29951.68 + 200000 = 230398.72 متر بر ثانیه > 80 سال = 2.52458 > 2.52455 > 239 ثانیه 2.52455e9 ثانیه = 5.8165309e+14 متر > 5.8165309e+14 متر = 3888.11076 واحد نجومی یا 0.0614820933 نور > سال. ویرایش 3: پاسخ زیر از @Johannes > 371000 m/s * 2.52455e9 ثانیه = 9.3660805e+14 متر > 9.3660805e+14 متر = 6260.83811 واحد نجومی یا 0.06350 سال نوری ویرایش 4: من تازه متوجه شدم که باید هر 4 مورد را اضافه کنم (چرخش زمین + چرخش به دور خورشید + چرخش به دور کهکشان + و سرعت حرکت خوشه کهکشانی نسبت به CMB). > 5.8165309e+14 متر + 9.3660805e+14 متر = 1.5182611e+15 متر > 1.5182611e+15 متر = 10148.9489 واحدهای نجومی = 0.160481 سال نوری ~ 6% طول عمر یک سال نوری.
|
انسان در طول عمر خود چه مسافتی را طی می کند؟
|
83883
|
چگونه هیگز می تواند این همه کوپلینگ یوکاوا داشته باشد؟ آیا این تقریباً مشابه این نیست که بگوییم هیگز برای هر جفت مختلف نیرو یا بار دارد؟ آیا این نشانه ای از زیرساخت هیگز است یا نوعی اختلاط با دیگر ذرات خنثی اسکالر که هنوز پیدا نشده اند؟
|
چگونه هیگز می تواند این همه کوپلینگ یوکاوا داشته باشد؟
|
47665
|
پس از خواندن راهنمای نسبیت عام، به این فکر کردم که یک توپ بولینگ روی یک ورقه لاستیکی بزرگ چه شکلی ایجاد می کند. برای سادگی، من می خواهم فرض کنم که قانون هوک در مورد لاستیک اعمال می شود. کاری که من تاکنون انجام دادهام این است: قاب 1 بعدی یک جرم $M$ است که در وسط یک نوار لاستیکی با طول $L$ و ثابت فنر $k$ معلق است. در این حالت، نوار یک شکل V ایجاد میکند، که در آن زاویه در وسط (بین نوار و افقی) توسط $2Tsin(\theta) = Mg$ محدود میشود، و کشش مربوط به مقدار کشش است. قانون هوک، به دادن $T = k \Delta L = k (\sqrt{L^2 + (L\ tan\ \theta)^2 } - L)$. با این حال، من مطمئن نیستم که چگونه در مورد 2 بعدی اقدام کنم. آیا در نظر گرفتن یک ورق لاستیکی به عنوان مش بی نهایت ظریف از نوارهای لاستیکی معتبر است؟ به طور شهودی، در فاصله ای $r$ از نقطه جرم، به نظر می رسد که جرم باید به طور مساوی توسط ماده در دایره شعاع $r$ پشتیبانی شود، بنابراین $2\pi r T sin(\theta_r) = خواهیم داشت. Mg$. با این حال، این بدان معنی است که به عنوان $r\rightarrow 0$، $T\rightarrow\infty$ داریم که فیزیکی نیست (فکر میکنم کشش باید در همه جای صفحه ثابت باشد.) روش صحیح مدلسازی شکل چیست. از یک ورق لاستیکی با جرم نقطه ای روی آن؟
|
توپ بولینگ روی یک ورق لاستیکی
|
71887
|
در سرن - به لحظه برخورد ذرات (رویداد) در شتاب دهنده ذرات با هم چه می گویید؟ در سرن، ذرات مختلف را با هم میکوبند و آنچه را که بیرون میآید اندازهگیری میکنند. نام رویداد (لحظه) برخورد ذرات در تونل چیست؟ آیا نامی برای خود رویداد یا خود تصادف وجود دارد؟
|
در سرن - به لحظه برخورد ذرات (رویداد) در شتاب دهنده ذرات با هم چه می گویید؟
|
94437
|
آیا بدن انسان ما می تواند با سرعت نور در یک شاتل فضایی حرکت کند؟ در واقع، آیا هر جسم مادی با جرم غیر صفر می تواند با سرعت نور نسبت به یک قاب اینرسی معتبر حرکت کند؟ اگر نه، چرا که نه؟
|
آیا انسان می تواند با سرعت نور حرکت کند؟
|
88642
|
من سعی می کنم بفهمم آیا تصویری که در یک میکروسکوپ نوری مرکب تشکیل شده است در بی نهایت است یا خیر. هر جا که نگاه می کنم پاسخ های متناقضی می گیرم.
|
تصویر در یک میکروسکوپ نوری مرکب تشکیل شده است
|
33377
|
سکینو و ساسکیند استدلال کردهاند که سیاهچالهها اطلاعات را سریعتر از هر نظریه میدان کوانتومی در این مقاله به هم میزنند. مکانیسم چنین درهمکاری چیست؟
|
مکانیسم درهم آمیختن سریع اطلاعات توسط سیاهچاله ها چیست؟
|
89590
|
من برای امتحانم آماده می شوم، اما در درک اینکه چرا در فرمول فاصله $d=\frac{1}{2}در^2$، $\frac{1}{2}$ وجود دارد، مشکل دارم؟
|
چرا یک $\frac{1}{2}$ در فرمول فاصله $d=\frac{1}{2}در^2$ وجود دارد؟
|
8265
|
من چندین نسخه خوب برای خرید پیدا کرده ام، اما همه نسخه های رایگان یا لاتین، انگلیسی قدیمی یا پیکسلی هستند. من در گوگل جستجو کردم و فقط توانستم موارد رایگانی که از صفحه ویکی پدیا در Philosophiæ Naturalis Principia Mathematica به آنها پیوند داده شده اند را پیدا کنم.
|
آیا ترجمه انگلیسی مدرن خوبی از Philosophiæ Naturalis Principia Mathematica نیوتن برای مشاهده یا دانلود رایگان موجود است؟
|
122110
|
اصل پائولی می گوید: تابع موج دو فرمیون یکسان باید کاملاً ضد متقارن باشد. من می دانم که برای یک تابع موج ضد متقارن، $(-1)^L*(-1)^{S+1}*(-1)^{I+1}=-1$ کاملاً ضد متقارن به معنای این رابطه یا یعنی این 3 رابطه: $(-1)^L=-1$ و $(-1)^{S+1}=-1$ و $(-1)^{I+1}=-1$ باید به طور همزمان تأیید شود؟
|
تابع موج کاملاً ضد متقارن: توضیح در مورد اصطلاحات
|
123241
|
من یک بار شنیدم که یک ساختمان بلند، فرض کنید 10 طبقه، در واقع به دلیل وجود ساده، باعث وزش باد می شود. همچنین گفته شد که به همین دلیل است که مناطق مرکزی شهر معمولاً بادخیز هستند. حقایق مربوط به تینز چیست؟
|
یک ساختمان بلند چه نیرویی به هوا وارد می کند؟
|
94430
|
بهترین راه برای توزیع نویز از بیش از یک منبع (من سیستمی با تعداد زیادی را متصور هستم)، در داخل یک گنبد، با زمین به عنوان هدف اصلی آن، در فرکانس ها و حجم های بهینه برای ایجاد حداکثر ارتعاش در زمین چیست؟ فکر کنید، این تصویر - http://hyperphysics.phy- astr.gsu.edu/hbase/acoustic/imgaco/foc3.gif \- اما با بیش از یک منبع.  من فرض میکنم که شما میخواهید گنبد کاملاً دایرهای باشد و نقطهای باشد که دیوار گنبد با زمین برخورد میکند. در شیب کمی (بر خلاف عمودی) بنابراین تمام صدا به سمت زمین می ماند. توپ تنیس را تصور کنید که از وسط نصف شده، اما درست قبل از خط استوا تقسیم شده است. طرف کوچکتر را بردارید و آن را برگردانید. این چیزی است که من تصور می کنم. من فقط از روی نقاشی بالا قضاوت می کنم که شما می خواهید منابع صدا تا حد امکان نزدیک به مرکز گنبد قرار گیرند، تا جایی که می توانید آن را طراحی کنید، و شاید به گونه ای هدایت شوند که همه آنها به آن اشاره داشته باشند. مرکز نواحی مستقل و به اندازه خودشان (گنبد کل سطح سطحی است که صدا به آن اشاره می کند). به نظر می رسد اگر بتوانید تمام صدا را در نقطه ای از تکینگی قرار دهید و آن را در مرکز گنبد قرار دهید، و سپس به نحوی آن را رها کنید - این ایده آل خواهد بود (اگرچه بسیار پیچیده به نظر می رسد). در مورد فرکانس یا حجم مطمئن نیستم.
|
صدا - برای اهداف ارتعاش
|
95885
|
اگر دمای اتاق را 20 درجه سانتیگراد فرض کنیم، کدام یک از سیالات گرما را بهتر هدایت می کند و چرا؟
|
کدام یک گرما را بهتر هدایت می کند: آب یا هوا؟
|
126747
|
آیا کتاب یا مرجعی وجود دارد که به طور جامع مقاطع مقطعی را برای فرآیندهای مختلف در QED یا فیزیک ذرات فهرست کند؟ فکر میکنم چنین کتابی مرجع بسیار مفیدی خواهد بود، و بهویژه میخواهم استخراج مقاطع متقاطع را تمرین کنم.
|
خلاصه مقطعی؟
|
65149
|
با توجه به ورودی ویکیپدیا در مورد ثابت ساختار ریز: > در واقع، α یکی از حدود 20 پارامتر تجربی در مدل استاندارد > فیزیک ذرات است که مقدار آن در استاندارد > مدل تعیین نمیشود. اما، لیست پارامترهای ویکیپدیا، α را ذکر نکرده است: me جرم الکترون 511 keV mμ جرم میون 105.7 MeV mτ جرم Tau 1.78 GeV mu جرم کوارک بالا μMS = 2 GeV 1.9 MeV md جرم کوارک پایین میکرومتر = 2 GeV 4.4 MeV کوارک عجیب جرم μMS = 2 GeV 87 MeV mc جرم کوارک جذاب μMS = mc 1.32 GeV mb جرم کوارک پایین μMS = mb 4.24 GeV mt جرم کوارک بالا طرح روی پوسته 172.7 گیگا الکترون ولت θ12 CKM 12-زاویه اختلاط 13.1 درجه θ23 CKM 23- زاویه اختلاط 2.4 درجه زاویه اختلاط 2.4 درجه θ13xM CKM ناقض CP فاز 0.995 g1 یا g'U(1) کوپلینگ گیج μMS = mZ 0.357 g2 یا g SU(2) کوپلینگ گیج μMS = mZ 0.652 g3 یا gs SU(3) کوپلینگ گیج μMS = mZ 1.221 خلاء زاویه θQCD QCD 0 v مقدار انتظار خلاء هیگز 246 GeV mH جرم هیگز ~ 125 GeV (آزمایشی) آیا α یکی از پارامترهای اساسی مدل استاندارد است؟ اگر نه، پس آیا یک فرمول ساده برای α از نظر این پارامترهای دیگر وجود دارد؟ (حدس من این است که α را می توان از g1/g2/g3 مشتق کرد. با این حال، من تا کنون نتوانسته ام یک فرمول صریح پیدا کنم.)
|
آیا ثابت ساختار ریز پارامتری از مدل استاندارد است؟
|
122118
|
در تئوری پراکندگی، میتوان یک کمیت ثابت لورنتس را با $\epsilon_{\mu 1 2\nu}P^{\mu}_{1}P^{\nu}_{2}$ تشکیل داد که واقعاً $1 است. وضعیت 1$s spin 0. آیا چنین استدلالی وجود دارد که نشان دهد $\epsilon_{\alpha\beta\mu\nu}$ نیز تحت تبدیل لورنتس ثابت است بدون اینکه تعیین کننده تبدیل لورنتس 1 باشد.
|
یک سوال در مورد جبر چرخشی
|
76827
|
من فقط ابتدا مشکل را لیست می کنم و سپس توضیح می دهم که در مورد چه چیزی به کمک نیاز دارم. > توزیع بار استوانه ای را در نظر بگیرید که از $r = 0$ تا $r = > 8.2 $cm چگالی شارژ $\rho = r/a_0$، که در آن $a_0 = 21 سانتی متر · m^3/μC$ است. این توزیع بار استوانه ای توسط یک پوسته دی الکتریک با ثابت دی الکتریک 6.72 دلار احاطه شده است که شعاع داخلی آن 17.7 سانتی متر دلار و شعاع بیرونی آن 25.9 سانتی متر دلار است. به نظر نمی رسد فرمولی برای یافتن میدان الکتریکی در یک فاصله معین پیدا کنم. پیشنهادی وجود دارد که از کجا شروع کنیم؟
|
توزیع بار استوانه ای
|
121355
|
من یک پاسخ غیر ریاضی می خواهم. فکر میکنم بدون ریاضیات، درک نسبتاً خوبی از فیزیک دارم، که متأسفانه از درک من دوری میکند. شاید اگر ریاضیات را می فهمیدم جواب واضح بود، اما نمی دانم. همانطور که من می بینم، افق رویداد برای هر اندازه سیاهچاله خاصیت یکسانی دارد. این نقطه ای است که نور نمی تواند از آن فرار کند. با توجه به اینکه این خاصیت بدون توجه به اندازه سوراخ یکسان است، منطقی به نظر می رسد که شدت تابش هاوکینگ در واحد سطح افق ثابت باشد. میدونم اشتباه میکنم ولی نمیدونم چرا توضیح غیر ریاضی قدردانی می شود.
|
چرا شدت تابش هاوکینگ به اندازه سیاهچاله ای که از آن می آید بستگی دارد؟
|
126740
|
من جایی خواندم که مردم به دلیل پیشنهاداتشان گرادیان را به شکل کوواریانت می نویسند. من فکر میکنم گرادیان در مبنای کوواریانت $i$، $j$، $k$ گسترش یافته است، بنابراین با توجه به ماهیت تغییرناپذیری بردارها، جزء گرادیان باید به شکل متناقض باشد. با این حال ما با خواص تبدیل و قانون چانه می دانیم که یک بردار کوواریانت است. چه بلایی سرم اومده؟ سوال دوم من این است: اگر گرادیان به صورت کوواریانت نوشته شده است، شکل گرادیان مغایر چیست؟
|
گرادیان کوواریانت است یا متضاد؟
|
126748
|
 چرخی را در نظر بگیرید که بلبرینگ و میله محور روی زمین هموار می چرخد. اگر بخواهم به چرخ کمک کنم تا به حرکت بیشتر (یا سرعت بیشتر) کمک کنم، آیا باید با حرکت دادن بدنه سوار در جلو یا پشت میله محور چرخ وزن اضافه کنم؟
|
وزن را در جلو یا پشت چرخ متحرک اضافه کنید؟
|
87396
|
من در حال خواندن QFT: جلد 1 توسط واینبرگ هستم و یک سوال (شاید بی اهمیت) در مورد جمله ای که او در صفحه 63 بیان می کند دارم. \mu U(\Lambda) |p,\sigma \rangle = \Lambda^\mu{}_\rho p^\rho U(\Lambda) |p,\sigma \rangle \end{equation} که در آن برچسب $\sigma$ علاوه بر چهار تکانه، تمام درجات آزادی دیگر را نیز نشان میدهد. اکنون، می توانم ببینم که، در پرتو معادله (2.5.1)، معادله فوق به این معناست: \begin{equation} U(\Lambda) |p,\sigma \rangle \propto |\Lambda p,\sigma \rangle \end{equation} و بنابراین مینویسم: \begin{equation} U(\Lambda) |p,\sigma \rangle = C |\Lambda p,\sigma \rangle \end{equation} که در آن $C$ ثابت عادی سازی است که باید تعیین شود. با این حال، مطابق با واینبرگ، معادله (2.5.2) دلالت دارد: \begin{equation} U(\Lambda)|p,\sigma\rangle = \sum_{\sigma'} C_{\sigma' \sigma}(\Lambda ,p)|\Lambda p, \sigma'\rangle \end{equation} حالا من نمیفهمم معادله بالا دقیقاً به چه معناست. $\sigma'$ چه چیزی را نشان می دهد و چرا ما روی آن جمع می کنیم؟ پیشاپیش ممنون
|
سوال در مورد اشتقاق واینبرگ از حالت های تک ذره ای تحت گروه پوانکر
|
120055
|
فرض کنید که جهان همگن و همسانگرد است و معادله زیر برقرار است: \begin{equation}R_{00}-\frac{1}{2}g_{00}R=8\pi GT_{00}; \space \space \nabla_{\mu}T^{\mu 0}=0.\end{equation} چگونه ثابت کنم که معادلات زیر یکسان هستند، مشروط بر اینکه دو مورد بالا راضی باشند؟ \begin{equation}R_{0i}-\frac{1}{2}g_{0i}R=8\pi GT_{0i}; \space \space R_{ij}-\frac{1}{2}g_{ij}R=8\pi GT_{ij}; \space \space \nabla_{\mu}T^{\mu i}=0.\end{equation} رویکرد من نوشتن $g_{00}=1$ و $g_{ij}=-a^2\ بود gamma_{ij}$ و تانسورهای Ricci و غیره را ارزیابی کنید، اما من میدانم که این راهی برای انجام آن نیست. کسی میتونه راهی رو به من پیشنهاد کنه؟
|
اثبات یک معادله میدان به دیگری منجر می شود
|
7579
|
من داشتم محاسبات کوانتومی را میخواندم که برای مادرم توضیح داده شده بود، که ادعای زیر را دارد > فرض 2 یک سیستم فیزیکی بسته در حالت V، پس از مدت زمان معینی با توجه به W = UV که در آن U یک n است، به یک حالت جدید > W تبدیل میشود. × n > ماتریس واحد اعداد مختلط. در اینجا، «V» یک ماتریس ستونی با ردیف «n» است. آیا کسی می تواند این فرض را توجیه کند؟
|
نمایش تبدیل های کوانتومی به عنوان ماتریس
|
123249
|
ریاضیدانان فیزیکدانان را افرادی می دانند که از ریاضیات صرفاً به عنوان ابزار استفاده می کنند، اما به نوعی، فرض کنید، نادرست هستند، زیرا فیزیکدانان تمایل دارند در ریاضیات خود فرضیات زیادی داشته باشند و شواهد تجربی را تعمیم یا استفاده کنند، در حالی که ریاضیدانان پر از دقت و دقت ریاضی هستند. و اثبات جایی که تقریباً هیچ نقشی از آزمایش وجود ندارد. ریاضیدانان تمایل دارند که فیزیکدانان را از نظر دقت و دقت پایین تر از آنها بدانند. سوال من این است که چه کسی در درک نحوه عملکرد جهان بهتر است؟ کاربرد واقعی این همه سخت گیری ریاضی در زندگی واقعی چیست؟ اگر من باید به این ترتیب یک ریاضیدان یا یک فیزیکدان باشم، به هر دو علاقه دارم، اما گیج هستم.
|
ریاضیدان یا فیزیکدان
|
7576
|
همیشه بحثی در مورد ساعت زمین هر سال وجود دارد و طرف مقابل ساعت زمین معمولاً ادعا می کند که > کاهش (ناگهانی) و افزایش مصرف برق در شروع و پایان > ساعت زمین باعث اتلاف انرژی بسیار بیشتر می شود. صرفه جویی در مصرف برق)، و > حتی به سیستم منبع تغذیه آسیب وارد کند. آیا این گفته درست است؟ تا چه حد؟ خیلی ممنون.
|
آیا ساعت زمین به سیستم منبع تغذیه آسیب می رساند؟
|
65141
|
در مقالات فیزیک، آیا درست است که بگوییم وقتی از مولدها نام برده می شود، واقعاً منظور آنها مولدهای جبر Lie است تا مولدهای گروه Lie؟ به عنوان مثال من منابعی را دیده ام که می گویند که $SU(N)$ _group_ دارای مولدهای $N^2-1$ است، اما در واقع اینها مولدهایی برای جبر Lie هستند، اینطور نیست؟ آیا این در مورد نمایندگی ها نیز صادق است؟ وقتی می گوییم یک میدان در تکرار الحاقی است، آیا این معمولاً به معنای تکرار الحاقی جبر است نه گروه سنج؟
|
آیا ژنراتورها به گروه Lie تعلق دارند یا جبر Lie؟
|
101080
|
آیا اصولاً می توان اصل طرد را به معنای محلی به عنوان ویژگی فضای مماس در یک نقطه یا یک فیبر منفرد از یک بسته چرخشی تعریف کرد؟ یا نیاز به توصیف کلی دارد، به عنوان مثال. اپراتورهای میدانی بدون مختصات؟ به عنوان یک مثال فرضی برای درک روح این سوال، آیا احتمال بی نهایت کوچک و جریان های اسپین می توانند به شیوه ای آشکارا انحصاری با هم تعامل داشته باشند؟ من نفسم را حبس نمیکنم، زیرا با همه چیزهایی که میدانم، «محلی» که به آن اشاره میکنم، تا حد تفسیر نامشخص است و با ده قضیه مختلف ممنوعه منتفی است. :)
|
آیا طرد پائولی را می توان به صورت محلی توصیف کرد؟
|
65147
|
اگر بخواهیم جریان الکتریکی را برای مسافت طولانی انتقال دهیم، باید گرمایی را که به دلیل مقاومت آزاد می شود به حداقل برسانیم. ما نمی توانیم یک کابل عریض بسازیم زیرا گران است و عظیم خواهد بود. بنابراین، باید یک جریان را کاهش دهیم زیرا $Q = I^2R\Delta t$. توانی که می خواهیم انتقال دهیم ثابت است، $P = UI$، بنابراین باید ولتاژ را افزایش دهیم. با این وجود، $Q = \frac{U^2}{R}\Delta t$، بنابراین اگر ولتاژ را افزایش دهیم، گرما نیز افزایش مییابد. و برای جمع، $U = IR$، بنابراین اگر جریان را کاهش دهیم، ولتاژ نیز کاهش می یابد. میشه با جزییات توضیح بدید در کجا اشتباه دارم. P.S. متاسفم برای انگلیسی من، من یک زبان مادری نیستم.
|
انتقال قدرت الکتریکی
|
89598
|
معادله موج 1 بعدی با $\frac{\partial ^2 p}{\partial t^2}=c^2 \frac{\partial^2 p}{\partial x^2}$ به دست میآید. من در یک مرجع دریافتم که برای یک گاز ناپایدار، که در آن هر دو سرعت گاز و صدا تابعی از $x,t$ هستند، معادله را می توان به صورت: \begin{align*} &\frac{\partial^2 a\ نوشت: left(x,t\right)}{\partial t^2}+2u\left(x,t\right)\frac{\partial^2 a\left(x,t\right)}{\partial x \partial t}+\left[u^2\left(x,t\right)-a^2\left(x,t\right)\right]\frac{\partial^2 a\left(x,t \right)}{\partial x^2}=0\\\ &\frac{\partial^2 u\left(x,t\right)}{\partial t^2}+2u\left(x,t\right)\frac{\partial^2 u\left(x,t\right)}{\partial x \partial t}+\left[u^2\left (x,t\right)-a^2\left(x,t\right)\right]\frac{\partial^2 u\left(x,t\right)}{\partial x^2}=0 \end{align*} که $a(x,t)$ و $u(x,t)$ به ترتیب سرعت صدا و سرعت گاز هستند. من هیچ مرجعی با اثبات این دو معادله آخر پیدا نمی کنم. هر گونه کمکی قدردانی خواهد شد.
|
معادله موج 1 بعدی به عنوان تابعی از سرعت صوت
|
41629
|
من سعی کردم این معادله را ثابت کنم: $$ \delta G_{\alpha\beta}=-\frac{1}{2}\left(\square\bar{h}_{\alpha\beta}+2R{}_{\gamma\alpha\delta\beta}\ bar{h}^{\gamma\delta}\right)+\frac{1}{2}\le ft(\bar{h}_{\alpha;\gamma\beta}^{\gamma}+\bar{h}_{\beta;\gamma\alpha}^{\gamma}-g_{\alpha\beta }\bar{h}^{\rho\delta}{}_{;\rho\delta}\right)، $$ برای تانسور مرتبه اول اینشتین، جایی که $\bar{h}_{\alpha\beta}:=h_{\alpha\beta}-\frac{1}{2}g_{\alpha\beta}\ چپ [g_{\gamma\delta}h^{\gamma\delta}\right]$. من ده ها بار آن را امتحان کرده ام و همیشه این عبارت را دریافت می کنم: $$ \delta G_{\alpha\beta}=-\frac{1}{2}\left(\square\bar{h}_{\alpha\beta}-2R{}_{\gamma\alpha\delta\beta}\ bar{h}^{\gamma\delta}\right)+\frac{1}{2}\le ft(\bar{h}_{\alpha;\gamma\beta}^{\gamma}+\bar{h}_{\beta;\gamma\alpha}^{\gamma}-g_{\alpha\beta }\bar{h}^{\rho\delta}{}_{;\rho\delta}\right). $$. آیا کسی می تواند عبارت درست را از: $$ \delta اثبات کند G{}_{\alpha\beta}=\frac{1}{2}\left(-h_{\gamma;\beta\alpha}^{\gamma}+h_{\beta;\alpha\gamma}^ {\g amma}+h_{\alpha;\beta\gamma}^{\gamma}-h_{\alpha\beta}{}^{;\gamma}{}_{;\gamma}\right)-\frac{1 }{ 4}g{}_{\alpha\beta}\left[g{}^{\gamma\delta}\left(-h_{\rho;\delta\gamma}^{\rho}+h_{\delta; \گام a\rho}^{\rho}+h_{\gamma;\delta\rho}^{\rho}-h_{\delta\gamma}{}^{;\rho}{}_{;\rho}\ راست)\راست]. $$ متشکرم
|
معادلات خطی شده اینشتین
|
87640
|
وقتی یک قرقره جرم دارد، چرا کشش در هر دو طرف متفاوت است؟ چرا وقتی قرقره بدون جرم است، چرخش آن را در نظر نمی گیریم؟
|
کشش در دو طرف یک قرقره عظیم؟
|
96289
|
آیا قانون سوم حرکت نیوتن در جایی از جمله فیزیک ذرات و سایر موضوعات پیشرفته شکست می خورد؟
|
آیا قانون سوم حرکت نیوتن در جایی شکست می خورد؟
|
96288
|
چیزی که برای مدت طولانی در تعجب بودم: در چه نقطه ای از پرواز، استرس در هواپیما بالاتر است؟ آیا در هنگام برخاستن، فرود یا در هنگام آشفتگی (سبک/متوسط/شدید) است؟ منظورم از استرس بار وارد شده به سازه هواپیما است.
|
چه زمانی بیشترین استرس در هواپیما وجود دارد؟
|
90276
|
در یادداشت های درس دینامیک سیالات من بیان شده است که یک تغییر در سرعت نسبی را می توان تجزیه کرد: $$\delta \mathbf{v} = \left\\{ \begin{pmatrix} \Delta & 0 \\\ 0 & \Delta \end {pmatrix} + \begin{pmatrix} D_1 & D_2 \\\ D_2 & -D_1 \end{pmatrix} + \begin{pmatrix} 0 & -\xi \\\ \xi & 0 \end{pmatrix}\right\\} \frac{1}{2} \begin{pmatrix} \delta x \\\ \delta y \ end{pmatrix} $$ که در آن $ \Delta = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}، D_1 = \frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}, D_2 = \frac{\partial u}{\partial y} + \frac{\partial v}{\ x جزئی}, \xi = \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}$ من نتوانستم مرجعی برای این به صورت آنلاین پیدا کنم. آیا این تجزیه نامی دارد؟ چگونه مشتق شده است؟
|
تجزیه با سرعت نسبی
|
44814
|
اگر به $P=VI$ نگاه کنیم، میبینیم که اگر جریان دو برابر شود، اختلاف پتانسیل نصف میشود، اما به نظر میرسد با توجه به $V=IR$ این منطقی نیست. اگر به آن معادله نگاه کنیم، از آنجایی که مقاومت ثابت می ماند، دوبرابر کردن جریان باید اختلاف پتانسیل را افزایش دهد. آیا کسی می تواند توضیح دهد که من در اصطلاح ساده چه چیزی را اشتباه می فهمم؟
|
سردرگمی در مورد P=VI و V=IR
|
47668
|
یک سیاهچاله دمایی خواهد داشت که تابعی از جرم، تکانه زاویه ای و بار الکتریکی است. برای یک جرم ثابت، تکانه زاویه ای و بار الکتریکی توسط شرایط انتهائی $$M^2 - a^2 - Q^2 \gt 0$$ محدود می شوند دقیقاً در مرز منتهی الیه، هر دو آنتروپی و دما صفر هستند. فرض کنید من یک سیاهچاله با یک جبهه موج کروی متقارن و ورودی از تابش الکترومغناطیسی **در حالت کوانتومی خالص** ایجاد می کنم (یعنی ماتریس چگالی ویژگی $\rho^2 = \rho$ را برآورده می کند). جبهه موج به گونه ای شکل می گیرد که کل انرژی بسته در داخل شعاع شوارتزشیلد قرار می گیرد که یک افق رویداد را تشکیل می دهد. از آنجایی که بسته موج تقریباً به همان اندازه خالص است که از نظر فیزیکی امکان ایجاد آن وجود دارد، آنتروپی کوانتومی (فون نیومن) صفر یا تقریباً صفر است. اما تشکیل سیاهچاله نه آنتروپی ایجاد می کند و نه از بین می برد، بنابراین سیاهچاله باید دارای آنتروپی صفر یا نزدیک به صفر نیز باشد. بنابراین سیاهچاله به نظر می رسد خارج از حد است (دمای صفر دارد) اما با این وجود هیچ تکانه زاویه ای ندارد (از جبهه موجی با قطبش خالص صفر در کل کره تشکیل شده است) و هیچ باری ندارد (تابش الکترومغناطیسی خنثی). > **سؤال:** چه مویی سیاهچاله ای دارد که از چنین حالت خالصی تشکیل شده است، به طوری که می تواند فوق العاده باشد و هنوز تکانه زاویه ای یا بار الکتریکی نداشته باشد (که همان موهای کلاسیک است که ما می آییم). انتظار از > نسبیت عام کلاسیک) _این سوال جهش این سوال است، اما در حالی که آن سوال خاص سعی می کند ببیند که حالت های سیاه چاله چه ورودی خروجی خاصی ایجاد می کنند (هاوکینگ) حالتهای تشعشعی که از نظر آماری از حرارتی دور هستند، این سوال در مورد مازادی است که با تکانه زاویه ای و بار ارتباطی ندارد.
|
سیاهچاله فوق العاده بدون تکانه زاویه ای و بدون بار الکتریکی
|
82919
|
راکتورهای هسته ای با استفاده از میله های کنترلی که نوترون ها را جذب می کنند از بحرانی بودن دور می شوند. در صورت گرم شدن بیش از حد و ذوب هسته، میله های کنترل ممکن است دیگر وارد نشوند و منجر به فاجعه شود. یک جرم زیر بحرانی را می توان با قرار دادن مواد بازتابنده نوترون در اطراف آن حیاتی ساخت. بنابراین سوال من این است که چرا راکتورهای هسته ای با این نوع محافظ بازتابی به جای میله های کنترل کار نمی کنند؟ سپر می تواند به گونه ای طراحی شود که از حداکثر دما قبل از تصادف / سوختن / ذوب شدن راکتور را به دور از بحرانی به طور خودکار به روشی کاملاً غیرفعال پشتیبانی کند. چه چیزی را از دست داده ام؟
|
مواد بازتابنده نوترون در راکتورهای هسته ای
|
44810
|
در این مقاله، نویسندگان طیف تحریک را در یک ضد فرومغناطیس هایزنبرگ $J_1$-$J_2$ با استفاده از تئوری موج اسپین اصلاح شده در نمایش Dyson-Maleev حل می کنند. به عنوان یک مرحله میانی، نویسندگان همبستگان اسپین همسایه $\left<\vec{S}_i\cdot \vec{S}_j\right>$ را محاسبه کردند، همانطور که در معادله نشان داده شده است. (4). از آنجایی که محورهای کوانتیزاسیون اسپینهای همسایه با زاویه دلخواه $\phi_{ij}$ از هم جدا میشوند، به نظر میرسد که همبستههای اسپین همیشه شامل عباراتی از توان ششم در عملگرهای بوزون هستند. با این حال، چنین عباراتی شکل درجه دوم معادله را ایجاد نمی کنند. (4). من اینجا چه چیزی را از دست داده ام؟
|
$J_1$-$J_2$ ضد فرومغناطیس هایزنبرگ
|
91087
|
من یک سوال جالب دارم که به این صورت است: فرض کنید یک میله استوانه ای بلند داریم که از یک ماده شفاف ساخته شده است (تصویر زیر را ببینید). منبع نقطه ای $O$ که روی محور میله قرار دارد، نور را در همه جهات ساطع می کند. نور تا حدی منعکس شده و تا حدی منکسر می شود (یعنی به هوا می رود). سوال این است که پرتوهای نور به کدام نقاط خواهند رسید؟ (1) فقط A، (2) فقط A و B (3) همه چهار نقطه (4) اطلاعات کافی نیست طبق کتاب، پاسخ درست (3) است، اما من چندان مطمئن نیستم که این درست باشد - از یک طرف، نور در تمام جهات ممکن ساطع می شود، اما از طرف دیگر، دوست من فکر می کند که ممکن است وجود داشته باشد. انعکاس کلی درونی در یک نقطه در هر دو مورد، هیچ دلیل دقیقی برای هر یک از پاسخ ها وجود ندارد. به هر حال، هیچ اطلاعاتی در مورد موقعیت ها، شاخص های شکست و غیره وجود ندارد.
|
تعیین کنید که آیا نور به نقاط خاصی می رسد یا خیر
|
106242
|
بسط حالت یک میدان اسکالر (کاایرال) محدود به یک دیسک با محیط L را در نظر بگیرید: $$ \phi(x) = \phi_{0} + p_{\phi} \frac{2\pi}{L} x + \sum_{n=1}^{\infty} \frac{1}{\sqrt{n}} e^{-(k_{n}a)/2} \left(e^{-ik_{n}x} \ b_{n}^{\dagger}+e^{ik_{n}x} \ b_{n}\right) $$ با $k_{n}= \frac{2\pi n}{L}$ , $\phi_{0}$ مقداری حالت صفر، $p_{\phi}$ مقداری محرک مزدوج و $a$ مقداری فاصله کوتاه قطع کردن عملگرها روابط کموتاسیون بوزونی زیر را برآورده می کنند $$ \left[b_{n}^{\dagger} , b_{n'}\right]=\delta_{n,n'} \quad\text{and}\quad \ چپ[\phi_{0},p_{\phi}\right]=i عملگرهای راس $$ (فرمیونیک) با $$ تعریف میشوند V_{\alpha}(x)=:e^{i\alpha\phi(x)}: $$ با $: \ ... \ :$ نشان دهنده ترتیب عادی است. با وارد کردن بسط حالت $\phi(x)$ در تعریف عملگر راس، به کمترین مرتبه در $\frac{a}{L}$: $$ :e^{i\alpha\phi(x)} میرسد. : = \left(\frac{L}{2\pi a}\right)^{\Delta(\alpha)} e^{i\alpha\phi(x)} $$ با scaling dimension $\Delta(\alpha)=\frac{\alpha^{2}}{2}$. پیش فاکتور در سمت راست در مقابل نمایی گاهی اوقات ضریب کلاین نامیده می شود. حالا سؤالات من اینجاست (ممکن است واقعاً سؤالات «تازه کار»-CFT باشند؛) ): 1. از آنجایی که سمت راست فقط تقریبی از $:e^{i\alpha\phi(x)}:$ است. به پایینترین مرتبه، نمیدانم که آیا سمت چپ در همه موارد کموتاتورهای فرمونی درست (مثلاً) را بازتولید میکند و آیا سمت دست فقط تا حدی فرمونیک صحیح را بازتولید میکند. تعویض کننده ها؟ 2. اگر سمت راست فقط تا حدی روابط کموتاسیون صحیح را بازتولید می کند، چگونه می توانیم بگوییم که محصول خاصی از عملگرهای فرمیونی (مثلاً حاصلضرب 3 عملگر فرمیونی) در واقع از جابجایی کننده های موعظه ای درست زمانی که به زبان بوزونی نوشته می شود اطاعت می کند. ? 3. اهمیت عبارت های مرتبه بالاتر در $\frac{a}{L}$ در بسط عملگر راس چیست؟ 4. آیا همه اینها ساختار کلی تری در CFT است؟ من مشتاقانه منتظر پاسخ های شما هستم!
|
عوامل کلاین و نظریه میدان همسان
|
69820
|
من یک سیستم میکروسکوپی دارم که به شرح زیر تنظیم شده است: * DSLR با ضریب برش 1.6x (معادل بزرگنمایی، من معتقدم) * یک آداپتور نوری، برای اتصال DSLR به میکروسکوپ، که به عنوان بزرگنمایی 2 برابر ذکر شده است * یک هدف روی میکروسکوپ، که در حال حاضر با بزرگنمایی 4 برابر تنظیم شده است، من از یک جسم 2 میلی متری عکس گرفته ام و متوجه شدم که 14.24 میلیمتر روی سنسور (طول 3618 پیکسل در سنسور عریض 5184 پیکسلی با طول 22.3 میلیمتر). با این کار بزرگنمایی کل سیستم رو 7.12x حساب میکنم. من بر 4 تقسیم می کنم تا هدف حذف شود و 1.78 باقی می ماند و سپس آن را بر 1.6 تقسیم می کنم تا ضریب برش دوربین به 1.113 برسد. این بسیار کمتر از 2x ذکر شده توسط آداپتور است. علاوه بر این، آداپتور همچنین می گوید: بسته به دوربین شما، بین 12x و 16x بزرگنمایی خواهید داشت، که بسیار مبهم است، زیرا اهداف میکروسکوپ از 4x تا 100x یا بیشتر متغیر است. بنابراین، میخواهم بدانم اگر کار اشتباهی انجام میدهم، چرا 2x برای آداپتور دریافت نمیکنم، و این 12x به 16x از کجا میآید. هر گونه کمک بسیار قدردانی می شود!
|
محاسبه بزرگنمایی یک سیستم میکروسکوپ نوری
|
5482
|
خوشحال می شوم اگر کسی بتواند این بحث را برای من توضیح دهد که چرا شکست ابرتقارن لزوماً با ظهور فرمیون بدون جرم، یعنی گلدستینو همراه است. (و همچنین چرا این یک اثر غیر اغتشاشگر است) اجازه دهید در اینجا دو خط از جلد سوم کتابهای QFT توسط واینبرگ را نقل کنم، جایی که او سعی دارد این پدیده را توضیح دهد، * _(وقتی ابرتقارن شکسته شود)..هر n - حالت ذرات با 2 حالت انرژی و تکانه یکسان و آمار متضاد همراه است که حاوی یک گلداستین 0 تکانه اضافی از چرخش به بالا یا پایین و با حالت دیگری از همان است. انرژی و تکانه و همان آمار، شامل دو گلدستینوی 0 تکانه اضافی با اسپین مخالف._ * _به ویژه هنگامی که ابرتقارن بطور خود به خود شکسته می شود، حالت خلاء انرژی غیر صفر دارد، بنابراین باید با حالت فرمیونی جفت شود. همان انرژی و تکانه صفر به طور دقیق تر، خلاء و حالت حاوی دو گلدستینو با تکانه صفر با دو حالت جفت می شوند. من نمی توانم دو استدلال بالا را درک کنم و خوشحال می شوم اگر کسی بتواند کمک کند.
|
شکستن ابرتقارن و گلدستینو
|
65495
|
فاصله نزدیکترین رویکرد در این مقاله ویکی پدیا چقدر است؟ به نظر می رسد نمی توانم تعریف آن را پیدا کنم، و این سوال دیگر پاسخی ندارد که بتوانم آن را بفهمم.
|
چگونه فاصله نزدیکترین رویکرد را برای ژئودزیک شوارتزشیلد پیدا کنیم؟
|
126742
|
در $T=0K$، آیا همه الکترون ها جفت کوپر را تشکیل می دهند یا فقط الکترون های نزدیک به سطح فرمی؟
|
آیا تمام الکترون ها در صفر مطلق جفت کوپر را تشکیل می دهند؟
|
134200
|
سحابی بومرنگ اغلب بهعنوان یکی از سردترین مکانهای طبیعی در کیهان در 1 K ذکر میشود، اما این سحابی حدود 10 مرتبه از آنچه در آزمایشگاه ایجاد شده است فاصله دارد. آیا مکانیسمهای نظری وجود دارد که ذاتاً میتواند بر تسلط (ظاهری) ما بر سرما غلبه کند یا سردترین مکان در جهان احتمالاً آزمایشگاه یک دانشمند (اینجا یا جای دیگر) است؟
|
آیا احتمالاً سردترین مکان در جهان مصنوعی است یا طبیعی؟
|
16163
|
دامنه انتقال تابع موج $\phi(x)=e^{ikx}(\tanh x -ik)$ چقدر است؟ من فکر می کردم که $\tanh x -ik$ است زیرا این عامل مربوط به حرکت رو به جلو $e^{ikx}$ است، اما از آنجایی که ضریب بازتاب $0$ است، احتمال انعکاس آن $0$ است. ، اما $|\tanh x-ik|^2$ به $x$ وابسته است، بنابراین یکسان نیست $=1$؟ کجا اشتباه کردم؟
|
انتقال و انعکاس
|
60515
|
> س: _سرعت فرار برای جسمی که به صورت عمودی از سطح زمین به سمت بالا پرتاب می شود 11 کیلومتر بر ثانیه است. اگر بدن در زاویه > $45^\circ$ با عمودی پرتاب شود، سرعت فرار خواهد بود؟_ رویکرد من: سرعت عمودی جدید $u * \sin(45^\circ)$ = $u / خواهد بود. \sqrt2$ **محاسبه عبارت برای سرعت فرار:** $$\frac{1}{2} mv^2 = \frac{GMm}{r}$$ $$\frac{1}{4} mu^2 = \frac{GMm}{r}$$ $$u = 2\sqrt\frac{GMm}{r}$$ بنابراین سرعت فرار جدید = $\sqrt2 * 11 دلار کیلومتر در ثانیه. با این حال، **پاسخ صحیح** 11 کیلومتر بر ثانیه است.
|
پرتابه ها و سرعت فرار
|
120050
|
من یک دانش آموز دبیرستانی با سابقه قوی در فیزیک، مهندسی و علوم کامپیوتر هستم. من بسیار علاقه مند به تحقیق و فرمول بندی اکتشافات خودم هستم تا درباره ترکیب این موضوعات بیشتر بیاموزم و اینکه چگونه می توانم روزی علایقم را در یک پروژه تحقیقاتی بلندمدت ترکیب کنم. در حالت ایدهآل، من میخواهم علایقم را با ایجاد یک شبیهسازی رایانهای از یک مسئله و سپس ایجاد تنظیماتی برای جمعآوری نتایج واقعی و تجزیه و تحلیل آنها ترکیب کنم. در مورد چه نوع موضوعاتی می توانم از طریق این روش اکتشافات جدید و غیر پیش پاافتاده را شکل دهم؟
|
یک دانش آموز دبیرستانی می تواند درگیر چه نوع تحقیقات فیزیک باشد و در آن اکتشافات جدیدی ایجاد کند؟
|
86116
|
اگر $|ψ\rangle$ حالت یک سیستم متشکل از دو ذره غیرقابل تشخیص باشد، در این صورت یک عملگر مبادله P داریم که حالات دو ذره را تغییر می دهد. از آنجایی که دو ذره قابل تشخیص نیستند، وضعیت فیزیکی تحت عمل عملگر مبادله نمی تواند تغییر کند، بنابراین باید $P|ψ\rangle=λ|ψ\rangle$ را داشته باشیم که در آن $|λ|=1$ است. بدیهی است که با تغییر حالت دو ذره، و سپس تعویض مجدد آنها، ذرات حالت اولیه خود را باقی میگذارند، بنابراین $P^2|ψ\rangle=(λ^2)|ψ\rangle=|ψ\rangle$، بنابراین $λ=±1$، و بنابراین وضعیت سیستم باید با توجه به مبادله متقارن یا ضد متقارن باشد. حالا من شنیده ام که این استدلال برای دو بعد صدق نمی کند، که منجر به احتمال هر کسی می شود، که می توانید $λ$ چیزی غیر از 1 یا -1 باشد. در دنیا چگونه ممکن است؟ نقص یا نظارت در استدلال فوق کجاست که باعث می شود مورد دوبعدی حذف شود؟ در کجای برهان فوق، فضا را سه بعدی فرض می کنیم؟ هر گونه کمکی بسیار قدردانی خواهد شد. پیشاپیش از شما متشکرم ویرایش: اجازه دهید من اثبات را به صورت گام به گام ارائه کنم، تا خطا راحت تر شناسایی شود: 1. برای هر حالت $|ψ_1\rangle$ و $|ψ_2\rangle$، $P|ψ_1\ را تعریف کنید. rangle|ψ_2\rangle$ $|ψ_2\rangle|ψ_1\rangle$ 2. برای ذرات یکسان، $P |\psi \rangle$ و $|\psi \rangle$ با همان حالت فیزیکی (یعنی اشعه) مطابقت دارد، بنابراین ما باید $P |\psi \rangle = \lambda |\psi \rangle$ برای برخی از عدد مختلط $\lambda$ داشته باشیم. 3. با دوبار اعمال تعریف $P$ در مرحله 1، $P^2|ψ_1\rangle|ψ_2\rangle=PP|ψ_1\rangle|ψ_2\rangle=P|ψ_2\rangle|ψ_1\rangle = | ψ_1\rangle|ψ_2\rangle$، بنابراین برای هر حالت دو ذره ای $|\psi\rangle$، $P^2|\psi داریم \rangle = |\psi \rangle$. 4. با دو بار اعمال مرحله 2، $P^2|ψ\rangle = PP|ψ\rangle = P \lambda |ψ\rangle = \lambda P |ψ\rangle = \lambda^2 |ψ\rangle$ 5 داریم. در مراحل 3 و 4، $\lambda^2 = 1$ داریم و بنابراین $\lambda = ±1$ فرض میکنم مشکل به نوعی مربوط به مرحله 3 است، اما. من مطمئن نیستم مشکل چیست، زیرا مستقیماً از تعریف مرحله 1 ناشی می شود. آیا مشکل با تعریف مرحله 1 است؟ اما چگونه ممکن است یک تعریف اشتباه باشد؟
|
چگونه هر کسی ممکن است؟
|
44816
|
من به خاصیت قطبش دایره ای نور فکر می کنم. من دو پرتو قطبی دایره ای دارم، یکی در جهت مثبت گرد است، دیگری منفی است. وظیفه من این است که بفهمم: 1. اگر آن دو پرتو قطبی شده دایره ای هستند (من می توانم برای این کار از آشکارساز قطبی کننده دایره ای استفاده کنم). 2. من باید بررسی کنم که آیا آن دو پرتو قطبی شده دقیقاً مخالف یکدیگر هستند یا خیر. من هیچ ایده ای ندارم اما به این فکر می کنم که آیا آن دو پرتو را اضافه کنم، اگر دایره ای هستند اما متضاد هستند، دامنه پرتو روی هم قرار گرفته باید واقعی باشد (زیرا قسمت خیالی از بین می رود). با این حال، در این مرحله، من نمی دانم چگونه از آن اطلاعات برای تعیین اینکه آیا پرتوها دو قطبی دایره ای مخالف هستند استفاده کنم؟ 3. برای اضافه کردن دو پرتو، آیا فقط با تابش دو پرتو به یک آشکارساز عکس کار می کند؟ یا برای اضافه کردن تیرها ابتدا باید از جمع کننده استفاده کنم؟
|
قطبش دایره ای: خواص و تشخیص
|
51957
|
من با ارقام زیادی برخورد کرده ام که کارایی نوری طیفی را به عنوان تابعی از طول موج نشان می دهد (به معنای حساسیت چشم انسان به طول موج های مختلف) http://www.yorku.ca/eye/photopik.htm اما من نتوانستم معادله ای که این تابع را می دهد را پیدا کنید تا بتوانم خودم آن را رسم کنم.
|
بازده نوری طیفی به عنوان تابعی از طول موج
|
65494
|
بیایید بگوییم که یک آزمایش باید تعداد میون کیهانی را در سطح دریا تعیین کند. تجهیزات مناسب برای اندازه گیری نرخ شمارش آماده است. من می توانم به دو راه فکر کنم 1. 10 دقیقه بشمار تا خطای مربوطه کاهش یابد. 2. 10 بار بشمارید (1 دقیقه/اندازه گیری) بهترین اندازه گیری کدام است؟ آیا آنها برابر هستند؟
|
زمان اندازه گیری در مقابل تعداد اندازه گیری ها
|
90932
|
می دانیم که آب بسیار خالص جریان الکتریسیته را هدایت نمی کند، اما آب نمک رسانای مناسبی است. این معمولاً با گفتن اینکه یونها جریان را از طریق محلول حمل می کنند توضیح داده می شود، توضیحی که واقعاً منطقی نیست زیرا مشخص نیست وقتی همه یون ها به الکترودها مهاجرت کنند چه اتفاقی می افتد. توضیحات بهتر رسانایی از طریق محلول نمکی (مثل این یا این یکی) هدایت الکتریسیته را بر حسب واکنش کاهشی که در آند و واکنش اکسیداسیون در کاتد انجام میشود، توضیح میدهد. در مورد آب نمک، گاز کلر (Cl2) در آند و گاز هیدروژن (H2) در کاتد تشکیل می شود. این توضیح برای من منطقی است، اما به این معناست که رسانش الکتریسیته از طریق یک محلول اساساً با رسانش الکتریسیته از طریق یک سیم متفاوت است. یک سیم مسی پس از عبور برق از آن به هیچ وجه تغییر نمی کند. در مقابل، در آب نمک، ما در حال انجام دو واکنش شیمیایی (یکی در هر الکترود) هستیم که اساساً مواد ترکیب را تغییر میدهند. این به این معنی است که برای یک محلول آبی امکان رسانایی الکتریسیته برای همیشه وجود ندارد. از آنجایی که ما در حال انجام یک واکنش شیمیایی هستیم، یا با تشکیل گاز (یا قرار دادن آن روی الکترودها) نمک خود را مصرف می کنیم یا با تشکیل گاز H2 یا O2 آب را مصرف می کنیم. این برای من تعجب آور است (به دلایلی). بنابراین، من میپرسم آیا فکر من درست است: **آیا ممکن است یک محلول نمک برای همیشه جریان الکتریسیته را هدایت کند**، یا همیشه در نهایت واکنشدهندهها را مصرف میکند و همانطور که من حدس میزدم متوقف میشود؟
|
آیا محلول آب شور می تواند برای همیشه الکتریسیته را هدایت کند؟
|
51958
|
من می دانم که افق رویداد شوارتزشیلد یک سطح پوچ است که توسط ژئودزیک های پوچ ایجاد می شود. اما در واقع از نظر مسیر پرتو نوری که به آن می رسد چه معنایی دارد؟ آیا این بدان معناست که مسیر ژئودزیکی نور روی سطح در امتداد سطح خواهد بود؟ پرتو نور به کدام سمت خواهد رفت؟ و چه معادله ای این را نشان می دهد؟
|
واقعاً برای یک پرتو نور در افق سیاهچاله شوارتزشیلد چه اتفاقی می افتد؟
|
60517
|
من همین الان مقاله ویکی پدیا در مورد خورشید را خواندم. در بخش هسته خورشیدی آمده است > چگالی آن تا 150 گرم بر سانتی متر مکعب است[47][48] (حدود 150 برابر چگالی > آب) ذرات (اتمی و زیر اتمی) موجود در هسته خورشیدی را انجام دهید. با همان سرعتی که اگر در خلاء بودند حرکت کنند؟ ویرایش: فقط مقاله مربوط به میانگین مسیر آزاد را بخوانید. من قبلاً آن را خوانده بودم و فراموش کردم به هر حال، میانگین سرعت مسیر آزاد ذرات زیر اتمی شبیه چیزی است که من در ذهن دارم.
|
آیا ذرات موجود در هسته خورشیدی با همان سرعتی که در خلاء حرکت می کنند حرکت می کنند؟
|
69790
|
قانون حرکت ارسطو، که نادرست است، بیان می کند که > > _سرعت یک جسم $\vec v$ مستقیماً با نیرویی که بر آن وارد می شود مرتبط است > $\vec F$_ > > یا $\vec F \propto \ vec v$ > > یا $\vec F = R\vec v$، > > که در آن $R$ ثابت تناسب است که مقاومت در برابر حرکت است. من می خواهم بدانم چگونه می توانیم این معادله $\vec F = R\vec v$ را تفسیر کنیم؟ آیا این معادله نشان می دهد که $\vec F$ و $\vec v$ یک جهت دارند؟ اگر اینطور است، پس چگونه از طریق این معادله این را بفهمیم؟ آیا مساوات به این معناست که هم جهت باشند؟ کتابی که من واقعاً این معادله را در آن دیدم، این معادله را به این صورت نوشت: $\vec v = \frac {\vec F}{R}$.
|
تفسیر معادله $\vec F = R\vec v$
|
116562
|
هوایی که ما تنفس می کنیم از گازهای نیتروژن و اکسیژن تشکیل شده است. آب موجود در حوضچه از یک مولکول هیدروژن/اکسیژن تشکیل شده است. اگر کشش سطحی بالای آب نبود، مولکولهای اکسیژن میتوانند وارد آب شده و فضای کنار مولکولهای هیدروژن/اکسیژن را اشغال کنند. سوال من این است: اگر همه چیز برابر باشد، اکسیژن بیشتر جذب آب می شود یا هوا؟
|
جذب هوا در مقابل آب مولکول های اکسیژن
|
69827
|
ما چند مثال داشتیم که قرار بود تبدیل متعارف (CT) را محاسبه کنیم، اما هرگز در مورد شرایطی صحبت نکردیم که تعیین میکند یک تبدیل متعارف است یا خیر. اجازه دهید مثالی برای شما بزنم: ما این تبدیل را داشتیم: $$P=q \cdot \cot(p), \qquad Q=\ln (\frac{\sin(p)}{q}).$$ چگونه من می بینم که آیا این تحول یک تحول شرعی است یا نه؟ شما مجبور نیستید محاسبه کامل را انجام دهید، اما شاید بتوانید به من اشاره کنید که چه چیزی را باید در اینجا نشان دهم؟
|
چگونه بفهمیم که یک تبدیل یک تبدیل متعارف است؟
|
69828
|
تا آنجا که من می دانم قضیه هم ارزی بیان می کند که ماتریس S تحت پارامترسازی مجدد میدان ثابت است، بنابراین اگر من یک عمل $S(\phi)$ داشته باشم، تغییر متعارف متغیر $\phi \ به \phi +F(\phi)$ ماتریس S را ثابت می گذارد. در کتاب Itzykson اکنون تمرینی وجود دارد که در آن باید نشان دهید که تابع مولد $$Z^\prime(j)=\int \mathcal{D}[\phi] \exp{\\{iS(\phi )+i\int d^4x\hspace{0.2cm} j(x)(\phi +F(\phi)\\}}$$ همان ماتریس S را به دست می دهد. تابعی معمولی که فقط $\phi$ به دلیل شرایط تماس ناپدید می شود، می نویسد که این قضیه هم ارزی را ثابت می کند، که فرض کنید من این تغییر متعارف متغیر را نمی فهمم یک اقدام جدید $S^\prime(\phi)=S(\phi+F(\phi))$ و یک تابع تولیدی $$Z(j)=\int \mathcal{D}[\phi] \exp\\{iS(\phi+F(\phi))+i\int d^4x\hspace{0.2cm} j(x)\phi\\} $$ اگر اکنون $\phi+F(\phi)=\chi$ را جایگزین می کنم $$Z(j)=\int \mathcal{D}[\chi] \det\left(\frac{\partial \phi}{\partial \chi}\right) \exp\\{iS(\chi)+i\int d^4x\hspace{0.2cm} j(x)\ phi(\chi)\\} $$ با $\phi(\chi)=\chi + G(\chi)$ معکوس $\chi(\phi)$ بنابراین مقایسه $Z(j)$ و $Z^\prime(j)$ یک دترمینان ژاکوبین اضافی دریافت می کنم. اشتباه من کجاست یا چرا باید تعیین کننده 1 باشد؟ پیشاپیش از شما متشکرم
|
قضیه هم ارزی ماتریس S
|
119577
|
در شبیهسازی دینامیک مولکولی (MD)، میانگین جابجایی مربع $\text{MSD}$ با $$\text{MSD}(\delta t) = \left\langle\left|\vec{r}(\ داده میشود. دلتا t)-\vec{r}(0)\right|^2\right\rangle،$$ که $\vec{r}$ بردار موقعیت یک اتم است و $\delta t$ یک مرحله زمانی است. اغلب وابستگی به گام زمانی $\text{MSD}$ حذف میشود، که به نظر میرسد به سوال من مربوط میشود، اما تاکنون مشکلی وجود ندارد. با این حال، محاسبه عملی میانگین گروه $\langle\ldots\rangle$ معمولاً تا حدودی مبهم توضیح داده میشود و به نظر میرسد بستگی به این دارد که کجا نگاه میکنید. این منبع بیان میکند که ما باید در تمام اتمها _و_ چند گام زمانی میانگین بگیریم (من تمام مراحل زمانی را در یک شبیهسازی معین فرض میکنم). این و این منبع از سوی دیگر فقط میانگین تمام اتم ها را ذکر می کنند (اگرچه دومی نشان دهنده یک وابستگی زمانی (مرحله ای) است). به نظر می رسد این آخرین منبع منبع اول را پشتیبانی می کند. توجه داشته باشید که هم منبع اول و هم آخرین منبع $\text{MSD}$ به مرحله زمانی بستگی دارد. تعبیر من این است. من انتظار دارم $\text{MSD}$ وابستگی به مرحله زمانی داشته باشد، بنابراین تمایل دارم اولین و آخرین منبعی را که نقل کردهام دنبال کنم. بنابراین در مورد شبیهسازی MD از اتمهای $N$ که در کل زمان $N_{k\tau}k\tau$ را در بر میگیرد، میتوان جابجایی میانگین مربع $k\tau$ را به صورت $$\text{MSD}(k) محاسبه کرد \ tau) = \frac{1}{N}\frac{1}{N_{k\tau}}\sum_{n=1}^{N}{\sum_{i=1}^{N_{k\tau}}{ \بزرگ|\ vec{r}_n\big(ik\tau\big)-\vec{r}_n\big((i-1)k\tau\big)\Big|^2}}.\qquad(*)$$ سوال من واقعاً این است: آیا این درست است؟ و اگر بله، چه تفاوتی با دو منبع دیگری که ذکر کردم چیست؟ چرا میانگین گیری در مراحل زمانی را ذکر نمی کنند؟ آیا آنها به سادگی فرمول یک مرحله زمانی را مورد بحث قرار می دهند؟ (یعنی $N_{k\tau} = 1$)
|
درک میانگین جابجایی مربع در دینامیک مولکولی
|
65146
|
آزمایش بقای تکانه به صورت تجربی ساده نیست، و بسیاری از آزمایشهایی که به نظر آزمایش میرسند واقعاً اینطور نیستند. برای مثال، در یک سیستم نیوتنی از ذرات یکسان که از طریق برخورد برهم کنش دارند، بقای تکانه صرفاً از تغییر ناپذیری گالیله و تقارن برخوردها در مرکز قاب جرم ناشی میشود. به دلایلی مانند این، بسیاری از آزمونهای فیزیک دانشجوی سال اول در مورد بقای تکانه ممکن است واقعاً آن را آزمایش نکنند، حتی به طور تقریبی - یعنی ممکن است حتی امکان منطقی جعل قانون بقا را ارائه ندهند. یک مشکل اضافه این است که هر دو نظریه بنیادی فیزیک، مکانیک کوانتومی و نسبیت عام، بقای موضعی انرژی- تکانه چهار بردار را کاملاً در ساختارهای خود جای داده اند. به طور کلی، آزمایش یک فرضیه سخت است، مگر اینکه شما یک نظریه آزمایشی داشته باشید که با شکست فرضیه سازگار باشد. در مورد GR، ما فرمالیسم PPN را داریم، که اگرچه واقعاً یک نظریه علمی نیست، اما امکان عدم حفظ تکانه را فراهم می کند. بهترین آزمایشی که در این چارچوب می شناسم، آزمایش برد لیزر ماه توسط بارتلت (1986) است که برابری جرم گرانشی فعال و غیرفعال را با دقتی در حدود 10^{-10}$ تأیید کرد. اعتبار این آزمایش به ناهمگنی ماه بستگی دارد - در غیر این صورت، به دلایلی مشابه مواردی که در پاراگراف اول توضیح داده شد، شتاب غیرعادی توسط تقارن ممنوع است. مشاهدات جدیدتر تپ اخترها، پارامتر PPN غیرقابل حفظ تکانه $|\alpha_3|$ را به کمتر از $5\times10^{-16}$ محدود می کند (Bell 1995). در مورد آزمایشات در مقیاس میکروسکوپی، در بخش الکترومغناطیسی چطور؟ البته تصور تئوری سخت است که چگونه بقای تکانه ممکن است شکست بخورد، زیرا به نظر می رسد مستقیماً از عدم تغییر ترجمه و قضیه نوتر ناشی می شود. اما این همان تأیید آزمایشی آن نیست. آیا آزمایشهای غیر گرانشی در مقیاس ماکروسکوپی وجود داشته است، به عنوان مثال، محدودیتهای تجربی در مورد شتابهای خود به خودی تودههای ناهمگن در مقیاس کیلوگرم؟ (به نظر می رسد کاری که گروه Eot-Wash انجام می دهد.) تفسیر این نوع چیزها به این بستگی دارد که آیا نظریه آزمون شما اجازه نقض لورنتس را می دهد یا خیر. به عنوان مثال، فرمالیسم PPN صراحتاً امکان عدم حفظ حرکت و نقض لورنتس را فراهم می کند. اگر تغییر ناپذیری لورنتز معتبر باشد، هر آزمونی برای بقای انرژی نیز آزمون پایستگی تکانه است. بنابراین ممکن است یک محدودیت برای عدم حفظ تکانه وجود داشته باشد، اگر شما ثابتناپذیری لورنتس را فرض نکنید، و محدودیت دیگری، اگر انجام دهید، محدودتر است. [ویرایش] به نظر میرسد که آزمایشهای فیزیک اتمی معمولاً بهعنوان آزمونهای تغییرناپذیری موقعیت محلی (LPI) توصیف میشوند، اگرچه با قضیه نوتر که معادل بقای انرژی-تکانه است. آزمایشها با بالاترین دقت، نرخهای ساعتهای اتمی گونههای اتمی مختلف را مقایسه میکنند و به دنبال تغییر در نسبت نرخهای آنها در طول زمان هستند. همچنین میتوان جهانی بودن جابهجاییهای گرانشی به سرخ را آزمایش کرد، یا ساعتهای اتمی (میکروسکوپی) را با تشدیدگرهای الکترومغناطیسی (ماکروسکوپی) مقایسه کرد. برخی از مقالات اخیر Guéna 2012 و Agachev 2010 هستند. وقتی این سوال را پرسیدم، واژه جستجوی مناسبی را برای یافتن این آزمایشها انتخاب نکرده بودم. من همچنان علاقه مند به دیدن یک پاسخ سینوپتیک هستم، یا پاسخی که بر بخش نیروی قوی تاثیر می گذارد، یا پاسخی که مروری جالب از تاریخچه چنین آزمایش هایی ارائه می دهد. آگاچف 2010، http://link.springer.com/article/10.1134%2FS0202289311010026#page-1 بارتلت و ون بورن، فیزیک. کشیش لِت 57 (1986) 21، خلاصه شده در Will، http://relativity.livingreviews.org/Articles/lrr-2006-3/ Bauch، http://ebookbrowse.com/2002-bauch-weyers-phys-rev-d65- pdf-d370051021 بل، محدودیت محکم تر در گرانش پس از نیوتنی با استفاده از تپ اخترهای میلی ثانیه، http://arxiv.org/abs/astro-ph/9507086 Guéna 2012، http://arxiv.org/abs/1205.4235
|
بهترین مرزهای فعلی در مورد عدم حفظ تکانه؟
|
18729
|
روز قبل یکی به من گفت که برای مثال تعاریف مطلقی از گرما و سرما وجود دارد. شما همیشه می توانید بگویید a گرمتر از b است، مهم نیست کجا هستید. اما او گفت، هیچ تعریف مطلقی برای راست (یعنی نه چپ) وجود ندارد. او به من گفت که آنها آزمایشی را ارائه کردند که می توانید آن را در مقابل خود قرار دهید و چیزی به سمت راست می رود. و اگر دستگاه را بچرخانید باز هم به سمت راست شما می رود. من گفتم نمی توانم این را باور کنم، زیرا با دو ناظر شکست می خورد و حق کاملاً خودسرانه است. اگر منظور او تعریفی از راست به نوعی کایرالیته بود، هر چیزی که در آن ضربدری باشد باید به او اجازه دهد که سیستم مختصات راست دست را از چپ جدا کند. او بار دیگر گفت که «آنها یک تعریف مطلق از حق ارائه کردند. فقط از من نپرسید که چگونه این کار را کردند» که واقعاً اجازه یک گفتگوی اساسی را نمی داد. آیا چنین چیزی وجود دارد؟
|
تعریف مطلق جهت راست (یعنی نه چپ).
|
100119
|
معادله دیراک ممکن است به عنوان عمل عملگر پیشبینی $\frac{1 - \Delta}{2}\Psi = 0$ تفسیر شود، که در آن $$ \Delta = \begin{pmatrix} 0 & \Delta_{b \dot { a}} \\\ \Delta^{\dot {b}a} & 0 \end{pmatrix}، \quad \Delta_{b \dot {a}} = \frac{i}{m}p_{b \dot {a}}, \Delta_{b \dot {a}}\Delta^{\dot {a} c} = \delta^{c }_{b} \Rightarrow \Delta^{2} = 1. $$ در اینجا $\Delta_{a \dot {b}}$ شاخص نقطهدار را به بدون نقطه تغییر میدهد (تبدیل $\left( \frac{1}{2}, 0\right)$ به $\left( 0, \frac{1}{2} \right)$). دو عملگر پیشبینی $\frac{1 + \Delta }{2}، \quad \frac{1 - \Delta}{2}$ وجود دارد، بنابراین $\frac{1 - \Delta}{2}\Psi = 0 , \quad \frac{1 + \Delta }{2}\Psi = \Psi$ یا برعکس. این عملگر تنها دو جزء مستقل از spinor $\Psi$ را باقی میگذارد، اما به طور رسمی همچنان به مجموع مستقیم $\left( \frac{1}{2}, 0\right) + \left( 0, \frac{ اشاره میکند. 1}{2} \right)$. دو عملگر دیگر نیز وجود دارد $\frac{1 + \gamma^{5}}{2}, \quad \frac{1 - \gamma_{5}}{2}$ که اسپینور را نیز بر روی یکی از زیرفضاها پخش میکند. . من کاملاً متوجه نمی شوم که چه تفاوتی بین این جفت اپراتورها وجود دارد. شاید اولی اسپینور را بهعنوان نمایش مجموع مستقیم رها کند و دومی فقط یکی را ترک کند، $\left( \frac{1}{2}, 0\right)$ یا $\left( \frac{1} {2}، 0\راست)$؟ آیا می توانید درک آن را واضح تر بیان کنید؟
|
دو جفت عملگر پروجکشن معادله دیراک
|
16169
|
چرا پلاریزاسیون غیرخطی مرتبه دوم فقط در مواد کریستالی با ساختار کریستالی غیرمتقارن اتفاق می افتد؟ (اثرات غیرخطی در سطوح کریستالی یک استثنا هستند). چرا قطبی شدن مرتبه سوم اساساً در همه رسانه ها اتفاق می افتد؟ پاسخی که در اینجا یافت شد http://www.rp- photonics.com/nonlinear_polarization.html کمکی نکرد (حداقل در حال حاضر).
|
پلاریزاسیون غیرخطی ( مرتبه دوم و سوم)
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.