_id
stringlengths 1
6
| text
stringlengths 0
5.02k
| title
stringlengths 0
170
|
|---|---|---|
104278
|
آیا می توان نور سفید را در فیبر نوری تک حالته متمرکز کرد؟ من فکر کردم نه، زیرا برای تمرکز باید راه حلی برای معادله هلمهولتز باشد، اما در مورد آن خیلی مطمئن نیستم. همچنین از آنجایی که معادله دارای عدد موج است، آیا نباید غیرممکن باشد؟
|
فیبرهای تک حالته
|
130583
|
فرض کنید ما در 3 بعدی هستیم و از $(-++)$ استفاده کنید. اگر متریک $$ds^2=-dt^2+dr^2+r^2df^2(t),$$ را داشته باشیم، اگر دو مختصات اول $t$ و $r$ باشند، مختصات سوم چیست؟ $$X^iX_i=-t^2+r^2+؟$$
|
طول در مختصات قطبی
|
37886
|
آیا چرخش/انقلاب زمین توسط سیارات دیگر (و بالعکس) به هیچ وجه تنظیم می شود؟ چگونه؟
|
آیا سیارات دیگر در چرخش و چرخش زمین تأثیر دارند؟
|
78682
|
پارادوکس فایروال یک موضوع بسیار داغ در حال حاضر است (1207.3123v4). به نظر می رسد هرکسی که در فیزیک نظری کسی باشد، وارد عمل می شود (مالداسینا، پولچینسکی، ساسکیند به نام چند مورد). با این حال، من قادر به دیدن پارادوکس نیستم. به نظر من، وضوح پارادوکس اطلاعاتی هاوکینگ (hep-th/0507171) به اصطلاح پارادوکس فایروال را نیز حل می کند. هاوکینگ هرگز نمی گوید که اطلاعات در پس زمینه سیاه چاله ثابت از بین نمی رود. در واقع او برعکس می گوید. او می گوید (صفحه 3): بنابراین در نهایت همه به نوعی حق داشتند. اطلاعات در معیارهای توپولوژیکی غیر پیش پا افتاده مانند سیاهچاله ها از بین می رود. این مربوط به اتلاف است که در آن فرد وضعیت دقیق را از دست می دهد. از سوی دیگر. اطلاعات مربوط به وضعیت دقیق در معیارهای بی اهمیت توپولوژیکی حفظ شده است. برای حدس زدن، در گرانش کوانتومی شما نمی دانید که آیا واقعاً یک سیاهچاله دارید یا نه، بنابراین باید توپولوژی های بی اهمیت، از جمله مواردی که سیاهچاله ای در آنجا وجود ندارد، در دامنه بگنجانید. تنها در این صورت است که وحدت را بازیابی کنید. به نظر من خطای بچه های AMPS این است که از یک پس زمینه سیاه چاله ثابت استفاده می کنند و حفظ اطلاعات را فرض می کنند (یعنی تابش دیررس حداکثر با تابش زمان اولیه درهم می آمیزد). جای تعجب نیست که آنها به یک تناقض منجر می شوند. آنها به سادگی دوباره پارادوکس اطلاعات را انجام می دهند. آنها فهرستی از مفاهیم را به صورت انتزاعی ارائه می دهند: (1) تابش هاوکینگ در حالت خالص است، (2) اطلاعات حمل شده توسط تابش از ناحیه نزدیک به افق ساطع می شود، با نظریه میدان موثر کم انرژی که فراتر از فاصله میکروسکوپی معتبر است. از افق، و (iii) ناظر در حال سقوط با هیچ چیز غیرعادی در افق مواجه نمی شود. اما راه حل واضح این است که (i) اشتباه است. تابش، در محاسبات نیمه کلاسیک که آنها آن را محاسبه می کنند (یعنی نه گرانش کوانتومی)، غیر واحد است. بنابراین سوال من این است که چرا این یک پارادوکس است؟ «استادان» فیزیک مطمئناً نمیتوانند چیزی بسیار واضح را نادیده بگیرند. بنابراین من دوست دارم نظرات شما را بشنوم.
|
آیا پارادوکس فایروال واقعا یک پارادوکس است؟
|
131180
|
شار حرارتی = 10 مگاوات دمای آب ورودی = 28 درجه سانتیگراد برای خنک سازی از طریق لوله ای که از مرکز بلوک مستطیلی به طول 50 میلی متر، ارتفاع 30 میلی متر و عرض 30 میلی متر قطر داخلی لوله = 10 میلی متر و قطر خارجی = لوله 12 میلی متر عبور می کند. از مس ساخته شده است. ضریب انتقال حرارت آب را در 42 بار و دمای داده شده پیدا کنید عدد ناسلت و عدد رینولد را پیدا کنید.
|
انتقال حرارت به یک مکعب از یکی از وجوه
|
111990
|
می خواستم بدانم اگر فردی در استخر بزرگ باشد یا در دریای که از طریق منبع برق وصل است دچار برق گرفتگی می شود؟ از آنجایی که آب دریا شور است، جریان الکتریسیته را هدایت می کند، آیا خطرناک خواهد بود!؟
|
اگر یک منبع برق را در یک آب بزرگ وصل کنیم، آیا خطرناک خواهد بود؟
|
22348
|
من یک سوال خیلی ساده دارم. همه باید رنگین کمان را بعد از باران دیده باشند. بر اساس این تئوری، رنگین کمان به دلیل عبور نور خورشید از قطرات کوچک آب در جو (به معنی پراکندگی نور) ایجاد می شود. اکنون آنچه من می خواهم بدانم این است که پس از باران قطرات باران در کل جو وجود دارد. بنابراین کل فضا باید رنگارنگ به نظر برسد. چرا فقط یک شکل نیم دایره تشکیل می شود (یا رنگارنگ است).
|
چرا شکل رنگین کمان بعد از باران نیم دایره است چرا کل جو رنگارنگ نیست؟
|
86821
|
وقتی در مورد کار و گشتاور مطالعه می کنم، متوجه شدم که واحد آنها یکی است. اما چرا به جای نیوتن متر (واحد گشتاور) از ژول (واحد کار) استفاده نمی کنیم؟ از آنجایی که $\mathrm{1\ Joule = 1\Nm}$، چرا نمی توان آنها را تعویض کرد؟
|
چرا واحدهای کار و گشتاور قابل تعویض نیستند؟
|
92579
|
1. منظور از مختصات تعمیم یافته در مکانیک کلاسیک چیست؟ 2. فرمالیسم لاگرانژی چه تفاوتی با فرمالیسم همیلتونی دارد؟ 3. ارتباط آنها با اصل همیلتون چگونه است؟ 4. ارتباط آنها با معادله اویلر-لاگرانژ چگونه است؟
|
مکانیک کلاسیک و مختصات
|
93620
|
دوگانگی موج - ذره وجود دارد. بر اساس این نظریه، نور یک موج و یک ذره است. میدان مغناطیسی چطور؟ آیا ممکن است که آن هم یک موج و ذره باشد، اما این ذره هنوز کشف نشده باشد؟ آیا میدان مغناطیسی گسسته است؟ 
|
آیا میدان مغناطیسی در دوگانگی موج-ذره قرار دارد؟
|
131186
|
این مسئله 2.6 (ب) در گریفیث است، _مقدمه QM:_ > یک ذره در یک چاه مربع نامتناهی تابع موج اولیه خود را دارد یک ترکیب زوج از دو حالت ثابت اول: > > $\Psi(x,0) = A[\psi_1(x) + \psi_2(x)]$. در اینجا بخشی از مشکل است که من با آن مشکل کمی دارم: > (ب) $\Psi(x,t)$ و $|\Psi(x,t)|^2$ را پیدا کنید. دومی را به صورت سینوسی > تابع زمان بیان کنید، مانند مثال 2.1. برای ساده کردن نتیجه، اجازه دهید $\omega > \equiv \frac{\pi^2 \hbar}{2ma^2}$ مطابق کلید پاسخ، حتی پس از $t=0$، تابع موج همچنان مخلوط باشد. از دو حالت ساکن اول چرا اینطور است؟ من در درک این موضوع کمی مشکل دارم. چرا نمی تواند یک مخلوط جدید باشد؟ آیا سوالات من به اندازه کافی روشن است؟
|
تعیین تابع موج از شرایط اولیه
|
35622
|
در طول تجزیه و تحلیل محدودیت یک نظریه، فرض کنید همیلتونی متعارف من $$H_c=P^A\dot{A}+P^B\dot{B}-L$$ باشد که در آن $P^A=\frac{\جزئی L }{\partial \dot A}$ and $P^B=\frac{\partial L}{\partial \dot B}$ در این مورد، کموتاسیون $[P^A,P^B]=0$؟
|
محاسبه Commutation در تحلیل محدودیت
|
28610
|
اگر کسی به من بگوید چگونه cft روی یک منیفولد فشرده شده (مثلاً با استفاده از شرایط مرزی دوره ای) می تواند معنادار باشد، خوشحال می شوم؟ تغییر ناپذیری منسجم جهانی به دلیل مقیاسی که منیفولد در آن فشرده شده است (به عنوان مثال دوره) شکسته می شود. بیتغییر همشکل محلی البته هنوز به طور کلاسیک وجود دارد، اما برای مثال، برای یک مورد ساده از یک میدان روی یک استوانه، ردیابی تانسور تنش-انرژی غیر صفر میشود (به نسبت بار مرکزی). از این رو ظاهرا فشرده سازی منیفولد فضا-زمان در تضاد با داشتن تقارن منسجم است.
|
زمینه های منطبق بر روی منیفولدهای فشرده شده؟ یک پارادوکس ظاهری!
|
26648
|
اخیراً این نوشته دکتر فیل پلیت (با نام مستعار اخترشناس بد) را خواندم. او در مورد دریاچه ای از آب صحبت می کند که در لایه یخی اروپا قرار دارد. > دریاچه به طور کامل در پوسته یخی فرو رفته است. به طور کلی، یخ بسیار ضخیم است که ظاهر معمول سطح اروپا را توضیح می دهد. اما در برخی از نقاط، درست زیر یخ، یخ ذوب شده است. یخ بالای این > دریاچه زیرزمینی بسیار نازک تر است، شاید تنها 3 کیلومتر (حدود 2 مایل) ضخامت داشته باشد، > سطح آشفته در آن نقاط محلی را توضیح می دهد. مانند تصور این هنرمند:  دکتر پلیت در مورد اهمیت این کشف صحبت می کند، اما در مورد چگونگی این اتفاق نمی پردازد. آیا مقاله، فرضیه یا حدس در مورد چگونگی ساخت این دریاچه (و احتمالاً موارد مشابه دیگر) انجام شده است؟
|
آب مایع در میان یخ در اروپا. مکانیزم؟
|
23695
|
ما می دانیم که الکترونی که توسط هسته به دام افتاده است، مانند سیستم هیدروژن، با حالت کوانتومی توصیف می شود و هرگز به هسته نمی افتد. بنابراین آیا وضعیت مشابهی در مورد الکترون در نزدیکی سیاهچاله وجود دارد اما در آن نیفتاده است؟ و هنگام در نظر گرفتن مکانیک کوانتومی سقوط در گرانش به چه معناست؟ اصل هم ارزی در موارد کوانتومی به چه معناست؟
|
اصل هم ارزی در موارد کوانتومی به چه معناست؟
|
23690
|
یک ماهواره هواشناسی ($m_s = 4350$ کیلوگرم) در مدار دایره ای پایدار به دور زمین قرار دارد ($m_E = 5.97 \cdot 10^{24}$ کیلوگرم). هر 2 ساعت و نیم یک بار یک مدار را کامل می کند. (در مورد این 2 جواب مطمئنم) ماهواره در چه فاصله ای از مرکز زمین می چرخد؟ $r_i = 9.35 \cdot 10^6$ m سرعت زاویه ای ماهواره چقدر است؟ $\omega_i = 6.98 \cdot 10^{-4}$ rad/s (من در تهیه این قسمت مشکل دارم:) اپراتورهای ماهواره تصمیم میگیرند راکتهای مانور را شلیک کنند و ماهواره را به مداری با شعاع 5% بزرگتر منتقل کنند. اگر قدر اولیه انرژی مکانیکی ماهواره $E_{m,i} = 9.26 \cdot 10^{10}$ J بود و با همان سرعت ادامه مییابد، موشکها چقدر کار در انتقال ماهواره به ماهواره انجام دادهاند. مدار بالاتر؟ من شعاع بزرگتر را محاسبه کردم r_f= 9.86 \cdot 10^6$ m. با استفاده از $v = \sqrt{\frac{GM_e}{r}}$، $v_i = \sqrt{\frac{GM_e}{r_i}} = 6529.7$ m/s پیدا کردم. به همین ترتیب، $v_f=6371.5$ متر بر ثانیه. با استفاده از قضیه انرژی کار، می دانم که $W_i+K_i+W_{other}=W_f+K_f$. از آنجا که کل انرژی مکانیکی داده می شود، $E_{m,i}+W_{other}=W_f+K_f$. تنها کاری که روی جسم انجام می شود انرژی پتانسیل ناشی از گرانش است، بنابراین $E_{m,i}+W_{other}=-\frac{GM_em_s}{r_f}+\frac{1}{2}m_sv_f^2 \ دلالت دارد W_{other}=-\frac{GM_em_s}{r_f}+\frac{1}{2}m_sv_f^2-E_{m,i} = -1.80 \cdot 10^{11}J$، که واضح است پاسخ اشتباه آیا کسی می تواند بفهمد که من کجا را خراب می کنم؟
|
کار انجام شده توسط راکت ها در حرکت مداری
|
81661
|
من سعی می کنم به یک کودک کمک کنم تا در مورد یک پروژه علمی در مورد تبرید تحقیق کند. تازه کردن مهارت های ترمودینامیک بسیار زنگ زده من.... قانون گاز ایده آل: $PV=nRT$. بیایید هوا را در STP بگیریم: $P = 101\,kPa$ V = 1\,L = 0.001\,m^3$R $R = 8.3\,J/mol\cdot K$T $T = 298\,K$ $n=PV/RT = (101000) (.001) / (8.3 \cdot 298) = 0.04\، خال دلار؟ اگر هوا را به صورت آدیاباتیک به ~7atm فشرده کنیم $P_2 = 7P$، فکر می کنم حجم به $\frac{1}{7V}$ V_2 = \frac{V}{7}$ می رود، پس انتظار دارم که گاز داغ تر باشد اما واضح است که من گیج شده ام زیرا با آن فشار و حجم، دما به وضوح یکسان است. من فرض میکنم که اشتباه میکنم در مورد حجم یک گاز ایدهآل اگر به 7$\,atm فشردهسازی کنم؟$T_2 = \frac{P_2V_2}{nR} = ???$ گرمای ویژه هوا : $c_p = 1.006\,kJ/kg\cdot K$ البته هوا کاملا ایده آل نیست. همچنین از کسی که توضیح دهد رفتار غیر ایده آل ناشی از چیست، سپاسگزارم. به اختلاط ربطی داره؟ نوعی برهمکنش شیمیایی بین اجزای مختلف؟ آنچه من می خواهم بدانم این است که چگونه دمای یک گاز را با توجه به دمای اولیه، فشار، ظرفیت گرمایی و فشار نهایی به صورت آدیاباتیک محاسبه کنم.
|
رفتار گازها، ایده آل و غیره
|
95610
|
فوراً می گویم که منظور من اسفالرون های مدل استاندارد نیست، منظورم اسفالرون های برخی از پسوند های مدل استاندارد است. دلیل حتی فکر کردن به این موضوع مقاله سال گذشته فرامپتون و هانگ (بحث) است که پیشنهاد می کند جرم هیگز ممکن است 126 گیگا ولت باشد زیرا مقیاس های زمانی برای واپاشی خلاء و واپاشی پروتون ناشی از لحظه یکسان است. به طور دقیق تر: مقیاس زمانی واپاشی خلاء ناشناخته است، اما اگر با مقیاس زمانی رخداد خود به خودی یک اسفالرون در یک پروتون یکسان باشد، نشان دهنده وجود جرم هیگز در نزدیکی جرم مشاهده شده است. (این آنقدرها هم که به نظر می رسد قابل توجه نیست: جرم هیگز درست در لبه ای است که خلاء را واقعاً پایدار می کند، بنابراین _هر_ عمر بسیار طولانی برای خلاء مطابق با جرم هیگز نزدیک به مقداری است که ما می بینیم.) مدل علی منسجم داشته باشد. اما یکی از راههای کارکرد آن این است که واپاشی پروتون باعث واپاشی خلاء شود. این باید مشکلاتی را با کیهانشناسی جهان اولیه ایجاد کند، اما فعلاً آن را کنار بگذارید، شاید راهی برای دور زدن آن وجود داشته باشد. آنچه من می خواهم بدانم این است که آیا ایده واپاشی پروتون باعث واپاشی خلاء می شود یا خیر. آنچه من در نظر دارم یک توسعه مدل استاندارد با اسکالرهای جدید است که در عمل اسفالرون _و_ در پتانسیل گسترده بخش هیگز ظاهر می شود. شاید اسکالر جدید یک VEV خاص خود را داشته باشد، عمل اسفالرون تخریب کننده پروتون زمانی که آن VEV تغییر می کند به حداقل می رسد، اما VEV جدید به نوبه خود VEV هیگز موجود را بی ثبات می کند و آن را به یک حداقل واقعی جدید سوق می دهد. تأثیر یک اسکالر اضافی بر پایداری خلاء ضعیف یک موضوع فعلی تحقیق است، و بخش 4 این مقاله نشان میدهد که اسنوترینوها به طور اسمی در عمل اسفالرون در گسترش MSSM نقش دارند (اگرچه در اینجا سهم آنها ناچیز است).
|
آیا فروپاشی پروتون ناشی از اسفالرون نیز می تواند باعث فروپاشی خلاء شود؟
|
25695
|
در مقالهای که اخیراً از ناسا منتشر شده، آمده است که آنها ستارههایی را پیدا کردهاند که دمای آنها به اندازه بدن انسان است. این چگونه ممکن است؟ آیا همجوشی هنوز در این ستاره ها رخ می دهد؟
|
چگونه ستاره های کوتوله Y می توانند چنین دمای پایینی داشته باشند؟
|
114176
|
کمبود نوترینوی خورشیدی برای اولین بار در اواخر دهه 1960 مشاهده شد. و نظریه نوسان نوترینو در سال 1967 توسعه یافت. اما در سال 2001، اولین شواهد قانع کننده از نوسانات نوترینو خورشیدی در SNO ارائه شد. چرا نزدیک به 35 سال طول کشید تا نوسان نوترینو تایید شود؟ مرجع: http://en.wikipedia.org/wiki/Neutrino_oscillation
|
مشکل نوترینوهای خورشیدی در سال 1968 و تأیید تجربی نوسانات نوترینو در سال 2001. چرا تأخیر عظیم؟
|
94281
|
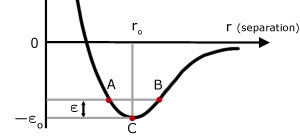 من سعی می کنم این منحنی را بهتر درک کنم، اما نمی توانم کاملاً بفهمم انرژی پتانسیل منفی به چه معناست. نمودار باید مولکولی را توصیف کند که بین $A$ و $B$ در نوسان است، اما در جایی که من در استدلال گیر کرده ام این است که PE در $A$ و $B$ برابر است، اما پس چرا این به این معنی است که $r$ خواهد بود. افزایش $A$ (دفع) و کاهش در $B$؟
|
منحنی انرژی پتانسیل برای فاصله بین مولکولی
|
23962
|
رفتار جالب همبستگی قوی بین الکترون ها در فلزاتی با اوربیتال های d یا f تا حدی پر (فلزات گذار) رخ می دهد. چرا این همبستگی های قوی برای مثال با عناصری با مدار p یا s ناقص ظاهر نمی شوند؟
|
اوربیتال های تا حدی پر شده و الکترون های همبستگی قوی
|
79553
|
من سعی می کنم نسبت سطح به حجم یک کره را با کران بکنشتاین مرتبط کنم. از آنجایی که نسبت سطح به حجم با افزایش حجم کاهش مییابد، میتوان حدس زد که در هر واحد حجم، یک فضای کوچک نسبت به فضای بزرگ از نظر اطلاعات غنیتر است. این چگونه می تواند باشد و چگونه می تواند برای سیاهچاله های با اندازه های مختلف کار کند؟ خیلی ممنون آقای رنی. از پاسخ شما قدردانی می کنم و بررسی کرده ام. به نظر می رسد که من با مکاتبات AdS/CFT آشنا هستم و درک کافی از ریاضیات دارم (فقط به سختی) که مجذوب حدس و گمان و البته نظریه هولوگرافی باشم. اگر تناظر فقط برای یک سیاهچاله با قطر معین کار کند، به نظر من حدس ضعیف به دلیل تغییر نسبت سطح به حجم یک کره است. برای من، به نظر می رسد، به احتمال زیاد، یک کنجکاوی یا تصادفی ریاضی است. با این حال، اگر از جنبهای که من نمیفهمم، این مطابقت برای قطرهای مختلف، در واقع تمام قطرهای سیاهچالهها برقرار باشد، در واقع بسیار شگفتانگیز به نظر میرسد. پس از مدتی جستجو، یک بار مقداری را دیدم که بهعنوان بیاهمیت و احتمالاً در نمونهای دیگر توصیف شده است، که ممکن است ربطی به افزونگی اطلاعاتی داشته باشد. من می ترسم که نتوانم این منابع را سایت کنم، زیرا آنها خیلی کوتاه بودند و نمی توانستند کمکی کنند.
|
نسبت سطح به حجم یک کره و مرز بکنشتاین
|
128403
|
بنابراین در QFT، عملگر میدان کوانتومی $\psi$ وجود دارد. به نظر می رسد $\psi$ نقش تابع موج در QM را بر عهده می گیرد که اکنون بر اساس حالت خلاء عمل می کند. سپس در لاگرانژی نظریه های مختلف میدان کوانتومی، $\psi$ ظاهر می شود، اما اکنون به آن میدان کوانتومی می گویند. پس آیا عملگر میدان کوانتومی با میدان کوانتومی اینجا فرقی ندارد؟ اگر متفاوت نیست، پس چگونه $\psi$ میتواند $|\psi|$ اسکالر را در هر فرضی داشته باشد، زیرا فقط در حالت خلاء عمل میکند؟ با فرض اینکه حالت خلاء با مقداری $n \times 1$ بردار نمایش داده می شود (بگذارید فعلاً بعد بی نهایت را فراموش کنیم)، عملگر باید به شکل $n \times n$ باشد.
|
آیا عملگر میدان کوانتومی $\psi$ با میدان کوانتومی $\psi$ یکی است؟
|
86225
|
تصور کنید دختر/پسر کوچکی روی یکی از صندلی های چرخ و فلک نشسته است. او سنگی را بیرون می اندازد و می بیند که سرعت **v** را تجربه می کند. در همین حال، ناظر دیگری که روی زمین ایستاده است، می بیند که سنگ با سرعت افقی **u** پرتاب می شود. چه ارتباطی بین **u** و **v** وجود دارد؟ (امیدوارم آنچه را که در ذهنم است به خوبی توضیح داده باشم.)
|
چرخ و پرتابه
|
51163
|
فرض کنید یک حلقه سیم دایره ای داریم و یک شیر برقی بلند و کامل داخل آن قرار می دهیم که به منبع ولتاژ متناوب متصل است به طوری که میدان مغناطیسی داخل آن شروع به تغییر در زمان کند، آیا این میدان مغناطیسی متغیر یک emf را در حلقه ما القا می کند. طبق قانون استقرا فارادی؟ (فرض کنید که شعاع شیر برقی بسیار کوچکتر از شعاع حلقه دایره ای باشد) آیا این یک نوع غیرمحلی مانند اثر آهارونوف-بوم را نشان می دهد؟ یا من فقط مفهوم را اشتباه متوجه شده ام؟
|
محلی در مقابل غیرمحلی
|
104822
|
بیایید Dirac spinor $\Psi (x)$ داشته باشیم. تبدیل به $\left( \frac{1}{2}, 0 \right) \oplus \left( 0, \frac{1}{2} \right)$ از گروه لورنتس میشود: $$ \Psi = \begin{pmatrix} \psi_{a} \\\ \kappa^{\dot {a}}\end{pmatrix}, \quad \Psi {'} = \hat {S}\Psi . $$ بیایید spinor $\bar {\Psi} (x)$ داشته باشیم که به $\left( \frac{1}{2}, 0 \right) \oplus \left( 0, \frac{1} نیز تبدیل میشود. {2} \right)$، اما به عنوان cospinor: $$ \bar {\Psi} = \begin{pmatrix} \kappa^{a} & \psi_{\dot {a}}\end{pmatrix}، \quad \bar {\Psi}{'} = \bar {\Psi} \hat {S}^{-1}. $$ چگونه به طور رسمی نشان دهیم که $$ \bar {\Psi}\Psi = inv؟ $$ منظورم این است که اگر $\Psi \bar {\Psi}$ به محصول مستقیم اشاره دارد (لطفا تصحیح کنید، اگر اشتباه کردهام) $$ \left[\left( \frac{1}{2}، 0 \right) \oplus \left( 0, \frac{1}{2} \right) \right]\otimes \left[\left( \frac{1}{2}, 0 \right) \oplus \left( 0, \frac{1}{2} \right) \right], $$ چه عملیات گروهی با $\bar {\Psi} \Psi$ مطابقت دارد؟ این سوال به شدت با این سوال مرتبط است.
|
چگونه می توان ماهیت ثابت برخی از ارزش ها را با نمایش های نظریه گروه نشان داد؟
|
56622
|
اگر $ از قرارداد علامت $(+،-،-،-)$ استفاده کند، آنگاه چهار موقعیت، چهار سرعت مثبت میشوند اما چهار شتاب منفی! $x_{\mu}x^{\mu}=\tau^2c^2،$$U_{\mu}U^{\mu}=c^2،$a_{\mu}a^{\mu }=-(a\gamma^3)^2,$ در دست های دیگر اگر از قرارداد علامت $(-،+،+،+)$ استفاده کنم، چهار موقعیت، چهار سرعت منفی می شود، اما شتاب چهار مثبت می شود! $x_{\mu}x^{\mu}=-\tau^2c^2، $U_{\mu}U^{\mu}=-c^2، $a_{\mu}a^{ \mu}=(a\gamma^3)^2,$ درست نیست!؟
|
نسبیت خاص علامت و چهار شتاب
|
35627
|
به نظر می رسد این ادعا که جهان جوان در حالت آنتروپی پایین قرار دارد با * حداکثر آنتروپی تعادل حرارتی و * جهان جوان در تعادل گرمایی در تضاد است. من به برخی از پاسخهای دیگر نگاه کردهام و آنها برای من خیلی فنی هستند، اما فکر میکنم دلیل اصلی این را فهمیدهام: «آنتروپی پایینتر بود زیرا جهان کوچکتر بود». آیا این درست است؟
|
ساده کردن توضیح بیگ بنگ با آنتروپی پایین
|
128409
|
چندین سال پیش، من روی تختم دراز کشیده بودم و یک دیسک پلاستیکی شفاف به شکل سی دی (که یک پشته 100 سی دی را می پوشاند) داشتم، اساساً یک سی دی شفاف. نمیدونم چرا ولی گوشیمو برداشتم و از سوراخ اون دیسک پلاستیکی از لامپ اتاقم عکس گرفتم. نتیجه این است:  چرا اینطور به نظر می رسد؟ آیا ربطی به تداخل لایه نازک دارد؟ و آیا اگر سوراخی در وسط وجود نداشته باشد، به همین شکل خواهد بود؟
|
آیا این نتیجه تداخل لایه نازک است؟
|
56626
|
من مرتباً متوجه می شوم که می فهمم محتوای میدانی در یک مقاله فیزیک خاص از کجا آمده است، اما سپس یک لاگرانژی یا عمل یا ابرپتانسیل بیان می شود و نمی دانم چگونه مشتق شده است. اگر از قبل محتوای میدانی نظریه را میدانید، آیا مجموعهای از قوانین کلی برای ساخت یک لاگرانژی/عمل/فوق پتانسیل وجود دارد؟ هر گونه پیشنهادی از منابعی که نحوه انجام این کار را توضیح دهد بسیار استقبال می شود زیرا من در یافتن موارد کمک کننده مشکل کمی دارم.
|
آیا کسی منبع خوبی می شناسد که توضیح دهد (به طور کلی) چگونه ما لاگرانژها/عملکردها/فوق پتانسیل ها را برای محتوای زمینه های مختلف تشکیل می دهیم؟
|
93621
|
به خوبی شناخته شده است که قطبش پذیری پیچیده کره دی الکتریک یکنواخت با شعاع $r$ و گذردهی پیچیده $\hat\epsilon_{in}(\omega)$ در محیطی با گذردهی پیچیده $\hat\epsilon_{out}(\omega )$ تحت میدان الکتریکی همگن با فرکانس دایره ای $\omega$ با (در سیستم واحدهای CGS) تعریف می شود: $$\hat\alpha(\omega)=r^3 {\hat\epsilon_{in}(\omega)-\hat\epsilon_{out}(\omega)\over \hat\epsilon_{in}(\omega )+2\hat\epsilon_{out}(\omega)}$$ این رابطه برای حالت استاتیک در بسیاری از کتابهای درسی در مورد الکترواستاتیک مشتق شده است (نمونه مرتبط را اینجا ببینید). در مورد کیس پویا چطور؟
|
قطبش پذیری پیچیده یک کره دی الکتریک در یک میدان الکتریکی همگن
|
79604
|
من با اصطلاحات فیزیک خیلی خوب نیستم، پس لطفا با من به عنوان یک نادان رفتار کنید. من سعی می کنم ضریب میرایی را به صورت دینامیکی برای درب کنترل شده هیدرولیک که در اثر فشار هیدرولیک باز و بسته می شود (باز/بستن) محاسبه کنم. فرمولی که من به ضریب میرایی خود نیاز دارم این است: viscous_fric_mom = $C \times \omega \times 2/\pi$; تقسیم $\pi/2$ به این دلیل است که حداکثر زاویه ای که در را می توان با آن باز کرد $\pi/2$ (یعنی 90 درجه) است، $\omega$ سرعت زاویه ای در است که بر حسب $\rm است. راد/s$. و $C$ ضریب میرایی است که باید آن را به صورت پویا محاسبه کنم. سیستم مشخص می کند که واحد ضریب میرایی من در $\rm N m s$ است! من فکر کردم $\rm N s /m$ باشد، زیرا معمولاً Force*time/distance است. ظاهرا من اشتباه می کنم. کسی میتونه راهنمایی کنه که برای محاسبه این ضریب میرایی چی باید در نظر بگیرم؟ من واقعاً در ریاضی بد هستم و بهتر از این نمی دانم. **به روز رسانی** من در حال تلاش برای ایجاد یک مدل نرم افزاری از درب هیدرولیک هستم. با توجه به اعمال فشار موثر جک هیدرولیک درب باز می شود. همین امر در هنگام بسته شدن درب صدق می کند، یعنی باید فشار انقباض جک هیدرولیک موثری اعمال شود. من از ادغام دو قسمتی (ادغام شتاب و سرعت) برای بدست آوردن موقعیت زاویه ای فعلی درب، یعنی از حالت قفل استفاده می کنم. فرض فعلی من این است که درب دارای شتاب $\pi/2$ یا $-\pi/2$ خواهد بود (یعنی باز یا بسته شدن). اگر من آن را ادغام کنم، سرعت را دریافت می کنم و ادغام مضاعف موقعیت را به من می دهد. اگر موقعیت زاویه ای را بگیرم و آن را به ماشین حساب ضریب میرایی خود برگردانم، باید کار کند، درست است؟
|
ضریب میرایی برای یک درب با کنترل هیدرولیک
|
66210
|
من فکر می کردم الکترونیک عمدتا در رشته های مهندسی بحث می شود. اما در دانشگاه من الکترونیک و الکترونیک دیجیتال برای رشته های فیزیک اجباری است. من برنامه درسی دیگران را جستجو کردم، اما هیچ درس الکترونیک پیدا نکردم. در MIT opencourseware نیز هیچ دوره الکترونیکی در فیزیک وجود ندارد. آیا پدیده ای در الکترونیک وجود دارد که در درک ما از جهان اساسی باشد؟
|
آیا الکترونیک موضوع اصلی در فیزیک است؟
|
74794
|
آیا سرعت جذب یک پرتو ذرات نباید به شدت به زاویه بین پرتو و محور کریستال ماده مورد نظر (اگر ماده هدف یک بلور باشد) بستگی دارد؟ در زوایای معین، تمام هستهها پشت هم قرار میگیرند و سطح مقطع بسیار کوچکی را ارائه میدهند، در حالی که جهتگیریهای دیگر، همه هستهها را بدون هیچ سایهزنی در معرض دید قرار میدهند. با این حال، من هیچ اشاره ای به این موضوع در جداول مقطعی نمی بینم، بنابراین حدس می زنم که مهم نباشد. چرا این است؟
|
آیا سطح مقطع واکنش هسته ای به زاویه بین پرتو فرودی و کریستال هدف بستگی دارد؟
|
83016
|
برای چاه بی نهایت: $$U(x)=\quad\infty : x \leq 0\quad 0 : 0 < x < L\quad \infty : x \geq L$$ $\psi_n=$$\sqrt{ \frac{2}{L}}\sin{\frac{n\pi x}{L}}$ $\Delta x_n$ را پیدا کنید، عدم قطعیت در موقعیت برای برخی eigenstate دلخواه psi.n بنابراین تلاشی که برای انجام این کار انجام دادم این بود که با استفاده از $\Delta x_n=\sqrt{<x^2>-<x>^2}$ را پیدا کنم و $$<x^2> را پیدا کردم. =L^2(\frac{1}{3}-\frac{1}{2\pi^2})$$ و $$<x>^2=\frac{L^2}{4}$$ این منجر به نتیجه نهایی $$L\sqrt{\frac{2\pi^2-12}{24\pi^2}}$$ وقتی به قسمت بعدی سوال رفتم و $\Delta p_n=\frac را پیدا کردم {\pi\hbar}{L}$ و سپس از این با $\Delta x_n$ برای تأیید اصل عدم قطعیت استفاده کردم، شکست خوردم. من چه کار اشتباهی انجام داده ام، نمی توانم آن را ببینم. من از کتابم برای تأیید انتگرال ها استفاده کردم.
|
محاسبات عدم قطعیت معیوب برای یک ذره حالت زمین در یک چاه بی نهایت
|
23696
|
من یک سوال در مورد کتاب والد دارم: نسبیت عام. در پیوست E معادله انیشتین را با در نظر گرفتن عبارت سطحی (GHY) به دست آورد. من نمی فهمم بعد از معادله (E.1.38) چه گفت. در واقع او این را در نظر میگیرد که $h^{bc}\nabla_c(\delta g_{ab})=0$، زیرا ما $\delta g_{ab}=0$ را در سطح ثابت میکنیم، اما بنابراین چرا عبارت دیگر در (E .1.38) پوچ نیست، عبارت $h^{bc}\nabla_a(\delta g_{bc})$. آنها برای من یکسان به نظر می رسند، و بعد از مقداری جبر، جایی که مشتق کوواریانت را با مشتق سازگار با متریک روی سطح جایگزین می کنیم، باید یک عبارت مشتق کل در سطح داشته باشیم که بتوانیم آن را ادغام کنیم. پیشاپیش ممنون
|
توضیح در مورد کتاب والد
|
78351
|
من یک دانش آموز دبیرستانی هستم که در مورد فرکانس های تشدید صفحات Chladni با مواد و اندازه های مختلف تحقیقی در IB Extended Essay انجام می دهم. لطفاً کسی تعریف گره های شعاعی و قطری ($n$ و $m$) و نحوه تعیین آنها را توضیح دهد؟ علاوه بر این، آیا کسی مایل است مشتق معادله Chladni را ارائه دهد $$f \sim (m + 2n)^2؟$$ در اینجا پیوندی با منابع ریاضی مرتبط وجود دارد: http://www.nhn.ou.edu/ ~johnson/Education/Juniorlab/Chladni/2001-ChladniPlates- CurtisParry.pdf
|
ریاضیات بشقاب کلادنی
|
51169
|
آیا کسی می تواند به من بگوید چه معادلاتی را می توانم از چگالی لاگرانژی $${\cal L}(\phi,\,\,\phi_{,i},\,\,A_i, \dot A_i,\,\,A_ بدست بیاورم {i,j})~=~\frac{1}{2}|\dot A+\nabla\phi|^2-\frac{1}{2}|\nabla \times A|^2-\rho\phi+J\cdot A$$ توسط معادلات اویلر-لاگرانژ؟
|
الکترودینامیک و چگالی لاگرانژی
|
65979
|
من به تازگی یادگیری نظریه M(atrix) و اصول فشرده سازی ابعاد اضافی را به پایان رساندم. 6 بعد اضافی نظریه ابر ریسمان را می توان روی 3 منیفولد Calabi-Yau فشرده کرد (زیرا 6 بعد واقعی به معنای 3 بعد پیچیده است). با این حال، وقتی صحبت از نظریه M می شود، نمی توان روی منیفولدهای 3.5 Calabi-Yau فشرده سازی کرد، بنابراین پس از فشرده سازی 6 بعد، بعد 1 اضافی کجا می رود؟ آیا فقط روی یک دایره فشرده می شود یا چیزی شبیه به آن؟
|
منیفولدهای Calabi-Yau و فشرده سازی ابعاد اضافی در نظریه M
|
28618
|
من یک سوال در مورد الکترودینامیک کلاسیک جکسون دارم. معادله $$\varphi \left ( x\right )=\tfrac{1}{4\pi\epsilon _{0}} \int_V \frac{\varrho ( x )}{R}d^{3} را در نظر بگیرید x+\tfrac{1}{4\pi} \oint_{\partial V} \left(\frac{1}{R}\frac{\partial }{\partial n}\varphi -\varphi \frac{\partial }{\partial n}\frac{1}{R} \right)dS.$$ این پتانسیل الکترواستاتیکی را به دلیل توزیع بار $\varrho$ در یک متن محدود بیان میکند. حجم $V$ با شرایط مرزی مشخص. انتگرال اول بار داخل یک حجم در فضا را بیان می کند. انتگرال دوم شرایط مرزی روی سطح این حجم را کد می کند. اولین سوال من: آیا این بدون توجه به هر باری که خارج از ولوم قرار می دهید یا حذف می کنید، پتانسیل کل را کاملاً در داخل آن حجم مشخص می کند؟ یا تغییر در توزیع بار در خارج از حجم باعث تغییر در شرایط مرزی (پتانسیل و مشتق نرمال آن در سطح) می شود؟ سوال دوم من: از نظر ریاضی می توانم درک کنم که پتانسیل خارج از حجم باید صفر باشد، اما نمی توانم بفهمم که چرا اینقدر از نظر فیزیکی است. همچنین، اگر مقداری شارژ خارج از ولوم قرار دهید، پتانسیل صفر در خارج تغییر خواهد کرد، درست است؟
|
یک سوال از الکترودینامیک جکسون
|
61295
|
چه تغییرات انرژی هنگام استفاده از جت اسکی رخ می دهد؟
|
چه تغییرات انرژی هنگام استفاده از جت اسکی رخ می دهد؟
|
53950
|
بهترین کتاب های مقدماتی برای توپولوژی، هندسه جبری، منیفولدها و غیره که برای تئوری ریسمان مورد نیاز است کدامند؟
|
توپولوژی برای فیزیکدانان
|
24479
|
> **تکراری احتمالی:** > بهترین کتاب ها برای پیشینه ریاضی؟ من به دنبال یک کتاب درسی در مورد نظریه گروه/بازنمایی برای یک دانش آموز فیزیکدان هستم. سؤالات اصلی مورد علاقه بازنمایی SO، SU و گروه لورنتس/پوانکر در ابعاد مختلف (یا شاید برخی موضوعات دیگر که از قلم انداخته ام اما برای فیزیک ذرات مهم هستند) است.
|
کتاب های تئوری بازنمایی
|
56623
|
خورشید منبع اصلی تشعشعات الکترومغناطیسی است. سپس اگر منبع یکسان است، امواج EM مختلف با طول موج های متفاوت چگونه تولید می شوند؟
|
تولید امواج EM با طول موج های متفاوت
|
25524
|
http://hpiers.obspm.fr/eop-pc/models/constants.html بیان می کند که سال گرمسیری 365.242190402 دلار روز است. میانگین سال تقویم میلادی 365.2425 دلار روز است (هر چهارمین سال یک سال کبیسه، به جز هر 100 سال، به جز هر 400 سال). تفاوت 0.000309598 دلار در روز است که به 26.7493 دلار در ثانیه می رسد. این بسیار بیشتر از 1 ثانیه کبیسه ای است که هر 2-3 سال یا بیشتر اضافه می کنیم. چه چیزی را از دست داده ام؟
|
سال گرمسیری 27 ثانیه از سال میلادی فاصله دارد؟
|
33222
|
فکر میکنم این سوال اینجا جای خود را دارد زیرا مطمئن هستم که برخی از شما متخصصان خودآموخته هستید و میتوانید کمی مرا در این روند راهنمایی کنید. با توجه به این که : * من اصلاً سابقه ی فیزیکدان ندارم. * من کمی پیش زمینه ریاضی دارم اما هیچ چیز خیلی پیچیده ای مانند حساب دیفرانسیل و انتگرال ندارم * من یک دانش آموز سریع هستم و حاضرم برای یادگیری فیزیک تلاش های زیادی انجام دهم * من یک برنامه نویس کامپیوتر و تحلیلگر هستم و علاقه مند به قوانین فیزیک، نظریه ها، مطالعات و هر چیز دیگری هستم. به من کمک میکند تا بفهمم همه چیز چگونه کار میکند یا باعث میشود دیدگاهم را در اطرافم تغییر دهم. از کجا شروع کنم؟ منظورم این است که آیا حتی یک نقطه شروع وجود دارد؟ آیا من مطلقاً باید یک نوع فیزیک را انتخاب کنم؟ آیا امکان یادگیری فیزیک به تنهایی وجود دارد؟ من می دانم که این یک سوال کلی است، اما مطمئن هستم که شما درک می کنید که من در اینجا کمی در تاریکی هستم.
|
چگونه خودآموز فیزیک را شروع می کنید؟
|
23697
|
چرا وقتی با کفشهایتان کوبیده میشوید، بارها حرکت میکنند (از آنجایی که الکترومتر به جلو و عقب حرکت میکند)، اما اگر کفشهایتان را نپوشید، الکترومتر حرکت نمیکند. در اینجا ویدیو مربوطه با جزئیات این رویداد است. http://www.youtube.com/watch?v=cJSp8v0YJrA از ابتدا در حدود 47 دقیقه ویدیو است. من منطق پشت آن را درک نمی کنم.
|
اگر پارچه را با کفشهایتان کوبید، شارژ حرکت میکند
|
2489
|
> **تکراری احتمالی:** > آیا مدل های فعلی فیزیک ذرات خواص شیمیایی > عناصر/ترکیبات را توضیح می دهند؟ آیا قانون/الگو یا قوانین و/یا الگوهای متعددی وجود دارد که ویژگی های یک عنصر را با توجه به تعداد پروتون ها و نوترون های آن توصیف کند؟ به عنوان مثال، یک اتم کربن که دارای 6 پروتون و 6 نوترون است، چگونه می توانید بفهمید که چگونه عمل می کند، واکنش پذیری، اگر یک نوار کربن وجود داشت، چگونه می توان آنها را مرتب کرد و خواص آن مانند قدرت چگونه بود. اما قوانین برای هر تعداد پروتون و نوترون کار می کنند.
|
آیا [مجموعه ای از] قوانین/الگوهایی وجود دارد که برای عناصر اعمال می شود؟
|
74000
|
در حال حاضر در حال انجام دوره های مکانیک کلاسیک پیشرفته هستم. به دلیل فقدان دانش در جبر خطی، حساب دیفرانسیل و انتگرال چند متغیره و سایر فصول، درک آن برایم سخت است. آیا کسی می تواند یک کتاب ریاضی که برای آموزش تمام ریاضیاتی که در فیزیک استفاده می شود اختصاص دهد؟
|
کتاب های یادگیری ریاضی در فیزیک؟
|
32934
|
در ادامه با یک سری سؤال در مورد فشردن کوانتومی، اجازه دهید سؤال دیگری را اضافه کنم: فشردن کوانتومی خلاء یک حالت انتشار واقعی میدان است، می توان آن را روشن و خاموش کرد، فشردن را می توان تغییر داد و اطلاعات را می توان برای تعدیل آن ارسال کرد. بنابراین، باید درجاتی از آزادی واقعی در توضیحات فیلد QED وجود داشته باشد که فشردگی را توضیح دهد. اما فشردن بر خود میدان تأثیر نمی گذارد، بلکه بر عدم قطعیت های مرتبط تأثیر می گذارد. میدان کوانتومی الکترومغناطیسی معمولاً به عنوان نوسانگرهای کوانتومی روی یک عدد موج $k$ و یک عدد پلاریزاسیون (یا 1- یا 1) توصیف میشود. بنابراین سؤال این است: درجات آزادی که یک میدان فشرده را توصیف می کند کجاست؟ آیا آنها به سادگی گم شده اند؟ این سؤال به دنبال بحث از این سؤالات است: اینجا و اینجا
|
شرح میدان کوانتومی فشردن
|
93627
|
من در منیفولدهای لورنتزی کار می کنم، به طور کلی در منیفولدهای شبه ریمانی و کاربردهای نسبیت عام. من تعاریف فیلدهای بردار همسان، کشنده و همتز را در ابرسطوح های ریمانی می دانم. آیا این کمیت ها در ابرسطح های شبه ریمانی به همین صورت تعریف می شوند؟ اهمیت فیزیکی این مقادیر چیست؟
|
آیا میدانهای بردار منسجم، Killing و همتتیک در منیفولدهای شبه ریمانی یکسان هستند؟
|
57236
|
من به دنبال اشتقاقی از عبارت چگالی انرژی در هر نقطه از میدان مغناطیسی ساکن بودم. من میدانم که $\dfrac {1}{2 \mu_0}\left|\vec{B}\right|^2$ است -- من فقط فکر میکردم آیا یک مشتق وجود دارد که بتوان آن را ساخت چگالی انرژی $\dfrac {\epsilon_0}{2}\left|\vec{E}\right|^2$ را در هر نقطه از یک میدان _الکتریکی، با در نظر گرفتن انرژی مورد نیاز برای ساخت به دست میآورد. بیت به بیت شارژ «منبع» را افزایش دهید. به نظر می رسد هر مدرکی که من پیدا کرده ام _القایی_ را به تصویر می آورد -- آیا راهی برای انجام آن بدون آن وجود دارد؟ می پرسم چون اثبات مربوطه برای میدان الکتریکی به نظر نمی رسد جایی به تعریف ظرفیت نیازی داشته باشد... ممنون...
|
چگالی انرژی مغناطیسی - مشتق بدون معرفی ایندچانس؟
|
27272
|
این سوال از مکالمه من و جو فیتزسیمون ایجاد شد. آیا یک نمایش تثبیت کننده مختصر برای حالت های متقارن، در سیستم های _n_ spin-1/2 یا (به طور کلی) _n_ ذرات اسپین بالاتر وجود دارد؟ منظور من از نمایش تثبیت کننده این است که: * هر حالت متقارن (یا برخی از خانواده های قابل توجه و غیر پیش پا افتاده از آنها که بیشتر از حالت های محصول فقط شامل می شود) به عنوان یک حالت ویژه +1 یک عملگر یا مفصل منحصر به فرد نشان داده می شود. +1-حالت ویژه فهرستی از عملگرها، که در آن * هر عنصر از این مجموعه از عملگرهای تثبیت کننده را می توان به طور خلاصه توصیف کرد، به عنوان یک عملگر در فضای بزرگتر هیلبرت ( _یعنی_ نه تنها به عنوان یک تبدیل محدود به خود زیرفضای متقارن، و * که در آن عملگرهای تثبیت کننده به روشی زیبا در تصویر هایزنبرگ تحت واحدهای محلی متقارن تغییر می کنند (_یعنی تبدیلات واحد به شکل _U ⊗ n_). در حالت ایدهآل، میتوان انواع دگرگونیها را بین حالتهای متقارن مختلف توصیف کرد. اما نمی توان همه چیز را داشت. محدودیت منحصر به فرد بودن یک حالت ویژه از لیست عملگرهای تثبیت کننده نیز می تواند مشمول محدودیت بودن حالت متقارن باشد. (به عنوان مثال، بسیاری از حالات در ذرات _n_ spin-1/2 توسط یک عملگر σz در یک اسپین تثبیت می شوند، اما دقیقاً یک حالت متقارن توسط آن عملگر تثبیت می شود. نه اینکه من انتظار داشته باشم که چنین عملگر لزوماً در فرمالیسم ایجاد شود. ...) آیا نمایشی با ویژگی های فوق (یا نزدیک به آن) وجود دارد؟
|
فرمالیسم تثبیت کننده برای حالت های اسپین متقارن؟
|
11478
|
ما معمولاً می گوییم که نیروها باعث شتاب معکوس با جرم می شوند. آیا کمتر صحیح است که بگوییم شتاب باعث ایجاد نیروهایی متناسب با جرم می شود؟ چرا؟ (توجه داشته باشید که سؤال اساسی در ذهن من - اساساً آنچه علت را از معلول متمایز می کند - بسیار کلی تر است. اما به نظر می رسد این مکان خوبی برای شروع باشد.)
|
چه چیزی باعث می شود که نیروها علت و شتاب معلول باشند؟
|
27277
|
من از فکر کردن در مورد اخترفیزیک نظری لذت می برم زیرا می خواهم سیاهچاله ها را درک کنم. با توجه به اینکه هیچ کس سیاهچاله ها را درک نمی کند، من دوست دارم به نزدیک ترین چیز به سیاهچاله فکر کنم: یک ستاره نوترونی! من در سراسر وب برای بحث های آموزشی در مورد ساختار ستاره های نوترونی مانند این پیوند از ناسا جستجو کرده ام: http://heasarc.nasa.gov/docs/objects/binaries/neutron_star_structure.html، اما به نظر می رسد هیچ کدام در سطح پیشرفته ای نیستند. سطح کافی برای میل من مشکل این است که نمی دانم چه ادبیاتی را باید بخوانم تا بیشتر یاد بگیرم. وضعیت فعلی تحقیقات ستاره نوترونی چگونه است؟ چند مقاله مروری خوب چیست؟ به طور خاص، من در مورد پیشبینیهای نظری برای «ستارهزلزلهها» که در پیوند بالا به آنها اشاره شده است، و اینکه چگونه به یک ناظر روی زمین نگاه میکنند، کنجکاو هستم. من همچنین علاقه مندم که بفهمم چه اتفاقی برای سقوط گاز در یک ستاره نوترونی می افتد -- به ویژه، اگر سول توسط ستاره نوترونی به سمت مرگ خود مارپیچی می رود.
|
مقدمه ای بر فیزیک ستاره های نوترونی
|
117195
|
سلام من می خواهم شروع به یادگیری حساب چند متغیره به طور خاص برای یادگیری الکترودینامیک کنم. چند کتاب درسی خوب چیست؟
|
کتاب محاسبات چند متغیره
|
89736
|
آیا وب سایت هایی برای خودآموزی ریاضیات پیشرفته وجود دارد؟ به عنوان مثال، محققان پیرامونی برای مطالعه خود فیزیک نظری وجود دارد، اما من وبسایتهای خوبی را پیدا نکردم که ویدیوهای سخنرانی ریاضیات را ارائه دهند، به عنوان مثال، چند سخنرانی عالی هندسه دیفرانسیل، گروه دروغ، جبر دروغ، توپولوژی جبری، معادلات دیفرانسیل جزئی و به همین ترتیب
|
آیا وب سایت هایی برای خودآموزی ریاضیات پیشرفته وجود دارد؟
|
93624
|
با توجه به پتانسیل زیر: $$V(\theta,\phi)=\frac{Q}{a}\left(\sin\theta \cos\phi+\frac{1}{2}\cos^2\theta\ راست)$$ روی سطح کره ای به شعاع $a$ من سعی می کنم معادله لاپلاس را خارج از کره (جایی که هیچ باری وجود ندارد) حل کنم. من میدانم که راهحل کلی معادله لاپلاس در خارج از کره به صورت زیر به دست میآید: $$\phi(r,\theta,\phi)=\sum_{l=0}B_l r^{-l-1}P_l(\cos\ تتا). آیا مرحله بعدی شامل بیان پتانسیل داده شده به عنوان چند جمله ای لژاندر است؟ ممنون میشم راهنمایی کنید
|
هارمونیک های کروی
|
61294
|
من معیاری از شکل زیر را در نظر میگیرم (امضای $(+,-,-,-)$): $$ds^2 = (F(r,t)-G(r,t))dt^2 - (F(r,t)+G(r,t))dr^2 - r^2(d\Omega)^2$$ که در آن $F(r,t)$ و $G(r,t)$ هستند توابع اسکالر دلخواه من در تلاش برای یافتن یک تغییر مختصات و/یا هماهنگ به یکی از فرمهای «استاندارد» رابرتسون-واکر هستم، به عنوان مثال. $$ds^2 = dT^2 - a(T)^2/(1-kR^2)dR^2 - R^2(d\Omega)^2$$ برای هر $k=0,-1، +1$، یا نشان دهید که وجود ندارد. هر راهنمایی؟
|
تحولات هماهنگ و منسجم متریک FRW
|
27274
|
* اگر $\Phi$ یک میدان اسکالر چند جزئی است که در برخی از نمایشهای یک گروه سنج تغییر شکل میدهد، مثلاً $G$، پس چقدر میتوان یک دلیل کلی برای استدلال اینکه پتانسیل فقط تابعی از G-Invariant است ارائه داد. تابع، $\Phi^\Dagger \Phi$؟ این موضوع به ویژه زمانی گیجکنندهتر میشود که نگاه کنیم به موقعیتهایی که $\Phi_{[ij]}$ یک تانسور ضد متقارن رتبه-2 در نظر گرفته میشود. سپس فکر میکنم ادعا این است که تنها شکل ممکن پتانسیل این است که $V = \frac{m^2}{2}\Phi^{*ij}\Phi_{ij} + \frac{\lambda}{32 }(\Phi^{*ij}\Phi_{ij})^2 +\frac{\lambda'}{8}\Phi^{*ij}\Phi_{jk}\Phi^{*kl}\Phi_{li}$ * این عبارت است که در بالا تنها پتانسیلی است که $ است G-$نامتغیر برای هر $G$ و چنین $\Phi$؟ {..نزدیک ترین چیزی که می توانم به آن فکر کنم این است که فضای همه تانسورهای رتبه-2 ضد متقارن، $\Phi_{[i,j]}، i,j = 1,2,..,N$, از نمایش طبیعی گروه $SU(N)$ پشتیبانی می کند.. اما چه؟..}
|
پتانسیل های اسکالر ثابت را اندازه گیری کنید
|
28616
|
با توجه به این بررسی > تابع موج فوتون. ایوو بیالینیکی-بیرولا. _پیشرفت در اپتیک_ **36** V > (1996)، ص 245-294. arXiv:quant-ph/0508202، یک تابع موج صفحه کلاسیک EM یک تابع موج (در فضای هیلبرت) از یک فوتون منفرد با تکانه معین (c.f بخش 1.4) است، اگرچه یک تفسیر احتمالی ساده و ساده قابل استفاده نیست. با این حال، آنچه من در برخی منابع دیگر آموخته ام (مانند QM پیشرفته ساکورای، فصل 2) این است که فیلد EM کلاسیک با گرفتن مقدار انتظار عملگر فیلد به دست می آید. سپس طبق گفته ساکورای، میدان $E$ یا $B$ کلاسیک یک حالت فوتون منفرد با تکانه p معین توسط $\langle p|\hat{E}(یا \hat{B})|p\rangle$ داده میشود. ، که در کل فضا 0 دلار است. به نظر میرسد که این با دیدگاه اول در تضاد است، اما هر دو دیدگاه با استدلالهای خودشان به یک اندازه برای من حس خوبی دارند، پس چگونه میتوانم آنها را با هم تطبیق دهم؟
|
تابع موج EM و تابع موج فوتون
|
74246
|
فرض کنید یک سلول ولتی داریم. در یک نیم سلول، ما یک الکترود روی (یا هر دیگری) و در دیگری یک الکترود هیدروژن (یا هر دیگری) داریم. حالا اگر بگویم پتانسیل الکترود روی 5 ولت است، آیا این (5 ولت) در واقع اختلاف پتانسیل بین دو الکترود یعنی روی و هیدروژن است؟
|
پتانسیل الکترود یک الکترود
|
74248
|
در کتاب _Arthur Beiser - Concepts of Modern Physics [صفحه 213]_ نویسنده متغیرهای معادله شرودینگر قطبی را با این فرض جدا می کند: $$\psi_{nlm}=R(r)\Phi(\phi)\Theta(\theta) $$ سپس عبارتی وجود دارد که فضای دیفرانسیل od در سیستم مختصات قطبی عبارت است از: $$dV=(dr)\cdot (d\theta r)\cdot (r\sin\theta d\phi)$$ من این را درک می کنم، اما در صفحه بعد عبارتی وجود دارد: > As $\Phi$ و $\Theta$ توابع نرمال شده هستند، احتمال واقعی > $P(r)dr$ برای یافتن الکترون در اتم هیدروژن جایی در پوسته کروی بین $r$ و $r+dr$ از هسته عبارت است از: $$P(r)dr=r^2|R(r)|^2dr\,\int\limits_{0}^{\pi}|\Theta(\theta) |^2\sin\theta d\theta \, \int\limits_{0}^{2\pi}|\Phi|^2 d\phi=r^2|R(r)|^2dr$$ در این معادله می توانم دیفرانسیل حجمی که در بالا توضیح داده شد و تابع موج $\psi_{nlm}=R(r)\Phi(\phi)\ را تشخیص دهم. تتا(\تتا)$. من هم میدونم که نرمال شدن توابع زاویه ای روی زوایا 1 برمیگرده ولی نمیفهمم چرا قسمت شعاعی ادغام نمیشه...کسی میتونه کمی توضیح بده؟
|
احتمال یافتن الکترون در اتم H
|
25527
|
من همیشه به فضا و نجوم علاقه داشتم (در جوانی - می خواستم فضانورد شوم). با این حال، به دلایل مختلف، من هرگز کاملا شروع نکردم. من اکنون می خواهم شروع کنم - کوچک اما پیوسته. من در شهری زندگی می کنم، بنابراین: آلودگی نوری یک مشکل است - با این حال، من می خواهم یک تلسکوپ (شاید یک تلسکوپ دست دوم اما یک ساخت خوب) تهیه کنم، شاید به یک باشگاه نجوم محلی بپیوندم؟ در یک دنیای ایده آل، من یک تلسکوپ خوب دریافت خواهم کرد که دارای ویژگی های زیر باشد: 1. می توان آن را گسترش داد تا به تدریج قدرتمندتر شود. عکس بگیرید آیا کسی می تواند یک سری مراحل را به من ارائه دهد تا در نهایت رویای رصد آسمان را به واقعیت تبدیل کنم؟ توجه: من می دانم که به احتمال زیاد مجبور خواهم شد با یک تلسکوپ کوچک دستی شروع کنم - اما ایده تلسکوپی را دوست دارم که با من رشد کند - اگر اصلاً امکان پذیر باشد.
|
چگونه در نجوم (مستقر در انگلستان) شروع کنیم
|
56624
|
$\ زاویه I +\ زاویه E=\ زاویه A +\ زاویه D $ زاویه تابش + زاویه ظهور = زاویه منشور (به طور معمول $60^\circ$) + زاویه انحراف. اگر مجموع آنها برابر نباشد، در انجام آزمایش با منشور دچار خطای شخصی شدیم. لطفا این معادله را معنا کنید.
|
این معادله از کجا آمده است ∠I+ ∠E = ∠A+ ∠D؟
|
104226
|
ما در جهانی زندگی می کنیم که بسیار بزرگتر از دنیای کوانتومی است. قوانین فیزیک کوانتوم معتبر نیستند. در حالی که کلیدهای لپ تاپم را فشار می دهم، 100٪ مطمئن هستم که آنچه را که واقعاً می خواهم می نویسم. پس چنین دنیای میکروسکوپی چگونه بر من تأثیر می گذارد؟ دنیای کوانتومی کاملاً متفاوت است، شاید بهترین گزینه برای آن بیگانگان باشد. پس چرا باید نگران عدم قطعیت و سایر مواردی باشم که در مقیاس بی نهایت کوچک اتفاق میافتند؟
|
دنیای کوانتومی چگونه بر ما تأثیر می گذارد و چرا باید به آن اهمیت بدهم؟
|
70548
|
## بیان مسئله، همه متغیرها و دادههای داده شده/مشخص، ترتیب زیر را در نظر بگیرید:  کار انجام شده توسط کشش روی 2 کیلوگرم را محاسبه کنید. بلوک در طول حرکت خود در مسیر دایره ای از نقطه $A$ تا نقطه $B$. ## تلاش برای یک راه حل می دانیم که کار انجام شده توسط یک نیرو محصول نیرو و جابجایی است. ما جابجایی نقطه کاربرد را 4 متر می دانیم. چگونه می توان کار انجام شده توسط کشش را پیدا کرد زیرا ثابت نیست، متغیر است! تلاش دوم (رویکرد حسابداری) بلوک 2 کیلوگرمی در امتداد دایره حرکت می کند، بنابراین سرعت آن Rdθ/dt است. ریسمان را می کشد، طول رشته بین نقطه O و بلوک را می توانیم با هندسه ساده در هر موقعیت θ (بدون توجه به اندازه قرقره) بدست آوریم. طول کل رشته بدون تغییر است، بنابراین سرعت بلوک 1 کیلوگرمی dL/dt است. http://imgur.com/PbpBpOB آیا می توانید بعد از این کمک کنید
|
کار انجام شده توسط تنش
|
130580
|
با توجه به وظیفهام در نوشتن روالهای پیشبینی مدار، سعی میکنم چارچوبهای مرجع و نحوه استفاده از آنها را بهتر درک کنم (مخصوصاً برای مدارهای زمین). فکر میکنم متوجه شدهام که ECI (اینرسی مرکز زمین) در مورد چیست. اما چند چیز در مورد J2000 نامشخص است. آیا من درست فکر می کنم که J2000 یک فریم ECI است، فقط با متغیر زمان اضافه شده است؟ اگر چنین است، اگر موقعیت ماهواره را نسبت به سطح زمین (طول جغرافیایی، طول جغرافیایی و فاصله از سطح/مرکز زمین) می دانید، چگونه موقعیت ماهواره خاصی را در یک لحظه معین در فریم J2000 نشان می دهید؟ جدای از توضیحات کلی، من همچنین قدردانی می کنم که تبدیل مختصات و هر محاسبات دیگری که برای انجام کار لازم است را بدانم.
|
چگونه موقعیت ماهواره را در J2000 از عرض، طول و فاصله از زمین تعیین کنیم؟
|
70542
|
آیا می توانیم سرعت را تغییر مسافت در زمان_ بنامیم؟ علاوه بر این، آیا ظرفیت گرمایی را به عنوان _تغییر گرما در هر دما_ یا _تغییر دما در هر گرما_ بیان می کنید؟ دلیل این سوال این است که برخی از افراد ظرفیت گرمایی را با _تغییر دما در هر گرما_ می دانند و اگر بخواهم معادله ای را بر اساس آن فرمول بنویسم، آن را به صورت $C_{[p|V]} = \ می نویسم. left( \frac{\partial T}{\partial U}\right)_{[p|V]}$، که معمولاً نوشته نمیشود.
|
سرعت و ظرفیت گرمایی ترجمه
|
26646
|
بنابراین من امروز صبح داشتم در مورد GN-108036 مطالعه می کردم و به دلایلی به چیزی فکر کردم که نمی توانم کاملاً سرم را دور آن بپیچم و بفهمم. صبح زود است، پس شاید هنوز قهوه نیامده است. اگر با یک انفجار بزرگ مرکزی شروع شود و ما اکنون به چیزی نگاه کنیم که 12.9 میلیارد سال نوری از ما فاصله دارد، چگونه میتوانیم اینجا باشیم تا نور را مشاهده کنیم اگر جهان تقریباً باشد. 13 میلیارد ساله؟ به عبارت دیگر: بیگ بنگ، چیزها شروع به گسترش می کنند. آنچه که GN-108036 را تشکیل می دهد بخشی از آن است آنچه در نهایت زمین را تشکیل می دهد بخشی از آن است. هنوز هیچ چیز نمی تواند سریعتر از نور حرکت کند. 12.9 میلیون سال پس از آن که ما در این نقطه از نور GN-108036 پیشتر هستیم تا نوری که به ما می رسد را ببینیم؟
|
سال نوری و انتقال به سرخ از دیدگاه ما. چگونه می توانیم آن را ببینیم؟
|
72051
|
اگر میدان الکتریکی نه لزوماً همگن توزیع بار در یک الکترولیت داشته باشم و میخواهم بفهمم میدان الکتریکی در مکانی در الکترولیت چقدر است. آیا معادله ای وجود دارد که بتوانم از آن استفاده کنم تا غربالگری الکتریکی توسط یون ها را نیز در نظر بگیرم تا میدان الکتریکی متفاوتی بدست بیاورم که با غربالگری کاهش می یابد؟ بنابراین اساساً من به دنبال معادله ای هستم که یک میدان الکتریکی یا پتانسیل را بگیرد و یک مورد غربال شده را به من بدهد.
|
غربالگری میدان الکتریکی برای شارژ خودسرانه
|
27279
|
با $Y_{lm}(\vartheta,\varphi)$ که هارمونیک های کروی هستند و $z_l^{(j)}(r)$ که توابع بسل کروی هستند ($j=1$)، توابع نویمان ($j=) 2$) یا توابع Hankel ($j=3,4$) را تعریف می کند $$\psi_{lm}^{(j)}(r,\vartheta,\varphi)=z_l^{(j)}(r)Y_{lm}(\vartheta,\varphi)،$$ بازنمودها چیست از تبدیل های پوانکاره اعمال شده به هارمونیک های کروی برداری $$\vec L_{lm}^{(j)} = \vec\nabla \psi_{lm}^{(j)}،\\\ \vec M_{lm}^{(j)} = \vec\nabla\times\vec r \psi_{lm}^{(j)}،\ \\ \vec N_{lm}^{(j)} = \vec\nabla\times\vec M_{lm}^{(j)}$$ ? آیا هیچ نشریهای تمام تبدیلهای پوانکره، یعنی نه تنها ترجمهها و چرخشها، بلکه تقویتهای لورنتس را نیز پوشش میدهد؟ به دلیل نرمال سازی های مختلف که گاهی اوقات استفاده می شود، یک نشریه را ترجیح می دهم که همه تغییرات را به طور همزمان پوشش دهد.
|
یک نمای کلی (و شاید اشتقاق) از تبدیل پوانکاره هارمونیک های کروی برداری
|
57570
|
اندازه یک قاب اینرسی چقدر است؟ میله بزرگی را در نظر بگیرید که حول یک نقطه ثابت در یک صفحه می چرخد، طول آن 1 سال نوری است. بنابراین نور از انتهای نزدیکتر به نقطه ثابت تا انتهای دورتر از نقطه ثابت یک سال طول می کشد تا به آن برسد. اکنون سرعت زاویه ای نقطه نزدیکتر به نقطه ثابت بسیار کندتر از سرعت زاویه ای نقطه دورتر است. بنابراین انتهای نزدیکتر به نقطه ثابت دارای سرعت نسبی به انتهای دورتر است. در نقطهای از زمان، ساعتهای دو انتها با ارسال یک سیگنال نوری به هر دو طرف دقیقاً از مرکز میله (نیم سال نوری از هر نقطه) هماهنگ میشوند. سوال من این است که آیا دو سر میله در یک قاب اینرسی هستند؟ آیا ممکن است 1 جسم به طور همزمان در دو قاب اینرسی قرار گیرد؟ یه سوال ساده تر طول یک میله 1 سال نوری است و با سرعت c/2 در طول خود حرکت می کند. انقباض طول میله توسط گاما وجود خواهد داشت. حالا یک منبع نور را در یک سر میله تصور کنید. نور یک انتها یک سال طول می کشد تا به انتهای دیگر برسد (همانطور که توسط هر دو انتها اندازه گیری می شود)، زمانی که میله ساکن است. اکنون از آنجایی که فاصله زمانی که میله در حال حرکت است منقبض می شود، بنابراین باید زمان متفاوت باشد (در مقایسه با ناظری که به این میله نگاه می کند) برای دو سر میله زیرا نور باید با سرعت یکسان در هر دو سر اندازه گیری شود. زمان باید در هر دو انتها از نظر تقارن یکسان باشد، بنابراین آنها در واقع در یک چارچوب اینرسی هستند. با این حال، اگر انقباض طول وجود داشته باشد، آنها یک سال نوری اندازه گیری نمی کنند، هر کدام باید کمتر از یک سال نوری اندازه گیری کنند. یک ناظر خارجی با مشاهده این میله، فاصله را کمتر از یک سال می بیند. اما برای اندازهگیری همان سرعت نور، باید همان زمان انتهای میله را نیز اندازهگیری کرد، بنابراین به این معنی است که ناظر در همان قاب میله است؟ بخش دوم سوال من این است. در گرانش صفر، شخص توپی را در دست می گیرد. بنابراین فرد و توپ در یک چارچوب اینرسی قرار دارند. سپس فرد توپ را «پرتاب» می کند و در نتیجه، هر دو و توپ و فرد اکنون سرعت نسبی نسبت به یکدیگر (عمل و واکنش) به دست می آورند. آیا این دو در یک قاب اینرسی هستند؟ بخش سوم سوال من این است. آیا در گرانش صفر، یک کشتی و یک ناظر در کشتی می توانند در یک چارچوب اینرسی باشند؟ یعنی شتاب مشترک دارند؟ با فرض اینکه کشتی یک هواپیما است، وقتی هواپیما شتاب می گیرد، شخص در اطراف شناور است، بنابراین شخص و کشتی نمی توانند شتاب مشترکی داشته باشند مگر اینکه فرد به کشتی بسته شود. بنابراین در گرانش صفر، هر جسم باید چارچوب اینرسی خود را داشته باشد؟
|
اندازه یک قاب اینرسی چقدر است؟
|
91301
|
من در حال گذراندن مقطع کارشناسی ارشد در برنامه های کاربردی کامپیوتر هستم. من هیچ پیش زمینه رسمی ریاضی و فیزیک ندارم، اما برای کنکور کارشناسی ارشد، ریاضیات سطح دبیرستان را با برخی از ریاضیات سطح کالج مقدماتی مانند حساب دیفرانسیل و انتگرال چند متغیره، جبر خطی پیشرفته و غیره خوانده ام، اما 2 سال قبل بود. به نظر شخصی من برنامه نویسی کامپیوتر کار یکنواختی است که من را از 2 سال گذشته (بعد از مطالعه ریاضی) خسته می کند و میل شدیدی به خودآموزی ریاضی و فیزیک دارم. ریاضیات پیش نیازی برای محاسبات به خصوص مباحث پیشرفته (الگوریتم ها، هوش مصنوعی و غیره) و فیزیک است، بنابراین تصمیم گرفتم ابتدا این مباحث ریاضی را پوشش دهم **1.** جبر خطی با استفاده از مقدمه ای بر جبر خطی از گیلبرت استرنگ **2.* * مثلثات با استفاده از مثلثات توسط Charles P. McKeague و Mark D. Turner **3.** هندسه مختصات **( _نیاز به توصیه برای کتاب برای پوشش این مبحث_ )** **4**. حساب دیفرانسیل و انتگرال **( _آشکار شدم از کدام کتاب از حساب دیفرانسیل و انتگرال توماس یا استوارت یا برخی دیگر استفاده کنم. بنابراین من نمی خواهم هیچ اشتباهی در انتخاب متن اشتباه برای newB انجام دهم. آیا می توانید با معرفی چند کتاب خوب که می توانم با یا به جای کتاب های ذکر شده در بالا از آنها استفاده کنم و یک استراتژی مناسب برای رسیدن به هدف به موازات مطالعه منظم خود به من کمک کنید.
|
توصیه هایی برای شروع خودآموزی فیزیک از ابتدا
|
74795
|
این سوال از سوال دیگر من ترتیب زمان و مشتق زمانی در فرمالیسم انتگرال مسیر و فرمالیسم عملگر به ویژه از بحث با دریک بیرون می آید. پست اصلی تا حدودی بد نوشته شده است، زیرا حاوی سوالات بسیار زیادی است، و تا امروز من در نهایت به اندازه کافی پرانرژی شدم تا سوال دیگری بنویسم که امیدوارم آنچه در آن پست پرسیده شده را روشن کند. من با تمام مشتقات کتاب درسی DSE مشکلی ندارم، اما پس از تغییر دیدگاه، بسیار کنجکاو شدم که DSE واقعاً کار می کند، معادله حرکت (EOM) تابع گرین مرتب شده با زمان کلین-گوردون آزاد را در نظر می گیرم. KG) را به عنوان مثال وارد کنید و منظور من را در واقع توضیح دهید. EOM تابع سبزهای سفارشی KG T رایگان $$(\partial^2+m^2)\langle T\\{\phi(x)\phi(x')\\}\rangle=-i\delta است. ^4(x-x')\cdots\cdots(1).$$ تابع دلتا از این واقعیت ناشی می شود که $\partial^2$ حاوی مشتقات زمانی است و با آن رفت و آمد نمی کند. نماد سفارش T به طور کلی برای عملگرهای بوسونیک $$\partial_t \langle T\\{A(t)\,B(t')\\}\rangle=\langle T \\{ \dot A(t)B(t')\ rangle+\delta (t-t')\,\langle [A(t),B(t')]\rangle \cdots\cdots(2)،$$$(1)$ را می توان از $(2)$ و رابطه کموتاسیون متعارف زمان برابر فیلدها. با این حال $(1)$ از رویکرد انتگرال مسیر چندان واضح نیست: $$(\partial^2+m^2)\langle T\\{\phi(x)\phi(x')\\}\rangle =(\partial^2+m^2)\int\mathcal{D}\phi e^{iS}\phi(x)\phi(x')\\\\\quad \quad \quad \qquad \qquad \qquad \qquad =\int\mathcal{D}\phi e^{iS}[(\partial^2+m^2)\phi(x)]\phi(x')\cdots\cdots (3).$$ حالا اگر به طور رسمی و ساده لوحانه فکر کنیم $$\int\mathcal{D}\phi e^{iS}[(\partial^2+m^2)\phi(x)]\phi(x')=\langle T\\{[(\partial^2+m^2)\phi(x )]\phi(x')\\}\rangle\cdots\cdots(4)، $$ **با علامت $\langle\cdots\rangle$ که همیشه مقدار انتظار را در رویکرد عملگر نشان میدهد**. سپس نتیجه نهایی به جای $-i\delta^4(x-x')$ 0 خواهد بود (به دلیل معادله میدان) و نمی توان نتیجه ای مانند معادله (2) به دست آورد. همانطور که دریک اشاره کرده است، این به دلیل ابهام در تعریف محصول عملگر زمان برابر است، زمانی که مشتق زمانی در انتگرال مسیر وجود دارد، بسیار مهم است (به عنوان مثال CCR در انتگرال مسیر) به وضوح مشتق زمانی را در شبکه زمانی تعریف کنیم. یعنی گسسته سازی. 3 تعریف ممکن برای $\dot \phi$ (با حذف متغیرهای فضایی) وجود دارد: (الف) مشتق رو به جلو $\dot \phi(t)=\frac{\phi(t+\epsilon^+)-\phi(t )}{\epsilon^+}$; (ب) مشتق عقب $\dot \phi(t)=\frac{\phi(t)-\phi(t-\epsilon^+)}{\epsilon^+}$ (c)مشتق مرکز $\dot \phi(t)=\frac{\phi(t+\epsilon^+)-\phi(t-\epsilon^+)}{2\epsilon^+}=\frac{1}{2}(\text{ forward}+\text{backward})$ این گسستهسازیهای زمانی مختلف منجر به سفارشهای متفاوت اپراتورهای همزمان میشود (پاسخ ران میمون را در این پست ببینید)، به ترتیب عبارتند از: (a)$\int\mathcal{D}\phi e^{iS}\dot \phi(t)\phi(t)=\langle \dot \phi(t)\phi(t)\rangle$ (b )$\int\mathcal{D}\phi e^{iS}\dot \phi(t)\phi(t)=\langle \phi(t)\dot \phi(t)\rangle$ (c)$\int\mathcal{D}\phi e^{iS}\dot \phi(t)\phi(t)=\frac{1}{2}[\langle \dot \phi(t)\phi(t)\rangle+\langle \phi(t)\dot \phi(t)\rangle]$ با در نظر گرفتن این موارد، اکنون میتوانیم معادله $(1)$ را بدست آوریم. از مسیر انتگرال (من فقط آن را برای نقطه زمان مساوی نشان میدهم، زیرا برای $t\neq t'$ هیچ ناسازگاری وجود ندارد): ابتدا تعریف (c) را برای $\dot \phi$ میگیرم، اما $\ddot\phi$ را با استفاده از مشتق جلو تعریف کنید (که موافقم ساختگی است)، بنابراین $\int\mathcal{D}\phi e^{iS}\ddot داریم \phi(t)\phi(t)\equiv\int\mathcal{D}\phi e^{iS}\frac{1}{\epsilon^+}[\dot \phi(t+\epsilon^+)- \dot \phi(t)]\phi(t) =\frac{1}{\epsilon^+}\\{\langle\dot \phi(t+\epsilon^+)\phi(t)\rangle-\frac{1}{2}\langle \dot \phi(t)\phi(t)\rangle-\frac{1}{2} \langle \phi(t)\dot \phi(t)\rangle\\}\\\ =\frac{1}{\epsilon^+}\\{\langle \dot \phi(t+\epsilon^+)\phi(t)\rangle-\langle \dot \phi(t)\phi(t)\rangle+\frac{1}{2}\langle [\dot \phi(t ),\phi(t)]\rangle\\}\\\ =\langle \ddot \phi(t)\phi(t)\rangle+\frac{1}{2\epsilon^+ }\langle[\dot \phi(t),\phi(t)]\rangle=\langle \ddot \phi (t)\phi(t)\rangle+\frac{1}{2\epsilon^+ }\delta^3(\mathbf{x}-\mathbf{x'})\cdots\cdots(5)$ اکنون میتوانیم به طور رسمی فکر کنیم $\lim_{\epsilon^+\ به 0}\frac{1}{ 2\epsilon^+}=\delta(0)$ زیرا $\delta (t)= \lim_{\epsilon^+\to 0}\,{1\over 2\epsilon^+}\,e^{-\pi\,t^2/(4\,{\epsilon^+}^2)}$. بنابراین $(5)$ می شود $$\int\mathcal{D}\phi e^{iS}\ddot \phi(t)\phi(t)=\langle \ddot \phi(t)\phi(t) \rangle+\delta(0)\delta^3(\mathbf{x}-\mathbf{x'})\cdots\cdots(6)$$ بقیه ساده است، فقط مشتقات فضایی را اعمال کنید، آن را به $(6)$ اضافه کنید و معادله میدان را اعمال کنید، سپس $(1)$ بازتولید خواهد شد. اشتقاق فوق بیشتر به دلیل دریک، به شکل سازمان یافته تر است. اکنون واضح است که تعریف دقیق گسسته سازی مشتق زمانی برای به دست آوردن نتیجه صحیح بسیار مهم است، گسسته سازی اشتباه به ما $(1)$ نمی دهد. با این حال، اشتقاق DSE مطلقاً هیچ اشاره ای به هیچ طرح گسسته سازی نمی کند، اما همیشه یک نتیجه سازگار با رویکرد اپراتور می دهد، چرا اینقدر خوب کار می کند؟ با تشکر فراوان از کسانی که به اندازه کافی صبور هستند تا بخوانند
|
یک مسئله کنجکاو در مورد معادله دایسون-شوینگر (DSE): چرا آنقدر خوب کار می کند؟
|
91888
|
آیا کتاب حساب دیفرانسیل و انتگرال اسپیوک و آپوستول حتی از نظر فیزیک برای یادگیری حساب دیفرانسیل و انتگرال خوب است؟ من درک اولیه ای از حساب دیفرانسیل و انتگرال دارم اما می خواهم فیزیک عمیق تری یاد بگیرم و برای این کار به حساب دیفرانسیل و انتگرال بیشتری نیاز دارم.
|
بهترین کتاب حساب دیفرانسیل و انتگرال برای فیزیک
|
13790
|
اگر موج الکترومغناطیسی فرودی به صورت زیر داده شود: $$\begin{align*}E_i&=A_e \cos(\omega t + bz)\\\ H_i&=A_h \cos(\omega t + bz)\end{align*}$ $ چه رابطه ای برای موج REFLECTED وجود دارد؟ اینجوری میشه؟ $$\begin{align*}E_r&=A_e \cos(\omega t - bz)\\\ H_r&=A_h \cos(\omega t - bz)\end{align*}$$
|
رابطه موج الکترومغناطیسی منعکس شده
|
30791
|
> **تکراری احتمالی:** > بهترین کتاب ها برای پیشینه ریاضی؟ من یک سال آخر کالج هستم و به امید اینکه یک فیزیکدان نظری شوم، برای تحصیلات تکمیلی درخواست می کنم. یکی از چیزهایی که استاد من دائماً از آن ناامید است، توانایی من در انجام محاسبات دشوار است. من نمیپرسم آیا کسی در آنجا کتاب یا منبع آنلاین خوبی را میشناسد که اساساً پر از مشکلات عملی حسابداری پیشرفته باشد. مواردی مانند بسط های تیلور آشفته، انتگرال های گاوسی، انتگرال های برداری، جایگزینی های غیر آشکار و غیره.
|
کتاب تمرین حساب دیفرانسیل و انتگرال برای فیزیکدانان
|
15495
|
داشتم درباره عمق فوکوس مطالعه میکردم و به این فکر میکردم که آیا عینک روی عمق فوکوس تأثیر میگذارد یا خیر. اگر بله، آیا برای کاربر قابل توجه است؟
|
آیا عینک عمق تمرکز را کاهش می دهد؟
|
78689
|
معلم فیزیک من در مورد ملاقات 2 خط موازی صحبت کرد و گفت ممکن است در بینهایت اتفاق بیفتد یا چیز دیگری. من می دانم که 2 خط موازی می توانند در هندسه کروی به هم برسند (به لطف مبادله پشته ریاضی)، اما آیا چنین چیزی در فیزیک ممکن است رخ دهد؟ (من واقعاً می خواهم بدانم تا بتوانم به او بگویم).
|
آیا دو خط موازی می توانند به هم برسند؟
|
78353
|
من روی این آزمایشگاه کار می کنم که شامل جمع آوری داده ها از دو منبع مختلف است. این شامل جمع آوری زمان واکنش از یک دستگاه و از یک برنامه وب است که در مجموعه داده های ما قرار داده شده است. پرسش در مورد رویدادهای پیشبینیشده و اینکه آیا آنها با عدم قطعیت تجربی موافق بودند یا خیر. پس از جستجوی این عبارات در گوگل، من هنوز توضیحات را بسیار نامشخص یافتم. آیا کسی می تواند توضیح دهد که چگونه می توانم به این پاسخ پاسخ دهم؟
|
رویدادهای پیش بینی شده و عدم قطعیت تجربی چیست؟
|
75708
|
بدیهی است که به حساب تک و چند متغیره و جبر خطی نیاز دارد، اما چه چیز دیگری؟ و پیشنهاد میکنید از کجا این پسزمینه را دریافت کنید؟
|
پیش نیاز سخنرانی های فاینمن؟
|
73013
|
من یک مهمانی دارم. فرض کنید من میخواهم یک یخچال پر از بطریهای آبجو سرد (6$~^\circ\text{C}$ یا پایینتر) در کوتاهترین زمان ممکن داشته باشم. یخچال نشان می دهد که 4$~^\circ\text{C}$ (و احتمالاً در حال حاضر) را هدف قرار داده است. قیمت تمام بطریها در حال حاضر 30$~^\circ\text{C}$ است، که دمای خارج از یخچال است، و بطریها با هم یخچال را کاملا پر میکنند (مانند بطریهای دیگر نمیتوان در آن قرار داد). بهترین استراتژی برای رسیدن به این هدف چیست؟ (آیا باید همه بطری ها را به یکباره در آن قرار دهم؟ آیا باید بطری ها را در زمان های مختلف در آن قرار دهم؟ و اگر چنین است، باید آنها را لمس کنم یا در ابتدا تا حد امکان از هم جدا نگه دارم؟ آیا حتی باید در نظر داشته باشم که برخی از بطری ها را در مدتی و بعداً آنها را دوباره در آن قرار دهید (این واقعاً عجیب خواهد بود.) اگر چنین است، آیا باید آن بطری ها را خنک کنم که هنوز در یخچال نبوده اند؟) * * * نکته 1: من فریزر در دسترس ندارم. نکته 2: فرض کنید که من می دانم چگونه بطری های بیشتری را در یخچال قرار دهم (بدون شکستن). * * * _اندازه گیری ها:_ 1 بطری آبجو: $0.61~\text{kg}$، 1 بطری خالی (با درپوش): $0.28~\text{kg}$، 1 بطری خالی (بدون درپوش): $0.28~\text{ kg}$، محتویات 1 بطری: $0.33~\text{l}$. حدس من این است که می توانم 72 بطری را در یخچال بگذارم.
|
بهترین استراتژی برای پر کردن کامل یخچال با بطری های آبجو و خنک کردن همه آنها چیست؟
|
75118
|
من در مورد یونیزاسیون حرارتی صحبت می کنم، آیا ساخت هر ماده ای امکان پذیر است یا عنصری وجود دارد که بتوان در دمای مثلا 20 درجه سانتیگراد یونیزه کرد؟ من یک مهندس کامپیوتر هستم و تا این حد به علم علاقه دارم، اما این فقط کنجکاوی است، لطفاً اگر بیهوده صحبت می کنم، مرا اصلاح کنید. **ویرایش:** همانطور که میدانم رشتهای از یک لامپ با اعمال گرما فوتون تولید میکند. منظور من این است که آیا می توانیم هر ماده ای بسازیم که در دمای کمتر از اتاق فوتون تولید کند و از اثر فوتوالکتریک برای گرفتن انرژی فوتون و تبدیل آن به الکتریسیته استفاده کنیم.
|
آیا می توانیم ماده ای بسازیم که در دمای پایین یون تولید کند؟
|
98104
|
در یک مورد الکترواستاتیک واضح است که در فضای محصور با یک هادی (بدون بار در آن) میدان الکتریکی صفر است. این اغلب در نمایشهای فیزیک مانند تصویر زیر نشان داده میشود:  به هر حال روشنایی دارید که جریانی در هوا میگذرد. و از طریق قفس بنابراین دیگر در وضعیت الکترو**استاتیک** نیستیم زیرا جریان داریم، یعنی بارهای متحرک. چگونه می توان در این توضیح به درستی حساب کرد که ما هزینه های متحرک داریم؟ برخی افراد می گویند که این واقعیت که مرد داخل قفس در امان است، کاری به قفس فارادی ندارد، فقط به این دلیل است که قفس رسانای بهتری است. گاهی به اثر پوستی نیز اشاره می شود. پس چه چیزی درست است. خیلی خوب است که توضیح دقیق و درستی در این مورد داشته باشید. آیا مرجع خوبی دارید؟
|
چرا قفس فارادی از شما در برابر جریان های زیاد محافظت می کند؟
|
116271
|
آیا قرار دادن دو ماژول Peltier کارآمدتر است یا قرار دادن آنها در کنار هم؟ و چرا؟ من یک جعبه کوچک دارم که میخواهم آن را حدود 20 کلوین پایینتر از محیط خنک کنم - سرد، اما نه زیر صفر. (من می خواهم دوربینم را خنک نگه دارم، بنابراین این جعبه خنک را قرار می دهم. دوربین از طریق یک پنجره شیشه ای تخت در یک طرف جعبه نگاه می کند). هیت سینکی که من در دست دارم تقریباً دو برابر عریض ترین ماژول Peltier است که در ابتدا قصد استفاده از آن را داشتم. بنابراین جا برای قرار دادن 2 ماژول Peltier در کنار هم در زیر هیت سینک وجود دارد. یا می توانم پشته ای از 2 ماژول Peltier را زیر هیت سینک قرار دهم. کدام ترتیب کارآمدتر است؟ برای چیدمان کنار هم باید سوراخ بزرگتری در عایق ایجاد کنم، بنابراین گرمای ناخواسته ای که از طریق آرایش کنار هم جریان می یابد بدتر است. از سوی دیگر، اثرات دیگر برای آرایش انباشته بدتر است. (آیا http://electronics.stackexchange.com/ مکان بهتری برای ارسال سوالات در مورد کولرهای Peltier است؟)
|
آیا قرار دادن دو ماژول Peltier کارآمدتر است یا قرار دادن آنها در کنار هم؟
|
41339
|
من روی خواص انتقال گاز الکترون دو بعدی در ساختارهای ناهمسان نیمه هادی کار می کنم و به طول مشخصه و مقیاس های زمانی سیستم مانند زمان و طول پراکندگی الاستیک، طول پیوستگی فاز، طول حرارتی و غیره علاقه مند هستم. لطفاً یک مقاله مروری خوب پیشنهاد کنید. در توضیح اهمیت هر یک از این مقیاس ها در رابطه با طول موج فرمی و تأثیر آنها در سنجش خواص انتقال الکترونیکی به عنوان تابعی از ابعاد سیستم ما (مانند [بالستیک (XOR) انتشاری] (AND) [رژیمهای کوانتومی کلاسیک (XOR)]). از آنجایی که هر تجزیه و تحلیل خاصیت خاصی از **سیستم ماده متراکم** مستلزم **مقیاس های طول و زمانی مشخصه** است، ممنون می شوم اگر مرجعی را پیشنهاد دهید که به مشکل یافتن مقیاس ها در یک چارچوب یکپارچه می پردازد. . در غیر این صورت حتی یک مرجع که به طور رضایت بخشی به مسئله انتقال الکترون می پردازد نیز مفید خواهد بود.
|
مرجع درک طول مشخصه و مقیاس های زمانی در یک سیستم (به ویژه حمل و نقل الکترونیکی)
|
134466
|
البته این یک سوال کاملا نظری است و در وهله اول برای حرکت آهنربا انرژی لازم است، اما زمانی که در خلاء فضا حرکت می کند، بدون گرانش یا میدان مغناطیسی در نزدیکی، می تواند تقریبا برای همیشه بچرخد (مانند میلیاردها سال) یک میدان مغناطیسی تولید می کند که از آن می توانید الکتریسیته بگیرید؟ اگر این کار نمی کند، چرا که نه؟
|
اگر آهنربایی را در فضا دور از هر میدان مغناطیسی بچرخانید، آیا برای همیشه می چرخد و می تواند برای همیشه الکتریسیته تولید کند؟
|
41333
|
سوال این است: اگر * یک توپ بولینگ و یک توپ پینگ پنگ * با **تحرک یکسان** * حرکت کنند و شما **همین نیرو** را برای متوقف کردن هر کدام اعمال کنید * که زمان بیشتری طول می کشد؟ یا برخی؟ * کدام فاصله توقف طولانی تری خواهد داشت؟ * * * بنابراین فکر می کنم می توانم به این شکل فکر کنم: $$F = \frac{dp}{dt} = m \cdot \frac{v_i - 0}{\Delta t} = \frac{p_i}{\Delta t}$$ از آنجایی که هر دو دارای تکانه یکسان هستند، با توجه به نیروی و تکانه یکسان، زمان یکسان خواهد بود؟ آیا این درست است؟ * * * پس چگونه فاصله توقف یک را انجام دهم؟
|
حرکت یکسان، جرم متفاوت
|
91724
|
من می خواهم یک فرآیند فیزیکی (تجربی) را ببینم که بتواند بسیاری از تبدیل مختصات را به این روش ریاضی توضیح دهد. (واقعاً دو تغییر، اما من فکر می کنم که در اینجا یک عدد بزرگ است)
|
معنای فیزیکی متریک Eddington - Finkelstein چیست؟
|
35626
|
خوب، آیا واقعاً امکان حفظ چنین دماهای پایین مورد نیاز برای ابررساناها (با در نظر گرفتن ابررسانایی در دمای بالا) در فواصل زیاد وجود دارد؟ چیزی که من می گویم این است - حتی اگر بتوانیم جریان را از ابررساناها عبور دهیم، برای حفظ مقاومت صفر باید آنها را دائماً خنک کنیم. از این رو برای خنک کردن، به قدرت نیاز داریم. اونوقت ابررساناها اگه مزیتی نداشته باشن اینجوری لازم نیس..؟ یا آیا رویکرد جدیدی برای غلبه بر این معایب وجود دارد؟
|
مسائل عملی با ابررسانایی
|
99858
|
من حدس میزنم که به یک حرکت در جهت درست نیاز دارم (این یک سؤال تکلیف نیست). من می خواهم طول کل یک پرتو را از یک تابشگر به یک هدف که از یک دال با ویژگی های شناخته شده عبور می کند محاسبه کنم. داده شده: * موقعیت امیتر و هدف $P_\text{منبع}، P_\text{Dest}$ * ضریب شکست دال و محیط اطراف $n_1، n_2$ * موقعیت و ضخامت دال $d_1$، $d_2 $, $d_3$  سوال: 1. چه زاویه تابش $\theta_i$ لازم است تا پرتو پرتویی از $P_{source}$ برای تقاطع $P_\text {dest}$؟ 2. مسیری که پرتو در واقع طی می کند چقدر است؟ می دانم که پرتو فرودی بسته به زاویه تابش و ضریب شکست به موازات جابجا می شود. من همچنین معادله ای برای تعیین افست پیدا کرده ام، اما هنوز مطمئن نیستم که چگونه آن را برای مشکل خود اعمال کنم: $$ \begin{equation}\tag{1} \Delta y = d_2 \tan \theta_i \left ( 1- \frac{\cos \theta_i}{\sqrt{n^2 - \sin^2 \theta_r}}\right) \end{equation} $$ که در آن $\Delta_y$ جبران پرتوی است که از دال بیرون میآید. میشه چندتا راهنمایی بهم بدی
|
نحوه جبران جابجایی پرتو ناشی از شکست در دال شیشه ای
|
57579
|
فرض کنید که مجموعهای از واحدهای شناختهشده $U_1,...,U_n$ داریم که بهطور تصادفی از معیار Haar انتخاب شدهاند و فرض کنید که هر واحد با احتمال $\frac{1}{n}$ در یک حالت ورودی $\rho اعمال میشود. $ که خالص است و در فضای هیلبرت $d$-بعدی زندگی می کند. برای $n\rightarrow\infty$ واضح است که: \begin{equation} \lim_{n\rightarrow\infty}H(\frac{1}{n}\sum_{i=1}^nU_i\rho U_i^ +)=\log d \end{معادله} که در آن $H$ آنتروپی فون نویمان است. با این حال، برای $n$ کوچک چگونه آنتروپی حالت را به صراحت محاسبه می کنید؟ من تعدادی اعداد را برای نشان دادن یک مثال وصل می کنم: اگر اجازه دهیم $n=2$، $d=2$، این معادل محاسبه میانگین زیر خواهد بود: \begin{equation} E_U\left[H\left(\ فراکس{1}{2} U_1|0\rangle\langle0|U_1^++\frac{1}{2}U_2|0\rangle\langle0|U_2^+\right)\right] \end{معادله} من نوشتم $|0\ rangle\langle0|$ از آنجایی که با تقارن، هر حالت خالص آنتروپی یکسانی خواهد داشت، میانگین خارج از تابع آنتروپی است زیرا بر اساس فرضیه مجموعه واحدها شناخته می شوند، به این معنی که ما میتوانیم بین هر مجموعه از واحدها تمایز قائل شویم، حتی اگر ندانیم کدام واحد از مجموعه اعمال شده است.
|
آنتروپی حالتی که تابع مجموعه ای از واحدهای تصادفی است
|
3452
|
اگر کسی یک دسته چوب را به کوهها برد تا انرژی بالقوه آن افزایش یابد، آیا با سوزاندن آن گرمای بیشتری بدست می آید؟
|
آیا انرژی پتانسیل گرانشی در آتش آزاد می شود؟
|
57907
|
من در مورد خطوط میدان الکتریکی برای توزیع پیوسته شک دارم. خوب، اگر فقط چند بار نقطهای وجود داشته باشد، میدانم که میدان از موارد مثبت (یا در بینهایت) شروع میشود، به بارهای منفی (یا در بینهایت) ختم میشود و تعداد خطوط متناسب با تعداد بارها است. این خوب است، اما دستورالعمل برای ترسیم خطوط میدان زمانی که توزیع پیوسته است چیست؟ به نظر من بعضی جاها خطوط را ترسیم میکنند و فقط تصور میکنند که توزیع پیوسته همان توزیع متناهی هزینههای کوچک $dq$ است، اما مطمئن نیستم که این روش انجام شود. کسی میتونه راهنمایی کنه که چطوری با این کار کنیم؟ پیشاپیش متشکرم
|
خطوط میدان الکتریکی برای توزیع مداوم
|
24351
|
من در حال ساختن یک هواپیما (Super Baby Great Lakes) هستم و در مورد ایرفویل ها فکر می کنم. به طور خاص (این هواپیما پوشیده از پارچه است)، من در مورد نیروهای بالابر روی بال های اصلی تعجب می کنم. من چیزهایی در مورد این موضوع خوانده ام که بسیار مهم است که پارچه به خوبی در بالای بال به دنده ها بچسبد تا پارچه هنگام بالا رفتن از هم جدا نشود. سوال من این است: فشار مستقیم جریان لغزشی به پایین بال به دلیل زاویه حمله بالا در مقابل میزان نیروی مکیدن به دلیل فشار کم در بالای بال چقدر بالابر ایجاد می شود؟ آیا جاروبرقی بالای بال صرفاً به دلیل کمبود فشار اتمسفر است، یا واقعاً یک نیروی مکنده است، مانند یک جاروبرقی قدرتمند که می تواند به عنوان مثال، ورق را از یک نوت بوک جدا کند؟ ممنون، جی
|
نیروهای روی یک ایرفویل
|
26643
|
در حین خواندن با پسرم در مورد چگونگی برخورد سیاره ای شبیه به مریخ با زمین اولیه که منجر به ماه فعلی ما شد، گفت که بقایای اولیه نیز یک حلقه تشکیل داده است، اما آن حلقه در نهایت توسط زمین و ماه جذب شد. من نتوانستم به سوال او پاسخ دهم که چرا زحل هنوز حلقه دارد. آیا حلقه های زحل نباید در قمرها جمع شوند یا جذب گرانش زحل شوند؟
|
چرا حلقههای زحل در قمرها جمع نمیشوند؟
|
74240
|
فرض کنید چرخ ها را زیر یک مخزن هوای فشرده  قرار داده اید تا بتواند به صورت افقی به سمت راست و چپ حرکت کند. فرض کنید در سمت راست مخزن یک نازل وجود دارد (در صورت تمایل در تصویر پشت آن). اگر مخزن با هوای پرفشار پر شود و نازل را باز کنید، مخزن به سمت چپ حرکت می کند. موشک ها اینگونه کار می کنند و به راحتی می توان آن را تصور کرد. **وقتی مخزن با خلاء پر میشود و نازل را باز میکنید چه اتفاقی میافتد؟** اولین برداشت من این بود که مخزن به سمت راست حرکت میکند اما یکی به من گفت که ثابت میماند. آیا این حقیقت دارد؟ توضیح شهودی برای آن چیست؟
|
اگر موشک به جای هوای پرفشار با خلاء پر شود چه اتفاقی می افتد؟
|
75968
|
اخیراً من در حال مطالعه گروه تقارن تصویری (PSG) و مفهوم مرتبط نظم کوانتومی هستم که برای اولین بار توسط prof.Wen پیشنهاد شد. در مقاله ون، آخرین خط معادله (8) را ببینید، تبدیل گیج محلی SU(2) برای عملگرهای اسپینور به صورت $\psi_i\rightarrow G_i\psi_i$، جایی که $\psi_i=(\psi_{1i}) تعریف شده است. ,\psi_{2i})^T$ عملگرهای فرمیونی هستند و $G_i\در SU(2)$. چرا اینطور تعریف می کنیم؟ همانطور که می دانیم، نمایش فرمیون Shcwinger برای spin-1/2 را می توان به صورت $\mathbf{S}_i=\frac{1}{4}tr(\Psi_i^\dagger\mathbf{\sigma}\Psi_i نوشت )$، جایی که $\Psi_i=\begin{pmatrix} \psi_{1i} & -\psi_{2i}^\dagger \\\ \psi_{2i} & \psi_{1i}^\dagger \end{pmatrix}$ و $G_i\Psi_i$ که همان تبدیل فوق است $\psi_i\rightarrow G_i\psi_i$ در واقع یک چرخش چرخشی است. از $\mathbf{S}_i$، در حالی که $\Psi_iG_i$ چرخش را _نه_ تغییر می دهد اصلاً $\mathbf{S}_i$. بنابراین در معادله (8)، چرا تبدیل گیج SU(2) را به جای $\Psi_iG_i$ به صورت $G_i\Psi_i$ تعریف می کنیم؟
|
یک سوال ساده در مورد تبدیل گیج $SU(2)$ در مقالات ون در مورد گروه تقارن تصویری (PSG)؟
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.