_id
stringlengths 1
6
| text
stringlengths 0
5.02k
| title
stringlengths 0
170
|
|---|---|---|
71542
|
وقتی چیزی جدید می گویم به چیزی که قبلا ساخته شده است مانند H، O و غیره اشاره نمی کنم و وقتی منظورم چیز جدیدی است، به تبدیلی مانند تریتیوم به هلیوم و طلا اشاره نمی کنم. اگر بله چگونه؟ (منظورم این است که آیا راه خاصی برای انجام آن وجود دارد؟)
|
آیا امکان ایجاد عنصر جدیدی وجود دارد که در جهان وجود ندارد؟
|
39525
|
معادلات فریدمن می گوید که چگالی های عظیم ماده منجر به نرخ انبساط عظیم می شود. در گرانش نیوتنی، دو ذره نقطه ای عظیم که با فاصله بینهایت کوچک از هم جدا شده اند، نیروی عظیمی را تجربه خواهند کرد. پس چه تفاوتی در مورد سیاهچاله وجود دارد؟
|
چرا تکینگی های سیاهچاله پایدار هستند؟
|
107493
|
تصور کنید این سال 1960-1970 است.....یک کشور قبلا نیروگاه های هسته ای دارد (برای مقاصد صلح آمیز) حالا اگر آنها فناوری سانتریفیوژهای گازی را دریافت کنند، برای ساختن دو موشک هسته ای کوچک در یک سال به چه چیزهایی نیاز خواهند داشت؟ و اگر بخواهند این را مانند یک بمب ساعتی منفجر کنند، آیا ممکن است؟
|
چند سانتریفیوژ گازی برای ساخت دو هسته کوچک در یک سال نیاز است؟
|
112386
|
آیا تحقیقات بعدی یا پاسخی از اعماق فضای بیرونی به هر شکلی با این تصاویر و صداها انجام شده است؟
|
رکورد طلایی وویجر
|
31734
|
من در جستجوی فهرستی جامع و تا حدودی کامل از نمادهای استاندارد پیشنهادی هستم (نمادهایی که باید در فیزیک (نظری) و همچنین ریاضیات استفاده کرد). آیا چنین مجموعه ای وجود دارد، آیا کسی در مورد آن فکر کرده است یا باید خودم آن را انجام دهم؟
|
مرجع نشانه گذاری استاندارد
|
21180
|
من در حال تماشای برنامه ای در مورد آمادگی در برابر بلایا بودم، و پیشنهاد شد که محفظه فلزی یک کانتینر حمل و نقل مشترک (از نوع چندوجهی) برای محافظت از محتویات آن در برابر یک پالس بزرگ الکترومغناطیسی (نوعی که می تواند کل منطقه یا منطقه را تحت تاثیر قرار دهد) کافی است. قاره). من شک دارم که این درست باشد، زیرا به نظر می رسد یک سوء تفاهم از نحوه عملکرد پالس های الکترومغناطیسی است - اما من نمی توانم هیچ منبع قابل اعتمادی در مورد این موضوع پیدا کنم. فیزیک در این مورد چه می گوید؟ **آیا یک محفظه فلزی (مانند یک کانتینر حمل و نقل) از محتویات خود در برابر تأثیرات یک پالس الکترومغناطیسی به اندازه کافی بزرگ برای تأثیرگذاری بر یک منطقه جغرافیایی بزرگ محافظت می کند؟**
|
آیا یک محفظه فلزی (مانند کانتینر حمل و نقل) از محتویات آن در برابر تأثیرات یک پالس الکترومغناطیسی محافظت می کند؟
|
15142
|
اساساً من فکر می کنم آلبرت انیشتین (A.E.) در تلاش بود تا تبدیلی پیدا کند که: > 1. همیشه یک حرکت با سرعت ثابت را به یک حرکت با سرعت ثابت > تبدیل کنید. > 2. همیشه یک حرکت با سرعت نور را به یک حرکت با سرعت نور تبدیل کنید. > 3. اگر یک شی با سرعت $v$ در قاب $A$، در قاب $B$ استراحت کند، آنگاه > هر شیء استراحت در $A$ دارای سرعت $-v$ در $B$ است. > A.E داده است: $$x'=\frac{x-ut}{\sqrt{1-u^2/c^2}},$$ $$t'=\frac{t-(u/c^2 )x}{\sqrt{1-u^2/c^2}}.$$ اما بیش از یک تبدیل وجود دارد که می تواند این کار را انجام دهد. یک ضریب را ضرب کنیم، می توانیم یک عامل دیگر بدست آوریم: $$x'=\frac{x-ut}{\sqrt{1-u^2/c^2}}(1+u^2)، $$ $$t '=\frac{t-(u/c^2)x}{\sqrt{1-u^2/c^2}}(1+u^2).$$ هر سه فرض داده شده را برآورده می کند. پس چرا دومی نمی تواند تبدیل لورنتس باشد؟
|
چرا تبدیل لورنتس در نسبیت خاص باید اینگونه باشد؟
|
113073
|
من لاگرانژی زیر را برای میدان الکترومغناطیسی آزاد دارم، $$\mathcal{L} = -\frac{1}{4} F^{\mu \nu}F_{\mu \nu}، $$ و تنش متعارف تانسور است $$T^{\alpha \beta}=\frac{\partial \mathcal{L}}{\partial \left(\partial_{\alpha} A^{\lambda}\right)}\partial^{\beta} A^{\lambda}-g^{\alpha \beta}\mathcal{L}.$$ $T^{0i}$ من است، $T^{0i} = (\vec{E}\times \vec{B})_{i}$ اما تانسور تنش متقارن است، و من باید آن را پیدا کنم: $$T^{0i} = (\vec{E}\times \vec{B})_{i} + \nabla \cdot (A_{i}\vec{E})$$ من نمیدانم این اصطلاح واگرایی از کجا آمده است. چگونه می توانم این تانسور نامتقارن $T^{0i}$ را انجام دهم؟ (فقط برای مرجع، نگاه کنید به جکسون - الکترودینامیک کلاسیک، ویرایش سوم - صفحه 606)
|
تانسور تنش متعارف برای میدان الکترومغناطیسی آزاد
|
39524
|
من همه جا در پایگاه های داده ای که مدرسه ام ارائه می کند، جستجوهای گوگل، سوالات مطرح شده در انجمن های فیزیک و اینجا را جستجو کرده ام. همانطور که میدانم، پروتکل اصلی QT (تلپورت کوانتومی) که توسط بنت در نظر گرفته شده بود، با حالتهای پلاریزاسیون فوتونها «تحقق» یافته است که اثبات فوقالعادهای است. QT را تأیید می کند زیرا حالت قطبش درهم تنیده نور یک آنالوگ کامل است. با این حال، دقیقاً محقق نشده است زیرا به نظر می رسد با چرخش انجام نشده است! آیا واقعاً هیچ مقاله ای در مورد انتقال از راه دور حالت اسپین یک ذره وجود ندارد؟
|
تحقق تجربی دورپورت کوانتومی اسپین، نه قطبش، نه یون یا اتم
|
133866
|
وقتی مردم فعل و انفعالات نوترینو را توصیف می کنند، آنها را به عنوان نادر/نادر توصیف می کنند، زیرا نوترینوها از نظر الکتریکی خنثی هستند و جرم کمی دارند، در صورت وجود. خوب، چرا فوتون با توجه به خنثی بودن و بی جرم بودن آن بسیار قوی تر است؟ چه اختلافی بین این دو وجود دارد؟ چرا نوترینو بسیار گریزان است، در حالی که نور بسیار رایج است؟ آیا این احتمالاً ربطی به این واقعیت دارد که یک نوترینو یک فرمیون است در حالی که یک فوتون یک بوزون است؟
|
چرا نوترینوها ضعیف تر از نور تعامل دارند؟
|
119528
|
یک سوال از متخصصان در فرمالیسم ضعیف اندازه گیری: در مقاله معروف چگونه نتیجه اندازه گیری یک جزء از اسپین یک ذره اسپین-1/2 می تواند 100 شود توسط آهارونوف، آلبرت و ویدمن توضیح می دهند. معادله (4) تحت چه شرایطی فرمالیسم اندازه گیری ضعیف برقرار است: $$ \Delta \ll \underset{n}{\text{max}} \frac{\langle \psi_{f}|\psi_i\rangle}{\langle \psi_{f}|A^n|\psi_i\rangle^{1/n}} $$ که در آن $\Delta$ اسپرد است از تابع اشاره گر طبق معمول $\psi_f$، $\psi_i$ حالت اولیه و پس از انتخاب و $A$ قابل مشاهده است که باید اندازه گیری شود. مشکل من این است که تابع اشاره گر یک تابع گاوسی است. آیا کسی می داند که آیا تعمیم هایی برای این عبارت وجود دارد به این معنا که تابع اشاره گر کلی تر است و گاوسی نیست؟
|
فرمالیسم اندازه گیری ضعیف: ارزش ضعیف می تواند خیلی بزرگ باشد؟
|
71544
|
مهم نیست که نور قاب داخل آن باشد، همیشه در یک خط مستقیم در آن قاب حرکت می کند. چرا اینطور است؟ به نظر من چیزی نیست که لزوماً درست باشد. اگر کسی به جلو می دود و چیزی عمود بر حرکت خود می فرستد، چرا باید با آنها به جلو حرکت کند - سرعت منبع را حمل نمی کند.
|
چرا نور همیشه در یک خط مستقیم حرکت می کند؟
|
25749
|
برنامه من این بود که قدر ظاهری ماه را در طول کل ماه گرفتگی ژوئن 2011 مشاهده و تخمین بزنم، اما ابرها دقیقاً در همان لحظه وارد شدند، بنابراین نمیتوانم تخمین مفیدی داشته باشم. قدر ظاهری چقدر بود؟
|
قدر ظاهری ماه گرفتگی 15 ژوئن 2011 چقدر بود؟
|
107495
|
من به دنبال مجموعه ای از مثال ها هستم تا رابطه دما و رنگ اجسام درخشنده را به تصویر بکشم. این باید به ایجاد درک شهودی از این رابطه اجازه دهد، بنابراین در مورد طیف نیست، بلکه فقط رنگ از نظر ظاهر بصری است. در صورت امکان، نمونه ها باید مادون قرمز را تا جایی بالاتر از نور بصری پوشش دهند (یا دلایلی که ممکن نیست). * * * چند نمونه خوب دما/رابطه با رنگ از نظرات/پاسخ ها: یک مثال برای حدود **2500K** می تواند **سیم تنگستن** یک لامپ رشته ای باشد. همانطور که سی تاون اسپرینگر در پاسخ خود توضیح می دهد، این مثال خوبی نیست زیرا سیم موجود در گاز مدل خوبی برای بدن سیاه نیست. او یک کوره الکتریکی** را به عنوان مثال برای حدود **1400K** ارائه می دهد که تقریب بسیار خوبی با بدنه سیاه ارائه می دهد. همانطور که گفته شد، این در مورد تصویر است، نه در مورد تطابق کامل با طیف یک جسم سیاه - به اندازه کافی شبیه به یکسان به نظر می رسد واجد شرایط است. از نظر رابین، **خورشید** می تواند به عنوان مثال برای حدود **5800K** خوب باشد.
|
مثال هایی برای نشان دادن تابش وابسته به دما با مثال هایی از رابطه دما به رنگ
|
69003
|
فرض کنید یک ذره توسط یک حالت کوانتومی داده شده است که به گونه ای ساخته شده است که به همان اندازه احتمال دارد که آن را در هر نقطه ای از بازه ثابت $(0,L)$ پیدا کند اما سرعت دلخواه پایینی دارد. ذره تقریباً در حال استراحت است اما موقعیت آن هنوز تصادفی است! من برای چنین حالت کوانتومی ساختنی خواهم داد. اجازه دهید $$\psi(x) = B(x)e^{ikx}، $$ که در آن $B(x)$ یک تابع با برش صاف است که تقریباً شبیه یک تابع مربع است که $1$ در $(0 است. ,L)$ و صفر در هر جای دیگر. (من $B(x)$ را بر روی تابع مربع معرفی کرده ام تا آرگومان های مربوط به تداوم $\psi(x)$ را حذف کنم). محتمل ترین تکانه این ذره $k$ با عدم قطعیت قابل مدیریت است. اگر $L$ را در مقدار بالایی مشخص کنیم، آنگاه عدم قطعیت در حرکت در مقدار کم ثابت می شود. حال سوال این است که در تنظیم بالا میتوانیم $k$ را بهطور دلخواه کوچک و با عدم قطعیت تقریباً یکسان انتخاب کنیم و همچنان موقعیت آن به طور مساوی در یک بازه کامل $(0,L)$ توزیع شود. در اصل ما یک حالت کوانتومی معتبر داریم که در آن یک ذره تقریباً در حالت سکون است، اما موقعیت آن در یک بازه کاملاً تصادفی است. اگرچه من در مکانیک کوانتومی تازه کار هستم، اما تصور چنین وضعیت دنیای واقعی برایم بسیار جالب و تقریباً سخت است. آیا این یک نقص احتمالی در QM است؟ از نظرات و توضیح شما در مورد هر گونه اشکال در این استدلال سپاسگزارم.
|
ذره ای کوانتومی که تقریباً در حال سکون است اما موقعیتش تصادفی است!
|
102787
|
سوال من این است: شکل گیری یک برهمکنش اسپین-اسپین موثر برای اصطلاح مبادله در تحلیل تغییرات هلیوم چیست؟ آیا این اصطلاح هیچ اهمیتی جز دلایل زیبایی شناختی دارد، به عنوان مثال. آیا این اصطلاح اسپین اسپین در مسائل مشابه بوجود می آید؟ در دور اول تجزیه و تحلیل تغییرات اتم هلیوم، معمولاً برهمکنش الکترون-الکترون را نادیده می گیریم و معادله شرودینگر را حل می کنیم تا حالت هایی حاصل شود که حاصل توابع موج هیدروژن هستند. پس از این، برهمکنش الکترون-الکترون را دوباره اضافه می کنیم و مقدار تغییر انرژی را محاسبه می کنیم و چیزی شبیه $\left< V_{ee} \right> = J_{n,l}\pm K_{n,l} بدست می آوریم. $ که در آن $J_{n,l}$ سهم ناشی از برهمکنش کولن چگالی بار الکترونها است، و $K_{n,l}$ عبارت مبادلهای است. سپس انرژی حاصل از برهمکنش الکترون-الکترون را می بینید که به صورت زیر نوشته می شود: $\left< V_{ee} \right> = J_{n,l}-\frac{1}{2}(1+\frac{4} {\hbar^{2}}\vec{S}_{1}\cdot\vec{S}_{2})K_{n,l}$ برای من، این روشی هوشمندانه به نظر میرسد صراحتاً تمایز سهگانه/تفرد را در فرمول مثبت/منفی بنویسید. آیا این است یا من یک مفهوم گسترده تر را از دست داده ام؟
|
برهمکنش موثر اسپین در هلیم
|
76015
|
مشکل کامل اینجاست: > _سرعت قطاری که در یک مسیر تراز حرکت می کند دیفرانسیل > معادله $\mathrm{d}V/\mathrm{d}t = kv^2$ را برآورده می کند. سرعت اولیه قطار > $v(0)=10~\text{m/s}$ است و سرعت با نرخ > $-1~\text{m/s}^2$ کاهش مییابد که $ v=5~\text{m/s}$. چقدر طول می کشد تا سرعت قطار به $1~\text{m/s}$ کاهش یابد؟ با این مدل قطار > کی می ایستد؟ من به مرکز آموزشی مدرسه ام می رفتم اما در حال حاضر در تعطیلات روز کارگر هستیم. -_- ویرایش 1: من چند بار آن را امتحان کردهام و این پاسخ من است: $vknot=10~\text{m/s}، v=5~\text{m/s}، a=-1~\ text{m/s}^2$ من $k = -1/25$ را پیدا کردم و به ادغام $\mathrm{d}V/\mathrm{d}t = kv^2$ ادامه دادم. معادله ای که من دریافت کردم $v=kv^2t + vknot$ بود و تمام شرایط من را به آن متصل کرد. پاسخ من $t=5~\text{s}$ بود. نمیدانم درست میگویم یا نه، زیرا مشکلات کلمات همیشه من را ناامید میکنند. ویرایش 2: من k=-1/25 را با وصل کردن به معادله dV/dt پیدا کردم. dV/dt همان شتاب است و بیان شده است که شتاب ما -1m/s^2 است که منجر به این می شود: $-1 = k(5)^2$ ===> $-1 = 25k$ === > $-1/25 = k$. نمیدانم که آیا این کار معتبر بود یا نه، اما مطمئن نبودم که چگونه به آن نزدیک شوم، بنابراین این فرض را کردم که معتبر است. ویرایش 3: بعد از اینکه متوجه خطای ادغام من شدم، پس از ادغام فرمول $v=v(vknot)kt + vknot$ را دریافت کردم. پس از وصل کردن اطلاعات من، زمان t=2.5 بود. حالا نمی دانم چگونه بفهمم قطار چه زمانی می ایستد...
|
چقدر طول می کشد تا سرعت قطار به $1~\text{m/s}$ کاهش یابد؟
|
39526
|
من در حال خواندن بررسی عالی از اریک پواسون هستم که در اینجا یافت شده است. در حین مطالعه آن به اثباتی رسیدم که نمی توانم بسازم... راهی برای رفتن از معادله (19.3) به قبل از معادله (19.4) (که بدون شماره است) پیدا نمی کنم. من توانستم پیشرفتی داشته باشم (که در زیر ارائه می کنم)، اما نمی توانم پاسخ درستی دریافت کنم... لطفاً یکی به من کمک کند. واقعا ناامید کننده است... با توجه به تانسور انرژی-ممنتوم متشکرم$$T^{\alpha\beta}\left(x\right)=m{\displaystyle \int_{\gamma}\frac{g^{\alpha}{}_{\mu}\left(x,z\right)g^{\beta}{}_{\nu}\left(x,z \راست)\dot{z}^{\mu}\do t{z}^{\nu}}{\sqrt{-g_{\alpha\beta}\dot{z}^{\alpha}\dot{z}^{\nu}}}\delta_{4}\ چپ (x,z\right)d\lambda,}$$ می توان واگرایی را گرفت\begin{alignedat}{1}\nabla_{\beta}T^{\alpha\beta} و =m{\displaystyle \int_{\gamma}\nabla_{\beta}\left[\frac{g^{\alpha}{}_{\mu}g^{\beta}{}_{\nu}\dot{z}^ {\mu}\dot{z}^{\nu} }{\sqrt{-g_{\alpha\beta}\dot{z}^{\alpha}\dot{z}^{\nu}}}\delta_{4}\left(x,z\right)\ راست]d\lambda}=\\\ & =m{\displaystyle \int_{\gamma}\nabla_{\beta}\left[\frac{g^{\alpha}{}_{\mu}g^{\beta}{}_{\nu}\dot{z}^ {\mu}\dot{z}^{\nu}}{\sqr t{-g_{\alpha\beta}\dot{z}^{\alpha}\dot{z}^{\nu}}}\right]\delta_{4}\left(x,z\right)d \lambda+m{\displaystyle \int_{\gamma}\frac{g^{\alpha}{}_{\mu}g^{\beta}{}_{\nu}\dot{z}^{\mu}\dot{z} ^{\nu}}{\sqrt{-g_{\alpha\ بتا}\dot{z}^{\alpha}\dot{z}^{\nu}}}\nabla_{\beta}\left[\delta_{4}\left(x,z\right)\right] d\lambda.}} \end{alignedat} اما با استفاده از معادله 13.3 مرجع متوجه میشویم که واگرایی تانسور انرژی-تکانه نیز توسط\begin{alignedat}{1}\nabla_{\beta}T^{\alpha\beta} به دست میآید. & =m{\displaystyle \int_{\gamma}\nabla_{\beta}\left[\frac{g^{\alpha}{}_{\mu}g^{\beta}{}_{\nu}\dot{z}^ {\mu}\dot{z}^{\nu} }{\sqrt{-g_{\alpha\beta}\dot{z}^{\alpha}\dot{z}^{\nu}}}\delta_{4}\left(x,z\right)\ راست]d\lambda}=\\\ & =m{\displaystyle \int_{\gamma}\nabla_{\beta}\left[\frac{g^{\alpha}{}_{\mu}\dot{z}^{\mu}\dot{z}^{\nu }}{\sqrt{-g_{\alpha\beta }\dot{z}^{\alpha}\dot{z}^{\nu}}}\right]g^{\beta}{}_{\nu}\delta_{4}\left(x,z \right)d\lambda-m{\displaystyle \int_{\gamma}\frac{g^{\alpha}{}_{\mu}\dot{z}^{\mu}\dot{z}^{\nu}}{\sqrt{-g_{ \alpha\beta}\do t{z}^{\alpha}\dot{z}^{\nu}}}\nabla_{\nu}\left[\delta_{4}\left(x,z\right)\right]d\lambda ,}} \end{alignedat} یعنی $$m{\displaystyle \int_{\gamma}\frac{g^{\alpha}{}_{\mu}g^{\beta}{}_{\nu}\dot{z}^{\mu}\dot{z} ^{\nu}}{\sqrt{-g_{\alpha\beta}\d ot{z}^{\alpha}\dot{z}^{\nu}}}\nabla_{\beta}\left[\delta_{4}\left(x,z\right)\right]d\lambda =-m{\displaystyle \int_{\gamma}\frac{g^{\alpha}{}_{\mu}\dot{z}^{\mu}\dot{z}^{\nu}}{\sqrt{-g_{ \alpha\beta}\dot {z}^{\alpha}\dot{z}^{\nu}}}\nabla_{\nu}\left[\delta_{4}\left(x,z\right)\right]d\lambda, }}$$ بنابراین باید صفر باشد (لطفا اگر اشتباه می کنم اصلاح کنید). سپس، با استفاده از معادلات (5.14) و (13.3)، واگرایی تانسور انرژی- تکانه به سادگی \begin{alignedat}{1}\nabla_{\beta}T^{\alpha\beta} & =m{\ است. نمایش سبک \int_{\gamma}\nabla_{\beta}\left[\frac{g^{\alpha}{}_{\mu}g^{\beta}{}_{\nu}\dot{z}^ {\mu}\dot{z}^{\nu} }{\sqrt{-g_{\alpha\beta}\dot{z}^{\alpha}\dot{z}^{\nu}}}\right]\delta_{4}\left(x,z\ راست)d\lambda}=\\\ & =m{\displaystyle \int_{\gamma}\frac{D}{d\lambda}\left[\frac{g^{\alpha}{}_{\mu}\dot{z}^{\mu}}{\sqrt{ -g_{\ alpha\beta}\dot{z}^{\alpha}\dot{z}^{\nu}}\right]\delta_{4}\left(x,z\right)d\lambda}+\\ \ & \,\,\,+m{\displaystyle \int_{\gamma}\frac{g^{\alpha}{}_{\mu}\dot{z}^{\mu}}{\sqrt{-g_{\alpha\beta}\dot{z} ^{\alpha}\dot{z}^{ \nu}}}\nabla_{\beta}\left[g^{\beta}{}_{\nu}\dot{z}^{\nu}\right]\delta_{4}\left(x, z\right)d\lambda.} \end{alignedat} اگر کاری که من انجام دادهام درست باشد، در مقایسه با نتیجه مرجع، جمله آخر باید صفر باشد. کسی میتونه فکر کنه چرا؟ من فکر کردم که چون مشتق کوواریانت در نقطه $x$ گرفته می شود، پس $g^{\beta}{}_{\nu}\nabla_{\beta}\dot{z}^{\nu}$ صفر است اما پس از آن، چه چیزی منع می کند $g^{\alpha}{}_{\mu}g^{\beta}{}_{\nu}\dot{z}^{\nu}\nabla_{\beta}\dot{z}^{ \mu}$ به همان اندازه صفر باشد؟
|
معادله ژئودزیکی از بقای انرژی - تکانه
|
107149
|
سرعت ظاهری جسمی که با سرعت واقعی $v$ به ما نزدیک می شود چقدر خواهد بود؟ من میدانم که $cv/c-v$ یک پاسخ ممکن است، اما در اینجا یک استدلال دیگر وجود دارد - آیا سرعت نباید تغییر داپلر $$v\left(\frac{c+v}{c-v} \right)^{1/2} باشد. $$ برابر سرعت واقعی؟
|
سرعت ظاهری یک جسم در حال نزدیک شدن
|
133849
|
فرض کنید می خواهم رشته بیت 010110 را برای کسی ارسال کنم. آیا یک حد پایین نظری برای انرژی مورد نیاز برای انجام این کار وجود دارد؟
|
آیا حداقل محتوای انرژی اطلاعات به غیر از 0 ژول وجود دارد؟
|
99037
|
آیا می توان یک نمایندگی الحاقی برای گروه لورنتس ساخت؟
|
نمایندگی مشترک گروه لورنتس
|
33771
|
من واقعاً نمیدانم ناهمدوسی کوانتومی چیست، اما شنیدهام که از آن برای توضیح اینکه چرا اجسام ماکروسکوپی ظاهراً از دینامیک کوانتومی پیروی نمیکنند استفاده میشود. آیا کسی میتواند توضیح سادهای درباره چیستی ناهمدوسی بدهد و چرا از آن نتیجه میشود که اجرام ماکروسکوپی ظاهراً از دینامیک کوانتومی پیروی نمیکنند.
|
ناهمدوسی کوانتومی و پدیده های ماکروسکوپی
|
78143
|
> _به یک توپ فولادی اجازه داده می شود که از حالت سکون به سمت پایین شیب به طول 20 متر و روی سطحی به طول بیش از 25 متر غلت بخورد. 4.0 ثانیه طول می کشد تا از شیب پایین بیایید. > سرعت پایین شیب را محاسبه کنید._ من میانگین سرعت در شیب را 50 متر بر ثانیه یافتم. اما، من مطمئن نیستم که از چه فرمولی برای یافتن سرعت در پایین شیب استفاده کنم.
|
شتاب یکنواخت
|
39521
|
آیا کسی می تواند به من یک نمای کلی از نحوه استفاده از ایالت های OAM در ارتباطات بدهد؟ استفاده از حالت های حرکت زاویه ای مداری موضوعی داغ برای ارتباطات به نظر می رسد. من چند مقاله در مورد اصول اولیه و آزمایش های انجام شده در ایتالیا خواندم که از حالت های OAM برای دو برابر کردن ظرفیت یک لینک بی سیم استفاده می کنند. همچنین اگر کسی می داند کجا می توان یک آموزش خوب در مورد وضعیت های OAM یا هر مکان خوب دیگری پیدا کرد تا به دنبال اطلاعات بیشتر، آزمایش ها، داده ها و غیره مرتبط با این موضوع باشد که به من کمک زیادی می کند :).
|
حالت های OAM برای ارتباطات بی سیم
|
76012
|
من اخیراً به این جمله جالب برخوردم که اکثر تعاریف سانسور کیهانی (_CC_) و اکثراً برای اثبات آن کار می کنند، چیزی را که هاوکینگ آن را رعد و برق می نامد رد نمی کند (پنروز 1978، هاوکینگ 1993، پنروز 1999). پنروز شرح شفاهی را به شرح زیر ارائه می دهد. > ... پیشنهادهای سانسور [با ماهیت معینی]... امکانی را که هاوکینگ (1993) از آن به عنوان صاعقه یاد می کند، که برای اولین بار در پنروز (1978) در نظر گرفته شد، حذف نمی کند. این وضعیت فرضی است که بر اساس آن یک فروپاشی گرانشی منجر به موج تکینگی می شود که از منطقه فروپاشی بیرون می آید، که جهان را در حین حرکت ویران می کند! در این تصویر، کل فضا-زمان می تواند در سطح جهانی هذلولی باقی بماند، زیرا همه چیز فراتر از حوزه وابستگی برخی ابرسطح اولیه، توسط موج منفرد قطع شده است (ویران می شود). یک ناظر، چه در بینهایت > چه در مکان محدودی در فضا-زمان، درست در لحظهای که تکینگی قابل مشاهده میشد، نابود میشود[...] برای راحتی، تعاریف فنی مربوطه را بیان میکنم. در اینجا: * $S$ - مجموعه گذشته، مجموعه ای که ماضی علّی آن $J^-(S)$ همان خودش است. * $IP$ - مجموعه گذشته غیرقابل تجزیه، مجموعه گذشته که اتحاد دو مجموعه گذشته نیست. * $PIP$ - $IP$ مناسب، یک $IP$ که معادل $J^-(x)$ برای یک نقطه $x$ است. * $TIP$ - $IP$ که یک $PIP$ نیست، همچنین به عنوان نقطه ایده آل شناخته می شود. * $TIP_\infty$ - $TIP$، ایجاد شده توسط یک منحنی زمان مانند، که تا بی نهایت در آینده گسترش می یابد. * $TIP_S$ - $TIP$ مفرد، که $TIP_\infty$ نیست. یکی از اظهارات احتمالی سانسور کیهانی این است که هیچ $TIP_\infty$ حاوی $TIP_S$ نیست. این تعریف خاص صاعقه را رد می کند. Penrose 1999 تفسیر را کمی مورد بحث قرار می دهد و این تصور را ایجاد می کند که این بیانیه _CC_ ممکن است قوی باشد و بنابراین پیشرفت در آن برای افراد بسیار سخت است. **آیا از سال 1999 پیشرفتی در اثبات هر نسخه ای از _CC_ که صاعقه را رد می کند، حاصل شده است؟** لطفاً پیشاپیش عذرخواهی من را بپذیرید اگر صاعقه Penrose ما را محو کرد قبل از اینکه بتوانم به پاسخ مفید شما رأی مثبت بدهم. **منابع:** * Penrose (1978). اصول نظری در اخترفیزیک و نسبیت، ویرایش. لیبوویتز و همکاران * هاوکینگ (1993). رنسانس نسبیت عام (به افتخار D. W. Sciama)، ویرایشها. الیس و همکاران. * Penrose (1999). The Question of Cosmic Censorship, _J. Astrophys. Astr. (1999)، 233-248
|
وضعیت فعلی پنروز-هاوکینگ رعد و برق؟
|
68502
|
سنگاپور به دلیل دود ناشی از آتش سوزی جنگل ها، قسمتی از فصل مه آلود معمولی خود را سپری می کند. برخی از افراد احتمالاً به دلایل سلامتی از ماسک های جراحی مانند آنچه در پایین این پست نشان داده شده است استفاده می کنند. من می دانم که ماسک باید از عبور ذرات ناخواسته جلوگیری کند. اما در عین حال باید هوای کافی را برای تنفس وارد کند. من میدانم که چگونه میتوان از بیمار شدن افراد جلوگیری کرد - بالاخره، باکتریها بسیار بزرگتر از مولکولهای هوا هستند، بنابراین میتوانید سوراخهای کوچکی داشته باشید که هوا را از آن عبور میدهند، اما باکتریها را بیرون نگه میدارد. **اما آیا ذرات دود آنقدر ریز نیستند که بتوان از این طریق جلوی آنها را گرفت؟** من دود را به عنوان یک گاز تصور می کنم (مطمئناً اینطور به نظر می رسد، مثلاً بیرون آمدن از یک شمع یا یک تکه بخور سوزان). آیا ذرات دود به کوچکی مولکول هایی هستند که برای زنده ماندن باید تنفس کنم؟ اگر چنین هستند، چگونه این ماسک می تواند بین مثلاً اکسیژن و دود تفاوت قائل شود؟ 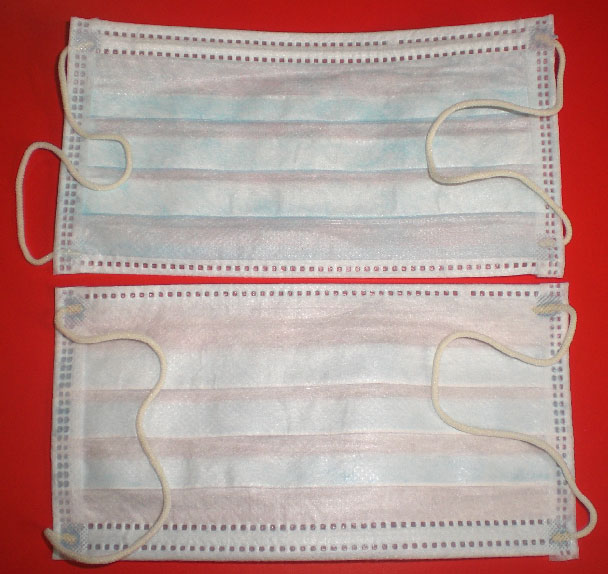
|
آیا ماسک جراحی صورت می تواند ذرات آلودگی دود را به طور موثر فیلتر کند؟
|
112034
|
مقاله زیر همیلتونی گاز دایمر کوانتومی دوبعدی را نشان می دهد (صفحه 2) http://www-thphys.physics.ox.ac.uk/people/ClaudioCastelnovo/Talks/050209_MIT.pdf در اینجا چند سوال وجود دارد. * چرا یک اصطلاح جنبشی و دیگری بالقوه است؟ از آنجایی که همه چیز در مورد حالت های مجرد است، آیا همه آنها بالقوه نیستند؟ * اهمیت متغیرهای t و v چیست؟ * حالات eignenstate هامیلتونی مذکور چیست؟ من همچنین مطمئن نیستم که چگونه گاز دایمر 2 بعدی در نتیجه اثر هال کوانتومی کسری می آید. کسی می تواند آن را برای من توضیح دهد؟
|
آیا کسی می تواند Rocksar-Kivelson Hamiltonian را برای من توضیح دهد؟
|
112994
|
نمودارهای نابودی ($e^+ e^-\rightarrow 2\gamma$) هستند  فقط تعجب می کنم که آیا دامنه ها باید $$(-ie)^2\left[\bar باشد v(p_2)\gamma^b\epsilon_b^*\frac{-i(-(\gamma^\mu p_{1\mu}-\gamma^\nu p_{3\nu})+m)}{( p_1-p_3)^2+m^2-i\epsilon}\gamma^a\epsilon_a^* u(p_1)+ \\\ \bar v(p_2)\gamma^a\epsilon_a^*\frac{-i(-(\gamma^\mu p_{1\mu}-\gamma^\nu p_{4\nu})+m)}{( p_1-p_4)^2+m^2-i\epsilon}\gamma^b\epsilon_b^* u(p_1)\right]$$ به طور خاص، قطبش هستند بردارهای فوتون های خروجی درست است؟ به طور کلی، آیا فوتون های خارجی همیشه بردار پلاریزاسیون و $\gamma^a$ را با هم منقبض می کنند؟ همچنین، اگر $\epsilon^a\rightarrow\epsilon^a+\alpha k^a$ برای ثابت $\alpha$، چرا دامنه بدون تغییر است و این به چه معناست؟
|
بردارهای پلاریزاسیون در دامنه های پراکندگی
|
31731
|
در حالی که محاسبه توابع پارتیشن در مدلهای مکانیک آماری (مثلاً) روی یک شبکه دو بعدی معمولاً از شرایط مرزی دایرهای استفاده میکند که بنابراین توپولوژی شبکه یک چنبره را به دست میدهد. این عبارات و محاسبات را ساده تر می کند. و معمولاً فرض می شود که در محدوده حجم نامتناهی اثرات مرزی ناچیز خواهد بود. با این حال، من هرگز از طریق هیچ مدرک کلی برای این استدلال فیزیکی نیافته ام. چه می شود اگر شناسایی مرزهای پیچیده تری را انتخاب کنیم تا شبکه دارای توپولوژی سطح جنس بالاتر باشد؟ چگونه بر پاسخ نهایی برای تابع پارتیشن یا سایر توابع همبستگی تأثیر می گذارد؟
|
تاثیر شرایط مرزی بر توابع پارتیشن
|
51783
|
IT اغلب بیان می کند که جریان با Re بالا همسانگرد نیست، به این معنی که هیچ جهت یکنواخت یا غالب جریان وجود ندارد. اما این به نظر من اشتباه است - در حالی که مطمئناً مواردی وجود دارد که هیچ جهت غالب جریان را نمی توان در موقعیت های بسیار متلاطم تشخیص داد، برای مثال جریان از طریق لوله ها یا در امتداد جسم سریع حرکت می کند که در آن به وضوح ناهمسانگردی قوی وجود دارد. حتی یک گرداب در یک فنجان قهوه هم زده جهت جریان به راحتی قابل تشخیص است. عدد رینولدز رابطه بین نیروهای اینرسی و ویسکوز را به من می گوید - آیا عدد یا متریکی وجود دارد که به من بگوید یک جریان چقدر غیر همسانگرد است؟
|
آیا ارتباط دادن جریان غیر همسانگرد زیاد با عدد رینولدز اشتباه است و آیا متریک بهتری وجود دارد؟
|
31735
|
من Wiki: http://en.wikipedia.org/wiki/Barn_(unit) را در این مورد خواندم و محاسبات زیر تبدیل از واحدهای مربع پیشوند SI درست به نظر نمی رسند. آیا 1fm^2 = 10 مگابایت است؟ (یا 1b = 100m^2) . کدام یک صحیح است و چگونه آن را محاسبه می کنید؟ با تشکر
|
تبدیل واحد انباری به متر مربع؟
|
39298
|
مفهوم از دست دادن اطلاعات معمولاً با توجه به سیاهچاله مورد بحث قرار می گیرد. درک من این است که هر ماده ای را که در سیاهچاله قرار دهید، فقط 3 مو دارد و بنابراین، تنها با تعیین ویژگی های سیاهچاله، مکانیسم تشکیل سیاهچاله را نمی دانید. تحولات زیادی رخ داده است و بسیاری از مردم اکنون بر این باورند که اطلاعات واقعاً از بین نمی روند، بلکه درهم می روند و غیره. اگر یک ذره و یک ضد ذره دارید که به دو فوتون تبدیل می شود، بگویید؛ با مشاهده فوتون ها نمی توانید سرعت دو ذره را بازسازی کنید. آیا در این مورد اطلاعاتی را از دست داده اید؟ آیا این مفهوم از اطلاعات با تعریف شانون یکسان است؟ اگر نابودی واحد باشد، با حفظ آنتروپی، میدانم که اطلاعات شانون نیز حفظ میشود. اما، ما نمیتوانیم به حالت اولیه منحصربهفرد برگردیم، آیا میتوانیم؟ (سرعت تغییر ناپذیر لورنتس نیست، اما اجازه دهید بگوییم که همه چیز در یک قاب اینرسی انجام می شود.) به طور کلی، من نمی دانم چگونه اطلاعات در بسیاری از فرآیندهایی که چند به یک هستند از بین نمی روند. به دلیل ماهیت فیزیک ذرات و اینکه چرا این با سناریوی سیاهچاله ها متفاوت است.
|
از دست دادن اطلاعات در نابودی
|
31730
|
اگر بخواهم انرژی یک دترمینانت اسلاتر را با توجه به قید متعامد بودن اوربیتالهای اسپین به حداقل برسانم (مانند تقریب هارتری-فوک)، میتوانم از روش لاگرانژ از ضربکننده نامشخص، یعنی $$L[\\{\chi_ استفاده کنم. {a}\\}] = E_{0}[\\{\chi_{a}\\}]-\sum_{a=1}^{N}\sum_{b=1}^{N}\varepsilon_{ba}([a|b ]-\delta_{ab})$$ که $\\{\chi_{a}\\}$ اوربیتالهای اسپین هستند، $E_{0}$ انرژی حالت پایه، $[a|b]$ است همپوشانی انتگرال بین اوربیتال های اسپین $\chi_{a}$ و $\chi_{b}$ و $\varepsilon_{ba}$ یک ضریب لانگرانژ است. با تنظیم اولین تغییر $L$ روی صفر، می توانم انرژی یک تعیین کننده را به حداقل برسانم $|\Psi_0\rangle=|\chi_{1}\chi_{2}\cdots\chi_{a}\chi_{ b}\cdots\chi_{N}\rangle$. مشکلی در شیمی کوانتومی مدرن: مقدمه ای بر نظریه ساختار الکترونیکی پیشرفته سابو و اوستلوند از من می خواهد ثابت کنم که ضرب کننده های لاگرانژ عناصر یک ماتریس هرمیتی هستند، یعنی $\varepsilon_{ba} = \varepsilon_{ab}^{*} $، با توجه به اینکه $L$ واقعی و $[a|b] = است [b|a]^{*}$. چگونه می توان این را ثابت کرد؟ جایی که من در حال حاضر شروع می کنم این است که از آنجایی که $L$ واقعی است، پس $L = L^{*}$. اگر $L^{*}$ را پیدا کنم، آنگاه مساوی کردن آن با $L$ نشان میدهد که لازم است ضربکنندههای لاگرانژ عناصر یک ماتریس هرمیتی باشند. با این حال، به نظر نمی رسد که دنبال کردن این موضوع مرا به جایی برساند که بتوانم بگویم $\varepsilon_{ba} = \varepsilon_{ab}^{*}$.
|
به حداقل رساندن انرژی یک تعیین کننده اسلاتر: چرا عناصر ضریب لاگرانژ یک ماتریس هرمیتی هستند؟
|
76019
|
من یک خط سیال دارم که سیال با چگالی بالا را با قیمت 60 $ \text{psi}$ عبور می دهد. در انتها یک دریچه وجود دارد. من یک افت فشار دینامیکی 30 دلاری \text{psi} دلار در شیر خط دارم که فشار برگشتی برابر با 10 دلار \text{psi} دلار ایجاد می کند. چگونه افت فشار خود را بدون تغییر پارامترهای لوله کاهش دهم؟
|
چگونه افت فشار را در یک لوله 5/16 ss کاهش دهیم
|
102839
|
درک من از امواج مایکروویو این بود که به دلیل فرکانس بالا به راحتی در هر ماده ای جذب می شوند. هرچه مواد شل تر باشد، جذب آن آسان تر است. می دانم که روشن کردن مایکروویو در حالت خالی خطرناک است، بیشتر به این دلیل که چیزی وجود ندارد که مایکروویوها را جذب کند و ممکن است باعث ایجاد طوفان مغناطیسی در داخل شود :) اما امروز شنیدم که استفاده از مایکروویو برای گرم کردن بشقاب ها به همان اندازه خطرناک است. می خواهم بدانم که آیا و چرا درست است؟ من فکر می کنم که بشقاب مانند مواد دیگر است. اما به دلیل چگالی بالا، مایکروویو را کندتر از یک لیوان شیر جذب می کند. و همچنین ارتعاشات ممکن است باعث شکستن آن پس از مدت زمان طولانی شود.
|
آیا پیش گرم کردن صفحات در مایکروویو خطرناک است؟ اگر چنین است، چرا؟
|
68506
|
سوالات مشابهی برای من در این سایت وجود دارد، اما کاملاً آن چیزی نیست که من می پرسم (فکر می کنم). روابط د بروگلی برای انرژی و تکانه $$ \lambda = \frac{h}{p}، \\\ \nu = E/h .$$ یک فرکانس و طول موج خاص را با یک ذره برابر میکند، اما میدانیم که یک موج بسته ترکیبی خطی از محدوده بی نهایت فرکانس و طول موج است. چگونه است که ما (یا طبیعت) یک فرکانس و طول موج را خارج از محدوده انتخاب می کنیم؟ آیا این ربطی به فروپاشی بسته موج در هنگام اندازه گیری دارد؟ و اگر چنین است، آیا فرکانس اندازه گیری شده نتیجه تصادفی است؟ به طور مشابه، هنگامی که یک الکترون از یک سطح انرژی به سطح انرژی دیگر در یک اتم می پرد، فوتونی با فرکانس $$ \ \nu = \Delta E/h .$$ ساطع می کند. از آنجایی که فوتون یک موج سینوسی خالص نیست، چگونه می تواند فرکانس به فوتون نسبت داده می شود؟
|
فرکانس مشخصی برای یک بسته موج وجود ندارد؟
|
32640
|
با توجه به تقسیم یک سیستم به دو سیستم کوچکتر، انرژی $U$ به $U_1$ و $U_2$، با $$U=\mathcal{P}(U_1,U_2):=U_1+U_2,$$ تقسیم می شود. به طوری که $U_2$ توسط $U-U_1$ داده می شود. در اینجا عملیات $\mathcal{P}$ نشان دهنده قانون پارتیشن است. آنچه در بالا نوشتم اساساً وسعت انرژی است و تا حدودی ایده بسته های انرژی یا ذرات را تقویت می کند. ایده گستردگی ارتباط نزدیکی با افزودنی دارد. سپس یک جریان انرژی کوچک از سیستم یک به سیستم دو از طریق $$U_1\rightarrow \mathbb{fl}^-(U_1):= U_1-\epsilon, \\\ U_2\rightarrow \mathbb{fl}^+( U_2):=U_2+\epsilon.$$ چیزی که نمی خواهیم کاهش دهیم، صرفه جویی در انرژی است، به طوری که $$U=\mathcal{P}(U_1,U_2)=\mathcal{P}(\mathbb{fl}^-(U_1)،\mathbb{fl}^+(U_2))، $$ جایی که $\mathbb {fl}^\pm$ تعریف میکند که جریان انرژی به چه معناست، و به دلیل حفظ انرژی، این توابع تا حدی توسط $\mathcal{P}$ تعیین میشوند. > آیا دلایل خوبی وجود دارد که چرا در ترمودینامیک یا در فیزیک آماری کلاسیک، قوانین ضمنی این نوع تقسیم بندی باید با علامت مثبت فرموله شوند (به غیر از این واقعیت که نظریه های خوبی وجود دارد که این ایده در آنها عمل می کند) ? به هر حال، برخی مدلها وجود دارند که مفاهیم گستردگی یا افزایشی برای همه کمیتها چندان واضح نیستند (مثلاً برخی از تعاریف آنتروپی دهههای گذشته). * * * روابط $$\mathcal{P}(U_2,U_1)=\mathcal{P}(U_1,U_2),$$ $$\mathcal{P}(\mathbb{fl}^-(U_1)،\mathbb{fl}^+(U_2))=\mathcal{P}(\mathbb{fl}^+(U_1)،\mathbb {fl}^-(U_2))، $$ نیز بسیار طبیعی به نظر می رسد - اگرچه این ممکن است کاملاً ضروری نباشد، زیرا مقادیر $U_1$ و $U_2$ عناصر واقعی هستند و بنابراین سفارش داده شده / قابل تشخیص همچنین، من فکر میکنم ترتیب کنار هم قرار دادن زیرسیستمها نمیتواند مهم باشد $$\mathcal{P}(U_1,\mathcal{P}(U_2,U_3))=\mathcal{P}(\mathcal{P}(U_1, U_2)،U_3).$$ باید از این نوع محدودیت ها بیشتر باشد. * * * بنابراین برای مثال، اولین ansatz این است که می توان $$U=\mathcal{P}(U_1,U_2):=U_1U_2,$$ را در نظر گرفت تا $$\mathbb{fl}^-(U_1) \equiv\tfrac{U_2}{\mathbb{fl}^+(U_2)}U_1.$$ یک تحقق از آن (که به گونه ای ساخته شده است که تغییر از طریق $\mathbb{fl}^-$ مانند حالت افزودنی است) $$U_1\rightarrow \mathbb{fl}^-(U_1):= \left(1-\tfrac{\epsilon} {U_1}\right)U_1 =U_1-\epsilon، \\\ U_2\right arrow \mathbb{fl}^+(U_2):= \left(1-\tfrac{\epsilon}{U_1}\right)^{-1}U_2 =U_2+\left(\tfrac{U_2}{U_1}\right)\epsilon+ O\left((\tfrac{\ epsilon}{U_1})^2\right).$$
|
آیا وسعت انرژی در ترمودینامیک ضروری است؟
|
64993
|
یک سیم حامل جریان میدان مغناطیسی در اطراف خود ایجاد می کند. ما می توانیم جهت را با قانون دست راست فلمینگ پیدا کنیم. می دانیم که تغییر در سوله الکتریکی میدان مغناطیسی ایجاد می کند و تغییر در میدان مغناطیسی میدان الکتریکی ایجاد می کند. رابطه متقابل است. **سوال من این است که آیا شرایطی وجود دارد که حلقه یا سیم حامل جریان میدان مغناطیسی تولید نکند**
|
آیا یک حلقه یا سیم حامل جریان می تواند میدان مغناطیسی تولید نکند؟
|
47265
|
من سعی می کنم یک مشکل نسبتاً پیش پاافتاده را حل کنم، اما به نظر نمی رسد خودم را متقاعد کنم که پاسخی که دریافت می کنم درست است. من دو تا سناریو دارم **سناریو 1.** _یک موج صوتی از متوسط W به متوسط G._ W متوسط ¦ G متوسط **سناریو 2.** _یک موج صوتی از W متوسط به P متوسط تا G متوسط منتشر می شود._ W متوسط ¦ متوسط P ¦ متوسط G اکنون **W** نشان دهنده آب، **P** نشان دهنده مقداری پلیمر و **G** است. به نوعی شیشه اشاره می کند. من فکر می کنم که انتقال از آب به شیشه به دلیل عدم تطابق امپدانس آکوستیک بالا کم باشد. من همچنین فکر می کنم که انتقال از آب به پلیمر زیاد باشد، به دلیل عدم تطابق امپدانس آکوستیک کم. با این حال، با استفاده از $$T = \frac{2Z_1}{Z_1 + Z_0}$$ که در آن Z1 رسانه ای است که فیلد در آن منتشر می شود، دریافتم که انتقال در سناریوی 1 88.56٪ و در سناریو 2 42.35٪ است. . من از یک امپدانس صوتی (واحد Pa.s.m-1) استفاده می کنم: آب 1,480,000 پلیمر 2,758,460 شیشه 23,676,565 آیا کسی می تواند حدس بزند که چرا انتقال در سناریوی 2 بسیار کمتر است؟
|
چرا عدم تطابق امپدانس آکوستیک کوچکتر انتقال کمتری ایجاد می کند؟
|
91366
|
وقتی فلز مذاب در یک میدان مغناطیسی قوی سرد می شود چه اتفاقی می افتد؟ نمی دانم بیشتر چه بگویم، در کتاب های درسی دانشگاه من چیزی مرتبط با این موضوع به خاطر نداشته باشید.
|
وقتی فلز مذاب در یک میدان مغناطیسی قوی سرد می شود چه اتفاقی می افتد؟
|
119529
|
من در حال حاضر در حال تلاش برای درک نظریه دو بعدی یانگ-میلز هستم و به نظر نمی رسد توضیحی برای محاسبه مقدار انتظار حلقه های ویلسون متقاطع پیدا کنم. ویتن در تئوریهای دوبعدی سنج کوانتومی خود محاسبهای عجیب انجام میدهد: برای سه تکرار $\alpha,\beta,\gamma $، پایهای از فضای محصول تانسور متعلق به $\alpha \otimes \beta\ را ثابت میکنیم. otimes \gamma$ به نام $\epsilon_\mu(\alpha\beta\gamma)^{ijk}$ ($\mu$ نمایه بردار پایه $\mu$-th، $i,j,k$ شاخصهایی از تکرارهای اصلی هستند) با این ویژگی که $$ \int \mathrm{d}U {\alpha(U)^i}_i' {\beta(U)^j}_j' {\gamma(U)^k}_k' = \epsilon_\mu(\alpha\beta\gamma)^{ijk}\bar{\epsilon}_\mu(\alpha\beta\gamma)_{i'j'k'}$$ یک سوال جزئی این است که چرا این امکان پذیر است - اگر بپذیرم که همیشه می توانم برخی از بردارها را پیدا کنم که این رابطه را برآورده می کنند خوب است، اما چرا آنها یک مبنا هستند؟ بخش واقعی که من نمی فهمم اکنون می آید: با توجه به موارد بالا، هر لبه پلاک مقداری $\epsilon_\mu$ را حمل می کند، و در تقاطع دو خط، ما چهار تا از اینها از لبه ها می آیند و چهار عدد دیگر. تکرار $\delta^{j}_c$ (j از 1 تا 4 اجرا می شود) متعلق به خود پلاک ها. بدون هیچ محاسباتی صریح، ویتن اکنون به سادگی می گوید که پس از جمع کردن $\epsilon$ روی همه شاخص های آنها (همانطور که توسط تجزیه یک ردیابی از قبل لازم است)، یک عامل محلی مرتبط با این راس $G(\alpha_i,\delta) دریافت می کنیم. ^{(j)}_c,\epsilon)$، که نماد 6j ویگنر است (اما او برای نشان دادن دلیلش مکث نمی کند). من نمی توانم هیچ منبعی را پیدا کنم که این رابطه را بیان کند، یعنی نشان دهد که چرا ما دقیقاً نمادهای 6j را در این محاسبه به دست می آوریم (اگرچه ارتباط آنها با همبسته حاصلضرب تانسور باعث می شود که ما این کار را انجام دهیم). سوال واقعی این است - نماد 6j که این چه ارتباطی است، و چگونه می توان این را ثابت کرد؟ از هر کسی که بتواند این موضوع را برای من توضیح دهد یا مرا به مرجعی راهنمایی کند که در آن با جزئیات بیشتری در مورد آن بحث شده است بسیار سپاسگزار خواهم بود.
|
حلقه های ویلسون متقاطع در دوبعدی یانگ میلز
|
72229
|
طبق اطلاعات من، درجات آزادی هر سیستم فیزیکی، تعداد کمیتهای مستقل (مختصات) است که باید مشخص شوند تا وضعیت یک سیستم به طور منحصر به فرد مشخص شود. با این حال، سوال من این است که چرا برای هر سیستمی تعداد درجات آزادی منحصر به فردی وجود دارد؟ یا به بیان دیگر، اگر مجموعهای از $n$ مختصات مستقل وضعیت سیستم را به طور کامل توصیف میکند، چرا درست است که هر مجموعه دیگر از $n$ مختصات مستقل نیز وضعیت سیستم را به طور کامل توصیف میکند؟ و چرا نمیتوان مجموعهای از $m$ مستقل وجود داشته باشد که وضعیت سیستم را به طور کامل توصیف کند، جایی که $m>n$ ?
|
منحصر به فرد بودن تعداد درجات آزادی
|
18511
|
ایزوسپین فوتون ها چیست؟ چرا کتاب PDG به ازای $I(J^{PC})$ $0، 1(1^{--})$ می گوید؟ 0 دلار، 1 دلار در اینجا به چه معناست؟ آیا ایزواسپین ها مشخص نیستند و می توانند 0 یا 1 باشند؟
|
ایزوسپین فوتون ها چیست؟
|
31739
|
تنظیم: دو فن روبروی هم، فاصله حدود 1 متر. هر دو روشن هستند. در بین آنها یک هواپیمای کاغذی ساده قرار دهید و طبق این ویدیو پرواز می کند. http://www.bieraffe.com/1184/videos/papierflieger-schwebt-trick/ آیا این واقعا درست است؟ اگر بله، فیزیک پشت آن چیست؟ به نظر می رسد فن که از پشت می وزد با دور کمتری کار می کند.
|
هواپیمای کاغذی بین دو فن - آیا این امکان پذیر است؟
|
105433
|
من در حال حاضر در دبیرستان در حال یادگیری نسبیت خاص هستم و ما در درجه اول به این می پردازیم که وقتی یک جسم با سرعت نسبیتی ثابت حرکت می کند چه اتفاقی می افتد. اما اگر شیء سرعتش را تا حد توقف کند کند چه؟ من انقباض طول را برای یک جسم در سرعت های نسبیتی مشاهده می کنم، وقتی که به حالت ثابت برمی گردد، آیا به طول اولیه خود باز می گردد؟
|
وقتی اثرات نسبیتی متوقف می شود چه اتفاقی می افتد؟
|
108340
|
هنگامی که یک حباب هوا در داخل آب تشکیل می شود، و در حالی که هنوز داخل آب است، آیا نیرویی به دلیل کشش سطحی روی آن وارد می شود؟ چرا و کجا این نیرو عمل می کند؟ در جایی خواندم که اگر نیروی شناوری از نیروی ناشی از کشش سطحی بیشتر شود، یک حباب از ته ظرف پر از مایع جدا می شود. اگر کشش سطحی خاصیت یک سطح مایع است، چرا در پایین، خوب در داخل مایع کار می کند؟ من فکر می کنم از یک چیز بسیار ابتدایی ناشی می شود، اما من نمی توانم آن را درک کنم. ویرایش: فکر کنم متوجه شدم. آیا به این دلیل است که مایع لایه مایع اطراف حباب را می کشد؟
|
تأثیر کشش سطحی بر حباب هوا در داخل آب چیست؟
|
72226
|
در QFT همانطور که خواندم به طور طبیعی ظاهر می شود. با جبر پوانکاره مرتبط است، اینطور نیست؟ __ به عنوان توضیح قسمت اصلی سوال. عملگر تکانه زاویه ای مداری نسبیتی با اپراتور 4 تانسوری و 4 ضربه ای جبر پوانکر را ایجاد می کند. بنابراین مقادیر ویژه بردار عملگر تکانه زاویه ای از طریق مقادیر کامل یا نیم صحیح (در واحد $\hbar $) بیان می شود. اما استفاده از عملگر تکانه مداری باعث می شود که فقط مقادیر صحیح داشته باشیم. ما میتوانیم عملگر را بهطور مصنوعی اضافه کنیم که یک نمایش کاهشناپذیر را پیادهسازی میکند، بنابراین با نمایش مختصات مرتبط نیست و ممکن است مقادیر نیمه صحیح داشته باشد. اما این روش مصنوعی است، زیرا بدون اثبات تجربی وجود اسپین ما به راحتی میتوانیم تنها با تکانه زاویهای مداری عمل کنیم. در مقابل، در تئوری میدان کوانتومی، اسپین به طور طبیعیتر اتفاق میافتد (؟).
|
اسپین چگونه در QFT ظاهر می شود؟
|
83402
|
در این موج پیشرونده باید تفاوت فاز را دریابیم. اگر آن را با $\phi$ در فاصله x تعریف کنیم، دریافت می کنیم. $$\phi = \frac{2 \pi}{\lambda}x$$ اما وقتی معادله موج پیشرونده را مینویسیم، $$y= A \sin (\omega t - \phi)$$ A نویسنده می گوید که این اختلاف فاز کمتر از اختلاف فاز در سمت چپ است. مشکل من این است که می توانیم علامت + را نیز وارد کنیم. اما فیزیک برای درج علامت مثبت یا منفی چیست. با تشکر
|
مشکل در موج پیشرونده
|
68501
|
پدیده بسیار آشنا شارژ از طریق القاء شامل آوردن یک جسم باردار به یک کره بدون بار برای ایجاد جدایی بارها در آن و سپس زمین کردن بار (همانطور که بار بدن نزدیک شده است) است که در انتها از کره دور است. یکی که در آن جسم نزدیک می شود. اما سوال من: - واقعیت این است که میدان الکتریکی حاصل در هر رسانایی صفر است و یک سطح هم پتانسیل است. بنابراین قبل از زمین، میدان به دلیل جسم باردار نزدیک شده است (مثلا +)، بار منفی القایی (مثلا q-)، و به دلیل بار القایی مثبت (q+) در انتهای دیگر یک میدان صفر در داخل می دهد. کره اما وقتی q+ زمین شود، آیا میدان حاصل از دو بار باقیمانده غیرصفر نمی شود زیرا باری که زمین شده بود سهمی در صفر کردن میدان داشت. سؤال بعدی، «زمینسازی» زمانی اتفاق میافتد که زمین تقریباً در پتانسیل صفر است و بنابراین وقتی جسم باردار با پتانسیل بالاتر یا پایینتر به زمین متصل میشود، بار به داخل و خارج جریان مییابد تا در نهایت جسم را در پتانسیل صفر قرار دهد. اما در مثال القایی بالا، بار مثبت به دلیل اختلاف پتانسیل زمین شد اما بار منفی نشد. چرا آیا بار منفی نیز نباید زمین شود؟
|
شارژ از طریق القاء (و زمین)؟
|
113071
|
من سعی می کنم به راحتی طول بین kpoint های ویژه در BZ گروه های 32 نقطه ای در یک سیستم کریستالی را محاسبه کنم. من طول ها را محاسبه می کنم تا نمونه برداری از K نقطه را در طول این مسیرها برای محاسبات ساختار الکترونیکی مقیاس کنم. من میتوانم از بردارهای شبکه متقابل برای محاسبه هر نقطه تقارن خاص برای هر شبکه Bravais برای بدست آوردن طولها استفاده کنم، اما نمیدانم که آیا راه آسانی برای حداقل یافتن نسبت بین طولهایی که فقط از دست دادهام وجود دارد. من برای مثال میخواهم طول مسیرها را برای کریستال شبکه Rhombohedral Bravais پیدا کنم، بنابراین از مسیرها استفاده میکنم  اما برای قسمتهای کوتاهتر از از مسیرهایی که میخواهم از k نقطه کمتر نمونهبرداری کنم و برای مسیرهایی که طولانیتر هستند، بیشتر نمونهبرداری میکنم (به طوری که در بیشتر موارد به طور مساوی پخش شوند) میتوانم این نقاط و طول مسیر را با اما قصد من این است که فرآیند را خودکار کنم تا بتوانم بردارهای شبکه متقابل و نوع شبکه را ورودی تابعی داشته باشم که طول بین هر یک از نقاط را به طور خودکار به من می دهد. من این تصور را دارم که از آنجایی که مختصات کسری برخی از این نقاط به بردارهای شبکه متقابل سلول وابسته است، برخی از طول مسیرها با تغییر بردارهای شبکه تغییر می کنند. بنابراین من می خواهم یک راه آسان برای بدست آوردن این طول ها بدون کدگذاری سخت تمام معادلات با دستور if/else داشته باشم. می ترسم فقط مجبور باشم این کار را انجام دهم. امیدوارم بتوانید غیر از این به من بگویید!
|
نحوه محاسبه آسان طول (یا طول نسبی) مسیرهای بین نقاط تقارن در BZ
|
108343
|
سوال این است: فرض کنید میدان داخل یک قطعه بزرگ دی الکتریک $E(0)$ باشد به طوری که $D(0) =$$\epsilon(0)E(0)$ + $P$. اکنون یک حفره کروی کوچک از مواد توخالی شده است. جابجایی ($D$) را در مرکز حفره بر حسب $D(0)$ و $P$ پیدا کنید. اکنون، این سؤال یک اشاره داشت: حک کردن یک حفره مانند قرار دادن جسمی با همان شکل اما قطبش مخالف است. با استفاده از آن اشاره میدان در مرکز کره = $E(0)$ - میدان به دلیل قطبش یکنواخت کره. بنابراین، $E=E(0)+P/(3\epsilon(0))$ برای بدست آوردن $D$ باید $\epsilon(0)E$ باشد نه $\epsilon(0)E$ + $P$. چرا اینطور است؟ ما یک میدان $E(0)$ داریم که باعث قطبش $P$ ماده دی الکتریک می شود. بنابراین ما $D(0)$ را دریافت می کنیم. بنابراین اکنون در حالی که $D$ را در مرکز محاسبه می کنیم، چرا $P$ را در نظر نمی گیریم؟ آیا به این دلیل است که اگر من $P$ را در نظر بگیرم، به نوعی سهم آن را دو بار در نظر خواهم گرفت؟
|
سوال در مورد کره دی الکتریک
|
79234
|
آیا این حرکت است؟ اما تکانه $\rm{Ns}$ است، نه $\rm{N}$. http://www.skepticforum.com/viewtopic.php?f=32&t=14624 > مطمئن نیستم که 3430 نیوتن لزوما فراتر از توانایی انسان باشد. بوکسور > ضربه مشت فرانک برونو بیش از 6000 نیوتن بود. واحد تکانه $\rm{Ns}$ است، نه $\rm{N}$. آیا این بدان معناست که مشت فرانک برونو می تواند نیرویی معادل 6$\,\rm{kN}$ اعمال کند؟  یعنی با یک دست او می تواند نیروی کافی برای بلند کردن 0.6 دلار تن وزن ایجاد کند؟ مشکل این تفسیر این است که مقدار نیروی وارد شده توسط یک دست بسیار به نحوه توزیع تکانه پانچ در طول زمان بستگی دارد. یک دست آهنی نیروی عظیمی تولید می کند در حالی که یک دستکش لاستیکی نیروی بسیار کمی تولید می کند حتی اگر تکانه یکسان باشد. باشه برگرد به سوال به هر حال منظور از نیروی پانچ $6\,\rm{kN}$ چیست؟
|
این که برونو می تواند $6\,\rm{kN}$ را بزند به چه معناست؟
|
131990
|
همانطور که در تلاش برای یافتن پاسخ برای یک مشکل دیگر بودم، به من اطلاع دادند که معادله ای که استفاده می کنم کار نمی کند. معادله ای که من استفاده کردم $$F = (NI)^2\mu_0\frac{\text{Area}}{2g^2}$$ بود. من مدتی را صرف تلاش کردم تا بفهمم چه چیزی اشتباه است، و به نظر نمی رسد مشکل را پیدا کنم. به نظر من، تنها مشکل من همان چیزی است که در سوال اصلی خود در مورد آن پرسیدم. TIA، به هر کسی که می تواند این مشکل را روشن کند. **ویرایش:** شاید خودم مشکلم را حل کرده باشم. فکر می کنم ممکن است در سوال دیگرم معادله را اشتباه نوشته باشم. وقتی به آن نگاه میکنم، نمیدانم چگونه قبلاً این را از دست دادهام، به نظر میرسد آن را به صورت $$F = (NI)\mu_0\frac{\text{Area}}{2g^2}$$ نوشتهام و نه معادله صحیح $$F = (NI)^2\mu_0\frac{\text{Area}}{2g^2}$$ در حالی که من فکر میکنم این درست است، لطفاً کسی میتواند تأیید کند؟ من قصد دارم آن را دوباره مرتب کنم تا تعداد سیم پیچ هایی را که در شیر برقی نیاز دارم پیدا کنم و واقعاً نمی خواهم این اشتباه را متوجه شوم. **ویرایش:** بنابراین، برای کمک به این امر، میخواهم یک مثال انجام دهم. علاوه بر این، من سؤال دیگرم را میپرسیدم، زیرا وقتی از مقدار Area گرفتهشده از صفحه **b** استفاده میکردم، اعداد خندهداری را از این موضوع میگرفتم. راهاندازی: بنابراین، اگر استوانهای به طول 25 میلیمتر و دور آن 5 میلیمتر ارائه شود، و از من خواسته شود که تعداد چرخشهای شیر برقی را که مجموعاً نیرویی معادل 1 نیوتن بر ثانیه روی سیلندر در فاصله 5 میلیمتری وارد میکند، بیابم. که از جریان 3 آمپری استفاده می کند که باید داشته باشد، من با تنظیم مجدد معادله نیروی شیر برقی خود شروع می کنم. $$F = (NI)^2\mu_0\frac{\text{Area}}{2g^2}$$ * * * $$\frac{F}{\mu_0} = (NI)^2\frac{ \text{Area}}{2g^2}$$ * * * $$\frac{F}{\mu_0\frac{\text{Area}}{2g^2}} = (NI)^2$$ * * * $$\sqrt{\frac{F}{\mu_0\frac{\text{Area}}{2g^2}}} = NI$$ * * * $$\sqrt{\frac{F}{ \mu_0\frac{\text{Area}}{2g^2}}}/I = N$$ جایی که F نیروی وارد شده به سیلندر بر حسب نیوتن است، N تعداد دورها است، I جریانی است که از سیم پیچ عبور می کند، μ₀ 4π x 10^-7 است، مساحت is مساحت استوانه در صفحه **b** است (عکس را ببینید)، و g فاصله جداسازی است. سیلندر از سیم پیچ نمونه ای از هواپیماهایی که از یک استوانه عبور می کنند.  * * * $$\sqrt{\frac{(1)}{(4π · 10^{-7})\frac{ \text{Area}}{2(15)^2}}}/(3) = N$$ * * * $$\sqrt{\frac{1}{4π · 10^{-7}·\frac{\text{(19.634375)}}{2(15)^2}}}/3 = N$$ و می دانیم مساحت _about_ 19.634375 است زیرا مساحت π·r^2 است و شعاع 2.5 میلی متر بود. * * * $$\sqrt{\frac{1}{4π · 10^{-7}· 19.634375}}/3 = N$$ * * * $$\sqrt{\frac{1}{0.000024673283}}/ 3 = N$$ * * * $$\sqrt{40529.66927830399}/3 = N$$ * * * $201.3198183942753/3 = N$$ * * * $$N = 67.1066061314251$$ * * * $$N = 67.1 \text{ چرخش}$$ فکر نمیکنم چیزی را از دست دادهام، اما اگر من کار اشتباهی کرد لطفا به من بگویید امیدوارم این کمک کند که آیا این معادله درست است یا خیر. **ویرایش:** فکر نمی کنم کسی بتواند ریاضی من را بررسی کند؟
|
نیروی یک سلونوئید بر یک ماده فرومغناطیسی
|
21565
|
آیا کتابی وجود دارد که به عمق توابع همبستگی بپردازد؟ کتاب/مقاله ای که به جزئیات رابطه توابع همبستگی با تقارن ها را توضیح می دهد و اینکه چگونه می توان ارتباط بین استفاده از توابع همبستگی و اندازه گیری ها را در آزمایشگاه درک کرد، علاقه مندم. من به مثالهای تجربی/نظریهای علاقهمندم که به کوانتوم محدود نمیشود، بلکه به همه نمونههای فیزیک که از تابع همبستگی استفاده میکنند، علاقهمندم.
|
توابع همبستگی، تقارن ها و اندازه گیری ها
|
4229
|
آیا می توان از هیچ چیزی جز فلز خالص فیلتری ساخت که فقط از تابش قطبی دایره ای سمت راست عبور کند و تابش قطبی دایره ای سمت چپ را منعکس کند؟ چه شکلی خواهد بود؟ فنر مارپیچ در لوله؟ در مورد یک نوار فلزی پیچ خورده در داخل یک لوله رسانای دایره ای چطور؟ یک آنتن مارپیچ حالت محوری تابش قطبی دایره ای را منتقل می کند. اگر یک آنتن حالت محوری (شاید با بار مقاومتی؟) را در یک موجبر قرار دهم، آیا می توانم فیلتری ایجاد کنم که فقط تابش قطبی دایره ای سمت چپ را عبور دهد؟ من در حالت ایده آل دوست دارم این کار را فقط با مواد رسانا (یعنی نه مقاومتی) انجام دهم. من همچنین می خواهم که تابش قطبش دایره ای مخالف را منعکس کند (نه جذب کند). آیا کسی می تواند به من بگوید چگونه این کار را انجام دهم؟
|
آیا می توان یک فیلتر موج رادیویی قطبی دایره ای حالت محوری با مواد صرفا رسانا ساخت؟
|
31192
|
 اجازه دهید $\bf{n}'$ یک بردار واحد در جهت بردار موج در قاب استراحت پلاسما باشد و $ \bf{B'}$ یک بردار واحد در امتداد میدان مغناطیسی در قاب استراحت پلاسما باشد. میدان الکتریکی یک موج الکترومغناطیسی قطبی شده خطی در امتداد بردار واحد $\hat{e}=\bf{n'} \times \hat{B'}$ هدایت میشود و میدان مغناطیسی موج در امتداد بردار واحد است. $\hat{b'}=\bf{b}\times \hat{e'}$، به طوری که شار Poynting در امتداد $\hat{e'}\times باشد \hat{b'}$ در امتداد $\bf{n'}$ هدایت شد. ما یک تقویت لورنتس به قاب انفجار می دهیم تا میدان الکتریکی $e$ را در آنجا پیدا کنیم، آن را به حالت یکپارچگی نرمال کنیم، و e$$ را در یک جهت معین (مثلاً در امتداد طرح محور جریان در صفحه آسمان) پیش بینی کنیم. . میدانهای موج که بر حسب جهت فوتون در قاب انفجار بیان میشوند $\bf{n}$ است \begin{equation} \hat{e'} ~=~\frac{\bf{b} \times \ کلاه{B'}}{\Gamma (1-\bf{n}\cdot\bf{v})}+\frac{1+\Gamma (1-\bf{n}\cdot \bf{v})}{(1+\Gamma(1-\bf{n}\cdot \bf{v}))} \end{equation} که در آن $\Gamma =\frac{1}{\sqrt{1-v^2/c^2}}$ فاکتور عمده لورنتس است. آیا کسی می تواند به استنباط معادله فوق کمک کند؟
|
تبدیلات لورنتس بردار پلاریزاسیون
|
43049
|
یک سوال پراکنده دیگر بنابراین من این شبکه Bravais از سایتهای R را دارم که با برخی حالتهای معمولی با دامنه جابجایی کوچک $u_o$، مقداری بردار موج k و مقداری فرکانس $\omega$ میلرزد. ما می توانیم به وضوح $u(R)=u_o \cos(k R - \omega t)$ را توصیف کنیم. اگر پرتویی از تابش از شبکه را با تغییر بردار موج q پراکنده کنیم، دامنه در آشکارساز $$\psi(t)=\Lambda e^{-i \Omega t} \sum_{\vec{R است. }} e^{i\vec{q}\vec{r}(\vec{R},t)}$$ جایی که $\Omega$ فرکانس این موج فرود است، $\vec{r} (\vec{R},t)$ موقعیت اتم R و زمان t است. بنابراین من باید بردارهای موج q را پیدا کنم که به طور منسجم در نتیجه ارتعاشات پراکنده شده اند. $u_o$ کوچک فرض میشود، بنابراین میتوانیم بگوییم برای همه q مورد علاقه، $q u_o << 1$. بنابراین ما در اینجا به Scattering تامپسون علاقه مندیم. آیا کسی می تواند به من راهنمایی کند که چگونه پارامترهای خود را تنظیم کنم و از آن شروع کنم؟ چیزی که من را گیج می کند این است که چگونه می توان همه بردارهای موج q را عملیاتی کرد و مطمئن شد که آنها فقط q هستند که به طور منسجم پراکنده شده اند. فکر میکنم این بدان معناست که من باید شرایطی را روی q تنظیم کنم، سپس بردارهای موج خود را ارزیابی کنم. اگر آنها به طور منسجم پراکنده باشند، فکر میکنم این بدان معناست که من مجموعه بردارهای موجی را میخواهم که به تداخل سازنده قلهها کمک کنند. با تشکر
|
پراکندگی غیر کشسان و پراکندگی منسجم
|
23742
|
در مدل سیگما شکست تقارن خود به خود، حالات خلاء منحط داریم. اما اگر مقدار خاصی از VEV را انتخاب نکنیم، هیچ گونه شکست تقارنی نخواهیم داشت. همانطور که از یک کتاب خواندم، در نظریه میدان در حجم محدود، مشکلی وجود نخواهد داشت. اما در حجم بی نهایت، مجبور می شویم مقداری از فیلد $\pi$ را انتخاب کنیم. اما چرا؟
|
چرا در پدیده Nambu-Goldstone مجبور به انتخاب مقدار خاصی برای فیلد $\pi$ هستیم؟
|
133840
|
چگونه می توانم مشتق تابعی این تابع را محاسبه کنم؟ $$F[x(t)] = \int_{0}^{t}x(t_1)a(t_1)\ چپ \\{ \int_{0}^{t_1}x(t_2)b(t_2) \ ,dt_2\right \\} dt_1 .$$ که در آن $a(t)$ و $b(t)$ توابع ثابت واقعی هستند. طبق روش معمول، من $$\frac{\delta F\left [ x \right ]}{\delta x(s) } = \int_{0}^{s}\left [ a(t') دریافت می کنم )b(s)+a(s)b(t') \right ]x(t')dt'.$$ که عجیب به نظر می رسد زیرا آن هم تابعی است و من فکر می کنم که باید تابعی را دریافت کنم.
|
چگونه این مشتق تابعی را محاسبه کنیم؟
|
31194
|
من در اینجا نابغه فیزیک نیستم، من فقط به بوزون هیگز علاقه داشتم، بنابراین داشتم این مقاله را می خواندم: چگونه کشف بوزون هیگز می تواند فیزیک را بشکند. *وزن 125 گیگاالکترون ولت (GeV)** – یا حدود 125 برابر بیشتر از یک > پروتون – به این معنی که دقیقاً همان جایی است که مدل استاندارد انتظار داشت > باشد. چگونه می توان وزن را با الکترون ولت اندازه گیری کرد؟
|
جرم بوزون هیگز در الکترون ولت؟
|
72227
|
یک سوال مرتبط وجود دارد (چرا شیشه شفاف است؟) اما من فقط از معادلات ماکسول به آن می پردازم. اگر وابستگی فرکانس را نادیده بگیرم، می توان عمق پوست $δ$ را برای هادی های ضعیف مانند آب (خالص) و شیشه با استفاده از (به ویکی پدیا مراجعه کنید) تعیین کرد. گذردهی (فقط برای به دست آوردن محدوده تخته برای عمق پوست شیشه)، با استفاده از مقادیر مناسب برای مقاومت ρ (آب = $2.5×10^5$ Ω∙m و شیشه = $10^{10}−10^{14}$ Ω∙m)، گذردهی الکتریکی ($ε=ε_0ϵ_r$) و نفوذپذیری مغناطیسی ($μ ≈ μ_0$)، من محاسبه می کنم که $$δ( آب) =10^4m$$$δ(شیشه) =10^8-10^{12} m$$ Maxwell's معادلات رفتار امواج الکترومغناطیسی را در رساناها (و همچنین هادی های ضعیف) تعیین می کند، بنابراین اگر شیشه و آب دارای چنین عمق پوستی بیشتری هستند، پس این دلیل شفافیت نور برای این دو رسانه است - درست است؟ اگر چنین است، پس من دو سؤال مرتبط دارم: 1. از نظر ریاضی، نشان دادن اینکه عمق پوست مستقل از فرکانس است، کاملاً ساده است. با این حال، آیا توضیح فیزیکی وجود دارد که چرا عمق پوست برای هادی های ضعیف مستقل از فرکانس است اما برای هادی های خوب نه؟ 2. حداقل در فرکانس های نوری، عمق پوست عمدتاً به مقاومت ماده بستگی دارد. از آنجایی که شیشه مقاومت بیشتری نسبت به آب دارد (رسانای ضعیف تری است)، امواج الکترومغناطیسی به دورتر از شیشه نفوذ می کنند. بنابراین، کلید درک اینکه چرا شیشه شفافتر از آب است، درک فیزیکی چرا δ∝ ρ است؟ من کتاب های گریفیث و جکسون را برای کمک در این مورد جستجو کردم و چیزی پیدا نکردم. پیشاپیش از هرگونه راهنمایی در مورد این سوالات سپاسگزارم. **اصلاح و ویرایش به دلیل نظر یوهانس در زیر برای سوال 2**
|
چرا شیشه بسیار شفاف تر از آب است؟
|
131994
|
یک هادی مغناطیسی با سطح مقطع استوانه ای را تصور کنید که توسط سیم پیچی با جریان متغیر زمانی احاطه شده است $$I = I_0\cdot \cos (2\pi f t)$$ هادی به دو قسمت تقسیم شده است، قسمت اول دارای رسانایی است. و نفوذپذیری نسبی $\kappa، \mu$، دوم با $4\kappa، \mu$. یک میدان مغناطیسی $B$ از طریق هادی وجود دارد که ناشی از تغییر جریان و در نتیجه زمان نیز می باشد: $$B = B_0\cdot \cos (2\pi f t)$$  تغییر این میدان مغناطیسی ولتاژی را در داخل ماده القا می کند و باعث چگالی جریان $J$ می شود. این چگالی جریان دارای مقدار $J_1$ در سطح هادی چپ و $J_2$ در سمت راست است. عمق پوست $\delta$ با فاصله از سطح که در آن $J = 0.37 \cdot J_1$، به ترتیب $J = 0.37 \cdot J_2$، با $0.37 = 1/e$ و همچنین: $$\delta = \frac{1}{\sqrt{\pi f\kappa\mu}} = \frac{\sqrt{2j}}{\alpha}$$ که در آن $\alpha$ ثابت انتشار است. من با شبیه سازی دریافتم که در مرز بین هر دو ماده، آبی و نارنجی، اعمال می شود: $$\frac{1}{\delta_{12}} = \frac{1}{2}(\ frac{1}{\delta_{1}}+\frac{1}{\delta_{2}})$$ و بنابراین $$\alpha_{12} = \frac{1}{2}(\alpha_1 + \alpha_2)$$ اما من واقعاً در تلاش برای اثبات آن هستم. آیا کسی می تواند به من نکاتی بدهد که چگونه می توانم این روابط را به صورت تحلیلی بدست بیاورم؟ * * * در اینجا نمودار دیگری: نمودار بالایی چگالی جریان را در سطح نشان می دهد. مورد دوم خط کانتور را نشان می دهد که در آن چگالی جریان حدود 63$\% = عمق پوست $ کاهش یافته است. در $z=0$ مرز بین هر دو ماده است. اگرچه چگالی جریان یک تابع پله ای است، اما عمق پوست پیوسته است و مقدار $\delta_{12}=\frac{2}{\frac{1}{\delta_{1}}+\frac{1}{1}{1} را دارد. \delta_{2}}}$ در $z=0$. 
|
عمق پوست چگالی جریان در هادی مغناطیسی در مرز بین دو ماده مختلف
|
107145
|
اگر دو رویداد فضازمان با $(dx,dy,dz,dt),(dx',dy',dz',dt)$ در دو قاب مرجع به ترتیب $K,K'$ از هم جدا شوند که حرکت نسبی آنها صرفاً در امتداد پس محور $x$، صرفاً به این دلیل است که $$dx^2+dy^2+dz^2-c^2dt^2=dx'^2+dy'^2+dz'^2-c^2dt'^2.....(*)$ $ نتیجه می شود که $$dx'=dx\cosh\phi+cdt\sinh\phi.....(1)$$ $$cdt'=cdt\cosh\phi+dx\sinh\phi.....(2)$$ برای $\phi \in \mathbb{R}.$ از نظر ریاضی، هر $\phi\in \mathbb{ R}$ $(*)$ را برآورده می کند، اگرچه اگر $K,K'$ و دو رویداد فضازمان مشخص شده باشند، $\phi$ باید ثابت شود. **سوال:** در لاندو و لیفشیتز، به نظر می رسد نویسندگان به طور ضمنی فرض می کنند که $\phi$ صرفاً تابعی از $K,K'$ است و نه از دو رویداد فضا-زمان مورد مطالعه. آنها این فرض را به این ترتیب میکنند: آنها $\phi$ را برای حالت خاص دو رویداد که $dx=0$ را برآورده میکند (یعنی ذرهای که بین دو رویداد حرکت میکند با سرعت $0$ نسبت به $K$ حرکت میکند) پیدا میکنند، اما سپس وارد میکنند. این مقدار برای $\phi$ به $(1)،(2)$ میرسد، که این را توجیه نمیکند. این چه توجیهی دارد؟ _نکته_: در لاندو و لیفشیتز، آنها معادلات x',x,t',t$ را تجزیه و تحلیل میکنند، نه معادلات مربوط به دیفرانسیلهای آنها، اما بعداً دیفرانسیلهای $(1)، (2)$ را میگیرند، بنابراین در نهایت همان کاری را انجام میدهند. در بالا توضیح دادم
|
چرا $\phi$ در تبدیل های لورنتس هذلولی ثابت است؟
|
113923
|
در این ویدیوی یوتیوب، یک کوسه استخری به طور مداوم توپ نشانه را میگیرد تا در اواسط فیلم (یعنی پس از ضربه زدن به آن) به شدت تغییر جهت دهد. آیا این از نظر تئوری بدون استفاده از توپ های ترفند امکان پذیر است؟ اگر چنین است، چگونه؟ اگر نه، چرا که نه؟ **توجه: من نمیپرسم که آیا ویدیوی خاص جعلی است یا خیر، من میپرسم که آیا چنین عکسهایی _ممکن_ هستند.**
|
آیا توپ استخر می تواند در اواسط رول تغییر جهت دهد؟
|
99966
|
ما می دانیم که اگر فردی ماده ای را مانند یک ریسمان ارتعاش دهد، رشته با فرکانس طبیعی خود نوسان می کند. اما من فکر میکنم فرکانس بستگی به سرعتی دارد که عاملی مانند دست یک مرد روی سیم ارتعاش میکند. اما کتاب من می گوید فرکانس طبیعی فقط به ویژگی های رشته بستگی دارد. لطفا توضیح دهید.
|
آیا فرکانس یک ماده ارتعاشی مانند یک ریسمان به خواص آن بستگی دارد یا صرفاً به عاملی که رشته را ارتعاش می کند بستگی دارد؟
|
112991
|
داشتم در مورد معادلات انتگرال می خواندم و این گزیده را در ویکی پدیای پرتغالی پیدا کردم: > معادلات انتگرال برای تعیین موقعیت در همه موارد یک جسم، در صورت شناخته شدن، سرعت لحظه ای آن در همه زمان ها عمل می کنند اما خواندن در مورد اصل عدم قطعیت، من این گزیده را پیدا کردم: برای مثال، در سال 1927، ورنر هایزنبرگ بیان کرد که موضع برخی ذره تعیین می شود، تکانه آن را کمتر می توان شناخت، و بالعکس. نتیجه گیری من چه اشکالی دارد؟ واقعا این دو اصل با هم تضاد دارند؟
|
معادلات انتگرال با اصل عدم قطعیت تناقض دارند؟
|
15147
|
آیا کسی می داند که چگونه فاصله بین آشکارسازها در آزمایش نوترینو معروف اکنون اندازه گیری می شود؟ همچنین زمان پرواز چگونه اندازه گیری شد؟
|
فاصله بین آشکارساز ژنو و گرن ساسو چگونه اندازه گیری می شود؟
|
132712
|
من بردار poynting را برای یک موج ساده محاسبه می کنم و کمی شک دارم. $$ \bar S = \frac 1 2 \bar E \times \bar H^* = ... = \frac {| \bar E|^2} {2 \zeta} \hat i_k $$ حالا اگر حجم استوانهای را در نظر بگیرم و قضیه واگرایی را اعمال کنم، $$ \int_{s_1} Re \,\, \bar S \,\, به دست میآید. \hat i_n dS = - \frac {| \bar E|^2} {2 \zeta} A$$ $$ \int_{s_2} Re \,\, \bar S \,\,\hat i_n dS = \frac {| \bar E|^2} {2 \zeta} A$$ $$ \int_{s_l} Re \,\, \bar S \,\,\hat i_n dS = 0$$ که $s_1$ وجه چپ است $s_2$ وجه سمت راست و $s_l$ وجه جانبی سیلندر است. بنابراین باید $$ \int_{S} Re \,\, \bar S \,\,\hat i_n dS = - \frac {| \bar E|^2} {2 \zeta}A +\frac {| \bar E|^2} {2 \zeta} A = 0$$ آیا ممکن است؟
|
موج ساده بردار Poynting
|
73578
|
من در خواندن نظریه ریسمان پولچینسکی جلد اول ص 123، در مورد کوانتیزاسیون کوواریانت قدیمی سوالی دارم. گفته می شود > ... $\langle 0;k | 0; k' \rangle = (2\pi)^D \delta^D (k-k') \tag{4.1.15}$ > به شرح زیر از بقای حرکت. برانگیختگی زمانی یک هنجار > منفی دارد. چگونه می توان تحریک زمانی یک هنجار منفی دارد را دید؟ آیا تابع دلتای دیراک در RHS معادله است. (4.1.15) یا $0$ یا $\infty$؟
|
نحوه مشاهده برانگیختگی زماندار دارای یک هنجار منفی از کوانتیزاسیون کوواریانت قدیمی است.
|
91365
|
آیا چیزی بزرگتر از یک مولکول و همچنان تصادفی در طبیعت وجود دارد؟ من می دانم که فروپاشی یک اتم ناپایدار قابل پیش بینی نیست، فقط می توان احتمال فروپاشی را محاسبه کرد. مولکول هایی که در یک مایع حرکت می کنند نیز می توانند تصادفی باشند. اما آیا چیزی بزرگتر از آن وجود دارد که غیر قطعی باشد؟ آیا تصادفی بودن در سطح مولکولی متوقف می شود؟
|
آیا همه فرآیندهای طبیعی که بزرگتر از یک مولکول هستند نیز قطعی هستند؟
|
73574
|
اگر مکعبی داشته باشم که با سرعت $v$ حرکت می کند و با سرعت زاویه ای $\omega$ می چرخد، چگونه می توانم بردار سرعت لحظه ای یکی از رئوس مکعب را تعیین کنم؟ اگر مکعب در حال شتاب گرفتن باشد چه؟ و اگر شتاب زاویه ای داشته باشد، $\alpha$ چه؟ آیا این روش محاسبه را تغییر می دهد؟ آیا می توان بردار شتاب را بدست آورد؟
|
به دست آوردن بردار سرعت یا شتاب نقطه روی جسم صلب؟
|
79233
|
به ویژه، من می خواهم نقل قول زیر را از مقاله ای توسط ویتن درک کنم: Nucl.Phys. B188 (1981) 513 (ص. 515 در بالا) بیانیه او: > این به این دلیل است که در ابر تقارن جهانی، ابرجبرها همیشه با تقارن سنج جابجا می شوند. کموتاتور، اگر صفر نباشد، یک ابرتقارن > تبدیل بسته به تعداد نامتناهی پارامترهای گیج > تقارن خواهد بود، بنابراین باید ابرتقارن محلی باشد. لطفاً کسی می تواند آخرین گزاره در مورد تعداد نامتناهی پارامترها را به طور واضح تر توضیح دهد؟
|
چرا ابر تقارن جهانی با دگرگونی های گیج جابجا می شود؟
|
77051
|
شاید یک سوال احمقانه باشد زیرا جستجوی من چیزی برنمیگرداند. با فرض حالت کم انرژی، یک پروتون (ساخته شده توسط کوارک های قرمز رو به بالا، آبی رو به بالا و سبز پایین) با یک ضد نوترون (ساخته شده توسط یک کوارک ضد سبز، یک ضد قرمز و یک کوارک ضد آبی پایین) ملاقات می کند. . آیا آنها به دلیل هزینه های رنگی بی همتا بدون نابودی در کنار هم خواهند ماند؟ یا گلوئون ها برای تغییر رنگ ساطع می شوند تا نابودی اتفاق بیفتد؟
|
چه اتفاقی بین یک پروتون و یک ضد نوترون با بارهای رنگی بی همتا خواهد افتاد؟
|
131991
|
کتاب من میگوید که بین سطح تماس بین دو جسم، نیروهای تماسی بین یکدیگر اعمال میشوند (میزان آنها برابر هستند اما جهت مخالف دارند، مطابق قانون سوم نیوتن) به دلیل برهمکنش الکترومغناطیسی. مولفه عمود نیروی تماس نیروی نرمال است در حالی که جزء موازی نیروی اصطکاک است. اصطکاک ناشی از جوش سرد یعنی. ایجاد پیوند بین نواحی تماس میکرو هنگامی که آنها به دلیل نیروی خارجی منحرف می شوند، امواج ارتعاشی ایجاد می کنند که میرا شده و گرما آزاد می شود. اما در مورد مکانیسم اصطکاک استاتیک، چگونگی وقوع آن در سطح میکروسکوپی صحبت نکرد. با افزایش نیروی خارجی بر روی بدن، نیروی اصطکاک ایستا نیز مقدار آن را افزایش می دهد (تا یک سطح). نیروی اصطکاک ساکن چگونه افزایش می یابد؟ علت آن در سطح میکروسکوپی چیست؟ آیا پیوند قوی تر می شود؟ چگونه این افزایش در اصطکاک استاتیک اتفاق می افتد؟
|
چگونه اصطکاک استاتیک با افزایش نیروی اعمالی افزایش می یابد؟
|
110715
|
توضیح استاندارد برای انتقال به سرخ کیهانی این است که فوتونهایی که از کهکشانهای دور ساطع میشوند، با حرکت در جهان در حال انبساط، طول موجهایشان افزایش مییابد. اما شاید فوتونها هنگام حرکت انرژی خود را از دست ندهند، بلکه اتمهای آشکارسازهای ما در مقایسه با اتمهایی که این فوتونها را برای مدت طولانی در گذشته ساطع کردهاند، پرانرژیتر هستند و منجر به یک اثر انتقال آشکار به سرخ میشوند؟ **اضافه** (با تبادل نظر با @rob، به زیر مراجعه کنید): فرضیه من این است که جرم پلانک $M_{pl} \propto a(t)$ که $a(t)$ ضریب مقیاس جهانی است . **ضافه 2** البته اگر جرم پلانک $M_{pl}$ در حال تغییر است، آنگاه $G=1/M^2_{pl}$ در حال تغییر است به طوری که دیگر GR استاندارد نداریم! من قبلاً این سؤال را پرسیده ام، به تفسیر انتقال به سرخ کیهان شناسی مراجعه کنید، اما این بار برای تأیید فرضیه خود کمی تئوری اضافه می کنم. برای سادگی، یک متریک شعاعی FRW مسطح فرض کنیم: $$ds^2=-dt^2 + a^2(t)\ dr^2$$ مسیر ژئودزیکی صفر پرتو نور با $ds=0$ را در نظر بگیرید. که داریم: $$dt = a(t)\ dr\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)$$ حال در حال حاضر $t_0$ تعریف می کنیم ضریب مقیاس $a(t_0)=1$ به طوری که داریم: $$dt_0 = dr\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)$$ جایگزین معادله (2 ) در معادله (1) داریم: $$dt = a(t)\ dt_0$$ برای اینکه بازه زمانی $dt$ ثابت بماند با افزایش ضریب مقیاس $a(t)$، باید بازه متناظر زمان کنونی $dt_0$ برعکس با ضریب مقیاس متفاوت است: $$dt_0 \propto \frac{1}{a(t)}$$ بنابراین با افزایش زمان کیهانی $t$، و انبساط جهان، برابر است فواصل زمان کیهانی $dt$ مطابق با فواصل کوچکتر و کوچکتر زمان فعلی $dt_0$ است. اکنون انرژی یک سیستم با فرکانس نوسان آن متناسب است که به نوبه خود با دوره نوسان آن نسبت معکوس دارد: $$E(t) \propto \frac{1}{dt}$$ انرژی متناظر سیستم در شرایط عصر حاضر $t_0$ توسط $$E(t_0) \propto \frac{1}{dt_0}$$ $$E(t_0) \propto داده شده است a(t)$$ بنابراین یک اتم در زمان $t$ عاملی است $a(t)$ برابر پرانرژی تر از همان اتم در زمان $t_0$. از آنجایی که مقیاس انرژی در نهایت توسط جرم پلانک تنظیم می شود، جرم پلانک باید با انبساط جهان افزایش یابد: $M_{pl} \propto a(t)$. این اثر به تنهایی دلیل انتقال گرانشی به سرخ کهکشان های دور است بدون این فرض که فوتون هایی که از آن کهکشان ها حرکت می کنند به دلیل انبساط طول موج انرژی خود را از دست می دهند. علاوه بر این: من معتقدم این فرضیه منجر به گسترش کیهانی خطی $a(t)\propto t$ می شود (به نظرات زیر مراجعه کنید).
|
آیا انتقال به سرخ کیهانی ناشی از جرم پلانک افزایش می یابد؟
|
131902
|
من سعی می کنم درک کاملی از رابطه بین بسیاری از واحدهایی که در فیزیک جنبشی استفاده می شوند را بدست بیاورم. من دریافتم که می توان یک نمودار ون تهیه کرد که عوامل بسیاری از واحدها را نشان دهد: ضربه در مرکز، نیرو و سرعت بین دو دایره و جرم، شتاب و زمان در خارج. تنها فضایی که در نمودار وجود ندارد ضرب جرم در زمان است. آیا چیزی به نام کیلوگرم ثانیه وجود دارد؟ آیا برای چیزی در فیزیک استفاده می شود؟
|
آیا مقداری در کیلوگرم ثانیه اندازه گیری می شود؟
|
74061
|
در زمینه اپتیک کوانتومی، موج دوار همیلتونی را می توان نوشت: $\hbar\begin{pmatrix} -\Delta & \Omega/2\\\ \Omega/2 & 0 \end{pmatrix}$ سپس مقادیر ویژه میتوانند به روش متعارف محاسبه شود، به دست می آید: $\hbar\frac{1}{2} \left(-\Delta -\sqrt{\Delta ^2+\Omega ^2}\right)$ and $\hbar\frac{1}{2} \left(-\Delta +\sqrt{\Delta ^2+\Omega ^2} \راست)$. تا اینجای کار خیلی خوبه. سوال من این است که چگونه از اینجا به بردارهای ویژه $\\{\sin(\theta),\cos(\theta)\\}$ و $\\{\cos(\theta),-\sin(\ برسیم تتا)\\}$ با: $\tan(2\theta)=-\Omega/\Delta$؟ من بارها شاهد استفاده از این نتیجه بدون اثبات بوده ام (بالاخره ما فقط فیزیکدان هستیم)، اما هیچ جا نمی توانم توجیه مناسبی پیدا کنم. من فرض میکنم که ربطی به گناه و متعارف بودن دارد، اما شفافیت خوشایند است :-). P.S. من این سوال را در ریاضیات نیز پرسیدم - مطمئن نیستم که آیا راه خوبی برای ارجاع متقابل بین سایت ها وجود دارد؟
|
آیا خودسرانه از Sin و Cos به عنوان توابع ویژه هامیلتونی استفاده می کنید؟
|
31738
|
در مقاله http://arxiv.org/pdf/math-ph/0005029v2.pdf فرمول 23 Voros تابع تتا /(نیمه کلاسیک) طیفی زیر را ارزیابی کرده و به دست می آورد $ \sum (E_{n}+\lambda )^{- s}= \frac{\Gamma (s-1/2)}{\Gamma(s)\sqrt \pi}\int_{0}^{\infty}\frac{dx}{(V(x)+\lambda)^{s-1/2})}= \zeta (s، \lambda)$ $ H =p^{2}+V(x). $ من معتقدم که او از هویت برای تابع گاما استفاده کرده است $ \Gamma (s-1/2)a^{1/2-s} = \int_{0}^{\infty} dt t^{s-1/ 2}e^{-at} $ اما چگونه می توانم مشتق $ \frac{ \partial }{\partial s}\zeta (s, \lambda)$ را در $ s=0 $ محاسبه کنم. تمام اصطلاحات واگرا را نادیده بگیرید و به سادگی قسمت محدود را انتخاب کنید ?? با تشکر
|
تابع زتا بعدی Voros onde
|
113381
|
من سعی میکنم مفاهیمی را که برای ناویر-استوکس استخراج شدهاند، مانند معادلات، به معادلات ماکسول برای رسانای بینقص بیان کنم. در نقطه ای خاص، من می خواهم فرض کنم که میدان الکتریکی $\mathbf E$ در فضای Sobolev $H_0^1(\Omega)$ است، یعنی $E$ قابل تفکیک wrt است. متغیرهای فاصله و $E=0$ در مرز. این با مفروضات رایجی که $\mathbf E$ را در $H_0(curl;\Omega)$ قرار می دهد متفاوت است، یعنی $\mathbf E$ کمی صاف تر است و فقط جزء مماسی آن، یعنی $n\times E=0 است. $، در مرز صفر است. از آنجایی که $H_0^1(\Omega) \subset H_0(curl;\Omega)$، فرض من محدودتر است. **سوال من**: آیا این فرض که $E=0$ در مرز، انواع رایج میدان های الکتریکی را حذف می کند؟ من نگران شرایطی هستم که $E=0$ روی مرز باشد، نه در مورد صافی اضافی. به عبارت دیگر: آیا منطقی است که میدان مغناطیسی را در یک مرز صفر فرض کنیم؟
|
آیا $H_0^1$ چیزی معقول برای میدان الکتریکی برای یک هادی کامل است؟
|
76663
|
برخی از پلاسماها دارای ضریب شکست کمتر از 1 هستند. در این پلاسماها سرعت فاز نور می تواند سریعتر از سرعت نور باشد. اما خود فاز اطلاعات را منتقل نمی کند، بنابراین هیچ تناقضی در اینجا رخ نمی دهد. اما اگر یک لوله پر از پلاسما با یک مشعل در یک سر و یک حسگر فوتون در طرف دیگر بسازم چه می شود. وقتی می بینم پرتوی نور قرمز از کنارم می گذرد، مشعل را روشن کردم و مردی در انتهای دیگر می تواند بداند که قبل از رسیدن چراغ قرمز نور قرمز به سمت او می آید. آیا این یک مناسبت FTL نیست؟
|
سریعتر از نور در پلاسما
|
53925
|
اجازه دهید با این شروع کنم که من این سوال را اینجا نیز ارسال کرده ام. من آن را در اینجا پست کردم زیرا فکر می کنم سؤالاتی که پرسیده ام مربوط به فیزیک مولکول ها است. بنابراین من سعی می کنم درک عمیق تری از نحوه عملکرد طیف سنجی جرمی به دست بیاورم. اکثر آموزشها و کتابهای درسی که من با آنها مواجه شدهام، جزئیات خاصی را در مورد فرآیند حذف میکنند و امیدوارم کسی که این فرآیند را درک میکند بتواند شکافها را پر کند. من با توضیح روشی که در حال حاضر این فرآیند را درک می کنم شروع می کنم و سپس فهرستی از جایی که شروع به گیج شدن می کنم، می کنم. 1 ابتدا یک مولکول خاص با پرتوی از الکترون بمباران می شود (مرحله یونیزاسیون). این مرحله برای آزاد کردن یک الکترون از مولکول تحت تجزیه و تحلیل که یک کاتیون تولید می کند، عمل می کند. **نکته**: یادآوری این نکته مهم است که تنها دلیل یونیزه شدن این مولکول استفاده از میدان مغناطیسی برای خم کردن جهت آن است. فقط یون ها تحت تأثیر این میدان مغناطیسی قرار می گیرند که به ما امکان می دهد مولکول مورد نظر را مشخص کنیم. 2 سپس، این یون ها توسط یک میدان الکتریکی به سمت یک میدان مغناطیسی شتاب می گیرند که یون های متحرک را به مقدار مشخصی خم می کند. > سوال 1: تفاوت بین میدان الکتریکی و میدان مغناطیسی چیست؟ و چرا میدان مغناطیسی یون ها را خم می کند در حالی که میدان الکترونی خم نمی کند. آیا این فقط نتیجه شکل دستگاه است؟ > آیا می توانید از یک میدان مغناطیسی برای شتاب بخشیدن به یک ذره و یک میدان الکتریکی > برای انجام خمش استفاده کنید؟ من فقط در مورد تفاوت بین میدان های الکتریکی و میدان های مغناطیسی واقعا گیج شده ام. 3 یون هایی که خم می شوند تا حد مشخصی در اطراف یک لوله حرکت می کنند و به آشکارساز برخورد می کنند. مقدار خمش جرم یک مولکول خاص را به ما می گوید. مولکول های سنگین تر کمتر خم می شوند و مولکول های سبک تر بیشتر خم می شوند. > سوال 2: من به آموزشی برخوردم که می گوید آنچه این آشکارساز در واقع اندازه گیری می کند نسبت جرم به بار است. چگونه این کالیبره شده است و > چگونه این مرحله به ما امکان می دهد جرم یک مولکول را اندازه گیری کنیم. آیا چندین ذره به طور همزمان به آشکارساز برخورد نمی کنند، آیا این روی خوانش جرم یک مولکول خاص تأثیری نخواهد داشت؟ من فقط در مورد این مرحله نهایی و اینکه چگونه می توانیم یک جرم دقیق برای یک مولکول خاص بدست آوریم گیج شده ام. هر گونه کمکی برای درک این مفهوم قدردانی خواهد شد.
|
درک نحوه عملکرد طیف سنجی جرمی
|
87874
|
چرا در مدل استاندارد نوترینوها بدون جرم هستند؟ آیا با این واقعیت تجربی مرتبط است که نوترینوها همیشه فقط یک جهت پرتاب اسپین در جهت حرکت دارند؟
|
چرا مدل استاندارد نوترینوها را بدون جرم پیش بینی می کند؟
|
73571
|
من میخواهم حالتهای محدود (در واقع فقط حالت پایه مورد نیاز است) معادله شرودینگر مستقل از زمان را با یک چاه مربع مستطیل شکل 2 بعدی ** محدود** \begin{equation}V(x,y)=\cases{0,& حل کنم. $ |x|\le a \text{ و } |y|\le b$ \\\ V_0،&\text{در غیر این صورت}}.\tag{1}\end{equation} $$\Big[-\frac{\hbar^2}{2m}(\partial_x^2+\partial_y^2)+V (x,y)\Big]\psi(x,y)=E\psi(x,y)$$ در نگاه اول این مشکل ساده است. به نظر می رسد که راه حل متغیر-جداپذیر است و می تواند به صورت $\psi(x,y)=f(x)g(y)$ نوشته شود. سپس $$ \frac{f''(x)}{f(x)}+\frac{g''(y)}{g(y)}+\frac{2m}{\hbar^2}(E-V )=0.$$ اجازه دهید $E=E_x+E_y$ و $V=V_x+V_y$، سپس مشکل به دو مسئله 1 بعدی کاهش می یابد. $$\cases{f''(x)+\frac{2m}{\hbar^2}(E_x- V_x)f(x)=0\\\g''(y)+\frac{2m}{ \hbar^2}(E_y-V_y)g(y)=0}.$$ با این حال، چگونه می توان $V_x$ و $V_y$ را در فضای دوبعدی تعیین کرد؟ یک روش قطعاً اشتباه، ساختن $$ V_x=\cases{0,&$|x|\le a$\\\V_1,&$|x|>a$}\text{ و }V_y=\cases{0، &$|y|\le b$\\\V_2,&$|y|>b$}\tag{2}.$$ در واقع، معادله بالقوه. (2) معادل دو مسئله مستقل چاه مربع محدود 1 بعدی در جهت $x$ و $y$ است. با این حال، یک خواننده دقیق متوجه خواهد شد که معادله بالقوه (2) با معادله (1) متفاوت است، به این معنی که معادله (2) بالقوه آن چیزی نیست که ما می خواهیم. این یک چاه مستطیلی نیست، بلکه به شکل زیر است. سپس، متوجه شدم که یک حالت کران متغیر قابل تفکیک برای چاه مربع 2 بعدی محدود وجود ندارد. اگرچه راهحلهای تحلیلی در هر منطقه با پتانسیل ثابت وجود دارد، اما هنگام تطبیق شرایط مرزی برای حفظ تداوم $\psi(x,y)$، مشکلات رخ میدهد. بر خلاف شرایط مرزی تطبیق در نقاط مشخص در 1D، در 2D باید شرایط مرزی را در امتداد خطوط مطابقت دهیم، به عنوان مثال، $$ f_1(a)g_1(y)=f_2(a)g_2(y)$$ در مرز بین $x <a$(منطقه 1) و $x>a$ (منطقه 2). این منجر به $$ g_1(y)/g_2(y)=f_2(a)/f_1(a)=constant می شود.$$ مطابقت دادن همه مرزها به این روش منجر به این می شود که $\psi(x,y)$ باید باشد 0 خارج از چاه اما این به خوبی مورد INFINITE است. این راه حل چاه محدود نیست. سپس من فکر می کنم هیچ راه حلی تحت روش متغیر جداسازی وجود ندارد. سپس، سوال این است که فراتر از روش جداسازی متغیر، چگونه این مشکل را حل کنیم؟ BTW: آیا کسی می داند که چه نوع (شکل) چاه دو بعدی برای حالت های محدود قابل حل است و چگونه؟ (پتانسیل با تقارن دایره ای مستثنی است، زیرا می دانم چگونه آن را حل کنم. می خواهم شکل دیگری از چاه دو بعدی پیدا کنم که قابل حل باشد.)
|
چگونه حالت های محدود مربع مستطیلی متناهی دوبعدی را به خوبی حل کنیم؟
|
132713
|
این یک سوال اساسی است که من نمی توانم آن را حل کنم و به نظر می رسد که در وب به آن پرداخته نشده است. متاسفم برای مهارت های من در نقاشی.  فرض کنید یک آونگ فوکو معلق در قطب شمال داریم. محور درست بالای محور چرخش است (به صفحه آونگ اجازه می دهد در هر جهتی نسبت به دستگاه قرار گیرد). قبل از اینکه آونگ شروع به چرخیدن کند، آونگ توسط یک رشته کوچک به یکی از میله های نگهدارنده (خطوط سیاه) متصل می شود. برای شروع حرکت آونگ، آن رشته را می سوزانید (این مکانیزمی است که فوکو استفاده می کند). در حالی که آونگ به میله های نگهدارنده متصل است که با دستگاه حرکت می کند، بنابراین دارای یک سرعت و شتاب است، در لحظه رها شدن، سرعت اولیه در جهت چرخش دارد. _این سرعت چه می شود؟؟_ تمام توضیحات و تصاویری که می بینم، از ابتدا فرض را بر این می گذارند که صفحه آونگ در قطب شمال نسبت به ستاره های ثابت ثابت است (من از بحث های فلسفی آگاهم)، به نوعی غفلت می کنم. آن سرعت اولیه حدس میزنم که درک درستی از مکانیسم محوری ندارم، بنابراین اگر کسی بتواند سؤال من و مکانیسم محور را روشن کند، بسیار سپاسگزار خواهم بود! # ویرایش: فکر میکنم در مورد سؤال و توضیح وضعیتم چندان واضح نیستم. من یک مقاله ویکی باورنکردنی پیدا کردم: آونگ فوکو در زیر این بخش: حرکت نسبی صفحه آونگ به سمت سطح زمین، در قطب شمال: > هنگامی که باب از محور مرکزی آونگ جابه جا می شود و سپس > دیگر نیرویی بر باب وارد نمی شود که باعث می شود حول محور مرکزی آونگ بچرخد و بچرخد (چرخش) با > زمین. همانطور که از نمای انتهایی باب در حال چرخش مشاهده می شود، تاب > باب همیشه به سمت یک ستاره قرار می گیرد یا به سمت یک ستاره می چرخد (درست مانند محور نقاط زمین در یک ستاره برای دوره های زمانی در نظر گرفته شده) همانطور که باب نوسان می کند. > از طریق محور مرکزی آونگ. اگر شرایط اولیه حرکت زاویهای لغو نشود اما دیگر نیرویی بر روی باب وارد نشود که باعث شود بعد از رها شدن باب سرعت زاویهای داشته باشد، میتواند یک نوسان جزئی بیضوی وجود داشته باشد. صفحه نوسان آونگ > باب اکنون مستقل از سطح زمین است که قبل از رها شدن (از طریق نقطه نگهدارنده) به باب نیرویی وارد می کرد. همانطور که قبلاً اشاره شد، باب همچنان با زمین در حال چرخش است (لکه ای از باب با زمین می چرخد)، حتی اگر باب دیگر با زمین نمی چرخد. بنابراین زمین به چرخش در زیر تاب آونگ ادامه می دهد در حالی که چرخش آونگ در صفحه ثابتی باقی می ماند که > نمی چرخد (چرخش). نکته حائز اهمیت این است که نیرویی که سرعت زاویهای به باب از پیش آزاد شده وارد میکند، دیگر روی باب در حال چرخش اثر نمیگذارد. در قطب شمال، این نیرو یک روز طول می کشد تا جهت > نیرو یک دایره کامل کامل کند، زیرا یک روز طول می کشد تا زمین > بچرخد. تکانه زاویه ای اولیه در اینجا به وضوح ذکر شده است و باید لغو شود، آیا فوکو آن را لغو کرد؟
|
سرعت اولیه آونگ فوکو
|
116607
|
فیزیک S.E. ممکن است برای این سوال اشتباه باشد، اما من نمی دانم چه اتفاقی برای ارتعاش در سیلندر شکسته، ترک خورده یا آسیب دیده می افتد. فرض کنید یک استوانه فولادی به طول 1 متر دارید، آن را به دو قسمت می شکنید و سپس قطعات را دوباره روی هم قرار می دهید (بدون جوش یا هیچ چیز دیگری). سپس در یک انتها یک ارتعاش سینوسی قرار داده و در انتهای دیگر فرکانس و دامنه را اندازه گیری کنید. تا آنجا که من می توانم بگویم، فرکانس تغییر نمی کند، بلکه فقط دامنه تغییر می کند، زیرا انرژی موج فرکانس در انتقال از استوانه فولادی کامل به سیلندر آسیب دیده و دوباره به سیلندر کامل از دست می رود. آیا این تعبیر صحیح است؟ اگر چنین است، سیلندری که فقط ترک خورده یا خم شده است چگونه رفتار می کند؟ می دانم که از لرزش برای عیب یابی موتورها و پروانه ها استفاده می کنند.
|
لرزش در یک سیلندر شکسته
|
74503
|
در کتاب تئوری میدان آماری و کوانتومی لو بلاک، ثابت دوباره عادی سازی $Z_3$ با معادله $$ \Gamma^{(2)}_R(k^2, m^2, g) = Z_3 \Gamma^{ معرفی شده است. (2)}(k^2، m_0^2، g_0؛ \Lambda) $$ که $m_0$ و $g_0$ هستند جرم خالی و جفت و $m$ و $g$ جرم و جفت مجدد نرمال شده هستند. اندکی بعد، نویسنده می نویسد که با تحلیل ابعادی، $Z_3$ می تواند تنها تابعی از $g$ و $\Lambda/m$ باشد ($Z_3 = Z_3(g,\Lambda/m$)). برای من فوری نیست که چرا اینطور است. کسی می تواند آن را توضیح دهد؟
|
چگونه تعیین کنیم که ثابت مجدد عادی سازی $Z_3$ باید فقط به $g$ و $\Lambda/m$ بستگی داشته باشد
|
135296
|
با توجه به یک معادله موج، مثلاً بگویید $\Psi(x,y,z,t) = a \cos\left(\omega t -\vec{k}\cdot \vec{r} \right)$، چه شرایطی باید برای $\Psi$ برای نشان دادن یک موج **صفحه** ملاقات کرد؟
|
شرایط برای توصیف یک موج به عنوان موج صفحه
|
74501
|
> سینگ هوات خودرویی را با سرعت اولیه 30 کیلومتر در ساعت و شتاب 2 کیلومتر بر ساعت > به سمت تی می راند که جابجایی آن 200 متر از او فاصله دارد. در همان زمان، تی > با سرعت اولیه 50 کیلومتر بر ساعت و > شتاب 3 کیلومتر بر ساعت، ماشین دیگری را به سمت سینگ هوات می راند. فاصله محل اولیه Sing > Huat را پیدا کنید، جایی که این دو ماشین به هم می رسند. http://i.stack.imgur.com/WlyV0.jpg من تعجب می کنم که آیا تی همزمان با دو ماشین رانندگی می کند؟ اگر چنین است، فاصله را از محل اولیه Sing Huat پیدا کنید، جایی که این دو خودرو به هم می رسند. سوال با کدام دو ماشین می خواهد مقایسه کند؟
|
فاصله از محل اولیه را پیدا کنید
|
130710
|
برای یک گاز همونتروپیک تراکم پذیر آیا سرعت جریان خروجی از لوله با سرعت داخل لوله برابر است؟
|
سرعت جریان خروجی از لوله
|
77054
|
آیا این درست است که تابع دو نقطه برای نظریه بوزون بدون جرم در بعد 2 یک ثابت است؟ یعنی مستقل از فاصله بین دو نقطه است؟
|
تابع دو نقطه برای بوزون بدون جرم در 2 بعدی
|
132711
|
چرا سلف برخلاف خازن که در جهت مخالف شارژش تخلیه می شود (جهت جریان در تخلیه معکوس می شود) در همان مسیر (همان جهت جریان) تخلیه می شود. دلیل فیزیکی آن چه می تواند باشد (برای قانون لنز)
|
شارژ و تخلیه سلف
|
74505
|
آیا کسی می تواند به من بگوید که کجا می توانم مرجعی برای محاسبه ضرایب هسته حرارتی در منیفولد با تکینگی های مخروطی پیدا کنم؟ من سعی می کنم آنتروپی درهم تنیدگی را برای میدان های گیج با استفاده از هسته حرارتی و روش زاویه کسری مخروطی محاسبه کنم. میخواستم بدانم چگونه میتوانم اصطلاحات (در آنتروپی درهمتنیدگی) را فراتر از واگرای UV پیشرو بر حسب انحناهای ثابت ساخته شده از انحنای بیرونی و درونی ناحیه درهمتنیدگی بیان کنم. منتظر پاسخ هستیم.
|
گسترش هسته حرارتی برای آنتروپی درهم تنیدگی
|
74500
|
اگر یک گروه تقارن $G$ (بیایید برای سادگی بگوییم متناهی) بر روی یک نظریه شبکه تنها با عمل کردن بر روی متغیرهای رأس عمل کند، من آن را ultralocal می نامم. هر تقارن فوق محلی را می توان اندازه گیری کرد. با این حال، به طور کلی تقارن های گسسته ای وجود دارد که نمی توان آنها را اندازه گیری کرد. به عنوان مثال، Freed و Vafa در http://link.springer.com/article/10.1007%2FBF01212418 در مورد اینکه چگونه در 1+1d نیاز به عقب نشینی یک کلاس خاص در $H^3(G,U(1))$ است، بحث می کنند. برای داشتن دوره های بی اهمیت بنابراین، آیا برعکس این موضوع درست است - که اگر $G$ را بتوان اندازهگیری کرد، فرمولبندی این تئوری وجود دارد که در آن $G$ به صورت فرامحلی عمل میکند؟ به عبارت دیگر، آیا تقارن بدون عمل فرامحلی لزوماً غیرعادی است؟ و اگر چنین است، آیا میتوانیم این ناهنجاری را به عنوان یک کلاس صریح در $H^3(G,U(1))$ برای نظریههای 1+1d ببینیم؟ به نظر من پاسخ مثبت است. اگر هیچ ناهنجاری نداشته باشیم و جلو برویم و $G$ را اندازه گیری کنیم، می توانیم نتیجه را روی شبکه ای قرار دهیم که فیلد گیج $G$ روی لبه ها قرار می گیرد. این متغیرهای لبه دارای شرایط مسطح هستند که متغیرهای راس شروع و پایان با عملکرد متغیر لبه (یک عنصر G$) متفاوت هستند. به نظر میرسد که $G$ نباید در جای دیگری عمل کند، زیرا به نوعی اندازهگیری $G$ نوعی ضریب چربی نظریه توسط $G$ است. بنابراین، اگر این فرمول شبکه را بگیریم و میدان گیج را فراموش کنیم، دوباره به نظریه اصلی میرسیم، اما اکنون با یک عمل فوقمحلی $G$. آنچه باقی می ماند این است که چگونه می توان این ناهنجاری را در گروه cohomology تعیین کرد.
|
ناهنجاری برای تقارن گیج گسسته در محل
|
86833
|
لاگرانژیان مدل QED، QCD و استاندارد را چگونه می خوانید؟ همه نمادها و تانسورها چه چیزی را نشان می دهند؟ و چگونه می توانید آنها را به تنهایی استخراج کنید؟
|
چگونه Lagrangians مدل QED، QCD و استاندارد را درک کنیم؟
|
24307
|
آیا ثابت های فیزیکی به طور تصادفی توسط طبیعت انتخاب شده اند یا توسط منبعی از… _ماده_ (؟) تعیین شده است. من واقعا ایده ای ندارم اگه بتونی کمکم کنی خیلی عالی میشه
|
آیا ثابت های فیزیکی به طور تصادفی توسط طبیعت انتخاب شده اند؟
|
130717
|
با در نظر گرفتن آزمایش دو شکاف با یک ذره باردار، آیا پس از عبور ذره از شکاف ها، آیا دو قسمت تابع موج، جاذبه الکترومغناطیسی قسمت دیگر را احساس می کنند؟ به طور کلی تر، آیا عبارت بالقوه در معادله شرودینگر می تواند به خود تابع موج وابسته باشد؟ از یک طرف می توان تصور کرد که موج الکترونی از هم جدا می شود و هر قسمت نسبتی از بار را حمل می کند. از طرف دیگر، تابع موج یک توزیع احتمال است که نشان می دهد هیچ تعاملی وجود ندارد.
|
آیا یک تابع موج با خودش تعامل دارد؟
|
108346
|
ما به لطف نیوتن می دانیم که: $$F=G\frac{m_1\cdot m_2}{r^2}$$ که در آن $G$ ثابت گرانشی است که در حدود 6.673$ است\cdot10^{-11}$m_1$ و $m_2$ جرم دو جسم مختلف است $r$ فاصله بین آنهاست. ما همچنین می دانیم که $F=ma$ پس آیا می توانیم این را بنویسیم؟ : $$ma=G\frac{m_1\cdot m_2}{r^2}$$ اگر چنین است $m$ در جمله اول معادله چیست؟ $m_1$ یا $m_2$؟ خیلی ممنون برای کمک!!!
|
نیروی گرانش بین دو جسم با جرم متفاوت
|
68217
|
از $E=mc^2$ به نظر می رسد جرم و انرژی قابل تعویض هستند. من می توانم بفهمم که جرم قابل تشخیص است، یک نوع از نوع دیگر، مانند پروتون ها و الکترون ها. اما در فرآیند معکوس، چگونه ممکن است انرژی که به یک ذره تبدیل شده است، کاملاً غیرقابل تشخیص از انرژی است که به یک نوع ذره دیگر تبدیل شده است. آیا نباید فقط یک نوع ذره وجود داشته باشد؟ آیا این بدان معناست که انرژی نوعی چیز ترکیبی با پتانسیل این یا آن است، مانند یک سلول بنیادی در زیست شناسی. یا یک چیز ساده است؟ یک موج الکترومغناطیسی (فوتون) را به عنوان مثال در نظر بگیرید (که بدون جرم است). کاملاً از فوتون دیگری با همان فرکانس قابل تشخیص نیست. با این حال، یکی می تواند به یک نوع ذره و دیگری به نوع دیگری متراکم شود. اگر هر دو فوتون کاملاً غیرقابل تشخیص باشند این چگونه ممکن است؟
|
انرژی ساده است یا ترکیبی؟
|
112037
|
در حرکت دایره ای یکنواخت، اگر خودرویی با سرعت معینی منحنی را گرد کند و زاویه جاده به خودرو اجازه دهد تا با آن سرعت دور بزند، به آن سرعت «سرعت طراحی» می گویند. اگر اندازهگیری زاویه θ، شعاع r، سرعت طراحی d و ضریب اصطکاک استاتیک روی لاستیکها μs باشد، تغییر سرعت خودرو چگونه بر حداقل ضریب اصطکاک استاتیک مورد نیاز برای حفظ تأثیر میگذارد. ماشین در همان مسیر؟
|
حرکت دایره ای یکنواخت با جاده و ماشین کرانه دار
|
74504
|
این حکمت عمومی پذیرفته شده است که یک ال سی دی Twisted Nematic همیشه باید با استفاده از AC به جای DC هدایت شود، زیرا DC ظاهراً LC را دناتور می کند. من دو سوال دارم: 1. آیا این اثر فقط در ولتاژهای درایو معمولی 8 ولت تا 9 ولت اتفاق می افتد؟ اگر ال سی دی با ولتاژ پایین تر، حدود 3 ولت هدایت شود، آیا تخریب آن بد نیست؟ 2. در ولتاژ 3 ولت چند ساعت طول می کشد تا LC خراب شود؟ من یک آزمایش را به مدت 500 ساعت انجام دادم که هیچ اثر بدی نداشت. با تشکر
|
کریستال مایع نماتیک پیچ خورده: میزان تخریب ناشی از درایو DC؟
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.